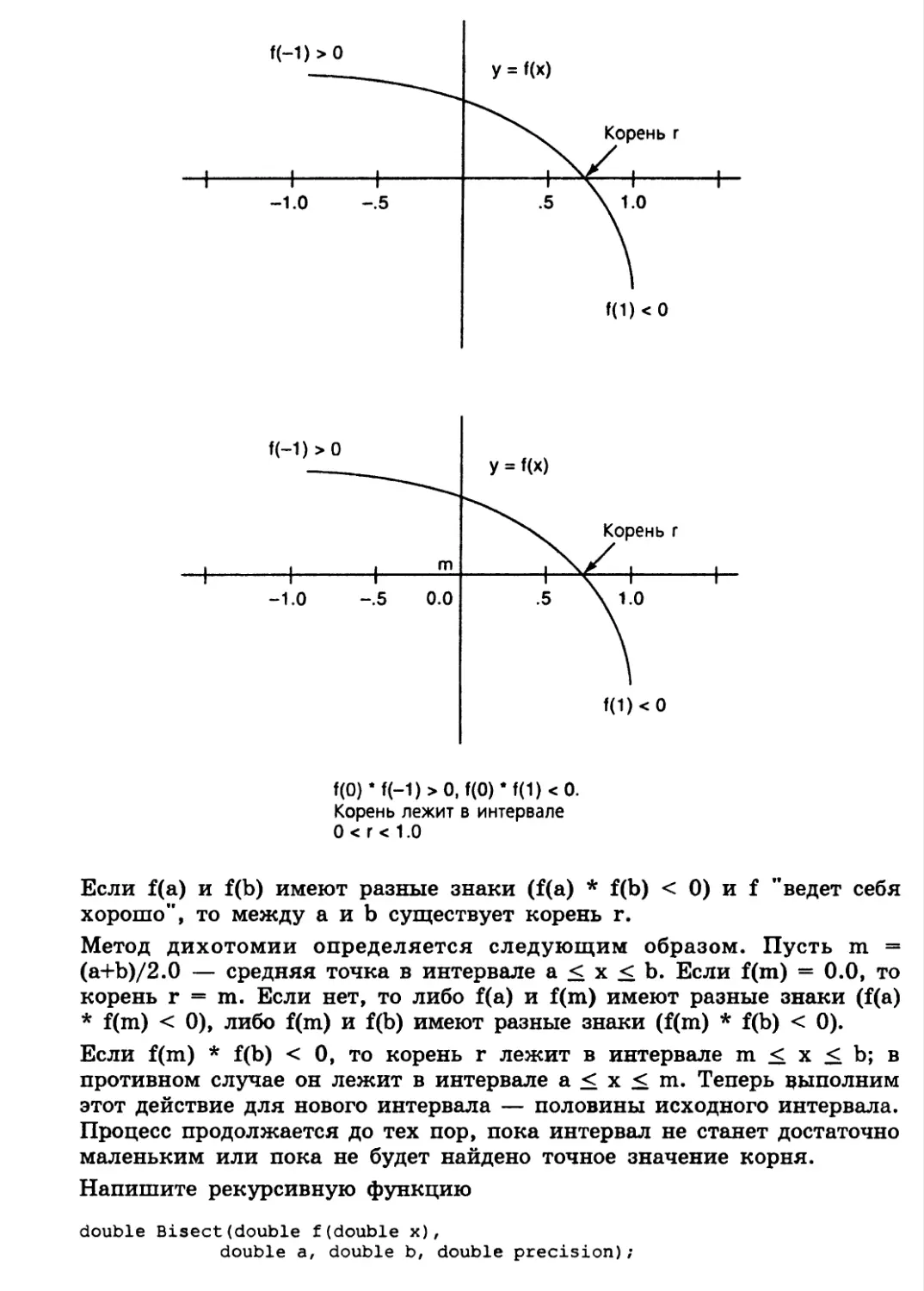
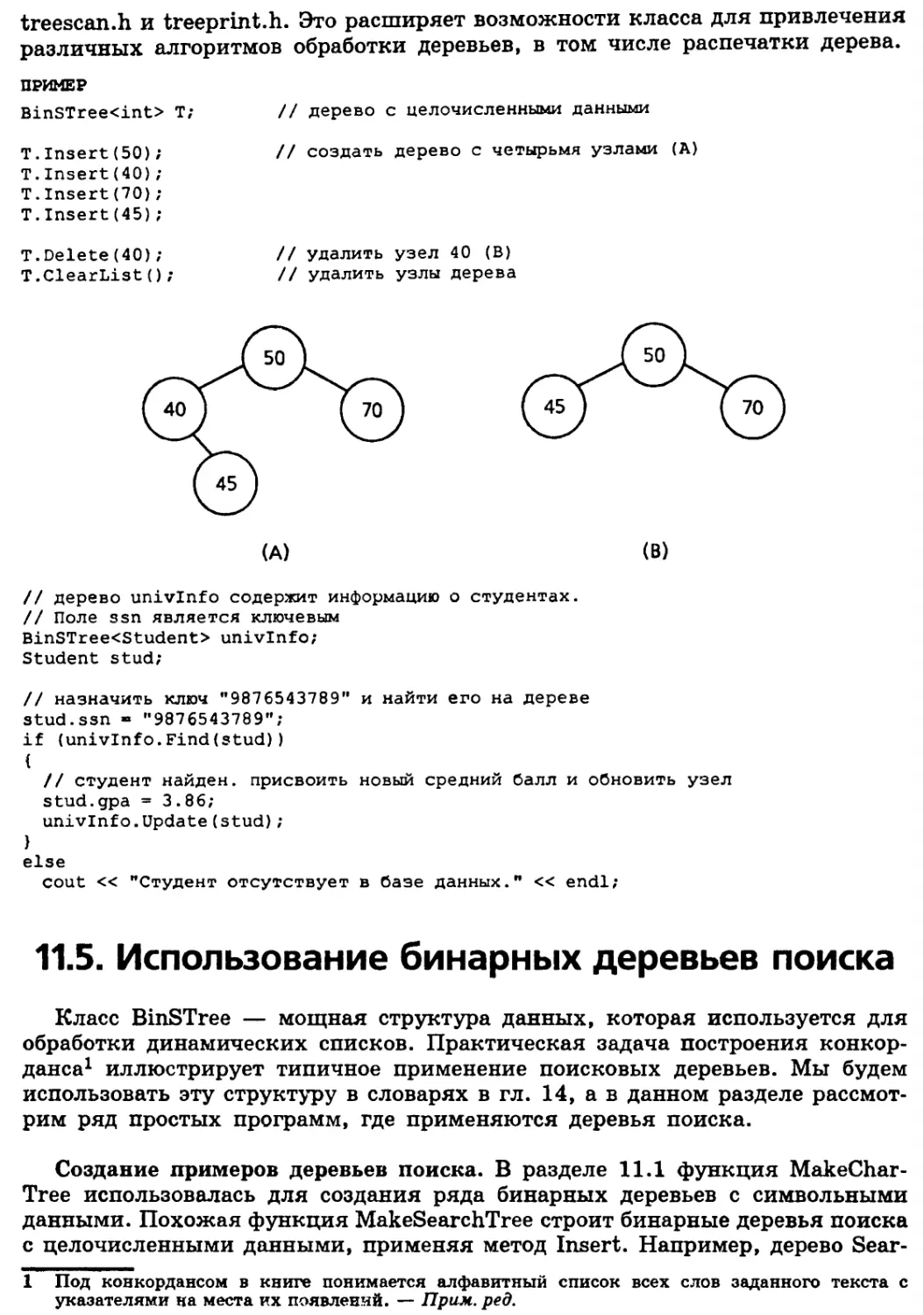
Tags: программирование на эвм компьютерные программы программирование язык программирования c++
ISBN: 5-7989-0017-7
Year: 1999
Text
СТРУКТУРЫ ДАННЫХ
в C++
Уильям Топп
Уильям Форд
БИНОМ
Data Structures
with C++
William Ford
University of the Pacific
William Topp
University of the Pacific
Prentice-Hall International, Inc.
Уильям Топп, Уильям Форд
Структуры данных
в C++
Перевод с английского
под редакцией
В. Кузьменко
Москва
ЗАО «Издательство БИНОМ»
199 9
УДК 004.422
ББК 32.973
Т58
Уильям Топп, Уильям Форд.
Структуры данных в C++: Пер. с англ. — М.: ЗАО «Издательство
БИНОМ», 1999. - 816 с: ил.
В книге на основе так называемых абстрактных структур данных (ADT)
рассматриваются как встроенные, так и определяемые пользователем типы данных
в языке C++. Подробно излагаются вопросы организации структур данных для
эффективной их обработки методами сортировки и поиска информации,
построением стеков, очередей и деревьев.
Книга будет интересна всем категориям программистов — от начинающих до
профессионалов.
Все права защищены. Никакая часть этой книги не может быть воспроизведена в любой
форме или любыми средствами, электронными или механическими, включая
фотографирование, магнитную запись или иные средства копирования или сохранения информации без
письменного разрешения издательства.
ISBN 5-7989-0017-7 (рус.)
ISBN 0-13-320938-5 (англ.)
Authorized translation from
the English language edition.
© Original copyright. Prentice Hall, Inc.
A Simon & Schuster Company
© Издание на русском языке
ЗАО «Издательство БИНОМ*, 1999.
Содержание
Предисловие 13
Глава 1. Введение 19
1.1. Абстрактные типы данных 20
ADT — формат Г 21
1.2. Классы C++ и абстрактные типы 24
Инкапсуляция и скрытие информации 24
Передача сообщений 25
1.3. Объекты в приложениях C++ 25
Приложение: класс Circle 25
1.4. Разработка объектов . 28
Объекты и композиция 28
C++ геометрические классы 30
Объекты и наследование 30
Наследование в программировании . 31
Упорядоченные списки и наследование 34
Повторное использование кода 35
Спецификации класса SeqList и OrderedList 36
1.5. Приложения с наследованием классов 37
1.6. Разработка объектно-ориентированных программ 38
Анализ задачи/определение программы 39
Разработка 39
Кодирование 40
Тестирование 40
Иллюстрация программной разработки: Dice график 40
1.7. Тестирование и сопровождение программы 45
Объектное тестирование 45
Тестирование управляющего модуля 45
Программное сопровождение и документирование 46
1.8. Язык программирования C++ 47
1.9. Абстрактные базовые классы и полиморфизм 48
Полиморфизм и динамическое связывание 48
Письменные упражнения 50
Глава 2. Базовые типы данных 53
2.1. Целочисленные типы 54
Компьютерное хранение целых чисел 56
Данные в памяти 57
Представление целых в языке C++ 58
2.2. Символьные типы 58
Символы ASCII 58
2.3. Вещественные типы 60
Представление вещественных чисел 60
2.4. Типы перечисления 62
Реализация типов перечисления C++ 62
2.5. Указатели 63
Указатели ADT 63
Значения указателя 65
2.6. Массив (array) 65
Встроенный тип массива C++ 66
Сохранение одномерных массивов 66
Границы массива 67
Двумерные массивы 68
Сохранение двумерных массивов 69
2.7. Строковые константы и переменные 71
Строки C++ 73
Приложение: перестановка имен 74
2.8. Записи 76
Структуры C++ 77
2.9. Файлы 77
Иерархия потоков C++ 80
2.10. Приложения массива и записи 82
Последовательный поиск 82
Обменная сортировка 85
Подсчет зарезервированных слов C++ 87
Письменные упражнения 90
Упражнения по программированию 96
Глава 3. Абстрактные типы данных и классы 99
3.1. Пользовательский тип — КЛАСС 100
Объявление класса 100
Конструктор 101
Объявление объекта 102
Реализация класса 102
Реализация конструктора 103
Создание объектов 104
3.2. Примеры классов 107
Класс Temperature 108
Класс случайных чисел 110
3.3. Объекты и передача информации 114
Объект как возвращаемое значение 115
Объект как параметр функции 115
3.4. Массивы объектов 116
Конструктор умолчания 117
3.5. Множественные конструкторы 117
3.6. Практическое применение: Треугольные матрицы 120
Свойства верхней треугольной матрицы 121
Класс TriMat 124
Письменные упражнения 129
Упражнения по программированию 133
Глава 4. Классы коллекций 143
4.1. Описание линейных коллекций 146
Коллекции с прямым доступом 147
Коллекции с последовательным доступом 148
Универсальная индексация 151
4.2. Описание нелинейных коллекций 152
Коллекции групп 153
4.3. Анализ алгоритмов 155
Критерии эффективности 155
Общий порядок величин 159
4.4. Последовательный и бинарный поиск 161
Бинарный поиск 162
4.5. Базовый класс последовательного списка 166
Методы модификации списка 169
Письменные упражнения 175
Упражнения по программированию 178
Глава 5. Стеки и очереди 181
5.1. Стеки 182
5.2. Класс Stack 184
5.3. Оценка выражений 193
Постфиксная оценка 194
Применение: постфиксный калькулятор 195
5.4. Очереди 198
5.5. Класс Queue 201
5.6. Очереди приоритетов 212
Класс PQueue 214
Приложение: службы поддержки компании 217
5.7. Практическое применение:
Управляемое событиями моделирование 220
Разработка приложения 221
Информация моделирования 224
Установка параметров моделирования 226
Выполнение задачи моделирования 226
Письменные упражнения 232
Упражнения по программированию 236
Глава 6. Абстрактные операторы 239
6.1. Описание перегрузки операторов 241
Определяемые пользователем внешние функции 241
Члены класса 242
Дружественные функции 244
6.2. Система рациональных чисел 245
Представление рациональных чисел 245
Арифметика рациональных чисел 246
Преобразование рациональных чисел 247
6.3. Класс Rational 247
6.4. Операторы класса Rational как функции-члены 249
Реализация операторов класса Rational 249
6.5. Операторы потока класса Rational как дружественные функции . 250
Реализация операторов потока класса Rational 251
6.6. Преобразование рациональных чисел 252
Преобразование в объектный тип 252
Преобразование из объектного типа 253
6.7. Использование рациональных чисел 254
Письменные упражнения 258
Упражнения по программированию 265
Глава 7. Параметризованные типы данных 269
7.1. Шаблонные функции . . . « 270
Сортировка на базе шаблона 273
7.2. Шаблонные классы 273
Определение шаблонного класса 274
Объявление объектов шаблонного класса 274
Определение методов шаблонного класса 274
7.3. Шаблонные списковые классы 276
7.4. Вычисление инфиксного выражения 277
Письменные упражнения 285
Упражнения по программированию 286
Глава 8. Классы и динамическая память 289
8.1. Указатели и динамические структуры данных 291
Оператор new для выделения памяти 292
Динамическое выделение массива 292
Оператор delete освобождения памяти 293
8.2. Динамически создаваемые объекты 293
Освобождение данных объекта: деструктор 295
8.3. Присваивание и инициализация 297
Проблемы присваивания 297
Перегруженный оператор присваивания 299
Указатель this 300
Проблемы инициализации 300
Создание конструктора копирования 301
8.4. Надежные массивы 303
Класс Array 303
Выделение памяти для класса Array 305
Проверка границ массива и перегруженный оператор [] 306
Преобразование объекта в указатель 307
Использование класса Array 309
8.5. Класс String 310
Реализация класса String 315
8.6. Сопоставление с образцом 320
Процесс Find 320
Алгоритм сопоставления с образцом 321
Анализ алгоритма сопоставления с образцом 325
8.7. Целочисленные множества 325
Множества целочисленных типов 326
Побитовые операторы C++ 327
Представление элементов множества 329
Решето Эратосфена 332
Письменные упражнения 336
Упражнения по программированию 345
Глава 9. Связанные списки 349
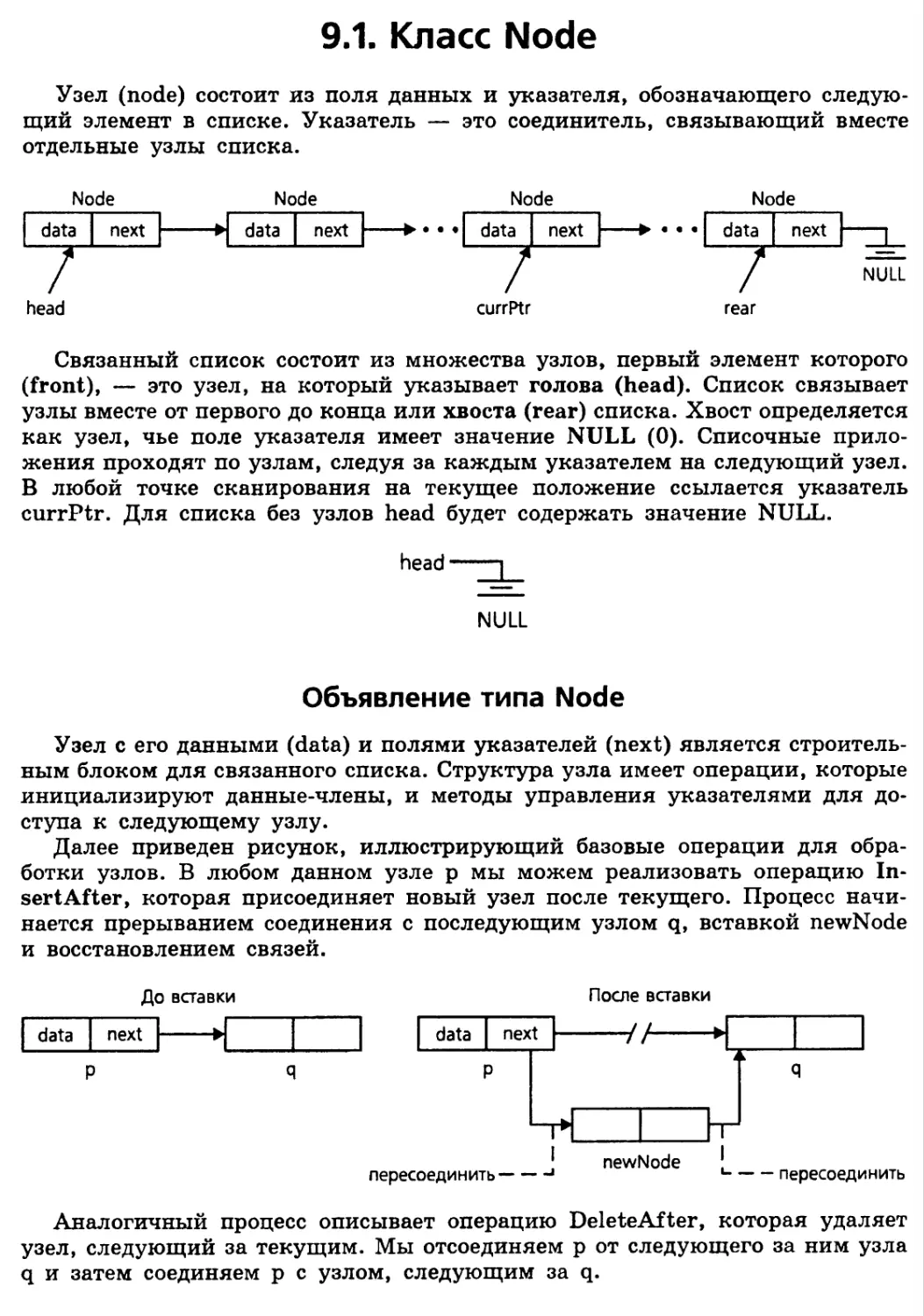
Описание связанного списка 351
Обзор главы 352
9.1. Класс Node 353
Объявление типа Node 353
Реализация класса Node 356
9.2. Создание связанных списков 358
Создание узла 358
Вставка узла: InsertFront 358
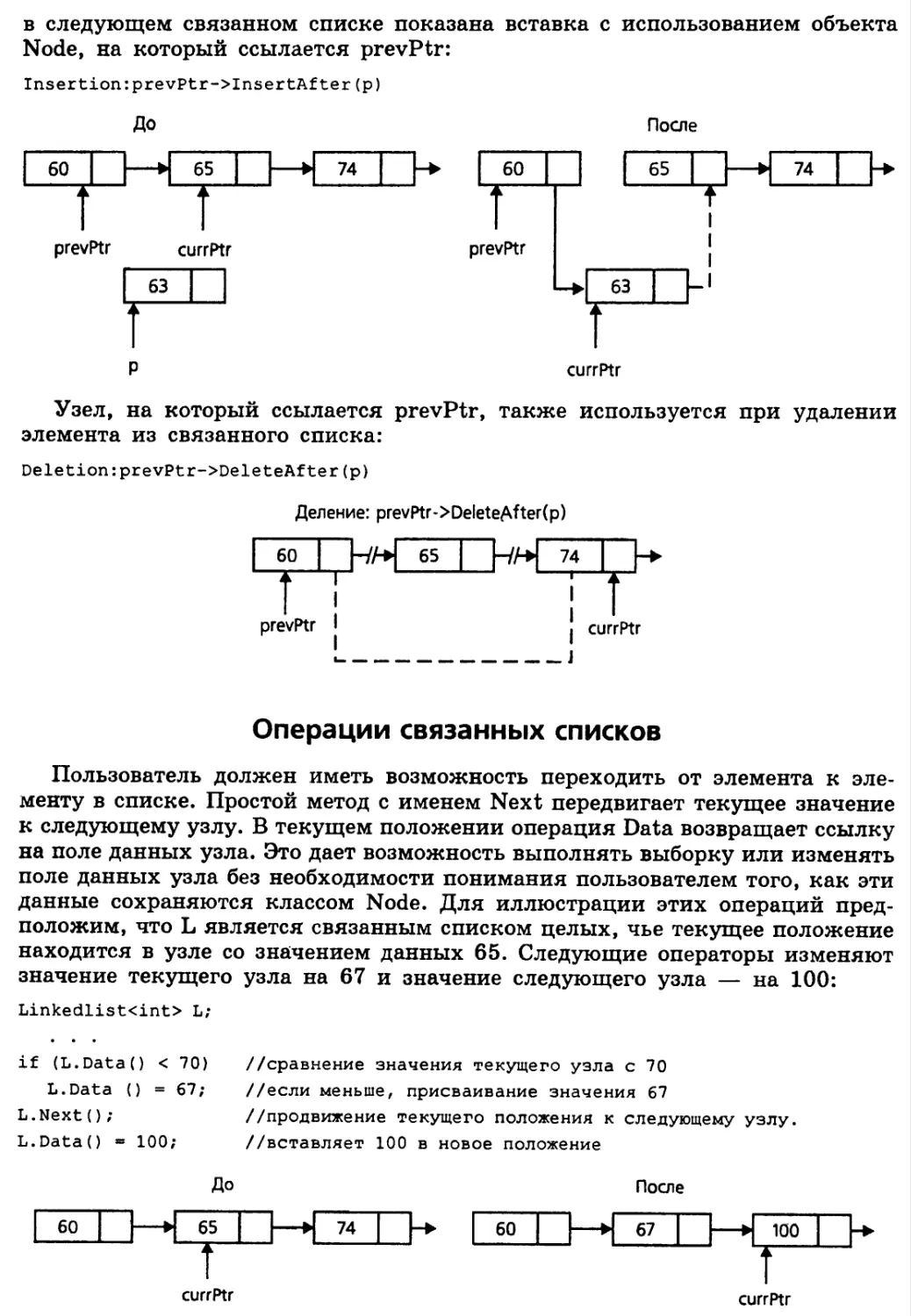
Прохождение по связанному списку 359
Вставка узла: InsertRear 361
Приложение: Список выпускников 365
Создание упорядоченного списка 367
Приложение: сортировка со связанными списками 369
9.3. Разработка класса связанного списка 371
Данные-члены связанных списков 371
Операции связанных списков 372
9.4. Класс LinkedList 374
Конкатенация двух списков 377
Сортировка списка 377
9.5. Реализация класса LinkedList 381
9.6. Реализация коллекций со связанными списками 388
Связанные очереди 389
Реализация методов Queue 390
Использование объекта LinkedList с классом SeqList 391
Реализация методов доступа к данным класса SeqList 392
Приложение: Сравнение реализаций SeqList 392
9.7. Исследовательская задача: Буферизация печати 394
Анализ проблемы 394
Разработка программы 395
Реализация метода UPDATE для класса Spooler 397
Методы оценки системы буферизации печати 398
9.8. Циклические списки 400
Реализация класса CNode 402
Приложение: Решение задачи Джозефуса 403
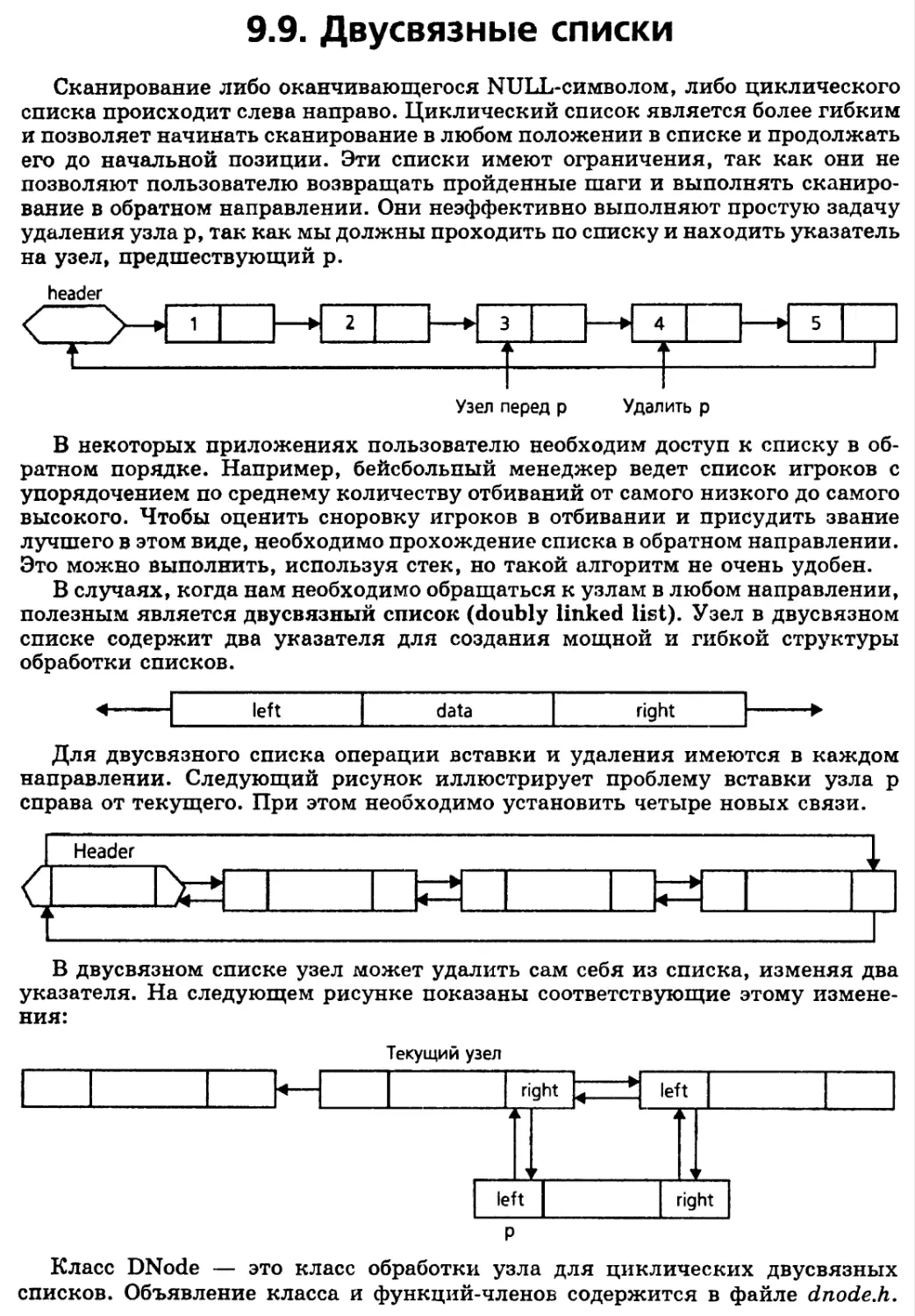
9.9. Двусвязные списки 406
Приложение: Сортировка двусвязного списка 408
Реализация класса DNode 410
9.10. Практическая задача: Управление окнами 411
Список окон 412
Реализация класса WindowList 415
Письменные упражнения 418
Упражнения по программированию 426
Глава 10. Рекурсия 431
10.1. Понятие рекурсии 432
Рекурсивные определения 433
Рекурсивные задачи 435
10.2. Построение рекурсивных функций 439
10.3. Рекурсивный код и стек времени исполнения 443
Стек времени исполнения 444
10.4. Решение задач с помощью рекурсии 445
Бинарный поиск 446
Комбинаторика: задача о комитетах 448
Комбинаторика: перестановки 451
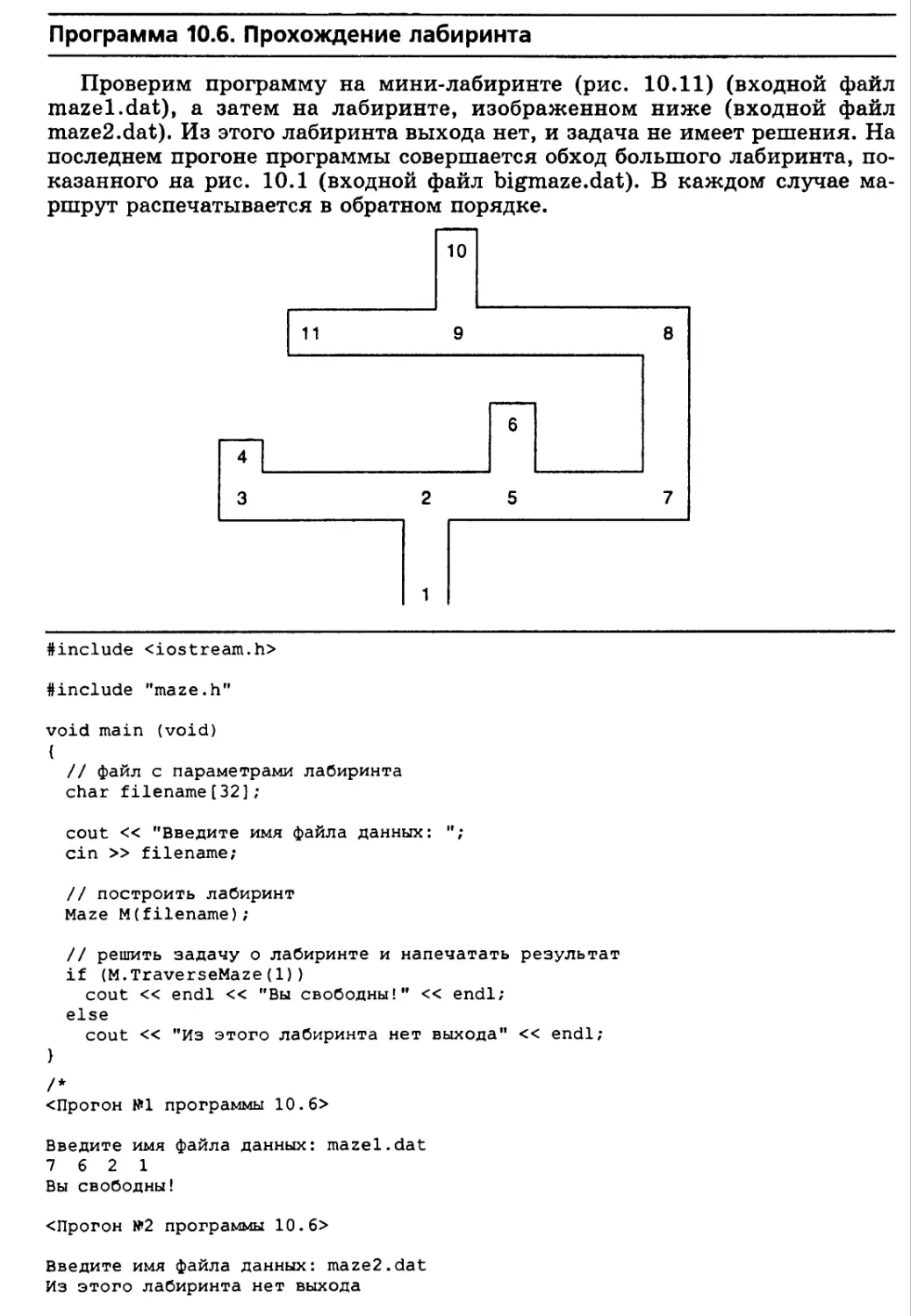
Прохождение лабиринта 460
Реализация класса Maze 463
10.5. Оценка рекурсии 466
Письменные упражнения 470
Упражнения по программированию 473
Глава 11. Деревья 477
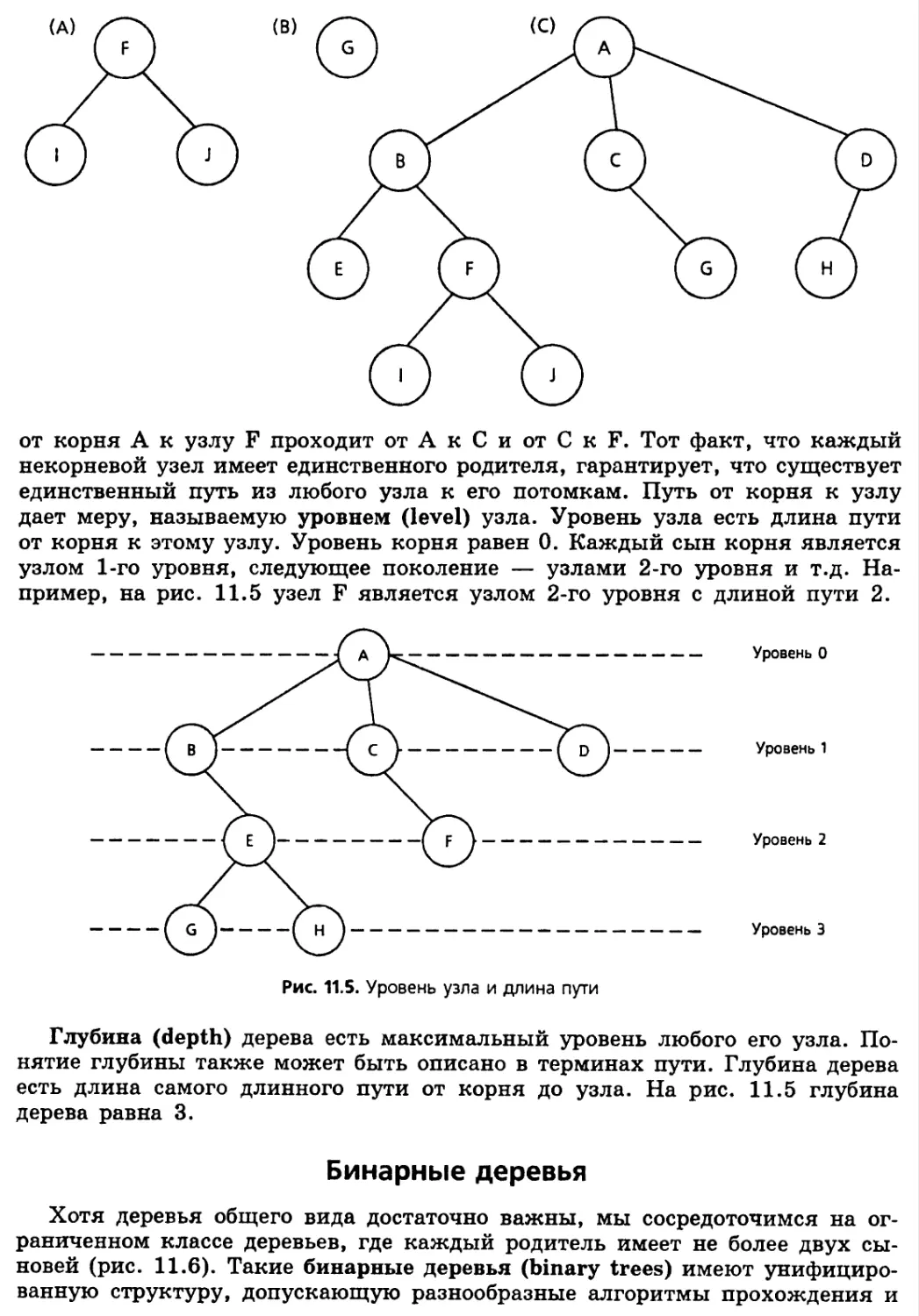
Терминология деревьев 479
Бинарные деревья 480
11.1. Структура бинарного дерева 483
Проектирование класса TreeNode 483
Построение бинарного дерева 485
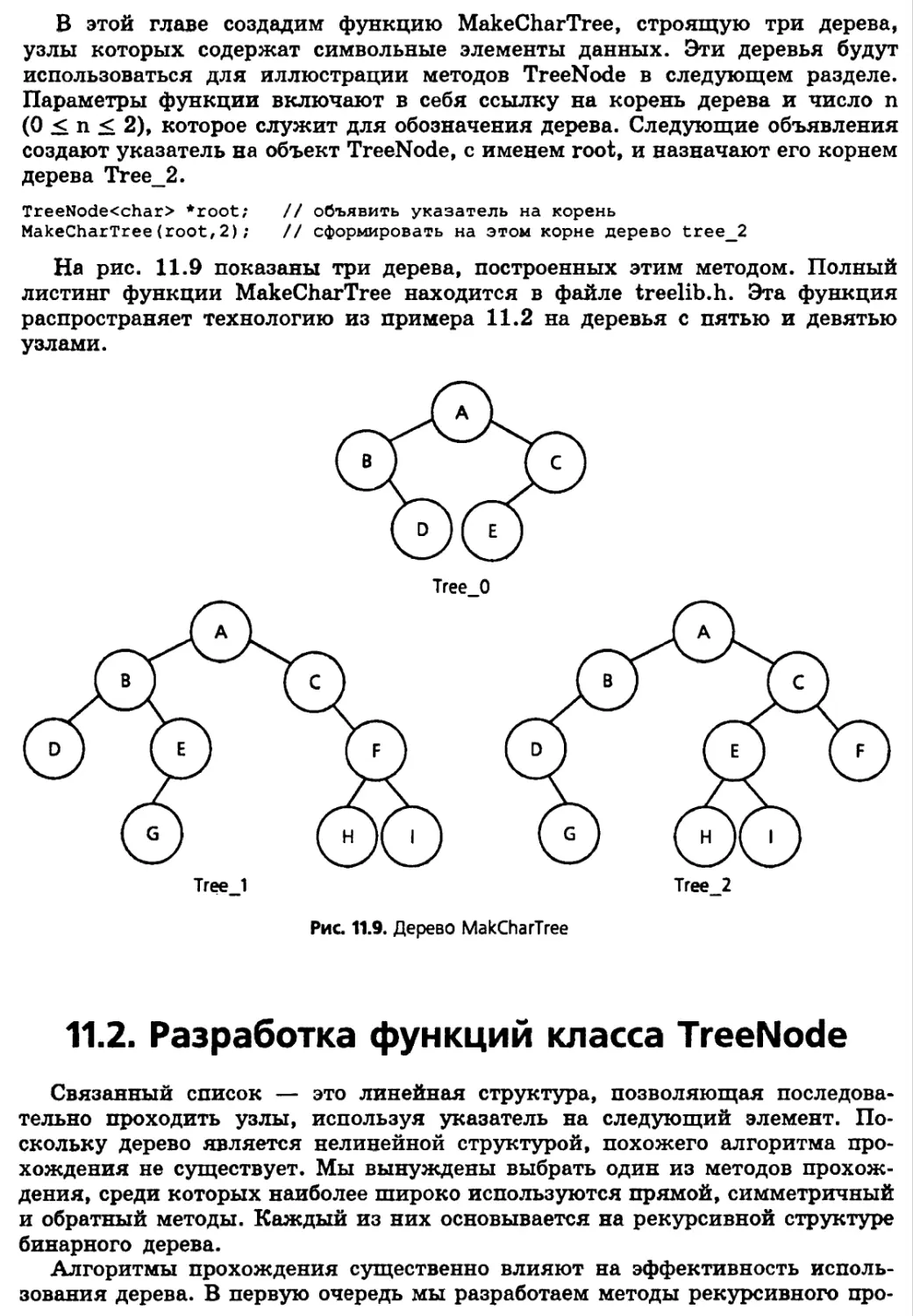
11.2. Разработка функций класса TreeNode 487
Рекурсивные методы прохождения деревьев 489
Симметричный метод прохождения дерева 489
11.3. Использование алгоритмов прохождения деревьев 492
Приложение: посещение узлов дерева 492
Приложение: печать дерева 493
Приложение: копирование и удаление деревьев 495
Приложение: вертикальная печать дерева 500
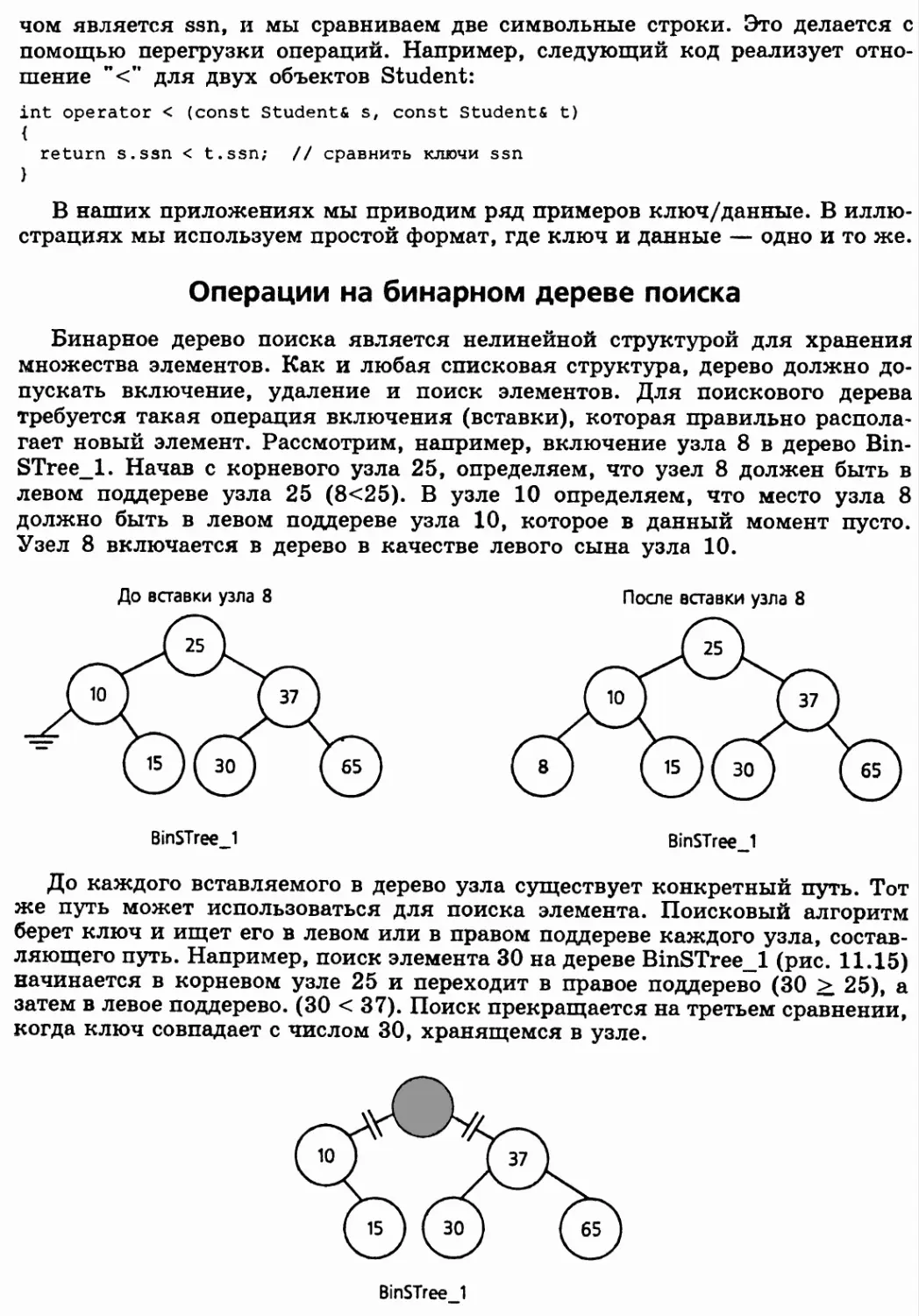
11.4. Бинарные деревья поиска 503
Ключ в узле бинарного дерева поиска 505
Операции на бинарном дереве поиска 506
Объявление абстрактного типа деревьев 507
11.5. Использование бинарных деревьев поиска 510
Дублированные узлы 513
11.6. Реализация класса BinSTree 515
Операции обработки списков 516
11.7. Практическая задача: конкорданс 525
Письменные упражнения 529
Упражнения по программированию 536
Глава 12. Наследование и абстрактные классы 539
12.1. Понятие о наследовании 540
Терминология наследования 542
12.2. Наследование в C++ 543
Конструкторы и производные классы 544
Что нельзя наследовать 550
12.3. Полиморфизм и виртуальные функции 550
Демонстрация полиморфизма 553
Приложение: геометрические фигуры и виртуальные методы . . .556
Виртуальные методы и деструктор 558
12.4. Абстрактные базовые классы 559
Абстрактный базовый класс List 560
Образование класса SeqList из абстрактного базового класса List . 561
12.5. Итераторы 563
Абстрактный базовый класс Iterator 564
Образование итераторов для списка 564
Построение итератора SeqList 565
Итератор массива 569
Приложение: слияние сортированных последовательностей 570
Реализация класса Arraylterator 574
12.6. Упорядоченные списки 575
12.7. Разнородные списки 579
Разнородные массивы 579
Разнородные связанные списки 581
Письменные упражнения 586
Упражнения по программированию 595
Глава 13. Более сложные нелинейные структуры 599
13.1. Бинарные деревья, представляемые массивами 600
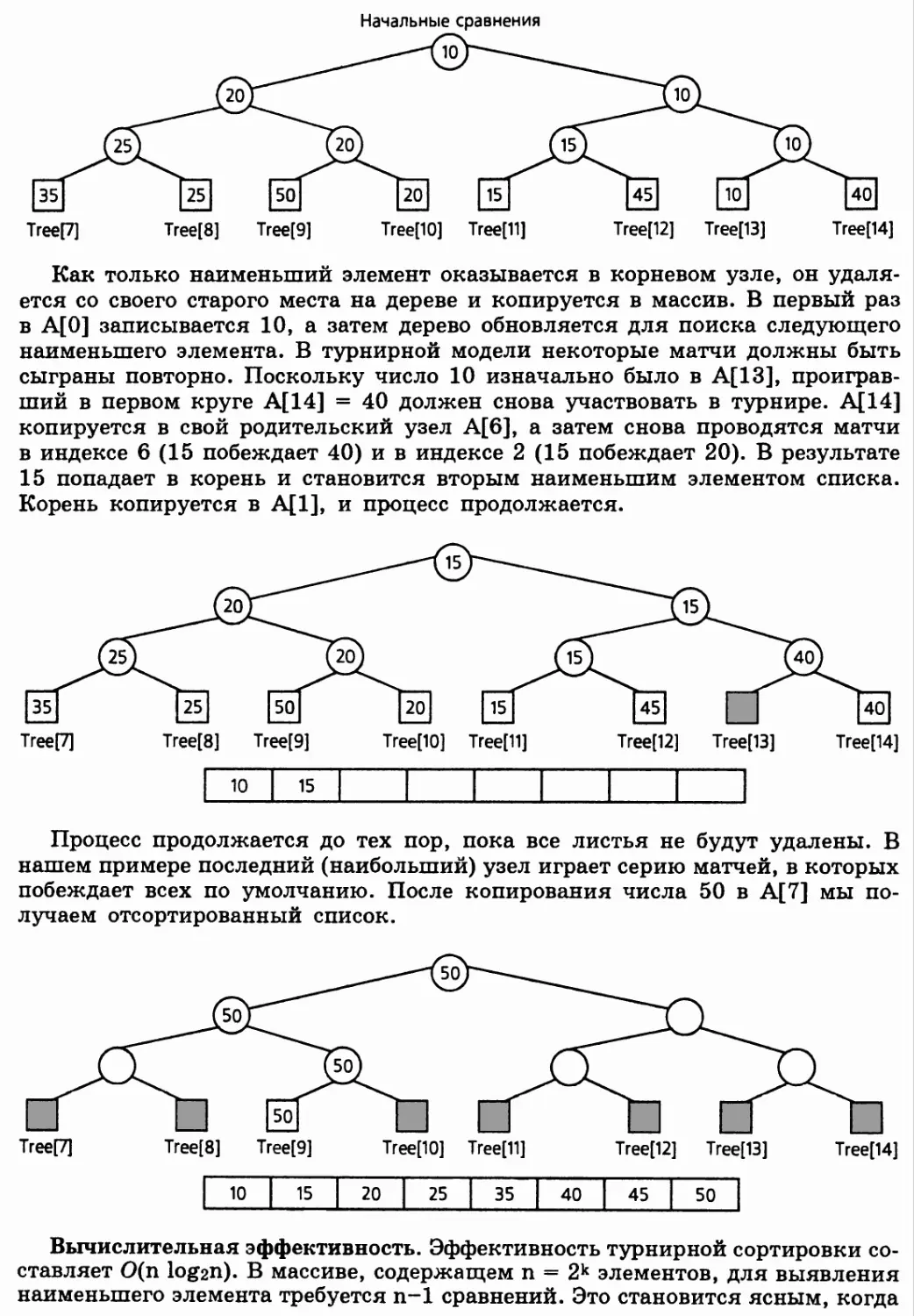
Приложение: турнирная сортировка 602
13.2. Пирамиды 607
Пирамида как список 607
Класс Heap 609
13.3. Реализация класса Heap 612
Приложение: пирамидальная сортировка 618
13.4. Очереди приоритетов 621
Приложение: длинные последовательности 622
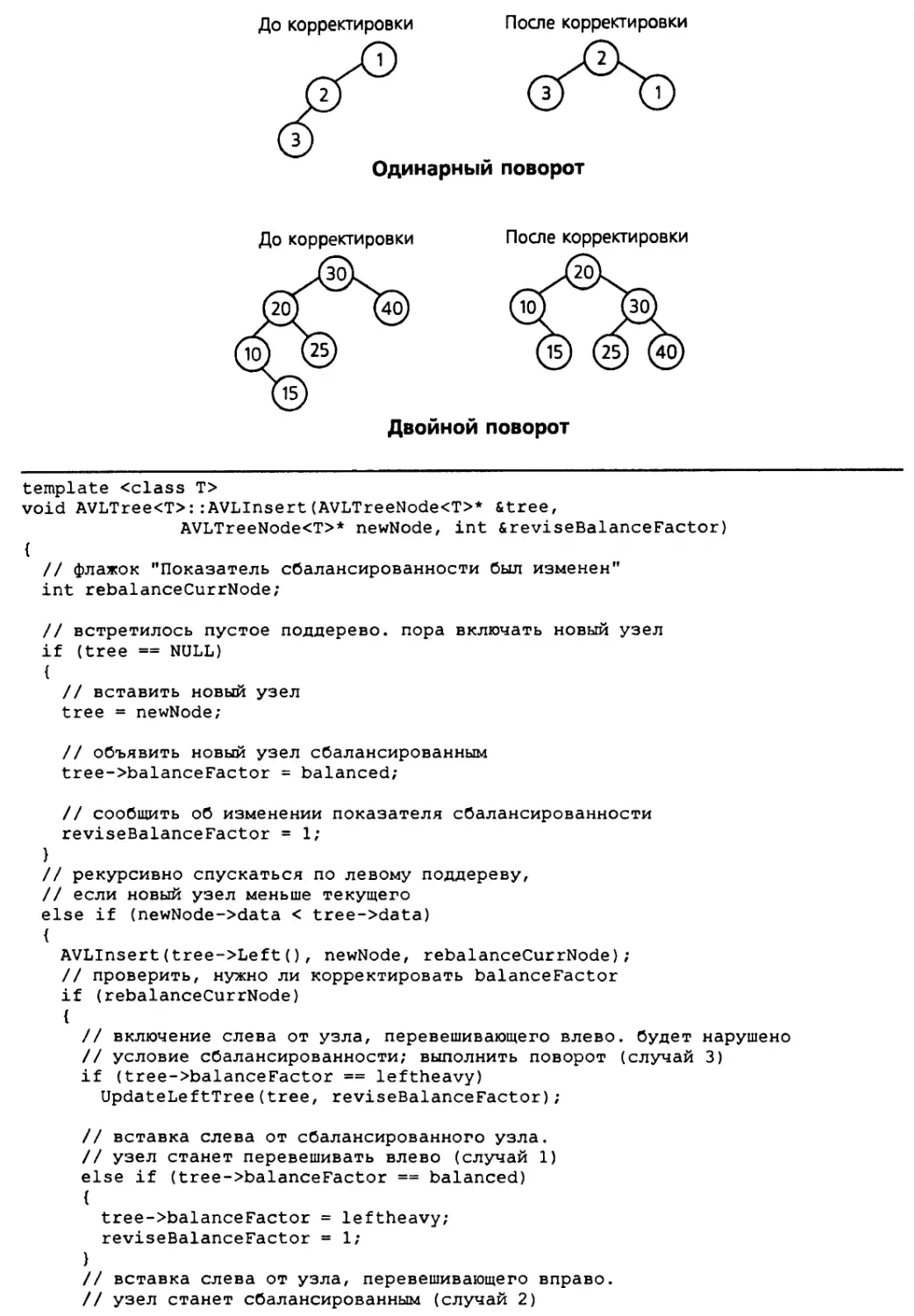
13.5. AVL-деревья 627
Узлы AVL-дерева 628
13.6. Класс AVLTree 631
Распределение памяти для AVLTree 633
Оценка сбалансированных деревьев 640
13.7. Итераторы деревьев 642
Итератор симметричного метода прохождения 643
Реализация класса Inorderlterator . 644
Приложение: алгоритм TreeSort 646
13.8. Графы 647
Связанные компоненты 648
13.9. Класс Graph 649
Объявление абстрактного типа данных Graph 649
Реализация класса Graph 653
Способы прохождения графов 656
Приложения 659
Достижимость и алгоритм Уоршалла 666
Письменные упражнения 669
Упражнения по программированию 678
Глава 14. Организация коллекций 683
14.1. Основные алгоритмы сортировки массивов 684
Сортировка посредством выбора 684
Сортировка методом пузырька 686
Вычислительная сложность сортировки методом пузырька 688
Сортировка вставками 688
14.2. "Быстрая сортировка" 690
Описание "быстрой сортировки" 690
Алгоритм Quicksort 693
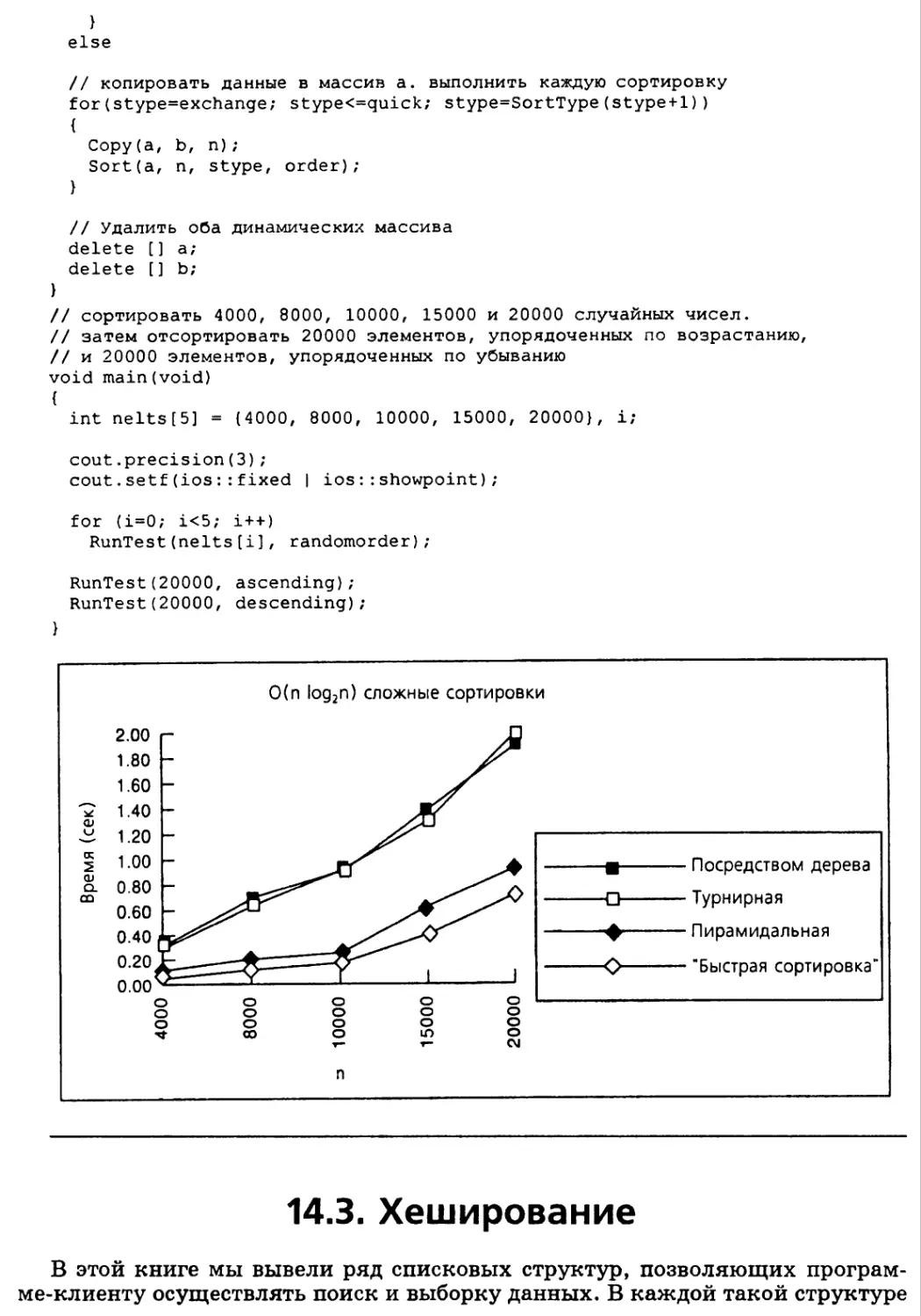
Сравнение алгоритмов сортировки массивов 696
14.3. Хеширование 700
Ключи и хеш-функция 701
Хеш-функции 702
Другие методы хеширования ". . 704
Разрешение коллизий 704
14.4. Класс хеш-таблиц 707
Приложение: частота символьных строк 709
Реализация класса HashTable 711
Реализация класса HashTablelterator 712
14.5. Производительность методов поиска 714
14.6. Бинарные файлы и операции с данными на внешних носителях 715
Бинарные файлы 716
Класс BinFile 718
Внешний поиск 723
Внешняя сортировка 727
Сортировка естественным слиянием 729
14.7. Словари 735
Письменные упражнения 742
Упражнения по программированию 748
Приложение.
Ответы на избранные письменные упражнения 753
Предметный указатель 775
Index 795
Предисловие
Книга посвящается Дэвиду Джонстоуну, редактору.
Он разделял наше видение предмета. Несмотря на его трагическую гибель
в результате акта бессмысленного насилия, мы сохранили это видение в
нашей работе. Мы надеемся, что это — вклад, достойный его памяти.
Решение проблемы
Разработка программы
Структуры
данных
Программирование
Алгоритмы
Эта книга предназначена для представления основных структур данных
с точки зрения объектно-ориентированной перспективы. Изучение структур
данных является ядром курса обучения информатике. Оно предоставляет
богатый контекст для изучения методов решения задач и разработки
программ и использует мощные конструкции и алгоритмы программирования.
Эта книга использует гибкий язык C++, классы и
объектно-ориентированные конструкции которого конкретно предназначаются для эффективной
реализации структур данных. Хотя существует ряд
объектно-ориентированных языков, C++ имеет преимущество вследствие его развития из
популярного языка программирования С и использования многими продавцами
программного обеспечения. Мы развиваем каждую структуру данных вокруг
понятия абстрактного типа данных (abstract data type, ADT), которое
определяет как организацию данных, так и операции их обработки. Нас
поддерживает C++, обеспечивающий тип класса для представления ADT и
эффективное использование этих структур в каком-либо объекте.
Структура книги
Книга "Структуры данных в C++" организует изучение структур данных
вокруг классов коллекций, которые включают списки, деревья, множества,
графы и словари. В процессе изучения мы охватываем основные темы
структур данных и разрабатываем методологию объектно-ориентированного
программирования. Эти структуры и методология реализуются в ряде
законченных программ и практических задач. Для оценки эффективности алгоритмов
мы вводим понятие записи "Big-O".
В главах 1-11 излагаются традиционные темы первого курса по структурам
данных (CS 2). Формальная трактовка наследования и виртуальных функций
приводится в главе 12, и эти темы используются для реализации структур
данных повышенной сложности в главах 13 и 14. Материал в главах 12-14
определяет темы, традиционно излагаемые в курсе по структурам
данных/алгоритмам повышенной сложности (CS 7) и в курсе по продвинутому
программированию. Мы включаем подробную разработку шаблонов и перегрузку
операторов для поддержки общих структур и применяем эти мощные
конструкции языка C++, чтобы упростить использование структур данных.
Профессиональный программист может использовать "Структуры данных
в C++" как самоучитель по структурам данных, который сделает возможным
понимание большинства библиотек классов, научно-исследовательских статей
и профессиональных изданий повышенной сложности.
Описание глав
В большинстве глав книги разрабатываются абстрактные типы данных и
описывается их реализация как класса C++. Объявление каждого класса и
его ключевых методов также включены в эту книгу. Во многих случаях
приводится полное определение, в некоторых случаях даются определения
избранных методов классов. Полная реализация классов включена в
программное приложение.
Глава 1. Введение
Эта глава является обзорной и знакомит с абстрактными типами данных
и объектно-ориентированным программированием с использованием C++.
Разрабатывается понятие ADT и относящиеся к нему атрибуты инкапсуляции
данных и скрытия информации. Глава также знакомит с наследованием и
полиморфизмом, которые формально излагаются в главе 12.
Глава 2. Базовые типы данных
Языки программирования предоставляют простые числовые и символьные
типы, которые охватывают целые числа и числа с плавающей точкой,
символьные данные и определяемые пользователем перечислимые типы. Простые
типы объединяются для создания массивов, записей, строковых и файловых
структур. Эта глава описывает ADT для типов языков, используя C++ в
качестве примера.
Глава 3. Абстрактные типы данных и классы
В этой книге в целом формально рассматриваются абстрактные типы
данных и их представление в качестве классов C++. Конкретно эта глава
определяет основные понятия класса, включая данные-члены, конструкторы и
определения методов.
Глава 4. Классы коллекций
Коллекция — это класс памяти с инструментами обработки данных для
добавления, удаления или обновления элементов. Изучение классов
коллекций находится в центре внимания этой книги. Поэтому в данной главе
содержится пример различных типов коллекций, представленных в книге.
Глава включает простое введение в запись "Big-O", которая позволяет
определить эффективность какого-либо алгоритма. Эта запись используется на
протяжение всей книги для сравнения и сопоставления различных
алгоритмов. Глава завершается изучением класса SeqList, являющегося прототипом
общей списочной структуры.
Глава 5. Стеки и очереди
В этой главе обсуждаются стеки и очереди, которые являются основными
классами, поддерживающими данные в порядке LIFO ("последний пришел —
первый вышел") и FIFO ("первый пришел — первый вышел"). В ней
разрабатывается также очередь приоритетов, модифицированная версия очереди,
в которой клиент всегда удаляет из списка элемент с наивысшим
приоритетом. В практическом примере используются очереди приоритетов для
управляемого событиями моделирования.
Глава 6. Абстрактные операторы
Абстрактный тип данных определяет набор методов для инициализации
и управления данными. В этой главе мы расширяем определяемые языком
программирования операторы (например, +, *, < и так далее) до абстрактных
типов данных. Процесс, называемый перегрузкой операторов, переопределяет
стандартные символы операторов для реализации операций в ADT. Полностью
разработанный класс рациональных чисел иллюстрирует перегрузку
операторов и преобразование типов, а также введение дружественных функций
для перегрузки стандартных операторов ввода/вывода C++.
Глава 7. Параметризованные типы данных
C++ использует шаблонный механизм для предоставления
параметризованных функций и классов, поддерживающих различные типы данных.
Шаблоны обеспечивают мощную параметризацию структур данных. Эту
концепцию иллюстрирует основанная на шаблоне версия класса Stack и ее
применение в вычислении инфиксного выражения.
Глава 8. Классы и динамическая память
Динамические структуры данных используют память, выделяемую
системой во время исполнения приложения. Они позволяют определять структуры
без ограничений по размеру и увеличивают возможность использования
классов. Однако их применение требует особого внимания. Мы вводим
конструктор копирования, перегруженный оператор присваивания и методы
деструктора, позволяющие правильно копировать и присваивать динамические данные,
а затем освобождать их при удалении объекта. Возможности динамических
данных иллюстрируют классы Array, String и Set. Эти классы используются
и далее в книге.
Глава 9. Связанные списки
Использование списков для хранения и выборки данных является темой,
обсуждаемой на протяжение всей книги, поскольку списки очень важщ^ для
разработки большинства приложений данных. Эта глава знакомит со
связанными списками, позволяющими выполнять динамическую обработку списков.
Мы используем двойной подход, при котором сначала разрабатывается
базовый класс узлов и создаются функции для добавления и удаления элементов
из списка. Более абстрактный подход создает класс связанных списков со
встроенным механизмом прохождения для обработки элементов в списке.
Класс LinkedList используется для реализации класса SeqList и Queue. В
каждом случае объект связанного списка включается композицией. Этот
подход предоставляет мощный инструмент для разработки структур данных. В
этой главе обсуждаются также циклические и двусвязные списки, имеющие
интересное применение. Глава содержит также практическую задачу очереди
для принтера.
Глава 10. Рекурсия
Рекурсия — это важный инструмент решения задач как в информатике,
так и в математике. Мы описываем рекурсию и показываем ее использование
в различном контексте. Ряд приложений используют рекурсию с
математическими формулами, комбинаторикой и головоломками. Последовательность
Фибоначчи используется для сравнения эффективности рекурсивного
алгоритма, итеративного алгоритма или прямых вычислений при определении
терма последовательности.
Глава 11. Деревья
Связанные списки определяют множество узлов с последовательным
доступом, начиная с головы. Эта структура данных называется линейным
списком. Во многих приложениях объекты сохраняются в нелинейном порядке,
в котором элемент может иметь множество последователей. В главе 11 мы
вводим базовую нелинейную структуру, называемую деревьями, в которой
все элементы данных происходят из единого источника — корня. Дерево
является идеальной структурой для описания иерархической структуры,
такой как компьютерная файловая система или таблица бизнес-отчета. В
этой главе мы ограничиваем анализ бинарными деревьями, в которых
каждый узел имеет самое большее два наследника. Мы разрабатываем класс
TreeNode для реализации этих деревьев и представляем приложения,
включающие классические алгоритмы прямого, симметричного и обратного
сканирования. Бинарные деревья находят применение в качестве списочной
структуры, эффективно сохраняющей большие объемы данных. Эта
структура, называемая деревом бинарного поиска, реализуется в классе BinSTree.
Класс представлен в практической задаче, которая разрабатывает конкорданс.
Глава 12. Наследование и абстрактные классы
Наследование является основным понятием объектно-ориентированного
программирования. В этой главе обсуждаются основные свойства
наследования, подробно разрабатывается его реализация в C++ и вводятся виртуальные
функции как инструменты, использующие возможности наследования.
Разрабатывается также понятие абстрактного базового класса с чистыми
виртуальными функциями. Виртуальные функции являются основными для
объектно-ориентированного программирования и используются последующими
темами в этой книге. Глава знакомит с итераторами, определяющими
однородный и общий механизм прохождения для различных списков и
завершается примером наследования и виртуальных функций для разработки
неоднородных массивов и связанных списков.
Глава 13. Нелинейные структуры повышенной сложности
Эта книга продолжает разработку бинарных деревьев и вводит
дополнительные нелинейные структуры. В ней описываются основанные на массиве
деревья, моделирующие массив как законченное бинарное дерево.
Предоставляется также обширное изучение пирамид, и это понятие используется для
реализации пирамидальной сортировки и очередей приоритетов. Хотя деревья
бинарного поиска обычно являются хорошими структурами для реализации
списка, вырожденные случаи могут быть неэффективными. Структуры
данных предоставляют различные структуры со сбалансированной высотой,
обеспечивающие быстрое среднее время поиска. Используя наследование,
выводится новый класс дерева поиска, называемый AVL-деревьями. Глава
завершается введением в графы, представляющим ряд классических алгоритмов.
Глава 14. Организация коллекций
В этой главе рассматриваются алгоритмы поиска и сортировки для общих
коллекций и разрабатываются классические основанные на массиве
алгоритмы сортировки выбором, пузырьковой сортировки и сортировки вставками.
Наше исследование включает известный алгоритм "быстрой сортировки"
Quicksort. В этой книге особенно выделяются данные, сохраняемые во
внутренней памяти. Для более обширных множеств данные могут сохраняться
на диске. Можно также использовать внешние методы для поиска и
сортировки данных. Мы разрабатываем класс BinFile для прямого файлового
доступа и используем его методы для иллюстрации как алгоритма внешнего
индексного последовательного поиска, так и алгоритма внешней сортировки
слиянием. Раздел, посвященный ассоциативным массивам, обобщает понятие
индекса массива.
Необходимая подготовка
Эта книга предполагает, что читатель закончил первый курс
программирования и свободно владеет базовым языком C++. Глава 2 определяет простые
структуры данных C++ и показывает их использование в нескольких
законченных программах. Эта глава может использоваться как стандарт для
определения необходимых предпосылок C++. Для заинтересованного читателя
авторы предоставляют учебник по C++, определяющий простые типы языка
и синтаксис для массивов, управляющих структур, ввода/вывода, функций
и указателей. Учебник включает обсуждение каждой темы вместе с
примерами, законченными программами и упражнениями.
Приложения
Полные листинги исходных кодов для всех классов и программ доступны
через канал Internet ftp из University of the Pacific, где работают авторы.
Код C++ в этой книге протестирован и выполнен с использованием новейшего
компилятора фирмы "Borland". За очень небольшими исключениями, эти
программы можно компилировать и выполнять в системе Macintosh,
используя Symantec C++ и в системе Unix, используя GNU C++.
Те, кто имеют канал Internet, используйте адрес ftp.cs.uop.edu. После
соединения с системой ваше логическое имя является анонимным а ваш
пароль — это ваш mail-адрес Internet. Программное обеспечение находится
в каталоге "/риЬ/С-Ь+".
Читатели могут обращаться непосредственно к авторам для получения
копии учебника. Информация для заказа предоставляется по электронной
почте: посылайте запрос по адресу "billf@uop.edu", или по международной
почте: пишите Bill Тор, 456 S. Regent Stockton, CA 95204.
Благодарности
Во время подготовки книги "Структуры данных в C++" авторам оказывали
поддержку друзья, студенты и коллеги. University of the Pacific щедро
предоставлял ресурсы и поддержку для завершения проекта. Издательство
"Prentice Hall" обеспечило преданную делу команду профессионалов, выполнивших
дизайн и производство книги. Мы особенно благодарны редакторам Элизабет
Джоунз, Биллу Зобристу и Алану Апту и выпускающему редактору Байани
де Леону. Выпуск реализован совместно Spectrum Publisher Services и Prentice
Hall. Большую помощь нам оказали Келли Риччи и Кристин Миллер из
Spectrum.
Студенты проявили ценный критицизм при обсуждении рукописи,
обеспечивая обратную связь и непредвзятый взгляд на работу. Наши рецензенты
оказывали помощь в начале работы над книгой, предоставляя комментарии
как по содержанию, так и по педагогическим аспектам. Мы учли большинство
из их рекомендаций. Особая благодарность Хамиду Р. Арабниа (University
of Georgia), Рхода А. Ваггс (Florida Institute of Technology), Сандре Л. Барлетт
(University of Michigan — Ann Arbor), Ричарду Т.Клоузу (U.S. Coast Guard
Academy), Дэвиду Куку (U.S. Air Force Academy), Чарльзу Дж. Доулингу
(Catonsville (Baltimore County) Community College), Дэвиду Дж. Хаглину
(Mancato State University), Джиму Мерфи (California State University — Chico)
и Герберту Шилдту. Наши коллеги Ральф Эутон (University of Texas — El
Paso) и Дуглас Смит (University of the Pacific) внесли большой вклад в эту
работу. Их взгляды и поддержка были бесценны для авторов и значительно
улучшили окончательную структуру книги.
Уильям Форд
Уильям Топп
глава
1
Введение
1.1. Абстрактные типы данных
1.2. Классы C++ и абстрактные типы
1.3. Объекты в приложениях C++*
1.4. Разработка объектов
1.5. Приложения с наследованием
классов
1.6. Разработка
объектно-ориентированных программ
1.7. Тестирование и сопровождение
программ
1.8. Язык программирования C++
1.9. Абстрактные базовые классы и
полиморфизм*
Письменные упражнения
В этой книге разрабатываются структуры данных и алгоритмы в контексте
объектно-ориентированного программирования с использованием языка C++.
Мы разрабатываем каждую структуру данных как абстрактный тип, который
определяет и организацию, и операции обработки данных. Структура,
называемая абстрактный тип данных (abstract data type, ADT), — это абстрактная
модель, описывающая интерфейс между клиентом (пользователем) и этими
данными. Используя язык C++, мы разрабатываем представление каждой
абстрактной структуры. Язык C++ поддерживает определяемый
пользователем тип, называемый классом (class), для представления ADT и элементы
этого типа, называемые объектами (objects), для хранения и обработки
данных в приложении.
В данной главе вводится понятие ADT и относящихся к нему атрибутов,
называемое инкапсуляцией данных и скрытием информации. С помощью
серии примеров мы показываем разработку ADT и создаем формат для
определения организации данных и операций.
Понятие конструктора класса в C++ является фундаментальным в нашем
изучении структур данных и формально разрабатывается в главе 3. В данной
главе мы начинаем с обзора класса C++ и рассматриваем его использование
для представления какого-либо ADT. Необязательные разделы, помеченные
символом звездочки (*), содержат примеры классов C++. В этой главе дается
обзор разработки объектов, которая включает композицию объектов и
наследование. Эти понятия являются строительными блоками
объектно-ориентированного программирования. Глава включает основы разработки программ для
построения более крупных приложений и изучения этой книги. Наследование
и полиморфизм расширяют возможности объектно-ориентированного
программирования и позволяют разрабатывать большие системы программирования
на основе библиотек классов. Эти темы тщательно разрабатываются в главе 12
и используются выборочно для представления улучшенных структур данных.
В данной главе предварительно рассматриваются темы, представленные в
книге. Вы познакомитесь с ключевыми структурами данных и
объектно-ориентированными понятиями до их формального рассмотрения.
1.1. Абстрактные типы данных
Абстракция данных — центральное понятие в разработке программ.
Абстракция определяет область и структуру данных вместе с набором операций,
которые имеют доступ к данным. Абстракция, называемая абстрактным
типом данных (ADT), создает определяемый пользователем тип данных, чьи
операции указывают, как клиент может манипулировать этими данными.
ADT является независимым от реализации и позволяет программисту
сосредоточиться на идеализированных моделях данных и оперяттхтстх над ними.
Пример 1.1
1. Программа учета для малого предприятия сопровождает
инвентаризационную информацию. Каждый элемент в описи представлен
записью данных, которая включает идентификационный номер этого
элемента, текущий уровень запаса, ценовую информацию и
информацию упорядочивания. Набор операций по обработке списка об-
новляет различные информационные поля и инициирует
переупорядочивание запаса, когда его уровень падает ниже определенного
порога. Абстракция данных описывает какой-либо элемент как
запись, содержащую серию информационных полей и операций,
необходимых менеджеру компании для инвентаризационного
сопровождения. Операции могут включать изменение значения Stock on
Hand (имеющийся запас) при продаже этого товара, изменение Unit
Price (цены за единицу) при использовании новой ценовой политики
и инициализации упорядочивания при падении уровня запаса ниже
уровня переупорядочивания (Reorder Level).
Данные
Identification
Stock on Hand
Unit Price
Reorder Level
Операции
UpdatestoekLevel
AdjustUnitPrice
Reorderltem
2. Игровая программа моделирует бросание набора костей. В этой
разработке игральные кости описываются как абстрактный тип данных,
которые включают число бросаемых костей, сумму очков в
последнем бросании и список со значениями очков каждой кости в
последнем бросании. Операции включают бросание костей (Toss),
возвращение суммы очков в одном бросании (Total) и вывод очков для
каждой отдельной кости (DisplayToss).
Данные
N
diceTotai
Dice List
Операции
Toss
Total
DisplayToss
ADT — формат
Для описания ADT используется формат, который включает заголовок с
именем ADT, описание типа данных и список операций. Для каждой операции
определяются входные (input) значения, предоставляемые клиентом,
предусловия (preconditions), применяемые к данным до того, как операция может быть
выполнена, и процесс (process), который выполняется операцией. После
выполнения операции определяются выходные (output) значения, которые
возвращаются клиенту, и постусловия (postconditions), указывающие на любые
изменения данных. Большинство ADT имеют инициализирующую операцию
(initializer), которая присваивает данным начальные значения. В среде языка C++ такой
инициализатор называется конструктором (constructor). Мы используем этот
термин для упрощения перехода от ADT к его преставлению в C++.
APT — формат
ADT ADTJName
Данные
Описание структуры данных
Операции
Конструктор
Начальные значения: Данные, используемые для инициализации объекта
Процесс: Инициализация объекта
Операция2
Вход: Данные от клиента
Предусловия: Необходимое состояние системы
перед выполнением операций
Процесс: Действия, выполняемые с данными
Выход: Данные, возвращаемые клиенту
Постусловия: Состояние системы после выполнения операций
Операция2
* • •
Операцияп
* • •
Конец ADT
Пример 1.2
1. Данные абстрактного типа Dice включают счетчик N числа
игральных костей, которые используются в одном бросании, общую сумму
очков и список из N элементов, который содержит значения очков,
выпавших на каждой кости.
ADT Dice
Данные
Число костей в каждом бросании — целое, большее либо равное 1. Целое
значение, содержащее сумму очков всех костей в последнем бросании.
Если N — число бросаемых костей, то число очков находится в диапазоне
от N до 6N. Список, содержащий число очков каждой кости в бросании.
Значение любого элемента списка находится в диапазоне от 1 до 6.
Операции
Конструктор
Начальные значения: Число бросаемых костей
Процесс: Инициализировать данные, определяющие число
костей в каждом бросании
Toss
Вход: Нет
Предусловия: Нет
Процесс: Бросание костей и вычисление общей суммы очков
Выход: Нет
Постусловия: Общая сумма содержит сумму очков в бросании,
а в списке находятся очки каждой кости
DieTotal
Вход: Нет
Предусловия: Нет
Процесс: Находит значение элемента, определяемого как
сумма очков в последнем бросании
Выход: Возвращает сумму очков в последнем бросании
Постусловия: Нет
DisplayToss
Вход: Нет
Предусловия: Нет
Процесс: Печатает список очков каждой кости
в последнем бросании
Выход: Нет
Постусловия: Нет
конец ADT Dice
2. Окружность определяется как набор точек, равноудаленных от
точки, называемой центром. С целью графического отображения
абстрактный тип данных для окружности включает как радиус
(radius), так и положение центра. Для измеряющих приложений
абстрактному типу данных требуется только радиус. Мы
разрабатываем Circle ADT и включаем операции для вычисления площади
(area) и длины окружности (circumference). Этот ADT применяется
в следующем разделе для иллюстрации описания класса C++ и
использования объектов при программировании приложений.
radius
radius
Circumference
Area
ADT Circle
Данные
Неотрицательное действительное число, определяющее радиус окружности.
Операции
Конструктор
Начальные значения: Радиус окружности
Процесс: Присвоить радиусу начальное значение
Area
Вход: Нет
Предусловия Нет
Процесс: Вычислить площадь круга
Выход: Возвратить площадь круга
Постусловия: Нет
Circumference
Вход: Нет
Предусловия Нет
Процесс: Вычислить длину окружности
Выход: Возвратить длину окружности
Постусловия: Нет
конец ADT Circle
1.2. Классы C++ и абстрактные типы
Язык C++ поддерживает определяемый пользователем тип классов для
представления абстрактных типов данных. Класс состоит из членов
(members), которые включают значения данных и операции по обработке этих
данных. Операции также называются методами (methods), поскольку они
определяют методы доступа к данным. Переменная типа класса называется
объектом (object). Класс содержит две отдельные части. Открытая (public)
часть описывает интерфейс, позволяющий клиенту манипулировать
объектами типа класса. Открытая часть представляет ADT и позволяет клиенту
Класс
private:
Данные-члены: переменнаяь переменнаяг
Внутренние операции
public:
Конструктор
Операция1
Операцияг
использовать объект и его операции без знания внутренних деталей
реализации. Закрытая (private) часть содержит данные и внутренние операции,
помогающие в реализации абстракции данных. Например, класс для
представления ADT Circle содержит один закрытый член класса — radius.
Открытые члены включают конструктор и методы вычисления площади круга
и длины окружности
Circle Класс
private:
radius
public:
Конструктор
Area
Circumference
Инкапсуляция и скрытие информации
Класс инкапсулирует (encapsulates) информацию, связывая вместе члены
и методы и обращаясь сними как с одним целым. Структура класса скрывает
реализацию деталей и тщательно ограничивает внешний доступ как к
данным, так и к операциям. Этот принцип, известный как скрытие информации
(information hiding), защищает целостность данных.
Класс использует свои открытую и закрытую части для контроля за
доступом клиентов к данным. Члены внутри закрытой части используются
методами класса и изолированы от внешней среды. Данные обычно
определяются в закрытой части класса для предотвращения нежелательного доступа
клиента. Открытые члены взаимодействуют с внешней средой и могут
использоваться клиентами.
Например, в Circle-классе radius является закрытым членом класса, доступ
к которому может осуществляться только тремя методами. Конструктор
присваивает начальное значение члену radius. Каждый из других методов
использует radius. Например, area = р * raduis2. Здесь методы являются
открытыми членами класса, которые могут вызываться всеми внешними
единицами программы.
Передача сообщений
В приложении доступ клиентов к открытым членам какого-либо объекта
может быть реализован вне этого объекта. Доступом управляют главная
программа и подпрограммы (master control modules), которые наблюдают за
взаимодействием между объектами. Управляющий код руководит объектом
для доступа к его данным путем использования одного из его методов или
операций. Процесс управления деятельностью объектов называется передачей
сообщений (message passing). Отправитель передает сообщение получающему
объекту и указывает этому объекту выполнить некоторую задачу.
В нужный момент отправитель включает в сообщение информацию,
которая используется получателем. Эта информация передается как данные
ввода для операции. После выполнения задачи получатель может возвращать
информацию отправителю (данные вывода) или передавать сообщения другим
объектам, запрашивая выполнение дополнительных задач. Когда
получающий объект выполняет операцию, он может обновлять некоторые из его
собственных внутренних значений. В этом случае считается, что происходит
изменение состояния (state change) объекта и возникают новые постусловия.
1.3. Объекты в приложениях C++*
Абстрактный тип данных реализует общее описание данных и операций
над данными. Класс C++ обычно вводится сначала объявлением этого класса
без определения функций-членов. Это известно как объявление класса (class
declaration) и является конкретным представлением ADT. Фактическое
определение методов дается в реализации класса (class implementation),
отдельной от объявления.
Реализация классов C++ и использование объектов иллюстрируются
следующей завершенной программой, которая определяет стоимость планировки
бассейна. Программа объявляет Circle класс и показывает, как определяются
и используются объекты. В коде содержатся определения открытого и
закрытого разделов класса и используются функции C++ для определения
операций. Главная программа — это клиент, который объявляет объекты,
и затем использует их операции для выполнения вычислений. Главная
программа отвечает за передачу всех сообщений в приложении.
Приложение: класс Circle
Объекты Circle используются для описания плавательного бассейна и
дорожки вокруг него. С помощью методов Circumference (вычисление длины
окружности) и Area (вычисление площади круга) мы можем вычислить
стоимость бетонирования дорожки и строительства ограды вокруг бассейна. К
нашему приложению применяются следующие условия.
Строительные правила требуют, чтобы плавательный бассейн окружала
бетонная дорожка (темная область на следующем рисунке) и вся территория
была огорожена. Текущая стоимость ограды составляет $ 3,50 за погонный
фут, а стоимость бетонирования — $ 0,5 за кв. фут. Приложение
предполагает, что ширина дорожки, окружающей бассейн, составляет, 3 фута и что
клиент указывает радиус круглого бассейна. В качестве результата
приложение должно определить стоимость строительства ограды и дорожки при
планировании бассейна.
Pool
PoolRim
Мы объявляем объект Circle с именем Pool, описывающий площадь
плавательного бассейна. Второй объект — PoolRim, — это объект Circle,
включающий как бассейн, так и окружающую дорожку. Конструктор вызывается
при определении объекта. Для объекта Pool клиент задает радиус в качестве
параметра, и затем использует радиус плюс 3 фута для определения объекта
PoolRim.
Для вызова операции класса задайте имя объекта, за которым следует
точка (.) и операция. Например, Роо1.Агеа() и Circumference() вызывают
операции Circle для Pool.
Ограда располагается вдоль наружной стороны PoolRim. Вызовите
операцию вычисления окружности PoolRim.Circumference() для вычисления
стоимости ограды.
FenceCost = PoolRim.Circumference() * 3.50
Площадь бетонной поверхности определяется вычитанием площади Pool
из внешней площади PoolRim.
ConcreteCost = (PoolRim.Area() - Pool.Area()) * 0.5
Программа 1.1. Конструкция и использование класса Circle
Программа 1.1 реализует приложение для бассейна. Для оказания
помощи в чтении кода C++ в тексте имеются комментарии. Объявление
класса Circle показывает представление Circle ADT и использование
закрытых и открытых директив для контроля за доступом к членам класса.
Главная программа запрашивает клиента ввести радиус бассейна. Это
значение используется для объявления объекта Pool. Второй объект —
PoolRim объявляется как имеющий дополнительные три фута к его
радиусу для размещения дорожки вокруг бассейна. Стоимость строительства
ограды и стоимость бетонирования дорожки выводятся для печати.
Вне главного модуля программа определяет класс Circle. Читатель может
обратить внимание на использование спецификатора const для указания на
то, что функция-член не изменяет данные. Этот спецификатор используется
с методами Circumference и Area в их объявлении и определении. Стоимость
строительных материалов для сетки ограды и стоимость бетона задаются
как константы.
// рг01_01.срр
#include <iostream.h>
const float PI = 3.14152;
const float FencePrice - 3.50;
const float ConcretePrice = 0.50;
// Объявление класса Circle, данных и методов
class Circle
{
private:
// член класса radius — число с плавающей запятой
float radius;
public:
// конструктор
Circle(float r);
// вычисляющие функции
float Circumference(void) const;
float Area(void) const;
};
// class implementation
// конструктор инициализирует член класса radius
Circle::Circle(float r): radius(r)
{ )
// возвратить длину окружности
float Circle::Circumference(void) const
{
return 2 * PI * radius;
}
// возвратить площадь круга
float Circle::Area(void) const
{
return PI * radius * radius;
}
void main()
{
float radius;
float FenceCost, ConcreteCost;
// настраивает поток вывода на выдачу двух знаков
// после десятичной точки
cout.setf(ios::fixed);
cout.setf(ios::showpoint);
cout.precision(2) ;
// запрос па ввод радиуса
cout « "Введите радиус бассейна: ";
cin » radius;
// объявить объекты Circle
Circle Pool (radius) ;
Circle PoolRim(radius + 3) ;
// вычислить стоимость ограды и выдать ее значение
FenceCost = PoolRim.Circumference() * FencePrice;
cout « "Стоимость ограды: $" « FenceCost « endl;
// вычислить стоимость бетона и выдать ее значение
ConcreteCost = (PoolRim.Area() - Pool.Area{))*ConcretePrice;
cout « "Стоимость бетона: $" « ConcreteCost « endl;
}
/*
Запуск программы pr01_01. cpp
Введите радиус бассейна: 40
Стоимость ограды: $945.60
Стоимость бетона: $391.12
*/
1.4. Разработка объектов
В этой книге разрабатываются структуры данных с классами и объектами.
Мы начинаем с классов, которые определяются простыми данными-членами
и операциями класса. Для более сложных структур классы могут содержать
члены класса, которые сами являются объектами. Результирующие классы,
созданные посредством композиции (composition), имеют доступ к
функциям-членам в составляющих объектах. Использование композиции объектов
расширяет понятия инкапсуляции и скрытия информации и обеспечивает
повторное использование кода. Объектно-ориентированные языки также
позволяют классу быть порожденным из других классов путем наследования
(inheritance). Это дает возможность разработчику создавать новые классы
как усовершенствования других классов и повторно использовать код,
который был разработан ранее. Наследование является фундаментальным
средством объектно-ориентированного программирования на языке C++. Эта тема
вводится формально в главе 12 и используется для разработки и реализации
улучшенных структур данных.
Объекты и композиция
Геометрические фигуры состоят из наборов точек, которые образуют линии,
прямоугольники и т.д. Основными строительными блоками фигур являются
точки, сочетающиеся с серией аксиом для определения геометрических
объектов. В данном разделе мы рассматриваем точку как примитивный
геометрический объект, а затем описываем линии и прямоугольники. Эти
геометрические фигуры используются для иллюстрации объектов и композиции.
Точка — это местоположение на плоской поверхности. Мы предполагаем,
что объект точка расположена на сетке с координатами, которые измеряют
горизонтальное (х) и вертикальное (у) расстояние от базовой точки. Например,
точка р (3,1) находится на 3 единицы измерения правее и 1 единицу ниже
базовой точки.
Линия образуется из точек, а две точки определяют линию. Последний
факт используется для создания модели отрезка (line segment), который
определяется своими конечными точками pi и р2 [Рис. 1.1 (А)].
базовая точка
Прямоугольник — это четырехсторонняя фигура, чьи смежные стороны
встречаются в прямых углах. Для рисования прямоугольник определяется
двумя точками, которые отмечают верхний левый угол (ul) и нижний правый
угол (1г) рамки [Рис. 1.1 (В)].
(А) Отрезок Цр1, р2)
(В) Прямоугольник R(ul, lr)
Рис. 1.1. Отрезок и прямоугольник
Мы используем эти факты для создания классов Point, Line и Rectangle.
Члены в классах Line и Rectangle являются объектами типа Point.
Композиция — это важный инструмент в создании классов с объектами из других
классов. Заметьте, что каждый класс имеет метод Draw для отображения
рисунка на поверхности рисования. Класс Point содержит функции-члены
для доступа к координатам х и у точки.
Класс Point
private:
х у координаты
public
Конструктор, Draw,
GetX, detY
Класс Line
private:
Point pi, p2
public
Конструктор,
Draw
Класс Rectangle
private:
Point ul, lr
public:
Конструктор,
Draw
Пример 1.3
Определите геометрический объект, задавая фигуру, за которой следуют
имя объекта и параметры для указания объекта.
1. Point p(l,3); // объявляет объект point (1,3)
2. Point pl(4,2), p2(5,lb-
Line 1(р1,р2); // линия: от (4,2) до (5,1)
3. Point pl(4,3), р2(6,4);
Rectangle r(pl,p2); // прямоугольник: от (4,3) до р2(б,4)
4. Метод Draw в каждом классе делает наброски рисунка на
поверхности рисования.
p.DrawO; l.DrawO; r.DrawO;
Методы Draw
C++ геометрические классы*
Далее следуют объявления C++ для классов Point и Line. Заметьте, что
конструктору для класса Line передаются координаты двух точек,
определяющих линию. Каждый класс имеет функцию-член Draw, отображающую
рисунок в области рисования.
Спецификация класса Point
ОБЪЯВЛЕНИЕ
class Point
{
private:
float x, у; // горизонтальная и вертикальная позиция
public:
Point (float h, float v);
float GetX(void) const; // возвратить координату х
float GetY(void) const; // возвратить координату у
void Draw(void)Jconst; // нарисовать точку (х,у)
>;
Класс посредством композиции Line включает два объекта Point. Эти
объекты инициализируются конструктором.
Спецификация класса Line
ОБЪЯВЛЕНИЕ
class Line
{
private:
Point PI, P2; // две конечные точки отрезка
public:
Line (Point a, Point b);// инициализировать PI и Р2
void Draw(void) const; // нарисовать отрезок
};
Объекты и наследование
Наследование — это интуитивное понятие, из которого мы можем
извлекать примеры, основанные на каждодневном опыте. Все из нас наследуют
Проиллюстрируем наследование класса с помощью линейного списка,
названного SeqList, который сохраняет информацию в последовательном
порядке. Список — это важная и знакомая структура, используемая для ведения
инвентаризационных записей, графика деловых встреч, типов и количества
необходимых гастрономических товаров и т.д. Наследование возникает, когда
мы объявляем упорядоченный список, который является особым типом
последовательного списка. Упорядоченный список использует все базовые методы
обработки списка из последовательного списка и обеспечивает свою
собственную операцию вставки для того, чтобы элементы списка сохранялись в
возрастающем порядке.
В линейном списке, содержащем N элементов, любой элемент занимает
одно из положений от 0 до N-1. Первое положение является передним, а
последнее — конечным. На рис. 1.3 показан неупорядоченный список целых
чисел с шестью элементами.
Рис. 1.3. Неупорядоченный линейный список
Базовые операции SeqList включают операцию Insert, которая добавляет
новый элемент в конец списка (Рис. 1.4), и операцию Delete, которая удаляет
первый элемент списка, соответствующий ключу. Вторая функция удаления,
называемая DeleteFront, удаляет первый элемент в списке (Рис. 1.5).
Структура определяет размер списка с помощью ListSize и предоставляет операцию
Find, выполняющую поиск элемента в списке. Для управления данными
пользователь может определить, является ли список пустым, и удалить его
операцией ClearList.
Insert (10)
Рис. 1.4. Вставка значения 10
Delete (45)
DeleteFront
Рис. 1.5. Удаление элемента 45 и удаление первого элемента в списке
Данный класс предоставляет метод GetData, позволяющий клиенту читать
значение любого элемента списка. Например, для нахождения максимального
значения в списке мы можем начать сканирование списка с нулевого
элемента. Процесс заканчивается при достижении конца списка, который
определяется с помощью ListSize. В каждом положении следует обновлять
максимальное значение, если текущее значение (GetData) больше, чем текущий
максимум. Например, для второго элемента списка число 22 сравнивается с
характерные черты от своих родителей такие, как раса, цвет глаз и тип
крови. Мы можем думать о родителе как о базе, из которой мы наследуем
характерные черты. Взаимосвязь иллюстрируется двумя объектами,
связанными стрелкой, острие которой направлено к базовому объекту.
Зоология формально изучает наследование у животных. На рис. 1.2
показана иерархия животных для млекопитающих, собак и колли.
Млекопитающее — это теплокровное животное, которое имеет шерсть и вскармливает
своих детенышей молоком. Собака — это млекопитающие, которое имеет
клыки, ест мясо, имеет определенное строение скелета и является
общественным животным. Колли — это собака с заостренной мордой, имеющая
белый с рыжим окрас и хорошо развитые пастушеские инстинкты.
Млекопитающее
Теплокровное животное, имеет шерсть, вскармливает детенышей молоком
Собака
Имеет клыки, ест мясо, имеет определенное строение скелета, является
общественным животным
Колли
Имеет заостренную морду, белый с рыжим окрас, хорошо развитые
пастушеские инстинкты
Рис. 1.2. Цепочка наследования у животных
В иерархической цепочке класс наследует все характерные черты своего
класса-предка. Например, собака имеет все черты млекопитающего плюс те,
которые отличают ее от кошек, слонов и т.д. Порядок расположения классов
указывает что
Колли есть собака. Собака есть млекопитающее
В этой цепочке класс млекопитающих определяется в качестве базового
класса (base class) для собаки, а собака называется производным классом
(derived class). Используя аналогию семейного наследования, мы говорим о
базовом и производном классах как о родительском классе и
классе-наследнике, соответственно. В случае расширенной цепочки наследник наследует
характерные черты своего родительского и прародительского класса.
Наследование в программировании
Объектно-ориентированное программирование предоставляет механизм,
посредством которого производному классу разрешается наследовать данные и
операции от базового класса. Этот механизм, называемый наследование класса (class
inheritance), позволяет производному классу использовать данные и операции,
которые были определены ранее в базовом классе. Производный класс может
добавлять новые операции или переписывать некоторые операции, так как он
устанавливает методы для обработки его данных. Аналогично, ребенок может
наследовать дом или автомашину от его (или ее) родителя. Затем он может затем
использовать этот дом или автомашину. Если необходимо, наследник может
модифицировать дом, чтобы он соответствовал его (или ее) особым условиям.
предыдущим максимумом, равным 3, поэтому текущее максимальное
значение заменяется на 22. В конечном счете, число 23 определяется как
максимальный элемент в списке.
3 <22
Новым максимумом будет 22
ADT SeqList
Данные
Неотрицательное целое число, указывающее количество элементов, находящихся в
данный момент в списке (размер), и список элементов данных.
Операции
Коне труктор
Начальные значения: Нет
Процесс: Установка размера списка на О
ListSize
Вход: Нет
Предусловия: Нет
Процесс: Чтение размера списка
Выход: Размер списка
Постусловия: Нет
ListEmpty
Вход: Нет
Предусловия: Нет
Процесс: Проверка размера списка
Выход: Возвращать TRUE, если список пустой;
в противном случае — возвращать FALSE.
Постусловия: Нет
ClearList
Вход: Нет
Предусловия: Нет
Процесс: Удаление всех элементов из списка и установка
размера списка на 0.
Выход: Нет
Постусловия: Список пустой
Find
Вход: Элемент, который необходимо найти в списке.
Предусловия: Нет
Процесс: Сканирование списка для нахождения соответствующего
элемента.
Выход: Если соответствующий элемент списка не найден,
возвращать FALSE; если он найден, возвращать TRUE
и этот элемент.
Постусловия: Нет
Insert
Вход: Элемент для вставки в список
Предусловия: Нет
Процесс: Добавление этого элемента в конец списка.
Выход: Нет
Постусловия: Список имеет новый элемент; его размер
увеличивается на 1.
Delete
Вход: Значение, которое должно быть удалено из списка.
Предусловия: Нет
Процесс: Сканирование списка и удаление первого найденного
элемента в списке. Не выполнять никакого действия,
если этот элемент не находится в списке.
Выход: Нет
Постусловия: Если соответствующий элемент найден, список
уменьшается на один элемент.
DeleteFront
Вход: Нет
Предусловия: Список не должен быть пустым.
Процесс: Удаление первого элемента из списка.
Выход: Возвращать значение удаляемого элемента
Постусловия: Список имеет на один элемент меньше.
GetData
Вход: Положение (pos) в списке.
Предусловия: Генерируется ошибка доступа, если pos меньше О
или больше 0 (размер -1)
Процесс: Получать значение в положении pos в списке.
Выход: Значение элемента в положении pos.
Постусловия: Нет
Конец ADT SeqLlst
Упорядоченные списки и наследование
Упорядоченный список — это особый тип списка, в котором элементы
сохраняются в возрастающем порядке. Как абстрактный тип данных этот
особый список получает большинство своих операций из класса SeqList, за
исключением операции Insert, которая должна добавлять новый элемент в
положение, сохраняющее упорядочение (Рис. 1.6).
insert(8)
23
45
Рис. 1.6. Упорядоченный список: Вставка элемента (8)
Операции ListSize, ListEmpty, ClearList, Find и GetData независимы от
любого упорядочения элементов. Операции Delete и DeleteFront удаляют
элемент, но сохраняют остающиеся элементы упорядоченными. Далее следует
ADT, отражающий сходство операций упорядоченного списка и SeqList.
ADT OrderedList
Данные
те же, что и для SeqList ADT
Операции
Конструктор выполняет конструктор базового класса
ListSize тот же, что и для SeqList ADT
ListEmpty тот же, что и для SeqList ADT
ClearList тот же, что и для SeqList ADT
Find тот же, что и для SeqList ADT
Delete тот же, что и для SeqList ADT
DeleteFront тот же, что и для SeqList ADT
GetData тот же, что и для SeqList ADT
Insert
Вход: Элемент для вставки в список.
Предусловия: Нет
Процесс: Добавление элемента в положение, сохраняющее упорядочение.
Выход: Нет
Постусловия: Список имеет новый элемент, и его размер увеличивается на 1.
Конец ADT OrderedList
Класс OrderedList является производным от класса SeqList. Он наследует
операции базового класса и модифицирует операцию Insert для упорядоченной
вставки элементов.
Класс SeqUst
private:
детали реализации
public
Коструктор Find
ListEmpty Delete
ClearList DeleteFront
ListSize GetData
Класс OrderedList
private:
public
Конструктор. Insert
Повторное использование кода
Объектно-ориентированный подход к структурам данных способствует
повторному использованию кода, который уже был разработан и протестирован,
и может быть вставлен в ваше приложение. Мы уже рассматривали повторное
использование кода с композицией. Наследование также является мощным
инструментом для этой цели. Например, реализация класса упорядоченного
списка требует от нас написания только методов Insert и конструктора. Все
другие операции задаются кодом из класса SeqList. Повторное использование
кода является важнейшим преимуществом в объектно-ориентированной
разработке, поскольку оно сокращает время разработки и способствует
однородности приложений и вариантов программного продукта. Например, при
модернизации операционной системы к ней добавляются новые функции. В то же
время, эта модернизация должна позволять выполнение существующих
приложений. Одним из подходов является определение оригинальной
операционной системы в качестве базового класса. Модернизированная система действует
как производный класс с его новыми функциями и операциями.
Спецификации класса SeqList и OrderedList*
Формальное описание класса SeqList приводится в главе 4. В этом разделе
мы даем только спецификацию класса для того, чтобы вы могли соотнести
этот класс и его методы с очень общим ADT. Класс OrderedList определяется
для иллюстрации наследования. Тип элемента данных в списке представлен
параметрическим именем DataType.
Спецификация класса SeqList
ОБЪЯВЛЕНИЕ
class SeqList
{
private:
// массив для хранения списка и число элементов текущего списка
DataType listitem[ARRAYSIZE];
int size;
public:
// конструктор
SeqList(void);
// методы доступа списка
int ListSize(void) const;
int ListEmpty(void) const;
int Find (DataType& item) const;
DataType GetData (int pos) const;
// методы модификации списка
void Insert (const DataType& item) ;
void Delete (const DataType& item) ;
DataType DeleteFront (void);
void ClearList (void);
);
ОПИСАНИЕ
Методы ListSize, ListEmpty, Find и GetData завершаются словом const
после объявления функции. Они называются постоянными функциями,
поскольку не изменяют состояние списка. Функции Insert, Delete имеют слово
const как часть списка параметров. Этот синтаксис C++ передает ссылку на
элемент, но указывает, что значение этого элемента не изменяется.
C++ использует простой синтаксис для объявления производного класса
В заголовке базовый класс указывается после двоеточия (:). Далее следует
объявление класса OrderedList. Особенности описываются в главе 12, в
которой содержится формальное введение в наследование.
Спецификация класса OrderedList
ОБЪЯВЛЕНИЕ
class OrderedList: public SeqList // наследование класса SeqList
{
public:
OrderedList (void); // инициализировать базовый класс
// для создания пустого списка
void Insert (const DataType& item) ; // вставить элемент по порядку
};
ОПИСАНИЕ
Insert замещает метод базового класса с тем же именем. Она проходит
по всему списку и вставляет элемент в положение, сохраняющее
упорядочение списка.
1.5. Приложения с наследованием классов
Понятие наследования класса имеет важное применение в
программировании графического пользовательского интерфейса (grafical user interface —
GUI) и системах баз данных. Графические приложения фокусируют внимание
на окнах, меню, диалоговых окнах и так далее. Базовое окно — это структура
данных с данными и операциями, являющимися общими для всех типов
окон. Операции включают открытие окна, создание или изменение заголовка
окна, установку линеек прокрутки и областей перетаскивания и т.д.
Приложения GUI состоят из классов диалога, классов меню, классов текстовых
окон и так далее, которые наследуют базовую структуру и операции от
базового класса окна. Например, следующая иерархия класса включает класс
Dialog и класс TextEdit, порожденные от класса Window.
Класс Window
Класс Dialog
Класс TextEdit
Этот пример класса Window показывает одиночное наследование, в
котором производный класс имеет только один базовый класс. Однако при
множественном наследовании (multiple inheritance) класс порождается от двух
или более базовых классов. Некоторые приложения GUI используют это
свойство. Программа текстового процессора объединяет редактор (editor) с
менеджером просмотра (view manager) для пролистывания текста в некотором
окне. Редактор читает строку символов и вносит изменения, вставляя и
удаляя строки, и вводя информацию форматирования. Менеджер просмотра
отвечает за копирование текста на экран с использованием информации о
шрифте и окне. Редактор экрана может быть определен как производный
класс, использующий класс Editor (редактора) и класс View (менеджера
просмотра) в качестве базовых классов.
Множественное наследование
Класс View
Класс Editor
Класс Screen Editor
1.6. Разработка объектно-ориентированных
программ
Большие программные системы становятся все более сложными и требуют
новых подходов к разработке. Традиционная разработка использует модель
управления, которая предполагает наличие администратора верхнего уровня
(top administrator), понимающего систему и поручающего задачи менеджерам.
Такая нисходящая программная разработка (top-down program design)
рассматривает систему как набор подпрограмм, состоящий из нескольких слоев.
Главная программа
Подпрограмма!
Подпрограмма2
ПодпрограммаЗ
На верхнем уровне главная программа управляет работой системы,
выполняя последовательность вызовов подпрограмм, которые производят
вычисления и возвращают информацию. Эти подпрограммы могут далее поручать
выполнение некоторых задач другим подпрограммам. Элементы нисходящей
программной разработки необходимы для всех систем. Однако, когда задача
становится слишком большой, этот подход может оказаться неудачным,
поскольку его сложность подавляет способность отдельного человека управлять
такой иерархией подпрограмм. Кроме того, простые структурные изменения в
подпрограммах около вершины иерархии могут потребовать дорогих и
занимающих длительное время изменений в алгоритмах для подпрограмм,
находящихся в нижней части диаграммы.
Объектно-ориентированное программирование использует другую модель
системной разработки. Оно рассматривает большую систему как набор объектов
(агентов), которые взаимодействуют для выполнения задач. Каждый объект
имеет методы, управляющие его данными.
Целью программной разработки является создание читабельной и
поддерживаемой архитектуры, которая может быть расширена, как диктует
необходимость. Хорошо организованные системы легче понимать, разрабатывать
и отлаживать. Все философии разработки пытаются преодолеть сложность
программной системы с помощью принципа разделения и подчинения.
Нисходящая программная разработка рассматривает систему как набор
функциональных модулей, состоящий из слоев. Объектно-ориентированное
программирование использует объекты как основу разработки. Не существует
единственного способа программной разработки и строго определенного процесса,
которому необходимо следовать. Разработка программ — это вид деятельности
человека, который должен включать творческую свободу и гибкость. В этой
книге мы обсуждаем общий подход, определяющий методологию разработки
программного продукта (software development methodology). Этот подход
включает отдельные фазы разработки программного продукта, среди которых
анализ задачи и определение программы, разработка объекта и процесса,
кодирование, тестирование и поддержка (сопровождение)
Анализ задачи/определение программы
Программная разработка начинается, когда клиент обозначит некоторую
задачу, которая должна быть решена. Эта задача часто определяется свободно,
без ясного понимания, какие именно данные имеются в наличии (вход) и какая
новая информация должна быть получена в результате (выход). Программист
анализирует задачу вместе с клиентом и определяет, какую форму должны
принять вход и выход и алгоритмы, которые используются при выполнении
вычислений. Этот анализ формализуется в фазе разработки программы.
Разработка
Программная разработка описывает объекты, которые являются основными
строительными блоками программы. Разработка описывает также
управляющие модули, руководящие взаимодействием между объектами.
В фазе объектной разработки определяются объекты, которые будут
использоваться в программе, и пишется объявление для каждого класса. Класс
тестируется путем его использования с какой-либо небольшой программой,
тестирующей методы класса при управляемых условиях. Тот факт, что классы
могут тестироваться отдельно, вне области большого приложения, является
одной из важнейших возможностей объектно-ориентированной разработки.
Фаза разработки управления процессом использует нисходящую
разработку путем создания главной программы и подпрограмм для управления
взаимодействием между объектами. Главная программа и подпрограммы
образуют каркас разработки (design framework).
Главный управляющий модуль соответствует главной функции в
программе C++ и отвечает за поток данных программы. При нисходящей
программной разработке система делится на последовательность действий, которые
выполняются как независимые подпрограммы. Главная программа и ее
подпрограммы организуются в нисходящую иерархию модулей, называемую
структурным деревом (structure tree). Главный модуль является корнем этого
дерева. Каждый модуль заключается в прямоугольник, а каждый класс,
который используется модулем, заключается в овал. Мы представляем
каждый модуль, указывая имя функции, входные и выходные параметры и
краткое описание ее действия.
класс
Главная
класс
Подпрограмма
Подпрограмма
Подпрограмма
Подпрограмма
класс
класс
Подпрограмма
Кодирование
В фазе кодирования пишутся главная программа и подпрограммы,
реализующие каркас программной разработки.
Тестирование
Реализация и тестирование объектов выполняются в течение фазы
объектной разработки. Это позволяет нам сосредоточить внимание на разработке
управляющего модуля. Мы можем проверять кодирование программы,
тестируя взаимодействие каждого объекта с управляющими модулями в каркасе
разработки.
Иллюстрация программной разработки: Dice график
Разработку и реализацию объектно-ориентированной программы
иллюстрирует использование графика для записи частоты результатов бросания
при игре в кости. В последующих разделах описывается каждая фаза в
жизненном цикле программы.
Анализ задачи. Предположим, событие — это бросание двух костей. Для
каждого бросания сумма лежит в диапазоне от 2 до 12. Используя повторное
бросание костей, мы определяем эмпирическую вероятность того, что сумма
равна 2, 3 ... , 11 или 12, и строим диаграмму, которая отражает вероятность
каждого возможного результата.
Замечание
Эмпирическая вероятность определяется моделированием большого количества
событий и записью результатов. Отношение количества появлений некоторого события
к количеству всех моделируемых событий представляет эмпирическую вероятность
того, рассматриваемое событие произойдет. Например, если бросание костей
повторится 100000 раз и сумма 4 возникнет 10000 раз, то эмпирическая вероятность этой
суммы равна 0,10.
эмпирическая
вероятность
Прежде всего следует ясно определить задачу. Этот процесс включает
понимание входа, выхода и промежуточных вычислений. В фазе анализа задачи
клиент формирует серию требований к системе. Они включают контроль за
вводом данных, указание вычислений и используемых формул и описание
желаемого выхода.
Определение программы. Программа запрашивает пользователя ввести
число N — количество бросаний двух костей. Поскольку бросание костей
имеет случайный результат, используем для моделирования N бросаний
случайные числа. Программа ведет запись количества появлений каждой воз-
можной суммы S (2 < S < 12). Эмпирическая вероятность определяется
делением количества результатов S на N. Что касается выхода, это дробное
значение используется для определения высоты прямоугольника на нашей
диаграмме. Результаты выводятся на экран как столбцовая диаграмма.
Объектная разработка. Программа использует класс Line для создания осей
координат и класс Rectangle — для построения столбцов. Эти классы вводятся
в разделе 1.4 Разработка объектов. Бросание костей — это метод в классе Dice,
который обрабатывает две кости. Далее следует объявление класса Dice. Его
реализация и тестирование приводятся в программе вместе с реализацией и
тестированием классов Line и Rectangle.
#include random.h
class Dice
{
private:
// данные-члены
int diceTotal/ // сумма двух костей
int diceList[2]; // список очков двух костей
// класс генератора случайных чисел, используемый для
// моделирования бросаний
RandcmNumber rnd;
public:
// конструктор
Dice(void);
// методы
void Toss(void);
int Total(void) const;
void DisplayToss(void) const;
};
Разработка управления процессом. Для построения диаграммы бросания
костей главный модуль вызывает три подпрограммы, которые выполняют
основные действия программы. Функция SimulateDieToss использует методы из
класса Dice для бросания костей N раз. Draw Axes вызывает метод Draw в классе
Line для рисования осей координат графика, a Plot рисует серию
прямоугольников, которые образуют столбцовую диаграмму. Функция Plot вызывает Мах
для определения максимального количества появлений любой возможной
суммы. Это значение позволяет нам вычислить относительную высоту каждого
прямоугольника диаграммы. Структурное дерево этой программы показано на
рис. 1.8. Далее следуют объявления для каждого управляющего модуля в
структурном дереве.
Главная
SimulateDieToss
DrawAxes
Plot
Dice
Line
Rectangle
Max
Рис. 1.8. Древовидная структура программы Dice Graph
main
Передаваемые параметры:
Нет
Выполнение:
Запросить у пользователя количество бросаний костей в моделировании.
Вызвать функцию SimulateDieToss для выполнения бросаний и записать количество
раз, когда возникает каждая возможная сумма: (2 < Total <. 12). Нарисовать
оси координат функцией DrawAxes и создать столбцовую диаграмму функцией Plot.
Возвращаемые параметры:
Нет
SimulateDieToss
Передаваемые параметры:
tossTotal Массив tossTotal содержит количество появлений каждой суммы
в диапазоне от 2 до 12. tossTotal [i] — это количество
появлений суммы i при бросании костей tossCount раз.
tossCount Количество бросаний N при моделировании.
Выполнение:
Создать объект Dice и использовать его для бросания костей указанное
количество раз, записывая в массив tossTotal количество раз, когда возникает
сумма 2, количество раз, когда возникает сумма 3, . . . , количество раз,
когда возникает сумма 12.
Возвращаемые параметры:
Массив tossTotal с количеством раз, когда возникает каждая сумма.
DrawAxes
Передаваемые параметры:
Нет
Выполнение:
Создать два объекта Line: один — для вертикальной оси (оси у) и один — для
горизонтальной оси (оси х) . Ось у — это линия от (1.0, 3.25) до (1.0, 0.25)
Ось х — это линия от (0.75, 3.0) до (7.0, 3.0) . Вертикальный диапазон
графика равен 2,75.
Возвращаемые параметры:
Нет
Мах
Передаваемые параметры:
а Массив, содержащий длинные значения данных,
п Количество значений данных в а.
Выполнение:
Найти максимальное значение элементов в массиве а.
Возвращаемый параметр:
Максимальное значение в массиве.
Plot
Передаваемый параметр:
tossTotal Массив, содержащий количество появлений каждой возможной суммы,
вычисленной в SimulateDieToss.
Выполнение:
Поиск максимальной суммы (maxTotal) в массиве tossTotal для диапазона
индекса 2—12. Затем каждый элемент в массиве генерирует соответствующую
часть (tossTotal [i]/ maxTotal) вертикального'диапазона графика. Разделить
6-дюймовый интервал оси х от (1.0, 3.0) до (7.0, 3.0) на 23 равных сегмента
и построить соответствующие прямоугольники, чьи высоты — это функция
(tossTotal [i]) / maxTotal*2.75, 2 < i й 12.
Возвращаемые параметры:
Нет
Кодирование*. Завершает разработку программы кодирование
управляющих модулей. Например, следующей программой задаются управляющие
модули для dice-диаграммы:
Программа 1.2. Диаграмма бросания костей
Главная программа запрашивает пользователя ввести количество
бросаний костей для моделирования. Наш запуск программы тестирует случай
500 000 бросаний костей. В конце выполнения задачи система ожидает
нажатия клавиши или щелчка кнопкой мыши для завершения работы.
Классы Line и Rectangle содержатся в файле figures.h, а класс Dice
содержится в файле dice.h. Подпрограммы рисования графических примитивов
находятся в graphlib.h.
#include <iostream.h>
#include "figures.h"
#include "dice.h"
iinclude "graphlib.h"
// Бросание двух костей tossCount раз.
// Запись числа выпавших "двоек" в tossTotal[2],
// "троек" — в tossTotal[3] и так далее
void SimulateDieToss( long tossTotal[], long tossCount )
{
long tossEvent;
int i;
Dice D;
// очистить каждый элемент массива tossTotal
for (i=2; i 12; i++)
tossTotal[i] = 0;
// Бросание костей tossCount раз
for (tossEvent = 1; tossEvent tossCount; tossEvent++ )
{
D.TossO; // бросание костей
tossTotal[D.Total()]++; // увеличение счетчика
}
}
// Нахождение максимального значения в массиве их п элементов
long Max (long а [], int п)
{
long lmax - а[0] ;
int i;
for (i=l; i n; i++)
if (a [i] lmax)
lmax = a[i];
return lmax;
}
// Рисование двух осей
void DrawAxes (void)
{
const float vertspan = 3.0;
Line VerticalAxis(Point(1.0, vertspan+0.25),Point(1.0,0.25));
VerticalAxis.Draw();
Line HorizontalAxis(Point(0.75,vertspan),Point(0.75,vertspan));
HorizontalAxis.Draw();
}
// Рисование графического столбца
void Plot (long tossTotal [ ])
{
const float vertspan = 3.0, scaleHeight = 2.75;
float x, rectHeight, dx;
long maxTotal;
int i;
// Нахождение максимального значения в массиве tossTotal.
// Поиск для индексов в диапазоне 2-12
maxTotal =Мах(&tossTotal[2], 11) ;
// теперь создаем прямоугольники
dx = 6.0/23.0;
х = 1.0 + dx;
// Цикл — 11 раз.
//В цикле:
// определяется высота столбца для рисования в текущем положении;
// создается объект Rectangle для соответствующего
// положения, высота и ширина;
// рисуется столбец и происходит переход к следующему столбцу
for (i=2; i 12; i++)
{
rectHeight = (float(tossTotal[i])/maxTotal)*scaleHeight;
Rectangle CurrRect(Point(x,vertspan-rectHeight), Point(x+dx,vertspan));
CurrRect.Draw();
x += 2.0*dx;
}
)
void main (void)
{
long numTosses;
long tossTotal [13] ;
// запрос числа моделирования бросаний
cout « "Введите число бросаний: ";
cin » numTosses;
SimulateDieToss(tossTotal, numTosses); //бросание
InitGraphics (); // инициализация графической системы
DrawAxes (); // рисование осей
Plot (tossTotal); // построение графика
ViewPause (); // ожидание нажатия клавиши или щечка мышью
ShutdownGraphi.es (); // закрытие графической системы
}
/*
Запуск программы рг01_02.срр
Введите число бросаний: 50000
*/
1.7. Тестирование и сопровождение программы
Использование объектно-ориентированного программирования
способствует созданию систем, позволяющих выполнять независимое тестирование
объектов и повторно использовать написанные ранее классы. Эти преимущества
уменьшают риск появления ошибок при создании сложных программных систем,
поскольку они развиваются, расширяясь из меньших систем, в которых вы
уверены. Тестирование выполняется в процессе разработки программной системы.
Объектное тестирование
Тип класса — это самодостаточная структура данных, которая может
передавать информацию внешнему компоненту программы и от него. Мы можем
тестировать каждый класс, создав короткую программу, вызывающую каждый
public-метод. Эта дополнительная программа иллюстрирует тестирование
методов в классе Dice.
Тестирование управляющего модуля
Программа должна быть до конца протестирована путем ее выполнения с
тщательно отобранными данными. Перед началом выполнения этой задачи
правильность программы часто может быть оценена с помощью структурного
сквозного контроля (structure walk-through), в котором программист
показывает полную структуру и реализацию другому программисту и объясняет, что
именно происходит, от объектной разработки и до разработки управляющих
модулей. Этот процесс часто вскрывает концептуальные ошибки, проясняет
логику программы и подсказывает тесты, которые могут быть выполнены.
Современные компиляторы поддерживают отладчик на уровне исходного
кода (source-level debugger), который позволяет отслеживать отдельные
команды и останавливает работу в выбранных контрольных точках. Во время
управляемого выполнения значения переменных могут отображаться на экране,
позволяя сравнивать выборочные части программы до и после возникновения
ошибки.
Основной проверкой правильности программы является ее выполнение с
наборами хорошо подобранных данных. Выполняя тестирование,
программист убеждается в правильности программы. Программисту следует также
использовать неверные входные данные для проверки кода на устойчивость
к ошибкам (robustness), которая определяет способность программы
идентифицировать неверные данные и возвращать сообщения об ошибках.
Данные для тестирования отбираются с помощью различных подходов.
Одним из методов является так называемый метод "надеюсь и молюсь",
когда программист запускает программу несколько раз с простыми данными
и, если она работает, то он (или она) продолжает разработку. Более разумным
подходом является выбор серии входных данных, которая тестирует
различные алгоритмы в программе. Ввод должен включать простые, типовые и
экстремальные данные, которые тестируют специальные случаи в nporpaiv ме,
и неверные данные, проверяющие способность программы реагировать на
ошибки ввода.
Полностью структурированный тест рассматривает логическую структуру
программы. Этот подход предполагает, что программа не тестируется до
конца, если некоторая часть кода не была уже выполнена. Исчерпывающее
тестирование требует от программиста выбора данных для проверки
различных алгоритмов в программе: каждого условного оператора, каждой
конструкции цикла, каждого вызова функции и так далее. Некоторые
компиляторы предоставляют функции протоколирования, которые указывают
количество вызовов функций в программе.
Программное сопровождение и документирование
Для удовлетворения дополнительным требованиям компьютерные программы
часто нуждаются в обновлении. Объектно-ориентированное программирование
упрощает программное сопровождение. Наследование классов делает
возможным повторное использование существующих программ. Эти инструменты
эффективны при поддержке хорошим программным документированием,
описывающим классы и управляющие модули для того, чтобы помогать
пользователям понимать программу и ее правильное выполнение. Большие
программы обычно поддерживаются руководством пользователя, которое
включает информацию по установке программного обеспечения и одну или более
обучающие программы для иллюстрации центральных возможностей
программного продукта.
Объектные спецификации и структурные диаграммы управляющих
модулей являются превосходными инструментами программного
документирования. В исходном программном коде комментарии описывают действие
отдельных функций и классов. Комментарии также помещаются там, где
логика какого-либо алгоритма является особенно трудной.
1.8. Язык программирования C++
Эта книга знакомит читателя со структурами данных, используя язык
объектно-ориентированного программирования C++. Несмотря на существование
ряда объектно-ориентированных языков, C++ обладает преимуществом,
благодаря своим корням в популярном языке программирования С и качеству
компиляторов.
Язык С был разработан в начале 70-х годов как структурный язык для
системного программирования. Он содержал средства для вызова системных
подпрограмм низкого уровня и реализации конструкций высокого уровня.
С годами быстрые и эффективные компиляторы С появились на большинстве
компьютерных платформ. Вся операционная система Unix, кроме небольшой
части, написана на языке С, и С является основным языком
программирования в среде Unix. Язык программирования C++ был разработан в Bell
Laboratories Бьярном Страуструпом в качестве развития языка С.
Использование языка С означало, что C++ не пришлось разрабатывать с самого начала,
и эта связь с С дала новому языку широкую аудиторию квалифицированных
программистов. Первоначально C++ назывался "С с классами" и стал
доступен для пользователей в начале 80-х годов. Были написаны трансляторы
для преобразования исходного кода С с классами в код С перед вызовом
компилятора С для создания машинного кода.
Название C++ было придумано Риком Масситти в 1983г. Он использовал
оператор приращения ++ языка С, чтобы отразить его эволюцию из языка
С и то, что он расширяет язык С. Многие спрашивали, должен ли C++
сохранять совместимость с С, в частности, поскольку C++ разрабатывает
новые мощные конструкции и средства, которые не присутствуют в С. На
практике этот язык, вероятно, будет продолжать оставаться развитием языка
С. Количество существующих программ на языке С и количество функций
библиотеки С будет заставлять разработчиков C++ сохранять крепкую связь
с языком С. Определение C++ продолжает обеспечивать то, что общие
конструкции С и C++ имеют одно и то же значение на обоих языках.
Идеи многих конструкций C++ развивались в 70-е годы из языков Си-
мула-67 и Алгол-68. Эти языки ввели в употребление серьезную проверку
типов, понятия класса и модульность. Министерство обороны содействовало
разработке Ада, который привел в систему многие ключевые идеи
конструкции компилятора. Язык Ада стимулировал использование параметризации
для возможности появления обобщенных классов. C++ использует похожую
шаблонную конструкцию и имеет также общие с языком Ада механизмы
обработки особых ситуаций.
Популярность C++ и его миграция на многие платформы привели к
необходимости стандартизации. Компания AT&T активно развивает этот язык.
Сознательные усилия прилагаются для связи тех, кто пишет компилятор
C++, с разработчиками оригинального языка и с растущей популяцией
пользователей. AT&T развивает свой успех с Unix и работает совместно с
пользователями для координации разработки стандартов ANSI C++ и
опубликования окончательного справочного руководства по C++. Ожидается, что
стандарт ANSI (Американский национальный институт стандартов) по C++ станет
частью стандарта ISO (Международная организация по стандартам).
1.9. Абстрактные базовые классы
и полиморфизм*
Наследование классов объединяется с абстрактными базовыми классами
(abstract base classes) для создания важного инструмента разработки
структуры данных. Эти абстрактные базовые классы определяют открытый
интерфейс класса, независимый от внутренней реализации данных класса и
операций. Открытый интерфейс класса определяет методы доступа к данным.
Клиент хочет, чтобы открытый интерфейс оставался постоянным, несмотря
на изменения во внутренней реализации. Объектно-ориентированные языки
подходят к этой проблеме, используя абстрактный базовый класс, который
объявляет имена и параметры для каждого из public-методов. Абстрактный
базовый класс предоставляет ограниченные детали реализации и
сосредотачивает внимание на объявлении public-методов. Это объявление форсирует
реализацию в производном классе. Абстрактный базовый класс C++
объявляет некоторые методы как чистые виртуальные функции (pure virtual
functions). Следующее объявление определяет абстрактный базовый класс List,
который задает операции списка. Слово "virtual" и присвоение нуля операции
определяют чистую виртуальную функцию.
template <class T>
class List
{
protected:
// число элементов в списке.
// обновляется производным классом
int size size;
public:
// конструктор
List(void);
// методы доступа
virtual int ListSize(void) const;
virtual int ListEmpty(void) const;
virtual int Find(T& item) = 0;
// методы модификации списка
virtual void Insert(const T& item) = 0;
virtual void Delete(const T& item) = 0;
virtual void ClearList(void) = 0;
};
Этот абстрактный базовый класс предназначен для описания очень общих
списков. Он используется как база для серии классов наборов (структур
списков) в последующих главах. Использование абстрактного класса в
качестве базы требует, чтобы наборы реализовывали общие методы класса List.
Для иллюстрации этого процесса класс SeqList снова рассматривается в главе
12, где он порождается от List.
Полиморфизм и динамическое связывание
Концепция наследования поддерживается в языке C++ рядом мощных
конструкций. Мы уже рассмотрели чистые виртуальные функции в
абстрактном базовом классе. Общая концепция виртуальных функций поддерживает
наследование в том, что позволяет двум или более объектам в иерархии
наследования иметь операции с одним и тем же объявлением, выполняющие
различные задачи. Это объектно-ориентированное свойство, называемое
полиморфизм (polymorhism), позволяет объектам из множества классов отвечать
на одно и то же сообщение. Получатель этого сообщения определяется
динамически во время выполнения. Например, системный администратор может
использовать полиморфизм для обработки резервных файлов в
многосистемной среде. Предположим, что администратор имеет подсистему с магнитной
лентой 1/2 дюйма и компактный магнитофон с лентой 1/4 дюйма. Классы
HalfTape и QuarterTape являются производными от общего класса Таре и
управляют соответствующими лентопротяжными устройствами. Класс Таре
имеет виртуальную операцию Backup, содержащую действия, общие для всех
лентопротяжных устройств. Производные классы имеют (виртуальную)
операцию Backup, использующую специфическую внутреннюю информацию о
лентопротяжных механизмах. Когда администратор дает указание выполнить
системное резервное копирование, каждый лентопротяжный механизм
принимает сообщение Backup и выполняет особую операцию, определенную для
его аппаратных средств. Объект типа HalfTape выполняет резервное
копирование на 1/2-дюймовую ленту, а объект типа QuarterTape — на
1/4-дюймовую ленту.
Концепция полиморфизма является фундаментальной для
объектно-ориентированного программирования. Профессионалы часто говорят об
объектно-ориентированном программировании как о наследовании с полиморфизмом
времени исполнения. C++ поддерживает эту конструкцию, используя
динамическое связывание (dynamic binding) и виртуальные функции-члены
(virtual member functions). Эти понятия описываются в главе 12. Сейчас же мы
концентрируем внимание на этих понятиях, не давая технической
информации о языковой реализации.
Динамическое связывание позволяет многим различным объектам в
системе отвечать на одно и то же сообщение. Каждый объект отвечает на это
сообщение определенным для его типа способом. Рассмотрим работу
профессионального маляра, когда он (или она) выполняет малярную работу с
различными типами домов. Определенные общие задачи должны быть
выполнены при покраске дома. Допустим, что они описываются в классе House.
Кроме общих задач требуются особые методы работы для различных типов
домов. Покраска деревянного дома отличается от покраски дома с наружной
штукатуркой или дома с виниловой облицовкой стен и так далее. В контексте
House
Paint
WoodFrame
Stucco
VinylSided
Paint
Paint
Paint
объектно-ориентированного программирования особые малярные задачи для
каждого вида дома задаются в производном классе, который наследует
базовый класс House. Допустим, что каждый производный класс имеет
операцию Paint. Класс House имеет операцию Paint, которая задается как
виртуальная функция. Предположим, что BigWoody — это объект типа Wood-
Frame. Мы можем указать BigWoody покрасить дом, вызывая явно операцию
Paint. Это называется статическим связыванием (static binding).
BigWoody. Paint ( ); // static binding
Допустим, однако, что подрядчик имеет список адресов домов, которые
нуждаются в покраске, и что он передает сообщение своей команде маляров
пойти по адресам в списке и покрасить эти дома. В данном случае каждое
сообщение привязано не к определенному дому, а скорее — к адресу дома-
объекта в списке. Команда маляров приходит к дому и выбирает правильную
малярную операцию Paint, после того, как она увидит тип дома. Этот процесс
известен как динамическое связывание (dynamic binding).
(House at address 414) .Paint ( ); // dynamic binding
Процесс вызывает операцию Paint, соответствующую дому по данному
адресу. Если дом по адресу 414 является деревянным, то выполняется
операция Paint( ) из класса WoodFrame.
При использовании структур наследования в C++ операции, которые
динамически связываются с их объектом, объявляются как виртуальные
функции-члены (virtual member functions). Генерируется код для создания
таблицы, указывающей местоположения виртуальных функций какого-либо
объекта и устанавливается связь между объектом и этой таблицей. Во время
выполнения, когда на положение объекта осуществляется ссылка, система
использует это положение для получения доступа к таблице и выполнения
правильной функции.
Понятие полиморфизма является фундаментальным в
объектно-ориентированном программировании. Мы используем его с более совершенными
структурами данных.
Письменные упражнения
1.1 Укажите различие между инкапсуляцией и скрытием информации для
объектов.
1.2
(а) Разработайте ADT для цилиндра. Данные включают радиус и высоту
цилиндра. Операциями являются конструктор, вычисление площади и
объема.
(б) Разработайте ADT для телевизионного приемника. Данными являются
настройки для регулирования громкости и канала. Операциями
являются включение и выключение приемника, настройка громкости и
изменение канала.
(в) Разработайте ADT для шара. Данными являются радиус и его масса в
фунтах. Операции возвращают радиус и массу шара.
(г) Разработайте ADT для Примера 1.1, часть 2.
1.3 Геометрическое тело образовано высверливанием круглого отверстия с
радиусом rh через центр цилиндра с радиусом г и высотой h.
(а) Используйте ADT Cylinder, разработанный в упражнении 1.2(a), для
нахождения объема геометрического тела.
(б) Используйте ADT Circle, разработанный в тексте, и ADT Cylinder для
вычисления площади этого геометрического тела. Площадь должна
включать площадь боковой поверхности внутри отверстия.
1.4 Опишите несколько сообщений которые могут передаваться для ADT
Television Set из упражнения 1.2(b). Что делает приемник в каждом
случае?
1.5 Разработайте класс Cylinder, реализующий ADT из упражнения 1.2(a).
1.6 Нарисуйте цепочку наследования, включающую следующие термины:
транспортное средство, автомобиль, грузовой автомобиль, автомобиль с
откидным верхом, Форд и грузовой полуприцеп.
1.7 Какова структура разработки программного продукта?
1.8 Приведите три причины растущей популярности C++.
1.9 Какова связь между С и C++?
1.10 Перечислите некоторые компиляторы C++ общего использования. К
каким компиляторам вы имеете доступ? Для каждого компилятора
укажите, предоставляет ли он интегрированную среду разработки (IDE),
в которой имеются редактор, компилятор, компоновщик, отладчик и
исполняющая система. Альтернативой является компилятор с
командной строкой.
1.11
(а) Объясните, что подразумевается под полиморфизмом.
(б) Графическая система инкапсулирует операции окна в базовом классе
Twindow. Производные классы реализуют окна главной программы,
диалоги и элементы управления. Каждый класс имеет метод Setup
Window, который инициализирует различные компоненты окна. Должен
ли использоваться полиморфизм в объявлении SetupWindow в базовом
классе?
глава
Базовые типы данных
2.1. Целочисленные типы
2.2. Символьные типы
2.3. Вещественные типы данных
2.4. Типы перечисления
2.5. Указатели
2.6. Массивы
2.7. Строчные константы и переменные
2.8. Записи
2.9. Файлы
2.10. Приложения с массивами
и записями
Письменные упражнения
Упражнения по программированию
Эта глава знакомит с серией базовых типов данных, которые включают
числа, символы, определенные пользователем типы перечисления1 и
указатели. Эти типы являются естественными для большинства языков
программирования. Каждый базовый тип данных включает данные и операции, компоненты
абстрактного типа данных (ADT). В этой главе мы предоставляем ADT для
целочисленных, литерных типов, типов real number, типов перечисления и
указателей. Языки программирования реализуют ADT на компьютере,
используя различные представления данных, включая двоичные числа и символы в
коде ASH (American Standard Code for Information Interchange). В этой книге
язык C++ используется для иллюстрации реализации абстрактных типов
данных.
Численные, литерные типы и указатели описывают простые данные, потому
что объекты этих типов не могут быть разделены на меньшие части. Наоборот,
структурированные типы данных имеют компоненты, построенные из простых
типов по правилам, определяющим связи между компонентами.
Структурированные типы включают массивы, строки, записи, файлы, списки, стеки,
очереди, деревья, графы и таблицы, которые определяют основные темы этой
книги. Большинство языков программирования предоставляют
синтаксические конструкции или библиотечные функции для обработки массивов, строк,
записей и файловых структур. По существу, мы определяем их как встроенные
(built-in) структурированные типы данных. Мы предоставляем абстрактные
типы данных для этих встроенных структур и обсуждаем их реализацию в
C++.
Мы также представляем серию приложений для встроенных
структурированных типов, которые вводят важные алгоритмы последовательного поиска
и обменной сортировки. Одно из приложений иллюстрирует реализацию типа
строки с использованием библиотеки строк C++. C++ использует иерархию
наследования для реализации файлов. Другое приложение показывает
обработку трех различных типов файлов.
.1. Целочисленные типы
Целые числа — это положительные или отрицательные целые числа,
состоящие из знака и последовательности цифр. О целых числах говорят, как о
знаковых (signed) числах. Например, далее следуют специфические
целочисленные значения, называемые целочисленные константами (integer constants):
+35 -278 19 (знак +) -28976510
Вы знакомы с элементарной арифметикой, в которой определяется серия
операторов, имеющих результатом новые целые значения. Операторы,
принимающие один операнд (унарный оператор) или два операнда (бинарный
оператор) создают целые выражения:
(Унарный +) +35 = 35 (Вычитание -) 73 — 50 = 23
(Сложение +) 4+6 = 10 (Умножение *) -3*7 = -21
Целые выражения могут использоваться с арифметическими операторами
сравнения для получения результата, который является True или False.
(Сравнение меньше, чем) 5 < 7 (True)
(Сравнение больше, чем или равно ) 10 >= 18 (False)
1 Термины "типы перечисления" и "перечислимые типы" встречаются в русских источниках
одинаково часто. — Прим. ред.
Теоретически, длина целых чисел не имеет ограничения, — факт,
подразумевающийся в определении ADT.
ADT, которые мы предусматриваем для простых типов, предполагают, что
читатель знаком с предусловиями, входом и постусловиями для каждой
операции. Например, полной спецификацией для операции деления целых
(Integer Division) является:
Integer Division
Вход: Два целых значения и и v.
Предусловия: Знаменатель v не может быть равен 0.
Процесс: Разделить v на и, используя операцию Integer Division.
Выход: Значение частного.
Постусловия: Возникает условие ошибки, если v =* 0.
В нашей спецификации мы используем нотацию оператора C++ вместо
родовых названий операций и только описываем процесс.
ADT Integer
Данные
Целое число N со знаком
Операции
Предположим, что и и v являются целыми выражениями, а N - целая переменная.
Присваивание
= N - и Присваивает значение выражения и переменной N
Бинарные арифметические операции
+ u + v Сложение
u — v Вычитание
* u * v Умножение
/ u / v Деление нацело
% u % v Остаток от деления нацело
Унарные арифметические операции
-и Изменение знака (унарный минус)
+ +и То же, что и и (унарный плюс)
Операции отношения
(Выражение отношения — это истинность заданного условия)
=* и == v Результат — TRUE, если и эквивалентно v
!=* и != v Результат — TRUE, если и не эквивалентно v
< и < v Результат — TRUE, если и меньше v
<= и <= v Результат — TRUE, если и меньше, либо равно v
> и > v Результат — TRUE, если и больше v
>= и >== v Результат — TRUE, если и больше, либо равно v
Конец ADT Integer
Пример 2.1
3+5 (выражение имеет значение 8)
val =25/20 (val - 1)
rem * 25 % 20 (rem = 5)
Компьютерное хранение целых чисел
Реализация целых чисел обеспечивается описаниями типа языка
программирования и компьютерными аппаратными средствами. Компьютерные
системы сохраняют целые числа в блоках памяти с фиксированной длиной.
Результирующая область значений лежит в ограниченном диапазоне. Длина
блока памяти и диапазон значений зависят от реализации. Для того, чтобы
способствовать некоторой стандартизации, языки программирования
предоставляют простые встроенные типы данных для коротких и длинных целых.
Когда требуются очень большие целые значения, приложение должно
предоставлять библиотеку подпрограмм для выполнения операций. Библиотека
целых операций может расширить реализацию целых до любой длины, хотя
эти подпрограммы значительно снижают эффективность системы,
исполняющей приложения.
В компьютере целые хранятся как двоичные (бинарные) числа (binary
numbers), состоящие из различных последовательностей цифр 0 и 1. Это
представление моделируется на базе 10 (или десятичной системы, которая
использует цифры 0, 1, 2 ,..., 9). Десятичное число сохраняется как набор
цифр d0 , d2 , d2f и т.д., представляющий степени 10. Например, й-разрядное
число
Nw = dki dk2 „di... d2 d0 , для О < dt < 9
представляет
Nio = dk.jflO*11)* dk.2(10k2)+...+di(10i)+...+ drflO'J+do (10°)
Индекс 10 указывает на то, что N записано как десятичное число.
Например, десятичное целое из четырех цифр 2589 представляет
258910 = 2(103)+ 5(102)+ 8(10!)+ 9(10°)
= 2(1000)+ 5(100)4- 8(10)+ 9
Двоичные целые используют цифры 0 и 1 и степени 2-х (2° = 1, 21 = 2,
22 = 4, 23 = 8, 24 — 16 и так далее). Например, 1310 имеет двоичное
представление
1310 = 1(23) + 1(22) + 0(2Х) + 1(2°) = 11012
Двоичная цифра называется бит (bit), сокращение, включающее Ы от
binary и t — от digit. В общем виде /г-разрядное или fe-битовое двоичное
число имеет представление:
N2 ^ ^А-1 &fe-2 ••• Ь} ... bj bp
= bk.1(2kl)+bk2(2k'2)+... +Ь^2г;+... +b1(21)+b0(2°), 0 <bx< 1
Следующее 6-битовое число дает двоичное представление 42. Десятичное
значение двоичного числа вычисляется добавлением членов в сумме:
1010102= 1(25) + 0(24) + 1(23) + 0(22) + Ц21) + 0(2°) = 4210
Пример 2.2
Вычислить десятичное значение двоичного числа:
1101012= 1(25) + 1(24) + 0(23) + 1(22) + 0(2*) + 1(2°) = 5310
100001102=1(27) + 1(22) + Ц21) = 13410
Преобразование десятичного числа в его двоичный эквивалент может быть
выполнено нахождением самой большой степени 2-х, которая меньше, чем
это число или равна этому числу. Прогрессия степеней 2-х включает значения
1, 2, 4, 8, 16, 32, 64 и так далее. Это дает ведущую цифру в этом двоичном
представлении. Остающиеся степени 2-х заполняются по убывающей до 0.
Например, рассмотрим значение 35. Числом с самой большой степенью 2-х,
меньшим, чем 35, является 32 = 25, это подразумевает, что 35 является
6-разрядным двоичным числом:
3510=1(32) + 0(16) + 0(8) + 0(4) + 1(2) + 1 = 1000112
Чистые двоичные числа являются просто суммой степеней 2-х. Они не
имеют знака, ассоциированного с ними, и о них говорят как о беззнаковых
числах (unsigned numbers). Эти числа представляют положительные целые.
Отрицательные целые используют либо представление точного дополнения,
либо — величины со знаком. В любом формате специальный бит, называемый
знаковым битом (sign bit), указывает знак числа.
Данные в памяти
Числа сохраняются в памяти как последовательности двоичных цифр
фиксированной длины. Распространенные длины включают 8, 16, и 32 бита.
Последовательность битов измеряется 8-битовой единицей, называемой байт
(byte).
0 0 10 0 0 11
Число 35 как байт
В таблице 2.1 приводится диапазон беззнаковых чисел и чисел со знаком
для этих распространенных длин.
Таблица 2.1
Диапазоны чисел и размер в байтах
Размер
8 (1 байт)
16 (2 байта)
32 (4 байта)
Диапазон беззнакового числа
0 .. 255=28 " 1
0 .. 65535=216Н
0 .. 4294967295=232-1
Диапазон числа со знаком
-27 =-128 .. 127=27-1
-215=-32768 .. 32767=215Н
-231 .. 231-1
Компьютерная память — это последовательность байтов, к которой
обращаются с помощью адресов 0, 1, 2, 3 и так далее. Адрес (address) целого в
памяти — это местоположение первого байта последовательности. Рис.2.1
иллюстрирует вид памяти с числом 8710 = 10101112, находящимся в одном байте
с адресом 3, и числом 50010 = 00000001111101002 с адресом 4.
Адрес
0
1
2
01010111
3
00000001 11110100
4 5
Рис. 2.1. Вид памяти
Представление целых в языке C++
Целыми типами в языке C++ являются: int, short int и long int. Тип
short int (short) предоставляет 16-битовые (2-байтные) целые значения в
диапазоне от -32768 до 32767. Тип long int (long) предоставляет самый широкий
диапазон целых значений и в большинстве систем реализуется с 32 битами
(4 байтами), и поэтому его диапазон составляет от -231 до 231 - 1.
Общий тип int идентифицирует целые, чья длина в битах зависит от
компьютера и компилятора. Обычно компиляторы используют 16-битовые
или 32-битовые целые. В некоторых случаях пользователь имеет возможность
выбирать длину целого в качестве опции. Целые типы данных устанавливают
область значений данных и задают арифметические операторы и операторы
отношения. Каждый тип данных задает реализацию целого ADT с
ограничением, что целые значения находятся в некотором конечном диапазоне.
2.2. Символьные типы
Символьные данные включают алфавитно-цифровые элементы, которые
определяют заглавные и строчные буквы, цифры, знаки пунктуации и
специальные символы. Компьютерная индустрия использует различные
представления символов для приложений. Набор символов ASCII из 128 элементов
имеет самое широкое применение для текстовой обработки, ввода и вывода
текста и передачи данных. Мы используем набор ASCII для нашего
символьного ADT. Подобно целым, символы ASCII включают отношение порядка,
определяющее набор операторов отношения. В случае алфавитных символов
буквы следуют словарному порядку. В этом отношении все заглавные буквы
меньше, чем строчные:
T<W, b<d, T<b
ADT Character
Данные
Набор символов ASCII
Операции
Присваивание
Значение символа может присваиваться символьной переменной.
Операция отношения
Шесть стандартных операций отношения применяются к символам
с использованием ASCII словарного отношения порядка.
Конец ADT Character
Символы ASCII
Большинство компьютерных систем используют стандартную систему
кодирования ASCII для символьного представления. Символы ASCII хранятся
как 7-битовый целый код в 8-битовом числе. 27 = 128 различных кодов
подразделяются на 95 печатаемых и 33 управляющих символа. Управляющий
символ используется при передаче данных и вызывает выполнение
управляющей функции устройством, например, перемещение курсора дисплея на
одну строку вниз.
В таблице 2.2 показан печатаемый набор символов ASCII. Символ "пробел"
представлен как ♦. Десятичный код для каждого символа задается
десятичной позицией, которой соответствует номер строки, и единичной, — которой
соответствует номер столбца. Например, символ "Т" имеет ASCII-значение
8410 и хранится в двоичном виде как 010101002.
В символьном наборе ASCII десятичные цифры и алфавитные символы
находятся в правильно определенных диацазонах (табл. 2.3). Это делает более
легким преобразование между заглавными и строчными буквами и
преобразование цифры ASCII ('0' ... '9') в соответствующее число (0 ... 9).
Набор печатаемых символов ASCII
Таблица 2.2
Левая цифра
3
4
5
6
7
8
9
10
11
12
Правая цифра
0
(
2
<
F
Р
Z
d
п
X
1
)
3
=
G
Q
[
е
о
У
2
♦
*
4
>
Н
R
\
f
Р
z
3
j
+
5
•
I
S
]
g
q
{
4
-
г
6
@
J
T
л
h
г
5
#
•
7
A
К
U
i
s
}
6
$
/
8
В
L
V
>
j
t
-
7
%
0
9
С
M
w
a
k
u
8
&
1
•
D
N
X
b
I
V
9
i
*
E
0
Y
с
m
w
Коды 00-31 и 127 - управляющие символы, которые являются непечатаемыми.
Таблица 2.3
Символьные диапазоны ASCII
Символы ASCII
Пробел
Десятичный знак
Символ верхнего регистра
Символ нижнего регистра
Десятичный
32
48-57
65-90
97-122
Двоичный
00100000
00110000-00111001
01000001-01011010
01100001-01111010
Пример 2.3
1. ASCII-значение для цифры '0' — это 48. Цифры упорядочены в
диапазоне 48 — 57:
ASCII-цифра '3' — это 51 (48 + 3)
Соответствующая численная цифра получается вычитанием '0*
(ASCII 48):
Численная цифра: 3 = '3' — '0' = 51 — 48
2. Для преобразования заглавного символа в строчный добавьте 32 к
ASCII-значению символа:
ASCII ('А') = 65 ASCII (V) = 65 + 32 = 97
Для хранения символа в C++ используется простой тип char. Коды ASCII
находятся в диапазоне от 0 до 127; однако, для использовалия остающихся
значений диапазона часто определяются машинно-зависимые расширенные
символы. Как целый тип, значение является кодом для символа.
2.3. Вещественные типы
Целые типы, о которых говорят как о дискретных типах (discrete types),
представляют значения данных, которые могут быть продолжены, например:
-2, -1, 0, 1, 2, 3 и так далее. Многие приложения требуют чисел, которые
имеют дробные значения. Эти значения, называемые вещественными числами
(real numbers), могут быть представлены в формате с фиксированной точкой
(fixed-point format) с целой и дробной частью:
9.6789 -6.345 +18.23
Вещественные числа могут быть также записаны как числа с плавающей
точкой в экспоненциальном формате (scientific notation). Этот формат
представляет числа как серию цифр, называемых мантиссой (mantissa) и порядком
(exponent), который представляет степень 10-и. Например, 6.02е23 имеет
мантиссу 6.02 и порядок 23. Число с фиксированной точкой является просто
особым случаем числа с плавающей точкой с порядком 0. Как в случае с целыми
и символами, вещественные числа составляют абстрактный тип данных.
Стандартные арифметические и операции отношения применяются к вещественным
числам, используемым вместо целых.
ADT Real
Данные
Числа, описанные в формате с фиксированной или плавающей точкой.
Операции •
Приев аивание
Вещественное выражение может быть присвоено действительной переменной.
Арифметические операторы
Стандартные двоичные и унарные арифметические операции применяются к
вещественным числам вместо целых. Никаких других операторов не имеется
Операции отношения
К вещественным числам применяются шесть стандартных операций
отношения.
конец ADT Real
Представление вещественных чисел
Как и для целых чисел, область вещественного числа не имеет предела.
Значения вещественных чисел являются безграничными и в отрицательном, и
в положительном направлении, а мантисса распределяет действительные числа
на последовательность точек числовой оси. Вещественные числа реализуются
в конечном блоке памяти, ограничивающем диапазон значений и образующем
дискретные точки числовой оси.
В течение многих лет специалисты использовали разнообразные форматы
для хранения чисел с плавающей точкой. Формат IEEE (Института инженеров
по электротехнике и радиоэлектронике) является широко используемым
стандартом. Вы знакомы с вещественными числами, которые используют формат
с фиксированной точкой. Таким является число, разделяемое на целую часть
и дробную, цифры которой умножаются на 1/10, 1/100, 1/1000 и так далее.
Десятичная точка разделяет эти части:
25.638 = 2(10!) + 5(10°) 4- 6(101) + 3(10'2) +8(10"3)
Как в случае с целыми числами, имеются соответствующие двоичные
представления для вещественных чисел с фиксированной точкой. Эти числа содержат
целую и двоичную дробную части и двоичную точку с дробными цифрами,
соответствующими 1/2, 1/4, 1/8 и т. д. Общая форма такого представления:
N = ьп... Ъ0 . fe-i^". = Ъп2п + ... + Ъ02° + Ь^2г + Ъ-22~2 +...
Например:
1011.1102 = 1(23) + Ц21) + 1(2°) + Ц2-1) + 1(2"2) + 1(2~4)
= 8 + 2+1 +0.5 + 0.25 + 0.0625
= 11.812510
Преобразование десятичных и двоичных чисел с плавающей точкой
использует алгоритмы, подобные разработанным для целых чисел. Преобразование в
десятичные числа выполняется сложением произведений цифр и степеней 10-и.
Обратный процесс является более сложным, поскольку десятичное число
может потребовать бесконечного двоичного представления для создания
эквивалентного числа с плавающей точкой. В компьютере количество цифр
ограничено, так как используются только числа с плавающей точкой
фиксированной длины.
Пример 2.4
Преобразовать двоичное число с фиксированной точкой в десятичное
число:
1. 0.011012 = 1/4 + 1/8 + 1/32
= 0.25 + 0.125 + 0.03125 - 0.4062510
Преобразовать десятичное число в двоичное число с плавающей точкой:
2. 4.3125ю = 4 + 0.25 + 0.0625 = 100.01012
3. Десятичное число 0.15 не имеет эквивалентной двоичной дроби
фиксированной длины. Преобразование десятичной дроби в двоичную
требует бесконечного двоичного расширения. Поскольку
компьютерная память ограничена числами фиксированной длины, хвост
бесконечного расширения отсекается, и частичная сумма является
приближением десятичного значения:
0.15ю = 1/8+1/64+1/128+1/1024+ ... =0.0010011001 ...2
Большинство компьютеров хранят вещественные числа в двоичной форме,
используя экспоненциальный формат со знаком, мантиссой и порядком:
N = ±£>nDni - - • DjD0 . d2d2. . . dn x 2е
C++ поддерживает три вещественных типа данных: float, double и long
double. Тип long double применяется для вычислений, требующих высокой
точности и не используется в этой книге. Часто тип float реализуется с
помощью 32-битового формата IEEE с плавающей точкой, тогда как
64-битовый формат используется для типа double.
2.4. Типы перечисления
Набор символов ASCII использует целое представление символьных
данных. Сходное целое представление может быть использовано для описания
определяемых программистом наборов данных. Например, вот перечень
месяцев, длина которых составляет 30 дней:
Апрель, июнь, сентябрь, ноябрь
Этот набор месяцев образует тип перечисления (enumerated data type).
Для каждого типа упорядочение элементов определяется так, как эти
элементы перечислены. Например:
Цвет волос
черные // первое значение
белокурые // второе значение
каштановые // третье значение
рыжие // четвертое значение
черные
белокурые
каштановые
рыжие
Этот тип поддерживает операцию присваивания и стандартные операции
отношения. Например:
черные < рыжие //черные находятся перед рыжими
каштановые >= белокурые //каштановые находятся после белокурых
Тип перечисления имеет данные и операторы и, следовательно, является
ADT.
ADT Enumerated
Данные
Определяемый пользователем список N отдельных элементов.
Операции
Присваивание
Переменной типа перечисления может быть присвоен любой
из элементов в списке.
конец ADT Enumerated
Реализация типов перечисления C++
C++ имеет тип перечисления, определяющий отдельные целые значения,
на которые ссылаются именованные константы.
Пример 2.5
1. Булев тип может быть объявлен типом перечисления. Значением
константы False является 0, а значение True — это 1. Переменная
Done определяется как булева с первоначальным значением False.
enum Boolean (False, True);
Boolean Done = False;
2. Месяцы года объявляются как тип перечисления. По умолчанию
первоначальным значением Jan является 0. Однако, целая
последовательность может начинаться с другого значения путем
присваивания этого значения первому элементу. В этом случае Jan является
1, и месяцы соответствуют последовательности 1, 2,. . . , 12.
enum Month {Jan=l/Feb/ Mar, Apr, May, Jun, Jul, Aug, Sep, Oct, Nov, Dec};
Month Mon = Dec;
2.5. Указатели
Тип указателей является основным в любом языке программирования.
Указатель (pointer) — это беззнаковое целое, представляющее адрес памяти.
Указатель служит также в качестве ссылки на данные по адресу. В адресе
указателя тип данных называется базовым типом (base type) и используется
в определении указателя. Например, указатель Р имеет значение 5000 в
каждом случае на рис. 2.2. Однако, в (а) указатель ссылается на символ, а
в (Ь) указатель ссылается на короткое целое.
Указатель делает возможным эффективный доступ к элементам в списке
и является фундаментальным для разработки динамических структур
данных, таких как связанные тексты, деревья и графы.
Рис. 2.2. Тип указатель
Указатели ADT
Как число, указатель использует некоторые арифметические операторы и
операторы отношения. Арифметические операции требуют особого внимания.
Указатель может быть увеличен или уменьшен на целое значение для ссылки
на новые данные в памяти. Добавление 1 обновляет указатель для ссылки
на следующий элемент этого типа в памяти. Например, если р указывает
на объект char,, то р + 1 указывает на следующий байт в памяти. Добавление
к > 0 перемещает указатель на к позиций данных вправо. Например, если
р указывает на double, р + к ссылается на double:
N = sizeof (double) * k байтов вправо от р.
Тип данных
j char
| int (2 байта)
| double (4 байта)
Текущий адрес
р = 5000
р = 5000
р = 5000
Новый адрес
р + 1 = 5001
р + 3 = 5000 + 3*2 = 5006
р - б = 5000 -6*4 = 4976 |
Указатель использует адресный оператор "&", который возвращает адрес в
памяти элемента данных. Напротив, оператор "*" ссылается на данные,
ассоциированные со значением указателя. Упорядочение указателей происходит
путем сравнения их беззнаковых целых значений.
Динамическая память (dynamic memory) — это новая память
распределяемая во время выполнения программы. Динамическая память отличается от
статической памяти (static memory), чье наличие определяется до начала
выполнения программы. Динамическая память описывается в главе 8. Оператор
new принимает тип Т, динамически выделяет память для элемента типа Т и
возвращает указатель на память, которую он выделил. Оператор delete
принимает указатель в качестве параметра и освобождает динамическую память,
выделенную ранее по этому адресу.
ADT Pointer
Данные
Набор беззнаковых целых, который представляет адрес памяти для элемента
данных базового типа Т.
Операции
Предположим, что и и v — это выражения-указатели, i — это целое выражение,
ptr — это переменная pointer, a var — это переменная типа Т.
Адрес
& ptr = &var Присваивает ptr адрес переменной var.
Присваивание
= ptr = u Присваивает ptr значение указателя и.
Разыменовывание
* var = *ptr Присваивает элемент типа Т, на который ссылается
ptr, переменной var.
Выделение и освобождение динамической памяти
new ptr = new Т Создает динамическую память для элемента типа Т
и присваивает ptr его адрес.
delete delete ptr Освобождает динамическую память, выделенную
по адресу ptr.
Арифметическая
+ u + i Указывает на элемент, размещенный на i элементов
данных правее элемента, на который ссылается и.
~ и — i Указывает на элемент, размещенный на i элементов
левее элемента, на который ссылается и.
~~ и — v Возвращает число элементов базового типа,
которые находятся между двумя указателями.
Отношения
К указателям применяются шесть стандартных операторов отношения путем
сравнения их беззнаковых целых значений.
Конец ADT Pointer
Значения указателя
Значение указателя — это адрес памяти, использующий 16, 32 или более
битов в зависимости от машинной архитектуры. В качестве примера: PC — это
указатель на char (1 байт), а РХ — это указатель на short int (2 байта).
char str[] = ABCDEFG;
char *PC = str; //PC указывает на строку str
short X = 33;
short *PC = &X; // РХ указывает на Х типа short
Следующие операторы иллюстрируют основные операции с указателями.
cout « *РС « endl; // напечатать 'А'
РС+= 4; // сдвинуть PC вправо на четыре символа
cout « *РС « endl; // напечатать 'Е'
PC—; // сдвинуть PC влево на один символ
cout « *РС « endl; // напечатать 'D'
cout « *РХ + 3 « endl; // напечать 36 = 33 + 3
Операции new и delete обсуждаются в главе 8.
2.6. Массив (array)
Массив является примером набора данных. Одномерный массив — это
конечный, последовательный список элементов одного и того же типа данных —
однородный массив (homogeneous array). Последовательность определяет первый
элемент, второй элемент и так далее. С каждым элементом ассоциирован целый
индекс (index), определяющий позицию элемента в списке. Массив имеет
оператор индекса, который делает возможным прямой доступ (direct access) к
элементам в списке при сохранении или возвращении какого-либо элемента.
А0 А, А2 А3
ADT Array
Данные
Набор N — элементов одного и того же типа данных; индексы выбираются из
диапазона целых от 0 до N — 1, которые определяют позицию элементов
в списке и обеспечивают прямой доступ к элементам. Индекс 0 ссылается
на первый элемент в этом списке, индекс 1 ссылается на второй элемент и т.д.
Операции
Индексирование [ ]
Вход: Индекс
Предусловия: Индекс находится в диапазоне от 0 до N — 1.
Процесс: В правой части оператора присваивания оператор
индексирования возвращает данные из элемента; в левой
части оператора присваивания оператор индексирования
возвращает адрес элемента массива, который сохраняет
правую часть выражения.
Выход: Если операция индексирования находится в правой части
оператора присваивания, то операция выбирает данные
из массива и возвращает эти данные клиенту.
Постусловия: Если операция индексирования находится в левой части,
то заменяется соответствующий элемент массива.
Конец ADT Array
Встроенный тип массива C++
В качестве части своего базового синтаксиса C++ предоставляет
встроенный тип статического массива, который определяет список элементов одного
и того же типа. Явное объявление задает постоянный размер массива N и
указывает, что индексы находятся в диапазоне от 0 до N-1. Объявление в
примере 2.6 определяет статический массив C++. В главе 8 мы будем
создавать динамические массивы, используя указатели.
Пример 2.6
1. Объявить два массива типа double. Массив X имеет 50 элементов,
а массив Y — 200 элементов:
double X [ 50 ], Y [ 200 ];
2. Объявить длинный массив А с размером, задаваемым целой
константой ArraySize = 10.
const int ArraySize - 10;
long A[ArraySize];
Индекс массива в диапазоне от 0 до ArraySize - 1 используется для доступа
к отдельным элементам массива. Элемент с индексом i имеет представление
A[i].
Индексирование массива фактически выполняется путем использования
оператора индексирования ([]). Это двоичный оператор, левый операнд
которого является именем массива, а правый — позицией элемента в массиве.
Доступ к элементам массива может осуществляться в любой части оператора
присваивания:
A[i] ■ х; // присвоить (сохранить) х как данные для элемента массива
t e A[i] ; // возвратить данные из A[i] и присвоить их переменной t
A[i] - A[i + 1] = х;
// присвоить х элементу A[i +1]. Второе присваивание
сохраняет данные из A[i +1] в A[i].
Сохранение одномерных массивов
C++ одномерный массив А логически сохраняется как последовательное
упорядочение элементов в памяти. Каждый элемент относится к одному и тому
же типу данных.
А[0]
A[i]
t i
Address A[0] Address A[i]
В C++ имя массива является константой и рассматривается как адрес
первого элемента этого массива. Так, в объявлении
Type A[ArraySize];
имя массива А является константой и местоположением в памяти первого
элемента А[0]. Элементы А[1], А[2] и т.д. следуют за ним последовательно.
Допустим, что sizeof(Type) = М, весь массив А занимает М * ArraySize байтов.
А[0] А[1] А[2] А[3]
Компилятор задает таблицу, называемую дескриптор массива (dope vector),
для ведения записи характеристик массива. Таблица включает информацию о
размере каждого элемента, начальный адрес массива и количество элементов
в этом массиве:
Начальный адрес: А
Количество элементов массива: ArraySize
Размер типа: М = sizeof(Type)
Эта таблица используется компилятором также для реализации функции
доступа (access function), которая определяет адрес элемента в памяти.
Функция ArrayAccess использует начальный адрес массива и размер типа данных
для установки индекса I по адресу А[1]:
Adress A[I] « ArrayAccess (A, I, M)
ArrayAccess задается:
ArrayAccess (А, I, М) = А + I * М;
Пример 2.7
Предположим, что float сохраняется с использованием 4 байт
(sizeof(float) = 4) и массив Height начинается в памяти по адресу 20000.
float Height [35];
Элемент массива Height[18] размещается по адресу
20000 + 18 * 4 = 20072
Границы массива
ADT массива предполагает, что индексы находятся в целом диапазоне от 0
до N — 1, где N — это размер массива. То же самое и в C++. В действительности,
большинство компиляторов C++ при доступе к элементу массива не генерируют
код, который тестирует, находится ли индекс вне пределов массива. Например,
следующая последовательность будет приниматься большинством компиляторов:
int V = 20;
int A[20]; //размер массива 20; индексный диапазон 0—19
A[V] =0; //индекс V больше, чем верхний предел
Массив занимает память в области данных пользователя. Функция доступа
к массиву определяет адрес в памяти для отдельного элемента, и обычно не
производится проверки того, находится ли адрес на самом деле в диапазоне
элементов массива. В результате C++ программа может использовать индексы,
находящиеся вне указанного диапазона. Адреса для элементов, которые
находятся вне диапазона массива, могут все же находиться в области данных
пользователя. В процессе выполнения программа может замещать другие
переменные и вызывать нежелательные ошибки. На рисунке 2.3 показан вид
программы в памяти.
System Memory
User Program
User Data Block
int N
int arr[20];
float D;
Array
Space
Рис 2.З. Размещение памяти в интервале данных пользователя
Некоторые компиляторы реализуют проверку индекса массива, генерируя
код времени исполнения для проверки того, находятся ли индексы массива
внутри диапазона. Поскольку дополнительный код замедляет выполнение,
большинство программистов используют проверку массива только во время
программной разработки. Как только код отлажен, эта опция выключается,
и программа перекомпилируется на более эффективный код. Другим
подходом к проблеме является разработка "надежного массива", который реагирует
на неправильные индексные ссылки и выводит сообщение об ошибке.
Надежные массивы разрабатываются в главе 8.
Двумерные массивы
Двумерный массив, часто называемый матрицей, является
структурированным типом данных, который создается путем вложения одномерных
массивов. Доступ к элементам выполняется по индексам строк и столбцов.
Например, на следующем рисунке представлен массив Т из 32 элементов с 4
строками и 8 столбцами. Значение 10 доступно с помощью пары индексов
(строка, столбец) (1, 2), а -3 — с помощью индексов (2, 6).
Концепция двумерного массива может быть расширена для охвата
основных многомерных массивов, элементы в которых доступны с помощью трех
или более индексов. Двумерные массивы имеют примененние в таких
различных областях, как обработка данных и численное решение
дифференциальных уравнений в частных производных.
Столбец
Строка
В С+4- объявление двумерного массива Т определяет количество строк,
количество столбцов и тип данных элементов массива:
type T [RowCount] [ColumnCount];
Ссылка на элементы массива Т производится с помощью индексов строки
и столбца:
T[i] [j], 0 <= i <= RowCount - 1, 0 <= j <= ColumnCount — 1
Например, матрица Т — это массив целых размером 4x8:
int T[4] [8];
Значение Т[1][2] = 10 и Т[2][6] = -3.
Мы можем представлять двумерный массив как список одномерных
массивов. Например, Т[0] — это строка 0, которая состоит из ColumnCount
отдельных элементов. Данная концепция полезна, когда двумерный массив
передается в качестве параметра. Нотация int Т[][8] указывает на то, что Т
является списком из 8-элементных массивов.
Сохранение двумерных массивов
Двумерный массив может инициализироваться присваиванием элементам
по одной строке каждый раз. Например, массив Т задает таблицу размером 3x4:
int T[3] [4] = {{20, 5, - 30, 0}, {-40, 15, 100, 80}, {3, 0, 0 -1)};
Как массив, элементы сохраняются в следующем порядке: первая строка,
вторая строка, третья строка (рис. 2.4).
Для доступа к элементу в памяти компилятор расширяет дескриптор
массива для включения информации о количестве столбцов и длине каждой строки
и использует новую функцию доступа, называемую Matrix Access, для
возвращения адреса элемента.
Столбец
S
*
20
-40
3
5
15
0
-30
100
0
0
80
-1
Начальный адрес: Т
Количество арок: RowCount
Количество столбцов: ColumnCount
Размер типа: М = sizeof(Type)
Длина строки: RS = M*ColumnCount //длина всей строки
Функция MatrixAccess принимает пару индексов строки и столбца (I,J)
и возвращает адрес элемента T[I][J]:
Address T[I] [J] = MatrixAccess (T, I, J)
- T + (I * RS) + (J * M)
Значение (I * RS) дает количество байтов, необходимое для хранения I
строк данных. Значение (J * М) дает количество байтов для хранения первых
J элементов в строке I.
Построчное хранение массива
20
5
-30
0
Строка#0
-40
15
100
80
Строка#1
3
0
0
-1
Строка#2
Рис 2.4. Хранение матрицы Т
Пример 2.8
Пусть Т будет матрицей 3x4 на рис. 2.4. Предположим, что длина
целого равна 2, и матрица хранится в памяти по адресу 1000.
Начальный адрес: 1000
Количество строк: 3
Количество столбцов: 4
Размер типа: 2 = sizeof(int)
Длина строки: 8 = 2*4// длина всей строки
20
5
-30
0
/ Строка#0
-40
15
100
80
/ Строка#1
3
0
0
-1
/ Строка#2
1. Адреса для строк в памяти следующие:
Строка 0: Адрес 1000
Строка 1: Адрес 1000 + 1*8 = 1008 (строка — это 8 байт)
Строка 2: Адрес 1000 + 2*8 = 1016
2. Адресом Т[1][3] является:
ArrayAccess (Т, 1, 3)= 1000 + (1 * 8) + (2 * 3)
= 1014
2.7. Строковые константы и переменные
Массив — это структурированный тип данных, содержащий однородный
список элементов. Особая форма массива содержит символьные данные,
которые определяют имена, слова, предложения и так далее. Структура,
называемая строкой (string), обращается с символами как с одним
объектом и предоставляет операции для доступа к последовательностям символов
в строке. Строка является важнейшей структурой данных для большинства
приложений, использующих алфавитно-цифровые данные. Эта структура
необходима для управления текстовой обработкой с ее операциями
редактирования, ее алгоритмами поиска/замены и т. д. Например, лингвисту
может потребоваться информация о количестве появлений определенного
слова в документе, или программист может использовать шаблоны
поиска/замены для изменения исходного кода в документе. Большинство
языков объявляют строковые структуры и предоставляют встроенные
операторы и библиотечные функции для управления строками.
Для определения длины строки структура может включать 0 в конце
строки (строка с нулевым завершающим символом или NULL-символом —
NULL-terminated string) или отдельный параметр длины. Следующие
представления строки содержат 6-символьную строку STRING.
Строка с нулевым символом в конце
S
т
R
1
N
G
NULL
Строка со счетчиком длины
6
S
т
R
1
N
G
Длина
Серия операций обрабатывает строку как единый блок символов.
Например, мы можем определить длину строки, копировать одну строку в другую,
объединять строки (конкатенация) и обрабатывать подстроки операциями
вставки, удаления и отождествления* Строки имеют также операцию
сравнения, позволяющую их упорядочивать. Эта операция использует
ASCII-упорядочивание. Например:
"Baker" меньше, чем "Martin" // В следует перед М
"Smith" меньше, чем "Smithson"
"Barber" следует перед "barber" //заглавная В предшествует строчной b
"123Stop" меньше, чем "AAA" //числа предшествуют буквам
ADT String
Данные
Строка является последовательностью символов с ассоциированной длиной.
Строковая структура может иметь NULL-символ или отдельный параметр длины.
Операции
Длина
Вход: Нет
Предусловия: Нет
Процесс: Для строки с NULL-символом подсчитать символы
до NULL-символа; для строки с параметром длины
возвращать значение длины.
Выход: Возвращать длину строки
Постусловия: Нет
Копирование
Вход: Две строки: STR1 и STR2. STR2 - это источник,
a STR1 — это место назначения.
Предусловия: Нет
Процесс: Копирование символов из STR2 в STR1.
Выход: Возвращать доступ к STR1
Постусловия: Создается новая строка STR1 с длиной и данными,
полученными из STR2.
Конкатенация
Вход: Две строки STR1 и STR2. Соединить STR2 с хвостом STR1
Предусловия: Нет
Процесс: Нахождение конца STR1. Копирование символов из STR2
в конец STR1. Обновление информации о длине STR1.
Выход: Возвращать доступ к STR1.
Постусловия: STR1 изменяется.
Сравнение
Вход: Две строки: STR1 и STR2.
Предусловия: Нет
Процесс: Применение ASCII-упорядочения к этим строкам.
Выход: Возвращать значение следующим образом:
STR1 меньше, чем STR2: возвращать отрицательное значени
STR1 равна STR2: возвращать значение О
STR1 больше, чем STR2: возвращать положительное значени
Постусловия: Нет
Индексация
Вход: Строка STR и одиночный символ СН
Предусловия: Нет
Процесс: Поиск STR для входного символа СН
Выход: Возвращать адрес места, содержащего первое появление
СН в STR или 0, если этот символ не найден.
Постусловия: Нет
Правый индекс
Вход: Строка STR и одиночный символ СН
Предусловия: Нет
Процесс: Поиск STR для последнего появления символа СН.
Выход: Возвращать адрес места, содержащего последнее появление
СН в STR или 0, если этот символ не найден.
Постусловия: Нет
Чтение
Вход: Файловый поток, символы которого считываются, и строка
STR для сохранения символов.
Предусловия: Нет
Процесс: Считывание последовательности символов из потока в строку STR.
Выход: Нет
Постусловия: Строке STR присваиваются считываемые символы
Запись
Вход: Строка, которая содержит символы для выхода, и поток,
в который символы записываются.
Предусловия: Нет
Процесс: Пересылка строки символов в поток.
Выход: Выходной поток изменяется.
Постусловия: Нет
Конец ADT String
Строки C++
Глава 8 содержит спецификацию и реализацию C++ класса String. Этот
класс содержит расширенный набор операторов сравнения и операций
ввода/вывода. В этой главе мы используем строки с NULL-символами и C++
строковую библиотеку для реализации ADT.
Строка в C++ — это строка с нулевым завершающим символом, в которой
NULL-символ обозначается символом 0 в коде ASCII. Компилятор определяет
строковую константу (string literal) как последовательность символов,
заключенную в двойные кавычки. Строковая переменная (string variable) —
это символьный массив, который содержит последовательность символов с
NULL-символом в конце. Следующее объявление создает символьный массив
и присваивает строковую константу массиву:
char STR[9] = МА String";
Строка "A String" сохраняется в памяти как символьный массив из 9
элементов:
А
S
t
г
i
п
9
NULL
STR
C++ предоставляет ряд операторов ввода/вывода текста для потоков: cin
(клавиатура), cout (экран), сегг (экран) и определяемых пользователем
файловых потоков.
Строковые функции C++ и примеры
Таблица 2.4
char sl[20]="dir/bin/appl", s2[20] - "file.asm", s3[20];
char *p; int result;
1. Длина int etrlen(char *s);
cout << strlen(sl) « endl; // выходное значение равно 12
cout « strlen(s2) « endl; // выходное значение равно 8
2. Копирование char* etrcpy(char *sl, *s2);
strcpy(s3,sl); // s3 = "dir/bin/appl"
3. Конкатенация char *etrcat(char *sl, *s2);
strcat(s3, /);
strcat(s3, s2); // s3="dir/bin/appl/file.asm"
4. Сравнение int strcmp(char *sl, *s2);)
result - strcmp("baker", "Baker"); // result > 0
result - strcmp("12"/ "12"); // result = 0
result = strcmp("Joe", "Joseph"); // result < 0
5. Индекс char *etrchr(char *s, int c);
p = strchar(s2, ' .'); II V указывает на '/' после bin
if (P)
strcpy(p, ".cpp"); // s2 « "file.cpp"
6. Правый индекс char *etrrchr(char *s, int c);
p = strrchr(sl, '/'); II P указывает на ' /' после bin
if (p)
*p =■ 0; // закончить строку после bin; s2 = "dir/bin"
7. Считать StreamVariable » s
8. Записать StreamVariable << s
cin > si; // если входная строка - "hello world", то si
ccut < si; // указывает на строку
// "hello world"
// выход - "hello world"
Строковая библиотека C++ <string.h> содержит гибкий набор функций
строкового управления, который непосредственно реализует большинство
операций ADT. В таблице 2.4 перечислены ключевые строковые функции C++.
Приложение: перестановка имен
Строковая прикладная программа иллюстрирует использование строковых
библиотечных функций C++. В этом приложении функции strchr(), strcpy() и
strcat() объединяются для копирования имени такого, как "John Doe" в "Doe",
"John", в строку Newname. Следующие операторы реализуют этот алгоритм:
char Name[10] = "John Doe", Newname[30];
char *p;
Оператор 1: p * strchrfName, ' ');
Возвратить указатель р на первый пробел в переменной Name.
Первая буква фамилии находится по адресу р+1.
J
1
О
h
п
D
0
е
NULL
Name
Р
Оператор 2: *р = 0; // заменить пробел на нулевой символ
J
0
h
n
NULL
D
0
e
NULL
Name p
Оператор 3: strcpy(Newname, p+1); // копировать фамилию в Newname
J
t
Name
D
0
0
h
e
n
NULL
p+1
NULL
D
0
e
NULL
Newname
Оператор 4: strcat (Newname, ", " ); // добавить ',' и пробел к Newname
D
О
e
i
NULL
Newname
Оператор 5: strcat (Newname, Name); // добавить к Newname имя
J
0
h
n
NULL
' t
Name
D
0
e
•
J
0
h
n
null:
Newname
Программа 2.1. Перестановка имени
Данная программа использует операторы 1 — 5 для перестановки
имени. Эти шаги содержатся в функции ReverseName. Цикл главной
программы тестирует алгоритм на трех строках ввода. Выходом в каждом
случае является переставленное имя.
// рг02_01.срр
iinclude <iostream.h>
♦include <string.h>
// перестановка имени и фамилии и разделение их запятой
// результат копируется в Newname
void ReverseName(char *name, char *newName)
{
char *p;
// поиск первого пробела в name и замена пробела
// NULL-символом
р = strchr(name,' ' ) ;
*р« 0;
// копировать фамилию в Newname, добавить ", "и
// присоединить к Newname имя
strcpy(newName,p+1);
streat(newName,", ");
streat(newName,name);
*p = '
}
void main (void)
{
char name [ 32 ], newName [ 32 ];
int i;
// считать и обработать три имени
for (i = 0; i < 3; i++)
{
cin.getline(name,32,'\n');
ReverseName(name,newName);
cout << "Переставленное имя: " « newName « endl « endl;
}
}
/*
Оапуск программы pr02_01. cpp>
Abraham Lincoln
Переставленное имя: Lincoln, Abraham
Debbie Rogers
Переставленное имя: Rogers, Debbie
Jim Brady
Переставленное имя: Brady, Jim
*/
2.8. Записи
Запись (record) — это структура, которая связывает элементы различных
типов в один объект. Элементы в записи называются полями (fields). Подобно
массиву, запись имеет оператор доступа, который делает возможным прямой
доступ к каждому полю. Например, Student — это структура записи,
содержащая информацию о студенте, посещающем колледж. Эта информация
включает имя (Name), адрес (Local Address), возраст (Age), профилирующую
дисциплину (academic major) и среднюю успеваемость (grade-point average, GPA).
Name
Строка
Local Address
Строка
Age
Целое
T
Major
ип перечисления
GPA
Действительное
Поля Name и Local Address содержат строковые данные. Age и GPA
являются численными типами, a Major — это тип перечисления. Полагая, что
Том — студент, мы получаем доступ к отдельным полям, объединяя записи
имени и поля с использованием оператора доступа ".":
Tom.Name Tom.Age Tom.GPA Тот.Major
«
Запись позволяет объединять данные различных типов (неоднородные
типы — heterogeneous types) в структуре. В отличие от массива, запись
описывает единственное значение, а не список значений.
ADT Record
Данные
Элемент, содержащий набор полей неоднородного типа. Каждое поле имеет имя,
обеспечивающее прямой доступ к данным в поле.
Операции
Оператор доступа
Вход: Имя записи (recname) и поле
Предусловия: Нет
Процесс: Доступ к данным в поле
Выход: При нахождении данных возвращать значение поля клиенту.
Постусловия: При сохранении данных запись изменяется
Конец ADT Record
Структуры C++
C++ имеет встроенный тип struct, представляющий запись. Эта структура
заимствована из языка С и сохраняется для совместимости. C++ определяет
тип struct как особый случай класса, в котором все члены являются
открытыми. Мы используем тип struct в этом тексте только, когда имеем дело со
структурой записи.
Пример 2.9
struct Student
{
int id;
char name [30];
}
Student S = {555, "Davis, Samuel"};
cout « S.id «" "< S.name < endl;
2.9. Файлы
Большинство тем в этой книге концентрируют внимание на разработке и
реализации внутренних структур данных (internal data structures), которые
обращаются к информации, постоянно находящейся в памяти. Для
приложений, однако, мы часто предполагаем, что данные доступны на устройстве
внешней памяти, таком как диск. Это устройство (физический файл) сохра-
Клавиатура
Память
компьютера
Входной поток
Запоминающее устройство
большой емкости
Рис. 2.5. Поток данных ввода
няет информацию в символьном потоке, и операционная система
предоставляет ряд операций для передачи данных в память и из нее. Это позволяет
нам выполнять ввод и вывод данных, которые могут постоянно храниться
на внешнем устройстве. Сохраняемые данные вместе с операциями передачи
определяют структуру данных, называемую (логическим) файлом (file),
которая имеет важное преимущество сохранения большего количества
информации, чем обычно находится постоянно в памяти.
Языки программирования предоставляют высокоуровневые операции
управления файлами для того, чтобы избавить программиста от необходимости
использовать низкоуровневые вызовы операционной системы. Файловые
операции используют поток (stream) данных, логически соединений с файлом.
Stream ассоциирует поток данных с файлом. Для ввода поток позволяет данным
последовательно перемещаться от внешнего устройства к памяти (рис.2.5). Та
же программа может выводить информацию в файл, используя поток вывода
(рис.2.6).
Полезно определить ADT для файла. Данные состоят из
последовательности символов, которые представляют текстовые данные или байты в виде
двоичных данных. Для текста данные сохраняются как последовательность
символов в коде ASCII, разделяемых newline-символами. Операции ADT
задаются в большинстве случаев с концентрацией внимания на простых
операциях ввода/вывода. Операция ввода Read извлекает последовательность
символов из потока. Родственная операция вывода Write вставляет
последовательность символов в поток. Специальные операции Get и Put управляют
вводом/выводом одного символа.
Поток управляет файловым указателем (file pointer), который определяет
текущую позицию в потоке. Операция Input продвигает файловый указатель
к следующему несчитанному элементу данных в потоке. Операция Output
устанавливает файловый указатель в следующую позицию вывода. Операция
установки Seek позволяет устанавливать файловый указатель в нужную по-
Память
компьютера
Монитор
Выходной поток
Запоминающее устройство
большой емкости
зицию в файле. Эта операция предполагает, что мы имеем доступ ко всем
символам в файле и можем перемещаться в переднюю, заднюю и
промежуточную позицию. Чаще всего операция установки используется для
дисковых файлов.
Файл обычно присоединяется к потоку в одном из трех режимов: read-only,
write-only и read-write. Режимы read-only и write-only указывают на то, что
поток используется для ввода или вывода, соответственно. Режим read-write
обеспечивает поток данных в обоих направлениях.
ADT File
Данные
Определение внешнего файла и направления потока данных. Последовательность
данных, которые считываются из файла или записываются в файл.
Операции
Орел
Вход: Имя файла и направление потока.
Предусловия: Для ввода должен существовать внешний файл.
Процесс: Связывание потока с файлом.
Выход: Флажок, указывающий на успешность операции.
Постусловия: Данные могут последовательно перемещаться между внешним
файлом и системной памятью посредством потока.
Close
Вход: Нет
Предусловия: Нет
Процесс: Отделение потока от файла.
Выход: Нет
Постусловия: Данные больше не могут перемещаться посредством потока
между внешним файлом и системной памятью.
Чтение
Вход: Массив размером N для хранения блоков данных.
Предусловия: Поток должен быть открыт в направлении только для чтения
или чтения-записи.
Процесс: Ввод N символов из потока в массив.
Остановка в конце файла.
Выход: Возвращать количество символов, которые считываются.
Постусловия: Файловый указатель перемещается вперед на N символов.
Запись
Вход: Массив; count N
Предусловия: Поток должен быть открыт с направлением только для
записи или для чтения-записи.
Процесс: Вывод N символов из массива в поток.
Выход: Возвращать количество символов, которые записываются.
Постусловия: Поток содержит данные вывода, и файловый указатель
перемещается вперед на N символов.
Установка
Вход: Параметры для переустановки файлового указателя.
Предусловия: Нет
Процесс: Переустановка файлового указателя.
Выход: Возвращать флажок, указывающий на успешность установки.
Постусловия: Устанавливается новый файловый указатель.
Конец ADT File
Иерархия потоков C++
C++ обеспечивает файловое управление с потоковой системой
ввода/вывода, которая реализуется путем использования иерархии классов, как
частично показано на рис. 2.7. Поток C++ является объектом, соответствующим
классу в этой иерархии. Каждый поток определяет файл и направление
потока данных.
Корневым классом в иерархии является ios, содержащий данные и
операции для всех производных классов. Этот класс содержит флажки, которые
определяют специфические атрибуты потока и методы форматирования,
которые действительны для ввода и вывода. Например:
cout.setf(ios:: fixed);
устанавливает режим отображения для вещественных чисел на
фиксированный формат, а не на экспоненциальный.
Классы istream и ostream предоставляют базовые операции ввода и вывода
и используются как базовые классы для остальной части потоковой иерархии
ввода/вывода.
Класс istream_withassign — это вариант istream, который позволяет
выполнять объектное присваивание. Предопределенный объект cin является
объектом этого класса. Предопределенные объекты cout и сегг — это объекты типа
класса ostream_withassign. Во время выполнения эти три потока открыты для
ввода с клавиатуры и вывода на экран. Объявления этих классов включены в
файл <iostream.h>.
Класс ifstream является производным класса istream и используется для
дискового файлового ввода; аналогично of stream используется для дискового
файлового вывода. Эти классы объявляются в файле <fstream.h>. Оба класса
содержат операцию Open для присоединения файла к потоку и операцию Close
для отделения потока от файла.
Двумя типами дисковых файлов являются текстовые файлы (text files)
и бинарные файлы (binary files). Текстовый файл содержит символы ASCII
и является печатаемым, тогда как бинарный файл содержит чистые бинарные
данные. Например, редактор использует текстовые файлы, а программа —
электронная таблица создает и использует бинарные файлы. Пример текс-
ios
istream
ostream
istrstream
istream_
withassign
ifstream
iostream
ofstream
ostream_
withassign
ostrstream
fstream
strstream
Рис.2.7. Иерархия потоковых классов
тового файлового ввода/вывода дается в программе 2.2, а бинарные файлы
разрабатываются как класс в главе 14. Класс бинарных файлов используется
для реализации алгоритмов внешнего поиска и сортировки.
Класс fstream позволяет создавать и сопровождать файлы, которые
требуют доступа и для чтения, и для записи. Класс fstream описывается вместе
с приложениями в главе 14.
Ввод/вывод на базе массива реализуется классами istrstream и ostrstream
и объявляется в файле <strstream.h>. Здесь данные считываются из массива
или записываются в массив вместо внешнего устройства. Текстовые
редакторы часто используют ввод/вывод на базе массива для выполнения сложных
операций форматирования.
Программа 2.2. Файловый ввод/вывод
Данная программа представляет потоки C++, включающие текстовый
файл и ввод/вывод на базе массива.
Программа использует cout и сегг, которые включены в <iostream.h>.
Ввод текстового файла и вывод на базе массива используют файлы
<fstream.h> и <strstream.h>, соответственно. Программа открывает файл и
считывает каждую строку, содержащую пары переменная/значение в
формате Name Value. С использованием потоковой операции на базе массива эта
пара записывается в массив outputstr в формате
name = Value
и затем выводится на экран оператором cout. Например, строки ввода
start 55
stop 8.5
выводятся на экран как строки
start = 55 stop =8.5
// pr02_02.cpp
#include <iostream.h>
#include <fstream.h>
#include <strstream.h>
#include <stdlib.h>
#include <string.h>
void main(void)
{
// ввести текстовый файл, содержащий имена и значения
ifstream fin;
char name[30], outputstr[256];
//декларировать выходной поток, основанный на массиве и
// использующий outputstr
ostrstream outs(outputstr, sizeof(outputstr));
double value;
// открыть для ввода файл 'names.dat',
// убедиться в его существовании
fin.open("names.dat", ios::in | ios::nocreate);
if (!fin)
{
cerr « "Невозможно открыть файл 'names.dat' " « endl;
exit(1);
}
// читать имена и значения,
// записывать в поток outs как 'имя = значение '
while(fin >> name)
{
fin >> value;
outs « name « " = " « value « " ";
}
// NULL-символ для выходной строки
outs << ends;
cout << outputstr « endl;
}
/*
<•' names, da t">
start 55
breakloop 225.39
stop 23
Оапуск программы pr02_02 . cpp>
start = 55 breakloop = 225.39 stop = 23
*/
2.10. Приложения массива и записи
Массивы и записи являются встроенными структурами данных в
большинстве языков программирования. Данная глава знакомит с ADT для этих
структур и описывает их реализацию C++. Мы используем эти структуры
для разработки важных алгоритмов во всей книге. Массив является основной
структурой данных для списков. Во многих приложениях мы используем
утилиты search и sort для нахождения элемента в списке на базе массива
и для упорядочения данных. Этот раздел знакомит с последовательным
поиском и обменной сортировкой, которые легко кодировать и понимать.
Последовательный поиск
Последовательный поиск предназначен для поиска элемента в списке с
использованием целевого значения, называемого ключом (key). Этот алгоритм
начинает с индекса, предоставляемого пользователем, называемого start, и
проходит через остальные элементы в списке, сравнивая каждый элемент с
ключом. Сканирование продолжается, пока не будет найден ключ или список
не будет исчерпан. Если ключ найден, функция возвращает индекс
соответствующего элемента в списке; в противном случае возвращается значение
-1. Для функции SeqSearch требуются четыре параметра: адрес списка,
начальный индекс для поиска, количество элементов и ключ. Например,
рассмотрим следующий список целых, содержащихся в массиве А:
А: 8 3 6 2 6
Key = 6, Start = 0, n = 5. Искать с начала списка, возвращая индекс
первого появления элемента 6.
Кеу=б
N=5
8
3
6
2
6
А-список
Возвращаемое значение
2. Key = 6, Start = 3, n = 2. Начинать с А[3] и искать в списке, возвращая
указатель на первое появление элемента 6.
Кеу=6
N=2
8
3
6
2
6
*
А
список Возвращаемое значение
3. Key = 9, Start = 0, n = 5. Начинать с первого элемента и искать в
списке число 9. Когда оно не найдено, возвращать значение -1.
Кеу=9
N=5
8
3
6
2
6
А=список
Возвращаемое значение = -1
Алгоритм последовательного поиска применяется к любому массиву, для
которого оператор "==" определяется для типа элемента. Общий алгоритм
поиска требует шаблонов и перегрузки операторов. Эти темы обсуждаются
в главах 6 и 7. Следующая функция реализует последовательный поиск для
массива целых:
Функция последовательного поиска
int SeqSearch(int list[], int start, int n, int key)
{
for (int i=start; i < n; i++)
if (list [i] == key)
return i;
}
return -1;
}
Программа 2.З. Повторяемый поиск
Данная программа тестирует функцию последовательного поиска,
подсчитывая количество появлений ключа в списке. Главная программа
сначала вводит 10 целых чисел в массив А и затем запрашивает ключ.
Программа выполняет повторяемые вызовы SeqSearch, используя
различный начальный индекс. В исходном положении мы начинаем с индекса
О, начала массива. После каждого вызова SeqSearch счетчик количества
появлений увеличивается, если ключ находится; в противном случае поиск
прекращается, и счетчик является возвращаемым значением. Если ключ
найден, возвращаемое значение определяет его позицию в списке.
Следующий вызов SeqSearch выполняется со значения start, равного
положению элемента, находящегося непосредственно справа от последнего
найденного.
// рг02__03.срр
#include <iostream.h>
// поиск в массиве из п целых значений элемента по ключу;
// возвратить указатель на этот элемент или NULL, если элемент не найден
int SeqSearch(int list[], int start, int n, int key)
{
for(int i=start;i < n; i++)
■ if (list[ij == key)
return i; // возвратить индекс соответствующего элемента
return -1; // неудачный поиск, возвратить -1
}
void main(void)
{
int A[10];
int key, count = 0, pos;
// запрос на ввод списка 10-ти целых чисел
cout << "Введите список из 10 целых чисел: ";
for (pos=0; pos < 10; pos++)
cin >> A[pos];
cout « "Введите ключ: ";
cin » key;
// начать поиск с первого элемента массива
pos = 0;
// продвигаться по списку, пока ключ находится
while ((pos = SeqSearch(A,pos,10,key)) != -1)
{
COUnt++;
// продвинуться к следующему целому после найденного
pos++;
}
cout << key « " появляется " « count
« " раз(а) в этом списке." << endl;
}
/*
Запуск программы рг02_03.срр
Введите список из 10 целых чисел: 5298158753
Введите ключ:5
5 появляется 3 раз(а) в этом списке.
*/
Обменная сортировка
Упорядочение элементов в списке является важным для многих
приложений. Например, некоторый список может сортировать записи по их
инвентарным номерам для обеспечения быстрого доступа к элементу, словарь
сохраняет слова в алфавитном порядке и регистрационные порядковые записи
студентов — по их номерам социального страхования.
Для создания упорядоченного списка мы вводим алгоритм сортировки,
называемый ExchangeSort, который упорядочивает элементы в возрастающем
порядке. Этот алгоритм иллюстрируется списком 8, 3, 6, 2 и создает
упорядоченный список 2, 3, 6, 8.
Индекс 0: Рассмотрим полный список 8, 3, 6, 2. Элемент с индексом О
сравнивается с каждым последующим элементом в списке с индексами 1, 2
и 3. Для каждого сравнения, если последующий элемент меньше, чем элемент
с индексом 0, эти два элемента меняются местами. После выполнения всех
сравнений наименьший элемент помещается в позицию с индексом 0.
Индекс 0
Исходный список
Действие
Обмен
Нет обмена
Обмен
Полученный список
Индекс 1: При уже помещенном в позицию с индексом 0 самом маленьком
элементе рассмотрим подсписок 8, 6, 3. Принимаются во внимание только
элементы от индекса 1 до конца списка. Элемент с индексом 1 сравнивается с
последующими элементами с индексами 2 и 3. Для каждого сравнения, если
больший элемент находится в позиции с индексом 1, то два элемента меняются
местами. После выполнения сравнений второй наименьший элемент в списке
сохраняется в позиции с индексом 1.
Индекс 1
Исходный список
Действие
Полученный список
Обмен
Обмен
Индекс 2: Рассмотрим подсписок 8, 6. Этот процесс продолжается для
подсписка из двух элементов с индексами 2 и 3. Между элементами выполняется
простое сравнение, в результате которого происходит обмен.
Индекс 2
Исходный список
Действие
Полученный список
Обмен
У нас остался только один элемент с индексом 3, и список отсортирован.
Отсортированный список
2 3
6
8
В C++ функция ExchangeSort использует вложенные циклы. Предположим,
что размер списка задается значением п. Внешний цикл приращивает индекс
i в диапазоне от 0 до п-2. Для каждого индекса i сравним последующие
элементы при j=i+l, i+2, ..., п-1. Выполним сравнение и поменяем местами
элементы, если listfi] > list[j].
Программа 2.4. Сортировка списка
Эта программа иллюстрирует алгоритм сортировки. Список из 15 целых
в диапазоне от 0 до 99 заполняет list. ExchangeSort упорядочивает список,
используя функцию Swap для того, чтобы поменять местами два элемента
массива. Программа выдает на экран список до и после сортировки.
// рг02_04.срр
#include <iostream.h>
// поменять значения двух переменных целого типа х и у
void Swap(int & х, int & у)
{
int temp - х; // сохранить первоначальное значение х
х = у; // заменить х на у
у - temp; // присвоить переменной у
// первоначальное значение х
}
// сортировать целый массив n-элементов а в возрастающем порядке
void ExchangeSort(int а[], int n)
{
int i, j;
// реализовать n — 1 проходов.найти правильные значения
// в а[],...,а[п-2].
for(i = 0; i < n-1; i++)
// поместить минимум из а[п+1]...а[п-1] в a[i]
for(j = i+1; j < n; j++)
// заменить if a[i] > a[j]
if (a[i] > a[j])
Swap(a[i], a[j]);
}
// пройти по списку, печатая каждое значение
void PrintList(int a[], int n)
{
for (int i = 0; i n; i++)
cout « a[i] < " ";
cout « endl;
}
void main(void)
{
int list[15] - {38,58,13,15,51,27,10,19,
12,86,49,67,84,60,25);
int i;
cout « "Исходный список \n";
PrintList(list,15);
ExchangeSort(list,15);
cout « endl «"Отсортированный список" « endl;
PrintList(list,15);
)
/*
Оапуск программы pr02_04 . cpp>
Исходный список
38 58 13 15 51 27 10 19 12 86 49 67 84 60 25
Отсортированный список
10 12 13 15 19 25 27 38 49 51 58 60 67 84 86
V
Подсчет зарезервированных слов C++
В разделе 2.8 обсуждается тип записи, который реализуется в C++ как
struct. В качестве иллюстрации записей программа подсчитывает количество
раз, когда в файле появляются зарезервированные слова "else", "for", "if",
"include" и "while". Эта программа использует строковые переменные также,
как массив записей.
Основной структурой данных программы является struct Key Word, чьи
поля состоят из строковой переменной keyword и count типа integer:
struct Keyword
{
char keyword[20];
int count;
}/
В массиве KeyWordTable создается таблица для пяти зарезервированных
слов. Каждый элемент в этой таблице инициализируется указанием
зарезервированного слова и начального значения счетчика count=0. Например,
первый инициализатор массива {"else", 0} приводит к тому, что элемент Кеу-
WordTable[0] содержит строку "else" со значением счетчика 0:
Keyword KeyWordTable[ ] =
{
{"else", 0}, {"for", 0}, {"if", 0}, {"include", 0}, {"while", 0}
};
Программа читает отдельные слова в файле с помощью функции Get Word.
Словом является любая последовательность символов, которая начинается с
буквы и продолжается произвольным количеством букв или цифр. Например,
когда представлена строка
Expression: 3+5=8 (N1 + N2 = N3)
GetWord извлекает слова "Expression", "Nl", "N2", и "N3" и отбрасывает
другие символы.
Функция SeqSearch сканирует таблицу, выполняя поиск соответствия
ключевому слову. Когда поиск завершается успешно, функция возвращает индекс
соответствующей записи, увеличивая на единицу поле count.
Программа 2.5. Подсчет зарезервированных слов
Эта программа читает собственный исходный код в качестве ввода. В
цикл читается каждое слово и вызывается функция SeqSearch для
определения того, соответствует ли ввод зарезервированному слову в KeyWordTable.
Если так, поле count в записи увеличивается на единицу. После завершения
ввода, количество появлений каждого ключевого слова выводится на экран.
Программа имеет интересный оператор, который динамически
вычисляет количество элементов в массиве KeyWordTable с помощью выражения
sizeof (KeyWordTable)/ sizeof (Keyword)
Это выражение предоставляет независимый от системы метод
вычисления количества элементов в каком-либо массиве. Если другие ключевые
слова добавляются к этой таблице, последующая компиляция генерирует
новый подсчет элементов.
// рг02_05.срр
#include <Iostream.h>
#include <fstream.h>
#include <string.h>
#include <ctype.h>
#include <stdlib.h>
// объявление структуры слова
struct Keyword
{
char keyword[20];
int count;
};
// объявление и инициализация таблицы слов
Keyword KeyWordTable[]=
{
{"else", 0), {"for", 0}, {"if", 0}, {"include", 0}, {"while", 0}
);
// настраиваемый алгоритм поиска слов
int SeqSearch(Keyword *tab, int n, char *word)
{
int i;
// сканировать список, сравнивать word с keyword в текущей записи
for (i=0; i < n; i++, tab++)
if (strcmp(word, tab-keyword) == 0)
return i; // при совпадении вернуть индекс
return -1; // к сожалению, нет совпадения
}
// извлечь слово, начинающееся с буквы и, возможно,
// другие буквы/цифры
int GetWord(ifstreams fin, char w[])
{
char c;
int i = 0;
// пропустить не алфавитный ввод
while ( fin.get(с) && lisalpha(c) ) ;
// вернуть 0 (Неудача) в конце файла
if (fin.eof () )
return 0;
// записать первый символ word
w[i++] =с;
// собирать буквы, цифры и символ окончания строки
while ( fin.get (с) && ( isalpha(c) | | isdigit(c) ) )
w[i++] = с;
w[i] =
'Nonreturn 1; // вернуть 1 (Успех)
}
void main (void)
{
const int MAXWORD = 50; // максимальный размер любого слова
// объявить и инициализировать размер таблицы
const int NKEYWORDS = sizeof(KeyWordTable)/sizeof(Keyword);
int n;
char word [MAXWORD] , c;
ifstream fin;
// открыть файл с проверкой ошибки
fin.open("pr02_05.cpp", ios::in | ios::nocreate);
if (!fin)
{
cerr « "Невозможно открыть файл 'pr02_05.cpp' " « endl;
exit (1) ;
}
// извлекать слова до конца файла
while (GetWord(fin,word))
// при совпадении с таблицей keyword увеличивать счетчик
if ((n= SeqSearch(KeyWordTable,NKEYWORDS,word)) != -1)
KeyWordTable[n].count++;
// сканировать таблицу keyword и печатать поля записи
for (n = 0; n < NKEYWORDS; n++)
if (KeyWordTable[n].count > 0)
{
cout « KeyWordTable[n].count;
cout « " " « KeyWordTable[n].keyword « endl;
}
fin.close();
}
*/
Запуск программы pr02_05 . cpp
1 else
3 for
6 if
6 include
4 while
*/
Письменные упражнения
2.1 Вычислите десятичное значение каждого двоичного числа:
(а) 101 (б) 1110 (в) 110111 (г) 1111111
2.2 Напишите каждое десятичное число в двоичном представлении:
(а) 23 (б) 55 (в) 85 (г) 253
2.3 В современных компьютерных системах адреса обычно реализуются на
аппаратном уровне как 16-битовые или 32-битовые двоичные значения.
Естественно работать с адресами в двоичном представлении, а не
преобразовывать их в десятичную систему. Поскольку числа такой длины
затруднительно записывать как строку двоичных цифр, в качестве
основания используется 16 или шестнадцатиричные (hexadecimal) числа.
Такие числа, упоминаемые как hex numbers, являются важным
представлением целых чисел и позволяют легко выполнять преобразования
в двоичную систему и наоборот. Большинство системных программ
имеет дело с машинными адресами в шестнадцатиричной системе.
Шестнадцатиричные числа строятся на базе числа 16 с цифрами в
диапазоне 0-15 (десятичном). Первые 10 цифр являются производными
от десятичных чисел: 0, 1, 2, 3, . . ., 9. Цифры от 10-15 представлены
буквами А, В, С, D, Е и F. Степени 16: 16° = 1, 161 = 16, 162 = 256,
163 = 4096 и так далее. В форме позиционной нотации примерами
шестнадцатиричных чисел являются 17Е, 48 и FFFF8000. Числа
преобразуются в десятичную форму расширением степеней 16 точно так
же, как степени 2-х расширяются для двоичных чисел.
Например, шестнадцатиричное число 2A3Fi6 преобразуется в десятичное
расширением степеней 16-и.
2A3F16 = 2(1б3) + А(1б2 ) +3 (161) +F(16°)
= 2(4096) +10 (256) +3 (16) +15 (1)
- 8192 + 2560 +48 +48 + 15 = 1018510
Преобразуйте каждое шестнадцатиричное число в десятичное
(а) 1А (б) 41F (в) 10ЕС (г) FF (д) 10000
Преобразуйте каждое десятичное число в шестнадцатиричное
(е) 23 (ж) 87 (з) 115 (и) 255
2.4 Основной причиной введения шестнадцатиричных чисел является их
естественное соответствие двоичным числам. Они обеспечивают
компактное представление двоичных данных и адресов памяти.
Шестнадцатиричные цифры имеют 4-битовое двоичное представление в
диапазоне 0-15. Следующая таблица показывает соответствие между
двоичными и шестнадцатиричными цифрами:
Шестнадцатиричные
0
1
2
3
4
5
6
7
Двоичные
0000
0001
0010
0011
0100
0101
0110
0111
Шестнадцатиричные
8
9
А
В
С
D
Е
F
Двоичные
1000
1001
1010
1011
1100
1101
1110
1111
Для представления двоичного числа в шестнадцатиричном формате
начинайте с правого конца числа и разделяйте биты на группы из четырех
битов, добавляя начальный 0 слева в последней группе, если
необходимо. Запишите каждую группу из 4-х битов как шестнадцатиричное
число. Например:
1111000111011102 » 0111 1000 1110 1110 = 78ЕЕ1б
Для преобразования шестнадцатиричного числа в двоичное выполните
обратное действие и запишите каждое шестнадцатиричное число как
4 бита. Рассмотрим следующий пример:
А7891б = 1010 0111 1000 1001 = 10100111100010012
Преобразуйте двоичные числа в шестнадцатиричные:
(а) 1100 (б) 1010 ОНО (в) 1111 0010
(г) 1011 1101 1110 ООН
Преобразуйте шестнадцатиричные числа в двоичные:
(д) 061016 (е) AF2016
2.5 C++ позволяет программисту вводить и выводить числа в
шестнадцатиричном представлении. При помещении манипулятора "hex" в поток
режим ввода или вывода чисел становится шестнадцатиричным. Этот
режим действует до тех пор, пока он не поменяется на десятичный с
помощью манипулятора "dec". Например:
cin >> hex » t » dec » u; // t читается как шестнадцатиричное;
u — как десятичное
<ввод 100 25б> t = 1001б и и = 25б10
cout « hex « 100 « t « u; // вывод 64 100 100
cout « dec « 100 << t « u; // вывод 100 256 256
Рассмотрим следующее объявление и выполняемые операторы:
int i, j, k;
cin » i ;
cin » hex » j » dec;
cin >> k;
(а) Предположим, ввод является 50 50 32. Каков вывод для оператора?
cout « hex « i « " " « j « " " « dec « k « endl;
(б) Предположим, ввод является 32 32 64. Каков вывод для этого
оператора?
cout « dec « i « " " « hex << j « " " « k « endl;
2.6 Напишите полную спецификацию для оператора % в целом ADT.
Выполните то же для оператора сравнения !=.
2.7 Булев тип определяет данные, которые имеют значения True или False.
Некоторые языки программирования определяют базовый булев тип с
рядом встроенных функций для обработки этих данных. C++
ассоциирует булево значение с каждым числовым выражением.
(а) Определите булев ADT, описывающий область данных, и его операции.
(б) Опишите реализацию этого ADT, используя языковые конструкции
C++.
2.8
(а) Какой символ ASCII соответствует десятичному числу 78?
(б) Какой символ ASCII соответствует двоичному числу 1001011г?
(в) Каковы коды ASCII для символов "*", "q" и возврата каретки? Дайте
ответы в десятичном и шестнадцатиричном представлении.
2.9 Что печатается следующим фрагментом кода?
cout « char (86) « " " « int ( ' q' ) « " " «
char( int ("0") + 8) « endl;
2.10 Объясните, почему оператор % (остаток) не дается в ADT для
вещественных чисел.
2.11 Преобразуйте каждое двоичное число с фиксированной точкой в
десятичное:
(а) 110.110
(б) 1010.0101
(в) 1110.00001
(г) 11.111 . . . 111 . . . (Совет: Используйте формулу для суммы
геометрического ряда).
2.12 Преобразуйте каждое десятичное число с фиксированной точкой в
двоичное:
(а) 2.25
(б) 1.125
(в) 1.0875
2.13
(а) Существует ли наименьшее положительное действительное число в ADT
для вещественных чисел? Почему да или почему нет?
(б) Когда в компьютере следует использовать вещественное числа,
существует ли наименьшее положительное вещественное число? Почему да
или почему нет?
2.14 Формат IEEE с плавающей точкой сохраняет знак числа отдельно, а
порядок и мантиссу — как беззнаковые числа. Нормализованная форма
позволяет получить уникальное представление для каждого числа с
плавающей точкой.
Нормализованная форма: Число с плавающей точкой задается так, что
имеет одну не равную нулю цифру слева от двоичной точки
N = ± 1 .d1d2 • • • dn_x 2е
Число с плавающей точкой 0.0 сохраняется со знаком, порядком и
мантиссой 0.
В качестве примера: два двоичных числа преобразуются в представление
в нормализованной форме.
Двоичное число Нормализованная форма
1101.101 х 21 1.1011010 х 24
0.0011 х 2б 1.1 х 23
Тридцати-двух-битовые числа с плавающей точкой сохраняются в
нормализованной форме с использованием внутреннего формата IEEE.
Знак Самый левый бит используется для знака. "+" имеет
знаковый разряд 0, и "-" имеет знаковый разряд 1.
Порядок Порядок задается 8-ю битами. Для обеспечения сохранения
всех порядков как положительных (беззнаковых) чисел,
формат IEEE задает использование нотации "excess -127"
для порядка. Сохраняемый порядок (Ехр3) создается
добавлением 127 к реальному порядку.
Exps = Exp + 127
Истинный порядок Сохраняемый порядок
Диапазон Диапазон
-127 < Ехр < 128 0< Exps < 255
Мантисса Допустим, что число сохраняется в нормализованной форме,
начальная цифра 1 скрыта, дробные цифры сохраняются в
23-битовой мантиссе, задается точность 24 бита.
Знак
1 бит
Порядок
8 битов
Мантисса
23бита
В качестве примера вычислим внутреннее представление -0.1875.
Нормализованная форма (-) 1.100 * 2~3
Знак 1
Порядок Exps = -3 + 127 = 124 = 011111002
Мантисса <1>1000000 ... 0
-0.1875 - 10111110010000000000000000000000
Запишите каждое число в 32-битовой форме IEEE с плавающей точкой:
(а) 7.5
(б) -1/4
Каково значение следующих 32-битовых чисел в формате IEEE в
десятичной форме? Каждое число дается в шестнадцатиричной форме.
(в) С1800000
(г) 41Е90000
2.15
(а) Перечислите в календарном порядке месяцы года, которые имеют
символ "р" в имени. Это перечислимый тип.
(б) Напишите реализацию C++ для перечислимого типа.
(в) Какой месяц соответствует целому числу 4 в реализации C++? Какова
позиция октября?
(г) Напишите это перечисление в алфавитном порядке. Имеют ли какие-
либо месяцы одну и ту же позицию в обоих списках?
2.16 Добавьте операции successor и predecessor к ADT для перечислимых
типов. Используйте полные спецификации. Successor возвращает
следующий элемент в списке, и predecessor возвращает предыдущий
элемент. Будьте осторожны при определении того, что происходит на
границах списка.
2.17 С учетом следующих объявлений и операторов укажите содержимое X,
Y и А после выполнения этих операторов:
int X =4, Y=7, *РХ = &Х, *PY;
double А[ ] = {2.3, 4.5, 8.9, 1.0, 5.5, 3.5}, *РА - А;
PY = &Y; (*РХ)--; *PY += *РХ; PY = РХ;
*PY = 55; *РА += 3.0; РА++; *РА++ =* 6.8;
РА+= 2;
*++РА = 3.3;
2.18
(а) А объявляется как А[5];
short A[5];
Сколько байтов выделяется для массива А? Если адрес массива А =
6000, вычислите адрес А[3] и А[1].
(б) Предположим такое объявление:
long А[ ] - {30, 500000, -100000, 5, 33};
Если длинное слово занимает 4 байта и адрес А равен 2050,
□ Каково содержимое с адресом 2066?
D Удвойте содержимое с адресом 2050 и адресом 2062. Выпишите
массив А.
□ Какой адрес у А[3]?
2.19 Предположим, что А — это массив размером mxn с индексами строк
в диапазоне 0 — (ш-1) и индексами столбцов в диапазоне 0 — (п-1).
Генерируйте функцию доступа, вычисляющую адрес A[row] [col],
полагая, что элементы сохраняются столбцами.
2.20 А объявляется как
short А[5] [б];
(а) Сколько байтов выделено для массива А?
(б) Если адрес массива А = 1000, вычислите адрес А[3] [2] и А[1] [4].
(в) Какой элемент массива помещается по адресу 1020? По адресу 1034?
2.21
(а) Объявите строку Name с вашим именем в качестве начального значения.
(б) Рассмотрите объявления строковой переменной:
char sl[50], s2[50];
и операторы ввода:
cin » SI >> S2;
Каково значение SI и S2 для строки ввода "Джордж спешит!"?
Каково значение S1 и S2 при вводе следующего текста (Ф— это пустой
символ, а 1| — это конец строки.)?:
Next*
^^<->Word
2.22 Рассмотрим следующие строковые объявления:
char SI[30] = "Stockton, CA", S2[30] = "March 5, 1994м, *р;
char S3 [30];
(а) Каково значение *p после выполнения каждого следующего оператора?
р = strchr (SI, 't');
р = strrchr (SI, 't');
p = strrchr (S2, '6');
(б) Каково значение S3 после выполнения:
strcpy (S3,SI);
strcat (S3, ",");
strcat (S3,S2);
(в) Какое значение возвращается вызовом функции strcmp (S1.S2)?
(г) Какое значение возвращается вызовом функции strcmp (&Sl[5],"ton")?
2.23 Функция
void strinsert (char *s, char *t, int i);
вставляет строку t в строку s в позиции с индексом i. Если i больше
длины s, вставка не выполняется. Реализуйте strinsert, используя
библиотечные функции C++ strlen, strcpy и strcat. Вам потребуется
объявить временную строковую переменную для хранения оригинальных
символов в s с индекса i до индекса strlen(s) -1. Вы можете полагать,
что этот хвост никогда не превышает 127 символов.
2.24 Функция:
void strdelete(char *s, int i, int n) ;
удаляет последовательность п символов из строки s, начиная с индекса
i. Если индекс i больше, чем длина s или равен ей, то никакие символы
не удаляются. Если i+/z больше, чем длина s или равено ей, то удаляется
конец строки, начиная с индекса i. Реализуйте strdelete, используя
библиотечные функции C++ strlen и strcpy.
2.25 Альтернативой использованию строк с NULL-символом является
помещение счетчика символов в первый элемент символьного массива. Это
называется форматом со счетчиком байтов, и такие строки часто
называют строками Паскаля, поскольку программные системы на языке
Паскаль используют этот формат для строк.
(а) Реализуйте функцию strcat, полагая, что строки сохраняются в формате
со счетчиком байтов.
(б) Функции PtoCStr и CtoCStr выполняют преобразование этих двух
строковых форматов:
void PtoCStr(char *s); // конвертировать s из Pascal в C++
void CtoPStr(char *s); // конвертировать s из C++ в Pascal
Реализуйте эти две функции.
2.26 Добавьте оператор присваивания "=" к ADT записи, используя полную
спецификацию. Точно определите, какое действие выполняется во
время присваивания.
2.27 Комплексное число имеет форму х + iy, где i2 = -1. Комплексные числа
имеют широкое применение в математике, физике и технике. Они
имеют арифметику, управляемую рядом правил, включая следующие:
Пусть и = а + ib, v = с + id
u + v = (а + с) + i <b + d)
u — v = (a — с) + i (b — d)
u
v
ac + bd
c2 + d2
+ i
be - ad
c2 + d2
Представьте комплексное число, используя следующую структуру:
struct Complex
{
float real;
float imag;
}
и реализуйте следующие функции, которые выполняют операции с
комплексными числами:
Complex cadd(Complex& х, Complex& у); // х + у
Complex csub{Complex& x, Complex& у); // х — у
Complex cmul(Complex^ х, Complex& у); // х * у
Complex cdiv(Complex& х, Complexs у); // х / у
2.28 Добавьте операцию FileSize к ADT для потоков. Она должна возвращать
количество символов в файле. Точно укажите, для каких предусловий
эта операция имеет смысл. (Совет: Как насчет cin/cout?)
2.29 Четко различайте текстовый и двоичный файл. Как вы думаете,
возможно ли разработать программу, принимающую имя файла в качестве
входа и определить текстовый он или бинарный?
Упражнения по программированию
2.1 Напишите функцию
void BaseOut(unsigned int n, int b)
которая выводит п с основанием b, 2 < b <. 10. Напечатайте каждое
число в диапазоне 2 < п < 50 с основанием 2, 4, 5, 8 и 9.
2.2 Напишите функцию
void Octln(unsigned int& n);
которая читает число с основанием 8 (восьмеричное) и присваивает его
п. Используйте Octln в главной программе, которая читает следующие
восьмеричные числа и печатает десятичные эквиваленты:
7, 177, 127, 7776, 177777
2.3 Напишите программу, которая объявляет три целые переменные i, у,
k. Введите значение для i в десятичной форме и значения для у и ft —
в шестнадцатиричной. Напечатайте все три переменные и в
шестнадцатиричной, и в десятичной форме.
2.4 Изучите дискретность представления вещественных чисел на вашем
компьютере путем вычисления 1 + D для D = 1/10, 1/100, 1/1000,
..., 1/10п до тех пор, пока 1 + D == 1.0. Если вы имеете доступ более,
чем к одной машинной архитектуре, попробуйте выполнить это на
других машинах.
2.5 Рассмотрим перечислимый тип
enum DaysOfWeek {Sun, Mon, Tue, Wed, Thurs, Fri, Sat};
Напишите функцию
void GetDay(DaysOfWeek& day);
которая читает имя дня с клавиатуры как строку и присваивает дню
соответствующее значение элемента перечисления. Напишите также
функцию
void PutDay(DaysOfWeek day)
которая записывает значение элемента перечисления на экране.
Разработайте главную программу для тестирования этих двух функций.
2.6 Введите ряд слов до конца файла, преобразуя каждое в слово на ломаной
латыни. Если слово начинается с согласного, переместите первый
символ слова на последнюю позицию и присоедините "ау". Если слово
начинается с гласного, просто присоедините "ау". Например:
Вход: this is simple
Выход: histay isay implesay
2.7 Строка текста может быть зашифрована с использованием табуляцион-
ного соответствия, которое ассоциирует каждую букву алфавита с
уникальной буквой. Например, табуляционное соответствие
abcdefghijklmnopqrstuvwxyz ==> ngzqtcobmuhelkpdawxfyivrsj
устанавливает соответствие между "encrypt" и "tkzwsdf".
Напишите программу, которая читает текст до конца файла и выводит
зашифрованную форму.
2.8 Создайте свою программу табуляционного соответствия, которая
выполняет установку соответствия, обратную той, которая использовалась
в упражнении 2.7. Введите зашифрованный файл и выведите на экран
его расшифрованную форму.
2.9 Напишите программу, которая вызывает выход за границы одного или
более индексов массива. Доведите программу до такого состояния, чтобы
она "разрушалась". Притворитесь, что вы не знаете, в чем заключается
проблема. Используйте любой имеющийся в вашем распоряжении
отладчик и диагностируйте причину такого поведения.
2.10 Измените сортировку обмена так, чтобы она сортировала список в
порядке убывания. Протестируйте новый алгоритм, написав главную
программу, подобную программе 2.4.
2.11 Рассмотрим объявление записи
struct Month
{
char name[10]; // имя месяца
int monthnum; // число дней в месяце
};
(а) Напишите функцию
void SortByName(Month months[ ], int n) ;
которая сортирует массив с элементами типа Month, сравнивая имена
(используйте функцию strcmp в C++). Напишите также функцию
void SotrByDays (Month months[ ], int n);
которая сортирует список, сравнивая количество дней в месяце.
Напишите главную программу, которая объявляет массив, содержащий все
месяцы года и сортирует его, используя обе функции. Выведите на
экран каждый отсортированный список.
(б) Заметьте, что сортировка списка месяцев по количеству дней создает
связи соперничества. Когда это происходит, метод сортировки может
использовать вторичный ключ (secondary key) для устранения этих
связей. Напишите функцию
void Sort2ByDays(Month months[ ], int n);
которая сортирует список, сравнивая сначала количество дней, и, если
связь возникает, разбивает ее, сравнивая имена. Используйте эту
функцию в главной программе для распечатки упорядоченного списка всех
месяцев года, упорядоченных по количеству дней в месяце.
2.12 Напишите программу, которая читает текстовый файл и выводит на
экран счетчик количества появлений знаков пунктуации(. , ! ?).
2.13 Используя cin.getline, читайте строку, начинающуюся с имени функции
из одного символа, за которым следуют последовательности "х" с
символами "+" и "-", вставленными в промежутки. Строка не может
заканчиваться символом "+" или "-". Образуйте строку в форме:
SingleCharFuncName (х) = х**п ± х**щ±. . .
в массиве, используя выход на базе массива. Если порядком является
равным 1, то опустите "**1". Запишите каждую строку в файл
"funcs.val". Например, строки
Fxxx + xx — x
Gxx — xxx + xxxx
создают файл "funcs.val", имеющий строки
F(x) = х**3 + х**2 - х
G(x) = х**2 - х**3 +х**4
2.14 Напишите программу, которая вводит N х N матрицу А целых значений
и выводит на экран след матрицы. След матрицы определяется как
сумма диагональных элементов
Trace (А) = А[0, 0} +А[1, 1] + . . . + A[N - 1, N - 1]
2.15 Это упражнение использует результаты упражнения 2.27 из
предыдущего раздела "Упражнения". Напишите функцию f(z), вычисляющую
комплексную полиномиальную функцию:
z3 - 3z2 + 4z - 2
Определите полиномиал для следующих значений z:
z = 2 +3i, -1 + i, 1 + i, 1 - i, 1 + Oi
Заметьте, что последние три значения являются корнями от f.
глава
Абстрактные типы данных
и классы
Т
3.1. Пользовательский тип - КЛАСС
3.2. Примеры классов
3.3. Объекты и передача информации
3.4. Массивы объектов
3.5. Множественные конструкторы
3.6. Практическое применение:
треугольные матрицы
Письменные упражнения
Упражнения по программированию
В главе 1 были даны абстрактные типы данных (ADT) и их представление
в качестве классов C++. Это введение описывает структуру класса, которая
обеспечивает инкапсуляцию данных и скрытие информации. В этой главе
содержится более полное описание базовых концепций класса. Мы
рассматриваем разработку и использование конструкторов класса, реализацию методов
класса и использование классов с другими структурами данных. Для
обеспечения хорошего понимания классов читателем мы разрабатываем широкий
диапазон примеров и используем их в законченных программах. Выбранные
соответствующим образом ADT иллюстрируют связь между абстрактной
структурой и объявлением класса.
3.1. Пользовательский тип — КЛАСС
Класс — это определяемый пользователем тип с данными и функциями
(методами), называемыми членами (members) класса. Переменная типа класс
называется объект (object). Класс создает различные уровни доступа к его
членам, разделяя объявление на части: private, protected и public. Часть private
(закрытая) объекта может быть доступна только для функций-членов в этом
классе. Часть public (открытая) объекта может быть доступна для внешних
элементов программы, в области действия которых находится этот объект (рис.
3.1). Protected (защищенные) члены используются с производными классами
и описываются в главе 12, посвященной наследованию.
Члены класса
private:
Данные
Операторы
public:
Данные
Операторы
Внешние программные
единицы
Рис. 3.1. Доступ к методам класса
Объявление класса
Объявление класса начинается с заголовка класса (class head), состоящего
из зарезервированного слова class, за которым следует имя класса. Члены
класса определяются в теле класса (class body), которое заключается в
фигурные скобки и заканчивается точкой с запятой. Зарезервированные слова public
и private разделяют члены класса, и эти спецификаторы доступа заканчиваются
двоеточием. Члены класса объявляются как переменные C++, а методы задаются
как объявления функций C++. Общая форма объявления класса такова:
class Имя_класса
{
private:
// Закрытые данные
// Объявление закрытых методов
//
public:
// Открытые данные
// Объявление открытых методов
//
};
Следует, по возможности, помещать члены класса в закрытую секцию. В
результате этого значение данных обновляется только функцией-членом
класса. Это предотвращает нежелательные изменения в данных кодом
использующего класс приложения.
Пример 3.1
Класс Rectangle
При геометрических измерениях прямоугольник определяется его
длиной и шириной. Это позволяет нам вычислять периметр и площадь
фигуры. Параметры длины и ширины и операции объединяются для
образования абстрактного типа данных прямоугольной фигуры. Мы
оставляем спецификацию ADT в качестве упражнения и разрабатываем
класс Rectangle C++, который реализует этот ADT. Класс содержит
конструктор и набор методов — GetLength, PutLength, Get Width и PutWidth,
имеющих доступ к закрытым членам класса. Объявление класса
Rectangle следующее:
class Rectangle
{
private:
//длина и ширина прямоугольного объекта
float length, width;
public:
// конструктор
Rectangle(float 1=0, float w = 0);
// методы для нахождения и изменения закрытых данных
float GetLength(void) const;
void PutLength(float 1);
float GetWidth(void) const;
void PutWidth(float w);
// вычислять и возвращать измерения прямоугольника
float Perimeter(void) const;
float Area(void) const;
};
Обратите внимание, что методы GetLength, Get Width, Perimeter и Area
имеют ключевое слово const после списка параметров. Это объявляет
каждый метод как константный. В определении константного метода
никакой элемент данных не может быть изменен. Другими словами,
выполнение метода, объявленного как const, не изменяет состояния объекта
Rectangle.
Если первый спецификатор доступа опускается, начальные члены в
классе являются закрытыми по умолчанию. Члены класса являются
закрытыми до первого появления открытой или защищенной
спецификации. C++ позволяет программисту чередовать закрытую, защищенную
и открытую секции, хотя это обычно не рекомендуется.
Конструктор
Функция, называемая конструктором (constructor) класса, имеет то же имя,
что и класс. Подобно другим функциям C++, конструктору могут передаваться
параметры, используемые для инициализации одного или более данных-членов
класса. В классе Rectangle конструктору дается имя Rectangle, и он принимает
параметры 1 и w, используемые для инициализации длины и ширины объекта,
соответственно. Заметьте, что эти параметры имеют значения, по умолчанию,
которые указывают, что используется значение 0, когда параметр 1 или w не
передается явно.
Пример 3.1 иллюстрирует объявление класса (class definition), так как
методы описываются только объявлениями функций. Код C++ для
определения отдельных функций создает реализацию класса (class implementation).
Объявление объекта
Объявление класса описывает новый тип данных. Объявление объекта
типа класс создает экземпляр (instance) класса. Это делает реальным объект
типа класс и автоматически вызывает конструктор для инициализации
некоторых или всех данных-членов класса. Параметры для объекта передаются
конструктору заключением их в скобки после имени объекта. Заметьте, что
конструктор не имеет возвращаемого типа, поскольку вызывается только во
время создания объекта:
ClassName object(<parameters>); //список параметров может быть пустым
Например, следующие объявления создают два объекта типа Rectangle:
Rectangle room(12, 10);
Rectangle t; //использование параметров по умолчанию (0, 0).
Каждый объект имеет полный диапазон данных-членов и методов,
объявляемых в классе. Открытые члены доступны с использованием имени
объекта и имени члена, разделяемых "." (точкой). Например:
х - room.Area(); // присваивает х площадь = 12 * 10 = 120
t.PutLength(20); // присваивает 20 как длину объекта Rectangle
// Текущая длина равна 0, так как используются
// параметры по умолчанию,
cout < t.GetWidthO; // выводит текущую ширину, которая = 0 по умолчанию
В объявлении объекта Room конструктор первоначально устанавливает
значение длины, равным 12, а ширины — 10. Клиент может изменять
размеры, используя методы доступа PutLength и PutWidth:
room.PutLength(15); // изменение длины и ширины на 15 и 12
room.PutWidth(12) ;
Объявление класса не обязательно должно включать конструктор. Это
действие, которое не рекомендуется и не используется в этой книге, оставляет объект
с неинициализированными данными в точке его объявления. Например, класс
Rectangle может не иметь конструктора, а клиент мог бы задать длину и
ширину с помощью открытых методов доступа. Включая в класс конструктор,
мы обеспечиваем правильную инициализацию важных данных. Конструктор
позволяет объекту инициализировать его собственные данные-члены класса.
Класс Rectangle содержит члены класса типа float. В общем, класс может
содержать элементы любого допустимого типа C++, даже других классов.
Однако, класс не может содержать объект его собственного типа в качестве члена.
Реализация класса
Каждый метод в объявлении класса должен быть определен. Определения
функций могут быть заданы в теле класса (встроенный код) или вне его.
При помещении функции вне тела имя класса, за которым следует два двое-
точия, должно предшествовать имени этой функции. Символ "::" называется
операцией разрешения области действия (scope resolution operator) и
указывает на то, что функция принадлежит области действия класса. Это
позволяет всем операторам в определении функции иметь доступ к закрытым
членам класса. В случае с классом Rectangle идентификатор "Rectangle::"
предшествует именам методов.
Далее следует определение GetLength(), когда она записана вне тела класса
Rectangle:
float Regtangle::GetLength(void) const
<
return length; // доступ к закрытому члену length
}
Заметьте, что при определении константного метода может быть такэке
использован квалификатор const.
Функция-член класса может быть записана внутри тела класса. В этом
случае код является расширенным встраиваемым (expanded inline), а операция
разрешения области действия не используется, так как код находится в области
действия тела класса. Встраиваемое определение операции GetLength имеет
вид:
class Rectangle
{
private:
float length;
float width;
public:
• • *
float GetLength(void) const // код задается как inline
{
return(length);
}
* • •
};
В этой книге обычно функции-члены определяются вне тела класса для
того, чтобы придать особое значение различию между объявлением и
реализацией класса. Inline-код используется в этой книге редко.
Реализация конструктора
Конструктор может быть определен как inline или вне тела класса.
Например, следующий код определяет конструктор Rectangle:
Rectangle::Rectangle(float 1, float w)
{
length « 1;
width = w;
}
C++ предоставляет специальный синтаксис для инициализации членов
класса. Список инициализации членов (member initialization list) — это список
имен данных-членов класса, разделенных запятыми, за каждым из которых
следует начальное его значение, заключенное в скобки. Начальные значения
обычно являются параметрами конструктора, которые присваиваются
соответствующим данным-членам класса в списке. Список инициализации членов
помещается после заголовка функции и отделяется от списка параметров двоеточием:
ClassName: :ClassName (parm list) : datax (parir^), . . . , datantparn^)
Например, параметры конструктора 1 и w могут быть присвоены данным-
членам класса length и width:
Rectangle::Rectangle(float 1, float w) : length (1), width(w)
{}
Создание объектов
Один объект может использоваться для инициализации другого в каком-
либо объявлении. Например, следующий оператор является правильным:
Rectangle square(10, 10), yard = square, S;
Объект square создается с length и width, равными 10. Второй объект yard
создается с начальными данными, копируемыми из объекта square. Объект S
имеет length и width, по умолчанию равными 0.
Объекты могут свободно присваиваться один другому. Если только
пользователь не создает пользовательский оператор присваивания, присваивание
объекта может выполняться побитовым копированием данных-членов класса.
Например, присваивание
S = yard;
копирует все данные из объекта yard в объект S. В этом случае length и
width объекта yard копируются в length и width объекта S.
Объект может быть создан ссылкой на его конструктор. Например,
объявление Rectangle(10,5) создает временный объект с lengh = 10 и width = 5. В
следующем операторе операция присваивания копирует данные из временного
объекта в rectangle S:
S = Rectangle(10,5);
Пример 3.2
1. Операторы
S = Rectangle(10,5);
cout « S.Area О « endl;
приводят к выводу в поток cout числа 50.
2. Оператор
cout « Rectangle(10,5).GetWidth() « endl;
ВЫВОДИТ ЧИСЛО 5.
Программа 3.1. Использование класса Rectangle
В этой программе вычисляется относительная стоимость отделочных
работ передней стороны гаража. Пользователь задает размеры передней
стороны гаража, а программа выдает различные размеры и стоимость
двери. Пользователь замечает, что при выборе большей двери требуется
меньше материала для обшивки и опалубки для кладки бетона. Учитывая
стоимость пиломатериалов большая дверь может быть более экономичной.
Предположим, что опалубка проходит по периметру передней стороны
и периметру проема двери. Мы запрашиваем у пользователя размер
передней стороны гаража и затем вводим цикл, позволяющий выбрать размер
двери. Цикл заканчивается, когда пользователем выбирается опция "Quit".
Для каждого выбора двери программа определяет стоимость отделки
передней стороны гаража и выводит это значение. Мы задаем константами
стоимость деревянной обшивки $2 за кв. фут и стоимость опалубки на
$0.50 за погонный фут.
Опалубка
Обшивка
Дверь
Длина опалубки равна сумме периметров передней стороны гаража и
двери. Стоимость обшивки равна площади передней стороны гаража минус
площадь двери.
// рг03_01.срр
#include <iostream.h>
class Rectangle
{
private:
// длина и ширина прямоугольного объекта
float length,width;
public:
// конструктор
Rectangle(float 1=0, float w = 0);
// методы для получения и модификации закрытых данных
float GetLength(void) const;
void PutLength(float 1);
float GetWidth (void) const;
void PutWidth(float w);
// вычисление характеристик прямоугольника
float Perimeter(void) const;
float Area(void) const;
>;
// конструктор, выполняет присваивания: length=l, width=w
Rectangle::Rectangle (float 1, float w) : length(1), width(w)
{}
// возвратить длину прямоугольника
float Rectangle::GetLength (void) const
{
return length;
}
// изменить длину прямоугольника
void Rectangle::PutLength (float 1)
{
length = 1;
}
// возвратить ширину прямоугольника
float Rectangle: :GetWidth (void) const
return width; //
// изменить ширину прямоугольника
void Rectangle: :PutWidth (float w)
width = w;
// вычислить и возвратить периметр прямоугольника
float Rectangle::Perimeter (void) const
return 2.0* (length + width);
// вычислить и возвратить площадь прямоугольника
float Rectangle: :Area (void) const
return length*width;
void main (void)
// стоимости обшивки и опалубки — постоянные
const float sidingCost = 2.00, moldingCost = 0.50;
int completedSelections = 0;
// опция из меню, выделенная пользователем
char doorOption;
// длина/ширина и стоимость двери
float glength, gwidth, doorCost;
// общая стоимость, включая дверь, обшивку и опалубку
float totalCost;
cout « "Введите длину и ширину гаража: ";
cin » glength » gwidth;
// создать объект garage (гараж) с размерами по умолчанию
// создать объект door (дверь) с размерами по умолчанию
Rectangle garage (glength, gwidth) ;
Rectangle door;
while (!completedSelections)
{
cout << "Введите 1-4 или ' q' для выхода" << endl « endl;
cout << "Дверь 1 (12 x 8; $380) "
« "Дверь 2 (12 x 10; $420) " « endl;
cout « "Дверь 3 (16 x 8; $450) "
« "Дверь 4 (16 x10; $480)" « endl;
cout « endl;
cin »doorOption;
if (doorOption « ' q' )
completedSelections = 1;
else
{
switch (doorOption)
{
case ' 1' :door.PutLength(12); // 12 x 8 ($380)
door.PutWidth(8);
doorCost = 380;
break;
case'2':door.PutLength(12) ; //12x10 ($420)
door.PutWidth(lO);
doorCost =420;
break;
case '3':door.PutLength(16); // 16 x 8 ($450)
door.PutWidth(8);
doorCost = 450;
break;
case '4':door.PutLength(12); // 16 x 10 ($480)
door.PutWidth(lO) ;
doorCost = 480;
break;
}
totalCost = doorCost +
moldingCost*(garage.Perimeter()+door.Perimeter())
+ sidingCost*(garage.Area()-door.Area());
cout « "Общая стоимость двери, обшивки и опалубки: $"
« totalCost « endl « endl;
}
}
}
/*
Оапуск программы 3 . 1>
Введите длину и ширину гаража: Введите 1-4 или ' q' для выхода
Дверь 1 (12 х8; $380) Дверь 2 (12 х 10; $420)
Дверь 3 (16 х8; $450) Дверь 4 (16 х 10; $480)
Общая стоимость двери, обшивки и опалубки: $720
Введите 1-4 или ' q' для выхода
Дверь 1 (12 х8; $380) Дверь 2 (12 х 10; $420)
Дверь 3 (16 х8; $450) Дверь 4 (16 х 10; $480)
q
*/
3.2. Примеры классов
Следующие два примера классов иллюстрируют конструкторы класса в C++.
Класс Temperature поддерживает записи значений высокой и низкой
температуры. В качестве приложения объект мог бы иметь высокую (точка кипения)
и низкую (точка замерзания) температуры воды. ADT RandomNumber
определяет тип для создания последовательности целых или с плавающей точкой
случайных чисел. В реализации C++ конструктор позволяет клиенту самому
инициализировать последовательность случайных чисел или использовать
программный способ получения последовательности с системно-зависимой
функцией времени.
Класс Temperature
Класс Temperature содержит информацию о значениях высокой и низкой
температуры. Конструктор присваивает начальные значения двум закрытым
данным-членам highTemp и lowTemp, которые являются числами с
плавающей точкой. Метод UpdateTemp принимает новое значение данных и
определяет, должно ли обновляться одно из значений температуры в объекте.
Если отмечается новое самое низкое значение, то обновляется lowTemp.
Аналогично, новое самое высокое значение изменит highTemp. Этот класс имеет
два метода доступа к данным: GetHighTemp возвращает самую высокую
температуру, a GetLowTemp возвращает самую низкую температуру.
Спецификация класса Temperature
ОБЪЯВЛЕНИЕ
class Temperature
{
private:
float highTemp, lowTemp; // закрытые данные-члены
public:
Temperature (float h, float 1);
void UpdateTemp(float temp);
float GetHighTemp(void) const;
float GetLowTemp(void) const;
};
ОБСУЖДЕНИЕ
Конструктору должны быть переданы начальные высокая и низкая
температуры для объекта. Эти значения могут быть изменены методом
UpdateTemp. Методы GetLowTemp и GetHighTemp являются константными
функциями, так как они не изменяют никакие данные-члены в классе. Класс
описан в файле "temp.h".
ПРИМЕР
/Уточка кипения/замерзания воды по Фаренгейту
Temperature fwater{212, 32);
//точка кипения/замерзания воды по Цельсию
Temperature cwater(100, 0);
cout « Вода замерзает при << cwater .GetLowtemp « " С"
<< endl;
cout « Вода кипит при « fwater.GetHighTemp « " F" « endl;
Выход: Вода замерзает при 0 С
Вода кипит при 212 F
Реализация класса Temperature
Каждый метод в классе записывается вне тела класса с использованием
оператора области действия. Конструктор принимает начальные показания
высокой и низкой температуры, которые присваиваются полям highTemp и
lowTemp. Эти значения могут изменяться только методом UpdateTemp, когда
новая высокая или низкая температура передаются в качестве параметра.
Функции доступа GetHighTemp и GetLowTemp возвращают значение высокой
и низкой температуры.
//конструктор, присвоить данные: highTemp=h и lowTemp=l
Temperature::Temperature(float h, float 1): highTemp(h),
lowTemp(1)
{}
//обновление текущих показаний температуры
void Temperature::UpdateTemp (float temp)
{
if (temp> highTemp)
highTemp = temp;
else if (temp < lowTemp)
lowTemp = temp;
}
// возвратить high (самая высокая температура)
float Temperature::GetHighTemp (void) const
{
return highTemp;
}
// возвратить low (самая низкая температура)
float Temperature::GetLowTemp (void) const
{
return lowTemp;
}
Программа З.2. Использование класса Temperature
// pr03_02.cpp
#include <iostream.h>
#include "temp.h" //
void main(void)
{
//
Temperature today (70,50);
float temp;
cout « "Введите температуру в полдень: ";
cin » temp;
// обновить объект для включения дневной температуры
today.UpdateTemp(temp);
cout « "В полдень: Наивысшая :" << today.GetHighTemp ();
cout « " Низшая " « today.GetLowTempO « endl;
cout « "Введите вечернюю температуру: ";
cin » temp;
// обновить объект для включения вечерней температуры
today.UpdateTemp(temp);
cout << "Сегодня наивысшая :" « today.GetHighTemp();
cout « " Низшая " « today.GetLowTempO « endl;
}
/*
Оапуск программы pr03_02.cpp>
Введите температуру в полдень: 80
В полдень: Наивысшая :80 Низшая 50
Введите вечернюю температуру: 40
Сегодня наивысшая :80 Низшая 40
*/
Класс случайных чисел
Для многих приложений требуются случайные данные, представляющие
случайные события. Моделирование самолета, тестирующее реакцию летчика
на непредвиденные изменения в поведении самолета, карточная игра,
предполагающая, что дилер использует тасованную колоду, и изучение сбыта,
предполагающее вариации в прибытии клиентов, — все это примеры
компьютерных приложений, которые опираются на случайные данные.
Компьютер использует генератор случайных чисел (random number generator),
который выдает числа в фиксированном диапазоне таким образом, что числа
равномерно распределяются в этом диапазоне. Генератор использует
детерминистический алгоритм, который начинается с начального значения
данных, называемого значением, инициализирующим алгоритм, или
seed-значением. Алгоритм манипулирует этим значением для генерирования
последовательности чисел. Этот процесс является детерминистическим, так как
он берет начальное значение и выполняет фиксированный набор инструкций.
Выход является уникальным, определенным данными и инструкциями. По
существу, компьютер не производит истинные случайные числа, а создает
последовательности псевдослучайных чисел (pseudorandom numbers),
которые распределяются равномерно в диапазоне. Вследствие начальной
зависимости от seed-значения, генератор создает ту же последовательность при
использовании одного и того же seed-значения. Способность повторять
случайную последовательность используется в исследованиях моделирования, где
в приложении необходимо сравнить различные стратегии, реагирующие на
один и тот же набор случайных условий. Например, имитатор полета
использует одну и ту же последовательность случайных чисел для сравнения
эффективности реакции двух летчиков на аварию самолета. Каждый летчик
подвергается одному и тому же набору событий. Однако, если seed-значение
изменяется каждый раз при запуске имитатора, мы имеем уникальное
моделирование. Эта уникальность свойственна игре, которая обычно создает
различную последовательность событий каждый раз в процессе игры.
Большинство компиляторов предоставляют библиотечные функции,
реализующие генератор псевдослучайных чисел. К сожалению, вариация этой
реализации в зависимости от компилятора является значительной. Для
предоставления генератора случайных чисел, переносимого из системы в систему,
мы создаем класс RandomNumber. Этот класс содержит seed-значение, которое
должно инициализироваться клиентом. В соответствии с начальным seed-
значением генератор создает псевдослучайную последовательность. Класс
обеспечивает автоматический выбор seed-значения, когда конструктору не
передается никакого значения, и позволяет клиенту создавать независимые
псевдослучайные последовательности.
Спецификация класса RandomNumber
ОБЪЯВЛЕНИЕ
♦include <time.h>
// используется для генерации случайного числа
//по текущему seed-значению
const unsigned long maxshort - 65536L;
const unsigned long multiplier = 1194211693L;
const unsigned long adder = 12345L;
class RandomNumber
{
private:
// закрытый член класса, содержащий текущее seed-значение
unsigned long randSeed;
public:
// конструктор, параметр 0 (по умолчанию) задает автоматический
// выбор seed-значения
RandomNumber(unsigned long s » 0);
// генерировать случайное целое в диапазоне [0, п-1]
unsigned short Random(unsigned long n);
// генерировать действительное число в диапазоне [0, 1.0]
double fRandom(void);
};
ОПИСАНИЕ
Начальное seed-значение — это беззнаковое длинное число. Метод Random
принимает беззнаковый длинный параметр п < 65536 и возвращает 16-битовое
беззнаковое короткое значение в диапазоне 0,. . • , п - 1. Заметьте, что если
возвращаемое методом Random значение присваивается целой переменной со
знаком, то это значение может интерпретироваться как отрицательное, если
п не будет удовлетворять неравенству п < 215 = 32768. Функция fRandom
возвращает число с плавающей точкой в диапазоне 0 < fRandom() < 1.0.
ПРИМЕР
RandomNumber rnd; //seed-значение выбирается автоматически
RandomNumber R(l); //создает последовательность с seed пользователя 1
cout « R.fRandomO; //выводит действительное число в диапазоне 0—1
//выводит 5 случайных целых чисел в диапазоне 0—99
for (int i = 0; i < 5; i++)
cout « R.Random(lOO) « " "; // <sample> 93 21 45 5 3
Пример 3.3
Создание случайных данных
1. Значение грани кости находится в диапазоне 1 — 6 (шесть вариантов).
Для имитации бросания кости используйте функцию die.Random(6),
которая возвращает значения в диапазоне 0 — 5. Затем прибавьте
1 для перевода случайного числа в нужный диапазон.
RandomNumber Die //использует автоматич. seeding
dicevalue = die.Random(б) +1;
2. Объект FNum использует автоматическое задание seed-значения для
создания случайной последовательности:
RandomNumber FNum;
Для вычисления плавающего значения в диапазоне 50 <, х < 75
генерируйте случайное число в диапазоне 0 — 25, умножая
результат fRandom на 25. Это расширяет диапазон случайных чисел от
1-й единицы (0 < х < 1) до 25 единиц (0 < х < 25). Преобразуйте
нижнюю границу нового диапазона, добавив 50:
value = FNum. fRandom() *25 + 50; //умножение на 25; прибавление 50
Реализация класса RandomNumber
Для создания псевдослучайных чисел мы используем линейный
конгруэнтный алгоритм. Этот алгоритм использует большой нечетный постоянный
множитель и постоянное слагаемое вместе с seed-значением для итеративного
создания случайных чисел и обновления seed-значения:
const unsigned long maxshort = 65536;
const unsigned long multiplier = 1194211693;
const unsigned long adder = 12345;
Последовательность случайных чисел начинается с начального значения
для длинного целого randSeed. Задание этого значения называется настройкой
(seeding) генератора случайных чисел и выполняется конструктором.
Конструктор позволяет клиенту передавать seed-значение или использовать
для его получения машинно-зависимую функцию time. Мы подразумеваем, что
функция time объявляется в файле <time.h>. При вызове конструктора с
параметром 0 функция time возвращает беззнаковое длинное (32-битовое) число,
указывая количество секунд, прошедших после базового времени.
Используемое базовое время включает полночь 1-го января 1970 года и полночь 1-го
января 1904 года. В любом случае, это большое беззнаковое длинное значение:
//генерация seed-значения
RandomNumber::RandomNumber (unsigned long s)
{
if (s == 0)
randSeed = time(0); //использование системной функции time
else
randSeed = s; //пользовательское seed-значение
}
В каждой итерации используем константы для создания нового беззнакового
длинного seed-значения:
randSeed = multiplier * randSeed + adder;
В результате умножения и сложения верхние 16 битов 32-битового значения
randSeed являются случайными ("хорошо перемешанными") числами. Наш
алгоритм создает случайное число в диапазоне от 0 до 65535, сдвигая 16 битов
вправо. Мы отображаем это число на диапазон 0 ... п - 1, беря остаток от
деления на п. Результатом является значение Random(n).
//возвращать случайное целое 0 <= value <= п-1 < 65536
unsigned short RandomNumber::Random (unsigned long n)
{
randSeed = multiplier * randSeed + adder;
return (unsigned short) ((randSeed) » 16) % n) ;
}
Для числа с плавающей точкой сначала вызываем метод Random(maxshort),
который возвращает следующее случайное целое число в диапазоне от 0 до
maxshort — 1. После деления на double(maxshort) получаем действительное
число в интервале 0 < fRandom() < 1.0.
double RandomNumber::fRandom (void)
{
return Random(maxshort)/double(maxshort);
}
Объявление и реализация RandomNumber содержится в файле "random.h".
Приложение; Частота выпадения лицевой стороны при бросании монет.
Класс RandomNumber используется для имитации повторяемого бросания 10
монет. Во время бросания некоторые монеты падают лицевой стороной (head)1
вверх, а другие — обратной. Бросание десяти монет имеет результатом число
падений лицевой стороной в диапазоне 0-10. Интуитивно вы подразумеваете,
что 0 лицевых сторон или 10 лицевых сторон в бросании 10 монет — это
относительно невероятно. Более вероятно, что количества выпадений разных
сторон будут примерно равными. Число лицевых сторон будет находиться
где-нибудь в середине диапазона 0—10, скажем, 4—6. Мы проверим это
интуитивное предположение большим числом (50 0000) повторений бросания.
Массив head ведет подсчет количества раз, когда соответствующий подсчет
лицевых сторон составляет 0, 1, . . ., 10.
Значение head[i] (0 <. i < 10) — это количество раз в 50 000 повторениях,
когда ровно i лицевых сторон выпадает во время бросания 10 монет.
Программа 3.3. График частоты
Бросание 10 монет составляет событие. Метод Random с параметром 2
моделирует одно бросание монеты, интерпретируя возвращаемое значение
0 как обратные стороны, а возвращаемое значение 1 — как лицевые стороны.
Функция TossCoins объявляет статический объект coinToss типа Random-
Number, использущий автоматическое задание seed-значения. Так как этот
объект является статическим, каждый вызов TossCoins использует
следующее значение в одной последовательности случайных чисел. Бросание
указанного количества монет выполняется суммированием 10 значений,
выдаваемых CoinToss.Random(2). Возвращаемый результат приращивает
соответствующий счетчик в массиве лицевых сторон.
Выходом программы является частотный график количества лицевых
сторон. График с числом лицевых сторон на оси х и относительным числом
событий (occurences) — на оси у обеспечивает наглядное представление того,
что известно как биномиальное распределение. Для каждого индекса i
относительное число событий, при которых лицевые стороны выпали ровно i
раз, составляет
heads[i]/float(NTOSSES)
Это значение используется для помещения символа * в относительном
местоположении между 1-й и 72-й позицией строки. Результирующий
график является аппроксимацией биномиального распределения.
#include <iostream.h>
#include <iomanip.h>
#include "random.h" // включает генератор случайных чисел
// "бросить" numberCoins монет и возвратить общее число
// выпадений лицевой стороны
int TossCoins(int numberCoins)
{
static RandomNumber coinToss;
int i, tosses = 0;
1 Здесь под лицевой стороной подразумевается та сторона монеты, на которой изображен монарх
или президент. — Прим. ред.
for (i«0;i < numberCoins;i++)
// Random(2) * 1 индицирует лицевую сторону
tosses += coinToss.Random(2);
return tosses;
}
void main (void)
{
// число монет в бросании и число бросаний
const int NCOINS = 10;
const long NTOSSES = 50000;
// heads [0]=сколько раз не выпало ни одной лицевой стороны
// heads [1]=сколько раз выпала одна лицевая сторона и т.д.
long i, heads[NCOINS + 1];
int j, position;
// инициализация массива heads
for (j=0; j <= NCOINS+l;j++)
heads[j] = 0;
// "бросать" монеты NTOSSES раз и записывать результаты в массив heads
for (i=0;i< NTOSSES;i++)
heads[TossCoins(NCOINS)]++;
// печатать график частот
for (i=0;i < NCOINS+l;i++)
{
position = int(float(heads[i])/float(NTOSSES) * 72);
cout « setw(6) « i « " ";
for (j=0;j <position-1;j++)
cout « " " ;
// ' *' относительное число бросаний с i лицевыми сторонами
cout « ' *' « endl;
}
}
/*
Оапуск программы рг03_03 . срр>
0 *
1 *
2 *
3 *
4 *
5 *
6 *
7 *
8 *
9 *
10 *
*/
33. Объекты и передача информации
Объект является экземпляром типа данных и как таковой может
передаваться в качестве параметра функции или возвращаться как значение
функции. Подобно другим типам C++, объектный параметр может передаваться
по значению или по ссылке. Положения этого раздела иллюстрируются
примерами из класса Temperature.
Объект как возвращаемое значение
Любой тип класса может быть возвращаемым типом функции. Например,
функция SetDailyTemp принимает в качестве параметра массив чисел,
представляющий показания температуры, извлекает максимальное и
минимальное показания из списка и возвращает объект Temperature с этими крайними
значениями.
Temperature SetDailyTemp (float readingf], int n)
{
//создание t с 1-ми значениями high и low
Temperature t(reading[0], reading[0]);
//обновление high или low, если необходимо
for (int i = 1; i < n; i ++)
t.UpdateTemp(reading[i]);
//возвращение t с крайними температурами этого дня
return t;
}
Массив reading содержит шесть температурных значений. Для определения
высокой и низкой температур вызовите SetDailyTemp и присвойте результат
объекту today. Чтобы вывести эти температуры на экран, используются
методы GetHighTemp и GetLowTemp.
float reading[6) = {40, 90, 80, 60, 20, 50};
Temperature today = SetDailyTemp(reading,6);
cout « "Сегодняшние высокая и низкая температуры такие"
« today.GetHighTemp () « "и"
« today.GetLowTemp() « endl;
Объект как параметр функции
Объекты могут передаваться как параметры функции по значению или
по ссылке. Следующие примеры иллюстрируют соответствующий синтаксис.
Функция TemperatureRange использует вызов по значению (call by value)
параметра Т типа Temperature и возвращает разницу между самой высокой
и самой низкой температурами. При выполнении этой функции вызывающий
элемент копирует объект типа Temperature (фактический параметр) в Т.
float TemperatureRange(Temperature T)
{
return T.GetHighTemp() - Т.GetLowTemp();
}
Функция Celsius использует вызов по ссылке (call by reference) параметра
Т типа Temperature, который, как первоначально подразумевалось, содержит
значения по Фаренгейту. Функция создает объект типа Temperature, чьи
самое высокое и самое низкое показания преобразуются в значения по
Цельсию, и присваивает его объекту Т.
void Celsius(Temperatures T)
{
float hi, low;
//с = 5/9 * (f-32)
hi - float (5)/9 * (T.GetHighTempO -32);
low = float(5)/9 * (T.GetLowTempO -32);
T = Temperature(hi, low);
}
Пример: объект Water содержит точку кипения (212° по Фаренгейту) и
точку замерзания (32° по Фаренгейту) воды в качестве самого высокого и
самого низкого температурных значений. Результат использования функции
TemperatureRange показывает, что 180° — это диапазон для воды по шкале
Фаренгейта. С помощью функции Celsius преобразуем эти температуры в
значения по Цельсию и вызовем TemperatureRange, чтобы показать, что
100° — это соответствующий диапазон по шкале Цельсия.
Temperature Water(212, 32); //кипение при 212F, замерзание при 32F
cout <<"Температурный диапазон воды по шкале Фаренгейта"
« TemperatureRange(Water) « endl;
Celsius(Water); //преобразование температуры по Фаренгейту
//в температуру по Цельсию
cout «"Температурный диапазон воды по шкале Цельсия"
« TemperatureRange(Water) « endl;
3.4. Массивы объектов
Тип элемента массива может включать не только встроенные типы данных,
такие как int или char, но также определяемые пользователем типы класса.
Результирующий массив объектов может использоваться для создания
списков, таблиц и так далее. Однако, использование объектных массивов требует
осторожности. Объявление массива вызывает конструктор для каждого
объекта в списке. Сравните простое объявление одного объекта Rectangle и
массива из 100 объектов Rectangle. В каждом объявлении конструктор
вызывается для создания объекта, который задает длину и ширину. В случае
массива конструктор вызывается для каждого из 100 объектов.
Rectangle pool(150, 100); //создание бассейна 150 х 100
Rectangle room[100]; //конструктор вызывается для
//комната[0] .. [99]
Объявление объекта pool передает начальные значения конструктору.
Объекты room фактически имеют начальные значения, поскольку конструктор
Rectangle присваивает нулевые значения по умолчанию длине и ширине
объекта:
Rectangle(float 1=0, float w=0); //параметры по умолчанию
После объявления массива длина и ширина каждого объекта roomfi] имеют
нулевые значения:
cout « room[25].GetLengh() //выход 0;
cout « room[25].GetWidth() //выход 0;
room[25].PutLengh(lO) //установка длины комнаты[25] на 10
room[25].PutWidth(5) //установка ширины комнаты[25] на 5
Объявление массива объектов Rectangle поднимает важную проблему,
касающуюся массиЕов и классов. Если конструктор класса Rectangle не имеет
параметров по умолчанию, объявление массива room вызовет ошибку, потому
что каждый массив будет требовать параметры. Объявлению потребуется
список инициализаторов массива, который управляет каждым элементом в
массиве. Например, для объявления массива room из 100 элементов и установки
параметров длины и ширины на 0 потребуется список инициализаторов 100
объектов Rectangle. В действительности это на практикуется.
Rectangle room[100] = {Rectangle(0, 0), . . . , Rectangle(0, 0)};
Для объявления массива объектов мы предоставляем конструктору
значения по умолчанию или просто создаем конструктор без параметров.
Конструктор умолчания
Конструктор умолчания (default costructor) — это конструктор, не
требующий никаких параметров. Это бывает, когда конструктор не имеет параметров
или когда каждый параметр имеет значение по умолчанию. В этой главе класс
Rectangle содержит конструктор умолчания, тогда как класс Temperature
требует параметров при объявлении объекта.
Класс Rectangle
КОНСТРУКТОР
Rectangle(float 1=0, float w=0);
Конструктор содержит параметры 1 и w со значением по умолчанию 0. При
создании массива Rectangle значения по умолчанию присваиваются каждому
объекту.
Rectangle R[25]; //каждый элемент имеет значение Rectangle(0, 0)
Класс Temperature
КОНСТРУКТОР
Temperature(float h, float 1);
Класс Temperature не содержит конструктор по умолчанию. Вместо этого,
объекту должно быть дано начальное значение для высокой и низкой
температуры. Объявление объектов today и week является недействительным!
Temperature today; //недействительно: отсутствуют параметры
Temperature week[7]; //Temperature не имеет конструктора по умолчанию
3.5. Множественные конструкторы
До сих пор в наших классах мы разрабатывали как default-, так и nonde-
fault-конструкторы1. В результате предыдущих рассуждений вы можете
предположить, что они являются взаимоисключающими, поскольку все классы
имели одиночный конструктор. C++ "признает" нашу потребность в
разнообразии способов инициализации объекта и позволяет определять
множественные конструкторы в одном и том же классе. Компилятор использует перегрузку
функции для выбора правильной формы конструктора, когда мы создаем
объект. Концепция перегрузки функции и ее правила обсуждаются в главе 6.
Multiple-конструкторы добавляют большие возможности классу. Особый тип
multiple-конструктора, называемый конструктором копирования (copy
constructor), используется со многими классами, содержащими динамические
данные-члены. Конструктор копирования описывается в главе 8.
1 Следует отметить, что в русских изданиях термин default constructor встречается как
конструктор умолчания или default-конструктор. В то же время под термином nondefault
constructor (или nondefault-конструктор) следует понимать конструктор с самым обычным
синтаксисом, из которого не следуют никакие дополнительные свойства конструктора. — Прим. ред.
месяц
1 < m < 12
день
1 < d < 31
год
1900 <, у £ 1999
Класс Date иллюстрирует использование multiple конструкторов. Этот
класс имеет три данных-члена, которые обозначают месяц, день и год в дате.
Один конструктор имеет три параметра, соответствующие трем
данным-членам. Действием конструктора является инициализация этих переменных.
Второй конструктор позволяет клиенту объявлять дату как строку в форме
"mm/dd/yy", читает эту строку и преобразует пары символов "mm" в месяц,
"dd" в день и "уу" в год. Для каждого конструктора мы подразумеваем, что
параметр, задающий год — это значение из двух цифр в диапазоне 00-99.
Фактический год сохраняется добавлением 1900 к начальному значению:
year - 1900 + уу
Класс Date имеет метод, который выводит на экран полную дату с
названием месяца, дня и значением года. Например, первый день в двадцатом
веке был
1 января 1900
Спецификация класса Date
ОБЪЯВЛЕНИЕ
#include <string.h>
#include <strstream.h>
class Date
{
private:
// закрытые члены, которые определяют дату
int month, day, year/
public:
// конструкторы, дата по умолчанию — Январь 1, 1900
Date (int m = 1, int d = 1, int у = 0);
Date (char *dstr);
// вывод данных в формате "месяц день, год"
void PrintDate (void);
};
ОПИСАНИЕ
Для построения Date-объектов используются два конструктора,
отличающиеся параметрами. Компилятор выбирает конкретный конструктор во время
создания Date-объекта. Следующие примеры демонстрируют создание
объектов.
ПРИМЕРЫ
Date dayl(6, 6, 44); // 6 июня 1944
Date day2; // значение по умолчанию для 1 января 1990
date day3("12/31/99"); // 31 декабря 1999
Реализация класса Date
Сердцевиной класса Date являются два его конструктора, которые
определяют дату, передавая значения месяца, дня и года или строки "mm/dd/yy".
Первый конструктор имеет три параметра со значениями по умолчанию,
соответствующими 1 января 1900 года. Со значениями по умолчанию
конструктор квалифицируется как конструктор умолчания:
// конструктор, day и year задаются как целые ram dd yy
Date::Date (int m, int d, int y) : month(m), day(d)
{
year = 1900 + у; // у — год в 20-м столетии
);
Альтернативная форма конструктора принимает строковый параметр.
Строка имеет форму "mm/dd/yy". Для преобразования пар данных мы используем
ввод на базе массива, который преобразует символьные пары "mm" в целое
значение месяца и так далее. Копируем строку параметра в массив inputBuffer
и затем читаем символы в таком порядке:
month — ch — day -ch — year
Ввод ch удаляет два разделителя "/" из строки ввода.
// конструктор
// month, day и year задаются в виде строки "mm/dd/yy"
Date::Date (char *dstr)
{
char inputBuffer[16];
char ch;
// копирование в inputBuffer
strcpy(inputBuffer,dstr);
istrstream input(inputBuffer, sizeof(inputBuffer));
// чтение данных из входного потока ch используется в качестве символа '/'
input » month » ch » day » ch »year;
year += 1900/
);
При выводе метод Print дает текст полной даты, включающий название
месяца, дня и год. Массив months содержит пустую строку (индекс 0) и 12
названий для календарных месяцев. Значение месяца используется как индекс
в массиве для печати названия месяца.
// печать даты с полным названием месяца
void Date::PrintDate (void)
{
// статический массив с названиями месяцев
static char *Months[] = {"","Январь","Февраль",
"Март","Апрель","Май",
"Июнь","Июль","Август",
"Сентябрь","Октябрь",
"Ноябрь","Декабрь"};
cout « Months [month] « " " « day « ", "« year ;
};
Программа 3.4. Дата двадцатого века
Тестовая прграмма использует конструкторы для установки
демонстрационных объектов. Получаемые в результате данные печатаются. Класс Date
содержится в файле "date.h".
#include <iostream.h>
#include "date.h" // включение класса Date
void main(void)
{
// Date-объекты с целыми, умалчиваемыми и строчными параметрами
Date dayl(6,6,44) ; // Июнь б, 1944
Date day2; // Январь 1, 1900
Date day3("12/31/99"); // Декабрь 31, 1999
cout « "День Д во Второй Мировой войне — ";
dayl.PrintDate();
cout « endl;
cout « "Первый день 20-ого века — ";
day2.PrintDate();
cout << endl;
cout « "Последний день 20-ого века — ";
day3.PrintDate();
cout « endl;
}
/*
<Выполнение программы 3.4>
День Д во Второй Мировой войне — Июнь б, 1944
Первый день 20-ого века — Январь 1, 1900
Последний день 20-ого века — Декабрь 31, 1999
*/
3.6. Практическое применение:
Треугольные матрицы
Двумерный массив, часто называемый матрицей (matrix), предоставляет
важную для математики структуру данных. В этом разделе мы исследуем
квадратные матрицы (square matrices — матрицы с одинаковым числом
строк и столбцов), чьи элементы данных являются действительными
числами. Мы разрабатываем класс TriMat, определяющий верхние
треугольные матрицы (upper triangular matrices), в которых все элементы,
находящиеся ниже диагонали, имеют нулевые значения.
В математических терминах, Ау=0 для j<i. Верхний треугольник
определяется элементами Ау для j>i. Эти матрицы имеют важные алгебраические
свойства и используются для решения систем уравнений. Реализация операций
верхней треугольной матрицы в классе TriMat показывает способ эффективного
хранения треугольной матрицы в виде одномерного массива.
Свойства верхней треугольной матрицы
Если верхняя треугольная матрица имеет л2 элементов, приблизительно
половина из них являются нулевыми и нет необходимости сохранять их явно.
Конкретно, если мы вычитаем п диагональных элементов из суммы п2
элементов, то половина оставшихся элементов являются нулевыми. Например, при
л=25 имеется 300 элементов со значением 0:
(П2 _ п)/2 = (252 _ 25)/2 = (625 — 25)/2 = 300
Далее следует набор операций для треугольных матриц. Мы определяем
сложение, вычитание и умножение матриц, а также детерминант, который
имеет важное применение для решения уравнений.
Сумма или разность двух треугольных матриц А и В получается в результате
сложения или вычитания соответствующих элементов матриц.
Результирующая матрица является треугольной.
Сложение С = А + В
где С — это треугольная матрица с элементами Ctj = Ац + Bij.
Вычитание С = А — В
где С — это треугольная матрица с элементами dj = Aij - Bq.
Умножение С = А * В
Результирующая матрица С — это треугольная матрица с элементами С*,/,
значения которых вычисляются из элементов строки i матрицы А и столбца у
матрицы В:
Citr(Aii0*B0,j) + (Au*Bltj) + (Ait2*B2J) + . . . + (Aitnl*Bn.u)
Например, если
Со,2 — это сумма произведений элементов строки 0 матрицы А и колонки 2
матрицы В.
1*4+1*1+0*3=5
Произведение матриц А и В:
Для общей квадратной матрицы детерминант является сложной для
вычисления функцией, однако вычислить детерминант треугольной матрицы
не трудно. Просто получите произведение элементов на диагонали.
Хранение треугольной матрицы
Применение для хранения верхней треугольной матрицы стандартного
двумерного массива требует использования всей памяти размером л2,
несмотря на прогнозируемые нули, расположенные ниже диагонали. Для
исключения этого пространства мы сохраняем элементы из треугольной матрицы
в одномерном массиве М. Все элементы ниже главной диагонали не
сохраняются. Таблица 3.1 показывает количество элементов, которые сохраняются
в каждой строке.
Таблица 3.1
Хранение треугольной матрицы
Строка
0
1
2
...
п-2
п-1
Число элементов
п
п-1
п-2
ф •»
2
1
Элементы
(Ао, о . . ■ Ао, n-i)
(Ai( i . . . Ai, n-i)
(A2, 2 . . . A2, n-i)
• • •
(An-2. n-2 • • • An-2, n-i)
(An-1, n-i)
Алгоритму сохранения требуется функция доступа, которая должна
определять местоположение в массиве М элемента Ау. Для j < i элемент Ay
является равным 0 и не сохраняется в М. Для j > i функция доступа использует
информацию о числе сохраняемых элементов в каждой строке вплоть до строки
i. Эта информация может быть вычислена для каждой строки i и сохранена в
массиве (rowTable) для использования функцией доступа.
Строка
0
1
2
3
rowTable
rowTable[0] = 0
rowTable[1] = n
rowTable [2] = n + n-1
rowTable [3] = n + n-l+n-2
Замечание
0 элементов перед строкой 0
п элементов перед строкой 1 (от строки 0)
п + п-1 элементов перед строкой 2
элементы перед строкой 3
n-1
rowTable[n-1] = n + n-1 + ... +2
Строка
0
1
2
rowTable
rowTable[0] «■ 0
rowTable[1] - 3
rowTable[2] - 5
Замечание
0 элементов, сохраненных перед строкой 0
3 элемента строки 0 (110)
5 элементов из строк 0 и 1 (11021)
Row Table
Элементы треугольной матрицы сохраняются по строкам в массиве М.
Массив М
Элементы
строки 0
Элементы
строки 1
Элементы
строки 2
С учетом того, что элементы треугольной матрицы сохраняются построчно
в массиве М, функция доступа для Ац использует следующие параметры:
Индексы i и j,
Массив rowTable
Алгоритм доступа к элементу Ау заключается в следующем:
1. Если j<i, Aij = 0 и этот элемент не сохрдняется.
2. Если j>i, то получается значение rowTable[i], являющееся количеством
элементов, которые сохраняются в массиве М, для элементов до строки
L В строке i первые i элементов являются нулевыми и не сохраняются
в М. Элемент Aij помещается в M[rowTable[i] + (j — i)].
Пример 3.4
Рассмотрим матрицу X размера 3x3
Пример 3.5
Рассмотрим треугольную матрицу Х[3][3] из примера 3.4:
1. X0t2 =M[rowTable[0] + (2 — 0)]
=М[0 + 2]
=М[2] = 0
2. Xi,o не сохраняются
3. Xlt2 =M[rowTable[l] + (2 — 1)]
=М[3 4- 1]
=М[4] = 1
Класс TriMat
Класс TriMat реализует ряд операций треугольной матрицы. Вычитание и
умножение треугольной матрицы оставлены для упражнений в конце главы.
Учитывая то ограничение, что мы должны использовать только статические
массивы, наш класс ограничивает размер строки и столбца числом 25. При
этом мы будем иметь 300 = (252 — 25)/2 нулевых элементов, поэтому массив
М должен содержать 325 элементов.
Спецификация класса TriMat
ОБЪЯВЛЕНИЕ
#include <iostream.h>
#include <stdlib.h>
// максимальное число элементов и строк
// верхней треугольной матрицы
const int ELEMENTLIMIT = 325;
const int ROWLIMIT = 25;
class TriMat
{
private:
// закрытые данные-члены
int rowTable[ROWLIMIT]; // начальный индекс строки в М
int n; // размер строки/колонки
double М[ELEMENTLIMIT];
public:
// конструктор с параметрами
TriMat(int matsize);
// методы доступа к элементам матрицы
void PutElement (double item, int i, int j);
double GetElement(int i, int j) const;
// матричные арифметические операции
TriMat AddMat(const TriMat& A) const;
double DelMat(void) const;
// матричные операции ввода/вывода
void ReadMat(void);
void WriteMat(void) const;
// получить размерность матрицы
int GetDimension(void) const;
};
ОПИСАНИЕ
Конструктор принимает число строк и столбцов матрицы. Методы PutEle-
ment и GetElement сохраняют и возвращают элементы верхней треугольной
матрицы. GetElement возвращает 0 для элементов ниже диагонали. AddMat
возвращает сумму матрицы А с текущим объектом. Этот метод не изменяет
значение текущей матрицы. Операторы ввода/вывода ReadMat и WriteMat
работают со всеми элементами матрицы п х п. Сам метод ReadMat сохраняет
только верхне-треугольные элементы матрицы.
ПРИМЕР
#include trimat.h // включить класс TriMat
TriMat A(10), В(10), С(10); // треугольные матрицы 10x10
A.ReadMat(); // ввести матрицы А и В
В.ReadMat();
С = A.AddMat(В); // вычислить С = А + В
С.WriteMat(); // печатать С
Реализация класса TriMat
Конструктор инициализирует закрытый член п параметром matsize. Таким
образом задается число строк и столбцов матрицы. Этот же параметр
используется для инициализации массива rowTable, который используется для
доступа к элементам матрицы. Если matsize превышает ROWLIMIT, выдается
сообщение об ошибке и выполнение программы прерывается.
// инициализация п и rowTable
TriMat::TriMat(int matsize)
{
int storedElements = 0;
// прервать программу, если matsize больше ROWLIMIT
if (matsize > ROWLIMIT)
{
cerr « "Превышен размер матрицы" « ROWLIMIT «
« "x" « ROWLIMIT « endl;
exit (1);
}
n = matsize;
// задать таблицу
for(int i = 0; i < n; i++)
{
rowTable[i] = storedElements;
storedElements += n — i;
}
}
Матричные методы доступа. Ключевым моментом при работе с
треугольными матрицами является возможность эффективного хранения ненулевых
элементов в линейном массиве. Чтобы достичь такой эффективности и все
же использовать обычные двумерные индексы i и j для доступа к элементу
матрицы, нам необходимы функции PutElement и GetElement для сохранения
и возвращения элементов матрицы в массиве.
Метод GetDimension предоставляет клиенту доступ к размеру матрицы. Эта
информация может использоваться для обеспечения того, чтобы методам
доступа передавались параметры, соответствующие правильной строке и столбцу:
// возвратить размерность матрицы п
int TriMat::GetDimension(void) const
{
return n;
}
Метод PutElement проверяет индексы i и j. Если j > i, мы сохраняем
значение данных в М, используя функцию доступа к матрице для треугольных
матриц: Если i или j не находится в диапазоне 0 . . (п-1), то программа
заканчивается:
// записать элемент матрицы [i,j] в массив М
void TriMat::PutElement (double item, int i, int j)
{
// прервать программу, если индексы элемента вне индексного диапазона
if ((i < О | I i >- п) II (j < О I | j >= n))
{
cerr « "PutElement: индекс вне диапазона 0 — "
« n-1 « endl;
exit (l);
}
// все элементы ниже диагонали игнорируются
if (j >= i)
M[rowTable[i] + j-i] = item;
}
Для получения любого элемента метод GetElement проверяет индексы i и j.
Если i или j не находится в диапазоне 0 . . (п — 1), программа заканчивается.
Если j<i, то элемент находится в нижней треугольной матрице со значением 0.
GetElement просто возвращает несохраняемое значение 0. В противном случае,
j>i, и метод доступа может возвращать элемент из массива М:
// получить матричный элемент [i, j] массива М
double TriMat::GetElement(int i, int j) const
{
// прервать программу, если индексы вне индексного диапазона
if ((i < 0 | | i >= n) || (j < 0 | I j >- n))
<
cerr « "GetElement: индекс вне диапазона 0 — "
« n-1 « endl;
exit (1);
}
if (j >- i)
// вернуть элемент, если он выше диагонали
return M[rowTable[i] + j-i];
else
// элемент равен 0, если он ниже диагонали
return 0;
}
Ввод/вывод матричных объектов. Традиционно, ввод матрицы
подразумевает, что данные вводятся построчно с полным набором значений строк, и
столбцов. В объекте TriMat нижняя треугольная матрица является нулевой и
значения не сохраняются в массиве. Тем не менее, пользователю предлагается
ввести эти нулевые значения для сохранения обычного матричного ввода.
// читать элементы матрицы построчно, клиент должен ввести
// все (п х п) элементов
void TriMat::ReadMat(void)
{
double item;
int i, j;
for (i = 0; i < n; i++) // сканировать строки
for (j = 0; j < n; j++) // для каждой строки сканировать столбцы
{
cin >> item; //читать [i, j ] -й элемент матрицы
PutElement (item, i, j ); // сохранить этот элемент
}
}
// построчная выдача в поток элементов матрицы
void TriMat::WriteMat(void) const
{
int i, j;
// установка режима выдачи
cout.setf(ios::fixed);
cout.precision(3) ;
cout.setf(ios::showpoint);
for (i =0; i < n; i++)
{
for (j = 0; j < n; j++)
cout « setw(7) « GetElement (i,j) ;
cout << endl;
}
}
Матричные операции. Класс TriMat имеет методы для вычисления суммы
двух матриц и детерминанта матрицы. Метод AddMat принимает
единственный параметр, который является правым операндом в сумме. Текущий объект
соответствует левому операнду. Например, сумма треугольных матриц X и Y
использует метод AddMat для объекта X. Предположим, сумма сохраняется в
объекте Z. Для вычисления
Z = X + Y
используйте оператор
Z = X.AddMat(Y);
Алгоритм сложения двух объектов типа TriMat возвращает новую матрицу
В с элементами By = CurrentObjecty + Ay:
// возвращает сумму текущей и матрицы А.
// текущий объект не изменяется
TriMat TriMat::AddMat (const TriMat& A) const
{
int i,j;
double itemCurrent, itemA;
TriMat B(A.n); // в В будет искомая сумма
for (i « 0; i < n; i++) // цикл по строкам
{
for (j - i; j < n; j++) // пропускать элементы ниже диагонали
{
itemCurrent = GetElement(i,j);
itemA = A.GetElement(i,j);
B.PutElement (itemCurrent + itemA, i, j);
}
}
return B;
Метод DetMat возвращает детерминант текущего объекта. Возвращаемое
значение — это действительное число, которое является произведением
элементов диагонали. Полный текст кода для реализации класса TriMat можно
найти в программном приложении.
Программа 3.5. Операции с классом TriMat
Тестовая программа иллюстрирует класс TriMat с операциями
ввода/вывода, а также матричного суммирования и определения детерминанта.
Каждая секция программы снабжена комментариями.
#include <iostream.h>
#include <iomanip.h>
#include "trimat.h" // включить класс TriMat
void main(void)
{
int n;
// задать размер однородной матрицы
cout << "Каков размер матрицы? ";
cin >> п;
// объявить три матрицы размером (n x п)
TriMat A(n), B(n), C(n);
// читать матрицы А и В
cout « "Введите некоторую " << п « " х " « п
« " треугольную марицу" << endl;
A.ReadMat();
cout << endl;
cout << "Введите некоторую " << n << " x " << n
<< " треугольную марицу" << endl;
B.ReadMatO ;
cout « endl;
// выполнить операции и напечать результат
cout « "Сумма А + в" << endl;
С = A.AddMat(В);
C.WriteMatO ;
cout « endl;
cout « "Детерминант A+B= " « С.DetMat{) « endl;
}
/*
<Выполнение программы 3.5>
Каков размер матрицы? 4
Введите некоторую 4x4 треугольную марицу
12-45
0 2 4 1
0 0 3 7
0 0 0 5
Введите некоторую 4x4 треугольную матрицу
14 6 7
О 2 б 12
0 0 3 1
0 0 0 2
Сумма. А + В
2.000 6.000 2.000 12.000
0.000 4.000 10.000 13.000
0.000 0.000 6.000 8.000
0.000 0.000 0.000 7.000
Детерминант А+В= 336.000
*/
Письменные упражнения
3.1 Разработайте ADT Coins для набора из п монет. Данные включают
количество монет, общее количество лицевых сторон в последнем бросании
и список значений монет в последнем бросании. Операции должны
включать инициализацию, бросание монет, возвращение общего количества
выпадений лицевых сторон и печать значений в последнем бросании.
3.2
(а) Разработайте ADT для коробки. Включите в этот ADT инициализацию
и операции, которые возвращают длины сторон и вычисляют площадь
и объем.
(б) Напишите класс Box, реализующий этот ADT.
(в) Обхват коробки — это периметр прямоугольника, образованного двумя
сторонами. Коробка имеет три возможных значений обхвата. Почтовая
длина определяется обхватом плюс расстояние третьей стороны.
Упаковка пригодна для пересылки по почте, если какая-либо из ее длин
меньше 100. Напишите фрагмент кода для определения, пригоден ли
объект В для пересылки по почте.
3.3 Определите все ошибки синтаксиса в определениях класса:
(а) class X
{
private int t;
private int q;
public
int X(int a, int b)/
{
t = a; q = b;
}
void printX(void);
}
(б) class Y
{
private:
int p;
int q/
public
Y (int n, int m) : n(p) q(m);
{
}
};
3.4
(а) Объявите спецификацию для класса X, который имеет следующее:
Закрытые члены: Целые переменные а, Ь, с.
Открытые члены: Конструктор, который присваивает значения
переменным а, Ъ, с; значения по умолчанию будут равны 1. Функцию F,
возвращающую максимум переменных а, Ь, с.
(б) Напишите конструктор для класса X пункта (а).
(в) Напишите открытую функцию F, поместив ее определение вне класса.
3.5 Предположим следующее объявление:
class Student
{
private:
int studentid;
intgradepts, units;
float gpa;
float ComputeGPA(void);
public;
Student(int studid; int studgradepts, int studunits);
void ReadGradelnfo(void);
void PrintGradelnfo(void);
void UpdateGradeInfo(int newunits, int newgradepts);
};
Этот класс ведет запись отметок для студента. Переменные gradepts и
units используются методом ComputeGPA для присваивания средней
успеваемости студента переменной gpa. Используйте формулу:
gpa = gradepts/units
Напишите код для этой функции-члена. Конструктор и ComputeGPA
должны быть выполнены как код in-line.
3.6 ADT Calendar содержит элементы данных year и логическое значение
leapyr. Его операции следующие:
Конструктор Инициализирует данные-члены year и leapyr.
NumDays(mm.dd) Возвращение количества дней с самого начала
года до заданного месяца mm и дня dd.
Leapyear(void) Указывает, является ли год високосным.
PrintDate(ndays) Печатает дату ndays в year в формате
mm/dd/yy.
(а) Напишите ADT формально
(б) Реализуйте ADT Calendar как класс.
3.7 Разработайте объявление для класса, который имеет следующие
данные-члены. Объявите операции, соответствующие объекту этого типа.
(а) Имя студента, профилирующая дисциплина, предлагаемый год
окончания учебы, средняя успеваемость.
(б) Штат, столица, население, площадь, губернатор
(в) Цилиндр. Сделайте возможными изменения радиуса и высоты и
включите вычисление площади поверхности и объема.
3.8 Следующий код является объявлением для класса, представляющего
колоду карт:
class CardDeck
{
private:
//колода карт реализуется как массив
//целых от 0 до 51.
int cards[52];
int currentCard;
public:
//конструктор, тасование колоды карт
CardDeck(void);
//тасование колоды карт
void Shuffle(void);
//возвращать следующую карту в колоде. СОВЕТ: вы
//должны установить текущее местоположение в колоде.
int GetCard(void);
//трефы 0-12., бубны 13-25, черви 26-38,
//пики 39-51. В каждом диапазоне первая карта — это
//туз, а последние три карты — это валет, дама, король.
//запишите карту с как масть, значение карты
void PrintCard(int с);
};
(а) Реализуйте эти методы. СОВЕТ: Для тасования карт используйте цикл
со сканированием 52-х карт. Для карты i выберите случайное число в
диапазоне от i до 51 и поменяйте местами карту с этим случайным
индексом и карту с индексом i.
(б) Запишите функцию
void DealHand(CardDeck& d, int n) ;
которая сдает п карт из d, сортирует их и печатает их значения.
3.9 Используя класс Temperature из раздела 3.2, напишите функцию:
Temperature Average( temperature a[ ], int n);
которая возвращает объект типа Temperature, содержащий среднюю
низкую и высокую температуры п показаний.
3.10 Используйте класс Date из раздела 3.5.
(а) Измените класс Date для включения метода IncrementDate. Он
принимает положительное число дней в диапазоне 0-365, добавляет его к
текущей дате и возвращает объект, имеющий новую дату.
(б) Сделайте так, чтобы параметр для IncrementDate мог принимать
отрицательные значения.
3.11 Покажите использование класса случайных чисел для моделирования
следующего:
(а) Одна пятая часть автомобилей штата не соответствует стандартам по
вредным эмиссиям. Используйте fRandom, чтобы определить, отвечает
ли этим стандартам случайно выбранная автомашина.
(б) Вес особи в популяции варьируется в пределах 140-230 фунтов.
Используйте Random для выбора веса какого-либо человека в этой
популяции.
3.12 Рассмотрите класс Event, которому передано начальное значение для
нижнего и верхнего предела времени какого-либо события. Границы
принимают значение по умолчанию 0 и 1. Операции:
Конструктор Инициализировать границы данных. Если нижняя
граница выходит за верхнюю границу, печатать
сообщение об ошибке и выходить из программы.
GetEvent Получать случайное событие в диапазоне:
нижняя граница — верхняя граница.
(а) Реализуйте этот класс, используя код in-line.
(б) Реализуйте этот класс, определяя функции-члены вне объявления класса.
(в) Приложение требует массив из пяти объектов Event, где каждый
элемент принимает значение в диапазоне от 10 до 20. Как вы
инициализируете массив? Проще ли решается данная задача, если диапазон для
каждого объекта будет 0-1?
3.13 Напишите функцию Datelnterval, которая принимает два объекта
класса Calendar из письменного упражнения 3.6 и возвращает число дней
между двумя этими датами.
3.14* Матрицы могут использоваться для решения систем уравнений с п
неизвестными. Мы показываем алгоритм для системы с тремя
неизвестными.
В этой системе уравнений элементы Ау являются коэффициентами
неизвестных Хо, Xi и Хг.
В правой части уравнений даются элементы Q.
Эти уравнения могут быть описаны одним матричным уравнением
где матрица называется матрицей коэффициентов (coefficient matrix).
Например, система уравнений
1Х0 + 1ХХ + 0Х2 = 4
-ЗХ0 - lXj + 1Х2 = -11
2Х0 + 2Х: + 2Х2 « 14
соответствует матричному уравнению
Теорема математики утверждает, что эти уравнения могут быть сведены
к системе эквивалентных уравнений, в которой матрица коэффициентов
является треугольной. В нашем примере:
1. Исключите элемент Аю = -3.
Умножьте элементы в строке 0 на константу 3 и сложите элементы
строки 0 с элементами строки 1.
2. Исключите элемент Аго = 2.
Умножьте элементы строки 0 на константу -2 и сложите элементы
строки 0 с элементами строки 2. В этом процессе исключается также
член Агь
Матричное уравнение для новой системы имеет треугольную матрицу
коэффициентов.
(а) Сведите алгебраическую систему к уравнению, включающему
треугольную матрицу коэффициентов
(б) Найдите детерминант этой матрицы коэффициентов.
Упражнения по программированию
3.1 Многие программные приложения используют постоянно обновляемый
сумматор (accumulator). В качестве простого примера абстрактного типа
данных предположим, что Accumulator — это тип данных, которые
обновляются операцией сложения и выводятся с использованием
операции печати.
ADT Accumulator
Данные
Действительное значение для суммирования
Операции
Initialize
Вход: Действительное значение N.
Предусловия: Нет
Процесс: Присваивание N в качестве значения суммы.
Выход: Нет
Постусловия: Сумма инициализируется.
Add
Вход: Действительное число N.
Предусловия: Нет
Процесс: Сложение N с суммой.
Выход: Нет
Постусловия: Сумма обновляется.
Print
Вход: Нет
Предусловия: Нет
Процесс: Чтение суммы.
Выход: Печать суммы.
Постусловия: Нет
Конец ADT Accumulator
Банковское приложение считывает начальный баланс и
последовательность операций. Отрицательная операция определяет дебет, а
положительная — кредит. Используются три объекта типа Accumulator. Объект
Balance определяется со стартовым балансом в качестве параметра
конструктора. Объекты Debits и Credits имеют начальное значение 0 и
используются для поддержки определения текущей суммы дебетных и
кредитных операций. Оператор Add обновляет сумму в объектах.
Считайте последовательность операций, заканчивающихся на операции
0.00. Печатайте окончательные значения баланса, дебетов и кредитов.
3.2 Напишите main-функцию, которая использует класс, реализованный в
письменном упражнении 3.5 со следующими данными:
Студент Id
1047
3050
| 0020
Grade Points
120
75
100
Units |
40
20
_75 J
(а) Печатайте информацию по каждому студенту.
(б) Последний студент (ID 0020) имеет дополнительные записи из летней
школы. Обновите запись со следующими новыми данными:
успеваемость 40 при 10 часах. Печатайте новые данные для этого студента.
3.3 Расширьте класс Circle из раздела 1.3 для вычисления площади сектора.
Площадь сектора определяется по формуле (Q/360)*7ir2.
Сектор
Используйте этот класс для решения следующей задачи:
Круглая игровая площадка определяется как объект с радиусом 100
футов. Программа определяет стоимость ограждения этой площадки.
Стоимость ограждения $2,40 /фут. Площадь поверхности площадки в
основном травяная. Один сектор, измеряемый углом в 30°, не является
лужайкой. Программа определяет стоимость лужайки для катания:
$4,00 за полосу 2 х 8(16 кв.фута).
Fencing
Cost = Circumference * 2,40
Lawn
Lawn_Area - Area — Sector_Area
Number_Rolls = Lawn__Area/16
Cost = Number_Rolls* 4,00.
3.4 Напишите класс, содержащий индикатор пола (М или F), возраст и
ID-номер в диапазоне от 0 до 100. Операции включают Read, Print и
функции Getld/GetAge/GetGender, которые возвращают ID, возраст и
пол человека, сохраняемые в объекте.
Напишите программное приложение, определяющее объекты Young-
Women и OldMen. Программа вводит информацию о ряде людей и
присваивает данные о самых молодых женщинах в YoungWomen и
самых старых мужчинах в OldMen. Ввод завершается ID-номером О.
Используя Print, выполните вывод данных из этих объектов.
3.5 Реализуйте класс Geometry, закрытые данные которого содержат два
(2) элемента данных VI и V2 типа double и переменную figuretype
типа Figure.
Этот класс должен содержать два конструктора, которые принимают 1
или 2 параметра, соответственно, метод Border, возвращающий
периметр объекта, метод Area, возвращающий площадь и метод Diagonal,
вычисляющий диагональ.
Enum Figure (Circle, Rectangle)
class Geometry
{
private:
double VI, V2;
Figure figuretype;
public:
Goemetry(double radius); // для окружности
Geometry(double 1, double w); // для прямоугольника
double Border(void) const;
double Area(void) const;
double Diagonal(void) const;
}
(а) Реализуйте класс Geometry, используя внешние функции. Первый
конструктор для окружности будет иметь один параметр и следовательно
присваивать объект типа Circle переменной figuretype. Другой
конструктор, будет присваивать этой переменной объект типа Rectangle.
Вычисляющие методы должны проверять тип figuretype перед
вычислением возвращаемого значения.
(б) Пользователь вводит внутренний радиус, который затем используется
для создания маленькой окружности. Используйте эту информацию
для объявления описывающего окружность прямоугольника и внешней
окружности, описывающей этот прямоугольник. Печатайте периметр,
площадь и диагональ каждого объекта.
радиус
Вычислите площадь внешней полосы между двумя окружностями
(площадь вне маленькой окружности, но внутри большой окружности).
Вычислите периметр маленькой области, помеченной символом "X".
3.6 Класс Ref подсчитывает количество положительных (>0) и
отрицательных (<0) чисел, "представленных на рассмотрение". Конструктор не
имеет параметров и инициализирует элементы данных positiveCount и
negativeCount нулевыми значениями.
class Ref
{
private:
int positiveCount;
int negativeCount;
public:
Ref(void);
void Count(int x) ;
void Write(void) const;
>;
Объект типа Ref передается функции, которая использует его для
записи количества положительных и отрицательных чисел в
последовательность ввода из пяти целых чисел. Две версии функции
иллюстрируют различие между передачей объектов по значению и по ссылке.
В первой версии объект передается по значению.
void PassByValue(Ref V)
{
int num;
for(int i = 0; i<5; i++)
{
cin > num;
if (num! = 0)
v.Count (num);
}
}
Вторая версия функции передает параметр по ссылке.
void PassByReference (Ref & V)
{
int num;
* • *
}
Реализуйте Ref и создайте main-программу, которая вызывает каждую
функцию и использует метод Write для печати результатов. В каждом
экземпляре данными являются 1, 2, 3, -1 и -7. Объясните, почему
PassByValue работает неправильно, a PassByReference выполняется
успешно.
3.7 Рассмотрим следующее объявление класса:
class Grade
{
private:
char name[30];
float score;
public:
Grade(char student[], float score);
Grade(void);
int Compare(char s[]);
void Read(void);
Write(void);
};
Напишите функцию main по частям от (а) до (е):
(а) Напишите реализацию для функций-членов. Используйте строковую
функцию strcpy для присваивания имени в первом конструкторе.
Заметьте, что второй конструктор является конструктором умолчания.
Он устанавливает переменную name в NULL-строку, a score — в 0.0.
Метод Compare возвращает 1, если s равна имени, в противном случае
возвращается 0. Используйте функцию strcmp.
(б) В функции main объявите массив Students из пяти объектов с
начальными значениями:
{Grade("Johnп, 78.3), Grade("Sally", 86.5),
Grade("Bob", 58.9), Grade("Donna", 98.3)};
(в) Пятый объект, Students[4], вводится с использованием функции-члена
Read().
(г) Запишите функцию
int Search(Grade Arr)[ ], int n, char keyname[ ];
которая ищет массив Arr из п элементов и возвращает индекс объекта,
имя которого соответствует ключу. Если ключ не найден в Arr,
возвращается -1.
(д) Вызывайте Search три раза с разными именами для проверки
правильности ее работы.
3.8 Используйте класс CardDeck, разработанный в письменном упражнении
3.8, для карточной игры под названием Hi-Low. Сдайте пять карт. Для
каждой карты спросите игрока, будет ли случайно вытащенная из
оставшихся карт в колоде карта больше или меньше данной карты. Туз —
самая большая карта любой масти, и масти упорядочены от трефовой
до пиковой. Печатайте количество удачных догадок.
3.9 В данном упражнении используйте класс Calendar, разработанный в
письменном упражнении 3.6. Запишите функцию
int Daylnterval(Calendar С, int mml, intddl, intmm2/ int dd2);
возвращающую количество дней между двумя данными. Напишите
функцию main, выполняющую следующее:
1. Печатает, является ли текущий год високосным.
2. Использует NumDays для определения количества дней от начала
года до Рождества.
3. Передает результат (2) функции PrintDate и проверяет правильность
печати даты.
4. Включает вычисление количества дней от сегодняшнего дня
до Рождества.
5. Вычисляет количество дней между 1 февраля и 1 марта.
3.10 Расширьте класс Dice из главы 1 до бросания п костей, п<:20. Если
количество костей не дается конструктору, он устанавливается на
значение по умолчанию 2. Используйте класс Dice для решения следующей
задачи:
Объявите массив из 30 объектов Dice. Инициализируйте каждый
элемент для бросания пяти (5) костей. Вам понадобиться использовать
конструктор умолчания в объявлении, а затем — цикл для
инициализации каждого элемента пяти костей.
Выполните Toss для каждого элемента.
Сканируйте список и определите, сколько раз была брошена 5 или 12.
Укажите, сколько раз сумма повторялась в следующем бросании.
Например, 8 8 8 считается как два повтора.
Сканируйте список и найдите самую большую сумму, отображая
стороны со значениями кости.
Сортируйте список, считая и печатая суммы.
3.11 Объявите перечисление:
enum unit {metric, English}/
Класс Height содержит следующие закрытые данные-члены:
char name[20];
unit measureType;
float h; //высота в единицах measureType (футы или см).
Операции включают:
//конструктор:имя параметров, высота, тип измерения
Height(char nm[ ], float ht, unit m);
PrintHeight(void); //печать высоты в соответствующих единицах
//ввод имени, типа измерения и высоты
ReadHeight(void);
float GetHeight(void); //возвращение высоты
void Convert(unit m); //преобразование h в измерение m
(а) Реализуйте этот класс. Один дюйм равен 2,54 см.
(б) Напишите функцию, сканирующую список и преобразующую элементы
в единицы измерения, заданные как параметр. Подразумевается, что
объекты выражены в других единицах измерения.
(в) Напишите функцию, которая сортирует массив объектов Height.
Подразумевается, что каждый объект использует одну и ту же единицу
измерения.
(г) Напишите функцию, сканирующую массив и возвращающую объект,
представляющий самого высокого человека. Считайте, что все объекты
используют одну и ту же единицу измерения.
(д) Напишите программу для тестирования класса, создав список из пяти
элементов типа Height. Инициализируйте первые три из них в
объявлении и считайте последние два. Используйте функции, разработанные
в частях (Ь), (с) и (d).
3.12 В банке с одним только кассиром заметили, что клиентские операции
занимают интервал времени 5-10 минут. Очередь из 10 клиентов
образовалась в момент открытия. Используйте класс Event,
разработанный в письменном упражнении 3.12 для вычисления времени,
необходимого кассиру, чтобы обслужить 10 клиентов.
3.13 Эллипс или овал определяется описывающим прямоугольником,
размеры которого 2а х 2Ь.
Константы а и b называются полуосями эллипса. Эллипс, полуоси
которого имеют одну и ту же длину, являетя окружностью.
Математическое уравнение эллипса имеет вид:
(х - х0)2/а2 + (у - у0)2/Ь2 = 1
и его площадь равна nab. Разработайте класс Ellipse, функции-члены
которого состоят из конструктора и метода Area. Используйте Ellips и
класс Rectangle для решения следующей задачи:
Необходимо построить овальный плавательный бассейн, полуоси
которого являются длинами 30 и 40, внутри прямоугольной площади
80 х 60. Стоимость бассейна $25 000. Площадь снаружи бассейна
необходимо зацементировать. Стоимость цемента составляет
$50/кв.фут. Вычислите общую стоимость строительства.
3.14 Данные о бейсболисте включают номер игрока (number), количество
раз, когда он отбивающий (times at bat), количество ударов по мячу
(hits) и средний результат (NumberHits/ NumberAtBats). Эта
информация сохраняется как данные-члены в закрытой секции класса Baseball.
Все параметры конструктора имеют значения по умолчанию: номер
униформы устанавливается равным -1, а значения числа отбиваний и
ударов — 0. Применение для номера униформы значения по умолчанию
подразумевает, что номер униформы игрока, количество ударов и
количество раз, когда игрок является отбивающим, считываются с ис-
пользованием ReadPlayer. Для известного номера униформы функция-
член ReadPlayer вводит количество ударов и количество отбиваний.
Метод GetBatAve возвращает средний результат отбиваний. Закрытый
метод ComputeBatAve используется как утилита конструктором, a
ReadPlayer — для задания данного-члена, содержащего средний результат
отбиваний. Метод WritePlayer выводит всю информацию об игроке в
формате:
Player <UniformNo> Average < BattingAvg>
Средний результат выводится как целое число из трех цифр. Например,
если количество ударов 30, а количество раз, когда игрок был
отбивающим, равно 100, то средний результат выводится методом WritePlayer
как 300.
Объявление класса Baseball
class Baseball
{
private:
int playerno;
int atbats;
int hits;
float batave;
//ComputeBatAve дается с inline-кодом.
float ComputeBatAve (void) const //закрытый метод
{
if(playerno == -1 atbats == 0)
return(0);
else
returne(float(hits)/atbats);
{
public:
Baseball (int n = -1, int ab - 0, int h = 0) ;
void ReadPlayer(void) ;
void WritePlayer(void) const;
float GetBatAve(void) const;
};
Реализуйте класс Baseball и используйте его в функции main
следующим образом:
1. Объявите четыре объекта:
Catcher Номер униформы 10, 100 отбиваний, 10 ударов
Shortstop Имеется только номер униформы 44
Centerfielder Нет никакой информации
Maxobject Нет никакой информации
2. Считайте необходимую информацию для объектов shortstop
и centerfielder.
3. Выпишите всю информацию для объектов catcher, shortstop
и centerfielder.
4. Используя операцию GetBatAve и присваивание объекта, присвойте
игрока с самым высоким средним результатом объекту maxobject
и распечатайте информацию.
3.15 Добавьте вычитание и умножение треугольной матрицы к классу TriMat
и протестируйте их в программе, подобной программе 3.5.
3.16 При решении общей n x n системы алгебраических уравнений ряд
операций сводит задачу к решению уравнения треугольной матрицы.
Уравнение треугольной матрицы имеет единственное решение, при
условии, что детерминант матрицы коэффициентов является ненулевым.
Набор алгебраических уравнений получают умножением каждой строки
в матрице коэффициентов на столбцовый массив неизвестных. Решая
уравнения в порядке от п — 1 до 0, мы получаем единственное решение
для переменных Xn-i, Xn-2, ..., Xi,Xo. Например, треугольная система
уравнений, описанная в письменном упражнении 3.14, решается
применением этого метода:
Уравнение 0: ix0 + ixx + ox2 = 4
Уравнение 1: 2х1 + ix2 =1
Уравнение 2: 2х2 = б
Решение для Х2 В уравнении 2 х2 = 6/2 = з
Решение для Хх: В уравнении 1 подставьте 3 для Х2;
решите уравнение для неизвестного Хх.
2Х1 + 3 = 1
Решение для Х0: В уравнении 0 подставьте -1 для Хг и 3 для Х2;
решите уравнение для неизвестного Х0.
Х0 - 1 = 4
Х0 = 5
Окончательное решение: Хо =5, Xi = -1, Х2 = 3.
Объедините эти идеи и разработайте функцию
void SolveEqn(const TriMat& A, double X[ ], double C[ ]);
Она определяет единственное решение, если оно существует, общего
уравнения треугольной матрицы
(а) Используйте SolveEqn в программе для решения примера системы
уравнений.
(б) Решите систему уравнений в письменном упражнении 3.14 (а).
глава
Шеф
Классы коллекций
4.1. Линейные коллекции
4.2. Нелинейные коллекции
4.3. Анализ алгоритмов
4.4. Последовательный и бинарный
поиск
4.5. Базовый класс последовательного
списка
Письменные упражнения
Упражнения по программированию
В главе 2 описываются базовые типы данных, которые непосредственно
поддерживаются языком программирования и включают примитивные
числовые и символьные данные, а также массивы, строки и записи. Эти
структурированные типы данных являются примерами коллекций (collections),
которые сохраняют данные и предоставляют операции доступа, добавляющие,
удаляющие или обновляющие элементы данных. Изучению типов коллекций
уделяется основное внимание в данной книге.
Коллекции подразделяются на две основные категории: линейные и
нелинейные. На рис. 4.1 приводятся методы доступа к данным для дальнейшего
деления категорий и перечисления структур данных, представленных в этой
книге. В данной главе приводится краткий обзор каждой коллекции вместе с
описанием ее данных, операций и некоторых случаев практического
использования.
Линейная (linear) коллекция содержит список элементов, упорядоченных
по положению (рис.4.2). В этом списке имеется первый элемент, второй и
т.д. Массив с индексом, отражающим порядок элементов, является основным
примером линейной коллекции.
Нелинейная (nonlinear) коллекция определяет элементы без позиционного
упорядочения. Например, цепочка управления рабочими на заводе или
комплект мячей в сетке — это нелинейные коллекции (рис. 4.3).
Эта глава включает также исследование эффективности алгоритмов. Мы
описываем факторы, определяющие эффективность и вводим нотацию Big-0
(большая О) в качестве ее критерия. Этот критерий используется на
протяжение всей книги для сравнения и сопоставления различных алгоритмов.
Класс SeqList из главы 1 является основным типом коллекций. В данной
главе описывается реализация этого класса на базе массива. Этот класс
рассматривается также в главе 9, когда мы определяем реализацию связанного
списка. В главе 12 SeqList используется с наследованием для создания
упорядоченного списка.
Когда C++ реализует коллекции как классы, компилятор требует
параметры функции, чтобы иметь специфические типы данных, и выполняет
тщательную проверку типа на предмет совместимости. Для наиболее общей
реализации типов коллекций мы вводим классы шаблонов (template) C++ в
Коллекции
Линейные
Нелинейные
С индексным
доступом
С прямым
доступом
С
последовательным доступом
Иерархические
Групповые
Словарь
Hash-
таблица
Массив
Запись
Файл
Список
Стек
Очередь
Очередь
приоритетов
Дерево
Heap-
дерево
Набор
Граф
Рис. 4.1. Иерархия коллекций
главе 7. Классы шаблонов пишутся с использованием параметризованного
имени, такого как Т для типа данных, управляемых коллекцией. Когда
объявляется какой-либо объект, фактический тип для Т задается как
параметр. Шаблоны являются мощным инструментом C++, позволяющим
выполнять параметризованное объявление классов. Например, предположим, что
класс коллекции имеет массив из 10 элементов.
Первый элемент
Второй элемент
Третий элемент
Последний элемент
Рис. 4.2. Линейная коллекция
Менеджер завода
Менеджер производства
Менеджер сбыта
Рабочий
Рабочий
Рабочий
Рабочий
Рабочий
Рис. 4.3. Нелинейные коллекции
Первое объявление определяет массив целых. Версия шаблонов не
предполагает определенного типа, а позволяет классу использовать
параметризованное имя Т для типа элемента массива. Фактический тип указывается во
время объявления объекта.
Объявление 1
class Collection
{
• • • *
int A[10]; //массив целых является данным-"членом
}
Collection object; //A — это массив целых
Объявление 2
template <class T>
class Collection
{
* • • •
Т А[10] ; //параметризованное объявление массива
//задает Т при объявлении объекта
}
Collection<int> object; //А — это массив целых
Collection<char> object; //A — это массив символов
4.1. Описание линейных коллекций
Метод доступа для элементов различает линейные коллекции, показанные
на рис. 4.1. С помощью прямого доступа (direct access) мы можем выбирать
элемент непосредственно, не обращаясь сначала к предшествующим
элементам в списке. Например, символы в строке могут быть доступны
непосредственно. Третья буква в слове LIMEAR употреблена ошибочно. Первые две
буквы написаны правильно. Мы можем исправить третью букву, не
обращаясь сначала к первым двум буквам. В некоторых линейных коллекциях,
называемых последовательными списками (sequential lists), прямой доступ
невозможен. Вы обращаетесь к элементу, начиная с начала списка и двигаясь
по списку до нужного элемента. Например, в бейсболе отбивающий
благополучно достигает третьего пункта (base) только после первого и второго.
Пример парковочного гаража может служить для сравнения списков с
возможным прямым доступом и последовательных списков. Следующая
диаграмма описывает гараж, в котором рядом с машинами имеется свободный
проход. Служащий может выводить машину 3 из гаража, садясь
непосредственно в нее и используя свободный проход.
#0 #1 #2 #3 #4
Прямой доступ к машине 3
Следующая диаграмма иллюстрирует гараж с последовательной
парковкой, в котором все машины паркуются в один ряд. Служащий имеет только
последовательный доступ к машине. Чтобы вывести машину 3, он должен
переместить машины 0 — 3 в таком порядке:
#0 #1 #2 #3 #4
Последовательный доступ к машине 3
Коллекции с прямым доступом
Массив (array) — это коллекция элементов, имеющих один и тот же тип
данных, с прямым доступом посредством целого индекса.
Aq A, A2 •• Aj •• An.-|
Коллекция Array
Данные
Коллекция объектов одного и того же (однородного) типа.
Операции
Данные в каждом местоположении в массиве доступны непосредственно
с помощью целого индекса.
Статический массив (static array) содержит фиксированное количество
элементов и задается в памяти во время компиляции. Динамический массив
(dynamic array) создается с использованием методов динамического
распределения памяти и его размер может быть изменен.
Массив — это структура данных, которая может использоваться для
хранения списка. В случае с последовательным списком массив позволяет
выполнять эффективное добавление элементов в конец списка. Эта структура
менее эффективна при удалении элемента, поскольку мы должны часто
сдвигать элементы. Такой же сдвиг происходит, когда новые элементы
вставляются в массив, хранящий упорядоченный список.
Список M5I 201301 351401
Список 115 1201301351401
Вставить 25 45 120
на
301351401
Удалить 20 СШ 130135140
т
Глава 8 знакомит с классом Array, расширяющим концепцию простого
массива. Этот класс предоставляет новый индексный оператор, который
перед сохранением или возвращением данных проверяет, находится ли
соответствующий этим данным индекс в допустимом диапазоне. Класс,
реализующий такие безопасные массивы (safe arrays), позволяет клиенту
динамически распределять массив во время исполнения приложения.
Символьная строка (character string) — это массив символов с
ассоциированными операциями, которые определяют длину строки, склеивают
(конкатенируют) две строки, удаляют подстроку и так далее. Общий класс
String, имеющий расширенный набор строковых операций, разработан в
главе 8.
Коллекция String
Данные
Коллекция символов с известной длиной
Операции
Имеются операции для определения длины строки, копирования одной строки
в другую или их конкатенации, сравнения двух строк, выполнения
сопоставления с образцом, ввода и вывода из строк.
Запись (record) — это базовая структура коллекций для сохранения
данных, которые могут состоять из разных типов. Для многих приложений
различные элементы данных ассоциированы с одним объектом. Например,
авиабилет включает такие данные, как номер рейса, номер места, имя
пассажира, стоимость, данные об агенте и так далее. Единственный билетный
объект — это набор полей разных типов. Коллекция записи связывает поля
при обеспечении прямого доступа к данным в отдельных полях.
Коллекция Record
Данные
Элемент с коллекцией полей, возможно, различных типов.
Операции
Точечный оператор (dot operator) обеспечивает прямой доступ к данным в поле.
Коллекции с последовательным доступом
Более общей коллекцией является список, сохраняющий элементы в
последовательном порядке. Структура, называемая линейным списком (linear list),
содержит произвольное число элементов. Размер списка изменяется
добавлением или удалением элемента из этого списка, а ссылка на элементы в списке
выполняется по их положению. Первый элемент находится в голове или в
начале списка, последний элемент находится в конце списка. Каждый элемент,
за исключением последнего, имеет единственный последующий элемент.
1-й
2-й
3-й
4-й
• • •
п-й
передний последний
Коллекция List
Данные
Произвольная коллекция объектов одного и того же (однородного) типа.
Операции
Для ссылки на отдельные элементы мы должны идти по списку от его начальной
точки, проходя от элемента к элементу до достижения нужного местоположения.
Вставки и удаления изменяют размер списка.
Коллекция линейного списка может иметь любое количество элементов и
подразумевает, что эта коллекция будет расширяться или сужаться по мере
добавления новых элементов в список или удаления резидентных элементов.
Эта структура списка является ограничивающей, когда необходим доступ к
произвольным элементам, так как в ней нет прямого доступа. Для доступа
к элементам списка необходимо выполнять прохождение элементов от
начальной точки в списке. В зависимости от используемого метода, мы можем
перемещаться одним из двух способов: слева направо или в обоих
направлениях. В этой главе мы разрабатываем класс, который реализует
последовательный список, используя массив. Результирующий список
ограничивается размером массива. Более мощная реализация, описанная в главе 9,
снимает все ограничения на размер использованием связанных списков и
динамических структур.
Список покупок является примером последовательного списка. Покупатель
первоначально создает список, записывая названия товаров. Делая покупки,
он вычеркивает названия из списка, когда товары найдены или больше не
нужны.
Упорядоченный линейный список (ordered linear list) — это линейный
список, данные которого упорядочены относительно друг друга. Например, список
3, 5, 6, 12, 18, 33
расположен в числовом порядке, а список
1, 6, 2, 5, 8
— нет.
Бинарный поиск, описываемый в этой главе, является алгоритмом,
использующим упорядоченный список.
Стеки и очереди — это особые версии линейного списка с ограниченным
доступом к элементам данных. В стеке (stack) элементы добавляются и
удаляются только в один конец списка, называемый вершиной (top). Полка для
подносов в столовой — это знакомый пример. Операция удаления элемента
из списка называется извлечением из стека (popping the stack). О добавлении
элемента в список говорится как о помещении (pushing) элемента в стек.
вершина вершина
Поместить
в стек
Извлечь из
стека
При помещении элемента в стек все другие элементы, находящиеся в
данный момент в стеке, опускаются вниз, уступая место на вершине новому
элементу. Когда элементы удаляются из стека, они перемещаются в обратном
порядке. Последний элемент, помещенный в стек, является первым
извлекаемым из стека. О таком типе хранения элементов говорят как о магазинном
порядке (last -in/first-out (LIFO) — последним пришел/первым ушел).
Коллекция Stack
Данные
Список элементов, которые могут быть доступны только на вершине списка.
Операции
Список поддерживает операции push и pop. Push добавляет новый элемент
в вершину списка, и pop удаляет элемент из вершины списка.
Мы вводим стеки в ряд приложений, которые включают оценку выражений,
рекурсию и прохождение дерева. В этих случаях мы просматриваем элементы
и затем обращаемся к ним в порядке LIFO. При помощи стека компиляторы
передают параметры функциям, а также используют стек для хранения
локальных переменных.
Очередь (queue) — это список с доступом только в начале и в конце
списка. Элементы вставляются в конец списка и удаляются из начала. При
использовании обоих концов списка элементы оставляют очередь в том же
порядке, в каком они поступают. Хранение элементов соответствует порядку
поступления (first-in/first-out (FIFO) — первым пришел/первым утел).
Q-вставка
последний
Q-удаление
передний
Коллекция Queue
Данные
Список элементов с доступом в начале и в конце списка.
Операции
Добавление элемента в конец списка и удаление элемента из начала списка.
Очередь является полезной коллекцией для ведения списков
очередников. Моделью очереди является очередь обслуживания в банке или
обслуживание покупателей в продовольственном отделе. Очереди находят
машинное применение в моделирующих исследованиях и осуществляют
планирование заданий в рамках операционной системы.
Для некоторых приложений мы изменяем структуру очереди,
устанавливая очередность элементов. При удалении объекта из списка
определяется элемент с наивысшим приоритетом. Эта коллекция, называемая
очередью приоритетов (priority queue), имеет операции insert (вставить) и
delete (удалить). Где вставляются данные, является несущественным.
Важным является то, что операция delete выбирает элемент с наивысшим
приоритетом. В больничном отделении скорой помощи используется очередь
приоритетов. Пациенты обслуживаются в порядке поступления, если только
их состояние не является угрожающим для жизни, что дает им наивысший
приоритет и первоочередной доступ к экстренной медицинской помощи.
Коллекция Queue Priority
Данные
Список элементов, такой, что каждый элемент имеет приоритет.
Операции
Добавление элемента в список. При удалении элемента извлекается элемент
с наивысшим приоритетом.
Очереди приоритетов используются для планирования заданий в рамках
операционной системы. Задания с наивысшим приоритетом должны
выполняться в первую очередь. Очереди приоритетов используются также в
моделировании, управляемом прерываниями (event-driven simulation).
Например, в практическом приложении в главе 5 выполняется моделирование
потока клиентов в банк и из банка. Каждый тип события ( появление
или уход) вставляется в очередь приоритетов. Самое раннее по времени
событие удаляется и обслуживается первым.
В машинной системе файл (file) — это внешняя коллекция, которая
имеет ассоциированную структуру данных, называемую потоком (stream).
Мы приравниваем file к его stream и сосредоточиваем внимание на потоке
данных. Прямой доступ осуществляется только к дисковому файлу,
ленточные же файлы являются последовательными. Операция read удаляет
данные из потока ввода, а операция write добавляет новые данные в конец
потока вывода. Файл часто используется для хранения большого
количества данных. Например, во время компиляции программы генерируются
большие таблицы и часто сохраняются во временных файлах.
Коллекция File
Данные
Последовательность байтов, ассоциированная с внешним устройством.
Данные перемещаются посредством потока к устройству и из него.
Операции
Открытие файла, считывание данных из файла, запись данных в файл,
поиск указанного адреса в файле (прямой доступ), закрытие файла.
Универсальная индексация
Массив — это классическая коллекция, позволяющая иметь прямой доступ
к каждому элементу, посредством целого индекса. Для многих приложений
мы связываем с записью данных некоторый ключ, использующийся для
доступа к записи. Когда вы звоните в банк или в страховую компанию для
получения информации, вы даете ваш номер банковского счета, который
становится ключом для нахождения записи этого счета. Коллекция,
называемая хеш-таблица (hash table), сохраняет данные, связанные с ключом.
Ключ трансформируется в целый индекс, используемый для нахождения
данных. В одном часто используемом методе хеш-таблиц целое значение —
это индекс в массиве коллекций. После преобразования ключа в индекс
выполняется поиск ассоциированной коллекции. Ключ не обязательно должен
быть целым числом. Например, запись данных может состоять из имени,
классификации работы, количества лет работы в компании, жалования и
так далее.
"Уилсон, Сандра Р."
3
15
42500
В этом случае строка, указывающая имя, является ключом.
Обычный словарь — это коллекция слов и их определений. Вы ищете
слово, используя его как ключ. В структурах данных, коллекция, называемая
словарем (dictionary), состоит из набора пар ключ-значение, называемых
ассоциациями (associations).
Ключ
Значение
Ассоциация
Например, ключом может быть слово, а значением — строка,
указывающая определение слова. К значению в ассоциации осуществляется прямой
доступ с использованием ключа в качестве индекса. В результате, словарь
подобен массиву, за исключением того, что индексы не должны быть целыми
значениями. Например, если Diet является коллекцией dictionary, ищите
определение слова dog, ссылаясь на Dict[dog]. Словари часто называют
ассоциативными массивами (associative arrays), потому что они связывают
(ассоциируют) общий индекс со значением данных.
above
dog
long
Значение . . .
1
Значение . . .
■ • •
Значение . . .
count « Dict[dog] « endl;
4.2. Описание нелинейных коллекций
На рис. 4.1 показано, что нелинейные коллекции разделяются на
иерархические и групповые структуры. Иерархическая коллекция (hierarchical
collection) — это масса элементов, которые разделяются по уровням.
Элементы на данном уровне могут иметь несколько наследников на следующем
уровне. Мы вводим особую иерархическую коллекцию, называемую деревом
(tree), в которой все элементы данных происходят из одного источника,
называемого корнем (root). Элементы в дереве называются узлами (nodes),
каждый из которых указывает на нисходящие узлы, называемые детьми
(children). Каждый элемент, за исключением корня, имеет единственного
предка. Пути вниз по дереву начинаются в корне и развиваются по
направлению к нижним уровням от родителя к ребенку.
Корень
Дерево является идеальной структурой для описания файловой системы
с каталогами и подкаталогами. Модель для дерева — это организационная
схема в бизнесе, определяющая цепочку управления, начиная с босса (СЕО,
президента), и далее — к вице-президентам, супервайзерам и так далее.
В этой книге мы рассматриваем особую форму дерева, в котором каждый
узел имеет самое большее два потомка. Такая структура, бинарное дерево
(binary tree), имеет важное применение в оценке арифметических выражений
и в теории компиляции. С дополнительным упорядочением дерево становится
деревом бинарного поиска (binary search tree), которое эффективно сохраняет
большие объемы данных. Деревья бинарного поиска обеспечивают быстрый
доступ к элементам, располагая узлы так, что данные можно находить,
перемещаясь вниз по короткому пути из корневого узла. На рис. 4.4 показано
дерево с 16 узлами. Самый длинный путь от корня к узлу включает четыре
ветви. Предположим, что дерево относительно заполнено узлами, отношение
узлов к длине пути значительно улучшается по мере того, как мы
увеличиваем размер дерева. Пример: если дерево бинарного поиска имеет 220 — 1
= 1 048 575 узлов, которые расположены на минимальном количестве
уровней, то элемент данных можно найти, посещая не более, чем 20 узлов. Особое
дерево бинарного поиска — это AVL-дерево, гарантирующее равномерное
распределение узлов и обеспечивающее очень короткое время поиска.
Корень
Рис. 4.4. Дерево с 16 узлами
Коллекция Tree
Данные
Иерархическая коллекция узлов, происходящих из корня. Каждый узел указывает
на узлы-сыновья, которые сами являются корнями поддеревьев.
Операции
Структура дерева позволяет добавлять и удалять узлы. Несмотря на то, что
дерево — это нелинейная структура, алгоритмы прохождения деревьев
позволяют нам посещать отдельные узлы и осуществлять поиск ключа.
Heap-дерево — это особая версия дерева, в котором самый маленький
элемент всегда занимает корневой узел. Операция delete удаляет корневой
узел, и обе операции insert и delete вызывают такую реорганизацию дерева,
что самый маленький элемент вновь занимает корень такого дерева. Heap-
дерево использует очень эффективные алгоритмы реорганизации,
просматривая только короткие пути от корня вниз к концу дерева. Heap-дерево
может использоваться для упорядочения списка элементов. Вместо
использования медленных алгоритмов сортировки мы упорядочиваем их, повторно
удаляя корневой узел из heap-дерева. Это позволяет получить быструю
сортировку (heap-сортировку). Кроме того, при использовании heap-дерева
наиболее часто реализуется очередь приоритетов.
Коллекции групп
Группа (group) представляет те нелинейные коллекции, которые содержат
элементы без какого-либо упорядочения. Множество уникальных элементов
является примером группы. Операции над коллекцией типа множество
включают объединение (union) и пересечение (intersection). Другие операции над
множеством тестируют на членство и отношение подмножеств. В главе 8 мы
вводим класс Set с перегрузкой операторов для реализации операций над
множествами.
S » {1.2.3}. Т » {3.8.5}
S объединение Т-{1,2,3,8,5}
5 пересечение Т -{3}
Коллекция Set
Данные
Неупорядоченная коллекция объектов без дубликатов.
Операции
Бинарные операции членства, объединения, пересечения и дифференциации,
которые возвращают новое множество. Ряд операторов, тестирующих отношения
подмножеств.
Множество (set) — это коллекция, находящая применение, когда данные
являются неупорядоченными и каждый элемент данных является
единственным в своем роде, уникальным. Например, группа регистрации
избирателей составляет банк телефонных номеров для того, чтобы звонить лицам,
находящимся в списке. Каждый раз, когда группа контактирует с человеком
из банка номеров, его имя помещается в список номеров, по которым
позвонили, и удаляется из банка. Конечно, группа людей, которым еще не
позвонили, тоже является множеством. Группа регистрации избирателей
продолжает звонить, пока множество номеров, по которым не позвонили, не
будет пустым, или не будет сделано разумное количество попыток позвонить.
Граф (graph) — это структура данных, задающая набор вершин и набор
связей, соединяющих вершины. Графы находят применение в планировании
заданий, транспортировании и так далее. Например, строитель дома должен
заключать контракты на этапы строительной работы. План работы должен
быть составлен так, чтобы обеспечить выполнение всей подготовительной
работы к моменту, когда начнется новый этап строительства. Например,
кровельщики не могут начать свою работу, пока строители не завершат работу
по сооружению дома, а строительные работы не могут быть выполнены, пока
не будет заложен бетонный фундамент.
Подвод водоснабжения
Начало
Подвод коллектора
Сантехнические работы
Строительные работы
Закладка фундамента
Кровельные работы
Коллекция Graph
Данные
Набор вершин и набор соединительных связей.
Операции
Как коллекция вершин и связей граф имеет операции для добавления и удаления
этих элементов. Алгоритмы просмотра начинаются в заданной вершине и находят
все другие вершины, которые достижимы из начальных вершин. Другие алгоритмы
просмотра выполняют оба просмотра графа — в глубину и в ширину.
Сеть (network) — это особая форма графа, которая присваивает вес каждой
связи. Вес указывает стоимость использования связи при прохождении графа.
Например, в следующей сети вершины представляют города, а вес,
присваиваемый связям, — это расстояния между парами городов.
752
Salt Lake City
604
San Francisco
.648
763
504
San Diego )~355
Phoenix
Albuquerque
4.3. Анализ алгоритмов
В этой книге мы разрабатываем, классы реализующие коллекции данных.
Для реализации методов класса часто используются классические алгоритмы.
Мы часто описываем подробно разработку и реализацию этих алгоритмов и
анализируем их эффективность.
Клиент судит о программе по ее корректности, легкости исцользования
и эффективности. Легкость использования и корректность программы зависит
от процедур разработки и тестирования. На эффективность программы влияет
множество факторов, которые включают внутреннюю машинную систему,
количество памяти, имеющейся для управления данными и сложность
алгоритмов. Мы кратко рассматриваем эти факторы и затем сосредоточиваем
внимание на вычислительной сложности алгоритмов. Мы разрабатываем
критерии эффективности, позволяющие нам измерять эффективность какого-либо
алгоритма в терминах размера коллекции. Критерии не зависят от
определенной машинной системы и измеряют абстрактные характеристики
эффективности алгоритмов. Для создания численной меры эффективности нами
используется нотация Big-0.
Критерии эффективности
Алгоритм, в конечном счете, выполняется в машинной системе со
специфическим набором команд и периферийными устройствами. Для отдельной
системы какой-либо алгоритм может быть разработан для полного
использования преимуществ данного компьютера и поэтому достигает высокой
степени эффективности. Критерий, называемый системной эффективностью
(system efficiency), сравнивает скорость выполнения двух или более алгоритмов,
которые разработаны для выполнения одной и той же задачи. Выполняя эти
алгоритмы на одном компьютере с одними и теми же наборами данных, мы
можем определить относительное время, используя внутренние системные
часы. Оценка времени становится мерой системной эффективности для
каждого из алгоритмов.
При работе с некоторыми алгоритмами могут стать проблемой ограничения
памяти. Процесс может потребовать большого временного хранения,
ограничивающего размер первоначального набора данных, или вызвать требующую
времени дисковую подкачку. Эффективность пространства (space
efficiency) — это мера относительного количества внутренней памяти,
используемой каким-либо алгоритмом. Она может указать, какого типа компьютер
способен выполнять этот алгоритм и полную системную эффективность
алгоритма. Вследствие увеличения объема памяти в новых системах, анализ
пространственной эффективности становится менее важным.
Третий критерий эффективности рассматривает внутреннюю структуру
алгоритма, анализируя его разработку, включая количество тестов сравнения,
итераций и операторов присваивания, используемых алгоритмом. Эти типы
измерений являются независимыми от какой-либо отдельной машинной системы.
Критерий измеряет вычислительную сложность алгоритма относительно п,
количества элементов данных в коллекции. Мы называем эти критерии
вычислительной эффективностью (computational efficiency) алгоритма и
разрабатываем нотацию Big-О для построения измерений, являющихся функциями п.
Нотация Big-O. Интуитивно вычислительная эффективность алгоритма
измеряется количеством обрабатываемых им данных для определения
ключевых операций алгоритма. Эти операции могут зависеть от типа коллекции
данных, количества данных и их начального упорядочения.
Нахождение минимального элемента в массиве — это простой алгоритм,
основная операция которого включает сравнение элементов данных. Для
массива с п элементами алгоритм требует п — 1 сравнений и мера эффективности
пропорциональна п. Другие алгоритмы являются более сложными. Для
обменной сортировки, описанной в главе 2, обработка данных включает серию
сравнений в каждом прохождении. Если А — это массив из п элементов, то
обменная сортировка выполняет п — 1 проходов. На рис. 4.5 показан этот алгоритм.
После прохода элементы с X сохраняются
Проход 1
п-1 сравнений
Проход 2
п-2 сравнений
Проход i
n-i сравнений
Проход N-1
1 сравнение
Рис. 4.5. Проходы в обменной сортировке
Проход 1: Сравнение п-1 — элементов А[1] . . . А[п — 1] с А[0] и, если
необходимо, такой обмен элементов, чтобы А[0] всегда имел
наименьшее значение.
Проход 2: Сравнение п-2 — элементов А[2] . . . А[п — 1] с А[1].
Проход i: Для общего случая, сравнение п4 — элементов A[i] . . . A[n — i]
с A[i — 1].
Общее число сравнений в сортировке обмена задается арифметическим
рядом f(n) от 1 до п-1:
f(n) = (п — 1) + (п — 2) + . . . + 3 + 2 + 1 = п(п — 1)/2
Количество сравнений зависит от п2.
Для обработки данных общих классов коллекций таких, как
последовательные списки и деревья, мы используем сравнения в качестве меры
эффективности алгоритмов.
Алгоритмы зависят также от начального упорядочения данных. Например,
нахождение минимального значения в массиве значительно упрощается, если
мы знаем, что эти данные упорядочены. В возрастающем списке минимальное
значение занимает первую позицию. Это значение находится в конце
убывающего списка. В этих случаях вычислительная сложность включает
единственный доступ к данным, который может быть выполнен в постоянную единицу
времени. В примере с сортировкой, если список упорядочен, не требуется
никакого обмена. Это условие наилучшего случая, и оно представляет наиболее
эффективное выполнение алгоритма. Однако, если список отсортирован в
обратном порядке, каждое сравнение приводит к обмену. Это условие наихудшего
случая для сортировки. Общий случай предполагает некоторое промежуточное
количество обменов в зависимости от порядка данных в списке. Для
алгоритмов поиска и сортировки в классе коллекций мы используем количество
сравнений как доминантное действие и меру вычислительной эффективности. Наш
анализ определяет также начальное упорядочение данных, в котором можно
различать наилучший случай (best case), наихудший случай (worst case) и
средний случай (average case) для алгоритма. Средний случай — это
ожидаемая эффективность алгоритма, если он выполняется много раз со случайным
набором значений данных.
Определяя вычислительную эффективность алгоритма, мы ассоциируем
функцию f(n) с количеством сравнений. В действительности, точная форма
функции может быть трудна для определения, и поэтому мы используем
методы аппроксимации для определения хорошей верхней границы функции.
Мы определяем простую функцию g(n) и константу К так, что K*g(n)
превышает f(n) по мере того, как п значительно возрастает. Для большого
значения п поведение f(n) ограничивается произведением функции g(ri) на
некоторую константу. Мы используем эту математическую концепцию,
называемую нотацией Big-О, чтобы дать меру вычислительной эффективности.
Определение: Функция /(п) имеет порядок 0(£(л)), если имеется константа
К и счетчик л0, такие, что f(n) < K*g(n), для п > /г0.
Интуитивно это означает, что функция g в конечном счете превышает
значение функции /. Мы говорим, что вычислительная сложность (computational
complexity) (или порядок) алгоритма равна 0(g(n)).
Традиционно значение Big-О для алгоритма структур данных выбирается
среди небольшого набора полиномиальных, логарифмических и
экспоненциальных функций. Для классических структур данных эти функции дают
наилучшие верхние границы вычислительной сложности алгоритмов.
Kg(n)
f(n)
В примере с обменной сортировкой мы ищем функцию gf которая
ограничивает f(n). В таблице 4.1 рассматриваются g(n) = х/2 п2 и f(n) для разных
значений л.
В конечном счете, функция f(n) ограничивается величиной l/2 g(n), где
g(n) = п2. В этом случае возможное условие появляется непосредственно
при п0 = 1 и К = 1/2.
f(n) < l/2 п2 для всех п >_ 1
Мы говорим, что f(n) имеет порядок 0(g(n)) = 0(n2), поэтому
вычислительная сложность обменной сортировки составляет 0(п2). Анализ
наилучшего и наихудшего случаев также приводит к той же мере сложности, так
как обменная сортировка всегда требует 1/2 п(п — 1) сравнений. Этот
алгоритм сортировки требует порядка 0(п2) единиц времени для вычисления
независимо от начального порядка данных.
В нашем исследовании сортировки мы обнаружим, что некоторые
алгоритмы имеют вычислительную сложность (порядок) 0(п log2n) для
достаточно большого п0-
Количество сравнений < К п log2 п для п > п0.
В таблице 4.1 сравниваются значения л2 и п log2n. Заметьте, насколько
более эффективным является алгоритм сортировки 0(п log2n), чем обменная
сортировка. Например, в случае со списком из 10 000 элементов количество
сравнений для обменной сортировки ограничивается величиной 100 000 000,
тогда как более эффективный алгоритм имеет количество сравнений,
ограниченное величиной 132 000. Новая сортировка приблизительно в 750 раз
более эффективна.
Таблица 4.1
п
10
100
1000
5000
10000
(1/2)п2
50
5.000
500.000
12.500.000
50.000.000
S(n) = n2/2 - п-2
45
4.950
499.500
12.497.500
49/995.000
п
5
10
100
1000
10000
п2
25
100
10000
1000000
100000000
п !одгп
11,6
33,2
664,3
9965,7
132877,1
При выполнении Big-O-аппроксимации функции f(n) мы используем
термин доминирование для определения вычислительной сложности. Небольшой
опыт работы с неравенствами дает возможность математически проверить
эту стратегию. Например, в случае функции
f(n) = п + 2
терм п является доминирующим. Функция g(n) = n используется в следующем
неравенстве для проверки того, что / имеет порядок О(п).
f(n) = и + 2</1 + гс = 2*л для п > 2
/ также имеет порядок 0(п2) или 0(п3), так как g(n) = п2 и £(п) = п3
ограничивают /(я). Мы выбираем О(п), что представляет наилучшую оценку
для этой функции.
Пример 4.1
1. f(n) = п2 + п + 16 Доминирующий терм — п29 а / имеет порядок
0(п2).
f(n) = п2 + п + 1 < п2 + п2 + п2 = Зп2 для п > 1
2. f(n) = sqrt(n+3) Доминирующий терм — sqrt(n), a / имеет порядок
0(sqrt(n))
f(n) = sqrt(n+3) < sqrt(n+n)=sqrt(2n)=sqrt(2)*sqrt(n) для п >, 3
3. /fra,) = 2Л + л + 2 Доминирующий терм — 2n, a / имеет порядок
0(2п).
f(n) = 2п + п + 2
< 2п + 2п +2п
= 3*2П, для п > 1
Сложность алгоритма. Big-O-оценка дает меру времени выполнения
(runtime) алгоритма. Обычно алгоритм имеет разную вычислительную
эффективность для наилучшего и наихудшего случаев, поэтому мы вычисляем
конкретное значение Big-О для каждого случая. В разделе 4.4 излагается метод
нахождения времении выполнения для последовательного и бинарного поиска.
Каждый алгоритм имеет порядок для наилучшего и наихудшего случая,
которые различны. Наилучший случай для алгоритма часто не важен, так как эти
обстоятельства являются исключительными и неподходящими для решения о
выборе какого-либо алгоритма. Наихудший случай может быть важен, так как
эти обстоятельства будут наиболее негативно влиять на ваше приложение.
Клиент может не допускать наихудшего случая и может предпочесть, чтобы
вы выбрали алгоритм, который имеет более узкий диапазон эффективности. В
общем, довольно трудно математически определить среднюю эффективность
какого-либо алгоритма. Мы будем использовать только очень простые
измерения ожидаемых значений и оставим математические детали для курса по
теории сложности.
Общий порядок величин
Небольшой набор различных порядков определяет сложность большинства
алгоритмов структур данных. Мы определяем различные порядки и описываем
алгоритмы, приводящие в результате к таким оценкам.
Если алгоритм — порядка 0(1), то этот порядок не зависит от количества
элементов данных в коллекции. Этот алгоритм выполняется за постоянную
единицу времени (constant time). Например, присваивание некоторого
значения элементу списка массива имеет порядок 0(1), при условии, что вы
храните индекс, который определяет конец списка. Сохранение этого
элемента включает только простой оператор присваивания.
Прямая вставка в конец списка
начало
конец
Алгоритм О(п) является линейным (linear). Сложность этого алгоритма
пропорциональна размеру списка. Например, вставка элемента в конец списка
п элементов будет линейной, если мы не храним ссылку на конец списка.
Подразумевая, что мы можем просматривать элемент за элементом, алгоритм
требует, чтобы мы протестировали п элементов перед определением конца
списка. Порядком этого процесса является О(п). Нахождение максимального
элемента в массиве из п элементов — это О(п), потому что должен быть
проверен каждый из п элементов.
Последовательная вставка в конец списка
начало конец
Ряд алгоритмов имеют порядок, включающий log2n, и называются
логарифмическими (logarithmic). Эта сложность возникает, когда алгоритм
неоднократно подразделяет данные на подсписки, длиной 1/2, 1/4, 1/8, и так
далее от оригинального размера списка. Логарифмические порядки
возникают при работе с бинарными деревьями. Бинарный поиск, изложенный в
разделе 4.4, имеет сложность среднего и наихудшего случаев O(log2n). В
главах 13 и 14 описываются алгоритмы сортировки с использованием дерева
и быстрая сортировка порядка 0(п log2n).
Алгоритмы, имеющие порядок 0(гс2), являются квадратическими
(quadratic). Наиболее простые алгоритмы сортировки такие, как обменная
сортировка, имеют порядок 0(п2). Квадратические алгоритмы используются на
практике только для относительно небольших значений п. Всякий раз, когда
п удваивается, время выполнения такого алгоритма увеличивается на
множитель 4. Алгоритм показывает кубическое (cubic) время, если его порядок
равен 0(л3), и такие алгоритмы очень медленные. Всякий раз, когда п
удваивается, время выполнения алгоритма увеличивается в восемь раз.
Алгоритм Уоршела, применимый к графам, — это алгоритм порядка 0(п3).
Алгоритм со сложностью 0(2п) имеет экспоненциальную сложность
(exponential complexity). Такие алгоритмы выполняются настолько медленно,
что они используются только при малых значениях п. Этот тип сложности
часто ассоциируется с проблемами, требующими неоднократного поиска
дерева решений.
В таблице 4.2 приводятся линейный, квадратичный, кубический,
экспоненциальный и логарифмический порядки величины для выбранных
значений п. Из таблицы очевидно, что следует избегать использования кубических
и экспоненциальных алгоритмов, если только значение п не мало.
Таблица 4.2
Оценка порядка алгоритмов
п
2
4
8
16
32
128
1024
65536
1од2П
1
2
3
4
5
7
10
16
п !од2П
2
8
24
64
160
896
10240
1048576
п2
4
16
64
256
1024
16384
1048576
4294967296
п3
8
64
512
4096
32768
2097152
1073741824
2.8 х 1014
2П
4
16
256
65536
4294967296
3.4 х 1038
1.8 х 10308
Избегайте!
4.4. Последовательный и бинарный поиск
Теперь познакомимся с последовательным поиском в целях нахождения
некоторого значения в списке. Предположим, что мы ищем пределы списка
целых с использованием этого алгоритма. В действительности, мы можем
выполнять поиск в массиве любого типа, для которого определен оператор ==.
Необходимо модифицировать последовательный поиск для ссылки на
параметризованный тип DataType, который является псевдонимом фактического типа.
Мы создаем этот псевдоним, используя ключевое слово typedef. Например:
typedef int DataType; //DataType это int
или
typedef double DataType: //DataType это double
Если предположить, что программист имеет определенный тип DataType,
то код для общего алгоритма последовательного поиска следующий:
// поиск в массиве а из п элементов для нахождения соответствия с ключем
// использовать последовательный поиск, возвращать индекс
// соответствующего элемента массива или — 1, если нет соответствия
int SeqSearch(DataType list[ ], int n, DataType key)
{
for (int i=0; i < n; i++)
if (list[i] == key)
return i; //возвращать индекс соответствующего элемента
return -1; //поиск неудачный, возвращать -1
}
При определении порядка алгоритма последовательного поиска различают
поведение наилучшего и наихудшего случаев. Наилучшему случаю
соответствует нахождение ключа в первом элементе списка. Время выполнения
алгоритма при этом составляет 0(1). Наихудший случай имеет место, когда этот
ключ не находится в списке или обнаруживается в конце списка. Он требует
проверки всех п элементов и имеет порядок О(л). Средний случай требует
небольшого количества вероятностных рассуждений. Для случайного списка
совпадение с ключом может с одинаковой вероятностью появиться в любой
позиции списка. После выполнения проверок большого количества элементов
средняя позиция совпадения — это срединный элемент (midpoint) п/2. Эта
промежуточная точка анализируется после п/2 сравнений, что определяет
ожидаемую стоимость поиска. По этой причине мы говорим, что средняя
эффективность последовательного поиска составляет О(п).
Бинарный поиск
Последовательный поиск применим для любого списка. Если список
является упорядоченным, алгоритм, называемый бинарный поиск (binary search),
предоставляет улучшенный метод поиска. Ваш опыт по нахождению номера в
большом телефонном справочнике — это модель такого алгоритма. Зная
нужные имя и фамилию, вы открываете справочник ближе к началу, середине или
концу, в зависимости от первой буквы фамилии. Вам может повезти, и вы
сразу попадете на нужную страницу. В противном случае вы переходите к более
ранней или более поздней странице в справочнике в зависимости от
относительного местоположения имени человека по алфавиту. Например, если имя
человека начинается с буквы R, а вы находитесь на странице с именами на
букву Т, вы переходите на более раннюю страницу. Процесс продолжается до
тех пор, пока вы не найдете соответствие или не обнаружите, что этого имени
нет в справочнике. Соответствующая идея применима к поиску в
упорядоченном списке. Мы идем к середине списка и ищем быстрое соответствие ключа
значению срединного элемента. Если нам не удается найти соответствия, мы
смотрим на относительный размер ключа и значение срединного элемента и
затем перемещаемся в нижнюю или верхнюю половину списка. В общем, если
мы знаем, как упорядочены данные, мы можем использовать эту информацию,
чтобы сократить время поиска.
Следующие шаги описывают алгоритм. Предположим, что список
упорядочен, как массив. Индексами в концах списка являются: low = 0 и high = п — 1,
где п — это количество элементов в массиве.
1. Сравнить индекс срединного элемента массива:
mid * <low+high)/2.
2. Сравнить значение в срединном элементе с key (ключ).
key
key
low mid high low mid high low mid high
Совпадение найдено Поиск в левой половине Поиск в правой половине
Если совпадение найдено, возвращать индекс mid для нахождения ключа,
if (A[mid] -- key)
return(mid);
key
Если AJmid] < key, совпадение должно происходить в диапазоне индексов
mid-fl . . . high, в правой половине рассматриваемого списка. Это верно,
потому что список упорядочен. Новыми границами являются low=mid+l и
high.
Если key < A[mid], совпадение должно происходить в диапазоне индексов
low . . . mid-1, в левой половине списка. Новыми границами являются low
и high=mid-l.
key
key
low mid - 1 = high low = mid + 1 high
Проверка левой половины Проверка правой половины
Алгоритм уточняет местоположение совпадающего с ключом элемента,
деля пополам длину интервала, в котором может находиться этот элемент,
и затем выполняя тот же алгоритм поиска в меньшем подсписке. В конце
концов, если искомый элемент не находится в списке, low превысит high,
и алгоритм возвращает индикатор сбоя — 1 (совпадение не произошло).
Пример 4.2
Рассмотрим массив целых А. Этот пример дает выборку алгоритма
для заданного ключа 33.
low = О
high = 8
mid = (0 + 8)/2 « 4
33 > A[mid]
low — 5
high = 8
mid = (5 + 8)/2 = 6
33 > A[mid]
low = 7
high «= 8
mid = (7 + 8)/2 = 7
33 > A[mid] Success!
Заметьте, что этот алгоритм требует трех (3) сравнений. При
линейном поиске в списке требуется восемь (8) сравнений.
Реализация бинарного поиска
Функция использует параметризованное имя DataType, которое должно
поддерживать оба оператора: равенства (==) и меньше чем (<)• Первоначально low
равно 0, a high — (п-1), где п — число элементов в этом массиве. Функция
возвращает номер удовлетворяющего условию элемента массива или -1, если
такой элемент не найден (low>high).
// dsearch.h
// просмотреть сортированный массив на предмет совпадения
// с ключом, используя бинарный поиск, возвращать индекс
// совпадающего элемента массива или -1, если совпадение
//не происходит
int BinSearch(DataType list[], int low, int high, DataType key)
{
int mid;
DataType midvalue;
while (low <= high)
{
mid = (low+high)/2; // mid-индекс в подсписке
midvalue = list[mid]; // значение при mid-индексе
if (key == midvalue)
return mid; // совпадение имеется, возвращаем
// его положение в массиве
else if (key < midvalue)
high = mid-1; // перейти в нижний подсписок
else
low = mid+1; // перейти в верхний подсписок
}
return -l; // элемент не найден
}
Реализация последовательного и бинарного поиска включена в файл
dsearch.h. Так как эта функция зависит от класса DataType, определение
DataType должно предшествовать включению этого файла.
Программа 4.1. Сравнение последовательного и бинарного поиска
Программа сравнивает время вычисления последовательного и бинарного
поиска. Массив А заполняется 1000 случайными целыми числами в
диапазоне 0 . • 1999 и затем сортируется. Второму массиву В присваиваются 500
случайных целых чисел в том же диапазоне. Элементы в массиве В
используются как ключи для алгоритмов поиска. Временная функция TickCount
определяется в файле ticks.h и возвращает количество 1/60-х секунд со
времени запуска системы. Мы измеряем время, которое занимает
выполнение 500 поисков, используя каждый алгоритм. Выходная информация
включает время в секундах и количество соответствий.
#include <iostream.h>
typedef int DataType; // данные типа integer
#include "dsearch.h"
#include "random.h"
#include "ticks.h"
// сортировать целый массив из п элементов
// в возрастающем порядке
void ExchangeSort(int a[], int n)
{
int i, j, temp;
for (i=0;i < n-l; i++)
// поместить минимум элементов a[i] . . .a[n-1] в a[i]
for (j = i+1; j < n; j++)
// если a [ j ] < a[i], выполнить их замену
if (a[j] <a[i])
{
temp = a[i] ;
a[i] = a[j] ;
a[j] •= temp;
}
}
void main (void)
{
//А содержит список для поиска, В содержит ключи
int А[1000], В[500];
int i, matchCount;
// используется для данных времени
long tcount;
RandomNumber rnd;
// создать массив А из 1000 случайных чисел со значениями
// в диапазоне 0. . 1999
for (i - 0; i < 1000; i++)
A[i] = rnd.Random(2000);
ExchangeSort(A,1000);
// генерить 500 случайных ключей из того же диапазона
for (i« 0; i < 500; i++)
B[i] - rnd.Random(2000) ;
cout « "Время последовательного поиска" << endl;
tcount = TickCount (); // время начала
matchCount = 0;
for (i = 0; i < 500; i++)
if (SeqSearch(A,1000, B[i]) !=-l)
matchCount++;
tcount = TickCount() — tcount; //
cout « "Последовательный поиск занимает " « tcount/60.0
« " скунд для " « matchCount « " совпадений." « endl;
cout « "Время бинарного поиска"« endl;
tcount = TickCount() ;
matchCount = 0;
for (i = 0; i < 500; i++J
if (BinSearch(A/0,999,B[i]) !=-1)
matchCount++;
tcount=TickCount() —tcount; //
cout « "Бинарный поиск занимает " « tcount/60.0
« " секунд для " « matchCount « " совпадений." « endl;
}
/*
<Выполнение программы 4 . 1>
Время последовательного поиска
Последовательный поиск занимает 0.816667 секунд для 181 совпадений.
Время бинарного поиска
Бинарный поиск занимает 0.016667 секунд для 181 совпадений.
*/
Неформальный анализ для бинарного поиска. Наилучший случай имеет
место, когда совпадающий с ключом элемент находится в середине списка.
При этом порядок алгоритма составляет 0(1 )f так как требуется только одно
тестирующее сравнение равенства. При наихудшем случае, когда элемент не
находится в списке или определяется в последнем сравнении, имеем порядок
0(log2n). Мы можем интуитивно вывести этот порядок. Наихудший случай
возникает, когда мы должны уменьшать подсписок до длины 1. Каждая
итерация, которая не находит соответствие, уменьшает длину подсписка на
множитель 2. Размеры подсписков следующие:
п п/2 п/4 п/8 ... 1
Разделение на подсписки требует т итераций, где т — это приблизительно
log2n (см. подробный анализ). Для наихудшего случая мы имеем начальное
сравнение в середине списка и затем — ряд итераций log2n. Каждая итерация
требует одну операцию сравнения:
Total Comparisons = 1 + log2n
В результате наихудшим случаем для бинарного поиска является 0(log2ri).
Этот результат проверяется имперически программой 4.1. Отношение времени
выполнения последовательного поиска ко времени выполнения бинарного
поиска равно 49,0. Теоретическое отношение ожидаемого времени
приблизительно составляет 500/(log2l000)= 50,2.
Формальный анализ бинарного поиска. Первая итерация цикла имеет дело
со всем списком. Каждая последующая итерация делит пополам размер
подсписка. Так, размерами списка для алгоритма являются
п п/21 п/22 п/23 п/24 . . . п/2т
В конце концов будет такое целое т, что
п/2ш<2 или n<2m+1
Так как m — это первое целое, для которого n/2m<2, то должно быть
верно
n/2m-l>2 или 2m<n
Из этого следует, что
2m<n<2m+1
Возьмите логарифм каждой части неравенства и получите /о^г^действи-
тельному числу х:
m<\og2n=x<m+1
Значение m — это наибольшее целое, которое .<х и задается int(x).
Например, если n=50, log250=5,644. Следовательно,
m=int(5,644)= 5
Можно показать, что средний случай также составляет 0(log2n).
4.5. Базовый класс последовательного списка
Товары для покупки, автобусное расписание, телефонный справочник,
налоговые таблицы и инвентаризационные записи являются примерами списков.
В каждом случае объекты включают последовательность элементов. Во многих
приложениях ведется какой-либо список. Например, перечень товаров пред-
приятия содержит информацию о поставках и заказах, персонал офиса создает
платежную ведомость для списка работников компании, ключевые слова для
компилятора сохраняются в списке зарезервированных слов и так далее.
В главе 1 описывался ADT для базового последовательного списка. Операции
базового списка включают вставку нового элемента в конец списка, удаление
элемента, доступ к элементу в списке по позиции и очистку списка. Мы имеем
также операции для тестирования, является ли список пустым, или находится
ли какой-либо элемент в списке. В качестве примера этому из реальной жизни
рассмотрим список продуктов для покупки в универсаме (Рис.4.6). Когда вы
идете по универсаму, вы решаете купить дополнительные товары и добавляете
их в конец списка. Когда товар найден, вы удаляете его из списка. Список с
этими простыми операциями может использоваться для решения
существенных задач. Приложение описывает отдел видеотоваров, в котором ведется
список имеющихся фильмов и список клиентов. Когда какой-либо фильм выдается
клиенту, он переходит из списка имеющихся фильмов в список клиентов. При
возврате фильма происходит обратный процесс.
Первоначальный
список
Вычеркнули
картофель
Добавили
рыбу
Вычеркнули
хлеб
Добавили
молоко
Рис.4.6. Список покупок
Список ADT описывает однородные списки (homogeneous lists), в которых
каждый элемент имеет один и тот же тип данных, называемый DataType.
В определении ADT не упоминается о том, как хранятся элементы. Для
этого может использоваться массив или связанный список с применением
динамического распределения памяти. Реализации операций Insert, Delete и
Find зависят от метода, используемого для хранения элементов списка.
В главе 1 приводится лишь набросок спецификации этого класса. В данном
разделе мы приводим реализацию класса SeqList, который сохраняет
элементы в массиве. В главе 9 мы разрабатываем новую реализацию этого класса,
используя связанные списки, и выводим этот класс из абстрактного базового
класса List в главе 12. В главах 11, 13, и 14 разрабатываются классы сходной
структуры для деревьев бинарного поиска, хеш-таблиц и словарей.
Спецификация класса SeqList
ОБЪЯВЛЕНИЕ
#include <iostream.h>
#include <stdlib.h>
typedef int DataType;
const int MaxListSize = 50;
class SeqList
{
private:
// массив для списка и число элементов текущего списка
DataType listitem[MaxListSize];
int size;
public:
// конструктор
SeqList(void) ;
// методы доступа
int ListSize(void) const;
int ListEmpty(void) const;
int Find (DataType& item) const;
DataType GetData(int pos) const;
// методы модификации списка
void Insert(const DataType& item);
void Delete(const DataTypefc item);
DataType DeleteFront(void);
void ClearList(void);
>;
ОПИСАНИЕ
Объявление и реализация находятся в файле aseqlist.h. Имя DataType
используется для представления общего типа данных. Перед включением класса
из файла используйте typedef для связывания имени DataType с конкретным
типом. Переменная size поддерживает текущий размер списка. Первоначально
размер установлен на 0. Так как статический массив используется для
реализации списка, константа MaxListSize является верхней границей размера
списка. Попытка вставить больше, чем MaxListSize элементов в список приводит
к сообщению об ошибке и завершению программы.
Реализация класса SeqList
Данная реализация класса SeqList использует массив listitem для
сохранения данных. Коллекция распределяет память для MaxListSize числа элементов
типа DataType. Количество элементов в списке содержится в size (член класса).
Файлы iostream.h и stdlib.h включены для обеспечения выдачи сообщения об
ошибках и для завершения программы, если Insert приведет к тому, что размер
превысит MaxListSize.
Закрытый член size содержит длину списка для операций Insert и Delete.
Значение size является центральным для конструктора и методов ListSize,
ListEmpty и ClearList. Мы включаем конструктор, устанавливающий размер
на 0.
// конструктор, устанавливает size в 0
SeqList::SeqList (void) : size(0)
{}
Методы модификации списка
Метод Insert добавляет новый элемент в конец списка и увеличивает длину
на 1, Если при этом превышается размер массива listitem, то метод выводит
сообщение об ошибке и завершает программу. Ограничение на размер списка
снимается в главе 9, где класс реализуется с использованием связанного
списка.
вставка (10)
Элемент параметра передается в качестве ссылки константе. Если размер
DataType большой, использование ссылочного параметра позволяет избежать
неэффективного копирования данных, которое необходимо в вызове
параметра по значению. Ключевое слово const указывает на то, что фактический
параметр не может быть изменен. Этот же тип передачи параметра
используется методом Delete.
Insert
// вставить элемент в хвост списка, прервать выполнение
// программы, если размер списка превысит MaxListSize
void SeqList::Insert(const DataTypeS item)
{
// проверка размера списка
if (size+1 > MaxListSize)
{
cerr «"Превышен максимальный размер списка" « endl;
exit(1);
>
// индекс хвоста равен размеру текущего списка
listitem[sizej = item;
size++;
}
Метод Delete определяет первое появление в списке заданного элемента.
Функция требует, чтобы был определен оператор сравнения (==) для DataType.
В некоторых случаях для этого может потребоваться, чтобы пользователь
предоставил особую функцию, которая переопределяет оператор == для
конкретного DataType. Эта тема формально излагается в главе 6. Если элемент
не обнаруживается при индексе i, операция спокойно заканчивается без
изменения списка. Если элемент найден, он удаляется из списка перемещением
всех элементов с индексами i+1 к концу списка влево на одну позицию.
Например, удаление элемента со значением 45 из списка приведет к
смещению влево хвостовых элементов 23 и 8. Длина списка изменяется с 6 на
5. Удаление элемента со значением 30 оставляет список неизменным.
Delete
// поиск и удаление элемента item из списка
void SeqList::Delete(const DataTypefc item)
{
int i = 0;
// поиск элемента
while (i < size && «(item == listitem[i]))
i++;
if (i < size)
{
// передвинуть хвост списка на одну позицию влево
while (i < size-1)
{
listitem[i] = listitem[i+i];
i++;
}
size—; // уменьшение size на 1
}
}
Методы доступа к списку. Метод GetData возвращает значение данных в
позицию pos в списке. Если pos не находится в диапазоне от 0 до size-1,
печатается сообщение об ошибке, и программа завершается.
// возвращает значение элемента списка для индекса pos. если pos
// не находится в диапазоне индексов списка, программа заканчивается
//с сообщением об ошибке
DataType SeqList::GetData(int pos) const
{
// прервать программу, если pos вне диапазона индексов списка
if (pos < 0 || pos >= size)
{
cerr « "pos выходит за диапазон индексов!" « endl;
exit(1);
}
return listitem[pos];
}
Метод доступа Find принимает параметр, который служит в качестве ключа,
и последовательно просматривает список для нахождения совпадения. Если
список пустой или совпадение не найдено, Find возвращает 0 (False). Если
элемент обнаруживается в списке в позиции с индексом i, Find присваивает
запись из listitem[i] соответствующему элементу списка и возвращает 1 (True).
Для данных, совпадающих с ключом, процесс присваивания значения
данных элемента списка параметру является важнейшим в приложениях,
касающихся записей данных. Например, предположим, что DataType — это
структура с полем ключа и полем значения, и что оператор == тестирует
только поле ключа. При вводе элемент параметра может определять только
поле ключа. При выводе элемент присваивается обоим полям.
ключ
ключ
значение
элемент (вводг
^элемент (вывод)
SeqList
ключ
значение
ключ
значение
ключ
значение
Совпадение
Find
// использовать item в качестве ключа для поиска в списке.
// возвращать True, если элемент item находится в списке, и
// False — в противном случае, если элемент найден, присвоить
// его значение параметру item, передаваемому по ссылке
int SeqList::Find(DataTypefi item) const
{
int i - 0;
if (ListEmptyO )
return 0; // возвратить False, если список пуст
while (i < size && ! (item » listitem[i]))
i++;
if (i < size)
{
item » listitem[i]; // присвоить item значение элемента списка
return 1; // возвратить True
}
else
return 0; // возвратить False
}
Класс SeqList не предоставляет метода для непосредственного изменения
значения какого-либо элемента. Для выполнения такого изменения мы
должны сначала найти этот элемент и возвратить запись данных, удалить этот
элемент, изменить запись и вставить новые данные в список. Конечно, это
изменяет положение элемента в списке, потому что новый элемент
помещается в конец списка.
Пример 4.3
Запись Inventoryltem содержит номер детали и количество деталей
в запасе. Оператор == сравнивает две записи Inventoryltem, сравнивая
поля partNumber. Выполняется поиск SeqList-объекта L для нахождения
записи с partNumber 5. Если объект найден, запись обновляется
увеличением поля count.
struct Inventoryltem
{
int partNumber;
int count;
}
int operator— (Invntoryltem x, Invntoryltem y)
{
return x.partNumber == у.partNumber;
}
typedef Inventoryltem DataType;
#include "aseqlist.h"
* * *
SeqList L;
Inventoryltem item;
• • •
item.partNumber = 5;
if(L.Find(item))
{
L.Delete(item);
item.count++;
L.Insert(item);
)
Так как любой элемент всегда вставляется в хвост списка, порядок (время
выполнения) метода Insert зависит от п и равен O(l). Find выполняет
последовательный поиск, поэтому среднее время его работы будет О(л). На
протяжение многих проб метод Delete должен проверить в среднем п/2 элементов
списка и должен перемещать в среднем п/2 элементов. Это означает, что
среднее время выполнения для Delete составляет О(л). Порядок наихудшего
случая для обоих методов Find и Delete также составляет О(п).
Применение. Объекты SeqList используются для ведения списка
имеющихся фильмов, и списка фильмов, взятых для просмотра клиентами в
видеомагазине. Каждый элемент в списке является записью, которая состоит
из названия фильма и (для проката) имени клиента.
// структура записи для хранения данных о фильме и клиенте
struct FilmData
{
char filmName[32];
char customerName[32];
}
Так как метод Find в классе SeqList требует определения оператора
сравнения ==, мы перегрузим этот оператор для структуры FilmData. Этот
оператор проверяет имя файла, используя функцию C++ strcmp.
// перегрузка ==
int operator -= (const FilmData &A, cost FilmData *B)
{
return strcmp(A.filmName, B.filmName);
)
Чтобы использовать FilmData с классом SeqList, включите объявление
typedef FilmData DataType;
Определение оператора == для FilmData и DataType находятся в файле
video.h.
В видеомагазине ведется инвентаризационный список фильмов. Для
простоты мы полагаем, что в магазине имеется только одна копия каждого
фильма. Новый фильм добавляется в инвентаризационный список функцией
Insert. Для проверки наличия фильма в списке используется функция Find.
Если фильм найден, он удаляется из инвентаризационного списка фильмов
и вставляется в список фильмов, отданных для просмотра.
Программа 4.2. Видеомагазин
Main-программа эмулирует операции видеомагазина. Первоначально
весь перечень фильмов считывается из файла films и сохраняется в списке
с именем inventory List. Мы наблюдаем короткий промежуток времени
деятельности видеомагазина и рассматриваем заказы четырех клиентов на
прокат фильмов. В каждом случае мы вводим имя клиента и заказ фильма и
определяем, имеется ли этот фильм в наличии в настоящее время. Если да,
то мы удаляем его из инвентаризационного списка и добавляем клиента в
список лиц, взявших фильмы напрокат. Если фильма нет в наличии, клиент
уведомляется об этом.
#include <iostream.h>
#include <fstream.h>
#include <stdlib.h>
#include <string.h>
tinclude "video.h" // объявления видео-данных
#include "aseqlist.h" // включить класс SeqList
// читать таблицу фильмов с диска
void SetupInventoryList(seqList sinventoryList)
{
ifstream filmFile;
FilmData fd;
// открыть файл, с проверкой ошибок
filmFile.open("Films", ios::in | ios::nocreate);
if (!filmFile)
{
cerr « "Файл 'films' не найден!" « endl;
exit(1);
}
// читать строки до конца файла;
// вставлять наименования фильмов в инвентаризационный список
while(filmFil.e.getline(fd.filmName,32,'\n'))
inventoryList.Insert(fd);
}
// печать наименовании фильмов
void PrintlnvemtoryList(const SeqList &inventoryList)
{
int i;
FilmData fd;
for (i - 0; i < inventoryList.ListSize (); i++)
{
fd «= inventoryList.GetData(i) ; //
cout « fd.filmName « endl; //
}
>
// цикл по списку клиентов, печать клиентов и фильмов
void PrintCustomerList(const SeqList &customerList)
{
int i
FilmData fd;
for (i « 0; i < customerList.ListSize (); i++)
fd = customerList.GetData(i); //
cout « fd.customerName « " (" « fd.filmName « ") " « endl;
}
}
void main (void)
{
//
SeqList invemtoryList, customerList;
int i;
//
FilmData fdata;
char customer [20];
SetupInventoryList (inventoryList); // читать файл с фильмами
// запрос имени клиента и названия фильма.
// если запрошенный фильм имеется в наличии, он вносится в список клиентов
//и удаляется из списка фильмов; в противном случае выдается
// сообщение об отсутствии фильма
for (i = 0; i < 4; i++)
{
// ввод имени клиента и названия фильма
cout « "Имя клиента: ";
cin.getline(customer,32,'\n');
cout « "Запрашиваемый фильм: " ;
cin.getline(fdata.filmName,32,'\n');
if (inventoryList.Find(fdata))
{
strcpy(fdata.customerName, customer);
// вставить название фильма в список клиентов
customerList.Insert(fdata);
// удалить из списка фильмов
inventoryList.Delete(fdata);
}
else
cout « "Сожалею! " « fdata. filmName
« " отсутствует." « endl;
}
cout << endl;
// печать списков клиентов и фильмов
cout « "Клиенты, взявшие фильмы для просмотра" « endl;
PrintCustomerList(customerList);
cout « endl;
cout « "Фильмы, оставшиеся в ведомости:"« endl;
PrintlnventoryList(inventoryList);
}
/*
<Входной файл "Films">
Война миров
Касабланка
Грязный Гарри
Дом животных
Десять заповедей
Красавица и зверь
Список Шиндлера
Звуки музыки
La Strata
Звездные войны
<Выполнение программы 4.2>
Имя клиента: Дон Бекер
Запрашиваемый фильм: Дом животных
Имя клиента: Тери Молтон
Запрашиваемый фильм: Красавица и зверь
Имя клиента: Деррик Лопез
Запрашиваемый фильм: La Strata
Имя клиента: Хиллари Дэн
Запрашиваемый фильм: Дом животных
Сожалею! Дом животных отсутствует.
Клиенты, взявшие фильмы для просмотра
Дон Бекер (Дом животных)
Тери Молтон (Красавица и зверь)
Деррик Лопез (La Strata)
Фильмы, оставшиеся в ведомости:
Война миров
Касабланка
Грязный Гарри
Десять заповедей
Список Шиндлера
Звуки музыки
Звездные войны
*/
Письменные упражнения
4.1 Объясните различие между линейной и нелинейной структурой данных.
Дайте пример каждой.
4.2 Определите, какая структура данных является соответствующей для
следующих ситуаций:
(а) Сохранить абсолютное значение числа в элементе 5 целого списка.
(б) Пройти по списку студентов в алфавитном порядке и напечатать отметки.
(в) Когда арифметический оператор найден, два предыдущих числа
удаляются из коллекции.
(г) В исследовании с использованием моделирования каждое событие
вставляется в коллекцию и удаляется в порядке его вставки.
(д) Когда ферзь на шахматной доске может переместиться в какую-либо
позицию, эта позиция вставляется в коллекцию.
(е) Одно поле структуры данных является целым, другое —
действительным значением, а последнее поле — это строка.
(ж) Постоянно сохраняйте выходные данные программы, чтобы рассмотреть
их позже.
(з) Если ключ меньше, чем текущее значение в списке, рассмотрите
предыдущие значения.
(и) Минимальное значение всегда переходит в вершину списка.
(к) Строка используется в качестве ключа для нахождения записи данных,
находящейся где-то в коллекции.
(л) Слово используется в качестве индекса для нахождения его определения
в коллекции.
(м) В праздники телефонная сеть перегружена. Определите альтернативный
набор путей для наилучшего распределения вызовов.
4;3 Ниже приведены меры сложности наихудшего случая для трех
алгоритмов, которые решают одну и ту же задачу:
Алгоритм 1 Алгоритм 2 Алгоритм 3
0(п2) 0(п log2n) 0(2n)
Какой метод предпочтителен и почему?
4.4 Выполните анализ Big-О для каждой из следующих функций:
(а) п + 5
(б) п2 +6п +7
(в) Vn + 3
(г) п3 + п2 - 1
п + 1
4.5
(а) Для какого значения п>1, 2п становится больше, чем и3?
(б) Покажите, что 2п +п3 имеет порядок 0(2п).
(в\ п2 + 5
v ' Дайте Big-O-оценку для — + 6 \og2n ?
л + 3
4.6 Список целых ведется в массиве. Каков порядок алгоритма печати
первого и последнего элемента в массиве?
4.7 Объясните, почему алгоритм порядка 0(log2n) имеет также порядок 0{п).
4.8 Каждый цикл является главным компонентом для алгоритма.
Используйте нотацию Big-O, чтобы выразить время вычисления наихудшего
случая для каждого из следующих алгоритмов как функции п.
(а) for (dotprd=0.0,i=0;i < n;i++)
dotprd +=a[i] * b[i];
(б) for (i=0;i<n;i++)
if(a[i] == k)
return 1;
return 0;
(в) for (i=0;i<n;i++)
for (j=0;j<n;j++)
b[i] [j] *= c;
(r) for (i=0;i<n;i++)
for(j=0;j<n;j++)
{
entry= 0.0;
for (k=0;k<n;k++)
entry +=a[i] [k] * b[k] [j];
c[i,j] = entry;
}
4.9 Следующие коллекции из п элементов используются для сохранения
данных. Каков порядок алгоритма нахождения минимального значения
(а) в стеке?
(б) в очереди приоритетов?
(в) в дереве бинарного поиска?
(г) в последовательном списке с упорядочением по возрастанию?
(д) в списке с возможностью прямого доступа к элементам с упорядочением
по убыванию?
4.10 Последовательность чисел Фибоначчи имеет вид:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, . , .
Первые два числа являются 1, и каждое последующее число Фибоначчи
является суммой двух предшествующих. Эта последовательность
описывается рекуррентным отношением
fl = 1, f2=l, fn = fn-2 + fn-1, ДЛЯ П > 3
Следующая функция вычисляет n-ное число Фибоначчи. Каков ее
порядок?
long Fibonacci(int n)
{
long fnm2=l, fninl^l, fn;
int i;
if (n<« 2)
return 1;
for (i-~3;i<= n;i++)
{
fn - fnm2 + fnml;
fnm2 - fnml;
fnml - fn;
}
return fn;
}
В главе 10 рекурсивная функция записывается для вычисления п-ного
числа Фибоначчи. Метод имеет экспоненциальный порядок. Ясно, что
рекурсивное решение неприемлемо!
4.11
(а) Последовательный поиск используется в списке из 50000 элементов.
□ Какое наименьшее количество сравнений выполнит этот поиск?
□ Какое необходимо максимальное количество сравнений?
□ Каково ожидаемое количество сравнений?
(б) Бинарный поиск используется в списке из 50000 элементов
□ Какое наименьшее количество сравнений выполнит этот поиск?
D Какое максимальное количество сравнений необходимо?
4.12 Предположим, SeqList-объект L состоит из элементов:
34 11 22 16 40
(а) Задайте элементы в списке после каждой из следующих команд:
п « L.DeleteFront();
L.Insert(n);
if (L.Find(L.GetData(0)*2)
L.Delete(16);
(б) Используя объект L, приведите выход для следующей
последовательности команд:
for (int i=0; i <5; i++)
{
L.Insert(L.DeleteFront());
cout « L.GetData(i) << ;
}
4.13 Напишите функцию для реализации указанной задачи
(а) Добавить SeqList-объект L в хвост объекта К.
void Concatenate(SeqListfi К, SeqList& L);
(б) Поменяйте на обратный порядок элементов в SeqList-объекте L.
void Reverse (SeqList& L);
4.14 Функция Ques берет SeqList-объект L, элементы которого все являются
положительными целыми.
Каково действие функции над списком?
{1, 3, 7, 2, 15, 0, 12}?
Почему L должен передаваться по ссылке?
typedef int DataType;
#include "aseqlist.h"
int M(const SeqList &L)
{
int i, nival, length « L.ListSize ();
if (length == 0)
{
cerr « Список пустой << endl;
return -1;
}
mval = L.GetData(O);
for (i= 1; i< length; I++)
if (L.GetData(i) > mval)
mval « L.GetData(i);
return mval;
}
void Ques(SeqList &L)
{
int mval = M(L);
L.Delete(mval);
}
4.15 Объясните, почему необходима пересылка данных при реализации
метода Delete в классе SeqList на базе массива.
Упражнения по программированию
4.1 Используйте класс SeqList с DataType int для создания utility функции
InsertMax:
void InsertMax(SeqList& L, int elt);
InsertMax помещает elt в список L, только если он больше всех
существующих элементов в списке.
Напишите main-программу, которая читает 10 целых и вызывает In-
sertMax для каждого. Напечатайте список.
4.2 Объявите запись
struct Person
{
char name [20];
int age;
char gender;
};
и вызовите класс SeqList следующим образом:
#inclucle <string.h>
//needed for SeqList class method Find
int operator»* (Person x, Person y)
{
return strcmp(x.name, y.name)-* 0;
}
typedef Person DataType;
tinclude "aseqlist.h"
(а) Напишите функцию
void PrintByGender(const SeqListS L, char sex);
которая проходит по списку L и печатает все записи, имеющие заданный
пол.
(б) Напишите функцию
int InList (const SeqList&, char *nm, Persons p);
которая определяет, существует ли в списке L запись с полем имени
nm. Выполните это, создав объект Person с полем имени nm и используя
метод Find. Нет необходимости инициализировать поля age и gender
записи. Сравнение двух записей выполняется сравнением полей имени.
Если совпадение происходит, присвоить запись параметру р и
возвратить 1; в противном случае возвратить 0. Параметр р не должен
изменяться, если только не будет найдено совпадение.
(в) Напишите main-программу для тестирования этих функций.
4.3 Напишите программу, которая запрашивает у пользователя целое п,
генерирует массив из п случайных целых в диапазоне 0 ... 999 и
сортирует список, используя обменную сортировку. Задайте время
выполнения сортировки, используя функцию TickCount, определенную в
файле ticks.h. Выполните программу, используя п= 50, 500, 1000 и
10000. Это является экспериментальным подтверждением того, что
обменная сортировка имеет порядок 0(п2).
Примечание: Так как локальный массив из 1000 или 10000 элементов
может превысить объем динамической области системы, выделить
динамический массив со следующим синтаксисом для хранения
элементов. Вы можете использовать общую нотацию массива a[i] с
динамической структурой.
int *a; //определяет указатель
• • •
а = new int [n]; //п равен 50, 500, 1000 или 10000
Напишите программу, которая запрашивает у пользователя целое п,
генерирует массив из п случайных целых в диапазоне 0 ... 999 и
сортирует список, используя обменную сортировку. Задайте время
выполнения сортировки. Выполните программу, используя п = 50, 500,
1000 и 10000. Это является экспериментальным подтверждением того,
что обменная сортировка имеет порядок 0(п2).
4.4 Это упражнение расширяет применение Программы 4.2 (Видеомагазин)
для включения возврата фильмов. Спросите клиента, берет ли он фильм
напрокат или возвращает. Если фильм возвращается, удалите его из
списка фильмов, взятых напрокат, и вставьте его в
инвентаризационный список.
4.5 Ситуация тестирования содержит пример структуры SeqList. Студенты
сдают контрольные работы на стол преподавателя титульной стороной
вниз (вставка в конец списка). Предположим, что взволнованный студент
обнаруживает правильный ответ на какой-либо вопрос и хочет проверить,
как он (или она) ответил. Преподаватель должен перевернуть стопку
контрольных работ так, чтобы первая работа оказалась титульной стороной
вверх, просмотреть работу, пока не будет найдена работа этого студента,
и затем удалить контрольную работу из списка. После того, как студент
закончит проверку работы, преподаватель вставляет ее в коцец списка.
Напишите программу, которая использует класс SeqList для
моделирования этой ситуации. Ассоциируйте студента с контрольной работой,
используя следующую запись:
struct Test
{
char name [30];
int testNumber;
};
Цикл в main-программе управляет выполнением, читая целое:
1=Сдать контрольную работу 2=Позволить студенту проверить работу
З-Возвратить взятую работу 4=Выйти из программы
Выполните следующие действия:
Ввод 1: Запросите имя и номер работы; вставьте работу в список sub-
mittedTests.
Ввод 2: Запросите только имя, удалите работу из submitted-Tests и
вставьте ее в список borrowedTests.
Ввод 3: Запросите имя, удалите запись из borrowedTests и вставьте ее
в submittedTests.
Ввод 4: Преподаватель готов уйти, и все взятые на время работы должны
быть возвращены. Удалите все элементы из borrowedTests, вставляя
их в submittedTests. Печатайте окончательный список.
Вы должны определить оператор ==, чтобы определить, равны ли две
записи Test. Выполните это, используя функцию
#include <string.h>
int operator== (const Test& tl, Tests t2)
{
return strcmp(tl.name/ t2.name) -= 0;
}
глава
Стеки и очереди
5.1. Стеки
5.2. Класс Stack
5.3. Оценка выражения
5.4. Очереди
5.5. Класс Queue
5.6. Очереди приоритетов
5.7. Практическое применение:
управляемое событиями
моделирование
Письменные упражнения
Упражнения по программированию
В этой главе мы обсуждаем более подробно классический стек и очередь,
являющиеся структурами данных, сохраняющими и возвращающими
элементы из защищенных частей списка. Описывается также очередь
приоритетов, модифицированная версия очереди, в которой из списка удаляется
элемент с наивысшим приоритетом. Стек, очередь и очередь приоритетов
реализуются как классы C++. Основные идеи этой главы иллюстрируют два
практических примера. Демонстрируется действие RPN-калькулятора со
стеком операндов. Пример обслуживания очереди клиентов кассирами в банке
показан с помощью событийного моделирования. Это приложение использует
очередь приоритетов и знакомит с важным инструментом управления в
бизнесе.
5.1. Стеки
Стек является одной из наиболее используемых и наиболее важных
структур данных. Стеки применяются очень часто. Например, распознавание
синтаксиса в компиляторе, как и оценка выражений, основано на стеке. На
нижнем уровне стеки используются для передачи параметров функциям,
выполнения вызова функции и возвращения из нее.
Стек (stack) — это список элементов, доступных только в одном конце
списка. Элементы добавляются или удаляются из списка только в вершине
(top) стека. Подносы в столовой или стопка коробок являются моделями
стека.
Стек предназначен для хранения элементов, доступных естественным
путем в вершине списка. Представим шампур, на который нанизаны
нарезанные овощи, подготовленные для шашлыка. На рис. 5.1 овощи на
шампуре 1 расположены в порядке: лук, грибочек, зеленый перец и лук.
Перед приготовлением шашлыка гость сообщает, что он не ест грибов, и
их необходимо убрать. Эта просьба означает удалить лук (шампур 2), уда-
лить грибочек (шампур 3) и затем вновь нанизать лук (шампур 4). Если
гость не любит зеленый перец или лук, это доставит повару больше
проблем.
В структуре стека важнейшее место занимают операции, добавляющие и
удаляющие элементы. Операция Push добавляет элемент в вершину стека.
Об операции удаления элемента из стека говорят как об извлечении (to pop
the stack) из стека. На рис. 5.2 показана последовательность операций Push
и Pop. Последний вставленный в стек элемент является первым удаляемым
элементом. По этой прцчине о стеке говорят, что он имеет порядок LIFO
(last-in/first-out) (последний пришел/первый ушел).
Лук
Зеленый перец
Грибы
Рис. 5.1. Стек овощей
Абстрактное понятие стека допускает неопределенно большой список.
Логически подносы в столовой могут складываться бесконечно. В
действительности подносы находятся на полке, а овощи нанизаны на коротких шампурах.
Когда полка или шампур переполнены, мы не можем добавить (Push) еще
один элемент в стек. Стек достигает максимального количества элементов,
которыми он может управлять. Эта ситуация поясняет значение условия
полного стека (stack full). Другая крайность — вы не можете взять поднос
с пустой полки. Условие пустого стека (stack empty) подразумевает, что вы
не можете удалить (Pop) элемент. Описание ADT Stack включает только
условие пустого стека. Условие полного стека является уместным в том
случае, если реализация содержит верхнюю границу размера списка.
Push A Push В Push С Pop Pop Push D
Рис. 5.2. Помещение в стек и извлечение из него
ADT Stack
Данные
Список элементов с позицией top, указывающей на вершину стека.
Операции
Конструктор
Начальные значения: Нет
Процесс: Инициализация вершины стека.
StackEmpty
Вход: Нет
Предусловия: Нет
Процесс: Проверка, пустой ли стек.
Выход: Возвращать True, если стек пустой,
иначе возвращать False.
Постусловия: Нет
Pop
Вход: Нет
Предусловия: Стек не пустой.
Процесс: Удаление элемента из вершины стека.
Выход: Возвращать элемент из вершины стека.
Постусловия: Элемент удаляется из вершины стека.
Push
Вход: Элемент для стека.
Предусловия: Нет
Процесс: Сохранение элемента в вершине стека.
Выход: Нет
Постусловия: Стек имеет новый элемент в вершине.
Peek
Вход: Нет
Предусловия: Стек не пустой.
Процесс: Нахождение значения элемента в вершине стека.
Выход: Возвращать значение элемента из вершины стека.
Постусловия: Стек неизменный.
ClearStack
Вход: Нет
Предусловия: Нет
Процесс: Удаление всех элементов из стека
и переустановка вершины стека.
Выход: Нет
Постусловия: Стек переустановлен в начальные условия.
Конец ADT Stack
5.2. Класс Stack
Члены класса Stack включают список, индекс или указатель на вершину
стека и набор стековых операций. Для хранения элементов стека используется
массив. В результате размер стека не может превысить количества элементов
в массиве и условие полного стека является релевантным. В главе 9 мы
снимаем это ограничение, когда разрабатываем класс Stack, используя
связанный список.
Объявление объекта типа Stack включает размер стека, который
определяет максимальное количество элементов в списке. Размер имеет значение
по умолчанию MaxStackSize = 50. Список (stacklist), максимальное
количество элементов в стеке (size) и индекс (top) являются закрытыми членами,
а операции — открытыми.
top
Реализация стека
Первоначально стек пуст и top = -1. Элементы вводятся в массив (функция
Push) в возрастающем порядке индексов (top = 0, 1, 2) и извлекаются из
стека (функция Pop) в убывающем порядке индексов (top = 2, 1, 0).
Например, следующий объект является стеком символов (DataType = char). После
нескольких операций Push/Pop индекс top = 2, а элемент в вершине стека —
это stacklist[top] = С.
top-
top«=2
Возрастающий индекс
Пример 5.1
Данный пример иллюстрирует целый массив из 5 элементов с
последовательностью операций Push 10; Push 25; Push 50; Pop; Pop. Индекс
top увеличивается на 1 при операции Push и уменьшается на 1 при
операции Pop.
Пустой стек
top = -1
Push 10
top = 0
Push 25
top = 1
Push 50
top = 2
Pop
top = 1
Pop
top =0
Спецификация класса Stack
ОБЪЯВЛЕНИЕ
#include <iostream.h>
tinclude <stdlib.h>
const int MaxStackSize « 50;
class Stack
{
private:
// закрытые данные-члены, массив стека и вершина (индекс)
DataType stacklist[MaxStackSize];
int top;
public:
// конструктор; инициализирует вершину
Stack (void);
// операции модификации стека
void Push (const DataType& item);
DataType Pop (void);
void ClearStack(void);
// доступ к стеку
DataType Peek (void) const;
// методы проверки стека
int StackEmpty(void) const;
int StackFull(void) const; // реализация массива
};
ОПИСАНИЕ
Данные в стеке имеют тип DataType, который должен определяться с
использованием оператора typedef. Пользователь должен проверять, полный ли
стек, перед попыткой поместить в него элемент и проверять, не пустой ли стек,
перед извлечением данных из него. Если предусловия для операции push или pop
не удовлетворяются, печатается сообщение об ошибке и программа
завершается.
StackEmpty возвращает 1 (True), если стек пустой, и 0 (False) — в противном
случае. Используйте StackEmpty, чтобы определить, может ли выполняться
операция Pop.
StackFull возвращает l(True), если стек полный, и 0 (False) — в противном
случае. Используйте StackFull, чтобы определить, может ли выполняться
операция Push.
Clear Stack делает стек пустым, устанавливая top — -1. Этот метод позволяет
использовать стек для других целей.
ПРИМЕР
Объявление стека и реализация содержатся в файле astack.h*
typedef int DataType;
#include astack.h; // включить описание класса Stack
Stack S; // объявить объект типа Stack
S.Push(10); // поместить в стек S значение 10
cout « S.Peek() « endl; // напечатать 10
// вытолкнуть 10 из стека и оставить стек пустым
if (!S.StackEmpty())
temp * S.Pop();
cout « temp « endl;
S.ClearStackO; // очистить стек
Реализация класса Stack
Конструктор Stack присваивает индексу top значение -1, что эквивалентно
условию пустого стека.
//инициализация вершины стека
Stack::Stack (void) : top(-l)
{ >
Операции стека. Две основные операции стека вставляют (Push) и удаляют
(Pop) элемент из стека. Класс содержит операцию Peek, позволяющую
клиенту выбирать данные из элемента в вершине стека, не удаляя в
действительности этот элемент.
Для того, чтобы поместить элемент в стек, увеличьте индекс top на 1 и
присвойте новый элемент массиву stacklist. Попытка добавить элемент в
полный стек приведет к сообщению об ошибке и завершению программы.
// поместить элемент в стек
void Stack::Push (const DataType& item)
{
// если стек полный, завершить выполнение программы
if (top == MaxStackSize-1)
{
cerr « "Переполнение стека!" « endl;
exit(l);
}
// увеличить индекс top и копировать item в массив stacklist
top++;
stacklist[top] « item;
}
Перед вставкой элемента
После вставки элемента
top
item
top = top + 1
Операция Pop извлекает элемент из стека, копируя сначала значение из
вершины стека в локальную переменную temp и затем увеличивая top на 1.
Переменная temp становится возвращаемым значением. Попытка извлечь
элемент из пустого стека приводит к сообщению об ошибке и завершению
программы.
Перед операцией Pop
После операции Pop
item
item
top
top = top - 1
Возвратить
// взять элемент из стека
DataType Stack::Pop (void)
{
DataType temp;
// стек пуст, завершить программу
if (top == -1)
{
cerr << "Попытка обращения к пустому стеку! м << endl;
exit(l);
}
// считать элемент в вершине стека
temp = stacklist[top] ;
// уменьшить top и возвратить значение из вершины стека
top—;
return temp;
}
Операция Peek в основном дублирует определение Pop с единственным
важным исключением. Индекс top не уменьшается, оставляя стек нетронутым.
// возвратить данные в вершине стека
DataType Stack::Peek (void) const
{
// если стек пуст, завершить программу
if (top == -1)
{
cerr << "Попытка считать данные из пустого стека!" << endl;
exit(l);
}
return stacklist[top];
}
Условия тестирования стека. Во время своего выполнения операции стека
завершают программу при попытках клиента обращаться к стеку неправильно;
например, когда мы пытаемся выполнить операцию Peek над пустым стеком.
Для защиты целостности стека класс предусматривает операции тестирования
состояния стека.
Функция StackEmpty проверяет, является ли top равным -1. Если — да,
стек пуст и возвращаемое значение — l(True); иначе возвращаемое значение —
О (False).
// тестирование стека на наличие в нем данных
int Stack:-.StackEmpty (void) const
{
// возвратить логическое top == -1
return top == -1;
}
Функция StackFull проверяет, равен ли top значению MaxStackSize-1. Если
так, то стек заполнен и возвращаемым значением будет 1 (True); иначе,
возвращаемое значение — 0 (False).
// проверка, заполнен ли стек
int Stack::StackFull(void) const
{
return top == MaxStackSize-1;
)
Метод ClearStack переустанавливает вершину стека на -1. Это
восстанавливает начальное условие, определенное конструктором.
// удалить все элементы из стека
void Stack::ClearStack<void)
{
top = -1;
}
Стековые операции Push и Pop используют прямой доступ к вершине
стека и не зависят от количества элементов в списке. Таким образом, обе
операции имеют время вычисления 0(1).
Применение: Палиндромы. Когда DataType является типом char,
приложение обрабатывает символьный стек. Приложение определяет палиндромы,
являющиеся строками, которые читаются одинаково в прямом и обратном
порядке. Пробелы не включаются. Например, dad, sees и madam im adam
являются палиндромами, a good — нет. Программа 5.1 использует класс
Stack для тестирования входной строки на наличие палиндрома.
Программа 5.1. Палиндромы
Эта программа читает строку текста, используя функцию cin.getlineQ,
и вызывает функцию Deblank для удаления всех пробелов из текста.
Функция Deblank копирует непустые символы во вторую строку программы,
сканируя строку дважды, проверяет, является ли строка, лишенная
пробелов, палиндромом. Во время первого просмотра каждый символ
помещается в стек, создается список, содержащий текст в обратном порядке.
Во время второго просмотра каждый символ сравнивается с элементом,
который удаляется из стека. Просмотр завершается, если два символа не
совпадают, в случае чего этот текст не является палиндромом. Если
сравнения остаются правильными до тех пор, пока стек не будет пуст, этот
текст является палиндромом.
Исходная строка = "dad"
Палиндром
top
Исходная строка = "good"
Не палиндром
top
#include <iostream.h>
ipragma hdrstop
typedef char DataType; // элементы стека - символы
#include "astack.h"
// создает новую строку
void Deblank(char *s, char *t)
i
// цикл до тех пор, пока не встретится NULL-символ
while(*s != NULL)
{
// если символ - не пробел, копировать в новую строку
if (*s != ' ' )
*t++ = *s;
s-*- + ; // передвинуться к следующему символу
}
*t = NULL; // добавить NULL в конец новой строки
}
void main (void)
{
const int True = 1, False = 0;
Stack S;
char palstring[80], deblankstring[80), c;
int i = 0;
int ispalindrome = True; // полагаем, что строка - палиндром
// считать в полную строку
cin.getline(palstring/80,' \n' );
// удалить пробелы из строки и поместить результат в deblankstring
Deblank(palstring,deblankstring) ;
// поместить символы выражения без пробелов в стек
i-0;
while(deblankstring[i] != 0)
{
S.Push(deblankstring[i]);
i++;
}
// сравнение вершины стека с символами из оригинальной строки
i- 0;
while (!S.StackEmpty())
{
с = S. Pop () ; // получить следующий символ из стека
// если символы не совпадают, прервать цикл
if (с != deblankstring[i]j
{
ispalindrome = False; // не палиндром
break;
}
i++;
}
if (ispalindrome)
cout « ' \"' « palstring « ' V"
« " - палиндром" « endl;
else
cout « ' \n' « palstring « ' \M/
« " - не палиндром" << endl;
}
/*
Оапуск 1 Программы 5 . 1>
madam im adam
"madam im adam" - палиндром
< Запуск 2 Программы 5. 1>
a man a plan a canal panama
"a man a plan a canal panama" - палиндром
< Запуск 3 Программы 5 . 1>
palindrome
"palindrome" - не палиндром
*/
Применение: Вывод данных с различными основаниями. Операторы
вывода многих языков программирования печатают числа в десятичном формате
как значения по умолчанию. Стек может использоваться для печати чисел
с другими основаниями. Бинарные (с основанием 2) числа описаны в главе 2,
и мы полагаем, что вы можете применить рассмотренные там принципы для
других оснований.
Пример 5.2
В этом примере десятичные числа преобразуются в числа с заданным
основанием.
1. (Основание 8) 28ю = 3*8+4 = 34в
2. (Основание 4) 72ю = 1*64+0*16+2*4+0 = 1020*
3. (Основание 2) 53ю =1*32+1*16+0*8+1*4+0*2+1 =1101012
Задача отображения на экране числа с недесятичным основанием
решается с использованием стека. Мы описываем алгоритм для
десятичного числа п, которое печатается как число с основанием В.
1. Крайняя правая цифра п — это п%В. Поместите ее в стек S.
2. Остальные цифры п задаются как п/В. Замените п на п/В.
3. Повторяйте шаги 1-2 до тех пор, пока не будет выполнено л=0 и
не останется ни одной значащей цифры.
4. Теперь в стеке имеется новое представление N как числа с базой
В. Выбирайте и печатайте символы из S до тех пор, пока стек не
будет пуст.
На рис. 5.3 показано преобразование п = 3553ю в число с основанием 8.
Рисунок отображает рост стека при создании четырех восьмеричных цифр
для п. Завершим алгоритм выборкой и затем печатью каждого символа
из стека. Выходом является число 6741.
п = 355310
Пустой стек
п = 3553
п%8 = 1
п/8 = 444
п = 444
п%8 = 4
п/8 = 55
п = 55
п%8=7
п/8 = 6
п = б
п%8 = 6
п/8 = 0
п-0
Рис. 5.3. Использование стека для печати числа в восьмеричном формате
Программа 5.2. Печать числа по любому основанию
Программа представляет функцию выхода, которая принимает
неотрицательное длинное целое num и основание В в диапазоне 2 - 9 и отображает
num на экране как число с основанием В. Main-программа запрашивает
у пользователя три неотрицательных целых числа и основания, а затем
выводит эти числа с соответствующими основаниями.
#include <iostream.h>
#pragma hdrstop
typedef int DataType;
#include "astack.h"
// печать целого num с основанием В
void MultibaseOutput(long num, int B)
{
Stack S;
// извлечение чисел с основанием В справа налево
//и помещение их в стек S
do
{
S.Push(int(num % В));
num /= В;
} while (num != 0) ;
while (!S.StackEmpty())
cout « S.Pop();
}
void main(void)
{
long num; // десятичное число
int В; // основание
// читать 3 положительных числа и приводить к основанию 2 <= В <= 9
for(int i=0;i < 3;i++)
{
cout << "Введите неотрицательное десятичное число и основание "
<< "(2<=В<=9): ";
cin >> num >> В;
cout << num << " основание " << В << " - ";
MultibaseOutput(num, В);
cout << endl;
}
}
/*
Оапуск программы 5.2>
Введите неотрицательное десятичное число и основание (2<-В<=9) : 72 4
72 основание 4 - 1020
Введите неотрицательное десятичное число и основание (2<=В<=9): 53 2
53 основание 2 - 110101
Введите неотрицательное десятичное число и основание (2<=В<=9): 3553 8
3553 основание 8 - 6741
*/
5.3. Оценка выражений
Электронные калькуляторы иллюстрируют одно из основных применений
стека. Пользователь вводит математическое выражение с числами
(операндами) и операторы, а калькулятор использует один стек для вычисления
числовых результатов. Алгоритм калькулятора предусматривает ввод
выражения в определенном числовом формате. Такое выражение, как
-8 + (4*12 + 5А2)/3
содержит бинарные операторы (binary operators) (+, *, /, "), операнды
(operands) (8, 4, 12, 5, 2, 3) и круглые скобки (parantheses), которые создают
подвыражения. Первая часть выражения включает унарный оператор (unary
operator) отрицания, который действует на один операнд (например, - 8).
Другие операторы называются бинарными, потому что они требуют двух
операндов. Оператор Л создает выражение 52 = 25.
Выражение записывается в инфиксной (infix) форме, если каждый
бинарный оператор помещается между его операндами и каждый унарный оператор
предшествует его операнду. Например,
-2 + 3*5
является инфиксным выражением. Инфиксный формат является наиболее
общим для записи выражений и используется в большинстве языков
программирования и калькуляторов. Инфиксное выражение вычисляется алгоритмом,
который использует два стека для различных типов данных: один — для
хранения операндов, другой — для хранения операторов. Так как класс Stack
в astack.h требует единственного определения DataType, мы не можем
реализовать вычисление инфиксного выражения в данном разделе. Эта тема
описывается в главе 7, где определяются шаблоны и реализуется шаблон класса
Stack. Этот класс позволяет использовать два или более объектов типа Stack с
различными типами данных.
Альтернативной рассмотренной форме является постфиксное (postfix)
представление, в котором операнды предшествуют оператору. Этот формат
называется также RPN или Польской инверсной нотацией (Reverse Polish
Notation). Например, инфиксное выражение "а + Ь" записывается в
постфиксной форме как "a b +". В постфиксной форме переменные и числа
вводятся по мере их появления, а оператор — там, где имеются два его
операнда. Например, в следующем выражении знак * вводится
непосредственно после его двух операндов b и с. Знак 4- вводится после того, как
имеются его операнды а и (Ь*с). В постфиксном формате используется
приоритет операторов. Оператор * появляется перед -К
Infix: а + Ь*с = а + (Ь * с) Postfix: a b с * +
Скобки в постфиксном формате не обязательны. Далее следует ряд
инфиксных выражений и их постфиксные эквиваленты.
Инфиксное выражение
а*Ь + с
a*b*c*d*e*f
а + (b*c +d)/e
(b*b - 4*а*с)/(2*а)
Постфиксное выражение
а Ь*с +
a b*c*d*e*f*
a b c*d + e/+
b b*4a*c* - 2а*/
Постфиксная оценка
Постфиксное выражение оценивается алгоритмом, который просматривает
выражение слева направо и использует стек. Для этого примера мы полагаем,
что все операторы являются бинарными. Унарные операторы мы охватываем
в упражнениях.
Выражение в постфиксном формате содержит только операнды и
операторы. Мы читаем каждый терм и в зависимости от его типа выполняем
действия. Если терм является операндом, помещаем его значение в стек.
Если терм является оператором <ор>, дважды выполняем выборку из стека
для возвращения операндов X и Y. Затем оцениваем выражение, используя
оператор <ор> и помещаем результат X<op>Y обратно в стек. После чтения
каждого терма в выражении вершина стека содержит результат.
Пример 5.3
Инфиксное выражение 4+3*5 записывается в постфиксной форме как
4 3 5*+. Для его оценки требуется пять шагов.
Шаги 1-3: Читать операнды 4 3 5 и помещать каждое число в стек.
Шаг!
Шаг 2
ШагЗ
top
top
top
Push 4
Push3
Push 5
Шаг 4: Читать оператор * и оценить выражение выборкой верхних
двух операндов 5 и 3 и вычислением 3*5. Результат 15 поместить
обратно в стек.
top
Шаг 4
Шаг 5: Читать оператор + и оценить выражение выборкой операндов
15 и 4 и вычислением 4+15 = 19. Результат 19 поместить обратно в
стек, возвратить в качестве результата полученное выражение.
top
Шаг 5
Применение: постфиксный калькулятор
Мы иллюстрируем вычисление постфиксного выражения, моделируя
работу с RPN-калькулятором, имеющим операторы +,-,*,/ и л (возведение
в степень). Калькулятор принимает данные с плавающей точкой и вычисляет
выражения. Данные калькулятора и операции включаются в класс Calculator,
а простая main-функция вызывает его методы. Класс Calculator содержит
открытые функции-члены, которые вводят выражение и очищают
калькулятор. Для оценки выражения используется ряд закрытых функций-членов.
Спецификация класса Calculator
ОБЪЯВЛЕНИЕ
enum Boolean {False, True};
typedef double DataType; // калькулятор принимает числа типа double
#include "astack.h" // включить файл с описанием класса Stack
class Calculator
{
private:
// закрытые члены: стек калькулятора и операторы
Stack S;
void Enter{double num);
Boolean GetTwoOperands(doubles opndl, doubles opnd2);
void Compute(char op);
public:
// конструктор
Calculator(void);
// вычислить выражение и очистить калькулятор
void Run(void);
void Clear(void);
};
ОПИСАНИЕ
Конструктор умолчания создает пустой стек калькулятора. Так как
калькулятор работает постоянно, пользователь должен вызывать Clear для
очистки стека калькулятора и обеспечения последующего вычисления нового
выражения.
Операция Run позволяет вводить выражение в RPN-формате. Ввод символа
"=" завершает выражение. Отображается только конечное значение
выражения.
Сообщение об ошибке Missing operand (Отсутствует операнд) выводится,
когда оператор не имеет двух операндов. Попытка разделить на ноль также
вызывает сообщение об ошибке. В любом другом случае калькулятор очищает
стек и готовится к новому вводу.
ПРИМЕР
Calculator CALC; //Создает объект CALC
CALC.Run();
<Пример работы>
4 3* =
12 // оезультат выражения 4*3
Реализация класса Calculator
Функции калькулятора выполняются рядом методов, которые позволяют
клиенту вводить число, выполнять вычисление и печатать результат на экране.
Определение класса находится в файле calc.h.
Calculator::Calculator(void)
{}
Метод Enter принимает аргумент с плавающей точкой и помещает его в
стек.
//сохраняем значение данных в стеке
void Calculator::Enter(double num)
{
S.Push(num);
}
Функция GetTwoOperands используется методом Compute для получения
операндов из стека калькулятора и присваивания их параметрам выхода
operandi и operand 2. Этот метод выполняет проверку ошибок и возвращает
значение, которое указывает, существуют ли оба операнда.
// извлекать операнды из стека и назначать из параметрам
// печатать сообщение и возвращать False,
// если нет двух операндов
Boolean Calculator::GetTwoOperands(doubles opndl, doubles opnd2)
{
if (S.StackEmpty()) // проверить наличие операнда
{
cerr << "Missing operand!". « endl;
return False;
}
opndl = S.Pop (); // извлечь правый операнд
if (S.StackEmpty())
{
cerr « "Missing operand.1" « endl;
return False;
}
opnd2 = S.Pop(); // извлечь левый операнд
return True;
}
Все внутренние вычисления управляются методом Compute, который
начинается вызовом GetTwoOperands для выборки двух верхних стековых значений.
Если GetTwoOperands возвращает False, мы имеем неправильные операнды и
метод Compute очищает стек калькулятора. Иначе Compute выполняет операцию,
указанную символьным параметром ор ('+', '-', '*', '/\ ,А') и помещает результат
в стек. При попытке деления на 0 печатается сообщение об ошибке, и стек
калькулятора очищается. Для возведения в степень используется функция
double pow(double х, double у);
которая вычисляет ху. Она определяется в C++ библиотеке <math.h>.
// выполнение операции
void Calculator::Compute(char op)
{
Boolean result;
double operandi, operand2;
// извлечь два операнда и получить код завершения
result = GetTwoOperands(operandi, operand2);
// при успешном завершении, выполнить оператор
// и поместить результат в стек
// иначе, очистить стек, проверять деление на 0.
if (result » True)
switch(op)
{
case '+': S.Push(operand2+operandl);
break;
case '-': S.Push(operand2-operandl);
break/
case '*': S.Push(operand2*operandl);
break;
case '/': if (operandi »* 0.0)
{
cerr « "Деление на ноль!" « endl;
S,ClearStack();
}
else
S.Push(operand2/operandi);
break;
case 'Л': S.Push(pow(operand2,operandi));
break;
}
else
S.ClearStackO; // ошибка! очистить калькулятор
}
Основное действие калькулятора реализуется открытым методом Run,
который выполняет оценку постфиксного выражения. Главный цикл в методе
Run читает символы из потока ввода и завершается, когда считывается символ
"=". Символы пробела игнорируются. Если символ является оператором (Ч-\
*-'» **\ 7*> '"')» соответствующая операция выполняется вызовом метода
Compute. Если символ не является оператором, Run полагает, что проверяется
первый символ операнда, поскольку поток должен содержать только операторы
и операнды. Run помещает символ обратно в поток ввода, чтобы он мог быть
последовательно считан как часть операнда с плавающей точкой.
// считывать и оценивать постфиксное выражение
// при вводе '=' остановиться
void Calculator::Run(void)
{
char с;
double newoperand;
while(cin » с, с !~ '■') // читать до символа '«' (Выход)
{
switch(с)
{
case '+': // определение нужного оператора
case '-':
case '*':
case '/':
case 'Л':
Compute(с); // имеется оператор; вычислить его
break;
default:
//не оператор, возможно, операнд; вернуть символ
cin.putback(c);
// читать операнд и передавать его в стек
cin » newoperand;
Enter(newoperand);
break;
}
)
// ответ, сохраняемый в вершине стека печатать с использованием Peek
if (!S.StackEmpty())
cout « S.Peek() « endl;
}
// очистить стек операндов
void Calculator::Clear(void)
{
S.ClearStackO ;
}
Программа 5.З. Постфиксный калькулятор
Объект CALC — это калькулятор. Первый запуск вычисляет длину
гипотенузы прямоугольного треугольника со сторонами 6, 8 и 10. Два других
запуска иллюстрируют обработку ошибок.
#include "calc.h"
void main (void)
{
Calculator CALC;
CALC.RunO;
}
/*
Оапуск 1 программы 5.3>
88*66* + .5 Л =
10
Оапуск #2 программ*! 5.3>
3 4 + *
Missing operand!
3 4 + 8* =
56
Оапуск 3 программы 5.3>
10/-
Деление на 0!
*/
5.4. Очереди
Очередь (queue) — это структура данных, которая сохраняет элементы в
списке и обеспечивает доступ к данным только в двух концах списка (рис. 5.4).
Элемент вставляется в конец списка и удаляется из начала списка.
Приложения используют очередь для хранения элементов в порядке их поступления.
1-й
2-й
3-й
4-й
|ПоследЛ
Начало
Рис.5.4. Очередь
А
начало конец
А
В
начало конец
А
в
с
начало конец
В
с
начало конец
С
Конец
Добавление А
Добавление В
Добавление С
Удаление А
Удаление В
начало конец
Рис.5.5. Операции очереди
Элементы удаляются из очереди в том же порядке, в котором они
сохраняются и, следовательно, очередь обеспечивает FIFO (first-in/first-out) или FCFS-
упорядочение (first-come/first-served). Обслуживание клиентов в очереди и
буферизация задач принтера в системе входных и выходных потоков
принтера — это классические примеры очередей.
Очередь включает список и определенные ссылки на начальную и конечную
позиции (рис. 5.5). Эти позиции используются для вставки и удаления
элементов очереди. Подобно стеку, очередь сохраняет элементы параметризованного
типа DataType. Подобно стеку, абстрактная очередь не ограничивает
количество элементов ввода. Однако, если для реализации списка используется
массив, может возникнуть условие полной очереди.
ADT Queue
данные
Список элементов
front: позиция первого элемента в очереди
rear: позиция последнего элемента в очереди
count: число элементов в очереди в любое данное время
Операции
Конструктор
Начальные значения: Нет
Процесс: Инициализация начала и конца очереди.
QLength
Вход: Нет
Предусловия: Нет
Процесс: Определение количества элементов в очереди
Выход: Возвращать количество элементов в очереди.
Постусловия: Нет
QEmpty
Вход: Нет
Предусловия: Нет
Процесс: Проверка: пуста ли очередь.
Выход: Возвращать 1 (True), если очередь пуста и 0 (False)
иначе. Заметьте, что это условие эквивалентно
проверке, равна ли QLength 0.
Постусловия: Нет
QDelete
Вход: Нет
Предусловия: Очередь не пуста.
Процесс: Удаление элемента из начала очереди.
Выход: Взвращать элемент, удаляемый из очереди.
Постусловия: Элемент удаляется из очереди.
Qlnsert
Вход: Элемент для сохранения в очереди.
Предусловия: Нет
Процесс: Запись элемента в конец очереди.
Выход: Нет
Постусловия: Новый элемент добавляется в очередь
QFront
Вход: Нет
Предусловия: Очередь не пуста.
Процесс: Выборка значения элемента в начале очереди.
Выход: Возвращать значение элемента в начале очереди.
Постусловия: Нет
ClearQueue
Вход: Нет
Предусловия: Нет
Процесс: Удаление всех элементов из очереди и восстановление
начальных условий.
Выход: Нет
Постусловия: Очередь пуста.
Конец ADT Queue
Пример 5.4
На рис. 5.6 показаны изменения в очереди из четырех элементов во
время последовательности операций. В каждом случае приводится
значение флажка QEmpty.
Очереди широко используются в компьютерном моделировании, таком
как моделирование очереди клиентов в банке. Многопользовательские
операционные системы поддерживают очереди программ, ожидающих
выполнения, и заданий, ожидающих печати.
Операция
Список очереди Признак пустого списка
Qlnsert (A)
Qlnsert (В)
QDelete О
front
rear
А
front rear
А
В
front
В
rear
TRUE
FALSE
FALSE
FALSE
front rear
Рис.5.6. Изменения в очереди из четырех элементов во время операций
5.5. Класс Queue
Класс Queue реализует ADT, используя массив для сохранения списка
элементов и определяя переменные, которые поддерживают позиции front и
rear. Так как для реализации списка используется массив, класс содержит
метод Qfull для проверки, заполнен ли массив. Этот метод будет устранен,
в главе 9, где представлена реализация очереди со связанным списком.
Спецификация класса Queue
ОБЪЯВЛЕНИЕ
#include <iostream.h>
#include <stdlib.h>
// максимальный размер списка очереди
const int MaxQSize = 50;
class Queue
{
private:
// массив и параметры очереди
int front, rear, count;
DataType qlist[MaxQSize];
public:
// конструктор
Queue (void); // initialize integer data members
// операции модификации очереди
void Qlnsert(const DataTypes item);
DataType QDelete(void);
void ClearQueue(void);
// операции доступа
DataType QFront(void) const;
// методы тестирования очереди
int QLength(void) const;
int QEmpty(void) const;
int QFull(void) const;
};
ОПИСАНИЕ
Параметризованный тип DataType позволяет очереди управлять
различными типами данных. Класс Queue содержит список (qlist), максимальный размер
которого определяется константой MaxQSize.
Данное-член count содержит число элементов в очереди. Это значение также
определяет, является ли очередь полной или пустой.
Qlnsert принимает элемент item типа DataType и вставляет его в конец
очереди, a QDelete удаляет и возвращает элемент в начале очереди. Метод
QFront возвращает значение элемента в начале очереди.
Очередь следует тестировать при помощи метода QEmpty перед удалением
элемента и метода QFull перед вставкой новых данных для проверки, пуста ли
очередь или заполнена. Если предусловия для Qlnsert или QDelete нарушаются,
программа печатает сообщение об ошибке и завершается.
Объявление очереди и реализация содержатся в файле aqueue.h.
ПРИМЕР
typedef int DataType;
♦include aqueue.h
Queue Q; //объявляем очередь
Q.Qlnsert(30); //вставляем 30 в очередь
Q.Qlnsert(70); //вставляем 70 в очередь
cout «Q.QLength()«endl; //печатает 2
cout «Q.QFront () «endl; //печатает 30
if (!Q.QEmpty( ))
cout «Q.QDelete( ); //печатает значение 30
cout «Q.QFront ( ) «endl; //печатает 70
Q/ClearQueue( ); //очистка очереди
Реализация класса Queue
Начало очереди определяется первым клиентом в очереди. Конец очереди —
это место непосредственно за последним элементом очереди. Когда очередь
полна, клиенты должны идти к другой расчетной очереди. На рис. 5.7
показаны изменения в очереди и некоторые проблемы, которые влияют на
реализацию. Предположим, очередь ограничивается четырьмя клиентами. Вид 2
показывает, что после того, как клиента А обслужили, клиенты В и С
перемещаются вперед. Вид 3: клиента В обслужили и С перемещается вперед. Вид 4:
клиенты D, Е и F встают в очередь, заполняя ее, а клиент G должен встать в
другую очередь.
Эти виды отражают поведение клиентов в расчетной очереди. После того,
как одного клиента обслужили, другие в очереди перемещаются вперед. В
терминологии списка, элементы данных смещаются вперед на одну позицию
каждый раз, когда какой-либо элемент покидает очередь. Эта модель не
обеспечивает эффективную компьютерную реализацию. Предположим,
очередь содержит 1000 элементов. Когда один элемент удаляется из начала,
999 элементов должны переместиться влево.
Наша реализация очереди вводит круговую модель. Вместо сдвига
элементов влево, когда один элемент удаляется, элементы очереди организованы
логически в окружность. Переменная front всегда является местоположением
первого элемента очереди, и она продвигается вправо по кругу по мере вы-
Вид№1
Ввести клиентов
А, В, С
Вид №2 Обслужить клиента А
Вид №3 Обслужить клиента В
Вид №4
Добавить клиентов
D, E, F
А
front
В
front
С
front
С
В
С
rear
D
С
rear
Е
rear
F
front
G
rear
Рис. 5.7. Очередь из четырех элементов
полнения удалений. Переменная rear является местоположением, где
происходит следующая вставка. После вставки rear перемещается по кругу вправо.
Переменная count поддерживает запись количества элементов в очереди, и
если счетчик count равен значению MaxQSize, очередь заполнена. На рис. 5.8
показана круговая модель очереди.
размер = 4 count » 3
размер = 4 count ■= 2
размер = 4 count » 3
rear
front
rear
rear
front
front
Очередь заполнена
размер - 4 count = 4
Удалить А
размер • 4 count ■ 3
Вставить D
rear
front
front
rear
Вставить Е Удалить В
Рис, 5.8. Круговая модель очереди
Реализуем круговое движение, используя операцию остатка от деления:
Перемещение конца очереди вперед: rear = (rear+l)%MaxQSize;
Перемещение начала вперед: front - (front+l)%MaxQSize;
Пример 5.5
Используем целый массив qlist (размер = 4) из четырех элементов
для реализации круговой очереди. Первоначально count = 0, и индексы
front и rear имеют значение 0. На рис. 5.9 показана последовательность
вставок и удалений круговой очереди.
count * 0
3
Вставить 3
count «= 1
3
Вставить 5
count = 2
5
front =
rear «
*0
0
Вставить б
count - 3
3
5
6
front = 0 rear = 3
Удалить 5
count = 2
6
2
rear * 0 front = 2
Удалить 2
count = 1
8
front = 0 rear = 1
Удалить 3
count * 2
front = 0 rear = 2
Вставить 2
count = 3
5 6
5 6 2
front - 1
rear = 3
rear = 0 front = 1
8
Вставить 8
count = 3
6
2
8
Удалить 6
count = 2
2
rear = 1 front = 2
rear = 1 front = 3
Удалить 8
count = 0
front = 1
rear = 1
front = 0 rear = 1
Рис 5.9. Последовательность вставок и удалений круговой очереди
Конструктор Queue. Конструктор инициализирует элементы данных front,
rear и count нулевыми значениями. Это задает пустую очередь
// инициализация данных-членов: front, rear, count
Queue::Queue (void) : front(0), rear(0), count(0)
О
Операции класса Queue. Для работы с очередью предоставляется
ограниченный набор операций, которые добавляют новый (метод Qlnsert) или
удаляют (метод Qdelete) элемент. Класс имеет также метод QFront, который
позволяет делать выборку первого элемента очереди. Для некоторых
приложений эта операция позволяет определять, должен ли элемент удаляться из
списка.
В этом разделе описываются операции обновления очереди, вставляющие
и удаляющие элементы списка. Другие методы имеют модели в стековом
классе и их можно найти в программном приложении в файле aqueue.h.
Перед началом процесса вставки индекс rear указывает на следующую
позицию в списке. Новый элемент помещается в это место, и переменная
count увеличивается на 1.
qlist[rear] - item;
count++;
После помещения элемента в список индекс rear должен быть обновлен
для указания на следующую позицию [Рис. 5.10 (А)]. Так как мы используем
круговую модель, вставка может появиться в конце массива (qlist[size-l]) с
перемещением rear к началу списка [рис. 5.10(B)].
Вычисление выполняется с помощью оператора остатка (%).
rear - (rear+1) % MaxQSize;
Qlneert
// вставить item в очередь
void Queue::Qlnsert (const DataType& item)
{
// закончить программу, если очередь заполнена
if (count == MaxQSize)
{
cerr « "Переполнение очереди!" « endl;
exit(1);
}
// увеличить count, присвоить значение item элементу массива
// изменить значение rear
count++;
qlist[rear] = item;
rear = (rear+1) % MaxQSize;
}
(A)
До Qlnsert: count = 2
После Qlnsert: count = 3
■
t
front
■
t
rear
■
t
front
■
элемент
t
rear
(B)
До Qlnsert: count = 2
После Qlnsert: count = 3
■
t
front
■
t
rear
t
rear
■
t
front
ж
элемент
Рис 5.10. Метод Qinsert
Операция QDelete удаляет элемент из начала очереди, позиции, на которую
ссылается индекс front. Мы начинаем процесс удаления, копируя значение
во временную переменную и уменьшая счетчик очереди.
item = qlist[front];
count—;
В круговой модели необходимо перенести front в позицию следующего
элемента в списке, используя оператор остатка от деления (%) (рис. 5.11).
front = (front + 1) % MaxQSize;
Значение из временной позиции становится возвращаемым значецием.
QDelete
// удалить элемент из начала очереди
// и возвратить его значение
DataType Queue::QDelete(void)
{
DataType temp;
// если очередь пуста, закончить программу)
{
cerr « "Удаление из пустой очереди!" « endl;
exit(l);
)
// записать значение в начало очереди
temp » qlist[front];
// уменьшить count на единицу
// продвинуть начало очередии возвратить прежнее значение
//из начала
count—;
front - (front+1) % MaxQSize;
return temp;
(A)
До QDelete: count = 3
После QDelete: count =2
(B)
■
элемент
■
■
T T
front rear
До QDelete: count = 3
■
элемент
A A
■
T T т
rear front front
■
■
т
front
После QDelete: count =2
■
T
rear
t
rear
элемент
возвратить
в
элемент
озврати
ть
Рис. 5.11. Метод QDelete
Операции Qlnsert, QDelete и QFront имеют эффективность 0(1)9 поскольку
каждый метод имеет прямой доступ к элементу либо в начале, либо в конце
списка.
Программа 5.4. Партнеры по танцу
Танцы организуются в пятницу вечером. По мере того, как мужчины
и женщины входят в танцевальный зал, мужчины выстраиваются в один
ряд, а женщины — в другой. Когда танец начинается, партнеры
выбираются по одному из начала каждого ряда. Если в этих рядах неодинаковое
количество людей, лишний человек должен ждать следующего танца.
Данная программа получает имена мужчин и женщин, читая файл
dance.dat. Каждый элемент данных файла имеет формат
Sex Name
где Sex — это один символ F или М. Все записи считываются из файла,
и организуются очереди. Партнеры образуются удалением их из каждой
очереди. Этот процесс останавливается, когда какая-либо очередь
становится пустой. Если есть ожидающие люди, программа указывает, сколько
их и печатает имя первого человека, который будет танцевать в следующем
танце.
iinclude <iostream.h>
♦include <iomanip.h>
iinclude <fstream.h>
#pragma hdrstop
// record that declares a dancer
struct Person
{
char name[203;
char sex; // ' F' (женщина) ; 'М' (мужчина)
};
// очередь содержит список объектов типа Person
typedef Person DataType;
iinclude "aqueue.h"
void main(void)
{
// две очереди для разделения на партнеров по танцу
Queue maleDancers, femaleDancers;
Person p;
char blankseparator;
// входной файл для танцоров
ifstream fin;
// открыть файл с проверкой на его существование
fin.open("dance.dat");
if (!fin)
{
cerr « "He возможно открыть файл!" « endl;
exit (1);
}
// считать входную строку, которая включает
// пол, имя и возраст
while(fin.get(p.sex)) // цикл до конца файла
{
fin.get(blankseparator);
fin.getline(p.name,20,' \n');
// вставить в соответствующую очередь
if (p.sex »- ' F')
femaleDancers.Qlnsert(p);
else
maleDancers.Qlnsert(p);
}
// установить пару танцоров, получением партнеров
//из двух очередей
// закончить, когда одна из очередей окажется пустой
cout « "Партнеры по танцу: " « endl « endl;
while (!femaleDancers.QEmpty() && !maleDancers.QEmptyО)
{
p * femaleDancers.QDeleteO;
cout « p.name « " "; // сообщить имя женщины
p « maleDancers.QDelete();
cout « p.name « endl; // сообщить имя мужчины
}
cout « endl;
// если в какой-либо очереди кто-либо остался,
// сообщить имя первого (первой) из них
if (!femaleDancers.QEmpty())
{
cout « "Следующего танца ожидают "
« femaleDancers.QLength()
« " дамы" « endl;
cout « femaleDancers.QFront().name
« " первой получит партнера." « endl;
}
else if (!maleDancers.QEmpty())
{
cout « "Следующего танца ожидают "
« maleDancers.QLength()
<< " кавалера." « endl;
cout « maleDancers.QFront().name
« " первым получит патнера." « endl;
}
}
/*
<Файл "dance.dat">
M George Thompson
F Jane Andrews
F Sandra Williams
M Bill Brooks
M Bob Carlson
F Shirley Granley
F Louise Sanderson
M Dave Evans
M Harold Brown
F Roberta Edwards
M Dan Gromley
M John Gaston
<Выполнение программы 5.4>
Партнеры по танцу:
Jane Andrews George Thompson
Sandra Williams Bill Brooks
Shirley Granley Bob Carlson
Louise Sanderson Dave Evans
Roberta Edwards Harold Brown
Следующего танца ожидают 2 кавалера.
Dan Gromley первым получит патнера.
*/
Применение: использование очереди для сортировки данных. На заре
компьютеризации для упорядочения стопки перфокарт использовался
механический сортировщик. Следующая программа моделирует действие этого
сортировщика. Для объяснения процесса предположим, что перфокарты
содержат числа из двух цифр в диапазоне 00-99, и сортировщик имеет десять
бункеров с номерами 0-9. При сортировке выполняются два прохода для
обработки сначала по позициям единиц, а затем — десятков. Каждая
перфокарта попадает в соответствующий бункер. Такая сортировка называется
поразрядной сортировкой (radix sort) и может быть расширена до сортировки
чисел любого размера.
Начальный список: 91 46 85 15 92 35 31 22
В проходе 1 перфокарты распределяются по позициям единиц.
Перфокарты выбираются из бункеров в порядке от 0 до 9.
Список после прохода 1: 91 31 92 22 85 15 35 46
В проходе 2 перфокарты распределяются по позициям десятков.
Перфокарты выбираются из бункеров в порядке от 0 до 9.
Список после прохода 2: 15 22 31 35 46 85 91 92
После двух проходов список становится упорядоченным. Интуитивно
проход 1 приводит к тому, что все перфокарты с меньшими единичными цифрами
предшествуют перфокартам с большими единичными цифрами. Например,
все числа, заканчивающиеся на 1, предшествуют числам, заканчивающимся
на 2 и так далее. Для прохода 2 предположим, что две перфокарты имеют
значение 3s и 3t при s<t. Они попадают в бункер 3 в таком порядке, что
за 3s следует 3t (помните, что все перфокарты, заканчивающиеся на s
предшествуют перфокартам, заканчивающимся на t после прохода 1). Так как
каждый бункер является очередью, перфокарты покидают бункер 3 в порядке
FIFO. Если после прохода 2 перфокарты снова собрать, они будут
упорядочены.
Программа 5.5. Поразрядная сортировка
Данная программа выполняет поразрядную сортировку чисел из двух
цифр. Последовательность из 50 случайных чисел сохраняется в списке,
представленном массивом L.
int L(50); //содержит 50 случайных целых
Массив очередей моделирует 10 сортировочных бункеров;
Queue digitQueue[10]; // 10 очередей целых
Функции Distribute передается массив чисел, массив очередей digitqueue
и определенный пользователем дескриптор ones или tens для указания того,
выполняется ли сортировка по позициям единиц (проход 1) или десятков
(проход 2).
В проходе 1 используется выражение L[i]%10 для доступа к цифре
единиц, а затем — полученное значение для передачи L[i] соответствующей
очереди.
digitQueue[L[i] % 10].Qlnsert(L[i])
В проходе 2 используется выражение L[i]/10 для доступа к цифре
десятков, а затем — полученное значение для передачи L[i] соответствующей
очереди.
digitQueue[L[i] / 10].Qlnsert(L[i])
Функция Collect просматривает массив очередей digitQueue в порядке
цифр 0 — 9 и извлекает все элементы из каждой очереди в список L.
while (!digitQueue[digit].QEmpty())
L[i++] = digitQueue[digit].QDelete();
Функция Print записывает числа в списке. Числа печатаются по 10 в
строке с каждым числом, использующим пять позиций печати.
#include <iostream.h>
#pragma hdrstop
#include "random.h" // объявление генератора случайных чисел
typedef int DataType;
#include "aqueue.h"
enum DigitKind {ones,tens};
void Distribute(int L[],Queue digitQueue[],int n,
DigitKind kind)
{
int i;
// цикл для массива из п элементов
for {i =0; i < n; i++)
if (kind == ones)
// вычислить цифру единиц и использовать ее как номер очереди
digitQueue[L[i] % 10].Qlnsert(L[i]);
else
// вычислить цифру десятков и использовать ее как номер очереди
digitQueue[L[i] / 10].Qlnsert(L[i]);
}
// собрать элементы из очередей в массив
void Collect(Queue digitQueue[], int L[])
{
int i = 0, digit = 0;
// сканировать массив очередей,
// используя индексы 0, 1, 2, и т.д.
for (digit = 0; digit < 10; digit++)
// собирать элементы, пока очередь не опустеет,
// копировать элементы снова в массив
while (!digitQueue[digit].QEmpty())
L[i++] = digitQueue[digit].QDelete();
}
// сканировать массив из п элементов и печатать каждый элемент.
// в каждой строке печатать 10 элементов
void PrintArray(int L[],int n)
{
int i = 0;
while(i < n)
{
cout.width(5) ;
cout << L[i];
if (++i % 10 == 0)
cout « endl;
}
cout « endl;
}
void main(void)
{
// 10 десять очередей для моделирования бункеров
Queue digitQueue[10];
// массив из 50 целых
int L[50];
int i = 0;
RandomNumber rnd;
// инициализировать массив случайными числами
// в диапазоне 0-99
for (i = 0; i < 50; i++)
L[i] =* rnd.Random(100) ;
// распределить в 10 бункеров по цифрам единиц;
// собрать и распечатать
Distribute(L, digitQueue, 50, ones);
Collect(digitQueue, L);
PrintArray(L,50);
// распределить в 10 бункеров по цифрам десятков;
// собрать и распечатать отсортированный массив
Distribute(L,digitQueue, 50, tens);
Collect(digitQueue,L);
PrintArray(L,50);
}
/*
Оапуск программы 5.5>
40
62
3
25
88
3
24
52
69
83
70
72
73
16
98
7
25
54
69
84
20
82
33
46
68
11
27
55
70
85
51
82
54
86
69
12
29
59
72
86
11
62
24
36
79
15
33
62
72
88
81
72
84
67
89
16
36
62
73
89
21
52
55
17
29
17
40
63
79
92
12
83
15
27
69
20
46
65
81
97
52
63
65
7
99
21
51
67
82
98
92
23
85
97
59
23
52
68
82
99
*/
Каждый проход выполняет О(п) операций, состоящих из деления, вставки
в очередь и удаления из нее. Так как выполняется два прохода, порядок
алгоритма поразрядной сортировки чисел из двух цифр составляет 0(2п) и также
является линейным. Поразрядная сортировка может быть расширена до
сортировки п чисел, каждое из которых имеет т цифр. В этом случае сложность
составляет О(тп), так как поразрядная сортировка выполняет т проходов,
каждый включающий О(п) операций. Этот алгоритм превосходит алгоритмы
сортировки, имеющие порядок 0(п \og2n), такие как heapsort и quicksort,
которые описываются в главах 13 и 14. Однако, поразрядная сортировка имеет
меньшую эффективность по использованию памяти, чем эти in-place-сортиров-
ки. Алгоритмы in-place-сортировок сортируют данные в оригинальном
массиве и не используют временную память. Поразрядная сортировка требует
использования 10 очередей. Каждая очередь имеет свою локальную память
для front, rear, queue count и массива. Кроме того, поразрядная сортировка
менее эффективна, если числа содержат много цифр, так как при этом
возрастает произведение тп.
5.6. Очереди приоритетов
Как уже описывалось, очередь — это структура данных, которая
обеспечивает FIFO-порядок элементов. Очередь удаляет самый старый элемент из
списка. Приложения часто требуют модифицированной версии памяти для
очереди, в которой из списка удаляется элемент с высшим приоритетом. Эта
структура, называемая очередью приоритетов (priority queue), имеет
операции PQInsert и PQDelete. PQInsert просто вставляет элемент данных в список,
а операция PQDelete удаляет из списка наиболее важный элемент (с высшим
приоритетом), оцениваемый по некоторому внешнему критерию, который
различает элементы в списке. Например, предположим, компания имеет
централизованную секретарскую группу для обеспечения выполнения персоналом
определенных задач. Политика компании рассматривает задание, выданное
президентом компании, как имеющее высший приоритет, за которым следуют
задания менеджеров, затем — задания супервайзеров и так далее. Должность
человека в компании становится критерием, который оценивает
относительную важность задания. Вместо управления заданиями на основе порядка
first-come/first-served (очередь), секретарская группа выполняет задания в
порядке их важности (очередь приоритетов).
Очереди приоритетов находят применение в операционной системе, которая
записывает процессы в список и затем выполняет их в порядке приоритетов.
Например, большинство операционных систем присваивают более низкий, чем
другим процессам, приоритет выполнению печати. Приоритет 0 часто
определяется как высший приоритет, а обычный приоритет имеет большее значение,
такое как 20. Например, рассмотрим следующий список задач и их приоритетов:
Задача № 1
20
Задача № 2
0
Задача № 3
40
Задача № 4
30
Задача № 5
10
Порядок хранения
Задачи выполняются в порядке 2, 5, 1, 4 и 3.
Задача № 2 Задача № 5 Задача № 1 Задача № 4 Задача № 3
Порядок выполнения
В большинстве приложений элементы в очереди приоритетов являются
парой ключ-значение (key-value pair), в которой ключ определяет уровень
приоритета. Например, в операционной системе каждая задача имеет
дескриптор задачи и уровень приоритета, служащий ключом.
Уровень приоритета
Дескриптор задачи
При удалении элемента из очереди приоритетов в списке могут находиться
несколько элементов с одним и тем же уровнем приоритета. В этом случае мы
можем потребовать, чтобы эти элементы рассматривались как очередь. В
результате элементы с одним и тем же приоритетом обслуживались бы в порядке
их поступления. В следующем ADT мы не делаем никаких допущений по
поводу порядка элементов с одним и тем же уровнем приоритета.
Очередь приоритетов описывает список с операциями для добавления или
удаления элементов из списка. Имеется серия операций, которая определяет
длину списка и указывает, пуст ли список.
ADT PQueue
Данные
Список элементов.
Операции
Конструктор
Начальные значения: Нет
Процесс: Инициализация количества элементов списка
нулевым значением
PQLength
Вход: Нет
Предусловия: Нет
Процесс: Определение количества элементов в списке.
Выход: Возвращать количество элементов в списке.
Постусловия: Нет
PQEmpty
Вход: Нет
Предусловия: Нет
Процесс:- Проверка/ является ли количество элементов
списка равным 0.
Выход: Возвращать l(True), если в списке нет элементов,
и 0 (False) — иначе.
Постусловия: Нет
PQInsert
Вход: Элемент для сохранения в списке.
Предусловия: Нет
Процесс: Сохранение элемента в списке. Это увеличивает длину
списка на 1.
Выход: Нет
Постусловия: Список имеет новые элемент и длину.
PQDlelete
Вход: Нет
Предусловия: Очередь приоритетов не пуста.
Процесс: Удаление элемента с высшим приоритетом из списка.
это уменьшает длину списка на 1.
Выход: Возвращать элемент, удаленный из списка.
Постусловия: Элемент удаляется из списка, который теперь имеет
на один элемент меньше.
ClearPQ
Вход: Нет
Предусловия: Нет
Процесс: Удаление всех элементов из очереди приоритетов
и восстановление начальных условий.
Выход: Нет
Постусловия: Очередь приоритетов пуста.
Конец ADT PQueue
Класс PQueue
В этой книге приводятся различные реализации очереди приоритетов. В
каждом случае выделяется объект list для сохранения элементов. Мы
используем параметр count и методы доступа к списку для вставки и удаления
элементов. В этой главе элементы, сохраняемые в массиве, имеют
параметризованный тип DataType. В последующих главах используются упорядоченные
списки и динамические области для сохранения элементов в очереди
приоритетов.
Спецификация класса PQueue
ОБЪЯВЛЕНИЕ
#include <iostream.h>
#include <stdlib.h>
// максимальный размер массива очереди приоритетов
const int MaxPQSize = 50;
class PQueue
{
private:
// массив очереди приоритетов и счетчик
int count;
DataType pqlist[MaxPQSize];
public:
// конструктор
PQueue (void);
// операции, модифицирующие очередь приоритетов
void PQInsert(const DataType& item);
DataType PQDelete(void);
void ClearPQ(void)/
// тестирующие методы
int PQEmpty(void) const;
int PQFull(void) const;
int PQLength(void) const;
}/
ОПИСАНИЕ
Константа MaxPQSize определяет размер массива pqlist.
Метод PQInsert просто вставляет элементы в список. В спецификации не
делается никаких допущений о том, где элемент помещается в списке.
Метод PQDelete удаляет элемент с высшим приоритетом из списка. Мы
полагаем, что элемент с высшим приоритетом — это элемент с наименьшим
значением. Наименьшее значение определяется с использованием оператора
сравнения "<", который должен быть определен для DataType.
ПРИМЕР
typedef int DataType;
PQueue PQ;
PQ.PQInsert(20);
PQ.PQInsert(10);
cout « PQ.PQLengthO « endl; // печать 2
N » PQ.PQDelete(); // извлечь N * 10
Реализация класса Pqueue
Операции очереди приоритетов. Подобно обычной очереди, очередь
приоритетов имеет операцию для вставки элемента. ADT не делает никаких
допущений о том, в какое место списка помещается элемент, оставляя этот вопрос в
качестве детали реализации в методе PQInsert. В данном случае мы сначала
тестируем, заполнен ли список, и завершаем программу при этом условии. В
противном случае, новый элемент вставляется в конец списка, местоположение
которого указывается с помощью счетчика (count).
До PQInsert: count = 4 После PQInsert: count = 5
20
40
10
30
20
40
10
30
50
Вставить 50 \
pqllst[4]
PQInsezt
// вставить элемент в очередь приоритетов
void PQueue::PQInsert (const DataTypeb item)
{
// если уже све элементы массива pqlist использованы,
// закончить завершить программу
if (count « MaxPQSize)
{
cerr « "Переполнение очереди приоритетов!" << endl;
exit(l)/
}
// поместить элемент в конец списка
//и увеличить count на единицу
pqlist[count] = item;
count++;
)
Метод PQDelete удаляет из списка элемент с высшим приоритетом. Это
условие не подразумевает, что мы выбираем первый элемент, когда имеются
два или более элементов, как и не подразумевает, что элементы сохраняют
какой-либо порядок во время процесса удаления. Это все — детали
реализации. В данном случае мы сначала определяем, является ли список пустым,
и завершаем программу, если условие является равным True. В противном
случае, мы ищем минимальное значение и удаляем его из списка, уменьшая
длину очереди (count) и заменяя этот элемент последним элементом в списке.
Индекс последнего элемента становится новым значением count.
В следующем примере минимальное значение (10) имеет элемент с
индексом 2. Метод удаляет этот элемент, уменьшая длину списка на 1 и заменяя
его последним элементом в списке (pqlist[count]). Затем удаляется 15,
который находится в конце списка.
count=5
Минимальный элемент с индексом 2
count=4
Минимальный элемент заменить последним
Удалить 10
20
40
10
Т
pqlistp]
15
50
20
40
50
15
Вставить 50
count=4
Минимальный элемент с индексом 3
count=3
Минимальный элемент заменить последним
Удалить 15
20
40
50
Т
pqlistP]
15
20
40
50
15
PQDelete
// удаляет элемент из очереди приоритетов
/У и возвращает его значение
DataType PQueue::PQDelete(void)
{
DataType min;
int i, minindex =0;
if (count > 0)
{
// найти минимальное значение и его индекс в массиве pqlist
min = pqlist[0]/ // предполагаем, pqlist[0] - это минимум
// просмотреть остальные элементы
// изменяя минимум и его индекс
for (i = 1; i < count; i++)
if (pqlist[i] < min)
{
// новый минимум в элементе pqlist[i]. новый индекс - i
min = pqlist[i];
minindex = i;
}
// переместить хвостовой элемент на место минимального
//и уменьшить на единицу count
pqlist[minindex] = pqlist[count-1];
count--;
}
// массив qlist пуст, завершить программу
else
{
cerr << "Удаление из пустой очереди приоритетов!" << endl;
exit(l);
}
// возвратить минимальное значение
return min;
}
Операция PQInsert имеет время вычисления (порядок) 0(1), так как она
непосредственно добавляет элемент в конец списка. С другой стороны,
операция PQDelete требует начального просмотра списка для определения
минимального значения и его индекса. Эта операция имеет время вычисления 0(п)у
где п — это текущая длина очереди приоритетов.
Данное-член count содержит количество элементов в списке. Это значение
используется в реализации методов PQLength, PQEmpty и PQFull. Код этих
методов находится в программном приложении в файле apqueue.h.
Приложение: службы поддержки компании
Сотрудники компании определяются по категориям: менеджер, супервайзер
и рабочий. Создав тип enum с различными категориями, мы имеем
естественное упорядочение, дающее каждой уровень приоритета при заявке на
выполнение работ.
//уровень приоритета сотрудника (менеджер = 0, и т.д.)
enunv Staff{Manager, Supervisor, Worker}; // Менеджер =0, и т. д.
Работа службы поддержки компании выполняется общей секретарской
группой. Каждый сотрудник Может сделать заказ на выполнение задания,
заполнив форму, которая включает информацию о категории служащего,
подающего заявку на выполнение работы, ID-номер задания, и указывая время,
за которое будет выполнена работа. Эта информация сохраняется в записи
JobRequest. Заявки на выполнение работ вводятся в очередь приоритетов с
приоритетом, определяемым по категории сотрудника. Это упорядочение
используется, чтобы определить операцию < для объектов типа JobRequest.
// структура, определяющая запрос
struct JobRequest
{
Staff staffPerson;
int jobid;
int joTime;
};
// перегрузка оператора < для сравнения
// двух объектов JobRequest
int operator < (const JobRequest& a, const JobRequest& b)
{
return a.staffPerson < b.staffPerson;
}
Файл job.dat содержит список заявок на выполнение заданий, которые
загружаются в очередь приоритетов. Приложение подразумевает, что заявки
помещены заранее и ожидают выполнения. Элементы извлекаются из очереди
приоритетов и выполняются. Массив jobServicesUse содержит общее
количество времени, потраченное на обслуживание каждого из различных типов
сотрудников:
//время, потраченное на работу для каждой категории сотрудников
int jobServicesUse[3] = {0, 0, 0}/
Функции печати PrintJoblnfo и PrintSupportSummary выдают
информацию о каждом задании и об общем количестве минут, потраченных на
обслуживание каждой категории служащих в компании:
// печать одной записи структуры JobRequest
viod PrintJoblnfo(JobRequest PR)
{
switch (PR.staffPerson)
{
case Manager: cout « Manager ;
break;
case Supervisor: cout « Supervisor ;
break;
case Worker: cout « Worker ;
break;
}
#include <iomanip.h>
// печать общего времени работы,
// выделенного каждой категории служащих
void PrintJobSummery(int jobServiceUse[))
{
cout « ХпВремя обслуживания по категориями;
cout « Manager « setw(3) «
cout « jobServicesUse[0] « endl;
cout « Supervisor « setw(3) «
cout « jobServicesUse[1] << endl;
cout « Worker « setw(3) «
cout « jobServicesUse[2] << endl;
Программа 5.6. Выполнение заданий
Каждая заявка на выполнение работы сохраняется как запись в файле
job.dat. Эта запись задает категорию сотрудника (*М\ 43 \ 'W') и ID-номер
задания, и время для выполнения. Записи читаются, пока не достигается
конец файла, и каждая запись вставляется в очередь приоритетов jobPool.
На выходе каждое задание извлекается из очереди приоритетов, и его
информация печатается функцией PrintJoblnfo. Программа завершается
печатью резюме по выполненным заданиям вызовом функции PrintJob-
Summary. Структура JobRequest и функции работы с ней находятся в
файле job.h.
#include <iostream.h>
#include <fstream.h>
#pragma hdrstop
#include "job.h"
// элементы очереди приоритетов имеют тип JobRequest
typedef JobRequest DataType;
#include "apqueue.h" // включить класс PQueue
void main()
{
// обрабатывает до 25 заданий
PQueue jobPool;
// требуемые задания читаются из потока
// с дескриптором fin
ifstream fin;
// время облуживания каждой категории служащих
int jobServicesUse[3] = {0, 0, 0);
JobRequest PR;
char ch;
// открыть файл job.dat для ввода
// при ошибке завершить работу программы
fin.open("job.dat", ios::in | ios:inocreate);
if (!fin)
{
cerr « "Невозможно открыть файл job.dat" « endl;
exit(l);
}
// читать файл.
// вставлять каждое задание в очередь приоритетов jobPool.
// каждая строка начинается с символа, характеризующего
// служащего
while (fin » ch)
{
// полю staffPerson присвоить категорию служащего
switch(ch)
{
case 'M' : PR.staffPerson = Manager;
break;
case 'S': PR.staffPerson = Supervisor;
break;
case ' W : PR.staffPerson *= Worker;
break;
default: break;
}
// читать идентификатор задания
//и поле jobTime (время на выполнение задания)
fin » PR.jobid;
fin >> PR.jobTime;
// вставить задание в очередь приоритетов
jobPool.PQInsert(PR);
}
// удалять задания из очереди приоритетов
//и печатать эту информацию
cout « " Категория Номер Время\п\п";
while (!jobPool.PQEmpty())
{
PR = jobPool.PQDeleteO ;
PrintJoblnfo(PR);
// накапливать время для выполнения заданий
// каждой категории служащих
jobServicesUsefint(PR.staffPerson)] += PR.jobTime;
}
PrintJobSummary(jobServicesUse);
}
/*
<Входной файл job.dat>
M 300 20
W 301 30
M 302 40
S 303 10
S 304 40
M 305 70
W 306 20
W 307 20
M 308 60
S 30$ 30
Категория
Manager
Manager
Manager
Manager
Supervisor
Supervisor
Supervisor
Worker
Worker
Worker
Номер
300
302
308
305
309
303
304
306
307
301
Время
20
40
60
70
30
10
40
20
20
30
Время обслуживания по категориям
Manager 190
Supervisor 80
Worker 70
*/
5.7. Практическое применение:
управляемое событиями моделирование
Задачей моделирования является создание модели реальной ситуации для
лучшего ее понимания. Моделирование позволяет вводить различные условия
и наблюдать их результаты. Например, имитатор полета побуждает летчика
реагировать на неблагоприятные условия и измеряет скорость и соответствие
реакции. При изучении рынка сбыта моделирование часто используется для
измерения текущей деятельности или оценки расширения бизнеса. В этом
разделе рассмотрены модели прихода и ухода клиентов банка по мере того,
как они проходят через одну из п>2 очередей к кассиру. В заключении
оценивается эффективность обслуживания вычислением среднего времени
ожидания каждого клиента и времени занятости каждого кассира в процен-
тах. Используя моделирование, мы можем создать различные модели
обслуживания и оценить их с точки зрения стоимости и эффективности. Такой
подход выполняет управляемое событиями моделирование (event-driven
simulation), которое определяет объекты для представления банковской
деятельности. Мы используем вероятностные значения, описывающие
различные Ьжидаемые частоты прихода клиентов и различное ожидаемое время
обслуживания клиента кассиром. Моделирование позволяет использовать
генератор случайных чисел для отражения прихода и ухода клиентов в течение
рабочего дня в банке.
Моделирование позволяет также изменять параметры и таким образом
измерять относительное влияние на обслуживание, если мы изменяем
поведение клиента или кассира. Например, предположим, что отделение
маркетинга считает, что поощрительные подарки увеличат приход клиентов на
20%. Исследование с использованием моделирования повысит ожидаемые
темпы прихода клиентов и эффективность работы кассира. В некоторый
момент банку понадобятся дополнительные кассиры для поддержания
приемлемого обслуживания, а дополнительный расход может свести к нулю
прибыль от поощрительной кампании. Это моделирование снабжает банковского
менеджера параметрами для оценки обслуживания клиентов. Если среднее
время ожидания будет слишком долгим, менеджер может использовать еще
одного кассира. Это моделирование можно повторять снова и снова, просто
изменяя условия.
Разработка приложения
По мере выполнения приложение отслеживает приход и уход отдельных
клиентов. Например, предположим, 50-й клиент приходит в банк в 2:30
(приход) для получения вида услуг, требующего 12 минут времени кассира.
Данное моделирование подразумевает, что каждый кассир наглядно
предоставляет график своей работы, так что новый клиент может определить, кто
из кассиров его будет обслуживать и когда может начаться обслуживание.
[Занят до 2:40|
БАНК
Свободен
{Кассир 11 | Кассир 21
time(departure) = time(arrival) + servicetime
time(departure) = 2:30 + 0:12 = 2:42
Событие
Время
Приход
Уход
Время прихода
Время ухода
Обслуживание
Рассмотрим различные обстоятельства для 50-го клиента. Предположим,
что два кассира заняты, и клиент должен занять место в очереди и ожидать
обслуживания. Если Кассир 1 освобождается в 2:40, а Кассир 2 будет свободен
в 2:33, новый клиент выбирает Кассира 2. После 3 минут ожидания и 12
минут совершения операции клиент уходит в 2:45, что близко ко времени,
когда освобождается Кассир 2.
time(departure) = time(arrival) + waittime + servicetime
time(departure) » 2:30 + 0:03 +0:12 = 2:45
Приход
Уход
Событие
Время
Время прихода
Время ухода
ожидание
обслуживание
В нашем моделировании клиент выбирает кассира, который затем
обновляет на окне вывеску следующего свободного времени для обслуживания.
Занят до 2:40
БАНК
|3анят до 2:33]
[Занят до 2:40|
БАНК
ранят до 2:45|
1 Кассир 1| (Кассир 2| ) ( 1 Кассир Ц | Кассир 2]
До прихода клиента
После прихода клиента
Ключевыми компонентами в этом моделировании обслуживания в банке
являются события, включающие как приход, так и уход клиента, а реальное
время рассматривается как последовательность случайных событий, которые
отражают приход, обслуживание и уход клиента. Событие объявляется как
класс C++ с закрытыми данными-членами, которые определяют и клиента,
и кассира, а также поддерживают информацию о времени появления события,
типе события (приход или уход), продолжительности обслуживания клиента
и количестве времени, которое клиент вынужден провести в очереди, ожидая
обслуживания.
time
etype
customerlD
tellerlD
waittime
servicetime
Когда клиент входит в банк, мы имеем событие прихода (arrival event).
Например, если клиент 50 приходит в 2:30, соответствующей записью будет:
Данные события прихода
2:30
Приход
50
—
—
—
time
etype
customerlD
tellerlD
waittime
servicetime
Поля tellerlD, waittime и servicetime не используются для события
прихода. Эти поля определяются после того, как генерируется событие ухода.
После того, как клиент проверит, свободен ли кассир, мы можем
определить событие ухода (departure), которое описывает, когда клиент покинет
банк. Этот объект может использоваться для преобразования истории клиента
в банковской системе. Например, далее следует событие ухода для клиента,
который приходит в 2:30, ожидает 3 минуты Кассира 2 и уходит после
12-минутного обслуживания:
Данные события ухода
2:45
Уход
50
2
3
12
time
etype
customerlD
tellerlD
waittime servicetime
Поля данных объекта описывают всю соответствующую информацию,
которая относится к потоку клиентов в системе. Методы класса обеспечивают
доступ к полям данных, используемым для сбора информации об общей
эффективности обслуживания.
Спецификация класса Event
ОБЪЯВЛЕНИЕ
#include <iostream.h>
♦include random.h
enum EventType {arrival, departure};
class Event
{
private:
// данные-члены
int time; // время события
EventType etype; // тип события
int customerlD; // номер клиента
int tellerlD; // номер кассира
int waittime; // время ожидания
int servicetime; // время обслуживания
public:
Event(void);
Event(int t, EventType et, int en, int tn, int wt, int st);
int GetTime(void);
EventType GetEventType(void);
int GetCustomerlD(void) const;
int GetTellerlD(void) const;
int GetWaitTime(void)const;
int GetServiceTime(void)const;
};
ОПИСАНИЕ
Конструктор умолчания позволяет объявлять объект Event, чтобы позже
можно было инициализировать (присваиванием) его данные-члены. Второй
конструктор позволяет задать каждый параметр при объявлении события.
Остальные Методы возвращают значения данных-членов.
ПРИМЕР
Время задается в минутах от начала выполнения моделирования.
Event e; // объявление события конструктором умолчания
// клиент 3 уходит в 120 минут. После 10 минут ожидания,
//клиент затрачивает 5 минут на совершение операции.
е = Event(120, departure, 3, 1, 10, 5);
cout«e.GetService(); //выводится время обслуживания 5
Информация моделирования
Во время выполнения моделирования мы накапливаем информацию о
каждом кассире, указывающую общее количество клиентов, которых обслужил
кассир, время, которое клиенты провели в ожидании и общее время
обслуживания клиентов кассиром в течение дня. Вся эта информация
накапливается в записи TellerStats, содержащей также поле finishServi.ee,
представляющее значение вывески в окне.
Запись TellerStats
finishService
totalCustomerCount
totalCustomerWait
totalService
//Структура для информации о кассире
struct TellerStats
{
int finishService; //когда кассир может обслуживать
int totalCustomerCount; //общее количество обслуженных клиентов
int totalCustomerWait; //общее время ожидания обслуживания клиентами
int totalService; //общее время обслуживания клиентов
};
При моделировании генерируется событие прихода и ухода для каждого
клиента. Время всех событий отмечается, и они помещаются в очередь
приоритетов. Событие с высшим приоритетом в очереди приоритетов — это
событие с самой ранней отметкой времени. Структура списка позволяет
удалять события, так чтобы мы перемещались в возрастающей временной
последовательности с приходом и уходом клиентов.
Моделирование обслуживания в банке использует генератор случайных
чисел для определения следующего прихода клиента и времени текущего
обслуживания клиента. Генератор обеспечивает то, что любой результат в
диапазоне значений одинаково возможен. Если при моделировании текущее
событие прихода возникает в Т минут, следующий приход происходит
произвольно в диапазоне от T+arrivalLow до T+arrivalHigh минут, а общее время
обслуживания, необходимое для клиента, находится в диапазоне от serv-
iceLow до serviceHigh минут. Например, предположим, что некоторый клиент
приходит в 2 минуты и диапазон времени прихода следующего клиента
составляет от arriveLow=6 до arriveHigh=14 минут. Существует вероятность
1/9 того, что будет наблюдаться любой из результатов б, 7, . . . , 14 минут.
Текущий приход
Следующий приход
arrivalLow=4
arrivalLow=12
Если мы знаем что, последующее событие (приход другого клиента) будет в
9 минут, можно создать это событие и поместить его в очередь приоритетов для
будущей обработки.
Данные для моделирования и методы, реализующие эту задачу, содержатся
в классе Simulation. Данные-члены включают продолжительность (length)
моделирования (в минутах), количество кассиров, номер следующего клиента,
массив записей TellerStats, содержащих информацию о каждом кассире, и
очередь приоритетов, которая содержит список событий. Класс также содержит
границы диапазонов для следующего прихода и для текущего обслуживания
клиента.
Спецификация класса Simulation
ОБЪЯВЛЕНИЕ
class Simulation
{
private:
// данные для моделирования
int simulationLength; // продолжительность моделирования
int numTellers; // число кассиров
int nextCustomer; // номер следующего клиента
int arrivalLow, arrivalHigh; // диапазон прихода нового клиента
int serviceLow, serviceHigh; // диапазон обслуживания
TellerStats tstat[ll]; // максимальное число кассиров - 10
PQueue pq; // очередь приоритетов
RandomNumber rnd; // использовать для времени прихода
// обслуживания
// закрытые методы, используемые функцией RunSimulation
int NextArrivalTime(void);
int GetServiceTime(void);
int NextAvailableTeller(void);
public:
// конструктор
Simulation(void);
void RunSimulation(void);
void PrintSimulationResults(void);
};
ОПИСАНИЕ
Конструктор инициализирует массив типа TellerStats и член класса пех-
tCustomer, который начинается с 1. Индекс 0 в массиве tstat не используется.
Таким образом, номер кассира является и индексом в массиве tstat.
Конструктор запрашивает пользователя ввести данные для задачи
исследовательского моделирования. Данные включают продолжительность
моделирования в минутах, количество кассиров и диапазон времени прихода и
времени обслуживания. Класс предусматривает до 10 кассиров.
Для каждого события прихода мы вызываем метод NextArrivalTime, чтобы
определить, когда в банк придет следующий клиент. В то же время мы
вызываем GetServiceTime, чтобы определить, как долго будет продолжаться текущее
обслуживание клиента кассиром, и метод NextAvailableTeller для определения
кассира, который будет обслуживать клиента.
Метод RunSimulation выполняет задачу исследовательского моделирования,
a PrintSimulationResults выводит окончательную статистику.
Установка параметров моделирования
Конструктор инициализирует данные и запрашивает у пользователя
параметры моделирования.
Simulation::Simulation(void)
{
int i;
Event firstevent;
// инициализация информационных параметров кассиров
for(i - 1; i <« 10; i++)
{
tstat[i].finishService « 0;
tstat[i].totalService - 0;
tstat[ij.totalCustomerWait * 0;
tstat[ij.totalCustomerCount - 0;
)
nextCustomer - 1;
cout « "Введите время моделирования в минутах: ";
cin » simulationLength;
cout « "Введите число кассиров банка; ";
cin » numTellers;
cout « "Введите диапазон времени приходов в минутах: ";
cin » arrivalLow » arrivalHigh;
cout << "Введите диапазон времени обслуживания в минутах: ";
cin » serviceLow » serviceHigh;
// генерить событие первого прихода клиента
pq.PQInsert(Event(0,arrival,1,0,0,0));
)
Выполнение задачи моделирования
Продолжительность моделирования (simulationLength) используется для
определения, следует ли генерировать событие прихода для другого клиента.
Если банк будет закрыт в планируемое время прихода нового клиента (arrival
time>simulationLengtb), новые клиенты не принимаются, и моделирование
завершается обслуживанием клиентов, остающихся в банке. Данное-член
nextCustomer — это счетчик, ведущий запись количества клиентов.
Метод NextArrivalTime возвращает интервал времени до прихода
следующего клиента. Метод использует генератор случайных чисел и параметры
arrivalLow и arrivalHigh для генерирования возвращаемого значения.
Сходный метод GetServiceTime использует параметры serviceLow и serviceffigh
// определить случайное время следующего прихода
int Simulation::NextArrivalTime(void)
{
return arrivalLow+rnd.Random(arrivalHigh-arrivalLow+l);
>
// определить случайное время обслуживания клиента
int Simulation::GetServiceTime(void)
{
return serviceLow+rnd.Random(serv^ceHigh-serviceLow+l);
}
В этой задаче клиент приходит, смотрит на окно кассира и читает вывеску,
указывающую, когда каждый кассир будет свободен. Исходя из этой
информации, клиент выбирает кассира, который предоставит ему банковские
услуги. Значение данных finishService в записи каждого кассира представляет
вывеску, висящую в окне. Функция NextAvailableTeller просматривает массив
кассиров и возвращает номер кассира с минимальным значением
finishService. Если все кассиры будут заняты вплоть до времени закрытия банка,
клиенту назначается произвольный кассир.
// возвратить номер первого доступного кассира
int Simulation: .'NextAvailableTeller (void)
{
// вначале предполагается, что все кассиры
// освобождаются ко времени закрытия банка
int minfinish = simulationLength;
// назначить случайного кассира клиенту, пришедшему
//до закрытия, но имеющему возможность получить обслуживание
// после закрытия банка
int minfinishindex - rnd.Random(nuraTellers) + 1;
// найти кассира, который освобождается первым
for (int i = 1; i <== numTellers; i++)
if (tstat[i].finishService < minfinish)
{
minfinish = tstat[i].finishService;
minfinishindex = i;
}
return minfinishindex;
}
Основная функция в задаче моделирования — это метод RunSimulation,
который управляет очередью приоритетов событий. Первоначально очередь
имеет единственное событие прихода, возникающее, когда банк открывается.
С этого момента и далее процесс является непрекращающимся. Метод Run-
Simulation является циклом, который извлекает события из очереди
приоритетов. Такой цикл определяется как событийный (event loop), и он завершается
при пустой очереди. Кассиры банка продолжают обслуживать клиентов после
истечения времени работы банка (time>simulationLength) с учетом того, что
клиенты пришли до закрытия банка. В заключительном резюме simulation-
Length обновляется, чтобы предоставить время ухода последнего клиента, с
учетом того, что этот уход наступает после времени закрытия банка. Если
переменная е является объектом Event, содержащим последнее событие дня,
e.GetTime() возвращает время события, а продолжительность задачи
моделирования вычисляется с использованием оператора:
simulationLength = (e.GetTimeO <=simulationLength)
? simulationLength : e.GetTimeO;
ПРИХОД
1. Объект вновь пришедшего клиента отвечает за генерирование
следующего события прихода, которое затем помещается в очередь приоритетов
для последующей обработки. Если следующий приход должен
наступить после завершения задачи моделирования, это событие не
учитывается.
//вычисление времени следующего прихода,
nexttime = e.GetTimeO + NextArrivalTime ();
if (nexttime > simulationLength)
//обрабатывать события, но новые не генерировать
continue;
else
{
//генерировать приход следующего клиента и помещать в
queue nextCustomer++;
newevent - Event(nexttime, arrival,
nextCustomer, 0, 0, 0) ;
pq.PQInsert(newevent);
}
2. После создания следующего события прихода обновляется информация
TellerStats, а затем создается событие ухода. Мы начинаем с
инициализации значения servicetime, которое определяет количество времени,
необходимого на обслуживание текущего клиента, и затем определяем
первого кассира, свободного для обслуживания следующего клиента.
//время, затрачиваемое на клиента
servicetime = GetServiceTime();
//кассир, который обслуживает клиента
tellerlD - nextAvailableTeller();
Теперь рассмотрим поле finishService кассира, который будет работать
с клиентом. Если finishService не 0, то это — время, когда кассир
освобождается для обслуживания другого клиента. Если значение
finishService равно 0, то кассир свободен. В этом случае установим
finishService на текущее время, чтобы отразить тот факт, что кассир будет
теперь обслуживать клиента. Определим время, в течение которого
клиент должен ожидать (waittime), вычитая текущее время из finishService.
//если кассир свободен, заменить время на вывеске на текущее время
if (tstat[tellerlD].finishService == 0)
tstat [tellerlD] . finishService = e.GetTimeO;
//вычислить время, когда клиент ожидает, вычитая
//текущее время из времени на вывеске кассира
waittime = tstat[tellerlD].finishService - e.GetTimeO;
Этими значениями мы обновляем информацию TellerStats для кассира,
который обслуживает клиента. Поле finishService увеличивается на
время обслуживания, необходимое для текущего клиента. Оно теперь
содержит время, когда кассир закончит обслуживание всех его (ее)
текущих клиентов.
//обновлять статистику кассира
tstat[tellerlD].totalCustomerWait +=waittime;
tstat[tellerlD].totalCustomerCount++;
tstat[tellerlD].totalService +=servicetime/
tstat[tellerlD].finishService +=servicetime;
3. Конечная задача включает определение события ухода и помещение
его в очередь приоритетов. Мы имеем все необходимые параметры для
создания события.
Элемент данных события
time
etype
customerlD
tellerlD
waittime
servicetime
Передаваемый параметр
tstat[tellerlD].finishService
departure
e.GetCustomerlDO
tellerlD
waittime
servicetime
newevent = Event(tstat[tellerlD] . finishService,
departure, e.GetCustomerlD(),tellerlD,
waittime, servicetime);
pq.PQInsert(newevent);
УХОД
Событие ухода дает нам доступ к истории деятельности клиента во
время нахождения в банке. В задаче исследовательского моделирования
эта информация может выводиться на экран. Для события ухода мы
должны обновить поле finishService, если у кассира нет других
клиентов. Это наступает, если текущее значение finishService равно времени
ухода. В этом случае finishService устанавливается на 0.
tellerlD = e.GetTellerlDO;
//если никто не ждет кассира, отметить, что кассир свободен
if (e.GetTimeO -- tstat[tellerlD] .finishService)
tstat[tellerlD] .finishService = 0/
Резюме задачи моделирования. Для завершения моделирования вызываем
функцию PrintSimulationResults. Она печатает резюме данных о клиентах и
отдельных кассирах. Данные собираются из записей TellerStats, содержащих
информацию о количестве клиентов, которых обслужил каждый кассир, и
суммарное время ожидания клиентами обслуживания.
for (i = 1; i<=numTellers; I++)
{
cumCustomers += tstat[i].totalCustomerCount;
cumWait += tstat[i]. totalCustomerWait;
}
Окончательное резюме дает среднее время ожидания клиента и время
занятости каждого кассира в процентах.
cout « endl;
cout « ******** Simulation Summary ******** « endl;
cout « Simulation of « simulationLength
<< minutes << endl;
cout « No. of Customers: « cumCustomers << endl;
cout « Average Customer Wait:;
avgCustWait = float(cumWait)/cumCustomers + 0.5;
cout « avgCustWait « minutes « endl;
for(i*l;i<« numTellers;i++)
{
cout « n Teller # " « i « % Working: ;
//отображать значение в процентах, округленное до ближайшего целого
tellerWork * float(tstatfi].totalService)/simulationLength;
tellerWorkPercent - tellerWork * 100.0 + 0.5;
cout « tellerWorkPercent « endl;
}
Пример задачи моделирования. Main-программа определяет объект
моделирования S и затем выполняет цикл event с использованием метода Run-
Simulation. После завершения цикла event вызывается метод PrintSimula-
tionResulte.
Пример 5.6
Мы следим за задачей моделирования после определения этих
параметров:
simulationLength * 30 (минут) numTellers= 2
arriveLow » б arriveffigh = 10
serviceLow -» 18 serviceffigh * 20
Клиент 1 приходит в 0 минут
Прмиод
customerlD 1
tellerlD -
waittime -
servicetime -
Клиент 1 генерирует событие прихода для клиента 2 в 7 минут и
генерирует свое собственное событие ухода в 19 минут
Приход
customerlD 2
tellerlD -
waittime -
servicetime -
Клиент 2 приходит в 7 минут.
Уход
customerlD 1
tellerlD 1
waittime 0
servicetime 19
19
Уход
customerlD 1
tellerlD 1
waittime 0
servicetime 19
19
Клиент 2 генерирует событие прихода для клиента 3 в 16 минут и
генерирует свое событие ухода в 25 минут.
Приход
Уход
Уход
customerlD 3
tellerlD -
waittime -
servicetime -
customerlD 1
tellerlD 1
waittime 0
servicetime 19
customerlD 2
tellerlD 2
waittime 0
servicetime 18
16
19
25
Клиент З приходит в 16 минут.
Клиент 3 генерирует событие прихода, которое наступает после
закрытия банка, что прекращает создание событий прихода. Клиент 3
должен ожидать 3 минуты кассира 1 и генерирует свое событие ухода
в 37 минут.
Уход
Уход
customerlD 1
tellerlD 1
waittime 0
servicetime 19
customerlD 2
tellerlD 2
waittime 0
servicetime 18
19
25
События ухода удаляются из очереди приоритетов в таком порядке:
клиент 1 — в 19 минут, клиент 2 — в 25 минут и клиент 3 — в 37 минут.
Уход
customerlD 1
tellerlD 1
waittime 0
servicetime 19
Уход
customerlD 2
tellerlD 2
waittime 0
servicetime 18
Уход
customerlD 3
tellerlD 1
waittime 3
servicetime 18
19 25 37
Банк закрывается после 37 минут обслуживания.
Программа 5.7 Код и выполнение
Эта программа запускается дважды. Данные первого запуска
соответствуют данным в примере 5.6. Во втором запуске используется
продолжительность задачи 480 минут (8 часов). Метод вывода PrintSimulation-
Results указывает количество постоянных клиентов (patrons), среднее
время ожидания для каждого клиента и общее время занятости каждого
кассира. Реализация классов Event, TellerStats и Simulation содержится
в файле sim.h.
#include "sim.h"
void main(void)
{
// S - объект для моделирования
Simulation S;
// запустить моделирование
S.RunSimulation();
// печатать результаты
S.PrintSimulationResults();
}
/*
<Прогон 1 программы 5.7>
Enter the simulation time in minutes: 30
Enter the number of bank tellers: 2
Enter the range of arrival times in minutes: б 10
Enter the range of service times in minutes: 18 20
Time: 0 arrival of customer 1
Time: 7 arrival of customer 2
Time: 16 arrival of customer 3
Time: 19 departure of customer 1
Teller 1 Wait 0 Service 19
Time: 25 departure of customer 2
Teller 2 Wait 0 Service 18
Time: 37 departure of customer 3
Teller 1 Wait 3 Service 18
******** Simulation Summary ********
Simulation* of 37 minutes
No, of Customers: 3
Average Customer Wait: 1 minutes
Teller #1 % Working: 100
Teller #2 % Working: 49
<Прогон 2 программы 5.7>
Enter the simulation time in minutes 480
Enter the number of bank tellers 4
Enter the range of arrival times in minutes 2 5
Enter the range of service times in minutes 6 20
<arrival and departure of 137 customers>
******** Simulation Summary ********
Simulation of 521 minutes
No. of Customers: 137
Average Customer Wait: 2 minutes
Teller #1 % Working: 89
Teller #2 % Working: 86
Teller #3 % Working: 83
Teller #4 % Working: 86
*/
Письменные упражнения
5.1 Подчеркните правильное. СЩК — это структура, реализующая порядок:
(a) first-in/last-out (b) last-in/first-out (с) first-come/first-serve
(d) first-in/first-out (e) last-in/last-out
5.2 Напишите два программных приложения для стеков.
5.3 Какой выход имеет следующая последовательность операций стека?
(DataType = int):
Stack S
int x = 5, у = 3;
S.Push (8);
S.Push(9);
S.Push(y);
x = S.Pop{);
S.Push(18);
x = S.Pop();
S.Push(22);
while (! S.StackEmpty())
{
у = S.Pop();
cout « у « endl;
}
cout « x <<endl;
5.4 Напишите функцию
void StackClear(Stacks S) ;
которая очищает стек S. Почему важно, чтобы объект S передавался
по ссылке?
5.5 Что выполняет следующая функция? (DataType = int):
void Ques5(Stacks S)
{
int ar'r[64], n = 0, I;
int elt;
while (!S.StackEmpty())
a[n++] = S.PopO ;
for(i=0;i< n;i++)
S.Push(a{i] ;
}
5.6 Что выполняет следующий сегмент кода?
Stack SI, S2, tmp;
DataType x;
while (!Sl.StackEmpty())
{
x = Sl.PopO ;
tmp. Push (x) ;
}
while (!tmp.StackEmpty())
{.
x = tmp.Pop();
Sl.Push(x);
S2.Push(x);
}
5.7 Напишите функцию
int StackSize(Stack S);
которая использует операции стека, чтобы возвращать количество
элементов в стеке S.
5.8 Что выполняет следующая функция Ques8? (DataType = int):
void Ques8(Stacks S, int n)
{
Stack Q/
int I;
while(!S.StackEmpty())
{
i = S.Pop();
if (I !=n)
Q.Push(i);
}
while(!Q.StackEmpty())
{
i * Q.PopO ;
S.Push(i);
)
}
5.9 Если DataType является int, напишите функцию
void SelectItem(Stack& S, int n) ;
которая использует операции стека для нахождения первого появления
элемента в стеке S и перемещает его в вершину стека. Поддерживайте
упорядочение для других элементов.
5.10 Преобразуйте следующие инфиксные выражения в постфиксные:
(а) а 4- Ь*с
(б) (a+)/(d-e)
(в) (Ь2 - 4*а*с)/(2*а)
5.11 Напишите следующие выражения в инфиксной форме:
(а) a b + с*
(б) a b с + *
(в) a b с d e ++**e f - *
5.12 Подчеркните правильное. Очередь — это структура, реализующая
порядок:
(а) first-in/last-out
(б) last-in/first-out
(в) first-come/first-serve
(г) first-in/first-out
(д) last-in/last-out
5.13 Очередь — это структура данных, применимая для (подчеркнуть все
возможные варианты)
(а) оценки выражений
(б) планирования задач операционной системы
(в) моделирования очередей ожидания
(г) печати списка в обратном порядке.
5.14 Какой выход имеет следующая последовательность операций очереди?
(DataType = int):
Queue Q;
DataType x - 5, у * 3;
Q.QInsert (8);
Q.QlnsertO);
Q.QInsert(y);
x e Q.QDeleteO ;
Q.QInsert(18);
x * Q.QDeleteO ;
Q.QInsert(22);
while <!Q.QEmptyO)
{
у - Q.QDeleteO ;
cout « у « endl;
}
cout « x « endl;
5.15 Что выполняет следующая функция? (DataType = int):
void QueslS(Queues Q, int n - 50)
{
Stack S;
int elt;
while (IQ.QEmptyO)
{
elt - Q.QDeleteO ;
S.Push<elt);
)
while (!S.StackEmpty())
{
elt - S.PopO;
Q.QInsert(elt);
)
)
Почему важно, чтобы объект Q передавался по ссылке?
5.16 Что выполняет следующий сегмент кода?
(DataType « int)
Queue Ql, Q2;
int n « 0, x;
• * *
while (JQl.QEmptyO)
{
x «Ql.QDeleteO ;
Q2.QInsert (x);
n++;
}
for (int i-0;i <n;i++)
{
x » Q2.QDelete О;
Ql.QInsert(x);
Q2.QInsert(x);
)
5.17 Предположим, что список очереди приоритетов содержит целые
значения с оператором "меньше, чем" (<), определяющим очередь
приоритетов. Текущий список содержит элементы.
Записывая методы PQDelete и PQInsert в классе Pqueue, опишите этот
список после выполнения каждой из следующих инструкций:
45
15
50
25
65
30
(a) Item = pq.PQDelete() Item * List:
(b) pq.PQInsert(20) List:
(c) Item « pq.PQDelete() Item = List:
(d) Item * pq.PQDelete() Item = List:
5.18 Перепишите подпрограмму PQDelete для обеспечения FIFO-порядка
элементов на том же самом уровне приоритетов.
Упражнения по программированию
5.1 Добавьте метод
void Qprint (void);
который приводит к печати очереди, по 8 элементов в строке. Напишите
программу, которая вводит 20 значений double из файла pq.dat в
очередь. Печатайте элементы.
5.2 Считайте 10 целых в массив, поместив каждый в стек. Напечатайте
оригинальный список и затем напечатайте стек, извлекая элементы.
Конечно, вторая печать перечисляет элементы в обратном порядке.
5.3 Стек может использоваться для распознавания определенных типов
образов. Рассмотрим образец STRING1#STRING2, где никакая строка не
содержит "#" и STRING2 должна быть обратна STRING 1. Например,
строка "123&~a#a~&321" совпадает с образцом, но строка "a2qd#dq3a" —
нет. Напишите программу, которая считывает пять строк и указывает,
совпадает ли каждая строка с образцом.
5.4 Во второй модели стека стек растет в направлении уменьшения индексов
массива. Первоначально стек пуст и Тор=21. После помещения трех
символов в стек индекс Тор — 18, и элемент в вершине стека — это
LIST[TOP] = С.
top
top
Убывающий индекс
В этой модели индекс Тор уменьшается с каждой операцией Push.
Напишите реализацию для класса Stack, используя эту модель.
Протестируйте свою работу, запуская программу 5.1.
5.5 Массив может использоваться для сохранения двух стеков, один,
растущий с левого конца, второй, уменьшающийся с правого конца.
top.
top2
Возрастание стека
Возрастание стека
(а) Каково условие для того, чтобы Si был пуст? Когда S2 пуст?
(б) Каково условие для того, чтобы Si был полным? Когда S2 полный?
(в) Реализуйте класс DualStack, объявление которого задается с помощью
const int MaxDuaiStackSize = 100
class DualStack
{
private:
int topi, top2;
DataType stackStorage[MaxDuaiStackSize];
public:
DualStack(void);
//помещаем elt в стек п
void Push(DataType elt, int n);
//извлекаем из стека п
DataType Pop(int n);
//выборка в стеке п
DataType Peek(int n);
//стек п пуст?
int StackEmpty(int n );
//стек п полный?
int StackFull(int n);
//очистка стека п
void ClearStack(int n);
};
(г) Напишите main-программу, считывающую последовательность из 20
целых, помещая все четные целые в один стек, и нечетные — в другой.
Печатайте содержимое каждого стека.
5.6 Считайте строку текста, помещая каждый непустой символ и в очередь,
и в стек. Проверьте, не является ли текст палиндромом.
5.7 Расширьте постфиксный калькулятор, добавив унарный минус,
представленный символом "@". Например, введите выражение
7
@
12
+
<Display>5
5.8 Это упражнение расширяет класс постфиксного калькулятора для
включения оценки выражений с переменной. Новое объявление следующее:
class Calculator
{
private:
Stack S;
struct component //NEW
{
short type;
float value;
};
int expsize: //NEW
component expComponent[50]; //NEW
int GetTwoOperands(doubles operandi,
doubles operand2);
void Enter(double num);
void Compute(char op);
public:
Calculator(void);
void Run(void);
void Clear(void);
void Variable(void); //NEW
double Eval(double x); //NEW
};
Операция Variable позволяет пользователю вводить постфиксное
выражение, содержащее переменную х, равно как числа и операторы.
Например, введите выражение
хх*Зх* + 5 +
когда вам необходимо оценить инфиксное выражение х2 + Зх + 5. Когда
каждый компонент считан, выполните ввод в массив expComponent.
Поле типа каждого элемента ввода устанавливается так: 1= число, 2
— переменная х, 3 = +, 4 = -, 5 = *, 6 = /. Если тип = 1, то число
сохраняется в поле значения. Увеличивайте expsize на единицу для
каждого нового элемента ввода.
Функция-член Eval выполняется циклично для членов expsize массива
expComponent и использует стек для оценки выражения. Всякий раз,
когда какой-либо элемент имеет поле типа 2, помещайте параметр х
в стек.
Напишите main-программу, оценивающую выражение
(х2 + 1)/ (х4 + 8х2 + 5х + 3)
для х =0, 101, 102, 103, . . . , 1(R
5.9 Измените задачу моделирования в программе 5.7, чтобы она включала
следующую информацию:
(а) Выводить среднее время, которое клиент проводит в банке. Время
клиента измеряется от прихода до ухода.
(б) В настоящее время все кассиры остаются в банке до тех пор, пока не
уходит последний клиент. Это обходится дорого, если кассиры
задерживаются после закрытия банка для обслуживания пришедшего поздно
клиента. Дайте возможность кассиру уйти, если банк закрывается и
нет ожидающих обслуживания клиентов. Совет: добавьте поле к записи
TellerStat, которое указывает общее время, которое кассир проводит в
банке. Используйте эту переменную для вычисления времени в
процентах, в течение которого кассир занят.
5.10 Предположим, в банке создается отдельная очередь к каждому кассиру.
Когда клиент приходит, он (или она) выбирает самую короткую очередь,
а не оценивает загруженность кассиров. Измените программу
моделирования 5.7 для указания среднего времени ожидания клиента и объема
работы, выполненной каждым кассиром. Сравните результаты с
моделью банковского обслуживания с единственной очередью к кассирам.
глава
Абстрактные операторы
6.1. Описание перегрузки операторов
6.2. Система рациональных чисел
6.3. Класс Rational
6.4. Операторы класса Rational как
функции-члены
6.5. Операторы потока класса Rational
как дружественные функции
6.6. Преобразование рациональных
чисел
6.7. Использование рациональных
чисел
Письменные упражнения
Упражнения по программированию
Абстрактный тип данных определяет набор методов для инициализации
и управления данными. С классами язык C++ вводит мощные средства для
реализации ADT. В этой главе мы расширяем определенные языком
операторы (например, +, [] и так далее) для абстрактных типов данных. Процесс,
называемый перегрузка оператора (operator overloading), переопределяет
стандартные символы операторов для реализации операций для абстрактного
типа. Перегрузка оператора — это одна из наиболее интересных возможностей
объектно-ориентированного программирования. Эта концепция позволяет
использовать стандартные операторы языка с их приоритетом и свойствами
ассоциативности как методы класса. Например, предположим, класс Matrix
определяет операции сложения и умножения, используя AddMat и MultMat.
При перегрузке мы можем использовать знакомые инфиксные операторы
"+" и "*". Предположим, что Р, Q, R, S — это объекты типа Matrix:
Стандартные методы класса
R = P.AddMat (Q);
S = R.MultMat (Q.AddMat(P));
Перегруженные операторы
R = Р + Q
S = R * (Q + Р)
Реляционные выражения определяют порядок между элементами. Мы
говорим, что целое 3 является положительным или что 10 меньше, чем 15.
3 >=0 10 < 15
Концепция порядка применима к структурам данных, отличным от чисел.
В классе Data в главе 3, например, две даты (объекты) могут сравниваться
по хронологии года.
Date(б, б, 44) < (Date(12, 25,80) //День-Д наступил раньше рождества 1980
Date(4, 1, 99) == Date {"4/1/99") //Два способа создать дату 1 апреля
Date(7, 1, 94) < Date("8/1/94") //июль наступает перед августом
C++ позволяет выполнять перегрузку большинства присущих ему
операторов, включая операторы потока. Программист не может создавать новые
символы оператора, а должен перегружать существующие операторы C++.
Метод PrintDate в классе Date принимает объект D и выводит его поля
в стандартном формате. Тот же метод может быть переписан как оператор
"«" и использоваться в потоке cout. Например, Date-объект D(12,31,99)
определяет последний день двадцатого века. Чтобы создать выходную строку
Последний день 20-го века — 31 декабря 1999
мы можем использовать метод print из главы 3 или перегрузить оператор
вывода.
PrintDate Method:
cout <<"Последний день 20-го века -"
D.PrintDate();
Overloaded "«" Method:
со1^<<"Последний день 20-го века -"<< D;
Перегрузка операторов — это тема, которая описывается в нескольких
главах. В данной главе мы разрабатываем класс рациональных чисел для
иллюстрации ключевых понятий. Вы, конечно, знакомы с "дробями" и имеете
школьный опыт работы с операциями. Класс Rational дает хороший пример
арифметических и операций отношения, преобразования типов между
целыми значениями и действительными числами и простого определения для
перегруженного потока ввода/вывода.
6.1. Описание перегрузки операторов
Термин перегрузка операторов (operator overloading) подразумевает, что
операторы языка, такие как +,!=,[] и = могут быть переопределены для типа
класса. Этот тип класса дает возможность реализации операций с
абстрактными типами данных с использованием знакомых символов операций. C++
предоставляет различные методы определения перегрузки операторов, включающие
определяемые пользователем внешние функции, члены класса и
дружественные функции. C++ требует, чтобы по крайней мере один аргумент
перегруженного оператора был объектом или ссылкой на объект.
Определяемые пользователем внешние функции
В классе SeqList методы Find и Delete требуют определения оператора
отношения "==" для DataType. Если оператор не присущ этому типу, пользователь
должен явно задать перегруженную версию. Объявление использует
идентификатор "operator" и символ "==". Так как результатом операции является
True или False, возвращаемое значение будет типа int:
int operator==(const DataTypei a, const Datatypes b);
Например, предположим, список содержит записи Employee, которые
состоят из поля ID и другой информации, включающей имя, адрес и так далее.
struct Employee
{
int ID;
• • •
}
ID
Имя
Адрес
■ ■ ■
Операция отношения "равно" сравнивает поля Ю:
int operator == (const Employees a, const Employees b)
{
return a.ID ==b.ID; //сравнение ID-полей
}
Перегруженный оператор должен иметь аргумент типа класс. Заметьте, что
следующая попытка перегрузить "==" для строк C++ будет неудачной, потому
что никакой аргумент не является объектом или ссылкой на объект.
int operator==(char *s, char *t)//неверный оператор
{
return strcmp(s, t)== 0;
}
Когда оператор отношения "равно" будет объявлен, пользователь может
использовать функции Find или Delete класса SeqList:
typedef Employee DataType; //тип данных Employee
#include "aseqlist.h"
■ * •
SeqList L;
Employee emp; //объявляем объект SeqList.
• л т
emp.ID=1000; //ищем служащего с ID=1000
if (L.Find(emp))
L.Delete(emp); //если найден, удаляем этого служащего
Чтобы использовать класс SeqList, пользователь должен иметь технические
знания для определения оператора "==" как внешней функции. Это является
дополнительным, но обязательным требованием, поскольку оператор "=="
присоединяется к типу данных, а не к классу.
Члены класса
Арифметические операторы и операторы отношения происходят из систем
счисления. Они позволяют программисту объединять операнды в выражениях,
используя инфиксную запись. Класс может иметь методы, объединяющие
объекты сходным образом. В большинстве случаев методы могут записываться как
перегруженные функции-члены с использованием стандартных операторов
С4--К Когда левый операнд является объектом, оператор может выполняться
как метод, который определяется для этого объекта. Например, двумерные
векторы имеют операторы, включающие сложение, отрицание и скалярное
произведение векторов.
Сложение векторов
Сложим два вектора u=(ui,U2) и v=(vi,V2), образуя вектор, компоненты
которого являются суммой компонентов каждого вектора (см. часть (а) рис. 6.1).
u+v = (ux+v^i^+va)
Отрицание векторов
Образуем отрицание векторов u=(ui,U2), беря отрицательное значение
каждого компонента. Новый вектор имеет ту же величину, но противоположное
направление (см. часть (Ь) рис. 6.1).
-(ui,u2)=(-iii, -u2)
Скалярное произведение векторов
Вектор u=(ui,U2), умноженный на вектор u=(vi,V2), является числом,
полученным сложением произведений соответствующих компонентов (см. часть (с)
рис. 6.1). Скалярное произведение векторов является произведением модулей
векторов (magnitude) на косинус угла между ними.
v*w=u1v1+u2v2=magnitude(v)*magnitude(w)*cos(q)
(VI, V2)
(U1, U2)
u + v
Ul * V1 + U2 * V2
(а) Сложение (б) Вычитание (с) Произведение
Рис. 6.1. Векторные операции
Мы объявляем класс векторов Vec2d с координатами х и у как закрытыми
данными-членами. Этот класс имеет конструктор, два бинарных оператора
(сложение, скалярное произведение) и унарный оператор (отрицание) в
качестве функций-членов, а также дружественные функции, определяющие
умножение вектора на скаляр и потоковый вывод. Использование дружественных
функций описывается в следующем разделе.
class Vec2d
{
private:
double xl,x2 //компоненты
public:
//конструктор со значениями по умолчанию
Vec2d(double h=0.G, double v=0.0);
//функции-члены
Vec2d operator-(void); //вычитание
Vec2d operatori-(const Vec2d& V); //сложение
double operator*(const Vec2d& V); //скалярное произведение
//дружественные функции
friend Vec2d operator*(const double c,const Vec2d& V);
friend ostreams operator<<(ostream& os, const Vec2d& U);
>;
Как в функциях-членах в операторах сложения, отрицания и скалярного
произведения предполагается, что текущий объект является левым операндом
в выражении. Предположим, U и V- это векторы.
Сложение. Выражение U + V использует бинарный оператор "+", связанный
с объектом U. Метод operator4- вызывается с параметром V.
U.operator+(V) //возвращает значение Vec2d(x+V.x, у + V.y)
Отрицание. Выражение -U использует унарный оператор "-". Метод
operator- выполняется для объекта U.
U.operator- () //возвращает значение Vec2d(-x, -у)
Скалярное произведение. Подобно сложению, выражение U*V использует
бинарный оператор *'*", связанный с объектом U. Произведение вычисляется
методом текущего объекта U и параметра V.
U.operator*(V) //возвращает значение х * V.x +y * V.y
Пример с объектами:
Vec2d U(l, 2), V(2, 3);
U + V = (1, 2) + (2, 3) « (3, 5)
-U - -(1, 2) = (-1, -2)
U *V = (1, 2) * (2, 3) = 8
Перегрузка операторов требует соблюдения определенных условий.
1. Операторы должны соблюдать приоритет операций, ассоциативность и
количество операндов, диктуемое встроенным определением этого
оператора. Например, "*" — это бинарный оператор и должен всегда,
когда он перегружается, иметь два параметра.
2. Все операторы в C++ могут быть перегружены, за исключением
следующих:
, (оператор "запятая") sizeof :: (оператор области действия)
?: (условное выражение)
3. Перегруженные операторы не могут иметь аргументов по умолчанию;
другими словами, все операнды для оператора должны присутствовать.
Например, следующее объявление оператора является неправильным:
double Vec2d::operator* (vec2d V = Vec2d(l,l));
4. Когда оператор перегружается как функция-член, объект, связанный
с этим оператором, всегда является крайним слева операндом.
5. Как функции-члены унарные операторы не принимают никаких
аргументов, а бинарные операторы принимают один аргумент.
Дружественные функции
Обычно объектно-ориентированное программирование требует, чтобы
только функции-члены имели доступ к закрытым данным какого-либо класса. Это
обеспечивает инкапсуляцию и скрытие информации. Этот принцип следует
расширить до перегрузки оператора везде, где возможно. В некоторых ситуациях,
однако, использование перегрузки с функцией-членом невозможно или слишком
неудобно. Поэтому необходимо использовать дружественные функции (friend
functions), которые определяются вне класса, но имеют доступ к закрытым
данным-членам. Например, умножение вектора на скаляр является еще одной
формой умножения векторов, где каждый компонент вектора умножается на числовое
значение. Число (скаляр) с, умноженное на вектор u=(ui,ui), является вектором,
компоненты которого образуются умножением каждого компонента и на с:
c*u=(cu1,cu2)
Это естественная операция перегрузки с использованием оператора '*'.
Однако, перегрузка оператора с использованием функции-члена не
позволяет помещать скалярное значение С как левый операнд. Левым операндом
должен быть вектор.
Мы определяем, что '*' является оператором вне класса, имеющим
параметры С и U, и имеет доступ к закрытым членам х и у параметра U. Это
выполняется определением оператора как дружественного внутри объявления
класса. Дружественная функция объявляется помещением ключевого слова
friend перед объявлением функции в классе.
friend Vec2d operator * (const double с, const Vec2d& U);
Так как дружественная функция является внешней для класса, она не
находится в области действия класса и реализуется как стандартная функция.
Заметьте, что ключевое слово friend не повторяется в объявлении функции.
Vec2d operator* (double с, Vec2d U)
{
return Vec2d(c*U.x, c*U.y);
}
При использовании умножения вектора на скаляр оператору '*' передаются
оба аргумента, и скаляр должен быть левым параметром.
Vec2d 7(8,5), Z;
Z = 3.0 * Y; //результатом является (24,15)
Использование дружественных функций и права доступа к ним
описываются в следующем перечне правил
1. Объявление дружественной функции выполняется помещением
объявления функции внутрь класса, которому предшествует ключевое слово
friend. Фактическое определение дружественной функции дается вне
блока класса. Дружественная функция определяется подобно любой
обычной функции C++ и не является членом класса.
2. Ключевое слово friend используется только в объявлении функции в
классе, а не с определением функции.
3. Дружественная функция имеет доступ к закрытым членам класса.
4. Дружественная функция получает доступ к членам класса только при
передаче ей объектов как параметров и использовании записи с точкой
для ссылки на члена.
5. Для перегрузки унарного оператора как друга в качестве параметра
передается операнд. При перегрузке бинарного оператора как друга в
качестве параметров передаются оба операнда. Например:
friend Vec2d operator-(Vec2d X); //унарный "минус"
friend Vec2d operator+(Vec2d X, Vec2d Y); //бинарное сложение
6.2. Система рациональных чисел
Рациональные числа — это множество частных P/Q, где Р и Q — это целые,
a Q * 0. Число Р называется числителем или нумератором (numerator), а число
Q — знаменателем или деноминатором (denominator).
2/3 -6/7 8/2 10/1 0/5 5/0 (неверно)
Представление рациональных чисел
Рациональное число — это отношение числителя к знаменателю, и
следовательно, представляет один член коллекции эквивалентных чисел (equivalent
numbers). Например:
2/3 = 10/15 = 50/75 //эквивалентные рациональные числа
Один член коллекции имеет редуцированную форму (reduced form), в
которой числитель и знаменатель не имеют общего делителя. Рациональное число
в редуцированной форме является наиболее репрезентативным значением из
коллекции эквивалентных чисел. Например, 2/3 — это редуцированная форма
в коллекции 2/3, 10/15, 50/75 и так далее. Чтобы создать редуцированную
форму какого-либо числа, числитель и знаменатель нужно разделить на их
наибольший общий делитель (GCD, greatest common denominator). Например:
10/15 = 2/3
(GCD(10,15) = 5; 10/5 = 2 15/5 = 3)
24/21 = 8/7
(GCD (24,21) = 3; 24/3 = 8 21/3 = 7)
5/9 - 5/9
(GCD(5,9) - 1; рациональное число уже в редуцированной форме)
В рациональном числе и числитель, и знаменатель могут быть
отрицательными целыми. Мы используем термин нормализованная форма (standardized
form) с положительным деноминатором.
2/-3 * -2/3 //-2/3 — это нормализованная форма
-2/-3 = 2/3 //2/3 — это нормализованная форма
Арифметика рациональных чисел
Читатель знаком со сложением, вычитанием и сравнением дробей с
использованием общих деноминаторов и правил умножения и деления этих чисел.
Далее приводятся несколько примеров, которые предлагают формальные
алгоритмы для реализации операций в классе рациональных чисел.
Сложение/Вычитание. Сложим (вычтем) два рациональных числа, создав
эквивалентную дробь с общим знаменателем. Затем сложим (вычтем) числители.
I 5 8*1 3*5 8*1+3*5 23
(+) 3*8~3*8 + 3*8~ 3*8 "24
I _ А - 1 * 8 _ 3*5 _ 1*8-3*5 _ -7
^ 3 8"з*8 3 * 8 ~ 3*8 ~ 24
Умножение/Деление. Умножим два рациональных числа, умножая
числители и знаменатели. Выполним деление, инвертируя второй операнд (меняя
местами числитель и знаменатель) и перемножая члены дробей.
W 3*8 3*8 24
(/) 1/5 = 1,8=_8_
1 } 3 8 3 5 15
Сравнение. Все операторы отношения используют один и тот же принцип:
Создаем эквивалентные дроби и сравниваем числители:
/ч15 1*85*3
(<) 77 < ■=■ эквивалентно отношению ——г- <
38 3*88*3
Данное отношение ВЕРНО (TRUE), так как 1*8 < 3*5 (8<15)
Пример 6.1
Этот пример иллюстрирует операции с рациональными числами.
Предположим, U = 4/5, V = -3/8 и W = 20/25.
l' U + V 5 + 8 40 Ч 40 40
v ) \ )
и „4 * ( 3) ~12
V 5 8 40
QO 1 К
U > V, так как ^ > - 4£ (32 > -15)
40 40
0 тт ,„ 4 100 20 100
2. U = = W, таккак 5=-^ ^ = 125
Преобразование рациональных чисел
Множество рациональных чисел включает целые как подмножество. В
представлении целого как рационального числа используется деноминатор 1.
Следовательно,
(целое) 25 = 25/1 (рациональное)
Более сложное преобразование касается действительных и рациональных
чисел. Например, действительное число 4,25 — это 4+1/4, что соответствует
рациональному числу 17/4. Алгоритм для преобразования действительного
числа в рациональное приводится в разделе 6.6. Обратное преобразование
рационального числа в действительное включает простое деление нумератора
на деноминатор. Например:
3/4 = 0,75 //делим 3,0/4,0
6.3. Класс Rational
Идеи, изложенные в разделе 6.2, могут быть прекрасно реализованы в
классе, использующем данные-члены нумератор и деноминатор для описания
рационального числа и объявляющем базовые арифметические и операторы
отношения как перегруженные функции-члены. Операторы потокового ввода
и вывода реализуются с использованием перегрузки дружественной функции.
Преобразование между целыми (или действительными) и рациональными
числами и преобразование между рациональными и действительными
числами творчески использует функции конструктора и операторы
преобразования C++.
Спецификация класса Rational
ОБЪЯВЛЕНИЕ
♦include <iostream.h>
♦include <stdlib.h>
class Rational
<
private:
// определяет рациональное число как числитель/знаменатель
long num, den;
// закрытый коструктор, используемый
// арифметическими операторами
Rational(long num, long denom);
// функции-утилиты
void Standardize(void);
long gcd(long m, long n) const;
public:
// конструкторы преобразуют:
// int->Rational, double->Rational
Rational(int num=0, int denom=l);
Rational(double x);
// ввод/вывод
friend istream& operator» (istreamft istr,
Rational &r);
friend ©streams operator« (ostream& ostr,
const Rationale d);
// бинарные операторы:
// сложить, вычесть, умножить, разделить
Rational operator+ (Rational r) const/
Rational operator- (Rational r) const;
Rational operator* (Rational r) const;
Rational operator/ (Rational r) const;
// унарный минус (изменяет знак)
Rational operator- (void) const;
// операторы отношения
int operator< (Rational r) const;
int operator<= (Rational r) const;
int operator== (Rational r) const;
int operator!= (Rational r) const;
int operator> (Rational r) const;
int operators (Rational r) const;
// оператор преобразования: Rational -> double
operator double(void) const;
// методы-утилиты
long GetNumerator(void) const;
long GetDenominator(void) const;
void Reduce(void);
);
ОПИСАНИЕ
Закрытый метод Standardize преобразует рациональное число в
"нормальную форму" с положительным деноминатором. Конструкторы используют
Standardize для преобразования числа в нормальную форму. Мы также
используем этот метод при чтении числа или при делении двух чисел, поскольку
эти операции могут привести к результату с отрицательным деноминатором.
Сложение и вычитание не вызывают Standardize, потому что два знаменателя
операндов уже являются неотрицательными. Закрытый метод gcd возвращает
наибольший общий делитель двух целых тип.
Открытая функция Reduce преобразует объект рациональное число в его
редуцированную форму вызовом gcd.
Два конструктора для этого класса действуют как операции
преобразования целого (long int) и действительного (double) числа в рациональное
(Rational) число. Они описываются в разделе, посвященном операторам
преобразования типа.
Для приложений мы используем методы-утилиты GetNumerator и
GetDenominator для доступа к данным-членам рационального числа.
Оператор ввода « является дружественной функцией, которая считывает
рациональное число в форме P/Q. При выводе это число имеет форму P/Q.
Попытка ввести рациональное число с деноминатором 0 вызывает ошибку и
завершение программы.
пример
Rational A(-4,5), В, С; // А - это -4/5, В и С - это 0/1
cin » С; // при вводе -12/-18
// Standardize сохраняет 12/18
cout « С.GetNumerator(); // печать числителя 12
С.Reduce О; // привести С к форме 2/3
В = С + А; //В - это 2/3 + (-4/5) = -2/15
cout « -В; // вызвать оператор минус; вывести 2/15
cout « float(A); // конвертировать в действительное число;
// вывести -.8
cout « .5 + Rational(3); // преобразовать .5 в 1/2;
// вывести сумму: 1/2 + 3/1 = 7/2
6.4. Операторы класса Rational
как функции-члены
Класс Rational объявляет арифметические операторы и операторы
отношения как перегруженные функции-члены. Каждый бинарный оператор
имеет параметр, который является правым операндом.
Предположим, u, v и w — это объекты типа Rational в выражении:
w = u + v
Перегруженный оператор + является членом объекта и (левый операнд)
и принимает v в качестве параметра. Возвращаемым значением является
объект типа Rational, который присваивается w. Технически w — u + v
оценивается как w = u. + (v)
Для выражения v — -и. C++ выполняет оператор "-" для объекта и
(единственный операнд). Возвращаемым значением является объект Rational,
который присваивается v. Технически v = -и оценивается как v = u.-()
Реализация операторов класса Rational
В программном приложении содержится весь код класса Rational. Мы
реализуем сложение и деление, реляционное равенство и отрицание для
иллюстрации перегрузки членов. Пусть имеются следующие объявления:
Rational u(a,b), v(c,d);
Чтобы сложить ("+") рациональные числа, найдем общий деноминатор
для операндов. Фактическое сложение производится объединением
нумераторов.
а с а * d Ь * с а * d + b * с
(+) ы + у=_+_=__+_=___
Для реализации а и b — это данные-члены num и den левого операнда,
который является объектом, связанным с оператором "+". Числа end
являются данными-членами v.num и v.den правого операнда:
// Rational-суммирование
Rational Rational::operator+ (Rational r) const
{
return Rational(num*r.den + den*r.num, den*r.den);
}
Деление ("/") выполняется инвертированием правого операнда и затем
перемножением членов. Числа а и b соответствуют данным-членам левого
операнда. Числа end относятся к данным-членам в объекте v, правом
операнде. Так как результат может иметь отрицательный деноминатор,
частное нормализуется.
( } и~Ъ d~Ъ* с"ъ*с
II Rational-деление
Rational Rational::operator/ (Rational r) const
<
Rational temp = Rational(num*r.den, den*r.num);
// убедиться, что деноминатор - положительный
temp.Standardize();
return temp;
}
Для оценки оператора отношения сравним нумераторы после приведения
рациональных чисел к общему деноминатору. Тогда для оператора отношения
"равно" ("==") возвращаемым значением является True, когда нумераторы
равны. Далее следуют операторы логического эквивалента (<^>).
^^а с
а * d b * с
<=> = =
b * d b * d
Протестируйте условие a * d === b * c:
II отношение равно
int Rational::operator== (Rational r) const
{
return num*r.den *- den*r.num;
}
Унарный оператор минус "-" работает с данными-членами единственного
операнда, определяющего эту операцию. Вычисление просто делает
отрицательным нумератор:
// минус для Rational
Rational Rational::operator- (void) const
{
return Rational(-num, den);
}
6.5. Операторы потока класса Rational как
дружественные функции
Файл <iostream.h> содержит объявления для двух классов с именами
ostream и istream, которые обеспечивают потоковый вывод и потоковый ввод,
соответственно. Потоковая система ввода/вывода предоставляет определения
для потоковых операторов ввода/вывода "»" и "«" в случае элементарных
типов char, int, short, long, float, double и char*. Например:
Ввод Вывод
istream & operator»(short v) ; ostream & operator«(short v);
istream & operator»(double v) ; ostream & operator«(double v);
Потоковые операторы можно перегружать для реализации ввода/вывода
определяемого пользователем типа. Например, с классом Date операторы "«"
и "»" могут обеспечивать потоковый ввод/вывод тем же способом, который
использовался для простых типов. Например:
Date D;
cin»D //<ввод>10/5/75
cout«D //<вывод> October 5, 1975
Если бы операторы для класса Date должны были быть перегруженными
как функции-члены, их было бы необходимо объявлять явно в <iostream.h>.
Классу ostream пришлось бы иметь перегруженную версию "«", которая
принимает параметр Date. Это явно непрактично, и поэтому мы используем
дружественную перегрузку, которая определяет этот оператор вне класса, но
позволяет ему иметь доступ к закрытым данным-членам в классе.
Перегрузка потокового оператора использует структурированный формат,
который далее показан для общего типа класса CL.
class CL
{
■ • •
public:
• • •
friend istreamfi operator>>(istream& istr, CL& Variable);
friend ostream& operator<<(ostream& ostr, const CL& Value);
}
Параметр istr представляет поток ввода, такой как cin, и ostr представляет
поток вывода, такой как cout. Так как процесс ввода/вывода изменяет
состояние потока, параметр должен передаваться по ссылке.
Для ввода, элементу данных Variable присваивается значение из потока,
поэтому оно передается по ссылке. Функция возвращает ссылку на istream,
чтобы оператор мог использоваться в такой последовательности как
cin » m » n;
В случае вывода Value копируется в поток вывода. Так как данные не
изменяются, Value передается как константная ссылка. Это позволяет
избежать копирования возможно большого объекта по значению. Функция
возвращает ссылку на ostream (output), чтобы оператор мог использоваться в
такой последовательности как
cout « m « n;
Реализация операторов потока класса Rational
Ввод и вывод рациональных чисел реализуется перегрузкой потоковых
операторов. С вводом мы считываем число в форме P/Q, где Q*0. Программа
завершается, если введенный деноминатор равен 0.
// перегрузка оператора ввода потока, ввод в форме P/Q
istreamfi operator >> (istreamb istr, Rationale r)
{
char с; // для чтения разделителя ' /'
// как друг оператор ">>" имеет доступ
// к номинатору и деноминатору объекта г
istr >> r.nura » с >> r.den;
// проверка деноминатора на равенство нулю
if (r.den === 0)
I
cerr « "Нулевой деноминатор!\n";
exit(1);
)
// приведение объекта г к стандартной форме
г.Standardize();
return istr;
}
Перегруженный потоковый оператор вывода записывает рациональное
число в форме P/Q.
// перегруженный оператор вывода потока, форма: P/Q
ostream& operator « (ostream& ostr, const Rationalb r)
{
// как друг оператор "»" имеет доступ
// к номинатору и деноминатору объекта г
ostr << r.num << '/' << r.den;
return ostr;
}
6.6. Преобразование рациональных чисел
Класс Rational иллюстрирует операторы преобразования типа.
Программист может реализовать пользовательские операторы преобразования,
аналогичные операторам, предусмотренным для стандартных типов. Конкретнее,
мы сосредотачиваем внимание на преобразовании между объектами типа
класс и соответствующего типа данными C++.
Преобразование в объектный тип
Конструктор класса может использоваться для построения объекта. Как
таковой, конструктор принимает его параметры ввода и преобразует их в
объект.
Класс Rational имеет два конструктора, которые служат в качестве
операторов преобразования типа. Первый конструктор преобразует целое в
рациональное число, а второй преобразует число с плавающей точкой в
рациональное число.
При вызове конструктора с единственным целым параметром num он
преобразует целое в эквивалентное рациональное num/1. Например, рассмотрим
эти объявления и операторы:
Rational P(7), 0(3,5), R, S; // явное преобразование 7 в 7/1
R - Rational(2); // явное преобразование 2 в 2/1
S = 5; // построить Rational(5)
//и присвоить новый объект переменной S
Объявления Q и R создают объекты Q=3/5 и R=0/1. Присваивание R =
Rational(2) явно изменяет значение R на 2/1. Присваивание S = 5 приводит
к преобразованию типа. Компилятор принимает S = 5 как оператор S =
Rational(5).
// конструктор, рациональное число в форме num/den
Rational::Rational(int p, int q): num(p), den(q)
{
if (den == 0)
{
cerr « "Нулевой деноминатор!" « endl;
exit(1);
}
>
Второй конструктор преобразует действительное число в рациональное.
Например, следующие операторы создают рациональные числа А=3/2 и
В=16/5:
Rational А = Rational(1.5), В; // явное преобразование
В = 3.2; // преобразовать 3.2 в Rational(1 б,5)
Для преобразования необходим алгоритм, который аппроксимирует
произвольное число с плавающей точкой в эквивалентное рациональное.
Алгоритм включает сдвиг десятичной точки в числе с плавающей точкой. В
зависимости от количества значащих цифр в действительном числе результат
может быть только приближенным. После создания рационального числа
вызываем функцию Reduce, сохраняющую рациональное число в более
читабельной редуцированной форме.
// конструктор, преобразует х типа double
// к типу Rational
Rational::Rational(double x)
{
double vail, val2;
vail = 100000000L*x;
val2 = 10000000L*x;
num = long(vall-val2);
den = 90000000L;
Reduce();
}
Преобразование из объектного типа
Язык C++ определяет явные преобразования между простыми типами.
Например, чтобы напечатать символ с в коде ASCII, мы можем использовать
код:
cout << int(с) << endl; // преобразовать char в int
Между типами также определяются неявные преобразования. Например,
если I — это целое long, a Y — это double, то оператор
Y = I; //у = double (I)
преобразует I в double и присваивает результат переменной Y. Класс может
содержать одну или более функций-членов, которые преобразуют объект в
значение другого типа данных. Для класса CL предположим, что нам
необходимо преобразовать объект в тип с именем NewType. Оператор NewTypeQ
принимает объект и возвращает значение типа NewType. Искомый тип New-
Type часто является стандартным типом, таким как int или float. Являясь
унарным, оператор преобразования не содержит параметр. Так же, оператор
преобразования не имеет возвращаемого типа, потому что он находится неявно
в имени NewType. Объявление принимает форму:
class CL
{
* • ■ •
operator NewType(void);
>;
Оператор преобразования используется следующим образом:
NewType a;
CL obj;
а - NewType(obj); //явное преобразование
а » obj; //неявное преобразование
Класс Rational содержит оператор, преобразующий объект в double. Этот
оператор позволяет выполнять присваивание рациональных данных
переменным с плавающей точкой. Преобразователь принимает рациональное число
рЛь делит нумератор на деноминатор и возвращает результат как число с
плавающей точкой. Например:
3/4 это 0.75 4/2 это 2.0
// преобразовать: Rational -> double
Rational::operator double(void) const
{
return double(num)/den;
}
Пример 6.2
Пусть имеются объявления
Rational R(l,2), S(3,5)
double Y,Z;
1. Оператор Y = double(R) осуществляет явное использование
преобразователя. Результат: Y = 0.5
2. Оператор Z = S осуществляет неявное преобразование к
рациональному числу. Результат: Z = 0.6.
6.7. Использование рациональных чисел
Перед тем, как разрабатывать приложения для рациональных чисел,
опишем алгоритм для генерирования редуцированной формы дроби. Этот
алгоритм включает нахождение наибольшего общего делителя (gcd) нумератора
и деноминатора.
Для создания редуцированной формы рационального числа метод Reduce
использует закрытую функцию-член gcd, которая принимает два
положительных целых параметра и возвращает наибольший из их общих делителей.
Функция gcd реализуется в программном приложении. Для ненулевого
рационального числа метод Reduce делит нумератор и деноминатор на их gcd:
void Rational::Reduce(void)
{
long bigdivisor, tempnumerator;
// tempnumerator — модуль от num
tempnumerator = (num < 0) ? -num : num;
if (num == 0)
den *= 1; // приведение к 0/1
else
{
// найти GCD положительных чисел:
// tempnumerator и den
bigdivisor = gcd(tempnumerator, den),
if (bigdivisor > 1)
{
num /= bigdivisor;
den /= bigdivisor;
)
}
)
Программа 6.1. Использование класса Rational
Эта программа иллюстрирует основные возможности класса Rational.
Здесь показаны различные методы преобразования, включая
преобразование целого числа в рациональное и рационального числа в действительное.
Демонстрируется также сложение, вычитание, умножение и деление
рациональных чисел. Программа заканчивается неявным преобразованием
числа с плавающей точкой в рациональное и наоборот — в число с
плавающей точкой. Реализация класса Rational содержится в файле rational.h.
♦include <iostream.h>
#pragma hdrstop
tinclude "rational.h"
// каждая операция сопровождается выводом
void main(void)
{
Rational rl(5), r2, r3;
float f;
cout << "1. Rational-значение 5 is " << rl « endl;
cout « "2. Введите рациональное число: ";
cin >> rl;
f = float(rl);
cout << " Эквивалент с плавающей запятой: " « f « endl;
cout « "3. Введите два рациональных числа: ";
cin » rl » r2;
cout « " Результаты: " « (rl+r2) « " ( + ) "
« (rl-r2) « " (-) " « (rl*r2) « и (*) п
« (rl/r2) « " (/) " « endl;
if (rl < r2)
cout « " Отношение (меньше чем) : " « rl « " < "
« r2 « endl;
else if (rl == r2)
cout « " Отношение (равно): " « rl « " == "
<< r2 « endl;
else
cout « " Отношение (больше чем) : " << rl « " > "
« r2 « endl;
cout << "4. Введите число с плавающей запятой: ";
cin >> f;
rl = f;
cout « " Преобразование к Rational " << rl « endl;
f = rl;
cout « " Преобразование к float " « f « endl;
}
/*
<Run of Program 6.1>
1. Rational-значение 5 is 5/1
2. Введите рациональное число: -4/5
Эквивалент с плавающей запятой: -0.8
3. Введите два рациональных числа: 1/2 -2/3
Результаты: -1/6 (+) 7/6 (-) -2/6 (*) -3/4 (/)
Отношение (больше чем): 1/2 > -2/3
4. Введите число с плавающей запятой: 4.25
Преобразование к Rational 17/4
Преобразование к float 4.25
*/
Приложение: Утилиты для рациональных чисел. Читатель научился
работать с дробями еще в начальной школе. Для иллюстрации приложения
класса Rational описывается ряд функций, выполняющих вычисления с
дробями.
Функция PrintMixedNumber записывает дробь как смешанное число:
Дробь
10/4
-10/4
200/4
Смешанное число
2 1/2
-2 1/2
50
В алгебре основной задачей является решение общего уравнения дроби
2/ЗХ + 2 = 4/5
Процесс включает изоляцию члена X перестановкой 2 в правую часть
уравнения:
2/ЗХ = -6/5
Решение получают, разделив обе части уравнения на рациональное число
2/3, коэффициент X. Реализуем этот процесс в функции SolveEquation.
х = -6/5 * 3/2 = -18/10 = -9/5 (редуцированное)
Программа 6.2. Утилиты для рациональных чисел
Программа использует ряд утилит для рациональных чисел при
выполнении некоторых вычислений.
PrintMixedNumber // печатать число как смешанное
SoiveEquation // решить общее уравнение
// (a/b)X + (c/d) - <e/f)
Действие каждого оператора явно описывается в операторе вывода.
#include <iostream.h>
#include <stdlib.h>
#pragma hdrstop
#include "rational.h"
// печатать Rational-число как смешанное: <+/-)N p/q
void PrintMixedNumber (Rational x)
{
// целая часть Rational-числа х
int wholepart * int(x.GetNumerator() / x.GetDenominator());
// сохранить дробную часть смешанного числа
Rational fractionpart = х - Rational(wholepart);
// если дробной части нет, печатать целую
if (fractionpart ==* Rational (0))
cout << wholepart « " ";
else
{
// вычислить дробную часть
fractionpart.Reduce();
// печатать знак без целой части
if (wholepart < 0)
fractionpart ■ -fractionpart;
if (wholepart !*= 0)
cout « wholepart « " " « fractionpart « " ";
else
cout << fractionpart « " ";
}
}
// решить ax + b - с, где a, b, с — рациональные числа
Rational SoiveEquation(Rational a, Rational b, Rational c)
{
// проверить а на равенство нулю
if (a « Rational(0))
{
cout « "Уравнение не имеет решений." << endl;
// возвратить Rational(0), если решений нет
return Rational(0);
}
else
return (c-b)/a;
}
void main(void)
{
Rational rl, r2, r3, ans;
cout « "Введите коэффициенты для "
"'a/b X + c/d = e/f : ";
cin » rl » r2 » r3;
cout « "Приведенное уравнение: " « rl «"Xя "
« (r3-r2) « endl;
ans - SolveEquation(rl,r2,r3);
ans.Reduce ();
cout « "X » " « ans « endl;
cout « "Решение как смешанное число: ";
PrintMixedNumber(ans);
cout « endl;
>
Л
Оапуск 1 программы 6.2>
Введите коэффициенты для 'a/b X + c/d « e/f : 2/3 2/1 4/5
Приведенное уравнение: 2/3 X - -6/5
X - -9/5
Решение как смешанное число: -1 4/5
Оапуск 2 программы 6.2>
Введите коэффициенты для ' а/Ь X + c/d = e/f : 2/3 -7/8 -3/8
Приведенное уравнение: 2/3 X * 32/64
X = 3/4
Решение как смешанное число: 3/4
*/
Письменные упражнения
6.1 C++ позволяет двум или более функциям в программе иметь одно и
то же имя при условии, что их списки аргументов достаточно отличны
друг от друга, чтобы компилятор мог различать вызовы функций.
Компилятор оценивает параметры в вызывающем блоке и выбирает
правильную функцию. Этот процесс называется перегрузкой функции
(function overloading). Например, математическая библиотека C++
<math.h> определяет две версии функции sqr, которая возвращает
квадрат ее аргумента.
integer version: int sqr (long); //выбор целой версии
float version: double sqr(double); //выбор версии действительного числа
Ряд правил определяет правильную перегрузку операторов. Эти правила
следующие:
Правило 1: Функции должны иметь отдельный список параметров,
независимый от возвращаемого типа, и значения по умолчанию.
Правило 2: Перечислимые типы — это отдельные типы с целью
перегрузки. Ключевое слово typedef не влияет на перегрузку.
Правило 3: Если параметр не совпадает точно с формальным параметром
в наборе перегружаемых функций, применяется алгоритм совпадения
для определения "наиболее совпадающей" функции. Преобразование
выполняется, если необходимо. Например, при передаче переменной
short перегруженной функции, которая имеет целые параметры, ком-
пилятор может создавать совпадение, преобразуя эту переменную в int.
Компилятор не выполняет преобразование параметра, если выбор
приводит к неоднозначности.
Для каждого из следующих примеров укажите правило, которое
применимо. Если правило нарушается, опишите ошибку.
(а) Предположим, что следующие сегменты кода используются для
перегрузки функции f.
<function 1>
int f(int x, int у)
{
return x*y;
)
<function 3
int f(int x=l, int y=7)
{
return x + у + x*y;
}
<function 2>
double f(int x, int y)
{
return x*y;
}
(б) Функция max перегружается четырьмя отдельными определениями
<function 1>
int max(int x, int y)
(
return x>y? x : y;
)
<function 3>
int шах(int x, int y, int z)
{
int lmax *x;
if(y>lmax)
lmax=»y;
if (z > lmax)
lmax - z;
return lmax;
}
<function 2>
double max(double x, double y)
{
return x>y? x : y;
)
<function 4>
int max (void)
{
int a, b;
cin »a»b;
return abs(a) > abs(b)?
a : b;
)
(в) Эти три версии функции read предназначены для различения ввода
данных целого и перечисляемого типа.
<function 1>
void read(int& х)
{
cin»x;
>
<function 3>
typedef int Logical;
<function 2>
enum Boolean{FALSE,TRUE};
void read(Boolean& x)
(
char c;
cin» c;
x = (c«'T') ? TRUErFALSE;
}
const int TRUE=1, FALSE^O;
void read(Logical& x)
{
char c;
cin>>c;
X=(C«'T') ? TRUE:FALSE;
}
6.2 Используйте функцию max из письменного упражнения 6.1(b) и
предположите, что пользователь вводит значения т=-29 и п=8. Укажите,
какая функция вызывается и какое будет возвращаемое значение.
(a) cin » m » n; (б) max(); (в) max(m, -40, 30);
max (m, n) ;
6.3 При использовании max из письменного упражнения 6.1(b) каков выход
каждого из операторов?
int а=5, Ь«99, с=153
int m,n;
double hl= .01, h2= .05;
long t = 3000, u= 70000, v= -100000;
cout «"Максимум а и b равен "<<max(a,b);
cout <<"Максимум a, b и с равен "<<ma:-;(a,b,c) ;
cout «"1.0 + max (hi, h2) -"«1.0 + max (hi, h2);
cout «"Максимум t, u и v равен "« max(t,u,v);
6.4 Являются ли следующие функции различными с целью перегрузки?
Почему?
(а) enum El{one, two}; (6) type def double scientific;
enum E2{three,four);
int f(int x, El y) ; double f(double x);
int f(int x, E2 y); scientific f(scientific x);
6.5 Напишите перегруженные версии функции Swap, которая может
принимать два int, float и string(char*) параметра.
void Swap(int& a, int&b);
void Swap(float& x, floats y);
void Swap(char *s, char *t);
6.6 Объясните различие между перегрузкой оператора с использованием
функции-члена и дружественной функции.
6.7 Класс ModClass имеет единственный целый данное-член dataval в
диапазоне 0 . . .6. Конструктор принимает любое положительное целое v
и присваивает данному-члену dataval остаток от деления на 7.
dataval=v% 7
Оператор сложения складывает два объекта, суммируя их данные-члены
и находя остаток после деления на 7. Например:
ModClass a(10)/ //dataval в а равен 3;
ModClass b(6); //dataval в b равен 6;
ModClass c; // c-a + b имеет значение (3+6) % 7 -2
class ModClass
{
private:
int dataval;
public:
ModClass{int v * o) ;
ModClass operator+(const ModClassS x);
int GetValue(void) const;
};
(а) Реализуйте методы этого класса.
(б) Объявите и реализуйте оператор "*" как друга ModClass. Оператор
умножает поля значений в двух объектах ModClass и находит остаток
после деления на 7.
(в) Напишите функцию
ModClass Inverse(ModValue& x);
которая принимает объект х с ненулевым значением и возвращает
значение у, так что х*у=1 (у называется обратным значением х). (Совет:
неоднократно умножайте х на объекты со значениями от1 до 6. Один
из этих объектов является обратным).
(г) Перегрузите потоковый вывод для ModClass и добавьте этот метод к
классу.
(д) Замените GetValue, перегрузив оператор преобразования int(). Этот
оператор преобразует объект ModClass в целое, возвращая dataval.
operator int (void);
(е) Напишите функцию
void Solve(ModClass a, ModClass& x, ModClass b);
которая решает уравнение ах = b для х, вызывая метод Inverse.
6.8 Добавьте полный набор операторов отношения в класс Date из главы 3.
Две даты необходимо сравнить по хронологии года. Например:
Date(5,5,77) > Date(10,24,73)
Date(12/25/44) <= Date(9,30,82)
Date(3,5,99) !=Date(3,7,99)
6.9 Комплексное число имеет форму х + iy, где i2 = -1. Комплексные
числа имеют широкое применение в математике, физике и технике.
Они имеют арифметику, управляемую рядом правил, включающих
следующие:
Пусть u =a+ ib, v = с +id
Величина (u) =sqrt(a2+b2)
Комплексное число, соответствующее действительному числу f,
равно f+iO
Вещественная часть u = a
Мнимая часть u=sqrt(a2+b2)
u + v = (а + с) + i(b + d)
u - v = (а - с) 4- i(b - d)
u*v = (ас - bd) + i(ad 4- be)
ac + bd /be - adN
u/v = — —- + l — —-
c2 + d2 c2 + d2
v J
-u = -a 4- i(-b)
Реализуйте класс Complex, объявление которого является следующим:
class Complex
{
private:
double real;
double imag;
public:
Complex (double x = 0.0, double у » 0.0);
//бинарные операторы
Complex operator* (Complex x) const;
Complex operator- (Complex x) const;
Complex operator* (Complex x) const;
Complex operator/ (Complex x) const;
//Отрицание
Complex operator- (void) const;
//Оператор потокового ввода/вывода
//вывод в формате (real, imag)
friend ostream& operator« (ostream& ostr,const Complex& x) ;
};
6.10 Добавьте методы GetReal и Getlmag в класс Complex из письменного
упражнения 6.9. Они возвращают вещественную и мнимую части
комплексного числа. Используйте эти методы для написания функции
Distance, которая вычисляет расстояние между двумя комплексными
числами.
double Distance (const Complex &a, const Complex &b);
6.11
(а) Добавьте преобразователь в класс Rational, который возвращает объект
ModClass.
(б) Добавьте преобразователь в ModClass, который возвращает объект
Rational
6.12
(а) Реализуйте класс Vec2d из раздела 6.1
(б) Добавьте функцию-член в класс Vec2d, который обеспечивает скалярное
произведение, где операнд скаляра находится в правой части.
Реализуйте оператор и как функцию-член, и как дружественную функцию.
Пример:
Vec2d v(3,5);
cout«v*2«" "<<2*v«endl;
<output>
(6,10) (6,10)
6.13 Множество — это коллекция объектов, которые выбраны из группы
объектов, называемой универсальным множеством. Множество записывается
как список, разделяемый запятыми и заключенный в фигурные скобки.
X = {Ii, I2, 1з, . . . , Im}
В данной задаче элементы множества выбраны из целых в диапазоне
от 0 до 499. Класс поддерживает ряд бинарных операций для множеств
X и Y.
D Множество Union(isJ) XUY — это множество, содержащее все
элементы в X и все элементы bY без дублирования.
□ Множество Intersection(O) X О Y — это множество, содержащее
все элементы, которые находятся и в X, и в Y.
XUY
ХПУ
X - (0. 3. 20, 55}, Y - {4. 20. 45. 55}
X U У - {0. 3. 4. 20. 45. 55} ХП Y - {20. 55}
Множество Membership^) nGX является True, если элемент п
является членом множества X; иначе оно равно False.
X ={0, 3, 20, 55}//20 G X является True, 35 € X является False
Спецификация класса Set
В этом объявлении множество — это список элементов, выбранных из
диапазона целых 0 ...SETSIZE -1, где SETSIZE является 500. Операции
ввода/вывода, объединения, пересечения и принадлежности элементов
определяют управление множеством.
отьявлжниж
const int SETSIZE » 500;
const int False ■ 0, True ■ 1;
class Set
{
private:
// данные-члены класса set
int member[SETSIZE];
public:
// конструктор, создает пустое множество
Set(void);
// конструктор, создает множество с начальными
// элементами а[0], . . . , а[п-1]
Set(int all, int n) ;
// операторы объединения {+), пересечения (*), принадлежности (А)
Set operator+ (Set x) const;
Set operator* (Set x) const;
friend int operator* (int elt, Set x);
// методы вставки и удаления
void Insert (int n); // добавить элемент п к множеству set
void Delete(int); // удалить элемент п
// операторы вывода Set
friend ostreamfi operator« (ostream& ostr, const Sets x) ;
>;
ОПИСАНИЕ
Первый конструктор просто создает пустое множество. Элементы
добавляются во множество с использованием Insert. Второй конструктор
присваивает п целых значений в массиве а этому множеству. Каждый элемент
проверяется на нахождение в диапазоне.
Элемент я находится во множестве, при условии, что соответствующий
элемент массива является равным True.
п€х если и только если элемент [п] является True
Например, множество X ={1, 4, 5, 7} соответствует массиву с элементами
member[l], member[4], member[5], member[7] равными True, и другими
элементами, равными False.
false
true
false
false
true
true
false
true
false
false
0123456789 499
Потоковый оператор вывода должен печатать множества с элементами,
разделяемыми запятыми и заключенными в фигурные скобки. Например:
int setvalsf ] = {4, 7, 12};
Set S, T(setvals, 3);
S.Insert(5);
cout « S « endl;
cout « T « endl;
<output>
{5}
{4, 7, 12)
(а) Реализуйте конструкторы Set.
(б) Реализуйте функцию-член множества в ('"'). Возвращается True, если
member[n] является равными True; иначе возвращается False. Так как
приоритет оператора '"' является относительно низким, выражение,
включающее '"' следует заключать в скобки для надежности. Например:
Set A;
• • *
if ({0 Л А) == 0) //проверка на нахождение 0 во множестве А
(в) S — это множество {1, 4, 17, 25} и Т — это множество {1,8,25,33,53,63}.
Выполните следующие операции:
(I) S + Т (ii) S * Т (ш) 5^S
(iv) 4* (S+T) (v) 25Л (S*T)
(г) Укажите действие следующей последовательности операторов:
int a[] * {1,2,3,5};
int b[] = {2,3,7,8,25};
int n;
Set A(a,4), Bib,5), C;
С = A+B; cout « C;
С « A*B; ccut « C;
cin >> n; // введите 55
A.Insert(n);
if (пЛА)
cout << Удачно « endl;
(д) Реализуйте остальные методы Set
Упражнения по программированию
6.1 Эта программа использует результат письменного упражнения 6.5.
Напишите программу, которая берет два целых и два числа с плавающей
точкой, печатает их значения и затем вызывает соответствующую
функцию Swap для записи этих значений в обратном порядке. Эта же
программа должна вводить две символьные строки, менять местами их
значения с использованием Swap и печатать результирующие строки.
6.2 Эта программа тестирует класс ModClass, разработанный в письменном
упражнении 6.7. Напишите программу для проверки дистрибутивного
закона для объектов ModClass.
а*(Ь+с) = а*Ь + а*с
Определите три объекта a, b и с, имеющие параметры конструктора
10, 20 и 30, соответственно. Ваша программа должна выводить значение
из выражений в каждой части уравнения.
6.3 Используйте ModClass и функцию Solve, разработанные в письменном
упражнении 6.7. Сформируйте массив
ModClass а[ ] = {ModClass(4), ModClass(10), ModClass(50)};
Программа должна выполнять цикл
for(int i=0; i<3; i++)
cout « a[i] « " " « int(a[i]) « endl;
Используйте функцию Solve для печати решения уравнения
ModClass (4) * х = ModClass(3)
6.4 Эта программа использует операторы класса Date из письменного
упражнения 6.8. Напишите функцию
Date Min(const Date& x, const Dates y);
которая возвращает более раннюю из двух дат. Определите четыре
объекта от D1 до D4, которые соответствуют
D1 — это 6/6/44 D2 - это день Нового года в 1999
D3 — это Рождество 197 6 D4 — это 4 июля 1976
Протестируйте функцию, сравнивая объекты D1 и D2, D3 и D4.
6.5 Рассмотрим следующие свойства векторов с двумя измерениями:
(а) u*(v+w)=u*v + u*w (дистрибутивное свойство)
(б) Два вектора перпендикулярны; их скалярное произведение равно 0.
(в) c*v=v*c, где с — действительное число.
Используя класс Vec2d, разработанный в письменном упражнении 6.12,
дайте явные примеры, иллюстрирующие (а) и (с). Эта программа должна
также считывать два действительных числа х и у и проверять, чтобы
векторы (х, у) и (-у, х) были перпендикулярными.
6.6 Это упражнение использует класс Complex number, разработанный в
письменном упражнении 6.9. Программа должна выполнять следующие
действия:
(а) Проверьте, чтобы -i2 = 1.
(б) Напишите функцию f(z), оценивающую комплексную полиномиальную
функцию:
2з _ 3z2 + 4z — 2
Вычислите полиномиал для следующих значений z:
z = 2+3i, -1+i, 1+i, 1-i, l+0i
Заметьте, что последние три значения являются корнями из f.
6.7 Используйте класс Rational и его операторы преобразования для
выполнения следующего сравнения действительных и рациональных
чисел. Объявите действительное число pi= 3.14159265 и приближение
рационального числа Rational(22,7), которое часто используется
студентами. Напишите программу, которая выполняет два следующих
вычисления и печатает результаты.
(а) Вычислите разность между двумя числами как рациональными
числами.
Rational(pi) — Rational(22,7)
(б) Вычислите разность между двумя числами как действительными
числами, pi — float(Rational(22,7))
6.8 В главе 8 описывается класс экстенсивной строковой обработки,
использующий указатели и динамическую память. Это упражнение
разрабатывает простой строковый класс, который сохраняет данные,
используя массив. Рассмотрим объявление
Class String
I
private:
char str[256];
public:
String(char s[] « " ")
int Length(void) const; // длина строки
void CString(char s[) const; // копировать строку в массив C++
// **********потоковый ввод/вывод ***********
friend ostrearafi operator« (ostream& ostr, const Strings s);
// Читать строки, разделенные пробелами
friend istream& operator» (istream& istr, Strings s);
// ******* оператор отношения: String « String *****
int operator-* (Strings s) const;
// ***** объединение *****
String operator+ (Strings s) const;
};
Реализуем класс и протестируем его, запуская следующую программу
void main(void)
{
String SI("Это n), S2("прекрасный день!"), S3;
char s[30];
if (SI ==String(3TO a))
cout «"Тестирование на равенство удачное" «endl;
else
cout «"Тестирование на равенство неудачное, "«endl;
cout «"Длина Sl= "«SI. Length () « endl;
cout «"Ввод строки S3: ";
cin » S3;
S3 « SI + S2;
cout «"Конкатенация SI и S2 равна"
« S3 « endl;
S3. Cstring(s);
cout «"Строка C++, сохраняемая в S3 следующая"
« s «"' "« endl;
}
6.9 Это упражнение тестирует класс Set из письменного упражнения 6.13.
Рассмотрим множества
S = {1,5,7,12,24,36,45,103,355,499}
Т = {2,3,5,7,8,9,12,15,36,45,56,103,255,355,498}
U - {1,2,3,4,5, ..., 50}
Создайте множества S, Т и U. Используйте Insert для инициализации
множества U. Выполните следующие вычисления:
(1) Вычислите и печатайте S+T.
(2) Вычислите и печатайте S*T.
(3) Вычислите и печатайте S*U.
(4) Удалите 8, 36, 103 и 498 из Т и печатайте это множество.
(5) Генерируйте случайное число от 1 до 9, печатайте его
и затем проверьте, находится ли оно во множестве Т.
6.10 В этом упражнении используется класс Set для моделирования
вероятности получения пяти отдельных случайных чисел в диапазоне от 0
до 4 в пяти последовательных жеребьевках. Математическая
вероятность этого события равна
1 • 4/5 • 3/5 • 2/5 • 1/5 - .0384
Напишите функцию
int fillSet(void);
которая выполняет эксперимент жеребьевки пяти чисел и вставляет
их во множество S. Протестируйте, находятся ли 0 ... 4 в этом
множестве, проходя цикл пять раз и используя оператор ,Л\ Если все
целые находятся в этом множестве, возвращайте 1, иначе
возвращайте О,
Напишите main-программу, вызывающую fillSet 100000 раз и
записывающую количество случаев, когда выбираются все пять чисел.
Разделите результат на 100000 для определения моделируемой вероятности.
гла в а
7
Параметризованные типы
данных
7.1. Шаблонные функции
7.2. Шаблонные классы
7.3. Шаблонные классы списков
7.4. Вычисление инфиксных выражений
Письменные упражнения
Упражнения по программированию
Определения классов SeqList, Stack и Queue предназначены для родового
(параметризованного) типа, называемого DataType. Перед использованием
какого-либо класса клиент получает конкретный тип для DataType, используя
директиву typedef. К сожалению, это ограничивает возможности клиента
единственным типом с любым из классов. В приложении не может использоваться
стек целых и стек записей в одной и той же программе. Так как использование
родового DataType сильно ограничивает клиента, лучшим подходом было бы
связать тип данных с объектом, а не с программой. Например:
SeqList<int> А; //Список целых
Stack<float> В; //Стек действительных чисел
Queue<CL> С; //Очередь объектов CL
C++ предоставляет такую возможность директивой шаблона (template),
которая позволяет использовать параметры общего типа для функций и
классов. Использование шаблонов с классом коллекций дает возможность
определять родовые параметры и выполнять два или более вызовов функций с
параметрами времени исполнения различных типов. Шаблоны обеспечивают
мощным средством обобщения структуры данных. Мы излагаем эту тему в
данной главе, сначала вводя шаблонные функции и затем расширяя эти
понятия до шаблонных классов. Для приложений разрабатывается
последовательный поиск как шаблонная функция и использование шаблонов для
перезаписи класса Stack. Множественные стеки являются основной
структурой данных в изложенном в этой главе практическом применении,
описывающем вычисление инфиксных выражений.
7.1. Шаблонные функции
Алгоритм часто предназначается для обработки некоторого диапазона типов
данных. Например, алгоритм последовательного поиска принимает ключ и
просматривает список элементов на предмет совпадения. Этот алгоритм
подразумевает, что оператор отношения "==" определяется для некоторого типа
данных и может использоваться для просмотра списка целых, символов или
объектов. До этого момента в книге мы обсудили несколько приложений для
алгоритма последовательного поиска. В каждом случае указывалась
конкретная версия функции SeqSearch для типа элементов в списке. Мы уже создали
множество версий этой функции для реализации того же самого родового
алгоритма. Теперь нам хотелось бы написать родовой код, который может
применяться с различными списками. C++ делает это возможным с помощью
шаблонов, основные элемепты синтаксиса которых рассматриваются далее.
Объявления шаблонной функции начинаются со списка параметров
шаблона в форме
template <class Tlt class T2, . . . class Tn>
За ключевым словом template следует непустой список параметров типов,
заключенный в угловые скобки. Типам предшествует ключевое слово class.
Идентификатор Ti является общим именем для конкретного типа данных C++,
которое передается как параметр при использовании шаблонной функции.
Ключевое слово class присутствует только для указания на то, что имя Ti
представляет собой тип. Вы можете читать class как "type". При использовании
шаблона Ti может быть стандартным типом, таким как int, или определяемым
пользователем типом, таким как класс. Например, в следующих списках
параметров шаблона имена Т и U ссылаются на типы данных.
template <class T> //T - это тип
template <class T, class U> //T и U оба являются типами
После определения списка параметров шаблона функция следует обычному
формату и имеет доступ ко всем типам в списке. Например, определение
SeqSearch как шаблонной функции следующее:
// используя ключ, ищет совпадение в массиве из п элементов.
// если совпадение обнаружено, возвращает индекс совпадения;
// иначе возвращает -1
template<class T>
int SeqSearch(T list[ ], int n, T key)
{
for(int i*0; i<n; i++)
if (listfi] -= key)
return i; //возвращает индекс совпадающего элемента
return -1; //поиск неудачный, возвращает -1
}
Когда программа вызывает шаблонную функцию, компилятор указывает
типы данных фактических параметров и связывает эти типы с элементами в
списке параметров шаблона. Например, в вызове функции SeqSearch
компилятор различает целые и действительные параметры,
int А[10], Aindex, Mindex;
float M[100], fkey « 4.5;
Aindex = SeqSearch(A, 10, 25); //поиск 25 в А
Mindex - SeqSearch(M, 100, fkey); //поиск fkey 4.5 в М
Компилятор создает отдельный экземпляр функции SeqSearch для каждого
отдельного списка параметров времени исполнения. В первом случае
шаблонный тип Т будет целым (int), и SeqSearch просматривает список целых,
используя оператор сравнения целых "==". Во втором случае параметр типа Т будет
действительным (float), и используется оператор сравнения чисел с плавающей
точкой == .
При вызове основанной на шаблоне функции с конкретным типом все
операции должны определяться для этого типа. Если функция использует
операцию, не являющуюся присущей этому типу, программист должен предоставить
свою версию этой операции или использовать нешаблонную версию такой
функции, Например, C++ не определяет оператор сравнения "==" для stuct или класса.
Параметризованная версия функции SeqSearch не может упорядочивать объекты
класса, если только оператор не определяется (перегружается) пользователем.
В качестве примера рассмотрим тип записи Student, включающий как целое
поле, так и поле с плавающей точкой. Оператор "==" перегружается для
применения функции SeqSearch.
//запись о студенте, содержащая его ID и средний балл
struct Student
{
int studID;
float gpa;
};
// перегружает ==, сравнивая id студента
int operator ■■ (Student a, Student b)
{
return a.studID « b.studID;
}
Объявление записи Student и оператор "==и находятся в файле student.h.
C++ строковый тип char* создает пользователю некоторые проблемы.
Оператор "==" сравнивает значения указателей, а не фактические строки
посимвольно. Так как char* не является структурой или классом, мы не можем
определять перегруженный оператор "==" для этого типа. Пользователь
должен использовать нешаблонную версию функции SeqSearch, которая
применима к строковому типу C++.
// просмотреть массив строк для нахождения совпадения со строкой-ключом
int SeqSearch(char *list[ ], int n, char *key)
I
for (int is=0;i<n;i++)
// сравнить, используя строковую библиотечную функцию C++
if (strcmpdist [i], key) == 0)
return i; // возвратить индекс совпадающей строки
return -1; // при неудаче возвратить -1
}
Главная тема этого раздела проиллюстрирована в программе
параметризованного поиска. Код для шаблонной функции SeqSearch и специфическая
версия для строк C++ содержится в файле utils.h.
Программа 7.1. Параметризованный поиск
Эта программа иллюстрирует последовательный поиск для трех
отдельных типов данных.
□ Массив list инициализируется 10-ю целыми значениями. Мы
определяем индекс элемента массива со значением 8.
D Перегрузка оператора используется с типом записи Student. Запись
{1550, 0} используется как ключ для поиска в списке и определения
ID студента. Возвращаемый индекс обеспечивает доступ к GPA 2,6.
П Для массива строк компилятор использует нешаблонную функцию
SeqSearch с типом данных "char*". Ведется поиск строки "two", которая
находится в позиции с индексом 2.
♦include <iostream.h>
ipragma hdrstop
// включить код шаблонной функции SeqSearch и
// специфической версии для строк C++
// search function specific to C++ strings
#include "utils.h"
// объявление структуры Student и операции "=-" для Student
linclude "student.h"
void main()
{
// три массива с различными типами данных
int listriO] = {5, 9, 1, 3, 4, 8, 2, 0, 7, 6};
Student studlist[3] - {{1000, 3.4),{1555, 2.6},{1625, 3.8}};
char *strlist[5] = {"zero","one","two","three","four"};
int i, index;
// ключ для поиска в массиве studlist
Student studentKey * {1555t 0);
if ((i = SeqSearchdist, 10,8)) >= 0)
cout « "Значение 8 находится в элементе: " « i « endl;
else
cout « "Элемент со значением 8 не найден" « endl;
index - SeqSearch(studlist, 3, studentKey);
cout « "Студент с ID, равным 1555, имеет GPA: " « studlist[index].gpa
« endl;
cout << "Строка 'two' — в элементе: "
« SeqSearch(strlist,5,"two") « endl;
>
/*
<Run of Program 7.1>
Значение 8 находится в элементе: 5
Студент с ID, равным 1555, имеет GPA: 2.6
Строка 'two' — в элементе: 2
*/
Сортировка на базе шаблона
Обменная сортировка предоставляет алгоритм для упорядочения элементов в
списке с использованием оператора сравнения "<". Этот алгоритм реализуется
основанной на шаблоне функцией ExchangeSort, которая использует
единственный параметр шаблона Т. Оператор "<" должен определяться для типа данных,
который соответствует Т, или в качестве перегруженного оператора пользователя.
// сортировка п элементов массива а с использованием обменной сортировки
template <class T>
void ExchangeSort(T a[], int n)
{
Т temp;
int i, j/
// выполнить n-1 проходов
for (i = 0; i < n-1; i++)
// наименьшее из a[i+l]...a[n-1] поместить в a[ij
for (j » i+1; j < n; j++)
if (a[j] < a[i])
{
// поменять значения элементов a[i] и a[j]
temp ■ a[i];
a[i] = a[j];
a(j] = temp;
}
}
Для удобства функция ExchangeSort находится в файле utils.h.
7.2. Шаблонные классы
Обсудим основанный на шаблоне класс Store, содержащий значение
данных, которое перед использованием класса должно инициализироваться. В
процессе обсуждения мы проиллюстрируем главные концепции основанных
на шаблоне классов.
Определение шаблонного класса
При определении шаблонного класса (template class) его объявлению
предшествует список параметров шаблона. Для объявления элементов данных и
функций-членов в определении шаблона используются имена параметризиро-
ванного типа. Далее следует объявление шаблонного класса Store:
#include <iostream.h>
♦include <stdlib.h>
template <class T>
class Store
{
private:
T item/ // объект, содержащий данные
int haveValue; // флаг, устанавливаемый при инициализации
public:
// конструктор умолчания
Store(void);
// операции получения и сохранения данных
Т GetElement(void);
void PutElement(T x);
>;
Объявление объектов шаблонного класса
Типы этому классу передаются при создании объекта. Объявление связывает
тип с экземпляром класса. Следующие объявления создают объекты типа Store:
//данное-член в X имеет тип int.
Store<int> X;
//создает массив из 10 объектов Store с данными char
Stdre<char> S[10];
Определение методов шаблонного класса
Метод шаблонного класса может быть определен как код in-line или вне
тела класса. При внешнем определении метод должен рассматриваться как
шаблонная функция со списком параметров шаблона, включенным в
определение функции. Все ссылки на класс как тип данных должны включать
шаблонные типы, заключенные в угловые скобки. Это применяется к имени
класса с оператором области видимости класса:
ClassName<T>::
Например, следующий код определяет функцию GetElement для класса Store:
// получение элемента, если он инициализирован
template <class T>
Т Store<T>::GetElement(void)
{
// прервать программу при попытке доступа к неинициализированным данным
if (haveValue *~ 0)
{
cerr « "Нет элемента!" « endl;
exit(1);
}
return item; // возвратить элемент
}
В методе Putltem подразумевается, что присваивание является правильной
операцией для элементов типа Т:
// сохранить элемент в памяти
template <class T>
void Store<T>::PutElement(const T&x)
{
haveValue+4; // haveValue = TRUE
item = x; // сохранить х
>
Для внешнего определения конструктора используется имя класса с
оператором области видимости класса и имя метода конструктора. В качестве типа
класса используйте параметр шаблона. Например, типом класса является
Store<T>, тогда как именем конструктора является просто Store.
// объявление Оез инициализации элемента данных
template<class T>
Store<T>::Store(void):haveValue(0)
{ )
Объявление и реализация класса Store находится в файле store.h.
Программа 7.2. Использование шаблонного класса Store
Эта программа использует шаблонный класс Store для объектов типа
integer, записи Student и объектов типа double. В первых двух случаях
значения данным присваиваются с использованием PutElement и
печатаются с использованием GetElement. Когда типом данных является double,
делается попытка выборки значения данных, которое не инициализировано,
и программа завершается.
♦include <iostream.h>
♦pragma hdrstop
♦include "store.h"
♦include "student.h"
void main(void)
{
Student graduate » {1000, 23};
Store<int> A, B;
Store<Student> S;
Store<double> D;
A.PutElement(3);
B.PutElement(-7);
cout « A.GetElement () « " " « B.GetElement () « endl;
S.PutElement(graduate);
cout « "ID студента: " « S.GetElement (). studID
« endl;
// D не инициализировано
cout « "Получение объекта D: " << D.GetElement() « endl;
)
Л
<Run of Program 7.2>
3 -7
ID студента: 1000
Получение объекта D: Нет элемента!
*/
7.3. Шаблонные списковые классы
Мы расширяем возможности коллекций в этой книге, используя шаблонные
классы. В данном разделе переопределяется класс Stack с шаблонами, который
используется в разделе 7.4 для вычисления инфиксного выражения.
Шаблонная версия этого класса включена в программное приложение в файл tstack.h.
Переопределение класса Stack включает простую шаблонную технику.
Начинаем объявление, помещая список параметров шаблона перед объявлением
класса и заменяя DataType на Т.
Спецификация шаблонного класса Stack
ОБЪЯВЛЕНИЕ
#include <iostreara.h>
#include <stdlib.h>
const int MaxStackSize = 50;
template <class T>
class Stack
{
private:
// закрытые данные-члены
T stacklist[MaxStackSize];
int top;
public:
// конструктор
Stack(void);
// стековые методы доступа
void Push(const T& item);
T Pop(void);
T Peek(void);
// методы тестирования и очистки
int StackEmpty(void) const;
int StackFull(void) const;
void ClearStack(void);
};
Реализация класса Stack, основанного на шаблоне
Каждый метод класса определяется как внешняя шаблонная функция. Это
требует помещения списка параметров шаблона перед каждой функцией и
замены класса типа Stack на Stack<Т>. В фактическом определении функции
мы должны заменить параметризованный тип DataType на шаблонный тип Т.
Следующий листинг задает новое определение для методов Push и Pop.1
1 Данный код взят из программного приложения, так как он значительно отличается от
приведенного в оригинале книги. — Прим. ред.
// constructor
template <class T>
Stack<T>::Stack(void)
{}
// uses the LinkedList method ClearList to clear the stack
template <class T>
void Stack<T>::ClearStack(void)
{
stackList.ClearList();
)
// use the LinkedList method InsertFront to push item
template <class T>
void Stack<T>::Push(const T& item)
{
stackList.InsertFront(item);
}
// use the LinkedList method DeleteFront to pop stack
template <class T>
T Stack<T>::Pop(void)
{
// check for an empty linked list
if (stackList.ListEmptyO)
{
cerr « "Popping an empty stack" « endl;
exit(l);
}
// delete first node and return its data value
return stackList.DeleteFront();
}
// returns the data value of the first first item on the stack
template <class T>
T Stack<T>::Peek(void)
{
// check for an empty linked list
if (stackList.ListEmpty())
{
cerr « "Calling Peek for an empty stack" « endl;
exit(l);
}
// reset to the front of linked list and return value
stackList.Reset();
return stackList.Data();
}
// use the LinkedList method ListEmpty to test for empty stack
template <class T>
int Stack<T>::StackEmpty(void) const
{
return stackList.ListEmpty();
}
7.4. Вычисление инфиксного выражения
В главе 5 показано использование стеков при вычислении выражений
постфиксной или польской инверсной записи (Reverse Polish Notation, RPN). Тема
вычисления инфиксных выражений была умышленно опущена, так как их
реализация требует использования двух стеков: одного для операндов, и дру-
гого — для операторов. Поскольку в двух стеках находятся данные различных
типов, при инфиксном вычислении эффективно используются шаблоны. В этом
разделе разрабатывается алгоритм вычисления инфиксного выражения,
который реализуется с шаблонным стековым классом.
Вы знакомы с выражениями, объединяющими арифметические операции.
Например, следующие выражения объединяют унарный оператор —,
бинарные операторы +, -, *, /, скобки и операнды с плавающей точкой:
8.5 + 2 * 3 -7 * (4/3 - 6.25) + 9
Эти выражения используют инфиксную запись с бинарными операторами,
расположенными между операндами. Пара скобок создает подвыражение,
вычисляемое отдельно.
В языках высокого уровня существует порядок выполнения операций
(order of precedence) и ассоциативность (associativity) между операторами.
Оператор с высоким приоритетом выполняется первым. Если более одного
бинарного оператора имеют один и тот же приоритет, первым выполняется
крайний слева оператор в случае левой ассоциативности (+, -, *, /) и крайний
правый оператор — в случае правой ассоциативности (унарный плюс,
унарный минус).
Порядок выполнения операций
(от низкого к высокому)
1
2
3
Оператор
+. -
•./
унарный плюс, унарный минус
Пример 7.1
1. 8.5 + 2*3= 14.5 // * выполняется перед +
2. (8.5 + 2) * 3 = 31.5 // скобки создают подвыражение
3. 9 6 » 15 // унарный минус имеет высший приоритет
Ранг выражения. Алгоритм для вычисления инфиксного выражения
использует понятие ранга (rank), который присваивает значение -1, 0, или 1
каждому терму выражения:
Ранг операнда с плавающей точкой равен 1
Ранг унарных операторов +, - равен О
Ранг бинарных операторов +, -, *, / равен -1.
Ранг левой скобки равен 0.
Когда мы просматриваем термы в выражении, ранг определяет неправильно
расположенные операнды или операторы, которые могут сделать выражение
неверным. С каждым термом выражения мы ассоциируем суммарный ранг
(cumulative rank), который является суммой ранга отдельных термов от
первого символа до данного терма. Суммарный ранг используется для контроля
за тем, чтобы каждый бинарный оператор имел два окружающих операнда и
чтобы никакие операнды в выражении не существовали без инфиксного
оператора. Например, в простом выражении
2 + 3
последовательные значения ранга такие:
Сканирование 2: суммарный ранг = 1
Сканирование +: суммарный ранг = 1 + -1 = О
Сканирование 3: суммарный ранг = 1
Правило: Для каждого терма в выражении суммарный ранг выражения
должен быть равен 0 или 1. Ранг полного выражения должен быть равен 1.
Пример 7.2
Следующие выражения являются неверными, что определяется
функцией rank:
Выражение
1. 2.5А + 3
2. 2.5 + 1 3
3. 2.5 + 3 -
Неверный ранг
Ранг 4 = 2
Ранг * - -1
Конечный ранг = 0
Причина
Слишком много последовательных операндов
Слишком много последовательных операндов
Нет одного операнда
Алгоритм инфиксного выражения. Алгоритм инфиксного выражения
использует стек операндов (operand stack) — стек значений с плавающей точкой
для хранения операндов и результатов промежуточных вычислений. Второй
стек, называемый стеком операторов (operator stack) содержит операторы и
левые скобки и позволяет реализовать порядок приоритетов. При
сканировании выражения термы помещаются в соответствующие стеки. Операнд
помещается в стек операндов, когда он встречается в процессе сканирования
и извлекается (popped) из стека, когда он необходим для операции. Оператор
помещается в стек только тогда, когда уже были оценены все операторы с
более высоким или равным приоритетом, и освобождается из стека, когда
наступает время его выполнения. Это происходит при вводе последующего
оператора с более низким или равным приоритетом или в конце выражения.
Рассмотрим выражение
2 + 4 — 3*6
Ввод 2: Поместить 2 в стек операндов.
Ввод +: Поместить + в стек операторов.
Ввод 4: Поместить 4 в стек операндов.
Операнд Оператор
Ввод -: Оператор - имеет тот же порядок приоритетов, что и оцератор
+ в стеке. Сначала извлечь 4- из стека операторов, извлечь два операнда и
выполнить операцию сложения. Результат (2 + 4 = 6) поместить обратно в
стек операндов.
Поместить - в стек операторов.
Операнд Оператор
Ввод 3: Поместить 3 в стек операндов.
Ввод *; Оператор * имеет более высокий приоритет, чем оператор — в
стеке. Поместить * в стек операторов.
Ввод 6: Поместить 6 в стек операндов.
Операнд Оператор
Выполнить: Извлечь * и выполнить операцию с операндами 6 и 3 из
стека операндов. Поместить результат 18 в стек операндов.
Операнд Оператор
Извлечь из стека и выполнить операцию — с операндами 18 и 3 из стека
операндов. 6 - 18 = -12. Это результат.
Приоритет оператора определяется дважды: сначала при вводе оператора,
затем, — когда он находится в стеке. Начальное значение, называемое
входным приоритетом (input precedence), используется для сравнения
относительной важности оператора с операторами в стеке. Как только оператор
помещается в стек, ему задается новый приоритет, называемый стековым
приоритетом (stack precedence). Различие между входным и стековым
приоритетом используется для скобок и правых ассоциативных операторов. В
этих случаях стековый приоритет меньше, чем входной приоритет. Когда
обнаруживается оператор с тем же приоритетом и ассоциативностью, входной
приоритет превышает стековый приоритет оператора в вершине стека.
Первый оператор не извлекается, а новый оператор помещается в стек. Порядок
вычисления задается справа налево.
В таблице 7.1 приводится входной и стековый приоритет и ранг,
используемые для вычисления инфиксного выражения. Эти операторы включают
скобки и бинарные операторы Н-, -, *, и /. Бинарные операторы являются
левыми ассоциативными и имеют равный входной и стековый приоритет.
Алгоритм вычисления выражений становится немного сложнее при
наличии скобок. Когда обнаруживается левая скобка, она представляет начало
подвыражения и, следовательно, должна быть немедленно помещена в стек.
Это выполняется присваиванием левой скобке входного приоритета, который
больше приоритета любого из операторов. Если левая скобка помещена в
стек, она может быть удалена только тогда, когда находится соответствующая
ей правая скобка, и подвыражение вычисляется полностью. Приоритет левой
скобки в стеке должен быть меньше, чем приоритет любого оператора, чтобы
она не извлекалась из стека при вычислении всех термов в подвыражении.
Алгоритм. Алгоритм реализуется с двумя стеками. Стек операндов содержит
числа с плавающей точкой, в то время как элементами стека операторов
являются объекты класса типа MathOperator.
Входной и стековый приоритет с рангом
Таблица 7.1
Символ
+ - (бинарный)
V
(
)
Приоритет
Входной приоритет
1
2
3
0
Стековый приоритет
1
2
-1
0
Ранг
-1
-1
0
0
// класс, управляющий операторами в стеке- операторов
class MathOperator
{
private:
// оператор и два его значения приоритета
char op;
int inputprecedence;
int stackprecedence;
public:
// конструктор; включает конструктор умолчания и
// конструктор, инициализирующий объект
MathOperator(void);
MathOperator(char ch);
// функции-члены для управления оператором в стеке
int operators (MathOperator a) const;
void Evaluate (Stack<float> &OperandStack);
char GetOp(void);
}.;
Объект MathOperator сохраняет оператор и значения приоритета, связанные
с этим оператором. Конструктор задает как входной, так и стековый приоритет
оператора.
MathOperator::MathOperator(char ch)
{
op = ch;
switch(op)
{
// '+' и '-' имеют входной и стековый приоритет 1
case ' +' :
case '-': inputprecedence = 1;
stackprecedence = 1;
break;
// '*' и '/' имеют входной и стековый приоритет 2
case '*' :
case '/': inputprecedence = 2;
stackprecedence « 2;
break;
// ' (' имеет входной приоритет 3 и стековый приоритет -1
case ' С : inputprecedence = 3;
stackprecedence = -1;
break;
// ')' имеет входной и стековый приоритет О
case ')' : inputprecedence « 0;
stackprecedence «■ 0;
break;
}
>
Класс MathOperator перегружает C++ оператор ">", используемый для
сравнения значений приоритетов.
// перегрузить оператор >= сравнением стекового
// приоритета текущего объекта и входного приоритета а.
// используется при чтении оператора для определения
// того, следует ли вычислять операторы из стека перед тем,
// как поместить в него новый оператор
int MathOperator::operator>= (MathOperator a) const
<
return stackprecedence >* a.inputprecedence;
)
Этот класс содержит функцию-член Evaluate, которая отвечает за
выполнение операций и извлекает два операнда. После выполнения операции результат
помещается обратно в стек операндов.
void MathOperator::Evaluate (Stack<float> &OperandStack)
{
float operandi = OperandStack.Pop(); // получить левый операнд
float operand2 = OperandStack.Pop{); // получить правый операнд
// выполнить оператор и поместить результат в стек
switch (op) // выбрать операцию
{
case '+' : OperandStack.Push(operand2 + operandi);
break;
case '-': OperandStack.Push(operand2 - operandi);
break;
case '*': OperandStack.Push(operand2 * operandi);
break;
case '/': OperandStack.Push(operand2 / operandi);
break;
}
}
Алгоритм вычисления инфиксного выражения считывает каждый терм
выражения, помещает его в соответствующий стек и обновляет суммарный
ранг. Ввод завершается в конце выражения или, если ранг находится вне
диапазона. Следующие правила применимы при считывании термов:
Ввод операнда: Поместить операнд в стек операндов.
Ввод оператора: Извлечь из стека все операторы, имеющие приоритет
больший или равный входному приоритету текущего оператора. Выполнить
сравнение, используя метод класса MathOperator ">=". Когда операторы
будут удалены из стека, выполнить оператор, используя метод Evaluate.
Ввод правой скобки "/' ' Извлечь и выполнить все операторы в стеке,
имеющие стековый приоритет больший или равный входному приоритету
скобки ")", который равен 0. Заметьте, что стековый приоритет скобки ")" равен
-1, так что процесс останавливается, когда встречается скобка "(".
Выполнением является вычисление всех операторов меясду скобками. Если никакой
скобки "(" не обнаружено, выражение является неверным ( "нет левой
скобки").
В конце выражения очистить стек операторов: Ранг должен быть 1. Если
ранг меньше 1, это означает, что не хватает операнда. Если при очистке стека
обнаруживается "(", то выражение является неверным ("нет правой скобки").
Когда операторы удаляются из стека, функция Evaluate выполняет каждое
вычисление. Конечный результат выражения находят выборкой из стека операндов.
Программа 7.3. Вычисление инфиксного выражения
Данная программа иллюстрирует вычисление инфиксного выражения. Мы
считываем каждый терм выражения, пропускаем все символы пробелов, пока
не находим "в". Во время этого процесса выполняется проверка ошибок с
печатью специальных сообщений об ошибках. После завершения ввода
вычисляются оставшиеся термы выражения и его значение выводится для печати.
♦include <iostream.h>
#include <stdlib.h>
♦include <ctype.h> // используется для функции isdigit
♦pragma hdrstop
♦include "tstack.h"
♦include "mathop.h"
// проверить: оператор или скобка
int isoperator<char ch)
{
if (ch — '+' || ch ~ '-' || ch — '*' ||
ch ~ '/' II ch -- ' (')
return 1;
else
return 0;
}
// проверить: является ли символ пробелом
int iswhitespace(char ch)
{
if (ch -- ' ' || ch — ' \t' II ch — '\n')
return 1;
else
return 0;
}
// функция сообщений об ошибках
void error(int n)
{
// таблица сообщений об ошибках
static char *errormsgs[] ■ {
"Отсутствует оператор",
"Отсутствует операнд",
"Нет левой скобки",
"Нет правой скобки",
"Неверный ввод"
);
// параметр п - это индекс ошибки.
// печатать сообщение и закочить программу
cerr « errormsgs[n] « endl;
exit(1);
)
void main(void)
{
// объявить стек операторов с объектами типа MathOperator
Stack<MathOperator> Operatorstack;
// объявить стек операндов
Stack<float> OperandStack;
MathOperator oprl,opr2;
int rank - 0;
float number;
char ch;
// выполнять до знака '='
while (cin.get(ch) && ch !« '*=')
i
// ******** обработка операнда с плавающей точкой ********
if (isdigit(ch) || ch -- ' .' )
{
// возвратить знак или '.' и читать число
cin.putback(ch);
cin >> number;
// ранг операнда равен 1. суммарный ранг должен быть равен 1
rank++;
if (rank > 1)
error(OperatorExpected);
// поместить операнд в стек операндов
OperandStack.Push(number);
>
// ********* обработка оператора **********
else if (isoperator(ch))
{
// ранг каждого оператора, отличного от 'С, равен -1.
// суммарный ранг должен быть равен 0
if (ch !- ' (') // ранг ' (' равен 0
rank—;
if (rank < 0)
error(OperandExpected);
oprl ■ MathOperator(ch);
while(!OperatorStack.StackEmpty() &&
(opr2 * OperatorStack.PeekO ) >■= oprl)
{
opr2 - OperatorStack.PopO ;
opr2.Evaluate(OperandStack);
}
OperatorStack.Push(oprl);
)
// ********* обработка правой скобки **********
else if (ch « rightparenthesis)
{
oprl » MathOperator(ch);
while(!OperatorStack.StackEmpty() &&
(opr2 * OperatorStack.PeekO) >« oprl)
{
opr2 = OperatorStack.PopO;
opr2.Evaluate(OperandStack);
)
if(OperatorStack.StackEmpty())
error(MissingLeftParenthesis);
opr2 e OperatorStack.PopO; // get rid of ' ('
}
// ********* имеем неверный беод **********
else if (liswhitespace(ch))
error(Invalidlnput);
}
// ранг вычисленного выражения должен быть равен 1
if (rank != 1)
error(OperandExpected);
// заполнить стек операторов и завершить вычисление выражения,
// если найдена левая скобка, а правая отсутствует,
while (!OperatorStack.StackEmpty())
{
oprl = OperatorStack.Pop();
if (oprl.GetOpO -= leftparenthesis)
error(MissingRightParenthesis);
oprl.Evaluate(OperandStack);
}
// значение выражения - в вершине стека операндов
cout « "Значение равно: " « OperandStack.Pop() « endl;
}
/*
Оапуск 1 программы 7.3>
.2.5 + 6/3 * 4 - 3 -
Значение равно: 7.5
Оапуск 2 программы 7. 3>
(2 + 3.25) * 4 =
Значение равно: 21
Оапуск 3 программы 7.3>
(4 + 3) - 7) -
Нет левой скобки
*/
Письменные упражнения
7.1
(а) Напишите код для параметризованной функции Мах, которая
возвращает большее из двух значений.
(б) Напишите перегруженную версию функции Мах, которая работает со
строками C++. Передайте указатели символам как параметры и
возвращайте указатель большей строке.
7.2 Напишите шаблонный класс DataStore, который имеет следующие методы:
int insert (т eit); Вставляет elt в закрытый массив dataElements,
имеющий пять элементов типа Т. Индекс
следующей доступной позиции в dataElements задается
данным-членом 1ос, который также является
количеством значений данных в dataElements.
Возвращает 0, если больше не остается места в dataElements.
int Find(T eit); Выполняет поиск элемента elt в dataElement и
возвращает его индекс, если он найден, и -1, если нет.
int NumEits(void); Возвращает количество элементов, сохраняемых в
dataElements.
т& GetDatadnt n) / Возвращает элемент в позиции п в dataElements.
Генерирует сообщение об ошибке и выходит, если
п<0 или п>4.
7.3 Напишите функцию
template<class T>
int Max(T Arr[ ], int n) ;
которая возвращает индекс максимального значения в массиве.
7.4 Реализуйте функцию
template<class T>
int BinSearch(T A[ ], T key, int low, int high);
которая выполняет бинарный поиск ключа в массиве А.
7.5 Напишите функцию
template <class T>
void InsertOrder(T A[ J, int n, T elem);
которая вставляет elem в массив А, так что список сохраняет
возрастающий порядок. Заметьте, что, когда позиция находится для elem, вы
должны передвинуть все остальные элементы на одну позицию вправо.
7.6
(а) Дайте основанное на шаблоне объявление класса SeqList.
(б) Для шаблонного класса реализуйте конструктор и методы DeleteFront
и Insert.
(в) Перед объявлением объекта SeqList<T> какие операторы должны
определяться для типа Т?
(г) Объявите S как объект Stack, в котором элементами стека являются
объекты SeqList.
Упражнения по программированию
7.1 Протестируйте функции Мах из письменного упражнения 7.1,
используя их в main-программе. Включите в main-программу две строки C++.
7.2 Напишите шаблонную функцию Сору с объявлением
template<class T>
void Copy(T А[ ], Т В[ ], int n) ;
Эта функция копирует п элементов из массива В в массив А. Напишите
main-программу для тестирования функции Сору. Включите, по
крайней мере, следующие массивы:
(a) int Aint[6], Eint[6] = {1, 3, 5, 7, 9, 11};
(b) struct Student
{
int fieldl;
double field2;
);
Student AStudent[3];
Student BStudent[3] - {{1, 3.5}# {3,0}, {5, 5.5}};
7.3 В этом упражнении используется шаблонный класс DataStore,
разработанный в письменном упражнении 7.2. Напишите перегруженный
оператор "«", который печатает данные объекта DataStore, используя
метод GetData. Пусть записью будет Person:
struct Person
{
char name [50];
int age;
int height;
};
Перегрузите оператор "==" для Person так, чтобы он сравнивал поля
имен.
Напишите программу, которая вставляет элементы данных типа Person
до тех пор, пока объект DataStore не будет заполненным. Включите
следующий элемент р типа Person в ваш ввод:
"John"
25
72
Выполните поиск р и затем печатайте результат поиска. Используйте
"«" для вывода объекта.
7.4 Расширьте программу 7.3 для операции возведения в степень, которая
представлена символом "~". Возведение в степень является правым
ассоциативным. Например:
2 А 3 - 8 //23 - 8
2Л2Л3«2Л(2Л3)~ 256.
Для вычисления аь включите математическую библиотеку <math.h>
и используйте функцию pow следующим образом:
ab - pow (a, b)
7.5 Во время последовательного поиска выполняется сканирование списка
и поиск совпадения с ключом. Для каждого элемента у нас имеется
двойная задача: проверка на совпадение и проверка достижения конца
списка. Модифицированная версия поиска, называемая быстрый
последовательный поиск (fast sequential search), совершенствует алгоритм,
добавляя ключ в конец списка. Расширенный список гарантирует
наличие совпадения, так как имеется по крайней мере один "ключевой"
элемент в списке.
Исходный список
Ключ
А[0] А[1]
А{п-1] А[п]
В процессе поиска просто выполняется тестирование на совпадение и
поиск завершается, когда ключ найден в списке.
(а) Напишите код для
template <class T>
int FastSeqSearch(T A[ ], int n, T key)/
(б) Перепишите программу 7.1, используя FastSeqSearch.
7.6 Mode — это значение, которое чаще всего наблюдается в списке. Чтобы
собрать такую информацию для списка произвольных типов данных,
определите класс Datalnfo, поддерживающий два поля данных: value
и frequency.
template <class T>
class Datalnfo
{
private:
T data; // значение данных
int frequency; // появления значения данных
public:
// увеличение frequency
void Increment(void);
// операторы отношения =- и < должны
// соответствовать типу Т
// сравнение значений
int operator— (const DataInfo<T>& w);
// сравнение счетчиков частоты
int operator< (const DataInfo<T>& w);
// операторы потоков << и » должны
// соответствовать типу Т
friend istreamb operator» (istreamfi is, DataInfo<T> &w) ;
friend ostream& operator« (ostreams os, DataInfo<T> &w);
};
Этот класс имеет метод Increment, который увеличивает счетчик на 1,
и потоковый выходной оператор, который выводит объект в формате
"value:count". Запись с начальным значением и начальный счетчик 1
создается выполнением перегруженного потокового входного оператора
"»", который считывает значение данных из входного потока. Эти
операторы отношения добавляются, чтобы облегчить поиск
определенного значения данных в списке объектов Datalnfo и сортировку списка
в частотном порядке.
(а) Реализуйте Datalnfo в файле datainfo.h.
(б) Напишите main-программу, запрашивающую у пользователя количество
элементов, которое будет введено в целый список. Когда этот размер
будет известен, считайте фактические целые значения и создайте
DataInfo<int> — массив с именем dataList. Используйте функцию
SeqSearch, чтобы определить, находится ли значение ввода в массиве
dataList. Возвращаемое значение -1 указывает на то, что новое значение
было считано и, следовательно, должно быть сохранено в массиве
dataList. Иначе, вводимый элемент уже имеется в массиве, и его частота
должна обновляться. Завершите программу, вызывая ExchangeSort для
сортировки dataList, и затем печатайте каждое значение и частоту.
7.7 Модифицируйте упражнение по программированию 7.6 так, чтобы
список Datalnfo сохранял порядок, а для определения того, встречалось
ли уже какое-либо значение, использовался бинарный поиск.
Воспользуйтесь функциями, разработанными в письменных упражнениях 7.4
и 7.5. Конечно, нет необходимости выполнять сортировку.
глава
8
Классы и динамическая
память
8.1. Указатели и динамические
структуры данных
8.2. Динамически создаваемые объекты
8.3. Присваивание и инициализация
8.4. Надежные массивы
8.5. Класс String
8.6. Сопоставление с образцом
8.7. Целочисленные множества
Письменные упражнения
Упражнения по программированию
До этого момента в книге мы использовали только статические структуры
данных (static data structures) для реализации классов коллекций.
Обсуждение включало статические массивы для реализации классов SeqList, Stack и
Queue. Использование статического массива имеет свои недостатки, так как
его размер определяется на этапе компиляции и может быть изменен во время
исполнения приложения. Каждый класс должен запрашивать приемлемо
большое количество элементов, чтобы удовлетворять диапазону потребностей
пользователя. Поэтому во многих приложениях некоторая часть памяти
расходуется напрасно. В некоторых же случаях размер массива может оказаться
недостаточным, и пользователь вынужден будет обращаться к исходному коду
программы, чтобы увеличить размер массива и перекомпилировать программу.
В этой главе мы знакомимся с динамическими структурами данных
(dynamic data structures), которые используют память, полученную из системы
во время исполнения. У нас имеется некоторый опыт распределения памяти
при работе с блочной структурой программ. Компилятор распределяет
глобальные данные и создает автоматические переменные, для которых при
входе в блок выделяется ресурс памяти, а при выходе из блока —
освобождается. Например, в следующей последовательности кода компилятор C++
распределяет глобальные данные, параметры и локальные переменные:
int global =8; // переменная доступна для всей программы
// резервирование памяти в системном стеке для параметров х и у
void subtask (int x, long *y)
{
int z; // выделение ресурса для локальной переменной z
... // при выходе из блока ресурс памяти освобождается
}
Тип и размер каждой переменной известен во время компиляции.
Компиляторы также предоставляют пользователю возможность создавать
динамические данные. Оператор new выделяет ресурс памяти из
динамической области для использования во время выполнения программы, а оператор
delete возвращает ресурс памяти в динамическую область для последующего
выделения. Динамические структуры данных находят важное применение в
приложениях, потребности в памяти которых становятся известными только
во время исполнения этих приложений. Использование динамических
структур является основным в общем изучении коллекций и эффективно снимает
ограничения на размеры, возникающие при объявлении статических
коллекций. Например, в классе Stack его максимальный размер ограничивается
параметром по умолчанию MaxStackSize, а от клиента требуется выполнение
проверки условия заполненности стека перед добавлением (помещением)
нового элемента. Динамическая память повышает возможности использования
класса Stack, поскольку при этом класс запрашивает достаточный ресурс
памяти для удовлетворения потребностей приложения. Приложения баз
данных часто используют временную память для хранения таблиц и списков,
которые создаются по запросу пользователя. Ресурс памяти может выделяться
в ответ на запрос и освобождаться после выполнения запроса.
Использование динамической памяти имеет ограничения и некоторые
неудобства. Приложение может быть предназначено для работы с данными
переменного размера, распределяемыми динамически, но при его выполнении
может быть сделано достаточно запросов, чтобы в конце концов исчерпать
имеющуюся в наличии память. В этом случае пользователь получит сообщение
"Out of memory", а приложение может даже вынуждено завершиться. Такая
проблема чаще всего возникает при выполнении приложения с графическим
интерфейсом, поскольку обычно диалоговая программа использует ряд окон
для отображения данных, установки меню и так далее. Даже если программа
хорошо структурирована, пользователь может иметь слишком много активных
графических структур, из-за чего в конце концов прекратится выделение
имеющейся памяти. При использовании динамической памяти мы должны
понимать, что память — это ресурс, который должен эффективно управляться
программистом. Память, выделяемая динамически, должна освобождаться,
как только в ней отпадает необходимость. Компилятор следует этой политике
при выделении памяти для параметров и локальных переменных.
Программист должен следовать этой же политике, используя оператор delete.
C++ предоставляет ряд методов для обработки динамических данных.
Метод, называемый деструктором (destructor) удаляет динамическую память,
зарезервированную объектом, при удалении этого объекта. Кроме того, класс
может иметь конструктор копирования (copy constructor) и перегруженный
оператор присваивания (overloaded assignment operator), которые
используются для копирования или присваивания одного объекта другому. Эти методы
класса находятся в центре внимания в данной главе. Для введения новых
методов в большинстве примеров мы используем простой класс DynamicClass.
Динамические массивы позволяют выделять блоки памяти во время
исполнения приложений. Для большинства приложений при создании массивов
мы знаем необходимые размеры. Однако в особых случаях нам может
понадобиться расширить границы массива и изменить его размер. Для
обеспечения этой возможности здесь разрабатывается класс Array, который создает
списки произвольного размера и реализует границы массива, проверяя и
изменяя размер списков. Этот класс предоставляет мощную структуру данных
и иллюстрирует использование деструктора, конструктора копирования и
перегруженного оператора присваивания. Мы перегружаем индексный
оператор [ ], поскольку хотим, чтобы объект Array выглядел подобно
стандартному массиву C++.
Строки являются основной структурой данных. В действительности,
некоторые языки определяют встроенный строковый тип. В этой главе
разрабатывается и используется для решения задачи сопоставления с образцом
полный класс String, который затем часто применяется в оставшихся главах
книги.
Множества (sets) очень часто используются в математической теории. В
компьютерных приложениях множества являются мощной нелинейной
структурой данных, применяемых в таких областях, как текстовый анализ,
исправление орфографических ошибок и реализация графов и сетей. Класс Set,
сохраняющий данные интегрального типа, разрабатывается с использованием
битовых операторов C++. Этот подход обеспечивает превосходную
эффективность использования памяти и времени исполнения. Класс Set применяется
для реализации известного алгоритма при нахождении простых чисел,
называемого решетом Эратосфена (Sieve of Eratosthenes).
8.1. Указатели и динамические структуры данных
Указатели как структура данных вводятся в главе 2. В этом разделе
переменные-указатели объединяются с операторами C++ new и delete для
выделения и освобождения ресурса динамической памяти.
Оператор new для выделения памяти
C++ использует оператор new для выделения ресурса памяти данным во
время выполнения программы. "Зная" размер данных, оператор запрашивает
у системы необходимое количество памяти для сохранения данных и
возвращает указатель на начало выделенного участка. Если память не может
быть выделена, оператор возвращает О (NULL).
В следующем примере оператор new принимает тип данных Т в качестве
параметра и резервирует память для переменной типа Т, возвращая адрес
памяти.
Т *р; // объявление р как указателя на T
р = new T; // р указывает на только что
// созданный объект типа Т
Далее переменные ptrl и ptr2 указывают на данные типа int и long,
соответственно.
int *ptrl; // размером int является 2
long *ptr2; // размером long является 4
В следующем примере оператор new присваивает адрес int-переменной
ptrl и адрес long-переменной ptr2.
ptrl = new int; // ptrl указывает на целое в памяти
ptr2 = new long; // ptr2 указывает на длинное целое б памяти
Системная память
целое
длинное целое
ptrl
ptr2
Здесь, ptrl содержит адрес 2-х, a ptr2 — 4-х байтовых целых в памяти.
По умолчанию содержимое памяти не имеет начального значения. Если такое
значение необходимо, оно должно указываться в качестве параметра при
использовании оператора new:
р - new T(value);
Например, операция
ptr2 = new long(100000);
резервирует память для длинного целого и присваивает ему значение 100000.
Динамическое выделение массива
Преимущества динамического выделения памяти особенно очевидны при
запросе целого массива. Предположим, что в некотором приложении размер
массива становится известен только во время исполнения приложения.
Оператор new может резервировать память для массива, используя запись со
скобками []. Пусть, р указывает на данные типа Т. Тогда оператор
р = new Т [п] ; // выделение массива п элементов типа Т
предписывает р указывать на первый элемент массива. Массив, созданный
таким способом, не может быть инициализирован.
Пример 8.1
В следующем примере оператор new выделяет память для массива из
50 длинных целых при условии, что имеется достаточно памяти. Если
указателю р присваивается значение NULL, оператору new не удалось
выделить память и программа завершается.
long *p;
р * new long [50]; // выделить массив для 50 длинных целых
if (p == NULL)
{
cerr << "Ошибка выделения памяти! "«endl;
exit(l); // завершение программы
>
Оператор delete освобождения памяти
Управление памятью является обязанностью программиста. В C++ имеется
оператор delete для освобождения (возвращения в системный ресурс) памяти,
предварительно выделенной оператором new. Синтаксис delete прост и
основывается на том факте, что система времени исполнения C++ сохраняет
информацию о каждом вызове оператора new. Предположим, р и q указывают на
динамически выделяемую память:
Т *р, *q; // р и q являются указателями на тип Т
р = new T; // р указывает на один элемент
q = new T[n]; // q указывает на массив п элементов
Функция delete использует указатель для освобождения памяти. В случае
освобождения массива delete применяется с оператором [].
delete р; // освобождает память переменной, на которую указывает р
delete [] q; // освобождает весь массив,
// на который указывает q
Пример 8.2
Оператор delete освобождает память, указателем на которую является р:
long *p;
р = new long[50]; // выделение массива для 50 длинных целых
delete [] р; // освобождение памяти 50 длинных целых
8.2. Динамически создаваемые объекты
Подобно любой переменной, объект типа класс может объявляться как
статическая или создаваемая динамически (с использованием new) переменная. В
каждом случае обычно вызывается конструктор для инициализации
переменных и динамического выделения памяти для одного или более данных-членов.
Синтаксис использования оператора new подобен синтаксису выделения
памяти для простых типов и массивов. Оператор new выделяет память для объекта
и инициирует вызов конструктора класса, если он существует. Конструктору
передаются любые необходимые параметры.
Для знакомства с динамическим созданием объектов используется
основанный на шаблоне класс DynamicClass, имеющий статические и динамические
данные-члены. Далее следует объявление класса, методы которого
разрабатываются в этом и в разделе 8.3. Класс DynamicClass находится в файле dynamic.h
программного приложения:
frinclude <iostream.h>
template <class T>
class DynamicClass
{
private:
// переменная типа Т и указатель на тип Т
Т member1;
Т *member2;
public:
// конструкторы
DynamicClass (const T& ml, const T& m2);
DynamicClass(const DynamicClass<T>& obj);
// деструктор
^DynamicClass(void)/
// оператор присваивания
DynamicClass<T>& operator^ (const DynamicClass<T>& rhs);
);
Этот простой класс с его двумя данными-членами иллюстрирует основное
действие функций-членов в обработке динамически распределяемых объектов.
Класс предназначен только для демонстрационных целей и не имеет реального
применения.
Конструктор этого класса использует параметр ml для инициализации
статического данного-члена member 1. Для данного-члена member2 требуется
выделение памяти типа Т и инициализация ее значением т2:
// конструктор с параметрами для инициализации данного-члена
template <class T>
DynamicClass<T>::DynamicClass(const T& ml, const T& m2)
{
// параметр ml инициализирует статический член класса
memberl = ml;
// выделение динамической памяти и инициализация ее значением т2
member2 * new T(m2);
cout «"Конструктор:" « memberl « '/' « *member2 « endl;
}
Пример 8.3
Следующие операторы определяют статическую переменную staticObj
и указатель-переменную dynamicObj. Объект staticObj имеет параметры
1 и 100, которые инициализируют данные-члены:
// объект типа DynamicClass
DynamicClass<int> staticObj(1, 100);
Объект, на который указывает dynamicObj, создается оператором new.
Параметры 2 и 200 передаются конструктору в качестве параметров. При
создании объекта *dynamicObj конструктор класса инициализирует
данные-члены значениями 2 и 200:
// переменная-указатель
DynamicClass<int> *dynamicObj;
// создание объекта
dynamicObj - new DynamicClass<int> (2, 200);
Системная память
100
тетЬег1=1
member1=*2
member2
200
тетЬег2
dynamicObj
staticObj
Освобождение данных объекта: деструктор
Рассмотрим функцию DestroyDemo, которая создает объект DynamicClass,
имеющий целые данные.
void DestroyDemo (int ml, int iti2)
{
DynamicClass<int> obj(ml, m2);
}
При возвращении из DestroyDemo объект obj уничтожается, однако, процесс
не освобождает динамическую память, связанную с объектом. Эта ситуация
показана на рис. 8.1.
До удаления объекта obj
Системная память
После удаления объекта obj
Системная память
гл2
member1=m1
m2
member2
meW>er1=m1 \ тетмс2
Рис. 8.1. Необходимость использования деструктора
Для эффективного управления памятью необходимо освобождать
динамические данные объекта в то же самое время, когда уничтожается объект. Нам
следует выполнить действие конструктора в обратном порядке, который
первоначально распределял динамические данные. Язык C++ предоставляет
функцию-член, называемую деструктором (destructor), которая вызывается при
уничтожении объекта. Для DynamicClass деструктор имеет следующее
объявление:
-DynamicClass(void);
Символ "~" представляет "дополнение", поэтому -DynamicClass — это
дополнение конструктора. Деструктор никогда не имеет параметра или
возвращаемого типа. В данном простом случае деструктор отвечает за освобождение
динамических данных для member2:
// деструктор.освобождает память, выделенную конструктором
template<class T>
DynamicClass<T>:: ^DynamicClass(void)
{
cout«"Деструктор:"« memberl «'/'
« *member2 « endl;
delete member2;
}
Деструктор вызывается всякий раз при уничтожении какого-либо объекта.
Когда программа завершается, все глобальные объекты или объекты,
объявленные в main-программе, уничтожаются. Для локальных объектов,
создаваемых внутри блока, деструктор вызывается при выходе программы из
блока.
Программа 8.1. Деструктор
Эта программа иллюстрирует определение и использование деструктора.
Программа тестирования включает три объекта. Obj_l является
переменной, объявляемой в main-программе, a Obj__2 ссылается на динамический
объект. В программу включена ранее обсуждавшаяся функция Destroy-
Demo, которая объявляет локальный объект obj. На рис. 8.2 отмечены
различные случаи использования конструкторов и деструкторов объектов.
( void DestroyDemo(int m1( int m2)
DynamicClass<int> Obj (m1,m2) ц Конструктор для Obj (3300)
| < Деструктор для Obj
void main (void)
DynamicClass<int>Obj _1(1,100),*Obj_2; < Конструктор для Obj J (1.100)
Obj_2 - new DynamicClass<int>(2,200);« Конструктор для *Obj_2 (2.200)
DestroyDemo(3,300);
delete Obj_2; * Деструктор для Obj_2
| < Деструктор для Obj_1
Рис. 8.2. Инициализация для DynamicClass А(3,5), В = А
#include <iostream.h>
#pragma hdrstop
linclude "dynamic.h"
void DestroyDemo(int ml, int m2)
{
DynamicClass<int> obj(ml,m2);
}
void main(void)
{
// создать объект Obj_l с memberl=l и *member2=100
DynamicClass<int> Obj_l(1,100);
// объявить указатель на объект
DynamicClass<int> *Obj_2;
// создать объект с memberl = 2 и *member2 = 200,
//на который будет указывать Obj__2
Obj_2 = new DynamicClass<int>(2,200);
// вызвать функцию DestroyObject с параметрами 3, 300
DestroyDemo(3,300);
// полное удаление Obj_2
delete Obj_2;
cout << "Программа готова к завершению" << endl;
}
/*
<Выполнение программы 8.1>
Конструктор: 1/100
Конструктор: 2/200
Конструктор: 3/300
Деструктор: 3/300
Деструктор: 2/200
Программа готова к завершению
Деструктор: 1/100
*/
8.3. Присваивание и инициализация
Присваивание и инициализация являются базовыми операциями,
применяемыми к любому объекту. Присваивание Y = X приводит к побитовому
копированию данных из объекта X в данные объекта Y. Инициализация
создает новый объект, который является копией другого объекта. Эти
операции показаны на примерах с объектами X и Y:
// создать объекты X и Y типа DynamicClass
// данные объекта Y инициализируются данными X
DynamicClass Х(20, 50), Y = X;
Y -X; // данные объекта Y переписываются из данных X
Особое внимание необходимо уделить динамической памяти, чтобы
избежать нежелательных ошибок. Мы должны создавать новые методы,
управляющие присваиванием и инициализацией объектов. В этом разделе сначала
обсуждаются потенциальные проблемы, а затем создаются новые методы класса.
Проблемы присваивания
Конструктор для DynamicClass инициализирует member 1 и выделяет
динамические данные, на которые указывает member2. Например, в объявлении
объектов А и В мы создаем два объекта и два связанных блока памяти с
использованием оператора new.
Системная память Системная память
*A.member2
memberl
member2
*B.member2
memberl
member2
А В
Оператор присваивания В « А приводит к тому, что данные объекта А
копируются в В.
// копировать статические данные из А в В:
// memberl объекта В ■ memberl объекта А
// копировать указатель из А в В
// member2 объекта В = meraber2 объекта А
Так как значению указателя member2 в объекте В присваивается значение
указателя member2 в объекте А, оба указателя теперь ссылаются на один и
тот же участок памяти, а на динамическую память, первоначально
присвоенную В, ссылки теперь нет. Предположим, что оператор присваивания
появляется в функции F.
void F(void)
{
DynamicClass<int> A<2,3), B(7,9);
• * •
В * А; // присваивание объекта А объекту В
Неправильное присваивание: В=А
*A.member2
*B.member2
member! I member2
memberl member2
При возвращении из функции F все объекты, созданные в блоке,
уничтожаются вызовом деструктора класса, освобождающего динамическую
память, на которую указывает member2. Предположим, объект В уничтожается
первым. Деструктор освобождает память, на которую указывает В.member2
(и одновременно A.member2), При уничтожении объекта А вызывается его
деструктор для освобождения памяти, связанной с указателем-переменной
A. member2, но этот блок памяти ранее уже был освобожден при уничтожении
B, поэтому использование операции delete в деструкторе для А является
ошибкой! Во многих случаях это — фатальная ошибка.
Проблема заключается в операторе присваивания В = А. Указатель
member 2 в А копируется в указатель member2 в В. На самом деле мы хотим,
чтобы содержимое, на которое указывает member2 из А, было скопировано
в участок памяти, на который указывает member2 из В.
Правильное присваивание: В=А
*A.member2
копировать
содержимое
*B.member2
memberl member?
memberl member2
Перегруженный оператор присваивания
Для правильного выполнения присваивания объектов в случаях, когда
это касается динамических данных, C++ позволяет перегружать оператор
присваивания = как функцию-член. Синтаксис для перегруженного оператора
присваивания в DynamicClass следующий:
DynamicClass<T>& operator» (const DynamicClass<T>& rhs);
Бинарный оператор реализуется как функция-член с параметром rhs,
представляющим операнд в правой части оператора. Например
В = А;
Перегруженный оператор = выполняется для каждого оператора
присваивания, включающего объекты типа DynamicClass. Вместо простого
побитового копирования данных-членов из объекта А в В, перегруженный оператор
отвечает за явное присваивание всех данных, включая закрытые и открытые
данные-члены, а так же данные, на которые указывают эти члены. Параметр
rhs передается по константной ссылке. Таким образом, мы избегаем
копирования в этот параметр того, что могло бы быть большим объектом в правой
части, и не допускаем никакого изменения объекта. Заметим также, что где
бы ни использовалось имя шаблонного класса как типа, необходимо добавлять
"<Т>" в конец имени класса.
Для DynamicClass оператор = должен присваивать значение данных mem-
berl объекта rhs значению данных memberl текущего объекта и копировать
содержимое, на которое указывает member2 объекта rhs, в участок памяти,
на который указывает member2 текущего объекта:
// перегруженный оператор присваивания.
// возвращает ссылку на текущий объект
template<class T>
DynaraicClass<T>& DynamicClass<T>::operator=»(const DynamicClass<T>& rhs)
{
// копирование статического данного-члена из rhs
//в текущий объект
memberl » rhs.memberl;
// содержимое динамической памяти должно быть тем же,
// что и содержимое rhs
*member2 = *rhs,member2;
cout «"Оператор присваивания:" <<memberl«' /'
<< *member2 << endl;
return *this;
}
Зарезервированное слово this используется для возвращения ссылки на
текущий объект и обсуждается в следующем разделе. Операторы,
переносящие данные из объекта rhs в текущий объект, гарантируют правильное
выполнение оператора присваивания
В * А;
Поскольку оператор = возвращает ссылку на текущий объект, мы можем
эффективно связывать вместе два или более операторов присваивания.
Например:
С - В - А; // результат (В я А) присваивается С
Указатель this
Каждый объект C++ имеет указатель с именем this, определяемый
автоматически при создании объекта. Идентификатор является
зарезервированным словом и может использоваться только внутри функции-члена класса.
Он является указателем на текущий объект, a *this — это сам объект.
Например, в объекте А типа DynamicClass
// *this — это объект А;
// this->memberl — это memberl, значение данных в А
// this->member2 — это member2, указатель в А
Для оператора присваивания возвращаемое значение является ссылочным
параметром. Выражение "return *this" возвращает ссылку на текущий объект.
Проблемы инициализации
Инициализация объекта — это операция, создающая новый объект,
который является копией другого объекта. Подобно присваиванию, когда объект
имеет динамические данные, эта операция требует особую функцию-член,
называемую конструктором копирования (copy constructor). Мы можем,
забегая вперед, обсудить действие конструктора копирования на примере:
DynamicClass<int> А{3,5), В * А; // инициализация объекта В данными объекта А
Это объявление создает объект А, начальными данными которого являются
member 1 = 3 и *member2 = 5, и объект В с двумя данными-членами, которые
затем структурируются для сохранения тех же значений данных, которые
помещены в А. Процесс инициализации должен включать копирование
значения 3 из объекта А в member 1 объекта В, выделение памяти для данных,
на которые указывает member2 объекта В, и затем копирование значения 5
из * A. member 2 в динамически распределяемые данные объекта В.
Инициализация DynamicClass: В=А
*A.member2
memberl member2
№3: копировать
содержимое
*B.member2
memberl member2
№2: выделить память
для *member 2
№1: копировать содержимое
Инициализация осуществляется не только при объявлении объектов, но и
при передаче объекта функции в качестве параметра по значению, и при
возвращении объекта в качестве значения функции. Например, предположим, что
функция F имеет передаваемый по значению параметр X типа Dynamic-
Class<int>.
DynamicClass<int> F(DynamicClass<int> X) // параметр передаваемый
//по значению
{
DynamicClass<int> obj;
• • • •
return obj;
>
Когда вызывающий блок использует объект А как фактический параметр,
локальный объект X создается копированием объекта А:
DynamicClass<int> A(3,5), В(0,0); // объявление объектов
В = F(A); // вызов F копированием А в X
При выполнении возврата из F создается копия obj, вызываются
деструкторы для локальных объектов X и obj и копия obj возвращается как значение
функции.
Создание конструктора копирования
Чтобы правильно обращаться с классами, которые выделяют
динамическую память, C++ предоставляет конструктор копирования для выделения
динамической памяти новому объекту и инициализации его значений данных.
Мы иллюстрируем эту идею, разрабатывая конструктор копирования для
DynamicClass.
Конструктор копирования является функцией-членом, которая
объявляется с именем класса и одним параметром. Поскольку это — конструктор,
он не имеет возвращаемого значения:
DynamicClass(const DynamicClass <T>& X); // конструктор копирования
Конструктор копирования DynamicClass копирует данные из memberl
объекта X в текущий объект. Для динамических данных конструктор
копирования выделяет память, на которую указывает member2, и инициализирует
ее на значение содержимым *Х. member 2:
// конструктор копирования.
// инициализирует новый объект теми же данными, что и в X
template <class T>
DynamicClass<T>::DynamicClass(const DynamicClass<T>& X)
{
// копировать статический данное-член из X
// в текущий объект
memberl = X.memberl;
// выделить динамическую память и инциализировать ее
// значением *X.member2.
member2 = new T(*X.member2);
cout « "Конструктор копирования: " « memberl
« '/' « *member2 « endl;
}
Если класс имеет конструктор копирования, этот конструктор
используется компилятором всякий раз при выполнении инициализации. Конструктор
копирования используется только тогда, когда создается объект.
Несмотря на свое сходство, присваивание и инициализация являются,
несомненно, различными операциями. Присваивание выполняется, когда
объект в левой части уже существует. В случае инициализации создается
новый объект копированием данных из существующего объекта. Более того,
во время процесса инициализации перед копированием динамических данных
для выделения памяти должен использоваться оператор new.
Параметр в конструкторе копирования должен передаваться по ссылке.
Невыполнение этого может привести к катастрофическим последствиям, если
компилятор не распознает ошибку. Предположим, что мы объявляем
конструктор копирования с передаваемым по значению параметром:
DynamicClass(DynamicClass<T> X);
Конструктор копирования вызывается всякий раз, когда параметр
функции указывается как передаваемый по значению. Предположим, что объект
А в конструкторе копирования передается параметру X по значению.
DynamicClassfDynamicClass X)
Так как мы А передаем в X по значению, должен вызываться конструктор
копирования для выполнения копирования А в X. Этот вызов, в свою очередь,
нуждается в конструкторе копирования, и мы имеем бесконечную цепь
вызовов конструктора копирования. К счастью, эта потенциальная проблема
распознается компилятором, который указывает, что параметр должен
передаваться по ссылке. Кроме того, ссылочный параметр X должен объявляться
константным, так как мы определенно не хотим изменять объект, который
копируем.
Программа 8.2. Использование DynamicClass
Эта программа иллюстрирует действие функций-членов DynamicClass с
использованием целых данных.
linclude <iostream.h>
finclude "dynamic.h"
template <class T>
DynamicClass<int> Demo(DynamicClass<T> one,
DynamicClass<T>& two, T m)
{
// вызов конструктора с (memberl»» m, *member2* m)
DynamicClass<T> obj(m,m);
// копирование для obj выполнено.
// возвратить его как значение функции
return obj;
}
void main()
{
/* A(3,5) вызывает конструктор с (member1=3, *member2=5)
В « А вызывает конструктор копирования для
инициализации В данными объекта А:
(memberl=3, *member2-5)
объект С вызывает конструктор с (memberl=0, *member2»0) */
DynamicClass<int> A(3, 5) , В ■= А, С(0,0);
/* вызов функции Demo, конструктор копирования создает параметр one
(member1=3, *member2-5) копированием из А. параметр two передается по
ссылке, поэтому конструктор копирования не вызывается, при возращении
создается копия локального объекта obj, который
присваивается объекту С */
С * Demo (А, В, 5) ;
// остальные объекты удаляются при выходе из программы
}
/*
< Выполнение программы 8.2>
Конструктор: 3/5
Конструктор копирования: 3/5
Конструктор: 0/0
Конструктор копирования: 3/5
Конструктор: 5/5
Конструктор копирования: 5/5
Деструктор: 5/5564
Деструктор: 3/5556
Оператор присваивания: 5/5
Деструктор: 5/5
Деструктор: 5/5
Деструктор: 3/5
Деструктор: 3/5
*/
8.4. Надежные массивы
Статический массив — это коллекция, содержащая фиксированное
количество элементов, ссылка на которые выполняется индексным оператором.
Статические массивы являются основной структурой данных для реализации
списков. Несмотря на свою важность, статические массивы создают
определенные проблемы. Их размер устанавливается во время компиляции и не
может изменяться во время исполнения приложения.
В ответ на ограничения, свойственные статическим массивам, мы создаем
основанный на шаблоне класс Array, содержащий список последовательных
элементов любого типа данных, размер которого может быть изменен во время
выполнения приложения. Этот класс содержит методы, реализующие
индексацию и преобразование типа указателя. Чтобы был возможен индексный
доступ к элементам в списке, мы перегружаем индексный оператор (index
operator) []. Более того, мы проверяем, чтобы каждый индекс соответствовал
элементу в списке. Это свойство, называемое проверкой границ массива (array
bounds checking), генерирует сообщение об ошибке, если индекс находится вне
границ. Полученные в результате объекты называются надежными массивами
(safe arrays), поскольку мы реагируем на неверные индексные ссылки. Для
того, чтобы объект массива мог использоваться с функциями, принимающими
стандартные параметры массива, мы определяем общий оператор
преобразования указателя (pointer conversion operator) T*, связывающий объект Array
с обычным массивом, элементы которого — это элементы типа Т.
Класс Array
Основанный на шаблоне класс Array поддерживает список элементов
любого типа данных.
0 12 3 size-1
alist данные типа Т
Спецификация класса Array
ОБЪЯВЛЕНИЕ
#include <iostream.h>
#include <stdlib.h>
#ifndef NULL
const int NULL = 0;
#endif
enum ErrorType
{invalidArraySize, memoryAllocationError, indexOutOfRange};
char *errorMsg[] =
{
"Неверный размер массива", "Ошибка выделения памяти",
"Неверный индекс: "
};
template <class T>
class Array
{
private:
// динамически выделяемый список размером size
Т* alist;
int size;
// метод обработки ошибок
void Error(ErrorType error,int badlndex^O) const;
public:
// конструкторы и деструктор
Array(int sz = 50);
Array(const Array<T>& A);
-Array(void);
// присваивание, индексация и преобразование указателя
Array<T>& operator= (const Array<T>& rhs);
T& operator[](int i);
operator T* (void) const;
// операции с размером массива
int ListSize(void) const; // читать size
void Resize(int sz); // обновлять size
};
ОБСУЖДЕНИЕ
Использование перегруженного индексного ([]) и оператора преобразования
позволяет объекту Array функционировать подобно обычному, определенному
языком программирования, массиву. Оператор присваивания расширяет
возможности массива, реализуя присваивание одного объекта Array другому. Для
определенных же языком программирования массивов присваивание является
неверной операцией.
Метод Resize позволяет изменять размер списка. Если параметр sz больше,
чем текущий размер массива (size), старый список сохраняется и к массиву
добавляются дополнительные элементы. Если sz меньше, чем текущий размер,
сохраняются первые sz элементов в массиве, остальные — удаляются.
ПРИМЕР
Array<int> A(20); // массив из 20 целых
cout « A.SizeO; // вывод текущего размера 20
for(int i«=0/ i<20; i++) // доступ к массиву с использованием []
A[i] = i/
А[25] = 50; // неверный индекс
A.Resize(30); // размер массива увеличивается на 30;
А[25] = 50; // теперь верный индекс
ExchangeSort(а, 30); // преобразование позволяет использовать
// параметр Array
Выделение памяти для класса Array
В этом разделе показаны конструктор, деструктор и конструктор
копирования, выполняющие необходимую проверку наличия ошибок.
Конструктор класса выделяет динамический массив, элементы которого —
это элементы типа Т. Начальный размер массива определяется параметром sz,
который имеет значение по умолчанию 50:
// конструктор
template<class T>
Array<T>::Array(int sz)
{
// проверка на наличие параметра неверного размера
if(sz<= 0)
Error(invalidArraySize);
// присваивание размера и выделение памяти
size = sz;
alist e new T[size];
// убеждаемся в том, что система выделяет необходимую память,
if (alist == NULL)
Error(memoryAllocationError);
}
Деструктор освобождает память, выделенную для массива alist:
// деструктор
template<class T>
Array<T>::-Array(void)
{
delete [] alist;
}
Конструктор копирования делает возможными операции, которые
недоступны для определенных языком программирования массивов, позволяя
инициализировать один массив элементами другого массива (X) и передавать объект
Array какой-либо функции по значению. Для этого извлекается размер объекта
X, выделяется соответствующий объем динамической памяти и копируются
элементы объекта X в текущий объект.
текущий объект
alist
объект X
X.alist
X.size -1
// конструктор копирования
template <class T>
Array<T>::Array(const Array<T>& X)
{
// получить размер объекта X и присвоить текущему объекту
int n - X.size;
size - n;
// выделить новую память для объекта с проверкой
// возможных ошибок
alist - new T[n]; // динамически созданный массив
if (alist — NULL)
Error(memory^llocationError);
// копировать элементы массива объекта X в текущий объект
Т* srcptr ■ X.alist; // адрес начала X.alist
Т* destptr « alist; // адрес начала alist
while (n—)// копировать список
*destptr++ - *srcptr++;
}
Проверка фаниц массива и перегруженный оператор []
Ссылка на индекс массива выполняется с использованием оператора [] и
появляется в выражении, имеющем форму
Р[п)
где Р — это указатель на тип Т, а п — это целое выражение. Фактически, это —
оператор, называемый в языке C++ оператором индексации массива (array
indexing operator). Этот оператор имеет два операнда (Р и п) и возвращает
ссылку на данные в позиции Р + п.
Р[п]
Р[0]
Р[1]
Р Р+1 Р+п
Оператор может быть перегруженным только как функция-член и
обеспечивает индексированный доступ к данным объекта.
Мы перегружаем индексный оператор для класса Array. Предположим, что
А — это объект Array целого типа. Доступ к элементам массива получаем
использованием записи А[п]. Например, оператор
А[0] - 5
присваивает значение 5 первому элементу в массиве (alist[0] = 5).
Объявление функции-члена [ ] принимает форму
Т& operator [ ] (int n) ;
где Т — это тип данных, хранящихся в объекте, an — это индекс. Тот факт,
что перегруженный оператор [] возвращает ссылочный параметр, означает, что
оператор индексации может находиться в левой части оператора присваивания.
value « А[п]; // переменной value присваивается А[п]
A[n] « value/ // элементу п массва А присваивается
// значение value
Для класса Array перегруженный оператор индексации предоставляет
доступ к надежному массиву, проверяя, находится ли индекс п в диапазоне
индексов массива (от 0 до size-1). Если он не находится в этом диапазоне,
выводится сообщение об ошибке и программа завершается. Иначе оператор
возвращает значение alist[n].
// перегруженный индексный оператор
template<class T>
Т& Array<T>;:operator[ ] (int n)
{
// выполнение проверки границ массива
if (n<0 n>size-l)
Error(indexOutOfRange,n);
// возвращается элемент из закрытого списка массива
return alist[n];
)
Преобразование объекта в указатель
Преобразованием указателя пользователь получает возможность
использовать объект Array как параметр времени исполнения в любой функции,
определяющей обычный массив. Это выполняется перегрузкой оператора
преобразования Т*(), которая преобразует объект в указатель. В данном случае
мы преобразуем объект Array в начальный адрес массива alist.
size
alist
Объект А
Например, функции ExchangeSort и SeqSearch принимают параметр
массива. Для объекта А шаблонного целого типа следующие операторы функции
являются верными:
//сортировать A (size () элементов)
ExchangeSort(A,A.size О)/
// поиск ключа в А
index « SeqSearch(A,A.size(), int key);
В вызове функции объект А передается формальному параметру Т*агг.
Объявление; ExchanqeSort(T*arr,int n)
/ /
Вызов: ExchangeSort (A,A.sizeO);
Это приводит к выполнению оператора преобразования и присваиванию
указателя alist переменной агт. Переменная агг указывает на массив объекта А:
// оператор преобразования указателя
template<class T>
Array<T>::operator T*(void) const
{
// возвращает адрес закрытого массива в текущем объекте
return alist;
}
Операторы изменения размера. Класс Array предоставляет метод List Size,
возвращающий текущее количество элементов в массиве. Более динамичным
является метод Resize, который изменяет количество элементов массива в
объекте. Если требуемое количество элементов sz равно размеру текущего
объекта, выполняется простой возврат; иначе выделяется новое пространство
памяти. Если размер списка уменьшается (sz<size), первое sz количество
элементов копируется в новый массив.
Уменьшение
размера
новый list
старый list
sz
sz -1
X.size -1
Если мы увеличиваем размер массива, старые элементы копируются в
новый список и в наличии остается некоторая неиспользованная часть списка.
В каждом из двух случаев память для старого массива удаляется.
Увеличение
размера
новый list
старый list
X.size -1
srcptr = &X.alist[size]
// оператор изменения размера (resize-рператор)
template <class T>
void Array<T>::Resize(int sz)
{
// проверка нового размера массива;
// выход из программы при sz <= О
if (sz <= 0)
Error(invalidArraySize);
// ничего не делать, если размер не изменился
if (sz « size)
return;
// запросить память для нового массива и проверить ответ системы
Т* newlist = new T[sz];
if (newlist == NULL)
Error(memoryAllocationError);
// объявить п и инициализировать значением sz или size
int n = (sz <= size) ? sz : size;
// копировать п элементов массива из старой в новую память
Т* srcptr = alist; // адрес начала alist
Т* destptr = newlist; // адрес начала newlist
while (n—) // копировать список
*destptr++ = *srcptr++;
// удалить старый список
delete[] alist;
// переустановить alist, чтобы он указывал на newlist
// и обновить член класса size
alist - newlist;
size = sz;
}
Использование класса Array
Реализация класса Array иллюстрирует большинство идей этой главы.
Пользователь может использовать класс Array вместо определенных языком
программирования массивов и пользоваться преимуществами надежности и
гибкости, обеспечиваемыми возможностью изменения размера.
Программа 8.3. Изменение размера массива
Пусть Array-объект А определяет список из 10 целых, в котором мы
сохраняем простые числа:
Определение: Простое число — это положительное целое 2, которое
делится только на себя и на 1.
Данная программа определяет все простые числа в диапазоне 2..N, где
N — это предоставляемая пользователем верхняя граница. Так как мы
не можем заранее установить размер массива на необходимый, программа
проверяет условие "список полный", сравнивая текущее количество
простых чисел (primecount) с размером массива. Когда список полный, мы
изменяем размер списка и добавляем еще 10 элементов. Программа
завершается печатью списка простых чисел по 10 в строке.
#include <iostream.h>
#include <iomanip.h>
#pragma hdrstop
#include "array.h"
void main(void)
{
// начальный размер массива А равен 10
Array<int> A(10);
// пользователь задает верхнюю границу диапазона поиска
int upperlimit, primecount = 0, i, j;
cout « "Введите число >= 2 как верхную границу диапазона: ";
cin » upperlimit;
A[primecount++] -2; // 2 — простое число
for(i = 3; i < upperlimit; i++)
{
// если список простых чисел полный, добавить к нему еще 10 элементов
if (primecount == A.ListSize ())
A.Resize(primecount + 10);
// четные числа > 2 — непростые.
// перейти к следующей итерации
if (i % 2 «■ 0)
continue;
// проверить нечетные делители 3,5,7,... до i/2
J - 3;
while (j <= i/2 && i % j !- 0)
j +- 2;
// i - простое, если не делится на 3,5,7,... до i/2
if (j > i/2)
A[primecount++] - i;
}
for (i я 0; i < primecount; i++)
{
cout « setw(5) « A[i];
// вывести новую строку из 10 простых чисел
if (U+1) % 10 « 0)
cout « endl;
}
cout « endl;
}
/*
<Выполнение программы 8.3>
Введите число >= 2 как верхную границу диапазона: 100
2 3 5 7 11 13 17 19 23 29
31 37 41 43 47 53 59 61 67 71
73 79 83 89 97
*/
8.5. Класс String
Строки являются основным компонентом многих нечисловых алгоритмов.
Они используются в таких областях, как сопоставление с образцом,
компиляция языков программирования и обработка данных. По существу, полезно
иметь строковый тип данных, который инкапсулирует разнообразные
операции обработки строк и делает возможными расширения. Строковые
переменные C++ являются массивами символов с нулевым символом в конце.
Каждая система программирования C++ предоставляет библиотеку функций
в <string.h> для сопровождения операций обработки строк. В руках опытного
программиста функции являются мощным средством реализации
эффективных строковых алгоритмов. Однако для многих приложений функции
являются чем-то техническим и неудобным для использования.
Некоторые языки программирования, подобные языку BASIC, определяют
операторы для обработки строк. Например, строковая переменная BASIC
заканчивается символом "$и и поддерживает присваивание оператором = и
сравнение строк оператором <. Строковый тип является частью определения
языка BASIC:
NAME$ *» JOE // присваивание
IF NAME$ < STUDENTPRES$ THEN ... // сравнение
Для некоторых языков программирования компиляторы предоставляют
расширения, которые обеспечивают возможность улучшенной обработки
строк. Большинство программистов C++ хотели бы получить такое
расширение для более гибкого доступа к строкам.
В этом разделе описывается класс String, определяющий строковый тип и
предоставляющий мощный набор строковых методов. Объекты используют
динамическую память для сохранения строк переменной длины и перегруженные
операторы для создания строковых выражений. Класс String предоставляет
пользователю альтернативный строковый тип и тем не менее обеспечивает
полное взаимодействие со стандартными строками C++ (C++String). Класс
String используется в последующих главах этой книги, и вы найдете достойной
его простоту. Для иллюстрации использования класса String рассмотрим
задачу сравнения и присваивания строк S и Т. Следующие операторы сопоставляют
использование библиотеки функций C++ и класса String. Мы присваиваем
меньшую строку переменной firststring.
Решение строковой библиотеки C++ Решение класса String
if ( strcmpt S, T ) < 0 ) firststring = ( S < Т ) ? S : Т;
strcpyt firststring, S );
else
strcpyt firststring, T );
Этот раздел включает полный листинг объявления класса String. Здесь
обсуждается реализация избранных методов и предоставляется программа
тестирования. Полный листинг класса String находится в файле strclass.h
программного приложения. Раздел 8.6 знакомит с алгоритмом сопоставления
с образцом, который широко используется в классе String.
Спецификация класса String
ОБЪЯВЛЕНИЕ
#ifndef STRING_CLASS
#define STRING__CLASS
#include <iostream.h>
#include <string.h>
♦include <stdlib.h>
Hfndef NULL
const int NULL - 0;
#endif // NULL
const int outOfMemory « 0, indexError я 1;
class String
{
private:
// указатель на динамически создаваемую строку.
// длина строки включает NULL-символ
char *str;
int size;
// функция сообщения об ошибках
void Error(int errorType, int badlndex = 0) const;
public:
// конструкторы
String(char *s - "");
String(const Strings s) ;
// деструктор
-String(void);
// операторы присваивания
// String = String, String = O+String
Strings operator= (const Strings s);
Strings operator= (char *s);
// операторы отношений
// String—String, String==C++String, C++String==String
int operator== (const Strings s) const;
int operator™ (char *s) const;
friend int operator== (char *str, const Strings s);
// String!=String, String!=C++String, C++String!=String
int operator!= (const Strings s) const;
int operator!= (char *s) const;
friend int operator!3 (char *str, const Strings s);
// String<String, String<C++String, C++String<String
int operator< (const Strings s) const;
int operator< (char *s) const;
friend int operator< (char *str, const Strings s);
// String<=String, String<=C++String, C++String<=String
int operator<= (const Strings s) const;
int operator<= (char *s) const;
friend int operator<= (char *str, const Strings s);
// String>String, String>C++String, C++String>String
int operator> (const Strings s) const;
int operator> (char *s) const;
friend int operator> (char *str, const Strings s);
// String>=String, String>=C++String, C++String>=String
int operator>~ (const Strings s) const;
int operator>= (char *s) const;
friend int operator>= (char *str, const Strings s);
// операторы String-конкатенации
// String+String, String+C++String, C++String+String
// String += String, String += C++String
String operator+ (const Strings s) const;
String operator+ (char *s) const;
friend String operator+ (char *str,const Strings s);
void operator+= (const Strings s);
void operator+= (char *s);
// String-функции
// начиная с первого индекса, найти положение символа с
int Find(char с, int start) const;
// найти последнее вхождение символа с
int FindLast(char с) const;
// выделение подстроки
String Substr(int index, int count) const;
// вставить объект String объект String
void Insert(const Strings s, int index);
// вставить строку типа C++String в строку типа String
void Insert(char *s, int index);
// удалить подстроку
void Remove(int index, int count);
// String-индексация
chars operator[] (int n);
// преобразовать String в C++String
operator char* (void) const;
// String-ввод/вывод
friend ostream& operator« (ostream& ostr,
const Strings s);
friend istream& operator>> (istreams istr,
Strings s);
// читать символы до разделителя
int ReadString{istreams is=cin,
char delimiter='\n');
// дополнительные методы
int Length(void) const;
int IsEmpty(void) const;
void Clear(void);
};
ОПИСАНИЕ
Объекты класса String могут взаимодействовать со строками C++ (char*).
Например, следующие три функции предназначены для конкатенации
строковых переменных с использованием оператора +:
// String + String
String operator* ( const Strings s );
// String + C++String
String operator* ( char *s ) ;
// C++String + String
friend String operator* ( char *str,const Strings s );
Класс String имеет деструктор, конструктор копирования и два
перегруженных оператора присваивания, позволяющие пользователю присваивать
объект типа String или строку C++ новому объекту String:
String S (Hello ) , T = S, R; // T = Hello , R - NULL-строка
R = "World!";
Класс реализует разнообразные операторы конкатенадии строк, включая
оператор += для конкатенации строки в текущую строку:
R = Т + "World!"; // R = "Hello World!"
R +« ;
R += S; // R = "Hello World! Hello "
Ряд операторов сравнения используют упорядочение ASCII для сравнения
двух строк:
string U("Smith"), V("Smithsonian"), W("Thomas");
if (U>= V) . . . // FALSE
if (W « "Thomas") ... // TRUE
if ("Tom" !=W) . . . // TRUE
Класс String предоставляет несколько мощных и полезных строковых
операций, включающих возможность поиска определенного символа в строке,
извлечение подстроки, вставку одной строки в другую и удаление подстроки.
Для каждого символа в строке имеется индексный доступ как для простого
символьного массива.
int sindex;
String V(Smithsonian);
// поиск 's', начиная с позиции с индексом О
sindex - V.FindCs' ,0) ;
R - V.Substr(sindex,3); // R - "son"
V.Remove (sindex, 6); // V - "Smith"
R[0] - 'S'; // R - "Son"
R.Insert("ilvert", 1); // R - "Silverton"
Оператор ввода » использует пробел для разделения строкового ввода:
cin » S » Т » R;
<Ввод> Separate by blanks
S ="Separate" T * "by"R * "blanks"
Метод ReadString считывает символы до ограничительного символа,
который заменяется на NULL-символ:
R.ReadString(cin);
<Ввод> The fox leaped over the big brown dog<newline>
R = "The fox leaped over the big brown dog"
Программа 8.4. Использование класса String
Эта программа иллюстрирует избранные методы класса String. Каждая
операция включает оператор вывода, описывающий ее действие.
#pragma hdrstop
#include "strclass.h"
#define TF(b) ((b) ? "TRUE" : "FALSE")
void main(void)
{
String si("STRING "), s2("CLASS");
String s3;
int i;
char c, cstr[30];
s3 * si + s2;
cout « si « "объединена с " « s2 « " = "
« s3 « endl;
cout « "Длина " « s2 « " = " « s2.Length0 « endl;
cout << "Первое вхождение 'S' в " « s2 « " =» " «
s2.Find('S' ,0) «endl;
cout « "Последнее вхождение 'S' в " « s2 « " — " «
s2.FindLast('S') « endl;
cout « "Вставить 'OBJECT ' в s3 в позицию 7." « endl;
s3.Insert("OBJECT ",1);
cout « s3 « endl;
si * "FILE1.S";
for(i=0;i < sl.LengthO;i++)
{
с «■ s 1 [ i ];
if (c >= 'A' && с <= 'Z' )
{
с +- 32; // преобразовать в нижний регистр
si[i] « с;
}
)
cout « "Строка 'FILE1.S' преобразована в нижний регистр: ";
cout « si « endl;
cout « "Тестирование операций отношения: ";
cout « "si » 'ABCDE' s2 = '3CF'" « endl;
si » "ABCDE";
s2 - "BCF";
cout « "si < s2 - " « TF(sl < s2) « endl;
cout « "si »= s2 - " « TF(sl ** s2) « endl;
cout « "Используйте 'operator char* ()' для получения si"
" как строки C++: ";
strcpy(cstr,si);
cout « cstr « endl;
}
/*
^Выполнение программы 8.4>
STRING объединена с CLASS = STRING CLASS
Длина CLASS = 5
Первое вхождение 'S' в CLASS = 3
Последнее вхождение 'S' в CLASS — 4
Вставить 'OBJECT ' в s3 в позицию 7.
STRING OBJECT CLASS
Строка 'FILE1.S' преобразована в нижний регистр: filel.s
Тестирование операций отношения: si = 'ABCDE' s2 - 'BCF'
si < s2 - TRUE
si « s2 - FALSE
Используйте 'operator char* О' для получения si как строки C++: ABCDE
*/
Реализация класса String
Данный раздел содержит обзор реализации класса String.
Данными-членами являются переменная-указатель str, содержащая адрес строки с
нулевым завершающим символом, и size, содержащая длину строки + 1, где
дополнительный байт обычно хранит символ NULL. Значение size, таким
образом, является фактическим количеством байт памяти, используемым для
строки. Если какая-либо операция изменяет размер строки, старая память
освобождается и динамически выделяется новая память для сохранения
измененной строки.
Поле str в классе String является адресом строки C++. Добавление поля
size и, конечно, доступ к богатому источнику функций памяти отличают
переменную String (объект) от строковой переменной C++ (C++String).
Конструкторы и деструктор. Конструктор создает объект типа String,
принимая в качестве параметра строку C++. Во время процесса инициализации
он присваивает размер, выделяет динамическую память и копирует строку
C++ в создаваемый динамически данное-член str. По умолчанию
присваивается NULL-строка. Конструктор копирования следует той же процедуре, но
копирует строку из начального объекта String, а не из строки C++.
Деструктор удаляет символьный массив, который содержит эту строку.
// конструктор, выделяет память и копирует в строку C++
String::String(char *s)
{
// длина включает NULL символ
size = strlen(s) +1;
str - new char [size];
// программа завершается, если память исчерпана.
if (str == NULL)
Error(outOfMemory);
strcpy(str,s);
}
Перегруженные операторы присваивания. Оператор присваивания
позволяет присваивать либо объект String, либо строку C++ объекту String.
Например:
String S("I am a String variable"), T;
// присваивает объект String объекту String
Т = S;
// присваивает строку C++ объекту String
Т= "I am a C++ String";
Для того, чтобы присвоить новый String-объект s текущему объекту,
сравнивается длина двух строк. Если они различные, оператор удаляет
динамическую память текущего объекта и снова (оператором new) выделяет s.size
символов. Затем s.str копируется в новую память.
// оператор присваивания: String в String
Strings String::operator=(const Strings s)
{
// если размеры различные, удаление текущей
// строки и выделение нового массива
if (s.size != size)
{
delete [] str;
str = new char [s.size];
if(str == NULL)
Error(outOfMemory);
// назначение размера, равного размеру s
size = s.size;
}
// копируется s.str и возвращается ссылка на текущий объект
strcpy(str,s.str);
return *this;
}
Операторы сравнения. Класс String предоставляет полный набор операторов
сравнения строк в соответствии с кодом ASCII. Эти операторы сравнивают два
объекта String или объект String с С++String. Например:
String S("Cat")/ T("Dog");
//сравнение строк
if(S==T)... // условие FALSE
if (T<"Tiger") ... // условие TRUE
if ("Aardvark">= T) . . . // условие FALSE
Реляционный оператор == проверяет равенство строки C++ объекта типа
String. Заметим, что версия =—, которая позволяет строковой переменной C++
появляться в качестве левого операнда, должна быть перегруженной как
дружественная функция:
// C++String == String, дружественная функция
// так как C++String находится в левой части
friend int operator== (char *str, const Stringi s)
{
return strcmp(str, s.str) == 0;
}
String-операторы. Этот класс имеет набор функций, используемых для
конкатенации строк. Конкатенация выполняется перегрузкой операторов + и •+•=.
В первом случае возвращается новая строка. Во втором — происходит
добавление к текущей строке. Например, строка "Cool Water" создается с
использованием трех версий оператора конкатенации:
String SC'Cool"), T("Water"), U, V;
U = S + T; // конкатенация двух String
V = S + Water; // конкатенация String и C++String
S += T; // S теперь - это "Cool Water"
Следующий код реализует версию "String + String" оператора
конкатенации. Функция возвращает объект String, являющийся конкатенацией
текущего объекта String и String справа от +. В этом алгоритме мы сначала создаем
String-объект temp, содержащий size-fs.size-1 символов, включая NULL-сим-
вол. Заметим, что когда объявляется temp, мы сначала удаляем NULL-строку,
созданную конструктором, а затем выделяет память (размером size+s.size-1).
Метод копирует символы из текущего объекта в новую строку и конкатенирует
символы из s. Строка temp представляет собой возвращаемое значение.
// конкатенация: String + String
String String:: operator+ (const Strings s) const
{
// создание новой строки temp с длиной len
String temp;
int len;
// удаление NULL string, созданной при объявлении temp
delete [] temp.str;
// вычисление длины результирующей строки
//и выделение памяти в temp
len = size + s.size -1; // только один NULL-символ
temp.str = new char [len];
if (temp.str == NULL)
Error(outOfMemoryO;
// установка размера результирующей строки
// и создание строки
temp.size = len;
strcpy(temp.str,str); // копирование str в temp
strcat(temp.str, s.str); // конкатенация
return temp; // возвратить temp
}
String-функции. Метод Substr возвращает подстроку текущей строки,
которая начинается с позиции index и имеет длину count:
String Substr(int index, int count);
Этот оператор широко используется в алгоритмах сопоставления с образцом.
Например:
String SC'Cool Water"), U;
U = S.Substr(1,2); // извлекает 'оо' из Cool
Если индекс выходит за позицию последнего строкового символа, функция
возвращает NULL-строку. Количество символов в строке от элемента index до
конца строки равно size-index-1. Если count превышает это значение,
используется хвост строки как подстрока, а параметру count присваивается значение
size-index-1. Для реализации этого метода выделяется память для count+1
символов в объекте temp. В эту память копируется count символов объекта
String, начиная с позиции index, и нулевой завершающий символ. Данному-
члену temp.size присваивается значение count+1, temp возвращается в качестве
значения функции.
// возвращает подстроку с позиции index и
// длиной count
String String:;Substr(int index, int count) const
{
// число символов от index до конца строки
int charsLeft * size-index-1,i;
// создать подстроку в temp
String temp;
char *p, *q;
// возвратить NULL-строку, если index слишком велик
if (index >« size-1)
return temp;
// если count > charsLeft, возвращать оставшиеся символы
if (count > charsLeft)
count » charsLeft;
// удалить NULL-строку, созданную при объявлении temp
delete [] temp.str;
// выделить память для подстроки
temp.str = new char [count+1];
if (temp.str == NULL)
Error(outOfMemory);
// копировать count символов из str в temp.str
for(i*0,p~temp.str,q»&str[index];i < count;i++)
*p++ » *q++;
// последний NULL-символ
*p = 0;
temp.size • count+1;
return temp;
}
Substr(3,3)
Текущий объект
char*str;
int size; (=7)
v.
temp
char*str;
int size; (=4)
ъ._^
NULL
Функции-члены Find и FindLast выполняют поиск вхождения какого-либо
символа в строке. Обе возвращают -1, если этот символ не находится в
строке. Метод
int Find(char C, int stsrt) const;
начинает с начальной позиции и выполняет поиск первого вхождения символа
С. Если символ найден, Find возвращает его позицию в строке. Метод
int FindLast(char С) const;
выполняет поиск последнего вхождения символа С. Если этот символ найден,
FindLast возвращает его позицию в строке.
// возвратить индекс последнего вхождения С в строке
int String::FindLast(char C) const
{
int ret;
char *p/
// использование библиотечной функции C++ strrchr.
// возвращает указатель на последнее вхождение символа С в строке
р = strrchr(str,С);
if (p l« NULL)
ret * int(p-str); // вычисление индекса
else
ret - -1; // возвратить -1 при неудаче
return ret;
}
Строковый ввод/вывод. Строковые потоковые операторы » и «
реализуются использованием операций потокового ввода и вывода для строк C++.
Оператор » читает разделяемые пробелами слова текста.
Метод ReadString читает строку текста (до 255 символов или до указанного
ограничительного символа) из текстового файла и включает ее в объект
String. Если не передается никакого файлового параметра, по умолчанию
символы принимаются из стандартного потока cin. Ввод завершается на
ограничителе, который не сохраняется в строке. В качестве ограничителя по
умолчанию используется символ новой строки С\п')« Например,
String S, Т;
cin» S; // пропускает пробелы; читает следующую лексему
T.ReadStringO; // читает до конца строки
cout «"Компоненты:" « S « " и " « Т « endl;
<Ввод>
Super! Grade A // пробел после ! является частью Т
<Вывод>
Компоненты: Super! и Grade A
Метод использует функцию getline для считывания до ограничителя или
до 255 символов из входного потока istr в символьный массив tmp. Если
getline указывает на конец файла, возвращается -1; иначе удаляется
существующий динамический массив str и выделяется другой — размером
size=strlen(tmp)+l. Массив tmp копируется в новый массив, и функция
возвращает количество считанных символов (size-1).
// читать строку текста из потока istr
int String::ReadString (istream& istr, char delimiter)
{
// читать строку в tmp
char tmp[256];
// если не конец файла, читать строку до 255 симвлов
if (istr.getline(tmp, 256, delimiter))
{
// удалить текущую строку и выделить массив для новой
delete [] str;
size = strlen(tmp) + 1;
str e new char [size];
if (str == NULL)
Error(outOfMemory);
// копировать tmp. возвращать число считанных символов
strcpy(str,tmp);
return size-1;
}
else
return -1; // возвратить -1, если конец файла
}
8.6. Сопоставление с образцом
Общая проблема сопоставления с образцом включает поиск одного или
более вхождений строки в текстовом файле. Большинство текстовых
редакторов имеют меню Search, содержащее несколько элементов поиска
подстроки, таких как Find, Replace и Replace All.
Search
Find ...
?ir;3 Ac*:.Jx
«Hewlett* *г>д h'Xz.-d Aflrain
5iad i& ife»t iriln
Go to Top
Go to Bottom
Go to Line #
Процесс Find начинает с текущего местоположения в файле и выполняет
поиск следующего вхождения подстроки по направлению вперед или назад.
Replace заменяет подстроку, совпавшую при выполнении процесса Find,
другой подстрокой. Replace All проходит по файлу и заменяет все вхождения
подстроки-образца на подстроку-замену.
Процесс Find
Рассмотрим процесс Find для простой ситуации. Даны строковые
переменные S и Р, начинаем в заданной позиции в S и ищем подстроку Р. Если
она существует, возвращаем индекс в строке S первого символа подстроки
Р. Если Р не существует в S, возвращаем -1. Например:
1. Дана строка S="aaacabc" и P="abc", подстрока Р расположена в S,
начиная с позиции 4.
2. Если S="Blue Bar ranch lies outside the city of the animals" и P="the",
то Р появляется в S дважды в позициях с индексами 28 и 40.
3. Подстрока Р="аса" не присутствует в строке S="acbaccacbcbcac".
Программа 8.5 иллюстрирует алгоритм сопоставления с образцом,
использующий класс String.
Алгоритм сопоставления с образцом
Этот алгоритм реализуется функцией FindPat, которая начинает с позиции
startindex строки S и выполняет поиск первого вхождения подстроки Р. Мы
приводим сначала код, так как наш анализ алгоритма ссылается на
переменные этой функции.
int FindPat(String S, String P, int startindex)
{
// первый и последний символы образца и его длина
char patStartChar, patEndChar;
int patLength;
// индекс последнего символа образца
int patlnc;
// начинать с searchlndex искать совпадение с первым
// символом образца, переменной matchStart присвоить
// индекс совпавшего символа строки S. проверить,
//не совпадает ли символ строки S для индекса matchEnd
//с последним символом образца
int searchlndex, matchStart, matchEnd;
// индекс последнего символа в S. matchEnd должен быть <=
// этого значения
int lastStrlndex;
String insidePattern;
patStartChar = P[0]; // первый символ образца
patLength = P.LengthO; // длина образца
patlnc = patLengtn-1; // индекс последнего символа образца
patEndChar = P[patlnc]; // последний символ образца
// если длина образца > 2, получить все символы образца,
// кроме первого и последнего
if (patLength > 2)
insidePattern = P.Substr(l,patLength-2);
lastStrlndex = S.Length()-1; // индекс последнего символа в S
// начать поиск отсюда до совпадения первых символов
searchlndex = startindex;
// искать совпадение с первым символом образца
matchStart « S.Find(patStartChar,searchlndex);
// индекс последнего символа возможного совпадения
matchEnd = matchStart + patlnc;
// повторно искать совпадение первого символа и проверять,
// чтобы последний символ не выходил за строку
while(matchStart != -1 && matchEnd <= lastStrlndex)
{
// это первое или последнее совпадение?
if (S[matchEnd]==patEndChar)
{
// если совпадают один или два символа, имеем совпадение
if (patLength о 2)
return matchStart;
// сравнить все символы, кроме первого и последнего
if (S.Substr(matchStart+l,patLength-2) ~ insidePattern)
return matchStart;
}
// образец не найден, продолжать поиск со следующего символа
searchlndex * matchStart+1;
matchStart - S.Find(patStartChar,searchlndex);
matchEnd ■ matchStart+patlnc;
}
return -1; // совпадение не найдено
)
Следующие шаги описывают этот алгоритм в общих чертах. Делаются
ссылки на пример строки:
S*badcabcabdabc
и образец
Р ■ a b с
1. Образец — это блок текста с начальным символом patStartChar = Р[0],
длиной patLength « P.Length(), приращением patlnc = patLength-1,
которое дает индекс последнего символа в образце, и конечным
символом patendChar = P[patlnc]. Как мы увидим в шагах 3 и 4, алгоритм
сравнивает первый и последний символы текстового блока в S длиной
patLength с первым и последним символами в Р. Если длина Р
(patLength) превышает 2, извлекаем подстроку символов, которая не
включает первый и последний символы (P.Substr(l, patLength-2)) и
присваиваем эту строку переменной insidePattern.
Р = a b с
parStartChar = *а' patlnc * 2 patEndChar = 'с'
patLength ■» 3
insidePattern - "b"
2. Чтобы отметить конец строки S, присваиваем переменной lastStrlndex
индекс последнего символа (S.Length()-l). Начальный индекс (startln-
dex) может быть нулевым (поиск от начала строки) или некоторым
положительным значением, если вам необходимо начинать поиск
внутри строки. Инициализируем переменную searchlndex значением startln-
dex. Эта переменная служит как точка запуска для сопоставления с
первым символом образца.
3. Начиная с searchlndex, используем метод Find класса String для
выполнения поиска символа в строке, совпадающего с patStartChar.
Присваиваем индекс совпадения переменной matchStart. Переменная
matchEnd (matchStart+patlnc) — это индекс последнего символа строки
S, который может совпадать с patEndChar. Поиск завершается неудачей,
если Find не находит совпадения с patStartChar или matchEnd
превышает lastStrlndex.
4. Сравниваем patEndChar с последним символом текстового блока в S
(S[matchEnd] == patEndChar). Если эти символы не совпадают, мы должны
перейти к шагу 5 и выполнить еще ряд сравнений. Сравнение последних
символов является оптимизирующей функцией, освобождающей нас от
ненужного тестирования для образцов, которые не могут совпадать. Если
длина образца равна 1 или 2 (patLength<= 2), лш имеем совпадение и
возвращаем индекс matchStart. Иначе сравниваем символы в текстовом
блоке, исключая первый и последний (S.Substr(matchStart+l, patLength-2))
со строкой insidePattern. Если они совпадают, возвращаем matchStart. В
примере matchStart=l и matchEnd = 3. Строковый блок и образец
совпадают на концах. Строки insidePattern ="b" и S.Substr(2,l) = "d" не
совпадают.
S = b a d с a b с a b d a b с
а Ь с
matchStart = 1 matchEnd ж 3
5. Повторяем шаги 3 и 4, но на этот раз начинаем в позиции с индексом
searchlndex= matchStart+1. В нашем примере следующее совпадение с
первым символом Р имеется в позиции с индексом 4.
S = b a d c_a bcabdabc
а Ь с
matchStart * 4 matchEnd « 6
Последний символ Р и последний символ текстового блока совпадают,
и совпадают также S.Substr(5,l) и insidePattern. Возвращаем индекс 4
(matchStart).
6. Для нахождения множества вхождений образца вновь вызываем
функцию с начальным индексом, большим на единицу, чем индекс,
возвращаемый функцией FindPat, Например, продолжение поиска "abc" дает
следующие результаты:
Поиск возможного совпадения в позиции с индексом 7 неудачен.
Start Index = 5
S = b a d с a b с a_b d a b с
a b с
matchStart = 7 matchEnd = 9
Поиск возможного совпадения в позиции с индексом 10 является
удачным. Возвращается значение 10.
S = badcabcabd_abc
а Ь с
matchStart =* 10 matchEnd * 12
Программа 8.5. Поиск подстрок
Функция FindPat реализует только что описанный алгоритм
сопоставления с образцом и находится в файле findpat.h.
Эта программа читает образец строкового объекта pattern и затем
начинает чтение строки linestr до тех пор, пока не будет достигнут конец
файла. Функция FindPat вызывается для нахождения количества
вхождений образца в каждой строке, а затем выводит количество вхождений
вместе с номером строки.
#include <iostream.h>
#pragma hdrstop
#include "strclass.h"
#include "findpat.h"
void main()
{
// определить строку-образец и строку для поиска
String pattern, lineStr;
// параметры поиска
int lineno = 0, lenLineStr, startSearch, patlndex;
// число совпадений в текущей строке
int numberOfMatches;
cout « "Введите подстроку для поиска: ";
pattern.ReadString();
cout « "Введите строку или EOF:" « endl;
while(lineStr.ReadString() != -1)
{
lineno++;
lenLineStr = lineStr.Length();
startSearch = 0;
numberOfMatches = 0;
// поиск до конца строки
while(startSearch <= lenLineStr-1 &&
(patlndex = FindPat(lineStr, pattern,startSearch)) != -1)
{
numberOfMatches+-i-;
// продолжать поиск до следующего вхождения
startSearch = patlndex+l;
}
cout « "Число совпадений: " « numberOfMatches « "в строке: "
« lineno « endl;
cout << "Введите строку или EOF:" « endl;
}
}
/*
^Выполнение программы 8.5>
Введите подстроку для поиска:: iss
Введите строку или EOF:
Alfred the snake hissed because he missed his Missy.
Число совпадений: 3 в строке: 1
Введите строку или EOF:
Mississippi
Число совпадений: 2 в строке: 2
Введите строку или EOF:
Не blissfully walked down the sunny lane.
Число совпадений: 1 в строке: 3
Введите строку или EOF:
It is so.
Число совпадений: 0 в строке: 4
Введите строку или EOF:
*/
Анализ алгоритма сопоставления с образцом
Предположим, что образец имеет m символов, а строка имеет п символов.
Если первые m символов в S совпадают с Р, мы находим совпадение после
m сравнений. Оценкой наилучшего случая для алгоритма является О(т).
Для определения оценки наихудшего случая предположим, что мы не
используем оптимизирующую функцию, в которой сравниваются последние
символы. Более того, допустим, что у нас всегда совпадают первые символы,
но никогда — образец. Например, это верно, если
Р = "abc" и S = "аааааааа" (т = 3, п = 8)
В этом примере т = 3 символа образца "abc" должны сравниваться с
текстовыми блоками в S в сумме n ~ m+l=6 раз. В общем случае мы должны
сравнивать m символов по n-m+1 раз, т.е. всего выполнить m(n-m+l)
сравнений.
m символов
m символов
0 1 2 n-m n-1
n —m+1 блоков, каждый требует m сравнений
Так как
m(n-m+l) < m(n-m+m) = mn,
оценкой наихудшего случая для алгоритма будет О(тп).
Сопоставление с образцом — это очень важная тема в компьютерной науке,
и она широко изучается в литературе. Например, алгоритм сопоставления с
образцом Кнута-Морриса-Прата (Knuth, 1977) имеет вычислительное время
0(т+п), т.е. является более эффективным, чем только что представленный
простой алгоритм.
8.7. Целочисленные множества
Множество — это группа объектов, выбранная из коллекции, называемой
универсальным множеством (universal set). Множество записывается как
список, разделяемый запятыми и заключенный в фигурные скобки.
X = {Iifl2> I3» • * * » ^m/
D Объединение множеств ( u ) X u Y — это множество, содержащее все
элементы в X и все элементы в Y без дублирования.
D Пересечение множеств ( п ) X n Y — это множество, содержащее все
элементы, которые находятся в обоих множествах X и Y.
XUY XHY
X = {0, 3, 20, 55}. Y = {4, 20, 45, 55}
X U Y = {0. 3, 4, 20, 45, 55} ХП Y = {20, 55}
□ Вхождение во множество (е) nGX равно TRUE, если элемент п является
элементом множества X; иначе оно равно FALSE.
Х={0, 3, 20, 55} //20 € X равно TRUE, 35 Е X равно FALSE
Множества целочисленных типов
Целочисленный тип (integer type) — это любой тип, элементы которого
представлены целыми значениями. Типы char, int всех размеров и
перечисления являются целочисленными типами. Например, набор символов
кода ASCII соответствует 8-битовым целым в дипазоне от 0 до 127. Тогда
как приложения используют традиционное представление символов 'А', 'В',
..., для их внутреннего хранения применяются целые коды 65, 66 и так
далее. Программист имеет возможность выбирать любое представление.
char chl - 'A', ch2 « 97, ch3;
Ch3 - chl + 4; // ch3 - 'E'
cout « ch2 « " " « int('A'); // печать: а 65
В этом разделе разрабатываются множества с элементами
целочисленного типа. Универсальное множество имеет соответствие "один-к-одному"
с беззнаковыми целыми в диапазоне от 0 до setrange-1, где setrange —
это количество элементов множества. Рассмотрим следующие множества:
Множество цифр = {0,1,2,3,4,5,6,7,8,9}
соответствует диапазону 0 ... 9
Множество символов кода ASCII={. . . , 'А', 'В\ . . . , *Z\ . . . }
соответствует диапазону 0 ... 127
enum Color (красный, белый, синий)
множество Color соответствует диапазону 0 ... 2
Мы можем реализовать тип Set, с помощью массива значений нулей и
единиц (0 и 1). В этом массиве значение в позиции i равно 1 (TRUE), если
элемент i находится в данном множестве, или — О (FALSE), если он отсутствует
в нем. В письменном упражнении 6.13 описывается метод для реализации
множества целых значенией с использованием статического массива. Этот
подход использует одно целое значение для каждого возможного элемента
множества. Мы можем выделять память для этого массива целых динамически.
// объявление множества с элементами в диапазоне от 0 до setrange-1
class Set
{
private:
int *member: // указатель на массив set
int setrange;
• * •
public:
// конструктор для распределения массива set
Set(int n):setrange (n)
{
member ■ new int [setrange];
• • •
}
};
• » •
Set S{20); // множество {0, . . . , 19)
n£S «■> S.member[n] == 1 // элемент равен 1, если п принадлежит Set
Требуемая память значительно уменьшается, если мы поддерживаем массив
с использованием побитовых операторов C++. Более того, мы можем обобщить
этот подход до обработки любого целого типа, применяя шаблоны.
Побитовые операторы C++
Операторы OR (||), AND (&&) и NOT (!) используются в логических
выражениях для объединения целочисленных операндов и возвращение результата
TRUE (1) или FALSE (0). Одни и те же операнды могут вычисляться с
эквивалентными арифметическими операторами, которые применяются к их
отдельным битам. Битовые операторы OR(|), AND (&), NOT (-) и EOR С) определены
для отдельных битов и возвращают значения 0 и 1. Эти операторы приведены
в таблице 8.1. Из них только EOR может оказаться для вас новым. Он
возвращает 1, только если оба бита не равны.
Таблица 8.1
Битовые операции
X
0
0
1
1
У
0
1
0
1
-X
1
1
0
0
х)у
0
1
1
1
х&у
0
0
0
1
Хлу
0
1
1
0
Битовые операции применяются к n-битовым значениям выполнением
операций над каждым битом. Допустим,
а " an-ian-2 ■ • • а2а1ао Ь ■ bn-!bn_2 . . . Ьзк^Ьо
Результат с = a op b задается следующим образом:
с = cn,!Cn_2 • • • CjCiCo ** a^a^ . . . a2a!a0 op bn_xbn_2 . . . ^b^Q
где
Ci = аА op bi; 0 < i < n-1 и op = ' |', ' &' / ' л'
Унарный оператор '-' инвертирует биты операнда.
Пример 8.4
8-битовые числа х =11100011 и у = 01110110 используются с
операциями а) х OR у, Ь) х AND у, с) х EOR у и d) ~х.
а) х 11100011 Ь) х 11100011 с) х 11100011
OR у 01110110 AND у 01110110 EOR у 01110110
11110111 01100010 10010101
d) -х = 00011100
В C++ имеются также операторы сдвига, которые сдвигают биты
операнда влево («) или вправо (»). Выражение а « п умножает а на 271,
выражение а » п делит а на 2П. Обычно, использование битового
оператора ускоряет любое вычисление, включающее умножение или деление
целого значения на степень двойки.
Битовые операторы обычно используются с беззнаковыми целыми
операндами. Мы будем их использовать только для этого.
Пример 8.5
Предположим, что переменные х, у и z определяются следующим
образом:
// каждая переменная — 16 битовая
unsigned short x = 10, у = 13r z;
Пункты а — d иллюстрируют использование битового оператора.
a. z = х | у; // z - ХЪ
b. х = х & у; // z = 8
c. z = ~0 « 2; // z = 65532
d. z = ~х & (у » 2) ; // z = 1
Спецификация класса Set
В нашем классе Set-объект состоит из списка элементов, взятых в
диапазоне 0..setrange-l целых чисел. Целочисленный тип определяется именем
шаблонного типа Т. Мы полагаем, что для типа Т определен преобразователь
int и что целое значение может быть преобразование явно в тип Т. Например,
пусть val будет элементом типа Т, а I — целой переменной:
Т val;
int I;
Если I — это целый эквивалент элемента данных val, то
I = int(T), a val = Т(1)
Пример 8.6
a. Char — это целый тип.
char с = ' А' ;
int i;
i = int(с); // i = 65
с - char(i); //с - 'A'
b. Перечислимый тип — это целый тип.
enum Days {Sun, Mon, Tues, Wed, Thurs, Fri, Sat};
Days day = Thurs;
int d;
d = int (day) ; //d «= 4
day = Days (d); // day = Thurs
Представление элементов множества
При определении битовых операторов C++ для эффективной реализации
объекта Set используются отдельные биты в слове. Диапазон значений множества
(0..setrange-l) хранится в динамическом массиве из 16-битовых беззнаковых
целых. Массив с именем member связывает целые числа в диапазоне 0..setsize-l
как цепочку битов. Каждый бит представляет один элемент множества, и элемент
находится в этом множестве, если соответствующий бит равен 1. Нулевой элемент
множества представлен крайним правым битом первого элемента массива, а 15
представляется крайним левым битом первого элемента массива. Далее
продолжаем крайним правым битом второго элемента массива, представляющим 16, и
так далее. Схема хранения в памяти показана на следующем рисунке.
15 14 13 12 11 10 9 8 7 6 5 4 3 2 10 31 30 29 28 27 26 25 24 23 22 21 20 19 18 17 16
i|o|o|olo|o|i|o|o|oli|o|o|o|o|T| |o|o|o|i|o|o|o|o|o|o|o|o|o|o| 1 Го~|• ■ •
member[0] member[1]
В этом случае целые значения 0, 5, 9, 15, 17 и 28 принадлежат этому
множеству.
ОБЪЯВЛЕНИЕ
iinclude <iostream.h>
#include <stdlib.h>
enum ErrorType
{
InvalidMember, ExpectRightBrace, MissingValue,
MissingComma, InvalidChar, MissingLeftBrace,
InvalidlnputData, EndOfFile, OutOfMemory,
InvalidMemberRef, SetsDifferentSize
};
template <class T>
class Set
{
private:
// максимальное число элементов множества
int setrange;
// число байтов битового массива и указатель на массив
int arraysize;
unsigned short *member;
// обработка ошибок
void Error(ErrorType n) const;
// реализация распределения элементов множества
//по битам внутри 16-битовых целых
int Arraylndex(const T& elt) const;
unsigned short BitMask(const T& elt) const;
public:
// конструктор, создает пустое сножество
Set(int setrange);
// конструктор копирования
Set(const Set<T>& x);
// деструктор
-Set(void);
// оператор присваивания
Set<T>& operator» (const Set<T>& rhs);
// вхождение в текущее множество
int isMember(const T& elt);
// эквивалентность
int operator-» (const Set<T>& x) const;
// объединение
Set operator+ (const Set<T>& x) const;
// пересечение
Set operator* (const Set<T>& x) const;
// вставка/удаление
void Insert(const T& elt);
void Delete(const T& elt);
// ввод/вывод
friend istreamfc operator>> (istream& istr,
Set<T>& x);
friend ostream& operator« (ostrearafi ostr,
const Set<T>& x);
};
ОПИСАНИЕ
Шаблонный класс Set реализует множество целочисленных значений. Тип
Т может быть любым типом, для которого применимы операции i — int(v) и
v = T(i), где v и i задаются объявлениями
Т v;
int i;
Конструктор создает пустое множество Set, а арифметические операторы
используются для определения операций над множествами: объединение (+),
пересечение (*) и равенство (==). Методы Insert и Delete, так же как и оператор
присваивания, используются для обновления Set.
Операции ввода/вывода вводят и печатают множества, заключаемые в
фигурные скобки и разделяемые запятыми.
ПРИМЕР:
// набор целых чисел в диапазоне 0..24
Set<int> S(25);
// набор символов в коде ASCII
Set<char> T<128), U(128);
cin » S; // ввести {4, 7, 12}
S.Insert(5);
cout « S « endl; // вывод {4, 5, 7, 12}
cin << T; // ввести {a, e, i, о, u, у)
U = T; // U =» {a, e, i, о, u, у}
T.Delete('y');
cout « T « encll/ // вывод {a, e, i, o, u}
if (T*U — T)
cout « T « п- подмассив" « U « endl;
Код, реализующий класс Set, находится в файле set.h.
Класс Set предоставляет клиенту возможность создания множества объектов
определяемых пользователем перечислимых типов и стандартных
целочисленных типов, таких как int и char. Если требуется ввод/вывод множества для
перечислимых типов, потоковые операторы должны быть перегружены.
Пример 8.7
Рассмотрим следующий перечислимый тип
enum Days {Sun,Mon,Tues,Wen,Thurs,Fri, Sat};
В программном приложении содержится перегруженный оператор
« для этого типа. Он находится вместе с main-функцией в файле
enumset.cpp.
Следующие объявления и операторы иллюстрируют использование
этих инструментов.
// объявить 4 объекта, которые представляют различные
// множества дней
Set<Days> weekdays(7), weekend(7), week(7);
// массивы wd и we определяют списки дней в неделе.
// эти списки инициализируют множества объектов weekdays и weekend
Days wd[] * {Mon,Tues,Wen,Thurs, Fri}, we[] *» {Sat, Sun};
// вставить элементы массива в множества
for(int i«0; i<5; i++)
weekdays.Insert(wd[i]);
for(int i*0; i<5; i++)
weekend.Insert(we[i]);
// печатать множества
cout « weekdays « endl/
cout « weekend « endl/
// формировать и печать объединение двух массивов
week ■ weekdays + weekend/
cout « week « endl;
<Выполнение программы>
{Mon, Tues, Wen, Thurs, Fri}
{Sat, Sun}
{Sun, Mon, Tues, Wen, Thurs, Fri, Sat}
Решето Эратосфена
Греческий математик и философ Эратосфен жил в 3 в. до н.э. Он открыл
увлекательный метод использования множеств для нахождения всех простых
чисел, меньших, чем или равных целому значению п. Этот алгоритм
начинается инициализацией множества, содержащего все элементы в диапазоне 2..п.
Путем повторяемых проходов по элементам во множестве мы "просеиваем
элементы сквозь решето". В конечном счете, остаются только простые числа.
Решето начинает действие со своего наименьшего числа m = 2, которое служит
ключевым значением. Мы сканируем множество и удаляем все большие и
кратные ключу 2*т, 3*т, . . . , к*т, которые остаются в этом множестве. Эти
кратные не могут быть простыми числами, так как они делятся на т.
Следующее число в решете — это ключ т=3, являющийся простым числом. Как в
случае с начальным значением 2, мы удаляем все большие и кратные 3-м,
начиная с 6. Так как 6, 12, 18 и так далее уже были удалены как кратные 2,
этот проход удаляет 9, 15, 21... Продолжая процесс, переходим к следующему
большему числу множества, являющемуся простым числом 5. Помните, что
число 4 было удалено как кратное 2-м. В случае с 5 мы проходим по элементам
и удаляем всякое большее кратное 5 (25, 35, 55 ...). Процесс продолжается до
тех пор, пока пока мы не просканируем все множество и не удалим кратные
для каждого ключевого значения. Числа, которые остаются в решете, являются
простыми в диапазоне 2..п.
Пример 8.8
На этом рисунке показано решето Эратосфена выполняющее поиск
всех простых чисел в диапазоне 2 . . 25.
Решето Эратосфена: п=25
!ХеыхИ 21 i2|3N5N7N9NnNl3Nl5Nl7N^N2l|X|23N25
Г?аТЛнГ 31 |2|3| |5| |7| |\| \п\ Цз| |Х| |Т7| Ц9| [XI И Щ
У=е.ПТГз| Ы |7| | | Н |13| | | н н | i |23| ы
7,11,13,17,19, и 23 не содержат кратных в этом множестве
Простые числа {2,3,5,7,11,13,19,23}
Решето работает, пока не удалит все числа, не являющиеся простыми.
Для того, чтобы проверить это, предположим, что составное (не простое)
число m остается в решете. Такое число может быть записано как
m = p*k, р>1
где р является простым числом в диапазоне от 2 до т-1. В алгоритме
решета р было бы ключевым значением, и m было бы удалено, так как
оно является кратным р.
Программа 8.6. Решето Эратосфена
Функция PrintPrimes реализует решето. Алгоритм использует функцию
оптимизации, проверяя ключевые значения в диапазоне 2 < т < V/Г. Это
ограниченное число ключевых значений удаляет всё непростые числа из
множества. Для проверки этого факта предположим, что некоторое
составное число t = p*q остается. Если бы оба сомножителя (р и q) были
больше, чем п, то
t = p*q > VJT * V/Г = n
и t не находилось бы в этом множестве. Таким образом, один сомножитель
р должен быть < Vrc~. Этот меньший сомножитель был бы ключевым
значением или кратным ключевому значению и, следовательно, t было бы
удалено как кратное ключу. Вместо вычисления корня квадратного от п мы
проверяем все числа т, которые m*m < п.
#include <iostream.h>
#include <iomanip.h>
#pragma hdrstop
#include "set.h" // использовать класс Set
// вычислять и печатать все простые <- п, используя
// алгоритм Решето Эратосфена
void PrintPrimes(int n)
{
// множество содержит числа в диапазоне 2..п
Set<int> S(n+1);
int m, k, count;
// вставить все значения из 2..п в это множество
for(m=2;m <= n;m++)
S.Insert(m);
// проверять все числа от 2 до sqrt(n)
for(m=2;m*m <= n;m++)
// если m в S, удалить все кратные m из множества
if(S.IsMember(m))
for(k=m+m;k <= n;k += m)
if (S.IsMember(k))
S.Delete(k);
// все оставшиеся в S числа — простые.
// печатать простые числа по 10 в строке
count - 1;
for<m=2;m <= n;m++)
if (S.IsMember(m))
{
cout « setw(3) « m « " ";
if (count++ % 10 == 0)
cout « endl;
}
cout « endl;
}
void main(void)
{
int n;
cout « "Введите п: и;
cin » n;
cout « endl;
PrintPrimes(n);
)
/*
<Выполнение программы 8.б>
Введите п: 100
2 3 5 7 11 13 17 19 23 29
31 37 41 43 47 53 59 61 67 71
73 79 83 89 97
*/
Реализация класса Set
Закрытые методы Arraylndex и BitMask реализуют схему хранения в
памяти массива целых. Arraylndex определяет элемент массива, которому
принадлежит параметр elt простым делением на 16 с использованием
эффективного сдвига на 4 бита вправо:
template <class T>
int Set<T>::Arraylndex(const T& elt) const
{
// преобразовать elt к типу int и сдвинуть
return int(elt) » 4/
}
Если обнаруживается правильный индекс массива, BitMask возвращает
беззнаковое короткое значение, содержащее 1 в битовой позиции, задаваемой
значением elt. Эта маска (mask) может использоваться для задания или
очистки бита.
// создать беззнаковое короткое целое с 1 в битовой elt-позиции
template <class T>
unsigned short Set<T>::BitMask(const T& elt) const
{
// использовать & для нахождения остатка от деления на 16.
//0 попадает в крайний правый бит, 15 — крайний левый
return 1 « (int(elt) & 15);
}
Обработка ошибок. Класс реагирует на группу ошибок, вызывая
закрытую функцию-член Error. ErrorType типа enum используется для удобного
задания наименований возможных ошибок. Функции передается параметр
ErrorType, который используется в операторе выбора для определения
ошибки и завершения программы. Реализация метода Error приведена в
программном приложении.
Конструкторы класса Set. Класс имеет два конструктора, создающие
объект Set: один — создающий пустое множество, другой — конструктор
копирования. Пустое множество создается определением количества
беззнаковых коротких элементов массива arraysize, необходимых для
представления диапазона значений данных, выделением массива и заполнением его
значениями 0.
// конструктор, создает пустое множество
template <class T>
Set<T>::Set(int sz): setrange(sz)
{
// число беззнаковых коротких целых для задания множества
arraysize = (setrange+15) » 4;
// выделить массив
member « new unsigned short [arraysize];
if (member == NULL)
Error(OutOfMemory);
// создать пустое множество, заполняя его нулями
for (int i = 0; i < arraysize; i++)
member[i] = 0;
}
Set-операторы. Бинарные операции объединения и пересечения
реализуются перегрузкой операторов + и * языка C++. Для оператора объединения (+)
создается объект множества tmp (содержащий элементы в диапазоне 0..set-
range-1) побитовой операцией OR над элементами массива, представляющими
текущее множество, и элементами множества х. Этот новый объект
возвращается в качестве значения метода. Заметьте, что мы сообщаем об ошибке, если
оба множества (операнды) имеют разные размеры.
// формировать и возвращать объединение
// текущего множества с множеством х
template <class T>
Set<T> Set<T>::operator* (const Set<T>& x) const
{
// множества должны иметь одинаковые размеры
if (setrange != x.setrange)
Error(SetsDifferentSize);
// формировать объединение в tmp
Set<T> tmp(setrange);
// каждый элемент множества tmp — результат побитового OR
for (int i * 0; i < arraysize; i++)
tmp.member[i] = member[i] | x.memberti];
// возвратить объединение
return tmp;
}
Подобно объединению операция пересечения (*) создает объект множества
tmp, являющийся пересечением, использованием побитовой операции AND
над элементами массива текущего множества и множества х. Возвращается
новое множество как значение метода.
Метод IsMember определяет вхождение в текущее множество и возвращает
TRUE, если бит, соответствующий elt, равен 1, и FALSE — в противном случае:
template <class T>
int Set<T>::IsMember(const T& elt)
{
// находится ли int(elt) в диапазоне 0..setrange-1 ?
if (int(elt) < 0 || int(elt) >= setrange)
Error(InvalidMemberRef);
// возвратить бит, соответствующий elt
return member[Arraylndex(elt)] & BitMask(elt);
}
Операции вставки и удаления. Операция Insertion реализуется заданием
бита, соответствующего параметру elt:
template <class T>
void Set<T>::Insert(const T& elt)
{
// находится ли int(elt) в диапазоне 0..setrange-1 ?
if (int(elt) < 0 || int(elt) >= setrange)
Error(InvalidMemberRef);
// находится ли int(elt) в диапазоне 0. .setrange-1 ?
member[Arraylndex(elt)3 |= BitMask(elt);
}
Операцией удаления убирается бит, соответствующий elt. Метод использует
оператор AND и маску, содержащую все 1, кроме заданного elt-бита. Маска
создается с использованием операции побитового отрицания (~).
// удалить elt из множества
template <class T>
void Set<T>::Delete(const T& elt)
{
// находится ли int(elt) в диапазоне 0..setrange-1 ?
if (int(elt) < 0 || int(elt) >= setrange)
Error(InvalidMemberRef);
// очистить бит, соответствующий elt
member[Arraylndex(elt)] &= -BitMask(elt);
}
Ввод/вывод, Потоковые операторы » и « перегружаются для реализации
потокового ввода/вывода для типа Set. Оператор ввода (») читает множество
х в формате {io, ii, . . . im}. Элементы множества заключены в фигурные скобки
и разделены запятыми. Каждое целочисленное значение in представляет
элемент множества. Оператор вывода («) записывает множество х в формате
{io, ii, . . . im}, где io< ii< . . . <im являются элементами этого множества.
Метод Input является наиболее трудным для реализации. Он пропускает
пробел, используя функцию get для ввода одиночного символа, а затем
проверяет, является ли текущий символ символом "{". Если — нет, вызывается
метод error, который выводит сообщение об ошибке и завершает программу.
Когда начальная скобка найдена, метод проходит по разделенному запятыми
списку целочисленных значений и добавляет каждый элемент в текущее
множество. Выполняется проверка того, что запятые правильно размещены и что
элементы множества остаются в диапазоне от 0 до setrange-1. Для разделения
элементов в списке может использоваться любое количество пробелов.
Письменные упражнения
8.1 Объявите массив из 10 целых и указатель на int:
int a[10], *р;
Рассмотрите следующие операторы:
for(i=0; i<2; i++)
{
p=new int[5];
for(j=0;j<5;j++)
a[5*i+j] = *p++ = i+j;
}
(а) Укажите выход для операторов:
for(i=0; i<10; i++)
cout « a[i] « " ";
cout « endl;
(б) Определите переустанавливает ли оператор
р = р - 10;
указатель р в начало ранее выделенного динамического массива.
(в) Предположим, что q — это указатель на первоначальный динамический
массив. Производит ли этот код тот же выход, что и в пункте (а)?
for(i=0; i<10; i++)
cout « *(q+i) « " ";
cout << endl;
8.2 Для каждого объявления используйте оператор new, чтобы динамически
выделять указанную память.
(а) int* px;
Создайте целое, на которое указывает рх, имеющее значение 5.
(б) long *а;
int n;
cin >> п;
Создайте динамический массив из длинных целых, на который
указывает а.
(в) struct DemoC
{
int one;
long two;
double three;
}
DemoC *p;
Создайте узел, на который указывает р. Затем задайте поля {1, 500000,
3.14}
(г) struct DemoD
{
int one;
long two;
double three;
char name[30] ;
};
DemoD *p;
Создайте динамически узел, на который указывает р, и задайте поля
{3, 35, 1.78, "Bob C++").
(д) Задайте операторы, которые освобождают память для каждого пункта
а) — d).
8.3 Конструктор класса Dynamiclnt использует новый оператор для
динамического выделения целого и присваивания его адреса указателю рп.
Открытые методы GetVal и SetVal сохраняют и извлекают данные из
динамической памяти.
class Dynamiclnt
{
private:
int *pn;
public:
// конструктор и конструктор копирования
Dynamiclnt(int n e 0) ;
Dynamiclnt(const Dynamiclntfi x);
// деструктор
-Dynamiclnt(void);
// оператор присваивания
Dynamiclnt& operator» (const Dynamiclnt& x);
// методы управления данными
int GetVal(void); // получить целое значение
void SetVal(int n); // установить целое значение
// оператор преобразования
operator int(void); // возвращает целое
// потоковый ввод/вывод
friend ostream& operator« (ostream& ostr, const Dynamiclnt& x);
friend istream& operator» (istreams istr, Dynamiclnts x);
};
(а) Напишите код для реализации методов конструктора и деструктора.
(б) Напишите методы, которые перегружают оператор = и реализуют
конструктор копирования.
(в) Реализуйте GetVal, оператор int, и SetVal.
(г) Реализуйте функции потокового ввода/вывода, так чтобы они
считывали и записывали значение *рп.
8.4 Используйте объявление Dynamiclnt из письменного упражнения 8.3
для следующих упражнений:
(а) Dynamiclnt *р;
Задайте объявление для выделения одного объекта с начальным
значением 50.
(б) Dynamiclnt *p;
Выделите массив р с тремя элементами. Каково значение каждого
объекта в массиве?
(в) Dynamiclnt a[10];
Укажите, как бы вы объявили массив из 10 объектов типа Dynamiclnt
и инициализировали каждый элемент значением 100?
(г) Задайте операторы delete, освобождающие динамическую память,
используемую в упражнениях (а) — (с).
8.5 Запишите класс Dynamiclnt из письменного упражнения 8.3 как
шаблонный класс DynamicType.
template <class T>
class DynamicType
{
private:
T *pt;
public:
// конструктор и конструктор копирования
DynamicType(T value);
DynamicType(const DynamicType<T>& x);
// деструктор
-DynamicType(void);
// оператор присваивания
DynamicType<t>& operator* (const DynamicType<T>& x);
// методы управления данными
T GetVal(void); // получить значение
void SetVal(T value); // установить значение
// оператор преобразования
operator T(void); // возвратить значение
// потоковый ввод/вывод
friend ostream& operator« (ostream& ostr,
const DynamicType<T>& x);
friend istream& operator» (istreamfi istr, DynamicType<T>& x);
};
8.6 В этом упражнении используются классы Dynamiclnt и DynamicType,
разработанные в письменных упражнениях 8.3 и 8.5. Объявите объект:
DynamicType<DynamicInt> D(Dynamiclnt(5));
Каков выход для следующих операторов?
cout « D « endl;
cout « D.GetValO .GetValO) « endl;
cout « int(D.GetValO ) « endl;
cout « Dynamiclnt(D) « endl;
cout « int(Dynamiclnt(D)) « endl;
8.7 Рассмотрите класс ReadFile со следующим объявлением:
class ReadFile
{
private:
// чтение символов из потока fin для динамического
// выделения буферного массива размером bufferSize
ifstream fin;
char *buffer;
int bufferSize;
public:
// конструктор принимает имя файла и размер буфера
ReadFile(char *name, int size);
// выдача сообщения об ошибке и выход
ReadFile(const ReadFilefi f);
// удаление буфера и закрытие потока fin
-ReadFile(void);
void operator* (const ReadFile x);
// чтение следующей строки из файла.
// возвращает 0, если конец файла
int Read(void);
// копирование текущей строки в буфер
void CopyBuffer(char *buf);
// печать текущей строки в поток cout
void Printbuffer(void);
);
(а) Реализуйте этот класс.
(б) Напишите функцию
void LineNum(ReadFile& f) ;
которая читает f и распечатывает соответствующий файл с номерами
строк.
8.8 Класс DynamicType разработан в письменном упражнении 8.5.
Предположим следующие объявления:
DynamicType<int> *р, Q;
DynamicType<char> *c;
Ответьте на каждый вопрос:
(а) Напишите оператор, создающий объект класса DynamicType со
значением 5, на который указывает р.
(б) Печатайте значение 5, на которое указывает р, используя три
различных метода.
(в) Является ли каждый оператор верным? Если да, каково его действие?
с * new DynamicType<char> [65];
с = new DynamicType<char> (65);
(г) Если вводится число 35, каким будет выход?
cin » *р;
Q = *р;
cout « Q « endl;
(д) Используя значение Q из упражнения (d), рпределите, каков выход.
DynamicType<int> R(Q);
cout « Q << endl;
(е) Каков выход?
Q = DynamicType<int> (68);
с - DynamicType<char> (char(int (Q)));
cout « с « char(с) « int(c) « endl;
(ж) Напишите операторы, удаляющие объекты *р и *с. Что произойдет,
если вы выполните?
delete Q;
8.9
(а) Если CL является классом, объясните, почему вы не можете объявить
его конструктор копирования следующим образом:
CL(const CL х) ;
(б) Объясните, почему вообще не нужно объявлять оператор присваивания
для CL следующим образом:
void operator» (const CL& х);
8.10
(а) Каково значение ключевого слова this? Объясните, почему оно верно
только внутри функции-члена.
(б) Назовите основное применение ключевого слова this.
8.11 Класс Rational из главы 6 реализует арифметику рациональных чисел.
Оператор += должен быть добавлен в этот класс. Объясните, почему
следующая реализация является правильной:
Rational& Rational::operator+= (const Rationalu r)
{
♦this = *this + r;
return *this;
}
8.12 Класс ArrCL реализует границы массива, проверяя использование
перегруженного оператора индексации массива [] и преобразование
указателя. Он содержит массив из 50 элементов и поле длины. При создании
объекта типа ArrCL пользователь может указать максимальную длину
для списка и передавать это значение конструктору как параметр.
const int ARRAYSIZE = 50;
template <class T>
class ArrCL
{
private:
T arr[ARRAYSIZE] ;
int length;
public:
// конструктор
ArrCL9int n = ARRAYSIZE);
// получение размера списка
int ListSize(void) const;
// индексный оператор, реализующий надежный массив
Т& operator[] (int n);
// преобразование указателя. Возвращает адрес arr.
operator T* (void) const;
}
Размер встроенного списка arr ограничивается значением ARRAY-
SIZE = 50. Если пользователь пытается зарезервировать массив
большего размера, конструктор устанавливает размер на ARRAYSIZE и
выдает предупреждение.
(а) Напишите объявления, резервирующие массив А из 20 целых, массив
В из 50 элементов типа char и массив С из 25 элементов типа float.
(б) Имеется ли ошибка в этом цикле?
ArrCL<long> A(30);
for(int i=0; i<= 30; i++)
A[iJ « 0;
(в) Объясните, почему выходом будет 420 420
int Suml (const ArrCKint>& A)
{
int s = 0;
for(int i*0; i<A.ListSize (); i++)
s += A[i];
return s;
}
int Sum2(int *A, int n)
{
int s = 0;
for(int i-0; i<n; i++)
s += *A++;
return s;
}
• • *
ArrCL<int> arr(20);
for(int i=0; i<20; i++)
arr[i] = 2*(i+l);
cout « Suml(arr) « " " « Sum2(arr, 20) « endl;
(г) Реализуйте этот класс.
8.13 Рассмотрите объявления
String A("Have а ", В("nice day!")/ С(A), D=B;
(а) Каково значение С?
(б) Каково значение D?
(в) Укажите значение D = А + В;
(г) Укажите значение С+=В.
8.14 Рассмотрите строки:
String S{"abcl2xya52cba"), Т;
(а) Каково значение S.FindLast(V)?
(б) Каково значение S[6]?
(в) Каково значение S[3]?
(г) Каково значение S[24]?
(д) Каково значение Т = S.Substr(5,6)?
(е) Каково значение Т после выполнения операторов:
Т - S;
Т.Insert("ABC", 5);
8.15 Сделайте следующие объявления:
#define TF(b) ((b)? "TRUE" : "FALSE")
String si("STRING") , s2 ("CLASS");
String s3;
int loc, I;
char c, cstr[30];
Определите выход каждой последовательности операторов:
(а) s3 - si + s2;
cout << si « "объединенная с " << s2
« « ш " « 83 « endl;
(б) cout « "Длина " « s2 « " = "
« s2.Length() « endl;
(в) cout « "Первое вхождение 'S' в " « s2
« » = » « s2.Find('S',0) « endl;
cout « "Последнее вхождение 'S' в " « s2
« » = " « S2.FindLast('S') « endl;
(r) cout « "Вставить 'OBJECT ' в строку s3 в позицию 7."
« endl;
S3 = si + s2;
s3.Insert("OBJECT ", 7);
cout « s3 « endl;
(д) si = FILE1.S;
for(i=0; i < sl.LegthO; i++)
{
с ■ si[i];
if (с >= 'A' && с <« 'Z'}
{
с +- 32;
sl[i] = с;
}
}
cout « si « endl;
(e) si = "ABCDE";
s2 ■ "BCF";
cout « "si < s2 * " « TF(sl < s2) « endl;
cout « "si « s2 - " « TF(sl «« s2) « endl;
(ж) si « "Проверка оператора преобразования указателя";
strcpy(cstr, si);
cout « cstr << endl;
8.16 Предположим, что переменные x, у и z определены следующим образом:
unsigned short х » 14, у = 11, z;
Какое значение присваивается переменной z в результате выполнения
каждого следующего оператора?
(а) z - х | у;
(б) z * х & у;
(в) z =* -0 « 4;
(г) z * -х & (у » 1);
(д) 2 » (1 « 3) & х;
8.17 В этом упражнении представлены четыре функции, выполняющие
битовые преобразования. Сопоставьте каждую функцию с одной из
следующих описательных фраз:
(а) Определение количества битов в int для определенной машины.
(б) Возвращение числового значения п битов, начиная с бита в позиции р.
(в) Инвертирование п битов, начиная с бита в позиции р. В позиции О
находится крайний левый бит целого значения.
(г) Битовый сдвиг целого по часовой стрелке.
unsigned int one(unsigned int n, int b)
{
int rightbit;
int lshift - three () - 1;
int mask = (unsigned int) -0 » 1;
while (b—)
{
rightbit « n & 1;
n - (n » 1) & mask;
rightbit - rightbit « lshift;
n « n | rightbit;
}
return n;
}
unsigned int two(unsigned int x, int p, int n)
{
unsigned int mask = (unsigned int) ~(~0 << n);
return (x » (p-n+1)) & mask;
}
int three(void)
{
int i;
unsigned int u ■= (unsigned int) ~0;
for (i-l;u « u »l;i++);
return i;
}
unsigned int four(unsigned int x, int p, int n)
{
unsigned int mask;
mask = -0;
return x л (-(mask » n) » p);
}
8.18 Добавьте оператор разности (-) в класс Set. Этот оператор принимает
два параметра типа множество, X и Y, и возвращает множество,
состоящее из элементов в X, которые не находятся в Y. Необходимо,
чтобы два эти множества имели одно и то же количество элементов.
х-y
X - {0, 3, 7, 9), Y - {4, 7, 8, 10, 15}
X - У - {0, 3, 9)
template <class T>
Set<T> Set<T>::operator - (const Set<T> &x);
(Совет: Вычислите diff.member[i] = member[i] & ~x.member[i])
8.19 Добавьте оператор побитового отрицания (~) в класс Set. Этот унарный
оператор возвращает множество, состоящее из всех значений в
универсальном множестве, которые не находятся в X.
Set<int> Х(10), У(10);
for(int i=0; i < 10; i += 2)
X.Insert(i);
Y - -X; // X - {1,3,5,7,9}
8.20
(а) Используйте оператор побитового отрицания для создания
универсального множества в качестве объекта Set.
(б) Реализуйте оператор разности из письменного упражнения 8.18 с
операторами побитового отрицания и пересечения.
Упражнения по программированию
8.1 В этом упражнении используется класс Dynamiclnt, разработанный в
письменном упражнении 8.3.
(а) Перегрузите оператор < для Dynamiclnt как внешнюю функцию. Она
должна быть дружественной этому классу.
(б) Напишите функцию
Dynamiclnt *Initialize(int n);
которая возвращает указатель на массив динамически выделенных
объектов. Инициализируйте значения объектов, чтобы они были
случайными целыми числами в диапазоне 1..1000.
(в) Main-функция должна считывать целое п и использовать Initialize для
создания массива объектов типа Dynamiclnt. Используйте основанную
на шаблоне обменную сортировку из главы 7 для сортировки списка.
Напечатайте результирующий список.
8.2 Данная программа использует класс ReadFile из письменного
упражнения 8.7. Используйте функцию LineNum для чтения файла и вывода
на экран строк с номерами.
8.3 В этой программе используется класс ReadFile из письменного
упражнения 8.7.
(а) Напишите функцию
void CapLine(ReadFilefc f, char *capline);
которая считывает следующую строку из файла f, печатает ее
прописными буквами и возвращает эту строку в capline.
(б) Используйте эту функцию для чтения файла и печати его в верхнем
регистре.
8.4 Это упражнение использует класс ArrCL из письменного упражнения
8.12. Создайте надежный массив из 10 целых и затем запросите
пользователя ввести 10 элементов данных. После вызова основанной на
шаблоне обменной сортировки (в файле arrsort.h) печатайте
упорядоченный список. Попытайтесь обратиться к А[10], чтобы вызвать
сообщение об ошибке и завершение программы.
8.5 Это упражнение модифицирует основанный на шаблоне класс Stack,
разработанный в главе 7 (stack.h). Замените данное-член статического
массива stacklist объектом Array, первоначально содержащим Мах-
StackSize элементов. Удалите параметр размера стека из конструктора
и перепишите метод Push так, чтобы размер стека при необходимости
возрастал. Протестируйте ваши изменения, помещая целые значения
1..100 в стек и затем удаляя их, печатая каждое 10-е значение.
8.6 Считайте файл, используя потоковый метод getline, и сохраните строки
в объекте Array, называемом строковым пулом. Вставьте строку в этот
пул, выполняя операцию Resize, чтобы добавить достаточное
пространство в пул, и поместите начальный индекс этой строки в массив
строковых индексов, изменяя при необходимости его размер. Этот массив
будет определять начальное положение каждой последующей строки в
пуле. Введите целое N и печатайте последние N строк файла. Если
файл имеет меньше строк, чем N, печатайте весь файл.
Массив строковых индексов
indexO indexl I index2 I index3
Строковый пул
indexO indexl inoex2 Index3
8.7 Измените программу 8.3, сохраняя список всех простых чисел, которые
вы вычислили до этого времени. Для следующего целого п в
последовательности проверяйте только простые числа в списке, а не все
делители от 3 до п/2. Если п не делится ни на какое простое число, то
п — это новое простое число, которое может быть добавлено в список.
Этот факт является математическим результатом того, что любое число
может быть записано, как произведение его простых делителей.
8.8
(а) Напишите функцию
void Replace(Strings S, int pos, const Strings repstr);
которая заменяет repstr.Length() символов из S, начиная с индекса рое.
Если в хвосте строки S символов меньше, чем repetr.Length, вставьте
все символы repstr.
8.8
(а) Напишите функцию
void Center(Strings S);
которая вызывает Replace для печати S с центрированием внутри 80-
символьной строки.
Напишите main-функцию, тестирующую функции из пунктов (а) и (Ь).
8.9 Считайте целое п, представляющее количество строк текста в
документе. Динамически выделите место для п указателей на объекты String.
Читайте п объектов String, используя ReadString.
Строки текста могут содержать специальные символы "#" и "&",
например:
Уважаемый #
Ваш счастливый подарок находится в &. Если Вы пойдете в &
и укажете Ваше имя, служащий вручит Вам Ваш приз. Спасибо
# за Ваш интерес к нашему конкурсу.
С уважением,
Мистер Стринг
Введите строку poundstr, которая заменяет все вхождения "#" в вашем
документе. Введите строку ampstring, которая заменяет все вхождения
"&". Пройдите по массиву строковых указателей и выполните
подстановки. Печатайте окончательный документ.
8.10 Напишите программу, которая инициализирует два 10-элементных
массива intA и intB и использует их для создания множеств А и В. Оператор
разности множества (-) определяется в письменном упражнении 8.18.
Эта программа должна вычислить А-В и напечатать результат.
Программа должна также проверить, что
А + В = А-В + В-А + А*В
8.11 Функция
template <class>T
Set <T> TxclusiveUnion(const Set<T>& X, const Set<T>& Y);
возвращает множество, содержащее все элементы, которые находятся
либо в X, либо в Y, но не в обоих множествах.
(а) Используйте графический аргумент, чтобы показать, что ExclusiveUnion
может вычисляться с использованием любой из следующих формул:
1. (X-Y) + (Y-X)
2. X* -Y + ~X*Y
Операции разности множества (-) и дополнения (~) определяются в
письменных упражнениях 8.18 и 8.19.
(б) Реализуйте ExclusiveUnion, используя формулу 2. Протестируйте вашу
работу, используя множества:
X = {1,3,4,5,7,8,12,20}, Y = {3,5,9,10,12,15,20,25}
для которых
ExclusiveUnion(X,Y) = {1,4,7,8,10,15,25}
8.12 Два ферзя на шахматной доске должны быть атакующими, если один
может переместиться в позицию второго, то есть, если они находятся
в одном и том же ряду, столбце или диагонали. На следующем рисунке
показан пример атакующих и неатакующих ферзей.
Атакующие ферзи
Не атакующие ферзи
Учитывая позицию каждого ферзя, рассмотрим проблему определения
множества всех возможных перемещений каждого из них и, являются
ли ферзи атакующими.
Любая позиция на шахматной доске может рассматриваться с
использованием номера строки и номера столбца, каждый в диапазоне от О
до 7. Каждой клеточке доски может быть присвоен единственный номер
между 0 и 63 назначением каждой паре строка/столбец (i,j) целого
значения i*8+j. Мы можем теперь рассматривать шахматную доску как
множество из 64 целых в диапазоне от 0 до 63.
Напишите функцию
void ComputeQeenPositions(Set<int>& Board, int rowq, int colq);
которая принимает множество Board, позицию ферзя (int rowq, int
colq) и присваивает множеству все клеточки, на которые ферзь может
переместиться.
Напишите функцию
void PrintQueenPositions(Set<int> Queen,int Qrow,int Qcol,
int QOtherRow,int QOtherCol);
Первый ферзь находится в позиции (Qrow, Qcol), a Queen — это
множество позиций, на которые этот ферзь может переместиться. Другой
ферзь находится в позиции (QOtherRow, QOtherCol). Функция печатает
доску, помещая символ "X" в каждую клеточку, на которую может
переместиться первый ферзь, и символ " — в другие клеточки. Если
один из ферзей находится в клеточке, печатается "Q".
Напишите функцию
int AttackingQeens(int QlRow, int QlCol,
int Q2Row, int Q2Col);
которая принимает позицию двух ферзей и определяет, являются ли
они атакующими. Это выполняется определением того, находятся ли
они в одной и той же строке, столбце или диагонали.
Напишите main-функцию, читающую позиции двух ферзей и
печатающую множество возможных положений, на которые каждый ферзь
может переместиться. Сообщение указывает, являются ли ферзи
атакующими.
глава
Связанные списки
9.1. Класс Node
9.2. Построение связанных списков
9.3. Разработка класса связанного
списка
9.4. Класс LinkedList
9.5. Реализация класса LinkedList
9.6. Реализация коллекций со
связанными списками
9.7. Исследовательская задача:
Буферизация печати
9.8. Циклические списки
9.9. Двусвязные списки
9.10. Практическая задача:
Управление окнами
Письменные упражнения
Упражнения по программированию
Мы уже определили класс коллекций, которые реализованы на базе
массивов. Коллекции включали стеки, очереди и более общий класс SeqList,
поддерживающий последовательный список элементов. В этой главе
разрабатываются связанные списки, которые предоставляют более гибкие методы
добавления и удаления элементов.
Массив может использоваться с простыми приложениями сохранения
списков. Например, многие авиалинии продают незарезервированные билеты,
которые могут быть выкуплены клиентами как посадочный билет. Во время
предварительной продажи билетов авиалиния ведет список клиентов,
добавляя в него их имена. Перед полетом каждого клиента регистрирует служащий
авиакомпании, который удаляет имя из билетного списка и добавляет его в
список пассажиров. С помощью таких списков авиакомпания имеет доступ
к количеству пассажиров на борту самолета и к количеству клиентов с еще
неоплаченными билетами.
Списки, основанные на массиве, недостаточно эффективны для
приложений, требующих более гибких методов обработки. Рассмотрим пример
ресторана, в котором выполняется резервирование мест. Метрдотелю необходимо
вводить имена в список с упорядочением по времени и пользоваться
несколькими критериями для удаления имени из списка. Немедленное удаление
происходит, если клиент звонит по телефону и отменяет заказ или, если
клиент приходит и занимает место. Периодически метрдотель должен
просматривать список и удалять имена клиентов, которые потеряли
резервирование, не появившись в ресторане в течение 15 минут после времени заказа.
Ресторан
Jones
Dolan */
$;45
Banks
Dal porto
1Ш
Johnson
Ресторан
6:30
Jones V'
Dolan S
6;45
Banks
Dal porto i/
7:00
Johnson
Ресторан
6:30
Jones S
Dolan i/
6;45
Banks i/
Dal porto v
7:00
Johnson
Время 6:15
(Dolan - отменил)
Время 6:40
(Jones, Dal porto - пришли)
Время 7:05
(Banks - удалить)
Основанный на массиве список не может эффективно работать с
ресторанной системой резервирования. Имена должны вставляться в различные
места в списке с учетом различного времени прихода клиентов. Для этого
необходимо, чтобы имена были сдвинуты вправо. Удаления требуют, чтобы
имена сдвигались влево. Работники ресторана не могут предвидеть количество
зарезервированных мест и должны выделять преувеличенный объем памяти
для обработки экстренных случаев. Когда начинается обслуживание, список
резервирования становится очень динамичным с быстрым движением имен
в список и из него. Массивы с их непрерывной памятью не отвечают этим
динамическим изменениям. В последующем обсуждении рассматриваются
некоторые из этих проблем с массивами и разрабатываются решения, которые
используют динамические связанные списки.
Массив — это структура фиксированной длины. Даже динамический
массив имеет фиксированный размер после операции изменения размера.
Например, массив А создается динамически как массив целых из 6 элементов:
А = new int [б];
| 74 | 60 | 25 | 82 | 65 | 23 |
Когда массив заполнен, мы можем добавлять элементы только после
изменения размера списка — процесс, требующий копирования каждого
элемента в новую память. Частое изменение размера больших списков может
существенно повлиять на эффективность приложения.
Массив сохраняет элементы в смежных ячейках памяти, что делает
возможным прямой доступ к элементу, но не позволяет эффективно выполнять
добавление и удаление элементов, если только эти операции не выполняются
в конце массива. Например, предположим, что вы удаляете элемент 60 из
второй позиции в следующем списке:
| 74 | 60 | 25 | 82 | 65 | 23
индекс 1
Для сохранения непрерывного порядка элементов в списке мы должны
сдвинуть четыре элемента влево.
74 | 25 | 82 | 65 | 23
Предположим, что мы добавляем новый элемент 50 в позицию с индексом
2. Так как массив сохраняет элементы в непрерывном порядке, мы должны
освободить участок в списке, сдвигая три элемента на одну позицию вправо:
| 74 | 25 | 50 | 82 | 65 | 23 |
индекс 2
Для списка из N элементов вставка и удаление элемента в конце списка
требуют времени вычисления 0(1). Однако для общего случая ожидаемое
количество сдвигов равно N/2, а время вычисления — O(N).
Описание связанного1 списка
Проблема эффективного управления данными является важнейшей для
любой реализации списка. Нам необходимо разработать новую структуру,
которая освободит нас от непрерывного порядка сохранения данных. Мы
можем использовать модель звеньев в цепи.
1 В литературе часто используется термин "связный список". — Прим. ред.
Длина списка может увеличиваться без ограничений при добавлении новых
звеньев. Более того, новые элементы могут быть вставлены в список простым
разрывом соединения, добавлением нового звена и восстановлением
соединения.
До вставки После вставки
Элементы удаляются из списка разрывом двух соединений, удалением
звена и затем повторным соединением цепи.
До удаления После удаления
В этой главе разрабатывается структура данных, называемая связанный
список (linked list), для реализации последовательного списка. Связанные
списки предоставляют эффективные методы обработки и снимают многие
ограничения, отмеченные при описании массивов.
Обзор главы
Независимые элементы в связанном списке называются узлами (nodes).
Мы разрабатываем класс Node, определяющий отдельные объекты узла и
предоставляющий методы обработки связанных списков. В частности, мы
реализуем методы узла, которые вставляют и удаляют узлы после текущего
узла, разрабатываем алгоритмы, позволяющие использовать отдельные узлы
и создавать связанный список, сканировать узлы и обновлять их значения.
Мы создаем класс LinkedList, который инкапсулирует основные алгоритмы
узла в структуре класса, и используем этот класс для реализации классов
Queue и SeqList, снимая тем самым ограничения списков, основанных на
массиве. Этот класс применяется для решения множества интересных
проблем, включая удаление всех дублированных данных-значений из списка.
Класс LinkedList используется в разработке двух практических задач: для
моделирования системы буферизации печати и при построении динамических
оконных списков.
Разработка списка как круговой системы содержит как концептуальные
преимущества, так и преимущества кодирования. Двусвязные списки находят
применение, когда нам необходимо выполнять поиск элементов в обоих
направлениях. Мы определяем классы CNode и DNode, реализующие круговые
и двусвязные списочные структуры.
9.1. Класс Node
Узел (node) состоит из поля данных и указателя, обозначающего
следующий элемент в списке. Указатель — это соединитель, связывающий вместе
отдельные узлы списка.
Node
Node
Node
Node
data
next
data
next
• • • data next
• • • data next
NULL
head
currPtr
rear
Связанный список состоит из множества узлов, первый элемент которого
(front), — это узел, на который указывает голова (head). Список связывает
узлы вместе от первого до конца или хвоста (rear) списка. Хвост определяется
как узел, чье поле указателя имеет значение NULL (0). Списочные
приложения проходят по узлам, следуя за каждым указателем на следующий узел.
В любой точке сканирования на текущее положение ссылается указатель
currPtr. Для списка без узлов head будет содержать значение NULL.
head
NULL
Объявление типа Node
Узел с его данными (data) и полями указателей (next) является
строительным блоком для связанного списка. Структура узла имеет операции, которые
инициализируют данные-члены, и методы управления указателями для
доступа к следующему узлу.
Далее приведен рисунок, иллюстрирующий базовые операции для
обработки узлов. В любом данном узле р мы можем реализовать операцию 1п-
sertAfter, которая присоединяет новый узел после текущего. Процесс
начинается прерыванием соединения с последующим узлом q, вставкой newNode
и восстановлением связей.
До вставки
data next
data next
После вставки
newNode
пересоединить
пересоединить
Аналогичный процесс описывает операцию DeleteAfter, которая удаляет
узел, следующий за текущим. Мы отсоединяем р от следующего за ним узла
q и затем соединяем р с узлом, следующим за q.
До удаления
data next
разъединить
После удаления
data next
пересоединить
Структура узлов с операциями вставки и удаления описывает абстрактный
тип данных. Для каждого узла эти операции относятся непосредственно к
его последующему (следующему) узлу.
ADT Nod*
Данные
Поле данных используется для хранения данных, кроме инициализации, значение не
используется ни в какой другой операции. Поле next является указателем на
последующий узел. Если next — это NULL, то следующего узла нет.
Операции
Конструктор
Начальные значения: Значение данных и указатель на следующий узел.
Процесс: Инициализация двух полей.
NextNode
Вход: Нет
Предусловия: Нет
Процесс: Выборка значения поля next
Выход: Возвращение значения поля next.
Постусловия: Нет
InsertAfter
Вход: Указатель на новый узел.
Предусловия: Нет
Процесс: Переустановка значения next для указания на новый
узел и установка значения next в новом узле для
ссылки на узел, следующий за текущим.
Выход: Нет
Постусловия: Узел теперь указывает на новый узел
DeleteAfter
Вход: Нет
Предусловия: Нет
Процесс: Отсоединение следующего узла и присваивание значения
next для ссылки на узел, который следует
за следующим узлом.
Выход: Указатель на удаленный узел.
Постусловия: Узел имеет новое значение next.
Конец ADT Node
ADT Node описывается основанным на шаблоне классом C++.
Спецификация класса Node
ОБЪЯВЛЕНИЕ
template <class T>
class Node
{
private:
// next указывает на адрес
// следующего узла
Node<T> *next;
public:
// открытые данные
Т data;
// конструктор
Node (const T& item, Node<T>* ptrnext ■ NULL);
// методы модификации списка
void InsertAfter(Node<T> *p);
Node<T> *DeleteAfter(void);
// получение адреса следующего узла
Node<T> *NextNode(void) const;
};
ОПИСАНИЕ
Значение поля next — это указатель на Node. Класс Node является
самоссылающейся (self-referencing) структурой, в которой указатель-член (pointer
member) ссылается на объекты своего собственного типа.
Мы используем объекты Node для разнообразных классов коллекций,
таких как словари и хеш-таблицы, и объявляем поле открытых данных для
обеспечения удобного доступа к ним. Такой подход менее затруднителен для
пользователя, чем использование пары функций-членов, таких как Get-
Data/SetData. Преимущества становятся очевиднее, когда необходимо
наличие ссылки на данное-член. Это необходимо при реализации более
продвинутых классов, таких как словари. Поле next остается закрытым, и доступ
к нему обеспечивается функцией-членом NextNode. Оно изменяется только
методами InsertAfter и DeleteAfter.
Конструктор для класса Node инициализирует поле открытых данных и
поле закрытых указателей. По умолчанию значение next устанавливается на
NULL.
ПРИМЕР
Node<int> t(10); // создание узла t с данными
// значене * 10, next = NULL
10
NULL
P = &t
Node<int> *u;
u« new Node<int>(20); //выделяет объект в и
//value - 20 и next - NULL
Node<char> *p, *q, *r;
q - new Node<char>('B'); // q имеет данные 'В'
p « new Node<char>('A',q); // объявление узла р с данными 'А'
// поле next указывает на q
г * new Node<char>('C ); // объявление узла г с данными 'С
q->InsertAfter(r); // вставка г в хвост списка
cout « p->data; // печать символа 'А'
р = p->NextNodeО; // переход к следующему узлу
cout « p->data; // печать символа 'В'
cout « endl;
г = q->DeleteAfter(); // отделение хвостасписка;
// присваивание значения г
Реализация класса Node
Класс Node содержит как открытый, так и закрытый данные-члены.
Открытый данное-член предназначается для того, чтобы пользователь и классы
коллекций могли иметь прямой доступ к его значению. Поле next является
закрытым, и доступом к этому полю указателя управляют функции-члены.
Только методам InsertAfter и DeleteAfter позволяется изменять значение
поля next. Если сделать это поле открытым, пользователь получит
возможность нарушать связь и уничтожать связанный список. Класс Node содержит
функцию-член NextNode, которая позволяет клиенту проходить по
связанному списку.
// конструктор, инициализация данных и указателя
template <class T>
Node<T>::Node(const T& item, Node<T>* ptrnext) :
data(item), next(ptrnext)
{}
Списковые операции. Метод NextNode предоставляет клиенту доступ к
полю указателя next. Этот метод возвращает значение next и используется
для прохождения по списку.
// возвратить закрытый член next
template <class T>
Node<T> *Node<T>::NextNode(void) const
{
return next;
}
Функции InsertAfter и DeleteAfter являются основными операциями
создания списков. В каждом случае процесс включает только изменения
указателей.
InsertAfter принимает узел р в качестве параметра и добавляет его в
список в качестве следующего узла. Первоначально текущий объект
указывает на узел, адресом которого является q (значение в поле next). Алгоритм
изменяет два указателя. Поле указателей р устанавливается на q, а полю
указателей в текущем объекте присваивается значение р.
До После
Текущий
объект
Текущий
объект
// вставить узел р после текущего узла
template <class T>
void Node<T>::InsertAfter(Node<T> *p)
{
// p указывает на следующий за текущим узел,
// а текущий узел — на р.
p->next = next;
next = р;
}
Порядок присваиваний указателей очень важен. Предположим, что
операторы присваивания имеют обратный порядок.
next = р; // Узел, следующий за текущим объектом,
// потерян!
p->next e next
После
текущий
объект
Остаток списка потерян!
DeleteAfter удаляет узел, который следует за текущим объектом и
связывает его поле указателей со следующим узлом в списке. Если после
текущего объекта нет никакого узла (next == NULL), функция возвращает NULL.
Иначе, функция возвращает адрес удаленного узла для случая, если
программисту необходимо освободить память этого узла. Алгоритм DeleteAfter
сохраняет адрес следующего узла в tempPtr. Поле next узла tempPtr
определяет узел в списке, на который должен теперь указывать текущий объект.
Возвращается указатель на узел tempPtr. Процесс требует присваивания
только одного указателя.
До После
next h—H next г—И next next Wm next hH next
текущий
объект
tempPtr
текущий
объект
tempPtr
// удалить узел, следующий за текущим, и возвратить его адрес
template <class T>
Node<T> *Node<T>::DeleteAfter(void)
{
// сохранить адрес удаляемого узла
Node<T> *tempPtr = next;
// если нет следующего узла, возвратить NULL
if (next =« NULL)
return NULL;
// текущий узел указывает на узел, следующий за tempPtr.
next = tempPtr->next;
// возвратить указатель на несвязанный узел
return tempPtr;
}
9.2. Создание связанных списков
Для создания связанных списков мы используем класс Node. В процессе
обсуждения этой темы вводятся основные алгоритмы связанных списков,
применяемых в большинстве приложений. Материал этого раздела важен
для понимания связанных списков, поскольку здесь вы узнаете, как создавать
списки и обращаться к узлам. Мы реализуем алгоритмы связанных списков
как независимые функции. Овладение этим фундаментальным материалом
поможет вам, когда эти методы будут использоваться для создания общего
класса связанных списков. Для простоты в нашем обсуждении
подразумевается, что узлы списка содержат целые данные.
Связанный список начинается с указателя узла, который ссылается на
начало списка. Мы называем этот указатель головой, так как он указывает
на начало списка. Первоначально значением головы является NULL для
указания пустого списка.
Мы можем создать связанный список различными способами. Начнем с
изучения случая, когда каждый новый узел помещается в голову списка.
Позже мы рассмотрим случай, когда узлы добавляются в хвост списка или
в промежуточные позиции.
Создание узла
Мы реализуем создание узла с использованием основанной на шаблоне
функции GetNode, которая принимает начальные данное-значение и
указатель и динамически создает новый узел. Если выделение памяти происходит
неудачно, программа завершается, иначе, функция возвращает указатель на
новый узел.
// выделение узла с данным-членом item и указателем nextPtr
template <class T>
Node<T> *GetNode(const T& item, Node<T> *nextPtr - NULL)
{
Node<T> *newNode;
// выделение памяти при передаче item и NextPtr конструктору.
// завершение программы, если выделение памяти неудачно
newNode ш new Node<T>(item, nextPtr);
if (newNode «- NULL)
{
cerr << "Ошибка выделения памяти!" « endl;
exit(1);
}
return newNode;
)
Вставка узла: InsertFront
Операция вставки узла в начало списка требует обновления значения
указателя головы, так как список должен теперь иметь новое начало. Проблема
сохранения головы списка является основной для управления списками. Если
вы потеряете голову, вы потеряете список!
Перед началом вставки голова определяет начало списка. После вставки
новый узел займет положение в начале списка, а предыдущее начало списка
займет вторую позицию. Следовательно, полю указателей нового узла
присваивается текущее значение головы, а голове присваивается адрес нового
узла. Назначение выполняется с использованием GetNode для создания нового
узла,
head - GetNode(item,head);
head
head указывает на р
head
Пустой список
item
item NULL
newNode
newNode
Функция InsertFront принимает текущую голову списка, которая является
указателем, определяющим список, а также принимает новое значение
данных. Она вставляет значение данных в узел в начале списка. Так как голова
будет изменяться этой операцией, она передается как ссылочный параметр.
// вставка элемента в начало списка
template <class T>
void InsertFront(Node<T>* & head, T item)
{
// создание нового узла, чтобы он указывал на
// первоначальную голову списка
// изменение головы списка
head e GetNode (item, head);
)
Эта функция и GetNode находятся в файле nodelib.h.
Прохождение по связанному списку
Начальной точкой любого алгоритма прохождения является указатель
головы, так как он определяет начало списка. При прохождении по списку,
мы используем указатель currPtr для ссылки на текущее положение в списке.
Первоначально currPtr устанавливается на начало списка:
currPtr ■ head;
Во время сканирования нам необходим доступ к полю данных в текущем
положении. Так как data — это открытый член, у нас есть возможность
выполнить выборку значения data или присвоить этому члену класса новое
значение.
currentDataValue ■» currPtr->data/
currPtr->data « newdata;
Например, простой оператор cout может быть включен в алгоритм
прохождения списка для печати значения каждого узла:
cout « currPtr->data;
В процессе сканирования мы непрерывно перемещаем currPtr к
следующему узлу до тех лор, пока не достигнем конца списка.
currPtr ■ currPtr->nextNode();
Прохождение по списку завершается, когда currPtr становится равным
NULL. Например, функция PrintList печатает значение данных каждого узла.
Голова передается в качестве параметра для определения списка. Второй
параметр пользовательского типа AppendNewline указывает на TOj должны
ли следовать за выводом два пробела или символ newline. Функция
содержится в файле nodelib.h.
enum AppendNewline {noNewline,addNewline};
// печать связанного списка
template <class T>
void PrintList(Node<T> *head, AppendNewline addnl = noNewline)
{
// currPtr пробегает по списку, начиная с головы
Node<T> *currPtr = head;
// пока не конец списка, печатать значение данных
// текущего узла
while(currPtr != NULL)
{
if(addnl == addNewline)
cout « currPtr->data « endl;
else
cout « currPtr->data « " ";
// перейти к следующему узлу
currPtr = currPtr->NextNode();
}
}
Программа 9.1. Сопоставление с ключом
Программа генерирует 10 случайных чисел в диапазоне от 1 до 10 и
вставляет эти значения как узлы в голову связанного списка, используя
InsertFront. Для отображения списка используется Printlist.
Программа содержит код, который подсчитывает количество вхождений
ключа в список. У пользователя сначала запрашивается ключ, который
при прохождении по списку сравнивается с полем данных в каждом узле
списка. Выводится общее количество вхождений этого ключа.
#include <iostream.h>
#pragma hdrstop
#include "node.h"
#include "nodelib.h"
#include "random.h"
void main(void)
{
// установить голову списка в NULL
Node<int> *head = NULL, *currPtr;
int i, key, count = 0;
RandomNumber rnd;
// ввести 10-ть случайный чисел в начало списка
for (i=0;i < 10;i++)
InsertFront(head, int(1+rnd.Random(10)));
// печать исходного списка
cout « "Список: ";
PrintList(head,noNewline);
cout « endl;
// запросить ввод ключа
cout « "Введите ключ: ";
cin » key;
// цикл по списку
currPtr = head;
while (currPtr != NULL)
{
// если данные совпадают с ключом, увеличить count
if (currPtr->data — key)
count++;
// перейти к следующему узлу
currPtr = currPtr->NextNode();
}
cout « "Значение " « key « " появляется " « count
« " раз(а) в этом списке" << endl;
}
/*
<Выполнение программы 9.1>
Список: 365752459 10
Введите ключ: 5
Значение 5 появляется 3 раз(а) в этом списке
*/
Вставка узла: InsertRear
Помещение узла в хвост списка требует начального тестирования для
определения, пуст ли список. Если да, то создаем новый узел с нулевым указателем
поля и присваиваем его адрес голове. Операция реализуется функцией Insert-
Front. При непустом списке мы должны сканировать узлы для обнаружения
хвостового узла (в котором поле next содержит значение NULL).
currPtr->NextNode() == NULL;
currPtr
item NULL
newMode
Вставка выполняется следующим образом: сначала создается новый узел
(GetNode), затем он вставляется после текущего объекта Node (InsertAfter).
Так как вставка может изменять значение указателя головы, голова
передается как ссылочный параметр:
// найти хвост списка и добавить item
template <class T>
void InsertRear(Node<T>* & head, const T& item)
Node<T> *newNode, *currPtr - head;
// если список пуст, вставить item в начало
if (currPtr « NULL)
InsertFront(head,item) ;
else
{
// найти узел с нулевым указателем
while(currPtr->NextNode() !- NULL)
currPtr » currPtr->NextNode();
// создать узел и вставить в конец списка
// (после currPtr)
newNode * GetNode(item);
currPtr->InsertAfter(newNode);
}
}
InsertRear содержится в файле nodelib.h.
Программа 9.2. Головоломка
В этой программе беспорядочно смешиваются буквы слова для создания
слова-путаницы. Процесс сканирует каждый символ в строке и произвольно
помещает его либо в начало, либо в хвост списка. Для каждого символа
вызываем random(2). Если возвращаемое значение является равным 0,
вызываем InsertFront, иначе — InsertRear. Например, с вводом j-u-m-b-1-e и
последовательностью случайных чисел 0110 01 получаем результирующий
список lbjume. Программа читает и записывает четыре слова-головоломки.
♦include <iostream.h>
tpragma hdrstop
♦include "random.h"
♦include "strclass.h"
♦include "nodelib.h"
void main(void)
{
// список узлов для символов головоломки (Jumbled)
Node<char> *jumbleword = NULL;
// входная строка, генератор случайных чисел, счетчики
String s;
RandomNumber rnd;
int i, j;
// ввести четыре строки
for (i - 0; i < 4; i++)
{
cin » s;
// использование Random(2) для определения направления движения
// символа:в начало (value «0), или в конец (value « 1) списка
for (j « 0; j < s.LengthO; j++)
if (rnd.Random(2))
InsertRear(jumbleword, s[j]);
else
InsertFront(jumbleword, s[j]);
// печать входной строки и ее перепутанного варианта
cout « "String/Jumble: n « s « " ";
PrintList(jumbleword);
cout « endl « endl;
ClearList (jumbleword);
}
}
/*
<Выполнение программы 9.2>
pepper
String/Jumble: pepper r p p e p e
hawaii
String/Jumble: hawaii i i h a w a
jumble
String/Jumble: jumble e b m j u 1
C++
String/Jumble: C++ + С +
*/
Удаление узла. В этом разделе уже обсуждались алгоритмы для
сканирования списка и для вставки новых узлов. Третья списочная операция, удаление
узла из списка, знакомит с рядом новых проблем. Нам часто бывает необходимо
удалять первый узел в списке. Операция требует, чтобы мы изменяли голову
списка для указания на последующий узел за бывшим начальным узлом.
head
next
head
head-» NextModeO
Функция DeleteFront, которой передается голова списка как ссылочный
параметр, отцепляет от списка первый узел и освобождает его память:
// удалить первый узел списка
template <class T>
void DeleteFront(Node<T>* & head)
{
// сохранить адрес удаляемого узла
Node<T> *p * head;
// убедиться в том, что список не пуст
if (head !» NULL)
{
// передвинуть голову к следующему узлу и удалить оригинал
head ■ head->NextNode();
delete p;
}
}
Общая функция удаления проверяет список и удаляет первый узел, чье
значение данных совпадает с ключом. Устанавливаем prevPtr на NULL, a
currPtr — на голову списка. Затем перемещаем currPtr по списку в поисках
совпадения с ключом и сохраняем prevPtr, так чтобы он ссылался на
предыдущее значение currPtr.
prevPtr
key
currPtr
Указатели prevPtr и currPtr перемещаются по списку совместно до тех пор,
пока currPtr не станет равным NULL или не будет найден ключ (currPtr->data
== key).
while (curPtr != NULL && currPtr->data !=key)
{
// перемещение prevPtr вперед к currPtr
prevPtr = currPtr;
// перемещение currPtr вперед на один узел
currPtr = currPtr->NextNode();
}
Совпадение возникает, если мы выходим из оператора while с currPtr!=NULL.
Тогда мы можем удалить текущий узел. Существует две возможности. Если
prevPtr — это NULL, удаляем первый узел в списке. Иначе, удаляем узел,
выполняя DeleteAfter для узла prevPtr.
if (prevptr == NULL)
head = head->NextNode();
else
prevPtr->DeleteAfter{);
Если ключ не найден, метод Delete просто завершается. Так как удаление
в начале списка приводит к изменению головы, мы должны передавать голову
по ссылке.
// удаление первого элемента, совпадающего с ключем
template <class T>
void Delete (Node<T>* & head, T key)
{
Node<T> *currPtr = head, *prevPtr = NULL;
// завершить функцию, если список пустой
if (currPtr == NULL)
return;
// прохождение по списку до совпадения с ключем или до конца
while (currPtr !- NULL && currPtr->data !- key)
{
prevPtr * currPtr;
currPtr = currPtr->NextNode();
}
// если currPtr не равно NULL, ключ в currPtr.
if (currPtr != NULL)
{
// prevPtr == NULL означает совпадение в начале списка
if(prevPtr == NULL)
head = head->NextNode();
else
// совпадение во втором или последующем узле
// prevPtr->DeleteAfter() отсоединяет этот узел
prevPtr->DeleteAfter();
// удаление узла
delete currPtr;
}
}
Приложение: Список выпускников
Запись StudentRecord содержит имя и средний балл кандидата на выпуск
из университета. Мы приступаем к созданию списка студентов, которые
пройдут через выпускную церемонию. Список кандидатов на выцуск считывается
из файла studrecs и вставляется в начало списка. Так как по университетским
правилам студент со средним баллом ниже, чем 2.0, не допускается к выпуску,
мы просматриваем список и удаляем всех кандидатов, средний балл которых
не удовлетворяет минимальным требованиям. Второй список из файла noattend
представляет студентов, которые не собираются присутствовать на выпускной
церемонии, и используется для удаления дополнительных имен из выпускного
списка. Оставшиеся элементы представляют собой список студентов,
получивших квалификацию и планирующих принять участие в выпускной церемонии.
struct StudentRecord
{
String name;
float gpa;
};
Программа 9.З. Список выпускников университета
Каждая запись, считываемая из файла studrecs, вставляется в начало
связанного списка graduateList с использованием функции InsertFront
библиотеки Node. Указатели prevPtr и currPtr используются для сканирования
списка и удаления всех студентов, средний балл которых ниже, чем 2.0.
После удаления имен студентов, которым не присвоена квалификация, мы
считываем имена из файла noattend и удаляем из полученного ранее списка
студентов, не принимающих участия в выпускной церемонии. В заключение
выводим полученный список.
#include <iostream.h>
#include <fstream.h>
#include <stdlib.h>
#include <iomanip.h>
tpragma hdrstop
#include "node.h"
#include "nodelib.h"
#include "studinfo.h"
void main(void)
{
Node<StudentRecord> *graduateList=NULL,
*currPtr, *prevPtr,
*deletedNodePtr;
StudentRecord srec;
ifstream fin;
fin.open("studrecs",ios::in | ios: mocreate);
if (!fin)
{
cerr « "Невозможно открыть файл studrecs." « endl/
exit(1);
}
// вывод среднего балла (gpa)
cout.setf(ios::fixed);
cout.precision(1);
cout.setf{ios:rshowpoint);
while(fin » srec)
{
// вставить srec в голову списка
InsertFront(graduateList,srec);
)
prevPtr « NULL;
currPtr « graduateList;
while (currPtr !» NULL)
{
if (currPtr->data.gpa < 2.0)
{
if (prevPtr ■- NULL) // запись в начале списка?
{
graduateList * currPtr->NextNode();
deletedNodePtr - currPtr;
currPtr ■ graduateList;
}
else // удалить узел внутри списка
{
currPtr » currPtr->NextNode();
deletedNodePtr « prevPtr->DeleteAfter();
)
delete deletedNodePtr;
)
else
{
// нет удаления, передвинуть указатели вниз
prevPtr - currPtr;
currPtr = currPtr->NextNode();
>
}
fin.close ();
fin.open("noattend",ios: :in I ios: mocreate) ;
if (!fin)
{
cerr « " Невозможно открыть файл noattend." « endl;
exit(l);
>
while(srec.name.ReadString(fin) !« -1)
Delete(graduateList,srec);
cout << "Пристствующие на выпускной церемонии:и « endl;
PrintList(graduateList,addNewline);
}
/*
<Файл "studrecs,,>
Julie Bailey
1.5
Harold Nelson
2.9
Thomas Frazer
3.5
Bailey Harnes
1.7
Sara Miller
3.9
Nancy Barnes
2.5
Rebecca Neeson
4.0
Shannon Johnson
3.8
<Файл "noattend">
Thomas Frazer
Sara Miller
<Выполнение программы 9.3>
Присутствующие на выпускной церемонии:
Shannon Johnson 3.8
Rebecca Neeson 4.0
Nancy Barnes 2.5
Harold Nelson 2.9
V
Создание упорядоченного списка
Во многих приложениях нам необходимо поддерживать упорядоченный
список данных с узлами, приведенными в возрастающем или убывающем
порядке. Для этого алгоритм вставки должен сначала сканировать список
для определения правильного положения, в которое будет добавляться новый
узел. Последующее обсуждение иллюстрирует процесс создания списка с
возрастающим порядком.
Для ввода значения данных X мы сначала сканируем список и
устанавливаем currPtr на первый же узел, значение данных которого больше, чем
X. Новый узел со значением X должен вставляться непосредственно слева
от currPtr. Во время сканирования указатель prevPtr перемещается совместно
с currPtr и сохраняет запись предыдущей позиции.
Следующий пример иллюстрирует этот алгоритм. Предположим, что
список L первоначально содержит целые 60, 65, 74 и 82.
Вставка 50 в список: Поскольку 60 является первым узлом в списке,
большим, чем 50, мы вставляем 50 в голову списка.
head=currPtr
newNode
insertFront(head,50);
Вставка 70 в список: 74 — это первый узел в списке, больший, чем 70.
Указатели prevPtr и currPtr обозначают узлы 65 и 74, соответственно.
:head;
prevPtr currPtr
newNode
newNode = GetNode(70);
prevPtr->InsertAfter(newNode);
Вставка 90 в список: Мы сканируем весь список и не можем найти узел,
больший, чем 90 (currPtr ==NULL). Новое значение больше, или равно всем
другим значениям в списке и, следовательно, новое значение должно быть
помещено в хвост списка. Когда сканирование завершается, вставляем новый
узел после prevPtr.
prevPtr
currPtr
newNode
newNode = GetNode(90);
prevPtr->InsertAfter(newNode);
Следующая функция реализует общий алгоритм упорядоченной вставки.
Для списка из п элементов, эффективность наихудшего случая имеет место при
вставке нового элемента в конец списка. В этом случае должно быть выполнено
п сравнений, поэтому наихудший случай имеет порядок О(п). В среднем
ожидается, что для нахождения места вставки мы просматриваем половину списка.
В результате средний случай имеет порядок О(п). Конечно, наилучший случай
имеет порядок 0(1).
// вставить item в упорядоченный список
template <class T>
void InsertOrder(Node<T>* & head, T item)
{
// currPtr пробегает по списку
Node<T> *currPtr, *prevPtr, *newNode;
// prevPtr == NULL указывает на совпадение в начале списка
prevPtr = NULL;
currPtr = head;
// цикл по списку и поиск точки вставки
while (currPtr != NULL)
{
// точка вставки найдена, если item < текущего data
if (item < currPtr->data)
break;
prevPtr = currPtr;
currPtr = currPtr->NextNode();
}
// вставка
if (prevPtr == NULL)
// если prevPtr == NULL, вставлять в начало
InsertFront(head,item) ;
else
{
// вставить новый узел после предыдущего
newNode = GetNode(item);
prevPtr->InsertAfter (newNode) ;
}
}
Приложение: сортировка со связанными списками
InsertOrder может использоваться для сортировки коллекции элементов,
при условии, что оператор сравнения "<" определяется для типа данных Т.
Функция LinkSort принимает массив А из п элементов и вставляет эти
элементы в упорядоченный связанный список. Затем выполняется прохождение
списка, и уцорядоченные элементы копируются обратно в массив. Вызов функции
ClearList освобождает память, ассоциированную с каждым узлом в списке.
Функция проходит по списку и для каждого узла записывает его адрес,
перемещается к следующему узлу и затем удаляет исходный узел. ClearList входит
в файл nodelib.h.
// удаление свех узлов в связанном списке
template <class T>
void ClearList(Node<T> * &head)
{
Node<T> *currPtr, *nextPtr;
currPtr = head;
while(currPtr != NULL)
{
// записать адрес следующего узла, удалить текущий узел
nextPtr = currPtr->NextNode();
delete currPtr;
currPtr = nextPtr;
}
// пометить как пустой
head = NULL;
)
Программа 9.4. Сортировка вставками
Данная программа принимает в качестве параметра массив целых А из
10 элементов и сортирует список, используя шаблонную функцию LinkSort.
Полученный в результате упорядоченный массив, выводится с помощью
PrintArray.
#include <iostream.h>
#pragma hdrstop
♦include "node.h"
♦include "nodelib.h"
template <class T>
void LinkSort(T a[], int n)
{
Node<T> *ordlist - NULL, *currPtr;
int i;
// вставлять элементы из массива в список с упорядочением
for (i«0;i < n;i++)
InsertOrder(ordlist, a[i]);
// сканировать список и копировать данные в массив
currPtr e ordlist;
i = 0;
while(currPtr != NULL)
{
a[i++] = currPtr->data;
currPtr « currPtr->NextNode();
}
// удалить все узлы, созданные в упорядоченном списке
ClearList(ordlist);
}
// сканировать массив и печатать его элементы
void PrintArray(int a[], int n)
{
for(int i=0;i < n;i++)
cout « a[i] « " ";
}
void main(void)
{
// инициализировать массив с 10 целыми значениями
int A[10] = {82,65,74,95,60,28,5,3,33,55};
LinkSort(А,10); // сортировать массив
cout « " Отсортированный массив: ";
PrintArray(А,10); // печать массива
cout « endl;
>
Л
<Выполнение программы 9.4>
Отсортированный массив: 3 5 28 33 55 60 65 74 82 95
*/
При анализе эффективности времени исполнения алгоритма LinkSort
следует принимать во внимание начальное упорядочение элементов массива.
Наихудший случай соответствует списку, который уже отсортирован по
возрастанию. Каждый элемент вставляется в конец этого списка. Первая вставка
выполняется без сравнений, вторая вставка выполняется с одним сравнением, третья —
с двумя сравнениями и так далее. Общее количество сравнений составляет
(п — 1) * п
0 + 1 + 2 + . . . + - y
что имеет порядок 0(п2). Другая крайность — список, который отсортирован
в убывающем порядке, требует только п — 1 сравнений, так как каждый
элемент массива вставляется в начало списка. Поэтому наилучший случай
имеет порядок О(п), а наихудший — 0(п2). Интуитивно, средний случай имеет
п вставок с j-тым элементом ввода, требующим ожидаемых j/2 сравнений.
Общее количество сравнений равно 0(п2). В отличие от сортировки типа in-place
(такой как ExchangeSort), LinkSort требует дополнительной памяти для всех
п элементов данных, а также памяти для указателей в связанном списке.
9.3. Разработка класса связанного списка
Программист может использовать класс Node вместе с утилитными
функциями, находящимися в nodelib.h, для работы с приложениями связанных
списков. Такой подход вынуждает программиста создавать каждый узел и
выполнять непосредственно списочные операции низкого уровня. Более
структурированный подход определяет класс связанных списков, который
организует базовые списочные операции как функции-члены. В этом разделе
обсуждается тип данных-членов и операций, которые должны быть включены
в класс связанных списков, с использованием знаний, приобретенных при
разработке алгоритмов с классом Node. Мы также заранее оговариваем тот
факт, что наш класс связанных списков будет использоваться для реализации
других списочных коллекций, которые включают связанные стеки, очереди
и класс SeqList. В следующем разделе мы объявляем класс LinkedList и
определяем его функции-члены.
Данные-члены связанных списков
Связанный список состоит из множества объектов Node, связанных вместе
от начала до конца списка. Список имеет начальный узел, называемый
головой, который определяет первый узел списка. Последний узел в списке
имеет поле указателей со значением NULL, и на него ссылаются как на
указатель-хвост. Нам необходимо, чтобы класс связанных списков содержал
указатели на начало и на хвост списка, так как это полезно для многих
приложений и важно при реализации связанной очереди.
Связанный список предоставляет последовательный доступ к элементам
данных и использует указатель для задания текущего положения прохождения
в списке. Наш связанный список содержит указатель currPtr для ссылки на
это текущее положение в терминах его места в списке. Первый элемент в списке
имеет позицию (position) 0 со следующим элементом в позиции 1 и так далее.
Количество элементов в связанном списке содержится в переменной size. Это
позволяет нам определять пустой список или возвращать счетчик количества
элементов в списке. В следующем списке текущим положением является
элемент со значением 90, расположенный в позиции 3:
Адрес prevPtr используется для вставки и удаления узла в текущем
положении с использованием Node-методов InsertAfter и DeleteAfter. Например,
Данные связанного списка
front
rear
prevPtr
currPtr
position * 3
size«5
position
60 next W 20 next W 30 next W 90 next Ы 10 NULL
prevPtr
currPtr
в следующем связанном списке показана вставка с использованием объекта
Node, на который ссылается prevPtr:
Insertion:prevPtr->InsertAfter(p)
До После
prevPtr currPtr prevPtr
Р currPtr
Узел, на который ссылается prevPtr, также используется при удалении
элемента из связанного списка:
Deletion:prevPtr->DeleteAfter(p)
Деление: prevPtr->DeleteAfter(p)
prevPtr 1 . currPtr
Операции связанных списков
Пользователь должен иметь возможность переходить от элемента к
элементу в списке. Простой метод с именем Next передвигает текущее значение
к следующему узлу. В текущем положении операция Data возвращает ссылку
на поле данных узла. Это дает возможность выполнять выборку или изменять
поле данных узла без необходимости понимания пользователем того, как эти
данные сохраняются классом Node. Для иллюстрации этих операций
предположим, что L является связанным списком целых, чье текущее положение
находится в узле со значением данных 65. Следующие операторы изменяют
значение текущего узла на 67 и значение следующего узла — на 100:
Linkedlist<int> L;
• • •
if (L.Data() < 70) //сравнение значения текущего узла с 70
L.Data () = 67; //если меньше, присваивание значения 67
L.Next (); //продвижение текущего положения к следующему узлу.
L.Data() = 100; //вставляет 100 в новое положение
До После
60 И 65 И 74 Ь* 60 И 67 И 100
currPtr
currPtr
В приложениях нам иногда необходимо устанавливать текущее положение
в определенное место в списке. Это выполняет метод Reset. Он принимает
параметр pos и перемещает текущее положение списка в эту позицию.
Значением по умолчанию параметра pos является 0, которое устанавливает
текущее положение на первый элемент списка. От него приложение может
сканировать узлы, используя Next. Сканирование списка завершается, когда
условие EndOfList является равным TRUE. Например, простой цикл выводит
элементы в списке. Перед сканированием списка мы сначала проверяем
условие ListEmpty (пустой список):
L.Reset О; // установка currPtr в положение первого
// элемента списка
if (L.ListEmpty()) // пуст ли список?
cout « "Empty list\n";
else
while(IL.EndOfList()) // сканирование до конца списка
{
cout « L.Data () « endl; // вывод значения данных
L.Next(); // перемещение к следующему узлу
}
Пользователь имеет доступ к текущей позиции списка при помощи метода
CurrentPosition. Метод Reset может применяться для возвращения указателей
списка в исходное положение. Эта возможность используется в таких задачах,
как нахождение максимального значения в списке и установка списка на
этот узел для последующего удаления или вставки.
//сохранение текущей позиции
int currPos = L.CurrentPosition();
<команды, которые сканируют список вправо от currPos>
// переустановка текущего положения в
// бывшую позицию currPos.
L.Reset(currPos);
Добавление и удаление узлов являются основными операциями в
связанном списке. Эти операции могут выполняться в начале и хвосте списка или
в текущем положении.
Операции вставки. Операции вставки создают новый узел с новым полем
данных. Затем узел помещается в список в текущее положение или
непосредственно после него.
Операция InsertAfter помещает новый узел после текущей позиции и
присваивает currPtr новому узлу. Эта операция служит той же цели, что и
метод InsertAfter в классе Node.
Метод InsertAfter помещает новый узел в текущее положение. Новый
узел помещается непосредственно перед текущим узлом. Текущая позиция
устанавливается на новый узел. Эта операция используется при создании
упорядоченного списка.
Класс упорядоченных списков имеет операции Insertfront и InsertRear
для добавления новых узлов в голову и в хвост списка. Эти операции
устанавливают текущую позицию на новый узел.
Операции удаления. Операции удаления удаляют узел из списка. DeleteAt
удаляет узел в текущей позиции, a DeleteFront удаляет первый узел в списке.
Пример: Linked List<int> L;
L.InsertFront(100); // список содержит 100
L.InsertAfter(200); // список содержит 100 200
L.InsertAtpOO); // список содержит 100 300 200
L.InsertRear(50); // список содержит 100 300 200 50
L.Reset(l); // установка currPtr на 300
L.DeleteAt(); // список содержит 100 200 50
L.DeleteAt(); // список содержит 100 50
L.DeleteAtO; // список содержит 100;
Другие методы. Класс связанных списков создает динамические данные,
поэтому он должен иметь конструктор копирования, деструктор и
перегруженный оператор присваивания. Пользователь может явно очистить список
с помощью оператора ClearList.
9.4. Класс LinkedList
В данном разделе представлен класс LinkedList как простой, но мощный
инструмент для динамической обработки списков. Основное внимание
уделяется спецификации класса и примерам программ, иллюстрирующим его
использование. Объявление класса и его реализация находятся в файле link.h.
Спецификация класса LinkedList
ОБЪЯВЛЕНИЕ
♦include <icstreara.h>
♦include <stdlib.h>
♦include "node.h"
template <class T>
class LinkedList
{
private:
// указатели для доступа к началу и концу списка
Node<T> *front, *rear;
// используются для извлечения, вставки и удаления данных
Node<T> *prevPtr, *currPtr;
// число элементов в списке
int size;
// положение в списке, используется методом Reset
int position;
// закрытые методы создания и удаления узлов
Node<T> *GetNode(const T& item,Node<T> *ptrNext=NULL);
void FreeNode(Node<T> *p);
// копирует список L в текущий список
void CopyList(const LinkedList<T>& L);
public:
// конструктор
LinkedList(void);
LinkedList(const LinkedList<T>& L) ;
// деструктор
-LinkedList(void);
// оператор присваивания
LinkedList<T>& operator= (const LinkedList<T>& L);
// проверка состояния списка
int ListSize(void) const;
int ListEmpty(void) const;
// методы прохождения списка
void Reset(int pos = 0);
void Next(void);
int EndOfList(void) const;
int CurrentPosition(void) const;
// методы вставки
void InsertFront(const T& item);
void InsertRear(const T& item);
void InsertAt(const T& item);
void InsertAfter(const T& item);
// методы удаления
T DeleteFront(void);
void DeleteAt(void);
// возвратить/изменить данные
T& Data(void);
// очистка списка
void ClearList(void);
};
ОБСУЖДЕНИЕ
Класс использует динамическую память, поэтому ему необходимы
конструктор копирования, деструктор и перегруженный оператор присваивания.
Закрытые методы GetNode и FreeNode выполняют все выделения памяти
для этого класса. Если при выделении памяти происходит ошибка, метод
GetNode завершает программу.
Класс поддерживает размер списка, доступ к которому обеспечивается
использованием методов ListSize и ListEmpty.
Закрытые данные-члены currPtr и prevPtr поддерживают запись текущегр
положения при прохождении списка. Методы вставки и удаления отвечают
за изменение этих значений после выполнения операции. Метод Reset явно
задает значение currPtr и prevPtr.
Класс содержит гибкие методы прохождения, Reset принимает
позиционный параметр и устанавливает текущее положение в эту позицию. Он имеет
параметр по умолчанию 0 для того, чтобы при его использовании без
аргументов, метод устанавливал текущую позицию в голову списка. Метод Next
продвигается к следующему узлу списка, a EndOfList указывает, был ли
достигнут конец списка. Например, для списка L цикл FOR осуществляет
последовательное сканирование списка.
for (L.Reset (); !L.EndOfList (); L.NextO)
<посещение текущего положения>
CurrentPosition возвращает текущее положение при прохождении списка.
Для посещения текущего узла позже сохраните возвращаемое значение и
впоследствии передайте его как параметр методу Reset.
Вставки могут производиться в любом конце списка с использованием
InsertFront и InsertRear. InsertAt вставляет новый узел в текущую позицию
в списке, a Insert After вставляет узел после текущей позиции. Если текущее
положение находится в конце списка (EndOfList == True), то и InsertAt, и
InsertAfter помещают новый узел в хвост списка,
DeleteFront удаляет первый элемент из списка, a DeleteAt удаляет узел
в текущей позиции списка. Для любого из этих двух методов попытка
удаления из пустого списка завершает программу.
Метод Data используется для чтения или изменения данных в текущей
позиции в списке. Так как Data возвращает ссылку на данные в узле, он
может использоваться в правой или левой части оператора присваивания.
// выборка данного из текущего узла и увеличение его
// значения на 5
L.DataO = L.DataO + 5;
ClearList удаляет все узлы списка и помечает список как пустой.
ПРИМЕР
LinkedList<int> L/ К; // объявление списков целых L, К
// добавление 25 целых к этим спискам
for(i=0; i<25; i++)
{
cin » num;
L.InsertRear(num); // узлы вставляются в порядке ввода
К.InsertFront(num); // узлы в порядке, обратном вводу
}
// сканирует список L, изменяя каждый узел на его
// абсолютное значение
for(L.Reset(); !L.EndOfList();L.Next())
// если данное отрицательное, сохранение нового значения
if (L.DataO < 0)
L.DataO = -L.DataO;
К.InsertFront(100); // сохранение 100 в начале К
К.InsertAfter (200); //вставка 200 после 100
К.InsertAt(150); //вставка 150 между 100 и 200
// вывод списка L
void PrintList(LinkedList<int>& L)
{
// перемещение в голову списка L и прохождение списка с
// выводом каждого элемента
for(L.Reset() ; ! L. EndOfList (); L.Next О)
cout « L.DataO « " ";
)
Перед реализацией класса LinkedList мы иллюстрируем его основные
возможности в серии примеров. Функция конкатенации объединяет два списка,
присоединяя второй список к хвосту первого. Второй пример реализует
версию сортировки выбором связанного списка. Классическая версия алгоритма
сортирует массив на месте. В нашей реализации широко используются
вставки и удаления со связанными списками. Раздел завершается алгоритмом,
который удаляет узлы-дубликаты из списка.
Конкатенация двух списков
Функция конкатенирует два списка, выполняя упорядочение узлов во
втором списке и вставляя каждое из его значений в хвост первого списка.
Функция используется в законченной программе concat.cpp в программном
приложении.
Функция ConcatLists сканирует второй список и методом Data извлекает
из каждого узла значение данных, которое затем используется для добавления
нового узла в хвост первого списка с использованием метода InsertRear.
template <class T>
// добавление списка L2 в конец L1
void ConcatLists(LinkedList<T>& LI, LinkedList<T>& L2)
{
// переустановка обоих списков на начало
LI.Reset();
L2.Reset();
// прохождение L2. вставка каждого значения данных в
// хвост L1
while (!L2.End0fList())
{
LI. InsertRear(L2.Data());
L2.Next();
}
}
Сортировка списка
Мы реализуем версию сортировки выбором для связанного списка,
используя два отдельных связанных списка. Первый список L содержит
неотсортированное множество данных. Второй список К создается как копия
списка L со значениями в отсортированном порядке. Алгоритм удаляет
элементы из списка L в порядке от наибольшего до наименьшего элемента и
вставляет их в начало списка К, который становится упорядоченным списком.
Сортировка выбором требует многократного сканирования списка. Мы
используем функцию FindMax для сканирования списка и установки текущей
позиции на максимальный элемент. После выборки значения данных из этой
позиции вставляем новый узел с этим значением в начало списка К, используя
InsertFront, и затем удаляем этот максимальный узел из списка L, используя
DeleteAt.
Рассмотрим следующий пример:
Список L содержит элементы 57, 40, 74, 20, 62
Cfront
Шаг 1: Находим максимальное значение 74. Удаляем из L и добавляем в К.
L <front
57
* 40
* 20
62
К <f ront
74
57
40
74
20
62
Шаг 2: Находим максимальное значение 62. Удаляем из L и добавляем в К.
L <front
57
40
20
К <f ront.
62
74
Программа 9.5. Сортировка списков выбором
Эта программа создает список L с 10 случайными числами в диапазоне
от 0 до 99. После вывода начального списка функцией PrintList мы
используем алгоритм сортировки выбором для переноса элементов из списка
L в список К. В конце программы снова вызывается PrintList для вывода
значений из К, который содержит элементы в возрастающем порядке.
#include <iostream.h>
#pragma hdrstop
#include "link.h"
linclude "random.h"
// установка L на его максимальный элемент
template <class T>
void FindMax(LinkedList<T> &L)
{
if (L.ListEmptyO )
{
cerr « "FindMax: Список пустой!" « endl;
return;
}
// вернуться на начало списка
L.Reset();
// записать первое значение списка как текущий максимум
// с нулевой позицией
Т max = L.Data();
int maxLoc = 0;
// перейти к следующему узлу и сканировать список
for (L.Next (); IL.EndOfList(); L.NextO)
if (L.DataO > max)
{
// новый максимум, записать значение и
// положение в списке
max = L.Data();
maxLoc = L.CurrentPosition();
}
L.Reset(maxLoc);
}
// печатать список L
template <class T>
void PrintList(LinkedList<T>& L)
{
// перейти к началу списка L.
// проходить список и печатать данные каждого узла
for(L.Reset(); IL.EndOfList(); L.Next О)
cout « L.Data() « " ";
}
void main(void)
{
// список L размещается в сортированном порядке в списке К
LinkedList<int> L, К;
RandoraNumber rnd;
int i;
// L — это список из 10-ти случайных целых в диапазоне 0-99
for(i«0; i < 10; i++)
L.InsertRear(rnd.Random(100));
cout « "Исходный список: ";
PrintList(L);
cout « endl;
// удалить данные из L, вставляя их в К
while (!L.ListEmpty())
{
// найти максимум оставшихся элементов
FindMax(L);
// вставить максимум в начало К и удалить его из L
K.InsertFront(L.Data());
L.DeleteAt();
}
cout « "Отсортированный список: ";
PrintList(К);
cout « endl;
}
/*
<Выполнение программы 9.5>
Исходный список: 82 72 62 3 85 33 58 50 91 26
Отсортированный список: 3 26 33 50 58 62 72 82 85 91
*/
Удаление дубликатов. Алгоритм удаления дубликатов в списке является
интересным приложением класса LinkedList. После создания списка L
начинаем сканирование его узлов. В каждом узле записываем позицию узла и
его значение данных. Это дает нам ключ для начала поиска дубликатов в
оставшемся списке, а также — позицию для возвращения после удаления
дубликатов. От текущей позиции сканируем хвост списка, удаляя все узлы,
значение данных которых совпадает с ключом, затем переустанавливаем
текущее положение сканирования в позицию исходного значения и переходим
вперед на один узел для продолжения этого процесса.
текущая позиция
5 Ь-* 7 Н-М 5
4 Ь-* 5
, сканировать подсписок и удалять все узлы со значением 5 |
новая текущая позиция
7
4
Программа 9.6. Удаление дубликатов
В этой программе используется алгоритм удаления дубликатов.
Начальный список имеет 15 случайных значений в диапазоне 1—7. После вывода
списка вызываем функцию RemoveDuplicates, удаляющую дубликаты из
списка. Получаемый в результате список выводится с использованием
функции PrintList, которая включена в link.h.
#include <iostream.h>
#pragma hdrstop
#include "link.h"
#include "random.h"
// печать списка L
template <class T>
void PrintList(LinkedList<T>& L)
{
// перейти к началу списка L.
// прохождение списка и печать каждого элемента
for (L. Reset () ; IL.EndOfListО; L.NextO)
cout « L.Data() « " ";
}
void RemoveDuplicates(LinkedList<int>& L)
{
// текущее положение в списке и значение данных
int currPos, currValue;
// перейти к началу списка
L.Reset ();
// цикл по списку
while(IL.EndOfList())
{
// записать данные текущего положения в списке
//и это положение
currValue = L.DataO;
currPos = L.CurrentPositionO;
// перейти к узлу справа
L.NextO;
// двигаться вперед до конца списка, удаляя все появления currValue
while(IL.EndOfList())
// если узел удален, текущее положение — это следующий узел
if (L.DataO == currValue)
L.DeleteAtO ;
else
L.Next(); // перейти к следующему узлу
// перейти к первому узлу со значением currValue.
// идти вперед
L.Reset(currPos);
L.Next();
}
}
void main(void)
{
LinkedList<int> L;
int i;
RandomNumber rnd;
// вставить 15 случайных целых в диапазоне 1-7 и печатать список
for(i=0; i < 15; i++)
L.InsertRear(1+rnd.Random(7));
cout << " Исходный список: ";
PrintList(L);
cout « endl;
// удалить все значения-дубликаты и печатать новый список
RemoveDuplicates(L);
cout << " Окончательный список: ";
PrintList(L);
cout « endl;
}
/*
<Выполнение программы 9. 6>
Исходный список: 177151272166364
Окончательный список: 17 5 2 6 3 4
V
9.5. Реализация класса LinkedList
Спецификация класса LinkedList ссылается на класс Node. Реализация
класса LinkedList использует много методов, описанных разделе 9.1 с классом
Node. Алгоритмы, использующемые функциями в nodelib.h, являются основой
для разработки класса LinkedList. Однако мы должны знать о дополнительной
сложности поддержания указателей front и rear, которые определяют доступ
к списку, указателей currPtr и prevPtr, которые сохраняют информацию о
текущем положении прохождения, местонахождения данных и size (размера
списка). Методы LinkedList отвечают за изменение этих данных всякий раз,
когда изменяется состояние списка.
Закрытые данные-члены. Класс ограничивает доступ к данным, так как
эта информация используется только функциями-членами. Связанный список
состоит из множества объектов Node, связанных вместе от начала до хвоста
списка. Мы определяем начало или голову списка как данные-члены. Для
более легкого выполнения вставок в хвост списка этот класс поддерживает
указатель rear на последний узел списка. Это избавляет от сканирования
всего списка для нахождения положения хвоста. Переменная size содержит
количество узлов в списке. Это значение используется для определения,
является ли список пустым, и для возвращения количества значений данных
в списке. Переменная position делает более легкой переустановку текущего
положения при прохождении списка методом Reset.
Объект LinkedList содержит два указателя, определяющих текущее
(currPtr) и предыдущее положение (prevPtr) в списке. Указатель currPtr
ссылается на текущий узел списка и используется методом Data и методом
вставки InsertAfter. Указатель prevPtr используется методами DeleteAt и
InsertAt, действующими для текущего положения. При выполнении вставок
и удалений этот класс изменяет поля front, rear, position и size объекта
списка.
Данные класса LinkedList
front
rear
prevPtr
currPtr
position - 2
size=4
data next f-W data next Ы data next Ш data NULL
Методы выделения памяти. Класс выполняет все вставки и удаления.
Конструктор копирования и методы вставки выделяют узлы, тогда как Clear-
list и методы удаления уничтожают узлы. Класс LinkedList мог бы
использовать операторы new и delete непосредственно в этих методах. Однако
функции GetNode и FreeNode предоставляют более структурированный доступ для
управления памятью.
Метод GetNode делает попытку динамического создания узла с
передаваемыми ему значением данных и полем указателя. Если выделение памяти
происходит без ошибки, он возвращает указатель на новый узел; иначе,
печатается сообщение об ошибке и программа завершается. Метод FreeNode
просто удаляет память, занятую узлом.
Конструкторы и деструктор. Конструктор создает пустой список со всеми
значениями указателей, установленными на NULL. В этом начальном
состоянии size устанавливается на 0, а значение position — на -1:
// создать пустой список
template <class T>
LinkedList<T>::LinkedList(void): front(NULL), rear(NULL),
prevPtr(NULL),currPtr(NULL), size(O), position(-1)
{}
Конструктор копирования и оператор присваивания копируют объект L
класса LinkedList. Для этой цели класс реализует метод CopyList, проходящий
по списку L и вставляющий каждое значение данных в хвост текущего
списка. Эта закрытая функция вызывается только тогда, когда текущий
список пуст. Она назначает параметры прохождения prevPtr, currPtr и
position так, чтобы текущий список был той же конфигурации, что и список
L. Таким образом, два эти списка имеют одно и то же состояние прохождения
после присваивания или инициализации.
// копировать L в текущий список (предполагается пустым)
template <class T>
void LinkedList<T>::CopyList(const LinkedList<T>& L)
{
// p — указатель на L
Node<T> *p * L.front;
int pos;
// вставлять каждый элемент из L в конец текущего объекта
while (p !» NULL)
{
InsertRear(p->data);
р - p->NextNode{);
}
// выход, если список пустой
if (position -= -1)
return;
// переустановить prevPtr и currPtr в новом списке
prevPtr = NULL;
currPtr « front;
for (pos * 0; pos != position; pos++)
{
prevPtr * currPtr;
currPtr * currPtr->NextNode<);
}
}
ClearList проходит связанный список и уничтожает все узлы, используя
алгоритм, разработанный в разделе 9.1. Деструктор реализуется простым
вызовом Clearlist.
template <class T>
void LinkedList<T>::ClearList(void)
{
Node<T> *currPosition, *nextPosition;
currPosition = front;
while(currPosition !- NULL)
{
// получить адрес следующего узла и удалить текущий
nextPosition = currPosition->NextNode();
FreeNode(currPosition);
currPosition = nextPosition; // перейти к следующему узлу
}
front - rear ~ NULL;
prevPtr « currPtr = NULL;
size =
Opposition « -1;
}
Методы прохождения списка. Reset устанавливает текущее положение
прохождения в позицию, обозначенную параметром pos. В то же время, этот
метод изменяет положение как currPtr, так и prevPtr. Если pos не находится
в диапазоне 0..size-l, то выводится сообщение об ошибке и программа
завершается. Для установки currPtr и prevPtr функция различает случаи,
когда pos является головой списка и внутренней позицией в списке.
pos == 0: Переустановка текущего положения на начало списка путем
установки prevPtr на NULL, currPtr — на front и position — на 0.
pos! = 0: Так как случай, когда pos == 0 уже рассматривался, мы можем
предположить, что значение pos должно быть больше 0 и что прохождение
списка должно устанавливаться на внутреннюю позицию. Для изменения
позиции currPtr начинаем во втором узле списка и перемещаемся к
положению pos.
template <class T>
void LinkedList<T>::Reset(int pos)
{
int startPos;
// если список пустой, выход
if (front == NULL)
return;
// если положение задано не верно, закончить программу
if {pos < 0 || pos > size-1)
{
cerr « "Reset: Неверно задано положение: " « pos
« endl;
return;
}
// установить механизм прохождения в pos
if(pos == 0)
{
// перейти в начало списка
prevPtr = NULL;
currPtr = front;
position = 0;
}
else
// переустановить currPtr, prevPtr, и startPos
{
currPtr = front->NextNode();
prevPtr = front;
startPos = 1;
// передвигаться вправо до pos
for(position=startPos; position != pos; position++)
{
// передвинуть оба указателя прохождения вперед
prevPtr = currPtr;
currPtr = currPtr->NextNode();
}
)
}
Для последовательного сканирования списка мы перемещаемся от элемента
к элементу, выполняя метод Next. Функция перемещает prevPtr к текущему
узлу, a currPtr — на один узел вперед. Если мы прошли все узлы в списке,
переменная position имеет значение size, и currPtr устанавливается на NULL.
// переустановить prevPtr и currPtr вперед на один узел
template <class T>
void LinkedList<T>::Next(void)
{
// выйти, если конец списка или
// список пустой
if (currPtr != NULL)
{
// переустановить два указателя на один узел вперед
prevPtr = currPtr;
currPtr = currPtr->NextNode();
position++;
}
}
Доступ к данным. Используйте метод Data для доступа к значению данных
в списочном узле. Если список пуст или прохождение достигло конца списка,
выводится сообщение об ошибке и программа завершается; иначе, Data
возвращает currPtr->data.
// возвратить ссылку на данные текущего узла
template <class T>
Т& LinlcedList<T>: : Data (void)
{
// ошибка, если список пустой или прохождение закончено
if (size == 0 || currPtr == NULL)
{
cerr « "Data: Неверная ссылка!" « endl;
exit (1);
)
return currPtr->data;
}
Методы вставки для списка. Класс LinkedList имеет ряд операций для
добавления узла в начало или хвост списка (InsertFront, InsertRear) или
относительно текущей позиции (Insert At и Insert After). Методам вставки
передается значение данных, используемое для инициализации поля данных
нового узла.
Insert At вставляет узел со значением данных в текущую позицию в списке.
Метод использует GetNode для выделения узла со значением данных item,
имеющим адрес newNode, увеличивает размер списка и устанавливает
текущее положение на новый узел. Алгоритм должен обрабатывать два случая.
Если вставка имеет место в начале списка (prevPtr == NULL), обновляется
front для указания на новый узел. Если вставка имеет место внутри списка,
новый узел помещается после prevPtr Node-методом InsertAfter. Если элемент
вставляется в пустой список или в хвост непустого списка, должна
выполняться специальная обработка указателя rear.
// вставка item в текущую позицию списка
template <class T>
void LinkedList<T>::InsertAt(const T& item)
{
Node<T> *newNode;
// два случая: вставка в начало или внутрь списка
if (prevPtr == NULL)
{
// вставка в начало списка, помещает также
// узел в пустой список
newNode = GetNode(item,front);
front = newNode;
}
else
{
// вставка внутрь списка, помещает узел после prevPtr
newNode = GetNode(item);
prevPtr->InsertAfter(newNode);
}
InsertAt (пустой список)
front
rear
prevPtr
currPtr
position (-1)
size (0)
front
rear
prevPtr
currPtr
position (0)
size (1)
item
InsertAt (вставка в конец)
front
rear
prevPtr
currPtr
position (3)
size (4)
front
rear
prevPtr
currPtr
position (4)
size (5)
item
// при prevPtr *» rear, имеем вставку в пустой список
// или в хвост непустого списка; обновляет rear и position
if (prevPtr == rear)
i
rear - newNode;
position = size;
}
// обновить currPtr и увеличить size
currPtr = newNode;
size++;
}
Методы удаления. Для удаления узла имеются две операции, которые
удаляют узел из начала списка (DeleteFront) или из текущей позиции
(DeleteAt).
DeleteAt удаляет узел с адресом currPtr. Если currPtr является равным
NULL, то список пуст, или весь список уже пройден. В этом случае функция
выводит сообщение об ошибке и завершает программу. Иначе, алгоритм
обрабатывает два случая. Если удаляется первый узел списка (prevPtr
==NULL), изменяется указатель front. Если это последний узел списка, front
становится равным NULL. Второй случай имеет место при prevPtr^NULL, и
удаляемый узел находится внутри списка. Используйте метод DeleteAfter
класса Node для отсоединения от списка узла, следующего за prevPtr.
Как и в случае с методом InsertAfter, следует обратить особое внимание
на указатель rear. Если узел, который мы удаляем, находится в хвосте списка
(currPtr —= rear), то новым хвостом теперь будет являться prevPtr, значение
position уменьшается, a currPtr становится равным NULL. Во всех других
случаях position остается без изменения. Если мы удаляем последний узел
в списке, rear становится равным NULL, а значение position изменяется с
О на -1. Вызываем FreeNode для удаления узла из памяти и уменьшаем
размер списка.
DeleteAt (список становится пустым)
front
rear
prevPtr
currPtr
position (0)
size (1)
front
rear
prevPtr
currPtr
position (-1)
size (0)
DeleteAt (currPtr - это rear)
front
rear
prevPtr
currPtr
position (3)
size (4)
front
rear
prevPtr
currPtr
position (2)
size (3)
// удаление узла в текущей позиции списка
template <class T>
void LinkedList<T>::DeleteAt(void)
{
Node<T> *p;
// ошибка, если список пустой или конец списка
if (currPtr -= NULL)
{
cerr << "Ошибка удаления!" « endl;
exit(l);
}
// удалаять можно только в начале и внутри списка
if (prevPtr « NULL)
{
// сохранить адрес начала, но не связывать его. если это -
// последний узел, присвоить front значение NULL
р = front;
front « front->NextNode();
}
else
// не связывать внутренний узел после prevPtr.
// запомнить адрес
р = prevPtr->DeleteAfter();
// если хвост удален, адрес нового хвоста в prevPtr,
// a position уменьшается на 1
if (p == rear)
{
rear = prevPtr;
position--;
}
// установить currPtr на последний удаленный узел.
// если р — последний узел в списке,
// currPtr становится равным NULL
currPtr = p->NextNode();
// освободить узел и уменьшить значение size
FreeNode(p);
size—;
}
9.6. Реализация коллекций со связанными
списками
До этого раздела в книге мы использовали основанные на массиве
реализации классов Stack, Queue и SeqList. В каждом случае список элементов
сохраняется в массиве, который определяется как закрытый данное-член
этого класса. В этой главе разрабатывается класс LinkedList, который
предоставляет мощную структуру динамической памяти вместе с разнообразными
методами добавления и удаления элементов и обновления значений данных.
Сохраняя элементы в объекте связанного списка, а не в массиве, мы получаем
новую стратегию реализации, которая увеличивает возможности и
эффективность базовых списочных классов. Используя различные методы в классе
LinkedList, мы имеем инструменты для простой и понятной реализации
операций stack, queue и list.
В данном разделе разрабатываются новые реализации для классов Queue
и SeqList с использованием связанных списков. Для класса SeqList мы
сравниваем эффективности динамического хранения связанного списка и списка,
основанного на массиве. Класс Queue используется в следующем разделе при
разработке задачи моделирования буферизации печати (printer spooler).
Реализация связанного списка класса Stack опущена как самостоятельное
упражнение.
Связанные очереди
Объект LinkedList является гибкой структурой памяти для сохранения
списка элементов. Класс Queue предоставляет простую реализацию очереди,
используя композицию (структуру) для включения объекта LinkedList. Этот
объект производит Queue-операции, выполняя эквивалентные операции
LinkedList. Например, объект LinkedList позволяет выполнять вставку
элемента в хвост списка (InsertRear) и удаление элемента из головы списка
(DeleteFront). Переустанавливая текущий указатель на голову списка (Reset),
мы можем определить операцию Qfront, извлекающую значение данных из
головы списка. Другие Queue-методы оценивают состояние списка — задача,
управляемая списочными операциями ListEmpty и ListSize. Очередь
очищается простым вызовом списочного метода ClearList.
Спецификация класса Queue (с использованием объекта LinkedList)
ОБЪЯВЛЕНИЕ
#include <iostream.h>
#include <stdlib.h>
#include "link.h"
template <class T>
class Queue
{
private:
// объект связанного списка
// для хранения элементов очереди
LinkedList<T> queueList;
public:
// конструктор
Queue(void);
// методы обновления
void Qlnsert(const T& elt);
T QDelete(void);
// доступ к очереди
T QFront(void);
// методы тестирования
int QLength(void) const;
int QEmpty(void) const;
void QClear(void);
};
ОПИСАНИЕ
Объект queueList класса LinkedList содержит элементы очереди. Он
предоставляет полный набор операций связанного списка, которые используются
для реализации открытых методов Queue.
Класс Queue не имеет собственных деструктора, конструктора копирования
и оператора присваивания. Эти методы не являются обязательными, так как
они реализуются для объекта queueList. Компилятор реализует присваивание
и инициализацию, выцолняя оператор присваивания или конструктор
копирования для объекта типа queueList. Деструктор для queueList вызывается
автоматически при уничтожении объекта Queue.
Так как элементы сохраняются в связанном списке, размер очереди не
ограничивается константой реализации, такой как MaxQueueSize
ПРИМЕР
Queue<int> Q1,Q2; // объявление двух очередей целых значений
Ql.QInsert(10); // добавление 10, а затем 50 в Q1
Ql.Qlnsert(50);
cout « Ql.QFrontO; // вывод значения 10 в начале очереди
Q2 * Q1; // использование оператора = для queueList
Ql.QClearO; // очистка очереди и освобождение памяти
Реализация связанного списка класса Queue находится в файле queue.h.
Реализация методов Queue
Для иллюстрации реализации методов Queue мы определяем методы
модификации очереди Qlnsert и QDelete, а также метод доступа QFront. Каждый
из них непосредственно вызывает эквивалентный метод LinkedList.
Операция Qlnsert добавляет элемент в хвост очереди, используя LinkedList-
операцию InsertRear.
// LinkedList-метод вставляет элемент в хвост
template<class T>
void Queue<T>::Qlnsert(const T& elt)
{
queueList.InsertRear(elt);
}
QDelete сначала проверяет состояние очереди и завершает программу при
пустом списке. Иначе, при помощи списочной операции DeleteFront
выполняется операция отсоединения первого элемента от очереди, удаления памяти
и возврата значения данных.
// LinkedList-метод DeleteFront удаляет элемент из
// головы очереди
Т Queue<T>::QDelete(void)
{
// проверка, пустой ли список, и завершение, если — да
if (queueList.ListEmpty())
{
cerr « "Qdelete вызвана для пустой очереди!" « endl/
exit (1);
}
return queueList.DeleteFront();
}
Операция QFront выполняет выборку значения данных из первого
элемента queueList. Для этого требуется изменение позиции текущего указателя
на голову списка и считывание его значения данных. Попытка вызвать эту
функцию при пустой очереди вызывает сообщение об ошибке и завершение
программы.
// возвратить значение данных первого элемента в очереди
template <class T>
Т Queue<T>::QFront(void)
{
// если очередь пуста, завершить программу
if (queueList.ListEmpty())
{
cerr << "QFront вызвана для пустой очереди!" « endl;
exit(l);
}
// перенастроиться на голову очереди и возвратить данные
queueList.Reset{);
return queueList.Data();
}
Использование объекта LinkedList с классом SeqList
Класс SeqList определяет ограниченную структуру памяти, позволяющую
вставлять элементы только в хвост списка и удаляющую только первый
элемент в списке или элемент, который совпадает с ключом. Пользователь
имеет возможность доступа к данным в списке с использованием метода Find
или с помощью позиционного индекса для чтения значения данных в узле.
Как в случае со связанной очередью, мы можем использовать объект
LinkedList для сохранения данных при реализации класса SeqList. Более
того, этот объект предоставляет мощный набор операций для реализации
методов класса.
Спецификация класса SeqList
ОБЪЯВЛЕНИЕ
tinclude <iostream.h>
#include <stdlib.h>
♦include "link.h"
template <class T>
class SeqList
{
private:
// объект связанного списка
LinkedList<T> Hist;
public:
// конструктор
SeqList(void);
// методы доступа
int ListSize(void) const;
int ListEmpty(void) const;
int Find (T& item);
T GetData(int pos);
// методы модификации
void Insert(const T& item);
void Delete(const T& item);
T DeleteFront(void);
void ClearList(void);
)/
ОПИСАНИЕ
Методы этого класса идентичны методам, определенным для основанной на
массиве версии в файле aseqlist.fi. Нет необходимости определять деструктор,
конструктор копирования и оператор присваивания. Компилятор создает их,
используя соответствующие операции в классе LinkedList. Класс находится в
файле seqlistl.h.
ПРИМЕР
SeqList<int>chList; // выделение динамического списка целых
chList.Insert (40); // добавление 40 в конец списка
cout « chList.DeleteFront () « endl; // вывод значения 40
Реализация методов доступа к данным класса SeqList
Класс SeqList дает возможность пользователю иметь доступ к данным по
ключу, с помощью метода Find, или по позиции в списке. В первом случае
для сканирования списка и поиска ключа используется механизм
прохождения класса LinkedList.
// использовать item как ключ для поиска в списке.
// возвратить True, если элемент — в списке, и — False
//в противном случае.
template <class T>
int SeqList<T>::Find (T& item)
{
int result - 0;
// поиск item в списке, если — найден, result = True
for (Hist.Reset () ; ! Hist. EndOf List () ;llist .Next () )
if (item == Hist.DataO )
{
result++;
break;
}
// если result равно True, обновить item и возвратить True;
// иначе — возвратить False
if (result)
item = Hist.DataO;
return result;
}
Метод GetData используется для доступа к элементу данных по его
положению в списке. Здесь используется LinkedList-метод Reset для установки
механизма прохождения в нужное положение в списке и выполняется метод
Data для извлечения данных:
// возвратить значение данных элемента в положении pos
template <class T>
Т SeqList<T>::GetData(int pos)
{
// контроль правильности pos
if (pos < 0 || pos >= Hist .ListSize () )
{
cerr << "pos вне диапазона!" « endl;
exit(l);
}
// установить текущее положение связанного
// списка в pos и возвратить значение данных
Hist. Reset (pos) ;
return Hist.DataO;
}
Приложение: Сравнение реализаций SeqList
Основанная на массиве версия класса SeqList требует значительных усилий
для удаления элемента, так как все элементы, находящиеся в хвосте списка,
должны быть сдвинуты влево. В случае с реализацией связанного списка те
же операции имеют место с простым отсоединением указателей. Для
иллюстрации результата использования структуры памяти для хранения
связанного списка сравним версию, основанную на массиве, и версию связанного
списка класса SeqList. После создания начального списка с 500 членами при
тестировании неоднократно удаляется элемент из головы списка и затем
вставляется элемент в хвост списка. Процесс повторяется 50 000 раз и
представляет собой наихудший случай для объекта основанного на массиве класса
SeqList.
Мы выполняем две эквивалентные программы на одной и той же
компьютерной системе и вычисляем время выполнения 50 000 операций
вставки/удаления в секундах.
Программа 9.7а. (Класс List — реализация массива)
Эта задача тестирования использует основанный на массиве класс
SeqList, находящийся в файле aseqlist.h. Только для этой программы
константа ARRAYSIZE изменяется так, чтобы список мог содержать 500
элементов. Задача выполняется за 55 секунд.
#include <iostream.h>
#pragma hdrstop
// DataType = int (список хранит целые значения)
typedef int DataType;
// включение класса SeqList
#include "aseqlist.h"
void main(void)
{
// список с 500 целыми
SeqList L/
long i;
// инициализация списка значениями 0 .. 499
for (i = 0; i < 500; i++)
L.Insert(int(i));
// выполнение операций удаления/вставки 50000 раз
cout « " Начало программы!" « endl;
for (i = 1; i <= 50000L; i++)
{
L.DeleteFront();
L.Insert(O);
}
cout « " Программа выполнена! « endl;
}
/*
<Выполнение программы 9.7а>
Начало программы!
Программа выполнена! // 55 секунд
*/
Программа 9.7b. (Класс List — реализация связанного списка)
Эта программа тестирует версию связанного списка класса SeqList,
находящегося в файле seqlistLh. Задача выполняется за 4 секунды!
tinclude <iostream.h>
#pragma hdrstop
// включить реализацию связанного списка (SeqList)
♦include "seqlistl.h"
void main(void)
{
// определить список целых
SeqList<int> L;
long i;
// инициализировать список значениями 0 .. 499
for (i - 0; i < 500; i++)
L.Insert(int(i));
// выполнение операций удаления/вставки 50000 раз
cout « " Начало программы!" « endl;
for (i « 1; i <- 50000L; i++)
{
L.DeleteFront();
L.Insert(0);
}
cout « " Программа выполнена!" « endl;
}
/*
<Выполнение программы 9.7b>
Начало программы!
Программа выполнена! // 4 секунды
*/
9.7. Исследовательская задача:
Буферизация печати
Очереди используются для реализации систем буферизации печати в
операционных системах. Система буферизации (буферизатор) печати принимает
запрос на печать и вставляет файл, который должен печататься, в очередь.
При освобождении принтера буферизатор удаляет задание из очереди и
печатает этот файл. Действие буферизатора позволяет осуществлять печать на
фоне выполнения пользователями других задач на переднем плане.
Анализ проблемы
В этой задаче разрабатывается класс Spooler, операции которого
моделируют ситуацию добавления пользователем новых заданий в очередь печати
и проверки статуса заданий, уже имеющихся в очереди. Задание на печать —
это структура, содержащая целый номер задания, имя файла и число страниц.
struct PrintJob
{
int number;
charfilename[20];
int pagesize;
};
В задаче моделирования подразумевается, что принтер работает
непрерывно со скоростью 8 страниц в минуту.
Следующая таблица иллюстрирует ситуацию, когда пользователь
направляет в систему буферизации три задания на печать.
Задание
45
6
70
Имя
Тезисы
Письмо
Записи
Количество страниц
70
5
20
Пользователь добавляет эти три задания в течение 12 минут и дважды
запрашивает печать заданий в очереди. Элементы 4, 1, 5 и 2 представляют
время между операциями пользователя. Значения 70, 38, 35, 20 и 4
указывают количество страниц, оставшихся для печати, в момент каждой операции
пользователя.
Добавить
Задание 45
Запрос
списка
заданий
Добавить
Задание 6
Добавить
Задание 70
Запрос
списка
заданий
70 38 35 20 4
Оставшиеся для печати страницы
На рисунке 9.1 перечислены операции системы буферизации печати от 0
до 12 минут. В каждом событии распечатывается количество страниц в бу-
феризаторе, общее количество уже распечатанных страниц и очередь печати.
Разработка программы
Буферизатор печати является списком, в котором сохраняются записи
PrintJob. Так как задания обрабатываются на основе порядка first-come/first-
served, мы рассматриваем список как очередь с запросами на выполнение
заданий, вставляемых в хвост списка, и фактической печатью, управляемой
удалением запросов на выполнение заданий из начала списка. В нашем
исследовании мы выполняем задачи, которых нет в наличии в формальной
коллекции очередей. В списке сканируются запросы на выполнение заданий
и распечатывается их статус. При обновлении данных изменяется размер в
страницах текущего задания без его удаления из списка. Для того, чтобы
иметь гибкий доступ к заданиям на печать, мы реализуем буферизатор как
связанный список.
Эта исследовательская задача для управления моделированием использует
события. Событие может включать добавление задания на печать в систему
буферизации, распечатку заданий в буферизаторе и проверку того, остается
ли определенное задание для печати. Случайно выбранные блоки времени в
диапазоне от 1 до 5 минут отделяют события. Для моделирования
непрерывной печати заданий в фоновом режиме используется вхождение события
для обновления очереди печати. Информация о продолжительности времени
между событиями сохраняется для того, чтобы можно было узнать, сколько
страниц уже распечатано. Допустим, что время, прошедшее с момента
последнего события, равно deltaTime, тогда количество страниц, которые были
напечатаны, равно
pagesPrinted = deltaTime * 8
Время (мин.)
Операция
Страниц в задании
Страниц в буфере
Напечатанные страницы
О Добавить задание 45 70 70 0
Печатать очередь 45 Тезисы 70 |
4 Запрос списка 38 32
Печатать очередь 45 Тезисы 38
5 Добавить задание 6 5 35 40
Печатать очередь 45 Тезисы 30 6 Письмо 5
10 Добавить задание 70 20 20 75
Печатать очередь 70 Записи 20
12 Запрос списка 4 91
Печатать очередь 70 Записи 4
Рис. 9.1. Отслеживание операций системы буферизации печати
Хранение заданий на печать и функции доступа к системе буферизации
определяются классом Spooler.
Спецификация класса Spooler
ОБЪЯВЛЕНИЕ
#include <iostream.h>
// включить генератор случайных чисел и класс LinkedList
#include "random.h"
#include "link.h"
// скорость печати — 8 страниц в минуту
const int PRINTSPEED = 8;
// класс буферизатора печати
class Spooler
{
private:
// очередь, которая содержит задания
LinkedList<PrintJob> jobList;
// deltaTime содержит случайное число в диапазоне 1—5
// минут для имитации прошедшего времени
int deltaTime;
// метод обновления информации о задании
void UpdateSpooler(int time);
RandomNumber rnd;
public:
// констуктор
Spooler(void) ;
// добавление задания в буферизатор
void AddJob(const PrintJob& J);
// методы оценивания
void ListJobs(void);
int Chec)cJob(int jobno);
int NumberOfJobs(void);
>;
ОПИСАНИЕ
Закрытый данное-член deltaTime моделирует количество минут, за которые
выполнялась печать со времени последнего события в системе буферизации.
В начале каждого события вызывается операция UpdateSpooler с deltaTime
в качестве параметра. Эта функция изменяет jobList для отражения того
факта, что распечатка происходила в фоновом режиме в течение deltaTime
минут. Каждый открытый метод отвечает за присваивание нового значения
deltaTime. Значение, создаваемое генератором RandomNumber в диапазоне
от 1 до 5, указывает количество минут перед следующим событием.
Задания на печать добавляются в систему буферизации с использованием
метода AddJob. Две операции ListJobs и Check Job предоставляют информацию
о статусе задания, находящегося в буферизаторе. В любое время список заданий
в буферизаторе распечатывается вызовом ListJobs. Метод Check Job принимает
номер задания и возвращает информацию о его статусе в буферизаторе. Он
возвращает количество страниц, оставшихся для печати. Объявление PrintJob,
PRINTSPEED и реализация класса буферизатора содержатся в файле spooler.h.
Реализация метода UPDATE для класса Spooler
Процесс обновления удаляет все задания, суммарное количество страниц
которых меньше, чем количество распечатанных страниц. Если количество
нераспечатанных страниц меньше или равно потенциальному общему
количеству страниц печати, то все задания выполнены и очередь пуста. Иначе
из очереди могут быть удалены одно или более заданий и распечатаны
несколько страниц текущего задания. Обновление оставляет текущее задание
не полностью выполненным.
// обновление буферизатора. предполагается, что при печати
// страниц проходит некоторое время, метод удаляет
// законченные задания и изменяет число оставшихся страниц
// для задания, выполняемого в текущий момент времени
void Spooler::UpdateSpooler(int time)
{
PrintJob J;
// число страниц, которые следует напечатать
// в соответствии с time
int printedpages = time*PRINTSPEED;
// использовать printedpages и сканировать
// список заданий в очереди.
// обновлять очередь печати
jobList.Reset();
while (!jobList.ListEmpty() && printedpages > 0)
{
// найти первое задание
J * jobList.Data О;
// если напечатанных страниц больше, чем
// страниц в задании, обновить счетчик печатаемых
// страниц и удалить задание
if (printedpages >* J.pagesize)
{
printedpages -« J.pagesize;
j obList.DeleteFront();
}
// часть задания выполнена;
// изменить оставшееся число страниц
else
{
J.pagesize -= printedpages;
printedpages = 0;
jobList.Data() ■ J;
}
}
}
Методы оценки системы буферизации печати
Методы оценки системы буферизации печати дают информацию
пользователю в ответ на запрос о заданиях, которые ожидают печати, и статусе
отдельного задания. Методы ListJobs и CheckJob выполняют последовательное
сканирование списка буферизатора. Мы приводим функцию ListJobs; другие
методы читатель может найти в файле spooler,h.
// обновление буферизатора и выдача списка всех заданий
//в очереди
void Spooler::ListJobs(void)
{
PrintJob J;
// обновить очередь
UpdateSpooler(deltaTime);
// генерировать время до следующего события
deltaTime * 1 + rnd.Random(5);
// перед сканированием проверить, не пуста ли очередь
if (jobList.ListSize() ■- 0)
cout « "Очередь печати пуста!\п";
else
{
// перейти к началу списка и использовать
// цикл для сканирования списка, остановиться
//в конце списка, выводить информационные поля
// для каждого задания
for(jobList.Reset(); !jobList.EndOfList();
jobList.Next())
{
J - jobList.Data0;
cout << "Задание " « J.number « ": " « J.filename;
cout « " " « J.pagesize « " страниц осталось"
« endl;
)
}
)
Программа 9.8. Буферизатор печати
Эта main-программа определяет Spooler-объект spool и создает
интерактивный диалог с пользователем. В каждой итерации пользователю
предоставляется меню из четырех пунктов. Пункты 'А' (добавить задание), 'L'
(список заданий) и 'С* (информация о задании) обновляют очередь печати
и выполняют определенную операцию системы буферизации. Пункт 'Q'
завершает программу. Пункты 'I/ и 'С* не выводятся, если очередь печати
пуста.
#include <iostreara.h>
tinclude <ctype.h>
#pragma hdrstop
♦include "spooler.h"
void main(void)
{
// объект типа Spooler
Spooler spool;
int jnum, jobno ■ 0, rempages;
char response - 'C;
PrintJob J;
for (;;)
{
// выдача меню
if (spool.NumberOfJobs() != 0)
cout « "Add(A) List(L) Check(C) Quit(Q) «=> ";
else
cout « "Add(A) Quit(Q) -*> ";
cin » response;
// преобразовать ответ к верхнему регистру
response - toupper(response);
// действие, продиктованное ответом
switch(response)
{
// добавить новое задание со следующим номером,
// используемым как идентификационный (id); читать
// имя файла и число страниц.
case 'A':
J.number = jobno;
jobno++;
cout << "Имя файла: ";
cin » J.filename;
cout « "Число страниц: ";
cin » J.pagesize;
spool.AddJob(J);
break;
// Печать информации каждого оставшегося задания
case ' I/ :
spool.ListJobs();
break;
// ввести id-задания; сканировать список с этим ключом.
// указать, что задание.выполнено или число оставшихся
// для печати страниц
case 'С :
cout « "Введите номер задания: ";
cin » jnum/
rempages - spool.CheckJob(jnum) ;
if (rempages > 0)
cout << "Задание в очереди. " « rempages
<< " страниц осталось напечатать\n";
else
cout « "Задание выполнено\п";
break;
// выход для ответа ' Q'
case 'Q':
break;
// сообщить о неправильном ответе и
// перерисовать меню
default:
cout « "Неправильная команда!\п";
break;
}
if (response == ' Q')
break;
cout << endl;
}
}
/*
<Выполнение программы 9.8>
Add (A) Quit (Q) ==> a
Имя файла: notes
Число страниц: 75
Add (A) List(L) Check (C) Quit (Q) «> a
Имя файла: paper
Число страниц: 25
Add (A) List(L) Check (C) Quit (Q) «> 1
Задание 0: notes 19 страниц осталось
Задание 1: paper 25 страниц осталось
Add (A) List(L) Check (С) Quit (Q) «> с
Введите номер задания: 1
Задание в очереди. 20 страниц осталось напечатать
Add (A) List(L) Check (С) Quit (Q) ==> 1
Очередь печати пуста!
Add (A) Quit (Q) «»> q
*/
9.8. Циклические списки
Оканчивающийся NULL-символом связанный список — это
последовательность узлов, которая начинается с головного узла и заканчивается узлом, поле
указателя next которого имеет значение NULL. В разделе 9.1 разработана
библиотека функций для сканирования такого списка и для вставки и удаления
узлов. В этом разделе разрабатывается альтернативная модель, называемая
циклическим связанным списком (circular linked list), которая упрощает раз-
работку и кодирование алгоритмов последовательных списков. Многие
профессиональные программисты используют циклическую модель для реализации
связанных списков.
Пустой циклический список содержит узел, который имеет
неинициализированное поле данных. Этот узел называется заголовком (header) и
первоначально указывает на самого себя. Роль заголовка — указывать на первый
реальный узел в списке и, следовательно, на заголовок часто ссылаются как
на узел-часовой (sentinel). В циклической модели связанного списка пустой
список фактически содержит один узел, и указатель NULL никогда не
используется. Мы приводим схему заголовка, используя угловые линии в качестве
стоны узла.
header
next
Заметьте, что для стандартного связанного списка и циклического
связанного списка тесты, определяющие, является ли список пустым, различны.
Стандартный связанный список: head == NULL
Циклический связанный список: header->next == header
При добавлении узлов в список последний узел указывает на заголовочный
узел. Мы можем представить циклический связанный список как браслет с
заголовочным узлом, служащим застежкой. Заголовок связывает вместе
реальные узлы в списке.
header
next
В разделе 9.1 был описан класс Node и использовались его методы для
создания связанных списков. В этом разделе мы объявляем класс Cnode,
создающий узлы для циклического списка. Этот класс предоставляет
конструктор по умолчанию, допускающий неинициализированное поле данных.
Конструктор используется для создания заголовка.
Спецификация класса CNode
ОБЪЯВЛЕНИЕ
template <class T>
class CNode
{
private:
// циклическая связь для следующего узла
CNode<T> *next;
public:
// данные — открытые
Т data;
// конструктор
CNode(void);
CNode (const T& item);
// методы модификации списка
void InsertAfter(CNode<T> *p);
CNode<T> *DeleteAfter(void);
// получить адрес следующего узла
CNode<T> *NextNode(void) const;
};
ОПИСАНИЕ
Этот класс подобен классу Node в разделе 9.1. В действительности все
члены этого класса имеют то же имя и те же функции. Детали открытых
членов класса приводятся в следующем разделе, в котором описывается
реализация класса. Класс CNode содержится в файле cnode.h.
Реализация класса CNode
Конструкторы инициализируют узел его указанием на самого себя, поэтому
каждый узел может служить в качестве заголовка для пустого списка.
Указатель на самого себя — это указатель this, и, следовательно, присваивание
становится следующим:
next = this;
Для конструктора по умолчанию поле data не инициализируется. Второй
конструктор принимает параметр и использует его для инициализации поля
data.
Никакой конструктор не требует параметра, определяющего начальное
значение для поля next. Все необходимые изменения поля next выполняются
с использованием методов Insert After и Delete After.
// конструктор, который создает пустой список
//и инициализирует данные
template<class T>
CNode<T>::CNode(const T& item)
{
// устанавливает узел для указания на самого себя и
// инициализирует данные
next ■> this;
data = item;
}
Операции класса CNode. Класс CNode предоставляет метод NextNode,
который используется для прохождения по списку. Подобно методу класса
Node функция NextNode возвращает значение указателя next.
Insert After добавляет узел р непосредственно после текущего объекта. Для
загрузки узла в голову списка не требуется никакого специального алгоритма,
так как мы просто выполняем Insert After (header).
До
header
next
next
header После
next
P
// вставка узла р после текущего узла
template<class T>
void CNode<T>::InsertAfter(CNode<T> *p)
{
// p указывает на следующий узел за текущим.
// текущий узел указывает на р.
p->next = next;
next = р;
}
Удаление узла из списка выполняется методом DeleteAfter. DeleteAf ter
удаляет узел, следующий непосредственно за текущим узлом, и затем возвращает
указатель на удаленный узел. Если next равно this, то в списке нет никаких
других узлов, и узел не должен удалять самого себя. В этом случае операция
возвращает значение NULL.
// удалить узел, следующий за текущим и возвратить его адрес
template <class T>
CNode<T> *CNode<T>::DeleteAfter(void)
{
// сохранить адрес удаляемого узла
CNode<T> *tempPtr = next;
// если в next адрес текущего объекта (this)/ он
// указывает сам на себя, возвратить NULL
if (next =» this)
return NULL;
// текущий узел указывает на следующий за tempPtr.
next - tempPtr->next;
// возвратить указатель на несвязанный узел
return tempPtr;
}
Приложение: Решение задачи Джозефуса
Задача Джозефуса является интересной программой, предоставляющей
изящное решение циклического связанного списка. Далее следует версия
задачи:
Агент бюро путешествий выбирает п клиентов для участия в розыгрыше
бесплатного кругосветного путешествия. Участники становятся в круг и затем
из шляпы выбирается число m (m < n). Розыгрыш производится агентом,
который идет по кругу по часовой стрелке и останавливается у каждого т-ного
участника. Этот человек удаляется из игры, и агент продолжает счет, удаляя
каждого m-ного человека до тех пор, пока не останется только один участник.
Этот счастливчик выигрывает кругосветное путешествие.
Например, если п = 8, и m = 3, то участники удаляются в следующем
порядке: 3, 6, 1, 5, 2, 8, 4 и участник 7 выигрывает круиз.
Программа 9.9. Задача Джозефуса
Эта программа эмулирует розыгрыш кругосветного путешествия.
Функция CreateList создает циклический список 1,2,...п, используя CNode-метод
InsertAfter.
Процесс выбора управляется функцией Josephus, которая принимает
заголовок циклического списка и случайное число т. Она выполняет п-1
итераций, отсчитывая каждый раз m последовательных элементов в списке
и удаляя m-ый элемент. Когда мы продолжаем обходить список по кругу,
мы выводим номер каждого участника, который удаляется. При завершении
цикла остается один элемент.
Main-программа запрашивает количество участников розыгрыша п и
использует CreateList для создания циклического списка. Генерируется
случайное число m в диапазоне 1..п, и вызывается функция Josephus для
определения порядка удаления участников и победителя в розыгрыше круиза.
#include <iostream.h>
#pragma hdrstop
#include "cnode.h"
#include "random.h"
// создать циклический список с заданным узлом
void CreateList(CNode<int> *header, int n)
{
// начать вставку после головы списка
CNode<int> *currPtr = header, *newNodePtr;
int i;
// построить п-ый элемент списка
for(i=l;i <= n;i++)
{
// создать узел со значением i
newNodePtr = new CNode<int>(i);
// вставить в конец списка и продвинуть currPtr к концу
currPtr->InsertAfter(newNodePtr);
currPtr = newNodePtr;
}
}
// для списка из п элементов решить задачу Джозефуса
// удалением каждого m-го элемента, пока не останется один
void Josephus(CNode<int> *list, int n, int m)
{
CNode<int> *prevPtr = list, *currPtr = list->NextNode();
CNode<int> *deletedNodePtr;
// удалить из списка всех, кроме одного
for(int i=0;i < n-l;i++)
{
// вычисление для currPtr, обработать m элементов.
// следует продвигать т-1 раз
for(int j=0;j < m-l;j++)
{
// передвинуть указатели
prevPtr = currPtr;
currPtr = currPtr->NextNode();
// если currPtr указывает на голову, снова передвинуть указатели
if (currPtr == list)
{
prevPtr = list;
currPtr = currPtr->NextNode();
}
}
cout << "Удалить участника: " « currPtr->data << endl;
// записать удаляемый узел и продвинуть currPtr
deletedNodePtr = currPtr;
currPtr = currPtr->NextNode();
// удалить узел из списка
prevPtr->DeleteAfter();
delete deletedNodePtr;
// если currPtr указывает на голову,
// снова передвинуть указатели
if (currPtr == list)
{
prevPtr = list;
currPtr = currPtr->NextNode();
}
}
cout << endl « "Участник " « currPtr->data
<< " выиграл круиз." « endl;
// удалить оставшийся узел
deletedNodePtr = list->DeleteAfter();
delete deletedNodePtr;
}
void main(void)
{
// список участников
CNode<int> list;
int n, m;
RandomNumber rnd; // для генерации случайных чисел
cout << "Введите число участников: и;
cin >> п;
// создать циклический список из участников 1, 2, ... п
CreateList(&list,n);
m = 1+rnd.Random(n);
cout « "Сгенерированное случайное число: " « m « endl;
// ришить задачу Джозефуса и напечатать выигравшего круиз
Josephus(&list,n,m) ;
}
Л
<Выполнение программы 9.9>
Введите число участников: 10
Сгенерированное случайное число: 5
Удалить участника: 5
Удалить участника: 10
Удалить участника: б
Удалить участника: 2
Удалить участника: 9
Удалить участника: 8
Удалить участника: 1
Удалить участника: 4
Удалить участника: 7
Участник 3 выиграл круиз.
*/
9.9. Двусвязные списки
Сканирование либо оканчивающегося NULL-символом, либо циклического
списка происходит слева направо. Циклический список является более гибким
и позволяет начинать сканирование в любом положении в списке и продолжать
его до начальной позиции. Эти списки имеют ограничения, так как они не
позволяют пользователю возвращать пройденные шаги и выполнять
сканирование в обратном направлении. Они неэффективно выполняют простую задачу
удаления узла р, так как мы должны проходить по списку и находить указатель
на узел, предшествующий р.
header
Узел перед р Удалить р
В некоторых приложениях пользователю необходим доступ к списку в
обратном порядке. Например, бейсбольный менеджер ведет список игроков с
упорядочением по среднему количеству отбиваний от самого низкого до самого
высокого. Чтобы оценить сноровку игроков в отбивании и присудить звание
лучшего в этом виде, необходимо прохождение списка в обратном направлении.
Это можно выполнить, используя стек, но такой алгоритм не очень удобен.
В случаях, когда нам необходимо обращаться к узлам в любом направлении,
полезным является двусвязный список (doubly linked list). Узел в двусвязном
списке содержит два указателя для создания мощной и гибкой структуры
обработки списков.
left
data
right
Для двусвязного списка операции вставки и удаления имеются в каждом
направлении. Следующий рисунок иллюстрирует проблему вставки узла р
справа от текущего. При этом необходимо установить четыре новых связи.
Header
В двусвязном списке узел может удалить сам себя из списка, изменяя два
указателя. На следующем рисунке показаны соответствующие этому
изменения:
Текущий узел
right
left
left
right
Класс DNode — это класс обработки узла для циклических двусвязных
списков. Объявление класса и функций-членов содержится в файле dnode.h.
Текущий узел
right
left
right
left
Спецификация класса DNode
ОБЪЯВЛЕНИЕ
template <class T>
class DNode
{
private:
// циклические связи влево и вправо
DNode<T> *left/
DNode<T> *right;
public:
// данные — открытые
T data;
// конструкторы
DNode(void);
DNode (const T& item);
// методы модификации списка
void InsertRight(DNode<T> *p);
void InsertLeft(DNode<T> *p);
DNode<T> *DeleteNode(void);
// получение адреса следующего (вправо и влево) узла
DNode<T> *NextNodeRight(void) const;
DNode<T> *NextNodeLeft(void) const;
};
ОПИСАНИЕ
Данные-члены подобны членам односвязного класса CNode, за исключением
того, что здесь используются два указателя next. Имеются две операции
вставки (по одной для каждого направления) и операция удаления, которая удаляет
текущий узел из списка. Значение закрытого указателя возвращается с
помощью функций NextNodeRight и NextNodeLeft.
ПРИМЕР
DNode<int> dlist; // двусвязный список
// сканировать список, выводя значения узла, до тех
// пор, пока мы не вернемся к заголовочному узлу
DNode<int> *p = &dlist; // инициализация указателя
р = p->NextNodeRight(); // установка р на первый узел в списке
while (р != Slist)
{
cout « p->data « ; // вывод значения данных
р « p->NextNodeRight(); // установка р на следующий узел в списке
}
DNode<int> *newNodel(10); // создание узлов со значениями
DNode<int> *newNode2(20); // 10 и 20
DNode<int> *p - sdlist; // р указывает на заголовочный узел
p->InsertRight(newNodel); // вставка в начало списка
p->InsertLeft(newNode2); // вставка в хвост списка
Приложение: Сортировка двусвязного списка
Функция InsertOrder используется в программе 9.4 для создания
отсортированного списка. Алгоритм начинается в головном узле и сканирует список
в поисках места для вставки. Имея дело с двусвязным списком, мы можем
оптимизировать этот процесс, поддерживая указатель currPtr, определяющий
последний узел, который был помещен в список. Для вставки нового элемента
мы сравниваем его значение с данным в текущем положении. Если новый
элемент меньше, используйте левые указатели для сканирования списка в
направлении вниз. Если новый элемент больше, используйте правые указатели
для сканирования списка вверх. Например, предположим, что мы только что
сохранили 40 в списке dlist.
dlist: 10 25 30 40 50 55 60 75 90
Для добавления узла 70 сканируем список по направлению вверх и
вставляем 70 справа от 60. Для добавления узла 35 сканируем список по
направлению вниз и вставляем 35 слева от 40.
Программа 9.10. Сортировка в двусвязных списках
DLinkSort использует двусвязный список для сортировки массива из п
элементов, создавая упорядоченный список и затем копируя элементы
обратно в массив. Функция InsertHigher добавляет новый узел справа от
текущей списочной позиции. Симметричная по отношению к InsertHigher
функция InsertLower добавляет новый узел слева от текущей позиции.
Алгоритм функции DLinkSort:
Вставить элемент (item) 1
вызвать InsertRight с головой и сохранить а[0]
Вставить элементы 2—10
если item < currPtr->data, вызвать InsertLower
если item > currPtr-<data, вызвать InsertHigher
В следующей программе с использованием функции DLinkSort
сортируется список из 10 целых. Отсортированный список выводится с помощью
функции PrintArray.
#include <iostream.h>
#pragma hdrstop
#include "dnode.h"
template <class T>
void InsertLower(DNode<T> *dheader, DNode<T>* scurrPtr, T item)
{
DNode<T> *newNode= new DNode<T>(item) , *p;
// найти место вставки
p «= currPtr;
while (p != dheader && item < p->data)
p = p->NextNodeLeft();
// вставить элемент
p->InsertRight(newNode);
// переустановить currPtr на новый узел
currPtr = newNode;
}
template <class T>
void InsertHigher(DNode<T>* dheader, DNode<T>* & currPtr, T item)
{
DNode<T> *newNode= new DNode<T>(item), *p;
// найти место вставки
p = currPtr;
while (p != dheader && p->data < item)
p = p->NextNodeRight();
// вставить элемент
p->InsertLeft(newNode);
// переустановить currPtr на новый узел
currPtr = newNode;
}
template <class T>
void DLinkSort(T a[], int n)
{
// задать двусвязный список для элементов массива
DNode<T> dheader, *currPtr;
int i;
// вставить первый элемент в список
DNode<T> *newNode = new DNode<T>(a[0]);
dheader.InsertRight{newNode);
currPtr = newNode;
// вставить оставшиеся элементы в список
for (i=l;i < n;i++)
if (a[i] < currPtr->data)
InsertLower(&dheader,currPtr,a[i]);
else
InsertHigher(sdheader,currPtr,a[i]);
// сканировать список и копировать данные в массив
currPtr = dheader.NextNodeRight();
i = 0;
while(currPtr != sdheader)
{
a[i++] = currPtr->data;
currPtr = currPtr->NextNodeRight();
}
// удалить все узлы списка
while(dheader.NextNodeRight() != &dheader)
{
currPtr = (dheader.NextNodeRight())->DeleteNode();
delete currPtr;
}
}
// сканировать массив и выводить его элементы
void PrintArray(int a[], int n)
{
for(int i=0;i < n;i++)
cout « a[i] « " ";
}
void main(void)
{
// инициализированный массив из десяти целых
int A[10] = {82,65,74,95,60,28,5,3,33,55};
DLinkSort(A,10)/ // сортировать массив
cout « " Отсортированный массив: ";
PrintArray{A,10); // печатать массив
cout « endl;
}
/*
<Выполнение программы 9.10>
Отсортированный массив: 3 5 28 33 55 60 65 74 82 95
*/
Реализация класса DNode
Конструктор создает пустой список, присваивая адрес узла this обоим
(левому и правому) указателям. Если конструктору передается параметр item,
данному-члену узла присваивается значение item.
// конструктор, который создает пустой
// список и инициализирует данные
template<class T>
DNode<T>::DNode(const T& item)
<
// установить узел для указания на самого себя и
// инициализировать данные
left = right = this;
data = item;
}
Списочные операции. Для вставки узла р справа от текущего узла
необходимо назначить четыре указателя. На рисунке 9.2 показано соответствие между
операторами C++ этими новыми связями. Заметим, что присваивания не могут
выполняться в произвольном порядке. Например, если (4) выполняется
первым, то связь к узлу, следующему за текущим, теряется.
Текущий узел right
right
(1) р -> right = right;
(2) right -> left = p;
(3) p -> ieft = this;
(4) right = p;
Рис. 9.2. Вставка узла справа в циклическом двусвязном списке
Читателю следует проверить, что этот алгоритм работает правильно в случае
вставки в пустой список.
// вставить узел р справа от текущего
template <class T>
void DNode<T>::InsertRight<DNode<T> *p)
{
// связать р с его предшественником справа
p->right = right;
right->left = p;
// связать р с текущим узлом
p->left = this;
right = p;
}
Метод InsertLeft выполняет вставку узла слева аналогично вставке справа
в алгоритме для InsertRight.
// вставить узел р слева от текущего
template <class T>
void DNode<T>::InsertLeft(DNode<T> *p)
{
// связать р с его предшественником слева
p->left = left;
left->right « p;
// связать р с текущим узлом
p->right = this;
left = p;
)
Для удаления текущего узла должны быть изменены два указателя, как
показано на рис. 9.3. Читателю следует проверить, что алгоритм работает
правильно в случае, когда удаляется последний узел списка. Метод
возвращает указатель на удаленный узел.
// отсоединить текущий элемент от списка и возвратить его адрес
template <class T>
DNode<T> *DNode<T>::DeleteNode(void)
{
left->right = right;
right->left = left;
return this;
}
left
right
Текущий узел
(1) left -> right = right;
(2) right -> left = left;
Рис. 9.З. Удаление узла в циклическом двусвязном списке
9.10. Практическая задача: Управление окнами
Графический пользовательский интерфейс (Graphical User Interface, GUI)
поддерживает на экране многочисленные окна. Они организованы слоями,
причем переднее окно считается активным окном (active window). Некоторые
приложения ведут список текущих открытых окон. Список доступен из меню
и позволяет пользователю выделять наименование окна и делать его передним
или активным. Это может быть особенно полезным, когда необходимо
активизировать заднее окно, которое в данный момент времени является невидимым.
Например, на рис. 9.4 показаны три окна, где (слева) Window_0 — это активное
окно. Выбор Window_l из списка меню активизирует это окно и делает его
передним.
Select Window 1
Window 0 active
Windows
Windows_l active
Zoora
Layer
Tile
Closo &11
Save All
Full P&thnatoe
Show Clipboard
Window_0
Window 1
Window 2
Рис. 9.4 Списки окон
Каждое окно на экране ассоциируется с каким-либо файлом. Окно
создается при открытии соответствующего файла и уничтожается, когда этот файл
закрывается. Мы используем связанный список для хранения списка окон.
С каждой файловой операцией связываем соответствующую операцию в
списке окон. Файловая операция New создает переднее окно, которое добавляется
в начало списка. Операции Close и Save As применимы к активному окну
в начале списка. Общая операция, такая как Close All, может быть
реализована удалением окна из списка и закрытием как окна, так и
соответствующего ему файла.
Рассмотрим практическую задачу, которая ведет список окон для
приложения GUI. Приложение поддерживает следующие файловые и списочные
операции:
New: Вставляет окно с именем Untitled.
Close: Удаляет переднее окно.
CloseAll: Закрывает все окна, очищая список.
Save As: Сохраняет содержимое окна под другим именем
и обновляет заголовок в элементе ввода окна.
Quit: Завершает приложение.
Menu Display: Оконное меню отображает номер и имя каждого
окна в порядке расположения окон слоями.
Пользователь может вводить номер и
активизировать окно, перемещая его в начало списка окон.
Список окон
В любой момент времени допускается одновременное открытие максимум
10 окон. Каждое открытое окно имеет соответствующий номер в диапазоне
от 0 до 9. Когда окно закрывается, этот номер становится доступным для
операции New, которая создает новое открытое окно. За управление
отдельными окнами и изменение текущего активного окна отвечают методы Close,
Close All, Save As и Activate. Каждое окно представлено объектом окна,
который определяет имя окна и его номер (index) в списке имеющихся в
наличии окон.
Объект окна описывается классом Window, который содержит поля win-
dowTitle и windowNumber. Класс имеет функции-члены для изменения
заголовка окна, получения номера окна и вывода информации в формате
Зато л овок[номер окна] (Title[window number]). Перегруженный оператор равно
(==) сравнивает две Window-записи по номеру окон.
Спецификация класса Window
ОБЪЯВЛЕНИЕ
// класс, содержащий информацию об отдельном окне
class Window
{
private:
// window-данные включают заголовок окна и
// индекс в таблице доступных окнон
String windowTitle;
int windowNumber;
public:
// конструкторы
Window(void) ;
Window(const Strings title, int wnum) ;
// методы доступа к данным
void ChangeTitle(const Strings title);
int GetWindowNumber(void);
// перегруженные операторы
int operator== (const Windows w);
friend ostream& operator« (ostreams ostr,
const Windows w);
>;
Полная реализация класса Window находится в файле windlist.h. Список
окон и операции для создания, хранения и активизации объектов окна
определяются классом WindowList.
Спецификация класса WindowList
ОБЪЯВЛЕНИЕ
#include "link.h"
// структура связанного списка для Window-объектов
class WindowList
{
private:
// список активных окон
LinkedList<Window> windList;
// список доступных окон и число открытых
int windAvail[10];
int windCount;
// функции получения и освобождения окон
int GetWindowNumber(void);
int FindAndDelete(Windows wind);
// печать списка открытых окон
void PrintWindowList(void);
public:
// конструктор
WindowList(void);
// методы window-меню
void New(void);
void Close(void); // закрыть переднее окно
void CloseAll(void); // закрыть все окна
void SaveAs(const Strings name); // изменить имя
void Activate(int windownum); // активизировать окно
// моделировать управление окнами
void Selectltem(int& item, Strings name);
>;
ОПИСАНИЕ
Конструктор присваивает окнам начальные данные. Он устанавливает
счетчик окон на нуль и отмечает каждое доступное окно в диапазоне 0-9. New
получает окно из списка имеющихся в наличии окон и присваивает индекс
в качестве номера окна. Окну передается заголовок Untitled. Новое окно
вставляется в начало списка открытых окон.
Класс WindowList поддерживает дополнительные операции: Close, Close
All, Save As и Activate, которые обеспечивают реакцию на соответствующие
опции меню.
Операция Selectltem реализует меню. Пользователь может ввести с
клавиатуры либо буквенный символ N (New), С (Close), A (Close All), S (Save
As), Q (Quit), либо цифру 0,1.... Метод возвращает входной выбор и
сгенерированный внутри номер пункта, обозначающий операцию. Следующая
таблица соотносит номер пункта и выбор:
Номер пункта
1
2
3
4
5
6
7
15
Имя
New
Close
Close All
Save As
Quit
WindowName[iol
WindowNamefh]
. . .
WindowNamepg]
Символьный код для выбора
n(N)
с(С)
а(А)
s(S)
q(Q)
i0
i1
i9
Пункты меню 2—4 выводятся только в том случае, если имеется, по
крайней мере, одно открытое окно. Вывод имен и номеров окон управляется
закрытым методом Print WindowList. Пункты с 6-го и далее соответствуют
списку текущих открытых окон. Пункт 6 — это переднее окно с номером
окна i0; пункт 7 — это второе окно с номером ij и так далее. Окно помещается
в начало списка вводом с клавиатуры его номера. Новым окнам дается
наименьший имеющийся в наличии номер в диапазоне 0—9. Например, если
номера 0, 1, 3 и 5 используются в данный момент и 0-е окно закрывается,
следующее новое окно создается с номером окна 0. Функция GetWindowNum-
ber осуществляет выполнение алгоритма для распределения номеров окон.
ПРИМЕР
В следующей таблице приводится последовательность оконных команд.
После завершения какой-либо операции мы задаем список окон с первым эле-
ментом ввода, являющимся активным окном. Для команды SaveAs
последующий ввод заключается в круглые скобки.
Выбор
N
N
S (One)
О
N
С
С
N
А
Q
Номер пункта
1
1
4
7
1
2
2
1
3
5
Действие
новое окно
новое окно
сохранить как One
активизировать 0
новое окно
закрыть
закрыть
новое окно
закрыть все
выход
Список окон
Untitled[0]
Untitled[1] Untit!ed[0]
One[1] Untitled[0]
Untitled[0] 0ne[1]
Untitled[2] Untitled[0] 0ne[1]
Untit!ed[0] One[1]
One[1]
Untitled[0] 0ne[1]
< пусто >
завершение работы приложения
Реализация класса WindowList
Полный листинг методов WindowList содержится в файле windlist.h. Мы
приводим здесь код только нескольких функций для иллюстрации
использования связанного списка при ведении списка открытых окон и выполнении
опций меню. Функция GetWindowNumber проходит массив windAvail в
поисках имеющегося в наличии номера окна и возвращает первый найденный
номер. В результате все новые окна получают наименьший возможный номер.
// получить первое свободное окно из списка доступных окон
int WindowList::GetWindowNumber(void)
{
for(int i«0;i < 10;i++)
// если окно доступно, выделить его
// сделать его недоступным,
if (windAvail[i])
{
windAvail[i] = 0;
break;
}
return i; // return window index
}
Закрытая функция PrintWindowList сканирует список окон и выводит
заголовок и номер для каждого окна. Метод реализует простое последовательное
сканирование списка, начиная с первого (Reset) и переходя от окна к окну
(Next) до достижения конца списка (EndOf List). Оператор « из класса Window
выводит данные окна в формате Заголовок[номер] (Title[#]).
// вывод оконной информации для всех активных окон
void WindowList::PrintWindowList(void)
{
for(windList.Reset(); !windList.EndOfList();
windList.Next 0)
cout « windList.Data() ;
}
Списочные операции окон. Для создания какого-либо окна метод New
присваивает Window-объекту win заголовок Untitled. Вызовом
GetWindowNumber этому объекту присваивается номер окна, и он вставляется в
список окон; счетчик окон увеличивается.
//получение нового окна и передача ему заголовка 'untitled'
void WindowList::New(void)
{
//проверка, имеется ли в наличии окно, если
//нет, просто — возврат
if (windCount ==10)
{
cerr « "Нет больше окон в наличии, пока одно не будет закрыто" « endl;
return;
}
// получить новое окно с заголовком 'Untitled' вызовом
// функции getWindowNumber
Window win(Untitled, GetWindowNumber());
// сделать его активным, вставляя в начало списка
windList.InsertFront(win);
windCount++;
}
Для активизации окна, расположенного за другими окнами, мы должны
сначала найти это окно, используя его номер в качестве ключа, а затем удалить
этот элемент из списка. При вставке окна в начало списка, оно становится
активным. Вызывается закрытый метод FindAndDelete, который сканирует
список, выполняя поиск совпадения с номером окна. Когда окно обнаружено,
метод отсоединяет его от списка и возвращает данные окна. Эта информация
затем используется для создания нового окна, которое вставляется в начало
списка.
int WindowList::FindAndDelete(Windows wind)
{
int retval;
// цикл по списку для поиска wind
for(windList.Reset();!windList.EndOfList();windList.Next())
// window-оператор == сравнивает номера окон.
// при совпадении прервать цикл
if(wind == windList.Data())
break;
// совпадение имеется?
if(!windList.EndOfList())
{
// присвоить wind значение, удалить запись и возвратить 1 (успешно)
wind = windList.Data();
windList.DeleteAt();
retval =1/
}
else
retval - 0; // возвратить О (неуспешно)
return retval;
}
void WindowList::Activate(int windownum)
{
Window win("Формальное имя", windownum);
if (FindAndDelete(win))
windList.InsertFront(win);
else
cerr « "Некорректный номер окна.\п";
}
Программа 9.11. Управление списком окон
Эта main-программа определяет WindowList-объект windops,
содержащий список открытых окон. Цикл событий вызывает функцию Selectltem
и выполняет действия, соответствующие значению, возвращаемому
функцией. Цикл продолжается до тех пор, пока пользователь не выберет Q
(Quit).
#include <iostream.h>
// включить классы Window и WindowList
#include "windlist.h"
// очистка входного буфера
void ClearEOL(void)
{
char с;
do
cin.get(c);
while (c != '\n');
}
void main(void)
{
// список доступных программе окон
WindowList windops;
// window-заголовки
String wtitle, itemText;
// done = 1, если пользователь ввел символ q
int done = 0, item;
// моделировать до введения пользователем символа 'q'
while(!done)
{
// выдать меню и принять ответ пользователя
windops.Selectltem(item,itemText);
// при выборе числа активизировать окно
if (item >= б)
windops.Activate(itemText[0] — '0');
// иначе выбирать из опций 0—5.
// вызвать метод для обработки запроса
else
switch(item)
{
case 0: break;
case 1: windops.New();
break;
case 2: windops.Close();
break;
case 3: windops.CloseAll();
break;
case 4: cout « "Заголовок нового окна: ";
ClearEOL();
wtitle.ReadString();
windops.SaveAs(wtitle);
break;
case 5: done *
Inbreak;
}
}
)
/*
<Выполнение программы 9.11>
New Quit: n
New Close Close All Save As Quit Untitled[0] : n
New Close Close All Save As Quit Untitledfl] Untitled[0]: s
Заголовок нового окна: one
New Close Close All Save As Quit one[l] Untitled[0]: 0
New Close Close All Save As Quit Untitled[0] one[l]: s
Заголовок нового окна: two
New Close Close All Save As Quit two[0] one[l]: n
New Close Close All Save As Quit Untitled[2] two[0] one[l]:s
Заголовок нового окна: three
New Close Close All Save As Quit three[2] two[0] one[l]: 0
New Close Close All Save As Quit two[0] three[2] one[l]: с
New Close Close All Save As Quit three[2] one[lJ: a
New Quit: q
*/
Письменные упражнения
9.1 Предположим, что выполняется следующая последовательность
операторов:
Node<int> *pl, *р2;
pi * new Node<int>(2);
р2 * new Node<int>(3);
Что выводится каждым сегментом программы?
(а) cout « pl->data « " " « p2->data « endl;
(б) pl->data - 5;
pl->InsertAfter(p2);
cout « pl->data « " " « pl->NextNode()->data « endl;
(в) pl->data * 7;
p2->data * 9;
p2 - pi;
cout « pl->data « n n « p2->data « endl;
(r) pl->data - 8;
p2->data * 15;
p2->InsertAfter(pi);
cout « pl~>data « n " « p2->NextNode () ->data « endl;
(д) pl->data - 77;
p2->data ■ 17;
pl->InsertAfter<p2);
p2->InsertAfter(pl) ;
cout « pl->data « " n « p2->NextNode ()->data « endl;
9.2 Имеется следующий связанный список объектов Node и указателей Р1,
Р2, РЗ и Р4. Для каждого сегмента кода нарисуйте аналогичный
рисунок, указывающий, как изменяется список.
Head
(а) P2 = Pl->NextNode();
(б) head = Pl->NextNode();
(в) P3->data = Pl->data;
(r) P3->data - Pl->NextNode()->data;
(д) Р2 *= Pl->DeleteAfter();
delete P2/
(е) P2->InsertAfter(new Node<int>(3));
(ж) Pl->NextNode()->NextNode()->NextNode()->data » Pl->data;
(з) Node<int> *P = PI;
while (P !*= NULL)
{
P->data *= 3;
P * P->NextNode();
}
(и) Node<int> *P = PI;
while(P->NextNode() !* NULL)
{
P->data *=* 3;
P ~ P->NextNode();
}
Head
9.3 Напишите сегмент кода, создающий связанный список со значениями
данных 1..20.
9.4 Распечатайте содержимое связанного списка после каждого из
следующих операторов. Для оператора cout укажите выход.
Node<char> *head, *р, *q;
head e new Node<char>(*B');
head * new Node<char>(*A',head);
q * new Node<char>(yC);
p = head;
p = p->NextNode();
p->InsertAfter(q);
cout « p->data « " " « p->NextNode()->data « endl;
q я p->DeleteAfter();
delete q;
q ■ head;
head = head->NextNode();
delete q;
9.5 Напишите функцию
template <class T>
Node<T> *Copy(Node<T> *p);
которая создает связанный список, являющийся копией списка,
начинающегося с узла р.
9.6 Предположим, что вы пишете метод класса Node и таким образом,
можете изменять следующий данное-член. Опишите результат
выполнения этих операторов. Так как код встречается в методе, вы имеете
доступ к указателям next и this.
Node<T> *p;
(а) р « next;
p->next = next;
(б) р = this;
next->next « р;
(в) next * next->next;
(г) р = this;
next->next = p->next;
9.7 Вместо использования указателя на голову связанного списка объектов
Node мы можем поддерживать заголовочный узел. Его значение данных
не считается частью списка, и его следующий данное-член указывает
на первый узел данных в этом связанном списке. Заголовок называется
узлом-часовым и позволяет избежать пустого списка.
Header
Filler
Data1
Предположим, что ведется связанный список целых с использованием
заголовочного узла:
Node<int> header(0);
(а) Напишите последовательность кода для вставки узла р в начало списка.
(б) Напишите последовательность кода для удаления узла из начала списка.
9.8 Это упражнение предполагает, что связанные списки создаются и
поддерживаются с использованием класса Node. Два упорядоченных
списка: L1 и L2 могут быть объединены в третий список L3
последовательным прохождением двух этих списков и вставкой узлов в третий список.
В любом месте вы рассматриваете одно значение из L1 и одно из L2,
вставляя меньшее значение в хвост L3. Например, рассмотрим
следующую последовательность вставок. Текущие элементы, которые
рассматриваются в Ы и L2, обведены кружком.
1 Поскольку значение данных в этом узле не используется, такие данные названы здесь
данные-заполнитель. — Прим. ред.
Напишите функцию
void MergeLists(Node<T> *L1, Node<T>* L2, Node<T>* &L3);
для объединения LI и L2 в L3.
9.9 Каково действие этой последовательности кода?
while(currPtr != NULL)
{
currPtr->data +* 7;
currPtr ■ currPtr->NextNode();
}
9.10 Опишите действие функции F:
template <class T>
void F(Node<T>* &head)
{
Node<T> *p, *q;
if (head ! + NULL&& head->NextNode() !-NULL)
{
q * head;
head = p = head->NextNode();
while(p->NextNode() !» NULL)
p ~ p->NextNode();
p->InsertAfter(q);
}
}
9.11 Напишите функцию
template <class T>
int CountKey(const Node<T> *head, T key);
которая подсчитывает количество вхождений ключа в списке.
9.12 Напишите функцию
template <class T>
void DeleteKey(Node<T>* shead, T key;
которая удаляет из списка все вхождения ключа.
Шаг!
Шаг 2
ШагЗ
Шаг 4
9.13 Измените функцию InsertOrder в разделе 9.2, так чтобы значения
данных добавлялись в начало последовательности копий.
9.14 Для каждого из пунктов (а) — (d) каков список, получающийся
выполнением заданной последовательности команд:
LinkedList<int> L;
int i, val;
(а) for(i«l;i <- 5;i++)
L.InsertFront (*I);
(б) for(i«l;i <- 5;i++)
L.InsertAfter(2*i)/
(B) for(i=l/i <- 5;i++)
L.InsertAt(2*i)
(r) for(i-l;i <- 5;i++)
{
L.InsertAt(i);
L.NextO /
L.InsertAt(2*i)
val » L.DeleteFront(>;
}
(д) Используя InsertFront, напишите оператор for для создания списка:
50, 40, 30, 20, 10
(е) Повторите пункт (е), используя InsertRear и InsertAfter.
9.15 Предположим следующие объявления:
LinkedList<int> L;
int i, val/
Допустим, что связанный список L содержит значения 10, 20, 30 ...,
100. Каковы значения данных в списке после выполнения каждого из
следующих пунктов?
(а) L.Reset();
for(i«l/i <« 5;i+)
L.DeleteAtO;
(б) L.Reset О;
for(i«l;i <« 5;i++)
{
L.DeleteAtO;
L.NextO/
}
(в) L. Reset 0 ;
for(i-l;i <* 3;i++)
{
vail - L.DeleteFront();
L.NextO;
L.InsertAt(val)/
)
9.16 Напишите функцию
template <class T>
void Split(const LinkedList<T>& L, LinkedList<T>& LI, LinkedList<T>& L2)/
которая принимает список L и создает два новых списка L1 и L2* L1
содержит первый, третий, пятый и последующие нечетные узлы. L2
содержит четные узлы.
9.17 Предположим, что L — это список целых. Напишите функцию
void OddEven(const LinkedList<int>& L, LinkedList<int>& LI,
LinkedList<int>& L2);
которая принимает связанный список L и создает два новых списка
L1 и L2. Список L1 содержит узлы списка L, значения данных которых
являются нечетными числами. L2 содержит узлы, значения данных
которых являются четными числами. Используйте итератор.
9.18 Напишите метод класса List
int operator* (const List<T>& L);
который конкатенирует список L на конец текущего списка.
Возвращается 1, если оператор выполнен правильно или 0, если память для
новых узлов не могла быть выделена. Не допускайте конкатенацию
списка на самого себя. В этом случае должен возвращаться 0.
9.19 Напишите функцию
template <class T>
void DeleteRear(LinkedList<T>& L);
которая удаляет хвост списка L.
9.20 Нарисуйте рисунок связанного стека
Stack<int> L;
целых данных после серии операций:
Push(l), Push<2), Pop, Push(5), Push(7), Pop, Pop.
9.21 Реализуйте класс Stack, включая объект LinkedList с помощью
композиции.
9.22 Реализуйте класс Stack, сопровождая связанный список объектов Node.
9.23 Каково действие этой функции?
template <class T>
void Actions(LinkedList<T>& L)
{
Stack<T> S;
for( L.ResetO; IL.EndOfList (); L.NextO )
S.Push(L.Data());
L.Reset();
While( !S.StackEmpty() )
{
L.DataO = S.PopO ;
L.NextO;
)
}
9.24 Нарисуйте рисунок связанной очереди
Queue<int> Q;
целых данных после серии операций
Qlnsert(l), QInsert(2), QDelete, QInsert(5), QInsert(7), QDelete, QInsert(9).
Обязательно включите указатель rear в рисунок.
9.25 Каково действие этой функции?
template <class T>
void ActionQ(LinkedList<T>& L, Queue<T>& Q)
{
Q.QClear();
for( L.Reset(); !L.EndOfList();L.Next() )
Q.Q. Insert (L.DataO ) ;
}
9.26 Измените класс Queue в разделе 9.6, так чтобы он содержал функции-
члены
Т PeekFront(void);
Т PeakRear(void);
которые возвращают значения данных в начале и в хвосте очереди,
соответственно.
9.27 Класс Queue не имеет явного оператора присваивания. Объясните,
почему два Queue-объекта Objl и Obj2 могут появиться в операторе
Obj2 = Objl;
9.28 Реализуйте функцию Replace, выполняющую поиск значения данных
в циклическом связанном списке.
template <class T>
CNode<T> *Replace(CNode<T> *header, CNode<T> *start, T elem,
T newelem);
Начиная в узле start, сканируйте список, выполняя поиск elem. Если
elem будет найден, замените его новым значением данных newelem и
возвратите указатель на совпадающий узел; иначе, возвращайте NULL.
Примечание: при сканировании вы можете проходить заголовок.
9.29 Реализуйте функцию
template <class T>
void InsertOrder(CNode<T> *header, CNode<T> *elem) ;
которая вставляет узел elem в циклический список, так чтобы данные
были упорядочены.
9.30 Рассмотрите структуру
template <class T>
struct Clist
{
CNode<T> header;
CNode<T> *rear;
>;
Она определяет циклический список с указателем rear.
header.next
rear
Разработайте функции
// вставить узел р в начало списка L
template <class t>
void InsertFront(CList<T>& L, CNode<T> *p);
// вставить узел р в хвост списка L
template <class t>
void InsertRear(CList<T>& L, CNode<T> *p);
// удалить первый узел списка L
template <class t>
CNode<T> *DeleteFront(CList<t>& L);
Обеспечьте правильное поддержание rear, так чтобы в любое время он
указывал на последний узел списка.
9.31
(а) Напишите функцию
template <class T>
void Concat(CNode<T>& s, CNode<T>& t);
которая конкатенирует циклический список с заголовком t на конец
циклического списка с заголовком s.
(б) Напишите функцию
template <class T>
int Lenght(CNode<T>& s)/
которая определяет количество элементов в циклическом списке с
заголовком s.
(в) Напишите функцию
template <class T>
CNode<T> *Index(CNode<T>& s, T elem);
которая возвращает указатель на первый узел в циклическом списке
с заголовком s, содержащий значение данных elem. Возвращайте
заголовок, если elem не найден.
(г) Напишите функцию
template <class T>
void Remove(CNode<T>& s, T elem);
которая удаляет все узлы из списка s, содержащего значение данных
elem.
9.32 Напишите функции-члены
DNode<T> *DeleteNodeRight(void);
DNode<T> *DeleteNodeLeft(void);
для класса двусвязных узлов. DeleteNodeRight удаляет узел справа от
текущего узла, a DeleteNodeLeft удаляет узел слева от него.
Упражнения по программированию
9.1 Это упражнение расширяет функции-утилиты для узлов в файле node-
lib.h. Напишите функции, имеющие следующие объявления:
// удаление хвостового узла в списке;
// возврат указателя на удаленный узел
template <class T>
Node<T> *DeleteRear(Node<T> * & head);
// удаление всех вхождений клю^а в списке
template <class T>
void DeleteRear(Node<T> * & head, const T& key);
Напишите программу для тестирования этих функций.
□ Введите 10 целых и сохраните их в списке, используя функцию
InsertFront. Используйте PrintList для вывода списка.
D Введите целое, которое служит в качестве ключа. Используйте
DeleteKey для удаления из списка всех вхождений ключа.
Распечатайте итоговый список.
□ Удалите все узлы списка, используя DeleteRear. Для каждого
удаления выводите значение данных.
9.2 Для этого упражнения используйте класс Node. Полем данных для
упражнения является структура IntEntry.
struct IntEntry
{
int value; // целое число
int count; // вхождения значения
};
Введите 10 целых и создайте упорядоченный список IntEntry узлов,
использующих поле count для указания дубликатов в списке.
Распечатайте итоговую информацию об узлах, которая должна включать
отдельные целые значения и количество вхождений каждого целого в
списке. Вам следует изменить функцию InsertOrder, чтобы при
нахождении дубликата обновлялись значения данных узла.
Введите ключ и удалите все узлы, значение данных которых больше,
чем ключ» Распечатайте итоговый список.
9.3 Для этого упражнения используйте класс Node. Данные представляют
служащего: его имя (name), id-номер (idnumber) и почасовую оплату
его труда (hourlypay).
struct Emplyee
{
char name[20];
int indnumber;
float hourlypay;
};
Перегрузите операторы ввода/вывода « и » для служащего и
используйте PrintList для вывода списка. Введите следующие записи
данных и сохраните их в связанном списке.
40 9.50 Dennis Williams
10 6.00 Harold Barry
25 8.75 Steve Walker
Реализуйте следующие операции обновления, изменяющие список:
(а) Считайте id-номер и выполняйте поиск записи данного служащего в
списке. Если запись найдена, увеличьте почасовую оплату на $3,00.
Выведите итоговый список. (Вам необходимо перегрузить оператор ==.)
(б) Сканируйте список и удаляйте всех служащих, получающих более
$9,00 в час. Выведите итоговый список.
9.4 Два списка L = {Lo» La, . . . Li} и М = {Mo, Mi, . . . Mj} могут быть
объединены по парам для получения списка {Lo,Mo, Li,Mi, . . . Li,Mi,
• . . Lj,Mj}, j > i. Напишите программу, используя класс Node, которая
генерирует список Lei числами (i < i < 10) и список М с j числами
(1 < j < 20). Элементы ввода в списке L являются случайными числами
в диапазоне от 0 до 99, а элементы ввода в М — это случайные числа
в диапазоне от 100 до 199. Программа выводит начальные списки L
и М, объединяет их в новый список N и выводит его.
9.5 Повторите упражнение 9.4, используя два LinkedList-объекта L и М.
9.6 Используя класс Node, напишите программу, вводящую 5 целых в
связанный список, используя следующий алгоритм:
Каждое вводимое N вставлять в голову списка. Сканировать оставшийся
список, удаляя все узлы, которые меньше, чем N.
Выполните программу три раза, используя следующие входные данные.
Распечатайте итоговый список.
1, 2, 3, 4, 5
5, 4, 3, 2, 1
3, 5, 1, 2, 4
9.7 Класс LinkedList содержит как конструктор копирования, так
перегруженный оператор присваивания. Напишите тестирующую программу,
которая оценивает правильность этих двух методов.
9.8 Используйте класс String из главы 8 для считывания разделенных
пробелами значащих символов текста. Введите строку, которая может
включать строки, начинающиеся с '-'. Например:
// t и includelist являются опциями
run -t -includelist linkdemo
В этом примере строки включают опции (символы, начинающиеся с
'-') и символы, не являющиеся опциями. Используя класс LinkedList,
сохраните незначащие символы в связанном списке tokenlist и
символы-опции — в связанном списке optionlist. Распечатайте символы из
каждого списка.
9.9 Положительное целое п (п>1) может быть записано единственным
образом как произведение простых чисел. Это называется разложением
числа на простые числа. Например,
12 = 2*2*3 18 = 2*3*3 11 = 11
Функция LoadPrimes использует структуру записей IntEntry из
упражнения по программированию 9.2 для создания связанного списка,
который определяет различные числа и количество вхождений простых
чисел в разложение числа. Например, в случае с 18 простое число 2
встречается 1 раз, а простое число 3 встречается 2 раза.
void LoadPrimes(LinkdList<IntEntry> &L, int n)
{
int i = 2;
int nc =0; // счетчик повторений
do
{
if (n % i == 0)
{
nc++;
n = n/i;
}
else
{
if (nc > 0)
Оагрузить i и nc как узла в хвост списка>
nc » 0;
I++;
}
}
while {n > 1);
}
Напишите программу, которая вводит два целых М и N и использует
функцию LoadPrimes для создания связанного списка простых чисел.
Сканируйте список и выводите разложение каждого числа на простые
числа.
Создайте новый список, состоящий из всех простых чисел, общих для
списков М и N. Когда вы определите каждое такое простое число,
возьмите минимальный счетчик в двух узлах и используйте как счетчик
в узле для нового списка. Например, 2 является простым множителем
60-ти, и 2 — это простой множитель 18-ти.
18 =2*3*3 //2 имеет счетчик 1
60 =2*2*3*5 //2 имеет счетчик 2
В новом списке 2 является значением со счетчиком 1 (минимум 1, 2).
Результирующее число является наибольшим общим делителем
значений М и N, GCD(M,N).
9.10 Полином n-ной степени является выражением в форме
f(x) = anxn + an.!Xn+1 + ... + а2х2 + аххх + а0х°
где термы ai называются коэффициентами. Используйте класс
LinkedList для этого упражнения с записью данных Term, содержащей
коэффициент и показатель степени х для каждого терма.
struct Terra
{
double coeff;
int power;
};
В программе введите полином как ряд пар коэффициентов и
показателей степени. Завершайте программу при вводе коэффициента 0.
Сохраните каждую пару (коэффициент/показатель степени) в связанном
списке, упорядоченном по показателю степени.
(а) Напишите каждый терм результирующего полинома в форме
аА * xAi
(б) Введите 3 значения х и вызовите функцию
double poly(LinkedList<Term>& f);
которая вычисляет полином для значения х и выводит результат.
9.11 Это упражнение использует функции, разработанные в письменных
упражнениях 9.12 и 9.13. Считайте упорядоченный список из 10 целых
значений и распечатайте его. Запросите у пользователя какое-либо
значение данных и, используя CountKey, определите, сколько раз это
значение встречается в списке. Используйте DeleteKey для удаления из
списка всех вхождений этого значения. Выведите новый список.
9.12 Протестируйте функцию MergeLists в письменном упражнении 9.8,
используя целые данные. Включите списки L1={1,3,4,6,7,10,12,15} и
L2={3,5,6,8,11,12,14,18,22,33,55} в свои тесты.
9.13 Используйте класс CNode для разработки класса Queue. Объявите
заголовочный узел в закрытой секции класса и выполните вставки и
удаления следующим образом:
Qlnsert: InsertAfter текущий узел и перейти к новому узлу.
QDelete: Delete After заголовочный узел. Будьте осторожны и
выполняйте проверку на удаление из пустой очереди.
Пустая очередь
front, rear
front
rear
Протестируйте вашу реализацию, вставляя целые значения 1, 2, ...,
10 в очередь. Сделайте очередь пустой и распечатайте значения.
9.14 Мы можем реализовать класс Set с элементами типа Т, сохраняя
уникальные элементы данных в связанном списке. Реализуйте эти две
функции
template <class T>
LinkedList<T> Union(LinkedList<T>& x, LinkedList<T>& y);
template <class T>
LinkedList<T> Intersection(LinkedList<T>& x, LinkedList<T>& y);
Union возвращает связанный список, представляющий множество всех
элементов, которые найдены, по крайней мере, в одном х или у.
Intersection возвращает связанный список, представляющий множество всех
элементов, находящихся как в х, так иву. Пусть А будет множеством
целых {1,2,5,8,12,33,55}, а В — множеством {2,8,10,12,33,88,99}.
Используйте эти две функции для вычисления и вывода
A U В - {1, 2, 5, 8, 10, 12, 33, 55, 88, 99}
и
АГ1 В - {2, 8, 12, 33}
9.15 Начнем с пустого циклического двусвязного списка целых. Введите 10
целых, вставляя положительные числа непосредственно справа от
заголовка, а отрицательные числа — слева. Распечатайте этот список.
Разделите список на два односвязных, содержащих положительные и
отрицательные числа, соответственно. Распечатайте каждый список.
9.16 Это упражнение изменяет класс Window из раздела 9.10. Добавьте
метод Save All. Он должен проходить список окон от переднего окна до
заднего и выводить заголовок каждого окна и сообщение Заголовок:
<window-3amnoBOK>. Если окно в текущий момент является окном без
заголовка (Untitled), выдайте запрос на ввод заголовка.
глава
ю
Рекурсия
10.1. Понятие рекурсии
10.2. Построение рекурсивных функций
10.3. Рекурсивный код и стек времени
исполнения
10.4. Решение задач с помощью
рекурсии
10.5. Оценка рекурсии
Письменные упражнения
Упражнения по программированию
Рекурсия является важным инструментом решения вычислительных и
математических задач. Она широко используется для определения синтаксиса
языков программирования, а также в структурах данных при разработке
алгоритмов сортировки и поиска для списков и деревьев. Математики
применяют рекурсию в комбинаторике для разного рода подсчетов и вычисления
вероятностей. Рекурсия — важный раздел, имеющий теоретическое и
практическое применение в общей теории алгоритмов, моделях исследования
операций, теории игр и теории графов.
В данной главе мы даем общее введение в рекурсию и иллюстрируем ее
применение различными приложениям. В следующих главах рекурсия будет
использоваться для изучения деревьев и сортировки.
10.1. Понятие рекурсии
Для большинства людей рекурсивное мышление не является характерным.
Если вас, допустим, попросят определить степенную функцию хп, где х —
действительное число, an — неотрицательное целое, то типичным ответом
будет следующий:
хп = х * х * х * ... * х * х
I I
п множителей
Вот, например, различные значения степеней двойки:
2° = 1 //по определению
21 = 2
22 . 2 * 2 = 4
23 =2*2*2=8
24 = 2*2*2*2 = 16
Функция S(n) вычисляет сумму первых п положительных целых — задача,
которая решается путем многократного сложения.
п
S(n)=]Ti = l + 2 + 3+...+ n-1 + п
1
Например, для S(10) мы складываем первые 10 целых, чтобы получить
ответ 55:
ю
S(10) = £i = l + 2 + 3+...+9 + 10=55
l
Если мы применим этот же алгоритм для вычисления S(ll), процесс
повторит все эти сложения. Более практичным подходом было бы использовать
предыдущий результат для S(10), а затем добавить к нему 11, чтобы получить
ответ S(ll) = 66:
11
S(ll) = £ i = S(10) + 11 = 55 + 11 = 66
l
При таком подходе для получения ответа используется предыдущий
результат вычислений. Мы называем это рекурсивным процессом.
Вернемся к степенной функции и представим ее с помощью рекурсивного
процесса. Подсчитывая последовательные степени двойки, мы заметили, что
предыдущее значение может быть использовано для вычисления следующего.
Например,
23 =2* 22 =2*4=8
24 * 2 * 23 - 2 * 8 - 16
Поскольку мы имеем начальную степень двойки (2° = 1), последующие
ее степени есть всего лишь удвоение предыдущего значения. Процесс
использования меньшей степени для вычисления очередной приводит к
рекурсивному определению степенной функции. Для действительного х значение
хп определяется как
' 1, при п = О
хп = |
х * х*""1*, при п > О
Похожее рекурсивное определение описывает функцию S(n), дающую
сумму первых п целых чисел. Для простого случая S(l) сумма равна 1.
Сумма S(n) может быть получена из S(n-l):
{1, при п = 1
n + S(n-l), при п > 1
Рекурсия имеет место, когда вы решаете какую-то задачу посредством
разбиения ее на меньшие подзадачи, выполняемые с помощью одного и того
же алгоритма. Процесс разбиения завершается, когда мы достигаем
простейших возможных решаемых подзадач. Мы называем эти задачи условиями
останова. Рекурсия действует по принципу "разделяй и властвуй".
Алгоритм определен рекурсивно, если это определение состоит из
1. Одного или нескольких условий останова, которые могут быть
вычислены для определенных параметров.
2. Шага рекурсии, в котором текущее значение в алгоритме может быть
определено в терминах предыдущего значения. В конечном итоге шаг
рекурсии должен приводить к условиям останова.
Например, рекурсивное определение степенной функции имеет
единственное условие останова для случая п = 0 (х° =1). Шаг рекурсии описывает
общий случай
хп = х * х&л\ при п > О
Рекурсивные определения
В языках программирования применяются разнообразные рекурсивные
методы определения синтаксиса. Большинство читателей знакомо с
синтаксическими диаграммами. Приведенная ниже диаграмма описывает
идентификатор (identifier), который состоит из начальной буквы и необязательно
следующей за ней цепочки букв и цифр. Например, class, float и var4 —
допустимые идентификаторы, которые могут встречаться в программе на
C++, в то время как Х++ и 2team идентификаторами не являются.
буква
буква
цифра
Пройдите эту диаграмму слева направо, двигаясь по стрелкам. Во время
движения включайте каждый символ, содержащийся в прямоугольнике.
Например, простейший проход по диаграмме заключается в движении от входа
к выходу через первый прямоугольник "буква". Это соответствует однобуквен-
ному идентификатору, например, A, n, t и т.д. Для каждого из приведенных
ниже идентификаторов описан путь по диаграмме.
Идентификатор
А
XY3
7А
Путь
Войти в прямоугольник "буква (А)", выйти из диаграммы.
Войти в прямоугольник "буква (X)", пройти по стрелке через
прямоугольник "буква (Y)", пройти через прямоугольник "цифра
(3)", выйти из диаграммы.
Недопустимый идентификатор; нет выхода из диаграммы.
Несмотря на то, что синтаксические диаграммы эффективны для описания
некоторых языков, синтаксис фактически всех языков программирования
описывается с помощью рекурсивной нотации, называемой формой Бэкуса-
Наура (Bakus-Naur Form, BNF). Она была разработана для определения
Алгола 60 и состоит из правил подстановки, определяющих, как
нетерминальный символ может быть замещен другим нетерминальным или терминальным
символом. В правилах подстановки используется знак "|" для разделения
альтернативных подстановок. Нетерминальные символы заключены в
угловые скобки "о" и представляют собой такие языковые конструкции, как
идентификаторы и выражения. Терминальные символы определяют
фактические знаки в языке. Например, BNF-определение идентификатора
представляется приведенным ниже правилом. Символ "идентификатор" —
нетерминальный символ, расположенный слева от оператора "::=".
<идентификатор> ::- <буква> | <идентификатор> <буква> |
<идентификатор> <цифра>
<буква> ::-a|b|c|d|e|f|g|h|i|j|k|l|m|n|o|p|q|r|s|t|u|v|w|x|y|z
<цифра> ::= 0|1|2|3|4|5|6|7|8|9
Эти правила указывают, что идентификатор есть буква или буква с
последующей цепочкой букв или цифр. Обратите внимание, что идентификатор
определяется в терминах самого себя, поэтому его определение рекурсивно.
Интерпретация рекурсивных определений является естественным
применением для рекурсивных функций. Например, некоторые компиляторы
используют для трансляции программ в машинный код BNF-определение
грамматики языка и алгоритмы рекурсивного спуска. Различные правила
подстановки кодируются как функции, которые могут завершаться вызовом
самих себя или других правил. Процесс может заключать в себе косвенную
рекурсию (inderect recursion), когда, например, правило Р вызывает правило
Q, которое завершается вызовом правила Р.
Пример 10.1
Упрощенные арифметические выражения, допускающие только
бинарные операторы +, -, * и /, имеют следующую BNF-формулировку:
<выражекие> ::= <терм> + <терм> | <терм> - <терм> | <терм>
<терм> : :* <множитель> * <множитель> j <множитель> / <множитель> | <множитель>
<множитель> ::* (<выражение>) j <буква> | <цифра>
Примерами выражений являются:
А + 5; В*С + D; 2*(3+4+5); (A+B*C)/D
Эти правила применяют косвенную рекурсию. Например, выражение
может быть термом, который может быть множителем, который может
быть выражением, заключенным в скобки. Следовательно, выражение
косвенно определено в терминах самого себя.
Рекурсивные задачи
Сила рекурсии обеспечивает весьма простые и изящные решения ряда
проблем. Приведем обзор задач и методов их решения, использующих рекурсию.
Ханойская башня. Любители головоломок долго были увлечены задачей о
ханойской башне.
Шпиль А
Шпиль В
Шпиль С
Согласно легенде, у жрецов храма Брахмы есть медная платформа с тремя
алмазными шпилями. На одном шпиле А нанизано 64 золотых диска, каждый
из которых немного меньше того, что под ним. Конец света наступит, когда
жрецы переместят диски со шпиля А на шпиль С. Однако задача имеет весьма
специфические условия. За один раз можно перемещать только один диск, и
при этом ни разу диск большего размера не должен лечь на диск меньшего
размера. Несомненно, жрецы все еще работают, так как задача включает в себя
264 — 1 хода. Если тратить по одной секунде на ход, то потребуется 500
миллиардов лет.
Ханойская башня — тяжелое испытание для решателя головоломок. Между
тем опытный программист видит быстрое рекурсивное решение. Мы
проиллюстрируем проблему на шпилях, содержащих шесть дисков. Начнем, сосредо-
Шпиль А
Шпиль В
Шпиль С
точившись на перемещении верхних пяти дисков на шпиль В и последующего
перемещения самого большого диска на шпиль С.
Осталась более простая задача перемещения только пяти дисков со шпиля
В на шпиль С. Применяя тот же самый алгоритм, сосредоточим внимание на
верхних четырех дисках и вытащим их из стопки. Затем перенесем самый
большой диск со шпиля В на шпиль С. Осталась еще меньшая стопка из
четырех дисков. Процесс продолжается до тех пор, пока не останется один
диск, который в конечном счете перемещается на шпиль С.
Шпиль А
Шпиль В
Шпиль С
Очевидно, что данное решение носит рекурсивный характер. Проблема
разбивается на последовательность меньших подзадач одного и того же типа.
Условием останова является простая задача перемещения одного диска.
Лабиринт. Каждый знаком с проблемой перехода через лабиринт с
возможностью бесконечного числа альтернатив, приводящих в тупики и
окончательному запутыванию. Психологи используют лабиринт с приманкой в виде сыра
для исследования поведенческих моделей у крыс. Мы полагаем, что неудачи
зверька в деле поиска сыра следуют из его неспособности мыслить рекурсивно.
Рассмотрите рис. 10.1 и обдумайте стратегию, гарантирующую надежный
способ пройти до "Конца". Мы представляем важное средство решения задач,
называемое возвратами (backtracking).
Конец
Начало
Рис. 10.1 Обход лабиринта
Лабиринт есть связанное множество перекрестков. Каждый перекресток
имеет три связанных с ним значения: налево, прямо и направо. Если некоторое
значение равно 1, то движение в данном направлении возможно. Нуль
показывает, что движение в данном направлении заблокировано. Множество из
трех нулей представляет мертвую точку, или тупик. Проход по лабиринту
считается успешным, когда мы достигаем точки "Конец". Процесс включает
ряд рекурсивных шагов. В каждом перекрестке мы исследуем наши варианты.
Если возможно, то сначала идем налево. Достигнув очередного перекрестка,
мы снова рассматриваем свои варианты и пытаемся идти налево. Если выбор
левого направления заводит в тупик, мы возвращаемся и выбираем движение
прямо, если это направление не заблокировано. Если этот выбор заводит в
тупик, мы возвращаемся и идем направо. Если все альтернативы движения из
данного перекрестка ведут в тупики, мы возвращаемся к предыдущему
перекрестку и делаем новый выбор. Эта довольно скучная и консервативная стратегия не
побьет рекорды эффективности, но гарантирует, что в конце концов мы найдем
выход из лабиринта. Рассмотрим первые 10 вариантов в нашем лабиринте.
Комбинаторика. Рекурсия находит широкое применение в
комбинаторике — разделе математики, касающемся подсчета объектов. Предположим, мы
бросаем три игральные кости и записываем общий итог. Одним из вопросов
комбинаторики является количество различных способов, которыми можно
набрать 8 очков. Рекурсивный подход пытается свести проблему к постепенно
упрощающимся задачам и использовать эти результаты для решения более
сложной проблемы. В нашем случае три игральные кости считаются сложной
проблемой, и мы фокусируем внимание на более простом случае бросания двух
игральных костей. Мы предполагаем, что можем взять две игральные кости и
любой результат N в диапазоне от 2 до 12 и определить все различные способы
выпадения N. В случае трех костей, дающих в сумме 8, мы бросаем первую
кость и записываем значение в таблице вместе со значением N,
представляющим оставшееся количество очков, которое должно быть набрано двумя
следующими костями. Например, если на первой кости выпало 3, следующие две
должны дать в сумме 5. Используя наши навыки с двумя игральными костями,
определяем, что есть четыре возможных исхода бросания двух костей, дающих
5. Объединяя эти исходы с тройкой на первой кости, мы имеем как минимум
четыре способа получить восьмерку на трех костях.
В следующей таблице перечислены все 15 способов выпадения восьмерки
на трех игральных костях. Поскольку количество бросаний невелико, мы
можем перечислить все варианты, не прибегая к рекурсии. Мы проверим по-
хожые случаи, когда решение с помощью таблицы практически
неосуществимо.
Перекресток Выбор
1:
2:
3:
7:
3:
4:
6:
4:
5:
2:
прямо
налево
налево
тупик; вернуться к 3
прямо
прямо
тупик; вернуться к 4
прямо
тупик; вернуться к 4, 3, 2
прямо
• ■ •
Результирующий
перекресток
2
3
7
3
4
б
4
5
2
8
Кость1
1
2
3
4
5
б
№
7
б
5
4
3
2
Различные исходы на двух костях
(3.3) (4,2) (2,4) (5,1) (1,5)
(4,1) (3,2) (1,4) (2,3)
(3,1) (2,2) (1,3)
(2,1) (1,2)
(1.1)
Количество
0
5
4
3
2
1
15
Чтобы подсчитать вероятность выпадения восьмерки на трех костях,
следует разделить 15 на общее число различных исходов бросания трех костей.
Это число равно б3 = 216. Таким образом, вероятность выбросить восьмерку
равна 15/216, или 7%.
Синтаксические деревья. На этапе нашего изучения стеков вводятся
инфиксный и постфиксный (RPN) форматы записи арифметических выражений.
Эти форматы можно сравнить между собой, запоминая операторы и операнды
в виде узлов бинарного дерева. Операнды помещаются в листовые узлы на
конце ветви. Предшествование оператора отражается его уровнем на дереве.
Оператор на более глубоком уровне дерева должен быть выполнен до
оператора менее глубокого уровня. Например, выражение
а * b + c/d
представляется соответствующим деревом с семью узлами:
Как и в случае с лабиринтом, мы можем разработать методы рекурсивного
прохождения, выбирающие те или иные варианты в каждом узле дерева.
Предположим, мы руководствуемся следующими правилами:
Если возможно, идти по левой ветви.
Выписать значение, содержащееся в узле.
Если возможно, идти по правой ветви.
Поскольку мы выписываем значение узла в между директивами
прохождения, назовем это симметричным прохождением (inorder scan). Ниже
приводится последовательность прохождения узлов синтаксического дерева1.
Условие останова возникает, когда нельзя пройти ни по левой ни по правой
ветви.
1 В книге Д.Кнута "Искусство программирования для ЭВМ", т.1, Основные алгоритмы, этот
метод называется концевым от оригинального enorder. — Прим. ред.
Действие
Начать с корня
Идти по левой ветви
Идти по левой ветви
(нет левой ветви из а)
Выписать значение
(нет правой ветви из а)
(возврат к узлу *; движение влево завершено)
Выписать значение
Идти по правой ветви
(нет левой ветви из Ь)
Выписать значение
(нет правой ветви из Ь)
(возврат к узлу +; движение влево завершено)
Выписать значение
Идти по правой ветви
Идти по левой ветви
(нет левой ветви из с)
Выписать значение
(нет правой ветви из с)
(возврат к узлу /; движение влево завершено)
Выписать значение
Идти по правой ветви
(нет левой ветви из d)
Выписать значение
(нет правой ветви из d)
Результирующий узел
+
*
а
b
/
с
d
Вывод
а
а*
а*Ь
а*Ь+
а*Ь+с
а*Ь+с/
a*b+c/d
После того как все узлы пройдены, проход завершается и мы имеем
инфиксную форму выражения.
Другой порядок рекурсивного прохождения определяется следующими
правилами:
Если возможно, идти по левой ветви.
Если возможно, идти по правой ветви.
Выписать значение, содержащееся в узле.
Поскольку выписывание значения узла происходит после обеих директив
обхода, назовем это обратным прохождением (postorder scan). В результате
узлы будут выписаны в следующем порядке:
a b * с d / +
Это постфиксная, или RPN-форма записи выражения.
Рекурсия является мощным средством определения и прохождения
деревьев. Мы будем использовать разнообразные рекурсивные алгоритмы в гл. 11.
В гл. 13 разработаем итерационные эквиваленты этих алгоритмов для создания
итераторов дерева.
10.2. Построение рекурсивных функций
Структура рекурсивной функции иллюстрируется задачей вычисления
факториала неотрицательных целых чисел. Мы рассмотрим эту структуру,
разработав как рекурсивное, так и итерационное определение функции.
Факториал неотрицательных целых чисел, Factorial(N), определяется как
произведение всех положительных целых чисел, меньших или равных N.
Число, обозначаемое NI, представляется следующим образом:
N! = N * (N-l) * (N-2) * ... * 2 * 1
Например,
Factorial (4) =41=4*3*2*1 = 24
Factorial (6) =61=6*5*4*3*2*1 = 720
Factorial (1) = 1! = 1
Factorial(0) = 0! = 1 //по определению
Итерационная версия этой функции реализуется посредством возврата 1, если
п=0, и циклом перемножения членов последовательности в противном случае.
// итерационная форма факториала
long Factorial(long n)
{
int prod =1, i;
// для n == 0 вернуть prod = 1, в противном случае
// вычислить prod = 1*2*..*n
if (n > 0)
for (i = 1; i <= n; i++)
prod *= i;
return prod;
}
Рассмотрение членов последовательности в различных примерах
факториала приводит к рекурсивному определению функции Factorial(N). Для 41 первое
число равно 4, а остальные — (3*2*1) — равны 31. То же справедливо и для
61, являющегося произведением 6 и 5!.
Рекурсивное определение любого неотрицательного целого п включает в
себя как условие останова, так и шаг рекурсии:
{1, при п = 0 // условие останова
п * (п-1)!, при п > 1 // шаг рекурсии
Можно представить себе функцию Factorial(n) как n-машину,
вычисляющую п! путем п * (п-1)!. Чтобы машина функционировала, она должна быть
связана с рядом других машин, передающих информацию вперед и назад.
0-машине ассистирует другая машина. Опишем необходимые связи и
взаимодействие машин для 4-машины, вычисляющей 4!.
4-машина (4*3!) должна запустить 3-машину
3-машина (3*2!) должна запустить 2-машину
2-машина (2*1!) должна запустить 1-машину
1-машина (1*0!) должна запустить 0-машину
Работа отдельных машин описывается на рис. 10.2. Как только
активизируется 0-машина, мы сразу в результате получаем единицу, которая
передается в 1-машину. У 1-машины теперь есть информация, чтобы завершить
умножение и передать результат 2-машине.
1*01=1*1=1
Необходимые передаваемые значения становятся доступными
последовательно от 1-машины до 4-машины.
1-машина использует значение 1 из 0-машины и вычисляет 1 * 0! = 1
2-машина использует значение 1 из 1-машины и вычисляет 2 * 1! = 2
3-машина использует значение 2 из 2-машины и вычисляет 3 * 2! = 6
4-машина использует значение 6 из 3-машины и вычисляет 4 * 3! = 24
Начать 3!
Начать 2!
Начать 1!
Начать О!
►
4*(4-1)!
4! = 24
3*<3-1)!
3! = б
1
2*(2-1)!
2! = 2
1*(М)!
1! = 1
О! = 1
Рис 10.2. Факториал-машины
При вычислении N! нужно четко различать случай 0!, представляющий
условие останова, и другие случаи (N>0), представляющие шаги рекурсии. Это
различие является фундаментальным для построения рекурсивного алгоритма.
Программист реализует распознавание данной ситуации с помощью оператора
IF ... ELSE. Блок IF обрабатывает условие останова, а блок ELSE выполняет
шаг рекурсии. Для факториала блок IF вычисляет единственное условие
останова N = 0 и возвращает единицу. Блок ELSE выполняет шаг рекурсии,
вычисляя выражение N * (N-l)I, и возвращает результат.
// Рекурсивная форма факториала
long Factorial (long n)
{
// условием останова является п == 0
if (n =*= 0)
return 1;
else
// шаг рекурсии
return n * Factorial (п-1);
}
На рис. 10.3 описана последовательность вызовов функции при вычислении
Factorial(4). Предположим, что первоначально функция вызывается из главной
программы. Внутри блока функции выполняется оператор ELSE с параметрами
3, 2, 1 и 0. На последнем вызове выполняется оператор IF с п = 0. По
достижении условия останова рекурсивная цепочка вызовов прерывается и начина-
Параметр
0
Параметр
1
Параметр
2
Параметр
3
Параметр
4
Действие
Вычислить: 0! = 1
Действие
Вычислить: 1* Factorial (0)
Действие
Вычислить: 2* Factorial (1)
Действие
Вычислить: 3* Factorial (2)
Действие
Вычислить: 4* Factorial (3)
Возврат
1
Возврат
1
Возврат
2
Возврат
6
Возврат
24
Передаваемые
параметры
Возвращаемые
значения
Главная программа
Рис. 10.3. Набор факториалов
ется серия вычислений в порядке 1*1, 2*1, 3*2 и 4*6. Последнее значение 24
возвращается в главную программу.
Пример 10.2
Конструкция IF..ELSE различает условие останова и шаг рекурсии
при вычислении степенной функции и суммы из раздела 10.1. Для
степенной функции значение power(0,0) не определено, и в этом случае
выдается сообщение об ошибке.
1. Степенная функция (рекурсивная форма)
// вычислить х в степени п, используя рекурсию
float power(float x, int n)
{
// условием останова является п =- 0
if (n «• 0)
// 0 в степени 0 не определен
if (х — 0)
{
cerr « "power(0,0) не определено" « endl;
exit(1);
}
else
// x в степени 0 равен 1
return 1;
else
// шаг рекурсии:
// power(х, n) = х * power(x, n-1)
return x * power(x, n-1);
)
2. Функция суммирования (рекурсивная форма)
// вычислить 1+2+ ... +п рекурсивно
int S(int n)
{
// условием останова является п -- 1
if (n ==» 1)
return 1;
else
// шаг рекурсии: S(n) = n + S(n-l)
return n + S(n-1);
}
Программа 10.1. Использование функции Factorial
Эта программа иллюстрирует рекурсивную форму факториальной
функции. Пользователь вводит четыре целых числа и получает их факториалы.
#include <iostream.h>
// вычислить п! « п (п-1) (п-2) ... (2) (1) при 0! = 1 рекурсивно
long Factorial(long n)
{
// если n == 0, то 0! = 1; иначе п! *= п*(п-1) !
if (n =»« 0)
return 1;
else
return n * Factorial(n-1);
}
void main (void)
{
int i, n;
// ввести 4 положительных числа и вычислить п! для каждого из них
cout « "Введите 4 положительных целых числа: ";
for (i - 0; i < 4; i++)
{
cin » n; cout « n « " !- "« Factorial (n) « end;
}
}
/* <Выполнение программы 10.1>
Введите 4 положительных целых числа: 0 7 14
0! - 1
7! - 5040
1! = 1
4! = 24
V
10.3. Рекурсивный код и стек времени
исполнения
Функция — это последовательность инструкций, выполняемых в ответ на
ее вызов. Процесс выполнения начинается с того, что вызывающий блок
заполняет активизирующую запись (activation record), которая включает
список параметров и местоположение следующей инструкции, подлежащей
выполнению после возврата из блока.
Параметры
<фактические параметры>
Местоположение
<следующая инструкция>
Активизирующая запись
При вызове функции данные из активизирующей записи заталкиваются
в стек, организуемый системой (стек времени исполнения). Данные
объединяются с локальными переменными и образуют активизирующий фрейм,
доступный функции.
Активизирующая
запись
Локальные переменные
Адрес возврата
Параметры
Активизирующий
фрейм
При выходе из функции устанавливается местоположение следующей
инструкции (рис. 10.4), а данные в стеке, соответствующие активизирующей
записи, уничтожаются. Рекурсивная функция повторно вызывает саму себя,
используя всякий раз модифицированный список параметров. При этом
последовательность активизирующих записей заталкивается в стек до тех пор,
пока не будет достигнуто условие останова. Последовательное выталкивание
этих записей и дает нам наше рекурсивное решение. Функция вычисления
факториала иллюстрирует использование активизирующих записей.
Вызывающий блок
Функциональный блок
<следующая инструкция>
F(<cnncoK параметров>):
<Возврат>
Рис. 10.4. Вызов функции и возврат
Стек времени исполнения
С помощью примера вычисления факториала от 4 мы проиллюстрируем
использование активизирующих записей и стека, создаваемого во время
выполнения рекурсивной функции. Начальный вызов факториала производится
из главной программы. После выполнения функции управление возвращается
в точку RetLockl, где переменной N присваивается значение 24(4!):
void main (void)
{
int N;
// поместить в стек запись с помощью вызова FACTORIAL(4)
// RetLockl — адрес присвоения N == FACTORIAL(4)
N = FACTORIAL(4);
RetLockl *
}
Рекурсивные вызовы в функции FACTORIAL возвращают управление в
точку RetLock2, где вычисляется произведение n * (n-l)I. Результат
вычисления запоминается в переменной temp, чтобы помочь читателю проследить код
и продемонстрировать стек времени исполнения:
long FACTORIAL(long n)
{
int temp;
if (n == 0)
return 1; // вытолкнуть из стека активизирующую запись
else
{
// поместить в стек активизирующую запись с помощью вызова FACTORIAL(n-1)
// Retlock2 - адрес вычисления п * FACTORIAL(n-1)
temp = n * FACTORIAL(n-1);
RetLock2 1
return temp; // вытолкнуть из стека активизирующую запись
}
}
Вызывающий блок
FACTORIALO)
FACTORIALO)
FACTORIALO)
FACTORIALO)
Главная программа
Параметр о
Параметр 1
Параметр 2
Параметр 3
Параметр 4
Возврат: RetLock2
Возврат RetLock2
Возврат. RetLock2
Возврат RetLock2
Возврат RetLockl
Рис 10.5. Стек времени выполнения
Для функции FACTORIAL активизирующая запись имеет два поля.
Выполнение FACTORIAL(4) инициирует последовательность из пяти
вызовов. На рис. 10.5 показаны активизирующие записи для каждого вызова.
Записи входят в стек снизу вверх вместе с вызовом из главной процедуры,
занимая нижнюю часть стека.
Параметры
long n
Местоположение
<следующая инструкция>
Активизирующая запись
При обращении к функции FACTORIAL с параметром 0 возникает условие
останова, и начинается выполнение последовательности операторов возврата.
Когда из стека выталкивается самая верхняя активизирующая запись,
управление передается в точку возврата. Очистка стека от активизирующих
записей описывается следующими операциями.
Параметр
0
1
2
3
4
Адрес возврата
RetLoc2
RetLoc2
RetLoc2
RetLoc2
RetLod
Инструкции возврата
RetLoc2 temp = 1 * 1; // 1 from FACTORIAL(O)
return temp; // temp ~ 1;
RetLoc2 temp = 2 * 1; // 1 from FACTORIALO)
return temp; // temp = 2;
RetLoc2 temp = 3 * 2; // 2 from FACTORIAL(2)
return temp; // temp = 6;
RetLoc2 temp = 4 * 6; // 6 from FACTORIALO)
return temp; // temp = 24;
RetLoc2 N = FACTORIALS); // возврат к главной процедуре
10.4. Решение задач с помощью рекурсии
Многие вычислительные задачи имеют весьма простую и изящную
формулировку, которая непосредственно переводится в рекурсивный код. В раз-
деле ЮЛ рассмотрен ряд примеров, включая Ханойскую башню, лабиринт
и комбинаторику. В этом разделе мы расширим диапазон примеров и
рассмотрим рекурсивное определение алгоритма бинарного поиска, решение
некоторых комбинаторных задач, разгадку Ханойской башни, а также
сконструируем класс Maze для работы с общими задачами лабиринтного типа.
Бинарный поиск
При бинарном поиске берется некоторый ключ и просматривается
упорядоченный массив из N элементов на предмет совпадения с этим ключом.
Функция возвращает индекс совпавшего с ключом элемента или -1 при
отсутствии такового. Алгоритм бинарного поиска может быть описан
рекурсивно.
Допустим, отсортированный список А характеризуется нижним
граничным индексом low и верхним — high. Имея ключ, мы начинаем искать
совпадение в середине списка (индекс mid).
mid - {low+high)/2 Сравнить A[mid] с ключом
Если совпадение произошло, мы имеем условие останова, что позволяет
нам прекратить поиск и возвратить индекс mid.
Если совпадение не происходит, можно воспользоваться тем фактом, что
список упорядочен, и ограничить диапазон поиска "нижним подсписком"
(слева от mid) или "верхним подсписком" (справа от mid).
Если ключ < A[mid], совпадение может произойти только в левой половине
списка в диапазоне индексов от low до mid-1.
Если ключ > A[mid], совпадение может произойти только в правой
половине списка в диапазоне индексов от mid+1 до high.
Шаг рекурсии направляет бинарный поиск для продолжения в один из
подсписков. Рекурсивный процесс просматривает все меньшие и меньшие
списки. В конце концов поиск заканчивается неудачей, если подсписки
исчезли. Это происходит тогда, когда верхний предел списка становится меньше
чем нижний предел. Условие low>high — второе условие останова. В этом
случае алгоритм возвращает -1.
Бинарный поиск (рекурсивная форма). В шаблонной версии бинарного
поиска в качестве параметров используется массив элементов типа Т,
значение ключа, а также верхний и нижний граничные индексы. Оператор IF
обрабатывает два условия останова: 1) совпадение произошло; 2) ключевого
значения нет в списке. В блоке ELSE оператора IF выполняется шаг рекурсии,
который направляет дальнейший поиск в левый (ключ<А[пш1]) или в правый
подсписок (ключ>А[п^]). Тот же алгоритм применяется по принципу
"разделяй и властвуй" к последовательности все меньших интервалов, пока не
произойдет успех (совпадение) или неудача.
// рекурсивная версия бинарного поиска ключевого значения
//в упорядоченном массиве А
template <class T>
int BinSearch(T А[], int low, int high, T key)
{
int mid;
T midvalue;
// условие останова: ключ не найден
if (low > high)
return (-1);
// сравнить ключ с элементом в середине списка.
// если совпадения нет, разделить на подсписки.
// применить процедуру бинарного поиска к подходящему подсписку
else
{
mid* (low+high)/2;
midvalue * A[mid];
// условие останова: ключ найден
if (key « midvalue)
return mid; // ключ найден по индексу mid
// просматривать левый подсписок, если key < midvalue;
// в противном случае — правый подсписок
else if (key < midvalue)
// шаг рекурсии
return BinSearch(A, low, mid-1, key);
else
// шаг рекурсии
return BinSearcMA, mid+1, high, key);
}
}
Программа 10.2. Тестирование функции бинарного поиска
Эта программа считывает список слов из файла vocab.dat в массив
Wordlist. Список слов отсортирован в алфавитном порядке. Запрашивается
ключевое слово. Если оно будет найдено, печатается его индекс в списке.
В противном случае выдается сообщение об отсутствии ключевого слова
в данном списке. Функция поиска находится в файле search.h.
#include <iostream.h>
#include <fstream.h>
#include "strclass.h"
#include "search.h"
void main(void)
{
// поиск производится в массиве упорядоченных строк из потока fin
String wordlist[50];
ifstream fin;
String word;
int pos, i;
// открыть файл vocab.dat, содержащий упорядоченные слова
fin.open("vocab.dat");
// читать до конца файла и инициализировать wordlist
i = 0;
while(fin » wordlist[i])
i++;
// запросить слово
cout « "Введите слово: ";
cin » word;
// бинарный поиск введенного слова
if ((pos = BinSearch(wordlist,0,i,word)) != -1)
cout « word « " есть в списке по индексу "
« pos « endl;
else
cout « word « " отсутствует в списке." « endl;
)
/*
<Входной файл vocab.dat>
array
class
file
struct
template
vector
<1-й прогон программы 10.2>
Введите слово: template
template есть в списке по индексу 4
<2-й прогон программы 10.2>
Введите слово: mark
mark отсутствует в списке.
*/
Комбинаторика: задача о комитетах
К комбинаторным относятся алгоритмы подсчета числа способов
наступления того или иного события. В классической задаче о комитетах требуется
определить число C(N,K), где N и К — неотрицательные целые, равное
количеству способов формирования комитетов по К членов в каждом из
общего списка N людей.
Исследуем решение общей задачи на примере cN = 5hK = 2. Этот
упрощенный случай можно применить к маленькой организации и быстро
составить исчерпывающий перечень десяти различных вариантов. Обозначим
членов этой организации как А, В, С, D и Е. Возможные комитеты
изображены вокруг группы людей.
Этот подход не годится для большего числа членов, и нам нужно
использовать стратегию "разделяй и властвуй", чтобы разбить задачу на более
простые подзадачи.
Упростим проблему, исключив член А из общей группы. Теперь осталось
четыре человека: В, С, D и Е.
Подзадача 1:
Попросите четверку оставшихся сформировать все возможные комитеты
по 2 человека. Получается шесть различных подкомитетов.
Список 1: (В,С), (B,D), (B,E), (C,D), (C,E), (D,E)
Заметьте, что ни один из новых комитетов не включает отсутствующий
член А.
Подзадача 2:
Попросите четырех членов группы сформировать все возможные
комитеты по одному человеку.
(В), (С), (D), (Е)
В каждом из этих комитетов не хватает одного человека. Добавим в
них член А.
Список 2: (А,В), (А,С), (A,D), (A,E)
Требуется, чтобы комитеты из двух человек, сформированные в подзадачах
1 и 2, охватили все возможные комитеты первоначальной задачи. Приведенный
ниже рисунок описывает оба случая.
Подзадача 1
Комитеты из К = 2 членов
Подзадача 2
Комитеты из К = 1 членов
Шесть групп в списке 1 представляют все комитеты, не содержащие член
А. Четыре группы в списке 2 представляют все комитеты, содержащие член
А. Поскольку комитет должен либо содержать, либо не содержать А, десять
комитетов в двух списках представляют собой все возможные варианты
комитетов по два человека.
Разработка алгоритма. В анализе по принципу "разделяй и властвуй"
(рекурсивном) мы имеем дело с общей проблемой подсчета количества комитетов
из К членов, которые можно сформировать из N людей. Удалим персону А и
рассмотрим оставшиеся N-1 человек. Общее число комитетов складывается из
числа комитетов по К членов, выбранных из N-1 человек (член А не
включается), и числа комитетов по К-1 членов, выбранных из N-1 человек (включая
А). Первая группа насчитывает C(N-1,K), а вторая — C(N-1,K-1) вариантов.
Меньший комитет из К-1 членов во второй группе расширится до комитета из
К членов, если член А присоединится к этой группе.
C(N,K) = C(N-1,K-1) + C(N-1,K) // шаг рекурсии
Условия останова состоят из нескольких экстремальных случаев, которые
можно проанализировать непосредственно.
Если К > N, то нет достаточного числа людей для формирования комитетов.
Число возможных комитетов по К членов, сформированных из N человек,
равно нулю.
Если К — 0, то формируется пустой комитет и это можно сделать лишь
одним способом.
Если К = N, все должны оказаться в одном комитете. Это может произойти
только выбором всех членов списка в этот комитет.
C(N,N) = 1 C(N,0) - 1 C(N/K) = 0 при К > N
Объединяя условия останова и шаг рекурсии, можно реализовать
рекурсивную функцию comm(n,k) = C(n,k). Эта функция расположена в файле
comm.h.
// определить число комитетов из к членов,
// которые можно сформировать из п человек
int comm (int n, int k)
{
// условие останова: слишком мало народа
if (k > n)
return 0;
// условие останова: в комитете все или никого
else if (n -« к || к — 0)
return 1;
else
// шаг рекурсии: все комитеты без персоны А
// плюс все комитеты с персоной А
return comm(n-l,k) + comm(n-l, k-1);
}
Программа 10.3. Формирование комитетов
Пользователь вводит число кандидатов п и число человек в комитете
к. На выходе выдается число С(п,к) возможных вариантов комитетов.
♦include <iostream.h>
#include "comm.h"
void main (void)
<
int n, k;
cout « "Введите число кандидатов и число членов комитета: ";
cin » n » к;
cout « "Число возможных комитетов: "
« comm(n,k) « endl;
}
/*
<Прогон Н»1 программы 10.3>
Введите число кандидатов и число членов комитета: 10 4
Число возможных комитетов: 210
<Прогон №2 программы 10.3>
Введите число кандидатов и число членов комитета: 9 0
Число возможных комитетов: 1
*/
Комбинаторика: перестановки
Многие интересные рекурсивные алгоритмы предполагают наличие
массивов. В этом разделе мы рассмотрим задачу генерации всех перестановок
из N элементов. В алгоритме предусматривается передача массива по
значению, а поскольку в C++ все массивы передаются по адресу, должно быть
выполнено копирование массива.
Перестановка (permutation) из N элементов (1, 2, ..., N) есть
упорядоченное расположение этих элементов. Для N = 3 (1 3 2), (3 2 1) (12 3) —
различные перестановки. В комбинаторике установлено, что число
перестановок равно N!. Это интуитивно понятно, если взглянуть на отдельные
позиции в перестановке. Для позиции 1 существуют N вариантов, так как все
N элементов доступны. Для позиции 2 имеются N-1 вариантов, так как один
элемент используется для позиции 1. Число вариантов уменьшается на
единицу по мере продвижения по позициям списка.
Число вариантов
Поз 1 Поз 2 Поз 3 Поз п - 1 Поз п
Общее число перестановок есть произведение числа вариантов в каждой
позиции.
Permulation(N) = N * (N-1) * (N-2) * ... * 2 * 1 = N!
Более интересный рекурсивный алгоритм генерирует перечень всех
перестановок из N элементов для N >= 1. Для демонстрационных целей
сформируем вручную 24 (4!) перестановки из четырех элементов. Перестановки
с одинаковыми первыми элементами записываются в отдельный столбец.
Каждый столбец в дальнейшем делится на три пары с одинаковыми вторыми
элементами.
1
1234
1243
1324
1342
1423
1432
2
2134
2143
2314
2341
2413
2431
3
3124
3142
3214
3241
3412
3421
4
4123
4132
4213
4231
4312
4321
Алгоритм вычисления числа перестановок иллюстрируется иерархическим
деревом, которое содержит упорядоченные пути, соответствующие
перестановкам. В исходном положении имеется четыре варианта — 1, 2, 3 и 4 —
соответствующие четырем столбцам. По мере продвижения вниз по дереву
низ лежащие уровни разделяются на 3, 2 и 1 элемент, соответственно. Общее
число путей (перестановок) равно
4*3*2*1 = 4!
Алгоритм генерации всех перестановок моделирует проход по путям
дерева. Продвигаясь от уровня к уровню, мы тем самым указываем очередную
позицию в перестановке. Этот процесс представляет собой шаг рекурсии.
Индекс 0:
Итерационный процесс проверяет все возможные первые элементы для
индекса 0. В нашем примере существует N=4 возможных первых элемента.
Индекс 1:
1
2
3
4
На следующем уровне дерева каждый узел дает начало N-1 узлам,
содержащим N-1 отличных от первого элементов. Например, узел 1
соответствует перестановкам, которые начинаются с единицы в первой (индекс
0) позиции. Путь, ведущий к узлу 2 следующего уровня, соответствует
перестановкам с 1 и 2 в первых двух позициях и т.д. Можно итерационно
определить второй элемент перестановки перебором узлов 2, 3 и 4.
Индекс 2:
1
2
1
3
1
4
На следующем уровне дерева каждый узел разветвляется на два пути,
которые представляют перестановки из двух элементов. Например, в
узле 2 элементами являются [3,4], и их упорядоченными
расположениями являются
Результирующие перестановки из четырех элементов:
Индекс 3:
Перестановки на [3,4]
Поскольку третий член перестановки зафиксирован, последний элемент
определяется однозначно, т.к. перестановка не допускает
повторяющиеся значения. Это становится условием останова. Каждый узел завершает
отдельную перестановку.
Разработка алгоритма. Программа на C++, реализующая этот алгоритм,
запоминает каждую перестановку в виде массива из N элементов. Перед
каждым вызовом рекурсивная функция создает копию этого массива, с тем чтобы
по возвращении из шага рекурсии значения оставались в тех же самых
позициях массива. Помните, что для N = 4 программа должна в конечном итоге
создать 24 различных массива. Вначале мы создаем четыре массива,
содержащих 1, 2, 3 и 4 в своих первых позициях. На следующем уровне каждый из
четырех существующих массивов создает три массива, которые запоминают
первый элемент из базового массива и т.д.
void copy(int х[], int y[], int n)
{
for (int i=0; i<n; i++)
x[i] = y[i];
}
Рекурсивный алгоритм постепенно помещает элементы в массив permlist,
по индексам 0, 1, 2, ..., N-1.
1. Условие останова возникает на индексе N-1. В этот момент N-элемент-
ная перестановка завершается и массив распечатывается.
2. Шаг рекурсии: На шаге рекурсии происходит продвижение вперед по
индексам массива от 0 до N-2.
Для индекса k (0<=k<N-l) первые к элементов массива permlist уже
сформированы. Мы итерационно просматриваем другие элементы и
помещаем их в permlist[k]. Это делается путем обменивания каждого
элемента в оставшейся части списка с числом permlist[k]. Допустим,
N = 4, к = 1 и permlist[k] = 1. Во время итерационных шагов числа
2, 3 и 4 помещаются по индексу 1.
Сдвиг 2 с permlist[1]
Сдвиг 3 с permlist[1]
Сдвиг 4 с permlist[1]
1
I 1
1
2
2
I
3
3
3
I
2
4 I
4 I
4 I
Новый список
Новый список
Новый список
1
2
3
4 I
1
3
2
4 I
1
4
2
3
После каждого чередования результирующий список копируется во
временный список и передается в рекурсивную функцию permute вместе
со следующим индексом и параметром N. На рис. 10.6 показан вызов
permute с permlist[l] == 2.
По индексу 1: поместить 2
12 3 4
Вызвать permute
с индексом 2
По индексу 2
L^
2
: поместить 3
3
4 I
По индексу 3:
сг
2
3
4
Вызвать permute
с индексом 3
Условие останова
Напечатать 12 3 4
По индексу 2
1
2
: поместить 4
4
3 |
По индексу 3:
[ 1
2
4
3 |
Вызвать permute
с индексом 3
Условие останова
Напечатать 12 3 4
Рис. 10.6. Перестановка 1 2 х X
По индексу 1: поместить 3
1 | 3
2
4 |
Вызвать permute
с индексом 3
По индексу 2
1
3
: поместить 3
2
4
По индексу 3:
i 1
3
2
4
Вызвать permute
с индексом 3
Условие останова
Напечатать 12 3 4
По индексу 2
1
3
: поместить 3
4
2 J
По индексу 3:
1
3
4
2
Вызвать permute
с индексом 3
Условие останова
Напечатать 12 3 4
Рис. 10.7. Перестановки 1 3 х х
Перестановки создаются в порядке (1234) и (1243). Рис, 10.7 иллюстрирует
вызов permute, когда в permlist[l] помещается 3. Затем на шаге итерации в
permlist[l] помещается 4, и рекурсивный процесс продолжается с массивом 1423.
Рекурсивная функция Permute
// UpperLimit - максимальное число элементов перестановки
const int UpperLimit = 5;
// копирование п элементов массива у в массив х
void copy(int х[], int y[], int n)
{
for (int i*=0; i<n; i++)
x[i] « y[i];
}
// permlist есть п-элементный массив целых чисел.
// генерировать перестановки элементов, индексы которых находятся в диапазоне
// start <= i <= п-1. по заполнении перестановки распечатывать весь массив.
.// чтобы переставить все п элементов, начинать с start = О
void permute(int permlist[], int start, int n)
{
int tmparr[UpperLimit];
int temp, i;
// условие останова: достигнут последний элемент
if (start « n-1)
{
// распечатать перестановку
for (i=0; i<n; i++)
cout « permlist[i] « " ";
cout « endl;
}
else
// шаг рекурсии: поменять местами permlist[start] и permlist[i]; скопировать
// массив в tmparr и переставить элементы tmparr от start+1 до1конца массива,
for (i=start; i<n; i++)
{
// поменять permlist[i] с permlist[start]
temp = permlist[i];
permlist[i] = permlist[start];
permlist[start] = temp;
// создать новый список и вызвать permute
copy (tmparr, permlist, n);
permute (tmparr, start+1, n);
}
}
Программа 10.4. Перестановки
Эта задача о перестановках запускается с N = 3. Функции копирования
и перестановки хранятся в файле permute.h.
#include <iostream.h>
#include "permute.h"
void main(void)
{
// permlist содержит п чисел, подлежащих перестановке
int permlist[UpperLimit]/
int n, i;
cout « "Введите число в диапазоне от 1 до "
« UpperLimit « ": ";
cin » n;
// инициализировать permlist множеством {1,2, 3, . . . ,n}
for (i=0/ i<n; i++)
permlist[i] = i+1;
cout « endl;
// распечатать перестановки элементов массива permlist по индексам от 0 до п-1
permute(permlist, 0, п);
}
/*
<Выполнение программы 10.4>
Введите число в диапазоне от 1 до 5: 3
12 3
13 2
2 13
2 3 1
3 12
3 2 1
V
Ханойская башня. Задача о ханойской башне, рассмотренная в разделе
10.1, является примером рекурсивного алгоритма, который просто решал
проблему, не углубляясь в детали. В этом разделе для перекладывания дисков
разрабатываются шаги рекурсии и условия останова.
Формулировка задачи. На платформе расположены три стержня:
начальный (start), средний (middle) и конечный (end). На начальный
стержень нанизано N дисков в порядке возрастания размера, т.е. самый
большой диск лежит внизу. Цель головоломки — переместить все N
дисков с начального стержня на конечный. Каждый раз можно
перемещать лишь один диск, и никогда диск большего размера не должен
лежать на диске меньшего размера.
На рис. 10.8 показаны перемещения дисков для N = 3. Стержни помечены
буквами S (начальный), Е (конечный) и М (средний). Мы используем этот
относительно простой случай, чтобы определить рекурсивный процесс.
Рекурсивный алгоритм дается в терминах N стержней.
Алгоритм Hanoi. Пример с тремя дисками может быть обобщен до трех-
шагового рекурсивного алгоритма (рис. 10.9). В функции Hanoi стержни
Исходная башня из трех дисков на стержне S
Стержень S Стержень М Стержень Е
Шаг 1: Переместить маленький диск на стержне Е (S->E)
Стержень S Стержень М Стержень Е
Шаг 2: Переместить средний диск на стержне М (S->M)
Стержень S Стержень М Стержень Е
Шаг 3: Переместить маленький диск на стержне М (Е->М)
Стержень S Стержень М Стержень Е
Шаг 4: Переместить большой диск на стержне Е (S->E)
Стержень S Стержень М Стержень Е
Шаг 5: Переместить маленький диск на стержне S (M->S)
Стержень S Стержень М Стержень Е
Рис. 10.8. Ханойская башня (N = 3)
Шаг б: Переместить средний диск на стержне Е (М->Е)
Стержень S Стержень М Стержень Е
Шаг 4: Переместить маленький диск на стержне Е (S->E). Башня из трех дисков построена
Стержень S Стержень М Стержень Е
Рис. 10.8. Продолжение
объявляются как объекты типа String. В списке параметров порядок
переменных следующий:
startpeg — middlepeg — endpeg
Предполагается, что мы перемещаем диски с начального стержня на
конечный, используя средний для временного хранения дисков. Если N = 1,
мы имеем специальное условие останова, которое может быть обработано
путем перемещения единственного диска с начального стержня на конечный.
cout « "переместить " « startpeg « " на " « endpeg « endl;
В ином случае мы имеем трехшаговый процесс перемещения N дисков с
начального стержня на конечный. На первом шаге алгоритма перемещается
N-1 дисков с начального стержня на средний с использованием конечного
стержня в качестве промежуточного. Отсюда порядок параметров в
рекурсивном вызове функций таков: startpeg, endpeg и middlepeg:
// использовать конечный стержень для временного хранения
Hanoi (n-1, startpeg, endpeg, middlepeg);
На втором шаге самый большой диск просто перемещается с начального
стержня на конечный:
cout « "переместить " « startpeg « " на " « endpeg « endl;
На третьем шаге N-1 дисков перемещаются со среднего стержня на
конечный с использованием начального стержня для временного хранения.
Отсюда порядок параметров в рекурсивном вызове функций таков: middlepeg,
startpeg и endpeg:
// использовать начальный стержень для временного хранения
Hanoi (n-1, middlepeg, startpeg, endpeg);
Шаг 1: Переместить N-1 дисков с S на М
Стержень S Стержень М Стержень Е
До
Стержень S Стержень М Стержень Е
После
Шаг 2: Переместить 1 диск с S на Е
Стержень S
Стержень М
До
Стержень S
Стержень М
После
Стержень Е
Стержень Е
Шаг 3: Переместить N-1 диск с М на Е
Стержень S Стержень М Стержень Е
До
Стержень S Стержень М Стержень Е
После
Рис. 10.9. Перемещение дисков ханойской башни
Программа 10.5. Ханойская башня
Три стержня представляются строками "start", "middle" и "end",
которые передаются в функцию в качестве параметров. Вначале программа
запрашивает число дисков N. Рекурсивная функция Hanoi вызывается
для распечатки перечня ходов при перемещении N дисков со стержня
"start" на стержень "end".
Алгоритм требует 2N - 1 хода. Для 10 дисков, задача решается за 1023
хода. Для нашего теста N = 3 число ходов равняется 23 — 1 — 7.
#include <iostream.h>
♦include "strclass.h"
// переложить п дисков с начального стержня на конечный, используя
// средний как промежуточный
void hanoi (int n, String startpeg, String middlepeg,
String endpeg)
{
// условие останова: перемещение одного диска
if (n — 1)
cout « "переместить " « startpeg « " на " << endpeg « endl;
// переместить n-1 дисков на средний стержень,
// переместить нижний диск на конечный стержень, затем переместить
// п-1 диск со среднего стержня на конечный
else
{
hanoi(n-1, startpeg, endpeg, middlepeg);
cout « "переместить " « startpeg « " на " « endpeg << endl;
hanoi(n-1, middlepeg, startpeg, endpeg);
}
}
void main()
{
// Число дисков и названия стержней
int n;
String startpeg ■ "start ",
middlepeg = "middle",
endpeg = "end ";
// запросить п и решить задачу для п дисков
cout « "Введите число дисков: ";
cin » п;
cout « "Решение для п ■ " « n « endl;
hanoi(n, startpeg, middlepeg, endpeg);
}
/*
<Выполнение программы 10.5>
Введите число дисков: 3
Решение для п = 3 переместить start на end
переместить start на middle
переместить end на middle
переместить start на end
переместить middle на start
переместить middle на end
переместить start на end
*/
Прохождение лабиринта
Многие рекурсивные алгоритмы используют принцип перебора с
возвратами (backtracking). Этот принцип применяется, когда мы сталкиваемся с
некоторой проблемой, требующей каких-то шагов и решений. Пытаясь
достичь конечной цели, мы шаг за шагом принимаем ряд частичных решений,
которые кажутся согласующимися с конечной целью. Если мы выполняем
шаг или принимаем решение, которые не согласуются с конечной целью,
мы возвращаемся на один или несколько шагов назад к последнему
согласующемуся частичному решению. Как по старой поговорке: шаг вперед —
два шага назад. Иногда возврат может повлечь за собой один шаг вперед и
п шагов назад, где п достаточно велико. В этом разделе мы рассмотрим
возвраты в уже знакомом контексте лабиринтов. В нашем анализе
подразумевается, что лабиринт не содержит циклов, которые позволили бы нам
ходить по кругу. Это ограничение не является обязательным. Возвраты
применимы и к лабиринтам с циклами, поскольку мы сохраняем карту,
показывающую, какие узлы уже были пройдены. На рис. 10.10 изображен
лабиринт с циклом, включающим перекрестки 2, 3, 4 и 5.
Рис. 10.10. Лабиринт с циклом
Анализ алгоритма. Лабиринт есть множество перекрестков. Двигаясь в
некотором направлении, путешественник попадает на перекресток и движется
далее по одному из трех путей: налево, прямо или направо. Путь
идентифицируется номером следующего перекрестка. Если некоторое направление
заблокировано, оно обозначается нулем. Перекресток без выходов является
тупиком, или мертвой точкой.
Полный авантюризма и готовности к возвратам путешественник входит в
лабиринт через начальную точку и смело начинает поиски цели — конечного
перекрестка и, следовательно, свободы. Каждый перекресток на его пути
представляет собой частичное решение. К сожалению, дух авантюризма
может завести в тупик, и тогда потребуется возврат к предыдущему
перекрестку.
Чтобы как-то организовать выбор вариантов на каждом перекрестке, будем
придерживаться рекурсивной стратегии. Сначала попробуем свернуть налево
(если это направление не заблокировано) и проложить путь к конечной точке.
Перекресток
1
2
3
4 (тупик)
3 (тупик)
2
5 (тупик)
2
6
Действие
Идти прямо
Идти налево
Идти направо
Возврат
Возврат
Идти прямо
Возврат
Идти направо
Идти налево
Результат
Перекресток 2
Перекресток 3
Перекресток 4
Перекресток 3
Перекресток 2
Перекресток 5
Перекресток 2
Перекресток 6
Перекресток 7 (конец)
Рис. 10.11. Мини-лабиринт
Этот вариант становится несовместимым с нашей целью лишь в том случае,
если заводит в тупик. Оттуда мы возвращаемся к перекрестку и пытаемся
пойти прямо до самого конца. Очередной тупик делает это решение
несовместимым, и мы выбираем движение направо. Если и этот выбор
заканчивается неудачей, то мы в тупике и должны возвратиться к предыдущему
"совместимому" перекрестку. Эту стратегию относительно просто описать и
запрограммировать в виде рекурсивной функции. Задача создания
итерационной версии этой функции будет ясна из частичного прохода по лабиринту
с семью перекрестками, показанному на рис. 10.11. Здесь путь, ведущий к
выходу из лабиринта, проходит через перекрестки 1 — 2 — 6 — 7.
Стратегия обхода гарантирует, что если путешественник выходит из
какого-то перекрестка, то возврата назад не будет до тех пор, пока не будут
проверены все возможные альтернативы, возникающие далее вдоль пути, и
не встретится тупик. Кроме того, перекресток официально не включается в
итоговый маршрут, пока не будет гарантии, что из него существует путь к
выходу из лабиринта. Как только путешественник достигает конечной точки,
мы можем проследить историю его прогулки и идентифицировать все
перекрестки на маршруте.
Класс Maze. Класс Maze — это структура, состоящая из данных
(перекрестков) и методов, позволяющих формировать лабиринт и совершать
прохождение его перекрестков, используя нашу стратегию. Допустим, что
каждый перекресток представляется записью с полями, показывающими
результаты движения из этой точки налево, прямо или направо. Целое число в
поле определяет следующий перекресток при движении в данном
направлении. Нуль обозначает, что направление заблокировано. Эта запись
реализуется структурой Intersection.
// запись, описывающая соседние перекрестки, на которые вы попадете,
// если отправитесь из данной точки налево, прямо или направо
struct Intersection
{
int left;
int forward;
int right;
Класс Maze включает целые значения, показывающие размер лабиринта,
конечную точку и список перекрестков, который размещается в
динамическом массиве. Доступ ко всем данным обеспечивается конструктором,
выполняющим построение лабиринта, и методом, выполняющим прохождение
лабиринта. Данные читаются из файла, который содержит количество
перекрестков, по три числа на каждый перекресток и номер точки выхода из
лабиринта. Точка выхода не считается перекрестком. Например, данные для
мини-лабиринта на рис. 10.11 таковы:
6 // число перекрестков
0 2 0 // 1: вперед до перекрестка 2
3 5 6 //2: налево к 3; прямо к 5; направо к 6
0 0 4 // 3: направо к 4
0 0 0 //4: тупик
0 0 0 //5: тупик
7 0 0 //6: налево к точке выхода
7 // номер точки выхода
Спецификация класса maze
ОБЪЯВЛЕНИЕ
#include <iostream.h>
#include <fstream.h>
#include <stdlib.h>
class Maze
{
private:
// число перекрестков лабиринта и номер точки выхода
int mazesize;
int EXIT;
// массив перекрестков лабиринта
Intersection *intsec
public:
// конструктор; чтение данный из файла <filename>
Maze(char *filename);
// прохождение лабиринта
int TraverseMaze(int intsecvalue);
>;
ОПИСАНИЕ
В конструктор передается имя файла, содержащего данные о лабиринте.
В этом процессе мы указываем число перекрестков и можем распределить
память под динамический массив intsec.
TraverseMaze — рекурсивная функция, которая находит выход из
лабиринта. Параметр intsecvalue вначале равен 1, показывая тем самым, что
путешественник входит в лабиринт в точке 1. Во время рекурсивного процесса
эта переменная хранит номер текущего перекрестка. Объявление и
реализация класса Maze находятся в файле maze.h.
Реализация класса Maze
Конструктор отвечает за формирование лабиринта. Так, например, он
открывает входной файл, считывает размер лабиринта, инициализирует массив
перекрестков и назначает точку выхода.
// построить лабиринт, введя перекрестки и номер точки выхода из файла filename
Maze::Maze{char *filename)
{
ifstream fin;
int i;
// открыть filename, завершить выполнение, если файл не найден
fin.open(filename, ios::in | ios:rnocreate);
if (!fin)
{
cerr « "Невозможно открыть файл описания лабиринта " « filename
« endl;
exit(l);
}
// первое число в файле — количество перекрестков
fin > mazesize/
// выделить память для массива перекрестков, мы не используем
// нулевой индекс и поэтому должны распределить mazesize+1 запись.
intsec ■ new Intersection[mazesize+l];
// ввести перекрестки из файла
for (i = 1; i <= mazesize; i++)
fin » intsec[i].left » intsec[i].forward
» intsec[i].right
// ввести номер точки выхода и закрыть файл
fin » EXIT;
fin.close();
}
Рекурсивная стратегия управляется методом TraverseMaze, который
принимает в качестве параметра число перекрестков (intsecValue). Эта функция
вызывается из предыдущего перекрестка и возвращает 1 (TRUE), если из
текущего перекрестка существует путь к точке выхода. Если intsec Value = 0, мы
наткнулись на стену и немедленно возвращаемся с нулем (FALSE).
Сердцевиной метода является дерево решений, позволяющее
путешественнику выбрать с помощью некоторых условий то направление, которое
завершится точкой выхода.
Случай 1. Если intsec Value == EXIT, то цель успешно достигнута. Мы
печатаем номер перекрестка и возвращаем TRUE предыдущему
перекрестку на этом пути, который ждет результата проверки на успешность.
Случай 2. Если это не точка выхода, мы поворачиваем налево и ждем
сообщения TRUE или FALSE, указывающего на результат тестирования
левого направления. Получив TRUE, мы печатаем номер текущего
перекрестка и возвращаем TRUE предыдущему перекрестку.
Случай 3. Этот случай похож на случай 2 за исключением того, что
попытка повернуть налево не увенчалась успехом. Теперь мы
отправляемся прямо и ждем сообщения TRUE или FALSE в качестве резуль-
тата тестирования прямого направления. Если возвращается TRUE, мы
печатаем номер текущего перекрестка и возвращаем TRUE
предыдущему перекрестку.
Случай 4. Этот случай идентичен случаям 2 и 3, но обрабатывает правый
поворот.
Если ни один из перечисленных случаев не возвратил сообщение TRUE,
значит текущий перекресток является тупиком. Чтобы зафиксировать этот
факт, возвращается сообщение FALSE. Способность передавать информацию
назад в предыдущий перекресток (в предыдущий экземпляр TraverseMaze)
обусловлена рекурсивной структурой кода. В конце концов TraverseMaze(l)
возвращает TRUE или FALSE в главную программу, показывая тем самым,
можно ли пройти данный лабиринт.
__!__■ | ■■ Mill .. _ . ■!._■■ .. _. . ■- ■ — —* I I I —
// обход с возвратами произвольного лабиринта
int Maze::TraverseMaze(int intsecvalue)
{
// если intsecvalue = 0, то мы в тупике.
// в противном случае мы пытаемся найти допустимое направление
if (intsecvalue > 0)
{
// условие останова: обнаружена точка выхода
if (intsecvalue == EXIT)
{
// печатать номер перекрестка и возвратить TRUE
cout « intsecvalue << " ";
return 1;
}
// попытка повернуть налево
else if (TraverseMaze(intsec[intsecvalue].left))
{
// печатать номер перекрестка и возвратить TRUE
cout « intsecvalue « " ";
return 1;
}
// поворот налево завел в тупик. Попробуем пойти вперед
else if (TraverseMaze(intsec[intsecvalue].forward))
{
// печатать номер перекрестка и возвратить TRUE
cout « intsecvalue « " ";
return 1;
}
// направления налево и прямо ведут в тупик, попробуем свернуть направо
else if (TraverseMaze(intsec[intsecvalue].right))
{
// печатать номер перекрестка и возвратить TRUE
cout « intsecvalue « " ";
return 1;
}
}
// это тупик, возвратить FALSE
return 0;
}
Программа 10.6. Прохождение лабиринта
Проверим программу на мини-лабиринте (рис. 10.11) (входной файл
mazel.dat), а затем на лабиринте, изображенном ниже (входной файл
maze2.dat). Из этого лабиринта выхода нет, и задача не имеет решения. На
последнем прогоне программы совершается обход большого лабиринта,
показанного на рис. 10.1 (входной файл bigmaze.dat). В каждом случае
маршрут распечатывается в обратном порядке.
#include <iostream.h>
#include "maze.h"
void main (void)
{
// файл с параметрами лабиринта
char filename [32];
cout « "Введите имя файла данных: ";
cin » filename;
// построить лабиринт
Maze M(filename);
// решить задачу о лабиринте и напечатать результат
if (M.TraverseMaze(l))
cout « endl << "Вы свободны!" << endl;
else
cout « "Из этого лабиринта нет выхода" << endl;
}
/*
<Прогон №1 программы 10.6>
Введите имя файла данных: mazel.dat
7 6 2 1
Вы свободны!
<Прогон №2 программы 10.б>
Введите имя файла данных: maze2.dat
Из этого лабиринта нет выхода
<Прогон №3 программы 10.б>
Введите имя файла данных: bigmaze.dat
19 17 16 14 10 9 8 2 1.
Вы свободны!
*/
10.5. Оценка рекурсии
Часто рекурсия не является эффективным методом решения проблемы.
Рассмотрим задачу вычисления факториала. Итерационный алгоритм
использует цикл, а не повторные вызовы функции. Рекурсия может сыграть злую
шутку. Она часто упрощает разработку алгоритма и кода для того лишь,
чтобы потерпеть фиаско на этапе выполнения по причине недостаточной
эффективности. Этот конфликт иллюстрируется с помощью чисел Фибоначчи:
1, 1, 2, 3, 5, 8, 13, 21, 34, ...
Члены этой последовательности F(n) определяются рекурсивно для п >=
1. Первые два члена равны 1 по определению. Начиная с третьего, каждый
член последовательности равен сумме двух предыдущих.
г 1, если п = 1 или 2
F(n) = «
.F(n-l) + F(n-2) если n > 2
Это определение сразу переводится в рекурсивную функцию.
Предположим, что F(n) есть n-ый член последовательности Фибоначчи, где п>=1.
Тогда
Условие останова: F(l) - 1 F(2) = 1
Шаг рекурсии: Для N £. 3, F(n) - F(n-l) + F(n-2);
Функция Fib на языке C++ реализует рекурсивную функцию F. Она имеет
единственный целочисленный параметр п и возвращает длинный целый
результат.
// рекурсивная генерация n-го числа Фибоначчи
long Fib(int n)
{
// условие останова: fl = f2 = 1
if (n -» 1 | | n « 2)
return 1;
// шаг рекурсии: Fib(n) « Fib(n-l) + Fib(n-2)
else
return Fib(n-l) + Fib(n-2);
}
Сразу заметно, что функция Fib много раз вызывает сама себя с одним
и тем же параметром. Пусть, например, N = 6. Выражение Fib(N-l) + Fib(N-2)
формирует иерархическое дерево вызовов функции Fib для N = 5, 4, 3, 2
и 1 (рис. 10.12).
Обратите внимание, что Fib(3) вычисляется три раза, a Fib(2) — пять раз.
Пятнадцать узлов дерева представляют количество рекурсивных вызовов,
требующихся для вычисления Fib(6) — 8.
Рис 10.12. Дерево рекурсивных вызовов при вычислении Fib(6)
Пусть NumCall(k) — число рекурсивных вызовов, необходимых для
вычисления Fib(k).
NumCall(k) - 2 * Fib(k) - 1
Например,
NumCall(6) - 2 * Fib (6) -1«2*8-1 = 15
NumCall(35) - 2 * Fib(35) -1 = 2* 9277465 - 1 - 18,554,929
Вычислительная эффективность алгоритма — 0(2n), т.е. время счета растет
по экспоненте.
Числа Фибоначчи: итерационная форма. При итерационном вычислении
n-го числа Фибоначчи используется простой цикл. Эта функция имеет
вычислительную эффективность О(п).
// вычислить n-е число Фибоначчи с помощью итераций
long Fiblter(int n)
{
long twoback - 1, oneback = 1, current;
int i;
// Fiblter(l) = Fiblter(2) = 1
if (n « 1 || n « 2)
return 1;
// current - twoback + oneback, n >= 3
else
for (i~3; i<=n; i++)
{
current - twoback + oneback;
twoback * oneback;
oneback - current;
}
return current;
}
Для k-го числа Фибоначчи (k >= 3) итерационная форма требует k-2
сложений и один вызов функции. Для к = 35 эта форма требует 33 сложения,
в то время как рекурсивная функция — более 18,5 миллиона вызовов!
Вычисление чисел Фибоначчи по формуле. Эффективнее всего вычислять
числа Фибоначчи непосредственно по формуле, выводимой из рекуррентных
соотношений. Вывод этой формулы выходит за рамки данной книги.
F(n) = VT ~2 ГТ"
1Л J V ) J
Поскольку функции квадратного корня и возведения в степень имеются
в библиотеке <math.h> языка C++, n-ое число Фибоначчи может быть
вычислено непосредственно с эффективностью 0(1) при помощи кода:
#include <math.h>
const double sqrtS = sqrt(5.0);
// вычислить n-oe число Фибоначчи по алгебраической формуле
double FibFormula(int n)
{
double pi, p2;
// библиотечная функция языка C++
// double pow(double x, double y);
// вычисляет x в степени у
pi *= pow{l+sqrt5)/2.0, n);
p2 = pow(l-sqrt5)/2.0, n);
return (pi - p2)/sqrt5;
}
Программа 10.7. Оценка рекурсии (на примере чисел Фибоначчи)
Эта программа хронометрирует вычисление 35-го числа Фибоначчи с
помощью формулы, итерационной функции и рекурсивной функции из
файла fib.h. Нерекурсивные программы выполняются доли секунды, в то
время как рекурсивная функция требует более 82 секунд.
tinclude <iostream.h>
#include "fib.h"
void main (void)
{
int i;
// распечатать результат FibFormula в виде десятичного числа
// с фиксированной точкой без дробной части
cout.setf(ios::fixed);
cout.precision(0);
// вычислить 35-е число Фибоначчи тремя способами
cout « FibFormula (35). « endl;
cout « Fiblter(35) « endl;
cout « Fib(35) « endl;
}
/*
<Выполнение программы 10.7>
92274 65 <формула заняла менее 1 секунды>
92274 65 <итерационная функция заняла менее 1 секунды>
92274 65 <рекурсивная функция заняла более 82 секунд>
*/
Издержки рекурсии. Пример с числами Фибоначчи должен подготовить
вас к потенциальным проблемам при использовании рекурсии. Избыточность
вызовов в простой рекурсивной функции может серьезно ухудшить
производительность программы. Еще более серьезно то, что рекурсивный вызов
может породить наслоение целой последовательности рекурсивных вызовов,
которые выходят из-под контроля программиста и делают запросы,
превышающие размер стека. Числа Фибоначчи являются экстремальным случаем.
Здесь легко можно реализовать итерационную версию.
Со сделанными оговорками рекурсия остается важным инструментом
программирования. Многие алгоритмы проще сформулировать и
запрограммировать с помощью рекурсии. Они естественным образом адаптируются к
рекурсивной реализации, где выделяются условия останова и шаг рекурсии.
Например, использование возвратов в задаче о лабиринте облегчается
посредством рекурсии.
Хотя рекурсия не является объектно-ориентированным понятием, для нее
характерны некоторые черты объектно-ориентированного проектирования.
Она позволяет программисту управлять ключевыми логическими
компонентами алгоритма и скрывать некоторые сложные детали реализации. Не
существует жесткого правила, когда можно использовать рекурсию, а когда
нельзя. Вы должны взвесить эффективности разработки и выполнения.
Используйте рекурсию, когда разработка алгоритма усложняется, а реализация
позволяет достичь приемлемого быстродействия и затрат памяти.
Задняя рекурсия. Если последним действием функции является
рекурсивный вызов, мы говорим, что эта функция использует заднюю рекурсию
(tail recursion). Этот рекурсивный вызов требует затрат на создание
активизирующей записи и ее запоминание в стеке. Когда рекурсивный процесс
доходит до условия останова, мы должны выполнить серию возвратов,
которые выталкивают активизирующие записи из стека. Мы просто помещаем
записи в стек и вынимаем их оттуда, не используя для существенных
вычислений.
Исключение задней рекурсии может значительно повлиять на
эффективность рекурсивной функции. Эту проблему иллюстрирует простой пример,
где предлагается типичное решение. Рассмотрим рекурсивную функцию
recfunc, которая распечатывает элементы массива от индекса п до индекса
0. Этот пример не имеет практического значения и выбран для простоты
иллюстрации.
void recfunc(int А[], int n)
{
if (n >= 0) // идти вперед, если индекс п не вышел за предел
{
cout « A[n] « " ";
n—; // декремент индекса п
recfunc(А, п);
}
}
Пусть массив А[] = {10, 20, 30}. Тогда вызов recfunc(A,2) начинается с
п = 2 и создает вывод 10 20 10.
Функция recfunc иллюстрирует типичную ситуацию задней рекурсии. Эту
проблему можно показать на логической схеме, где п > 0 интерпретируется
как условие, требующее дальнейшего рекурсивного вызова.
—* if <рекурсивное условие> < n >■ О
Выполнить задачу < вывод А[п]
Обновить условие < декремент п
' Вызвать recfunc
Эта логическая схема эквивалентна циклу WHILE, проверяющему простое
условие п > 0. В функции recfunc управление передается оператору проверки
условия с помощью менее эффективной рекурсивной операции.
Г while <условие> < п >« 0
Выполнить задачу < вывод А[п]
Обновить условие < декремент п
В нашем примере рекурсивная функция recfunc может быть заменена
функцией iterfunc, которая использует эквивалент оператора WHILE.
Проблема исключения задней рекурсии может оказаться немного запутанной.
Надежнее будет построить логическую схему для рекурсивной функции и
затем создать такую же итерационную схему с использованием WHILE.
// итерационная функция, исключающая заднюю рекурсию
void iterfunc(int А[), int n)
{
while (n >- 0)
{
cout « "While-значение " « A[n) «endl;
n—;
}
}
Письменные упражнения
10.1 Объясните, почему выполнение следующей функции может дать
неверный результат.
long factorial(long n)
{
if (n ■■ 0 | | n ■■ 1)
return 1;
else
return n * factorial(—n);
}
Результат зависит от порядка оценивания операндов компилятором.
Если п = 3 и левый операнд вычисляется первым, результатом будет
3 * 2! = 6. Если первым вычисляется правый операнд, результатом
будет 2 * 2! = 4.
10.2 Какая числовая последовательность порождается следующей
рекурсивной функцией?
long f(int n)
{
if (n =« 0 || n « 1)
return 1;
else
return 3*f(n-2) + 2*f(n-l);
}
10.3 Какая числовая последовательность порождается следующей
рекурсивной функцией?
int f(int n)
{
if (n « 0)
return 1;
else if (n == 1)
return 2;
else
return 2*f(n-2) + f(n-l);
}
10.4 Каким будет результат выполнения следующей программы, если
входными данными являются 5 3?
#include <iostream.h>
long f(int b, int n)
{
if (n « 0)
return 1;
else
return b*f(b, n-1);
}
void main(void)
{
int b, e;
cin » b » e;
cout « f (b, e) « endl;
}
10.5 Каким будет результат выполнения следующей программы, если
входными данными является строка "Это перекресток"?
#include <iostream>
void Q(void)
{
char с;
cin.get(с);
if (c !« '\n')
QO;
cout « c;
}
void main(void)
{
cout « "Введите текстовую строку: " « endl;
QO;
cout « endl/
}
10.6 Требуется рекурсивно вычислить максимальный элемент п-злементного
массива. Определите функцию
int max (int a[], int у);
которая возвращает максимальное из двух целых х и у. Определите
функцию
int arraymax(int a[], int n);
которая использует рекурсию, чтобы возвратить максимальный элемент
массива а.
Условие останова: п == 1
Шаг рекурсии: arraymax = max(max(a[0], ... a[n-2]), a[n-l])
10.7 Напишите рекурсивную функцию
float avg{float a[], int n);
которая возвращает среднее из п элементов массива чисел с плавающей
точкой.
Условие останова: п == 1
Шаг рекурсии: avg — ((п-1)/п)*(среднее из п-1 элементов) + (п-ый
элемент)/п
10.8 Напишите рекурсивную функцию
int rstrlen(char s[]);
которая вычисляет длину строки.
Условие останова: s[0] == 0
Шаг рекурсии: 14-length(noflCTpoKa, начинающаяся со 2-го символа)
10.9 Напишите рекурсивную функцию, которая проверяет, является ли
строка палиндромом. Палиндром — это строка, не содержащая пробелов,
которая одинаково читается справа налево и слева направо. Например,
dad level did madamimadam1 кабак чинзванмечемнавзнич
Используйте следующее объявление
int pal(char A[], int s, int e);
где pal определяет, является ли палиндромом цепочка символов в А,
начинающаяся с индекса s и заканчивающаяся индексом е.
Условия останова: s >= е (успех); A[s] != A[e] (неудача)
Шаг рекурсии: Является ли строка A[s4-1] ... А[е-1] палиндромом?
10,10 Коэффициенты C(n,k), использующиеся при разложении формулы
(х+1)п, называются биномиальными.
(х+1)п = СП/П хп + СП/П_! х""1 + Сп,п_2 хп"2 + ... + Сп,2 х2 + СП/1 х1 + СП/0 х°
Для любого п С(п,п) = С(п,0) = 1. Рекуррентные соотношения для
биномиальных коэффициентов таковы:
С(п,0) = 1
С(п,п) - 1
C(n,k) - C(n-l,k-l) + C(n-l,k)
Заметьте, что каждый коэффициент C(n,k), 0<k<n, является решением
задачи о комитетах, рассмотренной нами выше. Биномиальные
коэффициенты C(n,k) определяют, сколькими способами можно выбрать к
элементов из п элементов.
1 Madam, Гт Adam. — Прим. перев.
Эти коэффициенты образуют знаменитый треугольник Паскаля. В этом
треугольнике столбец 0 содержит все единицы, как и диагональ.
Каждый из остальных элементов является суммой двух элементов,
расположенных на строку выше в том же столбце и столбце слева.
1
1 1
12 1
13 3 1
14 6 4 1
Напишите функцию, которая строит треугольник Паскаля для
заданного п. Выше приведен пример для п = 4.
10.11 Напишите рекурсивную функцию
int qcd(int a, int b);
для вычисления наибольшего общего делителя положительных целых
а и Ь. См. процедуры для итерационной версии этой функции в гл. 6.
10.12 Следующие данные представляют собой входной файл описания
лабиринта. Нарисуйте лабиринт и найдите решение, прослеживая
рекурсивный алгоритм по шагам.
11 // число перекрестков
0 2 0// перекресток 1: (налево, прямо, направо)
4 3 6
0 0 0
0 0 5
0 0 0
7 0 0
8 11 9
0 0 0
0 0 10
0 0 0
12 0 0
12 // точка выхода
Упражнения по программированию
10.1 Используйте функцию arraymax из письменного упражнения 10.6 для
выполнения следующих действий:
1. Сгенерируйте 10 случайных целых чисел в диапазоне 1—20000 и
сохраните их в массиве.
2. Рапечатайте массив.
3. Примените функцию arraymax и распечатайте результат. Проверьте
его правильность.
10.2 Сумма первых п целых чисел находится по формуле
1 + 2 + 3 + ... + n = n(n+l)/2
Занесите в массив А первые 50 чисел. Тогда средним для этих элементов
будет значение 51/2 = 25,5. Проверьте свое решение, обработав массив
А программой из письменного упражнения 10.7,
10.3 Испытайте свою функцию rstrlen из письменного упражнения 10.8,
вводя пять строк с клавиатуры с помощью cin.getline и распечатывая
длину строки как посредством rstrlen, так и с помощью библиотечной
функции C++ strlen.
10.4 Читайте символьные строки до конца файла с помощью оператора »,
чтобы получить отдельные "слова". К каждому слову примените
функцию pal из письменного упражнения 10.9, чтобы определить, является
ли оно палиндромом. Если да, то запишите его в строковый массив.
По окончании ввода файла распечатайте все найденные палиндромы
по одному в строке.
10.5 Классической арифметической задачей является представление целого
значения в различных системах счисления:
N = 45 Основание = 2 Выход: 101101 [32 + 8 + 4 + 1]
N = 90 Основание = 8 Выход: 132 [1(64) + 3(8) + 2(1)]
N = 75 Основание = 5 Выход: 300 [3(52) + 0(5) + 0(1)]
В обычном алгоритме преобразования в другую систему счисления
используется многократное деление на ее основание. Если
N = dn_x dn.2 dn_3 ... dx d0
то последовательность остатков дает цифры числа N в порядке d(0) ...
d(n-l).
Определите рекурсивную функцию
void intout(long N, int В);
для печати N в системе счисления по основанию В, подразумевая
В <, 10. Испытайте эту функцию в главной процедуре, которая вводит
пять пар чисел N,B и распечатывает каждое N в системе счисления
по основанию В.
10.6 Введите положительное целое п < 10. Обратитесь к письменному
упражнению 10.10 и распечатайте разложение полинома (х+1)п.
10.7 Разработайте рекурсивную функцию для подсчета количества п-разряд-
ных двоичных чисел, не имеющих двух идущих подряд единиц.
(Подсказка: Число начинается либо с нуля либо с единицы. Если оно
начинается с нуля, количество вариантов определяется оставшимися п-1
цифрами. А если с единицы, то какой должна быть следующая цифра?)
10.8 Довольно часто возникает задача нахождения корня действительной
функции. Если f(x) — функция, ее корень г есть действительное число
такое, что f(r) = 0. В некоторых случаях корни могут быть вычислены
по алгебраической формуле. Например, все корни квадратного
уравнения f(x) = ах2 + Ьх + с находятся по формуле
, , Vb2 - 4ас
г = -Ь ± ~
2а
Для общего случая формулы нет, и корни должны находиться
численными методами.
f(-1)>0
У = f (x)
Корень г
f(1)<0
f(-1)>0
У = f (x)
Корень г
1(1) < О
f(0)M(-1)>0,f(0)M(1)<0.
Корень лежит в интервале
О < г < 1.0
Если f(a) и f(b) имеют разные знаки (f(a) * f(b) < 0) и f "ведет себя
хорошо", то между а и b существует корень г.
Метод дихотомии определяется следующим образом. Пусть m =
(a+b)/2.0 — средняя точка в интервале а < х < Ь. Если f(m) = 0.0, то
корень г = т. Если нет, то либо f(a) и f(m) имеют разные знаки (f(a)
* f(m) < 0), либо f(m) и f(b) имеют разные знаки (f(m) * f(b) < 0).
Если f(m) * f(b) < 0, то корень г лежит в интервале m < х < Ь; в
противном случае он лежит в интервале а < х < т. Теперь выполним
этот действие для нового интервала — половины исходного интервала.
Процесс продолжается до тех пор, пока интервал не станет достаточно
маленьким или пока не будет найдено точное значение корня.
Напишите рекурсивную функцию
double Bisect(double f(double x),
double a, double b, double precision);
вычисляющую и возвращающую баланс после выплачивания простого
процента по заданной величине капитала с месячной ставкой nmonths.
Используйте метод дихотомии для расчета платежей по ссуде $150000
под 10% годовых на 25 лет.
10.9 Запустите программу 10.6 с данными из письменного упражнения
10.12. Проверьте свое решение этого упражнения.
глава
11
Деревья
11.1. Структура бинарного дерева
11.2. Разработка функций класса
TreeNode
11.3. Использование алгоритмов
прохождения деревьев
11.4. Бинарные деревья поиска
11.5. Использование бинарных
поисковых деревьев
11.6. Реализация класса BinSTree
11.7. Практическая задача: конкорданс
Письменные упражнения
Упражнения по программированию
Дед
Рис. 11.1. Генеалогическое дерево
Массивы и связанные списки определяют коллекции объектов, доступ к
которым осуществляется последовательно. Такие структуры данных
называют линейными (linear) списками, поскольку они имеют уникальные первый
и последний элементы и у каждого внутреннего элемента есть только один
наследник. Линейный список является общим описанием для таких структур,
как массивы, стеки, очереди и связанные списки.
Во многих приложениях обнаруживается нелинейный порядок объектов,
где элементы могут иметь нескольких наследников. Например, в фамильном
дереве родитель может иметь нескольких потомков (детей). На рис. 11.1
показаны три поколения семьи. Подобное упорядочение описывает и
управляющий аппарат компании, во главе которой стоит президент, а далее идут
начальники отделов и менеджеры (рис. 11.2). Такое упорядочение называют
иерархическим, поскольку это название происходит от церковного
распределения власти — от епископа к пасторам, дьяконам и т.д.
В этой главе мы рассмотрим нелинейную структуру, называемую деревом
(tree), которая состоит из узлов и ветвей и имеет направление от корня к
внешним узлам, называемым листьями. В гл. 13 представлены графы,
описывающие нелинейную структуру, в которой два или более узла могут
переходить в один и тот же объект. Эти структуры подобны коммуникационной
сети, показанной на рис. 11.3, требуют особых алгоритмов и применяются
в специальных приложениях.
отец
дядя
тетя
брат
ребенок
сестра
Менеджер
по производству
Президент
Менеджер
по сбыту
Начальник
отдела кадров
Снабжение
Склад
Поставки
Рис. 11.2. Иерархическая структура
Станция В
Станция А
Станция С
Станция D
Рис. 11.3. Ретрансляционные телефонные станции
Терминология деревьев
Древовидная структура характеризуется множеством узлов (nodes),
происходящих от единственного начального узла, называемого корнем (root).
На рис. 11.4 корнем является узел А. В терминах генеалогического дерева
узел можно считать родителем (parent), указывающим на 0, 1 или более
узлов, называемых сыновьями (children). Например, узел В является
родителем сыновей Е и F. Родитель узла Н — узел D. Дерево может представлять
несколько поколений семьи. Сыновья узла и сыновья их сыновей называются
потомками (descendants), а родители и прародители — предками (ancestors)
этого узла. Например, узлы Е, F, I, J — потомки узла В. Каждый некорневой
узел имеет только одного родителя, и каждый родитель имеет 0 или более
сыновей. Узел, не имеющий детей (Е, G, H, I, J), называется листом (leaf).
Рис. 11.4. Дерево общего вида
Каждый узел дерева является корнем поддерева (subtree), которое
определяется данным узлом и всеми потомками этого узла. Ниже показаны три
поддерева дерева на рис. 11.4. Узел F есть корень поддерева, содержащего
узлы F, I и J. Узел G является корнем поддерева без потомков. Это
определение позволяет говорить, что узел А есть корень поддерева, которое само
оказывается деревом.
Прохождение от родительского узла к его дочернему узлу и к другим
потомкам осуществляется вдоль пути (path). Например, на рис. 11.5 путь
от корня А к узлу F проходит от А к С и от С к F. Тот факт, что каждый
некорневой узел имеет единственного родителя, гарантирует, что существует
единственный путь из любого узла к его потомкам. Путь от корня к узлу
дает меру, называемую уровнем (level) узла. Уровень узла есть длина пути
от корня к этому узлу. Уровень корня равен 0. Каждый сын корня является
узлом 1-го уровня, следующее поколение — узлами 2-го уровня и т.д.
Например, на рис. 11.5 узел F является узлом 2-го уровня с длиной пути 2.
Уровень О
Уровень 1
Уровень 2
Уровень 3
Рис. 11.5. Уровень узла и длина пути
Глубина (depth) дерева есть максимальный уровень любого его узла.
Понятие глубины также может быть описано в терминах пути. Глубина дерева
есть длина самого длинного пути от корня до узла. На рис. 11.5 глубина
дерева равна 3.
Бинарные деревья
Хотя деревья общего вида достаточно важны, мы сосредоточимся на
ограниченном классе деревьев, где каждый родитель имеет не более двух
сыновей (рис. 11.6). Такие бинарные деревья (binary trees) имеют
унифицированную структуру, допускающую разнообразные алгоритмы прохождения и
(А) Глубина 3 (В) Глубина 4
Рис. 11.6. Бинарные деревья
эффективный доступ к элементам. Изучение бинарных деревьев дает
возможность решать наиболее общие задачи, связанные с деревьями, поскольку
любое дерево общего вида можно представить эквивалентным ему бинарным
деревом. Этот вопрос рассматривается в упражнениях.
У каждого узла бинарного дерева может быть 0, 1 или 2 сына. По
отношению к узлу слева будем употреблять термин левый сын (left child), а по
отношению к узлу справа — правый сын (right child). Наименования "левый"
и "правый" относятся к графическому представлению дерева. Бинарное
дерево является рекурсивной структурой. Каждый узел — это корень своего
собственного поддерева. У него есть сыновья, которые сами являются корнями
деревьев, называемых левым и правым поддеревьями соответственно. Таким
образом, процедуры обработки деревьев естественно рекурсивны. Вот
рекурсивное определение бинарного дерева:
Бинарное дерево — это такое множество узлов В, что
а) В является деревом, если множество узлов пусто (пустое дерево — тоже
дерево);
б) В разбивается на три непересекающихся подмножества:
{R} корневой узел
{Li, L2, ..., Lm} левое поддерево R
{Ri, R2, ..., Rm} правое поддерево R
На любом уровне п бинарное дерево может содержать от 1 до 2П узлов.
Число узлов, приходящееся на уровень, является показателем плотности
дерева. Интуитивно плотность есть мера величины дерева (число узлов) по
отношению к глубине дерева. На рис. 11.6 дерево А содержит 8 узлов при
глубине 3, в то время как дерево В содержит 5 узлов при глубине 4.
Последний случай является особой формой, называемой вырожденным
(degenerate) деревом, у которого есть единственный лист (Е) и каждый нелистовой
узел имеет только одного сына. Вырожденное дерево эквивалентно
связанному списку.
Деревья с большой плотностью очень важны в качестве структур данных,
так как они содержат пропорционально больше элементов вблизи корня, т.е.
с более короткими путями от корня. Плотное дерево позволяет хранить
большие коллекции данных и осуществлять эффективный доступ к элементам.
Левое поддерево Правое поддерево
Быстрый поиск — главное, что обусловливает использование деревьев для
хранения данных.
Вырожденные деревья являются крайней мерой плотности. Другая
крайность — законченные бинарные деревья (complete binary tree) глубины N,
где каждый уровень 0...N-1 имеет полный набор узлов и все листья уровня
N расположены слева. Законченное бинарное дерево, содержащее 2N узлов
на уровне N является полным (full). На рис. 11.7 показаны законченное и
полное бинарные деревья.
Законченное дерево (глубина 3) Полное дерево (глубина 2)
Рис 11.7. Классификация бинарных деревьев
Законченные и полные бинарные деревья дают интересные математические
факты. На нулевом уровне имеется 2° узлов, на первом — 21, на втором — 22
и т.д. На первых к-1 уровнях имеется 2к1 узлов.
1 + 2 + 4 + ... + 2к1 = 2к1
На к-ом уровне количество дополнительных узлов колеблется от 1 до 2к
(полное). В полном дереве число узлов равно
1 4- 2 + 4 + ... + 2" + 2к = 2к+1 — 1
Число узлов законченного бинарного дерева удовлетворяет неравенству
2к < N < 2к+1 — 1 < 2к+1
Решая его относительно к, имеем
к < log2 (N) < к+1
Например, полное дерево глубины 3 имеет
24 — 1 = 15 узлов
Пример 111
1. Максимальная глубина дерева с 5-ю узлами равна 4 [рис. 11.6 (В)].
Минимальная глубина к дерева с 5-ю узлами равна
к < log2 (5) < к+1
log2 (5) - 2,32 и к - 2
2. Глубина дерева есть длина самого длинного пути от корня к узлу.
Для вырожденного дерева с N узлами наибольший путь имеет длину
N-1.
Для законченного дерева с N узлами глубина равна целой части от
log2N. Этому же значению равен максимальный путь. Пусть дерево
имеет N = 10000 элементов, тогда максимальный путь равен
int(log2 10000) - int(13,28) - 13
11.1. Структура бинарного дерева
Структура бинарного дерева построена из узлов. Как и в связанном списке,
эти узлы содержат поля данных и указатели на другие узлы в коллекции. В
этом разделе определяются узлы дерева и операции для его построения и
прохождения. Подобно представлению класса Node в гл. 9, объявляется класс
TreeNode, а затем разрабатывается ряд функций, использующих узлы дерева
для построения бинарного дерева и прохождения индивидуальных узлов.
Узел дерева содержит поле данных и два поля с указателями. Поля
указателей называются левым указателем (left) и правым указателем (right),
поскольку они указывают на левое и правое поддерево, соответственно. Значение
NULL является признаком пустого дерева.
TreeNode
left
данные
right
left
данные
right
Корневой узел определяет входную точку дерева, а поле указателя — узел
следующего уровня. Листовой узел содержит NULL в поле правого и левого
указателей (рис. 11.8).
Проектирование класса TreeNode
В этом разделе разрабатывается класс TreeNode, в котором объявляются
объекты-узлы бинарного дерева. Узел состоит из поля данных, которое
является открытым (public) элементом, т.е. к которому пользователь может
обращаться непосредственно. Это позволяет клиенту читать или обновлять данные
во время прохождения дерева, а также допускает возвращение ссылки на
данные. Последняя особенность используется более сложными структурами
данных, такими как словари. Два поля с указателями являются закрытыми
(private) элементами, доступ к которым осуществляется посредством функций
Left() и Right(). Объявление и определение класса TreeNode содержатся в файле
treenode.h.
Дерево
left
А
right
left
В
right
left
с
right
left
D J right
left
E
right
left
G
right
Структура TreeNode
Рис. 11.8. Узлы бинарного дерева
Спецификация класса TreeNode
ОБЪЯВЛЕНИЕ
// BinSTree зависит от TreeNode
template <class T>
class BinSTree;
// объявление объекта для узла бинарного дерева
template <class T>
class TreeNode
{
private:
// указатели левого и правого дочерних узлов
TreeNode<T> *left;
TreeNode<T> * right;
public:
// открытый элемент, допускающий обновление
Т data;
// конструктор
TreeNode (const T& item, TreeNode<T> *lptr = NULL,
TreeNode<T> *rptr = NULL);
// методы доступа к полям указателей
TreeNode<T>* Left(void) const;
TreeNode<T>* Right(void) const;
left
u_
right
left
H I right j
// сделать класс BinSTree дружественным, поскольку необходим
// доступ к полям left и right
friend class BinSTree<T>;
};
ОПИСАНИЕ
Конструктор инициализирует поля данных и указателей. С помощью
пустого указателя NULL узлы инициализируются как листья. Имея указатель
Р объекта TreeNode в качестве параметра, конструктор присоединяет Р как
левого или правого сына нового узла.
Методы доступа Left и Right возвращают соответствующий указатель.
Класс BinSTree объявляется дружественным классу TreeNode и может
модифицировать указатели. Другие клиенты должны использовать конструктор
для создания указателей и методы Left и Right для прохождения дерева.
ПРИМЕР
// указатели целочисленных узлов дерева
TreeNode<int> *root, *lchild, *rchild;
TreeNode<int> *p;
// создать листья, содержащие 20 и 30 в качестве данных
lchild - new TreeNode<int> (20);
rchild » new TreeNode<int> (30);
// создать корень, содержащий число 10 и двух сыновей
root * new TreeNode<int> (10, lchild, rchild);
root->data =50; // присвоить корню 50
Реализация класса TreeNode Класс TreeNode инициализирует поля
объекта. Для инициализации поля данных конструктор имеет параметр item.
Указатели назначают узлу левого и правого сына (поддерево). При отсутствии
сына используется значение NULL.
// конструктор инициализирует поля данных и указателей
// значение NULL соответствует пустому поддереву
template <class T>
TreeNode<T>::TreeNode(const T& item, TreeNode<T> *lptr,
TreeNode<T> *rptr):data(item), left(lptr), right(rptr)
{}
Методы Left и Right возвращают значения полей левого и правого
указателей. Благодаря этому клиент имеет доступ к левому и правому сыновьям узла.
Построение бинарного дерева
Бинарное дерево состоит из коллекции объектов TreeNode, связанных
посредством своих полей с указателями. Объект TreeNode создается динамически
с помощью функции new.
TreeNode<int> *p; // объявление указателя
//на целочисленный узел дерева
р - new TreeNode(item); // левый и правый указатели равны NULL
left
Р
right
Вызов функции new обязательно должен включать значение данных. Если
в качестве параметра передается также указатель объекта TreeNode, то об
используется вновь созданным узлом для присоединения дочернего узла.
Определим функцию GetTreeNode, принимающую данные и ноль или более
указателей объекта TreeNode, для создания и инициализации узла бинарного
дерева. При недостаточном количестве доступной памяти программа
прекращается сразу после выдачи сообщения об ошибке.
// создать объект TreeNode с указательными полями lptr и rptr.
//по умолчанию указатели содержат NULL.
template <class T>
TreeNode<T> *GetTreeNode(T item, TreeNode<T> *lptr « NULL,
TreeNode<T> *rptr - NULL)
{
TreeNode<T> *p;
// вызвать new для создания нового узла
// передать туда параметры lptr и rptr
р - new TreeNode<T> (item, lptr, rptr);
// если памяти недостаточно, завершить программу сообщением об ошибке
if (p «- NULL)
{
cerr « "Ошибка при выделении памяти!\п";
exit(l);
}
// вернуть указатель на выделенную системой память
return p;
}
Функция FreeTreeNode принимает указатель на объект TreeNode и
освобождает занимаемую узлом память, вызывая функцию C++ delete.
// освободить динамическую память, занимаемую данным узлом
template <class t>
void FreeTreeNode(TreeNode<T> *p)
{
delete p;
}
Обе эти функции находятся в файле treelib.h вместе с функциями
обработки бинарного дерева, представленными в разделе 11.2.
Пример определения дерева. Функция GetTreeNode может быть
использована для явного построения каждого узла дерева и, следовательно, всего
дерева. Это было продемонстрировано на дереве с тремя узлами, содержащими
10, 20 и 30. Для более крупного экземпляра процесс будет немного
утомительным, так как вы должны включить в дерево все значения данных и
указателей.
В этой главе создадим функцию MakeCharTree, строящую три дерева,
узлы которых содержат символьные элементы данных. Эти деревья будут
использоваться для иллюстрации методов TreeNode в следующем разделе.
Параметры функции включают в себя ссылку на корень дерева и число п
(О < п < 2), которое служит для обозначения дерева. Следующие объявления
создают указатель на объект TreeNode, с именем root, и назначают его корнем
дерева Тгее_2.
TreeNode<char> *root; // объявить указатель на корень
MakeCharTree(root,2); // сформировать на этом корне дерево tree_2
На рис. 11.9 показаны три дерева, построенных этим методом. Полный
листинг функции MakeCharTree находится в файле treelib.h. Эта функция
распространяет технологию из примера 11.2 на деревья с пятью и девятью
узлами.
Tree О
Tree 1 Tree 2
Рис 11.9. Дерево MakCharTree
11.2. Разработка функций класса TreeNode
Связанный список — это линейная структура, позволяющая
последовательно проходить узлы, используя указатель на следующий элемент.
Поскольку дерево является нелинейной структурой, похожего алгоритма
прохождения не существует. Мы вынуждены выбрать один из методов
прохождения, среди которых наиболее широко используются прямой, симметричный
и обратный методы. Каждый из них основывается на рекурсивной структуре
бинарного дерева.
Алгоритмы прохождения существенно влияют на эффективность
использования дерева. В первую очередь мы разработаем методы рекурсивного про-
хождения, а затем на их основе создадим алгоритмы печати, копирования
и удаления, а также определения глубины дерева. Мы также рассмотрим
поперечный метод (breadth first) прохождения, который использует очередь
для запоминания узлов. Этот метод сканирует дерево уровень за уровнем,
начиная с корня и передвигаясь к первому поколению сыновей, затем ко
второму и т.д. Метод находит важное применение в административных
иерархиях, где власть распределяется от главы к другим уровням управления.
Наша реализация метода прохождения предусматривает
параметр-функцию visit, которая осуществляет доступ к содержащимся в узле данным.
Передавая в качестве параметра функцию, можно указать некоторое действие,
которое должно выполняться в каждом узле в процессе прохождения дерева.
template <class T>
void <Метод_прохода> (TreeNode<T> *t, void visit(T& item));
Всякий раз при вызове метода клиент должен передавать имя функции,
выполняющей некоторое действие с данными, имеющимися в узле. По мере
того как метод перемещается от узла к узлу, вызывается эта функция и
выполняется предусмотренное действие.
Замечание. Понятие параметра-функции является относительно простым,
но требует некоторого пояснения. В общем случае функция может быть
аргументом, если указать ее имя, список параметров и возвращаемое ею
значение. Пусть, например, функция G имеет параметр-функцию f. В этом
параметре указывается имя функции (f), список параметров (int x) и
возвращаемый тип (int).
Список параметров
i 1
int G(int t, int f (int x))
int G(int t, int f(int x) ) // параметр-функция f
{
// вычислить f (t) с помощью функции f и параметра t.
// возвратить произведение этого значения и t
return t * f(t)/
}
Вызывая функцию G, клиент должен передать функцию для f с той же
структурой. Пусть в нашем примере клиент определил функцию XSquared,
вычисляющую х2.
// XSquared — целочисленная функция с целочисленным параметром х
int XSquared(int x)
{
return x*x;
}
Клиент вызывает функцию G с целочисленным параметром t и
параметром-функцией XSquared. Оператор
Y = G<3, XSquared)
вызывает функцию G, которая в свою очередь вызывает функцию XSquared с
параметром 3. Оператор cout печатает результат 27.
cout « G(3.0, XSquared) « endl;
возвращаемый тип
имя функции
список параметров
Рекурсивные методы прохождения деревьев
Рекурсивное определение бинарного дерева определяет эту структуру как
корень с двумя поддеревьями, которые идентифицируются полями левого и
правого указателей в корневом узле. Сила рекурсии проявляется вместе с
методами прохождения. Каждый алгоритм прохождения дерева выполняет в
узле три действия: заходит в узел, рекурсивно спускается по левому поддереву
и по правому поддереву. Спустившись к поддереву, алгоритм определяет, что
он находится в узле, и может выполнить те же три действия. Спуск
прекращается по достижении пустого дерева (указатель == NULL). Различные
алгоритмы рекурсивного прохождения отличаются порядком, в котором они
выполняют свои действия в узле. Мы изложим симметричный и обратный
методы, в которых сначала осуществляется спуск по левому поддереву, а затем по
правому. Другие методы оставляем вам в качестве упражнений.
Симметричный метод прохождения дерева
Симметричный метод прохождения начинает свои действия в узле спуском
по его левому поддереву. Затем выполняется второе действие — обработка
данных в узле. Третье действие — рекурсивное прохождение правого
поддерева. В процессе рекурсивного спуска действия алгоритма повторяются в каждом
новом узле.
Итак, порядок операций при симметричном методе следующий:
1. Прохождение левого поддерева.
2. Посещение узла.
3. Прохождение правого поддерева.
Мы называем такое прохождение LNR (left, node, right). Для дерева Tree_0
в функции MakeCharTree "посещение" означает печать значения из поля
данных узла.
Тгее_0
При симметричном методе прохождения дерева Тгее__0 выполняются
следующие операции.
Действие Печать Замечания
Спуститься от А к В: Левый сын узла В равен NULL
Посетить В; В
Спуститься от В к D: D — листовой узел
Посетить D; D Конец левого поддерева узла А
Посетить корень А: А
Спуститься от А к С:
Спуститься от С к Е: Е — листовой узел
Посетить Е; Е
Посетить С; С Готово!
Узлы посещаются в порядке В D А Е С, Рекурсивная функция сначала
спускается по левому дереву [t—>Left()], а затем посещает узел. Второй шаг
рекурсии спускается по правому дереву [t—>Right()].
// симметричное рекурсивное прохождение узлов дерева
template <class T>
void Inorder (TreeNode<T> *t, void visit(T& item))
{
// рекурсивное прохождение завершается на пустом поддереве
if (t !- NULL)
{
Inorder(t->Left(), visit); // спуститься по левому поддереву
visit(t->data); // посетить узел
Inorder(t->Right(), visit); // спуститься по правому поддереву
)
}
Обратный метод прохождения дерева. При обратном прохождении
посещение узла откладывается до тех пор, пока не будут рекурсивно пройдены
оба его поддерева. Порядок операций дает так называемое LRN (left, right,
node) сканирование.
1. Прохождение левого поддерева.
2. Прохождение правого поддерева.
3. Посещение узла.
При обратном прохождении дерева Тгее_0 узлы посещаются в порядке
D В Е С А.
Замечания
Левый сын узла В равен NULL
D — листовой узел
Все сыновья узла В пройдены
Левое поддерево узла А пройдено
Е — листовой узел
Левый сын узла С
Правый сын узла А
Готово!
Функция сканирует дерево снизу вверх. Мы спускаемся вниз по левому
дереву [t->Left()], а затем вниз по правому [t->Right()]. Последней операцией
является посещение узла.
// обратное рекурсивное прохождение узлов дерева
template <class T>
void Postorder (TreeNode<T> *t, void visit (T& item) )
{
// рекурсивное прохождение завершается на пустом поддереве
if (t !* NULL)
{
Postorder(t->Left(), visit); // спуститься по левому поддереву
Postorder(t->Right(), visit); // спуститься по правому поддереву
visit(t->data); // посетить узел
}
}
Действие
Спуститься от А к В:
Спуститься от В к D:
Посетить D;
Посетить В;
Спуститься от А к С:
Спуститься от С к Е:
Посетить Е;
Посетить С;
Посетить корень А:
Печать
D
В
Е
С
А
Прямой метод прохождения определяется посещением узла в первую
очередь и последующим прохождением сначала левого, а потом правого его
поддеревьев (NLR).
Ясно, что префиксы pre, in и post в названиях функций показывают,
когда происходит посещение узла. В каждом случае сначала осуществлялось
прохождение по левому поддереву, а уже потом по правому. Фактически
существуют еще три алгоритма, которые выбирают сначала правое поддерево
и потом левое. Для печати дерева будем использовать RNL-прохождение.
Алгоритмы прохождения посещают каждый узел дерева. Они дают
эквивалент последовательного сканирования массива или связанного списка.
Функции прямого, симметричного и обратного методов прохождения содержатся
в файле treescan.h.
Пример 11.2
1. Для символьного дерева Тгее_2 имеет место следующий порядок
Тгее_2
посещения узлов.
Прямой: ABDGCEHI F
Симметричный: DGBAHEI CF
Обратный: GDBHI EFCA
2. Результат симметричного прохождения дерева Тгее_2 производится
следующими операторами:
// функция visit распечатывает поле данных
void PrintChar(char& elem)
{
cout «elem « " n;
}
TreeNode<char> *root;
MakeCharTree(root, 2); // сформировать дерево Tree_2 с корнем root
// распечатать заголовок и осуществить прохождение, используя
// функцию PrintChar для обработки узла
cout < "Симметричное прохождение: ";
Inorder (root, PrintChar);
11.3. Использование алгоритмов прохождения
деревьев
На рекурсивных алгоритмах прохождения основаны многие приложения
деревьев. Эти алгоритмы обеспечивают упорядоченный доступ к узлам. В
данном разделе демонстрируется использование алгоритмов прохождения для
подсчета количества листьев на дереве, глубины дерева и для печати дерева. В
каждом случае для посещения узлов мы должны применять ту или иную
стратегию прохождения.
Приложение: посещение узлов дерева
Для многих приложений требуется просто обойти узлы дерева, неважно в
каком порядке. В этих случаях клиент волен выбрать любой алгоритм
прохождения. В данном приложении функция CountLeaf проходит дерево с целью
подсчета его листьев. При распознавании очередного листа происходит
приращение параметра count.
// эта функция использует обратный метод прохождения.
// во время посещения узла проверяется, является ли он листовым
template CountLeaf (<TreeNode<T> *t, int& count)
{
// Использовать обратный метод прохождения
if (t != NULL)
{
CountLeaf(t->Left(), count); // пройти левое поддерево
CountLeaf(t->Right (), count); // пройти правое поддерево
// Проверить, является ли данный узел листом.
// Если да, то произвести приращение переменной count
if (t->Left() == NULL && t->Right() == NULL)
COunt++;
)
}
Функция Depth использует обратный метод прохождения для вычисления
глубины бинарного дерева. В каждом узле вычисляется глубина его левого и
правого поддеревьев. Итоговая глубина на единицу больше максимальной
глубины поддеревьев.
// эта функция использует обратный метод прохождения для вычисления глубины
// левого и правого поддеревьев узла и возвращает результирующее
// значение глубины, равное 1 + max(depthLeft, depthRight).
// глубина пустого дерева равна -1
template <class T>
void Depth (TreeNode<T> *t)
{
int depthLeft, depthRight, depthval;
if (t === NULL)
depthval = -1;
else
{
depthLeft = Depth(t->Left());
depthRight = Depth(t->Right());
depthval - 1 + (depthLeft > depthRight?depthLeft:depthRight);
}
return depthval;
}
Программа 11.1. LeafCount и Depth
Эта программа иллюстрирует использование функций LeafCount и Depth
для прохождения символьного дерева Тгее_2. Итоговые значения LeafCount
и Depth распечатываются.
#include <iostream.h>
// включить класс TreeNode и библиотеку функций
#include "treenode.h"
#include "treelib.h"
void main(void)
{
TreeNode<char> *root;
// использовать дерево Тгее_2
MakeCharTree(root, 2);
// переменная, которая обновляется функцией CountLeaf
int leafCount =0;
// вызвать функцию CountLeaf для подсчета числа листьев
CountLeaf(root, leafCount);
cout « "Число листьев равно " « leafCount « endl;
// вызвать функцию Depth для вычисления глубины дерева
cout « "Глубина дерева равна "
« Depth(root) « endl;
}
/*
<Выполнение программы 11.1>
Число листьев равно 4
Глубина дерева равна 3
V
Приложение: печать дерева
Функция печати дерева создает изображение дерева, повернутое на 90
градусов против часовой стрелки. На рис. 11.10 показано исходное дерево Тгее_2
(слева) и распечатанное. Поскольку принтер выводит информацию построчно,
алгоритм использует RNL-прохождение и распечатывает узлы правого
поддерева раньше узлов левого поддерева. Узлы дерева Тгее__2 печатаются в порядке
FCIEHABGD.
Функция PrintTree распечатывает поле данных узла и уровень узла.
Вызывающая программа передает корень с уровнем 0. На каждом рекурсивном
вызове функции PrintTree нужно делать отступ для уровня узла. В нашем
формате величина отступа вычисляется как indentBlock * level, где indentBlock —
константа 6, задающая число пробелов, которое приходятся на один уровень
узла. Чтобы распечатать узел, сначала вычисляется число пробелов в отступе,
соответствующее уровню этого узла, а затем выводится поле данных.
Поскольку функция PrintTree использует стандартный поток cout, для типа Т должен
быть определен оператор «. На рис. 11.11 показаны уровни и пробелы,
предшествующие каждому узлу дерева Тгее_2.
Tree 2
Printed Tree_2
Рис 11.10. Распечатанное дерево Tree_2
Отступ
0
12
6
18
12
18
0 A
6
18
12
Уровни
1 2
F
С
E
В
D
3
I
H
G
Рис. 11.11. Печать дерева Tree_2
Код функции PrintTree находится в файле treeprint.h.
// промежуток между уровнями
const int indentBlock - 6;
// вставить num пробелов на текущей строке
void IndentBlanks(int num)
{
for (int i * 0; i < num; i++)
cout « и и;
)
// распечатать дерево Ооком, используя RNL-прохождение
template <class T>
void PrintTree (Treenode<T> *t, int level)
{
// печатать дерево с корнем t, пока t != NULL
if (t !« NULL)
{
// печатать правое поддерево узла t
PrintTree(t->Right(), level+1);
// выровнять текущий уровень и вывести поле данных
IndentBlanks(indentBlock * level);
cout « t->data « endl;
// печатать левое поддерево
PrintTree(t->Left(), level+1);
}
}
Приложение: копирование и удаление деревьев
Утилиты копирования и удаления всего дерева вводят новые понятия и
подготавливают нас к проектированию класса деревьев, который требует
деструктор и конструктор копирования. Функция СоруТгее принимает исходное
дерево и создает его дубликат. Процедура DeleteTree удаляет каждый узел дерева,
включая корень, и высвобождает занимаемую узлами память. Функции,
разработанные для бинарных деревьев общего вида, находятся в файле treelib.h.
Копирование дерева. Функция СоруТгее использует для посещения узлов
обратный метод прохождения. Этот метод гарантирует, что мы спустимся по
дереву на максимальную глубину, прежде чем начнем операцию посещения,
которая создает узел для нового дерева. Функция СоруТгее строит новое дерево
снизу вверх. Сначала создаются сыновья, а затем они присоединяются к своим
родителям, как только те будут созданы. Этот подход использовался в функции
MakeCharTree. Например, порядок операций для дерева Тгее__0 следующий:
Тгее_0
d « GetTreeNode('D');
e « GetTreeNode('E');
b = GetTreeNode('B', NULL, d)/
с = GetTreeNode('С, e, NULL);
a =• GetTreeNode {'A' , b, c);
root - a;
Сначала мы создаем сына D, который затем присоединяется к своему
родителю В при создании узла. Создается узел Е и присоединяется к своему
родителю С во время рождения (или создания) последнего. Наконец, создается
корень и присоединяется к своим сыновьям В и С.
Алгоритм копирования дерева начинает с корня и в первую очередь строит
левое поддерево узла, а затем — правое его поддерево. Только после этого
создается новый узел. Тот же рекурсивный процесс повторяется для каждого
узла. Соответственно узлу t исходного дерева создается новый узел с
указателями newlptr и newrptr.
При обратном методе прохождения сыновья посещаются перед их
родителями. В результате в новом дереве создаются поддеревья, соответствующие
t->Left() и t->Right(). Сыновья присоединяются к своим родителям в момент
создания последних.
Исходное дерево
Новое дерево
left
data
right
newlptr
data
newrptr
newnode
t->Left()
t->Right()
newnode->Left()
newnode->Right()
CopyTree(t->Left()))
CopyTree(t->Right())
newlptr = CopyTree(t->Left());
newrptr = CopyTree(t->Right());
// создать родителя и присоединить к нему его сыновей
newnode = GetTreeNode(t->data, newlptr, newrptr);
Суть посещения узла t в исходном дереве заключается в создании нового
узла на дереве-дубликате.
Символьное дерево Тгее__0 является примером, иллюстрирующим
рекурсивную функцию CopyTree. Предположим, что главная процедура определяет
корни rootl и root2 и создает дерево Тгее_0. Функция CopyTree создает новое
дерево с корнем root2. Проследим алгоритм и проиллюстрируем процесс
создания пяти узлов на дереве-дубликате.
TreeNode<char> *rootl, *root2; // объявить два дерева
MakeCharTree(rootl, 0); // rootl указывает на Tree_0
root2 = CopyTree(rootl); // создать копию дерева Тгее_0
rootl root2
Tree_0 Дубликат
1. Пройти потомков узла А, начиная с левого поддерева в узле В и далее
к узлу D, который является правым поддеревом узла В. Создать новый
узел с данными, равными D, и левым и правым указателями, равными
NULL [рис. 11.12 (А)].
2. Сыновья узла В пройдены. Создать новый узел с данными, равными
В, левым указателем, равным NULL, и правым указателем,
указывающим на узел D [рис. 11.12 (В)].
3. Поскольку левое поддерево узла А пройдено, начать прохождение его
правого поддерева и дойти до узла Е. Создать новый узел с данными
из узла Е и указательными полями, равными NULL.
4. После обработки Е перейти к его родителю и создать новый узел с
данными из С. В поле правого указателя поместить NULL, а левому
указателю присвоить ссылку на дочерний узел Е [рис. 11.13 (А)].
rootl root2 rootl root2
Рис. 11.12. Копирование левого поддерева узла А
rootl root2
(А)
rootl root2
(В)
Рис. 11.13. Копирование правого поддерева узла А
5. Последний шаг выполняется в узле А. Создать новый узел с данными
из А и присоединить к нему сына В слева и сына С справа [рис. 11.13 (В)].
Копирование дерева завершено.
Функция СоруТгее возвращает указатель на вновь созданный узел. Это
возвращаемое значение используется родителем, когда тот создает свой
собственный узел и присоединяет к нему своих сыновей. Функция возвращает корень
вызывающей программе.
// создать дубликат дерева t и возвратить корень нового дерева
template <class T>
TreeNode<T> *CopyTree(TreeNode<T> *t)
{
// переменная newnode указывает на новый узел, создаваемый
// посредством вызова GetTreeNode и присоединяемый в дальнейшем
// к новому дереву, указатели newlptr и newrptr адресуют сыновей
// нового узла и передаются в качестве параметров в GetTreeNode
TreeNode<T> *newlptr, *newrptr, *newnode;
// остановить рекурсивное прохождение при достижении пустого дерева
if (t « NULL)
return NULL;
// CopyTree строит новое дерево в процессе прохождения узлов дерева t. в каждом
// узле этого дерева функция CopyTree проверяет наличие левого сына, если он
// есть, создается его копия, в противном случае возвращается NULL. CopyTree
// создает копию узла с помощью GetTreeNode и подвешивает к нему копии сыновей.
if (t->Left() != NULL)
newlptr - CopyTree(t->Left ());
else
newlptr - NULL;
if (t->Right() !=* NULL)
newrptr - CopyTree(t->Right());
else
newrptr ■ NULL;
// построить новое дерево снизу вверх, сначала создавая
// двух сыновей, а затем их родителя
newnode » GetTreeNode(t->data, newlptr, newrptr);
// вернуть указатель на вновь созданное дерево
return newnode;
)
Удаление дерева. Когда в приложении используется такая динамическая
структура, как дерево, ответственность за освобождение занимаемой им
памяти ложится на программиста. Для бинарного дерева общего вида
разработаем функцию DeleteTree, в которой применяется обратный метод
прохождения. Это гарантирует, что мы посетим всех сыновей родительского узла,
прежде чем удалим его. Операция посещения заключается в вызове функции
FreeTreeNode, удаляющей узел.
// использовать обратный алгоритм для прохождения узлов дерева
//и удалить каждый узел при его посещении
template <class T>
void DeleteTree(TreeNode<T> *t)
{
if (t !« NULL)
{
DeleteTree(t->Left ());
DeleteTree(t->Right());
FreeTreeNode(t);
)
)
Более общая процедура удаления дерева удаляет узлы и сбрасывает корень.
Функция ClearTree вызывает DeleteTree для удаления узлов дерева и
присваивает указателю на корень значение NULL.
// вызвать функцию DeleteTree для удаления узлов дерева.
// затем сбросить указатель на его корень в NULL
template <class T>
void ClearTree(TreeNode<T> &t)
{
DeleteTree(t);
t = NULL;
// теперь корень пуст
>
Программа 11.2. Тестирование функций СоруТгее и DeleteTree
Эта программа использует дерево Тгее_0 и создает копию, которая
адресуется указателем root2. Мы осуществляем обратный проход вновь
созданного дерева, преобразуя букву в поле данных каждого узла из прописной в
строчную. Результат распечатывается с помощью функции PrintTree.
♦include <iostream.h>
♦include <ctype.h>
♦include <stdlib.h>
♦include "treescan.h"
♦include "treelib.h"
♦include "treeprnt.h"
// функция преобразования прописной буквы в строчную
void Lowercase(char &ch)
{
ch ■ tolower(ch);
}
void main(void)
{
// указатели на исходное дерево и его дубликат
TreeNode<char> *rootl, *root2;
// создать дерево Tree_0 и распечатать его
MakeCharTree(root1, 0);
PrintTree (rootl, 0);
// копировать дерево
cout « endl « "Копия:" « endl;
root2 - СоруТгее(rootl);
// выполнить обратное прохождение и распечатать дерево
Postorder(root2, Lowercase);
PrintTree(root2, 0);
)
*/
<Выполнение программы 11.2>
С
E
A
D
В
Копия:
с
e
a
d
b
*/
Приложение: вертикальная печать дерева
Функция PrintTree создает повернутое набок изображение дерева. На
каждой строке узел распечатывается в позиции, определяемой его уровнем. Хотя
такое дерево воспринимается трудно, этот прием позволяет распечатывать
большие деревья. На 80-колоночном листе неограниченной длины можно
изобразить дерево с216 — 1 =65535 узлами, если промежуток между уровнями
indentBlock равен пяти пробелам. Вертикальная распечатка дерева более
ограничена, так как элементы данных и межуровневые промежутки будут
располагаться по ширине листа. Но для относительно небольших деревьев такая
картинка более реалистична и привлекательна. В данном приложении мы
разработаем инструменты для реализации функции PrintVTree (см. файл treeprint.h).
Функция PrintVTree требует нового алгоритма прохождения, который
сканирует дерево уровень за уровнем, начиная с корня на уровне 0. Этот метод,
называемый поперечным прохождением или прохождением уровней (level
scan), не спускается рекурсивно вдоль поддеревьев, а просматривает дерево
поперек, посещая все узлы на одном уровне, и затем переходит на уровень ниже.
В отличие от рекурсивного спуска здесь более предпочтителен итерационный
алгоритм, использующий очередь элементов. Для каждого узла в очередь
помещается всякий непустой левый или правый указатель на сына этого узла. Это
гарантия того, что одноуровневые узлы следующего уровня будут посещаться в
нужном порядке. Символьное дерево Тгее_2 иллюстрирует этот алгоритм.
PrintTree PrintVTree
Уровень 0:
Уровень 1:
Уровень 2:
Уровень 3:
Посещение А
Посещение В, С
Посещение D, Е, F
Посещение G, Н, I
Тгее_2
Алгоритм поперечного прохождения
Шаг инициализации:
Поместить в очередь корневой узел.
Шаги итерации:
Прекратить процесс, если очередь пуста.
Удалить из очереди передний узел р и распечатать его значение.
Использовать этот узел для идентификации его детей на следующем
уровне дерева.
if (p->Left() != NULL) // проверить наличие левого сына
Q.QInsert(p->Left());
if (p->Right() !* NULL) // проверить наличие правого сына
Q.QInsert(p->Right());
Пример 11.3
Алгоритм поперечного прохождения иллюстрируется на дереве Тгее_0.
Тгее_0
Инициализация: Вставить узел А в очередь.
1: Удалить узел А из очереди.
Печатать А.
Вставить сыновей узла А в очередь.
Левый сын = В
Правый сын = С
2: Удалить узел В из очереди.
Распечатать В.
3: Удалить узел С из очереди.
Левый сын = Е
4: Удалить узел D из очереди.
Распечатать D.
Узел D не имеет сыновей.
5: Удалить узел Е из очереди.
Алгоритм завершается. Очередь пуста.
// Прохождение дерева уровень за уровнем с посещением каждого узла
template <class T>
void LevelScan(TreeNode<T> *t, void visit(T& item))
{
// запомнить сыновей каждого узла в очереди, чтобы их
// можно было посетить в этом порядке на следующем уровне
Queue<TreeNode<T> *> Q;
TreeNode<T> *p;
// инициализировать очередь, вставив туда корень
Q.Qinsert(t);
// продолжать итерационный процесс, пока очередь не опустеет
while(!Q.QEmpty())
{
// удалить первый в очереди узел и выполнить функцию visit
р = Q.QDelete() ;
visit(p->data);
// если есть левый сын, вставить его в очередь
if (p->Left() != NULL)
Q.Qinsert(p->Left());
// если есть правый сын, вставить его в очередь
if (p->Right() != NULL)
Q.Qinsert(p->Right{));
}
}
Алгоритм PrintVTree. В функцию вертикальной печати дерева передается
корень дерева, максимальная ширина данных и ширина экрана:
void PrintVTree(TreeNode<T> *t, int dataWidth, int screenWidth)
Параметры ширины позволяют организовать экран. Пусть dataWidth = 2 и
screenWidth = 64 = 26. Тот факт, что значение ширины равно степени двойки,
позволяет описать поуровневую организацию данных. Поскольку мы не знаем
структуру дерева, то полагаем, что места должно хватать для полного
бинарного дерева. Узлы строятся в координатах (уровень, смещение).
Уровень 0:
Корень рисуется в точке (0,32).
Уровень 1:
Поскольку корень смещен на 32 позиции, следующий уровень имеет
смещение 32/2 = 16 = screenWidth/22. Два узла первого уровня
располагаются в точках (1, 32-смещение) и (1, 324-смещение), т.е. в точках
(1,16) и (1,48).
Уровень 2:
На втором уровне смещение равно screenWidth/23 = 8. Четыре узла
второго уровня располагаются в точках (2, 16-смещение), (2, 16+сме-
щение), (2, 48-смещение), (2, 48+смещение), т.е. в точках (2,8), (2,24),
(2,40) и (2,56).
Уровень i:
Смещение равно screenWidth/2i+1. Позиция каждого узла данного
уровня определяется во время посещения его родителя на уровне i-1. Пусть
позиция родителя равна (i-1, parentPos). Если узел i-ro уровня является
левым сыном, то его позиция равна (i, parentPos-смещение), а если
правым — (i, parentPos4-смещение).
Уровень 0
Уровень 1
Уровень 2
Уровень 3
PrintVTree использует две очереди и поперечный метод прохождения узлов
дерева. В очереди Q находятся узлы, а очередь QI содержит уровни и позиции
печати в форме записей типа Info. Когда узел добавляется в очередь Q,
соответствующая ему информация о печати запоминается в QI. Элементы
удаляются в тандеме во время посещения узла.
// запись для хранения координат (х,у) узла
struct Info
{
int xlndent, yLevel;
};
// Очереди для хранения узлов и информации о печати
Queue<TreeNode<T> * Q;
Queue<Info> QI;
Программа 11.3. Вертикальная печать дерева
Эта программа распечатывает символьное дерево Тгее_2 на 30- или на
60-символьном листе. Ширина данных для вывода dataWidth = 1.
♦include <iostream.h>
// включить функцию PrintVTree из библиотеки
♦include "treelib.h"
♦include "treeprnt.h"
void main (void)
{
// объявить символьное дерево
TreeNode<char> *root;
// назначить дереву Tree_2 корень root
MakeCharTree(root, 2);
cout « "Печать дерева на 30-символьном экране" « endl;
PrintVTree(root, 1, 30);
cout « endl « endl;
cout « "Печать дерева на 60-символьном экране" « endl;
PrintVTree(root, 1, 60);
}
/*
<Выполнение программы 11.3>
Печать дерева на 30-символьном экране
Печать дерева на 60-символьном экране
11.4. Бинарные деревья поиска
Обычное бинарное дерево может содержать большую коллекцию данных и
все зке обеспечивать быстрый поиск, добавление или удаление элементов.
Одним из наиболее важных приложений деревьев является построение классов
коллекций. Нам уже знакомы проблемы, возникающие при построении общего
класса коллекций из класса SeqList и его реализации с помощью массива или
связанного списка. Главную роль в классе SeqList играет метод Find,
реализующий последовательный поиск. Для линейных структур сложность этого
алгоритма равна O(N), что неэффективно для больших коллекций. В общем
случае древовидные структуры обеспечивают значительно большую
производительность, так как путь к любым данным не превышает глубины дерева.
Эффективность поиска максимизируется при законченном бинарном дереве и
составляет 0(log2N). Например, в списке из 10000 элементов предполагаемое
число сравнений при последовательном поиске равно 5000. Поиск же на
законченном дереве потребовал бы не более 14 сравнений. Бинарное дерево
представляет большие потенциальные возможности в качестве структуры хранения
списка.
Линейный связанный список 5000 сравнений
Бинарное дерево
14 сравнений в худшем случае
Чтобы запомнить элементы в виде дерева с целью эффективного доступа,
мы должны разработать поисковую структуру, которая указывает путь к
элементу. Эта структура, называемая бинарным деревом поиска (binary search
tree), упорядочивает элементы посредством оператора отношения "<". Чтобы
сравнить узлы дерева, мы подразумеваем, что часть или все поле данных
определено в качестве ключа и оператор "<" сравнивает ключи, когда размещает
элемент на дереве. Бинарное дерево поиска строится по следующему правилу:
Для каждого узла значения данных в левом поддереве меньше, чем в
этом узле, а в правом поддереве — больше или равны.
На рис. 11.14 показан пример бинарного поискового дерева. Это дерево
называется поисковым потому, что в поисках некоторого элемента (ключа)
мы можем идти лишь по совершенно конкретному пути. Начав с корня, мы
сканируем левое поддерево, если значение ключа меньше текущего узла. В
Рис. 11.14. Дерево бинарного поиска
противном случае сканируется правое поддерево. Метод создания дерева
позволяет осуществлять поиск элемента по кратчайшему пути от корня.
Например, поиск числа 37 требует четырех сравнений, начиная с корня.
Текущий узел Действие
Корень = 50 Сравнить ключ = 37 и 50
поскольку 37 < 50, перейти в левое поддерево
Узел = 30 Сравнить ключ = 37 и 30
поскольку 37 >= 30, перейти в правое поддерево
Узел = 35 Сравнить ключ = 37 и 35
поскольку 37 >= 35, перейти в правое поддерево
Узел = 37 Сравнить ключ = 37 и 37. Элемент найден.
На рис. 11.15 показаны различные бинарные деревья поиска.
Ключ в узле бинарного дерева поиска
Ключ в поле данных работает как этикетка, с помощью которой можно
идентифицировать узел. Во многих приложениях элементы данных являются
записями, состоящими из отдельных полей. Ключ — одно из этих полей.
Например, номер социальной страховки является ключом,
идентифицирующим студента университета.
Номер социальной страховки
(9-символьная строка)
Имя студента
(строка)
Средний балл
(число с плавающей точкой)
Ключевое поле
struct Student
{
String ssn;
String name;
float gpa;
}
Ключом может быть все поле данных и только его часть. На рис. 11.5
узлы содержат единственное целочисленное значение, которое и является
ключом. В этом случае узел 25 имеет ключ 25, и мы сравниваем два узла
путем сравнения целых чисел. Сравнение производится с помощью
целочисленных операторов отношения "<" и "==". Для студента университета клю-
BinSTree 1 BinSTree_2
Рис. 11.15. Примеры деревьев бинарного поиска
чом является ssn, и мы сравниваем две символьные строки. Это делается с
помощью перегрузки операций. Например, следующий код реализует
отношение "<" для двух объектов Student:
int operator < (const Students s, const Students t)
{
return s.ssn < t.ssn; // сравнить ключи ssn
}
В наших приложениях мы приводим ряд примеров ключ/данные. В
иллюстрациях мы используем простой формат, где ключ и данные — одно и то же.
Операции на бинарном дереве поиска
Бинарное дерево поиска является нелинейной структурой для хранения
множества элементов. Как и любая списковая структура, дерево должно
допускать включение, удаление и поиск элементов. Для поискового дерева
требуется такая операция включения (вставки), которая правильно
располагает новый элемент. Рассмотрим, например, включение узла 8 в дерево
BinSTree^. Начав с корневого узла 25, определяем, что узел 8 должен быть в
левом поддереве узла 25 (8<25). В узле 10 определяем, что место узла 8
должно быть в левом поддереве узла 10, которое в данный момент пусто.
Узел 8 включается в дерево в качестве левого сына узла 10.
До вставки узла 8
После вставки узла 8
BinSTree 1
BinSTree 1
До каждого вставляемого в дерево узла существует конкретный путь. Тот
же путь может использоваться для поиска элемента. Поисковый алгоритм
берет ключ и ищет его в левом или в правом поддереве каждого узла,
составляющего путь. Например, поиск элемента 30 на дереве BinSTree__l (рис. 11.15)
начинается в корневом узле 25 и переходит в правое поддерево (30 > 25), а
затем в левое поддерево. (30 < 37). Поиск прекращается на третьем сравнении,
когда ключ совпадает с числом 30, хранящемся в узле.
BinSTree 1
В связанном списке операция удаления отсоединяет узел и соединяет его
предшественника со следующим узлом. На бинарном дереве поиска подобная
операция намного сложнее, так как узел может нарушить упорядочение
элементов дерева. Рассмотрим задачу удаления корня 25 из BinSTree_l. В
результате появляются два разобщенных поддерева, которым требуется новый
корень.
На первый взгляд напрашивается решение выбрать сына узла 25 —
скажем, 37 — и заменить его родителя. Однако это простое решение терпит
неудачу, так как некоторые узлы оказываются не с той стороны корня.
Поскольку данное дерево относительно невелико, мы можем установить, что
15 или 30 являются допустимой заменой корневому узлу.
Неудачное решение: 30 не на месте
Удачное решение
BinSTree 1
BinSTree 1
Объявление абстрактного типа деревьев
Абстрактный тип данных (ADT) для списка строится по образцу класса
SeqList. Тот факт, что бинарное дерево поиска хранит элементы данных в
виде нелинейного списка, становится существенной деталью реализации его
методов. Заметим, что этот ADT является зеркальным отражением ADT для
класса SeqList, но имеет дополнительный метод Update, позволяющий
обновлять поле данных, и метод GetRoot, предоставляющий доступ к корневому
узлу, а следовательно, и функциям прохождения из treescan.h и к функциям
печати из treeprint.h. Обратите внимание, что метод GetData класса SeqList
отсутствует, так как он относится к линейному списку.
APT для бинарных деревьев поиска
Данные
Список элементов, хранящийся в виде бинарного дерева, и значение size,
определяющее текущее число элементов в списке. Дерево содержит указатель
на корень и ссылку на последний обработанный узел — текущую позицию.
Операции
Конструктор <Тот же, что и в ADT для класса SeqList>
ListSize <Тот же, что и в ADT для класса SeqList>
ListEmpty <Тот же, что и в ADT для класса SeqList>
ClearList <Тот же, что и в ADT для класса SeqList>
Find
Вход: Ссылка на значение данных
Предусловия: Нет
Процесс: Осуществить поиск на дереве путем сравнения элемента
с данными, хранящимися в узле. Если происходит совпадение,
выбрать данные из узла.
Выход: Возвратить 1 (True), если произошло совпадение, и присвоить
данные из совпавшего узла параметру.
В противном случае возвратить 0 (False).
Постусловия: Текущая позиция соответствует совпавшему узлу.
Insert
Вход: Элемент данных
Предусловия: Нет
Процесс: Найти подходящее для вставки место на дереве.
Добавить новый элемент данных.
Выход: Нет
Постусловия: Текущая позиция соответствует новому узлу.
Delete
Вход: Элемент данных
Предусловия: Нет
Процесс: Найти на дереве первый попавшийся узел, содержащий элемент
данных. Удалить этот узел и связать все его поддеревья так,
чтобы сохранить структуру бинарного дерева поиска.
Выход: Нет
Постусловия: Текущая позиция соответствует узлу, заменившему удаленный.
Update
Вход: Элемент данных
Предусловия: Нет
Процесс: Если ключ в текущей позиции совпадает с ключом элемента
данных, присвоить элемент данных узлу. В противном случае
вставить элемент данных в дерево.
Выход: Нет
Постусловия: В списке может оказаться новое значение.
GetRoot
Вход: Нет
Предусловия: Нет
Процесс: Получить указатель на корень.
Выход: Возвратить указатель на корень.
Постусловия: Не изменяется
Конец ADT для бинарных поисковых деревьев
Объявление класса BinSTree. Мы реализовали ADT для бинарных
поисковых деревьев в виде класса с динамическими списковыми структурами. Этот
класс содержит стандартный деструктор, конструктор копирования и
перегруженные операторы присваивания, позволяющие инициализировать объекты и
играющие роль операторов присваивания. Деструктор отвечает за очистку
списка, когда закрывается область действия объекта. Деструктор и операторы
присваивания вместе с методом ClearList вызывают закрытый метод DeleteTree.
Мы также включили сюда закрытый метод СоруТгее для использования в
конструкторе копирования и перегруженном операторе.
Спецификация класса BinSTree
ОБЪЯВЛЕНИЕ
#include <iostream.h>
iinclude <stdlib.h>
#include "treenode.h"
template <class T>
class BinSTree
{
protected: // требуется для наследования в гл. 12
// указатели на корень и на текущий узел
TreeNode<T> *root;
TreeNode<T> *current;
// число элементов дерева
int size;
// распределение/освобождение памяти
TreeNode<T> *GetTreeNode(const T& item,
TreeNode<T> *lptr, TreeNode<T> *rptr);
void FreeTreeNode(TreeNode<T> *p);
// используется конструктором копирования и оператором присваивания
void DeleteTree(TreeNode<T> *t);
// используется деструктором, оператором присваивания
// и функцией ClearList
TreeNode<T> *FindNode(const T& item,
TreeNode<T>* & parent) const;
public:
// конструктор и деструктор
BinSTree(void);
BinSTree(const BinSTree<T>& tree);
-BinSTree(void);
// оператор присваивания
BinSTree<T>& operator= (const BinSTree<T>& rhs);
// стандартные методы обработки списков
int Find(T& item);
void Insert(const T& item);
void Delete(const T& item);
void ClearList(void);
int ListEmpty(void) const;
int ListSize(void) const;
// методы, специфичные для деревьев
void Update(const T& item);
TreeNode<T> *GetRoot(void) const;
}
ОПИСАНИЕ
Этот класс имеет защищенные данные. Они представляют конструкцию
наследования, которая обсуждается в гл. 12. Защищенный доступ
функционально эквивалентен закрытому доступу для данного класса. Переменная root
указывает на корневой узел дерева. Указатель current ссылается на точку
последнего изменения в списке. Например, current указывает положение
нового узла после операции включения, а метод Find заносит в current ссылку
на узел, совпавший с элементом данных.
Стандартные операции обработки списков используют те же имена и
параметры, что и определенные в классе SeqList.
Класс BinSTree содержит две операции, специфические для деревьев.
Метод Update присваивает новый элемент данных текущему узлу или
включает в дерево новый элемент, если тот не совпадает с данными в текущей
позиции. Метод GetRoot предоставляет доступ к корню дерева. Имея корень
дерева, пользователь получает доступ к библиотечным функциям из treelib.h,
treescan.h и treeprint.h. Это расширяет возможности класса для привлечения
различных алгоритмов обработки деревьев, в том числе распечатки дерева.
ПРИМЕР
BinSTree<int> T; // дерево с целочисленными данными
T.Insert(50); // создать дерево с четырьмя узлами (А)
T.Insert(40);
T.Insert(70);
Т.Insert(45);
Т.Delete(40); // удалить узел 40 (В)
T.ClearListO; // удалить узлы дерева
(А)
(В)
// дерево univlnfo содержит информацию о студентах.
// Поле ssn является ключевым
BinSTree<Student> univlnfo/
Student stud;
// назначить ключ "9876543789" и найти его на дереве
stud.ssn - "9876543789";
if (univlnfo.Find(stud))
(
// студент найден, присвоить новый средний балл и обновить узел
stud.gpa = 3.86;
univlnfo.Update(stud);
}
else
cout « "Студент отсутствует в базе данных." « endl;
11.5. Использование бинарных деревьев поиска
Класс BinSTree — мощная структура данных, которая используется для
обработки динамических списков. Практическая задача построения
конкорданса1 иллюстрирует типичное применение поисковых деревьев. Мы будем
использовать эту структуру в словарях в гл. 14, а в данном разделе
рассмотрим ряд простых программ, где применяются деревья поиска.
Создание примеров деревьев поиска. В разделе 11.1 функция MakeChar-
Tree использовалась для создания ряда бинарных деревьев с символьными
данными. Похожая функция MakeSearchTree строит бинарные деревья поиска
с целочисленными данными, применяя метод Insert. Например, дерево Sear-
1 Под конкордансом в книге понимается алфавитный список всех слов заданного текста с
указателями на места их появлений. — Прим, ред.
chTree_0 использует шесть элементов заранее определенного массива аггО,
чтобы сконструировать дерево с помощью объекта Т класса BinSTree.
int arr0[6] = {30, 20, 45, 5, 10, 40};
for (i = 0; i < 6; i++)
T.Insert(arr0[i]); // добавить элемент к дереву
SearchTree 0
MakeSearchTree создает второе восьмиэлементное дерево и дерево с десятью
случайными числами из диапазона 10-99 (рис. 11.16). Параметры функции
содержат объект класса BinSTree и параметр type (0 < type < 2), служащий
для обозначения дерева. Код MakeSearchTree находится в файле makesrch.h.
SearchTree 1 SearchTree 2
Рис. 11.16. Деревья, созданные с помощью функции MakeSearchTree
Симметричный метод прохождения. При симметричном прохждении
бинарного дерева сначала посещается левое поддерево узла, затем — сам узел
и наконец правое поддерево. Когда этот метод прохождения применяется к
бинарному дереву поиска, узлы посещаются в сортированном порядке. Этот
факт становится очевидным, когда вы сравниваете узлы в поддеревьях
текущего узла. Все узлы левого поддерева текущего узла имеют меньшие
значения, чем текущий узел, и все узлы правого поддерева текущего узла больше
или равны текущему узлу. Симметричное прохождение бинарного дерева
гарантирует, что для каждого узла, который мы посещаем впервые, меньшие
узлы находятся в левом поддереве, а большие — в правом. В результате
узлы проходятся в возрастающем порядке.
Программа 11.4. Использование дерева поиска
Эта программа использует функцию MakeSearchTree для создания
дерева SearchTree_l, содержащего числа
50, 20, 45, 70, 10, 60, 90, 30
С помощью метода GetRoot мы получаем доступ к корню этого дерева,
что позволяет вызвать функцию PrintVTree. Метод GetRoot позволяет
также распечатать элементы по возрастанию, используя функцию Inorder
с параметром-функцией Printlnt. Программа заканчивается удалением
элементов 50 и 70 и повторной печатью дерева.
♦include "makesrch.h" // функция MakeSearch
♦include "treescan.h"
♦include "treeprnt.h" // функция PrintVTree
♦include "bstree.h" // функция Inorder
// печать целого числа, используется функцией Inorder
void Printlnt(int& item)
{
cout « item « " ";
}
void main(void)
{
// объявить целочисленное дерево
BinSTree<int> Tree;
// создать дерево поиска ♦in распечатать его вертикально
// при ширине в 40 символов
MakeSearchTree(Tree, l);
PrintVTree (Tree.GetRoot (), 2, 40);
// симметричное прохождение обеспечивает
// посещение узлов по возрастанию
// хранящихся в них чисел
cout « endl « endl « "Сортированный список: ";
Inorder(Tree.GetRoot(), Printlnt);
cout « endl;
cout « endl « "Удаление узлов 70 и 50." « endl;
Tree.Delete(70);
Tree.Delete(50);
PrintVTree(Tree.GetRoot(), 2, 40);
cout « endl;
}
/*
<Выполнение программы 11.4>
50
20 70
10 45 60 90
30
Сортированный список: 10 20 30 45 50 60 70 90
Удаление узлов 70 и 50.
45
20 60
10 30 90
*/
Дублированные узлы
Бинарное дерево поиска может иметь дублированные узлы. В операции
включения мы продолжаем сканировать правое поддерево, если наш новый
элемент совпадает с данными в текущем узле. В результате в правом поддереве
совпавшего узла возникают дублированные узлы. Например, следующее дерево
генерируется из списка 50 70 25 90 30 55 25 15 25.
Многие приложения не допускают дублирования узлов, а используют в
данных поле счетчика экземпляров элемента. Это — принцип конкорданса,
когда отслеживаются номера строк, в которых встречается некоторое слово.
Вместо того чтобы несколько раз размещать слово на дереве, мы обрабатываем
повторные случаи употребления этого слова путем помещения номеров строк
в список. Программа 11.5 иллюстрирует лобовой подход, когда счетчик
дубликатов хранится как отдельный элемент данных.
Список: 50 70 25 90 30 55 25 15 25
Программа 11.5. Счетчики появлений
Запись IntegerCount содержит целую переменную number и поле count,
которое используется для запоминания частоты появлений целого числа в
списке. Поле number работает в качестве ключа в перегруженных
операторах "<" и "==", позволяющих сравнить две записи IntegerCount. Эти
операторы используются в функциях Find и Insert.
Программа генерирует 100000 случайных чисел в диапазоне 0-9 и
связывает каждое число с записью IntegerCount. Метод Find сначала определяет,
есть ли уже данное число на дереве. Если есть, то значение поля count
увеличивается на единицу и мы обновляем запись. В противном случае новая запись
включается в дерево. Программа завершается симметричным прохождением
узлов, в процессе которого происходит печать чисел и их счетчиков. Все
генерируемые случайным образом числа от 0 до 9 равновероятны.
Следовательно, каждый элемент может появиться приблизительно 10000 раз.
Запись IntegerCount и два ее оператора находятся в файле intcount.h.
♦include <iostreara.h>
♦include "random.h" // генератор случайных чисел
♦include "bstree.h" // класс BinSTree
♦include "treescan.h" // функция Inorder
♦include "intcount.h" // запись IntegerCount
// вызывается функцией Inorder для распечатки записи IntegerCount
void PrintNumberdntegerCounti N)
i
cout « N. number « ' :' « N. count « endl;
}
void main(void)
{
// объявить дерево, состоящее из записей IntegerCount
BinSTree<IntegerCount> Tree;
// сгенерировать 100000 случайный целых чисел в диапазоне 0..9
for (n - 0; n < 100000L; п++);
{
// сгенерировать запись IntegerCount со случайным ключом
N.number * rnd.Random(10);
// искать ключ на дереве
if (Tree.Find(N))
{
// ключ найден, увеличить count и обновить запись
N. count++;
Tree.Update(N);
)
else
{
// это число встретилось впервые, вставить его с count=l
N. count - 1;
Tree.Insert(N);
}
}
// симметричной прохождение для распечатки ключей по возрастанию
Inorder(Tree.GetRoot(), PrintNumber);
}
/*
<Выполнение программы 11.5>
0:10116
1:9835
2:9826
3:10028
4:10015
5:9975
6:9983
7:10112
8:10082
9:10028
*/
11.6. Реализация класса BinSTree
Класс BinSTree описывает нелинейный список и базовые операции
включения, удаления и поиска элементов. Помимо методов обработки списков важную
роль при реализации класса играет управление памятью. Частные методы
СоруТгее и DeleteTree используются конструктором, деструктором и
оператором присваивания для размещения и уничтожения узлов списка в
динамической памяти.
Элементы данных класса BinSTree. Бинарное дерево поиска определяется
своим указателем корня, который используется в операциях включения
(Insert), поиска (Find) и удаления (Delete). Класс BinSTree содержит элемент
данных root, являющийся указателем корня и имеющий начальное значение
NULL. Доступ к root осуществляется посредством метода GetRoot,
разрешающего вызовы функций прохождения и печати. Второй указатель, current,
определяет на дереве место для обновлений. Операция Find устанавливает current
на совпавший узел, и этот указатель используется функцией Update для
обновления данных. Методы Insert и Delete переустанавливают current на новый
узел или на узел, заменивший удаленный. Объект BinSTree является списком,
размер которого все время изменяется функциями Insert и Delete. Текущее
число элементов в списке хранится в закрытом элементе данных size.
// Указатели на корень и на текущий узел
TreeNode<T> *root;
TreeNode<T> *current;
// Число элементов дерева
int size;
Управление памятью. Размещение и уничтожение узлов для методов Insert
и Delete, а также для утилит СоруТгее и DeleteTree выполняется посредством
GetTreeNode и FreeTreeNode. Метод GetTreeNode создан по образцу функций
из treelib.h. Он распределяет память и инициализирует поля данных и
указателей в узле. FreeTreeNode непосредственно вызывает оператор удаления для
освобождения памяти.
Конструктор, деструктор и оператор присваивания. Класс содержит
конструктор, который инициализирует элементы данных. Конструктор
копирования и перегруженный оператор присваивания с помощью метода СоруТгее
создают новое бинарное дерево поиска для текущего объекта. Алгоритм
функции СоруТгее был разработан нами для класса TreeNode в разделе 11.3. В
том же разделе мы рассматривали алгоритм удаления узлов дерева, который
реализован в классе BinSTree функцией DeleteTree и используется как
деструктором, так и методом Clear List.
Перегружаемый оператор присваивания копирует объект, стоящий справа,
в текущий объект. После проверки того, что объект не присваивается самому
себе, функция очищает текущее дерево и с помощью СоруТгее создает
дубликат того, что стоит в правой части оператора (rhs). Указателю current
присваивается указатель root, копируется размер списка и возвращается
ссылка на текущий объект.
// оператор присваивания
template <class T>
BinSTree<T>& BinSTree<T>::operator =* (const BinSTree<T>& rhs)
{
// нельзя копировать дерево в само себя
if (this ~ &rhs)
return *this;
// очистить текущее дерево, скопировать новое дерево в текущий объект
ClearList();
root = CopyTree(tree.root);
// присвоить текущему указателю значение корня и задать размер дерева
current = root;
size = tree.size;
// возвратить ссылку на текущий объект
return *this;
}
Операции обработки списков
Методы Find и Insert начинают с корня и проходят по дереву уникальный
путь. Используя определение бинарного дерева поиска, алгоритм идет по правому
поддереву, когда ключ или новый элемент больше или равен значению текущего
узла. В противном случае прохождение продолжается по левому поддереву.
Операция Find (поиск). Операция Find использует закрытый
элемент-функцию FindNode, принимающую в качестве параметра ключ и осуществляющую
прохождение вниз по дереву. Операция возвращает указатель на совпавший
узел и указатель на его родителя. Если совпадение происходит в корневом узле,
родительский указатель равен NULL.
// искать элемент данных на дереве, если найден, возвратить адрес
// совпавшего узла и указатель на его родителя, иначе зозвратить NULL
template <class T>
TreeNode<T> *BinSTree<T>::FindNode(const T& item,
TreeNode<T>* & parent) const
{
// пробежать по узлам дерева, начиная с корня
TreeNode<T> *t = root;
//у корня нет родителя
parent = NULL;
// прерваться на пустом дереве
while (t !== NULL)
{
// остановиться по совпадении
if (item == t->data)
break;
else
{
// обновить родительский указатель и идти направо или налево
parent = t;
if (item < t->data)
t = t->left;
else
t = t->right;
}
}
// возвратить указатель на узел; NULL, если не найден
return t;
}
Информация о родителе используется операцией Delete (удаление). В методе
Find нас интересует только установление текущей позиции на совпавший узел и
присвоение ссылки на этот узел параметру item. Метод Find возвращает True (1)
или False (0), показывая тем самым, удался ли поиск. Для сравнения данных в
узлах методу Find требуются операторы отношения "==" и "<". Эти операторы
должны быть перегруженными, если они не определены для этого типа данных.
// искать item, если найден, присвоить данные узла параметру item
template <class T>
int BinSTree<T>::Find(T& item)
{
//мы используем FindNode, который принимает параметр parent
TreeNode<T> *parent;
// искать item, назначить совпавший узел текущим
current = FindNode (item, parent);
// если найден, присвоить данные узла и возвратить True
if (current != NULL)
{
item » current->data/
return 1;
}
else
// item не найден, возвратить False
return 0;
}
Операция Insert (вставка). Метод Insert принимает в качестве параметра
новый элемент данных и вставляет его в подходящее место на дереве. Эта
функция итеративно проходит путь вдоль левых и правых поддеревьев, пока
не найдет точку вставки. На каждом шаге этого пути алгоритм сохраняет
запись текущего узла (t) и родителя этого узла (parent). Процесс
прекращается по достижении пустого поддерева (t == NULL), которое показывает,
что мы нашли место для включения нового элемента. В этом месте новый
узел включается в качестве сына данного родителя. Например, следующие
шаги вставляют число 32 в дерево, изображенное на рис. 11.17.
1. Метод начинает работу в корневом узле и сравнивает 32 с корневым
значением 25 [рис. 11.17 (А)]. Поскольку 32 >. 25, переходим к правому
поддереву и рассматриваем узел 35.
t = узел 35; parent = узел 25
2. Считая узел 35 корнем своего собственного поддерева, сравниваем 32
и 35 и переходим к левому поддереву узла 35 [рис. 11.17 (В)].
t = NULL; parent = 35
3. С помощью GetTreeNode мы можем создать листовой узел, содержащий
значение 32, а затем вставить новый узел в качестве левого сына узла
35 [рис. 11.17 (С)]:
// присвоение указателю left возможно,
// т.к. BinSTree является дружественным TreeNode
newNode = GetTreeNode(item, NULL, NULL);
parent->left - newNode;
Указатели parent и t являются локальными переменными,
изменяющимися по мере нашего продвижения по пути в поисках точки вставки.
Parent
(A)
Шаг 1: Сравнить 32 и 25.
Перейти к правому поддереву
parent
parent
(В)
(С)
Шаг 2: Сравнить 32 и 35.
Перейти к левому поддереву
Шаг 3: Вставить 32 в качестве
левого сына узла parent
Рис 11.17. Вставка в дерево бинарного поиска
// вставить item в дерево поиска
template <class T>
void BinSTree<T>::Insert(const T& item)
{
// t — текущий узел, parent — предыдущий узел
TreeNode<T> *t •» root, *parent » NULL, *newNode;
// закончить на пустом дереве
while(t !* NULL)
{
// обновить указатель parent и идти направо или налево
parent - t;
if (item < t->data)
t - t->left;
else
t - t->right;
}
// если родителя нет, вставить в качестве корневого узла
if (parent ~ NULL)
root - newNode;
// если item меньше родительского узла, вставить в качестве левого сына
else if (item < parent-> data)
parent->left * newNode;
else
// если item больше или равен родительскому узлу,
// вставить в качестве правого сына
parent->right - newNode;
// присвоить указателю current адрес нового узла и увеличить size на единицу
current - newNode;
size++;
}
Операция Delete (удаление). Операция Delete удаляет из дерева узел с
заданным ключом. Сначала с помощью метода FindNode устанавливается
место этого узла на дереве и определяется указатель на его родителя. Если
искомый узел отсутствует, операция удаления спокойно завершается.
Удаление узла из дерева требует ряда проверок, чтобы определить, куда
присоединять сыновей удаляемого узла. Поддеревья должны быть заново
присоединены таким образом, чтобы сохранилась структура бинарного дерева
поиска.
Функция Findnode возвращает указатель DNodePtr на узел D, подлежащий
удалению. Второй указатель, PNodePtr, идентифицирует узел Р — родителя
удаляемого узла. Метод Delete "пытается" подыскать заменяющий узел R,
который будет присоединен к родителю и, следовательно, займет место
удаленного узла. Заменяющий узел R идентифицируется указателем RNodePtr.
Алгоритм поиска заменяющего узла должен рассмотреть четыре случая,
зависящие от числа сыновей удаляемого узла. Заметьте, что если указатель
на родителя равен NULL, то удаляется корень. Эта ситуация учитывается
нашими четырьмя случаями и тем дополнительным фактором, что корень
должен быть обновлен. Поскольку класс BinSTree является другом класса
TreeNode, у нас есть доступ к закрытым элементам left и right.
Ситуация А: Узел D не имеет сыновей, т.е. является листом.
Обновить родительский узел так, чтобы его поддерево оказалось пустым.
До После
Удалить листовой узел 17: Замена не нужна
PNodePtr->left есть DNodePtr PNodePtr->left есть NULL
Обновление совершается путем установки RNodePtr в NULL. Когда мы
присоединяем NULL-узел, родитель указывает на NULL.
RNodePtr = NULL;
• • •
PNodePtr->left = RNodePtr;
Ситуация В: Узел D имеет левого сына, но не имеет правого сына.
Присоединить левое поддерево узла D к его родителю.
Обновление совершается путем установки RNodePtr на левого сына узла
D и последующего присоединения узла R к родителю.
RNodePtr ~ DNodePtr->left;
PNodePtr->right = RNodePtr;
До
После
Удалить узел 20, имеющий только левого сына:
Узлом R является левый сын
Присоединить узел R к родителю
Ситуация С: Узел D имеет правого сына, но не имеет левого сына.
Присоединить правое поддерево узла D к его родителю.
До
После
Удалить узел 15, имеющий только правого сына:
Узлом R является правый сын
Присоединить узел R к родителю
Как и в ситуации С, обновление может быть совершено путем установки
RNodePtr на правого сына узла D и последующего присоединения узла R к
родителю.
RNodePtr = DNodePtr->right;
■ * *
PNodePtr->left = RNodePtr;
Ситуация D: Удаление узла с двумя сыновьями.
Демонстрационное дерево
Удалить узел 30
"Осиротевшие" поддеревья
Узел с двумя сыновьями имеет в своих поддеревьях элементы, которые
меньше, больше или равны его собственному ключевому значению. Алгоритм
должен выбрать тот заменяющий узел, который сохранит правильный порядок
элементов. Рассмотрим следующий пример.
Удалив узел 30, мы создали два "осиротевших" поддерева, которые
должны быть вновь присоединены к дереву. Для этого требуется стратегия выбора
заменяющего узла из оставшейся совокупности узлов. Результирующее дерево
должно удовлетворять определению бинарного дерева поиска. Применим мак-
симинный (max-min) принцип.
Выберите в качестве заменяющего самый правый узел левого поддерева.
Это — максимальный из узлов, меньших чем удаляемый. Отсоедините этот
узел R от дерева, присоедините его левое поддерево к его родителю, а затем
поставьте R на место удаляемого узла. В демонстрационном дереве
заменяющим является узел 28. Мы присоединяем его левого сына (26) к его
родителю (25) и заменяем удаленный узел (30) заменяющим (28).
Для отыскания самого правого узла левого поддерева используется
следующий простой алгоритм.
Шаг 1: Поскольку заменяющий узел R меньше, чем удаляемый узел D,
перейти к левому поддереву узла D. Спуститься к узлу 25.
Шаг 2: Поскольку R является максимальным узлом левого поддерева,
найти его значение, спустившись вниз по правому поддереву. Во время спуска
следите за предшествующим узлом PofRNodePtr. В нашем примере
спуститесь к узлу 28. PofRNodePtr указывает на узел 25.
Спуск вниз по правому поддереву предполагает два случая.
Если правое поддерево пусто, то текущей точкой является заменяющий
узел R и PofRNodePtr указывает на удаляемый узел D. Мы присоединяем
правое поддерево узла D в качестве правого поддерева узла R, а родителя
Р удаляемого узла присоединяем к R.
PofRNodePtr = DNodePtr
Правое поддерево
Правое поддерево
RNodePtr->right = DNodePtr->right;
PNodePtr->left = RNodePtr;
Если правое поддерево непусто, проход завершается листовым узлом или
узлом, имеющим только левое поддерево. В любом случае отсоединить узел
R от дерева и присоединить сыновей узла R к родительскому узлу
PofRNodePtr. В каждом случае правый сын узла PofRNodePtr
переустанавливается оператором
(**) PofRNodePtr->right = PofRNodePtr->left;
1, R является листом. Отсоединить его от дерева. Поскольку RNodePtr->left
равен NULL, оператор (**) устанавливает правого сына узла PofR-
NodePtr в NULL.
Правое поддерево
RofRNodePtr
Правое поддерево
RofRNodePtr
2. R имеет левое поддерево. Оператор (**) присоединяет это поддерево в
качестве правого сына узла PofRNodePtr.
Правое поддерево
PofRNodePtr
PofRNodePtr
Правое поддерево
Левое поддерево
Левое поддерево
Алгоритм заканчивается заменой удаляемого узла узлом R. Сначала
сыновья узла D присоединяются в качестве сыновей узла R. Затем узел R
замещает узел D как корень поддерева, образованного узлом D.
RNodePtr->left = DNodePtr->left;
RNodePtr->right «= DNodePtr->right;
Завершите присоединение к родительскому узлу Р.
// удаление корневого узла, назначение нового корня
if (PNodePtr — NULL)
root * RNodePtr;
// присоединить R к Р с правильной стороны
else if (DNodePtr->data < PNodePtr->data)
PNodePtr->left - RNodePtr;
else
PNodePtr->right « RNodePtr;
Альтернативным способом замены узла D на узел R является копирование
R в D. Однако, если данные занимают много места в памяти, это может быть
дорогостоящей операцией. Наш способ предусматривает изменение лишь двух
указателей.
Метод Delete
// если элемент находится на дереве, удалить его
template <class T>
void BinSTree<T>::Delete(const T& item)
{
// DNodePtr — указатель на удаляемый узел D
// DNodePtr — указатель на родительский узел Р узла D
// RNodePtr — указатель узел R, замещающий узел D
TreeNode<T> *DNodePtr, *PNodePtr, *RNodePtr;
// найти узел, данные в котором совпадают с item.
// получить его адрес и адрес его родителя
if ((DNodePtr - FindNode (item, PNodePtr)) « NULL
return;
// если узел D имеет NULL-указатель, то заменяющим
// узлом является тот, что находится на другой ветви
if (DNodePtr->right =- NULL)
RNodePtr * DNodePtr->left;
else if (DNodePtr->left « NULL)
RNodePtr = DNodePtr->right;
// узел D имеет двух сыновей
else
{
// найти и отсоединить заменяющий узел R для узла D.
//в левом поддереве узла D найти максимальный узел
// из всех узлов, меньших чем узел D.
// отсоединить этот узел от дерева.
// PofRNodePtr — указатель на родителя заменяющего узла
TreeNode<T> *PofRNodePtr = DNodePtr;
// первой возможной заменой является левый сын узла D
RNodePtr = DNodePtr->left;
// спуститься вниз по правому поддереву левого сына узла D,
// сохраняя записи текущего узла и его родителя.
// остановившись, мы будем иметь заменяющий узел
while (RNodePtr->right != NULL)
{
PofRNodePtr = RNodePtr;
RNodePtr = RNodePtr->right;
}
if (PofRNodePtr == DNodePtr)
// левый сын удаляемого узла является заменяющим
// присоединить правое поддерево узла D к узлу R
RNodePtr->right = DNodePtr->right;
else
{
// мы спустились вниз по правой ветви как минимум на один узел.
// удалить заменяющий узел из дерева,
// присоединив его правую ветвь к родительскому узлу
PofRNodePtr->right = RNodePtr->left;
)
}
// завершить присоединение к родительскому узлу.
// удалить корневой узел, назначить новый корень,
if (RNodePtr == NULL)
root * RNodePtr;
// присоединить узел R к узлу Р с правильной стороны
else if (DNodePtr->data < PNodePtr->data)
PNodePtr->left = RNodePtr;
else
PNodePtr->right = RNodePtr;
// удалить узел из памяти и уменьшить размер списка
FreeTreeNode(DNodePtr);
size—;
}
Метод Update. После использования метода Find при желании можно
обновить поля данных в этом (текущем) узле. Для этого мы предоставляем метод
Update, имеющий значение данных в качестве входного параметра. Если
текущий узел найден, Update сравнивает значение текущего узла со значением
данных и, если они равны, производит обновление узла. Если текущий узел
не определен или элемент данных не совпал, новое значение данных
включается в дерево.
// если текущий узел определен и элемент данных (item) совпал
// с данными в этом узле, переписать элемент данных в узел.
// иначе включить item в дерево
template <class T>
void BinSTree<T>::Update( const T& item)
{
if (current != NULL && current->data == item)
current->data = item;
else
Insert(item);
}
11.7. Практическая задача: конкорданс
Обычной проблемой анализа текстов является определение частоты и
расположения слов в документе. Эта информация запоминается в конкордансе,
где различные слова перечислены в алфавитном порядке и каждое слово
снабжено ссылками на строки текста, в которых оно встречается. Рассмотрим
следующую цитату.
Peter Piper picked a peck of pickled peppers. A peck of pickled peppers
Peter Piper picked. If Peter Piper picked a peck of pickled peppers, where
is the peck that Peter Piper picked?
Слово "piper" встречается здесь 4 раза в строках 1, 2 и 3. Слово "pickled"
встречается 3 раза в строках 1 и 3.
В этой задаче создается конкорданс для текстового файла с помощью
следующего проекта:
Вход: Открыть документ как текстовый файл и ввести текст по словам,
отслеживая текущую строку.
Действие: Определить запись, которая состоит из слова, счетчика
появлений и списка номеров строк, содержащих это слово. При первой встрече
некоторого слова в тексте создать запись и включить ее в дерево. Если слово уже
есть на дереве, обновить его частоту и список номеров строк.
Выход: После ввода файла распечатать слова в алфавитном порядке вместе
со счетчиками частоты и упорядоченными списками строк, где встречается
каждое слово.
Структуры данных
Данными каждого узла является объект Word, содержащий символьную
цепочку, счетчик частоты и связанный список номеров строк текста. Объект
Word содержит также номер строки, где данное слово встретилось последний
раз. Это гарантирует, что мы сможем обработать несколько случаев появлений
слова в строке и только один раз занести номер этой строки в список.
wordText
count
LinkedUst<int>
LineNumbers
LastLineNo
Функции-члены класса Word перегружают операторы отношения "==" и
"<" и стандартные операторы потокового ввода/вывода.
class Word
{
private:
// wordText — слово из текста; count — его частота
String wordText/
int count;
// счетчик строк разделяется всеми объектами Word
static int lineno;
// номер последней строки, где встретилось данное слово.
// используется для того, чтобы знать, когда вставлять
// номер строки в lineNumbers
int lastLineNo;
LinkedList<int> lineNumbers;
public:
// конструктор
Word(void);
// открытые операции класса
void CountWord (void);
Strings Key(void);
// операторы сравнения, используемые классом BinSTree
int operator== (const Word& w) const;
int operator< (const Words w) const;
// Операторы потока
friend istreams operator» (istream& istr, Words w);
friend ostreams operator» (ostream& ostr, Words w);
>;
Реализация класса Word
Для каждого слова конструктор устанавливает начальное значение частоты
в 0 и номер последней строки в -1. Перегружаемые операторы отношения
"<" и "==" непроходимы для операций вставки и поиска на деревьях и
реализуются путем сравнения символьных последовательностей двух
объектов. Код этих функций находится в файле word.h.
В этом классе объявляется статический элемент данных lineno. Это
закрытая переменная, доступная только элементам класса и друзьям. Однако
под именем Word::lineno она фактически определяется внешней по
отношению к классу. Следовательно, она совмесно используется всеми
словами-объектами. И это правильно, так как всем этим объектам нужен доступ к номеру
текущей строки входного файла. Статические элементы данных допускают
совместное использование с одновременным контролем доступа и поэтому
более предпочтительны, чем глобальные переменные.
Оператор ввода "»". Оператор ввода считывает данные из потока по
одному слову за раз. Слово должно начинаться с буквы, за которой
необязательно идет последовательность букв и цифр. Ввод слова начинается с
чтения и выбрасывания всех небуквенных символов. Это гарантирует, что
все межсловные промежутки и знаки пунктуации будут пропущены. Процесс
ввода прекращается по достижении конца файла. Если встречается символ
конца строки, происходит увеличение переменной lineno на единицу.
// пропустить все предшествующие пробелы и небуквенные символы
while (istr.get(с) && !isalpha(c))
// если встретился конец строки, увеличить счетчик строк текста
if (с — '\п')
w.lineno++;
Когда распознается начало слова, оператор "»" накапливает символы,
читая буквы и цифры до тех пор, пока не встретится неалфавитноцифровой
символ. Буквы слова преобразуются в строчные и запоминаются в локальной
переменной wd. Это позволяет сделать наш конкорданс нечувствительным к
регистру букв, из которых состоит слово. Если после очередного слова следует
символ конца строки, он снова помещается в поток и обнаруживается во
время ввода следующего слова. Функция завершается копированием
переменной wd в wordText, сбросом счетчика count и присвоением переменной
lastLineNo значения lineno.
// если не конец файла, ввести слово
if (listr.eof())
{
// преобразовать первую букву в строчную, занести ее в wd
с ■ tolower(с);
wd[i++] - с;
// последовательно считывать буквы или цифры, преобразуя их в строчные
while (istr.get(c) && (isalpha(c) II isdigit(c)))
wd[i++] ~ tolower(c);
// завершить символьную последовательность нулем
wd[i] - '\0';
// если после текущего слова встретился конец строки,
// сохранить его для следующего слова
if (с »* '\п')
istr.putback(c);
// заключительные установки
w.wordText « wd;
w.count ■ 0;
w.lastLineNo * w.lineno;
}
Функция CountWord. После считывания слова из текста вызывается
функция CountWord, которая обновляет значение частоты и список номеров строк.
Вначале значение счетчика count увеличивается на единицу. Если count =» 1,
то слово — новый элемент дерева, и номер строки, где впервые встретилось это
слово, добавляется в список. Если слово уже есть в списке, то проверяется,
изменился ли номер строки с момента последнего появления данного слова.
Если да, то номер текущей строки заносится в список и используется для
обновления lastLineNo.
// записать случай вхождения слова
void Word::CountWord (void)
{
// увеличить частоту вхождения слова
count++;
// если это слово встретилось впервые или на новой строке,
// вставить его в список и присвоить переменной lastLineNo
// номер текущей строки,
if (count — 1 || lastLineNo !- lineno)
{
lineNumbers.InsertRear(lineno) ;
lastLineNo e lineno;
)
}
Оператор вывода "«". Оператор потокового вывода распечатывает слово и
частоту, вслед за которыми идет упорядоченный список номеров строк, где это
слово встречается.
<слово> <частота>: nl, п2, пЗ, ...
// вывести объект класса Word в поток
ostream& operator« (ostreami ostr, Words w)
I
// вывести слово
ostr « w.wordText;
// вывести выровненный вправо счетчик частоты.
// заполнить промежуток точками.
ostr.fillC .' );
ostr « setw(25-w.wordText.Length{)) « w.count « ": ";
ostr.fillC '); // снова назначить пробел символом-заполнителем
// пройтись по списку и распечатать номера строк
for(w.lineNumbers.Reset(); Iw.lineNumbers.EndOfList();
w.lineNumbers.Next())
ostr « w.lineNumbers.Data() « " ";
ostr « endl;
return ostr;
}
Программа 11.6. Конкорданс
В программе определено бинарное дерево поиска concordTree, в котором
хранятся объекты класса Word. После открытия текстового файла соп-
cord.txt оператор ввода потока считывает слова, пока не встретится конец
файла. Каждое слово либо включается в дерево, либо используется для
обновления информации о себе, если оно уже встречалось ранее. После того
как все слова обработаны, выполняется симметричное прохождение, в
процессе которого слова распечатываются в алфавитном порядке. Класс Word
находится в файле word.h.
iinclude <iostream.h>
#include <fstream.h>
#include <stdlib.h>
#include "word.h" // класс Word
#include "bstree.h" // класс BinSTree
iinclude "treescan.h" // метод Inorder
// используется функцией Inorder
void PrintWord(Words w)
{
cout « w;
}
void main(void)
{
// объявить дерево объектов Word; читать из потока fin
BinSTree<Word> concordTree;
ifstream fin;
Word w;
// открыть файл concord.txt
fin.open("concord.txt", ios::in | ios::nocreate);
if (!fin)
{
cerr « "He могу открыть concord.txt" « endl;
exit(1);
}
// читать объекты Word из потока fin, пока не встретится конец файла
while(fin » w)
{
// найти w на дереве
if (concordTree.Find(w) == 0)
{
// w нет на дереве, обновить частоту слова и включить его в дерево
w.CountWordO ;
concordTree.Insert(w);
}
else
{
// w на дереве, обновить информацию о слове
w.CountWordO ;
concordTree.Update(w);
}
}
// распечатать дерево в алфавитном порядке
Inorder(concordTree.GetRoot(), PrintWord);
}
/*
<Файл concord.txt>
Peter Piper picked a peck of pickled peppers. A peck of pickled
peppers Peter Piper picked. If Peter Piper picked a peck of
pickled peppers, where is the peck that Peter Piper picked?
<Выполнение программы 11.б>
a 3: 1 2
if 1: 2
is 1: 3
of 3: 1 2
peck 4: 12 3
peppers 3: 1 2 3
peter 4: 12 3
picked 4: 12 3
pickled 3: 1 3
piper 4: 12 3
that 1: 3
the 1: 3
where 1: 3
*/
Письменные упражнения
11.1 Объясните, почему дерево является нелинейной структурой данных.
11.2 Какова минимальная глубина дерева, содержащего
а) 15 узлов
б) 5 узлов
в) 91 узел
г) 800 узлов
11.3
а) Нарисуйте бинарное дерево, содержащее 10 узлов и имеющее глубину 5.
б) Нарисуйте бинарное дерево, содержащее 14 узлов и имеющее глубину 5.
11.4 Пусть бинарное дерево содержит числа 1 3 7 2 12.
а) Нарисуйте два дерева максимальной глубины, содержащие эти данные,
б) Нарисуйте два законченных бинарных дерева, у которых родительский
узел больше, чем любой из его сыновей.
11.5 Нарисуйте все возможные деревья, состоящие из трех узлов.
11.6 Действительно ли бинарное дерево с п узлами должно иметь ровно п-1
ребер (ненулевых указателей)?
11.7 Рассмотрим следующее бинарное дерево.
а) Если в дерево вставляется число 30, какой узел будет его родителем?
б) Если в дерево вставляется число 41, какой узел будет его родителем?
в) Осуществите прямой, симметричный и обратный метод прохождения
этого дерева.
11.8 Опишите действие функции F. Подразумевается, что F является
функцией-членом класса BinSTree.
template <class T>
void F(TreeNode<T>* & t, T item)
{
if (t — NULL)
t = GetTreeNode(item);
else if (item < t->data
F(t->left, item);
else
F(t->right, item);
}
Почему так важно передавать параметр t по ссылке?
11.9 Нарисуйте бинарное дерево поиска для каждой из приведенных
последовательностей символов и осуществите его прохждение прямым,
обратным и симметричным методами.
а) М, Т, V, F, U, N
б) F, L, О, R, I, D, А
г) R, О, Т, A, R, Y, С, L, U, В
11.10 Осуществите прохождение каждого дерева из предыдущего
упражнения в порядке RLN, RNL и NRL, а также поперечным методом.
11.11 Нарисуйте бинарное дерево поиска для каждой из приведенных
числовых последовательностей и осуществите его прохождение прямым,
обратным, симметричным и поперечным методами.
а) 30, 20, 10, 6, 5, 35, 56, 1, 32, 40, 48
б) 60, 25, 70, 99, 15, 3, 110, 30, 38, 59, 62, 34
в) 30, 20, 25, 22, 24, 23
11.12 Осуществите прохождение каждого дерева из предыдущего
упражнения в порядке RLN, RNL и NRL.
11.13 Модифицируйте функцию MakeCharTree таким образом, чтобы она
построила следующие деревья в качестве 3-го и 4-го вариантов.
Дерево (А) Дерево (В)
11.14
а) В каком порядке будет проходится дерево, если алгоритм поперечного
прохождения будет запоминать узлы не в очереди, а в стеке?
Проиллюстрируйте свой анализ на дереве Тгее_2 из раздела 11.1.
б) Пусть узлы включаются в очередь с приоритетами, определяемыми
полями данных. Используя этот алгоритм, покажите порядок
прохождения дерева Тгее_2.
11.15 Используйте MakeCharTree как образец для функции MakelntTree,
которая строит следующие бинарные деревья поиска. Проследите
построение каждого узла.
Дерево (А)
Дерево (В)
11.16
а) Приведенная ниже числовая последовательность получена путем
прямого прохождения бинарного дерева поиска. Постройте это дерево.
50 45 35 15 40 46 65 75 70
б) Постройте бинарное дерево поиска, которое в результате
симметричного прохождения давало бы следующую последовательность узлов:
40 45 46 50 65 70 75
11.17 Дано следующее бинарное дерево поиска:
Выполните следующие действия, используя каждый раз исходное
дерево:
а) Покажите дерево после включения узлов 1, 48, 75, 100.
б) Удалите узлы 5, 35.
в) Удалите узел 45.
г) Удалите узел 50.
д) Удалите узел 65 и вставьте его снова.
11.18 На основе функции СоруТгее создайте функцию ТСоруТгее, которая
имела бы параметр target. Эта функция должна копировать только те
узлы, значения которых больше, чем target. Меньшие по значению
узлы должны копироваться в качестве листьев. Имейте в виду, что в
процессе копирования вам придется удалять все узлы в обоих
поддеревьях каждого будущего листа.
TreeNode<T> *TCopyTree (TreeNode<T> *t, T target);
11.19 Напишите функцию
TreeNode<T> *ReverseCopy(TreeNode<T> *tree);
которая копирует дерево, попутно меняя местами все левые и правые
указатели.
11.20 Напишите функцию
void PostOrder_Right(TreeNode<T> *t, void visit(T& item);
которая осуществляет RNL-прохождение дерева.
11.21 Напишите функцию
void *InsertOne(BinSTree<T>&t, T item);
которая включает item в бинарное дерево поиска t, если его там еще
нет. В противном случае функция завершается, не выполняя
включение нового узла.
11.22 Напишите функцию
TreeNode *Max(TreeNode *t);
которая возвращает указатель на максимальный узел бинарного дерева
поиска. Сделайте ее итерационной.
11.23 Напишите функцию
TreeNode *Min(TreeNode *t);
которая возвращает указатель на минимальный узел бинарного дерева
поиска. Сделайте ее рекурсивной.
11.24 Числа 1-9 используются для построения бинарного дерева поиска с
9-ю узлами без дублирования данных.
а) Покажите возможное значение корня, если глубина дерева равна 4.
б) Сделайте то же самое для глубины 5, 6, 7 и 8.
11.25 Для каждого из приведенных ниже буквенных списков нарисуйте
бинарное дерево поиска, которое получается, когда буквы вставляются
в указанной последовательности.
а) D, A, E, F, В, К
б) G, J, L, М, Р, А
в) D, Н, Р, Q, Z, L, М
г) S, J, К, L, X, F, E, Z
11.26 Напишите итерационную функцию
template <class T>
int NodeLevel(const BinSTree<T>& T, const T£ elem);
которая определяет глубину elem на дереве и возвращает -1, если его
нет на дереве.
11.27
а) Пусть в узлах дерева находятся символьные строки. Постройте
бинарное дерево поиска, которое получается в результате вставки следующих
ключевых слов в данном порядке:
for, case, while, class, protected, virtual, public, private, do, template,
const, if, int
б) Осуществите прохождение этого дерева прямым, обратным и
симметричным методами.
11.28
а) Иногда узлы бинарного дерева могут содержать указатель на своего
родителя. Модифицировав TreeNode, создайте класс PTreeNode для
поддержки этого указателя.
б) Напишите функцию
template <class T>
void PrintAncestors(PTreeNode<T> *t);
которая распечатывает данные из цепочки узлов, начинающейся от
узла t и заканчивающейся на корне.
в) используя технологию MakeCharTree, постройте дерево Tree_J2,
содержащее объекты PTreeNode.
11.29 Некоторые задачи, например компьютерные игры, имеют дело с
деревьями общего вида, т.е. такими, узлы которых могут иметь более двух
сыновей. Ниже приведено дерево, где максимальное число сыновей
равно 3 (тернарное дерево).
а) Может ли симметричный метод прохождения быть однозначно
определен на дереве общего вида?
б) Реализуйте прямой и обратный методы прохождения тернарного дерева.
в) Дерево общего вида может быть преобразовано в бинарное дерево с
помощью следующего алгоритма:
1) Левый указатель каждого узла бинарного дерева указывает на самого
левого сына соответствующего узла на дереве общего вида.
2) Правый указатель каждого узла бинарного дерева указывает на брата
(узел, имеющий того же родителя) этого узла на дереве общего вида.
Рисуя бинарное дерево, располагайте каждого сына прямо под его
родителем, а его братьев располагайте справа. Вот бинарное дерево,
соответствующее только что приведенному примеру дерева общего вида:
Если это дерево повернуть на 45 градусов по часовой стрелке,
получится белее знакомое изображение:
Осуществите прохождение этого дерева прямым, обратным и
симметричным методами. Что общего вы находите между ними и
соответствующими методами для дерева общего вида?
г) Для приведенного ниже дерева общего вида выполните следующее:
1) Осуществите его прохождение прямым и обратным методами.
2) Постройте соответствующее ему бинарное дерево.
3) Осуществиет прохождение бинарного дерева прямым, обратным и
симметричным методами.
11.30 Поскольку бинарное дерево с п узлами имеет п+1 нулевых указателей,
половина выделенной для указателей памяти тратится впустую.
Хороший алгоритм использует эту память. Действительно, пусть при
симметричном прохождении каждый левый пустой указатель
указывает на своего предшственника, а каждый правый — на преемника.
Такая структура называется прошитым деревом (threaded tree), а сами
указатели — нитями (threads). Узел прошитого дерева может быть
представлен несложным расширением класса TreeNode. Добавьте
закрытую логическую переменную rightThread, показывающую, являет-
ся ли соответствующий указатель нитью, и методы LeftThread и Right-
Thread, которые возвращают значения этих указателей. Назовем этот
новый класс ThreadedTreeNode. Напишите итерационную функцию
template <class T>
void Threadedlnoraer(ThreadedTree<T> *t);
которая осуществляет симметричное прохождение дерева t и
распечатывает данные из его узлов.
Упражнения по программированию
11.1 Напишите функцию
int CountEdges(TreeNode<T> *tree);
которая подсчитывает число ребер (ненулевых указателей) бинарного
дерева. Испытайте эту функцию на дереве Тгее__1 из treelib.h.
11.2 Напишите функцию
void RNL(TreeNode<T> *tree, void visit(T& item));
которая посещает узлы дерева в порядке RNL. Введите 10 целых чисел
и разместите их на бинарном поисковом дереве, используя класс Bin-
STree. Осуществите RNL-прохождение этого дерева. Как
упорядочиваются данные при таком методе?
11.3 Используя функции, разработанные вами в письменном упражнении
11.15 а) и б), напишите main-программу, которая распечатывает эти
два дерева. Распечатайте дерево из а), применяя PrintTree, и дерево
из б), применяя PrintVTree.
11.4 Возьмите функцию InsertOne из письменного упражнения 11.21. В
тестовой программе постройте дерево с восемью узлами. Входные
данные должны дублироваться. Распечатайте получившееся дерево с
помощью PrintTree.
11.5 В main-программе используйте класс BinSTree для создания дерева с
500 узлами, содержащими случайные целые числа в диапазоне от 1
до 10000. С помощью функций Мах и Min из письменных упражнений
11.22 и 11.23 вычислите максимальный и минимальный узлы.
11.6 Модифицируйте задачу о конкордансе (программа 11.6) таким образом,
чтобы число встреч каждого слова в каждой строке распечатывалось
в следующем формате:
номер строки (число встреч)
Например,
<Вход> one two one two three
<Выход> one 2: 1(2)
three 1: 1(1)
two 2: 1(2)
11.7
а) Напишите функцию
void LinkedSort(Array<int>& A);
которая сортирует массив А путем включения его элементов в
упорядоченный связанный список и копирования отсортированных данных
обратно в А.
б) Напишите функцию
void TreeSort(Array<int>& A);
которая сортирует массив А путем включения его элементов в бинарное
дерево поиска, симметричного прохождения этого дерева и копирования
отсортированных данных обратно в А. (Совет: Для симметричного
прохождения и присвоения значений элементам массива напишите
рекурсивную функцию
void InorderAssign(TreeNode<int> *t, Array<int>& A, int i);
в) Напишите главную процедуру, создающую массив 10000 случайных
целых чисел и использующую системный таймер для определения
быстродействия функций а) и б). Обе функции должны сортировать одни
и те же данные.
11.8 Арифметическое выражение, включающее бинарные операторы
сложения (+), вычитания (-), умножения (*) и деления (/), может быть
представлено в виде бинарного дерева, где каждый оператор имеет двух
сыновей — операнд или подвыражение. Листовой узел содержит
операнд, а не листовой — бинарный оператор. Левое и правое поддеревья
оператора описывают подвыражения, которые вычисляются и
используются в качестве операндов этого оператора. Например, выражению
a+b*c/d-e соответствует следующее бинарное дерево:
а) Выполните прямой, симметричный и обратный методы прохождения
этого дерева. Какая связь существует между этими методами и
префиксной, инфиксной и постфиксной записями данного выражения?
б) Для каждого из приведенных ниже арифметических выражений
постройте соответствующее бинарное дерево. Осуществив прохождение
дерева, выдайте префиксную, инфиксную и постфиксную формы выра-
жения*
(l)a + b = c*d + e
(2) / а - b * с d
(3) a b с d / - *
(4) * - / + a b с d e
в) Можно разработать рекурсивный алгоритм ввода выражения в
префиксной форме и построения соответствующего бинарного дерева.
Если элемент выражения является операндом, используйте его значение
для создания листового узла, в котором поля указателей содержат
NULL.
Если элемент выражения является оператором, назначьте его в качестве
данных узлу дерева, а затем создайте его левого и правого сыновей.
Напишите функцию
void BuildExpTree(TreeNode<char> *t, char * & exp);
которая строит бинарное дерево по префиксной форме выражения,
содержащейся в строке ехр. Предполагается, что операнды являются одно-
буквенными идентификаторами в диапазоне от а до z, а операторы
представлены символами Ч-\ '-*, **' и */\
г) Напишите main-программу, которая вводит выражение и создает
бинарное дерево. Распечатайте дерево вертикально с помощью PrintVtree
и выдайте инфиксную и постфиксную формы этого выражения.
11.9 Используя функцию ТСоруТгее из письменного упражнения 11.18,
создайте в главной программе бинарное дерево поиска с 10-ю узлами,
содержащими целые числа. Задайте значение параметра target и
скопируйте узлы дерева с помощью ТСоруТгее. Распечатайте исходное
дерево и копию, используя PrintVTree.
лава
12
Наследование и абстрактные
классы
12.1. Понятие о наследовании
12.2. Наследование в C++
12.3. Полиморфизм и виртуальные
функции
12.4. Абстрактные базовые классы
12.5. Итераторы
12.6. Упорядоченные списки
12.7. Разнородные списки
Письменные упражнения
Упражнения по программированию
Наследование — фундаментальное понятие в объектно-ориентированном
программировании. В этой главе развиваются ключевые свойства
наследования, о которых кратко было упомянуто в гл. 1. Мы сосредоточимся на
концепции наследования и ее реализации в C++ с помощью базового класса
Shape и семейства производных от него классов геометрических фигур.
Полиморфизм и виртуальные функции популярно обсуждаются в разделе
12.3 и применяются в задаче отображения свойств геометрических объектов.
В разделе 12,4 развивается концепция абстрактного базового класса. В
дополнение к обеспечиваемой им функциональности абстрактный базовый
класс обязывает реализовывать свои чистые виртуальные функции в
производных от него классах. В качестве примера разрабатывается абстрактный
базовый класс линейных и нелинейных списков общего вида.
Итератор — это объект, который осуществляет обход таких структур
данных, как массивы, связанные списки или деревья. В качестве такового он
является абстракцией элемента управления (control abstraction). В разделе
12.5 итераторы разрабатываются путем определения абстрактного базового
класса и образования на его основе итераторов для классов SeqList и Array.
Итератор Array используется для сортировки слиянием
последовательностей — методики, используемой также в гл. 14.
В разделе 12.6 наследование применяется для порождения класса
упорядоченных списков из версии класса связанных списков SeqList,
разработанного в гл. 9. Этот класс используется как фильтр для создания сортированных
последовательностей, сливаемых при сортировке внешнего файла.
Необязательный для чтения раздел 12.7 показывает, как можно
использовать наследование и полиморфизм для разработки массивов и связанных
списков, содержащих объекты различных типов. Когда это полезно и
приемлемо, наследование используется в последующих главах для разработки
структур данных.
12.1. Понятие о наследовании
С точки зрения зоологии, наследование описывает общие признаки и
особые характеристики видов. Например, пусть класс "Животные"
представляет животных, включая обезьян, кошек, птиц и т.д. Несмотря на то
что все они имеют признаки животных, существуют различные семейства
с особыми характеристиками. Все животные в дальнейшем подразделяются
на виды. Например, к семейству кошачьих относятся львы, тигры, гепарды
и т.д.
Животные
Обезьяны
Лев
Кошачьи
Птицы
Тигр
Гепард
Все существующие животные могут быть описаны иерархией от царства
до вида. "Семейство кошачьих принадлежит к царству животных", "тигр
принадлежит к семейству кошачьих" и т.д. Более высокий уровень
обнаруживает признаки, присущие элементам более низкого уровня. Отношения
сохраняются и через несколько уровней — "тигр принадлежит к царству
животных".
Иерархия наследования существует и в программировании. Можете вновь
вернуться к разделу 1.4, где разрабатываются объекты типа Point, Line и
Rectangle и устанавливаются отношения между ними с помощью
наследования. Эти классы включали в себя методы Draw, которые из базовой точки
рисовали на экране фигуры. В данном разделе мы разработаем подобные
классы для замкнутых фигур, таких, как окружности, прямоугольники и
т.д., а также общие для всех этих классов изолированные методы.
У наших геометрических объектов есть общие признаки. Все они являются
формами, которые могут быть нарисованы на экране, и каждая фигура имеет
базовую точку, фиксирующую ее положение. Например, мы очерчиваем
окружность вокруг центра и позиционируем прямоугольник по его левому
верхнему углу. Кроме того, каждая фигура заштриховывается (заполняется) по
некоторому образцу, определяемому целочисленным значением. В
большинстве графических библиотек отсутствие штриховки специфицируется нулем.
Например, следующий график предусматривает вычерчивание окружности
вокруг точки (xl, yl) со сплошным заполнением. Прямоугольник рисуется
из точки (х2, у2) с образцом штриховки в виде кирпичной кладки.
Из коллекции геометрических классов мы выделяем общие признаки —
базовую точку и образец штриховки — и определяем класс Shape, который
содержит эти элементы данных. Этот класс содержит также методы для
получения координаты базовой точки, ее позиционирования и для выбора
или смены образца заполнения. Системно-зависимый метод Draw
инициализирует графическую систему таким образом, что операции построения
различных геометрических фигур будут использовать указанный образец
заполнения. Метод Draw является виртуальной функцией (virtual function), т.е.
специально созданной для того, чтобы переопределяться в виртуальном
классе. Виртуальные функции обсуждаются в разделе 12.3.
В первой главе мы разработали класс Circle вместе с операциями
измерения площади и периметра (длины окружности). Эти операции могут
применяться ко всем замкнутым фигурам, и поэтому мы включаем их в класс
Shape. Методы в классе Shape не определяются, а служат шаблоном для
своего определения в производных классах. Они называются чистыми
виртуальными функциями (pure virtual functions), a Shape — абстрактным
классом (abstract class). Мы приводим здесь эскиз описания класса Shape, хотя
многие концепции развиваются в разделах 12.3 и 12.4. Различные элементы,
включенные в описание класса, анонсируют тему данной главы.
class Shape
{
protected:
float x, у; // координаты базовой точки
int fillpat;
public: // конструктор, действующий по умолчанию
Shape (float h*=0, float v=0, int fill=0);
// виртуальная функция, вызываемая методом Draw в производном
// классе, инициализирует образец заполнения
virtual void Draw(void) const;
// производные классы должны определять методы
// для вычисления площади и периметра
virtual float Area(void) const - 0;
virtual float Perimeter(void) const = 0;
}
Мы используем класс Shape в иерархии наследования. В каждом случае наш
производный класс использует методы класса Shape и создает свои
специфические методы, которые перекрывают родовые методы абстрактного класса.
Например, объект типа Circle есть Shape (базовая точка в центре) с радиусом.
Он содержит метод Draw для отображения заштрихованной окружности на
поверхности чертежа. Этот класс имеет свои особые методы Area и Perimeter,
использующие радиус и константу PI. В цепочке наследования Circle является
производным от Shape.
Аналогично объект типа Rectangle есть Shape (базовая точка в левом
верхнем углу) с длиной и шириной. Метод Draw строит прямоугольник, используя
его длину и ширину и заштриховывая его внутри по заданному образцу.
Формулы
area = length * width
perimeter «= 2 * (length + width)
являются базисом для методов Area и Perimeter. В цепочке наследования
Rectangle является производным от Shape.
Форма
Окружность
Прямоугольник
Терминология наследования
В C++ наследование определяется для классов. Эта концепция
предполагает, что производный класс (derived class) наследует данные и операции
базового класса (base class). Производный класс сам может являться базовым по
отношению к другому слою наследования. Система классов, которая
использует наследование, образует иерархию наследования (class hierarchy).
Базовый класс
Производный/базовый класс
Производный класс
Производный класс часто называют подклассом (subclass)
соответствующего базового класса, который, в свою очередь, называется также
суперклассом (superclass).
12.2. Наследование в C++
Базовый класс, являющийся родоначальником цепочки наследования,
имеет обычное объявление. В объявлении производного класса указывается
родство с базовым классом.
БАЗОВЫЙ КЛАСС
// объявление обычного класса для языка C++
class BaseCL
{
<данные и методы>
}
ПРОИЗВОДНЫЙ КЛАСС
// объявление производного класса со ссылкой на его базовый класс
class DerivedCL: public BaseCL
{
<данные и методы>
}
Здесь BaseCL — это наименование базового класса, который наследуется
классом DerivedCL. Ключевое слово public указывает, что используется
открытое наследование. Производный класс в C++ может определяться с открытым
(public), закрытым (private) и защищенным (protected) наследованием. В
большинстве программных проектов используется открытое наследование.
Защищенный тип наследования применяется редко. Закрытый тип рассматривается
в упражнениях.
Пример 12.1
1. Класс Shape является базовым для производного класса Circle.
class Shape
{<Элементы>}
class Circle: public Shape // Класс Circle наследует класс Shape
{<Элементы>}
2. В цепочке наследования Животные-Кошачьи-Тигр объявление
классов таково:
class Animal
{<Элементы>}
class Cat: public Animal
{<Элементы>}
class Tiger: public Cat
{<Элементы>}
При открытом наследовании закрытые элементы базового класса остаются
закрытыми и доступны только функциям-членам базового класса. К открытым
элементам базового класса могут обращаться все функции-члены производного
класса и любая программа, использующая производный класс. Кроме того, для
открытых и закрытых элементов в C++ определяются защищенные (protected)
элементы, которые имеют особое значение в базовом классе. При наследовании
базового класса его защищенные элементы доступны только через методы
производного класса.
class BaseCL
{
private:
{<Элементы>} // доступны только элементам BaseCL
protected:
{<Элементы>} // доступны как элементам DerivedCL,
// так и BaseCL
public:
{<Элементы>} // доступны всем программам-клиентам
}
В иерархической цепочке, содержащей несколько производных классов,
каждый из них сохраняет доступ ко всем защищенным и общедоступным
элементам базовых классов более высокого уровня. На рис. 12.1 показаны
один и два производных класса. Стрелки слева указывают доступ элементов
производного класса к данным различных видов базового класса. Правая
сторона каждой структурйой схемы показывает, что клиент может
обращаться только к открытым членам базового и производных классов.
Один производный класс
BaseCL
Private_Members
Protected_Members
Public Members
DerivedCL
Private_Members
Protected _M em bers
Public Members
КЛИЕНТ
Два производных класса
BaseCL
Private_Members
Protected _ M em bers
Public Members
DerivedKL
Private_Members
Protected_Members
Public Members
Derived2CL
Private_Members
Protected _M em bers
Public Members
КЛИЕНТ
Рис.12.1. Доступ к элементам данных базового класса при открытом наследовании
Конструкторы и производные классы
В цепочке наследования производный объект наследует данные и методы
базового класса. Мы говорим, что базовый класс является подтипом произ-
водного класса. Ресурсы производного объекта включают в себя ресурсы
базового объекта.
Данные базового класса
т м^^ ма^ ^мм «■» ^пш втлш шшшя ^мм а^вшв tmamm ^шшш ^м
Данные производного класса
Производный объект
При создании производного объекта вызывается его конструктор для
инициализации элементов данных производного объекта. Одновременно объект
наследует данные базового класса, которые инициализируются конструктором
базового класса. Поскольку конструктор вызывается в момент объявления
объекта, должно происходить взаимодействие между конструкторами базового и
производного классов. Когда объявляется производный объект, сначала
выполняется конструктор базового класса, а затем — производного класса.
Интуитивно ясно, что начало цепочки наследования должно быть построено базовы-
мым классом, так как производный класс часто использует данные базового
класса. Если цепочка длиннее, чем два класса, процесс инициализации
начинается с самого первого базового класса и распространяется далее по цепочке
производных классов:
DerivedCL obj; // вызывается конструктор BaseCL;
//а затем конструктор DerivedCL
Когда конструктору базового класса требуются параметры, конструктор
производного класса должен явно вызвать базовый конструктор и передать ему
необходимые параметры. Это делается путем размещения имени конструктора
и параметров базового класса в списке инициализации параметров
конструктора производного класса. Если у базового класса есть конструктор,
выполняемый по умолчанию, и предполагаются его значения по умолчанию, то
производному классу, в принципе, не нужно явно вызывать такой конструктор.
Однако хорошо бы все-таки это делать.
Пример 12.2
Пусть конструктор базового класса объявляется следующим образом:
BaseCL(int n, char ch); // конструктор, имеющий два параметра
В общем случае список параметров для конструктора производного
класса включает в себя параметры базового класса.
// список параметров конструктора включает в себя как минимум
// два параметра конструктора базового класса
DerivedCL{int n, char ch, int sz);
Производный конструктор должен инициализировать объект базового
класса путем явного вызова конструктора базового класса в списке
инициализации. Вот пример реализации конструктора производного класса.
// вызвать конструктор BaseCL(n, ch) в списке инициализации
// Выражение data(sz) — стандартное присвоение значения sz
// элементам данных
DerivedCL::DerivedCL(int n, char ch, int sz) :
BaseCL(n, ch), data(sz)
{}
Деструкторы в цепочке наследования вызываются в порядке, обратном
вызовам конструкторов. В первую очередь вызывается деструктор для
производного класса, затем деструкторы для объектов, затем деструкторы для
базовых классов в порядке, обратном появлению этих классов. Интуитивно
понятно, что производный объект создается после базового и поэтому должен
быть ликвидирован раньше. Если у производного класса нет деструктора, а
у базового есть, то деструктор для производного класса генерируется
автоматически. Этот деструктор уничтожает элементы производного класса и
запускает деструктор базового класса.
Разрешение конфликтов имен при наследовании. В цепочке наследования
классы могут содержать элементы с идентичными именами. Области действия
элемента производного класса и элемента базового класса различны, несмотря
на то что имена этих элементов одинаковы. Объявление элемента в
производном классе скрывает объявление элемента с тем же именем в базовом
классе, но не перегружает его. Для ссылки на метод базового класса с тем
же именем, что и в производном, должен использоваться оператор области
действия класса "::".
Рассмотрим цепочку
class BaseCL class DerivedCL: public BaseCL
{ {
public: public:
• • • • • •
void F(void); void F(void);
void G(int x); void G(float x);
• • ■ » • •
}; );
Предположим, что из функции G в производном классе происходит
обращение к функции G базового класса. Тогда в производном классе следует
применить оператор BaseCL::, чтобы получить доступ к методу G базового класса.
void DerivedCL::G(float x)
{
• * *
BaseCL::G(x) // оператор области действия в функции-члене
• • •
};
Для программы, использующей производный объект, обращение к F
обрабатывается методом F из класса DerivedCL. Вызов функции F базового
класса должен сопровождаться оператором области действия.
derived OBJ;
Вызовы из программы, использующей OBJ
0BJ.FO; // обращение к F производного класса
OBJ.base::F(); // обращение к F базового класса
Приложение: наследование класса Shape. В разделе 12.1 мы представили
класс Shape как пример абстрактного базового класса. Его методы и данные
могут использоваться классами геометрических фигур Circle и Rectangle.
Проиллюстрируем технические детали наследования, объявив класс Shape в
качестве базового, а затем образовав на его основе класс Circle. Производный
класс Rectangle рассматривается в разделе 12.3 при обсуждении виртуальных
функций.
Спецификация класса Shape
ОБЪЯВЛЕНИЕ
// это родовой класс, определяющий точку, образец заполнения и методы доступа
// к этим параметрам, этот класс наследуется классами геометрических фигур,
// которые выдают рисунок фигуры, а также вычисляют ее площадь и периметр,
class Shape
{
protected:
// горизонтальная и вертикальная экранные координаты точки,
// измеряемые в пикселах, используются методами производных классов
float х, у;
// образец заполнения для графических функций
int fillpat;
public:
// конструктор
Shape(float h=0, float v=0, int fill=0);
// методы доступа к координатам базовой точки
float GetX(void) const; // возвращает координату х
float GetY(void) const; // возвращает координату у
void SetPoint(float h, float v); // изменяет базовую точку
// чистые виртуальные функции, производный класс обязан
// определить свои методы Area и Perimeter
virtual float Area(void) const - 0;
virtual float Perimeter(void) const « 0;
// виртуальная функция, вызываемая методом Draw в производном
// классе, инициализирует образец заполнения.
virtual void Draw(void) const;
>
ОПИСАНИЕ
По умолчанию конструктор задает базовую точку (0,0) в левом верхнем углу
окна. Нулевой образец заполнения обычно предполагает его отсутствие.
Методы GetX и GetY возвращают координаты х и у базовой точки. SetPoint
позволяет клиенту изменять базовую точку. Похожие методы GetFill и SetFill
обеспечивают доступ к образцу заполнения.
Метод Draw инициализирует графическую систему таким образом, что
фигуры заполняются по образцу fillpat. Предполагается, что клиент сам несет
ответственность за открытие графического окна и закрытие поверхности
чертежа. Методы Area и Perimeter являются чистыми виртуальными функциями.
Они объявляются в классе Shape и ведут себя, как шаблоны. Эти методы
должны определяться во всех производных классах, наследующих Shape.
Реализация класса Shape
Полное объявление класса Shape находится в файле geometry.h. В этом
разделе детально описывается конструктор и функция Draw.
Конструктору требуются координаты базовой точки и образец заполнения.
Клиент может изменять их значения с помощью методов SetPoint и SetFill.
// конструктор задает начальные значения координат и образец заполнения
Shape::Shape(float h, float v, int fill);
x(h), y(v), fillpat(fill)
Метод Draw вызывает графическую функцию SetFillStyle. Когда
производный класс рисует конкретную фигуру, используется данный стиль заполнения.
void Shape::Draw(void) const
{
SetFillStyle(fillpat); // вызов функции графической системы
}
Производный класс Circle
В первой главе мы объявили класс Circle, чтобы иметь радиус и методы для
вычисления площади и периметра. Радиус передавался конструктору в момент
создания объекта и не был доступен. В этом разделе мы расширим класс,
включив сюда возможности рисования и методы доступа к радиусу. Методы
рисования наследуют базовую точку и образец заполнения из класса Shape.
Заполнение
f radius
(радиус>
Базовая точка
ОБЪЯВЛЕНИЕ
// константа, используемая методами Area и Perimeter
const float PI = 3.14159;
// объявление класса Circle на основе класса Shape
class Circle: public Shape
{
protected:
// если класс Circle становится базовым, то производные
// классы могут иметь доступ к радиусу
float radius;
public:
// конструктор, параметрами являются координаты центра,
// радиус и образец заполнения
Circle(float h=0, float v=0, float radius=0, int fill = 0);
// методы доступа к радиусу
float GetRadius(void) const;
void SetRadius(float r);
// метод Draw для окружности вызывает Draw из базового класса
virtual void Draw(void) const;
// измерительные методы
virtual float Area(void) const;
virtual float Perimeter(void) const;
};
ОПИСАНИЕ
Метод Draw рисует окружность вокруг базовой точки (х,у) с радиусом г.
Объявление и реализация класса находятся в файле geometry.h.
Реализация класса Circle
Реализация класса Circle предполагает наличие файла geometry.h,
содержащего графические операции нижнего уровня. Конструктору класса Circle
передаются параметры для инициализации базового класса Shape и его дан-
ное-член — radius.
// конструктор
// параметры h и v задают начальное положение базовой
// точки в классе Shape. Point(h,v) представляет центр окружности.
// параметр fill задает начальный образец заполнения для класса Shape.
// параметр г используется исключительно классом Circle.
// базовый объект класса Shape инициализируется конструктором
// Shape(h, v, fill) в списке инициализации
Circle:rCircle(float h, float v, float r, int fill):
Shape(h, v, fill), radius(r)
{}
Операция рисования Вызывайте метод Draw из базового класса (Shape: :Draw),
чтобы задавать образец заполнения. Поскольку данные в базовом классе имеют
тип доступа protected, метод Draw класса Circle может к ним обращаться.
Однако программа, использующая объект, не имеет непосредственного доступа
к координатам базовой точки.
// нарисовать окружность заданного радиуса с центром (х,у)
void Circle::Draw(void) const
{
Shape::Draw(); // задает образец заполнения
DrawCircle(x,у, radius);
}
Программа 12.1. Вычерчивание окружностей
Эта программа демонстрирует применение классов Shape и Circle. После
объявления двух Circle-объектов выполняется ряд методов из классов
Shape и Circle.
#include <iostream.h>
#include "graphlib.h"
#include "geometry.h"
void main(void)
{
// объявить объекты С с заполнением 7 и D без заполнения
Circle С(1.О, 1.0, 0.5, 7), D(2.0, 1.0, 0.33);
char eol; // используется для задержки перед рисованием фигур
cout « "Координаты С: " « C.GetXO « " и "
« C.GetYO « endl;
cout << "Периметр С: " « С.Perimeter () « endl;
cout « "Площадь С: " « C.AreaO « endl;
cout « "Нажмите Enter, чтобы увидеть фигуры: ";
cin.get(eol); // ждать нажатия клавиши Enter
// системный вызов для инициализации поверхности чертежа
InitGraphics();
// нарисовать окружность С с радиусом 0.5 и заполнением 7
С.Draw();
// для окружности D задать центр=(1.5, 1.8), радиус=0.25,
// образец заполнения =11
D.SetPoint(1.5, 1.8);
D.SetRadius(.25) ;
D.SetFill(ll);
D.Draw();
// выдержать паузу и закрыть графическую систему
ViewPause()/
ShutdownGraphics();
}
/*
<Выполнение программы 12.1>
Координаты С: 1 и 1
Периметр С: 3.14159
Площадь С: 0.785398
Нажмите Enter, чтобы увидеть фигуры:
*/
Что нельзя наследовать
В то время как производный класс наследует доступ к защищенным
данным-членам базового класса, некоторые члены и свойства базового класса
по наследству не передаются. Не наследуются конструкторы. Следовательно,
они не объявляются как виртуальные методы. Если конструктору базового
класса требуются параметры, то производный класс должен иметь свой
собственный конструктор, который вызывает конструктор базового класса.
Дружественность тоже не наследуется. Если функция F является дружественной
для класса А и класс В образован из А, то F не становится автоматически
дружественной для В.
12.3. Полиморфизм и виртуальные функции
Понятие полиморфизма с нетехнической точки зрения обсуждалось в
разделе 1.3, и было бы полезно перечитать тот материал. В данном разделе мы
расширим наше представление о полиморфизме и приведем некоторые
примеры.
Объектно-ориентирование программирование вводит в обращение некое
свойство, называемое полиморфизмом (polymorphism). Этот термин взят из
древнегреческого и означает "много форм". В программировании
полиморфизм означает то, что один и тот же метод может быть определен для объектов
различных типов. Конкретное поведение метода будет зависеть от типа
объекта. C++ поддерживает полиморфизм с помощью динамического связывания
(dynemic binding) и виртуальных функций-членов (virtual member functions).
Динамическое связывание позволяет различным объектам в системе реаги-
ровать на одни и те же сообщения в специфической для их типа манере.
Приемник сообщения определяется динамически во время исполнения.
Чтобы использовать полиморфизм, объявите в базовом классе функцию-
член как виртуальную, поставив ключевое слово virtual впереди объявления.
Например, в классе BaseCL функции F и G объявлены виртуальными:
class BaseCL
{
private:
* • •
public:
• • •
virtual void F(int n);
virtual void G(long m);
■ ■ *
};
Во время объявления производного класса в него должны быть включены
функции-члены F и G с точно такими же списками параметров. В
производном классе слово virtual не является обязательным, так как атрибут
виртуальности переходит по наследству от базового класса. Тем не менее указание
virtual в производном классе приветствуется, чтобы не вынуждать читателя
заглядывать в базовый класс для выяснения этого вопроса.
class DerivedCL: public BaseCL
{
private:
* • •
public:
• • •
virtual void F(int n);
virtual void G(long m);
• • •
};
Поскольку цепочка наследования и виртуальные функции определены, мы
можем обсудить новые условия доступа для наших членов класса. Пусть DObj
есть объект типа DerivedCL:
DerivedCL DObj;
Числовая функция F в производном классе доступна с помощью имени
объекта. Функция F в базовом классе доступна с помощью имени объекта и
оператора области действия базового класса:
DObj.F(n); // функция-член производного класса
DObj.BaseCL::F(n); // функция-член базового класса
Эти вызовы являются примерами статического связывания (static binding).
Компилятор представляет себе, что клиент каждый раз вызывает особую
версию F — из базового класса и из производного. Однако полиморфизм
проявляется лишь тогда, когда используются указатели или ссылки. Рассмотрим
объявление
BaseCL *P, *Q;
BaseCL BObj;
DerivedCL DObj;
Поскольку производный класс является подтипом базового, производный
объект может быть присвоен базовому. В процессе этого присваивания
копируется та часть данных производного объекта, которая присутствует в базовом
классе.
BObj = DObj;
Данные базового класса
Данные производного класса
Производный объект
В то же время присвоение базового объекта производному недопустимо, так
как некоторые элементы данных производного класса могут оказаться
неопределенными. В качестве примера рассмотрим следующие операторы
присваивания.
BObj = DObj; // копирует базовую часть данных в BObj
DObj = BObj; // недопустимо, т.к. часть данных, относящаяся
// к производному классу остается неопределенной
В контексте указателей и ссылок указатель базового класса может
указывать на производный объект, поэтому допустимы следующие присваивания:
Q *= &Bobj; // присваивает адрес объекта типа BaseCL указателю класса BaseCL
Р = &DObj; // присваивает адрес объекта типа DerivedCL указателю класса BaseCL
Оператор
Q->F(n); // вызов метода F базового класса
вызывает функцию F базового класса. Подобный оператор для указателя Р
иллюстрирует суть полиморфизма, поскольку он вызывает метод F
производного класса, хотя Р является указателем на класс BaseCL.
P->F(n); // вызов метода F производного класса
Когда доступ осуществляется через указатель или ссылку, C++ определяет,
какую версию функции вызывать, основываясь на конкретном объекте,
адресуемом данным указателем или ссылкой. Этот процесс называется
динамическим связыванием.
Каждый объект, имеющий как минимум одну виртуальную функцию,
содержит указатель на таблицу виртуальных функций (virtual function table).
Эта таблица содержит начальные адреса всех виртуальных функций,
объявленных в классе. Когда виртуальная функция вызывается по указателю или
по ссылке, система использует адреса объектов для обращения к указателю на
таблицу виртуальных функций, отыскивает там адрес функции и вызывает ее.
Данные производного класса
Базовый объект
Копирование членов
базового класса
class DerivedCL: public BaseCL
Таблица виртуальных функций
virtual void F(int n);
virtual int Gflong m);
В нашем примере Р указывает на объект типа DerivedCL, поэтому
вызывается версия F, определенная в классе DerivedCL. Это позволяет создать
разнообразные объекты, адресуемые указателем базового класса. Во время выполнения
виртуальной функции вызывается та ее версия, которая соответствует
фактическому типу объекта. Полиморфизм позволяет повторно использовать
функции, принимающие в качестве аргументов указатель или ссылку базового
класса, вместе с новыми версиями виртуальных функций в производных классах.
Демонстрация полиморфизма
Мы начали эту главу простым примером наследования в зоологической
иерархии. От царства животных мы перешли к семейству кошачьих и далее к
конкретному виду — тигру. Тигр "принадлежит к" кошачьим, кошачьи
"принадлежат к" животным. Приведенные ниже классы моделируют эту иерархию
с помощью классов Animal, Cat и Tiger. Каждый класс содержит символьную
строку, которая инициализируется конструктором и предусмотрена для
специфической информации об объекте. Каждый класс имеет метод Identify,
распечатывающий эту информацию.
Животные
Кошачьи
Тигр
Объявление класса Animal
class Animal
{
private:
char animalName[20];
public:
Animal(char nma[])
{
strcopy (animalName, nma);
}
virtual void Identify(void)
{
cout « "Я " « animalName « " животное" « endl;
}
}
Объявление класса Cat
class Cat: public Animal
{
private:
char catName[20];
public:
Cat(char nmc[], char nma[]): Animal (nma)
{
strcopy(catName, nmc);
}
virtual void Identify(void)
{
Animal::Identify();
cout « "Я " « catName « " кот" « endl;
}
}
Объявление класса Tiger
class Tiger: public Cat
{
private:
char tigerName[20];
public:
Tiger(char nmt[], char nmc[], char nma[]): Cat (nmc, nma)
{
strcopy(tigerName, nmt);
}
virtual void Identify(void)
{
Cat::Identify();
cout « "Я п « tigerName « " тигр" « endl;
}
}
Программа 12.2. Полиморфизм класса Animal
Эта программа иллюстрирует статическое и динамическое связывание
двух функций — Announce 1 и Announce2 — которые вызывают метод
Identify для объекта, переданного им в качестве параметра. Используются
два различных способа передачи параметров.
Передача объекта Animal в функцию Announce 1 по значению
void Announcel (Animal a)
{
// пример статического связывания, компилятор управляет
// выполнением метода Identify — члена объекта типа Animal
cout « "Вызов функции Identify в статической Announcel:"
« endl;
a.Identify();
cout « endl/
>
Передача объекта Animal в функцию Announce2 по ссылке
void Announce2 (Animal *pa)
{
// пример динамического связывания, вызывается метод Identify
// того объекта, на который указывает ра
cout << "Вызов функции Identify в динамической Announce2:"
« endl;
pa->Identify();
cout « endl;
}
В main-программе объявляется объект А типа Animal, объект С типа Cat
и объект Т типа Tiger. С помощью функций Announce иллюстрируется
эффект различного способа передачи параметров. Статическое связывание
рассматривается на примере передачи в Announcel объекта Т типа Tiger.
Полиморфизм демонстрируется тремя отдельными вызовами функции Ап-
nounce2, в которую передаются указатели на объекты А, С и Т. Еще одним
примером полиморфизма является обращение к методу Identify через
указатель класса Animal, указывающий на объект типа Cat. В результате
вызывается метод Identify для класса Cat. Оставшаяся часть кода
демонстрирует присвоение производного объекта базовому. Данные производного
объекта, унаследованные от базового класса, копируются в правую часть.
Упомянутые классы и функции Announce находятся в файле animal.h.
#include <iostream.h>
#include <string.h>
♦include "animal.h"
void main(void)
{
Animal A("млекопитающее"), *p;
Cat С("домашний", "теплокровное");
Tiger T("бенгальский", "дикий", "хищное");
// статическое связывание. Announcel имеет параметр Т типа Tiger
// и выполняет метод Identify из Animal
Announcel(T); // статическое связывание; вызов метода Animal
// примеры полиморфизма, поскольку параметр является указателем,
// Announce2 использует динамическое связывание для выполнения
// метода Identify фактического параметра-объекта.
Announce2(&A); // динамическое связывание; вызов метода Animal
Announce2(&C); // динамическое связывание; вызов метода Cat
Announce2(&T); // динамическое связывание; вызов метода Tiger
// непосредственное обращение к методу Identify класса Animal
A.Identify(); // статическое связывание
cout << endl;
// динамическое связывание, вызов метода Cat
р - &С;
p->Identify();
cout « endl;
// присвоение объекта типа Tiger объекту типа Animal.
// копируются данные, наследуемые от Animal
А - Т;
A.IdentifyO; //
cout « endl;
}
*/
<Выполнение программы 12.2>
Вызов функции Identify при статическом связывании:
Я хищное животное
Вызов функции Identify при динамическом связывании:
Я млекопитающее животное
Вызов функции Identify при динамическом связывании:
Я теплокровное животное
Я домашний кот
Вызов функции Identify при динамическом связывании:
Я хищное животное
Я дикий кот
Я бенгальский тигр
Я млекопитающее животное
Я теплокровное животное
Я домашний кот
Я хищное животное
Приложение: геометрические фигуры и виртуальные методы
Класс Shape может быть использован в качестве базового для ряда
производных геометрических классов, включая Circle и Rectangle. В данном
приложении мы дадим спецификацию класса Rectangle и применим его
вместе с классом Circle в одной программе для иллюстрации виртуальных
функций.
length (длина)
width (ширина)
В классе Rectangle базовой точкой является верхний левый угол объекта.
Подобно классу Circle, Rectangle подменяет метод Draw базового класса своим
собственным виртуальным методом Draw, отображающим прямоугольник. В
классе Rectangle также определяются методы Area (длина * ширина) и
Perimeter ( 2 * (длина+ширина)) вместе с методами для получения и изменения
значений длины и ширины. Мы представляем объявление класса и отсылаем
читателя к файлу geometry.h в программном приложении.
// производный класс Rectangle; наследует класс Shape
class Rectangle: public Shape
{
protected:
// защищенные элементы данных, описывающие прямоугольник
float length, width;
public:
// конструктор, получающий в качестве параметров
// координаты базовой точки, длину, ширину и образец заполнения
Rectangle(float h=0, float v=0, float 1=0,
float w=0, int fill = 0) ;
// методы
float GetLength(void) const;
void SetLength(float 1) ;
float GetWidth(void) const;
void SetWidth (float w);
// подменить виртуальные функции базового класса
virtual void Draw(void) const; // визуальное отображение прямоугольника
virtual float Area(void) const;
virtual float Perimeter(void) const;
};
Программа 12.3. Геометрические классы и виртуальные функции
Эта программа иллюстрирует динамическое связывание и полиморфизм
для базового класса Shape и производных от него классов Circle и Rectangle.
Объект С типа Circle является статическим, а переменные one, two и three —
указателями на объекты типа Shape.
При использовании статического связывания площадь и длина
окружности объекта С вычисляются методами С.Агеа() и C.Perimeter().
Указателям класса Shape присваиваются адреса динамически создаваемых объектов
типа Circle и Rectangle. При использовании динамического связывания,
площадь и периметр объекта вычисляются методами Area/Perimeter из
соответствующего производного класса. Указателю three присваивается адрес
Circle-объекта С. Таким образом мы динамически связываемся с
соответствующими методами класса Circle при вызове функций для вычисления
площади и периметра объекта С.
Динамическое связывание позволяет использовать три указателя
базового класса, чтобы выполнить метод Draw для трех фигур.
#include <iostream.h>
#include "graphlib.h"
#include "geometry.h"
void main(void)
{
// окружность С с центром в точке (3,1) и радиусом 0.25
// переменная three является указателем типа Shape на окружность С
Circle C(3,l/ .25, 11);
Shape *one, *two, *three = &С;
char eol;
// окружность *опе имеет центр в точке (1,1) и радиус 0.5
// прямоугольник *two базируется в точке (2,2)
// и имеет длину и ширину, равные 0.5
one = new Circle(1,1, .5, 4);
two = new Rectangle(2,2, .5, .5, 6);
cout « "Площадь/периметр С и фигур 1—3:" « endl;
cout « "С: " « С.Area() « " " « С. Perimeter () « endl;
cout « "1: " « one->Area() « " "
« one->Perimeter<) << endl;
cout << "2: " « two->Area() « " "
« two->Perimeter() « endl;
cout « "3: " « three->Area() « " "
« three->Perimeter() « endl;
cout « "Нажмите Enter, чтобы увидеть фигуры: ";
cin.get(eol); // ждать нажатия клавиши Enter
// инициализация графической системы
InitGraphics();
one->Draw<); // нарисовать окружность
two->Draw(); // нарисовать прямоугольник
three->Draw(); // нарисовать окружность
// выдержать паузу и закрыть графическую систему
ViewPause();
ShutdownGraphics();
}
/*
<Выполнение программы 12.3>
Площадь/периметр С и фигур 1—3:
С: 0.196349 1.570795
1: 0.785398 3.14159
2: 0.25 2
3: 0.196349 1.570795
Нажмите Enter, чтобы увидеть фигуры:
*/
Виртуальные методы и деструктор
Деструктор класса должен быть определен, когда класс распределяет
динамическую память. Если класс будет использоваться в качестве базового, его
деструктор должен быть виртуальным. Этот тонкий, но важный момент должен
учитываться при сохранении списков объектов по указателям базового класса.
Если деструктор базового класса не является виртуальным, то базовый класс,
ссылающийся на объект производного класса не будет вызывать деструктор
этого класса. Эта проблема иллюстрируется следующей ситуацией. Пусть
конструктор базового класса BaseCL динамически размещает массив из семи целых
чисел. Для освобождения памяти должен быть разработан деструктор.
class BaseCL
{
public:
BaseCL (...); // разместить 7-элементный массив
-BaseCL (void); // деструктор (не виртуальный)
}
Класс DerivedCL наследует BaseCL и выполняет те же действия.
class DerivedCL
{
public:
DerivedCL (...); // разместить 7-элементный массив
-DerivedCL (void); // деструктор (не виртуальный)
}
Предположим, что р является указателем класса BaseCL, которому
присваивается динамический объект типа DerivedCL, и затем мы вызываем
функцию delete:
BaseCL *p « new DerivedCL(); // построить новый объект типа DerivedCL
delete p; // вызвать деструктор базового класса
Динамические данные, порожденные производным классом, не
уничтожаются. Если же деструктор базового класса объявлен виртуальным, вызывается
деструктор производного класса. Деструктор базового класса тоже
вызывается, но не раньше производного.
В общем случае, если класс будет использоваться в качестве базового в
иерархии наследования, он обязательно должен иметь виртуальный
деструктор, даже если этот деструктор ничего не будет делать. Например,
virtual BaseCL::~BaseCL(void)
{}
12.4. Абстрактные базовые классы
Наше обсуждение наследования привело к использованию виртуальных
методов базового класса одновременно с методами, имеющими те же имена,
но принадлежащими к производным классам. Поскольку базовый метод
определяется как виртуальный, можно использовать динамическое связывание
и гарантировать таким образом вызов правильной версии. Например, в классе
Shape определяется виртуальный метод Draw, имеющий примитивную задачу
установки образца заполнения. Каждый из наших производных
геометрических классов имеет свой собственный метод Draw, подменяющий базовый
и рисующий конкретную фигуру. В том же классе Shape мы определили
виртуальные методы для вычисления площади и периметра. Эти операции
не имеют смысла для объектов типа Shape, которые состоят из базовой точки
и образца заполнения. Подразумевается, что эти операции будут подменяться
в производных геометрических классах. Объявляя эти операции в базовом
классе как виртуальные методы, мы гарантируем, что динамическое
связывание будет вызывать корректную версию метода для конкретного
геометрического объекта. Определим функции, возвращающие 0.
// Определение функции-заглушки в базовом классе
float Shape::Area(void) const
{
return 0.0; // площадь точки
}
float Shape::Perimeter(void) const
{
return 0.0; // периметр точки
}
Вместо того чтобы вынуждать программиста создавать подобные заглушки,
C++ допускает использование чистых виртуальных функций (pure virtual
functions), путем добавления м=0" к определению. Например,
virtual float Area(void) const = 0;
virtual float Perimeter(void) const = 0;
Применение чистой виртуальной функции в базовом классе подразумевает,
что немедленной ее реализации не будет. В то же время это объявление
предписывает реализацию функции в каждом производном классе. Например,
в каждом производном геометрическом классе должны быть определены
методы Area и Perimeter. Включая чистые виртуальные функции в класс Shape,
мы тем самым гарантируем невозможность создания отдельных объектов
типа Shape. Этот класс может лишь служить базовым для другого класса.
Класс с одной или несколькими чистыми виртуальными функциями
называется абстрактным (abstract class). Любой класс, образованный от
абстрактного класса обязан обеспечить реализацию каждой чистой виртуальной
функции, иначе он также будет абстрактным и не сможет порождать объекты.
Пример 12.3
Абстрактный класс BaseCL содержит две чистые виртуальные
функции и поэтому является абстрактным базовым классом.
class BaseCL
{
• • •
public:
virtual void F(void) - 0; // чистая виртуальная функция
virtual void G(void) = 0; // чистая виртуальная функция
>;
Производный класс DerivedCL определяет F, но не G и поэтому
остается абстрактным.
class DerivedCL: public BaseCL
<
public:
// поскольку функция G не определена, нельзя объявить
// объект типа DerivedCL. класс остается абстрактным
// базовым классом для другого производного класса,
//в котором будет определена функция G
virtual void F(void);
>;
Следующее объявление повлечет за собой ошибку компиляции:
DerivedCL D;
Ошибка:
Нельзя создать экземпляр абстрактного класса 'DerivedCL'
Абстрактный базовый класс List
Абстрактный класс служит шаблоном для своих производных классов. Он
может содержать данные и методы, совместно используемые всеми
производными классами. С помощью чистых виртуальных функций он обеспечивает
объявления общедоступных методов, которые должны быть реализованы
производными классами. В качестве примера мы разрабатываем абстрактный
класс List как шаблон для списковых коллекций. Этот класс имеет переменную
(член класса) size, используемую для определения методов ListSize и
ListEmpty. Эти функции доступны каждому производному классу,
обеспечивающему корректное сохранение size при включении или удалении элементов,
а также при очистке списка. Несмотря на то что методы ListSize и ListEmpty
представляются в базовом классе, они могут быть либо подменены в
производном классе, либо восприняты по умолчанию. Остальные методы объявляются
как чистые виртуальные функции базового класса и должны подменяться в
производном классе. Функция Insert зависит от конкретного класса
коллекций. В одном образовании Insert может помещать данные в последовательный
список, а для бинарного дерева или словаря требуется совершенно иной
алгоритм включения.
Спецификация класса List
template <class T>
class List
{
protected:
// число элементов списка, обновляемое производным классом
int size;
public:
// конструктор
List(void);
// методы доступа к списку
virtual int ListSize(void) const;
virtual int ListEmpty(void) const;
virtual int Find (T& item) «= 0;
// методы модификации списка
virtual void Insert (const T& item) - 0;
virtual void Delete (const T& item) = 0;
virtual void ClearList (void) = 0;
};
Реализация методов класса List
В любом производном классе методы модификации списка должны
поддерживать size — член базового класса. Начальное значение 0 присваивается этой
переменной конструктором класса List.
// конструктор устанавливает size в 0
template <class T>
int List<T>::List(void): size(0)
{}
Методы ListSize и ListEmpty класса List зависят только от значения size.
Они реализуются в базовом классе и затем используются любым производным
классом.
// возвратить размер списка
template <class T>
int List<T>::List(void) const
{
return size;
}
// проверить, пуст ли список
template <class T>
int List<T>::ListEmpty(void) const
{
return size == 0;
}
Образование класса SeqList из абстрактного базового класса List
Первый раз мы представили класс SeqList в гл. 1 и в последующих главах
показали реализацию массива и связанного списка. Теперь мы снова
рассмотрим SeqList в качестве класса, образованного от абстрактного класса
List. Методы DeleteFront и GetData отсутствуют в абстрактном классе, так
как они применимы только к последовательному списку.
Спецификация класса SeqList
ОБЪЯВЛЕНИЕ
template <class T>
class SeqList: public List
{
protected:
// связанный список, доступный производным классам
LinkedList<T> Hist;
public:
// конструктор
SeqList(void);
// методы доступа к списку
virtual int Find (T& item);
T GetData(int pos);
// методы модификации списка
virtual void Insert (const T& item);
virtual void Delete (const T& item);
T DeleteFront(void);
virtual void ClearList (void);
// для объекта типа SeqListlterator требуется доступ к Hist
friend class SeqListIterator<T>;
};
ОПИСАНИЕ
Являясь наследником абстрактного класса List, класс SeqList должен
поддерживать указанные в List операции. Поскольку SeqList реализует
последовательный список, в этот производный класс должны быть добавлены метод
GetData, принимающий позицию элемента в качестве параметра, и метод
DeleteFront, удаляющий первый элемент списка.
Методы Insert, Delete и ClearList поддерживают защищенный элемент данных
базового класса size, поэтому методы ListSize и ListEmpty подменять не нужно.
Прохождение объекта типа SeqList можно выполнить с помощью средства,
называемого итератором (iterator). Этот инструмент, объявляемый как объект
типа SeqListlterator, должен иметь доступ к Hist, что обеспечивается
объявлением класса SeqListlterator дружественным. Итераторы обсуждаются в
следующем разделе. Производная версия класса SeqList вкючена в файл seqlist2.h.
Реализация производной версии класса SeqList
Основная часть работы по реализации этого класса была сделана в гл. 9.
Нам необходимо определить функции Insert, Delete, ClearList и Find. Мы
повторяем их определения, сделанные в классе LinkedList, но добавляем
поддержку значения size из класса List. Например, метод Insert выглядит
следующим образом:
// использовать метод InsertRear для включения элемента в хвост списка
template <class T>
void SeqList<T>::Insert{const T& item)
{
Hist. InsertRear (item) ;
size++; // обновить size в классе List
}
Конструктор производного класса SeqList вызывает конструктор класса
List, который обнуляет size.
// конструктор умолчания
// инициализация базового класса
template <class T>
SeqList<T>::SeqList(void): List<T>{)
{}
12.5. Итераторы
Многие алгоритмы обработки списков предполагают, что мы сканируем
элементы и попутно совершаем какое-то действие. Производный от List класс
предоставляет методы для добавления и удаления данных, В общем случае в
нем отсутствуют методы, специально предназначенные для прохождения
списка. Подразумевается, что прохождение осуществляет некий внешний процесс,
который поддерживает номер текущей записи списка.
В случае массива или объекта L типа SeqList мы можем выполнить
прохождение, используя цикл и индекс позиции. Для объекта L типа SeqList доступ
к данным класса осуществляется посредством метода GetData.
for (pos - 0; pos < ListSizeO; pos++)
cout « L.GetData (pos)« " ";
Для бинарных деревьев, хешированных таблиц и словарей процесс
прохождения списка более сложен. Например, прохождение дерева является
рекурсивным и должно выполняться рекурсивным прямым, обратным или
симметричным методами. Эти методы могут быть добавлены в класс
обработки бинарных деревьев. Однако рекурсивные функции не позволяют
клиенту остановить процесс прохождения, выполнить другую задачу и
продолжить итерацию. Как мы увидим в гл. 13, итерационное прохождение может
быть выполнено путем сохранения указателей на узлы дерева в стеке. Классу
деревьев не потребуется содержать итерационную версию для каждого способа
прохождения, даже если клиент не может выполнить прохождение дерева
или может постоянно использовать один метод прохождения.
Предпочтительно отделять абстракцию данных от абстракции управления. Решением
проблемы прохождения списка является создание класса итераторов, задачей
которого будет прохождение элементов таких структур данных, как
связанные списки или деревья. Итератор инициализируется так, чтобы указывать
на начало списка (на голову, корень и т.д.). У итератора есть методы Next()
и EndOfList(), обеспечивающие продвижение по списку. Объект-итератор
сохраняет запись состояния итерации между обращениями к Next.
С помощью итератора клиент может приостановить процесс прохождения,
проверить содержимое элемента данных, а также выполнить другие задачи.
Клиенту дается средство прохождения списка, не требующее сохранения
внутренних индексов или указателей. Имея класс, включающий дружественный
ему итератор, мы можем связывать с этим классом некоторый подлежащий
сканированию объект и обеспечивать доступ к его элементам через итератор.
При реализации методов итератора используется структура внутреннего
представления списков.
В этом разделе дается общее обсуждение итераторов. С помощью
виртуальных функций мы объявляем абстрактный базовый класс, используемый
в качестве основы для конструирования всех итераторов. Этот абстрактный
класс предоставляет общий интерфейс для всех операций итератора, несмотря
на то что производные итераторы реализуются по-разному.
Абстрактный базовый класс Iterator
Мы определяем абстрактный класс Iterator как шаблон для итераторов
списков общего вида. Каждый из представляемых далее итераторов образован из
этого класса, который находится в файле iterator.h.
Спецификация класса Iterator
ОБЪЯВЛЕНИЕ
template <class T>
class Iterator
{
protected:
// флажок, показывающий, достиг ли итератор конца списка.
// должен поддерживаться производными классами
int iterationComplete;
public:
// конструктор
Iterator(void);
// обязательные методы итератора
virtual void Next(void) = 0;
virtual void Reset(void) = 0;
// методы для выборки/модификации данных
virtual T& Data(void) = 0;
// проверка конца списка
virtual int EndOfList(void) const;
};
ОБСУЖДЕНИЕ
Итератор является средством прохождения списка. Его основные методы:
Reset (установка на первый элемент списка), Next (установка позиции на
следующий элемент), EndOfList (обнаружение конца списка). Функция Data
осуществляет доступ к данным текущего элемента списка.
Реализация класса Iterator
Этот абстрактный класс имеет единственный элемент данных,
iterationComplete, который должен поддерживаться методами Next и Reset в каждом
производном классе. Из функций реализованы только конструктор и метод EndOfList.
// конструктор, устанавливает iterationComplete в 0 (False)
template <class T>
Iterator<T>::Iterator(void): iterationComplete(0)
{}
Метод EndOfList просто возвращает значение iterationComplete. Этот
флажок устанавливается в 1 (True) производным методом Reset, если список пуст.
Метод Next в производном классе должен устанавливать iterationComplete в 1
при выходе за верхнюю границу списка.
Образование итераторов для списка
Класс SeqList широко использовался в этой книге и послужил основой
для разработки абстрактного класса List. Ввиду его важности мы начнем с
итератора последовательных списков. Этот итератор хранит указатель listPtr,
указывающий на сканируемый в данный момент объект типа SeqList.
Поскольку SeqListlterator является дружественным по отношению к
производному классу SeqList, допускается обращение к закрытым элементам данных
класса SeqList.
Спецификация класса SeqListlterator
ОБЪЯВЛЕНИЕ
// SeqListlterator образован от абстрактного класса Iterator
template <class T>
class SeqListlterator: public Iterator<T>
{
private:
// локальный указатель на объект SeqList
SeqList<T> *listPtr;
// по. мере прохода по списку необходимо хранить предыдущую и текущую позицию
Node<T> *prevPtr, *currPtr;
public:
// конструктор
SeqListlterator (SeqList<T>& 1st);
// обязательные методы прохождения
virtual void Next(void);
virtual void Reset(void);
// методы для выборки/модификации данных
virtual T& Data(void);
// установить итератор для прохождения нового списка
void SetList(SeqList<T>& 1st);
}
ОБСУЖДЕНИЕ
Этот итератор реализует виртуальные функции Next, Reset и Data, которые
были объявлены как чистые виртуальные функции в базовом классе Iterator.
Метод SetList является специфичным для класса SeqListlterator и позволяет
клиенту присваивать итератор другому объекту типа SeqList. Класс SeqList
вместе с итератором находятся в файле seqlist2.h.
ПРИМЕР
SeqList<int> L; // создать список
SeqListIterator<int> iter(L); // создать итератор и присоединить к списку L
cout « iter.Data (); // распечатать текущее значение данных
iter.Next{); // перейти на следующую позицию в списке
// цикл, выполняющий проход по списку и распечатывающий его элементы
for (iter.Reset(); liter.EndOfList(); iter.NextO )
cout « iter.Data() « " ";
Построение итератора SeqList
Итератор, создаваемый конструктором, ограничен определенным классом
SeqList, и все его операции применимы к последовательному списку. Итератор
хранит указатель на объект типа SeqList.
После присоединения итератора к списку мы инициализируем iterationCom-
plete и устанавливаем текущую позицию на первый элемент списка.
SeqListlterator
HstPtr
Hist
prevPtr
currPtr
// конструктор, инициализировать базовый класс и локальный указатель SeqList
template <class T>
SeqListIterator<T>::SeqListlterator(SeqList<T>& 1st):
Iterator<T>(), listPtr(&lst)
{
// выяснить, пуст ли список
iterationComplete «= listPtr->llist.ListEmpty();
// позиционировать итератор на начало списка
Reset();
}
Reset устанавливает итератор в начальное состояние, инициализируя
iterationComplete и устанавливая указатели prevPtr и currPtr на свои позиции в
начале списка. Класс SeqListlterator является также дружественным по
отношению к классу LinkedList и, следовательно, имеет доступ к члену класса front.
// перейти к началу списка
template <class T>
void SeqListIterator<T>::Reset(void)
{
// переприсвоить состояние итерации
iterationComplete « listPtr->llist.ListEmpty<);
// вернуться, если список пуст
if (listPtr->llist.front -» NULL)
return;
// установить механизм прохождения списка с первого узла
prevPtr * NULL;
currPtr - listPtr->llist.front;
}
Метод SetList является эквивалентом конструктора времени исполнения.
Новый объект 1st типа SeqList передается в качестве параметра, и теперь
итератор идет по списку 1st. Переназначьте listPtr и вызовите Reset.
// сейчас итератор должен проходить список 1st.
// переназначьте listPtr и вызовите Reset,
template <class T>
void SeqListIterator<T>::SetList(SeqList<T>& 1st)
{
listPtr - &lst;
// инициализировать механизм прохождения для списка 1st
Reset();
}
Итератор получает доступ к данным текущего элемента списка с помощью
метода Data(). Эта функция возвращает значение данных текущего элемента
списка, используя currPtr для доступа к данным узла LinkedList. Если список
пуст или итератор находится в конце списка, выполнение программы
прекращается после выдачи сообщения об ошибке.
// возвратить данные, расположенные в текущем элементе списка
template <class T>
void SeqListIterator<T>::Data(void)
{
// ошибка, если список пуст или прохождение уже завершено
if (listPtr->llist.ListEmpty() I I currPtr «= NULL)
{
cerr « "Data: недопустимая ссылка!" « endl;
exit(l);
)
return currPtr->data;
}
Продвижение от элемента к элементу обеспечивается методом Next. Процесс
сканирования продолжается до тех пор, пока текущая позиция не достигнет
конца списка. Это событие отражается значением члена iterationComplete
класса Iterator, который должен поддерживаться функцией Next.
// продвинуться к следующему элементу списка
template <class T>
void SeqListIterator<T>::Next(void)
{
// если currPtr == NULL, мы в конце списка
if (currPtr ==* NULL)
return;
// передвинуть указатели prevPtr/currPtr на один узел вперед
prevPtr = currPtr;
currPtr = currPtr->NextNode();
// если обнаружен конец связанного списка,
// установить флажок "итерация завершена"
if (currPtr =- NULL)
iterationComplete * 1;
Программа 12.4. Использование класса SeqListlterator
Некая компания ежемесячно создает записи Salesperson, состоящие из
личного номера продавца и количества проданного товара. Список salesList
содержит накопленные за некоторый отрезок времени записи Salesperson.
Во втором списке, idList, хранятся только личные номера служащих. Из
файла sales.dat вводится информация о продажах за насколько месяцев, и
каждая запись включается в salesList. Поскольку записи охватывают
несколько месяцев, одному продавцу может соответствовать несколько записей.
Однако в список idList каждый сотрудник включается только единожды.
После ввода данных соответствующим спискам назначаются итераторы
idlter и saleslter. Сканируя список idList, мы идентифицируем каждого
служащего по его личному номеру и передаем этот номер в качестве
параметра функции PrintTotalSales. Эта функция сканирует список salesList и
подсчитывает суммарное количество товара, проданного сотрудником с
данным личным номером. В конце распечатывается личный номер служащего
и суммарное количество проданного им товара.
#include <iostream.h>
#include <fstream.h>
finclude "seqlist2.h"
// использовать класс SeqList, наследующий класс List, и SeqListlterator
// запись, содержащая личный номер продавца и количество проданного товара
struct Salesperson
{
int idno;
int units;
);
// оператор =* сравнивает служащих по личному номеру
int operator » (const Salesperson &a, const Salesperson &b)
{
return a.idno « b.idno;
}
// взять id в качестве ключа и пройти список.
// суммировать количество товара, проданное сотрудником с личным номером id
// печатать результат
void PrintTotalSales(SeqList<SalesPerson> & L, int id)
{
// объявить переменную типа Salesperson и инициализировать поля записи
Salesperson salesP = {id, 0};
// объявить итератор последовательного списка
// и использовать его для прохождения списка
SeqListIterator<SalesPerson> iter(L);
for(iter.Reset О; !iter.EndOfList(); iter.NextO )
// если происходит совпадение с id, прибавить количество товара
if (iter.DataO *= salesP)
sales.P += (iter.Data()).units;
// печатать личный номер и суммарное количество продаж
cout « "Служащий " « salesP.idno
« " Количество проданного товара " « salesP.units
« endl;
)
void main(void)
{
// список, содержащий записи типа Salesperson,
//и список личных номеров сотрудников
SeqList<SalesPerson> SalesList;
SeqList<int> idList;
ifstreaiti salesFile; // Входной файл
Salesperson salesP; // Переменная для ввода
int i;
// открыть входной файл
salesFile.open("sales.dat", ios::in | ios::nocreate);
if (JsalesFile)
{
cerr « "Файл sales.dat не найден!";
exit(1);
}
// читать данные в форме "личный номер количество товара"
//до конца файла
while (!salesFile.eof())
{
// ввести поля данных и вставить в список salesList
salesFile » salesP.idno >> salesP.units;
salesList.Insert(salesP);
// если id отсутствует в idList, включить этот id
if (!idList.Find(sales?.idno))
idList.Insert(salesP.idno);
}
// создать итераторы для этих двух списков
SeqListIterator<int> idlter(idList);
SeqListIterator<SalesPerson> saleslter(salesList);
// сканировать список личных номеров и передавать каждый номер
// в функцию PrintTotalSales для добавления количества // проданного
товара к общему числу его продаж
for(idlter.Reset(); !idlter.EndOfList(); idlter.Next () )
PrintTotalSales(salesList, idlter.Data());
}
/*
<Файл sales.dat>
300 40
100 45
200 20
200 60
100 50
300 10
400 40
200 30
300 10
<Прогон программы 12.4>
Служащий 300 Количество проданного товара 70
Служащий 100 Количество проданного товара 95
Служащий 200 Количество проданного товара 110
Служащий 400 Количество проданного товара 40
V
Итератор массива
Стремясь привязать итераторы к классам списков, мы, возможно,
упустили из виду класс Array. Между тем итератор массивов является весьма
полезной абстракцией. Настроив итератор так, чтобы тот начинался и
заканчивался на конкретных элементах, можно исключить работу с индексами.
Кроме того, один и тот же массив может обрабатываться несколькими
итераторами одновременно. Здесь приводится пример использования нескольких
итераторов при слиянии двух отсортированных последовательностей,
находящихся в одном массиве.
Спецификация класса Arraylterator
ОБЪЯВЛЕНИЕ
#include "iterator.h"
template <class T>
class Arraylterator: public Iterator<T>
{
private:
// начальная, текущая и конечная точки
int startlndex;
int currentIndex;
int finishlndex;
// адрес объекта типа Array, подлежащего сканированию
Array<T> *arr;
public:
// конструктор
Arraylterator(Array<T>& A, int start=0, int finish=-l);
// стандартные операции итератора, обусловленные базовым классом
virtual void Next(void);
virtual void Reset(void);
virtual T& Data(void);
};
ОБСУЖДЕНИЕ
Конструктор связывает объект типа Array с итератором и инициализирует
начальный и конечный индексы массива. По умолчанию начальный индекс
равен 0 (итератор находится на первом элементе массива), а конечный индекс
равен -1 (верхней границей массива является индекс последнего элемента).
На любом шаге итерации currlndex является индексом текущего элемента
массива. Его начальное значение равно startlndex. Класс Arraylterator
находится в файле arriter.h.
Класс Arraylterator имеет минимальный набор общедоступных функций-
членов, подменяющих чистые виртуальные методы базового класса.
ПРИМЕР
// массив 50 чисел с плавающей точкой от 0 до 49
Array<double> A(50);
// итератор массива сканирует А от 3-го до 10-го индекса
ArrayIterator<double> arriter(Arr, 3, 10);
// печатать массива с 3-го по 10-й элемент
for (arriter.Reset(); !arriter.EndOfList (); arriter.Next () )
cout « arriter.Data() « " ";
Приложение: слияние сортированных последовательностей
В главе 14 формально изучаются алгоритмы сортировки, включая и
внешнюю сортировку слиянием, которая упорядочивает файл данных на диске.
Этот алгоритм разделяет список элементов на сортированные подсписки,
называемые последовательностями (runs).
ОПРЕДЕЛЕНИЕ
В списке Х0, Хх, ..., Хп_х последовательностью является подсписок Ха,
Xa+i> •••! Хъ, где
Xi<Xi+i при a<i<b
Xa-i>Xa при а>0
Хь+1<Хъ при Ь<п—1
Например, ПОДСПИСОК Л.2 ••• Л5 есть последовательность в массиве X
X: 20 35 15 25 30 65 50 70 10
В процессе слияния последовательности вкладываются друг в друга,
создавая тем самым более длинные упорядоченные подсписки до тех пор,
пока в результате не получится отсортированный массив.
Список А: 3 б 23 35 2 4 6
I I I I
Последовательность #1 Последовательность #2
Это приложение реализует лишь очень ограниченную часть полного
алгоритма. Предполагается, что данные хранятся в виде двух
последовательностей в N-элементном массиве. Первая последовательность заключена в
диапазоне от 0 до R-1, вторая — от R до N-1. Например, в семиэлементном
массиве А последовательности разделяются на индексе R = 4.
Поэлементное слияние порождает сортированный список. Текущая точка
прохождения устанавливается на начало каждой последовательности.
Значения в текущей точке сравниваются, и наименьшее из них копируется
в массив. Когда значение в последовательности обработано, выполняется
шаг вперед к следующему числу и сравнение продолжается. Поскольку
подсписки изначально упорядочены, элементы копируются в выходной
массив в сортированном порядке. Когда одна из последовательностей
заканчивается, оставшиеся члены другой последовательности копируются в
выходной массив.
Этот алгоритм изящно реализуется с помощью трех итераторов: left,
right и output. Итератор left проходит первую последовательность, right —
вторую, a output используется для записи данных в выходной массив.
Пример работы алгоритма показан на рис. 12.2.
Программа 12.5. Слияние сортированных последовательностей
Функция Merge получает две последовательности, расположенные в
массиве А, и сливает их в выходной массив Out. Этот используют
итераторы left и right, которые инициализируются параметрами lowlndex,
endOfRunlndex и highlndex. Итератор output записывает
отсортированные данные в Out. Процесс прекращается по достижении конца одной
из последовательностей. Функция Сору дописывает данные, оставшиеся
в другой последовательности, в массив Out. После сбрасывания
итератора output в начальное состояние отсортированный список копируется
обратно в А.
Эта программа вводит 20 целых чисел из файла rundata. В процессе ввода
мы сохраняем данные в массиве А и распознаем индекс конца
последовательности, который потребуется функции Merge. Функция Merge сортирует
массив, который затем распечатывается.
♦include <iostream.h>
♦include <fstream.h>
♦include "array.h"
♦include "агг^ег.п"
// копирование одного массива в другой с помощью их итераторов
void Copy(ArrayIterator<int>& Source, ArrayIterator<int>& Dest)
Шаг!
Шаг 2
ШагЗ
Шаг 4
Шаг 5
left
right
left
right
left
right
left
right
left
right
Шаг 6
Шаг 7
left
right
left
right
output
output
output
output
output
right достиг конца
последовательности
output
оставшиеся члены
первой
последовательности
переписываются в выходной
массив
output !
Рис 12.2. Слияние сортированных последовательностей
{
while ( !Source.EndOfList() )
{
Dest.DataO = Source.Data() ;
Source.Next();
Dest.Next();
}
}
// слияние сортированных последовательностей в массиве А.
// первая последовательность заключена в диапазоне индексов
// lowlndex..endOfRunlndex-l, // вторая — в диапазоне endOfRunlndex..highln-
dex
void Merge(Array<int>& A, int lowlndex, int endOfRunlndex,
int highlndex)
{
// массив, в котором объединяются сортированные последовательности
Array<int> Out (A.ListSizeO );
// итератор left сканирует 1-ю последовательность;
// итератор right сканирует 2-ю последовательность;
ArrayIterator<int> left(A, lowlndex, endOfRunlndex-l);
ArrayIterator<int> right(A, endOfRunlndex, highlndex);
// итератор output записывает отсортированные данные в Out
ArrayIterator<int> output(Out);
// копировать, пока не кончится одна или обе последовательности
while (!left.EndOfList() && !right.EndOfList())
{
// если элемент "левой" последовательности с итератором left меньше или
// равен элемент "правой" последовательности, то записать его в массив Out.
// перейти к следующему элементу "левой" последовательности
if (left.DataO <= right .Data () )
{
output. Data () = left.DataO;
left.NextO ;
)
// иначе записать в Out элемент "правой" последовательности
//и перейти к следующему элементу "правой" последовательности
else
{
output.Data() = right.Data();
right.Next();
}
output.Next{); // продвинуть итератор выходного массива
}
// если одна из последовательностей не обработана до конца,
// скопировать этот остаток в массив Out
if (!left.EndOfList())
Copy(left, output);
else (!right.EndOfList())
Copy(right, output);
// сбросить итератор выходного массива и скопировать Out в А
output.Reset() ;
ArrayIterator<int> final(A); // массив для копирования обратно в А
Copy(output, final);
}
void main(void)
{
// массив для сортированных последовательностей, введенных из потока fin
Array<int> A(20);
ifstream fin;
int i;
int endOfRun = 0;
// открыть файл rundata
fin.open("rundata", ios::in | ios::nocreate);
if (!fin)
{
cerr « "Нельзя открыть файл rundata", « endl;
exit(1);
}
// читать 20 чисел, представленных в виде двух
// сортированных последовательностей
fin » А[0];
for (i=l; i<20; i++)
{
fin » A[i] ;
if (A[i] < A[i-1])
endOfRun = i;
}
// слияние последовательностей
Merge(A, 0, endOfRun, 19);
// распечатать отсортированный массив по 10 чисел в строке
for (i»0; i<20; i++)
{
cout « A[iJ « " ";
if (i -- 9)
cout « endl;
}
}
/*
<Файл rundata>
1 3 6 9 12 23 33 45 55 68 88 95
2 8 12 25 33 48 55 75
<Выполнение программы 12.5>
1 2 3 6 8 9 12 12 23 25
33 33 45 48 55 55 68 75 88 95
V
Реализация класса Arraylterator
Конструктор задает начальное состояние итератора. Он привязывает
итератор к массиву и инициализирует три индекса. Если для индексов startlndex
и finishlndex используются значения по умолчанию (0 и -1), то итератор
проходит через весь массив.
// конструктор, инициализирует базовый класс и данные-члены
template <class T>
ArrayIterator<T>::Arraylterator(Array<T>& A, int start,
int finish): arr(&A)
{
// последний доступный индекс массива
int ilast » A.ListSizet) - 1;
// инициализировать индексы, если finish ■■ -1,
//то сканируется весь массив
currentlndex - startlndex - start;
finishlndex e finish !« -1 ? finish : ilast;
// индексы должны быть в границах массива
if (!<(startlndex>«0 && startlndex<-ilast) &&
(finishIndex>-0 && finishlndex<~ilast) &&
(startlndex <= finishlndex)))
{
cerr « "Arraylterator: Неверные параметры индекса!"
« endl;
exit(1);
}
}
Reset переустанавливает текущий индекс на стартовую точку и обнуляет
iterationComplete, показывая тем самым, что начался новый процесс
прохождения.
// сброс итератора массива
template <class T>
void ArrayIterator<T>::Reset(void)
{
// установить текущий индекс на начало массива
currentlndex « startlndex;
// итерация еще не завершена
iterationComplete = 0;
}
Метод Data использует currentlndex для доступа к данным-членам. Если
текущая точка прохождения заходит за верхнюю границу списка,
генерируется сообщение об ошибке и программа прекращается.
// возвратить значение текущего элемента массива
template <class T>
Т& ArrayIterator<T>::Data(void)
{
// если весь массив пройден, то вызов метода невозможен
if (iterationComplete)
{
cerr « "Итератор прошел весь список до конца!"
« endl;
exit(1);
}
return (*arr) [currentlndex]/
}
Если итерация завершается, метод Next просто возвращает управление. В
противном случае он увеличивает currentlndex и обновляет логическую
переменную базового класса iterationComplete.
// перейти к следующему элементу массива
template <class T>
void ArrayIterator<T>::Next (void)
{
// если итерация не завершена, увеличить currentlndex
// если пройден finishlndex, то итерация завершена
if (!iterationComplete)
<
currentIndex++;
if (currentlndex > finishlndex)
iterationComplete ■ 1;
}
}
12.6. Упорядоченные списки
Класс SeqList создает список, элементы которого добавляются в хвост. В
результате получается неупорядоченный список. Однако во многих
приложениях требуется списковая структура с таким условием включения, при котором
элементы запоминаются в некотором порядке. В этом случае приложение
сможет эффективно определять наличие того или иного элемента в списке, а также
выводить элементы в виде отсортированных последовательностей.
Чтобы создать упорядоченный список, мы используем класс SeqList в
качестве базового и образуем на его основе класс OrderedList, который вставляет
элементы в возрастающем порядке с помощью оператора "<". Это пример
наследования в действии. Мы переопределяем только метод Insert, поскольку
все другие операции не влияют на упорядочение и могут быть унаследованы
от базового класса.
Спецификация класса OrderedLlst
ОБЪЯВЛЕНИЕ
#include "seqlist2.h"
template <class T>
class OrderedList: public SeqList<T>
{
public:
// конструктор
OrderedList(void);
// подменить метод Insert для формирования упорядоченного списка
virtual void Insert (const t& item) ;
};
ОПИСАНИЕ
Все операции, за исключением Insert, взяты из SeqList, так как они не
влияют на упорядочение. Поэтому должен быть объявлен только метод Insert,
чтобы подменить одноименный метод из SeqList. Эта функция сканирует
список и включает в него элементы, сохраняя порядок.
Класс OrderedList находится в файле ordlist.h.
Реализация класса OrderedList
В классе OrderedList определяется конструктор, который просто вызывает
конструктор класса SeqList. Тем самым инициализируется этот базовый
класс, а он в свою очередь инициализирует свой базовый класс List. Мы
имем пример трех-классовой иерархической цепи.
// конструктор, инициализировать базовый класс
template <class T>
OrderedList::OrderedList(void): SeqList<T>()
{}
В этом классе определяется новая функция Insert, которая включает
элементы в подходящее место списка. Новый метод Insert использует встроенный
в класс LinkedList механизм поиска первого элемента, большего, чем
включаемый элемент. Метод InsertAt используется для включения в связанный список
нового узла в текущем месте. Если новое значение больше, чем все имеющиеся,
оно дописывается в хвост списка. Метод Insert отвечает за обновление
переменной size, определенной в базовом классе List.
// вставить элемент в список в возрастающем порядке
template <class T>
void OrderedList::Insert(const T& item)
{
// использовать механизм прохождения связанных списков
// для обнаружения места вставки
for( Hist. Reset (); ! Hist. EndOf List () ; Hist.NextO )
if (item < Hist.DataO )
break;
// вставить item в текущем месте
Hist. InsertAt (item);
size++;
)
Приложение: длинные последовательности. В программе 12.5 описана
часть алгоритма сортировки слиянием, который включал слияние двух сор-
тированных последовательностей в одну, тоже сортированную. В программе
предполагалось, что ваши входные данные уже заранее разбиты на две
последовательности. Сейчас мы обсудим методику фильтрации (предварительной
обработки) данных для получения более длинных последовательностей.
Предположим, что большой блок данных хранится в случайном порядке в
массиве или на диске. Тогда эти данные можно представить в виде ряда
коротких последовательностей. Например, следующее множество из 15-и символов
состоит из восьми последовательностей.
CharArray: [a k] [g] [с m t] [e n] [1] [с г s] [с b f]
Попытка использовать сортировку слиянием для упорядочения этих данных
была бы тщетной ввиду значительного числа коротких последовательностей,
подлежащих объединению. В нашем примере четыре слияния дают следующие
последовательности.
[a g к] [с е m t] [с 1 г s] [b с f]
Сортировка слиянием предписывает объединить на следующем проходе
эти четыре последовательности в две и затем создать полностью
отсортированный список. Алгоритм работал бы лучше, если бы изначально
последовательности имели разумную длину. Этого можно достичь путем
сканирования элементов и объединения их в сортированные подсписки. Алгоритм
внешней сортировки должен противостоять относительно медленному времени
доступа к диску и часто включает в себя фильтр для предварительной
обработки данных. Мы должны постараться, чтобы время, затраченное на
фильтрацию данных, повышало бы общую эффективность алгоритма.
Упорядоченный список является примером простого фильтра.
Предположим, что исходный массив или файл содержит N элементов. Мы вставляем
каждую группу из к элементов в некоторый упорядоченный список, а затем
копируем этот список обратно в массив. Этот фильтр гарантирует, что
последовательности будут иметь длину, по крайней мере, к. Например, пусть к=5,
и мы обрабатываем данные массива CharArray. Тогда результат будет таким:
{а с g k m] [с е 1 n t] [b с £ г s]
Усовершенствованная версия этого фильтра приводится в гл. 13.
Программа 12.6. Длинные последовательности
Эта программа фильтрует массив 100 случайных целых чисел в диапазоне
от 100 до 999 в последовательности, по крайней мере, из 25 элементов,
используя упорядоченный список. Каждой новое случайное число
вставляется в объект L типа OrderedList. Для каждых 25 элементов функция Сору
удаляет эти элементы из списка L и вставляет их обратно в массив А.
Программа заканчивается печатью результирующего массива А.
#include <iostream.h>
#include "ordlist.h"
#include "array.h"
#include "arriter.h"
#include "random.h"
// пройти целочисленный массив и распечатать каждый элемент
// по 10 чисел в строке
void PrintList(Array<int>& A)
{
// использовать итератор массива
ArrayIterator<int> iter(A);
int count;
// прохождение и печать списка
count * 1;
for(iter.Reset(); !iter.EndOfList(); iter.NextO, count++)
{
cout « iter.Data() « " ";
// печатать по 10 чисел в строке
if (count % 10 -= 0)
cout « endl;
}
}
// удалять элементы из упорядоченного списка L и вставлять, их в массив А.
// обновить loadlndex, указывающий следующий индекс в А
void Copy(OrderedList<int> &L, Array<int> &A, int &loadIndex)
{
while (IL.ListEmpty())
A[loadIndex++] =» L.DeleteFront();
)
void main(void)
{
// создать последовательности в А с помощью упорядоченного списка L
Array<int> А(100);
OrderedList<int> L;
// генератор случайных чисел
RandomNumber rnd;
int i, loadlndex = 0;
// сгенерировать 100 случайных чисел в диапазоне от 100 до 999.
// отфильтровать их через 25-элементный упорядоченный список.
// после заполнения списка копировать его в массив А
for (i-1; i<«100; i++)
{
L.Insert(rnd.Random(900) + 100);
if (i % 25 — 0)
Copy(L, A, loadlndex);
)
// печатать итоговый массив А
PrintList(A);
}
/*
<Выполнение программы 12.б>
110
500
850
205
513
296
725
940
343
641
116
532
903
216
524
375
728
990
368
739
149
578
929
221
604
412
771
991
372
774
152
601
947
243
634
437
799
992
434
784
162
715
958
287
641
457
803
994
443
829
240
730
105
348
730
466
815
101
489
875
345
732
132
350
784
507
859
118
515
883
370
754
139
445
940
550
879
123
529
922
422
815
139
466
969
594
909
155
557
967
492
833
190
507
982
652
915
310
574
972
*/
12.7. Разнородные списки
Коллекция, хранящая объекты одинакового типа называется однородной
(homogeneous). До сих пор мы рассматривали только однородные коллекции.
Коллекция, содержащая объекты различных типов, называется разнородной
(heterogeneous). Поскольку типы данных в C++ определяются в момент
компиляции, мы должны представить новую методику для реализации
разнородных коллекций. В данном разделе мы реализуем разнородные массивы и
связанные списки, предполагая, что все имеющиеся там объекты образованы от
общего для всех них базового класса.
Разнородные массивы
Всеобъемлющее обсуждение разнородных массивом выходит за рамки
данной книги. Мы ограничимся массивами указателей на объекты различных
типов. Рассмотрим еще раз пример из гл. 1, иллюстрирующий полиморфизм.
Ради удобства сформулируем его снова.
Имеется набор базовых операций, необходимых для покраски любого дома.
Дома различных типов требуют различной технологии покраски. Например,
деревянные стены можно шлифовать, а пластиковую облицовку можно мыть.
В контексте объектно-ориентированного программирования эти дома
представляют собой различные классы, образованные от базового класса (House) дом,
который содержит общие для всех операции покраски. Технология покраски
(метод Paint) ассоциируется с каждым классом.
Дом (House)
Paint
Деревянный дом
Оштукатуренный дом
Дом с пластиковой облицовкой
Paint
Paint
Paint
Базовый класс House содержит идентификационную строку "дом" и
виртуальный метод Paint, который распечатывает ее. Каждый производный класс
подменяет метод Paint и показывает тип дома, подлежащего покраске.
// базовый класс в иерархии технологий покраски домов
class House
{
private:
String id; // идентификатор дома
public:
// конструктор, присвоить идентификатору дома значение "дом"
House (void)
{
id - "дом";
}
// виртуальный метод, печатает символьную строку "дом"
virtual void Paint(void)
{
cout « id;
}
);
Каждый производный класс содержит символьную строку,
идентифицирующую тип дома. Виртуальный метод Paint распечатывает эту строку и
вызывает базовый метод Paint. Объявление класса WoodFrameHouse
приводится в качестве модели. Полное описание классов домов находится в файле
houses.h.
class WoodFrameHouse: public House
{
private:
// идентификатор дома
String id;
public:
// конструктор.
WoodFrameHouse(void): House()
{
id - "деревянный"
}
// виртуальный метод, распечатывает id
// и вызывает Paint базового класса
virtual void Paint(void)
<
cout « "Покрасить " « id « " ";
House::Paint();
}
};
Чтобы описать понятие разнородного массива, определим массив
contractor List (подрядчики), состоящий из пяти указателей на базовый класс House.
Массив инициализируется посредством случайной выборки В массив
заносится случайная выборка объектов, имеющих тип WoodFrameHouse
(деревянный), StuccoHouse (оштукатуренный) или VinylSidedHouse (пластиковый).
Например, такая:
contractorList
VinylSidedHouse
WoodFrameHouse
StuccoHouse
WoodFrameHouse
VinylSidedHouse
Можно рассматривать этот массив указателей как список адресов пяти
домов подлежащих покраске. Подрядчик распределяет работы по бригадам.
В нашем примере подрядчик дает каждой бригаде адрес дома и полагает,
что они сообразят, как покрасить дом, когда увидят, какого он типа.
Программа 12.7. Разнородный массив
Эта программа проходит массив contractorList и вызывает метод Paint
для каждого объекта. Поскольку каждый объект адресуется указателем,
динамическое связывание гарантирует, что будет выполнен именно тот
Paint, который нужен. Это соответствует выписыванию нарядов на
малярные работы.
#include <iostream.h>
♦include "random.h" // датчик случайных чисел
#include "houses.h" // иерархия покрасочных технологий
void main(void)
{
// динамический список адресов объектов
House *contractorList[5];
RandomNumber rnd;
// построить список пяти домов, подлежащих покраске
for (int i=0; i<5; i++)
// выбрать случайным образом дом типа 0, 1 или 2.
// создать объект и занести его адрес в contractorList
switch(rnd.Random{3))
{
case 0: contractorList[i] ■ new WoodFrameHouse;
break;
case 1: contractorList[i] - new StuccoHouse;
break;
case 2: contractorList[i] ■ new VinylSidedHouse;
break;
}
// покрасить дома с помощью метода Paint, поскольку он виртуальный,
// используется динамическое связывание и вызывается правильный метод
for (i-0; i<5; i++)
contractorList[i]->Paint();
}
/*
<Прогон программы 12.7>
Покрасить деревянный дом
Покрасить оштукатуренный дом
Покрасить пластиковый дом
Покрасить оштукатуренный дом
Покрасить деревянный дом
*/
Разнородные связанные списки
Как и в разнородных массивах, каждый объект в разнородном списке
образован от общего для всех базового класса. Каждая базовая составляющая
объекта содержит указатель на следующий объект в списке. Благодаря
полиморфизму указатель используется для выполнения методов производного
объекта, невзирая на его тип.
Проиллюстрируем эти понятия на связанном списке геометрических
объектов, образованных от варианта класса Shape.
Спецификация класса NodeShape
ОБЪЯВЛЕНИЕ
#inclucie "graphlib.h"
class NodeShape
{
protected:
// координаты базовой точки, образец заполнения
//и указатель на следующий узел
float х, у;
int fillpat;
NodeShape *next;
public:
// конструктор
NodeShape(float h=0, float v=0, int fill=0);
// виртуальная функция рисования
virtual void Draw(void) const;
// методы обработки списков
void InsertAfter(NodeShape *p);
NodeShape *DeleteAfter(void);
NodeShape *Next(void);
>;
ОПИСАНИЕ
Координаты (х,у) задают базовую точку для производного объекта,
который должен быть нарисован и заштрихован по образцу fillpat. Метод Draw
инициализирует образец заполнения в графической системе и указатель next,
указывающий на следующий объект типа NodeShape в связанном списке.
Методы InsertAfter и DeleteAfter поддерживают кольцевой список
посредством включения или удаления узла, следующего за текущим. Метод Next
возвращает указатель на следующий узел.
Класс NodeShape находится в файле shapelst.h.
Реализация класса NodeShape
Реализация класса NodeShape сделана по образцу класса CNode (см. гл.
9). Так как предполагается кольцевой список, конструктор должен создать
начальный узел, который указывает на самого себя.
х, У
fillpat
next
// конструктор, задает начальные значения базовой точки,
// образца заполнения и указателя next
NodeShape::NodeShape(float h, float v, int fill):
x(h), y(v), fillpat(fill)
{
next = this;
}
Образование связанных геометрических классов. Геометрические, классы
CircleFigure и RectangleFigure являются производными от класса NodeShape.
В дополнение к методам базового класса они содержат метод Draw,
перекрывающий виртуальный метод Draw базового класса. Методы Area и Perimeter
не включаются. Мы используем класс CircleFigure для иллюстрации понятий.
// Класс CircleFigure, образованный от класса NodeShape
class CircleFigure: public NodeShape
{
protected:
// радиус окружности
float radius;
public:
// конструктор
CircleFigure(float h, float v, float r, int fill);
// виртуальная функция рисования окружности
virtual void Draw(void) const;
};
// конструктор, инициализирует базовый класс и радиус
CircleFigure::CircleFigure(float h, float v, float r, int fill):
NodeShape(h, v, fill), radius(r)
{}
// задать образец заполнения посредством вызова базового метода Draw
//и нарисовать окружность
void CircleFigure::Draw(void) const
{
NodeShape::Draw();
DrawCircle(x, y, radius);
}
Мы также включили в файл shapelst.h новый геометрический класс Right-
Triangle, который описывает прямоугольный треугольник с помощью
координат самой левой точки его гипотенузы, базы и высоты.
высота
база
Чтобы сформировать связанный список, объявим заголовок, имеющий тип
NodeShape и имя listHeader. Начиная с этого заголовка, будем динамически
создавать узлы и с помощью InsertAfter включать их в список
последовательно друг за другом. Например, следующая итерация создает четырехэле-
ментный список, в котором чередуются объекты-окружности и
объекты-треугольники:
listHeader
next
Объект
Shape
—►
next
Объект
Circle
—►
next
Объект
RightTriangle
—►
next
Объект
Circle
—►
next
Объект
RightTriangle
// заголовок списка и указатель для создания нового списка
NodeShape listHeader, *р;
float x, у, radius, height;
// установить р на начало списка
р = slistHeader;
// включить 4 узла в список
for (int i-0; i<4; i++)
{
// координаты базовой точки
cout « "Введите х и у: ";
cin » х » у;
if (i % 2 « 0) // если i четное, добавить окружность
{
cout « "Введите радиус окружности: ";
cin » radius;
// включить объект с заполнением i в список
p->InsertAfter(new Circle(х,у,radius,i));
}
else // если i нечетное, добавить прямоугольный треугольник
{
cout « "Введите базу и высоту для прямоугольного треугольника: ";
cin » base » height;
p->InsertAfter(new RightTriangle(x,y,radius,i));
}
// передвинуть р на только что созданный узел
р - p->Next();
}
Динамическое связывание имеет принципиальное значение во время
прохождения списка и визуального отображения содержащихся в нем объектов.
В приведенном ниже фрагменте кода указатель р указывает либо на объект
типа Circle, либо на объект типа RightTriangle. Поскольку Draw является
виртуальной функцией, выполняется метод Draw того или иного производного
класса.
р = listHeader.Next();
while (p != slistHeader)
{
p->Draw();
p - p->Next();
}
Теперь мы готовы поставить задачу создания и управления разнородными
списками целиком.
Программа 12.8. Разнородные списки
Эта программа создает связанный список, состоящий из объектов типа
Circle, Rectangle и RightTriangle. Файл figures содержит элементы этого
списка в следующем формате:
<фигура> <координаты базовой точки> <параметры фигуры>
Фигура описывается буквой с (окружность), г (прямоугольник) или t
(прямоугольный треугольник). Координатами базовой точки является пара
чисел с плавающей точкой. Параметрами являются окружность или
стороны. Ниже приводится пример входных записей.
с 0.5 0.5 0.25 // окружность с центром (1/2, 1/2) и радиусом 1/4
г 1.0 0.25 .5 .5 // прямоугольник с базовой точкой (1, 1/4)
// и сторонами 1/2, 1/2
t 2.0 0.75 .25 .5 // прямоугольный треугольник с базовой точкой (2, 3/4)
// и сторонами 1/4, 1/2
Программа читает файл и формирует связанный список геометрических
объектов. В процессе прохождения списка фигуры отображаются
визуально.
#include <iostream.h>
#include <fstream.h>
#include <stdlib.h>
#include "graphlib.h"
#include "shapelst.h"
void main(void)
{
// listHeader — заголовок кольцевого списка форм
NodeShape listHeader, *p, *nFig;
// фигуры: с (окружность), г (прямоугольник), t (прямоугольный треугольник)
char figType;
// начальный образец заполнения — нет заполнения
int pat = 0;
float x, у, radius, length, width, tb, th;
// входной поток fin
ifstream fin;
// открыть файл figures, содержащий описания фигур
fin.open("figures", ios::in | ios::nocreate);
if (!fin)
{
cerr « "Нельзя открыть файл figures" « endl;
exit(1);
}
// установить р на начало списка
p = slistHeader;
// прочитать файл до конца и построить связанный список фигур
while (!fin.eof())
{
// ввести тип фигуры и координаты базовой точки
fin » figType;
if (fin.eofO)
break;
fin » x » y;
// построить конкретную фигуру
switch(figType)
{
case 'c':
// ввести радиус и включить окружность в список
fin » radius;
nFig = new CircleFigure(x,у,radius,pat);
p->InsertAfter(nFig);
break;
case 'r':
// ввести длину и ширину и включить прямоугольник в список
fin » length » width;
nFig ■ new RectangleFigure(x,у,length,width,pat);
p->InsertAfter(nFig);
break;
case 't' :
// ввести базу и высоту и включить прямоугольный треугольник
fin » tb » th;
nFig = new RightTriangleFigure(x,у,tb,th,pat);
p->InsertAfter(nFig);
break;
)
// сменить образец заполнения, продвинуть указатель
pat « (pat+1) % 12;
р - p->Next();
}
// инициализировать графическую систему
InitGraphics();
// начиная с 1-й фигуры, пройти по списку и нарисовать каждую фигуру
р - listHeader.Next();
while (p Iя* &listHeader)
{
p->Draw();
р = p->Next();
}
// организовать паузу для просмотра фигур и закрыть графическую систему
ViewPause();
ShutdownGraphics() ;
}
/*
<Прогон программы 12.8>
<см. график>
*/
Письменные упражнения
12.1
а) По образцу зоологической иерархии из раздела 12.1 постройте
иерархическое дерево для следующих понятий:
Транспортное средство, автомобиль, дизель, газ, самолет,
электромобиль, турбовинтовой, реактивный.
б) Задайте базовые классы для классов "Электромобиль" и "Реактивный".
в) Перечислите все классы, являющиеся одновременно и базовыми, и
производными.
г) Какие классы образованы от класса "Транспортное средство"?
12.2 Пусть даны следующие объявления
class BASE
{
private:
Base_Priv;
protected:
Base_Prot;
public:
Base_Pub
};
class DERIVED: public BASE
{
private:
Derived_Priv;
protected:
Derived_Prot;
public:
Derived_Pub
};
а) Представленные базовый и производный класс содержат закрытые,
защищенные и открытые члены. Заполните приведенную ниже таблицу,
показав тем самым права доступа клиента или объекта к этим членам.
Крестик в строке говорит о том, что объект имеет доступ к члену
класса. Например, представитель производного класса имеет доступ к
защищенным членам базового класса, а клиент может обращаться к
открытым членам базового класса.
BASE
DERIVED
КЛИЕНТ
Base_Priv
Base_Prot
X
Base_Pub
X
Derived_Priv
Derived _Prot
Derived_Pub
б) Класс может быть образован с использованием закрытого наследования.
В этом случае открытые и защищенные члены базового класса являются
доступными для производного класса. Однако для клиента производного
класса (программы, использующей данный производный класс)
открытые члены базового класса считаются закрытыми и недоступны. Этот
тип наследование иногда применяется, когда базовый класс служит
просто связующим звеном для производных классов. Заполните таблицу
для этого типа наследования.
BASE
DERIVED
КЛИЕНТ
Base_Priv
Base_Prot
Base_Pub
Derived _Priv
Derived_Prot
Derived _ Pub
12.3 Дана схема класса Base. Укажите ошибки в объявлениях производных
классов.
class Base
<
public:
Base (int a, int b);
■ • •
};
а) class DerivedCLl: public Base
{
private:
int q;
public:
DerivedCLl (int z): q(z);
{}
• • •
};
б) class DerivedCL2: public Base
{
private:
• • • r
public:
// DerivedCL2 не имеет конструктора
• • •
};
12.4 Даны следующие схемы базового и производного классов:
class BaseCL
{
protected:
int datal;
int data2;
public:
BaseCL(int a, int b=0): datal (a), data2(b)
{}
BaseCL(void): datal(0), data2(0)
{}
• • •
};
class DerivedCL
{
private:
int data3;
public:
// Конструктор #1
DerivedCL(int a, int b, int c=0)/
// Конструктор #2
DerivedCL(int a);
• * •
};
а) Напишите конструктор #1 таким образом, чтобы а предназначалось
производному классу, а Ъ и с — базовому.
б) Напишите конструктор #2 таким образом, чтобы а предназначалось
производному классу и при этом использовался конструктор базового
класса, действующий по умолчанию.
в) Подразумевая определение конструктора класса DerivedCL, покажите
значения datal, data2 и data3 в следующих объектах:
DerivedCL obj1(1,2), obj2(3,4/5), obj3(8);
12.5 Следующая программа иллюстрирует порядок выполнения
конструкторов и деструкторов в цепочке наследования. У каждого из трех классов
Basel, Base2 и Derived есть конструктор и деструктор. Покажите, что
выдаст эта программа на выходе.
tinclude <iostream.h>
class Basel
{
public:
Basel(void)
{
cout « "Вызван конструктор Basel." « endl;
}
-Basel(void)
{
cout « "Вызван деструктор Basel." « endl;
}
};
class Base2
{
public:
Base2(void)
{
cout « "Вызван конструктор Base2." « endl;
}
~Base2(void)
{
cout « "Вызван деструктор Base2." « endl;
}
};
class Derived: public Basel, public Base2
{
public:
Derived(void): Basel(), Base2()
{
cout << "Вызван конструктор Derived." « endl;
}
-Derived(void)
{
cout « "Вызван деструктор Derived." « endl;
}
};
void main(void)
{
Derived objD;
{
Basel objBl;
{
Base2 objB2;
}
}
}
12.6 Дана следующая цепочка наследования:
class Base
{
• • •
public:
void F(void);
void G(int x);
• • •
};
class Derived: public Base
{
• • *
public:
void F(void);
void G(float x);
• • •
};
void Derived::G(float x)
{
• • •
Base::G(10); // использование оператора спецификации области действия
• • •
>;
Рассмотрим объявление
Derived OBJ;
а) Как клиент обращается к функции F базового класса?
б) Как клиент обращается к функции F производного класса?
в) Как компилятор будет реагировать на оператор OBJ.G(20)?
Замечание: Как было показано в разделе 12.5, нежелательно
перекрывать невиртуальные функции базового класса.
12.7 В разделе 12.2 была построена цепочка наследования, состоящая из
абстрактного базового класса Shape и класса Circle. Приведенная ниже
программа использует эти классы. Прочитайте программу и ответьте
на вопросы, приведенные далее.
#include <iostreara.h>
#include "graphlib.h"
#include "geometry.h"
void main(void)
{
Circle C;
C.SetPoint(l,2);
C.SetRadius(0.5);
cout « C.GetXO « " " « C.GetYO « endl;
C.SetPoint(C.GetX{), 3) ;
cout « C.GetXO « " " « C.GetYO « endl;
C.SetFill(ll);
InitGraphics О;
С.Draw();
ViewPause ();
ShutdownGraphics() ;
}
а) Почему функцию GetX можно вызывать из производного класса?
б) Почему к х можно обращаться из метода Draw?
в) Что будет на выходе этой программы?
г) Почему оператор
C.SetPoint(3,5);
является допустимым, а операторы
С.х = 3;
Су « 5;
нет?
12.8 Что будет на выходе этой программы?
#include <iostream.h>
#include <string.h>
class Base
{
private:
char msg[30];
protected:
int n/
public:
Base (char s[], int m=0) : n(m)
{
strcopy(msg, s);
}
void output(void)
{
cout « n « endl « msg « endl;
}
};
class Derivedl: public Base
{
private:
int n;
public:
Derivedl(int m«l): Base ("Base", m-1), n(m)
{}
void output(void)
{
cout « n « endl;
Base::output();
}
};
class Derived2: public Derivedl
{
private:
int n;
public:
Derived2(int m=2): Derivedl (m-1), n(m)
{}
void output(void)
{
cout « n « endl;
Derivedl::output();
}
);
void main(void)
{
Base B("Base Class", 1);
Derived2 D;
В.output();
D.output ();
}
12,9 Почему методы Area и Perimeter класса Shape являются чистыми
виртуальными функциями?
12.10 Даны следующие объявления классов:
class Base
{
private:
int x,y;
* • •
};
class Derived: public Base
{
private:
int z;
• * •
);
Рассмотрим объявления
Base В;
Derived D;
а) Допустимо ли присвоение
В = D;
Почему? Проиллюстрируйте свой ответ картинкой.
б) Допустимо ли присвоение
D = В;
Почему? Проиллюстрируйте свой ответ картинкой.
12.11 Даны следующие классы:
class BaseCL
{
protected:
int one/
public:
BaseCL(int a): one(a)
{}
virtual void Identify(void)
{
cout << one « endl;
}
);
class DerivedCL: public BaseCL
{
protected:
int two;
public:
DerivedCL(int a, int b) : BaseCL(a), two(b)
{}
virtual void Identify(void)
{
cout « one « " " « two « endl;
}
};
и функции:
void Announce1(BaseCL x)
x.Identify();
void Announce2(BaseCL& x)
x.Identify();
void АппоипсеЗ(BaseCL *x)
x->Identify();
Покажите, что будет на выходе следующего фрагмента кода:
BaseCL A<7), *р, *arr[3];
DerivedCL В(3,5), С(2,4);
Announce1(А);
Announce1(С);
Announce2(В);
АппоипсеЗ(&С);
р = &С;
p->Identify();
for (int i=0; i<3; i++)
if (i—1)
arr[i] = new BaseCL(7);
else
arr[i] * new DerivedCL(i, i+1);
for (i=0; i<3; i++)
arr[i]->Identify();
12.12 Объясните, почему деструктор должен объявляться виртуальным в
любом классе, который может служить базовым.
12.13 Разработайте абстрактный базовый класс StackBase, в котором
объявляются стековые операции Push, Pop, Peek и StackEmpty. Базовый
класс должен содержать защищенную целочисленную переменную nu-
mElements и метод StackEmpty, возвращающий значение этой
переменной. Производный класс Stack должен увеличивать numElements
с каждой операцией Push и уменьшать ее с каждой операцией Pop.
Реализуйте производный класс Stack двумя разными способами: с
помощью массива и с помощью связанного списка.
12.14 Выполните предыдущее упражнение для абстрактного класса Queue-
Base, описывающего очередь. Этот класс должен содержать как
минимум один метод, не являющийся чистой виртуальной функцией.
12.15 Что такое итератор? Почему итератор часто должен быть
дружественным по отношению к классу, элементы которого он обрабатывает?
Как понимать то, что итератор является абстракцией управления?
12.16 Разработайте класс Queue, образуя его от абстрактного класса Queue-
Base (см. упр. 12.14) и используя объект типа SeqList. Образуйте из
класса SeqListlterator класс Queuelterator и сделайте его
дружественным по отношению к QueueBase. Для этого нужен лишь конструктор.
12.17 Напишите функцию
template <class T>
Т GetRear(Queue<T>& q);
которая возвращает последний в очереди элемент. Если очередь пуста,
выдайте сообщение об ошибке и завершите программу. Используйте
Queuelterator, разработанный в предыдущем упражнении.
12.18 Пусть имеется массив символьных строк. С помощью Arraylterator
просканируйте массив и замените все символы табуляции четырьмя
пробелами.
12.19 Напишите функцию
void RemoveDuplicates(Array<int>& A);
которая удаляет из массива все дубликаты данных и соответствующим
образом изменяет размер объекта. Например, если исходный массив
А имеет 20 элементов
А - {1, 3, 5, 3, 2, 3, 1, 4, 6, 3, 5, 4, 2, 6, 7, 8, 1, 3, 9, 7},
то после вызова RemoveDuplicates
А « {1, 3, 5, 2, 4, 6, 7, 8, 9} (A.ListSizeO = 9)
12.20 Напишите функцию
template <class T>
Т Max(Iterator<T>& colllter);
которая ищет максимальное значение среди данных в той коллекции,
для которой существует итератор colllter. Предполагается, что оператор
">" определен для типа Т. Заметьте, что эта функция использует тот
факт, что методы итератора являются виртуальными.
12.21 Покажите, как можно использовать виртуальные функции для
формирования массива указателей на объекты Circle и Rectangle
(разнородный массив), а также для прохождения массива и распечатки
площади и периметра фигур.
Упражнения по программированию
12.1 Реализуйте цепочку наследования из письменного упражнения 12.1.
Каждый конструктор класса должен содержать метод Identify,
распечатывающий информацию о своем базовом классе и о себе самом.
Напишите тестовую программу, в которой объявляются объекты
каждого типа.
12.2 Из прямоугольных поверхностей можно построить короб.
длина
высота
ширина
ширина
длина
Напишите классы Rectangle и Box, которые реализуют эту иерархию.
Класс Rectangle имеет методы для вычисления площади и объема,
причем в последнем случае всегда возвращается нулевой объем. Класс
Box также имеет методы для вычисления площади и объема.
Испытайте эти классы в главной процедуре, которая запрашивает тип
фигуры и ее размеры. Определите объект каждого типа и распечатайте
площадь и объем фигуры.
12.3 Из класса SeqList образуйте производный класс MidList с помощью
следующего объявления:
template <class T>
class MidList: public SeqList<T>
{
public:
<Конструктор>
virtual void Insert(const T& elt);
virtual void Delete(const T& elt);
};
Метод Insert включает elt в середину списка. Метод Delete удаляет
элемент из середины списка. При этом подразумевается, что
пользователь сам контролирует размер списка и гарантирует, что хотя бы один
элемент там есть. Реализуйте класс Midlist и используйте его в
следующей тестовой программе:
Ввести пять целых чисел и включить их в список с помощью Insert.
Распечатать список.
Удалить два числа из списка. Еще раз распечатать список и его размер.
12.4 В этом упражнении требуется разработать иерархическую структуру
для задачи обработки данных. Класс Employee содержит элементы
данных name (имя) и ssn (номер страховки), конструктор и операцию
PrintEmployeelnfo, которая распечатывает поля name и ssn. Эти данные
связаны с информацией о служащих с постоянными окладами.
Производный класс SalaryEmployee содержит поле salary (месячный оклад)
и операцию PrintEmployeelnfo, которая распечатывает данные как из
базового, так и из производного класса. В дополнение к информации,
имеющейся в базовом классе Employee, данные по временным
сотрудникам включают в себя почасовую ставку и количество отработанных
в данном месяце часов. Эта информация хранится в классе TempEm-
ployee, который состоит из элементов hourlypay и hours worked и
операции PrintEmployeelnfo.
Реализуйте эту иерархию и поместите в файл employee.h. Напишите
главную процедуру, в которой объявляются объекты для окладников
и почасовиков и для каждого объекта вызывается PrintEmployeelnfo.
Класс Employee
name
ssn
Данные
Операции
Employee
Класс SalaryEmployee I PrintEmployeelnfo
Класс TempEmployee
Данные
salary
Операции
SalaryEmployee
PrintEmployeelnfo
Данные
hourlypay
hoursworked
Операции
TempEmployee
PrintEmployeelnfo
12.5 Создайте новую реализацию класса Array как класса, образованного от
класса List. При этом вы должны столкнуться с важной проблемой
структурирования. Базовый класс List содержит ряд чистых
виртуальных методов, которые обязаны перекрываться в производном классе
Array. Некоторые из них, возможно, не имеют смысла для производного
класса. Следующая таблица показывает проблемные методы и поможет
вам при повторном определении.
ListSize
Возвращает число элементов объекта Array
ListEmpty
Возвращает False, поскольку предполагается, что массив никогда не пуст
ClearList
Ошибка! Операция не имеет смысла для массивов
Find
Выполняет последовательный поиск элемента данных
Insert
Ошибка! Массив есть структура прямого доступа.
Операция вставки неопределена для массивов.
Delete
Ошибка! Операция удаления элемента неопределена для массивов.
Проверьте свою реализацию, запустив программу 12.5.
12.6 Используйте любую реализацию класса Stack, разработанную в
письменном упражнении 12.13, для чтения символьной строки и
распознавания палиндрома.
12.7 В этом упражнении используются классы Queue и Queuelterator,
разработанные в письменных упражнениях 12.14 и 12.16. В тестовой
программе вводите список целых чисел, пока не встретите 0. Попутно
вставляйте положительные числа в одну очередь, а отрицательные —
в другую. Используйте объекты Queuelterator для сканирования и
распечатки обеих очередей.
12.8 Напишите программу для тестирования функции GetRear,
разработанной в письменном упражнении 12.17.
12.9 В главной программе введите несколько строк из файла и каждую из
них запишите в массив символьных строк. Используйте Array Iterator
для сканирования массива, в ходе которого все символы табуляции
заменяются четырьмя пробелами. Распечатайте модифицированные
строки. Обратите внимание, что в этом упражнении используется
результат письменного упражнения 12.18.
12.10 Проверьте функцию RemoveDuplicates, реализованную вами в
письменном упражнении 12.19, на следующей главной программе.
void main(void)
{
Array<int> A(20);
int data[] = {1, 3, 5, 3, 2, 3, 1, 4, 6, 3, 5, 4, 2, 6, 7, 8, 1, 3, 9, 7);
for (int i=0; i<20; i++)
A[i] = data[i];
RemoveDuplicates(A);
for (i=0; i<A.ListSize(); i++)
cout « A[i] « " ";
cout « endl;
}
/*
<Прогон программы>
135246789
*/
12.11 Определите объект Array<int>, содержащий целые числа 1..10, и
объект SeqList<char>, содержащий буквы 'а\.'е\ С помощью функции
Мах из письменного упражнения 12.20 распечатайте максимальное
значение для каждого из списков.
12.12 Добавьте методы Area и Perimeter в классы NodeShape, CircleFigure,
RectangleFigure и RightTriangleFigure (см. раздел 12.7). В базовом
классе NodeShape определите методы для возврата нуля. По образцу
программы 12.8 разработайте программу, которая создает разнородный
список производных объектов. Программа должна проходить по этому
списку и распечатывать площадь и периметр каждой фигуры. На
втором проходе должны быть нарисованы сами фигуры.
глава
13
Более сложные нелинейные
структуры
13.1. Бинарные деревья,
представляемые массивами
13.2. Пирамиды
13.3. Реализация класса Heap
13.4. Приоритетные очереди
13.5. AVL-деревья
13.6. Класс AVLTree
13.7. Итераторы деревьев
13.8. Графы
13.9. Класс Graph
Письменные упражнения
Упражнения по программированию
В этой главе мы продолжим изучение бинарных деревьев и познакомимся
с новыми нелинейными структурами. В гл. 11 деревья представлялись в виде
динамически порождаемых узлов. В настоящей же главе описываются деревья,
которые моделируют массивы в виде законченных бинарных деревьев. Они
используются в приложениях, связанных с пирамидальными структурами и
турнирной сортировкой. Мы подробно остановимся на пирамидах и рассмотрим
их применение в пирамидальной сортировке и очередях приоритетов.
Деревья бинарного поиска реализуют списки и обеспечивают среднее время
поиска порядка 0(log2n). Однако на несбалансированных деревьях
эффективность поисковых алгоритмов снижается. Мы рассмотрим новый тип деревьев,
называемых сбалансированными или AVL-деревьями1, в которых
поддерживаются хорошие поисковые характеристики бинарного дерева.
В гл. 12 были представлены итераторы, с помощью которых реализованы
классы SeqListlterator и Arraylterator. В данной главе концепция итераторов
распространяется на деревья и графы. Это мощное средство сканирования
позволяет осуществлять прохождение нелинейных структур с помощью простых
методов, применяемых обычно к линейным спискам. Здесь мы разрабатываем
симметричный итератор дерева, который расширяет возможности деревьев.
Это используется для реализации алгоритма сортировки с помощью дерева.
Обобщением иерархической структуры является граф, который состоит из
вершин и ребер, соединяющих вершины. Графы — важный раздел дискретной
математики. Они играют основную роль в целом ряде классических
алгоритмов, широко применяющихся в исследовании операций. Эта глава завершается
изложением основ теории графов и разработкой класса Graph, который будет
использоваться во многих приложениях.
13.1. Бинарные деревья, представляемые
массивами
В гл. 11 для построения бинарных деревьев мы используем узлы дерева.
Каждый узел имеет поле данных и поля указателей на правое и левое
поддеревья данного узла. Пустое дерево представляется нулевым указателем.
Вставки и удаления производятся путем динамического размещения узлов и
присвоения значений полям указателей. Это представление используется для
целой группы деревьев от вырожденных до законченных. В данном разделе
вводится последовательное представление деревьев с помощью массивов. При
этом данные хранятся в элементах массива, а узлы указываются индексами.
Мы выявим очень близкое родство между массивом и законченным бинарным
деревом — взаимосвязь, используемую в пирамидах и очередях приоритетов.
Вспомним из гл. 11, что законченное бинарное дерево глубины п содержит
все возможные узлы на уровнях до п-1, а узлы уровня п располагаются слева
направо подряд (без дыр). Массив А есть последовательный список, элементы
которого могут представлять узлы законченного бинарного дерева с корнем
А[0]; потомками первого уровня А[1] и А[2]; потомками второго уровня А[3],
А[4], А[5] и А[6] и т.д. Корневой узел имеет индекс 0, а всем остальным узлам
индексы назначаются в порядке, определяемом поперечным (уровень за
уровнем) методом прохождения. На рис. 13.1 показано законченное бинарное
дерево для массива А из десяти элементов.
int А[10] * {5, 1, 3, 9, 6, 2, 4, 7, О, 8}
1 По фамилиям их изобретателей — Г. М. Адельсона-Вельского и Е. М. Ландиса [1]. — Прим. перев.
Рис 13.1. Законченное бинарное дерево для 10-элементного массива А
Бинарные деревья
Эквивалентное представление в виде массива
Несмотря на то, что массивы обеспечивают естественное представление
деревьев, возникает проблема, связанная с отсутствующими узлами, которым
должны соответствовать неиспользуемые элементы массива. В следующем
примере массив имеет четыре неиспользуемых элемента, т.е. треть занимаемого
деревом пространства. Вырожденное дерево, имеющее только правые
поддеревья, дает в этом смысле еще худший результат.
Преимущества представляемых массивами деревьев обнаруживаются тогда,
когда требуется прямой доступ к узлам. Индексы, идентифицирующие сыновей
и родителя данного узла, вычисляются просто. В таблице 13.1 представлено
дерево, изображенное на рис. 13.1. Здесь для каждого уровня указаны узлы,
а также их родители и сыновья.
Для каждого узла A[i] в N-элементном массиве индекс его сыновей
вычисляется по формулам:
Индекс левого сына = 2*i (неопределен при 2*i + 1 > N)
Индекс правого сына = 2*i + 2 (неопределен при 2*i + 2 > N)
Таблица 13.1
| Уровень
0
1
2
3
Родитель
0
1
2
3
4
5
б
7
8
9
Значение
А[0] = 5
А[1] = 1
А[2] = 3
А[3] = 9
А[4] = 6
А[5] = 2
А[б] = 4
А[7] = 7
А[8] = 0
А[9] = 8
Левый сын
1
2
5
7
9
11=NULL
13=NULL
-
-
-
Правый сын |
2
4
6
8
1CNNULL
12=NULL
14=NULL
-
-
-
Поднимаясь от сыновей к родителю, мы замечаем, что родителем узлов
А[3] и А[4] является А[1], родителем А[5] и А[6] — А[2] и т.д. Общая
формула для вычисления родителя узла A[i] следующая:
Индекс родителя = (i-l)/2 (неопределен при i=0)
Пример 13.1
Во время прохождения последовательно представленного дерева
можно идти вниз к сыновьям или вверх к родителю. Ниже приводятся
примеры путей для следующего дерева:
1. Начиная с корня, выбрать путь, проходящий через меньших
сыновей.
Путь: А[0] = 7, А[2] = 9, А[6] - 3
2. Начиная с корня, выбрать путь, проходящий через левых сыновей.
Путь: А[0] = 7, А[1] - 10, А[3] = 12, А[7] - 3
3. Начиная с А[10], выбрать путь, проходящий через родителей.
Путь: А[10] = 2, А[4] = 2, А[1] = 10, А[0] - 7
Приложение: турнирная сортировка
Бинарные деревья находят важное применение в качестве деревьев
принятия решения, в которых каждый узел представляет ситуацию, имеющую
два возможных исхода. В частности, для представления спортивного турнира,
проводимого по схеме с выбываниями. Каждый не листовой узел соответствует
победителю встречи между двумя игроками. Листовые узлы дают стартовый
состав участников и распределение их по парам. Например, победителем
теннисного турнира является Дэвид, выигравший финальную встречу с
Доном. Оба спортсмена вышли в финал, выиграв предварительные матчи.
Дон победил Алана, а Дэвид — Мэнни. Все игры турнира и их результаты
могут быть записаны в виде дерева.
Дон
Алан
Мэнни
Дэвид
Дон
Дэвид
Дэвид
Победитель
Победитель
Дэвид
Дон
Дэвид
Дон
Алан
Мэнни
Дэвид
В турнире с выбываниями победитель определяется очень скоро.
Например, для четырех игроков понадобится всего три матча, а для 24 = 16
участников — 24 - 1 = 15 встреч.
Турнир выявляет победителя, но со вторым лучшим игроком пока не все
ясно. Поскольку Дон проиграл финал победителю турнира, он может и не
оказаться вторым лучшим игроком. Нам нужно дать шанс Мэнни, так как тот
играл матч первого круга с, быть может, единственным игроком, способным
его победить. Чтобы выявить второго лучшего игрока, нужно исключить
Дэвида и реорганизовать турнирное дерево, устроив матч между Доном и Мэнни.
Второй
Мэнни
Третий
Дон
Мэнни
Четвертый
Дон
Алан
Мэнни
Как только определится победитель этого матча, мы сможем правильно
распределить места.
Выиграл Мэнни: Места Дэвид Мэнни Дон Алан
Выиграл Дон: Места Дэвид Дон Мэнни Алан
Турнирное дерево может использоваться для сортировки списка из N
элементов. Рассмотрим эффективный алгоритм, использующий дерево,
представленное в виде массива. Пусть имеется последовательно представленное дерево,
содержащее N элементов — листовых узлов в нижнем ряду. Эти элементы
запоминаются на уровне к, где 2к > N. Предположим, что список сортируется
по возрастанию. Мы сравниваем каждую пару элементов и запоминаем
меньший из них (победителя) в родительском узле. Процесс продолжается до тех
пор, пока наименьший элемент (победитель турнира) не окажется в корневом
узле. Например, приведенное ниже дерево задает следующее начальное
состояние массива из N = 8 целых чисел. Элементы запоминаются на уровне
3, где 23 = 8.
А[8] = {35, 25, 50, 20, 15, 45, 10, 40}
Исходное Tree
Тгее[7] Тгее[8] Тгее[9] Тгее[10] Тгее[11] Тгее[12] Тгее[13] Тгее[14]
Со второго уровня начинаются "игры" — в родительские узлы помещаются
наименьшие значения в парах. Например, "игру" между элементами Тгее[7]
и Тгее[8] выигрывает меньший из них, и значение 25 записывается в Тгее[3].
Подобные сравнения проводятся также на втором и первом уровнях. В
результате последнего сравнения наименьший элемент попадает в корень дерева
на урозне 0.
Начальные сравнения
Тгее[7] Тгее[8] Тгее[9] Тгее[10] Тгее[11] Тгее[12] Тгее[13] Тгее[14]
Как только наименьший элемент оказывается в корневом узле, он
удаляется со своего старого места на дереве и копируется в массив. В первый раз
в А[0] записывается 10, а затем дерево обновляется для поиска следующего
наименьшего элемента. В турнирной модели некоторые матчи должны быть
сыграны повторно. Поскольку число 10 изначально было в А[13],
проигравший в первом круге А[14] = 40 должен снова участвовать в турнире. А[14]
копируется в свой родительский узел А[6], а затем снова проводятся матчи
в индексе 6 (15 побеждает 40) и в индексе 2 (15 побеждает 20). В результате
15 попадает в корень и становится вторым наименьшим элементом списка.
Корень копируется в А[1], и процесс продолжается.
Тгее[7] Тгее[8] Тгее[9] Тгее[10] Тгее[11] Тгее[12] Тгее[13] Тгее[14]
Процесс продолжается до тех пор, пока все листья не будут удалены. В
нашем примере последний (наибольший) узел играет серию матчей, в которых
побеждает всех по умолчанию. После копирования числа 50 в А[7] мы
получаем отсортированный список.
Тгее[7] Тгее[8] Тгее[9] Тгее[10] Тгее[11] Тгее[12] Тгее[13] Тгее[14]
10
15
20
25
35
40
45
50 ]
Вычислительная эффективность. Эффективность турнирной сортировки
составляет 0(n log2n). В массиве, содержащем n = 2k элементов, для выявления
наименьшего элемента требуется п-1 сравнений. Это становится ясным, когда
мы замечаем, что половина участников выбывает после каждого круга по мере
продвижения к корню. Общее число матчей равно
2k-i + 2k"2 + ... + 21 + 1 = n-1
Дерево обновляется, и оставшиеся п-1 элементов.обрабатываются
посредством к-1 сравнений вдоль пути, проходящего через родительские узлы. Общее
число сравнений равно
(п-1) + (к-1)*(п-1) = (п-1) + (n-l)*(log2n-l) = (п-1) log2n
Хотя количество сравнений в турнирной сортировке составляет 0(п log2n),
использование пустот значительно менее эффективно. Дереву требуется 2 * п-1
узлов, чтобы вместить к-1 кругов соревнования.
Алгоритм TournamentSort. Для реализации турнирной сортировки
определим класс DataNode и создадим представленное массивом дерево из объектов
этого типа. Членами класса являются элемент данных, его место в нижнем
ряду дерева и флажок, показывающий, участвует ли еще этот элемент в
турнире. Для сравнения узлов используется перегруженный оператор "<=".
template <class T>
class DataNode
{
public:
// элемент данных, индекс в массиве, логический флажок
Т data;
int index;
int active;
friend int operator <= (const DataNode<T> &x,
const DataNode<T> &y);
};
Сортировка реализуется с помощью функции TournamentSort и утилиты
UpdateTree, которая производит сравнения вдоль пути предков. Полный
листинг функций и переменных, обеспечивающих турнирную сортировку,
находится в файле toursort.h.
// сформировать последовательное дерево, скопировать туда элементы массива;
// отсортировать элементы и скопировать их обратно в массив
template <class T>
void TournamentSort (T a[], int n)
{
DataNode<T> *tree; // корень дерева
DataNode<T> item;
// минимальная степень двойки, большая или равная п
int bottomRowSize;
// число узлов в полном дереве, нижний ряд которого
// имеет bottomRowSize узлов
int treesize;
// начальный индекс нижнего ряда узлов
int loadindex;
int i, j;
// определить требуемый размер памяти для нижнего ряда узлов
bottomRowSize « PowerOfTwo(n);
// вычислить размер дерева и динамически создать его узлы
treesize - 2 * bottomRowSize - 1;
tree = new DataNode<T>[treesize];
// скопировать массив в дерево объектов типа DataNode
j - 0;
for (i=loadindex; i<treesize; i++)
{
item.index - i;
if (j < n)
{
item.active = 1;
item.data = a[j++];
)
else
item, active =
Octree [i] = item;
}
// выполнить начальные сравнения для определения наименьшего элемента
i = loadindex;
while (i > 0)
{
3 - i'
while (j < 2*i); // обработать пары соревнующихся
{
// проведение матча, сравнить tree[j] с его соперником tree[j+l]
// скопировать победителя в родительский узел
if (!tree[j+1].active || tree[j] < tree[j+l])
tree[(j-l)/2] = tree[j];
else
treet(j-l)/2] = tree[j+l];
j +* 2; // перейти к следующей паре
}
// обработать оставшиеся п-1 элементов, скопировать победителя
// из корня в массив, сделать победителя неактивным, обновить
// дерево, разрешив сопернику победителя снова войти в турнир
for (i=0; i<n-l; i++)
{
a[i] ~ tree[0].data;
tree[tree[0].index].active = 0;
UpdateTree(tree, tree[0].index);
}
// скопировать наибольшее значение в массив
a[n-l] = tree[0].data;
}
В функцию UpdateTree передается индекс i, указывающий исходное
положение наименьшего текущего элемента в нижнем ряду дерева.
Это—удаляемый узел (становится неактивным). Значению, которое "проиграло"
предварительный раунд последнему победителю (наименьшему значению),
разрешается снова войти в турнир.
// параметр i есть начальный индекс текущего наименьшего элемента
// в списке (победителя турнира)
template <class T>
void UpdateTree(DataNode<T> *tree, int i)
{
int j;
// определить соперника победителя, позволить ему продолжить
// турнир, копируя его в родительский узел,
if (i % 2 — 0)
tree [(i-l)/2] = tree[i-l]; // соперник - левый узел
else
tree [(i-l)/2] = tree[i+l]; // соперник — правый узел
// переиграть те матчи, в которых принимал участие
// только что исключенный из турнира игрок
i = (i-l)/2;
while (i > 0)
{
// соперником является правый или левый узел?
if (i % 2 ==* 0)
j - i-1;
else
j = i+1;
// проверить, является ли соперник активным
if (!tree[i].active I I !tree[j].active)
if (tree[i].active)
tree[(i-l)/2] =tree[i];
else
tree[(i-l)/2] - treefj];
// устроить соревнование.
// победителя скопировать в родительский узел
else
if <tree[i] < tree[j])
tree[(i-l)/2] = tree[i];
else
tree[(i-l)/2] =tree[j];
// перейти к следующему кругу соревнования (родительский уровень)
i = (i-l)/2;
}
// Турнир с новым соперником закончен.
// очередное наименьшее значение находится в корневом узле
}
13.2. Пирамиды
Представляемые массивами деревья находят применение в имеющих
большое значение приложениях с пирамидами (heaps), являющимися
законченными бинарными деревьями, имеющими упорядочение узлов по уровням. В
максимальной пирамиде (maximum heap) родительский узел больше или равен
каждому из своих сыновей. В минимальной пирамиде (minimum heap)
родительский узел меньше или равен каждому из своих сыновей. Эти ситуации
изображены на рис. 13.2. В максимальной пирамиде корень содержит
наибольший элемент, а в минимальной — наименьший. В этой книге рассматриваются
минимальные пирамиды.
Пирамида как список
Пирамида является списком, который хранит некоторый набор данных в
виде бинарного дерева. Пирамидальное упорядочение предполагает, что
каждый узел пирамиды содержит значение, которое меньше или равно значению
любого из его сыновей. При таком упорядочении корень содержит наименьшее
значение данных. Как абстрактная списковая структура пирамида допускает
добавление и удаление элементов. Процесс включения не подразумевает, что новый
элемент занимает конкретное место, а лишь требует, чтобы поддерживалось
пирамидальное упорядочение. Однако при удалении из списка выбрасывается
наименьший элемент (корень). Пирамида используется в тех приложениях, где
клиенту требуется прямой доступ к минимальному элементу. Как список
пирамида не имеет операции поиска и осуществляет прямой доступ к
минимальному элементу в режиме "только чтение". Все алгоритмы обработки пирамид
сами должны обновлять дерево и поддерживать пирамидальное упорядочение.
(С) Максимальная пирамида (9 узлов)
(D) Максимальная пирамида (4 узла)
Рис. 13.2. Максимальные и минимальные пирамиды
Пирамида является очень эффективной структурой управления списками,
которая пользуется преимуществами полного бинарного дерева. При каждой
операции включения или удаления пирамида восстанавливает свое
упорядочение посредством сканирования только коротких путей от корня вниз до
конца дерева. Важными приложениями пирамид являются очереди
приоритетов и сортировка элементов списка. Вместо того чтобы использовать более
медленные алгоритмы сортировки, можно включить элементы списка в
пирамиду и отсортировать их, постоянно удаляя корневой узел. Это дает
чрезвычайно быстрый алгоритм сортировки.
Обсудим внутреннюю организацию пирамиды в нашем классе Heap.
Алгоритмы включения и исключения элементов представляются в реализации
методов Insert и Delete. Пример 13.2 исследует пирамиды и иллюстрирует
некоторые операции над ними.
Пример 13.2
1. Создание пирамиды. Массив имеет соотвествующее представление в
виде дерева. В общем случае это дерево не является пирамидой.
Пирамида создается переупорядочением элементов массива.
Исходный список: 40 10 30
Пирамида: 10 40 30
2. Вставка элемента. Новый элемент добавляется в конец списка, а
затем дерево реорганизуется с целью восстановления пирамидальной
структуры. Например, для добавления в список числа 15
производятся следующие действия:
Записать 15 в А[3]
Переупорядочить дерево
3. Удаление элемента. Удаляется всегда корень дерева (А[0]).
Освободившееся место занимает последний элемент списка. Дерево
реорганизуется с целью восстановления пирамидальной структуры.
Например, для исключения числа 10 производятся следующие
действия:
Удалить 10 из А[10]
Переместить 40 из А[3]
Восстановить дерево
Класс Heap
Как и любой линейный или нелинейный список, класс пирамид имеет
операции включения и исключения элементов, а также операции, которые
возвращают информацию о состоянии объекта, например, размер списка.
Спецификация класса Heap
ОБЪЯВЛЕНИЕ
#include <iostream.h>
#include <stdlib.h>
template <class T>
class Heap
{
private:
// hlist указывает на массив, который может быть динамически создан
// конструктором (inArray == 0) или передан как параметр (inArray == 1)
Т *hlist;
int inArray;
// максимальный и текущий размеры пирамиды
int maxheapsize;
int heapsize; // определяет конец списка
// функция вывода сообщений об ошибке
void error(char errmsg[]);
// утилиты восстановления пирамидальной структуры
void FilterDown(int i);
void FilterUp(int i);
public:
// конструкторы и деструктор
Heap (int maxsize); // создать пустую пирамиду
Heap (T arr[], int n); // преобразовать arr в пирамиду
Heap (const Heap<T>& H); // конструктор копий
-Heap(void); // деструктор
// перегруженные операторы: "=м, "[]", "т*"
Неар<Т> operator= (const Heap<T>& rhs);
const T& operator[] (int i);
// методы обработки списков
int ListSize(void) const;
int ListEmpty(void) const;
int ListFull(void) const;
void Insert(const T& item);
T Delete(void);
void ClearList(void);
};
ОПИСАНИЕ
Первый конструктор принимает параметр size и использует его для
динамического выделения памяти под массив. В исходном состоянии пирамида
пуста, и новые элементы включаются в нее с помощью метода Insert.
Деструктор, конструктор копирования и оператор присваивания поддерживают
использование динамической памяти. Второй конструктор принимает в
качестве параметра массив и преобразует его в пирамиду. Таким образом,
клиент может навязать пирамидальную структуру любому существующему
массиву и воспользоваться свойствами пирамиды.
Перегруженный оператор индекса "[]" позволяет клиенту обращаться к
объекту типа пирамиды как к массиву. Поскольку этот оператор возвращает
ссылку на константу, доступ осуществляется лишь в режиме "только чтение".
Методы ListEmpty, ListSize и ListFull возвращают информацию о текущем
состоянии пирамиды.
Метод Delete всегда исключает из пирамиды первый (наименьший)
элемент. Метод Insert включает элемент в список и поддерживает пирамидальное
упорядочение.
ПРИМЕР
Heap<int> H(4); // 4-элементная пирамида целых чисел
int A[] = {15, 10, 40, 30); // 4-элементный массив
Heap<int> К(А, 4); // преобразовать массив А в пирамиду К
Н.Insert (85); // вставить 85 в пирамиду Н
Н.Insert(40); // вставить 40 в пирамиду Н
cout « Н.Delete (); // напечатать 40 — наименьший элемент в Н
// распечатать массив, представляющий пирамиду А
for (int i=0; i<4; i++)
cout « K[i] « " "; // напечатать 10 15 40 30
K[0] = 99; // недопустимый оператор
Программа 13.1. Иллюстрация класса Heap
Эта программа начинается с инициализации массива А, а затем
преобразует его в пирамиду.
А: 50, 20, 60, 65, 15, 25, 10, 30, 4, 45
Массив А
Пирамида А
Элементы исключаются из пирамиды и распечатываются до тех пор, пока
пирамида не опустеет. Поскольку пирамида реорганизуется после каждого
исключения, элементы распечатываются по возрастанию.
#include <iostream.h>
#include "heap.h"
// распечатать массив, состоящий из п элементов
template <class T>
void PrintList (T А[], int n)
{
for (int i=0; i<n; i++)
cout « A[i] « " ";
cout « endl;
}
void main(void)
{
// исходный массив
int A[10] = {50, 20, 60, 65, 15, 25, 10, 30, 4, 45}
cout « "Исходный массив:" « endl;
PrintList(A, 10);
// преобразование А в пирамиду
heap<int> H(A,10);
// распечатать новую версию массива А
cout << "Пирамида:" « endl;
PrintList(A, 10);
cout « "Удаление элементов из пирамиды:" « endl;
// непрерывно извлекать наименьшее значение
while {!H.ListEmpty())
cout « Н.Delete() « " ";
cout « endl;
}
/*
<Прогон программы 13.1>
Исходный массив:
50 20 60 65 15 25 10 30 4 45
Пирамида:
4 15 10 20 45 25 60 30 65 50
Удаление элементов из пирамиды:
4 10 15 20 25 30 45 50 60 65
*/
13.3. Реализация класса Heap
Здесь мы подробно обсудим операции вставки и удаления для пирамид,
а также методы FilterUp и FilterDown. Эти вспомогательные методы отвечают
за реорганизацию пирамиды при ее создании или изменении.
Операция включения элемента в пирамиду. Вначале элемент добавляется
в конец списка. Однако при этом может нарушиться условие пирамидаль-
ности. Если новый элемент имеет значение меньшее, чем у его родителя,
узлы меняются местами. Возможные ситуации представлены на следующем
рисунке.
Родитель
Родитель)
Новый
i элемент)
Брат
Новый
элемент
Новый элемент является левым сыном
меньшим, чем родительский узел
Новый элемент является правым сыном
меньшим, чем родительский узел
Этот обмен восстанавливает условие пирамидальности для данного
родительского узла, однако может нарушить условие пирамидальности для
высших уровней дерева. Теперь мы должны рассмотреть нового родителя как
сына и проверить условие пирамидальности для более старшего родителя.
Если новый элемент меньше, следует переместить его выше. Таким образом
новый элемент поднимается вверх по дереву вдоль пути, проходящего через
его предков. Рассмотрим следующий пример для 9-элементной пирамиды Н:
Н.Insert(8); // вставить элемент 8 в пирамиду
Вставить 8 в А[9]. Вставить новый элемент в конец пирамиды. Эта
позиция определяется индексом heapsize, хранящим текущее число элементов
в пирамиде.
Н[9]
Отправить значение 8 по пути предков. Сравнить 8 с родителем 20.
Поскольку сын меньше своего родителя, поменять их значения местами (А).
Продолжить движение по пути предков. Теперь элемент 8 меньше своего
родителя Н[1]=10 и поэтому меняется с ним местами. Процесс завершается, так
как следующий родитель удовлетворяет условию пирами дальности.
(А) (В)
Процесс включения элементов сканирует путь предков и завершается,
встретив "маленького" (меньше чем новый элемент) родителя или достигнув
корневого узла. Так как у корневого узла нет родителя, новое значение помещается
в корень.
Чтобы поместить узел в правильную позицию, операция вставки использует
метод Filter Up.
// утилита для восстановления пирамиды, начиная с индекса i,
// подниматься вверх по дереву, переходя от предка к предку.
// менять элементы местами, если сын меньше родителя
template <class T>
void Heap<T>::FilterUp (int i)
{
int currentpos, parentpos/
T target;
// currentpos — индекс текущей позиции на пути предков.
// target — вставляемое значение, для которого выбирается
// правильная позиция в пирамиде
currentpos = i;
parentpos = (i-l)/2;
target = hlist[i];
// подниматься к корню по пути родителей
while (currentpos != 0)
{
// если родитель <= target, то все в порядке,
if (hlist[parentpos] <= target)
break;
else
// поменять местами родителя с сыном и обновить индексы
// для проверки следующего родителя
{
// переместить данные из родительской позиции в текущую.
// назначить родительскую позицию текущей.
// проверить следующего родителя
hlist[currentpos] = hlist[parentpos];
currentpos = parentpos;
parentpos = (currentpos-1)/2;
}
}
// правильная позиция найдена, поместить туда target
hlist[currentpos] = target;
}
Открытый метод Insert проверяет сначала заполненность пирамиды, а
затем начинает операцию включения. После записи элемента в конец
пирамиды вызывается FilterUp для ее реорганизации.
// вставить в пирамиду новый элемент и восстановить ее структуру
template <class T>
void Heap<T>:-.Insert (const T& item)
{
// проверить, заполнена ли пирамида и выйти, если да
if (heapsize == maxheapsize)
error ("Пирамида заполнена");
// записать элемент в конец пирамиды и увеличить heapsize.
// вызвать FilterUp для восстановления пирамидального упорядочения
hlist[heapsize] = item;
FilterUp(heapsize);
heapsize++;
}
Удаление из пирамиды. Данные удаляются всегда из корня дерева. После
такого удаления корень остается ничем не занятым и сначала заполняется
последним элементом пирамиды. Однако такая замена может нарушить
условие пирами дальности. Поэтому требуется пробежать по всем меньшим
потомкам и найти подходящее место для только что помещенного в корень
элемента. Если он больше любого своего сына, мы должны поменять местами
этот элемент с его наименьшим сыном. Движение по пути меньших сыновей
продолжается до тех пор, пока элемент не займет правильную позицию в
качестве родителя или пока не будет достигнут конец списка. В последнем
случае элемент помещается в листовой узел. Например, в приведенной ниже
пирамиде удаляется корневой узел 5.
Удалить корневой узел 5 и заменить его последним узлом 22.
Последний элемент пирамиды копируется в корень. Новый корень может не
удовлетворять условию пирами дальности, и требуется отправиться по
пути, проходящему через меньших сыновей, чтобы подыскать для
нового корня правильную позицию.
Удалить 5
Исходная пирамида
Заменить корень значением 22
Передвигать число 22 от корня вниз по пути, проходящему через
меньших сыновей. Сравнить корень 22 с его сыновьями. Наименьший
из двух сын Н[1] меньше, чем 22, поэтому следует поменять их местами
(А). Находясь теперь на первом уровне, новый родитель сравнивается
со своими сыновьями Н[3] и Н[4]. Наименьший из них имеет значение
11 и поэтому должен поменяться местами со своим родителем (В).
Теперь дерево удовлетворяет условию пирамидальности.
(А) (В)
Метод Delete. Чтобы поместить узел в правильную позицию, операция
удаления использует метод FilterDown. Эта функция получает в качестве
параметра индекс i, с которого начинается сканирование. При удалении метод
FilterDown вызывается с параметром 0, так как замещающее значение
копируется из последнего элемента пирамиды в ее корень. Метод FilterDown
используется также конструктором для построения пирамиды.
// утилита для восстановления пирамиды, начиная с индекса i,
// менять местами родителя и сына так, чтобы поддерево,
// начинающееся в узле i, было пирамидой
template <class T>
void Heap<T>::FilterDown (int i)
{
int currentpos, childpos;
T target;
// начать с узла i и присвоить его значение переменной target
currentpos = i;
target = hlist[i]/
// вычислить индекс левого сына и начать движение вниз по пути,
// проходящему через меньших сыновей до конца списка
childpos = 2 * i + 1;
while (childpos < heapsize) // пока не конец списка
{
// индекс правого сына равен childpos+1. присвоить переменной
// childpos индекс наименьшего из двух сыновей
if ((childpos+1 < heapsize) &&
(hlist[childpos+1] <= hlist[childpos]))
childpos = childpos + 1;
// если родитель меньше сына, пирамида в порядке, выход
if (target <= hlist[childpos])
break;
else
{
// переместить значение меньшего сына в родительский узел.
// теперь позиция меньшего сына не занята
hlist[currentpos] = hlist[childpos];
// обновить индексы и продолжить сканирование
currentpos = childpos;
childpos = 2 * currentpos + 1;
}
}
// поместить target в только что ставшую незанятой позицию
hlist{currentpos] = target;
}
Открытый метод Delete копирует значение из корневого узла во временную
переменную, а затем замещает корень последним элементом пирамиды. После
этого heapsize уменьшается на единицу. FilterDown реорганизует пирамиду.
Значение, сохраненное во временной переменной, возвращается клиенту.
// возвратить значение корневого элемента и обновить пирамиду.
// попытка удаления элемента из пустой пирамиды влечет за собой
// выдачу сообщения об ошибке и прекращение программы
template <class T>
Т Неар<Т>::Delete(void)
{
Т tempitem;
// проверить, пуста ли пирамида
if (heapsize « 0)
error ("Пирамида пуста");
// копировать корень в tempitem. заменить корень последним элементом
// пирамиды и произвести декремент переменной heapsize
tempitem = hlist[0];
hlist[0] = hlist[heapsize-l];
heapsize—;
// вызвать FilterDown для установки нового значения корня
FilterDown(0);
// возвратить исходное значение корня
return tempitem;
}
Преобразование массива в пирамиду. Один из конструкторов класса Heap
использует существующий массив в качестве входного списка и преобразует
его в пирамиду. Ко всем нелистовым узлам применяется метод FilterDown.
Индекс последнего элемента пирамиды равен п-1. Индекс его родителя равен
(п - 1) - 1 п - 2
currentpos = - = —-г—
и определяет последний нелистовой узел пирамиды. Этот индекс является
начальным для преобразования массива. Если применить метод FilterDown ко
всем индексам от currentpos до 0, то можно гарантировать, что каждый
родительский узел будет удовлетворять условию пирамидальности. В качестве
примера рассмотрим целочисленный массив
int A[10] = {9, 12, 17, 30, 50, 20, 60, 65, 4, 19}
Индексы листьев: 5, 6, ..., 9
Индексы родительских узлов: 4, 3, ..., 0
Исходный список
Приведенные ниже рисунки иллюстрируют процесс преобразования
пирамиды. Для всех вызовов FilterDown соответствующее поддерево выделено на
рисунках треугольником.
FilterDown(4). Родитель Н[4] = 50 больше своего сына Н[9] = 19 и
поэтому должен поменяться с ним местами (А).
Поставить на место число 50 с помощью FilterDown(4)
(А)
FilterDown(3). Родитель Н[3] = 30 больше своего сына Н[8] = 19 и
поэтому должен поменяться с ним местами (В).
Поставить на место число 30 с помощью FilterDownO)
(В)
На уровне 2 родитель Н[2] = 17 уже удовлетворяет условию пирами-
дальности, поэтому вызов FilterDown(2) не производит никаких
перестановок.
FilterDown(l). Родитель Н[1] = 12 больше своего сына Н[3] = 19 и
поэтому должен поменяться с ним местами (С).
FilterDown(O). Процесс прекращается в корневом узле. Родитель
Н[0] = 9 должен поменяться местами со своим сыном Н[1].
Результирующее дерево является пирамидой.
(D)
КОНСТРУКТОР
// конструктор преобразует исходный массив в пирамиду.
// этот массив и его размер передаются в качестве параметров
template <class T>
Неар<Т>::Неар(Т arr[], int n)
{
int j, currentpos;
// n <- 0 является недопустимым размером массива
if (n <= 0)
error ("Неправильная размерность массива");
// использовать п для установки размера пирамиды и максимального размера пирамиды.
// копировать массив агг в список пирамиды
maxheapsize = п;
heapsize = п;
hlist » arr;
// присвоить переменной currentpos индекс последнего родителя.
// вызывать FilterDown в цикле с индексами currentpos..0
currentpos « (heapsize-2)/2;
while (currentpos >= 0)
{
// выполнить условие пирамидальности для поддерева
// с корнем hlist[currentpos]
FilterDown(currentpos);
currentpos—;
)
// присвоить флажку inArray значение True
inArray * 1;
}
Приложение: пирамидальная сортировка
Пирамидальная сортировка имеет эффективность 0(n log2n). Алгоритм
использует тот факт, что наименьший элемент находится в корне (индекс 0) и
что метод Delete возвращает это значение.
Для осуществления пирамидальной сортировки массива А объявите объект
типа Heap с массивом А в качестве параметра. Конструктор преобразует А в
пирамиду. Сортировка осуществляется последовательным исключением А[0] и
включением его в A[N-1], A[N-2], ..., А[1]. Вспомните, что после исключения
элемента из пирамиды элемент, бывший до этого хвостовым, замещает корневой
и с этого момента больше не является частью пирамиды. Мы имеем возможность
скопировать удаленный элемент в эту позицию. В процессе пирамидальной
сортировки очередные наименьшие элементы удаляются и последовательно
запоминаются в хвостовой части массива. Таким образом, массив А сортируется по
убыванию. В качестве упражнения читателю предлагается построить класс
максимальных пирамид, с помощью которого массив сортируется по возрастанию.
Пирамидальная сортировка пятиэлементного массива А осуществляется
посредством следующих действий:
int A[] = {50, 20,75, 35, 25}
Исходная пирамида
Удалить 20 и запомнить в А[4] Удалить 25 и запомнить в А[3]
Удалить 35 и запомнить в А[2] Удалить 50 и запомнить в А[1]
Поскольку единственный оставшийся элемент 75 является корнем, массив
отсортирован: А = 75 50 35 25 20.
Ниже приводится реализация алгоритма пирамидальной сортировки.
Функция HeapSort находится в файле heapsort.h.
Функция HeapSort
tinclude "heap.h" // класс Heap
// отсортировать массив А по убыванию
template <class T>
void HeapSort (T A[], int n)
{
// конструктор, преобразующий А в пирамиду
Неар<Т> Н(А, п);
Т elt;
// цикл заполнения элементов А[п-1] ... А[1]
for (int i=n-l; i>=l; i—)
{
// исключить наименьший элемент из пирамиды и запомнить его в A[i]
elt = H.DeleteO ;
A[i] = elt;
}
}
Вычислительная эффективность пирамидальной сортировки. Массив,
содержащий п элементов соответствует законченному бинарному дереву
глубиной k = log2n. Начальная фаза преобразования массива в пирамиду требует
п/2 операций FilterDown. Каждой из них требуется не более к сравнений.
На второй фазе сортировки операция FilterDown выполняется п-1 раз. В
худшем случае она требует к сравнений. Объединив обе фазы, получим
худший случай сложности пирамидальной сортировки:
k*f + k*(n-l) = k*^-l) = log2nxf^-lj
Таким образом, сложность алгоритма имеет порядок 0(n log2n).
Пирамидальная сортировка не требует никакой дополнительной памяти,
поскольку производится на месте. Турнирная сортировка является алгоритмом
порядка 0(n log2n), но требует создания последовательно представляемого мае-
сивом дерева из 2(к+1) узлов, где к — наименьшее целое, при котором n < 2к.
Некоторые 0(n log2n) сложные сортировки дают 0(п2) в худшем случае.
Примером может служить сортировка, рассмотренная в разделе 13.7.
Пирамидальная сортировка всегда имеет сложность 0(n log2n) независимо от исходного
распределения данных.
Программа 13.2. Сравнение методов сортировки
Массив А, содержащий 2000 случайных целых чисел, сортируется с
помощью функции HeapSort (пирамидальная сортировка). В целях
сравнения массивы В и С заполняются теми же элементами и сортируются с
помощью функций TournamentSort (турнирная сортировка) и ExchangeSort
(обменая сортировка). Функция ExchangeSort находится в файле arrsort.h.
Сортировки хронометрируются функцией TickCount, которая возвращает
число 1/60 долей секунды, прошедших с момента старта системы.
Сортировка обменом, имеющая сложность 0(п2), позволит четко представить
быстродействие турнирного и пирамидального методов, имеющих
сложность 0(n log2n). Функция PrintFirst_Last распечатывает первые и
последние пять элементов массива. Код этой функции не включен в листинг
программы. Его можно найти в программном приложении в файле
prgl3__2.cpp.
#include <iostream.h>
#include "random.h"
ffinclude "arrsort.h"
iinclude "toursort.h"
#include "heapsort.h"
#include "ticks.h"
enum SortType {heap, tournament, exchange};
void TimeSort (int *A, int n, char *sortName, SortType sort)
{
long tcount;
// TickCount — системная функция.
// возвращает число 1/60 долей
// секунды с момента старта системы
cout « "Испытывается " « sortName « ":" « endl;
// засечь время, отсортировать массив А. подсчитать затраченное
// время в 1/60 долях секунды
tcount = TickCount ();
switch(sort)
{
case heap: HeapSort(A,n);
break;
case tournament: TournamentSort(A, n);
break;
case exchange: ExchangeSort(A, n);
break;
)
tcount = TickCount() - tcount;
// распечатать 5 первых и 5 последних элементов
// отсортированного массива
for (int i«0; i<5; i++)
cout « A[i] « " ";
cout « ".. . ";
for (i=n-5; i<n; i++)
cout « A[i] « " "/
cout « endl;
cout << "Продолжительность " « tcount « "\n\n";
}
void main(void)
{
// указатели массивов А, В и С
int *А, *В, *С;
RandomNumber rnd;
// динамическое выделение памяти и загрузка массивов
А = new int [2000];
В = new int [2000];
С = new int [2000];
// загрузить в массивы одни и те же 2000 случайных чисел
for (int i=0; i<2000; i++)
A[iJ = B[i] = C[i] = rnd.Random(10000);
TimeSort(A/ 2000, "пирамидальная сортировка ", heap);
delete [] A;
TimeSort(B, 2000, "турнирная сортировка ", heap);
delete [] B;
TimeSort(C, 2000, "сортировка обменом ", heap);
delete [] C;
}
/*
<Прогон программы 13.2>
Испытывается пирамидальная сортировка :
9999 9996 9996 9995 9990 ... 11 10 9 6 3
Продолжительность 16
Испытывается турнирная сортировка :
3 6 9 10 11 ... 9990 9995 9996 9996 9999
Продолжительность 36
Испытывается сортировка обменом :
3 6 9 10 11 ... 9990 9995 9996 9996 9999
Продолжительность 818
*/
13.4. Очереди приоритетов
Очереди приоритетов рассматривались в гл. 5 и использовались в задаче
моделирования событий. Клиенту был предоставлен доступ к оператору
вставки и оператору удаления, который удалял из списка элемент с наивысшим
приоритетом. В главе 5 для реализации списка, лежащего в основе объекта
PQueue, использовался массив.
В этом разделе очередь приоритетов реализуется с помощью пирамиды.
Поскольку мы используем минимальную пирамиду, предполагается, что
элементы имеют возрастающие приоритеты. Операция удаления из пирамиды
возвращает наименьший (с наивысшим приоритетом) элемент очереди
приоритетов. Пирамидальная реализация обеспечивает высокую эффективность
метода PQDelete, так как требует только 0(log2n) сравнений. Это соизмеримо с О(п)
сравнениями в реализации с помощью массива.
Данный раздел завершается рассмотрением фильтра, преобразующего
массив элементов в длинные последовательности1. Такой фильтр, используя
очередь приоритетов, существенно повышает эффективность сортировки
слиянием при упорядочении больших наборов данных файла. Эта тема
обсуждается в гл. 14.
Спецификация класса PQueue (пирамидальная версия)
ОБЪЯВЛЕНИЕ
#include "heap.h"
template <class T>
class PQueue
{
private:
// пирамида, в которой хранится очередь
Неар<Т> *ptrHeap;
public:
// конструктор
PQueue (int sz) ;
// операции модификации очереди приоритетов
void PQInsert(const T& item);
Т PQDelete(void);
void ClearPQ(void);
// методы опроса состояния очереди приоритетов
int PQEmpty(void) const;
int PQFull(void) const;
int PQLength(void) const;
};
ОПИСАНИЕ
В конструктор передается параметр sz, который используется для
динамического размещения структуры, адресуемой указателем ptrHeap. Методы
реализуются простым вызовом соответствующего метода в классе Heap.
Например, PQDelete использует метод исключения элемента из пирамиды.
// удалить первый элемент очереди посредством удаления корня
// соответствующей пирамиды, возвратить удаленное значение
template <class T>
Т PQueue<T>::PQDelete(void)
{
return ptrHeap->Delete ();
}
Реализация PQeue находится в файле pqueue.h.
Приложение: длинные последовательности
Сортировка слиянием является основным алгоритмом упорядочения
больших файлов. Его эффективность возрастает, если данные фильтруются, т.е.
предварительно преобразуются в длинные последовательности. В гл. 12 мы
уже видели один такой фильтр, который вводит сразу к элементов данных
и сортирует их. В этом случае минимальная длина последовательностей равна
1 Другие названия: серии» отрезки, цепочки. — Прим, пер.
к. В данном приложении используется к-элементная очередь приоритетов и
создаются последовательности, длины которых часто существенно превышают
к. Алгоритм читает элементы из исходного списка А и пропускает их через
фильтр очереди приоритетов. Элементы возвращаются в исходный список в
форме длинных последовательностей.
Проиллюстрируем алгоритм на примере. Пусть массив А имеет 12 целых
чисел, а приоритетная очередь PQ1 является фильтром с к=4 элементами.
PQ1 хранит элементы, которые в конечном счете попадут в текущую
последовательность. Вторая приоритетная очередь, PQ2, содержит элементы для
следующей последовательности. Для сканирования массива используются два
индекса. Переменная loadlndex указывает элемент, который вводится в
данный момент. Переменная currlndex указывает последний элемент,
покинувший очередь PQ1 и вернувшийся в исходный массив. В нашем примере
массив А изначально разбит на шесть последовательностей, самая длинная
из которых содержит три элемента:
А = [13] [6 61 96] [26] [1 72 91] [37] [25 97] [21]
После фильтрации получатся три последовательности, самая длинная из
которых будет содержать семь элементов.
Вначале в PQ1 загружаются элементы А[0]...А[3]. Так как очередь
приоритетов удаляет элементы в возрастающем порядке, у нас уже есть средство
для сортировки, по крайней мере, четырех элементов последовательности.
Но мы поступим даже лучше. Исключим из PQ1 первый элемент (с
минимальным значением) и присвоим его A[currIndex] = А[0] = 6. Это число
начинает первую последовательность, а в PQ1 остается незаполненное место.
Поскольку первые четыре элемента массива А были скопированы в PQ1,
продолжим с четвертого элемента (loadlndex = 4). На каждом шаге
сравниваются A[currlndex] и A[loadIndex]. Если первый из них больше, он в конце
концов попадет в текущую последовательность и поэтому запоминается в
PQ1. В противном случае он попадет в следующую последовательность и
поэтому запоминается в PQ2. Опишем это действие для каждого элемента в
нашем примере. После обработки некоторого элемента мы используем
следующий формат для перечисления загруженных элементов в А, элементов
которые еще должны считываться, и содержимое обеих очередей приоритетов:
А: Олементы, загружаемые в последовательности> A[loadIndex]:
Оставшиеся элементы>
PQ1: <содержимое текущей последовательности> PQ2: <содержимое
следующей последовательности>
Выполнить по шагам: Элемент А[4]=26 > A[currlndex]=6. Запомнить
26 в PQ1; и удалить 13 из PQ1; поместить 13 в А[1].
А: 6 13 А[5]...А[11]: 1 72 91 37 25 97 21
PQ1: 61 96 26 PQ2: <пусто>
Элемент А[5]=1 < A[currlndex]=13. Поэтому 1 принадлежит следующей
последовательности. Запомнить 1 в PQ2; исключить 26 из PQ1;
поместить 26 в А[2].
А: 6 13 26 А[6]...А[11]: 72 91 37 25 97 21
PQ1: 61 96 PQ2: 1
Элемент А[6]=72 больше, чем элемент 26 в текущей последовательности.
Запомнить А[6] в PQ1; исключить 61 из PQ1. Аналогично, следующий
элемент 91 попадает в PQ1 прежде, чем произойдет исключение
элемента 72 и запись его в текущую последовательность по индексу cur-
rlndex=4.
А: 6 13 26 61 72 А[8]...А[11]: 37 25 97 21
PQ1: 91 96 PQ2: 1
Элементы А[8]=37 и А[9]=25 больше, чем 72 и попадут в следующую
последовательность. Они запоминаются в PQ2. Одновременно из PQ1
исключаются два элемента и помещаются в массив, а очередь PQ1
остается пустой,
А: 6 13 26 61 72 91 96 А[10]...А[11]: 97 21
PQ1: <пусто> PQ2: 1 37 25
Мы сформировали текущую последовательность и можем начинать
следующую. Скопируем PQ2 в PQ1 и исключим наименьший элемент из
вновь заполненной очереди PQ1. В нашем примере удаляем 1 из PQ1
и начнем следующую последовательность.
А: 6 13 26 61 72 91 96 1 А[10]...А[11]: 97 21
PQ1: 25 37 PQ2: <пусто>
Элемент А[10]=97 > 1 и запоминается в PQ1. Затем минимальное
значение 25 исключается из PQ1.
А: 6 13 26 61 72 91 96 1 25 А[11]: 21
PQ1: 37 97 PQ2: <пусто>
Элемент А[11]=21 < 25 и должен ждать следующую последовательность.
Он запоминается в PQ2, а 37 исключается из PQ1.
А: 6 13 26 61 72 91 96 1 25 37 <весь список пройден>
PQ1: 97 PQ2: 21
Сканирование исходного списка завершено. Исключить все элементы
из PQ1 и поместить их в текущую последовательность. Затем все
элементы из PQ2 поместить в следующую последовательность.
Последовательность 1: 6 13 26 61 72 91 96
Последовательность 2: 1 25 37 97
Последовательность 3: 21
Алгоритм Runs. Алгоритм порождения длинных последовательностей
реализуется с помощью класса LongRunFilter. Его закрытые данные-члены
включают массив и две приоритетные очереди, содержащие текущую и
следующую последовательности. Конструктор связывает объект данного класса
с массивом и создает соответствующие очереди приоритетов. Алгоритм
поддерживается закрытыми методами LoadPQ, который включает элементы
массива в очередь PQ1, и CopyPQ, который копирует элементы из PQ2 в PQ1.
ОБЪЯВЛЕНИЕ
template <class T>
class LongRunFilter
{
private:
// указатели, определяющие ключевые параметры в фильтре
// список А и две очереди приоритетов — PQ1 и PQ2 Т *А;
PQueue<T> *PQ1, *PQ2;
int loadlndex;
// размер массива и очередей приоритетов
int arraySize;
int filterSize;
// копирование PQ2 в PQ1
void CopyPQ (void);
// загрузка массива А в очередь приоритетов PQ1
void LoadPQ (void);
public:
// конструктор и деструктор
LongRunFilter(T arr[], int n, int sz);
~LongRunFilter(void);
// создание длинных последовательностей
void LoadRuns(void);
// оценка последовательностей
void PrintRuns(void) const;
int CountRuns(void) const;
};
ОПИСАНИЕ
Конструктор инициализирует данные-члены и загружает элементы из
массива в PQ1, формируя таким образом элементы первой последовательности.
Метод LoadRuns является главным алгоритмом, преобразующим элементы
массива в длинные последовательности.
Методы PrintRuns и CountRuns служат для иллюстрации алгоритма. Они
используются для сравнения последовательностей до и после вызова Load-
Runs.
Полная реализация класса LongRunFilter находится в файле longrun.h.
// сканировать массив А и создать длинные последовательности,
// пропуская элементы через фильтр
template <class T>
void LongRunFilter<T>::LoadRuns(void)
{
T value/
int currIndex; = 0/
if (filterSize == 0)
return;
// начать с загрузки наименьшего элемента из PQ1 в А
A[currlndex] = PQl->PQDelete();
// заполнить PQ1 элементами из А
// теперь просмотреть элементы, оставшиеся в А
while (loadlndex < arraySize)
{
// рассмотреть очередной элемент списка
value = A[loadLndex++];
// если элемент больше или равен Afcurrlndex],
//он принадлежит текущей последовательности
//и попадает в PQ1. в противном случае он копируется
//в PQ2 и в конечном счете попадает в следующую последовательность
if (Afcurrlndex] <= value)
PQl->PQInsert(value);
else
PQl->PQInsert(value);
// если PQ1 пуста, текущая последовательность сформирована.
// скопировать PQ2 в PQ1 и начать следующую последовательность
if (PQl->PQEmpty())
CopyPQO;
// взять элемент из PQ1 и включить его в последовательность
if (!PQl->PQEmpty()>
A[++currIndex] = PQl->PQDelete;
}
// удалить элементы из текущей последовательности,
//а затем из следующей
while (!PQl->PQEmpty())
A[++currIndex] * PQl->PQDelete;
while (!PQ2->PQEmpty())
A[++currIndex] = PQ2->PQDelete;
}
Программа 13.3. Длинные последовательности
Эта программа иллюстрирует применение фильтра. В первом примере
берется небольшой массив из 15 элементов и фильтруется с помощью
4-элементных очередей приоритетов. На выход выдается перечень
последовательностей до и после вызова фильтра. В более практическом примере
обрабатывается 10000-элементный массив, который фильтруется с
помощью 5-, 50- и 500-элементных очередей приоритетов. В каждом случае
распечатывается число итоговых последовательностей.
#include <iostream.h>
#include "random.h"
♦include "longrun.h"
// копирование массива А в массив В
void CopyArray(int A[], int B[], int n)
{
for (int i=0; i<n; i++)
B[i] = A[i];
}
void main()
{
// исходный 15-элементный массив для иллюстрации фильтра
int demoArray[15];
// большие 10000-элементные массивы для подсчета последовательностей
int *А = new int [10000], *В « new int [10000];
RandomNumber rnd;
// создать 15 случайных чисел; сформировать фильтр
for (i=0; i<15; i++)
demoArray[i] = rnd.Random(100);
LongRunFilter<int> F(demoArray, 15, 4);
// распечатать список до и после создания длинных последовательностей
//с помощью 4-элементного фильтра
cout « "Исходные последовательности" « endl;
F.PrintRuns();
cout « endl;
F.LoadRuns();
cout « "Отфильтрованные последовательности" « endl;
F.PrintRuns();
cout « endl;
// сформировать массив из 10000 случайных чисел
for (i=0; К10000; i++)
A[i] « rnd.Random(25000);
cout << "Последовательности, полученные с помощью 3-х фильтров"
« endl;
LongRunFilter<int> LR(A, 10000, 0) ;
cout « "Число последовательностей в исходном массиве: "
« LR.CountRuns() « endl;
// тестирование 5- , 50- и 500-элементных фильтров
for (i=0; i<3; i++)
{
CopyArray(A, В, 10000);
LongRunFilter<int> LR(B, 10000, filterSize);
// создать длинные последовательности
LR.LoadRuns{);
cout « " Число последовательностей после фильтра "
« filterSize « " = " « LR.CountRuns () « endl;
// 10-кратное увеличение размера фильтра
filtersize *= 10;
}
}
/*
<Прогон программы 13.3>
Исходные последовательности
Отфильтрованные последовательности 22 26 36 44 44 66 79 81 84 86 88
2 19 40 47
Последовательности, полученные с помощью 3-х фильтров
Количество последовательностей в исходном массиве: 5077
Число последовательностей после фильтра 5 = 991
Число последовательностей после фильтра 50 = 101
Число последовательностей после фильтра 500 =11
*/
36
22 79
26 84
44 88
44 66 81
19 86
40
2 47
13.5. AVL-деревья
Бинарные деревья поиска предназначены для быстрого доступа к данным.
В идеале дерево является разумно сбалансированным и имеет высоту порядка
0(log2n). Однако при некоторых данных дерево может оказаться вырожден-
ным. Тогда высота его будет О(п), и доступ к данным существенно замедлится.
В этом разделе мы рассмотрим модифицированный класс деревьев,
обладающих всеми преимуществами бинарных деревьев поиска и никогда не
вырождающихся. Они называются сбалансированными или AVL-деревьями. Под
сбалансированностью будем понимать то, что для каждого узла дерева высоты
обоих его поддеревьев различаются не более чем на I1.
Новые методы включения и исключения в классе AVL-деревьев
гарантируют, что все узлы останутся сбалансированными по высоте. На рис. 13.3
показаны эквивалентные представления массива AVL-деревом и бинарным
деревом поиска. Верхняя пара деревьев представляет простой пятиэлемент-
ный массив А, отсортированный по возрастанию. Нижняя пара деревьев
представляет массив В. Бинарное дерево поиска имеет высоту 5, в то время
как высота AVL-дерева равна 2. В общем случае высота сбалансированного
дерева не превышает 0(log2n). Таким образом, AVL-дерево является мощной
структурой хранения, обеспечивающей быстрый доступ к данным.
А[5] = {1,2,3,4,5} В[8] - {20, 30, 80, 40, 10, 60, 50, 70}
В этом разделе используется подход, принятый в гл. 11, когда поисковое
дерево строилось отдельно от своих узлов. Сначала мы разработаем класс
AVLTreeNode, а затем используем объекты этого типа для конструирования
класса AVLTree. Предметом пристального внимания будут методы Insert и
Delete. Они требуют тщательного проектирования, поскольку должны
гарантировать, что все узлы нового дерева останутся сбалансированными по высоте.
Узлы AVL-дерева
AVL-деревья имеют представление, похожее на бинарные деревья поиска.
Все операции идентичны, за исключением методов Insert и Delete, которые
должны постоянно отслеживать соотношение высот левого и правого
поддеревьев узла. Для сохранения этой информации мы расширили определение
объекта TreeNode, включив поле balanceFactor (показатель сбалансированности),
которое содержит разность высот правого и левого поддеревьев.
left
data
balanceFactor
right
AVLTreeNode
balanceFactor-height(right subtree)- height(left subtree)
Если balanceFactor отрицателен, то узел "перевешивает влево", так как
высота левого поддерева больше, чем высота правого поддерева. При
положительном balanceFactor узел "перевешивает вправо". Сбалансированный по
высоте узел имеет balanceFactor = 0. В AVL-дереве показатель сбалансированности
должен быть в диапазоне [-1, 1].
На рис. 13.4 изображены AVL-деревья с пометками -1, 0 и +1 на каждом
узле, показывающими относительный размер левого и правого поддеревьев.
-1: Высота левого поддерева на 1 больше высоты правого поддерева.
0: Высоты обоих поддеревьев одинаковы.
1 Строго говоря, этот критерий нужно называть AVL-сбалансированностью в отличие от
идеальной сбалансированности, когда для каждого узла дерева количества узлов в левом и правом
поддеревьях различаются не более чем на 1. В этой главе всегда подразумевается AVL-сбалан-
сированность. — Прим. перев.
+1: Высота правого поддерева на 1 больше высоты левого поддерева.
Бинарное дерево поиска
AVL-дерево
Бинарное дерево поиска
AVL-дерево
Рис. 13.3. Представление массива с помощью бинарного дерева поиска и AVL-дерева
Используя свойства наследования, можно образовать класс AVLTreeNode
на базе класса TreeNode. Объект типа AVLTreeNode наследует поля из класса
TreeNode и добавляет к ним поле balanceFactor. Данные-члены left и right
класса TreeNode являются защищенными, поэтому AVLTreeNode или другие
производные классы имеют к ним доступ. Класс AVLTreeNode и все
сопровождающие его программы находятся в файле avltree.h.
Спецификация класса AVLTreeNode
ОБЪЯВЛЕНИЕ
// наследник класса TreeNode
template <class T>
class AVLTreeNode: public TreeNode<T>
{
private:
// дополнительный член класса
int balanceFactor/
// используются методами класса AVLTree и позволяют
// избегать "перевешивания" узлов
AVLTreeNode<T>* & Left(void);
AVLTreeNode<T>* & Right(void);
public:
// конструктор
AVLTreeNode(const T& item, AVLTreeNode<T> *lptr = NULL,
AVLTreeNode<T> *rptr = NULL, int balfac = 0);
// возвратить левый/правый указатель узла типа TreeNode,
//в качестве указателя узла типа AVLTreeNode; выполнить
// приведение типов
AVLTreeNode<T> *Left(void) const;
AVLTreeNode<T> *Right(void) const;
// метод для доступа к новому полю данных
int GetBalanceFactor(void);
// методы класса AVLTree должны иметь доступ к Left и Right
friend class AVLTree<T>;
};
ОПИСАНИЕ
Элемент данных balanceFactor является закрытым, так как обновлять его
должны только сбалансированные операции включения и исключения.
Параметры, передаваемые в конструктор, содержат данные для базовой
структуры типа TreeNode. По умолчанию параметр balfac равен 0.
Доступ к полям указателей осуществляется с помощью методов Left и Right.
Новые определения для этих методов обязательны, поскольку они возвращают
указатель на стуктуру AVLTreeNode.
Основные причины, по которым деструктор объявляется виртуальным,
обсуждались в разделе 12.3. Поскольку класс AVLTree образован на базе класса
BinSTree, будем использовать деструктор базового класса и ClearList. Эти
методы удаляют узлы с помощью оператора delete. В каждом случае указатель
ссылается на объект типа AVLTreeNode, а не TreeNode. Если деструктор
базового класса TreeNode виртуальный, то при вызове delete используется
динамическое связывание и удаляется объект типа AVLTreeNode.
ПРИМЕРЫ
AVLTreeNode<char> *root; // корень AVL-дерева
// эта функция создает AVL-дерево, изображенное ниже.
// каждому узлу присваивается показатель сбалансированности
void MakeAVLCharTree(AVLTreeNode<char>* &root)
{
AVLTreeNode<char> *a, *b, *c, *d, *e;
e = new AVLTreeNode<char>(/E', NULL, NULL, 0);
d = new AVLTreeNode<char>('D', NULL, NULL, 0);
с = new AVLTreeNode<char>('C, e, NULL, -1);
b = new AVLTreeNode<char>('B', NULL, d, 1) ;
a * new AVLTreeNode<char> (' A' , b, c, Ob-
root = a;
}
Реализация класса AVLTreeNode. Конструктор класса AVLTreeNode
вызывает конструктор базового класса и инициализирует balanceFactor.
// конструктор, инициализирует balanceFactor и базовый класс.
// нулевые начальные значения полей указателей
// (по умолчанию) инициализируют узел как лист, template <class T>
AVLTreeNode<T>::AVLTreeNode (const T& item,
AVLTreeNode<T> *lptr, AVLTreeNode<T> *rptr, int balfac):
TreeNode<T>(item, lptr, rptr), balanceFactor(balfac)
{}
Методы Left и Right в классе AVLTreeNode упрощают доступ к полям
данных. При попытке обратиться к левому сыну с помощью базового метода
Left возвращается указатель на объект типа TreeNode. Чтобы получить
указатель на узел сбалансированного дерева, требуется преобразование типов.
Например,
AVLTreeNode<T> *р, *q;
q = p->Left(); // недопустимая операция
q = (AVLTreeNode<T> *)p->Left(); // необходимое приведение типа
Во избежание постоянного преобразования типа указателей мы определяем
методы Left и Right для класса AVLTreeNode, возвращающие указатели на
объекты типа AVLTreeNode.
template <class T>
AVLTreeNode<T>* AVLTreeNode::Left(void)
{
return ((AVLTreeNode<T> *)left;
}
13.6. Класс AVLTree
AVL-дерево представляет списковую структуру, похожую на бинарное
дерево поиска, с одним дополнительным условием: дерево должно оставаться
сбалансированным по высоте после каждой операции включения или
удаления. Поскольку AVL-дерево является расширенным бинарным деревом
поиска, класс AVLTree строится на базе класса BinSTree и является его
наследником.
Методы Insert и Delete должны подменяться для выполнения AVL-условия.
Кроме того, в производном классе определяются конструктор копирования
и перегруженный оператор присваивания, так как мы строим дерево с
большей узловой структурой.
Спецификация класса AVLTree
ОБЪЯВЛЕНИЕ
// Значения показателя сбалансированности узла
const int leftheavy = -1;
const int balanced =1;
const int rightheavy =1;
// производный класс поисковых деревьев
template <class T>
class AVLTree: public BinSTree<T>
{
private:
// выделение памяти
AVLTreeNode<T> *GetAVLTreeNode(const T& item,
AVLTreeNode<T> *lptr, AVLTreeNode<T> *rptr);
// используется конструктором копирования и оператором присваивания
AVLTreeNode<T> *CopyTree(AVLTreeNode<T> *t) ;
// используется методами Insert и Delete для восстановления
// AVL-условий после операций включения/исключения
void SingleRotateLeft (AVLTreeNode<T>* &p);
void SingleRotateRight (AVLTreeNode<T>* &p);
void DoubleRotateLeft (AVLTreeNode<T>* &p);
void DoubleRotateRight (AVLTreeNode<T>* &p);
void UpdateLeftTree (AVLTreeNode<T>* &tree,
int &reviseBalanceFactor);
void UpdateRightTree (AVLTreeNode<T>* &tree,
int SreviseBalanceFactor);
// специальные версии методов Insert и Delete
void AVLInsert(AVLTreeNode<T>* &tree,
AVLTreeNode<T>* newNode, int SreviseBalanceFactor);
void AVLDelete(AVLTreeNode<T>* &tree,
AVLTreeNode<T>* newNode, int sreviseBalanceFactor);
public:
// конструкторы
AVLTree(void);
AVLTree(const AVLTree<T>& tree);
// оператор присваивания
AVLTree<T>& operator^ (const AVLTree<T>i tree);
// стандартные методы обработки списков
virtual void Insert(const T& item);
virtual void Delete(const T& item);
};
ОПИСАНИЕ
Константы leftheavy, balanced и rightheavy используются в операциях
вставки/удаления для описания показателя сбалансированности узла.
Метод GetAVLTreeNode управляет выделением памяти для класса. По
умолчанию balanceFactor нового узла равен нулю.
В этом классе заново определяется функция СоруТгее для использования
с конструктором копирования и перегруженным оператором присваивания.
Несмотря на то, что алгоритм идентичен алгоритму для функции СоруТгее
класса BinSTree, новая версия корректно создает расширенные объекты типа
AVLTreeNode при построении нового дерева.
Функции AVLInsert и AVLDelete реализуют методы Insert и Delete,
соответственно. Они используют закрытые методы наподобие SingleRotateLeft.
Открытые методы Insert и Delete объявлены как виртуальные и подменяют
соответствующие функции базового класса. Остальные операции наследуются
от класса BinSTree.
ПРИМЕР
AVLTree<int> avltree; // AVLTree-список целых чисел
BinSTree<int> bintгее; // BinSTree-список целых чисел
for (int i=l; i<=5; i++)
(А) (В)
{
bintree.Insert(i); // создать дерево А
avltree.Insert(i); // создать дерево В
}
avltree.Delete(3); // удалить 3 из AVL-дерева
// функция AVLPrintTree эквивалентна функции вертикальной распечатки
// дерева из гл. 11. кроме собственно данных для каждого узла
// распечатываются показатели сбалансированности, дерево (С) есть дерево (В)
// без удаленного узла 3. AVLPrintTree находится в файле avltree.h
AVLPrintTree((AVLTreeNode<int> *)avltree.GetRoot(), 0);
Распределение памяти для AVLTree
Класс AVLTree образован от класса BinSTree и наследует большинство его
операций. Для создания расширенных объектов типа AVLTreeNode мы
разработали отдельные методы выделения памяти и копирования.
// разместить в памяти объект типа AVLTreeNode. прервать программу,
// если во время выделения памяти произошла ошибка
template <class T>
AVLTreeNode<T> *AVLTree<T>::GetAVLTreeNode(const T& item,
AVLTreeNode<T> *lptr, AVLTreeNode<T> *rptr)
{
AVLTreeNode<T> *p;
p - new AVLTreeNode<T> (item, lptr, rptr);
if (p == NULL)
{
cerr « "Ошибка выделения памяти!" « endl;
exit(1);
}
return p/
}
Для удаления узлов AVL-дерева достаточно методов базового класса. Метод
DeleteTree из класса BinSTree задействует виртуальный деструктор класса
TreeNode.
Метод Insert класса AVLTree. Преимущество AVL-деревьев состоит в их
сбалансированности, которая поддерживается соответствующими
алгоритмами вставки/удаления. Опишем метод Insert для класса AVLTree, который
перекрывает одноименную операцию базового класса BinSTree. При
реализации метода Insert для запоминания элемента используется рекурсивная
функция AVLInsert. Сначала приведем код метода Insert на C++, а затем
сосредоточим внимание на рекурсивном методе AVLInsert, реализующем
алгоритм Адельсона-Вельского и Ландиса.
template <class T>
void AVLTree<T>::Insert(const T& item)
{
// объявить указатель AVL-дерева, используя метод
// базового класса GetRoot.
// произвести приведение типов для указателей
AVLTreeNode<T> *treeRoot = (AVLTreeNode<T> *)GetRoot()/
*newNode;
// флажок, используемый функцией AVLInsert для перебалансировки узлов
int reviseBalanceFactor = 0;
// создать новый узел AVL-дерева с нулевыми полями указателей
newNode = GetAVLTreeNode(item, NULL, NULL);
// вызвать рекурсивную процедуру для фактической вставки элемента
AVLInsert(treeRoot, newNode, reviseBalancefactor);
// присвоить новые значения элементам данных базового класса
root = treeRoot;
current = newNode;
size++;
}
Ядром алгоритма включения является рекурсивный метод AVLInsert. Как
и его аналог в классе BinSTree, этот метод осуществляет прохождение левого
поддерева, если item меньше данного узла, и правого поддерева, если item
больше или равен данному узлу. Эта закрытая функция имеет параметр с
именем tree, в котором находится запись текущего узла при сканировании,
новый узел для вставки в дерево, флажок revisebalanceFactor. При
сканировании левого или правого поддерева некоторого узла, этот флажок является
признаком изменения любого параметра balanceFactor в поддереве. Если да,
то нужно проверить, сохранилась ли AVL-сбалансированность всего дерева.
Если в результате включения нового узла она оказалась нарушенной, то мы
обязаны восстановить равновесие. Данный алгоритм рассматривается на ряде
примеров.
Алгоритм AVL-вставки. Процесс включения является почти таким же, что
и для бинарного дерева поиска. Осуществляется рекурсивный спуск по левым
и правым сыновьям, пока не встретится пустое поддерево, а затем производится
пробное включение нового узла в этом месте. В течение этого процесса мы
посещаем каждый узел на пути поиска от корневого к новому элементу.
Поскольку процесс рекурсивный, обработка узлов ведется в обратном
порядке. При этом показатель сбалансированности родительского узла можно
скорректировать после изучения эффекта от добавления нового элемента в
одно из поддеревьев. Необходимость корректировки определяется для
каждого узла, входящего в поисковый маршрут. Есть три возможных ситуации.
В первых двух случаях узел сохраняет сбалансированность и реорганизация
поддеревьев не требуется, а нужно лишь скорректировать показатель
сбалансированности данного узла. В третьем случае расбалансировка дерева
требует одинарного или двойного поворотов узлов.
Случай 1. Узел на поисковом маршруте изначально является
сбалансированным (balanceFactor = 0). После включения в поддерево нового
элемента узел стал перевешивать влево или вправо в зависимости от
того, в какое поддерево было произведено включение. Если элемент
был включен в левое поддерево, показателю сбалансированности
присваивается -1, а если в правое, то 1. Например, на пути 40-50-60
каждый узел сбалансирован. После включения узла 55 показатели
сбалансированности изменяются.
До включения узла 55 После включения узла 55
Случай 2. Одно из поддеревьев узла перевешивает, и новый узел
включается в более легкое поддерево. Узел становится сбалансированным.
Сравните, например, состояния дерева до и после включения узла 55.
До включения узла 55 После включения узла 55
Случай 3. Одно из поддеревьев узла перевешивает, и новый узел
включается в более тяжелое поддерево. Тем самым нарушается условие
сбалансированности, так как balanceFactor выходит за пределы -1..1.
Чтобы восстановить равновесие, нужно выполнить поворот.
Рассмотрим пример. Предположим, дерево разбалансировалось слева и мы
восстанавливаем равновесие, вызывая одну из функций поворота вправо. Раз-
балансировка справа влечет за собой симметричные действия.
Сказанное иллюстрируется следующими рисунками. При разработке
алгоритма поворота мы включили дополнительные детали.
Метод AVLInsert. Продвигаясь вдоль некоторого пути для вставки нового
узла, этот рекурсивный метод распознает все три указанных выше случая
корректировки. При нарушении условия сбалансированности восстановление
равновесия осуществляется с помощью функций UpdateLeftTree и Up-
dateRightTree.
До корректировки
После корректировки
Одинарный поворот
До корректировки После корректировки
Двойной поворот
template <class T>
void AVLTree<T>: .-AVLInsert (AVLTreeNode<T>* &tree,
AVLTreeNode<T>* newNode, int ^reviseBalanceFactor)
{
// флажок "Показатель сбалансированности был изменен"
int rebalanceCurrNode/
// встретилось пустое поддерево, пора включать новый узел
if (tree == NULL)
{
// вставить новый узел
tree = newNode;
// объявить новый узел сбалансированным
tree->balanceFactor = balanced;
// сообщить об изменении показателя сбалансированности
reviseBalanceFactor = 1;
}
// рекурсивно спускаться по левому поддереву,
// если новый узел меньше текущего
else if (newNode->data < tree->data)
{
AVLInsert(tree->Left(), newNode, rebalanceCurrNode);
// проверить, нужно ли корректировать balanceFactor
if (rebalanceCurrNode)
{
// включение слева от узла, перевешивающего влево, будет нарушено
// условие сбалансированности; выполнить поворот (случай 3)
if (tree->balanceFactor == leftheavy)
UpdateLeftTree(tree, reviseBalanceFactor);
// вставка слева от сбалансированного узла.
// узел станет перевешивать влево (случай 1)
else if (tree->balanceFactor == balanced)
{
tree->balanceFactor = leftheavy;
reviseBalanceFactor = 1;
}
// вставка слева от узла, перевешивающего вправо.
// узел станет сбалансированным (случай 2)
else
{
tree->balanceFactor = balanced;
reviseBalanceFactor = 0;
}
}
else
// перебалансировка не требуется, не опрашивать предыдущие узлы
reviseBalanceFactor = 0;
}
// иначе рекурсивно спускаться по правому поддереву
else if (newNode->data < tree->data)
{
AVLInsert(tree->Right(), newNode, rebalanceCurrNode);
// проверить, нужно ли корректировать balanceFactor
if (rebalanceCurrNode)
{
// вставка справа от узла, перевешивающего вправо, будет нарушено
// условие сбалансированности; выполнить поворот (случай 3)
if (tree->balanceFactor == rightheavy)
UpdateRightTree(tree, reviseBalanceFactor);
// вставка справа от сбалансированного узла.
// узел станет перевешивать вправо (случай 1)
else if (tree->balanceFactor == balanced)
{
tree->balanceFactor = rightheavy;
reviseBalanceFactor = 1;
}
// вставка справа от узла, перевешивающего влево.
// узел станет сбалансированным (случай 2)
else
{
tree->balanceFactor = balanced;
reviseBalanceFactor = 0;
}
}
else
// перебалансировка не требуется, не опрашивать предыдущие узлы
reviseBalanceFactor = 0;
}
}
Метод AVLInsert распознает случай 3, когда нарушается AVL-условие. Для
выполнения перебалансировки используются методы UpdateLeftTree и
UpdateRightTree. Они выполняют одинарный или двойной поворот для
уравновешивания узла, а затем сбрасывают флажок reviseBalanceFactor. Перед тем как
обсудить специфические детали поворотов, приведем программный код
функции UpdateLeftTree.
template <class T>
void AVLTree<T>::UpdateLeftTree(AVLTreeNode<T>* &p,
int reviseBalanceFactor)
{
AVLTreeNode<T> *lc;
lc = p->Left();
// перевешивает левое поддерево?
if (lc->balanceFactor == leftheavy)
{
SingleRotateRight(p); // однократный поворот
reviseBalanceFactor = 0;
}
// перевешивает правое поддерево?
else if (lc->balanceFactor == rightheavy)
{
// выполнить двойной поворот
DoubleRotateRight(p);
// теперь корень уравновешен
reviseBalanceFactor - 0;
}
}
Повороты. Повороты необходимы, когда родительский узел Р становится
расбалансированным. Одинарный поворот вправо (single right rotation)
происходит тогда, когда родительский узел Р и его левый сын LC начинают
перевешивать влево после включения узла в позицию X. В результате такого
поворота LC замещает своего родителя, который становится правым сыном. Бывшее
правое поддерево узла LC (ST) присоединяется к Р в качестве левого поддерева.
Это сохраняет упорядоченность, так как узлы в ST больше или равны узлу LC,
но меньше узла Р. Поворот уравновешивает как родителя, так и его левого сына.
// выполнить поворот по часовой стрелке вокруг узла р.
// сделать 1с новой точкой вращения
template <class T>
void AVLTree<T>::SingleRotateRight (AVLTreeNode<T>* &p)
{
// левое, перевешивающее поддерево узла р
AVLTreeNode<T> *lc;
// назначить 1с левым поддеревом
lc = p->Left();
// скорректировать показатель сбалансированности для
// родительского узла и его левого сына
p->balanceFactor = balanced;
lc->balanceFactor = balanced;
// правое поддерево узла 1с в любом случае должно оставаться справа
// от 1с. выполнить это условие, сделав st левым поддеревом узла р
p->Left() = lc->Right();
// переместить р в правое поддерево узла 1с.
// сделать 1с новой точкой вращения.
lc->Right() = р;
р - 1с;
}
Попытка включить узел 5 в изображенное ниже AVL-дерево нарушает AVL-
условие для узла 30 из равновесия. Одновременно левое поддерево узла 15 (LC)
становится перегруженным. Для переупорядочения узлов вызывается
процедура SingleRotateRight. В результате родительский узел (30) становится
сбалансированным, а узел 10 — перевешивающим влево.
Исходное дерево
Показатели
сбалансированности до поворота
После включения узла 5
Двойной поворот вправо (double rigyn rotation) происходит тогда, когда
родительский узел (Р) становится перевешивающим влево, а его левый сын
(LC) — перевешивающим вправо. NP — корень правого перевешивающего
поддерева узла LC. Тогда в результате поворота узел NP замещает родительский
узел. На следующих далее рисунках показаны два случая включения нового
узла в качестве сына узла NP. В обоих случаях NP становится родительским
узлом, а бывший родитель Р становится правым сыном NP.
На верхней схеме мы видим сдвиг узла Xlt после того как он был вставлен
в левое поддерево узла NP. На нижней схеме изображено перемещение узла
Х2 после его включения в правое поддерево NP.
// двойной поворот вправо вокруг узла р
template <class T>
void AVLTree<T>::DoubleRotateRight (AVLTreeNode<T>* &p)
{
// два поддерева, подлежащих повороту
AVLTreeNode<T> *lc, *np;
// узел lc <= узел np < узел р
lc = p->Left(); // левый сын узла р
пр = lc->Right(); // правый сын узла 1с
// обновить показатели сбалансированности в узлах р, 1с и пр
if (np->balanceFactor == rightheavy)
{
p->balanceFactor = balanced;
lc->balanceFactor = rightheavy;
}
else
{
p->balanceFactor = rightheavy;
lc->balanceFactor = balanced;
}
np->balanceFactor = balanced;
// перед тем как заменить родительский узел р,
// следует отсоединить его старых детей и присоединить новых
lc->Right() =np->Left();
np->Left() = lc;
p->Left() = np->Right();
np->Right() = p;
p - np;
}
Двойной поворот иллюстрируется на изображенном ниже дереве. Попытка
включить узел 25 разбалансирует корневой узел 50. В этом случае узел 20 (LC)
приобретает слишком высокое правое поддерево и требуется двойной поворот.
Новым родительским узлом (NP) становится узел 40. Старый родительский
узел становится его правым сыном и присоединяет к себе узел 45, который
также переходит с левой стороны дерева.
До включения узла 25 После включения узла 25
Оценка сбалансированных деревьев
Ценность AVL-деревьев зависит от приложения, поскольку они требуют
дополнительных затрат на поддержание сбалансированности при включении
или исключении узлов. Если в дереве постоянно происходят вставки и
удаления элементов, эти операции могут значительно снизить быстродействие. С
другой стороны, если ваши данные превращают бинарное дерево поиска в
вырожденное, вы теряете поисковую эффективность и вынуждены
использовать AVL-дерево.
Для сбалансированного дерева не существует наихудшего случая, так как
оно является почти полным бинарным деревом. Сложность операции поиска
составляет 0(log2n). Опыт показывает, что повороты требуются примерно в
половине случаев включений и удалений. Сложность балансировки
обусловливает применение AVL-деревьев только там, где поиск является
доминирующей операцией.
Программа 13.4. Оценка AVL-деревьев
Эта программа сравнивает сбалансированное и обычное бинарное дерево
поиска, каждое из которых содержит N случайных чисел. Они хранятся
в едином массиве и включаются в оба дерева. Для каждого элемента
массива осуществляется его поиск в обоих деревьях. Длины поисковых
путей суммируются, а затем подсчитывается средняя длина поиска по
каждому дереву.
Программа прогоняется на 1000- и на 10000-элементном массивах.
Обратите внимание, что на случайных данных поисковые характеристики
AVL-дерева несколько лучше. В самом худшем случае вырожденное дерево
поиска, содержащее 1000 элементов, имеет среднюю глубину 500, в то
время как средняя глубина AVL-дерева всегда равна 9.
#include <iostream.h>
#include "bstree.h"
#include "avltree.h"
#include "random.h"
// загрузить массив, бинарное поисковое дерево и AVL-дерево
// одинаковыми множествами, состоящими из п случайных чисел от 0 до 999
void SetupLists(BinSTree<int> fiTreel, AVLTree<int> &Tree2,
int A[], int n)
{
int i;
RandomNumber rnd;
// запомнить случайное число в массиве А, а также включить его
// в бинарное дерево поиска и в AVL-дерево
for (i=0; i<n; i++)
{
A[i] = rnd.Random(1000);
Treel.Insert(A[i]);
Tree2.Insert(A[i]);
}
}
// поиск элемента item на дереве t. накапливается суммарная длина поиска
template <class T>
void PathLength(TreeNode<T> *t, long &totallength, int item)
{
// возврат, если элемент найден или отсутствует в списке
if (t == NULL I| t->data « item)
return;
else
{
// перейти на следующий уровень.
// увеличить суммарную длину пути поиска
totallength++;
if (item < t->data)
PathLength(t->Left{), totallength, item);
else
PathLength(t->Right(), totallength, item);
}
}
void main(void);
{
// переменные для деревьев и массива
BinSTree<int> binTree;
AVLTree<int> avlTree;
int *A;
// суммарные длины поисковых путей элементов массива
//в бинарном дереве поиска и в AVL-дереве
long totalLengthBintree = 0, totalLengthAVLTree = 0;
int n, i;
cout « "Сколько узлов на дереве? ";
cin » n;
// загрузить случайными числами массив и оба дерева
SetupLists(binTree, avlTree, A, n);
for (i=0; i<n; i++)
{
PathLength(binTree.GetRoot(), totalLengthBintree, A[i]);
PathLength((TreeNode<int> *)avlTree.getRoot(),
totalLengthAVLTree, A[i]);
}
cout « "Средняя длина поиска для бинарного дерева = "
« float(totalLengthBintree)/n « endl;
cout « "Средняя длина поиска для сбалансированного дерева - "
« float(totalLengthAVLTree)/n « endl;
>
/*
<Прогон #1 программы 13.4>
Сколько узлов на дереве? 1000
Средняя длина поиска для бинарного дерева = 10.256
Средняя длина поиска для сбалансированного дерева = 7.901
<Прогон #2 программы 13.4>
Сколько узлов на дереве? 10000
Средняя длина поиска для бинарного дерева = 12.2822
Средняя длина поиска для сбалансированного дерева = 8.5632
*/
13.7. Итераторы деревьев
Мы уже убедились в силе итераторов, применяемых для обхода таких
линейных структур, как массивы и последовательные списки. Сканирование
узлов дерева более сложно, так как дерево является нелинейной структурой и
существует не один порядок прохождения. Утилиты класса TreeNode из гл. 11
реализуют прямой, симметричный и обратный алгоритмы рекурсивного
прохождения. Проблема каждого из этих методов прохождения состоит в том, что
до завершения рекурсивного процесса из него невозможно выйти. Нельзя
остановить сканирование, проверить содержимое узла, выполнить какие-нибудь
операции с данными, а затем вновь продолжить сканирование со следующего
узла дерева. Используя же итератор, клиент получает средство сканирования
узлов дерева, как если бы они представляли собой линейный список, без
обременительных деталей алгоритмов прохождения, лежащих в основе процесса.
Итератор симметричного метода прохождения
В гл. 12 мы разработали абстрактный класс Iterator для создания
множества базовых методов прохождения списков. Класс Iterator задает общий
формат для методов прохождения независимо от деталей их реализации в
базовом классе. В данном разделе на основе этого базового класса строится
итератор симметричного бинарного дерева. Симметричное прохождение
бинарного дерева поиска, в процессе которого узлы посещаются в порядке
возрастания их значений, является полезным инструментом.
Конструирование итераторов прямого, поперечного и обратного методов прохождения
предлагается в качестве упражнений.
ОБЪЯВЛЕНИЕ
// итератор симметричного прохождения бинарного дерева.
// использует базовый класс Iterator
template <class T>
class Inorderlterator: public Iterator<T>
{
private:
// поддерживать стек адресов узлов
Stack< TreeNode <T> * > S;
// корень дерева и текущий узел
TreeNode<T> *root, *current;
// сканирование левого поддерева, используется функцией Next
TreeNode<T> *GoFarLeft(TreeNode<T> *t);
public:
// конструктор
Inorderlterator(TreeNode<T> *tree);
// реализации базовых операций прохождения
virtual void Next(void);
virtual void Reset(void);
virtual T& Data(void);
// назначение итератору нового дерева
void SetTree(TreeNode<T> *tree);
};
ОПИСАНИЕ
Класс Inorderlterator построен по общему для всех итераторов образцу.
Метод EndOfList определен в базовом классе Iterator. Конструктор
инициализирует базовый класс и с помощью GoFarLeft определяет начальный узел
сканирования. Класс Inorderlterator находится в файле treeiter.h.
ПРИМЕР
TreeNode<int> *root; // бинарное дерево
Inorderlterator treeiter(root); // присоединить итератор
// распечатать начальный узел сканирования.
// для смешанного прохождения это самый левый узел дерева
cout << treeiter.Data();
// сканирование узлов и печать их значений
for (treeiter.Reset О; !treeiter.EndOfList(); treeiter.Next ())
cout « treeiter.Data () « " ";.
Реализация класса Inorderlterator
Итерационный симметричный метод прохождения эмулирует рекурсивное
сканирование с помощью стека адресов узлов. Начиная с корня, осуществляется
спуск вдоль левых поддеревьев. По пути указатель каждого пройденного узла
запоминается в стеке. Процесс останавливается на узле с нулевым левым
указателем, который становится первым посещаемым узлом в симметричном
сканировании. Спуск от узла t и запоминание адресов узлов в стеке выполняет метод
GoFarLeft. Вызов этого метода с t=root определяет первый посещаемый узел.
Указатель, возвращаемый
функцией GoFarLeft
// вернуть адрес крайнего узла на левой ветви узла t.
// запомнить в стеке адреса всех пройденных узлов
template <class T>
TreeNode<T> *InorderIterator<T>::GoFArLeft(TreeNode<T> *t)
{
// если t=NULL, вернуть NULL
if (t == NULL)
return NULL;
// пока не встретится узел с нулевым левым указателем,
// спускаться по левым ветвям, запоминая в стеке S
// адреса пройденных узлов, возвратить указатель на этот узел
while (t->Left() != NULL)
{
S.Push(t);
t = t->Left() ;
}
return t;
}
После инициализации базового класса конструктор присваивает элементу
данных root адрес корня бинарного дерева поиска. Узел для начала
симметричного сканирования получается в результате вызова функции GoFarLeft с
root в качестве параметра. Это возвращаемое значение становится текущим
для указателя типа TreeNode.
// инициализировать флажок iterationComplete. базовый класс
// сбрасывает его, но дерево может оказаться пустым, начальным
// узлом сканирования является самый крайний слева узел,
template <class T>
InorderIterator<T>::Inorderlterator(TreeNode<T> *tree):
Iterator<T>(), root(tree)
{
iterationComplete = (root == NULL);
current = GoFarLeft(root);
}
Метод Reset по существу является таким же, как и конструктор, за
исключением того, что он очищает стек.
Перед первым обращением к Next указатель current уже указывает на
первый узел симметричного сканирования. Метод Next работает по следующему
алгоритму.
1. Если правая ветвь узла не пуста, перейти к его правому сыну и
осуществить спуск по левым ветвям до узла с нулевым левым указателем,
попутно запоминая в стеке адреса пройденных узлов.
2. Если правая ветвь узла пуста, то сканирование его левой ветви, самого
узла и его правой ветви завершено. Адрес следующего узла,
подлежащего обработке, находится в стеке. Если стек не пуст, удалить
следующий узел. Если же стек пуст, то все узлы обработаны и сканирование
завершено.
Итерационное прохождение дерева, состоящего из пяти узлов,
изображено на следующем рисунке.
Обработка
узла В
Обработка
узла Е
t Обработка
узла D
Обработка
узла А *
Обработка
узла С
t = NULL
Алгоритм
завершен
template <class T>
void InorderIterator<T>::Next(void)
{
// ошибка, если все узлы уже посещались
if (iterationComplete)
{
cerr « "Next: итератор прошел конец списка!" « endl;
exit(l);
}
// current - текущий обрабатываемый узел.
// если есть правое поддерево, спуститься до конца по его левой ветви,
// попутно запоминая в стеке адреса пройденных узлов
if (current->Right() != NULL)
current = GoFarLeft(current->Right());
// правого поддерева нет, но в стеке есть другие узлы,
// подлежащие обработке, вытолкнуть из стека новый текущий адрес
else if (IS.StackEmpty()) // продвинуться вверх по дереву
current = S.PopO;
// нет ни правого поддерева ни узлов в стеке, сканирование завершено
else
iterationComplete = 1;
}
Приложение: алгоритм TreeSort
Когда объект типа Inorderlterator осуществляет прохождение дерева поиска,
узлы проходятся в сортированном порядке и, следовательно, можно построить
еще один алгоритм сортировки, называемый TreeSort. Этот алгоритм
предполагает, что элементы изначально хранятся в массиве. Поисковое дерево служит
фильтром, куда элементы массива копируются в соответствии с алгоритмом
включения в бинарное дерево поиска. Осуществляя симметричное
прохождение этого дерева и записывая элементы снова в массив, мы получаем в
результате отсортированный список. На рис. 13.5 показана сортировка 8-элементного
массива. Указанный алгоритм реализуется функцией TreeSort, которая
находится в файле treesort.h.
Рис 13.5. Алгоритм TreeSort
#include "bstree.h"
♦include "treeiter.h"
// использование бинарного дерева поиска для сортировки массива
template <class T>
void TreeSort(T arr[], int n)
{
// бинарное дерево поиска, в которое копируется массив
BinSTree<T> sortTree;
int i;
// включить каждый элемент массива в поисковое дерево
for (i=0; i<n; i++)
sortTree.Insert(arr[i]);
// объявить итератор симметричного прохождения для sortTree
InorderIterator<T> treeSortlter(sortTree.GetRoot());
// выполнить симметричное прохождение дерева.
// скопировать каждый элемент снова в массив
i = 0;
while (!treeSortlter.EndOfList())
{
arr[i++] * treeSortlter.Data();
treeSortlter.Next();
}
}
Эффективность сортировки включением в дерево. Ожидаемое число
сравнений, необходимых для включения узла в бинарное дерево поиска, равно
0(log2n). Поскольку в дерево включается п элементов, средняя эффективность
должна быть 0(n log2n). Однако в худшем случае, когда исходный список
отсортирован в обратном порядке, она составит 0(п2). Соответствующее дерево
поиска вырождается в связанный список. Покажем, что худший случай требует
0(п2) сравнений. Первое включение требует 0 сравнений. Второе включение —
двух сравнений (одно с корнем и одно для определения того, в какое поддерево
следует вставлять данное значение). Третье включение требует трех сравнений,
4-е — четырех, ..., п-е включение требует п сравнений. Тогда общее число
сравнений равно:
0 + 2 + 3+ ... +п= {1 + 2 + 3+ ... +п) - 1 =* п(п+1)/2 -1 - 0(п2)
Для каждого узла дерева память должна выделяться динамически, поэтому
худший случай не лучше, чем сортировка обменом.
Когда п случайных значений повторно вставляются в бинарное дерево
поиска, можно ожидать, что дерево будет относительно сбалансированным.
Наилучшим случаем является законченное бинарное дерево. Для этого случая
можно оценить верхнюю границу, рассмотрев полное дерево глубиной d. На
i-ом уровне (l<i<Ld) имеется 21 узлов. Поскольку для помещения узла на уровень
i требуется i+1 сравнение, сортировка на полном дереве требует (i+1) * 21
сравнений для включения всех элементов на уровень i. Если вспомнить, что п =
2<d+1)-l, то верхняя граница меры эффективности выражается следующим
неравенством:
d d
X (i + x)2i * (d + J) X 2i e (d + l)(2d+1 - 2) - (d + l)(2d+1 - 1 - 1)
i=l i=l
= (d + l)(n - 1) = (n - 1) log2(n + 1) = 0(n log2n)
Таким образом, эффективность алгоритма в лучшем случае составит 0(n log2n).
13.8. Графы
Дерево есть иерархическая структура, которая состоит из узлов, исходящих
от корня. Узлы соединяются указателями от родителя к сыновьям. В этом
разделе мы познакомимся с графами, которые являются обобщенными
иерархическими структурами. Граф состоит из множества элементов данных,
называемых вершинами (vertices), и множества ребер (edges), соединяющих эти
вершины попарно. Ребро Е = (Vi, Vj) соединяет вершины Vi и Vj.
Вершины = {V0, Vlf V2, V3, ..., V^}
Ребра = {E0, Ei, E2, E3, ..., En.i)
Пусть вершины обозначают города, а ребра — дорожное сообщение между
ними. Движение по дорогам может происходить в обоих направлениях, и поэ-
Солт-Лэйк-Сити
Сан-Франциско
Сан-Диего
Феникс
Альбукерк
Направленный граф
Ненаправленный граф
Вершины V = {A,B,C,D,E}
Ребра Е = {(A,C)I(AID),(B,A),(B/D),(D,E),(E,B)}
Вершины V = {A,B,C,D,E}
Ребра Е = {(A,B),(A,C),(A,D),(B,A),(B,D).(B,E),
(C,A),(D,B),(D,E),(E,B),(E,D)}
Рис.13.6. Направленный и ненаправленный графы
тому ребра графа G не имеют направлений. Такой граф называется
ненапрвленным (undirected graph).
Если ребра представляют систему связи с однонаправленными
информационными потоками, то граф в этом случае становится направленным графом
(directed graph), или орграфом (digraph). На рис. 13.6 показаны графы
обоих типов. Мы сосредоточим внимание на орграфах.
В орграфе ребро задается парой (Vi9 Vj), где VA — начальная вершина, а
Vj — конечная вершина. Путь (path) P(VS, VE) есть последовательность
вершин VS=VR, VR+1, ..., VR+T=VE, где Vs — начальная вершина, VE — конечная
вершина, а каждая пара членов последовательности есть ребро. В орграфе
указывается направленный путь от VB к VE, но пути от VE к VB может и
не быть. Например, для орграфа на рис. 13.6
Путь(А,В) = {A,D,E,B}
Путь(Е,С) = {Е,В,А,С}
Путь(В,А) = {В,А}
Путь(С,Е) = {} // пути нет
Связанные компоненты
С понятием пути связано понятие связанности орграфа. Две вершины V*
и Vj связаны (connected), если существует путь от Vi к Vj. Орграф является
сильно связанным (strongly connected), если в нем существует направленный
путь от любой вершины к любой другой. Орграф является слабо связанным
(weakly connected), если для каждой пары вершин Vt и Vj существует
направленный путь P(Vi, Vj) или P(Vj, Vi). Связанность графов иллюстрируется
на рис. 13.7.
(А) Не сильно или слабо связанный
(В) Сильно связанный
(С) Слабо связанный
Рис. 13.7. Сильно и слабо связанные компоненты орграфа
Мы расширили понятие сильносвязанных вершин до сильно связанной
компоненты (strongly connected component) — максимального множества вершин
{VJ, где для каждой пары Vi и Vj существует путь от Vi к Vj и путь от Vj к Vi.
Цикл (cycle) — это путь, проходящий через три или более вершины и
связывающий некоторую вершину саму с собой. В ориентированном графе (С) на
рис. 13.7 существуют циклы для вершин А (А->С->В->А), В и С. Граф, не
содержащий циклов, называется ациклическим (acycle).
Во взвешенном орграфе (weighted digraph) каждому ребру приписано
значение, или вес. На транспортном графе веса могут представлять расстояния
между городами. На графе планирования работ веса ребер определяют
продолжительность конкретной работы.
Прокладка внешнего
трубопровода
5 дней
15 дней
Прокладка внутреннего
трубопровода
1 день
Начало
8 дней
Возведение
стен
3 дня
7 дней
6 дней
2 дня
Конец
8 дней
2 дня
Бетонирование
Подключение
канализации
Покрытие
крыши
13.9. Класс Graph
В этом разделе мы опишем структуру данных для взвешенного орграфа.
Начнем с математического определения графа как основы абстрактного типа
данных (ADT) Graph. Вершины задаются в виде списка элементов, а ребра —
в виде списка упорядоченных пар вершин.
Объявление абстрактного типа данных Graph
Взвешенный орграф состоит из вершин и взвешенных ребер. ADT включает
в себя операции, которые будут добавлять или удалять эти элементы данных.
Для каждой вершины VA определяются все смежные с ней вершины Vj,
которые соединяются с V\ ребрами E(Vi, Vj).
ADT Graph
Данные
Множество вершин {Vt} и ребер {Е±}. Ребро есть пара (Vif Vj), которая
указывает на связь вершины V± с вершиной Vj. Приписанный каждому ребру
вес определяет стоимость прохождения по этому ребру.
Операции
Конструктор
Вход: Нет
Обработка: Создает граф в виде множества вершин и ребер.
InsertVertex
Вход: Новая вершина.
Предусловия: Нет
Обработка: Вставить новую вершину в множество вершин.
Выход: Нет
Постусловия: Список вершин увеличивается.
InsertEdge
Вход: Пара вершин VL и Vj с весом W.
Предусловия: VL и Vj должны принадлежать множеству вершин, а ребро
(Vif Vj) не должно принадлежать множеству ребер.
Обработка: Вставить ребро {Vit Vj) с весом W в множество ребер.
Выход: Нет
Постусловия: Множество ребер увеличивается.
DeleteVertex
Вход: Ссылка на вершину VD.
Предусловия: Входная вершина должна принадлежать множеству вершин.
Обработка: Удалить вершину VD из списка вершин. Удалить все входящие
и исходящие ребра этой вершины.
Выход: Нет
Постусловия: Множество вершин и множество ребер модифицируются.
DeleteEdge
Вход: Пара вершин VA и Vj.
Предусловия: Входные вершины должны принадлежать множеству вершин.
Обработка: Если ребро {Vif Vj) существует,
удалить его из множества ребер.
Выход: Нет
Постусловия: Множество ребер модифицируется.
GetNeighbors
Вход: Вершина V.
Предусловия: Нет
Обработка: Идентифицировать все смежные с V вершины VE, такие,
что (V, VE) есть ребро.
Выход: Список смежных вершин.
Постусловия: Нет
GetWeight
Вход: Пара вершин Vi и Vj.
Предусловия: Входные вершины должны принадлежать множеству вершин.
Обработка: Выдать вес ребра (Vif Vj), если оно существует.
Выход: Вес ребра или 0, если ребра не существует.
Постусловия: Нет
Конец ADT Graph
Представление графов. Существует много способов представления
орграфов. Можно просто хранить вершины в виде последовательного списка
Vo, Vi, ..., Vm-l, а ребра задавать квадратной матрицей размером m x m,
называемой матрицей смежности (adjcency matrix). Здесь строка i и
столбец j соответствуют вершинам Vi и Vj. Каждый элемент (i, j) этой матрицы
содержит вес ребра Eij = (Vi, Vj) или 0, если такого ребра нет. Для
невзвешенного орграфа элементы матрицы смежности содержат 0 или 1,
показывая отсутствие или наличие соответствующего ребра. Ниже
приводятся примеры орграфов со своими матрицами смежности.
В другом способе представления графов каждая вершина ассоциируется
со связанным списком смежных с ней вершин. Эта динамическая модель
хранит информацию лишь о фактически принадлежащих графу вершинах.
Для взвешенного орграфа каждый узел связанного списка содержит поле
веса. Примеры спискового представления орграфов даны ниже.
Вершины Список смежных вершин
Вершины
Список смежных вершин
Класс Graph, рассматриваемый в этом разделе, использует матричное
представление ребер. Мы используем статическую модель графа, которая
предполагает конечное число вершин. Матричное представление упрощает
реализацию класса и позволяет сосредоточиться на целом ряде алгоритмов
обработки графов. Реализация на основе связанных списков предлагается в
упражнениях. Основными особенностями класса Graph являются
представление ADT Graph, метод ReadGraph и ряд поисковых алгоритмов,
осуществляющих прохождение вершин способами "сначала в глубину" и "сначала
в ширину". Данный класс включает также итератор списка вершин для
использования в приложениях.
Спецификация класса Graph
ОБЪЯВЛЕНИЕ
const int MaxGraphSize =25;
template <class T>
class Graph
{
private:
// основные данные включают список вершин, матрицу смежности
//и текущий размер (число вершин) графа
SeqList<T> vertexList;
int edge [MaxGraphSize];
int graphsize;
// методы для поиска вершины и указания ее позиции в списке
int FindVertex(SeqList<T> &L, const T& vertex);
int GetVertexPos(const T& vertex);
public:
// конструктор
Graph(void);
// методы тестирования графа
int GraphEmpty(void) const;
int GraphFull(void) const;
// методы обработки данных
int NumberOfVertices(void) const;
int NumberOfEdges(void) const;
int GetWeight(const T& vertexl, const T& vertex2);
SeqList<T>& GetNeighbors(const T& vertex);
// методы модификации графа
void InsertVertex(const T& vertex);
void InsertEdge(const T& vertexl, const T& vertex2, int weight);
void DeleteVertex(const T& vertex);
void DeleteEdge(const T& vertexl, const T& vertex2);
// утилиты
void ReadGraph(char *filename);
int MinimumPath(const T& sVertex, const T& sVertex);
SeqList<T>& DepthFirstSearch(const T& beginVertex);
SeqList<T>& BreadthFirstSearch(const T& beginVertex);
// итератор для обхода вершин
friend class VertexIterator<T>;
};
ОПИСАНИЕ
Данные-члены класса включают вершины, хранящиеся в виде
последовательного списка, ребра, представленные двумерной целочисленной матрицей
смежности, и переменную graphsize, являющуюся счетчиком вершин.
Значение graphsize возвращается функцией NumberOfVertices.
Утилита FindVertex проверяет наличие вершины в списке L и используется
в поисковых методах. Метод GetVertexPos вычисляет позицию вершины vertex
в vertexList. Эта позиция соответствует индексу строки или столбца в матрице
смежности.
Методу ReadGraph передается в качестве параметра имя файла с входным
описанием вершин и ребер графа.
Класс Vertexlterator является производным от класса SeqListlterator и
позволяет осуществлять прохождение вершин. Итератор упрощает приложения.
ПРИМЕР
Graph <char> G; // граф с символьными вершинами
G.ReadGraph("graph.dat"); // ввести данные из graph.dat
// Пример входного описания графа
<Количество вершин> 4
ВершинаО А
Вершина1 В
Вершина2 С
ВершинаЗ D
<Количество ребер> 5
РеброО ВесО А С 1
Ребро1 Bed A D 1
Ребро2 Вес2 В А 1
РеброЗ ВесЗ С В 1
Ребро4 Вес4 D А 1
VertexIterator<char> viter(G); // итератор для вершин
SeqList<char>L;
for (viter.Reset(); !viter.EndOfList(); viter.Next())
{
cout « "Вершины, смежные с вершиной " « viter.DataO « ": ";
L - G.GetNeighbors(viter.DataO);
// распечатать смежные вершины
SeqListIterator<char> liter(L); // список смежных вершин
for (liter.Reset(); Iliter.EndOfListО; liter.Next())
cout « liter.Data() « " ";
}
Реализация класса Graph
Конструктор класса Graph "отвечает" за инициализацию матрицы
смежности размера MaxGraphSize x MaxGraphSize и обнуление переменной graphsize.
Конструктором обнуляется каждый элемент матрицы для указания на
отсутствие ребер.
// конструктор, обнуляет матрицу смежности и переменную graphsize
template <class T>
Graph<T>::Graph(void)
{
for (int i=0; i<MaxGraphSize; i++)
for (int j=0; j<MaxGraphSize; j++)
edgefi][j] - 0;
graphsize = 0;
}
Подсчет компонентов графа. Переменная graphsize хранит размер списка
вершин. Обращение к этому закрытому члену класса осуществляется посредством
метода NumberOfVertices. Оператор GraphEmpty проверяет, пуст ли список.
Доступ к компонентам графа. Компоненты графа содержатся в списке
вершин и матрице смежности. Итератор вершин, являясь дружественным по
отношению к классу Graph, позволяет сканировать список вершин. Этот
итератор — наследник класса SeqListlterator.
template ass T>
class Vertexlterator: public SeqListIterator<T>
{
public:
Vertexlterator(Graph<T>& G) ;
);
Конструктор просто инициализирует базовый класс для прохождения
списка вершин vertexList.
template ass T>
VertexIterator<T>::Vertexlterator(Graph<T>& G):
SeqListIterator<T> (G.vertexList)
{}
Итератор сканирует элементы vertexList и используется для реализации
функции GetVertexPos, которая осуществляет сканирование списка вершин и
возвращает позицию вершины в этом списке.
template ass T>
int Graph<T>::GetVertexPos(const T& vertex)
{
SeqListIterator<T> liter(vertexList);
int pos * 0;
while(!liter.EndOfList () && liter.Data() !« vertex)
{
pos++;
liter.Next();
}
return pos;
}
Метод GetWeight возвращает вес ребра, соединяющего vertexl и vertex2.
Чтобы получить позиции этих двух вершин в списке, а следовательно, и строку
со столбцом в матрице смежности, используется функция GetVertexPos. Если
любая из двух вершин отсутствует в списке вершин, метод возвращает -1.
Метод GetNeighbors создает список вершин, смежных с vertex. Этот список
является выходным параметром и может быть просканирован с помощью
итератора последовательных списков. Если vertex не имеет смежных вершин,
метод возвращает пустой список.
// возвратить список смежных вершин
template <class T>
SeqList<T>fi Graph::GetNeighbors(const T& vertex)
{
SeqList<T> *L;
SeqListIterator<T> viter(vertexList);
// создать пустой список
L = new SeqList<T>;
// позиция в списке, соответствующая номеру строки матрицы смежности
int pos ■ GetVertexPos(vertex);
// если вершины vertex нет в списке вершин, закончить
if (pos -« -1)
{
cerr << "GetNeighbors: такой вершины нет в графе." « endl;
return *L; // вернуть пустой список
}
// сканировать строку матрицы смежности и включать в список
// все вершины, имеющие ребро ненулевого веса из vertex
for (int i=0; Kgraphsize; i++)
{
if (edge[pos][i] > 0)
L->lnsert(viter.Data() ) ;
viter.Next();
}
return *L;
}
Обновление вершин и ребер. Чтобы вставить ребро, мы используем
GetVertexPos для проверки наличия vertexl и vertex2 в списке вершин. Если
какая-либо из них не будет обнаружена, выдается сообщение об ошибке и
осуществляется возврат управления. Если позиции posl и pos2 получены,
метод InsertEdge записывает вес ребра в элемент (posl, pos2) матрицы
смежности. Эта операция выполняется за время О(п), поскольку каждый вызов
GetVertexPos требует О(п) времени.
Метод Delete Vertex класса Graph удаляет вершину из графа. Если вершины
нет в списке, выдается сообщение об ошибке и осуществляется возврат
управления. В противном случае удаляются все ребра, соединяющие удаляемую
вершину с другими вершинами. При этом в матрице смежности должны быть
скорректированы три области. Поэтому эта операция выполняется за время
0(п2), так как каждая область является частью матрицы n x п.
pos
pos
Область I: Сдвинуть индекс столбца влево
Область II: Сдвинуть индекс строки вверх и индекс столбца влево
Область III: Сдвинуть индекс строки вверх
// удалить вершину из списка вершин и скорректировать матрицу
// смежности, удалив принадлежащие этой вершине ребра
template <class T>
void Graph<T>::DeleteVertex(const T& vertex)
{
// получить позицию вершины в списке вершин
int pos = GetVertexPos(vertex);
int row, col;
// если такой вершины нет, сообщить об этом и вернуть управление
if (pos == -1)
{
cerr « "DeleteVertex: вершины нет графы" « endl;
return;
}
// удалить вершину и уменьшить graphsize
vertexList.Delete(vertex);
graphsize--;
// матрица смежности делится на три области
for (row=0; row<pos; row++) // область I
for (col=pos+l; col<graphsize; col++)
edge[row][col-1] = edge[row][col];
for (row=pos+l; row<graphsize; row++) // область II
for (col=pos+l; col<graphsize; col++)
edge[row-1][col-1] = edge[row][col];
for (row=pos+l; row<graphsize; row++) // область III
for {col=0; col<pos; col++)
edge[row-1][col] = edge[row][col];
}
Удаление ребра производится путем удаления связи между двумя
вершинами. После проверки наличия вершин в vertexList метод DeleteEdge присваивает
данному ребру нулевой вес, оставляя все другие ребра неизменными. Если
такого ребра нет в графе, процедура выдает сообщение об ошибке и
завершается.
Способы прохождения графов
Для прохождения нелинейных структур требуется разработать стратегию
доступа к узлам и маркирования узлов после обработки. Поисковые методы
для бинарных деревьев имеют свои аналоги для графов. В нисходящем обходе
бинарного дерева применяется такая стратегия, при которой сначала
выполняется обработка узла, а затем уже продвижение вниз по поддереву.
Обобщением прямого метода прохождения для графов является поиск "сначала в
глубину" (depth-first). Начальная вершина передается в качестве параметра и
становится первой обрабатываемой вершиной. По мере продвижения вниз до
тупика смежные вершины запоминаются в стеке, с тем чтобы можно было к
ним вернуться и продолжить поиск по другому пути в случае, если еще
остались необработанные вершины. Обработанные вершины образуют множество
всех вершин, достижимых из начальной вершины.
Характерное для деревьев поперечное сканирование начинается с корня, а
обход узлов осуществляется уровень за уровнем сверху вниз. Аналогичная
стратегия применяется при поиске "сначала в ширину" (breadth-first) на гра-
фах, когда, начиная с некоторой начальной вершины, производится обработка
каждой смежной с ней вершины. Затем сканирование продолжается на
следующем уровне смежных вершин и т.д. до конца пути. При этом для запоминания
смежных вершин используется очередь. Проиллюстрируем оба поисковых
алгоритма на следующем графе. В данном случае начальной вершиной является А.
Поиск "сначала в глубину". Для хранения обработанных вершин
используется список L, а для запоминания смежных вершин — стек S. Поместив
начальную вершину в стек, мы начинаем итерационный процесс выталкивания
вершины из стека и ее обработки. Когда стек становится пустым, процесс
завершается и возвращает список обработанных вершин. На каждом шаге
используется следующая стратегия.
Вытолкнуть вершину V из стека и проверить по списку L, была ли
она обработана. Если нет, произвести обработку этой вершины, а также
воспользоваться удобным случаем и получить список смежных с ней
вершин. Включить V в список L, чтобы избежать повторной обработки.
Поместить в стек те смежные с V вершины, которых еще нет в списке L.
В нашем примере предполагалось, что вершина А является начальной.
Поиск начинается с выталкивания А из стека и обработки этой вершины. Затем
А включается в список обработанных вершин, а смежные с ней вершины В и
G помещаются в стек. После обработки А стек S и список L выглядят
следующим образом:
Стек S
Список L
Итерация продолжается. Вершина G выталкивается из стека. Так как этой
вершины пока нет в списке L, она включается в него, а в стек помещается
единственная смежная с ней вершина F:
Стек S
Список L
Вытолкнув из стека вершину F и поместив ее в список L, мы достигаем
тупика, поскольку смежная с F вершина А уже находится в L. В стеке остается
вершина В, которая была идентифицирована как смежная с А на первой фазе
поиска:
Стек S
Список L
Вершины В и С обрабатываются в указанном порядке. Теперь стек содержит
вершины D и Е, являющиеся смежными с вершиной С:
Стек S
Список L
У вершины Е две смежные вершины: D и F, и обе они являются
подходящими для записи в стек. Однако F уже была обработана на пути A-G-F и
поэтому пропускается. Зато вершина D помещается в стек дважды, поскольку
наш алгоритм не "знает", что D достижима из С:
Стек S Список L
Поиск завершается после обработки вершины D. Второй экземпляр D в стеке
игнорируется, так как эта вершина уже находится в списке L:
Список L
// начиная с начальной вершины, сформировать список вершин,
// обрабатываемых в порядке обхода "сначала в глубину"
template <class T>
SeqList <T> & Graph<T>::DepthFirstSearch{const T& beginVertex)
{
// стек для временного хранения вершин, ожидающих обработки
Stack<T> S;
// L - список пройденных вершин. adjL содержит вершины,
// смежные с текущей. L создается динамически, поэтому можно
// возвратить его адрес
SeqList<T> *L, adjL;
// iteradjL - итератор списка смежных вершин
SeqListIterator<T> iteradjL(adjL);
Т vertex;
// инициализировать выходной список.
// поместить начальную вершину в стек
L = new SeqList<T>;
S.Push(beginVertex);
// продолжать сканирование, пока не опустеет стек
while (IS.StackEmpty())
{
// вытолкнуть очередную вершину
vertex = S.PopO ;
// проверить ее наличие в списке L
if (!FindVertex(*L, vertex))
{
// если нет, включить вершину в L,
//а также получить все смежные с ней вершины
(*L).Insert(vertex);
adjL = GetNeighbors(vertex);
// установить итератор на текущий adjL
iteradjL.SetList(adjL);
// сканировать список смежных вершин.
// помещать в стек те из них, которые отсутствуют в списке L
for (iteradjL.Reset(); !iteradjL.EndOfList()/ iteradjL.Next())
if (!FindVertex(*L, iteradjL.Data()))
S.Push(iteradjL.Data());
}
}
// возвратить выходной список
return *L;
}
Поиск "сначала в ширину". Как и в поперечном прохождении бинарного
дерева, при поиске "сначала в ширину" для хранения вершин используется
очередь, а не стек. Итерационный процесс продолжается до тех пор, пока
очередь не опустеет.
Удалить вершину V из очереди и проверить ее наличие в списке
обработанных вершин. Если вершины V нет в списке L, включить ее в этот
список. Одновременно получить все смежные с V вершины и вставить в
очередь те из них, которые отсутствуют в списке обработанных вершин.
Если применить этот алгоритм к рассмотренному в предыдущем примере
графу, то вершины будут обрабатываться в следующем порядке:
А В G С F D Е
Анализ сложности. В описанных алгоритмах поиска посещение каждой
вершины требует времени вычислений О(п). При добавлении вершины в
список обработанных вершин для обнаружения смежных с ней вершин
проверяется строка матрицы смежности. Каждая строка — это О(п),
следовательно общее время вычислений равно п*0(п) = 0(п2). Число сравнений,
требующихся в случае матричного представлении графа, не зависит от
количества ребер в графе. Даже если в графе относительно мало ребер
("разреженный граф"), мы обязаны произвести п сравнений для каждой вершины.
В списковом представлении графа быстродействие алгоритма поиска зависит
от плотности ребер в графе. В лучшем случае ребер нет и длина каждого
списка смежных вершин равна 1. Тогда время вычислений для каждого
поиска будет 0(п+п) = О(п). В худшем случае каждая вершина связана с
каждой и длина каждого списка смежных вершин равна п. Тогда алгоритм
поиска имеет порядок 0(п2).
Приложения
Вспомним, что орграф является сильно связанным, если существует
направленный путь от любой его вершины к любой другой. Сильная компонента
(strong component) есть подмножество вершин, сильно связанных друг с
другом. Сильно связанный граф имеет одну сильную компоненту, но всякий
граф может быть разбит на ряд сильных компонент. Например, на рис. 13.8
граф разбит на три сильных компоненты.
В теории графов для определения сильных компонент используются
классические алгоритмы. В данном приложении мы используем для этого поиск
"сначала в глубину". Функция PathConnect проверяет существование
направленного пути от вершины v к вершине w и возвращает булевские TRUE и
FALSE, соответственно.
Компоненты
А,В,С
D,F,G
Е
template <class T>
int PathConnect (Graph<T> &G, T v, T w)
{
SeqList<T> L;
// найти вершины, связанные с v
L = G.DepthFirstSearch(v);
// если w в их числе, вернуть TRUE
if (L.Find(w))
return 1;
else
return 0;
}
Функция ConnectedComponent начинает работу с пустого списка вершин с
именем markedList. Этот список все время содержит коллекцию вершин,
которые были обнаружены в сильной компоненте. Итератор осуществляет обход
вершин графа. Каждая вершина V проверяется на наличие в списке markedList.
Если ее там нет, то должна быть построена новая сильная компонента,
содержащая V. Список scList, который будет содержать новую сильную компоненту,
очищается, и с помощью поиска "сначала в глубину" формируется список L
всех вершин, достижимых из V. Для каждой вершины списка L с помощью
функции PathConnect проверяется существование пути обратно к V. Если
таковой существует, вершина включается в scList и в markedList. Обратите
внимание, что вершина вставляется в оба этих списка. Поскольку существует путь
от V к каждой вершине из scList и путь от каждой вершины из scList обратно
к V, то, следовательно, существует путь между любыми двумя вершинами из
scList. Эти вершины и есть очередная сильная компонента. Так как каждая
вершина в scList црисутствует также в markedList, она не будет
рассматриваться повторно.
template <class T>
void ConnectedComponent (Graph<T> &G)
{
VertexIterator<T> viter(G);
SeqList<T> markedList, scList, L, K;
for (viter.Reset(); !viter.EndOfList(); viter.Next())
{
// проверять в цикле каждую вершину viter.Data ()
if (JmarkedList.Find(viter.Data()))
// если не помечен, включить в сильную компоненту
{
scList.ClearList();
// получить вершины, достижимые из viter.Data()
L = G.DepthFirstSearch(viter.Data());
// искать в списке вершины, из которых достижима вершина viter.Data ()
SeqListIterator<T> liter(L);
for (liter.Reset(); Iliter.EndOfList(), liter.Next())
if (PathConnect(G, liter.Data(), viter.Data()))
{
// вставить вершины в текущую сильную компоненту и в markedList
scList.Insert(liter.Data());
markedList.Insert(liter.Data());
}
PrintList(scList); // распечатать сильную компоненту
cout « endl;
}
}
)
Программа 13.5. Сильные компоненты
Эта программа находит сильные компоненты в графе, изображенном
на рис. 13.8. Граф вводится из файла sctest.dat с помощью ReadGraph.
Функции PathConnect, ConnectedComponent и PrintList находятся в файле
conncomp.h.
#include <iostream.h>
#include <fstream.h>
#include "graph.h"
#include "conncomp.h"
void main(void)
{
Graph<char> G;
G.ReadGraph("sctest.dat");
cout « "Сильные компоненты:" « endl;
ConnectedComponent(G);
}
/*
<Прогон программы 13.5>
Сильные компоненты:
ABC
D G F
E
*/
Минимальный путь. Методы прохождения "сначала в глубину" и "сначала
в ширину" находят вершины, достижимые из начальной вершины. При этом
движение от вершины к вершине не оптимизируется в смысле минимального
пути. Между тем во многих приложениях требуется выбрать путь с
минимальной "стоимостью", складывающейся из весов ребер, составляющих путь.
Для решения этой задачи мы представляем класс Pathlnfo. Объект,
порождаемый этим классом, описывает путь, существующий между двумя
вершинами, и его стоимость. Объекты типа Pathlnfo запоминаются в очереди
приоритетов, которая обеспечивает прямой доступ к объекту с минимальной
стоимостью.
template <class T>
struct Pathlnfo
{
Т startV, endV;
};
template <class T>
int operator <= (const PathInfo<T>& a, const PathInfo<T>& b)
{
return a.cost <= b.cost;
}
Так как между вершинами графа может существовать несколько разных
путей, объекты типа Pathlnfo могут соответствовать одним и тем же вершинам,
но иметь разные стоимости. Например, в показанном ниже графе между
вершинами А и D существуют три пути с различными стоимостями.
Путь
А- С - D
А- В - D
А- В - С- D
Стоимость
13
14
11
Для сравнения стоимостей в классе Pathlnfo определен оператор "<=".
Алгоритм проверяет объекты типа Pathlnfo, хранящиеся в очереди
приоритетов, и выбирает объект с минимальной стоимостью. Определение
минимального пути между начальной (sVertex) и конечной (eVertex) вершинами
иллюстрируется на следующем графе. Если между ними нет вообще никакого
пути, алгоритм завершается выдачей соответствующего сообщения. Пусть
вершина А будет начальной, a D — конечной.
Начать с создания первого объекта типа Pathlnfo, соединяющего
начальную вершину саму с собой при нулевой начальной стоимости. Включить
объект в очередь приоритетов.
Очередь приоритетов
Для нахождения минимального пути мы следуем итерационному процессу,
который удаляет объекты из очереди приоритетов. Если конечная вершина
в объекте есть еVertex, то мы имеем минимальный путь, стоимость которого
находится в поле cost. В противном случае просматриваем все вершины,
смежные с текущей конечной вершиной endV, и в искомый путь,
начинающийся из sVertex, включается еще одно ребро.
В нашем примере мы хотим найти минимальный путь от А до D. Удаляем
единственный объект Pathlnfo, в котором endV = А. Если бы вершина А
являлась заданной конечной вершиной еVertex, процесс завершился бы с
нулевой минимальной стоимостью. Поскольку вершина А не есть еVertex,
она запоминается в списке L, содержащим все вершины, до которых
минимальный путь из А известен. Смежными с А вершинами являются вершины
В, С и Е. Для каждой из них создается объект типа Pathlnfo, и все эти
объекты помещаются в очередь приоритетов. Стоимость пути из А до каждой
из этих вершин равна
стоимость (A, endV) + sectendV, <смежная вершина>)
Объект Pathlnfo
0А,в
0А,с
Од,Е
startV
А
А
А
endV
В
С
Е
Стоимость
4
12
4
Объекты включаются в очередь приоритетов в следующем порядке:
Очередь приоритетов
На следующем шаге объект 0АВ удаляется из очереди приоритетов. В
нем вершина В есть endV с минимальной стоимостью 4. Поскольку вершины
В нет в списке L, она включается в него. Ясно, что не существует
последующего пути от А к В со стоимостью меньшей, чем 4. Если бы существовал
путь А-Х-...-В и смежная с А вершина X находилась бы от нее на расстоянии
меньшем, чем 4, то вершина X оказалась бы первой в очереди приоритетов
и была бы удалена оттуда раньше вершины В.
Смежными с В вершинами являются А, С и D. Так как А уже в списке
L, объекты типа Pathlnfo создаются для вершин С и D и включаются в
очередь приоритетов.
Объект Pathlnfo
0Б.с
Ob,d
startV
В
В
endV
С
С
Стоимость
10=4+6
12=4+8
Результирующая очередь приоритетов содержит четыре элемента. Обратите
внимание, что два разных объекта заканчиваются в вершине С. Минимальный
из них, имеющий стоимость 10, был только что добавлен в очередь
приоритетов и представляет путь А-В-С. Прямой путь А-С, определенный на первом
шаге, имеет стоимость 12.
Очередь приоритетов
После удаления объекта 0АЕ и установления минимальной стоимости пути
от А к Е равной 4 создается объект 0E)D стоимостью 14.
Очередь приоритетов
После очередного удаления объекта с минимальной стоимостью, которым
являлся Овс, вершина С может быть добавлена в список L, так как 10
является минимальной стоимостью пути от А к С.
Поскольку конечной вершиной искомого минимального пути является D,
мы ожидаем удаления объекта с endV=D. У вершины С есть смежные
вершины В и D. Так как В уже обработана, в очередь приоритетов включается
только объект Oc,d*
Объект Pathlnfo
Oc>d
startV
С
endV
D
Стоимость
24=10+14
После удаления объекта 0А)С из очереди приоритетов он отбрасывается,
так как С уже есть в списке. Теперь очередь приоритетов имеет три элемента.
Очередь приоритетов
Удаляя 0b,d из очереди приоритетов, мы тем самым устанавливаем
минимальную стоимость пути от А к D равной 12.
template <class T>
int Graph<T>::MinimumPath(const T& sVertex, const T& eVertex)
{
// очередь приоритетов, в которую помещаются объекты,
// несущие информацию о стоимости путей из sVertex
PQueue< PathInfo<T> > PQ(MaxGraphSize);
// используется при вставке/удалении объектов Pathlnfo
// в очереди приоритетов
PathInfo<T> pathData/
// L — список всех вершин, достижимых из sVertex и стоимость
// которых уже учтена. adjL — список вершин, смежных с посещаемой
// в данный момент, для сканирования adjL используется итератор
// adjLiter
SeqList<T> L, adjL;
SeqListIterator<T> adjLiter(adjL);
T sv, ev;
int mincost;
// сформировать начальный элемент очереди приоритетов
pathData.startV = sVertex;
pathData.endV = sVertex;
// стоимость пути из sVertex в sVertex равна О
pathData.cost = 0;
PQ.PQInsert(pathData);
// обрабатывать вершины, пока не будет найден минимальный путь
// к eVertex или пока не опустеет очередь приоритетов
while ( IPQ.PQEmptyO )
{
// удалить элемент приоритетной очереди и запомнить
// его конечную вершину и стоимость пути от sVertex
pathData = PQ.PQDelete();
ev = pathData.endV;
mincost = pathData.cost;
// если это eVertex,
// то минимальный путь от sVertex к eVertex найден
if (ev =« eVertex)
break;
// если конечная вершина уже имеется в L,
// не рассматривать ее снова
if (!FindVertex(L, ev))
{
// Включить ev в список L
L.Insert(ev);
// найти все смежные с ev вершины. Для тех из них,
// которых нет в L, сформировать объекты Pathlnfo с начальными
// вершинами, равными ev, и включить их в очередь приоритетов
sv = ev;
adjL = GetNeighbors(sv);
// новый список adjL сканируется итератором adjLiter
adjLiter.SetList(adjL);
for (adjLiter.Reset(); ladjLiter.EndOfList(); adjLiter.Next())
{
ev = adjLiter.Data();
if (!FindVertex{L,ev))
{
// создать новый элемент приоритетной очереди
pathData.startV = sv;
pathData.endV = ev;
// стоимость равна текущей минимальной стоимости
// плюс стоимость перехода от sv к ev
pathData.cost = mincost + GetWeight (sv, ev);
PQ.PQInsert(pathData);
}
}
}
}
if (ev « eVertex)
return mincost;
else
return -1;
}
Программа 13.6. Система авиаперевозок
Транспортная система авиакомпании имеет список городов на
некотором маршруте полетов. Пользователь вводит исходный город, а процедура
определения минимального пути выдает кратчайшие расстояния между
этим городом и всеми прочими пунктами назначения. Эта авиалиния
соединяет главные города на Западе.
Солт-Лэйк-Сити
Сан-Франциско
Сан-Диего
Феникс
Альбукерк
#include <iostream.h>
#include <fstream.h>
#include "strclass.h"
#include "graph.h" // метод MinimumPath
void main(void)
{
// вершины типа символьных строк (названия городов)
Graph<String> G;
String S;
// ввод описания транспортного графа
G.ReadGraph("airline.dat");
// запросить аэропорт отправления
cout « "Выдать мин. расстояние при отправлении из ";
cin » S;
//с помощью итератора пройти список городов и определить
// мин. расстояния от точки отправления
VertexIterator<String> viter(G);
for (viter.Reset(); !viter.EndOfList(); viter.Next())
cout « "Минимальное расстояние от аэропорта " << S «
« " до аэропорта " « viter.Data() « " = "
« G.MinimumPath(S, viter.Data()) « endl;
}
/*
<Прогон #1 программы 13.6>
Выдать минимальное расстояние при отправлении из Солт-Лэйк-Сити
Мин. расстояние от аэропорта Солт-Лэйк-Сити до аэропорта Солт-Лэйк-Сити = О
Мин. расстояние от аэропорта Солт-Лэйк-Сити до аэропорта Альбукерк =» 604
Мин. расстояние от аэропорта Солт-Лэйк-Сити до аэропорта Феникс =648
Мин. расстояние от аэропорта Солт-Лэйк-Сити до аэропорта Сан-Франциско =752
Мин. расстояние от аэропорта Солт-Лэйк-Сити до аэропорта Сан-Диего = 1003
<Прогон #2 программы 13.б>
Выдать мин. расстояние при отправлении из Сан-Франциско
Мин. расстояние от аэропорта Сан-Франциско до аэропорта Солт-Лэйк-Сити = 752
Мин. расстояние от аэропорта Сан-Франциско до аэропорта Альбукерк = 1195
Мин. расстояние от аэропорта Сан-Франциско до аэропорта Феникс =763
Мин. расстояние от аэропорта Сан-Франциско до аэропорта Сан-Франциско = 0
Мин. расстояние от аэропорта Сан-Франциско до аэропорта Сан-Диего = 504
*/
Достижимость и алгоритм Уоршалла
Для каждой пары вершин некоторого графа говорят, что Vj достижима
из Vj тогда и только тогда, когда существует направленный путь от Vi к Vj.
Это определяет отношение достижимости R (reachability relation R). Для
каждой вершины Vi поиск "сначала в глубину" находит все вершины,
достижимые из Vie При использовании поиска "сначала в ширину" получается
серия списков достижимости, которые образуют отношение R:
Vi: <Список достижимости для Vi>
V2: <Список достижимости для V2>
* • •
Vn: <Список достижимости для Vn>
Это же отношение можно также описать с помощью матрицы
достижимости (reachability matrix) размером n x n, которая содержит 1 в позиции
(U), представляя тем самым VA R Vj. В следующем примере показаны списки
и матрица достижимости для изображенного здесь графа.
Списки достижимости
А: А В С D
В: В D
С: С В
D:
Матрица достижимости
1111
0 10 1
0 110
0 0 0 1
Матрицу достижимости можно использовать для проверки существования
пути между двумя вершинами. Если элемент (ij) равен 1, то существует
минимальный путь между V\ и Vj. Вершины в списке достижимости можно
использовать для наращивания ребер в исходном графе. Если существует
путь из вершины v к вершине w (w достижима из v), мы добавляем ребро
E(v,w), соединяющее эти две вершины. Расширенный граф G1 состоит из
вершин V графа G и ребер, связывающих вершины, которые соединены
направленным путем. Такой расширенный граф называется транзитивным
замыканием (transitive closure). Ниже приводится пример графа и его
транзитивного замыкания.
Задача нахождения списка достижимости с помощью поиска "сначала в
глубину" предлагается читателю в качестве упражнения. Более изящный
подход применяется в знаменитом алгоритме Стефана Уоршалла. Матрица
достижимости некоторого графа может быть построена путем присвоения 1
каждой паре вершин, связанных общей вершиной. Предположим, мы строим
матрицу достижимости R и вершинам а, Ь, с соответствуют индексы i, j, k.
Если R[i][j] = 1 и R[i][k] = 1, установить R[i][j] = 1.
Алгоритм Уоршалла проверяет все возможные тройки с помощью трех
вложенных циклов по индексам i, j и к. Для каждой пары (i,j) добавляется ребро
E(vi,Vj), если существует вершина Vk, такая, что ребра E(vi,Vk) и E(vk,Vj)
находятся в расширенном графе. Повторяя этот процесс, мы соединяем
дополнительными ребрами любую пару достижимых вершин. В результате получается
матрица достижимости.
Предположим, что вершины v и w достижимы через направленный путь,
связывающий пять вершин. Тогда существует последовательность вершин,
формирующих путь
v = хь х2, х3, х4, х5 = w
Имея путь от v до w, мы должны показать в матрице достижимости, что
алгоритм Уоршалла в конце концов даст тот же путь. С помощью трех
вложенных циклов мы проверяем все возможные тройки вершин. Допустим,
вершины идут в порядке Хх-х5. В процессе просмотра различных троек
вершина х2 идентифицируется как общий узел, связывающий хх и х3.
Следовательно, согласно алгоритма Уоршалла мы вводим новое ребро Е(х!,х3). Для
пары xlf x4 общей связующей вершиной является х3, так как путь, соединяющий
X! и х3, был найден на предыдущем шаге итерации. Поэтому мы создаем ребро
Е(х!,х4). Таким же образом х4 становится общей вершиной, связывающей хх
и х5, и мы добавляем ребро Е(х1,х5) и присваиваем элементу R[l][5] значение 1.
Проиллюстрируем алгоритм Уоршалла на следующем графе. Здесь
дополнительные ребра, добавленные для формирования транзитивного замыкания,
изображены пунктиром.
Исходный граф
Транзитивное замыкание
Матрица достижимости
1110 1
0 110 1
0 0 10 0
11111
0 0 10 1
Алгоритм Уоршалла имеет время вычисления 0(п3). При сканировании
матрицы смежности применяются три вложенных цикла. Списковое
представление графа также дает сложность 0(п3),
Программа 13.7. Использование алгоритма Уоршалла
Алгоритм Уоршалла используется для создания и печати матрицы
достижимости.
#include <iostream.h>
#include <fstream.h>
#include "graph.h"
template <class T>
void Warshall(Graph<T>& G)
{
VertexIterator<T> vi(G), vj(G);
int i, j, k;
int WSM[MaxGraphSize][MaxGraphSize]; // матрица Уоршалла
int n - G.NumberOfVertices();
// создать исходную матрицу
for (vi.Reset(); i=0; !vi.EndOfList(); vi.Next(), i++)
for (vj . Reset (); i=0; !vj .EndOfList () ; vj.NextO, j++)
if (i == j)
WSM[iJ [i] = 1;
else
WSM[i][j] = G.GetWeight(vi.Data(), vj.DataO);
// просмотреть все тройки, записать 1 в WSM, если существует ребро
// между vi и vj или существует тройка vi-vk-vj, соединяющая
// vi и vj
for (i=0; i<n; i++)
for <j=0; j<n; j++)
for (k=0; k<n; k++)
WSM[i][j] |=WSM[iJ[k] &WSM[k]j];
// распечатать каждую вершину и ее строку из матрицы достижимости
for {vi.Reset (); i=0; !vi .EndOfList () ; vi.NextO, i++)
{
cout « vi.DataO « ": ";
for (j=0; j<n; j++)
cout « WSM[i][j] « " ";
cout « endl;
}
}
void main(void)
{
Graph<char> G;
G.ReadGraph("warshall.dat") ;
cout « "Матрица достижимости:" << endl;
Warshall(G);
}
/*
<Прогон программы 13.7>
Матрица достижимости:
A: 1 1 1 0 1
В: 0 1 1 0 1
С: 0 0 1 0 0
D: 1 1 1 1 1
Е: 0 0 1 0 1
*/
Письменные упражнения
13.1 Нарисуйте законченное дерево для каждого из следующих массивов:
а) int А[8] = {5, 9, 3, 6, 2, 1, 4, 7}
б) char *B = "array-based tree"
13.2 Для каждого из изображенных ниже деревьев задайте соответствующий
массив.
13.3 Напишите функцию, выполняющую а) прямое и б) симметричное
прохождение представленного массивом дерева. В качестве образца
используйте ранее разработанный код для спискового представления деревьев.
13.4 Пусть А есть массив, состоящий из 70 элементов и представляющий
дерево.
а) Является ли А[45] листовым узлом?
б) Какой индекс у первого листового узла?
в) Кто родитель узла А[50]?
г) Кто является сыном узла А[10]?
д) Имеет ли какой-нибудь узел только одного сына?
е) Какова глубина этого дерева?
ж) Сколько листьев у этого дерева?
13.5
а) Напишите функцию, которая принимает N-элементный массив типа Т
и выполняет поперечное прохождение представляемого им дерева. Для
запоминания элементов ваша процедура должна использовать очередь.
Распечатайте элементы по уровням (один уровень на строке).
б) Сможете ли вы разработать более простую версию поперечного обхода,
используя тот факт, что дерево представлено в виде массива?
13.6 Покажите, что в законченном бинарном дереве число листовых узлов
больше и равно числу не листовых узлов. Покажите, что в полном
бинарном дереве число листовых узлов больше, чем не листовых.
13.7 Законченное бинарное дерево, содержащее 50 узлов, представлено в
виде массива.
а) Сколько уровеней в этом дереве?
б) Сколько узлов являются листовыми? Нелистовыми?
в) Какой индекс у родителя узла В[35]?
г) Какие индексы у сыновей узла В[20]?
д) Какой индекс у первого листового узла? У первого узла, имеющего
одного сына?
е) Какие индексы у узлов четвертого уровня?
13.8 Распишите по шагам турнирную сортировку массива А = {7, 10, 3,
9, 4, 12, 15, 5, 1, 8}.
13.9 Модифицируйте турнирную сортировку так, чтобы листовые и
нелистовые узлы содержали фактические данные из массива. Оформите
модифицированный код в виде функции ModTournamentSort.
13.10 Скажите, являются ли приведенные ниже бинарные деревья
пирамидами (минимальными или максимальными)?
13.11 Для каждого дерева, не являющегося пирамидой, из предыдущего
упражнения создайте минимальную и максимальную пирамиды. Для
каждой минимальной (максимальной) пирамиды создайте
соответствующую максимальную (минимальную) пирамиду.
13.12 С помощью FiterDown и конструктора сделайте из следующего дерева
минимальную пирамиду.
13.13 Даны пирамида А и пирамида В. Над каждой из них последовательно
произведите указанные ниже операции.
Пирамида А
а) вставить 15
б) вставить 35
в) удалить 10
г) вставить 40
д) вставить 10
Пирамида В
а) удалить 22
б) вставить 35
в) вставить 65
г) удалить 15
д) удалить 27
е) вставить 5
13.14
а) Каково наибольшее число узлов, которое может существовать в дереве,
являющемся минимальной пирамидой и бинарным деревом поиска
одновременно? Дублирующиеся значения не допускаются.
б) Каково наибольшее число узлов, которое может существовать в дереве,
являющемся максимальной пирамидой и бинарным деревом поиска
одновременно? Дублирующиеся значения не допускаются.
13.15 Для следующей пирамиды перечислите узлы, составляющие
указанный путь.
а) Путь родителей, начинающийся в узле 47.
б) Путь родителей, начинающийся в узле 71.
в) Путь через минимальных сыновей, начинающийся в узле 35.
г) Путь через минимальных сыновей, начинающийся в узле 10.
д) Путь через минимальных сыновей, начинающийся в узле 40 на первом
уровне.
13.16 Постройте минимальную пирамиду, для каждого из перечисленных
ниже массивов.
а) int A[10] = {40, 20, 70, 30, 90, 10, 50, 100, 60, 80};
б) int А[8] = {3, 90, 45, 6, 16, 45, 3, 88};
в) char *В = "heapify";
г) char *B = "minimal heap";
13.17 Реализуйте класс очередей приоритетов PQueue с помощью класса Bin-
STree. (Совет. Модифицируйте метод PQDelete для поиска и удаления
минимального элемента дерева.)
13.18 Постройте AVL-дерево для каждой из указанных последовательностей.
а) <int> 30, 50, 25, 70, 60, 40, 55, 45, 20
б) <int> 44, 22, 66, 11, 0, 33, 77, 55, 88,
в) <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
г) <String> tree, AVL, insert, delete, find, root, search
д) <String> class, object, public, private, derived, base, inherit, method,
constructor, abstract
13.19 Разработайте итерационную функцию прямого сканирования Preor-
der_I. Она должна эмулировать следующую рекурсивную функцию
Preorder.
template <class T>
void Preorder (TreeNode<T> *t, void visit (T& item))
{
while (t != NULL)
{
visit(t->data);
Preorder<t->Left{), visit);
t = t->Right();
}
}
После обработки узла обрабатывается сначала левое, а затем правое
поддеревья. Итерационное прямое прохождение должно эмулировать
рекурсивное сканирование с помощью стека адресов узлов.
Предположим, мы обработали узел А бинарного дерева. Теперь мы должны
обработать его левое поддерево и вернуться к предыдущей точке, чтобы
обработать его правое поддерево. Чтобы помнить необходимость
посещения правого поддерева, мы помещаем правый указатель узла А в
стек. После обработки всех, узлов левого поддерева А этот указатель
выталкивается из стека, и мы возвращаемся к прохождению правого
поддерева. Описанные ситуации показаны на следующих рисунках.
Обработать А.
Перейти к левому поддереву
Поместить С в стек
вершина
стека
Вытолкнуть С из стека
вершина
стека
Вытолкнуть С из стека
и обработать
Алгоритм итерационного прохождения состоит из следующих шагов.
Начиная с корня, выполнять в цикле
1. Посетить узел
2. Сохранить адрес его правого сына в стеке адресов.
3. Перейти к его левому сыну.
Всякий раз, когда в цикле встречается нулевой узел, обрабатываются
правые сыновья, адреса которых последовательно выталкиваются из
стека. Цикл прекращается, когда встретится нулевой указатель и в
стеке больше нет правых сыновей.
13.20 Функция PostorderJ осуществляет восходящее прохождение дерева.
Однако задача более сложна, чем просто восходящее или смешанное
прохождение. Требуется различать спуск по левому поддереву
(состояние 0) и возврат к родительскому узлу (состояние 1). При движении
вверх по дереву возможны два действия — посещение правого поддерева
узла или обработка самого узла. Состояние хранится в целочисленной
переменной state. Если state == 0, происходит движение вниз по дереву.
Если state == 0, происходит движение вверх. Когда мы попадаем в
узел сверху, родитель этого узла находится на вершине стека. Чтобы
определить, пришли ли мы слева, нужно сравнить указатель текущего
узла с левым указателем родительского узла. Если они согласуются и
у родителя есть правое поддерево, следует перейти в это поддерево. В
противном случае нужно обработать узел и продолжить движение вверх.
Пройти левое поддерево
Обработать узел и подняться вверх
Пройти правое поддерево
Нарисуйте несколько диаграмм, как те, что на рис. 13.5 и 13.6, чтобы
проиллюстрировать работу этого алгоритма, реализованного следующей
программой.
#include <iostream.h>
#include "treenode.h"
#include "treelib.h"
#include "stack.h"
void printchar(char& item)
{
cout « item « " ";
}
template <class T>
void Postorder_I(TreeNode<T> *t, void visit(T& item))
{
Stack<TreeNode<T> *> S;
TreeNode<T> *child;
int state = 0, scanOver = 0;
while (!scanOver)
{
if (state == 0)
{
if (t != NULL)
{
S.Push(t);
t = t->Left();
}
else
state « 1;
}
else
{
if (S.StackEmptyO )
scanOver = 1;
else
{
child = t;
t = S.PeekO ;
if (child == t->Left() && t->Right() != NULL)
{
t = t->Right();
state = 0;
}
else
{
visit(t->data);
S.Pop();
}
}
}
}
}
void main(void)
{
TreeNode<char> *root;
MakeCharTree(root, 0);
PrintTree(root, 0);
cout « endl;
Postorder_I(root, printchar);
cout « endl;
}
<Прогон>
С
A
D
В
D В Е С А
13.21 Для каждого из приведенных ниже графов задайте матрицу смежности
и списки смежности.
13.22 Используйте графы из предыдущего упражнения и ответьте на
следующие вопросы, касающиеся путей. Если пути не существует, отвечайте:
"Пути нет".
а) Найти в графе (А) направленный путь от Е к В.
б) Найти в графе (В) направленный путь от А к Е.
в) Найти в графе (С) направленные пути от В к Е и от Е к В.
г) Найти в графе (В) все узлы, смежные с А (с Е).
д) Найти в графе (С) такие узлы X, для которых имеется путь Р(А,Х) и
Р(Х,А).
е) Перечислите связанные компоненты в каждом графе.
ж) Какой из этих графов является сильно связанным (слабо связанным)?
13.23 Возьмите графы из письменного упражнения 13.21. Перечислите
вершины в порядке их прохождения методом "сначала в глубину" и
методом "сначала в ширину".
а) В графе (А), начав с вершины А.
б) В графе (В), начав с вершины А.
в) В графе (С), начав с вершины А.
г) В графе (В), начав с вершины В.
13.24 Создайте частичную реализацию класса Graph, основанного на
списковом представлении графов. Определите класс Vertexlnfo,
содержащий имя вершины и связанный список смежных с ней вершин.
Информация о смежных вершинах должна храниться в виде структуры,
включающей имя конечной вершины и вес ребра, соединяющего
начальную и конечную вершины. Для сравнения наименований вершин
следует добавить в класс Vertexlnfo перегруженный оператор
сравнения.
а) Реализуйте конструктор.
б) Реализуйте методы GraphEmpty, NumberOfVertices, GetNeighbors,
Insert Vert ex, InsertEdge и DepthFirstSearch.
13.25
а) Модифицируйте функцию MinimumPath, чтобы создать функцию
MinimumLength, которая находит путь между двумя вершинами,
содержащий минимальное число вершин. Если не существует вообще
никакого пути, возвращайте -1.
б) Создайте функцию VertexLength, которая принимает в качестве
параметров граф G и начальную вершину V и распечатывает вершины
графа, а также длины путей до этих вершин от V. Используйте
функцию MinimumLength из упражнения а).
13.26 Опишите действие следующей функции:
template <class T>
SeqList<T> RV(Graph<T> &G)
{
SeqList<T> L;
VertexIterator<T> viter(G);
ListIterator<T> liter(L);
for (viter.Reset(); !viter.EndOfList(); viter.Next())
{
cout « viter.Data() « ":
L = G.BreadthFirstSearch(viter.Data());
liter.SetList(L);
PrintList(L);
cout « endl;
}
}
13.27 Постройте соответствующий граф по каждой из следующих матриц
смежности. Считайте, что вершины являются буквами А, В, С и т.д.
а) 0 1 1 1
10 11
110 1
1110
б) 0 110 0
0 0 0 10
10 0 0 1
10 0 10
0 10 10
13.28 Для каждого из следующих графов задайте матрицу достижимости.
(В)
Упражнения по программированию
13.1 С помощью функций, разработанных вами в письменном упражнении
13.3, определите число листовых узлов, число узлов, имеющих по
одному сыну и число узлов, имеющих по два сына. Используйте глобальные
переменные nochild, onechild и twochild в программе, которая тестирует
и распечатывает следующие глобальные данные:
int А[50]; // хранит данные 0, 1, 2, ..., 49
int А[100]; // хранит данные 0, 1, 2, . .., 99
13.2
а) Разработайте тестовую программу для упорядочения с помощью
турнирной сортировки следующих символьных строк. Создайте массив
объектов типа String и передайте его в функцию TournamentSort.
class, object, public, private, derived, base, inherit, method,
constructor, abstract
б) Создайте массив из 100 случайных чисел от 0 до 999 и отсортируйте
его по возрастанию с помощью модифицированной функции турнирной
сортировки ModTournamentSort из письменного упражнения 13.3.
Распечатайте результирующий массив.
13.3 Модифицируйте класс Heap, приспособив его для создания
максимальных пирамид. Вызовите этот новый класс МахНеар и протестируйте
его операции с помощью варианта программы 13.3, сортирующей
элементы массива.
13.4 Реализуйте функции FilterUp и FilterDown класса Heap рекурсивным
способом. Протестируйте их на массиве из 15 случайных чисел в
диапазоне от 0 до 99. Используйте функцию HDelete для удаления N
элементов из пирамиды и печати их значений.
13.5 В некоторой компьютерной системе каждой работающей программе
(процессу) назначается приоритет. Наивысшим приоритетом является
О, а самым низким — 39. Когда приходит время выполнить некоторый
процесс, в очередь приоритетов вставляется запись запроса на
обработку. Когда ЦП свободен, запись удаляется и соответствующий процесс
запускается на выполнение. Запись запроса на обработку имеет
следующий формат:
struct ProcessRequestRecord
{
int priority;
String name;
);
Поле name идентифицирует конкретный процесс. Сгенерируйте
случайным образом 10 записей запроса на обработку с именами "Process A",
"Process В", ..., "Process J" и приоритетами в диапазоне от 0 до 39.
Распечатайте каждую запись, а затем включите их в приоритетную
очередь. Потом удаляйте из очереди и распечатывайте каждую запись.
13.6 Определите структуру, содержащую значение данных и приоритет.
template <class T>
struct PriorityData
{
Т data;
int priority;
>;
Используйте эту структуру и очередь приоритетов для реализации
класса Queue. (Совет. Объявите очередь как список записей типа Priority-
Data. Элементы запоминаются в очереди приоритетов в порядке,
определяемом полем priority каждой записи. Определите целочисленную
переменную PL, увеличивающуюся на единицу всякий раз, когда
очередной элемент включается в очередь. Пусть значение PL и будет
приоритетом очередной включаемой в очередь записи.)
Протестируйте свою очередь, введя пять целых чисел и запомнив их
в очереди с помощью Qlnsert. Затем последовательно удаляйте и
распечатывайте элементы, пока очередь не опустеет.
13.7 Используйте модель из предыдущего упражнения и класс МахНеар из
упражнения 13.3 для реализации стека с помощью очереди приоритетов.
Испытайте новый класс, введя пять целых чисел и запомнив их в стеке
с помощью Push. Затем последовательно удаляйте с помощью Pop и
распечатывайте элементы, пока очередь не опустеет.
13.8 Разработайте класс итераторов ArrPreorderlterator для прямого
прохождения представленных массивами деревьев. Объявите его
следующим образом:
template <class T>
class ArrPreorderlterator: public Iterator<T>
{
private:
Stack<int> S;
T *A;
int arraySize;
int currents-
public:
ArrPreorderlterator(T *Arr, int n);
virtual void Next(void);
virtual void Reset(void);
virtual T& Data(void);
};
Протестируйте этот класс с помощью дерева, представленного в виде
следующего массива:
int А[15] = {1, 4, 6, 2, 8, 9, 12, 25, 23, 55, 18, 78, 58, 14, 45);
и распечатайте его по уровням и в нисходящем порядке.
13.9 Унарный оператор ++ может быть перегруженным только в качестве
функции-члена класса. Итераторная функция Next реализуется с
помощью этого оператора естественным образом. Ниже приводится
объявление этого оператора и пример его использования.
void operator++ (void);
Прохождение бинарного дерева поиска.
BinSTree<T> *tree;
• * •
InorderIterator<T> inorderlter(tree.GetRoot());
while (!inorderlter.EndOfList())
{
• • •
inorderIter++;
}
Реализуйте метод Next класса Inorderlterator с помощью "++" и
испытайте его в программе, которая включает 25 случайных целых чисел
в бинарное дерево поиска, а затем сортирует их с помощью функции
TreeSort.
13.10 Разработайте класс итераторов Levelorderlterator для поперечного
прохождения бинарного дерева поиска. Объявление этого класса выглядит
следующим образом:
template <class T>
class Levelorderlterator: public Iterator<T>
{
private:
Queue<TreeNode<T> *> S;
TreeNode<T> *root, *current;
public:
Levelorderlterator(TreeNode<T>* 1st);
virtual void Next(void);
virtual void Reset(void);
virtual T& Data(void);
};
В главной программе создайте бинарное дерево поиска, содержащее
следующие данные:
int data[] = {100, 55, 135, 145, 25, 106, 88, 90, 5, 26, 67, 45, 99, 33);
Распечатайте это дерево. с помощью PrintTree, а затем осуществите
его поперечный обход с помощью Levelorderlterator.
13.11 Разработайте класс Postorderlterator по следующему алгоритму.
Инициализировать итератор посредством помещения адресов всех
узлов в стек в процессе NRL-обхода. Во время прохождения текущий
узел всегда находится на вершине стека, и очередной узел можно
получить посредством операции выталкивания из стека.
Испытайте итератор, осуществив прохождение и печать узлов дерева
из предыдущего упражнения.
13.12 Разработайте класс Postorderlterator путем модификации алгоритма
обратного прохождения из письменного упражнения 13,20. Испытайте
итератор, осуществив прохождение и печать узлов дерева из
упражнения 13.10.
13.13 С помощью ReadGraph создайте файл данных для графов А и В.
Напишите главную программу, которая вводит эти данные, а затем
использует функцию VertexLength из письменного упражнения 12.25 для
распечатки расстояния каждой вершины от А. Испытайте свою
программу на приведенных ниже графах.
13.14 Примените алгоритм Уоршалла к графам из предыдущего упражнения
и распечатайте матрицу достижимости для каждого графа.
глава
14
Организация коллекций
14.1. Основные алгоритмы сортировки
массивов
14.2. "Быстрая сортировка"
14.3. Хеширование
14.4. Класс хеш-таблиц
14.5. Производительность методов
поиска
14.6. Бинарные файлы и операции
с данными на внешних носителях
14.7. Словари
Письменные упражнения
Упражнения по программированию
Мы завершаем нашу книгу общей главой по организации данных. Здесь
будет рассмотрен ряд классических алгоритмов сортировки. В предыдущих
главах сортировка служила иллюстрацией возможностей списковых структур.
Например, поразрядная сортировка была представлена как приложение
очередей. Теперь же мы сосредоточимся на сортировке массивов и познакомимся
с классическими алгоритмами сортировки посредством выбора, сортировки
методом пузырька и сортировки вставками, которые требуют 0(п2) сравнений.
Хотя эти алгоритмы на практике не слишком эффективны для большого
количества элементов, они иллюстрируют основные подходы к сортировке
массивов. Последним будет рассмотрен знаменитый алгоритм "быстрой
сортировки".
В гл. 4 были представлены алгоритмы последовательного и бинарного
поиска, являющиеся базовыми алгоритмами поиска в списках. В настоящей
главе мы пополним наше знание о поиске и изучим хеширование, при
котором для быстрого доступа к элементам данных используется ключ, а
сложность поиска имеет порядок 0(1). Мы разработаем обобщенный класс хеш-
таблиц, допускающий произвольные типы данных.
В этой книге внимание было сосредоточено на данных, размещаемых в
оперативной памяти. Для больших наборов данных, хранимых на диске,
требуются методы внешнего доступа. Мы рассмотрим класс BinFile,
предназначенный для обработки двоичных файлов, и на его методах
проиллюстрируем алгоритм внешнего индексно-последовательного поиска и алгоритм
внешней сортировки слиянием.
Раздел, посвященный ассоциативным массивам, или словарям, обобщает
понятие индекса массива, что позволяет организовать данные с помощью
нечисловых индексов. Мы воспользуемся ассоциативными массивами для
построения небольшого словаря.
14.1. Основные алгоритмы сортировки
массивов
Начнем с трех алгоритмов, составляющих основу методики сортировки
"на месте" по возрастанию. Для каждого алгоритма оценим его
вычислительную эффективность.
Сортировка посредством выбора
Сортировка выбором моделирует наш повседневный опыт. Воспитатели
детского сада часто используют эту методику, чтобы выстроить детей по
росту. При этом самый маленький ребенок выбирается из неупорядоченной
группы детей и перемещается в шеренгу, выстраиваемую по росту. Этот
процесс, иллюстрируемый следующими несколькими рисунками,
продолжается до тех пор, пока все дети не окажутся в упорядоченной шеренге.
Для компьютерного алгоритма предполагается, что п элементов данных
хранятся в массиве А и по этому массиву выполняется п-1 проход. В нулевом
проходе выбирается наименьший элемент, который затем меняется местами
с А[0]. После этого неупорядоченными остаются элементы А[1] ... А[п-1]. В
следующем проходе просматривается неупорядоченная хвостовая часть
списка, откуда выбирается наименьший элемент и запоминается в А[1]. В еле-
Выбрать Рона
Выбрать Тома
Начальная шеренга
Том Дебби Майк Рон
Том Дебби Майк
Упорядоченная шеренга
Рон
Рон Том
Выбрать Майка
Выбрать Дэбби
Дебби Майк
Рон Том Майк
Дебби
Рон Том Майк Дебби
дующем проходе производится поиск наименьшего элемента в подсписке А[2]
... А[д-1]. Найденное значение меняется местами с А[2]. Таким образом
выполняется п-1 проход, после чего неупорядоченный хвост списка сокращается
до одного элемента, который и является наибольшим.
Рассмотрим сортировку посредством выбора на массиве, содержащем пять
целых чисел: 50, 20, 40, 75 и 35.
I 50
20
40
1
проход 0
1 20
50
40
1 1
проход 1
I 20
35
40
1 ^
75
75
' I
проход 2
| 20 |
35
40
75
35
\ 35
50
50 j
1 1
проход 3
| 20
35
40
50
75
Проход 0: Выбрать 20
Поменять местами 20 и А[0]
Проход 1: Выбрать 35
Поменять местами 35 и А[1]
Проход 2: Выбрать 40
Поменять местами 40 и А[2]
Проход 3: Выбрать 50
Поменять местами 50 и А[3]
Отсортированный список
В i-ом проходе сканируется подсписок A[i] ... А[п-1] и переменной smallln-
dex присваивается индекс наименьшего элемента в этом подсписке. Затем
элементы A[i] и A[smalllndex] меняются местами. Функция SelectionSort и
утилита Swap находятся в файле arrsort.h.
// отсортировать n-элементный массив типа Т,
//с помощью алгоритма сортировки посредством выбора
template <class T>
void SelectionSort(T A[], int n)
{
// индекс наименьшего элемента на каждом проходе
int smalllndex;
int i, j;
for (i=0; i<n-l; i++)
{
// начать проход с индекса i; установить smalllndex в i
smalllndex =i;
for (j=i+l; j<n; j++)
// обновить smalllndex, если найден меньший элемент
if (Alj] < A[smalllndex])
smalllndex = j;
//по окончании поместить наименьший элемент в A[i]
Swap(A[ij, A[smalllndex]);
}
}
Вычислительная сложность сортировки посредством выбора. Сортировка
посредством выбора требует фиксированного числа сравнений, зависящего
только от размера массива, а не от начального распределения в нем данных.
В i-ом проходе число сравнений с элементами A[i+1] ... А[п-1] равно
(п-1) - (i+1) + 1 = п - i - 1
Общее число сравнений равно
п-2 п-2
X(n-l)-i = (n-l)^-Xi-(n-l)2-(n"1)2(n"2)=|n(n-l)
О О
Сложность алгоритма, измеряемая числом сравнений, равна 0(п2), а число
обменов равно О(п). Наилучшего и наихудшего случаев не существует, так как
алгоритм делает фиксированное число проходов, в каждом из которых
сканируется определенное число элементов. Пирамидальная сортировка, имеющая
сложность 0(n log2 n), является обобщением метода сортировки посредством
выбора.
Сортировка методом пузырька
В гл. 2 мы познакомились с обменной сортировкой, требующей п-1
проходов и фиксированного числа сравнений в каждом из них. В этом разделе
мы обсудим пузырьковую сортировку, при которой также в каждом проходе
выполняется ряд обменов.
Для сортировки n-элементного массива А методом пузырька требуется до
п-1 проходов. В каждом проходе сравниваются соседние элементы, и если
первый из них больше или равен второму, эти элементы меняются местами.
К моменту окончания каждого прохода наибольший элемент поднимается к
вершине текущего подсписка, подобно пузырьку воздуха в кипящей воде.
Например, по окончании прохода 0 хвост списка (А[п-1]) отсортирован, а
головная часть остается неупорядоченной.
Рассмотрим эти проходы подробнее. Переменная lastExchangelndex хранит
последний участвующий в обмене индекс и приравнивается нулю в начале
каждого прохода. В нулевом проходе сравниваются соседние элементы (А[0],
А[1]), (А[1], А[2]), ...,(А[п-2], А[п-1]). В каждой паре (A[i], A[i+1]) элементы
меняются местами при условии, что A[i+1] < A[i], а значение lastExchange-
Index становится равным i. В конце этого прохода наибольшее значение
оказывается в элементе А[п-1], а значение lastExchangelndex показывает, что
все элементы в хвостовой части списка от A[lastExchangeIndex+l] до А[п-1]
отсортированы. В очередном проходе сравниваются соседние элементы в
подсписке А[0]—A[lastExchangeIndex]. Процесс прекращается при
lastExchangelndex = 0. Алгоритм совершает максимум п-1 проход.
Рассмотрим пузырьковую сортировку на массиве, содержащем пять целых
чисел: 50, 20, 40, 75 и 35.
проход 0
50
|
20
20
20
20
20
1
50
1
40
' 40
40
40
40
1
50
1
50
50
75
75
75
1
75
1
35
35
35
35
35
! 1
75
Поменять местами 50 и 20
Поменять местами 50 и 40
50 и 75 упорядочены
Поменять местами 75 и 35
75 - наибольший элемент
LastExchangelndex = 3
Поскольку lastExchangelndex не равен нулю, процесс продолжается. В
проходе 1 сканируется подсписок от А[0] до A[3]=A[lastExchangeIndex]. Новым
значением lastExchangelndex становится 2.
проход 1
20
1
20
20
20
40
1
40
1
40
40
50
50
1
50
1
35
35
35
35
1
50
75
75
75
75
20 и 40 упорядочены
40 и 50 упорядочены
Поменять местами 50 и 35
50 - наибольший элемент
lastExchangelndex = 0
В проходе 2 сканируется подсписок от А[0] до А[2] и элементы 40 и 35
меняются местами. lastExchangelndex становится равным 1.
проход 2
20
1
20
40
1
35
1
35
40
1
50
50
75
75
20 и 40 упорядочены
Поменять местами 40 и 35
lastExchangelndex = 1
В проходе 3 выполняется единственное сравнение (20 и 35). Обменов нет,
lastExchangelndex = 0, и процесс прекращается.
проход 3
20
I
20
35
I
35
40
40
50
50
75
75
20 и 35 упорядочены
Упорядоченный список
lastExchangelndex = 0
// BubbleSort принимает массив А и его размер п.
// сортировка выполняется посредством ряда проходов, пока lastExchangelndex О
template <class T>
void BubbleSort (T А[], int n)
{
int i, j;
// индекс последнего элемента, участвовавшего в обмене
int lastExchangelndex;
// i — индекс последнего элемента в подсписке
i = п-1;
// продолжать процесс, пока не будет произведено ни одного обмена
while (1 > 0)
{
// начальное значение lastExchangelndex lastExchangelndex = 0;
// сканировать подсписок A[0]--A[i]
for (j=0; j < i; j++)
// менять местами соседние элементы и обновить lastExchangelndex
if <A[j+l] < A[j])
{
Swap(A[j], A[j+1]);
lastExchangelndex = j;
}
// присвоить i значение индекса последнего обмена, продолжить сортировку
i = lastExchangelndex;
}
}
Вычислительная сложность сортировки методом пузырька
При пузырьковой сортировке сохраняется индекс последнего обмена во
избежание избыточного просмотра. Это придает алгоритму заметную
эффективность в некоторых особых случаях. Самое замечательное — это то, что
пузырьковая сортировка совершает всего один проход по списку, уже
упорядоченному по возрастанию. Таким образом, в лучшем случае эффективность
равна О(п). Худший случай для пузырьковой сортировки — когда список
упорядочен по убыванию. Тогда необходимо выполнять все п-1 проходов.
В i-ом проходе производится (п - i - 1) сравнений и (п - i - 1) обменов.
Сложность наихудшего случая составляет 0(п2) сравнений и 0(п2) обменов.
Анализ общего случая затруднен из-за возможности пропуска некоторых
проходов. Можно показать, что среднее количество проходов к равно О(п) и,
следовательно, общее число сравнений равно 0(п2). Даже если пузырьковая
сортировка выполняется менее чем за п-1 проходов, это требует, как правило,
большего числа обменов, чем при сортировке посредством выбора, и поэтому
ее средняя производительность меньше. В общем случае сортировка
посредством выбора превосходит пузырьковую за счет меньшего числа обменов.
Сортировка вставками
Сортировка вставками похожа на хорошо всем знакомый процесс
тасования карточек с именами. Регистратор заносит каждое имя на карточку
размером 127x76, а затем упорядочивает карточки по алфавиту, вставляя
карточку в верхнюю часть стопки в подходящее место. Опишем этот процесс
на примере нашего пятиэлементного списка А = 50, 20, 40, 75, 35.
50
Обработка 20
Обработка 40
Обработка 75
Обработка 35
Начать с элемента 50
Вставить 20 в позицию 0; передвинуть 50 в позицию 1
Вставить 40 в позицию 1; передвинуть 50 в позицию 2
Элемент 75 на месте
Вставить 40 в позицию 1;
сдвинуть хвост списка вправо
В функцию InsertionSort передается массив А и длина списка п. Рассмотрим
i-ый проход (l<i:<n-l). Подсписок А[0]—A[i-1] уже отсортирован по
возрастанию. В качестве вставляемого (TARGET) выберем элемент A[i] и будем
продвигать его к началу списка, сравнивая с элементами A[i-1], A[i-2] и т.д. Просмотр
заканчивается на элементе A[j], который меньше или равен TARGET или
находится в начале списка (j = 0). По мере продвижения к началу списка каждый
элемент сдвигается вправо (A[j] = A[j-1]). Когда подходящее место для A[i]
будет найдено, этот элемент вставляется в точку j.
// Сортировка вставками упорядочивает подсписки A[0]...A[i],
// 1 <- i <= п-1. Для каждого i A[i] вставляется в подходящую
// позицию А[j]
template <class T>
void InsertionSort(T A[], int n)
{
int i, j;
T temp;
// i определяет подсписок А[0]...A[i]
for (i=l; i<n; i++)
{
// индекс j пробегает вниз по списку от A[i] в процессе
// поиска правильной позиции вставляемого значения
j = i;
temp = A[i] ;
// обнаружить подходящую позицию для вставки, сканируя подсписок,
// пока temp < A[j-1] или пока не встретится начало списка
while (j > 0 && temp < A[j-1])
{
// сдвинуть элементы вправо, чтобы освободить место для вставки
A[j] = A[j-1];
j—;
}
// точка вставки найдена; вставить temp
A[j] = temp;
}
}
Вычислительная эффективность сортировки вставками. Сортировка
вставками требует фиксированного числа проходов. В п-1 проходах включаются
элементы А[1]—А[п-1]. В i-ом проходе включения производятся в подсписок
А[0]—A[i] и требуют в среднем i/2 сравнений. Общее число сравнений равно
1/2 + 2/2 + 3/2 + ... + (n-2)/2 + (n-l)/2 = n(n-l)/4
В отличие от других методов, сортировка вставками не использует обмены.
Сложность алгоритма измеряется числом сравнений и равна 0(п2). Наилучший
случай — когда исходный список уже отсортирован. Тогда в i-ом проходе вставка
производится в точке A[i], а общее число сравнений равно п-1, т.е. сложность
составляет 0(п). Наихудший случай возникает, когда список отсортирован по
убыванию. Тогда каждая вставка происходит в точке А[0] и требует i сравнений.
Общее число сравнений равно п(п-1)/2, т.е. сложность составляет 0(п2).
14.2. "Быстрая сортировка11
К этому моменту мы рассмотрели ряд 0(п2)-сложных алгоритмов
сортировки массивов "на месте". Алгоритмы, использующие деревья (турнирная
сортировка, сортировка посредством поискового дерева), обеспечивают
значительно лучшую производительность 0(n log2n). Несмотря на то, что они
требуют копирования массива в дерево и обратно, эти затраты покрываются
за счет большей эффективности самой сортировки. Широко используемый
метод пирамидальной сортировки также обрабатывает массив "на месте" и
имеет эффективность 0(n log2n). Однако "быстрая сортировка", которую
изобрел К. Хоар, для большинства приложений превосходит пирамидальную
сортировку и является самой быстрой из известных до сих пор.
Описание "быстрой сортировки"
Как и для большинства алгоритмов сортировки, методика "быстрой
сортировки" взята из повседневного опыта. Чтобы отсортировать большую стопку
алфавитных карточек по именам, можно разбить ее на две меньшие стопки
относительно какой-нибудь буквы, например К. Все имена, меньшие или
равные К, идут в одну стопку, а остальные — в другую. Затем каждая стопка снова
делится на две. Например, на рис. 14.1 точками разбиения являются буквы F и
R. Процесс разбиения на все меньшие и меньшие стопки продолжается.
В алгоритме "быстрой сортировки" применяется метод разбиения с
определением центрального элемента. Так как мы не можем позволить себе
удовольствие разбрасывать стопки по всему столу, как при сортировке алфавитных
карточек, элементы разбиваются на группы внутри массива. Рассмотрим
алгоритм "быстрой сортировки" на примере, а затем обсудим технические детали.
Пусть дан массив, состоящий из 10 целых чисел:
А = 800, 150, 300, 600, 550, 650, 400, 350, 450, 700
Точка разбиения = К
Точка разбиения = R
Точка разбиения =
Рис. 14.1. Разбиение для «быстрой сортировки»
Фаза сканирования. Массив простирается от индекса low = 0 до индекса
high = 9. Его середина приходится на индекс mid = 4. Первым центральным
элементом является A[mid] = 550. Таким образом, все элементы массива А
разбиваются на два подсписка: Sj и Sh. Меньший из них (S^ будет содержать
элементы, меньшие или равные центральному. Подсписок Sh будет содержать
элементы большие, чем центральный. Поскольку заранее известно, что
центральный элемент в конечном итоге будет последним в подсписке 8\9 мы
временно передвигаем его в начало массива, меняя местами с А[0] (A[low]).
Это позволяет сканировать подсписок А[1]—А[9] с помощью двух индексов:
scanllp и scanDown. Начальное значение scanUp соответствует индексу 1
(low+1). Эта переменная адресует элементы подсписка S^ Переменная scan-
Down адресует элементы подсписка Sh и имеет начальное значение 9 (high).
Целью прохода является определение элементов для каждого подсписка.
150
300
600
800
650
400
350
450
700
scanUp scanDown
Оригинальность "быстрой сортировки" заключается во взаимодействии
двух индексов в процессе сканирования списка. Индекс scanUp перемещается
вверх по списку, a scanDown — вниз. Мы продвигаем scanUp вперед и ищем
элемент A[scanUp] больший, чем центральный. В этом месте сканирование
останавливается, и мы готовимся переместить найденный элемент в верхний
подсписок. Перед тем как это перемещение произойдет, мы продвигаем
индекс scanDown вниз по списку и находим элемент, меньший или равный
центральному. Таким образом, у нас есть два элемента, которые находятся
не в тех подсписках, и их можно менять местами.
Swap (AfscanUp), A[scanDown]); // менять местами партнеров
Этот процесс продолжается до тех пор, пока scanUp и scanDown не зайдут
друг за друга (scanUp = 6, scanDown = 5). В этот момент scanDown
оказывается в подсписке, элементы которого меньше или равны центральному.
Мы попали в точку разбиения двух списков и указали окончательную
позицию для центрального элемента. В нашем примере поменялись местами
числа 600 и 450, 800 и 350, 650 и 400.
550 I | 150 | 300 | 600 | 800 | 650 | 400 | 350 | 450 | 700 |
scanDown scanUp
Затем происходит обмен значениями центрального элемента А[0] с A[scan-
Down]:
Swap (А[0], A[scanDown]);
В результате получился подсписок А[0]—А[4], элементы которого меньше
элементов подсписка А[6]—А[9]. Центральный элемент (550) разделяет два
подсписка, каждый из которых равен примерно половине исходного списка.
Оба подсписка обрабатываются по одному и тому же алгоритму. Мы называем
это рекурсивной фазой.
400 150 300 450 350 550 650 800 600 700
А[0]-А[4]
А[б]-А[9]
Рекурсивная фаза. Одним и тем же методом обрабатываются два
подсписка: S2 (A[0]—А[4]) и Sh (А[5]—А[9]).
Подсписок Si. Подсписок определяется диапазоном от индекса low = 0 до
high = 4. Его середина приходится на индекс mid = 2. Центральным
элементом является A[mid] = 300. Поменять местами центральный элемент с
A[low] и присвоить начальные значения индексам scanUp и scanDown:
scanUp = 1 = low + 1
scanDown = 4 = high
Сканирование вверх останавливается на индексе 2 (А[2] > центрального элемента)
Сканирование вниз останавливается на индексе 1 (А[1] < центрального элемента)
Начальные значения
После сканирования
300 | | 150
400
450
350
300 | | 150
400
450
350
scanUp
scanDown
scanDown
scanUp
Так как scanDown < scanUp, процесс останавливается. При этом scanDown
является точкой разделения двух еще меньших подсписков: А[0] и А[2]—А[4].
Завершить обработку, поменяв местами A[scanDown] = 150 и A[low] = 300.
Заметьте, что положение центрального элемента дает нам одноэлементный и
трехэлементный подсписки. Рекурсивный процесс прекращается на пустом
или одноэлементном подсписках.
150 В00 | 400 | 450 | 350
А[0]
А[2]-А[4]
Подсписок Sh. Диапазон подсписка — от индекса low = 6 до high = 9. Его
середина приходится на индекс mid = 7. Центральным элементом является
A[mid] = 800. Поменять местами центральный элемент с A[low] и присвоить
начальные значения индексам scanUp и scanDown:
scanUp = 7 = low + 1
scanDown = 9 = high
Сканирование вверх останавливается по достижении конца списка (scanUp=10)
scanDown остается на начальной позиции
Начальные значения
После сканирования
800
650
600
700J
800 650 600 700 конец списка
scanUp scanDown
scanDown scanUp
Так как scanDown < scanUp, процесс останавливается. При этом scanDown
является точкой вставки центрального элемента. Завершить обработку, по-
меняв местами A[scanDown] = 700 и A[low] = 800. Обратите внимание, что
положение центрального элемента дает нам трехэлементный и пустой
подсписки. Рекурсивный процесс прекращается на пустом или одноэлементном
подсписках.
700
650
600
800
Завершение сортировки
Обработать подсписок 400, 450, 350 (А[2]—А[4]). Центральным
элементом является 450.
На фазе сканирования элементы выстраиваются в порядке 350, 400,
450. Для двухэлементного подсписка 350, 400 понадобится еще один
рекурсивный вызов.
Обработать подсписок 700, 650, 600 (А[6]—А[8]). Центральным
элементом является 650.
После сканирования элементы выстраиваются в порядке 600, 650, 700.
Числа 600 и 700 образуют два одноэлементных подсписка.
"Быстрая сортировка" завершена. Результатом является следующий
сортированный список:
А = 150, 300, 350, 400, 450, 550, 600, 650, 700, 800
Алгоритм Quicksort
Этот рекурсивный алгоритм разделяет список A[low]—A[high] по
центральному элементу, который выбирается из середины списка:
pivot = A[mid]; // mid = (high+low)/2
После обмена местами центрального элемента с A[low], задаются начальные
значения индексам scanUp = low + 1 и scanDown = high, указывающих на
начало и конец списка, соответственно. Алгоритм управляет этими двумя
индексами. Сначала scanUp продвигается вверх по списку, пока не превысит
значение scanDown или пока не встретится элемент больший, чем
центральный.
// индекс scanUp пробегает по элементам,
// меньшим или равным центральному
while (scanUp <e scanDown && A[scanUp] <= pivot)
scanup++; // перейти к следующему элементу
После позиционирования scanUp индекс scanDown продвигается вниз по
списку, пока не встретится элемент, меньший или равный центральному.
// сканировать верхний подсписок в обратном направлении.
// остановиться, когда scanDown укажет на элемент, меньший
// или равный центральному, сканирование должно прекратиться
// при A[low] = pivot
while (pivot < A[scanDown])
scanDown—;
По окончании этого цикла (и при условии что scanUp < scanDown) оба
индекса адресуют два элемента, находящихся не в тех подсписках. Эти
элементы меняются местами.
// поменять местами больший элемент из нижнего подсписка
// с меньшим элементом из верхнего подсписка
Swap (A[scanUp], AfscanDown]);
Обмен элементов прекращается, когда scanDown становится меньше, чем
scanUp. В этот момент scanDown указывает начало левого подсписка, который
содержит меньшие или равные центральному элементы. Индекс scanDown
становится центральным. Взять центральный элемент из A[low]:
Swap(A[low], А[scanDown]);
Для обработки подсписков используется рекурсия. После обнаружения
точки разбиения мы рекурсивно вызываем Quicksort с параметрами low, mid-1
и mid+1, high. Условие останова возникает, когда в подсписке остается менее
двух элементов, так как одноэлементный или пустой массив всегда упорядочен.
Функция Quicksort находится в файле arrsort.h.
// Quicksort принимает в качестве параметров массив
// и предельные значения его индексов
template <class T>
void Quicksort(T A[], int low, int high)
{
// локальные переменные, содержащие индекс середины mid,
// центральный элемент и индексы сканирования
t pivot;
int scanUp, scanDown;
int mid;
// если диапазон индексов не включает в себя как минимум два элемента, вернуться
if (high - low <= 0)
return;
else
// если в подсписке два элемента, сравнить их между собой
// и поменять местами при необходимости
if (high - low == 1)
{
if (A[high] < A[low])
Swap(A[low], Afhigh]);
return;
}
// получить индекс середины и присвоить указываемое им значение
// центральному значению
mid = (low + high)/2;
pivot « A[mid];
// поменять местами центральный и начальный элементы списка
// и инициализировать индексы scanUp и scanDown
Swap (A[mid], A[low]);
scanUp = low + 1;
scanDown = high;
// искать элементы, расположенные не в тех подсписках.
// остановиться при scanDown < scanUp
do
{
// продвигаться вверх по нижнему подсписку; остановиться,
// когда scanUp укажет на верхний подсписок или если
// указываемый этим индексом элемент > центрального
while (scanUp <= scanDown && A[scanUp] <= pivot)
scanUp++;
// продвигаться вниз по верхнему подсписку; остановиться,
// если scanDown укажет элемент <= центрального.
// остановка на элементе A[low] гарантируется
while (pivot < A[scanDown])
scanDown—;
// если индексы все еще в своих подсписках, то они указывают
// два элемента, находящихся не в тех подсписках.
// Поменять их местами
if (scanUp < scanDown)
{
Swap (AfscanUp], AEscanDown]);
}
}
while (scanUp < scanDown);
// копировать центральный элемент в точку разбиения
A[low] = A[scanDown];
A[scanDown] = pivot;
// если нижний подсписок (low...scanDown-1) имеет 2 или более
// элементов, выполнить рекурсивный вызов
if (low < scanDown-1)
Quicksort(A, low, scanDown-1);
// если верхний подсписок (scanDown+1...high) имеет 2 или более
// элементов, выполнить рекурсивный вызов
if (scanDown+1 < high)
Quicksort(A, scanDown+1, high);
}
Вычислительная сложность "быстрой сортировки". Общий анализ
эффективности "быстрой сортировки" достаточно труден. Будет лучше показать ее
вычислительную сложность, подсчитав число сравнений при некоторых
идеальных допущениях. Допустим, что п — степень двойки, n = 2к (к = log2n),
а центральный элемент располагается точно посередине каждого списка и
разбивает его на два подсписка примерно одинаковой длины.
При первом сканировании производится п-1 сравнений. В результате
создаются два подсписка размером п/2. На следующей фазе обработка каждого
подсписка требует примерно п/2 сравнений. Общее число сравнений на этой
фазе равно 2(п/2) = п. На следующей фазе обрабатываются четыре подсписка,
что требует 4(п/4) сравнений, и т.д. В конце концов процесс разбиения
прекращается после к проходов, когда получившиеся подсписки содержат по
одному элементу. Общее число сравнений приблизительно равно
п + 2(п/2) 4- 4(п/4) 4- ... + n(n/n) = n + n+... + n = n*k = n* log2n
Для списка общего вида вычислительная сложность "быстрой сортировки"
равна 0(п \og2n). Идеальный случай, который мы только что рассмотрели,
фактически возникает тогда, когда массив уже отсортирован по возрастанию.
Тогда центральный элемент попадает точно в середину каждого подсписка.
Список отсортированный по возрастанию
10
20
30
40
50
60
70
80
пограничный
элемент
Если массив отсортирован по убыванию, то на первом проходе центральный
элемент находится в середине списка и меняется местами с каждым
элементом как в нижнем, так и в правом подсписке. Результирующий список почти
отсортирован, алгоритм имеет сложность порядка 0(n log2n).
Список отсортированный по убыванию
80
70
60
50
40
30
20
10
Поменять местами A[low] и A[mid]. Выполнить проход
После первого прохода
50
70
60
80
40
30
20
10
40
10
20
30
50
80
60
70
Наихудшим сценарием для "быстрой сортировки" будет тот, при котором
центральный элемент все время попадает в одноэлементный подсписок, а все
прочие элементы остаются во втором подсписке. Это происходит тогда, когда
центральным всегда является наименьший элемент. Рассмотрим
последовательность 3, 8, 1, 5, 9. В первом проходе производится п сравнений, а больший
подсписок содержит п-1 элементов. В следующем проходе этот подсписок
требует п-1 сравнений и дает подсписок из п-2 элементов и т.д. Общее число
сравнений равно
п + п-1 + п-2 + ... + 2 = п(п+1)/2 - 1
Сложность худшего случая равна 0(п2), т.е. не лучше, чем для сортировок
вставками и выбором. Однако этот случай является паталогическим и
маловероятен на практике. В общем, средняя производительность "быстрой
сортировки" выше, чем у всех рассмотренных нами сортировок.
Алгоритм Quicksort выбирается за основу в большинстве универсальных
сортирующих утилит. Если вы не можете смириться с производительностью
наихудшего случая, используйте пирамидальную сортировку — более
устойчивый алгоритм, сложность которого равна 0(n log2n) и зависит только от
размера списка.
Сравнение алгоритмов сортировки массивов
Мы сравнили алгоритмы сортировки, испытав их на массивах, содержащих
4000, 8000, 10000, 15000 и 20000 целых чисел, соответственно. Время
выполнения измерено в тиках (1/60 доля секунды). Среди всех алгоритмов порядка
0(п2) время сортировки вставками отражает тот факт, что на i-ом проходе
требуется лишь i/2 сравнений. Этот алгоритм явно превосходит все прочие
сортировки порядка 0(п2). Заметьте, что самую худшую общую
производительность демонстрирует сортировка методом пузырька. Результаты испытаний
показаны на рис. 14.2.
п = 4000
п = 8000
п = 10000
п = 15000
п = 20000
Обменная
сортировка
12.23
49.95
77.47
173.97
313.33
Сортировка
выбором
17.30
29.43
46.02
103.00
185.05
Пузырьковая
сортировка
15.78
64.03
99.10
223.28
399.47
Сортировка
вставками
5.67
23.15
35.43
80.23
143.67
Обменная
Выбором
Пузырьковая
Вставками
Рис. 14.2. Сравнение сортировок порядка 0(п2)
Для иллюстрации эффективности алгоритмов сортировки в экстремальных
случаях используются массивы из 20000 элементов, отсортированных по
возрастанию и по убыванию. При сортировке методом пузырька и сортировке
вставками выполняется только один проход массива, упорядоченного по
возрастанию, в то время как сортировка посредством выбора зависит только от
размера списка и выполняет 19999 проходов. Упорядоченность данных по
убыванию является наихудшим случаем для пузырьковой, обменной и
сортировки вставками, зато сортировка выбором выполняется, как обычно.
Сортировки сложности 0(п ) упорядоченных массивов
п = 8000 (упорядочен
по возрастанию)
п = 8000 (упорядочен
по убыванию)
Обменная
сортировка
185.27
526.17
Сортировка
выбором
185.78
199.0
Пузырьковая
сортировка
.03
584.67
Сортировка
вставками
.05
286.92
В общем случае Quicksort является самым быстрым алгоритмом.
Благодаря своей эффективности, равной 0(n log2n), он явно превосходит любой
алгоритм порядка 0(п2). Судя по результатам испытаний, приведенных на
рис. 14.3, он также быстрее любой из сортировок порядка 0(n log2n),
рассмотренных нами в гл. 13. Обратите внимание, что эффективность "быстрой
сортировки" составляет 0(n log2n) даже в экстремальных случаях. Зато
сортировка посредством поискового дерева становится в этих случаях 0(п2)
сложной, так как формируемое дерево является вырожденным.
сортировки порядка 0(п2)
Время (сек)
Сортировки порядка 0(п 1одгп)
п = 4000
п = 8000
п = 10000
п = 15000
п = 20000
п = 8000 (упорядочен
по возрастанию)
п = 8000 (упорядочен
по убыванию)
Турнирная
сортировка
0.28
0.63
0.90
1.30
1.95
1.77
1.65
Сортировка
посредством
дерева
0.32
0.68
0.92
1.40
1.88
262.27
275.70
Пирамидальная
сортировка
0.13
0.28
0.35
0.58
0.77
0.75
0.80
"Быстрая
сортировка"
0.07
0.17
0.22
0.33
0.47
0.23
0.28
Рис. 14.3. Сравнение сортировок порядка 0(п Ьдгп)
Программа 14.3. Сравнение сортировок
Эта программа осуществляет сравнение алгоритмов сортировки данных,
представленных на рис. 14.2 и 14.3. Здесь дается только базовая структура
программы, а полный листинг находится в файле prgl4_l.cpp.
Хронометраж производится с помощью функции TickCount, возвращающей число
1/60 долей секунды, прошедших с момента старта программы. Эта
функция находится в файле ticks.h.
tinclude <iostream.h>
tinclude "arrsort.h"
// перечислимый тип, описывающий начальное
// состояние массива данных
enum Ordering {randomorder, ascending, descending};
// перечислимый тип, идентифицирующий алгоритм сортировки
enum SortType {exchange, selection, bubble, insertion,
tournament, tree, heap, quick};
// копировать n-элементный массив у в массив х
void Copy(int *x, int *y, int n)
{
for (int i=0; i<n; i++)
•x++ = *y++;
}
// общая сортирующая функция, которая принимает исходный массив
//с заданной упорядоченностью элементов и применяет указанный
// алгоритм сортировки
void Sort(int a[], int n, SortType type, Ordering order)
{
long time;
cout << "Сортировка " « n;
// вывести тип упорядоченности
switch(order)
{
case random: cout « " элементов. ■■;
break;
case ascending: cout « " элементов, упорядоченных по возрастанию. ";
break;
case descending: cout « " элементов, упорядоченных по убыванию. ";
break;
}
// засечь время
time = TickCount();
// вывести тип сортировки и выполнить ее switch(type)
{
case exchange: ExchangeSort (a, n);
cout « "Сортировка обменом: ";
break;
case selection: SelectionSort(a, n);
cout « "Сортировка выбором: ";
break;
case bubble:
case insertion:
case tournament:
case tree:
case heap:
case quick:
}
// подсчитать время выполнения в секундах
time = TickCount () - time;
cout « time/60.0 « endl;
}
// запустить сортировки для п чисел,
// расположенных в заданном порядке
void RunTest(int n, Ordering order)
{
int i;
int *a, *b;
SortType stype;
RandomNumber rnd;
// выделить память для двух n-элементных массивов а и b
а = new int [n];
b = new int [n];
// определить тип упорядоченности данных
if (order = randomorder)
// заполнить массив b случайными числами
for (i=0; i<n; i++)
{
b[i] = rnd.Random(n);
}
else
// данные, отсортированные по возрастанию
for (i=0; i<n; i++)
{
b[i] = i;
}
else
// данные, отсортированные по убыванию
for (i=0; i<n; i++)
{
b[ij - n - 1 - i;
}
else
// копировать данные в массив а. выполнить каждую сортировку
for(stype=exchange; stype<=quick; stype=SortType(stype+1))
{
Copy(a, b, n);
Sort(a, n, stype, order);
}
// Удалить оба динамических массива
delete [] а;
delete [] b;
}
// сортировать 4000, 8000, 10000, 15000 и 20000 случайных чисел.
// затем отсортировать 20000 элементов, упорядоченных по возрастанию,
// и 20000 элементов, упорядоченных по убыванию
void main(void)
{
int nelts[5] = {4000, 8000, 10000, 15000, 20000}, i;
cout.precision(3);
cout.setf(ios::fixed | ios::showpoint);
for (i=0; i<5; i++)
RunTest(nelts[i], randomorder);
RunTest(20000, ascending);
RunTest(20000, descending);
}
0(n log2n) сложные сортировки
Время (сек)
Посредством дерева
Турнирная
Пирамидальная
"Быстрая сортировка"
14.3. Хеширование
В этой книге мы вывели ряд списковых структур, позволяющих
программе-клиенту осуществлять поиск и выборку данных. В каждой такой структуре
метод Find выполняет обход списка и ищет элемент данных, совпадающий с
ключом. При этом эффективность поиска зависит от структуры списка. В
случае последовательного списка метод Find гарантированно просматривает
О(п) элементов, в то время как в случае бинарных поисковых деревьев и при
бинарном поиске обеспечивается более высокая эффективность 0(log2n). В
идеале нам хотелось бы выбирать данные за время 0(1). В этом случае число
необходимых сравнений не зависит от количества элементов данных. Выборка
элемента осуществляется за время 0(1) при использовании в качестве индекса
в массиве некоторого ключа. Например, блюда из меню в закусочной в целях
упрощения бухгалтерского учета обозначаются номерами. Какой-нибудь
деликатес типа "бастурма, маринованная в водке" в базе данных обозначается
просто #2. Владельцу закусочной остается лишь сопоставить ключ 2 с записью
в списке.
Ключ
2
Наименование Цена
1 Бастурма, маринованная в водке! $3.50
Продано штук
1 43
GZ.
м
L2
L3
Ln-2
Ln-1
Элементы меню
Мы знаем и другие примеры. Файл клиентов пункта проката видеокассет
содержит семизначные номера телефонов. Номер телефона используется в
качестве ключа для доступа к конкретной записи файла клиентов.
| Номер телефона | Имя клиента, название фильма и т. д. |
Ключи не обязательно должны быть числовыми. Например, формируемая
компилятором таблица символов (symbol table) содержит все используемые
в программе идентификаторы вместе с сопутствующей каждому из них
информацией. Ключом для доступа к конкретной записи является сам
идентификатор.
Ключи и хеш-функция
В общем случае ключи не настолько просты, как в примере с закусочной.
Несмотря на то, что они обеспечивают доступ к данным, ключи, как правило,
не являются непосредственными индексами в массиве записей. Например,
телефонный номер может идентифицировать клиента, но вряд ли пункт
проката хранит десятимиллионный массив.
0 12 i 9999998 9999999
Запись клиента
В большинстве приложений ключ обеспечивает косвенную ссылку на
данные. Ключ отображается во множество целых чисел посредством
хеш-функции (hash function). Полученное в результате значение затем используется
для доступа к данным. Давайте исследуем эту идею.
Предположим, есть множество записей с целочисленными ключами. Хеш-
функция HF отображает ключ в целочисленный индекс из диапазона О...п-l.
С хеш-функцией связана так называемая хеш-таблица (hash table), ячейки
которой пронумерованы от 0 до п-1 и хранят сами данные или ссылки на
данные.
Хеш-таблица
Запись
nfdcmon) = i
Пример 14.1
Предположим, Key — положительное целое, a HF(Key) — значение
младшей цифры числа Key, Тогда диапазон индексов равен 0—9.
Например, если Key = 49, HF(Key) = HF(49) = 9. Эта хеш-функция в
качестве возвращаемого значение использует остаток от деления на 10.
// Хеш-функция, возвращающая младшую цифру ключа
int HF(int key)
{
return key % 10;
}
Часто отображение, осуществляемое хеш-функцией, является
отображением "многие к одному" и приводит к коллизиям (collisions). В примере 14.1
HF(49) = HF(29) = 9. При возникновении коллизии два или более ключа
ассоциируются с одной и той же ячейкой хеш-таблицы. Поскольку два ключа
не могут занимать одну и ту же ячейку в таблице, мы должны разработать
стратегию разрешения коллизий. Схемы разрешения коллизий обсуждаются
после знакомства с некоторыми типами хеш-функций.
Хеш-функции
Хеш-функция должна отображать ключ в целое число из диапазона О...п-l.
При этом количество коллизий должно быть ограниченным, а вычисление
самой хеш-функции — очень быстрым. Некоторые методы удовлетворяют
этим требованиям.
Наиболее часто используется метод деления (division method), требующий
двух шагов. Сперва ключ должен быть преобразован в целое число, а затем
полученное значение вписывается в диапазон О...п-l с помощью оператора
получения остатка. На практике метод деления используется в большинстве
приложений с хешированием.
Пример 14.2
1. Ключ — пятизначное число. Хеш-функция извлекает две младшие
цифры. Например, если это число равно 56389, то HF(56389) = 89.
Две младшие цифры являются остатком от деления на 100.
int HF(int key)
{
return key % 100 // метод деления на 100
}
Эффективность хеш-функции зависит от того, обеспечивает ли она
равномерное рассеивание ключей в диапазоне О...п-l. Если две
последние цифры соответствуют году рождения, то будет слишком
много коллизий при идентификации подростков, играющих в
юношеской бейсбольной лиге.
2. Ключ — символьная строка языка C++. Хеш-функция отображает
эту строку в целое число посредством суммирования первого и
последнего символов и последующего деления на 101 (размер таблицы).
// хеш-функция для символьной строки.
// возвращает значение в диапазоне от 0 до 100
int HF(char *key)
{
int len ** strlen(key), hashf = 0;
// если длина ключа равна 0 или 1, возвратить key[0].
// иначе сложить первый и последний символ
if (len <= 1)
hashf = key[0];
else
hashf = key[0] + key[len-l];
return hashf % 101;
}
Эта хеш-функция приводит к коллизии при одинаковых первом и
последнем символах строки. Например, строки "start" и "slant"
будут отображаться в индекс 29. Так же ведет себя хеш-функция,
суммирующая все символы строки.
int HF(char *key)
{
int hashf * 0;
// просуммировать все символы строки и разделить на 101
while (*key)
hashf +* *key++;
return hashf % 101;
}
Строки "bad" и "dab" преобразуются в один и тот же индекс. Лучшие
результаты дает хеш-функция, производящая перемешивание битов
в символах. Пример более удачной хеш-функции для строк
представлен вместе с программой 14.2.
В общем случае при больших п индексы имеют больший разброс.
Кроме того, математическая теория утверждает, что распределение
будет более равномерным, если п — простое число.
Другие методы хеширования
Метод середины квадрата (midsquare technique) предусматривает
преобразование ключа в целое число, возведение его в квадрат и возвращение в
качестве значения функции последовательности битов, извлеченных из середины
этого квадрата. Предположим, что ключ есть целое 32-битовое число. Тогда
следующая хеш-функция извлекает средние 10 бит возведенного в квадрат
ключа.
// возвратить средние 10 бит произведения key*key
int HF(int key);
{
key *= key; // возвести ключ в квадрат
key »= 11; // отбросить 11 младших бит
return key % 1024 // возвратить 10 младших бит
}
При мультипликативном методе (multiplicative method) используется
случайное действительное число f в диапазоне 0<f<l. Дробная часть
произведения f*key лежит в диапазоне от 0 до 1. Если это произведение умножить
на п (размер хеш-таблицы), то целая часть полученного произведения даст
значение хеш-функции в диапазоне от 0 до п-1.
// хеш-функция, использующая мультипликативный метод;
// возвращает значение в диапазоне 0...700
int HF(int key) ;
{
static RandomNumber rnd;
float f;
// умножить ключ на случайное число из диапазона 0...1
f = key * rnd.fRandom();
// взять дробную часть
f - f - int(f);
// возвратить число в диапазоне О...п-l
return 701*f;
}
Разрешение коллизий
Несмотря на то, что два или более ключей могут хешироваться одинаково,
они не могут занимать в хеш-таблице одну и ту же ячейку. Нам остаются
два пути: либо найти для нового ключа другую позицию в таблице, либо
создать для каждого значения хеш-функции отдельный список, в котором
будут все ключи, отображающиеся при хешировании в это значение. Оба
варианта представляют собой две классические стратегии разрешения
коллизий — открытую адресацию с линейным опробыванием (linear probe open
addressing) и метод цепочек (chaining with separate lists). Мы
проиллюстрируем на примере открытую адресацию, а сосредоточимся главным образом
на втором методе, поскольку эта стратегия является доминирующей.
Открытая адресация с линейным опробыванием. Эта методика
предполагает, что каждая ячейка таблицы помечена как незанятая. Поэтому при
добавлении нового ключа всегда можно определить, занята ли данная ячейка
таблицы или нет. Если да, алгоритм осуществляет "опробывание" по кругу,
пока не встретится "открытый адрес" (свободное место). Отсюда и название
метода. Если размер таблицы велик относительно числа хранимых там клю-
чей, метод работает хорошо, поскольку хеш-функция будет равномерно
рассеивать ключи по всему диапазону и число коллизий будет минимальным.
По мере того как коэффициент заполнения таблицы приближается к 1,
эффективность процесса заметно падает. Проиллюстрируем линейное опробы-
вание на примере семи записей.
Пример 14.3
Предположим, что данные имеют тип DataRecord и хранятся в 11-
элементной таблице.
struct DataRecord
{
int key;
int data;
};
В качестве хеш-функции HF используется остаток от деления на 11,
принимающий значения в диапазоне 0—10.
HF(item) = item.key % 11
В таблице хранятся следующие данные. Каждый элемент помечен
числом проб, необходимых для его размещения в таблице.
Список: {54,1}, {77,3}, {94,5}, {89,7}, {14,8}, {45,2}, {76,9}
Хеш-таблица
77(1)! 3
0
89(1)! 7
1
45(2)! 2
2
14(1)! 8
3
76(6)! 9
4
5
94(1)! 5
6
7
8
9
54(1)! 1
10
Хеширование первых пяти ключей дает пять различных индексов,
по которым эти ключи запоминаются в таблице. Например, HF({54,1})
= 10, и этот элемент попадает в ТаЫе[10]. Первая коллизия возникает
между ключами 89 и 45, так как оба они отображаются в индекс 1.
Элемент данных {89,7} идет первым в списке и занимает позицию
ТаЫе[1]. При попытке записать {45,2} оказывается, что место ТаЫе[1]
уже занято. Тогда начинается последовательное опробывание ячеек
таблицы с целью нахождения свободного места. В данном случае это
ТаЫе[2]. На ключе 76 эффективность алгоритма сильно падает. Этот
ключ хешируется в индекс 10 — место, уже занятое. В процессе оп-
робывания осуществляется просмотр еще пяти ячеек, прежде чем будет
найдено свободное место в ТаЫе[4]. Общее число проб для размещения
в таблице всех элементов списка равно 13, т.е. в среднем 1,9 проб на
элемент.
Реализация алгоритма открытой адресации дана в упражнениях.
Метод цепочек. При другом подходе к хешированию таблица
рассматривается как массив связанных списков или деревьев. Каждая такая цепочка
называется блоком (bucket) и содержит записи, отображаемые хеш-функцией
в один и тот же табличный адрес. Эта стратегия разрешения коллизий
называется методом цепочек.
Хеш-таблица
Блок 0
Блок 1
Блок п-1
Ключ
Данные
• ••
Ключ
Данные
Если таблица является массивом связанных списков, то элемент данных
просто вставляется в соответствующий список в качестве нового узла. Чтобы
обнаружить элемент данных, нужно применить хеш-функцию для определения
нужного связанного списка и выполнить там последовательный поиск.
Пример 14.4
Проиллюстрируем метод цепочек на семи записях типа DataRecord
и хеш-функции HF из примера 14.3.
Список: {54,1}/ {77,3}, {94,5}, {89,7}, {14,8}, {45,2}, {76,9}
HF(item) = item.key % 11
Каждый новый элемент данных вставляется в хвост соответствующего
связанного списка. В следующей таблице каждое значение данных
сопровождается числом проб, требуемых для запоминания этого значения
в таблице.
нт[о] е
НТ[1] С
НТ[2]
нт[3] Е
НТ[4]
НТ[5]
НТ[б] Е
НТ[7]
НТ[8]
НТ[9]
нт[Ю] Е
77<1)
89(1)
14(1)
94(1)
54(1)
|з
|7|
8
|5
И
NULL
NULL
NULL
► 45(2) I 2 NULL
► 76(2) 9 I NULL
Заметьте, что если считать пробой вставку нового узла, то их общее
число при включении семи элементов равно 9, т.е. в среднем 1,3 пробы
на элемент данных.
В общем случае метод цепочек быстрее открытой адресации, так как
просматривает только те ключи, которые попадают в один и тот же табличный
адрес. Кроме того, открытая адресация предполагает наличие таблицы
фиксированного размера, в то время как в методе цепочек элементы таблицы
создаются динамически, а длина списка ограничена лишь количеством памяти.
Основным недостатком метода цепочек являются дополнительные затраты
памяти на поля указателей. В общем случае динамическая структура метода
цепочек более предпочтительна для хеширования.
14.4. Класс хеш-таблиц
В этом разделе определяется общий класс HashTable, осуществляющий
хеширование методом цепочек. Этот класс образуется от базового абстрактного
класса List и обеспечивает механизм хранения с очень эффективными
методами доступа. Допускаются данные любого типа с тем лишь ограничением, что
для этого типа данных должен быть определен оператор ==. Чтобы сравнить
ключевые поля двух элементов данных, прикладная программа должна
перегрузить оператор ==.
Мы также рассмотрим класс HashTablelterator, облегчающий обработку
данных в хеш-таблице. Объект типа HashTablelterator находит важное
применение при сортировке и печати данных.
Объявления и реализации этих классов находятся в файле hash.h.
Спецификация класса HashTablelterator
ОБЪЯВЛЕНИЕ
#include "array.h"
#include "list.h"
#include "link.h"
#include "iterator.h"
template <class T>
class HashTablelterator;
template <class T>
class HashTable: public List<T>
{
protected:
// число блоков; представляет размер таблицы
int numBuckets;
// хеш-таблица есть массив связанных списков
Array< LinkedList<T> > buckets;
// хеш-функция и адрес элемента данных,
//к которому обращались последний раз
unsigned long (*hf)(T key);
Т *current;
public:
// конструктор с параметрами, включающими
// размер таблицы и хеш-функцию
HashTable(int nbuckets, unsigned long hashf(T key));
// методы обработки списков
virtual void Insert(const T& key);
virtual int Find(T& key);
virtual void Delete(const T& key);
virtual void ClearList(void);
void Update(const T& key);
// дружественный итератор, имеющий доступ к
// данным-членам
friend class HashTableIterator<T>
}
ОПИСАНИЕ
Объект типа HashTable есть список элементов типа Т. В нем реализованы
все методы, которые требует абстрактный базовый класс List. Прикладная
программа должна задать размер таблицы и хеш-функцию, преобразующую
элемент типа Т в длинное целое без знака. Такой тип возвращаемого значения
допускает хеш-функции для широкого диапазона данных. Деление на размер
таблицы осуществляется внутри.
Методы Insert, Find, Delete и ClearList являются базовыми методами
обработки списков. Отдельный метод Update служит для обновления элемента,
уже имеющегося в таблице.
Методы ListSize и ListEmpty реализованы в базовом классе. Элемент
данных current всегда указывает на последнее доступное значение данных. Он
используется методом Update и производными классами, которые должны
возвращать ссылки. Пример такого класса дан в разделе 14.7.
ПРИМЕР
Предположим, что NameRecord есть запись, содержащая поле
наименования и поле счетчика.
struct NameRecord
{
String name;
int count;
>;
// 101-элементная таблица, содержащая данные типа NameRecord
//и имеющая хеш-функцию hash
HashTable<NameRecord> HF(101,hash);
// вставить запись {"Betsy",1} в таблицу
NameRecord rec; // переменная типа NameRecord
rec.name = "Betsy"; // присвоение name = "Betsy
rec.count =1; //и count = 1
HF.Insert(rec); // Вставить запись
cout « HF.ListSize (); // распечатать размер таблицы
// выбрать значение данных, соответствующее ключу "Betsy",
// увеличить поле счетчика на 1 и обновить запись
rec.name = "Betsy";
if (HF.Find(rec) // найти "Betsy"
{
rec.cout +=1; // обновить поле данных
HF.Update(rec); // обновить запись в таблице
}
else
cerr « "Ошибка: \"Ключ Betsy должен быть в таблице.\"\п;
Класс HashTablelterator образован из абстрактного класса Iterator и
содержит методы для просмотра данных в таблице.
Спецификация класса HashTablelterator
ОБЪЯВЛЕНИЕ
template <class T>
class HashTablelterator: public Iterator<T>
{
private:
// указатель таблицы, подлежащей обходу
HashTable<T> *HashTable;
// индекс текущего просматриваемого блока
//и указатель на связанный список
int currentBucket;
LinkedList<T> *currBucketPtr;
// утилита для реализации метода Next
void SearchNextNode(int cb);
public:
// конструктор
HashTablelterator (HashTable<T>& ht);
// базовые методы итератора
virtual void Next(void);
virtual void Reset(void);
virtual T& Data(void);
// подготовить итератор для сканирования другой таблицы
void SetList(HashTable<T>& 1st);
};
ОПИСАНИЕ
Метод Next выполняет прохождение таблицы список (блок) за списком,
проходя узлы каждого списка. Значения данных, выдаваемые итератором,
никак не упорядочены. Для обнаружения очередного списка, подлежащего
прохождению, метод Next использует функцию SearchNextNode.
ПРИМЕР
// объявить итератор для объекта HF типа HashTable
HashTableIterator<NameRecord> hiter(HF);
// сканировать все элементы базы данных
for (niter.Reset(); !niter.EndOfList; hiter.Next())
{
rec = hiter.Data();
cout « rec.name « ": " « rec.count << endl;
}
Приложение: частота символьных строк
Класс HashTable используется для хранения множества символьных строк
и определения частоты их появления в файле. Каждая символьная строка
хранится в объекте типа NameRecord, содержащем наименование строки и
частоту ее повторяемости.
struct NameRecord
{
String name;
int count;
};
Хеш-функция перемешивает биты символов строки путем сдвига текущего
значения функции на три бита влево (умножая на 8) перед тем, как прибавить
следующий символ. Для n-символьной строки СоСх.-.с^Сл.!
п-1
hash(s) = X ci 8n"bl
i=l
Такое вычисление предотвращает проблемы хеширования символьных
строк, рассмотренные в примере 14.2.
// функция для использования в классе HashTable
unsigned long hash (NameRecord elem)
{
unsigned long hashval = 0;
// сдвинуть hashval на три бита влево и
// сложить со следующим символом
for (int i=0; i<elem.Length(); i++)
hashval - (hashval << 3) + elem.name [i];
return hashval;
}
Программа 14.2. Вычисление частот символьных строк
Эта программа вводит символьные строки из файла strings.dat и
запоминает их в 101-элементной таблице. Каждая символьная строка вводится
из файла и, если еще не встречалась ранее, помещается в таблицу. Для
дублирующихся строк из хеш-таблицы выбирается соответствующая
запись, где и производится увеличение на единицу поля счетчика. В конце
программы определяется итератор, который используется для просмотра
и печати всей таблицы. Определения NameRecord, хеш-функции и
оператора == для данных типа NameRecord находятся в файле strfreq.h.
#include <iostream.h>
#include <fstream.h>
#include <stdlib.h>
#include "hash.h"
♦include "strclass.h"
♦include "strfreq.h"
void main(void)
{
// ввести символьные строки из входного потока
ifstream fin;
NameRecord rec;
String token;
HashTable<NameRecord> HF(101, hash);
fin.open("strings.dat"), ios::in | ios::nocreate);
if (!fin)
{
cerr « "Невозможно открыть V'strings,dat\"!" « endl;
exit(1);
}
while (fin >> rec.name)
{
// искать строку в таблице, если найдена, обновить поле count
if (HF.Find(rec))
{
rec.count += 1;
HF.Update(rec);
}
else
{
rec.count = 1;
HF.Insert(rec) ;
}
}
// печатать символьные строки вместе с частотами
HashTableIterator<NameRecord> niter(HF);
for(hiter.Reset(); Ihiter.EndOfList(); niter.Next())
{
rec = hiter.Data();
cout « rec.name « ": " « rec.count « endl;
}
}
/*
<Файл strings.dat>
Columbus Washington Napoleon Washington Lee Grant
Washington Lincoln Grant Columbus Washington
<Прогон программы 14.2>
Lee: 1
Washington: 4
Lincoln: 1
Napoleon: 1 Grant: 2
Columbus: 2
*/
Реализация класса HashTable
Данный класс образован от абстрактного класса List, предоставляющего
методы ListSize и ListEmpty. Мы обсудим элементы данных класса HashTable
и операции, реализующие чистые виртуальные функции Insert, Find, Delete и
ClearList.
Ключевым элементом данных класса является объект buckets типа Array,
который определяет массив связанных списков, образующих хеш-таблицу.
Указатель функции hf определяет хеш-функцию, a numBuckets является
размером таблицы. Указатель current идентифицирует последний элемент
данных, к которому осуществлялся доступ тем или иным методом класса. Его
значение задается методами Find и Insert и используется методом Update для
обновления данных в таблице.
Методы обработки списков. Метод Insert вычисляет значение хеш-функции
(индекс блока) и ищет объект типа LinkedList, чтобы проверить, есть ли уже
такой элемент данных в таблице или нет. Если есть, то Insert обновляет этот
элемент данных, устанавливает на него указатель current и возвращает
управление. Если такого элемента в таблице нет, Insert добавляет его в хвост списка,
устанавливает на него указатель current и увеличивает размер списка.
template <class T>
void HashTable<T>::Insert(const T& key)
{
// hashval — индекс блока (связанного списка)
int hashval = int(hf(key) % numBuckets);
// 1st — псевдоним для buckets[hashval].
// помогает обойтись без индексов
LinkedList<T>& 1st = buckets[hashval];
for (Ist.ResetO ; ! 1st .EndOfList () ; Ist.NextO)
// если ключ совпал, обновить данные и выйти
if (Ist.DataO == key)
{
1st.Data() = key;
current = &lst.Data();
return;
}
// данные, соответствующие этому ключу, не найдены, вставить элемент в список
1st.InsertRear(key);
current - &lst.Data();
size++;
}
Метод Find применяет хеш-функцию и просматривает указанный в
результате список на предмет совпадения с входным параметром. Если совпадение
обнаружено, метод копирует данные в key, устанавливает указатель current на
соответствующий узел и возвращает True. В противном случает метод
возвращает False.
template <class T>
int HashTable<T>::Find(T& key)
{
// вычислить значение хеш-функции и установить 1st
// на начало соответствующего связанного списка
int hashval = int(hf(key) % NumBuckets);
LinkedList<T>& 1st = buckets[hashval];
// просматривать узлы связанного списка в поисках key
for (1st.Reset (); list .EndOf List (■) ; Ist.NextO)
// если ключ совпал, получить данные, установить current и выйти
if (Ist.DataO == key)
{
key = Ist.DataO ;
current = &lst.Data();
return 1; // вернуть True
}
return 0; // иначе вернуть False
}
Метод Delete просматривает указанный список и удаляет узел, если
совпадение произошло. Этот метод (вместе с методами ClearList и Update) находится
в файле hash.h.
Реализация класса HashTablelterator
Этот класс должен просматривать данные, разбросанные по хеш-таблице.
Поэтому он более интересен и более сложен с точки зрения реализации, чем
класс HashTable. Обход элементов таблицы начинается с поиска непустого
блока в массиве списков. Обнаружив непустой блок, мы просматриваем все
узлы этого списка, а затем продолжаем процесс, взяв другой непустой блок.
Итератор заканчивает обход, когда просмотрен последний непустой блок.
Итератор должен быть привязан к списку. В данном случае переменной hash-
Table присваивается адрес таблицы. Поскольку класс HashTablelterator является
дружественным по отношению к HashTable, он имеет доступ ко всем закрытым
данным-членам последнего, включая массив buckets и его размер numBuckets.
Переменная currentBucket является индексом связанного списка, который
просматривается в данный момент, a currBucketPtr — указателем этого списка. Прохождение
каждого блока осуществляется итератором, встроенным в класс LinkedList. На рис.
14.4 показано, как итератор проходит таблицу с четырьмя элементами.
Метод SearchNextNode вызывается для обнаружения очередного списка,
подлежащего прохождению. Просматриваются все блоки, начиная с cb, пока
hashTablelterator
hashTable<T> *hashTable;
Объект типа HashTable
Buckets[0]
Buckets[1]
Buckets[2]
Buckets[3]
Buckets[4]
hf(x) = x
Empty
Empty
Итератор извлекает 10 2 22 29
Рис. 14.4. Итератор хэш-таблиц
не встретится непустой список. Переменной currentBucket присваивается
индекс этого списка, а переменной currBucketPtr — его адрес. Если непустых
списков нет, происходит возврат с currentBucket = -1.
// начиная с cb, искать следующий непустой список для просмотра
template <class t>
void HashTableIterator<T>::SearchNextNode(int cb)
{
currentBucket = -1;
// если индекс cb больше размера таблицы, прекратить поиск
if (cb > hashTable->numBuckets)
return;
// иначе искать, начиная с текущего списка до конца таблицы,
// непустой блок и обновить частные элементы данных
for (int i=cb; i<hashTable->numBuckets; i++)
if (!hashTable->buckets[i].ListEmptyO)
{
// перед тем как вернуться, установить currentBucket равным i
//ив currBucketPtr поместить адрес нового непустого списка
currBucketPtr = &hashTable->buckets[i];
currBucketPtr ->Reset();
currentBucket = i;
return;
}
}
Конструктор инициализирует базовый класс Iterator и присваивает
закрытому указателю hashTable адрес таблицы. Непустой список обнаруживается с
помощью вызова SearchNextNode с нулевым параметром.
// конструктор, инициализирует базовый класс и класс HashTable
// SearchNextNode идентифицирует первый непустой блок в таблице
template <class T>
HashTableIterator<T>::HashTablelterator(HashTable<T>& hf):
Iterator<T>(hf), HashTable(&hf)
{
SearchNextNode(0);
}
С помощью метода Next осуществляется продвижение вперед по текущему
списку на один элемент. По достижении конца списка функция SearchNextNode
настраивает итератор на следующий непустой блок.
// перейти к следующему элементу данных в таблице
template <class T>
void HashTableIterator<T>::Next(void)
{
// продвинуться к следующему узлу текущего списка
currBucketPtr->Next();
// по достижении конца списка вызвать SearchNextNode
// для поиска следующего непустого блока в таблице
if (currBucketPtr->EndOfList())
SearchNextNode(++currentBucket);
// установить флажок iterationComplete, если непустых списков
// больше нет
iterationComplete = currentBucket == -1;
)
14.5. Производительность методов поиска
Мы представили в этой книге четыре метода поиска: последовательный,
бинарный, поиск на бинарном дереве и хеширование. Быстродействие того или
иного метода обычно зависит от среднего числа сравнений, необходимых для
обнаружения элемента данных. Мы показали, что эффективность
последовательного поиска равна О(п), а бинарного поиска и поиска на дереве — 0(log2n).
Анализ производительности хеширования более увлекательный. Здесь
производительность зависит от качества хеш-функции и от размера таблицы.
Хорошая хеш-функция дает равномерное распределение значений. При
относительно большой таблице число коллизий сокращается. Размер таблицы
влияет на коэффициент заполнения (load factor) таблицы. Если таблица
состоит из m ячеек, п из которых заняты, то коэффициент заполнения X
определяется следующим образом:
X = n/m
Когда таблица пуста, X = 0. По мере того как данные добавляются в таблицу,
X растет, как и вероятность коллизий. При открытой адресации X достигает
своего максимального значения, равного 1, когда таблица заполнена (т = п).
При использовании метода цепочек списки могут быть как угодно длинными,
поэтому X может превысить 1.
Для оценки сложности хеширования по методу цепочек можно выдвинуть
следующие интуитивные соображения. Наихудшим случаем является тот,
при котором все элементы данных отображаются в один и тот же табличный
адрес. Если связанный список содержит п элементов, время поиска составит
О(п), т.е. в худшем случае производительность равна О(п).
Для среднего случая при относительно равномерном распределении
значений хеш-функции мы ожидаем X = n/m элементов в каждом связанном списке.
Следовательно, время поиска в каждом связанном списке равно 0(Х) = 0(n/m).
Если предполагается, что количество элементов, размещаемых в таблице,
ограничено некоторым числом, скажем R*m, то время поиска в каждом списке
равно 0(R*m/m) = O(R) = 0(1), т.е. метод цепочек имеет порядок 0(1). Доступ
к данным в хеш-таблице, реализованной по методу цепочек, производится за
фиксированное время, не зависящее от количества данных.
Формальный математический анализ хеширования выходит за рамки этой
книги. В табл. 14.1 для каждого метода хеширования даны формулы
приблизительного расчета числа проб, необходимых при успешном и
безуспешном поиске в достаточно большой таблице. Каждая формула есть функция
коэффициента заполнения X. Подробное обсуждение этих и других
результатов можно найти в [19]. Когда X = 1, успешный поиск требует в среднем
т/2 проб, а безуспешный — т проб.
Формулы для оценки сложности методов хеширования
Таблица 14.1
Открытая
адресация
Метод цепочек
Число проб при успешном поиске
1 1 i «
—-—— + ■=:, x*^
2(1 -А) 2
л X
1 + 2
Число проб при безуспешном поиске
1 1 1 ,
2(1-Л)2 + 2'Л*1
е~х + Х
Из этой таблицы следует, что метод открытой адресации достаточно хорош
при небольшом коэффициенте заполнения. В общем случае метод цепочек
лучше. Например, когда m = n (X = 1), то методу цепочек требуется только
1,5 пробы для успешного поиска, в то время как при открытой адресации
просматривается вся таблица и требуется в среднем т/2 проб. Когда таблица
заполнена наполовину, метод цепочек требует 1,25 проб при успешном
поиске, а открытая адресация — 1,5.
Очевидно, что хеширование является чрезвычайно быстрым методом
поиска. Однако каждый из четырех поисковых методов имеет свое применение.
Последовательный поиск эффективен при малом числе элементов и в тех
случаях, когда данные не нужно сортировать. Бинарный поиск очень быстр,
но требует чтобы массив данных был отсортирован. Этот метод не годится
для данных, значения которых определяются во время выполнения
программы (например, таблица символов в компиляторе), поскольку упорядоченный
массив — далеко не благоприятная среда для операций удаления и вставки.
Для этих задач подходят бинарное дерево поиска и хеширование. Бинарное
дерево поиска не столь быстрое, но обладает привлекательным эффектом
упорядочения данных при выполнении симметричного прохождения. Когда
нужен быстрый доступ к неупорядоченным данным, хеширование — лучший
метод.
14.6. Бинарные файлы и операции с данными
на внешних носителях
Во многих приложениях требуется доступ к данным, расположенным в
файлах на диске. В этом разделе дается обзор ввода/вывода бинарных файлов
с помощью класса fstream (файл fstream.h). Мы рассмотрим класс BinFile,
содержащий методы для открытия и закрытия бинарных файлов, для доступа
к отдельным записям файла и для блочного ввода/вывода. Большие наборы
данных могут содержать миллионы записей, которые невозможно разместить
в памяти одновременно. Для управления ими нужны алгоритмы внешней
сортировки и поиска. Мы дадим лишь краткое введение в эту тему, поскольку
детальное обсуждение файлов, а также внешней сортировки и поиска выходит
за рамки данной книги.
Бинарные файлы
Текстовый файл содержит строки ASCII-символов, разделенные символами
конца строки. Бинарный файл состоит из записей, которые варьируются от
одного байта до сложных структур, включающих целые числа, числа с
плавающей точкой и массивы. С аппаратной точки зрения записи файла
представляют собой блоки данных фиксированной длины, хранящиеся на диске.
Блоки, как правило, несмежные. Однако с логической точки зрения записи
располагаются в файле последовательно. Файловая система позволяет
осуществлять доступ как к отдельным записям, так и ко всему файлу целиком,
рассматривая последний как массив записей. Во время ввода/вывода данных
система поддерживает файловый указатель (file pointer) — текущую позицию
в файле.
Файл как структура прямого доступа
*о
0
Ri
1
R2
2
R3
3
R4
4
Ri
Текущая позиция
Rn-2
n-2
Rn-1
n-1
Файл является также последовательной структурой, которая сохраняет
файловый указатель в текущей позиции внутри данных. Операции
ввода/вывода обращаются к данным в текущей позиции, которая затем продвигается
к следующей записи.
Файл как структура последовательного доступа
Начало
Текущая позиция
Конец
Встроенный в C++ класс fstream описывает файловые объекты, которые
могут использоваться как для ввода, так и для вывода. Создавая объект,
мы используем метод open для назначения файлу физического имени и
режима доступа. Возможные режимы определены в базовом классе ios.
Режим
in
out
trunc
nocreate
binary
Действие
открыть файл для чтения
открыть файл для записи
удалить запись до чтения или записи
если файл не существует, не создавать пустой файл;
возвратить ошибочное состояние потока
открыть файл, считая его бинарным (не текстовым)
Пример 14.5
#include <fstream.h>
fstream f; // объявление файла
// открыть текстовый файл Phone для ввода.
// если такого файла нет, сообщить об ошибке
f.open("Phone", ios::in | ios: mocreate) ;
fstream f; // объявление файла
// открыть бинарный файл для ввода
f.open("DataBase", ios::in | ios::out | ios:ibinary);
Каждый файловый объект имеет ассоциированный с ним файловый
указатель, который указывает на текущую позицию для ввода или вывода. Функция
tellg() возвращает смещение в байтах от начала файла до текущей позиции во
входном файле. Функция tellp() возвращает смещение в байтах от начала файла
до текущей позиции в выходном файле. Функции seekg() и seekp() позволяют
передвинуть текущий файловый указатель. Все эти функции принимают в
качестве параметра смещение, измеряемое числом байтов относительно начала
файла (beg), конца файла (end) или текущей позиции в файле (cur). Если файл
используется как для ввода, так и для вывода, пользуйтесь функциями tellg
и seekg.
смещение смещение смещение смещение
BEG CUR END
Следующий код иллюстрирует действие функций seekg и tellg:
// Бинарный файл целых чисел
fstream f;
f.open("datafile", ios::in | ios::nocreate | ios::binary);
// сбросить текущую позицию на начало файла
f.seekg(0, ios::beg);
// установить текущую позицию на последний элемент данных
f.seekg(-sizeof(int), ios:rend);
// передвинуть текущую позицию к следующей записи
f.seekg(-sizeof(int), ios::cur);
• • *
// переместиться к концу файла
f.seekg(0, ios::end);
// распечатать число байтов в файле
cout « f.tellg() << endl;
// распечатать число элементов данных в файле
cout << f.tellg()/sizeof(int);
Класс fstream имеет базовые методы read и write, выполняющие ввод/вывод
потока байтов. Каждому методу передаются адрес буфера и счетчик
пересылаемых байтов. Буфер является массивом символов, в котором данные
запоминаются в том виде, каком они принимаются или посылаются на диск. Операции
ввода/вывода данных несимвольного типа требуют приведения к типу char.
Например, следующие операции передают блок целых чисел:
fstream f; // объявление файла
int data = 30, A[20];
// записать число 30 как блок символов длиной sizeof(int)
f.write((char*) &data, sizeof(int));
// прочитать 20 чисел из файла f в массив А
f.read((char*)A, 20*sizeof(int));
Класс BinFile
Файловый ввод/вывод используется во многих приложениях. В этом
разделе мы абстрагируем файл от какого бы то ни было приложения и определяем
некоторый класс, обеспечивающий общие операции обработки бинарных
файлов. Это пример класса, полностью скрывающего от пользователя системные
детали нижнего уровня. Поскольку этот класс определен как шаблон,
порождаемые им файлы могут содержать различные типы данных.
Спецификация класса BinFile
ОБЪЯВЛЕНИЕ
// системные файлы, содержащие методы для обработки файлов
#include <iostream.h>
#include <fstream.h>
#include <stdlib.h>
#include "strclass.h"
// тип доступа
enuiri Access {IN, OUT, INOUT};
// тип смещения в операциях поиска
enum SeekType {BEG, CUR, END};
template <class T>
class BinFile
{
private:
// файловый поток со своим именем и типом доступа
fstream f;
Access accessType; // тип доступа
String fname; // физическое имя файла
int fileOpen; // файл открыт?
// параметры, характеризующие файл как структуру прямого доступа
int Tsize; // размер записи
int filesize; // число записей
// выдает сообщение об ошибке и завершает программу
void Error{char *msg);
public:
// конструкторы и деструктор
BinFile(const Strings fileName, Access atype = OUT);
-BinFile(void);
// конструктор копирования.
// объект должен передаваться по ссылке.
// завершает программу
BinFile(BinFile<T>& bf);
// утилиты обслуживания файла
void Clear(void); // очистить файл от записей
void Delete(void); // закрыть файл и удалить его
void Close(void); // закрыть файл
int EndFile(); // проверить условие конца файла
long Size(); // вернуть число записей в файле
void Reset(void); // установить файл на первую запись
// переместить файловый указатель на pos записей относительно
// начала файла, текущей позиции или конца файла
void Seek(long pos, SeekType mode);
// блочное чтение п элементов данных в буфер с адресом А
int Read{T *A, int n);
// блочная запись п элементов данных из буфера с адресом А
void Write(T *А, int n);
// Еыбрать запись, расположенную в текущей позиции
Т Peek(void);
// копировать data в запись, расположенную в позиции pos
void Write (const T& data, long pos);
// читать запись по индексу pos
Т Read (long pos);
// записать запись в конец файла
void Append(T item);
};
ОПИСАНИЕ
Конструктор отвечает за открытие файла и инициализацию параметров
класса. Создавая объект типа BinFile, программа должна указывать режим
доступа к файлу (IN, OUT или INOUT). Если файл открывается в режиме OUT,
он очищается. Файл, открывающийся в режиме IN, должен существовать,
иначе будет выдано сообщение об ошибке с последующим завершением
программы. Если файл объявлен как INOUT, то записи можно как вводить, так и
выводить. Открыв такой файл, конструктор устанавливает fileOpen в 1 (True),
показывая тем самым, допускается операция чтения.
При вызове конструктора копий выдается сообщение об ошибке. В момент
создания файловому объекту приписывается физический файл. Допуская
копирование файла, можно было бы потребовать, чтобы новый объект
обязательно открывал тот же самый файл. Однако на некоторых системах это
невозможно, а если и допускается, то может привести к опасной ситуации. Объект типа
BinFile должен передаваться по ссылке.
Файл может обрабатываться как структура прямого доступа. Методы Read и
Write принимают в качестве параметра индекс записи pos и вводят или выводят
элемент данных по этой позиции. Методы блочного чтения/записи используются
для ввода/вывода сразу нескольких записей. Блочный Read возвращает число
прочитанных записей или 0, если встретился конец файла. Возможна ситуация,
когда в файле остается менее п записей. Следовательно, возвращаемое значение
может быть меньше п. В качестве параметров передаются адрес буфера данных и
число записей. Передача начинается с текущей позиции в файле. Метод Peek
позволяет выбрать текущую запись, не продвигая файловый указатель.
Метод EndFile возвращает логическое значение, сигнализирующее о том,
был ли достигнут конец файла. Используйте этот метод только для входных
файлов. Для файлов других типов проверяйте в цикле индекс текущей записи
и останавливайтесь, когда переменная цикла превысит индекс последней записи.
Метод Close закрывает поток, но не удаляет физический файл. Используйте
Close, если файл должен быть открыт другим объектом, возможно, в другом
режиме.
Метод Clear очищает файл от записей, оставляя его открытым и имеющим
нулевой размер. Метод Delete закрывает файл и удаляет его с диска. Эти методы
сбрасывают флажок fileOpen в 0. После этого любая попытка обратиться к
файлу заканчивается прекращением программы. Метод Seek позволяет пере-
местить файловый указатель. Параметр mode указывает базу, относительно
которой отсчитывается смещение pos, и соответствует началу файла, текущей
позиции или концу файла.
ПРИМЕР
// файл целых чисел, предназначенный для ввода/вывода;
// физическое имя demofile
BinFile<int> BF("demofile", INOUT);
BinFile<int> BG("outfile", OUT); // файл для вывода целых чисел
int i, m = 5, n = 10, A[10]; // переменные целого типа
// Эти данные будут выведены в demofile
int vals[] = {30,40,50,60,70,80,90,100};
for (i=0; i<5; i++)
BF.Write(&i,l);
BF.Append(m) ; // записать 5 в конец файла
BF.Reset(); // встать на начало файла
BF.Write(п,0) // записать 10 в начало файла
cout « BF.SizeO « endl; // распечатать размер файла (6)
cout « BF.Read(3) « endl; // распечатать третью запись
BF.Read(A,2); // ввести два числа в массив А
cout « А[0] « " " « А[1]; // и распечатать их
BF.Reset(); // встать на начало файла
cout « BF.PeekO « endl; // распечатать текущую запись (10)
BF.Read(A,4); // ввести четыре числа в массив А
BG.Write(А, 4); // вывести А[0]~А[3] в файл BG
А[0] *= 2; // удвоить А[0]
BG.Write(А[0],0); // вывести новое значение в первую запись
BF.Seek(2,beg); // переместиться ко второй записи файла BF
BF.Write(vals,8) ; // записать 30..100 в файл,
// начиная со второй записи
BF.Reset(); // вернуться к началу файла demofile
// Читать и распечатывать demofile
for (i=0; i<BF.Size(); i++)
{
BF.Read(&m,1);
cout « m « " ";
}
cout « endl;
BF.Delete(); // удалить файл BF
BG.Close(); // закрыть outfile
BinFile<int> BH("outfile", IN) // открыть outfile для ввода
while (IBH.EndFile ()) // читать и распечатывать outfile
{
BH.ReadUm, 1);
cout << m « " ";
}
cout « endl;
BH.CloseO; // закрыть outfile
<Результирующая распечатка>
б
3
4 5
10
10 1 30 40 50 60 70 80 90 100
20 1 2 3
Реализация класса BinFile
Полная реализация класса содержится в файле binfile.h. В этом разделе мы
обсудим конструктор, метод прямого чтения, блочный вывод п записей и
утилиту Clear,
Конструктор отвечает за открытие файла и инициализацию параметров
класса. Создавая объект, мы передаем конструктору имя файла и тип доступа.
// конструктор, открывает файл с заданным именем и типом доступа
template <class T>
BinFile<T>::BinFile(const Strings fileName, Access atype)
{
// операция открытия потока зависит от типа доступа.
// для IN файл не создается, если он не существует.
// для OUT все существующие в нем данные удаляются.
// для INOUT файл пригоден и для ввода, и для вывода
if (atype «« IN)
f.open(fileName, ios::in 1 ios::trunc | ios::binary;
else if (atype == OUT)
f.open(fileName, ios::out | ios::trunc ! ios::binary;
else
f.open(fileName, ios::in | ios::out I ios::binary;
if (!f)
Error("Конструктор BinFile: не могу открыть файл");
else
fileOpen - 1/
accessType * atype;
// подсчитать число записей в файле
// Tsize — размер типа данных Т (длина записи)
Tsize = sizeof(T);
if (accessType =- IN I I accessType » INOUT)
{
// подсчитать число записей во входном файле, переместившись
//к его концу, вызвав tellg и затем разделив полученную длину
// файла в байтах на длину записи
f.seekg(0, ios::end);
fileSize * f.tellgO/Tsize;
f.seekg(0, ios::beg);
}
else
fileSize =0; // размер для выходного файла
// записать имя физического файла в fname
fname =« fileName;
}
Доступ к файлу. С помощью метода seekg файл можно рассматривать как
массив прямого доступа. Метод Read имеет параметр pos. Комбинируя размер
записи и параметр pos, метод seekg перемещает файловый указатель на
конкретную запись и извлекает ее из файла.
// метод Read возвращает запись, идущую в файле под номером pos
template <class T>
Т BinFile<T>::Read (long pos)
{
// переменная для хранения записи
Т data;
if (IfileOpen)
Error ("BinFile Read(int роз): файл закрыт");
// метод Read недопустим для выходных файлов
if (accessType » OUT)
Error("Недопустимая операция доступа к файлу")/
// проверить попадание pos в диапазон 0..fileSize-1
else if (pos < 0 || pos >= fileSize)
Error("Недопустимая операция доступа к файлу");
// переместить файловый указатель и извлечь, данные
//с помощью метода read класса fstream
f.seekg(pos*Tsize, ios::beg);
f.read((char *)&data,Tsize);
// если файл входной и мы прочитали все записи,
// установить флажок конца потока
if (accessType « IN)
if (f.tellgO/Tsize >- fileSize)
f.clear(ios::eofbit); // установить бит eof
return data;
)
Когда файл используется как устройство последовательного доступа, метод
Write можно определить так, чтобы он копировал в файл сразу несколько
записей. Адрес выводимых данных и число записей передаются в качестве
параметров. Метод write класса fstream копирует поток байтов в выходной
файл. Поскольку вывод может начинаться не с начала файла, следует
позаботиться о правильном значении fileSize.
// выводит п-элементный массив А в файл
template <class T>
void BinFile<T>::Write(T *A, int n)
{
long previousRecords;
// для входных файлов операция записи недопустима
if (accessType «=* IN)
Error("Недопустимая операция доступа к файлу");
if (IfileOpen)
Error ("BinFile Write(T *A, int n): файл закрыт");
// вычислить новый размер файла, вызвать tellg для подсчета
// числа записей, предшествующих точке вывода, определить,
// увеличился ли размер файла, если да, увеличить fileSize на
// число добавляемых записей
previousRecords - f.tellg()/Tsize;
if (previousRecords + n > fileSize)
fileSize +« previousRecords + n - fileSize;
// число выводимых Сайтов равно n * Tsize
f.write((char *)A, Tsize*n);
)
Утилиты. В данном классе имеется целый ряд полезных методов для
управления файлом. Метод Clear удаляет все имеющиеся в файле записи,
сперва закрывая файл, а затем вновь открывая его в режиме trunc,
используя набор параметров файла, которые хранятся как частные данные-
члены класса.
// метод Clear удаляет записи файла, сначала закрывая его,
// а затем открывая вновь
template <class T>
void BinFile<T>::Clear(void)
{
// входной файл очищать нельзя
if {accessType -= IN)
Error("Недопустимая операция доступа к файлу");
// закрыть, а затем вновь открыть файл
f.close();
if (accessType *» OUT)
f.open(fname, ios::out I ios::trunc | ios::binary);
else
f.open(fname, ios::in | ios::out | ios::trunc I ios::binary)/
if (!f)
Error("BinFile Clear: не могу повторно открыть файл");
fileSize - 0;
}
Внешний поиск
Ранее мы рассмотрели ряд внутренних списковых структур хранения
данных. Подобный набор структур можно определить для данных, хранящихся
в файле. Эффективность методов внешней сортировки и поиска зависит от
организации записей файла. Мы распространим концепцию хеширования на
файловые структуры и используем методы класса BinFile для доступа к
данным.
Методика хеширования обеспечивает высокую эффективность поиска и
может быть применена к внешним структурам. Хеш-функция ставит в
соответствие каждой записи целое число из диапазона О...п-l. Это число может
служить индексом в массиве записей, где данные запоминались методом
открытой адресации. В более эффективном методе цепочек это число может
использоваться как индекс в массиве списков. Оба этих метода хранения
можно применить к файлам. В этом разделе мы будем иметь дело с методом
цепочек, при котором файл содержит связанные списки записей. Мы создадим
в памяти хеш-таблицу и с ее помощью будем обращаться к более медленному
дисковому устройству.
Пусть запись содержит данные вместе с файловым индексом.
data
nextlndex
FaleOataRecord
Эти записи хранятся на диске в виде связанного списка. Поле nextlndex
указывает позицию следующей записи файла. Чтобы сформировать связанные
списки, создадим в памяти хеш-таблицу, которая ссылается на связанные
списки в файле. Хеш-функция отображает каждую запись в табличный индекс.
int hashtable[n]; // массив файловых индексов
Хеш-таблица представляется в памяти в виде n-элементного массива.
Изначально таблица пуста (каждая ячейка содержит -1), показывая тем самым, что
записей в файле нет. Как только мы вводим запись из базы данных,
хеш-функция определяет индекс в таблице. Если соответствующая ячейка таблицы
пуста, мы запоминаем саму запись на диске, а ее позицию в файле — в таблице.
Хеш-таблица
(в памяти)
Записи FileDataRecord на диске
хеш-адрес
Данные
Запись#3
Записи FileDataRecord на диске
Теперь ячейка таблицы содержит дисковый адрес первой отображаемой в эту
ячейку записи. Этот адрес можно использовать для доступа к
соответствующему связанному списку и вставить туда цовую запись. Процесс вставки
заключается в выводе записи на диск и обновлении указателя в поле nextlndex.
Проиллюстрируем этот процесс на простом примере, который, тем не
менее, выражаетет главные особенности. Пусть наши данные имеют целый
тип и запоминаются в файле в виде списка записей FileDataRecord.
// узел списка, в котором хранится запись
struct FileDataRecord
{
// в нашем примере поле data есть целое число, на практике
// чаще всего поле data является сложной записью
int data;
int nextlndex; // ссылка на следующую запись в файле
>;
Хеш-функция отображает каждое значение данных в другое целое число,
выражаемое младшей цифрой исходного числа.
h(data) = data % 10; // h{456) = 6; h(891) = 1; h(26) = 6
В нашем примере в файле запоминаются следующие данные:
456 64 84 101 144
Первые два числа отображаются в пустые ячейки таблицы и,
следовательно, могут быть сразу вставлены в файл в качестве узлов. Первый узел
запоминается в позиции 0, а второй — в позиции 1. Номера позиций
заносятся в соответствующие ячейки таблицы.
Таблица
Ячейка таблицы, соответствующая числу 84, содержит 1 — номер записи
файла, являющейся первой в некотором связанном списке записей. Новая
запись (84) вставляется в начало этого списка.
Таблица
После загрузки чисел 101 и 104 файл содержит пять записей
FileDataRecord, которые логически представляют собой три связанных списка. Головы
этих списков содержатся в известных ячейках таблицы.
В данном методе хранения эффективно используется прямой доступ к
файлу. Файл формируется путем последовательного добавления записей и
обновления соответствующих ячеек таблицы. Часто сама таблица
запоминается в виде отдельного файла и загружается оттуда в память, когда требуется
поработать с основным файлом.
Программа 14.3. Внешнее хеширование
Эта программа иллюстрирует ранее рассмотренный алгоритм внешнего
хеширования. Функция LoadRecord добавляет в файл новую запись, а
функция PrintList распечатывает связанный список записей, соответствующий
некоторому хеш-адресу. Каждая запись вставляется в начало своего
связанного списка. Исключение дубликатов не производится. Главная процедура
включает в файл 50 случайных чисел от 0 до 999. У пользователя
запрашивается какой-нибудь хеш-индекс, а затем распечатываются элементы
соответствующего связанного списка.
#include <iostream.h>
#include "random.h"
#include "binfile.h"
const long Empty = -1;
// узел списка, в котором хранится запись
struct FileDataRecord
{
//в нашем примере поле data есть целое число, на практике
// чаще всего поле data само является сложной записью
int data;
int nextIndex; // ссылка на следующую запись в файле
};
// startindex — индекс в таблице, передается по ссылке, чтобы
// можно было обновлять голову списка
void LoadRecord(BinFile<FileDataRecord> &bf, long &startindex,
FileDataRecord &dr)
{
// если таблица не пуста, startindex указывает на первую запись
// списка, в противном случае startindex = 1
dr.nextlndex « startindex;
startindex = bf.SizeO;
// добавить в файл новую запись
bf.Append(dr);
}
// сканировать узлы списка в файле и распечатывать значения данных
void PrintList(BinFile<FileDataRecord> &bf, long &startindex)
{
// index — индекс первой записи списка
long index * startindex;
FileDataRecord rec;
// index продвигается к концу списка (до index = -1)
while (index !=» Empty)
{
// прочитать запись, распечатать поле данных и перейти к следующей записи
rec « bf.Read(index);
cout « rec.data « " ";
index =* rec.nextlndex;
}
cout « endl;
)
void main(void)
{
// таблица голов списков записей в файле.
// область значений хеш-функции равна 0..9
long HashTable[10];
// генератор случайных чисел и запись с данными
RandomNumber rnd;
FileDataRecord dr;
int i, item, request;
// открыть файл DRfile для ввода/вывода
BinFile<FileDataRecord> dataFile{"DRfile", INOUT);
// инициализировать таблицу пустыми ячейками
for (i*»0; i<10; i++)
hashTable[i] ■ Empty;
// ввести 50 случайных чисел от 0 до 999
for (i*0; i<50; i++)
{
item » rnd.Random(1000);
// сформировать запись и вывести ее в файл
dr.data e item;
LoadRecord(dataFile, hashTable[item % 10], dr);
}
// запросить индекс в хеш-таблице
// и распечатать соответствующий список
cout « "Введите номер ячейки хеш-таблицы: ";
cin » request;
cout « "Печать элементов данных, хещируемых в число "
« request « endl;
PrintList(dataFile, hashTable[request]);
// удалить файл
dataFile.Delete();
)
/*
<Прогон программы 14.3>
Введите номер ячейки хеш-таблицы: 5
Печать элементов данных, хешируемых в число 5
835 385 205 185 455 5
*/
Внешняя сортировка
Сортировка данных на внешних носителях составляет специальную
проблему, когда файл настолько велик, что не умещается в оперативной памяти.
Поскольку все данные нельзя расположить в одном массиве, мы должны
использовать для их хранения временные файлы. В этом разделе
рассматривается вцешняя сортировка слиянием с помощью трех файлов. Мы обсудим
алгоритмы как прямого, так и естественного слияния, использующего
длинные последовательности. Эти алгоритмы могут быть расширены до п-путевого
слияния, в котором задействовано более чем 3 файла.
В гл. 12 мы рассмотрели простое слияние, которое объединяет два
упорядоченных списка в один. Сортировка прямым слиянием использует этот
подход, объединяя подсписки фиксированной длины. Пусть сортируемые
элементы хранятся в файле fC, а файлы fA и fB являются временными и
служат для разбиения данных. Тогда алгоритм сортировки можно
представить последовательностью следующих шагов:
1. Разбить fC пополам, попеременно записывая его элементы то в fA, то
в fB. Таким образом в каждом новом файле создается
последовательность одноэлементных подсписков,
2. Сопоставить подсписки. Выбрать один элемент из fA и один элемент
из fB. Объединить их в двухэлементный подсписок и записать в fC.
Продолжать до тех пор, пока все элементы в обоих файлах не будут
снова скопированы в fC.
3. Повторить шаг 1, попеременно записывая двухэлементные подсписки
файла fC в файлы fA и fB.
4. Попарно слить все двухэлементные подсписки файлов fА и fВ в четы-
рехэлементные подсписки файла fC.
5. Повторять шаг, на котором fC разбивается пополам, образуя четырех-,
восьми- и т.д. -элементные подсписки в файлах fA и fB. Затем сливать
каждую пару подсписков в восьми-, шестнадцати- и т.д. -элементные
подсписки файла fC. Процесс завершается в тот момент, когда в fА и
fВ образуется по одному упорядоченному списку, которые окончательно
сливаются в отсортированный файл fC.
Проиллюстрируем сортировку прямым слиянием на примере двадцати
целых чисел.
5 15 35 30 20 45 35 5 65 75 40 50 60 70 30 40 25 10 45 55
Файл f A
файл fB
Файл fC
На первом шаге fC разбивается на два временных файла по 10
одноэлементных подсписка в каждом. На втором шаге посредством слияния создается
файл упорядоченных пар fC.
Файл fA
Файл fB
Файл fC
На третьем шаге файл упорядоченных пар fC разбивается пополам на
файлы fA и fB, которые затем попарно сливаются в файл упорядоченных
четверок fC.
Разбиение и последующее попарное слияние файлов происходит еще три
раза. В этих проходах в fC создаются упорядоченные 8-, 16- и наконец
20-элементные подсписки. После финального прохода fC становится
отсортированным файлом. При создании 8- и 16-элементных подсписков в хвосте
файла fA остается "непарный" подсписок, который просто копируется снова
в fC. В финальном проходе 16-элементный подсписок в fA сливается с 4-
элементным подсписком в fВ и процесс завершается.
8-элементные
подсписки
16 -элементные
подсписки
20-элементный
подсписок
Анализ сортировки прямым слиянием. Сортировка прямым слиянием
состоит из серии проходов, начинающейся с одноэлементных подсписков. На
каждом проходе длина подсписков удваивается, пока не достигнет своего
предельного значения s > п. Для этого требуется log2n отдельных проходов,
во время которых все п элементов копируются сначала во временные файлы,
а затем снова в fC. Таким образом, сортировка прямым слиянием требует
2 * n * log2n обращений к данным, что составляет сложность порядка 0(n log2n).
Сортировка естественным слиянием
Сортировка прямым слиянием использует упорядоченные подсписки с
начальной длиной 1, удваивающейся на каждом проходе. В конце концов
упорядоченные подсписки охватывают весь файл, и сортировка завершается. При
этом несоизмеримое количество времени тратится на короткие подсписки —
на их разбиения и последующие слияния. Эффективность алгоритма намного
возрастает на длинных подсписках, так как требуется меньше проходов и
файловые операции не должны выполняться столь часто. В данном разделе мы
модифицируем сортировку прямым слиянием таким образом, чтобы она
начиналась с относительно длинных подсписков и, следовательно, стала более
эффективной. Усовершенствованному алгоритму требуется файл fC и буфер в
оперативной памяти для создания упорядоченных подсписков. Данные исходного
файла читаются в буфер поблочно. Каждый блок сортируется с помощью какого-
нибудь быстрого алгоритма внутренней сортировки (например, Quicksort).
Отсортированные блоки попеременно копируются в файлы f А и fB. Слияние начинается
с подсписков, которые уже с самого начала имеют большую длину.
Чтобы оценить влияние длины исходных подсписков, сравните по табл. 14.2
времена сортировок 30000 случайных чисел при различных размерах блока.
Реализация естественного слияния. Функция MergeSort создает два
временных файла и осуществляет серию проходов, разбивающих исходный файл на
файлы fA и fB, которые затем снова сливаются в исходный файл fC. Это
продолжается до тех пор, пока в файле fC не окажется единственная
отсортированная последовательность.
// функция для сортировки файла fC, использующая последовательности
// длиной blockSize. сначала блоки данных вводятся и сортируются с
// помощью алгоритма "быстрой сортировки", а затем записываются в качестве
// последовательностей во временные файлы fA и fB
template <class T>
void MergeSort(BinFile<T>& fC, int blockSize)
{
// временные файлы для разбиения исходного файла
BinFile<T> fACfileA", INOUT);
BinFile<T> fB("fileB", INOUT);
// длина файла и длина блока
int size = int (fC.SizeO), n = blockSize;
int k = 1, useA = 1, readCount;
T *A;
// установить файл fC на начало
fС.Reset();
// если файл маленький, ввести данные из fC, отсортировать
// и скопировать обратно
if (size <= blockSize)
{
// создать буфер для блока данных и выполнить блочное чтение
А = new T[size];
if (A == NULL)
{
cerr << "MergeSort: ошибка распределения памяти" « endl;
exittl);
}
fС.Read(A.size);
// отсортировать блок данных
Quicksort(А, 0, (int)size-l);
// очистить файл и снова записать туда отсортированные данные
fC.ClearO;
fC.Write(A, size);
// освободить память, выделенную под буфер, и вернуться
delete [J A;
return;
)
else
{
// создать буфер для блока данных и читать блоки до конца файла
А * new Т[blockSize];
if (A «= NULL)
{
cerr « "MergeSort: ошибка распределения памяти" << endl;
exit (1);
}
while (IfC.EndFileO)
{
readCount * fC.Read(A, blockSize);
if (readCount =» 0)
break;
// сортировать блоки и попеременно записывать отсортированные
// последовательности в файлы fA и fB
QuickSort(A, 0, readCount-1);
if (useA)
fA.Write(A, readCount);
else
fB.Write(A, readCount);
useA * JuseA;
}
delete [] A;
}
// слить отсортированные последовательности обратно в файл fC
Merge(fA, fB, fC, blockSize);
// удвоить размер отсортированных последовательностей
к *- 2;
п •• к * blockSize;
// если п больше или равно длине файла, то в fC только одна
// последовательность, т.е. файл отсортирован
while (n < size)
{
// на каждом проходе разбивать последовательности и снова
// сливать их в последовательности удвоенной длины
Split(fA, fB, fC, k, blockSize);
Merge{fA, fB, fC, n);
k *« 2;
n - k * blockSize;
)
// удалить временные файлы
fA.Delete();
fВ.Delete();
)
В каждом проходе функция Split сканирует файл f С и поочередно копирует
его последовательности в файлы fA и fB. При каждом вызове этой функции
размер подсписков уже удвоен и равен k * blockSize. Поскольку blockSize
представляет собой длину буфера, подсписок выводится в файл в виде к
блоков. Процесс прекращается, когда все последовательности файла fC
скопированы во временные файлы.
// сканировать файл fC и поочередно копировать его последовательности
// в файлы fА и fB. на текущем проходе длина последовательностей
// равна k * blockSize
template <class T>
void Split(BinFile<T> &fA, BinFile<T> &fB, BinFile<T> &fC,
int k, int blockSize)
<
int useA * 1;
int i - 0;
int readCount/
// для блочного ввода/вывода размер блока равен blockSize
Т *А * new T[blockSize];
if (A — NULL)
{
cerr « "MergeSort: ошибка распределения памяти" « endl;
exit(l);
}
// инициализация файлов перед разбиением
f A. Clear О;
fБ.Clear();
fС.Reset();
// распределить последовательности файла fC
while (JfC.EndFileO)
{
// ввести блок данных в динамический массив
// readCount — число введенных элементов данных
readCount - fC.ReadfA, blockSize);
// если readCount равен нулю, достигнут конец файла
if {readCount « 0)
break;
// если useA-True, записать блок в fA; иначе — в fВ
if (useA)
fA.Write(Af readCount);
else
fB.Write(A, readCount);
// сменить выходной файл после вывода к блоков
if (++i » k)
{
i « 0;
useA - luseA;
}
}
// освободить динамическую память
delete [] A;
)
Как только последовательности скопированы во временные файлы, можно
начинать их слияние. Этот процесс управляется функцией Merge, которая
объединяет пары последовательностей из временных файлов, создавая из
каждой пары одну упорядоченную последовательность. Если в файле fA
оказывается лишняя последовательность, она просто копируется в fС с помощью
CopyTail.
// слить последовательности длиной п из файлов fA и fB в файл fC
template <class T>
void Merge (BinFile<T> &fA, BinFile<T> &fB,
BinFile<T> &fC, int n)
{
// currA и currB — текущие позиции в последовательностях,
// взятых из каждого файла
int currA = 1, currB - 1;
// элементы данных, введенные из fA и fB соответственно.
// флажки haveA/haveB показывают, откуда был введен элемент данных
Т dataA, dataB;
int haveA, haveB;
// инициализировать файлы перед слиянием
fA.Reset();
fВ.Reset{);
fС.Clear();
// взять по одному элементу из каждого файла
fA.Read(&dataA, 1);
fB.Read(&dataB, 1);
for (;;)
{
// если dataA<=dataB, скопировать dataA в fC и обновить
// текущую позицию в текущей последовательности из файла fA
if (dataA <= dataB)
{
fC.WriteUdataA, 1) ;
// взять следующий элемент из fA. если элемент не найден,
// достигнут конец файла и хвост fB должен быть скопирован
// в fС. если текущая позиция больше п, то последовательность
// из fA просмотрена и в fC следует скопировать хвост файла fB
if ((haveA = fA.Read(&dataA,1)) == 0 I I ++currA > n)
{
// скопировать dataB в fC. обновить текущую позицию в fB
fC.Write(&dataB, 1);
currB++;
CopyTail(fB, fC, currB, n) ;
// размер файла fA больше или равен размеру файла fB
// если конец файла fA, дело сделано
if (!haveA)
break;
// иначе новая последовательность, сбросить текущую позицию
currA = 1;
// взять следующий элемент из fB. если там ничего нет,
// то в fA остается только одна последовательность, которую
// следует скопировать в fC. скопировать текущий элемент из
// файла fA, перед тем как выйти из цикла
if ((haveB = fB.Read(&dataB,1)) == 0)
{
fC.Write UdataA, 1);
currA = 2;
break;
}
// иначе сбросить текущую позицию в последовательности из fB
CurrB = 1;
}
}
else
{
// скопировать dataB в fС и обновить текущую позицию в fB
fC.Write(&dataB, 1);
// поверить конец последовательности из fB или конец файла fB
if ( (haveB = fB.Read(&dataB,1)) ===== 0 | i ++currB > n)
{
// если конец, записать элемент, который уже прочитан из fA,
// обновить его позицию, а затем записать хвост последовательности
fC.Write UdataA, 1)
currA++;
CopyTail(fA, fC, currA, n) ;
// если в fB больше нет элементов, сбросить текущую позицию
// в fA и подготовиться к копированию последней последовательности
// из fA
currB = 1;
if ((haveA = fA.Read(&dataA, 1) ) == 0)
break;
currA =1;
}
}
}
// скопировать хвост последней последовательности из fA,
// если таковой существует
if (haveA && lhaveB)
CopyTail(fA, fC, currA, n);
}
Сливая две последовательности, мы достигаем конца одной из них раньше,
чем другой. Функция CopyTail копирует в выходной файл хвост другой
последовательности .
// п - текущий размер последовательности, скопировать хвост
// последовательности из файла fX в файл fY. переменная
// currRunPos — текущий индекс в последовательности
template <class T>
void CopyTail (BinFile<T> &fX, BinFile<T> &fY,
int &currRunPos, int n)
{
T data;
// копировать каждый элемент, начиная с текущей позиции
// до конца последовательности
while (currRunPos <= n)
{
// если вводить больше нечего, достигнут конец файла
// и, следовательно, конец последовательности
if (fX.Read(&data, 1) == 0)
return;
// обновить текущую позицию и записать элемент в файл fY
currRunPos++;
fY.Write(&data,l);
}
}
Программа 14.4. Тестирование функции MergeSort
Эта программа сортирует методом естественного слияния файл,
содержащий 1000 случайных чисел, используя 100-элементные последовательности.
Файл создается функцией LoadFile. С помощью PrintFile распечатываются
первые 45 элементов исходного и отсортированного файлов.
♦include <iostream.h>
♦include <iomanip.h>
♦include "binfile.h"
finclude "merge.h"
♦include "random.h"
// распечатать элементы файла f по 9 элементов в строке
void PrintFile (BinFile<int> &f, long n)
// инициализировать п по размеру файла
int data;
long i;
n » (f.SizeO < n) ? f.SizeO : n;
// установить файловый указатель на начало файла
f.Reset О;
// последовательное сканирование файла, читать и распечатывать
// каждый элемент, начинать каждый 10-й элемент с новой строки
for (i=0; i<n; i++)
{
if (i % 9 — 0)
cout « endl;
f .ReadUdata, 1);
cout « setw(5) « data « " ";
}
cout << endl;
}
// создать файл, содержащий n случайных чисел в диапазоне 0—32767
void LoadFile(BinFile<int> &f, int n)
{
int i, item;
RandomNumber rnd;
// инициализировать файл
f.Reset();
// заполнить файл случайными числами
for (i=*0; i<n; i++)
{
item =• rnd.Random(32768L) ;
f.Write(bitem, 1);
}
1
void main(void)
<
// файл fC заполняется случайными числами и сортируется
BinFile<int> fC("fileC", INOUT);
// создать файл 1000 случайных чисел
LoadFile(fC, 1000);
// распечатать первые 45 элементов исходного файла
cout « "Первые 45 элементов исходного файла:" « endl;
PrintFile(fC, 45);
cout « endl;
// выполнить сортировку слиянием
MergeSort(fC, 100);
// распечатать первые 45 элементов отсортированного файла
cout « "Первые 45 элементов отсортированного файла:" « endl;
PrintFile(fC, 45);
// удалить файл
fС.Delete<);
)
/*
<Прогон программы 14.4>
Первые 45 элементов исходного файла:
14879 26060 28442 20710 19366 10959 17112 7880 22963
16103 22910 6789 4976 19024 1470 25654 31721 28709
997 23378 14186 14986 21650 7351 25237 28059 5942
9593 20294 27928 8267 9837 17191 8398 18261 21620
5139 964 10393 16777 15915 18986 22175 2697 20409
Первые 45 элементов отсортированного файла:
19 76 94 98 106 119 188 192 236
259 308 344 346 371 383 424 463 558
570 605 614 714 741 756 794 861 864
891 910 923 964 979 997 1000 1007 1029
1051 1079 1112 1223 1232 1347 1470 1515 1558
*/
14.7. Словари
Доступ к элементу массива осуществляется по индексу, который указывает
позицию элемента в массиве. Например, если А — массив, то элемент А[п]
расположен в n-ой ячейке массива. Индекс не хранится как часть данных.
Словарь (таблица, ассоциативный массив) есть индексируемая структура
данных, подобная массиву. Однако как индексы, так и сами словарные данные могут
быть любого типа. Например, если Common Words — словарь, то Common-
Words["decide"] может быть определением сдова "decide". В отличие от массивов,
словарный индекс, скорее, связан с элементом данных, чем точно указывает,
где этот элемент хранится. Кроме того, число элементов словаря не ограничено.
Словарь называют ассоциативной структурой, поскольку он хранит список
ключей и ассоциируемых с ними значений данных. Например, толковый
словарь является таблицей слов (ключей) и их дефиниций (значений). Словари
отличаются от массивов тем, что фактическое расположение их элементов
скрыто. Доступ никогда не производится путем прямого указания позиции в
списке, а осуществляется только по ключу.
Данные запоминаются в словаре в виде множества пар ключ-значение,
называемых также ассоциациями. Эти пары могут храниться в связанном
списке, дереве или хеш-таблице. Если данные упорядочены по ключам, то говорят,
что таблица упорядочена. Рис. 14.5 иллюстрирует смысл всех этих понятий.
"for
DicEntryfforj-
"is"
•what"
"and"
]
'but"
■at"
I "so"
Связанный список, дерево, хеш-таблица, ...
Рис. 14.5. Словарь (ассоциативный массив)
Чтобы реализовать пригодный для работы словарь, следует сперва
разработать методы хранения пар ключ-значение в рамках класса KeyValue. Каждая
пара ключ-значение есть объект типа KeyValue с постоянным ключом. Любые
два таких объекта можно сравнивать посредством операторов == и <.
Сравнение происходит по ключам. Это будет нашим первым шаблоном класса,
имеющим два параметра: К — тип ключа и Т — тип значения, ассоциируемого с
ключом.
Спецификация класса KeyValue
ОБЪЯВЛЕНИЕ
template <class К, class T>
class KeyValue
{
protected:
// после инициализации ключ не может быть изменен
const К key;
public:
// словарные данные являются общедоступными
Т value;
KeyValue(К KeyValue, T datavalue);
// операторы присваивания, не изменяют ключ
KeyValue<K,T>& operator^ (const KeyValue<K,T>& rhs) ;
// операторы сравнения, сравнивают два ключа
int operator— (const KeyValue<K,T>& value) const;
int operator— (const K& keyval) const;
int operator< (const KeyValue<K,T>& value) const;
int operator< (const K& keyval) const;
// метод доступа к ключу
К Key(void) const;
};
ОПИСАНИЕ
Конструктор создает пару ключ-значение. Конструктора по умолчанию нет.
Если объект создан, ключ изменять нельзя. Оператор присваивания
затрагивает только собственно данные (не ключ), а оператор отношения сравнивает
ключи (а не сами данные). Метод Key предназначен для чтения ключа.
ПРИМЕР
Определяется пара ключ-значение, содержащая номер социальной
страховки в качестве символьного ключа и запись типа Data в качестве значения.
struct Data
{
char name[30];
int yearsThisCompany;
int jobclass;
float salary;
};
Data empData « {"Джордж Уильяме", 10, 5, 45000.00};
KeyValue<String, Data> Employee("345789553", empData);
Реализация этого класса очень проста, несмотря на довольно изощренную
концепцию словаря. Выберем класс для хранения объектов типа Key Value. Для
хранения упорядоченных пар ключ-значение подойдут классы OrderedList,
BinSTree и AVLTree, а для неупорядоченных — SeqList или HashTable. Все эти
классы имеют методы Insert, Delete, Find и т.д. Чтобы создать словарь мы
должны дополнить этот набор оператором индексирования []. Этот оператор
связывает ключ, указываемый в качестве индекса, с полем данных
соответствующего объекта KeyValue. В этой книге мы использовали наследование для
выражения отношения "является". Еще одно применение наследования —
расширение функциональности базового класса. Мы дополним с помощью
наследования коллекцию пар ключ-значение оператором индексирования и
другими специфическими словарными операциями. На рис. 14.6 показано, как
класс Dictionary может быть образован из нескольких базовых классов.
OrderedList
BinSTree
HashTable
ListSize
ListEmpty
ClearList
Find (KeyValue<K,T>& item)
lnsert(const KeyValue<K,T& item)
Delete(const KeyValue<K,T>& item)
ListSize
ListEmpty
ClearList
Find (KeyValue<K,T>& item)
lnsert(const KeyValue<K,T& item)
Delete(const KeyValue<K,T>& item)
T& operator[] (const K& index);
int lnDictionary(const K& keyval);
void DeleteKeyteonst K& keyval);
ListSize
ListEmpty
ClearList
Find (KeyValue<K,T>& item)
lnsert(const KeyValue<K,T& item)
Delete(const KeyValue<K,T>& item)
T& operator[] (const K& index);
int lnDictionary(const K& keyval);
void DeleteKey(const K& keyval);
T& operatorQ (const K& index);
int lnDictionary(const K& keyval);
void DeleteKey (const K& keyval);
Классы упорядоченных словарей Неупорядоченный словарь
Рис. 14.6. Расширение коллекции объектов ключ-значение до словаря
Спецификация класса Dictionary
ОБЪЯВЛЕНИЕ
#include "keyval.h"
#include "bstree.h"
#include "treeiter,h"
template <class K, class T>
class Dictionary: public BinSTree< KeyValue<K,T> >
{
// значение, присваиваемое элементу словаря по умолчанию.
// используется оператором индексирования, а также методами
// InDictionary и DeleteKey
private:
Т defaultValue;
public:
// конструктор
Dictionary(const T& defval);
// оператор индексирования
T& operator!] (const K& index);
// дополнительные словарные методы
int InDictionary(const K& keyval);
void DeleteKey(const K& keyval);
};
ОПИСАНИЕ
Оператор индексирования выполняет большую часть работы. Он проверяет
наличие заданного ключа в словаре. Если словарный элемент с таким ключом
существует, оператор возвращает ссылку на этот элемент. Если нет, то
создается новая словарная статья и возвращается ссылка на нее. Таким образом,
любое создание или обновление словарных данных происходит с помощью
оператора индексирования. Поскольку для класса KeyValue не создается
конструктор, действующий по умолчанию, ключ и данные должны быть указаны.
Поэтому при создании объекта оператор [] должен иметь некоторое значение
словарной статьи по умолчанию. Оно передается в конструктору качестве
параметра. Это значение следует выбирать с осторожностью, так, чтобы новый
словарный элемент мог участвовать в выражениях.
Например, словарь может содержать символьный ключ — слово — и
символьное значение — дефиницию этого слова. Тогда объект BasicDict типа
Dictionary объявляется следующим образом:
// словарная статья по умолчанию пуста
DictionaryOtring, String> BasicDict ('');
Предположим, что следующий оператор употребляется впервые:
BasicDict["секстет"] +« "Группа из шести исполнителей";
Оператор [] создает пустую словарную статью с ключом "секстет".
Строковый оператор +в сцепляет с пустой строкой строку "Группа из шести
исполнителей", создавая тем самым дефиницию слова "секстет".
Метод InDictionary проверяет наличие в словаре пары ключ-значение с
ключом keyval, а метод DeleteKey удаляет словарную статью, имеющую ключ
keyval. Методы ListEmpty, ListSize и Clear List определены в базовом классе.
Методы Insert, Find и Delete также могут непосредственно работать с объектами
типа KeyValue, но сам факт их использования для словарей является несколько
необычным.
В большинстве приложений требуется итератор словаря, чтобы собирать
данные для вывода. Поскольку объект типа Dictionary образуется из класса
BinSTree, класс Dictionarylterator можно вывести иЗ класса Inorderlterator.
template <class К, class T>
class Dictionarylterator: public InorderIterator<KeyValue<K,T>
{
public:
// конструктор
Dictionarylterator(Dictionary<K,T>& diet);
// начать итерацию нового словаря
void SetList(Dictionary<K,T>& diet);
};
// конструктор, diet "расширяет" объект BinSTree и использует его
// общедоступный метод GetRoot для инициализации базового класса
// Inorderlterator
template <class К, class T>
DictionaryIterator<K,T>::DictionaryIterator(Dictionary<K/T>& diet):
lnorderIterator< KeyValue<K,T> >
(dict.GetRootO )
{}
// использовать метод SetTree базового класса
template <class K# class T>
void DictionaryIterator<K,T>::SetList(Dictionary<K,T> & diet)
{
SetTree(diet.GetRoot());
)
Реализации классов Dictionary и Dictionarylterator находятся в файле
dict.h.
Программа 14.5. Построение толкового словаря
Эта программа создает объект wordDictionary типа Dictionary со
строковым ключом и данными. Значением словарной статьи по умолчанию
является пустая строка. Файл defs.dat содержит список слов и их
дефиниций. Ключевое слово находится в начале строки и завершается
пробелом. Остальная часть строки содержит дефиницию. Слова вводятся в цикле
и используются в качестве ключей для добавления своих дефиниций в
словарь.
Словарный итератор dictlter используется для прохождения словаря, во
время которого для каждой найденной пары ключ-значение вызывается
функция PrintEntry для распечатки словарной статьи. Эта функция сначала
распечатывает ключевое слово и следующее за ним тире, а затем построчно
выводит его дефиницию по 65 символов в строке без переносов по слогам.
♦include <fstream.h>
♦include <stdlib.h>
♦include "keyval.h" // итератор, просматривающий объекты KeyValue
♦include "dict.h" // класс Dictionary
♦include "strclass.h" // пары ключ-значение имеют тип String
// распечатать объект KeyValue, содержащий ключевое слово word
// и его дефиницию(и)
void PrintEntry(const KeyValue<String,String>& word)
{
KeyValue<String,String> w « word;
// поскольку после ключевого слова выводится " - ",
// дефиниция распечатывается с позиции, равной Length(word) + 3
int linepos * w.Key().Length() + 3;
int i;
// распечатать слово и " - "
cout « w.KeyO " - ";
// распечатать дефиницию на 65-символьных строках
while (!w.value. IsEmptyO)
{
// определить, умещается ли еще не распечатанная часть в 65-символьной
// строке, вычислить индекс последнего символа в строке
if (w.value.Length() > 65-linepos)
{
// текст не умещается в строке, двигаясь в обратном направлении,
// найти первый пробел, не переносить слова по слогам.
i * 64-linepos;
while(w.value[i] != ' ')
<
д.—;
}
else
// текст умещается в строке
i « w.value.Length {) - 1;
// вывести часть текста дефиниции, которая умещается в строке
cout « w.value.Substr(0, i + 1) « endl;
// удалить только что распечатанную часть текста.
// приготовиться к переходу на новую строку
w.value.Remove(0, i+1);
linepos = 0;
}
}
void main(void)
{
// входной поток данных
ifstream fin;
String word, definition;
// словарь
Dictionary<String,String> wordDictionary("");
// открыть файл defs.dat ключевых слов и их дефиниций
fin.open("defs.dat", ios::in | ios::nocreate);
if (!fin)
{
cerr « "Файл defs.dat не найден" « endl;
exit(l);
}
// прочитать слово и его дефиницию, с помощью оператора индексирования
// включить статью в словарь или обновить существующую дефиницию,
// дополнив ее текущей
while (fin » word)
{
if (fin.eofO)
break;
// прочитать пробел, следующий за ключевым словом
definition.ReadString(fin);
wordDictionary[word] += definition;
}
// объявить итератор для нисходящего обхода словаря
DictionaryIterator<String,String> dictlter(wordDictionary) ;
// просматривать словарь, распечатывать каждое ключевое слово
// и его дефиницию(и)
cout « "Толковый словарь:" « endl « endl;
for (dictlter.Reset(); !dictlter.EndOfList(); dictlter.Next())
{
PrintEntry(dictlter.Data());
cout << endl;
}
wordDictionary.ClearList();
}
/*
<Файл defs.dat>
Программа Последовательность операций, выполняемых компьютером.
Финишировать Заканчивать, завершать.
Причина То, из чего следует результат.
Секстет Группа из шести исполнителей.
Программа Перечень действий, приветственных речей, музыкальных пьес и т.п.
Скорость Быстрота, проворность.
Скорость Перемещение за единицу времени.
Секстет Музыкальная композиция для шести инструментов.
Шапка Головной убор.
Шапка Газетный заголовок шириной на всю полосу.
<Прогон программы 14.5>
Толковый словарь:
Причина - То, из чего следует результат.
Программа - Последовательность операций, выполняемых компьютером.
Перечень действий, приветственных речей, музыкальных пьес и т.п.
Секстет - Группа из шести исполнителей.
Музыкальная композиция для шести инструментов.
Скорость - Быстрота, проворность. Перемещение за единицу времени.
Финишировать - Заканчивать, завершать.
Шапка - Головной убор. Газетный заголовок шириной на всю полосу.
*/
Реализация класса Dictionary
Конструктор инициализирует базовый класс и задает значение словарной
статьи по умолчанию.
// конструктор, инициализирует базовый класс и задает значение
// словарной статьи по умолчанию
template <class К, class T>
Dictionary<K,T>::Dictionary(const T& defaultval):
BinSTree< KeyValue<K,T> >(), defaultValue(defaultval)
{)
Оператор индексирования создает объект targetKey типа KeyValue с
заданным ключом и значением данных по умолчанию и ищет этот ключ на дереве.
Если ключ не найден, targetKey вставляется в дерево. Элемент базового класса
current устанавливается на только что найденный или вставленный узел.
Оператор возвращает ссылку на значение данных в этом узле.
// оператор индексирования, здесь делается почти вся работа
template <class К, class T>
Т& Dictionary<K,T>::operator[] (const K& index)
{
// определить целевой объект типа KeyValue, содержащий
// данные задаваемые по умолчанию
KeyValue<K,T> targetKey(index, defaultValue);
// искать ключ, если не найден, вставить targetKey
if (!Find(targetKey))
Insert(targetKey);
// возвратить ссылку на найденные или вставленные данные
return current->data.value;
}
Функция InDictionary создает объект tmp типа KeyValue с заданным
ключом и значением данных по умолчанию, ищет этот ключ на дереве и
возвращает результат поиска.
// проверить, существует ли объект типа KeyValue
//с данным ключом
template <class К, class T>
int Dictionary<K,T>::InDictionary(const K& keyval)
{
// определить целевой объект типа KeyValue, содержащий
// данные задаваемые по умолчанию
KeyValue<K,T> tmp(index, defaultValue);
int retval ■ 1;
// искать tmp на дереве, вернуть результат
if (!Find(tmp))
retval - 0;
return retval;
}
Функция DeleteKey создает объект tmp типа KeyValue с заданным ключом
и значением данных по умолчанию и удаляет этот словарный элемент из
дерева.
// удалить оОъект типа KeyValue с данным ключом из словаря
template <с1азз к, class т>
void Dictionary<K,T>::DeleteKey(const K& keyval)
{
KeyValue<K,T> tmp(index, defaultValue);
Delete (tmp);
>
Письменные упражнения
14.1
а) Отсортируйте числовую последовательность 8, 4, 1, 9, 2, 1, 7, 4
посредством выбора. Отображайте состояние списка после каждого
прохода.
б) Повторите пункт а) для символьной последовательности V, В, L, А,
Z, I, С, XI» S, S, В, Н.
14.2 В предыдущем упражнении выполните сортировку вставками.
14.3 Отсортируйте символьную последовательность С, А, М, Т, В, В, A, L
методом включения. Проследите каждый шаг сортировки.
14.4
а) Какова эффективность сортировки посредством выбора, в случае
массива п одинаковых элементов?
б) Ответьте на вопрос а) для случаев сортировки вставками и методом
пузырька.
14.5 Отсортируйте массив А, используя метод пузырька. После каждого
прохода показывайте сам список и подсписок, подлежащий сортировке.
А = 85, 40, 10, 95, 20, 15, 70, 45, 40, 90, 80, 10
14.6 Отсортируйте массив А с помощью "быстрой сортировки". Выбирайте
центральный элемент из середины списка. Во время каждого прохода
фиксируйте все обмены элементов между нижним и верхним
подсписками. Показывайте состояние последовательности после каждого прохода.
А - 790, 175, 284, 581, 374, 799, 852. 685, 486, 347
14.7 В другой версии алгоритма "быстрой сортировки" в качестве
центрального элемента выбирается A[low], а не A[mid]. Эта версия тоже
является 0(п log2n)-cлoжнoй, но поведение худшего случая изменяется.
Как?
14.8 Массив А следует отсортировать посредством включения его элементов
в двусвязный список. Вставьте элемент в текущую точку и
перемещайте его вперед по списку, если новый элемент больше текущего,
или назад, если меньше. Напишите функцию DoubleSort,
реализующую этот метод сортировки.
template <class T>
void DoubleSort (T а[], int n);
Голова Хвост
14.9 Оцените алгоритмическую сложность метода сортировки из предыдущего
упражнения. Рассмотрите наилучший, наихудший и средний случаи.
14.10 Какой из основных алгоритмов сортировки (выбором, вставками или
пузырьковый) наиболее эффективен для обработки уже
отсортированного списка? А если этот список отсортирован в обратном порядке?
14.11 В настоящей книге мы рассмотрели следующие методы сортировки:
включением в бинарное дерево, пузырьковый, обменный,
пирамидальный, вставками, поразрядный, выбором, турнирный.
Для каждой из этих сортировок укажите сложность, потребности в
памяти и дайте некоторые комментарии по поводу ее эффективности.
В комментариях можно отразить следующие моменты: возможность
досрочного окончания процесса в случае уже отсортированного списка,
вероятность наихудшего случая, число обменов и величину константы
пропорциональности (большое О).
14.12 Метод сортировки называют устойчивым (stable), если на любом шаге
алгоритма два одинаковых элемента не меняются местами друг
относительно друга. Например, в пятиэлементном массиве
5i 55 12 52 33
устойчивая сортировка гарантирует, что результирующая
последовательность будет иметь следующий порядок:
5i 52 12 33 55
Классифицируйте методы сортировки из предыдущего упражнения с
точки зрения их устойчивости.
14.13 Покажите, что хеш-функция
hash(x) ■ х % m
неприемлема при четном т. Изменится ли ситуация при нечетном т?
(Совет. Рассмотрите распределение четных и нечетных случайных
чисел.)
14.14 Предположим, что хеш-функция имеет следующие характеристики:
Ключи 257 и 567 отображаются в 3
Ключи 987 и 313 отображаются в 6
Ключи 734, 189 и 575 отображаются в 5
Ключи 122 и 391 отображаются в 8
Ключи вставляются в таблицу в следующем порядке: 257, 987, 122,
575, 189, 734, 567, 313, 391.
а) Покажите позиции этих данных в таблице, если коллизии
разрешаются методом открытой адресации.
НТ
О 1 2 3 4 5 6 7 8 9 10
б) Покажите позиции этих данных в таблице, если коллизии
разрешаются методом цепочек.
НТ
0123456789 10
14.15 Повторите предыдущее упражнение при обратном порядке вставки в
таблицу.
14.16 Для отображения данных в табличные индексы используйте
хеш-функцию hashf(x) = х % 11. Данные вставляются в таблицу в следующем
порядке: 11, 13, 12, 34, 38, 33, 27, 22.
а) Постройте хеш-таблицу методом открытой адресации.
б) Постройте хеш-таблицу методом цепочек.
в) Для обоих методов определите коэффициент заполнения, среднее число
проб, необходимое для обнаружения элемента в таблице и среднее
число проб для констатации отсутствия элемента в таблице.
14.17 Покажите, что хеш-функция, отображающая символьные строки в
целые числа посредством суммирования символов в строке, не является
хорошей. Рассмотрите, как с помощью сдвигов можно исправить
ситуацию.
14*18 При разработке хеш-функции иногда применяется метод свертки
(folding). Ключ разбивается на части, которые затем комбинируются таким
образом, чтобы получилось меньшее число. Это число используется в
качестве значения хеш-функции или уменьшается еще раз посредством
деления. Предположим, в некоторой программе в качестве ключа
используется номер социальной страховки. Разобьем ключ на три группы
по три цифры и сложим их. Получится некоторое число в диапазоне
0..2997. Например, номер 523456795 даст индекс 523 + 456 + 795 =
1774. Напишите хеш-функцию
int hashf(char *ssn);
реализующую этот метод. (Совет. Нужно извлечь подстроки и
преобразовать их в целое число.)
14.19 Дана следующая хеш-функция:
unsigned short hash(unsigned short key)
{
return (key » 4) % 256;
}
а) Каков размер хеш-таблицы?
б) Чему равны hashf(16) и hashf(257)?
в) Что вообще делает эта хеш-функция?
14.20 Дана следующая хеш-функция:
unsigned long hash(unsigned long key)
{
return (key » 8) % 65536;
}
а) Каков размер хеш-таблицы?
б) Чему равны hashf(16) и hashf( 10000)?
в) Что вообще делает эта хеш-функция?
14.21 Проблемой открытой адресации является скопление (clustering)
конфликтующих ключей.
Скопление
Скопление
Скопление
TableSize-1
Предположим, в таблице есть N ячеек. Если хеш-функция хорошая,
то какова вероятность хеширования в индекс р? Если ключ попал в
ячейку р, то ячейка р+1 может быть занята ключом, хешированным
в р или в р+1, Какова вероятность занятия ячейки р+1? Какова
вероятность занятия ячейки р+2? Объясните, почему вообще возникают
скопления.
14.22 Если ключ отображается в занятую ячейку таблицы с номером index,
метод открытой адресации по схеме линейного опробывания выполняет
функцию
index * (index+1) % m; // проверить следующий индекс
Эта функция называется функцией рехеширования (rehash function),
а метод разрешения коллизий — рехешированием (rehashing). Линей-
ное опробывание благоприятствует скоплению ключей. Однако
функция рехеширования может рассеивать ключи лучше. Два целых числа
р и q называются взаимно простыми, если не имеют общего делителя,
иного чем 1. Например, 3 и 10 — взаимно простые числа, как и 18
и 35.
Пусть в методе открытой адресации используется следующая функция
рехеширования:
index « (index + d) % m;
где d и m — взаимно простые числа1. Последовательное применение
этой функции порождает индексы от 0 до т-1. При линейном опро-
бывании d = 1.
а) Если d и т не являются взаимно простыми, некоторые ячейки таблицы
пропускаются. Покажите, что при d = 3 и m - 93 функция
index « (index +3) % 93
попадает лишь в каждую третью ячейку таблицы.
б) Покажите, что если m — простое число и d < m, то вся таблица
покрывается функцией рехеширования.
в) Выполните упражнение 14.16а, используя функцию рехеширования
index = (index + 5) % 11
14.23 Хеш-таблицы хорошо подходят для тех приложений, где основной
операцией является поиск и выборка. Запись вставляется в таблицу,
а затем много раз выбирается оттуда. Однако хеширование методом
открытой адресации не слишком удобно для тех приложений, где
требуются удаления данных из хеш-таблицы.
Рассмотрим следующую таблицу из 101 ячейки и хеш-функцию
hashf(key) = key % 11.
а) Удалите ключ 304, поместив в ячейку 1 число -1. Что произойдет при
поиске ключа 707? Объясните, почему для решения задачи удаления
в общем виде недостаточно просто пометить ячейку как незанятую?
б) Решение этой проблемы предусматривает запись в ячейку,
содержащую удаляемый элемент, ключа DeletedData. При поиске ключа все
ячейки, содержащие DeletedData, пропускаются. Для удаленных
ключей используйте значение -2. Покажите, что при таком подходе
удаление ключа 304 не помешает корректному поиску ключа 707.
Операции вставки и выборки в алгоритме открытой адресации должны
быть модифицированы с учетом удалений.
в) Опишите алгоритм удаления табличного элемента.
г) Опишите алгоритм обнаружения элемента в таблице.
д) Опишите алгоритм включения элемента в таблицу.
14.24 Еще одним методом разрешения коллизий, который иногда
применяется, является связывание в срастающиеся списки. Этот метод подобен
1 Этот метод разрешения коллизий называют еще открытой адресацией по схеме случайного
опробывания. — Прим. перев.
открытой адресации, но конфликтующие ключи, которые должны
располагаться в таблице ниже и т.д. по кругу, сцепляются вместе с
помощью связанного списка. Возможны ситуации, когда цепочка
содержит ключи, первоначально хеширующиеся в разные ячейки таблицы.
Тогда говорят, что эти списки срастаются. Например, если hashf(x) =
х % 7 и в таблицу включаются 12, 3, 5, 20 и 7, мы имеем следующую
картину:
-1 обозначает пустую ячейку и NULL-указатель
а) Выполните упражнение 14.16а, используя метод связывания в
срастающиеся списки.
б) Как вы думаете, сравним ли данный метод с методами открытой
адресации и методом цепочек с точки зрения быстродействия?
Классифицируйте все эти методы по быстродействию.
в) Проще ли решается проблема удаления, чем в методе открытой
адресации? Поясните.
14.25 Даны множество ключей ко, кь ..., kn-i и совершенная хеш-функция
(perfect hashing function) H — хеш-функция, не порождающая коллизий.
Нет смысла искать совершенную хеш-функцию, если множество ключей
не является постоянным. Однако для таблицы символов компилятора
(содержащую зарезервированные слова while, template, class и т.д.)
совершенная хеш-функция крайне желательна. Тогда для определения
того, является ли некоторый идентификатор зарезервированным
словом, потребуется лишь одна проба.
Найти совершенную хеш-функцию даже для конкретного набора
ключей очень сложно. Обсуждение этого предмета выходит за рамки данной
книги. Кроме того, если данный набор ключей пополнится новыми
ключами, совершенная хеш-функция, как правило, перестает быть
совершенной.
а) Даны множество целочисленных ключей 81, 129, 301, 38, 434, 216,
412, 487, 234 и хеш-функция
Н(х) = (х+18)/63
Является ли данная хеш-функция совершенной?
б) Дан набор символьных ключей
Bret, Jane, Shirley, Bryce, Michelle, Heather
Придумайте совершенную хеш-функцию для 7-элементной таблицы.
14.26 Дано следующее описание класса текстовых файлов, в котором
моделируются файловые операции языка Паскаль. Реализуйте этот класс
с помощью операций класса fstream языка C++,
enum Access {IN, OUT} // определяет поток данных файла
class PascalTextFile
private:
fstream f; // файловый поток Си++
char fname[64]; // имя файла
Access accesstype; // входной или выходной поток
int isOpen; // используется методом Reset
void Error(char *msg); // используется для печати ошибок
public:
PascalTextFile(void); // конструктор
void Assign(char *filename); // задает имя файла
void Reset(void); // открывает файл для ввода
void Rewrite(void); // открывает файл для вывода
int EndFile(void); // читает флаг конца файла
void Close(void); // закрывает файл
int PRead(T А[], int n); // читает п символов в А
void PWrite(T А[], int n); // записывает п символов в А
};
Упражнения по программированию
14.1 Напишите программу, создающую упорядоченный список N случайных
чисел из диапазона 0—1000 с помощью алгоритма включения в дву-
связный список из письменного упражнения 14.8. Распечатайте
отсортированную последовательность.
14.2 Реализуйте следующий алгоритм:
Разбить n-элементный список пополам. Отсортировать каждую
половину с помощью сортировки выбором, а затем слить обе половины.
а) Проанализируйте сложность этой сортировки.
б) Используйте этот алгоритм для сортировки 20000 случайных чисел и
измерьте время выполнения программы.
г) Запустите ту же программу, но использующую обычную сортировку
посредством выбора. Какая версия работает быстрее?
14.3 В разделе 14.6 обсуждалась сортировка файлов прямым слиянием.
Реализуйте внутреннюю версию этого алгоритма для сортировки п-эле-
ментного массива. Отсортируйте с помощью этой программы 1000
случайно сгенерированных чисел с двойной точностью. Распечатайте
первые и последние 20 элементов отсортированного массива.
14.4 Дана следующая структура:
struct TwoKey
{
int primary;
int secondary;
};
Создайте массив из 100 записей этого типа. Поле primary содержит
случайное число в диапазоне 0..9, а поле secondary — в диапазоне
0..100. Модифицируйте алгоритм сортировки вставками для
упорядочения по двум ключам. Новый алгоритм должен производить
сортировку по вторичному ключу для каждого фиксированного значения
первичного ключа. Отсортируйте с его помощью ранее созданный
массив. Распечатайте массив в формате primary (secondary).
14.5 Сортировка Шелла, названная так по имени своего изобретателя
Дональда Шелла, является простым и довольно эффективным алгоритмом.
Она начинается с разбиения исходного n-элементного списка на к
подсписков:
а[0], a[k+0], а[2к+0], ...
а[1], а[к+1], а[2к+1], ...
...
а[к-1], а[к+(к-1)], а[2к+(к-1)], ...
Подсписок начинается с первого элемента a[i] в диапазоне а[0] ... а[к-1]
и включает в себя каждый последующий k-ый элемент. Например, при
к = 4 следующий массив разбивается на четыре подсписка:
7586249130
Подсписок #0 7 2 3
Подсписок #1 5 4 0
Подсписок #2 8 9
Подсписок #3 6 1
Отсортируйте каждый подсписок сортировкой вставками. В нашем
примере получатся следующие подсписки:
Подсписок #0 2 3 7
Подсписок #1 0 4 5
Подсписок #2 8 9
Подсписок #3 16
и частично отсортированный массив 2081349675.
Повторите процесс с к = к/3. Продолжайте так до к = 1, при котором
список получается отсортированным. Оптимальный выбор начального
значения к — задача теории алгоритмов. Алгоритм является успешным,
поскольку обмен данных происходит в несмежных сегментах массива.
В результате элемент перемещается гораздо ближе к своей
окончательной позиции, чем при обмене соседних элементов в сортировке
простыми вставками.
Создайте в главной процедуре массив 100 случайных целых чисел в
диапазоне 0—999. Для сортировки Шелла возьмите начальное значение
к = 40. Распечатайте исходный и отсортированный списки по 10 чисел
в строке.
14.6 В этом упражнении разрабатывается простая программа
орфографического контроля. В программном приложении к этой книге имеется файл
words, который содержит 500 наиболее часто употребляющихся слов.
Прочитайте этот файл и вставьте все имеющиеся там слова в
хеш-таблицу. Прочитайте текстовый документ и разбейте его на отдельные
слова с помощью следующей несложной функции:
// извлечь слово, начинающееся с буквы и состоящее из букв и цифр
int GetWord (ifstream& fin, char w[[])
{
char с;
int i - 0;
// пропустить все не буквы
while (fin.get(с) && !isalpha(c));
// возвратить 0 по окончании файла
if (fin.eofO)
return 0;
// записать первую букву слова
w[i++] * с;
// собрать буквы и цифры. Завершить слово нулем
while (fin.get(с) && (isalpha(c) II isdigit(с))}
w[i++] * с;
w[i] »
'Nonreturn 1;
}
Используя хеш-таблицу, распечатайте слова, в которых могут быть
орфографические ошибки.
14.7 Разработайте классы OpenProbe и OpenProbelterator, поддерживающие
хеш-таблицы, которые используют метод открытой адресации. Ниже
дана спецификация класса OpenProbe. Для реализации класса
используйте письменное упражнение 14.23.
// формат записей таблицы
template <class T>
struct TableRecord
{
// доступен (да или нет)
int available;
Т data;
};
template <class T>
class OpenProbe: public List<T>
{
protected:
// динамически создаваемая таблица и ее размер
TableRecord<T> *table;
int tableSize;
// хеш-функция
unsigned long (*hf) (T key);
// индекс ячейки, к которой последний раз было обращение
int lastlndex;
public:
// конструктор, деструктор
OpenProbe(int tabsize, unsigned long hashf(T key));
-OpenProbe(void);
// стандартные методы обработки списков
virtual void Insert(const T& key);
virtual void Delete(const T& key);
virtual int Find(T& key);
virtual void ClearList(void);
// обновить ячейку, к которой последний раз было обращение
void Update(const T& key);
friend class OpenProbeIterator<T>;
};
Используйте эти классы в программе 14.2.
14.8 Поместите объявление класса PascalTextFile из письменного
упражнения 14.27 в файл ptf.h. Напишите программу, которая с помощью
этого класса читает файл ptf.h, преобразует каждую строчную букву
в прописную и записывает их в файл ptf.uc. Используйте
соответствующую команду вашей операционной системы для распечатки
содержимого файла ptf.uc.
14.9 Используйте класс BinFile для следующих программ.
а) Запись Person определяет последовательность полей в некоторой базе
данных.
struct Person
{
char first[20]; // имя
char last[20]; // фамилия
char id[4]; // четырехзначный идентификатор
>;
Определите функцию DelimRec, параметрами которой являются запись
Person и буфер.
void DelimRec (const Person &p, char *buffer);
Эта функция преобразует каждое поле записи в символьную строку
переменной длины, заканчивающуюся разделителем "р. Три поля
сцепляются друг с другом в буфере. Например,
Person: first Tom
last Davis
id 6192
Буфер: Tom|Davis|6192|
Напишите программу, которая вводит пять записей Person по одному
полю в строке и создает файл символов reel.out. Для каждой записи
создайте компактный буфер длиной п и выведите в файл размер этого
буфера в виде двухбайтового короткого целого и п символов,
находящихся в буфере. Распечатайте содержимое reel.out с помощью утилиты
шестнадцатеричного дампа, если таковая имеется в вашей системе.
б) Напишите программу, которая вводит последовательные записи из
файла reel.out, расширяя каждое поле до его фиксированной длины,
определенной в записи Person. Если нужно, дополняйте поле
пробелами справа. Теперь запись Person имеет длину 44 байта. Выведите
новые записи в файл rec2.out.
в) Напишите программу поиска заданного четырехзначного
идентификатора в файле rec2.out. В случае удачи распечатайте имя и фамилию
найденного человека.
14.10 Дан следующий тип записи:
struct CharRec
{
char Key;
int count;
};
С помощью класса BinFile создайте файл letcount из 26 таких записей,
содержащих в поле key буквы от 'А* до 'Z' и 0 в поле count. Прочитайте
текстовый файл, преобразуя каждую букву в прописную и обновляя
поле count в соответствующей записи бинарного файла letcount.
Распечатайте частоту каждой буквы. Отсортируйте записи по полю count
методом естественного слияния (см. раздел 14.6) с длиной блока,
равной 4. Распечатайте отсортированный файл.
14.11 Образуйте класс упорядоченных словарей из класса OrderedList.
Используйте этот класс, а также связанный с ним итератор в
программе 14*5.
14.12 Образуйте класс словарей из класса HashTable. Используйте этот класс,
а также связанный с ним итератор в программе 14.5. Распечатайте
словарные объекты в порядке извлечения итератором. Отсортируйте
результаты обхода и распечатайте словарные объекты в алфавитном
порядке.
Приложение
Ответы на избранные
письменные упражнения
Глава 1
1.2
a) ADT Cylinder
Данные
Радиус и высота цилиндра представляются положительными числами
с плавающей точкой.
Операции
Конструктор
Начальные значения: Радиус и высота цилиндра.
Обработка: Задать начальные значения радиуса
и высоты цилиндра.
Area
Вход: Нет
Предусловия: Нет
Обработка: Вычислить площадь цилиндра по заданным
радиусу и высоте.
Выход: Возвратить величину площади
Постусловия: Нет
Volume
Вход: Нет
Предусловия: Нет
Обработка: Вычислить объем цилиндра по заданным
радиусу и высоте.
Выход: Возвратить величину объема.
Постусловия: Нет
Конец ADT Cylinder
1.3 Пусть Cyl и Hole — цилиндры с радиусами R и Rh, а С — окружность
с радиусом Rh.
а) Результирующий объем геометрического тела равен CyLVolumeQ —
Hole.Volume().
б) Площадь этого геометрического тела равна Cyl.Area() + Hole.AreaQ —
4*С.Агеа().
1.5 const float PI = 3.14159;
class Cylinder
{
private:
float radius, height;
public:
Cylinder(float r, float h): radius(r), height(h) {}
float Area(void)
{return 2.0*PI*radius(radius+height);)
float Volume(void)
{return Pl*radius*radius*height;)
);
1.11
а) Два или более объектов в некоторой иерархии наследования классов
имеют одноименные методы, выполняющие разные задачи. Это свойство
позволяет объектам различных классов отвечать на одно и то же
сообщение. Приемник сообщения определяется динамически в процессе
выполнения программы.
Глава 2
2.1
а) 5;
б) 14;
в) 55;
г) 127
2.3
а) 26;
б) 1055;
в) 4332;
г) 255;
д) 65536;
е) 17;
ж) 57;
з) 73;
и) FF
2.4
а) С;
б) А6;
в) F2;
г) BDE3;
д) 11000010000;
е) 1010111100100000
2.5
а) 32 50 32;
б) 32 32 40
2.8
а) 'N';
б) *К';
в) '*':42ю, IOIOIO2 'q':113io, HHOOOI2 <сг>:13ю, 11012
2.9 V 113 8
2.11
а) 6.75
л\ i„ 111 1 , mn
eJ .111 ... Ill ... =^ + j + jT+...+ — +... = 1 - -g
При стремлении п к бесконечности дробная часть стремится к 1.
Следовательно десятичный эквивалент равен 3 + 1 = 4.
2.12
б) 1.001
2.14
а) 4Of00000;
г) 29.125
2.17 X = 55, Y = 10, А - {5.3, 6.8, 8.9, 1, 5.5, 3.3}
2.18
а) (1) Для А выделяется 10 байт. (2) &А[3] = 6000 + 2*3 = 6006, &А[1]
= 6000 + 2*1 = 6002
б) (1) 33 (2) А = {60, 50000, -10000, 10, 33} (3) &А[3] - 2050 + 4*3 -
2062
2.20
а) 30 * 2 = 60 байт.
б) &А[3][2] = 1000 + 3*12 + 2*12 - 1040, &А[1][4] - 1000 + 1*12 + 4*2
= 1020
2.22
а) Ч\ Ч\ NULL;
б) Stockton, C.A. March 5, 1994;
в) 1;
г) 1
2.23 void strinsert (char *s, char *t, int i)
{
char tmp[128]; // хранит хвост s
if (i > strlen(s)) // выход по достижении хвостового нуля
return;
strcpy(tmp, &s[i]); // скопировать хвост s в tmp
strcpy(&s[i], t); // скопировать t на место хвоста
strcpy(s, tmp); // сцепить с хвостом из tmp
}
2.25
б) void PtoCStr(char *s)
{
int n = *s++; // взять счетчик байтов
while (n—) // передвинуть каждый символ влево
*(s-l) = *s++; // на одну позицию
*s *= 0; // завершить формирование строки
)
2.27 Complex cadd(Complex& х, Complex& у)
{
Complex sum = {x.real+y.real, x.imag+y.imag};
return sum;
}
Complex cmul(Complexs x, ComplexS y)
{
Complex product = {x.real*y.real - x.imag*y.imag,
x.real*y.imag + x.imag*y.real};
return product;
}
Глава 3
3.2
6) class Box
{
private:
float length, width, height;
public:
Box(float 1, float w, float h);
float GetLength(void) const;
float GetWidth(void) const;
float GetHeight(void) const;
float Area(void) const;
float Volume(void) const;
};
Box::Box(float 1, float w, float h): length(1), width(w), height(h) {}
float Box::Area(void)
{
return 2.0 * (l*w + l*h + w*h);
}
в) Напишите функцию Qualify (Box В), которая возвращает 0, если ящик
бракованный, или 1 - в противном случае.
if ( (2*(B.GetLength() + B.GetWidth()) + В.GetHeight()) < 100 )
return 1; // и т.д.
3.3
а) private и public должны заканчиваться двоеточием ":". Последняя
закрывающая фигурная скобка "}" должна заканчиваться точкой с за-
пятой ; .
б) Y(int n, int m): p(n), q(m) {}
3.4
а) class x
{
private:
int a, b, c;
public:
X(int x=l, int y-1, int z=l);
int f(void);
};
б) X:X(int x, int y, int z): a(x), b(y), c(z) {}
3.5 class Student
{ ...
public:
Student(int id, int studgradepts, int studunits):
studentid(id), gradepts(studgradepts), units(studunits)
{ComputeGPAO ;}
• • •
};
void Student::UpdateGradeInfо(int newunits, int newgradepts)
{
units +* newunits;
gradepts += newgradepts;
ComputeGPA();
}
3.8
a) CardDeck::CardDeck(void)
{
for (int i=0; i<52; i++)
cards[i] = i;
currentCard = 0;
)
void CardDeck::Shuffle(void)
{
static RandomNumber rnd;
int randlndex, tmp;
for (int i=0; i<52; i++)
{
randlndex = i + rnd.Random(52-i);
tmp * cards[i];
cards[ij = cards[randlndex];
cards[randlndex] = tmp;
}
currentCard = 0;
}
б) В DealHand объявить локальный целочисленный массив размером 52.
С помощью GetCard записать в массив п значений карт. Отсортировать
массив, используя, например обменную сортировку, которая описана в
гл. 2. Распечатать массив в цикле с помощью PrintCard.
3.9 Temperature Average(Temperatures a[], int n)
{
float avgLow =0.0, avgHigh = 0.0;
for (int i=0/ i<n/ i++)
{
avgLow +~ a[i].GetLowTemp();
avgHigh += a[i].GetHighTemp();
}
avgLow /= n;
avgHigh = /= n;
return Temperature(avgLow, avgHigh);
}
3.11 RandomNumber rnd;
а) int (rnd.fRandom() <= 0.2) ...
б) int weight; weight = 140 + rnd.Random(91);
3.12
а) Замечание. Статический член класса определяется вне класса, но может
быть доступен только для функций-членов класса. Все объекты
разделяют значение статического элемента данных класса.
#include "random.h"
class Event
{
private:
int lowTime, highTime;
static RandomNumber rnd;
public:
Event (int low = 0, int high = 1) : lowTime
(low), highTime(high)
{ if (lowTime > highTime)
{ cerr « "Нижняя граница превышает верхнюю."
« endl;
exit(1);
}
}
int GetEvent(void)
{return lowTime + rnd.Random(highTime-lowTime+1);}
>;
// rnd — статический элемент данных класса Event
RandomNumber Event::rnd;
в) Event A[5] = {Event(10,20), Event(10,20), Event(10,20),
Event(10,20), Event(10,20)};
// использовать конструктор по умолчанию
Event B[5]; // lowTime = 0; highTime = 1
3.14
"l 2 3~
0 -7 -8
0 0-4
*
x."
xx
x,
-
"б"
-14
0
6) Determinate - (1) (-7) (-4) = 28
Глава 4
4.2
а) массив;
в) стек;
д) множество;
ж) файл;
и) пирамида;
к) словарь.
4.4
б) п2 + 6п 4- 7 < п2 + п2 + п2 - 3n2, n > 6
Г) П8 + П2 - 1 ^ П3 + П2 - 1 2 1 ^ 2 ^ ^ о 2 ^1
< = n2 + n <n2 + n< 2n2, n > 1
п +1 п п
4.5
а) п = 10 б) 2П + п3 < 2П + 2П = 2 (2n), n > 10
4.7 К log2n < Kn, n >. 1, поэтому этот алгоритм также имеет порядок О(п).
4.8
б) О(п);
в) 0(п2).
4.11
а) (3) п/2, т.е. О(п);
б) (1) 1
4.14 Удаляет из списка максимальный элемент. L должен передаваться по
ссылке, поэтому внутренний программный стек обновляется.
Глава 5
5.3 <строка 1> 22 <строка 2> 9 <строка 3> 8 <строка 4> 18
5.4 void StackClear(Stacks S)
{
while (!S.StackEmpty())
S.Pop ();
}
5.6 Копирует стек SI в S2 с помощью промежуточного стека tmp.
5.7 int StackSize(Stack S)
{
int size - 0;
// S передается по значению, программный стек не изменяется
while (!S.StackEmpty())
{ size++;
S.Pop();
}
return size;
}
5.9 void SelectItem(Stack& S, int n)
{
Stack Q;
int i, foundn ■ 0;
while (!S.StackEmpty())
{
i = S.Pop();
if S.PopO ;
{ foundn++;
break;
}
Q.Push(i);
}
while (!Q.StackEmpty())
S.Push(Q.Pop());
if (foundn)
S.Push(n);
}
5.10
6) a b + d e - /
5.11
6) a*(b + c)
5.14 <строка 1> З <строка 2> 18 <строка 3> 22 <строка 4> 9
5.15 Выстраивает очередь в обратном порядке. Переменная Q должна
передаваться по ссылке, чтобы параметр менялся в процессе выполнения
программы.
5.18 DataType PQueue::PQDelete(void)
{
DataType min;
int i, minindex » 0;
if (count > 0)
{
min * pqlist[0]; // положить pqlist[0] минимальным
// обработать остальные элементы, обновляя значение и индекс
// минимального элемента
for (i^O; Kcount; i++)
if (pqlistfi] < min)
// новый минимальный элемент равен pqlistfi]
// новый индекс минимального элемента равен i
{ min e pqlistfi];
minindex = i;
}
// сдвинуть влево pqlist[minindex+1]..pqlist[count-1]
i = minindex;
while (i < count-1)
{ pqlist[i] = pqlist[i+1];
i++;
}
count—; // уменьшить счетчик
}
// pqlist пуст; завершить программу
else
{
cerr « "Попытка удаления из пустой приоритетной очереди!"
« endl;
exit(1);
}
return min; // возвратить минимальное значение
}
Глава 6
ел
а) Правило #1. Списки параметров не отличаются друг от друга. Функции
1 и 2 имеют одинаковые списки, и задаваемые по умолчанию параметры
функции 3 не перегружаются.
б) Правило #1. Списки параметров различны. Перегрузка сделана
правильно.
в) Правило #2. Функции 1 и 2 допустимы, так как тип enum считается
отличающимся от других типов. Однако typedef в функции 3 не
оказывает никакого влияния. Компилятор полагает список параметров
имеющим форму "int& х" — такую же, что и для функции 1.
6.3 Максимум из а и b равен 99. Максимум из a, b и с равен 153. 1.0 +
max(hl, h2) = 1.05. Максимум из t, u и v равен 70000.
6.5 Обмен символьных строк языка C++.
void Swap(char *s, char *t)
// предполагается, что s и t содержат не более 7 9 символов
{
char tmp[80];
strcpy(tmp, s);
strcpy(s, t);
strcpy(t, tmp);
}
6.7
а) ModClass::ModClass (int v): dataval(v % 7) {}
ModClass ModClass::operator+ (const ModClass& x)
{ return ModClass(dataval+x.dataval); }
б) ModClass::operator* (const ModClass& x, const ModClass& y)
{ return ModClass(x,dataval * y.dataval); }
в) ModClass Inverse(const ModClassfc x)
{
ModClass prod value;
for (int i=0; i<7; i++)
{ value «■ ModClass (i);
prod = x * ModClass(i);
if (prod.GetValueO == 1)
break;
}
return value;
)
6.9 Complex::Complex(double x, double y): real(x), imag(y) {}
Complex Complex::operator+ (Complex x) const
{ return Complex(real+x.real, imag+x.imag);
}
Complex Complex: .-operator/ (Complex x) const
{ double denom - x.real*x.real + x.imag*x.imag;
return Complex((real*x.real + imag*x.imag)/denom,
(imag*x.real - real*x.imag)/denom);
}
// вывод в формате (real, imag)
ostream& operator« (ostream& ost, const Complex& x)
{
ostr « ' (' « x.real « ',' « x.imag « ')';
return ostr;
}
6.11
а) return ModClass(num/den);
б) return Rational(dataval);
6.13
а) Set::Set(int a[], int n)
{
for (int i*0; KSETSIZE; i++)
member[i] = FALSE;
for (i=0; i<n; i++)
member[a[i]] = TRUE;
}
б) int operator" (int n, Set x)
{ if (n<0 || n>=SETSIZE)
{ cerr « "Оператор А: неверный операнд" « n « endl;
exit(l);
}
return (x.member[n]);
}
в) (i) {1, 4, 8, 17, 25, 33, 53, 63}; (ii) {1,25}; (iii) 0; (iv) 1
г) <выход> <строка 1> {1,2,3,5,7,9,25} <строка 2> {2,3} <строка 3> 55
<строка 4> 55 is in A
Д) Set Set::operator+ (Set x) const
{
int i;
Set tmp;
for (i=0; KSETSIZE; i++)
tmp.member[i] = member[i] + x.member[i];
return tmp;
}
void Set::Insert(int n)
{
if (n<0 || n>=SETSIZE)
{ cerr « "Insert: неверный параметр " « n « endl;
exit(1);
}
member[n] = TRUE;
}
Глава 7
7.1
a) template <class T>
T Max(const T &x, const T &y)
{ return (x<y) ? у : x; }
6) char *Max(char* x, char* y)
{ return (strcmp(x,y) < 0) ? у : x; )
7.3 template <class T>
int Max{T Arr[], int n)
{
T currMax - Arr[0]; // подразумевается n>0
int currMaxIndex * 0;
for (int i*0; i<n; i++)
if (curMax < Arr(i])
{
currMax « Arrfi];
CurrMaxIndex - i;
}
return currMaxIndex;
}
7.5 template <class T>
void InsertOrder(T A[], int n, T elem)
{
int i - 0; // подразумевается n>0
while (i<n && A[i]<elem) // найти позицию вставки
i++;
if (i < n)
for (int j=n; j>i; j —) // сдвинуть хвост вправо
ACj] - A[j-1];
A[i] - elem;
}
Глава 8
8.1
а) 0123412345
б) Нет. Указателю р присваивается два разных адреса при обращении к
новой функции. Чтобы р-10 указывал на начало первого списка десяти
целых чисел, новая функция должна выделить память в
последовательных блоках.
8.2
а) int *px e new int (5);
б) а * new long[n]/
в) р ~ new DemoC; p->two - 500000; p->three » 3.14;
г) р - new DemoD; p->one; p->two = 35; p->three * 1.78;
strcpy (p->name, "Bob C++");
Д) delete px; delete [] a; delete p; delete p;
8.3
а) Dynamiclnt::DynamicInt(int)
{pn - new int(n);)
б) Dynamiclnt::Dynamiclnt(const Dynamiclnt &x)
(pn e new int(*x.pn);}
в) Dynamiclnt::operator int(void) // возвратить целое значение
{return *pn;}
г) istreams operator» (isteram istr, Dynamiclnt& x)
{
istr » *(x.pn);
return istr;
}
8.4
a) p = new Dynamiclnt(50);
б) г = new Dynamiclnt[3]; // каждый элемент имеет нулевое значение
в) for (int i=0; i<10; i++) a[i].SetVal(100); // или a[i] = DynamicInt(lOO);
r) delete p; delete [] q;
8.8
a) DynamicType<int> *p = new DynamicType<int> (5);
б) cout « *p; // используется перегруженный оператор «
cout « p->GetValue(); // используется функция-член класса
cout « int(p); // используется оператор преобразования в целое
в) Выделяет память под массив 65-ти объектов типа PynamicType<char>.
Каждый элемент этого массива равен NULL.
Выделяет память под один объект типа DynamicType<char> и
присваивает ему значение 'А'.
г) 35;
Д) 35;
е) D D 68;
ж) delete p; delete с; delate Q; // ошибка: переменная Q не создавалась
динамически
8.9
а) Параметр х передается по значению, и, следовательно, будет вызываться
конструктор копирования. Конструктор копирования постоянно
вызывал бы самого себя в программе, выполняющей бесконечный цикл.
б) Вы не могли бы иметь цепочку операторов присваивания С = В = А;
8.11 Оператор '+=' прибавляет правую часть г к текущему объекту Rational,
а затем присваивает результат этому же объекту. Текущий объект
задается с помощью *this. Значение "*this + г" присваивается текущему
объекту (*this) и возвращается в точку вызова.
8.12
а) ArrCL<int> A(20); ArrCL<char> В; ArrCL<float> C(25);
б) Класс ArrCL выполняет проверку границ массива. А[30] выходит за
границы.
в) 20-элементный массив агг содержит элементы 2, 4, 6, 8, ..., 40, сумма
которых (20 * 42)/2 = 10 * 42 = 420. Обе функции вычисляют одно
и то же значение,
8.13
а) "Have a";
б) "nice day!";
в) "Have a nice day!";
г) "Have a nice day!"
8.14
a) 10;
б) у;
в) 1;
г) Индекс 24 находится вне диапазона.
д) хуа52с;
ж) abcl2ABCxya52cba
8.16
а) 15;
б) 10;
в) 65520;
г) 1;
Д) 8
8.17 (1) соответствует функции three; (4) соответствует функции one
8.19 template <class T> Set<T> Set<T>::operator- (void) const
{
Set<T> tmp(setrange);
for (int i^O; i<arraysize; i++) // сформировать универсальное множество
tmp.member[i] = ~tmp.member[i]; // присвоить каждому элементу tmp
// значение 0=111...Ill
return tmp-*this; // возвратить разность между универсальным
// и текущим множествами
}
8.20
а) Set<T> UniversalSet(n); UniversalSet = -UniversalSet;
б) template <class T>
Set<T>Difference(const Set<T>& S, const Set<T>& T) {return S* ~T;}
Глава 9
9.1
а) 2 3;
б) 5 3;
в) 7 7;
г) 15 15;
Д) 17 17
9.3 Node<int> *head = NULL, *p;
for (int i=20; i>0; i—)
{ p = new Node<int>(i, head);
head = p;
}
p = head;
while (p != NULL)
{
cout « p->data « " ";
p = p->NextNode();
}
9.6
б) Следующий узел снова ссылается на р.
в) Следующий узел ссылается сам на себя.
9.7
a) template <class T>
void InsertFront(Node<T> header, T item)
{
Node<T> *p - new Node<T>(item) ;
header.InsertAfter(p);
}
9.9 Начиная с текущего узла, сканировать оставшуюся часть списка и
прибавлять 7 к содержимому каждого узла.
9.10 Удаляет из списка первый узел и вставляет его в конец списка.
9.11 template <class T>
int CountKey(Node<T> *head, T key)
{
Node<T> *p = head;
int count = 0;
while (p != NULL)
{
if (p->data == key)
count++;
p = p->NextNode();
}
return count;
}
9.14
а) 10 8 6 4 2;
б) 2 4 6 8 10;
в) 10 8 6 4 2;
г) 10 8 6 4 2
9.15
а) 60 70 80 90 100;
б) 20 40 60 80 100;
в) 20 10 30 40 50 60 70 80 90 100
9.17 void OddEven(LinkedList<int>& L, LinkedList<int>& Ll,
LinkedList<int>& L2)
{
L.Reset();
while (!L.EndOfList())
{
if {L.DataO % 2 == 1)
Ll.InsertAfter(L.Data{));
else
L2. InsertAf ter (L.DataO ) ;
L.NextO ;
}
}
9.19 template <class T>
void DeleteRear(LinkedList<T>& L)
{
L.Reset();
for (int i=0; i<L.ListSize()-1; i++)
L.NextO ;
L.DeleteAtO ;
}
9.23 Переставляет элементы связанного списка в обратном порядке, копируя
их в промежуточный стек, а оттуда обратно в связанный список.
9.27 Каждая очередь имеет объект типа LinkedList, включенный посредством
объединения. Когда объекты очереди присваиваются друг другу,
вызывается перегруженный оператор из класса LinkedList и один список
копируется в другой.
9.29 template <class T>
void InsertOrder(CNode<T> *header, Cnode<T> *newNode)
{
CNode<T> *curr = header->NextNode(), *prev = header;
while (curr !- header && curr->data < newNode->data)
{
prev = curr;
curr «■ curr->NextNode ();
}
prev->InsertAfter(newNode);
}
9.32 template <class T>
DNode<T> *DNode<T>::DeleteNodeRight(void)
{
DNode<T> *tempPtr « next/ // сохранить адрес узла
if (next »- this)
return NULL; // указывает на самого себя; выйти!
// текущий узел указывает на преемника tempPtr
.right - tempPtr->right;
// преемник tempPtr снова указывает на текущий узел
tempPtr->right->left - this;
)
Глава 10
10.1 Результат зависит от того, в каком порядке компилятор вычисляет
операнды. Если п=3 и левый операнд вычисляется первым,
результатом будет 3*2! = 6. Если в первую очередь вычисляется правый
операнд, в результате получается 2*21 = 4.
10.2 1 1 5 13 41 121 365 1093 3281 984 ...
10.4 125
10.5 котсеркереп отЭ
10.7 float avg(float а[], int n)
{
if (n -- 1)
return a[0];
else
return float (n-1)/n*avg(a, n-1) + a[n-l]/n;
)
10.8 int rstrlen(char *s)
{
if (*s — 0)
return 0;
else
return l+rstrlen(s+l);
}
10.12 Решение: 1 2 6 7 11 12
Глава 11
11.2
а) 3;
б) 2
11.6 Да
11.7
а) 15;
б) 42;
в) Прямое прохождение: 50 45 35 15 5 40 38 36 42 43 46 65 75 70 85
11.8 Вставляет узлы в бинарное дерево поиска. Передача указателя по
ссылке позволяет изменять корень и поля указателей узлов.
11.9
а) Прямое прохождение: М F Т N V U
б) Обратное прохождение: A D I R О L F
11.10
а) RNL-прохождение: V U Т N М F
б) RLN-прохождение: R О I L A D F
в) Поперечное прохождение: ROTARYCUBL
11.14
a)ACFEIHBDG
11.20 template <class T>
void PostOrder_Right (TreeNode<T> *t, void visit(T& item))
{
if (t != NULL)
{
// рекурсивное прохождение завершается на пустом поддереве
PostOrder_Right(t->Right(), visit); // пройти правое поддерево
PostOrder_Right<t->Left(), visit); // пройти левое поддерево
visit(t->data); // обработать узел
}
}
11.22 template <class T>
TreeNode<T> *Max(TreeNode<T> *t)
{
while (t->Right() != NULL)
t » t->Right();
return t;
)
11.26 template <class T>
int NodeLevel(TreeNode<T> *t, const T& elem)
{
int level = -1;
while (t != NULL)
{
level++;
if (t->data =■» elem)
break;
else if (elem < t-> data)
t » t->Left();
else
t « t->Right();
}
if (t == NULL)
level = -1;
return level;
}
Глава 12
12.2
BASE
DERIVED
КЛИЕНТ
Base Priv
X
Base Prot
X
X
Base Pub
X
X
Derived Priv
X
Derived Prot
X
Derived _Pub
x 1
X
12.3
а) Конструктор производного класса не вызывает конструктор базового
класса.
12.4
а) DerivedCL::DerivedCL(int a, int b, int с): data3(a), BaseCL(b,c){}
б) DerivedCL::DerivedCL(int a): data3(a), BaseCL() {}
в) datal data2 data3
objl 2 0 1
obj2 4 5 3
obj3 0 0 8
12.5 Вызван конструктор Basel.
Вызван конструктор Base2.
Вызван конструктор Derived.
Вызван конструктор Basel.
Вызван конструктор Base2.
Вызван деструктор Base2.
Вызван деструктор Basel.
Вызван деструктор Derived.
Вызван деструктор Base2.
Вызван деструктор Basel.
12.7
а) GetX — открытый метод класса Shape.
б) Так как х является защищенным элементом данных в классе Shape,
к нему можно обращаться из производных классов, но не из
программы-клиента.
12.8 <строка 1> 1 <строка 2> Base Class <строка 3> 2 <строка 4> 1 <строка
5> 0 <строка 6> Base
12.11 <строка 1> 7 <строка 2> 2 <строка 3> 3 5 <строка 4> 2 4 <строка
5> 2 4 <строка 6> 0 1 <строка 7> 7 <строка 8> 2 3
12.13 template <class T>
class StackBase
{
protected:
int numElements;
public:
StackBase(void): numElements(0) {}
virtual void Push(const T& item) = 0;
virtual T Pop(void) - 0;
virtual T Peek(void) = 0;
virtual int StackEmpty(void)
{ return numElements == 0 }
};
Реализуйте производный класс Stack с помощью массива (гл. 5) или
связанного списка (гл. 9).
12.19 int LookForMatch(Array<int>& A, int end, int elem)
{
ArrayIterator<int> aiter(A, 0, end-1);
while (!aiter.EndOfList())
{
if (aiter.DataO == elem)
return 1;
aiter.Next();
}
return 0;
}
void RemoveDuplicates(Array<int>& A)
{
ArrayIterator<int> assign(A), march(A);
int assignlndex;
if (A.ListSizeO <= 1)
return;
assign.Next();
march.Next();
assignlndex = 1;
while (march.EndOfList())
{
if (!LookForMatch(A, assignlndex, march.Data()))
(
assign.Data() = march.Data90;
assign.Next();
assignlndex++;
}
march.Next();
}
A.Resize(assignlndex);
}
12.20 template <class T>
int Max(Iterator<T>& colllter, T& maxval)
// перейти к первому элементу
{
colllter.Reset();
// если это конец списка, то список пуст
if (colllter.EndOfList())
return 0;
// взять первый элемент списка и начать сравнения
maxval *= colllter .Data () ;
for(colllter.Next(); !colllter.EndOfList(); colllter.Next())
if (colllter.Data() > maxval)
maxval = colllter.Data();
return 1; // успешный выход
}
Глава 13
13.1 Дерево (В): 60 30 80 65 40 5 50 10 90 15 70
13.3 template <class T>
void Preorder (T A[], int currindex, int n, void visit(T& item)
{
if (currindex < n)
{
visit (A[currindex]); // обработать узел
Preorder(A, 2*currindex+l, n, visit); // обход левого поддерева
Preorder(A, 2*currindex+2, n, visit); // обход правого поддерева
}
}
13.4
а) Да;
в) А[24];
д) Да А[34]
13.6 Последний уровень имеет 2П элементов. Число нелистовых узлов равно
1 + 2 + 4 + ... + 2nl « 2*n - 1.
13.7
а) 5;
г) 41 и 42;
е) 15—30
13.10 Дерево (Ь) является минимальной пирамидой, а дерево (f) —
максимальной.
13.13 Начальное состояние пирамиды А: 5 10 20 25 50
Вставить 15: 5 10 15 25 50 20
Вставить 35: 10 15 25 50 20 35
Удалить 5: 10 25 15 35 50 20
Вставить 40: 10 25 15 35 50 20 40
Вставить 10: 10 10 15 25 50 20 40 35
13.15
а) 47 45 40 10;
в) 35 40 45
13.16
б) 3, 6, 33, 88, 16, 45, 45, 90;
в) "aehpify"
13.21 Для графа (В)
Матрица смежности
А
В
С
D
Е
А
0
0
0
0
1
В
0
0
0
0
0
С
1
1
0
0
1
D
1
1
0
0
1
Е
0
0
0
0
0
Представление в виде списков смежности
А: С D
В: С D
С:
D:
Е: А С D
13.22
б) Пути нет;
г) Из А существует путь в С и D.
13.23
б) Прохождение "сначала в глубину": А Е D С; прохождение "сначала
в ширину" : А С D Е.
13.26 Проходит граф методом "сначала в ширину", распечатывая попутно
каждую вершину.
Глава 14
14.1
а) Проход 0: 14892174
Проход 1: 11892474
Проход 2: 11298474
Проход 3: 11248974
Проход 4: 11244978
Проход 5: 11244798
Проход 6: 11244789
14.2 Проход 0: 48192174
Проход 1: 14892174
Проход 2: 14892174
Проход 3: 12489174
Проход 4: 11248974
Проход 5: 11247894
Проход 6: 11244789
14.7 Когда список уже отсортирован по возрастанию или по убыванию,
алгоритм имеет порядок 0(п2).
14.13 Если г = х % m и q — частное от х/т, то х = mq + г и г = х - mq.
Поскольку m четно, то при четном х значение хеш-функции четно.
Все четные ключи хешируются в четные табличные индексы. Хеш-
коды недостаточно рассеяны по таблице.
14.14
01 2 3 4 5 6789 10
а) НТ 391 Пусто Пусто 257 567 575 987 189 122 734 313
НТ
5) 012345678910
NULL NULL NULL j NULL | i NULL . NULL NULL
14.19
6) hashf(16) = 1; hashf(257) - 16
14.21 Если хеш-функция хорошая, вероятность хеширования в ячейку i
равна 1/N. Когда ключ занял i-ю ячейку таблицы, вероятность
заполнения ячейки i+1 равна 2/N. Вероятность заполнения ячейки i+2
равна 3/N. Скопление происходит из-за того, что вероятность
попадания в группу смежных ячеек становится больше, чем вероятность
попадания в одиночную ячейку таблицы.
14.22
а) Покажем, что если хеширование происходит в индекс i, то
последовательное рехеширование снова приводит нас к этому индексу. Пусть
i = (i+3k) % 93 для некоторого к. Это значит, что i+3k = 93q+i для
некоторого q и, следовательно, 3k = 93q. Минимальным решением
этого уравнения являются к=31 и q=l. После 31-й итерации функция
рехеширования снова возвращается к i, т.е. покрывает только 1/3
таблицы.
б) Если d < m, to d и т — взаимно простые и вся таблица покрывается
функцией рехеширования.
14.24
14.25
а) Да;
б) int H(char *s) {return (s[2] - 'a') % 7;}
14.26 void PascalTextFile::Assign(char *filename)
{strcpy(fname, filename);}
void PascalTextFile::Reset(void);
{
if (isOpen)
f.seek(0, ios::beg);
else
{
accesstype * IN;
f.open(fname, ios::in | ios:mocreate);
if (f !- NULL)
isOpen++;
else
Error("Невозможно открыть файл");
}
}
void PascalTextFile::PWrite(char A[], int n)
{
if (accesstype == IN)
Error ("Недопустимая операция доступа к файлу");
if (!isOpen)
Error ("Файл закрыт");
f.write(A,n);
}
Список литературы
1. Адельсон-Вельский Г. М., Ландис Е. М. Один алгоритм организации
информации. — Доклады АН СССР. Серия математическая, т. 146,
1962, N 2 — с. 263—266.
2. Aho А. V., Hopcroft J. E., Ullman J. D. Data structures and algorithms. —
Reading, MA: Addison-Wesley, 1983.
3. Baase S. Computer algorithms (2nd ed.). — Reading, MA: Addison-Wesley,
1988.
4. Bar-David T. Object oriented design for C++. — Englewood Cliffs, NJ:
Prentice Hall, 1993.
5. Booch G. Object oriented design. — Redwood City, CA: Benjamin/Cum-
mings, 1991.
6. Budd T. A. Classical data structures in C++. — Reading, MA: Addison-
Wesley, 1994.
7. Carrano F. M. Data abstraction and problem solving with C++, walls and
mirrors — Redwood City, CA: Benjamin/Cummings, 1995.
8. Collins W. J. Data stuctures, an object-oriented approach. — Reading,
MA: Addison-Wesley, 1992.
9. Dale N., Lilly S. C. Pascal plus data structure, algorithms and advanced
programming (3rd ed,). — Lexington, MA: D. C. Heath, 1991.
10. Decker R., Hirshfield S. Working classes, data structures and algorithms
using C++. — Boston, MA: PWS, 1996.
11. Ellis M. A., Stroustrup B. The annotated C++ reference manual. —
Reading, MA: Addison-Wesley, 1992.
12. Flaming B. Practical data structures in C++. — New York: Wiley, 1993.
13. Flaming B. Turbo C++: Step-by-step. — New York: Wiley, 1993.
14. Headington M. R., Riley D. D. Data abstraction and structures using
C++. — Lexington, MA: D. C. Heath, 1994.
15. Horowitz E., Sahni S., Mehta D. Fundamentals of data structures in
C++. — New York, W. H. Freeman, 1995.
16. Horstman C. S. Mastering object-oriented design in C++. — New York:
Wiley, 1995.
17. Knuth D. E. The art of computer programming, vol. 1: Fundamental
algorithms (2nd ed.). — Reading, MA: Addison-Wesley, 1973.
18. Knuth D. E. The art of computer programming, vol. 2: Seminumerical
algorithms (2nd ed.). — Reading, MA: Addison-Wesley, 1973.
19. Knuth D. E. The art of computer programming, vol. 3: Sorting and
searching (2nd ed.). — Reading, MA: Addison-Wesley, 1973.
20. Kruse R. L. Data structures and program design. — Englewood Cliffs,
NJ: Prentice Hall, 1994.
21. Lewis T. G. Smith M. Z. Applying data structures (2nd ed.). — Boston:
Houghton-Miffin, 1982.
22. Martin R. Designing object-oriented C++ applications using the Booch
method. — Englewood Cliffs, NJ: Prentice Hall, 1995.
23. Model M. Data structures, data abstraction. — Englewood Cliffs, NJ:
Prentice Hall, 1994.
24. Murray R. B. C++ strategies and tactics. — Reading, MA: Addison-
Wesley, 1993.
25. Naps T. L. Introduction to data structures and algorithm analysis. — St.
Paul, MN: West, 1992.
26. Pohl I. Object-oriented programming in C++. — Redwood City, CA: Ben-
jamin/Cummings, 1993.
27. Pothering G. J., Naps T. L. Introduction to data structures and algorithm
analysis with C++. — St. Paul, MN: West, 1995.
28. Schildt H. C++: The complete reference. — Berkeley, CA: Osborne
McGraw-Hill, 1991.
29. Sedgewich R. Algorithms in C++. — Reading, MA: Addison-Wesley, 1992.
30. Standish T. A. Data structures, algorithms, and software principles. —
Reading, MA: Addison-Wesley, 1994.
31. Stroustrup B. The C++ programming language (2nd ed.). — Reading,
MA: Addison-Wesley, 1991.
32. Stubbs D. F., Webre N. W. Data structures with abstract data types and
С — Pacific Grove, С A: Brooks/Cole, 1989.
33. Tenenbaum A. M., Langsam Y., Augenstein M. J. Data structures using
С — Englewood Cliffs, NJ: Prentice Hall, 1990.
34. Weiss M. A. Data structures and algorithms analysis in C++. — Redwood
City, CA: Benjamin/Cummings, 1994.
35. Winder R. Developing C++ software. — New York: Wiley, 1991.
36. Wirth N. Algorithms + data structures = programs. — Englewood Cliffs,
NJ: Prentice Hall, 1976.
37. Wirth N. Algorithms and data structures. — Englewood Cliffs, NJ:
Prentice Hall, 1986.
Предметный указатель
А
абстрактный базовый класс abstract base class 48,559
- класс - class 48,541,560
- списковый класс - list class 560-563
- тип данных - data type 2
абстракция элемента управления control abstraction 540
адрес, память address, memory 57
активизирующая запись activation record 443
алгебраическое выражение algebraic expression 193
инфиксное infix 193
постфиксное postfix 193
префиксное prefix 537
алгоритм Уоршалла Warshall algorithm 666
алгоритмы деревьев tree algorithms 489-503
вычисление глубины computing the depth 492
вычисление количества листовых counting leaf nodes 492
узлов
горизонтальная печать дерева horizontal tree printing 493
копирование дерева copying a tree 495
обратное сканирование postorder scan 490
поперечное сканирование breadth-first csan 500
по уровневое сканирование level-order scan 500
симметричное сканирование inorder scan 489
удаление дерева deleting a tree 498-499
алгоритмы сортировки sorting algorithms
"быстрая" quiksort 690
treesort-сортировка treesort 646
вставками insertion sort 688
двусвязного списка doubly linked list sort 408
методом пузырька bubble sort 686
обменная exchange sort 85
поразрядная radix sort 209
сортировка посредством выбора selection sort 684
со связанными списками linked list sort 369
турнирная tournament sort 602
анализ наилучшего случая best case analysis 157
- наихудшего случая (алгоритма) worst case analysis 157
- сложности (алгоритма) complexity analysis 155-159
алгоритм Уоршалла Warshall algorithm 667
поиск "сначала в ширину" breadth-first search 659
сравнение 0(n log2n)-copTHpoeoK compare 0(n log2n) sorts 697
"быстрая сортировка" quicksort 695
- - AVL-дерево - - AVL tree 628
алгоритм сопоставления с образцом pattern matching algorithm 325
бинарное дерево поиска binary search tree 504
бинарный поиск search 166
законченное бинарное дерево complete binary tree 482
обменная сортировка exchange sort 155
операции с очередью queue operations 206
операции с очередью приоритетов priority queue operations 217
операции со стеком stack operations 189
пирамидальная сортировка heapsort 619
поиск "сначала в глубину" depth-first search 659
поразрядная сортировка radix sort 212
последовательный поиск sequential search 161
сортировка включением в дерево tree sort 646
сортировка вставками isertion sort 689
сортировка методом пузырька bubble sort 688
сортировка посредством выбора selection sort 686
сортировка прямым слиянием straight merge sort 728
сортировка со связанными списками linked list sort 370
сравнение 0(п )-сортировок compare 0(n ) sorts 696
турнирная сортировка tounament sort 604
хеширование hashing 714
числа Фибоначчи Fibonacci numbers 466-468
ассоциативность операций associativity of operators 278
ассоциативные массивы associative arrays 151
Б
базовый класс base class 31
байт byte 57
бинарное дерево binary tree 479-482
вертикальная печать upright (vertical) tree printing 500
вырожденное degenerate 481
горизонтальная печать — horizontal tree printing 493
законченное complete 482
класс TreeNode TreeNode class 483
копирование дерева copy a tree 495
левый-правый сын left-right child 481
описание description 479
определение definition 479
полное full 482
поперечное сканирование breadth first scan 500
построение building 485
по уровневое сканирование level scan 500
симметричный метод прохождения inorder traversal 489
(порядок) - - LNR, LRN, etc. 489
структура узла node structure 483
удаление дерева deleting a tree 498
бинарные деревья, представляемые array-based binary trees 600-602
массивами
бинарный оператор binary operator 193
- поиск - search 503
неформальный анализ informal analysis 166
рекурсивная форма recursive form 443-445
сравнение последовательного и compare sequential 164
бинарного методов
формальный анализ formal analysis 166
биномиальные коэффициенты Binomial coefficients 472
бит bit 57
битовые операции bit operations 327-328
и and 327
исключающее или exclusive or 327
не not 327
или or 327
блок (метод цепочек при хешировании) bucket 705
буферизация печати print spooler 394-400
быстрая сортировка quicksort 690
в
верхняя треугольная матрица upper triangular matrix 120
вершина графа vertex of graph 647
- стека top of stack 182
вещественное число real number
- - ADT - - ADT 60
мантисса mantissa 60
научный формат scientific notation 60
определение definition 60
порядок (экспонента) exponent 60
представление representation 60
вещественные типы данных - data types 60
взвешенный орграф weighted digraph 649
виртуальная функция virtual function 550-552
деструктор destructor 558
и полиморфизм and polymorphism 550
описание description 49-50,541
таблица table 552
чистая pure 541, 559
внешние структуры данных external data structures 77
внешний файловый поиск - file search 723
внутренние структуры данных internal data structures 77
возврат (прохождение лабиринта) backtracking 436
возможности программного program design features
конструирования
объектная разработка object design 38
сквозной стуктуированный structured walkthrough 45
контроль
структурное дерево structure tree 39
тестирование объектов object testing 40,45
устойчивость к ошибкам robustness 46
вращение AVL-дерева rotation in AVL tree
двойное double 639
единичное single 638
входной приоритет input precedence 280
вызов по значению call by value 115
- по ссылке - reference 115
выражение expression
- вычисление (оценка) - evaluation 193
- деревья - trees 438
Г
глубина дерева depth of a tree 480
голова связанного списка head of a linked list 353, 358
граф graph 647
- ADT - ADT 649
- ациклический - acyclic 649
- вершины - vertices 647
- взвешенный орграф - weighted digraph 649
- матрица достижимости - reachability matrix 666
смежности - adjacency matrix 650
- направленный (орграф) - directed (digraph) 648
- ненаправленный - undirected 648
- приложение: сильные компоненты - application: strong components 659
- путь - path 648
- ребра - edges 647
- связанные вершины - connected vertices 648
- сильно связанный - strongly connected 648
- сильные компоненты - strong components 659
- слабо связанный - weakly connected 648
- транзитивное замыкание - transitive closure 667
- цикл - cycle 649
группа group 153
Д
двоичные числа binary numbers 56
двоичный файл - file 715
двумерный массив two-dimensional array
определение definition 68
хранение storage 69
двусвязный список doubly linked list 410
приложение: сортировка вставками application: insertion sort 406
дерево tree 479-480
- бинарного поиска binary search tree 503-507
ADT ADT 508
вставка узла inserting a node 517
класс BinStree BinStree class 508
ключ key 505
описание description 503
приложение: конкорданс application: concordance 525
симметричное прохождение inorder traversal (sort) 511
(сортировка)
счетчики появлений application: occurrence counts 513
удаление узла deleting a node 519
- бинарное дерево - binary tree 480
- высота, см. глубина - height, see depth
- глубина - depth 480
- корень - root 479
- левый сын - left child 481
- лист - leaf 479
- описание - description 479
- определение - definition 479
- поддерево - subtree 479
- правый сын - right child 479
- предки-потомки - ancestors-descendents 479
- путь - path 479
- сын-родитель - children-parent 479
- терминология - terminology 479
- тип коллекции - collection type 152
- узел - node 483
- уровень - level 480
деструктор destructor 295-296,
291
динамический dynamic 408
- выделение массива - array allocation 292
- массив - array 147
- объект - object 293-297
- память - memory 64
- связывание - binding 49
- структуры данных - data structures 291
дискретный тип discrete type 60
длинная последовательность long run 577
сортировка слиянием merge sort 729
доступ, см. прямой доступ, access, see direct access, sequential
последовательный доступ access
дружественные функции friend functions 244-245
3
заголовочный узел header node 401
задача Джозефуса Josephus problem 403
- о комитетах committee problem 448-450
задняя рекурсия tail recursion 469
закрытое наследование private inheritance 587
запись (как набор данных) record
ADT - ADT 77
определение - definition 76
защищенные методы protected members 544
знаковый бит sign bit 57
И
изменение состояния state change 25
индекс, массив index, array 65
инициализатор, см. конструктор initializer, see constructor
инкапсуляция encapsulation 24
инфиксный infix
- вычисление выражения - expression evaluation 277-285
- формат - notation 193
итератор iterator 563
итераторы дерева tree iterators 642
К
каркас разработки design framework 39
квадратичное время (0(n2)) quadratic time (0(n )) 160
квадратная матрица square matrix 120
класс class
- (в книге): Queue (связанный список) - (in book): Queue (linked list) 388
Animal Animal 553-555
Array Array 303
Calculator Calculator 195
Circle (производный) Circle (derived) 548
CNode CNode 401
Date Date 118
Dice Dice 40
DNode DNode 410
DynamicClass DynamicClass 293
Event Event 223
Heap Heap 612
Iterator (абстрактный) Iterator (abstract class) 564
Line Line 30
LinkedList LinkedList 374
List (абстрактный) List (abstract) 560
MathOperator MathOperator 281
Maze Maze 462
Node Node 353
NodeShape NodeShape 582
OrderedList OrderedList 36
Point Point 29
PQueue PQueue 214
RandomNumber RandomNumber 111-112
Rational Rational 247
Rectangle Rectangle 101
SeqList SeqList 36,168
SeqList (производный) SeqList (derivde) 561
SeqList (связанный список) SeqList (linked list) 391
Shape Shape 546
Simulation Simulation 225
Spooler (для печати) Spooler (print) 396
Stack Stack 184
Stack (шаблонный) Stack (template) 276
String String 310
Temperature Temperature 108
TriMat TriMat 12-129
Vec2d Vec2d 243
Window Window 412
- Array Array class
деструктор destructor 305
конструктор constructor 305
конструктор копирования copy constructor 305-306
метод Resize Resize method 308-309
объявление declaration 303
оператор индексации index operator 306
преобразования указателя pointer conversion operator 307-309
- Arraylterator Arraylterator class 574
- AVLTree AVLTree class 631-641
метод UpdateLeftTree UpdateLeftTree method 637
AVLInsert Avllnsert method 636
DoubleRotation DoubleRotation method 639
GetAVLTreeNode - - GetAVLTreeNode method 633
Insert Insert method 634
объявление declaration 631
- AVLTreeNode AVLTreeNode class 629-631
конструктор constructor 631
метод Left Left method 631
объявление declaration 629
реализация implementation 631
- Binfile BinFile class 718
конструктор constructor 721
- метод Clear Clear method 719
EndFile - - EndFile method 719
Peek - - Peek method 719
Read Read method 721
(блочный) (block) method 721
Write - - Write method 722
(блочный) (block) method 722
объявление declaration 718
реализация implementation 721
- BinSTree BinSTree class 508-510,
515-524
конструктор constructor 515
метод Delete Delete method 523
Find - - Find method 516
FindNode - - FindNode method 516
Insert Insert method 517
Update Update method 524
объявление declaration 510
оператор присваивания assignment operator 515
реализация implementation 515
управление памятью memory management 515
- Calculator Calculator class 202
метод Run Run method 197
Compute Compute method 196
объявление declaration 195
реализация implementation 196
- Circle Circle class 548
объявление declaration 548
описание description 548
реализация implementation 548
- CNode CNode class
DeleteAfter метод DeleteAfter method 403
InsertAfter метод InsertAfter method 403
конструктор constructor 402
объявление declaration 401
реализация implementation 402
- Date Date class 118
- Dice - class 41
- Dictionary Dictionary class 737
конструктор constructor 741
метод DeleteKey DeleteKey method 742
InDictionary InDictionary method 742
объявление declaration 737
реализация implementation 741
- DNode DNode class 407
метод DeleteNode DeleteNode method 411
реализация implementation 410
конструктор constructor 410
метод InsertLeft InsertLeft method 411
InsertRight InsertRight method 411
- DynamicClass DynamicClass class
деструктор destructor 295
конструктор constructor 293-294
конструктор копирования copy constructor 300
оператор присваивания assignment operator 297
- Event Event class 223
- Graph Graph class 652
конструктор constructor 653
метод DeleteVertex DeleteVertex method 655
GetNeighbors GetNeighbors method 654
GetVertexPos GetVertexPos method 654
GetWeight - - GetWeight method 654
InsertEdge InsertEdge method 654
Vertexlterator Vertexlterator class 654
минимальный путь minimum path 661
объявление declaration 652
прохождение "сначала в глубину" depth-first graph traversal 656
"сначала в ширину" (метод) breadth-first traversal 656
реализация implementation 653
- HashTable HashTable class 707
метод Find Find method 712
Insert Insert method 711
объявление declaration 707
реализация implementation 711
- HashTablelterator HashTablelterator class 711
конструктор constructor 713
метод Next Next method 714
SearchNextNode SearchNextNode method 713
объявление declaration 708
реализация implementation 712
- Heap Heap class 609
конструктор constructor 618
метод Delete Delete method 615
FilterDown FilterDown method 615
FilterUp - - FilterUp method 613
Insert Insert method 614
объявление declaration 609
пирамидальная сортировка heapsort 618
реализация implementation 612
- ifstream if stream class 80
- Inorderlterator Inorderlterator class
конструктор constructor 644
метод Next Next method 645
объявление declaration 643
реализация implamentation 644
- Ios Ios class 80
- Istream Istream class 80
- Istrtream Istrtream class 81
- KeyValue KeyValue class 736
- Line Line class 30
- LinkedList LinkedList class 371-376,
381-388
конструктор constructor 382
метод InsertAt InsertAt method 385
ClearList - - ClearList method 383
CopyList CopyList method 383
Data Data method 385
DeleteAt - - DeleteAt method 387
Next - - Next method 384
Reset Reset method 384
методы выделения памяти memory allocation methods 382
объявление declaration 374
описание операций describing operations 372-374
приложение: конкатенированные application: concatenating lists 377
списки
сортировка выбором selection sort 378
удаление дубликатов removing duplicates 379
проектирование списка designing the class 371
реализация implementation 381
указатель на первый узел front pointer 371
на последний узел rear pointer 371
на предыдущий узел previous pointer (prevPtr) 371
на текущий узел current pointer (currPtr) 371
- List (абстрактный) List class (abstract) 560-563
объявление declaration 561
реализация implementation 561
- MathOperator MathOperator class
конструктор constructor 281
метод Evaluate Evaluate method 282
объявление declaration 281
оператор сравнения comparison operator 282
- Maze Maze class
объявление declaration 462
реализация imlementation 463
- Node Node class 353-358
конструктор constructor 356
метод Delete After DeleteAfter method 357
InsertAfter InsertAfter method 357
NextNode NextNode method 356
объявление declaration 355
реализация implementation 356
- NodeShape NodeShape class 582
- ofstream ofstream class 80
- OperandList OperandList class 35
метод Insert Insert method 576
объявление declaration 576
реализация implementation 576
- Ostream Ostream class 80
- Ostrstream Ostrstream class 81
- Point Point class 29-30
- Pqueue PQueue class 214-217
метод Pqdelete Pqdelete 216
Pqinsert Pqinsert 215
объявление declaration 214
(пирамидальная версия) (heap version) 622
реализация implementation 215
- Queue (массив) Queue class (array) 199
конструктор constructor 204
метод Qdelete Qdelete method 206
Qinsert Qinsert method 205
объявление declaration 201
реализация implementation 202
(связанный список) (linked linked) 389-392
объявление declaration 389
реализация implementation 390
- RandomNumber RandomNumber class 110-114
конструктор constructor 111-112
метод fRandom fRandom method 112
Random Random method 112
объявление declaration 110
реализация implementation 112
- Rational Rational class 247-258
метод Reduce Reduce method 255
объявление declaration 247
операторы (как дружественные) operators (as friends) 247
(как члены) (as members) 249
(преобразование типа) (type conversion) 252
потоковые операторы stream operators 248
- Rectangle Rectangle class 101-107
- SeqList (массив) SeqList class (array) 168-175
метод Delete Delete method 170
Find Find method 171
GetData GetData method 170
Insert Insert method 169
объявление declaration 168
реализация implementation 168
(производный) (derived) 561-563
объявление declaration 562
реализация implementation 562
(связанный список) (linked list) 391-392
объявление declaration 391
приложение: сравнение application: efficiency 392-394
эффективности comparison
реализация implementation 392
- SeqListlterator SeqListlterator class
объявление declaration 565
реализация implementation 565
- Shape Shape class
- объявление declaration 547
описание description 546
реализация implementation 547
- Simulation Simulation class
конструктор constructor 226
метод NextArrvalTime NextArrvalTime method 227
объявление declaration 225
- Spooler (печать) Spooler (print) class
объявление declaration 396
реализация implementation 397
- Stack Stack class 184-189
конструктор constructor 187
метод ClearStack ClearStack method 188
Peek - - Peek method 188
Pop - - Pop method 187
Push - - Push method 187
StackEmpty StackEmpty method 188
StackFull - - StackFull method 188
объявление declaration 186
реализация implementation 187
- String String class 310-320
ввод/вывод I/O 319
- - FindLast - - FindLast 319
конкатенация concatenation 314
конструктор constructor 315
метод ReadString ReadString method 319
Substr - - Substr method 318
объявление declaration 311
оператор присваивания assignment operator 316
приложение: тестовая программа application: test program 314
реализация implementation 315
сравнение строк string comparison 316
- Temperature Temperature class 108
- TreeNode TreeNode class 484
конструктор constructor 485
метод FreeTreeNode FreeTreeNode method 486
GetTreeNode - - GetTreeNode method 486
объявление declaration 484
- TriMat TriMat class 124-129
- Vec2d Vec2d class 243
объявление declaration 244
операторы (как дружественные) operators (as friends) 243
(как члены класса) (as members) 262
скалярное произведение scalar multiplication
- Window Window class
объявление declaration 413
реализация implementation 415
- заголовок class: head 100
- закрытая часть - private part 100
- защищенная часть - protected part 100
- иерархия - hierarchy 542
- инкапсуляция - encapsulation 24
- конструктор - constuctor 101
- методы - methods 24,100
- наследование - inheritance 31
- объект - object 100
- объявление - declaration 25
- оператор разрешения области действия - scope resolution operator 103
- открытая часть - puplic part 100
- реализация - imlementation 25Д02
- скрытие информации - information hiding 24
- список инициализации - member initialization list 103
- члена класса - members 24,100
- тело - body 100
классы животных animal classes 553-555
- итераторов iterator classes
- Arraylterator Arraylterator 569
Inorderlterator Inorderlterator 643
SeqListlterator SeqListlterator 565
Vertexlterator Vertexlterator 652
ключ key 82
коллизия collision
- определение - definition 704
- разрешение - resolution 704
комбинаторика combinatories 437
композиция объектов composition of objects 28-30
компонента постусловий ADT ADT Postconditions component 21
- предусловий ADT - Preconditions component 21
- процесса ADT - Process component 21
конкатенация списков concatenating lists 377
конкорданс concordance 525-529
конструирование функций узлов дерева tree node function desing 486
конструктор constructor 21
- копирования copy constructor 291,300-
302
- умолчания default constructor 117
корень дерева root of tree 152,479
косвенная рекурсия inderact recursion 434
коэффициент заполнения load factor 714
кубическое время (0(n )) cubic time (0(n )) 160
Л
линейная коллекция linear collection 144-152
линейное время - time (o(n)) 160
линейный -
- последовательный список - sequential list 148
листовой узел leaf node 479
логарифмическое время (0(log2n), logarithmic time (0(log2n), 0(nlog2n)) 160
0(nlog2n))
M
максимальная пирамида maximum heap 608
массив: ADT Array ADT 65
- границы - index bounds 67
- дескриптор - dope vector 67
- проверка границ - bounds checking 303-305
- тип - type 65-71
коллекции - collection type 147
- хранение - storage 66
матрица matrix 120
- достижимости reachability matrix 666
- коэффициентов coefficient matrix 132
- смежности adjacency matrix 650
метод Peek (стековый) Peek (stack) method 188
- вставки insertion method
- - BinFile (Write) - - BinFile (Write) 722
- - HastTable (Insert) - - HastTable (Insert) 711
LinkedList (InsertRear) LinkedList (InsertRear) 375
Queue (Qlnsert) Queue (Qlnsert) 205
- - String (Insert) - - String (Insert) 312
- - AVLTree (AVLInsert) - - AVLTree (AVLInsert) 636
(Insert) (Insert) 634
- - BinSTree (Insert) - - BinSTree (Insert) 518
- - Graph (InsertEdge) - - Graph (InsertEdge) 652
(InsertVertex) (InsertVertex) 652
- Heap (Insert) Heap (Insert) 614
- - LinkedList (InsertAfter) - - LinkedList (InsertAfter) 375
(InsertAt) (InsertAt) 385
(InsertFront) (InsertFront) 375
OrderedList (Insert) OrderedList (Insert) 575
- - PQueue (PQInsert) - - PQueue (PQInsert) 215
- - SeqList (Insert) - - SeqList (Insert) 169
- - Set (Insert) - - Set (Insert) 366
- - Stack (Push) - - Stack (Push) 187
String (operator+) String (operator+) 312,317
- деления (хеширование) division method (hashing) 702
- середины квадрата (хеширование) midsquare technique (hashing) 704
- удаления deletion method
- - BinSTree (Delete) - - BinSTree (Delete) 523
Dictionary (DeleteKey) Dictionary (DeleteKey) 742
- - Graph (DeleteEdge) - - Graph (DeleteEdge) 652
- - SeqList (Delete) - - SeqList (Delete) 170
- - Set (Delete) - - Set (Delete) 336
- - Stack (Pop) - - Stack (Pop) 187
Graph (DeleteVertex) Graph (DeleteVertex) 655
- - HashTable (Delete) - - HashTable (Delete) 707
- - Heap (Delete) - - Heap (Delete) 615
- - LinkedList (DeleteAt) - - LinkedList (DeleteAt) 387
(DeleteFont) (DeleteFont) 375
PQueue (PQDelete) - - PQueue (PQDelete) 216
- - Queue (QDelete) Queue (QDelete) 206
- цепочек (хеширование) chaining with separate lists 704
методы класса method in a class 24
- поиска retrieval methods
- - BinFile (block Read) - - BinFile (block Read) 721
(Read) (Read) 721
- - BinSTree (Find) - - BinSTree (Find) 515
- - NasTable (Find) - - NasTable (Find) 712
Queue (Qfront) - - Queue (Qfront) 201
- - SeqList (Find) - - SeqList (Find) 171
- - Set (IsMember) - - Set (IsMember) 335
- - Stack (Peek) - - Stack (Peek) 188
- - String (Find) - - String (Find) 312
(FindLast) (FindLast) 319
(Substr) (Substr) 317
методы прохождения дерева tree traversals 489
минимальная пирамида minimum heap 608
минимальный путь - path 661
множественное наследование multiple inheritance 37
множественные конструкторы - constructors 117
множество set
- Set (integral type) Set class (integral type) 334
operator+ (объединение) operator+ (union) 335
конструктор constructor 329
метод Delete Delete method 330
Insert Insert method 335
IsMember IsMember method 335
объявление declaration 336
описание description 336
потоковые операторы I/O stream operatos 334
ввода/вывода
реализация implementation 336
- класс Set (модель массива) set: Set class (array model) 263
(целочисленный тип) (integral type) 328
- описание (целочисленный тип) - description (integral type) 325-327,329
- решето Эратосфена - application: Sieve of Eratosthenes 332
- тип коллекции - collection type 154
моделирование simulation 220-232
- событие прихода - arrival event 223
ухода - departure event 223
мультипликативный метод (хеширование) multiplicative method (hashing) 704
H
набор символов кода ASCII ASCII character set 59
надежные массивы safe arrays 303
наибольший общий делитель GCD (Greatest Common Devisor) 254
направленный граф directed graph 648
наследование inheritance
- абстрактный класс - abstract class 541
- базовый класс - base class 542
- виртуальная функция - virtual function 541
функция-член member function 550
- динамическое связывание - dynamic binding 550
- защищенные члены (класса) - protected members 544
- иерархия класса - class hierarchy 542
- концепция - concept 28
- множественное (наследование) - multiple 37
- определение - definition 540
- открытое наследование - public inheritance 543
- подкласс - subclass 543
- полиморфизм - polymorphism 550
- приложение: геометрические фигуры - application: geometric figures 556
- производный класс - derived class 542
- статическое связывание - static binding 551
- суперкласс - superclass 543
- чистая виртуальная функция - pure virtual function 541
начало связанного списка front of linked list 353
нелинейная коллекция nonlinear collection 144,152-155
ненаправленный граф undirected graph 648
нисходящая программная разработка top-down program disign 38
нотация Big-0 Big-0 notation 156
О
обменная сортировка exchange sort 85-86
обратная польская запись Reverse Polish notation 193
обратный метод прохождения postorder traversal 490
объект object
- как возвращаемое значение - as a return value 115
- как параметр функции - as a function parameter 115
- композиция - composition 28
- наследование - inheritance 28,31-32
- определение - definition 20
- тестирование - testing 45
объектно-ориентированное object-oriented programming
программирование
виртуальная функция virtual function 49
абстрактный базовый класс abstract base class 48
Бъярн Страуструп Stroustrup, Bjarne 47
динамическое связывание dynamic binding 550
композиция composition 28
множественное наследование multiple inhritance 37
наследование inheritance 28, 31
повторное использование кода reusability of software 35
полиморфизм polimorphism 550
построение программы program design 38-43,45-46
тестирование testing 45
чистая виртуальная функция pure virtual function 49
объекты и передача информации objects and information passing 115
объявление (класса) declaration, class 25
однородный homogeneous
- массив - array 65
- список - list 166
оператор delete delete operator 64
описание description 290
определение definition 293
- new new operator
описание description 290
определение definition 64
ошибка выделения памяти insufficient memory error 292
- адреса & address operator & 64
- индекса [] index operator [] 303,306
- преобразования типа type conversion operator
к типу объекта to object type 252
из объектного типа from object type 253
- присваивания assignment operator 297
операция извлечения (из стека) pop operation
метод Stack Stack method 187
описание description 149,182
- помещения в стек push operator
метод Stack Stack method 187
описание description 149,182
- разрешения области действия scope resolution operator 103
определение AVL-дерева AVL tree: definition 627
орграф, см. направленный граф digraph, see directed graph
открытая адресация с линейным linear probe open addressing 704
опробованием
- секция класса public class section 24
открытое наследование - inheritance 543
отладчик на уровне кода source level debugger 46
очередь queue 198-206
- приоритетов priority queue 212-217
- - ADT - - ADT 213
класс Pqueue PQueue class 214
(пирамидальная версия) (heap version) 622
определение definition 212
приложение: длинные applicaion: long runs 622
последовательности
моделирование, управляемое event-driven simulation 220
событиями
сервисная поддержка support services 217
- ADT queue: ADT 199
- определение - definition 198
- приложение: партнеры по танцу - application: dance partners 206
поразрядная сортировка radix sort 209
- реализация - implementation 202
- тип коллекции - collection type 149
п
палиндром palindrome 189
первым вошел-первым вышел first-in-first-out 199
перегрузка overloading
- оператора operator overloading 241
потока stream operator overloading 251
- функции function overloading 258
- внешние функции overloading: external function 241
- дружественными функциями - with friend functions 244
- оператор индекса [ ] - index operator [ ]
присваивания — - assignment operator e 299
- оператора - operator 241
- операторы потока - stream operators 250-252
преобразования - conversion operators 252-254
- функциями-членами класса - with class members 242
передача сообщения message passing 25
перестановки permutations 451-455
пирамида heap 607-612
- максимальная - maximum 608
- минимальная - minimum 608
- определение - definition 607
- порядок - order 607
пирамидальная сортировка heapsort 618
повторное использование кода reusability of software 35
поддерево subtree 479
поиск "сначала в ширину" breadth-first search 657
полиморфизм polimorfism 48-50
полное бинарное дерево full binary tree 482
поля записи fields of a record 76
поперечное сканирование level-order scan 500
поразрядная сортировка radix sort 209
последним пришел-первым вышел last-in-first-out 183
последовательный доступ sequential access
массив array 65
- - файл - - file 77
- поиск - search 82,161-162
алгоритм algorithm 161
быстрый fast 287
сравнение с бинарным compare binary search 164
- список - list 166-175
- - ADT - - ADT 33
класс SeqList SeqList class 36,168,391
описание description 32,166
приложение: хранение application: video store 173
видео-фильмов
тип коллекций collection type 146
постоянная единица времени (0(1)) constant time (0(1)) 160
постфиксный postfix
- вычисление - evaluation 193
- форма представления - notation 193
поток cerr cerr stream 80
- stream (стандартный вывод) cout stream 80
- ввода cin stream 80
- описание stream, description 78, 150
потоки в C++ C++ streams 77-78
потоковый класс stream class
f stream f stream 81
ifstream ifstream 80
ios ios 80
istream istream 80
ofstream ofstream 80
ostream ostream 80
- объект - object
cerr (стандартный поток ошибок) cerr 80
cin (стандартный ввод) cin 80
cout (стандартный вывод) cout 80
предусловия, см. ADT precondition, See ADT
приоритет операции precedence of perators
входной приоритет input precedence 280
стековый приоритет stack precedence 280
производный класс derived class 31
прохождение "сначала в глубину" depth-first graph traversal 656
прошитые деревья threaded trees 535
прямой доступ direct access
массив array 147
определение definition 146
- - файл - - file 715
путь в графе path in a graph 648
- в дереве - in a tree 479
P
разделяй и властвуй (метод) divide and conquer 433
разнородный heterogeneous
- массив - array 579
- список - list 579
- тип - type 77
разработка программного продукта software development
методология methodology 38
повторное использование reusability of software 35
ранг rank 278
распределение памяти memory allocation
динамическое dynamic 290,292
статическое static 290
рациональное число rational number 245-247
нормализованная форма standardized form 246
представление representation 245
приложение: решение лин. уравнений application: solving linear equations 256
редуцированная форма reduced form 245
ребро графа edge of graph 647
рекурсия recursion 432-439
- бинарный поиск - binary search 446
- биномиальные коэффициенты - binomial coefficients 472
- задача о комитетах - committee problem 448-450
- задняя рекурсия - tail recursion 469
- комбинаторика - combinatorics 438
- лабиринт - maze 436,460
- определение - recursive definition 433
- перестановки - permutations 451-455
- синтаксические деревья - expression trees 438
- стек времени исполнения - runtime stack 443-445
- степенная функция - power function 442
- треугольник Паскаля - Pascal's triangle 473
- факториал - factorial 439
- Ханойская башня - Tower of Hanoi 435,455
- числа Фибоначчи - Fibonacci numbers 466
- шаг рекурсии - recursive step 433
Решето Эратосфена Sieve of Eratosthenes 332
родитель parent 479
родительский узел - node 479
С
самоссылающаяся структура self-referencing structure 335
сбалансированное дерево balanced (AVL) tree 628
связанный connected 647
- список linked list 358-361,
363-364
удаление узла deleting a node 364
введение introduction 350
вставка в начало inserting at front 358
голова head 358
описание description 351
приложение: буферизация печати application: print spooler 394
головоломка word jumble 362
список выпускников graduation 365
управление окнами window management 411
прохождение traversal 359
создание узла creating a node 358
упорядоченного списка an ordered list 367
сортировка с использованием sorting using ordered list 369
связанного списка
удаление начального элемента deleting a front 363
элементов списка clearing a list 369
- вершины графа connected: graph vertices 647
- граф, сильно связанный strongly 648
слабо связанный weakly 648
связный список: вставка в хвост linked list: inserting at rear 361
печать списка printing a list 360
сеть network 155
сильно связанный граф strongly connected graph 648
символьный тип character type 58-60
симметричный метод прохождения inorder traversal 58
системная эффективность system efficiency 155
скрытие информации information hiding 24
слабо связанный граф weakly connected graph 648
слияние merge
- сортировка прямым слиянием - straight merge sort 727
- сортированных последовательностей - sorted runs 570-574
словарь dictionary 735
- ассоциативная структура - association structure 735
- класс Dictionarylterator - Dictionarylterator class 738
- определение - definition 151
- приложение: построение толкового - application: word building 739
словаря
случайное число random number
seed-значение seed 110
генератор generator 110
класс RandomNumber RandomNumber class 110
событие прихода (событийное arrival event 223
моделирование)
- ухода (событийное моделирование) departure event 223
сопоставление с образцом pattern matching 320
сортировка вставками insertion sort 688
- методом пузырька bubble sort 686
- на месте in-place sorting 212
- посредством выбора selection sort 684
- при помощи внешнего файла external file sort 727
спецификатор const (константы) const qualifier 27
список инициализации членов (класса) member initialization list 103
статическая: память static: memory 64
статические: структуры данных - data structures 290
статический static
- массив - array 147
статическое: связывание - binding 551
стек stack 182-189
- времени исполнения runtime stack 443
- операнда operand stack 278
- операторов operator stack 279
- ADT stack: ADT 184
- описание - description 182
- определение - definition 182
- полный - full 183
- приложение: вывод (чисел) с - application: multibase output 191
различными основаниями
вычисление выражения expression evaluation 193
инфиксное выражение, оценивание infix expression, evaluation 279
палиндром palindrome 189
постфиксный калькулятор — postfix calculator 195
- пустой - empty 183
- тип коллекции - collection type 149
степенная функция (рекурсивная форма) power function (recursive form) 442
строка в C++ String type (C++) 73
- ADT string ADT 72
- описание - description 71
строки в C++ C++ strings 73-74
T
текстовый файл text file 77-80
типы данных (определяемые языком) data types (language-defined)
- двоичный файл — binary file 80
двумерный массив two dimensional array 68
действительный real 60
запись record 77
массив array 65
перечисления enumerated 62
символьный character 58
строки C++ C++ strings 73
строчный string 72
структура C++ C++ struct 77
текстовый файл text file 79
указатель pointer 64
целочисленный integer 55
бинарное дерево binary tree 152
граф graph 154
запись (как данные) record 148
линейный список linear list 148
массив array 147
множество set 154
очередь queue 149
приоритетов priority queue 150
последовательный список sequential list 36
словарь dictionary 151
случайные числа random numbers 110
стек stack 149
строка string 147
- - файл - - file 150
хеш-таблица hash table 151
типы перечисления enumarated types 62-63
транзитивное замыкание transitive closure 667
треугольные матрицы trangular matrices 120-129
У
узел node
- ADT - ADT 354
- в дереве - in a tree 152
- в связанном списке - in linked list 351-352
- определение - definition 352
узел-часовой sentinel node 401
узлы AVL-деревьев AVL tree: nodes 628
указатель pointer
- this this pointer 300
- ADT pointer: ADT 64
- операция преобразования - conversion operator 303
- определение - definition 63
унарный оператор unary operator 54,193
универсальное множество universal set 325
упорядоченный список ordered list 149
- - ADT - - ADT 34
алгоритм создания creation algorithm 367
приложение: длинные application: long runs 577
последовательности
управление окнами window management 411-418
управляемое событиями моделирование, event-driven simulation, see simulation
см. моделирование
уровень дерева level in a tree 480
условие останова (цикла) stopping condition 433
Ф
файл file 77-79
- потоковый метод seekp - seekp stream method 717
tellg - tellg stream method 717
- ADT - ADT 79
- внешнее хеширование - external hashing 725
- внешний поиск search 723
- двоичный файл - binary file 715
- класс BinFile - BinFile class 718
- последовательный - sequential 717
- потоковый метод seekg - seekg stream method 717
tellp - tellp stream method 717
- режим (записи/чтения) - mode 716
- сортировка прямым слиянием - straight merge sort 727
- текстовый файл - text file 80
- тип коллекции - collection type 150
- указатель - pointer 716
- файловый указатель - file pointer 78
фактор сбалансированности AVL-дерева AVL tree: balance factor 628
форма Бэкуса Наура Bakus-Naur form 434
функция (MakeSearchTree building a tree search (MakeSearchTree) 511
- доступа access function 67
к массиву array access function 67
- факториала (рекурсивная форма) factorial function (recursive form) 442
X
хвост связанного списка rear of linked list 353
хеширование hashing 700
- класс HashTable - HashTable class 707
- коллизии - collisions 702
- метод деления - division metod 702
- свертки - folding method 744
середины квадрата - midsquare technique 704
цепочек - chaining with separate lists 704
- мультипликативный метод - multiplicative method 704
- описание - description 700
- открытая адресация с линейным - linear probe open addressing 704
опробованием
- рехеширование - rehashing 745
- хеш-таблица - hash table 701
- хеш-функция — function 701
хеш-таблица hash table
- анализ сложности complexity analysis 714
- итератор iterator 708
- определение definition 700
хеш-функция - function 701
Ц
целочисленный тип integer types 54-57
цикл, в графе cycle, in a graph 649
циклический circular 400
- связанный список - linked list 400-403
класс Cnode Cnode class 400
приложение: Джозефус application: Josephus 403
4
числа Фибоначчи Fibonacci numbers 466
число без знака unsigned number 57
- с фиксированной точкой fixed point number 60
чистая виртуальная функция, см. pure virtual function, see virtual
виртуальная функция function
Ш
шаблон template 270-275
- ключевое слово - keyword 270
- метод - method 274
- объект - object 274
- объявление класса - class declaration 274
- синтаксис - syntax 270
- класс Stack - Stack class 276-277
- список параметров - parameter list 270
- функция - function 270-273
шестнадцатеричный hexadecimal 90
Э
экземпляр класса instance of a class 102
экспоненциальное время (0(2n)) exponential time (0(2n)) 160
эффективность использования памяти space efficiency 156
Я
язык C++ C++ language 47
Бьярн Страуструп Stroustrup, Bjarne 47
историческое развитие historical development 47
определение -— definition 47
Index
A
abstract base class абстрактный базовый класс 48, 559
- class - класс 48,541,560
- data type - тип данных 2
- list class - списковый класс 560-563
access function функция доступа 67
access, see direct access, sequential доступ, см. прямой доступ,
access последовательный доступ
activation record активизирующая запись 443
address operator & оператор адреса & 64
- memory адрес, память 57
adjacency matrix матрица смежности 650
ADT Accumulator ADT Accumulator 133
- Array - Array 65
- Binary Search Tree - бинарного дерева 507
- Character - Character 58
- Definition - Definition 20
- Enumerated - Enumerated 62
- File - File 79
- Format - Format 21-22
- Graph - Graph 649
- Input component - Вход 21
- Integer - Integer 55
- Node - Node 354
- OrderedList - OrderedList 35
- Output component - Выход 21
- Pointer - Pointer 64
- Postconditions component компонента постусловий ADT 21
- PQueue ADT PQueue 213
- Preconditions component компонента предусловий ADT 21
- Process component - процесса ADT 21
- Queue ADT Queue 199
- Real - Real 60
- Record - Record 77
- SeqList - SeqList 33
- Stack - Stack 184
- String - String 72
algebraic expression алгебраическое выражение 193
infix инфиксное 193
postfix постфиксное 193
prefix префиксное 537
animal classes классы животных 553-555
array access function функция доступа к массиву 67
Array ADT массив: ADT 65
- class класс Array
constructor конструктор 305
copy constructor копирования 305-306
declaration объявление 303
destructor деструктор 305
index operator оператор индексации 306
pointer conversion operator преобразования указателя 307-309
Resize method метод Resize 308-309
array: bounds checking массив: проверка границ 303-305
- collection type - тип коллекции 147
- dope vector - дескриптор 67
- index bounds - границы 67
- storage - хранение 66
- type - тип 65-71
array-based binary trees бинарные деревья, представляемые 600-602
массивами
Arraylterator class класс Arraylterator 574
arrival event событие прихода (событийное 223
моделирован ие)
ASCII character set набор символов кода ASCII 59
assignment operator оператор присваивания 297
associative arrays ассоциативные массивы 151
associativity of operators ассоциативность операций 278
AVL tree AVL-дерево 627
balance factor фактор сбалансированности AVL-дерева 628
compare with BinSTree AVL tree: сравнение с BinSTree 641
definition определение AVL-дерева 627
nodes узлы AVL-деревьев 628
AVLTree class класс AVLTree 631-641
SingleRotation method AVLTree class: метод SingleRotation 638
Avllnsert method класс AVLTree: метод AVLInsert 636
declaration объявление 631
DoubleRotation method метод DoubleRotation 639
- - GetAVLTreeNode method GetAVLTreeNode 633
Insert method Insert 634
- - UpdateLeftTree method UpdateLeftTree 637
AVLTreeNode class класс AVLTreeNode 629-631
constructor конструктор 631
declaration объявление 629
implementation реализация 631
Left method метод Left 631
В
backtracking возврат (прохождение лабиринта) 436
Bakus-Naur form форма Бэкуса Наура 434
balanced (AVL) tree сбалансированное дерево 628
base class базовый класс 31
best case analysis анализ наилучшего случая 157
Big-0 notation нотация Big-0 156
binary file двоичный файл 715
- numbers двоичные числа 56
- operator бинарный оператор 193
- search - поиск 503
tree дерево бинарного поиска 503-507
ADT ADT 508
application: concordance приложение: конкорданс 525
occurrence counts счетчики появлений 513
description описание 503
BinStree class класс BinStree 508
deleting a node удаление узла 519
inorder traversal (sort) симметричное прохождение 511
(сортировка)
inserting a node вставка узла 517
key ключ 505
compare sequential бинарный поиск: сравнение 164
последовательного и бинарного методов
formal analysis формальный анализ 166
informal analysis неформальный анализ 166
recursive form рекурсивная форма 443-445
- tree бинарное дерево 479-482
breadth first scan поперечное сканирование 500
complete законченное 482
copy a tree копирование дерева 495
deleting a tree удаление дерева 498
horizontal tree printing горизонтальная печать 493
inorder traversal симметричный метод прохождения 489
left-right child левый-правый сын 481
level scan по уровне вое сканирование 500
LNR, LRN, etc. симметричный метод прохождения 489
(порядок)
node structure структура узла 483
TreeNode class класс TreeNode 483
upright (vertical) tree printing вертикальная печать 500
building построение 485
definition определение 479
degenerate вырожденное 481
description описание 479
full полное 482
BinFile class класс Binfile 718
Clear method метод Clear 719
constructor конструктор 721
declaration объявление 718
- - EndFile method - - метод EndFile 719
implementation реализация 721
Peek method метод Peek 719
Read (block) method Read (блочный) 721
method 721
- - Write (block) method Write (блочный) 722
method 722
Binomial coefficients биномиальные коэффициенты 472
BinSTree class класс BinSTree 508-510,
515-524
assignment operator оператор присваивания 515
constructor конструктор 515
declaration объявление 510
Delete method метод Delete 523
- - Find method Find 516
FindNode method FindNode 516
implementation реализация 515
Insert method метод Insert 517
memory management управление памятью 515
Update method метод Update 524
bit бит 57
- operations битовые операции 327-328
- - and - - и 327
exclusive or исключающее или 327
- - not - - не 327
or -— или 327
BNF, see Bakus-Naur form BNF, см. форма Бэкуса Наура
breadth-first search поиск "сначала в ширину" 657
bubble sort сортировка методом пузырька 686
bucket блок (метод цепочек при хешировании) 705
building a tree search функция (MakeSearchTree 511
(MakeSearchTree)
byte байт 57
с
C++ language язык C++ 47
definition определение 47
historical development историческое развитие 47
Stroustrup, Bjarne Бьярн Страуструп 47
- streams потоки в C++ 77-78
- strings строки в C++ 73-74
Calculator class класс Calculator 202
Compute method метод Compute 196
declaration объявление 195
implementation реализация 196
Run method метод Run 197
call by reference вызов по ссылке 115
- by value - по значению 115
cerr stream поток cerr 80
chaining with separate lists метод цепочек (хеширование) 704
Character ADT ADT Character 58
- type символьный тип 58-60
cin stream поток ввода 80
Circle class класс Circle 548
declaration объявление 548
description описание 548
implementation реализация 548
circular циклический 400
- linked list - связанный список 400-403
application: Josephus приложение: Джозефус 403
Cnode class класс Cnode 400
class класс
- (in book): Animal - (в книге): Animal 553-555
Array Array 303
Calculator Calculator 195
Circle (derived) Circle (производный) 548
- - CNode - - CNode 401
- - Date - - Date 118
Dice Dice 40
- - DNode - - DNode 410
- DynamicClass DynamicClass 293
Event Event 223
Heap Heap 612
Iterator (abstract class) Iterator (абстрактный) 564
Line Line 30
LinkedList LinkedList 374
List (abstract) List (абстрактный) 560
MathOperator MathOperator 281
Maze Maze 462
- - Node - - Node 353
NodeShape NodeShape 582
OrderedList OrderedList 36
- - Point - - Point 29
PQueue PQueue 214
Queue (linked list) Queue (связанный список) 388
RandomNumber RandomNumber 111-112
- - Rational - - Rational 247
Rectangle Rectangle 101
- - SeqList - - SeqList 36,168
(derived) (производный) 561
(linked list) (связанный список) 391
Shape Shape 546
- Simulation — Simulation 225
Spooler (print) Spooler (для печати) 396
- - Stack - - Stack 184
(template) (шаблонный) 276
- - String - - String 310
- Temperature Temperature 108
- - TriMat - - TriMat 12-129
- - Vec2d - - Vec2d 243
Window Window 412
- body - тело 100
- constuctor - конструктор 101
- declaration - объявление 25
- encapsulation - инкапсуляция 24
- head - заголовок 100
- hierarchy - иерархия 542
- imlementation - реализация 25,102
- information hiding - скрытие информации 24
- inheritance - наследование 31
- member initialization list - список инициализации 103
- members - члена класса 24,100
- methods - методы 24,100
- object - объект 100
- private part - закрытая часть 100
- protected part - защищенная часть 100
- puplic part - открытая часть 100
- scope resolution operator - оператор разрешения области действия 103
CNode class - CNode
constructor конструктор 402
declaration объявление 401
DeleteAfter method DeleteAfter метод 403
implementation реализация 402
InsertAfter method InsertAfter метод 403
coefficient matrix матрица коэффициентов 132
collection types типы коллекций
array массив 147
binary tree бинарное дерево 152
dictionary словарь 151
- - file - - файл 150
graph граф 154
hash table хеш-таблица 151
linear list линейный список 148
priority queue очередь приоритетов 150
queue очередь 149
random numbers случайные числа 110
record запись (как данные) 148
sequential list последовательный список 36
set множество 154
stack стек 149
string строка 147
collision коллизия
- definition - определение 704
- resolution - разрешение 704
combinatories комбинаторика 437
committee problem задача о. комитетах 448-450
complexity analysis анализ сложности (алгоритма) 155-159
- - AVL tree - - AVL-дерево 628
binary search бинарный поиск 166
tree бинарное дерево поиска 504
breadth-first search поиск "сначала в ширину" 659
bubble sort сортировка методом пузырька 688
compare 0(n log2n) sorts сравнение 0(n log2n)-copTnpoBOK 697
О 9
0(n ) sorts 0(n )-сортировок 696
complete binary tree законченное бинарное дерево 482
depth-first search поиск "сначала в глубину" 659
exchange sort обменная сортировка 155
Fibonacci numbers числа Фибоначчи 466-468
hashing хеширование 714
heapsort пирамидальная сортировка 619
isertion sort сортировка вставками 689
linked list sort со связанными списками 370
pattern matching algorithm алгоритм сопоставления с образцом 325
priority queue operations операции с очередью приоритетов 217
queue operations с очередью 206
quicksort "быстрая сортировка" 695
radix sort поразрядная сортировка 212
selection sort сортировка посредством выбора 686
sequential search последовательный поиск 161
stack operations операции со стеком 189
straight merge sort сортировка прямым слиянием 728
tounament sort турнирная сортировка 604
tree sort сортировка включением в дерево 646
Warshall algorithm алгоритм Уоршалла 667
composition of objects композиция объектов 28-30
concatenating lists конкатенация списков 377
concordance конкорданс 525-529
connected связанный 647
- graph vertices - вершины графа 647
strongly - граф, сильно связанный 648
weakly слабо связанный 648
const qualifier спецификатор const (константы) 27
constant time (0(1)) постоянная единица времени (0(1)) 160
constructor конструктор 21
control abstraction абстракция элемента управления 540
copy constructor конструктор копирования 291,
300-302
cout stream поток stream (стандартный вывод) 80
cubic time (0(n3)) кубическое время (0(п3)) 160
cycle, in a graph цикл, в графе 649
D
data types (language-defined) типы данных (определяемые языком)
array массив 65
binary file двоичный файл 80
C++ strings строки C++ 73
struct структура C++ 77
character символьный 58
enumerated перечисления 62
integer целочисленный 55
pointer указатель 64
real действительный 60
record запись 77
string строчный 72
text file текстовый файл 79
two dimensional array двумерный массив 68
Date class класс Date 118
declaration, class объявление (класса) 25
default constructor конструктор умолчания 117
delete operator оператор delete 64
definition определение 293
description описание 290
deletion method метод удаления
- - BinSTree (Delete) - - BinSTree (Delete) 523
Dictionary (DeleteKey) Dictionary (DeleteKey) 742
- - Graph (DeleteEdge) - - Graph (DeleteEdge) 652
(DeleteVertex) (DeleteVertex) 655
- - HashTable (Delete) - - HashTable (Delete) 707
- - Heap (Delete) - - Heap (Delete) 615
- - LinkedList (DeleteAt) - - LinkedList (DeleteAt) 387
(DeleteFont) (DeleteFont) 375
- - PQueue (PQDelete) - - PQueue (PQDelete) 216
Queue (QDelete) Queue (QDelete) 206
- - SeqList (Delete) - - SeqList (Delete) 170
- - Set (Delete) - - Set (Delete) 336
- - Stack (Pop) - - Stack (Pop) 187
departure event событие ухода (событийное моделирование) 223
depth of a tree глубина дерева 480
depth-first graph traversal прохождение "сначала в глубину" 656
derived class производный класс 31
design framework каркас разработки 39
destructor деструктор 291,
295-296
Dice class класс Dice 41
dictionary словарь 735
Dictionary class класс Dictionary 737
constructor конструктор 741
declaration объявление 737
DeleteKey method метод DeleteKey 742
implementation реализация 741
InDictionary method метод InDictionary 742
- application: word building словарь: приложение: построение 739
толкового словаря
- association structure - ассоциативная структура 735
- definition - определение 151
- Dictionarylterator class - класс Dictionarylterator 738
digraph, see directed graph орграф, см. направленный граф
direct access прямой доступ
array массив 147
definition определение 146
- - file - - файл 715
directed graph направленный граф 648
discrete type дискретный тип 60
divide and conquer разделяй и властвуй (метод) 433
division method (hashing) метод деления (хеширование) 702
DNode class класс DNode 407
constructor конструктор 410
DeleteNode method метод DeleteNode 411
implementation реализация 410
InsertLeft method метод InsertLeft 411
InsertRight method InsertRight 411
doubly linked list двусвязный список 410
application: insertion sort приложение: сортировка вставками 406
dynamic динамический 408
- array - массив 147
allocation - выделение массива 292
- binding - связывание 49
- data structures - структуры данных 291
- memory - память 64
- object - объект 293-297
DynamicClass class класс DynamicClass
assignment operator оператор присваивания 297
constructor конструктор 293-294
copy constructor копирования 300
destructor деструктор 295
E
edge of graph ребро графа 647
encapsulation инкапсуляция 24
enumerated types типы перечисления 62-63
Enumerated ADT Enumerated ADT 62
Event class класс Event 223
event-driven simulation, see simulation управляемое событиями моделирование,
см. моделирование
exchange sort обменная сортировка 85-86
exponential time (0(2n)) экспоненциальное время (0(2п)) 160
expression выражение
- evaluation - вычисление (оценка) 193
- trees - деревья 438
external data structures внешние структуры данных 77
- file search внешний файловый поиск 723
sort сортировка при помощи внешнего файла 727
F
factorial function (recursive form) функция факториала (рекурсивная форма) 439
Fibonacci numbers числа Фибоначчи 466
fields of a record поля записи 76
FIFO, see first-in-first-out FIFO, см. первым вошел-первым вышел
file файл 77-79
- ADT - ADT 79
- binary file - двоичный файл 715
- BinFile class - класс BinFile 718
- collection type - тип коллекции 150
- external hashing - внешнее хеширование 725
search - внешний поиск 723
- file pointer - файловый указатель 78
- mode - режим (записи/чтения) 716
- pointer - указатель 716
- seekg stream method - потоковый метод seekg 717
- seekp stream method seekp 717
- sequential - последовательный 717
- straight merge sort - сортировка прямым слиянием 727
- tellg stream method - потоковый метод tellg 717
- tellp stream method tellp 717
- text file - текстовый файл 80
first-in-first-out первым вошел-первым вышел 199
fixed point number число с фиксированной точкой 60
friend functions дружественные функции 244-245
front of linked list начало связанного списка 353
full binary tree полное бинарное дерево 482
function overloading перегрузка функции 258
G
GCD (Greatest Common Devisor) наибольший общий делитель 254
graph граф 647
Graph class класс Graph 652
breadth-first traversal прохождение "сначала в ширину" 656
(метод)
constructor конструктор 653
declaration объявление 652
Delete Vertex method метод Delete Vertex 655
GetNeighbors method GetNeighbors 654
GetVertexPos method GetVertexPos 654
- - GetWeight method GetWeight 654
implementation реализация 653
InsertEdge method метод InsertEdge 654
minimum path минимальный путь 661
Vertexlterator class метод Vertexlterator 654
depth-first graph traversal прохождение "сначала в глубину" 656
graph: acyclic граф: ациклический 649
- adjacency matrix - матрица смежности 650
- ADT - ADT 649
- application: strong components - приложение: сильные компоненты 659
- connected vertices - связанные вершины 648
- cycle - цикл 649
- directed (digraph) - направленный (орграф) 648
- edges - ребра 648
- path - путь 648
- reachability matrix - матрица достижимости 666
- strong components - сильные компоненты 659
- strongly connected - сильно связанный 648
- transitive closure - транзитивное замыкание 667
- undirected - ненаправленный 648
- vertices - вершины 647
- weakly connected — слабо связанный 648
- weighted digraph - взвешенный орграф 649
group группа 153
H
hash function хеш-функция 701
- table хеш-таблица
complexity analysis - анализ сложности 714
definition - определение 700
iterator - итератор 708
hashing хеширование 700
- chaining with separate lists - метод цепочек 704
- collisions - коллизии 702
- description - описание 700
- division metod - метод деления 702
- folding method свертки 744
- hash function - хеш-функция 701
table - хеш-таблица 701
- HashTable class - класс HashTable 707
- linear probe open addressing - открытая адресация с линейным 704
опробованием
- midsquare technique - метод середины квадрата 704
- multiplicative method - мультипликативный метод 704
- rehashing — рехеширование 745
HashTable class класс HashTable 707
declaration объявление 707
Find method метод Find 712
implementation реализация 711
Insert method метод Insert 711
HashTablelterator class - HashTablelterator 711
constructor конструктор 713
declaration объявление 708
implementation реализация 712
Next method метод Next 714
SearchNextNode method SearchNextNode 713
head of a linked list голова связанного списка 353, 358
header node заголовочный узел 401
heap пирамида 607-612
Heap class класс Heap 609
constructor конструктор 618
declaration объявление 609
Delete method метод Delete 615
FilterDown method FilterDown 615
- - Filter Up method FilterUp 613
heapsort пирамидальная сортировка 618
implementation реализация 612
Insert method метод Insert 614
heap: definition пирамида: определение 607
- maximum - максимальная 608
- minimum - минимальная 608
- order - порядок 607
heapsort пирамидальная сортировка 618
heterogeneous разнородный
- array - массив 579
- list - список 579
- type - тип 77
hexadecimal шестнадцатеричный 90
homogeneous однородный
- array - массив 65
- list однородный: список 166
I
ifstream class класс ifstream 80
inderact recursion косвенная рекурсия 434
index operator [] оператор индекса [] 303, 306
- array индекс, массив 65
infix инфиксный
- expression evaluation - вычисление выражения 277-285
- notation - формат 193
information hiding скрытие информации 24
inheritance наследование
- abstract class - абстрактный класс 541
- application: geometric figures - приложение: геометрические фигуры 556
- base class - базовый класс 542
- class hierarchy - иерархия класса 542
- concept - концепция 28
- definition - определение 540
- derived class - производный класс 542
- dynamic binding - динамическое связывание 550
- multiple - множественное (наследование) 37
- polymorphism - полиморфизм 550
- protected members - защищенные члены (класса) 544
- public inheritance - открытое наследование 543
- pure virtual function - чистая виртуальная функция 541
- static binding - статическое связывание 551
- subclass - подкласс 543
- superclass - суперкласс 543
- virtual function - виртуальная функция 541
member function функция-член 550
initializer, see constructor инициализатор, см. конструктор
inorder traversal симметричный метод прохождения 58
Inorderlterator class класс Inorderlterator
constructor конструктор 644
declaration объявление 643
implamentation реализация 644
Next method метод Next 645
in-place sorting сортировка на месте 212
input precedence входной приоритет 280
insertion method метод вставки
- - AVLTree (AVLInsert) - - AVLTree (AVLInsert) 636
(Insert) (Insert) 634
- - BinFile (Write) - - BinFile (Write) 722
- - BinSTree (Insert) - - BinSTree (Insert) 517
- - Graph (InsertEdge) Graph (InsertEdge) 652
(InsertVertex) (InsertVertex) 652
- - HastTable (Insert) - - HastTable (Insert) 711
Heap (Insert) Heap (Insert) 614
Linkedlist (InsertAfter) LinkedList (InsertAfter) 375
(InsertAt) (InsertAt) 385
(InsertFront) (InsertFront) 375
(InsertRear) (InsertRear) 375
OrderedLdst (Insert) OrderedList (Insert) 575
- - PQueue (PQInsert) - - PQueue (PQInsert) 215
Queue (Qlnsert) Queue (Qlnsert) 205
SeqList (Insert) SeqList (Insert) 169
- - Set (Insert) - - Set (Insert) 366
- - Stack (Push) - - Stack (Push) 187
- - String (Insert) - - String (Insert) 312
(operator+) (operator*) 312, 317
insertion sort сортировка вставками 688
instance of a class экземпляр класса 102
Integer ADT Integer ADT 55
integer types целочисленный тип 54-57
internal data structures внутренние структуры данных 77
Ios class класс Ios 80
Istream class - Istream 80
Istrtream class - Istrtream 81
iterator итератор 563
Iterator (abstract class) Iterator (абстрактный класс)
declaration объявление 564
implementation реализация 564
iterator classes классы итераторов
Arraylterator Arraylterator 569
Inorderlterator Inorderlterator 643
SeqListlterator SeqListlterator 565
Vertexlterator Vertexlterator 652
J
Josephus problem задача Джозефуса 403
К
key ключ 82
KeyValue class класс KeyValue 736
L
last-in-first-out последним пришел-первым вышел 183
leaf node листовой узел 479
level in a tree уровень дерева 480
level-order scan поперечное сканирование 500
LIFO, see laat-in-first-out UFO, см. последним пришел-первым
вышел
Line cites класс Line 30
linear линейный 32
- collection линейная коллекция 144-152
- probe open addressing открытая адресация с линейным 704
опробованием
- time (o(n)) линейное время 160
- sequential list линейный: последовательный список 148
linked list связанный список 358-361,
363-364
- application: graduation приложение: список выпускников 365
print spooler буферизация печати 394
window management управление окнами 411
word jumble головоломка 362
clearing a list удаление элементов списка 369
creating a node создание узла 358
an ordered list упорядоченного списка 367
deleting a front удаление начального элемента 363
a node узла 364
description описание 351
head голова 358
inserting at front вставка в начало 358
at rear в хвост 361
introduction введение 350
printing a list печать списка 360
sorting using ordered list сортировка с использованием 369
связанного списка
traversal прохождение 359
LinkedList class класс LinkedList 371-376,
381-388
application: concatenating lists приложение: конкатенированные 377
списки
removing duplicates удаление дубликатов 379
selection sort сортировка выбором 378
ClearList method метод ClearList 383
constructor конструктор 382
CopyList method метод CopyList 383
current pointer (currPtr) указатель на текущий узел 371
Data method метод Data 385
declaration объявление 374
Delete At method метод DeleteAt 387
describing operations описание операций 372-374
designing the class проектирование списка 371
front pointer указатель на первый узел 371
implementation реализация 381
InsertAt method метод InsertAt 385
memory allocation methods методы выделения памяти 382
Next method метод Next 384
previous pointer (prevPtr) указатель на предыдущий узел 371
rear pointer на последний узел 371
Reset method метод Reset 384
List class (abstract) класс List (абстрактный) 560-563
declaration объявление 561
implementation реализация 561
load factor коэффициент заполнения 714
logarithmic time (O(log2n), 0(nlog2n)) логарифмическое время (0(log2n), 0(nlog2n)) 160
long run длинная последовательность 577
merge sort сортировка слиянием 729
м
MathOperator class класс MathOperator
comparison operator оператор сравнения 282
constructor конструктор 281
declaration объявление 281
Evaluate method метод Evaluate 282
matrix матрица 120
maximum heap максимальная пирамида 608
Maze class класс Maze
declaration объявление 462
imlementation реализация 463
member initialization list список инициализации членов (класса) 103
memory allocation распределение памяти
dynamic динамическое 290, 292
static статическое 290
merge слияние
- sorted runs - сортированных последовательностей 570-574
- straight merge sort - сортировка прямым слиянием 727
message passing передача сообщения 25
method in a class методы класса 24
midsquare technique (hashing) метод середины квадрата (хеширование) 704
minimum heap минимальная пирамида 608
- path минимальный путь 661
multiple constructors множественные конструкторы 117
- inheritance множественное наследование 37
multiplicative method (hashing) мультипликативный метод (хеширование) 704
N
network сеть 155
new operator оператор new
definition определение 64
description описание 290
insufficient memory error ошибка выделения памяти 292
node узел
Node class класс Node 353-358
constructor конструктор 356
declaration объявление 355
DeleteAfter method метод DeleteAfter 357
implementation реализация 356
Insert After method метод InsertAfter 357
NextNode method NextNode 356
node: ADT узел: ADT 354
- definition - определение 352
- in a tree - в дереве 152
- in linked list - в связанном списке 351-352
NodeShape class класс NodeShape 582
nonlinear collection нелинейная коллекция 144,
152-155
NULL pointer NULL-указатель 353
О
object объект
- as a function parameter - как параметр функции 115
- as a return value - как возвращаемое значение 115
- composition - композиция 28
- definition - определение 20
- inheritance - наследование 28, 31-32
- testing - тестирование 45
object-oriented programming объектно-ориентированное
программирование
abstract base class абстрактный базовый класс 48
composition композиция 28
dynamic binding динамическое связывание 550
inheritance наследование 28, 31
multiple inhritance множественное наследование 37
polimorphism полиморфизм 550
program design построение программы 38-43,
45-46
pure virtual function чистая виртуальная функция 49
reusability of software повторное использование кода 35
Stroustrup, Bjarne Бъярн Страуструп 47
testing тестирование 45
virtual function виртуальная функция 49
objects and information passing объекты и передача информации 115
ofstream class класс ofstream 80
operand stack стек операнда 278
OperandList class класс OperandList 35
operator overloading перегрузка оператора 241
- stack стек операторов 279
ordered list упорядоченный список 149
- - ADT - - ADT 34
application: long runs приложение: длинные 577
последовательности
creation algorithm алгоритм создания 367
OrderedList class implementation класс OrderedList: реализация 576
Insert method метод Insert 576
declaration объявление 576
Ostream class класс Ostream 80
Ostrstream class - Ostrstream 81
overloading перегрузка
- assignment operator = - оператор присваивания — 299
- conversion operators - операторы преобразования 252-254
- external function - внешние функции 241
- index operator [ ] - оператор индекса [ ]
- operator - оператора 241
- stream operators - операторы потока 250-252
- with class members - функциями-членами класса 242
- with friend functions - дружественными функциями 244
P
palindrome палиндром 189
parent родитель
- node родительский: узел 479
path in a graph путь в графе 648
- in a tree - в дереве 479
pattern matching сопоставление с образцом 320
Peek (stack) method метод Peek (стековый) 188
permutations перестановки 451-455
Point class класс Point 29-30
pointer указатель
- ADT - ADT 64
- conversion operator - операция преобразования 303
- definition - определение 63
polimorfism полиморфизм 48-50
pop operation операция извлечения (из стека)
description описание 149, 182
Stack method метод Stack 187
postfix постфиксный
- evaluation - вычисление 193
- notation - форма представления 193
postorder traversal обратный метод прохождения 490
power function (recursive form) степенная функция (рекурсивная форма) 442
PQueue class класс Pqueue 214-217
declaration объявление 214
(heap version) (пирамидальная версия) 622
implementation реализация 215
Pqdelete метод Pqdelete 216
Pqinsert Pqinsert 215
precedence of perators приоритет операции
input precedence входной приоритет 280
stack precedence стековый приоритет 280
precondition, See ADT предусловия, см. ADT
print spooler буферизация печати 394-400
priority queue очередь приоритетов 212-217
- - ADT - - ADT 213
applicaion: long runs приложение: длинные 622
последовательности
support services сервисная поддержка 217
event-driven simulation приложение: моделирование, 220
управляемое событиями
definition определение 212
PQueue class класс Pqueue 214
(heap version) (пирамидальная версия) 622
private inheritance закрытое наследование 587
PRN, see Reverse Polish notation PRN, см обратная польская запись
program design features возможности программного
конструирования
object design объектная разработка 38
testing тестирование объектов 45
robustness устойчивость к ошибкам 46
structure tree структурное дерево 39
structured walkthrough сквозной стуктуированный контроль 45
testing тестирование объектов 40
protected members защищенные методы 544
public class section открытая секция класса 24
- inheritance открытое наследование 543
pure virtual function, see virtual чистая виртуальная функция, см.
function виртуальная функция
push operator операция помещения в стек
description описание 149, 182
Stack method метод Stack 187
Q
quadratic time (0(n2)) квадратичное время (0(п2)) 160
queue очередь 198-206
Queue class (array) класс Queue (массив) 199
constructor конструктор 204
declaration объявление 201
implementation реализация 202
Qdelete method метод Qdelete 206
Qinsert method Qinsert 205
(linked linked) (связанный список) 389-392
declaration объявление 389
implementation реализация 390
queue: ADT очередь: ADT 199
- application: dance partners - приложение: партнеры по танцу 206
radix sort поразрядная сортировка 209
- collection type - тип коллекции 149
- definition - определение 198
- implementation - реализация 202
quicksort быстрая сортировка 690
R
radix sort поразрядная сортировка 209
random number случайное число
generator генератор 110
RandomNumber class класс RandomNumber 110
seed seed-значение 110
RandomNumber class класс RandomNumber 110-114
constructor конструктор 111-112
declaration объявление 110
fRandom method метод fRandom 112
implementation реализация 112
Random method метод Random 112
rank ранг 278
Rational class класс Rational 247-258
declaration объявление 247
operators (as friends) операторы (как дружественные) 247
(as members) (как члены) 249
(type conversion) (преобразование типа) 252
Reduce method метод Reduce 255
stream operators потоковые операторы 248
rational number рациональное число 245-247
application: solving linear приложение: решение линейных 256
equations уравнений
reduced form редуцированная форма 245
representation представление 245
standardized form нормализованная форма 246
reachability matrix матрица достижимости 666
real data types вещественные типы данных 60
- number вещественное число
- - ADT - - ADT 60
definition определение 60
exponent порядок (экспонента) 60
mantissa мантисса 60
representation представление 60
scientific notation научный формат 60
rear of linked list хвост связанного списка 353
record запись (как набор данных)
- ADT ADT 77
- definition определение 76
Rectangle class класс Rectangle 101-107
recursion рекурсия 432-439
- binary search - бинарный поиск 446
- binomial coefficients - биномиальные коэффициенты 472
- combinatorics - комбинаторика 438
- committee problem - задача о комитетах 448-450
- expression trees - синтаксические деревья 438
- factorial - факториал 439
- Fibonacci numbers - числа Фибоначчи 466
- maze - лабиринт 436, 460
- Pascal's triangle - треугольник Паскаля 473
- permutations - перестановки 451-455
- power function - степенная функция 442
- recursive definition - определение 433
step - шаг рекурсии 433
- runtime stack - стек времени исполнения 443-445
- tail recursion - задняя рекурсия 469
- Tower of Hanoi - Ханойская башня 435, 455
retrieval methods методы поиска
- - BinFile (block Read) - - BinFile (block Read) 721
(Read) (Read) 721
- - BinSTree (Find) - - BinSTree (Find) 515
- - NasTable (Find) - - NasTable (Find) 712
- - Queue (Qfront) Queue (Qfront) 201
- - SeqList (Find) - - SeqList (Find) 171
- - Set (IsMember) - - Set (IsMember) 335
- - Stack (Peek) - - Stack (Peek) 188
- - String (Find) - - String (Find) 312
(FindLast) (FindLast) 319
(Substr) (Substr) 317
reusability of software повторное использование кода 35
Reverse Polish notation обратная польская запись 193
root of tree корень дерева 152, 479
rotation in AVL tree вращение AVL-дерева
- ■ double двойное 639
single единичное 638
runtime stack стек времени исполнения 443
S
safe arrays надежные массивы 303
scope resolution operator операция разрешения области действия 103
selection sort сортировка посредством выбора 684
self-referencing structure само ссылающаяся структура 335
sentinel node узел-часовой 401
SeqList class (array) класс SeqList (массив) 168-175
declaration объявление 168
Delete method метод Delete 170
Find method Find 171
GetData method GetData 170
implementation реализация 168
Insert method метод Insert 169
(derived) (производный) 561-563
declaration объявление 562
implementation реализация 562
(linked list) (связанный список) 391-392
application: efficiency приложение: сравнение 392-394
comparison эффективности
declaration объявление 391
implementation реализация 392
SeqListlterator class - SeqListlterator
- - declaration объявление 565
implementation реализация 565
sequential access последовательный доступ
array массив 65
- - file - - файл 77
- list - список 166-175
- - ADT - - ADT 33
application: video store приложение: хранение видео фильмов 173
- - collection type тип коллекций 146
description описание 32,166
SeqList class класс SeqList 36,168,
391
- search - поиск 82,
161-162
algorithm алгоритм 161
compare binary search сравнение с бинарным 164
fast быстрый 287
set множество
Set class (integral type) - Set (integral type) 334
constructor конструктор 329
declaration объявление 336
Delete method метод Delete 330
description описание 336
I/O stream operatos потоковые операторы 334
ввода/вывода
implementation реализация 336
Insert method метод Insert 335
IsMember method метод IsMember 335
operator* (union) operator* (объединение) 335
set: Set class (array model) - класс Set (модель массива) 263
(integral type) (целочисленный тип) 328
- application: Sieve of Eratosthenes - решето Эратосфена 332
- collection type - тип коллекции 154
- description (integral type) - описание (целочисленный тип) 325-327,
329
Shape class класс Shape
declaration объявление 547
description описание 546
implementation реализация 547
Sieve of Eratosthenes Решето Эратосфена 332
sign bit знаковый бит 57
simulation моделирование 220-232
Simulation class класс Simulation
constructor конструктор 226
declaration объявление 225
NextArrvalTime method метод NextArrvalTime 227
simulation: arrival event моделирование: событие прихода 223
- departure event ухода 223
software development разработка программного продукта
methodology методология 38
reusability of software повторное использование 35
sorting algorithms алгоритмы сортировки
bubble sort методом пузырька 686
doubly linked list sort двусвязного списка 408
exchange sort обменная 85
insertion sort вставками 688
linked list sort сортировка со связанными списками 369
quiksort "быстрая" 690
radix sort поразрядная 209
-— selection sort сортировка посредством выбора 684
tournament sort турнирная 602
treesort treesort-сортировка 646
source level debugger отладчик на уровне кода 46
space efficiency эффективность использования памяти 156
Spooler (print) class класс Spooler (печать)
declaration объявление 396
implementation реализация 397
square matrix квадратная матрица 120
stack стек 182-189
Stack class класс Stack 184-189
ClearStack method метод ClearStack 188
constructor конструктор 187
declaration объявление 186
implementation реализация 187
Peek method метод Peek 188
- - Pop method Pop 187
- - Push method Push 187
StackEmpty method StackEmpty 188
- - StackFull method StackFull 188
stack precedence стековый приоритет
- ADT стек: ADT 184
- application: expression evaluation - приложение: вычисление выражения 193
infix expression, evaluation инфиксное выражение, оценивание 279
multibase output вывод (чисел) с различными 191
основаниями
palindrome палиндром 189
postfix calculator постфиксный калькулятор 195
- collection type - тип коллекции 149
- definition - определение 182
- description - описание 182
- empty - пустой 183
- full - полный 183
state change изменение состояния 25
static статический
- array - массив 147
- binding статическое: связывание 551
- data structures статические: структуры данных 290
- memory статическая: память 64
stopping condition условие останова (цикла) 433
stream class потоковый класс
f stream f stream 81
ifstream ifstream 80
ios ios 80
istream istream 80
ofstream of stream 80
ostream ostream 80
cerr cerr (стандартный поток ошибок) 80
cin cin (стандартный ввод) 80
cout cout (стандартный вывод) 80
- operator overloading перегрузка оператора потока 251
- description поток, описание 78,150
String class класс String 310-320
application: test program приложение: тестовая программа 314
assignment operator оператор присваивания 316
concatenation конкатенация 314
constructor конструктор 315
declaration объявление 311
- - FindLast - - FindLast 319
I/O ввод /вывод 319
implementation реализация 315
ReadString method метод ReadString 319
string comparison сравнение строк 316
Substr method метод Substr 318
- type (C++) строка в C++ 73
string: ADT - ADT 72
- description - описание 71
strongly connected graph сильно связанный граф 648
subtree поддерево 479
system efficiency системная эффективность 155
т
tail recursion задняя рекурсия 469
Temperature class класс Temperature 108
template шаблон 270-275
- class declaration - объявление класса 274
- function - функция 270-273
- keyword - ключевое слово 270
- method - метод 274
- object - объект 274
- parameter list - список параметров 270
- Stack class - класс Stack 276-277
- syntax - синтаксис 270
text file текстовый файл 77-80
this pointer указатель this 300
threaded trees прошитые деревья 535
top of stack вершина стека 182
top-down program disign нисходящая программная разработка 38
trangular matrices треугольные матрицы 120-129
transitive closure транзитивное замыкание 667
tree дерево 479-480
- algorithms алгоритмы деревьев 489-503
breadth-first csan поперечное сканирование 500
computing the depth вычисление глубины 492
copying a tree копирование дерева 495
counting leaf nodes вычисление количества листовых 492
узлов
deleting a tree удаление дерева 498-499
horizontal tree printing горизонтальная печать дерева 493
inorder scan симметричное сканирование 489
level-order scan по уровневое сканирование 500
postorder scan обратное сканирование 490
- iterators итераторы дерева 642
- node function desing конструирование функций узлов дерева 486
- traversals методы прохождения дерева 489
- ancestors-descendents дерево: предки-потомки 479
- binary tree - бинарное дерево 480
- children-parent - сын-родитель 479
- collection type - тип коллекции 152
- definition - определение 479
- depth - глубина 480
- description - описание 479
- height, see depth - высота, см. глубина
- leaf - лист 479
- left child - левый сын 481
- level - уровень 480
- node - узел 483
- path - путь 479
- right child - правый сын 479
- root - корень 479
- subtree - поддерево 479
- terminology - терминология 479
TreeNode class класс TreeNode 484
constructor - конструктор 485
declaration объявление 484
FreeTreeNode method метод FreeTreeNode 486
GetTreeNode method GetTreeNode 486
treesort treesort-сортировка 646
TriMat class класс TriMat 124-129
two-dimensional array двумерный массив
definition определение 68
storage хранение 69
type conversion operator оператор преобразования типа
from object type из объектного типа 253
to object type к типу объекта 252
U
unary operator унарный оператор 54,193
undirected graph ненаправленный граф 648
universal set универсальное множество 325
unsigned number число без знака 57
upper triangular matrix верхняя треугольная матрица 120
V
Vec2d class класс Vec2d 243
declaration объявление 244
operators (as friends) операторы (как дружественные) 243
(as members) (как члены класса) 262
scalar multiplication скалярное произведение 262
vertex of graph вершина графа 647
virtual function виртуальная функция 550-552
and polymorphism и полиморфизм 550
description описание 49-50, 541
destructor деструктор 558
pure чистая 541,559
table таблица 552
W
Warshall algorithm алгоритм Уоршалла 666
weakly connected graph слабо связанный граф 648
weighted digraph взвешенный орграф 649
Window class класс Window
declaration объявление 413
implementation реализация 415
window management управление окнами 411-418
worst case analysis анализ наихудшего случая (алгоритма) 157
Научно-популярное издание
Уильям Топп, Уильям Форд
Структуры данных в C++
Компьютерная верстка Свиридова К.А.
Подписано в печать 15.03.99. Формат 70x100 V\e. Усл. печ. л. 66,3
Гарнитура Школьная. Бумага газетная. Печать офсетная.
Тираж 3000 экз. Заказ 100
ЗАО «Издательство БИНОМ», 1999 г.
103473, Москва, Краснопролетарская, 16
Лицензия на издательскую деятельность № 065249 от 26 июня 1997 г.
Отпечатано с готового оригинал-макета в типографии ИПО Профиздат
109044, Москва, Крутицкий вал, 18.































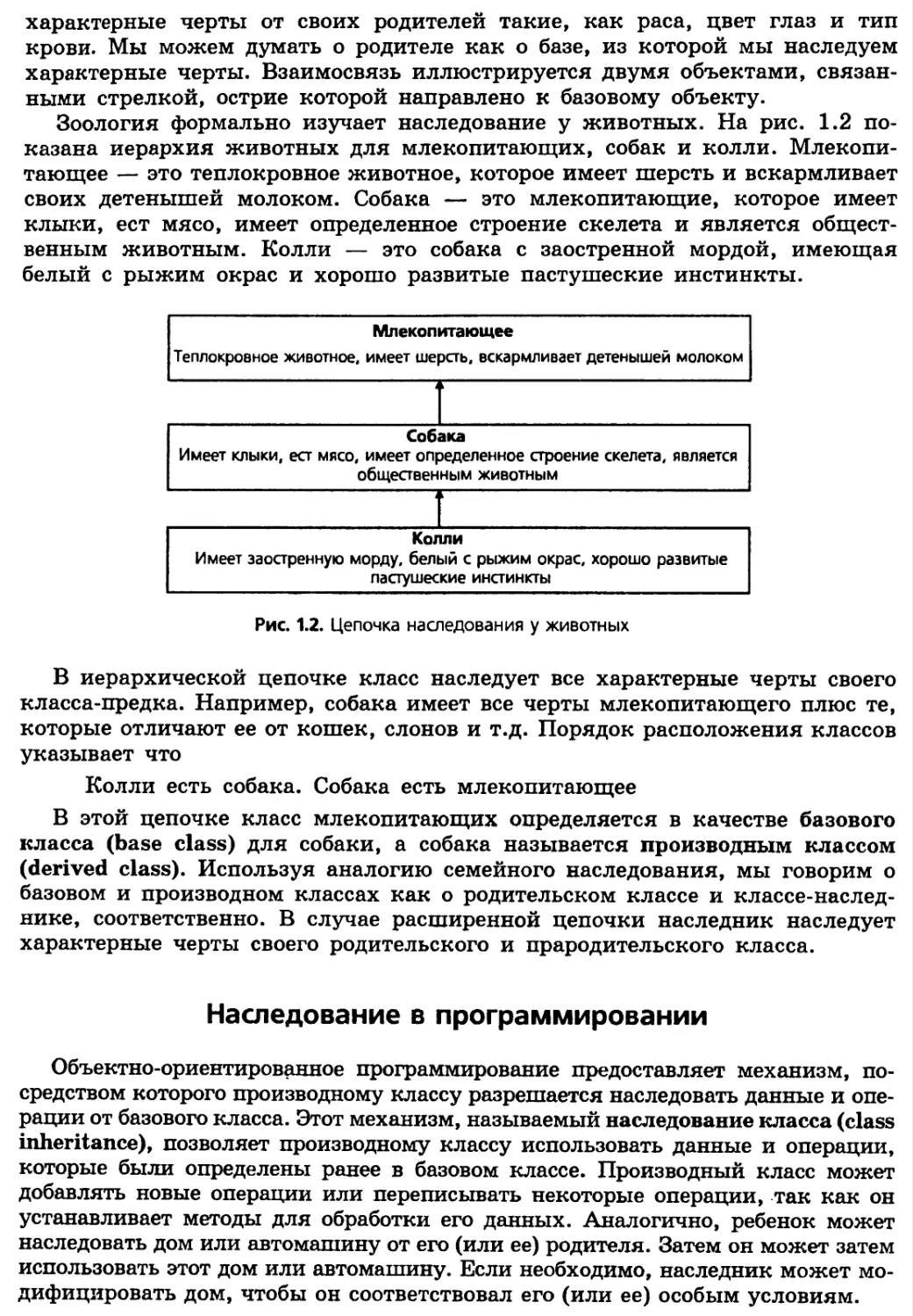




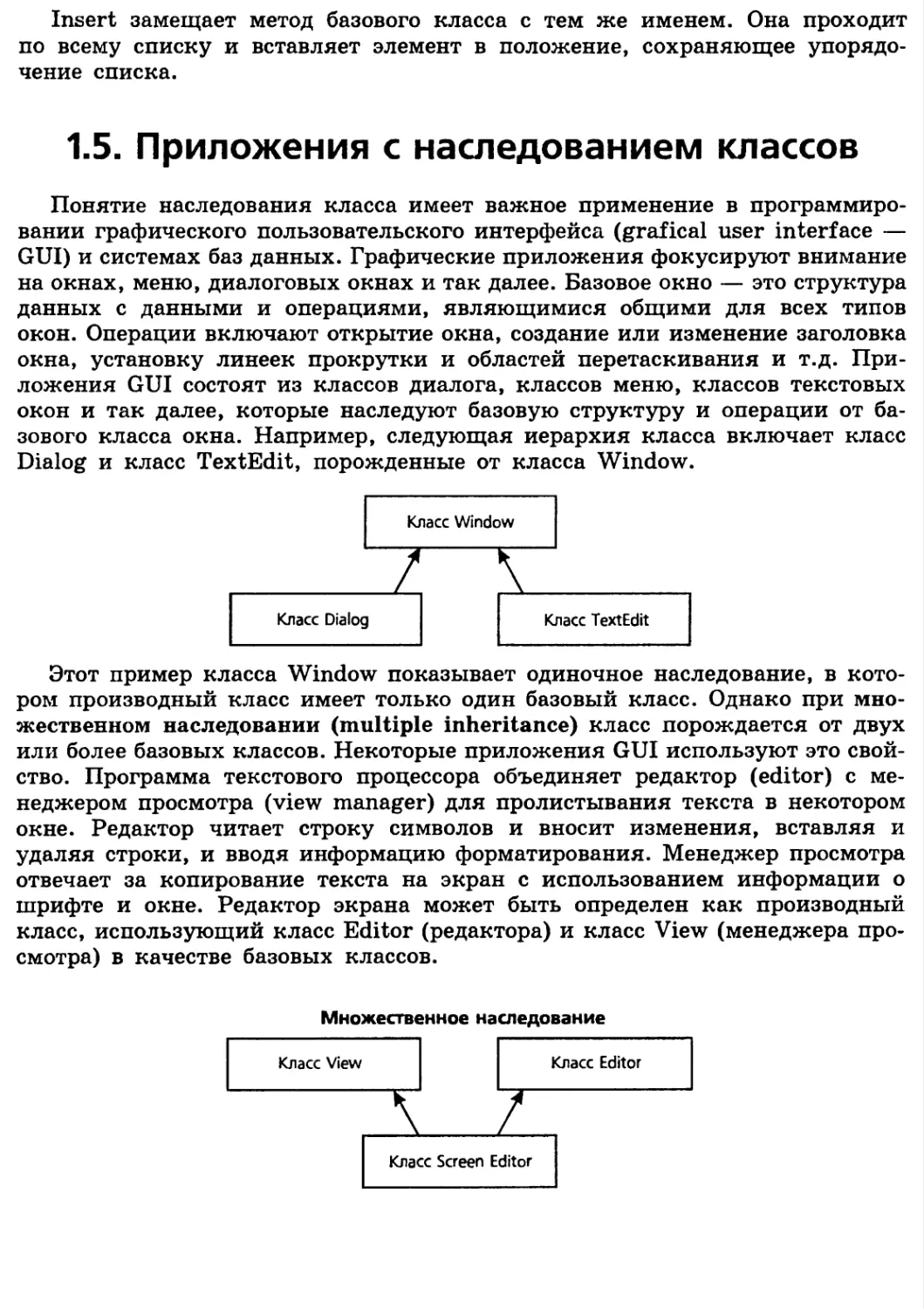







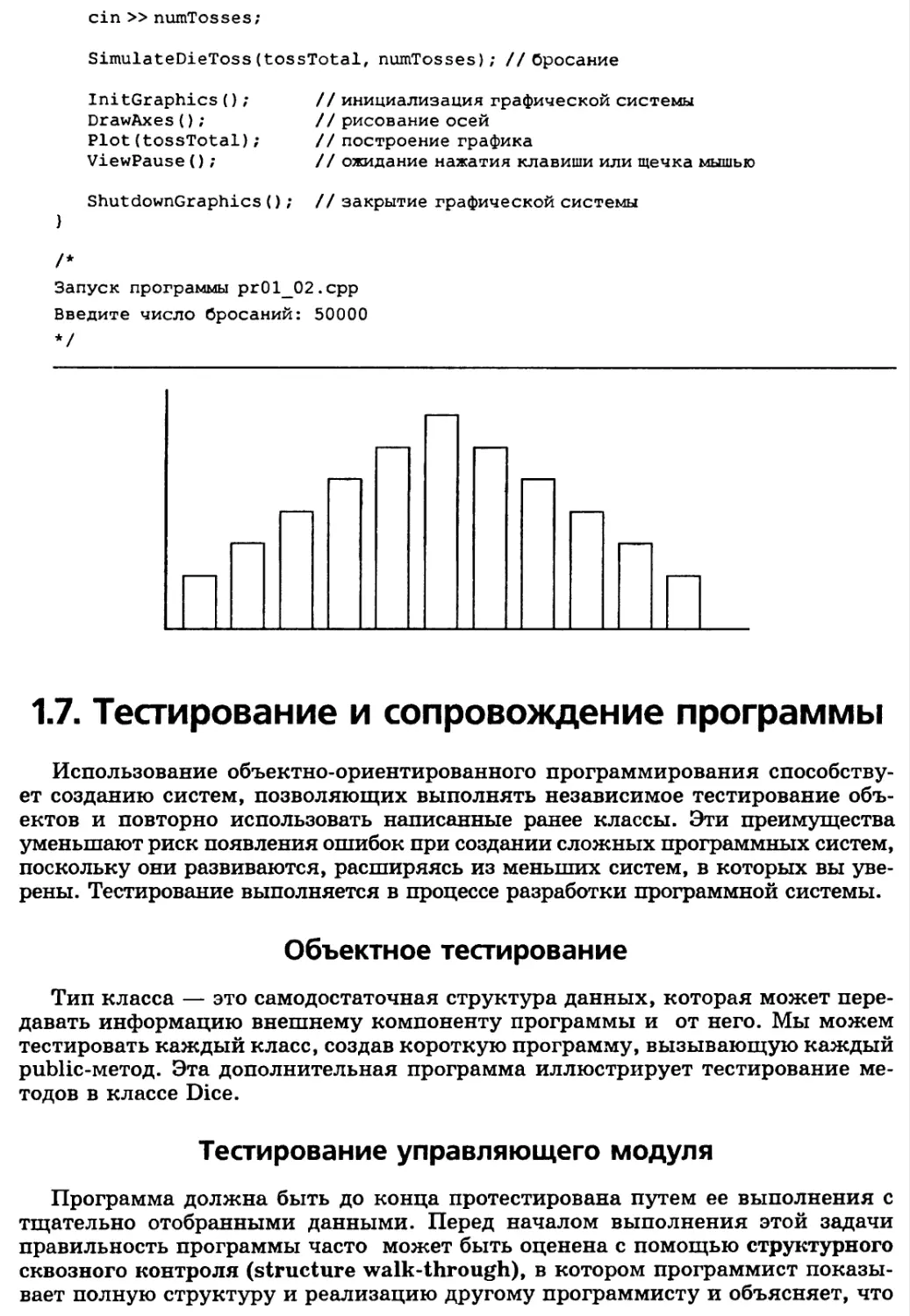










































































































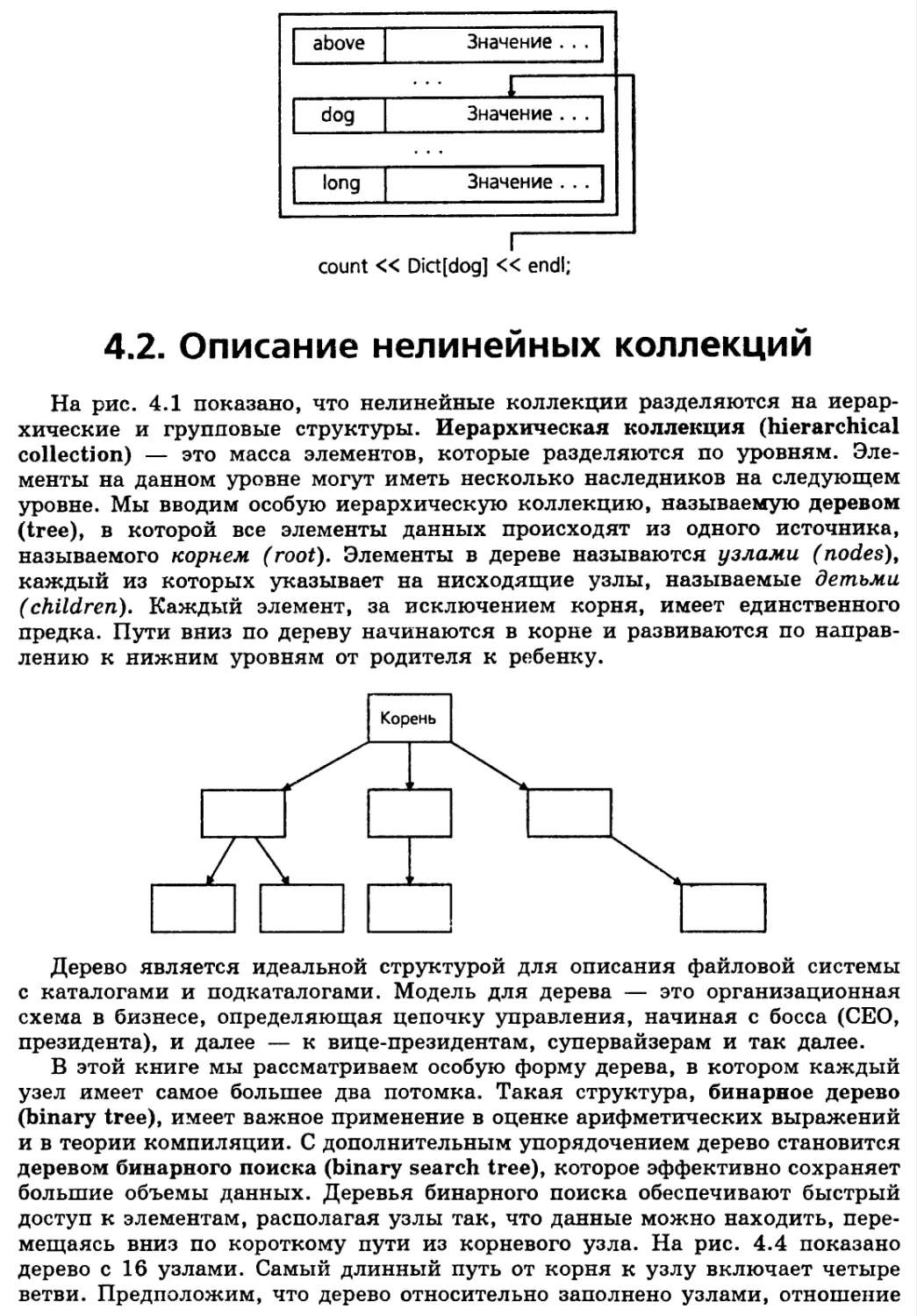

























































































































































![Проверка границ массива и перегруженный оператор []](https://djvu.online/jpg/C/i/q/CiqRypuMuS7yo/306.webp)