Author: Кириллов А.А. Гвишиани А.Д.
Tags: анализ физико-математические науки математика задачи по математике функциональный анализ
ISBN: 5-02-013797-9
Year: 1988
Text
А. А. КИРИЛЛОВ
А. Д. ГВИШИАНИ
ТЕОРЕМЫ И ЗАДАЧИ
ФУНКЦИОНАЛЬНОГО
АНАЛИЗА
ИЗДАНИЕ ВТОРОЕ,
ПЕРЕРАБОТАННОЕ И ДОПОЛНЕННОЕ
Допущено Министерством
высшего и среднего специального образования СССР
в качестве учебного пособия
для студентов вузов, обучающихся по специальностям
«Математика» и «Прикладная математика»
МОСКВА «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
1988
ББК 22.162
К43
УДК 517.5
Кириллов А. А., Гвишиани А. Д.
Теоремы и задачи функционального анализа:
Учеб. пособие для вузов.— 2-е изд., перераб. и
доп.— М.: Наука. Гл. ред. физ.-мат. лит., 1988.—
400 с- ISBN 5-02-013797-9
Книга состоит из трех разделов. Первый
раздел представляет собой изложение теорети-
теоретического материала, входящего в курс лекций,
читаемых на механико-математическом факуль-
факультете МГУ. Второй раздел книги содержит зада-
задачи по этому курсу, многие из которых предла-
предлагались на семинарских занятиях. Третий раздел
содержит указания к решению задач.
Для студентов и аспирантов университетов,
изучающих функциональный анализ; может
быть использована преподавателями в качестве
пособия при подготовке различных курсов ана-
анализа.
Табл. 1. Илл. 18. Библиогр. 55 назв.
Рецензент
член-корреспондент АН СССР
Л, Д. Кудрявцев
1702050000—057 пг оо © Издательство «Наука».
Псо/п9\ оо 75-88 Главная редакция
udo \V6) -оо физико-математической
литературы, 1979;
с изменениями, 1988
ISBN 5-02-013797-9
ОГЛАВЛЕНИЕ
Предисловие ко второму изданию ?
Предисловие '*
Глава I. Сведения из теории множеств и топологии ;. ?
§ 1. Отношения. Аксиома выбора и лемма Цорна ... 9
Теория (9). Задачи A87). Указания B88).
§ 2. Метрические пространства и их приложения ... 12
Теория A2). Задачи A90). Указания B91).
§ 3. Категории и функторы 18
Теория A8). Задачи A93). Указания B93).
Глава II. Теория меры и интеграла 23
§ 1. Теория меры 23
1. Алгебра множеств 23
Теория B3). Задачи A99). Указания B9S).
2. Продолжение меры 25
Теория B5). Задачи B01). Указания C00).
3. Конструкции мер 31
Теория C1). Задачи B03). Указания C02).
§ 2. Измеримые функции 31
1. Свойства измеримых функций 33
Теория C(>). Задачи B05). Указания C04).
2. Сходимость измеримых функций 37
Теория C7). Задачи B07). Указания C06).
§ 3. Интеграл 39
1. Интеграл Лебега 39
Теория C9). Задачи B10). Указания C08).
2. Функции ограниченной вариации и интеграл Ле-
Лебега — Стнлтьеса 44
Теория D4). Задачи B13). Указания C13).
3. Свойства интеграла Лебега 47
Теория D7). Задачи B16). Указания C16). •
Глава III. Линейные топологические пространства и ли-
линейные операторы 56
§ 1. Нормированные пространства . 56
1. Основные определения 56
Теория E6). Задачи B19). Указания C19).
1* 3
2. Сопряженные пространства 59
Теория E9). Задачи B21). Указания C21).
3. Операторы в нормированных пространствах ... 60
Теория F0). Задачи B22). Указания C23).
4. Конструкции банаховых пространств 62
Теория F2). Задачи B23). Указания C23).
§ 2. Линейные топологические пространства .... 63
1. Топология, выпуклость и полунормы 63
Теория F3). Задачи B25). Указания C25)
2. Сопряженные пространства 68
Теория F8). Задачи B28). Указания C27).
3. Теорема Хана — Банаха 69
Теория F9). Задачи B28). Указания C27).
§ 3. Линейные операторы 73
1. Пространство линейных операторов 73
Теория G3). Задачи B31). Указания C29).
2. Компактные множества и компактные операторы » 73
Теория G8). Задачи B32). Указания C30).
3. Теория фредгольмовых операторов 84
Теория (84). Задачи B34). Указания C32).
§ 4. Функциональные пространства и обобщенные функции 93
1. Пространства интегрируемых функций . . 93
Теория (93). Задачи B38). Указания C34).
2. Пространства непрерывных функций .... 94
Теория (94). Задачи B40). Указания C37).
3. Пространства гладких функций 97
Теория (97). Задачи B43). Указания C41).
4. Обобщенные функции 107
Теория A07). Задачи B46). Указания C44).
5. Действия над обобщенными функциями . . . . 111
Теория A11). Задачи B47). Указания C45).
5 5. Гильбертовы пространства , « .,,... 115
1. Геометрия гильбертова пространства 115
Теория A15). Задачи B49). Указания C46).
2. Операторы в гильбертовом пространстве .... 122
Теория A22). Задачи B52). Указания C48).
Глава IV. Преобразование Фурье и элементы гармониче-
гармонического анализа . . • • • • • t . 128
§ 1. Свертки на коммутативной группе 128
1. Свертки основных функций . . # ^28
Теория A28). Задачи B57). Указания C51).
2. Свертки обобщенных функций . . • . . 133
Теория A33). Задачи B60). Указания C53).
§ 2. Преобразование Фурье 13^
1. Характеры коммутативной группы 138
Теория A38). Задачи B61). Указания C54).
2. Ряды Фурье 143
Теория A43). Задачи B64). Указания C56).
3. Интеграл Фурье 145
Теория A45). Задачи B66). Указания C59).
4. Преобразование Фурье обобщенных функций . . 150
Теория A50). Задачи B69). Указания C62).
Глава V. Спектральная теория операторов 153
§ 1. Функциональное исчисление 153
1. Функции операторов в конечномерном пространстве 153
Теория A53). Задачи B70). Указания C63).
2. Функции ограниченных самосопряженных операто-
операторов 155
Теория A55). Задачи B73). Указания C65).
3. Неограниченные самосопряженные операторы . . 162
Теория A62). Задачи B75). Указания C66).
4. Расширения операторов 166
Теория A66). Задачи B77). Указания C67).
§ 2. Спектральное разложение операторов 171
1. Приведение оператора к виду умножения на функцию 171
Теория A71). Задачи B78). Указания C69).
2. Спектральная теорема 175
Теория A75). Задачи B80). Указания C70).
§ 3. Математическая модель квантовой механики . . . 180
Теория A80). Задачи B84). Указания C72).
Послесловие # # 379
Основная литература 385
Дополнительная литература 387
Список обозначений 389
Предметный указатель 392
ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
При подготовке второго издания мы несколько реор-
реорганизовали материал книги. В частности, были изъяты
простые задачи на вычисление. Они будут включены в
готовящийся нами специальный сборник задач и упраж-
упражнений по функциональному анализу. В то же время мы
постарались уточнить и несколько упростить теоретиче-
теоретические задачи.
Расширен теоретический раздел книги. Добавлены
приложения функционального анализа в математическом
прогнозировании, а также математическая модель кван-
квантовой механики. В большем объеме изложена спектраль-
спектральная теория, добавлена теория расширений операторов.
В настоящем виде книга полностью охватывает програм-
программу кандидатского экзамена по функциональному анализу.
Первое издание книги было переведено на англий-
английский, французский, итальянский и венгерский языки.
При подготовке этих переводов было сделано достаточно
много исправлений и добавлений. Все они учтены в на-
настоящем издании книги. Кроме того, существенно пере-
переработаны указания к решению задач.
А. А. Кириллов, А. Д. Гвишиани
ПРЕДИСЛОВИЕ
Уже простейшая математическая абстракция явлений
реальной действительности — прямая линия — рассматри-
рассматривается с разных точек зрения различными математиче-
математическими дисциплинами. Так, алгебраический подход к изу-
изучению этого объекта состоит в описании его свойств как
множества, к элементам которого можно применять «опе-
«операции», и в получении его алгебраической модели на ос-
основании этих свойств, абстрагируясь от свойств тополо-
топологических. С другой стороны, топология абстрагируется
от алгебраической структуры объекта и строит формаль-
формальную модель прямой линии, выделяя в качестве основы
модели ее непрерывность. Анализ рассматривает прямую
и функции на прямой в единстве всей системы их ал-
алгебраических и топологических свойств, получая свои
основные выводы путем использования взаимосвязи алгеб-
алгебраической и топологической структур.
Такая же картина наблюдается и на более высоких
ступенях абстракции. Алгебра изучает линейные прост-
пространства, группы, кольца, модули и т. д. Топология —
различного рода структуры на произвольных множест-
множествах, придающие математический смысл понятиям предела,
непрерывности, окрестности и т. д. Функциональный
анализ рассматривает топологические линейные простран-
пространства, топологические группы, нормированные кольца,
модули представлений топологических групп в топологи-
топологических линейных пространствах и т. д. Таким образом,
основным предметом изучения функционального анализа
следует считать объекты, наделенные согласованными
алгебраической и топологической структурами.
Курс функционального анализа, впервые прочитанный
на механико-математическом факультете МГУ А. Н. Кол-
Колмогоровым и традиционно включающий в себя теорию
меры и интеграла Лебега, в основном посвящен класси-
классическим разделам функционального анализа. Предлагае-
Предлагаемая читателю книга является результатом попытки обоб-
7
щения и систематизации опыта преподавания авторами
этого курса на механико-математическом факультете
МГУ и преследует следующие цели.
Изложить необходимые теоретические сведения по
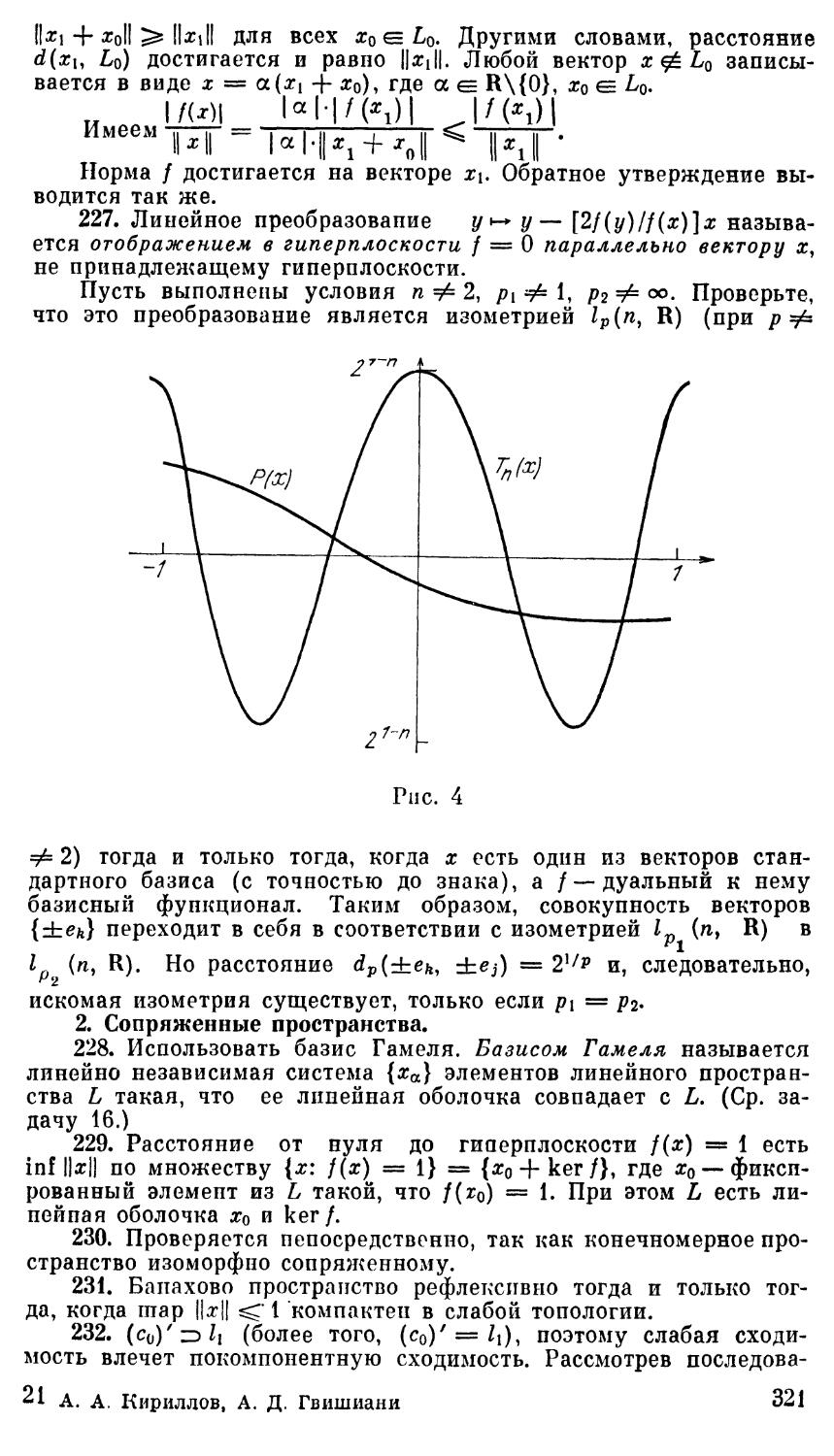
кУРсу функционального анализа в объеме программы
математических факультетов университетов.
Снабдить преподавателей, читающих лекции и веду-
ведущих упражнения по функциональному анализу, а также
студентов, изучающих этот предмет, пособием, органи-
органически соединяющим в себе учебник и задачник с доста-
достаточно подробными указаниями к решениям задач.
Дать читателю представление о некоторых элементах
аппарата, используемого для решения задач современ-
современного функционального анализа (категории, функторы,
пространства когомологий, характеры групп и т. д.).
Снабдить читателя пособием, пригодным для само-
самостоятельного изучения классических глав функционально-
функционального анализа и освоения методики решения соответствую-
соответствующих задач.
Книга делится на три тесно связанные между собой
части — теорию, задачи и указания к решению задач.
Соответствующие разделы каждой из трех частей объеди-
объединены общим названием. Главы подразделяются на парагра-
параграфы, а параграфы (как правило)—на пункты (кроме гла-
главы I). Система деления книги на пункты может быть ре-
рекомендована в качестве схемы примерного распределения
материала по семинарским занятиям, где на материал каж-
каждого пункта отводится 1—3 занятия в зависимости от
направленности курса, уровня подготовки студентов и их
интересов. По каждому пункту приводятся задачи раз-
различной трудности, причем те, которые составляют не-
необходимый минимум, помечены кружочком, а сложные —
звездочкой. Небольшое число особо трудных задач отме-
отмечено двумя звездочками. Решения этих задач могут быть
изложены преподавателем либо предложены студентам
как темы индивидуальных докладов. С другой стороны,
задачи с кружочком разумно рекомендовать для пись-
письменных контрольных работ.
Авторы благодарны С. М. Агаяну, А. В. Зелевинско-
му и А. В. Трусову за помощь в составлении указаний
к решениям задач.
А. А. Кириллов, А. Д. Гвишиани
РАЗДЕЛ I
ТЕОРИЯ
ГЛАВА I
СВЕДЕНИЯ ИЗ ТЕОРИИ МНОЖЕСТВ
И ТОПОЛОГИИ
§ 1. Отношения. Аксиома выбора и лемма Цорна
Пусть X — множество, R — подмножество в XXX.
Говорят, что точки х и у из X находятся в отношении R,
и пишут xRy, если (х, y)^R.
Примеры отношении. 1) Отношение равенства:
2) Отношение порядка на вещественной прямой:
R = {{x, у)\х>у).
3) Отношение линейной зависимости в линейном про-
пространстве L над полем К:
R = Цх, у) Iг/ = 0 либо х = Ху, %^К}.
Отношение R называется отношением эквивалентно-
эквивалентности, если оно обладает свойствами:
1) рефлексивности: (х, x)^R ViceX (или
R^Ax);
2) симметричности: (х, у)^ R => (г/, х)^ R (или
Д' = Л, где R' означает транспонированное отношение:
()(y));
3) транзитивности: (х, y)^R и (г/, г)еД=>
=> {х, z)^R (или R°R<^R, где знак ° означает компо-
композицию отношений:Rx о R2 = {(х, z) \ Зу: {х, у)е Д1э (г/, z)is
Пусть 7? — отношение эквивалентности. В этом случае
будем писать я ~ у вместо xRy и говорить, что х эквива-
6
лентен у. Обозначим через R(x) совокупность всех эле-
элементов из X, эквивалентных х. Из свойств 1), 2), 3)
вытекает, что подмножества вида R(x) исчерпывают все
X и попарно либо не пересекаются, либо совпадают.
Эти подмножества называются классами эквивалентности.
Совокупность классов эквивалентности обозначается Х(Л)
н называется фактормножеством X по отношению R.
Примеры. 1) Проективное пространство P(L), свя-
связанное с данным линейным пространством L. 2) Фактор-
пространство LJL2 линейного пространства L{ по под-
подпространству Ьг (для х, у ^ L{ считаем, что х ~ у, если
x — y^L2). 3) Совокупность вычетов по модулю п. 4) Со-
Совокупность положительных рациональных или всех це-
целых чисел как классов эквивалентности .пар натуральных
чисел.
Отношение R на множестве X называется отношением
частичного порядка, если оно обладает свойствами:
1) транзитивности (/?°/?с:/?);
2) антисимметричности (R П Rf сг &х).
Вместо xRy обычно пишут х ^ у и говорят «х следует
за у». Знак > (читается «х строго следует за у») мы
будем употреблять для обозначения отношения R{ =
= R\&x. Таким образом, х>у означает х ^ у и х?=у.
Если, кроме того, выполняется свойство
3) i?Ui?' = XXX (т. е. любые два элемента сравни-
ум), то отношение R называется отношением порядка.
Примеры. 1) Обычное отношение порядка на ве-
вещественной прямой. 2) Отношение включения для под-
подмножеств данного множества (это отношение обозначают
знаком с:)? которое является отношением частичного по-
порядка (но не порядка). 3) Отношение делимости для
целых чисел (обычно обозначаемое знаком I), также яв-
являющееся отношением частичного порядка.
Подмножество Y в частично упорядоченном множе-
множестве X называется ограниченным сверху (снизу), если
оно допускает мажоранту (миноранту), т. е. такой эле-
элемент хеХ, что у^х (соотв. у > х) для всех у е= Y.
Множество X с отношением частичного порядка R
называется направленным множеством, если R обладает
свойством R'°R = XXX (другими словами, для любых
х и у из X найдется элемент z, следующий и за х, и за
у). Если (X, R) —направленное множество, Д/— произ-
произвольное множество, то отображение X в М называется
направленностью или сетью в М. Это понятие является
обобщением понятия последовательности, к которому оно
10
сводится, если X — натуральный ряд с обычным отно-
отношением порядка.
В курсах высшей математики нередко говорят, что
понятие множества «является настолько общим, что ему
трудно дать какое-либо определение», и поэтому ограни-
ограничиваются указанием ряда синонимов: набор, совокупность,
семейство и т. д. На самом деле существует строгая тео-
теория множеств, в которой это понятие точно определяется
(разумеется, не сведением к другим, более простым или
общим понятиям, а описанием тех свойств, которыми об-
обладает понятие множества). При этом оказывается, что
вовсе не всякие «набор», «совокупность», «семейство» и
т. д. можно считать множеством. (Например, понятие
множества всех множеств, как известно, противоречиво.)
Том не менее существуют непротиворечивые теории с до-
достаточно богатым запасом множеств.
Для большинства разделов математики достаточно,
чтобы рассматриваемый запас множеств содержал хотя
бы одно бесконечное множество и допускал следующие
операции:
1) объединение U ^а;
а =а
2) пересечение П ^а;
3) разность X\Y;
4) построение множества отображений X в Y, обозна-
обозначаемого Yx\
5) произведение Ц Ха.
Здесь X, F, А и все Ха, а<^А, являются множества-
множествами, и мы предполагаем, что результатом операции также
является множество.
Последняя операция заслуживает более подробного
обсуждения. Пусть А — некоторое множество и каждому
элементу а^А поставлено в соответствие непустое мно-
множество Ха. По определению, элементом множества Ц Ха
а=А
является такое отображение я,*-*ха множества А в [} Ха,
а=А
что ха <= Ха для всех а^А. Если множество А беско-
бесконечно, то существование такого отображения неочевидно
(и, как сейчас известно, не может быть выведено из его
существования для конечных А и других естественных
аксиом). Поэтому утверждение о непустоте JJ Ха для
A
непустых Ха принимают в качестве самостоятельной ак-
аксиомы. Она получила название аксиомы выбора или an-
сиомы Цермело. Приведем два утверждения, эквивалент-
эквивалентные аксиоме выбора.
Лемма Цорна. Если в частично упорядоченном
множестве X всякое упорядоченное подмножество ограни-
ограничено сверху (снизу), то в X есть хотя бы один макси-
максимальный (минимальный) элемент х0.
Замечание. Термин «максимальный элемент» не
означает, что х0 > х для всех х^Х (такой элемент мы
будем называть наибольшим). Максимальность х0 озна-
означает лишь, что в X нет элемента, строго следующего за х0.
Теорема Цермело. Каждое множество можно
вполне упорядочить, т. е. ввести на нем такое отноше-
отношение порядка, при котором любое подмножество содержит
наименьший элемент.
Оба эти утверждения являются, по существу, обоб-
обобщением известного принципа математической индукции
и заменяют этот принцип в тех случаях, когда прихо-
приходится иметь дело с несчетными множествами.
Читателю, желающему подробнее познакомиться с ос-
основами теории множеств, мы рекомендуем просмотреть
«Сводку результатов» книги [6], а также предисловия
автора и редактора перевода к этой книге; см. так-
также [20*].
§ 2. Метрические пространства и их приложения
Важнейшие понятия анализа — предел и непрерыв-
непрерывность — опираются на понятие расстояния между точка-
точками числовой оси. Формализация этого понятия приводит
к определению метрического пространства.
Определение. Метрическим пространством назы-
называется множество X вместе с вещественной функцией d
на XXX, обладающей свойствами:
1) d(x} y)>0; d(x, г/)=0, если и только если х = у;
2) d(x, y) = d(y, x) (симметричность);
3) d(x, y)+d(y, z)>d(x, z) (неравенство треуголь-
треугольника).
Функция d называется расстоянием или метрикой
на X.
Мы предоставляем читателю убедиться, что опреде-
определения предела числовой последовательности и непрерыв-
непрерывности вещественной функции от вещественного аргумен-
аргумента можно дословно перенести на последовательности то-
точек метрического пространства и отображения одного
метрического пространства в другое.
12
Приведем еще несколько определений, связанных с
понятием расстояния и имеющих смысл в любом метри-
метрическом пространстве.
Замкнутым шаром с центром а и радиусом г в метри-
метрическом пространстве (X, d) называется подмножество в
X, состоящее из точек х, находящихся на расстоянии <г
от точки аеХ. Мы будем обозначать этот шар В (а, г).
Если в определении замкнутого шара заменить неравен-
неравенство d(a, х)<г на строгое неравенство d(a, х)<г, то
получится определение открытого шара, обозначаемого
В (а, г).
Точка а называется точкой прикосновения для мно-
множества А, если для любого г>0 в шаре В (а, г) есть
точки множества А.
Множество А называется замкнутым, если оно со-
содержит все свои точки прикосновения, и открытым, если
вместе с каждой точкой а оно содержит некоторый шар
В(а, г) с г>0.
Читателю, который впервые знакомится с этими по-
понятиями, полезно будет самостоятельно доказать, что
замкнутый шар является замкнутым множеством, а от-
открытый шар — открытым множеством.
Метрическое пространство X называется полным, если
всякая фундаментальная последовательность имеет пре-
предел в X.
Полные пространства обладают важным свойством:
в них справедливы два утверждения, служащие основой
для вывода многочисленных «теорем существования» в
анализе.
Теорема о стягивающихся шарах. Пусть
{BJ — последовательность замкнутых шаров в метриче-
метрическом пространстве (X, d), обладающая свойствами:
1) Bt ^> В2 ^ ... => Вп =>. .. (г. е. каждый шар содер-
содержится в предыдущем);
2) радиусы шаров стремятся к нулю.
Тогда если X — полное пространство, то все шары Вп
имеют роено одну общую точку.
Принцип сжимающих отображений. Пусть
/: X -*• X — отображение метрического пространства в
себя, обладающее свойством: для некоторого числа Х<1
выполняется неравенство
d(f(x), f(y))<M(x, у)
для $сех х, у^Х,
13
Тогда если X полно, то отображение / имеет ровно
одну неподвижную точку х <= X (т. е. такую, что
По существу, эти два утверждения являются харак-
тери€тическтш свойствами полных пространств (см. за-
задачу 18). Однако часто приходится иметь дело с непол-
неполными пространствами. Существует замечательная кон-
конструкция, позволяющая изготовить из каждого неполного
пространства соответствующее ему полное пространство,
присоединяя «недостающие» точки.
Определение. Пусть X — метрическое простран-
пространство. Пополнением X называется метрическое простран-
пространство У, обладающее свойствами:
1) У—полное пространство;
2) в У есть подмножество Уо, изометричное X;
3) Уо плотно в У (т. е. замыкание Уо совпадает с У;
другими словами, каждая точка из У является точкой
прикосновения для Уо).
Пример. Множество R вещественных чисел явля-
является пополнением множества О рациональных чисел с
обычным расстоянием.
Теорема 1. Каждое метрическое пространство X
допускает пополнение У. Для любых двух пополнений У
и У" пространства X существует изометрия Yr на Y",
оставляющая на месте точки X.
Доказательство состоит в явной конструкции попол-
пополнения. Пусть F — множество всех фундаментальных по-
последовательностей точек из X. Если х = {хп} и у = {уп} —
две точки из F, то числовая последовательность d(xn, уп)
будет фундаментальной, так как \d(xn, yv)—d(xm, ym)\ ^
^d(xn, xm) + d(yn, ym). Значит, эта последовательность
имеет предел, .который мы обозначим d(x, у). Величина
d{xt) у) обладает почти всеми свойствами расстояния.
В" самом деле, неравенства d(x, y)>0, d{x, y)<d(x, z) +
-\-d(y, z) и равенства d(x, x)==0, d(x, y) = d(y, x) легко
получаются предельным переходом из. соответствующих
неравенств и равенств, где вместо х, у, z стоят хп, г/„, zn.
Не выполняется лишь свойство отделимости: d(x, #)=0
не означает, вообще говоря, что х = у.
Введем на F отношение /? = {(?, y)\d{x, г/)=^О}."Из
приведенных выше свойств величины d(x, у) следует, что
R — отношение эквивалентности. Положим У = F(R) и оп-
определим расстояние на У, полагая d{R(x), R(y)) =
= d(x, у). Проверка корректности этого определения пре-
предоставляется читателю,
14
Покажем теперь, что У—пополнение X. Для этого
рассмотрим отображение ф: X -*- У, которое каждой точке
х ставит в соответствие класс Ц)(х), содержащий постоян-
постоянную (и, следовательно, фундаментальную) последователь-
последовательность х=(х, х, х, . . ., х, ...). Ясно, что отображение ф
изометрично. Мы обозначим через Уо образ X при отоб-
отображении ф. Далее, пусть у — любой элемент из У и
{xj ef- какая-нибудь последовательность из класса у.
Тогда
lim d(q>(xn), у) = lim lim d(xn, xm) = 0.
Это значит, что у является пределом последовательности
{ф (.?„)} и, значит, точкой прикосновения для Уо.
Докажем полноту У. Пусть {уп} — фундаментальная
последовательность в У. Так как Уо плотно в У, можно
указать такую последовательность {(р(хп)} в Уо, что
d{q>(xn), уп)-*0. Ясно, что {yj и {у(хп)} сходятся или
расходятся одновременно. Но последовательность {(р(хп)}
имеет своим пределом точку у — класс последовательно-
последовательности {xj. В самом деле,
lim d(<p(xn), у) = lim lim d(xn, xm) = 0.
71 —> oo Ti~><x> 771 —* <x>
Пусть теперь У и Y" — два пополнения X и ф': Х->
-^Л'о, ф": Х->У6 —соответствующие изометрические ото-
отображения. Рассмотрим отображение г|з0 = ф' °(ф" )~х из Уо
в Уо. Оно изометрично и, значит, переводит фундамен-
фундаментальные последовательности в фундаментальные. По-
Поскольку У и Y" полны, фундаментальные последователь-
последовательности в Уо (Уо) являются сходящимися в Yf(Y"). Это
позволяет однозначно нродолжить изометрию г|э0: Y'o-+Yo
до изометрии г|э: Y" ->• У, полагая г);(lim г/п) = lim i|?o(^n).
Теорема доказана.
Практически пополнение чаще строится с помощью
другой конструкции.
Теорема 2. Пусть М — полное метрическое прост-
пространство и X — подмножество в М. Тогда X полно тогда
и только тогда, когда оно замкнуто в М. В частности,
в качестве пополнения X можно взять его замыкание в М.
(По поводу доказательства см. задачу 25.)
Пример. Пополнением интервала (а, Ь) относи-
относительно обычного расстояния является отрезок [а, Ь] — за-
замыкание интервала (а, Ъ) в R.
15
Понятие метрического пространства имеет много хо-
хорошо известных приложений в анализе, дифференциаль-
дифференциальных уравнениях, теории функций и других разделах ма-
математики.
Например, специальный класс метрических прост-
пространств используется в прикладных исследованиях по
распознаванию образов и математическому прогнозиро-
прогнозированию. Приведем соответствующие определения.
Обозначим через Qn множество всех векторов со =
= (о)A), ..., (д(п)) с двоичными координатами о(/)
(? = 1, ..., п). Введем в Qn метрику по формуле
п
d° К со') = 2 041 <>> @ ~ <*>' (О I где о = (оц ..., о„)',
Oi > 0 (/ = 1, ..., п) — вектор весов. Метрическое про-
пространство (Qn, da\ называется пространством Хемминга.
Это пространство играет важную роль в алгоритмиче-
алгоритмическом распознавании.
Приведем пример. Пусть W — конечное множество объ-
объектов, t е [То, Tt] — параметр, имеющий смысл времени
(Г^оо). Предположим, что при всех t имеется разбие-
г
ние pit): W= uWi(t) множества W на г непересе-
кающихся классов. Иными словами, задано отображение
^: WX[T0, Г|]-*И, ..., г}.
В каждый момент времени объекты w e W характе-
характеризуются значениями некоторых двоичных параметров,
т. е. имеется отображение Ф: WX[T0, T{] -*¦ Qn , (коди-
(кодировка).
Пусть фиксирован момент времени t, в который ре-
решается задача. Исходную информацию в динамической
задаче распознавания составляют данные о поведении си-
системы на отрезке времени [TOi t]. Таким образом, функ-
функции ? и Ф предполагаются известными для некоторых
подмножеств из WX[TQy t], составляя материал обуче-
обучения 0{t).
Рассмотрим другой момент времени t', такой, что t<
< t' < 7\. Под решением динамической задачи распозна-
распознавания или прогнозом понимается алгоритмическое опре-
т
деление классификации W = LJ W\ (tf) на основе мате-
риала обучения O(t). Иными словами, П(?, tr) есть прог-
прогноз неизвестных на данный момент значений функции Ч?
на множестве WX {?'}.
16
Зависимость классификации от времени позволяет вы-
выделить класс наиболее достоверных прогнозов, обладаю-
обладающих свойством стабильности. При этом используются до-
довольно тонкие свойства метрических пространств. Опре-
Определение стабильности сводится к следующему. Допустим,
что в момент времени ?0, исходя из разбиения P(tQ),
с помощью некоторого алгоритма А мы получили прог-
прогноз П(?о, t'). Затем мы стали решать ту же задачу в
более поздний момент времени t{ (to< tk< t'). Разбие-
Разбиение P(ti) назовем допустимым, если возможны такие
переходы объектов, что в моменты времени t0, U, f мно-
множество W представляется соответственно разбиениями
P(t0), P(t{), U(tQ, t'). Прогноз П(*о, t') называется ста-
стабильным, если для любого tt такого, что to<tx< t\ и лю-
любого допустимого разбиения P(ti) алгоритм А, исходя из
разбиения P(ti), дает прогноз П(?1э t'), совпадающий
с П(*в, О-
Стабильность прогноза означает, что любое измене-
изменение со временем материала обучения, не противоречащее
сделанному прогнозу, не меняет его результата. Тем са-
самым нестабильные прогнозы внутренне противоречивы и
их не следует рассматривать как достоверные при по-
поиске точной классификации.
В геофизических приложениях, связанных с сейсми-
сейсмическим районированием, особое значение имеет случай,
когда г = 2. Соответствующие разбиения будем обозна-
обозначать через W = B(t) LJ H(t) (высокосейсмичные и низко-
низкосейсмичные объекты). Здесь мы имеем возможность пере-
перехода объектов только из класса U(t) в класс B(t). (Низ-
(Низкосейсмичные области после сильного землетрясения мо-
могут стать высокосейсмичными, но не наоборот.)
Алгоритмы дихотомии (разбиение на два класса) осу-
осуществляют представление Qn в виде непересекающегося
объединения множеств Лв и Лн (или, что то же самое,
представление множества W в виде JF = BuH, где В =»
= Ф (Лв), Н = Ф (Лн)), основываясь па информации
о кодировке Ф и множествах Во и Но, составляющих
исходное разбиение. Дадим формулировку алгоритма
ГЭП-1, простейшего из класса алгоритмов ГНП [8*].
Введем следующие обозначения: ах (соответственно bh
ch dt) — число объектов w^BQ (соответственно Но, Во,
Но) таких, что 1-я компонента вектора со = Ф(н;) равна
нулю (соответственно 0, 1, I); Г/ = {о): со(/) = ()}, ?!=*
= {со: со (/)=!>, Д^ф-^г,), Л^ = Ф-1 (п). Как легко ви-
видеть, Qn = rx LJ тх (здесь и ниже чертой обозначен пе-
2 А, А. Кириллов, А. Д. Гвишиани 17
реход к_ дополнению)^ az = \В0 П #Л, Ь,= |Н0ПЛ/1, с, =
= I Во П Д/1, d, = I Но П Л/1. Таким образом, отношения
а,/(^ + С/) и bl/(bl-\- d,) характеризуют частоту встречае-
встречаемости нулей в Z-ом разряде для объектов из Во и Но
соответственно.
Определим вектор z e Qn следующим образом: z(l) =
а, Ь,
= 0, если—-г—^ , , , и z(l)=i в противном случае.
ai ~т~с1 °i* ai
Вектор z называется ядром класса В. Рассмотрим в мет-
метрическом пространстве Хемминга (Qn, pa) шар B(z, R) =
= {(о: р(со, z)^R) и положим AB = B(z, R). Алгоритм
ГЭП-1 осуществляет представление множества объектов
ввидеП(*0, Тг): Ж = ВиН, где В = Ф (Лв), Н = W\B.
Шар B(z, R) в (Qn, p°) может иметь яе один, а не-
несколько центров (см. задачу 37). Множество всех цент-
центров шара будем называть его центроидом. Достаточные
условия стабильности прогноза, полученного алгоритмом
ГЭП-1, дает следующая
Теорема 3. Для стабильности прогноза П(/о): W —
= В (?0) LJ Н (?0), полученного алгоритмом ГЭП-1, до-
достаточно, а если отображение Ф сюръективпо, то и не-
необходимо, чтобы при любом допустимом исходном раз-
биении Р ядро z(P) принадлежало центроиду шара Лв(?0).
Для того чтобы провести в этом случае конструктив-
конструктивную проверку стабильности, надо иметь классификацию
всех центроидов в пространстве (Qn, p°). Такая класси-
классификация дается в задаче 42.
Стабильность можно проверить и для произвольного
алгоритма класса ГНП. Методы такой проверки разра-
разработаны в [8*].
§ 3, Категории и функторы
Многие определения и конструкции, употребляемые в
математике, удобно получать из небольшого числа общих
понятий, которые в последнее время составили особую
область исследования — теорию категорий. Мы познако-
познакомим читателя с элементами этой теории.
Говорят, что задана категория К, если задана совокуп-
совокупность (вообще говоря, не множество, см. § 1) ОЪ(К) объ-
объектов категории и для каждой пары объектов А, В ука-
указано множество Мог(Л, В) морфизмов категории из А
в В. При этом морфизмы можно перемножать, т. е. за-
задано отображение Мог(Л, В)ХМот(В1 С)-* Мог (А, С):
18
образ пары морфизмов /^Мог(Л, В) и geMorE, С)
принадлежит Мог (Л, С) и обозначается g°j. Предпола-
Предполагается, что он обладает обычными свойствами компози-
композиции отображений: h °(g ° /) = (Ь g)° / для /^Мог(Л, В),
g^Mor(B, С), h e Мог (С, D). Кроме того, в множестве
Мог (Л, А) выделен так называемый единичный морфизм,
обозначаемый \А и обладающий свойствами: 1А°/ = /,
go/i-A=g для всех /^Мог(Я, Л), #еМог(Л, В). Часто
для наглядности объекты категории обозначают точками,
а морфизмы — стрелками, соединяющими эти точки.
Примеры. 1) Категория множеств (объекты — мно-
множества, морфизмы — отображения множеств).
2) Категория групп (соотв. колец, алгебр) (объекты —
группы (соотв. кольца, алгебры), морфизмы — гомомор-
гомоморфизмы).
3) Категория топологических пространств (объекты —
топологические пространства, морфизмы — непрерывные
отображения).
4) Категория линейных пространств над данным по-
полем К (объекты — линейные пространства над К, морфиз-
морфизмы — линейные операторы).
Два объекта А и В категории К называются изоморф-
изоморфными, если существуют такие морфизмы /^Мог(Л, В)
и ge= Мог (В, Л), что f°g = Ь, g° /= 1д.
Объект А в категории К называется универсальным
отталкивающим *) объектом, если для любого объекта В
из К множество Мог (Л, В) состоит ровно из одного эле-
элемента. (Выражаясь наглядно: из точки А в любую дру-
другую точку В ведет ровно одна стрелка.)
Покажем в качестве упражнения на введенные поня-
понятия, что любые два универсальных отталкивающих объ-
объекта А и В изоморфны (если они существуют). В самом
деле, пусть /—единственный морфизм из Л в В и g —
единственный морфизм из В в Л. Тогда /cg^MorE, В),
#°/еМог(Л, Л). Но Мог(В, В) содержит единственный
элемент 1В (поскольку В универсален), а Мог (Л, Л) —
единственный элемент. 1л (поскольку Л универсален).
Значит, / о g = 1Вч g о / = 1А.
Покажем теперь, что понятия фактормножества и по-
пополнения являются частными случаями понятия универ-
универсального объекта. В первом случае мы рассмотрим сле-
*) Слово «отталкивающий» мы для краткости будем иногда
опускать.
2* 13
дующую категорию /?, построенную по множеству X и от-
отношению R. Объектом К будем считать отображение ф
множества X в какое-нибудь другое множество У (свое
для каждого объекта), обладающее свойством: xRy =>•
=>- ф(#) = ф(г/). Морфизмом объекта ф*. X ->¦ У в объект
г|з: X ->- Z назовем такое отображение %: У -> Z, для кото-
которого коммутативна диаграмма
A)
Последнее означает, что % ° ф == г|). (Вообще, коммутатив-
коммутативность диаграммы, составленной из объектов и морфизмов
некоторой категории, означает, что для любого пути из
одной точки диаграммы в другую по стрелкам этой диаг-
диаграммы произведение соответствующих морфизмов зависит
только от начального и конечного объектов, а не от вы-
выбора пути. В приведенном выше примере есть два пути
из X в Z, что и дает условие % ° ф = if).)
Проверим, что каноническая проекция р: X-*X(R)
является универсальным объектом в категории К. Пусть
ф: Х-> У-—объект из К. Рассмотрим диаграмму
Легко убедиться, что условие коммутативности одно-
однозначно определяет отображение, соответствующее пунк-
пунктирной стрелке. Это значит, что Мог(/?, ф) состоит из од-
одного элемента. Поэтому р: X ->¦ X{R) — универсальный
объект.
Разберем теперь конструкцию пополнения. Пусть X —
метрическое пространство. Рассмотрим категорию К, объ-
объектами которой являются изометрические отображения
ф: Х.-> У, где У—полное метрическое пространство
(свое для каждого объекта). Морфизмом из ф: Х->У в
ty: X-+Z назовем такое изометрическое отображение
%: Y-+Z, для которого коммутативна диаграмма A).
Проверим, что каноническое вложение ф простран-
пространства X в его пополнение У является универсальным объ-
объектом. В самом деле, для любого объекта г|г. X-*Z
20
диаграмма
B)
может быть единственным образом достроена до комму-
коммутативной диаграммы вида A). Искомое отображение %
определяется на подмножестве Ц)(Х) по формуле % =
= if ° ф (условие коммутативности) а дальше распро-
распространяется по непрерывности:
Отметим, что единственность пополнения (с точностью
до изометрии) вытекает из доказанной выше общей тео-
теоремы об изоморфизме универсальных объектов.
Одно из основных понятий в теории категорий — по-
понятие функтора.
Определение. Ковариантным функтором из кате-
категории Ki в категорию Кг называется отображение F,
которое каждому объекту А из К{ ставит в соответствие
объект F(A) из К2, а каждому морфизму ф из
Мог(Л, ?) — морфизм F(cp) из Мог(^(Л), F(B)), при-
причем выполняются условия:
)
2) iW) {q)($)
Часто также встречаются отображения F категорий,
ставящие в соответствие каждому морфизму ф е
^Мог(^, В) морфизм /Чф)€=Мог(^E), F(A)) и удов-
удовлетворяющие вместо условия 2) условию
2') ^(фо1|,) = ^(ф)о^(ф).
Они называются контравариантными функторами.
Примеры. 1) Переход от метрического простран-
пространства к его пополнению является ковариантным функто-
функтором из категории метрических пространств в категорию
полных метрических пространств (морфизмами в обеих
категориях являются изометрические отображения).
2) Переход от линейного пространства L над полем К
к двойственному пространству V (пространству Х-ли-
нейных функционалов на L) является контравариантным
функтором из категории линейных пространств над К
в себя.
3) Для любой категории К отображения А -*¦ Мог(», А)
(А -> Мог(.4, •)) продолжаются до ковариантного (кон-
травариантного) функтора из Я б категорию множеств.
21
Для этого нужно морфизму cpe=Mor(,4i, Аг) поставить
в соответствие отображение Мог(-, Ах) в Мог(-, А2)
(Mor(A2i •) в Mor(Ali •)), состоящее в умножении слева
(справа) на морфизм ф.
Совокупность ковариантных функторов из Кх в К2
сама образует категорию Со\(Ки К2). Морфизмами в
ней являются так называемые функторные морфизмы
или естественные преобразования функторов. Они опре-
определяются так: пусть /^ и F2 — функторы из Кх в К2.
Морфизмом ф из F{ в F2 называется такой набор отображе-
отображений ф (А) е Могк9 (F^A), F2(A)) (где А пробегает
ОЪ{Кг)), что для "любого г|> е Мог^ D, В) коммутативна
диаграмма
F2<4»
Аналогично определяется категория Cont(/ifi, K2)
контравариантных функторов из К{ в К2.
Многие утверждения о функторах достаточно доказы-
доказывать только в случае ковариантных функторов в силу
следующего общего приема. Для любой категории К оп-
определим дуальную категорию К°, для которой ОЬ(/?°) =
= ОЬ(#), МогяоD, В) — Могк (В, А), а произведение /°g
в категории К0 определяется как произведение g ° / в
категории К. Иногда говорят, что К0 получается из К
обращением стрелок. Ясно, что контравариантный функ-
функтор из Ki в К2 — это то же самое, что ковариантный
функтор из К\ в К2 (или из К1 в К\).
Две категории К{ и К2 называют эквивалентными,
если существуют такие ковариантные функторы F: Ki -*•
-^ К2, G: K2-+Ki, что функторы F°G и G°F изоморфны
тождественным функторам в категориях Cov(K2, K2) и
Cov(Ku К^ соответственно.
Пример. Знаменитые три теоремы Софуса Ли вме-
вместе с теоремой Эли Картана по существу утверждают
эквивалентность трех категорий: категории односвязных
групп Ли, категории локальных групп Ли и категории
вещественных алгебр Ли.
Более простой пример: категория дискретных то-
топологических пространств (в которых псе подмножества
открыты) эквивалентна категории множеств,
22
Хорошей иллюстрацией к понятию эквивалентности
категорий является
Теорема 4. Если в категории К все объекты изо-
изоморфны, то К эквивалентна категории Ко, состоящей
из одного объекта Ао^ ОЪ(К) и всех морфизмов из
Moyk(Aq, AQ).
Примером такой категории может служить категория
и-мерных линейных пространств над данным полем иди
категория всех групп из р элементов (р — простое число).
Доказательство. Выберем для каждого объекта
А <= Ob К фиксированный изоморфизм а(А)\ А -> Ао и
построим функтор F: К-*К0 следующим образом: F(A) =
==А о для всех А е Ob К; если (} е Мог (^4, В\, то положим
F($)= a(fi)° p°a(i4)~1 еМог(Л0, Ло). Кроме того, обоз-
обозначим через G функтор вложения /?0 в X. Ясно, что
F°G = 1K , G о F — F. Покажем, что функторы F и \к изо-
изоморфны. Для этого определим функторные морфизмы ср:
F -+ \к п ty: 1к -* F так, чтобы ф°'ф = 'фоф = 1. По опре-
определению функторного морфизма, для любого (} следующие
диаграммы должны быть коммутативны:
аЛв аЛв
А Л Л Л
AQ—> Ло Ло—> Ло
Кроме того, должны выполняться соотношения
Ф (А) о гр (А) = 1А, г() (А) ° ф (А) = 1Aq. Ясно, что этого мож-
можно добиться, полагая ф(^4) = а(А)~\ ty(A)= а(А). Тео-
Теорема доказана.
ГЛАВА И
ТЕОРИЯ МЕРЫ II ИНТЕГРАЛА
§ 1. Теория меры
1. Алгебра множеств. Пусть X—некоторое множество.
Через Р{Х) будем обозначать совокупность всех подмно-
подмножеств множества X.
Определение. Кольцом подмножеств множества X
называется непустое семейство R<=^P(X), замкнутое от-
относительно операций объединения, пересечения и раз-
разности.
23
В этом случае R замкнуто также относительно опера-
операции симметрической разности А А В = (А U В)\(А П 5) =
= (А\В)[}(В\А).
Усиления структуры кольца. 1) Алгеброй
множеств называется кальцо RczP(X), содержащее в
качестве элемента все множество X.
2) о-колъцом называется кольцо R, замкнутое отно-
относительно операции счетного объединения.
3) 8-колъцом называется кольцо, замкнутое относи-
относительно операции счетного пересечения.
4) о-алгеброй (соотв. 8-алгеброй) называется кольцо,
которое одновременно является алгеброй и а-кольцом
(соотв. б-кольцом).
Ослабление структуры кольца. Полуколь-
Полукольцом называется семейство S^P(X), замкнутое относи-
относительно пересечения и обладающее свойством: если А,
B^S, то существуют такие d, ..., Cn^S, что А\В =
= Сх LJ С2 LJ . .. LJ Сп (символ LJ означает дизъюнктное
объединение, т. е. объединение непересекающихся мно-
множеств).
Примеры. 1) Совокупность S всех полуинтервалов
вида [а, Ь) на вещественной прямой является полуколь-
полукольцом, но не кольцом.
2) Если Л1с=Р(Х1) и i?2dP(X2) —кольца множеств,
то семейство
Я4 X R2 = {А X В е Р (X X Y) \А е Ль В е RJ
является полукольцом (но, вообще говоря, не кольцом).
То же верно, если Rt и R2 — полукольца (см. задачу 81).
Если S — любое семейство подмножеств X, то среди
колец (соотв. о-колец), содержащих 5, имеется мини-
минимальное. Оно обозначается R(S) (соотв. Ra(S)) и назы-
называется кольцом (соотв. g-колъцом) , порожденным S (см.
задачу 78).
Пусть А — подмножество в X. Характеристической
функцией подмножества А называется функция %А на X,
заданная условием
если же4,
если х ф А.
Удобно считать, что значения характеристической
функции — не числа, а вычеты по модулю 2. В этом слу-
случав будут справедливы равенства (см. задачу 87)
24
Пусть X — топологическое пространство (см. гл. I,
§ 4), С/ с Р (X) — семейство открытых множеств в X.
Элементы R(,(U) называются борелевскими подмноже-
подмножествами в X.
Пример. Множество всех рациональных точек от-
отрезка [0, 1] является борелевским множеством на веще-
вещественной прямой.
2. Продолжение меры.
Определение. Мерой на полукольце S <= Р (X)
называется вещественная неотрицательная функция р, на
Sy обладающая свойством аддитивности:
Мера \х называется счетно-аддитивной (или о-аддитив-
ной), если она обладает свойством:
(оо \ оо
IIЛ =2 и М*). A)
оо
(Более точно: если все Ah и А = J][ Ah принадлежат S,
то правая часть равенства A) сходится и ее сумма равна
левой части.)
Примеры. 1) Пусть х0 — фиксированная точка X.
Для любого множества А а X положим
{1, если xo^Af
О, если хо^?А,
Это — о-аддитивная мера на Р(Х).
2) Пусть S — рассмотренное выше полукольцо полу-
полуинтервалов вида [а, Ъ) на R. Положим \i{[a, b))= b — а.
Тогда |ы — мера на S. Счетная аддитивность этой меры
будет установлена ниже.
Теорема 1. Всякая мера \х' на полукольце S одно-
однозначно продолжается до меры \х на кольце R(S). Если
исходная мера счетно-аддитивна, то тем же свойством
обладает и ее продолжение.
25
Доказательство. Воспользуемся тем, что каж-
п
дое множество А е R(S) имеет вид ^4 = Jjf ^4fe (Ak e S)
ft=i
(см. задачу 77). Поэтому величина [i(A) (если она оп-
п
ределена) должна равняться 2 Н<' И*)- Покажем, что это
А
А1
равенство действительно определяет меру \х на R{S).
1) Корректность определения. Пусть Ак,
т п
Bi^S, ЦВ1= JjAk= А. Положим Chl = Akt\BL. Тогда
ясно, что Ак = П СЛ/, Я, = П Chi- Поэюму 2 ^ (Ак) =
П hi
n
2) Аддитивность. Пусть 4 = Ц 4А (ЛА е Л E)).
N(fe)
Положим -4ft = ТТ Cfeb где Cki^S. Тогда Л = ЦСА/ и
/=1 ft.Z
ЛГ(Л) п
И И) = 2 ^' (Cw) =2 2^' (Cw) = 2 Ц (Л). Остается
проверить о-аддитивность продолженной меры jli, если
оо
исходная мера о-аддитпвна. Пусть А = ?J ЛА (A, Ak^
€= Л E)). Тогда Л = П Si. Л = И Sfc/i где 5„ Д« е 5.
г=1 г=-1
Положим Сш = Bid Bkt. Имеем
и (А)=S и' (во = 2 2 ц' (с,А,) - 2 2 и' (с»ы) = 2 (* (Л).
г г ft,/ ft i,Z ft
(Мы воспользовались соотношениями Вг = ДС^, ЛЛ =
ft,/
== II ^ife^ и возможностью менять порядок суммирования
г,/
в рядах с неотрицательными членами.) Теорема доказана.
Важным свойством счетно-аддитивных мер является
счетная монотонность: если A, Ak^S и Л с: [}Ak, то
Оказывается, счетно-аддитивная мера, заданная на по-
полукольце S, продолжается не только на кольцо R(S) и
даже не только на о-кольцо R0(S), но на гораздо более
широкую совокупность так называемых измеримых мно-
множеств.
26
Определение. Пусть задано множество X, полу-
полукольцо S^P(X) и о-аддитивиая мера ji на S. Для лю-
любого А^Р(Х) определим внешнюю меру [i*(A) равен-
равенством
ц* (А) = inf 2 И (А), А<=1) \, A
h
Назовем подмножество А^Р(Х) измеримым по Ле-
Лебегу относительно меры jli, если для любого е>0 най-
найдется такое множество В е R(S), что [х*(ЛДВ)<е.
(В дальнейшем множества, измеримые по Лебегу отно-
относительно меры \х, будут для краткости называться просто
измеримыми или ^-измеримыми, если надо подчеркнуть,
о какой мере ji идет речь.)
Пусть теперь кольцо R (S) является алгеброй (т. е. со-
содержит максимальный элемент X). В этом случае спра-
справедлива
Теорема Лебега. Совокупность LE, ji) измери-
измеримых множеств образует о-алгебру, на которой ji* являет-
является с-аддитивной мерой.
Доказательство. Проверим сначала, что для мно-
множеств из исходного полукольца 5 (соотв. R(S)) внешняя
мера ji* совпадает с исходной мерой р/ (соотв. с ее про-
оо
должением \х). В самом деле, если A ^R(S) и A cz (J Ah,
оо
то \х (А) <; 2 № (Ah) в силу счетной монотонности меры \i.
Переходя к нижней грани по всем покрытиям, мы полу-
получаем отсюда, что \i{A)^ jj.*(Л). С другой стороны, по-
п
скольку А ^ R (S), можно представить А в виде А = JjBb,
п
где Bh^ S. Поэтому ц* (А)^ 2 И (^н) = I11 И)- Отметим,
что из самого определения внешней меры легко выводится
сю
ее счетная монотонность: если^сп (J Ak, то |л*(Л)^
h=l
11
Оставшуюся часть доказательства теоремы можно
кратко описать следующим образом. Элементы кольца
R{S) образуют некоторое неполное метрическое простран-
пространство, на котором мера |д является равномерно непрерыв-
27
ной функцией. Измеримые множества — это точки попол-
пополнения, а мера ji* — продолжение по непрерывности функ-
функции ji (см. задачу 95).
Перейдем к деталям. Определим расстояние между
множествами А и В формулой d(A, В) = р,*(Л А В). Для
проверки обычных свойств расстояния полезно отметить,
что само множество А А В можно рассматривать как свое-
своеобразное «расстояние» между А и 5, принимающее зна-
значения не в числах, а в множествах. Аксиома треуголь-
треугольника для этого расстояния имеет вид (см. задачу 73)
А А5с:(Л AC)U(BAC),
Отсюда и из монотонности ji* непосредственно следует
обычная аксиома треугольника: d(A1 B)^d(A, C) +
+ d(B, С). Свойства d(A, B) = d(B, А) и d(A, B)>0
очевидны. Последнее свойство d(A, В) = О =>- А =5, во-
вообще говоря, не выполняется. Стандартный выход из это-
этого затруднения состоит в том, что мы объявляем Множе-
Множества А и В эквивалентными, если d(A, B) = 0. Функция
d переносится на классы эквивалентных множеств и об-
обладает там всеми свойствами расстояния.
Теперь определение измеримого множества можно
сформулировать так: множество А измеримо, если оно с
любой точностью приближается множествами В из R(S).
Другими словами, совокупность L (S) измеримых множеств
совпадает с замыканием R{S) в построенном метрическом
пространстве. Можно показать (см. задачу 95), что про-
пространство Р(Х) (точнее, соответствующее факторпрост-
ранство классов эквивалентных множеств) полно. Поэто-
Поэтому L(S) можно также рассматривать как пополнение
R(S).
Прежде всего проверим, что L(S) является алгеброй.
Пусть А{ и Аг измеримы, т. е. для любого е>0 най-
найдутся такие множества В{ и В2 из R(S), что [i*(Ai А В{)<
<е и [i*(A2 А В2)< 8. Тогда (см. задачу 74) будут спра-
справедливы оценки
что доказывает измеримость множеств Ах U А2, А1пА1 и
АМг.
28
Покажем теперь, что L(S) есть а-алгебра. Пусть Ак&
оо
eiE) и А = U Ah. Для любого е >0 существуют такие
ft=l
множества Bk^R(SI что \х*(А А В)< е/2\ Положим
5= U 5А. Из включения |J Ah\ /\\[]
А=1 \ft=l У \ft=l
оо °°
cz [j (Ah A Bk) вытекает, что fx* (А Д 5) <! ^ -^- = е.
*=1 /г=1 2
Далее, пусть S^-S^^U^U ... U#ft-i)
(X)
= 5Г Тогда В1еЛE)иВ=и 5^. Поскольку ряд
fe=l ft
сходится (его частичные суммы ограничены числом [i(X)),
оо
существует такой номер N, что 2 М-(^/г)<8- Положим
k=N+l
N
В' = U 5ft. Тогда B'^R(S) и jr*(SAS')<e. Отсюда
=i
H*DAB')<[i*(iAS)+[i*(BAS')<2e, что и доказы-
доказывает измеримость А.
Проверим, что ц* — счетно-аддитивная мера на L(S).
Лемма. ||л*(Л)-|л*(ЯI ^*(Л А 5).
Другими словами, функция [х* равномерно непрерывна
относительно расстояния d(A, S) = [i*(A A 5).
Доказательство вытекает из монотонности р,* и вклю-
включений АаВ[)(А А 5), ВсЛ и (Л А 5).
Пусть теперь Л19 Л2е?E) и А = A1[jA2. Для любо-
любого е>0 выберем St и 52 из R(S) так, чтобы й(Лг-, Вг)<г
(г = 1, 2). Тогда d(i4, BIUZ?2)<2e. Поэтому |ц*(Л)-
- ц* (J9i U Вг) I < 2е. С другой стороны, ц* Et U В2) =
= |iEiUBa)=|i(fl1)+|i(Ba)-|iE1nB2). Но \1(В1ПВг)^
= d(Bi(]B2, 0) = d(BlC\B2, Л1ПЛ2)<2е, значит, I^^U
U В2) — [ii(Bi) — \i(B2) I < 2e. Соединяя все полученные и
исходные неравенства, получаем, что Iц*(А) — jlx*(Л1) —
— jj,*(Л2) I < бе. Поскольку это верно для всех е >0, это
значит, что [i*(A)= [i*(A{)+ р,*(Л2), т. е. р,* аддитивна
на L(S).
Наконец, докажем счетную аддитивность [х* на L(S).
ОО (X)
Пусть 4 = П Л- Неравенство [х* И)< 2 И* (Л) сле"
ft=i ft=i
дует из счетной монотонности р,*. Неравенство fx* (Л) ^
оо
получается предельным переходом из нера-
29
венства \i* {А) ^ ^ u.* (AkI которое вытекает из копеч-
ной аддитивности и монотонности \i. Теорема доказана.
Условие X^R(S) оказывается в ряде случаев слиш-
слишком сильным. Рассмотрим более слабое условие X е
сю
ейоE). Тогда X =г-ЦХП, где Xn^S; таким образом, все
h=l
пространство является счетным объединением множеств
из полукольца. Мера [х в этом случае называется о-ко-
печной.
Определение. Множество А называется измери-
измеримым по Лебегу относительно оконечной меры \х, если
измеримы все множества А П Xt (? = 1, 2, ...). Мерой А
оо
называется сумма ряда 2 И** {А П Хг), если он сходится,
и +оо в противном случае.
Нетрудно проверить, что измеримые множества по-
прежнему образуют о-алгебру, а определенная выше мера
ц* является о-аддитивной (с очевидно11 поправкой: обе
части равенства ^ (Ц Ah) = ^ \i (Ak) могут быть беско-
бесконечны).
Знакопеременным аналогом мер являются заряды.
Определение. Пусть А7 — множество и /? cz P(X) —
некоторое о-колыдо. Вещественная (соотв. комплексная)
функция v на R называется зарядом (соотв. комплексным
зарядом), если она счетно-аддитивна в следующем смыс-
оо
ле: для любых Ak e R из того, что А = Q Ak принадлежит
Z
R, следует, что ряд Zj v (Ah) абсолютно сходится и его
сумма равна \(А) (ср. с задачей 117).
Пример. Любая линейная комбинация о-аддитивных
мер на й с вещественными (соотв. комплексными) коэф-
коэффициентами является зарядом (соотв. комплексным за-
зарядом).
Оказывается, справедливо и обратное утверждение.
Теорема 2. Всякий заряд {соотв. комплексный за-
заряд) v может быть записан в виде v = ^i — \х2 (соотв.
v = jLii — |я2 + Щз — ф4), где \ih — счетно-аддитивные мерч.
Определение. Вариацией заряда v на множестве
А называется величина
30
Пример. Если v — jii — ц2,то Ivl (А)< iit(A)+ \i2{A).
Это неравенство превращается в равенство, если меры
jj,! и \i2 дизъюнктны на А (т. е. существует такое раз-
разложение А = Axi_jA2, что ii2(Ai)= lii{A2) = 0).
Теорема 3. Функция Ivl является счетно-аддитив-
счетно-аддитивной мерой на R. (См. задачу 124.)
3. Конструкции мер. Рассмотрим полукольцо 5, состо-
состоящее из всех полуинтервалов вида [а, Ъ) на веществен-
вещественной прямой. Совокупность всех мер на этом полукольце
допускает простое описание. А именно, сопоставим каж-
каждой мере \л на S функцию F^ на вещественной прямой R,
определенную формулой
И([О, *)) при *>0,
0 при * = 0,
1-Й!*, 0)) при *<0.
Очевидно, что функция F» — неубывающая. Обратно,
если F — неубывающая функция на R, то можно опреде-
определить меру juip на S, полагая jaf([#, b)) = F(b) — F(a).
(Проверка аддитивности jiiF предоставляется читателю.)
Соответствие между мерами на 5 и неубывающими функ-
функциями на R становится взаимно-однозначным, если рас-
рассматривать лишь функции с дополнительным условием
)
Теорема 4. Для того чтобы мера \х на S была
счетно-аддитивной, необходимо и достаточно, чтобы соот-
соответствующая функция F на R была непрерывна слева,
т. е. F{t-O) = F(t) для всех ieR.
Доказательство. Необходимость следует из соот-
соотношения F(t) - F{t - 0) = lim |i {[t - 6, *))=O.(Cp. с за-
дачей 94.) Для доказательства достаточности предполо-
оо
жим, что [а, Ь) = JI \-aki ЬА). Тогда для любого N спра-
N
ведливо включение [a, b) zd JJ [ak, bh) и, следовательно,
N
[i ([a, 6)) ^ 2j ^ {l^ki bk)) в силу аддитивности и монотон-
ности \х. Устремляя /V к бесконечности, получаем
оо
|я ([а, Ь)) ^ 2 ^([^/и bk)). ДокажвхМ обратное неравен-
ство. Для любого е > 0 выберем положительные числа
б, 6i, б2, ... так, чтобы выполнялись неравенства F(b) —
31
-F(ft-6)<e, F(ak)-F(ah-6h)<e/2\ Это можно сде-
сделать, так как F непрерывна слева. Заметим теперь, что
отрезок [а, Ь — б] покрывается целиком интервалами
(afe — 6ft, bh). Значит, существует такое N, что уже пер-
первые N интервалов покрывают этот отрезок*). Отсюда
N
\L([a, Ъ — 6)Х2[г([аЛ — бЛ, ЬЛ)), поскольку [a, fe — б) с:
N N
с [а, Ь — б] с П fafe — бЛ, ЬЛ) с: П [аЛ—бЛ, бЛ). Вместе
с написанными выше неравенствами это дает ц ([а} b)) ^
^ 2 ^(t^/i» ^ft)) + 2e. Теорема доказана.
Отметим важный пример: F(t)^t. В этом случае
мера на 5 совпадает с обычной длиной, а ее продолже-
продолжение \i* на L(S) называется мерой Лебега на R.
Другой пример: пусть [t] — целая часть t, т. е.
наибольшее целое число, не превосходящее t. Положим
F(t)=—[~t]. Легко проверить, что F(t) непрерывна сле-
слева. Соответствующая мера продолжается на все подмно-
подмножества R по формуле
[i(A) — число целых точек в А.
Опишем теперь все заряды, определенные на RoiS),
где S — рассмотренное выше полукольцо полуинтервалов.
Для каждого заряда v положим
( v([0,*)) при *>0,:
Fv (t) == I 0 при t = 0r B)
l-v([/, 0)) при *<0.
Чтобы описать множество функций Fv на R, соответ-
соответствующих зарядам v, нам понадобится
Определение. Вариацией функции / на отрезке
[а, Ь] называется величина
= sup "S | / (Е*) — / (E*+i) I,
где верхняя грань берется по всем конечным наборам
точек |ь ..., |„ на отрезке [a, b]. Множество функций
ограниченной вариации обозначается через У [а, Ь\.
*) Здесь используется компактность отрезка (см. гл. III, § 2).
32
Теорема 5. Вещественная функция f на отрезке
[а, Ь] имеет ограниченную вариацию тогда и только
тогда, когда она представила в виде разности двух моно-
монотонных функций.
Доказательство. Для монотонных функций ва-
вариация совпадает с приращением: Vara / = | /(&)—/ (a) |
(см. задачу 181). Поэтому все монотонные функции и их
линейные комбинации имеют ограниченную вариацию.
Обратно, пусть Var^/< оо. Положим ф(?) = Уага/. Ясно,
что ф — неубывающая функция. Кроме того, рассматривая
простейший набор точек |i = a, \г = Ъ, мы видим, что
Var*/>|/F)-/(a)|. Отсюда ф(д - ф(*2) = Var?/>
^ I / (*i) ~~" / (У 1ПРИ U > *а. Это значит, что функция
<ф(О==ф(О""/@ — также неубывающая. Поэтому f(t) =
= ф@*~ ^@ — разность двух монотонных функций.
Теорема 6. Для того чтобы функция F на R соот-
соответствовала некоторому заряду v no формуле B), необ-
необходимо и достаточно, чтобы она удовлетворяла условиям:
1) F@) = 0;
2) F непрерывна слева;
3) F имеет ограниченную вариацию на любом от-
отрезке.
Доказательство. Достаточность следует из тео-
теорем 4 и 5. В самом деле, представим F в виде разности
двух неубывающих функций F+ и F_. Ясно, что если F
удовлетворяет условиям 1) и 2), то Ff и F. можно вы-
выбрать так, чтобы они тоже удовлетворяли этим условиям.
По теореме 4 функции F+, F_ соответствуют некото-
некоторым счетно-аддитивным мерам ц+, \i~. Тогда функция
F = F+ — F- соответствует заряду jiif — ц-.
Необходимость условия 1) очевидна, необходимость 2)
доказывается так же, как и в теореме 4. Докажем необ-
необходимость 3). Для этого заметим, что по определению
вариации заряда v справедливо равенство VaraFv ==
= | v | ([а, Ь)).Таким образом, нужное нам утверждение
является частным случаем общей теоремы о конечности
вариации заряда (см. задачу 124). Теорема доказана
Пусть X и Y — два множества, 5с Р(Х) и Г с: P(Y) —
два полукольца, a \i и v — меры на S и Г. Рассмотрим
полукольцо SXjTcP(IXF), состоящее из множеств
вида АХ В, A^S, B^T (см. задачу 81), и определим
на нем функцию [iXv, полагая (\х X v) (A X В)= \х(А)Х
Xv(fi). Легко проверить, что эта функция аддитивна.
3 А. А. Кириллов, А. Д. Гвишиани 33
Теорема 7. Если меры ц, и v счетно-аддитивны, то
этим свойством обладает и мера \х X v.
Доказательство этой теоремы мы отложим до построе-
построения теории интегрирования (см. гл. II, § 3).
Ясно, что аналогичная теорема верна для произведе-
произведения любого конечного числа мер. Оказывается, что при
небольших добавочных ограничениях она справедлива и
для бесконечного произведения.
Пусть задано некоторое множество индексов А и для
каждого а е А заданы непустое множество Ха, полу-
полукольцо 5а<=Р(Ха) и счетно-аддитивная мера \ха на Sa.
Предположим, что для всех а^А, кроме конечного чис-
числа, полукольцо Sa содержит Ха и |иа(Ха)=1. Положим
% = П Ха и назовем цилиндрическими подмножества
Y с: X вида
У= П YaX П Ха,: C)
A AA
где AQ — любое конечное подмножество в А, содержащее
все индексы а, для которых [i(Xa)?=l, а Ya — любое под-
подмножество из Sa. Для Y вида C) положим
ИП= П М^а)<
а=А0
Теорема 8. Цилиндрические подмножества обра-
образуют полукольцо S, на котором |и является счетно-адди-
счетно-аддитивной мерой.
Доказательство см., например, в книге [29].
Есть один важный случай, когда счетная аддитивность
меры-произведения (и даже более общих мер) устанав-
устанавливается весьма просто.
Лемма. Пусть A=N и все Хп (neN)- конечные
множества. В этом случае соотношение Y = JJ Yk для
и
непустых цилиндрических множеств возможно, лишь если
сумма конечна.
Следствие. Всякая аддитивная мера на полуколь-
полукольце S счетно-аддитивна.
Доказательство леммы. Мы введем в Х =
оо
5=3 И %п такую метрику, что все цилиндрические мно-
жества будут открыты, замкнуты и компактны. Утверж-
Утверждение леммы будет тогда следовать из леммы о конечном
покрытии. Искомая метрика может быть задана так.
34
Будем записывать элемент х е X в виде последователь-
последовательности {xj, хп^Хп. Положим
О, если х = у,
d(x, у) = < 1/кх где к — наименьший номер, для
которого хкфук.
Ясно, что замкнутый шар радиуса \Jk с центром в точке
х совпадает с открытым шаром радиуса 1/(& + 1) и яв-
является цилиндрическим множеством. Отсюда следует от-
открытость и замкнутость цилиндрических множеств. Ком-
Компактность их следует из компактности X, которая в свою
очередь легко доказывается предъявлением конечной е-
сети для любого е > 0 и тривиальной проверкой полноты
X. (По поводу компактности см. гл. III, § 3, п. 2.)
Пример. На множестве X бесконечных десятичных
дробей вида х = 0, х{ х2 х3... можно определить меру
описанным выше способом, полагая ХА = {0, 1, 2, ..., 9},
Sh = Р (Xh), \ik (У) = ^ card У, где card У — число элемен-
элементов множества У. Можно проверить, что лебеговское про-
продолжение этой меры по существу совпадает с мерой
Лебега на отрезке [0, 1].
Очень интересный пример меры возникает из физи-
физических приложений (броуновское движение). В простран-
пространстве С [а, Ь] непрерывных функций на отрезке [а, Ь]
рассмотрим подмножества вида
где Zi ^ t2 < ... < tn — точки отрезка [a, b], a Дь ..., Дп —
интервалы на вещественной оси. Легко проверить, что
такие множества образуют полукольцо S. Оказывается,
формула
1-П 71-1
\i (X (tx, ..., tn; Дх, .. ., Дп)) = я 2 JJ (tk+1 — ^)~1 2 X
задает на S счетно-аддитивную меру. При д = 1 эту фор-
формулу надо понимать так:
зз
Лебеговское продолжение меры jn называется мерой Ви-
Винера на С [а, Ь]. Эта мера обладает многими интересны-
интересными свойствами. Отметим, например, что функции, диффе-
дифференцируемые хотя бы в одной точке отрезка [а, Ь], обра-
образуют множество нулевой меры.
Физическая интерпретация меры Винера (точнее, свя-
связанной с ней меры jli0, см. задачу 179)—вероятность
того, что частица, совершающая броуновское блуждание
по прямой, в моменты tu t2, ..., tn находится в интерва-
интервалах Ai, Д2, ..., An соответственно. Таким образом, гра-
график движения этой частицы с вероятностью 1 является
нигде не дифференцируемой непрерывной функцией на
[а, Ь] (см. [6*]).
§ 2. Измеримые функции
1. Свойства измеримых функций. Пусть задано мно-
множество X и с-алгебра 31<=Р(Х). Вещественная функция
/ на X называется %-измеримой, если для любого с ^ R
множество
Ec(f)={xe=X: f(x)<c]
(так называемое лебеговское множество функции /) при-
принадлежит 31. Можно показать (см. задачу 125), что в
этом определении знак < можно заменить любым из
знаков ^, >, ^ (но не знаком =).
Комплекснозначная функция /(#)= и(х)+ iv(x) на-
называется ^-измеримой, если таковыми являются ее ве-
вещественная часть и(х) и мнимая часть v(x). Более общо:
вектор-функция ^(х) со значениями в конечномерном
вещественном линейном пространстве L называется ^-из-
^-измеримой, если для некоторого базиса е{, ..., еп в L в раз-
разложении *Е,{х) = \i{x)e{ + ... + \п{х)еп все коэффициенты
\г{х) являются St-измеримыми функциями. Это определе-
определение не зависит от выбора базиса в L (см. задачу 142).
Часто, когда речь идет о пространстве X с мерой |и,
определенной на с-алгебре 9t<=P(X), вместо «31-измери-
мая» говорят «ii-измеримая» или просто измеримая функ-
функция. Основные свойства измеримых функций описывает
Теорема 9. Множество измеримых функций обра-
образует алгебру, замкнутую относительно сходимости почти
всюду.
Доказательство. Если функция / измерима, то
функции X/, 1/1 и /2 измеримьг в силу следующей общей
леммы.
36
Лемма. Пусть f — измеримая, a g — непрерывная
функции. Тогда композиция g{f{x)) измерима.
Доказательство вытекает из утверждения задачи 128.
Пусть функции /i и /2 измеримы. Докажем измеримость
суммы /i + /2. Для этого заметим, что лебеговское мно-
множество Ec(fl + f2) можно представить в виде объединения
счетного числа измеримых множеств:
^c(/l + /2)= U (?г(/1)П?с-Л/2)),
где Q — множество рациональных чисел.
Далее, измеримость произведения Д/2 следует из вы-
,4 (/i + /2J (Л-А>J
шесказанного и из тождества /х/2 = / 4 "
1 1
Аналогично, тождество max (fv /2) =-^ (Д + /2) + -g |/i— /2I
показывает, что максимум двух, а значит, и любого ко-
конечного числа измеримых функций измерим. Пусть {/„} —
невозрастающая последовательность измеримых функций
и / — ее предел. Тогда множество Ec(f) является объеди-
объединением множеств Ec(fn) и, следовательно, измеримо.
Таким образом, алгебра измеримых функций замкнута
относительно монотонных предельных переходов. Но, как
известно, всякий предельный переход можно заменить
двумя монотонными. А именно,
Km in (x) = lira lim max {fn (x), fn+1 (x), ..., fn+k (*)}.
Очевидно, что если Д измерима, а /2 совпадает с Д
почти всюду, то /г также измерима. Теорема доказана.
2. Сходимость измеримых функций. Для измеримых
функций можно определить несколько разных типов схо-
сходимости. Наиболее употребительны следующие три типа:
1) Равномерная сходимость на множестве X обозна-
обозначается /„ =*¦ / и означает, что
sup |/п (я) — / (я) |-* 0 при гг->оо.
X -л
2) Сходимость почти всюду (относительно меры \х)
обозначается /п —* / и означает, что
fn(x)-+f(x) При П-+оо
для всех точек х вне некоторого подмножества меры нуль.
М-
3) Сходимость по мере обозначается fn~*f и означа-
означает, что для любого е>0 мера множества ^(е)^
37
= ЬеХ: \fn{^) — f{x)\> г) стремится к нулю при
П -> оо.
Перечисленные типы сходимости связаны между со-
собой. Ясно, что из равномерной сходимости вытекает схо-
сходимость почти всюду и сходимость по мере.
Теорема 10. Если последовательность fn сходится
к / почти всюду на X и \х(Х)< «^ то fn~* f-
Доказательство. Пусть Лп(е)= {х^X: \fn(x) —
— f(x)\> г). Положим Вп(г) = (J Ak(e). Ясно, что
оо
fli(e) = ft(e) = ...=^B(e) = ... Пусть В(в) = Г|Д„(е).
71=1
Если жеВ(е), то о? принадлежит Ап(г) для сколь угодно
больших номеров п. Отсюда следует, что /п(#) не сходит-
сходится к f(x) при гг->«). Значит, множество В(г) имеет
меру нуль. Ho\i(B(e)) = lim\i(Bn(e)), так как (X)
(см. задачу 94). Так как ц,(Лп(е))< \х(Вп(г)), мы видим,
что \х(Ап(г))-+0 при п ->- оо, т. е. fn~*f- Теорема до-
доказана.
Итак, равномерная сходимость влечет сходимость поч-
почти всюду, а сходимость почти всюду влечет (на множе-
множестве конечной меры) сходимость по мере. Обратные
утверждения неверны (см. задачи 143, 144, 148). Инте-
Интересный и важный факт состоит в том, что эти утвержде-
утверждения становятся верными, если «подправить» последова-
последовательность {/J или множество X. А именно, имеет место
Теорема Егорова. Если fn—*f на X и \i(X)<
< оо? то для любого а > 0 существует такое подмножество
Еа а X, что ii (Eа) <о и fn=> f вне Еа.
Теорема И. Если /n-^ fна X, то существует та-
такая подпоследовательность {nh} натурального ряда, что
fnk -V / на X при к ->¦ оо,
Доказательство теоремы Егорова. Вос-
Воспользуемся обозначениями Ап(г) и Вп(г) из доказатель-
доказательства теоремы 10. Мы видели, что для любого 8 > 0
jn(J?n(e))-> 0 при п-+ оо. Поэтому для любого к найдется
такой номер N(k), что \i(BN{h)(l/k))<G/2k. Возьмем в
с»
качестве Еа множество [J Вщк)(\/к). Тогда \i(Ea)<G и
ft=i
38
при n>N(k) справедливо равенство !/*(#) — /(#) I <
вне Еа*
Доказательство теоремы 11. В тех же обо-
обозначениях, что и выше, выберем для каждого к такой
номер nh, чтоц(^пА A/&)) < 1/2\ Покажем, что подпосле-
подпоследовательность nh — искомая. В самом деле, множество тех
точек х, в которых /n/t (х) не стремится к f(x) при к-> °°,
содержится в Нт АПк (l/к) и, следовательно, имеет меру
нуль.
§ 3. Интеграл
1. Интеграл Лебега. Пусть заданы множество X, о-ал-
гебра 2t<=P(X) и счетно-аддитивная мера \х на SI. Изме-
Измеримая (вещественная или комплексная) функция / на I
называется простой, если она принимает не более чем
счетное множество значений. Такая функция может быть
записана в виде счетной линейной комбинации характе-
характеристических функций:
п,— X
причем можно предполагать, что все Ак измеримы и
fei
Замечание. Если все значения ch попарно различ-
различны, то измеримость Ак следует из измеримости /. Кроме
того, при этом условии представление / в виде D) одно-
однозначно. Однако мы предпочитаем не требовать разли-
различия сл.
Функция / вида D) называется суммируемой на X,
если сходится ряд
2КЫЛ). E)
Можно проверить, что это определение, как и следую-
следующее ниже определение интеграла, не зависит от выбора
представления D) (см. задачу 165). Пусть Лс$(; опре-
определим интеграл f(x) по множеству А формулой
= 2^ИПЛ). F)
Сходимость этого ряда вытекает из суммируемости /.
39
Совокупность всех суммируемых простых функций на
X мы будем обозначать S(X, \i) или просто S(X)r если
из контекста ясно, о какой мере \х идет речь. Когда нуж-
нужно подчеркнуть, что мы рассматриваем вещественные или
комплексные функции, мы будем использовать обозначе-
обозначения Sn(X), SC(X). Основные свойства простых функций
описывает
Теорема 12. 1) Множество S(X) является линей-
линейным пространством.
2) Соответствие / •-* J / {x) d\i является линейным
А
функционалом на S(X).
3) Соответствие А*-+ \ f (x) d\i является зарядом
А
на St.
4) Величина dx (/, g) = j | / (х) — g (x) \ d\i {x) обладает
х
всеми свойствами расстояния, кроме, быть может, отде-
отделимости.
*i (/. 8) для
5) Справедлива оценка j / d\i — J g d\i
I a a
всех /, g^ S(x) и всех А ^ St.
Доказательство. Утверждения 1), 2), 4) и 5)
выводятся непосредственно из определения (ср. с зада-
задачей 162). Докажем 3). Если / — характеристическая
функция некоторого множества В е St, то соответствие
A -^j/g?|i = \i(Af\ В) является счетно-аддитивной мерой и,
А
следовательно, зарядом на St. В силу задачи НО анало-
аналогичное утверждение верно для конечных линейных ком-
комбинаций характеристических функций и их пределов в
смысле расстояния dY. Теорема доказана.
В дальнейшем мы будем отождествлять функции, сов-
совпадающие почти всюду, как правило, не оговаривая этого
особо. После такого отождествления множество S(X)
превращается в метрическое пространство с расстоянием
dY. Легко убедиться, что это пространство может быть
неполно (см. задачу 166). Как мы увидим ниже, попол-
пополнение S(X, fx) допускает явную реализацию в виде не-
некоторого пространства функций на X (точнее, в виде
классов эквивалентности таких функций).
Определение. Функция / на X называется сумми-
суммируемой по мере \i, если существует такая последователь-
последовательность {/п}с=5(Х, |д), что
40
1) последовательность {/п} фундаментальна в S(X, \i)
в смысле расстояния dt;
2) fn -*¦ / почти всюду относительно меры jn на X.
Ясно, что если функция / суммируема, a g эквива-
эквивалентна /, то g также суммируема (достаточно рассмот-
рассмотреть ту же самую последовательность (/J). Пространство
классов эквивалентности суммируемых функций обозна-
обозначается Li (X, \i).
Покажем, что если [i(X)<oo, T0 всякая ограниченная
измеримая функция / принадлежит Ь{(Х, [х). В самом
деле, пусть Ekn(f)={x^X: kin < f(x)<(k+ 1)/п}. По-
оо
ложим fn {я) —^ ~ %е (х)-(Фактически, в силу ограни-
— со
ченности /, эта сумма конечна.) Ясно, что !/„(#) — f(x)\ <
< l/п, так что fn => f и тем более /п —* /• Кроме того,
{fj фундаментальна, так как dl (/n, fm) == J | /п (х) —
х
A 1 \
^ ~т Iя W* (^ы пользуемся утвержде-
утверждением в) задачи 162.)
Полученный результат допускает обобщение. Назовем
измеримую функцию / на X существенно ограниченной,
если найдется такая константа С, что \f(x)\^C почти
всюду на X.
Наименьшая из таких констант (докажите ее суще-
существование!) называется существенной верхней гранью
функции 1/1 и обозначается ess sup l/(^r) I. Величина
^»(/, g) = ess sup \f(x)— g(x) I обладает всеми свойствами
расстояния, кроме отделимости. Соответствующее фактор-
пространство, состоящее из классов эквивалентности су-
существенно ограниченных функций, обозначается L^ (X, \i).
Это пространство полно относительно расстояния cL.
Суммируемость существенно ограниченной функции на
множестве конечной меры доказывается так же, как и
суммируемость ограниченной функции. Поэтому при
loo мы имеем включение
Построим теперь интеграл для суммируемых функций.
Для этого нам понадобится
Лемма. Если {fj и {gn} — две фундаментальные по-
последовательности в S(X, pi), которые почти всюду сходят-
41
ся к одной и той же функции h^Lt(X, pi), то di(fn,gn)-+
-> 0 При П ~> оо.
Доказательство. Пусть фп = fn — gn- Тогда {фп} —
п.в.
фундаментальная последовательность в S(X, jli) и фп-^0.
Мы должны доказать, что j | фп|й(и->0. Предположим,
х
что это не так. Тогда найдется такое число б > 0 и такая
подпоследовательность {%}, что j | српн I ф ^ б для всех А.
X
Произведя перенумерацию и умножив все функции на
б, мы можем считать, что для исходной последователь-
последовательности выполняются неравенства J | фп | ф ^ 1 для всех п.
х
Теперь выберем из {фп} так называемую «быстро схо-
сходящуюся» подпоследовательность {фпй}г обладающую свой-
свойством
Для этого достаточно в качестве nh взять тот номер,
начиная с которого члены последовательности {фпУ от-
отстоят друг от друга не более чем на 1/2\ Произведя еще
раз перенумерацию, мы можем считать, что выполняются
оценки di(<pn, фп+i)^ 1/2п+2. Вспомним теперь, что <pt—
простая функция вида D):
<Pi W = i
Поскольку 2 | cA 1 (i (ЛА) = ) | ф! {x) I ф (x) ^ 1, существует
fc=i x
N
такой номер N, что 2 I ch If1 Иа)^3/4. Положим Л =
^, и пусть С= max |cft| = max| фх (а:) |- По тео-
Н
реме Егорова в множестве А можно указать такое под-
подмножество Е, что \i{E)< 1/DC) и фп=^0 на множестве
В = А\Е. Тогда j |фп|ф->0. С другой стороны,
в
Е
А
J | ф« | d|X — J I ф„+1 | ф < ^ (ф„, ф„+1)
42
Поэтому
n-1
_. -ll
*=Ч В В
n-l
J
^ 2
ft.—l
Полученное противоречие доказывает лемму.
Следствие. Функционал 1А (/)=)/ (х) d\i (x), опре-
А
деленный для любого А^ЧЬ на пространстве S(X, \х),
продолжается по непрерывности до функционала на про-
пространстве Li(Z, \i).
В самом деле, если f^Li(X1 \х) и {/п} — фундамен-
фундаментальная последовательность в S(X, \x), сходящаяся к /
почти всюду, то можно положить
1AU)= Hm
В силу доказанной леммы предел в правой части не
зависит от выбора последовательности {/п}.
Построенный таким образом функционал называется
интегралом Лебега от суммируемой функции / по множе-
множеству А и обозначается J f(x)d\i(x).
А
Теорема 13. 1) Множество Li(X^ \л) является ли-
линейным пространством.
2) Для любого множества А^% соответствие / •->
»-*• J / (x) d[i (x) является линейным функционалом на
U(X, ц).
3) Для любой функции /^Z/t(Z, \i) величина v(^4) =
= J / (х) d\i (х) является зарядом на ЭС.
А f
4) Величинаdx(f, g)=^) \f—g\d\i обладает на Ll(X,\i)
х
всеми свойствами расстояния.
Доказательство. Пусть / и g — суммируемые
функции, {/„} и {gn) — сходящиеся к ним почти всюду
фундаментальные последовательности простых функций.
Тогда последовательность (a/n + $gj фундаментальна и
43
сходится почти всюду к а/ + jig. Это доказывает утверж-
утверждение 1). Утверждение 2) следует из J (а/ + Р#) d\i =
= lim f (а/n + pgn) ф, = a lim f/nd[i + piim f gn d(x =
* a n a n a
= aj /dfi + pj gcfyi. Утверждение З) доказывается так
A A
A A
же, как аналогичное утверждение теоремы 12. Наконец,
4) выводится переходом к пределу из соответствующих
свойств di в пространстве S(X, \i).
Замечание 1. Ниже мы покажем, что простран-
пространство Z/t(X, pi) полно относительно расстояния dt. Отме-
Отметим, что во многих вопросах функционального анализа
пространство Z/t(X, \x) естественно возникает как попол-
пополнение того или иного класса функций относительно ин-
интегральной метрики di. Тот факт, что точки этого про-
пространства можно реализовать классами эквивалентности
суммируемых функций, играет подчиненную роль.
Замечание 2. Распространение интеграла с про-
простых функций на суммируемые можно проводить многи-
многими способами (см. по этому поводу задачи 171—173).
2. Функции ограниченной вариации и интеграл Лебе-
Лебега — Стилтьеса. Пусть ф и / — две вещественные функции
на отрезке [а, Ь]. Для любого разбиения T = (to = a<
< ti < ... < tn-i <tn = b) отрезка [a, b] и любого набора
точек l = (li, ..., |п), удовлетворяющего условиям ft_4 <
^ Ъ ¦< ti (г=1, 2, ..., п) составим интегральную сумму
Римана — Стилтьеса:
S (Г, 6, /, Ф) = j|/(b) [<р(*0 - q>(*i-i)]- G)
Назовем величину Х(Т) = max (ti — ^-i) диаметром
разбиения Т. Если существует предел
Inn S (Г, 6,/, Ф), (8)
то он называется интегралом Римана — Стилтьеса и обо-
обозначается
ь
Классическая теорема Стилтьеса утверждает, что для
существования этого интеграла достаточно, чтобы функ-
44
ция ф имела ограниченную вариацию на отрезке [а, Ь],
а функция / была непрерывна на этом отрезке. Отметим,
что в частном случае, когда ф(?)=^ интеграл Римана —
Стилтьеса превращается в обычный интеграл Римана.
Условие ограниченности вариации для ф является есте-
естественным: иначе уже для кусочно-постоянных функций
/, принимающих значения ±1, выражение G) будет не-
неограниченным. Поэтому в дальнейшем мы будем рассмат-
рассматривать в качестве ф только функции с ограниченной ва-
вариацией. Далее, если функции / и ф имеют общую точку
разрыва, то легко убедиться, что предел (8) не сущест-
существует. Если же функция / непрерывна в точке разрыва
функции ф, то значение ф в этой точке не влияет на
величину G) (см. задачу 194). Значит, мы можем в даль-
дальнейшем считать функцию ф непрерывной слева. Каждой
такой функции ф соответствует некоторый заряд v (см.
теорему 6).
Интеграл функции / по этому заряду называется ин-
интегралом Лебега — Стилтьеса. Мы будем обозначать его
ь
\ f (x) dv (х). Справедлива
а
Теорема 14. Интеграл Римана — Стилтьеса
ь
J / (х) dy (x) существует тогда и только тогда, когда /
а
ограничена и почти всюду непрерывна на [а, Ь] относи-
относительно меры Ivl. В этом случае определен также интег-
ь
рал Лебега — Стилтьеса J / (х) dv (x) и его значение совпа-
а
дает со значением интеграла Римана — Стилтьеса.
Доказательство. Необходимость. Предста-
Представим ф в виде суммы непрерывной функции ф0 и функции
скачков ф! (см. задачу 186). Тогда заряд v также будет
суммой зарядов v0 и v4. Уже отмечалось, что функция /
должна быть непрерывной в точках разрыва ф. Поэтому
множество Q/ точек разрыва / имеет нулевую lvj-меру.
Покажем, что оно имеет нулевую |vol-Mepy. Пусть
со/[а, р] означает колебание функции J на отрезке [a, [J],
а со/ (х) = lim со/ [х — е, х + е] — колебание / в точке х.
е-»о
Обозначим через ?2/F) множество точек, где колебание
функции / не меньше б:
Q/(8)=be[a, b]: со/(я)^6}.
45
00 / 1 \
Ясно, что Qf = U Qf(8)= U Q/f— ). Поэтому доста-
б>0 n=l v п I
точно доказать, что каждое из множеств Й/(б) при б>0
имеет lvol-меру нуль. Пусть задано г > 0. Существует
настолько мелкое разбиение Т = (t0 = а.< tt < ... < tn = b),
что
2l9o(*i)-To(«i-i)l>|vo|ae, Ц)-в.
Тогда
2 (I v01 ([«i-ь ti]) - | Фо (^) - Фо (*i-i) 1} < e. (9)
Измельчая, если нужно, разбиение Г, мы можем счи-
считать, что справедливо неравенство
п
2 «у [?i_b ЭД | ф0 (гг) — ф0 (^_х) | < ббг A0)
г=1
так как функция / интегрируема, а выражение в левой
части A0) можно представить в виде
sup [S (Г, lv /, ф) - S (Г, 6Я, /, ф)].
Рассмотрим те слагаемые в сумме A0), которые соот-
соответствуют отрезкам разбиения [U-i, U], содержащим
внутри себя точки множества Q/F). Для этих слагаемых
величина со/ [U-u ti] ограничена снизу константой 6. По-
Поэтому из A0) следует, что
где символ S7 означает, что сумма распространяется на
указанные выше отрезки разбиения.
Из (9) следует, что S7lv0l ([f<-i, ?i])<2e, т. е. суммар-
суммарная lvol-мера указанных отрезков меньше 2е.
Но эти отрезки покрывают все множество ?2/F), кро-
кроме, быть может, конечного числа точек, совпавших с
точками разбиения Т. Так как lvol-мера точки равна ну-
нулю (функция фо непрерывна), мы видим, что
lvo(Q/F))l <2e.
Достаточность. Пусть заряд v представлен в ви-
виде ц+ — li_, где |ы+ и \х! — конечные меры на отрезке
[а, Ь] и lv! = ц+ + \i—
Если Ivl (Qy) = O, то ^(Q/)=|i_(Q/) = 0. С другой
стороны, если функция ф [1+-интегрируема и ^--интегри-
46
руема, то она и v-лштегрируема. Это показывает, что
в доказательстве достаточности мы можем ограничиться
случаем положительного заряда (или монотонной функ-
функции ф). В этом случае, как и в обычной теории интег-
интеграла Римана, мы можем воспользоваться критерием Дар-
Дарбу: для интегрируемости / достаточно, чтобы нижняя
грань по Т выражений в левой части A0) была равна
нулю.
Пусть задано е > 0. Обозначим через М колебание /
на [а, Ь] и через V вариацию функции ф на [а, Ь]. Мно-
Множество ?2/F) при любом 6 >0 имеет меру нуль. Кроме
того, это множество замкнуто и, следовательно, компакт-
компактно. Значит, его можно покрыть конечным числом отрезков
общей jn-меры <г/BМ). На оставшейся части отрезка
[а, Ь] колебание / во всех точках меньше б. Легко пока-
показать (аналог теоремы о равномерной непрерывности функ-
функции, непрерывной на отрезке), что существует такое раз-
разбиение этого множества на конечное число отрезков, что
колебание / на каждом из отрезков разбиения будет ^б.
Выберем в качестве б величину e/BF). Тогда для по-
построенного разбиения Т левую часть A0) можно оценить
константой М' ^ + 2у*У == ?* Теорема доказана.
Для практического вычисления интегралов Римана —
Стилтьеса и Лебега — Стилтьеса удобно пользоваться
свойствами, описанными в задачах 191, 194, 195, 196.
3. Свойства интеграла Лебега. Некоторые важные
свойства интеграла Лебега были уже описаны выше (см.
теорему 13); мы будем постоянно пользоваться этими
результатами. Здесь мы рассмотрим свойства интеграла,
связанные с предельными переходами, произведениями
мер и дифференцированием зарядов.
Теорема 15. (Теорема Лебега об ограниченной схо-
сходимости.) Пусть {/„} — последовательность ^-суммируе-
^-суммируемых функций на множестве X, ограниченная по модулю
фиксированной неотрицательной [х-суммируемой на X
функцией ф и сходящаяся \х-почти всюду на X к функ-
функции /.
Тогда f ^-суммируема на X и
lim )/пф= \fd\i
»-"»а а
для любого ^-измеримого множества А.
47
Доказательство. Положим для любого измери-
измеримого множества A v (А) = j фф (х). По теореме 13 v —
А
конечная мера на X.
Лемма. Если функция g измерима и ограничена на
X, то функция / = ф# ^-суммируема и J / (х) ф (х) =
А
— \ g (x) dv (х) для любого ^-измеримого множества А.
А
Доказательство. Рассмотрим множество М тех
функций g на X, для которых утверждение леммы спра-
справедливо. Очевидпо, М содержит все характеристические
функции измеримых множеств. В самом деле, если g = %в,
то
I V(A П В) =
АГ)?
Значит, Д/ содержит и конечные линейные комбинации
таких функций. Пусть теперь g — любая ограниченная
измеримая функция на X. Положим g- (х) =— [гг^ (х)]г
g+ (х) = g_ (я) + -^. Тогда g±
Поэтому J g-dv = J ф^_ (ж) ф (х) <J ф^ф< j ф?+ф = j g+dVs
А А А А А
При п -*¦ оо первый и последний члены этого соотноше-
соотношения стремятся к J grfv. Значит, g e Д/? и лемма доказана.
А
Вернемся к доказательству теоремы 15. Определим
функции
_ {fn(x)/y{x), если ф^^О^
gnW~l 0, еслиФИ = 0,
f/ И/Ф И, если ф (х) ф О,
gW~ I 0, если ф(х) = 0.
По предположению теоремы, функции ?л(.г) обладают
свойствами \gn(x)\ < 1, ^n(^) "^ g. Мы должны доказать,
что lim j /п(#)ф == /ф.В силу леммы, это равносиль-
п^°°А А
но утверждению lim \gn (x) dv = lgdv. Таким образом, мы
п-о а а
свели доказательство теоремы Лебега к частному случаю,
48
когда мера пространства X конечна, а рассматриваемые
функции ограничены по модулю одной и той же констан-
константой. В этом случае утверждение теоремы без труда выво-
выводится из теоремы Егорова.
Теорема 16. (Теорема Б. Леей о монотонной схо-
сходимости,) Пусть {/„}—монотонно возрастающая последо-
последовательность ^-суммируемых функций на множестве X.
Положим / (х) = lim fn{x)(допуская значение +«>).
П-»оо
1) Если интегралы) fn(x)d\i(x) ограничены в совокуп-
кх
ности, то j(x) суммируема и \ f(x)d\i(x)= lim J fn(x) d\i (x).
X П-+00 x
2) Если lim ]/п(х)ф(х) = + oo2 то функция f(x) не-
суммируема.
Доказательство. 1) Вычитая из всех /„ и из /
функцию /i, мы можем считать, что /„ > 0 и / > 0. Пусть
Е — множество, где f(x) принимает значение +°°. Тогда
Е = П U Enu, где ENn = {igI: /n(о:)>ЛГ}. Имеем
JV n
(ENn). Так как J /n (л:) ф ^ С для всех nf
X
мы получаем \i(E^n)^.C/N; отсюда [i(E)= lim lim
= 0.
Итак, функция / почти всюду конечна. Докажем, что
она суммируема. Проще всего воспользоваться результа-
результатом задачи 173. Пусть А — такое множество конечной
меры, на котором f(x) ограничена сверху. Тогда
А п^°° А п->°° X
что и доказывает суммируемость /. Оставшаяся часть
утверждения 1) и утверждение 2) вытекают из теоремы
Лебега об ограниченной сходимости.
Лемма Фату. Если последовательность {fn} ^-сум-
^-суммируемых неотрицательных функций обладает свой-
свойствами:
1) » fn (#) d\i ^ С для всех щ
х
2) /п(^)~>/(^) почти всюду на X,
то / — ii-суммируемая функция и ) f d\x ^ С,
х
4 А. А. Кириллов, А. Д. Гвишиани 49
Замечание. Сходимость fnd\i-+- ) fd\i в условиям
X X
леммы Фату может не иметь места.
Доказательство. Заменим предельный переход
/п -* / двумя монотонными предельными переходами
А именно, положим
gkn (х) = min {fn (x), fn+i (xI ..., fn+h (x)},;
gn(x) = limgkn(x).
Тогда lim gn (x) = f (x) для почти всех х. Из монотонности
интеграла следует, что ] gnd^^C^ а из теоремы 16 выте-
х
кает, что / суммируема и ) / d\i ^ С, что и доказывает
лемму.
Выведем из полученных свойств интеграла упоминав-
упоминавшуюся выше полноту пространства L^X, \x).
Теорема 17. Пространство L{(X, \i) полно.
Доказательство. Пусть ifj — фундаментальная
последовательность в L^X, \x). Переходя, если нужно,
к подпоследовательности, можно считать, что {fj облада-
обладает свойством di(fn, /n+i)< l/2n. Положим ф± = /lf фп =
оо
¦= /п — /n-i при п > 2. Ряд 2 | ф?г (я) I по теореме 16 схо-
п=1
дится всюду к некоторой почти всюду конечной сумми-
суммируемой функции ф(х). Значит, ряд 2 фп (х) сходится поч-
почти всюду к некоторой функции f(x). Отсюда вытекает,
что /п "^ / почти всюду на X. Кроме того, все функции /п
ограничены по модулю функцией ф(#). По теореме об
ограниченной сходимости (см. теорему 15) lim | /п (х) —
|=O. Значит, /„-> / в пространстве ^ p)
Теорема доказана.
Еще одно полезное свойство интеграла Лебега — его
так называемая абсолютная непрерывность.
Теорема 18. Пусть f^L^X, \х). Тогда для любого
е > 0 существует такое б > 0, что из \i(A) < б следует
|J|
Доказательство. Утверждение теоремы означает
по существу непрерывность отображения //: А -> 1 / (х)
А
60
действующего из метрического пространства Ь(Х) изме-
измеримых множеств (см. задачу 95) в R. Если % —- характе-
характеристическая функция измеримого подмножества конечной
меры в X, то отображение /х, очевидно, непрерывно. То
же самое верно для //, если / — линейная комбинация
характеристических функций. Далее, если /п -* / в
Li(X1 ц), то Ifn-*If равномерно на L(X). Остается вос-
воспользоваться известным фактом: равномерный предел
непрерывных функций является непрерывной функцией.
Теорема доказана.
Вернемся теперь к доказательству теоремы 7 § 1, п. 3,
о произведении мер. Пусть (X, S, \х), (У, Г, v) означают
то же, что и в указанной теореме. Для каждого множе-
множества С =*АХВ из полукольца S X Т положим /с (х) =
= Ха (х) v (В). Ясно, что (|i X v) (С) = \i (A) X v (В) =
= J/с(#)Ф- Если множество С представлено в виде
х
00
С = Ц Сhi Ch^S X Тх то из счетной аддитивности v
вытекает равенство /с (%) = 2 fck (^)-По теореме Лебега
об ограниченной сходимости отсюда следует равенство
/с (*) Ф (х) = 2 f fck (x) d\i (x)f
J
х
и значит,
(I* X v) (С) = 5 ((i X v) (Ck).
Теорема 7 доказана.
Изучим подробнее отображение С »->• /с, определенное
выше. Распространим его на кольцо R(SXT) по фор-
формуле
/ п =2 /СА.
II ft
Легко проверяется оценка
IIК - /с2 ||li(x^) < (|i X v) (С, Л Ся).
(В самом деле, если Сг = Ax\_j В, С2 = А2 |_j В, где
Б = С1 П С2, то /Cl — /с2 = /^j — /л2, /c^Cg = /лх + /л2.)
Поэтому соответствие d~+fc продолжается до отобра-
отображения всей о-алгебры (\х Xv)-измеримых множеств
4* 51
L(XXY) в Li(X, \x) по формуле /nmcn = lim fcn (первый
n n
предел рассматривается bL(XXF), второй — в Li(X, \x)).
Лемма. Пусть СеL(XXY). Для почти всех х^Х
множество Сх с: У, задаваемое формулой С* = iy e У:
(#? у)ЕС}} измеримо по мере v u v(Cx) = /c(.r).
Доказательство. Для элементарных множеств
(т. е. множеств из кольца R(SXT)) это верно по опре-
определению /с. Далее, если {С(п)} — монотонная последова-
последовательность множеств, то в силу счетной аддитивности меры
v справедливо равенство v(lim C$cn)) = lim v (C^n)). По-
n n
этому свойство v(Cx) = fc{x) сохраняется при монотон-
монотонных предельных переходах. Но всякое измеримое мно-
множество С может быть с точностью до множества меры
нуль получено из элементарных множеств двумя моно-
монотонными предельными переходами. В самом деле, пусть
Сп — элементарное множество, аппроксимирующее С с точ-
оо оо
ностью до 2"п по мере [iXv. Положим С = П U Сп+ъ-
П=1 /1=1
Тогда (fx X v) Л U Cn+h = 0, foX v) ( fj
Отсюда ([xXv)(C?AC) = 0.
Значит, fc и /g- совпадают почти всюду и, следователь-
следовательно, для почти всех х&Х fc {х) = /g- (ж) = v(Сх) = v(Сж).
Лемма доказана.
Теорема 19. Пусть \х и v — а-конечные меры,
С — (jlx X v)-измеримое подмножество в X X У. Положим
Сх= {уеУ: (#, i/)eC}, Тогда для \х-почти всех х&Х
множество Сх v-измеримо, функция fc(x) = v(Cx) ^-изме-
^-измерима и справедливо равенство
(\iXv)(C)=Uc(x)dlx(x), (И)
в котором обе части могут одновременно принимать зна-
значение +оо.
Доказательство. Если множество С имеет конеч-
конечную меру, то утверждения теоремы вытекают из дока-
доказанной выше леммы и из того факта, что равенство A1)
сохраняется при переходе к пределу (слева в простран-
пространстве L(XXY), справа в пространстве Lx (X, jli)).
Если мера множества С бесконечна, то существует
возрастающее семейство подмножеств копечной меры
Сп^С, для которого [)Сп = С и (fi X v) (С„)-* °°. Тогда
52
/с (х) = lim /с„ (х) и
П
Поэтому /с измерима и несуммируема. Теорема до-
доказана.
Эта теорема, в частности, обосновывает хорошо изве-
известный способ вычисления площадей плоских фигур (со-
(соответственно объемов пространственных тел) с помощью
интегрирования длин (соответственно площадей) их се-
сечений.
Замечание 1. Поскольку пространства (X, \х) и
(У, v) входят в условие теоремы 19 симметрично, заклю-
заключение теоремы останется верным, если поменять их ме-
местами. Таким образом,
OiXv)(C) = J^(c;)dv'y)t (И')
Y
где Су = {х^ X: (#, i/)gC}. Отсюда следует также, что
{Cy)dv^). A2)
Замечание 2. Аналогичная теорема справедлива
для произведения любого конечного числа пространств.
В случае трех пространств (X, jli), (F, v), (Z, Я) она
имеет вид
(li X v X Я) (С) -
= J ^(Cxfy)d(|iXv)(«>j,) = J(^Xv)(Cz)^(z)l A3)
XXY Z
где
Теорема Фубини. Пусть f(x, у)—суммируемая
функция на произведении пространств (X, \i) и (У, v).
Тогда справедливы следующие утверждения:
1) Для \х-почти всех х^Х функция f(x, у) суммиру-
суммируема на У и ее интеграл по У является суммируемой
функцией на X.
2) Для v-почти всех y^Y функция f(x, у) суммиру-
суммируема на X, а ее интеграл по X является суммируемой
функцией на У,
53
3) Справедливы равенства
f(x,y)d(liXv)(x,y) =
XxY
= j (J
J / (*,j,) dv (у) j dp (x) = J f f / (*,*,) ф (*)) dv (y). A4)
4) Для неотрицательных (fxXv) -измеримых функций
существование одного из повторных интегралов в A4)
влечет суммируемость f на XX Y.
Доказательство. Разложение / = /+->/_ сводит
доказательство к случаю неотрицательной функции. Рас-
Рассмотрим произведение пространств (X, |i), (У, v), (КД),
где Х = dz — обычная мера Лебега, и множество С с X X
X У X R, заданное условием
С = {(я, ^ z)e=XX7XR: 0<2</(л:, г/)}.
Применим к этому случаю соотношение A3). Имеем
G* = {zeR: 0<2</(^, у)}; Х(Сху) = /(^, I/),
(^, у)};
Отсюда непосредственно вытекают все утверждения тео-
теоремы.
Отметим существенность условий суммируемости / в
пп. 1), 2), 3) и условия неотрицательности в п. 4).
Определение. Пусть заданы множество X, о-алгеб-
ра §(с:Р(Х), о-конечная мера jut и конечный заряд v на
St. Заряд v называется абсолютно непрерывным относи-
относительно [х, если из условия \х(А) = 0 следует v(-4) = 0. Два
заряда Vt и v2 называются эквивалентными, если условие
|vil(-4) = 0 равносильно условию lv2l(<4) = 0.
Теорема Радона —Никодим а. Всякий конеч-
конечный заряд v, абсолютно непрерывный относительно меры
[X, имеет вид
v(A) = $f(x)dii(x), A5)
А
где j—некоторая функция из L{(X, \i). Функция f (как
элемент пространства /^(Х, fx)) однозначно определяется
зарядом v.
Доказательство. Для любого рационального чис-
числа г положим vr = v — rfx. В силу результата задачи 122
54
множество X представляется в виде Ar \__\АГ так, что за-
заряд vr неотрицателен на А* и неположителен на А^. Для
любого вещественного числа с положим Ас = (J Af. Ясно,
г>с
что {Ас} — убывающее семейство измеримых множеств:
ACiczAC2 при с1>с2. Покажем, что Л.» = [) Ас и до-
дополнение к Аоо = (J Ас имеют меру нуль. В самом деле,
с
если А сгЛ-оо, то vr(A)^0 для всех г, что возможно лишь
при \х(А) = 0. Если же А^ХХА^, то vr(-4)^0 для всех
г, что также возможно лишь при |л(Л) = 0. Далее, семей-
семейство {AJ по построению непрерывно справа: Ас =
= U Ас+е. Поэтому существует такая функция / на X,
8>0
что Ас = {х^Х: f(x)>c]. Функция / измерима, так как
все множества Ас измеримы по построению.
Пусть теперь Е — любое множество конечной меры.
Тогда (см. задачу 163)
Г
/ (х) ф = lim ^ 7 И [Е П Ak\Ak+1\ =
= lim ^ ^ И ^ Л
С другой стороны, по определению Ае, справедливы
оценки
n
п
Чтобы доказать суммируемость / на Е, положим Е =»
= Е+ 1—1 ?_, где для всех х^Е+ f(x)>0, а для всех
х<^Е- f(x)<0. Проведенное рассуждение показывает,
J
что J
Е+
+
образом, f^Li(E, \i). Это доказывает A5) для множеств
конечной меры. Действительно,
2
"I
так как v абсолютно непрерывен, а ц (Х\Х) = 0. Теперь
55
из копечпостп заряда v (см. задачу 120) вытекает сум-
суммируемость и справедливость A5) в общем случае. Един-
Единственность / (как элемента L^ (X, jn)) следует из резуль-
результата задачи 168. Теорема доказана.
Следствие. Если \х — мера на X, v — конечный за-
заряд, абсолютно непрерывный по мере jut, то для любого
е>0 существует такое б > 0, что из \i(A)<8 следует
М(А)<в.
В самом деле, по теореме Радона — Никодима суще-
существует такая функция f^L^X, |i), что v(i4)=J/dfi.
А
Тогда | v | (А) — j | / | d\L и утверждение вытекает из
А
теоремы 18.
ГЛАВА III
ЛИНЕЙНЫЕ ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
И ЛИНЕЙНЫЕ ОПЕРАТОРЫ
§ 1. Нормированные пространства
1. Основные определения. Наиболее интересные и по-
полезные математические понятия получаются, когда на
одном и том же множестве вводят несколько структур,
согласованных между собой. Пусть, например, на мно-
множестве L заданы структура линейного пространства (ве-
(вещественного или комплексного) и структура метрического
пространства. Естественные условия согласования состоят
в том, чтобы выполнялись соотношения:
1) d(x, y) = d(x + а, у + а) для любого ае?;
2) d(Xx, ky)=\X\d(x, у) для любого числа X из ос-
основного поля /?(=R или С).
Из первого условия видно, что расстояние d(x, г/),
т. е. функция на LXL, полностью определяется функ-
функцией р(х) = d@, x) на L, а именно d(x, y) = р(х — у).
Функция р обладает следующими свойствами, выте-
вытекающими из 1), 2) и из свойств расстояния:
3) р(х)^0, причем р(х) — 0 только при х==0;
4) ()\\()
5)
Такие функции получили название нормы, а линейные
пространства, снабженные нормой,— название нормиро-
56
ванного пространства. Каждое нормированное простран-
пространство является метрическим, а значит, и топологическим
пространством. Тем самым к нормированным простран-
пространствам применимы методы и алгебры и анализа, что и
объясняет богатство теории этих пространств и большое
число их приложений.
Определение. Банаховым пространством называ-
называется полное нормированное пространство.
Это понятие, введенное в 1931 г. львовским математиком Сте-
Стефаном Банахом, быстро превратилось в рабочий инструмент,
используемый почти во всех разделах математики. С него начина-
начинается история функционального анализа как самостоятельной об-
области. Изучение банаховых пространств и линейных операторов
в них составляет основу линейного функционального анализа и
продолжается до сих пор. Кроме того, в банаховых пространствах
справедливы теоремы об обратной и неявной функциях, на кото-
которые опираются многие результаты нелинейного функционального
анализа.
Приведем основные примеры нормированных и бана-
банаховых пространств.
Начнем с конечномерных пространств. Самым изве-
известным примером банахова пространства является про-
пространство 12{п, К), К = Л или С. Оно состоит из всех
векторов x = (xi, ..., хп)^Кп, а норма в нем определя-
определяется формулой
1*1= V 21
A)
Если /f = R, а /г = 1, 2 или 3, мы получаем хорошо из-
известные из элементарной геометрии евклидову прямую,
плоскость или пространство.
Естественным обобщением этого примера является
пространство 1Р{п, К). Оно также состоит из векторов
х е Кп, а норма имеет вид
п \1/р
) • B)
При р ->• оо выражение в правой части имеет предел,
равный
1*1,0= max \xk\. B')
Оказывается, величина ЫР обладает свойствами нор-
нормы, когда р принадлежит сегменту [1, оо], включая кон-
57
цы. Доказательство этого утверждения не очевидно и
приведено в решении задачи 217.
Пространство 1Р(п, К) допускает бесконечномерные
обобщения. Простейшее из них — пространство 1р(К)>
состоящее из всех последовательностей {xj в К со свой-
оо
ством 2l^n|P<oo. (Для р = о° обозначим через 1оо(К)
п=1
пространство ограниченных последовательностей в К.)
Положим
\\Ы\\Р = B I *» гI/Р для 1 < р < «о, C)
\п=1 /
К^пЦоо = SUP | Хп | ДЛЯ р = 00. C')
п
Оказывается (см. задачи 218, 221), что 1Р (К) — бана-
банаховы пространства для всех р е [1, оо].
Пусть теперь X — пространство с мерой [х. Обозначим
через LP(X, \х) A < р < оо) пространство классов эквива-
эквивалентности измеримых функций (две функции эквивален-
эквивалентны, если они совпадают почти всюду по мере |я) на X,
для которых р-я. степень суммируема по мере jut.
Положим для /eLp(Z, fx)
Определение пространства ЬЖ(Х, jli) несколько слож-
сложнее. Оно сострит из всех существенно ограниченных из-
измеримых функций на I с нормой
||/Цоо = esssup|/|. D')
х
Пространства ЬР(Х, jn) также являются банаховыми
при 1 ^ р ^ оо.
Еще один важный пример. Пусть X — любой компакт,
С(Х, К) — пространство непрерывных /?-значных функ-
функций на X (здесь, как обычно, К = Л или С) с нормой
К/1 = max |/ (х) |. E)
Х
Из основных свойств компактов вытекает, что правая
часть в E) существует. Легко проверяется, что она обла-
обладает свойством нормы. Кроме того (см. задачу 219), про-
пространство С(Х, К) оказывается банаховым. Символ К
часто опускают. Так, С [а, Ь] означает пространство не-
58
прерывных функций на отрезке [а, Ь] с вещественными
или комплексными значениями в зависимости от кон-
контекста.
Большой запас нормированных (но, вообще говоря,
не банаховых) пространств получается, если рассматри-
рассматривать линейные подпространства одного из введенных вы-
выше пространств. Отметим среди них подпространство
1р(К) финитных последовательностей в 1Р(К) (т. е. по-
последовательностей, у которых лишь конечное число эле-
элементов отличны от нуля) и подпространство &*[а, b]cz
а С [а, 6], состоящее из многочленов от одного перемен-
переменного х с нормой
|Р|= max \P(x)\.
2. Сопряженные пространства. Основным объектом
изучения являются не сами нормированные пространства,
а операторы в них, т. е. отображения одного простран-
пространства в другое. Среди них особую роль играют линейные
непрерывные функционалы.
Определение. Линейным непрерывным функцио-
функционалом на нормированном пространстве L называют ли-
линейное непрерывное отображение L в основное поле К.
Совокупность всех линейных непрерывных функцио-
функционалов на L обозначается V и называется сопряженным
пространством к L. В дальнейшем элементы U будут
называться просто функционалами.
Ясно, что если L — линейное пространство над К, то
V — также линейное пространство над К: линейные не-
непрерывные отображения можно складывать и умножать
на числа. Кроме того, в V можно ввести норму, полагая
F)
(ср. с задачей 229), где WzWL означает норму элемента
Теорема 1. Для любого нормированного простран-
пространства L сопряженное пространство V полно (и, следова-
следовательно, является банаховым).
Доказательство. Пусть {fj — фундаментальная
последовательность в L''. Из определения нормы F) вы-
вытекает полезное неравенство
G)
59
Отсюда видно, что для любого x^L числовая после-
последовательность {{п{х)} фундаментальна и, следовательно,
имеет предел, который мы обозначим f(x). Линейность
построенной функции x-^f(x) получается предельным
переходом из линейности /п. Докажем непрерывность /.
Для этого воспользуемся следующим утверждением, пред-
представляющим самостоятельный интерес.
Теорема 2. 1) Непрерывность линейного функцио-
функционала f на нормированном пространстве L равносильна его
ограниченности на единичном шаре этого пространства,
2) Справедливо равенство
\i\v= sup |/(s)|. (8)
Последовательность {fj фундаментальна; поэтому
последовательность ||/п||г/ ограничена. Значит, ограни-
ограничены значения jn{x) на единичном шаре пространства L,
а стало быть и значения предельной функции f{x). Это
доказывает, что f^L'. Далее, для любого 8 >0 и доста-
достаточно больших пит справедливо неравенство II/„ — /JI <
<е. Поэтому для х из единичного шара \fn(x) —fm(x)\ <г.
Переходя к пределу при т-+°о, получаем, что II/п — /II <
< е для достаточно большого п. Тем самым /п ->• / в L'
и теорема 2 доказана.
Линейные нормированные пространства и линейные
непрерывные операторы в них образуют категорию N,
а банаховы пространства — подкатегорию В в N. Соответ-
Соответствие L -*¦ U можно продолжить до контравариантного
функтора из N в В. А именно, каждому оператору
A: Li~+L2 поставим в соответствие сопряженный опера-
оператор А'\ Ь2-+Ьх, действующий по формуле
, (9)
где /е= Z/2, ^eii-
Для любого нормированного пространства L сущест-
существует естественное отображение его во второе сопряжен-
сопряженное пространство L"=(L')': каждый элемент x^L за-
задает функционал Fx на V по формуле /гх(/) = /(^), это
отображение является изометрическим вложением (см.
теорему 8). Если оно является изоморфизмом на все L",
то пространство L называется рефлексивным.
3. Операторы в нормированных пространствах. Сово-
Совокупность линейных непрерывных операторов из норми-
нормированного пространства Lx в нормированное простран-
пространство Ьг обозначим 3?(Lu L2). Ясно, что S {Lu L2) —
60
линейное пространство над основным полем К. Введем в
SB (Li, L2) норму, полагая
Заметим, что это определение является обобщением F),
поскольку при L2 = K SB (Lu L2) превращается в LL.
Полезным следствием формулы A0) является неравен-
неравенство
,L2).|H|v A1)
обобщающее G). Индексы у норм в этом неравенстве
часто опускаются (обычно их легко восстановить из кон-
контекста), и неравенство (И) приобретает легко запоми-
запоминающийся вид \\AxW <; IL4II1Ы1.
Теоремы 1 и 2 для линейных функционалов обобща-
обобщаются на случай линейных операторов. А именно, спра-
справедливы
Теорема 3. Если Lj — нормированное, a L2 — бана-
банахово пространство, то 9? (L{, L2) — банахово пространство.
Теорема 4. Пусть Li и L2 — нормированные про-
пространства.
1) Линейный оператор А из Li в L2 непрерывен тогда
и только тогда, когда ограничены в L2 его значения на
единичном шаре в L{.
2) Справедливо равенство
И||= supUArfl. A2)
11*11 <i
Доказательства этих теорем полностью аналогичны
доказательствам теорем 1 и 2. Мы оставляем их читателю.
Замечание. Линейный оператор А, для которого
ограничена правая часть в A2), называется ограничен-
ограниченным. Не следует путать этот термин с ограниченностью
А как функции из Lt в L2 (в этом смысле линейный
оператор никогда не бывает ограниченным, если только
он не нулевой).
Помимо обычных свойств нормы в линейном прост-
пространстве операторная норма обладает полезным мульти-
мультипликативным свойством: если Lu L2, L3 — нормированные
пространства, A=3?(L2, L3), В = SB (Llf L2), то АВ s
S>(Llf L,) и
WABW^WAW -WBW. A3)
61
4. Конструкции банаховых пространств. Приведем те-
теперь несколько конструкций, позволяющих строить но-
новые банаховы пространства из имеющихся.
1. Пополнение любого нормированного пространства
является банаховым пространством.
2. Если L — банахово пространство, a Lo — его замкну-
замкнутое подпространство, то Lo само является банаховым про-
пространством.
3. Пусть Lo — замкнутое подпространство в банаховом
пространстве L, L{ = L/Lo — соответствующее факторпро-
странство. Тогда L{ является банаховым пространством
относительно нормы \\x\\L = inf ||y\\L. (См. задачи 256,
257.)
4. Пусть Li и t2 — два банаховых пространства, Li ®
® L2 — их алгебраическое тензорное произведение, (На-
(Напомним определение Lt ® L2 (см. также задачу 56). Пусть
Li О L2 — совокупность всех формальных линейных ком-
комбинаций символов х П г/, где х^ Lu у е L2; Lt ° L2 — под-
подпространство в Lt ? L2, порожденное выраженияхми вида
а) (#i + я2) Е # — ?i ? у - я2 ? г/,
б) хП(У1 + уг)-хиух-хиУ1,
в) Х^ ? ^лг/ — Хц (.г ? г/); X, \х е Z.
Тогда L,® L2=(L1DL2)/(L1oL2). Если ^t,, i/gL2,
то класс эквивалентности, содержащий а:Пг/, обознача-
обозначают я ® г/.)
Замечание. Не следует думать, что каждый эле-
элемент пространства L{ ® L2 имеет вид х® у (см., напри-
например, задачу 262).
Если Li конечномерно и имеет базис еи ..., еп, то,
как легко проверить, каждый элемент а ^ Lt ® L2 одно-
71
значно записывается в виде 2 *ь ® Уь« Если L2 также
конечномерно и имеет базис /i, ..., /m, то элементы е{ ® /^
A ^ i < w, 1 ^ у ^ га) образуют базис в Lj ® L2. В Lj ® L
можно различными способами вводить норму. При этом
естественно потребовать, чтобы эта норма р обладала
свойством р(х® y) = Pi{x)p2(y), где x^Lu у е= L2, a /?!
и р2 — нормы в пространствах L{ и L2 соответственно.
Такие нормы называются кросс-нормами.
Заметим теперь, что пространство Lx <g> L2 естественно
отображается в {Ь^®Ь2)'\ элементу fx ® /2 е ЬХ®Ь'2 со-
соответствует линейный функционал / на Lt ® L2, опреде-
определяемый формулой f(x®y) — fi(x)-f2(y). Потребуем от
62
2
нормы р в Li ® Ьг выполнения условия р' (/) = pi (fx) X
Хр2 (/г)? ГДе/Л Pi» P2~"нормы в пространствах (Lt®L2)',
Lx, L2 соответственно. Такие нормы называют равномер-
равномерными кросс-нормами. Оказывается, что среди всех кросс-
норм есть наибольшая — она обозначается рх <?> р2, а сре-
среди равномерных кросс-норм есть наименьшая — она обо-
обозначается рх ® р2. Пополнения Z/4 ® L2 по этим нормам
обозначаются L1 ® L2 и Lx ® L2 соответственно.
5. Если L, и L2 — банаховы пространства, то в их
прямой сумме Li Ф L2 можно определить норму формулой
lbt Ф sall = \\xj\i + 11х2112.
Полученное пространство также будет банаховым.
Отметим, что топологически эквивалентное (но не изо-
метричное) пространство можно получить, если поло-
положить
, ад2).
§ 2. Линейные топологические пространства
1. Топология, выпуклость и полунормы. Мы будем
рассматривать линейные пространства L над полями R
и С. В тех случаях, когда утверждение не зависит от
выбора поля, мы будем вместо R или С писать К. Если
А я В — два подмножества в L, а X и \х — два числа из К,
то через ХА + \хВ мы будем обозначать множество эле-
элементов zei вида Хх + \iy, где х е А, у е J5.
Определения. Отрезком (соотв. интервалом) в L
с концами в точках х и г/ называется совокупность точек
zeL вида z = та + A — т)г/ @ ^ т^ 1) (соотв. 0< т< 1).
Множество Z? <= L называется выпуклым, если оно
вместе с любыми двумя точками содержит целиком отре-
отрезок с концами в этих точках.
Для любого множества Е <= L существует наименьшее
выпуклое множество, его содержащее (см. задачу 281).
Оно обозначается со(Е) и называется выпуклой оболоч-
оболочкой множества Е. Множество Е с= L называется уравно-
уравновешенным, если для любого а^К, \а\ < 1, справедливо
включение аЕ с Е.
Множество Е d L называется поглощающим, если
U kE = L.
63
Полунормой называется функция р на L, принимаю-
принимающая неотрицательные значения (допускается значение
р(х) = оо) и обладающая свойствами:
1) Р(^)= Шр(х), Х^К, x^L. Считается, что
О • оо = 0 (однородность);
2) р(х + у)< р(ос) +р(у) (полуаддитивность).
Из условия 1) следует, что /?@)==0.
Нормой называется такая полунорма, которая для лю-
любого ненулевого x^L принимает конечное ненулевое
значение.
Единичным шаром для полунормы р называется мно-
множество Вр = {х е L: р(х)<:1}.
Функционалом Минковского множества В с= L называ-
называется функция рв (я) = inf Я (если х&\В ни при ка-
ком Х>0, то полагаем рв(х) = +°°).
Оказывается, соответствия р *— Вр и В •-•> рв почти об-
ратны друг к другу, если р пробегает множество полу-
полунорм в L, а В — множество выпуклых уравновешенных
множеств. Оговорка «почти» связана с тем, что разные
множества В могут иметь один и тот же функционал
Минковского рв (см. задачу 280).
Теорема 5. 1) Если р — полунорма, то ее единич-
единичный шар Вр — выпуклое уравновешенное множество.
2) Если р —норма, то Вр — поглощающее множество,
не содержащее целиком никакой прямой (т. е. одномер-
одномерного подпространства) в L.
3) Если В — выпуклое уравновешенное множество, то
рв — полунорма.
4) Если В — выпуклое, уравновешенное, поглощаю-
поглощающее множество, не содержащее ни одной прямой, то рв —
норма.
5) Для любой полунормы р справедливо равенство
Рвр = р.
Доказательство. Утверждения 1) и 2) непосред-
непосредственно вытекают из определений. Докажем 3). Однород-
Однородность функционала рв очевидна. Пусть В — выпуклое
множество. Докажем, что рв — полуаддитивная функция.
Пусть х, у е L. Если рв(х) или рв(у) бесконечны, дока-
доказывать нечего. Если рв(х) = 0, то Хх^В при всех Х>0.
Поэтому из г/^В следует, что A — е) у + х = A —е) у +
+ ?'-еВ при 1 > е > 0. Таким образом, неравенство
рв(у)<1 влечет рв(A — г)у + х)^ 1 при всех е^@,1).
Отсюда следует, что рв(у 4- х)^ рв(у). Остается исследо-
64
вать случай, когда рв(х) и рв(у) отличны от нуля. Рас-
1—8 1-е гт
смотрим векторы хе = —— х и уг = —т— у. По опреде-
Рв v*J Рв \У)
лению функционала Минковского имеем хе, у*^В при
е > 0. Так как В выпукло, отсюда следует, что тхг +
+ A — ч)уге=В при 0^т^1. В частности, при т =
= —гтн гт получаем — ~ 8 (х + г/) е В. Зна-
Рб (*) + Рв (у) Рв (*) + Рв (У)
чит, рв (х + у) ^ з : при е > 0, откуда и следует
полуаддитивность рв. Утверждения 4) и 5) теоремы про-
проверяются без труда.
Определение. Линейным топологическим про-
пространством (сокращенно ЛТП) называется линейное про-
пространство L над полем К, снабженное топологией, отно-
относительно которой операции сложения и умножения на
число непрерывны.
Пример 1. Пусть р — конечная полунорма в L\ при-
примем в качестве базы топологии в L совокупность откры-
о
тых шаров Вр(х, г)= {у е L: р(х — у)<г}.
Проверим, что таким образом получается линейное то-
топологическое пространство. В самом деле, пусть х,у е L
и U — окрестность точки x + y^L. По определению то-
топологии множество U содержит некоторый шар вида
ВР (х + у, г) (г > 0). Положим U, = Вр (х, г/2), U2 =
о
= Вр(у1 г/2). Тогда ?Л и U2 открыты и Ui + U2<=:
о
с= Вр(х+ г/, г)с=[7 в силу полуаддитивности р. Тем са-
самым доказана непрерывность операции сложения.
Пусть теперь x^L, Х^К и U—окрестность точки
о
b^L. Тогда U содержит шар вида Bp(kx, r) (г>0).
Положим V, = {\x^K: \X-\x\<e}1 U6 = Bp(x, б). Если
\х е Ув1 у е С/в1 то
р (Ах - до) < р (^ - |хл:) + р (fix - до) < ер (я) + (Ш + е) б.
Ясно, что для достаточно малых положительных е и
б последнее выражение будет меньше г. Поэтому VeU6 a
о
<=Bp(kx, r)<^U, и мы доказали непрерывность умно-
умножения.
Пример 2. Пусть ipa)a^A — любое семейство конеч-
конечных полунорм в L. Примем в качестве базы топологии в
о
L совокупность шаров ВГа(х, г) (аеЛ, л?е?1г>0) и их
5 А. А. Кириллов, А. Д. Гвишиани 65
конечных пересечений. Как и в примере 1, можно про-
проверить, что эта топология превращает L в линейное то-
топологическое пространство. Такие ЛТП называют по-
поли нормированными.
Замечание 1. Каждая конечная полунорма в про-
пространстве L определяет отображение L в множество R+,
состоящее из всех вещественных неотрицательных чисел.
Определенная выше топология — это слабейшая тополо-
топология, относительно которой все полунормы семейства
{pJa&A непрерывны.
Замечание 2. Непрерывность полунормы р равно-
о
сильна открытости шара ВР@, 1).
Определение. Локально выпуклым линейным то-
топологическим пространством (сокращенно ЛВП) назы-
называется такое ЛТП, которое обладает базой топологии, со-
состоящей из выпуклых множеств.
Ясно, что ЛТП из примеров 1 и 2 являются ЛВП.
Оказывается, что ЛТП примера 2 является самым общим
примером ЛВП. А именно, справедлива
Теорема 6. Во всяком ЛВП L топология может
быть определена с помощью семейства полунорм {ра}аеА.
В качестве такого семейства можно взять совокупность
всех непрерывных полунорм на L.
Доказательство основано на следующем утверждении.
Лемма. Всякая окрестность нуля в ЛВП L содер-
содержит открытое выпуклое уравновешенное множество.
Доказательство леммы. Пусть U — произволь-
произвольная, a D ' с= U — открытая выпуклая окрестности нуля в L.
Из непрерывности операции умножения на число в L
вытекает, что существует такое число е > 0 и такая от-
открытая окрестность нуля V <= L, что Ве • V <=О, где Вг =
=={Х^К: Ш < е). Пусть W означает выпуклую оболочку
множества BeV. Тогда множество W открыто, выпукло,
уравновешено и содержится в V <= U. Лемма доказана.
Доказательство теоремы 6. В силу леммы и
утверждения 3) теоремы 5 на L определено некоторое
непустое семейство непрерывных полунорм, обладающее
свойством, описанным в примере 2. Введем в L топологпю
полинормированного пространства, взяв в качестве семей-
семейства {ра)а*А СОВОКУПНОСТЬ ВСвХ НвПрврЫВНЫХ ПОЛуНОрМ
на L. Ясно, что эта топология не сильнее исходной, так
о
как все шары В а (х, г) открыты в исходной топологии.
С другой стороны, в каждую окрестность нуля в исходной
топологии можно вписать выпуклое уравновешенное от-
крытое множество И7, а значит, н шар BPw@, 1). Таким
образом, топология полинормированного пространства не
слабее исходной. Теорема доказана.
Обычно рассматривают лишь отделимые или хаусдор-
фовы ЛТП, т. е. такие, в которых любые две различные
точки обладают непересекающимися окрестностями.
Те о р е м а 7. В любом ЛТП L существует и единст-
единственно такое подпространство Lo, что
1) любая непустая окрестность точки x^L содержит
множество х + Lo;
2) факторпространство L/Lo, снабженное естественной
фактортопологией, отделимо.
Доказательство. Пусть Lo — пересечение всех
окрестностей нуля. Из непрерывности операций сложения
и умножения на число вытекает, что Lo — подпростран-
подпространство и что справедливо утверждение 1). Далее, если
х и у — две различные точки факторпространства L/Lo,
то существует окрестность нуля U в L/Lo, не содержащая
х — у. Из непрерывности операции вычитания вытекает,
что существует такая окрестность нуля V, что V— V а
с= U. Тогда х+ V и у + V — непересекающиеся окрестно-
окрестности точек хну. Теорема доказана.
Пример. В полинормированном пространстве
(L, {ра}а^л) Lo совпадает с множеством, где все полу-
полунормы ра обращаются в нуль.
Одна и та же топология в ЛВП L может задаваться
азными наборами полунорм. Два набора полунорм
Ja^A и {q^)^B называются эквивалентными, если они
определяют одну и ту же топологию. Можно показать,
что два набора полунорм эквивалентны тогда и только
тогда, когда любая полунорма одного набора мажори-
мажорируется конечной линейной комбинацией полунорм друго-
другого набора и обратно.
В дальнейшем, как правило, будут рассматриваться
лишь отделимые полинормированные пространства. Среди
них особенно важны пространства (L, {/?а5аел), для кото-
которых семейство А конечно или счетно. Если А конечно,
то можно заменить набор полунорм одной полунормой
Р = 2 Ра, которая задает ту же топологию, что и весь на-
бор. Для отделимости L необходимо и достаточно, что-
чтобы полунорма р была нормой. Такие ЛТП называются
нормируемыми, а если норма р, задающая топологию,
фиксирована,— нормированными. Если А счетно, то,
5* 67
вообще говоря, L не является нормируемым. Однако
всякое счетно-нормированное ЛТП метризуемо. Более
того, метрику можно считать инвариантной относительно
сдвигов. Такова функция
d(x и) - ^2-" р«{х~у)
Множество Е с= L ограничено, если оно поглощается
любой окрестностью нуля в Е.
Для полинормированных пространств это определение
эквивалентно следующему более естественному:
Множество Е ограничено, если его элементы ограни-
ограничены по каждой из полунорм, определяющих тополо-
топологию в Е.
2. Сопряженные пространства. Линейные топологиче-
топологические пространства образуют категорию, морфизмами ко-
которой являются линейные непрерывные отображения
(операторы). Как и выше, мы обозначим через 3? (Lu L2)
совокупность всех морфизмов из ЛТП Lx в ЛТП L2. Яс-
Ясно, что 3? (Lb L2) — линейное пространство над К. Осо-
Особый интерес представляет случай Ь2 = К. Для любого
ЛТП L пространство 2'(L, К) мы обозначим через V
и назовем пространством, сопряженным к L.
В сопряженном пространстве можно ввести много
разных топологий (см., например, [7, 18*]), из которых
мы укажем лишь три наиболее важных.
Слабая топология определяется для любого ЛТП L
системой полунорм Pt{x) = \f(x) |, где / пробегает сопря-
сопряженное пространство L'; для слабой сходимости последо-
последовательностей используют обозначение хп-^х\
*-слабая топология определяется в пространстве L',
сопряженном к L, системой полунорм px(f)= \f{z)\, где
х пробегает L\
сильная топология в пространстве V\ сопряженном
к L, определяется системой полунорм ре (/) = sup | / (х) |,
где Е пробегает все ограниченные подмножества в L.
Отметим, что для нормированного пространства L
каждое ограниченное подмножество содержится в неко-
некотором шаре и поэтому сильная топология в V совпадает
с топологией нормы, введенной в § 1.
Как и для нормированных пространств, существует
естественное вложение ЛВП L во второе сопряженное про-
пространство L". Если оно является изоморфизмом, L назы-
называется рефлексивным ЛВП. В этом случае слабая и
¦-слабая топологии в V совпадают.
68
Соответствие L -*¦ L', как и в случае нормированных
пространств, продолжается до контрвариантного функто-
функтора в категории ЛТП, и сопряженный оператор опреде-
определяется той же формулой.
3. Теорема Хана — Банаха. Если ЛТП Lt и L2 отде-
отделимы и конечномерны, то всякое линейное отображение
из L{ в L2 непрерывно (см. задачу 294) и, следовательно,
dim S7 (Li, L2) = dim Lt • dim L2. В частности, dimZ/ =
=dimL. В бесконечномерном случае это не так. Извест-
Известно (см. задачу 314), что бывают такие отделимые беско-
бесконечномерные ЛТП L, для которых V = {0}. Оказывается,
в ЛВП такой неприятности не возникает.
Теорема Хана —Банаха. Пусть р —полунорма
на L, Lo — подпространство в L а /0 — линейный функ-
функционал на Lo, обладающий свойством \fo(xo)\ ^Р(^о) для
всех х0 е Lo. Тогда существует линейный функционал f
на L, совпадающий с /0 на Lo и обладающий свойством
\f{x)\ ^р(х) для всех xe=L.
Доказательство. Рассмотрим совокупность 3?
всех пар (Llf Д), где L{ — подпространство в L, содержа-
содержащее Lo, a /i — линейный функционал на Lt, обладающий
свойством \fi(xi) I ^ р{%\) (xt^Li) и совпадающий с /0
на Lo. Отметим, что 2? непусто, так как содержит пару
(Lo, /0). Определим на множестве 2 частичный порядок,
полагая (Lt, /,)<(L2, /2), если Lt cz L2 и ограничение /2
на Lj совпадает с /ь Множество S' удовлетворяет усло-
условиям леммы Цорна: всякое его упорядоченное подмноже-
подмножество {(La, /a)} (a^A) имеет мажоранту: (ULa, /), ae
е^, где /—функционал, совпадающий^ с /а на La. Зна-
Значит, в 3? есть максимальный элемент (L, f).
Предположим, что Г Ф L. Пусть х ^ L — элемент, не
лежащий в L. Построим продолжение ft функционала
f на пространство Г^ = Г + Кх, полагая fi(x + kx) =
= f(x) + kc. Выпишем условия, которым должна удовлет-
удовлетворять константа с е К для того, чтобы это продолжение
обладало свойством \fi(x)\^p(x) (x^E{):
\f(x) + kc\ <р{х + Хх), х^Г, К^К.
Заменяя х на — Ку и деля обе части неравенства на
Ш, мы приходим к равносильному условию
\c-f(y)\<p(x-y), y^Z.
Разберем сначала случай К = R. В этом случае мы
должны проверить, что семейство отрезков [f (у) — Р (я — У)>
69
f{y)~^pXx~~y)\ У^Е, имеет общую точку. Для этого
достаточно проверить, что левый конец любого отрезка
лежит левее, чем правый конец любого другого отрезка.
Искомой точкой будет тогда верхняя грань всех левых
концов.
Итак, осталось проверить неравенство
-У2), Уи
Но оно сразу следует из неравенства
Непосредственное перенесение этого рассуждения на
комплексный случай может быть проведено с помощью
теоремы Хелли (см. задачу 313). Мы укажем здесь более
простой обходной путь. Рассмотрим пространство Ei как
вещественное. Тогда его можно получить из Г, последо-
последовательно присоединяя R • х и R • ix. Последовательные
продолжения функционала f приведут нас к веществен-
нолинейному функционалу ф, совпадающему с f на Г,
обладающему свойством |ф(#) I ^ р(х) для х^Еи Ясно,
что теми же свойствами обладает и функционал г|)(#) =
= —iq)(ix). Наконец, полагая fi(x) =——g г мы по-
получим искомое продолжение:! j1 (х) \ = *— ^——^р {х)
У /• \ Ф {ix) — iw (—х) г^ / \ тт
и fiiix) = ^ = г/х (х).Итак, мы построили па-
пару (Ег, fj, следующую за (Г, f), что противоречит
максимальности последней. Значит, предположение Е ?= L
неверно, и теорема доказана.
Следствие 1. В любом отделимом полинормиро-
ванном пространстве L имеется достаточно много линей-
линейных непрерывных функционалов, чтобы разделить любые
две точки.
В самом деле, если x,y^L, хФу, то по лемме п. 1
существует выпуклая уравновешенная окрестность нуля
С/, не содержащая х — у. Положим р = Ри, Lo = К(х — у),
fo(x — у)= 1. По теореме Хана — Банаха существует та-
такой функционал f^L\ что /(#) — /(*/)= 1 и \f(x) \ <
^Ри(х).
Следствие 2. Для любого нормированного про-
пространства (L, р) и любого вектора x^L, x?=0 существу-
существует такой ненулевой функционал f^(L\ p'), что
f(x) = p'(f)p(x). C')
70
Следствие 3. Для любого нормированного прост-
пространства (L, р) естественное вложение L в L" [переводя-
щее x^L в функционал x(f) = f(x)) изометрично. (Ср. с
задачами 297, 298 и с теоремой 8.)
Замечание. В доказательстве теоремы Хана — Ба-
Банаха свойство полунормы р использовались не полностью.
А именно, можно показать, что все рассуждения остаются
в силе, если от р потребовать полуаддитивности и поло-
положительной однородности: p(kx)='kp(x) для 2-^0.
Кроме того, можно ослабить условия теоремы, потре-
потребовав выполнения неравенства fo(x)< р(х) (т. е. функ-
функционал ограничивается лишь сверху); при этом для
функционала j(x) также гарантируется односторонняя
оценка f(x)^ р(х).
Приведем геометрическую интерпретацию теоремы
Хана — Банаха.
Определение. Пусть L и М — линейные простран-
пространства. Линейным многообразием в линейном пространстве
L называется прообраз точки при линейном отображении
A: L-+M. Если образ L в М при отображении А имеет
размерность п, то говорят, что линейное многообразие
А~х(х) (x^A(L)) имеет коразмерность п. Многообразие
коразмерности 1 называется гиперплоскостью. Таким об-
образом, гиперплоскости — это множества уровня линейных
функционалов.
Геометрическая форма теоремы Хана —
Банаха. Пусть К = R. Если U — открытое выпуклое
множество в ЛТП L и S — линейное многообразие, не
пересекающее U, то существует гиперплоскость Т, содер-
содержащая S и не пересекающая U.
Доказательство. Будем считать, что U содержит
нуль. Пусть LQ — подпространство, порожденное 5, и /0 —
линейный функционал на Lo, определенный равенством
/о(х) = 1 для x^S (функционал /0 определен корректно,
поскольку S порождает Lo и не содержит нуля). Посколь-
Поскольку S не пересекает С/, функционал /0 обладает свойством
/о (х) ^ ри (х) для х е Lo. Функционал Минковского ри
полуаддитивен и положительно однороден: ри(Хх) =
= 'кри(х) при X > 0. В силу сделанного выше замечания,
этих свойств достаточно для справедливости аналога тео-
теоремы Хана — Банаха в вещественном случае. Продолжим
/о до функционала / во всем пространстве, обладающего
свойством f(x)^pu(x), и положим T = {x^L, f(x)=l].
Тогда Т — искомая гиперплоскость. В самом деле, на
V f(x)^l, а в силу открытости U f(x)<l для х^Е/,
71
Следствие. Пусть в ЛТП L заданы два выпуклых
непересекающихся множества С/4 и U2, одно из которых
открыто. Тогда существует гиперплоскость Г, разделяю-
разделяющая Ui и U2.
В самом деле, положим С/ = С/± — С/2, S = {0}. Тогда
U — выпуклое открытое множество, S — линейное много-
многообразие, не пересекающее U. Пусть То — гиперплоскость,
содержащая 5 и не пересекающая U. Поскольку Т содер-
содержит нуль, она задается уравнением /(#) = 0, где / — не-
некоторый линейный функционал на L. Так как U выпук-
выпукло и не пересекает Г, функционал / принимает на U
значения одного знака.
Пусть для определенности f(x)>0 для x^U. Вспо-
Вспоминая определение С/, мы видим, что f{x])'>f{x2) для
всех Xi^Ui, x2^U2. Пусть с = sup f{x2). Тогда гипер-
гиперплоскость Т = {х: f(x) = c) разделяет ?Л и U2.
Замечание. Требование открытости С/4 или U2 в
формулировке следствия существенно (см. задачу 295).
Другую теорему о разделении выпуклых множеств см.
в задаче 296.
Теперь мы в состоянии доказать утверждение об изо-
метричном вложении L в L"', о котором говорилось в
п. 2 § 1.
Теорема 8. Пусть L — нормированное пространство,
V — его сопряженное пространство и L" =(//)' — второе
сопряженное пространство. Каждому х е L поставим в
соответствие линейный функционал Fx на L', действую-
действующий по формуле
Тогда || Fx \Ln = \\ х \\l и тем самым отображение x<-»F
задает изометричное вложение L в L"'.
Доказательство. По определению нормы в L
имеем ||Fx||l»= sup |/(я)|. Поскольку |/ (х) |<||/||||||
l
отсюда следует, что Ц^Ц^^Л^^- Далее, в одномер-
одномерном пространстве LQ cz L, порожденном вектором х, зада-
зададим функционал /о формулой
Ясно, что ||/0|| / = 1. По теореме Хана — Банаха /0 про-
Lo
должается до функционала /t на L, причем |/||l' = 1.
Поэтому || Fx\\L» ^ | /х (х) | =-- || х \L. Теорема доказана.
72
§ 3. Линейные операторы
1. Пространство линейных операторов. Линейные то-
топологические пространства над данным полем К (К = В.
или С) образуют категорию 3?к, морфизмами которой
являются линейные непрерывные отображения, называе-
называемые обычно линейными непрерывными операторами. Если
Li и Z/2 — два ЛТП над полем /?, то совокупность всех
линейных непрерывных операторов из Lt в L2 обознача-
обозначается 2> (Li, L2) (см. гл. Ill, §2, п. 2). Ясно, что S?\L,,L2) —
линейное пространство над К\ если же ?4 = L2 = L, то
9? (L) или 3? (Lu L2), обозначаемое чаще End L, явля-
является к тому же алгеброй над полем К.
Пространство 2? {L\, L2) можно снабдить различными
топологиями. Наиболее употребительными являются сле-
следующие три.
1. Слабая топология. Базис окрестностей нуля*) в
этой топологии составляют множества
U(х, f) = {A^g (Llt L2): | /(A(x)) |< 1}, xe Lv f e h\.
Легко проверить, что последовательность {Ап} сходит-
сходится к Л в слабой топологии тогда и только тогда, когда
для любого х ^ Ь{ последовательность {Ап(х)} сходится
к А (х) в слабой топологии пространства L2. Это соотно-
соотношение записывают так: Ап-^-А или A =w-limAn.
2. Сильная топология. Базис окрестностей нуля состав-
составляют множества U(x, F)= {A e ?P (ib L2): 4jeF}, где
х s Li, a V—окрестность нуля в L2. Ясно, что сильная
сходимость Ап к А равносильна сходимости Апх к Ах
в топологии L2 для любого х е Ll# Это записывают так:
Лп -*¦ Л или Л = s-lim Ап.
3. Равномерная топология. Пусть Li и L2 — нормиро-
нормированные пространства с нормами р{ и /?2. Тогда в 3?(ЬЬ
можно ввести норму р по формуле
Р2
= sup V
Базис окрестностей нуля составляют множества
u L2): р{А)<г), е>0.
*) Для определения топологии в ЛТП достаточно задать базис
окрестностей нуля. В качестве такой системы можно рассматри-
рассматривать любое семейство подмножеств, содержащих нуль, сдвиги ко-
которых образуют базу топологии.
73
Тот факт, что последовательность Ап стремится к А
в равномерной топологии (т. е. р(Ап — А)^- 0 при п -> °°),
записывают так: Лп => Ап или 4 = u-lim An.
П-»оо
Несложное рассуждение показывает, что слабая топо-
топология слабее сильной, а сильная — слабее равномерной.
Отметим, что в конечномерном случае (т. е. когда
dim Z/t<oo, dimZ/2<°°) все три топологии совпадают.
В бесконечномерной ситуации это уже не так (ср. с зада-
задачами 316—318).
Отметим некоторую несогласованность описанной (об-
(общепринятой) терминологии с введенными раньше (и тоже
общепринятыми) понятиями слабой и сильной топологий
в пространстве L'= 3? (L, К). А именно, если рассматри-
рассматривать линейные функционалы /*=// как операторы из L
в К, то слабая и сильная операторные топологии соответ-
соответствуют *-слабой топологии в L'', а равномерная оператор-
операторная топология соответствует сильной топологии в L'.
Линейный функциональный анализ в основном поко-
покоится на трех китах — трех теоремах, связанных с именем
Стефана Банаха. Одна из них — теорема Хана — Бана-
Банаха— разобрана в § 2. Здесь мы приведем две другие.
Теорема Банаха — Штейнгауза. Пусть Ь{ —
полное линейное метрическое пространство, L2 — нормиро-
нормированное пространство и Ыт)теГ — семейство линейных не-
непрерывных операторов из Li в Ьг. Если для каждого
x^Li множество Ыт#}ТеГ ограничено в L2 (т. е. ||i4Y#(^
^ С (х) \fx g L2 (у G Г)), то семейство {AJ равномерно
ограничено на некотором шаре с центром в нуле в Li
(т. е. WA-ixW ^ С для всех ^ е Г и всех х из шара 5@, г)==
«fcreZ,,: d@, x)<r)).
Следствие. В условиях теоремы семейство Ыт} рав-
равностепенно непрерывно: V?>0 36>0: d(x1, x2) Ь
H4()A()ll Vr
H4(i)ABll y
Доказательство следствия. Пусть НЛтж11 < с
на шаре 5@, г). Выберем б настолько маленьким, чтобы
шар 5@, б) содержался в множестве —5@, г). (Это воз-
возможно в силу непрерывности операции умножения на
число в Ь{.) Тогда, если d{xu х2)<б, то ||-4V (xi) ~"
так как
74
Доказательство теоремы Банаха — Штейн-
гауза. Предположим, что семейство Ыт} неограничено
ни на каком шаре вида В (О, г) (г>0). Тогда оно неог-
неограничено ни на каком шаре вообще. В самом деле, пусть
В(хи Tj) —любой шар в ?ь Из инвариантности метрики
относительно сдвигов вытекает, что шар В(хи г1)=?1 +
+ #@, г4). Так как семейство Ыт} ограничено на векто-
векторе Xi и неограничено на шаре #@, г4), оно неограничено
на шаре В(хи г{).
Построим теперь последовательность шаров В{хп, гп)
и последовательность индексов {^J, обладающих следую-
следующими свойствами:
1) В{хп+и rn+l)czB(xn, г„); 2) г„+1<г„/2;
3) Mhl(z)W>n для всех х^В(хп, гп).
Положим х0 = 0, Го = 1 и воспользуемся тем, что се-
семейство {AJ неограничено на шаре В(х0, г0). Значит,
о
найдется такой индекс fi и такой элемент xl^B(x0, г0),
что 11 -4Y лг11| >-1. По непрерывности AVi существует такое
число г1? что |^4Vl^J^l для всех х^В(хи г4). Уменьшая,
если нужно, гь можно считать, что г{ < го/2 и В{хи r^cz
czB(x0, г0). Предположим, что шары #(?ft, rft) и индексы
^ уже выбраны для к^п— 1. Поскольку семейство Ыт}
неограыичено на В(хп-и fn-i), существует такой индекс "f№
о
и такой элемент хп^ В(хп-и rn_t), что l^vn^")! ^>n- По
непрерывности АУп существует такое число гп, что
||Луп^|^^гдля всех х<^В(хп, г„). Уменьшая, если нужно,
гп, можно добиться выполнения соотношений rn < rn-J2 и
Я(я„, гп)с=Д(а;п-1, rn-i).
Воспользуемся теперь полнотой Ь{. Пусть х — точка,
общая для всех шаров В(хп, гп). Такая точка найдется
по теореме о стягивающихся шарах (см. гл. I, § 2).
Тогда IL4Vn (x)W >п для любого п, что противоречит огра-
ограниченности семейства Ыт} па векторе х. Теорема до-
доказана.
Одно из важных следствий теоремы Банаха — Штейн-
гауза — слабая полнота пространства & (Lu L2) в случае,
когда Li — полное метрическое линейное пространство,
a L2 — банахово пространство. В частности, справедлива
Теорема 9. Если L — полное метрическое линейное
пространство, то сопряженное пространство U *-слабо
секвенциально полно.
Доказательство. Пусть ifj — слабо фундамен-
фундаментальная последовательность в Z/. Это значит, что для
75
любого x^L числовая последовательность ifn(%)} фунда-
фундаментальна и, значит, имеет предел, который мы обозна-
обозначим f(x). Для доказательства теоремы мы должны про-
проверить, что f^L'. Линейность / получается переходом
к пределу из линейности /„. Непрерывность / вытекает
из следствия теоремы Банаха — Штейнгауза. В самом де-
деле, семейство {/Л отображений L в К ограничено на каж-
каждом векторе iei, Значит, оно равностепенно непрерыв-
непрерывно. Поэтому для- любого е > 0 существует такое б > О,
что \fn(x)\ < б на шаре Я@, б). Переходя к пределу при
тг->оо? получаем, что \f(x)\ ^б на шаре #@, 6J, что и
доказывает непрерывность /.
Еще одно полезное следствие теоремы Банаха —
Штейнгауза формулируется так.
Теорема 10. В нормированном пространстве L вся-
всякое слабо ограниченное множество X (т. е. такое, что
\f(x)\^c(f) для любого х^Х и f e U) ограничено.
Доказательство. Рассмотрим элементы х^Х как
линейные функционалы на L'. По условию, семейство X
ограничено на каждом / s U. Так как L' полно, по тео-
теореме Банаха — Штейнгауза X ограничено на некотором
шаре 5@, г) в L', т. е. \f(x)\ <c для всех х^=Х и всех
/ей@, г). В силу следствия 3 теоремы Хана — Банаха
(см. § 2 гл. III) отсюда вытекает, что Ы1 < с/г для всех
jeX, т. е. X ограничено.
Третьим основным принципом линейного функциональ-
функционального анализа является
Теорема Банаха об обратном операторе.
Пусть Li и L2 — полные метрические линейные простран-
пространства, А — линейный непрерывный оператор, взаимно од-
однозначно отображающий Д на Ь2. Тогда обратный опе-
оператор Л: L2-^Li непрерывен.
Доказательство. Мы должны проверить, что для
о
любого г>0 образ шара #@, r)czL4 при отображении
А содержит окрестность нуля в L2, что и означает непре-
непрерывность А~\ Воспользуемся тем, что для любого е >0
объединение U пВ @, е) содержит Lim Поэтому объедине-
П=1
ние образов Хп = А(пВ@, е))__содержит L2. Пусть Хп —
замыкание Хп. Покажем, что Хп содержит целиком неко-
некоторый шар положительного радиуса в L2. В противном
случае дополнение Уп к Хп в L2 было бы всюду плотным
открытым множеством. В силу задачи 26 пересечение
76
П Уп было бы всюду плотно, в то время как оно на
n=i
самом деле пусто. Итак, существуют такие п е N, х0 e L2
о
и г0 > 0, что Хп=>В(х0, г0). Это значит, что замыкание
образа 5@, е) содержит шар B(xjn, ro/n). Выберем е
настолько малым, чтобы выполнялось условие 5@, г) —
о о
— 5@, е)<=#@, г). Это можно сделать в силу непрерыв-
непрерывности отображения {х, у)*-*- х— у- Мы доказали, что за-
о о
мыкание образа 5@, е) содержит шар В(хо/п, rjn).
Поэтому замыкание образа 5@, г) содержит множество
о о
В(хо/п, rjri) — B(xo/n, го/пI которое в свою очередь со-
о
держит 5@, rjri).
о
Итак, образ любого шара 5@, r)czL1, г>0, плотен
в некотором шаре вида 5@, р)<=?2. Пусть образ шара
5@, r/2n)czLl плотен в шаре 5@, рп)<=Ь2 (и= 1, 2, ...).
Не ограничивая общности, можно считать, что рп -*¦ 0.
Покажем, что образ шара 5@, г) содержит шар 5@, pt).
Пусть г/е=5@, pt). Поскольку образ 5@, г/2) плотен
о о
в 5@, Pi), найдется такой вектор #1^5@, г/2), что
d(y, Axi)<p2. Далее, поскольку образ 5@, г/4) плотен
в 5@, р2), найдется такой вектор #2^5@, г/4), что
d(y — Axu Ах2) < р3 и т. д. Ряд ^хп сходится в ?4
к некоторому вектору 1^5@, г). Имеем d(y,Ax) =
= d(^,2 Axn) = 0. Теорема доказана.
Эта теорема часто используется в такой ситуации.
Пусть в пространстве L заданы две нормы pt и р2, при-
причем р2 ^ сру и пространство L полно относительно каж-
каждой из норм. Тогда нормы р{ и р2 эквивалентны, т. е.
Pi ^ с рг для некоторой константы с . (Для доказатель-
доказательства достаточно рассмотреть тождественный оператор из
(L, р{) в (L, р2).)
Аналогичное рассуждение применимо и к двум счет-
счетным семействам полунорм, превращающих L в полное
метрическое пространство; если одна система полунорм
мажорирует другую, то эти системы задают одну и ту же
топологию. Этот факт широко используется в теории
обобщенных функций. (Ср. теорему 30 § 4 п. 3.)
77
2. Компактные множества и компактные операторы.
Понятия компактного и относительно компактного мно-
множеств предполагаем известными. (См. задачи 69—72.)
Из обычного курса анализа известно, что на веществен-
вещественной прямой относительная компактность множества рав-
равносильна его ограниченности. То же самое справедливо и
в любом конечномерном нормированном пространстве.
Теорема 11. Пусть L—конечномерное нормирован-
нормированное пространство, А — подмножество в L.
Тогда:
1) А относительно компактно тогда и только тогда,
когда оно ограничено;
2) А компактно тогда и только тогда, когда оно замк-
замкнуто и ограничено.
Доказательст bj>. Если А относительно компакт-
компактно, то его замыкание А — компакт. Норма —- непрерывна_я
функция, и, значит, она ограничена на А. Поэтому А,
а следовательно, и Л — ограниченные множества.
Пусть теперь А — ограниченное множество в L. По-
Построим для него конечную е-сеть. Пусть хи ..., хп —
координаты в L относительно какого-нибудь базиса et, ...
..., еп. Назовем кубом и обозначим Кс подмножество в L,
выделяемое условиями \хг\ ^с (i = 1, 2, ..., п).
Лемма. Существуют такие положительные числа М
и т, что единичный шар пространства L содержит куб
Кт и содержится в кубе Км.
Доказательство. Пусть дК{ — граница куба К{.
Она состоит из 2п кубов размерности (п— 1), задаваемых
условиями #г = =Н для некоторого i, \х}\ < 1 при j Ф i.
Индукцией по п легко доказать, что dKY — компакт. По-
Поэтому норма принимает на дК{ наибольшее значение В и
наименьшее значение Ъ. Заметим, что Ь > 0, так как О Ф
Ф- дКи Утверждение леммы будет выполнено, если поло-
положить М = Ь~\ т = В'\
Пусть теперь дано ограниченное подмножество A cz L.
По определению оно содержится в некотором шаре ра-
радиуса R и тем самым в кубе KRM. Разобьем этот куб на
Nn кубов, конгруэнтных KRMN-\.Каждый из них содер-
содержится в шаре радиуса RM/Nm. Выбирая JV> RM/гт,
получим искомую е-сеть, составленную из центров
маленьких кубов. Тем самым искомое утверждение до-
доказано.
Замечание. Число элементов в построенной е-сети
равно, как легко видеть, {RM/гтI1, т. е. имеет порядок
О(е~п) при ?-> 0. Показатель п здесь напоминает нам
78
о размерности пространства L, в котором лежит наше
множество. Важной и интересной характеристикой отно-
относительно компактного множества А является асимптоти-
асимптотическое поведение при е-»-О функции N(e)—числа эле-
элементов в минимальной е-сети для А. В частности, если
N (г) ~ С • е~т, то говорят, что А имеет аппроксимативную
размерность у. Можно показать, что в ^-мерном нормиро-
нормированном пространстве существуют относительно компакт-
компактные подмножества любой аппроксимативной размерности,
заключенной между 0 и п.
В бесконечномерных пространствах ограниченности,
как правило, уже недостаточно для того, чтобы множество
было относительно компактно.
Теорема 12. Пусть L—бесконечномерное линейное
нормированное пространство. Тогда единичный шар
В = {х <= L; Ы ^ 1} в L не является относительно ком-
компактным множеством.
Доказательство. Предположим, что В относи-
относительно компактен. Тогда он покрывается конечным чис-
числом шаров Ви ..., BN радиуса г< 1. Рассмотрим ^-мерное
подпространство Ln в L, содержащее центры этих шаров.
Такое подпространство заведомо существует при п > N.
Пусть В, Ei, ..., EN — пересечения шаров Б, Ви ..., Bs
с Ln. Ясно, что множества S, 5, являются шарами в ЬЛ
радиуса 1 и г соответственно. Пусть \х — мера Лебега в
Ln, нормированная условием (ы(Л)=1. Тогда |л(?г) = гп.
Так как В содержится в объединении Вх A ^ i ^N) спра-
справедливо неравенство Nrn~>l. Но при г<1 и достаточно
большом п это невозможно. Теорема доказана.
Некоторой компенсацией служит следующий ре-
результат.
Теорема 13. В нормированном рефлексивном про-
странстве L всякое слабо ограниченное множество слабо
относительно компактно.
Мы докажем эту теорему в предположении, что про.-
странство U сепарабельно, т. е. содержит счетное плот-
плотное подмножество {/J. (Общий случай требует примене-
применения теоремы Тихонова о компактности бесконечного про-
произведения компактов.) В этом случае слабая топология
на каждом слабо ограниченном подмножестве X^zL мет-
ризуема. В самом деле, если X слабо ограничено, то оно
и сильно ограничено по теореме 10. Значит, X содержится
в шаре радиуса г. Определим счетное семейство полунорм
Pn{x)^=\fn(x)\. Покажем, что это семейство определяет
слабую топологию на X. В самом деле, база слабой топо-
79
логип в множестве X состоит из мпожеств вида
U(x,f)={y<BX: \f{x-y)\<l}, xzeL, /gL',
и их конечных пересечений.
Пусть fi — функционал из плотного подмножества {/«),
обладающий свойством II/ — /JI < 1/Dг). Тогда подмноже-
подмножество тех у^Х, для которых pt(y — х)< 1/2, содержится
в ?/(*, /), так как |/ {х - у) \ = |А (я - у) + (/- /г) (ж -
-»)l<T+fc'2r==1-
Покажем теперь, что X—слабо предкомпактное мно-
множество. Для этого проверим, что из каждой последова-
последовательности {хп} cz X можно выбрать слабо сходящуюся в
замыкании X подпоследовательность. Так как числовая
последовательность fi{xn) ограничена при каждом i, то,
применяя стандартный диагональный процесс, можно вы-
выбрать подпоследовательность, сходящуюся по каждой по-
полунорме р(. Поскольку семейство {pj определяет слабую
топологию на X, эта подпоследовательность будет слабо
сходящейся. Теорема доказана.
Очень интересная и красивая область линейного функ-
функционального анализа— теория компактных выпуклых мно-
множеств. Мы приведем здесь лишь наиболее яркий и по-
полезный результат из этой теории — теорему Крейна —
Мильмана о крайних точках.
Точка ж, принадлежащая выпуклому множеству К
в ЛТП, называется крайней (или экстремальной), если
она не является серединой отрезка, целиком лежащего
в К. Например, крайние точки замкнутого шара в евкли-
евклидовом пространстве — это все точки ограничивающей его
сферы; крайние точки замкнутого куба — это его верши-
вершины; открытое множество вообще не имеет крайних точек.
Теорема 14 (Крейна—Мильмана). Пусть
L — ЛВП, К — выпуклый компакт в L, Е — совокупность
крайних точек К. Тогда К совпадает с замыканием вы-
пуклой оболочки Е.
Доказательство теоремы см. в задачах 329—333.
Одно из приложений этой теоремы — доказательство
неизоморфности различных банаховых пространств (ср.
с задачами 334—336); другое — изящное доказательство
де Бранжа теоремы Стоуна — Вейерштрасса (см. [28]).
Критерии компактности множеств в различных конк-
конкретных пространствах мы приведем ниже, но один слу-
случай— пространства С(Х)—разберем здесь, поскольку он
используется в общей теории нормированных пространств.
80
Теорема 15 (Арцела — А сколи). Пусть С(X) —
нормированное пространство вещественных непрерывных
функций на метрическом компакте X с нормой || /1| =
= max |/ (х) |. Для того чтобы семейство AczC(X) было
х
предкомпактным, необходимо и достаточно, чтобы оно
было 1) равномерно ограниченным (т. е. существовала бы
такая константа С, что \f(x)\ =^ С для f^A) и 2) равно-
степенно непрерывным (г. е. для каждого е > 0 существо-
вало бы такое 6 >0, что !/(#) — /(*/) I < 8, как только
d(x, г/)<б, для всех f^A).
Доказательство. Необходимость. Пусть А
предкомпактно. Тогда оио допускает конечную е/3-сеть
/i, ..., /#. Каждая из функций /,- непрерывна и, следова-
следовательно, ограничена на X. Отсюда следует равномерная
ограниченность А. Каждая из функций /< равномерно
непрерывна на X. Поэтому существует такое 6* > 0, что
\fi(x)-~ fi(y)\ <е/3 при d(x, y)<6t. Тогда из рассмотре-
рассмотрения четырехугольника /(я), 1х{х), /*(*/), /(*/) вытекает
требуемое свойство равностепенной непрерывности для
б = 111111F! . .. блг) .
Достаточность. Построим явно конечную е-сеть
для А, если известно, что семейство А равномерно огра-
ограничено и равностепенно непрерывно. Пусть б выбрано
так, чтобы выполнялось неравенство 1/(#) —/(у) I < е/3
при d(x, y)<6 для f^A. На компакте X существует
конечная б-сеть S = {хи ..., хп). Рассмотрим ограничение
функции /е4 на множество S как вектор пространства
loo(n, R). Образом А в Zoo (га, R) является некоторое огра-
ограниченное множество А. Значит, Л относительно компакт-
компактно и обладает конечной е/3-сетыо /t, ..., fN. Покажем,
что набор функций /1? ..., fN является е-сетью в А. Пусть
f^A. Ограничение / функции / на S отстоит не больше
чем на е/3 от некоторой /{ в смысле метрики /«.(га, R).
Оценим расстояние между / и /{ в С(Х). Пусть х — любая
точка изХи^еХ — ближайший к ней элемент S. Тогда
d(x,xh)<8. Поэтому 1/(я)-/(яЛI<в/Зи 1/г(*)-/*Ы I <
< е/3. Кроме того, \J(xk)— Ji(xk)\ <г/3 согласно выбору
/i. Значит, II/ — /JI < е. Теорема доказана.
Более общий результат см. в задаче 337.
Определение. Оператор А, действующий из норми-
нормированного пространства Li в нормированное пространство
?2, называется компактным (в другой терминологии —
вполне непрерывным), если он переводит всякое ограни-
ограниченное множество в относительно компактное.
А. А Кириллов, А Д. Гвишиани
81
Это понятие было введено Д. Гильбертом при изуче-
изучении интегральных операторов. Примером компактного опе-
оператора может служить любой ограниченный оператор ко-
конечного ранга (т. е. оператор с конечномерным образом).
В самом деле, в конечномерном пространстве всякое огра-
ограниченное множество относительно компактно. Совокуп-
Совокупность всех компактных операторов, действующих из Ь^ в
L2, мы будем обозначать Ж{Ьи L2).
Теорема 16. 1) Ж{Ь{, L2)—замкнутое по норме
подпространство в 2 (Lu L2).
2) Если A^g(U, Lt), В<=Ж{Ьи L2), C^g(U, L3),
то С ° В ° А <^Ж(Ь0, L3); e частности, Ж (L, L)—идеал
e g{L, L).
3) Если А^Ж(Ьи L2), то сопряженный оператор Аг\
L2—*Ll принадлежит Ж\Ь2,Ь1).
Доказательство. 1) Пусть А и В — компактные
операторы из Ь{ в L2, X — ограниченное подмножество
в L1# Множества АХ и ВХ предкомпактны. Поэтому пред-
компактно и множество аАХ + §ВХ. Значит, аА + $В е
^Ж{Ьи L2). Далее, пусть Ап^Ж(Ьи L2) и Ап=>А при
п -> оо. Покажем, что множество АХ предкомпактно. Пусть
задано в > 0. Выберем номер п таким, чтобы выполнялось
неравенство ИЛ - Л„II < е/BД), где R = sup[#||. Тогда
множество АпХ будет е/2-сетыо для множества ЛХ, так
как ИЛ# —ЛП#И < е/2 для х^Х. Множество АпХ по усло-
условию предкомпактно и, следовательно, имеет конечную
е/2-сеть S. Ясно, что 5 будет е-сетыо для АХ.
2) Пусть X—ограниченное множество в Lo. Тогда
АХ — ограниченное множество в Lu В°АХ—предком-
пактное множество в L2. Покажем, что С ° В ° АХ — пред-
компактное множество в Ья. В самом деле, если 5 — ко-
конечная е/НСН-сеть для В ° ЛХ, то CS — конечная е-сеть для
3) Пусть А^Ж(Ьи L2), M — ограниченное множество
в L2. Покажем, что множество А'М cz Lx предкомпакт-
предкомпактно. Для этого построим изометрическое вложение этого
множества в некоторое пространство типа С(Х). А имен-
именно, в качестве X мы возьмем захмыкание множества Л5,
где В — единичный шар в пространстве L{ (AB предком-
предкомпактно, так как Л — компактный оператор, В — ограни-
ограниченное множество). Каждому функционалу f^A'M мы
поставим в соответствие функцию f (x) на X по формуле
f(x) = g(x), где g^M выбирается так, чтобы выполня-
выполнялось равенство f = A'g. (Этим свойством g определяется,
82
вообще говоря, неоднозначно, но если / = A'gt = A'g2, то
для точек хе=АВ значения gi(x) и g2{x) совпадают. Та-
Таким образом, соответствие /•-*•/ определено корректно и,
очевидно, является вложением.) Покажем, что это соот-
соответствие изометрично. В самом деле,
= max |7 (х) | = sup | g (х) | = sup | g (Ay) | =
х=Х х&АВ у^В
= sup\A'g (y)\ = Snp\f (y)\ =\\f\\ ,.
В ^В Ll
Остается проверить, что функции f, соответствующие
функционалам f^A'M, образуют равномерно ограничен-
ограниченное и равностепенно непрерывное семейство. Это вытекает
из оценок
где diamik/" = sup \\g\\ ,. Теорема доказана.
Одно из самых полезных свойств компактных опера-
операторов описывает
Теорема 17. Компактные операторы переводят ела-
бо сходящиеся последовательности в сильно сходящиеся.
Доказательство. Пусть А: L^ -> L2 — компактный
оператор ж хп-^х в L4. По теореме 10 последовательность
{хп} ограничена по норме. Поэтому последовательность
{AxJ предкомпактна. Значит, существует подпоследова-
подпоследовательность {АгПк}, сходящаяся к некоторому вектору уе
е Ь2. Покажем, что и вся последовательность {AxJ схо-
сходится к у. Действительно, в противном случае нашлось
бы е>0 и бесконечная подпоследовательность (Armft),
обладающая свойством j|-4#mfe—у\^г. Так как {-4#mftj —
предкомпактное множество, оно обладает подпоследова-
подпоследовательностью, сходящейся к некоторому вектору z e Ьг.
Можно считать, что {^mft} и есть эта подпоследователь-
подпоследовательность. Ясно, что Wy — z\\> е. По следствию 1 из теоремы
Хана — Банаха существует такой линейный функционал
/ €= L'2, что f(y)^f (z). Пусть ф = A'fs=L[. Тогда ер (яЯл) =
= f(Axnk) ~+f(y), 4>(xmk) = f(Axmk)-+f(z). ЭТО ПрОТИВО-
речит сходимости последовательности ф(#п). Теорема
доказана.
0* 83
Замечание. В рефлексивных пространствах с се-
парабельным сопряженным доказанное свойство компакт-
компактных операторов является характеристическим: всякий ог-
ограниченный оператор, переводящий слабо сходящиеся
последовательности в сильно сходящиеся, является ком-
компактным. В самом деле, в этом случае слабая топология
на ограниченных множествах метризуема и поэтому опре-
определяется сходимостью последовательностей. Поэтому наш
оператор непрерывен на ограниченных множествах, если
снабдить Z/j слабой, а Ь2 сильной топологией. Так как
ограниченные множества слабо предкомпактны, их образы
сильно предкомпактны.
3. Теория фредгольмовых операторов. Пусть Li и L2 —
банаховы пространства и T^2?(LU L2). Уравнение
Т(х) = у, x<=Lu y^L2i A4)
является естественным обобщением системы линейных
алгебраических уравнений на бесконечномерный случай.
Оказывается, что при некоторых дополнительных предпо-
предположениях теория таких систем почти полностью анало-
аналогична конечномерной теории. Однако имеется и различие.
Помимо более сложных доказательств, в бесконечномер-
бесконечномерной ситуации возникает новое понятие — индекс линейно-
линейного оператора. Для введения этого понятия нам понадо-
понадобятся некоторые приготовления. Будем обозначать через
кегГ ядро оператора Г, т. е. совокупность всех решений
уравнения
Тх = 0, x^L,. A5)
Через im T обозначим образ оператора Г, т. е. сово-
совокупность тех у е L2, для которых разрешимо уравнение
A4). Ясно, что ker T—замкнутое подпространство (как
прообраз точки при непрерывном отображении). Множе-
Множество imT не всегда замкнуто (см. задачу 350). Мы будем
вместе с оператором Т рассматривать сопряженный опе-
оператор Т' = 2 (L'2i L[) и соответствующие уравнения
Гг = /, ?<=L'2, /gLI, A6)
Г* = 0, ^4 A7)
Если im Г и im 7" — замкнутые подпространства, то
можно определить банаховы пространства
coker Т — L2/im Г, сокег Т' = L'Jim T.
Они называются коядром операторов Г и Г' соответствен-
84
но. Положим
а(Т) = dim ker Г, р (Г) = dim coker Г,
Оператор Т назовем фредгольмовым, если числа а (Г),
Р(Г) конечны. В этом случае число i(T) называется ин-
индексом оператора Т.
В конечномерном случае, когда dimL1=iV1,
= N2i легко проверить равенства
которые в сочетании с равенством rang Т = rang T' (тео-
(теорема о ранге матрицы) дают соотношения
а(Г) = р(Г), Р(Г) = а(Г), i{T) = -i{T'). A9)
Цель этого пункта — доказать соотношения A9) в бес-
бесконечномерном случае (для фредгольмовых операторов) и
дать удобные критерии для вычисления индекса и для
разрешимости уравнений A4) —A7).
Пусть задана последовательность линейных прост-
пространств и линейных операторов:
с.. ->¦ Ьь-! —* Lk >¦ Lh+1 -> .., B0)
Эта последовательность называется точной в члене Lh,
если imTh = kerTh+l. Говорят, что последовательность
B0) точна, если она точна в каждом члене. Ясно, что
точность в члене Lh влечет равенство Th+l ° 7\ = 0. Послед-
Последнее свойство получило название полуточности. Если по-
последовательность B0) полуточна в члене Lft, то im7\c:
с= ker Tft+1. Факторпространство Hh = ker Th+J\m Th изме-
измеряет «отклонение от точности» в члене Lh. Оно называет-
называется k-м пространством погомологий последовательности
B0). Если Hh = {0) для всех &, то последовательность
B0) точна.
Нас будет интересовать случай, когда все пространства
Lh — банаховы, а операторы Th непрерывны. Основной
результат в этом случае
Теорема 18. Пусть дана точная последовательность
B0) банаховых пространств и непрерывных операторов.
85
Тогда сопряженная последовательность
, ^k , Tk+i ,
также точна.
Доказательство. Рассмотрим сначала один част-
частный случай. А именно, пусть последовательность B0)
имеет вид
0-^-^-0, B2)
где 0 означает тривиальное (нульмерное) пространство,
и соответственно последовательность B1) —вид
Оч-Li^L^O. B3)
Точность последовательности B2) означает, что кегГ =
= {0} и im T = L2, т. е. Т—изоморфизм линейных (но не
банаховых!) пространств Li и L2. По теореме Банаха об
обратном операторе, Г непрерывен и, следовательно, Т
осуществляет топологический изоморфизм (линейный го-
гомеоморфизм) банаховых пространств Li и Ьг. Поэтому
Тг — топологический изоморфизм Ь2 и Lx. Отсюда вы-
вытекает точность последовательности B3). Итак, справед-
справедливость теоремы 18 в этом простейшем частном случае
следует из теоремы Банаха. Можно проверить, что верно
и обратное: теорема Банаха является следствием рассмот-
рассмотренного случая теоремы 18.
Вернемся к рассмотрению общего случая. Полуточ-
ность сопряженной последовательности очевидна, так как
Th ° Th+i = (Tk+1 о Tky = 0. Остается доказать, что
im Th+i 13 ker Tk. Пусть /^kerT^. Это означает, что
функционал / е Lh обращается в нуль на im Tk = ker Th+i.
Значит, он определяет некоторый линейный функционал
Fo на подпространстве im 7\+1 cz Lfe+1 по формуле
Fo(Th+i(x)) = f(x). На пространстве im7\+1 есть две нор-
нормы: одна — заимствованная из Lh+l, другая — перенесен-
перенесенная из Lh/kerTh+i с помощью оператора Th+l. Так как Th+l
ограничен, первая норма мажорируется второй. По теоре-
теореме Банаха, эти нормы должны быть эквивалентны. Зна-
Значит, Fo непрерывен в топологии Lh+l и по теореме Хана —
Банаха допускает непрерывное продолжение до функцио-
функционала V е Lk+1. Ясно, что Tk+1F = /, и теорема доказана.
Эта теорема допускает обращение и обобщение (см,
задачи 355, 356).
86
Теорема 19. Пусть Т — фредголъмов оператор из
SB (Lu L2). Тогда Т' е 3? (Ь'2, Ь[) также фредголъмов и
справедливы равенства A9).
Доказательство. По определению пространств
ker T и coker T имеет место точность последовательности
где i — вложение, а р — естественная проекция. По теоре-
теореме 17 отсюда следует точность последовательности
0^- (ker ТУ ^L[?-L'2?- (coker T)' +-0.
А это означает, что имеют место изоморфизмы
ker Т' « (coker Т)', coker Т' « (ker T)'. B4)
Отсюда вытекает фредгольмовость Т' и справедливость
равенств A8) и A9).
Примером фредгольмова оператора может служить лю-
любой обратимый оператор Т<^3?(Ьи L2), т. е. такой, для
которого существует оператор S<^S?(L2, L{), обладающий
свойствами: Т oS = iL^ S <> Г == iL^. В этом случае а(Г) =
= р (Т) = 0. Оказывается, что фредгольмовы операторы
в определенном смысле близки к обратимым.
Назовем оператор T^3?(LU L2) почти обратимым,
если найдутся такие операторы Si и S2 в 3? (L2i Lj), что
S1oT = lLi + K1, ToS2 = lL2 + K21 B5)
где Кх е End Lx и K2 G End L2 — компактные операторы.
Теорема 20 (С. М. Никольский). Каждый
фредголъмов оператор почти обратим. Более того, опера-
торы Si и S2 можно выбрать так, чтобы К^ и К2 были
операторами конечного ранга.
Доказательство. Покажем, что существуют та-
такое замкнутое подпространство М cz Li и такое конечно-
конечномерное подпространство iV <= L2, что ?i = ker T ® M, L2-=
= im T Ф N. Выберем в ker T базис хи ..., ха{Т) и в
(ker Т)' — дуальный базис Д, /2, ..., /а(т). (Дуальность
этих базисов означает, что fi{Xj) = 8ц*) (i, / = 1, ...
..., а (Г)).) Продолжим по теореме Хана — Банаха функ-
функционалы fi до линейных непрерывных функционалов
, а(Т)
Fi^L± и положим М = П
i
*) Sij, как обычно, означает символ Кронекера: 6ц = 1, бц =
0 при i Ф ;\
87
Тогда для каждого х е L{ существует и единственно
представление в виде
а(Г)
х = 2 с.ж. + у, где у<=М. B6)
В самом деле, применяя к обеим частям равенства Fu
мы видим, что Ci = Fi(x). Обратно, при таком выборе ко-
коэффициентов ct вектор у обязан лежать в М. Значит,
L, = кег Т е М.
Пусть теперь zt, ..., zp(T) — базис в сокег Т = LJim 71,
и пусть Zi — представитель класса и. Обозначим через .V
линейную оболочку векторов zt (l^i^$(T)). Пусть z —
любой вектор из Д>, г — его образ в сокег Т. Тогда су-
Р(Л
ществует и единственно разложение 2 = 2 ciz^ откуда
следует существование и единственность представления
z в виде
Р(Г)
2= 2 *А+ *' где t^imT- B7)
Значит, L2 = imT ® N. По теореме Банаха оператор
Т\м осуществляет топологический изоморфизм М и im Т.
Обозначим через Т оператор, обратный к Т\м, и опреде-
определим оператор S^3?(L2, L{) равенством
f B8)
где z^L2 и t^imT связаны равенством B7). Операто-
Операторы ST и TS легко вычисляются в явном виде с помощью
разложений B6) и B7):
a(T)
T oS (z) = T о S [%c.z.
Отртпггя К 97* 1 г • г i-> У F-(r\r К TS 1г
i=l
z»-> —2 cjzp. где с^ —координаты вектора z в базисе {zj.
Теорема доказана.
Отметим, что операторы Ki и Х2, построенные в до-
доказательстве теоремы, являются проекторами (на прост-
ранство кег Т параллельно М и на пространство N па-
параллельно imT соответственно).
Теорема 21 (Ф. Рисе). Если Ke=EndL —ком-
—компактный оператор, то оператор T = i — K—фредголъмов.
Доказательство. Пространство кег Г состоит из
тех векторов х, для которых К(х) = х. Поэтому оператор
К в пространстве ker T является одновременно компакт-
компактным и единичным. Отсюда следует конечномерность ker T
(ср. с задачей 339).
Выберем, как и в доказательстве теоремы 20, замкну-
замкнутое подпространство М <= L, дополнительное к ker Г. Опе-
Оператор Т взаимно однозначно отображает М на im Т. Пусть
Т — обратное отображение. Покажем, что оператор Т ог-
ограничен (т. е. 11Г(у)Н/Иу11 <с<оо для всех y^imT).
В противном случае можно было бы найти последователь-
последовательность векторов единичной длины {хп} <= Л/, для которых
уп = Т(хп)-+ 0. Но Т(хп) = хп — К(хп). Последовательность
\хп) ограничена, и, следовательно, последовательность
{К(хп)} предкомпактна. Переходя, если нужно, к под-
подпоследовательности, мы можем считать, что {К(хп)} име-
имеет предел х. Так как Т(хп)-+0, отсюда следует, что хп -*•
-*•#. Вектор х лежит в М (так как М замкнуто), имеет
единичную норму (как предел хп) и обладает свойством
Т(х) = 0 (так как Т непрерывен, а Г(#п)->0). Значит,
х е М П ker Г, что невозможно. Мы доказали ограничен-
ограниченность Т. Выведем отсюда замкнутость im Т.
Пусть уп е im T и уп^ у. Тогда последовательность
уп фундаментальна и, значит, фундаментальна и последо-
последовательность хп = Т(уп). Поскольку М полно (см. теоре-
теорему 2 гл. I), существует х = lim хп. Тогда Т (х) =
П-»оо
= lim T (xn) =lim уп = у.Замкнутость im Т доказана. Ос-
П
талось доказать неравенство Р(Г)<°°, т. е. конечномер-
конечномерность сокегГ. Это следует из соотношений B4) и уже
доказанного утверждения о конечномерности ядра, при-
примененного к оператору Т'. (Мы используем здесь теорему
о том, что оператор К' компактен, если компак-
компактен К.)
Выведем теперь из всего сказанного выше
Критерий фредгольмовости. Оператор Ге
^9?(LU L2) фредголъмов тогда и только тогда, когда он
почти обратим.
Доказательство. Вторая часть критерия состав-
составляет утверждение теоремы 20. Докажем первую часть.
89
Пусть Т почти обратим, т. е. выполнены равенства
B5). Тогда кегГскег51вГ = кегA + ^1). Последнее
пространство конечномерно по теореме Рисса. Далее,
im Т => im Т ° S2 = im (I + К2). Последнее пространство
замкнуто и имеет конечную коразмерность в L2 по теоре-
теореме Рисса. Тогда \шТ обладает теми же свойствами (как
прообраз im Г/im Т ° S2 с: LJim T ° 52), что и завершает
доказательство критерия.
Обозначим множество всех фредгольмовых операторов
из Li в L2 через @~(LU L2).
Теорема 22. Множество 5?~{Ьи L2) открыто в
3* (Lu L2) [относительно равномерной топологии) и инва-
инвариантно относительно сдвигов на элементы Ж(Ьи L2).
Доказательство. Пусть Т<^@~(Ьи Ьг). Тогда Т
почти обратим и справедливы соотношения B5). Пусть
норма оператора A^S?{LU L2) строго меньше каждого
из чисел II5VI-1, IliSgH. Тогда операторы 1 + S{A и l+AS2
обратимы. (Если IIBH < 1, то в качестве A + fi) можно
сю
взять сумму сходящегося ряда 2 (— Щ •) Поэтому
(Т + A)St(i+ ASt)-1 =A
что доказывает почти обратимость оператора Т + А. Зна-
Значит, &~(Li, Lz) содержит окрестность точки Т.
Пусть теперь T<=&"(LU L2), К<=Ж(Ь{, L2). Равенства
(T + K)S2 = l + K2 + KS2 = l+K2
показывают почти обратимость Т ' + К. (Мы использовали
тот факт, что произведение компактного оператора на
ограниченный есть компактный оператор.) Теорема до-
доказана.
Теорема 23. Функция i (индекс) локально постоян-
постоянна на 3T(LU L2), не меняется при. сдвигах на элементы
Ж(Ьи L2) и обладает свойством i(АВ) = i(A) + i(В), где
Доказательство. Докажем сначала полезную тех-
техническую лемму, позволяющую иногда явно вычислить
индекс оператора. Пусть пространства Ь^ и L2 разложены
в прямые суммы замкнутых подпространств Lt = Мг® Nt
90
(? = 1, 2). Тогда каждый оператор T^3?(LU L2) может
быть записан в виде операторной матрицы второго поряд-
порядка: Г = (? *), где 4ei?№, N2), B^2>(MU N2),
{) {)
Лемма. Если оператор Т фредголъмов, a D обратим,
то i{T) = i(A-BD-xC).
Доказательство леммы. Заметим, что умноже-
умножение оператора Т слева или справа на обратимый опера-
оператор не меняет чисел ее(Т) и ${Т), а значит, и индекс Т.
Поэтому
BD-^C О
О D
)¦
Если оператор Т имеет вид I Q ^1 (его естественно
записать как 7\ Ф Г2), то ker Г = ker Ti Ф ker Г2, coker Г ==
= coker Т, Ф coker Г2. Отсюда 1{Т)=1{Т,)Л-1{Тг). В на-
нашем случае i(T) =i(A- BD~XC) + i (D) = г (Л - ШI?
Лемма доказана.
Пусть теперь Т0^?Г(Ьи L2). Положим iVi^
М2 = im Го и построим замкнутое подпространство Л/4 с: L{
и конечномерное подпространство N2^L2, как в доказа-
доказательстве теоремы 20. Тогда оператор То имеет вид
Р п , где DQ — обратимый оператор. Любой опера-
0 О/
тор Г, достаточно близкий по норме к Го, имеет вид
(А В\
\с Z)/' г^е ^ — обратимый оператор. В силу доказанной
леммы Т зависит только от размерности N{ и N2: i(T) =
= i(A -BD~lC) = dim N,- dim N2 (см. A8)).
Докажем второе утверждение теоремы. Пусть Ге
^&~(LU L2), К^Ж(Ьи L2). Рассмотрим функцию ф@==
= i(T + tK), определенную на всей вещественной прямой
(так как множество &~(LU L2) инвариантно относительно
сдвигов на элементы Ж(Ьи L2)). В силу уже доказанного
утверждения эта функция локально постоянна и, следо-
следовательно, постоянна на любом связном множестве, в част-
частности на прямой. Значит, i(T) = cp(O) = cp(l) = i(T-\-K).
Докажем третье утверждение. Для этого рассмотрим
вспомогательный оператор А Ф В, действующий из Lo Ф Lv
в L2 Ф LQ. Как уже отмечалось выше, i(A® B) = i(A) +
91
+ i(B). Далее,
равенство
i(A Q\ i( Л
¦v? -о
при
°\
в!
достаточно малом г справедливо
v ° ~*{Ч
Теорема доказана.
Альтернатива Фредгольма. Пусть L—бана-
L—банахово пространство, К — компактный оператор в L, X —
число, отличное от нуля. Рассмотрим четыре уравнения:
1) Кх~Хх = у,
2) Кх-Хх = 0,
3) K'f-kf = g,
4) *'/-*/ = О,
где ж, у ^ L, /, gel/. Тогда либо а) уравнения 2) и 4)
имеют лишь тривиальное решение, а уравнения 1) а 3)
однозначно и корректно разрешимы при любой правой
части, либо б) уравнение 2) имеет конечномерное прост-
ранство решений LiczL1 а уравнение 4) —конечномерное
пространство решений L2 с ¦?', причем dim L4 = dim L2.
Уравнение 1) разрешимо в точности для тех у е L, для
которых f(y) = O для всех / е L2. Уравнение 3) разреши-
разрешимо в точности для тех g^L\ для которых g(x) = Q для
всех х^ Li.
Доказательство. Оператор XI обратим и, следо-
следовательно, является фредгольмовым оператором с нулевым
индексом. Этими же свойствами по теореме 23 обладает
оператор Т = К — %i. Первый случай альтернативы соот-
соответствует равенству а(Г) = 0. Тогда $(Т) = а(Т)+ i(T) =
= 0, откуда а(Г7) =Р(Г7) ==0. Поэтому кегГ = кегГ =
= @), imr = L, imJ/ = L/. Корректная разрешимость
уравнений 1) и 3) (т. е. непрерывность Г и (Г'))
следует из теоремы Банаха.
Второй случай альтернативы характеризуется неравен-
неравенством а(Т)?=0. Тогда, поскольку Т фредгольмов, а(Т)<
<оо. Поскольку в силу формул A9) —i(T)=i(T') = Q,
мы имеем Р(Г) = а(Г), а(Г) = ${Т') = а(Т). Кроме того,
ker Tr =(im TI- *), im Tf = (ker Г)-1, Теорема доказана.
*) Если L — ЛТП, U — сопряженное пространство и X — под-
подмножество в L, то через X1- обозначается совокупность всех / е
е L1 таких, что f(x) =0 для всех х ^ X,
02
Отметим, что из альтерпативы Фредгольма вытекает
следующее спектральное свойство компактных операто-
операторов: если К Ф 0 — точка спектра (т. е. оператор К — XI
необратим), то к — собственное значение конечной
кратности.
§ 4. Функциональные пространства
и обобщенные функции
1. Пространства интегрируемых функций. Пусть X —
множество с мерой jx. Через LP(X, (i) (Кр<°°) Мы
обозначим совокупность классов эквивалентности [х-изме-
римых функций с сумхмирувхмой р-и степенью. Положим
для f^Lp(X, [i)
X
(Здесь мы не делаем различия между классом эквива-
эквивалентности f^Lp(X, |i) и конкретной функцией f(x)e=j.)
Априори не ясно, что LP(X, \i)—линейное нормирован-
нормированное пространство при рФ\. Этот факт является след-
следствием неравенства Минковского: II/ + gHp < И/ИР + Hg!lP,
которое в свою очередь вытекает из неравенства Гёльдера:
,, если —| = 1 (ср. с задачами 370,
371). В случае точечной о-конечной меры эти неравенства
превращаются в соответствующие неравенства для после-
последовательностей.
Введем еще пространство L0O(X, \i) существенно огра-
ограниченных ^-измеримых функций (ср. с п. 1 § 3 гл. II).
Теорема 24. Пространства LP(XJ ji) при 1^/?^°°
являются банаховыми. Пространство, сопряженное к
LV(X, |i), при 1 ^ р < оо изоморфно пространству Lq(Xy |i)t
еде 1+1 = 1.
р я
Доказательство. Пусть F — линейный непрерыв-
непрерывный функционал на LP(X, ji). Если А а X — множество
конечной меры, то его характеристическая функция Ха
принадлежит ?Р(Х, \i). Положим v(A) = F(%A) и прове-
проверим, что v — заряд на кольце измеримых подмножеств X.
Аддитивность v вытекает из линейности F. Абсолютная
непрерывность v относительно меры \х следует из оценки
| v (А) |< | F \\l, || ia \\Lp = | F ||l/ |i (AI/Pt По теореме Радо-
93
на — Никодима (см. гл. II, § 3, п. 3) существует такая
ji-измеримая функция g на X, что v (A) = J g (х) d\i (x)
А
для любого множества А конечной меры. Покажем, что
g^Lq(X, |i). Для этого заметим, что в силу замечания
к неравенству Гёльдера (см. задачу 370) для любой
ji-измеримой функции g справедливо равенство
I \
I х
B9)
Ясно также, что верхнюю грань в правой части B9)
достаточно брать по простым функциям / из LP(X, \i).
N
Но для функции вида / (х) = 2 cklE (х) имеем
X k=l Ek *=*
Поэтому правая часть в B9) ограничена числом
Значит, g<^Lq{X, |i). По неравенству Гёльдера выраже-
выражение Fg (/) = J / {х) g {x) d\x (x) является линейным непре-
х
рывным функционалом на ЬР(Х, |i). Так как F и Fg сов-
совпадают на простых функциях, они совпадают всюду на
LP(X, |i). Применяя еще раз соотношение B9), мы ви-
видим, что \\g\\q = 1^1 '• Тем самым доказан изоморфизм
LP
Lv (X, |i) = Lq(X, \i). Полнота LP(X, \i) в случае 1<
< p ^ с» следует теперь из общей теоремы о полноте со-
сопряженного пространства (см. гл. III). Полнота ?i(X, ji)
была доказана в гл. II, § 3.
Утверждение теоремы 24 об изоморфизме Lp (X, \i)
и Z/g(X, |i) при р = о© перестает быть верным. Простран-
Пространство LOO{X, ji) не изоморфно ^i(X, ji), за исключением
тривиального случая, когда оно конечномерно. Можно по-
показать, что бесконечномерное пространство L{{X, jli) для
неточечной меры |i вообще не является сопряженным
к какому-либо банахову пространству. (Ср. с задачей 390.)
2. Пространства непрерывных функций. Пусть X —
компакт. Пространство С{Х) состоит из всех непрерывных
функций на X. Норма в С{Х) определяется формулой
fl/|| = ma_x|/(*)|.
94
Легко проверяется (см. задачу 392), что С(Х) — бана-
банахово пространство.
Теорема 25. Всякое банахово пространство L изо-
изоморфно замкнутому подпространству в одном из прост-
пространств типа С(Х). Если L сепарабельно, то в качестве X
можно взять отрезок [О, 1].
Доказательство. Пусть X — единичный шар в
пространстве Z/, сопряженном к L. Тогда X —компакт в
*-слабой топологии (см. теорему 13 и [14]). Каждый эле-
элемент пространства L можно рассматривать как линейную
функцию на X. В силу сказанного в п. 2 § 1 получаемое
таким образом отображение L в С(Х) является изомор-
изоморфизмом на замкнутое подпространство всех линейных
функций на X. Пусть известно, что L сепарабельно. Тогда
X с: V — метризуемое топологическое пространство (см.
§ 2). Если X — выпуклый метрический компакт в л-иней-
ном пространстве, то существует непрерывное отображе-
отображение / отрезка [0, 1] на X (см. задачу 403). Определим
теперь отображение L в С [0,1]: ср»-* Ф(г) = [/ (t)] (cp).
В силу сказанного выше это отображение является изо-
изоморфизмом L на некоторое замкнутое подпространство
в С[0, 1].
Теорема 26. Пространство, сопряженное к С[0, 1],
изоморфно пространству V[0, 1] функций с ограниченной
вариацией на отрезке [0, 1], непрерывных слева всюду,
кроме, быть может, правого конца отрезка, и удовлетво-
удовлетворяющих условию g(Q) = Q, с нормой \\g\\ = Varjg.
Доказательство. Пусть g^V[0, 1], /еС[0, 1].
1
Положим Fg (/) = J / (х) dg (x). Для любого разбиения
о
0 = ?0 ^ ti ^ ... < tn = 1 и любых %i ^ [?*-!, t{] имеем
С другой стороны, для любого 8 > 0 существует такое
п
разбиение Т отрезка [0, 1], что 2 I g (*0 — g (h-i) I >
>Varog— 8. Мы можем и будем считать, что во внут-
внутренних точках разбиения Т функция g непрерывна. Пусть
{fn} — последовательность непрерывных функций таких,
что 1 fn (ж) К 1 и fn (x) ^T^sgn [g (tk)—g (/bl)],ie[^_i, h).
95
г п
Тогда lim J /я (х) dg(x) = 2 \g (h)—g (h-i) l Поэтому
П-юо 0 x=l
1
при достаточно большом n J /n dg (я) > Varjg — e. Отсюда
|[,П HM
Остается доказать, что любой линейный непрерывный
функционал F на С[0, 1] имеет вид Fg с некоторой g ^
е F[0, 1]. Продолжим F по теореме Банаха до функцио-
функционала F на пространстве В[0, 1] ограниченных функций
с нормой 11/11 = sup \f(x) I. Пусть Хо — характеристическая
функция полуинтервала [0, а). Положим g(a)=(F, %аУ.
Ясно, что ^@) = 0. Покажем, что Var0 g (я) < оо. Для лю-
любого разбиения Т положим 6r(^) = sgn [g(tk)~ g{th-i)\
п
х е |>А_„ th). Тогда (F, ег> = S U (*k) ~ « Ck-i) |> °™уда
|| I||
Для любой кусочно постоянной непрерывной справа
функции ф на [0, 1] имеем: (F, ф) = J y(x)dg(x). Henpe-
0
рывная функция / может быть равномерно приближена
такими ф„, как, например, фп(^)== f([nx]/n). Поэтому ра-
1
венство \F, // = J / (x) dg (x) верно для всех непрерывных
о
функций /. Остается заметить, что для непрерывных /
замена g(x) на g(x— 0) = lim g(x—г) не меняет интегра-
1
ла Стилтьеса J / (х) dg(x). Поэтому можно считать g не-
о
прерывной слева.
Замечание. Теорема 26 допускает следующую эк-
эквивалентную формулировку:
Всякий линейный непрерывный функционал на С[0, 1]
имеет вид
где v — некоторый борелевский заряд на [0, 1], причем
llfv|lc'Lo,u = Varjv,
95
В этой форме теорема 26 переносится на пространство
комплексных непрерывных функций (с заменой v на
комплексный заряд) и на пространство типа С(Х), где
X — любой метрический компакт. Для произвольного ком-
компакта X первое утверждение теоремы остается верным, но
соответствие между зарядахми и линейными непрерывны-
непрерывными функционалами перестает быть взаимно однозначным.
3. Пространства гладких функций. Пусть Q — область
(т. е. открытое подмножество) в Rn, Q — замыкание Q
в Rn. Мы будем использовать следующие стандартные
обозначения: x = (xi, ..., хп)—координаты в Rn, x =
= хх1... xnn,di = д/дх{ — оператор частной производной,
д1 = д[г...д1?, \к\ = кг+к2 + ... + кп. _ Через Cr(Q)
обозначается совокупность функций на Q, обладающих
частными производными до г-го порядка в точках Й,
причем dlf (Ul^r) продолжаются до ограниченных не-
непрерывных функций на Q. Определим норму в Cr(Q)
формулой
U
Таким образом, сходимость в Cr(Q) означает равно-
равномерную сходимость самих функций и их частных произ-
производных до г-го порядка включительно. Несложно прове-
проверить, что Cr(Q) — ба_пахово пространство.
Пространства Cr(Q) удобны в тех вопросах, в которых
от рассматриваемых функций требуется вполне опреде-
определенная конечная гладкость (т. е. наличие определенного
количества непрерывных производных). Есть, однако,
такие задачи, в которых требуется заранее неизвестная
или бесконечная гладкость. В этих задачах естественно
использовать пространства бесконечно дифференцируемых
функций. Эти пространства локально выпуклы, но, как
правило, ненормируемы, а иногда и неметризуемы.
Наибольшее применение находят три типа про-
пространств.
1. Пространство <§ (Q) состоит из всех бесконечно диф-
дифференцируемых функций в Q. Топология в <%(Q) опре-
определяется семейством полунорм pKi, где К — компакт в Q,
a Z = (Zi, ..., ln) — произвольный мультииндекс:
pKl(f)=m&x\d1f(x)\. C0)
хек
7 А. А. Кириллов, А. Д. Гвишиани 97
Теорема 27. Пространство &(Q) счетно-нормируе-
мо (и, следовательно, метризуемо) и полно.
Доказательство. Обозначим через Кт совокуп-
совокупность точек x^Q, обладающих свойствами: 1) расстояние
от х до границы области Q*) (т. е. множества <9Q = Q\Q)
не меньше 1/т; 2) расстояние от х до 0 не больше т.
Ясно, что Кт — компакт, что все точки Кт являются
внутренними для Km+i и что объединение Кт по всем т
исчерпывает область Q. Определим полунорму рт в ^T(Q)
формулой рт (/) = sup | dlf (x) |.
К
Пусть К— произвольный компакт в Q. Функция 6(х)~
c=d(x, Q\Q) непрерывна и положительна на К. Следо-
Следовательно, она достигает минимума б0 > 0. Функция
A(x) = d(x, 0) непрерывна на К и, значит, достигает мак-
максимума До. Если число т выбрать так, что выполняются
неравенства 1/т < б0, т > До, то Кт будет содержать
компакт /?. Если, кроме того, выполняется неравенство
тп^ |/|, то полунорма рт мажорирует полунорму рКи Мы
доказали, что семейство полунорм {рт} мажорирует се-
т
т
мейство {pKi). Обратное очевидно: рт (/) ^ 2 Рк г (/)•
/=о т
Осталось доказать полноту &{Q). Пусть {/„) — фунда-
фундаментальная последовательность. Тогда {fj фундаменталь-
фундаментальна по любой полунорме рт. Отсюда вытекает, что ограни-
ограничение {/J на Кт — фундаментальная последовательность
в Ст{Кт), Значит, существует такая функция Fm^
eCm(/{m), что fn\Km-+Fm в метрике Ст(Кт). Ясно, что
функции Fm согласованы в том смысле, что Fm+1|Km=Frn.
Поэтому существует единая функция /, совпадающая с
Fm на Кт. По построению, Pm(/n —/)-*0 при п -*-«>. Это
значит, что /^^(Q) и /п -^ / в топологии простран-
пространства S'(Q).
Замечание. Пространство &(Q) часто обозначают
C°°(Q). Если граница Q непуста, то <?f(Q) не совпадает
с пересечением Ch(Q) (функции из <^(й), вообще говоря,
не продолжаются до непрерывных функций на Q).
2. Пространство S)(Q) состоит из бесконечно диффе-
дифференцируемых финитных (т. е. равных нулю вне некото-
некоторого компакта) функций на Q. Носителем функции ф на-
*) Под расстоянием до границы мы, как обычно, понимаем
минимальное из расстояний до ее точек.
зшается замыкание множества тех точек, где ф отлична
от нуля. Носитель ф обозначается символом suppcp. Та-
Таким образом, 2)(Q) состоит из тех фе^(й), для
которых йиррф— компакт. Легко проверить, что 2)(Q)
не замкнуто в S'(Q) и, значит, неполно в тополо-
топологии &(п).
Пусть К—компакт в Q. Обозначим через &K(Q) под-
подпространство в <§T(Q), состоящее из тех ф, для которых
suppcp <=/?. Тогда 2)К(О>) с топологией, заимствованной
из ^(й), будет полным счетно-нормироваиным простран-
пространством (ср. с задачей 414). Определим теперь в &(Q) то-
топологию, более сильную, чем наследуемая из <?{Q).
А именно, будем считать выпуклое множество V^2)(Q)
открытым (соотв. замкнутым), если его пересечение с
2)(&) открыто (соотв. замкнуто) для любого компакта
Получаемую таким образом топологию можно также
задать с помощью семейства полунорм. Пусть {Кт} — си-
система компактов, построенная в доказательстве теоре-
теоремы 27. Обозначим символом а последовательность {N,n}
целых неотрицательных чисел и положим
SUP |0!ф(*)| C1)
К
(здесь Ко — пустое множество), Отметим, что для каждой
функции ф^2)(Й) ряд в правой части C1) содержит
лишь конечное число ненулевых слагаемых. Мы предо-
предоставляем читателю проверить, что введенная таким обра-
образом (несчетная) система полунорм определяет описанную
выше топологию.
Теорема 28. Последовательность {фп} сходится к ф
в 2)(Q) тогда и только тогда, когда
1) фп ->¦ ф в смысле & (Q).
2) все функции ф„ (а значит, и ф) принадлежат од-
одному подпространству 2)K(Q).
Доказательство. Достаточность условий 1} и 2)
очевидна так же, как и необходимость условия 1). До-
Докажем необходимость условия 2). Пусть последователь-
последовательность {ф„} такова, что носители фп не содержатся ни в
каком фиксированном компакте. Производя, если нужно,
перенумерацию, мы можем считать, что supp ут<?Кт.
Пусть хт — такая точка вне Кт, в которой фт отлична
от нуля. Рассмотрим множество V, состоящее из всех
функций ф <^ 3)(Q), удовлетворяющих условиям 1ф(^т) I <
<\ут{хт)\/т для m = l, 2, 3, ... Поскольку любой ком-
компакт #<=Q содержит лишь конечное число точек хт, пе-
пересечение V с SDK(Q) задается конечным числом условий
и, следовательно, открыто в S)K(Q). Значит, V открыто
в ?D(Q). Пусть pv — функционал Минковского для V. Лег-
Легко видеть, что V — выпуклое уравновешенное множество,
а тогда pv — непрерывная полунорма в S)(Q). Явный вид
пир (хт)
pv дается формулойpv (ср) = sup
фт (хт)
откуда вытекает,
что Рг(фт)^ т. Поэтому последовательность (ср™) не мо-
может быть сходящейся. Теорема доказана.
Теорема 29. Пространство 2)(Q) полно, неметри-
зуемо и обладает свойством Гейне — Бореля: всякое огра-
ограниченное*) подмножество в 2)(Q) предкомпактно.
Доказательство. Если последовательность {срп}
фундаментальна, то рассуждение, приведенное в доказа-
доказательстве теоремы 28, показывает, что вся эта последова-
последовательность лежит в одном подпространстве 3)к{&). По-
Поскольку 3)K(Q) полно, эта последовательность имеет пре-
предел. Предположим теперь, что S)(Q) метризуемо и пусть
{фт) — последовательность, для которой supp фт Ф Кт. Из
непрерывности умножения на число следует, что для
каждого т можно указать настолько малое число бт > О,
что d@, бтфт)<1/т. Это значит, что последовательность
{бтфш} стремится к нулю, что противоречит теореме 28.
Таким образом, 3){Q) неметризуемо. Пусть, наконец,
А — ограниченное подмножество в 3)(Q). Рассуждение,,
уже использовавшееся выше, показывает, что A<^?DK(Q)
для некоторого компакта K<=Q. Поскольку А ограничено
по каждой полунорме pKi, все функции из Л и все их
частные производные удовлетворяют условиям теоремы
Асколи — Арцела. Отсюда вытекает предкомпактность А-
в 2)K(Q), значит, и в 3)(Q). Теорема доказана.
Замечание. Вместо обозначения S)(Q) использу-
используется также С™ (Q).
3. Пространство S(Rn) состоит из бесконечно диффе-
дифференцируемых и быстро убывающих на бесконечности
функций в Rn. Топология в S(Rn) задается счетным се-
семейством полунорм
Р.р(/)= suplsV/tol, C2)
Rn
*) Ограниченным множеством в полинормированном простран-
пространстве называется множество, ограниченное по каждой из полунорм.
(Ср. п. 1 § 2.)
100
где приняты стандартные сокращенные обозначений
oft д 1 д п д1
(Пространство 5(R") состоит из всех /^^f(Rn), для ко-
которых /?аэ(/)<°° для всех а и [}.)
Иногда бывает удобно вместо набора полунорм C2)
рассматривать набор
Pap(/)= J hV/(x)|da: C2')
пли набор
у
Rn /
Теорема 30. Системы полунорм C2), C2') м C2")
эквивалентны.
Доказательство. Рассмотрим сначала более на-
наглядный случай п = 1. Справедливо равенство
| xkdlf (х) | < -i-j sup | (*» + 1) xhdlf (x) |.
1 + X 3C
Отсюда
Аналогично,
Таким образом, полунормы системы C2) мажорируют
полунормы систем C2') и C2"). Далее, применяя нера-
неравенство Коши — Буняковского к функциям
+ х%
101
получаем
PHlU)* =
= f j | xkdlf (x) I dx\2< j | xhdlf (x) |2 A + x2) dx j -^L_ =
j j
Значит, полунормы системы C2") мажорируют полу-
полунормы системы C2'). Остается оценить полунормы систе-
системы C2') через полунормы системы C2"). Воспользуем-
Воспользуемся тем, что для /^»S(R) функции xkdlf(x) при любых к
и I стремятся к нулю на бесконечности и поэтому спра-
справедливо равенство
х
xhdlf(x)= J [thdlf(t)]'dt. C3)
—сю
Отсюда
Phl(f)=suv\xhd1f(x)\<:§\[tkdlf(t)]'\dt^
х R
Случай n > 1 отличается лишь техническими услож-
Г dx п
нениями: вместо равенства 2 = n нужно использо-
использовать неравенство —^<°°> а вместо тождества
C3) — тождество
х1 хп
(* С ЯПСГ)
— СХ) —-ОО
справедливое для любой бесконечно дифференцируемой
функции, которая вместе со своими производными стре-
стремится к нулю на бесконечности. Теорема доказана.
По запасу функций и по топологии пространство
5(Rn) занимает промежуточное положение между & (Rn)
и S5(R"). Именно, имеют место непрерывные вложения
До сих пор мы не привели еще ни одного примера функ-
функции, принадлежащей .25 (Rn) или 5(Rn). Построение та-
таких примеров не вполне тривиально. Однако справедлива
102
Теорема 31. Пространство &{J{n) плотно в iP(Rn,
dx)*) при Кр<«>, в 5(Rn) и в <?(R"). Пространство
5(Rn) плотно в Lp(Rn, dx) при 1^р<°о и в S'(Rn).
Чтобы избежать технических сложностей, мы прове-
проведем доказательство подробно лишь для случая п = 1.
Начнем с конструкции нетривиальной функции в <2)(R).
Лемма 1. Функция
(О при х^ О,
{е1/х гсргг .г < О
бесконечно дифференцируема на всей прямой.
Доказательство. Всюду вне точки х = 0 утверж-
утверждение очевидно. Проверим, что q>{h)@) = 0 для к = 1,
2, ... Для этого заметим, что функция —^(е1/ос) имеет
вид Pk(x)x~zkeUx, где /\ — некоторый многочлен степени
<&\ (Это легко устанавливается по индукции.) Далее,
lim —^rellx== ^m Р1—~—Iте~1=0 для любого m и
любого многочлена Р, что легко установить с помощью
правила Лопиталя. Таким образом, lim ф(/?) (е) = 0 для
всех к. Применяя еще раз правило Лопиталя, получаем
утверждение леммы.
Лемма 2. Функция
_ |ехр {2/{х2 - 1)} при | х | < 1,
" 1 0 лгра \х\^1
принадлежит .25 (R).
В самом деле, эта функция обращается в нуль вне
отрезка [—1, 1] и бесконечно дифференцируема, так как
записывается в виде г|)(д;) = Ц){х— 1)ф(—х — 1), где ф —
функция из леммы 1.
Лемма 3. Для любого г > 0 полооким г|^ {х) =»
с / д. \ р
= —'Ф —/» г&е с~1 == Ф^) dx. Тогда функция гЬе(^У
обладает свойствами:
1) г|эв(я)>0;
2) supp\|)e = [-e, е];
3) J
¦) Как обычно, через dx мы обозначаем меру Лебега в Rn.
103
Доказательство очевидно.
Теперь мы в состоянии доказать первое утверждение
теоремы 31 (о плотности Ф(R) в LP(R, dx) при 1^р<
оо
<«>). Пусть /eLp(R, dx). Поскольку интеграл J \f\pdx
—оо
-JV
сходится, существует такое число N, что j | / \pdx -f-
— ОО
ОО
+ J | / \vdx < Ш\ Тогда функция
\х) при |*|<ЛГ,
О при | х | > N
имеет компактный носитель и II/ — fN\\p < е/2. Далее, по-
поскольку /#(#) непрерывна в среднем (см. задачу 386),
существует такое б > 0, что J | fN (х) — fN (х + t) |p<?z <
( г
при UI < б. Рассмотрим теперь функцию
оо
g(x)= \ fN(x-t)%(t)dt.
(Этот интеграл существует, поскольку \рб ограничена,
финитна и, следовательно, принадлежит Lq(R1 dx).) Оце-
Оценим расстояние между fN и g в ?/P(R, dx). Для этого
I Г
I Г
воспользуемся формулой ||/|р= sup м fhdx
. Имеем
= sup
= sup
I AN-g)hdx
-oo
oo
J ^e @ (/iv (« - 0 - /w (*)) Л («) rfx dt
oo / oo
-oo \-oo
—oo — oo
— \
Мы воспользовались равенством J ty6(t)dt = 1. I Послед-
104
нин интеграл допускает оценку
б / оо \
в силу выбора б. Итак, WfN — g\\p < г/2 и, следовательно,
"/~~^"р<е- Проверим, что g^2)(R). Финитность функ-
функции g вытекает из финитности jN и ty&: ясно, что suppgcz
с= supp/лг + supp'фб = [—N — б, yV + б]. Бесконечная диффе-
ренцируемость g вытекает из тождества
которое легко доказывается по индукции (ср. с § 1
гл. IV).
Докажем теперь, что 2) (Я) плотно в <^(R). Для этого
построим функцию %{^ 2) (R),
обладающую свойством: хЛх)~
^1 на [—1, 1]. В качестве та-
такой функции можно взять, на-
например, первообразную от функ- -^ ~/ д'
ции -ф1/2 (д: + 3/2) -я|I/2 (я - 3/2)
(рис. 1).
Положим у„ (х) - Yi ( 4г ). Рис> L
Тогда Xn(x)() ^()
= 1 при x^[-N, N]. Пусть /ear(R). Тогда x()
Проверим, что Хлг/"^ / в ^T(R) при 7V —^ оож Пусть К —
компакт на прямой. Тогда он содержится в [-N, N] при
достаточно большом N. Поэтому pkl (%Nf — /) = sup I (%Nf —
— f){l)(x)\ =0 при достаточно большом TV. Значит, х^/~^"
-* / в ^Г (R) при TV -> оо#
Оказывается, та же последовательность х*/ сходится
к / и в смысле пространства 5(R). Доказательство этого
опирается на оценку
^ при \x\>N, /eJ(R)t
которая непосредственно вытекает из определения нормы
105
pk+m, i. Имеем
sup
х~Я
I
\xkf>\
2 C\xkf>\x) (%N - \f~» (x)
3=0
I
Воспользуемся теперь соотношением
при xsR и
Тогда мы получим
Последнее выражение стремится к нулю при N ->*>.
Остальные утверждения теоремы следуют из уже дока-
доказанных.
Теорема Вейерштрасса. Пусть Q — ограничен-
ограниченная область в Rn. Тогда для любого натурального к про-
пространство Рп полиномиальных функций от п переменных
плотно в Ch(Q).
Доказательство теоремы мы отложим до § 1 гл. IV,
так как оно опирается на технику сверток.
Следствие 1. Для любой области Q с Rn прост-
пространство Рп полиномиальных функций от п переменных
плотно в $* (Q).
Доказательство следствия. Пусть заданы
функция /^<§f(Q) и полунорма pKk в ^T(Q). Покажем,
что для любого е > 0 существует такой многочлен q e Рп?
что ркн(я "~/)<е. Пусть V — ограниченная открытая ок-
окрестность компакта к. Ограничение / на V принадлежит,
очевидно, Ch(V). Применяя к этому ограничению теоре-
теорему Вейерштрасса, найдем такой многочлен q e Р^, что
||^ —/||с^(у)<е.Поскольку норма пространства Ch(V) ма-
мажорирует полунорму pRk, q — искомый многочлен.
Следствие 2. Пусть Q — область в Rn, К — ком-
компакт в О, фе55й(О), /e2)(Q) и f(x)*O для х^К.
Тогда найдется последовательность многочленов {pj cz Pn
такая, чго Pkf ~+У в iZ)(Q).
106
Для доказательства достаточно выбрать {ph} так, что-
чтобы ph -*¦ ф// в <§ (Q).
4. Обобщенные функции. Понятие обобщенной функ-
функции*) естественно возникает в различных вопросах мате-
математики и математической физики при желании распрост-
распространить некоторые естественные операции (дифференциро-
(дифференцирование, интегрирование, решение дифференциальных урав-
уравнений, преобразование Фурье и т. д.) на более широкую
область по сравнению с той, где эти операции первона-
первоначально определены. На первых порах это приводило к
парадоксальным и противоречивым определениям обоб-
обобщенных функций. Например, знаменитая б-функция Ди-
Дирака определялась следующими свойствами:
оо
б (х) = О при х ф О, б @) = оо, J б (х) dx = 1.
—оо
Другое определение той же функции:6(я) = ——(signer).
Ясно, что обычной функции с такими свойствами не су-
существует.
Оказалось, что эти и многие другие свойства пере-
перестают быть противоречивыми, если понимать обобщенную
функцию как элемент сопряженного пространства V\ где
L — некоторое пространство «пробных» или «основных»
функций. В качестве пространства L чаще всего исполь-
используют iZ)(Q), &(Q) или S(R"). Элементы пространств
2)'(Q), &'(Q) и 5"(R") получили название обобщенных
функций в области Q, обобщенных функций с компакт-
компактным носителем в области Q и обобщенных функций уме-
умеренного роста в Rn соответственно. Происхождение этих
названий выяснится ниже.
Покажем сначала, каким образом любую (не слишком
плохую) обычную функцию в Q можно рассматривать как
обобщенную функцию.
Теорема 32. Пусть f — локально суммируемая (т. е.
суммируемая на каждом компакте) по мере Лебега dx
функция в области Q. Соответствие гп ¦-* J ср (х) / (х) dx яв-
Q
ляется линейным непрерывным функционалом на 2D(Q).
Если, кроме того, f обращается в нуль вне некоторого
*) Вместо термина «обобщенная функция» иногда употребля-
употребляется термин «распределение» (distribution),
407
компакта K^Q, то это соответствие является линейным
непрерывным функционалом на & (Q).
Доказательство. В силу результата задачи 413
мы должны проверить, что из срЛ ->- 0 в 2)(Q) следует
J Фп(^) / (х) с'х-^д.Но это вытекает из определения схо-
Q
димости в 2D(Q) и теоремы Лебега о предельном перехо-
переходе под знаком интеграла. Для доказательства второго ут-
утверждения достаточно сослаться на теорему 15 гл. II.
Обобщенные функции типа, описанного в теореме 3,
назовем регулярными обобщенными функциями; они соот-
соответствуют обычным локально суммируемым функциям
f(x). Бывают, однако, и нерегулярные обобщенные функ-
функции. По аналогии с регулярным случаем значение обоб-
обобщенной функции F на основной функции ср часто запи-
записывают в виде | F (х) ф (х) dx = <F, cp>. Разумеется, эту за-
Q
пись нельзя понимать буквально — соответствующий инте-
интеграл расходится или вообще не имеет смысла.
Пусть Q — область в Rn, содержащая начало коорди-
координат. Определим функцию Дирака 8(х) как элемент про-
пространства ^T'(Q), задаваемый формулой
\6(x)q>(x)dx = ф@).
Поскольку 2)(Q) непрерывно вложено в &(Q), всякий
линейный функционал на ^(Q) порождает при ограни-
ограничении линейный функционал на 2D(Q). Из того, что
2)(Q) плотно в ^T(Q), вытекает, что естественное отобра-
отображение ^f'(Q) в 2) (Q) является вложением. Аналогич-
Аналогичные соображения показывают наличие непрерывных вло-
вложений
Другими словами, всякая обобщенная функция с ком-
компактным носителем является обобщенной функцией уме-
умеренного роста, а всякая обобщенная функция умеренного
роста является обобщенной функцией.
В отличие от обычных функций, обобщенные функ-
функции не имеют определенных значений в точке (впрочем,
этим свойством обладают уже известные нам элементы
пространств LP(X, \i)). Тем не менее для обобщенной
функции F & 2)' (Q) имеет смысл выражение «F(x) равна
нулю в области f/c=Q». По определению, это выражение
108
означает, что <F, ф> = О для всех пробных функций ф,
обладающих свойством supp ф cz U.
Пусть F^2Df(Q). Скажем, что х не принадлежит но-
носителю F, если F обращается в нуль в некоторой откры-
открытой окрестности точки х. Ясно, что носитель F является
замкнутым множеством (так как его дополнение откры-
открыто — это непосредственно вытекает из определения носи-
носителя). Обозначим его suppF и положим U = QXsuppF.
Докажем, что F обращается в нуль в области U. Пусть
Ф^2) (Q) и supp ф = К cz С/. Каждая точка х^К обладает
окрестностью Vx, в которой F обращается в нуль. Из по-
покрытия {Vx)xeK выделим конечное подпокрытие^, ...
• • • !^*п» и ПУСТЬ Ф1, •.., фп — соответствующее разбиение
п
единицы (см. задачу 415). Тогдаф =2 ФФг и (^, ф) -
г=1
п
5=58 S <^> ФФг> = О.Если У —любая область, в которой F
i=l
равна нулю, то все точки V не принадлежат supp F и,
значит, V cz U.
. Теперь выражение «обобщенная функция на Й с ком-
компактным носителем» мы можем понимать в двух смыслах:
1) как элемент пространства ?T'(Q);
2) как элемент ?е2)'(й)} для которого suppF —
компакт.
Эти два понятия на самом деле совпадают. А именно,
всякий элемент Fe^"(Q) определяет, как уже отмеча-
отмечалось выше, элемент 3)'(Q), который мы будем обозначать
той же буквой. Оказывается, таким образом получаются
в точности те элементы 3)'(Q), которые имеют компакт-
компактный носитель. Докажем это.
Пусть Fe^'(Q), Тогда F непрерывен относительно
одной из полунорм pKh, задающих топологию в &(Q)\
<F, ср> ^сркл(ср) для ф?^(Й).
Ясно, что ограничение F на 2)(Q) обращается в нуль на
Q\K. В самом деле, если фе2)(Ц) и suppфC=Q\^iL, го
Ркл(ф) = 0. Таким образом, suppFc:^ T. e. F как эле-
элемент 2D'(Q) имеет компактный носитель. Пусть теперь
F^2)'(Q) и supp F = Я—компакт в Q. Построим такой
функционал F на S'(Q), ограничение которого на 3)(Q)
совпадает с F. Для этого рассмотрим некоторую компакт-
компактную окрестность V множества К и построим функцию
Xve^(?2), обладающую свойством %v{x)^l для x&V
(см. задачу 415). Определим F формулой </f, /> = <^, %vft-
1ОЯГ
Это определение имеет смысл, так как %vf^@(Q) для
любой /e^(Q). Несложно также показать, что fe
Остается проверить, что F\gxQ) = F- Пусть
Тогда <F, ф> - <F, ф> = <F, Хуф-ф>==0, так
как
supp (хуФ — ф) <= Q\ V с QYK.
Теорема 33. Пространства 55'(Q), ?"(Q) и S"(Rn)
*-слабо полны. (Другими словами, если последователь-
последовательность {Fn} обобщенных функций такова, что числовая
последовательность i(Fn, ф>} фундаментальна для любой
пробной функции ф, то существует lim Fn = F, который
П-»оо
является обобщенной функцией того же типа, что и Fn.)
Доказательство. Определим F формулой <F, ф> =
= lim <Fn, ф>. Линейность F очевидна. Докажем непре-
П-»оо
рывность. В случае <§f(Q) и S(Rn) непрерывность выте-
вытекает из теоремы Банаха — Штейнгауза (ср. с § 3, п. 1),
так как <§T(Q) и S(Rn)—полные метрические линейные
пространства (см. задачи 427—430). Разберем случай
i0(Q). Ограничения Fn на 3)К{&) стремятся к некоторо-
некоторому элементу Fk е 3)к (^), так как &к{&) — полное мет-
метрическое линейное пространство. Определим теперь функ-
функционал Fe25'(Q), полагая его равным FK на &)к(Щ.
Корректность этого определения легко проверяется. (Если
supp ф е К, П К2, то<Рк ф> = lim <Fn, ф> = </г?х ф>.)Не-
прерывность F следует из задачи 413. Теорема доказана.
Пример. Обобщенные функции (х±Ю)~*. Пусть
оо
cpejZ)(R). Тогда интеграл \ , . ¦ rfx сходится при е >0
— оо
и имеет конечный предел при г\0 (см. задачу 439).
В силу теоремы 33 этот предел является обобщенной
функцией на прямой, которая обозначается (х±Ю)~1.
Всякая обобщенная функция с компактным носителем
в Q непрерывна по одной из полунорм pKt. Наименьшее I,
для которого это имеет место, называется порядком обоб-
обобщенной функции. Если обобщенная функция Fe^T'(Q)
имеет порядок I и носитель К, то она продолжается до
линейного непрерывного функционала на Cl(V), где У —
любая окрестность компакта К.
Говорят, что обобщенная функция F^3)'(Q) имеет
порядок <Z, если она продолжается до линейного непре-
«0
рывного функционала на Cl(Q). He всякий элемент Fe
^3)f(Q) имеет конечный порядок. Однако для любой
области Fczfi с компактным замыканием ограничение F
на 3)(V) имеет конечный порядок.
Всякая обобщенная функция умеренного роста F<=
eS'(Rn) непрерывна относительно одной из полунорм
n r=suppap(cM. п. 3). Порядком F называется наимень-
\a\<h
Ш1
шее Z, при котором это имеет место. Таким образом, вся-
всякая обобщенная функция умеренного роста имеет конеч-
конечный порядок. (Нетрудно проверить, что это определение
порядка эквивалентно данному выше в случае, когда Q =
*=R" и обобщенная функция / лежит в S' (Rn) с 3>'(Rn).)
5. Действия над обобщенными функциями. Мы пока-
покажем здесь, каким образом, основные действия над обыч-
обычными функциями — умножение на функцию, дифферен-
дифференцирование, замена переменных — переносятся на обобщен-
обобщенные функции.
Пусть L означает какое-либо из пространств 3)(Q\,
<§T(Q), ?(Rn), V — сопряженное пространство, Lo — не-
некоторое плотное подпространство в Z/, состоящее из ре-
регулярных обобщенных функций. В случае L = 2)(Q) или
<?(Q) в качестве Lo удобно взять iZ5(Q); в случае L =
= ?(Rn) можно в качестве L'o взять ^5(Rn) или S(Rn).
Предположим, что в Lo задан некоторый линейный опе-
оператор Ао и что этот оператор непрерывен в топологии Z/.
Тогда Ао продолжается до непрерывного оператора А в
L'. Это продолжение единственно, поскольку LQ плот-
плотно в Z/.
В нужных нам случаях непрерывность оператора Ао
может быть установлена следующим полезным приемом.
Пусть В — непрерывный оператор в i, В' — сопряженный
оператор в Z/. Если ограничение В' на L>0 совпадает
с AQ, to Ай непрерывен. В этом случае, очевидно, искомое
продолжение А совпадает с В\
Перейдем к конкретным приложениям описанной об-
общей схемы.
1) Умножение на функцию. Пусть /e#(Q);
покажем, что оператор M(f) умножения на / допускает
непрерывное продолжение с ?D(Q) на ?Df(Q). Положим
L = 3) (й) = LOi B = M(f). Ограничение оператора В' на
1/'о легко вычисляется, В самом деле, пусть фе^)(Й),
Ш
C Тогда
<B'g, Ф> = <*, 5ф> = <*, /Ф> = J g (x) f (x) Ф (x) dx.
2
Таким образом, оператор 5' на пространстве Lo действу-
действует как умножение на функцию /. Мы видим, что этот опе-
оператор допускает непрерывное продолжение (а именно,
Вг) на все пространство iZ)'(Q). Обозначая это продолже-
продолжение по-прежнему через M(f), мы получаем равенство
Пример. Вычислим произведение б-функции на
прямой на бесконечно дифференцируемую функцию /.
Имеем </6, ф> = <б, /ф> = / @) ср @). Отсюда /б = /@) б, что
согласуется с нашим интуитивным представлением о по-
поведении 6-функции при умножении.
2) Дифференцирование. Напомним, что через
д) мы обозначаем частную производную Ыдхи а через
d\k\
dk — оператор —; —. Покажем, что оператор dh до-
пускает непрерывное продолжение с S)(Q) на 2)'(Q)\
Достаточно рассмотреть случай оператора д}. Положим
В =—dj и вычислим ограничение В' на 2)(Q). Имеем
Итак, В' совпадает с д^ на ?D{Q). Поэтому оператор )
допускает непрерывное продолжение (а именно, В') на
2D (Q). Явный вид этого продолжения (которое мы обо-
обозначаем по-прежнему через dj) дается формулой
и вообще для любого к
Пример. Обобщенная функция 3Лб действует по
формуле
Замена переменных. Пусть у = у(х) — взаимно
однозначное бесконечно дифференцируемое отображение
области Q на себя, # = х(у) — обратное отображение.
В пространстве 2)(Q) определен оператор замены пере-
112
менных Т: (Ту) (у) = у(х(у)). Вычислим сопряженный
оператор Т' на пространстве ?D(Q). Имеем
Ф> = </
= J/ (У) Ф (* (У)) dy = lf{y (*)) Ф И l-g
Таким образом, оператор, сопряженный с 7\ является
композицией оператора Г обратной замены переменных
и оператора Ml \-^ I умножения на модуль якобиана
этой замены. Отсюда вытекает, что оператор Т допускает
непрерывное продолжение на 3)'(Q). Несложное вычис-
вычисление показывает, что оно задается формулой
<TF, cp> = <F
где У —якобиан отображения Т~\
Пример. Пусть а(х) — бесконечно дифференцируе-
дифференцируемое взаимно однозначное отображение прямой на себя.
Вычислим обобщенную функцию б (а (я)). Имеем
где Ь(х) —функция, обратная к а(х). В частности, спра-
справедливо равенство 8(ах + Ь)= |а|"б-ь/в(лг). (Через бь(х)
обозначается обобщенная функция, действующая по фор-
формуле <бь, Ф> = ф(&).)
Замечание. Определенные выше операции над
обобщенными функциями по построению являются непре-
непрерывными операторами. Следовательно, они перестановоч-
перестановочны с предельными переходами. В частности, сходящийся
ряд из обобщенных функций можно дифференцировать
почлейно любое число раз.
Покажем теперь, что совокупность всех обобщенных
функций с компактным носителем естественно возникает
из регулярных обобщенных функций применением опера-
операции дифференцирования. А именно, справедлива
Теорема 34. Всякая обобщенная функция F eJT' (Q)
может быть записана в виде
F-Pf, 'C4J
где к — некоторый мулътииндекс, a f — регулярная обоб-
обобщенная функция.
Доказательство. Удобно в качестве системы
полунорм в &(&), определяющей топологию в этом
8 А. А. Кириллов, А. Д. Гвишиани
пространстве, взять систему
кп
где {Кп} — семейство компактов, исчерпывающее область
(см. п. 3). Если обобщенная функция F непрерывна от-
относительно полунормы pnk, то в ?илу теоремы Хана —
Банаха и теоремы об общем виде линейного функционала
на L^Kn, dx) существует такая функция }^Ьх(Кп, dx),
что
<F, ф>= f dky(x)f(x)dx.
*п
Это равенство после замены / на (—l)|fei/ превраща-
превращается в искомое соотношение C4).
Замечания. 1. Приведенное доказательство обеспе-
обеспечивает лишь измеримость функции /. Увеличивая, если
нужно, мультииндекс /с, можно добиться, чтобы функция
/ была непрерывна на Q.
2. Можно показать, что функцию /. можно выбрать
совпадающей вне suppF с некоторым многочленом, анну-
аннулируемым оператором дк.
3. Аналогичным рассуждением доказывается
Теорема 35. Каждая обобщенная функция умерен-
умеренного роста F<=S'(Rn) допускает представление C4), где
/ — непрерывная функция умеренного роста на Rn.
Для построения и изучения обобщенных функций
в многомерных областях большую роль играет конструк-
конструкция прямого произведения обобщенных функций.
Пусть Qi — область в Rm, Q2 — область в Rn. Положим
Q = Qi X fi2 <= Rm+n. Если fi — регулярные обобщенные
функции в Qf, г = 1, 2, то можно определить регулярную
обобщенную функцию / в Q по формуле </, q>> =
*= J /х {х) /2 (у) ф (х,у) dx dy.Функция / называется прямым
а
произведением /4 и /2 и обозначается /4 X /2. По теореме
Фубини этот интеграл можно вычислять последовательно:
</, Ф> = I h (*) ($ /2 (У) Ф (*, У) dy\ dx -
v)d*\dy. C5)
114
Оказывается, эта конструкция сохраняет силу для любых
обобщенных функций.
Теорема 36. Пусть <р e2)(Q), /, e=^)'(Qt) (i = 1,2).
1) функция (pi(#)=</2, ф(^, •)> принадлежит
2) функция Фг (^/) = </i, ф(\ */)> принадлежит
3) справедливо равенство </ь ф.(> = </2, ф2>;
4) соответствие ф-*¦ </t, ф!> = </2, фг> является линей-
линейным непрерывным функционалом на 2)(Q).
Доказательство. Докажем финитность функции
ф1. Пусть Kc:Q — носитель функции ф, Кх— проекция К
в Qt. Тогда функция фх(*/) = ф(#, у) тождественно равна
нулю при х вне К{. Поэтому Ц){(х) = </2, ф*> = О для
х&Ки откуда биррф!^:/^^ Далее, отображение fit в
3) (Q2) по формуле х -*> фх бесконечно дифференцируемо.
Это влечет бесконечную дифференцируемость фь Итак,
ф1^.2)(й1), и мы доказали 1). Утверждение 2) доказы-
доказывается точно так же.
Для доказательства 3) рассмотрим сначала частный
случай, когда функция ф(.г, у) имеет вид <Pi(z)y2(y)t
В этом случае, очевидно, ($[(х) = ф! (д:) </2, ф2\ фг(^) =
~ф2(^/)^/ь Ф1^ и равенство 3) выполняется. Поскольку
линейные комбинации функции вида qi(z)(p2(y) плотны
в 2D(Q), остается проверить, что отображения ф-> </t, ф!>
и ф -*¦ </2> ф2> непрерывны в топологии 3)(Q). Это сле-
следует из непрерывности отображения ф -^ ф1 пространства
2D(Q) в пространство ^(Qi), проверяемой непосред-
непосредственно.
§ 5. Гильбертовы пространства
1. Геометрия гильбертова пространства. Линейное про-
пространство Н над полем /С =¦= R. или¦ С называется предгиль-
предгильбертовым, если в нем задано скалярное произведение*),
т. е. отображение Н ХН в К, обозначаемое ( , ) и обла-
обладающее свойствами:
1) (kiXi + KzXi, y)==^i(x^ У) + К(Х2, У) (линейность по
первому аргументу);
*) Название «скалярное произведение» возникло из работы
Гамильтона о теле кватернионов. Каждый кватернион q представ-
представляется в виде суммы «скалярной части» д0 и «векторной части»
Я. — Яг1 -\-Я21 + Чък. В соответствии с этим произведение двух
векторных кватернионов q и г является суммой скалярного
произведения (q, r) и векторного произведения [q, r]. В зарубежг
ной литературе вместо термина «скалярное произведение» часто
испрльзуется термин «внутреннее произведение».
8* 113.
2) (x, У) = (У, x) {эрмитова симметричность; черта оз-
означает комплексное сопряжение);
3) (х, х)>0 (положительная полуопределенность).
Предгильбертово пространство Я называется гильбер-
гильбертовым, если дополнительно выполняются условия:
3') (х, х)>0 при х^О;
4) Н полно в топологии, определяемой нормой 11x11 =
= У(.г, х).
(Тот факт, что это действительно норма, будет уста-
установлен ниже.)
Одним из важнейших следствий свойств скалярного
произведения является
Неравенство Коши — Буняковского:
\(х, у)\2^(х, х)(у, у).
Доказательство. Пусть сначала («г, у) — веще-
вещественное число. Для любого t ^ R имеем
0<(x + ty, x + ty) = (z, x)+2t(x, y)+t2(y, у).
Значит, этот квадратный трехчлен (от переменной t) име-
имеет неположительный дискриминант: (я, уJ— {х, х) •
• (у, г/)<0, что и требовалось. Общий случай получается
из разобранного умножением вектора х (или у) на подхо-
подходящее комплексное число, по модулю равное 1. При этом
(х, у) становится вещественным, не меняя, своей абсолют-
абсолютной величины, а (я, х) и (у, у) не изменяются.
Следствие. Величина \\x\\ = У (я, х) обладает свой-
свойствами полунормы (и даже нормы, если выполнено усло-
условие 3')).
В самом деле,
Х) + (у, у)^{х, Х) +
+ 21(х, у)\+(у, у)^(х,х)+2У(х,х)-(у, у) + (у, у) =
= (Ы + \\y\\J.
Из всякого предгильбертова пространства L можно
«изготовить» гильбертово пространство Е следующей кон-
конструкцией. Пусть Lo <=?/~ подмножество тех векторов х,
для Которых - (х, х) =0. Неравенство Коши — Буняков-
Буняковского показывает, что Lo — подпространство в L, В фак-
фактор-пространстве L/Lo естественным образом определяется
скалярное произведение: если х, y^L/L0, ъ. х^х, у^у—¦
представители классов х и у, то полагаем (х, г/) =
= (?, у). Предоставляем читателю убедиться в корректно-
116
сти этого определения и в том, что полученное скалярное
произведение обладает свойством 3'). Далее, если L/Lo не-
неполно, обозначим через Е его пополнение по норме 1Ы1 =
= У(х, х). Неравенство Коши — Буняковского показыва-
показывает, что скалярное произведение непрерывно в этой норме
и, следовательно, продолжается на L. Проверку свойств
1)—3) для продолженного скалярного произведения мы
опускаем.
Примеры. 1) Пусть L — пространство финитных
последовательностей ixj чисел из К со скалярным про-
оо
изведением(х, у) = ^хпуп. В этом случае L0 = {0), Е =
()
2) L = C [a, b] — скалярное произведение — задается
ь
формулой (/, g) = J / (х) g (x) dx. В этом случае Lo = {0>,
а
L = L2[a, b].
3) L — пространство измеримых ступенчатых функций
на множестве X с мерой jut, скалярное произведение име-
имеет вид (f,g)= | f (x) g{z)d\x. Здесь Lo состоит из функций,
х
почти всюду равных нулю по мере jut, Т, = L2(X, \i).
4) L — пространство многочленов от комплексного пе-
переменного 2, скалярное произведение задается формулой
Здесь L0 = @}, a L совпадает с совокупностью A2(D) всех
аналитических функций в единичном круге D, принадле-
принадлежащих Lz (A dxdy) (см. задачу 465).
В вещественном гильбертовом пространстве можно
определить угол ср е [0, п] между векторами х и у по
формуле
В частности, если (х, г/) = 0, то ф = я/2. В этом случае
говорят, что х и у ортогональны, и пишут х -J- у.
В комплексном гильбертовом пространстве угол не
определяется, но понятие ортогональности сохраняет
смысл. Если S — любое подмножество в гильбертовом
пространстве Я, то через S1- обозначают ортогональное
дополнение к 5, т. е. совокупность всех векторов х^Н,
ортогональных ко всем векторам у е 5. Очевидно, что
117
Sx всегда является замкнутым линейным подпростран-
подпространством в Я.
Одно из основных геометрических свойств гильбертова
пространства описывает
Теорема 37. Если К — непустое выпуклое замкну-
замкнутое подмножество в гильбертовом пространстве Я, то для
любой точки xetf существует единственная точка у еК,
ближайшая к х.
Доказательство. Пусть d = inf d(x, у), где
к
d{x, у) — расстояние, порожденное нормой 11*11 = У (ж, ж),
н пусть уп — последовательность точек из К, для которой
lim d (ж, уп) = d. Покажем, что iyj — фундаментальная
лоследовательность. Для этого нам будет полезно тож-
тождество параллелограмма:
\\х + г/И2 + Их - у\\2 - 2Ы2 + 2\\у\\2, C6)
справедливое в любом предгильбертовом пространстве
(см. задачу .475). Применив это тождество к параллело-
параллелограмму со сторонами х — уп и х — ут, получаем
\\уп - yj2 = 211* - yj2 + 211* - yj2 - 112* - уп - yJ2.
Заметим теперь, что 12х — уп — ут |j2 = 4 lx —' п т ^ Ad2,
Уп + Ут г v
так как ^—еЯ.Ьсли п и т достаточно велики, то
\\x-yn\\2^d2 + z, \\х-ут\\2^# + е, откуда Wyn-yJ2<
42 + 4f 4
( )
Мы доказали фундаментальность {г/п}. Пусть у =
= limz/-n. Тогда d(x, y) = limd(x, yn) = d. Существование
ближайшей точки доказано. Единственность вытекает из
тождества параллелограмма: если d(x, y) = d(x, y') = d,
то - Ц - у'\\2 = 211* - у\\г +' 211* - y'W2 - 112* -у- y'W2 < Ы2 -
— 4d2 = 0. Теорема доказана.
Теорема 38. Пусть Н — гильбертово пространство,
Н{ —его замкнутое подпространство,Н2 — Hf. Тогда Н
есть прямая сумма Н{ и Н2.
Доказательство. Пусть х<= Я, xt — ближайшая
к х точка из Hi. Положим хг = х — х{ и покажем, что
х2еЯ2. В самом деле, пусть y^Ht; мы знаем, - что
функция вещественного переменного t /@ е "* — *i + ty\\z
имеет минимум при ? = 0. Значит, /'@) = 0. Но
/' @) = lim l^ + ^iMKll2 = ( } + (у) } = 2Re ( )t
118
Поэтому Re (#2, у)=0. Заменяя у на iy, получаем
Im(;z2, у) = 0. Итак, (х2, г/)=0, т. е. х2^Н2. Мы доказа-
доказали, что Я является суммой Я4 и Я2. То, что эта сумма
прямая, вытекает из ортогональности Hi и Я2: если #е
effj П Я2, то (.г, #) = 0, т. е. х• = 0. Тот факт, что Я явля-'
ется прямой суммой двух ортогональных подпространств
Hi и Я2, записывают формулой Н = Hi® Я2.
Теорема 39. Всякий линейный непрерывный функ-
функционал / на гильбертовом пространстве имеет вид }(х) =
= (?, у) для некоторого у^Н.
Доказательство. Пусть Я4 = Кег / — совокуп-
совокупность всех векторов, аннулирующих /. Если Ht = Я, то
/ = 0 и можно положить у = 0. Если Hi Ф Я, то положим
Я2 = Я^» По теореме 38 Н = Hi® Я2. Покажем, что Я2
одномерно. Пусть у0 — ненулевой вектор из Я2. Тогда
/('Уо)^О, так как в противном случае г/0 принадлежал
бы Я4. Для любого г/i е Я2 вектор ^х — ,, \ г/0 принадле-
жит Hi П Я2 и, следовательно, равен нулю. Это доказыва-
/ (у )
ет, что {уо) — базис в Я2. Положим теперь у = ~. ^-т у0
и сравним функционал / с функционалом х •-> (х, у)*).
Оба функционала обращаются в нуль на Я4 и оба при-
принимают значение /(z/o) на у0. Поэтому они совпадают
всюду.
Замечание. Теоремы 37—39 перестают быть вер-
верными в предгильбертовом пространстве (см. задачу 473).
Система векторов {xJa&A в предгильбертовом про-
пространстве называется ортонормированной, если
при а = р,
при а Ф р.
Неравенство Бесселя. Для любой ортонорми-
рованной системы {ха)аеА и любого вектора х справедли-
справедливо неравенство
Сумма слева понимается как sup 21 (#» хо) |2, где верх-
Ао Ао
няя грань берется по всем конечным подмножествам Ао с:
¦) В комплексном случае у = —
119
czA. Нетрудно показать, что эта сумма может быть ко-
конечна лишь в том случае, когда не более счетного мно-
множества слагаемых отлично от нуля.
Доказательство. По определению суммы в левой
части C7) достаточно проверить это неравенство для ко-
конечного множества А. Пусть Я4 — подпространство в Н,
порожденное системой Ы,а?4, H2 = Hf. Тогда х =
= 2 caxa + У, где у е //2. Из ортонормированности {xj
сс~Л
и ортогональности #, и Я2 вытекают равенства
(Я, Я*) = Са, (X, X) = 2 I Са |2 + (у, у),
а~А
откуда немедленно следует C7).
Ортонормированная система {ха}аеА в гильбертовом
пространстве Н называется полной, если ее ортогональ-
ортогональное дополнение состоит из нуля.
Равенство Парсеваля (обобщение теоре-
теоремы Пифагора). Для любой полной ортонормирован-
ной системы balasA и любого вектора х справедливо ра-
равенство
(*,*)= 2 |(*,*«)|2. C3)
а~А
Доказательство. Пусть Ао — набор тех индексов,
для которых (х, ;ra)=^0. Как уже отмечалось выше, мно-
множество Ао счетно. Занумеруем его и будем писать хи
х2, ... вместо ха , Ха2, ... и сг, с2, ... вместо Сах, Са2, . ..
п
Рассмотрим последовательность сумм Sn — 2 сгхг* Так
n + h
как (l^^+fe — ^п ||2 = 2 kil2 и ряд 2кг12 сходится, по-
i=n+i i
следовательность {Sn} фундаментальна. Пусть S == lim Sn
и y = x — S. Покажем, что на самом деле у = 0. Для этого
достаточно проверить, что у ортогонален системе {^JasA.
Для а&А0 это очевидно по построению, а для а^А0 вы-
вытекает из равенства
(tf» xi) = {x —S, хг) = lim (^ — ^я, Хг) = 0.
Итак, 1/ = 0и, значит, а: = 5. Отсюда
п
(х, х) = lim E„, Sn) = Hm 2 | с, |2 = 2 к« |2-
Попутно нами доказана
Теорема 39. Всякая полная ортонормированная си-
система {ха}а<вА в гильбертовом пространстве Я является
гильбертовым базисом в том смысле, что любой вектор
х^Н однозначно записывается в виде
X = 2 са^а, Са = (х, Ха).
Замечание. Понятие гильбертова базиса отличается
от понятия базиса в линейном пространстве и совпадает
с ним только в конечномерном случае. Отличие состоит
в том, что допускаются бесконечные линейные комби-
комбинации, не имеющие смысла в чисто алгебраической си-
ситуации.
Теорема 41. Всякое гильбертово пространство об-
ладает гильбертовым базисом. Все базисы данного про-
странства Я равномощны. (Эта мощность называется
гильбертовой размерностью Я.)
Доказательство. Пользуясь леммой Цорна, легко
доказать существование максимальной ортонормирован-
ной системы в Я. Если бы она была неполна, то, присое-
присоединяя к этой системе единичный вектор из ее ортогональ-
ортогонального дополнения, мы получили бы противоречие с макси-
максимальностью системы. Значит, максимальная система пол-
полна и по теореме 40 является гильбертовым базисом в Я.
Равномощность двух базисов в конечномерном про-
пространстве следует из аналогичного алгебраического факта:
в этом случае понятия базиса и гильбертова базиса
совпадают.
Пус^ть теперь Я обладает счетным базисом {#n}n=N«
Тогда Я бесконечномерно (так как хп независимы) и се-
парабельно (т. е. обладает счетным всюду плотным под-
подмножеством; таковым является, например, совокупность
всех конечных линейных комбинаций базисных векторов
с рациональными коэффициентами). Всякий другой базис
{yJa&A содержит бесконечное число элементов. Если бы
А было несчетно, то в Я было бы несчетное множество
непересекающихся шаров радиуса 1 (достаточно взять
шары с центрами в точках 2уа (a^i)), что противоре-
противоречит сепарабельности Я.
Случай несчетной размерности требует дополнитель-
дополнительных сведений из теории множеств, и мы его опустим.
Для сепарабельных гильбертовых пространств сущест-
существование базиса можно доказать без использования леммы
Цорна с помощью процесса ортогонализации.
121
Пусть {-Zn}nsN — счетная система векторов в Н, орто-
ортогональное дополнение к которой состоит из одного нуля
(например, плотное в Я семейство векторов, существую-
существующее в силу сепарабельности Я). Удаляя «лишние» век-
векторы, мы можем считать, что хп линейно независимы.
Определим теперь новые последовательности векторов
{}, {zn}n=N следующим образом:
n-l
Уп-Хп~ ^ [Xn,Zt)Zu Zn-^
Легко видеть, что система {zn} ортонормирована и
линейная оболочка векторов zu ..., zn совпадает с линей-
линейной оболочкой векторов хи ..., хп. Поэтому {zn}a=N —
базис в Я. Заметим, что если первоначальная система
{хп} лежала в некотором (незамкнутом) подпространстве
HqCzH, то система {zj также лежит в Яо. Отсюда, в част-
частности, вытекает, что во всяком сепарабельном предгиль-
предгильбертовом пространстве есть базис.
Теорема 42. Два гильбертовых пространства изо-
изоморфны тогда и только тогда, когда они имеют одинако-
одинаковую гильбертову размерность.
Доказательство. Необходимость условия очевид-
очевидна. Докажем достаточность. Пусть Ht и Я2 имеют одина-
одинаковую размерность. Это значит, что в Я, и в Я2 есть рав-
номощные базисы {ха)а^л и iyJa^A. Определим оператор
U: Hi -> Я2 формулой U ( 2 Саха\ = 2 СаУа- Равенство
\А ] А
Парсеваля показывает, что этот оператор изометричен
(т. е. сохраняет скалярное произведение) и, следователь-
следовательно, отображает Ht в некоторое полное подпространство
L<=^H2. Поскольку L содержит базис {yJaeA, Z>-L = {0}.
Поэтому L = Я2. Теорема доказана.
Следствие. Все сепарабельные бесконечномерные
гильбертовы пространства изоморфны.
2. Операторы в гильбертовом пространстве. Как мы
видели в п. 1, каждый линейный непрерывный функцио-
функционал в гильбертовом пространстве Я может быть записан
122
в вйДё скалярного произведения. Отсюда вытекает, ЧТО
вещественное гильбертово пространство // естественно
отождествляется со своим сопряженным //': вектору у со-
соответствует функционал jy{x) = (x, у). Для комплексного
гильбертова пространства это соответствие является анти-
антиизоморфизмом, так как fy зависит от у антилинейно:
hlVl+k2y2 = ^^vx + ^242# ВвеДем пространство Я*, эрми-
эрмитово сопряженное к Н. Элементами Я* являются антили-
антилинейные непрерывные функционалы на Я. Пространства
Я и Я* естественно отождествляются: вектору х^Н со-
соответствует антилинейный функционал /х (у) = (#, */)•
Если Я, и Я2 — гильбертовы пространства, А — ли-
линейный оператор из Я| в Я2, то можно определить эрми-
эрмитово сопряженный оператор Л*, действующий из Н2=Н2
в Я* = Н1 по формуле
(А*х2, я,) = (#2, i4tfi), Xi&Hu
Соответствие А ¦-> Л* обладает свойствами:
Часто эрмитово сопряженные операторы называют
просто сопряженными. Мы тоже будем так делать, сохра-
сохраняя, однако, разницу в обозначении: сопряженный опе-
оператор обозначается Л', а эрмитово сопряженный— Л*.
Выделяются следующие классы операторов.
Самосопряженные (или эрмитовы) операторы А ха-
характеризуются свойством Л* = А.
Унитарные операторы характеризуются свойством
U* = С/-1. (Это равносильно условиям U*U = 1 = С/С/*.
В конечномерном случае достаточно одного из этих ра-
равенств.)
Нормальные операторы N характеризуются свойством
v* ;v*;v
Ортопроекторы Р характеризуются свойствами Р* =
= Р = Р2 (см. задачу 482).
Положительные операторы А характеризуются свой-
свойством (Ах, х)>0 для всех х^Н. Это свойство записыва-
записывается так: А > 0. В множестве End Я вводится частичный
порядок: А > 5, если А — В > 0.
Примеры. 1) Оператор А умножения на функцию
a^Loo(X, \x) в пространстве L2(X, \x) является самосо-
самосопряженным, если а(х) вещественна почти всюду, и уни-
унитарным, если |а(я)| =1 почти всюду. Этот оператор нор-
123
кален для любой функции а, ЯвЛЯетСЯ ортопроёктороМ,
если а принимает почти всюду значения 0 или 1, поло-
положителен, если аХ) почти всюду.
2) Оператор Т одностороннего сдвига в /2(R), действу-
действующий по формуле Т{хп) = {xn+J, обладает свойством
7Т* = 1, но не является унитарным, так как Г*Г = 1—
— Ри где Pi — проектор на подпространство, порожденное
первым базисным вектором.
3) Пусть А — интегральный оператор в L2(X1 \i) с яд-
ядром К(хи х2), т. e.Af{xx) = \ K(xv x2)f(x2)d\i (я2).Вычис-
х
лим сопряженный оператор Л*. Основное равенство
(Л/, g) = (/, A*g) в этом случае имеет вид
f ]
XX
1ч х2) / (х2) ТК) Ф (*i) d\i (х2) = J7 (x)(A*g) (x) dix (x),
X
откуда {A*g) (x) = ^K (x1, x) g(x1)d\x (хг). Итак, Л* — также
x
интегральный оператор с ядром К*(хи х2) = К(х2, Xi).
Отметим, что в частном случае, когда X состоит из
конечного числа точек единичной меры, мы получаем из-
весФное из линейной алгебры соотношение между элемен-
элементами матрицы А и эрмитово сопряженной матрицы Л*:
ih fii
Теорема 43. Линейный оператор А из гильбертова
пространства Н{ в гильбертово пространство Н2 компак-
компактен тогда и только тогда, когда он может быть равномер-
равномерно аппроксимирован операторами конечного ранга.
Доказательство. Достаточность условия спра-
справедлива в любом банаховом пространстве и была установ-
установлена выше (см. теорему 16). Необходимость доказывает-
доказывается так. Пусть А^Ж(Ни FI2), Bx — единичный шар в Я,.
Тогда ABi — предкомпактное множество в Н2. Возьмем
произвольное е > 0, пусть у^ ..., yN — конечная е-сеть
для АВи Но — линейная оболочка уи . . ., yN и Ро — орто-
проектор на Яо в Н2. Ясно, что Р0А — оператор конечно-
конечного ранга, поскольку im PQA с: im Po = Яо. С другой
стороны,
\А-Р0А\\= sup \\Ах-Р0Ах\\= sup \\у -
зс=вх г/sABj
так как
Иг/ -р„у\\ = \\у -yi-p0(y
124
(Последнее вытекает из того, что 1 — Д является, как
и Ро, ортопроектором и, следовательно, имеет норму 1.)
Теорема доказана.
Каждому эрмитову оператору А в гильбертовом про-
пространстве соответствует эрмитова (в вещественном про-
пространстве — квадратичная) форма QA (х) = (Ах, х).
Теорема 44. Для любого эрмитова оператора А
справедливо равенство sup | QA (x) | = || А ||; ес/ш верхняя
1М1
/ достигается в точке х0, то х0 — собственный вектор
оператора А с собственным значением dblL4ll.
Доказательство. Ясно, что IQA (x) I = I (Ax, x) I ^
< НЛд:11Ы1 ^ IUII при 1Ы1 = 1. Для получения обратной
оценки воспользуемся тождеством
которое легко выводится из определения QA. Пусть
sup \QA (x) | = с. Тогда из нашего тождества вытекает
неравенство
4 Re (Ах, у) < с\\х + у\\2 + с\\х - у\\2
пли, в силу тождества параллелограмма,
2Re(i4ar, y)< сЫ2 + с\\у\\\
Положим здесь у = гаТ\^х- Тогда мы получим 2ЫП14д:11 ^
IIЛХII
^ 2с11д:112 или \\AxW < clWI, что и требовалось. Другой вы-
вывод можно получить из задачи 484.
Пусть теперь sup \QA(x)\ достигается в точке х0. Обо-
Обозначим через z любой единичный вектор, ортогональный
к х0. Вектор xt = xQ cos t + z sin t при t = 0 совпадает с х0
и при любом t имеет единичную длину. Поэтому QA(xt)
имеет экстремум при ? = 0. Значит,-тт Qa (xM =0.
at u=0
Вычисляя эту производную, получаем 2Re(^^0, z) = 0.
Заменяя здесь z на iz, мы видим, что (Ах0, z) = 0.
Поэтому Axq^^Xq}1-I-, т. е. Axo = XxQ. Наконец,
?1 = (Лх0, Xq) = (Ax0, Хо)= ±\\А\\.
Теорема доказана.
Теорема 45. Если подпространство Hi с: Я инвари-
инвариантно относительно эрмитова оператора А, то ортогональ-
ортогональное дополнение Н2 = Н± также инвариантно относи-
относительно А.
125
Доказательство. Пусть Xi^Hh х2^Н2. Пока-
Покажем, что Ахг-L-Xi. Это следует из равенства (Ах2, #i) =
= {х2, Axi). Таким образом, АН2<^ Н2.
Теорема 46 (Гильберт). Пусть А — компактный
эрмитов оператор в гильбертовом пространстве Н. Суще-
Существует ортонормированный базис {х^}^в, "состоящий из
собственных векторов оператора А. Соответствующие соб-
собственные значения {Лр} вещественны, и для любого е>0
лишь конечное число их лежит в области IXl > 8.
Доказательство. С помощью леммы Цорна легко
устанавливается, что существует максимальная ортонор-
мированная система, состоящая из собственных векторов
оператора А. Покажем, что эта система является базисом
в Я. Если это не так, то пусть Но — ортогональное допол-
дополнение к этой системе. По теореме 45 Но инвариантно от-
относительно А. Ограничение Ао оператора А на Но — ком-
компактный эрмитов оператор, не имеющий ни одного соб-
собственного вектора (в силу максимальности исходной
системы). Покажем, что это противоречит теореме 44.
В самом деле, из компактности Ао вытекает, что Qa0
непрерывна в слабой топологии на единичном шаре Bt.
А именно, если хп -*¦ х, то
Qa0 (хп) — Qa0 И = {Аохп, хп) — (Аох, х) =
= (Ло (хп — х), хп) + (Ах, хп — х).
В первом слагаемом первый сомножитель сильно стре-
стремится к нулю ввиду компактности Ао, а второй ограни-
ограничен, так как хп е 5,. Поэтому первое слагаемое стремится
к нулю. Во втором слагаемом первый сомножитель фик-
фиксирован, а второй слабо стремится к нулю. Поэтому и
второе слагаемое стремится к нулю. Итак, QA — слабо не-
непрерывная функция на Si. Так как шар Bt — компакт
в слабой топологии, функция \QA\ достигает на В{ своей
верхней грани в некоторой точке х0 е Bt. По теореме 4
х0 — собственный вектор для Ау что и дает искомое про-
противоречие. Вещественность собственных значений вытека-
вытекает из соотношений
Докажем последнее утверждение теоремы. Пусть Вг <=
а В — совокупность тех индексов р, для которых 1Яр1 > 8,
#е — подпространство, порожденное {х$}$=ве- Простран-
Пространство #е инвариантно относительно А. Обозначим через Ай
126
ограничение А на Яв. Тогда А6 — обратимый компактный
оператор, что возможно, лишь если Я8 конечномерно и,
следовательно, В6 конечно. Теорема доказана.
Замечание. Доказательству теоремы Гильберта
можно придать конструктивный характер: мы последова-
последовательно находим собственные числа оператора А в поряд-
порядке убывания их абсолютных величин, пользуясь теорема-
теоремами 44 и 45.
Оказывается, не только максимальное (по абсолютной
величине) собственное значение эрмитова оператора А
имеет вариационный смысл. Справедлива
Теорема Куранта. Пусть А — компактный эрми-
эрмитов оператор в гильбертовом пространстве Я. Предполо-
Предположим, что его ненулевые собственные значения зануме-
занумерованы с учетом кратностей так, что выполняются
неравенства
^ .. . < 0 "^ . ... ^ Л2 ^ Ai.
Тогда
K = „inf X±T wF
Я^п= sup
где Яп-i пробегает все (п — 1) -мерные подпростран-
подпространства в Я.
Доказательство. Второе равенство вытекает из
первого после замены А на — А. Докажем первое. Пусть
о
Яп_! — линейная оболочка векторов хи ..., #n-i, соответ-
соответствующих собственным значениям Хи ..., Яп-1. Тогда в
о
Яп'-i максимальное собственное значение равно Хп. По-
Поэтому
С другой стороны, для каждого (тг— 1) -мерного подпро-
подпространства Нп-{ пространство Я^_х имеет ненулевое пе-
пересечение с пространством, натянутым на хи ..., хп.
Пусть
i27
Тогда
\*t 2Ы **.вп-г i*i
Теорема доказана.
Из этой теоремы вытекает полезный в приложениях
принцип промежуточности (см. задачу 494).
ГЛАВА IV
ПРЕОБРАЗОВАНИЕ ФУРЬЕ И ЭЛЕМЕНТЫ
ГАРМОНИЧЕСКОГО АНАЛИЗА
§ 1. Свертки на коммутативной группе
1. Свертки основных функций. Пусть G — конечная
группа, К — некоторое поле. Обозначим через К [G] сово-
совокупность формальных линейных комбинаций элементов
группы G с коэффициентами из К. Элементы K[G] име-
имеют вид
*=2я(г)г. где я(#)?=#• A)
На множестве K[G] естественно вводится структура
алгебры над полем К:
iSoa
2 a (g) g + 2,b(g)g= 1l(a(g) + b (g)) g, B)
B e
\tfSG
Удобно отождествлять элемент х е Я [G], заданный
формулой A), с функцией a(g) на группе G со значе-
значениями в К. При такой интерпретации умножение на чис-
число и сложение в K[G] становятся обычными операциями
над функциями. Операция умножения, однако, отличаит-
ся от обычного (поточечного) умножения. Она называет-
называется сверткой и обозначается *. Явный вид ее дается фор-
формулами
(а*Ь) (g) =
Ъ{*)Ъ(Ь)= ^a{h)b{}rlg)=, 2 a(gl)b(g2). C)
ftsG ftsG 8lgr=t
128
Множество К [G] с введенными в нем выше операция-
операциями называется групповой алгеброй группы G. Эта алгеб-
алгебра естественно возникает как универсальный объект в
подходящей категории (см. задачу 506) и играет большую
роль в теории линейных представлений групп.
В дальнейшем нас будут, как правило, интересовать
бесконечные группы G, снабженные некоторой мерой jx.
В этом случае сумму в формуле C) естественно заменить
на интеграл. Более точно, мы предположим, что G — ком-
коммутативная топологическая группа (последнее означает,
что в G определена хаусдорфова топология, относительно
которой групповые операции (gu g2) ~* gig2 и g-^g не-
непрерывны) и что на G задана борелевская мера jx, инва-
инвариантная относительно сдвигов и перехода к обратному
элементу. Групповую операцию в G мы будем обозначать
знаком +. Тогда свойство инвариантности меры \х можно
записать в виде
ц(Х + о) = ц(Х), ii(-X) = li(X) D)
для любого борелевского множества X^G и любого а^
е G. Известно, что такая мера \i существует тогда и толь-
только тогда, когда группа G локально компактна*) и в этом
случае инвариантная мера определена однозначно с точ-
точностью до числового множителя.
Основные примеры. 1) G = Rn, групповая опе-
операция — обычное сложение векторов, мера \х — обычная
мера Лебега в Rn,
d\x (х) = dxi dx2... dxn.
2) Zn — га-мерная целочисленная решетка в Rn, состо-
состоящая из векторов с целыми координатами. Групповая
операция — сложение, инвариантная мера \i имеет вид
lx(X) = cardX (число точек в множестве X).
3) Тп — /г-мерный тор. Мы будем рассматривать две
реализации Тп: либо как подмножество в Сп, состоящее
из векторов z = (zu ..., zn) с условием |zj = l A<A;<
^/г), и с операцией покоординатного умножения, либо
как факторгруппу RVZ", элементы которой можно зада-
задавать векторахми ?<^Rn с условием th^[0, 1) и с опера-
операцией сложения по модулю 1. Соответствие между реали-
зациями устанавливается формулой zh = е A
*) Топологическое пространство называется локально ком-
компактным, если любая его точка имеет относительно компактную
окрестность.
9 А. А. Кириллов, А. Д. Гвишиапи ^9
Инвариантная мера \х — обычная мера Лебега в коорди-
координатах tu ..., tn. Отметим, что эта группа компактна и что
(ТI
)
Свертка функций Д и Д на коммутативной группе G
с инвариантной мерой \х определяется формулами
(/i * /2) (*) = J /1 (х - у) /2
G
= J А (у)/»(*-») Ф (у), E)
G
J
G
которые являются точным аналогом C) (и превращают-
превращаются в C), если G конечна, а \х (X) = card X).
Теорема 1. ?Ъш Д, /2eIi(G, fi), ro интеграл E)
существует для почти всех x^G, функция Д * /2 принад-
принадлежит L,(Gf |i) и II/, * /2И < И/,П11/а11.
Доказательство. Если /,, Д е ^i (G, fi), то по тео-
теореме Фубини функция ф(х, у) = fi(x)f2(y) принадлежит
L,(GXG, цХц), причем НФН = НДННДП.
Рассмотрим теперь преобразование т пространства
GXG, переводящее точку (х, у) в (х + у, у). Это преоб-
преобразование измеримо (переводит борелевские множества
в борелевские) и сохраняет меру jxXjx. В самом деле,
если I = 4X5c=GXG — элементарное измеримое мно-
множество, то
GXG
IX X {х (т (X)) = f хт(х) (*' У) Ф И Ф (У)
GG
X d|i (у) = J (i И + У) d[i (у) = (i D) |i E) = |i X
Отсюда следует, что т порождает изометрическое пре-
преобразование Г пространства Li(GXGy \iX\i) по формуле
Гер (х, y) = (f (т-1 (ж, у)) = ф (х - у, у).
Применяя этот результат к функции cp(x, y) = Д (х)Д(г/),
получаем утверждение теоремы.
Замечание. Доказанное неравенство влечет непре-
непрерывность операции свертки в пространстве Li(G, jx).
Т • р о у " 2. Операция свертки коммутативна, ассо-
циинмпа и oucipидутиена относительно сложения.
Доказательство. Последнее утверждение сразу
следует из линейности интеграла. Первые два доказыва-
130
ются подходящей заменой переменных, сохраняющей ме-
меру ц. или ц. X ц. А именно,
/i * /2 И = J Л (« - у) /2 (у) Ф (у) =
G
= J Л (- 0) /. (* + </) Ф (У) = J /2 (* ~ </) /1
((/i * /2) * /з) (х) = f (Л • /,) (« - у) /з (у) Ф (у) =
G
11
G G
= || Д (х - z) /2 (г - у) /3
Пусть теперь Т(а) означает оператор сдвига на группе
G: (T(a)f) (x) = f(x + a). Ясно, что Г (а)—изометриче-
(а)—изометрический линейный оператор в Li(G, ji). Одно из важнейших
свойств свертки описывает
Теорема 3. Операция свертки перестановочна со
сдвигами на группе:
Т(а) (/, * U) = T(a)U * Н = А * ВД/.. (б)!
Доказательство. Имеем:
а - I/) /2 ((/) ф (у) =|Г (а) U (* -
Второе равенство следует из первого и коммутативности
свертки. В дальнейшем мы будем использовать обозначе-
обозначение S(f) для оператора свертки с функцией /: *Sr(/1)/2==
= /1 * /2. Утверждения теоремы 2 можно сформулировать
в виде тождеств
5 (А) 5 (А)-5 (А) 5 (А)-5 (А»/»), G)
а утверждение теоремы 3 — в виде тождества
f). (8)'
Теорема 4. ?Ъш qp^S5(Rn), ro 5(ф) — непрерыв-
непрерывный оператор из ?i(Rn, dx) в & (Кп) и из 2)(Rn)
в 2)(Rn).
9* 131
Доказательство. Пусть <р е=^5 (Rn), / е= Li (Rn, dx).
Покажем, что функция S(cp)f бесконечно дифференциру-
дифференцируема и справедливо равенство
' (9)
Очевидно, достаточно проверить это утверждение в
случае частной производной д; = d/dxj. Пусть е;- — базис-
базисный вектор в Rn. Оператор dj может быть записан в виде
Т ПеЛ — 1
lim . По теореме 3 последний оператор переста-
перестало *
новочен с S(f). Поэтому
д? (Ф) / (х) = djS (/) Ф (х) = lim 1Щ^1 S (/) ф (х) =
= lim S (/) ? {Uj) ~ 1 Ф (x) = S (/) д&.
Последнее равенство вытекает из того, что для q><^2)(Rn)
Т he.) — 1
функция ф равномерно стремится к 5jtp, а опе-
оператор S(f) сохраняет равномерную сходимость. Итак,
равенство (9) и бесконечная дифференцируемость S(cp)f
доказаны. Проверим, что 5(ф): Li(Rn, dx) -> 8 (Rn) —
непрерывный оператор. Для любой полунормы pKh в
S'(Rn) имеем
PKk (S (Ф) /) = SUP (dks (Ф) / (*)) = SUPIS (^ф) / И I <
< sup | д\ (x
Rn
что и требовалось.
Для доказательства последнего утверждения прове-
проверим, что для ф1? qJ^0(Rn) справедливо включение
supp (ф1 * ф2) <= supp ф! + supp ф2, A0)
где supp означает носитель, а + в правой части — ариф-
арифметическую сумму множеств: I+y = h + ^UeX, y^
^ У}. В самом деле, если х Ф supp ф! + supp ф2, то для
любого у ^ supp ф! вектор х — у Ф supp ф2. Поэтому в ин-
интеграле E), определяющем ф1*фг(#), подынтегральное
выражение тождественно равно нулю. Значит, ф! * ф2
обращается в нуль вне supp ф! + supp ф2. Последнее мно-
множество является компактом и, следовательно, содержит
зирр(ф1*ф2). Мы доказали, что 5(ф) переводит 2)(Rn)
в 2)(Rn). Непрерывность S(f) достаточно проверить на
132
подпространствах 2)к(Т{п), где она устанавливается той
же выкладкой, что и выше, учитывая, что S(q>) перево-
переводит &к{Яп) в S5Kl(Rn), где К, = К + suppф. Теорема до-
доказана.
2. Свертки обобщенных функций. Определение сверт-
свертки можно обобщить на тот случай, когда одинили оба
сомножителя являются не обычными, а обобщенными
функциями.
Пусть F^2>'(Rn), (pe=^)(Rn). Свертку F * <р можно
определить двумя способами.
Первый способ. Оператор S(qp), как мы знаем
(см. теорему 4), является непрерывным оператором в
пространстве 2)(Rn). Вычислим действие сопряженного
оператора S(cp)' на регулярную обобщенную функцию
/(#). Имеем
§ (И)
Rn Rn Rn
Введем обозначение ф(#) = ф(—х). Тогда последнее
выражение можно преобразовать так:
J J/ И Ф (У ~ *) Ш dy = J / * Ф Ы *(») dy = (S (ф) /, ф>.
R7l R7l R7l
Итак, мы установили равенство операторов »5(ф)/ =
= 5(ф) на регулярных обобщенных функциях. Отсюда
вытекает, что оператор S((p) допускает непрерывное про-
продолжение на ^'(Rn), а именно, оператор 5(ф)'. Это и
есть первое определение свертки. Запишем его в виде
формулы
<^*ф, -ф> = <iF, ф*ф>. A2)
Второй способ. Интеграл J у(х — у) F (у) йг/,зада-
Rn
ющий свертку в случае обычных функций, можно опре-
определить в случае, когда F ^ 2)' (Rn) как значение функ-
функционала F на основной функции г|?(г/) = ф(^г — г/). Исполь-
Используя ранее введенные обозначения, это определение мож-
можно выразить формулой
A3)
133
Таким образом, согласно второму определению сверт-
свертки F * ф является обычной функцией на Rn. Оказывается,
на самом деле оба определения совпадают. А именно,
справедлива
Теорема 5. Если Fe®'(R"), cpe=S5(Rn), то обоб-
обобщенная функция F * ф, определенная формулой A2), ре-
регулярна, бесконечно дифференцируема и может быть вы-
вычислена в точке ieR" no формуле A3).
Доказательство. Заметим прежде всего, что эле-
элемент Т(—х)<$ ^ 2)(Rn) непрерывно зависит от ?^R\
(Если хп -*- х в Rn, то Т(—Хп)у-+Т(—х)(р в топологии
пространства 2)(Rn).) Поэтому правая часть равенства
A3) —непрерывная функция. Рассмотрим ее как регу-
регулярную обобщенную функцию на R" и покажем, что она
совпадает с обобщенной функцией A2). Для этого мы
должны для любой ifeSJfR'1) проверить равенство
или
F(y)(
\Rn
= J
\Rn J
Покажем, что справедливо более общее равенство
J F (у) П а (х, y)dx\dy= \ (\ F (у) а (х, у) dy\dx, A4)
Rn \Rm J R^\Rn /
где Fe^fR»), ae2)(R"+m). Для этого заметим, что
множество тех a ^ 2) (Rm+n), для которых равенство A4)
верно, образует замкнутое линейное подпространство.
Это подпространство содержит все функции а вида
<*(*, г/)=РМтЫ, pe2>(Rn), Те2)(Г) и7 следова-
следовательно, совпадает с S)(Rw+n).
Для доказательства теоремы осталось проверить бес-
бесконечную дифференцируемость функции F * ф. Она сле-
следует из бесконечной дифференцируемости отображения
х и-* Т (— х) ф, которая проверяется непосредственно.
Аналогично определяется свертка F * ф в случае, когда
Ф и F принадлежат другим пространствам основных и
обобщенных функций (см. задачи 526, 527).
134
Пусть теперь Fe2)'(R»), /e=<y'(R»). Покажем, что
можно определить свертку F * /, которая будет элементом
пространства 3)'(Rn). Мы уже знаем, что оператор S(F)
свертки с Fe=0'(Rn) переводит 2)(Rn) в <^(Rn). Можно
проверить (см. задачу 526), что этот оператор непреры-
непрерывен. Далее, операцию V и соотношение A2) можно пере-
перенести на обобщенные функции. Отсюда вытекает, что
оператор S(F) имеет непрерывное продолжение (а имен-
именно, S(F)') на пространство <?f'(Rn) и отображает его в
3)'(Rn). Это и есть искомое определение свертки. Запи-
Запишем его в виде формулы
<F*f, ф> = </, /*ф>. A5)
Замечание. В этом определении сомножители F и
/ играют несимметричную роль. Можно было бы строить
продолжение оператора S(f): 2)(Rn)-^ 25(Rn) до непре-
непрерывного оператора в ?D' (Rn) (а именно, S(f)') и опре-
определять F * / как результат применения к F этого продол-
продолженного оператора. Мы получили бы формулу
<F * /, Ф> = <F, /* Ф>. A5')
Можно убедиться (ср. с доказательством теоремы 5),
что формулы A5) и A5') определяют одну и ту же
обобщенную функцию.
Приведем еще одну полезную формулу для свертки
обобщенных функций F и /:
<F*f, ф> = <FX/, ф>, A6)"
где FXf— прямое произведение обобщенных функций
F и / (см. § 4 гл. III), т. е. обобщенная функция в R2n,
заданная одним из эквивалентных равенств:
<FX/,a>= \f{x)( \j{y)a(x,y)dy\dx =
Rn \Rn /
' F(x)a(x,y)d%\ A7)
о
а через ф обозначена функция ф (#+*/). Доказательство
этой формулы предоставляется читателю (оно сводится
к замене переменных в интегралах, содержащих обоб-
обобщенные функции).
Приведем теперь «таблицу умножения» для операции
свертки в основных функциональных пространствах:
135
0(Rn)
s(Rn)
8' (R«)
S' (Rn)
a>> (Rn)
0(Rn)
*(R»)
!»(R»)
P* (R»)
*(R")
S(R")
5(Rn)
5(R«)
5(R")
PS (Rn)
—
го-,
g-(Rn)
—
*<R")
—
—
<?' (Rn)
2>(Rn)
5(Rn)
S' (R»)
5' (Rn)
Д>' (Rn)
5' (Rn)
PIT (Rn)
P^ (Rn)
5' (Rn)
—
—
S>' (Rn)
&(Rn)
—
ay (Rn)
—
—
Прочерк означает, что соответствующая операция
свертки не определена. Через P<?f(Rn) обозначено под-
подпространство в <?f(Rn), состоящее из функций, растущих
не быстрее многочлена. Для запоминания этой таблицы
полезно иметь в виду следующее правило: свертка опре-
определена, если хотя бы один сомножитель финитный, глад-
гладка, если хотя бы один сомножитель гладкий, и финитна,
если оба сомножителя финитны.
Теорема 6. Операторы свертки перестановочны друг
с другом {в тех случаях, когда их композиция имеет
смысл), с операторами сдвига и с операторами дифферен-
дифференцирования.
Доказательство. Прежде всего заметим, что пер-
первое утверждение теоремы влечет два остальных. Дело
в том, что операторы сдвига и дифференцирования явля-
являются частными случаями оператора свертки. А именно,
справедливы равенства
71(а)ф = ба*ф? A8)
«9*ф = <9*б*ф. A9)
Равенство A8) для основных функций ф вытекает из A3):
6а * ф (х) = 8а (х — у) ф (у) dy = (p(x + a) = T(a)q> (x).
Для обобщенных функций ф с компактным носителем
A8) вытекает из A5) и равенств 8а = 6-а, Т(а)' = Т(—а),
проверяемых непосредственно.
Равенство A9) доказывается индукцией по числу \к\.
Основная лемма в этом доказательстве — соотношение
доказывается так же, как и A8).
= dj8 *
136
Итак, осталось проверить равенство S(fi)S(f2)='
— S(fz)S(fi) в тех случаях, когда хотя бы одна из функ-
функций Д и /2 имеет компактный носитель. Пусть для опре-
определенности /1 = /^(r/(Rn), /2 = fG^(Rn), и мы дол-
должны проверить коммутативность диаграммы
По определению действия оператора свертки на обоб-
обобщенные функции это равносильно коммутативности диа-
диаграммы
которая вытекает из равенства A6). Теорема доказана.
Доказанная теорема о перестановочности операторов
свертки допускает следующее интересное и полезное об-
обращение.
Теорема 7. Пусть А — непрерывный оператор из
2)(Rn) в <?f(Rn). Следующие свойства А эквивалентны:
1) А перестановочен со сдвигами;
2) А перестановочен с операторами дифференциро-
дифференцирования;
3) А является оператором свертки с некоторой обоб-
обобщенной функцией f^3)'(Rn).
Доказательство. Согласно теореме 6 из свойства
3) следуют 1) и 2). Покажем, что из 2) вытекает 1).
Пусть (р^2)(Яп), aeR", /eR, Рассмотрим функцию ве-
вещественного переменного t •-> Т (— ta) AT (ta) ф со значе-
значениями в <?Г(Н/1). Производная этой функции по t легко
вычисляется, если учесть равенство
А Т (ta) = DaT (ta) = Т (ta) Da% B0)
справедливое для операторов сдвига в 2)(Rn) и <!f(Rn)
(через Da обозначена производная вдоль вектора а). Эта
производная имеет вид
[-Т (-ta)DaAT (ta)+ T (-ta)ADaT (ta)]cp,
что равно нулю в силу перестановочности А и Da. Поэто-
Поэтому наша функция постоянна. Приравнивая ее значения
137
при t = i и Z = 0, получаем Т(—а)АТ(а)ср = Лф, откуда
следует 1). Выведем теперь свойство 3) из 1). Для этого
заметим, что соответствие ср •-* Лф @) является линей-
линейным непрерывным функционалом на 3)(Rn). Обозначим
этот функционал через /. Теперь из 1) можно заключить,
что Ау(х) = Т(х)Ац@) = АТ(х)ц@)=<}, Г(.г)ф>=7*
) И 4S(
Ф()
Замечание. Утверждение теоремы и ее доказатель-
доказательство переносятся без изменения на случай, когда опера-
оператор А действует из S'(Rn) или 8'(Rn) в S'(Rn).
Свойство 3) при этом формулируется так: A=S(f),
где /e5"(Rn) или e#"(Rn) соответственно. Несколько
более сложно доказывается, что всякий оператор из
S)(Rn) в себя, перестановочный со сдвигами, имеет вид
5(/), где f^8'(Rn). Таким образом, операторы свертки
во всех этих случаях образуют максимальное коммута-
коммутативное семейство. Это свойство показывает, что семейство
операторов свертки похоже на семейство операторов
умножения на функции. Ниже мы увидим, что это сход-
сходство не случайно: оба семейства переходят друг в друга
при некотором преобразовании пространства.
§ 2. Преобразование Фурье
1. Характеры коммутативной группы. Пусть G — ком-
коммутативная группа. Характером этой группы называется
гомоморфизм G в группу Т, т. е. такая функция % на G
с комплексными значениями, равными 1 по абсолютной
величине, что
Х(* + 0) = Х(*)ХМ. B1)
Если G — топологическая группа, то, как правило,
термин «характер» означает «непрерывный характер».
Мы будем считать все рассматриваемые характеры непре-
непрерывными, не оговаривая этого особо. Если %i и %2 — ха-
характеры группы G, то их произведение %{%2 — также
характер; если % — характер, то х ==Х*)~ также харак-
характер. Таким образом, совокупность всех характеров данной
группы G образует группу относительно операции обыч-
обычного умножения функций. Эта группа обозначается G и
называется группой, двойственной к G. Группа G стано-
*) Черта, как обычно, означает комплексное сопряжение.
138
вится топологической группой, если определить сходи-
сходимость %п -* X как равномерную сходимость на каждом
компакте K^G.
Пример. Пусть G = Z — группа целых чисел. Ясно,
что каждый характер %<^ G определяется своим значени-
значением на образующем элементе 1 ^ G (не путать 1 с едини-
единицей группы, роль которой играет 0). В самом деле, из
B1) следует, что
ХИ = [ХA)]П Для всех п^Ъ. B2)
Значение ? = хA) может быть любым числом z^Т.
Тем самым множество G отождествляется в этом случае
с окружностью Т.
Теорема 8. Имеет место изоморфизм топологиче-
топологических групп Z = Т.
Доказательство. Мы уже видели, что множество
Z естественно отождествляется с Т. Покажем, что это со-
соответствие является изоморфизмом топологических групп.
Будем обозначать через %г характер, определяемый усло-
условием Xz(l) = 2, геТ. Равенство %Zl%z2 = Ъх*2 показывает,
что^ соответствие z-+%z является изоморфизмом групп Т
и Z. Осталось проверить, что это соответствие является
гомеоморфизмом. Поскольку группа Z дискретна, каж-
каждый компакт в Z состоит из конечного числа точек. Зна-
Значит, сходимость в Z является поточечной сходимостью.
Равенство B2) показывает, что %zn-*Xz тогда и только
тогда, когда %zn(l)-+%z{i), т. е. когда zn -> z. Теорема до-
доказана.
Теорема 9. Группа Т изоморфна Z.
Доказательство. Каждому /ieZ соответствует
характер %п группы Т, задаваемый равенством
Х»(*) = Л z^ Т. B3);
Мы покажем ниже (см. также задачу 546), что Т не име-
имеет других характеров, кроме тех, которые задаются фор-
формулой B3). Поэтому соответствие п-+%п устанавливает
эквивалентность множеств Z и Т. Равенство Xn%m=.Xn+m
показывает, что эта эквивалентность является изомор-
изоморфизмом групп. Осталось проверить, что она является го-
гомеоморфизмом топологических пространств. Для этого
проверим, что множество Т дискретно. Это следует из
13Э
равенства
max|XnB)-xmB)|2
при тфп.
Теорема доказана.
Мы видим, таким образом, что группы Z и Т двой-
двойственны друг к другу. Этот факт является частным слу-
случаем следующего результата.
Принцип двойственности Л. С. Понтря-
г и н а. Для любой локально компактной коммутативной
топологической группы G естественное отображение G в
G, которое элементу g^G ставит в соответствие харак-
характер fg на G по формуле
х^ё, B4)
является изоморфизмом топологических групп.
Заметим, что для общих коммутативных топологиче-
топологических групп этот принцип не всегда выполняется (см. за-
задачу 548).
Теорема 10. Группа R изоморфна R.
Доказательство. ^Каждому К е R поставим в со-
соответствие характер %л ^ R, задаваемый формулой
%,(x) = e2nikx. B5)
Покажем, что формула B5) дает все характеры груп-
группы R. Пусть % е R. Предположим сначала, что % — диф-
дифференцируемая функция. Тогда из B1), дифференцируя
по у и полагая у = 0, получаем %'(#) = с%(#), где с =
= %'((})• Это дифференциальное уравнение имеет един-
единственное решение, удовлетворяющее начальному условию
Х@)=1, а именно: %(х) = есх. Из условия |%(я)|=е=1 вы-
вытекает, что с чисто мнимо. Значит, % совпадает с одним
из характеров B5).
Теперь избавимся от предположения о дифференцируе-
мости х- Один из способов — рассмотреть % как элемент
3)' (R) (см. задачу 543). Другой способ — применить тех-
технику сглаживания. Пусть ф ^ 2)(R). Тогда функция х * Ф
бесконечно дифференцируема. С другой стороны, эта
функция пропорциональна % (см. задачу 544) с коэффи-
коэффициентом, отличным от нуля, для подходящей функции ф
(например, для достаточно далекого члена б-образной
последовательности). Отсюда вытекает, что всякий харак-
характер группы R — бесконечно дифференцируемая функция.
140
Итак, мы установили взаимно однозначное соответ-
соответствие R и R: Л ->- %х. Равенство х^Хм — Хм-ц показывает, что
это соответствие — изоморфизм групп. Докажем, что оно
является гомеоморфизмом. Если Лп -* Л, то ук -> %к рав-
равномерно на любом компакте в R, как следует из явного
вида х*. Обратно, пусть %х ~*%х равномерно на любом
отрезке. Тогда %к _к (х) -> 1 равномерно на отрезке
[О, 1]. Но
SUP I Ху _а (#) ~ 1 I = SUP | Sin Л (К — Л) Я I =«
[од] I Лп Л I [од]
1 при | К — Я | > 1/2,
sin л | Лп — Л | при |ЛП — Л|^1/2.
Отсюда вытекает, что Хп -*¦ Л. Теорема доказана.
Замечание 1. Группа R оказывается двойственной
самой себе в смысле Понтрягина. Однако канонического
изоморфизма R ->¦ R (в отличие от изоморфизма R -* R)
не существует. Наш выбор соответствия К -+¦ e2niXx дикту-
диктуется удобством определения преобразования Фурье в
L2(R) и формулы Пуассона (см. ниже). Часто использу-
используются другие соответствия: Л»-* eiKx или Л»-> e~i%x.
Замечание 2. Теперь мы можем доказать пропу-
пропущенное при доказательстве теоремы 9 утверждение о ха-
характерах группы Т. Пусть 5(^Т. Рассмотрим функции
Xi @ = Х(*2л1/.)- Ясно, что Xi ~ характер группы R. Зна-
Значит, %i(t) = e2ntkt для некоторого X е R. Поскольку Xi(l) =
= ХA)==1> число X должно быть целым. Отсюда Xi(^)==s
= е2лШ, т. е. %(z) = zn.
Мы предоставляем читателю доказать следующее об-
общее утверждение, содержащее теоремы 8—10 в качестве
частного случая.
Теорема 11. Пусть G = RnXZ*XT' — прямое про-
произведение групп. Тогда двойственная группа G изоморф-
изоморфна RnXZlX T\
Пусть G — локально компактная коммутативная груп-
группа с инвариантной мерой ju. Для любой функции /е
е Li(G1 \i) определим преобразование Фурье f формулой
J, %^G. B6)
G
Таким образом, преобразование Фурье переводит
функции на G в функции на двойственной группе G.
141
Примеры. 1) Если G = Z, то функция /^?t(
это суммируемая двусторонняя последовательность {cn}n
Преобразование Фурье ставит в соответствие этой после-
последовательности функцию / (Z) = 2 Сп%п на Т, называе-
n=Z
мую иногда производящей функцией последовательности
{}
}
2) Если G = T, j^L{(T, dt), то преобразование Фурье
функции / — не что иное, как последовательность коэф-
1
фициептов Фурье функции /: сп = 7(\) = J f (t)e~2mntdt.
о
3) Если G = R, /^Li(R, do:), то преобразование
Фурье / также является функцией на R, задаваемой ин-
интегралом Фурье: f (k) = ) / (^) e~2mkxdx. Основные свойства
R
преобразования Фурье на любой коммутативной группе
описывает
Теорема 12. Пусть G — локально компактная ком-
коммутативная группа с инвариантной мерой \i. Преобразо-
Преобразование Фурье переводит пространство L{(G, \i) в прост-
пространство непрерывных ограниченных функций на G. При
этом преобразовании свертка функций переходит в обыч-
обычное умножение:
(/.•/О~(Х) = /.(Х)-Д(Х), B7)
оператор сдвига Т (х) (xj=G) переходит в оператор умно-
умножения на характер fx^G (см. B4)):
B8)
оператор умножения на характер %^ G переходит в опе-
оператор сдвига Т(%~1) (в мультипликативной записи груп-
групповой операции на G):
(М (х)/Г (Xi) = Т (X'1)/foci) = 7 (x"xXi). B9)
Доказательство. Пусть %п ~+ % в G и / е Li (G, \i).
Для любого е > 0 найдется такой компакт К^ G, что
' |/|<7иО.По определению топологии в G функции
G\K
%п(х) равномерно на К стремятся к %{х). Поэтому, начи-
начиная с некоторого номера я(е), выполняется неравенство
142
<e для х^К. Отсюда
К
Мы доказали непрерывность f. Ограниченность f не-
непосредственно вытекает из оценки интеграла B6). Ра-
Равенства B7), B8) и B9) проверяются прямым вычисле-
вычислением с использованием замены переменных. Теорема
доказана.
2. Ряды Фурье. Разложение функции в ряд Фурье —
наиболее изученный случай преобразования Фурье на
коммутативной группе (в данном случае — группе Т).
Исследование рядов Фурье составляет отдельную обшир-
обширную область в теории функций. Мы здесь ограничимся
только основными фактами, наиболее важными для при-
приложений.
В дальнейшем для преобразования Фурье функции f
на Т мы будем вместо общего обозначения f(x) исполь-
использовать более традиционное обозначение
Теорема 13. Преобразование Фурье является уни-
унитарным оператором из ?2(Т, dt) в Z2(Z).
Доказательство вытекает из утверждения задачи 463
о том, что функции %n(t)= е2лШ образуют ортонормиро-
ванный базис в L2(T, dt), и из подсчета соответствующих
преобразований Фурье. Если через еп обозначить двусто-
двустороннюю последовательность, в которой на п-м месте
стоит единица, а на остальных местах — нули, то она бу-
будет в точности преобразованием Фурье функции %п. Так
как {en}n(=z—ортонормированный базис в Z2(Z), преобра-
преобразование Фурье унитарно (см. задачу 489).
Эта теорема является частным случаем следующего
общего факта:
Пусть G — компактная коммутативная группа, G —
двойственная к ней дискретная группа (см. задачу 541).
Будем считать, что инвариантные меры \х и \х на этих
143
группах нормированы условиями:
для
Тогда преобразование Фурье является унитарным опе-
оператором из L2(G, \x) в L2{G, \i).
Существует много результатов о связи гладкости функ-
функции / на Т с быстротой убывания ее коэффициентов
Фурье (см., например, задачи 561—564). Основой их вы-
вывода является
Теорема 14. Оператор дифференцирования перехо-
переходит при преобразовании Фурье в оператор умножения на
последовательность {2nin}n^Z'
Доказательство. Пусть /еС1 (Т); тогда коэффи-
коэффициенты Фурье с]г производной функции /' можно вычис-
вычислить, интегрируя по частям:
с\ = J /' (t) e-™inldt = е~2лШ/ (О IS - J /(О de-™int = 2nincn,.
0 0
1
где cn=\ f (t)e~~2mntdt— коэффициенты Фурье функции /.
о
Теорема доказана.
Распространим теперь преобразование Фурье на обоб-
обобщенные функции на Т. Пусть /е=#(Т). Естественно на-
назвать преобразованием ^Фуръе обобщенной функции / на-
набор коэффициентов с„ = </, e~2llint>.
Будем называть двустороннюю последовательность
{cn}n^z медленно растущей (или последовательностью
умеренного роста), если cn = O(nk) для некоторого к.
Пространство всех медленно растущих последовательно-
последовательностей обозначим P(Z).
Теорема 15. Преобразование Фурье задает изомор-
изоморфизм пространств (?Г'(Т) и P(Z), при котором свертка
переходит в обычное произведение, оператор сдвига
T(t)—e оператор умножения на последовательность
(е2Л111'}, дифференцирование по t—в оператор умножения
на последовательность Bяш), умножение на характер
е2лШ — в сдвиг на к.
Доказательство. Для гладких регулярных обоб-
обобщенных функций перечисленные свойства уже доказаны.
Остается сослаться на тот факт, что всякая обобщенная
функция на Т является конечной суммой производных
некоторого порядка от регулярных функций.
144
Рассмотрим теперь вопрос о восстановлении функции
/ по ее преобразованию Фурье {cn}n=z- Если /eL2(T,u),
то, как мы знаем,
/(*)= 2 *п*2я|я', C0)
причем ряд в правой части сходится в смысле простран-
пространства ?2(Т, dt). Если коэффициенты ch убывают достаточ-
достаточно быстро, то этот ряд сходится в более сильном смысле.
Например, если cn = O(n-h) для всех /с>0, то ряд схо-
сходится в топологии пространства <§Г(Т). Вопрос о сходи-
сходимости ряда Фурье занимает большое место в теории
функций. Мы не будем останавливаться на возникающих
здесь (иногда трудных) вопросах. (См. [23*].)
Сравним формулу C0) с определением преобразова-
преобразования Фурье на группе Z:
Мы видим, что эти преобразования получаются одно
из другого композицией с преобразованием ^ на Т или на Z:
{спГ = {с-п} или /@ в/(-0 •
Введем термин обратного преобразования Фурье для
композиции обычного (или прямого) преобразования
Фурье и преобразования ~ («птички»). Оказывается,
справедлив общий,принцип: прямое и обратное преобра-
преобразования Фурье являются взаимно обратными оператора-
операторами. Точная формулировка этого принципа с указанием
соответствующих друг другу классов функций на G и G
зависит от специфики группы G.
3. Интеграл Фурье. Преобразование Фурье для функ-
функций на вещественной прямой задается интегралом Фурье:
x. C1)
Напомним, что в п, 2 мы ввели понятие обратного
преобразования Фурье:
/(Л)= JfWe^dx. C2)
— оо
Теорема 16. Прямое и обратное преобразования
Фурье являются взаимно обратными преобразованиями
пространства S(R)
А. А. Кириллов, А. Д. Гвишиани
Доказательство. Покажем, что под действием
преобразования Фурье (и прямого, и обратного) про-
пространство S(R) переходит в себя. В сахмом деле, посколь-
поскольку функция /e5(R) и все ее производные суммируемы
и стремятся к нулю на бесконечности, интегрирование по
частям дает равенство
C3)
Далее, поскольку функции xkf(x) суммируемы при
любом /с, дифференцирование формулы C1) по X дает
равенство
fw = [f.(-2nix)h]~- C4)
Обозначая оператор преобразования Фурье через F,
мы можем переписать C3) и C4) в виде коммутацион-
коммутационных соотношений
FDk = MhF, F(-M)k = DhF, C5)
FDF-* = M, FMF-' = -Д C6)
где через D обозначен оператор дифференцирования d/dx,
а через М — оператор умножения на 2nix. Система полу-
полунорм, определяющая топологию в 5(R), имеет вид
/>„(/)= sup |*У°(*I-
По теореме 30 гл. III эта систвхма эквивалентна системе
Оценим полунорму рш([) через полунормы pmn{f)- Для
этого заметим, что рм (/) = Bя) ~hpOo (MkDlf) ,phi{f) = Bnyk x
Xp'Ql)(MkDlf). Далее, оценка интеграла C1) дает рооG)^
^Poo(f)- Отсюда
Ры (Г) = Bл) -%о (MkDlf) = Bл) "Voo ((DkMlf)~).
Остается переставить местами операторы Dk и М1, чтобы
получить требуемую оценку. По формуле Лейбница имеет
место тождество
Mk-'mi-niM*1''*''- C7)
Мы доказали непрерывность отображения F. Непрерыв-
Непрерывность обратного преобразования Фурье F доказывается
146
(,
точно так же с использованием коммутационных соотно-
соотношений
DiCF C57)'
или ^
FD{F)-1 = -М, FM{F)-X=D. C6')
Рассмотрим теперь композицию преобразований F и F.
Из соотношений C6) и C6') немедленно вытекает, что
эта композиция перестановочна с операторами D и М.
Лемма. Всякий непрерывный оператор в простран-
пространстве S(R), перестановочный с оператором М, является
оператором умножения на некоторую функцию.
Доказательство. Пусть оператор А в 5(R) пере-
перестановочен с М. Тогда он перестановочен с оператором
умножения на любой многочлен. Покажем, что для любой
функции cpeS(R) и любой точки aeR значение Ау(а)
зависит только от ф(а). В самом деле, если q)i(a)=(p2(a),
то разность tyi(x)— (p2(#) обращается в нуль в точке а и,
значит, имеет вид (х — а)$(х), где \|^S(R). Поэтому
Аф, (х) = А [ф2 + (х — a)\f] = Аф2 (х) + (х — а)А^ (х), по-
поскольку А перестановочен с умножением на х — а. Отсю-
Отсюда Aq)i(a) = Acp2(a), что и требовалось. Итак, для любой
точки a^R существует такое .число /(я), что Аср(а) —
= /(а)ф(а) для всех ф^5(Н). Значит, A=M(f). Лемма
доказана.
Замечание. Из приведенного доказательства нель-
нельзя сделать никаких выводов о структуре функции /. Но
мы знаем, что для любой функции ф^5(Р) функция /ф
также принадлежит 5(R). Отсюда следует, что / бесконеч-
бесконечно дифференцируема.
Вернемся к доказательству теоремы. Интересующие
нас операторы FF и FF, в силу доказанной леммы, яв-
являются операторами умножения. Кроме того, справедли-
справедливо соотношение
вытекающее из правил Лейбница. Поэтому оператор вида
М (/) перестановочен с оператором D только тогда, когда
/' = 0, т. е. / = const. Это показывает, что операторы FF
и FF скалярны: FF = CU FF = d. Для завершения дока-
доказательства теоремы остается проверить, что Ci = C2 = l.
Это вытекает, например, из явного подсчета преобразова-
преобразования Фурье какой-либо функции из 5(R).
10* 147
Теорема 17. Существует унитарный оператор в
L2(R, dx), ограничение которого на пространстве
L2(R, dx) П Li(R, dx) совпадает с преобразованием Фурье,
(В дальнейшем этот оператор мы будем обозначать, как
и прямое преобразование Фурье, буквой F.)
В частности, для любой функции /^S(R) справедли-
справедлива формула Планшереля:
l/jL,(H.d*)=l7||LI(H.«»M. C8)
Доказательство. Из теоремы 16 и общих свойств
преобразования Фурье (см. п. 1) вытекает, что преобра-
преобразование Фурье переводит умножение в свертку:
(/.A)~-/W*. C9)
Применим это равенство к частному случаю, когда Д (х) =
Поэтому C9) дает
f | / (
Полагая здесь Я = 0 и заменяя — \i на Я, получаем C8).
Поскольку 5(R) плотно в L2(R, dx), из C8) вытекает,
что оператор F имеет единственное унитарное продолже-
продолжение с S(R) на L2(R, dx). Остается проверить, что на под-
подпространстве L = L2(R, dx)P\Li(R, dx) это продолжение
задается интегралом C1). Пусть ф е L, cpn^5(R) ифп->
-> ф в смысле каждой из норм L2(R, dx) и Li(R, dx).
Тогда фп -*¦ ф равномерно и фп -> ^ф в смысле L2(R, dX).
Последнее влечет, что некоторая подпоследовательность
q>nk сходится к /чр почти всюду. Отсюда ^ф = ф, и теоре-
теорема доказана.
Замечание. Теорема 17 является частным случаем
общего утверждения: если G — локально компактная
коммутативная группа с инвариантной мерой (я, то суще-
существуют ^гакая инвариантная мера \i на двойственной
группе G и такой унитарный оператор F: L2(G, \i)-+
-> L2(G, \i), сужение которого на L2(G, (i)nL1(G, \i) сов-
совпадает с преобразованием Фурье.
Так же как и в случае окружности, гладкость функ-
функции / на прямой связана с убыванием на бесконечности
ее преобразования Фурье f. Так как группа R самодвой-
самодвойственна, имеет место двойственное утверждение: убывание
148
на бесконечности функции / связано с гладкостью f. Вот
один из вариантов точной формулировки.
Теорема 18. Если функция / и все ее производные
до порядка к суммируемы на R, то f удовлетворяет
оценке
\f(X)\=O{l
Если функция {1 + \x\)hf(x) суммируема на R, то f
имеет непрерывные ограниченные производные до по-
порядка к.
Доказательство вытекает из коммутационных соотно-
соотношений C5). (Мы предоставляем читателю убедиться, что
в предположениях теоремы 18 вывод этих соотношений
сохраняет силу.)
Требование быстрого убывания на бесконечности в
случае G = R можно сформулировать разными способа-
способами. Самое сильное условие такого сорта — финитность
функции /. Оказывается, это условие влечет аналитич-
аналитичность функции f на комплексной плоскости С, содержа-
содержащей прямую R.
Теорема Пэли — Винера. Преобразование Фурье
пространства L2(—a, а) (рассматриваемого как подпро-
подпространство в Z/2(R, dx)) состоит из всех целых аналити-
аналитических функций g(X), обладающих свойствами:
1) \g{X)\ <Ce2nalIml\ где константа С может быть
своя для каждой функции g;
2) ограничение g(X) на R принадлежит L2(R, dX).
Доказательство. Интеграл C1), определяющий
функцию / для f^L2(—a, а), сходится при всех Х^С.
Непосредственное вычисление показывает, что / (X) диф-
дифференцируема по комплексному переменному X и, следо-
следовательно, является целой функцией.
Необходимость условия 1) вытекает из оценки
/ (x) e~2JliKx dx
Необходимость условия 2) следует из теоремы 17.
Покажем достаточность этих условий. Поскольку огра-
ограничение g на R принадлежит L2(R, dX), существует такая
функция /eZ,2(R, dx), что g = f. Предположим сначала,
что g(X) достаточно быстро убывает на бесконечности:
?e2Ja\Iml\
Г"- Тогда g (X) суммируема на R и / может
1 + | К I
149
быть выражена через g обратным преобразованием Фурье:
/(*) =
По лемме Коши контур интегрирования можно сдвинуть
оо
в комплексную область: / (х) = j g (X + ib) e2nia+ib)x dx.
— оо
Пусть х>а. Тогда подынтегральное выражение при Ь >0
2Ь(а—х)
допускает оценку ~ и> следовательно, интере-
интересующий нас интеграл стремится к нулю. Поскольку зна-
значение интеграла на самом деле не зависит от Ь, мы по-
получаем, что f(x) = 0 при х>а. Аналогично, устремляя Ъ
к —оо, получаем, что f(x) = 0 при х < — а. Остается изба-
избавиться от условия убывания g(k) на бесконечности. Пусть
ф^^)(К) и suppqpc=[—e, е]. Тогда функция ф(Я) быст-
быстро убывает на бесконечности и удовлетворяет оценке
|ф(А,1 ^Се2ле]1тк] в силу уже доказанной части теоремы.
К функции ?1(^) = ?Г(?Оф(?О применимы изложенные вы-
выше соображения с заменой а на а + е. Значит, функция
/1(е) = /*ф принадлежит L2(—а — е, а + е). Отсюда без
труда выводится, что f^L2(—а, а). Теорема доказана.
4. Преобразование Фурье обобщенных функций. Пусть
/^«^(R). Интеграл, определяющий преобразование
Фурье функции /, можно рассматривать как значение
обобщенной функции / на характере Хя^^(К):
/(*)=¦</, Хх>. D0)
Более широкое определение преобразования Фурье
можно получить по схеме, описанной в п. 5 § 4 гл. III.
Если /e=Li(R, dx), q>e=S(R), то
<7, Ф> = f f e~2JXiKxf (х) ф (X) dx dX = </, ф>.
R R
Правая часть этого равенства имеет смысл для /<=5"(R).
Поэтому мы определим преобразование Фурье в простран-
пространстве S'(R) формулой
<Ь> = </, Ф>, Ф^5(R). D1)
В случае, когда /^^'(R), это определение эквивалентно
данному выше по формуле D0).
150
Теорема 19. Прямое и обратное преобразования
Фурье являются непрерывными взаимно обратными опе-
операторами в S'(Л).
Доказательство сразу вытекает из формулы D1), ко-
которая показывает, что преобразование Фурье в ?'(К)
является оператором, сопряженным к преобразованию
Фурье в S(R).
Преобразование Фурье обобщенных функций сохраня-
сохраняет основные свойства преобразования Фурье обычных
функций: оно переводит свертку в обычное умножение,
сдвиг — в умножение на характер, умножение на харак-
характер — в сдвиг, дифференциальный оператор с постоянны-
постоянными коэффициентами — в оператор умножения на много-
многочлен. Более точные формулировки см. в задачах соответ-
соответствующего пункта.
Замечание. Преобразование Фурье обобщенных
функций из 2)' (R) также можно определить по формуле
D1). Однако образом этого отображения уже не будут
обобщенные функции известных нам классов. Можно
показать, что образом 2){R) при преобразовании Фурье
является пространство аналитических функций g(X), ко-
которые для любого N и подходящих С и R удовлетворяют
оценке
Преобразования Фурье обобщенных функций из 3)'(К)
являются линейными функционалами на этом прост-
пространстве.
Пример. Регулярная обобщенная функция/ (х) = ех
имеет своим преобразованием Фурье линейный функ-
функционал
</,*>=-?-J *«
где интеграл берется по некоторому контуру С в комп-
комплексной плоскости X.
Некоторые полезные свойства обобщенных функций
можно доказать чисто алгебраическим способом, исполь-
используя коммутационные соотношения преобразования Фурье
с операторами сдвига и умножения на характер. Приме-
Примером является следующая формула суммирования Пуас-
Пуассона.
151
Теорема 20. Для любой функции 9^5(R) справед-
справедливо равенство
2 ф(*)=2ф(*). D2)
fe^Z h~Z
Доказательство. Равенство D2) равносильно
утверждению f = /, где / = 2 б (# — к). Обобщенная
k<=Z
функция / обладает свойствами: 1) ГA)/ = /, 2) Л/A)/ =
= /, где ГA)—сдвиг на 1, а МA) — оператор умножения
на %i=^e2nix. Свойства 1) и 2) переходят друг в друга
при преобразовании Фурье (задача 608). Покажем, что /
определяется этими свойствами с точностью до постоян-
постоянного множителя. В самом деле, из свойства 2) легко вы-
выводится, что носитель / содержится в Z и что в каждой
точке носителя / имеет нулевой порядок. Отсюда
^8(x — /с). Теперь из свойства 1) следует, что все
коэффициенты ch равны между собой и/ = с^ 6 (# —
ftZ
Остается вычислить константу с. Равенство / = / пока-
показывает, что с2 = 1. Поскольку в S(R) есть положительные
функции, преобразование Фурье которых положительно,
случай с = —1 невозможен. Теорема доказана.
Замечание 1. Условие (peS'(R) можно существен-
существенно ослабить. Достаточно, например, чтобы ф и ф допу-
допускали оценку вида O(UI~e).
Замечание 2. Формула Пуассона является част-
частным случаем более общего утверждения. Пусть
— точная последовательность локально компактных ком-
коммутативных групп и
0 +- Go «- G+- Gt +- 0
— двойственная последовательность. Тогда при подходя-
подходящем выборе инвариантных мер jj,0 на Go и jii на G4 спра-
справедливо равенство
152
ГЛАВА V
СПЕКТРАЛЬНАЯ ТЕОРИЯ ОПЕРАТОРОВ
§ 1. Функциональное исчисление
1. Функции операторов в конечномерном пространстве.
Линейные операторы можно рассматривать как обобще-
обобщение понятия числа. В одномерном случае эти два поня-
понятия совпадают. Уже в двумерном пространстве начина-
начинаются отличия, главное из которых— некоммутативность
операции умножения для операторов. Тем не менее мно-
многие свойства чисел сохраняются и при переходе к опера-
операторам в многомерных пространствах. Одно из этих
свойств — возможность подставлять операторы в качестве
аргументов в различные функции. Изучение функций от
операторных аргументов составляет предмет функцио-
функционального операторного исчисления. Мы ограничимся
функциями одного переменного. В этом случае не возни-
возникает затруднений, связанных с некоммутативностью*).
В этом пункте мы рассмотрим функции от оператора в
конечномерном пространстве.
Пусть А — линейный оператор в конечномерном ли-
линейном пространстве L над полем К = R или С. Простей-
Простейшие функции, в которые можно подставлять оператор А
в качестве аргумента,— это многочлены. Если р (х) =
п
= 2 Ck%ki то естественно определить р{А) равенством
fc=0
р(А)= %chA\ A)
условившись, что Л° = 1 (единичный оператор). Послед-
Последнее условие необходимо для того, чтобы выполнялись
естественные равенства
(hPi + X2P2) (А) = KiPl(A) + К2р2(А),
выражающие тот факт, что отображение р >-> р (А) явля-
является гомоморфизмом алгебры многочленов в алгебру опе-
операторов.
*) С одним из вариантов некоммутативного функционально-
функционального исчисления можно познакомиться по книге В. П. Маслова
[14*]. Другой вариант — теория представлений матричных групп,
см. [17],
153
Следующий, более широкий класс функций — рацио-
рациональные функции. Если r(x) = p(x)/q(x), где р и q —
многочлены, то мы определим г (А) формулой
г(А) = р(А)д(А)-> = д(А)-*р(А). C)
Это определение имеет смысл, только если q(А)— обрати-
обратимый оператор. В конечномерном случае обратимость q{A)
равносильна условию det q (A) Ф 0.
Наиболее важный пример — резольвента оператора
А — определяется формулой
/гх(Л) = (л-я.1)-1 = гя(Л), D)
где п(х)=1/(х-Х).
Соответствие г у-* г (А) является гомоморфизмом не-
некоторой подалгебры поля рациональных функций К(х)
в алгебру операторов. Можно проверить, что эта подал-
подалгебра состоит из всех рациональных функций, полюса ко-
которых лежат вне спектра (т. е. множества собственных
значений) оператора Л.
До сих пор мы не привлекали к нашим рассмотрени-
рассмотрениям топологию. Теперь предположим, что L — нормиро-
нормированное пространство и тем самым множество операторов
в L также снабжено нормой. Тогда мы можем определить
целую аналитическую функцию от оператора А формулой
E)
оо
если J (х) = 2 ?/А-В самом деле, если / — целая функ-
оо
ция, то числовой ряд 2 Ck\\A\\k сходится. Отсюда выте-
fc=o
кает, что последовательность частичных сумм ряда E)
фундаментальна и, следовательно, имеет предел в про-
пространстве операторов b>L.
Пример. Вычислим etA, где А — оператор поворота
на 90° в R2, a t — вещественный параметр. Поскольку
А2 = — 1, ряд для eiA принимает вид
/2 t* а /4 /5
*л 1 + ^И + 1 + 4
откуда etA = cos t • 1 + sin t А. В матричной форме это
/ 0 t\ I cos t sin t\
равенство принимает вид exp \^_ % QJ = y_ gin t cog J
154
Предположим теперь, что в пространстве многочленов
или целых аналитических функций введена некоторая
норма, относительно которой отображение / •-> / (А) не-
непрерывно. Тогда это отображение продолжается по непре-
непрерывности на пополнение пространства многочленов или
целых функций по этой норме.
Пример. Пусть оператор А задается диагональной
матрицей с вещественными числами на диагонали, при-
принадлежащими отрезку fa, b]. Тогда соответствие /•-> / (А)
непрерывно по норме С [а, Ь] и, следовательно, можно
определить f(A) для любой непрерывной функции
на fa, b].
В конечномерной ситуации вопрос о том, какие функ-
функции от оператора А имеют смысл, решается до конца
следующим образом. Пусть А,4, ..., \k —-набор комплекс-
комплексных чисел, пи ..., пк — набор натуральных чисел. Опре-
Определим в пространстве многочленов полунорму
ЛП тах I/
Если А — оператор в конечномерном комплексном линей-
линейном пространстве L, то через рА обозначим полунорму
в пространстве многочленов:
Теорема 1. Пусть А — оператор в конечномерном
линейном комплексном пространстве, Хи ..., Xh — корни
многочлена минимальной степени, аннулирующего опера-
оператор А, пи ..., nh— кратность этих корней. Тогда полу-
полунормы р. * .„ „ и рА эквивалентны.
Доказательство. Пусть L — пространство много-
многочленов, Lo ~ подпространство многочленов, имеющих в
точке ij корень кратности > п} (/ = 1, 2, ..., к). Обе по-
полунормы, о которых говорится в теореме, аннулируют
пространство Lo и порождают нормы в факторпростран-
стве L/Lq. Поскольку последнее конечномерно, любые две
нормы в нем эквивалентны.
Следствие 1. Если А — оператор с простыми соб-
собственными значениями, то выражение f(A) имеет смысл
для любой непрерывной функции /.
Следствие 2. Если А — оператор в п-мерном про-
пространстве, то выражение f(A) имеет смысл для любой
(п— 1)-кратно дифференцируемой функции.
2. Функции ограниченных самосопряженных операто-
операторов. Пусть А — ограниченный самосопряженный опера-
155
тор в гильбертовом пространстве Н над полем К = R или
С. Задача этого пункта — определить f(A) для любой бо-
релевской функции / на отрезке [—а, а], где а = НЛН.
Напомним, что спектром оператора А называется мно-
множество о(Л)<=С, состоящее из тех Х*=С, для которых
оператор А — X • 1 необратим. Дополнение к а (А) в С на-
называется резольвентным множеством и обозначается
р(А). Таким образом, резольвента оператора А, Гь(А) =
= (А —XI), определена при Х^ р(Л).
Теорема 2. Спектр ограниченного оператора явля-
является непустым компактным подмножеством в С.
Доказательство. Если IXI > ИЛII, то оператор
А — X •1 имеет обратный оператор г* (Л), задаваемый
рядом:
гх(Л)=-2Я.-*-1Л\ G)
Поэтому о(А) содержится в круге \Х\ <1Ш. Далее, если
в некоторой точке Хо е С существует резольвента гк (А) =
= 5, то в круге радиуса ШН сходится ряд
гк(А) = ^(Х-Х0)кВк+\ (8)
Это показывает, что резольвентное множество р(^)
открыто и, следовательно, а (А)—компакт. Попутно мы
установили, что норма резольвенты допускает следующую
оценку снизу:
(А) || > d (X, а D))-1- ( min (X - и)\~\ (9)
Остается доказать непустоту спектра. Предположим
противное, т. е. о(А) = 0. Тогда резольвента п(А) явля-
является целой аналитической функцией от X ^ С. Формула
G) показывает, что \\п(А)\\ -+ 0 при X -> «>. Значит,
Игх(-4)И ограничена на всей комплексной плоскости. Для
любых векторов х и у из Н величина (гк(А)х, у) явля-
является целой аналитической функцией от i, стремящейся к
нулю на бесконечности. Такая функция по теореме Лиу-
вилля тождественно равна нулю. Значит, гл(Л) = 0, что
невозможно. Теорема доказана.
Изучим теперь, как меняется спектр А, когда над
оператором А совершают те или иные преобразования.
Теорема 3. 1) Пусть г(х) —рациональная функция,
не имеющая полюсов на спектре оператора А. Тогда опе-
156
ратор г (А) определен и его спектр описывается формулой
A0)
2) Спектр сопряженного оператора А* связан со спек-
спектром А соотношением
= {Я: Х^о(А)}. (И)
Доказательство. Пусть r(x) = p(x)q(x)~\ где р
и q — взаимно простые многочлены. Если jiii, ..., \хт —
корни р(х), Xi, . . ., Хп — корни q(x) (учитывая кратно-
т п
сти), то г (х) = с JJ (х — аг) JJ (х -— Pj)~\ Отсюда г (А) =
т п
il il
Поскольку рациональная функция г(х)—\х обращается
в нуль при х = X, ее числитель имеет X корнем и, следо-
следовательно, содержит множитель х — К. Поэтому оператор
г (А)— \х -1 содержит множителем необратимый оператор
А — X • 1 и, следовательно, сам необратим. Значит, jii e
eo(r(i)). Мы доказали включение г(оD))<= о (г (А)).
Обратно, пусть \х^о(г(А)). Представим рациональ-
m
ную функцию г(х) — \х в виде произведения с JJ (х — аг) х
г=1
п
хП (х — Pj)- Если бы все a,i принадлежали рD), то
3=1
оператор г (А)— \х - 1 имел бы обратный оператор
m n
с-1 Ц га. D) Ц (А — fij-1), что неверно. Значит, одно из
чисел аг- принадлежит спектру 4. Но тогда г (a*)— jll = О,
т. е. \х^г(о(А)). Утверждение 1) доказано. Утвержде-
Утверждение 2) вытекает из равенства D)* =D*)~1, которое
влечет соотношение
Теорема 4. Пусть А — самосопряженный оператор.
Тогда
1) А имеет спектр на отрезке [—11411, II4II];
2) для любой рациональной функции г с полюсами
вне о (А) справедливо равенство
| г DI= max |г(Ь)|. A2)
157
Доказательство. Пусть X — невещественное чис-
число. Покажем, что существует п(А). Оператор А— XI не
имеет ядра, так как если х — единичный вектор из
кег(Л—XI), то \ = {Ах, х) = (х, Ах) = Х, что неверно.
Далее, образ оператора А— XI плотен в Я, так как
im (А-№)!- = кет {А -Х1)* = кег(Л -~Х1) = 0. Покажем,
что оператор (А— XI)", определенный на im(A— XI),
ограничен. Пусть X = а + ф, а, р *= R. Тогда
II(А -Xl)xW2 = ((A-al)x- i$x, (A-al)x- i$x) =
Отсюда \\А — ХШ < Р и г(Л) получается продолжени-
продолжением по непрерывности. (На самом деле, как можно прове-
проверить, из полученной оценки следует, что im(^4 — XI) = Н.)
Итак, о (А) лежит па вещественной оси. Утверждение
1) следует теперь из того, что о (А) лежит в круге ради-
радиуса Ы\\ (см. доказательство теоремы 2).
Доказательство утверждения 2) начнем со случая
г(х)^х. Тогда 2) сводится к равенству
IUII = sup{|Xl: Х^о(А)}. A3)
Величину, стоящую в правой части, называют спектраль-
спектральным радиусом оператора А и обозначают г (А). Имеет
место
Лемма. Для любого ограниченного оператора А
справедливо соотношение
гD) = Нт МТП; A4)
П-+оо
если А — самосопряженный оператор, то г(А)=\\А\\.
Доказательство. Существование предела в пра-
правой части равенства A4) вытекает из общих свойств по-
полуаддитивных последовательностей (см. задачу 621). Да-
Далее, разложение резольвенты в ряд Лорана в окрестности
бесконечно удаленной точки дается формулой G). По
формуле Адамара радиус сходимости этого ряда (равный,
очевидно, г (А)) связан с коэффициентами искомым соот-
соотношением A4). (Мы применяем здесь формулу Адамара
к операторной аналитической функции. Легко проверить,
что обычный вывод этой формулы полностью переносит-
переносится на этот случай.) Для любого оператора А справедливо
равенство
= sup (A*Ax, y) = sup д7ц'|Т = 1A f.
158
В частности, для самосопряженного А Ы'М =» 1Ш*. По-
Поэтому 1 А*п | = fl А |рп и, следовательно, lim | Ап |1/п =
Лемма доказана.
Вернемся к доказательству утверждения 2) в общем
случае. Пусть В = г(А). Тогда В* = г(А), где через г мы
обозначаем функцию r(z) = r(z). Легко проверить, что
г — рациональная функция, коэффициенты которой комп-
комплексно сопряжены коэффициентам г. Применяя уже дока-
доказанное утверждение к самосопряженному оператору
В*В= \г\2(А), получаем
= sup (ц)= sup
(последнее — в силу утверждения 1) теоремы 3). Теоре-
Теорема доказана.
Следствие. Для любого самосопряженного операто-
оператора А в гильбертовом пространстве Я существует единст-
единственный непрерывный гомоморфизм ф алгебры С [—а, а],
где a = IL4H, в алгебру ограниченных операторов в Я, об-
обладающий свойствами:
1) ф A) = 1 (здесь слева 1 означает функцию, тож-
тождественно равную 1, а справа — единичный оператор в Н);
2) () (/)*
3)
4)
Этот гомоморфизм обладает также свойством:
5) если AB = BA, то ф(/M = 5ф(/). (Другой вывод
этого утверждения см. в задачах 644, 645.)
Теперь мы распространим гомоморфизм ф на алгебру
В [—а, а] ограниченных борелевских функций на от-
отрезке [—а, а].
Теорема 5. Пусть А — ограниченный самосопря-
самосопряженный оператор в гильбертовом пространстве Я. Суще-
Существует единственный гомоморфизм ф алгебры В[—а, а]
ограниченных борелевских функций на отрезке [—а, а],
где a = IL4ll, обладающий свойствами:
2) <р(*) = 4;
3) если 1/п(#I < С и fn(t)-+ f(t) в каждой точке ?
[-а, а], то ф(/п)->ф(/).
Гомоморфизм ф обладает также свойствами:
4) ф(/) = ф(/)*;
5) Нф(/)И^ sup 1/@1, t = [-a,a];
159
6) ф(/M = 5ф(/) для любого оператора 5, перестано-
перестановочного с А.
Доказательство. На множестве С [—а, а] гомо-
гомоморфизм ф уже определен. Совокупность борелевских
функций получается из совокупности непрерывных функ-
функций поточечными предельными переходами; это влечет
единственность искомого гомоморфизма ф. Докажем его
существование. Пусть х, у *= Я. Определим линейный
функционал Fxy на С [—а, а] по формуле
Д*(/)-(ф(/)*. У). 'A5)
Поскольку \Fxy(f)\< Иф(/)ИЫ%11 < ll/llc[-.f.]WIII»ll,
Fxy — непрерывный функционал, норма которого не пре-
превосходит величины 1ЫШг/И. Значит, существует такой бо-
релевский заряд vxy на [—а, а], что
Fxv(f)= } f(t)dvxy(t), A6)
— а
причем Var!_av^!|#|||у[|. Пусть теперь /—ограниченная
борелевская функция на отрезке [-а, а]. Величина
a
Bj (х, у) = J / (t) dvxy (t) линейно зависит от х, антили-
—а
нейно —- от у и удовлетворяет оценке | Bf (х, у) \ ^
^ sup | / (t) \\\x\\\\ y\\. Отсюда следует, что существует
такой ограниченный оператор ф(/), что Bf(x, #) =
= (ф(/)^ y)i причем Нф(/)И ^sup l/(/)l, t^[-a,a\. Пусть
fn(t)~+f(t) для t<^[—а, а]. Тогда для любых х и у из //
мы имеем
a a
(Ф (/«) х, у) = j" /„ (t) dvxy @ -»- J / @ dvxy(t) = (Ф (/) x,y).
—a —a
Таким образом, ф(/„) слабо сходится к ф(/). Отсюда вы-
вытекает, что отображение ф — гомоморфизм. В самом деле,
равенства
справедливы, когда / и g принадлежат С [—а, а] и со-
сохраняются при поточечных предельных переходах. Это
же рассуждение показывает, что ф обладает свойством 4).
Теперь мы в состоянии доказать свойство 3). Пусть
/п@.-^/@ Д?я всех t^[~a, а] и |/п@1^С Тогда
160
1/п-/12@-*0 для всех t^[-a, а]. Поэтому ф^1/„ — /I2)'-*-
-> 0. Отсюда Нф (/п - /) х\\2 = (Ф (/п - /) *ф {fn - /) х, х) =
^(фО/п — Я2)#, я)-^0. Теорема доказана.
Основной пример. Пусть Н = L2(X, fi), Л — опе-
оператор умножения на функцию a^Loo{X, \x). В этом слу-
случае ф (/) — оператор умножения на функцию ф (а (х))
(проверьте это, проследив построение ф(/) на этом при-
примере). Универсальность этого примера выяснится ниже.
Построенное в теореме 5 функциональное исчисление
допускает следующее полезное обобщение.
Теорема 6. Пусть Аи ..., Ап — попарно перестано-
перестановочные ограниченные самосопряженные операторы в гиль-
гильбертовом пространстве Н,Т — параллелепипед в Rn, опре-
определенный условиями \ti\ < WAiW (z' = 1, 2, ..., п). Сущест-
Существует единственный гомоморфизм ф алгебры В(Т) ограни-
ограниченных борелевских функций на Т в алгебру ограничен-
ограниченных операторов в Я, обладающий свойствами:
1) AI
2) ц{) и
3) если \fh{t)\<C и fk(t)-+f(t) для всех t^T, то
)~^ф(/) в сильной операторной топологии.
Кроме того, гомоморфизм ф обладает свойствами:
4) (/) ()*
) ф(/) ф(/);
5) | Ф (/) || < sup 1/@1;
г
6) ф(/M = 5ф(/) для любого оператора В, перестано-
перестановочного с At, ..., Ап>
Доказательство. Пусть Bk(T)— подалгебра в
В(Т), состоящая из функций, зависящих от координа-
координаты tk. Тогда ограничение ф на Bh(T) совпадает с гомо-
гомоморфизмом фь, соответствующим по теореме 5 оператору
Ak. Обозначим через В0{Т) подалгебру ступенчатых
функций на Т, т. е. функций вида / (t) = 2 ck1 •. *
•.. Ckn%E1 (h) • • • %еп {^п)' Если искомый гомоморфизм ф
существует, то согласно сказанному выше на ступенчатой
функции / он должен задаваться формулой
Ф(/) = 2iCkv..knq>i(XE1) ... щ(%Еп). A7)
Отсюда вытекает единственность ф на BQ{T), а следова-
следовательно, и на В(Т) в силу свойства 3).
Докажем его существование. На подалгебре В0(Т) мы
определим отображение ф формулой A7). Поскольку
Ль ..., Ап попарно коммутируют, операторы 9i(/i),
ф2(/2), ..., фп(/п) также попарно коммутируют (утверж-
11 А. А. Киииллов. А. Л. Гвишиани 161
дение 6) в теореме 5). Поэтому отображение ср является
гомоморфизмом. Далее, гомоморфизм ф переводит поло-
положительные функции в положительные операторы, так как
если / ^ О, то f = gz для некоторой вещественной функ-
функции g^B0(T) и, значит, ф(/) = ф(#J >0. Это влечет
справедливость свойства 5) (см. задачу 645). Поэтому
гомоморфизм ф продолжается на алгебру С(Т) непрерыв-
непрерывных функций на Г и обладает там свойством 5). Вывод
отсюда теоремы проводится так же, как вывод теоремы 5
из следствия к теореме 4.
Отметим полезное
Следствие. Пусть А — нормальный оператор в
гильбертовом пространстве Н, Т — квадрат на комплекс-
комплексной плоскости с центром в нуле и стороной 211АII. Суще-
Существует единственный гомоморфизм алгебры В(Т) ограни-
ограниченных борелевских функций на Т в алгебру операторов
в Я, обладающий свойствами:
)
2)
3) Ф(/) Ф(/);
4) если |/„| ^С и fn(t)-+f для t^T, то
Этот гомоморфизм обладает также свойствами:
5) Иф(/)И<sup 1/@1;
6) ф(/)^==^ф(/) для любого оператора 5, перестано-
перестановочного с А и Л*.
В самом деле, если А — нормальный оператор, то
А = В + iC, где В и С — ограниченные самосопряженные
операторы, норма которых не превосходит нормы А.
Условия 2) и 3) влекут условие 2) ф(#) = #, <р(у) = С.
Теперь утверждение следствия вытекает из теоремы 6,
примененной к операторам В и С.
3, Неограниченные самосопряженные операторы.
В приложениях часто встречаются операторы А, опреде-
определенные не во всем гильбертовом пространстве Я, а толь-
только на некотором незамкнутом плотном подпространстве
3)А с: Я, и неограниченные на этом подпространстве. Для
такого оператора можно определить сопряженный опера-
оператор Л*, который также может быть не всюду определен
и неограничен. А именно, областью определения А* на-
называется (вообще говоря, незамкнутое) подпространство
&а*, состоящее из таких векторов i/^fl, для которых
линейный функционал х •-* (Ах, у) ограничен на 2)А-
В этом случае он однозначно продолжается до линейного
функционала на Я и может быть записан в виде х у-*
*-*ixiz)i z^H. Мы полагаем Л*г/ = 2. Таким образом,
162
равенство
(Ах, у) = (х, А*у), A8)
которое является определением А* для ограниченных А,
теперь остается справедливым лишь для х е ?DA, e 3)а*-
Можно дать другое, более «геометрическое» определе-
определение А*. Для этого заметим, что всякий (в том числе и не
всюду определенный и неограниченный) оператор А за-
задается своим графиком, т. е. подмножеством ГАСЯ®Я,
состоящим из векторов вида х® Ах, х^З)А* Ясно, что
ГА является линейным подпространством в Н ® Н, не со-
содержащим векторов вида 0®^, х Ф 0. Обратно, всякое
подпространство в Я®Я, не содержащее векторов вида
0 Ф х, хФО, является графиком некоторого оператора.
Обозначим через т преобразование # ® Я, переводя-
переводящее вектор х® у в — у®х (поворот на 90°).
Теорема 7. Графики операторов А и А* связаны
соотношением
Га* = т(Гл)*, A9)
Доказательство. Пусть у © z<= Га*. Это значит,
что для всех х^З)А выполняется соотношение (Ах,у) =
= (х, z) (см. A8)). Это соотношение — не что иное, как
условие ортогональности векторов у ® z и —Ах $ х в
Я ® #. Теорема доказана.
Назовем оператор А замкнутым, если ГА — замкнутое
подпространство в Я®Я, Оператор В называется замы-
канием оператора А, если Гв — замыкание подпростран-
подпространства ГА. Говорят, что В является расширением А, и пи-
пишут В => А, если Гв => ГА. Из теоремы 7 вытекает
Следствие. Для любого оператора А оператор А *
замкнут, а оператор (Л*)*, если он определен, совпадает
с замыканием Л.
Замечание. Не всякий оператор допускает замы-
замыкание. Например, оператор А, определенный на множест-
множестве финитных последовательностей в 12(R) и переводящий
еп в nei (п= 1, 2, ...) не имеет замыкания, так как сре-
среди предельных точек его графика есть точка 0 ® е4. Про-
Проверьте, что оператор А* определен на подпространстве
{^i}-1-, которое неплотно в Z2(R).
Оператор А называется самосопряженным, если
&а* = Фа B0)
и А =Л* на 3>А.
11* 163
Предостережение. Это свойство оператора не
эквивалентно более слабому условию
(Ах, у) = (х, Ау) для «г, у^3>л. B1)
Операторы, обладающие свойством B1), называют
симметрическими. Очевидно, B1) эквивалентно включе-
включению 4сЛ*.
Оператор А называется существенно самосопряжен-
самосопряженным, если его замыкание — самосопряженный оператор.
Примеры. 1) Пусть А — оператор умножения на х
в L2(R, dx) с областью определения 2)А = ?)(R). Най-
Найдем 2)а*- По определению, для / е Фа* должно выпол-
выполняться равенство
j ц (х) f{x)dx = j ф (я) Т(х) dx,
— оо —оо
где
Поскольку ?D(R) плотно в L2(R, dx), отсюда следует,
что g{x) = xf(x). Итак, Фа* состоит из всех /et2(R,&),
для которых xj(x)^ L2(R, dx). Оператор Л* состоит в
умножении на х. Вывод: оператор А симметричен, но не
самосопряжен. Можно проверить, что Л* самосопряжен
и, следовательно, А существенно самосопряжен.
2) Пусть А — оператор дифференцирования d/dx в
L2(R, dx) с областью определения S)(R). Найдем 3)а*.
Если / е 5?а*,то для всех <р е S5 (R)
с» оо
= J" q{x)J(*)dx, где g<=A*f,
Это равенство показывает, что g(.z) является обобщенной
производной от функции —f(x). Итак, 3)а* состоит из
таких функций /^Zv2(R, dx), у которых обобщенная про-
производная принадлежит L2(R, dx). Оператор А* совпадает
с —d/dx.
В приложениях оператор А часто задается в виде
дифференциального выражения. В этом случае у него
существует так называемая естественная область опреде-
определения ?DA<^ L2(Q, d\x), а именно, совокупность всех обоб-
обобщенных функций f<^2)'(Q), для которых / и Af принад-
принадлежат L2(Q, d\i). В приведенных выше примерах опера-
операторы Л* имели как раз естественную область опреде-
определения.
164
Теория самосопряженных операторов хорошо разрабо-
разработана. Для ее применения в приложениях нужно знать,
что тот или иной оператор самосопряжен или хотя бы
существенно самосопряжен. Необходимым условием для
этого является симметричность оператора, которая, как
правило, проверяется без труда. Для исследования сим-
симметрических операторов полезен следующий критерий.
Теорема 8. Пусть А — симметрический оператор
в гильбертовом пространстве Н. Тогда самосопряжен-
самосопряженность А эквивалентна каждому из условий:
1) А замкнут и кет(А*± il) = {0};
2) im(A±il) = H.
Существенная самосопряженность А равносильна каж-
каждому из условий:
3) кег(Л*±И) = {0};
4) im(A±il) плотно в Н.
Доказательство. Если А — самосопряженный
оператор, то он замкнут (так как А = Л*, а Л* замкнут).
Если х^ кег(Л^± ?1), то Ax = ix. Отсюда (Ах, х) =
= i\\x\\2 = (х, Ах)=— i\\x\\2, т. е. х = 0. Мы показали, что
для самосопряженного оператора А выполнены усло-
условия 1). Покажем, что 1) влечет 2). Сначала заметим, что
im(^ ± il)-1 = кег(Л* =F il). Поэтому из 1) вытекает, что
im(A±il) плотно в Я. Воспользуемся теперь замкну-
замкнутостью А. Пусть у — любой вектор из Н и {хп} — после-
последовательность из ?DA, для которой (А±И)хп-+ у. После-
Последовательность {(А ±И)хп) фундаментальна. Соотношение
II (А ± Н)х\\2 = (Ах ± ix, Ax ± ix) = \\Ах\\г + Ы2 > 1Ы12 пока-
показывает, что {хп} — также фундаментальная последователь-
последовательность. Пусть х = lim xn. Тогда ж®уе ТА±ц и, значит,
у ^im(A ± И).
Теперь покажем, что из 2) следует самосопряжен-
самосопряженность А. Так как 4ci*? нужно лишь проверить вклю-
включение 3)А* el S>а- Пусть у(=@)А*. Поскольку im(A±il) =
= #, существуют такие векторы x±^2DA, что (A±i\)x±=
*=(А* ±il)y. На подпространстве 2)А оператор Л* опре-
определен и совпадает с А, Поэтому (А* ± И) (у — х±) = 0. Но
кег(Л* ± il)= im(A =F il)-1 = 0. Значит, у = х± и y^?DA.
Предположим теперь, что А существенно самосопря-
самосопряжен. Тогда А* совпадает с замыканием А (задача 658) и,
следовательно, самосопряжен. Отсюда следует 3) в силу
уже доказанной части теоремы. Далее, из 4) следует 3)
(задача 671). Выведем теперь из условия 3) существен-
существенную самосопряженность А. Так как А симметричен, спра-
165
ведливо включение А с: А*._ Это показывает, что А допу-
допускает замыкание А и что А<=А* (так как Л* — замкну-
замкнутый оператор). Далее, из теоремы 7 следует, что А* =
= 4*. Значит, для оператора А выполнены условия 1).
Поэтому А самосопряжен, а А существенно самосо-
самосопряжен.
Пример. Пусть Л = г^-, Н = L2 (R, dx),ФА =*3>(К).
В этом случае симметричность А вытекает из равенства
С» 00
J ф' И 'ФИ dx = — J ф (j) г}O (л:) dz для <р, i|)
-—оо —оо
Сопряженный оператор А*, как мы видели выше, опре-
определен на множестве 3)а* cz L2 (R, dx), состоящем из
функций, имеющих обобщенную производную в L2(R, dx),
и равен id/dx. Найдем кег(Л* ± й). Если D*± il)/ = О,
т. е. &'(/'±/) = 0, то f = ce±x (задача 458). Поскольку эти
функции не лежат в ?2(R, ^#)» мы получаем кет(А*±
±tl) = {0}. Значит, Л существенно самосопряжен.
Пусть А — неограниченный, аи — ограниченный опе-
операторы. Говорят, что А и В перестановочны, если В пере-
переводит 2) А в себя и В Ах = АВх для х^З)А- Можно пока-
показать, что для самосопряженного оператора А это условие
равносильно перестановочности В и любого из ограничен-
ограниченных операторов [А ± i\)~\
4. Расширения операторов. Довольно часто встреча-
встречаются неограниченные симметрические операторы А, для
которых условия 3) и 4) теоремы 8 не выполняются
(и, следовательно, оператор А не является существенно
самосопряженным), однако А можно расширить до само-
самосопряженного оператора.
Существует простой способ выяснить, имеет ли дан-
данный симметрический оператор самосопряженное расшире-
расширение, и если да, то описать все такие расширения. Введем
понятие преобразования Кэли симметрического операто-
оператора А. По определению, это оператор V с областью опре-
определения im(i4 + il), действующий по формуле
V(A + il)x = {A-il)x. B2)
Из симметричности А следует, что кег(Л + г1) = 0, и по-
поэтому определение V по формуле B2) корректно. Кроме
того, как уже отмечалось в доказательстве теоремы 8,
ЦА +И)х\\ = \\(А— il)x\\ для всех x^D(A). Поэтому
оператор V изометричен: IIFi/II — IIг/II для всех yD(V)
166
Лемма. Преобразование Кэли устанавливает биек-
цию между множеством симметрических операторов А с
плотной областью определения и множеством изометри-
изометрических операторов V без неподвижных векторов. Спра-
Справедливы равенства
D {А) = im A - V), А = i A + V) A - V) ~\ B3)
Доказательство. Из B2) непосредственно следует,
что уравнение Vy = у не имеет ненулевых решений. Поэто-
Поэтому оператор V не имеет неподвижных векторов. Обратно,
пусть изометрический оператор V не имеет неподвиж-
неподвижных векторов. Тогда ker(l — F) = 0 и мы можем опреде-
определить оператор А так, чтобы выполнялись соотношения
B3). Пусть хи x2^D(A) и xk = (l-V)yk (k = 1,2).
Тогда (Ахи x2) = (i(l + V)yu {1-V)y2) = i(yu y2) +
+ 1{УУи Уг)—1(Уи Vy2)-i(Vyu Vy2). В силу изометрич-
ности V последнее выражение можно переписать в виде
{^Уи Уг)~^{Уи iVyz). Если Xi и х2 поменять местами, по-
последнее выражение заменится на комплексно сопряжен-
сопряженное. Это значит, что (Ах2, Xi) = (Axh x2) и оператор А
симметрический. Остается проверить, что преобразование
Кэли для построенного оператора А совпадает с исход-
исходным оператором V. Это вытекает из равенств
(А + И) A - V)у = Ну, (А - il) (l-V)y = 2iVy,
которые в свою очередь непосредственно следуют из B2)
и B3). Лемма доказана.
Значение этой леммы состоит в том, что она сводит
задачу о расширении симметрических операторов к за-
задаче о расширении изометрических операторов. В самом
деле, из определения преобразования Кэли следует, что
оно сохраняет отношение включения для операторов:
AiCiA2 равносильно Fj с: 172? а также операцию замыка-
замыкания. (Более наглядно эти свойства выводятся из другого
определения преобразования Кэли — см. задачу 676.)
Для замкнутых изометрических операторов V теория
расширений очень проста и описывается следующим об-
образом. Пусть L+=D(F)J-, L_ = Im(F)-L. Тогда имеет
место разложения H = D(V) $ L+ = im(F)® L_ и каждое
изометрическое расширение U оператора V имеет вид
U = V Ф W, где W — изометрический оператор из L+ в
?- с областью определения D(W)aL+. В самом деле,
всякий изометрический оператор в Я, расширяющий V,
обязан переводить векторы из L+ в пространство ?_, так
167
как сохранение нормы влечет сохранение скалярного
произведения.
Вспоминая определение F, можно выразить простран-
пространства L± в терминах исходного симметрического оператора
А. А именно, L± являются собственными подпространст-
подпространствами оператора Л*, отвечающими собственным значениям
±i. В самом деле,
L+=D{V)± = im(A + il)x = кег'(Л* -И);
L_ = im(F)-1- = im(A - П)^ = кег(Л* + И).
Поскольку пространства L± играют важную роль при
изучении расширений оператора А, они получили спе-
специальное название.
Определение. Пространства L± = кег(Л* Ч1 Ц) на-
называются дефектными подпространствами симметриче-
симметрического оператора Ау а их размерности l± — dimL± — чис-
числами дефекта.
Теперь мы можем сформулировать основную теорему
этого раздела.
Теорема фон Неймана. Пусть А — замкнутый
симметрический оператор, L± — его дефектные подпрост-
подпространства, 1± — числа дефекта. Все замкнутые симметри-
симметрические {соответственно самосопряженные) расширения А
описываются изометрическими (соответственно унитар-
унитарными) отображениями L+ в L_.
Следствие. Самосопряженные расширения А су-
существуют тогда и только тогда, когда /+ = /_; в этом слу-
случае они зависят от I2 вещественных параметров.
Доказательство. Искомое соответствие устанав-
устанавливается с помощью преобразования Кэли и сказанного
выше о расширениях изометрических операторов. Оста-
Остается заметить, что множество унитарных операторов в
Z-мерном пространстве описывается I2 вещественными па-
параметрами*).
Часто встречается простейший случай оператора А с
индексами дефекта A, 1). В этом случае множество само-
самосопряженных расширений А нумеруется точками окруж-
окружности (унитарный оператор в одномерном пространстве —
это комплексное число, равное по модулю единице).
В предыдущих рассуждениях выделенную роль играли
точки ±i на комплексной плоскости. На самом деле мож-
*) Более точная формулировка: это множество является глад-
гладким вещественным многообразием размерности I2 — см., напри-
например, [17].
168
но было бы заменить их любой парой чисел Я, \х соответ-
соответственно из верхней и нижней полуплоскости. Можно по-
показать (см. задачу 678), что число Z* = dimker(^4* — XI)
локально постоянно на C\R и, следовательно, постоянно
при im К > 0 и im К < 0.
Для многих приложений важно знать, когда симмет-
симметрический оператор А имеет равные числа дефекта 1+ — 1-.
Два достаточных условия приведены в задачах 679 и 681.
Одно из них состоит в том, что оператор А полуогра-
полуограничен сверху или снизу (т. е. (Ах, <г)^а1Ы12 или
(А х, х) > аЫ\2 для всех х е= D (А)).
Второе требует вещественности оператора А относи-
относительно подходящей вещественной структуры на Я. Бо-
Более точно, пусть Но — вещественное подпространство в
комплексном пространстве Я такое, что Н — Но + Шо.
Оператор А в пространстве Я называется вещественным
(относительно вещественной структуры, задаваемой под-
подпространством Яо), если он переводит Но в себя (ср. за-
задачу 680).
Оба сформулированных условия удобны для приме-
применения к неограниченным операторам, заданным с по-
помощью дифференциальных выражений.
Пример 1. Рассмотрим так называемый оператор
Штурма — Лиувилля, т. е. дифференциальное выражение
B4)
на интервале (а, Ь), — оо^а<Ь^оо# В качестве началь-
начальной области определения DQ рассмотррш пространство
С™ (а, Ъ) финитных гладких функций на (а, Ь). Пусть
Ао — оператор, задаваемый выражением B4) в Do. Если
q(t)—вещественная локально суммируемая функция, то
Ао будет симметрическим оператором. Обозначим через
А его замыкание. Можно проверить, что D(A) содер-
содержится в естественной области определения выражения
B4), a D(A*) совпадает с ней. Пространство Lx в дан-
данном случае состоит из квадратично интегрируемых на
(а, Ь) решений дифференциального уравнения
х" +{X-q)x = 0. B5J
Его размерность, очевидно, не превосходит 2.
Случай 1. Пусть а =»—«», Ъ == «>, q(t) = O. В этом
случае решения уравнения B5)—экспоненты, не при-
169
надлежащие L2(R). Ипдексы дефекта равпы нулю и опе-
оператор А самосопряженный.
Случай 2. Пусть а = 0, Ъ = °°, q{t) = O. Здесь, как
легко проверить, при любом вещественном К уравнение
B5) имеет только одно (с точностью до множителя) ре-
решение, принадлежащее ?2@, <»). Индексы дефекта рав-
равны A, 1).
Случай 3. Пусть аи 6 конечны, a q(t)—ограничен-
q(t)—ограниченная на [а, Ь] функция. Здесь все решения B5) лежат в
U {а, Ь). Индексы дефекта равны B, 2).
Теория расширений оператора Штурма — Лиувилля
была построена Г. Вейлем еще до возникновения общей
спектральной теории операторов. Некоторые факты тео-
теории Вейля см. в задачах 683—685.
Пример 2. Пусть А = i— — оператор в /7@, «>У с
п
областью определения С™ @, оо), Р (х) = 2 akXh — мно-
k=0
гочлен с вещественными коэффициентами. Тогда
п
P (A) = 2 akAh — симметрический оператор. Дефектное
пространство Lx для Р(А) определяется дифференциаль-
дифференциальным уравнением
п
2 CLkX^ @ — ^х (О*
Общий вид решения
где jit, ..., fin — корни алгебраического уравнения
Х. B6)
Поскольку коэффициенты Р вещественны, эти корни
не могут быть вещественными при X&R. Размерность
Lx равна числу корней уравнения B6), лежащих в ниж-
нижней полуплоскости. Из B6) следует, что Р(\х) = К. По-
Поэтому размерность L^ равна числу корней уравнения
B6) в верхней полуплоскости. При нечетном п отсюда
следует, что оператор Р(А) имеет разные числа дефек-
дефекта и, следовательно, не имеет самосопряженных расши-
расширений.
170
§ 2. Спектральное разложение операторов
1. Приведение оператора к виду умножения на функ-
функцию. В этом пункте мы покажем, что всякий самосопря-
самосопряженный оператор унитарно эквивалентен оператору
умножения. Более точно, имеет место
Теорема 9. Пусть А — самосопряженный оператор
в гильбертовом пространстве II. Существуют такое про-
пространство X с мерой jx, такая измеримая функция а на X
и такой унитарный оператор U из Н в L2(X, jj,), что
следующая диаграмма коммутативна:
B7)
(Здесь М(а)—оператор умножения на функцию а в
L2(X, \i) с областью определения SDm^), состоящей из
тех функций f^L2{X, ji), для которых af^L2(X, \x).)
Доказательство этой теоремы мы проведем в несколько
этапов. Предположим сначала, что оператор А ограничен
и что в пространстве Н есть циклический вектор для А,
т. е. такой вектор ?, что всякое замкнутое подпростран-
подпространство в Я, содержащее | и инвариантное относительно А,
совпадает с Н (см. задачу 611). В этом случае мы будем
называть А оператором с простым спектром (ср. с зада-
задачей 612).
Теорема 10. Пусть А — ограниченный самосопря-
самосопряженный оператор с простым спектром. Тогда для А спра-
справедливо утверждение теоремы 9, причем можно положить
[Ш IL4II]
[ ] () ()
Доказательство. Предположим, что теорема до-
доказана и |х — искомая мера на X. Пусть / — ограниченная
борелевская функция на X. Тогда из теоремы 5 вытекает,
что оператору /(^4) в Н соответствует оператор умноже-
умножения на f(x) в L2(X, ji), т. е.
Uf(A) = M(f)U. B8)
В самом деле, для f(x) = x B8) сводится к B7),
а общий случай получается, если проследить построение
оператора /(^4).
Отсюда следует равенство
(/ (А) 1,1)н = (Uf (А) 1, и1)цХМ = (/, 1к2(х,ю- B9)
Левую часть равенства B9) можно вычислить, зная толь-
171
ко оператор Л и вектор ?. Тем самым мы восстанавлива-
восстанавливаем меру |х. А именно, если Е — измеримое подмножество
в X и %Е — характеристическая функция Е, то
\i (Е) = (хе, 1)г.8(х,ю = (%е {Л) ?, 6)н. C0)
Пусть теперь задан самосопряженный оператор Л
с простым спектром в пространстве //, и пусть | — цикли-
циклический вектор для А. Определим функцию \х на борелев-
ских подмножествах отрезка Х = [—11ЛИ, ИЛИ] формулой
C0). Проверим, что [i — счетно-аддитивная мера. Прежде
всего, из равенств %е = %% = %е вытекает, что оператор
{А П ((Л) ) И(Л)Иа
р
%Е{А)— ортопроектор. Поэтому (хя(Л)|, |) =
^0. Далее, если/?=Ц #&, то %# = 2 ХяЛряд сходится
в каждой точке). Поэтому %е {А) = 2 %?& (^) '(в смысле
сильной сходимости) и, значит, \i (A) = (%E (A) g, I) =
/ оо \ со
= 2х^ь И) 5» 5 = 2 ^ (^л) • Определим теперь опера-
\ft=i / ft=i
тор С/ из Я в L2(X, fi) на векторах вида /(Л)| следую-
следующим образом:
Uf(A)l-f. C1)
Проверим, что этот оператор изометричен, т. е.
(Uf1 (A) I, UU (A) l)Lt(ZiVL) = (ft (A) I, U {А) 1)н. C2)
Если /х = %El, /2 =Xe2'TO C2) сводится к равенству
( ) (И 5 И) 5) (И)И)? 6)
^ 2) 8
справедливому по определению меры jli. По линейности
равенство C2) верно для ступенчатых функций Д и /2.
Наконец, это равенство сохраняется при поточечных
ограниченных предельных переходах. Тем самым изоме-
тричность U доказана. Поскольку векторы вида /(Л)|
плотны в Н (они образуют линейное пространство, содер-
содержащее | и инвариантное относительно Л), а функции /
плотны в L2(X, jn), оператор U продолжается до унитар-
унитарного оператора из II на L2(X, ji). Наконец, обозначая
xf(x) через g(x), по определению имеем
Отсюда UА = М (x)U па векторах вида /(Л)|, а значит,
и всюду. Теорема доказана.
Теперь освободимся от условия цикличности,
172
Теорема 11. Пусть А — ограниченный самосопря-
самосопряженный оператор в гильбертовом пространстве Я. Су-
Существует семейство подпространств {Яр}РеВ в Я, обладаю-
обладающее свойствами:
1) #р±.Я|у при Р=^Р';
2) 1>Щ = Н;
Реев
3) 4Ярс:Яр тг/ш всея E^5;
4) ограничение А на Яр имеет циклический вектор
для каждого р е 5.
Доказательство сразу следует из леммы Цорна, при-
примененной к совокупности всех систем {Я3}, обладающих
свойствами 1), 3), 4). Отметим также, что если Я сепа-
рабельно, то множество В не более чем счетно. Из теорем
10 и 11 вытекает справедливость для любого ограничен-
ограниченного самосопряженного оператора А теоремы 9 со сле-
следующим уточнением: в качестве множества X можно
взять объединение нескольких экземпляров отрезка
[—11411, ИЛИ], а в качестве функции а(х)—координатную
функцию х.
Мы предоставляем читателю вывести, следуя изложен-
изложенной выше схеме, более общий результат.
Теорема 12. Пусть Аи ..., Ап — ограниченные по-
парно перестановочные самосопряженные операторы в
гильбертовом пространстве Я. Существует такая реализа-
реализация Я в виде пространства L2(X, |li), что все операторы
Аи ..., Ап одновременно становятся операторами умно-
жения на вещественные функции а^х), ,.., ап(х)^
^ЬЖ(Х, ii).
Следствие. Пусть А — ограниченный нормальный
(в частности, унитарный) оператор в комплексном гиль-
гильбертовом пространстве Я. Существует такая реализация
Я в виде пространства ?2(Х, |i), при которой оператор А
переходит в оператор умножения на комплекснозначную
функцию a^Loo(X1 \x) (в случае унитарного оператора
\а(х)\ =1 почти всюду на X).
В самом деле, оператор А имеет вид В + 1С, где В и
С — перестановочные самосопряженные ограниченные опе-
операторы. Применяя к ним теорему 12, получаем нужное
утверждение. Если оператор А унитарен, то АА* = 1,
откуда \а(х)\2 = 1 почти всюду.
Разберем теперь случай неограниченного самосопря-
самосопряженного оператора А в пространстве Я. Рассмотрим его
преобразование Кэли V = (А +il) (A — il)~l. Оператор V
унитарен. По следствию из теоремы 12 существует такая
173
реализация пространства Я в виде L2(X, \i), при которой
V переходит в оператор умножения на измеримую функ-
функцию и(х), обладающую свойством: \и(х)\==1 почти всю-
всюду на X.
Покажем теперь, что значения и(х) отличны от 1
почти всюду. В противном случае оператор V имел бы
собственный вектор х0 с собственным значением 1 (тако-
(таковой в нашей реализации является любая функция, отлич-
отличная от 0 лишь на множестве, где v(x)=l). Равенство
Vxo = xo равносильно равенству Ау0 — iyo = Ayo + iy0,
откуда г/о — О и, значит, хо = О. Итак, и(х) отлично от 1
почти всюду. Значит, существует такая измеримая веще-
y / \ / \ а (#) ~\- i
ственная функция а(х), что v \х) = —т— г почти всюду;
п \Xj ~~~ I
/ \ • v (х) + 1 тт
достаточно положить а (х) = i . __ . Наконец докажем,
что S>A = S)(y_iri и A = i(V+l) (F-1)-1. Отсюда будет
следовать, что в нашей реализации А является операто-
оператором умножения на а(х).
По определению V имеем (V+i)x=Vx + x = Ay +
+ iy + Ay~ iy = 2Ау, (V - 1) х = Vx - х = А у + iy - А у +
+ iy = 2iy. Отсюда 3> (y_ir-i = im(F- 1) = 3>А и Ау =
= -j- (V + 1) х = i (V + 1) (V — 1) у. Теорема доказана.
Следствием этой теоремы является следующее обобще-
обобщение результатов п. 2 § 1.
Теорема 13. Пусть А — самосопряженный (быть
может, неограниченный) оператор в гильбертовом про-
пространстве Н. Существует единственный гомоморфизм
алгебры B(R) ограниченных борелевсаих функций на R
в алгебру End Я в Я, обладающий свойствами:
1) ФA)= 1;
2) ф(Й-|) = И+«1)И-*1Г1;
3) если \fn{t)\<C и fn(t)-*f(t) для всех ^R, то
ф(/п) сильно сходится к ф(/).
Кроме того, гомоморфизм ф обладает свойствами:
4) G) (*
) фG) ф(/);
5) ф (Я К «юр 1/(91-
Доказательство. Будем считать, что Я реализо-
реализовано в виде L2(X, \i). так, что оператор А состоит в ум-
умножении на измеримую вещественную функцию а(х).
Тогда оператор V = (A + И) (А — И) состоит в умноже-
, ч а (х) + i r\ » ^
нии на и (х) =———-:. Определим искомый гомоморфизм
174
Ф формулой ф(/) = Л/(/, а), где Л/(/, а)—оператор умно-
жения на функцию f(a(x)). Свойства 1)—5) проверяются
без труда. Докажем единственность ф. Из 2) следует, что
Тем самым ф однозначно определена на рациональных
Л2 —1 2t \
функциях вида Р l-g , -§ I» где Р — многочлен от
двух переменных. Используя теорему Вейерштрас-
са, можно доказать, что такими функциями равно-
равномерно приближается любая непрерывная функция на
прямой, для которой существуют и равны друг другу ко-
конечные пределы f(t) при Z->~+oo*). Наконец, последо-
последовательно применяя к таким f(t) поточечные ограничен-
ограниченные предельные переходы, можно получить любую функ-
функцию из B(R). Теорема доказана.
2. Спектральная теорема. Многие результаты теории
меры (см. гл. II) переносятся mutatis mutandis на слу-
случай, когда вместо обычных мер рассматриваются так на-
называемые проекционные меры.
Определение. Пусть задано множество X, некото-
некоторая о-алгебра В подмножеств X, содержащая X, и гиль-
гильбертово пространство Н. Отображение X: B-^EndH на-
называется проекционной мерой на {X, В) со значениями
в End Я, если выполнены условия:
1) %(Е) = К(Е)* для любого Е^В;
2) Х(Е10Е2) = Х(Е1)Х(Е2) для любых Еи Е2^В;
3) X(Ei U Е2) = Х{Ех)Л-Хг{Ег) для любых непересекаю-
непересекающихся Еи Е2^В;
4) если Еп ^ В и существует lim En = E (см. задачу
71->0О
71
82), то s-lim k(En) существует и равен
Пример. Пусть (X, В, \х)—- пространство с обычной
о-аддитивной мерой \х. Положим Н = L2(X, u,), %(E)=*
== М {%е)— оператор умножения на характеристическую
функцию множества Е<^В. Свойства 1)—3) здесь оче-
*) Достаточно воспользоваться заменой переменной
t2 — 1 2t
i->cosa, -_ -> sin a,
t2 -\-1 t2 + 1
175
видны, 4) следует из теоремы Лебега об ограниченной
сходимости.
Обсудим здесь некоторые свойства проекционных мер,
вытекающие из данного выше определения. Из условия
2) вытекает, что все операторы Х(Е), Е^В, попарно
перестановочны. Далее, условие 1) вместе с равенством
Х(ЕJ = Х(?), вытекающим из 2), показывают, что Х(Е)—*
ортопроектор.
Обозначим через НЕ подпространство ХB?)#, на кото-
которое Х(Е) проектирует //. Свойство 2) имеет следующий
геометрический смысл: Не^е2 = НЕ^ f| ##2. Из 3) легко
выводится более общее утверждение: Х{Е^\] E2)=X{Ei) +
+ X (Е2) — X (Z?j Л Е2). Геометрически это означает, что
Не1це2 = Не1 + Не2 и что HEiA-He2, если Et и Е2 не
пересекаются. Наконец, из 3) следует, что А,@) —О,
Х(Х)=1, т. е. #0 = {О}, НХ = Н.
Из проекционной меры X можно изготовить целое
семейство обычных мер и зарядов. А именно, пусть | и
ц — два вектора из //. Тогда отображение A,gn: В -> С,
заданное формулой
К1ч(Е)-(ЦЕI, л), C3)
будет комплексным зарядом на В. Если % = г|, то вместо
Хц мы будем писать просто Л$. Поскольку операторы
Х(Е) положительны, заряд Х$ является мерой. Тождество
^$ъ — ~ (Ч+п — Ц-ц + i^6—lTi — 1Ц+щ) C4)
показывает, что заряды Х$л, а следовательно, сама про-
проекционная мера X восстанавливаются по набору обычных
мер {^}6бН.
Проекционную меру X можно, как и обычную меру,
использовать для определения интеграла. Пусть / —В-из-
меримая ограниченная числовая функция на X. Интег-
Интегральной суммой Лебега для / назовем выражение
(
» (Л *) = 2 f
2
Легко проверяется, что если п{<п2, то Sn2{f) ^Sn (/)
(т. е. разность 5„ (/)—Sn (f)—положительный опера-
оператор). Кроме того, последовательность iSn(f)} ограничена
сверху оператором sup f(x)»l. Существует (см. задачу
хеХ
485) s-lim i^n (f)x который называется интегралом функ-
176
ции / по проекционной мере X и обозначается J / (х) дХ (#)«
х
Из свойств обычного интеграла Лебега вытекает, что
для любого вектора ? e H справедливо равенство
Отсюда и из тождества C4) вытекает справедливость
более общего равенства
(*) dX (x) g, n) = J/ (*) <&бп (*)• C6)
Наконец, можно определить интеграл А = J / (х) d!k (x)
х
для неограниченной В-измеримой функции / на X.
А именно, обозначим через 2)А совокупность векторов
?^#, для которых сходится интеграл \\f(z)\2dki(x).
х
(Из C4) можно вывести, что ®а — линейное подпрост-
подпространство в Я.)
Для | ^ 2)а определим оператор А равенством
(x)dKlri(x). C7)
Сходимость этого интеграла следует из неравенства
|Я5ч(Я)|2<Я5(Я)ЯчB?У, C8);
которое является частным случаем неравенства Коши —
Буняковского. А именно, для интегральной суммы интег-
интеграла C7) из C8) и неравенства Коши — Буняковского
следует оценка
откуда I j / (х) dXlr] (х) 2 < j | / (х) |2 [| n fd^. Таким обра-
обра||4?||<1/1
зом, ||-4?||
Отметим, что если функция / вещественна, то по опре-
определению оператора А выражение (Л^, ?) вещественно для
| е 2)А. Таким образом, оператор А — симметрический.
На самом деле этот оператор с областью определения
2)А, введенной выше, является самосопряженным. Это
следует из теоремы 8 и из явной конструкции операторов
12 а. А. Кириллов, А. Д. Гвишиани 177
(А±Н)~1: эти операторы можно определить интегралами
Г dX(x)
Jf(x)± Г
Теперь мы можем сформулировать основной результат
этого пункта.
Теорема 14. Пусть А — самосопряженный (не обя-
обязательно ограниченный) оператор в гильбертовом прост-
пространстве Я. Существует единственная борелевская проек-
проекционная мера X на R со значениями в End//, обладающая
свойством:
f(A)= $ f(x)dk(x) C9)
— оо
для любой ограниченной борелевской функции f на R.
Кроме того, справедливо равенство
А= §xd%(x). D0)
Доказательство. Единственность X сразу выте-
вытекает из C9), если положить / = Хя> гДе Е — борелевское
множество на прямой. Доказательство существования
очевидно, если перейти к той реализации Я, в которой
оператор А является оператором умножения на функцию.
Проекционная мера X называется спектральной мерой
оператора А, а равенство D0)— спектральным разложе-
разложением этого оператора.
В качестве следствия теоремы 14 мы получаем опре-
определение любых (в том числе неограниченных) борелев-
ских функций от любого самосопряженного оператора А:
они определяются интегралом C9) с теми предосторож-
предосторожностями, которые указаны выше. Можно проверить, что
/(Л)—всегда замкнутый оператор, нормальный в том
смысле, что А А* ж А* А имеют общую область определе-
определения и совпадают на ней. Примером применения этой
конструкции является описание однопараметрических
групп унитарных операторов.
Определение. Совокупность {V(?)}*ен унитарных
операторов в гильбертовом пространстве Я называется
однопараметрической группой, если выполнены условия:
1) V(t)V{s)=V(t + s) для*, sgR;
2) отображение t*^V(t) непрерывно в слабой опе-
операторной топологии,
178
Теорема -Стоуна. Всякая однопараметрическая
группа унитарных операторов в Н имеет вид
V(t) = eitA, D1)
где А — некоторый самосопряженный оператор в Н.
Доказательство. Отметим сначала, что формула
D1) действительно определяет однопараметрическую
группу, как сразу видно, если перейти к той реализации
Я, в которой А является оператором умножения на функ-
функцию; кроме того, в этой реализации легко проверяется
равенство
±V(t)l = iV(t)АЪ = iAV(t)I для g<= 3)A. D2)
Пусть теперь задана однопараметрическая группа
{F(?)}fGR. Определим 5DA как совокупность тех векто-
векторов ^Я, для которых функция t н-* V (t) g дифференци-
дифференцируема, и определим для | ^ 5DA оператор А равенством
А% = — ij7 V(t)^\t==0. Покажем, что 2DA плотно в Я.
Сначала заметим, что соответствие t •-> V (t) сильно не-
непрерывно. Пусть теперь {(pJ^S^R)—б-образная после-
последовательность. Тогда для любого |е Н последователь-
оо
ность In = J Чп(ъ)У(х)Ъс1т сходится к |. Проверим, что
—оо
Ьп е 3D а- В самом деле,
V(t)ln=
оо
Отсюда J- V (t) ln = - j Ф; (т - t) V (т) \ dr. (Дифферен-
—ос
цируемость интеграла по параметру t доказывается, как
в обычном анализе.)
Проверим теперь, что V(i) сохраняет подпространство
2)а и что справедливы равенства D2). Для этого доста-
достаточно заметить, что векторы V{t + i)% и V(x)V{t)\ сов-
совпадают. Дифференцируя их по т и полагая т = 0, полу-
получаем искомое соотношение.
Симметричность оператора А получается дифференци-
дифференцированием равенства {V{t)\, F(?)?)=l по t при ? = 0.
Наконец проверим, что А существенно самосопряжен.
Пусть т] ^кег(Л* ± И). Тогда для любого \^ЗЬА имеем
12* 179
г]) = (|, (А* ± jl)r]) = O. Поэтому функция
/() (()|, r\) удовлетворяет дифференциальному урав-
уравнению f'(t)±f(t) = O. Отсюда f(t) = ceTt. Но / ограни-
ограничена, так как V(t)—унитарный оператор. Значит, с —О
и (F(?)?, г]) = 0 для всех \^?DA. Поскольку ?DA плотно
в Я, то т] = 0. Итак, ker(^4* ± tl) = 0 _и, следовательно,
А существенно самосопряжен. Пусть А — его самосопря-
самосопряженное расширение. Сравним теперь операторы V(t) и
V (t) = eitA. Пусть I e 2>А с= 03. Рассмотрим функцию
/(?) —(^(~~0^@5» Л)- Дифференцируя эту функцию по
t и используя равенства D2), получаем
Отсюда /(*) —E. Л)» что Дает К(~0^@5 —5, т. е.
7@5== ^@5- Поскольку V(t) и F@ унитарны, а 3>А
плотно в Я, мы получаем V(t)=V(t). Теорема доказана.
§ 3. Математическая модель квантовой механики
Одно из самых замечательных приложений матема-
математики в естественных науках — построение строгой теории
квантовой механики. Основную роль при этом играет
спектральная теория операторов в гильбертовом прост-
пространстве.
Мы не будем останавливаться здесь на физических
основах квантовой механики и ее связи с механикой клас-
классической. Воспользуемся аксиоматическим методом, ко-
который легче усваивается студентами-математиками.
По определению, фазовым пространством (или прост-
пространством состояний) квантовомеханической системы яв-
является проективное пространство Ф = Р(#), соответст-
соответствующее некоторому комплексному гильбертову простран-
пространству Я. Другими словами, Ф — множество комплексных
прямых (одномерных подпространств) в Я. Точки про-
пространства Ф называются состояниями системы. Удобно
задавать состояние ф ^ Ф с помощью вектора единичной
длины Ч^Я, помня, однако, что коллинеарные векторы
Wi и Vz — cVi (где c = etoc — комплексное число, равное
по модулю единице) задают одну и ту же точку ф про-
пространства Ф.
Обычно пространство Я реализуется как пространство
функций, вектор V называется тогда волновой функ-
функцией.
180
Физической величиной или наблюдаемой называется
самосопряженный оператор А в пространстве Я.
В отличие от классической механики, наблюдаемая А
в состоянии ф принимает не фиксированное числовое зна-
значение, а является случайной величиной с известным рас-
распределением. Точная формулировка такова: вероятность
того, что значение наблюдаемой А в состоянии ф принад-
принадлежит подмножеству Е <= R, равна
U(E) = (k(E)V, ?), D3)
где Я — спектральная мера оператора А, а Ч? — единич-
единичный вектор из Я, задающий состояние ф.
Следствием этого определения является формула для
среднего значения (т. е. математического ожидания)
величины А в состоянии ф:
<А>* = (АЧГ, ЧГ). D4)
Отметим, что правые части в D3) и D4) не меня-
меняются при замене Чг на eiay?. Поэтому они зависят лишь
от состояния ф^ф, В дальнейшем мы иногда не будем
различать ф и ?, используя обозначение Ч? и для век-
вектора из Я, и для определяемого этим вектором состояния.
В некоторых случаях вероятностное распределение
D3) сосредоточено в одной точке aeR, Тогда говорят,
что величина А в состоянии Ч? принимает однозначно
определенное значение а. Это равносильно (см. задачу
720) тому, что Y — собственный вектор для А с собст-
собственным значением а.
Оператор А может не иметь вообще ни одного собст-
собственного вектора (случай непрерывного спектра), и тогда
наблюдаемая А ни в каком состоянии не определена
однозначно. Однако, как мы знаем (задача 708), всегда
существуют почти собственные векторы. Поэтому для
любой наблюдаемой есть состояния, в которых они почти
однозначно определены с любой наперед заданной точ-
точностью.
Для того чтобы две величины А и В принимали в со-
состоянии W определенные значения, вектор ЧГ должен
быть собственным одновременно для операторов А я В.
Это условие не выполняется для общих операторов,
даже если перейти от собственных векторов к почти соб-
собственным. Таким образом, две наблюдаемых величины
в квантовой механике, вообще говоря, не допускают
одновременного точного измерения.
181
Количественным выражением этого факта является
знаменитый принцип неопределенности Гейзенберга. Для
того, чтобы дать его математическую формулировку,
введем
Определение. Неопределенностью наблюдаемой А
в состоянии Ч* называется число
ДТD) = <D-<Л>Т)»>^. D5)
(Квадрат неопределенности в теории вероятностей на-
называется дисперсией соответствующей случайной вели-
величины.)
Принцип неопределенности Гейзенбер-
г а. Если операторы А и В удовлетворяют коммутацион-
коммутационному соотношению
AB-BA = i%i, %>0, D6)
то
D7)
для любого состояния Ч1".
Доказательство. Прежде всего заметим, что за-
замена А на Л — а • 1 иВ на В — ^ • 1, где a, fi ^ R, не ме-
меняет ни условия D6), ни заключения D7) теоремы.
В самом деле, коммутатор АВ — В А и неопределенности
Дчг(Л), A^(S) не изменяются при такой замене. Поэто-
Поэтому, полагая а=<АУЧг, $ = <#>?, мы можем ограничиться
в доказательстве теоремы случаем (АУ^ = (В)^ = 0.
Но тогда bv(A).b4r(B) \AVllBVl^\I{A4BV)\
Конкретные приложения этого принципа мы укажем
ниже.
Среди всех наблюдаемых особую роль играет одна,
называемая энергией (или гамильтонианом) и обозначае-
обозначаемая обычно буквой Я*). Постулируется, что состояние
системы меняется со временем так, что волновая функ-
функция удовлетворяет уравнению Шредингера:
ЛЧГ=ЯЧГ, D8)
где % — так называемая приведенная постоянная Планка,
а точка обозначает производную по времени.
*) Буква Н означает также и основное гильбертово простран-
пространство. Обычно из контекста бывает ясно, о чем идет речь. К тому
же, в приложениях всегда участвует какое-либо конкретное гиль-
гильбертово пространство, обозначаемое соответствующим образом,
182
В частности, состояние является стационарным, т. е.
не меняется со временем, тогда и только тогда, когда
вектор Y является собственным для оператора Я. Соот-
Соответствующее собственное значение обычно обозначают
буквой Е\ его физический смысл — энергия системы в
данном состоянии. Стационарное состояние удовлетворяет
стационарному уравнению Шредингера:
D9)
Заметим, что вектор Y вовсе не является постоянным
во времени. Из уравнения D8) следует, что он меняется
по закону
у (t) = rYV @), E0)
однако определяемое им состояние (т. е. точка проектив-
проективного пространства) остается неподвижным.
Кроме обычных собственных векторов в квантовой
механике часто используются обобщенные собственные
векторы, не принадлежащие исходному гильбертову про-
пространству. Общая схема определения таких векторов была
предложена И. М. Гельфандом и А. Г. Костюченко (см.
[12]). Она состоит в следующем. Пусть А — самосопря-
самосопряженный оператор в гильбертовом пространстве Я и Я —
его спектральная мера. Для любого вектора х^Н опре-
определена вектор-функция x(t) = X( (—<», t])x. Если бы эта
функция была дифференцируемой по ?, то были бы вер-
верны следующие легко проверяемые равенства:
оо
* = z(oo)= $x'(t)dtt E1)
—оо
Ax'(t)=±Ax(t)--=tx'(t)t E2)
которые дают разложение вектора х по собственным
векторам х (t) оператора А.
Оказывается, при подходящем ослаблении топологии
и соответствующем расширении пространства Я можно
добиться того, что функция x(t) станет дифференцируе-
дифференцируемой. В большинстве примеров достаточно в качестве
искомого расширения взять пространство *S'(Rn) (см.
гл. III, § 4).
Мы не будем останавливаться здесь на физической
интерпретации обобщенных состояний. Как правило, она
бывает ясна непосредственно из постановки задачи.
183
Чтобы применить описанную нами абстрактную схе-
схему к исследованию реальных физических систем, исполь-
используют так называемые правила квантования. Совокупность
имеющихся в настоящее время правил квантования, с од-
одной стороны, неполна (не позволяет «проквантовать» лю-
любую мыслимую классическую систему), с другой сторо-
стороны, противоречива (квантование по разным правилам мо-
может привести к различным результатам).
Этот факт объясняется тем, что классическая меха-
механика является более грубым описанием действительности,
чем квантовая. Она может быть получена предельным
переходом при Й -> 0. Поэтому правила квантования ана-
аналогичны попытке восстановить неизвестную последова-
последовательность по ее пределу. Понятно, что в общем случае
нельзя ожидать для такого рода задачи теоремы сущест-
существования и единственности.
Мы опишем теперь несколько простейших правил
квантования.
1. Пусть классическая механическая система состоит
из точечного объекта массы т, расположенного на пря-
прямой линии. Тогда классическое состояние этой системы
задается двумя числами q и р: q означает координату
точки на прямой, а р — ее импульс (который связан со
скоростью v = q = j- формулой p = mv). Все остальные
физические величины являются функциями от q и р.
Предположим, что энергия системы имеет вид
2
Н — ?^ + V (q) (первое слагаемое — так называемая
кинетическая энергия, второе — потенциальная энергия).
Тогда соответствующая квантовая система строится так.
В качестве основного гильбертова пространства берется
Z7(R, dq). Роль координаты играет оператор q умноже-
умножения на g в этом гильбертовом пространстве. В качестве
импульса выступает оператор р = ^т"« Оператор энер-
гпи имеет вид Н — ?- + V(q). Это — дифференциальный
оператор второго порядка, действующий на волновую
функцию W (q) по формуле
Уравнение D8), описывающее развитие системы во
184
времени, принимает вид
а стационарное уравнение D9) превращается в
2. Обобщением предыдущего правила является сле-
следующий общий принцип. Предположим, что исходная
классическая система описывалась 2дг-мерным фазовым
пространством с каноническими координатами q^ ,,., qn,
Ph • • •> Рп, удовлетворяющими соотношениям
iqu ?i> = {/>*, р,} = 0, {р<, &} = бг*
где {,} — скобка Пуассона. Тогда в соответствующей
квантовой системе роль координат и импульсов играют
операторы qu ..., qn; pu ..., рп, удовлетворяющие ком-
коммутационным соотношениям
Ыи qi\ = \Рь Р,] = 0, \ри ?J = ^б«-
Оказывается, что такой набор операторов определен,
по существу, однозначно. А именно, если предположить
дополнительно, что операторы qu ,.., qn, pu ..., рп по-
порождают всю алгебру операторов в гильбертовом прост-
пространстве (это квантовый аналог классического условия:
любая физическая величина является функцией от кано-
канонических координат qu ..., qn, pi, ..., рп), то можно
установить такой изоморфизм основного гильбертова про-
пространства с L2(Rn, dqi, ..., dqn)j при котором оператор q\
переходит в умножение на координату q^ а оператор
Pi — в дифференциальный оператор ih ^—-.
3. Если классическая система получается объедине-
объединением двух подсистем, то классическое фазовое простран-
пространство М будет произведением (как множеств) фазовых
пространств М1ч М2 соответствующих подсистем. В кван-
квантовой механике аналогом этой операции является гиль-
гильбертово тензорное произведение II = Н{® Ег (см. зада-
задачу 499).
Однако в квантовой ситуации возникает новое явле-
явление, не имеющее точного классического аналога.
Пусть, например, рассматриваемая система состоит из
двух попарно неразличимых частиц, каждая из которых
185
описывается вектором из гильбертова пространства //.
Тогда состояние всей системы, описываемое вектором
Xi ® х2 ^ Н ® Я, не должно меняться при перестановке
векторов хи х2. Значит, неразличимость частиц приводит
к тому, что вместо тензорного квадрата Я ® Я мы долж-
должны рассматривать другое гильбертово пространство, в ко-
котором векторы Xi ® х2 и х2 ® х{ пропорциональны. Есть
два кандидата на такое пространство: симметрический
квадрат ^(Я) и внешний квадрат Л2(Я).
Оказывается, обе схемы соответствуют реальным фи-
физическим ситуациям. Есть такие объекты (они получили
название бозонов), которые описываются симметриче-
симметрическими степенями пространства Я, и такие (называемые
фермионами), которые описываются внешними степе-
степенями.
РАЗДЕЛ II
ЗАДАЧИ
ГЛАВА I
СВЕДЕНИЯ ИЗ ТЕОРИИ МНОЖЕСТВ
И ТОПОЛОГИИ
§ 1. Отношения. Аксиома выбора и лемма Цорна
1°. Какие из следующих отношений являются отноше-
отношениями эквивалентности?
а) Отношение равенства двух чисел;
б) отношение подобия двух треугольников;
в) отношение порядка на вещественной прямой;
г) отношение линейной зависимости в линейном про-
пространстве L размерности п> 1;
д) отношение линейной зависимости в множестве
L* = L\{0}, где L — линейное пространство.
2. Назовем две положительные функции Д и /2 на
отрезке [0, 1] эквивалентными, если
Проверить, что это действительно отношение эквивалент-
эквивалентности и что соответствующее фактормножество несчетно.
3. Определим отношение /i > /2 для положительных
функций на отрезке [0, 1] условием Пт * = оо. Про-
Прозе-»0 '2 ^ '
верить, что это — отношение частичного порядка, и дока-
доказать, что любое счетное подмножество ограничено.
4°. Пусть X и У — частично упорядоченные множест-
множества. Определим на произведении X X У отношение
(#i, yi)>(%2, Уг) условием Xi^x2 и z/i^z/2. Доказать, что
это отношение частичного порядка. Будет ли оно отно-
отношением порядка, если X и У — упорядоченные мно-
множества?
187
5. Пусть X — частично упорядоченное множество.
Предположим, что частичный порядок на X обладает сле-
следующим свойством: множество М(х) = {у е X: у^х} ко-
конечно для всех х^Х. Для любой функции }(х) на X
положим
F(*)= 2/О/)-
Доказать, что функция f(x) восстанавливается по F(x)
с помощью формулы вида
/(*)= H[i(x,y)F{y).
У<Х
Функция [I определена однозначно и называется функ-
функцией Мёбиуса для частично упорядоченного множества X.
6. Найти функции Мёбиуса для следующих частично
упорядоченных множеств:
а) натурального ряда с обычным отношением по-
порядка;
б)* натурального ряда с отношением делимости;
в)* совокупности конечных подмножеств данного мно-
множества X с отношением включения;
г)** совокупности подпространств линейного дг-мер-
ного пространства над конечным полем с отношением
включения.
7*. Выразить через функцию Мёбиуса задачи 6, б)
следующие величины:
а) функцию Эйлера <р(гс), равную количеству нату-
натуральных чисел, меньших п и взаимно простых с п\
б)** величину Р(дг, q)— количество неразложимых
многочленов степени п с коэффициентами из конечного
поля Fq и со старшим коэффициентом 1;
в) предел C{N)/N\ iV-^oo, Где С{N)— число несокра-
несократимых дробей вида p/q, I ^ p <:N, I ^ q^N.
8. Пусть А — вполне упорядоченное множество и для
каждого а^А задано непустое упорядоченное множество
Ха. Определим в множестве X = JJ Ха лексикографиче-
ский порядок, полагая х > у, если ха > уа , где а0 — наи-
наименьший элемент Л, для которого х^ уа. Доказать, что
это — действительно отношение порядка.
9. Пусть пространство Rn упорядочено так, что
а) xx>yi и х2 > у2 => Xt + х2 > z/i + уг\
б) х>у и Х>0 влечет Хх > Ху для X е R;
в) х> у и у> х влечет х = у.
188
Доказать, что Rn изоморфно как упорядоченное прост-
пространство произведению п прямых (с обычным порядком),
на котором введен лексикографический порядок (см. за-
задачу 8).
10*. Назовем два вполне упорядоченных счетных мно-
множества эквивалентными, если между ними можно устано-
установить монотонное взаимно однозначное соответствие. Пусть
Ж — множество соответствующих классов эквивалентно-
эквивалентности. Определим на Ж отношение порядка, полагая
[I > v, если в классах [i и v есть такие представители
М и N, что М эквивалентно начальному отрезку в N
(т. е. множеству вида N(no)= {n^ N: п<п0}).
Доказать, что
&) в Ж имеется наименьший элемент [i0;
б) любые два элемента Ж сравнимы;
в) множество Ж вполне упорядочено;
г) множество Ж несчетно;
д)** любое несчетное множество содержит часть, рав-
номощную Ж.
11*. Пусть Ж— вполне упорядоченное множество,
описанное в задаче 10. Положим 31 = ^Х[0, 1) и опре-
определим на % лексикографический порядок: если a = (pi, x),
b=(v, у), то а^Ъ означает либо jx^v и \i?=v, либо
\i = v и х> у.
Доказать, что любой начальный отрезок (см. зада-
задачу 10) множества ЗС эквивалентен (как упорядоченное
множество) полуинтервалу [0, 1), в то время как само
множество 91 не эквивалентно этому полуинтервалу.
12*. Пусть ao=(jLio, 0) — минимальная точка мно-
множества 91 задачи И. Определим топологию на St0 = 9t\{a0},
принимая в качестве базиса открытых множеств «интер-
«интервалы» (а, Ъ) = {се=51о :а< с < Ь, с?=а, сФЪ). Доказать,
что
а) у каждой точки я^910 есть окрестность, гомео-
морфная обычному интервалу;
б) топологическое пространство %Q связно и не гомео-
морфно обычному интервалу.
Пространство 910 называется прямой Александрова и
служит примером одномерного многообразия, не обладаю-
обладающего счетной базой открытых множеств.
13°. Доказать, что в множестве кругов, содержащихся
в данном квадрате на плоскости, есть максимальный эле-
элемент, но нет наибольшего по включению.
14. Используя лемму Цорна, доказать, что в каждом
линейном пространстве есть базис.
189
15. Используя теорему Цермело, доказать, что для
любых двух множеств А я В существует либо взаимно
однозначное отображение А на часть В, либо взаимно
однозначное отображение В на часть А.
16. Вывести теорехму Цермело из леммы Цорна.
17. Доказать лемму Цорна, пользуясь теоремой Цер-
Цермело.
§ 2. Метрические пространства и их приложения
18*. Доказать, что справедливость теоремы о стяги-
стягивающейся последовательности замкнутых шаров является
характеристическим свойством полных метрических про-
пространств.
19°. Доказать, что всякая равномерно непрерывная
функция на метрическом пространстве X однозначно про-
продолжается до непрерывной функции на пополнении и это
продолжение равномерно непрерывно.
20. Доказать неполноту и построить пополнения сле-
следующих метрических пространств:
а) прямой R с расстоянием d(x, у)= larctg# — arctg г/1;
б) прямой R с расстоянием d{x, y)= \ex—ev\.
21. В множестве отрезков на прямой определим рас-
расстояние формулой d([a, b\, [с, d])= \а — с\ + \Ъ — d\. До-
Доказать неполноту и найти пополнение этого метрического
пространства.
22. В множестве {А} отрезков на прямой определим
расстояние как длину симметрической разности:
A2)=lAil + lA2l-2lAtnA2L
Доказать неполноту и найти пополнение этого метри-
метрического пространства.
23. Доказать полноту пространства В(Х) всех огра-
ограниченных функций на множестве X с расстоянием
24. Пусть X — ограниченное метрическое простран-
пространство. Доказать, что соответствие x+-*d{x, •) является
изометрическим отображением X в В(Х) (см. задачу 23).
25. Пусть X — подмножество в полном метрическом
пространстве У. Доказать, что:
а) X полно тогда и только тогда, когда оно замкнуто.
б) Пополнение X изометрично его замыканию в Y.
в) Вывести из задач 23, 24 и а), б) теорему о попол-
пополнении для ограниченных пространств.
190
26. Пусть X — полное метрическое пространство, У< —
открытые всюду плотные подмножества в X. Доказать,
оо
что П Y\ всюду плотно в X.
27. Доказать неполноту пространства многочленов от-
относительно расстояний:
а) d(PlQ) = max \P(x)~Q(x)\;
*=[o,i]
б) d(P,Q) = $\P(x)-Q(z)\dx;
о
В) d (Л (?) = 2 | d |, еСЛИ Р И - <? (X) = 2 **«.
i
28. В множестве С(Х, У) непрерывных отображений
метрического пространства X в ограниченное полное мет-
метрическое пространство У определим расстояние формулой
d {fv /2) = supdY (/1 (x), U И)-
Доказать полноту метрического пространства С(ХУ У).
29*. Пусть X — ограниченное полное метрическое про-
пространство с метрикой dx, a G — совокупность всех взаимно
однозначных и взаимно непрерывных отображений X на
себя. Определим в множестве G расстояние по формуле
d (Л, /2) = sup [dx (/x И, U И) + dx (/Г (х), П1 (х))\.
Доказать полноту метрического пространства G.
30. Пусть р — простое число. Определим р-адическую
норму на множестве рациональных чисел равенством
||r||p=p-k, если r = pk—x
где тип — целые числа, взаимно простые с р. Доказать
соотношения:
а) llr4r2llp = Hrillpllr2llp;
б) IIп + г2Нр < max {llrjlp, Иг2Нр};
в) если 11г111р< 11г211Р, то 11^-1^2^ = 11г211Р.
31*. Доказать, что множество Q рациональных чисел
с расстоянием dp(ru г2)= 11г4 —r2llp (см. задачу 30) явля-
является метрическим пространством. Пусть Qp — его попол-
пополнение. Доказать, что все арифметические операции в Q
продолжаются по непрерывности на QP. Получаемое та-
таким образом поле называется полем р-адических чисел.
32*. Доказать, что каждый элемент из поля Qp (см.
задачу 31) однозначно записывается в виде /ьичной
191
дроби вида
u-iCL-2 • • • Я-ft
где 0 ^ пг ^ р — 1; после запятой — конечное число зна-
знаков, а перед запятой — бесконечное. Другими словами,
каждый элемент х ^ Qp является суммой сходящегося
+«>
ряда S агР{- Доказать, что Qp^Q.
33*. Обозначим через Zp замыкание кольца целых
чисел Z в QP (множество целых р-адических чисел). До-
Доказать, что Zp — компактное множество. Построить взаим-
взаимно однозначное и взаимно непрерывное отображение Zp
на канторово совершенное множество.
34*. Доказать, что для любого х ^ Zp (см. задачу 33)
существует предел Нт х^п. Обозначим этот предел sgx\px.
П-»оо
Доказать, что полученная таким образом функция (р-ади-
ческий сигнум) принимает ровно р различных значений:
О и (р — 1) корней степени р — 1 из 1. Доказать тождество
sgnp (xy) = sgrip х • sgrip у.
35*. Определим расстояние на множестве N натураль-
натуральных чисел, полагая d(m, лг) = 1//с, если у чисел тип
совпадают последние к знаков в десятичной записи.
а) Доказать, что полученное метрическое пространство
неполно и его пополнение изоморфно (как кольцо) пря-
прямому произведению колец Z2 и Z5.
б) Доказать, что для любого натурального к сущест-
существует ровно четыре /с-значных окончания:
...000 000
...000 001
... 890 625
...109 376,
воспроизводящиеся при умножении. (Это значит, что если
числа iVj и N2 оканчиваются указанными к цифрами, то
произведение NiN2 оканчивается теми же к цифрами.)
36°. Пусть Qn — множество бинарных векторов 0 =
= (соA), ..., со (я)). Доказать, что вектор o^id, ..., о„)
п
определяет в Qn метрику ра (со, со') = 2 °г \ © @ — «' (i) \
тогда и только тогда, когда аг>0 при г = 1, ..., п.
192
37°. Показать, что в метрическом пространстве Хем-
минга существуют шары, имеющие несколько центров.
Привести пример шара в (йп, рст), совпадающего с мно-
множеством своих центров.
38. Пусть *? (w, t) —функция, определяющая динами-
динамическую задачу распознавания. Доказать, что Hm ^F (w, t)
при w^W существует, если граф допустимых переходов
Г не имеет циклов.
39°. Доказать, что при to<tl< V из стабильности
прогноза П(?о, V) вытекает стабильность прогноза
1, t'). Показать, что обратное утверждение неверно.
40. Назовем предельной динамическую задачу распо-
распознавания при 7\ = t' = °о. Пусть в предельной задаче граф
допустимых переходов имеет вид Г: В.«ч.Н и г = 2.
Введем множество S = Во(/о)\Во(/о), где B0(t0) определе-
определено исходным разбиением. Показать, что любое допустимое
разбиение P(ti) имеет вид (Во(?о) [)S') \_\ (U0(t0)\S') для
некоторого S' ^ S.
41°. Доказать, что ядро z = (z(l), ..., z(n)) класса В
в алгоритме ГЭП-1 может быть определено формулой
f (ai bi\
0, если det ^ 0,
\ci di/
1 в противном случае.
42*. Гранью размерности к, натянутой на ребра дли-
длины Oit, ..., oik, называется подмножество Г s Qn (см. за-
задачу 36), состоящее из всех векторов со е Qnj у которых
координаты с номерами ?ь ..., ik произвольны (т. е. рав-
равны 0 или 1), а остальные (и — к) координат фикси-
фиксированы.
Пусть о = (oi,..., о„) удовлетворяет условию 0 ^ Oi ^
^G2^...^on. Положим, кроме того, о0 = 0, оЛ+1 = °°.
k
Рассмотрим все такие к^{0, ..., п), что 2(Jj<%i-
i=0
Доказать, что множество центроидов в (Qn, p0) совпадает
с множеством граней, натянутых на ребра длины
§ 3. Категории и функторы
43. Построить контравариантный функтор из катего-
категории всех подмножеств данного множества в себя. Мор-
физмами в этой категории являются вложения.
13 А. А. Кириллов, А. Д. Гвишиани 193
44. Существует ли универсальный отталкивающий
объект в следующих категориях: групп, линейных прост-
пространств над данным полем, в категориях, дуальных к ка-
категориям групп и линейных пространств?
45. Пусть G{ — категория абелевых групп с отмечен-
отмеченной образующей (морфизмы — гомоморфизмы групп, пере-
переводящие отмеченную образующую в отмеченную). Ука-
Указать универсальный объект в Gle
46. Пусть G2 — категория групп с двумя отмеченными
образующими (морфизмы — гомоморфизмы групп, перево-
переводящие отмеченные образующие в отмеченные). Доказать,
что в G2 существует универсальный объект. Этот объект
называется свободной группой с двумя образующими.
47. Обозначим через AG2 полную подкатегорию в Gz
(см. задачу 46), объектами которой являются абелевы
группы с двумя отмеченными образующими. Доказать
существование универсального объекта в AG2. Этот
объект называется свободной абелевой группой с двумя
образующими.
48*. Обозначим через Ап(К) категорию ассоциативных
алгебр над полем К с п отмеченными образующими. До-
Доказать существование универсального объекта в Ап(К).
Этот универсальный объект есть тензорная алгебра над
я-мерным линейным пространством над полем К.
49*. Доказать существование универсального объекта
для полной подкатегории САп(К) в Ап(К), состоящей из
коммутативных алгебр.
50**. Доказать существование универсального объекта
для категории LAn(K) алгебр Ли над полем К с п отме-
отмеченными образующими. Этот объект называется свобод-
свободной алгеброй Ли с п образующими.
51*. Пусть Q—алгебра Ли над полем К характери-
характеристики нуль. Рассмотрим категорию Я(д), объектами кото-
которой являются линейные отображения ср пространства g
в ассоциативные алгебры (свою для каждого объекта),
обладающие свойством:
Морфизмом объекта ср: §-* А в объект г|з: д->5 назы-
называется такой гомоморфизм %: А -* В, для которого ком-
коммутативна диаграмма
1Q4
Доказать, что К($) обладает универсальным объектом
ф0: Й
Алгебра f/(g) называется ассоциативной оболочкой
или универсальной обертывающей алгеброй для д.
52*. Доказать, что ассоциативная оболочка (см. за-
задачу 51) свободной алгебры Ли с п образующими изо-
изоморфна тензорной алгебре над я-мерным пространством.
53*. Пусть {Ха) (а ^А) — семейство объектов ка-
категории К.
Рассмотрим категорию К, объектами которой явля-
являются наборы морфизмов фа^Мог(Ха, Y) (а ^ A) (Y —
некоторый объект из К, свой для каждого объекта из К).
Морфизмами в R являются наборы коммутативных диа-
диаграмм вида
Если категория R имеет универсальный отталкиваю-
отталкивающий объект, то соответствующий объект из К называется
суммой объектов и обозначается Ц Ха. Морфизмы
а~А
*а • Хот* II ^а называются каноническими вложениями
а зА
слагаемых в сумму.
Доказать, что в категории множеств и в категории
линейных пространств над данным полем определены
суммы любого семейства объектов.
54*. Определение произведения семейства объектов
{XJ (а^А) категории К получается из определения
суммы (см. задачу 53) с помощью обращения стрелок.
А именно, произведением U Ха называют сумму объ-
азА
ектов Ха в дуальной категории К°. Морфизмы ра'- И Ха-+
а=А
->Ха называют каноническими проекциями произведе-
произведения на сомножители.
Доказать, что в категориях множеств и линейных
пространств над данным полем определено произведение
любого семейства объектов.
55. Доказать, что в категории линейных пространств
п п
над данным полем сумма Ц Lk и произведение Ц Lh
конечного числа объектов изоморфны.
13* 195
56. Пусть Li и L2 — два линейных пространства над
полем К, Рассмотрим категорию, объектами которой яв-
являются билинейные отображения ф: LtX L2-+ L, где L —
некоторое линейное пространство (свое для каждого объ-
объекта ф). Морфизмом из объекта ф: L{X L2-+ L в объект
г|>: Li X L2 -> М назовем такое линейное отображение %:
Li -*- if, для которого диаграмма
коммутативна.
Доказать, что построенная таким образом категория
обладает универсальным отталкивающим объектом п:
(Lx х L2->- Lx <g) L2. Линейное пространство L4 ® L2 назы-
к
вается тензорным произведением пространств Lt и L2
над полем К.
57*. Пусть Gi и G2 — конечные абелевы группы. Рас-
Рассмотрим категорию всех отображений:
ф: Gi X G2 ->• G,
где G — некоторая конечная абелева группа, своя для
каждого объекта), которые являются гомоморфизмами по
каждому переменному. Морфизмами служат коммутатив-
коммутативные диаграммы вида
где х — гомоморфизм. Доказать, что в построенной кате-
категории существует универсальный объект
G1XGa-^Tor(GI| G2)
(так называемое произведение кручения двух групп).
Вычислить Тог (Цт, Цп), где Цт — циклическая группа
порядка т.
58**. Пусть заданы направленное множество А и не-
некоторая категория К. Предположим, что для каждого
а^4 указаны объект Ха е Ob К, а для каждой пары
а < р — морфизм фар е Мог (Ха, Хр), причем для любой
196
тройки а < Р < Tf диаграмма
коммутативна.
Рассмотрим категорию КА, объектами которой явля-
являются семейства морфизмов {фа: Ха -*¦ Х}аел, согласован-
согласованные с ф«э, где X— некоторый объект из К (свой для каж-
каждого семейства), а морфизмом из {фа: Ха-+ Х}а<=А в {г|за:
Ха-> 7}аел назовем такой морфизм %^Мог(Х, 7), что
для любого а е А диаграмма
коммутативна. Универсальный объект категории КА
(если он существует) называется индуктивным преде-
пределом семейства {Ха}а€вА. Двойственное понятие проектив-
проективного предела определяется как универсальный объект
в (КА)\
Доказать, что
а) аддитивная группа поля рациональных чисел явля-
является индуктивным пределом счетного семейства групп
целых чисел;
б)* кольцо Zp целых /ьадических чисел является
проективным пределом колец вычетов по модулю рп.
59. Каждое комплексное линейное пространство мож-
можно рассматривать как вещественное, а каждое комплекс-
комплексно-линейное отображение — как вещественно-линейное.
Доказать, что описанное соответствие является ковари-
антным функтором из категории L(C) линейных прост-
пространств над С в категорию L(R) линейных пространств
над R.
60. Доказать, что отображение L->Z/®RC (тензор-
(тензорное произведение над R в смысле задачи 54) порождает
ковариантный функтор из L(R) в L(C).
61. Доказать, что категории L(R) и Ь(С) (см. зада-
задачу 59) не эквивалентны.
62. Пусть заданы группа G и поле К. Рассмотрим
совокупность K[G] формальных линейных комбинаций
элементов G с коэффициентами из К. Относительно
естественных операций сложения, умножения на элемен-
197
ты К и произведения K[G] является алгеброй пад К
G^-алгеброп).
Доказать, что
а) соответствие G -> K[G] является ковариантньш
функтором из категории групп в категорию Z-алгебр;
б) K[G] является универсальным объектом в катего-
категории мультипликативных отображений группы G в К-
алгебры.
63. Сформулировать определение предела направлен-
направленности {xj (a^A) в топологическом пространстве.
64. Доказать, что:
а) для метрических пространств X, Y непрерывность
отображения /: X -> У равносильна условию f(\imxn) =
= lim/(^n) для любой сходящейся последовательности
ixj в X;
б)* для топологических пространств X, Y непрерыв-
непрерывность отображения /: X -> Y равносильна условию
/(lim ха) = Нш f(xa) для любой сходящейся направлен-
направленности {xJ<x<=a в X;
в)** верно ли утверждение б), если в нем заменить
направленности на обычные последовательности?
65. Проверить, что топологические пространства и не-
непрерывные отображения образуют категорию Г.
66. Построить функтор из категории М метрических
пространств (морфизмы — непрерывные отображения)
в категорию Т топологических пространств.
67**. Доказать, что в категории Т топологических
пространств определены сумма и произведение любого
семейства объектов.
68. Доказать эквивалентность двух определений замы-
замыкания М множества М:
а) М — пересечение всех замкнутых множеств, со-
содержащих М\
б) М — совокупность пределов всех сходящихся на-
правленностей с элементами из М.
69°. Доказать, что при непрерывном отображении /:
а) образ компактного множества компактен;
б) образ связного множества связен.
70°. Критерий Хаусдорфа. Пусть X — метрическое
пространство и А^Х: подмножество 5<=Х назовем
е-сетью для Л, если для любого а^А существует такой
х^ 5, что d(a, x)< г.
Доказать, что подмножество А предкомпактно тогда
и только тогда, когда для любого 8 > 0 существует конеч-
конечная е-сеть для А.
198
71. Пусть X— метрическое пространство и ЛсХ.
Доказать эквивалентность следующих утверждений:
а) А предкомпактно;
б) из всякой последовательности точек в А можно
выделить фундаментальную подпоследовательность.
72. Пусть X — метрическое пространство и А <= X.
Доказать эквивалентность утверждений:
а) А — компакт;
б) из всякой последовательности точек в А можно
выделить подпоследовательность, сходящуюся к некоторой
точке из А.
ГЛАВА II
ТЕОРИЯ МЕРЫ И ИНТЕГРАЛА
§ 1. Теория меры
1. Алгебра множеств.
73°. Доказать, что операция симметрической разности
удовлетворяет следующему условию:
(аналог неравенства треугольника для «расстояния»
d(A, B) = A&B, принимающего значения в множествах).
74. Доказать, что
а) (Л, U Аг) A (#i U Вг)<= (Л, А В,) \\{Аг А В2);
б) (А, П Аг) А (В, П В2) с (А, А в,) U (А2 А 52);
в) (Л ДЛ2) Л (ВДДз) с: D, А В,) и (Л2 А 52).
(Эти включения означают непрерывность операций объ-
объединения, пересечения и дополнения относительно «рас-
«расстояния» d(A, В), введенного в п. 2 § 1 гл. II).
75°. Показать, что система множеств, замкнутая от-
относительно операций объединения и пересечения, вообще
говоря, не является кольцом.
76. Доказать, что система множеств, замкнутая отно-
относительно операций объединения и разности, является
кольцом.
77°. Доказать, что множество всех отрезков (откры-
(открытых, замкнутых и полуоткрытых) на прямой является
полукольцом, но не кольцом.
78. Показать, что для любой непустой системы мно-
множеств S существует одно и только одно минимальное
кольцо R{S), т. е. такое кольцо множеств R E), что ?<=
193
() и R(S)czR для любого кольца Я, содержа-
содержащего S.
79. Доказать, что для полукольца S минимальное
п
кольцо совпадает с системой множеств вида А = JJ Ак
(Ah^S).
80°. Доказать, что любая о-алгебра является б-алгеб-
рой и, наоборот, любая б-алгебра является о-алгеброй.
81. а) Доказать, что прямое произведение полуколец
является полукольцом.
б) Показать, что прямое произведение колец может
не быть кольцом.
82. Верхним пределом последовательности множеств
Еп называется множество lim Еп = (| ( U Ек\ т. е. сово-
п п \к^п )
купность точек, принадлежащих бесконечному числу из
множеств Еп. Нижним пределом последовательности мно-
множеств Еп называется множество Нт Еп = [} ( f| ЕЛ. До-
— n \ft>n /
казать, что для любой последовательности множеств
Еп lim En g lim En. Если верхний и нижний пределы
~1Г п
равны, то их общее значение называется пределом после-
последовательности множеств Еп.
83. Привести пример последовательности множеств
Еп, для которой lim En=?limEn.
Т п
84. Пусть X — множество и {EJ — последовательность
множеств таких, что Еп^Х для любого п. Доказать фор-
формулу
85. Пусть {Еп) — последовательность множеств и
ixJ — последовательность их характеристических функ-
функций. Доказать, что характеристической функцией мно-
множества lim En является функция lim %n, а характеристиче-
п п
ской функцией множества Ит Еп — функция Ит %п-
п п
86. Доказать, что предел последовательности множеств
Еп существует тогда и только тогда, когда существует
предел характеристических функций множеств Еп.
87. Пусть А — некоторая система множеств и А — со-
совокупность характеристических функций множеств, при-
200
надлежащих А. Доказать, что А является кольцом мно-
множеств тогда и только тогда, когда А есть алгебраическое
кольцо относительно сложения и умножения по модулю 2.
88*. Борелевскими множествами на прямой называ-
называются множества, получающиеся из интервалов примене-
применением счетного числа операций объединения, пересечения
и разности. Доказать, что совокупность борелевских мно-
множеств имеет мощность континуума.
89. а) Пусть /: А ~+ В — отображение множеств, $Ф —
система подмножеств множества А, ^—система подмно-
подмножеств множества В. Положим
Доказать, что если $ — кольцо, то f~l(^) — также кольцо.
б) Показать, что /(^), вообще говоря, не обязано
являться кольцом, если s& — кольцо.
в) Доказать, что если 3& — а-алгебра, то f~l{$) —
также а-алгебра.
г) В обозначениях задачи 89 доказать равенство
R(tl (<%)) = Г (R(M)).
2. Продолжение меры.
90. Пусть X — пространство с конечной а-аддитивной
мерой \i, определенной на некоторой алгебре R^P(X).
Внутренней мерой множества А <= X называется число
[х* (А) = \х (X) — [х* (Х\Л), где \х* — внешняя мера мно-
множества А. Доказать, что
91*. В обозначениях задачи 90 доказать, что мно-
множество А а X измеримо по Лебегу тогда и только тогда,
когда
Vit(A) = v*(A).
92*. Доказать, что мощность множества измеримых по
Лебегу подмножеств отрезка [0, 1] больше мощности кон-
континуума.
93*. Обозначим через \i меру Лебега на отрезке [0, 1]
и введем на пространстве измеримых по Лебегу подмно-
подмножеств отрезка [0, 1] отношение эквивалентности, положив
А ~ 5, если \х(А АВ) = 0. Доказать, что множество клас-
классов эквивалентности имеет мощность континуума.
94*. Пусть \х — мера на S. Доказать, что следующие
условия эквивалентны, если S — кольцо, и могут быть не
эквивалентны, если S— полукольцо:
201
/ OO \ 00
а) счетная аддитивность \i ?J Ak I = 2 Iх Иа);
\/i=i / k=i
б) полунепрерывность сверху: если 4t =>42 ^ 43 =>...
OO
и Л = П Ak, то [x (A) = lim fx (Л);
в) полунепрерывность снизу: если ^t с Л2 с= Л3 <= ...
оо
и 4 - U 4, то (I (Л) = lim (i (Л);
г) непрерывность: [i Him Л/Л = lim (х (Л^).
\//-*ОО / П-»ОО
95. Пусть \х — счетно-аддитивная мера на полу-
полукольце *S<=P(X), |i* — соответствующая внешняя ме-
мера на Р(Х).
а) Доказать, что отношение |и*(ЛД5) = 0 является
отношением эквивалентности и что функция d(A, 5) =
= \i*(A&B) задает расстояние на соответствующем
фактормножестве М. (Здесь А и В — классы эквивалент-
эквивалентности, содержащие множества А и В.)
б)* Доказать, что метрическое пространство Л полно.
в) Обозначим через Я и L подпространства в Ж, со-
состоящие из классов элементарных (т. е. принадлежащих
R(S)) и измеримых множеств соответственно. Докажите,
что L совпадает с замыканием /?. (См. п. 2 § 1 гл. II.)
96. Пусть S — подкольцо интервалов вида fa, b) на
отрезке [О, 1], Ж — пространство, построенное в задаче
95. Доказать, что Л связно и некомпактно.
97. Пусть {EJ — последовательность измеримых по
Лебегу множеств на прямой. Являются ли измеримыми
множествами верхний и нижний пределы последователь-
последовательности {/?„}?
98. Пусть А а — последовательность измеримых мно-
множеств и 21 \х (Ап) < оо. Доказать, что \i(\im An) = 0.
99. а) Доказать, что борелевские множества измеримы
по Лебегу.
б) Доказать, что всякое измеримое по Лебегу множе-
множество на прямой есть объединение борелевского множества
и множества меры нуль.
100. Пусть X — единичный квадрат на плоскости и
S — полукольцо прямоугольников, принадлежащих X,
вида
Таъ = {а<х<Ъ, 0<г/<1).
Положим m(Tab)=b - а. Описать явный вид лебеговского
продолжения этой меры.
202
101. В условиях и обозначениях задачи 100 доказать,
что множество 7* = {0 <; # ^ 1, у = 1/2} неизмеримо, и най-
найти его внешнюю меру.
102*. Пусть мера \х задана на полукольце X с еди-
единицей и \х* — отвечающая ей внешняя мера. Множество
A cz X называется измеримым по Каратеодори, если для
любого подмножества Z с X имеет место равенство
Доказать, что множество А измеримо по Лебегу тогда
и только тогда, когда оно измеримо по Каратеодори.
103**. Пусть тп — исходная а-аддитивная мера, опре-
определенная на полукольце. Множество А называется мно-
множеством о-однозначности для меры т, если
1) существует а-аддитивное продолжение % меры т,
определенное на Л;
2) для всяких двух таких а-аддитивных продолжений
Xi и Х2 справедливо равенство
а) Доказать, что каждое множество Л, измеримое по
Лебегу, является множеством а-однозначности для исход-
исходной меры т.
б) Доказать, что система множеств, измеримых по Ле-
Лебегу, исчерпывает всю систему множеств а-однозначности
для исходной меры т.
104*. Пусть каждое из множеств Хп (п = 1, 2, 3,...)
состоит из цифр 0, 1, 2, ..., 9. Определим меру \хп на Хп,
полагая \in (Y) = -^ card Y. Пусть [х—мэра на X = JJ Хп,
являющаяся произведением мер jnn. Рассмотрим отобра-
отображение X в отрезок [0, 1]: {хп} ¦-> 0, х1 х2 х3 ... (бесконеч-
(бесконечная десятичная дробь). Доказать, что при этом отобра-
отображении мера \х переходит в обычную меру Лебега на
[0, 1].
3. Конструкции мер.
105*. Построить пример неизмеримого по Лебегу мно-
множества на прямой.
1С6*. Построить пример измеримого по Лебегу мно-
множества на плоскости, проекции которого на координат-
координатные оси неизмеримы.
107**. Пусть jLi — мера Лебега, X— измеримое подмно-
подмножество отрезка [0, 1]. Точка х^Х называется точкой
203
плотности множества X, если
1- \1{Хп(х — е, х + е)} ___ ,
11111 9р
Доказать, что почти все точки множества X есть точки
плотности.
108. Описать все подмножества Е отрезка [0, 1] та-
такие, что их характеристические функции %е(х) интегри-
интегрируемы по Риману.
109°. а) Пусть X — пространство с а-аддитивной ме-
мерой. Доказать, что подмножества нулевой меры в X об-
образуют а-кольцо.
б) Доказать, что счетные множества на прямой имеют
лебеговскую меру нуль. Привести пример несчетного
множества на прямой, имеющего лебеговскую меру нуль.
110. Доказать, что множество всех зарядов на а-ал-
гебре §1 является линейным пространством, полным отно-
относительно расстояния d (vv v2) = sup | vx (A) — v2 (A) |.
111*. Для любого подмножества М пространства Rn
обозначим через М — М множество
М — М = {х- у: х<^М, уе=М}.
Доказать, что если М измеримо и имеет положитель-
положительную лебеговскую меру, то множество М—М содержит
окрестность нуля в Rn.
112°. Пусть X = {xi4 х2, ..., хп, ...) — счетное мно-
множество и каждому его элементу х{ поставлено в соответ-
ствие число Pi^O так, что2рп = 1^ Положим для лю-
бого подмножества Аа X пг (А) — 2 Рп» гДв NA =
n^NA
= {i: x\ e A}.
Доказать, что m есть а-аддитивная мера на алгебре
всех подмножеств множества X.
ИЗ*. Привести пример конечно-аддитивной, но не
а-аддитивной меры.
114*. Вычислить меру Винера множества функций
/^С[<2, Ь], обладающих свойствами: /(<z)<0, /(fe)>0.
115. Определим меру \х на [0, 1] формулой fx([cc, Р)) =
1+ Р
Доказать, что эта мера сохраняется при преобразова-
преобразовании/: х ь> | — L где {•} означает дробную часть числа.
204
(То есть jlx (/ *(A)) = \i(A). He утверждается,
{f(A))(A))
f())v())
116. Каждое действительное число х е [0, 1] мо
разложить в непрерывную дробь х — -— (pai
нальным числам соответствуют конечные дроби, ирра]
нальным — бесконечные).
а) Доказать, что преобразование задачи 115 в Tej
нах последовательностей {пк} имеет вид {пк} *-+ {nk+l}.
б) Вычислить меру простейших цилиндрических i
жеств в пространстве последовательностей, соответсть
щую мере \х задачи 115.
117. Докажите, что условие абсолютной сходимс
ряда 2v (An) в определении заряда можно заменить
ловием простой сходимости (см. с. 30).
118. Вычислить вариацию комплексного заряда
= jlxi + tjjt2 на множестве Л, если а) известно, что м
jlx± и \i2 дизъюнктны на Л; б) |Lii = jll2 на ^4.
119. Пусть v — комплексный заряд на а-алгебре
<=Р(Х).
Доказать, что вещественная и мнимая части v яз
ются зарядами на §1.
120*. Пусть v — заряд на а-алгебре 51<=Р(Х). Дс
зать, что sup v (А) < + сю, inf v (A) > — оо.
121*. Доказать, что верхняя и нижняя грани, о
торых идет речь в задаче 120, достигаются на некото]
множествах А+ и А- из 31.
122*. В обозначениях задачи 120, 121 доказать,
функция v (соотв. —v) является а-аддитивной мерой
31ПР(Л+) (соотв. на ЯПР(Л_)).
123*. В обозначениях задач 120, 121 доказать, что
всякого А^% справедливо равенство v(A) = v(A Г\ А^
+ v(A0A-).
124*. Доказать, что вариация Ivl заряда v коне
и а-аддитивна.
§ 2. Измеримые функции
1. Свойства измеримых функций.
125. Пусть X — пространство с мерой и / — вещ<
веннозначная функция, определенная на множестве
Доказать, что следующие свойства функции / экве
лентны:
аH для любого fl^R множество {х^Х: f(x)>a) из-
измеримо;
б)° для любого fl^R множество {хе=Х: f(x)>a) из-
измеримо;
в)° для любого fl^R множество {х^Х: j(x)<a) из-
измеримо;
г)° для любого fl^R множество {х*=Х: f(x)^a) из-
измеримо;
д) для любого борелевского множества В <= R мно-
множество /~* (#) измеримо.
126. Пусть функция / измерима и не обращается
в нуль. Доказать, что функция 1// измерима.
127. Доказать, что 1/1—измеримая функция, если /
измерима.
128. Пусть f(ti, t2, ..., tn) — непрерывная вещественно-
значная функция, определенная на гс-мерном веществен-
вещественном пространстве, a g{ (x) gn {x) — измеримые функции.
Доказать, что функция h(x) = f(gi(x)...gn{x)) измерима.
129. Пусть g(x)— измеримая функция, определенная
на вещественной прямой, а / — непрерывная веществен-
вещественная функция. Показать, что функция h>(х) = g(f(x)), во-
вообще говоря, неизмерима.
130. Пусть f(x)— функция, всюду дифференцируемая
на отрезке [0, 1]. Доказать, что /'' (х) измерима по Ле-
Лебегу.
131*. Пусть f(x)—канторово взаимно-однозначное
отображение отрезка [0, 1] на квадрат: для двоично-ирра-
двоично-иррационального х = (хи х2, х3, ...)/(#) = (Уь г/2), #! =
= (^i, #з, ...); г/г = {х2, хк, ...). Доказать, что отображе-
отображение f(x) переводит любое измеримое подмножество от-
отрезка в измеримое подмножество квадрата и сохраняет
значение меры.
132*. Функция f(x), определенная на вещественной
прямой, называется борелевской, если для любого fl^R
множество {х ^ R: f(x)<a) — борелевское. Доказать, что
любая измеримая функция после «исправления» на мно-
множестве меры нуль становится борелевской.
133**. С-свойство Лузина. Пусть \х — мера Лебега на
отрезке [0, 1], а /—измеримая, почти всюду конечная
функция на этом отрезке. Доказать, что для любого
8>0 существует замкнутое множество F<=[0, 1] такое,
что ограничение функции / на множество F непрерывно
и h(F)>1-e.
134*. Пусть /—измеримая функция, определенная на
вещественной прямой. Точка хе R называется точкой
206
Лебега функции /, если существует измеримое по Лебегу
подмножество X a R, содержащее х и имеющее х своей
точкой плотности. При этом ограничение f\x непрерывно
в точке х. Доказать, что почти все точки прямой есть
точки Лебега для функции /.
135*. Пусть f(x) — непрерывная функция, определен-
определенная на отрезке [<z, Ь], и п(с) — число решений уравнения
f(x) = c. Доказать, что функция п(с) измерима по
Лебегу.
136°. Пусть /п(#)—последовательность измеримых
функций. Доказать, что функции sup fn (#) и inf fn (x) из-
п п
меримы.
137. Пусть {/J — последовательность измеримых
функций. Доказать, что множество тех точек х, где су-
существует lim fn (x), измеримо.
П->оо
138°. Пусть /—измеримая функция. Доказать, что ее
положительная часть /+ = тах(/, 0) и ее отрицательная
часть /~ = —min(/, 0)—измеримые функции.
139. Вещественные функции / и g, измеримые соответ-
соответственно относительно мер \х и v, называются равноизме-
римыми, если для любого с>0 \i{x: f(x)<c}=viy:
g(y)<c).
а) Доказать, что если /— функция, измеримая относи-
относительно меры \i, то существует непрерывная слева на от-
отрезке [0, |ы(^0] неубывающая функция g, равноизмери-
мая с /.
б) Доказать единственность функции g(x).
140. Комплекснозначная функция f (х) = и (х) + iv(x)
называется измеримой, если измеримы ее вещественная
часть и(х) и ее мнимая часть v(x). Доказать измеримость
модуля и аргумента f{x).
141. Доказать, что для измеримости комплекснознач-
ной функции f(x) необходимо и достаточно, чтобы были
измеримы все множества вида Ar,i = {x: \f{x) — z\ ^ г},
где z^C, r>0.
142. Вектор-функция / со значениями в конечномер-
конечномерном пространстве V называется измеримой, если изме-
измеримы координаты вектора f(x) относительно некоторого
базиса в V. Доказать, что это определение не зависит от
выбора базиса.
2. Сходимость измеримых функций.
143°. Доказать, что последовательность /п (<?) = -2 , 2
всюду на R сходится к нулю, но не равномерно.
207
144. Исследовать на сходимость и равномер-
равномерную сходимость последовательность fn{x) = xn на от-
отрезке [0, 1].
145 . Доказать, что две непрерывные функции на
отрезке эквивалентны относительно меры Лебега только
тогда, когда они тождественно равны.
146*. Построить измеримую по Лебегу функ-
функцию на отрезке, не эквивалентную никакой непрерыв-
непрерывной функции.
147°. Известно, что fn—W и /п ' *> g. Доказать, что
/ эквивалентна g.
148*. Занумеруем все рациональные числа отрезка
[О, 1] и запишем к-е число гк в виде несократимой дроби
Гк^Рн/Як. Положим fk(x) = exp{-(ph-xqhJ}.
а) Доказать, что /* -* О по мере Лебега на [0, 1] и
что lim fh (x) не существует ни в одной точке отрезка.
П->оо
б) Указать явно подпоследовательность, сходящуюся
к нулю почти всюду.
149. Определим функции f\ на отрезке [0, 1], по-
полагая
fl при
'О в остальных точках2
и пусть gn{x) = fih (x), где i и к подбираются из условия
п = -Ц,—- + i. Доказать, что gn -* О1 по мере, но
lim gn{x) не существует ни в одной точке.
150. Пусть jn~*h и fn~*g- Доказать, что h и g экви-
эквивалентны по мере \х.
151**. Теорема Лузина. Доказать, что вещественная
функция на отрезке [а, Ь] измерима по мере Лебега
тогда и только тогда, когда для любого 8 > 0 сущест-
существует непрерывная функция, отличающаяся от / на мно-
множестве меры меньше 8.
152**. Из теоремы Лузина (задача 151) вытекает, что
всякая измеримая на отрезке [а, Ь] функция / является
почти всюду пределом последовательности {/„} непрерыв-
непрерывных функций. Всегда ли можно эту последовательность
выбрать монотонной?
208
153. а) Показать, что функция Дирихле
{О, если х иррационально,
1, если х рационально,
может быть получена из непрерывных функций двукрат-
двукратным предельным переходом:
г|)(я) = lim lim [cos Bnn\ x)]m.
б)* Можно ли получить ее из непрерывных функций
одним предельным переходом?
154% Доказать, что простая функция (т. е. функция,
принимающая не более счетного множества значений)
измерима тогда и только тогда, когда измеримы все ее
множества уровня
Верно ли это для произвольных функций?
155. Доказать, что каждая измеримая функция может
быть представлена в виде равномерного предела измери-
измеримых простых функций.
156. Определим функцию f(x) на отрезке [0, 1] сле-
следующим образом. Если х = 0, п^щ ...— десятичная за-
запись числа х, то / {%) = шах щ.
а) Доказать, что f(x) измерима и почти всюду по-
постоянна.
б) Доказать, что функция / (х) = lim щ определена
всюду и почти всюду постоянна.
157. Пусть jLi — мера Винера на пространстве Х=*
= С[я, Ь]. Определим функцию / на X, полагая f(x) =
ь
= J x (t) dt,
a
Доказать, что / ц-измерима.
158*. Доказать измеримость относительно меры Ви-
Винера следующих функций:
ъ
а) / (х) = j Ф (х (Oi 0 ^i где Ф{х, у)— непрерывная
а
функция двух переменных;
б) / (х) = max x(t).
159*. Пусть X — множество целых р-адических чисел,
S — алгебра подмножеств X, которые одновременно от-
" А. А. Кириллов, А. Д. Гвишиани ^"
крыты и замкнуты в X, 5f = /?0Er). Доказать, что всякая
непрерывная функция на X §1-измерима.
160*. В условиях задачи 159 доказать, что всякое
множество А^S является объединением конечного числа
шаров. Определим меру \i на 5, полагая меру шара рав-
равной его радиусу (для шаров радиуса р~к (к = 0, 1,
2, ...))• Доказать, что мера \х счетно-аддитивна.
161. Доказать, что мера |i из задачи 160 обладает
свойствами:
а) ii(X)=l;
б) \х(А +я)= [i(A) для всех х^Х.
Доказать, что всякая мера на §1, обладающая свой-
свойствами а) и б), совпадает с |я.
§ 3. Интеграл
1. Интеграл Лебега.
162°. Доказать, что если fug — суммируемые про-
простые функции, то
a) J(/(*) + g(x)) ф = |
А А
б) J a/ (x) d\x = a \ f (x) d\x (а = const);
А А
в) если \f(x)\^M почти всюду на А и |и(Л)<<х>? то
li"
163. Пусть [i(X)<oo и /—суммируемая функция
•на X. Доказать, что интеграл Лебега J / (x) d\x может
быть вычислен по формуле
/ (x) dix = lim 2 6aH ({* е= X: tk < / < ^+1}), A)
\ МГ)-»о h
где Т = {tk} — разбиение вещественной оси, Я (Т) =
=sup|^—^/i+i|—диаметр разбиения Г, а {?л} — любой
/i
набор точек, удовлетворяющий условию ?л е [thi tk+i].
Выражение A) называется интегральной суммой Ле-
Лебега.
164*. Доказать, что утверждение задачи 163 остается
верным в случае |я(Х)=оо? если дополнительно потребо-
210
вать, чтобы ?ь = 0 для тех /с, для которых отрезок
[th, th+i] содержит точку 0.
165. Пусть измеримая простая функция / представле-
представлена двумя способами в виде линейных комбинаций харак-
характеристических функций дизъюнктных множеств:
/ И = 2 ckXAk ix) = 2 di%Bl (*).
Доказать, что ^ск\1(Ак) = 2c^fl№) в случае, если один
к I
из этих рядов абсолютно сходится.
166. Пусть /п — простая функция на [0, 1], опреде-
определенная формулой Jn (х) = — [гс.г],где [х] означает целую
часть числа х. Доказать, что последовательность {/„}
фундаментальна и не имеет предела в пространстве
5[0, 1] простых суммируемых функций с расстоянием
1
d1(f,g)=$\f-g\dx.
О
167. При каких значениях параметров аир функция
/(^) = ^asin^p, определенная на полуинтервале @, 1],
а) интегрируема по Лебегу,
б) несобственно интегрируема по Риману?
168°. Доказать, что интеграл от неотрицательной сум-
суммируемой функции / по множеству А
а) неотрицателен,
б) равен нулю только тогда, когда f(x) = O почти
всюду на А.
169. Пусть ф — монотонно возрастающая гладкая
функция на отрезке [а, 6], if — обратная к ней функция
на отрезке [ф(я), ф(&)]. Рассматривая интеграл как пре-
предел суммы Лебега, доказать тождество
ytf (У) dy.
a cp(a)
170. Доказать, что интеграл Лебега от неотрицатель-
неотрицательной функции ]{х) по отрезку [a, b] совпадает с мерой
Лебега множества Е на плоскости, заданного неравен-
неравенствами a<x<b, 0<y<f{x).
171. Доказать, что неотрицательная измеримая функ-
функция / суммируема на А тогда и только тогда, когда для
всех простых функций g, не превосходящих по модулю /,
14* 211
интегралы j g (x) d\i (x) ограничены одной и той же кон-
А
стантой.
172. Положим для любой вещественной функции /:
U(x) = (f(x)+\f(x)\)/2, f-(x) = (\f(x)\-f(x))/2. Дока-
Доказать, что функция / суммируема тогда и только тогда,
когда суммируемы функции /+ и /_.
173. Доказать, что измеримая неотрицательная функ-
функция / суммируема тогда и только тогда, когда
sup I / (x) d\i (x) < оо, где верхняя грань берется по всем
А
множествам А конечной меры, на которых функция /
ограничена сверху.
174. Пусть \х(Х)<°°. Доказать, что неотрицательная
измеримая функция / на I суммируема тогда и только
тогда, когда сходится ряд
п=о
175. Доказать, что неотрицательная ограниченная
функция на множестве X бесконечной меры суммируема
тогда и только тогда, когда сходится ряд
77=0
176*. Доказать, что функция на отрезке [а, Ь] интег-
интегрируема по Риману тогда и только тогда, когда она огра-
ограничена и почти всюду непрерывна.
177*. Доказать, что интеграл Лебега от функции
/ (#i, .. ., хп) = ехр {— 2 aijXiXj]
конечен тогда и только тогда, когда симметрическая мат-
матрица А = WuijW положительно определена. Доказать, что
интеграл в этом случае равен det(n -ЛI72.
178*. Вычислить интеграл по мере Винера на С[0, 1]
от функции
F(x) = ехр I— ах2 @) - b2 j x2 (t) dt\.
179**. Обозначим через С0[0, 1] пространство непре-
непрерывных функций x(t) на отрезке [0,1] с дополнительный
условием .г@) = 0. Доказать, что пространство С[0, 1]
212
можно так отождествить с произведением RXC0[0, 1],
что мера Винера \i перейдет в \ii X \i0, где jj, — обычная
мера Лебега на R, a \i0 — некоторая мера на С0[0, 1].
180**. Пусть \io — мера, построенная в задаче 179.
Вычислить интегралы:
(t)dt
в) j J *«(*)#
d\L0(x).
co[o,i]Lo
2. Функции ограниченной вариации и интеграл Ле-
Лебега — Стилтьеса.
181°. Установить следующие свойства полной ва-
вариации:
а) для любого постоянного а и функции / ограничен-
ограниченной вариации Vara (а/) = | а | Vai*a (/);
б) если / и g — функции ограниченной вариации, то
/ + g — также функция ограниченной вариации, причем
в) если а < Ь < с и / — функция ограниченной ва-
вариации на отрезке [а, с], то
г) если / —- монотонная функция, то
182. Доказать, что множество точек разрыва функции
ограниченной вариации на отрезке не более чем счетно
и состоит лишь из точек разрывов первого рода.
183. Доказать, что функция ограниченной вариации
на отрезке измерима по Лебегу.
184°. Доказать, что функция на отрезке, обладающая
ограниченной производной, является функцией ограни-
ограниченной вариации.
185*. Пусть функция / обладает интегрируемой по
Риману производной на отрезке [а, Ь]. Доказать формулу
213
186. Пусть Ф — непрерывная слева функция ограни-
ограниченной вариации на отрезке [а, Ь]. Доказать, что функ-
функция Ф однозначно представляется в виде суммы Ф =
= Фо + Ф4, где Фо — непрерывная функция ограничен-
ограниченной вариации, a Oi — так называемая функция скачков:
Фх (х) = 2 с$ (х — ak)i где {ak} — любое конечное или
h
счетное подмножество на [а, 6], 6(я)— функция Хеви-
J 0 при х^.0,
сайда, задаваемая формулой 9 (х) = \ . п
у х При X ^^ \),
a {ch} — любая числовая последовательность, удовлетво-
удовлетворяющая условию ]? 1 Ck | <С оо.
h
187. Доказать, что
а) произведение двух функций, ограниченной вариа-
вариации есть функция ограниченной вариации;
б) если f(x)^a>0 и /—функция ограниченной ва-
вариации, то и вариация функции 1// ограничена.
188. Будет ли функция ф(/) иметь ограниченную
вариацию на отрезке [0, 1], если функция / имеет огра-
ограниченную вариацию на отрезке [0, 1], а функция ф
а) непрерывна на всей числовой оси,
б) имеет ограниченную вариацию на всей число-
числовой оси?
189. Пусть Е — подмножество отрезка [0, 1], % — ха-
характеристическая функция множества Е. Доказать, что х
имеет ограниченную вариацию тогда и только тогда, ког-
когда граница Е — конечное множество.
190*. Пусть / и g — две непрерывные функции с
ограниченной вариацией на отрезке [а, Ь]. Доказать, что
множество if(x), g(x)}, x e [а, Ь], не может заполнить
квадрат. Верно ли это, если отказаться от требования
ограниченности вариации?
191°. Докажите следующие свойства интеграла Рима-
на — Стилтьеса:
а) если Ф — функция ограниченной вариации, а
функция / интегрируема по Ф, то
б) если Ot и Ф2- функции ограниченной вариации,
а функция / интегрируема по Ф1 и Ф2, то она иптегри-
214
руема и по Ф, где Ф = Oi + Ф2, и
ь ъ ъ
J / (х) йФ (х) = J / (х) dOx (х) + J / (*) <?Ф2 (*).
а а а
_J92. Пусть функция Ф имеет ограниченную вариацию
на отрезке [а, Ь] и разрывна в точке с^(а, Ь), а функ-
функция / интегрируема по Ф в смысле Римана — Стилтьеса.
Доказать, что функция / непрерывна в точке с.
193. Доказать, что если Ф — функция ограниченной
вариации на отрезке [а, Ь], отличная от нуля в конечном
или счетном числе точек, лежащих внутри (а, Ь), то для
любой функции /, непрерывной на отрезке [а, Ь],
194. Доказать, что если функция / непрерывна, то
ъ
интеграл Римана —- Стилтьеса J / (#) йФ (х) не зависит от
а
значений, принимаемых функцией Ф в точках разрыва,
лежащих внутри (а, Ь).
195. Доказать формулу интегрирования по частям для
интеграла Стилтьеса:
ь ъ ъ
\f{x)dg{x) = f{x)g{x) -\g{x)df{x).
а а
196. Пусть функция f(x) непрерывна на отрезке
[а, Ь], а функция g(x) имеет на [а, Ъ] всюду, кроме ко-
конечного числа точек си ..., ch, суммируемую по Риману
производную g'(x). Доказать, что при этих условиях су-
ъ
ществует интеграл Римана — Стилтьеса J / dg и что он
а
выражается формулой
ь ъ
j / dg = j fg' dx + / (a)[g(a + 0) - g(a)] +
a a
h
+ f (b) \g (b) - g Ф - 0)] + 2 / (Cm) [g (Cm + 0)-g (Cm-O)].
m=l
197°, Пусть щ — мера, порожденная монотонной не-
непрерывной функцией ф. Доказать, что интеграл Лебега
215
j xd\i<p равен интегралу Стилтьеса j xdcp(x)y и вычис-
[atb] a
лить его.
198*. Пусть j(x)—непрерывная функция на отрезке
[О, 1]. Индикатрисой Банаха Nf(y) функции / называет-
называется число корней уравнения f(x)=y (если оно бесконеч-
бесконечно, то полагаем Nfiy)^00)- Доказать, что Nf(y) — изме-
со
римая по Лебегу функция от у и J Nj (у) dy =Var0 (/)t
—оо
если хотя бы одна из частей последнего равенства имеет
смысл.
199*. Пусть (р(х)—канторова лестница, т. е. непре-
непрерывная монотонная функция на отрезке [0, 1], постоян-
постоянная на каждом интервале, дополнительном к канторову
совершенному множеству, и принимающая на интерва-
интервалах k-то ранга значения l/2ft, 3/2ft, 5/2\ ..., Bft — l)/2ft.
!\
1/2
/I I
r1 i I
' I I
О 1/9 2/91/3
2/3 7/9 8/9 си
Вычислить интегралы:
ill
a) J xkd(f (х)\ б) J e* dy (х); в) j sin nx dy (x).
ооо
3. Свойства интеграла Лебега.
200°. Доказать, что множество L{(X, \x) является мет-
метрическим пространством относительно расстояния
216
201е. Пусть последовательность /n e ?i (X, \i) сходит-
сходится равномерно к функции /(#). Доказать, что если
\i(X)<°°, то /п -*¦ / в пространстве Li(Z, ^i). Верно ли
это в случае ^i(X)=°°?
202. Построить последовательность функций /n e
е LJO, 1], обладающую свойствами:
а) /n(s)-*0 для всех #€=[0, 1];
1
б) J I /n (#) I dx ^ с > 0 для всех я;
о
в) последовательность {/п} не имеет предела в Ь{[0,1].
203. Пусть X — множество конечной меры \i. Для
любых измеримых функций / и g положим
а) Доказать, что функция d обладает всеми свойства-
свойствами расстояния, кроме отделимости, и что соответствую-
соответствующее метрическое пространство М[0, 1] состоит из клас-
классов эквивалентных функций.
б) Доказать, что сходимость в пространстве М\0, 1]
совпадает со сходимостью по мере и что пространство
Л/[0, 1] полно по метрике d(f, g).
в) Доказать, что функция
= f arctg | / (ж) — ^ (х) | ф (яг)
определяет метрику в пространстве Л/[0, 1] и что сходи-
сходимость по этой метрике совпадает со сходимостью по мере.
204. Пусть {/п} — последовательность неотрицатель-
неотрицательных суммируемых функций, сходящаяся почти всюду к
суммируемой функции /. Доказать, что если при п ->¦ <»
] /пф-> j fd\i, то /n -^ / в смысле сходимости в прост-
х х
ранстве L{(X, ji).
205*. Пусть /eLi(X, \i) и \i(X)=l. Доказать, что
существует такая монотонная функция g(t)& L^O, I],
что для любого t е [0, 1]
inf \f()v()
»(A)=tA о
1
sup f/(лг)ф(д:) = f g(x)dT,
217
206**. Пусть \i — ненулевая борелевская мера на
множестве вещественных чисел, обладающая следующим
свойством: для любого t e R мера \it, определенная фор-
формулой \it {А)= \х(А + ?), эквивалентна мере \х. (Такие
меры называют квазиинвариантными относительно сдви-
сдвигов.) Доказать, что мера \i эквивалентна мере Лебега.
207*. Пусть |i — мера на X и /i, /2 — две |1-суммст-
руемые вещественные функции на X. Определим заряды
Vi = fi\i формулой Vj (A) = j {г d\i (i = 1, 2). Доказать, что Vi
A
и v2 эквивалентны тогда и только тогда, когда
208*. Пусть \х — о-конечная мера на I, v- мера,
определенная на той же о-алгебре и абсолютно непре-
непрерывная относительно \х (т. е. ц(-4) = 0 =>• v(-4)= 0). До-
Доказать, что существует неотрицательная ^-измеримая
функция р, обладающая свойством v (A) = J p (x) d\i (x)
А
для любого измеримого множества А (обе части равенст-
равенства могут одновременно принимать значение +«>).
209*. Доказать, что на вещественной прямой R не
существует измеримого по Лебегу множества Л, обла-
обладающего свойством: для любого интервала Д
м Л4 П Д) = -— Li (Д).
210**. Пусть f^Li[a, b]. Доказать, что функция
X
F(x)=\f(x)d\i(x) почти всюду дифференцируема hF'(#) =
а
= f(x) для почти всех х е [а, Ь].
211**. Вещественная функция F на отрезке fa, b]
называется абсолютно непрерывной, если для любого
е > 0 существует такое б > 0, что для любого семейства
интервалов {Дг), &{=(аи Ь,-) (l^Kn) с суммой длин
п
<б справедлива оценка 2 \^(аг)—-^(Ьг)|<е. Доказать, что
г=1
а) абсолютно непрерывная функция F почти всюду
дифференцируема;
б) производная f(x) = F'(x) суммируема на отрезке
[а, Ь];
в) справедлива формула Ньютона — Лейбница
ь
218
212°. Доказать, что следующие множества плотны
в пространстве Li[0, 1]:
а) множество S@, 1) кусочно-постоянных функций
с конечным числом точек разрыва;
б) множество непрерывных кусочно-линейных функ-
функций с конечным числом точек излома;
N
в) множество многочленов Р (х) = ^ akxk;
г) множество тригонометрических многочленов
N
Т(х)= 2 cke™ikx.
k=-N
213. Доказать, что в пространстве ?i(R) плотны сле-
следующие множества:
а) кусочно-постоянных финитных функций;
б) непрерывных финитных функций;
в)* множество функций вида Р (х) е~х , где Р —
многочлен.
214. Пусть /^L1(R). Доказать, что ] | / (х + е) —
R
— / (х) | Лг-> 0 при е-^0. Другими словами, сдвиг яв-
является непрерывной операцией в Li(R).
215. Сверткой функций Д и /2 на прямой называется
функция /, задаваемая формулой
/(*)= J /i
а) Доказать, что если /i и /2 принадлежат Lt(R), то
подынтегральная функция суммируема для почти всех х
и свертка / также принадлежит пространству Lj(R).
б) Доказать, что если одна из функций Д или /2 огра-
ограничена, то свертка / непрерывна.
ГЛАВА III
ЛИНЕЙНЫЕ ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
И ЛИНЕЙНЫЕ ОПЕРАТОРЫ
§ 1. Нормированные пространства
1. Основные определения.
216. Два числа р и q из [1, °°) называются сопря-
сопряженными, если выполняется одно из следующих эквива-
эквивалентных условий:
219
2) (P— l)(g —1)—1;
3) P + q = pq.
а) Доказать неравенство Гелъдера
где x, у е 7Г\ а /? и g — сопряженные числа (/? = R
или С).
б) Выяснить, когда это неравенство превращается в
равенство.
217. Доказать неравенство Минковспого
\\х + у\\р < Ibllp + llffllp
для х, У^Кп, ре[1, оо).
218. Доказать полноту пространств 1Р(п, К) и 1Р(К)
при р s [1, оо).
219. Доказать полноту пространства С(Х, К).
220. Доказать, что при 1^/?<<х\ X = R или С, 1Р(К)
является сепарабельным банаховым пространством.
221. Доказать, что пространство 1оо{К) всех ограни-
ограниченных последовательностей {хп}, хп е К, К = R или С,
с нормой |{хп}|| = sup\xn\ — несепарабельное банахово
п
пространство.
222. Доказать, что нормированное пространство L
является банаховым тогда и только тогда, когда всякий
ряд 2-Ti, для которого 2l#ill<00» сходится в L.
223°. Доказать, что нормированное пространство L
несепарабельно тогда и только тогда, когда в нем есть
несчетное множество попарно непересекающихся шаров
радиуса единица.
224. Доказать, что в нормированном пространстве до-
достигается расстояние от данной точки до произвольного
конечномерного подпространства.
225*. Найти расстояние от точки хп^С[—1, 1] до под-
подпространства Рп-х с: С[—1, 1], состоящего из всех много-
многочленов степени <п.
226. а) Пусть L — банахово пространство и Lo c= L —
его замкнутое подпространство. Вектор х е L называется
г-перпендикуляром к Lo, если для любого у е Lo выпол-
выполняется неравенство \\х + у\\ >A — е)\\x\\. Доказать, что
при е > 0 любое собственное подпространство Ьй обла-
обладает е-перпендикуляром.
220
б) Вывести отсюда некомпактность единичного niaipa
в бесконечномерном банаховом пространстве.
в) Доказать, что существование нуль-перпендикуляра
к подпространству Lo, задаваемому уравнением )(х) = 0,
где / — линейный функционал на ?, равносильно суще-
существованию тах|/(#)|.
IMK1
227. Доказать, что при рг < р2 пространство lPl (n, R)
изометрично пространству Ip2{n, R), только если п = 2,
Pi = 1, Рг = °°.
2. Сопряженные пространства.
228. Доказать, что если L — бесконечномерное нор-
нормированное пространство, то на нем существует разрыв-
разрывный линейный функционал.
229. Доказать, что норма функционала j^L' обратна
к расстоянию в L от нуля до гиперплоскости /(#)= 1.
230°. Доказать, что любое конечномерное линейное
нормированное пространство рефлексивно.
231*. Доказать, что замкнутое подпространство реф-
рефлексивного пространства рефлексивно.
232. Доказать, что пространство с0 всех последова-
последовательностей вещественных чисел, стремящихся к нулю
с нормой р({хп})= max \хп\, нерефлексивно.
233°. Пусть L — бесконечномерное нормированное
пространство. Доказать, что слабая топология в L не сов-
совпадает с сильной.
234. Пусть L = /i(R)— пространство последователь-
оо
ностей вещественных чисел с нормой рх ({хп}) = S \хп\-
71=1
Доказать, что слабая сходимость в L совпадает с сильной.
235. Гиперплоскость Р называется опорной для вы-
выпуклого множества К, если имеет с ним общую точку и
все К расположено по одну сторону от Р. Доказать, что
множество опорных плоскостей к единичному шару в L
естественно нумеруется точками единичной сферы в Z/.
236. Пусть в нормированном пространстве L единич-
единичный шар В является выпуклым многогранником. По-
Построить естественное соответствие между ^-мерными
гранями В и (п — к) -мерными гранями единичного
шара В' в U.
237. Пусть с — пространство всех вещественных по-
последовательностей {хп}, для которых существует предел
lim^n с нормой \\{хп}\\ = sup \zn\, и с0 — подпространство
последовательностей, стремящихся к нулю. Доказать, что
221
пространства с и с0 изоморфны пространству Zt (R),
а пространства с и с0 неизоморфны друг другу.
238. Доказать изоморфизмы lp(K)'=lq(K), где р е
е[1, оо), д = р/(р— 1), # = R или С.
239. Доказать, что Z« (Я)' неизоморфно h(K), i? = R, С.
240. Пусть ?i и Z/2 — нормированные пространства,
элементы которых записываются в виде векторов-столб-
векторов-столбцов длины nY и п2 соответственно. Оператор А е
e^(Llt L2) можно тогда записать в виде матрицы из w4
столбцов и п2 строк, так что действие А на х ^ Lx со-
состоит в умножении слева А на Xi согласно правилам
матричного умножения. Показать, что пространства Lx и
L2 можно отождествить с пространствами векторов-строк
длины rii и п2 соответственно, так что действие сопря-
сопряженного оператора А' будет состоять в умножении спра-
справа на матрицу А.
241. Пусть линейный функционал определен на ве-
вещественном линейном нормированном пространстве и не
ограничен. Доказать, что в любой окрестности нуля он
принимает все вещественные значения.
242. Доказать, что линейный функционал в линейном
нормированном пространстве непрерывен тогда и только
тогда, когда его ядро замкнуто.
243. Доказать, что два непрерывных линейных функ-
функционала, определенные на одном и том же линейном
нормированном пространстве и имеющие общее ядро,
пропорциональны.
244. Доказать, что всякая гиперплоскость в линейном
нормированном пространстве или замкнута, или всюду
плотна в нем.
3. Операторы в нормированных пространствах.
245. Пусть банахово пространство L разложено в ал-
алгебраическую прямую сумму подпространств Li и L2. До-
Доказать, что оператор проектирования на L{ параллельно
L2 ограничен тогда и только тогда, когда L{ и L2 замкну-
замкнуты в L.
246. Доказать, что оператор Р в банаховом простран-
пространстве L является проектором на некоторое замкнутое под-
подпространство Lt параллельно замкнутому подпространст-
подпространству L2 тогда и только тогда, когда он ограничен и удов-
удовлетворяет соотношению Р2 = Р.
247*. Для каких функций а(х) оператор умножения
на а (х) является непрерывным оператором из Lp[0, 1]
в L,[0, 1J?
222
248. Пусть A (t)—дифференцируемая операторная
функция на Я, значения которой принадлежит EndL и
dim L < оо. Доказать, что все решения дифференциаль-
дифференциального уравнения A'(t) = CA(t), где С ^ EndL, имеют вид
A{t) = etcA0, где A0 ^
k=o
249. Пусть A(t)—непрерывная операторная функция
на R со значениями в EndL, dimL<°°. Доказать, что
все решения функционального уравнения A(t)A(s) =»
= A(t + .s) имеют вид A(t)= etc, где Се EndL.
250. Показать, что утверждение 249 перестает быть
верным в случае dimL = °°. (Ср. теорему Стоуна из
гл. V.)
251. Пусть К(х, у)—непрерывная функция на еди-
единичном квадрате в R2. Оператор А действует из Lp[0, 1]
в Lg[0, 1J, К р, q < оо, по формуле {Af) (х) =
= J К (х, у) •/ (у) dy. Найти сопряженный оператор
A'hq, [О, 1]->V [О, 1], где р'=р/(р - 1), q'=q/(q-l).
252. Пусть Р:С[О, 2]->С[0, 1] — оператор ограниче-
ограничения. Найти сопряженный оператор Р'\ V[0, 1}->F[O, 2].
253. Доказать, что оператор, отображающий линейное
нормированное пространство L в факторпространство
L/Lj (ставящий в соответствие элементу х е L содержа-
содержащий его класс смежности), является линейным и огра-
ограниченным.
254. Пусть А — линейный оператор, отображающий
линейное нормированное пространство X в линейное
нормированное пространство У. Пусть, кроме того, мно-
множество значений этого оператора образует конечномер-
конечномерное многообразие. Следует ли отсюда, что А — ограни-
ограниченный оператор?
255. Пусть А : X -+ Y — непрерывный линейный опе-
оператор, определенный на всем линейном нормированном
пространстве X и принимающий значения в линейном
нормированном пространстве У. Всегда ли существует
хе=Х, хФО такой, что Ых\\ = Ш Ы?
4. Конструкции банаховых пространств.
256. а) Пусть Lo — замкнутое подпространство бана-
банахова пространства L. Доказать, что формула ||#|i =
= inf || у || определяет норму на пространстве Ьг = Ь/Ь0.
б) Доказать, что пространство Ьг — банахово.
223
257*. Пусть L — нормированное пространство, Lo —
его замкнутое подпространство, Li — L/Lo и норма в Ь{
определена, как в предыдущей задаче. Верно ли, что
если Z/0 и Lj — банаховы пространства, то пространство
L — тоже банахово?
258*. Показать, что всякое сепарабельное банахово
пространство над полем К (К = R или С) является фак-
торпро'Странством 1г (К).
259. Подпространство Lo в банаховом пространстве L
называется дополняемым, если существует такое замкну-
замкнутое подпространство Ь{^Ь, что L — L0®Li (алгебраиче-
(алгебраическая прямая сумма). Доказать, что:
а) всякое конечномерное подпространство допол-
дополняемо;
б) всякое замкнутое подпространство конечной кораз-
коразмерности дополняемо;
в) пространство ^(К), K = R или С, дополняемо в
любом содержащем его банаховом пространстве;
г) если L/Lo изометрично h(K), то Lo дополняемо.
260*. Пусть Lx и L2 — линейные пространства над по-
полем К. Рассмотрим категорию К, объектами которой яв-
являются билинейные отображения А: /^ X Ь2 -*- L, где L —
некоторое линейное пространство над К (свое для каж-
каждого объекта). Морфизмом объекта A: Li X L2-> L в объ-
объект В: Li X L2 -*- М назовем линейное отображение
ф: L -> М, для которого коммутативна диаграмма
Доказать, что универсальным объектом в К является
Ао: L1xL2-+L1<8) L2: (xv x2) -* хг ® х2.
261*. Пусть Ь{ и L2 — банаховы пространства, К —
категория билинейных отображений A: L1xL2^* Lc нор-
нормой ^1. Морфизмы определяются, как в предыдущей за-
задаче с дополнительным условием НсрН < 1. Доказать, что
в категории К универсальным объектом является отобра-
отображение Ао: Lxx L2-+Lx ® L2: (xv х2) н- xt ® х2.
262*. Пусть Li = l2(nJ R), L2 = l2{m, R). Отождествим
пространство Li ® L2 с пространством матриц порядка
пХ т следующим образом. Будем записывать элементы
L2 в виде векторов-строк, а элементы Li — в виде векто-
векторов-столбцов. Тогда элементу х ® у мы поставим в соот-
соответствие матрицу х - у. Пусть элементу а е Li ® L2 соот-
224
ветствует матрица А. Доказать, что норма элемента а
в пространстве Lx ® L2 может быть вычислена по форму-
формуле ||а|| = si+ ... + sA , к = min (/г, т), где st — располо-
расположенные в порядке убывания собственные числа матри-
матрицы АА'(А'А), если к = п (соответственно к = т).
263. Доказать, что в условиях предыдущей задачи
норма элемента ае ^ ® L2 совпадает с нормой матрицы
А как оператора из h{m, R) в Z2(n, R) и равна числу sx 2.
264. Пусть Li и Ь2 — банаховы пространства. Пока-
Показать, что существует естественное изометрическое вложе-
вложение Li ® L2 в пространство 3?{LU L2).
265*. Доказать, что Zx (гг, R) ® Zx (m, R) изоморфно
hR)
266*. Доказать, что loo (л, R) ® Zoo (яг, R) изоморфно
§ 2. Линейные топологические пространства
1. Топология, выпуклость и полунормы.
267°. Доказать, что топология в ЛТП определяется
заданием системы окрестностей нуля.
268. Доказать, что в любом ЛТП замкнутое множе-
множество X и точка хФХ имеют непересекающиеся окрест-
окрестности.
269. Пусть в конечномерном линейном пространстве
заданы две нормы — р{(х) и р2{х). Доказать, что суще-
существует такая положительная константа С, что
270. Доказать, что в конечномерном линейном прост-
пространстве L есть только одна топология, относительно ко-
которой L является отделимым ЛТП.
271. Доказать, что если две нормы р{х) и q{x) мажо-
мажорируют друг друга: С~*р(х)^ q(x)< Ср(х) (?>0), то
о о
системы открытых шаров Вр и Bq определяют одну и ту
же топологию.
272°. а) Доказать, что если множество А открыто,
а В произвольно, что множество А + В открыто.
б) Доказать, что если множество А замкнуто, а В —
компакт, то множество А + В замкнуто.
273. Приведите пример замкнутых множеств А и S,
для которых А + В не является замкнутым множеством.
15 А. А. Кириллов, А. Д. Гвишиани 225
274°. Пусть Аи ..., Ап — выпуклые множества и
^i, ..., hn — фиксированные числа. Доказать, что множе-
п
ство А= 2 КАг выпукло.
г=1
275°. Доказать, что пересечение любого семейства вы-
выпуклых множеств выпукло.
276. Пусть А — любое ограниченное множество на
плоскости и В — единичный круг х2 + у2 < 1. Доказать,
что для любых положительных чисел а и р множество
осА + $В измеримо по Лебегу, а если А выпукло, то
+ рД) = 5а2 + Lap + л р2.
Каков смысл коэффициентов S и L?
277*. Пусть Аи ..., Ak — выпуклые ограниченные
множества в пространстве Rn. Доказать, что jw,(aH1 + ...
... + akAk) является однородным многочленом степени п
от переменных аи ..., ah.
278. Пусть L — линейное пространство над полем К,
Доказать, что среди всех отделимых топологий, превра-
превращающих L в ЛВП, есть самая сильная, которая назы-
называется ядерно-выпуклой топологией и обладает следую-
следующими свойствами:
а) всякий линейный функционал (т. е. линейное ото-
отображение /: L -*¦ К) непрерывен;
б) базис окрестностей нуля в L состоит из всех вы-
выпуклых множеств, содержащих нуль и пересекающихся
с каждой прямой, проходящей через нуль, по интервалу
положительной длины.
279. Доказать, что множество В является единичным
шаром для некоторой полунормы р тогда и только тогда,
когда оно выпукло, уравновешено и замкнуто в ядерно-
выпуклой топологии (см. задачу 278).
280. а) Доказать, что среди всех выпуклых множеств
5, содержащих 0 и имеющих данный функционал Мин-
ковского р, есть наибольшее Bt и наименьшее Во (по
включению).
б) Доказать, что Si является замыканием Во в ядер-
ядерно-выпуклой топологии.
281. Пусть А — любое множество в линейном прост-
пространстве L, d(А)— пересечение всех выпуклых множеств
в L, содержащих Л, с2(А)— совокупность всех векторов
п
вида х= 2т^ьгде ^jg4, а коэффициенты т* неотри-
226
цательны и обладают свойством 2 т* = 1. Доказать, что
Ci(A) = c2(A). Это множество называется выпуклой обо-
оболочкой и обозначается со (Л).
282. Доказать, что в полинормированном пространстве
(L, {ра)а<=А) множество М ограничено тогда и только
тогда, когда оно ограничено по каждой из полунорм
ра (а^А).
283. Доказать, что во всяком ЛВП выпуклая оболоч-
оболочка ограниченного множества ограничена. Привести при-
пример, показывающий, что в произвольном ЛТП это свой-
свойство может не выполняться.
284. Пусть R°° — пространство всех последователь-
последовательностей вещественных чисел с топологией покоординатной
сходимости. Доказать, что в R°° нет непустых открытых
ограниченных множеств.
285. В пространстве С (R) всех непрерывных веществен-
вещественных функций на прямой введем счетную систему полунорм
pN (/) = max | / (х) | и положим d (/, g) - 2 2~У 1?+р' uJg) •
Для каких г>0 шар радиуса г является выпуклым мно-
множеством в C(R)?
286. В пространстве C(R) всех непрерывных вещест-
вещественных функций на прямой определим расстояние фор-
формулой
-cup
Будет ли являться пространство C(R) с топологией,
определяемой этим расстоянием, ЛТП?
287°. Доказать, что подпространство BC(R) простран-
пространства C(R) из предыдущей задачи, состоящее из всех
ограниченных непрерывных функций на прямой, являет-
является нормируемым ЛТП.
288. Обозначим через R°° пространство всех последо-
последовательностей вещественных чисел с расстоянием
Доказать, что
а) R°° локально выпукло;
б) R°° счетно-нормируемо;
в)* R00 ненормируемо.
15* 227
2. Сопряженные пространства.
289°. Доказать, что если линейный функционал не-
непрерывен в какой-либо точке линейного топологического
пространства, то он непрерывен в каждой точке этого
пространства.
290. Пусть L — линейное топологическое простран-
пространство. Доказать, что
а) линейный функционал / на L непрерывен тогда и
только тогда, когда существуют такое открытое множе-
множество C/czL и такое число ?, что t не принадлежит мно-
множеству /(?/);
б) линейный функционал / на L непрерывен тогда и
только тогда, когда его нулевое подпространство Кег/ =
= {х: f(x) = O) замкнуто в L.
291*. Пусть в линейном топологическом пространстве
L существует определяющая система окрестностей нуля,
мощность которой не превосходит размерности L. Дока-
Доказать, что на L существует разрывный линейный функ-
функционал.
292. Выпуклое множество М в ЛТП L, для которого
множество {^GM|V^Gi3e(|/)GR: x + ty e M при
1*1 <г(У)} непусто, называется выпуклым телом. Назо-
Назовем выпуклые тела В и В' в Rn двойственными, если их
функционалы Минковского определяют в Rn структуры
сопряженных нормированных пространств. (Мы отождест-
отождествляем вектор {аи ..., ап) с функционалом
п
Доказать, что сечение В fc-мерной плоскостью Р двой-
двойственно ортогональной проекции В' на эту плоскость.
293**. Доказать, что не существует никакого нормиро-
нормированного пространства, для которого пространство С[а, Ъ\
было бы сопряженным.
3. Теорема Хана — Банаха.
294. Доказать, что если ЛТП LK отделимо и конечно-
конечномерно, то всякое линейное отображение ?А ->• L2, где L2—
произвольное ЛТП, непрерывно.
295. Пусть Р — пространство всех многочленов от х
с вещественными коэффициентами, U+ (соотв. [/_) —
подмножество многочленов с положительным (соотв. от-
отрицательным) старшим коэффициентом. Доказать, что
множества U+ и С/_ выпуклы, но не разделяются ника-
никакой гиперплоскостью.
228
296. Доказать, что выпуклые замкнутые непересека-
непересекающиеся множества А и В в ЛТП, одно из которых —
компакт, строго разделяются гиперплоскостью. (Это зна-
значит, что существуют такой непрерывный линейный
функционал / и такие константы ct < с2, что f(x)<cl
на Л и f(x) > c2 на В.)
297°. Пусть L — линейное нормированное пространст-
пространство с нормой /?, Z/ — сопряженное пространство с нор-
нормой р', L" — пространство, сопряженное к Z/, с нормой
р"'. Каждому x^L поставим в соответствие элемент
FX^L" по формуле Fx(f) = f(x) для f^L\ Доказать
равенство р" (Fx) = p{x)-
298. Пусть L — конечномерное нормированное прост-
пространство. Доказать, что L и L" изоморфны (т. е. су-
существует линейное изометрическое отображение L
на L").
299. Доказать, что всякое линейное нормированное
пространство изометрично подпространству некоторого
пространства вида С(Х), где С (X) — пространство непре-
непрерывных функций на компакте X с нормой ||/||=тах |/(#)|.
300*. Доказать, что всякое сепарабельное нормирован-
нормированное пространство L изометрично некоторому подпрост-
подпространству в С[0, 1].
301. Построить изометричное вложение /РB, R) в
пространство С[0, 1] для р = 1, 2, с».
302. Доказать, что существует изометрическое вложе-
вложение lP(n, R) в /оо (R).
303. Пусть /^(R)—пространство ограниченных веще-
вещественных последовательностей {хп} (п = 1, 2, ...). Дока-
Доказать, что существует линейный функционал LIM^Zoo (R) \
обладающий свойствами:
1) sup^n^ LIM {xj > inf xn;
2) если существует Нт хп = а, то LIM {хп) = а;
3) LIM {xn+i} = LIM {xj.
304. Доказать, что утверждения задачи 303 перено-
переносятся на случай двусторонних последовательностей {хп),
п*=Ъ.
305*. Пусть L — нормированное пространство, Т — ли-
линейный обратимый оператор в ?, обладающий свойством:
р (Тпх) ^ср{х) V^gL, п = 0, ± 1, ...
Доказать, что существует норма р в L, эквивалентная
Р, относительно которой преобразование Т изометрично.
229
306. Пусть L — ЛВП. Доказать, что L допускает не-
непрерывное вложение в произведение прямых Ra, где a —
достаточно высокая мощность. (Другими словами, всякое
ЛВП допускает координатное описание.)
307*. Пусть В(Rn) — совокупность ограниченных ве-
вещественных функций на Rn с нормой |/|| = sup \f (x)\.
n
Доказать, что существует линейный функционал LIM е
efifR")', обладающий свойствами:
а) inf / (х) < LIM / (х) < sup / (х);
Rn Rn
б) если существует lim/(;r) = a, то ЫМ/(ж)=а;
|Х|-»0О
в) для любого у е Rn LIM/(я + у) = LIM/(я).
308°. Доказать, что линейное подмногообразие X в
ЛВП L плотно тогда и только тогда, когда всякий линей-
линейный функционал /е?', равный нулю на X, обращается
в нуль тождественно.
309. Доказать, что всякое замкнутое выпуклое мно-
множество в вещественном ЛВП L является пересечением
некоторого семейства полупространств вида )(х)^с1 где
310. Представить единичный шар в Ьр(?г1 R) в виде
пересечения счетного числа полупространств.
311. Пусть IN — N-мерный куб, задаваемый в Rv
уравнениями |;rj < I (I <i<N). Доказать, что любое
выпуклое ограниченное множество на плоскости можно
с любой точностью аппроксимировать двумерным сече-
сечением IN. (Более точно, для любого е>0 и любого вы-
выпуклого множества V с= R2 существуют такое N и такое
вложение ср: R2 -*- RlV, что функционалы Минковского
множеств U и ^==Ф('ЛГ) связаны неравенствами
Pv
312. Построить изометрическое вложение lP(n, R) в
С [0, 1] ДЛЯ ЛЮбоГО р S [1, оо].
313. Теорема Хелли. Доказать, что если семейство
выпуклых множеств в R" таково, что любые /2+1 мно-
множеств семейства имеют общую точку, то все множества
семейства имеют общую точку.
314. Определим топологию в пространстве С [0, 1],
взяв в качестве базиса окрестностей нуля множества
f
С [0,1]: \V\f (x)\dx<z\. Доказать, что на по-
о J
230
лученном топологическом пространстве каждый непре-
непрерывный линейный функционал равен нулю.
315*. Пусть L — ЛВП, X — множество с мерой |i, / —
функция на X со значениями в L. Говорят, что / слабо
измерима, если числовая функция F(f(x)) ji-измерима
для всех F ^ V. Элемент cp^L называется слабым инте-
интегралом от / по мере \х на множестве X, если F (/) =
= J F (/ (х)) d\i (х) для всех F е= Z/. Доказать:
х
а) единственность слабого интеграла;
б) существование слабого интеграла в случае, когда
L — рефлексивное банахово пространство, а функция 11/11
суммируема по мере \х на X.
§ 3. Линейные операторы
1. Пространство линейных операторов.
316. Пусть в пространстве Z2(R) оператор Ph действу-
действует по формуле Pk({xn})= hnkxn}, где гпк — 1 при к < п и
е„й = 0 при к>п. Какие из следующих сходимостей
имеют место при &-><*>: a) Ph =>¦ 0, б) Ph -> 0, в) Pft-^0?
317. Пусть еи . . ., еп, . . .— естественный базис в про-
пространстве /2(R). Определим оператор Ап формулой
(ev если к = п,
Апвк = (о, если к Ф п.
Доказать, что \\Ап\\ = 1 и что Ап -> 0 при п -> с».
318. В условиях задачи 317 определим оператор Вп
формулой
(еп, если к = 1,
если й=^1.
Доказать, что \\Вп\\ = 1, Sn -^ 0 при гг -> с», но не су-
существует s-lim Bn.
319°. Доказать непрерывность операции умножения
операторов в равномерной топологии: если Ап =^ A
^L,, L2), Bn=>B^2?(L0, L,), то ЛЛЛВ
(, )
320. Пусть Li и L2 — банаховы пространства. Дока-
Доказать, что если Ап-*~ А <^ 2*(Lu L2), то нормы операторов
Лп ограничены в совокупности.
321. Доказать, что если Ап -> А е 3?(LUL2), Вп -> Be
^(L Li), то ЛпД„-> 4fie^(L0, L2).
231
322*. Доказать, что операция умножения операторов
а) не непрерывна в сильной топологии пространства
dL, если L бесконечномерно (сравнение с результатом
1,ачи 321 показывает, что сильная топология в End L
определяется сходящимися последовательностями);
б) непрерывна в сильной топологии на единичном
ipe пространства End L.
323. Привести пример последовательностей операто-
в Лп-^0, Вп -*¦ 0, для которых АпВп не сходится сла-
к 0.
324°. Доказать неравенство У fill < ИЛИ llfill для А е
S 2(
(U2), A )
325. Пусть Т(*)— оператор сдвига в LP(R) (К р <
оо): T(t)f(x) = f(x + t).
Доказать, что T(t)-+T(t0) при t -> t0. Верно ли, что
(*)=* T{U) при t-+ U!
326. Пусть А — линейный оператор из Lj в L2, пере-
>дящий всякую сильно сходящуюся последовательность
слабо сходящуюся. Доказать, что А ограничен.
327. Пусть А — оператор из Lt в L2, непрерывный в
1ысле слабых топологий Li и L2. Будет ли А непреры-
зн в смысле сильных топологий?
2. Компактные множества и компактные операторы.
328. Вычислить аппроксимативную размерность пап-
эрова совершенного множества X. (Множество X явля-
гся пересечением счетного числа множеств Хп, где Хп
олучается из отрезка [О, 1] выбрасыванием З" интер-
/Зк2 Зк-1\ 7 \
р
Зк-2 Зк
[, ] р
— , Л = 1, 2, ...,3 .
J J
алов вида ,
329. Пусть К — выпуклое множество в линейном про-
транстве L. Подмножество А ^ К называется крайним,
ели всякий отрезок, лежащий в К, середина которого
гринадлежит А, целиком лежит в А. Доказать, что пере-
-ечение любого семейства крайних подмножеств либо
густо, либо является крайним подмножеством.
330. Пусть К — выпуклый компакт. Доказать, что со-
юкупность его замкнутых крайних подмножеств (см. за-
задачу 329), упорядоченная по включению, имеет мини-
минимальный элемент.
331. Пусть К—замкнутое выпуклое ограниченное
подмножество в ЛВП L, А — минимальный элемент
семейства замкнутых крайних подмножеств в К (см. за-
задачу 330). Доказать, что А состоит из одной точки.
332. Доказать, что выпуклый компакт К в ЛВП L
имеет хотя бы одну крайнюю точку.
232
333*. Доказать теорему Крейна — Милъмана: всякий
выпуклый компакт К в ЛВП L совпадает с замыканием
выпуклой оболочки своих крайних точек.
334. Найти крайние точки единичного шара в про-
пространстве 1Р{п, R) A </?<<*>).
335. Найти крайние точки единичного шара в про-
пространствах с и с0.
336. Доказать, что пространства с и с0 не являются
сопряженными ни к какому линейному нормированному
пространству.
337. Доказать следующий аналог теоремы Асколи —
Арцела: пусть В(Т, X)—метрическое пространство всех
ограниченных функций на множестве Т со значениями
в компактном метрическом пространстве X; расстояние
в В(Т, X) определено как d(f, g) = supdx (/ (*)» ()
tGT
tGT
где dx — расстояние в X. Для того чтобы множество
MczB(T, X) было предкомпактным, необходимо и доста-
достаточно, чтобы выполнялись условия: для каждого г > О
существует такое конечное разбиение множества Т: Т =
— ^iLJ • • -LJ^n, что на каждой части Г, каждая функция
j^M изменяется не больше чем на е.
338. Найти крайние точкп множества S дважды сто-
стохастических матриц порядка п. (Матрица А называется
дважды стохастической, если ее элементы неотрицатель-
неотрицательны и сумма элементов каждой строки и каждого столб-
столбца равна 1.)
339. Доказать, что в бесконечномерном нормирован-
нормированном пространстве единичный оператор некомпактен.
340. Доказать, что в бесконечномерном нормирован-
нормированном пространстве компактный оператор не имеет огра-
ограниченного обратного оператора.
341. Пусть оператор А в /P(R) A<р<°о) задан
формулой A{xJ = ianxn}, где {aj — фиксированная огра-
ограниченная последовательность вещественных чисел. Дока-
Доказать, что оператор А компактен тогда и только тогда,
когда Hm an = 0.
342. Доказать некомпактность в пространстве С[0, 1]
оператора А, действующего по формуле Aj(x) =
= *•/(*).
343. Пусть L, и L2 — банаховы пространства, A s
^&{LU L2). Доказать, что из компактности сопряжен-
сопряженного оператора А' следует компактность А.
344. Пусть К(х, у)—непрерывная функция на еди-
единичном квадрате в R2. Доказать, что оператор А в С [0,1],
233
1
определенный формулой^/ (х) = \ К(х, у) f (у) dy, компак-
о
тен.
345. Пусть /{е!2(ХХ7, |uXv). Доказать, что опе-
оператор А, действующий из L2(Y, v) в L2(X, \i) по форму-
формуле Af (x) = j К (х, у) / (у) dv (г/), является компактным.
у
346*. Пусть оператор Т в пространстве Lp@, °°) (р >
1) задан формулой Т] (х) = — \ / (t) dt.
Доказать, что Т ограничен, но некомпактен. Найти
норму Т.
347*. Пусть пространство L рефлексивно. Доказать
компактность оператора Т ^ End L, переводящего всякую
слабо сходящуюся последовательность в сильно схо-
сходящуюся.
348. Пусть Q — область в Rn. Доказать, что оператор
вложения из Cftfl(Q) в Ch(Q) компактен.
349. Может ли компактный оператор А удовлетворять
п
алгебраическому уравнению 2 °кА = 0 (мы полагаем
k
)
3. Теория фредгольмовых операторов.
350. Пусть А — оператор в /P(R), действующий по
формуле А{хп) = {апхп}, где (ап) — фиксированная после-
последовательность вещественных чисел. При каком условии
на {aj подпространство im А замкнуто в /P(R)?
351. Пусть Т — оператор в /P(R), действующий по
формуле T{xJ = {xn+li. Найти ядро и коядро операторов
Г (fc = l, 2, ...).
352*. Пусть Р — многогранник в R3, Xk — множество
его ориентированных /с-мериых граней @-мерпые гра-
грани — вершины, 1-мерные грани — ребра, 2-мерные гра-
грани — обычные грани, 3-мерная грань — сам многогран-
многогранник), Lh — пространство вещественных функций на Xh.
Если Г ^ Xft-j, A ^ Хк, то можно определить число
е(Г, А), равное 0, если Г не лежит на границе А, и ±1
в противном случае. Знак е(Г, А) зависит от ориентации
Г и А. Пусть еи ..., ek-t базис, задающий ориентацию Г;
А, •. •, /а — базис, задающий ориентацию А и выбранный
так, что векторы fu ..., /ft_t лежат в плоскости Г, а век-
вектор fk трансверсален к Г и направлен вне А. Тогда
234
е(Г, А) равно знаку определителя матрицы перехода от
еи ..., eh-i к А, ..., Д-t. Определим оператор dh: Lh-i ->
->¦ Lk формулой
(ЙЛ/)(Д)= 2 е(Г, А)/(Г).
Доказать полуточность последовательности
с?^ с/о do
н вычислить ее когомологии для простейших многогран-
многогранников (симплекса, куба, куба с дыркой, куба с внутрен-
внутренней полостью).
353. Пусть Ch(Г)— пространство функций на окруж-
окружности Т, имеющих к непрерывных производных, с нормой
||/|= max ||/@|, |/' @1, ...,|/(
Доказать полуточность последовательности
где d — оператор дифференцирования, и вычислить ее
когомологии.
354. Пусть дана полуточная последовательность ко-
конечномерных пространств
и Hh — пространства ее когомологии для к = 0, 1, ..., п.
Доказать тождество Эйлера
2 (-i)*dimLfc= 2 (-l)
355**. Пусть задана последовательность
банаховых пространств и непрерывных операторов. До-
Доказать, что если сопряженная последовательность
, Tk г Th+\ f
...-<— Lk_x *— Lk < Lk+1 <- . . .
точна, то точна и исходная последовательность.
356*. Пусть дана полуточная последовательность
235
банаховых пространств и непрерывных отображений. До-
Доказать, что сопряженная последовательность полуточна
и пространства когомологий сопряженной последователь-
последовательности сопряжены к пространствам когомологий исходной
последовательности.
357. Построить почти обратный оператор для опера-
оператора Т из задачи 351.
358. Пусть Т — дифференциальный оператор вида
действующий из C*fn[0, 1] в С* [0, 1]. Доказать, что опе-
оператор Т — фредгольмов и найти его индекс.
359. Является ли фредгольмовым оператор умножения
на непрерывную функцию а(х) в пространстве С [0,1]?
360*. Пусть L — пространство гармонических непре-
непрерывных вплоть до границы функций в области Q <r R2,
ограниченной гладкой кривой Г. Доказать, что оператор
ограничения Р : L -> С (Г) является фредгольмовым,
ы найти его индекс.
361. Пусть Q — ограниченная область на комплексной
плоскости, #(Q)—пространство голоморфных в Q и не-
непрерывных в Q функций, а{2)Ф 0 — функция, голоморф-
голоморфная в некоторой окрестности Q. Доказать, что оператор
умножения на a(z) фредгольмов в #(Q), и найти его
индекс.
362. Пусть //0 = Z/2(R, dx), #t — пополнение про-
пространства S(R) по норме ||/|!i = ИР + II/'Но (здесь II Нв
означает норму в //0). Операторы рождения и уничто-
уничтожения в квантовой теории поля могут быть определены
как дифференциальные операторы из #t в Яо, действую-
действующие по формулам A±f = (^± «^1/. Доказать, что А± —
фредгольмовы и что ind A± = ±1.
363. а) Оператором Гильберта — Шмидта называется
интегральный оператор
ь
действующий в пространстве Ьг [а, Ь], ядро которого
удовлетворяет условию J ] | Ar(.9, t) |2 dsdt <сю. Доказать,
а а
что для оператора Гильберта — Шмидта выполнено не-
236
равенство
/"ъ~ь
б) Доказать, что соответствие А «-* К (s, t) между опе-
операторами Гильберта — Шмидта и их ядрами является
взаимно-однозначным с точностью до эквивалентности
измеримых функций.
364. Пусть дан оператор Гильберта — Шмидта, опре-
определенный ядром K(s, t) (см. задачу 363). Доказать, что
сопряженный к нему оператор определяется «сопряжен-
«сопряженным» ядром K(t, s).
365. Интегральным уравнением Фредголъма {второго
рода) с вырожденным ядром называется уравнение вида
ф (s) = J (g Л (s) Qt (*)) ф @ dt + / (S),
где Р{, Qi — функции из L2 [a, b]. Доказать, что общее pe-
peri
шение этого уравнения имеет впд ср (s) = 2 Qi^i (s) + f (s)
и что неопределенные коэффициенты q{ можно найти
пз некоторой системы алгебраических уравнений вида
366. Уравнением Волътерра (второго рода) называет-
называется интегральное уравнение
где K(s, ^—ограниченная измеримая функция на квад-
квадрате [а, 6]Х[а, Ь]. Доказать, что для любой функции
j^L2{a,b) уравнение Вольтерра имеет одно и только
одно решение.
367. Доказать, что произведение двух операторов
Гильберта — Шмидта с ядрами K(s, t), Q(s, t) (см. за-
задачу 363) есть оператор того же типа с ядром
ь
R (s, t) = \ К E, и) Q {и, t) du.
а
2У!
368. Пусть А — оператор Гильберта — Шмидта (см.
задачу 363), причем его ядро удовлетворяет соотношению
ъ ъ
JJl^fo t)\2dsdt= K2<oo.
а а
Доказать, что ядро Kn(s, t) оператора Ап удовлетворяет
оценке
ъ ь
§ 4. Функциональные пространства
и обобщенные функции
1. Пространства интегрируемых функций.
369. Доказать, что для любых измеримых функции
на множестве X с мерой \i справедливо неравенство
Гёльдера:
(*) g (х) | ф (х) < Q| / (х) f dii (^))lr(.[l e И
где числа р и q связаны соотношением 1 = 1.
370. Доказать, что для любой измеримой функции /
на множестве X с мерой jlx справедливо равенство
I / (*) Г Ф i*)YP = sup J | / (х) g (х) | ф (x),
где верхняя грань берется по всем функциям g{x), удов-
удовлетворяющим неравенству ] | g (x) \q d\i (х) ^ 1, а числа р
х
и q связаны соотношением 1 = 1.
371. Доказать интегральное неравенство Минковского
i / и г ф (х) J/p + Q i g
ДЛЯ 1 < р < оо.
372. Говорят, что мера ji па множестве X имеет счет-
ную базу, если существует такое счетное семейство {AJ
238
измеримых подмножеств в X, что для любого измеримого
подмножества В и любого е > О найдется такое множе-
множество Ап, что \i(An А В)< е.
Доказать, что пространство L\ (X \i) сепарабельтто
тогда и только тогда, когда \х имеет счетную балу.
373. Доказать, что пространство Lv(X,\x) A<р<°°)
сепарабельно тогда и только тогда, когда сепарабельно
374. Доказать, что пространство ЬОО(Х, \х) либо ко-
конечномерно, либо несепарабельно.
375. Пусть (я(Х)<оо. Доказать, что при p>q>l
пространство Lp (X, \i) содержится в пространстве Lq (X, \х).
376. Доказать, что при р Ф q ни одно из пространств
Z/P(R, dx), ?g(R, dx) не содержится в другом.
377. Пусть 0 < а < р < оо. При каких р функция
f(x) = ~oT*—К принадлежит пространству LP(R+, dx) (через
R+ обозначена положительная полупрямая)?
378. Пусть числа р, q, r связаны соотношением
7 + 7 + Т = 1' f^LP(X,\i),g^Lq(X,li),h^Lr(X,li).
Доказать, что функция fgh суммируема и что ll/gfelli <
< ll/llplljrll,HAIIr.
379. Пусть 1<р^г<д<оо. Доказать, что Lv (X, \х) П
flZ/g(X, ji) содержится в Lr(X, \x) и для всякой функции
/eLp(X, ji)nLg(X, \x) справедливо неравенство ||/[г^
а =
380. Пусть jli(X)<oo. Доказать, что ^^(Х, р) с
с Lv (X, ц) при всех р > 1 и что || / Ц» = Нт || / ||р.
р-^ос
381. Доказать, что в пространстве Lp[a, b] плотны
следующие множества функций:
а) множество S [а, Ь] всех кусочно-постоянных функ-
функций;
б) множество С [а, Ь] всех непрерывных функций;
в) множество & всех многочленов;
г) множество ^0 многочленов, равных нулю на кон-
концах отрезка.
382. Найти норму функции f(x)=xa в тех простран-
пространствах Lp[0, I] (l^p^°°), которым эта функция при-
принадлежит.
383. Построить в Li(R, dx):
а) бесконечномерное замкнутое подпространство, со-
состоящее из непрерывных функций;
239
б) бескопечномерпое замкнутое подпространство, не
содержащее ни одной ненулевой непрерывной функции.
384*. Пусть \х(Х)<°°, VczLl(X9 \i)— замкнутое бес-
бесконечномерное подпространство. Доказать, что V не мо-
может содержаться в LOO{X, \x).
385. Доказать, что множество C0(R) непрерывных
финитных функций плотно в ?P(R, dx) при 1 < р < «>.
386. Доказать, что функция /eip(R,fo) непрерывна
в среднем, т. е. для всякого г > 0 существует такое б > О,
что при UI < б выполняется неравенство
j \f(z + t) — f(x)\Pdx<E.
387. Доказать утверждение задачи 386 для прост-
пространства LP(Rn, dx).
388*. Пусть M<=:Lp(J\\dx) (Kp<oo). Доказать,
что для предкомпактности М необходимо и достаточно,
чтобы выполнялись условия:
а) существует такая константа с, что П/Пр < с для
всех / е М;
б) для любого е > 0 существует такое число /?(е), что
J \f(x)\J>dx<El
в) для любого е>0 существует такое число 8(е)>0,
что при UI <б(е) выполняется неравенство
389*. Доказать изоморфизм пространств
Ьг (X, ц) g Lx (Г, v) « Lt (X X ^ Ц X v).
390. Найти крайние точки единичного шара в Lv (X, \х]:
а) при /? = 1;
б) при 1 < р < <х>\
в) при р = оо.
391*. Доказать, что пространства Li [0,1] и 1Х не изо-
изоморфны.
2. Пространства непрерывных функций.
392°. Доказать, что для любого компакта X простран-
пространство С(Х) — банахово.
240
393. Доказать сепарабельность пространства С(Х),
где X — компакт, лежащий в R\
394. Назовем линейный функционал F на С(Х) поло-
положительным, если F(f)>0 для всех неотрицательных
функций f^C(X). Доказать, что всякий положительный
линейный функционал F непрерывен и его норма равна
F(l), где 1 — функция, тождественно равная 1 на X.
395. Доказать, что любой функционал F'еС (X)
можно записать в виде F = /^ — F2, где Fx nf2- поло-
положительные функционалы (см. задачу 394).
396. Пусть X — метрический компакт, F е С {X) —
положительный функционал (см. задачу 394). Положим
для любого компакта К а X [х (К) = inf F (ф) и для
X«1
борелевского множества Е с X [i (Е) = sup [i (К), где
каЕ
К — компакт. Доказать, что |л — счетно-аддитивпая
мера.
397. Первая теорема Хелли. Доказать, что последо-
1
вательность функционалов Fn (/) = J / (х) dgn (x), где gn s
о
е F[0, 1] имеет *-слабым пределом функционал F (/) =
1
= J f(x)dg(x), где ^е^[0, 1], тогда и только тогдя,
о
когда gn (х) -+ g (х) в каждой точке отрезка [0, 1] и
вариации всех функций gn ограничены в совокупности.
398*. Вторая теорема Хелли. Пусть М сг V [0, 1].
Доказать, что если все функции из М имеют ограни-
ограниченную в совокупности вариацию, то М содержит подпо-
подпоследовательность {gn(x)), сходящуюся в каждой точке
отрезка [0, 1].
399. Пусть 9* — подпространство многочленов в
С [О, 1J. Какие из следующих линейных функционалов
на 3* допускают непрерывное продолжение на С [0, 1]
degp
(через р обозначается многочлен 2 анх ):
a) Fi{p)=aQi
б) F2 (p) = 2 aht
fe=o
degp
в) F,(p)= 2 (-1L,
fc=o
А. А. Кириллов, А. Д. Гвишиаыи 241
N
г) ^4 (р) — 2 съ.а>к1 где fcj — фиксированный вектор
из R"?
400. Пусть X — связный компакт. Доказать, что еди-
единичный шар в пространстве С(Х) имеет всего две край-
крайние точки.
401*. Доказать, что крайними точками в единичном
шаре пространства С (X) являются точечные заряды
±[ix, igX, определенные формулой <\хх, /> = /(#).
402**. Теорема Стоуна — Вейерштрасса. Пусть X —
метрический компакт, А с С(Х)— замкпутая подалгебра
в С(Х), разделяющая точки (т. е. для любых двух раз-
различных точек хх и хг из X существует такая функция
Ф^Л, что (р(х{)?= (р(х2)) и содержащая функцию, тож-
тождественно равную 1.
а) Доказать, что А =С(Х).
б) Верно ли утверждение для алгебр, не содержащих
единицу?
403*. Пусть X — линейно связный метрический ком-
компакт. Построить непрерывное отображение отрезка [0, 1]
на X.
404. Построить непрерывное отображение отрезка
[0, 1] на единичный квадрат.
405. Построить изометрическое вложение ZPB, R)
в С[0, 1] с помощью непрерывного отображения отрезка
[0, 1] на единичную сферу пространства /РB, R).
406. Доказать изоморфизм пространстве [0, 1]§С [0, 1]
и С(П), где П — единичный квадрат в R2.
407*. Доказать, что для любых компактов X и К
в R* имеет место изоморфизм С (X) g С (Y) ж C(XxY).
408. Пусть А: С(Х)-> С(Y)— изоморфизм банаховых
пространств. Доказать, что А имеет вид (Af) (у) = а(у)Х
^/(ф(у))» гДе а — непрерывная функция на F, прини-
принимающая значения ±1, а ф- гомеоморфизм Y на X.
409. Доказать, что пространство всех функций вида
f{z)+g{y), где /, ge=C[0, 1], замкнуто в С(П), где
О — единичный квадрат в R2.
410**. Доказать, что пространство С[0, 1] обладает
счетным топологическим базисом {/п(^)}} т. е. такой си-
системой функций {/п(#)}, что любая функция /еС[0, 1]
однозначно представима в виде равномерно сходящегося
с»
ряда /(я) = 2 cnfn(x).
71=1
242
411*. Доказать, что система функций {е2л1П*}, п <= Z,
не является топологическим базисом (см. задачу 410)
в пространстве СР[0, 1] всех непрерывных функций на
[0, 1] с условием /@)=/A).
3. Пространства гладких функций.
412*. Пусть 2)(N)—пространство финитных последо-
последовательностей (т. е. последовательностей, у которых лишь
конечное число членов отлично от нуля). Для любой
последовательности a=(ai, a2, ...) положительных чи-
чисел определим полунорму ра в 2)(N) равенством
оо
Pa (W) = 2 «A I *fc I-
а) Доказать, что набор полунорм ра превращает
(N) в полное неметризуемое ЛВП. б) Описать сходи-
сходимость в этом пространстве, в) Доказать, что для любой
непустой области Q в 2)(Q) есть замкнутое подпрост-
подпространство, гомеоморфное 3)(N).
413. Пусть А — линейное отображение пространства
3)(Q) в локально выпуклое пространство L. Доказать
эквивалентность следующих утверждений:
а) А — непрерывное отображение;
б) А — ограниченное отображение (т. е. переводит
ограниченные множества в ограниченные);
в) А секвенциально непрерывно (т. е. из ф„ ->¦ 0 при
п -> оо следует Пт Ацп = 0);
П-»оо
г) ограничение А на любое подпространство 2)K(Q)<=z
<= 2) (Q) непрерывно.
414. Доказать, что 2)K(Q) замкнуто в ?D{Q).
415. Пусть К — компакт в области Q ci Rn и {С/Д —
открытое покрытие К. Доказать, что существуют такие
неотрицательные функции ср* е 2)(Q) (i = 1, ..., N), что
выполняются условия:
1) supp ф» с и{ для всех i\
N
2) 2 %(х) = 1 для х<== К.
Набор (фг) называется разбиением единицы на К.
416. Доказать, что 2)(Q) плотно в ^T(Q) для любой
области Q cz Rn.
417*. Доказать, что любое замкнутое подмножество
в R" является множеством нулей некоторой функции
/#(
16* 243
418*. Пусть icj — любая числовая последователь-
последовательность. Существует ли функция f^2)(R), для которой
рп)@) = сп (л = 0, 1, 2, ...).
419. Доказать, что операции дифференцирования
д/дх{ и умножения на независимую переменную х{ явля-
являются непрерывными операторами в пространствах
> RTR
(), (),()
420. Доказать, что если /e=25(Q), ge^(fi), то /ge
е S)(Q). Является ли билинейное отображение (/; g) ¦-* /g
из а>(Й)ХгГ(Й) в S>(Q):
а) непрерывным по каждому переменному;
б) непрерывным по совокупности переменных;
в) секвенциально непрерывным по совокупности пе-
переменных (т. е. из /п -*¦ / в &(Q), gn-+ g в <?f(Q) следу-
следует Ugn-^fg в 2>(Q))?
421. Пусть /—ограниченная бесконечно дифферен-
дифференцируемая функция на прямой. Будет ли умножение на /
непрерывным оператором:
а) в S)(R), г) из 3>(R) в S(R),
б) в 5(Д), д) из 2>(Д) в <Г(Я),
в) в гГ(Д), е) из S{R) в ^(Д)?
422. Обозначим через G(R2) подпространство в <?f(R2).
состоящее из функций g, обладающих свойством:
g{x+m, y + n)=eZnim»g{x, у), т, п е= Z.
Доказать, что оператор Л, действующий по формуле
переводит 5(R) в G(R2).
423**. Пространство 2)(Тп) бесконечно дифференци-
дифференцируемых функций на гс-мерном торе Tn« Rn/Zn опреде-
определяется как совокупность тех функций ф на Тп, для ко-
которых соответствующие функции на Rn Ф(^, ..., tn) =
= ф(в2я*Ч ..., е2л"") принадлежат ^(Rn). Доказать изо-
изоморфизмы:
2) (Тт) ® 3) (Тп) « Д) (Тш) § 2) (Тп) « Д) (Tm+n).
424. а) Пусть /^S)(R"). Доказать, что для любого
/ ( / )
Д,
»6R» направленность /, (х) - / (^ + W ~ / (*) имеет
дел в 2D(Rn) при ^ -> 0.
244
б) Пусть /e<§?(Rn). Доказать, что для любого y^Rn
х / \ f(x + ty) — f(x)
направленность U (х) — имеет предел в
<T(Rn) при t-+0.
425*. Пусть {6J — последовательность положитель-
оо
ных чисел, для которой сходится ряд 2 6л- Определим
h=l
последовательность функций {fj на прямой, полагая
х
/о (х) = sgn х, fn (x) = тг /п-1 И ^ при гс > 1. Дока-
зс-бп
зать, что последовательность fn равномерно сходится
к функции /е^Г(К), обладающей свойствами:
а) /(х)= —1 при дг<0, f(x) = +1 при д:> 2 6ft;
б) |/(п)(^I^2п(б1...бп)-1 для всех igR.
426*. Пусть счетно-нормированное пространство L
с системой полунорм {pk} обладает тем свойством, что
всякое ограниченное по полунорме ph+l множество пред-
компактно по полунорме pk.
а) Доказать, что L обладает свойством Гейне — Бо-
реля.
в) Вывести отсюда, что пространства S)K(Q)i <?Г(Й),
К) обладают свойством Гейне — Бореля.
427*. Пусть L — полное ЛВП, Q — область в Rn. Че-
Через §(Q, L) обозначим пространство бесконечно диффе-
дифференцируемых вектор-функций в области Q со значения-
значениями в L. Если ipJa^A — набор полунорм, определяющий
топологию в L, то в ^Г(Й, L) топология определяется се-
семейством полунорм рк1а, где К — компакт в й, I —
~(^i, ..., In)— мультииндекс, а^4:
Pleiad =Ырра{д1Ц)(х)).
х<=К
Доказать, что <^(Q, L)—полное ЛВП, метризуемое,
если метризуемо L.
428*. Пусть Qi — область в Rn, Q2 ~ область в Rn,
Qi X Q2 с Rm^n — их прямое произведение. В обозначе-
обозначениях задачи 427 доказать изоморфизмы:
429*. Доказать изоморфизмы:
% (Йх) i % (Qa) « 8 (Qx x i\) & S (Их) g S (Q2).
245
430**. Сформулировать и доказать аналоги утвержде-
утверждений задач 427—429 для пространств 2){п) и S(Rn).
4. Обобщенные функции.
431. Доказать, что пространство основных функций
(R) вкладывается в пространство обобщенных функ-
функций 3)'(R).
432. Существует ли limsin(,z/e) в пространстве
iZ)'(R)?
433. Пусть две локально суммируемые функции / и
g в области Q ci Rn определяют одну и ту же регуляр-
регулярную обобщенную функцию (т. е. ] / (х) ф (х) dx =
G
= ) 8 (х) Ф (х) dx для всех ф ^ 3) (Q)).
Доказать, что / и g совпадают почти всюду в Q.
434. Доказать, что б-функция Дирака, определенная
ОО
формулой J б (х) ф (х) dx = ф @), не является регулярной.
— оо
435. Обобщенные функции на ^-мерном торе Тп опре-
определяются как линейные непрерывные функционалы но
пространстве 2)(Тп) (см. задачу 423). Доказать, что ряд
из регулярных обобщенных функций 2-1 exP {2nikt} (здесь
I e Rn, kt = kiti + .. . + kntn; суммирование ведется по
всем к ^ Zn) сходится в смысле 3)' (Тп) к обобщенной
функции 6@, определенной равенством J 8(t)<p(t)dt =
= Ф(О).
436. Доказать, что каждая обобщенная функция на
торе Т" (см. задачу 435) имеет конечный порядок (т. е.
продолжается до непрерывного линейного функционала
на пространстве Ск(Тп) fc-гладких функций на Тп при
некотором к).
437. Доказать, что обобщенная функция F на прямой,
сю
заданная формулой <F, ф> = Zj <P(fe) (^)> не имеет конеч-
пого порядка.
438. Доказать тождество Сохоцкого п = ?Р—=F
439. Доказать, что функции х , /Q имеют порядок 1
в любой ограниченной области на прямой, содержа-
содержащей 0.
246
440. а) Пусть L — ЛВП, V — сопряженное к L про-
пространство, снабженное *-слабой топологией. Доказать,
что всякий линейный непрерывный функционал F e(Z/)'
имеет вид F(f) = /(ф), где ф е L.
б) Доказать, что регулярные обобщенные функции
*-слабо плотны в пространствах &'(Q), 2)'(Q), ^'(R").
441*. Пусть ф g2)(R).
а) Доказать, что функция
определенная при Re X > 0, допускает аналитическое
продолжение на левую полуплоскость.
б) Доказать, что при фиксированном ^е С соответ-
соответствие ф »-* /ф (^) является обобщенной функцией (кото-
(которую обычно обозначают х^Гг/Г (к)).
в) Вычислить определенную выше обобщенную функ-
функцию для значений параметра X = —п (лг = 0, 1, 2, ...).
442. Теорема о ядре. Доказать, что всякое не-
непрерывное линейное отображение A: 2)(Qi)-> ?D'(Q2)
имеет вид
<Лф1, ф2> = J К (ж, у) фх (х) ф2 (у) dx dy,
где #e=S>'(Q1XQ2).
443. В условиях задачи 442 пусть Qi = Q2 = R. Найти
явно обобщенную функцию К е 2)' (R2), если отобра-
отображение А:
а) является естественным вложением S)(R) в iZ)'(R);
б) имеет вид ф •-* ф (а) б^.
5. Действия над обобщенными функциями.
444. Доказать равенства:
а) 6(х)Х6(у)=6(х, у);
б) 6w(x)xbii){y) =
г) ±
— ОО
445°. Доказать, что обобщенная функция
обладающая свойством F' = 0, есть константа.
247
446. Доказать, что все решения уравнения xF = О
в обобщенных функциях Fg2)'(R) пропорциональны
б-функции.
447*. Доказать, что всякая обобщеппая функция на
прямой с носителем в точке ogR имеет вид Pi —)ба(^)Л
где Р — многочлен.
448. Пусть gel'(R) задает взаимно-однозначное ото-
отображение прямой на себя и /ie^(R)—обратное отобра-
отображение. Выразить явно через 8(х) и ее производные
функцию 6'(#(#)).
449. Обобщенная функция F на прямой называется
однородной степени (X, е), где Х^С, 8 = 0 или 1, если
для любого t ?= 0 справедливо равенство F(tx) =
= \t\2(sgnt)eF(x). Доказать, что однородная функция
степени (X, е) на прямой удовлетворяет дифференциаль-
дифференциальному уравнению xFf = XF.
450. Доказать, что для всех 1еС, е = 0, 1 сущест-
существует ровно одна с точностью до числового множителя
однородная обобщенная функция на прямой степе-
степени (X, г).
451*. Доказать, что единственными обобщенными
функциями на прямой, инвариантными относительно
сдвигов, являются константы.
452*. Пусть F — обобщенная функция на плоскости,
инвариантная относительно сдвигов вдоль осп Ох.
а) Доказать, что существует такая обобщенная функ-
функция / на прямой, что <F, ср> —//, J ц(х, у) dx
\ R
б) Выразить F в виде прямого произведения.
453*. Пусть F — обобщенная функция на плоскости
с носителем — отрезком [0, 1] на оси Ох.
а) Доказать, что существуют такое число N и такие
обобщенные функции на прямой /0, Д, ..., fN, что
б) Сформулировать это утверждение в терминах пря-
прямого произведения обобщенных функций.
454*. Доказать, что регулярная обобщенная функция
f(x)= exp {iex} принадлежит 5'(R), но ее производная
в смысле обобщенных функций не совпадает с /' {х) =
248
455. Решить уравнение sin:r •/(#) = 0 в обобщенных
функциях на прямой.
456*. Пусть обобщенная функция F в Rn удовлетво-
удовлетворяет соотношению/^ х\— R2\F(x) = 0n инвариантна от-
I * /
носительно вращений R". Доказать, что <F, ф> =
= с \ 4>{x)do (х), где с — константа, а о — стандартный
sR
элемент объема на сфере SR радиуса R в R\
457. Пусть обобщенная функция F на прямой обла-
обладает свойствами:
а) F(x+l) = F(x);
б) e2nixF(x) = F(x).
Доказать, что F(х) = с *? 6{х — к).
458. Доказать, что всякая обобщенная функция F на
прямой, удовлетворяющая уравнению. F'(x) = a (x)F(x) +
+ b(x), a, fre^(R), является регулярной (и, значит,
совпадает с обычным решением этого уравнения).
459**. Пусть F — обобщенная функция в Rn, у кото-
dhF . _ . ^
рои все частные производные вида —^-, 1 ^ i ^ щ
г
О ^ к ^ г, принадлежат Z/2(Rn, dz). Доказать, что при
г > -н- + I функция F совпадает почти всюду с функцией
класса Cl(Rn).
460*. При каком условии на коэффициенты {сп} ряд
2 cne2ninx сходится в S>'(R)?
n=Z
461. Можно ли определить операцию умножения
в iZ)'(R) так, чтобы она была непрерывна по каждому
переменному и совпадала с обычным умножением на ре-
регулярных функциях?
§ 5. Гильбертовы пространства
1. Геометрия гильбертова пространства.
462. а) Доказать, что соответствие L ->• 27, построенное
в п. 1 § 5 гл. III раздела «Теория», определяет ковариант-
ный функтор из категории предгильбертовых пространств
в категорию гильбертовых пространств.
б) Покажите, что L можно определить как универ-
универсальный объект в подходящей категории.
463. Доказать, что система функций еп (х) = е2лЫх,
ne=Z, является гильбертовым базисом в L2@, 1).
249
464*. Применить процесс ортогонализации к последо-
последовательности одночленов 1, х, х2, ... в следующих гильбер-
гильбертовых пространствах:
а) ?2([-1, 1], dx); в) La([0, оо), e~xdz);
б) L2([-l, 1], y=l); Г) M(-~f оо),*-1
465. Применить процесс ортогонализации к последо-
последовательности одночленов 1, z, z2, ... в предгильбертовых
пространствах многочленов со следующими скалярными
произведениями:
а) (Л<?)= f J P(z)QjI)dxdy;
\z\<R
б) iP*® =
l
с
466. Выразить линейный функционал Fx(f) = f(x) в
пространствах задачи 465 в виде скалярного произве-
произведения.
467*. Доказать, что пополнения предгильбертовых
пространств, рассмотренных в задаче 465, состоят из всех
аналитических функций с суммируемым квадратом по
мере dxdy в круге радиуса R в случае а) и суммиру-
суммируемых по мере е~№ dxdy на плоскости в случае б).
468*. Доказать, что ортогональное дополнение к си-
системе функций еп(х) = е2лЫх, п^Ъ, в пространстве
L2([a,b],dx)
а) равно нулю при \b — a\ ^ 1;
б) отлично от нуля при \Ь — а\ > I.
469*. Пусть Во — пространство всех тригонометриче-
тригонометрических полиномов (т. е. конечных линейных комбинаций
функций eiKx, X^R). Введем в Во скалярное произве-
произведение
А
А->+оо *л JA
а) Доказать, что соответствующее гильбертово про-
пространство В несепарабельно и имеет континуальный гиль-
гильбертов базис {eiKx}k(BR-
б)** Доказать, что В содержит пространство почти
периодических непрерывных функций, т. е. замыкание
Во по равномерной норме || /1| = sup | / (х) |, но не совпадает
с ним.
250
470*. Пусть \i — мера па прямой, определенная фор-
формулой \х (А) = card А (число точек в А). Доказать, что
L2(R, |li) несепарабельно и изоморфно пространству за-
задачи 469.
471. Доказать, что в Ьг[а, Ь] есть ортонормирован-
ные полные системы, состоящие из
а) многочленов;
б) ступенчатых функций;
в) тригонометрических многочленов;
г) функций, лежащих в наперед заданном плотном
подпространстве.
472. Найти в гильбертовом пространстве ?2@, 1) ор-
ортогональное дополнение к следующим множествам:
а) многочленов от х;
б) многочленов от х2;
в) многочленов с нулевым свободным членом;
г) многочленов с нулевой суммой коэффициентов.
473°. Найти в предгильбертовом пространстве С[— 1, 1]
всех непрерывных функций на [—1, 1] со скалярным
1
произведением (/, g) = 1 / (х) g (x) dx ортогональное допол-
-1
ненпе к пространствам:
а) функций, равных нулю при х ^ 0;
б) функций, равных нулю в точке х = 0.
Верна ли в этих случаях теорема об ортогональном
дополнении?
474. Пусть et — характеристическая функция отрезка
[0, t], t^Q. Найти углы между двумя хордами кривой et
bL2@, оо):
а) если хорды имеют общий конец и направлены в
разные стороны;
б) если хорды имеют общий конец п направлены в
одну сторону.
475. а) Доказать, что во всяком предгильбертовом
пространстве выполняется тождество параллелограмма:
\\х - у\\г + \\х + у\\2 = 21Ы12
б)* Показать, что во всяком нормированном линейном
пространстве над R или С, в котором выполняется это
тождество, можно ввести такое скалярное произведение,
что будет справедливо равенство 1Ы12=(х, х).
251
476. Доказать, что в комплексном гильбертовом про-
анстве справедливы равенства:
а\ (~, ,,\ *¦ \ || r I ?>2nik/N ж» ||2 yy2nik/N ттлтт /V ^"!> Ч*
/ \ > У) ДГ ^^ || «^ "Г С У || ^ 11_р*1 IT j;^> C»J
«)(*.»)-srJl*
О
477. Пусть в гильбертовом пространстве Н семейство
векторов Ixj обладает свойствами: \\хп\\ = 1, (#«, ят) = с
при тФп. Доказать, что существует слабый предел по-
последовательности {хп}.
478. Доказать, что для ортогональной системы векто-
векторов {хп} следующие условия равносильны:
а) 2 хп сильно сходится;
п
б) 2 хп слабо сходится;
п
в) 2II хп II2 сходится.
п
479°. Пусть 5 — любое подмножество в гильбертовом
пространстве Н. Доказать, что (*?-L)-L совпадает с замыка-
замыканием линейной оболочки S.
480. Пусть L — подпространство в гильбертовом прост-
пространстве //, /о — линейный непрерывный функционал на L.
Доказать, что /0 имеет единственное продолжение на Я
с сохранением нормы.
2. Операторы в гильбертовом пространстве.
481. а) Доказать, что всякий оператор А в комп-
комплексном гильбертовом пространстве Н однозначно пред-
представим в виде А = В + iC, где В и С — эрмитовы опера-
операторы. (Иногда пишут В = Re А, С = Im A.)
б) Проверьте, что А нормален тогда и только тогда,
когда Re Л и Im А перестановочны.
в) Доказать, что оператор А унитарен тогда и только
тогда, когда он нормален и (Re АJ + AтАJ = 1.
482°. Доказать, что
а) всякий оператор Р в гильбертовом пространстве,
обладающий свойством Р2 = Р* = Р, является ортопроек-
тором, т. е. оператором проектирования на замкнутое
подпространство //А параллельно его ортогональному до-
дополнению Нг,
б) всякий оператор S, обладающий свойством S'1 =
= S* = S, является ортогональным отражением в неко-
некотором подпространстве.
252
483. Доказать равенства \\А*А\\ = IL<L4*II = ИЛИ2 = IU*Ila
для любого ограниченного оператора А в гильбертовом
пространстве Я.
484. Пусть А — положительный оператор в предгиль-
предгильбертовом пространстве Я, х — любой вектор из Я.
а) Доказать, что числовая последовательность а(&) =
[ \
1 / ль \
= \п(Акх, х) выпукла, т. е. ay)
б) Доказать неравенство Ых\\2 ^QA(x)-WAW, где
QA(x) = (Ax,x).
485. Пусть \Ап} — монотонная ограниченная последо-
последовательность операторов в гильбертовом пространстве Я.
Доказать, что существует s-lim An.
П-»оо
486. Пусть Hi — замкнутое подпространство в гиль-
гильбертовом пространстве Я, Я2 = Я^, Р — ортопроектор на
Ни А — оператор в Я. Выразить в виде алгебраического
соотношения между А и Р следующие утверждения:
а) Н{ инвариантно относительно А]
б) Hi и Я2 инвариантны относительно А.
487. Пара конечномерных подпространств (L4, L2) в
гильбертовом пространстве Я (над R или С) называется
конгруэнтной паре (Ми М2), если существует такой уни-
унитарный оператор U в Я? который переводит L{ в Mt
и L2 в М2. Необходимыми условиями конгруэнтности
являются равенства dim Lv = dim Mu dim L2 = dim M2.
В дальнейшем они считаются выполненными. Пусть Pi —
ортопроектор на Lu Qi —ортопроектор на М{ B=1, 2).
а) Пусть dim L{ = dim M,{ = 1. Доказать, что для конг-
конгруэнтности пар (Lt, L2) и (Л/i, Л/2) в вещественном про-
пространстве необходимо и достаточно, чтобы были равны
углы между векторами, порождающими эти пространства.
б) Выразить угол между векторами, порождающими
пространства L{ и L2, через проекторы Р{ и Р2-
в) Найти критерий конгруэнтности двух пар одномер-
одномерных подпространств в комплексном пространстве.
488. В обозначениях задачи 487 пусть Xi, ... Хя, .. .—
собственные значения оператора РХР2РХ.
а) Доказать, что X* — веществе иные числа, заключен-
заключенные между 0 и 1.
б) Доказать, что отличных от нуля чисел Х< не боль-
больше чем k = min(dim Lb dimL2). Расположим их в поряд-
порядке убывания и положим ф,= arccos УХ< (?=1, 2, ..., Л).
Числа фг называются углами между подпространствами
Ьг и L2.
253
в) Если dim L{ = 1, dim M{ = 1, то имеется единствен-
единственный угол ф1 между Li и L2 и единственный угол ifi между
Mi и М2. Доказать, что пары (?,, ?2) и (Д/i, М2) кон-
конгруэнтны тогда и только тогда, когда cpi = ifi.
г)* Доказать общий критерий конгруэнтности: пара
(Lu L2) конгруэнтна паре (Ми М2) тогда и только тогда,
когда углы между L{ и L2 равны соответствующим уг-
углам между Mi и М2.
д) Раствором подпространств L{ и L2 называется чи-
число llPi — Р2И. Выразить это число через углы между
Ь^ и L2.
489. Доказать, что для унитарности оператора U&
&&(Ии Н2) необходимо, чтобы U переводил любой гиль-
гильбертов базис в Я! в базис в Я2, и достаточно, чтобы U
переводил некоторый базис в Hi в базис в /72.
490. Для любого оператора А в гильбертовом прост-
пространстве доказать соотношения:
а) *
б)
(черта означает замыкание).
491. Пусть последовательность операторов {Ап} в гиль-
гильбертовом пространстве // слабо сходится к А и, кроме
того, для любого х^П WAnxW -* WAxW. Доказать, что {AJ
сильно сходится к Л. В частности, это означает, что для
последовательностей унитарных операторов сильная и
слабая сходимости к унитарному пределу совпадают.
492. Пусть 2(Я)— алгебра ограниченных операторов
в гильбертовом пространстве Я. Доказать, что всякий
автоморфизм ^(Я), перестановочный с операцией сопря-
сопряжения, имеет вид A*-*>UAU~l, где U — унитарный опе-
оператор в Я.
493. Найти все замкнутые по норме идеалы в алгебре
2'(Я) (см. задачу 492) для сепарабельного гильбертова
пространства Я.
494. Вывести из теоремы Куранта следующий принцип
промежуточности. Пусть А — компактный эрмитов опера-
оператор в гильбертовом пространстве Я, Я4 — замкнутое под-
подпространство коразмерности 1 в Я (т. е. dimHi ~ i),
Р — ортопроектор на Яь Тогда для собственных чисел
{Xi) оператора А и собственных чисел {jxj оператора
РАР, занумерованных так же, как в теореме Куранта,
имеем
Х-1 < y-t < Л-* < ... < 0 < ... < На < Ла < Ht < Я,!.
254
495*. а) Доказать, что всякий положительный опера-
оператор А в гильбертовом пространстве имеет положительный
квадратный корень В, который может быть получен как
сильный предел последовательности 5„, определенной
начальным условием Во = О и рекуррентной формулой
Л -Л , А~Вп
б) Доказать единственность положительного квадрат-
квадратного корня В из положительного оператора А.
496. а) Доказать, что в конечномерном гильбертовом
пространстве Я всякий оператор А допускает запись в
виде A=RU и в виде А = VS, где R и V — положи-
положительные операторы, a U и V — унитарные. Эта запись
называется полярным разложением А. (В случае
dim# = l она сводится к записи комплексного числа а
в виде гегф.)
б) Доказать, что R и 5 определяются по оператору А
однозначно. Верно ли это относительно U и V?
в) Проверить, что оператор Т одностороннего сдвига
в 1г не допускает полярного разложения в смысле п. а).
497. Пусть U — оператор в гильбертовом пространстве
Я, Н^ — ортогональное дополнение к ker U, Я2 — замыка-
замыкание im U. Оператор U называется частично изо-
изометрическим, если он изометрично отображает Hi на Я2.
Выразить это свойство в терминах ортопроекторов Ри Р2
на Hi и Я2.
498. Пусть А — оператор в гильбертовом пространстве
Я; доказать, что существует единственное представление
А в виде А == RU, где R — положительный опера-
оператор, a U—частично изометрический оператор (см.
задачу 498), обладающий свойством kerf/ = ker4.
Э-to представление также называется полярным разло-
разложением А.
499. Оператор А называется оператором Гильберта —
Шмидта, если для некоторого гильбертова базиса \}
сходится ряд 2 II Ц II2
а) Доказать, что если А — оператор Гильберта —
Шмидта, то величина ||4|2 = / 2 || Ar,jV 2 не зависит от
выбора базиса и определяет норму в пространстве «2^2(//)
операторов Гильберта — Шмидта, мажорирующую обыч-
обычную норму оператора.
255
б) Доказать, что норма Н-Н2 порождается скалярным
произведением <4, Ву& ,н) = 2 j
r
v
любой гильбертов базис в Я.
в) Доказать, что всякий оператор Гильберта — Шмид-
Шмидта компактен.
г) Построить изоморфизм пространства 3?г(Н) и гиль-
гильбертова тензорного произведения Я на Я'.
д) Доказать, что всякий оператор Гильберта — Шмид-
Шмидта в Ь2(Х, |ы) является интегральным оператором с яд-
ядром K^L2(XXX, jbiXjn).
500. Оператор А в гильбертовом пространстве Я на-
называется ядерным, если он представим в виде Л=5С,
где В и С — операторы Гильберта — Шмидта.
Доказать, что
а) если А — ядерный оператор, то для любого базиса
{г/т}ТеГ в Я ряд 2 {АУу* Уу) сходится и его сумма не за-
зависит от выбора базиса; она обозначается tr А и назы-
называется следом оператора А;
б) если А — ядерный и В — ограниченный операторы,
то АВ и В А—ядерные операторы и tr AB = tr В А,
в) Совокупность всех ядерных операторов образует
банахово пространство 3?i(H) относительно нормы II-lit,
определяемой формулой \\AW=trR, где А = RU — поляр-
полярное разложение А.
г) Пусть Ж (Я)—пространство компактных операто-
операторов в Я с обычной нормой. Доказать изоморфизмы:
ЛГ(Я)'57(Я) 5(Я)/^(Я
()() ()()
501*. Пусть Я — гильбертово пространство, X—мно-
X—множество с мерой jh. Набор единичных векторов {ухеЛ из
Я называется непрерывным базисом (в другой терминоло-
терминологии— когерентной или переполненной системой), если
для любого | е Я функция х *-+ (?, ?х) (и-измерима и
справедливо равенство
ВЕР —
а) Построить непрорывные базисы в пространствах
задачи 465.
б) Доказать, что отображение ||-*E»Ы является
изометрическим отображением Я в Ьг(Х, \i).
в) Доказать равенство dim Я = }л(Х).
г)** Доказать равенство tr А = J (Л?х, 2jx) d|i (я) для
ядерного оператора А.
256
502**. Пусть А — ядерный интегральный оператор в
пространстве L2[Q, 1] с непрерывным ядром К(х1 у).
Доказать тождество
ГЛАВА IV
ПРЕОБРАЗОВАНИЕ ФУРЬЕ И ЭЛЕМЕНТЫ
ГАРМОНИЧЕСКОГО АНАЛИЗА
§ 1. Свертки на коммутативной группе
1. Свертки основных функций.
503. Пусть G — конечная группа, К — некоторое поле,
а) Доказать, что центр K[G] состоит из функций й?
, обладающих свойством a(gh) = a(hg) для любых
Kg
б) Классом сопряженных элементов в G называется
множество вида Ch = {ghg~\ g^G). Доказать, что число
различных классов сопряженных элементов в G равно
размерности центра K(G).
в) Известно, что алгебра K(G) коммутативна. Верно
ли, что коммутативна группа G?
504. Пусть Цп означает циклическую группу порядка п.
а) Доказать, что С(Цп) изоморфна прямой сумме п
экземпляров поля С.
б) Верно ли аналогичное утверждение для поля R?
505. Доказать изоморфизм R(S3) и R + R+Mat2R.
506. Доказать, что естественное вложение G в K(G)
является универсальным объектом для категории отобра-
отображений ф группы G в ассоциативные /v-алгебры с едини-
единицей, обладающих свойствами cp(gi?2) = ф(#1)ф(?г), фA) =
= 1 (морфизм объекта ф: G -> А в объект if: G-* В оп-
определен как гомоморфизм х- А -+¦ В такой, что диаграмма
коммутативна). Останется ли утверждение в силе, если
отказаться от условия фA)=1?
17 а. А. Кириллов, А. Д. Гвишиани 257
507. Пусть G = Rn или ТЛ. Доказать, что свертка двух
ограниченных функций из ?i(G, M<) является непрерыв-
непрерывной функцией.
508. Пусть функция ф в Rn финитна и к раз не-
непрерывно дифференцируема, а функция / принадлежит
Li(Rn, dx). Доказать, что свертка ф*/ имеет непрерыв-
непрерывные производные до к-то порядка.
509. Пусть L — некоторое банахово пространство функ-
функций на группе G с нормой II • HL, обладающей свойст-
свойствами:
1) ИГ (a) f\\L = II/IIL, где Т (а) — оператор сдвига:
T()f( f( + )
()f() f( );
2) 11Г(а)/-/11ь-*0 при а->0 в G.
Доказать, что оператор 5(ф), (p&Li(G, ju), переводит
пространство L в себя и имеет в этом пространстве норму,
не превосходящую ЦфЦц-
510. Говорят, что последовательность функций {/J на
топологическом пространстве X с борелевской мерой \х
является дельтообразной для точки а^Х, если выполня-
выполняются условия:
) H
2) [
х
3) для любой окрестности U точки а при к
Доказать, что следующие последовательности дельто-
дельтообразны для точки О е Rn:
а)* }п(х) = кпу(кх), где ф — любая борелевская функ-
функция на Rn, обладающая свойствами 1), 2);
о, N>i,
где ick} — подходящая последовательность констант.
511. Пусть G — коммутативная топологическая группа
с инвариантной мерой ц, {/J — дельтообразная последова-
последовательность для точки fleG (см. задачу 510), L — банахово
пространство функций на G, удовлетворяющее условиям
задачи 509.
Доказать, что S(fh)-*- Т(а) при к -> оо.
512. Пусть функция ф на Rn внутри шара радиуса R
совпадает с некоторым многочленом, а вне этого шара
равна нулю; функция ^^Li(Rn1 dx) имеет носитель в
шаре радиуса г < R.
258
Доказать, что свертка ф * ф имеет носитель в шаре
радиуса R + г и совпадает с некоторым многочленом
в шаре радиуса R — r. (Все шары имеют центром точ-
точку 0.)
513. Теорема Вейерштрасса. Доказать, что всякая не-
непрерывная функция в Rn может быть на любом компакте
равномерно аппроксимирована многочленом.
514. Пусть f^Lt(G, \x). Доказать, что 5(/)—ограни-
5(/)—ограниченный оператор в гильбертовом пространстве L2(G1 \x).
Вычислить сопряженный оператор 5(/)*.
515. Пусть /i и /2 принадлежат L2(G, ц). Доказать,
что свертка /А */2 определена и принадлежит LOO(G, \x).
516. Определим операцию * в пространстве функций
на группе G равенством /*(#) = /(— х).
Доказать, что
а) /Г * /* = (/i * /2)* Для /lf /2 е= Lx (G, ц);
б) (/i */*) @) = (Л, /2) для /lf /2 e L2 (G, ц).
517. Определим функцию eh на Тп формулой еА(^) =
= е2лт (здесь A;eZn- мультииндекс, Ы = A^t + ...
... + U).
Доказать тождества
ек * eh = efc, eA * ^ = 0 при к Ф /.
518. Тригонометрическим многочленом на Тп называ-
называется линейная комбинация функций ek, определенных в
задаче 517. Доказать, что совокупность тригономет-
тригонометрических многочленов образует идеал в алгебре
MTn, dt).
519*. Построить на торе Тп дельтообразную последо-
последовательность, состоящую из тригонометрических много-
многочленов.
520. Доказать, что тригонометрические многочлены
образуют плотное множество в СА(ТП) при любом к.
521*. Пусть /i и /2 — локально суммируемые функции,
носители которых ограничены слева. Тогда можно опре-
определить свертку /i * /2, которая обладает тем же свойством.
Вычислить явно свертки:
а) [9(*)*«]*[9(*)*<1];
б) [e"9(x)]*[ete9(x)].
522**. Пусть числа p^l, <Z^1, г>1 связаны равен-
равенством 1/р + l/q — 1/г = 1. Доказать, что
L,(G, v)»Lt(G, n).<=L,(G, ц)..
17* 259
2. Свертки обобщенных функций.
523. Записать в виде свертки дифференциальный опе-
п
ратор с постоянными коэффициентами L: /-> 2 cjj .
524°. Доказать тождество /*1 = </, 1> • 1 для любой
обобщенной функции / = <§f'(R).
525. Положим /(#) = /(--#)• Доказать тождество
(/i * /2)^ = /1 * /2' гДе А и /2 — обобщенные функции, одна
из которых имеет компактный носитель.
526*. Пусть /eS'(Rn), <pe=S(Rn). Свертка /*ф оп-
определяется формулой /*Ф=?(фO, т.е. </*ф, г|:> =
= </, ф * if>>. Доказать, что
а) / * ф— регулярная обобщенная функция;
б) (/*ф) (*)=</, Г(-*)ф>;
в) (/ 4 ф) (х) растет на бесконечности не быстрее мно-
многочлена от Ы.
527*. Пусть /e<T'(Rn), фе^И"). Свертка /*ф
определяется формулой /*Ф = ?(ф)/ (ср. с задачей 526).
Доказать, что:
а) / * ф — регулярная обобщенная функция;
б) /
в) /v()
г) оператор S(/): <^(Rn)-> <^(Rn) непрерывен.
528. Пусть /^^'(R77). Доказать непрерывность опе-
оператора S(f): ^(R^-^^iR71).
529. Пусть &(Тп)— пространство бесконечно диффе-
дифференцируемых функций на торе Тп (с топологией равно-
равномерной сходимости всех производных), <§' (Тп)-- сопря-
сопряженное пространство обобщенных функций. Определить
операцию свертки в <S'(Tn) и доказать, что ^(Т71)*
^(Т)^(Т)
()()
530. Доказать, что пространство тригонометрических
многочленов плотно в <zf (T).
531. Доказать утверждение задачи 530 для <?Г(ТП).
532*. Пусть /i и /2 — финитные непрерывные функции
на полупрямой [0, °°). Положим Ft = /г(У^2 + г/2).
Доказать, что свертка F = FX*F2 также имеет вид
F(x, y)=zi0x2 + У2), ГДе /—некоторая финитная непре-
непрерывная функция на [0, °°), и дать явное выражение /
через /i и /2.
533*. Пусть (В± [R] — подпространства в <^(R), состоя-
состоящие из функций с носителем, ограниченным слева или
справа, S>± (R) — аналогичные подпространства в 2)' (R).
260
а) Доказать изоморфизм{<S± (R))' = iZ) +(R)(сходимость
фп-> Ф в <^±(R) определяется условиями: эиррфп огра-
ограничены с одной стороны общей константой; фЛ -> ф в
смысле <§T(R)).
б) Определить операцию свертки в iZ)±(R).
в) Доказать, что S± (R) * S>± (R) cz #± (R).
534*, Положим при а>0 fa{x) = щ^ха~гв (х).
а) Проверить, что /а е S)+(R) при а> —1.
б) Доказать тождество /« * /э = /а+р.
в) Доказать тождество *^j/a = /a-i при a> 1.
г) Найти предел /а при а-* О в iZ)+ (R).
535*. Построить в 3)+ (R) семейство операторов /(а),
a^R, обладающее свойствами:
а) /(/ / /
X
б) / A) ф (х) - J ф (О Л для ф е ar'+ (R);
в) 7(-1)Ф(:г) = ф'(:г) для Фегг+(Н);
г) 7(a)/p = /a+p при Р>—1, а + ^>-1 (/а опреде-
определены в задаче 534).
Оператор /(а) называется оператором дробного ин-
интегрирования порядка а (или дробного дифференцирова-
дифференцирования порядка — а) и обозначается иногда через (d/dx)~a,
536*. Пусть обобщенная функция / на R2 имеет вид
2JI
/, ф> = 4г J ф
sin
Доказать, что / * / — регулярная обобщенная функция,
и вычислить ее.
537*. Вычислить свертку / * /, где / — обобщенная
функция на R3, задаваемая формулой </, ф> =
e JT I ' ^1? Х^ Х'^ ^a' Где ^ ~~ сФеРа "^" = ^i ^a "" эле"
мент площади сферы.
§ 2. Преобразование Фурье
1. Характеры коммутативной группы.
538. Найти явный вид характеров циклической груп-
группы Цп порядка п.
261
539. Доказать, что всякая конечная коммутативная
группа G изоморфна (не канонически) своей двойствен-
двойственной группе G.
540. Обобщенным или неунитарным характером груп-
группы G называют ее гомоморфизм в мультипликативную
группу поля комплексных чисел.
Доказать, что для компактной группы G все обобщен-
обобщенные характеры являются обычными. Найти обобщенные
характеры групп: a) Z, б) R, в) С, г) R*, д) С* (* озна-
означает мультипликативную группу).
541*. Доказать, что если группа G компактна, то двой-
двойственная группа G дискретна.
542*. Доказать, что если группа G дискретна, то
двойственная группа G компактна.
543. Пусть х — характер группы R, рассматриваемый
как элемент пространства iZ>'(R). Доказать, что х удов-
удовлетворяет дифференциальному уравнению х' = с%, где с —
некоторая константа.
544. Пусть % — характер группы G, f^Li(G1 \x). До-
Доказать, что х * / = CU гАе
545. Пусть G — компактная группа с инвариантной
мерой ц, нормированной условием jx(G)=l. Доказать,
что для любых двух характеров %и fc^G справедливо
соотношение
-
О, если
Xi, если
546. Доказать, что все характеры группы Тп исчерпы-
исчерпываются функциями ek(t) = е2лШ (ср. с задачей 517).
547*. Доказать, что соответствие G -> G определяет
контравариантиый функтор в категории топологических
абелевых групп.
548. Пусть L — ЛТП над нолем R, рассматриваемое
как топологическая абелева группа. Найти двойственную
к L группу L.
549**. Пусть QP — поле /?-адических чисел (см. задачу
38), Ър — подкольцо целых /?-адических чисел. Найти
двойственные группы к следующим группам: a) Qp, б) Zp,
в) Qp/Zp.
262
550**. Пусть Go — замкнутая подгруппа в G, d =
= G/Go — соответствующая фактор-группа. Это кратко за-
записывается в виде точной последовательности
где 0 — тривиальная группа из одного элемента. Дока-
Доказать, что двойственная последовательность
также точна.
551*. Найти двойственную группу G, если G = Q/Z.
(Группа G естественно отождествляется с группой всех
корней из единицы с помощью отображения х mod Z -*¦
-* elKix.)
оо
552. Пусть G = JX Ц2—группа всех последовательно-
последовательному
стей нулей и единиц (групповая операция — сложение по
модулю 2; топология определяется покоординатной схо-
сходимостью).
а) Доказать, что G компактна.
б) Доказать, что двойственная группа изоморфна
оо
счетной группе 2j Ц2 всех финитных последовательно-
последовательного i
стей нулей и единиц (групповая операция — сложение по
модулю 2; топология дискретна).
553. Пусть а — иррациональное число, /^LJT, dt) —
функция, обладающая свойством 1{t + a) = f{t) почти
всюду. Доказать, что / почти всюду постоянна.
554. а)° Пусть /eLt(R, dx). Доказать, что f(A,)->0
ПРИ X -> оо.
б) Пусть группа G имеет вид R" X Тт X Zh и М
^Lt(G, (j,). Доказать, что f{z)-+0 при х -> оо В G =
= R" X Zm X Т\
555**. Пусть G = Qp — аддитивная группа поля /?-ади-
ческих чисел. Обозначим через 3)(G) пространство фи-
финитных локально постоянных функций на G. Доказать,
что преобразование Фурье переводит пространство 2){G)
в себя.
556*. Пусть S (Z) — пространство двусторонних последо-
последовательностей {сп}, обладающих свойством сп = O(n~h) для
всех к. Топологию в 5(Z) зададим семейством норм
Рк (W) = sup I
n
263
Доказать, что преобразование Фурье устанавливает
изоморфизм линейных топологических пространств <У(Т)
и S(Z).
557. Непрерывная функция / на группе G называется
положительно определенной, если для любого конечного
набора #i, ..., хп элементов G матрица А с элементами
ahi = f(xk — Xj) положительно определена. Доказать следу-
следующие соотношения для положительно определенной
функции /:
а) !/(*)! </@),/(*)-/(-»);
б) \f(O)f(x-y)-f(x)f(y)\> <
/Ы12)
558. а) Доказать, что линейная комбинация характе-
характеров группы G с положительными коэффициентами явля-
является положительно определенной функцией на G.
б)* Доказать, что произведение двух положительно оп-
определенных функций является положительно определен-
определенной функцией.
в) Доказать, что если cp^Li(G, ц), то функция ф * ф*
(где ф*(#) = ф(—х)) положительно определена.
559. Пусть G — конечная группа. Доказать, что / по-
положительно определена на G тогда и только тогда, когда
функция f неотрицательна на G.
560. Пусть tp^Li(G, \х) и ф > 0. Доказать, что ф
положительно определена на G.
2. Ряды Фурье.
561°. Что можно сказать о коэффициентах Фурье
функции / на Т, если известно, что /
а) четна: f(t) = f(l-t),
б) нечетна: /(?) =-/A - 0,
в) вещественна почти всюду на Т?
562. Пусть функция / на Т имеет кусочно-дифферен-
кусочно-дифференцируемую к-ю производную. Каково максимальное число
Z, для которого можно гарантировать оценку \сп\ =
= о(\п\-1) для коэффициентов Фурье функции /?
563. Доказать, что образ пространства Ch(T) при пре-
преобразовании Фурье содержится в множестве последова-
последовательностей, обладающих свойством |сп| = o(\n\~h), и со-
содержит множество последовательностей, обладающих
свойством \сп\ =0(?г~*-1-е), е >0.
564. Пусть Wh(T)— совокупность функций на Т, у ко-
которых к-я обобщенная производная принадлежит Ь2(Т, dt).
Дайте описание этого пространства в терминах коэффи-
коэффициентов Фурье.
264
565. Выразить в терминах коэффициентов Фурье сле-
следующие свойства функции /:
а) /(*+1/2)-/@;
б) f(t+ l/k) = 'kf(t); при каких к е Z существуют не-
ненулевые функции, обладающие этим свойством?
566*. Точная последовательность 0 ->- Цп —> Т —> Т ->¦ О
задается вложением ?: Дп ->- Т по формуле i(kmodn) =
==e2jllft/n и проекцией р: Т -> Т по формуле p(z) = zn.
Описать двойственную точную последовательность.
567. Пусть функция / суммируема на отрезке [0, 1/4].
Как нужно продолжить / на отрезок [0, 1], чтобы ее коэф-
коэффициенты Фурье удовлетворяли соотношениям c2h = О,
Czu-i = —Ci-zh-
568°. Пусть {сп} — коэффициенты Фурье функции /е
eZ,4(T, d?). Найти коэффициенты Фурье {cn(h)} для
сглаженной функции (или функции Стеклова) fh(x) =
W J
J
569. Какими свойствами характеризуются последова-
последовательности {сп} коэффициентов Фурье:
а) тригонометрических многочленов,
б) многочленов от U),
в) многочленов от U—1/2}?
570*. Доказать, что непрерывная функция / на Т
положительно определена (см. задачу 557) тогда и толь-
только тогда, когда ее коэффициенты Фурье неотрицательны.
571. Последовательность {сп} (n^Z) называется поло-
положительно определенной, если для любой финитной после-
последовательности {zj (n^Z) справедливо неравенство
n,m
Доказать, что положительно определенная последова-
последовательность ограничена и обладает свойствами: сп = с_п,
572. Доказать, что всякая положительно определен-
определенная последовательность (см. задачу 571) является преоб-
преобразованием Фурье конечной борелевской меры \х на Т:
1
о
573. Пусть U — унитарный оператор в гильбертовом
пространстве Я, Ъ, е Я. Доказать, что последовательность
сп = (?/"!, |) положительно определена.
205
574. В условиях задачи 573 предположим, что 1 —
циклический вектор для U (т. е. линейная оболочка век-
векторов Un% (n^Z) плотна в Я). Построить изоморфизм
Н и L2(T, \х), где ji — преобразование Фурье последова-
последовательности {сп}, при котором оператор U переходит в ум-
умножение на e2nit.
575*. Пусть / — кусочно-дифференцируемая вещест-
п
венная функция на Т, Sn = 2 cke2nikt — частичная сум-
h=-n
ма ее ряда Фурье, Гп с Т X R — график функции Sn. Най-
Найти предельное множество для {Гп}, т. е. совокупность
всех предельных точек последовательностей {^п) G»еГп).
576. Доказать, что обобщенная функция Т определя-
определяется однозначно своими коэффициентами Фурье.
577. Обобщенная функция / на Т называется поло-
положительно определенной, если для любой функции ф е
е^Г(Т) справедливо неравенство </, ф*ф*>^0. Охарак-
Охарактеризовать положительно определенные обобщенные функ-
функции в терминах их коэффициентов Фурье.
578. Пусть а — иррациональное число, а X — измери-
измеримое подмножество Т, инвариантное относительно сдвига на
а. Докажите, что если ji — мера Хаара, то либо |i(X) = 0,
либо jui (X) = 1. (Это свойство для преобразований в про-
пространстве с мерой называется эргодичностью; преобразо-
преобразование называется эргодическим, если для любого изме-
измеримого подмножества либо оно само, либо его дополне-
дополнение имеют меру нуль.)
579*. Решить уравнение теплопроводности -гг = —%-
01 дх
ка Т с начальными условиями и @, х)=и(х) с помощью
метода Фурье.
3. Интеграл Фурье.
580. Пусть Dh = d/dxh, Mh — оператор умножения на
xk. Введем в пространстве 5(Rn) операторы Ah = iDh +
+ Mk, A*h = iDk — Mh (к = 1, 2, ..., n) (так называемые
операторы рождения и уничтожения в квантовой теории
поля).
а) Доказать, что система уравнений Akf = O A</с<
< п) имеет в 5(Rn) одномерное пространство решений.
б)* Пусть fo^S(Rn)—базисный вектор в пространстве
решений системы AJ = 0 A < к ^ п) (так называемый
вакуумный вектор). Доказать, что система функций fm ==
= (Al)mi ... DГП/О (^eN") плотна в 5(Rn).
266
n
в) Положим Nk = -^ A*kAk, N = ^ Nk (так называ-
емые операторы чисел заполнения и числа частиц). Дока-
Доказать, что функции jm (m^Zn) являются собственными
для операторов Nh и N, и вычислить соответствующие
собственные значения.
г)* Построить изоморфизм пространства 5(R") и про-
пространства га-кратных последовательностей {cm} (m^Nn),
обладающих свойством \ст\ = o(\m\~h) для всех /c^N.
д) Вычислить преобразование Фурье функций /w,
//г е N".
581. Доказать, что всякий непрерывный оператор в
пространстве S(Rn), перестановочный с операторами
Mk A < к < п) (см. задачу 580), является оператором ум-
умножения на функцию.
582. Доказать, что всякий непрерывный оператор
в S(R"), перестановочный с операторами Mh и Dh A<
^к^п) (см. задачу 580), является скалярным.
583. Доказать, что прямое и обратное преобразования
Фурье сохраняют пространство S(Rn) и являются в нем
взаимно обратными непрерывными преобразованиями.
584°. Что можно сказать о преобразовании Фурье
функции /, если известно, что функция /
а) четна,
б) нечетна,
в) вещественна,
г) удовлетворяет условию /(#) = /(—#)?
585. Функции / и g на Rn связаны равенством /(#) =
= g(Ax+ 6), где А —-линейный обратимый оператор в Rn,
bz=Rn. Как связаны преобразования Фурье / (X) и |(Я)?
586. Доказать, что если /^^(R71, dx) и /(Х)=0, то
f(x) = 0 почти всюду.
587. Пространство //S(R") определяется при s>0 как
пространство преобразований Фурье всех функций из
MRn, A + WS/2)A). Доказать, что при s > nil каждая
Функция f^IIs(Rn) совпадает почти всюду с некоторой
непрерывной ограниченной функцией.
588. Доказать непрерывность операторов Dh: Hs(Rn)-+-
-+H8-{(Rn) (i^k<n, s>l) (см. задачи 580 и 587).
589. Доказать, что свертка двух функций из 5(R")
также принадлежит 5(R").
590. Доказать, что свертка функций /х е Я^ (Rn) и
h ^ Hs2{Rn)(cM. задачу 587) принадлежит BCh(RnI если
267
Si + s2>k. (Через J9Cft(Rn) обозначается пространство
функций на R" с непрерывными ограниченными произ-
производными до порядка к. Норма в нем имеет вид
11/1= sup
591. Пусть Р — многочлен на R степени 2т, не имею-
имеющий вещественных корней.
а) Доказать, что преобразование Фурье функции
f(x)=l/P(x) бесконечно дифференцируемо всюду, кроме
точки Я = 0.
б) Доказать, что /(Я) имеет в точке Я = 0 односторон-
односторонние производные всех порядков. _
в) Каков порядок гладкости /(Я) (число непрерывных
производных)?
592. Пусть / е Li (R, dx) — рациональная функция.
Доказать, что для некоторых констант с > 0 и г > 0
справедлива оценка 1/(Я) |< се~вЩ (l,eR).
593. а) Известно, что /eS(R) и \ xnf(x)dx = 0 для
всех п е N. Следует ли отсюда, что /^0?
б) Известно, что cpeiZ>(R) и J д:пф (л:) йд: = 0 для всех
R
^г > тг0. Следует ли отсюда, что ф = 0?
594*. Доказать, что всякая непрерывная положительно
определенная функция / на прямой имеет вид f(x)=*
= J e~2Jlilxd\i (Я), где ji — некоторая конечная борелевская
R
мера на R.
595. Пусть W(t)} (ieR)—однопараметрическая груп-
группа унитарных операторов в гильбертовом пространстве
// (т. е. U(t) U(s)= U(t + s)), непрерывная по t в силь-
сильной операторной топологии. Доказать, что для любого
вектора |efl функция f(t) = (U(t)%, g) положительно
определена.
596. В условиях задачи 595 предположим, что вектор
? — циклический для U(t) (т. е. линейная оболочка век-
векторов Е/(?)? (^GR) плотна в //). Построить изоморфизм
пространств Я и L2(R, jx), при котором оператор С/(^)
переходит в оператор умножения на е2лШ.
597*. Теорема Пэли — Винера. Доказать, что преобра-
преобразования Фурье функций из 3)(R) образуют пространство
целых аналитических функций от Я ^ С, обладающих
свойством: существуют такое число а >0 и такие кон-
константы ск, что 1#(Х)| A+llft|
268
598*. Пусть /—непрерывная функция на Rn, убываю-
убывающая на бесконечности как 0AЫ1~П). Тогда для любого
аффинного^ подмногообразия L cz Rn размерности п — 1
ограничение / на L суммируемо на L относительно есте-
естественной меры Лебега \iL на L.
а) Доказать, что если J/ (х) d\iL (х) = 0 для всех L a R",
L
то /(s) = 0.
б)** Выразить явно f(x) через ф (Z/) = j f(x)d\iL(z)
L
в случае п = 3.
599**. Найти функцию /^S(R3), если известны инте-
интегралы этой функции по всем прямым, пересекающим дан-
данную прямую I с: R3.
4. Преобразование Фурье обобщенных функций.
600. Пусть /—однородная обобщенная функция сте-
степени (К, г). Доказать, что / также однородна, и найти
ее степень.
601. Пусть /—регулярная обобщенная функция на
окружности Т, F — обобщенная периодическая функция
на прямой, связанная с / соотношением (F9 ср> =
R
Как связаны преобразования Фурье функций F и /?
602*. Назовем непрерывную функцию / на Rn квази-
квазипериодической с периодом Z?, если ее интеграл по любому
шару радиуса R не зависит от положения центра шара.
а) Доказать, что для п = 1 квазипериодичность равно-
равносильна обычной периодичности.
б) Построить непостоянную квазипериодическую функ-
функцию на плоскости.
в) Может ли непостоянная квазипериодическая функ-
функция иметь два разных периода R{ и /?2?
603*. Найти преобразование Фурье обобщенной функ-
функции f(x) = е~л{Ах'х) в Rn, где А — симметрическая мат-
матрица с положительно определенной вещественной частью.
604. Найти преобразование Фурье обобщенной функ-
функции f(x) = ein{Ax'x) в R", где А — вещественная симмет-
симметрическая невырожденная матрица.
605. Доказать, что образом пространства <§f'(R) при
преобразовании Фурье является совокупность целых ана-
аналитических функций g(K) (ЯеС), удовлетворяющих
оценке
\g(X)\<C\l + \X\ \"eR-lIml],
269
где С, N, R — некоторые константы (свои для каждой
функции g). От каких свойств преобразуемой функции
зависят константы R и N?
606. Доказать, что уравнение Д/ = / не имеет ненуле-
п
2 г)
2
оператор Лапласа.)
607*, Пусть &(?, x)— решение уравнения теплопровод-
теплопроводности du/dt = д2и/дх2 с начальными данными н@, х) =
= v(x), i;gL,(R, dx). Показать, что u(t, x) имеет вид
v*ft(x), и найти функцию /*.
608. Пусть Т(а) — оператор сдвига на вектор a^Rn,
М (а)—оператор умножения на 2niax в пространстве
S"(Rn). Вывести коммутационные соотношения
где 2Г — преобразование Фурье.
609*, Обобщенная функция f^S'(R3) регулярна и
зависит только от радиуса г=Ы1, /(#) = Ф AЫ1). Пока-
Показать, что ее преобразование Фурье задается формулой
оо
= j * (Г1Ц) Ф (r) drx и найти функцию к.
о
ГЛАВА V
СПЕКТРАЛЬНАЯ ТЕОРИЯ ОПЕРАТОРОВ
§ 1. Функциональное исчисление
1. Функции операторов в конечномерном пространстве,
610°, Пусть А — оператор в ^-мерном пространстве L
над полем К, Доказать, что операторы 1, Л, А2, ..., Ап
линейно зависимы.
611, Доказать, что следующие свойства оператора А
в ^-мерном пространстве L над полем К = R или С экви-
эквивалентны друг другу:
а) операторы 1, А, Л2, ..., Ап~1 линейно независимы;
б) существует такой вектор ?^Ь, что ?, А\, ...
..., Ап~% — базис в L;
в) существует вектор |еД циклический для А (т. е.
такой, что всякое подпространство в L, содержащее ? и
инвариантное относительно А, совпадает с L).
270.
Операторы Л, обладающие перечисленными свойства-
свойствами, называются регулярными.
612. Доказать, что диагональная матрица задает регу-
регулярный оператор тогда и только тогда, когда все эле-
элементы, стоящие на главной диагонали, попарно различны.
613. Доказать, что следующие свойства матрицы А эк-
эквивалентны:
а) А задает регулярный оператор;
б) минимальный многочлен для А совпадает с харак-
характеристическим многочленом;
в) каждому собственному значению А отвечает только
одна жорданова клетка.
614. Доказать, что множество регулярных операторов
открыто и всюду плотно в множестве всех операторов.
615. Пусть Rn — совокупность матриц порядка п вида
0
0
0
аг
1
0
0
а2
0
1
0
а3
0
0
0
а*
... 0
... 0
... 1
... аг
Доказать, что
а) всякий регулярный оператор в га-мерном простран-
пространстве в подходящем базисе задается матрицей А ^ Rn;
б) каждая матрица A^Rn задает регулярный опе-
оператор;
в) две матрицы А и В из Rn подобны (т. е. А —
= С5С~1), только если А = В.
616. Доказать, что два регулярных оператора А и В
в и-мерном пространстве L над полем К = R или С по-
подобны тогда и только тогда, когда справедливы равенства
= 1, 2, ..., п.
617°. Пусть
[Я 1 О О
О Я 1 О
.0 V ' X.
— жорданова клетка порядка п с собственным значени-
значением X. Вычислить матрицы:
а) Лп, п = 2, о;
б) /?(Л), где р — многочлен;
в) f(A), где / — целая аналитическая функция;
271
г) г(Л), где г — рациопальиая функция, пе имеющая
полюса в точке А,.
618. Пусть 31 — алгебра над полем К = С или R.
Идемпотентом называется элемент x^3t, обладающий
свойством х2 = х. Прямой суммой алгебр Slt и 3t2 назы-
называется линейное пространство 914 ^ 912 с покомпонентной
операцией умножения. Доказать, что следующие свойства
алгебры 81 эквивалентны:
а) 31 изоморфна прямой сумме некоторых (ненулевых)
алгебр 3li и 3t2;
б) в алгебре 31 есть нетривиальный (отличный от ну-
нуля и единицы) идем поте ит.
Алгебры, не обладающие этими свойствами, называ-
называются примарными.
619. а) Доказать, что поле С является примарной ал-
алгеброй над R.
б) Доказать, что всякая примарная алгебра с едини-
единицей и с одной образующей над С изоморфна одной из
алгебр 31„ = С [.r]/(,rn) (факторалгебре многочленов от х
по идеалу, порожденному хп).
620. Доказать, что всякая конечномерная алгебра яв-
является прямой суммой примарных алгебр.
621°. Числовая последовательность {ап) обладает свой-
свойством 0 ^ ат+п ^ат + ап для всех т и га. Доказать, что
существует Ига (ап/п) и что он равен tnf (ап/п).
622. Пусть А — оператор в /2-мерном линейном прост-
пространстве L над полем К. Обозначим через 31 (А) алгебру
над К, порожденную 1 (единичный оператор) и А. Дока-
Докажите, что dim 31 (Л )< п.
623. Пусть К = С. Докажите, что алгебра 31(Л) при-
марна тогда и только тогда, когда оператор А имеет
единственное собственное значение.
624. Ilycib S — некоторое множество операторов в ли-
линейном пространстве L. Через 51 обозначается совокуп-
совокупность операторов в L, перестановочных со всеми опера-
операторами из S. Для каких операторов А справедливо ра-
равенство Я (ЛI = 21D)?
625°. Доказать, чго всякий многочлен от коэффициен-
коэффициентов матрицы 4, не меняющийся при преобразованиях
подобия А>~» САС~1, является многочленом от trA,
626*. Пусть А и В — матрицы второго порядка. Дока-
Доказать, что всякий многочлен от коэффициентов А и В, не
меняющийся при преобразованиях А -> САС~\ В -* СВС~\
272
имеет вид P(trAy trS, tr.42, tr Z?2, tr.45), где Р — неко-
некоторый однозначно определенный многочлен от пяти пе-
переменных.
627**. Пусть А и В — матрицы порядка п. Доказать,
что алгебра многочленов от коэффициентов А и В, инва-
риантных относительно преобразований А ->¦ САС~Х, В ->
-* СВС~\ содержит не менее п2 + 1 образующих.
628. Указать в пространстве матриц порядка 2п X 2п
подпространство размерности 1 + /г2, состоящее из попар-
попарно перестановочных матриц.
629. Пусть А — оператор в я-мерном пространстве
с единственным собственным значением X. Доказать, что
для любой функции /, (п— 1) -кратно дифференцируемой
в точке X, справедливо равенство / (^4) = ^ .— X
h0
Х()
630*. Пусть А — оператор в я-мерном пространстве
с различными собственными значениями А,ь ..., Хп. До-
Доказать формулу
631*. Пусть оператор А имеет собственные числа
?w, ..., Ха с кратностями ти ..., тп. Доказать формулу
п mh-l
НА) =Ъ 2 fU)(K)Bjk
и найти явный вид операторов Bjk.
632*. Пусть К — совокупность всех положительных
(см. задачу 643) операторов со следом 1 в конечномер-
конечномерном гильбертовом пространстве //. Доказать, что /? —вы-
—выпуклый компакт, и найти крайние точки К.
2. Функции ограниченных самосопряженных опера-
операторов.
633°. Пусть А — оператор умножения на непрерывную
вещественную функцию а(х) в пространстве ?г@, 1).
Доказать, что А — самосопряженный оператор, и найти
°М).
634°. Найти спектр оператора Л, действующего в
?г@, 1) по формуле Af(x)=*a(x)f(x), где a^L^O, 1).
635°. Пусть /Gti(R, dx). Найти спектр оператора
свертки S(f) в пространстве L2(R, dx).
° А. А. Кириллов, А. Д. Гвишиани 273
636°. Пусть /eLi(T, dt). Найти спектр оператора!
S(f) свертки с / в пространстве L2(T, dt). ]
637°. Доказать, что спектр унитарного оператора U
лежит на единичной окружности.
638. Пусть А — самосопряженный оператор. Доказать
унитарность оператора (А +Я1) (А + АЛ) для невещест-
невещественных X.
639. Известно, что оператор (A — il) обратим, а опе-
оператор (А + И)(А — И)~1 унитарен. Доказать, что А само-
самосопряжен.
640. Известно, что оператор U унитарен, a U—i
обратим. Доказать, что оператор А == i{UЛ-1) (U — I)
самосопряжен.
641. Вычислить спектральный радиус оператора Воль-
терра А в ?2@, 1), задаваемого формулой
о
642. Вычислить явно резольвенту оператора Вольтер-
ра (из задачи 641).
643. Оператор А в гильбертовом пространстве Н на-
называется положительным, если (Ах, х)^0 для всех
х<^Н, х?. Мы будем писать в этом случае А > 0.
Доказать, что для положительного оператора А справед-
справедлива формула
644*. Пусть А — самосопряженный оператор, удов-
удовлетворяющий условию а-1<Л<Ь-1, а многочлен р(х)
неотрицателен на отрезке [а, Ь]. Доказать, что р(А)>0.
645. Доказать, что отображение р -* р (А) непрерывно
относительно нормы С [а, Ь], если а • 1 < А < Ъ - 1.
646. Пусть А — ограниченный самосопряженный опе-
оператор. Доказать, что оператор U(t)=eitA при всех t^R
является унитарным оператором и что справедливы ра-
равенства U(t)U(s)=U(t + s), U(t)* = U{-t).
647. Доказать, что в условиях задачи 646 оператор-
операторная функция U(t) дифференцируема и U'{t) )
U()A
()
648*. Доказать, что всякая непрерывная в топологии
нормы операторная функция U(t), удовлетворяющая функ-
функциональным уравнениям U(t)U(s)= U(t + s), ?/(?)* =
= U(—t), имеет вид, указанный в задаче 646.
274
649. Найти полярное разложение оператора А умно-
умножения на функцию a^Loo(X, \i) в пространстве L2(X, \i).
650. Найти полярное разложение оператора односто-
одностороннего сдвига в /2(С): Т(хп) = хп-{.
651. Пусть А и В— перестановочные операторы,
A —RU — полярное разложение А.
а) Доказать, что R и U перестановочны с 5, если
В — унитарный оператор.
б) Верно ли это в общем случае?
652. Пусть А > В > 0 и В обратим. Доказать, что А
обратим и А~1 < В~1.
653*. Пусть Г —оператор сдвига в Z2(Z) (TixJ =
= {хп+1}). Доказать, что существует единственный само-
самосопряженный оператор А, обладающий свойствами:
1) Г = егА;
2) \\А\\<п.
654. Пусть Hi и #2 — подпространства в Я, Р4 и
Р2 — соответствующие им ортопроекторы. Доказать, что
lim (P^zO1 существует и равен ортопроектору на Ht Г) Н2.
655. Пусть А — оператор в ?2([0, °о), dx)y заданный
оо
формулой Af (х) = J j-p- йг/. Доказать, что Л перестано-
о
вочен с операторами растяжения L(a): f (x)*-* f (ах).
3. Неограниченные самосопряженные операторы.
656°. В обозначениях теоремы 7 гл. V доказать, что
т(ГаI- является графиком некоторого оператора тогда и
только тогда, когда DA плотно в Н.
657°. Пусть операторы А и А* плотно определены
(т. е. DA и Da* плотны в Я). Доказать, что (Л*)* сов-
совпадает с замыканием А.
658°. Доказать, что существенная самосопряженность
оператора А равносильна каждому из условий:
а) А* самосопряжен;
б) Л=Л*.
659°. В каких случаях оператор А = id/dx в про-
пространстве Я = 1/2@, 1) симметричен, существенно само-
самосопряжен, самосопряжен:
а) DA = C40, 1],
б) {1
б) Дл =
в) О
66
0, 1],
0, 1],
) ф , ], ф() ф()
660. Будет ли симметричным оператор Лапласа А =»
д2 д2
^^i + —2 в L2(R2, dx), если
1 2
18* 275
a) D* = S(W); 6) D*)
в) D± — естественная область определения.
661*. Докажите, что всякий симметрический оператор
А, для которого DA = H, ограничен.
662. Пусть А — самосопряженный оператор.
а) Доказать, что оператор (А + И) (А — il) = U
унитарен.
б) Доказать, что ker(?/—1 )= (О).
663..Пусть U унитарный оператор, для которого
ker(C/—1) = {0}. Докажите, что оператор A =i(U+ 1)Х
X(U— 1) с областью определения DA = irn(?/—1) са-
самосопряжен.
664*. Вычислить оператор А в условиях задачи 663,
если U—оператор сдвига на 1 в 12{Ъ).
665. Пусть /7 = /!2(С), DA состоит из всех финитных
последовательностей с нулевой суммой, оператор А зада-
задается матрицей А = НаЛН, где ajk = i sgn (/ — к).
а) Будет ли А симметрическим?
б) Будет ли А существенно самосопряженным?
666. Пусть Аг (г=1, 2) — операторы умножения на х
в Z/2(R, dx) с областями определения DAv Известно, что
А{ и А2 существенно самосопряжены. Могут ли подпро-
подпространства Da± и Da2 иметь нулевое пересечение?
667. Пусть оператор А плотно определен и положи-
положителен (см. задачу 643). Доказать, что существенная само-
самосопряженность А равносильна условию кег(Л* + 1) = 0.
668*. Доказать, что для любого замкнутого плотно
определенного оператора А оператор Т = А*А +1 с
областью определения Dr = {iG DA\ Ax e DA*} само-
самосопряжен.
669*. Пусть #i и Н2 — гильбертовы пространства,
Hi ® #2 — их гильбертово тензорное произведение. Дока-
Доказать, что если операторы А{ и А2 самосопряжены в Н{ и
#2 соответственно, то оператор At ® 1 + 1 ® А2 с областью
определения Da± ® ^л2 существенно самосопряжен в Я.
670°. Доказать, что спектр самосопряженного опера-
оператора лежит на вещественной оси.
671. а) Доказать соотношение (imАI- = кегЛ* для
плотно определенного оператора А в гильбертовом про-
пространстве.
б) Верно ли в этом случае соотношение (кегЛ)± =
= im
672. Доказать, что самосопряженный оператор А не
имеет симметрических расширений, отличных от А%
276
673. Пусть А — симметрический оператор. Доказать,
что оператор (А + i) (A — Q продолжается до изометри-
изометрического оператора U из im(^ — i) в im(A + i).
674. Пусть А — замкнутый симметрический оператор.
Доказать, что пространство im(A + il) замкнуто в Я.
675. Доказать, что замкнутый симметрический опера-
оператор А допускает самосопряженное расширение тогда и
только тогда, когда dimkerD* — г1) = сИткег(Л* + И).
4. Расширения операторов.
676. Пусть А — симметрический оператор, V — его
преобразование Кэли. Докажите, что графики этих опе-
операторов ГА и Ту связаны соотношением Ту = ТА\ ^ ^ .
(Здесь * А означает оператор в Я ® Я, переводящий
® ( + )®(i + ))
( )( ))
677. Доказать, что для замкнутого симметрического
оператора А и невещественного числа К пространство
im(A—X -1) замкнуто.
678. Пусть А — симметрический оператор, L% =
= кег(Л* — К • 1). Доказать, что функция Я н-* lk = dim L^
постоянна в некоторой окрестности точки Я, не лежащей
на вещественной оси.
679. Пусть А — симметрический оператор, полуогра-
полуограниченный снизу: (Ах, х) ^ а1Ы12. Доказать, что функция
^ *-+ 1% (см. предыдущую задачу) постоянна в области
С\[а, оо).
680. Пусть Я — комплексное пространство и С — анти-
антилинейный оператор в Я, обладающий свойством С2 = 1.
а) Докажите, что Н = Но + Шо, где Яо — веществен-
вещественное пространство, состоящее из С-неподвижных векторов.
б) Докажите, что условие АС = СА для линейного
оператора в Я равносильно условию АН0 ^ Яо.
681. Пусть А — симметрический оператор в Я. Пред-
Предположим, что существует антилинейный оператор С со
свойствами С2 = 1, АС = СА. Доказать, что индексы де-
дефекта у А равны.
682. Пусть А — замкнутый симметрический оператор
в пространстве Я, Lx = кег(Л* — X • 1). Доказать, что для
h^C\R пространства D(A), L% и L^ линейно независимы
и их сумма совпадает с D(A*).
В следующих трех задачах приняты следующие обо-
обозначения (ср. [22]): p{t)— положительная, q(t)— ве-
вещественная функции из С@, сю); А — дифференциальный
277
оператор, заданный равенством Ах = — (рх)' + qx\ для
каждой дифференцируемой комплексной функции x(t)
Г *@ 1
построим комплексную вектор-функцию g (t) = , ,, и
вещественную скалярную функцию f(t) = i,*(t)Ii,(tI где
/ = [J ;]; положим В = ВЬК) = [Я{°_Х '"Д
683. а) Доказать, что x(t) является решением уравне-
уравнения Ах^Хх тогда и только тогда, когда ^(t) удовлетво-
удовлетворяет уравнению %' — В%.
б) Проверить, что для любого ?^@, °°) условие
п х' (t)
= {) равносильно вещественности величины , ¦.
в) Доказать тождество
ь
\x (t) |2 Л
для любого решения x(t) уравнения Ах = Кх.
684. Пусть w(t)— решение матричного уравнения
w' = Bw с начальным условием г#@)=1.
а) Доказать, что общее решение уравнения Ах==Хх
fz\
имеет вид xz (t) = A, 0) w (t) 11), z e C.
б) Проверить, что det^(O= 1-
в) Пусть St — совокупность тех z^C, для которых
z ,,v e R. Проверить, что St — окружность, найти ее ра-
диус и доказать, что при ?2 > ^ ^<2 лежит внутри Stl.
685. Доказать, что при t -> o° окружность 5/ стремит-
стремится либо к предельной точке, либо к предельной окруж-
окружности, в зависимости от того, будет ли самосопряжен опе-
оператор А с областью определения D(A), заданной каким-
нибудь самосопряженным граничным условием в нуле:
ах @) + р*' @) = 0, где ос/р е R.
§ 2. Спектральное разложение операторов
1. Приведение оператора к виду умножения на функ-
функцию.
686. Пусть А — самосопряженный оператор в конечно-
конечномерном пространстве. Привести его к виду умножения
на функцию.
278
687. Оператор А в пространстве // = ?2[—1, 1] состоит
в умножении на функцию а(х) = х2. Доказать, что
а) в Я нет циклических векторов для А;
б) представить Я в виде суммы двух подпространств,
обладающих циклическими векторами для А.
688. Доказать, что если А — оператор с простым спект-
спектром в бесконечномерном гильбертовом пространстве Я,
то операторы 1, А, ..., Ап, ... линейно независимы.
689. Пусть В и С — ограниченные самосопряженные
операторы, перестановочные друг с другом. Доказать, что
существует такой ограниченный самосопряженный опера-
оператор А, что В и С являются функциями от А.
690. Пусть А — самосопряженный оператор с простым
спектром. Доказать, что всякий ограниченный оператор
5, перестановочный с А, является функцией от А.
691. Доказать, что ||/ D)|| == sup \f(t)\ для любой
ограниченной борелевской функции от самосопряженного
оператора А.
692. Привести к виду умножения на функцию опера-
операторов свертки 5(/), /eLj(R, dx). Для каких функций
этот оператор самосопряжен?
693. Может ли оператор свертки ?(/), /^Z/j(R, dx),
быть унитарным?
694*. Пусть G — коммутативная локально компактная
группа с инвариантной мерой ji. При каких условиях на
функцию f^L^G, \х) оператор свертки S(f) является:
а) самосопряженным;
б) унитарным;
в) компактным?
695. Пусть А — интегральный оператор в ?2@, 1),
1
заданный формулой Af (x) = j min (я, у) / (у) dy. Привести
о
этот оператор к виду умножения на функцию.
696. Пусть А — неограниченный самосопряженный
оператор в Я, ГА — график А в Я $ Я. Доказать, что ор-
ортогональным дополнением к ГА в Я $ Я является т(ГА).
697. В условиях задачи 696 обозначим проекцию век-
вектора х Ф 0 на ГА через {у® Ау), а проекцию этого векто-
вектора на Та1- — через — Az ® z. Доказать, что
а) соответствия х^-у и х •-> z являются ограничен-
ограниченными операторами в Я; обозначим их В и С соответ-
соответственно;
б) справедливы соотношения С = — АВ, A + А2)В = 1.
279
698. Доказать, что оператор конечной разности
(х) =-т-[ф (х + h) — ф (х)] является функцией от опе-
оператора дифференцирования.
699*. Пусть /—непрерывная функция на'окружности.
Написать явное выражение для оператора f(F), где F —
оператор Фурье: Ftp (у) = j e-2jlixyy(y)dy.
R
2. Спектральная теорема.
700. Пусть К — проекционная мера на отрезке [а, Ь]
со значениями в End Я, /—непрерывная функция на
[а, Ъ]. Для каждого разбиения Т = {а = t0 ^ tx ^ ... ^ tn =
= fo} и каждого набора точек g = {Ы, |fee[^ fA+i], опре-
определим интегральную сумму Римана
k=o
а) Доказать, что, когда диаметр разбиения б(Г) =
= max(^+i ~h)стремится к нулю, интегральные суммы
h
*?(/, Т, ?) стремятся по норме к некоторому оператору.
Этот оператор называется интегралом Римана от / по
мере К и обозначается
ъ
б) Доказать, что интеграл Римана R\f(x)dek(x) совпа-
а
Ъ
дает с интегралом Лебега J f(x)dX(x), определенным в
§ 2 гл.о V.
701°. Доказать следующие свойства интеграла от ог-
ограниченных функций по проекционной мере:
= a J М*) Л И + a J/2 (*
х х
б) j ihh) (x) dX (x) = j Д (*) dX (Ж) f /2 (г) (й (ж);
X XX
в) П/(*)^(ж) <sup|/(*)|;
280
г) П/(а
д) если fn(z)-*- f(x), \fn(x)\<C для всех х^Х, то
Г fn (x) dX (x) -»• j / (x) dX (x) сильно.
х х
702. а) Доказать, что свойство 3) в определении про-
проекционной меры можно заменить более слабым усло-
условием 3') X (Х\Е) = i — X (Е) и нормировочным условием
)
б) Доказать, что условие 2) в определении проекцион-
проекционной меры следует из условия 3), нормировочных усло-
условий А,@) = О, Х(Х)=1 и того, что значения меры X—
ортопроекторы.
703. Пусть #! = L2[0, 1], Я2 = ?2([0, 1]Х[0, 1]). Опре-
Определим проекционные меры Xi и Х2 со значениями в ЕпAЯ1
и End//2 соответственно, полагая Хг(Е) = М(%Е(х)). Су-
Существует ли такой изоморфизм U: Я4 -»- Я2, при котором
ki переходит в Я2?
704. Пусть заданы множество X с о-алгеброй В, гиль-
гильбертово пространство Я и для каждого | == Я конечная ме-
мера \ii на (X, В) так, что выполнены условия:
)llll2
)
2)
Верно ли, что существует такая проекционная мера X
на X со значениями в End Я, что щ = А,6 для всех | е Я?
705*. Пусть X — метрический компакт, Я — гильбер-
гильбертово пространство. Представлением алгебры С(Х) в Я на-
называется отображение ср: С(Х)-*- End Я, обладающее свой-
свойствами:
1) ф является гомоморфизмом алгебр;
2) ф(Л = ф(/)*;
3) фA)=1 (единица слева — функция на X, справа —
единичный оператор в Я).
Доказать, что существует единственная проекционная
мера X на X со значениями в End Я такая, что ср(/) =
706. Пусть А — самосопряженный оператор в гильбер-
гильбертовом пространстве Я, X — его спектральная мера, Е —
борелевское множество на прямой. Через НЕ обозначим
подпространство Х(Е)Н. Доказать, что
а) НЕ инвариантно относительно А\
б) если Е ограничено, то А \нЕ— ограниченный опе-
оператор;
281
в) если Е замкнуто, то о (А |Яе) с Е.
707. Доказать, что спектр самосопряженного опера-
оператора А состоит в точности из тех точек a^R, для ко-
которых К((а — е, а + г))?= 0 при любом е > 0. (Здесь К —
спектральная мера оператора А.)
708. Критерий Вейля. Доказать, что точка а принад-
принадлежит спектру самосопряженного ограниченного опера-
оператора А в гильбертовом пространстве Н тогда и только
тогда, когда существует последовательность единичных
векторов ?>п^Н, для которой L4gn — a|JI -+ 0 при п -* оо.
709. Определение существенного спектра ограниченно-
ограниченного самосопряженного оператора А получается из критерия
Вейля (см. задачу 708) наложением дополнительного ус-
условия: последовательность {|„} ортонормирована. Дока-
Доказать, что если оператор В самосопряжен и компактен, то
существенные спектры А и А + В совпадают.
710. Формула Стоуна. Пусть А — ограниченный само-
самосопряженный оператор. Доказать равенство
ь
s_lim — Г [{а - ЯJ + 821] -1 dX =
е->о л {
- ъЩа)) + Ц(а, Ь))+ I Ц{Ъ}) = 1 Л([а, Ь])+ | Л((а, Ъ)).
711. Пусть U — унитарный оператор в гильбертовом
пространстве Я. Доказать, что существует единственная
борелевская проекционная мера К на окружности Т со
значениями в End Я, для которой справедливо равенство
для любой борелевской ограниченной функции / на Т.
712. Эргодическая теорема фон Неймана. Пусть U —
унитарный оператор в гильбертовом пространстве Н. До-
N
казать, что s-lim -тг У, Uh существует и равен проекто-
N^oo k==1
ру на ker(C7— 1).
713. Пусть А — любой ограниченный оператор и / —
аналитическая функция в области Q, содержащей о (А).
282
Определим оператор f(A) равенством
где С —любой контур в Q, охватывающий о (А).
а) Доказать, что соответствие / •-> / (Л) является гомо-
гомоморфизмом алгебр.
б) Доказать, что для нормального оператора А это
определение f(A) совпадает с данным в п. 2 ~§ 1 гл. V.
714*. Доказать, что любое семейство попарно комму-
коммутирующих ограниченных самосопряженных операторов
в сепарабельном гильбертовом пространстве можно одно-
одновременно привести к виду умножения на функцию.
715*. Пусть А — самосопряженный оператор в гиль-
гильбертовом пространстве Я, К — его спектральная мера и
/ — борелевская функция на R. Определим f(A) фор-
формулой
оо
(/(ЛН, Г))= J /(Х)(й6л(х)
—с»
на подпространстве DA c= Я, состоящем из тех векторов
оо
1^Н, для которых J | / (х) |2 dki (х) < оо. Доказать, что
— оо
а) оператор B = f(A) замкнут и плотно определен;
б) операторы SB* и В*В имеют общую плотную об-
область определения и совпадают на этой области.
716. Найти оператор А в представлении V(t) = eitA
для однопараметрической группы в пространстве L2(R,dx),
заданной равенством F(?)/(x)= V(t + x).
717. Пусть однопараметрическая группа U(t) унитар-
унитарных операторов в гильбертовом пространстве Я обладает
свойством С/A) = 1. Доказать, что U(t) = eitA, где о(Л)с=
Z
718. Для всякого ли унитарного оператора U сущест-
существует такая однопараметрическая группа V{t), что
1) C7?
719*. Найти спектральное разложение самосопряжен-
ного расширения оператора А = ^ +х2 с первоначаль-
первоначальной областью определения D(A) = S(R).
283
§ 3. Математическая модель квантовой механики
720. Доказать, что среднее значение (АУ^ величины А
в состоянии Ч? меняется со временем по закону
где [Я, А] = НА —АН — коммутатор операторов Н и А.
721. а) Доказать, что всякий линейный функционал
на пространстве Matn(C) комплексных матриц п-го поряд-
порядка имеет вид
б) При каком условии на А этот функционал поло-
положителен (т. е. }А(Х)>0 для положительно определенных
матриц X) ?
722*. Пусть В(Н) означает банахово пространство
всех ограниченных линейных операторов в гильбертовом
пространстве Я. Доказать, что всякий положительный
линейный функционал / на В(Н) (т. е. f(X)>Q для по-
положительных операторов X) имеет вид
где А — положительный ядерный оператор (см. зада-
задачу 500).
723*. Пусть К — совокупность всех положительных
функционалов / на В(Н) (см. предыдущую задачу), об-
обладающих свойством /A)=1. Найти крайние точки мно-
множества К.
В задачах 724—728 речь идет об одномерных кванто-
квантовых системах, характеризуемых массой m и потенциа-
потенциалом V(x).
724. Пусть V(x)^0 (свободная частица). Найти
спектр операторов координаты, импульса и энергии. Ука-
Указать реализации, в которых эти операторы диагонализи-
руются (т. е. приводятся к виду умножения на функ-
функцию). Найти обобщенные собственные функции этих опе-
операторов.
725. В условиях предыдущей задачи найти закон из-
изменения со временем состояния
284
(О При |^|<<2,
. 11^ (частица между
-j- оо при | х I ^^ а
двумя непроницаемыми отталкивающими стенками).
Найти стационарные состояния и соответствующие уров-
уровни энергии.
(О при \х\ <Са,
727. Пусть V(x) = \lz n (частица в
1^о > и ПРИ Iх I ^ а
потенциальной яме конечной глубины). Найти стацио-
стационарные состояния и уровни энергии.
728. Пусть V (х) = -у ты2х2 (гармонический осцилля-
осциллятор). Найти стационарные состояния и уровни энергии.
В задачах 729—732 речь идет об элементах квантовой
теории рассеяния для одномерных частиц массы m на
прямой. Если потенциал V отличен от нуля лишь на ко-
конечном интервале Ы < а, то вне этого интервала обоб-
обобщенная собственная функция с энергией Е = —^— имеет
вид
{Аег + Ве~г х при x<Caf
Ceihx+De~ihx при х>а.
Коэффициенты А, В, С, D связаны соотношением
'А1 »„, И*) Ь(Щ
Матрица Г (А) называется матрицей перехода.
729. а) Доказать, что det Г(/с)= 1.
б) Доказать, что для вещественного потенциала V(x)
матрица перехода обладает свойствами:
c(k)=b(k),
730. Величины t(k) = a(k)-1 и г(к)=Ь(к)а(к)-1 на-
называются амплитудами рассеяния "вперед и назад соот-
соответственно. Доказать, что \t(k) I2 + \r(k) I2 = 1. (Величи-
(Величина \t(k)\z интерпретируется как вероятность того, что
частица пройдет потенциальный барьер, а величина
\г(к)\2 — как вероятность того, что она отразится от это-
этого барьера.)
731. Найти t{k) и г (к) в случае, когда V{x)^VQ>0
на отрезке \х\ ^ а и V(x) = 0 при \х\ > а.
285
732. Пусть в условиях предыдущей задачи а -> О,
Vo -* °° и 2aV0-+c. Найти пределы t(k) и г (к) (резуль-
(результат можно интерпретировать как рассеяние на полупро-
полупроницаемой перегородке, описываемой потенциалом V(z) =
= сЦх)).
733. Найти обобщенные собственные функции опера-
операторов координат, импульсов и энергии для свободной ча-
частицы массы т в пространстве Rn.
734. Найти стационарные состояния и уровни энергии
свободной частицы массы т:
а) на окружности Sl =R/Z;
б) на га-мерном торе Тт = Rm/Zm.
735. Найти стационарные состояния и уровни энергии
гармонического осциллятора в трехмерном пространстве,
для которого
736. Найти уровни энергии и стационарные состояния
системы п неразличимых одномерных гармонических ос-
осцилляторов, являющихся:
а) бозонами;
б) фермионами.
737. ~
Пусть X, У и Z — три оператора в конечномерном
пространстве F, подчиненные коммутационным соотно-
соотношениям
[X, Y] = Z, [Y,Z] = X, [Z,X] = Y.
а) Доказать, что оператор Д = X2 + Y2 + Z2 перестано-
перестановочен с X, У и Z.
б) Доказать соотношения (X± iY)Z = (Z± il)X
X(X±iY), [X + iY, X-iY] = -2iZ.
738. В условиях задачи 737 предположим дополни-
дополнительно, что пространство V неприводимо относительно
X, У, Z.(t. e. не содержит собственных подпространств,
инвариантных относительно всех этих операторов).
Доказать, что:
а) каждый из операторов X, У, Z имеет простой
спектр, состоящий из чисел {si, (s—l)i, ..., (l — s)i1 — sii,
dimF— 1
где s = -r целое или полуцелое число;
б) оператор Д сводится к умножению на число
s(i-s);
286
в) в подходящем базисе {r|J (& = 0, 1, ..., 2s) опера-
хоры X, Y и Z приводятся к каноническому виду
Х\ = -у 1С+ (к) Чи+х + с- (к) r\h_x],
Y\ = 4" [с~ W Yj/l-1 ~~ c
Zv\k~i(s-k)r\hi
где с-(/с) = Л, c+(k)=*k-2s.
739*. Пусть классическая система имеет в качестве
фазового пространства двумерную сферу S радиуса R со
скобкой Пауссона, задаваемой элементами площади.
Найти квантовые аналоги координат х, у, z на S. При
каких значениях радиуса эта задача разрешима?
740. Операторы момента импульса для частицы в R3
определяются формулами
Li = q2pz — ЦгРг, L2 = qsPi — QiPs, Ls = q{p2 —
где qu pi — координаты и импульсы частицы.
Доказать, что эти операторы удовлетворяют комму-
коммутационным соотношениям
[Lu L2] - ibL3i [L2i L3] = mLh [L3, LJ = ibL2.
741. В условиях предыдущей задачи оператор L2 =
=Ll + L% + L\ называется квадратом полного момента.
Если состояние 4х удовлетворяет условию Ь2Л? ==
= Ь21{1 — 1)^, то говорят, что частица в этом состоянии
имеет полный момент М.
Пусть даны две частицы с полными моментами Ы^ и
Ы2. Какой полный момент может иметь система, получен-
полученная объединением этих частиц?
742. Как изменится ответ в предыдущей задаче, если
считать частицы неразличимыми?
РАЗДЕЛ HI
УКАЗАНИЯ
ГЛАВА I
СВЕДЕНИЯ ИЗ ТЕОРИИ МНОЖЕСТВ
И ТОПОЛОГИИ
§ 1. Отношения. Аксиома выбора и лемма Цорна
1. Ответ: а), б), д)—отношения эквивалентности, в) иг) —
нет.
2. Определение переформулируется так: Я и /2 эквивалентны,
если существуют положительные числа а, Ь и е такие, что а <
< U(x)lh(x) < Ъ при 0 < х < е. Отсюда следует, что это — отно-
отношение эквивалентности. Несчетность фактормножества следует из
того, что все функции ха при а ^ О попарно не эквивалентны.
3. Пусть /i, /2, /3, ... — последовательность положительных
функций. Определим функции / и /, полагая / (х) = -г- min А (х),
= k max /t (s) при l/(fc + 1) < x < 1/fc. Тогда /</*</
для всех i = 1, 2, ...
4. Пример: X и У — множества патуральных чисел с обычным
отношением порядка. Тогда точки A, 2) и B, 1) в XX ^ не-
несравнимы.
5. Функция [i(x, t) находится из системы уравнений
SfO, если у ф х,
Iх (г, у) = \л
При вычислении \i(x, у) достаточно рассматривать элементы
множества X, предшествующие х. Поэтому можно считать, что X —
конечное множество, а х — его наибольший элемент. При подхо-
подходящей нумерации элементов X числа \iij = \x(xi, xj) образуют
треугольную матрицу М с единицами на главной диагонали. Обо-
Обозначим через N матрицу, определяемую условием
A, если х, < х-,
v- • = < J
lJ [0 в противном случае.
Тогда наша система записывается в виде N > М = 1, откуда
М = ЛМ.
6. a) \i(x, х) = 1, \х(х, х — 1) = — 1; во всех остальных слу-
случаях [1(х, у) = 0.
288
б) Ответ: [i(z, у) = \io(x/y), где [io— классическая функция
Мёбиуса (|хоA) = 1, |Хо(>1 • ... •/?*) = (—l)ft, где рь ..., рь — раз-
различные простые числа; в остальных случаях \io(n) = 0.
в) Ответ: ц(А, В) = (—1I*1-1*1, Где В < А < X, \А\ и |В| -
число элементов в А и В соответственно.
г) Пусть основное поле состоит из q элементов. Тогда
^(А, В) = (—l)d • ^(<*-1)/2, где d = dim Л — dim Bt План доказа-
ЛЛ
тельства: пусть [ I — число «-мерных подпространств в л-мерном
пространстве над полем из q элементов. Свойства коэффициентов
( аналогичны свойствам обычных биномиальных коэффициент
\k/q
тов (в которые они превращаются при q = 1). В частности,
(разделить все (/с + 1)-мерные подпространства (/г + 1)-мерного
пространства на два подмножества — содержащиеся и не содержа-
содержащиеся в данной гиперплоскости),
B)
(Эта формула выводится из A), так же как обычный бином Нью-
Ньютона — из основного свойства биномиальных коэффициентов.) Тре-
Требуемое равенство 2 V (С, В) =0 (см. указание к задаче 5)
следует из равенства B) при t = —1.
7. а) Проверить, что 2 Ф Й=л (ф№ равно количеству на-
нас/in
туральных чисел /«<пс НОД(лг, п) = /г/ d). Отсюда следует, что
ф(«) = 2'х(/г' d) d = ^\x {jild)d (см. указание к задаче 6 6).
d\n d\n
б) Сопоставим каждому неразложимому многочлену Р степени
d со старшим коэффициентом 1 ряд fp(X) = 1 + Xd + X2d + ...
Доказать, что коэффициент при Хп в JJ /р (X) (произведение по
р
всем неразложимым многочленам) равен числу всех многочленов
степени п со старшим коэффициентом 1, т. е. qn. Отсюда следует,
«О Hfp(x) = l + qX+q2X* +..; = _L_.. Но ПМ*) =
- п (VV)P(n'3)-так чт° п A -
п>1 \ 1 л / п>1
п>1 / п>1
Взяв логарифмическую производную от обеих частей этого равен-
равенства и разложив ее по степеням X, получить равенство
2j dP (g, d) — qn. Отсюда следует, что
d\n
7|2
d\n d\n
А. А Кириллов, А. Д. Гвишиани 289
в) Проверить, что С (N) =2 2 ф №) — 1. Используя равен-
Kh
ство задачи G), вывести равенство
- 2 s«[fP
dN L J \L
Г N1 N
где — — целая часть числа —. Отсюда следует, что
C(N) у V0(d)
lim о~ — Zj 2—• Это и есть искомое выражение.
Заметим, что вычисления можно продолжить: из основного
свойства функции Мёбиуса- (см. указание к задаче 5) легко выте-
v (%,(<*) /v 1 Vх
кает, что ?+ —2— = Ad ~~2~ » известно, что это число рав-
d^i * \n>i п J
но 6/я2.
8. Проверяется непосредственно.
9. Случай п = 1 легко исследуется. В случае п > 1 восполь-
воспользуемся тем, что нам известно, как устроено отношение порядка
на прямой, проходящей через начальную точку.
Разобьем Rn в дизъюнктную сумму трех подмножеств:
0+ = Int{* > 0}, О- = Int{* < 0}, Г « 0+ П 0-
(Int — внутренность множества, а Я — замыкание Л). Доказать,
что Г — линейное подпространство, множества О+ и О~ непусты и
любой путь из О+ в О~ пересекает Г. Вывести отсюда, что Г —
гиперплоскость в Rn, а О+ и О~ — ограничиваемые ею полупрост-
полупространства. Далее использовать индукцию.
10. а) Пусть jLi0 — класс эквивалентности, содержащий нату-
натуральный ряд N с естественным порядком. Если М — вполне упо-
упорядоченное счетное множество, то в нем есть наименьший эле-
элемент ти в множестве М\{гп])—наименьший элемент irt2 и т. д.
Пусть mос — наименьший элемент множества ^\{wj}S=i (е°ли
это множество пусто, то М эквивалентно натуральному ряду). Яс-
Ясно, что отрезок М(гпоо) множества М эквивалентен N. Значит,
класс М больше цо и jliq — минимальный элемент.
б) Пусть М и L — два вполне упорядоченных счетных мно-
множества. Назовем элемент тп^М допустимым, если отрезок М(тп)
эквивалентен некоторому отрезку в L. Если все элементы М допу-
допустимы, то можно построить монотонное отображение ф множеств
ва М на некоторый отрезок в L по следующему правилу: если для
всех тп < гп\ отображение ф определено, то ф(^1) определяется
как наименьший элемент L, не входящий в множество ^(M(mi)).
Если все L исчерпывается одним из множеств ф(Л/(лг)), то L и М
сравнимы и L < ill. Пусть теперь существуют недопустимые эле-
элементы, и пусть /по — наименьший из них. Разберите отдельно слу-
случай, когда у /п0 есть предшествующий элемент и когда такого эле-
элемента нет.
в) Пусть Jto с: Л. Выберем \i e J?q и представителя М клас-
класса [I. Если Mi — представитель класса jxi е Ло, то либо \i\ ^ ji,
либо М\ эквивалентен отрезку М{гп\). Мы получили монотонное
9QO
отображение \ix ¦-*• т1 той части Жо, которая лежит «левее» |х, на
подмножество в М. Так как М вполне упорядочено, это подмноже-
подмножество имеет минимальный элемент. Значит, минимальный элемент
есть и в Жо.
г) Предположим, что Ж счетно. Выберем в каждом классе
оо
[ii е Ж по представителю М\, и пусть М = U М^ Введем в М
отношение эквивалентности. Если \ii < JUj, то Mi отображается на
отрезок в Mj и мы говорим, что точка т е Mi эквивалентна свое-
своему образу в Mj. Проверьте, что построенное таким образом отно-
отношение будет действительно отношением эквивалентности, что соот-
соответствующее фактормножество М счетно, вполне упорядочено и
что его класс \х больше, чем все классы \х^Ж, что невозможно.
д) Воспользуйтесь теоремой Цермело.
11. Назовем |Х е Ж допустимым, если отрезок множества $, оп-
определяемый элементом (jx, 0), эквивалентен полуинтервалу [0, 1).
Докажите, что все элементы Ж допустимы, используя тот факт,
что каждый элемент йе! является мажорантой счетного семей-
семейства а\ ^ а2 ^ ...
Второе утверждение задачи вытекает из несчетности Ж (см.
задачу 10 г) и счетности базы топологии на [0, 1)).
12. См. указание к задаче 11.
13. Максимальные элементы — круги, касающиеся хотя бы двух
сторон квадрата. Среди них наибольшего в смысле включения не
существует.
14. Применить лемму Цорна к множеству всех линейно неза-
независимых систем векторов данного пространства, упорядоченному
по включению.
15. С помощью леммы Цорна показать, что любые два вполне
упорядоченных множества сравнимы (т. е. одно эквивалентно от-
отрезку другого).
16. Рассмотрите частично упорядоченное множество, элемен-
элементами которого являются подмножества данного множества X с от-
отношением полного порядка на них. Покажите, что условия леммы
Цорна выполнены и что максимальный элемент — это все мно-
множество X с отношением полного порядка.
17. Пусть X — частично упорядоченное множество, удовлетво-*
ряющее условиям леммы Цорна, У — множество мощности, боль-
большей, чем X (например, 'Р(Х)). По теореме Цермело У можно впол-
вполне упорядочить.
Предположим, что в X нет максимального элемента, и постро-
построим монотонное отображение ср множества У в X (что, очевидно,
невозможно). А именно, если ф уже определено на отрезке У(#о),
то полагаем ф(г/о) равным тому элементу xq e X, который мажо-
мажорирует ф(У(г/0)) (это множество упорядочено и по условиям лем-
леммы Цорна допускает мажоранту).
§ 2. Метрические пространства и их приложения
18. Пусть х\ч #2» хъ — фундаментальная последовательность. По
определению существует последовательность индексов щ < п2 <
"< и3 <; ... такая, что все точки хп при п >> пъ лежат в замкнутом
шаре Вк радиуса l/2ft с центром в одной из этих точек. Рассмотрим
шар Bk, концентрический Bk с вдвое большим радиусом. Прове-
19* 291
рить, что последовательность Въ. стягивающаяся и ее пересечение
есть lim xn*
П-*оо
19. Пусть / — равномерно непрерывная функция на X, х\,
х% • • •— фундаментальная последовательность их — отвечающая
ей точка пополнения. Тогда / {х) = lim / (х ) (предел существует
П->оо Ч '
в силу равномерной непрерывности / и полноты числовой пря-
прямой R).
20. а) Отображение х •-* arctg x изометрично отображает пря-
прямую с введенным расстоянием на интервал (—л/2, л/2) с обыч-
обычным расстоянием. Поэтому пополнение R изометрично отрезку
[-л/2, я/2].
б) Аналогично а) отображение х\-> выявляется изометрией на-
нашего пространства на луч @, оо). Пополнение изометрично по-
полупрямой [0, оо).
21. Пополнение получается добавлением «одноточечных отрез-
отрезков» [a, a] (aeR).
22. Прежде всего последовательность отрезков с длинами, стре-
стремящимися к 0, является последовательностью Коши — всем им со-
соответствует одна дополнительная точка в пополнении, расстояние
от которой до любого отрезка А равно |А|. Доказать, что пополне-
пополнение получается присоединением этой единственной точки. Для
этого доказать, что из любой фундаментальной последовательности
отрезков с длинами, не стремящимися к 0, можно выбрать под-
подпоследовательность, у которой все пересечения А* П Aj непусты.
Воспользоваться тем, что для пересекающихся отрезков расстоя-
расстояние совпадает с расстоянием, определенным в задаче 21.
23. Доказать, что для любой фундаментальной последователь-
последовательности {fn} предел / (х) = lim fn(x) существует при всех х е X и
П -*оо
что последовательность {/п} равномерно сходится к /. Для дока-
доказательства ограниченности / воспользоваться оценкой |/(я) —
-НУ)\< \f(x)-fn(x)\ + \fn(x) -fn(y)\ + \fn(y) ~f(y)\.
24. Воспользоваться неравенством треугольника.
25. а), б) Любая фундаментальная последовательность в X
сходится к точке в замыкании X. Обратно, любая точка замыка-
замыкания X есть предел некоторой фундаментальной последовательно-
последовательности в X.
в) В качестве пополнения X можно взять замыкание в В(Х)
его образа при изометрическом вложении задачи 24.
26. Доказать сперва непустоту пересечения всюду плотных от-
открытых множеств, построить подходящую стягивающуюся после-
последовательность замкнутых шаров, а затем вывести утверждение за-
задачи из непустоты пересечения.
27. Последовательность {Рк}, где ^ка^[~т) ' является Фун~
даментальной последовательностью для всех трех расстояний. По-
Показать, что никакой многочлен Р не может служить пределом этой
последовательности в смысле расстояний а), б) ив).
28. См. указание к задаче 23.
29. Пусть (fn) —последовательность Коши в G. Тогда (/~х) —
также последовательность Коши. В силу задачи 28 (/п) и (/п1)
равномерно сходятся к непрерывным отображениям / и g. Для до-
292
казательства того, что / и g взаимно обратны, воспользоваться
оценкой
dx (fg (*), х) < dx {fg (х) - ff-1 (x)) + dx (//-1 (x) - fj-1 (x)).
30. Непосредственно следует из определения.
31. Пусть (хп) и (уп) — последовательности Коши в Q отно-
относительно расстояния dp. Доказать, что (хп + уп) и (хпуп) — так-
также последовательности Коши; если хп А 0, т. е. ||яп||р > я Z> 0 для
достаточно больших п, то A/хп) —последовательность Коши (вос-
(воспользоваться оценкой
\\ху - «У Ир ^ \\x\\v\\y - у'\\р + \\у%\\х - х%
II 1 1 || U-x'\p \
и равенством | — — ~Р~1 = и^ц ц^ц—J. Относительно непол-
неполноты Q см. указание к задаче 32.
32. Доказать, что ряд 2 а{Р *» гДе 0 ^ а< ^ р — 1, сходится в
t=-ft
Qp (это следует из того, что его частичные суммы образуют после-
-foo оо
довательность Коши). Пусть х = 2 aiP%i У == 2 ^г^и ^ —на"
именьший индекс, для которого а\ Ф Ь\. Доказать, что dp(x, у) =
= р~1 (в частности, разложение в ряд по степеням р однозначно).
Вывести отсюда, что последовательность \xn=z 2 а\П^Рг }явля"
ется последовательностью Коши тогда и только тогда, когда для
любого индекса i последовательность а^ стабилизируется при
больших п. Отсюда следует, что множество элементов, представ-
представляющихся в виде суммы такого рода, замкнуто. Далее доказать,
что любое рациональное число г представляется в таком виде (до-
(достаточно рассмотреть случай г = т/п, где т, п — целые, п взаим-
взаимно просто с р\ построить по индукции целые числа m0, mi, т^ ...
и по, fli, й2, ... @ ^ at ^ р — 1) такие, что т0 — т, тщ — а\п =
оо
= rrii+ip при i ^ 0; тогда г — 2 агР% ~~ ПСК0Л1°е разложение). Ос-
талось сослаться на задачу 25.
Доказать, что число х е QP рационально тогда и только тогда,
когда соответствующая дробь периодична (вспомнить, как доказы-
доказывается аналогичное утверждение для вещественных чисел). Отсю-
Отсюда следует, что QP ф Q, т. е. что Q относительно р-адической мет-
метрики неполно.
33. Числа 0, 1, 2, ..., ph — 1 образуют р~к-сетъ в Z. Поэтому
компактность Zp вытекает из критерия Хаусдорфа. Далее исполь-
оо
зовать, что каждый элемент Zp имеет вид 2 aipt' гДе 0 ^ а{ ^
^ Р — 1, причем сходимость последовательностей элементов Zp
означает стабилизацию каждого коэффициента а*.
34. Доказать с помощью индукции по п, что хр =хр +рп«мп,
гДе un e Zp (при п = 1 воспользоваться малой теоремой Ферма).
293
Отсюда следует, что sgn (х) = lim xv = lim (x + ри + р2и +
1 П-*оо П-*оо V
+ ... + Рпип) существует и l|sgnp ж — #||р ^ р. Вывести из пос-
последнего неравенства, что числа sgnp а при а = О, 1, ..., р — 1 раз-
различные, т. е. sgnp принимает ^ /? значений. С другой стороны, вы-
вывести из определения sgnp, что (sgnp x)v = sgnp x для всех ж е Z^n,
и воспользоваться тем, что уравнение ур = у в поле QP не может
иметь больше чем р корней.
35. а) Доказать, что последовательность натуральных чисел
является последовательностью Коши относительно расстояния d
тогда и только тогда, когда она является последовательностью Ко-
Коши относительно 2-адического и 5-адического расстояний. Получа-
Получаемое отображение пополнения N по d в Z2XZ5 и есть искомый
изоморфизм.
б) В силу изоморфизма задачи а) бесконечные «окончания»,
воспроизводящиеся при умножении, соответствуют решениям урав-
уравнения х2 = х в кольце Z2 X Z5. Это уравнение имеет четыре реше-
ния: @, 0), @, 1), A, 0) и A, 1).
36. Проверяется непосредственно.
37. Все пространство Qn является шаром, имеющим любую
точку в качестве центра.
38. Так как граф Г конечен и не имеет циклов, функция
"Ф"(м?, t) при любом фиксированном w и f->oo может менять свои
значения лишь конечное число раз. Таким образом, при достаточ-
достаточно больших t функция ^(w, t) не зависит от t.
39. При to <C t\ < V стабильность прогноза Щ^, t') вытекает
из стабильности прогноза П(*о, О по определению. С другой сто-
стороны, нестабильный прогноз (П(?о, t')) может стабилизироваться
с течением времени (Tl(ti, t')).
40. Следует из того, что для любого t B(t) = W\H(t).
41. Воспользоваться формулой
bi
42. Подмножество а = (ii, ..., ik) будем называть Я-выборкой,
если ог +... + ог <Л; Я-выборку а будем называть полной,
X к.
если при добавлении к а любого индекса / е {1, ..., п}\а имеем
ог + •.. + Gi + °; > R- Пусть для данного R аь ..., ai — сово-
I
купность всех полных /?-выборок. Пересечение а = П а^ будем
называть /?-ядром. Утверждение задачи вытекает из лемм.
Лемма 1. Шар ^?(со0, R) есть объединение граней Га , ...
..., Га по всем полным R-выборкам аь ..., ai. Центроид шара
^(соо, R) есть пересечение Га , ..., Га , т. е. грань Га , где а0 —
R-ядро.
Лемма 2. Множество а ^ {1, ..., п) является R-ядром при
некотором R тогда и только тогда, когда а = {1, ..., к} и О{ + ..,
+
Подробное доказательство утверждения задачи приведено
в [8*].
294
§ 3. Категории и функторы
43. Каждому множеству сопоставить его дополнение.
44. Ответ на все вопросы — «да».
45. Универсальный отталкивающий объект в G\ — группа це-
целых чисел Z, а в GJ — единичная группа.
46. Универсальное свойство легко следует из любой известной
конструкции свободной группы. Приведем одну конструкцию сво-
свободной группы F2 с образующими а и Ь.
Пусть Ца и Ць — бесконечные циклические группы с образую-
образующими а и Ъ. Элементы F2 — это слова (х\, х2, ..., Яя), где хь. при
& = 1, 2, ..., п принадлежит одной из групп Ца или Ць, любые два
последовательных члена принадлежат разным группам и ни один
член не является единичным элементом своей группы; число п
назовем длиной слова. Длина слова может быть равна 0, т. е. F2
содержит пустое слово 0. Умножение слов определим с помощью
индукции по длине. Положим 0-0 = 0, 0-(хи ..., хп) = (#ь-..
..., хп)-0 = [х\, ..., хп) (т. е. 0 будет единичным элементом F2).
Произведение (xiy ..., хп)(уи ..., ут) определим отдельно в трех
случаях: f
1) если хп и у\ лежат в разных группах, то
(XU . . ., ХП) {УU - • ., Ут) = (*1, . . -, Хщ г/1, . . ., ут) \
2) если хп и г/1 лежат в одной группе и хпфу~х^ то
(XU . . ., Хп) B/1, • • ., Ут) = (*1, . . ., Xn-U ХпУи 2/2, . . ., Уп)\
3) если хп = г/, то
(Zl, . . ., ^п) (г/1, . • ., Ут) = (XU . . ., Хп-\) {У2, - . ., Ут)
(произведение в правой части определено в силу индуктивного
предположения).
Проверьте, что F2 с этим умножением является группой с дву-
двумя образующими а и Ь и что она и есть искомый универсальный
объект.
47. Свободная абелева группа с образующими а и Ь может
быть определена как прямое произведение бесконечных цикличе-
циклических групп Ца и Ць- Другой способ ее построения — взять фактор-
факторгруппу свободной группы с двумя образующими (см. задачу 46)
по ео коммутанту.
48. Приведем одну конструкцию универсального объекта. Рас-
Рассмотрим векторное пространство Лп над К с базисом ei, где / про-
пробегает конечные последовательности (кь ..., kN) (к{ = {1, 2, ...
• •., п})\ если рассматриваются алгебры с единицей, то допускает-
допускается пустая последовательность / = 0. Умножение в Лп, превраща-
превращающее ее в /^-алгебру, определяется правилом ej'ejf =zeiv> гДе Н'
получается приписыванием /' вслед за /. Проверить, что Лп яв-
является ассоциативной /^-алгеброй с п отмеченными образующими
e(i)? 6B), ..., ?(П) и что это и есть универсальный объект.
49. Универсальный объект в САп(К) может быть определен
как факторалгебра универсального объекта в Лп(К) (см. задачу
48) по двустороннему идеалу, натянутому на элементы вида
ХУ — ух,
295
50. Приведем конструкцию свободной алгебры Ли с и образу-
образующими еи ..., еп. Определим по индукции семейство множества
Еп (п"^ 1), полагая Ех = {еи ..., еп}, а при п ^ 2 Еп = JJ 2?fe X
X Ev Положим М = JJ Еп и определим умножение М X М t-> M
п
посредством отображений Ek X Ef-*Ek+l с: Af (стрелка — канониче-
каноническое включение, вытекающее из определения Eh+i). Пусть К[М] —
векторное пространство над К с базисом М\ введенное умножение
на М превращает К [М] в /f-алгебру. Свободная алгебра Ли с п
образующими может быть определена как факторалгебра К[М] по
двустороннему идеалу, натянутому на элементы вида а-а и (ab)c +
+ (bc)a +(ca)b. Проверьте универсальное свойство.
Заметим, что универсальные объекты задач 48 и 49 могут быть
получены аналогичной конструкцией, т. е. факторизацией К[М] по
подходящему двустороннему идеалу.
51. Определим F(g) как тензорную алгебру пространства д,
профакторизованную по двустороннему идеалу, натянутому на эле-
элементы ВИДа Хоу — уоХ — [X, у], X, !/?8.
Доказать универсальность F(g), исходя из универсальности
тензорной алгебры (см. задачу 48).
52. Пусть g — свободная алгебра Ли с п образующими. Исполь-
Используя универсальное свойство g (задача 50) и универсальное свой-
свойство F(g) (задача 56), доказать, что F(g) есть универсальный
объект в категории Ап(К) (см. задачу 48).
53. Сумма в категории множеств — дизъюнктивное объедине-
объединение; в категории линейных пространств — прямая сумма ( \\ V^ —
подпространство в декартовом произведении JJ Va, состоящее из
векторов, у которых лишь конечное число ненулевых компонент).
54. Произведение в категориях множеств и линейных прост-
пространств — обычное декартово произведение.
55. См. указания к задачам 53 и 54.
56. L\ (g> L2 может быть определено как факторпространство
L'IU\ где U — векторное пространство над К с базисом (е<а, ъ))
(а е L], бе Ь2) (т. е. множество индексов равно L\ X ?2, a L" —
подпространство в Z/, натянутое на векторы вида е<яа+цб,с) —
57. Пусть d — наибольший делитель чисел тип. Проверьте,
что Цл с каноническим морфизмом Цт X Цп -> Цл, переводящим
(a mod m, b mod n) в ab mod d, является универсальным объектом
(и, следовательно, Tor(ZJm, Цп) = Ца). В общем случае восполь-
воспользуйтесь тем, что любая конечная абелева группа является прямой
суммой циклических, и тем, что функтор Тог аддитивен по каж-
каждому аргументу.
58. а) Положим А равным множеству натуральных чисел и
превратим А в направленное множество с помощью делимости
(а ^ р, если а|Р). Пусть Ха = Z для всех а е А и фар при а < р
есть умножение на (J|oc. Проверить, что индуктивный предел этого
семейства изоморфен аддитивной группе Q (морфизмы фй: Ха -> Q
задаются формулами фа(/с) = к/а).
б) Доказать, что вложение Z->ZP индуцирует изоморфизм
296
59. Непосредственно следует из определения.
60. Если {|а}аел — базис в L (см. задачу 14), то он же явля-
является базисом в L 0дС.
61. Воспользоваться тем, что функтор F, осуществляющий эк-
эквивалентность категорий, задает изоморфизм полугруппы автомор-
автоморфизмов Aut(^) и Aut(F(A)), и тем, что полугруппа веществен-
вещественных чисел не изоморфна ни одной из полугрупп матриц с комп-
комплексными коэффициентами.
62. Следует из определений. '
63. Точка х е X является пределом направленности {ха}а е А,
если для любой окрестности U точки х существует такой элемент
Р g Л, что ха е С/ для всех р > а.
64. а) Пусть / непрерывна в точке х. Тогда для любого е > 0
существует такое б > 0, что |/(*/) — f{x) | < е, как только d(x, у) <
< б. Если х = lim xn, то существует такой номер iV, что
d(x, хп) < б при п > N. Отсюда видно, что f(xn) имеет своим
пределом f(x).
Если же / разрывна в точке х, то существует такое е > 0, что
как угодно близко от х найдется точка г/, для которой
\f(x)—/(*/) | ^е. Из таких точек у можно составить последова-
последовательность {хп}, сходящуюся к х. Соотношение j(\imxn) = lim/(;rn)
для этой последовательности не выполняется.
б) Переделайте рассуждения, приведенные в указании к п. а),
заменяя последовательности {хп} на направленности {ха}ае=А, где
А — множество окрестностей точки х, упорядоченное обратно вклю-
включению (т. е. U\ ^ С/г, если U] с= С/г).
в) Неверно. Противоречащие примеры (показывающие, что то-
топология пространства не определяется, вообще говоря, классом
сходящихся последовательностей) можно найти в теории интегра-
интеграла (теорема Лебега о переходе к пределу под знаком интеграла)
и в теории банаховых пространств (см. задачи 233, 234).
65. Непосредственная проверка определений. Единственное не-
нетривиальное утверждение: композиция двух непрерывных отобра-
отображений является непрерывным отображением. Это легко следует
из задачи 646).
66. В качестве базы топологии можно взять совокупность от-
открытых шаров.
67. В качестве суммы семейства объектов {Ха}а е а можно
взять их дизъюнктное объединение JJ Х^. Открытым множест-
а-з А
вом в этом объединении назовем множества вида JJ U^, где Ua —
а^ л
открытое подмножество в Х«.
В качестве произведения семейства {Ха}а е а можно взять тео-
теоретико-множественное произведение JJ Х^. В качестве базы то-
А
аеА
пологий нужно взять произведения вида JJ U^ где Ua — откры-
тое подмножество в Х«, причем Ua Ф Ха лишь для конечного мно-
множества индексов а.
68. Пусть М замкнуто и {ха}а е а — последовательность точек
Л/, сходящихся к х. Если х ф. М, то из открытости Х\М вытекает,
что хафМ для достаточно больших индексов а. Противоречие.
Обратно, пусть М незамкнуто. Тогда Х\М не открыто. Значит,
одна из точек х е Х\М обладает свойством: в любой ее окрестно-
297
сти U есть точки из М. Пусть xv — одпа из таких точек. Построй-
Постройте направленность {хи}, сходящуюся к х (см. задачу 64 6)).
69. а) Воспользуйтесь результатом предыдущей задачи.
б) Воспользуйтесь основным свойством непрерывных отобра-
отображений: прообраз открытого множества открыт.
70. Пусть А предкомпактно. Тогда А — компакт. Рассмотрим
покрытие А всевозможными открытыми шарами радиуса е. В си-
силу компактности А у этого покрытия есть конечпое подпокрытие.
Центры шаров, входящих в это подпокрытие, образуют искомую
е-сеть для А.
Обратно, пусть А — не компакт. Это значит, что существует
бесконечное открытое покрытие множества А, из которого нельзя
выбрать конечного подпокрытия. Рассмотрим теперь всевозможные
замкнутые шары в Л и назовем шар плохим, если он не покрыва-
покрывается никаким конечным числом элементов нашего покрытия. По
условию для любого е > 0 А можно представить в виде объедине-
объединения конечного числа шаров радиуса е. Хотя бы один из этих ша-
шаров должен быть плохим.
Получите противоречие, построив стягивающуюся последова-
последовательность плохих шаров.
71. а) =ф- б) Пусть А предкомпактно и {хп} — последователь-
последовательность точек из А. Назовем шар в А богатым, если он содержит
бесконечное число членов последовательности. Постройте стяги-
стягивающуюся последовательность богатых шаров, следуя методу, пред-
предложенному в указании к задаче 70.
б) =ф- а) Если А не предкомпактно, то для некоторого е > 0
оно содержит бесконечное число попарно непересекающихся ша-
шаров радиуса е. Центры этих шаров дают пример последовательно-
последовательности, из которой нельзя выбрать фундаментальную подпоследова-
подпоследовательность.
72. Следует из предыдущей задачи.
ГЛАВА II
ТЕОРИЯ МЕРЫ И ИНТЕГРАЛА
§ 1. Теория меры
1. Алгебра множеств.
73. Следует из того, что (А А В) = (А\В) [} {В\А), {А\В) с:
с (А\С) U (С\В), (В\А) с (С\А) [} (В\С).
74. а) Следует из включения (А{ [} А2)\{В1 [} В2) с: (Ai\B{) [}
U (А2\В2).
б) Введем обозначение для дополнения: Ее = (Ах\] А2\] Вх\]
U В2)\Е, тогда (Л,пА2) Д (^П*,) = (А[\} А%) Д (в\\)В%) с
<= ((Л1 A *i)nDA<))C = (лг Л Вг) U (Л2 Д Я2).
в) Следует из б), если учесть, что ^N^g ~ \ П ^2'
75. Рассмотреть систему, состоящую из одного непустого мно-
множества.
76. А П#= {А [}В)\((В\А) U Ц\В)), А А В = (А\В) [)
U (В\А).
77. Объединение двух непересекающихся отрезков не являет-
является отрезком.
298
78. Рассмотреть множество, состоящее из всех множеств, по-
получающихся из конечного числа элементов системы S путем при-
применения операций пересечения и дополнения.
п т
79. Пусть А = Ц Av В = Д В., Av Bj e= S. Тогда А\В =
п т
= JJ П (Ai\Bj)' Так как 5 — полукольцо, то существуют такие
„..€=?, что
80. Если Е — единица алгебры, то
81. а) Рассмотрим произведение двух полуколец S\ и S2 (для
большего числа сомножителей доказательство аналогично). Если
А = А\ X А2, В = Вх X ^2, где Л*, 5г е Л для i = 1, 2, то А П # =
= (i4ifl^i) Х.С^гП^г) e5iX52. Пусть B{czAu В2аА2; тогда
существуют ^^е S и ВB{)е *92 такие, что А± = B±U В[1)... B^fe)»
л2 = в2 и #
\j /
б) Пусть Р(Х) —алгебра подмножеств множества из двух эле-
элементов {а^а} U {6, Ъ) 0 Р(Х) X Р{Х).
82. lim^n есть совокупность точек, принадлежащих бесконеч-
бесконечному числу из множеств Еп\ Нт Еп — совокупность точек, принад-
принадлежащих всем множествам Ещ кроме, может быть, конечного чис-
числа из них.
83. Пусть А ф В\ верхний предел последовательности Ау В, А,
В, ... равен А [) В, нижний — А [\В.
84. Х\П( U Eh) = {J(X\ U
n\h>n^R) п\ h>n >
85. Рассмотрим X Aim En\ A (\\т ЕЛ рассматривается анало-
аналогично). Легко видеть, что условие %(х0) = 1 (т. е. х0 принад-
принадлежит бесконечному числу множеств из Еп) равносильно условию
86. Из задачи 85 следует, что условия lim En = Пш Еп и
' ~ п
lim Xn = lim %n равносильны.
п п
87. Пересечению множеств соответствует умножение харак-
характеристических функций, а симметрической разности — сложение
по модулю 2.
88. Каждому ji e Jt (см. задачу 10) поставим в соответствие
совокупность Яц борелевских множеств класса |х: В^ — совокуп-
совокупность интервалов; Вц — совокупность множеств, которые получа-
получаются из множеств класса < ]ы одной операцией счетного объеди-
объединения, счетного пересечения или дополнения. Докажите, что
В = U В.. и что все Ва имеют мощность континуума.
^Ж *
299
89. a) /-'(J7,) П/-'(У2) =t4Yi П F»), /"'(^i) Д /"'(^ =
б) Положим Л = {а, 6, с, d}, В = {a', 6', d'}, jtf = {0, {a, 6},
{c, d), {a, b, c, d}}, f(a) = a', f(b) = f(c) = 6', /(d) = d'.
Тогда/({a, 6}) П/({с, d})?/W
в) Если Е — единица в ^, то f~l (Е) — единица в / г C8) П
П=1
г) Для любых Уь У2 с: В выполняется /~!(^i) П /~т(^г) =
= f-^Y] П У2), f~l(Yi) Af'l(Y2) = tl(Yx А У2).
2. Продолжение меры.
90. В силу полуаддитивности внешней меры
91. Обозначим через S полукольцо интервалов, принадлежа-
принадлежащих отрезку [0, 1]. Пусть существует В е R(S) такое, что
[i*(A А В) < е; тогда \х (В) — е< ji* (Л) < ju* (Л) < ji E) + е, от-
откуда вытекает равенство \i* (Л) = ji* (Л). С другой стороны, пред-
предположим, что |i* (Л) = \х* (А). Тогда Ve > 0 существуют Вщ Ch e
CXI СХЭ / ОО \
е R(S) такие, что JJ Вп с: Л с: JJ Cft и У* I ТТ Дп 1 "~
n=i ft=i \n=i /
/00 \
— Н-* I JJ Cfe I < e. Легко доказать, что существует В ^R(S) та-
h=1**(Ip».
кое, что i^* / JJ Вп д В^ < е; тогда
)
92. Любое подмножество канторова множества, имеющего мощ-
мощность континуум, измеримо (его мера равна нулю).
93. В каждом классе эквивалентности существует борелевское
множество.
94. Очевидно, что а) -<=$* б), а) <=> в), г) =^ а). Если выполне-
выполнены б) ив), то имеют место следующие неравенства:
fifmnXWfn n
\ п ) \ h
(i (lim 4n\ = |x ( U П An)=\imii(r) A \ < lim |x (Ah),
{— ) \ ft n^h J h \n^h J ~
откуда следует импликация а) =^ г).
Рассмотреть следующий пример полунепрерывной сверху и
снизу, но не счетно-аддитивной меры на полукольце S подмно-
подмножеств [0, 1] П Q:
S = {sab = [а, Ъ) Л [0, 1) П Q}, VM =Ь-о.
95. Использовать неравенство jli*(Л АС) ^.\х*((А А В) [}
U (В А С)) ^ \х*(А А В) + \1*(В А С), которое следует из зада-
задачи 73 и полуаддитивности ц*.
300
б) Пусть {Жп} — фундаментальная последовательность элемен-
элементов из Ж, ЛпЩ^п.Тоща для любого п е N существует 1{п) gN
такое, что р BП,, 2П„) < 1/2п для любых /г' > /(/г), /г" > ?(/г).
Положим тA) = /A), mB) = max{m(l) + 1, 1B)}, mC) =
= max {mB) + 1, ЦЗ)} и т. д. Несложно доказать, что
ji (lim ^W(;-)\|22} ^mUn = ^ и» следовательно, {Яп} имеет предел.
\ i j J
Другое доказательство см. в задаче 236.
б) Если множество В измеримо, то по определению Ve > О
34 е R (S) такое, что \х*(А А В) < г.
.. \2k-i 2кЛ
96. Множества Ап = (J "~г^—» Туп задают такую совокупность
k=i[ * * J
{Яп}п=1,2 элементов из Ж, что p(^z, Am) = 1/2 для любых Z #
=И= т, откуда следует некомпактность JL. Для доказательства связ-
связности Ж используйте непрерывные отображения /~: [0, 1]->^,
задаваемые формулой /~ (t) = At, где Я* э [0, t] [\Е, Е ^Е.
Е
97. Да, так как измеримые множества образуют о-алгебру.
99. Измеримые множества образуют о-алгебру.
б) Пусть A aR измеримо. Из задачи 91 следует, что для лю-
любого е > 0 существует замкнутое множество В& а А такое, что
оо
\х*(А\В) < е. Тогда U Bi/n —искомое борелевское множество.
п=1
100. Подмножество квадрата измеримо тогда и только тогда,
когда оно имеет вид А X [0, 1], где A cz [0, 1] и измеримо по
Лебегу.
101. \х# (Т) =0, p,*(f) = 1, следовательно, Т измеримо.
102. Из измеримости множества А по Каратеодори следует, что
|х (X) = р* (А) + |х* (Х\А) = |х* (А) + ^ (А),
откуда следует измеримость А по Лебегу. С другой стороны, пусть
А измерима по Лебегу. Для любого подмножества Z аХ сущест-
существует измеримое по Лебегу множество Z\ такое, что X id Z\ id Z,
(x(Zi) = [i*{Z) (Zi — это пересечение последовательности счетных
покрытий множества Z элементами полукольца, для которой мера
\х (гс-го покрытия) меньше \i* (Z) + 1//г). Имеем
= |i(Z, П A) + \l(Z\A) ^ |i*(Z П Л) + i
откуда следует измеримость множества А по Каратеодори.
103. а) Если А измеримо по Лебегу, то Ve >0 осуществляет
такое В из минимального кольца, что \х*(А А В) < е. Отсюда сле-
следует, что Яг (Л А В) ^ р,*(Л А В) < е, следовательно, Я<(Л) —
— Xi(B) < е, где i = 1, 2. Так как Xi(Z?) = Я2E), то XiD) —
— Яг(Л) <С 2е, что и заканчивает доказательство.
б) Пусть а = \i# (У) < у < ja* (У) = Ъ. Построим лебеговское
расширение v лебеговской меры jx, порожденной т, такое, что Y
будет v-измернмо и v(Y) = у. Имеются такие ^.-измеримые мно-
множества Ei и 2?2» что
301
К системе jx-измеримых множеств добавим все подмножества
множества Е = Е2\Е\, имеющие вид С = A(Y\Ei) \J B(E2\Y), А с
а Е, ВаЕ, где А, В измеримы и однозначно с точностью до мно-
множества меры 0 определяются по множеству С. Положим
v (С) = pL-e ц (A) + U- lZL?
Ъ — а \ Ъ — а
(В).
104. Пусть V —мера Лебега на [0, 1]. Будем отождествлять
образы и прообразы при отображении /: Х->[0, 1] (так как / —
почти всюду биекция). Если Y = JJ Yn и для бесконечного мно-
п
жества индексов {к} Yk Ф Хн, то [i(Y) = v{Y) = 0. Если Y =
ft
= v(F), так как Г состоит из JJ card Y{ отрезков длиной 10~\
г=1
Рассмотрим теперь полукольцо множеств L вида (аНО"*, МО"*).
Легко видеть, что jx и v совпадают на L, а лебеговское продол-
продолжение с полукольца L совпадает с обычной мерой Лебега.
3. Конструкции мер.
105. Определим на интервале [0, 1] отношение эквивалентно-
эквивалентности: х ~ у, если i-|/eQ. Пусть А является подмножеством
@, 1], содержащим по одному элементу из каждого класса эквива-
эквивалентности. Для ге @, 1] определим множество Ar cz @, 1], полу-
получающееся из А сдвигом на г по модулю 1:
Аг^ ([г + А] и[(г-1)+Л]) П@, 1].
Легко видеть, что интервал @, 1] является объединением со-
совокупности попарно непересекающихся множеств {Аг}, где г е= Q f)
П @, 1]. Привести к противоречию предположение об измеримо-
измеримости А.
106. Пусть А а [0, 1) неизмеримо. Рассмотреть множество
{Л Х{0}} U {{0} X А} а [0, 1] X [0, 1].
107. По поводу указаний к решению этой задачи без исполь-
использования понятия интеграла читатель отсылается к книге [3], гл. V,
§ 6, упражнение 15. Отметим также, что если использовать поня-
понятие интеграла, то задача не представляет трудности, ибо если ф —
X
характеристическая функция множества А, Ф (х) = \ <р (t) dt, то
о
утверждение задачи легко следует из того, что Ф'(х) = ф(я) поч-
почти всюду.
108. Из теоремы Лебега об интегрируемости по Риману следу-
следует необходимое и достаточное условие: граница множества имеет
меру 0.
109. а) Тривиальная проверка.
б) Первая часть является следствием из задачи 109 а).
110. Для фундаментальной последовательности {vn} положим
( lim vn\ (A) — lim vn (А) для любого А е= 51. Счетная аддитив-
\п-»оо / п->оо
302
ность фупкции множеств lim v следует из равепства
П-»оо
lira 2 vn (АЛ = 2 lim vn Ш, где 4 = U Л4, Ак П 4, = 0
П-»оо | i П-»оо ч i
при кф\, которое следует из равномерной сходимости рядов
%vn(Ai) по »•
г
111. Непосредственно из определения измеримого множества
несложно доказать, что существует такой параллелепипед В, что
0,75^ (Я)
Доказать, что открытый параллелепипед В' с центром в точке
0 е Rn, гомотетичный параллелепипеду В с коэффициентом 1/2,
принадлежит М — М. Идея доказательства: если Ъ е В', то
(Ь + М П 5') П (Л^ П В') непусто, так как имеет положительную
меру.
112. Непосредственная проверка с использованием свойств
двойного абсолютно сходящегося ряда.
113. Пусть X = Q П [0, 1]. Рассмотреть кольцо подмножеств X,
порожденное отрезками, с обычной мерой; X состоит из счетного
числа точек, каждая из которых имеет меру 0.
114. Множество, о котором идет речь в задаче, является част-
частным случаем множества вида х(*ь h\ Ль Аг), при t\ = a, t2 = Ь,
дц = (—оо, 0), Дг = @, оо). Поэтому искомая мера равна
*= f ГеХр(-^121
nF-a) J J ^1 2(Ь-а
—оо О
О
115. Обозначим /: х-+{\/х}. Имеем
РГ1 ([а, Ь]) =
оо
= 2 [l0S2 (<* +"+*) + 1о§2 (Р + ") ~ 1о§2 (Р + « + 1) —
— log2 (а + п)] = log2 A + р) - log2 A + а) = ц ([а,
116. а)//" L__\=BLi +
^i + ^TT^J 1
Мера цилиндрического множества, состоящего из всех последова-
последовательностей, одна координата которых фиксирована: пь, = я, зада-
задается формулой р(п) = \og2(n + i)l(n(n + 2)).
117. Если сумма ряда не зависит от порядка суммирования, то
ряд сходится абсолютно.
118. a) |v| (X) = \i\(X) -f- \12(Х)\
б) |v|(X) = V2it,(X).
303
119. Определим комплексно сопряженпый заряд, положив
v"(il) = v(^) для любого AgI Тогда Rev=(v + v)/2, Imv =
= (v-"v)/2.
120. Для любого А е 51 положим f(A) = sup{|v(^') |: A'cz A,
А' е 51}. Предположим, что sup | v {А) \ = оо, тогда существует
Ло е= 5t, f(A0) = оо. По индукции выберем последовательность
Ао =э А\ =э А2 =э ... такую, что /(Лп) == °°, |v(i4n)|^«. (Пусть
Вс^4п-1 и |v(S)| ^ |v(i4n_i)| -f" Щ если /E) = оо, то положим
Ап — В, в противном случае Ап = Лп_Д5.)
По свойству непрерывности счетно-аддитивной функции полу-
П Ап I === 1*т v (^п)== оо, в то время как
п=0 ; »-«
С = П ^п е= 51 п, значит, v {С) Ф оо.
121. Множество ?g5( назовем отрицательным относительно v,
если v(? П ^) ^0 для любого F е= 51; аналогично определяется по-
положительное множество. Докажем существование отрицательного
множества А- такого, что А+ = Х\Л_ положительно, откуда сле-
следует утверждение задачи.
Пусть {Ап} — последовательность отрицательных множеств и
lim v (АЛ — а — inf (v(^): А отрицательно}. Тогда А = U Ап
П->оо П
отрицательно и v(A) = а. Если А+ = Х\А- неположительно, то
существует CqCzA+, v(Cq) < 0. Тогда существует наименьшее на-
натуральное &i, для которого существует С\ аС0, vFTj) ^ 1//с1# Повто-
Повторим операцию Cq\C\, получив Сч и А:2 ^ /fi, и т. д. Докажите, что
оо
множество FQ = Со\ [} С% непусто и отрицательно, что противо-
противоречит определению а. Значит, А+ положительно.
122. Любое подмножество А+ (соответственно А-.) является по-
положительным (соответственно отрицательным).
123. Если подмножество Е е= 51 лежит в Х\(Л+и^-), то
v(?) = 0.
124. v+(E) = \(E[]AiI v-(E) == —v{E(\A-). Применить за-
задачи 120—123.
§ 2. Измеримые функции
1. Свойства измеримых функций.
125. Цепочка следствий доказывается равенствами
ОО Г
{iel:/(x)>fl}= П UgI: f(x)>a-±
n=i I /г
{.г е= X: / (^) < a} =Z \{х е= X: / (х) > а},
@ .V: / (*)< а + ±
{ж е Z: / (Ж) > а} = Х\{х : / (х)< а}.
304
д) Всякий луч является борелевским множеством; наимень-
наименьшим а-кольцом, содержащим все лучи, является кольцо борелев-
ских множеств.
126. Lsl: JL>fl):
{хе=Х: 0 < / (х)< а}, еслп а > О,
{х <= X: 0 < / (а:) < оо), если а = О,
если а < 0.
127. {* е X: |/(*) | <а} = {х е= X: /(а:) < а} П {* е= X: /(*) >
}
>}
128. Очевидпо, что множество {(*i, ..., tn): f(t\, ..., tn) > о) от-
открыто и представимо в виде счетного объединения открытых па-
параллелепипедов из Rn вида (а^г), b{^) X ... X (о^\ ^П))*
Тогда
{xe=R: h(x)>a}= (J Q {x e R: a^ ^
ft—1 X—1
129. Построить непрерывную монотонно возрастающую функ-
функцию R -> R такую, что прообраз некоторого множества меры 0 яв-
является множеством X' положительной меры (используйте для это-
этого ряды из канторовых лестниц). Пусть ХаХ' — неизмеримое
множество, ф(#) —характеристическая функция множества j~x(x).
Тогда Ц>[{(х)] неизмерима.
130. Считая, что f(x) продолжена вправо от точки х = 1 диф-
дифференцируемым образом (например, f(i + a) =/(l) +a/'(l)), no-
( + ±)-f(z)
ложим Фп {х) = п
. Тогда f (х) является пределом
сходящейся последовательности непрерывных и, следовательно, из-
измеримых функций: /' (х) = lim Фп(ж).
\ m m -f- 1] Г / / -f- 1
131. Прообразом квадратаЯпЫ= —, -ттг" x k^"« "Т^Г
яв-
ляется интервал длиной 2~2п. Рассмотреть a-кольца, порожденные
Dnmi и f-l(Dnml).
132. Положим U{а) = (igR: /(я) < а). Каждое из счетной
совокупности множеств U ( - j становится борелевским после
выбрасывания некоторого множества меры 0. Объединение всех
выброшенных множеств — борелевское множество; можно на нем
положить, например, /(х) з= 0.
133. Доказать утверждение задачи для простых функций, при-
принимающих конечное число значений, доказав сначала, что для
любого измеримого множества А а [0, 1] выполняется: V6>0 су-
существует замкнутое В а А такое, что \х{А\В) < 6. Для любой
Функции ](х) существует последовательность простых функций
fn(x), сходящихся к ]{х). Тогда существует последовательность
8
замкнутых множеств {Кп}, \i (Кп) > 1 — —, /п(я) непрерывна на
А. А. Кириллов, А Д Гвишиани
305
Кп. На компактном мпожестве К — Р\ Кп последовательность не-
п
прерывных функций }п(х) равномерно сходится к f(x), откуда сле-
следует утверждение задачи.
134. Сведя задачу к случаю, когда f(x) задана на отрезке
[а, 6], в силу задачи 133 имеем: Ve >»0 существует измеримое
множество Хе с: [я, b], [i{XB) > Ъ — я — е такое, что f(x) непре-
непрерывна на Хе. Обозначим через Хе с Хе мпожество точек плотно-
плотности; можно показать, что jn (Х^) = ji (Х?), Очевидно, что все
точки Х'г являются точками Лебега функции /, откуда в силу
произвольности е следует утверждение задачи.
135. См. указания к задаче 198.
136./х: sup fn (x) > с) = U {x: fn{x)>c),
\ п } п=1
{х: inf fn (x) < с} = U {x: fn (x) < с}.
П—1
137. Искомое множество:
П U П {*¦¦ |/„(*)-/»+т(*) | <!/*}.
138. Следствие из задачи 136.
139. Положим F(c) = \л{х: f(x) < с}, тогда g (у) = inf с.
140. Следствие из задачи 128.
141. На множестве комплексных чисел круги и прямо-
прямоугольники
{геС: а < Re z ^ Ь, с < Im z ^ d}
порождают одну и ту же а-алгебру.
142. Координаты векторов в одном базисе непрерывно зави-
зависят от координат в другом базисе. Использовать задачу 128.
2. Сходимость измеримых функций.
143. Сходимость очевидна. Неравномерность сходимости сле-
следует из того, что fn(n) — 1/2.
144. Последовательность сходится к разрывной функции
ГО при 0<*<1,
/(*)==10пРи * = 1,
следовательно, сходимость неравномерная.
145. Несовпадение непрерывных функций в одной точке вле-
влечет несовпадение в некоторой окрестности.
146. t{x)=\*~l при °<*<1>
[0 при х — 0.
147. Пусть последовательность {/п} не сходится к / на множе-
множестве F, а к функции g — на множестве G. Тогда / и g могут от-
отличаться только на множестве F [) G.
148. Множество тех точек 3:eR, где /п(я) ^ е, при 0 < е < 1
является отрезком длины 2|/1п(е")/^. Эта величина стремится к
нулю при к -> оо. Значит, /* -*• 0 по мере.
306
Для любой точки х е [0, 1] рассмотрим подпоследовательность
рациональных чисел / гд |, для которой lim rfe существует и не
равен х. Тогда Срд ~ хЯи J">о° ПРИ я-* °° и» значит, fh (х)-*>0
при и->оо. Далее, существует подпоследовательность (г Л, для
i М
которой I р ,/д , — х\ ^ 1/д ,. Для этой подпоследовательности
I hnl hn I hn
f (з)^*". Значит, lim /n (ж) не существует.
k'n П-»оо
б) Выбрать {ki} (I = 1, 2, ...) так, чтобы отрезки, на кото-
которых fh > 1//,не пересекались.
149. Достаточно заметить, что самый естественный способ ну-
нумерации множества {/}** (х)} задается условием п = к (к — 1)/2+
+ i. Очевидно, что ]i (/? (ж) ^= 0) = 1/Л,
Tim gn(x) = I, limgu = 0.
150. Применить соотношения
= U ^(|Л-^|
п=1
151. Применить теорему Егорова.
152. Рассмотреть tg х на отрезке [—л/2, я/2]. Если |/i(z)| = М,
то хотя бы на одном из двух отрезков [—л/2, arctg M] или
[arctgAf, л/2] последовательность {fn(x)} не сходится к f(x).
Замечание. Используя теорему Леви, легко доказать, что
любую измеримую функцию f(x) = f+(x) — f-(x) такую, что
I f+.(x)dx= \ /_ {х) dx = + оо, нельзя представить в виде
[п,Ь] [а,Ъ]
монотонного предела последовательности суммируемых
функций.
153. Приведем к противоречию предположение о том, что
(х) = lim фп (х), где фп (х) непрерывны. Положим, Fn = Е(уп ^
П-»оо
^ 0,5) — это множество таких точек х, что фп(я)^0,5. Имеем
^ (ф <0,5) = lim Fn, что противоречит тому, что множество ир-
п
рациональных чисел не является объединением счетного числа
замкнутых множеств.
Замечание. Не непрерывные функции, представимые в ви-
Де предела последовательности непрерывных функций, называются
Функциями 1-го класса Бэра. Функция Дирихле принадлежит ко
2-му классу Бэра (двукратный предельный переход).
154. Необходимость (для любой измеримой функции) очевидна.
Достаточность следует из того, что прообраз любого борелевского
множества есть объединение не более чем счетного множества
Уровней. Рассмотреть следующий пример неизмеримой функции:
/е: R-*R, где Е cz R — неизмеримое множество:
/ = ( *' если х е Е>
1ь W "(„я, если хфЕ.
20* 307
155. Для функции f(x) рассмотреть последовательность
(Ы*)}, где fn(x) = т/п, если т/п ^ f(x) < (т + 1)/п (wgN,
ibgZ).
156. Мера множества чисел из [0, 1], в десятичной записи ко-
которых есть цифра 9, равна 10 + 9A0 + 9A0~3 + ...)) = 1.
б) f(x) измерима как предел измеримых функций и почти всю-
всюду равна 9.
157. 158. Функции f(x) непрерывны в топологии равномерной
сходимости, jx определена на борелевских множествах относитель-
относительно этой топологии.
159. Достаточно доказать, что любое открытое множество при-
принадлежит 51. Это следует из того, что каждый шар принадлежит
S, шары составляют базис окрестностей и что различных шаров
в X счетное число (различных радиусов счетное число, в каждом
шаре содержится натуральное число).
160. Из открытости множества А следует, что его можно пред-
представить в виде объединения некоторой совокупности шаров, из
которой можно выбрать конечное подпокрытие, так как А — замк-
замкнутое подмножество X и, следовательно, компактно. Счетную ад-
аддитивность \х достаточно проверить для полукольца всех шаров.
161. Свойства а) и б) достаточно проверить для полукольца
шаров. Единственность меры следует из того, что каждый шар ра-
радиуса p~h (к = 0, 1, 2, ...) состоит из р шаров радиуса р~(к+]), ме-
меры которых совпадают по свойству б).
§ 3. Интеграл
1. Интеграл Лебега.
162. Используйте свойства абсолютно сходящихся рядов.
163. Для каждого разбиения Т = {th} определим верхнюю и
нижнюю интегральные суммы Лебега: S(T) = ^ ^ft+iM' (ek)' $(T) =
h ~~
= 2 1№ (eft)' гДе еА = (^ G ^: ^ < /(ж) < *a+i}- Доказать, что ес-
— л
ли /(х) суммируема, то S(T) и ^(Т1) сходятся, S(T) ^ \ / (х) с?а <
<5(Г), |/(х)йц= lim 5G) = lim S (Т) (использовать оценку
164. Используя функции
{0, если "Вк такое, что / (х) и 0 принадлежат
отрезку [th, th+1],
/(х), если нет,
свести к задаче 163.
165. Использовать свойства абсолютно сходящихся рядов.
166. ?[0, 1] изометрически вкладывается в Lj[O, 1], где после-
последовательность fn(x) имеет пределом функцию f(x) =x&S[0, 1].
167. а) При а > -1 - р @ > 0) и а > -1 @< 0);
б) при а > —1 — |р|,
303
168. а) Очевидно;
6) |i ({*: / (*) > 0})
169. Имеем \л({х е [а, Ь]: *а<ф(*) < *fc+i}) = ФСа+i) — *(**)•
По теореме Лагранжа ф(^+1) — t|)(fft) = ф'(?л) (fo+i — **)•
170. В обозначениях указаний к задаче 163 определим изме-
измеримое множество на плоскости Е (Т) — [} {(х, у): f (x)&[tk, *ft+1),
0<y<th}.
Утверждение задачи следует из того, что \iE(T) = SJT),
\i(E АЕ(Т)) < ЦТ)(Ь — а).
172. Доказать, что из суммируемости f(x) следует суммируе-
суммируемость \f(x) |. Использовать равенство \ [g (x) + h (x)] d\i (x) =
А
= f g(x)dli(x)+\h(x)dli(x).
А А
173. Если }{х) не суммируема, то для любого с > 0 существу-
существует простая функция g(x) такая, что f(x) — 1 ^ g(x) ^f(x),
f d\i (x) > с.
Очевидно, что существует множество А, на котором g(x) при-
принимает конечное число значений, такое, что
J / (*)
А
J ^g (x) d\i (x) > с- 1.
А А
174. Положим ап = \i({x(?X, 2n z^f(x) <2п+*}). Суммируе-
оо
мость / равносильна сходимости каждого из рядов 2 ат?П и
2 an^n~lj Показать, что частичные суммы ряда, фигурирующего
п=о
в условии задачи, заключены между соответствующими частичны-
частичными суммами этих рядов.
175. Использовать метод решения задачи 174.
176. Интеграл Римана определяется только для ограниченных
функций. Введем последовательность разбиений отрезка [а, Ь] {Рп}
так, что Ph+i измельчает Рь. и диаметры разбиений стремятся к 0.
Пусть гпп(х) и Мп(х) —функции, соответствующие нижней и верх-
верхней суммам Дарбу для Рщ mn(x) < f(x) ^ М„(х). Положимт (х) =
= lim tnn(x), М (х) = lim Mn(x). Доказать, что f(x) интегрируе-
П-*со П^юо
ма по Риману тогда и только тогда, когда
ъ ъ
\т(х)йх=\м (х) dx.
а а
Последнее условие эквивалентно условию т(х) = М(х) поч-
почти всюду, что эквивалентно условию непрерывности f(x) почти
всюду.
309
177. Линейной ортогональной заменой переменных задач сво-
сводится к условию, когда матрица А диагональна.
178. Заменим интеграл \ х2 (t) dt интегральной суммой
о
п
— A^l —). Тогда подынтегральная функция уаьп(х) будет
ступенчатой и ее интеграл вычисляется по формуле
/п = я-"/»яп/« J ... J ехр {- п Я2 (тл+1 - ЧJ -
-оо -00
2
h=0
В силу задачи 177 справедливо равенство 1п = 1/ — (det
где Л —матрица размера (м + 1) X (л + 1), имеющая вид
l-t —,
-1,
0*
0,
0,
-1'
2+4.
-1,
o,
o,
o,
— 1,
2 + 4.
n
o,
o,
o,
o,
-1,
o,
o,
..., o,
...,o,
...,o,
..., -1,
..., o,
0,
o,
0,
2 + -
—
b2
n2'
1,
0
0
0
-.
Для вычисления det А можно поступить так. Обозначим через
DN(h, \х) определитель матрицы размера N X W, в которой на глав-
главной диагонали стоят числа X, а на двух соседних диагоналях —
числа (х (остальные компоненты равны нулю). Разлагая этот оп-
определитель по первой строке, получаем тождество: DN(X, \x) =
= \DN-i(X, \x) — \x2DN-2(K \x). Отсюда выводится по индукции,
r
что uN ^^ — _—__ , где ж+_ корни квадратного
Ъ2
уравнения х2 — Хх + и? — 0. Если X— 2 + —~i И = — 1, то х , =
310
Обозпачим DN(X, \х) при этпх X, \х просто через DN. Тогда
dot A = Dn+1 + ^т - -j - 1 j Dn + (- 1) Dn +
(разложение по первой и последней строкам). Пользуясь основ-
основным тождеством, это выражение можно привести к виду
а „ Ъ2
Вычислим Dn:
n+1 / h h2 \n+l
Dj)
exp {[A + о (n-2)](« +1)}- expf- [± + о (я)] (n + 1)]
ехр [ь + А + о (л-)]- ехр(— b - -А + о (п
\ п ) { п
sh b
— +chb + o A).
shb
Аналогично вычисляется ип__х = п ~у + о A). Отсюда
det A = ^-(ch Ь + о (l))+-ir[ п — ' -"Ч -« ch 1
Значит,
Итак,
311
Отсюда по лемме Фату следует , что функции (раЪ {х) =
= lim (pabn (х) будут fi-суммируемы при а > О, 6^0 или а ^ 0,
П->оо
Ъ > 0. Поскольку фаьп(я) <;1ш1фаьп(я) = фаь (х), отсюда вытекает,
что применима теорема Лебега и
J Фаьф = lim J Фв
179. Каждая функция хеС[0, 1] однозначно представляется
в виде x(t) -= с + y(t), где с = х@) — контанта, a j/gC0[0, 1].
Мера \хо на 6^0[0, 1] определяется форлхулой
4
*=i
где t0 = To = 0, а множество X(<i, ..., tn; Аь . • •, Дл) определяется
так же, как и раньше.
180. a)|i0(Co[0, 1]) = HO(*(V ...,/„; Я, ...,/?)) =
пс
Обозначив t^ — ta-i через ад, a h — h-i через sa, мы получим ве-
веf
личину я
"п/2
П
exP
al/*
б) Поскольку при отображении х -> —х мера jxo не меняется,
а подынтегральная функция меняет знак, то интеграл равен 0,
если он существует. Суммируемость подынтегральной функции сле-
следует из задачи 178 и неравенства Коши — Буняковского.
в) Пусть x(t) — c+y(t), #eC0[0, 1]. Результат задачи 178
можно сформулировать так. Если
то
фх (у) = J у @ «и» ф2 (у) == j / @ <*'.
о о
ехр { — ас2 — Ь2[с2 + 2сфх (у) -\- ф2 (#)] } rfc с/|_10(^)=г
ЛСо[о,1]
achb
Положим здесь с = П/д и устроим а к +». Тогда мы придем к
312
равенству
J J
R CJo.i
Ml
или
co[o.i]
Отсюда вытекает, что интегралы \ ф? {у) d\iQ (у) можно най-
найти из разложения в ряд Тейлора функции l/]/ch Ь. В частности,
Г * Г 2 — 7
J2 о 4'J2 ° 48'
Со[од] Со[од]
2. Функции ограниченной вариации и интеграл Лебега —
Стилтьеса.
181. Тривиальная проверка.
182, 183. Следует из справедливости утверждения задач для
монотонных функций.
184. Использовать теорему Лагранжа.
185. Использовать интегральные суммы Дарбу и теорему Ла-
Лагранжа.
186. {ац} — это точки разрыва,
+ 0) — Ф(ак).
187. 2. Используйте оценки:
a)|/-*(*n+i) -/•*(*»)! < \f(xn+l)g(xn+l) -
\f{*n)g(Xn + l) ~f{Xn)g{Xn)\ < |/(*»+1) -f{X
6)
|
188. а) Нет. Рассмотреть функции
10, с = 0.
б) Нет. Постройте монотонную функцию ф(х), чтобы ф| — )=
=— при и= 1, 2, 3, ..., ф@)= 0, и f(x)с ограниченным измене-
п
нием на отрезке [0, 1], чтобы для некоторой последовательности
1 > хх > ух > х2 > уг > ... > 0 выполнялось f(xn) = 2~п, /(г/п) =
= 0. Тогда неограниченность вариации ф(/) следует из расходимо-
сти ряда
313
189. Рассуждайте от противного.
190. Пусть ф: I = [a, b]^ S = [0, 1]Х[0, 1] является ото-
отображением на S, задаваемым формулой у(х) = (/(#), g{x)). Рас-
(к I \
—, — I, где к,1 = 1, ..., я, и их
прообразы а < х± < ... < хп2 < Ь, ф (х{) Ф ф(а^) при i Ф /.
Имеем
+ I g(xi+i) ~ ^ (^i) | ]
2
что противоречит ограниченности
вариаций f(x) и g(x).
Без требованрш ограниченности вариаций / и g утверждение
задачи неверно. Для п = 1, 2, 3, .., разбейте 5 и / на 4 равных
?23i...
tff
i
i
I
3
/i
J
' 5 '
I
" ~~Tnt
1С
-v
Рис. 2
замкнутых квадрата и интервала соответственно и установите со-
соответствие между этими квадратами и интервалами так, что если
некоторый квадрат соответствует некоторому интервалу, то его
подквадраты соответствуют подынтервалам указанного интервала
(рис. 2). Если же/, то х является точкой пересечения некоторой
последовательности замкнутых интервалов, которой соответствует
последовательность вложенных замкнутых квадратов, точку пере-
пересечения которых возьмите в качестве ф(х).
191. Проверить для интегральных сумм и перейти к пределу.
192. Из разрывности Ф(я) в точке с следует, что существуют
последовательности {ап} и {Ьп} такие, что а <С «i < a<i <C ... <
< с < ... < Ъ2 < Ь, < Ь, lim (Ьп - ап) = 0, | Ф (Ьп) ~ Ф (an) | >
> К > 0 V«. Из интегрируемости / по Ф следует, что
lim I Ф (Ъп) - Ф 1аЛ I / (х) |^п- 0. Таким образом / (х) \Ьп -+ 0,
что и означает непрерывность /(х) в точке с.
193. По задаче 191 б) f / (х) с?Ф (х) = f / (а) <2Ф^ (ж) +
а а
Ъ
+ \ f {х) с?ФЛ (а:), где Фл(х) отлична от нуля в первых N точках,
314
Флг(#)—в остальных точках. Очевидно, что первый интеграл ра-
равен нулю, ко второму интегралу применить оценку задачи 191 а).
194. Пусть ^? имеет ограниченную вариацию и отличается от
ф лишь в точках разрыва. Ф — У отлична от нуля не более чем
в счетном числе точек. Примените задачи 191 б) и 193.
195. Рассмотрите два разбиения: х0, хи. ..., хп и go = я, %\, ...
..., 1п+\ = Ь, где Xi-i ^ li < Xi при i = 1, ..., п.
Имеем
2 /&)[*(*,) -*(*,-!)] =
г=1
п+1
(Ь) - / И g («О - ^
196. Составьте интегральную сумму и рассмотрите отрезки раз-
разбиения, содержащие внутри себя точки {сн}.
ъ
197. См. задачи 194—195. Ответ: Ьц> (Ъ) — ац> (а) — \ ф (х) dx.
а
198. Разобьем отрезок [0, 1] на 2п равных частей и для у е
е [min/(a:), max f(x)] определим Nn(y) как число тех частей, в
которых есть хотя бы один корень уравнения }(х) = у. Функции
Nn(y) измеримы, так как имеют не более чем конечное число раз-
разрывов. Докажите, что Nf(y) = supWn(#). Равенство интеграла и
вариации проверяется непосредственно.
199. а) Обозначим \ хкйФ (х) через а*. Воспользуемся тем, что
о
функция Ф(х) обладает свойствами Ф|~з")=*2" Ф (*)» ^}("з+"з~)=3
1 1
= ~2" + -j- Ф (х), легко вытекающими из ее определения. Поэтому
=!
1/3
2/3
Г Х
= ^4 J
о
5==1
Отсюда a. = —A У Csk-2sa
Зная, что a0 = 1, получаем последовательно а\ = 1/2, a2 =
= 3/8, а3 = 5/16, a4 = 87/320, ...
l
б) Обозначим \ еахйФ (х) через Ч? (а) и воспользуемся мето-
o
315
дом решения задачи а). Имеем
1/3 1 1
ЦТ (а) = Г еахаФ (х) + Г eaxd<b (х) = -1 (V^rfO (у) +
О 2/3 О
1
» _1_ Г^2а/3+а^/3^ф (») 4-— (l-f-^2а/3)Ч;/—W^2a^3 ch —
2 J У>^ 2 ^ I3/ 3*^3
Итерируя полученную формулу, получаем
J h h
V (а) = e*W ... e-3-ft ch -J- ch -5-... ch jh V (j^.
При a->0, очевидно, ^(a) -> 1. Поэтому
в) Из результата задачи б) следует, что
Г sin л* <М> (х) =± [У (я/) - У (- яг)] = П cos [ —X
о
3. Свойства интеграла Лебега.
200. Проверяется непосредственно.
201. Нет. Рассмотрите пример: X = R, \i — мера Лебега,
202. U(oc) = х(о. i/i
203. а) Для вывода неравенства треугольника используйте не-
неравенство X ^ (ка + \ib)l(a + Ъ) ^ jit при Я ^ (л, а ^ 0, Ь ^ 0.
б) Фундаментальность по мере последовательности Коши из
М[0, 1] следует из неравенства
Р (/. 8) > Г^ И* е X: | / (ж) - g (ж) | > a}, a > 0.
Обратное очевидно. Полнота пространства Л/[0? 1] следует из того,
что из последовательности фундаментальной по мере, с помощью
теоремы И можно выбрать последовательность, сходящуюся поч-
почти всюду.
в) Решение аналогично задаче 203 а).
204. Пусть \ / (х) d[i = А. Для любого е > 0 существует под-
подмножество Е\ конечной меры в X, для которого \ / (х) й\л > А — е.
По теореме об абсолютной непрерывности интеграла существует
такое 6(е) > 0, что \ / (х) d\i < е для всех множеств Е меры
316
< б(е). По теореме Егорова сходимость /п к / равномерна на не-
некотором подмножестве Е2аЕи обладающем свойством \i(Ei\E2) <
< б(е). Далее, существуют такие номера п\(г) и гс2(е), что
[ | fN И — / И | dx < е при N > пх (е) и И /^ (я) dji — А <е при
я2 \х
iV>M2(e). Пусть Аг(е) == max{«i(e), гс2(е)}. Из всего предыдуще-
предыдущего следует, что
< e
X E2 X E2
< e + A + 8 — (A — 3e) + A — (A — 2e) = 7e при JV > n (e).
205. Пусть a e= R, Xa = {а: е= Х: /(ж) ^ а} и р(а) = jm(Xa). Тог-
Тогда p(a) —неубывающая функция на R, причем jo(a)->O при a->
-*—oo и p (a) ->¦ 1 при a ->¦ + °°.
Предположим сначала для простоты, что р(а) непрерывна. То-
Тогда существует обратная функция g(t), определенная на @, 1) и
обладающая свойством p(g(t)) = t. Покажем, что inf \ f (x) d\i
M(A)=t ^
достигается при А = Xg{t). В самом деле, любое множество А ме-
меры t получается выбрасыванием из Xg(t) некоторого подмножества
Y и добавлением к нему некоторого подмножества ZczX\X^(f),
причем ]ш(Г) = \i(Z).
Но в точках множества Y функция / не превосходит g(t), а в.
точках множества Z она больше g(t). Таким образом, в этом слу-
случае множество А, доставляющее нижнюю грань, определено одно-
однозначно с точностью до ц-нулевого множества.
Покажем теперь, что функция / на X и функция g на @, 1)
равноизмеримы, т. е. \io({t e @, 1): g(t) ^ a}) = \i({x e X:
f(x) ^ а}) для всех ogR, где (Ло означает обычную меру Лебега
на интервале @, 1). Левая часть этого равенства равна р(а), так
как неравенство g(t) ^ а равносильно t ^.р(а). Правая часть рав-
равна р(а) по определению.
Из равноизмеримости fug вытекает, что для любой борелев-
ской функции X I X (g (t)) dt — I X (/ (г)) d[i (x). В частности, по-
о х
лагая
*<*>-{?при
[h при
получаем искомое равенство. Случай разрывной функции р раз-
разберите самостоятельно. (Соответствующая функция g(t) будет
иметь интервалы постоянства.)
206. Пусть \io — мера Лебега, \i — квазиинвариантная мера и
X — любое борелевское подмножество на прямой. Рассмотрим мно-
множество Y на плоскости R2, состоящее из пар (х{, х2), для кото-
которых х\ — х2 е X. Применяя к этому множеству теорему Фубини
317
для произведения мер \х X М-о, получаем
Отсюда, если pio(^i —X) — \io(X) = 0, то pii(#2 + «X") = 0 для
почти всех х2 и, значит, \ii(X) = 0. Если же \io(X) ф 0, то слева
стоит iio(^OH'i(R) и, значит, \ii(x2 + X) Ф 0, т. е. \к\{Х) Ф 0. Таким
образом, меры \х и Цо эквивалентны.
207. Вариация заряда v* равна |v,-| = |/i|p.. Поэтому условия
|vi| (А) = 0 и |v2| (A) — 0 равносильны тогда и только тогда, ког-
когда равносильны условия \х(А f) N\) = 0 и (х(Л f| N2) = 0. Послед-
Последнее верно при всех А тогда и только тогда, когда [i(N\ Л N2) = 0.
208. Для каждого подмножества А конечной меры \х по теоре-
теореме Радона — Никодима существует измеримая функция Ра(я), об-
обладающая свойством v (В) — \ рА (х) d[i (x) для любого измеримо-
в
го В а А. Пусть теперь X = L№, М-№) < оо и рг = рх..Легко ви-
видеть, что функции рг и pj совпадают почти всюду на Хг- П Xj. По-
Поэтому существует измеримая функция р на X, совпадающая с р<
почти всюду на Х{. Она обладает нужным свойством.
209. Предположим противное. Тогда \х (А П [0, 1]) = 1/2 и су-
существует покрытие множества А П [0, 1] непересекающимися ин-
интервалами {Ап}п = i,2f... такое, что 211 (&п) < *• Получаем про-
п
тиворечие:
210. Воспользоваться тем, что F (х) = \ / (t) dt — абсолютно
о
непрерывная функция (это следует из абсолютной непрерывно-
непрерывности интеграла).
211. Воспользоваться теоремой Радона — Никодима.
212. а) Непосредственное следствие из определений, б) Этими
функциями можно приблизить любую функцию ф из S. в), г) Мно-
Многочлены и тригонометрические многочлены плотны (даже в смысле
равномерной сходимости) в пространстве непрерывных функций,
которые плотны в ?i[0, 1] по п. б).
213. а) Следует из определения метрики в Lj(R).
б) Заметить, что всякая кусочно-постоянная финитная функ-
функция приближается по метрике L\ (R) кусочно-линейной финитной
функцией, и воспользоваться п. а).
в) Рассмотрим совокупность Lo всех функций /gL2(R), обла-
обладающих свойством \ е~х xkf (x) dx = 0 для всех целых неотрица-
неотрицательных к. Покажем, что функции / характеризуются условием
318
для всех ^g^. В самом деле, из суммируемости функций
е-х +xxj ф и хе—х +hx j (х^ вытекает, что ф/(Я) дифференцируе-
дифференцируема при всех ^gC. Значит, она аналитична. Так как Ф^ @) =
= \ е~~х xhf (x) dx, условия / е Ьо и ф/ ^ 0 равносильны. Пусть
R
а (X) — любая суммируемая функция на R. Тогда 0= I a(X)q>f(iX)dX—
R
(X) e~x2+ilxf (x) dx dX = j е-Л (x) f (x) dx, где b (x) =
e^x
== 1 a (X) e^xdX. Покажем, что, подбирая подходящим образом
R
а(Х), можно в качестве Ь(х) получить любую непрерывную кусоч-
кусочно-линейную финитную функцию. Отсюда будет следовать, что
е / (х) = 0 почти всюду и, следовательно, f(x) =0 почти всюду.
Заметим, что умножение а(Х) на еш приводит к сдвигу Ь(х)
на U Кроме того, соответствие между а(X) и Ь(х) линейно. Поэто-
Поэтому достаточно в качестве Ь(х) получить элементарную функцию,
равпую 0 вне [—1, 1] и равную 1— \х\ на этом отрезке. Оказы-
Оказывается, для этого достаточно взять а (X) — -—. (Ср. теоре-
я X1
му 19 гл. IV и задачу 586.)
214. Докажите, что множество функций, для которых выполне-
выполнено условие непрерывности сдвига, замкнуто в Lj(R). Проверьте это
условие для непрерывных финитных функций.
215. а) Покажите, что fi(t)f2(x — t)— функция, измеримая отно-
относительно меры Лебега на плоскости (я, г), и примените теорему
Фубини для о-конечных мер. Использования теоремы Фубини мож-
можно избежать, рассмотрев сначала свертку на плотном в L\ прост-
пространстве непрерывных финитных функций, затем случай ограничен-
ограниченной функции fi(t) e Li, наконец, приближая /i@ ограниченными
функциями.
б) Рассмотрите неравенство
ГЛАВА III
sup | /х @| j | /2 (* + А) - /2 (о | dt.
ЛИНЕЙНЫЕ ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
И ЛИНЕЙНЫЕ ОПЕРАТОРЫ
§ 1. Нормированные пространства
1. Основные определения.
216. Если одно из чисел р или q равно оо, то искомое нера-
неравенство очевидно. Рассмотрим случай, когда р и q конечны. Вос-
Воспользуемся следующим вспомогательным результатом: если а ^ 0
и Ь > 0, а /) и з - сопряженные числа, то ab ^ a^lp + bv/q. Ана-
319
литическое доказательство этого неравенства легко получается, ес-
если вычислить частные производные функции q (х, у)= ху — х?1р —
— yqlq. Геометрический смысл неравенства виден на рис. 3. Из
этого же рисунка видно, что при а = Ь^~1 (или Ь = а?'1) нера-
неравенство превращается в равенство (см. также указание к зада-
задаче 369).
Докажем теперь неравенство Гельдера. Поскольку обе части
неравенства однородны по о: и по
у, достаточно рассмотреть случай
IWIp = 1 = \\y\\q. (ЕСЛИ ОДИН ИЗ
векторов х или у равен 0, то не-
неравенство становится очевид-
очевидным). Положим а = \х{\, Ь =
= \yi\ во вспомогательном нера-
неравенстве. МЫ ПОЛуЧИМ \Xiyi\ ^
^ \xi\plp + \yi\qlq. Суммируя по
г от 1 до п, получаем
Рис> 3 217—219. Подробное решение
этих задач изложено в книге
[19]. См. также указание к задаче 371.
220. Рассмотреть множество финитных последовательностей с
рациональными коэффициентами.
221. Рассмотреть множество последовательностей с элемента-
элементами из нулей и единиц. (Ср. задачу 223.)
222. Чтобы доказать, что последовательность Коши сходится,
достаточно показать, что сходится какая-либо ее подпоследова-
подпоследовательность. Воспользуйтесь «быстро сходящейся» подпоследователь-
подпоследовательностью \хп ], для которой || х — х || < 1/2\
I ft J II ft °~г 1 ||
223. Достаточность условия несепарабельности очевидна. Для
доказательства необходимости используйте лемму Цорна; доста-
достаточно доказать существование несчетного множества непересека-
непересекающихся шаров радиуса е, для некоторого е > 0.
224. Воспользоваться компактностью шара в конечномерном
пространстве.
225. Доказать от противного, что если Рп(х) —многочлен сте-
степени п со старшим коэффициентом 1, то шах | Рп (х) | ^
> max | Тп (х) | = 21~п, где Тп (х) = 2l~n cos (n arccos x) (на
рис. 4 изображен случай п = 4).
Если многочлен Р(х) имеет старший коэффициент 1 и
max \Р(х) | ^ 21-", то из рисунка видно, что графики Тп(х) п
Р(х) имеют по крайней мере п общих точек. Но разность Тп(х) —
— Р(х) есть многочлен степени п— 1 и потому тождественно рав-
равна нулю.
226. а) При факторотображении ср: L->L/L0 открытый еди-
единичный шар в L переходит в открытый единичный шар в L/Lo.
б) Выбрать последовательность 1/2 — перпепдикуляров уп к
L(yu ..., Уп-\).
в) Пусть к подпространству Lq = {х0 е L: f(x0) = 0} сущест-
существует нуль-перпендикуляр х\. Это равносильно утверждению
320
\\x\ + xo\\ ^ \\x\\\ для всех x0 e Lo. Другими словами, расстояние
d(;rb Lo) достигается и равно ||gil|. Любой вектор х & Lo записы-
записывается в виде х = а(х{ -f- ar0), где а е R\{0}, х0 е Lo-
MI'd)! J/()|
Норма / достигается на векторе х\. Обратное утверждение вы-
выводится так же.
227. Линейное преобразование у *-* у — [2f(y)/f(x)]x называ-
называется отображением в гиперплоскости / = О параллельно вектору х,
не принадлежащему гиперплоскости.
Пусть выполнены условия п ф 2, р\ Ф 1, р^Ф °°. Проверьте,
что это преобразование является изометрией /р(/г, R) (при р Ф
Ф 2) тогда и только тогда, когда х есть один из векторов стан-
стандартного базиса (с точностью до знака), а / — дуальный к нему
базисный функционал. Таким образом, совокупность векторов
{±еъ) переходит в себя в соответствии с изометрией lp (n, R) в
lp (n, R). Но расстояние dp(±ek, dszej) == 21/р и, следовательно,
искомая изометрия существует, только если р\ = /?2»
2. Сопряженные пространства.
228. Использовать базис Гамеля. Базисом Гамеля называется
линейно независимая система {ха} элементов линейного простран-
пространства L такая, что ее линейная оболочка совпадает с L. (Ср. за-
задачу 16.)
229. Расстояние от нуля до гиперплоскости f(x) = 1 есть
inf ||g|| по множеству {х: f(x) = 1} = {яо + ker/}, где х0 — фикси-
фиксированный элемепт из L такой, что /(г0) = 1. При этом L есть ли-
пейпая оболочка х0 и ker/.
230. Проверяется непосредственно, так как конечномерное про-
пространство изоморфно сопряженному.
231. Банахово пространство рефлексивно тогда и только тог-
тогда, когда тар ||#|| ^' 1 компактен в слабой топологии.
232. (со)':э/1 (более того, (с0)'= Zi), поэтому слабая сходи-
сходимость влечет покомпонентную сходимость. Рассмотрев последова-
21 А. А. Кириллов, А. Д. Гвишиани 321
тельность Xni = 1, i ^ n, xni = 0, i > n, доказать некомпактность
единичного шара в со в слабой топологии.
233. Базис слабой топологии состоит из множеств, не ограни-
ограниченных в сильной топологии.
234. Легко видеть, что (li)'^loo (более того, (h)' = I*,).
Пусть {.г(п)} — последовательность элементов в U, которая сходит-
сходится слабо и не сходится сильпо к нулю. Переходя к подпоследова-
подпоследовательности и умножая на константу, мы можем добиться того, что
||я(п)|| ^ 1 для всех п.
Будем говорить, что последовательность х е h сконцентриро-
сконцентрирована на интервале [к, I] в пределах е, если 2 | х{ | ^ A — е) | х\.
Переходя к подпоследовательности, мы можем предполагать, что
х{п) сконцентрирована на [кп, 1п], в пределах 1/4 и, более того,
эти интервалы не пересекаются для различных п. Пусть теперь
аг== sgn xi у если i e= [A:n, In] и «,=0 в противном случае.
Тогда
2и агхг ^ 2j \ хг I "" Zi I xi I
{=1 i=ftn i&hnjn]
. A || r(n) || i_ || „(n) || ^ J
что противоречит предположению о том, что х{п) -^ 0.
235. Докажите, что опорная плоскость единичного шара в L
задается уравнением f(x) = 1, где /gL'h ||/|| = 1.
236. Возьмем /с-мерную грань и (к + 1) вершину х{ (i =
= 1, 2, ..., к + 1) на этой граня (такие найдутся, так как вы-
выпуклый многогранник есть линейная оболочка своих вершин). По-
Поставим в соответствии этой /с-мерной грани множество {f^Bf:
'1(xi) = 1, * = 1, ..., ? + О- Доказать, что полученное множество
есть (п — к —1)-мерная грань В'.
237. Проверьте, что единичный шар в с0 не имеет крайних
точек, а единичпый шар в с имеет две крайние точки: хп == 1 и
хп 2=г —1. Изоморфизм между 1\ и cQ устанавливается формулой
оо
({ап}> {хп}У — 2 anxn'> a изоморфизм между h и с' —формулой
П=1
оо
({an}' {^n}) = ai ^m хп~Ь 2 an+ixn* Для вычисления нормы
{ап} в с' рассмотрите последовательности вида
(sgnai+1 при t<N,
х- = {
г lsgnax при i> N.
238. Использовать неравенство Гельдера.
239. Рассмотреть на сс/оо непрерывный функционал / ({xn}) =
= lim ~n и применить теорему Хана —Банаха.
П-»ос
240. Выбрать базисы ei (i = 1, ..., я^ и fj (/ = 1, ..., и2) в
L^ и L2, биортогональные соответственно к базисам е* (i =
= 1, ..., wO и fj (/ = 1, ..., л2) bZi и L2.
241. Проверяется непосредственно. (См. также задачу 290.)
322
242. При доказательстве достаточности применить задачу 241.
243. Проверяется непосредственно.
244. Воспользоваться задачами 241 и 242.
3. Операторы в нормированных пространствах.
245. Пусть Р — проектор на L{ параллельно L2. Тогда 1 — Р
есть проекция на L2 параллельно L\. Если Р непрерывно, то L\ и
Ь2 замкнуты. При этом L{ = ker A—-Р), L2 = ker P. Обратно, ес-
если L\ и L2 замкнуты, то непрерывность Р следует из теоремы Ба-
Банаха об обратном операторе. (Рассмотрите естественное отобра-
отображение Q: Lx ->- L/L2 и представьте Р в виде Q~l о я, где я — естест-
естественная проекция L на L/L2.)
246. Доказать, что kerP = im(l — Р), ker P f| im P = 0 и
L = ker P + im P.
247. Если р ^ q, то подходит любая функция а(х) е ?«>@,1);
при р < q подходит только а(х) == 0.
248. Воспользоваться теоремой единственности для обыкновен-
обыкновенных дифференциальных уравнений.
249. Воспользоваться методом доказательства теоремы 10 гл. IV.
250. Контрпример: рассмотрим оператор A(s): L2(R ->?2(R),
который задается формулой: (A (s)x) (t) = x(t + s), x(t)^L2(R).
251. Л': ^,[0,l]^Lp/[0,l]; M7) (*) = J if (y, x) f (y) dy.
253. Проверяется непосредственно по определению (задача 221).
254. Нет. Рассмотреть неограниченный функционал.
255. Ответ отрицательный. Рассмотрите оператор умножения
на функцию в пространстве ?2[0, 1].
4. Конструкции банаховых пространств.
256. а) Для доказательства ||я;|| = 0 ¦<=>- х = 0 использовать
замкнутость Lo в L.
б) Выбрать из фундаментальной в L\ последовательности уп
подпоследовательность уп так, чтобы У! bni~~ Упи \ь < °°* По-
и. Лшт^ || к At "Т" 1 И X
дожить ак— УпьГ~ Упк и выбрать й^еф;^) (ф — факторото-
бражение L->?i), так, чтобы |flft]|l<|]а&||l + 2~h- Рассмотреть
Sk = (ц + ... + ak. Доказать, что lim yk = ф(Пш Sk) + у\.
257. Пусть ф — факторотображение L на L\, zn — фундамен-
фундаментальная последовательность в L. Тогда уп = ф(^п) фундаменталь-
фундаментальна в Lu следовательно, существует у = lim уп, откуда || у — yn\\L ->•
-*- 0. Таким образом, существуют гп е ф (у — уп) = Ф (у) —
— ф~!(Уп) такие, что l|/*n||L-^0. Выберем в Ф-1(^) фиксированный
элемент /, тогда гп = / — /я, /n e ф'Ч^и)-
Следовательно, /п->/, но гпЕф'^п), поэтому /п — zn = хп —
фундаментальная последовательность в LQ.
258. Пусть X — сепарабельное банахово пространство,
{#i, •. •, хп, ...} — счетное всюду плотное множество в единич-
единичном шаре в X. Определим отображение 1\ (К) -> X, полагая
323
а) Докажите, что А непрерывно.
б) При данном #, \\x\\ = 1, выберем xn{i)i требуя, чтобы
U — 22~*+4i(i) <2~*- Отсюда imA = X.
в) Меняя в этой оценке число 2 на 3, 4, .,., покажите, что
A: li(K)/ker А -> X — изометрия.
259. Пусть L — банахово пространство, Lo — подпространство.
Тогда: 1) (LQ)' = L'/Lf, (L/LQ)' = L*, 2) Lo дополняемо <=>L0 =
= PL, где Р — непрерывный проектор.
а) Lo конечномерное. Выбрав базис lu ..., In в Lo, показать,
что существуют такие /ь ..., /n e L1, что (/г, ej) = 6ц. Рассмот-
Рассмотреть Р : L -+ Lo, ^ == 2 (Л» ж) ^г-
в) Пусть ф — изоморфизм 1ос(к) и ЬоаЬ, фг- = ^i-ф-1, где
е, — стандартный базис в ^ с= (Zoo)'. Обозначим через ф* продолже-
продолжение ф* на L без увеличения нормы. Тогда ||фг|| ^ Нф!! (i =
= 1, 2, ...). Определим отображение Р: L-+LQ по формуле Рх =
= ф({фг> #})• Доказать, что Р — непрерывный проектор.
б) и г) следуют из а), в) и 1), 2).
260. См. задачу 56.
261. Если S — произвольная (р, q)-кросс-норма, то S^p®q.
h h
262. Пусть п ^ иг, z = 2 ^i ® ^i' z "^ ^z = 2 ^г* Выберем
собственный базис 6i, ..., еп для оператора ^42-42» ej — базис
в L2.
^i}^hmei ej emek Z^ ^ij^km mjeieh jLJ ^ij^kj ik*
3
m
Положим aik = 2 ^ij^ftj» в СИЛУ того» что еи ..., en — собствен-
m
ный базис для AZA'Z, aik = O при i ф к; a{i = 2 ^ij^ij = 2 ^ii'
n m
Из представления ^ = 2 ei®Uv где У г = 2 ^ i/^?» следует, что
71
|| 21|= 2 |j/i| не меньше кросс-нормы на L{ ® L2. Осталось дока-
г1
зать, что || z|| — кросс-норма; тогда || • II — норма на Li (g> L2 в силу
предыдущей задачи.
263. Воспользоваться явным видом нормы на L\ ® L2.
264. Пространство Ь'г ® Ln при помощи соответствия х (& у -**
-+Ax>y^&(Lu Li); Ax>y(z) == {х, z)y, xgLJ, у е L2, zg^i
отождествляется с пространством операторов конечного ранга. До-
Доказать, что норма на L\ 0 Z>2 совпадает с обычпой нормой операто-
оператора (см. предыдущую задачу).
324
265. Доказать, что норма на l[(m-n, R) является кросс-нормой
для норм 1\{п, R) и l\(m, R) (см. также задачу 260).
266. Доказать, что норма на loo(m-n, R) является кросс-нор-
кросс-нормой на loo(n, R) и loo(m, R).
§ 2. Линейные топологические пространства
1. Топология, выпуклость и полунормы.
267. 268. Проверяется непосредственно, исходя из определений.
269. Воспользоваться теоремой 11 гл. III. (См. так-
также [19].)
270. Доказать индукцией по dim L, что всякий линейный изо-
изоморфизм L и KAim L (где К — поле скаляров) является гомеомор-
гомеоморфизмом.
271. Рассмотреть вложения окрестностей нуля.
272. а) А + Я- U (А + х).
х=В
б) Пусть а ф. А + В. Тогда для каждого igB множество
х + А замкнуто, следовательно, существует уравновешенная окре-
окрестность нуля U(x), для которой (a + U(x)) fl (x + А) = 0. Мно-
Множества х-\- — U (х) —открытое покрытие В. Пусть | xi + —U (х-^,
гс>— конечное подпокрытие и7= П -о- U (хЛ. Дока-
J кКп * х '
( V) (А + В) 0
J
зать, что (а + V) [\ (А + В) = 0.
273. Для каждого IeRh каждого целого га положим en{t) =
= ein*, /n = e_n + wen (n = 1, 2, ...). Будем рассматривать эти
функции как элементы пространства Z,2(—я, я).
Пусть Xi — наименьшее замкнутое подпространство в L2, со-
содержащее в0, ei, ..., а Х2 — наименьшее замкнутое подпространст-
подпространство в Z>2, содержащее /i, /2, ... Показать, что Х[ + Х2 всюду плотно
в ?г, по не замкнуто.
оо
Например, вектор х = ^ га—1^_п принадлежит ?г, но не
n=i
принадлежит Х\ + Х2.
274, 275. Следует из определения выпуклого множества.
276. Ответ: S = \х(А), L — периметр А.
277. Для простоты и наглядности приведем доказательство для
случая двух выпуклых множеств на плоскости. Предположим до-
дополнительно, что эти выпуклые множества Ах и А2 ограничены
гладкими кривыми Гу и Г2, не имеющими прямолинейных участ-
участков. Пусть множество А — oliAy -\- а2А2 ограничено кривой Г.
Выберем на кривых Гь Гг и Г специальную параметризацию.
А именно, каждой точке т <= [0, 2я1 поставим в соответствие ту
точку (ti(t), */i(t)) gFi, в которой достигает максимума величи-
величина х cos т + у sin т, когда (я, у) пробегает А{. (Другими словами,
(я(т), у(т)) — точка касания Г\ с опорной прямой, составляющей
угол т с осью у). Аналогично определяются параметризация
te(T), уг(т)) кривой Г2 и параметризация (х(т), у(т)) кри-
кривой Г. Покажем теперь, что эти параметризации связаны ра-
равенствами
х{т) == а^т) + а2*2(т),
У(т) = aiyi(T) +a2i/2(T).
325
В самом деле,
max (х cos т + у sin т) =
()A
= max [(a^x + а2я2) cos т + (a^ + a^) sin т] =
= max [ax (o:l cost + j/x sin x)+a2 (x2 cost -|-?/2 sin т)] =
= a. max (хл cos т + ?/, sin т) + a max Co:0cos x+wsin т),
откуда следует желаемое равенство.
Теперь остается воспользоваться известной формулой для пло-
площади множества Л, ограниченной кривой Г, заданной в парамет-
рической форме: |х (Л) = \ х (т) dy (т). Мы получим, что |х {А) =
= о«A (Лг)+«1(^) + га^-М (Л^ А2), где М (Av AJ -
2Л , ,
= I 1 2 —Li Jt. Последняя величина называется смешанной
о
площадью пары множеств А\ и Лг в смысле Минковского.
Точно так же доказывается, что для к выпуклых множеств
Ль ..., Лп на плоскости справедливо равенство
Для множеств в гс-мерном пространстве доказательство про-
проводится по тому же плану. Граница дА выпуклого множества Л
параметризуется точками единичной сферы S и Rnr после чего
используется формула для объема:
|х (Л) = j х± (т) dx2 (т) Л ... Л d*n (т).
S
При этом возникает понятие смешанного объема М(А\, ..., Лп)
набора из п выпуклых множеств в Rn, в терминах которого выра-
выражаются многие геометрические характеристики выпуклых тел.
278. Доказать, что ядерно-выпуклая топология задается систе-
системой всех вообще конечных полунорм на L.
а) pj = | f(x) | — полунорма для любого линейного функцио-
функционала / на L (не обязательно непрерывного).
б) Функционал Минковского выпуклого, уравновешенного и
поглощающего множества есть полунорма.
279. В пересекается с каждой прямой, проходящей через
нуль, по замкнутому в евклидовой топологии прямой интервалу,
когда В = {х: рв(х) ^ 1}, где рв — функционал Минковского мно-
множества В.
280. а) Рассмотреть множества Во = {х: рв(х) < 1} и В\ =
= {я: Рв(х) ^ 1}, где рв — функционал Минковского множе-
множества В.
б) Использовать предыдущую задачу.
326
281. c2(A) — выпуклое множество. Далее воспользоваться за-
задачей 275.
282. Базис окрестностей нуля в полинормированном прост-
пространстве L состоит из конечных пересечений множеств {ра(х) < е}
(иеД е>0).
283. Во всяком ЛВП есть базис окрестностей нуля, состоящий
из выпуклых множеств. Контрпример — пространство LP(X, ji) при
О </? ^ 1.
284. Доказать, что в топологии покоординатной сходимости
R°°— ЛВП с системой полунорм рп (п = 0,1,.. .);рп ({^iJi^H xnfi
далее использовать задачу 282.
285. Для г ^ 1 шар радиуса, г — выпуклое мзожество, так как
совпадает с С {К). При 0 < г < 1 шар радиуса г не является вы-
выпуклым множеством. Положим
0, |х]>1.
Рассмотрите функции вида hf(x) + ц}(х — п), гс > — log2r.
286. Шары SR = {fe=C(R), d(f, 0) < R) при R < 1 не явля-
являются поглощающими множествами, следовательно, в этой тополо-
топологии C(R) не есть ЛТП.
287. Нормой на BC(R) является функцией p(f) =sup|/(s)|.
288. Доказать, что топология в R°°, заданная метрикой d({xn},
{Уп}), есть топология покоординатной сходимости (см. задачу
284).
2. Сопряженные пространства.
289. Следует из линейности функционала и инвариантности
топологии ЛТП относительно сдвигов.
290. а) Свести задачу к случаю, когда U — уравновешенная
окрестность нуля.
б) кег/ замкнуто, следовательно, нигде не плотно, поэтому
существуют такие х е L и уравновешенная окрестность нуля F,
что ?+Fflker/=0. Доказать, что f(V) ф —j(x) и использо-
использовать а).
291. Из теоремы Хана — Банаха следует, что топология на L,
в которой непрерывны все функционалы, совпадает с ядерно-вы-
ядерно-выпуклой (см. задачу 278). Доказать, что мощность базиса окрестно-
окрестностей нуля ядерно-выпуклой топологии есть 2Э, где р — мощность
базиса Гамеля пространства L.
292. Выбрать базис в Р и дополнить его до базиса в Rn.
293. Единичный шар в пространстве С [а, Ь] имеет две крайние
точки: f(x) == 1 и f(x) s= —1. По теореме К'рейна — Мильмана сле-
следует, что он не является компактом ни в какой топологии.
3. Теорема Хана — Банаха.
294. Воспользоваться задачей 270.
295. Разделяющая гиперплоскость должна иметь вид /(я) = 0,
/ е Р'. Доказать, что / == 0.
296. Пусть А компактно; тогда существует выпуклая окрест-
окрестность нуля V такая, что (А + V) (] В = 0. Применить геометриче-
геометрическую форму теоремы Хана — Банаха к А + V и В и еще раз вос-
воспользоваться компактностью А.
297. Фиксируем isi; из теоремы Хана — Банаха следует, что
существует х* е L', \\х*\\ = 1, (х*, х) = ||ж||.
298. Изометрическое отображение L-+L", построенное в пре-
предыдущей задаче, является изоморфизмом в силу равенства раз-
размерностей пространств L и L'\
327
299. В качестве X взять единичный шар в сопряженном про-
пространстве со слабой топологией.
300.. Воспользуйтесь результатами п. 2 § 4, гл. III.
301. Воспользоваться полярными координатами.
302. Использовать сепарабельность lq(n, R).
303. Пусть L — подпространство в J«>(R), порожденное после-
последовательностями вида
у = хп+{ — хп, {хп} е *оо.
Докажите, что последовательность уп == 1 не лежит в L. Затем
примените теорему Хана — Банаха.
304. См. указания к предыдущей задаче.
305. р (х) = sup р (Тпх) (п = 0, ± 1, ...).
п
306. Рассмотреть пространство JJ R' (/ е L') и вложение
307. См. указания к задаче 303.
308. Применить теорему Хана — Банаха.
309. См. указания к задаче 308.
310. Рассмотреть гиперплоскости (х, /<) = 1, где U — счетное
всюду плотное подмножество единичного шара в Lq(n, R)
311. Можно считать, что данное выпуклое множество V со-
содержит нуль и пересечение V с каждой прямой, проходящей че-
через начало, есть замкнутое множество. Граница V задается в по-
полярных координатах (г, ф) уравнением выпуклой функции г(ф),
следовательно, г(ф) — непрерывная иа [0, 2я] функция, удовлет-
удовлетворяющая условию г@) = гBя). Доказать, что Ve > 0 3 много-
многоугольник Vn(e) такой, что |г(ф) —/Чф)! < 8, где г(ф) —функция
границы для Fn(e). Fn(e) задается пересечением полуплоскостей
вида atx + bijj ^i. Рассмотреть_ вложение ф: R2->Rn: (x, у) ->
-+xa+yb, где а= (аи ..., лп), 5= (Ьи ..., Ьп).
312. Построить изометрическое вложение сначала lP(n, R) в
Z«(R) (пользуясь сепарабельностью lP(n, R)), а затем построить
вложение U(R)->C[0, 1].
313. Проведем сначала индукцию по числу множеств. Пусть
N > п + 2 и для W—1 множеств утверждение доказано. Если
Хи ..., XN удовлетворяют условиям теоремы, то любые N — 1 из
них имеют общую точку по предположению индукции. Положим
Yi = Хг П XN (l<^i^/V— 1). Тогда любые /V-2 из множеств
Уi имеют общую точку. Поскольку N — 2 ^ п + 1, семейство У\
снова удовлетворяет условиям теоремы. Значит, все Yi имеют об-
общую точку, которая будет общей для всех Xit Осталось разобрать
случай N = п + 2. Проаедем теперь индукцию по размерности.
Предположим, что для размерностей <и теорома доказана, и рас-
рассмотрим множества Xi (I ^ i ^ п -\- 2) в R", каждые п + 1 из ко-
которых имеют общую точку. Если Хп+2 пе имеет общих точек с пе-
71+1
ресечением Z = J] Xit то существует гиперплоскость L, разде-
ляющая эти два выпуклых множества. Любые п множеств из Xi
(l^J^rt-f-1) имеют общую точку с Хп+ч и с Z. Поэтому они
имеют общую точку с L. Положим Yt = Xi f) L A ^r i ^ /г -f- 1).
Тогда, отождествляя L с R*-1, мы видим, по предположению ин-
328
n + 1
дукции, что П Ух непусто. Это противоречит определению L
П+1 ~~
как П Уг — % П L. Остается проверить теорему при п = О,
когда она тривиальна.
Замечание. Топологическими рассуждениями можно пока-
показать, что условие выпуклости в теореме Хелли можно заменить
условием: все множества вида Х{ П ... П Xt при к ^ п -\- 1
гомотопичеспи эквивалентны точке (т. е. стягиваются в точку).
314. Пусть Xi = i/n (i = 0, 1, ..., п) — разбиение отрезка
[О, 1]. Для любого е > 0 и любой /sC[0, 1] существует такое я,
.что \ ~Уп | / (х) | dx < e (i = 0, 1, ..., п — 1). Далее использовать
Н
представление фупкции f(x) в виде / (х) = ^ —L, где
г=о
315. a) U разделяет точки L.
б) Используя то, что
IJV (/(*))# (*) < \\F{f{x))\d\i{x)<i\\F\\^\\j\\d\i(x),
доказать непрерывность F(f) no F<
§ 3. Линейные операторы
1. Пространство линейных операторов.
316. Имеют место б) ив).
317. Пусть х = (хи х2, ..., #п, ...) eZ2(R), тогда Апх =
= xnh -+ 0.
318. (у, Впх) = ххуп, где х = (xh x2i ..., #„, ...) e^(R) и
У = (Уи У2, ..., Уп, . •.) е /2(R).
319. ЛПЯ„ — Л5 = ^ni5n — АпВ -f- ЛП5 — Л5 = (Лп — А)В +
-f- An(Bn — i5).
320. Воспользоваться теоремой Банаха — Штейнгауза.
321. См. указания к двум предыдущим задачам.
322. База сильной топологии на End L задается множеством
полунорм
Достаточно проверить непрерывность умножения в точке @, 0).
где 0 — нулевой оператор в End L.
323. См. задачи 317 и 318.
324. ||ЛК M«|I
IMKi
325. а) Проверить, что || / (х + /) — / (х) \\L -> 0 при t->0 для
непрерывных функций с компактным носителем.
б) \\T(t') — T(t")\\ = 2 при ? ф t". (Применить оператор к
функциям с достаточно малым носителем.)
329
326. Пусть ||xnll-*O и ||Лл;п|| А 0. Тогда существуют е > 0 и
подпоследовательность \хп } такие, что | Ах 1^ е. Из того, что
II хп || ">0» слеДУет существование а ->оо таких, что ankxnk "*"
->0. Тогда из того, что II AanhxnA "* °°» следует, что ^Aanjxn^
слабо не сходится.
327. В банаховых пространствах слабая и сильная ограничен-
ограниченности совпадают; непрерывность оператора равносильна его огра-
ограниченности. Ответ: будет.
2. Компактные множества и компактные операторы.
328. Канторово множество покрывается 2П отрезками длины
3~п и не может быть покрыто меньшим числом отрезков такой
длины. Поэтому при е = 3"n/2 iV(e) = 2\ Значит, N (б) =
= О (е 3 ) и аппроксимативная размерность равна log3 2 « 0,63.
329. Условие того, что А — крайнее подмножество К, выглядит
следующим образом: если х е= К, у е= К, хфу и (i+i/)/2g4
toig4 и yei
330. Пусть Р — семейство всех компактных крайних подмно-
подмножеств множества К. Так как К е= Р, то Р Ф 0. Из леммы Цорна
следует существование максимальной цепи Q, являющейся цент-
центрированной системой замкнутых подмножеств К. (Система мно-
множеств называется центрированной, если любая конечная подсис-
подсистема в ней имеет непустое пересечение.) Далее использовать тот
факт, что следующие свойства подмножества А в топологическом
пространстве эквивалентны:
а) А — компакт;
б) всякое бесконечное подмножество А содержит направлен-
направленность, сходящуюся к некоторому элементу из Л;
в) всякая центрированная система замкнутых подмножеств в
А имеет непустое пересечение.
331. Если А — крайнее подмножество К, AgL', ji — макси-
максимум Re Л на А и АА = {х е= A: ReA(x) = \i}, то АА — крайнее
подмножество К. Далее воспользоваться тем, что U разделяет
точки в L.
332. См. задачи 330 и 331.
333. Пусть Н — выпуклая оболочка крайних точек К. Так как
К компактно и выпукло, то замыкание Я с К. Поэтому Я ком-
компактно. Предположим, что некоторая точка х0 е= К и х0 §ё Я. При-
Применяя теорему Хана — Банаха к х0 и Я, показать, что КА ф П
(Л е= V — теорема Хана — Банаха. Но поводу обозначения КА см.
задачу 331). Таким образом мы получаем противоречие построе-
построению Я.
334. Все точки единичной сферы пространства lp(n, R).
335. Единичный шар пространства с0 не имеет крайних точек.
В пространстве с единичный шар имеет две крайние точки
A, 1, ..., 1, ...) и (-1, -1, ..., -1, ...).
336. Применить теорему Крейна — Мильмана (задача 333).
337. Пусть М — предкомпактное множество. Тогда оно облада-
обладает е/3-сетыо {/<} (l^i^N). Компакт X можно представить в
виде объединения конечного числа частей диаметра < е/3. Поэто-
Поэтому для каждого i существует разбиение Т на конечное число ча-
частей, на которых колебание /< не превосходит е/3. Взяв произве-
произведение этих разбиений, мы получим разбиение Т на такие части
{Tj} (^^/^и), что колебание U на Т\ не превосходит е/3 для
330
всех i и /. Если теперь / — любая функция из Л/, Д- — ближайшая
к / точке е/3-сети, a t и s — любые точки из Т$, то dx(j(t), f(s))^z
^dxU(t), fi(t))+dx(fi(t), /,(O)+<*x(M*). /(«))< «/3 + 8/3 +
+ е/3 = е. Необходимость условия доказана.
Пусть теперь задано е > 0 и существует такое разбиение
п
Т = ЛТР чт0 ®f(Ti) < 8/4 Для всех 1^м- (Здесь со/(Г;-) озна-
чает колебание функции / на множестве Tj.) Выберем в каждом
множестве Tj по точке tj и рассмотрим отображение ср: М-+Хп:
/->(/(^i), . •., /(^п)). Так как X — компакт, Хп — также компакт
(расстояние в Хп определяется формулойd(x, у)— max dx (хг, уг)).
l<:i<:n
Значит, образ М — предкомпактное множество. Выберем в ф(Л/)
конечную е/2-сеть ф(А), ..., ф(/п). Тогда /ь ..., /п — е-сеть для Л/.
В самом деле, если /-—любая функция из М, а ф(Д) — ближай-
ближайшая к ф(/) точка е/2-сети, то для t е Tj имеем
+ dx{U(tj), U(t) < e/4 + e/2 + e/4 = e.
338. Крайние точки — матрицы (aij), где aia{i) == 1; ац = О
для j Ф o(i), где og5 — симметрической группе n-го порядка.
Для п = 2 это очевидно. Пусть это доказано для к < п. Край-
Крайние точки множества стохастических матриц порядка п — это
сечение куба 0 ^ хц ^ 1 (?, / = п) плоскостью 2 xij == ^ (У ===
i
s= I,..., и). Отсюда следует, что каждая крайняя к ^xij—l (* =
= 1,..., и) точка должна содержать не менее п2 — 2п нулей. Про-
Проверить, что у крайней точки найдется ац == 1, и применить индук-
индукцию к матрице, у которой вычеркнуты i-я строка и /-й стол-
столбец.
339. Единичная сфера в этом случае ограничена, но не ком-
компактна.
340. Компактные операторы образуют идеал в End (L).
341. Если сц -> 0, то Ve > 0 3N: У/п > N I ап | < ё. Рассмот-
Д е I (R): <— ^ 1 \ (можно считать, что а* Ф 0)
III ЧИр J
и KN = К П L(eh ..., eN), выбрать е-сеть хи ..., хт в KN и дока-
доказать, что она есть 2е-сеть для К. Оператор А компактен тогда и
только тогда, когда К компактно.
342. На подпространстве L={/eC[0, 1], /|[o, i/2] = 0} опе-
оператор Af = xf обратим.
343. Пусть Л' — компактный оператор. Тогда оператор А"
компактен. Поэтому множество A "S", где S" — замкнутый единич-
единичный шар в пространстве L"v предкомпактно. Пространство L2 мо-
может быть изометрически вложено в L2. Отождествляя L2 с обра-
образом в b при этом вложении, получаем AS s A"S'\ следователь-
следовательно, множество AS предкомпактно в сильной топологии L, а по-
поэтому и в сильной топологии пространства ?г.
344. Применить теорему Арцела — Асколи.
331
345. Если {фг} и {\f>j} — полные ортонормированные системы
L2(X, \i) и L2(Y, v), то {fityj} — полная ортосистема в L2(^X Y,
Ц Xv).
X
346. Пусть F (х) = -1 Г / (О Л, / (О > О.
х J
о
Если 0 < \ < X, то имеем
J-
х
Отсюда || Ffp <JZIi\\f llp II FV-i \\q = ^ || /||-1| F fj\ Ответ: || Л| =
P_
~~ p — Г
347. L рефлексивно тогда и только тогда, когда единичный шар
S' слабо компактен.
348. Воспользоваться теоремой Асколи — Арцела.
349. Если с0 Ф 0, то нет. Если с0 = 0, то может. Примером
служит конечномерный проектор.
3. Теория фредгольмовых операторов.
350. Необходимое и достаточное условие: существует с > 0 та-
такое, что все отличные от нуля ап удовлетворяют условию \ап\ > с.
Далее применить теорему Банаха об обратном операторе.
351. imrA = Zp(R). Следовательно, coker Tk = 0, a ker Th по-
порождается первыми к базисными векторами.
352. а) Полуточность в членах Lo и L3 очевидна.
б) Полуточность в члене Lx. Пусть х — произвольная верши-
вершина Р, ех равна 1 на х и пулю на остальных вершинах. Тогда dxex
равна 1 на выходящих из х ребрах, —1 на входящих в х реб-
ребрах и 0 на остальных. Рассмотрим любую грань А, которой при-
принадлежит х\ тогда х принадлежит последовательно двум ребрам
1\ и Г2 грани А. Если Y\ и Г2 оба входящие в х или выходящие
из х ребра, то е(Гь А) = — е(Г2, А). Если одно ребро выходит, а
другое входит в х, то е(Гь А) = е(Г2, А). Отсюда следует, что
d2dx = 0.
в) Полуточность в члене L2. Рассмотрим любое ребро Г и
функцию /г, равную 1 на Г и нулю на остальных ребрах. Пусть
Ai и А2 — любая пара граней, которым принадлежит Г. Если
е(Г, АО =е(Г, А2), то е(Аь Р) = — е(А2, Р). Если е(Г, А,) =
= — е(Г, А2), то е(Аь Р) = е(А2, Р). Отсюда d3d2 = 0.
Для куба и симплекса Яо = R; Hi = Н2 = Я3 = 0. Для куба
с дыркой Но — Hi = R; Н2 = Я3 = 0. Для куба с внутренней по-
полостью Н\ = Я2 = R, Hi = Нъ = 0.
353. im d — подмножество в Ch~l(T), состоящее из функций /,
2Л
для которых j / @ dt =0. Оба пространства когомологий одно-
о
мерны.
332
354. Считая, что То = Тп+\ = 0, имеем
Hi в кег Гг+i/im Тц L,/ker Ti+l == im Ti+U t = 0, 1, ..., n,
откуда
dim Я» + dim im Г< = dim ker Ti+h
dim imJi+i + dim ker Ti+l = dim Lit
355. Сопряженная последовательность точна, следовательно,
im T'h замкнут в Lk_^, тогда im Тъ. замкнут в Lk. Если im Тъ. а
akerTk+h то по теореме Хана — Банаха существует такой
/ е= L'h, что / е= ker Trhn f ф im 7^+r
356. Будем через Х° с: ?' обозначать аннулятор множества
X a L, т. е. совокупность тех / е L', которые обращаются в нуль
на X. Пусть ф — факторотобрашение l!h -+ L^\(ker Tk+1)°, тогда
{Hk)' = (ker Tk+l/im Tk)' = Ф ((im rfc)«). Ho (ker rb+1)°=im r'ft+1'
так как im T'k+1 замкнут в *-слабой топологии =» L;/(ker rft+1)°=
= L'h/im T'k+V но (im Thf = ker r; = im fh+1 ^ Ф (im rft)° =
= kerr;/imr;+1.
357. Оператор сдвига вправо.
358. dim ker A = n, dim coker A = 0; ind Л = п.
359. Ответ: если а(х)Ф0 ни в одной точке отрезка [0, 1].
Пусть х0 е [0, 1], а(я0) =0и хп-+хо', можно считать, что а(хп)Ф
Ф0. Рассмотрим ДеС[0, 1] такую, что h(xn) = \a(xn) \*
@ < X < 1). Тогда Д независимы mod im A.
360. kerP ==0, imP = С(Г), так как любую непрерывную на
Г функцию и можно единственным образом гармонически продол-
продолжить в Q.
361. В силу теоремы единственности для голоморфных функ-
функций ядро оператора А умножения на a(z) —пулевое.
Пусть zu •. •» zn — нули a(z) на Q кратности ки ..., кп. Тогда
imi = {/Gff(Q), /Ш(*<) =0, / = 1 Л<; * — 1 /г},
п
ind Л = — 2 *г-
г=1
362. Пусть cpfe (х) = Hk (х) е~~х '2, где Hh — полиномы Эрмита.
Проверьте, что {ф&} является ортогональным базисом в Но и что
Л+фь = — 2&фь_, и Л^фй = фЛ+1.
363. а) Использовав теорему Фубини, доказать, что фупкция
•ф(s) = (Ay) (s) определена почти всюду. Применяя неравенство
Коши — Буняковского, получить оценку
ь
j|ff(*. t)\2dt.
Интегрируя это неравепство по s, приходим к искомой оценке,
б) Проверяется непосредственно, исходя из определений.
364. Применить теорему Фубини.
b b
365. Положить а{. = [ Qt (t) p. (t) dt, bj = J Qt (t) f (t) dt.
a a
333
366. Показать, что некоторая степень оператора, стоящего в
правой части уравнения, является сжимающим оператором и,
следовательно, однородное уравнение имеет единственное (триви-
(тривиальное) решение. Далее применить альтернативу Фредгольма.
367. Применить теорему Фубини и неравенство Коши — Буня-
ковского.
368. Воспользоваться результатом задачи 367 и применить ин-
индукцию.
§ 4. Функциональные пространства
и обобщенные функции
1. Пространства интегрируемых функций.
369. Докажите сначала для a, b ^ 0 числовое неравенство
al/Pbl/<* ^.a/p + b/q; рассмотрев функцию y(t) = tl/p — t/p, дока-
докажите неравенство (p(t) ^ фA) для t>0 и подставьте t = alb.
370. Из неравенства Гельдера следует, что
I J Н Ф < ( J I U I d[i\ < / [ | / ? ф V/P l]\g\qc
Следовательно, sup
\igty < ( J I / \v d\i\1/p. Подберите функ-
X \х )
цию g{x), для которой достигается неравенство.
371. Пусть q связано с р > 1 соотношением l/p,+ 1/q = 1.
Применяя неравенство Гельдера, имеем
[\f + g\pd\L< f | / I I / + g \p~* d[L+[\g\\f + g IP d[L <
XX X
X
i/q
откуда непосредственно следует доказываемое неравенство.
372. Пусть /г, fcgZ, wgN, % — характеристическая функция.
Если {Ап} — база, то конечные суммы функций fkmn (я) =
А:
= — X DП) — всюду плотное множество в L\(X, \i). Если gn(x)
{к к I
х е X
373. Решение аналогично задаче 372.
374. Рассмотрите несчетное множество функций, принимающих
значения 0 и 1.
334
— <gn{x)<-7r- -база.
375. Пусть р', qf удовлетворяют условиями р' = p/q; 1/р' +
+ IIq' = 1, / е Lp. Суммируемость |/|з следует из неравенства
Гельдера
х \х )
376. Пусть q > р, 1/р > к > 1/д. Рассмотрите функции
377. 1/р < />< 1/а.
378. Пусть — + — = —, тогда ^ + ^ = 1. Применяя два
раза неравенство Гельдера, имеем
\\fgh\h
379. Легко проверить, что 1/г = а/р + jVg, ос + р = 1. Ограня-
1 1
чимся случаем q < оо, /(я) > 0. Тогда 1 = рцщ + q/{r$y приме-
примените неравенство Гельдера к произведению /аг-/Рг.
380. Используйте очевидное неравенство
A1/11 оо - е)
где множество X' а X подбирается по е > 0 так, чтобы |/| ^
^ II/Hоо — е при х е= X', ^(Х7) Ф 0.
381. а) Используйте тот факт, что выпуклое подмножество X
в ЛВП L плотно тогда и только тогда, когда всякий линейный
функционал / е Z/, равный нулю на X, обращается в нуль тож-
тождественно.
б), в), г) —см. указания к задаче 213.
382. При а ф 0 —\/р < a lka||p = (ра + I)-1'*; при 1 < /> <
< оо ||*o||p = 1; при а ^ 0 1ка||оо = 1.
383. а) Подпространство ломаных с вершинами в точках О,
±1, ±2, ...
б) Функции из Lu удовлетворяющие условию f(x) = f([x]).
384. Пусть LczLoo(X, ц). Тождественное отображение из
?оо(X, ji) в L\(X, ji) непрерывно. По теореме Банаха об обратном
операторе, обратное отображение непрерывно на V. Следователь-
Следовательно, существует постоянная Мх такая, что 11/11» ^ Л/г II/H i при /е
е V. Из этого неравенства и неравенства Копти — Буняковского
следует оценка II/IU ^ Л/211/?Н при /gK Пусть фЬ ..., фп — орто-
нормированная система в V, соответствующая скалярному произ-
произведению в L2(X, ц). Тогда, если (си ..., сп) —единичный вектор в
h{n, R), имеем:
2 \\ 2 s w\ 2
II ft=i lloo II u=i h
Из этого следует, что для почти всех х е X вектор ((pi(я), .••
., фп(^)) имеет норму ^М2 в 12(п, R). Таким образом,
п
| фл w |2 ф < м^ (х) и dim v < °°-
=l
335
385. Для любого е > 0 и любой / €= LP(R, dx) существует от-
отрезок [а, Ь] такой, что ( \ | / (х) \ dx\ P < е.Примените за-
\R\[a,b]
дачу 381.
386. Проверьте непрерывность в среднем на пространстве
Co(R) из задачи 385.
387. Проверьте непрерывность в среднем на пространстве
<?o(Rn).
388. Пусть сначала М состоит из одной функции /. Тогда ус-
условие а) выполнено автоматически, условие б) вытекает из оп-
определения суммируемой функции, а условие в) — из задачи 380.
Далее, если М состоит из конечного числа функций /ь ..., /п, то
для каждой функции /< условия а), б), в) выполняются с кон-
константами с<, Ri(e), 6i(e) соответственно. Положим с = max c-v
R (e) = max йг (е), б (е) = min 6$ (е). Тогда для М выполнены усло-
условия а), б), в). Наконец, если М — любое предкомпактное множество,
для которого {fu ..., in) — е/3-сеть, то для М выполняются усло-
условия а), б), в) с константами с+ г/3, ЯBе/3), б(е/3). Это доказыва-
доказывает необходимость условий а), б), в).
Пусть теперь условия а), б), в) выполнены. Рассмотрим ото-
отображение фе множества М в подпространство ?[—#(е), R(e)] с
х+6(е)
с MR, dx) по формуле фе (/) (х) = jJ— j / (t) dt. Из условия
X
а) вытекает, что у(М) ограничено в С[—#(е), Я(е)];из условий
б) и в) —что расстояние в LP(R, dx) между / и фе(/) не превос-
превосходит 2е. Наконец, из в) следует, что функции ф(/), /еЛ/ равно-
равностепенно непрерывны. Поэтому ф(Л/) — предкомпакт вС[—/?(е),
/?(еI и, тем более, предкомпакт в LP(R, dx).
Если {ф(/0, ..., ф(/„)} — е-сеть в ф(Л/), то /ь ..., /п — Зе-
сеть в М. Поскольку е произвольно, М — предкомпакт.
389. Отображение f(x) <g> g(y) >->f(x)-g(y) продолжается по
непрерывности до отображения U(X, \i) ® LX(Y, v) в ^(IX^,
\х X v), не повышающего норму. Проверим, что это отображение
на самом деле изометрично. Пусть фе L{(XXY, jliXv). Тогда ф
п
аппроксимируется по норме функциями вида <р (х, у) =2 сг^е- х
i=i г
X (х) %Fi (у), где Ei, (Fi) — попарно дизъюнктные измеримые
подмножества в X(Y). Без ограничения общности можно считать,
что \i(Ei) и v(Ei) — рациональные числа, а тогда, умножая ф
на подходящее целое число, можно считать эти числа целыми.
Таким образом, наше утверждение сводится к частному случаю,
когда X и У состоят из конечного числа точек единичной меры.
Это значит, что мы должны установить изоморфизм пространства
Lx (n, R) ® Zj (m, R) и lx(mn, R). Пусть еи ..., еп — базис в
первом пространстве, /ь ..., /т — во втором; тогда в тензорном
произведении в качестве базиса можно взять е{ ® /;-. Пусть ga —
соответствующий базис в третьем пространстве. Надо доказать
IE vi ® /J =12 еН'т'е'inf2 s Iaf)'s 16^ =5' г« '•
II i; II II ij II a i j ij
336
где нижняя грань берется по всем представлениям вектора
2 cifi ® U В ВИДе СУММЫ 2 ^а ® *а' где Фа = 2 4°%» ^а =
ij а г
= 2 ^aVj« Оценка в одну сторону вытекает из равенства е^ =
з
==2 aia)^ja)* Оценка в другую сторону получается из рассмотре-
a
ния конкретного представления, в котором а пробегает все пары
h U фг-j = ctieu Фи = /j.
390. а) Назовем подмножество Е в пространстве X с мерой ц
атомом, если \х{Е) > 0 и любое измеримое подмножество FaE
либо имеет меру нуль, либо ji(F) = ц{Е). (Легко проверить, что
для борелевских мер ji атомы — это точки положительной меры.)
Докажите, что крайними точками в ЬХ(Х, ц) являются характери-
характеристические функции атомов и только они. (В частности, простран-
пространство 1\ имеет крайние точки, а Li[0, 1] — нет.)
б) Все граничные точки шара (для доказательства выясните,
когда неравенство Минковского превращается в равенство).
в) Множество таких /, что \1(х)\ = 1 почти для всех х.
391. 1Х является пространством, сопряженным к пространству
сходящихся к нулю последовательностей, а Ь\ [0, 1] не является
сопряженным ни к какому банахову пространству, так как в про-
противном случае единичный шар имел бы крайние точки вопреки
задаче 390. а) примените теорему Крейна — Мильмана,
2. Пространства непрерывных функций.
392. Для доказательства полноты рассмотрите поточечный пре-
предел фундаментальной в С(Х) последовательности.
393. Многочлены от п переменных с рациональными коэффи-
коэффициентами образуют всюду плотное множество в С(Х).
394. Если функция g принадлежит единичному шару в С(Х),
то положим
395. Если f(x) —неотрицательная функция, то положим Gf =
= {g: 0 ^ g{x) < j(x)}. Обозначим F, (/) = sup F (g). Неравен-
g^Gf
ства Fj(/) ^F(f) и Fx(f) >0 для />0 очевидны. Аддитивность
F\ следует из тождества Gf\ + /2 = Gf\ + Gf2 (включение Gfx +
+ Gf2 с Gf] + /2 очевидно, а обратное включение следует из тож-
тождества g = gni(U + /2) + gt*l{U + /2)).
396^ Будем обозначать через Ег е-окрестность множества Е и
через Е — замыкание Е. Покажем^ что для любого компакта К а
а X справедливо соотношение \i(KE) -* \i(K) при е->0. Для этого
фиксируем б>0 и выберем функцию феСA), обладающую
свойствами: %к(х) ^ ф(х) ^ 1, F(cp) ^ \i(K) — б.
Пусть L —множество тех точек х е X, для которых (р(х) ^
^1—6. Ясно, что L — компакт, не пересекающийся с К. Обозна-
Обозначим через d расстояние между К и L. Если е < d, то функ-
()
Ф (х)
ция г|) (х) = JZ75 °^лаДает свойствами у- (а;)< ty («)<1. Поэтому
F (Ф) М- (К) — б
\х (Я"е) < F (г|?) = 1 _ ^ = ^„ д . При б -v 0 последнее выраже-
выражение стремится к \i(K).
22 а. А. Кириллов, А. Д. Гвишиани 337
Отсюда легко вытекает равенство \i(K) -f ji(X\#) = 1, конеч-
конечная аддитивность, а также регулярность функции ji
\1 (А) = sup \i(K)=* inf fx (G),
KdA GZDA
где К означает компакт, aG- открытое множество.
/сю \ оо
Неравенство \х [ JJ ?п I > 2 ^ (^п) выводится непосред-
\п=1 I n=i
(п \
которое следует из определения \i{K).
Для вывода обратного неравенства воспользуемся регулярно-
оо
стью ji, введем компакт К а Е = JJ Еп и открытые множества
Gi zd Et так, чтобы
оо N
Из включения /iC с: (J ^п вытекает включение ^ с: U Gn
7Т=1 П=1
при некотором Л7. Теперь из конечной аддитивности ц следует
оценка ц (К) ^ 2 ^ (^п) и' следовательно, неравенство |i (E) ^
(
п=1
397. Для доказательства достаточности условия докажите, что
для любой ступенчатой функции S(x) выполняется
lim \s(x)dgn(x) - \ S(x)dg(x)
О О
Произвольную функцию f(x) gC[0, 1] приблизьте ступенчатыми.
398. Сведите задачу к случаю, когда М состоит из монотонно
неубывающих функций. Выбирая последовательность из Л/, схо-
сходящуюся в другой точке, и т. д., диагональным способом (из п-й.
подпоследовательности возьмите п-\\ член) получите подпоследо-
подпоследовательность {фп}, сходящуюся во всех рациональных точках от-
отрезка [0, 1]. Докажите, что {фп} сходится к некоторой неубываю-
неубывающей функции (р(х) всюду, кроме точек разрыва у(х) множество
которых не более чем счетно, что позволяет диагональным спосо-
способом выбрать из {фп} подпоследовательность, сходящуюся и в этих
точках.
399. а), б) Продолжением являются /@) и /A) соответствен-
соответственно; в), г) — продолжения нет, так как любую функцию /е
gC[0, 1] можно приблизить полиномами вида (х -f l)p\(x), для
которых F3 = 0, и полиномами вида p(xN+l), для которых F4(/) =
= со = /@). Проверьте, что эти продолжения не годятся.
400. /,(х) = 1, /2(х) = —1 (см. задачу 2Q3).
338
401. Пусть цх = тц\ + A — т) и.2, где т е @, 1), а ц\ и ц2 при-
принадлежат единичному шару в С'{Х). Обозначим через fx какую-
нибудь функцию из С(Х), которая равна 1 в точке х и принима-
принимает значение из [0, 1) в остальных точках (например, fx(y) =
= тах{1—<*(*, у), 0}). Тогда цхЦх) = \\fx\\ = 1, |fx,(/x)|^l,
|jul2(/a) I ^ 1. Поэтому jii(/x) = p«2(/*) = 1- Это возможно лишь в
случае \ii{{x}) = MW) = 1, т. е. щ = ц2 =цх. Значит, \хх —
крайняя точка.
Пусть теперь ^i — любая крайная точка в единичном шаре
С'(Х), f(x) — любая непрерывная функция на X, принимающая
значения из @, 1). Легко убедиться, что либо ji, либо (—и.) — по-
положительный заряд. Пусть для определенности ц > 0. Положим
/И- A - /) И _
Их = ПГТТ)' ^2 = 1 — и, (/) ' ТогДа ^1 и № лежат в единичном шаре
С'(Х) и
|1 = (!(/) ¦(!, + [1
Так как и. — крайняя точка, то jii и ^2 совпадают с [х. Отсюда лег-
легко выводится, что \x(fg) = \i(f)\i(g) для любых /, geC(Z), при-
принимающих значения из @, 1). Ввиду билинейности этого соотно-
соотношения, оно справедливо для всех /, g^C(X). Обозначим через L
ядро функционала ц. Это — замкнутый идеал коразмерности 1 в
С(Х). Л^гко показать, что существует точка х е X, в которой об-
обращаются в нуль все функции из L. (В противном случае X по-
покрывается конечным числом окрестностей ?/*, для которых най-
найдутся /,- е L такие, что /<(х) ^ 0 на ?/,. Тогда / = 2 | А |2 е ^
и / ф 0 па X, откуда L = С(АГ).) Условие codim L = 1 влечет
единственность такой точки. Теперь ясно, что ^i = [хх.
402. а) Вместе с любой функцией <р алгебра А содержит так-
также функцию Р(ф), где Р — полином. Из замкнутости А и теоремы
Вейерштрасса следует, что А содержит / ° ф для любой непрерыв-
непрерывной функции / на прямой. Используя это, последовательно дока-
докажите, что А содержит следующие типы функций:
1) для любых х Ф у\ х, у е X — функцию ф такую, что (р(х) —
= 0, ф(г/) =1 и 0^ Ф(г) <^ 1 для всех других z e X;
2) для каждой точки х е X и любой ее окрестности Z7 —
функцию ф такую, что ф(х) =0 и q>(z) = 1 для всех ze X\U;
3) для любых непересекающихся компактных множеств К\ и
#2 — функцию ф, которая равна нулю на К\, равна единице на
К2 и принимает значения между нулем и единицей в остальных
точках jg!
Используя функции последнего типа, покажите, что каждая
функция f^C(X) с нормой 1 может быть аппроксимирована с
точностью 2/3 функцией фЕ/1 о пормой 1/3.
б) Нет; рассмотрите
Ax^ = {f(x)\f(x)<=C(X), f(xQ)=0).
403. Пусть диаметр множества X равен 1 (что, очевидно, пе
ограничивает общности). Так как X — компакт, его можно пред-
представить в виде объединения конечного числа компактов X , ...
...,Хп диаметра 1/2. Каждый из X* (i = 1, ..., rci) можно пред-
представить в виде объединения конечного числа компактов
Xiv ..., Xin диаметра 1/4 и т. д. Отображение q> мы будем
22* 339
ссг
строить постепенно. Сначала разобьем отрезок [0, 1] на 2п — 1
равных отрезков Л1? ...? А2п _х и будем считать, что ф(А2А-0 с:
d Хг-, а ф(А2&) — путь, соединяющий некоторую точку Xh^Xk с
точкой Zfc+i e Хн+\. (Такой путь существует ввиду линейной связ-
связности X.) Отрезок А2&_1 мы разбиваем на 2п2 — 1 равных отрезков
А2ь_1 A < i < 2п2 — 1) и по-
полагаем, что ф(А2ь_1,2i-i) a
<=zXki, а ф(Л2й-1,2г)— путь,
соединяющий точку хм е
е Xkl С ТОЧКОЙ Xk, l + i е
е Xk, i+\. Продолжая этот
процесс, мы определим
отображение ф на некото-
некотором плотном подмножест-
подмножестве отрезка [0, 1], причем
это отображение будет рав-
равномерно непрерывно там,
где оно определено. Поэто-
Поэтому его можно продолжить
до непрерывного отображе-
отображения всего отрезка.
404. Утверждение этой
ос7
72
I©
L
Рис. 5
задачи — частный случаи
задачи 403. В этом случае
построение можно иллюст-
иллюстрировать чертежом (рис. 5).
Здесь числа пи п2, ...
все равны 4, в качестве представителя xi
xk квадрата
Xi »...,. берется его центр; четыре квадрата к-то ранга, лежащие
в одном квадрате (к — 1)-то ранга, проходятся по часовой стрел-
стрелке, начиная с левого нижнего.
405. Отображение t и* (| cos 2nt \2/q sgn cos 2nt, \ sin 2nt |2/g X
Xsgnsin2tt*) переводит [0,1] в единичную окружность в ZPB,R).
Соответствующее вложение ZpB, R) в С@, 1) имеет вид
(ОС, Р)м
Проверьте, пользуясь неравенством Гёльдера, что
(t) = a |cos 2nt\2lq sgn cos 2nt + p| sin 2nt \2/q sgnsin2n*.
max
te[o,i]
406. Рассмотрим естественное линейное отображение
С[0,
задаваемое формулой
Ясно, что это отображение инъективно, а из теоремы Вейерштрас-
са вытекает, что образ ф плотен в С(П). Остается проверить изо-
метричность ф. По определению нормы в тензорном произведении
2 и
i
= sup
| 2 I* (Л)
340
Достаточно брать верхнюю грань только по крайним точкам еди-
единичных шаров в С[0, 1]'. Поэтому (см. задачу 401)
I S h ® Si I ^ sup
II i 1 *.*
= sup
407. Воспользовавшись теоремой Стоуна — Веиерштрасса, до-
докажите, что С(Х) ($C(Y) плотно в С(АГ><У). Завершает доказа-
доказательство проверка того, что норма р % ® /;у, где рх и ру — нормы
в С(Х) и С(У), совпадает с нормой в С\Х X У).
408. Воспользуемся тем, что сопряженный оператор А' задает
изометрию единичного шара в С (У)' на единичный шар в С(Х)'.
Поэтому для каждой точки у е У существует такая точка я =
= Ц)(у) и такое число а (г/) = + J, что Л'ц^ = a(y)\ix. Отсюда
(Af)(y)=a(y)f(q){y)). Полагая / = const, мы видим, что ае
еС(У). Поэтому /офеС(У) для любой /еС(А'). Отсюда следует,
что ф — непрерывное отображение. Применяя это к оператору
Л, убеждаемся, что обратная функция также непрерывна.
409. Пусть Fn(x, у) = fn(x) + gn(у) — фундаментальная после-
последовательность в С(П). Тогда Fn @, у) =/п@) -j-#n(*/) фундамен-
фундаментальна в С[0, 1] и, следовательно, fn(z) — /п@) фундаментальная
lim ^n (г, у) = lim (/n (х) - /п @)) + lim (gn (у) + fn @)).
410. Пусть {гп} — всюду плотная в [0, 1] последовательность,
причем го = 0, п = 1. Рассмотрите систему {/п}, где fo(x) = 1,
f\(x) = х, а при гс ;> 1 /п(^) определяется следующим образом:
пусть гп принадлежит (rsl, rs2) — одному из (п — 1) интервалов,
на которые точки г2, ..., г„_, разбивают отрезок [0, 1]; тогда
/п@) = 0, /п(гв1) = 0, /п(гп) = 1, /п(г82) = 0, /пA) = 0,
а график fn(x) — четырехзвепная ломаная.
Замечание. Топологические базисы имеются также в про-
пространствах Z/P@, 1) и lv при 1 ^ р <с оо, в сепарабельном гиль-
гильбертовом пространстве, но не во всяком сепарабельном банаховом
пространстве.
411. Предположим, что для любой /еСР[0, 1] существует
тригонометрический ряд 2 ^k (/) e2rtl/iX>, который равномер-
но сходится к /. Тогда этот ряд сходится и в смысле Z»2@, 1).
Таким образом, числа Ck(f) есть коэффициенты Фурье функции /.
Пусть Sn (/)' = 2 ^ft M е2лг/?хв Из нашег0 предположения
h=-n
следует, что 5п->1. Это противоречит тому, что HSJI-> оо. (Про-
(Проверьте, что || Sn || = 1 I (sin Bп + 1) тех I sin пх \ dx. j
о /
3. Пространства гладких функций.
412. а) Неметризуемость следует из того, что для любой чис-
числовой нефинитной последовательности {кп} последовательность
{Япеп} не стремится к нулю в i?)(N),
341
б) Последовательность \х]^) сходится к {xh} при п -* <*>,
если и только если: 1) существует такое N, что я^ =0 при А: >
> iV п всех п; 2) г {*l) -* х/? при /с = 1, 2, ..., Я.
в) Пусть хА — последовательность точек в Q, не имеющая
предельной точки внутри Q\ {?/&} — набор попарно непересекаю-
непересекающихся окрестностей точек xh, фь — ненулевая функция с носите-
носителем в Uh. Искомое отображение &(N) в ?>{Q) можно задать
формулой
413. Импликация а)=^б) очевидна; б)=$> в), так как сходяща-
сходящаяся к нулю последовательность срп стремится к нулю по всем по-
полунормам; в)=^ г), так как 3)К{Ы) метризуемо; г)=^ а) по опре-
определению топологии в iZ)(Q).
414. ?DK(Q) является пересечением семейства замкнутых мно-
множеств 1Х = {rpeS>(Q): ф(.г) = 0}, где х пробегает п\К.
415. Сначала постройте конечный набор функции {if»*} A^
^ i ^ Лг), для которого sup фг a Ut и if = 2 ^i ^ ^ > 0 на ^«
Пусть теперь /е <^(R) такова, что f(x) = 0 при х < 6/2 и f(x) =
= \/х при .г ^ 6. Тогда ф< = if<*/(\f(a:)) —искомый набор.
416. Воспользуйтесь результатами задачи 415.
417. Представьте Q = Rn\/? в виде объединения счетного чис-
числа шаров. Воспользуйтесь тем, что любая функция из &(&), удов-
летворяющая оценке| Ф (х) I < ехр I — ^ . ^ |, продолжается (ну-
левыми значениями на К) до функции из
418. Существует.
419. В случае iZ)(Rn) проверьте, что ф* -> 0 влечет Яг-фА->0 и
0; в случае ^(R77), ^(Rn) дайте оценку соответствующих
полунорм.
420. а) да, б) пет, в) да.
421. а) да, б) пет, в) да, г) да, д) да, е) да.
422. Воспользуйтесь тем, что ряд 2 ^т/^ (# + /) сходит-
ся абсолютно и равномерно на отрезке [0, 1], если /
т, «gN.
423. Пусть ph — норма пространства CA(Tm), qh — норма про-
пространства 6й(Тп) и гА — норма пространства Ck(ln+n). Проверьте,
что норма ph <S> qk эквивалентна rh (пользуясь тем, что всякий
линейный непрерывпый функционал на Ch{Tn) имеет вид </, ф> =
= S 1 ^гф @ rfvj (<), где Vi — борелевские заряды с конечной
НК*тт
вариацией на Тт). Далее, из неравенства Коши — Буняковского
для k(Tm+n) выведите, что норма ph § qh межорируется нормой
г, при s> (т + пI2 + 2к. (Более точно, для /eCs(Tm+n) ряд
Фурье сходится к / по норме рк 0 я^)
342
Таким образом, системы норм {ph ® qk}, {rfe} и {ph ® qn} эк-
эквивалентны, что и доказывает нужное утверждение, если восполь-
воспользоваться теоремой Вейерштрасса о плотности тригонометрических
многочленов в ®(Тп).
424. а) Нужно проверить, что при t e [—1, 1] все функции
обращаются в нуль вне некоторого компакта К, не зависящего от
t, и что f{l) стремится равномерно на К к [dyf)^l\ где I — любой
мультииндекс, а ду означает частную производную по направле-
направлению у. Воспользуйтесь теоремой о конечном приращении.
б) Нужно проверить, что на любом компакте К с: Rn функции
f\1^ стремятся равномерно из Я" к dyfil\
425. Свойство а) очевидно; свойство б) доказывается по ин-
дукции, используя тождество Дг) (х) = — \ ДГ11 (х — t) dt, вер-
о
ное при г < п. Сходимость последовательности f? при w->oo и
фиксированном г следует из оценки
ог + 1
\ln Jn-i\ ^ 6Х ... 6г+1 п1
верной при п ^ г + 2.
426. а) Пусть М — ограниченное множество в L. Тогда оно
предкомпактно по любой полунорме рн, так как ограничено по
полунорме ph+i. Введем, как обычно, расстояние на L по формуле
оо
оо
d {/' 8) = 2 ~~hPk (f ~ 8)- Если {Д} — конечная 2~'-сеть для
l
М по полунорме 2 Рь> то она будет 21-г-сетью в смысле рас-
h=l
стояния d.
б) Разберем случай L = !g)K(Q), Q а Яп. По теореме Аско-
ли — Арцела, множество М, ограниченное по норме /?^+1 (/) =
= max | dlf (х) |, будет предкомпактным но норме ph, так как все
функции вида dlf, \l\ ^ к будут равномерно ограничены и равно-
равностепенно непрерывны в Q.
А27. Если фп — фундаментальная последовательность в & (Q,
L), то для любого мультииндскса / и любой точки х^п последо-
последовательность д1ц)п(х) фундаментальна в L. Пусть 'tyl(x)= lim дкрп (х).
Докажите, что tyi{x) = dltyo(x) и что фп-> "фо в топологии
S" (Q, L). Метризуемость & (Q, L) вытекает из наличия счетного
набора норм. (Если {р}} — счетный набор норм, задающий тополо-
топологию в L, а {/?{} — счетный набор компактов, исчерпывающий об-
область Q, то полунормы /?к.? определяют топологию в &(Q, L).)
428. Рассмотрите отображение <§T(Qi X ^2) в (^T(Qi), ^(^2)) по
формуле ф->/, где (f(x))(y) = ф(л:, ^). Воспользуйтесь результа-
результатами задачи 424.
429. Используйте результат задачи 423 и тот факт, что перио-
периодические функции плотны в ^T(Rn).
343
430. Для случая S(Rn) полезен результат задачи 426.
4. Обобщенные функции.
431. Нужно проверить, что если интеграл \ ср (я) г|? {х) dx равен
R
нулю для всех \pe^(R), то qpeiZ5(R) тождественно равна нулю.
432. Существует и равен 0.
433. Воспользуйтесь тем, что 2)(R) плотно в ?P(R, dx),
434. Пусть р (х) — локально суммируемая функция. Для лю-
любого отрезка [а, 6], не содержащего начала координат, существу-
существует последовательность фп е ^(R), сходящаяся к %[а, ь](#) и имею-
имеющая носитель в отрезке [а — е, Ь + е], также не содержащем на-
начала. Из равенства 0 = фп @) = 1 ф (х) р (х) dx вытекает, что
R
Ъ
\ р (х) dх — О для любых а и Ь одного знака. Но функция
х
q (х) = I p {t) dt непрерывна по х. Отсюда q(x) = const и р(х) =
о
= 0 почти всюду.
435. Заметим, что всякая функция фе^5(Тп) представляется
равномерно сходящимся рядом: Ф @ = 2 che2mkt* Поэтому
? Ф> = С_Л и /2 <2пШ> ч>\= 2 *-* = ф (°)-
\ks=Zn / k~Zn
436. В качестве определяющей системы полунорм в 2D(Tn)
можно взять нормы пространств Ck(Tn).
437. Пусть ф(ж) = е2х-®(х) е ^)(R), где со е ^(R) — функ-
функция с носителем [—1/3, 1/3], тождественно равная 1 на [—1/6, 1/6].
Рассмотрите действие F на сдвиги у(х ± А;).
438. Один из способов: разложите Ц(х ± Ю) в сумму четной и
нечетной компонент и воспользуйтесь тем, что
439. См. задачу 438.
440. Воспользуйтесь следующей леммой из линейной алгебры.
Пусть даны линейные функционалы /ь ..., /п и / на линейном
пространстве L. Если условия f\(x) =0, ..., /п(^) =0 влекут
/ = 0, то / является линейной комбинацией /ь ..., /п.
б) Воспользуйтесь п. а) и теоремой Хана — Банаха для ЛВП.
441. а) Примените интегрирование по частям.
б) Воспользуйтесь теоремой о слабой «-полноте ®'(R).
. /rk-l\ -А- 2
в) Воспользуйтесь соотношениями i -г i — -t-
dx\T(X)
и «начальным условием» Х\/Г W~ б (х)*
Ответ: х{-п~1)/Т (- л) = б(п) (х).
442. Используйте изоморфизм «^ (L1? L^) « (Lx ® Lg) и ре-
результаты задачи 430.
344
443. a) K(x, у) =в(*-у);
б) К(х, у) = 6(*-а) хб(у —6).
5. Действия над обобщенными функциями.
444. Проверяется непосредственно из определения прямого
произведения и производной обобщенных функций.
445. Докажите, что всякая функция фд^(К), обладающая
свойством \ ср (х) dx = 0, имеет вид ф = г|/, где i|)
446. Докажите, что всякая функция (peiZ>(R), обладающая
свойством ф@) =0, имеет вид у(х) = xty(x), ^e^(R).
447. Пусть искомая функция F на отрезке \а — е, а + е] яв-
является производной порядка к от непрерывной функции /. Дока-
Докажите, что f(x) совпадает с некоторым многочленом Р-(я) на
[а — 8, а] и с некоторым многочленом Р+(х) на (а, а-}-г], при-
причем cleg Р± < к.
Пусть Р(х) = Р+(ж) — Р-(х). Тогда
ft
[Р И 6 (х - а)] = 2 Ф(*~;) («) 6@ (* - «)•
448. б' (^ (а:)) = sgn Л' @) [-/*" @) б (а: — Л @)) + Л' @) 2б' X
Х(*-М0))].
449. Воспользуйтесь соотношением lim—( х) ~ ** \х) „ хр> ^^
t-*i t — 1
которое доказывается исходя из определения F(tx).
450. Воспользуйтесь задачей 441.
у
451. Пусть 9G^(R) и (p(x)dx = 0. Докажите, что суще-
R
^(R) иапЕ R, что
-lim [я|)п (ж + ап) - % (х)].
R
ствуют такие -фп е ^(R) иапЕ R, что
П->оо
(Например, можно положить ап = -L, -фп (х) = п \ ф (t) dt.)
п J
о
452. а) Докажите, что если фе=^^2) обладает свойством
ф (х, у) dx = 0 при всех у е= R7 то ф = 5i|)/^ для некоторой
|();
б) F = 1X/.
453. а) Обобщите метод, описанный в указании к задаче 452.
б) f = 2 Л х 6(i)-
454. Функция /'(я) не является регулярной обобщенной функ-
функцией умеренного роста, так как \f(x)\ = ex растет быстрее лю-
любого многочлена. К интегралу \ / (х) ф' (х) dx неприменима про-
«У
R
цедура интегрирования по частям.
455. Ответ: 2 ck6 (х — кк), где {ck} — любая числовая
Двусторонняя последовательность.
345
456. Пусть L — подпространство в iZ5(Rn), порожденное функ-
/ п \
циями вида
\ii
< / ^ и, (ре 0(Rn). Докажите, что F аннулирует L и что ? име-
имеет коразмерность 1 в ?D(Rn). (Для простоты разберите случай
и = 2.)
457. Воспользуйтесь результатом задачи 455.
458. Докажите, что функция ф = е~А(х) (F(x) —В(х)), где А и
В — первообразные для а \\ Ъ соответственно, удовлетворяет урав-
уравнению q/ = 0.
459. Воспользуйтесь преобразованием Фурье и формулой
Планшереля.
460. Существуют такие константы С и N% что | сп | ^ CnN при
п ф 0. (Или In (cn)/In n — ограниченная сверху последователь-
последовательность.)
461. Нет. (Например, lim фп (я) 6 (я), где {фп} — б-образная
последовательность, не существует.)
§ 5. Гильбертовы пространства
1. Геометрия гильбертова пространства.
462. б) Рассмотрите категорию изометрических отображений
данного предгильбертова пространства во всевозможные гильбер-
гильбертовы пространства.
463. Для доказательства полноты воспользуйтесь теоремой
Вейерштрасса.
464. Результатом ортогонализации являются с точностью до по-
постоянного множителя следующие специальные функции:
а) многочлены Лежандра Рп (х) =1 — I [(l — х2)п]\
б) многочлены Чебышева Тп(х) = cos (warccosz);
в) многочлены Лагерра Ln (х) = / f — 1 (е~ххп);
2 / 7 \ П 2
г) многочлены Эрмита Нп (х) — ех |— 1 е~~х .
465. a) fk (z) = ]/^~ («-У. где S = nR2 - площадь круга;
6,
укк\
466. Найдите разложение искомой функции gx(z) по базису
задачи 465.
Ответы:
a) gx (г)
g\ -. /д\ __ gXZ ^
346
467. С помощью результата задачи 465 докажите, что каждая
Сходящаяся в смысле L2 последовательность аналитических функ-
функций сходится равномерно на любом компакте, лежащем внутри
данной области.
468. а) Вложите L2{a, b) в L2@, 1).
б) Докажите, что произвольная функция из L2(a, 6—1) одно-
однозначно продолжается до функции из искомого ортогонального до-
дополнения в L2(a, b).
469. б) Докажите, что гильбертова норма оценивается че-
через равномерную норму п что обратное неверно, как следу-
п
ет из рассмотрения последовательности /п (х) = ^ — е1Нх,
h=i
где {Xk} — произвольная последовательность вещественных
чисел.
470. Пусть fx(x) —функция на R, равная 1 в точке А, и 0 в ос-
остальных точках. Тогда {/^}хек ~~ ортонормированный базис в
/>2(R, \i). Соответствие /л ¦«->¦ eiKx устанавливает изоморфизм ба-
базисов, а следовательно, и гильбертовых пространств.
471. Примените процесс ортогопализации.
472. Во всех случаях ортогональное дополнение равно нулю.
473. а) Пространство функций, равных нулю при х ^ 0;
б) {0}.
474. а) 90°,_
б) arccos Уд/6, где а — длпна меньшей хорды, Ъ — длина боль-
большей хорды.
475. а) Непосредственная проверка.
б) Пусть К = R. Определим; скалярное произведение фор-
формулой
Равенство (х + у, z) = (x, z) -f (у, z) равносильно соотношению
\\х + у+ z\P + Ы12 + Ы2 4- IUII2 = 112: + i/ll2 + 1^ + *H2 + Их + г||2.
Это соотношение получается из тождества параллелограмма, при-
примененного ко всем параллелограммам, которые можно составить
из вершин трехмерного параллелепипеда. Далее, индукцией по п
доказывается равенство (пх, z) = дг(х, г), а из него выводится,
что (\х, z) == 'h(x, z) для рациональных К. Поскольку (х, у) по
построению непрерывно зависит от х, равенство {Хх, у) =
= Х(х, у) справедливо для всех вещественных X. В случае комп-
комплексного поля мы можем сначала рассмотреть овеществление #R
гильбертова пространства Н (т. е. то же пространство Я, в кото-
котором допускаются только операции сложения и умножения на ве-
вещественное число). Тогда в силу уже доказанного в ffR сущест-
существует такое (вещественное) скалярное произведение (х, y)Ri что
|| я ||2 = {х, x)R. Определим скалярное произведение в Н форму-
формулой (я, у) = (х, y)R + ' (я» 7#)r- Проверьте, что это выражение
действительно обладает нужными свойствами. (Воспользуйтесь со-
соотношением (х, ix) R = ~ (|| х + ix ||2 — || х ||2 — || UII2) = 0, так как
11Ь:||2=_т21М1?.)
347
476. Воспользуйтесь тождеством \\х + eiey\\2eiQ — \\x\\2eiQ +
+ (х, у) + (у, x)e2iQ + \\y\\2eiQ u соотношением ^ ехр
N
/11
477. Проверьте, что существует сильный предел у последова-
п
1 V
тельности уп = — Ухх% и что векторы zt — xi — у ортогональ-
г=1
ны друг другу и вектору у.
478. 6)=^ в) по следствию из теоремы Банаха — Штейнгауза
(об ограниченности слабо сходящейся последовательности).
479. Пусть L(S)—замыкание линейной оболочки S. Тогда
L(SI- = 5-l. Поэтому (S-LI- = L(S) по теореме об ортогональном
дополнении.
480. Представьте Я в виде L Ф L1-.
2. Операторы в гильбертовом пространстве.
481. a) Re А = у (А + А*)> Im Л = Ti (i4 ~ Л*)#
б) АА* — А*А = 2Ц1тА-ЪеА — ЪеА-1тА)..
в) FF* = (ReFJ+ i(Im F-Re F—ReF-Im F)-f (Im FJ.
482. а) Положим Я, = РЯ, Я2 = A —Р)Я. Проверьте, что Я,
и Я2 ортогональны, в сумме дают Я и что Р — оператор проекти-
проектирования на Hi параллельно Я2.
S + 1
б) Положим Р = —g—• Проверьте, что Р — ортопроектор.
483. Воспользуйтесь равенством || Л || = sup LJ—' у ¦.
484. а) Если А; и Z четны, то искомое неравенство можно перепи-
переписать в виде (Ak/2x, Ali2x) < ||Л*/2л:||-М'/2л;||. Если же к и / нечет-
нечетны, то введем новое скалярное произведение (я, у)л = (Л.гг у)-
Тогда нужное нам неравенство примет вид:
б) Выведите из а) неравенство ЦЛ.г||2(п+1) ^ (Ах, хп) X
X (Ап+2х, х), а из него — искомое неравенство.
485. Докажите, что последовательность квадратичных форм
QАп № = (Апх* х) стремится поточечно к некоторой квадратич-
квадратичной форме Qa(x). Затем воспользуйтесь неравенством задачи
484 б).
486. а) АР = РАР, б) АР = РА.
487. а) Достаточно рассмотреть случай dim Я = 2.
б) cos2cp == ivPxP2Px = \\РХР2Р\\\.
в)Пусть единичные векторы g< порождают Ьи единичные век-
векторы rjt — Mi (i = 1, 2). Условием конгруэнтности пар (Lb L2) и
(Ми М2) является равенство \Ци g2) | = | (г|ь тJ)|, равносильное
равенству tr P\P2P\ = tr (?i(?2<?i •
488. а) Операторы РАЛ и 1 — PAPj = Рх A — P2)Pi +
+ A —Pi) положительны.
б) Ранг оператора P^Pi не превосходит рангов Pi и Р2.
348
в) При решении задачи можно считать, что L2 = М2, заменяя,
^и нужно, пару (М\, Л/г) конгруентной парой. Рассмотрите про-
проекции образующих векторов в L\ и М\ на Ь2 = М2 и на ортого-
грнальное дополнение к этому пространству.
г) Первый способ: развить соображения предыдущего пункта.
Второй способ. Назовем пару (Lx, L2) разложимой, если простран-
пространство Я представимо в виде Я = Н' Ф Н" так, что Ьг= Ь\® L\, где
Lj = L{ П Н', Ь"г = Ьг [\Н". В этом случае мы будем гово-
говорить, что пара (Li, L2) является суммой пар (?1? ?2) и yL'v L^J.
Покажите, что всякая пара является суммой неразложимых и
что неразложимые пары бывают только при dim Я = 1 или 2.
Последнее видно из того, что если \ — собственный вектор опера-
оператора Р\Р2Р\, то пространство Я', натянутое на % и Р2%, инвариант-
инвариантно относительно Pi и Р2. Значит, этим свойством обладает и Я" =
= (Н')-1-. Отсюда вытекает, что исходная пара разложима, если
только dim Я > 2.
д) Раствор равен sin ер, где ф — наибольший из углов между
L[ и L2.
489. а) Если U унитарен и {еа}аеА — базис в Н{, то {Uea}aeA —
ортонормированная система в Н2. Полнота ее следует из того, что
х JL Uea влечет U~lx J_ ea.
б) Если {ea}aeA — ортонормированный базис в Яь а
{Uea}a<=A — ортонормированный базис в Н2, то для любых i, j/e
е #i, имеем
х = 2 (*' еа) еы У = 2 (У. *ъ) %'
а 3
Поэтому Ux = 2 (я, «а) *7*а, С/у = 2 (^' ^р) ^Р и
а ji
( (р) (. ^р) = 2 (г' га) (*• еа) =^' »)'
а,р а
490. а) Условие г/ _L im А равносильно отношению (у, Ах) =
= 0 для всех хеЯ, а условие у е ker Л* — соотношению (А*у,
х) = 0 для всех j; g Я. Но (г/, Лх) = (Л*г/, х).
б) По теореме об ортогональном дополнении равенство
(кегЛ)-1-= (im Л*) равносильно равенству кегЛ = (imA*)±7 до-
доказанному в п. а) (с заменой Л на^А*).
491. Воспользуйтесь соотношением
|] (Ап - А)х\\* = \\Апх\\2 + \\Ax\\* - 2Re (Anx, Ах).
492. Пусть {ха} — базис в Я, ?ар — оператор, переводящий х$
в жа, а остальные базисные векторы — в нуль. Проверьте, что спра-
справедливы соотношения:
2) Eai^Eib = ?«б, если р = "f, а иначе Ea$Eu = 0;
3) если Р — ортопроектор, для которого ЕаР = Р, то Р = 0
ИЛИ /?а.
Докажите, что всякий набор операторов, обладающий этими
свойствами, устроен так; существует такой гильбертов базис
{2/а}, что Еар переводит г/р в г/а, а остальные-базисные векторы —
349
в нуль. Примените это утверждение к набору а(Еа$), где а — дан-
данный автоморфизм.
493. Если идеал / содержит хотя бы один ненулевой оператор,
то он содержит все операторы конечного ранга и, значит, все ком-
компактные операторы. Если / содержит некомпактный оператор, то
он содержит ортопроектор на бесконечное пространство и, следо-
следовательно, все операторы. Ответ: {0}, Ж(Н), 3?(Н).
494. Воспользуйтесь соотношениями
L
, х) ^ (АРх, Рх) JPx. Рх) sup (Ay, у)
X) L (Рх РХ) (X X) pL (у у)
sup
(X, X) x&L (Рх, РХ) (X, X) y^zpL (у, у)
sup [РАРх.
sap> up = up
xsL (л, х) х<=ЬПРН (х% х) x^LCiPH (x, х)
495. а) Докажите по индукции соотношения IUI|1/2-l > Вп >
> О, В*ь < А и воспользуйтесь результатом задачи 485.
б) Единственность сначала докажите для случая ker Л = 0,
пользуясь тем, что построенный квадратный корень В является
пределом многочлена от А и, следовательно, перестановочен с лю-
любым другим квадратным корнем С; это влечет равенство
{В + С) (В — С) х = 0, откуда {В — С)х = 0. Общий случай сле-
следует из соотношения кег С = кег С2, верного для любых С > 0.
496. б) Операторы R и S удовлетворяют соотношениям R2 =
= АА*, S2 = Л*Л. Оператор "К однозначно определен лишь на
im 5, оператор С/ определен по модулю ker R.
в) Операторы А, допускающие искомую запись, обладают
свойством dim ker A = dim ker А*. Однако dim ker Т ф dim ker T*.
497. U*U = Л; UU* = Р2.
498. Положим R = (АА*I/2 и определим U на im^4* равенст-
равенством UA*x = Rx.
499. а) Воспользуйтесь тем, что для любых двух базисов
{#р}р«=в и {ут}те г справедливо равенство:
211 л г 1J __ V» \1 1Мг г. \ I2 =
б) Сходимость ряда 2 (^v' Вуу)н вытекает из неравен-
ства Коши — Буняковского, примененного дважды: один раз для
скалярного произведения в Я, другой раз — для скалярного произ-
произведения в h(Г).
в) Пусть Го — конечное подмножество в Г, Pp. — проектор
на соответствующее подпространство в Н. Оцените норму разно-
разности А и РАР в L2(H).
г) Отображение Н (g) Н' в L2{H) переводит вектор х ® / в опе-
оператор A: y-+f(y)x.
д) Пусть {/рЬев — базис в L2(X, jx). Покажите, что А задает-
задается ядром К (х, х2) = ^ (Ah
_ 500. а) Следует из определения.
350
б) Докажите, что умножение справа на ограниченный опера-
оператор В е Ь2(Н) является ограниченным оператором в Ь2(Н). Обо-
Обозначим его М(В). Докажите, что М(В)* = М(В*).
в) Проверьте равенство || Л |L = sup \ tr U AV |, где U и V
1 Utv
пробегают совокупность всех частично изометрических операторов.
г) Каждый оператор А е 2?\ (Я) определяет линейный функ-
функционал fA на Ж(Н)\ 1а{К) = iv AK. Каждый ограниченный опера-
оператор В определяет линейный функционал FB на 2?\(Н): FB(A) =
= tr AB. Для доказательства того, что это полный набор функци-
функционалов, воспользуйтесь тем, что в Ж(Н) и в 2?\(Н) операторы ко-
конечного ранга образуют плотное множество.
501. а) Воспользуйтесь функциями gx(z), -построенными в за-
задаче 466.
в) Представьте dim Я в виде 2|?&|2> где {6*} — базис в Я.
k
г) Начните с операторов ранга 1.
502. Пусть ln(x) = e27linx — базис в L2 [0, 1],
+ N
n=-N JV=l
Докажите, что для А <= & (Я) lim sk (A) = tr А. Проверьте, что
fc-юо
для интегрального оператора с ядром К(х, у) справедливо соотно-
1 1
ШспИс 4fc\/il —¦ I I /V ^.?7 ыМ ———i——-^—————— UJL Cly. ДЛН Н clip С"
А JJ L sin я (ж — у) J
00
рывного ядра отсюда вытекает, что lim sk (А) = \ К (х, х) dx.
ГЛАВА IV
ПРЕОБРАЗОВАНИЕ ФУРЬЕ И ЭЛЕМЕНТЫ
ГАРМОНИЧЕСКОГО АНАЛИЗА
§ 1. Свертки на коммутативной группе
1. Свертки основных функций.
503. а) Обозначим через 6g элемент K[G], соответствующий
функции, равной 1 в точке g и 0 в остальных точках.
Выпишите явно условие перестановочности а ^ K[G] и б*.
б) Условие a(gh) = a(hg) можно переписать в виде a(h) =
= a(ghg-1).
в) Верно.
504. а) Пусть е = e2jlf/n, а — образующий элемент группы Цп
(в аддитивной записи). Положим eh — — N ek^ka- Проверьте
равенства ей * е> = 0 при к ф /, ей * eh = eh.
851
б) При п ^ 2 верно. При больших п неверно. Можно прове-
рить, что R [Ц2к] » R + R + С+ ... + С, R [Z?afc+1] = R +
ft
505. Каждой функции ah(g) поставим в соответствие числа
aQ = ^ а (?) и ах = 2 а ^) sSn ?» гДе sSn ? ~ четность пе-
рестановки g: sgn g = JJ g "; """ f ^'. Докажите, что отобра-
имения а->ао и a-+a,\ являются гомоморфизмами RE3) на R.
Далее, пусть еь е2, е3 — три вектора на плоскости, в сумме рав-
равные нулю. Каждому элементу g?-S3 соответствует линейпое пре-
преобразование плоскости T(g), действующее по формуле T(g)ei =
= е _1 y Докажите, что отображение а»-* ^ а (^) ^ (#) является
гомоморфизм R[53] на Mat2R. Используйте эти гомоморфизмы
для построения искомого изоморфизма.
506. Пусть ф — отображение G в ^-алгебру А с единицей, об-
обладающее свойствами ф(#1#2) = ф(#1)ф(#2) и фA) = !• Тогда
оно однозначно продолжается до гомоморфизма /: K[G\-*~A по
формуле а -*'2 а (Й Ф (#)•
Если отказаться от условия фA) = 1, то тривиальное отобра-
отображение G в нулевую алгебру становится универсальным объектом.
507. Свертка %[п, ъ] * Х[с,<п (х — характеристическая функция)
есть кусочно-линейная непрерывная финитная функция на пря-
прямой. График этой функции — ломаная с вершинами (а + с, 0),
(Ь + с, Ь — а), (а + d, b — a), (b + d, 0). (Здесь a <^ b, с ^ d,
b — a ^ d — с.) Для ступенчатых функций отсюда вытекает ис-
искомое утверждение. Общий случай получается из оценки ||/ * glloo^
<II/IL-Wi.
508. См. доказательство теоремы 4 гл. IV.
509. Установите равенство S (ф) = 1 ф (g) T (g) d\\, (g).
G
510. а) Свойство 3 следует из абсолютной непрерывности ин-
интеграла Лебега.
б) Свойство 3 достаточно проверить для шаровых окрестное
стей.
511. Представьте S(Д) - Т(а) в виде J/fe (g) [ Т (g)-T (a)] ф (g).
G
512. Воспользуйтесь формулой dk(y * г|)) = (дАф) * гр.
513. Используйте результаты задач 510—-512.
514. Используйте задачу 509. Ответ: ?(/)* = S(f(—x)) (ср.
задачу 516).
515. Существование /i * U вытекает из того, что при
каждом xf(x-y) принадлежит L2(G, \x) как функция у.
Измеримость следует из определения интеграла как предела
интегральных сумм, ограниченность — из неравенства Коши —
Буняковского.
516. Проделайте подходящие замены переменных.
517. Доказывается непосредственным вычислением.
518. Воспользуйтесь результатом задачи 517 и докажите ра-
равенство / * ek — (/, ek)ek для любой функции /е Li(G, ц),
352
519. Можно, например, положить fk (t) = Ц Ф& (*;)> где
2k
520. Используйте задачи 511, 519.
521. а) В(а + 1, 0 + l)9()+p+l
1
Ipbx ax
~ в (x) при а ф b,
b—a
xeaxQ (x) при а = b.
522. Покажите, что если / e LP(G, \i), g&Lq(G, \x), h&
e Ls(G, |x), то функция ф(х, i/) = f(x — y)g(y)h(x) принадлежит
Lt (G X ^, ^ X \i), где 2/« « 1/p + 1/q + Us. (Ср. задачу 378.)
Выведите отсюда нужное утверждение, полагая — = 1 — —,
2. Свертки обобщенных фупкций.
523. Lf =
524. Воспользуйтесь тождествами </, 1 # ф> = </ # 1, ф> и
1 *Ф= <1, ф>.1 для <pe0(R).
525. Можно воспользоваться формулой (f{ # /2, ф> = </i X /2,
Ф> и соотношениями /V х /V = (/х х /2)V, </V, фУ> = </? ф>.
526. 527. Докажите, что / # <р задает непрерывный функционал
на Li(R, dx).
528. Воспользуйтесь определением топологии в ^T(Rn) и
iZ)(Rn) и теоремой о представлении / в виде производной от регу-
регулярной функции.
529. Положите </х * /2, Ф> = j j /x @ /2 (в) Ф (f + s) dt ds.
530. Используйте результаты задачи 518.
531. Используйте указание к задаче 530.
532. Докажите, что / гыражается через /t и /2 с помощью
формулы / (г)=^ §K(rv г2; г) f1 (rj /2 (r2) dr^r^ где К(ги г2; г)-
0 0
некоторая локально суммируемая функция. Ответ: К(ги г2; г) =
= 0, если отрезки гь г2, г не образуют треугольника; К (г^ г2; г) =
= т^-, если отрезки ru r2, r образуют треугольник площади S.
533. а) Поскольку <ff+(R) содержит iZ)(R) в качестве плотного
подпространства, всякий линейный непрерывный функционал на
^T+(R) определяет некоторую обобщенную функцию /e^(R)
и сам однозначно определяется этой функцией. Пусть asl'-(R).
Тогда умножение на а является непрерывным оператором из
#*+(R) в iZ)(R). Значит, сопряженный оператор переводит iZ)'(R)
в <^+ (R). Отсюда следует, что &'+ (R) содержит ^L(R). Обратно,
23 а. А. Кириллов, А. Д. Гвишиани 353
если / г S)'_ (R) и а е *?- (R) — функция, тождественно рав-
равная 1 в окрестности supp /, то / ==-- а/ е <§Г+ (R).
о о
б) Первый способ: </j */2, ф> = </i X /2, Ф>, где ф(я, у) =
= ф(аг-{-*/). Здесь используется тот факт, что supp (/i X/2) име-
о- f
ет компактное пересечение с зиррф, если fv ^G^fR), а фЕ
Второй способ: определить сначала свертку 3)'^. (R) с <^±(R)
формулой (/ * ф) (х) — </, Г(—а:)ф^>, а затем положить
534. а), б) в) проверяются непосредственно.
г) Используйте результат п. в), непрерывную зависимость /«
от а при а>0 и непрерывность операции дифференцирования в
2)'+ (R). Ответ: lim /a — б.
535. Положите при а > — п /(а) =( —) S(fa+n)dx, где /а —
функции задачи 534. Проверьте независимость от выбора п (зада-
(задача 534 в)).
536. Используйте равенство / = — б (х2 + у2 — l). Ответ:
(/ * /) (ж, у) = -
О при х2 + у2 5* 4.
537. Используйте равенство / = ^" в (я2 + ?/2 + *2 — 0. Ответ:
при х2 + г/2 + z2 < 4,
0 при а;2 + у2 + 22 ^ 4.
§ 2. Преобразование Фурье
1. Характеры коммутативной группы.
538. Xkilmodn) = e2"thl'n (к = 1, 2, ..., п).
539. Используйте результат задачи 538 и тот факт, что всякая
конечная коммутативная группа является прямой суммой цикли-
циклических групп.
540. a) Xz(n) = 2n, zgC*;
°) ХЬ\Х) = е |ЛЕЦ
в) Xvw(z) = erz + wz, у, юеС;
г) Х^(^) = x\x(sgnx)e, Я е С, е = 0, 1;
541. Пусть Ue — окрестность характера Хо, задаваемая нера-
неравенством \х(х) — Хо(я)| < е для всех isG, Докажите, что при
е ^ УЗ эта окрестность не содержит точек G, отличных от Хо-
(Воспользуйтесь для этого тем, что множество комплексных чи-
чисел вида х(я)Хо(я) образуют подгруппу в Т.)
354
542. Докажите, что G отождествляется с замкнутым подмно-
подмножеством в произведении Т1 Т, которое является компактом от-
носительно покоординатной сходимости (теорема Тихонова).
543. Докажите, что обобщенная функция х(х) принадлежит
одномерному пространству, порожденному %(х).
544. Сделайте замену переменных в интеграле, определяющем
свёртку.
545. Воспользуйтесь результатом задачи 544.
546. Воспользуйтесь результатами задач 545 и 520.
547. Каждому гомоморфизму ср: G -> Н соответствует гомомор-
гомоморфизм ф: H-*G, действующий по формуле
548. Ответ: L совпадает с сопряженным пространством V.
Для доказательства рассмотрите ограничения характера на одно-
одномерные подпространства в L и докажите, что х имеет вид х(х) =
= eif(x\ где /eL'.
549. а) Всякий характер )(gQp имеет вид х* — е2лг{Хх), где
^eQp, а {•} — отображение Qp в QP/ZP cz Q/Z («дробная часть»).
Ответ: Qp = Qp.
б) Всякий характер %^ZP имеет вид %r(x) = e2ni{rx), где
г — рациональное число вида /т?//?п, определенное по modi. От-
Ответ: Zp~ Qp/Zp.
в) Характеры группы Qp/Zp отождествляются с характерами
группы Qp, тривиальными на Zp. Ответ: (Qp/Zp)^ « Zp.
550. Точность в члене G, означает, что р — мономорфизм, т. е.
каждый нетривиальный характер G\ = G[G0 определяет нетриви-
нетривиальный характер G. Точность в члене G означает, что в виде
р(%\) представимы те и только те характеры G, которые тривиаль-
тривиальны на Go. Наконец, точность в члене Go означает, что любой харак-
характер группы б?о получается ограничением из некоторого характера
г-руппы G. Это утверждение доказывается подобно теореме Хана —
Банаха с помощью трансфинитной индукции (группа Go расши-
расширяется до б? с помощью операций присоединения элемента и за-
замыкания).
551. Воспользуйтесь тем, что группа Q/Z изоморфна прямой
сумме групп Qp/Zp по всем простым числам р (каждая дробь
тп/п однозначно представима в виде суммы дробей, знамепатели
которых — степени простых чисел). Ответ: (Q/Z)^ » JJ Zp.
v
552. б) Воспользуйтесь разложением чисел отрезка [0, 1] в
бесконечную двоичную дробь.
553. Преобразование Фурье функции /инвариантно относи-
относительно умножения на последовательность {e2nina}.
554. Докажите требуемое утверждение для ступенчатых функ-
функций.
555. Пусть х — характеристическая функция множества
Zp с QP.
Всякий элемент @(G) является линейной комбинацией вида
2 сьУ- {акх + ьк)> гДе с*-е С» аь bh e Qp Докажите, что при отож-
23* 355
дествлении цР с Qp, указанном в задаче 549 а), функция % пере-
переходит в себя при преобразовании Фурье.
556. Воспользуйтесь эквивалентностью систем полунорм
Pft (/) = sup | /<*> (*) | и p'k(f)=\\fw(t)\dt.
x) /@)J
17@) f(x)]
557. а) Матрица положительно определена тог-
тогда и только тогда, когда /@)> 0, /(*) = /(—^) и /(ОJ— |/(ж) |2
>0.
б) Воспользуйтесь условием положительности матрицы
17@) fix) f(x-y)l
\f(-x) /@) /(-у) .
L/(y-*) /(У) /@) J
558. а) Положительная определенность матрицы А означает,
что 2 akizkzj ^ 0 для всех наборов {zk} e Сп.
б) Покомпонентное произведение положительно определен-
определенных матриц положительно определено. (Для доказательства вос-
воспользуйтесь тем, что положительно определенная матрица являет-
является суммой матриц ранга 1, обладающих тем же свойством.)
в) Преобразуйте выражение 2 (Ф * Ф*) (xk ~ xj) zkzj K ВПДУ
\\f(x) |2 dx, где / (у) =2 2^Ф (У ~ хкУ
i
559. Матрица Л, соответствующая набору всех элементов G,
является матрицей оператора ?(/). При преобразовании Фурье
этот оператор переходит в оператор умножения на /.
рр рд р
560. ^ Ф fox,-1) vj - \ ф
2 -?и (*).
2. Ряды Фурье.
561. а) сп == с_„; б) с„ = —с_„; в) сп = с_п.
562. Ответ: Z = к + 1. Представьте / в виде суммы (к + 1) —
гладкой функции и линейной комбинации модельных функций
(для к = 0 — функций вида | * — я |).
563. Достаточно разобрать случай & = 0. Первое утверждение
выводится из включения С[Т] с: L2(T, dt)\ второе — из равномер-
равномерной сходимости ряда Фурье.
564. Ответ: 2 * | сп|2 < °°-
565. a) xc2fe+i = 0, к е Z;
б) при Я = е2лг'т/\ /л eZ, cn = 0, если п Ф wi(mod ^).
566. 0-* Z -^ Z_J Z(n->0, где i —умножение на re, p—пере-
p—переход к вычетам.
567. Так, чтобы продолженная функция обладала свойствами
f(t + 1/2) = f(—t) = —f(t) (см. задачу 561 а) и 565 а)). Для этого
нужно положить
( /A/2-0 на [1/4, 1/2],
/(*) = {-/(«-1/2) на [1/2, 3/4],
1-/A-*) на [3/4, 1].
356
X
568. cn (h) = cn.*l"*jmn при п Ф 0; cQ (h) = cQ.
569. a) {cn} — финитная последовательность;
б) сп = P(i/n) при лг ф 0, где Р — некоторый многочлен;
в) сп = (—1)пРA/я) при дг Ф 0, где Р—многочлен.
570. Для доказательства необходимости выведите из положи-
Г С
тельной определенности /еС(Т) неравенство \ \ / (s — t) ф (s)
т т
Xф (t) ds dt ^ 0 для любой функции феС(Т). Примените это не-
неравенство к ф@ = e2jlint. Для доказательства достаточности вос-
воспользуйтесь тем, что / является пределом в С(Т) чезаровских
п к
1 V*
средних Сп = — > Sh, где Sk —
571. См. указание к задаче 557.
572. Рассмотрите линейный функционал F на пространстве
тригонометрических полиномов, принимающий на e2nint значение
с„. Докажите, что этот функционал положителен на полиномах
вида P(t) = \Q(t)\'\ где Q — также полином, и что всякий поло-
положительный тригонометрический полином представляется в таком
виде. (Воспользуйтесь принципом симметрии, согласно которому
корни полинома P(z), принимающего вещественные значения на
окружности \z\ = 1, симметричны относительно этой окружности:
вместе с корнем А, есть и корень А,-1.) Вывести отсюда, что F
имеет непрерывное продолжение на пространство С(Т) и, следо-
следовательно, представляется некоторой мерой \i.
573. 2j cn—mz z ~ \\ 2j ZrP Ь •
n,m || n II
574. Искомый изоморфизм V переводит вектор Un% e Я в
функцию е2лгп1 в L2(T, \i).
575. Если / — гладкая функция, то Sn =^ / и предельное мно-
множество совпадает с графиком /. Всякая кусочно-дифференцируе-
кусочно-дифференцируемая функция / представляется в виде суммы гладкой функции и
конечной линейной комбинации модельных функций вида f(t) =
= {t — а} (а е [0, 1)). Исследование в модельном случае сво-
п
дится к изучению суммы Sn = ^ ——-—, сходящейся к -—— {t[
при t e R/Z. Имеем
sin nt
о
en) = ± J si^dT + 0(en)
Таким образом, предельное множество содержит, кроме графика
1
функции / (t) = ~2~ — U}> вертикальный отрезок t = 0 длины 2Л,
357
где
а л
= sup J- Г 2*2* dx = ± f^
а П J X Л J X
0,588
(см. рис. 6).
Ответ: предельное множество содержит график функции / и
вертикальные отрезки в точках tk разрыва /. Длина отрезка в
-1
\
ч/г
У\
A'
4/2
V
\
A
\
t/з \
\
/ 07
>
Рис. 6
2А = 1,177 раз больше величины скачка / в tk, а центр отрезка
' / f('O) + f(t +0)\
^тот Факт полу-
полусовпадает с точкой Ufe» 2 Г
чил название явления Гиббса..
576. Воспользуйтесь тем, что тригонометрические полиномы
образуют множество, плотное в ^Г(Т) (задача 530).
577. сп ^ 0 для всех wgZ.
578. Пусть {ck} — коэффициенты Фурье характеристической
функции множества ХсТ: ch= j e~2Jllk1
1dt.
Если
X + а, то
X
Для иррациональных а равенство e-2nika ~ 1 возможно, если
только /с = 0. Таким образом, характеристическая функция X поч-
почти всюду постоянна.
579. Обозначим a(t, x) обобщенное решение уравнения с "на-
"начальными условиями а@, х) = Ь(х). Докажите, что искомое реше-
решение с начальными условиями и@, х) = и(х) имеет вид
tt(f, X) = f V{X-
T
y)<x{t,
358
Для вычисления a(t,x) представьте эту функцию рядом
Фурье по х:
fe<=z
Тогда уравнение принимает вид c'h (t) = — k2ck (t) с усло-
условием сл@) = 1. Соответственно ck (t) = e~k *. Для фиксирован-
фиксированного t функция
не может быть выражена в терминах элементарных функций
от х. В то же время она просто выражается через тэта-функ-
тэта-функцию Вейерштрасса
n~Z
Именно, a(f, x) = В(х + 1/2, е~*).
3. Интеграл Фурье.
580. а) После замены неизвестной функции / (х) »-* ф (
данные уравнения превращаются в систему -j— = 0
k
Отсюда у(х) = const.
б) Докажите тождество е~л^х~а^ = ехр | — illiiL 1 X
(Воспользуйтесь соотношениями fm = ел№\ дте-*л\Щ\ . j Проверь-
Проверьте, что ряд в правой части тождества сходится в тополо-
топологии S(R2n). Поэтому наименьшее замкнутое подпространство L а
czS(Rn), содержащее все функции /ffl(ffiGNn), содержит все
функции вида фа (х) — е~я1'х~а" = fQ (x — а). Выведите отсюда,
что для любой функции ф е 5(Rn) функция ф * фа принадлежит
L. Отсюда вытекает, что преобразование Фурье пространства L со-
содержит все функции вида ф1/0, где фе5(Кп). В частности, оно
содержит пространство 5)(Rn), плотное в S(Rn).
В) Nhfm=™<kfm- (ВоСПОЛЬЗуЙТеСЬ СООТНОШеНИЯМИ Akfm = /r7l + 8^?
Akfm = ck, m/m_E , где Efe~ базисные векторы в Nn. Для под-
подсчета констант Ckm используйте соотношение AkAk — AkAk == 4я.)
г) Каждой функции fs=S(Rn) соответствует последователь-
последовательность с = / (х) f (x) dx = (/, / ) ( у Оцените значения
полунорм, определяющих топологию S(Rn) на векторах /т, ис-
используя соотношения = —5-. 1, xk = -i. 5.
dxh 2i h Ш
359
д) fm = iiwl/m. (Воспользуйтесь соотношением FA*kF * =
= F (iDk + Mk) P'1 = iA*h = iMk ~ Dk-)
581. Покажите, что если /e?(Rn) и /(а) =0, a e Rn, то су-
существуют такие функции фА е iS(Rn) A ^ к <^ /г), что / (х) =
п / 1 \
- НапРимеР> Ф*(*) = I |?(a+T(a:--a))dT.
ft=l V ? h )
582. См. задачу 581 и доказательство теоремы для случая
тг = 1 в основном тексте.
583. Первый способ: обобщить рассуждения, приведенные в со-
соответствующем пункте раздела «Теория». Второй способ: восполь-
воспользоваться результатами задачи 580 г) ид).
584. а) f четна, б) f нечетна.
в) /Ч-А.) =/W,
г) f вещественна.
585. 7(W = I det А Г1/ (A'-lX) e^iXA~lb.
586. Воспользуйтесь соотношением/= Пт/*фп, где {ф„} —
П-*оо
дельтаобразная последовательность в ?D(Rn) (предел в норме
пространства Li(Rn, dx)). Проверьте, что в условиях задачи f (К)
суммируема (воспользуйтесь неравенством Коши — Буняковского
и тем фактом, что A+|^|2)8/2 е L2(Rn, dX) при s > /г/2).
587. Докажите, что при s > п/2 пространство L2(Rn, A +
+ l\k\\2)sdX) содержится в MRr\ d\). (Воспользуйтесь неравенст-
неравенством Коши — Буняковского для функций f(X) A + HWI2)l/2 и
(l + IIMI2)-*/2 и тем фактом, что A + 1Ш12)-*/2 е ^2(Rn, dX) при
s > /г/2.)
588. Перейдите к преобразованию Фурье.
589. Перейдите к преобразованию Фурье.
590. Воспользуйтесь результатами задач 587 и 588, а также
правилом дифференцирования свертки.
591. Воспользуйтесь разложением \/Р(х) на простейшие дро-
дроби вида 2 i ,2- Ответ в п. в): порядок гладкости равен
2/71-2.
592. Представьте / в виде суммы простейших дробей.
593. а) Не следует.
б) Следует (перейдите к преобразованию Фурье).
594. Рассмотрите функционал F на ?(R), действующий по
формуле <Л ф> = J / (К) ф (К) dk.
R
Докажите, что F неотрицателен на неотрицательных ф. (Вос-
(Воспользуйтесь тем, что если 9G^(R) и ф ^ 0, то ф = т|J, где i|? e
.) Выведите отсюда, что (F, ф> == I фф, где ц — векторная
R
мера на R.
595. См. указание к задаче 557.
596. См. указание к задаче 557,
360
597. Пусть / 6= Ф (R), supp / с [—Ь, 6] и g = F/. Тогда
tt)*(X) F(/i*>), откуда
(х) dx
-Ь
Bл)""* sup
Таким образом, g обладает требуемыми свойствами с константами
а = 2лЬ и г = Bя)~^ sup I /(ft) (я) |. Обратно, если g удовлетворяет
оценкам \g(X) | • \K\h < ckeallm *¦', то gE^ifR, dX) и можно опре-
определить непрерывную функцию / = ?g. Из тех же оценок следует,
что / бесконечно дифференцируема. Наконец, если \х\ > а/Bя),
то
\ e2niKxg (X) d%
R + i/sgnx
При t-^co эта величина стремится к нулю. Значит, supp / с:
с= [— а/2я, а/2п].
598. а) Пусть а е Rn, 5eR; положим ср {а, Ъ) = \ б (ая — Ь)Х
X / (.г) с?д:. Докажите тождества:
f Ф (а, 6) e~2nibdb = Г(«), Ф (а, Ь) - | а Г1 f / (x) d(iL (*),
R L
где L — гиперплоскость ах = &, | а | — |/ а2 + ... + а%. Если
последний интеграл равен нулю для всех ?, то ф(а, 6) = 0 при
Ои, значит, f = 0.
б) Найдем /@). По формуле обращения
/ @) = f Г(«) ^ = f ( f Ф (а.
* 3 U
Воспользуемся соотношением ф(тя, тб) = [r[~
щим из определения ф(а, 6) и тождества б(тя)
получим:
/ @) = J | J f f Ф (га, 6) e-2nibdb\ r2dr)da (a)
(a, 6),
6), вытекаю-
вытекаю| 2S . Мы
361
где г = [а|, а = [7j e ^> с?а (ос) — элемент площади сферы,
Р = r~lb. Если обозначить Dл) \ ф(а, $) do (а) через ф(Р), то
S2
оо
последнее выражение будет равно 4л I $ (г) r2dr = \|?" @). От-
J л
о
метим, что геометрический смысл величины ^(Р)—среднее зна-
значение интегралов от / по плоскостям, проходящим на расстоянии
Р от начала координат. Таким образом, для восстановления функ-
функции / в точке х нужно знать ее интегралы только по тем плоско-
плоскостям, которые пересекаются со сколь угодно малой окрестностью
точки х. Оказывается, что это свойство имеет место во всех не-
четномерных пространствах.
599. Пусть заданная прямая I является осью х в R3. Прямая,
пересекающая / в точке (t, 0, 0), имеет параметрическое представ-
представление х = / + as, у = $s, z = ys. Положим ф(а, р, к, 0 =
= \ / (t + as, Ps, ys) ds. Функция ср однородная степени —1 по пер-
R
вым трем переменным:
ф(ат, рт, чт» 0 = Iт|~ТФ(оь, Р, Ч, t).
Будем рассматривать ф как регулярную обобщенную функцию и
пусть ф(Х, \i, v, т) —ее преобразование Фурье. Можно проверить,
что ф регулярна вне прямой К — \i = v =0 в R4 и однородна сте-
степени —2 по первым трем переменным. Справедливо тождество
ф(Х, \i, v, т) = /(т, \хтК~\ vtX~1) \xK~2\.
(Для проверки примените обе части тождества к основной функ-
функции \fe5(R4) и воспользуйтесь определением ф и тождеством
<ф, г|)> = <ф, г()>.) Поэтому / можно выразить через ф.# f(a,b,c) =
= ф(а, 6, с, а) \а\. Отсюда
1
где интеграл следует понимать как значение обобщепной функции
\а\ на основной функции ip (a) --J* fф (я — 5, {/, г, t) e2nia{s'°dsdt.
4. Преобразование Фурье обобщенных функций.
600. Воспользуйтесь задачей 585. Ответ: (—1 — Л, е).
601. Ответ: F (%) = 2 Г № б & " Z)-
602. а) Воспользуйтесь тождеством
dx J
362
б) Функция еа* будет квазипериодической с периодом #,
если ^gR" удовлетворяет условию \ elKxdx = 0. Послед-
\
нее равносильно тому, что число R\\K\\ — корспь уравнении
Л/2
1пп(х) = 0, где Inn — Функция Бесселя, 1п (х) =— 1 cos 2nd X
, 1п (х) =— 1
о
Vi (— \)h I х \ +
Xcos(sin 0) с?6= > —- —- — . Известно, что это урав-
<« А:! {п + к)\ \ 2 /
пение имеет счетное число корней на положительной полуоси,
для которых справедлива асимптотическая формула хтп«
т -f- л при т -> оо. Если п нечетно, функция /п/2 вы-
ражается через элементарные. В частности, при п = 3
^ч/9 (л) — 1/ — I S1" Д ~~ cos * »так что уравнение на X принимает
Ли * пх \ х )
I
пх \ х
в этом случае вид
в) Может; см. указание к б).
G03. Ответ: J (I) = (det i4)-i/2e-n((A')-U^)) где аргумент
del А выбирается по непрерывности па пути, линейно соединяю-
соединяющем Л с единичной матрицей.
604. Ответ:? М = (det А)-1/2е1л*/4е~1л(А~1к*к\ где s — сигна-
сигнатура матрицы А (разность числа положительных и отрицатель-
отрицательных собственных значений).
605. Константа R связана с размерами носителя, а константа
7V — с порядком преобразуемой функции. (Ср. теорему Пэли—
Винера в задаче 597.)
606. Перепишите уравнение в терминах преобразований
Фурье.
607. Ответ: /((х)=^^
608. Проверьте эти соотношения в пространстве 5(R").
609. к {г) = B sin 2лг)/г.
ГЛАВА V
СПЕКТРАЛЬНАЯ ТЕОРИЯ ОПЕРАТОРОВ
§ 1. Функциональное исчисление
1. Функции операторов в конечномерном пространстве.
610. Воспользуйтесь тождеством Кэли Ра(А) =0, где Ра —
характеристический многочлеп матрицы А.
611. Импликации б) =^ в) =>- а) очевидны. Для вывода б) из
а) рассмотрим для каждого вектора | идеал /$ в кольце многочле-
многочлена от одного переменного, определяемый формулой /g =
363
= {P: P(A)% = 0}. Идеал /$ является главным (как любой идеал в
кольце многочленов от одного переменного), т. е. порождается неко-
некоторым многочленом Р%. Так как Pa cz /&, Pi есть делитель Ра-
Пусть Р|, ..., Ph — все различные делители РА степени <п со
старшим коэффициентом 1. Пусть Li =кегР*(А). Из а) следует,
что
. Тогда U
Таким образом, существует вектор
г1
? е L, который не аннулируется ни одним из операторов Р{(А),
ни, соответственно, одним из операторов вида Р(А), degP<n.
Отсюда следует б).
612. Воспользуйтесь формулой для определителя Вандер-
монда.
613. Действуйте по схеме а) =>- б) =>- в) =>- а).
614. Условие, что А нерегулярен, может быть записано систе-
системой алгебраических уравнений на матричные коэффициенты А
(выражающих линейную зависимость 1, А, ..., Ап~1).
615. а) Пусть | — циклический вектор для А. Запишите А в
базисе 6, А% Ап\.
б) Первый базисный вектор е\ является циклическим для А.
в) Коэффициенты {at} однозначно определяются характери-
характеристическим многочленом матрицы А.
616. Коэффициенты многочлена Р(х) = хп + а^"-*1 + ... + ап
п
— 2 ^ (& = 1, 2, ..., и) степе-
выражаются через суммы
г=1
ней его корней. (А именно, справедливы формулы Ньютона:
k-i
kak = — 2 aisk-V гДе ао = *•)
г=о
617. в) Ответ:
/(>-)
О
О
ГО)
2!
1!
О
-2)!
618. Если Я = Я] Ф Я2, ег- — единица в Я,-, то элементы е{ Ф 0 и
О Ф бг — нетривиальные идемпотенты. Обратно, если е — идемпо-
тент в Я, отличный от 0 и 1, то Я = Я] + Щ, где $И\ = еЯе, Щ =
-.A_„)ИA-е).
619. а) Уравнение X2 = X имеет в С лишь тривиальные реше-
решения 0 и 1.
б) Докажите, что образующий элемент х удовлетворяет урав-
уравнению (х — X • 1)п = 0, где X е С, а п = dim Я.
620. Рассуждайте от противного и рассмотрите алгебру ми-
минимальной размерности, неразложимую в сумму примарных.
621. Пусть А = inf ап/п. Тогда для любого е > 0 найдется пг
такое, что ап /пг < А + е. Представим произвольное iV ^в виде
N
Ьие + I, где 0 < ^ < ие. Тогда -дг
о. Отсюда следует утверждение задачи.
al
При
364
622. Воспользуйтесь задачей 610.
623. Воспользуйтесь задачей 619 б).
624. Для регулярных.
625. Воспользуйтесь задачами 614 и 616.
626. Докажите, что почти каждая пара матриц (Л, В) приво-
.[«01 \у е]
дитсяквиду Л^ J B ^ ]
627. Коразмерность орбиты действия группы PGL(n) равна в
этом случае 2п2 — (п2 — 1) = п2 + 1.
ГХ-1Л Л
628. Все матрицы вида I, где 1„ — единичная мат-
рица порядка п, попарно перестановочны.
629. Представьте А в виде X-1-J-/V, где Nn = 0, и проверьте
равенство для f(K) = № (к = 0, 1, ..., п — 1).
630. Проверьте, что f(A) линейно выражается через значения
/ в точках Х\, ..., Кп и найдите соответствующие (матричные) ко-
коэффициенты.
631. Проверьте, что f(A) линейно выражается через fu){kh)
(a^j^mk—\). Ответ: Bjk = Pjk(A), где Pjh{z) — многочлен
степени п — 1, обладающий свойствами:
1) Р^ (А|) = 0 для всех пар (s, ?) @ < s < пц — 1), кроме
пары (/, к);
632. Крайние точки К — положительные операторы ранга 1,
т. е. ортопроекторы на одномерные подпространства в Я.
2. Функции ограниченных самосопряженных операторов.
633. Множество о (А) совпадает с множеством значений, при-
принимаемых функцией а(х).
634. Спектр А — множество существенных значений функции
а(х), т. е. таких значений ^еС, что для любой окрестности U
точки К множество
Еи = {х€=Х: а(х) <= U}
имеет положительную меру.
635. Перейдите к преобразованию Фурье. Ответ: множество
значений преобразования Фурье функции /.
636. Перейдите к преобразованию Фурье. Ответ: совокупность
коэффициентов Фурье функции /.
637. Докажите, что спектры U и U~l лежат в единичном круге.
638. Проверьте изометричность отображения (Л + М) Ё*-*-
н* (А + М) Е и плотность im (A + И).
639. Пусть С/ = (Л + il) (Л — Л)-*. Тогда
D* + г1)-1D* — *1) = ?/*= С/-* = (Л — П)(А + П)-\
откуда
(Л* —а)(Л + il) = (А* + tl) (А — И) и Л=Л*.
640. Воспользуйтесь перестановочностью U+1 и (?/— I).
365
A.
641. Воспользуйтесь формулой Anf (x) = \ __ , } f (i) dt
о
и докажите неравенство | Л711 < , __ ^ ,. Ответ: г(А) = 0.
оо
642. Воспользуйтесь формулой Як (А) = — 2 X~~/i^fe'
ас
Ответ: Л^ (Л) / (х) = - Л/ (ж)— >Г2 j ^~1(x~°/ (/) ^^.
о
643. Воспользуйтесь задачей 484.
644. Докажите, что всякий многочлен, положительный на от-
отрезке [а, Ь], представим в виде суммы слагаемых вида Q\ (x),
(х — a) Q2 (х)^ (Ь — х) Q\t(x), где Qi — многочлены с вещественны-
вещественными коэффициентами. Указание:
(Ь — х) (х — а) = (Ь —
645. Докажите, что если а-1^Л ^^-1, то \\A\\ не превосхо-
превосходит {|а|, ш>.
646. Воспользуйтесь формулой еЧА == ^ ~"?f~ •
647. См. указание к задаче 646.
648. Докажите, что U(t) — дифференцируемая функция (см. ме-
метод сглаживания в доказательстве теоремы Стоуна). Затем выве-
выведите дифференциальное уравнение задачи 647 и докажите, что оно
имеет единственное решение с начальным условием U@) ~ 1.
649. А = RU, где R — оператор умножения на функцию
|а(я)|, a U — оператор умножения на функцию sgn (a(x)).
650. Оператор одностороннего сдвига Т обладает свойствами:
Т*Т = 1, ТТ* = Р, где Р — ортопроектор на ортогональное допол-
дополнение к первому базисному вектору. Ответ: Т = РТ.
651. а) А = BRB-lBUB~l — полярное разложение.
б) Неверно. Разберите случай, когда А и В — оператор одно-
одностороннего сдвига из задачи 650.
652. Разберите сначала случай В = 1, введя в рассмотрение
оператор А1/2.
653. Приведите Т к виду умножения на функцию.
654. Воспользуйтесь монотонностью последовательности
(ЛВД)П.
655. Проверяется непосредственно.
3. Неограниченные самосопряженные операторы.
656. Докажите эквивалентность соотношений ОфхЕТ(ГлI и
x±DA.
657. Воспользуйтесь перестановочностью операций т и J_,
а также результатом задачи 479.
658. Воспользуйтесь равенствами (А*) = А* и (А*)* = А (за-
(задача 657).
659. а) Не симметричен;
б) существенно самосопряжен;
в) симметричен, но не существенно самосопряжен.
660. Ответ: да, во всех трех случаях.
661. Докажите, что образ единичного шара при отображении А
слабо ограничен.
662. а) Проверьте равенство II (Л — Н)х\\ = \\(А + ti)x\].
б) Если xe=ker(U — 1) и х = (А — П)у, то х= (А + П)у,
^откуда у = 0.
663. Проверьте соотношение (тГд)-1 = Та-
664. Перейдите к преобразованию Фурье. Ответ:
/1=1
665. а) Да. б) Да. Проверьте, что im(A ± H) содержит все фи-
финитные последовательности.
666. Могут. Например, пространство D(R) и пространство сту-
ступенчатых функций.
667. Для доказательства достаточности воспользуйтесь неравен-
неравенством задачи 484 б) и покажите, что (i-f-Л)-1 продолжается с
im(A + 1) на все Я и имеет норму ^ 1.
668. Рассмотрите проекции вектора яфОеЯфЯ на Га и
Г^ = т (Гд*). Докажите, что A + А*А)~1 — ограниченный самоса-
пряженный оператор.
669. Воспользуйтесь критерием существенной самосопряжен-
самосопряженности или теоремой Стоуна.
670. Докажите ограниченность (А — Х1)~1 при невеществен-
невещественных К (замена А на аА +р, a, PeR сводит общий случай к слу-
случаю к = i).
671. б) Неверно. Может быть кег А = 0, но DA# = @). Для
этого достаточно в качестве ГА взять любое плотное в Я ф Я под-
подпространство, имеющее нулевое пересечение сЯфОисОфЯ.
672. Если А а А\, то А1С1А*1 причем оба включения одно-
одновременно строгие или нестрогие.
673. Проверьте равенство ||(Л + Н)х\\ = ||(Л — ii)x\\.
674. Докажите, что графики оператора А и оператора U из за-
задачи 673 получаются друг из друга линейными обратимыми пре-
преобразованиями пространства И Ф Я. Сравните графики А и А + И.
675. Каждому симметрическому расширению оператора А со-
соответствует изометрическое расширение оператора. U задачи 673.
Самосопряженному оператору соответствует унитарное рас-
расширение.
4. Расширения операторов.
676. Проверяется непосредственно.
677. Воспользуйтесь рассуждением из доказательства тео-
теоремы 8.
678. Предположим, что h > /д. Тогда в L\ найдется вектор,
ортогональный к ?й (см. доказательство теоремы 8). Из результа-
результата предыдущей задачи вытекает, что L^ = im (A — Я*1), L^ —
= im (A — jliI). Значит, есть вектор вида А у — [iy, ортогональ-
ортогональный Ау — Ху. Отсюда, пользуясь неравенством \Ау — jliz/|| ^
^ |Imp,| -Hz/ll, получите соотношение |Impi| ^r |pi —Я|. Последнее
невозможно, если расстояние между Лиц мало по сравнению с
их расстоянием до вещественной оси.
367
679. Повторить решение предыдущей задачи, воспользовавшись
неравенством \\Ау — ку\\ ^ dlfyll, где d — расстояние от точки X
до луча [а, оо),
680. а) Воспользоваться тождеством х = —-^— х + —2— х%
б) Если а: е= Яо и ЛС = СЛ, то САх = ЛСя = Ах, откуда Ах е=
еЯ0. Если AHqCzHq, то ЛС — С Л обращается в нуль на Яо, а в
силу антилинейности и на всем Я.
681. Проверить, что С переводит L% ъ L-.
682. Пусть x^D(A), (/ е= Lx, г е= ?- и х + у + z = 0. Приме-
няя_к этому равенству оператор Л* —XI, получаем (Л— ki)x +
+ (к — к)у = О. Так как xs=D(A), (Л* — XI) х = (Л—XI) х g=
е im (Л — XI) = L'?, С другой стороны, (X — Х)у g= Lx. Поэтому
У == о. Аналогично доказывается, что z = 0. Значит, данные прост-
пространства независимы. Далее, ясно, что все три пространства содер-
содержатся в D(A*). Следовательно, их сумма также содержится в
D(A*). Обратно, пусть ие=#(Л*). Запишем А*и — ки в виде сум-
суммы v' + у", где v' 6= Lx, v" 6= L'? = im (Л — XI), и положим v' =
= (Х—Х){/, у" = (Л — Х1)а\ Тогда А*и — ки = Ах — кх + (I — к)у,
откуда А*(и — х — у) = Х(и — д: — у). Значит, вектор 2 = и — х — у
принадлежит ?-.
683. а), б) Проверяется непосредственно.
в) Воспользоваться равенством B*J -\- JB =\
684. а) Если x(t) —решение уравнения Ах = кх и %(t) —со-
—соответствующая вектор-функция, то w~l (t) I (t) — постоянный век-
вектор, ибо (w-l%)' = —w-lw'w~ll + ы;!' = —w'B\ + w~lB% = 0.
б) Воспользоваться тождеством (det wf) = tr(w'w~l).
в) Перепишем условие в виде /2 (t) = %z (t) J%z (t) =0, где
\z (t) = w (t) I J. Тогда в силу задачи 683 в) справедливо равен-
t
ство /z @) = — 2 Im X I | хг (t) j2 dt. Но Д@)> как легко вычисляет-
о
ся, равно 2 Im z. Значит, уравнение St имеет вид
t
2 Im X Г | *г @ |2 dt + 2 Im z = 0. (¦)
Записывая xz(t) в виде zxx(t) +xo(t), мы видим, что (*) —урав-
—уравнение окружности. Соответствующий круг задается неравенством
368
Это показывает, что Kt 3 Кt при t2 > t\. Радиус S< равен
2 | Im X | j | хг (t) N .
685. Пусть имеет место случаи предельной окружности. Для
всех z e ?оо справедливо неравенство из указания к 684 в), пока-
показывающее, что хг е L2 @, оо). Отсюда следует, что оператор А
имеет числа дефекта A, 1). В случае предельной точки результат
задачи 684 в) показывает, что х\ §ё Z>2 @, оо). Поэтому есть единст-
единственное решение xz, z = Zoo уравнения Ах= Хх, лежащее в L2@, оо).
Оно не может удовлетворять самосопряженному грапичному усло-
условию в нуле ввиду монотонности функции fz . Значит, в этом слу-
случае оператор имеет нулевые числа дефекта.
§ 2. Спектральное разложение операторов
i. Приведение оператора к виду умножения на функцию.
686. Рассмотрите пространство X, состоящее из конечного чис-
числа точек.
687. а) Пусть / — любой вектор из Н. Положим g(x) = /(—#)•
•sgnz. Докажите, что вектор g ортогопален циклическому подпро-
подпространству, порожденному /.
б) Подпространства четных и нечетных функций — цикли-
циклические.
N
688. Предположим противное: 2 ch^ ~® и cN^=^t Тог-
k=o
да линейная оболочка оператора {^4fe}^=0 совпадает с линейной
оболочкой операторов {Ак}^~*. Поэтому для любого вектора ?g//
пространство, порожденное векторами {АЦ1}™=1, имеет размер-
размерность не выше iV. Значит, оператор А не может иметь циклическо-
циклического вектора.
689. Используйте тот факт, что квадрат и отрезок изоморфны
как пространства с мерой.
690. Всякий оператор в L2([a, b], и,), перестановочный с умпо-
жением на ж, является оператором умножения на функцию от х.
691. Воспользуйтесь теоремой о приведении оператора А к ви-
виду умножения на функцию а(х) в пространстве /^(Х, М-)- Докажи-
Докажите, что множество тех х е X, для которых а(х) ф. о (А), имеет ме-
меру нуль. Поэтому для почти всех ге! выполняется равенство
I/(a (*))|< sup f(t).
U)
692. Перейдите к преобразованиям Фурье. Условие самосопря-
женности: S(f): f(X)—вещественная функция (или: f(x)= f(—x)).
693. Нет, так как f (X) ->0 при Х->оо.
694. a) f(g) =/(-g);
б) |f(^)| ss= 1 (что возможно, лишь если группа G компактна,
a G дискретна);
в) когда группа G компактна.
2^ А. А. Кириллов, А, Д. Гвишпани 369
695. Найдите собственные векторы оператора Л, дважды про-
продифференцировав по х равенство Kf(x) = \ min (ж, у) f (у) dy.
о
696. Воспользуйтесь соотношением т (ТА) = ГА%1 которое
справедливо для любого оператора А и равносильно определе-
определению А*.
697. а) По определению проекции справедливо равенство
откуда ||ВЦ < 1, \\C\\ < 1.
б) Равенство х 0 0 = (у 0 Ау) + (—Az Ф z) влечет х = у — Az,
z = —Ay. Вспоминая, что у = Вх, г = Сх, получаем: х = Вх —
— ЛСх, Са; = — АВх или 1 = В — 4С, С = — А В.
Отсюда имеем: 1 = 5 + А2В, т. е. A + А2)В = 1.
698. Ал=
699. / (F):
. /(l)"i/W/(-l)i/K)^ . .
+ 4 Ф (*) +
Ф 4 Ф (— «) +
+ 4 Ф (— *).
2. Спектральная теорема.
700. а) Пусть w{t) — модуль непрерывности функции / (т. е.
\}(х) —f(y)\ < w(\x — y\)). Докажите оцепку
T, 6)-5(/, Г, т|)И<
б) Воспользуйтесь тем, что интегральная сумма ?(/, Г, ?) сов-
совпадает с интегралом Лебега от стуиенчатой функции
fe=o
701. Для доказательства свойств а), в), г) полезно использо-
использовать равенство
для любых g, Л е Я. Равенство б) проверьте спачала для характе-
характеристических функций, а затем используйте а). Для доказательства
свойства д) воспользуйтесь б) и задачей 491.
702. а) Воспользуйтесь соотношением
X\(El\jE2) = (X\?i)n(*\*2).
б) Рассмотрим сначала случай Е\ П Е2 = 0.
Пусть A,(/?i) = а и X(?) = Р. Поскольку аJ и а + Р~орто-
Р~ортогональные проекции, а2 = а, Р'= Р и (а + РJ == а + Р. Отсюда
370
следует, что ар + Р« = 0. Умножая это равенство слева, справа п
с обеих сторон на а, получаем ар + офа = 0, ара -f Ра == 0 и
2а[}а =з 0. Таким образом, ар = Ра = 0. Переходя к общему слу-
случаю, используем соотношения Е± = (ЕгГ\Е2) LJ (Е^Е^), Е2 =*
= (Ег[]Е2) LJ (E^EJ. Тогда K{Ei)l{E2) = [M#i 0 Е2) +
+ X{El\E2)][k(Ei(]E2)+Х(Е2\ЕХ)]. По доказанному выше, по-
последнее выражение равно К(Е} П Е2).
703. Существует. Воспользуйтесь отображением отрезка на
квадрат, сохраняющим меру (см. задачу 131).
704. Верно. Используйте тот факт, что соответствие %-*lii(E)
задает в Н полунорму, удовлетворяющую тождеству параллело-
параллелограмма.
705. Примените утверждение предыдущей задачи к мере \xi
представляющей функционал /-> (ф(/)?, |).
706. а) Следует из того, что К(Е) и А коммутируют, что, в свою
очередь, следует из конструкции X.
б), в) Следует из рассмотрения реализации, в которой А есть
оператор умножения на функцию.
707. Аналогично 706 в).
708. Если (А — аЛ)~х существует, то 1И? — а\\\"^
^ \\А — а-1||-"Ч1Ц1. Если точка а принадлежит спектру, восполь-
воспользуйтесь результатом задачи 707.
709. Используйте тот факт, что всякая ортонормированная сис-
система слабо сходится к нулю.
Ъ
71О.ПУсТЬ
Убедитесь прямым вычислением с помощью замены перемен-
переменных % -*~ (\ — t)/e, что
[0, если 1ф[а, Ь],
lim/?(/) = |l/2, если t = а или t = Ъ,
~* ll, если t e (а, 6).
711. Первый способ: представьте U в виде Re U + ilm U. Вто-
Второй способ: используйте результаты задач 662, 663.
712. Используйте результат задачи 711 и соотношение
*=i 1о прп
при N-+oo.
713. а) Для доказательства мультипликативности восполь-
RK (A) — R (А)
зуйтесь тождеством Гильберта R^(A)-R {А) = Т~И
и предположите, что контур С, пробегаемый переменной Я, содер-
содержит контур С\ пробегаемый переменной \х в интеграле
~ —2 I J /l W U ^ Rb ^ % (
4я с с,
24* 871
б) Воспользуйтесь том, что интеграл является пределом рима-
повых интегральных сумм и что соответствующие числовые ин-
интегральные суммы сходятся к интегралу — ——'- dX = / (t).
с
714. См. указания к задачам 300 и 689.
715. Рассмотрите сначала случай циклического подпростран-
подпространства.
716. Ответ: А = —id/dx.
717. Воспользуйтесь теоремой Стоуна и реализацией U(t) в ви-
виде оператора умножения на e2nit в прямой сумме пространств ви-
вида L2(R, M-).
718. Да. Используйте задачу 711.
719. Проверьте, что функция fQ (х) = е~х '2 является собст-
собственной для А и что оператор
переводит собственную функцию для А с собственным значением
X в собственную функцию с собственным значением X + 2. Ответ:
А = |j BЛ + 1) Pk,
fc=o
где Pk — проектор на подпространство, порожденное функцией
fh = BkfQ. Далее используйте задачи 464 г) и 213 в).
§ 3. Математическая модель квантовой механики
720. Воспользоваться равенством
d d
и уравнением Шредингера.
Результат этой задачи можно положить в основу альтернатив-
альтернативного описания квантовой системы. А именно, можно считать, что
векторы i|), описывающие состояния, не меняются со временем,
а операторы, описывающие физические величины, меняются по
dA
закону i'.% -jj = [//, А] (уравнение Гейзенберга).
Такой способ описания называется картиной Гейзенберга в от-
отличие от картины Шредингера, использованной нами в основном
тексте.
721. а) Функционалы указанного вида образуют линейное про-
пространство. Проверить, что его размерность равна /г2. Для этого до-
достаточно показать, что /а — 0 влечет А = 0. Но fA (A*)= tr AA* =
ik
б) При условии А > 0. Необходимость: М|, |) = tr(i4Ps) =
/(б)
Достаточность: /(Л') = 1г(АХ) = ^(Л^^Л1/2) ^ 0.
372
722. Воспользуйтесь результатом и методом решения зада-
задачи 500.
723. В силу задачи 722 К состоит из ядерных операторов со
следом 1. Покажите, что каждый проектор /% на единичный век-
вектор фд// является крайней точкой К. Пусть Р$ = тА\ +A —т)Л2,
где 0 < т < 1 и А \, А2<^ К. Тогда At ^ Р$. Отсюда следует (см.
ГЛ. III), ЧТО |(ЛгфЬ ф2)|2<(Л>ф1, ф2)(/Чф2, ф2)=|(ф1, ^)|2'
* I (ф2, Ф) I2 И, ЗНаЧИТ, А\ = CiP^.
Обратно, пусть А — крайняя точка в К. Оператор А по теоре-
теореме Гильберта представим в виде ^ ck^t> ' гДе ^h ~ некоторая ор-
k k
тонормироваииая система в //. Поскольку А ^> 0 и tr A — 1, имеем
Ck ^ 0 и ^ с^ ~ 1 • Теперь ясно, что А может быть крайней точ-
к
кой, лишь если среди коэффициентов си один равен единице, а ос-
остальные — нулю.
724. Оператор координаты q уже в исходном, координатном
представлении является оператором умножения на q. Его спектр
заполняет всю вещественную прямую. Обобщенные собственные
функции имеют вид b(q — q0).
оо
Преобразование Фурье я|э ->- г|? (к) = ,— I elkqty (q) dq при-
водит оператор импульса р к виду умножения на % /с, а оператор
энергии // = г>^~ к виду умножения па ~^' Это представление
называется импульсным. Спектр р — однократный и заполняет всю
прямую, а спектр // — двукратный и заполгшет положительную по-
полуось. Обобщенные собственные функции имеют вид е ° в ко-
координатном представлении и б (А- — Ао) —в импульсном представ-
представлении.
725. В импульсном представлении исходное состояние имеет
_4/Т Г ак2 \
вид 'фаЬ {к) = у -~- exp I— -~2~ + /6А-г• Учитывая результат за-
задачи 724, получаем:
*/Т \ «A-2 ilk2
%ь (*• 0 = У Т ехр Г Т - -ъГ1 + '
Переходя обратно к координатному представлению, получаем:
Таким образом, плотность вероятности распределения частицы
имеет вид
где Л = а + —2~.
/л а
373
726. Оператор // имеет вид — п— —о и его естественная об-
^пь dx
ласть определения в L2(—а, а) состоит из функций, у которых вто-
вторая обобщенная производная принадлежит L2(—a, а). Чтобы по-
получить самосопряженный оператор, эту область нужно сузить, на-
наложив дополнительные условия i|)(a) = г|э(—а) = 0. (Математиче-
(Математическая интерпретация физического условия непроницаемой оттал-
отталкивающей стенки.) Стационарное уравнение Шредингера прини-
принимает вид
2тЕ
V + Г V = 0, * (а) =я|> (- а)=0.
а
Отсюда г|) (х) = а ехр 1*У2тЕ Л + р еХр (- г 3^^ А что со-
2Л/2тЕ
—i a =0,
гласуемо с граничными условиями, лишь если sin—
т. е. ? = 2~, где л — натуральное число. Соответствующая
$П1п
собственная функция при нечетном п = 2к + 1 имеет вид
) = у^ cos Т (^ + т) ' а при четном n==2k ^2h И =
1 пкх
= —-;= sin .
727. Естественная область определения оператора энергии со-
состоит из функций, имеющих обобщенную вторую производную в
L2(R). Поэтому собственные функции должны иметь непрерывную
первую производную. Вне отрезка [—а, а] они удовлетворяют урав-
уравнению — |- V + (VQ — Е) я|) = 0. Так как i|)e=L2(R), должно
быть VQ~E > 0 ш
{с,е~1х при х > а,
при х <С — а,
щв1=—
Удобно исследовать отдельно четные и нечетные функции. (По-
(Поскольку оператор Н перестановочен с отражением ги —х, вся-
всякая собственная функция г|) представима в виде суммы чет-
я|) (х) + ф (— я)
ной и нечетной собственных функций: i|) {х) = 2 ~Ь
+ 2 • В нашем случае, когда спектр простой, каж-
каждая собственная функция либо четна, либо нечетна.) В четном
случае получаем:
с-е~1^ при | х\ >а,
с1 cos kx при | х \ < а,
374
где к = -г- уЪпЕ. Условия непрерывности \|? и г|/ в точке а дают:
ce~la = c\ cos ka,
cle~la = Ci& sin &a,
откуда к tg ka = I =
Это уравнение легко решается графически и имеет конечное
число решений, зависящее от характеристического параметра х =
= (LJL 2 . В нечетном случае рассмотрение аналогично.
/L
Отметим, что собственные функции ty отличны от нуля (хотя
и быстро убывают) вне потенциальной ямы. Это значит, что с по-
положительной, хотя и малой, вероятностью частица с энергией Е
может выскочить из ямы глубиной Vo > Е.
728. Уравнение Шредингера имеет вид
1 /~ т(д
= х I/ —
ъ 1 / т(д
Заменой аргумента у = х I/ — оно приводится к виду
Далее см. задачу 719. Ответ: Е = %to(n+ 1/2) (п = О, 1, 2, ...).
729. а) Пусть ф1 и ф2 — два линейно независимых решения
уравнения Шредингера. Докажите, что их вронскиан W (х) =*
ф (х) ф (х)
= det , , не зависит от х.
Pi (х) ф2 \х)
Воспользуйтесь тем, что если ф(я)—решение уравнения
Шредингера, то ф(х) —тоже решение.
730. Слодует из результатов задачи 729.
731. Нужно найти решение г|э(д;), имеющее вид eikx + r(k)e~ikx
при х < а и вид t(k)eikx при х > а.
Пусть па отрезке [—a, a] ty(x) = aeilx + ре~Пх, где I2 =*
0
==А: — 2 ¦ ^3 условия непрерывности if и ф7 в точках + а по-
К
лучаем уравнения
e-ika
t(k)e + ika =
kt(k)e+ika =
375
Отсюда
— i (l2 + к2) sin 2la + 21k cos 21a '
Im V' sin 2la
t{k).
kl
732. Ответ:
%2k — 2 Im (c)
%2k 4- 2 Im (с) ' Л + 2 Im (c) '
733. Для операторов координат обобщенные собственные функ-
функции имеют вид ty(z) = 6п(х — хо)\ для операторов импульса и
энергии — вид \|? (х) = eihx. (Здесь бп (х — xQ) = б (д:1 —- xj)...
... б ухп — x^J—/г-мерная б-функция, через кх кратко обозначе-
обозначена величина к{х] + ... + кпхп).
%2 d2
734. а) Оператор Шредппгера имеет вид Н = — ^ —2 и
действует в пространстве периодических функций с периодом 1.
Его собственные функции имеют вид tyn(x) = e2ninxy а соответ-
ствующие уровни Еп =
735. Разделением переменных задача сводится к одномерной.
Ответ: tykim(x, у, z) = ^k{x)^i (y)^m(z), где \|?г — собственные
tykim(, у, ) ^{)^i (y)^(), д |г
функции одномерного осциллятора. Eklm = tool > "" т* 1;
3
собственное значение Е = -т^ %(?>— простое, все прочие кратные.
/ , 3 ^ t (n + !)(» + 2)
Кратность значения (^"''"о") равна 2 •
736. Собственные функции имеют вид
где tfi — собственные функции одномерного осциллятора, ?(и) —
группа перестановок чисел 1, 2, ..., п, %(s) === 1 в случае бозонов
и 5сE) = sgn s в случае фермионов. Мультииндекс (ки ..., А:п) мо-
может быть любым в случае бозонов и состоящим из попарно раз-
различных чисел к{ в случае фермионов. Уровни энергии имеют вид
I iV + -r- ) ©Л, iV e N. Кратность такого уровня равна числу пред-
представлений числа N в виде суммы п любых натуральных (в слу-
случае бозонов) или п различных натуральных (в случае фермионов)
слагаемых.
37G
737. Воспользуйтесь правилом коммутации произведения (ана-
(аналог правила Лейбница для дифференцирования):
[А, ВС] = [Л, В]С + В[А% С].
738. а) Пусть % — собственный вектор оператора Z с собствен-
собственным значением Я. Из соотношений 737 б) следует, что вектор
(Х-?-?У)! либо нулевой, либо собственный для оператора Z с
собственным значением \-f-i. Выведите отсюда, что существует
такой собственный для Z вектор ?0 с собственным значением А,о,
что (X — iY)b,0 — 0. Положим ?ь = {X + iY)k^0 и пусть / — на-
наименьший номер, для которого %>i+\ = 0. Проверьте, что линейная
оболочка векторов |о» • • -, li инвариантна относительно всех трех
операторов X, У, Z и, следовательно, совпадает с V, Значит, I =
= dim V — 1 = 25. Далее, tr Z = tv(XY — YX) = 0. Но Z\h = X%h
?\ 2ь Bя + 1)
и Xfc = h - hi. Поэтому tr Z = 2^ Xk = Bs + 1) XQ ^—; /.
Отсюда Ko = si, Xk= (s — k)i.
б) Пусть 6 — собственное значение оператора Д. Тогда собст-
собственное подпространство, отвечающее этому собственному значе-
значению, инвариантно относительно X, У и Z (в силу 737 а)) и, следо-
следовательно, совпадает с V. Для вычисления б запишите оператор А в
виде А= (X -f iY) (X — iY) -f- Z2 -f iZ и примените его к векто-
вектору So (см. выше указапие к п. а)).
в) Соотношения (*) можно переписать в виде Zr\k = ХьГ|&,
(^ dz iY)*\k — c±(k)r\h±\. Поэтому для любого базиса {щ} вида
rjft — \Xk%k, ^k e С, соотношения (*) выполняются, причел!
Последнее из соотношений 737 б) в применении к вектору щ
дает с+(к — 1)с-(к) — с_(/с + 1)с+(Л) = — 2iXk = 2(s — k). Отсюда
и из равенства с+ Bs) = 0 выводится, что г+ (А:) с_ (к + 1) =
2.S
== ^ 2 (s - /) = (Аг + 1)(А:~2.9). Полагая р,п = (* + 1)!, полу-
чаем с_ (А) = fc, c+(A-) =k — 2s.
739. Функции ж, г/, 2 на 5 подчиняются соотношениям
{х, у} = zR~\ {у, z) = xR~\ {z, x) = yR~\ x2 + у2 + z2 = R\
Поэтому их квантовые аналоги X, У, Z должны удовлетворять со-
соотношениям
ih [X, У] = ZR~\ ih [У, Z] = ХЛ'1, ih [Z, X] = Т'Л-1,
Положим X = НИХ, Y = i%RY, Z = i%RZ. Тогда операторы
X, У, Z будут удовлетворять условиям задачи 737 и, кроме того,
равенству X2 + У2 + Z2 = —h2R2. В силу задачи 738 б) последнее
„2 *2 + *
возможно лишь при R = 2 1 гДе s ~ целое пли полуцелое
К
число.
Рассматривают ^также квантование, при котором жертвуют
условием X2 + У2 + Z2 = Л2, но требуют, чтобы максимальное соб-
377
ственное значение операторов X, F, Z было равно R. В этом слу-
случае для R возможны значения вида s/h, где s — полуцелое число.
Параметр s, однозначно характеризующий систему, называется ее
спином.
740. Первый способ: воспользоваться каноническими соотноше-
соотношениями коммутации координат и импульсов.
Второй способ: использовать координатные выражения
д д
741. Воспользуемся результатами задачи 737, введя операторы
Обозначим через Яг- пространство размерности 2U + 1, в котором
задано каноническое действие операторов X*, F*, Z\. Речь идет о
разложении пространства Н\ 0 Н2 на неприводимые подпростран-
подпространства относительно операторов
X = X: 0 1 + 1 0 Х2, Y = Y{ ® 1 + 1 0 F2, Z = Z: 0 1 + 1 0 Z2.
Пусть 60i •••i52/ и ^о' •"' ^2Z "" канонические базисы в
Hi и #2 соответственно. Тогда {?ь ® v|i} — базис в #i 0 Я2. Опера-
Оператор X— iF действует в этом базисе по формуле
(X — iY)lh ® r\i = Пк-1 ® Ц1 + Ilk ® Цг-и
Найдем ядро этого оператора. Для этого заметим, что если отож-
отождествить #i и #2 с пространствами многочленов от и и и соответ-
соответственно по формулам lh -<-> uk, r\i *->• у', то оператор X—iF пе-
перейдет в д/ди + d/ду (проверьте!). Поэтому ядро X—iF состоит
из многочленов от и — и.
Действие оператора Z в этой реализации сводится к
i [ 1± + 12~иди ~~~ v~dv )' Поэтому (и — v)h является собственным
вектором для Z с собственным значением i(^i -f- 52 — к). Число к
может меняться от 0 до minBZi, 2h). Каждый вектор (и — v)h по-
порождает неприводимое подпространство размерности 21\ + 2/2 —
— 2к + 1. Отсюда вытекает, что возможными значениями полного
момента объединенной системы являются числа
742. В решении предыдущей задачи нужно предположить, что
li = h, и на многочлены от и и v наложить дополнительно усло-
условие симметричности (для бозонов) или антисимметричности (для
фермионов). Это сводится к требованию четности или нечетно-
нечетности к. Ответ: для бозонов возможные значения момента 21 Л,
2{l — i)%, ..., 0; для фермионов {21 — 1I, B1 — 3)%, ..., К.
378
Функциональный анализ — часть
современного математического ана-
анализа, основной целью которой явля-
является изучение функций у = f(x), где
по крайней мере одна из перемен-
переменных х, у меняется по бесконечному
пространству.
Математическая энциклопедия, т. 5.
ПОСЛЕСЛОВИЕ
Дать точное определение функционального анализа
так же трудно (если вообще возможно), как и опреде-
определение всей математики. Таким образом, наиболее на-
надежный способ объяснить, что такое функциональный
анализ, состоит в том, чтобы познакомить читателя с
краткой историей его возникновения и развития.
Как и многие другие математические теории, функ-
функциональный анализ возник из конкретных задач и попы-
попыток обобщить их решения. Рождение функционального
анализа часто связывают с выходом в свет книги львов-
ского математика Стефана Банаха «Теория линейных
операций» (Варшава, 1932), а точнее, ее француз-
французского перевода иод названием «Курс функционального
анализа» A933). В этой книге содержалось системати-
систематическое изложение того, что сейчас называют линейным
функциональным анализом, т. е. теории линейных топо-
топологических пространств и линейных операторов в этих
пространствах.
Этому событию предшествовала почти столетняя ис-
история развития методов решения бесконечных систем
линейных уравнений. В 1836 г. были опубликованы ра-
работы Ш. Штурма и Ж. Лиувилля по теории колебаний
струны, описываемой обыкновенным дифференциальным
уравнением второго порядка с определенными граничными
условиями (задачи Штурма — Лиувилля). В течение 70
последующих лет многие выдающиеся математики зани-
занимались этой задачей. В частности, для ее решения были
изобретены методы ортогонализации Грама — Шмидта и
теория операторов и детерминантов Фредгольма. В 1906 г.
Д. Гильберт завершил значительную часть этой темы,
построив общую теорию самосопряженных вполне непре-
непрерывных операторов в пространстве, которое с тех пор
называется гильбертовым.
Еще более длинную историю имеет теория приближе-
приближения функций. Приближенные вычисления встречались в
379
математике со времен ее возникновения. Метод Ньютона
вычисления корней уравнения и метод наименьших квад-
квадратов К. Ф. Гаусса были первыми попытками внести
систему в такие вычисления.
Развитие метода Ньютона привело к появлению нели-
нелинейного функционального анализа, о котором речь пойдет
ниже. Метод Гаусса, по существу, сводится к ортого-
ортогональному проектированию на подпространство в евкли-
евклидовом пространстве. Он без труда переносится на беско-
бесконечномерное гильбертово пространство и до сих пор
играет основную роль в различных приложениях.
Теория наилучшего приближения в пространствах с
другой нормой существенно сложнее. Для равномерной
нормы такая теория была основана П. Л. Чебышевым в
середине прошлого века и развита его учениками Е.И.Зо-
Е.И.Золотаревым, А. Н. Коркиным и А. А. Марковым (стар-
(старшим). В 1885 г. итальянский математик В. Вольтерра
ввел понятие функционала как «функции от линии», а в
1906 г. французский математик М. Фреше определил об-
общее понятие метрического пространства в работе, оза-
озаглавленной «О некоторых вопросах функционального ис-
исчисления».
Таким образом, появление книги Банаха явилось ско-
скорее завершением целого этапа «утробного развития»
функционального анализа, чем началом этого направ-
направления. Основные определения книги Банаха, такие как
нормированное пространство, линейный функционал и
оператор, фундаментальные последовательности, полнота,
оказались очень удобными и вскоре были приняты по-
повсеместно.
Теория банаховых пространств и линейных операто-
операторов в них до сих пор привлекает внимание многих ис-
исследователей. Например, только недавно были решены
некоторые известные задачи, поставленные Банахом.
Отметим здесь отрицательное решение проблемы базиса
и проблемы аппроксимации, данные П. Энфло, а также
опровержение гипотезы о структуре множества сумм ус-
условно сходящегося ряда, полученное Е. М. Никишиным.
Большую роль в геометрической теории банаховых
пространств играет понятие выпуклого множества. Систе-
Систематическое исследование этого понятия сейчас состав-
составляет самостоятельное направление — выпуклый анализ,
имеющий важные приложения к вычислительной матема-
математике, линейному программированию, геофизике и другим
прикладным областям. В развитии этого направления
380
большой вклад принадлежит Л.В.Канторовичу, А. Н.Кол-
Н.Колмогорову и М. Г. Крейну.
Большое место в приложениях занимает теория гиль-
гильбертовых пространств и операторов в этих пространст-
пространствах. Достаточно отметить, что спектральная теория само-
самосопряженных операторов является языком квантовой
механики. Спектральная теория общих (в том числе и
неограниченных) самосопряженных операторов была
построена Дж. фон Нейманом и М. Стоуном в 1930 г.
Их результаты были сразу использованы в квантовой
теории.
Потребности математической физики постоянно сти-
стимулировали развитие спектральной теории. В частности,
под влиянием статистической физики в последние годы
были получены замечательные результаты в так назы-
называемой спектральной геометрии. Истоки этого направле-
направления лежат в известной работе Г. Вейля 1911 г. об асимп-
асимптотике собственных значений оператора Лапласа, задан-
заданного в плоской области. Физический смысл этой задачи
через 50 лет образно сформулирогал американский мате-
математик М. Кац, назвавший свой обзор по спектральной
геометрии так: «Можно ли услышать форму барабана?»
(дело в том, что уравнение Лапласа описывает колеба-
колебания мембраны, а собственные числа оператора Лапласа
соответствуют частоте звуковых воли, порождаемых эти-
этими колебаниями).
Изучение спектра дифференциальных операторов,
действующих в пространствах функций (пли векторных
полей, дифференциальных форм и других геометрических
объектов) на гладких многообразиях — одна из проблем
современного функционального анализа, решенная с при-
привлечением средств современной топологии. Прекрасным
достижением в этой области является полученное
М. Атьсй и И. Зингером в 1968 г. решение задачи
И. М. Гельфанда о вычислении индекса эллиптического
оператора, действующего в сечениях векторного рассло-
расслоения на многообразии. Формула Атьи — Зингера, связы-
связывающая анализ с геометрией и топологией, оказала боль-
большое влияние на развитие всех трех областей. Применя-
Применяется она и в современной математической физике: оказа-
оказалось, что именно на этом языке строится математическая
модель квантовой теории поля.
Еще одно направление функционального анализа по-
получило почти повсеместное приложение. Это — теория
обобщенных функций. Понятие обобщенной производной
381
было введено в математику С. Л. Соболевым в 1936 г.
Примерно в то же время П. Дирак ввел понятие дельта-
функции и ее производной, отражающее физическое
представление о точечном заряде и диполе. В 1950 г.
вышла монография Л. Шварца, в которой давалось си-
систематическое изложение теории обобщенных функций
(распределений) как линейных функционалов на тех или
иных пространствах «пробных функций». Эта книга
сыграла роль, подобную книге Банаха: обобщенные функ-
функции стали рабочим аппаратом. С 1958 г. И. М. Гель-
фанд, М. И. Граев, Г. Е. Шилов публикуют серию вы-
выпусков книг «Обобщенные функции», в которых система-
систематически излагаются теория обобщенных функций и ее
приложения к дифференциальным уравнениям, интег-
интегральной геометрии, теории представлений и современной
теории чисел. Сейчас обобщенные функции входят в обя-
обязательную программу университетского курса для мате-
математиков и физиков, хотя всего полвека назад они вос-
воспринимались с таким же недоверием, как комплексные
числа в эпоху Возрождения.
К предмету функционального анализа часто относят
такие классические разделы теории функций, как теорию
меры и интеграла Лебега. Эта теория была построена
Т. Стилтьесом и А. Лебегом, развивавшим идеи Э. Бо-
реля, и затем была дополнена результатами Дж. Фуби-
ни, Дж. Радона и О. Никодима. В окончательной форме
она была изложена в 1918 г. в монографии К. Каратео-
дори. Позже к этой теории были сделаны два сущест-
существенных с точки зрения функционального анализа добав-
добавления: теория интегрирования вектор-функций (сильный
интеграл Бохнера и слабый интеграл Гельфанда — Пет-
тиса), а также теория интегрирования в бесконечномер-
бесконечномерных пространствах. Последняя теория, по существу, была
начата уже в работах А. Эйнштейна и М. Смолуховского
по теории броуновского движения. В 1923 г. Н. Винер
показал, что средние в смысле Эйнштейна — Смолухов-
Смолуховского совпадают с интегралами по некоторой мере в
пространстве непрерывных функций. Эта мера получила
название меры Винера, а математическая модель броунов-
броуновского движения, построенная с помощью этой меры,—
винеровского процесса. В 1942 г. американский физик
Р. Фейнман ввел понятие интеграла по траекториям,
который сейчас называют интегралом Фейнмана. В от-
отличие от винеровского интеграла, он не является интег-
интегралом по «мере Фейнмана» (которую можно определить
382
аналогично мере Винера на цилиндрических множествах,
умножая показатель в экспоненте на мнимую единицу;
однако эта мера не будет счетно-аддитивной). Строгой
математической теории интеграла Фейнмана до сих пор
не существует несмотря на все усилия математиков и
физиков построить такую теорию.
В 1941 г. И. М. Гельфанд опубликовал статью «Нор-
«Нормированные кольца», с которой началось развитие тео-
теории банаховых алгебр — одного из ключевых направле-.
ний функционального анализа. Коммутативные банаховы
алгебры естественно появляются в теории функций,
в спектральной теории самосопряженных операторов,
в теории рядов и интегралов Фурье. Понятие максималь-
максимального идеала и связанное с ним «преобразование Гель-
фанда» лежит в основе всей этой теории. Среди неком-
некоммутативных банаховых алгебр выделяется класс так на-
называемых С*-алгебр (это алгебры с инволюцией * обла-
обладающей свойством \\аа*\ I = Mall2). И. М. Гельфанд и
М. А. Наймарн доказали, что Сх-алгебры, и только они,
допускают реализацию в виде сильно замкнутых алгебр
ограниченных операторов в гильбертовом пространстве с
обычной нормой и инволюцией (переход к сопряженному
оператору).
Примерно в это же время появляется серия работ
Дж. фон Неймана и Ф. Меррея по теории слабо замк-
замкнутых симметричных алгебр операторов в гильбертовом
пространстве. Эти алгебры получили впоследствии назва-
название алгебр Неймана. Среди них выделяются так назы-
называемые факторы, т. е. алгебры Неймана, центр которых
состоит только из скалярных операторов. Примером фак-
фактора является алгебра всех ограниченных операторов —
бесконечномерный аналог алгебры матриц. Были обна-
обнаружены и другие примеры факторов, не изоморфные при-
приведенному. Долгое время теория факторов не находила
применений. (Первоначальная идея Неймана состояла в
том, чтобы с помощью теории факторов решить пятую
проблему Гильберта об эквивалентности различных опре-
определений группы Ли; однако эта проблема решена другим
способом.) Лишь недавно обнаружилось, что факторы
естественно возникают в аксиоматической теории кван-
квантового поля. Это резко повысило интерес к ним и при-
привело к значительному прогрессу в их исследовании.
В работах А. Конна получена почти полная класси-
классификация факторов и намечена большая программа их
применения в геометрии и теории динамических систем.
383
Яркие результаты в теории факторов педавпо полу-
получены молодым американским математиком Ф. Джонсом,
обнаружившим, в частности, связь этой теории со старой
топологической проблемой классификации узлов в трех-
трехмерном пространстве.
Большое место в современном функциональном ана-
анализе занимает некоммутативный гармонический анализ,
основой которого является теория представлений групп.
Целью гармонического анализа является исследование
различных математических объектов (функциональных
пространств, операторов, уравнений), обладающих той или
иной симметрией. Как правило, эту симметрию можно
выразить в терминах действия на рассматриваемый
объект некоторой группы преобразований. Простейшие
объекты — линейные пространства, простейшие преоб-
преобразования — линейные операторы; поэтому на первый
плац выступает задача исследования линейных представ-
представлений групп, т. е. их реализаций линейными опера-
операторами.
Теория конечномерных представлений конечных групп
является, по существу, ветвью алгебры. В то же время
теория бесконечномерных представлений топологических
групп естественно относится к функциональному анализу.
Фундаментальные результаты в этой теории были полу-
получены советскими математиками.
Наконец, обширную область исследований состав-
составляет так называемый нелинейный функциональный ана-
анализ. Многие результаты в этой области являются беско-
бесконечномерными аналогами теорем обычного анализа. Та-
Таковы, например, многочисленные теоремы о неявных
функциях, о неподвижных точках, об экстремумах нели-
нелинейных функционалов и бифуркациях нелинейных опера-
операторов. Среди многочисленных направлений исследований
отметим здесь теорию особенностей гладких отображений,
в которой ряд сильных результатов получен В. И. Ар-
Арнольдом.
Все вышесказанное, разумеется, не исчерпывает пред-
предмета функционального анализа. Чтобы убедиться в этом,
читателю достаточно просмотреть оглавления нескольких
выпусков журнала «Функциональный анализ и его при-
приложения», выходящего уже свыше 20 лет.
Возможно, это наилучший способ ответа на вопрос
о том, что же такое современный функциональный
анализ.
Кириллов
384
ОСНОВНАЯ ЛИТЕРАТУРА
1. А х и е з е р Н. И., Глазмап И. М. Теория линейных опера-
операторов в гильбертовом пространстве.— М.: Наука, 1966.
2. Б е р е з и н Ф. А., Г в и ш и а н и А. Д., Г о р и н Е. А., Кирил-
Кириллов А. А. Сборник задач по функциональному анализу.— М.:
Изд-во МГУ, 1977.
3. В у р б а к и Н. Интегрирование. Меры, интегрирование мер.—
М.: Наука, 1967.
4. Б у р б а к и И. Интегрирование. Меры на локально компакт-
компактных пространствах. Меры на отделимых пространствах.— М.:
Наука, 1977.
5. Б у р б а к и Н. Спектральная теория.— М.: Мир, 1972.
6. Бурбаки Н. Теория множеств.—М.: Мир, 1965.
7. Б у р б а к и Н. Топологические векторные пространства.— М.:
ИЛ, 1959.
8. Владимиров В. С. Обобщенные функции в математической
физике.— М.: Наука, 1976.
9. Владимиров В. С, Михайлов В. П., В а ш а р и н А. А.,
Каримова X. X., Сидоров Ю. В., Шабуниц М. И.
Сборник задач по уравнениям матехматической физики.— М.:
Наука, 1974.
10. Г е л ь ф а н д И. М., Шилов Г. Е. Обобщенные функции.
Вып. 1. Обобщенные функции п действия над ними.— М.: Физ-
матгиз, 1959.
11. Гельфанд И. М., Шилов Г. Е. Обобщенные функции.
Вып. 2. Пространства основных и обобщенных функций.— М.:
Физматгиз, 1958.
12. Г е л ь ф а н д И. М., Шилов Г. Е. Обобщенные функции.
Вып. 3. Некоторые вопросы теории дифференциальных урав-
уравнений.— М.: Фпзматгиз, 1958.
13. Ге л ь ф а н д И. М., Виленкин II. Я. Обобщенные функции.
Вып. 4. Некоторые применения гармонического анализа. Осна-
Оснащенные гильбертовы пространства.— М.: Физматгиз, 1961.
14. Д а н ф о р д Н., Шварц Дж. Линейные операторы: Общая
теория.- М.: ИЛ, 1962.
15. Д а н ф о р д II., Шварц Дж. Линейные операторы: Спект-
Спектральная теория.— М.: Мир, 1966.
16. И оси да К. Функциональный анализ.—М.: Мир, 1967.
17. Канторович Л. В., А к и л о в Г. П. Функциональный ана-
анализ.— 2-е изд.— М.: Наука, 1977.
18. К и р и л л о в А. А. Элементы теории представлений.— М.: На-
Наука, 1972; второе издание— 1978.
19. Колмогоров А. П., Фомин С. В. Элементы теории функ-
функций и функционального анализа.— М.: Наука, 1977.
25 а. А. Кириллов, А. Д. Гвишиани 385
20. Кудрявцев Л. Д. Математический апализ. Т. 1, 2.— М.: На-
Наука, 1970.
21. Морен К. Методы гильбертова пространства.—М.: Мир, 1965.
22. Наймарк М. А. Линейные дифференциальные операторы.—
2-е изд.— М.: Наука, 1969.
23. П о н т р я г и н Л. С. Непрерывные группы.— 3-е изд.-— М.: На-
Наука, 1977.
24. Р и д М., Саймон Б. Методы современной математической
физики, вып. 1. Функциональный анализ.— М.: Мир, 1977.
25. Рид М., Саймон Б. Методы современной математической
физики, вып. 2. Гармонический анализ. Самосопряженность.—
М.: Мир, 1978.
26. Р и с с Ф., Надь Б. С. Лекции по функциональному анали-
анализу.— М.: ИЛ, 1954.
27. Р у д и н У. Осповы математического анализа.— 2-е изд.— М.:
Мир, 1976.
28. Рудин У. Функциональный анализ.—М.: Мир, 1975.
29. Халмош П. Теория меры.—М.:. ИЛ, 1953.
30. X ь ю и т т Э., Росс К. Абстрактный гармонический анализ.
Т. 1.— М.: Наука, 1975.
31. X ь ю и т т Э., Росс К. Абстрактный гармонический анализ.
Т. 2.- М.: Мир, 1975.
32. Ш и л о в Г. Е. Математический анализ: Второй специальный
курс— М.: Физматгиз, 1965.
33. Эдварде Р. Функциональный анализ.— М.: Мир, 1967.
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
1*. Александров П. С. Введение в теорию множеств и функ-
функций.— М.: Гостехиздат, 1948.
2*. Б а н а х С. Курс функционального анал!зу.— Кшв: Радяньска
школа, 1948.
3*. Б у р б а к и Н. Общая топология: Основные структуры.— М.:
Наука, 1968.
4*. Б у р б а к и Н. Общая топология: Использование веществен-
вещественных чисел в общей топологии. Функциональные пространства.
Сводка результатов.— М.: Наука, 1975.
5*. Винер Н. Интеграл Фурье и некоторые его приложения.—
М.: Физматгиз, 1963.
6*. Винер Н. Нелинейные задачи в теории случайных про-
процессов.—М.: ИЛ, 1961.
7*. Винер Н., Пэли Р. Преобразование Фурье в комплексной
области.— М.: Наука, 1964.
8*. Г в и ш и а н и А. Д., Г у р в и ч В. А. Динамические задачи
распознавания образов. 1. Условия стабильности для прогно-
прогноза мест сильных землетрясений / Математическое моделиро-
моделирование интерпретации геофизических данных. Вычислительная
сейсмология. Вып. 16.—М.: Наука, 1984.—С. 70—88.
9*. Д э й М. Линейные нормированные пространства.— М.: ИЛ,
1961.
10*. Дьедонне Ж. Основы современного анализа.— М.: Мир,
1964.
И*. Келли Дж. П. Общая топология.—М.: Наука, 1968.
12*. Лебег А. Интегрирование и отыскание примитивных функ-
функций.— М.; Л.: ГТТИ, 1934.
13*. Л ю м и с Л. Введение в абстрактный гармонический анализ.—
М.: ИЛ, 1956.
14*. М а с л о в В. П. Операторные методы.— М.: Наука, 1973.
15*. М их ли н С. Г. Лекции по интегральным уравнениям.— М.:
Физматгиз, 1959.
16*. П и ч А. Ядерные локально-выпуклые пространства.—М.: Мир,
1967.
17*. Плеснер А. И. Спектральная теория линейных операто-
операторов.— М.: Наука, 1965.
18*. Робертсон А., Робертсон В. Топологические вектор-
векторные пространства.— М.: Мир, 1967.
19*. Треногий В. А., Писаревский Б. М., Соболева Т. С.
Задачи и упражнения по функциональному анализу,— М.: На-
Наука, 1984.
10*. Френкель А., Бар-Хпллел И. Основания теории мно-
множеств,— М.: Мир, 1966.
!5* 387
21*. X а л м о ш П. Конечномерные векторные пространства.— М.:
Физматгиз, 1963.
22*. Шилов Г. Е., Фан Дик Т и н ь. Интеграл, мера и произ-
производная на линейных пространствах.— М.: Наука, 1967.
23*. Эдварде Р. Теория рядов Фурье.—М.: Мир, 1979.
Распределение литературы но главам
Глава I. [2, 6, 16, 18, 19, 23, 1*, 3*, 8*, 11*, 19*, 20*].
Глава II. [2, 3, 4, 19, 27, 29, 12*, 22*1.
Глава III. [1, 2, 7, 8, 9, 10, 11, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22,
23, 24, 26, 28, 32, 33, 2*, 4*, 8*, 13*, 14*, 15*, 16*, 18*].
Глава IV. [2, 8, 9, 16, 19, 23, 25, 28, 30, 31, 5*, 7*, 23*].
Глава V. [5, 12, 15, 16, 17, 28, 17*].
СПИСОК ОБОЗНАЧЕНИЙ
С — множество комплексных чисел
N — множество натуральных чисел
Q — множество рациональных чисел
R — множество вещественных чисел
Z — множество целых чисел
Qp — множество /?-адических чисел
Zp — множество целых /?-адических чисел
Далее три цифры, следующие за символом, означают соответ-
соответственно номер главы, параграфа и пункта части «Теория», в кото-
котором объясняется смысл этого символа
Пространства
A2(D) C.5.1) — пространство функций, аналитических в
круге D
В(Х) C.4.2) — пространство функций, ограниченных на мно-
множестве X
С(Х) C.1.1) — пространство непрерывных функций на мно-
множестве X
Cr(Q) C.4.3) — пространство г раз непрерывно дифференци-
дифференцируемых функций в Q
?D (Q) = С^° (Q) C.4.3) — пространство фипитных бесконечпо
дифференцируемых функций па Q
2D'(п) C.4.4) —пространство обобщенных функций
g (Q) = C°°(Q) C.4.3) — пространство бесконечно дифферен-
дифференцируемых функций
&'(Q) C.4.4) — пространство обобщенных функций с компакт-
компактным носителем
EndL = 2(U L)
@~(L\, L2) C.3.3) — пространство фредгольмовых операторов,
отображающих ЛТП L\ в ЛТП L2
II* C.5.2) — пространство, эрмитово сопряженное к гильбер-
гильбертову пространству //
Н\ Ф //2 C.5.1) —прямая сумма линейных пространств
II\ ® Но C.1.4) — тензорное произведение линейных прост-
пространств
Ж(Lb L2) C.3.2) — пространство компактпых операторов, ото-
отображающих ЛТП L\ в ЛТП L<i
3?{L\, L2) C.2.2) —пространство линейных непрерывных ото-
отображений из ЛТП L\ в ЛТП L2
V C.1.2) — пространство, сопряженное к ЛТП L
389
LP(X, |л) C.4.1) —пространство вещественнозначных функций
на множестве X с мерой [л, р-я степень которых ^-суммируема
Loo(X, [i) C.4.1) — пространство существенно ограниченных
функций на X
1Р(п, К) C.1.1) — /г-мерное пространство над полем К с нор-
нормой || а; || р
1Р(К) C.1.1) —пространство последовательностей над полем К
с нормой \\x\\p
(Qn, ра) A.2) — метрическое пространство Хеммипга
^[а, Ь] C.1.1) —пространство многочленов от одного перемен-
переменного с нормой max | <p (t) \
t^[a,b]
Р(Н) E.3)—фазовое пространство квантовомеханической
системы
Р(Ъ) D.2.2) — пространство медленна: растущих последова-
последовательностей
Р&(Rn) D.1.2) — подпространство в <^(Rln)), состоящее из
функций, растущих не быстрее многочлена
?(Rn) C.4.3)—пространство гладких быстро убывающих
функций
S'(Rn) C.4.4) —пространство медленно растущих обобщенных
функций
V[a, b] B.1.3) — пространство функции ограниченной вариа-
вариации на отрезке [а, Ь]
Сходимости
Ап => Л, А = u-lim Лп C.3.1) — равномерная сходимость ли-
линейных операторов
Ап-+А, ^ = s-lim^n C.3.1) — сильная сходимость опера-
операторов
Ап-^А, Л=лу-НтЛп C.3.1)—слабая сходимость опе-
операторов
/n zj / B.2.2) — равномерная сходимость функций
B.2.2) — сходимость функций почти всюду
fn-> f B.2.2) — сходимость функций по мере jx
Операторы
А' C.1.2) —оператор, сопряженный к оператору А
А* C.5.2) — оператор, эрмитово сопряженный к оператору А
Л_>0 C.5.2) —положительный оператор А
А E.1.3) —замыкание оператора А
А\ Ф А2 C.3.3) — прямая сумма операторов А\ и А2
В id A E.1.4) — оператор В есть расширение оператора А
сокегЛ C.3.3) —коядро оператора А
DA C.3.3) — область определения оператора А
д C.4.3) — оператор взятия частной производной
\{А) C.3.3) —индекс оператора А
imA C.3.3) —образ оператора А
кегЛ C.3.3) —ядро оператора А
M(f) C.4.5) — оператор умпожепия па функцию /
г(А) E.1.2) —спектральный радиус оператора А
390
т\(А) E.1.1) —резольвента оператора А
rang Л C.3.3) —ранг оператора А
S(f) D.1.1) —оператор свертки с функцией /
Т(а) D.1.1) — оператор сдвига на а
р(А) E.1.2) — резольвентное множество оператора А
а {А) E.1.2) —спектр оператора А
Другие обозначения
А А В B.1.1) —симметрическая разность множеств А и В
Л| |5 (или JJ A^j B.1.1)—дизъюнктное объединение
множеств;
о
В(х, г)(В(х, г)) C.2.1) —открытый (соотв. замкпутый) шар в
метрическом пространстве радиуса г с центром в точке х
Card Y B.1.3) —число элементов множества Y
Cont(/Ti, K2), Cow(Ku K2) A.3) —категория контравариаптных
(соотв., ковариантных) функторов из категории К\ в категорию К2
diam X C.3.2) — диаметр множества X
ess sup/ B.3.1) — существенная верхняя грань функции /
/ D.2.1) —преобразование Фурье функции /
/i X /2 C.4.5) — прямое произведение обобщенных функций
/i и /2
/i * /2 D.1.1) — свертка функций /i и /2
Ъ D.2.1) —группа, двойственная к группе G
K[G] D.1.1) —групповая алгебра группы G
К° A.3) —категория, дуальная к категории К
L(S, \i) B.1.2) —совокупность множеств, измеримых по мере \х
Мог (Л, В), Ob (К) A.3) — морфизмы и объекты категории К
Р(Х) B.1.1) —множество подмножеств X
Qa(X) C.5.2)—эрмитова (квадратичная) форма, соответству-
соответствующая оператору А
R(S) B.1.1) — кольцо, порожденное семейством множеств S
Ra(S) B.1.1) — а-кольцо, порожденное семейством множеств S
supp ф C.4.3) — носитель функции ф
Тп D.1.1) — гс-мерный тор
Var^/ B.1.3) —вариация функции / на отрезке [а, Ь]
X1- C.3.3) — ортогональное дополнение к X
хЛ. у C.5.1) —вектор х ортогонален вектору у
б(х) C.4.4) —функция Дирака (дельта-функция)
бь(х) C.4.5) —сдвинутая дельта-функция
6а C.3.3) — символ Кронекера
\i(A) B.1.2) —мера множества А
\i*(A) B.1.2) —верхняя мера множества А
v(A) B.1.2) —заряд
|v|D) B.1.2) — вариация заряда v
qT(x) D.1.2)-фМ =ср(-х)
%А B.1.1) —характеристическая функция множества А
Н E.3) — постоянная Планка
391
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Абсолютная непрерывность ин-
интеграла Лебега 50
Аксиома выбора (Цермело) 11
Алгебра множеств 24
— примариая 272
Альтернатива Фредгольма 92
Амплитуда рассеяния 285
Аннулятор множества 333
Антиизоморфизм 123
Антилинейность 123
Аппроксимативная размерность
79
Арифметическая сумма мно-
множеств 132
Атом 337
База топологии 65
Базис Гамеля 321
— гильбертов 121
Бозон 186
Борелевские подмножества 25
Быстро сходящаяся подпоследо-
подпоследовательность 42
Вакуумный вектор 266
Вариация заряда 30
— функции 32
Внутренняя мера 201
Выпуклая оболочка 63, 227
Выпуклое тело 228
Гармонический осциллятор 285
Гильбертова размерность 121
Гиперплоскость 71
— опорная 221
Гомотопическая эквивалент-
эквивалентность 329
Грань размерности к 193
График оператора 163
Групповая алгебра 129
Двойственная группа 138, 141
Двойственные выпуклые тела
228
392
Действительная часть операто-
оператора Й52
Дефектное подпространство 168
Дизъюнктное объединение 24
Динамическая задача распозна-
распознавания 16
Дифференцирование обобщен-
обобщенной функции 112
Длина слова 295
Естественная область определе-
определения оператора 164
Жорданова клетка 271
Замена переменной для обоб-
обобщенной функции 112
Замыкание оператора 163
Заряд 30
— абсолютно непрерывный 54
Заряды эквивалентные 54
Идемпотент 272
Измеримая вектор-функция 207
Измеримость по Каратеодори
203
Изоморфные объекты категории
19
Импульсное представление 373
Ипдекс оператора 85
Индикатриса Банаха 216
Индуктивный предел 197
Интеграл Лебега 43
от простой функции 39
— Лебега — Стилтьеса 45
— по проекционной мере 176
— Римана по проекционной ме-
мере 280
—- Римана — Стилтьеса 44
— Фурье 144
Интегральная сумма Лебега 176,
210, 211
Римана для проекционной
меры 280
Римана — Стилтьеса 44
Интегральное неравенство Мин-
ковского 238
— уравнение Фредгольма с вы-
вырожденным ядром 237
Канторова лестница 216
Картина Гейзенберга 372
Категории групп с отмеченны-
отмеченными образующими 194
— эквивалентные 22
Категория 18
— дуальная 22
Квадрат полного момента 287
Квадратичная форма 125
Квантовая теория рассеяния
285
Класс эквивалентности 10
Кодировка 16
Колебание функции в точке 45
на отрезке 45
Кольцо подмножеств 23
—, порожденное полукольцом 24
Коммутативная диаграмма 20
Композиция отношений 9
Конгруэнтные пары подпрост-
подпространств 253
Коразмерность 71
Коэффициенты Фурье 142
Коядро оператора 84
Крайняя (экстремальная) точка
80
Критерий Вейля 282
— Дарбу 47
— фредгольмовости 89
— Хаусдорфа 198
Кросс-норма 62
— равномерная 63
Куб гс-мерный 230
Лексикографический
188
Лемма Фату 49
- Цорна 12, 190
порядок
Мажоранта 10
Матрица дважды стохастиче-
стохастическая 233
— перехода 285
Медленно растущая двусторон-
двусторонняя последовательность 144
Мера 25, 30
— Винера 36
— внешняя 27
— квазиинвариантная относи-
относительно сдвига 48
— Лебега 32
— счетно-аддитивная 25
Меры дизъюнктные 31
Метрика 12
Минимальное кольцо 199
Миноранта 10
Мнимая часть оператора 252
Многочлены Лагерра 346
— Лежандра 346
— Чебышева 346
Множества, строго разделенные
гиперплоскостью 229
— эквивалентные 189
Множество борелевское 201
— вполне упорядоченное 189
— выпуклое 63
— замкнутое 13
— измеримое 27, 28, 30
— канторово совершенное 232
— лебеговское 36
— направленное 10
— ограниченное 68, 100
— открытое 13
— отрицательное 304
— поглощающее 63
— положительное 304
— резольвентное 156
— а-однозначности меры 203
— уравновешенное 63
— целых р-адических чисел 192
— цилиндрическое 34
Модуль непрерывности функ-
функции 370
Морфизм категории 18
единичный 19
— функторный 22
Направленность (сеть) 10
Неопределенность наблюдаемой
182
Непрерывность меры 202
Непрерывный базис 256
Неравенство Бесселя 119
— Гельдера 93, 220, 320
— Коши — Буняковского 116
— Минковского 220, 93
Норма 56, 64, 116
— в пространстве гладких
функций 97
— оператора 61
— р-адическая 191
393
Носитель обобщенной функции
109
— функции 98
Обобщенный (неунитарный) ха-
характер 262
Образ оператора 84
Обратное преобразование Фурье
145
Объект категории 18
— универсальный отталкиваю-
отталкивающий 19
Одномерные квантовые системы
284
Однопараметрическая группа
178
Оператор в гильбертовом прост-
пространстве 122
— Вольтерра 274
— Гильберта — Шмидта 236
— дробного интегрирования
(дифференцирования) 261
— замкнутый 163
— компактный (вполне непре-
непрерывный) 81
— конечного ранга 82
— Лапласа 270
— линейный ограниченный (не-
(непрерывный) 61, 73
— нормальный 123
— ортогонального отражения
252
— положительный 123, 274
— регулярный 271
— рождения (уничтожения)
236, 266
— самосопряженный (эрмитов)
123, 163
— симметрический 164
— сопряженный 60
— с простым спектром 171
— существенно самосопряжен-
самосопряженный 164
— унитарный 123
— фредгольмов 85
— частично изометрический 255
— чисел заполнения 267
— Штурма — Лиувилля 169
— эрмитово сопряженный 123
— ядерный 256
Ортогонализация 121, 122
Ортогональное дополнение 117
Ортогональность векторов 117
Ортонормированная система
векторов 119
Ортопроектор 123
Отношение 9
— порядка 10
— частичного порядка 10
— эквивалентности 9
Отображение в гиперплоскости
/ = 0 параллельно вектору
321
— ограниченное 243
— секвенциально непрерывное
243
Отрезок в линейном пространст-
пространстве 63
Подмножество изометричное 14
— крайнее 232
Подобные матрицы 271
Подпространство дополняемое
224
Поле /?-адических чисел 191
Полином Зрмита 333
Полная ортонормированная сис-
система векторов 120
— Я-выборка 294
Положительный функционал 241
Полукольцо 24
Полуиеирерывность меры свер-
сверху (снизу) 202
Полунорма 64, 116
Полуточная последовательность
операторов 85
Полярное разложение оператора
255
Пополнение 14
Порядок обобщенной функции
110, 111
Последовательность б-образная
258
— положительно определенная
265
Постоянная Планка 182
Потенциальный барьер 285
Правила квантования 184
Представление алгебры 281
Преобразование Кэли 166
— Фурье 141, 150
— — обобщенной функции 144
— эргоднческое 266
Принцип двойственности
Л. С. Понтряпша 140
— неопределенности Гейзенбер-
га 182
— промежуточности 254
— сжимающих отображений 13
Прогноз 16
Проективный предел 197
Проекционная мера 175
394
Произведение кручения 196
— функции и обобщенной функ-
функции 112
Пространство банахово 57
— бесконечно дифференцируе-
дифференцируемых функций 97
— — — быстро убывающих
функций 100
— финитных функций 93
— интегрируемых функций 93
— когомологий 85
— линейное метрическое 56
— — топологическое 65
— линейных операторов 61
— метрическое 12
— непрерывных функций 94
— нормированное 56
— отделимое (хаусдорфово) 67
— полинормированное 66
— полное 14
— почти периодических непре-
непрерывных функций 250
— предгильбертово 115
— рефлексивное 68
— сопряженное 59, 68
— суммируемых функций 40
— топологическое локально
компактное 129
— фазовое 180
— функций с ограниченной ва-
вариацией 95
— Хемминга 16
Процесс ортогонализации 121,
122
Прямая Александрова 184
— — подпространств 118, 119
Прямое произведение обобщен-
обобщенных функций 114
Равенство Парсеваля 120
Разбиение единицы 243
Рассеяние на полупроницаемой
перегородке 286
Расстояние 12
Раствор подпространств 254
Расширение оператора 163
Резольвента 154
Рефлексивность 9
Ряд Фурье 143
Свертка 128, 130, 133
— функций на группе 219
Свободная абелева группа 194
— алгебра Ли 194
— группа 194
— частица 284
Свойство Гейне — Бореля 100
Сигнатура матрицы 363
Сигнум /?-адический 192
Симметричность 9
Скалярное произведение 115
Слабый интеграл 231
След оператора 256
Слово 295
Смешанная площадь пары мно-
множеств 326
Смешанный объем набора из п-
выпуклых множеств 326
Сопряженные числа 219
Спектр оператора 156
Спектральная мера оператора
178
Спектральное разложение 178
Спектральный радиус 158
Стабильность прогноза 17
Стационарное уравнение Шре-
дингера 183
Сумма алгебр прямая 272
— объектов категории 195
' Существенная верхняя грань 41
Существенный спектр 282
Сходимость по мере 37
— почти всюду 36, 37
— равномерная 37
Счетная аддитивность меры 202
— монотонность меры 26
Таблица умножения для опера-
операции свертки 136
Тело кватернионов 115
Тензорная алгебра 194
Тензорное произведение бана-
банаховых пространств 62
— — линейных пространств 196
Теорема Арцела — Асколи 81
— Банаха об обратном операто-
операторе 76
— Банаха — Штейнгауза 74
— Вейерштрасса 106
— Гильберта 125
— Егорова 38
— Крейна — Мильмана 80, 233
— Куранта 127
— Лебега об ограниченной схо-
сходимости 47
— Леви о монотонной сходимо-
сходимости 49
— Лузина (С-свойство) 206, 208
— Никольского 87
— о ближайшей точке 118
— о гильбертовом базисе 121
395
Теорема о капопическом виде
линейного функционала на
гильбертовом пространстве
119
— о стягивающихся шарах 13
— о ядре 247
— Пэли — Винера 149, 268
— Радона — Никодима 54
— Рисса 89
— спектральная 178
— Стоуна 179
— Стоуна — Вейерштрасса 242
— Тихонова 355
— Ферма малая 293
— фон Неймана 168
— эргодическая 282
— Фубини 53
— Хана — Банаха 69, 71
— Хелли 230, 241
— Цермело 12, 190
Теория Вейля 170
Тождество Гильберта 371
— параллелограмма 118, 251
— Сохоцкого 246
— Эйлера 235
Топология равномерная 73
— сильная 68, 73
— слабая 68, 73
— #-слабая 68
Тор тг-мерный 129
Точка Лебега 207
— плотности множества 203, 204
— прикосновения 13
Точная последовательность опе-
операторов 85
Транзитивность 9
Транспонированное отношение
9
Тригонометрический многочлен
259
Тэта-функция Вейерштрасса 359
Угол между векторами в гиль-
гильбертовом пространстве 117
— — подпространствами 253
Уравнение Вольтерра 237
— Гейзенберга 372
— теплопроводности 266
— Шредингера 182
Фактормножество 10
Факторпространство 62
Фермион 186
396
Физическая величина (наблю-
(наблюдаемая) 181
Формула интегрирования по ча-
частям для интеграла Планше-
реля 148
Римана — Стилтьеса 215
— Стоуна 282
— суммирования Пуассона 151
Формулы Ньютона 364
Функтор ковариантный 21
— коптравариантный 21
Функции равноизмеримые 207
Функционал линейный непре-
непрерывный 59
— Минковского 64
Функциональное операторное
исчисление 153
Функция абсолютно непрерыв-
непрерывная 218
— Бесселя 362
— борелевская 206
— волновая 180
— Дирака 108
— Дирихле 209
— измеримая 36
— квазипериодическая 269
— локально суммируемая 107
— Мебиуса 188
— — классическая 289
— непрерывная в среднем 240
— обобщенная 107
— — однородная 248
регулярная 108
— — с компактным носителел!
107
умеренного роста 107
— ограниченной вариации 33
— 1-го класса Бэра 307
— положительно определенная
264
— производящая 142
— простая 39
— скачков 214
— слабо измеримая 231
— Стеклова 265
— суммируемая 39, 40
— существенно ограниченная 41
— Хевисайда 214
— Эйлера 188
Характер группы 138
Характеристическая функция
множества 24
Характеристическое свойство
полных метрических прост-
пространств 190
Целочисленная решетка тг-мер-
ная 129
Центрированная система мно-
множеств 330
Центроид шара 193
Циклический вектор 161, 266
Чезаровское среднее 357
Число дефекта 168
Шар замкнутый 13
— открытый 13
Энергия 182
— кинетическая 184
— потенциальная 184
Эрмитова форма 125
Явление Гиббса 358
Ядерно-выпуклая топология 226
Ядро оператора 84
Л-ядро 294
Г-функция 247, 344
б-алгебра 24
б-кольцо 24
е-периендикуляр 220
Кириллов Александр Александрович
Гвишиани Алексей Джерменович
ТЕОРЕМЫ И ЗАДАЧИ
ФУНКЦИОНАЛЬНОГО АНАЛИЗА
Редактор С. А. Смагин
Художественный редактор Г. М. Коровина
Технический редактор Л. В. Лихачева
Корректоры: Г. В. Подволъская, О. М. Березина
ИБ JSIS 32354
Сдано в набор 20.05.87. Подписано к печати 13.01.88.
Формат 84x108/32. Бумага книжно-журнальная. Гар-
Гарнитура обыкновенная. Печать высокая. Усл. печ.
л. 21. Усл. кр.-отт. 21. Уч.-изд. л. 24,13. Тираж
14 000 экз. Заказ Л° 835. Цена 1 р. 10 к.
Ордена Трудового Красного Знамени
издательство «Наука»
Главная редакция физико-математической литературы
117071 Москва В-71, Ленинский проспект, 15
4-я типография издательства «Наука»
630077 Новосибирск, 77, Станиславского, 25