ТЁЙ1 ВЕРОЯТНОЕ. ЕЙ
А.С.СОЛОДОВНИКОВ
А.С. солодовников
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Допущено
Министерством просвещения СССР в качестве учебного пособия для студентов педагогических институтов но математическим специальностям
Москва «Просвещение» 1983
ББК 22.171 С60
Рецензенты:
Кафедра геометрии МОПИ им. Н. К. Крупской (зав кафедрой, доктор физ.-мат. наук профессор Мантуров О. В.).
Доктор физ.-мат. наук, профессор Левин В. И. (МГПИ им. Ленина).
Солодовников А. С.
С 60 Теория вероятностей: Учеб, пособие для студентов пед. ин-тов по матем. спец.—М.: Просвещение, 1983.—207 с.
Учебное пособие по npoipaMMe физико-математических факультетов педагогических институтов содержит основные вопросы курса «Теория вероятностей», начиная с интуитивного подхода к понятиям случайного события и вероятности и кончая элементами математической статистики. Значительное место уделяется таким важнейшим фактам, как закон больших чисел и центральная предельная теорема, законы распределения случайных величин и их систем, числовые характеристики случайных величин. В книге на конкретных примерах показывается, как вероятностные еаконы применяются в практической деятельности.
с 4309010400 — 489
103 (03) — 83
223 — 83
ББК 22. 171
517. 8
© Издательство «Просвещение», 1983 г.
ОГЛАВЛЕНИЕ
Предисловие ................................................................................. 5
Глава 1. События и их вероятности ........................................................... 7
§ I.	Интуитивный подход к понятиям случайного события и вероятности ..................................................... —
§ 2.	Комбинации событий. Правило сложения вероятностей ...	12
§	3.	Аксиомы теории вероятностей .................................................... 17
§ 4.	Классический способ подсчета вероятностей ........................................ 24
§	5.	Геометрические вероятности ..................................................... 30
Глава	2. Комбинаторика ................................................................. 32
§	6.	Правила суммы и произведения ........................... —
§	7.	Размещения и перестановки	...................... 35
§	8.	Сочетания. Бином Ньютона	...................... 37
§	9.	Размещения данного состава.	Полиномиальная	формула	.	.	40
§	10.	Применение комбинаторики к	подсчету	вероятностей	....	43
'лава 3. Независимость событий. Простейшие формулы ......	47
§ 11.	Условная вероятность .............................................................. —
§ 12.	Независимые события и правило умножения вероятностей . .	50
§ 13.	Формула полной вероятности ....................................................... 55
§ 14.	Формула Байеса ................................................................... 57
лава 4. Схема Бернулли ..................................................................... 60
§ 15.	Схема Бернулли. Биномиальные вероятности .......................................... —
§ 16.	Наиболее вероятное число успехов. Среднее число успехов . .	64
§ 17.	Вероятности Pn(k) при больших значениях п. Приближенные формулы Лапласа ................................................ 67
§ 18.	Предельная теорема и приближенные формулы Пуассона ...	72
§ 19.	Цепи Маркова ..................................................................... 75
лава 5. Случайные величины и законы их распределения........................................ 84
§ 20.	Описательный подход к понятию случайной величины ....	—
§ 21.	Дискретные случайные величины .................................................... 86
§ 22.	Случайные величины общего вида. Функция распределения . .	89
§ 23.	Дискретные и непрерывные случайные величины. Плотность вероятности .................................................... 96
§ 24.	Закон равномерного распределения на отрезке и закон нормального распределения на прямой .............................. 101
§ 25.	Механическая модель случайной	величины ................ 105
Глава	6. Системы случайных величин	..................... 107
§ 26.	Формальное определение системы двух случайных величин. Система дискретного типа ........................................ —
§ 27.	Функция распределения системы (х, у). Плотность вероятности .......................................................   114
§ 28.	Независимые случайные величины .................................................. 117
§ 29.	Примеры двумерных распределений ................................................. 119
§ 30.	Функции случайной величины ...................................................... 124
3
§ 31.	Система любого числа случайных величин. Функции от нескольких случайных величин...................................... 129
Глава 7. Числовые характеристики случайных величин	......... 134
§ 32.	Математическое ожидание случайной величины	........... —
§ 33.	Свойства математическою ожидания..................... 144
§ 34.	Дисперсия случайной величины......................... 149
§ 35.	Дисперсия суммы случайных величин. Корреляционный	момент	154
Глава 8. Закон больших чисел и центральная предельная	теорема	.	.	156
§ 36.	Неравенство Чебышева ..................................... 157
§ 37.	Различные 4ормы закона больших чисел...................... 159
§ 38.	Центральная предельная теорема теории вероятностей ....	163
§ 39.	Применение центральной предельной теоремы ................ 166
§ 40.	Примеры задач на нормальный закон распределения ....	169
Глава 9. Элементы математической статистики ........................ 173
§ 41.	Вариационный ряд. Таблица частот. Гистограмма............. 174
§ 42.	Оценки параметров распределения .......................... 177
§ 43.	Доверительные оценки ..................................... 182
§ 44.	Оценка неизвестной вероятности по частоте ................ 187
§ 45.	Корреляция .............................................   189
§ 46.	Метод наименьших квадратов ............................... 193
Приложение 1. Условия, при которых наперед заданная функция F(x) является функцией распределения ......................... 196
Приложение 2. Теоремы сложения и умножения математических ожиданий ................................................. 199
Таблицы значений для функций ср (х) ='/==е	и
1 п-----1£
1 Г 2	•'
ФМ = Ж)е di.................'...................... 202
0	Xй
Таблица значений функции —е~^	.............. 204
«1
Предметный указатель.................................. 205
ПРЕДИСЛОВИЕ
Настоящая книга является учебным пособием для студентов физико-математических факультетов педагогических институтов по курсу «Теория вероятностей». В соответствии с учебным планом этот курс изучается в 6-м семестре.
Предмет теории вероятностей отличается большим своеобразием. Необычный характер теоретико-вероятностных, понятий явился причиной того, что долгое время подход к этим понятиям основывался только на интуитивных соображениях. Настоящее и по-современному строгое обоснование теории вероятностей появилось сравнительно недавно — в 30-х годах нашего века — в трудах советского математика академика А. Н. Колмогорова. С этого времени теория вероятностей превратилась в стройную дисциплину, в такой же мере безупречную, как, скажем, математический анализ или теория чисел.
Учебная литература по теории вероятностей довольно резко разделяется на книги двух категорий: те, что доступны читателю с солидной математической подготовкой, и книги, которые излагают предмет на интуитивном уровне, с использованием понятий, лежащих вне поля зрения математики. В настоящем пособии автор стремился избежать каждой из этих крайностей. Изложение ведется в нем достаточно строго; вместе с тем каждому новому понятию предшествует неформальное объяснение, вскрывающее существо вводимого понятия, его происхождение и реальный смысл.
Отметим некоторые особенности изложения в данной книге.
В § 3 главы 1 вводится понятие «вероятностная схема». Это синоним понятия «вероятностное пространство», принятого в большинстве пособий.
Главы 5—8 посвящены теории случайных величин. При этом само понятие случайной величины, а также ряд сопутствующих ему вводятся таким образом, чтобы избежать обращения к абстрактной теории меры и интеграла Лебега.
5
Доказательства нескольких важных теорем о случайных величинах вынесены за рамки основного текста книги и даны в виде приложений. Это касается теоремы о задании случайной величины некоторой функцией F(x), теорем сложения и умножения математических ожиданий (последние две теоремы в основном тексте доказаны только для дискретного случая).
По поводу обозначений, принятых в книге, заметим только следующее: случайные величины обозначаются жирными буквами латинского шрифта (х, у и т. д.), окончание доказательства каждой теоремы или леммы отмечается знаком И, а завершение решения примера или задачи — знаком А.
В целом книга соответствует действующей программе, но последовательность изложения несколько изменена по сравнению с программой. Главное изменение заключается в том, что все сведения, касающиеся математической обработки результатов наблюдений, отнесены в отдельную главу 9, посвященную элементам математической статистики.
Для более углубленного знакомства с предметом мы рекомендуем следующие книги: Гнеденко Б. В. Курс теории вероятностей. М., Наука, 1969, иБоровковА. А. Курс теории вероятностей. М., Наука, 1976.
Глава 1.
СОБЫТИЯ И ИХ ВЕРОЯТНОСТИ
Эта глава посвящена введению двух важнейших понятий теории вероятностей: понятия случайного события и понятия вероятности. Сначала мы рассмотрим (§ 1) чисто интуитивный, неформальный подход к этим понятиям. Он базируется на совершенно естественных, но вместе с тем не вполне строгих рассуждениях. Формализация основных понятий дается позже, в § 3, где рассматриваются аксиомы теории вероятностей.
§ 1. ИНТУИТИВНЫЙ ПОДХОД К ПОНЯТИЯМ СЛУЧАЙНОГО СОБЫТИЯ И ВЕРОЯТНОСТИ
1°. Случайные события и предмет теории вероятностей. На практике часто встречаются такие ситуации, когда исход проводимого нами опыта (эксперимента, испытания) нельзя предсказать заранее с полной уверенностью. Например, невозможно предсказать, какая сторона выпадет при бросании монеты, — на исход этого опыта влияет огромное число факторов, таких, как начальное положение монеты в момент броска, начальная скорость, сопротивление воздуха, особенности поверхности, на которую падает монета, и т. д. Аналогичным образом невозможно предсказать, останется ли исправной купленная нами в магазине электрическая лампа после тысячи часов работы, выпадет ли выигрыш на лотерейный билет с таким-то номером и т. д. Во всех подобных ситуациях мы вынуждены считать результат опыта зависящим от случая, рассматривать его как случайное событие.
Примем на первых порах такое определение.
Некоторое событие называется случайным по отношению к данному опыту, если при осуществлении этого опыта оно может наступить, а может и не наступить.
Примером случайного события может служить выпадение герба в опыте с бросанием монеты, выигрыш по данному лотерейному билету, совпадение дней рождения у двух наугад выбранных людей.
Случайные события обозначаются в дальнейшем А, В, С и т. д.
Сделаем сразу же одно замечание. Согласно данному выше определению, событие считается случайным, если его наступление в результате опыта представляет собой лишь одну из возможностей. Под это определение формально подходят и такие события, которые в результате данного опыта обязательно наступают', эти события
7
называют достоверными. Например, достоверным является событие, состоящее в том, что при бросании игральной кости выпадает целое число очков или что выбранное наугад слово из данной книги содержит не более 50 букв. Итак, достоверное событие можно рассматривать как одну из разновидностей случайного события.
Аналогичное замечание относится и к невозможным событиям, т. е. таким, которые никогда не наступают при осуществлении данного опыта. Невозможное событие тоже можно рассматривать как случайное. Примером невозможного события может служить получение двух выигрышей по одному лотерейному билету1.
В дальнейшем нас будут интересовать только такие опыты, которые можно повторить (в принципе) неограниченное число раз; именно такой характер носит опыт с бросанием монеты, с покупкой лотерейного билета, с обследованием изделия на годность или брак. Любое случайное событие, наступление которого возможно в такого рода опытах, называется массовым или статистическим.
Массовые случайные события следует отличать от единичных, исключительных, обладающих той особенностью, что опыт, с которым связаны эти события, принципиально невоспроизводим. Например, событие «1 мая 1975 года в Москве шел дождь» является в этом смысле исключительным, так как воспроизвести наступление указанного дня невозможно. В то же время собьпие «1 мая в Москве шел дождь» (без упоминания о годе) является, несомненно, массовым: ведь наблюдать погоду в Москве 1 мая можно в течение многих лет.
Теперь мы в состоянии ответить на вопрос, с которого, собственно, и должно начинаться знакомство с теорией вероятностей: чем занимается, какие задачи ставит перед собой эта дисциплина? В самых общих словах предмет теории вероятностей может быть определен следующим образом.
Теория вероятностей занимается изучением закономерностей, присущих массовым случайным событиям.
Столь общая характеристика предмета, разумеется, еще мало что говорит о его содержании; она лишь очерчивает тот круг явлений, с которым имеет дело теория вероятностей. Больше того, эта характеристика кажется на первый взгляд противоречивой. Действительно, само утверждение о том, что случайным явлениям свойственны закономерности, звучит довольно неожиданно. Однако такие закономерности реально существуют, и их значение в целом ряде случаев очень велико.
Простейший пример закономерности такого рода дает опыт с бросанием монеты. Предположим, что бросание производится много раз подряд. Исход каждого отдельного бросания является случайным, неопределенным. Однако средний результат большого числа
1 Включая достоверное и невозможное события в общее понятие случайного события, мы поступаем аналогично тому, как делают, например, в курсе аналитической геометрии,' когда прямую линию рассматривают как частный случай кривой, или в курсе математического анализа, когда постоянную величину рассматривают как частный случай переменной.
8
бросаний утрачивает случайный характер, становится закономерным. А именно: «доля» тех бросаний, при которых выпадает герб (т. е. отношение числа таких бросаний к числу всех бросаний) с увеличением числа бросаний приближается к —.
Приведем другой пример, весьма важный с практической точки зрения. В сосуде заключен газ. Находясь в беспрерывном движении, молекулы газа ударяются друг о друга и вследствие этого постоянно меняют величину и направление своей скорости. Казалось бы, отсюда следует, что давление газа на стенки сосуда, обусловленное ударами отдельных молекул о стенки, должно меняться случайным, неконтролируемым образом. Однако мы хорошо знаем, что это не так: давление газа подчиняется строгой закономерности (закону Бойля-Л1ариотта). Причина этой закономерности кроется в том, что давление газа на стенки сосуда есть средний результат воздействия большого числа молекул. Случайные особенности, свойственные движению отдельных молекул, в массе (поскольку молекул много) взаимно погашаются, нивелируются, и возникает некоторая средняя закономерность.
Именно эта устойчивость среднего результата, его независимость от колебаний отдельных слагаемых и обусловливают широту применений теории вероятностей. Статистическая физика, аэро- и гидродинамика, ядерная физика, биология, медицина, лингвистика и т. д. — все эти области науки используют (одни в большей степени, другие в меньшей) понятия и выводы теории вероятностей и родственных ей дисциплин (математической статистики, теории информации и т. д.).
С простейшим типом закономерностей в случайных явлениях мы ознакомимся уже в следующем пункте.
2°. «Статистическое определение» вероятности случайного события. Сравнивая между собой случайные события, мы часто говорим, что одно из них более вероятно (имеет больше шансов наступить, в большей степени возможно), чем другое. Например, выпадение герба при бросании монеты — событие более вероятное, чем, скажем, совпадение дней рождения у двух наугад выбранных людей; последнее же событие в свою очередь более вероятно, чем получение максимального выигрыша в «Спортлото».
Чтобы придать подобным сравнениям точный количественный смысл, необходимо с каждым событием связать число, выражающее степень возможности данного события. Наиболее естественный путь для введения такого числа состоит в следующем.
Пусть А — случайное событие по отношению к некоторому опыту. Предположим, что опыт произведен N раз и при этом событие А наступило в NA случаях. Составим отношение
9
Оно называется частотой наступления события Л в рассматриваемой серии опытов.
Для весьма многих (практически для всех) случайных событий частота обладает свойством устойчивости. Это означает, что с увеличением числа опытов частота стабилизируется, приближается к некоторой постоянной р (Л). Естественно считать, что эта постоянная и измеряет как раз степень возможности события А. Она называется вероятностью события А.
Итак, в полном соответствии с интуитивным представлением о вероятности мы принимаем такое определение:
Вероятность случайного события — это связанное с данным событием постоянное число, около которого колеблется частота наступления этого события в длинных сериях опытов.
Заметим, что устойчивость частоты представляет собой одну из простейших закономерностей, проявляющихся в сфере «случайного». Эта закономерность в конечном счете составляет основу всех приложений теории вероятностей к практике.
Приведенное выше определение часто называют «статистическим определением» вероятности. Оно не является, конечно, математическим в строгом смысле этого слова, так как опирается на чуждые математике понятия: «опыт», «наступление события», «колебание около числа». Однако мы вовсе и не собираемся строить теорию, исходя из этого определения. Путь, который мы изберем, будет другим; этот путь типичен для математических дисциплин. В следующем параграфе будут установлены некоторые простейшие свойства вероятности. После этого статистическое определение как основа для дальнейших построений перестанет быть необходимым: вся последующая математическая теория будет исходить только из этих свойств, носящих характер четких математических положений (аксиом теории вероятностей).
Впрочем, сказанное еще не означает, что статистическое определение является чем-то лишним. Напротив, оно играет чрезвычайно важную роль, но не для самой теории, а для ее приложений. В дальнейшем мы будем находить вероятности различных событий путем расчетов, не обращаясь к эксперименту; практическое же истолкование полученных вероятностен будет связано именно со статистическим определением. Другими словами, если найденная путем некоторого расчета (по формулам теории вероятностей) вероятность события А равна числу р, то реальная ценность этого результата состоит прежде всею в возможности такого предсказания: при большом числе опытов частота наступления события А будет близка к р.
Укажем некоторые факты, непосредственно вытекающие из данного выше статистического определения.
Так как частота р всегда удовлетворяет условиям 0 р 1, то в тех же пределах заключена и вероятность любого события:
О <р(А)< 1.
При этом, если событие А достоверно, т. е. наступает при каждом осуществлении опыта, то NA = N и, значит, р = 1; тем самым вероятность достоверного события равна 1. В другом крайнем
10
случае, когда событие А невозможно, имеем: NA = 0 и, значит, р. = 0; таким образом, вероятность невозможного события равна нулю.
Рассмотрим несколько примеров случайных событий и для каждого из них постараемся, исходя из интуитивных соображений, указать соответствующую вероятность р(Д).
1.	Опыт заключается в бросании монеты. Событие А — выпадение герба. Будем предполагать, что монета не деформирована (имеет правильную цилиндрическую форму), сделана из однородного материала и что чеканка на обеих ее сторонах не оказывает сколько-нибудь заметного влияния на распределение масс. Тогда естественно ожидать, что в длинных сериях бросаний герб и цифра будут появляться в среднем одинаково часто; как принято говорить в этом случае, обе стороны монеты «равноправны» («равновозможны»). Можно, таким образом, предполагать, что частота ц наступления события А будет колебаться около числа у. Отсюда напрашивается вывод, что р(А) =
2.	В урне лежат 10 шаров: 4 белых и 6 черных. Шары неотличимы на ощупь. Из урны наугад извлекают один шар. Какова вероятность того, что он окажется черным?
Допустим, что указанный опыт проделан большое число раз. Учитывая «равноправие» шаров, можно ожидать, что частота появления черного шара будет приблизительно равна «доле», которую сос-тавляют черные шары в урне, т. е. —. Отсюда ясно, что р(А) = —.
3.	Волчок приводится во вращение вокруг оси, после чего отпускается. Часть дискообразной поверхности волчка, —допустим, некоторый сектор, содержащий угол а (рис. 1), —закрашена. Событие А — касание волчком пола (после остановки) в точке, принадлежащей закрашенной части. Все те же соображения «равноправия» (на этот раз между различными точками окружности) подсказывают нам, что число наступлений события А будет составлять
примерно такую же долю от числа всех опытов, какую а составляет
от 2л; иначе говоря, что частота р будет колебаться около числа
а
2л”
Следовательно, р(Л) = —.
2л
Заметим, что последний пример можно свести к схеме извлечения шара из урны, частный случай которой был разобран в примере 2. В самом деле, представим себе, чго на окружности волчка каким-либо образом выделены с промежутками в один градус 3G0 точек. Час1ь из них, допустим k точек, приходится на закрашенный сектор. Пренебрегая дугами, меньшими 1°, будем считать, что точка соприкосновения волчка с полом является одной из выделенных точек. Тогда рассматриваемый опыт можно уподобить извлечению одного шара из урны,
Рис. 1
11
в которой находятся 360 шаров, причем k из них являются черными. Событие А в такой интерпретации будет означать извлечение черного шара. Вероятность k	а
этого события равна ——, т. е. ——.
1	360 2л
Приведенные примеры характерны тем, что в каждом из них для нахождения искомой вероятности не потребовалось проводить опыты: интересующее нас число р(А) можно было указать, исходя из интуитивно ясной идеи «равноправия». Разберем еще один пример: в нем вероятность случайного события уже не может быть вычислена иначе, чем с помощью серии опытов.
4.	Игральная кость имеет форму куба. На гранях, как обычно, написаны цифры от 1 до 6. Найти вероятность того, что при бросании кости выпадет цифра 1 (событие Л).
Если кость сделана из однородного материала, то опять-таки из соображений «равноправия» (между гранями) очевидно, что р(А) = —. Допустим, однако, что кость неоднородна (например, 6
где-то внутри нее запаян кусок свинца). Ясно, что в этом случае какие-то цифры будут выпадать чаще, чем другие. Для вычисления вероятности события А единственным способом является проведение большой серии бросаний. Найденная из этой серии частота п наступления события А может рассматриваться как приближенное значение для р(А).
§ 2.	КОМБИНАЦИИ СОБЫТИЙ. ПРАВИЛО СЛОЖЕНИЯ ВЕРОЯТНОСТЕЙ
При нахождении вероятностей приходится, естественно, учитывать связи между событиями. Формы таких связей весьма многообразны. Наиболее простые из них заключаются в том, что одни события являются комбинациями других. В этом параграфе мы ознакомимся с тремя основными видами комбинаций: суммой событий, произведением событий, противоположным событием.
1°. Сумма событий. Пусть с некоторым опытом связаны события А и В. Их суммой называется третье событие А + В, которое (по определению) считается наступившим тогда и только тогда, когда наступает хотя бы одно из событий А или В. Если мы условимся наступление события обозначать знаком «+», а ненаступле-ние — знаком «—», то полную характеристику события А + В будет давать следующая таблица:
12
(Таблица читается по строкам. Например, первая строка расшифровывается так: если наступает А и наступает В, то наступает и А + В.)
Из приведенной таблицы можно видеть, что операция сложения событий есть в сущности операция дизъюнкции для высказываний. Говоря точнее, высказывание «наступило А + В» есть дизъюнкция высказываний «наступило Л» и «наступило В».
Аналогично определяется сумма трех событий, четырех и т. д. Вообще, сумма любого множества событий есть событие, которое наступает в тех и только в тех случаях, когда наступает хотя бы одно из событий данного множества.
Приведем пример. Пусть опыт заключается в выборе наугад точки из области й, являющейся квадратом на плоскости (такой опыт осуществляет брошенный наугад биллиардный шар — после ряда отражений от бортов биллиардного стола шар останавливается в случайной точке). Если А обозначает попадание точки в верхнюю половину квадрата (рис. 2), а В — попадание в правую половину, то Л + В будет означать попадание в область, являющуюся объединением указанных половин.
Дцугой пример. Пусть в опыте с бросанием игральной кости событие А есть выпадение числа, кратного 2, а В — выпадение числа, кратного 3. Тогда А + В будет выпадение хотя бы одного из чисел 2, 3, 4, 6.
2°. Произведение событий. Пусть Л и В — два события. Их произведением называется третье событие АВ, которое считается наступившим тогда и только тогда, когда наступают оба события А и В. Другими словами, АВ есть совместное наступление событий Л и В.
Таблица, характеризующая событие АВ, имеет вид:
А	в	АВ
+	+	+
+	—	—
—	+	—
—	—	
Рис. 2
13
Аналогично определяется произведение любого множества событий. Это событие, заключающееся в совместном наступлении всех событий данного множества.
Если, например, А и В — события из указанного выше примера с выбором точки внутри квадрата, то АВ будет означать попадание точки в правую верхнюю четверть квадрата. В примере с бросанием игральной кости событие АВ означает выпадение 6 очков. Если в том же примере в качестве А принять выпадение четного числа очков, а в качестве В — выпадение нечетного числа очков, то АВ будет означать невозможное событие.
3°. Противоположное ^обытие. Противоположное событие для события А обозначается А. По определению А считается наступившим тогда и только тогда, когда А не наступает. Короче, А — это ненаступление А.
Например, если А есть выпадение четного числа очков при бросании игральной кости, то А — выпадение нечетного числа очков; если А — это попадание при выстреле, то А — промах; если А означает исправность всех элементов некоторой системы, то А — выход из строя хотя бы одного из элементов.
Таблица, характеризующая события А, выглядит так:
Мы видим, что операция перехода к противоположному событию есть, по сути дела, операция отрицания для высказываний.
Беря несколько событий А, В, С, D, ... и применяя к ним в любом порядке операции сложения и умножения, а также используя переход к противоположным событиям, можно строить различные комбинации, например: АВ + С, (АС + B)D и т. п. Читатель должен отчетливо понимать смысл подобных выражений, научиться быстро и безошибочно перечислять случаи наступления или не-наступления той или иной комбинации. Укажем, например, таблицу, дающую все случаи наступления и ненаступления события АВ + С:
АВЦ-С
+ + +
+ +
+ + + +
4-
4-
+ +
+ + +
Приведем еще один пример
14
Покупаются три лотерейных билета; событие означает выигрыш по первому билету, А2— выигрыш по второму, Аа— по третьему. Рассмотрим следующую комбинацию:
A^2 + А2А8 4- А^Ав-	(1)
Согласно определению операций сложения и умножения, событие (1) наступает в любом из трех случаев: выигрывают 1-й и 2-й билеты, выигрывают 2-й и 3-й, выигрывают 1-й и 3-й. Другими словами, событие (1) означает выигрыш не менее чем по двум билетам.
Аналогичным образом, рассмотрев комбинацию
4- AjAzA3 4~ AjA^Ag,	(2)
легко убедиться, что событие (2) означает выигрыш по двум билетам.
4°. Равенство между событиями. Некоторые замечания. В дальнейшем часто встречается запись А = В, означающая равенство между событиями А и В. Уточним смысл этой записи.
По определению события А и В считаются равными, если всякий раз, когда наступает одно из них, наступает и другое.
Разумеется, равные события могут иметь отличающиеся по форме словесные описания. Например, событие «не все студенты данного курса успешно сдали теорию вероятностей» и «по крайней мере один из студентов данного курса не сдал теорию вероятностей» равны, хотя и выражены различными оборотами речи.
Возвращаясь еще раз к операциям над событиями, выскажем ряд замечаний.
1. Выше уже говорилось о том, что операции сложения, умножения и перехода к противоположному событию равнозначны операциям дизъюнкции, конъюнкции и отрицания для высказываний. Отсюда следует, что все законы алгебры высказываний будут верны и для событий. Например, будут выполняться соотношения:
__________А = АВ + АВ,_
At + А2 4-	4~ Ал == AtA2 ... Ап,
АхА2 ... Ап — А{ + А2 + ••• 4- А„ и т. п.
2. Для наглядного истолкования различных соотношений между событиями удобно пользоваться так называемыми диаграммами Эйлера-Венна. В этом случае каждое событие рассматривается как попадание случайно брошенной точки в некоторую область на плоскости; иначе говоря, каждое событие задается некоторой фигурой на плоскости. При таком истолковании событие А + В будет не что иное, как попадание точки в область, являющуюся объединением фигур А и В (рис. 3), событие АВ — попадание в область, являющуюся пересечением фигур А и В, а событие А — попадание в область, дополнительную к фигуре А. Позже мы увидим, что такой подход является универсальным: с определенной точки зрения (см. § 3,
15
п. 2°) каждое событие можно истолковывать как некоторое множество, а операции А + В, АВ и А над событиями — как операции объединения, пересечения и дополнения для множеств.
5°. Правило сложения вероятностей. Согласно статистическому определению, вероятность случайного события можно оценить по частоте наступления этого события в большой серии опытов. Однако серию из большого числа опытов трудно осуществить практически. Поэтому непосредственное определение вероятности исходя из частоты возможно лишь в редких случаях. Как правило, вероятности различных событий стараются подсчитывать косвенным путем, не прибегая к эксперименту. Разработка правил для такого подсчета и составляет в значительной степени сод ер-
Рис. з	жание теории вероятностей. Общий смысл
этих правил состоит в том, что различные соотношения между событиями влекут за собой определенные зависимости между их вероятностями.
Самое простое и в то же время самое важное из правил такого рода называется правилом сложения вероятностей. Как мы увидим дальше, оно можег быть положено в основу всей теории вероятностей.
Условимся называть два события А и В несовместными, если они не могут наступить вместе в одном опыте. Так, например, в опыте с бросанием игральной кости выпадение четного числа очков (событие А) и выпадение нечетного числа очков (событие В) — два несовместных события; в то же время выпадение числа очков, кратного 2, и выпадение числа очков, кратного 3, — события совместные (они наступают вместе при выпадении 6).
Правило сложения вероятностей формулируется следующим образом.
Если события А и В несовместны, то вероятность их суммы равна сумме их вероятностей:.
р(А + В) = р(А) + р(В).	(3)
Приведем «доказательство» этого предложения (мы взяли слово «доказательство» в кавычки, желая этим подчеркнуть нестрогий характер рассуждений — ведь само понятие вероятности определено пока не вполне корректным образом).
Пусть опыт, с которым связаны данные события А и В, повторен N раз, при этом NA раз наступило событие А и NB раз — событие В. Ввиду несовместности событий А и В имеем:
16
*А+В = ^ +
Разделив обе части этого равенства на N, получим:
N, N
Л-|-£   л । в ~~N	N~ ‘ ~Л^'
С увеличением N дробь, стоящая в левой части, будет колебаться около числа р (А + В), а слагаемые правой части — соответственно около чисел р (Л) и р (В). Отсюда и «следует» формула (3).
Методом полной индукции можно распространить правило сложения на любое конечное число событий. Назовем события Лп Л 2, ..., Ап попарно несовместными, если из i ф j следует несовместность событий At и Aj. Правило сложения для п событий утверждает: если события Аг, Л2, , А„ попарно несовместны, то справедливо равенство
Р Иг + Л2 + ... + А„) — р (Л4) + р (Л2) + ••• + Р Ия).
Из правила сложения для двух событий вытекает одно простое, но важное следствие.
Сумма вероятностей противоположных событий равна единице:
Р (А) + р (А)	1.	(4)
Действительно, событие Л + Л достоверное (ибо при каждом осуществлении опыта событие Л либо наступает, либо не наступает), поэтому вероятность его равна 1. Учитывая, что события Л и А несовместны, и применяя правило сложения, получаем равенство (4).
Задачи на использование правила сложения будут рассмотрены позднее. Ограничимся пока простым примером.
Бросается игральная кость. Чему равна вероятность того, что выпадет четное число очков (событие Л)?
Обозначим через Лг выпадение t очков (i = 1, 2.... 6). Оче-
видно, событие А есть наступление хотя бы одного из событий Л2, Л4, Лв:
А — А2 А~ А± Ая.
Так как при этом события Л2, Л4, Ав попарно несовместны, то можно воспользоваться правилом сложения. Получим:
Р И) = Р (Л2) + р (Л4) 4 Р (Лв) =1+1 + 1=1. 6	6	6	2
§ 3. АКСИОМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
До сих пор мы исходили из представления о вероятности случайного события как о числе, к которому приближается частота наступления этого события с увеличением числа опытов. Такое представление не может, конечно, служить основой для строгой
17
математической теории, так как в нем участвуют привходящие понятия (опыт, появление события и т. д.); кроме того (и это, пожалуй, самое существенное), не вполне ясно, какой точный смысл имеет само утверждение об устойчивости частоты.
Чтобы придать понятиям теории вероятностей строгость, присущую другим математическим понятиям, можно воспользоваться широко распространенным в математике аксиоматическим методом. Он состоит в том, что с самого начала фиксируются первичные, не подлежащие определению понятия данной теории. Их основные свойства формулируются в виде ряда аксиом. После этого все предложения теории (иначе говоря, все теоремы) выводятся из аксиом строго логическим путем, без обращения к посторонним понятиям, наглядности, «здравому смыслу» и т. д. Современная аксиоматика теории вероятностей принадлежит советскому математику А. Н. Колмогорову.
1°. Предварительные соображения. Чтобы сделать понятной точку зрения А. Н. Колмогорова, заметим, что в каждой конкретной теоретико-вероятностной задаче среди допускаемых к рассмотрению случайных событий можно выделить такие, которые являются в определенном смысле простейшими, элементарными. Элементарные события характеризуются, во-первых, тем, что при каждом осуществлении опыта наступает одно и только одно из них; во-вторых, любое событие А, связанное с данным опытом, должно распадаться на элементарные, т. е. представляться в виде суммы некоторого множества элементарных событий.
Предоставляем читателю убедиться в том, что данная выше характеристика элементарных событий эквивалентна следующей: во-первых, при каждом осуществлении опыта обязательно наступает какое-либо из этих событий, во-вторых, элементарные события «неразложимы». Последнее означает, что представление любого элементарного события С в виде суммы двух событий возможно лишь тривиальным образом: С = С + С или С = С + V, где V — невозможное событие.
Например, в опыте с бросанием игральной кости события
At, Аг, А3, Л4, Л8, Ав,	(1)
где Ai означает выпадение i очков, являются элементарными. Действительно, любое событие, представляющее интерес в связи с бросанием игральной кости, формулируется как некоторое условие на число очков (например, «число очков четное», «число очков превосходит 2» и т. п.); напротив, любая информация, не касающаяся числа очков (скажем: «кость дважды ударилась об пол» или «кость закатилась под диван»), представляется несущественной. Отсюда ясно, что каждое событие, связанное с данным опытом, распадается на частные случаи из группы (1).
Рассмотрим еще один пример. Пусть опыт заключается в бросании маленького шарика в область Й на плоскости. Элементарное событие — это попадание шарика в определенную точку области й. Ясно, что суммами таких событий исчерпываются все мыслимые исходы опыта. В данном примере в отличие от предыдущего множе-18
ство элементарных событий бесконечно;
можно считать его совпадающим с мно-	''Х
жеством всех точек области Q.	о
Возвращаясь к общей ситуации, обо-	2	)
значим через Q множество всех элемен-"	1
тарных событий для данного опыта.
Каждому событию А, связанному с дан-
ным опытом, можно сопоставить подмно-	Рис 4
жество множества Q; это подмножество состоит из тех элементарных событий, на которые распадается А (иначе говоря, из тех элементарных событий, которые в сумме составляют Л). В аксиоматике А. Н. Колмогорова событие А отождествляется с соответствующим подмножеством. В такой интерпретации, например, событие «на игральной кости выпало четное число очков» есть подмножество {А2, Д4, Лв} множества (1), а событие «шарик попал в подобласть области Q, расположенную левее пунктирной черты на рисунке 4» есть подмножество множества Q, состоящее из всех точек указанной подобласти.
Такой подход к понятию события удобен еще и тем, что благодаря ему понятия суммы и произведения событий, а также противоположного события приобретают естественный теоретико-множественный смысл, а именно: сумма событий А и В превращается в объединение соответствующих подмножеств, произведение событий А и В — в пересечение тех же подмножеств, а противоположное событие А — в дополнение к подмножеству А (вй).
Мы переходим теперь к изложению аксиоматики А. Н. Колмогорова. Для большего удобства разобьем аксиомы на две группы: аксиомы событий и аксиомы вероятностей.
2°. Аксиомы событий. Мы исходим из того, что задано некоторое множество Q. Элементы этого множества называются элементарными событиями. Что представляют собой элементарные события, какова их конкретная природа, для нас сейчас безразлично; этот вопрос к математическому содержанию теории не имеет отношения.
Далее мы предполагаем, что фиксирована некоторая непустая совокупность подмножеств множества Q; эти подмножества названы просто событиями. События в дальнейшем обозначаются буквами А, В, С и т. д., а вся совокупность событий — буквой S.
К совокупности S предъявим следующие два требования (аксиомы событий):
/. Если множества Av Аг,... (в конечном или счетном числе) суть события, то их объединение тоже является событием.
II. Если множество А является событием, то его дополнение (до Q) есть тоже событие.
Множество Q называют пространством элементарных событий. Из аксиом I и II легко следует, что Q является событием: для доказательства достаточно взять любое событие А и рассмотреть объединение множества А и его дополнения.
19
Примем следующее соглашение. В тех случаях, когда число элементарных событий конечное (т. е. когда множество й состоит из конечною числа элементов), под событиями будем понимать все без исключения подмножества множества й (включая, разумеется, и пустое подмножество — оно является дополнением к Й и потому обязано быть событием). В этом случае аксиомы I и II становятся, конечно, ненужными — они выполняются автоматически.
Условимся операцию объединения множеств обозначать знаком «+» (знаком сложения), операцию пересечения множеств — знаком «•» (знаком умножения); наконец, если А — подмножество в Й, то дополнение к А будем обозначать А. Тогда аксиомы I и II запишутся следующим образом:
I. Ai £ S, А2 £ S, ... => Af + Д2 4- ... £ S;
II. А £ S => А С S.
Укажем одно следствие из аксиом I и II.
Если множества Аи Аг, ... суть события, то их пересечение — снова событие. Или в символической записи:
А{ $ S, А., £ S, ... => <4i<42 ... С S.’
Для доказательства воспользуемся соотношением
AtA2 ... = Ai + Аг + ...,	(2)
справедливым, как известно, для любых подмножеств А{, Аг, ... фиксированного множества Й. В силу аксиом II и I множество, записанное в правой части (2), есть событие; значит, и AtA2 ... — событие. Снова применяя аксиому II, получим, что Лр42 ... тоже событие.
Введем следующие определения.
Два события А и В, не имеющие (как два подмножества) общих элементов, называются несовместными. События А и А называются противоположными.
3°. Аксиомы вероятностей. Теперь мы можем сформулировать аксиомы, задающие само понятие вероятности.
1.	Каждому событию А поставлено в соответствие неотрицательное число р(А), называемое вероятностью события А.
2.	Если события А], А2, ... попарно несовместны, то р(А\ 4- Д2 + •••) = Р(А\) + Р(Д2) +••• •
Заметим, что при бесконечном числе событий At, А2 ... в правой части написанного равенства стоит сумма ряда.
Очевидно, если множество й является конечным, то любая совокупность попарно не пересекающихся подмножеств состоит лишь из конечного числа подмножеств. Отсюда ясно, что для случая конечного й аксиома 2 равнозначна такому (в общем случае более слабому) требованию:
2'. р(А 4- В) — р(А) 4- р(В), если А и В несовместны.
20
Чтобы подчеркнуть различие между аксиомами 2 и 2', часто называют аксиому 2' аксиомой аддитивности, а 2 — аксиомой счетной аддитивности.
3.	р(П) = 1.
Аксиомы 1—3 составляют основу всей теории вероятностей. Все теоремы этой теории, включая самые сложные, выводятся из них формально-логическим путем.
Укажем несколько примеров такою вывода.
Исходя из очевидного соотношения между подмножествами
А + А = И
и применяя аксиомы 2 и 3, получаем, что
Р (А) + р (А) = 1.
Отсюда, принимая во внимание неотрицательность чисел р (А) и р (А), находим:
Р (А) < 1
— факт, не содержащийся непосредственно ни в одной из аксиом 1 —3.
В качестве другого следствия аксиом выведем формулу
р (А + В) = р (А) + р (В) - р (АВ),	(3)
в которой события А и В могут быть как совместными, так и несовместными.
Формула (3) получается следующим образом. Рассмотрим очевидные соотношения между событиями (как между подмножествами множества Q):
А = АВ + АВ, А + В = В + АВ
(рис. 5). Применяя к обоим равенствам аксиому сложения, получим два числовых равенства:
р (А) = р (АВ) + р (АВ)Л р (А+В) = р (В) + р (АВ).
Вычитая из последнего равенства предыдущее, приходим к формуле (3).
Докажем теперь теорему, устанавливающую одно важное свойство величин р (А).
Теорема (о непрерывной зависимости числа р (А) от события А).
Пусть последовательность событий
А},А2... такова, чтоА1=>А2=оА3щ> ... (записаны включения для подмножеств).
Тогда Ишр(Ал) =р(А),	(4)
Л-*ОО
21
где А есть пересечение всех множеств А ь А 2 ... .
Доказательство. Рассмотрим произвольный элемент а С Аь Возможны только два случая:
1) а принадлежит любому из множеств А„, где п = 1, 2, ...;
2) а принадлежит некоторому Ап, но не принадлежит An+i, т- е. а С A„A„+i.
Из сказанного следует, что
At = А + А1/12 + А2А3 4* А3Л4 +
причем, как нетрудно видеть, слагаемые этой суммы попарно не пересекаются. По аксиоме 2 имеем:
Р ИО — Р И) + Р (AiA2) + р (Л2^з) + Р И3А4) +	(5)
Так как при любом п последовательность Ап, Ал+1 ... также удовлетворяет условиям теоремы, то к ней применимы те же рассуждения. Следовательно,
Р Ия) = Р И) + Р (АпАп+д + р (АплЛАп+2) + ... .	(6)
Обозначим через г,г сумму членов ряда (6), начиная со второго члена. Если мы докажем, что гп -> 0 при п->оо, то отсюда будет следовать (4). Но, как нетрудно видеть, гп совпадает с остатком ряда (5) после n-го члена; и так как ряд (5) сходится, то его остаток после п-го члена должен стремиться к О.И
4°. Вероятностные схемы. Предмет теории вероятностей. Аксиомы А. Н. Колмогорова дают весьма удобную математическую схему для исследования конкретных теоретико-вероятностных задач или, по-другому, для описания опытов со случайными исходами. В этой схеме содержится вся информация о данном опыте, представляющая интерес с точки зрения теории вероятностей. Схема включает в себя три объекта:
1)	множество Q (называемое пространством элементарных событий);
2)	систему S подмножеств множества Q (называемых событиями), удовлетворяющую аксиомам 1,11 пункта 2°;
3)	функцию р (А), определенную на S и удовлетворяющую аксиомам 1, 2, 3 п. 3°.
Совокупность этих трех объектов условимся называть вероятностной схемой данного опыта или просто вероятностной схемой. Упоминание об опыте может быть опущено, поскольку понятие вероятностной схемы является, как мы видим, чисто математическим понятием и не требует привязывания к какому-либо конкретному опыту.
С введением понятия вероятностной схемы появляется возможность определить предмет теории вероятностей в не вызывающих сомнений точных терминах, а именно: теория вероятностей занимается изучением всевозможных вероятностных схем. Естественно, что эту теорию должны интересовать как теоремы, справедливые в любой вероятностной схеме (таких теорем сравнительно немного, примером может служить доказанная выше теорема о непрерывно
22
сти функции р (Л) или, скажем, формула (3)), так и теоремы, относящиеся к вероятностным схемам тех или других специальных типов. В частности, одно из центральных мест в теории вероятностей занимает изучение вероятностных схем, в которых множество Q есть множество всех точек числовой оси, а событиями являются подмножества вида {х\х < а}, а также все подмножества, получаемые из них конечным или счетным числом операций объединения, пересечения и дополнения, — такие вероятностные схемы носят название случайных величин. Изучению случайных величин посвящена большая часть этой книги (главы 5—9).
5°. Вероятность как мера. Нетрудно видеть, что свойства вероятности, зафиксированные в аксиомах, напоминают свойства площадей и объемов. Действительно, если в качестве Q взять множество всех точек некоторой области на плоскости, имеющей площадь 1, назвать событиями всевозможные квадрируемые подмножества области Q и сопоставить каждому событию А число р (Л), равное площади соответствующего подмножества, то будут выполняться требования аксиом 1, 2', 3; если же расширить класс событий, включив в него все подмножества из Q, измеримые по Лебегу, то будет обеспечено и выполнение аксиомы 2.
Аналогичное замечание справедливо и в отношении объемов.
В общем случае неотрицательная функция р (Л), определенная для подмножеств и удовлетворяющая аксиоме 2, называется мерой, а именно мы говорим, что р (Л) есть мера подмножества А. Таким образом, понятие меры является обобщением понятия площади или объема. В известной степени всю теорию вероятностей можно рассматривать как один из разделов общей теории меры.
Сказанное выше относительно общего понятия меры нуждается в уточнениях. Пусть задана некоторая непустая система подмножества множества Q. Обозначим эту систему S; таким образом, запись А € S будет означать, что подмножество А множества Q принадлежит заданной системе S. Условимся называть S боре-левской1 системой подмножеств, если выполняются следующие условия:
1) Из А б S следует А g S (где А есть Q \ Л).
2) Из Л1 С S, А2 g S, ... следует Ai + Л2 + ... С S.
Другими словами, борелевская система подмножеств характеризуется тем, что операции объединения и дополнения, выполненные в конечном или счетном числе, не выводят за пределы этой системы. (Заметим, что из условий I) и 2) вытекает О € S, поскольку для любого подмножества А справедливо соотношение А + А = £2.)
Предположим далее, что каждому подмножеству А из борелевской системы S сопоставлено некоторое неотрицательное число или символ оо; и то и другое условимся обозначить р (Л). При этом потребуем, чтобы соответствие Л ->• р (Л) обладало следующим свойством, носящим название свойства счетной аддитивности'.
Р (Лг + Л2 + ...) = р (Л1) + р (Л2) + ...,
1 Эмиль Борель (1871—1956)—французский математик, один из творцов теории меры. Термин «борелевская система подмножеств» часто заменяется другим: «а — алгебра подмножеств».
23
если подмножества Ai, А2, ... (из системы S) попарно не имеют пересечений. Не исключается и такой случай, когда левая часть или какие-то слагаемые правой части равны оо; чтобы охватить этот случай, условимся считать:
со + р = оэ, оо -j- оо = оо, если р — конечное число.
При соблюдении всех указанных условий функция р (Л) называется мерой. Таким образом, мера есть счетно-аддитивная функция, определенная на бо-релевской системе подмножеств. Следует, однако, помнить, что допускаются и бесконечные значения меры, т. е. для некоторыхЛ £ S может быть р (Л) = оо.
Нетрудно видеть, что если р (Й) есть конечное число (а не оо), то при любом Л € S число р (Л) будет конечным (это следует из равенства р (Л) + р (Л)= = р (Й)). В этом случае мера называется конечной. Примером конечной меры может служить мера Лебега, если в качестве системы S рассмотреть систему всех измеримых множеств па прямой, принадлежащих некоторому фиксированному отрезку Й, или систему всех измеримых множеств на плоскости, принадлежащих данному фиксированному прямоугольнику Й.
Рассмотрим случай конечной меры, т. е. положим р (й) = с, где с — конечное число. Тогда вместо р (Л) можно ввести новую меру р* (Л), определив ее равенством р* (Л) = - — Для меры р*(Л) будет выполняться условие: о
р* (Й)= 1.
Любая мера, удовлетворяющая такому условию, называется нормированной. Как показывает система аксиом А. И. Колмогорова, теория вероятностей есть, по сути дела, не что иное, как теория нормированных мер.
Изложенные выше построения свидетельствуют о том, что язык современной теории вероятностей есть язык теории множеств, или, выражаясь точнее, язык теории меры. Между тем прикладные задачи формулируются на другом, «практическом» языке (читатель может для сравнения еще раз прочитать примеры из § 1, где вообще нет упоминания о множествах). Поэтому для придания теоретиковероятностным рассуждениям полной строгости желателен перевод с одного языка на другой. В дальнейшем при разборе конкретных задач мы, как правило, не будем делать такого перевода. Однако в тех случаях, когда отсутствие должной строгости может затруднить понимание вопроса, мы полностью опишем вероятностную схему, отвечающую данной задаче: укажем пространство Й элементарных событий, систем S подмножеств, играющих роль событий, и определим во всем объеме функцию р (Л).
§ 4. КЛАССИЧЕСКИЙ СПОСОБ ПОДСЧЕТА ВЕРОЯТНОСТЕЙ
Рассмотрим тот частный случай, когда множество й — пространство элементарных событий — является конечным множеством. Пусть элементы этого множества (элементарные события) суть <о2, ..., сол. Согласуясь со схемой, изложенной в § 3, будем считать, что каждому подмножеству А множества й, т. е. каждому событию, сопоставлено неотрицательное число р (А), причем выполнены требования, сформулированные в аксиомах 1—3, В частности, из этих требований следует:
р(А1) + р(А2) + ...+р(Ал) = 1,	(1)
где А; есть одноэлементное подмножество {со;}, (г — 1, 2, .... п);
24
чтобы получить это равенство, нужно к соотношению + ^2 + ••• + Аг =
применить аксиомы 2 и 3.
Нетрудно видеть, что весь набор чисел р (Д), где А — любое подмножество множества Й, определяется, если считать известными числа
р (А А, р (А), р (Ап).	(2)
Действительно, если событие А есть сумма каких-то k элементарных событий, скажем Ait А 2, ..., Ак, то в силу аксиомы 2 мы должны иметь:
р (А) = р (At) + р (Аг) + ... + р (Аа), что и решает вопрос о нахождении числа р (Л).
Рассмотрим более подробно тот случай, когда все числа (2) равны между собой:
р (А) = р (Д2) = ... = р (Аа), другими словами, когда все элементарные события равновероятны. Из соотношения (1) в этом случае вытекает:
Р(А) = ~,	= р(А) = -.
п	п	п
Следовательно, если какое-то событие А представляется в виде суммы k равновероятных элементарных событий, то справедливо равенство:
р (А) =	+ — (k слагаемых)
п п	п
или просто
=	(3)
Формула (3) позволяет решать многие задачи на нахождение вероятностей. В соответствии со сказанным ее применяют в тех случаях, когда для данного опыта можно указать группу из конечного числа событий Alt Л2, ..., Аа со следующими свойствами:
1) в результате опыта наступает каждый раз одно и только одно из этих событий',
2) указанные события по условиям данного опыта равновероятны.
Если выполнены эти условия, то, как показывают наши рассуждения, для любого события А, представимого в виде суммы каких-то k из указанных выше событий, будет справедливо равенство (3).
Обычно события Ль А2, ..., Ап, обладающие свойствами 1) и 2), называют элементарными исходами данного опыта (иногда шансами или случаями). При этом те элементарные исходы, которые в сумме составляют А, называют благоприятными для А, остальные элементарные исходы -неблагоприятными для А. В этой терминологии формула (3) читается так: вероятность собы
25
тия А равна отношению числа элементарных исходов, благоприятных для А, к общему числу элементарных исходов.
Способ подсчета вероятностей, основанный на формуле (3), получил название классического. Этим способом пользовались ученые XVII века, стоявшие у истоков теории вероятностей, -французские математики Блез Паскаль и Пьер Ферма, а также голландский математик Христиан Гюйгенс. Разумеется, в то далекое от нашей эпохи время трудно было предвидеть роль понятия вероятности, разнообразие и серьезность будущих приложений теории вероятностей к -естествознанию и технике. Первоначальным материалом, на котором «отрабатывались» простейшие факты теории, были азартные игры, весьма распространенные в обществе XVI — XVII веков. Названные выше ученые производили, в частности, подсчет вероятностей, с которыми может появиться та или иная комбинация карт (в карточной игре) или та или иная комбинация костей (при игре в кости). В переписке между ними, посвященной разбору конкретных задач, формировались . первые понятия теории вероятностей. Неудивительно, что с тех пор задачи о бросании игральной кости, об извлечении карт из колоды, шаров из урны и т. п. стали традиционными для теории вероятностей. Заметим, что и по сей день эти задачи сохраняют свою роль как тренировочные упражнения, а в некоторых случаях как наглядные модели для более серьезных вероятностных схем.
Историческая справка
Блез Паскаль (1623—1662)
Блез Паскаль (1623—1662)—французский математик, физик, отчасти философ. С его именем связан целый ряд понятий и фактов, ставших в науке классическими. Всем известен закон Паскаля в физике; широкой известностью пользуется теорема Паскаля в геометрии, арифметический треугольник Паскаля в комбинаторике.
Пьер Ферма (1601—1669)—французский математик, юрист по профессии. Прославился открытиями в теории чисел. Широкой публике Ферма известен как автор знаменитой «проблемы Ферма», не решенной до конца и в настоящее время. Известен принцип Ферма распространения света, согласно которому свет движется из одной точки в другую по такому пути, который требует наименьшей затраты времени.
Христиан Гюйгенс (1629—1695) — голландский математик и физик. Ему принадлежат исследования по колебанию маятника (заметим, что Гюйгенс был конструктором первых маятниковых часов). Гюйгенс — основоположник волновой теории света. Им же сделан ряд открытий в астрономии (кольца Сатурна, спутники Юпитера).
Рассмотрим ряд примеров, иллюстрирующих классический способ подсчета вероятностей.
Пример 1. В урне находятся 10 шаров: 4 белых и 6 черных. Из урны наудачу извлекают один шар, Какова
26
вероятность того, что он окажется черным (событие Л)?
Решение. Этот пример уже рассматривался ранее (§ 1) в рамках интуитивного подхода к понятию вероятности. Разберем его снова.
Представим себе, что шары снабжены номерами 1, 2, ..., 10, причем черные шары получили номера 1, 2, ..., 6.
Обозначим через Лг, где i — 1, 2, ..., 10, следующее событие: извлечение шара с номером I.
Тогда события Ль Л2, ..., Л1о будут элементарными исходами данного опыта; действительно, при каждом осуществлении опыта наступает одно и только одно из них, а оговорка «наудачу» в формулировке задачи служит указанием на то, что все события Л; равновероятны.
Интересующему нас событию Л благоприятны исходы Л2, ..., Лв. Значит, в данном случае п = 10, k = 6 и р (Л) =
= —.А
10
Замечание 1. При решении задач на подсчет вероятностей классическим способом решающее значение имеет правильный выбор элементарных исходов. Обычно такой выбор в условии задачи прямо не оговаривается, его приходится «домысливать», исходя из сюжета задачи. Например, в только что решенном примере условие, что выбор извлекаемого шара производится
истолковать как равновероятность исходов Лъ Л2, ..., Л1о.
Замечание 2. Приведенное выше решение примера 1 отличается некоторой громоздкостью. При соответствующем навыке можно рассуждать короче, например, так: опыт с извлечением шаров из урны имеет 10 равновероятных исходов, из них событию Л благоприятны 6 исходов, значит, р (Л) = —. Или еще короче: из 10 возможных случаев событию Л благоприятны 6, следовательно, р (Л) = —.
10
Рассмотрим следующий пример.
Пример 2. Дважды бросается игральная кость. Какова вероятность того, что сумма очков при обоих бросаниях окажется больше 6 (событие Л)?
Пьер Ферма (1601-1665)
Христиан Гюйгенс (1629—1695)
«наудачу», естественно
27
Решение. Через Aif обозначим событие, состоящее в том, что при первом бросании выпало j очков, а при втором /. Тогда 36 событий
Л() Л12 ... Л1Я
Л21 Л 22	Л26
^61 ^82 •••
можно рассматривать как элементарные исходы опыта, заключающегося в двукратном бросании игральной кости. Действительно, при каждом осуществлении опыта наступает одно и только одно из этих событий, а соображения «равноправия» (между гранями игральной кости, а также между первым и вторым бросаниями) позволяют считать указанные события равновероятными. Интересующему нас событию Л благоприятны исходы Л34, Л43, Л35, Л53, Л44, Л45, ^54’ -^48’ ^55> й4 (остальные неблагоприятны); следовательно, k = 10. Отсюда имеем:
р (Л) = - = - = п 36	18
Практический смысл полученного результата состоит в том, что если опыт с двукратным бросанием игральной кости производить 5 большое число раз, то частота наступления Л будет близка к —;
иначе говоря, в среднем в пяти опытах из 18 будет наступать событие Л. А
Пример 3. Десять книг наудачу расставляются на книжной полке. Какова вероятность того, что три конкретные из этих десяти книг (скажем, учебники математики, физики и химии) окажутся стоящими рядом (событие Л)?
Решение. Элементарным исходом опыта теперь следует считать любую расстановку десяти книг на полке; слово «наудачу» служит указанием на то, что всевозможные расстановки равновероятны. Число всех расстановок равно, очевидно, 10! Благоприятными для события Л являются расстановки, в которых данные три книги стоят рядом. Подсчитаем число таких расстановок.
Для этого представим, что данные три книги объединены в одну связку; условимся эту связку рассматривать как одну «большую» книгу. Тогда можно считать, что имеется всего 8 книг. Их расстановка возможна 8! способами. Теперь следует учесть, что внутри «большой» книги данные три книги могут переставляться 3! способами. Отсюда следует, что число благоприятных расстановок будет 8! • 3!. Таким образом, р(Л) = -! ' -- —	~ р- А
Пример 4. В лотерее разыгрывается 100 билетов. Выигрыши падают на 10 билетов. Некто покупает три билета. Какова вероятность того, что хотя бы один из них выиграет?
28
Решение. В данном случае опыт заключается в выборе наугад трех лотерейных билетов. Перенумеруем все возможные тройки билетов. В качестве номеров будут фигурировать числа 1, 2, ...
™	100 . 99 . 98 „ л л
п, где п = Cf00 = --— -------. Пусть At — событие, заключающееся в покупке тройки с номером i. Тогда события Ait А2..Ап
можно рассматривать как элементарные исходы данного опыта.
Интересующее нас событие А состоит в том, что хотя бы один из выбранных билетов оказался выигрышным. Благоприятными для А являются такие группы из трех билетов, которые содержат хотя бы один выигрышный билет, неблагоприятными — такие, в которых ни на один билет не падает выигрыш. Число неблагоприятных групп равно Сдо, следовательно, число благоприятных есть k = Cwo — — Сзо- Отсюда
Р(Л) = - = 1 п
С3
Г’З с100
90 • 89 - 88
100 -99-98
(4)
Полученное выражение приближенно .равно:
1 —
(0,9)3 = 0,271 ... .
Впрочем, выражение (4) нетрудно подсчитать точно. Такой подсчет дает р (Л) = 0,2735 ... . ▲
Рассмотрим в связи с последним примером еще один пример.
Пример 5. В условиях лотереи примера 4 выяснить, какое минимальное число билетов нужно купить, чтобы вероятность получения хотя бы выигрыша оказалась большей, чем 0,5.
Решение. Пусть покупаются т билетов. Обозначим вероятность выигрыша хотя бы по одному из них через рт. Понятно, что с ростом т число рт будет возрастать. Наша цель — найти наименьшее значение т, при котором это число больше 0,5.
Рассуждая, как в примере 4, получим:
Л	Л
Рт v ЮоД 99/ \
10
100 - (т — 1)
Следовательно, /	10 \т
При т — 6 правая часть больше 0,5 (проверьте!), следовательно, искомое значение т находится среди чисел 1, 2, 3, 4, 5, 6.
Непосредственным подсчетом по формуле (5) находим: Pi — 0,34 ...,	— 0,43 ... .
Оба написанных числа меньше 0,5. Таким образом, искомое значение т есть 6. А
29
§ 5.	ГЕОМЕТРИЧЕСКИЕ ВЕРОЯТНОСТИ
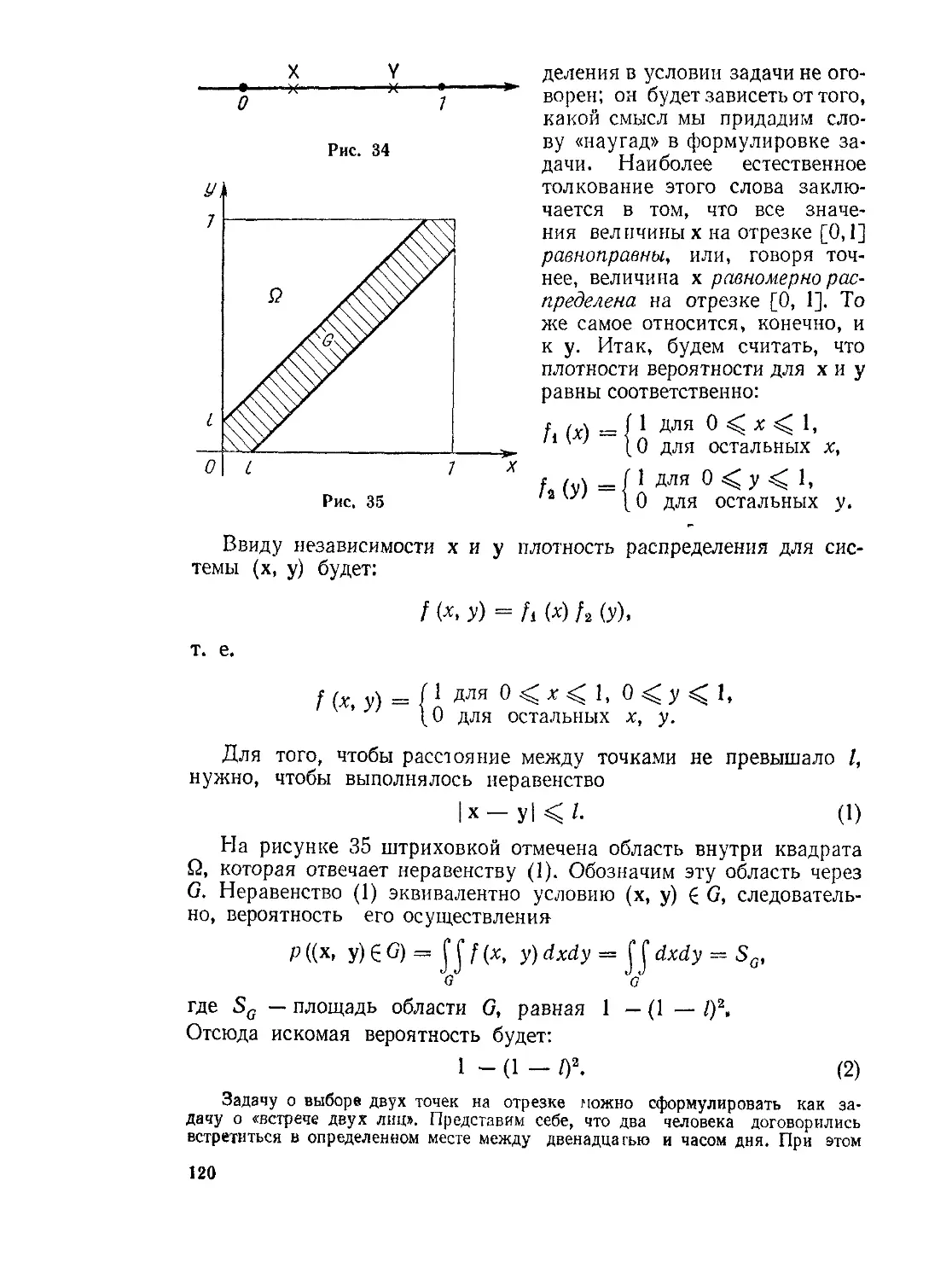
В § 3 мы ознакомили читателя с системой аксиом теории вероятностей. Конкретные реализации этой системы, возникающие при решении практических задач, могут быть самыми разными; например, в классической схеме рассматривается реализация, в которой пространство Q элементарных событий есть множество из конечного числа п элементов, причем вероятности этих элементов одинаковы. Рассмотрим теперь еще один интересный класс реализаций. В каждой из них пространство Q является бесконечным. По причинам, которые будут объяснены ниже, эти реализации называют геометрическими', соответственно этому вероятности р (Л) различных событий в таких реализациях называют геометрическими вероятностями.
Пусть Q — произвольное множество конечной лебеговой меры на прямой или в плоскости (более общо—в «-мерном арифметическом пространстве /?”). Условимся называть событиями всевозможные измеримые подмножества в Q. Каждому событию поставим в соответствие неотрицательное число
где р (А) обозначает (лебегову) меру множества А.
Все аксиомы — как для событий, так и для вероятностей, см. пп. 2° и 3° § 3 — будут в этом случае выполнены, и мы получим некоторую модель системы аксиом А. Н. Колмогорова. Особенностью этой модели является, конечно, ее геометрический характер; при этом существенно, что вероятность р (А) определяется не конкретной формой подмножества А, а единственно мерой А.
К указанной выше геометрической схеме сводится довольно большой круг задач. В каждой из них элементарное событие можно интерпретировать как случайный выбор точки в некоторой области Й. При этом условия задачи должны быть такими, чтобы все точки в й можно было считать «равноправными» (в смысле возможности их выбора).
В качестве примера рассмотрим следующую задачу.
Задача. Стержень длиной I произвольным образом ломают на три части. Какова вероятность того, что из этих частей можно составить треугольник?
Решение. Обозначим через х и у длины концевых частей стержня (рис. 6); длина третьей части будет, очевидно, I - (х + у). Возможные значения величин х и у связаны условиями:
О «С х I, О < у < I, х + у I.
Система написанных неравенств определяет на координатной плоскости хОу область Q, покрытую на рисунке 7 косой штриховкой. Любой разлом стержня равнозначен выбору точки в области Q.
30
Для того чтобы из трех частей стержня можно было сложить треугольник, необходимо и достаточно выполнение условий:
X < I — X,
У < I ~ У,	(2)
I - (х 4- у) < х + у
(мы записали, что каждая сторона треугольника должна быть меньше суммы двух других). Неравенства (2) выделяют из Q область А, зачерченную на рисунке двойной штриховкой.
Будем считать оправданным применение формулы (1) (основанием для этого служит «произвольность» разлома стержня). В этом случае можно записать:
р (д\ — площадь А = 2 А площадь Q 4
X Z-(X+Y) Y
Рис. 6
Глава 2.
КОМБИНАТОРИКА
В этой главе рассматриваются задачи комбинаторного характера. В каждой из них требуется подсчитать число различных вариантов, ответить на вопрос «сколько?» или «сколькими способами?». Например, интересно узнать, сколькими способами можно рассадить п людей в аудитории, где имеется п мест, сколько различных последовательно-параллельных соединений можно составить из п электрических ламп, каким количеством способов можно набрать на п вступительных экзаменах сумму баллов не ниже k, сколькими способами выпуклый n-угольник можно разбить на треугольники с помощью диагоналей.
Комбинаторика имеет весьма непосредственное отношение к теории вероятностей. Близость этих разделов обусловлена прежде всего классическим способом подсчета вероятностей. Формула
рИ) = -, п
где п — число всех элементарных исходов опыта, a k — число исходов, благоприятных для А, сводит вычисление р (А) к нахождению двух чисел п и k\ последняя задача во многих случаях носит явно комбинаторный характер. Кроме теории вероятностей, комбинаторика используется в теории вычислительных машин, теории автоматов, в некоторых задачах экономики, биологии и т. д.
§ 6.	ПРАВИЛА СУММЫ И ПРОИЗВЕДЕНИЯ
Решение многих комбинаторных задач основывается на двух фундаментальных правилах, называемых соответственно правилами суммы и произведения.
1°. Правило суммы. Правило суммы выражает вполне очевидный факт: если X и Y — два непересекающихся конечных множества, то число элементов, содержащихся в объединении этих множеств, равно сумме чисел элементов в каждом из них.
Если мы условимся число элементов конечного множества X обозначать |Х |, то правило суммы запишется следующим образом:
|Х + К| = |Х| + |К|,
если X и К не имеют общих элементов.
Обычно правило суммы формулируют несколько иначе: если некоторый объект х можно выбрать п способами, а объект у — т
32
способами, причем любой способ выбора объекта х отличен от любого способа выбора у, то выбор «х или у» можно сделать п + т способами.
Столь же очевидным является и обобщение правила суммы на любое число k множеств: если Х4, Х2, .... ХА — какие-то попарно непересекающиеся конечные множества, то
|Х, + Х2 + ... + ХА| = PGI + |Х2| + ... + |ХЙ|.
Задачи, которые можно решить применением одного лишь правила суммы, по большей части тривиальны. Обычно правило суммы используют вместе с правилом произведения.
2°. Правило произведения. Будем рассматривать последовательности данной длины k:
(хь х2, .... хД,
состоящие из некоторых элементов хь х2, .... xk (не обязательно различных). Условимся для краткости называть такие последовательности строками. Две строки (хь х2, .... хД и (уь у2, ..., уД будем считать различными в том и только в том случае, если хотя бы для одного номера i (из совокупности 1, 2, .... /г) элемент х, отличен от уг.
Правило произведения может быть сформулировано следующим образом.
Пусть элемент Xi может быть выбран П\ способами; при каждом выборе Х[ элемент х2 может быть выбран п2 способами; при каждом выборе пары Х\,х2 элемент х3 может быть выбран п3 способами и т. д.; наконец, при каждом выборе xlt х2, ..., хЛ_1 элемент xk может быть выбран nk способами. Тогда число различных строк (xi, Хг, ..., xk) равно произведению п^ ... nk.
Докажем это правило, используя индукцию по k.
Пусть k — 2. Обозначим через пь аг, .... ап, различные значения для Xi. Среди строк (хи х2) имеется ровно п2 строк, начинающихся с щ (т. е. строк вида (щ, х2)), ровно п2 строк, начинающихся с а2, и т, д. Следовательно, число всех строк (хь х2) будет:
П2		~ П1П2-
раз
Предположим теперь, что правило произведения справедливо для строк длины докажем тогда, что оно будет верно и для строк длины k + 1.
Любую строку {Xi, ...................... хк, хА+1)	(1)
можно рассматривать как строку из двух объектов: строки (xt, х2, ..., хД и элемента хА+1. Первый объект, по предположению индукции, может быть выбран прг2 ... nk способами; при любом из этих способов элемент хй+1 по условию может быть выбран пА+) способами. Применяя уже доказанное правило для строк длины 2,
2 А. С. Солодовников
33
находим, что число различных строк (1) будет
(/2^2... n^-nk^==nji2... /гА+1-И
Пример 1. Сколько различных «целых» прямоугольников (т. е. прямоугольников, составленных из целых клеток) имеется на шахматной доске?
Решение. На рисунке 8 изображен один из «целых» прямоугольников. Проектируя его
на указанную на том же рисунке ось Ох, получим «целый» отрезок (т. е. отрезок с целочисленными концами), содержащийся в [О, 8]; аналогично проекция прямоугольника на ось Оу есть «целый» отрезок из [0, 8]. Таким образом, каждому «целому» прямоугольнику отвечает строка (а, Р), где а — «целый» отрезок оси Ох, а р — «целый» отрезок оси Оу, причем каждый из отрезков содержится в [0, 8]. Обратно, любая строка (а, Р), где а и (5 — «целые» отрезки на осях (оба отрезка из [0, 8]), определяет «целый» прямоугольник. Следовательно, «целых» прямоугольников имеется столько же, сколько строк (а, Р) указанного вида. Но по правилу произведения число строк (а, Р) должно равняться N • N, где N есть число «целых» отрезков числовой оси, содержащихся в [0, 8]. Предоставляем читателю проверить, что N = = 84-7 + 6 + 5 + 4 4-34-2+1= 36 (имеется ровно восемь
«целых» отрезков с левым концом 0, семь отрезков с левым концом 1 и т. д.). Следовательно, искомое число «целых» прямоугольников равно 36 • 36 = 1296.А
Пример 2. Сколько различных подмножеств имеет множество А — {at, а2,	а„), состоящее из п эле-
ментов?
Решение. Пусть X — подмножество в А, Сопоставим этому подмножеству строку (хь хг, .... хп) длиной п — нечто вроде «шифра» подмножества X. А именно: положим хл равным 1 или 0, смотря по тому, входит или не входит элемент щ в подмножество X; положим х2 равным 1 или 0, смотря по тому, входит или не входит а2 в X, и так далее. В результате каждому подмножеству X будет соответствовать строка длиной п, состоящая из единиц и нулей. И обратно, любая строка длиной п, состоящая из единиц и нулей, однозначно определяет некоторое подмножество X (например, в случае п = 5 строка (0, 0, 0, 1, 1) определяет подмножество X = = {а4, а6}). Но число различных строк по правилу произведения равно 2 -2 •••2 = 2". Значит, число различных подмножеств множества А будет также 2", А
34
Пример 3. Сколько можно составить пятизначных чисел так, чтобы любые две соседние цифры числа были различны?
Решение. Пятизначному числу с цифрами xit xt, х3, х^, х5 можно сопоставить строку (хь х2, х3, х4, х5). При этом выбор цифры Xi возможен 9 способами; если xt выбрана, то для выбора х2 имеется тоже 9 возможностей (хг может быть любой из цифр 0, 1, 2, .... 9, отличной от X(); после выбора xt, х2 для х3 имеется снова 9 возможностей и т. д. Применяя правило произведения, находим, что искомое количество 'чисел есть 9"9-9-9-9 = 95. А
§ 7.	РАЗМЕЩЕНИЯ И ПЕРЕСТАНОВКИ
1°. Размещения с повторениями. При использовании правила произведения удобно считать, что элементы xit хг, .... хк, служащие для образования строки
(Х1, х2, .... хЛ),
берутся из одного и того же фиксированного множества X. В этом случае говорят о строках длиной k, составленных из элементов множества X. Например, числа натурального ряда (точнее, их десятичные записи) можно рассматривать как строки, составленные из элементов множества X = {О, I, 2,	9), слова русского языка
суть некоторые строки, составленные из элементов множества X = = {а, б, в, я) (множества букв русского алфавита). Вернувшись к примерам из пункта 2° предыдущего параграфа, читатель может убедиться, что и там мы имели дело со строками, составленными из элементов некоторого множества X (в примере 1 таким множеством было множество «целых» отрезков из [0, 8], в примере 2 — множество {0, 1’}, в примере 3 — множество {0, 1, 2, ..., 9}).
Пусть множество X состоит из п элементов; в дальнейшем такие множества будем иногда называть п-членными. Любая строка длиной k, составленная из элементов множества X, называется размещением с повторениями из п элементов по k. Словосочетание «с повторениями» подчеркивает тот факт, что в строке (хь х2, .... хА), где xlt х2, .... xk принадлежат X, некоторые элементы могут повторяться. Например, слово «папа» есть размещение с повторениями из двух элементов (п и а) по четыре.
Число всех размещений с повторениями из п элементов по k зависит, очевидно, только от л и А (а не от природы множества X). Обозначим это число А*. Из правила произведения следует, что
Ап — п- п •... • п = пк,
k pai
Пример 1. Сколькими способами k пассажиров могут распределиться по п вагонам, если для каждого пассажира существенным является только номер вагона, а не занимаемое им в вагоне место?
Решение. Перенумеруем всех пассажиров (т. е. условимся, кого из них мы считаем первым, кого вторым и т. д.). Пусть Xj — 2*	35
номер вагона, выбранного первым пассажиром, х2 — номер вагона второго пассажира и т. д. Строка (хх, х2, .... хА) полностью характеризует распределение пассажиров по вагонам. Каждое из чисел xt, х2...xk может принимать любое це-
лое значение от 1 до п. Таким образом, различных распределений по вагонам бу-
дет столько, сколько строк длиной k можно составить из элементов множества X — {1, 2, .... п}. Следовательно, их будет
П р и м е р 2, Из пункта А в пункт В ведут два шоссе, пере-' секаемые пятью поперечными дорогами (рис. 9). Сколькими способами можно проехать из А в В,
не проезжая дважды одно и то же место?
Решение. Применительно к рисунку 9 условимся одно шоссе называть «верхним», другое— «нижним». Поперечные дороги разбивают всю местность между А и В на 6 зон. Чтобы задать определенный маршрут движения от Л к В, нужно для каждой зоны выбрать одно из двух шоссе. Следовательно, любой маршрут задается строкой (хх, х2, х3, х4, х5, хв) длиной 6, составленной из элементов множества X = {в, н) (для краткости мы пишем «в» и «н» вместо «верхний» и «нижний»). На рисунке 9 жирной линией изображен один из маршрутов; ему отвечает строка (в, в, н, в, н, н). Так как имеется
взаимно-однозначное соответствие между множеством всех маршрутов и множеством строк длиной 6, то число различных маршрутов будет 26.А
2°. Размещения без повторений. Перестановки. Часто возникает необходимость в подсчете числа строк (той или другой длины), составленных из элементов данного множества X и подчиненных некоторым дополнительным ограничениям. Вот одна из подобных
задач.
Пусть множество X состоит из п элементов. Рассмотрим строки (хх, х2, .... хА) длиной k, удовлетворяющие следующему условию: все элементы хх, х2,.... xk различны. Разумеется, такие строки могут существовать только при k п. Любая строка такого рода называется размещением без повторений из п элементов по k или просто размещением из п элементов по k. Число всех размещений из п элементов по k обозначается А*.
Чтобы найти число заметим, что для выбора элемента хх имеется п возможностей; если хх выбран, то для х2 имеется п — 1 возможностей; если выбраны хх и х2, то для х3 имеется п — 2 возможностей и т. д. Пользуясь правилом произведения, находим отсюда, что
Л*=„. (/:-!). (п-2)... («-(£-!)).	(1)
Особо важным является частный случай, когда k = п, т. е. когда в строке участвуют все элементы из X (притом каждый по одному разу). Строки без повторений, составленные из всех элемен
36
тов n-членного множества X, называются, как известно, перестановками из п элементов. Пользуясь формулой (1), находим, что число различных перестановок из п элементов равно:
п • (п — 1) • (п — 2) ... 2 • 1 = п\
Добавим к этому равенство
О! = 1, которое принимают по определению.
§ 8.	СОЧЕТАНИЯ. БИНОМ НЬЮТОНА
1°. Числа Скп и их свойства. Пусть X — множество, состоящее из п элементов. Любое подмножество Y множества X, содержащее k элементов, называется сочетанием k элементов из п; при этом, разумеется, k п.
Число различных сочетаний k элементов из п обозначается С„. Одной из важнейших формул комбинаторики является следующая формула для числа С„:
п ~ k\ (п -k)\ '
Ее можно записать после очевидных сокращений следующим образом:
rk __ л (п — 1) (п — 2)... (л — (fe — 1)) П~	k\
В частности,
это вполне согласуется с тем, что в множестве X имеется только одно подмножество из 0 элементов — пустое подмножество.
Приведем доказательство формулы (2). Пусть Y — какое-либо подмножество множества X, содержащее k элементов. Составив всевозможные перестановки из этих элементов, получим kl различных строк длиной k. Если указанную операцию проделать с каждым подмножеством Y, содержащим k элементов, то получим всего С„ • kl различных строк длиной k. Но очевидно, что таким путем должны получиться все без исключения строки длиной k без повторений, которые можно составить из элементов множества X. Поскольку число таких строк равно А*, то имеем соотношение С„-kl =
.	k
= An, из которого следует Сп = _2L, т. е. формула (2). И kl
Числа Сп обладают рядом замечательных свойств. Эти свойства в конечном счете выражают различные соотношения между подмножествами данного множества X. Их можно доказывать непосредственно, исходя из формулы (1), но более содержательными являются доказательства, опирающиеся на теоретико-множественные рассуждения.
37
1)	Справедлива формула
С* = Спп~\	(3)
вытекающая из (1) очевидным образом. Смысл формулы (3) состоит в том, что имеется взаимно-однозначное соответствие между множеством всех /г-членных подмножеств из X и множеством всех (п — — й)-членных подмножеств из X: чтобы установить это соответствие, достаточно каждому /г-членному подмножеству Y сопоставить его дополнение в множестве X.
2)	Справедлива формула
С,°, + С\ + С* + ... + Спп = 2я.	(4)
Поскольку сумма, стоящая в левой части, выражает собой число всех подмножеств множества X (С° есть число 0-членных подмножеств, С\ — число 1-членных подмножеств и т. д.), то для доказательства формулы (4) достаточно сослаться на уже известный читателю факт (см. пример 2 на с. 34): число различных подмножеств n-членного множества X равно 2".
3)	При любом k, 1 k п, справедливо равенство
ckn = cLi +	.	(5)
Это равенство нетрудно получить с помощью формулы (1). В самом деле,
I Qk = (п ~ О1 । (п — 1)1	_ (п — 1)1 fe .
n_i-t- n-i -	_ 1)( (n _ -г	- k\(n_ky +"
=	{k + п _ k} =-----я]----= е
(л — ky k'.(n — k)l	’
Вывод формулы (5), основанный на теоретико-множественных соображениях, мы предоставляем провести читателю. Укажем, что для этого следует выделить какой-то определенный элемент а С X и все fe-членные подмножества разбить на две группы: подмножества, содержащий^, и подмножества, не содержащие а.
4)	Рассмотрим так называемый арифметический треугольник Паскаля.
Равенство (5) позволяет вычислять значения С„, если известны Сл-i и C£z}. Иными словами, с помощью этого равенства можно последовательно вычислять С„ сначала при п = I, затем при п = 2, п = 3 и т, д. Вычисления удобно записывать в виде треугольной таблицы:
1
1 1
1	2	1
13	3	1
1	4	6	4	1
1	5 10 10 5	1
88
В (п + 1) строке которой по порядку стоят числа С®, С„, ..., С*. При этом крайние числа строки, т. е. С° и С", равны 1, а остальные числа находятся по формуле (5). Поскольку C*Zi и C„_i располагаются в этой таблице строкой выше, чем число С£, и находятся в этой строке слева и справа от него, то для получения числа С„ надо сложить находящиеся слева и справа от него числа предыдущей строки.' Например, число 10 в шестой строке мы получаем, сложив числа 4 и 6 пятой строки.
Указанная таблица и есть как раз «арифметический треугольник Паскаля».
5) Задача. Пусть п и k — два целых числа, причем п > 0, k 0. Сколько существует различных строк длиной п, состоящих из букв а и Ь, с условием, что в каждой из этих строк буква а встречается k раз (и, следовательно, буква b— п — k раз)?
Решение. Пусть (х1( х2, хя) — одна из строк указанного вида. Рассмотрим все номера i, такие, что xz = а. Совокупность таких номеров является подмножеством множества М — {1, 2, ... .... п}, состоящим из k элементов. Обратно, если У — любое подмножество множества М, состоящее из k элементов, то, положив X; = а для всех i € У и х{ = b для всех i € У, получим строку (х,, х2, ..., хл) требуемого вида. Значит, число указанных в задаче строк равно числу fe-элементных подмножеств в n-элементном множестве М, т. е. равно числу С„. ▲
2°. Бином Ньютона. Из школьного курса читателю известны формулы:
(а + b)2 = а2 + 2аЬ + Ь2, (а + Ь)3 = а3 4- За2Ь + ЗаЬ2 + Ь3.
Обобщением этих формул является следующая формула, называемая обычно формулой бинома Ньютона'.
(а + Ь)п = С°па°Ьп +	+ С&Ь*-2 + ... + С^'а^Ь +
+ С"апЬ°.	(6)
В этой формуле п может быть любым натуральным числом.
Вывод формулы (6) несложен. Прежде всего запишем:
(а + Ь)п = (а + Ь) (а + Ь) ... (а + Ь),	(7)
где число перемножаемых скобок равно п. Из обычного правила умножения суммы на сумму вытекает, что выражение (7) равно сумме всевозможных произведений, которые можно составить следующим образом: любое слагаемое первой из сумм а + b умножается на любое слагаемое второй суммы а + Ь, на любое слагаемое третьей суммы и т. д. Например, при п = 3 имеем:
39
(a + b) (a + b) (a + b) = aaa + aab + aba + abb -f-+ baa + bab + bba + bbb.
Из сказанного ясно, что слагаемым в выражении для (а + Ь)п соответствуют (взаимно-однозначно) строки длиной п, составленные из букв а и Ь. Среди слагаемых будут встречаться подобные члены; очевидно, что таким членам соответствуют строки, содержащие одинаковое количество букв а. Но число строк, содержащих ровно k раз букву а, равно С„ (см. задачу в конце предыдущего пункта 1°). Значит, сумма всех членов, содержащих букву а множителем ровно k раз, равна	Поскольку k может принимать значе-
ния 0, 1, 2, .... п — 1, п, то из нашего рассуждения следует формула (6).
Заметим, что (6) можно записать короче:
(а + b)n =
Хотя формулу (6) называют именем Ньютона, в действительности она была открыта еще до Ньютона (например, ее знал Паскаль). Заслуга Ньютона состоит в том, что он нашел обобщение этой формулы на случай нецелых показателей.
Числа С„, Сп, ..., С", входящие в формулу (6), принято называть биномиальными коэффициентами. Из формулы (6) можно получить целый ряд свойств этих коэффициентов. Например, полагая а — 1, b = 1, получим: 2я = С„ + С„ + С„ + ... + С„, т. е. формулу (4). Если положить а = 1, b — —1, то будем иметь:
О = С° - С1п + С2п - Сп + ... + (-1)«С" или
С п+ Сп + Сп = Сп + Сп + Сп + ... .
§ 9. РАЗМЕЩЕНИЯ ДАННОГО СОСТАВА. ПОЛИНОМИАЛЬНАЯ ФОРМУЛА
1°. Состав строки. Размещения данного состава. Строки (а, Ь, а, а, Ь) и (а, а, Ь, Ь, а) различны, но имеют один и тот же «состав» — в каждую из них входят три буквы а и две буквы Ь. Уточним понятие состава строки.
Пусть а — строка длиной k, составленная из элементов п-член-ного множества X. Перенумеруем элементы этого множества, т. е. положим X — {аг, а2, .... ап}. Тогда каждому номеру i из совокупности 1, 2....п будет соответствовать число kh показывающее,
сколько раз элемент аг встречается в строке а. Выписывая по порядку эти числа, получаем новую строку (klt k2, .... kn), которую и называют составом строки а. Например, если X — {аг, а2, а3, с4} и а = (сц, а3,	а4, а3, aj, то строка а имеет состав (3, 0, 2, 1).
Две строки, имеющие один и тот же состав, могут отличаться друг от друга лишь порядком элементов. Из называют размещениями (с повторениями) данного состава.
40
Решим следующую комбинаторную задачу: найти число размещений, имеющих данный состав (An k2, ..., kn).
Способ решения поясним на примере. Пусть требуется найти число размещений, имеющих состав (3, 2, 2). Проще говоря, нужно найти число строк длиной 7 из букв а, а, а, Ь, Ь, с, с.
Представим себе для этого полку из 7 пронумерованных ящиков
1	2	3	4	5	6	7
Будем вписывать в ящики указанные 7 букв.
Три ящика для букв а, а, а можно выбрать Су способами. Рассмотрим один определенный выбор, скажем:
а	а а
1	2	3	4	5	6	7
Обозначим этот выбор хг. В оставшейся (свободной) части полки два ящика для букв b, b можно выбрать С% способами. Рассмотрим один определенный выбор, скажем:
b а Ь	а а
1	2	3	4	5	6	7 ~
Обозначим его х2. В оставшейся части полки два ящика для букв с, с можно выбрать Cf = 1 способами. Обозначим этот (единственный) выбор х3.
Всего, таким образом, нам придется сделать 3 последовательных выбора %!, х2, х3, что будет означать задание строки (xv х2, х3). В этой строке, как уже говорилось, элемент хх может быть выбран Су способами; если xt выбран, то х2 можно выбрать С% способами; если выбраны х1г х2, то х3 можно выбрать С2 способами. Согласно правилу произведения, число всех требуемых строк будет равно:
/->3	/~>2	/>2
Су • 1>4 • С2,
или	7!	. 41	. 2!
314! ' 212! ’ 2’0! '
После очевидных сокращений получаем число
Совершенно аналогично разбирается общий случай. Количество A (klt k2, .... kn) размещений с повторениями, имеющих состав (kv k2...kn), выражается формулой
А(^, k2.... k„) =	(1)
2 n’ k^....kn\
4!
Например, буквы слова «колос» можно размещать  *	-
способами. При этом будут получаться как осмысленные слова («колос», «сокол»), так и бессмысленные буквосочетания, например «лксоо».
2°. Полиномиальная формула. Рассмотрим выражение
(«1 + й2 + ••• + йл)*	(2)
или в более подробной записи
(аг 4- й2 + ... + ап) («1 + «2 + ••• + йл) (Й1 а2 +••• ... + ап)	(3)
(число перемножаемых сумм равно k). Из правила умножения суммы на сумму вытекает, что (3) будет равно сумме всевозможных произведений, составленных следующим образом: любое слагаемое первой из сумм (йх + а2 + ••• + йл) умножается на любое слагаемое второй суммы (йг + й2 + ... + йя), на любое слагаемое третьей суммы и т. д. Например,
(йх + Й2 + й3) (йх + й2 4~ й3) =
= a^Ctt + ЙХЙ2 + йхй3 + Й2ЙХ + й2й2 + й2й3 + й3йх + + й3й2 + й3й3.
Из сказанного ясно, что слагаемым в выражении для (йх + й2 + ... ... + й„)* соответствуют (взаимно-однозначно) строки длиной k, составленные из элементов множества X = {йх, й2, • ••, йл}. Среди слагаемых будут встречаться подобные члены; очевидно, что таким членам соответствуют строки одинакового состава. Но число строк, имеющих состав (klt k2, .... kn), мы обозначили выше A (klt k2, ... .... kn). Отсюда вытекает равенство
(йх + а2 + ... + йл)* = ZA(klt k2, ..., Йл)п?*й2а ••• йд", где суммирование распространяется на все составы, т. е. на все строки (klt k2, ..., kn), такие, что kY + k2 + ••• + kn = k. Принимая во внимание (1), приходим к формуле
(йх + й2 + + йл)а = V *’	 а*' а2г ...а„п.	(4)
... йл1
Подчеркнем еще раз, что суммирование в правой части производится по всевозможным наборам целых неотрицательных чисел ku k2, ... .... kn, таких, что ki + k2 + ... + kn = k.
Формулу (4) часто называют полиномиальной (в правой части стоит некоторый полином от йх, й2, .... йл).
Частным случаем формулы (4) является формула
(й + &)* = V1—~-ак< bk> (где kL + k2 = k), fk kl
которая лишь формой записи отличается от формулы бинома Ньютона.
3°. Некоторые дополнительные замечания о решении комбинаторных задач. Мы разобрали лишь основные схемы решения комбинаторных задач. При решении конкретной комбинаторной задачи целесообразно с самого начала выяснить, не
42
решается ли она непосредственным применением правил суммы и произведения. Если такое решение окажется затруднительным, то следует продумать математическую схему решаемой задачи, выяснив, идет ли в ней речь о составлении подмножеств или строк, какие при этом налагаются ограничения, допустимы или нет повторения и т. д.
Иногда для решения задачи может оказаться полезным составить для искомых чисел рекуррентное соотношение. Остановимся на этом несколько подробнее.
Рекуррентным соотношением для последовательности чисел с1г с2, с3, ... называется соотношение вида
f (сп> сл+1> •••> сл+д) = 0	(5)
(р — фиксированное, п — любое), связывающее между собой р + 1 соседних членов последовательности. Рекуррентное соотношение позволяет находить очередной член последовательности, если известны несколько предшествующих членов (из (5) можно найти сп+р, если известны сп, сп+1, .... cn+p^j). Поэтому обычно последовательность с1( с2, с3, ... считается заданной, если для нее указано рекуррентное соотношение типа (5) и в дополнение к нему числа clt сг, .... ср; дальнейшие члены последовательности могут быть найдены (в принципе) с помощью соотношения (5).
Рассмотрим пример. Пусть требуется найти число строк, которые можно составить из п нулей и единиц с условием, чтобы никакие две единицы не стояли подряд. Обозначим искомое число через сп. Пусть п > 2. Любая строка, удовлетворяющая поставленному условию, должна оканчиваться либо нулем, либо комбинацией 01. В первом случае впереди нуля может стоять любая строка длиной п — 1, составленная с тем же условием; во втором случае впереди комбинации 01 может стоять любая строка длиной п — 2 с тем же условием. Отсюда следует, что сп —	Это соотношение вместе с равенствами = 2,
с2 = 3 задает искомую последовательность чисел сп. В частности, с3 == 5, с4 = 8, с5 = 13, св = 21 и т. д.
§ 10.	ПРИМЕНЕНИЕ КОМБИНАТОРИКИ К ПОДСЧЕТУ ВЕРОЯТНОСТЕЙ
Многие задачи на подсчет вероятностей можно свести к так называемой схеме случайного выбора. Рассмотрим два основных варианта этой схемы: выбор с возвращением и выбор без возвращения.
1)	Выбор с возвращением. Представим себе, что в некотором ящике собрано п различных предметов alt а2, ап. Из ящика наугад извлекается один из предметов, регистрируется, затем кладется обратно в ящик. Если осуществить k таких извлечений, то получим некоторую строку длиной k, составленную из элементов множества X = {alt а2, .... ап}. Она называется выборкой объемом k из множества X. Число различных выборок объема k согласно § 7, 1° равно nk.
Описанная процедура носит название случайного выбора с возвращением. Слово «случайный» в этом названии означает нечто большее, нежели просто тот факт, что состав выборки предсказать заранее невозможно. Мы условимся вкладывать в это слово следующий смысл: все nh выборок равновероятны. Другими словами, вероятность появления любой конкретной выборки равна —.
К схеме случайного выбора с возвращением можно свести большое число опытов. Например, бросание монеты можно представить
43
как случайный выбор одного элемента из множества X = {герб, цифра}. Вместо двукратного бросания игральной кости можно рассматривать случайный выбор с возвращением двух элементов из множества X = {1, 2, 3, 4, 5, 6}. Выяснение дней рождения k случайных прохожих можно заменить случайным выбором с возвращением k элементов из множества X = {1, 2, 3,	365} и т. д.
2)	Выбор без возвращения. В этом случае выбранный предмет не кладется обратно в ящик и следующее извлечение производится из меньшего числа предметов. После k извлечений получаем строку длиной k без повторений. Число таких строк, как было показано в § 7, 2°, равно:
Akn = п (п — 1) (п — 2) ... (n - (k - 1)).
Случайный характер выбора понимается, как и выше, в том смысле, что все выборки данной длины имеют одну и ту же вероятность.
1
Последняя равна ~тъ.
А п
Пример 1. Пусть из совокупности п предметов извлекаются с возвращением k предметов. Найти вероятность того, что все предметы, составляющие выборку, окажутся различными (событие S).
В данном случае число всех элементарных исходов опыта равно nk, а число исходов, благоприятных для события S, равно Akn. Отсюда искомая вероятность
п/сх-	п(д-1)(п-2).. (п-(й-1))
Р W -	~к	• А U}
Остановимся на одном частном случае разобранного выше примера — этот частный случай известен как задача о днях рождения.
В кинозале собралось k человек. Какова вероятность того, что хотя бы у двух из собравшихся дни рождения совпадают (событие Т)?
Как уже отмечалось, выяснение дней рождения у k случайно собравшихся людей можно заменить случайным выбором с возвращением k элементов из множества X = {1, 2, ..., 365}. Нам необходимо найти вероятность события Т — совпадения дней рождения у каких-либо двух из собравшихся. Событие, противоположное Т, заключается в том, что все дни рождения различны — выше это событие было обозначено S. Формула (1) при п = 365 дает:
365 • 364 ... (365 — (fe— 1))
365* откуда следует:
.	365 • 364... (365 - (k -1))	.
₽(Г,“1----------------S'»----------'Ж (2)
Найденное нами выражение для р (Т) зависит, естественно, от k — числа собравшихся в зале. Подсчитав р (Т) для различных значений k, можно получить такую таблицу:
44
k	5	10	22	23	30	60
р(Т)	0,027	0,117	0,476	0,507	0,706	0,994
(все знаки после запятой, начиная с четвертого, отброшены). Из нее видно, что если в зале находятся всего лишь 23 человека, то уже и тогда имеется более половины шансов на то, что по крайней мере у двоих из них дни рождения совпадают!
Пример 2, Монету бросают 10 раз. Какова вероятность того, что герб при этом выпадет ровно 3 раза (и, следовательно, цифра выпадет 7 раз)?
Решение. Десятикратное бросание монеты можно рассматривать как составление строки длиной 10 (с повторениями) из элементов множества X — {г, ц}. Число всех строк такого рода равно 210. Строк, в которых элемент «г» встречается 3 раза, а «ц» входит 7 раз, будет Сю. Отсюда искомая вероятность
— Ci° _ 10,9,8 _ 15 А
Р ~ 2« “ 3! 210	“ 128’
Пример 3. Игральную кость бросают 10 раз. Какова вероятность, что при этом грани 1, 2, 3, 4, 5, 6 выпадут соответственно 2, 3, 1, 1, 1,2 раза (событие Л)?
Решение. Число всех строк длиной 10 из элементов множест-ва X = {1, 2, 3, 4, 5, 6} равно 610. Благоприятными для А будут строки, в которых элементы 1, 2, 3, 4, 5, 6 встречаются соответственно 2, 3, 1, 1, 1,2 раза, т. е. строки, имеющие состав (2, 3, 1, 1, 1, 2). Число таких строк, согласно § 9, 1°, равно:
(L+3 + 1 4-1 + 1.+ 2)! __ _10[ __ 2 . з . 5.7.8.9.10.
2131ШШ2!	4-6
Отсюда
р (Л) = -2’3'.1,7,8'.9‘ 10 = — = 0,002 ... ▲ ' ’	б10	6’
Пример 4. Слово «карета», составленное из букв-кубиков, рассыпано на отдельные буквы, которые затем сложены в коробке. Из коробки наугад извлекают буквы одну за другой. Какова вероятность получить при таком извлечении слово «ракета»?
Решение. Здесь нет схемы случайного выбора в прежнем понимании, так как буквы, сложенные в коробке, не все различны (три одинаковые буквы «а»). Представим себе, что одинаковые буквы (в данном случае а, а, а) индивидуализированы с помощью знаков 1, 2, 3 (превратились в ait а2, а3). Тогда число всех возможных выборок без возвращения будет 6'5-4«3«2-1 = 6!. Среди них благоприятными для слова «ракета» будут 3! выборок (число перестановок букв at, а2, аа). Следовательно,
45
р(Л) =
31
6i
1
4.5-6
1 120’
Приведем еще пример для иллющрации метода рекуррентных соотношений. Пример 5. В урне находятся 9 шаров: 3 белых, 3 зеленых и 3 желтых.
Из урны последовательно извлекаются с возвращением 5 шаров. Какова вероятность того, что в полученной выборке любые два соседних шара имеют разные цвета (событие Л)?
Решение. Обозначим шары условно ах, а2,	а9. Извлекая 5 шаров,
мы получаем строку длиной 5 из элементов множества X = {от, а2, ..., а9}. Число всех возможных строк равно 9“. Остается найти число строк, в которых любые два соседних шара имеют разные цвета, т. е. строк, благоприятных для А. Условимся называть такие строки разноцветными.
Число разноцветных строк длиной 5 обозначим с5. Вообще, через ck обозначим число разноцветных строк длиной k, k 1. Введем также следующие обозначения: с® — число разноцветных строк длиной k, начинающихся с белого шара, ск и ск определяются аналогично. Очевидно,
ck — ck + ck + cfeK-	(3)
поэтому достаточно научиться находить числа с®, с3к, с£.
Справедливо следующее рекуррентное соотношение:
ck = ck-\ + С*-Г	(4)
Чтобы его объяснить, достаточно заметить, что если из разноцветной строки длиной k, начинающейся с белою шара, удалить этот шар, то останется разноцветная строка длиной k — 1, начинающаяся с зеленого или желтого шара.
Примем теперь во внимание такое обстоятельство: ввиду симметрии между цветами (по условию в урне имеется одинаковое число белых, зеленых и жел. тых шаров) числа с®, c3k, с™ равны друг другу.Поэтому из (4) следует: = 2c®_j. Отсюда последовательно находим:
с® = 2с® = 4с® = 8с® = 16, после чего, возвращаясь к соотношению (3), находим с6:
с8 = Зс® = 48.
Искомая вероятность
Р0) =
48
95
Глава 3.
НЕЗАВИСИМОСТЬ СОБЫТИЙ.
ПРОСТЕЙШИЕ ФОРМУЛЫ
Одним из важнейших понятий теории вероятностей является понятие независимости событий. Настоящая глава посвящена, прежде всего, обсуждению этого понятия. Кроме того, в ней будут рассмотрены формулы, облегчающие в ряде случаев подсчет вероятностей.
§ 11.	УСЛОВНАЯ ВЕРОЯТНОСТЬ
При совместном рассмотрении двух случайных событий А и В часто возникает вопрос: насколько связаны эти события друг с другом, в какой мере наступление одного из них влияет на возможность наступления другого?
Простейшим примером связи между двумя событиями может служить причинная связь — когда наступление одного из событий ведет к обязательному осуществлению другого или же, наоборот, когда наступление одного события исключает шансы другого. Скажем, если событие А заключается в том, что выбранное наугад изделие данного предприятия не содержит брака, а событие В — в том, что изделие является первосортным, то ясно, что наступление В влечет за собой в обязательном порядке наступление Л; напротив, событие А исключает событие В.
Однако наряду с такими крайними случаями существует и много промежуточных, когда непосредственная причинная зависимость одного события от другого отсутствует, но некоторая зависимость все же имеется. Чтобы пояснить сказанное, приведем такой пример.
Бросается игральная кость. Событие А — выпадение четного числа очков, событие В — выпадение числа очков большего, чем 3. Очевидно, было бы неверно утверждать, что одно из этих событий влечет за собой другое или что, наоборот, одно из них исключает другое. В то же время между событиями А п В имеется какая-то зависимость. В самом деле, из трех случаев, к которым сводится В (выпадение 4, 5 или 6 очков), событию А будут благоприятны два; поэтому, если считать наступившим событие В, то шансы события А будут —. В то же время при отсутствии предварительной информации об исходе бросания шансы события А оцениваются отноше-3	2	3
нием — .Так как — > —, то следует признать, что наступление со-6	3	6
бытия В повышает шансы события А,
47
Для характеристики зависимости одних событий от других вводится понятие условной вероятности.
Определение. Пусть А и В — два случайных события по отношению к некоторому опыту а, причем р (В) ф 0. Число »<4В)	.
—~~у называется вероятностью события А при условии, что наступило событие В, или просто условной вероятностью события А.
Вероятность А при условии В обозначается р (А/В). Таким образом, по определению имеем следующее равенство:
Р(Л/В) = ^.	(!)
Чтобы понять реальный смысл числа5/? (A/В), обратимся к частотному истолкованию вероятности (§ 1, 2°). А именно, предположим, что опыт а произведен N раз, но во внимание приняты лишь те случаи, когда наступило событие В. Число таких случаев обозначим, как и ранее, NB. Составим отношение оно показывает, какую долю от числа опытов, в которых наступило событие В, составляет число таких опытов, в которых, помимо В, наступило также и А. Это отношение естественно называть частотой события А при условии, что наступило событие В, или просто условной частотой события А (в рассматриваемой серии опытов). Нетрудно видеть, что с увеличением N условная частота будет колебаться около числа р (A/В). Действительно,	: —, но дробь колебле-
Ав N N	N
тся около числа р (АВ), а дробь — — около числа р (В).
Итак, условная вероятность есть число, около которого колеблется условная частота в больших сериях опытов.
Для большей ясности укажем, что числа р (Л) и р (А/В) определяют вероятности события А по отношению к двум разным опытам о и о'. Если для опыта о пространство элементарных событий есть, положим, некоторое множество Й, то для а' таким пространством является В — подмножество в Q. Событиями по отношению к о' служат пересечения событий для о с В, а вероятности событий в опыте с' находятся путем деления вероятностей в опыте а на число р (В). Все аксиомы, обязательные для вероятностей (т. е. аксиомы I—3 пункта З9 § 3), будут справедливы для величин р (А/В). В самом деле, справедливость аксиом 1 и 3 очевидна, поскольку из определения условной вероятности тотчас следует; р (А/В) 0 и р (В/В) = 1. Аксиома 2 счетной аддитивности тоже выполняется: если 41, 42, ... — какие-то попарно непересекающиеся подмножества в В, то р (Ат + 42 + ...) = р (41) + р(Аг) + .... откуда делением обеих частей на р (В) находим:
р (41 + 43 + ... /В) — р (Ai/B ) + р AJB) + ... .
Из равенства (1), являющегося определением условной вероятности, следует:
р(АВ) = р(А[В)р(В).	(2)
48
Это значит, что вероятность произведения двух событий равна вероятности одного из этих событий при условии другого, умноженной на вероятность самого условия.
Если р (Л) #= 0, то наряду с равенством (2) имеет место
Р (ВА) = р (В!А) р(А).
Сравнивая эти равенства, мы видим, что
р (A/В) р(В) = р (В!А) р (Л).	(3)
Пример 1, Все грани игральной кости заклеены непрозрачной бумагой: грани I, 2, 3 — красной, грани 4, 5, 6 — черной. При бросании кости выпала черная грань. Какова вероятность того, что на этой грани стоит четное число?
Решение. Очевидно, мы должны найти условную вероятность р (AJB), где событие А есть выпадение четного числа очков, а событие В — выпадение числа очков, большего 3. Имеем:
£
р(Л/В) = ^ = 7 = Г р(В)	3	3
"б
Для сравнения отметим, что безусловная вероятность события А (просто р (Л)) равна —. ▲
Пример 2, Какова вероятность того, что вытащенная наугад кость домино окажется «дублем», если известно, что сумма очков на этой кости является четным числом?
Решение. Пусть событие В состоит в том, что сумма очков четна, а событие Л — в том, что вытащенная кость есть «дубль». Имеем:
7
р(Л/в) = <Щ2 = ?« = 1 ' р(В) 16	16
28
(следует учесть, что из 28 костей домино 16 имеют четную сумму у
очков). Заметим, что безусловная вероятность события Л равна —.А
Пример 3. Слово «лотос», составленное из букв-кубиков, рассыпано на отдельные буквы, которые затем сложены в коробке. Из коробки наугад извлекаются одна за другой три буквы. Какова вероятность того, что при этом появится слово «сто»?
Решение. Введем обозначения для событий:
Л1 — первой извлечена буква «с»;
49
Л2 — второй извлечена буква «т»;
Л3 — третьей извлечена буква «о»;
А — получилось слово «сто».
Очевидно, А = Л!Л2Л3. Имеем последовательно: р(А) = 4: '
р (Л2ЛХ) = р (Л2/Лх) р (Лх) = 1.1=1; 4 О ZO
9 1	1
р (Л3Л2ЛХ) = р (А./А.А.) р (Л2ЛХ) = 1.1=1
0 faU	UV
Итак, р (Л) = 1. А
30
§ 12.	НЕЗАВИСИМЫЕ СОБЫТИЯ И ПРАВИЛО УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ
1°. Независимость двух событий. Мы уже видели на примерах, что числа р (Л) и р (A/В), вообще говоря, различны; другими словами, наступление события В может изменять вероятность события Л. В связи с этим вводится следующее определение.
Определение. Мы говорим, что событие А не зависит от В, если выполняется равенство
р(Л/Д)=р(Л).	(1)
Таким образом, Л не зависит от В, если наступление В не оказывает влияния на вероятность Л (или, говоря проще, наступление В не меняет шансов Л).
Понятие независимости событий •— одно из центральных в теории вероятностей.
Из равенства
р (АВ) = р (AIB) р (В)	(2)
(см. (2) § 11) мы можем вывести теперь такое заключение.
Если событие А не зависит от В, то справедливо равенство
р (АВ) — р (А) р (В)	(3)
(вероятность произведения равна произведению вероятностей). Действительно, если в правой части равенства (2) заменить р (А/В) на р (Л), то придем к (3).
Указанное выше предложение называют обычно правилом умно
жения вероятностей.
Справедливо и предложение, в известном смысле обратное: если выполняется равенство (3), причем р (В) =Л= 0, то Л не зависит от В. Действительно, из (3) следует р (Л) =	 а значит, и
Р (Л) = р (AIB).
50
Согласно определению, данному в начале параграфа, говорить о независимости события А от В имеет смысл лишь при условии р (В) =/= 0. Однако в некоторых случаях такое ограничение представляется ненужным. Ввиду этого вводится более широкое понятие независимости, а именно: мы говорим, что событие А не зависит от В, если выполняется равенство (3). При этом уже безразлично, будет ли вероятность события В отлична от нуля или же будет р (В) = 0. В случае, когда вероятность В отлична от нуля, новое определение эквивалентно первоначальному.
В дальнейшем независимость А от В будет пониматься как выполнение равенства (3).
Заметим, что в случае, когда р (В) = 0, равенство (3) выполняется автоматически. Действительно, мы имеем всегда: р (В) = р (ВА) + р (ВД). Приняв р (В) = 0, получаем, что сумма двух неотрицательных чисел р (ВА) и р (ВА) равна нулю. Следовательно, каждое из них равно нулю в отдельности. Таким образом, если р (В) = 0, то р (ЛВ) = 0, что влечет (3).
Так как АВ = В А, то из равенства (3) следует также равенство р (ВА) = р (В) р (Я). Это означает, что если А не зависит от В, то и В не зависит от А. Иначе говоря, отношение независимости является симметричным. Поэтому в дальнейшем мы можем говорить просто о независимых событиях А и В.
Пример. Из колоды игральных карт наугад выбирают одну карту. Пусть событие А заключается в том, что вынутая карта является «тузом», а событие В — в том, что карта красной масти («бубновая» или «червовая»). Интуитивно ясно, что А не зависит от В (цена карты не зависит от масти). Проверим это подсчетом. Так как
р(Л) = A, p(B) = g, р(АВ) = ± оо	оо	оо
то равенство (3) выполняется. Следовательно, события А и В независимы.
Нетрудно видеть, что если события А и В независимы, то независимы также события А и В. Действительно, из (3) следует:
р(В) -р (АВ) = р (В) -р (Л) р (В)\ если еще учесть, что всегда справедливо равенство р (В) — р (АВ) + + р (АВ), то получим:
р(АВ) = р(В)-р(А)р(В).
Отсюда следует:
р (АВ) = р (В) (\-р (А)) = р (А) р (В), что означает независимость событий А и В.
Дважды применяя доказанное только что предложение, находим: если независимы события А и В, то независимы и события А и В.
al
В практических вопросах для установления независимости одного события от другого редко прибегают к проверке равенства (3). Обычно при этом довольствуются интуитивными соображениями. Так, например, если бросают подряд две монеты, то ясно, что выпадение той или другой стороны на одной монете не оказывает никакого влияния на условия бросания другой, и, значит, следующие два события: выпадение герба на одной монете (событие А) и выпадение герба на другой (событие В) — являются независимыми.
2°. Независимость п событий, п > 2. Дадим такое
Определение. События Аг, ..., Ап называются независимыми, если вероятность любого из них А; не меняется при наступлении какого угодно числа событий A/t j ф i, из той же совокупности.
Другими словами, события Ait А2, ..., Ап независимы, если выполняется следующее условие: каково бы ни было подмножество {z'i, ;2, ..., ik} множества {1, 2, .... л), событие A(j независимо от произведения событий Ait, Ai3, ..., A/k.
Как мы уже знаем, независимость А,, от А/,А;, ... AZft записывается в виде соотношения
р(Л,-АЛ, - Ла) = р(Л,)-р(ЛА - АЛ <4)
Если такое же соотношение записать для подмножества {i2, i8, ... ik}, то получим:
МЛ/А - Лл) = р(Л,)-р(Л, ... А).	(5)
Из (4) и (5), очевидно, следует:
Р(А(А.А, ... Alk) = p(Aii)p(Ai).p(Ai3 ... Aift).
Продолжив это рассуждение, придем в конце концов к следующему равенству:	.(
Р(ЛА ... Alk) =p(AZi)Z7(AG) ... p(A,k).	(6)
Итак, если события Ait А2, ...» Ап независимы, то для любого подмножества {/lt Z2, ik} множества (1, 2, ..., п\ справедливо равенство (6) («вероятность произведения равна произведению вероятностей»).
Это предложение мы будем называть правилом умножения вероятностей для п событий.
Из сказанного следует, что выполнение равенств (6) есть необходимое условие для независимости событий А1( А2, .... Ап. Но это же условие является и достаточным (поскольку из равенств (6) очевидным образом следуют равенства (4)). Отсюда ясно, что определение независимости для п событий можно было бы сформулировать по-другому: события Аь А2...Ап независимы, если для них
справедливы соотношения (6).
Заметим, что при п = 3 соотношения (6) принимают следующий вид:
52
Р (ЛИг) = р (ЛО р (Л2) р (ЛМз) = р (ло р (Л3) р (Л2Л3) = р (Л2) р (Лз)
(7)
р (ЛИИз) = р (ЛО р (Л2) р (Л8).	(8)
Может возникнуть предположение, что достаточно одних только равенств (7), т. е. что из (7) следует (8), иначе говоря, что попарная независимость событий (независимость Ai от Л2, затем Ai от Л3, наконец, А2 от Л3) гарантирует и независимость в совокупности. Приведем пример, показывающий, чтоэтоне1ак.
Бросаются две монеты. Рассмотрим следующие события:
Ai — на первой монете выпал герб;
Л2 — на второй монете выпал герб;
А3 — обе монеты упали на одну сторону,
Очевидно,
Р 0i) = Р 0а) = Р 0з) = 4
Л
и
Р (-402) = Р 00з) = Р 0алз) = 4’
следовательно, события Ai, А2, А3 попарно независимы. Но в то же время
р (Л1Л2Л3) = —,
4
так что условие (8) не выполняется.
Можно было бы показать, что из независимости событий 41( А2, ..., Ап вытекает, что любое из этих событий независимо от любой комбинации остальных. Мы рекомендуем читателю рассмотреть какой-либо частный случай этого утверждения: например, доказать, что из независимости событий Л1( Л2, А3 вытекает резависимость Ai от А2 + А3. В этом случае задача будет сводиться к тому, чтобы из соотношений (7), (8) вывести равенство
р {Ai  (Л2 + Л»)) = р (Л») • р (Л2 4-Л3).
Заключая обсуждение вопроса о независимости событий, еще раз подчеркнем, что в большинстве случаев основанием для вывода о независимости служат интуитивные соображения. Обычный ход рассуждений таков: из конкретных условий рассматриваемого опыта делается заключение о независимости тех или иных событий и затем на этом основании пишется равенство (3) (или равенства (6), если число событий больше двух).
Пример 1. Электрическая схема состоит из п последовательно соединенных блоков (рис. 10). Надежность (т. е. вероятность безотказной работы) каждого блока равна соответ-
ственно pi, р2,	рп.
Считая выходы из строя различных блоков независимыми событиями, найти надежность
Рис. 10
всей схемы в целом.
S3
Рис. 11
Рис. 12
Решение. Событие, заключающееся в исправной работе 1-го блока, обозначим А,; исправность схемы в целом обозначим Л. Так как блоки собраны последовательно, то А имеет место в том и только в том случае, когда имеют место все Лг. Поэтому
А = АхА2 ... Ап,
откуда в силу независимости событий Д±, А2, ..., Ап следует:
Р И) = piPt ... рп.
Та же самая задача для схемы из параллельно соединенных блоков (рис. 11) приводит к другому ответу. В этом случае выход схемы из строя происходит лишь в том случае, когда выходят из строя все блоки. Это значит, что
А = Л1Ла... Ап
и, следовательно,
Р И) = р (Л]) р (Л2) ... р (Ап) = (1 -рО (1 — р2)... (1 — р„).
Таким образом, надежность всей схемы оказывается равной
р(Л) = 1 ^-(1 -Р1)(1 -р2)...(1 -р„). А
Поставим в связи с последним примером такой вопрос. Пусть все блоки имеют одинаковую надежность р. Как велико должно быть число блоков п, чтобы надежность схемы, полученной путем параллельного соединения, превысила 0,99?
Чтобы получить ответ, необходимо решить неравенство 1 —• — (1 —• р)п > 0,99 или (1 — рУ1 < 0,01. Отсюда
2 п logm (1 — р) < —2, т. е. п >------------
10	logtoO-P)
(следует учесть, что log10 (1 — р) есть число отрицательное). Например, при р = 0,9 получаем: и > 2.
Пример 2. Найти надежность схемы, изображенной на рисунке 12.
Решение. Предложенную схему можно рассматривать как результат последовательного соединения трех блоков; на рисунке
54
эти блоки обведены пунктирами. Поэтому А = AiBAt, где В означает исправность второго блока. Согласно примеру 1, р (В) — 1 — — (1 — ра) (1 — р3). Окончательно имеем: р (Л) = р{ [1 — (1 — - Рг) (1 “ Рз)2 Pi-А
Отвлекаясь на время от примеров, сделаем одно замечание, полезное при решении задач. На практике правило умножения применяют чаще всего вместе с правилом сложения. При этом событие А, вероятность которого требуется найти, стараются представить в виде суммы нескольких попарно несовместных слагаемых — вариантов события А: А = At + Л2 + ... + А„, а каждый из вариантов в свою очередь в виде произведения нескольких независимых событий. Тогда последовательное применение правил сложения и умножения позволяет в большинстве случаев найти ответ.
Пример 3. Имеются две урны. В первой находятся 1 белый шар, 3 черных и 4 красных, во второй — 3 белых, 2 черных и 3 красных. Из каждой урны наугад извлекают по одному шару, после чего сравнивают их цвета. Найти вероятность того, что цвета вытащенных шаров совпадают (событие Л).
Решение. Обозначим событие, состоящее в извлечении из первой урны белого шара, через В(, черного — Ct, красного — Di. Аналогичные события для второй урны обозначим В2, С2, D2. Событие Л распадается на три варианта: В{В2, CtC2 kDiD2. Следовательно, Л = BiB2 + С1С2 + DiD2. Применяя сначала правило сложения, а затем правило умножения, получим:
р (Л) = р (ВО р (В2) + р (СО р (С2) + Р-(Р.) р (р2) ==
= 1.£_l£.Z_|_1.A==£! д
§ 13. ФОРМУЛА ПОЛНОЙ ВЕРОЯТНОСТИ
Одним из эффективных методов подсчета вероятностей является формула полной вероятности, с помощью которой решается широкий круг задач.
Предположим, что событие Л может наступить только вместе с одним из нескольких попарно несовместных событий Hi, Н2, ... ..., Нп. Условимся называть эти события (по отношению к Л) гипотезами. Имеет место следующая формула полной вероятности', р (А)-р (A/HJptHJ +р (A/HJp (Я2) + ... +р (А/Нп)р(Нп) (1)
Формула (1) читается так: вероятность события А равна сумме произведений условных вероятностей этого события по каждой из гипотез на вероятности самих гипотез.
Доказательство. По условию событие Л может произойти лишь вместе с одним из событий Hi, Н2, .... Нп, следовательно, А = AHi + ЛЯ? + ... + АНп. Так как Hi, Н2, .... Нп
55
попарно несовместны, то несовместны и события AHit АН2, .... АНп. Применяя правило сложения, находим: р (Л) = р (АН^ + + р (АН3) + ... + р (АНп)- Заменив каждое слагаемое р (AHt) правой части произведением р (AlHj) р (Ht), получаем требуемое равенство (!)
Пример 1. Имеются три урны. В первой находятся 5 белых и 3 черных шара, во второй — 4 белых и 4 черных, в третьей — 8 белых. Наугад выбирается одна из урн (это может означать, например, что сначала осуществляется выбор шара из вспомогательной урны, где находятся три шара с номерами 1, 2, 3 соответственно) и из нее наугад извлекается шар. Какова вероятность того, что он окажется черным (событие Д)?
Решение. Шар может быть вытащен из первой урны, либо из второй, либо из третьей; обозначим первое из этих событий Hit второе — Н2, третье — Н3. Так как имеются одинаковые шансы выбрать любую из урн, то р (ЯО — р (Н2) = р (Н3) = Далее находим вероятности события А при каждом из условий Я1( Н2, Н3:
р (A/HJ = {, р (А/Н3) = |, р (А/Н3) = ООО
Отсюда
Р И) = р (AIHD р (яа + р (А/Нг) р (Нг) + р (A/HJ р (Я3) =
13.14.10	7	.
• — । ~ • — н— • — == —. ж 3 8	3 8	3 8	24
В приведенном примере, как, впрочем, и во многих других задачах на формулу полной вероятности, рассматриваемый опыт можно представить как бы происходящим в два этапа; гипотезы Я1, Я2, .... Ял исчерпывают все возможные предположения относительно исхода первого этапа, событие же А есть один из возмож-
ных исходов второго этапа. В рассмотренном примере первый этап заключался в выборе урны, второй — в извлечении из нее шара.
Пример 2. Турист выходит из некоторого пункта О и на разветвлении дорог выбирает наугад один из возможных путей. Схема дорог изображена на рисунке 13. Какова вероятность того, что турист попадет в пункт а?
56
Решение. Как видно из рисунка, путь туриста обязательно проходит через один из промежуточных пунктов /г2, h3. Пусть Ht — событие, состоящее в том, что при своем движении турист попадает в пункт йг. События Hit Н2, Н3 по условию несовместны и равновероятны: ведь путь из точки О выбирается наугад. Поэтому р (Ht) — р (Н2) — р (Н3) = i-. Если обозначить через А событие —
приход туриста в пункт а, то будем иметь:
ptA/HJ = 1, р(А/Нг) = 1 р(А/Н3) = 1. «5	£	4
Отсюда: р(А) —	—— • —— • — = —. ▲
3 3	2 3	4 3	36
§ 14. ФОРМУЛА БАЙЕСА
В тесной связи с формулой полной вероятности находится так называемая формула Байеса1. Она относится к той же ситуации, что и формула полной вероятности (событие А может наступить только вместе с одним из п попарно несовместных событий Н{, Н2, ..., //„). Формула Байеса решает следующую задачу.
Пусть произведен опыт, и в результате него наступило событие А. Сам по себе этот факт еще не позволяет сказать, какое из событий /У2, ..., Нп имело место в проделанном опыте. Можно, однако, поставить такую задачу: найти вероятности
р (HJA), р (Н2/А)....р (Нп/А)
каждой из гипотез в предположении, что наступило событие А. Эту задачу и решает как раз формула Байеса. Понятно, что, вообще говоря, р (Ht!A) р (Hi). Так, в примере 1 из предыдущего параграфа вероятность гипотезы Нд (шар извлечен из третьей урны) до того, как произведен опыт, равнялась —. Однако если опыт произведен и наступило событие А — вытащенный шар оказался черным, то это снижает шансы гипотезы Н3 до нуля. Послеопытная, «апостериорная» вероятность гипотезы Н3 будет в данном случае ниже, чем доопытная, «априорная».
Вывод формулы Байеса весьма прост. Мы имеем:
р (AHt) = р (A/Hi) р (Hi),
а также
р (HiA) = р (HtlА) р (А).
Приравнивая правые части, получим:
р (HJА) р (А) — р (A/Hi) р (Hi),
1 Томас Байес (1702—1761) — английский ученый.
67
Откуда следует:
p(Ht/A) =	,
р(Д)
или, если воспользоваться формулой полной вероятности, p(HjA) =----------------------р ^Н{) р (Hi)---------------.
р (A/Hj) р (HJ + р (А/Н2) р (Н2) + ... 4- р (А/Нп) р (Н„)
Это и есть требуемая формула. Запомнить ее нетрудно: в знаменателе стоит выражение для полной вероятности события А, в числителе — одно из слагаемых в этом выражении.
Рассмотрим два примера на применение формулы Байеса.
Пример 1. В некоторой отрасли 60% продукции производится фабрикой I, 25% продукции —фабрикой II, а остальная часть продукции —фабрикой III. На фабрике I в брак идет 1% всей производимой ею продукции, на фабрике II — 1,5%, на фабрике III — 2%.
Купленная покупателем единица продукции оказалась браком. Какова вероятность того, что она произведена фабрикой I?
Решение. Введем обозначения для событий: А — купленное изделие оказалось браком; At — изделие произведено фабрикой I; А2 — изделие произведено фабрикой II; А3 — изделие произведено фабрикой III.
Имеем:
р = 0,30; р (Я2) = 0,25; р (Н3) = 0,45;
р (А/Hi) = 0,01; р (А/Н2) = 0,015; р (А/Н3) = 0,02;
р (Л) = 0,01 • 0,30 ф- 0,015 • 0,25 + 0,02 - 0,45 = 0,015;
р (HjA) = 0,01 '0’3° = 0,20. л v 1 '	0,015
Таким образом, из всех бракованных изделий отрасли в среднем 20% выпускаются фабрикой I. ▲
В данном примере послеопытная вероятность гипотезы Hi оказалась ниже доопытной (постарайтесь это объяснить).
Пример 21. При обследовании больного имеется подозрение на одно из двух заболеваний Hi и Н2. Их вероятности в данных условиях: р (Hi) = 0,6, р (Н2) = 0,4. Для уточнения диагноза назначается анализ, результатом которого является положительная или отрицательная реакция. В случае болезни Hi вероятность положительной реакции равна 0,9, отрицательной —0,1; в
1 Сюжет этого примера заимствован из популярной книги Б. В. Гнеденко и А. Я- Хинчина «Элементарное введение в теорию вероя1ностей». —М.: Наука, 1970.
58
случае Н2 положительная и отрицательная реакции равновероятны. Анализ произвели дважды, и оба раза реакция оказалась отрицательной (событие Л). Требуется найти вероятность каждого заболевания после проделанных анализов. Решение. В случае заболевания событие А происходит с вероятностью 0,1 -0,1 — 0,01, а в случае заболевания Н2 — с вероятностью 0,5 х 0,5 = 0,25. Следовательно, по формуле Байеса имеем:
р (HJA) =-----------------------------=--------2’01.А0>.в---о,О6,
1	'	0,01.0,6+0,25.0,4
р (Н2/А) =------°’-5 '--^4----да 0,94.
2	'	0,01.0,06 + 0,25.0,4
Отсюда видно, что полученные результаты анализов дают веские основания предполагать болезнь Н2. А
Глава 4.
СХЕМА БЕРНУЛЛИ
В приложениях теории вероятностей часто встречается некоторая стандартная схема, называемая схемой независимых испытаний или схемой Бернулли. Настоящая глава посвящена изучению этой схемы и связанных с нею теорем и задач.
г
Историческая справка. Якоб Бернулли (1654—1705) — один из старших представителей знаменитой семьи Бернулли, несколько поколений которой внесли важнейший вклад в науку. Я. Бернулли был современником Ньютона и Лейбница, его работы способствовали развитию применений только что возникших дифференциального и интегрального исчислений. Заметим, кстати, что название «интеграл», ставшее теперь рабочим математическим термином, впервые появилось в трудах Я. Бернулли. Я. Бернулли явился одним из создателей так называемого «вариационного исчисления».
Основной вклад Я. Бернулли в развитие теории вероятностей заключался в доказательстве теоремы, дававшей теоретическое обоснование одному из наиболее важных положений этой науки — факту сближения частоты и вероятности. Эта теорема, носящая теперь имя Я- Бернулли, будет рассмотрена в § 37.
§ 15. СХЕМА БЕРНУЛЛИ. БИНОМИАЛЬНЫЕ ВЕРОЯТНОСТИ
Якоб Бернулли (1654-1705)
1°. Описание схемы Бернулли. Пусть А — случайное событие по отношению к некоторому опыту о. Отвлекаясь от возможного разнообразия исходов опыта, будем интересоваться лишь тем, наступило или не наступило в результате опыта событие А. Это равнозначно принятию нами следующей точки зрения: пространство элементарных событий, связанное с опытом о, состоит только из двух элементов А и А. Обозначим вероятности этих элементов соответственно через р и q (р + q — 1).
Допустим теперь, что опытов неизменных условиях повторяется определенное число раз, скажем три раза. Условимся трехкратное осуществление о рассматривать как некий новый опыт S. Если по-прежнему интересоваться только наступлением или ненаступлением А, то следует, очевидно, принять, что пространство элементарных событий, отвеча
60
ющее опыту S, состоит из всевозможных строк длиной 3:
(Л, А, А), (Л, А, А), (А, А, Л), (Л, А, А), (А, А, А), (А, А, Л), (Л, Л, Л), (Л, А, А).	(1)
которые можно составить из Л и Л. Каждая из указанных строк означает ту или иную последовательность появлений или непоявлений события Л в трех опытах о; например, строка (Л, Л, Л) означает, что в первом из опытов наступило Л, а во втором и третьем — А. Постараемся теперь понять, какие вероятности следует приписать каждой из строк (1).
Условие, что все три раза опыт о проводится в неизменных условиях, по смыслу должно означать следующее: исход каждого из трех опытов не зависит от того, какие исходы имели место в остальных двух опытах. Другими словами, любая комбинация исходов трех опытов представляет собой тройку независимых событий. Но в таком случае, скажем, элементарному событию (Л, Л, Л) естественно приписать вероятность, равную р  q • q, событию (Л, Л, Л) — вероятность q • q • q и т. д.
Мы приходим, таким образом, к следующей вероятностной схеме для опыта S (т. е. для трехкратного осуществления а). Пространство й элементарных событий есть множество из 23 строк (1). Каждой строке сопоставляется в качестве вероятности число pkql, где показатели степеней k и / определяют, сколько раз символы Л и Л входят в выражение для данной строки.
Вероятностные схемы такого рода называются схемами Бернулли. В общем случае схема Бернулли определяется заданием двух чисел: натурального числа п и произвольного р, 0 р 1, Пространство Й состоит из всевозможных строк длиной п, составленных из символов А и А (число таких строк равно 2Л). Каждой строке приписывается вероятность pk (1 — р)‘, где k и I — число вхождений символов А и А в данную строку.
Реальное истолкование чисел п и р, задающих схему Бернулли, понятно из сказанного ранее: п есть число повторений опыта ст, гр— вероятность события Л по отношению к опыту ст.
Добавим ко всему сказанному одно замечание. Строго говоря, предположение о неизменности условий при каждом осуществлении опыта о содержит в себе некоторую идеализацию. В самом деле, воспроизвести в точном виде обстановку уже проделанного однажды опыта просто невозможно; в каких-то деталях условия второго опыта будут всегда отличаться от условий первого. Поэтому, вместо того чтобы говорить об n-кратном осуществлении одного и того же опыта, предпочитают говорить об п независимых опытах, понимая под этим следующее: любая комбинация исходов этих опытов представляет собой группу из п независимых событий. Разумеется, чтобы и в этой ситуации говорить о схеме Бернулли, нужно предположить, что вероятность события Л во всех п опытах одинакова.
61
Например, можно говорить о независимых опытах, если п раз бросается монета; п раз извлекается карта из колоды, причем каждый раз вынутая карта возвращается в колоду и карты заново перемешиваются; обследуются, с целью выяснения годности или бракован-ности, наугад выбранные п изделий данного производства и т. д.
2°. Вероятность заданного числа появлений события А. Со схемой Бернулли связана важная задача. Проиллюстрируем ее на примере.
Пример. Трижды бросается игральная кость. Какова вероятность того, что при этом ровно два раза выпадет максимальное число (т. е. 6) очков?
В соответствии со сказанным обозначим через S опыт, состоящий в трехкратном бросании игральной кости. Пространство элементарных событий для опыта S состоит из 23 строк (1), где А обозначает выпадение 6 очков.
Наша цель — найти вероятность того, что при трех бросаниях дважды наступит А. Очевидно, это событие можно представить в виде (А, Л, А) + (А, А, А) + (А, А, А), следовательно, его вероятность равна:
p2q 4- p2q + p-q = 3p2q = 3 •	• (j) = I. A
Реальное истолкование полученного ответа связано, как всегда, с частотным подходом к вероятности. Оно сводится к следующему: если опыт с трехкратным бросанием игральной кости выполнить много раз, то в среднем в 5 случаях из 72 будет наблюдаться интересующее нас событие: грань 6 выпадает ровно два раза.
Сформулируем теперь общую задачу, частным случаем которой является разобранный выше пример.
Производится п независимых опытов, в каждом из которых с одной и той же вероятностью р может наступить некоторое событие А. Требуется для заданного числа k найти вероятность следующего события: в п опытах событие А наступит ровно k раз. В предыдущем примере А заключалось в выпадении 6 очков.
Для большей наглядности условимся каждое наступление события А рассматривать как успех, ненаступление А —- как неудачу. Наша цель — найти вероятность того, что из п опытов ровно k окажутся успешными; обозначим это событие временно через В.
Событие В представляется в виде суммы ряда элементарных событий — вариантов события В. Чтобы фиксировать определенный вариант, нужно указать номера тех опытов, которые оканчиваются успехом. Например, один из возможных вариантов есть
(А, А.....А, А, А, .... А)
k	n—k
(успех в 1, 2, ..., /г-м опытах и неудача в остальных). Вообще, каждый вариант записывается в виде строки длиной п, в которой k компонент суть А, а остальные n—k компонент — А. Число всех
62
вариантов равно, очевидно, С„, а вероятность каждого варианта ввиду независимости опытов равна pkqn~k (где q = 1 — р). Отсюда вероятность события В будет Cknpkqn~k.
Чтобы подчеркнуть зависимость полученного выражения от п и k, обозначим его Итак,
P„(fc) = C>Vft-	(2)
Полученная формула носит название формулы Бернулли, а сами вероятности Pn(k) называются биномиальными вероятностями. Такое название связано с тем, что числа Рп (/е) имеют непосредственное отношение к формуле бинома Ньютона. Записав эту формулу в виде
(q + р)п =qn + CXnq^p + С^р* + ... + СГ^рп~" +
+ C^qp*-1 + р\
можно видеть, что выражение для Рп (k) совпадает с (k + 1)-м членом указанного бинома. Итак,
(<7 + Ру = Рп (0) + Рп (1) + ... + Рп (п - 1) + Рп (п).
Поскольку q + р = 1, то отсюда находим:
Рп (0) + Рп (1) + - + Рп (п - 1) + Рп (п) = 1 (постарайтесь объяснить это равенство, исходя из теоретико-вероятностных соображений!).
Приведем несколько примеров на применение формулы Бернулли.
Пример 1. Монета бросается 10 раз. Какова вероятность того, что герб выпадает при этом ровно 3 раза?
Решение. В данном случае успехом считается выпадение герба, вероятность р этого события в каждом опыте равна у. Отсюда
D /os	<-з I1 \3 ( 1 V	Ю-9-8	1	15	.
10v ’	\2/ \2 /	1-2-3	210	128
Пример 2. Вероятность того, что лампа останется исправной после 1000 часов работы, равна 0,2. Какова вероятность того, что из пяти ламп не менее трех останутся исправными после 1000 часов работы?
Решение. Рассматривая горение каждой лампы в течение 1000 часов как отдельный опыт, можно сказать, что производится 5 опытов, причем нас интересует вероятность события S = А3 + + Д4 + Л5, где А/, означает, что в результате пяти опытов успех (лампа осталась исправной) наступил ровно k раз; иначе говоря, Ak обозначает исправность k ламп из пяти. По формуле Бернулли имеем: Ръ (k) = С5 (0,2)ft (0,8)6-й, следовательно,
р (S) = Р5 (3) + Р5 (4) + Р6 (5) = Cl (0,2)3 (0>8)2 +
+ С5 (0,2)4 (0,8) + Cl (0,2)в = 10 • 0,008  0,64 + 5 х
X 0,0016  0,8 + 0,00032 = 0,05792 « 0,06. А
63
ПримерЗ. В урне находятся 6 белых и 9 черных ш-аров. Из урны извлекают шар, фиксируют его цвет, после чего возвращают шар обратно в урну. Указанный опыт повторяют трижды. Какова вероятность того, что из трех вытащенных при этом шаров ровно два окажутся белыми?
Решение. Поскольку все три опыта производятся в неизменных условиях, мы имеем дело со схемой Бернулли. Вероятность успеха (извлечения белого шара) в каждом из опытов равна —.
15
2 / 6 \2/ 9 \ Следовательно, искомая вероятность Р3 (2) = С3 1 — 1 1—1 = Зх
Х25 ’ 5	125* А
Если изменить условия предыдущего примера, потребовав, чтобы вынутый шар не возвращался в урну, то придем к другому ответу. В этом случае уже нельзя будет говорить о неизменности условий всех трех опытов, ибо после каждого извлечения состав шаров в урне будет меняться; как следствие этого будет меняться и вероятность успеха.
Чтобы все же ответить на поставленный вопрос, можно воспользоваться просто классическим способом подсчета вероятностей. Так как из урны извлекаются три шара, то число возможных исходов будет С^. Из них благоприятными для интересующего нас события будут Св • Сд исходов. Следовательно, искомая вероятность будет:
сб • 9 __ 6  5 • 9  3 _ 27
С? ~ 15-14-13 “ 91'
Мы видим, что в случае безвозвратной выборки вероятность получилась несколько большей, чем в случае выборки с возвращением.
§ 16. НАИБОЛЕЕ ВЕРОЯТНОЕ ЧИСЛО УСПЕХОВ. СРЕДНЕЕ ЧИСЛО УСПЕХОВ
Если п фиксировано, то Рп (/г) превращается в некоторую функцию от аргумента k, принимающего значения 0, 1, 2, .... п. Поставим вопрос: при каком значении аргумента эта функция достигает максимума, проще говоря, какое из чисел Рп (0), Рп (1), Рп (2), ... ..., Рп (п) является наибольшим? Итак, мы хотим выяснить, какое число успехов является наиболее вероятным при данном числе опытов п.
Из простых соображений можно предвидеть, что максимум достигается при значении k, близком к числу пр. Действительно, поскольку вероятность успеха, или, что то же самое, вероятность события А в одном опыте, равна р, то при n-кратном повторении опыта можно ожидать, что частота наступления события А будет близ
64
ка к р; следовательно, скорее всего число наступлений события А будет близко к пр.
Подтвердим наше предположение расчетом.
Для этой цели рассмотрим два соседних числа Рп (k) мРп (k + !)•
Между ними имеет место одно из трех соотношений:
Рп (/г) f Рп (k + 1)	(1)
(меньше, равно или больше) или, что эквивалентно,
_ML < 1.	(2)
Рп (k + 1) >
Подставляя вместо числителя и знаменателя их выражения по формулам
Рп (k) = Cknp<4f-b, Рп (k + 1) = C^p^-b-'
n = Cn • --------, получим вместо (2) соотноше-
k *4“ 1
НИЯ
k + 1 ,	।
n — k p >
или
(k + 1) q | (n — k)p.
Собирая все слагаемые c k и учитывая, что р + q = 1, получим эквивалентные (1) соотношения
пр — q,	(3)
Обозначим число пр — q через а. Тогда (3) перепишется: k а.
Таким образом, для всех значений k меньших, чем а, справедливо неравенство Рп (k) < Рп (k + 1), для k = а (это возможно только в том случае, когда а — целое число) имеет место равенство Рп (k) — — Рп (k + 1), наконец, при k > а выполняется неравенство Рп (k) > Рп (k Д 1). Тем самым при значениях k, меньших а, функция Рп (k) возрастает, а при значениях k, больших а, убывает. Следовательно, если число а не является целым, то функция имеет единственный максимум; он достигается при ближайшем к а справа целом значении k, т. е. при таком целом kg, которое заключено между а и а + 1:
пр — q < k0 < пр А- р-
Если же а — целое число, то два равных между собой максимума достигаются при £ = аи& = а+1. На рисунке 14 представлен график функции Рп (£) для двух случаев: п = 20, р = 0,7 (тогда а = 13,7) и п = 20, р = 0,1 (а = 1,1). Точки, из которых состоит график, для большей наглядности соединены отрезками.
Итак, ответ на вопрос, поставленный в начале параграфа, за-
3 А. С. Солодовников
65
ключается в следующем. Если число а = пр — q не является целым, то наиболее вероятное число успехов равно ближайшему к а справа целому числу. В случае, когда а есть целое число, наиболее вероятное число успехов имеет два значения', а и а + 1.
Отметим, что в любом случае наиболее вероятное число успехов отличается от а меньше чем на единицу.
Пример. Пусть игральную кость бросают 20 раз. Каково наиболее вероятное число выпадений грани «1»?
1	5
Решение. В данном случае п = 20, р = — , q = откуда 6	6
1	5
а = пр — q = 20 -------= 2,5. Поскольку а не является це-
6	6
лым числом, то наибольшим средн чисел Р20 (0), Рм (1), ..., Рао (20) будет Р2в (3). Следовательно, наиболее вероятное число выпадений грани «1» будет 3.
Найдем, чему равна вероятность такого числа выпадений. По формуле Бернулли имеем:
Р8о(3)=С10Ц)8(|У’ = О,249... . ▲
\ и / \ О /
66
При выяснении наиболее вероятного числа успехов в п опытах мы имели возможность убедиться в особой роли, которую играет в схеме Бернулли число пр. Эта роль заключалась в том, что одно из двух ближайших к пр целых чисел было наиболее вероятным числом успехов.
Оказывается, число пр допускает и другую интерпретацию, притом значительно более важную. А именно пр можно рассматривать в определенном смысле как среднее число успехов в п опытах.
Точная формулировка, а также строгое доказательство этого утверждения будут даны позднее, в главе 7 (см. задачу на с. 146); пока же ограничимся тем, что укажем его реальное содержание. При этом будем исходить из частотного истолкования вероятности (§ 1). Условимся для краткости называть n-кратное повторение данного опыта серией. Допустим, что мы произвели некоторое число серий, скажем, N серий. Пусть в первой серии было получено успехов, во второй — k2, ..., в А-й — kN. Составим среднее арифметическое этих чисел:
ki + k2 + ••• + kN	, „
N '	У '
Оказывается, что с увеличением N указанное среднее арифметическое приближается к некоторому постоянному значению, а именно к числу пр. Чтобы убедиться в этом, запишем (4) в виде*1 +
N • п
а затем примем во внимание следующее обстоятельство: произведя N серий, мы тем самым осуществляем данный опыт N • п раз. Написанная выше дробь со знаменателем N • п есть не что иное, как отношение общего числа успехов в этих N • п опытах к числу опытов. С увеличением N (а значит, и Nn) эта дробь будет приближаться к числу р — вероятности успеха. Следовательно, число (4) будет приближаться к рп, что и требовалось получить.
Пример. В условиях данного предприятия вероятность брака равна 0,05. Чему равно среднее число бракованных изделий на сотню?
Ответ: искомое число пр = 100 • 0,05 = 5.
§ 17. ВЕРОЯТНОСТИ Pn(k) ПРИ БОЛЬШИХ ЗНАЧЕНИЯХ п ПРИБЛИЖЕННЫЕ ФОРМУЛЫ ЛАПЛАСА
1°. В приложениях часто возникает необходимость в вычислении вероятностей Рп (k) для весьма больших значений п и k. Пусть, например, требуется решить такую задачу.
Задача. На некотором предприятии вероятность брака равна 0,02. Обследуются 500 изделий готовой продукции. Найти вероятность того, что среди них окажется ровно 10 бракованных (нетрудно видеть, что при указанной выше вероятности брака число 10 есть наиболее вероятное число бракованных изделий из 500).
3*
67
Рассматривая обследование каждого изделия как отдельный опыт, можно сказать, что производится 500 независимых опытов, причем в каждом из них событие А (изделие оказалось бракованным) наступает с вероятностью 0,02. По формуле Бернулли
Лоо (10) = cioo (0.02)10 (0,98)^°.
Непосредственный подсчет этого выражения представляет известную сложность, главным образом из-за громоздкости выражено
НИЯ ДЛЯ С500.
„10	500 • 499  498 ... 491
С500 ==	1 . 2 . 3 io—
Еще большую трудность нам пришлось бы испытать при попытке решить, например, такую задачу: в условиях последнего примера найти вероятность того, что число бракованных изделий среди 500 окажется в пределах, скажем, от 10 до 20. В этом случае потребовалось бы вычислить сумму РРС0 (10) + Л(10 (1 1) + ... + Р600 (20), что является, естественно, более сложным делом. Между тем задачи, подобные указанной, встречаются в приложениях весьма часто. Поэтому возникает необходимость в отыскании приближенных формул для вероятностей Рп (k), а также для сумм вида
%Pn(k)	(О
k=k,
при больших значениях п. Мы укажем четыре формулы такого рода. Первые две из них мы приведем без доказательства — эти приближенные формулы принадлежат Лапласу и основаны на так называемых предельных теоремах Лапласа (с формулировкой одной из них мы ознакомим читателя в §39, п. 2°). Две другие приближенные формулы носят имя Пуассон'а и основаны на предельной теореме Пуассона (см. § 18). Название «предельная» в обоих слу- < чаях связано с тем, что упомянутые теоремы устанавливают поведение вероятностей Рп (fe) (или сумм вида (1)) при определенных условиях, в число которых обязательно входит условие оо.
2°. Приближенные формулы Лапласа. Первая из этих формул дает оценку для вероятности Рп (k) при больших п. Эту формулу называют обычно «локальной».
Локальная приближенная формула Лапласа. При больших п справедливо приближенное равенство
Pn(k)^ -1=ф(х),	(2)
У npq
где х — а ср (х) обозначает следующую функцию: У npq
w (х) =	2.
’	/2л
68
Заметим, что для функции ср (%) составлена таблица ее значений (см. с. 202).
Обоснованием формулы (2) является, как уже отмечалось, одна из так называемых предельных теорем Лапласа; рассматривать ее здесь мы не будем. Таким образом, формулу (2) мы примем без доказательства.
Вторая приближенная формула Лапласа тесно связана с первой. Ее обычно называют «интегральной». Эта формула позволяет k=k
оценивать не отдельные вероятности Рп (k), а суммы 2 Рп (&)• k~fej
Иначе говоря, она дает приближенное выражение для величины р (kr / k / /г2) — вероятности того, что число наступлений события А в п опытах (число «успехов») окажется заключенным между заданными границами kr и k2.
Интегральная приближенная формула Ла пласа. При больших п справедливо приближенное равенство
p(k±
\ У npq }	\ У npq }
(3)
где Ф (х) обозначает следующую функцию'.
Ф{х)= j ср (/) dt = j е 2 dt. о	о
(4)
Формулу (3) мы также примем без доказательства.
Остановимся кратко па свойствах функции Ф (х). Из ее определения легко следует, что Ф (х) — нечетная функция: Ф (—х) = = —Ф (х). Далее, при возрастании х от 0 до <х> функция Ф (х) растет от 0 до числа
а = — Се 2 dt.
/2л J о
(5)
Если воспользоваться известным интегралом
со
С e~u*du = — Кя,
J	2
о
то легко получить, что число а равно Итак, при возрастании х от 0 до оо функция Ф (х) возрастает от 0 до . График Ф (х) изображен на рисунке 15.
Функция Ф(х) табулирована; таблица ее значений приведена
69
~ .	на с. 202 данной книги. Из
таблицы можно видеть, что
—--------------£_______уже при х = 5 значение Ф(х)
1
отличается от — меньше чем
Z	2
_____________/	на 3  10~8. По этой причине О_________________________х в таблице указаны значения
Ф (х) лишь для х в пределах ___.от 0 до 4.
-------------------------------- По поводу «точности» фор-- —-----------------------мул (2) и (3) мы укажем здесь
только следующее: точность
РИС. is	существенно зависит от взаи-
моотношения величин пир. Более определенно: точность улучшается с ростом произведения npq. Обычно формулами (2) и (3) пользуются, когда npq
10. Отсюда, между прочим, видно, что, чем ближе одно из чисел, р или q, к нулю (другое число в этом случае близко к единице), тем большим следует брать п. Поэтому в случае близости одной из величин р или q к нулю формулами (2) и (3) обычно не пользуются; для этого случая значительно более точными являются приближенные формулы Пуассона (см. следующий параграф).
Пример 1. Монету бросают 100 раз. Какова вероятность того, что при этом герб выпадет ровно 50 раз?
Решение. Имеем: пр (1 — р) — 100 •	• -^ = 25 > 10.
Воспользовавшись приближенной формулой (2), получим:
Из таблицы для функции ср (х) найдем, что ср (0) = 0,397... . Отсюда Pw (50) « 0,08.
Итак, если опыт, состоящий в 100 бросаниях монеты, выполнить много раз, то в среднем в 8% случаев герб будет выпадать 50 раз.А
Пример 2. Доведем до конца решение задачи из п. 1°, в которой требовалось найти Р800 (10), а также вероятность события 10 / k / 20.
Решение. В данном случае пр = 500 • 0,02 = 10, пр (1 — — р) — 500 • 0,02  0,98 = 9,8. Воспользовавшись приближенными формулами (2) и (3), получим:
d /1гл ~ 1	/10 — 10 X 1	,п.
1	(10)	—= ср  7=^ = ' 7— <р (0)
°00	/9,8 \ /9,8 )	/9,8
и
Р(10<^<20)^ф(2^)-ф(’|^^Ф(3)-Ф(0).
• Из таблиц для функций ср (х) и Ф (х) находим: ср (0) — 0,397... и
70
Ф (3) = 0,498... . Отсюда
Pwo (10)	0,124, р (10 < k < 20) « 0,499-Ж
Пример 3. Игральную кость бросают 300 раз. Пусть А обозначает выпадение грани «1» и k — число наступлений события А при 300 бросаниях.
k
Вообще говоря, дробь — — частота наступле-
ния события А —будет близка к— (вероятно-
6
сти события А при одном бросании). Однако, сколь тесной окажется эта близость, предугадать невозможно. Поставим следующую задачу; оценить вероятность события
т. е. вероятность того, что частота наступления события А в 300 опытах отклонится от вероятности события А не более чем на 0,01.
Решение. Написанное неравенство эквивалентно
47 < k < 53.
Применяя приближенную формулу (3), получим для данного случая:
/ 53 - 300 -2 \	/ 47 — 300 • 2 \
р (47 < k < 53) х Ф --_JL ) - Ф ------------------6- =
\ 1/ зоо • 2 • А /	\ 1/ зоо • 2.. 2 /
V	66/	\V 66/
= Ф f — ф/'—	~ ф (0,46) 4- Ф (0,46) « 0,35. ▲
\ 6	/	\	6	/
Историческая справка. Пьер Симон Лаплас (1749—1827) — крупнейший французский математик, механик и астроном. Автор знаменитого курса «Небесной механики», в котором впервые были поставлены ( и получили решение) фундаментальные проблемы динамики солнечной системы. «Уравнение Лапласа», «оператор Лапласа»— эти ставшие классическими математические понятия встречаются в математике и ее приложениях на каждом шагу.
В теории вероятностей с именем Лапласа связаны крупные сдвиги: он не только доказал ряд теорем первостепенной важности, но и дал первое систематическое изложение предмета в книге «Аналитическая теория вероятностей», вышедшей в 1812 году.
Отношение Лапласа к науке весьма ярко передает следующий эпизод. Когда Наполеон (бывший, кстати сказать, большим почитателем таланта Лапласа) обратился к ученому с вопросом, почему в
Пьер Симон Лаплас (1749-1827)
71
опубликованной им «Небесной механике» Het даже упоминания о боге, Лаплас ответил фразой, ставшей впоследствии знаменитой' «Эта типотеза мне не понадобилась».
§ 18. ПРЕДЕЛЬНАЯ ТЕОРЕМА И ПРИБЛИЖЕННЫЕ ФОРМУЛЫ ПУАССОНА
Как мы уже отмечали, точность приближенных формул Лапласа понижается по мере приближения одного из чисел, р или q, к нулю. Поэтому случай, когда р или q является малым числом, нуждается в особом исследовании. Будем считать для определенности, что мало р (в случае малого q нужно было бы просто изменить обозначения — вместо А рассмотреть событие А, при этом числа р и q поменяются ролями). Итак, нас интересует оценка для вероятности того или иного числа успехов, когда сам по себе успех является редким событием. Примеры таких событий указать нетрудно: рождение близнецов, достижение столетнего возраста, авария на городском транспорте, «сбой» в автоматическом соединении, опечатка в книге и т. п.
Разумеется, многие из подобных событий вовсе не являются «успехами»; скорее следовало бы рассматривать их как несчастья. Тем не менее мы сохраним принятую ранее терминологию и каждое наступление интересующего нас события А будем по-прежнему называть «успехом».
Искомую оценку для Pn (k) дает так называемая предельная теорема Пуассона. Разъясним ее содержание.
Выражение для Рп (k)
рп (k) = ckn Р* (1 - р)п~к представляет собой формально функцию трех переменных: п, р и k. Предположим, что k фиксировано, а п и р изменяются. Более точно: пусть п->оо, а р 0, притом так, что величина X = пр остается постоянной (X = const.).
Предельная теорема Пуассона. При указанных выше условиях справедливо равенство
НтРя(й) = ^Л	(1)
«!
Доказательство. Имеем:
рп {k} =	(1 _ ру
гЧ
К
и так как р — —, то п
Первое из подчеркнутых в правой части выражений представляет собой произведение k множителей, стремящихся к 1; поэтому и
72
все произведение стремится к 1. Третье подчеркнутое выражение также стремится к 1. Что касается второго, то его можно записать
в виде
1	о
1-----%	. Замечая, что выражение в квадратных скоэ-
п I J
ках имеет пределом число е = lim (1 + а)“ .получим окончательно: а-* О
Рп (&) = — где £	1. Отсюда тотчас следует равенство (1) И
Из предельной теоремы Пуассона вытекают следующие приближенные формулы Пуассона. При больших п и малых р справедливы приближенные равенства
k——k 2
k—kt

(2)
(3)
Исследование вопроса о точности формул (2) и (3) мы оставляем в стороне. Ограничимся лишь тем, чго приведем без доказательства неравенство
<пр2,
k 'Л	k VI
справедливое для любого множества М, принадлежащего {0, 1,
2, ...}. В частности, если М состоит из одного числа k, имеем:
I „ ... X*
\Рп(®--е
|	/г!
< пр2.
Обратим внимание читателя на замечательную особенность приближенного равенства (2): чтобы найти вероятность того или иного числа успехов, вовсе не требуется знать ни п, ни р. Все определяется в конечном счете числом X = пр, которое является не чем иным (см. конец § 16), как средним числом успехов.
Х/г
Для выражения — е~к, рассматриваемого как функция двух переменных k и X, составлена таблица значений; она приведена на с. 204.
Пример!. В тесто засыпают некоторое количество изюма, затем всю массу тщательно перемешивают, разрезают на равные доли и выпекают из них булочки с изюмом. Пусть N — число всех булок, а п — число всех изюмин. Требуется оценить вероятность того, чго в случайно выбранной булке окажется ровно k изюмин.
Решение. Рассматривая бросание каждой изюмины в тесто как отдельный опыт, можно утверждать, что производится п опытов. Событие А — попадание изюмины в выбранную нами булку.
73
Его вероятность р в каждом опыте равна — (условие, что тесто с изюмом тщательно перемешивается, означает для каждой изюмины одинаковую вероятность попадания в любую из булок, а число всех булок равно X). Так как обычно булок выпекается много, то можно считать р весьма малым числом. Что касается числа X = пр, то в данном случае оно есть —; это среднее число изюмин на одну булку, его реальное значение практически легко найти. Наша цель заключается в оценке вероятности Рп (&). Так как налицо все условия, при которых справедливо приближенное равенство (2), то можем записать ответ в виде

Например, для X — 8 находим:
Рп (0)	« 0,000,	Рп	(5)	«	0,092,	Рп	(10)	«	0,099,
Рп (1)	« 0,003,	Рп	(6)	«	0,122,	Рп	(11)	«	0,072,
Рп (2)	« 0,011,	Рп	(7)	«	0,139,	Рп	(12)	«	0,048,
Рп (3)	« 0,029,	Рп	(8)	«	0,139,	Рп	(13)	«	0,030,
Рп (4)	« 0,057,	Рп	(9)	«	0,124,	Рп	(14)	«	0,017
и Рп (k~) < 0,001 при k > 14.
Это означает, что из общего числа Л7 булок приблизительно 0,3% содержат по одной изюмине, 1,1% содержат по две изюмины и т. д. ▲
Как видно из решения данного примера, фактическое значение количества булок и числа изюмин не требуется для нахождения искомых вероятностей. Единственным числом, от которого зависит ответ, оказывается % =	— среднее число изюмин на булку.
Этот факт находится в полном согласии с общим замечанием, сделанным ранее к формуле (2).
Разобранный пример, несмотря на его специфическое содержание, носит довольно общий характер. Для иллюстрации приведем еще два подобных примера.
Пример 2. Под микроскопом наблюдается тонкий слой раствора серебра. Известно число X — среднее число крупинок серебра на 1 мм2. Какова вероятность того, что в поле зрения микроскопа, равном 1 мм2, будет обнаружено ровно k крупинок?
(Проводя сравнение с примером 1, можно уподобить раствор тесту, а участки площадью 1 мм2, на которые разбивается раствор, — булкам. Крупинки серебра играют роль «изюмин».)
ПримерЗ. В книге из 500 страниц имеется 50 опечаток. Какова вероятность того, что на случайно выбранной странице окажется ровно k опечаток? Список подобных примеров можно продолжить.
74
Мы не останавливаемся здесь на приложениях предельной теоремы Пуассона к задачам физического содержания, хотя эти приложения весьма серьезны и многообразны (процесс радиоактивного распада, эмиссия электронов и т. д.).
Историческая справка. Симеон Дени Пуассон (1781—1840) — выдающийся французский физик и математик. Его труды охватывают широкий круг вопросов — ог проблемы устойчивости солнечной системы до математической теории распространения тепла. Одна из главных заслуг Пуассона заключалась в разработке применений аппарата дифференциаль-
Симеон Дени Пуассон (1781—1840)
ных уравнений в частных производных к решению разнообразных задач математической физики. В этой связи особенно велика роль
«уравнения Пуассона», которому подчиняются многие физические явления.
Основным достижением Пуассона в теории верояпюстей явилось открытие им «закона распределения Пуассона» (см. § 21, п. 1°) и объяснение его роли в
науке и практике.
§ 19. ЦЕПИ МАРКОВА
1°. Определение и способ задания цепи Маркова. Изученная в предыдущих параграфах схема Бернулли базировалась на понятии независимых испытаний. Существует, однако, большой круг задач, в которых последовательно проводимые испытания не являются независимыми, а, наоборот, связаны между собой в определенного рода цепь. Один из вариантов такой связи будет описан ниже. Он получил название цепи Маркова, по имени выдающегося русского математика А. А. Маркова, впервые рассмотревшего такого рода связь.
В отличие от той ситуации, которая имела место в случае схемы Бернулли, где рассматривалась последовательность из заданного числа п испытаний, мы будем теперь считать, что производится бесконечная последовательность испытаний. Далее, мы примем, что имеются гп попарно несовместных событий Аи А2, •••, Ат (т — фиксированное число), таких, что в результате каждого испытания обязательно наступает одно из них. Это условие обобщает одно из требований к испытаниям в схеме Бернулли; напомним-, что в этой схеме для каждого испытания возможны лишь два исхода А или А. Наконец — и это самое существенное, — мы будем считать испытания связанными между собой некоторым специфическим образом. А именно вероятность наступления того или иного из событий А1Г А2, .... Ат при очередном, n-м испытании зависит от результата предыдущего, (п — 1)-го испытания, и только от него (тем самым она не зависит от результатов более ранних испытаний: (и — 2)-го, (п — 3)-го. 1-го).
75
Итак, неограниченная последовательность испытаний с возможными исходами А1Г А2, ..., Ат называется цепью Маркова, если вероятность наступления любого из этих исходов при очередном испытании однозначно определяется результатом предыдущего испытания.
Назовем прежде всего те величины, которые служат для задания цепи Маркова.
Наиболее существенные из них — это числа
р^ (i> / = 1, 2, ..., т; п = 2, 3, ...),
см&гсл которых состоит в следующем: р{? есть вероятность того, что при n-м испытании наступит событие Лу, если в предыдущем, (п — 1)-м испытании наступило Д;. Мы ограничимся изучением только таких цепей Маркова, для которых вероятности р^ не зависят от п, — такие цепи называют однородными. Вместо р\У мы можем, следовательно, писать просто рц. Итак, по своему смыслу ptj есть условная вероятность, и эта вероятность определяется только номерами i, /, но не зависит от п, т. е. от того, как далеко продвинулся процесс проведения испытаний.
Каждое из чисел ptj называют вероятностью перехода, имея в виду следующий переход:
Ai (в п — 1)-м испытании) А} (в n-м испытании).
В соответствии со сказанным матрица из чисел рц, т. е. матрица
/Р11 Р12 ••• Pirn \
р = | р21 Р22 ••• р2т> ],	(О
'Ptnl Pm2 ••• Pmm'
называется матрицей переходов (или матрицей перехода).
Для полного описания цепи Маркова недостаточно знания одной лишь матрицы Р. Необходимо еще задать «начальные данные», точнее, вероятность каждого из событий Дх, А2,  , Ат для первого испытания (ведь первому испытанию не предшествует никакое другое, поэтому числа pt} для первого испытания ничего не значат). Эти вероятности мы будем обозначать р°, р°2, ..., р°т и называть начальными вероятностями. Например, есть вероятность тою, что при первом испытании наступит событие А2.
Цепь Маркова считается заданной, если указаны вероятности переходов ptJ (Z, j = 1,2, ... т) и начальные вероятности р? ( /= = 1, 2, .... т).
Числа ptj и р° не могут выбираться произвольно — они должны удовлетворять некоторым обязательным соотношениям. Эти соотношения имеют вид:
О < р°( < 1, 0 < Plj <1 (i, / = 1, 2, .... m),	(2)
p° + pt + ... + An = 1,	(3)
Pn + Pi2 +	+ Pi,n = 1 (i = 1, 2....m).	(4)
76
Обязательность условий (2) очевидна. Соотношение (3) вытекает из того факта, что при первом испытании обязательно наступает одно из событий А,, Д2, • ••, Ат, причем эти события попарно несовместны; соотношения (4) следуют из того, что, каким бы ни был исход Ai первого испытания, при втором испытании обязательно наступает одно из событий Alt Аг, Ат.
Цепи Маркова бывает удобно описывать в несколько других терминах, чем это было сделано нами выше. Представим себе физическую систему, которая может находиться в любом из т различных состояний; обозначим эти состояния Аг, А2, , Ат. В определенные моменты времени — условно при t ~ t = 2, t ~ 3 и т. д. — происходят смены состояний. При этом вероятность смены At -> Aj, в какой бы момент она ни происходила, одна и та же и равна pj. Другими словами, р1} есть вероятность перехода системы за один шаг из состояния Az в состояние Aj. Бесконечная последовательность состояний, сменяющих друг друга с определенными вероятностями перехода, и есть, таким образом, цепь Маркова.
2°. Примеры марковских цепей.
I. Перекладывание книг. На письменном столе лежит стопка из N книг. Если обозначить книги номерами 1,2, ..., А, то порядок их следования сверху вниз запишется с помощью строки
(а1т а2,	(5)
представляющей собой перестановку из чисел 1, 2, ..., N. А именно есть номер книги, лежащей сверху, а2 — номер книги, лежащей под ней, и т. д. Каждое испытание заключается в том, что из стопки берется одна из книг и (после извлечения из нее нужной информации) кладется наверх. Предположим, что каждая книга берется с определенной вероятностью: книга i — с вероятностью (i == 1, 2, ..., А).
Состояние системы будем определять порядком расположения книг в стопке. Иначе говоря, состояние определяется перестановкой (5). Отсюда ясно, что число возможных состояний будет N\ ' При очередном шаге состояние (cq, а2, ..., aw) либо останется неизменным — что произойдет с вероятностью ра1 при выборе лежащей сверху книги с номером oq, либо заменится на одно из состояний (аА, cq.... aw), где k > I, —такая смена произойдет с
вероятностью рл при выборе й-й сверху книги с номером ak.
Перед нами, таким образом, цепь Маркова с А! состояниями и указанными выше вероятностями переходов.
Остановимся на частных случаях А = 2 и А = 3. При А = 2 имеются лишь два состояния: А1 = (1, 2), А2 — (2, 1), а вероятности переходов суть
Pll = Pl, Р12 = Р2,
Р21 = Pl, Р22 = Р2, следовательно, матрица переходов
77
р — (Pi Рг\ \Р1 Рг)
При N == 3 имеем шесть состояний:
At = (1, 2, 3), Л2 = (2, 3, 1), А3 = (3, 1, 2), Л4 = (1, 3, 2), Л5 = (3, 2, 1), Л = (2, 1, 3),
а матрица переходов
Например, р12 = 0, поскольку переход от состояния Лх — (1, 2, 3)кЛ2 = (2, 3, 1) (за один шаг) невозможен.
II. Суммирование случайных чисел «по модулю т». Зафиксируем некоторое натуральное число т. Пусть испытание заключается в выборе наугад какого-либо из чисел 0,1, 2, т — 1 (остатков от деления на т), причем каждое число выбирается с определенной вероятностью: число i (i — 0, 1, ..., tn — 1) — с вероятностью pi. Очевидно, должно быть
Ро + Pi + Рг + ••• + рт_л = 1.
Будем повторять указанное испытание, определяя состояние «системы» после каждого испытания суммой выбранных чисел, редуцированной по модулю т: последние слова означают, что берется не сама сумма, а ее остаток от деления на т. Таким образом, возможны tn различных состояний: Ло, Лх, Л2, •••, Лт_х, где состояние Л/ (после очередного, n-го испытания) означает, что остаток от деления на т суммы выбранных (за п шагов) чисел равен i. Например, если т = 8 и в результате последовательных испытаний выбирались числа 1, 3, 2, 2, 5, .... то последовательность состояний системы такова:
Лх, Л4, Ад, Ло, Л5, ...
Подсчитаем вероятности переходов. Пусть после п шагов система находится в состоянии Л,. Очередной, (п + 1)-й шаг заключается в выборе одного из чисел 0, 1, 2, ..., т — 1, что происходит с вероятностями р0, р1у ..., /?т_х соответственно; при этом, если выбрано число а, то состояние Лг сменяется Ajy где / есть остаток от деления i + а на т. Следовательно, если i + а < т, то j = i +>а и, значит, / i; если же i + а т, то j = i + а — лг и тем самым j < I (ибо а < т). На основании сказанного можем записать:
а = / — i, если j г,
а = т + (/ — i), если / < I,
78
а поскольку число а выбирается с вероятностью ра, то получаем следующие вероятности переходов:
р (рм, если />/,	(7)
Ьт+(7-9. если / </.
Положим, например, т — 5. В соответствии с (7) матрица переходов будет иметь в этом случае вид:
Ро Pi Рз
Р2
Pl Р2
Pl
Ро Pi
Рз
Р2 Рз Pi Pl Р2 Рз Ро Pi Pz Pl Ро Pi рз Pi Ро‘
(8)
Обратим внимание на интересную особенность матрицы (8), которая будет использована впоследствии: сумма элементов любого столбца равна р0 + pt + pz + Рз + Pi> т- е- равна 1. То же самое верно и для строк; однако равенство единице суммы элементов строки есть общий факт, справедливый для матрицы переходов любой марковской цепи (см. равенства (4)).
Оставим на время примеры и обратимся к рассмотрению типичных задач, возникающих при рассмотрении марковских цепей.
3°. Нахождение вероятностей переходов за несколько шагов. Пусть в результате n-го испытания наступило состояние At. Тогда вероятность того, что при следующем, (п + 1)-м испытании наступит Aj, равна р^. Мы выражаем этот факт в следующих словах: Ри есть вероятность перехода от Аг к Aj за один шаг.
Поставим теперь вопрос: чему равны вероятности переходов за два шага? Точнее, пусть после n-го испытания наступило Alt найдем тогда вероятность того, что после (п + 2)-го испытания, т. е. через два шага, наступит Aj. Обозначим эту вероятность/^у (2).
Интересующий нас переход от At к Ду за два шага может осуществиться т различными способами:
Л, -> Д! -> Ду, Дг —> А2 —> Ду,
Л m Aj-
Здесь запись Д( Д/г —Ду означает, что в результате (п + 1)-го испытания произошла смена Д; -> Ak, а в результате (п + 2)-го — смена Дй -> Ду. Вероятность осуществления такого «двойного» перехода легко найти, если воспользоваться уже известной нам формулой
р (АВ) = р (A/В) р (В);	(9)
эта вероятность равна plk pk]. Отсюда на основании правила сложения вероятностей будем иметь:
79
PlJ (2) = PnPl] + Pt2P2} + .•. + PlmPmr	(10)
что и решает поставленную нами задачу.
В правой части равенства (10) стоит сумма произведений Pik Pkj 1> 2. •••, tn). Первые множители pllt р12, ..., р,т этих произведений суть элементы i-й строки матрицы переходов Р, вторые множители р1}, p?j, ..., pmj — элементы /'-го столбца той же матрицы. Вспоминая известное правило умножения матриц, находим отсюда, что матрица, составленная из чисел ptj (2), т. е. матрица переходов за два шага, будет равна Р • Р = Р2.
Аналогичное рассуждение позволяет найти вероятности переходов за три шага. Событие А;А; (переход от At к Aj за три шага) распадается на следующие варианты:
А Дх -> Aj,
Aj —> —> А 2 -* Aj,
At -* Ат -> А}.
Применяя снова формулу (9), а также правило сложения вероятностей, находим отсюда вероятность перехода от At и Aj за три шага:
Рц (3) = Рп (21 р}] + ра (2) p2j + ... + p/m(2) pmi. (11)
Следовательно, матрица из чисел рц (3), т. е. матрица трехшаговых переходов, будет: Р2  Р = Р3.
Повторяя это рассуждение, найдем, что матрица Р (п) переходов за п шагов будет:
Р (п) = Р\	(12)
Полученная формула решает вопрос о нахождении вероятностей переходов за любое число шагов.
В качестве примера рассмотрим задачу о перекладывании книг (см. предыдущий пункт 2°). В простейшем случае N—2 мы имели:
Р = (Р1 Pz\
\Pi Рг)-
Учитывая, что pi + р2 = 1, находим отсюда:
Р2 = [Pi Рг\ [Pi Ръ\ — р.
\Pi Ра \Pi Pi)
Тем самым Рп — Р при любом п. Итак, в случае двух книг Р (п) = = Р для любого числа п шагов.
Если в той же задаче рассмотреть случай N = 3, то вычисление матрицы Р2, а гем более Р3, Р4 и т. д., становится весьма громоздким делом. Предоставляем читателю в качестве упражнения найти матрицу Р2, где Р есть матрица (6), и убедиться, что в этой матриц» нет нулей (если числа рт,р2.Дз строго положительны) Хорошим упражнением может служить и такая задача’ показать, что в случае любого V матрица Рп при достаточно высоком показателе степени п не будет им 1ь нулей.
80
4°. Предельные вероятности. Следующей важной задачей является исследование поведения вероятностей pi} (я) при неограниченном увеличении числа п. Решение этой задачи в целом ряде случаев может быть получено на основе следующей теоремы А. А. Маркова.
Теорема Маркова (о предельных вероятностях) Пусть существует такое число t шагов, что все вероятности pt/ (t) строго положительны. Тогда для каждого состояния Aj существует предельная вероятность его наступления, т. е. такое числор*, что независимо от t имеет место равенство
litnpzy (п) = Рр
Доказательство этой теоремы довольно сложно, и мы его не приводим. Отметим, однако, что смысл содержащегося в теореме утверждения интуитивно понятен: вероятность того, что система окажется в состоянии Aj, практически не зависит от того, в каком состоянии она находилась в далеком прошлом; эта вероятность мало отличается от предельной величины р*.
Возникает вопрос: если существуют предельные вероятности, то каким образом их можно найти? Покажем, что искомые числа pi, р*2, .... р‘т удовлетворяют следующей системе tn уравнений с m неизвестными:
Xj = МР1/ + x2p2j + ... + XmPmj (j = 1, 2, ..., m).	(13)
Чтобы установить этот факт, воспользуемся равенствами
Ру (м + 1) = Ра (п)р1} + р12 (tl)pi} 4- ... + ptm (n)pml, которые для частных случаев п ~ 2 и п = 3 уже рассматривались ранее (см. (10) и (11)). Переходя в этих равенствах к пределу при п оо, будем иметь:
Pi = Pl Pi) + Р$Ръ) + ••• + pmpm), что и требуется получить.
Помимо системы (13), числа р*, рЪ, рА должны удовлетворять еще одному уравнению:
*1 + *2 4" ••• 4- xm ~ 1.	(14)
Этот факт тоже проверяется весьма просто: нужно в соотношении
р 1 («) + Pl2 («) + ... + pirn (n) = 1
(объясните, почему справедливо такое равенство!) перейти к пределу при п -> оо.
Итак, предельные вероятности должны удовлетворять системе, состоящей из уравнений (13) и (14). Можно показать, что при условии существования предельных вероятностей эта система имеет только одно решение.
81
Вот доказательство этого утверждения. Пусть р*, р'2, .... р^ —предельные вероятности, a (xi, х2, .... хт) —любое решение системы (13). Запишем уравнения (13) короче:
т х)^ ’> 2....................т)- <15)
*=.!
Умножим обе части написанного равенства на pjk, где k — фиксированный т
номер, после чего просуммируем по j. Получим слева ^х ,/>;& = хд, а справа /=>
т	/ т	\	т
2 xl 2 PljPj/i = 2 xiP‘k(2)-
i=l	\/=1	/	i=l
Таким образом, вслед за (15) имеем:
т
xk ~ 2 xiPik (2)’
i=i
Рассуждая аналогично, получим при любом л:
т
*л=2 x‘P‘k(n).
1=1
Устремляя л к бесконечности, находим отсюда:
m	т
хь = 2 Wk = pZ • 2 = pt
/==1	i=l
что и требовалось доказать.
5°. Для иллюстрации сказанного выше исследуем цепь Маркова, возникающую при суммировании случайных чисел по модулю т (см. пример II в пункте 2°).
Для определенности положим т = 5. Матрица переходов Р имеет в этом случае вид (8). Если считать числа р0, plt р2, р3, р^ строго положительными, то все элементы матрицы Р, а значит, и матриц Рг, Р3 и т. д. тоже будут строго положительны. Мы видим, что условие теоремы Маркова выполняется. Следовательно, существуют предельные вероятности р3, pf, pj, pt Для их нахождения нужно решить систему (13), (14). Учитывая, что в данном случае состояния обозначаются До, Л(, Аг, А3, Д4 (а не Alt Д2, .... Ат), следует писать эту систему так:
х} = Харо) + XiPij + x2p2j 4- xsp3] + Xtfy (j = 0, 1, 2, 3, 4), (16)
Xq + Xt + хг + x3 + х^ = 1;	(17)
при этом, как уже отмечалось, мы можем быть заранее уверены, что решение системы единственно. Но в таком случае искомое решение будет:
11111
ХО = -, Xi = -, х2 = -, xs = -, х4 = -
82
Действительно, при подстановке этих значений в правые части уравнений (16) мы получаем: (p0J+ рц+Рц+Рз^+рцУ, О
но выражение, стоящее в скобках, представляет собой сумму элементов одного из столбцов матрицы Р и потому равно 1 (на это обстоятельство мы обращали внимание читателя при разборе примера II). Итак, все предельные вероятности равны между собой. Практически это означает, что при неограниченном продолжении испытаний состояния Ао, Ai, А2, А3, Л4 будут воз
Марков А. А. (1856—1922)
никать одинаково часто; иначе говоря,
суммы случайным образом выбираемых чисел из множества (0, 1, 2, 3, 4} будут с одинаковой частотой давать (при делении на 5) остатки О, 1, 2, 3, 4.
Историческая справка. Андрей Андреевич Марков (1856—1922) — выдающийся русский математик, труды которого существенно продвинули вперед теорию вероятностей. Важнейшее из его открьпий — понятие «цепи Маркова», оказавшееся чрезвычайно ценным в приложениях и вызвавшее большой поток исследований. Развитие идеи марковской цепи привело к созданию обширного и важного раздела теории вероятношей—теории так называемых случайных процессов, в которой главную роль сыграли труды советских математиков А. Н. Колмогорова, А. Я. Хинчина, Е. Е. Слуцкого и др.
А. А. Марков был не только крупным математиком, но и человеком передовых убеждений. Известен, например, такой эпизод: когда царские деятели отказали писателю А. М. Горькому в звании академика, Марков в знак протеста публично отказался от всех титулов и отличий, присвоенных ему Академией наук.
Глава 5.
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И ЗАКОНЫ ИХ РАСПРЕДЕЛЕНИЯ
§ 20.	ОПИСАТЕЛЬНЫЙ ПОДХОД К ПОНЯТИЮ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
Почти в каждом из примеров, с которыми мы встречались, дело обстояло таким образом, что в результате опьна возникало некоторое число. Например, при бросании игральной кости выпадало то или иное число очков, при обследовании партии готовых изделий обнаруживалось то или иное число единиц брака. Следует сказать, что такое положение типично для теории вероятностей. Среди решаемых ею задач исключительно много таких, в которых исход опыта выражается некоторым числом х. При этом случайный характер исхода влечет за собой случайность числа х; это означает, что при повторении опыта оно меняется непредвиденным образом. Приведем несколько примеров.
1.	Бросается игральная кость; х — выпавшее число очков.
2.	Покупается п лотерейных билетов; х — число выигрышей.
3.	Электрическая лампочка испытывается на длительность горения; х — полное время горения лампочки.
4.	Некто приходит на платформу станции метро, чтобы сесть в поезд; х — время ожидания ближайшего поезда.
Чтобы все примеры подобного рода уложить в единую схему, введем понятие случайной величины.
Определение. Случайной величиной, связанной с данным опытом, называется величина, которая при каждом осуществлении этого опыта принимает то или иное числовое значение, заранее неизвестно, какое именно (это зависит от случая).
Случайные величины мы будем обозначать в дальнейшем жирными буквами х, у и т. д.
Данное выше определение не претендует, конечно, на строгость; скорее его следует рассматривать как описание понятия случайной величины. Мы примем это описание в качестве «первого приближения».
Каждой случайной величине х соответствует некоторое множество чисел. Это множество значений, которые может принимать величина х. Так, в первом из наших примеров множество значений состоит из шести чисел: 1, 2, 3, 4, 5, 6, во втором — из чисел 0, 1, 2, ..., п, в третьем — х может принимать (в принципе) любое неотрицательное значение, наконец, в последнем примере множество значений есть отрезок [0, 2] числовой оси (поезда метрополитена следуют с интервалом в 2 минуты).
84
Различные случайные величины могут иметь одно и то же множество возможных значений. Чтобы проиллюстрировать это примером, представим себе, что имеются две игральные кости, причем одна сделана из однородного материала, а другая, скажем, склеена из двух кусков разной плотности. Обозначим через х число очков, выпадающих на первой кости, через у — число очков на второй. Случайные величины х и у имеют одно и то же множество возможных значений, а именно {1, 2, 3, 4, 5, 6}, однако ведут себя совершенно по-разному. Если много раз подряд бросать первую из костей, то частоты событий х=1, х = 2, ..., х = 6 будут близки к —; при 6 многократном же бросании второй кости частоты событий у = 1, у = 2, ..., у — 6 будут совсем другими. Этот пример показывает, что знания одного лишь множества возможных значений недостаточно для полного описания случайной величины. Необходимо еще знать, как часто случайная величина принимает то или другое из своих значений. Любое правило, устанавливающее связь между возможными значениями случайной величины и их вероятностями, называется законом распределения случайной величины.
Наиболее удобными для изучения являются так называемые дискретные случайные величины. Они характеризуются тем, что могут принимать лишь конечное или счетное множество значений. Среди примеров 1 —4, указанных в начале параграфа, очевидно, только первые два являются примерами дискретных случайных величин.
Для дискретной случайной величины х закон распределения может быть задан в форме таблицы:
Х1 | х2 | ...
Р1 | Рг | -
где xit х2, ... — возможные значения величины х, a pi, р2, ... — их вероятности. А именно pi есть вероятность значения лу (вероятность события х = лу), р2 есть вероятность значения х2 и т. д. Числа pit р2, ... связаны соотношением
Pi + Рг + ... = 1, которое вытекает из того факта, что события
X = Xi, х = х2, ...	(1)
попарно несовместны, а их сумма есть событие достоверное (при каждом осуществлении опыта величина х принимает одно и только одно из своих значений, т. е. наступает одно и только одно из событий (1)).
Подчеркнем еще раз, что рассуждения этого параграфа носят описательный характер. Точное определение понятия дискретной случайной величины будет дано в § 21, а случайной величины общего вида — в § 22.
85
§ 21. ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Определение. Мы говорим, что задана дискретная случайная величина х, если указано конечное или счетное множество чисел
X1, X 2, ...
и каждому из этих чисел xt сопоставлено некоторое положительное число pt, причем сумма всех равна 1.
Числа хх, х2, ... называются возможными значениями случайной величины х, а числа рх, р2, ••• —вероятностями этих значений есть вероятность значения х;).
Итак, дискретная случайная величина задается таблицей вида:
х2 -------------- (1)
Pi Рг j -
с условием, что числа pY, р2, ... положительны и их сумма равна 1.
С дискретной случайной величиной х, естественно, связывается вероятностная схема в смысле § 3. Пространством элементарных событий в ней является множество Q = {xlt х2, ...}, событиями являются всевозможные подмножества множества Q, а вероятность р (Л) события А определяется как сумма чисел для всех Х[ € А. Например, если А = {х2, хь}, то р (Л) = р2 + рь- Событие, заданное подмножеством Л, удобно записывать х € Л и выражать словами «случайная величина х приняла значение из множества Л».
Таблицу (1) обычно называют законом распределения дискретной случайной величины х.
Пример 1, По мишени стреляют один раз с вероятностью попадания р. Случайная величина х — число попаданий. Очевидно, х может принимать только два значения: 1 и 0, причем их вероятности равны соответственно р и 1 — р. Действительно, при выстреле возможны два исхода: попадание (тогда х = 1) и промах (х = 0); вероятности этих событий суть р и 1 — р. В итоге получаем следующую таблицу:
Значения х	1	0
Вероятности	Р	1 — Р
Пример 2. Дважды бросается игральная кость. Случайная величина х — сумма очков при обоих бросаниях. Возможные значения величины х суть числа 2, 3.................. 12. Вероятности этих значений легко
86
з подсчитываются. Например, /э (х = 10) = —, 36 так как из тридцати шести возможных исходов опыта событию х= 10 благоприятны три. Найдя все вероятности, получим следующую таблицу:
Значения х	2	3	4	5	6	7	8	9	10	11	12
Вероятности	£ 36	2 36	3 36	4 36	5 36	6 36	5 36	4 36	3 36	2 36	_1_ 36
Пример 3. Производится ряд независимых опытов, в каждом из которых с одной и той же вероятностью наступает событие А. Опыты продолжаются до первого появления события А, после чего прекращаются. Рассматривается случайная величина х — число произведенных опытов. Составить для нее закон распределения.
Решение. Возможные значения величины х суть 1, 2, 3, ... . Событие х = п (п — любое натуральное) означает, что в первых п — 1 опытах событие А не наступает, а в n-м опыте наступает. Вероятность такого исхода равна:
(1 —р) (1 —/?) ... (1 — р) • р = pqn~\
п—I раз
где <7 = 1 — р. Следовательно, закон распределения величины х-будет:
Значения х	1	2	3		п	
Вероятности	Р	РЧ	РЧ2	...	РЧ'1'1	
Пример 4. Монету бросают 5 раз. Случайная величина х — число выпадений герба. Возможные значения величины х суть 0, 1,2, 3, 4, 5. Их вероятности подсчитываются с помощью формулы Бернулли (§ 15), например:
/	04	/ 1 \з ! 1 \2 ю
р (х = 3) = С5 -	- =
Произведя все подсчеты, получим таблицу:
Значения х	0	1	2	3	4	5
Вероятности	2 | 32	_5 32	19 32	19 32	_5 32	1 32
Пример 5. Биномиальное распределение. Пусть производится определенное число п независимых опы-
«7
тов. В каждом из них с одной и той же вероятностью р может наступить некоторое событие А. Рассматривается случайная величина х — число наступлений события А в п опытах. Соответствующая таблица имеет вид:
Значения х	0	1	2	п — 1	п
Вероятности	Рл(0)	ДП1)	Р„(2)	...		Рп
(3)
где Pn(k) = Cnpk (1 — рУ~'г (k = 0, 1, 2....n). Это непосред-
ственно следует из формулы Бернулли.
Очевидно, таблица (2) есть частный случай таблицы (3). Этот частный случай соответствует значениям п — 5, р =
Закон распределения, характеризующийся таблицей (3), называют биномиальным. Такое название связано с уже известным читателю фактом: числа Р„(0), Р„(1), ..., Рл(п) являются членами бинома (<? + рУ, где q = 1 — р.
Пример 6. Распределение Пуассона. Мы говорим, что случайная величина х распределена по закону Пуассона, если соответствующая таблица имеет вид:
Значения х
О 1	2
Вероятности
(4)
где
pA = £V?“(& = 0, 1, 2, ...).
Здесь X — фиксированное положительное число (разным значениям X отвечают разные распределения Пуассона).
Легко проверить, что для написанной таблицы выполнено обязательное условие — сумма вероятностей всех возможных значений равна 1. Действительно,
Ро + Pi + Pi 4- ••• =6 z X х^+^+12+ ...ue-v=i. \0!	1!	21	)
На рисунке 16 показаны гра-фики функции pk = — е-ъ (как функции ot k) для различных значений параметрах. Каж
88
дый график представляет собой дискретный ряд точек; для большей наглядности точки соединены последовательно ломаной линией (так называемый многоугольник, распределения).
Распределение Пуассона заслуживает особого внимания, так как из всех дискретных распределений оно наиболее часто встречается в приложениях.
Одна из причин, обусловливающих важную роль пуассоновского распределения для практики, заключается в его тесной связи с биномиальным распределением. Напомним (§ 18), что если в выражении для биномиальных вероятностей
р„(й) = сУ(1-рГй
мы зафиксируем значение k и станем устремлять число опытов п к бесконечности, а вероятность р — к нулю, притом так, чтобы их произведение оставалось равным постоянному числу X (пр = Х), то будем иметь:
(5) /г!
Соотношение (5) показывает, что при описанном выше предельном переходе таблица (3) биномиального распределения переходит в таблицу (4) распределения Пуассона. Таким образом, распределение Пуассона является предельным для биномиального распределения при указанных выше условиях. Заметим, что с этим свойством распределения Пуассона — выражать биномиальное распределение при большом числе опытов и малой вероятности события — связано часто применяемое для него название закона редких явлений.
§ 22, СЛУЧАЙНЫЕ ВЕЛИЧИНЫ ОБЩЕГО ВИДА. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ
1°. Вступительная часть (о событиях, связанных со случайными величинами). Если при рассмотрении дискретных случайных величин мы могли ограничиться событиями, представляющимися в виде суммы конечного или счетного множества элементарных событий х = xt, то при переходе к случайным величинам общего вида нам следует прежде всего расширить класс событий. В необходимости такого расширения можно убедиться на примере. Пусть с испытательной целью определяется полное время работы электрической лампочки; для этого выпущенную заводом лампочку эксплуатируют без перерыва до выхода ее из строя. Результатом такого испытания является величина х — срок службы лампочки. Очевидно, эта величина является случайной — предсказать заранее ее значение невозможно. Элементарным событием в данном примере будет любое событие вида х = а, где а — неотрицательное число. Однако в отличие от дискретного случая каждое отдельно
89
взятое элементарное событие не представляет теперь большого интереса. Действительно, возможных значений для х существует несчетное множество, между тем в любой серии испытаний мы имеем дело всегда с конечным числом ламп. Поэтому ясно, что данное фиксированное значение а в серии испытаний, как правило, не будет встречаться вовсе или же будет наблюдаться чрезвычайно редко. Другими словами, вероятность события х = а будет равна нулю.
В то же время события, выражаемые при помощи неравенств, скажем х < 1000 (лампа перегорела, не прослужив 1000 часов), представляются значительно более важными. Вероятности таких событий дают существенную информацию о распределении значений величины х и тем самым о качестве ламп. Разумеется, вслед за событиями такого рода мы должны привлечь к рассмотрению и их комбинации, получаемые при помощи конечного или счетного числа операций сложения, умножения и перехода к противоположному событию.
2°. Борелевские множества на прямой.
Определение. Множество точек на числовой оси называется борелевским, если оно может быть получено из множеств вида{л: | х < а{применением конечного или счетного числа операций объединения, пересечения и дополнения.
Заметим, что операцию пересечения можно было бы из данного определения исключить, так как она сводится к операциям объединения и дополнения по формуле
Д1Дг--1 — Д1 + Дг ••• •
Класс борелевских множеств достаточно широк. В нем содержатся множества вида {х|х а) (дополнение к {х\х < а}), вся числовая ось (объединение {х\х<а} и {х| х а}), множества {х|я х < Ь} (пересечение {х|х и {х|х < Ь}), отдельные точки х — а (пересечение бесконечного числа полуинтервалов х| я х < я + —), где п — 1, 2, 3, ...), множества вида {х| я< н )
< х Ь}, {х|я < х < Ь}, {х|я х Ь}. Практически все встречающиеся в приложениях числовые множества являются боре-левскими.
Прежде чем сформулировать общее и математически строгое определение случайной величины, сделаем одно замечание. Если дана случайная (в нестрогом, интуитивном смысле, см. начало § 20) величина х, то можно говорить о вероятности событий х < а, а значит, и о вероятности событий х С Д, где А — любое борелевс-кое множество на прямой. Отсюда возникает идея: считать одной из форм задания случайной величины приписывание каждому бо-релевскому множеству А неотрицательного числа р (Д), истолковываемого как вероятность события х С А. Разумеется, числа р (Д) для различных А не могут выбираться произвольно; они
90
должны быть определенным образом согласованы друг с другом, как того требуют аксиомы для вероятностей (см. § 3, п. 3°).
3°. Общее определение случайной величины.
Определение. Мы говорим, что задана случайная величина х, если каждому борелевскому множеству А на числовой прямой R сопоставлено неотрицательное число р (Л), причем р (R) =1, и выполнено условие счетной аддитивности, т. е.
Р (^1 +	+ •••) = Р (Лх) + Р (^2> + ••• >	(1)
если множества Лъ Л2, ... (борелевские) попарно не пересекаются.
Знак «+» в левой части равенства (1) обозначает объединение множеств.
Для получения в дальнейшем следствий из условия (1) удобно придать этому условию несколько иную форму. Условие (1) объединяет два случая: первый — когда число множеств Лп Аг, • •• конечно, второй — когда имеется бесконечная последовательность множеств Лх, Л2, ••• • В первом случае условие (1) принимает вид:
р (Лх + Аг + ... + Л„) = р (Лх) + р (Л2) + ... + р (Ап\ (2) если A{Aj = 0 при i У= /. Рассмотрим теперь более подробно второй случай.
Положим,
Sn = А. + А2+ ... + Ап (и = 1,2, ...) и
5 = А{ + А2 + ... .
В правой части условия (1) стоит сумма бесконечного ряда чисел, т. е. предел последовательности частичных сумм. Но n-я частичная сумма ряда в силу (2) равна р (Sn). Таким образом, для случая бесконечной последовательности множеств Alt А2, ... условие (1) можно записать так:
limp(SJ = р (S),	(3)
если AtA} = 0 при i =А= j.
Сделаем еще одно замечание — на этот раз по поводу нашей дальнейшей речи. Чтобы приблизить данное выше определение случайной величины к практически сложившейся терминологии, условимся каждое борелевское множество А рассматривать как событие. Это событие будем обозначать либо А, либо
х € А	(4)
и выражать словами «случайная величина х приняла значение из множества Л». Число р (Л) будем называть вероятностью события А; наряду с записью р (А) будем использовать запись р (х С Л) (вероятность события х (: Л).
Впрочем, иногда событие (4) будем записывать по-другому. Например, если Л есть множество {х|х < а} (числовой луч), то вместо х£ Л будем писать х < а; если Л есть множество {х|а <х Ь}
91
(отрезок), то будем писать а х Ь\ если А состоит из единственной точки а, то будем записывать х = а.
Как показывает данное в начале этого пункта определение, задание случайной величины х означает задание некоторой вероятностной схемы (в смысле § 3, п. 4°). В этой схеме множество Q есть числовая прямая R, событиями служат всевозможные борелевские множества из R, а верояшости событий суть те самые числа р (А), с помощью которых определена величина х.
4°. Функция распределения случайной величины и ее свойства.
Способ, которым по определению задается случайная величина, не всегда удобен, поскольку счетно-аддитивная функция р (Л) представляет собой трудно обозримый объект. Возникает вопрос о более простых способах задания случайной величины. Один из них мы сейчас рассмотрим. Он состоит в задании так называемой функции распределения.
Каждой случайной величине х можно сопоставить некоторую функцию F, определенную на всей числовой оси. При любом х0 значение F (х0) задается равенством
F (х0) = р (х < х0),
т. е. F (х0) есть вероятность того, что случайная величина х примет значение меньшее, чем х0. Например, F (—1) = р (х < —1), F (3) = р (х < 3). Для большей отчетливости напомним, что в соответствии с принятыми ранее соглашениями р (х < х0) обозначает число р (А), где А есть множество {х|х < х0}.
Функция F называется функцией распределения случайной величины х.
В дальнейшем функцию F будем записывать F (х), следуя привычному способу обозначения функции.
Отметим прежде всего следующий факт: зная функцию F (х), можно найти вероятность любого события вида хг х < х2. Действительно, воспользуемся очевидным соотношением между событиями:
(х < х2) = (х < хх) 4- (%! < х < х2)
(см. рис. 17: луч, расположенный левее точки х2, есть объединение луча, расположенного левее х1( и полуинтервала [хп х2)). Если к этому соотношению применить (2) («правило сложения вероятностей»), то получим:
F (х2) = F (xj + р (хх < х < х2).
Следовательно,
р (хх < х < х2) = F (х2) — F (хх).	(5)
Рис. 17
Рис. 18
92
Формула (5) в дальнейших рассуждениях играет важную роль. Установим теперь некоторые свойства функции распределения. 1. Функция F (х) неубывающая, т. е. F (х2) F (хг), если х2 > хх. Это немедленно следует из формулы (5), если учесть, что величина, стоящая в левой «асти, неотрицательна (по самому определению случайной величины имеем р (Л)	0 для любого
борелевского Л).
2. Справедливы равенства:
lim F (л) = 1, lim F (х) = 0.	(6)
Х-*ОО	X-*— оо
Чтобы доказать первое из этих равенств, возьмем любую возрастающую последовательность чисел xv xit ..., для которой lim хп = оо, и рассмотрим последовательность событий: П-+ОЭ
Лр
Л 2* Лз:
X < X], Xt Д X < хг, Х2 < X < х3,
(см. рис. 18). Учитывая, что Л,Л;- = 0 при t =4= /, применим условие (3). В данном случае событие Sn Аг Ч- Л2 + ••• + Л„ есть, очевидно, х < хп, поэтому р (S„) = р (х < хп) — F (х„), а событие S есть х € R и, следовательно, р (5) = 1. Применив (3), получаем:
lim F (хл) = 1.
П-*00
Так как это равенство справедливо для любой последовательности х1( х2, уходящей в бесконечность, то этим доказано первое из равенств (6). Докажем теперь второе.
Пусть хп х2, ... — убывающая последовательность чисел, такая, что limx„ = —оо. Применим условие (3) к последовательно-
М->оо
сти событий Лц Л2, •••, показанной па рисунке 19. Так как теперь Sn есть событие хп+1 х < хг, то в силу формулы (5) р (Sn) — = F (rj) — F (хл+1); так как событие S есть х < хп то р (S) = F(xJ. Из (3) находим: F(x1)=lim [F(xx)—F (х„+1)], что дает: lim F(xn4,i)=O.
п -> ОО	П -> со
Очевидно, этим доказано второе из равенств (6).
Как известно, для неубывающей (вообще, для монотонной) функции F (х) при любом значении аргумента х существуют оба односторонних предела:
Рис. 20
93
F (x — 0) — lim F (x — a) a-»0,a>0
F (x + 0) — lim F (x + a)-
a-*-0,a>0
Оказывается, что в случае функции распределения первый из этих пределов совпадает со значением функции в самой точке х. А именно справедливо следующее свойство:
3. F (х — 0) = F (х) при любом х.	(7)
Как говорят в этом случае, функция F (х) непрерывна слева.
Для доказательства выберем какую-либо возрастающую последовательность чисел хп х2, сходящуюся к данному значению х0. Применим условие (3) к последовательности событий: Ар х <Xj, А 2  ^х <х2, А3: х2 х<х3 и т. д. (рис. 20). В этом случае S„ есть событие х < хп, так что р (S„) = F (хп), а S есть событие х < х0, так что р (S) = F (х0). Из (3) находим:
lim F (хл) = F (х0).	(8)
П-*со
Таким образом, каково бы ни было число х0, для любой возрастающей и сходящейся к х0 последовательности хп х2, ... справедливо равенство (8). Как известно из курса математического анализа, отсюда следует: F (х0 — 0) = F (х0), т. е. (7).
Представляет интерес вопрос о разрывах функции F (х). Точки разрыва соответствуют таким значениям х, для которых разность
F (х + 0) — F (х — 0)	(9)
отлична от нуля. Напомним, что в случае монотонной функции F (х) величина (9) называется скачком функции в точке х. Мы докажем сейчас, что при любом х справедлива формула
F (х + 0) — F (х — 0) = р (х = х),	(10)
Рис. 22
т. е. скачок функции распределения в точке х совпадает с вероятностью события х — х (рис. 21).
Чтобы вывести формулу (10), рассмотрим какую-нибудь убывающую последовательность хп х2, ..., сходящуюся в некоторой точке х0. Применим условие (3) к последовательности событий: Aj : х2 х < хн А 2 : х3 х< < х2, ... (рис. 22). В данном случае S„ есть событие х„+1^
х < хх, так что р (5Л) =
94
*=F (%]) — F (x„+1), a S есть событие x0 < x < xv Следовательно, имеем:
lim [F (xj — F (x„+1)] = p (x0 < x < xj. (11) n-*oo
Левую часть этого равенства можно записать как F (хг) — F (хо4-0). Что же касается правой части, то, рассмотрев очевидное соотношение между событиями:
(х0 < х < хг) = (х0 < х < xj + (х = х0)
и применив правило сложения вероятностей (условие (2)), получим:
F (xj — F (х0) = р (х0 < х < хх) + р (х = х0).
Следовательно, (11) перепишется:
F (хх) - F (х0 + 0) = (F (xj - F (х0)) - р (х = х0).
Если отбросить равные слагаемые F (xj и учесть, что F (х0) = = F (х0 — 0), то и придем к (10) (для х = х0).
Из формулы (10) можно извлечь такое следствие.
Если х0 есть точка непрерывности функции F (х), то вероятность события х = х0 равна нулю.
Как известно, точки разрыва монотонной функции всегда образуют конечное или счетное множество. В частности, множество точек разрыва функции F (х) не более чем счетно. Или, другими словами, имеется не более чем счетное множество точек х0, таких, что р (х = х0) =/= 0.
5°. Условия, при которых заданная функция F (х) является функцией распределения. Мы показали, что функция распределения обладает перечисленными выше свойствами 1—3. Возникает вопрос, являются ли эти свойства характеристическими. Иначе говоря, можно ли утверждать, что любая функция F (х), обладающая свойствами 1—3, является функцией распределения некоторой случайной величины х? Ответ на этот вопрос оказывается утвердительным. А именно справедлива следующая важная теорема.
Теорема. Пусть дана функция F (х), определенная для всех значений х и обладающая свойствами:
1)	F (х) не убывает;
2)	lim F(x) = 1, lim F (x) = 0;
Ж-*—ou
3)	F(х)непрерывна слева при любом х.
Тогда существует, и притом лишь одна, случайная величина х, функция распределения которой совпадает с F (х).
В более развернутой форме заключение теоремы можно сформулировать так.
Существует, и притом только одна, неотрицательная счетноаддитивная функция р(А), определенная на системе всех борелевских подмножеств числовой оси, удовлетворяющая условию р (R) ~ 1 (где R— числовая ось) и такая, что
x))*=F(x)
95
при всяком х, (Здесь (—оо, х) обозначает множество, состоящее из всех чисел, меньших х.)
Доказательство теоремы довольно сложно. Оно излагается отдельно в приложении 1 к данной книге (см. с. 196—198).
Сформулированная выше теорема имеет особое значение; опираясь на эту теорему, мы можем теперь при задании случайной величины использовать более простое средство, чем функция р (Л) борелевского множества А. Объектом, определяющим случайную величину, может служить, как мы теперь видим, любая числовая функция F (х), обладающая свойствами 1—3.
6°. Распределение случайной величины. Закон распределения. Согласно определению, задать случайную величину х означает задать неотрицательную счетно-аддитивную функцию р (Л), определенную на системе всех борелевских подмножеств числовой оси и удовлетворяющую условию р (R) = 1. Функцию р (Л) называют распределением величины х.
Однако, как мы видели, возможны и другие формы задания случайной величины, например с помощью функции распределения F (х).
Любая форма задания случайной величины хназывается законом распределения этой величины.
§ 23. ДИСКРЕТНЫЕ И НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ. ПЛОТНОСТЬ ВЕРОЯТНОСТИ
1°. Дискретная случайная величина и ее функция распределения. В § 21 мы дали определение дискретной случайной величины. Оно было сформулировано в несколько других терминах, чем введенное позже (в § 22) общее определение случайной величины. Чтобы устранить возникшую таким образом несогласованность, дадим теперь определение дискретной случайной величины в терминах функции р (Л).
Определение. Случайная величина х с распределением р (Л) называется дискретной, если существует такое конечное или счетное множество Q на прямой, что р (О) = 1.
Изучению дискретной случайной величины х предпошлем такую лемму.
Лемма. Пусть р (Л) — некоторое распределение и О — борелевское множество, для которого р (Q) = 1. Тогда для любого борелевского множества А справедливо равенство
р(Л) = р(Лй).	(1)
Доказательство. Обозначим, как обычно, дополнение к □ через Q. Так как р (Q) + р (Q) = р (Д) — 1, то р (Q) = 0. Следовательно, для любого борелевского подмножества В множества Q будет также р (В) = 0 (объясните почему!).
Пусть теперь А—любое борелевское множество. Имеем: А —
96
— AQ + 4Q, откуда следует: p (A) = p (ДЙ) + p (ЛЙ). Ho второе слагаемое правой части равно нулю, поскольку ЛП принадлежит й. Значит, р (Л) = /?(ЛЙ). 
Положим, й = {%!, Х2, •••} И Pl = Р ({%/}) (i — 1, 2, ...)• Из формулы (1) следует, что для любого борелевского А имеет место равенство
•р(Л)= 2 Pi,	(2)
{< I *АА}
здесь запись {i\xt б А} под знаком суммы указывает на то, что суммирование производится по всем номерам i, таким, что хг € А.
Формула (1) показывает, что функция р(А) полностью определяется заданием чисел xz и (t = 1, 2, Значит, таблица
Х1	Х2	...
Р|	Pt	
(3)
служит исчерпывающей характеристикой дискретной случайной величины х. Остается еще добавить, что из равенства /?(Й) == = р({^1}) + р(.{х2}) + ••• В силу р (й) = 1 следует:
Pl + Р2 + ••• — 1-
Этим полностью установлена равнозначность двух определений дискретной случайной величины — данного в этом пункте и определения из § 21.
Выясним теперь, какой вид имеет функция распределения дискретной случайной величины х, характеризуемой таблицей (3).
Пусть х0любое число. Среди чисел Xj, х2, ••• выделимте, которые меньше х0. Пусть ими будут х , х( , ... . Событие х < х0 является суммой событий х — х( х = х( , ..., поэтому его вероятность равна pt + р( + ... .
Итак,
F (х) = 2 Pi-	(4)
Формула (4) дает полную информацию о функции F(x). На рисунке 23 изображен график этой функции для частного случая, когдах принимает только три значения: хх, х2, х3. Можно при этом считать хг < <х2 <х3. График представляет собой ступенчатою ломаную со скачками в точках х1( х2, х3. Величины скачков равны соот-
Рис. 23
97
4 А. С. Солодовников
ветственно plt pz, ps. Левее xt график совпадает с осью Ох, правее xs — с прямой у = 1. Аналогичная ступенчатая ломаная будет получаться для любой дискретной случайной величины х.
2°. Непрерывные случайные Рис- 24	величины. Способ их построе-
ния.
В предыдущем пункте мы показали, что функция распределения дискретной случайной величины изменяет свои значения только скачками. Представляет интерес рассмотреть другой крайний случай — когда функция распределения вообще не имеет скачков, т. е. является непрерывной функцией.
Определение Случайная величина х называется непрерывной, если ее функция распределения F(x) непрерывна при всех значениях х.
Принимая во внимание формулу
F (х + 0) — F (х — 0) =- р (х = х0), доказанную в пункте 4° § 22, можно дать другое определение непрерывной случайной величины: случайная величина непрерывна, если вероятность каждого ее отдельного значения равна нулю. Существует простой способ построения примеров непрерывных случайных величин. Он заключается в следующем. Рассмотрим неотрицательную интегрируемую функцию f (х), определенную для всех значений х и удовлетворяющую условию:
со
Jf(x)dx=l.	(5)
—оо
Положим,
А(х)=	(6)
Определенная таким образом функция F(x) обладает всеми свойствами функции распределения. Действительно:
1)	F(x) не убывает — это вытекает из условия f (f)	0;
2)	lim F(x) = 1, lim F(x) — 0. Первое из этих равенств совпадает с условием (5), а второе вытекает из самой сходимости интеграла (5).
3)	F(x) непрерывна слева. Этот факт является следствием непрерывной зависимости определенного интеграла от переменного верхнего предела.
98
Из сказанного вытекает (см. теорему на с. 95), что функция F (х) является функцией распределения некоторой случайной величины х. Так как при этом F (х) непрерывна для всех значений х, то величина х будет непрерывной случайной величиной.
3°. Случайные величины, имеющие плотность вероятности. Рассмотренный выше способ построения непрерывных случайных величин дает повод к такому определению.
Определение. Мы говорим, что случайная величина х распределена с некоторой плотностью, если существует неотрицательная функция f (х), такая, что для всех х справедливо равенство (6) (где F (х) — функция распределения величины х).
Функция f (х), фигурирующая в этом определении, и называется как раз плотностью распределения или плотностью вероятности величины х.
Очевидно, что случайная величина, имеющая плотность вероятности, непрерывна. Обратное верно не всегда: можно привести примеры непрерывных случайных величин, для которых не существует плотности.
Очевидно также, что плотность вероятности должна удовлетворять условию (5) — это непосредственно следует из соотношения lim F (х) = 1, которому подчиняется функция распределения.
Таким образом, функция f (х) изображается графически с помощью кривой, лежащей в верхней полуплоскости и такой, что площадь, заключенная между ней и осью Ох, равна 1 (рис. 24).
Поясним смысл самого названия «плотность вероятности».
Согласно § 22 п. 4°, справедливо равенство р (хх х < х2) = — F (х2) — F (ху). Отсюда с учетом (6) находим:
#2
р (хх < X < х2) = J f (х) dx.	(7)
Х1
По теореме о среднем интеграл, стоящий в правой части, равен f (Е) (х2 — Хх), где g — некоторая точка из интервала (х1( х2). Отсюда
р (г, < х < х2) = ?
X, — Xj
Представим себе, что интервал (г,, х2) стягивается к некоторой точке х0, причем в этой точке функция f (х) непрерывна. То1да / (Е) будет стремиться к числу f (х0), и мы получим:
lim—-Х1^х<Хг) —/(х0).
х2 —Xj
Отношение, стоящее под знаком предела, есть своего рола «вероятность на единицу длины» интервала (хп х2>). Предел этого отношения естественно рассматривать как плотность вероятности в самой точке х0. Мы видим, таким образом, что во всякой точке
4*	69
х0, где f (x) непрерывна, число f (х~) совпадает с естественно понимаемой плотностью вероятности в точке х0. Отсюда и название для функции f (х) — «плотность вероятности».
В дальнейшем вместо формулы (7) мы будем писать обычно:
^2
Р (-4 < X < х2) = j f (х) dx.
Л1
(8)
Эквивалентность равенств (7) и (8) очевидна, поскольку р (х = = х2) — О-
Вернемся снова к формуле (6). С помощью этой формулы функция распределения F(x) выражается через плотность вероятности f(x). Однако во многих случаях важно знать выражение f(x) через F(x). Чтобы найти такое выражение, продифференцируем обе части равенства (6). Если точка х0 является точкой непрерывности функции f(x), то, как известно из курса математического анализа, производная правой части (т. е. производная определенного интеграла по переменному верхнему пределу) равна f(x0). Таким образом, во всякой точке непрерывности функции f(x) справедливо равенство
К*) = F'(x)
— плотность вероятности равна производной от функции распределения.
4°. Достаточное условие существования плотности. Введенное в пункте 3° определение случайной величины, имеющей плотность вероятности, оставляет открытым вопрос: когда, в каких случаях существует плотность?
Необходимым условием является, как уже отмечалось, условие непрерывности функции F(x) (функции распределения). Однако это условие не является достаточным. Можно было бы сформулировать условие, являющееся одновременно необходимым и достаточным (так называемая абсолютная непрерывность функции Г(х)), но это увело бы нас несколько в сторону. Ограничимся тем, что
укажем одно легко проверяемое
достаточное условие, а именно: если функция F (х) имеет, непрерывную производную всюду, за исключением разве лишь конечного числа точек, то существует плотность вероятности f (х).
Рекомендуем читателю доказать это предложение самостоятельно.
В заключение этого параграфа коснемся вопроса о взаимоотношениях между двумя классами случайных величин — диск
100
ретными и непрерывными случайными величинами.
Самое существенное для понимания этих взаимоотношений заключается в том, что любую непрерывную случайную величину можно получить предельным переходом из дискретных случайных величин.
Наглядное представление об этом дает рисунок 25, на котором ступенчатая ломаная изображает график функции распределения F (х) для дискретной случайной величины х. Если представить себе, что к множеству возможных значений величины х добавляются все новые точки, то число ступенек на кривой F (х) будет становиться все больше, а сами ступеньки — все мельче. Ступенчатая ломаная будет все более приближаться к плавной кривой, а дискретная случайная величина — к непрерывной.
§ 24. ЗАКОН РАВНОМЕРНОГО РАСПРЕДЕЛЕНИЯ НА ОТРЕЗКЕ И ЗАКОН НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ НА ПРЯМОЙ
В этом параграфе мы ознакомимся с двумя важными примерами непрерывных случайных величин. Соответствующие им законы распределения носят названия: закон равномерного распределения на отрезке и закон нормального распределения на прямой.
1°. Закон равномерного распределения на отрезке. Мы скажем, что случайная величина х равномерно распределена на отрезке [а, &], если она имеет плотность вероятности следующего специального вида:
f (Н = ( с для а х
1 ' '	(0 для х < а или х > b.	(1)
Значение постоянной с определяется из условия:
J f (х) dx — 1,
(2)
которому удовлетворяет любая плотность вероятности. В данном
случае это условие принимает вид:
с (Ь — а) = 1,
откуда следует:
1 с =------.
Ь — а
График f (х) изображен на рисунке 26.
Если какой-либо отрезок [а, р] целиком содержится в [а, Ь],
101
та вероятность попадания в него случайной величины х равна:
₽ ₽
f / (х) dx = i с dx = cl — ——»	(3)
J	J	ь — a
a	a
где I — длина отрезка [a, |3]. Таким образом, вероятность попадания в любую часть отрезка [а, Ь] пропорциональна длине этой части. В то же время вероятность попадания в любой отрезок, не перекрывающийся с fa, t>], очевидно, равна нулю.
Записав формулу (3) в виде
р (а < х < р)
длина [«, р] длина [а, Ь] *
(4)
мы узнаем в ней уже знакомую нам формулу геометрических вероятностей (см. § 5). Можно, следовательно, сказать, что геометрические вероятности порождаются равномерным распределением. Поз
же мы увидим, что это заключение справедливо не только для одномерного случая, но остается верным при любом числе измерений.
Охарактеризуем в общих чертах круг задач, приводящих к
равномерным распределениям.
Можно сказать, что с равномерным распределением мы сталкиваемся всякий раз, когда по условиям опыта величина х принимает значения в конечном промежутке [а, tf\, причем все значения из [а, Ь] возможны в одинаковой степени, ни одно из них не имеет в этом смысле преимуществ перед другими. Вот несколько примеров такого рода: 1) х — время ожидания на стоянке автобуса (величина х распределена равномерно на отрезке [0, /], где / -интервал движения между автобусами); 2) х — ошибка при взвешивании случайно выбранного предмета, получающаяся от округления результата взвешивания до ближайшего целого числа (величина
Г 1 11
х имеет равномерное распределение на отрезке ——, — , где за единицу принята цена деления шкалы); 3) х — угол между фиксированным радиусом приведенного во вращение волчка (рис. 27)
и радиусом, идущим в точку касания волчком пола после остановки (величина х распределена равномерно на отрезке [0,2л]).
Задача. Найти функцию распределения случайной величины х, распределенной равномерно на отрезке [а, Ь].
Решение. Связь между функцией распределения и плотностью вероятности дается формулой (6) § 23;
к
р(()Л,
«ПЗ
Подставляя сюда функцию / (/) из (1), получим:
для х < a F (х) = О, для а х < b X
F (х) = J cdx = с (х — а), а для х > Ь ь
F (х) = J cdx — с (b — а) = 1. а
График F (х) показан на рисунке 28. ▲
2°. Закон нормального распределения на прямой. Закон нормального распределения на прямой, или, иначе, нормальный закон, — наиболее ча^то встречающийся на практике закон распределения. О причинах, обусловливающих его широкую распространенность в природе, технике, на производстве и т. д., мы расскажем в главе 8; пока же просто дадим описание этого закона.
Определение. Мы говорим, что непрерывная случайная величина х подчиняется нормальному закону распределения, если она имеет плотность вероятности следующею специального вида:
f(x) = Ае~1{х~а>\
где А, X и а — постоянные, причем А > О, А. > 0.
Соотношение (2), которому должна удовлетворять функция /(х), показывает, что между параметрами А, К и а должна существовать некоторая связь:
со
A J e-4x-apdx = j
Если в последнем интеграле произвести замену ]/\ (х — а) = t, то получим соотношение
со
~ f е~** dt = 1.
Поскольку интеграл от функции по всей оси равен то имеем отсюда:
А /1 = 1.	<5>
103
Положим,
/. = £ (о > 0)
2а2
(т. е. введем вместо X другой параметр а), тогда из (5) будет следовать:
а У 2л ’
Окончательно имеем:
Это стандартная запись нормального закона распределения. В нее входят два параметра: а и ст. Их теоретико-вероятностный смысл будет указан позже.
На рисунке 29 показаны графики функции / (х) для различных значений параметра ст. Каждый из них имеет вид холма, склоны которого полого спускаются к оси Ох. Максимальная высота холма
1	V
равна 	1 она достигается при х = а. Если увеличивать зна-
чение параметра о, то вершина холма будет опускаться, но зато поднимутся склоны (ведь общая площадь между графиком и осью Ох должна остаться равной 1). Что касается параметра а, то его значение не влияет на форму графика; с изменением а график только смещается в направлении оси Ох.
Методами дифференциального исчисления нетрудно проверить, что график f (х) имеет две точки перегиба: одна отвечает значению х = а + ст, другая — значению х = а — а (рис. 30).
Решим теперь следующую задачу. Пусть случайная величина х распределена по нормальному закону с плотностью (6). Найдем вероятность попадания величины х в произвольный отрезок [а, 0].
Имеем;
₽
р (а х 0) = [ f (х) dx а
Рис. 29	Рис. 30
104
и, следовательно,
Р _ (х~а)г
р (а < х < (5) = —f е 2а2 dx.
\ \ г/ а /2л J а
Если в последнем интеграле произвести замену х-—- = t, то а
получим выражение Р—о о _Р_ 1 р 2 л	3 — а\ jl /сс ~~ а\
-т= \ е di или Ф ------ — Ф------ ,
/2л J	\ а )	\ а J
а—а а
где Ф (х) есть функция Лапласа, введенная в § 17:
X __р
Ф (х) = -U-- С е 2 di.
/2л.) о
Таким образом, справедлива формула
р(а =	ф/^Л	(7)
\ a j \ а /
которая и решает поставленную задачу.
В частности, вероятность попадания в отрезок [а — За, аф-За] равна:
Ф (3) - Ф ( -3) = 2Ф (3) = 0,997...;
как мы видим, эта вероятность отличается от 1 на весьма малую величину. Отсюда следует, что событие а — За х а ф- За является практически достоверным, т. е. что практически возможные значения величины х расположены на отрезке [а — За, а ф- За]. Этот факт носит название «правило трех сигм».
§ 25. МЕХАНИЧЕСКАЯ МОДЕЛЬ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
Для понимания свойств случайных величин, в особенности дискретных случайных величин, а также величин, имеющих плотность вероятности, весьма полезна так называемая механическая модель.
Представим себе некую массу, равную I (скажем, 1 кг густой краски). Будем рассматривать различные распределения этой массы вдоль оси Ох. Таких распределений имеется, конечно, бесчисленное множество.
Механической моделью случайной величины х называют такое распределение массы 1 вдоль числовой оси, при котором масса любого промежутка со равна вероятности попадания величины х в этот промежуток (вероятности события х б со).
105
Предположим, что величина х является дискретной и характеризуется таблицей:
X! х2
Р1 Рг
смысл которой известен читателю. Тогда механической моделью величины х будет служить следующее распределение массы: в точках xit хг, ... размещаются соответственно ри р2, ... единиц массы ( в механике такой тип распределения массы называют дискретным). Действительно, при таком распределении масса любого промежутка со будет равна 2 А и в точности такое же выражение {« |х/£со}, имеет вероятность события х С со.
Рассмотрим теперь другой крайний случай — когда величина х распределена с некоторой плотностью f (х). В этом случае моделью будет служить такое распределение массы (в механике его называют сплошным распределением), когда масса «размазывается» вдоль оси Ох с плотностью /(%). Действительно, в этом случае масса промежутка со будет равна J /(х) dx, но такое же выражение имеет (О и вероятность события х £ со.
Можно представить себе и более общий тип распределения, чем два указанных выше, а именно: масса 1 разбивается на две массы: Р и 1 — Р, причем масса Р распределяется дискретно, а масса 1 — Р — с некоторой плотностью f (х). Такое распределение массы служит моделью случайной величины смешанного типа.
Рекомендуем читателю попытаться, исходя из сказанного, дать определение случайной величины смешанного типа.
Глава 6.
СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИН
До сих пор мы рассматривали случайные величины изолированно друг от друга, не касаясь вопроса об их взаимоотношениях. Однако в практических задачах часто встречаются ситуации, при которых те или иные случайные величины приходится изучать совместно. В таких случаях говорят о системе нескольких случайных величин.
Систему двух случайных величин (х, у) можно истолковывать как случайную точку на плоскости, систему трех случайных величин (х, у, z) - как случайную точку в трехмерном пространстве. Мы ограничимся в основном двумерным случаем.
Интуитивный подход к понятию системы двух случайных величин связан с представлением об опыте, результатом которого является пара чисел х, у. Поскольку исход опыта мыслится как случайное событие, то предсказать заранее значения чисел х и у невозможно (при повторении опыта они меняются непредвиденным образом). Приведем несколько примеров.
Пример 1. Дважды бросается игральная кость. Обозначим через х число очков при первом бросании, через у — число очков при втором. Пара (х, у) будет системой двух случайных величин.
П р и м е р 2. Из некоторой аудитории наугад выбирается один человек; х — его рост (скажем, в сантиметрах), у — вес в (килограммах).
ПримерЗ. В данном сельскохозяйственном районе выбирается произвольно участок посева пшеницы площадью 1 га; х — количество внесенных на этом участке удобрений, у — урожай, полученный с участка.
Пример 4. Сравниваются письменные работы по математике и русскому языку; х — оценка за рабату по математике, у — за работу по русскому языку.
Список подобных примеров легко продолжить.
§ 26. ФОРМАЛЬНОЕ ОПРЕДЕЛЕНИЕ СИСТЕМЫ ДВУХ СЛУЧАЙНЫХ ВЕЛИЧИН. СИСТЕМА ДИСКРЕТНОГО ТИПА
1°. О борелевских множествах на плоскости. Прежде чем дать формальное определение системы двух случайных величин, остановимся кратко на вопросе о борелевских множествах на плоскости.
107
Определение. Множество точек на координатной плоскости R1 2 называется борелевскимесли оно может быть получено из множеств вида
Ra,b = {(*. у) ! X < а, у <b}	(1)
применением конечного или счетного числа операций объединения, пересечения и дополнения.
На рисунке 31 множество показано с помощью штриховки.
Предоставляем читателю показать, что класс борелевских множеств на.плоскости содержит, в частности, все множества вида {(х, у) |	< X < аг, bi-^y < b2},	(2)
где каждый из четырех символов -< может означать строгое или нестрогое неравенство (< или ^). При этом не исключается случай, когда какое-нибудь из чисел bi (или оба) равно — оо, а также когда какое-либо из чисел а2, Ь2 (или оба) равно оо; в каждом таком случае означает строгое неравенство.
Например, борелевскими множествами являются:
{(х, у) | -1 <х< 1, 2 <у <3}
—	заштрихованный прямоугольник на рисунке 32;
{(х, у) | 2 X оо, —оо < у < оо}
—	заштрихованная полуплоскость на том же рисунке;
{(х,у) | 1 <х< 1, 2 < у < 2}
точка с координатами 1, 2.
Частным случаем множества (2) является полуплоскость вида {(х, У) I — 00 < х < а, —оо < у < оо},
1 Мы пользуемся принятым в алгебре обозначением 7?2 для декартова про-
изведения множества R действительных чисел на себя, т. е. для множества пар (х, у), где х € R, у € R.
108
или, что то же самое, {(х, у) | х < а}. Разумеется, любое множество, полученное из таких полуплоскостей при помощи операций объединения, пересечения и дополнения (в конечном или счетном числе), тоже будет борелевским. Отсюда вытекает, что, каково бы ни было борелевское множество В на оси Ох, множество {(х, у) | х С В} будет борелевским множеством на плоскости.
2°. Определение системы двух случайных величин. Понятие системы двух случайных величин является непосредственным обобщением понятия случайной величины, рассмотренного в § 22.
Определение. Мы говорим, что задана система двух случайных величин (х, у), если каждому борелевскому множеству А на координатной плоскости /?2 сопоставлено неотрицательное число р (Д), причем р (/?2) = 1 и числа р (Д) удовлетворяют условию счетной аддитивности.
Заметим, что название система двух случайных величин (х, у) часто заменяется другим: случайная точка (х, у) на плоскости. Мы будем пользоваться в равной степени обоими названиями.
С каждой системой (х, у) можно связать вероятностную схему в смысле п. 4° § 3; событиями в ней являются борелевские множества А, а вероятности событий суть числа р(А), Событие А обозначается также
(х, у) € А
и характеризуется словами: «случайная точка (х, у) принадлежит А» (или каким-нибудь эквивалентным по смыслу оборотом речи, например «точка (х, у) попала в А» и т. и.).
Введенный нами термин система двух случайных величин (х, у) пока еще не вполне оправдан: исходя из данного выше определения системы, мы не можем ответить на вопрос, что представляет собой отдельно взятая величина х (а также у). Однако этот пробел легко восполнить. Как уже отмечалось, каждому борелевскому множеству В на числовой оси отвечает борелевское множество {(х, у) | х С В} на плоскости; обозначим это множество В*. Сопоставив множеству В число рх(В), равное р (В*), мы получим (в согласии с определением, данным в § 22, п. 2°) некоторую случайную величину х; действительно, рх (R) = 1 (ибо R* есть вся плоскость, и поэтому p(R*) = 1), а свойство счетной аддитивности для чисел рх (В) выполняется, поскольку этим свойством обладают числа р(В*).
Случайная величина х, определенная соглашением
р (х € В) = р ((х, у) С В*),
называется первой координатой (или первой компонентой) системы (х, у).
Аналогично определяется вторая координата у:
Р (У € В) = р ((х, у) £ В**),
109
где
В** = {(х, у) | у £ В}.
Таким образом, имеет смысл говорить не только о системе (х, у), но и об отдельных величинах хну — координатах данной системы.
Функция р (Л) борелевского множества А (на плоскости), задающая систему (х, у), называется распределением системы (х, у). Иногда распределение мы будем записывать р ( ), желая этим подчеркнуть, что речь идет о функции борелевского множества, а не о значении этой функции для данного множества А.
Так же как в случае одной случайной величины х, мы будем пользоваться для системы (х, у) термином «закон распределения», понимая под ним любой способ задания системы (х, у) (иначе говоря, любую совокупность данных, позволяющую однозначно восстановить функцию р (Л)).
3°. Система (х, у) дискретного типа. Понятие системы дискретного типа, или, по-другому, дискретной случайной точки, вводится по аналогии с понятием дискретной случайной величины.
Определение. Система (х, у) с распределением р (А) называется системой дискретного типа, если существует такое конечное или счетное множество й в /?2, что р (й) = 1.
Положим,
О = {(ъ, bi), (а2, b2), ...}	(1)
и
Pi = Р {(at, W = р (х = at, у = bz) (1=1, 2, ...).
Из формулы
Р (Л) = Р (Л Й)
(см. лемму на с. 96) следует, что для любого борелевского множества Л на плоскости имеет место равенство
рИ) = 2а	(2)
(Щаг. ьрел).
Таким образом, функция р (Л) полностью определяется заданием точек (az, bz) и чисел (i = 1, 2, ...).
Точки (щ, bz) называются возможными положениями случайной точки (х, у), а числа pt — их вероятностями. Как показывает равенство (2), для нахождения вероятности попадания случайной точки в то или иное множество Л следует из всех возможных положений выделить те, которые принадлежат Л, и просуммировать соответствующие им вероятности.
Очевидно, что каждая из двух компонент х и у дискретной случайной точки сама является дискретной случайной величиной. При этом возможные значения величины х суть числа ait а2, ... — первые координаты точек (1). Впрочем, среди этих чисел могут
по
оказаться совпадающие, поэтому правильнее будет сказать, что возможными значениями для х являются все не равные между собой числа из совокупности ait а2, ... . Обозначим их xlt х2, ... . Аналогично пусть уь у2, ... — возможные значения для у. Ясно, что возможные положения случайной точки (х, у) содержатся среди точек
(х„ Уу) («. / = h 2, ...).
Из сказанного вытекает, что исчерпывающей характеристикой (по-другому — законом распределения) системы дискретного типа может служить таблица:
означающая, что случайная точка (х, у) принимает положения (хг, уу) с вероятностями pij(i, j = 1,2, ...). Некоторые из чисел Ри могут быть равными нулю (это означает, что некоторые из точек (хг, Уу) могут не входить в первоначальное множество (1)), Сумма всех вероятностей рг?- равна 1.
Например, если множество возможных положений состоит из точек (1, 2), (1, 3), (2, 5), вероятности которых равны соответ-
1 1 X
3 ’ б’ 2’
ственно
то соответствующая таблица (3) будет:
В клетках (2, 2), (2, 3), (1, 5) поставлены нули, так как точки (2, 2), (2, 3), (1, 5) не являются возможными положениями случайной точки (х, у).
Для каждой из величин х и у в отдельности можно получить из таблицы (3) свой закон распределения. Поскольку событие х = xt является суммой событий
111
(X = Xb у = У1), (х = xt, у — у2), ....
то его вероятность
Г1 = Pli + Р(2 + ••• •
Найдя все числа гг, получим закон распределения величины х:
Значения х	«1	х2	
Вероятности	'1		...
Аналогичным образом находится закон распределения величины у:
Значения у	Ух	У г	
Вероятности	«J	$2	
где
Sj = Р (у = У7) = Ру + р2) + ••• (/ =- 1. 2, ...)
Числа г; и Sy можно найти из таблицы (3), суммируя числа в той или иной строке или в том или ином столбце таблицы.
Пример 1. В урне лежат четыре шара: 2 белых, 1 черный и 1 синий. Из урны наугад извлекают два шара. Пусть х — число черных, а у — число синих шаров в выборке. Составим для системы (х, у) закон распределения.
В данном случае множество возможных значений для х и у одно и то же — множество {0, 1}.
Имеем: -
Ро.о = р (х = 0, у = 0) = -
(событие х — 0, у = 0 наступает только при одном из С< = 6 исходов опыта),
о
Рол = р (х = 0, у = 1) = -
6
(событие х — 0, у = 1 наступает только при двух исходах),
Pt,о = Р (х = 0, у = 1) =
о
и
Р1.1 = р (X = 1, у = 1) = 1 о
112
Искомый закон распределения:
Пример 2. Монету бросают 5 раз. Если дважды подряд выпадает герб, то скажем, что имеет место повторение герба. Пусть х — число повторений герба, у - число повторений цифры при 5 бросаниях. Составим для системы (х, у) закон распределения.
Прежде всего поясним определение величин х и у. Пусть, например, при пятикратном бросании монеты выпала такая последовательность сторон: ц-ц-г-г-г (цифра-цифра-герб-герб-герб). В этой последовательности имеется одно повторение цифры и два повторения герба. Значит, при данном исходе опыта имеем: х = 2, У = 1-
Приступая к составлению таблицы, необходимо прежде всего выяснить, какие значения могут принимать х и у. В данном случае это совсем просто: так как производится 5 бросаний, то множество возможных значений для каждой из величин х и у есть {О, 1, 2, 3, 4}.
Остается найти вероятности
Pi.) = Р (х = г, у = /),
где i и / могут принимать любые значения из (0, 1, 2, 3, 4}. Подсчитаем для примера pl:i.
Событие х = 1, у == 1 означает, что при пятикратном бросании монеты герб и цифра повторились ровно по одному разу. Нетрудно видеть, что такому событию благоприятны четыре последовательности сторон, из них две начинаются с «ц»:
ц-г-г-ц-ц, ц-ц-г-г-ц,
и две с «г»: г-ц-ц-г-г, г-г-ц-ц-г.
4
Следовательно, pit = —. ’	25
Остальные числа phJ предоставляем найти читателю. В итоге должна получиться такая таблица:
113
(4)
Из таблицы (4) можно найти отдельные законы распределения для х и у. В обоих случаях получается таблица:
0	1	2	3	4
]3 32	10 32	£ 32	_2 32	32
§ 27. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ СИСТЕМЫ (X, У). ПЛОТНОСТЬ ВЕРОЯТНОСТИ
Напомним (§ 26, п. 1°), что символом Ra ь мы условились обозначать множество всех точек плоскости, абсциссы которых меньше числа а и ординаты меньше b (рис. 31).
Функция распределения системы (х, у) представляет собой функцию от двух аргументов. Она определяется формулой
F{x, У) — Р (Rx у) или в эквивалентной записи
F (х, у) = р (х < х, у < у).
В словесном описании F (х,у) есть вероятность попадания случайной точки в область
114
С помощью функции F {х, у) легко найти вероятность любого события вида
xt < х < х2, Ух < у < у2	(1)
(рис. 33). Для этого применим к событиям R и R формулу "1 > j 2	J’ z 1
р (Л + В) = р (4) + р {В) - р {АВ)
(см. § 3, п. 3°). Получим:
Р	~ Р + Р (^,У1) — Р =
= F (*х,У2) + F CWx)—F (*!.У1)-
Если теперь учесть, что события RXt у + Rv у и (1) несовместны и в сумме составляют событие R „ , то будем иметь:
Р {Xi < X < х2, У1 < у < у2) = Р {Вх2. уг) — р (Rx„ у, 4- Rx„ у,) =
= F{x2, У2)~ ^(*х, у2) —^и2, Ух) + ^(*х. У1).	(2)
что и решает поставленную задачу.
Формулу (2) легко запомнить: в правую часть входят со знаком «плюс» значения функции F {х, у) в двух противоположных вершинах прямоугольника (1) и со знаком «минус» —значения в двух других вершинах прямоугольника.
Так как число, стоящее в левой части (2), должно быть неотрицательным (это условие содержится в самом определении системы (х, у)), то отсюда сразу же получается важное свойство функции F {х, у):
1)	F (х2, у2) - F {xi, у2) — F (х2, уО + F (х1( yj) > О, если х{ < хг, yt < у2.	(3)
Перечислим еще ряд свойств функции F {х, у); их доказательства проводятся совершенно так же, как в случае одной случайной величины х (см. § 22).
Функция распределения:
2)	является неубывающей функцией по каждому из аргументов;
3)	непрерывна слева по каждому из аргументов;
4)	удовлетворяет соотношениям:
lim F {х, у) = 1, Х-*оо у-* СО
lim F {х, у) — 0 при любом у, X-*.—со
lim F {х, у) = 0 при любом х. у-*-—со
Свойства 1 —4, как можно показать, являются характеристическими свойствами функции распределения. Это значит, что
115
любая функция F(x, у) на плоскости, обладающая этими свойствами, является функцией распределения для некоторой системы случайных величин (х, у). Доказательство этою факта мы не приводим.
2°. Системы, имеющие плотность. Не останавливаясь на рассмотрении систем (х, у) с непрерывным распределением вероятностей (это означает, что функция F (х, у) является непрерывной функцией), обратимся к наиболее важному классу таких систем — системам, для которых существует плотность вероятности.
Определение. Мы скажем, что система (х, у) с функцией распределения F (х, у) имеет плотность вероятности, если существует неотрицательная функция f(x, у), такая, что
F(x, у) = J" J /(«, ©) dudv. — -хэ — оо
Функция f (х, у) и называется как раз плотностью вероятности (или плотностью распределения) системы (х, у).
В случае существования плотности формула (2) приобретает особенно наглядный вид. В ее правой части мы имеем такое выражение:
ч у,	х, у,	х, у,
J J f (и, и) dudv — J J / (и, у) dudv ~ U f (и< и) dudv + — ОО — ОО	—00 — ОО	—ОО— со
*1 У1
+ J у (и, v) dudv.
— 00 —ОО
Из сопоставления областей интегрирования (см. снова рис. 33) вытекает, что это выражение можно заменить одним интегралом по прямоугольнику (1). Таким образом,
Хе у,
р (Xi < х < х2, У1 < у < у2) = [ р(«, v)dudv. (4)
х. У,
Разумеется, вместо любого из неравенств < можно поставить — справедливость формулы (4) от этого не нарушится.
Итак, для системы (х, у), распределенной с плотностью f (х, у), справедлива формула
Р ((*, У) 6 G) = J f f (х, у) dxdy,	(5)
G
где G есть любой прямоугольник со сторонами, параллельными координатным осям. Поскольку и левая, и правая части этого равенства, рассматриваемые как функции от области G, обладают свойством аддитивности, то формула (5) справедлива для любой области G.
116
§ 28. НЕЗАВИСИМЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
1°. Общие замечания. Примеры. При рассмотрении системы двух случайных величин (х, у) необходимо иметь в виду, что свойства системы не всегда исчерпываются свойствами самих величин х и у. Иначе говоря, если мы знаем все о величине х и все о величине у, то это еще не значит, что мы знаем все о системе (х, у). Дело в том, что между величинами х и у может существовать зависимость, и без учета этой зависимости нельзя построить закон распределения системы (х, у).
Зависимость между случайными величинами в реальных условиях может быть различной, В некоторых случаях она оказывается столь сильной, что, зная, какое значение приняла величина х, можно в точности указать значение у. Применяя традиционную терминологию, можно сказать, что в этих случаях зависимость между х и у функциональная (впрочем, понятие функции от случайной величины еще нуждается в уточнениях; последние будут даны в § 30). С примерами такой зависимости мы постоянно встречаемся в природе и технике.
В то же время можно указать и примеры другого рода — когда зависимость между случайными величинами существует, но не носит строго выраженного функционального характера. Подобные примеры особенно характерны для таких областей науки и практики, как агротехника, биология, медицина, экономика и т. д., где развитие явлений, как правило, зависит от многих трудно поддающихся учету факторов. Известно, например, что обилие осадков в период созревания пшеницы приводит к повышению урожайности; однако это еще не означает, что связь между количеством х осадков и урожайностью у (скажем, в расчете на 1 га) является функциональной; кроме осадков, на урожайность оказывают влияние и другие факторы: тип почвы, количество внесенных удобрений, число солнечных дней и т. д. В подобных случаях, когда изменение одной величины влияет на другую лишь статистически в среднем, принято говорить о вероятностной связи между величинами. Не приводя пока точных определений, рассмотрим несколько примеров. Они иллюстрируют разные степени зависимости между случайными величинами — от сильной, почти функциональной зависимости до практической независимости.
Пример 1, Пусть х — рост наугад выбранного взрослого человека (скажем, в сантиметрах), а у •— его вес (в килограммах). Зависимость между ростом и весом является весьма сильной, в первом приближении ее можно даже считать функциональной. Формула, приближенно выражающая эту зависимость, пишется обычно:
у (кг) — х (см) — 100.
Пример 2. х — высота выбранного наугад дерева в лесу, у — диаметр его основания. И здесь зависимость
117
следует признать сильной, хотя и не в такой степени, как в предыдущем примере.
ПримерЗ. Из груды камней неправильной формы выбирают наугад один камень. Пусть х •— его масса, а у — наибольшая длина. Зависимость между х и у носит сугубо вероятностный характер.
Пример 4. х — рост выбранного наугад взрослого человека, у — его возраст. Наблюдения показывают, что эти величины практически независимы.
2°. Определение независимости случайных величин. Оставим пока в стороне вопрос о том, какими числами можно выразить степень зависимости между величинами х и у (этот вопрос будет обсуждаться в § 45). Ограничимся строгим определением независимости случайных величин.
Определение. Пусть задана система (х, у). Мы скажем, что величины х и у независимы, если независимы события х f Л и у С В, где А и В — любые два борелевских множества на прямой.
Иначе говоря, величины х и у, образующие систему (х, у), независимы, если для любых борелевских множеств Л и В на прямой справедливо равенство
Р (Л х В) = рх(А) • ру (В),	(1)
где р ( ), рх ( ), ру ( ) обозначают соответственно распределения системы (х, у), величины х и величины у, a А X В есть декартово произведение множеств А и В (т. е. совокупность точек (х, у), таких, что х С А, у £ В). Разумеется, равенство (1) можно записать и в такой форме:
р (х £ А, у С В) == р (х С Л) • р (у $ В).	(2)
3°. Случай системы дискретного типа. Если (х, у) — система дискретного типа, то условие независимости величин х и у можно представить в более обозримом виде:
Р (х = xh у = у,) = р (х =	• р(у = уу), (3)
где Х[ — любое возможное значение случайной величины х, а у У — любое возможное значение величины у.
В самом деле, необходимость уровня (3) очевидна (ибо (3) есть частный случай (2)). Проверим достаточность.
Пусть система (х, у) характеризуется таблицей:
118
причем
Pij = р(х = xt) • р(у = уу) (i, j = 1, 2, ...) (написанное равенство и есть как раз условие (3)). Тогда
Р(х€Д, у£В) =	2 pt/= 2 р(х = х,)Х
{l.px^A.yfBj	{l.px^A.y ^В]
х р (у = уj)=	2 р(х = ^) • 2 р (у = yj) =
{Дуусв}
= p(xgx) • р(уев), т. е. величины х и у независимы.
4°. Случай, когда существует плотность вероятности. Допустим, что каждая из величин х и у, составляющих систему (х, у), распределена с некоторой плотностью: х — с плотностью (х), у — с плотностью /2 (у). Постараемся для этого случая привести условие независимости х и у к более простому виду.
Пусть х и у независимы. Тогда
Р (х < х, у < у) = р (х <х) • р (у < у), откуда следует:
Р (х < х, у < у) = J Л («) du • j /2 (v) dv = J J A («) (y) dudv. —00	—co	—00—00
Наличие такого равенства (где х и у —• любые числа) означает, что система (х, у) имеет плотность и эта плотность равна (х) /2 (у). Итак, условием независимости величин х и у для рассматриваемого случая будет:
f (х, у) = fi(x) /2(у) — плотность распределения системы (х, у) равна произведению плотностей для х и у.
§ 29. ПРИМЕРЫ ДВУМЕРНЫХ РАСПРЕДЕЛЕНИЙ
1°. Равномерное распределение в плоской области Q. Начнем с разбора следующей задачи. На отрезке длиной 1 выбирают наугад и независимо друг от друга две точки. Какова вероятность того, что расстояние между ними окажется не больше I (где I < 1)?
Считая, что данный отрезок есть отрезок [О, 1] числовой оси, обозначим через х координату первой точки и через у — координату второй (рис. 34). Исходом опыта является пара чисел х, у, удовлетворяющих условиям:
О < х < 1, 0 < у < 1.
Иначе говоря, исход опыта — случайная точка квадрата Q, изображенного на рисунке 35.
Рассмотрим отдельно случайную величину х, Ее закон распре-
119
Рис. 34
L/k
деления в условии задачи не оговорен; он будет зависеть от того, какой смысл мы придадим слову «наугад» в формулировке задачи. Наиболее естественное толкование этого слова заключается в том, что все значения величины х на отрезке [0,1] равноправны, или, говоря точнее, величина х равномерно распределена на отрезке [0, 1]. То же самое относится, конечно, и к у. Итак, будем считать, что плотности вероятности для х и у равны соответственно:
Рис, 35
1 для 0	х	1,
0 для остальных х,
1 для 0	у	1,
0 для остальных у.
Ввиду независимости х и у плотность распределения для системы (х, у) будет:
f (х, у) = Л (х) /2 (у),
т. е.
(1 для	0 у	1,
[0 для остальных х, у.
Для того, чтобы расстояние между точками не превышало I, нужно, чтобы выполнялось неравенство
(1)
На рисунке 35 штриховкой отмечена область внутри квадрата Q, которая отвечает неравенству (1). Обозначим эту область через G. Неравенство (1) эквивалентно условию (х, у) С G, следовательно, вероятность его осуществления
где SG — площадь области G, равная 1 — (1 — /)2. Отсюда искомая вероятность будет:
1 - (1 - о2.
(2)
Задачу о выборе двух точек на отрезке можно сформулировать как задачу о «встрече двух лиц». Представим себе, что два человека договорились встретиться в определенном месте между двенадцатью и часом дня. При этом 120
было условлено, что пришедший на место свидания будет ждать другого только в течение 20 минут Какова вероятность того, что встреча состоится, если каждый из договорившихся приходит, когда ему вздумаекя (но между двенадцатью и часом дня), не согласуй свои действия с другим? Нетрудно понять, что математи-
ческое содержание этой задачи в точности такое же, как в задаче о выборе двух точек на отрезке [0, 1]; при этом задаваемый вопрос состоит в том, с какой веро-
ятностью расстояние между точками окажется не больше, чем •—. Действительно, «5
если обозначить через х время прихода одного и-» данных лиц и через у — время прихода второго, то условие встречи запишется:
|Х — У! < 4’
задачей о выборе точек становится очевидной. Полагая в найдем, что искомая вероятность встречи буде!
после чего аналогия с
1 выражении (2) I = —, О
£
9*
Распределение, с которым мы столкнулись в только что разобранной задаче, относится к числу равномерных распределений. В двумерном случае равномерное распределение задается с помощью области й конечной площади; при этом плотность вероятности постоянна в Q, а за пределами Q равна нулю:
f (х, у)
( с для (х, у) С Q, 10 в остальных точках.
Значение постоянной с можно определить из условия:
/ (х, у) dxdy = 1,
которое дает cSa = 1 области й.
1
ИЛИ С =	,
где Зд обозначает площадь
Если G — какая-либо часть области Q (рис. 36), то вероятность
попадания случайной точки (х, у) в область G равна интегралу по этой области от постоянной функции -4, следовательно,
Sr =	(3)
Заметим, что равномерное распределение можно рассматривать не только в двумерном случае, но и в случае пространства любого числа измерений. Равномерное распределение на отрезке прямой было введено в § 24; для этого случая мы имели
121
в упомянутом параграфе формулу (4), которую теперь запишем следующим образом:
, z- za длина G p(xgG) = *------,
длина U
где П есть отрезок числовой оси, представляющий собой множество всех возможных положений точки х, a G — любой отрезок, содержащийся в й. Аналогичным образом для равномерного распределения в пространственной области й имеем: ,,	. , л.. объем G
р ((х, у, z) е G) = -—-объем Q
(3')
(3")
Из рассмотрения формул (3), (3'), (3") можно сделать общее заключение: задачи, приводящие к равномерным распределениям, — это в точности задачи на геометрические вероятности. На это обстоятельство мы уже обращали внимание читателя в § 24, где равномерное распределение изучалось только для одномерного случая.
Пример. Иглу длиной I бросают на плоскость, в которой на расстоянии L друг от друга проведены параллельные линии. Определить вероятность пересечения иглой одной известна как знаменитый XVIII в.).
Решение. Введем в рассмотрение систему случайных величин (х, <р), где х есть расстояние от середины иглы до ближайшей линии, а ф — угол между иглой и линией (рис. 37). Исходя из условий задачи, естественно принять, что каждая из величин Га L х, ф распределена равномерно: первая — в промежутке 0, — , вторая — в промежутке [0, л]. Столь же естественно считать, что величины х и ф независимы. Итак, область возможных положений случайной точки (х, ф) есть прямоугольник Й:
из линий, если / <.А, Эта задача задача Бюффона (Жорж Бюффон — французский естествоиспытатель
122
а плотность распределения для системы (х, ф) равна произведению плотностей для х и ф в отдельности:
2	1
— • — при
• L л
О для
точка (х, ф)
О х , 0	® л,
остальных х, ф.
равномерно распределена в пря-
f (x> ф) =
Другими словами, моугольнике £2.
Нетрудно видеть, что пересечение иглой одной из_линий происходит только в том случае, когда
. / .
X < — sinro.
^2
Обозначим через G область, выделяемую из прямоугольника Q этим неравенством (рис. 38). Искомая вероятность р пересечения есть, следовательно, не что иное, как вероятность события (х, ф) б G. Отсюда
Р=д
Представляя площадь области G обычным образом в виде интеграла, получим:
JL
j sin ф dcp = I о
и, значит,
Z	2/
Р = — = зт/х	зтД,
(4)
что дает для р приближенное значение
0,637
L
В математической литературе упоминается о серии бросаний иглы, выполненной реально одним из еаествоиспыта гелей. Для эксперимента была взята игла длиной 7,2 см, в то время как расстояние между соседними параллельными прямыми равнялось 9 см. В этом случае формула (4) дает для искомой вероятности 8
значение —. Бросание производилось 500 раз; полученная при этом частота не-5л
ресечения оказалась равной 0,5064. Можно попытаться на основании этого ре-зулыата оценить приближенно число л, если положить
8
— = 0,5064.
5л
Таким путем получается: п == 3,1596, что довольно близко к истине.
2°. Нормальное распределение на плоскости. В случае плоское»
123
ти, как и на прямой, особое положение занимает нормальное распределение.
Определение. Мы говорим, что случайная точка М. на плоскости подчиняется нормальному закону распределения, если в некоторой системе координат хОу координаты точки М являются независимыми случайными величинами, распределенными (каждая в отдельности) по нормальному закону.
Пусть х и у — координаты точки М, а
_ (х—а)г
1 2о1
А (х) = ——=- е	— плотность для х
Щ у 2л и
(у—Ь) *
1	2о2
(у) — —е — плотность для у.
а2 У 2л
Тогда вследствие независимости величин х и у плотность для системы (х, у) будет:
Г(х—о)а (у—6)21
«	2а2 I
f (*>У) = Л (*) ft (у) =----— е L 1	2	(5)
GjOj • 2л
Разумеется, если систему координат изменить путем поворота осей на некоторый угол, то выражение для f (х, у) станет более сложным и уже не будет представляться в виде произведения функции от х на функцию от у; это означает, что в новой координатной системе координаты точки М уже не будут независимыми случайными величинами.-
Заметим, что при Of = сг2 распределение (5) называется круговым. В этом случае функция f(x, у) имеет вид:
_ U—о)2+(у—Ь)а
Написанное выражение, как нетрудно видеть, обладает круговой симметрией по отношению к точке S (а, Ь), т. е. оно не меняет своего значения при смещении точки (х, у) по окружности с центром S.
§ 30. ФУНКЦИИ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
1°. Определение функции у=<р (х). С чисто интуитивной точки зрения представляется естественным следующий подход к понятию функции от случайной величины х.
Пусть с некоторым опытом связана случайная величина х. Рассмотрим какую-нибудь (обычную числовую) функцию ср (х). Тогда можно определить новую случайную величину ср (х), связанную с тем же опытом. Величина <р (х) принимает свои значения
124
следующим образом. Пусть произведен опыт, и в результате него величина х приняла значение а. Тогда величина ср (х) по определению принимает в том же опыте значение ср (а). Ясно, что в рамках интуитивного подхода такое соглашение полностью определяет величину ср (х).
Дадим теперь формальное определение функции от случайной величины. Прежде условимся, что запись ср : Д -> Д (или просто ср) обозначает функцию, определенную на множестве R действительных чисел и принимающую значения снова в R. Условимся также называть функцию ср борелевской, если ее график, т. е. множество
= {(х, у) }у = <р (х)},	(1)
является борелевским множеством на плоскости. Практически все функции, с которыми приходится иметь дело, являются борелевс-кими.
Определение. Пусть даны система (х, у) и борелевская функция ср. Мы пишем
У = Ф(х)
и говорим, что величина у есть функция ср от величины х, если рСПр) = 1.
Здесь р ( ) обозначает, конечно, распределение системы (х, у).
Таким образом, запись у = ср (х) выражает тот факт, что с вероятностью 1 значения величин х и у связаны функциональной зависимостью у = ср (х).
Существование наперед заданной функции от случайной величины вытекает из следующей леммы.
Лемма. Для любой случайной величины х и любой борелевской функции ср существует, и притом единственная, система (х, у), такая, что:
1) величина х совпадает с х (имеет то же распределение, что и х);
2) у = ср(х).
Доказательство. Пусть А — борелевское множество из Д2. Определим множество А* из Д следующим образом: х £ А* тогда и только тогда, когда (х, ср (х)) £ А. Иначе говоря, Л* есть проекция множества ЛГф на ось
Ох (рис. 39). Далее, положим,
р (Л) = рх (Л*),	(2)	-----Д
где рх( ) обозначает распределе- "о/	v—	Д
ние величины х.	а*
Функция р (Л) обладает всеми
свойствами двумерного распре-	Рис. 39
125
деления. Действительно, если множества Л и В не пересекаются, то и соответствующие им множества А* и В* тоже не пересекаются; поэтому из счетной аддитивности функции рх ( ) следует счетная аддитивность р ( ). Далее, если А есть все Д2, то Л* есть все Д; поэтому р (Д2) = 1. Наконец, из рх(А*) 0 следует: р (Л) ^0.
Из сказанного вытекает существование системы (х, у) с распределением р (Л). Справедливость для этой системы утверждения 2 леммы проверяется просто: если в качестве А взять множество Гф, то Л* будет все Д, поэтому р (Г ) = px(R) = 1. Проверим теперь справедливость утверждения 1.
Пусть С — любое борелевское множество на оси Ох. По определению величины х (первой компоненты системы (х, у)) имеем: Р; (С) = р (С х Д).
Но если в качестве множества А в формуле (2) взять С х Д, то множество А* будет, очевидно, совпадать с С и, значит, р (С х. R) — = рх (С). Отсюда
= рх (С),
что и доказывает совпадение величин х и х.
Чтобы завершить доказательство леммы, осталось проверить единственность системы (х, у) со свойствами 1 и 2. Предположим, что имеется еще одна такая система, (х, у); ее распределение обозначим г (Л). Так как г (Г ) = 1 (это следует из у = <р (х)), то для любого борелевского множества А в Д2имеем: г (Л) = г (ДГср) (см. лемму на с. 96). Но множество А имеет, очевидно, такое же пересечение с Г , что и множество А* х Д, поэтому
г (Л) = г (Д* х Д).
Из последнего равенства следует:
г(Д) = г«(Д*).	(3)
X
Сравнивая (3) с (2) и учитывая, что распределения величин х и
х одинаковы, получим: г (Д) — р (Д). Ц
2°. Распределение функции. Согласно определению, данному в п. 1°, запись у = ср (х) предполагает, что величины х и у составляют систему (х, у). Однако это не мешает нам рассмотреть отдельно распределение величины у. Естественно ожидать, что оно выражается через распределение величины х и функцию ср. Найдем это выражение.
Для большей отчетливости распределение системы (х, у) будем обозначать рЛ,у( ) (а не р( ), как раньше). Если в формуле (2) в качестве А взять множество Д х Д, где Д — какое-либо
борелевское множество на прямой, то Л* будет представлять собой множество ф"1 (В) (рис. 40). Значит,
Рх.у (R X В) = рх (ср"1 (В)).
Отсюда следует, что
Ру (В) = рх (ф-1 (В)).	(4)
Полученная нами формула дает искомое выражение для распределения величины у.
Пример. Случайная величина х имеет нормальное распределение. Покажем, что величина у — а х + р, где аи^- постоянные, причем а =/= 0, тоже подчиняется нормальному закону.
Решение. По условию х имеет плотность вероятности вида
/У) = —
а У 2л
(х—а)2 2 а2
Рассмотрим сначала случай а > 0.
Пусть множество В задается условием х <с(с = const.) Поскольку в данном случае ф (х) = а х + р, то множество ф-1 (В) будет [х | х < ^—^1. Согласно (4), имеем:
I	а I
Р (у < с) = р X <
или
с—с—13 а	а	_ (х—а)*
р(у < с) = Г f (х) dx — 1 е г°‘ dx.
J	J а У2л
—оо	— оо
Производя в интеграле замену у = <хх + р, получим:
с	(у—gg—fl)2
Р(У<с) = f —е !(аа)‘ dy. J аа У 2л
Отсюда видно, что величина у распределена нормально с плот
ностью:
.	_ (у—(ga+fl))2
Д(у) = -----4= е 2(аа)2 .
1 (аа) У 2л
Случай а < 0 предоставляем рассмотреть читателю ▲
3°. Случай, когда величина х дискретная. Формула (4) дает закон распределения величины у = Ф (х) безотносительно к тому,
127
каков характер распределения величины х. Для случая, когда величина х дискретная, можно получить более конкретный результат.
Пусть xt, х2, ... — возможные значения величины х, a pit р2, ... — их вероятности. Положим,
Й = {%!, х2,
Множество ср (й) будет состоять из чисел ф (xj), ф (х2), ... (среди которых могут оказаться совпадающие). Согласно формуле (4),
Ру (ф (й)) = рх (М),
где М есть множество ф-1 (ф (Й)). Очевидно, М содержит й, поэтому рх (Л4) = 1. Итак,
Ру (<Р (&)) = 1-
Это показывает, что величина у тоже является дискретной и множество ее возможных значений есть ф (Й).
Подсчитаем теперь вероятности различных значений величины у.
Пусть с — любое число. Имеем:
Р (У = с) = р (х е ф-1 (с)) = р (х е ф-1 (с) П й)
(первое равенство написано на основании (4), второе — на основании леммы из § 23). Множество ф~х (с) П Й состоит из всех чисел xt й, таких, что ф (х;) = с. Значит,
Р (У = с) = 2 рь
Итак, чтобы найти вероятность события у — с, нужно из всех возможных значений xt величины х выбрать те, для которых Ф (xz) = с, и просуммировать их вероятности.
Пример. Пусть закон распределения величины х имеет вид:
Значения х	—2	— 1	0	1	2	3
Вероятности	0,1	0,2	0,4	0 02	0,15	0,13
Найдем закон распределения величины у = х2.
Возможные значения у будут (—2)2, (—I)2, О2, I2, 22, З2 т. е.
О, 1, 4, 9. Их вероятности:
Р (У	=	0)	=	р (х = 0)	=	0,4,
Р (У	=	О	=	Р (х = 1)	+	р (х	=	—1)=0,024-0,2=0,22,
Р (У	=	4)	=	р (х = 2)	4-	р (х	=	—2)=0,154-0,1=0,25,
р (у	=	9)	=	р (х = 3)	=	0,13.
Следовательно, закон распределения для у будет:
Значения у	0	1	4	9
Вероятности	0,4	0,22	0,25	0,13
128
§ 31. СИСТЕМА ЛЮБОГО ЧИСЛА СЛУЧАЙНЫХ ВЕЛИЧИН. ФУНКЦИИ ОТ НЕСКОЛЬКИХ СЛУЧАЙНЫХ ВЕЛИЧИН
1°. Распространение введенных ранее понятий на многомерный случай. Система п случайных величин, где п — любое число, большее 2, определяется по тому же образцу, что и система двух случайных величин. Вместо борелевских множеств в R2 приходится рассматривать борелевские множества в 7?я; в остальном определения, данные в § 26, п. 2°, остаются в силе.
При рассмотрении системы из п > 2 случайных величин возникает, впрочем, один новый момент. Это понятие подсистемы. Например, если дана система (х4, х2, х3) с распределением р ( ), то можно рассматривать подсистему (xf, х2); ее распределение, которое мы обозначим р, х ( ), задается формулой
PXi х (А) = р (А х R), лг
где А — любое борелевское множество в R2, а А х 7? есть совокупность точек (хь х2, х3) С R3, таких, что (хъ х2) С А.
Не останавливаясь на понятиях дискретного распределения, а также распределения, имеющего плотность (они вводятся по образцу таких же понятий в одномерном и двумерном случаях), обратимся к понятию функции от нескольких случайных величин. Для сокращения записей ограничимся функциями двух аргументов.
Пусть ср — функция, определенная на R2 и принимающая значения в R. Как и ранее, условимся называть ср борелевской функцией, если ее график, т. е. множество
Гф = {(xi, х2, у) I у = ср (хь х2)},
является борелевским множеством в R3.
Определение. Пусть даны система (хх, х2, у) и функция <р : R2 -> R. Мы пишем
у = ср (х1( х2)
и говорим, что у есть функция ср от величин хп х2, если
Р (Гф) = 1,
где р (	) есть распределение системы (хп х2, у).
Справедлива следующая лемма, обобщающая лемму из п. 1° § 30 на случай функции двух аргументов.
Лемма. Для любой системы (xlt х2) и любой борелевской функции ср : R2 -> R существует, и притом единственная, система (л\, х2, у), такая, что:
1) подсистема (хп х2) совпадает с (хп х2);
2) у = ср (хр £).
Доказательства мы не приводим, поскольку оно совершенно аналогично доказательству леммы из § 30. Отметим лишь, что
5 А. С. Солодовников
129
искомая система (х4, х2, У) имеет распределение р ( ), задаваемое формулой
Р И) = Pxt. х, (Л*)
(аналог формулы (2) из § 30), где рд х ( ) — распределение системы (xi, х2), а множество А* (из R2) связано с множеством А (из R3) следующим образом: (хь х2) С А* тогда и только тогда, когда (хь х2, <р (хь х2)) С А.
Обобщением формулы (4) из § 30 на случай функции двух аргументов служит формула
Ру (S) = Рх,. х, («Г* Ж	(1)
выражающая распределение величины у = <р (х4, х2) через распределение системы (xi, х2) и функцию <р. Вывод формулы (1) совершенно аналогичен выводу формулы (4) из § 30, и нет необходимости излагать его вторично.
2°. Закон распределения суммы двух случайных величин. Рассмотрим следующую важную задачу.
Задача. Пусть дана система двух случайных величин, распределенная с некоторой плотностью. Обозначим эту систему (х, у), а ее плотность /(х, у). Требуется найти закон распределения случайной величины
Z = X + у.
Решение. Подсчитаем вероятность события
Z < Z, где г  - некоторое число.
Hq авенство х + у < г определяет на координатной плоскости хОу некоторую область G - полуплоскость с граничной прямой х + у = z (на рис. 41 область G заштрихована).
Имеем:
р (х + у < z) = р ((х, у) С G) = j (7 (х, у) dxdy. d
Преобразуем полученный интеграл, сделав в нем замену переменных:
X + у = U, X — у = о.
Рис. 41
Относительно переменных и и v область G характеризуется неравенствами:
— оо < и < Z, —оо < V < оо, следовательно,
Jp(A У) dxdy = G
Z оо
= j du J - f ( u-^^dudv
130
j f(t, u — t) dt.
I
(множитель — есть якобиан перехода от х, у, к и, и). Во внутрен-
u 4- а ,	и — v , D
нем интеграле положим = t, тогда —— = u — t, В результате получим:
Z оо
f (х, у) dxdy = J du — оо
Итак, окончательно
р (z < z) = J ( J f (/, и — t) dt} du, — 00 —оо
т. е. вероятность попадания z в промежуток (—оо, г) равна интегралу по этому промежутку от функции
со
£(«) = J f(t, u — t)dt.	(2)
— 00
Эта функция и есть, следовательно, плотность распределения величины г.
Особого внимания заслуживает случай, когда складываемые величины х и у независимы. Тогда, как мы знаем,
f (.х, у) = Л (х) /2 (у),
где fx (х) — плотность для х, a f2 (у) — плотность для у. Формула (2) принимает вид:
ОО
И«) = pi (ОЛ	(3)
Отвлекаясь от существа решаемой задачи, можно заметить, что полученная нами формула (3) определяет весьма интересную операцию над функциями: каждой паре функций /1 (х) и /2 (х) ставится в соответствие новая функция | («), определяемая формулой (3). Эта операция называется свертыванием, а функция £(ц) — сверткой функций f{ (х) и /2 (х).
Пример 1. Найдем закон распределения для суммы х + у, если величины х и у независимы и каждая из них распределена равномерно на отрезке [О, Ц;
Для 0<х<1,
(О для остальных х
и
(У)
(1 для 0 у 1, (О для остальных у.
Решение.
Величина z = х + у принимает в этом слу-
5*
131
чае значения из промежутка [0, 2]; вне
этого промежутка ее плотность вероятности | (z) равна нулю.
При О z 1 имеем:
ОО
£(z) = pi Ш* -0 dt =
— оо
=J 1 • 1 dt = Z о
(интеграл по всей оси мы заменили интегралом по отрезку [0, z], так как при t < 0 равен нулю первый множитель (() подынтегрального выражения, а при t > z равен нулю второй множитель /2 (Z - 0).
При 1 z 2 имеем:
оо	1
Uz)= j* /1(0/2(г —0^ = J 1-1Л = 2-г
—со	2—1
(при t < z — 1 равен нулю второй множитель /г (z — Z), ибо тогда z — t > 1; при t > 1 равен нулю первый множитель (()). Итак,
&(*) =
' 0 вне [0, 2], z для 0 z	1,
2 — z для 1 < z 2.
График функции | (г) показан на рисунке 42. ▲
Пример 2. В качестве приложения формулы(3) установим следующий факт: сумма независимых случайных величин, каждая из которых подчиняется нормальному закону, сама имеет нормальное распределение.
Решение. Пусть г — х + у, где каждая из величин х и у подчинена нормальному закону:

_ (х—а,)г
1
----т=-е
}''2л
И
1	2°2
и
ОО	ОО —	_ <г~
Uz)= \	= —t— f е 20‘ dt.
—ОО	—ОО
132
Выражение, стоящее в показателе степени подынтегральной функции, после выполнения указанных в нем действий может быть представлено в виде
At2 + 2Bt + С,
где А, В, С — некоторые выражения, содержащие г. Выписывать эти выражения мы не будем, заметим только, что А < 0, причем в выражение А величина z не входит совсем, в выражение В входит в первой степени, а в С входит в квадрате.
Воспользуемся теперь формулой
оо	-----АС—в>
J eAt2+2Bi+c dt = у -^е А	(Л < 0),
— ОО
известной из курса математического анализа. Учитывая то, что сказано выше относительно А, В, С, получим, что | (г) есть функция вида
причем а < 0 (это видно, например, из сходимости интеграла оо
J | (z) dz = 1). Плотность | (г) такого вида соответствует нор-
мальному закону. Мы доказали, таким образом, что величина г имеет нормальное распределение.
Глава 7.
ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
Согласно изложенному выше, исчерпывающей характеристикой случайной величины является ее закон распределения. Но далеко не в каждой задаче нужно знать весь закон распределения. В ряде случаев можно обойтись одним или несколькими числами, отражающими наиболее важные особенности закона распределения, например числом, имеющим смысл среднего значения случайной величины, или же числом, характеризующим средний размер отклонения случайной величины от своего среднего значения, и т. д. Такого рода числа называют числовыми характеристиками случайной величины (или соответствующего закона распределения). Их роль в теории вероятностей чрезвычайно велика; многие задачи удается решить до конца, оставляя в стороне законы распределения и оперируя только числовыми характеристиками.
§ 32. МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
Наиболее важное место среди числовых характеристик занимает так называемое математическое ожидание или среднее значение случайной величины.
1°. Математическое ожидание дискретной случайной величины. Чтобы подойти естественным путем к понятию математического ожидания, будем рассуждать следующим образом. Пусть х—дискретная случайная величина. Придерживаясь неформальной точки зрения (см. § 20), будем считать, что величина х связана с некоторым опытом. Предположим, что опыт осуществлен N раз и при этом величина х:
Ni раз принимала значение х4, Nz раз принимала значение х2
и т. д. Найдем среднее арифметическое всех значений, принятых величиной х в данной серии опытов. Оно запишется:
*1^1 +	+ •••	_ v	I у ^2	|
--------------- = X,---f- Х„--^ ... .
N	1 N 2 N
Дробь есть частота, с которой появлялось значение xf, с увеличением числа опытов N эта дробь будет приближаться к -134
вероятности события х = Аналогичным образом дробь ~ будет приближаться к и т. д. В итоге получаем, что с увеличением N среднее арифметическое будет приближаться к числу
Xipi + х2р2 + ... ,
Дадим теперь такое определение.
Определение. Математическим ожиданием или средним значением дискретной случайной величины х с законом распределения
xi *.
Pl Р2
(1)
называется число
Ж [х] = х,/?, + х2р2 +... .	(2)
Таким образом, математическое ожидание дискретной случайной величины х равно сумме произведений возможных значений величины х на их вероятности.
Смысл числа Л4[х] ясен из приведенного выше рассуждения. Он заключается в том, что оком числа М [х] колеблется среднее арифметическое значений, принимаемых величиной х в больших сериях опытов.
В случае, когда таблица (1) состоит из бесконечного числа столбцов и, значит, в правой части (2) стоит сумма бесконечного ряда, к определению математического ожидания мы добавим следующее требование: ряд (2) должен сходиться абсолютно. Другими словами, должен сходиться ряд
1*11 Pi + Кг1 Р2 + ••• .
составленный из абсолютных величин членов ряда (2). Смысл этого требования очень прост. Если произвольным образом поменять местами столбцы таблицы (1), то измененная таблица будет по-прежнему задавать закон распределения величины х. В сумме (2) при этом произойдет перестановка слагаемых. Для того чтобы число М [х] оставалось неизменным, нужно, следовательно, потребовать, чтобы сумма ряда (2) не менялась при любой перестановке слагаемых. Как известно, таким свойством обладают только абсолютно сходящиеся ряды.
Число М [х] часто называют центром распределения случайной величины х. Это название связано с упоминавшейся ранее механической моделью случайной величины (§ 25). Если в точках xlt х.2, ... оси Ох сосредоточены массы mi, m2,... (соответственно), тс центром масс такой системы является точка
- _ х2т2 + х2т2 + ...
+ ni2 ...
135
Предположив, что суммма всех масс равна 1, получаем:
х — Х1Гп\ + хгпг2 + ••> что аналогично формуле для математического ожидания.
Из определения (2) непосредственно вытекает следующий факт.
Математическое ожидание постоянной величины равно ей самой.
Действительно, постоянную величину с можно рассматривать как дискретную случайную величину х, принимающую только одно значение с с вероятностью 1. Но тогда
М [х] = с • 1 = с.
Рассмотрим ряд примеров на нахождение математического ожидания.
Пример 1. Найти математическое ожидание числа очков, выпадающих при бросании игральной кости.
Л4 [х] =	1 • —	+ 2 • —	+ 3 • —	+ 4 • —	+ 5 • —	+ 6 • —	= 3,5. ▲
J 6	6	6	6	6	6
Пример 2. В ящике находятся п запакованных изделий, , каждое из которых с вероятностью р может оказаться дефектным. Из ящика необходимо выбрать исправное изделие. Для этого извлекаем из ящика наугад любое изделие, распаковываем его и подвергаем осмотру. Если при этом обнаруживается дефект, то извлекаем следующее изделие и т. д.
Рассматривается случайная величина х — число изделий, которое будет опробовано.Найти ее математическое ожидание.
Решение. Возможные значения для числа проб будут:
1, 2, 3, ..., п — 1, п,
а их вероятности
1 - Р, Р (1 - р), Р2 (1 - Р).	Р"”2 (1 - Р), Р"-1
(например, вероятность события х = 3 будет р2 (1 — р), поскольку это событие означает, что из трех выбранных изделий первые два оказались дефектными, а третье — исправным). Отсюда
М [х] = (1 - р) [1 + 2р + Зр2 + ... 4- (п 1) р^ + прп-\
136
Перемножив скобки и приведя подобные члены, будем иметь:
1 _ Пп
М[х] = 1 +р + р2 + ... +Рп~1 = —-
1 —Р
Смысл полученного ответа можно пояснить следующим рассуждением. Пусть имеется не один ящик, а большое число ящиков (в каждом по п изделий). Из каждого ящика с помощью некоторого числа проб выбирается исправное изделие. Если сложить все полученные таким образом числа и разделить на число ящиков, то должно получиться число, близкое к р-. ▲
Пример 3. Производится ряд независимых опытов, в каждом из которых с вероятностью р наступает событие А. Опыты продолжаются до первого появления А. Случайная величина х — число произведенных опытов. Вычислим М [х]
Решение. Закон распределения величины х был найден ранее (см. пример 3 на с. 87). Он имеет вид:
1	2	з		п	
р	pq	pq2		pqn~Y	
где q = 1 — р. Отсюда находим:
М [х] = 1 • р + 2 • pq + 3 • pq2 + ... + п • pq^1 ф- ... = = р (1 4- 2q + З72 + ... + nq"-1 + ...).
Ряд, записанный в скобках, получается почленным дифференцированием геометрической прогрессии
q + q2 + q3 + ... + qn + ... .
Следовательно,
MW = zJ_L__iy = p= х = A \i— q )	(i—?)2 p2 p
Пример 4. Найти математическое ожидание дискретной случайной величины х, распределенной по закону Пуассона.
Решение. Закон Пуассона задается таблицей:
0	1	2	3	
е~к		X2 -к — е Л 2'	X3 , — е~к 3!	...
Отсюда имеем:
137
Таким образом, параметр X, характеризующий данное пуассоновское распределение, есть не что иное, как математическое ожидание величины х. ▲
В заключение этого пункта решим следующую важную задачу.
Задача. Дискретная случайная величина у задана законом распределения (1). Найти математическое ожидание величины у = <р (х), где ф «— некоторая функция.
Возможными значениями величины у будут числа
У1 = ф (*i). у2 = ф (х2)...
При этом вероятность любого из этих значений с находится по формуле
Р(У = 0 = Pi
{< I Ф(-Щ=с}
(см. § 30, п. 3°).
Предположим сначала, что все числа yit у2, ... различны. Тогда р (у = yz) = pt, так что
М [у] = У1р! + у2р2 + ... .	(3)
Эта же формула для М [у] будет справедлива и в том случае, когда среди чисел уь у2, ... имеются равные. В самом деле, пусть, например, у4 и у2 равны одному и тому же числу с, а все остальные у; отличны от с. Тогда р (у = с) = р4 4- р2, следовательно, при подсчете М [у] сумму yrfi + у2р2 нужно заменить с (р£ + р2). Но так как в данном случае у iPi + у2рг = с (pt + р2), то равенство (3) сохраняется.
Итак, для нахождения М [ф (х)] имеем формулу (3) или, что то же, формулу
Л1 [ф (х)] = ф (хх) pj + ф (х2) р2 + ... = 2 Ф (*/) pt. (4) I
2°. е-приближение к случайной величине. Математическое ожидание случайной величины общего вида. Прежде чем дать определение математического ожидания в общем случае, введем понятие ^-приближения к случайной величине х.
Пусть 8 — положительное число. Рассмотрим на числовой оси бесконечную в обе стороны последовательность точек
.... а_2, а_1( а0, cq, а2, ....	(5)
где — is (рис. 43). Условимся называть такую последователь-
ность г-сетью.
Определим новую случайную
£ Е £ е Е £
Ct-j	ОС-; Р ОС; 0С2 CCj
Рис. 43
величину хЕ, которая принимает дискретный ряд значений (5), причем вероятность любого из них а; есть
р, = р (а, < х < а/+1)
(i = 0, ±1, ±2, ...).
138
Случайную величину xg будем называть ^-приближением к случайной величине х.
Заметим, что условие = 1, обязательное для дискретного распределения, выполняется, поскольку
1 = 00
S Pl = Р(— 00 < X < оо) = 1, /=—оо
Если предположить, что величина х связана с некоторым опытом, то взаимоотношения между х и хе можно истолковать следующим образом. Пусть произведен опыт, и в результате него величина х приняла значение, принадлежащее некоторому промежутку at х < «,+!. Тогда величина xg по определению принимает в том же опыте значение а;. При таком соглашении события хе = а; и х < будут равнозначны, и, следовательно, их вероятности будут совпадать; это как раз и соответствует данному выше определению величины хе. Итак, величина хе получается путем округления значений, принимаемых величиной х, до ближайших слева точек 8-сети.
Отсюда, между прочим, видно, что переход от случайной величины х к дискретной случайной величине xg имеет вполне реальный смысл. Например, такой переход совершается всякий раз, когда значения величины х считываются с измерительного прибора, причем показания прибора округляются до ближайшего слева деления шкалы.
Наши рассуждения показывают, что по мере приближения 8 к нулю различие между х8 и х становится все менее существенным. Естественно поэтому принять такое определение.
Определение. Математическим ожиданием случайной величины х называется число
М [х] = lim М [х ].	(6)
е-,0
Если указанный справа предел не существует, то математическое ожидание величины х также считается несуществующим.
Итак, согласно определению,
М [х] = lim 2 atP (ai х < a/+i)>	(7)
e-t-0 i=—х
где = «8 (i = ..., —2, —1, О, 1, 2, ...).
Важно отметить, что если величина х дискретна, то данное выше определение (7) математического ожидания эквивалентно первоначальному определению (из п. 1°).
В самом деле, пусть х—дискретная случайная величина. Для простоты будем считать, что множество возможных значений величины х конечно; обозначим эти значения xlt х2.х„, а их вероятности соответственно pi, р2, .... рп.
Для любого целого i имеем:
139
p(ai<x< az+1) = 2 Pk>
(i)
где символ (i) под знаком суммы означает, что суммируются только такие вероятности р/ц для которых хА принадлежит промежутку az х < az+1. Отсюда
(=Х)
М [Хе ] = 2	2 Рк-	(8)
i=—о©	(i)
Правая часть этого равенства представляет собой сумму членов вида azpft, причем любое из чисел рг, р.2, , Рп входит сомножителем в один и только один член (ибо любое из чисел х,, х2, .... хп принадлежит одному и только одному промежутку az^ х < az+1 ) и для каждого члена справедливо неравенство |az—х*| Таким образом, равенство (8) можно записать по-другому:
М [х8 ] = ptaZ1 + p2aZa + ... + p„aZ/!i
где каждое aik отличается от xZi не больше чем на в.
Сравним число М [хе] с математическим ожиданием величины х в смысле п. 1°. т. е. с числом
т = РЛ + РзЪ + ... + рпхп.
Имеем:
| М [хе ] — т | = | р, (aZ1 - xj + р2 (aZs — х2) + ... + рП (а1п — хп) | <
п
< Pi I а/х - 1 + р21 % — х21 4- ... + рп I а1п— хп | <е 3= в
п
(следует учесть, что 2pi ~ 1). Отсюда вытекает, что предел М [х ] при е->-0 i=i
равен т.
3°. Математическое ожидание случайной величины, имеющей плотность вероятности.
Теорема 1. Пусть х —непрерывная случайная величина, распределенная с некоторой плотностью f(x). Если сходится интеграл
со
J* (х|/(х) dx,	(9)
—GO
то существует М [(х) ] и справедлива формула
7ИЩ== j" xf(x)dx.	(10)
Другими словами, если интеграл (10) сходится абсолютно, то математическое ожидание величины х существует и равно этому интегралу.
В интересах дальнейшего изложения мы установим более сильную теорему, чем теорема 1. Вместо случайной величины х рассмотрим величину <р (х), где ф есть функция, удовлетворяющая
140
такому условию: для любого промежутка w (отрезка, интервала, полуинтервала) множество <р-1 (ы) есть объединение конечного или счетного числа попарно непересекающихся промежутков. Такие функции будем называть правильными', практически любая функция <р является правильной.
Теорема 2. Пусть х —непрерывная случайная величина, имеющая плотность f(x). Если сходится интеграл
оо
J \<f(x)\f(x)dx,	(11)
—оо
то существует 7И[ф(х)] и справедлива формула
Л4[ф(х)] = J q(x)f(x)dx.	(12)
Очевидно, теорема 1 есть частный случай теоремы 2, отвечающий функции ф (х) = х (разумеется, правильной).
Отметим также, что формула (12) есть своего рода интегральный аналог формулы (4).
Доказательство теоремы 2. В следующих ниже рассуждениях символ J, где Q есть объединение попарно непере-й
секающихся промежутков, означает сумму интегралов по всем промежуткам, составляющим Q.
Положим, у = ф (х). Рассмотрим величину уе — е-приближе-ние к у. Условимся, как и раньше, писать аг вместо ге (i —любое целое), а множество ф-1 (wz), где — полуинтервал [а;, а;+1), будем обозначать Qz.
Распределение ( ) величины у задается формулой (4) из § 30. Из этой формулы следует, что
Ру (®z) = Рх (^)= f f W dx.
Тем самым
i=CO	i=sCO р
м Су еЗ = . 5 чРу (и,) = 2 «J/й dx, (13) 1 =—ОО	1 =—оо
если только ряд, написанный справа, сходится абсолютно.
Убедимся в абсолютной сходимости ряда (13). Для этого рассмотрим соответствующий ряд из абсолютных величин:
2|а;|[/(х)^х	(14)
1=00
(для краткости мы пишем теперь вместо 2 ) и сопоставим его I	1=*—са
со сходящимся рядом
141
2 J | ф (x) | / (x) rfx,	(15)
сумма которого равна интегралу (11). Обозначив члены рядов (14) и (15), отвечающие номеру г, соответственно через at и bit а их разность через с;, будем иметь:
ct = — bt = J | at | f (x) dx — J | q> (x) | f (x) dx = £2/
= f (| a, | — | <p (x) I) f (x) dx. *
Так как на всем множестве Q; разность |aj— |ф (х)| по абсолютной величине не превосходит е, то
k;|<e р(х)</х.
Теперь заметим, что ряд, составленный из чисел e^(x)dx, схо-
дится: его сумма равна: оо
е • 2 j / (х) dx = е • J f (х) dx = е.
—оо
Следовательно, ряд из чисел тоже сходится. Отсюда, как из-вестно, вытекает сходимость ряда 2ср Поскольку, таким образом, из трех рядов 2ao Sfy, 2е/ второй и третий являются сходящими-I I i
ся, то сходится и первый ряд. Итак, ряд (14) сходится. Отсюда следует, что число Л4[уЕ] существует и, значит, справедливо равенство (13).
Совершенно так же, как сравнивались выше ряды (14) и (15), можно сравнить ряды
2 a J f	и 2 .f <₽ Wf W dx
i	i
и убедиться, что соответствующие (i-e) члены этих рядов отличаются не больше чем на е J f (x)dx\ следовательно, суммы рядов отли-
чаются не больше чем на е. Иначе говоря, число М [уе] отличается 00
от интеграла J <р (х) f (x)dx не больше чем на е. Отсюда вытекает, что предел М. [уе] при е -> 0 существует и равен указанному интегралу. Итак,
М [<р (х)] = J ф (х) f (х) dx. 
—00
142
Рассмотрим два важных примера на исйоЛьзование формулы (Ю).
Пример 1. Найти математическое ожидание случайной величины х, распределенной по нормальному закону с плотностью
(х-о)»
а У 2л
Решение. Имеем:
00	оо	(Ж—О)1
М [х]= С xf(x)dx =—-— С хе 2°2 dx. J	J
— ОО	— 00
В последнем интеграле произведем замену переменной:	= t.
а
Получим:
оо	ta	оо t9	ОО t*
М[х] = — f (ot + а) e~2dt = — f te~2dt +— f e~rdt.
/2л J	/2л J
— CO	—00	—00
Первый из двух интегралов правой части равен нулю ввиду нечетности подынтегральной функции, второй же интеграл подстановкой t — uV2 сводится к /^2 J e~u‘du = V2л.
В итоге получаем:
М [х] = а.	(16)
Этим выяснен теоретико-вероятностный смысл параметра а, входящего в выражение для нормального закона: параметр а совпадает с математическим ожиданием величины х.
Смысл второго параметра ст будет установлен позже. ▲
Равенство (16) можно было бы получить и более простым путем, используя одно соображение общего характера, а именно: если плотность f (х) четна относительно точки х — а (г. е. / (а — Z) = f (а + /) для всех /), то М [х] = а.
ОО
Действительно, если в интеграле Jx/(x) dx произвести замену х = a-j- t, то по-
СЮ
лучим интеграл J (а + /) f (а + /) dt или
a f f(a + t)dt+ ]tf(a + f)dt,	(17)
— ОО	—00
но первый из двух интегралов (17) равен 1, а второй равен нулю (ввиду нечетности функции f (а + /) относительно t = 0). Следовательно, М [х] = а.
Пример 2. Найти математическое ожидание случайной величины х, равномерно распределенной на отрезке [а, Ь].
143
Решение. Имеем:
Л4[х] = xf (х) dx = Г cdx,
где с — постоянная плотность вероятности на отрезке [а, 6], равная —!—. Отсюда
Ь — а
Мы получили, таким образом, что числу М [х] соответствует середина отрезка [a, ft]. Ввиду равномерности распределения х на отрезке Ea.bJ такой ответ можно было предвидеть заранее. ▲
§ 33. СВОЙСТВА МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ
В начале этой главы говорилось о важной роли числовых характеристик при решении разного рода задач на случайные величины. Чтобы сделать аппарат числовых характеристик более эффективным, необходимо изучить их свойства. Ранее был отмечен, например, такой факт: математическое ожидание постоянной величины равно ей самой. Добавим теперь к этому еще одно свойство:
Л1 [сх] = сМ [х]
(1)
— постоянный множитель с можно выносить за знак математического ожидания.
Для дискретной случайной величины равенство (1) очевидно: если х имеет закон распределения:
то сх будет иметь закон распределения:
откуда следует:
М [ex] = cxjPj + сх2р2 + ••• = с (х^! + Х2Р2 + • ••) = сМ[х]. Справедливость формулы (1) для произвольной случайной величины х (имеющей, однако, математическое ожидание) теперь легко вытекает из общего определения математического ожидания (§ 32, п. 2°).
1°. Математическое ожидание суммы. Наиболее существенным из всех свойств математического ожидания является следующий
144
факт, который часто называют теоремой сложения математических ожиданий.
Теорема. Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий:
ЛЕх4-у] = ЖМ + ЛКу].	(2)
'Доказательство этой теоремы мы приведем для случая, когда система (х, у) является системой дискретного типа.
Пусть xlt х2, ... — возможные значения величины х и У1, У2> ••• — возможные значения у. Возможные значения величины z = х + у будут содержаться среди чисел z вида xt + причем
p(z = z) = 2 Ру .	(3)
{i,/kz+y7=Z}
где рц есть вероятность события (х = xt, у — уу). В обоснование равенства (3) укажем, что событие z = z есть сумма событий (х = Х[, у = уу) для всех пар i, j, таких, что xt + уу = г.
Предположим сначала, что все числа вида xt + уу различны, т. е.
xt + у/ xv + у.,, если i #= Г' или /	j'.
Тогда сумма, стоящая в правой части (3), состоит только из одного слагаемого, и мы имеем:
Л4 [z] = 2 zp (z = z) = 5 (*/ + уу) Ру.	(4)
z	i, j
Покажем, что такое же выражение для М И получится и в том случае, когда среди чисел х, + у7 имеются равные.
Пусть, например, хт + у2 и х3 + у5 равны одному и тому же числу а, в то время как остальные числа x-t + уу отличны от а. Тогда в правой части равенства (4) вместо (хх + у2) р12 + (х3 + у6) рзъ следует написать а (р12 + /?3-), поскольку вероятность события z = а, согласно формуле (3), равна р12 + р3о. Но оба указанных выражения равны между собой:
(xi + у2) Р12 + (х3 + уБ) р3- = а (р12 + р35).
Следовательно, формула (4) остается справедливой.
Перепишем формулу (4) следующим образом:
Л4 [z] = 2 xtPtj + 2 У)Ру-i, i	( i
Первую сумму правой части можно представить в виде
I /
Выражение	или подробнее рп + pi2 + есть вероят*
/
ность того, что наступит какое-либо из событий
(х = х;, у = Ух) , (X = Xi, у = у2)..
6 А. С. Солодовников
145
т. е. в конечном счете, что х примет значение безотносительно к тому, какое значение примет у. Следовательно, это выражение равно р (х = х(). Отсюда
2 А А/ = 2 XtP (х = А) = Л1[х].
Аналогично покажем, что
2 yjpu = 2 yjp (у = у/) = м[у]. 1
В итоге имеем:
М [z] = М [х] + М [у].
что и требовалось получить. И
Если отказаться от предположения о дискретности системы (х, у), то доказательство теоремы существенно усложняется. Вывод формулы (2) для общего случая рассматривается в приложении 2 к данной книге (с. 199 — 200).
Методом математической индукции формула (2) переносится на любое конечное число слагаемых:
М [Х1 + х2 + ... + х„] = М И + М Ех2] + ... + М Ех„].
Заметим, что доказанные выше свойства математического ожидания
М Есх] = сМ [х] и
М Ех + у] = М Ex] + М [у] называют обычно свойствами линейности. Оба свойства линейности можно записать в виде одной формулы:
М Eax + by] = а М Ex] + b М [у].
Рассмотрим следующую важную задачу.
Задача. Производится п независимых опытов. В каждом из них с одной и той же вероятностью р может появиться некоторое событие А. Требуется найти математическое ожидание случайной величины х— числа наступлений события А в п опытах.
Решение. Обозначим через хг число наступлений события А в i-м опыте (i = 1, 2, ..., и). Очевидно,
X = хг + х2 + ... + х„.
Закон распределения каждой из величин х1( х2, ..., х„ один и тот же:
Значения хг	0	1
Вероятности		Р
146
где q — 1 — р. Следовательно, М [х(] = 0 • q + 1 • р = р. По теореме сложения математических ожиданий имеем:
М [х] = М FxJ + М Гх2] +	+ М Гхф1 = пр. (5)
Заметим, что тот же самый результат из более простых (однако нестрогих) соображений был получен в § 16, где решалась задача о нахождении «среднего числа успехов» в п опытах. А
Проиллюстрируем формулу (5) примером.
Пример 1. Случайное отклонение размера детали от стандарта подчиняется нормальному закону с параметрами а = 0, ст = 5 мк. Годными считаются детали, для которых отклонение не превышает 10 мк. Определить среднее число годных деталей из ста выбираемых наудачу.
Решение. Обозначим через А событие, состоящее в том, что деталь оказалась годной. Тогда
р (Л) = р (—10 < х < 10) = 2Ф (2) « 0,72
(см. формулу (7) на с. 105), где х обозначает отклонение размера детали от стандарта.
По условию выбирается 100 деталей. Если рассматривать выбор каждой детали как отдельный опыт, то можно сказать, что производится 100 опытов. Нас интересует среднее число наступлений события А в этих опытах.
Применив формулу (5), найдем, что это число равно пр == = 100-0,72 = 72. А
Разберем еще один пример, иллюстрирующий применение теоремы сложения математических ожиданий.
Пример 2. Игральную кость бросают до тех пор, пока не выпадут все шесть граней. Случайная величина х — число произведенных бросаний. Найти Л1 И.
Решение. Очевидно, имеем:
X = Xj + х2 + х3 + х4 + хв + хв, где х, — число бросаний до появления какой-либо из граней (т. е. х, = 1), х2 — число последующих бросаний до появления какой-либо другой грани, х3 — число последующих бросаний до появления третьей (еще не выпадавшей) грани и т. д. Например, если в результате серии бросаний появились грани
6, 1, 1, 1, 2, 3, 6, 5, 2, 3, 1, 2, 4, то в этом случае х = 13, а
Xj = 1, х2 = 1, х3 = 3, х4 = 1, х5 = 2, хв = 5.
По теореме сложения имеем:
6
В*	14?
Подсчитаем М [xj (i = 1, 2,	6). Если уже выпали i — 1
различных граней, то появление какой-либо новой грани есть со-бытие А, имеющее (при каждом бросании) вероятность р=--------
6
Величина xz есть не что иное, как число бросаний до первого наступления события Л. Но в таком случае, согласно примеру 3 на с. 137,
Итак,
ЛЦх2] = МЕх3] = 4, М[х41 = 4,
о	5	4	3
Мх5>-|, Л1Гхь>-|
и, значит,
Л1[х] = 6 М- + - + - + 1 + - + Й = ~. А \6	5	4	3	2 1 /	3
2°. Математическое ожидание произведения. Доказанная в предыдущем пункте формула (2) наводит па мысль о возможности аналогичной формулы для случайной величины ху:
М[ху] = Л4[х] МУ1	(6)
Однако формула (6) в общем случае неверна; чтобы в этом убедиться, достаточно взять в качестве х случайную величину с законом распределения:
-1 1
2	2
тогда х2 будет постоянной величиной 1 и равенство М [х2] — = М Гх] Л4 [х] выполняться не будет (1^0-0).
Докажем, что если случайные величины х и у независимы, то формула (6) справедлива.
Теорема. Если случайные величины х и у независимы, то математическое ожидание их произведения равно произведению их математических ожиданий, т. е.
М[ху]'==М[х]М[у].
Эту важную теорему часто называют теоремой умножения математических ожиданий.
При доказательстве ограничимся случаем, когда система (х, у) дискретного типа.
Доказательство. Возможные значения х обозначим,
148
как и ранее, хп х2, возможные значения у —у1( у2, ••• • Применив такие же рассуждения, как при выводе формулы (4), получим равенство
М [ху] = 2 х;у/А/>
где pLj есть вероятность события х = х;, у = у7-.
Ввиду независимости величин х и у имеем:
Р (х = xz, у = У/) = р (X = xz) р (у = у,).	(7)
Обозначив
Р (х = х;) = гг, р (у = у7) = sJt
перепишем равенство (7) в виде
А/ = r^j-
Итак,
Л1 Еху] = 2
Преобразуя полученное равенство, будем иметь:
Мху] = (2 V/) (2 Ул) = ЛЯх] Л1[у 1
что и требовалось получить. И
Доказательство теоремы для общего случая дается в приложении 2 к книге (с. 200—201).
§ 34. ДИСПЕРСИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
Различные случайные величины могут иметь одно и то же математическое ожидание. Рассмотрим, например, величины х и у, законы распределения которых заданы таблицами вида:
Значения х	—0,01	0,02
Вероятности	2 3	2 3
Значения у	— 100	100
Вероятности	Д 2	2 2
Математические ожидания их одинаковы (равны нулю):
М [х]= — 0,01 • - + 0,02.1 = 0, 3	3
м [у] = -100-1+ 100-1 =0.
Однако характер распределения величин х и у существенно различен. В то время как величина х может принимать лишь значения, мало отличающиеся от ее математического ожидания, значения величины у значительно удалены от М [у].
149
Аналогичных примеров можно привести много. В двух различных географических местностях могут оказаться одинаковые средние уровни осадков, в двух учреждениях с различным соотношением низкооплачиваемых и высокооплачиваемых служащих может оказаться одна и та же средняя заработная плата и т. д.
Укажем еще один пример. Пусть имеются два различных прибора для измерения одной и той же физической величины. Практически результат измерения никогда не совпадает точно с измеряемой величиной: каждое измерение сопровождается случайной ошибкой. Обозначим ошибку при измерении первым прибором через х, вторым — через у. Очевидно, х и у — случайные величины. Предполагая оба прибора исправными, будем иметь: М [х] = О, М [у] = 0 (написанные равенства означают, что измерения свободны от систематической ошибки). Однако сам по себе этот факт еще не означает одинаковой точности обоих приборов. Вполне может быть, что для одного из приборов ошибка (по абсолютной величине) принимает в среднем большие значения, чем для другого; проще говоря, один из приборов может оказаться более «разболтанным», давать большее рассеивание результатов измерения, чем другой.
1°. Определение дисперсии и среднего квадратичного отклонения. Рассмотренные в начале параграфа примеры убеждают нас в необходимости ввести еще одну числовую характеристику — для измерения степени рассеивания, разброса значений, принимаемых случайной величиной х, вокруг ее математического ожидания.
Обсудим вопрос о возможных подходах к оценке рассеивания.
На первый взгляд может показаться естественным в качестве характеристики рассеивания взять математическое ожидание разности х — т, где т — математическое ожидание величины х. Заметим, что случайную величину х — т называют отклонением (имеется в виду отклонение величины х от ее математического ожидания) и обозначают х:
х = х — т.
Оказывается, однако, что для характеристики рассеивания число О
М [х] ничего не дает — оно всегда равно нулю. Проверка этого факта тривиальна:
М [х] = М [х — т] = М [х] — М [т] — т — т = 0.
В действительности степень рассеивания, т. е. степень удаленности х от т, должна определяться не самим отклонением, а его абсолютной величиной |х — т\. Поэтому более логично в качестве меры рассеивания принять не М. [х — т\, а М [| х—т|]. Однако и такую меру рассеивания приходится отклонить, так как пользоваться ею не очень удобно; читатель по собственному опыту ьнает, сколь трудно оперировать с формулами, содержащими аб-130
солютные величины. Имеется и другое возражение против числа Л1Е1х — т|]; определенная таким образом мера рассеивания не обладает хорошими свойствами. В этом отношении она сильно уступает той мере рассеивания, которая вводится ниже и носит название дисперсии.
Определение. Дисперсией случайной величины х называется число
D[x] = M[(x-m)2].	(1)
Другими словами, дисперсия есть математическое ожидание квадрата отклонения.
Число
=	(2)
носит название среднего квадратичного отклонения величины х. Если дисперсия характеризует средний размер квадрата отклонения, то число о [х] можно рассматривать как некоторую среднюю характеристику самого отклонения, точнее, величины |х—т\.
Из определения (1) легко вытекают следующие два свойства дисперсии.
1. Дисперсия постоянной величины равна нулю.
Действительно, рассматривая постоянную величину с как дискретную случайную величину с единственным возможным значением с, получим:
D [с] = (с — М И)2 -1=0.
2. При умножении случайной величины х на постоянное число с ее дисперсия умножается на с2.
Действительно,
D [ex] = М [(ex — М Сех])2] = М [с2 (х — М [х])2] = = с2 М [(х — М [х])2] = c2D [х].
В заключение укажем весьма полезную общую формулу, вытекающую из определения дисперсии:
Д>[х]'л=Л! [х2]-Л12Ех].	(3)
Доказательство этой формулы основано на известных читателю свойствах математического ожидания. Мы имеем:
D [х] = М [(х — т)2] = УИ [х2 — 2mx + т2] = УИ [х2] — — 2т М. [х] + М [m2] = М [х2] — 2m2 + т2 = М [х2] — т2.
2°. Вычисление дисперсии. Так как дисперсия случайной величины представляет собой по определению математическое ожидание величины (х — т)2, то для вычисления дисперсии можно воспользоваться формулами, установленными в § 32. Согласно
151
формуле (4) указанного параграфа, для дискретной случайной величины х с законом распределения
	JC2	...
Pl	р2	...
будем иметь:
= 2(^- tri)2 рс,	(5)
согласно же формуле (12) § 32 для непрерывной случайной величины, распределенной с плотностью f (х), получим:
D [х] — [ (х — tri)2 f (х) dx.	(6)
— ОО
Несколько другие формулы для вычисления дисперсии можно получить, используя формулу (3), а именно:
О[х] = 2^(- т2,	(7)
если величина х дискретна, и
D W = J х2 f (х) dx — т2,	(8)
—сю
если х распределена с плотностью f (х).
Пример 1. Пусть х — число очков, выпадающих при бросании игральной кости. Распределение величины х описывается таблицей:
D[x] = I2 • - + 22 • + З2 • - + 42  1 + 52 • - + 62 • - — 6	6	6	6	6	6
35
12
Пример 2. Пусть величина х распределена равномерно на отрезке [а, Ь]. Воспользовавшись формулой (8), получим:
152
'а + Ь\2 . 2 /
b
D [x] = J x2c dx — a где c — постоянная плотность (на отрезке [a, tty, равная ——. Отсюда имеем:
Ь — а
Ь3 — а3 (а + Ь)2  b2 + ab + ci2 b2-'~ 2аЬ + а2  (Ь—а)2 .
3(6 — а) 4	3	4	12
Следующий пример заслуживает особого внимания.
Пример 3. Найти дисперсию случайной величины х, распределенной нормально с плотностью
(х-а/
Поскольку в данном случае М [х] совпадает с а (см. пример I на с. 143), то удобнее воспользоваться формулой (6), которая принимает следующий вид:
со	(X—(I)2
D [х] =----L- f (х — а)2 е dx.
а ]/2л J
—оо гг	х — а ,
Производя замену -----= t, получим:
О' оо №
D[x]=-^- [tte^dt.
Интеграл, стоящий в правой части, равен1 ]/2л. Следовательно, D Ех] = о2.
Тем самым выясняется смысл параметра о, входящего в выражение (9) для нормального закона; сг есть среднее квадратичное отклонение величины х. А
3°. Нормированные случайные величины.
Определение. Случайная величина у называется нормированной, если ее математическое ожидание равно нулю, а дисперсия — единице:
ЖЕу]=0, D[y] = l.
От любой случайной величины х можно перейти к нормированной случайной величине у с помощью линейною преобразования:
1 Применяя инте1рирование по частям, получим.
t2	/	i2\	t‘ « оо t2
J t2e 2 dt = — J td I e. 2 j = — te 2 | + J e dt =»
= j e dt = |/~2n.
153
X — tn
y= —
где tn — математическое ожидание, а <т — среднее квадратичное отклонение величины х. Нормированность у проверяется весьма просто:
М[у] = -7И[х — т] = 0, а
а2	с2
Отметим особо один частный случай. Для величины х, распределенной по нормальному закону с плотностью (9), нормированность означает: а = 0, <r = 1. Следовательно, в случае нормированного нормального закона плотность вероятности имеет вид:
_ ?!
. , . I 2
t (,х)---"zz: 6	•
у 2л
§ 35, ДИСПЕРСИЯ СУММЫ СЛУЧАЙНЫХ ВЕЛИЧИН. КОРРЕЛЯЦИОННЫЙ МОМЕНТ
Пусть х и у — две случайные величины. Положим,
Z = х + у.
По теореме сложения математических ожиданий будем иметь:
М И = м [х] + М [у].
Вычитая это равенство из предыдущего, получим:
ООО
Z = X + у,
где х обозначает, как и раньше, отклонение величины х. Отсюда
О О	О	О о
z2=x2 + у- + 2ху.
Найдем теперь дисперсию величины х + у:
D [х + у] = D [z] = М [z°2] = М [х2] + М [у2] + 2М [х у] =
= DLx] + D[y] + 2MLxy].	(1)
О о
Число М [ху] имеет особое значение для характеристики системы (х, у). Его называют корреляционным моментом или моментом связи случайных величин х и у и обозначают Д [х, у]. Таким образом, по определению
Д [х, у] = М[ху].
Формула (1) принимает теперь следующий вид:
154
D [x + у] = D [X] + D [у] + 2Л [x, уJ	(2)
— дисперсия суммы равна сумме дисперсий плюс удвоенный корреляционный момент.
Корреляционный момент, как свидетельствует его название (от латинского слова correlatio — соответствие, взаимосвязь), играет определенную роль при оценке зависимости х и у. Основное свойство корреляционного момента выражается следующим предложением.
Если величины х и у независимы, то их корреляционный момент равен нулю.
Действительно, пусть х и у независимы. Тогда, очевидно, величины х и у будут тоже независимы. Отсюда вытекает, что математическое ожидание произведения ху будет: М. [ху] = = М Щ М [у] = 0 • О - 0. и
Из доказанного предложения следует: если /С [х, у] 0, то величины х и у не могут быть независимыми. Таким образом, неравенство нулю корреляционного момента определенно свидетельствует о наличии связи между величинами х и у.
Из формулы (2) и доказанного выше свойства корреляционного момента получаем важное следствие, носящее название
Теорема сложения дисперсий.Если величины х и у не-зависимы, то дисперсия их суммы равна сумме их дисперсий:
D[x + y] = 0[x] + D[y].
Решим в заключение такую задачу.
Задача. Найти дисперсию случайной величины х, подчиненной биномиальному закону распределения.
Решение. Воспользовавшись представлением х в виде
х = Xj + х2 + ... + х„ (см. задачу в § 33, и. 1°) и применяя теорему сложения дисперсий, получим:
D [х] = D ЕхД + D [х2] + ... + D Схя].
Дисперсия любой из величин xz (i =1, 2, п) подсчитывается непосредственно:
D [xj == М [xf] - ЛР [xz] — О2 • (1 — р) + I2 • р — р2=р (1-р), Итак,
D [х] = пр (1 — р). ▲
Глава 8.
ЗАКОН БОЛЬШИХ ЧИСЕЛ И ЦЕНТРАЛЬНАЯ ПРЕДЕЛЬНАЯ ТЕОРЕМА
Предмет теории вероятностей, как мы знаем, составляют закономерности, свойственные массовым случайным событиям. Простейшая из них — устойчивость частоты — лежит в основе всех приложений теории вероятностей к практике. Если попытаться в немногих словах отразить общий смысл подобных закономерностей, то придем к такому заключению. Пусть производится большая серия однотипных опытов. Исход каждого отдельного опыта является случайным, неопределенным. Однако, несмотря на это, средний результат всей серии опытов утрачивает случайный характер, становится закономерным. Под законом больших чисел в теории вероятностей понимается ряд теорем, в каждой из которых устанавливается факт приближения средних характеристик большого числа опытов к некоторым определенным постоянным.
В основе доказательства этих теорем лежит важное неравенство, установленное в 1845 г. П. Л. Чебышевым.
Историческая справка. Пафнутий Львович Чебышев (1821—1894) — русский математик, один из крупнейших деятелей науки XIX столетия. Наиболее важные из его трудов посвящены теории чисел, математическому анализу и теории вероятностей. Открытия Чебышева в области теории чисел были настоящей сенсацией в математике: его работы о распределении простых чисел в натуральном ряду содержали, по сути дела, первые после Евклида фундаментальные результаты в этой области.
Главной проблемой в математическом анализе, интересовавшей Чебышева, была проблема приближения функций многочленами; здесь также Чебышев выступил в роли пионера, введя, в частности, свои знаменитые «многочлены, наименее отклоняющиеся от нуля». Основная заслуга Чебышева в развитии теории вероятностей состояла в том, что ему удалось придать понятиям случайной величины и математического ожидания ту основополагающую роль, которую эти понятия играют до сих пор.
От Чебышева ведет свое начало русская школа теории вероятностей,выдающимися представителями которой были А. А. Марков и А. А. Ляпунов. К этой школе идейно примыкают и труды ряда крупных советских математиков, таких, как С. Н. Бернштейн (1880-1968), А. Я. Хинчин (1894—1959), А. Н. Колмогоров, Б. В. Гнеденко. Советская школа теории вероятностей по всеобщему признанию занимает одно из первых мест в мировой математике.
Отличительной особенностью научного творчества Чебышева была прикладная направленность
Чебышев П. Л. (1821-1894)
156
его работ. Вот названия некоторых из них: «О зубчатых колесах», «О построении географических карт», «О кройке платьев». Особо выдающимся был вклад Чебышева в теорию конструирования механизмов.
Чебышев был одним из организаторов Московского математического общества, а также первого в России математического журнала «Математический сборник».
§ 36. НЕРАВЕНСТВО ЧЕБЫШЕВА
Пусть х —случайная величина с математическим ожиданием т. Выберем какое-либо положительное число е и рассмотрим событие
|х — т\ е.
(1)
Геометрический смысл этого события заключается в том, что значение случайной величины х попадает в область на числовой оси, получающуюся удалением из всей оси интервала от т — е до т + е (рис. 44). С возрастанием е эта область сужается, следовательно, вероятность попадания в нее (т. е. вероятность события (1)) становится все меньше. Неравенство Чебышева замечательно тем, что устанавливает для этой вероятности весьма простую оценку.
Неравенство Чебышева. Пусть имеется случайная величина х с математическим ожиданием т и дисперсией D. Каково бы ни было положительное число е, вероятность того, что величина х отклонится от своего математического ожидания не
D .
меньше чем на е,
ограничена
сверху' числом
Р(|х-4-е2
(2)
Доказательство. Неравенство (2) является следствием другого неравенства, также принадлежащего Чебышеву: если случайная величина х, для которой существует математическое ожидание т, может принимать только неотрицательные значения (т. е. р (х < 0) = 0), то вероятность того, что принятое ею значение окажется не меньше единицы, не превосходит числа riv.
р (х 1) m.
(3)
Докажем сначала неравенство (3).
Пусть х — дискретная случайная величина, принимающая неотрицательные значения xi( х2> с вероятностями рг, рг, ... соответственно. Имеем:
р(х> 1) =
—<-----«-------3—
/П-£	W	/7?+£
Рис. 44
157
Если каждое слагаемое р1 суммы, стоящей справа, умножить на соответствующее значение хг, то правая часть не уменьшится, поскольку Xi 1. Мы придем тогда к неравенству
xtPi-
Выражение, стоящее справа, опять-таки не уменьшится, если распространить суммирование на все возможные значения х: действительно, при этом добавятся неотрицательные слагаемые xtpt, отвечающие таким номерам i, для которых xt < 1. Итак, р(х > 1) <2 ад-t
Но последняя сумма по определению совпадает с М fxl. Тем самым неравенство (3) доказано для случая дискретной величины х.
Пусть теперь х— какая угодно случайная величина, удовлетворяющая, однако, условию р(х < 0) = 0 и имеющая математическое ожидание т. Взяв какое-либо е > 0, рассмотрим случайную величину хе — е-приближение к х (см. § 32, п. 2°) По доказанному р (хе > 1) < М [хь ]. Полученное неравенство имеет место для любого е > 0, в частности для е = —, где п — какое угод-п
но натуральное число. Поскольку в этом случае р (х8	1) = р (	1) (объяс-
ните!), то при любом натуральном п имеем: р (х 1) М [xj ]. При
п п->оо правая часть этого неравенства стремится к пределу, равному М [х]. Отсюда и следует (3).
Мы можем теперь вернуться к рассмотрению неравенства (2). Фигурирующее в нем событие |х — т\ е равносильно
(х — trip > । 82
Случайная величина —~- принимает лишь неотрицательные е2
значения, и к ней можно применить неравенство (3). Получим: p(|x-m|>s)>1)	=
= 1дН(х-т)> 4, е2	ь2
или в конечном итоге р(|х — т\	а
Неравенство Чебышева (2) можно записать в эквивалентной форме, если перейти от события |х — т\ е к противоположному событию |х — т\ < е. Тогда получим:
р (| х — m | < е) > 1 — —	(2')
ь2
158
Пример. Оценим вероятность события |х — т j < Зет, где <т — среднее квадратичное отклонение величины х.
Полагая в (2') е = Зо, получим в правой части неравенства D	8
число 1-----, т. е. —. Таким образом, вероятность события
9аI 2	9
т — Зег < х < m + Зо
8 не меньше чем —.
9
В действительности для подавляющего большинства встречающихся на практике случайных величин эта вероятность значи-х	8 тт
тельно ближе к единице, чем —. Например, для нормального распределения, как мы видели, она равна 0,997 ... .
Обычно, если закон распределения случайной величины неизвестен, но указаны параметры пг и о, принимают, что диапазон практически возможных значений случайной величины есть интервал (т — Зег, т + Зет) («правило трех сигм»).
§ 37. РАЗЛИЧНЫЕ ФОРМЫ ЗАКОНА БОЛЬШИХ ЧИСЕЛ
1°. Теорема Чебышева. Неравенство Чебышева позволяет доказать ряд важных теорем, объединенных общим названием «закон больших чисел». Основная из этих теорем принадлежит самому П. Л. Чебышеву.
Теорема Чебышева. Пусть имеется бесконечная последовательность
хР ха, ...
независимых случайных величин с одним и тем же математическим ожиданием ш и дисперсиями, ограниченными одной и той же постоянной:
7И[Х1 ] -= ТИ[х2] —... = tn, D[xJ < с, D [х2] < с, ... .
Тогда, каково бы ни было положительное число е, вероятность события
Iх1+.Х2+ш.+.1» _щ I < 8
I п	I
стремится к единице при п -> оо.
Доказательство. Положим, = xt + х2 + ... + х„
159
В силу свойств математического ожидания имеем:
= пг.
П	п
6=1
Далее, так как величины хх, х2, хл независимы, то
^[sJ = lyDLxJ<^ = ^.
П“	п2 п
Г = 1
Сопоставив полученное неравенство с неравенством Чебышева:
И|8л-М[5Л <е)>1-^,
е2
будем иметь:
j)(|s„ —m|< е) > 1 —(1) пеа
Это показывает, что с ростом п вероятность события |s„ — m|<8 стремится к 1.Я
Смысл теоремы Чебышева можно пояснить следующим примером. Пусть требуется измерить некоторую физическую величину т. В силу неизбежных при измерении ошибок результат измерения будет случайной величиной. Обозначим эту величину х; ее математическое ожидание будет совпадать с измеряемой величиной т, а дисперсия равна некоторой величине D (характеризующей точность измерительного прибора). Произведем п независимых измерений и обозначим:
хг — результат первого измерения, х2 — результат второго измерения
и т. д. Совокупность величин хп х2, ..., хл представляет собой систему п независимых случайных величин, каждая из которых имеет тот же закон распределения, что и сама величина х. Среднее арифметическое sn этих величин тоже является, конечно, случайной величиной. Однако с увеличением п эта величина почти перестает быть случайной, она все более приближается к постоянной т. Точная количественная формулировка этой близости и дается как раз теоремой Чебышева; она состоит в том, что событие | sn— ml <е становится как угодно достоверным при достаточно большом п.
Тем самым оправдывается рекомендуемый в практической деятельности способ получения более точных результатов измерений: одна и та же величина измеряется многократно, и в качестве ее значения берется среднее арифметическое полученных результатов измерений.
Близость к М [х] среднего арифметического опытных значений величины х уже подчеркивалась нами при самом введении понятия математического ожидания. Однако соответствующее рассуж
160
дение относилось только к дискретным случайным величинам; кроме того, само высказывание о близости мотивировалось соображениями эмпирического характера. В противоположность этому теорема Чебышева дает точную характеристику близости среднего арифметического к М [х], и притом для любой случайной величины.
2°. Теорема Бернулли. Из теоремы Чебышева в качестве следствия можно получить другую важную теорему, которая впервые была доказана Я. Бернулли и опубликована в 1713 году.
Теорема Бернулли. Пусть производится п независимых опытов, в каждом из которых с вероятностью р может наступить некоторое событие А. Рассмотрим случайную величину vn — число наступлений события А в п опытах. Каково бы ни было положительное число е, вероятность события
|--р|<8 I п I
стремится к единице при п	<х>.
Иначе говоря, как бы ни было мало е, с увеличением числа опытов становится сколь угодно достоверным тот факт, что частота наступления события А отличается от вероятности этого события меньше чем на е.
Чтобы вывести теорему Бернулли из теоремы Чебышева, достаточно заметить, что
V„ = Xj + х2 + ... + хя,
гдехг есть число наступлений события А в i-м опыте (г = 1,2, ..., п). Случайные величины хх, х2, ..., хл имеют один и тот же закон распределения:
Значения хг	0	1
Вероятности	q	Р
(где 7=1—р); для каждой из них математическое ожидание равно:
О . q + 1 • р = р,
а дисперсия
(° — р)2 7 + (1 — Р)2 Р = Рй (Р + 7) = Р7-
Таким образом, все условия теоремы Чебышева выполняются, и для среднего арифметического величин хх, х2, ..., хл, т. е. для
—, справедливо предельное соотношение п
limp (|^ — р| < 6^= 1. у
П-*ОО \ | П	I /
161
Отметим попутно следующий факт. Поскольку
М Г—1 — — М = — пр = р, I п I п	п
D п
1 г> г п 1	W
=	= -npq =
п2	п2	п
то неравенство Чебышева применительно к случайной величине
VZ2 — дает: п
\ I п. |	) пе?
(2)
Мы получаем, таким образом, оценку, хотя и весьма грубую, для вероятности того или другого отклонения частоты события А в серии из п опытов от вероятности события А в одном опыте.
3°. Заключительные замечания. Возвращаясь к вопросу о практическом значении изложенных выше теорем, заметим следующее. В каждой области человеческой деятельности, как правило, существует определенный «уровень значимости» вероятностей, т, е. такое граничное число а, что события, имеющие вероятность, меньшую а, считаются практически невозможными. Если в качестве примера взять, скажем, производство изделий бытового назначения, то указанный уровень будет находиться где-то в пределах 0,01—0,001. Действительно, известие о том, что вероятность брака в изделии имеет порядок 0,001, не заставит покупателя тревожиться за свою покупку; вероятность 0,001 мала настолько, что можно рассматривать бракованную лампу, часы, велоси-ред, пылесос и т. п. как практически невозможное явление. Однако та же самая вероятность 0,001 уже не устроила бы нас, если бы речь шла, скажем, об изготовлении частей авиационного двигателя; в этом случае уровень значимости должен быть много меньше, чем 0,001.
Если подойти с этой точки зрения, например, к неравенству (2), то можно сделать следующее заключение. Пусть дано число е > 0. Выберем п столь большим, чтобы величина была меньше2
ше того уровня значимости а, о котором шла речь выше. При таком выборе п событие
- -Р п
< е
будет практически достоверным. Иначе говоря, мы можем быть практически уверены, что при столь большом числе опытов частота наступления события А будет с точностью е совпадать с его вероятностью.
162
Обратим внимание читателя еще на один аспект теоремы Бернулли. Он связан с сопоставлением двух подходов к понятию вероятности: статистического, основанного на понятии частоты и не являющегося строго математическим, и чисто математического подхода, базирующегося на рассмотрении аксиом (во времена Я. Бернулли такой подход был неизвестен). Представим себе, что на множестве всех событий, связанных с данным опытом, определена функция р (Д), удовлетворяющая всем аксиомам теории вероятностей (аксиомам 1—3 § 3, и. 3°). Вслед за аксиомами будут, конечно, выполняться и их следствия, в частности теорема Бернулли. Возникает вопрос, соответствуют ли числа р (А) реальным частотам событий. Оказывается, что близость числа р (Д) к частоте вовсе не обязательно проверять для всякого события Д; достаточно убедиться в такой близости лишь для некоторых А. А именно рассмотрим те события Д, для которых р (Д) близко к 1. Тогда можно утверждать следующее: если для таких «формально достоверных» событий числа р (Д) будут близки к частотам (это означает, чго такие события будут практически достоверными), то и для любых событий числа р (Д) будут близки к частотам. Действительно, из теоремы Бернулли будет тогда следовать, что для всякого события А близость между р (Д) и частотой этого события (при большом числе опытов) является событием практически достоверным.
§ 38, ЦЕНТРАЛЬНАЯ ПРЕДЕЛЬНАЯ ТЕОРЕМА ТЕОРИИ ВЕРОЯТНОСТЕЙ
До сих пор мы говорили об устойчивости средних характеристик большого числа опытов, точнее, об устойчивости сумм вида
Xj +х2 + ...+хй 5Л = ---------------.
п
Однако не следует все же забывать, что величина sn — случайная, а значит, она имеет некоторый закон распределения. Оказывается, — и этот замечательный факт составляет содержание другой группы теорем, объединяемых общим названием «.центральная предельная теорема», — что при весьма общих условиях закон распределения s4 близок к нормальному закону.
Так как величина sn лишь постоянным множителем отличается от суммы
Х1 + х2 +	+ х«,	(1)
то в общих чертах содержание центральной предельной теоремы может быть высказано следующим образом.
Распределение суммы большого числа независимых случайных величин при весьма общих условиях близко к нормальному распределению.
Этим и определяется особая роль нормального закона, поскольку с суммами большого числа случайных слагаемых приходится иметь дело весьма часто как в самой теории вероятностей, так и в ее многочисленных приложениях. Чуть позже мы поясним этот факт примерами из разных областей.
Чтобы подготовить точную формулировку центральной предельной теоремы, поставим два вопроса:
1. Какой точный смысл содержится в утверждении о том, что закон распределения суммы (1) близок к нормальному закону?
163
2. При каких условиях имеет место эта близость?
Чтобы ответить на эти вопросы, рассмотрим не просто большое число, а бесконечную последовательность случайных величин:
Х1, х2....
Составим «частичные» суммы:
vn = хх + х2 + ... + хл (п = 1, 2, ...) .	(2)
От каждой из случайных величин vn перейдем к «нормированной» случайной величине (см. , 34, п. 3°):
- = Уя — 44 [ул]
П ’
математическое ожидание которой равно 0, а дисперсия 1. Ответ на первый из поставленных вопросов теперь можно сформулировать в виду равенства
Ъ х2
lim р (а v'n Ь) = —С е 2 dx	(3)
1/2л J
а
(где а и b — любые, а < Ь), означающего, что закон распределения случайной величины ч'п с ростом п приближается к нормальному закону распределения с математическим ожиданием 1 и дисперсией 0.
Разумеется, из того факта, что величина ул имеет приближенно нормальное распределение, следует, что и величина ул распределена приближенно нормально. Ведь связь между vn и v’n линейная:
v' = anvn + (где ап =	1	, Ря=----1
а, как мы знаем, нормальный характер распределения сохраняется при любом линейном преобразовании над случайной величиной (см. пример на с. 127).
По поводу условий, которые следует наложить на величины х1( х2, ..., можно высказать следующие соображения. Вычитая из равенства (2) равенство
М [vj = А4 ExJ + М [х2] + ... + М [хл],
получим:
ООО	о
v„=Xj+ х2 + ...+хл, о
где х, как обычно, означает отклонение случайной величины х от ее математического ожидания. Общий смысл условий, накладываемых на величины х„ х2...состоит в том, что отдельные откло-
О
нения xz (i = 1, 2, .... п) должны быть равномерно малы по сравнению с суммарным отклонением vn.
164
Точную формулировку условий, при которых справедливо предельное соотношение (2), дал в 1901 году выдающийся русский математик А. М. Ляпунов. Она заключается в следующем.
Пусть для каждой из величин х2 (i = 1, 2, ...) числа йг = <х?], /г2 = М[|х;^ конечны (заметим, что dt есть дисперсия случайной величины х2, a k, — так называемый «центральный момент третьего порядка»). Если при п -> оо п 2^ lim —1—-—j— = 0, п V 2 4 <=1 /
то будем говорить, что последовательность хп х2, ... удовлетворяет условию Ляпунова.
Простейший частный случай, когда выполняется условие Ляпунова, — это случай, когда все величины х2, х2, ... имеют один и тот же закон распределения. Тогда, разумеется, — d2 = ... —d ylJz1 = k2 = ... = k, следовательно,
п 2 ki 1=1	nk	k	1 n
-----T“—	при»-*».
V.V	M2	d2
4 J
На этом примере можно хорошо видеть, в чем находит свое проявление равномерная малость слагаемых х2: величина J} имеет л — 3
порядок п, а величина dt)2 — порядок п2 , тем самым от-г=1
ношение первой величины ко второй стремится к 0.
Теперь мы в состоянии сформулировать центральную предельную теорему в форме А. М. Ляпунова.
Теорема. Если последовательность хп х2, ... независимых случайных величин удовлетворяет условию Ляпунова, то справедливо предельное соотношение (3).
Иначе говоря, в этом случае закон распределения нормированной суммы v' сходится к нормальному закону с параметрами:
m = 0, <т = 1.
Отметим, что для доказательства своей теоремы А. М. Ляпунов разработал специальный метод, оказавшийся впоследствии полез
165
ным и в других разделах математики (метод так называемых характеристических функций). Рассмотрение этого метода выходит за рамки нашего курса.
§ 39. ПРИМЕНЕНИЕ ЦЕНТРАЛЬНОЙ ПРЕДЕЛЬНОЙ ТЕОРЕМЫ
1°. Обоснование роли нормального закона. Допустим, что производится измерение какой-либо физической величины. На результат измерения влияет огромное количество случайных факторов, таких, как колебание атмосферных условий, сотрясения измерительного прибора, усталость наблюдателя и т. п. Каждый из этих факторов, взятый в отдельности, порождает ничтожную ошибку х; в измерении данной величины. Результирующая ошибка v будет, следовательно, суммой огромного числа малых случайных величин хг; и хотя закон распределения каждой из этих величин нам неизвестен, тем не менее можно уверенно заключить, что вся сумма v будет иметь закон распределения, близкий к нормальному.
В полном соответствии со сказанным выше при математической обработке результатов измерений исходят из следующего постулата: случайная ошибка измерения подчиняется нормальному закону распределения. Из двух параметров этого закона один, а именно математическое ожидание, равен нулю. Второй параметр — среднее квадратичное отклонение — характеризует в известном смысле точность измерений.
Другой важный пример, иллюстрирующий роль нормального распределения в приложениях теории вероятностей, дает массовое производство, существующее во многих отраслях современной промышленности. В процессе массового производства изготовляются большие партии однотипных изделий. Все наиболее существенные характеристики выпускаемых изделий должны, естественно, соответствовать определенному стандарту. Однако в действительности наблюдаются отклонения от стандарта, которые порождаются причинами случайного характера (следует учесть, что выпуск изделия связан, как правило, с большим числом операций, некоторые из них не могут быть выполнены абсолютно точно). Каждая из этих причин сама по себе порождает лишь ничтожную ошибку xz, но, складываясь, такие ошибки могут давать вполне ощутимые отклонения от стандарта. И здесь, так же как в случае ошибок измерений, имеются все основания считать, что суммарное отклонение от стандарта следует нормальному распределению.
Подобных примеров можно привести очень много из самых различных областей науки и техники. Они объясняют, почему нормальный закон так часто возникает в задачах прикладного характера.
2°. Связь с приближенной формулой Лапласа. Пусть производится п независимых опытов, в каждом из которых с одной и той
166
же вероятностью р наступает событие А. Рассмотрим случайную величину v„ — число наступлений события А в п опытах. Очевидно,
v„ = Xi + х2 + ... + х„,
где хг обозначает число наступлений события А в i-м опыте (i = = 1,2, .... и). Случайные величины х; имеют один и тот же закон распределения, так что условия теоремы Ляпунова здесь налицо. Но тогда должна быть справедлива формула (3) § 38, которая в данном случае принимает вид:
Ь __
limp fa < -= -А Се 2 dx	(1)
\	V npq	1 У'2л J
а
(напомним, что М [v„] — пр, a D [vrt’J = npq, где q = 1 — р, см. с. 146 и 155). Это равенство носит название интегральной предельной теоремы Лапласа. Покажем, что из него следует интегральная приближенная формула Лапласа (формула (3) на с. 69).
Событие
У npq равнозначно
пр + а ]/" npq	С пР + V пРФ
Положим,
kL = пр + a Vnpq, k2 = пр + npq,
так что
а _ kr — np _ k2 — np
Vnpq ’	Vnpq '
Теперь левая часть формулы (1) запишется: lim р (kt < v„ < /?2),	(2)
П->00 правую же часть, учитывая соотношение Ь х2
{е~2 dx = Ф(Ь)—Ф(а)
V2л J а
(где Ф(х) — функция Лапласа, см. с. 69), можно представить как ф/А^Н ф)*сМ	(3)
\ у npq /	\ у npq /
Приравнивая выражение, стоящее под знаком предела в (2), к выражению (3), получаем приближенное равенство
167
которое есть не что иное, как интегральная приближенная формула Лапласа.
3°. Опыт Гальтона. Наглядной иллюстрацией центральной предельной теоремы служит эксперимент, предложенный английским статистиком Ф. Гальтоном (1822—1911).
Для эксперимента берется доска, в которую в шахматном порядке забиты гвоздики (рис. 45). Доска устанавливается в наклонном положении. Вверху доски имеется воронка, куда можно ссыпать шарики (например, ружейную дробь). Расстояние между любыми двумя соседними по горизонтали гвоздиками одно и то же. Это расстояние несколько больше диаметра шари-
ка, так что шарик может свободно проскакивать между гвоздиками. Выйдя из воронки, каждый шарик сталкивается с самым верхним из гвоздиков и отскакивает от него к одному из двух ближайших гвоздиков второго ряда, затем к одному из двух гвоздиков третьего ряда и т. д. У нижнего края доски сделаны бункеры, куда собираются шарики после всех столкновений-с гвоздиками.
Направим ось Ох вдоль нижнего ребра доски, поместив начало в центре указанного ребра; за единицу масштаба примем расстояние между соседними гвоздиками.
Рассмотрим траекторию одного из шариков. Обозначим через Xi смещение вдоль оси Ох, полученное шариком между первым и вторым столкновениями с гвоздиками, через х2 — смещение, полученное между вторым и третьим столкновениями, и т. д. Через х обозначим суммарное смещение, полученное после прохождения всех рядов гвоздиков. Очевидно, имеем:
X = Xj + х2 + ... + х„,
где п есть число горизонтальных рядов гвоздиков.
Каждая из величин х15 х2, ..., х„ представляет собой случайную величину, принимающую только два значения, -|-1 и —1, с вероятностями —; ее математическое ожидание равно 0, а дисперсия 1.
Предполагая число п достаточно большим, получим на основании центральной предельной теоремы, примененной к сумме большого числа одинаково распределенных независимых случайных вели
168
чин, что х имеет распределение, близкое к нормальному, с центром в точке 0 и средним квадратичным отклонением сг = У~п.
Если пропустить через воронку достаточно большое число N шариков, то количество шариков, проскочивших в х-й бункер (т. е. в бункер с абсциссой х), приближенно будет равно
N
_ У
1	„
. .	е
/ п У 2л
Иначе говоря, кривая, огибающая верхний ряд шариков, должна иметь приближенно уравнение вида
у = Аё~Кх*.
Проделав описанный эксперимент, можно убедиться, что кривая, составленная верхними шариками, действительно имеет указанную форму.
§ 40. ПРИМЕРЫ ЗАДАЧ НА НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ
Пример 1. Завод изготовляет шарики для подшипников. Каждый шарик должен иметь один и тот же диаметр d. Однако в силу ряда причин, неизбежных в условиях массового производства, фактический диаметр несколько отличается от d. Обо-
значим через х разность между фактическим диаметром и числом d. По соображениям, изложенным в п. 1° предыдущего параграфа, можно принять, что величина х подчиняется нормальному закону распределения с математическим ожиданием 0 и некоторым средним квадратичным отклонением о (характеризующим среднюю точность изготовления шариков).
Каждый шарик, сойдя с конвейера, проходит контроль. Последний состоит в том, что шарик пропускается через отверстия диаметром d — е и d + е (рис. 46). Все шарики, которые свободно проходят через большее отвер-стие, но застревают в меньшем, поступают в готовую продукцию; __________	.
остальные шарики бракуются.	I I
Найти вероятность того, что	j т d+8*
случайно выбранный с конвей-ера шарик будет забракован.	.
Решение. Условием ус-пешного прохождения шарика через контроль является вы-	”1 I
полнение неравенств	j d-e,* I
—е < х < е.	Рис. 46
169
Имеем (см. формулу (7) на с. 105):
р(— е<Сх^е) = ф( -—— ф( —-—- \ == 2Ф / — \ <т /	\ а /	\ о;
Поэтому вероятность того, что шарик окажется бракованным, равна 1 — 2Ф f—Y А
\ ° /
Пример 2. Для определения точности измерительного прибора произведено сравнение его показаний с показаниями контрольного (высокоточного) прибора. Это сравнение показало, что 75% всех ошибок данного прибора не превосходят по абсолютной величине 2 мк. Считая, что ошибка измерения подчиняется нормальному закону с математическим ожиданием 0, найти среднее квадратичное отклонение о.
Решение . Обозначим ошибку при измерении на данном приборе через х. По условию х есть случайная величина, подчиненная нормальному закону распределения с плотностью
а у 2л
В произведенной серии измерений событие —2 х 2 имело частоту 0,75. Считая, что число проделанных измерений достаточно велико, и заменяя частоту вероятностью, запишем:
р(— 2 <х <2) = 0,75.
Отсюда ф(—\ — ф(—-'l — 0 75, или 2ф(—'1 = 0,75. Решая \ о /	\	о i	\ о /
уравнение 2Ф (х) = 0,75 (с помощью таблицы значений функции Ф(х)), находим: = 1,15, откуда о = 1,74. А
Рис. 47.
170
Пример 3. Орудие обстреливает плоскость хОу (рис. 47). Цель находится в начале координат. Как известно, в реальных условиях стрельбы точка попадания снаряда не совпадает абсолютно точно с целью: при стрельбе неизбежны отклонения. Отклонения вызываются целым рядом причин: неточностью установки прицела, переменчивостью атмосферных условий, неравномерностью горения заряда и т. д. В теории стрельбы исходят из предположения, что точка попадания распределена по нормальному закону (причем центр распределения совпадает, разумеется, с местом положения цели). Основанием для такого предположения является множественность причин, вызывающих отклонение, и незначительность действия каждой из них в отдельности. Примем, что в данном случае распределение точки попадания является круговым нормальным распределением с центром в начале координат, т. е. что плотность распределения имеет вид:
х2+у2
/ (л 3') = -—jе 2а -2па2
Поскольку точка попадания является случайной точкой, ее расстояние до начала координат будет случайной величиной. Требуется найти для этой величины закон распределения.
Решение. Обозначим указанное расстояние через г. Вероятность события Ц < г < г2 равна интегралу от функции f (х, у) по области G, заключенной между концентрическими окружностями г = гх и г = г2- Переходя в этом интеграле от прямоугольных координат х, у к полярным г, ф, будем иметь:
г2 2л	г2	г,	г»
р (rr<	г < r2) = (	dr ( г —5— е	202dm	— ( — re	2a*dr.
' \	j j 2na2	r j a2
r, 0	r.
Отсюда видно, что плотность вероятности случайной величины г есть функция ла
— ге 202 при г > О, а2
<р(г) =
О при г< 0.	▲
Пример 4. Производится ряд независимых «выстрелов» По плоскости хОу. Рассеивание точек попадания то же, что и в предыдущем примере. Как много следует сделать выстрелов, чтобы с вероятно*
171
стью 0,99 попасть хотя бы раз в цель, имеющую вид круга радиуса ст с центром в начале координат?
Решение. Если производится один выстрел, то вероятность не попасть в указанный круг равна:
со Г2	Г2 co	1
,	_	. If- 2о* ,	— 2сР I	2*
р (о < г < оо) = — I ге аг=—е = е
°2 J	I
о	а
Если производится п независимых выстрелов, то вероятность не __L	__1
попасть ни разу в указанный круг равна (е 2 )п=е 2 . Следовательно, вероятность хотя бы одного попадания при п выстрелах будет п
1 — е 2, Для того чтобы выполнялось неравенство п
1 — <ГТ>0,99
или
е
п Т<0,01,
нужно взять и 8. Л
Глава 9.
ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Известно, какое значение в экономике, сельском хозяйстве, биологии, медицине и т. д. играют статистические методы изучения случайных явлений. Обычно к ним прибегают в тех случаях, когда требуется изучить распределение большой совокупности предметов (явлений, индивидуумов) по некоторому признаку. Например, можно интересоваться распределением множества людей по возрасту, множества животных данного вида по весу, распределением пахотных земель по урожайности, изделий определенного наименования по сортности, распределением больных гриппом по их реакции на данное лекарство.
Так как практически любой признак допускает количественную оценку, то, вместо того чтобы говорить о распределении предметов по признаку, можно говорить о распределении некоторой случайной величины х; опыт, с которым связана величина х, заключается в выборе наугад одного представителя данной совокупности, а значение, принимаемое х, есть значение признака для этого представителя.
Понятно, что исчерпывающее описание такого распределения можно получить, выяснив значения признака для всех без исключения представителей данной совокупности. В отдельных ситуациях так и поступают: например, данные о распределении жителей той или иной страны по полу, возрасту и т. д. получают при всеобщих переписях населения, производимых раз в несколько десятилетий. Однако такой способ «поголовного» обследования всей изучаемой совокупности связан с рядом трудностей. Одна из них — это (как правило) большой объем совокупности. В некоторых случаях имеется еще и трудность принципиального характера, заключающаяся в том, что рассматриваемая нами совокупность не существует в готовом виде, а является лишь воображаемой. Например, если нас интересует распределение ошибки, допускаемой измерительным прибором, то изучаемая совокупность представляет собой совокупность всех мыслимых измерений, которые можно произвести с помощью данного прибора. Ясно, что обследовать все элементы такой совокупности невозможно.
Чтобы обойти указанные трудности, поступают обычно так: обследование всей совокупности заменяют обследованием небольшой (притом выбранной наугад) ее части. Такую часть обычно называют выборкой', в противоположность ей вся совокупность назы
173
вается генеральной совокупностью. Разумеется, при этом желательно, чтобы результаты обследования выборки отражали характерные, основные черты изучаемого признака; для этого объем выборки не должен быть чрезмерно мал. Например, о распределении жителей Москвы по размерам носимой ими одежды нельзя судить по результатам обследования одной квартиры; в этом смысле данные, относящиеся к целому дому или группе домов, более показательны.
Разработка методов, позволяющих по результатам обследования выборки делать обоснованные заключения о распределении признака по всей совокупности, и есть одна из важнейших задач математической статистики.
§ 41. ВАРИАЦИОННЫЙ РЯД. ТАБЛИЦА ЧАСТОТ.
ГИСТОГРАММА
Итак, предположим, что изучается некоторая случайная величина х. С этой целью производится ряд независимых опытов, или, как принято говорить, наблюдений, в каждом из которых величина х принимает то или иное значение. Совокупность полученных значений
х2, .... хп	(1)
величины х (где п — число опытов) и есть произведенная нами выборка1. Эту совокупность часто называют статистическим рядом', последний играет роль исходного числового материала, подлежащего дальнейшей обработке и анализу.
Первый этап обработки ряда (1) — составление так называемого вариационного ряда. Его получают следующим образом: среди чисел (1) отбирают все различные и располагают их в порядке возрастания:
«!, а2, ..., ат,	(2)
где cq < а2 < ... < ат.
Пример 1. С помощью журнала посещаемости собраны данные о числе пропущенных занятий по математике (за один семестр) у 25 студентов I курса. В итоге получены значения:
2, 5, 0, 1, 6, 3, 0, 1, 5, 4, 0, 3, 3, 2, 1, 4, О, 0, 2, 3, 6, 0, 3, 0, 1.	(3)
Здесь вариационный ряд состоит из шести различных чисел:
О, 1, 2, 3, 4, 5, 6.
1 Обратим внимание читателя на одно расхождение в обозначениях между данной главой и главами 5—8, посвященными теории случайных величин. В главах 5—8, как правило, буквами Xi, х8, ... обозначались все возможные значения дискретной случайной величины х, В частности, это предполагало, что *1 <И» »} при i /, Для последовательности (1) такое условие уже не обязательно,
174
Следующий этап обработки ряда (1) — составление эмпирического закона распределения. Форма его записи зависит от характера изучаемой случайной величины х.
Пусть х — дискретная случайная величина. Тогда наиболее естественной формой эмпирического закона распределения является так называемая таблица частот, показывающая, с какой частотой наблюдалось то или иное значение. Таблица частот имеет
вид:
(4)
В первой строке записаны числа вариационного ряда (2), а во второй — их частоты, т. е. числа
цг = — (г = 1, 2, ... , /и), п
где п — число всех опытов, a kt — число опытов, в которых наступало событие х — at. Можно ожидать, что с увеличением числа п опытов таблица частот будет все более приближаться к истин
ному закону распределения величины х.
В качестве иллюстрации напишем таблицу частот для приведенного выше примера 1. Просматривая исходный статистический ряд (3), находим частоту появления каждого из чисел 0, 1, 2, 3, 4, 5, 6 (чисел вариационного ряда). Например, число 0 встречается 7
7 раз, значит, его частота равна —. Найдя таким же образом ос-25
тальные частоты, получим следующую таблицу частот:
0	1	2	3	4	5	6
7	4	3	5	2	2	2
 .		——	  и.  		—	и ——
25	25	25	25	25	25	25
Рассмотрим теперь другой крайний случай — когда величина х является непрерывной случайной величиной. Пользоваться таблицей частот в прежнем ее виде уже не имеет смысла, поскольку она мало показательна для изучаемого распределения. Действительно, характерной чертой непрерывного распределения является, как мы знаем, тот факт, что вероятность каждого отдельного значения равна нулю. Следовательно, в ряде (1), как правило, не будет повторений, и таблица частот примет вид:
Ясно, что такая таблица дает весьма малую информацию о распределении значений величины х.
175
Принимая во внимание сказанное, эмпирический закон распределения задают в этом случае по-другому. Его записывают с помощью так называемой интервальной таблицы частот, имею-
щей вид:
С1> С2		| СГ’ ci+i
1’1	1’2	'vi
(5)
Эта запись означает, что весь диапазон изменения величины х разбит на интервалы (границами i-ro интервала являются сг- и с(+1); число и; (i = l, 2, I) есть частота попадания в i-й интервал, т. е.
где ki — количество чисел в исходном ряде (1), приходящихся па i-й интервал. На практике число интервалов выбирается обычно в пределах одного-двух десятков; длины интервалов не обязаны быть одинаковыми.
Интервальная таблица частот часто изображается графически в виде так называемой гистограммы. Гистограмма представляет собой ступенчатую линию; основанием i-й ступеньки является интервал (сг, с(+1), а площадь этой ступеньки равна ц; (рис. 48).
Пример 2. Ниже приводится таблица, содержащая данные измерения роста 1000 школьников старших классов. В этой таблице в отличие от (5) интервалы размещены столбцом (технически это удобнее); кроме того, вместо чисел указаны kt (для нахождения рг нужно разделить kt на 1000).
Интервалы роста (в см)	Число школьников	Интервалы роста (в см)	Число школьников
143—146	1	167—170	170
146-149	2	170-173	120
149-152	8	173-176	64
152-155	26	176—179	27
155-158	65	179-182	10
158-161	120	182—185	3
161 — 164 164-167	181 201	185-188	1	ЮОО
Гистограмма, отвечающая этой таблице, показана на рисунке 49.
170
§ 42. ОЦЕНКИ ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ
По виду таблицы частот или гистограммы можно строить гипотезы об истинном характере распределения величины х. Например, получив гистограмму, изображенную на рисунке 49, естественно предположить, что распределение величины х является нормальным; из гистограммы же, указанной на рисунке 50, напрашивается вывод, что величина х имеет равномерное распределение на отрезке [0, 1].
На практике, однако, редко встречается такое положение, когда изучаемый нами закон распределения неизвестен полностью. Чаще всего дело обстоит так, что вид закона распределения ясен заранее (из каких-либо теоретических соображений), а требуется найти только некоторые параметры, от которых он зависит. Например, если заранее известно, что закон распределения случайной величины нормальный, то задача сводится к нахождению значений двух параметров а и ст. Впрочем, в некоторых задачах и сам вид закона распределения несуществен, а требуется найти только его числовые характеристики. Во всех подобных случаях можно обойтись сравнительно небольшим числом наблюдений — порядка одного или нескольких десятков.
1°. Требования, предъявляемые к оценкам параметров. Итак, допустим, что закон распределения случайной величины х со-держит некоторый параметр 0.	---- .
Численное значение этого параметра не указано (хотя оно и является вполне определенным числом). В связи с этим возникает такая задача: исходя из набора	-----------------
значений	°	?
Ч, ......хп	Рис. 50
7 А. С. Солодовников
177
величины х, полученного в результате п независимых опытов, оценить значение параметра 0.
Любая оценка для 0 —обозначим ее 0 —будет представлять собой, естественно, некоторое выражение, составленное из х1г хг, ..., хп:
0 = 0 (xlt х2,	х„).
Тем самым 0 будет случайной величиной (принимающей свои значения в результате п опытов над х). Ее закон распределения будет зависеть от закона распределения случайной величины х (последнему подчинена каждая из величин xlt хг,  , хп) и от числа опытов п.
Естественно предъявить к оценке 0 ряд требований.
1. Желательно, чтобы, пользуясь величиной 0 вместо 0, мы не делали систематических ошибок ни в сторону занижения, ни в сторону завышения, т. е. чтобы было
М [0] = 0.
Оценка, удовлетворяющая такому условию, называется несмещенной. Требование несмещенности особенно важно при малом числе опытов.
2. Желательно, чтобы с увеличением числа п опытов значения случайной величины 0 концентрировались около 0 все более тесно, т. е. чтобы было
D Г0] -> 0 при п->оо.
Оценку, обладающую таким свойством, условимся называть состоятельной.
На практике не всегда удается удовлетворить перечисленным требованиям, так как при прочих условиях желательно, чтобы выражение для функции 0 (Хц х2, ..., хп) было не слишком сложным. В некоторых случаях, например, применяют незначительно смещенные оценки.
2°. Оценка для математического ожидания. Рассмотрение конкретных оценок мы начнем с наиболее важного случая — оценки для математического ожидания т. В качестве такой оценки m естественно принять так называемое эмпирическое среднее, т. е. среднее арифметическое всех полученных значений величины х:
~ 1
m = “ 2Л’
п •«, i=l
178
Чтобы подчеркнуть случайный характер величины т, перепишем это равенство в виде
где через xz мы обозначаем значение случайной величины х, полученное в i-м опыте (в прежней записи лД.
Случайные величины х1т х2, хп имеют один и тот же закон распределения (он совпадает с законом распределения величины х), поэтому
~	1 n	1
-У/ИГхЛ =-пЛ1Ех] = ш	(1)
п	п
1=1
и оценка m является несмещенной. Дисперсия этой оценки
п	4
D А 2 D AnD=®
п2	п2 п
i=l
где D — дисперсия случайной величины х. Отсюда вытекает состоятельность оценки т.
3°. Оценки для дисперсии. Так как по самому определению дисперсия D есть математическое ожидание случайной величины (х — т)2, то естественной оценкой для D представляется выражение
— среднее арифметическое квадратов отклонений от эмпирического среднего гл; эту оценку условимся называть эмпирической дисперсией.
Можно показать, что D является состоятельной оценкой. Весьма неожиданным является, однако, то, что D смещена относительно D. Подсчет, который мы проведем в заключительной части параграфа, показывает, что математическое ожидание величины D не совпадает с числом D, а несколько меньше последнего:
MED] = —X-D.	(3)
Отсюда видно, что несмещенной оценкой дисперсии является величина
~ ~ } п ~
7*
179
Действительно,
AI[D] = _Д_ M[D] = D. n — 1
Оценку D условимся называть несмещенной эмпирической дисперсией.
Так как D отличается от D множителем ——, стремящимся к 1 п — 1
при оо, то при больших значениях п практически безразлично, какой из двух оценок мы пользуемся.
С чисто технической точки зрения вычисление оценки D удобно производить с помощью формулы
D ='rnl;> — (mJ2,	(4)
являющейся аналогом формулы
D [х] = М Сх2] — М2 И	(5)
из § 34 (см. с. 151). В правой части формулы (4) стоит разность между эмпирическим средним величины х2, т. е. числом —2х? (мы пи’ п
шем для краткости Jg вместо 2), и квадратом эмпирического сред-;=i
него величины х, т. е. числом — 2jx/ • \п /
Вывод формулы (4) аналогичен выводу формулы (5). Имеем:
D = - У (\ — m)2= -1 V (Х2 — 2тх; + т2) = П	П
= — (2 х»— 2т V хг|- пт2).
Отсюда следует:
D = тх,— 2 m m + m2 = тх! — т2 = т — (тЛ)2.
Пример. По данным четырех вступительных экзаменов составлена таблица:
Сумма баллов	12	13	14	15	16	17	18	19	20
Количество абитуриентов	1	3	7	15	21	30	12	8	3
180
Найти эмпирическое среднее и эмпирические дисперсии (смещенную и несмещенную) для величины х — суммы баллов.
Решение. В данном случае число всех наблюдений
п = 1 + 3 + 7 + 15 + 21 + 30 + 12 + 8 + 3 = 100
Отсюда находим:
т= —(12-1 + 13 - 3 + 14-7+ 15- 15 + 16-21 + 17- 30 + 100
+ 18-12 + 19-8 + 20-3) = — =16,48,
100
т . = — (122 - 1 + 133 - 3 + 142 - 7 + 15а • 15 + 162 - 21 + *100
+ 172 • 30 + 182 • 12 + 192 • 8 + 202  3) = — = 272,08,
-г	7	100
D = 272,08 — (16,48)2 = 0,4896,
D = — - D = —  0,4896 = 0,4945 ... . 99	99
Итак, искомые оценки: т = 16,48, D = 0,4896, D = 0,4945... .
4°. Смещенность оценки D. Приведем доказательство формулы (3).
На основании (4) можем записать:
М [D] = М
”	п L'-"	J
При дальнейших преобразованиях учтем, что
М [хг] = М Ex], М [х?] = М [х2] (i = 1, 2...... п),
а также
М Ех;ху] = М Ех;] М Еху] (i += /)
(ведь опыты по условию предполагаются независимыми, что влечет за собой независимость величин х; и х7). Кроме того, примем во внимание, что число произведений х;ху-, где i j, равно п (п — 1). Тогда будем иметь:
M[D] = - -пЛ4[х2] —- • пМ [х2] - -  п (п — 1) (М Ех]2) = п	п2	п2
= (1 — -UmEx2] — —-(М[х])2 = \ п J	п
= — (М Ех2] — М2 Ех]) = ^2 D.  п	п
Смещенность оценки б кажется на первый взгляд удивительным фактом До некоторой стегани дело может прояснить следующее замечание: п отклонений
xi — ш, х2 — т, х„ — т,
18!
входящих в выражение для D, не являются независимыми. Они связаны между собой соотношением
2 (х, — mj = О,
1=1
так что число независимых среди них равно п — 1. Это помогает понять, почему п
сумму 2 (х^ — m)a нужно делить на п — 1, а не на п.
i=l
§ 43. ДОВЕРИТЕЛЬНЫЕ ОЦЕНКИ
1°. Доверительные вероятности и доверительные интервалы. До сих пор мы ставили своей задачей оценить неизвестный параметр 0 одним числом 0. Такая оценка называется точечной. При большом числе опытов точечная оценка, как правило, близка к неизвестному параметру. Однако если число наблюдений мало, то случайный характер величины 0 может привести к значительному расхождению между 0 и 0. Тогда возникает задача о приближении параметра 0 не одним числом, а целым интервалом
(@1, ©з)
так, чтобы вероятность поглощения этим интервалом параметра 0, т. е. вероятность двойного неравенства
0, (хь .... х„) < 0 <02 (хх, ..., хл),	(1)
была не меньше заданного числа а.
Подчеркнем, что 0, и 02 суть случайные величины, в то время как 0 — некоторое вполне определенное (хотя и неизвестное нам) число, поэтому событие (1) является случайным событием, что дает право говорить о вероятности его наступления.
Если число а выбрать достаточно большим, например 0,95 или 0,99, то событие (1) можно считать практически достоверным; следовательно, получив опытные значения xlt х2, .... хп случайной величины х и построив по ним интервал (0Х, 02), можно быть практически уверенными в том, что неизвестный параметр 0 окажется заключенным в этом интервале.
Вероятность а называется доверительной вероятностью , а соответствующий интервал (0П 02) —доверительным интервалом (отвечающим доверительной вероятности а).
2°. Задача построения доверительного интервала для центра нормального распределения. Перейдем к вопросу о построении доверительного интервала. При этом ограничимся тем случаем, когда величина х имеет нормальное распределение с параметрами m (математическое ожидание) и а (среднее квадратичное отклонение). Для параметра m требуется на основе опытных данных построить
182
доверительный интервал, отвечающий доверительной вероятности а.
Эта задача имеет большое практическое значение, особенно при обработке результатов измерений. В самом деле, допустим, что производится серия независимых измерений для определения некоторой физической величины т. По соображениям, изложенным ранее (§ 39, п. 1°), обычно считают, что случайная ошибка измерения распределена по нормальному закону. Следовательно, и результат измерения
х = т + ошибка
имеет нормальное распределение. Если при этом отсутствует систематическая ошибка, то
М [х] = т.
Поэтому основная задача обработки результатов измерений — оценка истинного значения измеряемой величины — математически формулируется как задача оценки математического ожидания, или, по-другому, центра нормального распределения.
Частичное решение этой задачи дает эмпирическое среднее
однако если число п измерений невелико, то значительно больший интерес представляет доверительная оценка, т. е. такой интервал (mj, т2), который с заданной доверительной вероятностью (или, как говорят, с заданной надежностью) накрывает число т.
Задачу построения доверительного интервала для т мы решим в каждом из двух вариантов:
1) когда о известно;
2) когда о неизвестно.
3°. Доверительный интервал для т при известном ст.
Пусть ст известно. Примем во внимание, что случайная величи-п	~	j
на Ух;, от которой ш отличается лишь постоянным множителем —, п подчиняется нормальному закону (этот факт вытекает из предложения, доказанного в конце § 31: сумма независимых случайных величин, распределенных каждая по нормальному закону, сама имеет нормальное распределение). Следовательно, величина m тоже распределена нормально с математическим ожиданием т и средним квадратичным отклонением (см. формулы (1) и (2) предыдуще-
У п го параграфа). Рассмотрим нормированную случайную величину гл — т U = ------------------------------
о уТ
(2)
183
ее распределение тоже является нормальным с математическим ожиданием 0 и дисперсией 1. Пользуясь этим, можно по данному а найти такое число t , чтобы было
Р (—/а < u < ta) = а.
В самом деле, вероятность события —t < u < ta, согласно формуле (7) на с. 105, равна Ф (ta) — Ф (—ta), т. е. 2Ф (ta) (где Ф (х) — функция Лапласа); значит, для нахождения искомого числа t достаточно решить уравнение 2Ф (ta) — а. Получив ta, мы можем утверждать, что вероятность события —/ < u < ta или в более подробной записи события
“ п “	(3)
/п
равна а. Поскольку (3) эквивалентно
m — t < т < m ф- t	(4)
то можно, следовательно, утверждать, что вероятность события (4) равна а. Это означает, что интервал
+ (5’
будет доверительным интервалом для математического ожидания т, отвечающим доверительной вероятности а. Заметим, что длина 2t -£=. этого интервала оказалась постоянной (не зависящей от “у л
опытных данных), хотя, разумеется, она и зависит от взятого а;
центр интервала находится в случайной точке т.
Пример 1. Произведено 5 независимых опытов над случайной величиной х, распределенной нормально, с неизвестным параметром т и ст = 2. Результаты опытов приведены в таблице:
1	1	2	3	4	5
XI	—25	34	—20	10	21
Найти оценку m для математического ожидания, а также построить для него 90%-ный доверительный интервал (т. е. интервал, отвечающий доверительной вероятности а — 0,90).
Решение. Исходя из табличных данных, находим:
m = - (—25 + 34 — 20 + 10 + 21) = 4.
5
Далее, решая уравнение 2Ф (ta) = 0,9, получаем: ta — 1,65, от-
184
куда
Доверительный интервал будет:
(4 — 1,47; 4 + 1,47) = (2,53; 5,47). Д
Пример 2. Глубина моря измеряется прибором, системати-
ческая ошибка которого равна нулю, а случайные ошибки распределены нормально со средним квадратичным отклонением ст = 15 м. Сколько надо сделать независимых измерений, чтобы определить глубину с ошибкой не более 5 м при доверительной вероятности 90%?
Решение. В данном случае снова имеем: а = 0,9, и, значит,
/п = 3 • 1,65 = 4,95.
Следовательно, нужно сделать п = 25 измерений. А
4е. Доверительный интервал для Ш при неизвестном ст. Обратимся теперь к случаю, когда параметр ст неизвестен (он должен сам оцениваться по данным наблюдений). В этом случае рассмотрение величины и (см. формулу (2)) уже ничего не дает: в выражение для и входит не одно, а сразу два неизвестных (т и ст). Рассмотрим вместо нее величину
m —- т
Уп
где
7=
i=l
Оказывается, что ее закон распределения не зависит от значения параметра сг. Точнее, можно показать, что случайная величина s подчиняется так называемому закону распределения Стьюдента1 с п — 1 степенями свободы. Плотность вероятности для этого закона имеет вид:
sn_Af) = Bn(\ + -П
\ я — 1/
п
~2
где коэффициент Вп определяется из условия, что интеграл от функции s„_j (0 по всей числовой оси равен Г, выражение для Вп мы не приводим.
1 Этот факт был установлен (1908 г.) английским статистиком В. Госсетом, публиковавшим свои работы под псевдонимом Стьюдент (студент).
183
Исходя из сказанного, можно построить доверительный интервал для т.
Для этой цели находим такое t , чтобы было
Р < s < U = «;
тогда доверительный интервал для т будет:
m — t ——; m+ i —=. .
\ a]Pn ayn J
Чтобы найти t , мы должны решить уравнение
(6)
Г
J SZ!-1 (Т)	— а
~*а
или, учитывая, что функция sn_x (т) четная,
2] 8Л_1 (т) dx — а. о
Для интеграла, стоящего в левой части, как функции от t , составлены таблицы1; пользуясь ими, можно по данному а найти ta.
Пример. Срок службы осветительной лампы является нормально распределенной случайной величиной, параметры которой тио неизвестны. Для их оценки произведены контрольные испытания 16 ламп; исходя из этих испытаний, найдено, что
т = 3000 ч, ст = 20 ч.
Определить доверительный интервал для математического ожидания т с надежностью (доверительной вероятностью) 0,9.
Решение. С помощью таблицы распределения Стьюдента находим ta; в данном случае п — 1 = 15, а — 0,9, из таблицы по-
лучаем: ta = 1,753. Отсюда — 8,8 ч. Искомый доверительный интервал будет:
(3000 — 8,8; 3000 + 8,8) = (2991,2; 3008,8). А
Замечание. Сравнивая выражения (5) и (6) для доверительных интервалов при известном и неизвестном <т, мы видим, что они сходны между собой; различие в том, что в (6) коэффициент ta определяется исходя не из нормального закона распределения, а из закона распределения Стьюдента (и, кроме того, в (5) фигуриру
1 Эти таблицы можно найти, например, в упомянутой в предисловии книге Б. В. Гнеденко.
186
ет а, а в (6) а). Нетрудно видеть, что при п -> оо распределение Стьюдента переходит в нормальное распределение с параметрами т = 0, о = 1. Это непосредственно вытекает из соотношения
__п	_ Р
/ р \	2	2
lim 11 Я----)	= е
п-*оо \	-- 1 /
Поэтому при достаточно большом п (практически при п > 20) можно вместо распределения Стьюдента пользоваться нормальным распределением.
§ 44. ОЦЕНКА НЕИЗВЕСТНОЙ ВЕРОЯТНОСТИ ПО ЧАСТОТЕ
Задача построения доверительного интервала для математического ожидания имеет один особый частный случай, о котором следует сказать отдельно.
Пусть в результате n-кратного повторения данного опыта наступило k раз событие А. Тем самым частота наступления А оказалась равной
Требуется по известной частоте р оценить неизвестную вероятность р события А.
Рассмотрим случайную величину х — число наступлений события А в одном опыте. Ее закон распределения имеет вид:
Значения х	0	1
Вероятности	1 — Р	Р
Неизвестное число р входит сюда в качестве параметра. При этом МЕх! = 0 • (1 -р) + 1 • р = р, D Сх] = (0 - рУ (1 - р) + (1 - рУр = р (1 - р).
Мы видим, что параметр р есть не что иное, как математическое ожидание величины х.
Точечной оценкой для математического ожидания является, как мы знаем, эмпирическое среднее
Учитывая, что в данном случае у, xz есть число наступлений собы-1=1 ~
тия А в п опытах, мы получаем, что р есть частота наступления события А в п опытах, т. е. р.
187
При больших значениях п величину р можно считать распределенной приближенно нормально (это следует из центральной пре-п
дельной теоремы, примененной к сумме у х; одинаково распределен-
<=1
ных независимых случайных величин хх, х2, .... хл). Это позволяет нам в качестве доверительного интервала для искомой вероятности р принять интервал, обозначенный в предыдущем параграфе номером (5), т. е. интервал
1р — Р|
, о[х]
Возводя в квадрат обе части этого неравенства, а также учитывая, что = 1/Г р(1	, получим следующую запись доверитель-
У п V п ного интервала для р:
t2 (p-p)2<^p(l-p),	(1)
п
где t определяется из условия 2Ф (ta) — а. Относительно р соотношение (1) есть квадратное неравенство, решив его, найдем, что доверительный интервал для р есть
Pi < Р < Рг,
где p-L и р2 — корни квадратного уравнения, которое получается из (1) заменой знака < знаком равенства. Выражения для и р2 имеют довольно громоздкий вид:
При больших п эти выражения можно заменить более простыми:
Pi

188
(3)
Пример. При 100-кратном повторении опыта некоторое событие А наступило 78 раз. С надежностью 0,9 оценить неизвестную вероятность события А.
Решение. В данном случае ц = 0,78. Решая уравнение 2Ф (J = 0,9, находим: х = t = 1,65. Подставляя эти величины в (2) и (3), получаем: рх ~ 0,705, р2 = 0,840. Следовательно, доверительный интервал для р, отвечающий доверительной вероятности 0,9, будет (0,705; 0,840). А
§ 45. КОРРЕЛЯЦИЯ
Предположим, что в некотором опыте наблюдаются две случайные величины х и у.
То обстоятельство, что х и у обусловлены одним и тем же опытом, вообще говоря, создает между этими величинами некоторого рода связь; как принято говорить, х и у скоррелированы (согласованы) друг с другом.
Одной из характеристик корреляции служит рассмотренный в § 35 корреляционный момент
К [х, у] = М [х у] = М [(х — mJ (у — mJ], где тх и ту — математические ожидания величин х и у соответственно. Заметим, что справедлива формула
К [х, у] = М [ху] — тхту\ чтобы получить эту формулу, надо записать
(х — mJ (у — mJ = ху — тху — тух + тхту и приравнять друг к другу математические ожидания левой и правой частей.
Напомним следующий факт из § 35: если величины х и у независимы, то их корреляционный момент равен нулю. Поэтому неравенство нулю величины К [х, у] свидетельствует о наличии связи между х и у.
Случайные величины х и у, для которых корреляционный момент равен нулю, называются некоррелированными. Таким образом, из независимости величин х и у следует их некоррелированность. Обратное, вообще говоря, неверно: можно привести примеры величин х и у, для которых корреляционный момент равен нулю, между тем х и у связаны между собой (даже функционально).
Вот один из примеров такого рода. Пусть величина х распределена непрерывно, причем плотность вероятности f (х) симметрична относительно начала; величина у = х2. Тогда М И — 0 и
189
К [х, у] = М [ху] = М [х3] = J xsf (х) dx = 0.
Корреляционный момент, как следует из его определения, зависит от выбора единиц измерения для х и у; например, если при измерении х и у в килограммах было получено значение К = 5 кг2, то, приняв за единицу измерения 1 г, получим для корреляционного момента значение К = 5 • 106 г2. Это обстоятельство затрудняет сравнение корреляционных моментов различных систем случайных величин. Чтобы преодолеть такое затруднение, вводится другая характеристика связи между х и у — коэффициент корреляции.
Определение. Коэффициентом корреляции случайных величин х и у называется число
— отношение корреляционного момента к произведению средних квадратичных отклонений величин х и у.
Очевидно, коэффициент корреляции не зависит от выбора единиц измерения для велиин х и у (иначе говоря, г [х, у] есть величина безразмерная). Он не зависит также и от выбора начал отсчета при измерении х и у.
Докажем следующую теорему.
Теорема. Коэффициент корреляции всегда заключен между —1 и Г.
— 1 <г < 1.
В случае, когда г = 1, величины х и у связаны линейной зависимостью:
у = ах + b (a, b — const), причем а > 0; при г = — 1 между величинами х и у имеет место линейная зависимость с а < 0.
Доказательство. Рассмотрим математическое ожида-дание случайной величины
(У + /х)2,
где у — у — tny , х = х— tnx, a t — любое действительное число. Имеем:
М [(у + /х)2] = М [у2 + 2/ух + х2] = М [у2] +
+ 2Ш [ух] + М [х2] = D [у] + 2tK [х,у] + D [х].
Мы получили равенство вида
М [(у + Й] = at2 + 2₽/ + у,	(1)
где а = D [х], р = К [х,у], у ~ D [у]. Квадратный трехчлен,
190
стоящий в правой части этого равенства, при любом значении t неотрицателен (ибо он равен математическому ожиданию случайной величины, принимающей только неотрицательные значения). Отсюда вытекает, что дискриминант этого трехчлена, т. е. выражение Р2 — осу,
есть число неположительное. Итак, ^[x,y]-DCx]D[y] <0, или
[х,у]	<1
О[х]£>[у]
Мы пришли к неравенству г2 1, означающему, что величина г заключена в промежутке от —1 до 4-1.
Предположим теперь, что г2 = 1, т. е. г равно —1 или 1. В этом случае дискриминант указанного выше квадратного трехчлена равен нулю. Отсюда вытекает, что трехчлен имеет действительный корень, т. е. при некотором действительном значении t = —а выражение at2 4- 2₽/ 4- Y равно нулю. Но тогда в силу (1) мы должны иметь:
М [(у — ах)2] = 0,	(2)
а это в свою очередь означает1:
У — ах = 0,	(3)
или
у = ах 4- Ь.
Обратно, допустим, что между случайными величинами х и у имеет место такого рода соотношение. Изменив начало отсчета величины х (что не влияет на г), можно добиться, чтобы было b = 0, т. е. у = ах. В этом случае, как легко проверить, величина г будет равна —1, если а< 0, и 1, если а > 0. |
Установленные нами свойства коэффициента корреляции дают основание для некоторого качественного заключения, а именно: близость величины г2 к единице есть признак того, что зависимость между х и у близка к линейной. Если при этом г > 0, то с возрастанием х возрастает в среднем и у, тогда говорят о положительной корреляции между величинами х и у; если жег <0, то при возраста-
1 Переход от (2) к (3) нуждается в некотором разъяснении. Для обоснования этого перехода можно, например, воспользоваться предложением, доказанным на с. 157: если случайная величина z принимает только неотрицательные значения, то р (z 1)^ М [z]. В данном случае это предложение нужно применить к вели-
О о
чине z = k (у — ах)2, где k — любое положительное число. Тогда получим: / °	о 1 \
р (у — ах)* — =0, откуда ввиду произвольности k будет следовать: \	я /
о о	о о	о о
Р ((У — ах)2 > 0) = 0. Тем самым р ((у — ах)2 = 0)= 1, или просто у — ах=0<
191
У
сильная положительная корреляция
слабая положительная корреляция
отрицательная корреляция
Рис. 51
нии х величина у в среднем убывает (отрицательная корреляция). Иллюстрацией служит рисунок 51. Точки на этом рисунке изображают результаты наблюдений над системой (х, у); каждое наблюдение дает пару значений (х, у), т. е. точку на плоскости.
Одним из проявлений корреляции между случайными величинами х и у является следующий факт: при фиксированном значении х величины х величина у все еще остается случайной, но с законом распределения, зависящим от выбранного значения х. Поясним это на примере системы (х, у) дискретного типа.
Пусть величина х приняла некоторое значение X;. При этом условии вероятность любого из возможных значений у} величины у будет:
О = Р (У = У;/х = \) =
Р (х = хг, у = Уу) р (х = х;)
Таким образом, при фиксированном значении х = X/ величина у имеет закон
распределения:
(нетрудно видеть, что и + гв + ... = 1). Этот закон называют условным законом распределения величины у, роль условия играет х = х(
Располагая условным законом распределения для у, можно, разумеется, найти условное математическое ожидание у. Поскольку оно зависит от выбранного значения х — Xi, обозначим его ту (х(). Итак,
ту (х^ = ул + у2г2 + ... .
Условное математическое ожидание играет роль во многих вопросах. В частности, с его помощью можно сформулировать необходимое и достаточное условие, при котором у является некоторой функцией от х. С этой целью заметим, что Шу (х() есть на самом деле случайная величина (поскольку каждое значение х; принимается с определенной вероятностью). Рассмотрим дисперсию этой величины, т. е. число
М [ (ту (х) — Оту)2], и сравним ее с дисперсией самой величины у. Оказывается, всегда справедливо неравенство
м [(/Ну (х) - /Пу)2] < D [у],
192
причем равенство достигается в том и только в том случае, когда случайная величина у есть функция от случайной величины х.
Отметим, что число
2 _ м С(”Ь С*) ~ ту)23
Х ~ D [у]
называют корреляционным отношением у к х Из сказанного выше следует, что всегда 0 r]2y х 1, причем равенство Л2у,х = 1 является критерием того, чго у есть функция от х.
§ 46. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
Предположим, что зависимость между величинами х и у близка к линейной (коэффициент корреляции г близок к + 1 или —1). В этом случае естественно ставить вопрос о функции
у = ах + b,	(1)
которая наилучшим образом выражала бы зависимость у от х. Для нахождения такой функции существует хорошо разработанный метод, носящий название «метод наименьших квадратов».
Прежде всего уточним саму постановку вопроса.
Пусть над системой (х, у) произведено п независимых опытов, в результате чего получены «экспериментальные» точки
(Х1, У1), (х2, у2), .... (х„, уп).	(2)
Поставим задачу, найти такую прямую (1), чтобы сумма квадратов «отклонений-» экспериментальных точек от этой прямой, т. е. выражение
2Су,-(^ + 6)]2.	(3)
1=1
обращалась в минимум (на рис. 52 отклонения изображены в виде ряда вертикальных отрезков).
Обозначим выражение (3) через Ф (а, Ь):
Ф (а, Ь) = 2 ЕУг— (ах, + ЭД2.
i=i
Чтобы найти значения переменных а и Ь, обращающие это выражение в минимум, нужно приравнять нулю производные по а и Ь:
^==~22Cyi-(aXi+&)K=0,
~ = -2 2[yz-(«vH>)] = o.
1=1
После очевидных преобразований получаем:
193
— 0£х^ — b'ZXi — О, — а£х; — nb — О
п
(для упрощения записей мы пишем S вместо ). Это система двух
i=i
линейных уравнений с двумя неизвестными а и Ь. Разделив обе части каждого уравнения на п, получаем:
mrv — ат, — Ьт, — О,
ту — атх — b = 0.
Решив эту систему, находим значения неизвестных параметров а и Ь:
а —
тХу — тхту ~~гх
(4)
b — mv — атх.
Таким образом, искомая линейная зависимость у от х имеет вид: у = ах + (/пу — атх), или
у — ту = а(х — тх), .	(5)
где значение а указано выше.
Заметим что выражение тху — тхту , стоящее в числителе формулы (4), есть «эмпирический корреляционный момент» Кх у, знаменатель же тх, — т2х в силу формулы (4) из § 42 может быть заменен на Dx. Следовательно, для параметра а имеем выражение
а _ Кх, у „ «х, у _. «х, у . сту _ ~ Оу
D С х	Q х @ у &х	°х
где г — есть «эмпирический коэффициент корреляции». °хау
Мы рассмотрели метод наименьших квадратов применительно лишь к одному частному случаю, когда зависимость между величинами х и у является приблизительно линейной. Коснемся теперь более общего случая, когда рассматриваемая зависимость близка к некоторой функциональной зависимости (но уже не обязательно линейной); в этом случае тоже возникает задача о сглаживании ее методом наименьших квадратов.
Допустим, что тип разыскиваемой нами функциональной зави
194
симости у от х предписан заранее из каких-либо соображений; точнее, эта зависимость должна принадлежать семейству
у = <р (х; а, Ь, ...),	(6)
где ф — данная функция, в выражение которой входят некоторые параметры а, Ь, требуется подобрать значения этих параметров так, чтобы кривая (6) наименее уклонялась от экспериментальных точек.
Решение этой задачи методом наименьших квадратов заключается в отыскании таких значений параметров, для которых выражение
п
Ф(а, Ъ, ...)=	а, Ь, ...)]а
принимает наименьшее значение. И здесь, как ранее, задачу можно свести к решению системы уравнений
в которой число уравнений совпадает с числом неизвестных параметров.
Решить систему (7) в общем виде, конечно, нельзя; для этого необходимо задаться конкретным видом функции ф. В ряде случаев функцию ф задают в виде многочлена
а0 + aLx 4- а2хг + ...+ ййхА,
где роль параметров играют коэффициенты а0, alt ..., ak . В некоторых случаях ф выбирается как комбинация показательных функций
+ а2еа'х + ... + akeV,
где какие-то из чисел щ, а; могут быть заданы заранее, в то время как другие неизвестны (эти последние и играют роль параметров, подлежащих вычислению). Возможны, разумеется, и другие формы задания функции ф.
Приложение 1 УСЛОВИЯ, ПРИ КОТОРЫХ НАПЕРЕД ЗАДАННАЯ ФУНКЦИЯ F(x) ЯВЛЯЕТСЯ ФУНКЦИЕЙ РАСПРЕДЕЛЕНИЯ
Здесь мы изложим доказательство теоремы из § 22 о задании случайной величины с помощью некоторой функции F (х). Напомним формулировку теоремы.
Теорема. Пусть дана функция F (х), определенная для всех значений х и обладающая свойствами:
1)	F (х) не убывает;
2)	lim F(x) = 1, Hm F(x) = 0; X->oo	x->—°©
3)	F(x) непрерывна слева при любом х:
Тогда существует, и притом только одна, неотрицательная счетно-аддитивная функция р (А), определенная на системе всех борелевских подмножеств числовой оси R, удовлетворяющая условию р (/?) = 1 и такая, что
р((—оо, x)) = F(x)
при всяком X.
Доказательство. Для большей отчетливости разобьем последовательность рассуждений на ряд фрагментов.
1)	Рассмотрим график функции у — F (х). Дополним этот график отрезками, параллельными оси Оу, так, чтобы получилась линия без разрывов. А именно для каждого значения х — а, при котором F (х) имеет разрыв, дополним график отрезком
х = a, F (а — 0) < у < F (а + 0).
В итоге получим некоторую непрерывную линию Г (рис. 53).
Каждому множеству А на оси Ох можно через посредство линии Г сопоставить некоторое множество А* на оси Оу. Для этого образуем множество из всех точек линии Г, проекция которых на ось Ох принадлежит А; это множество в свою очередь проектируем на ось Оу и таким путем получаем множество А*.
На рисунке 54 показано множество А* для случая, когда А есть отрезок [а, р]; тогда А* есть отрезок [f(a), F(P + О)].
Из определения множества А* легко следует, что (А + В)* = А* + В*.
Установим также следующий факт: если АВ — 0, ю множество А*В* конечно или счетно.
196
В самом деле, пусть точка с принадлежит А* В*. Рассмотрим прямую у = с. На ней обязательно должна найтись точка и, проекция которой (на ось Ох) принадлежит А, и точка v, проекция которой принадлежит В. Поскольку АВ = 0, имеем: и и. Таким образом, и и v cyi ь две различные точки множества (х (х)= = с}. Но для функции F (х), обладающей свойствами 1 и 3, указанными в теореме, множество {х 1 F (х) = с] либо пусто, либо состоит из одной точки, либо является промежутком вида а < х Ь; последний естественно назвать промежутком постоянства функции F (х). Поскольку число промежутков постоянства всегда конечное или счетное (докажите!), то и точек с £ А*В* имеется не более чем счетное множество.
2)	Докажем теперь существование функции р (Л) с требуемыми свойствами.
Для этой цели определим р (Л) формулой
р(А)= И(Д*),
где р. (Д*) обозначает лебегову меру («длину») множества А*.
Счетная аддитивность р (Д) проверяется весьма просто. Пусть
А = Дт + Д2 -f- ...,
причем Д/Ду = 0 при i j. Согласно пункту 1), будем иметь:
д* = д;+ д;+ ....
причем каждое из множеств Д*Дj j) не более чем счетно. Ввиду счетной аддитивности лебеговой меры можем записать:
н(д*) = |х(д;) + р(л;) + ... .
Следовательно,
Р И) = Р (Д1) + Р (Д2) + ••• .
что и требовалось показать.
Равенство р (R) = 1 тоже проверяется очевидным образом: поскольку R* есть промежуток (интервал, полуинтервал или отрезок) от 0 до 1, то ц (Я*) = 1, значит, и р (R) = 1.
Наконец, пусть А есть луч (—оо, х). Тогда Д* есть промежуток от 0 до F (х), так чго р. (Д*) = F (х) и, следовательно, р (Д) = F (х).
Итак, существование функции р (Д) доказано.
3)	Установим теперь единственность функции р (Я), обладающей указанными в теореме свойствами.
Пусть pi (А) и р2 (Д) — две такие функции. Соответствующие им случайные величины обозначим xi и х2; обе эти величины имеют одну и ту же функцию распределения F (х). Наша цель — показать, что для любого борелевского множества А справедливо равенство
Pi (А) = р2 (А).	(1)
Прежде всего заметим, что равенство (1) справедливо для любого отрезка. Действительно, если А есть отрезок [а, р ], то
Pi (Д) = р (а < X! <₽) = F (Р + 0) - F (а), р2 (Д) = р (а < х2 <Р) = F (р + 0) - F (а)
(мы воспользовались известными читателю свойствами функции распределения случайной величины), следовательно, pi (А) = р2 (Д).
Обозначим через L класс всех борелевских множеств, для которых имеет место равенство (1). Мы должны показать, что L содержит все без исключения борелевские множества.
Укажем некоторые свойства класса L:
a)	L содержит все конечные объединения отрезков (это следует из того, что L содержит все отрезки, а также из аддитивности функций (Д) и р2 (Д));
б)	если множество А принадлежит L, то и его дополнение А принадлежит L (следует из равенств р2 (Д) + р2 (Д) = 1, р2 (Д) + рг (Д) = 1);
197
в)	если множества Ai, А2,из L образуют «убывающую» последовательность, т. е. Ai А2 до .... то их пересечение снова принадлежит L (следует из теоремы на с. 21); если множества Ai, А2, ... из L образуют «возрастающую» последовательность, т. е. Л с Л2 с ..., то их объединение принадлежит L (следует из свойства б) и теоремы на с. 21).
Теперь для завершения доказательства нам остается сослаться на следующий факт: любой класс борелевских множеств, обладающий свойствами а), б), в), совпадает с совокупностью всех борелевских множеств. Рекомендуем читателю попытаться доказать этот факт самостоятельно.
Для тех, кто не справится с такой задачей, укажем доказательство.
Пусть Н — минимальный класс борелевских множеств, обладающий свойствами а), б), в)1; очевидно, Н cL. Нам нужно показать, что Н содержит все борелевские множества. Поскольку Н обладает свойствами а), б), в), то достаточно показать следующее: класс Н счетно-аддитивен, т. е. объединение счетного числа множеств из Н снова принадлежит Н.
Установим сначала, что Н аддитивен, т. е. из Л € Н, В£Н следует: А-А-В^Н.
Пусть К — класс всех множеств, являющихся конечными объединениями промежутков (отрезков, полуинтервалов, интервалов), включая и промежутки с «концами» оо или — оо; очевидно, К cz Н. Далее , если А — борелевское множество, то обозначим Т (Л) класс всех борелевских множеств В, таких, что Л + В, Л + В, Л-J-B, Л+В принадлежат Н. Очевидно, Т (Л) обладает свойством б) и вслед за Н — свойством в). Если Л € К, то класс Т (Л) обладает еще и свойством а); следовательно, в этом случае Т (Л) содержит Н. Этому факту можно дать такое истолкование, для всякого В С Н класс Т (В) содержит любое множество А из К; другими словами, Т (В) обладает свойством а) Так как этот же класс обладает свойствами б) и в), то он содержит Н. Итак, если Л g Н и В € Н, то каждое из множеств А В, А В, А + В, А + В принадлежит Н, В частности, это означает, что класс Н аддитивен.
Проверка счетной аддитивности Н теперь осуществляется в несколько слов. Пусть Л1, Л2, ... принадлежат Н. Рассмотрим множество А = Лт + Л2 + ... . Очевидно, имеем: Л = Si + S2 + где S„ = Ai + Л3 + А„ (п= 1, 2, ,..). Поскольку класс Н аддитивен, все Sn принадлежат Н. Кроме того, последовательность множеств Si, S2, является «возрастающей». Учитывая, что класс Н обладает свойством в), находим отсюда, что Л € Н,
1 Это означает, что Н есть пересечения всех классов борелевских множеств со свойствами а), б), в).
Приложение 2
ТЕОРЕМЫ СЛОЖЕНИЯ И УМНОЖЕНИЯ МАТЕМАТИЧЕСКИХ ОЖИДАНИЙ
1°. Теорема сложения. Пусть х,, хг, ..., х, система п случайных величин. Если существует каждое из чисел М [хг j (i’. = 1, 2, .п), то существует и число М [хх + х2 + ... + хл], причем
М [Х1 + х2 + ... + х„] = М [Х1] 4- М [х2] + ... + Л/ [х„].
Для системы дискретного типа теорема доказана в § 33. Дадим теперь доказательство для произвольной системы (xi, х2.х„).
Очевидно, достаточно рассмотреть случай п — 2. Итак, будем доказывать формулу
M[x+y]=M[x]+M[y]	(1)
в предположении, что оба слагаемых правой части существуют.
При доказательстве будем опираться на следующую лемму, которая является аналогом леммы из § 30.
Лемма. Пусть даны система п случайных величин (хъ х2, ..., х/;) и несколько борелевских функций cpj, ф2, •••> Фт от аргументов (т. е. функций Rn~>R).
Тогда существует система (xlt х2, ..., хп, уь у2, ..., ут), такая, что;
1) подсистема (Х1, х2, ..., х„) совпадает с (Х1, х2, ..., х„);
2) Уг = ф; (хъ х2, ..., х„) (1 = 1, 2, .... т).
Доказательство вполне аналогично доказательству леммы из § 30. Распределение р искомой системы (xi....x„, yi, .... у,п) вводим при помощи форму-
лы
р(Д) = Рг,...х„(Л*)	(2)
— аналога формулы (2) из § 30. Здесь А — произвольное борелевское множество в Rn+m, рх,..... хп ( ) —распределение системы (xi, ..., х„), а множество А* (из Rn) связано с А условием:
(Х1, .... хп) € Д*<=> (Х1.хп, <р 1 (Х1.хп), .... фт (Х1, ..., хп)) € А.
Справедливость для построенной таким образом системы (xi..х„, yi, ..., ут)
утверждений 1 и 2 леммы проверяется очевидным образом.
Для доказательства теоремы сложения нам потребуется еще одно вспомогательное предложение. Оно относикя к случайной величине хе — е-прпбли-жению к величине х. Исходя из определения величины хе (см. п. 2° § 32), легко показать, что хЕ есть функция от величины х. А именно хе = Фв (х), где функция фе (х) определена условием: фЕ (х) = fee, если kz, х < (k + l)s (k — любое целое). График фЕ (х) приведен на рисунке 55.
Теперь мы располагаем всем необходимым, чтобы доказать теорему сложения.
Исходим из системы (х, у). Пусть е — какое-нибудь положительное число. По лемме (примененной для случая п = 2) существует система (х, у, г), где z = х+ у; опять-таки в силу леммы (для случая п= 3 ) существует система
(х, у, z, Хе , уЕ , zE ).	(3)
Рассмотрим величину1
1 Величины хе, ye, zE образуют систему (подсистему системы (3)), что дает нам право рассматривать любую функцию от этих величин, в частности хЕ |- у6 — zE. Эю замечание особенно важно в связи с последующим равенством (5).
199
поскольку для дискретных случайных Итак, имеем:
Хе + Уе — zE = <ре (х) + фе (у) — — фе (х + У)-	(4)
Так как
фе (х) + фе (У) — фе (х + у)=[фе (х)— — х] + [фе (у) — у] — [фе (х + у) —
— (х + У)]
и каждое из выражений, заключенных в квадратные скобки, по абсолютной величине не превосходите, то
|фв (х) + фв (У) — фе (х + у)| <3е.
Это означает, что все возможные значения дискретной случайной величины (4) не превосходят по абсолютной величине Зе. То же самое относится, следовательно, и к математическому ожиданию величины (4). Но
М [ Хе + Ув — Ze ] = М [хе ] +
М [ye ] - We .1,	(5)
величин доказываемая теорема верна.
—Зе < М [хЕ ] + М [уе ] — М [z8 ] < Зе.
(6)
Если теперь учесть, что при е -> О
Л4 [хе] -> М [х], М [уе] -> М [у], М [ze] М [z],
то из (6) будет следовать:
М [х] + М [у] — М [z] = 0. 
2°. Теорема умножения. Пусть (хр х2, ..., х„) — система п случайных величин. Если х]( х2, х„ независимы и существует каждое из чисел М [х;] (Z = 1, 2, ..., п), то существует и число М [х,х2 ... х„], причем
М [хл ... хл] = М [х,] М [х2] ... М [хя].
Для системы дискретного типа теорема доказана в § 33, рассмотрим теперь общий случай.
Снова примем п = 2, т. е. будет доказывать, что
М [ху] = М [х] М [у],	(7)
если величины х и у независимы и существует каждое из чисел М [х] и М [у], Пусть е > 0. Рассмотрим систему
(х, у, хе, уе),
существование которой обеспечивается леммой из п. 1°. Покажем прежде всего, что из независимости величин х и у следует независимость величин хе и уЕ.
Пусть Л1 и А2 — борелевские множества на прямой. Поскольку система (хе, Ув) является подсистемой в (х, у, хе, уе), то можем записать:
Рхе, Уе (^1	~ Рх, у, хе, уе Z? X Я, X Я2).	(8)
Но ввиду (2)
Рх, у, хе уЕ (Д X R X Я, X Я2) = у (Я*),	(9)
200
где А* состоит из точек (х, у), таких, что ф8(х) € А, <р8 (у) € Д2. Очевидно, А* = Bi X В2, где Bi =	В2 = Ф~‘(Л2).
Ввиду независимости х и у имеем:
Рх,у X В2) = Рх (Bi) Ру (В2).	(10)
Из (8), (9), (10) следует:
Рх£ уЁ (^1 "К ^г) = Рх (^1) Ру (^г)>
или
Рхе уЕ (A X А2) = рх^ (Aj) ру& (Л2),
что и доказывает независимость хЕ и у8.
Рассмотрим теперь случайную величину
х8у8 — ху,
которая представляет собой функцию ф8(х) фе (у) — ху от величин х и у. Воспользуемся тождеством
фе (х) фе (У) — ху = (х — фе (х)) (у — фе (у)) — (х — ф8 (х)) у — (у — Фс(у))х.
Первая часть этого тождества по абсолютной величине не превосходит е . е + + е |у| е |х|, следовательно,
— (е2 + е I у I + в | X |) < фе (х) фЕ (у) — ху < е2 + 8 I у I + е I X |.
Из этих неравенств вытекает, что1
— (е2 + ъМ [| у |] + еМ [| х |]) < М [хе у8 — ху] < е2 + ъМ [| у |] + еМ [| х |]
и тем самым
М [хЕуе—ху] —> 0 при s —> 0.	(11)
Поскольку для дискретных случайных величин считаем теорему доказанной, то можем записать, что
М [хе у8 ] = М [хе ] М [уЕ ].
С учетом этого равенства из (11) находим:
М [хе ] М [у8 ] — М [ху] -> 0 при 8	0.
Теперь остается учесть, что при 8 -> 0
М[хе ]-^Л1 [х], М[уЕ ]->Л1[у],
и приходим к (7). И
1 В этом месте мы используем следующий факт: если неравенство Д (х, у) Д (х> У) имеет место тождественно относительно х, у, то
Л1 [Д (х, у)] < М [Д (X, у)].
Доказательство предоставляется читателю.
Таблицы значений для функций
1	- Т*2	If"
ч(х) = ^е иф(х) = ЖГ dt-о
X	<р(х)	Ф'(х)	X	<р(х)	Ф(х)	X	<р(х)	Ф(х)
0,00	0,3989	0 ,0000	0,40	0,3683	0,1554	0,80	0,2897	0,2881
01	3989	0040	41	3668	1591	81	2874	2910
02	3989	0080	42	3653	1628	82	2850	2939
03	3988	0120	43	3637	1664	83	2827	2967
04	3986	0160	44	3621	1700	84	2803	2995
05	3984	0199	45	3605	1736	85	2780	3023
06	3982	0239	46	3589	1772	86	2756	3051
07	3980	0279	47	3572	1808	87	2732	3078
08	3977	0319	48	3555	1844	88	2709	3106
09	3973	0359	49	3538	1879	89	2685	3133
0,10	0,3970	0,0398	0,50	0,3521	0,1915	0,90	0,2661	0,3159
11	3965	0438	51	3503	1950	91	2637	3186
12	3961	0478	52	3485	1985	92	2613	3212
13	3956	0517	53	3467	2019	93	2589	3238
14	3951	0557	54	3448	2054	94	2565	3264
15	3945	0596	55	3429	2088	95	2541	3289
16	3939	0636	56	3410	2123	96	2516	3315
17	3932	0675	57	3391	2157	97	2492	3340
18	3925	0714	58	3372	2190	98	2468	3365
19	3918	0753	59	3352	2224	99	2444	3389
0,20	0 ,3910	0 ,0793	0,60	0 ,3332	0 ,2257	1,00	0,2420	0,3413
21	3902	0832	61	3312	2291	01	2396	3438
22	3894	0871	62	3292	2324	02	2371	3461
23	3885	0910	63	3271	2357	03	2347	3485
24	3876	0948	64	3251	2389	04	2323	3508
25	3867	0987	65	3230	2422	05	2299	3531
26	3857	1026	66	3209	2454	06	2275	3554
27	3847	1064	67	3187	2486	07	2251	3577
28	3836	1103	68	3166	2517	08	2227	3599
29	3825	1141	69	3144	2549	09	2203	3621
0,30	0,3814	0,1179	0,70	0,3123	0 ,2580	1 ,10	0,2179	0,3643
31	3802	1217	71	3101	2611	11	2155	3665
32	3790	1255	72	3079	2642	12	2131	3686
33	3778	1293	73	3056	2673	13	2107	3708
34	3765	1331	74	3034	2703	14	2083	3729
35	3752	1368	75	ЗОН	2734	15	2059	3749
36	3739	1406	76	2989	2764	16	2036	3770
37	3726	1443	77	2966	2794	17	2012	3790
38	3712	1480	78	2943	2823	18	1989	3810
39	3697	1517	79	2920	2852	19	1965	3830
202
Продолжение
X	Ф (х)	Ф х)	X	Ф W	Ф(х)	X	Ф W	Ф (х)
1 ,20	0,1942	0 ,3849	1 ,70	0,0940	0,4554	2,40	0,0224	0,4918
21	1919	3869	71	0925	4564	42	0213	4922
22	1895	3888	72	0909	4573	44	0203	4927
23	1872	3907	73	0893	4582	46	0194	4931
24	1849	3925	74	0878	4591	48	0184	4934
25	1826	3944	75	0863	4599	50	0175	4938
26	1804	3962	76	0848	4608	52	0167	4941
27	1781	3980	77	0833	4616	54	0158	4945
28	1758	3997	78	0818	4625	56	0151	4948
29	1736	4015	79	0804	4633	58	0143	4951
1 ,30	0,1714	0,4032	1 ,80	0,0790	0,4641	2,60	0,0136	0,4953
31	1691	4049	81	0775	4649	62	0129	4956
32	1669	4066	82	0761	4656	64	0122	4959
33	1647	4082	83	0748	4664	66	0116	4961
34	1626	4099	84	0734	4671	68	ОНО	4963
35	1604	4115	85	0721	4678	70	0104	4965
36	1582	4131	86	0707	4686	72	0099	4967
37	1561	4147	87	0694	4693	74	0093	4969
38	1539	4162	88	0681	4699	76	0088	4971
39	1518	4177	89	0669	4706	78	0084	4973
1 ,40	0,1497	0,4192	1,90	0 ,0656	0,4713	2,80	0 ,0079	0 ,4974
41	1476	4207	91	0644	4719	82	0075	4976
42	1456	4222	92	0632	4726	84	0071	4977
43	1435	4236	93	0620	4732	86	0067	4979
44	1415	4251	94	0608	4738	88	0063	4980
45	1394	4265	95	0596	4744	90	0060	4981
46	1374	4279	96	0584	4750	92	0056	4982
47	1354	4292	97	0573	4756	94	0053	4984
48	1334	4306	98	0562	4761	96	0050	4985
49	1315	4319	99	0551	4767	98	0047	4986
1 ,50	0,1295	0 ,4332	2,00	0 ,0540	0 ,4772	3,00	0,00443	0 ,49865
51	1276	4345	02	0519	4783			
52	1257	4357	04	0498	4793	3,10	00327	49903
53	1238	4370	06	0478	4803	3,20	00238	49931
54	1219	4382	08	0459	4812			
55	1200	4394	10	0440	4821	3,30	00172	49952
56	1182	4406	12	0422	4830	3,40	00123	49966
57	1163	4418	14	0404	4838			
58	1145	4429	16	0387	4846	3,50	00087	49977
59	1127	4441	18	0371	4854			
1 ,60	0,1109	0 ,4452	2,20	0 ,0355	0,4861	3,60	00061	49984
61	1092	4463	22	0339	4868	3,70	00042	49989
62	1074	4474	24	0325	4875	3,80	00029	49993
63	1057	4484	26	0310	4881			
64	1040	4495	28	0297	4887	3,90	00020	49995
65	1023	4505	30	0283	4893	4,00	0,0001338	499968
66	1006	4515	32	0270	4898			
67	0989	4525	34	0258	4904	4,50	0000160	499997
68	0973	4535	36	0246	4909	5,00	0000015	49999997
69	0957	4545	38	0235	4913			
'03
Таблица значений функции
‘V1 и
	Х==0,1	1=0,2	1=о,з	Х=0,4	К=0,5	Х=0,6	1=0,7	1=0,8	1=0,9	
0	0,9048	0,8187	0,7408	0,6703	0,6065	0,5488	0,4966	0,4493	0,4066	
1	0,0905	0,1637	0,2222	0,2681	0,3033	0,3293	0,3476	0,3595	0,3659	
2	0,0045	0,0164	0,0333	0,0536	0,0758	0,0988	0,1217	0,1438	0,1647	
3	0,0002	0,0011	0,0033	0,0072	0,0126	0,0198	0,0284	0,0383	0,0494	
4		0,0001	0,0003	0,0007	0,0016	0,0030	0,0050	0,0077	0,0111	
5				0,0001	0,0002	0,0004	0,0007	0,0012	0,0020	
6							0,0001	0,0002	0,0003	
ч		1=2	1=3	1=4	1=5	1=6	1=7	Х=8	1=9	1=10
0	0,3679	0,1353	0,0498	0,0183	0,0067	0,0025	0,0009	0,0003	0,0001	0,0000
1	0,3679	0,2707	0,1494	0,0733	0,0337	0,0149	0,0064	0,0027	0,0011	0,0005
2	0,1839	0,2707	0,2240	0,1465	0,0842	0,0446	0,0223	0,0107	0,0050	0,0023
3	0,0613	0,1804	0,2240	0,1954	0,1404	0,0892	0,0521	0,0286	0,0150	0,0076
4	0,0153	0,0902	0,1680	0,1954	0,1755	0,1339	0,0912	0,0572	0,0337	0,0189
5	0,0031	0,0361	0,1008	0,1563	0,1755	0,1606	0,1277	0,0916	0,0607	0,0378
6	0,0005	0,0120	0,0504	0,1042	0,1462	0,1606	0,1490	0,1221	0,0911	0,0631
7	0,0001	0,0034	0,0216	0,0595	0,1044	0,1377	0,1490	0,1396	0,1171	0,0901
8		0,0009	0,0081	0,0298	0,0653	0,1033	0,1304	0,1396	0,1318	0,1126
9		0,0002	0,0027	0,0132	0,0363	0,0688	0,1014	0,1241	0,1318	0,1251
10			0,0008	0,0053	0,0181	0,0413	0,0710	0,0993	0,1186	0,1251
11			0,0002	0,0019	0,0082	0,0213	0,0452	0,0722	0,0970	0,1137
12			0,0001	0,0006	0,0034	0,0126	0,0263	0,0481	0,0728	0,0948
13				0,0002	0,0013	0,0052	0,0142	0,0296	0,0504	0,0729
14				0,0001	0,0005	0,0022	0,0071	0,0169	0,0324	0,0521
15					0,0002	0,0009	0,0033	0,0090	0,0194	0,0347
16						0,0003	0,0014	0,0045	0,0109	0,0217
17						0,0001	0,0006	0,0021	0,0058	0,0128
18							0,0002	0,0009	0,0029	0,0071
19							0,0001	0,0004	0,0014	0,0037
20								0,0002	0,0006	0,0019
21								0,0001	0,0003	0,0009
22									0,0001	0,0004
23										0,0002
24										0,0001
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Аксиома аддитивности 21
—	счетной аддитивности 21
Аксиомы вероятностен 20
—	событий 19
о-алгебра подмножеств 23
Байес Т. 57
Бернулли Я. 60
Бернштейн С. Н. 156
Биномиальные вероятности 63
— коэффициенты 40
Борелевская система подмножеств 23
Борелевское множество на плоскости
108
--- на прямой 90
Борелевская функция нескольких переменных 129
--- одного переменного 125
Борель Э. 23
Вариационный ряд 174
Вероятностная схема 22
Вероятность (аксиоматическое определение) 20
—	(статистическое определение) 10
—	перехода 76
Выборка 173, 174
Гальтона опыт 168
Гальтон Ф. 168
Генеральная совокупность 174
Геометрические вероятности 30, 102,
122
Гистограмма 176
Гнеденко Б. В. 58, 156
Госсет В. 185
Гюйгенс X. 26
Диаграмма Эйлера — Венна 15
Дискретная случайная величина 85, 86, 96
Дисперсия случайной величины 151
	дискретной 152
-------, имеющей плотность 152
•	, нормально распределенной
153
Доверительная вероятность 182
Доверительный интервал 182
Достоверное событие 8
Задача о встрече двух лиц 120
Закон больших чисел 156, 159
—	редких явлений 89
—	распределения случайной величины 85, 86, 96
----системы случайных величин НО
Интегральная предельная теорема Лапласа 167
—	приближенная формула Лапласа 69
Интервальная таблица частот 176
Классический способ подсчета вероятностей 26
Колмогоров А. Н. 5, 18, 83, 156
Координаты случайной точки 109
Корреляционный момент 154
Корреляционное отношение 193
Корреляция 189
—	отрицательная 192
— положительная 191
Коэффициент корреляции 190
Лаплас П. 71
Локальная приближенная формула Лапласа 68
Марков А. А. 83
Массовое случайное событие 8
Математическое ожидание 'Дискретной случайной величины 135
----случайной величины, имеющей плотность 140
--------- нормально распределенной 143
--------общего вида 139
---- функции 138, 141
Матрица перехода марковской цепи 76
Метод наименьших квадратов 193
— характеристических функций 166
Механическая модель случайной величины 105
Многоугольник распределения 89
Невозможное событие 8
Независимость случайных величин 118
205
Независимость двух событий 50, 51 — любого числа событий 52
Некоррелированные случайные величины 189
Непрерывная случайная величина 98
Неравенство Чебышева 157
Несмещенная оценка 178
Несовместные события 16
Нормальное распределение круговое 124
---- на плоскости 123, 124
---- на прямой 103
Нормированная мера 24
— случайная величина 153
Опыт Гальтона 168
Отклонение случайной величины 150
Оценка параметра интервальная 182
----несмещенная 178
---- состоятельная 178
---- точечная 182
Паскаль Б. 26
Перестановка 37
Плотность вероятности (плотность распределения) системы случайных величин 116
---------случайной величины 99
Подсистема системы случайных величин 129
Полиномиальная формула 42
Правило произведения 33
— сложения вероятностей 16
— суммы 32
— трех сигм 159
Предельные вероятности 81
Предельная теорема Лапласа 68, 168
----Пуассона 72
Приближение к случайной величине (е-приближение) 139
Приближенные формулы Лапласа 68, 69
----Пуассона 72
Произведение событий 13
Пространство элементарных событий 19
Противоположное событие 14, 20
Равенство событий 15
Размещения без повторений 36
—	с повторениями 35
Распределение биномиальное 87
—	дискретное 96
—	непрерывное 98
—	Пуассона 88
—	равномерное 101, 119
—	случайной величины 96
—	Стьюдента 185
— функции от случайной величины 126, 130
Рекуррентное соотношение 43
Сеть (е-сеть) 138
Свертка 131
Свойства линейности (математического ожидания) 146
Система случайных величин 109 -------дискретного типа ПО --------------, имеющая плотность 116 -------, непрерывно распределенная
116
Случайная величина 84, 91
---дискретная 85, 86, 96
---имеющая плотность 99
---непрерывная 98
---смешанного типа 106
Слуцкий Е. Е. 83
Событие достоверное 8
—	невозможное 8
—	случайное 7, 19
—	элементарное 19
Состав строки 40
Состоятельная оценка 178
Сочетание 37
Среднее значение 134
—	квадратичное отклонение 151
—	число успехов 67
Статистическое определение вероятности 10
Строка 33
Стьюдент 185
Сумма событий 12
Схема Бернулли 61
—	случайного выбора 43
Счетно-аддитивная функция 24
Таблица частот 175
Теорема Бернулли 161
—	Ляпунова 165
— Маркова о предельных вероятностях 81
— о задании случайной величины 95, 196
— о непрерывной зависимости р (Л) от Л 21
— сложения дисперсий 155 — сложения математических ожиданий 145, 199
— умножения математических ожиданий 148, 200
—	Чебышева 159
Условие Ляпунова 165
Условная вероятность 48
—	- частота 48
Условный закон распределения 192
Ферма П. 26
Формула Байеса 57
—	Бернулли 63
206
—	полной вероятности 55
Функция Лапласа Ф (х) 69
—	нескольких случайных величин 129
—	случайной величины 125
—	распределения системы случайных величин 114
—	случайной величины 92
Хинчин А. Я. 58, 83, 156
Центр распределения 135
Центральная предельная теорема 163
Цепь Маркова 75, 76
— однородная 76
Чебышев П. Л. 156
Числовые характеристики 134
Элементарное событие 18
Элементарный исход 25
----благоприятный 25
----неблагоприятный 25
Эмпирическая дисперсия 179
----несмещенная 180
Эмпирический закон распределения 175
Эмпирическое среднее 178
Александр Самуилович Солодовников
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Редактор Т. В. Автономова
Художник Б. Л. Николаев
Художественный редактор Е. Н. Карасик Технический редактор Т. Н. Зыкина Корректор О. В. Ивашкина
ИБ № 7323
Сдано в набор 20 10 82 Подписано к печати 15 04 83. Формат 60x907ie Бум типограф № 2 Гарнит литературная Печать высокая Усл печ л 13 Усл кр отт 13,25 Уч -изд л 11,95 Тираж 39000 экз Заказ Де 459 Цена 55 коп
Ордена Трудового Красного Знамени издательство «Просвещение» Государственного коми* тета РСФСР по делам издательств, полиграфии и книжной торговли Москва, 3-й проезд Марьиной рощи, 41
Саратовский ордена Трудового Красного Знамени полиграфический комбинат Росглавполи графпрома Государственного комитета РСФСР по делам издательств, полиграфии и книжной торговли Саратов, ул Чернышевского, 59.