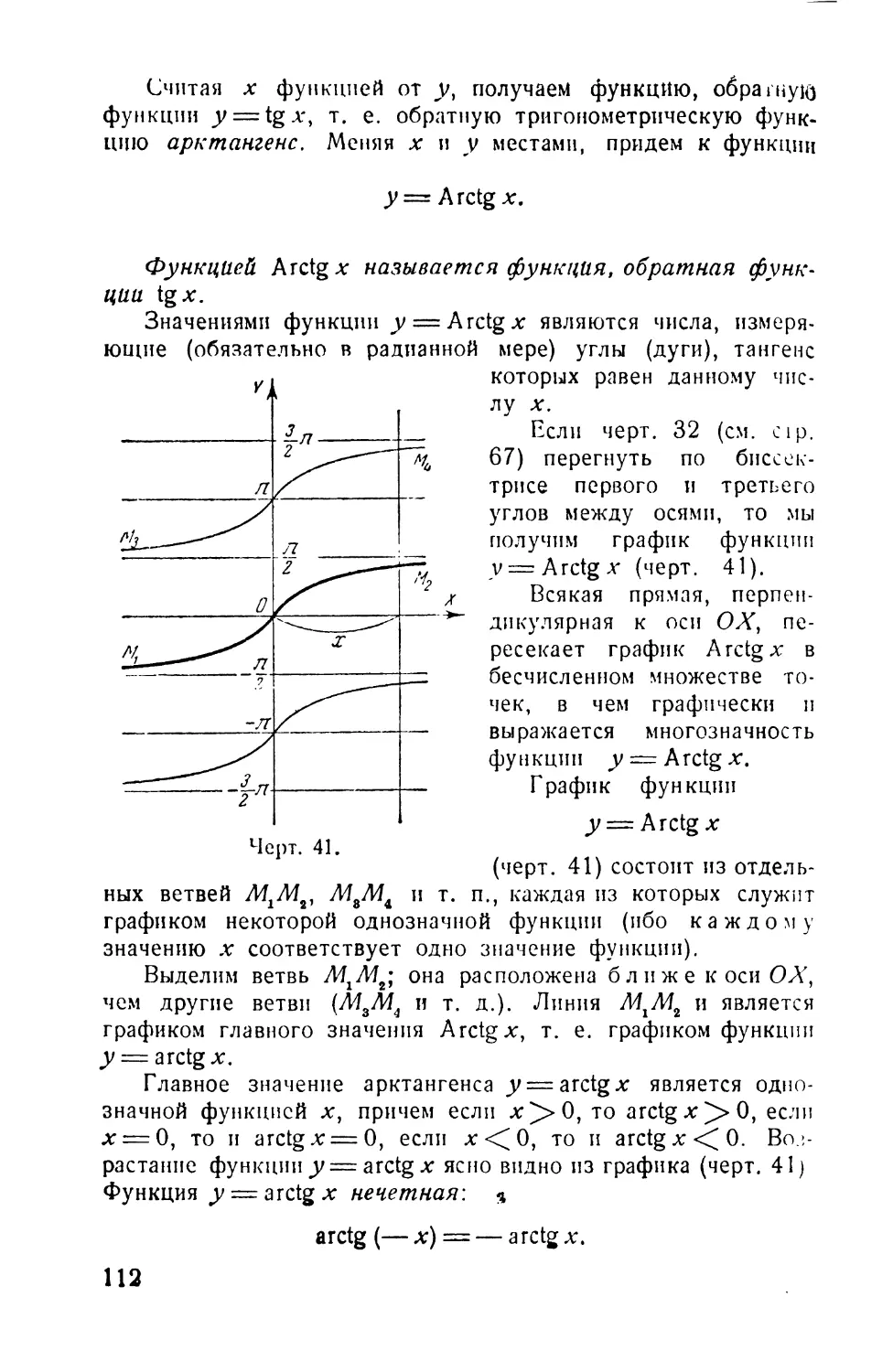
Text
А.Ф. БЕРМАНТи АА. ЛЮСТЕРНИК
ТРИГОНОМЕТРИЯ
А. Ф. БЕРМАНТ и Л. А. ЛЮСТЕРНИК
ТРИГОНОМЕТРИЯ
ИЗДАНИЕ ТРЕТЬЕ
СТЕРЕОТИПНОЕ
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1960
11-2-2
Бермант Анисим Федорович и Люстерник Лазарь Аронович
Тригонометрия.
Редакторы: А. 3. Рывкин и Л. Я. Цлаф.
Техн, редактор Н. Я- Мурашова. Корректор А. С. Бакулева
Печать с матриц. Подписано к печати 7/Ш 1960 г. Бумага 84\1081/з2-
Физ. печ. л. 5,63. Условн. печ. л. 9,23. Уч.-изд. л. 10,0. Тираж 55 000 экз. Т-02776.
Цена книги 3 руб.
Государственное издательство физико-математической литературы
Москва, В-71, Ленинский проспект, 15.
5-я типография Управле.пп полиграфической промышле ности Министерства
культуры Латвийской ССР. Рига, пл. 17 июня, 1. Заказ № 1073.
Отпечатано с матриц Первой образцовой тип. им. А. А. Жданова.
ОГЛАВЛЕНИЕ
Предисловие к первому изданию ............................ 6
ГЛАВА ПЕРВАЯ
ПРОИЗВОЛЬНЫЕ УГЛЫ
И ИХ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
§ 1. Тригонометрические функции острого угла............. 7
1. Понятие функции.................................... 7
2. Основные тригонометрические функции................ 8
3. Основные соотношения между, тригонометрическими функ-
циями ................................................11
4. Дополнительные углы и сходственные тригонометрические
функции ..............................................12
5. Таблица значений тригонометрических функций ..... 13
§ 2. Векторы.............................................16
6. Положительные и отрицательные отрезки на оси .... 16
7. Векторы и их проекции..............................17
8. Свойства проекций..................................18
§ 3. Обобщение понятий угла и дуги...................* . 19
9. Углы и дуги, меньшие 360°.........................19’
10. Углы и дуги, ббльшие 360° .......................21
11. Отрицательные углы и дуги. Суммы углов и дуг .... 22
§ 4. Тригонометрические функции и их простейшие свойства 23
12. Определение тригонометрических функций ........... 23
13. Знаки тригонометрических функций...................27
14. Значения тригонометрических функций некоторых углов . 29
15. Построение значений тригонометрических функции ... 30
§ 5. Некоторые важнейшие формулы..........................33
16. Основные формулы...................................33
17. Тригонометрические тождества.......................35
18. Изменение знака угла...............................36
19. Тригонометрические функции дополнительных углов ... 38
§ 6. Приведение к острому углу............................39
20. Приведение к углу, меньшему 360°...................39
1
3
21. Формулы приведения...............................39
22. Приведение к острому углу........................42
Задачи к главе I.........................................43
глава вторая
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
ЧИСЛОВОГО АРГУМЕНТА
§ 7. Тригонометрические функции числового аргумента и их
периодичность......................................54
23. Радианное измерение дуг и углов..................54
24. Определение тригонометрических функций числового
аргумента............................................56
25. Периодичность тригонометрических функций.........57
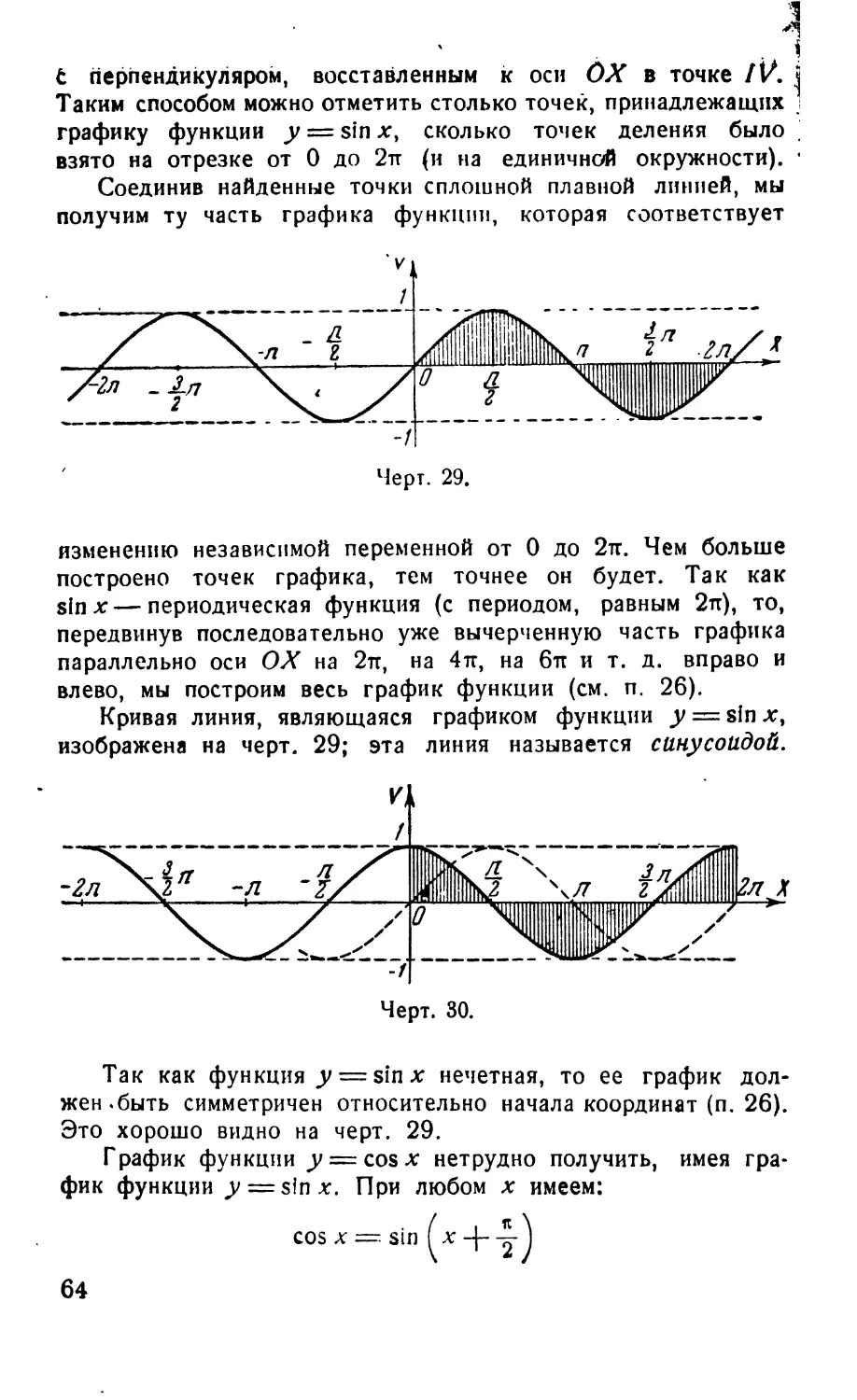
§ 8. Графики тригонометрических функций..................59
26. График функции...................................59
27. Графики функций sin х и cosx.....................63
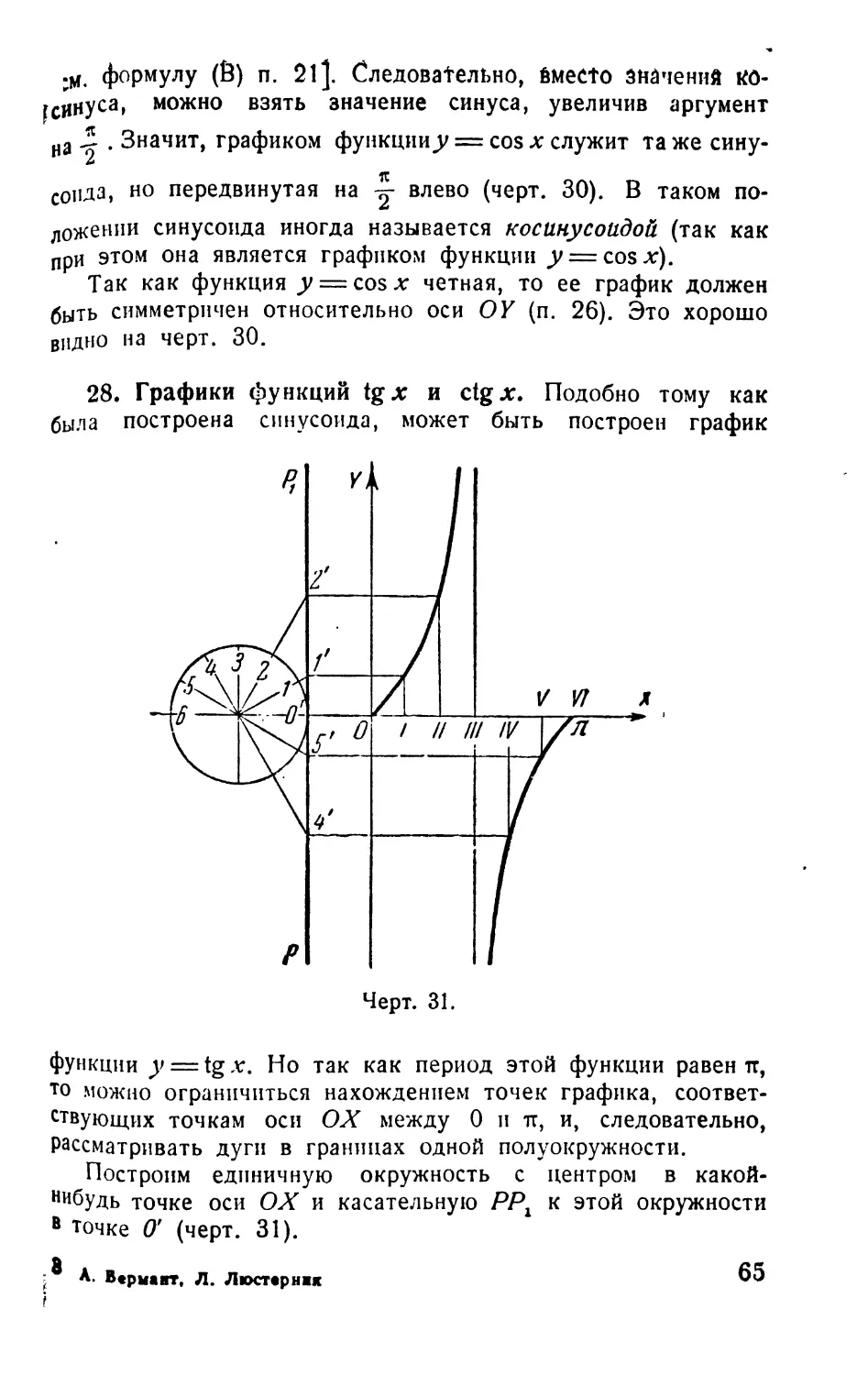
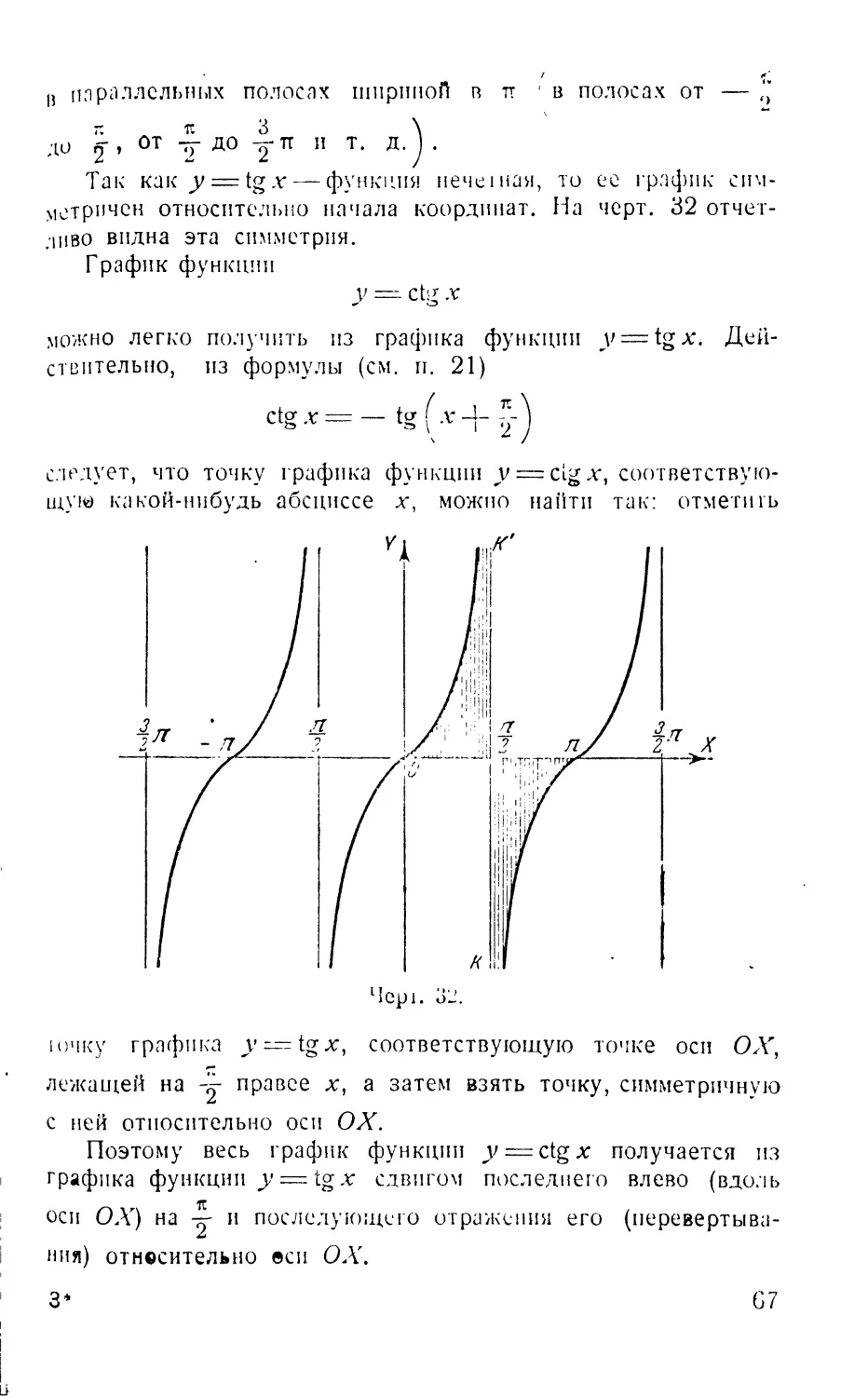
28. Графики функций tgx и ctgx.......................65
§ 9. Изменения тригонометрических функций ...............68
29. Характер изменения sin х и cos х.................68
30. Характер изменения tg х и ctg х .................69
§ 10. Гармонические колебания............................71
31. Простые гармонические колебания..................71
32. График простого гармонического колебания.........73
Задачи к главе II ......................................74
ГЛАВА ТРЕТЬЯ
ПРЕОБРАЗОВАНИЯ ТРИГОНОМЕТРИЧЕСКИХ
ВЫРАЖЕНИЙ
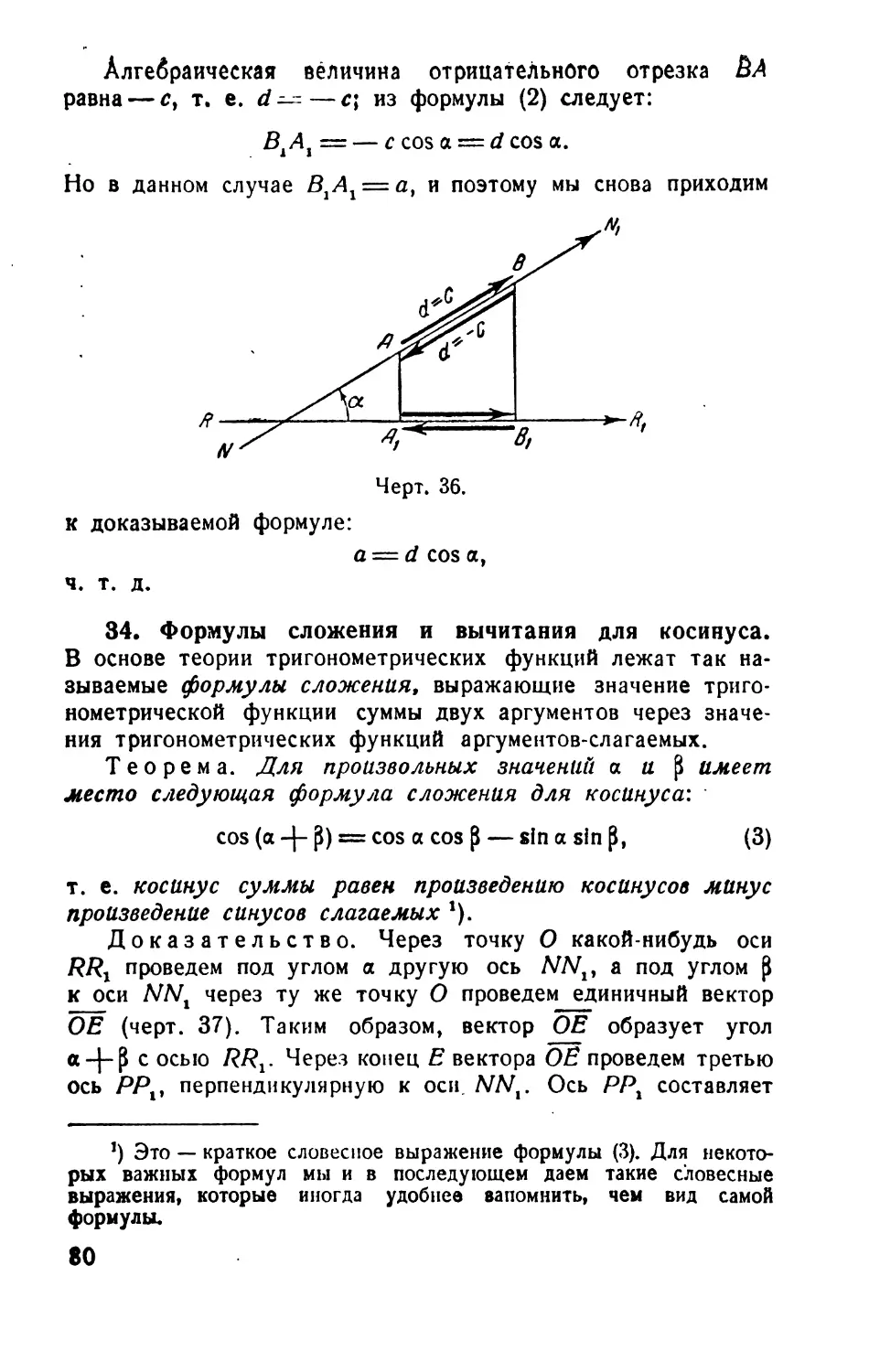
§ 11. Формулы сложения и вычитания.......................79
33. Обобщение формулы проекций .....................79
34. Формулы сложения и вычитания для косинуса.......80
35. Формулы сложения и вычитания для синуса.........82
36. Формулы сложения и вычитания для тангенса.......83
§ 12. Формулы для двойного и половинного аргументов . . 84
37. Тригонометрические функции двойного аргумента ... 84
38. Тригонометрические функции половинного аргумента . . 84
39. Выражение тригонометрических функций через тангенс
половинного аргумента ............................... 86
§ 13. Преобразования произведений тригонометрических
функций в сумму и обратные преобразования .... 87
40. Формулы для произведений синусов и косинусов . ... 87
41. Приведение к виду, удобному для логарифмирования . . 88
42. Преобразования с помощью вспомогательного аргумента 89
Задачи к главе III.......................................90
4
ГЛАВА ЧЕТВЕРТАЯ
ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ.
ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ
§ 14. Обратные тригонометрические функции................99
43. Определения и общий вид для значений обратных триго-
нометрических функций................................99
44. Главные значения обратных тригонометрических функций 102
§ 15. Изменения обратных тригонометрических функций . . 106
45. Общее понятие обратной функции..................106
46. Функция y = Arcsinx и ее график.................108
47. Функция y = Arccosjc и ее график ...............110
48. Функция y = Arctgx и ее график..................111
49. Функция y = Arcctgjc и ее график ................ИЗ
§ 16. Преобразования обратных тригонометрических функций 114
50. Простейшие преобразования.......................114
51. Дальнейшие преобразования ......................116
§ 17. Тригонометрические уравнения......................120
52. Определение.....................................120
53. Примеры уравнений ..............................121
54. Один общий метод................................126
Задачи к главе IV.......................................128
ГЛАВА ПЯТАЯ
ЭЛЕМЕНТЫ ТЕОРИИ ТРЕУГОЛЬНИКА
И РЕШЕНИЕ ТРЕУГОЛЬНИКОВ
§ 18. Основные зависимости между элементами треугольника 137
55. Постановка вопроса..............................137
56. Зависимость между углами треугольника ..........138
57. Теоремы синусов и косинусов.........'...........138
§ 19. Другие зависимости между элементами треугольника 141
58. Теорема тангенсов.................................141
59. Зависимости между площадью, периметром и другими
элементами треугольника ............................. 142
§ 20. Логарифмы тригонометрических функций.............145
60. Таблица логарифмов тригонометрических функций . . .145
61. Применения логарифмической линейки в тригонометри-
ческих вычислениях ...................................148
§ 21. Решение треугольников...............................150
62. Решение прямоугольных треугольников....150
63. Решение косоугольных треугольников................152
64. Измерения линий и углов на местности..............159
Задачи к главе V .........................................161
Сводка важных формул......................................168
Ответы....................................................172
ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
В основу книги мы положили учебник тригонометрии для
средней школы, написанный нами в 1938 г. по заданию
Наркомпроса РСФСР и издававшийся Учпедгизом РСФСР в 1940,
1947, 1950 годах, а также Учпедгизом Грузинской ССР в 1948 г.
За истекшие 17 лет учебник многократно обсуждался
в печати и педагогической и научной общественностью, был
предметом опытного преподавания в ряде школ. Все это,
а также анализ учебника в методической литературе (в книгах
В. М. Брадиса, Н. М. Бескина, В. Г. Чичигина и др.) послужили
нам для тщательной обработки книги при ее подготовке к
изданию.
После каждой главы в книге помещены задачи и примеры,
подобранные Р. И. Позойским.
Пользуемся случаем, чтобы выразить благодарность
А. 3. Рывкину, внесшему ряд ценных предложений по улуч-
шению текста.
Мы будем признательны читателям за замечания и за
сообщения об опыте работы с этой книгой.
А. Ф, Вермонт, Л, А. Люстерник
Москва,
ноябрь 1955 г.
ГЛАВА ПЕРВАЯ
ПРОИЗВОЛЬНЫЕ УГЛЫ
И ИХ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
§ 1. Тригонометрические функции острого угла
1. Понятие функции. Изучая различные вопросы мате-
матики, физики и других наук, мы замечаем, что некоторые
из рассматриваемых величин сохраняют одно и то же значе-
ние, другие же изменяют свои значения.
Так, например, наблюдая свободное падение тела в пустоте,
убеждаемся, что расстояние, пройденное телом, и его скорость изме-
f ПО1 СМ \
няются, а ускорение остается неизменным I равным 981 ) •
Величину, которая в данном вопросе сохраняет одно и
то же численное значение, называют постоянной} величину,
которая в данном вопросе принимает различные численные
значения, называют переменной.
В нашем примере ускорение — величина постоянная, а расстояние
и скорость — величины переменные.
Переменные величины чаще всего изменяются не совсем
произвольно, а в известной зависимости друг от друга: если
одной из них придавать значения по нашему усмотрению, то
вторая принимает не произвольные значения, а согласованные
со значениями первой величины.
Например, если указать расстояние, пройденное свободно падаю-
щим телом до некоторого момента времени, то скорость тела в этот
момент имеет уже вполне определенное значение, соответствующее
пройденному телом расстоянию.
Та из переменных, значения которой выбираются произ-
вольно, называется независимой переменной или аргумен-
том. Переменная же, значения которой находятся по зна-
7
чениям независимой переменной (аргумента), называется зави-
симой переменной или функцией.
В нашем примере расстояние, проходимое падающим телом, и
скорость тела находятся между собой в функциональной зависимости;
если расстояние принять за независимую переменную, то скорость
будет функцией l). С изменением пройденного расстояния меняется и
скорость тела, причем так, что каждому значению расстояния соот-
ветствует определенное значение скорости.
Определение. Функцией называется переменная
величина, изменяющаяся в зависимости от изменения дру-
гой переменной величины (независимой переменной, аргу-
мента), причем так, что каждому значению независимой
переменной соответствуют строго определенные значения
функции.
Тригонометрия изучает важный класс функций — так на-
зываемых тригонометрических, а также их применения в гео-
метрии. Само название «тригонометрия» (составлено из гре-
ческих слов: «тригонон» — треугольник и «метрезис» — изме-
рение) показывает, что этот раздел математики связан с за-
дачами решения треугольников, т. е. с задачами нахожде-
ния одних элементов треугольника по другим его известным
элементам. Исторически тригонометрия и возникла из таких
задач, но ими далеко не исчерпывается широкое применение
тригонометрических функций в самых различных разделах ма-
тематики, естествознания и техники.
2. Основные тригонометрические функции. Дадим прежде
всего определения четырех основных величин, рассматри-
рон такого прямоугольного
ваемых в тригонометрии: синуса,
косинуса, тангенса, котангенса,
для случая острого угла.
Возьмем прямоугольный тре-
угольник с заданным острым углом а
(черт. 1) и пусть с—гипотенуза,
а — катет, лежащий против угла а
(противолежащий катет), и
b — другой катет (прилежа-
щий катет). Указанные величины
определяются как отношения сто-
треугольника, а именно:
а
sina = — ,
с ’
(1)
*) Можно, наоборот, считать скорость независимой переменной,
тогда проходимое расстояние будет функцией.
8
т. е. синусом острого угла называется отношение проти-
волежащего катета к гипотенузе;
cosa = |, (2)
т. е. косинусом острого угла называется отношение при-
лежащего катета к гипотенузе;
tg«=y. (3)
т. е. тангенсом острого угла называется отношение про-
тиволежащего катета к прилежащему катету;
ctga = -^, И)
т. е. котангенсом острого угла называется отношение
прилежащего катета к противолежащему катету.
Значения синуса, косинуса, тангенса и котангенса для
данного острого угла а не зависят от длин сторон a, bt с
прямоугольного треугольника с углом а, взятого для нахож-
дения этих значений, а зависят только от угла а.
В самом деле, если мы имеем другой прямоугольный
треугольник, но с тем же острым углом а, то он будет по-
добен данному прямоугольному треугольнику и, следователь-
а b а Ъ
но, отношения сторон — , у , у , — останутся прежними.
Поэтому в обозначении синуса (sin а) участвует только обо-
значение угла.
Нужно заметить, что символ sin, стоящий перед символом,
обозначающим угол, сам по себе никакой величины не обо-
значает; он неотделим от символа а для угла. Вместе же
с ним он образует единый, нерасчленяемый символ, обозна-
чающий вполне определенное число, а именно: значение от-
fl
ношения -у при заданном угле а.
Это же замечание относится и к другим символам для
остальных величин: косинуса (cos а), тангенса (tg а), котан-
генса (ctga).
Мы видим, что каждая из величин: синус, косинус, тан-
генс, котангенс, имеет строго определенное значение для
каждого данного острого угла а, причем с изменением угла a
изменяются и значения этих величин. Таким образом, эти ве-
личины являются функциями угла.
9
Говорят, что sin a, cos а, tga, ctg а суть тригонометри-
ческие функции острого угла а, который служит их ар-
гументом.
Значениями тригонометрических функций являются отвле-
ченные числа.
Построив прямоугольный треугольник с острым углом a
и измерив его стороны, по формулам (1) — (4) можно получить
приближенные значения тригонометрических функций угла а.
Для углов а = 30°, 45°, 60° легко найти точные значения
тригонометрических функций:
sin3O°=4-, cos30oz=HJ tg30° = , ctg30°=|/3;
Z Z О
sin 45° = ^--, cos45o = KX, tg45°=l, ctg 45°= 1;
z z
sin60° = , cos60°=l, tg60° = /3, ctg60° = ^X
Z Z о
В прямоугольном треугольнике с острыми углами 30° и 60°
и гипотенузой с катет, противолежащий углу в 30° (и при-
лежащий к углу в 60°), равен ~ ; поэтому
с
sin 30° = cos 60° 1 = 1.
с 2
Другой катет, прилежащий к углу в 30° (и противоле-
жащии углу в 60 ), равен —-; поэтому
С^~
cos 30° = sin 60° = = КД.
с 2
Далее,
с
tg 30° = ctg 60°==4==Q;
/з /з 3
С 2
L 9 г —
ctg 30°= tg 60° = —р- = /3.
У
10
В прямоугольном треугольнике с двумя равными острыми
углами в 45 и гипотенузой с оба катета равны с ; по-
этому
С 2 Vo С 9
sin 45°— cos 45°= ——— =-Цт-; tg 45° = ctg 45° = —=!.
с 2 ° ® у 2
с —
Заметим, что, так как каждый катет всегда меньше гипо-
тенузы, то синус и косинус острого угла суть положи-
тельные числа, меныиие единицы. Что касается тангенса и
котангенса острого угла, то они могут быть любыми
положительными числами.
3. Основные соотношения между тригонометрическими
функциями. Четыре тригонометрические функции острого
угла а связаны между собой тремя соотношениями:
• 2 I 2 < , sin а . COS а
sin2 а 4- cos2 а = 1; tga =--; ctga = -—. (5)
Действительно, первое соотношение вытекает из теоремы
Пифагора:
а*-\-Ь* = с\
(а\ъ ( b V
У / + М=1’ т*е< (s,n a)’ + (cos a)* “ 1» что
записывают короче так:
sin2 аД- cos2 а — 1.
Итак, сумма квадратов синуса и косинуса одного и
того же острого угла равна единице.
Второе и третье соотношения непосредственно следуют
из определений:
a !L
L а с sin a . be COS а
tg а = -г — -г =----; ctg а — — = — = -— .
& b b cos а ь a a sin а
с с
Итак, тангенс острого угла равен частному от деления
синуса этого угла на его косинус, а котангенс острого угла ра-
вен частному от деления косинуса этого угла на его синус.
Из соотношений (5), которые называются основными, можно
вывести много других соотношений, например:
Ctga ——; sin2 a= . , ; cos2 a = .--т-,- -. (6)
& tg a ’ 1 -|- Ctg2 a ’ 1 + tg1 e
ll
Первое из этих соотношений (чевидно; второе получается
так: из третьего равенства (5) имеем cos а = ctg а • sin а, т. е.
cos2 а = ctg1 а • sin1 а, а подставляя сюда выражение для cos1 а,
находимое из первого равенства (5), получим 1—sin®a =
= ctg1 a-sin1 а, откуда и следует, что
таким же образом из второго и первого равенств (5) полу-
чается третье соотношение (6).
Пользуясь равенствами (5), а также следствиями из них,
например равенствами (6), можно находить значения всех три-
гонометрических функций данного угла по значению одной
из них. Например, пусть известно, что tga— -у. Из пер-
вого равенства (6) находим:
ctg « = = /3,
а из третьего равенства (6) и из первого равенства (5) по-
лучаем:
cos а —
Нетрудно заметить, что угол а при этом равен 30°.
Соотношения (5) и (6) являются примерами тригономет-
рических тождеств для острых углов, т. е. равенств, спра-
ведливых при любых значениях острого угла а.
4. Дополнительные углы и сходственные тригономет-
рические функции. Два острых угла а и (90° — а) назы-
ваются дополнительными. Сходственные тригонометриче-
ские функции (т. е. синус и косинус, тангенс и котангенс)
дополнительных углов равны между собой:
sin (90° — a) = cos a;
tg (90° — a) = ctg a;
cos (90° — a) = sin a;
ctg (90° — a) = tg a.
(7)
(7')
Эти соотношения сразу вытекают из рассмотрения прямо-
угольного треугольника с острым углом а на основании опре-
делений тригонометрических функций.
12
В самом деле, если в прямоугольном треугольнике один
острый угол равен а, то другой равен 90° — а (черт. 1).
Катет а, противолежащий углу а, есть прилежащий к углу
90°— а, катет Ь, прилежащий к углу а, есть противолежащий
углу 90° — а. Отсюда
sin (90°— а) = у = cos а, cos (90°— а) = у = sin а и т. п.
S. Таблица значений тригонометрических функций. Для
решения задач (например, для решения прямоугольных тре-
угольников, см. ниже) необходимо иметь значения тригоно-
метрических функций острых углов. На стр. 14 приведена
таблица таких значений (так называемая таблица нату-
ральных значений тригонометрических ф у н к-
ц и й). Она содержит значения тригонометрических функций
для всех острых углов, выражающихся целым числом граду-
сов (таблица через 1°). Значения даны с точностью
до 0,001 1).
Для того чтобы найти в ней значение тригонометрической
функции угла, меньшего 45°, нужно взять число, находя-
щееся на пересечении строки, в которой слева указано
данное число градусов, и столбца, в котором сверху ука-
зано наименование искомой функции.
Пример, tg 37° = 0,754.
Если же отыскивают значение тригонометрической функ-
ции угла, большего 45°, то нужно взять число, находя-
щееся на пересечении строки, в которой справа указано
данное число градусов, и столбца, внизу которого указано
наименование искомой функции.
Пример, cos 81° = 0,156.
Таблица дает возможность решать и обратную за-
дачу: по значению одной из тригонометрических функций
находить угол. Для этого среди чисел второго и пятого
столбцов, если дано значение синуса или косинуса, или
третьего и четвертого столбцов, если дано значение тангенса
или котангенса, разыскиваем число, равное данному. Тогда
число градусов, указанное в строке, в которой находится
заданное значение тригонометрической функции, показывает
величину искомого угла. Число градусов нужно брать еле-
вой стороны, если наименование заданной функции помещено
’) Заметим, что уже в XV веке в Самарканде были составлены
таблицы синусов через Г с точностью до 10“®.
13
Таблица значений тригонометрических функций
0 sin tg ctg cos о
1 0,017 0,017 57,290 0,9998 89
2 0,035 0,035 28,636 0,9994 88
3 0,052 0,052 19,081 0,9986 87
4 0,070 0,070 14,301 0,998 86
5 0,087 0,087 11,430 0,996 85
6 0,105 0,105 9,514 0,995 84
7 0,122 0,123 8,144 0,993 83
8 0,139 0,141 7,115 0,990 82
9 0,156 0,158 6,314 0,988 81
10 0,174 0,176 5,671 0,985 80
11 0,191 0,194 5,145 0,982 79
12 0,208 0,213 4,705 0,978 78
13 0,225 0,231 4,331 0,974 77
14 0,242 0,249 4,011 0,970 76
15 0,259 0,268 3,732 0,966 75
16 0.276 0,287 3,487 0,961 74
17 0,292 0,306 3,271 0,956 73
18 0,309 0,325 3,078 0,951 72
19 0,326 0,344 2,904 0,946 71
20 0,342 0,364 2,747 0,940 70
21 0,358 0,384 2,605 0,934 69
22 0,375 0,404 2,475 0,927 68
23 0,391 0,424 2,356 0,921 67
24 0,407 0,445 2,246 0,914 66
25 0,423 0,466 2,145 0,906 65
26 0,438 0,488 2,050 0,899 64
27 0,454 0,510 1,963 0,891 63
28 0,469 0,532 1,881 0,883 62
29 0,485 0,554 1,804 0,875 61
30 0,500 <0,577 1,732 0,866 60
31 0,515 0,601 1,664 0,857 59
32 0,530 0,625 1,600 0,848 58
33 0,545 0,649 1,540 0,839 57
34 0,559 0,675 1,483 0,829 56
35 0,574 0,700 1,428 0,819 55
36 0,588 0,727 1,376 0,809 54
37 0,602 0,754 1,327 0,799 53
38 0,616 0,781 1,280 0,788 52
39 0,629 0,810 1,235 0,777 51
40 0,643 0,839 1,192 0,766 50
41 0,656 0,869 1,150 0,755 49
42 0,669 0,900 1,111 0,743 48
43 0,682 0,933 1,072 0,731 47
44 0,695 0,966 1,036 0,719 46
45 0,707 1,000 1,000 0,707 45
о cos Ctg tg sin о
14
вверху столбца, и с правой стороны, если наименование
помещено внизу столбца.
Примеры, tgа = 0,649, а = 33°;
sin а = 0,743, а = 48°.
По нашей таблице нельзя найти значение тригонометри-
ческой функции, если угол выражается не целым числом
градусов. По ней нельзя найти также угол, если данного
значения тригонометрической функции в таблице нет. На
практике нередко заменяют данное значение угла (или три-
гонометрической функции) ближайшим к нему значением,
имеющимся в таблице. При этом будет получаться хотя и
приближенное значение искомой тригонометрической функции
(или угла), но иногда достаточное для целей задачи.
Пользуясь таблицей натуральных значений тригонометри-
ческих функций и формулами, можно решать прямоугольные
треугольники, т. е. зная некоторые из элементов такого
треугольника (гипотенуза с, катеты а и Ь. острые углы а и £>),
найти другие. Поясним это на примерах.
Пример 1. Известно: £ = 20иа = 33°. Найти: а, b и р.
В’силу формул (1) а = с sin a = 20-sin 33° 20-0,545
10,9 (значение sin 33° =5= 0,545 находим из таблицы);
b = c-cos a = 20-cos 33° 20-0,839 16,8. Кроме того,
р = 90°— a = 90°— 33° = 57°.
Пример 2. Известно: a =10,. a = 42°. Найти: b, с и
Имеем:
Ь = a ctg a = 10-ctg42° « 10- 1,111 = 11,11
a 10 iл л
с — -— 14,9;
sin a 0,669
P = 90°— a = 90°— 42° = 48°.
Пример 3. Известно: £=10, a = 6,3. Найти: £, a и jS.
Имеем:
sina = — = ^3= 0,63.
c 10
По таблице находим:
a = 39°;
p = 90°— a = 90°— 39° — 51 °;
b = c cos a =s 10• cos 39° 10-0,777 7,8.
15
Пример 4. Известно: л = 8, ^—10 Найти: <*, а и р.
Имеем: tg а = у = 0,8. Отсюда а 39°, далее;
р=90°— а ^90°— 39° = 51°;
с — 8 12 7
с ~ sin а sin 39° 0,63 ’ •
Прежде чем перейти к обобщению определений тригоно-
метрических функций на произвольные углы, обобщим само
понятие угла и введем понятие вектора и его проекции.
§ 2. Векторы
6. Положительные и отрицательные отрезки на оси.
На любой прямой можно различать два противоположных на-
правления. Например, на горизонтальной прямой — направле-
ния вправо и влево; на вертикальной прямой — направления
вверх и вниз. Одно из них называют положительным, дру-
гое — отрицательным.
Прямая, на которой указано положительное направле-
ние, отмечено начало отсчета длин и выбрана единица
длины (масштаб), называется осью. (Положительное направ-
ление обычно обозначается стрелкой.)
На прямолинейном отрезке направление определяется ука-
занием его начала и его конца. Отрезок с началом в
точке Лис концом в точке В обозначают через АВ.
Отрезок оси называется положительным, если его на-
правление совпадает с положительным направлением оси;
он называется отрица-
тельным, если его на-
правление противопо-
q 2 ложно положительному
направлению оси. На
черт. 2 отрезок АС положительный, отрезок АВ отрицательный.
Отрезок оси измеряется действительным числом, абсо-
лютная величина которого равна длине отрезка в выбран-
ном масштабе*, это число положительное, если отрезок
положительный, и отрицательное, если отрезок отрица-
тельный. Оно называется алгебраической величиной отрезка.
Алгебраические величины отрезков АВ и ВА отличаются
только знаками. Точку можно рассматривать как отрезок,
начало которого совпадает с концом; его алгебраической
величиной служит число нуль.
1
16
Равенство АЁ = а означает, чТо алгебраическая величина
отрезка АВ равна а (а — положительное или отрицаюльное
число, или нуль); равенство
| АВ '\ =с
означает, что длина отрезка АВ равна с. Очевидно: с = |а|.
Суммой от; езков АВ и ВС оси (черт. 3) называется
отрезок АС той же оси. Его алгебраической величиной
является сумма алгебраических величин данных отрезков.
Черт. 3.
Суммой отрезков В2В8, ..., Вп_хВп называют отре-
зок началом которого служит начало первого отрезка
и концом — конец последнего.
и Си на черт.
И
Черт. 4.
7. Векторы и их проекции. Прямолинейный отрезок АВ
плоскости, имеющий направление (от начала А к концу Б),
называется вектором и обозначается так\ АВ.
Многие физические величины (скорость, ускорение, сила
и т. п.) изображаются векторами. Длина отрезка АВ назы-
вается длиной (или модулем) вектора АВ и обозначается
через |ЛВ|.
Считается, что два непараллельных вектора имеют раз-
ные направления (например, векторы
Два вектора, параллельных или рас-
положенных на одной прямой, могут
иметь как одинаковые направле-
ния (векторы АВ и EF), так и про-
тивоположные (векторы АВ и GH,
см. черт. 4).
Векторы называются равными,
если они имеют одинаковые направ-
лена и равные длины.
Напомним теперь, что проекцией
точки на прямую называется осно-
вание перпендикуляра, опущенною из этой точки на прямую.
17
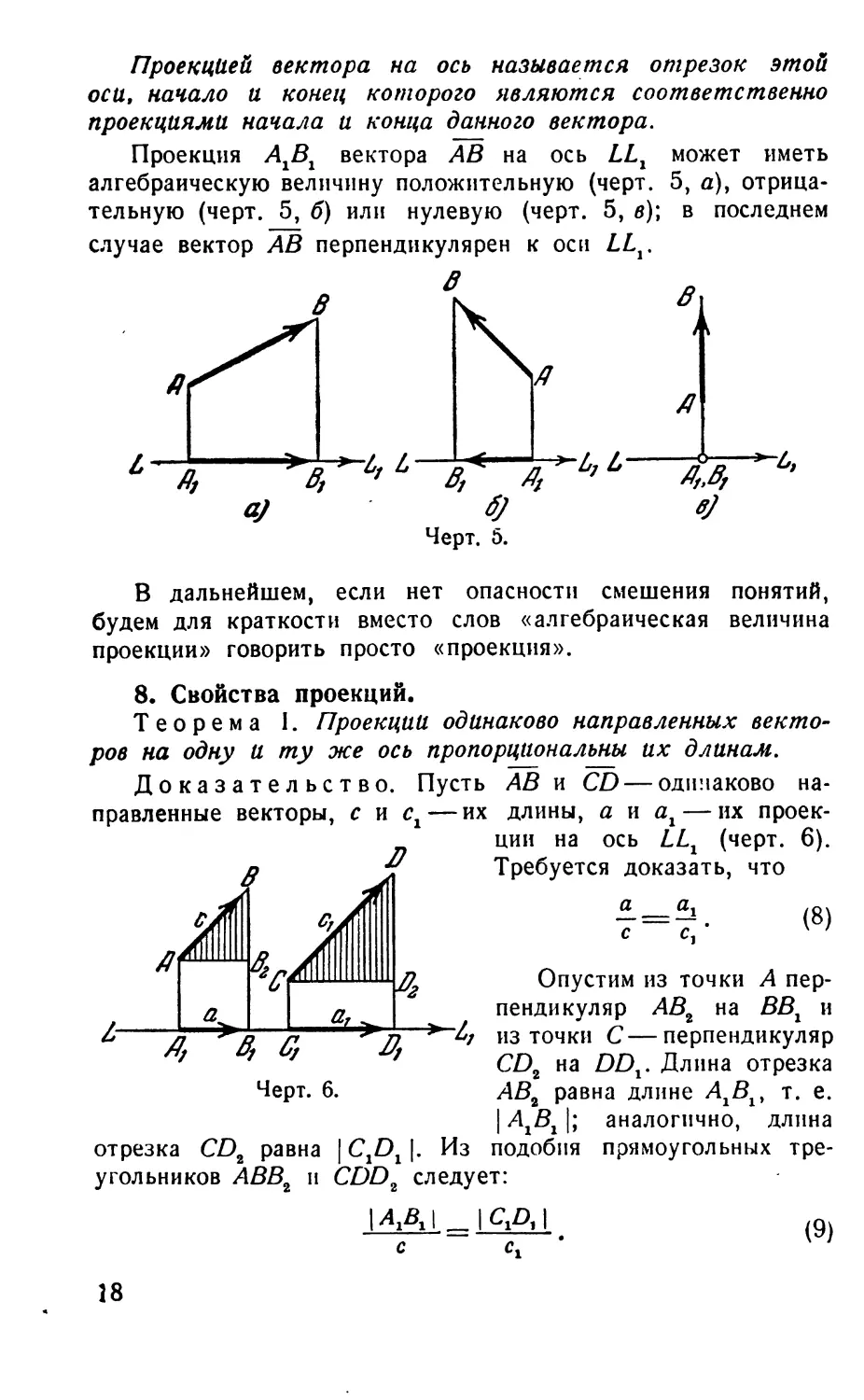
Проекцией вектора на ось называется отрезок этой
оси, начало и конец которого являются соответственно
проекциями начала и конца данного вектора.
Проекция А1В1 вектора АВ на ось LLX может иметь
алгебраическую величину положительную (черт. 5, а), отрица-
тельную (черт. 5, б) или нулевую (черт. 5, в); в последнем
случае вектор АВ перпендикулярен к оси LLt.
В дальнейшем, если нет опасности смешения понятий,
будем для краткости вместо слов «алгебраическая величина
проекции» говорить просто «проекция».
8. Свойства проекций.
Теорема 1. Проекции одинаково направленных векто-
ров на одну и ту же ось пропорциональны их длинам.
Доказательство. Пусть АВ и CD — одинаково на-
правленные векторы, с и сх— их длины, а и аг — их проек-
ции на ось LLr (черт. 6).
Требуется доказать, что
- = (8)
с с, ' '
Опустим из точки А пер-
пендикуляр АВ2 на ВВг и
из точки С—перпендикуляр
CD2 на DDr. Длина отрезка
АВ2 равна длине АХВГ, т. е.
| АгВг |; аналогично, длина
подобия прямоугольных тре-
угольников АВВ2 и CDD2 следует:
= (9)
с q *
Черт. 6.
СО оавна I C D I. Из
18
Проекции /AjBj и CJ[\ имеют на оси одинаковое
направление. Поэтому или обе они положительные, или обе —
отрицательные. В первом случае а==|41В1|1 al — и
пропорция (9) совпадает с пропорцией (8). Во втором слу-
чае а — — | |, at = — | ClDl | и пропорция (8) получится
из пропорции (9) умножением обеих частей на — 1. Теорема
доказана.
Следствие. Равные векторы имеют равные проекции.
Рассмотрим теперь ломаную AtA%A9.. .An_tAn (на черт. 7
взято /z = 5), составленную из векторов 4^, Д2Д8,..Дя-1 Ая.
Эти векторы называются
составляющими ломаной,
а вектор АгАп — замы-
кающим (он называется
также суммой данных
векторов).
Теорема 11. Проек-
ция замыкающего векто-
ра на ось равна сумме
проекций составляющих
векторов на ту же ось.
Доказательство. Черт. 7.
Обозначим через В2,
В3, ... , Вп_^ Вп проекции вершин 4Х, Д2, Д8, ... , Лп-1, Ап
ломаной на некоторую ось LLt. Проекциями составляющих век-
торов являются отрезки ВХВ2, В2Вг, ... , Вп_1Вп оси LLr
По правилу сложения отрезков оси (п. 6) сумма этих отрез-
ков есть отрезок ВхВп. Но ВгВп есть проекция замыкающего
вектора АхАп. Следовательно, алгебраическая величина про-
екции замыкающего вектора равна сумме алгебраических
величин проекций составляющих векторов, ч. т. д.
§ 3. Обобщение понятий угла и дуги
9. Углы и дуги, меньшие 360°. Так же как у отрезков
мы различаем начальную и конечную точки, мы будем теперь
различать у углов начальную и конечную стороны.
Через АОВ будем обозначать угол с начальной стороной ОА
и конечной ОВ. Мы будем считать, что угол АОВ образован
вращением подвижного луча вокруг точки О от начальной
стороны ОА № конечной стороны ОВ.
На плоскости возможны вращения в двух противополож-
ных направлениях: в направлении против движения
19
часовой стрелки и в направлении по движению
часовой стрелки. Пока мы будем рассматривать вращения
лишь против движения часовой стрелки.
Начальную сторону угла между вектором и осью мы
всегда считаем направленной по оси (в ее положительном
направлении). Иначе говоря, угол между вектором и осью
мы отсчитываем от оси.
Рассмотрим углы, образованные подвижным вектором ОЕ
с осью LLt (черт. 8). При вращении вектора ОЕ вокруг
точки О его конец Е описывает окружность с центром
в точке О.
Черт. 8. Черт. 9.
Проведем через точку О вторую ось ММХ под углом
в 90° к первой осп LLt. Обычно на чертежах ось LLX (от
которой отсчитываются углы) изображается горизонталь-
ной, направленной слева направо. Вторая ось изобра-
жается вертикальной, направленной снизу вверх.
Обе оси делят круг с центром в точке О на четыре
четверти: первая четверть АОВ. вторая — ВОС. третья —
COD и четвертая — DO А. Если сторона ОЕ угла АОЕ рас-
положена в первой, второй, третьей или четвертой четверти,
то угол АОЕ называется, соответственно, углом первой, вто-
рой, третьей или четвертой четверти.
Углы первой четверти (острые) заключены между 0° и
90°; углы второй четверти (тупые) заключены между 90° и
180°; углы третьей четверти заключены между 180° и 270°;
углы четвертой четверти заключены между 270° и 360°
(черт. 9).
20
Углы второй четверти можно представить в виде
или 180°—-jJ0, где а0 и ^ — острые углы (см. черт. 9);
углы третьей четверти — в виде 180°-(-а1 или 270° — plt
где а. и —острые углы; углы четвертой четверти — в виде
270° аг ИЛИ 36®° — |Де а2 и — острые углы.
Если вектор описывает угол АОЕ, равный а угловых гра-
дусов (см. черт. 8), то его конец описывает дугу АЕ окруж-
ности, равную а дуговым градусам. Точка /. является началь-
ной точкой этой дуги, а точка Е—ее конечной точкой.
Угол, равный 0° (нулевой угол), имеет совпадающие
стороны. Соответствующая ему дуга в 0° (нулевая дуга)
имеет совпадающие начальную и конечную точки.
Если точка Е опишет один раз всю окружность, то век-
тор ОЕ совершит вращение, равное полному обороту
(360°), и вернется к исходному положению.
10. Углы и дуги, большие 360°. До сих пор мы рассма-
тривали лишь вращения, не ббльшие полного оборота (360°).
Между тем часто приходится иметь дело с вращениями, ббль-
шими полного оборота, например с вращением ключа, охва-
тывающего гайку, вращением пропеллера и т. п. Таким образом,
понятие угла (и дуги) необходимо обобщить: ввести углы
(и дуги), ббльшие полного оборота (большие 360°).
Возьмем угол АОЕ—а, где 0^а<^360° (см. черт. 8).
Пусть подвижной вектор, вращаясь от положения ОА, сна-
чала сделает п полных оборотов, а затем опишет угол а.
Очевидно, он попадет в положение век юра ОЕ. Скажем,
что вектор описал угол, , равный л-360°4-&- Существует
бесконечное множество углов [I с начальной стороной ОА и
конечной стороной ОЕ. Они выражаются формулой
р = л-360°4-а, 0<а<360°, (10)
где п — любое целое число, положительное или нуль.
В технике углы измеряются иногда в частях полно! о
оборота. Если, например, лопасть винта сделала 7-i- пол-
ного оборота, то это значит, что она, сделав 7 полных обо-
ротов, повернулась еще на прямой угол (-i- полного оборота) .
У гол 7 ~ оборота в градусной мере равен 7 • 360° 90°= 2610°.
Когда вектор описывает угол £ = л •360°-|-а, ею конец
описывает дугу, равную сумме целого числа п полных
21
окружностей и дуги а. Существует бесконечное множе-
ство дуг, имеющих данное начало А и данный конец Е. Они
также выражаются формулой (10).
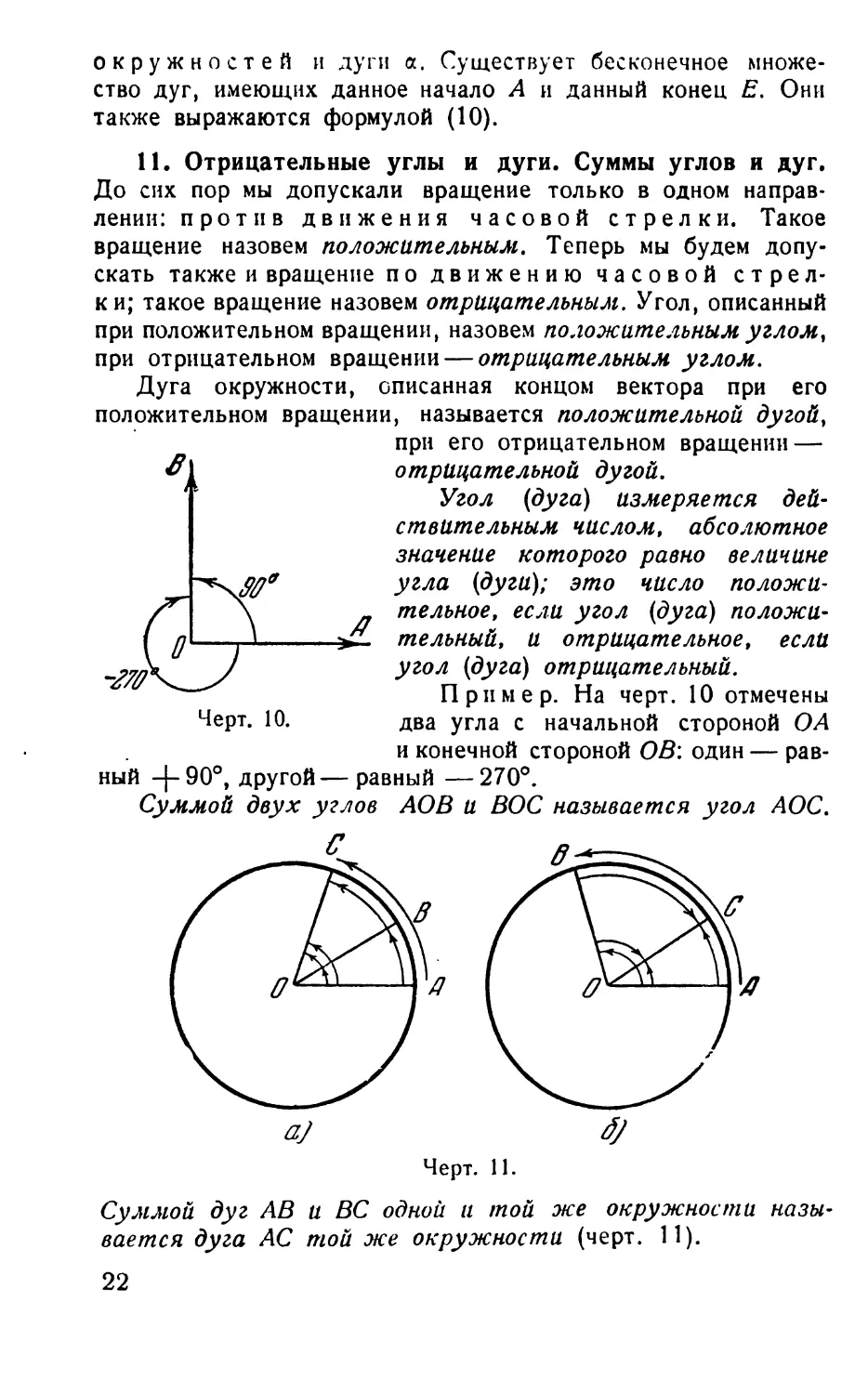
11. Отрицательные углы и дуги. Суммы углов и дуг.
До сих пор мы допускали вращение только в одном направ-
лении: против движения часовой стрелки. Такое
вращение назовем положительным. Теперь мы будем допу-
скать также и вращение по движению часовой стрел-
ки; такое вращение назовем отрицательным. Угол, описанный
при положительном вращении, назовем положительным углом,
при отрицательном вращении — отрицательным углом.
Дуга окружности, описанная концом вектора при его
положительном вращении, называется положительной дугой,
при его отрицательном вращении —
отрицательной дугой.
Угол (дуга) измеряется дей-
ствительным числом, абсолютное
значение которого равно величине
угла (дуги); это число положи-
тельное, если угол (дуга) положи-
тельный, и отрицательное, если
угол (дуга) отрицательный.
Пример. На черт. 10 отмечены
два угла с начальной стороной ОА
и конечной стороной ОВ: один — рав-
ный -|-90О> ДРУгой—равный —270°.
Суммой двух углов АОВ и ВОС называется угол АОС.
Суммой дуг АВ и ВС одной и той же окружности назы-
вается дуга АС той же окружности (черт. 11).
22
Сумма углов или дуг измеряется алгебраической суммой
чисел, измеряющих эти углы или дуги.
Если в формуле (10)
£ = п • 360° а, 0 а < 360°,
считать, что п есть не только положительное, но и отрица-
тельное целое число, то эта формула станет пригодной для
выражения любого как положительного, так и отрицатель-
ного угла.
Пример. —1000° = —3-360° 4-80° (л= —3, а = 80°).
Заметим, что все углы ft, выражаемые по формуле (10)
при различных л, но одном и том же а, имеют общие на-
чальную и конечную стороны. В силу этого построение
любого угла [J сводится к построению соответствующего
положительного (или нулевого) угла а, мень-
шего 360°.
§ 4. Тригонометрические функции
и их простейшие свойства
12. Определение тригонометрических функций. Рассмо-
трим на плоскости две оси: ось LLX (горизонтальная ось на
черт. 12) и ось ЛШХ, образующую с осью LLX угол 90°
(вертикальная ось на черт. 12).
Пусть вектор ОЕ длины с образует угол АОЕ*=а.
с осью LLX. Обозначим через ах его проекцию ОЕХ на
ось LLlt а через а2 — его проекцию ОЕ2 на ось ММг. Для
краткости будем называть ось LLX (от которой отсчитываются
углы) первой осью, ось МЩ — второй осью, а числа
ах и а2 — соответственно первой и второй проекциями
вектора ОЕ.
Если а — положительный острый угол (черт. 12, а), то
направления проекций ОЕХ и ОЕ2 совпадают с направлениями
соответственных осей: аг и а2— числа положительные, рав-
ные длинам отрезков ОЕг и ОЕ2.
В прямоугольном треугольнике ОЕХЕ гипотенуза ОЕт=с\
катет ОЕ1 = а1( = Ь)\ катет Е1Е=а2( — а} (см. стр. 8,9).
Из этого прямоугольного треугольника, в силу принятого
определения тригонометрических функций острого угла (см.
стр. 9), имеем:
а9 я, а, ., t.
sin а = у-, cos а = -у-, tga = ^, ctga=^. (11)
Исходя из равенств (II), мы 1еперь определим тригоно-
метрические функции произвольного угла.
23
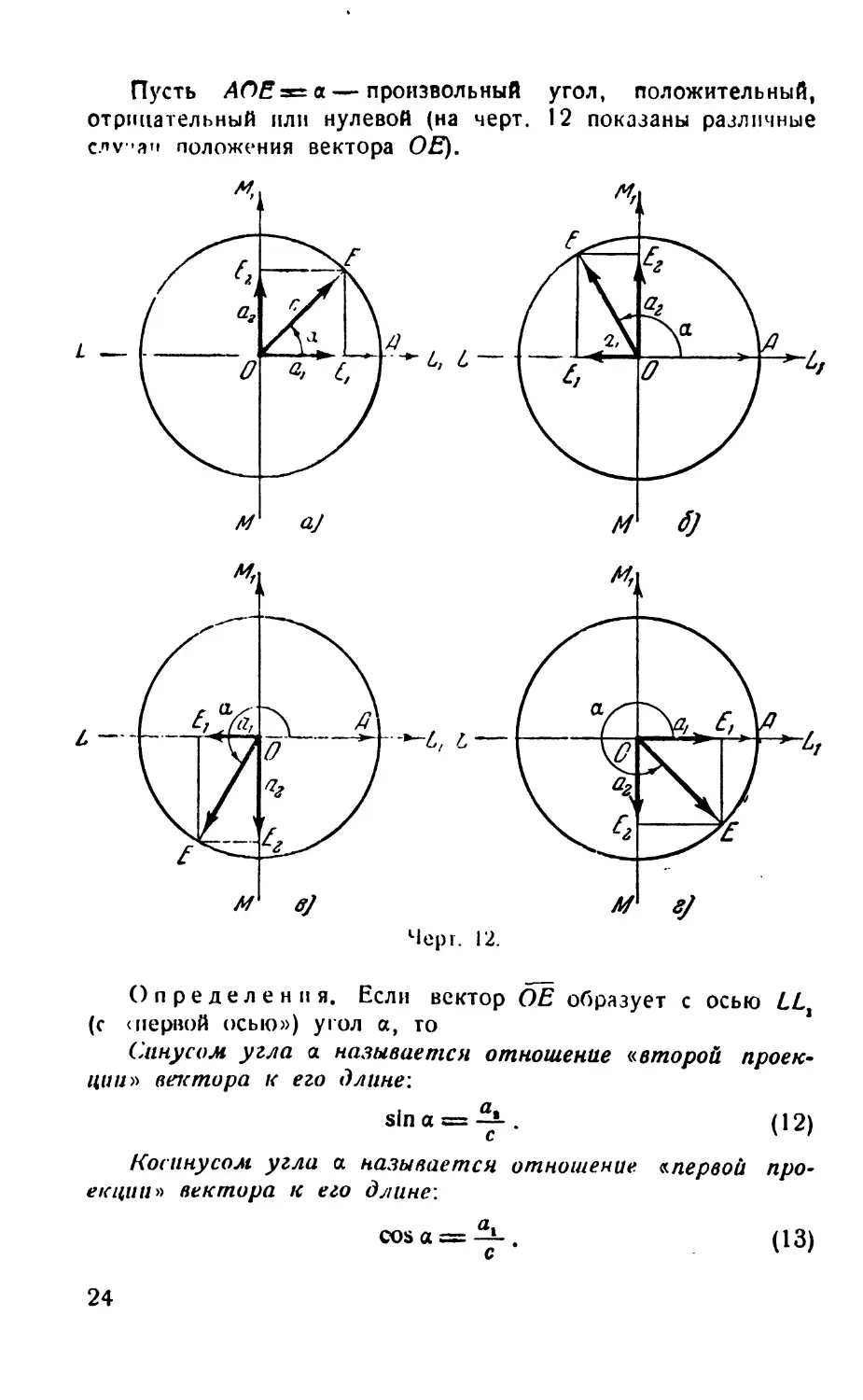
Пусть АОЕ== а — произвольный угол, положительный,
отрицательный или нулевой (на черт. 12 показаны различные
c.nv ’ап положения вектора ОЕ}.
Черт. 12.
Определения. Если вектор ОЕ образует с осью LL*
(с <первой осью») угол а, то
Синусом угла а называется отношение «второй проек-
ции» вектора к его длине:
slna = -^-. (12)
Косинусом угла а называется отношение, «первой про-
екции» вектора к его длине:
cosa = ^-. (13)
24
Тангенсом угла а называется отношение «второй про-
екции» вектора к его «первой проекции»*.
tga==^'' (,4)
Котангенсом угла а называется отношение «первой
проекции» вектора к его «второй проекции»:
ctga='§'- (15)
Аналогично определяются еще две тригонометрические
функции, так называемые секанс (sec...) и косеканс
(cosec.. .).
Секансом угла а называется отношение длины вектора
к его «net вой проекции»:
seca=-^-- (16)
Косекансом угла а называется отношение длины век-
тора к его «второй проекции»:
cosec a =— . (17)
&9
В последующем секанс и косеканс мы специально рассматри-
вать не будем, так как они очень просто выражаются через
синус и косинус:
sin a
, определяющие
cos a
Это прямо следует из определений.
Теорема. Отношения — , — ,
с с .
тригонометрические функции угла а, не зависят от длины
вектора ОЕ; они зависят только от угла а.
Доказательство. Рассмотрим наряду с вектором ОЕ
длины с вектор OF длины с\ образующий тот же угол a
с первой осью; обозначим через а' и a’t первую и вторую про-
екции вектора OF. В силу теоремы I п. 8 проекции аа и а\
векторов ОЕ и OF пропорциональны их длинам:
с с'
25
Аналогично:
_5_ = fL
с с'
Почленным делением этих равенств получаем также ра-
венства:
* а\ а ' at а
1 2
Мы видим, что значения sin a, cos а, tga, ctg а действи-
тельно не зависят от длины взятого вектора.
Если первая проекция оказывается равной нулю (ах = 0),
то тангенса угла а не существует. В самом деле, в этом
случае дробь , посредством которой определяется tga, не
имеет смысла.
Если вторая проекция оказывается равной нулю (аа = 0),
то по аналогичной причине не существует котангенса.
Пример, у/ АОЕ = а —— 45°. Имеем (черт. 13):
/2 /2
= а* = -с — ’
Находим!
• / V 2 , .-Оч а. У" 2
sin (— 45°) = -^ =---; cos (— 4о°) = ;
tg(-45°) «=£’=- 1; ctg(-45°)=^ = -l.
Дадим теперь важную формулу для проекции век-
тора на ось. Именно:
Проекция вектора на ось равна длине вектора, умно-
женной на косинус угла вектора с осью.
В самом деле, из формулы (13) непосредственно следует:
ах— fcosa. (19)
Эта формула означает, что проекция (ах) некоторого век-
тора (ОЕ) на ось (LLJ. с которой этот вектор образует не-
который угол (а), равна длине вектора, умноженной на ко-
синус угла между вектором и осью. ’
26
Формула (19) выведена в предположении, что начало
вектора (О) лежит на оси проекции. Однако эта формула
справедлива всегда. В самом деле, пусть задан любой вектор
длины с, образующий угол а
с осью проекции. Возьмем
другой вектор с началом в ка-
кой-нибудь точке оси проекции
и равный данному. Тогда этот
вектор имеет ту же длину с с
и образует тот же угол а с
осью проекции; в силу же
свойств проекций (см. п. 8) оба
вектора имеют равные проек-
ции на ось. Так как формула
(19) справедлива для второго
вектора, то она справедлива и
для данного вектора.
Замечание. Как мы знаем,
(20)
существует бесконечное
множество углов с начальной стороной ОА и конечной ОЕ.
Они выражаются формулой (10) (см. стр. 21):
Р = д.360°4-а (л = 0, ±1, ±2, ...).
Так как всем этим углам соответствуют одни и те же
числа ах, а2, с (проекции и длина одного и того же век-
тора ОЕ), то имеют место равенства:
sin (п • 360° а) = sin а;
cos (п • 360° а) = cos а;
tg (п • 360° 4- а) = tg а;
ctg (п • 360° а) = ctg а.
Обозначения этого параграфа мы сохраняем во всей главе.
13. Знаки тригонометрических функций. Выясним теперь
знаки тригонометрических функций для углов, заключенных
между 0° и 360° х).
Знак синуса. Синус положителен в первой и вто-
рой четвертях, отрицателен в третьей и четвертой чет-
вертях.
') Для краткости будем вместо выражения «т р и г о н о м е т р и-
ческал функция для углов в первой, во второй,...
четверти» употреблять выражение «тригонометрическая
Функция в первой, во второй, ... четверти».
27
В силу формулы (12)
а»
sma=:-
с
знак синуса совпадает со знаком с., = ОЕ2 (ибо длина с —
всегда положительное число).
В первой и второй четвертях проекция ОЕ2 направлена
вверх и, значит, а2 имеет знак плюс, а в третьей и в чет-
вертой четвертях проекция ОЕ2 направлена вниз и, значит,
а2 имеет знак минус.
Знак косинуса. Косинус положителен в первой и
четвертой четвертях, отрицателен во второй и третьей
четвертях.
В силу формулы (13)
а,
cos а = —
с
знак косинуса совпадает со знаком а1 = ОЕ1\ в первой и
четвертой четвертях ах положительно, так как проекция ОЕХ
направлена вправо, а во второй и третьей четвертях ах отри-
цательно, так как проекция ОЕХ направлена влево.
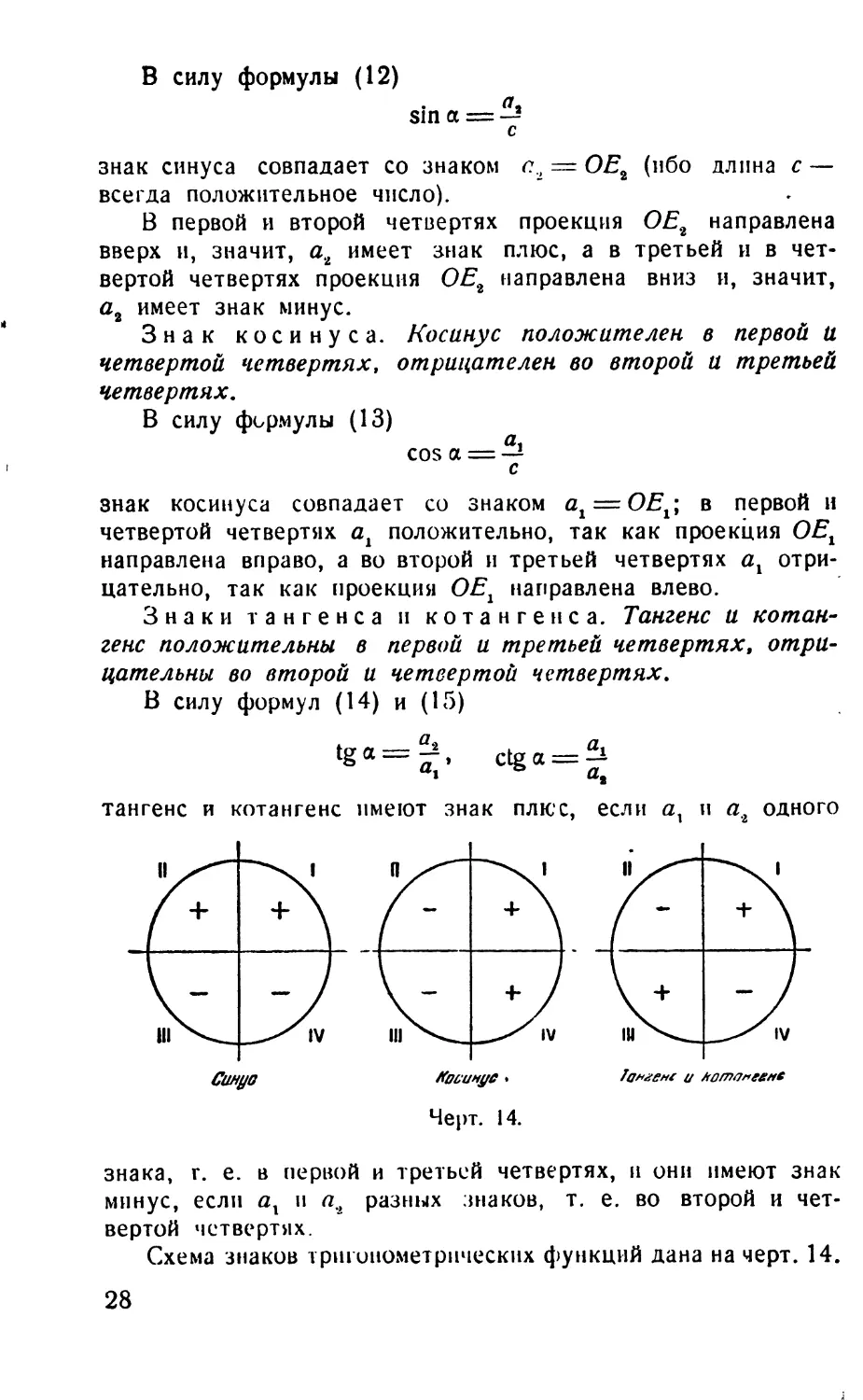
Знаки тангенса и котангенса. Тангенс и котан-
генс положительны в первой и третьей четвертях, отри-
цательны во второй и четвертой четвертях.
В силу формул (14) и (15)
‘ёа=Н;. ctga = ^i
тангенс и котангенс имеют знак плюс, если ау и а2 одного
Синуо косинус• Тангенс и го/панеенс
Черт. 14.
знака, г. е. в первой и третьей четвертях, и они имеют знак
минус, если ах и а2 разных знаков, т. е. во второй и чет-
вертой четвертях.
Схема знаков тригонометрических функций дана на черт. 14.
28
14. Значения тригонометрических функций некоторый
углов. ___________________________ ____________________
Угол 0°. Подвижной вектор ОЕ занимает положение ОА
(черт. 15), значит, ау = с, а2 = 0. Следовательно:
sin0° = —= 0; cosO°==—=1; tgO°=- = O.
С ’ С ’ ь с
Котангенса угла 0° не существует (так как л2 = 0).
Угол 90°. Подвижной вектор ОЕ занимает положение ОВ
(черт. 15), а1 = 0, а2 = с. Следовательно:
Sin 90°= ± = 1; cos90° = ^- = 0; ctg90° = ~^0.
Тангенса угла 90° не существует.
Угол 180°. Подвижной вектор ОЕ занимает положе-
ние ОС (черт. 15), аг — — с, а2 = 0. Следовательно:
sin 180° = —= 0, cos 180° = — — - 1, tgl80° = —= 0.
с ’ с — с
Котангенса угла 180° не существует.
Черт. 15.
Угол 270°. Подвижной вектор ОЕ занимает положе-
ние OD (черт. 15), а1=0, — — с. Следовательно:
sin 270° = — =— I, cos 270° = — = 0, ctg270°=— =0.
С ’ с ’ ь —с
Ташенса ума 270° не существует.
29
Приведем таблицу уже известных нам значений тригоно-
метрических функций для углов а = 0°, 30°, 45°, 60°, 90°,
180°, 270° (стр. 10 и 29).
0° 30° 45° 60° 90° 180° 270°
sin a 0 1 2 К2 2 r tel > 1 col 1 0 - 1
cos a 1 /3 2 /2 2 1 2 0 - 1 0
tga 0 Гз 3 1 /3 — 0 —
ctg а — /з 1 Гз 3 0 — 0
15. Построение значений тригонометрических функций.
Синус, косинус. Пусть теперь вектор ОЕ есть еди-
ничный вектору т. е. его длина в выбранном масштабе
равна 1(г=1). Формулы (12) и (13) примут вид:
sina = at; cosa = ax.
Находить значения sin а и cos а построением и измерением
особенно удобно на основании именно этих формул.
Построим (черт. 16) оси LLX и Л42И1; отложим единичный
вектор ОЕ под углом а к оси LLX\ проведем его проекции
ai—OE1 — EiE и аг = ОЕг =EtE.
Проекции ЕгЕ для различных углов и дают значения си-
нуса (на черт. 16, а они изображены жирными отрезками).
Проекции Е*Е (черт. 16, 6} дают значения косинуса.
Тангенс. Через точку А первой оси (черт. 17) прове-
дем вертикальную ось РРХ, направленную снизу вверх. Эта
ось касается в точке А единичной окружности (т. е.
окружности радиуса 1). Пусть вектор ОЕ образует угол a
с первой осью. Продолжим* прямую, на которой располо-
жен вектор ОЕ, до пересечения ее в точке G с осью РРХ.
Докажем, что алгебраическая величина d отрезка АО
оси РРг равна значению tga.
Рассмотрим отдельно два случая.
30
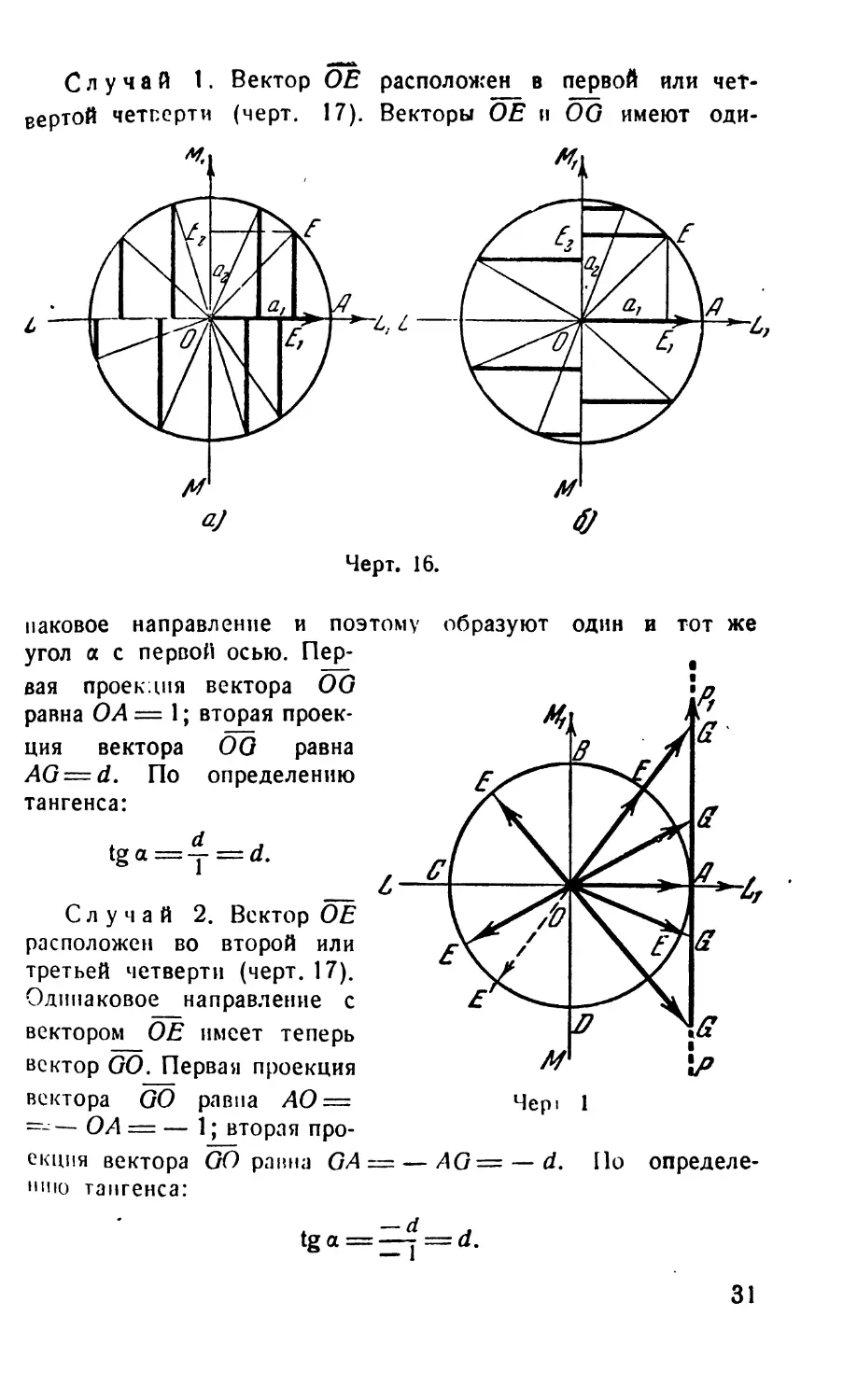
Случай 1. Вектор ОЕ расположен в первой или чет-
вертой четверти (черт. 17). Векторы ОЕ и OG имеют оди-
Черт. 16.
паковое направление и поэтому образуют один и тот же
угол а с первой осью. Пер-
вая проекция вектора 00
равна О А = 1; вторая проек-
ция вектора 00 равна
AG = d. По определению
тангенса:
, d а
tgb=-r = d.
_ L
Случай 2. Вектор ОЕ
расположен во второй или
третьей четверти (черт. 17).
Одинаковое направление с
вектором ОЕ имеет теперь
вектор 00. Первая проекция
вектора 00 равна АО =
--— О А = — 1; вторая про-
екция вектора GO равна GA —
нию тангенса:
AG= — d. По определе-
. ~d а
tga=-rf=d.
31
Итак, наше предложение доказано в обоих случая^.
Если а = 90° или а = 270°, то вектор ОЕ параллелен
оси РРХ и прямая, на которой он лежит, не пересекает ось
(точки G не существует). Это и является геометрической ил-
люстрацией того, что tg90° и tg270° не существует.
Из изложенного построения тангенса мы замечаем, что
тангенсы углов, отличающихся друг от друга на 180°, равны
между собой:
tg (180° + а) = tg а.
Действительно, векторы ОЕ и ОЕ\ образующие с первой
осью эти углы (см. черт. 17), лежат на одной прямой и
поэтому им соответствует одна и та же точка G, а значит,
и одно и то же значение tga.
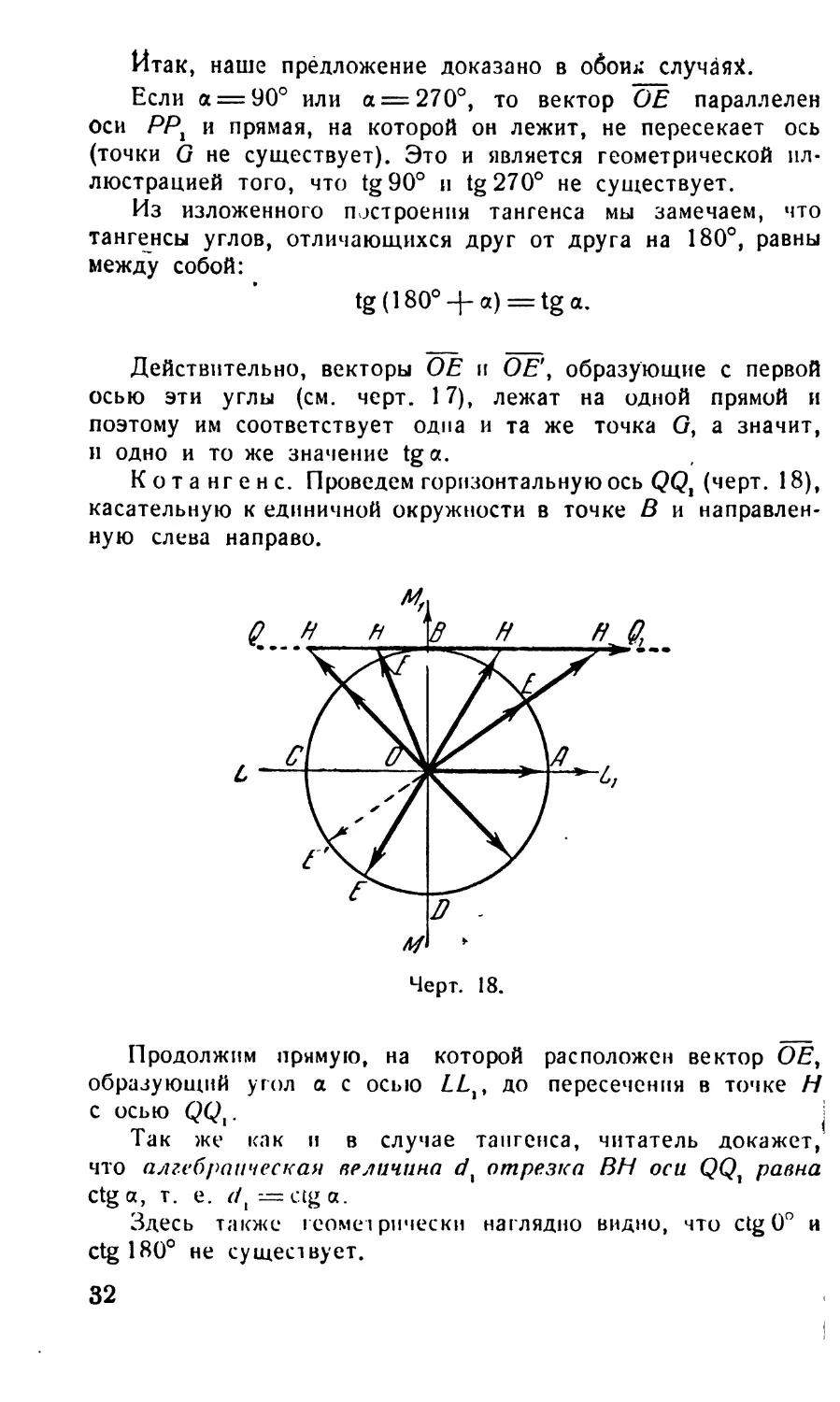
Котангенс. Проведем горизонтальную ось QQt (черт. 18),
касательную к единичной окружности в точке В и направлен-
ную слева направо.
Л/ ►
Черт. 18.
Продолжим прямую, на которой расположен вектор ОЕ,
образующий угол а с осью LLit до пересечения в точке Н
с осью QQX.
Так же как и в случае тангенса, читатель докажет,
что алгебраическая величина dx отрезка ВН оси QQX равна
ctg а, т. е. dx — ctg a.
Здесь также геометрически наглядно видно, что ctg 0° и
ctg 180° не существует.
32
Для котангенса, подобно тангенсу,
ctg (180° —а) = ctg а.
Эту формулу можно вывести также геометрически.
Из доказанных свойств тангенса и котангенса вытекают
следующие равенства:
tg(n-180°-|- а) — tga,
ctg (л • 180°a) — ctg а, /
где п — любое целое число пли нуль: л = 0, + 1, + 2. ...
В самом деле, раз углы, отличающиеся на один полуоборот
(180°), имеют одинаковые тангенс и котангенс, то углы, от-
личающиеся на любое целое число полуоборотов, также
имеют одинаковые тангенс и котангенс.
Рассмотрим теперь два примера обратной задачи: отыска-
ния углов по заданному значению тригонометрической функ-
ции. Эти примеры нам пригодятся в дальнейшем.
1. Найдем все углы а, для которых cos а = 1, т. е. для ко-
торых a1=OEl=z\ (см. п. 14). Это означает, что ОЕг со-
впадает с отрезком О А и угол а = ^АОЕ имеет совпадаю-
щие стороны. Следовательно, он равен целому числу п пол-
ных оборотов или нулю:
а = п»360°, л = 0, ±1, ±2, ...
2. Найдем все углы а, для-которых tgac=0. Из построе-
ния тангенса (см. черт. 17) следует, что если tga = O, то
отрезок AG есть нулевой отрезок п точка G совпадает
с точкой А. Вектор ОЕ при этом совпадает с вектором ОА
или вектором ОС. Значит, угол а = ^АОЕ равен целому
числу п полуоборотов; а = л-180°, п — 0, 4- 1, zb 2, ...
§ 5. Некоторые важнейшие формулы
16. Основные формулы.
Т е о р е м а. Между значениями тригонометрических
функций одного угла существуют соотношения [см. фор-
мулы (5)]:
• 21 2 1 sin a . cos a
sin a + cos a = 1, tga =------, ctg a — -—,
1 > ь cos я ’ ° sin a
называемые основными,
2 А. Бермант, Л, Люстерник 33
Доказательство. В п. 3 было доказано, что эти
соотношения имеют место для любого острого угла а.
Докажем теперь, что они справедливы для произволь-
ного угла а.
Пусть ОЕ — единичный вектор, образующий угол рс с пер-
вой осью (см. черт. 15). Значит, ах = ОЕг =з cos а, а2 = ОЕ2 =
= sina. В прямоугольном треугольнике ОЕгЕ имеем:
|О£|= 1, 10^ | = |cosa|, |£х£| = | 0Е21 = | sin а |.
Из теоремы Пифагора следует:
| sin a |* 4“ lcos a I* = 1-
При возвышении в квадрат знак абсолютной величины можно
опустить, и мы получаем:
sin* a cos* a = 1. (22)
Первая основная формула доказана.
Далее,
tga = —==—п-. (23)
® cosa Y '
Это — вторая основная формула.
Аналогично получаем третью основную формулу:
1 cos a
ctg a = -— . (24)
& sin a v '
Из основных формул (для произвольных углов а) можно
вывести ряд других формул. Например, из формул (23) и (24)
следует:
tg a = , ctg a = j-L. (25)
& ctg a’ & tga ' '
Точно так же из формул (23) и (22) вытекает:
. , sin8 a sin8 a
b cos2 a 1 — sinfc a
. sin8 a 1 — cos8 a
tg* a = —»------------•
& cos8a COS8a
Из последних формул получаем:
tg* a (1 — sin* a) = sin* a, tg* a cos2 a = 1 — cos* a,
откуда
sin* a = , cos* a = г-А . (26)
1 4“ tg2 a ’ 1 + tg2 a ' '
34
С помощью найденных формул можно отыскивать зна-
чения всех тригонометрических функций данного угла,
если известно значение одной из них.
В некоторых из употребляемых при этом формул встре-
чаются квадратные корни. Перед корнем может стоять тот
или другой из двух знаков в зависимости от величины угла.
Поэтому записывают, например, так:
cos а = 4- V1 — sin2 а, cos а =-.
— i/l+tg’a
Если угол а известен, то тем самым известны и знаки sin a,
cos a, tga и ctg a и перед квадратным корнем выбирается
соответствующий знак.
Пример, sin 135°= . Найти cos 135°, tgl35°,
ctg 135°.
Угол в 135° есть угол второй четверти, где косинус от-
рицательный. Следовательно:
cos 135° = —у 1—sin2 135°=— 1== —О;
и дальше:
ctg,35O=^=-1-
17. Тригонометрические тождества.
Определение. Тригонометрическим тождеством на-
зывается равенство, содержащее тригонометрические фун-
кции угла и справедливое при всех значениях этого угла.
Три основные формулы (22), (23) и (24) являются триго-
нометрическими тождествами; они справедливы для любого
угла а. Тождествами являются также и равенства (25) и (26).
Разумеется, при этом не принимаются в расчет
те значения угла а, для которых хотя бы одна
из входящих в равенство функций не существует.
Например, равенство tg a ctg a = 1 есть тригонометрическое
тождество, так как оно справедливо для всех углов а, за
исключением тех, для которых тангенс или котангенс не су-
ществует (0°, 90°, 180°, 270°, ...).
Из одних тригонометрических тождеств с помощью алгеб-
раических преобразований можно получить другие тригоно-
метрические тождества. Таким путем выведены, например,
тождества (25) и (26) из тождеств (22) — (24).
2*
85
О тождествах говорят, что они зависимы Друг о.
друга, если некоторые из них можно вывести из других!
В таком случае говорят также, что одни из них являются
следствиями других.
Из трех основных формул (22) — (24) можно образовать
сколько угодно формул, являющихся их следствиями. Но самг
основные формулы не зависят друг от друга: нельзя одну щ
них вывести из двух остальных. Основные формулы получа-
ются независимо одна от другой на основании самих опреде-
лений тригонометрических функций.
Три любых независимых тождества, связывающих четыре
тригонометрические функции, например одна из формул (25]
и формулы (26), позволяют по значению одной из них найти
значения остальных.
Иногда требуется доказать тождество, т. е. установить,
что данное равенство действительно является тригонометри-
ческим тождеством. Для этого нужно или посредством тож<
дествснных алгебраических преобразований и основных фор-
мул (22)— (24) привести заданное равенство к уже известному
тождеству или, исходя из какого-нибудь известного тождест-
ва, с помощью тождественных алгебраических преобразова-
ний и основных формул придти к данному равенству.
Пример. Доказать тождество
sin8 a (1 + ctg a) 4~ cos8 a (1 4“ tg a) = sin a cos a.
Заменим в левой части tga и ctgа их выражениями по
формулам (23) и (24). Получим:
sin8 a
cos a
.я sin a -4- cos a । 8 COS з + Sin a
= sin8 a-------г---— + cos8 a------!------=
Sin a 1 COS a
= sin9 a (sin a 4" cos a) -|- cos2 a (sin a 4“ cos a) =
— (sin2 a 4- cos2 a) • sin a 4“ cos a) = sin a 4~ cos a.
Последнее преобразование выполнено с помощью формулы
(22). Приходим к очевидному тождеству
sin a 4~ cos a = sin a 4~ cos a.
Этим доказано исходное тождество.
18. Изменение знака угла. Выразим теперь тригономет-
рические функции угла —а через тригонометрические функ-
ции угла а.
36
Теорема. При перемене знака угла значение косинуса
|f це меняется, а значения синуса, тангенса и котангенса
Линяют только свой знак.
Доказательство. Пусть дуга АЕ единичной окруж-
ности равна а; симметричная с ней относительно первой оси
LL дуга AF (черт. 19) равна —а. Соответствующие этим ду-
гам центральные углы
АОЕ и ЛО/7 равны соот-
ветственно а и—а. Так
как векторы ОЕ и OF
симметричны относитель-
но оси, то их пер-
вые проекции совпадают:
qE1 — OF1. Эти проекции £
равны соответственно cos а
и cos (— а); отсюда сле-
дует, что
cos (— а) = cos а. (27)
Вторые же проекции ОЕ2
и OF2 равны по абсолют-
ной величине в противо-
положны по знаку. Эти
проекции равны соответст:
следует, что
sin (— а) = — sin а. (28)
Далее находим:
а / \ sin ( — а) — sin а , \
< - °) - ~"Eosa = ~ ‘8 “ -
11 (29)
ctg (— а) = -г—.---. = —г— = — ctg а,
5 ' tg(—а) — tga 6 » ;
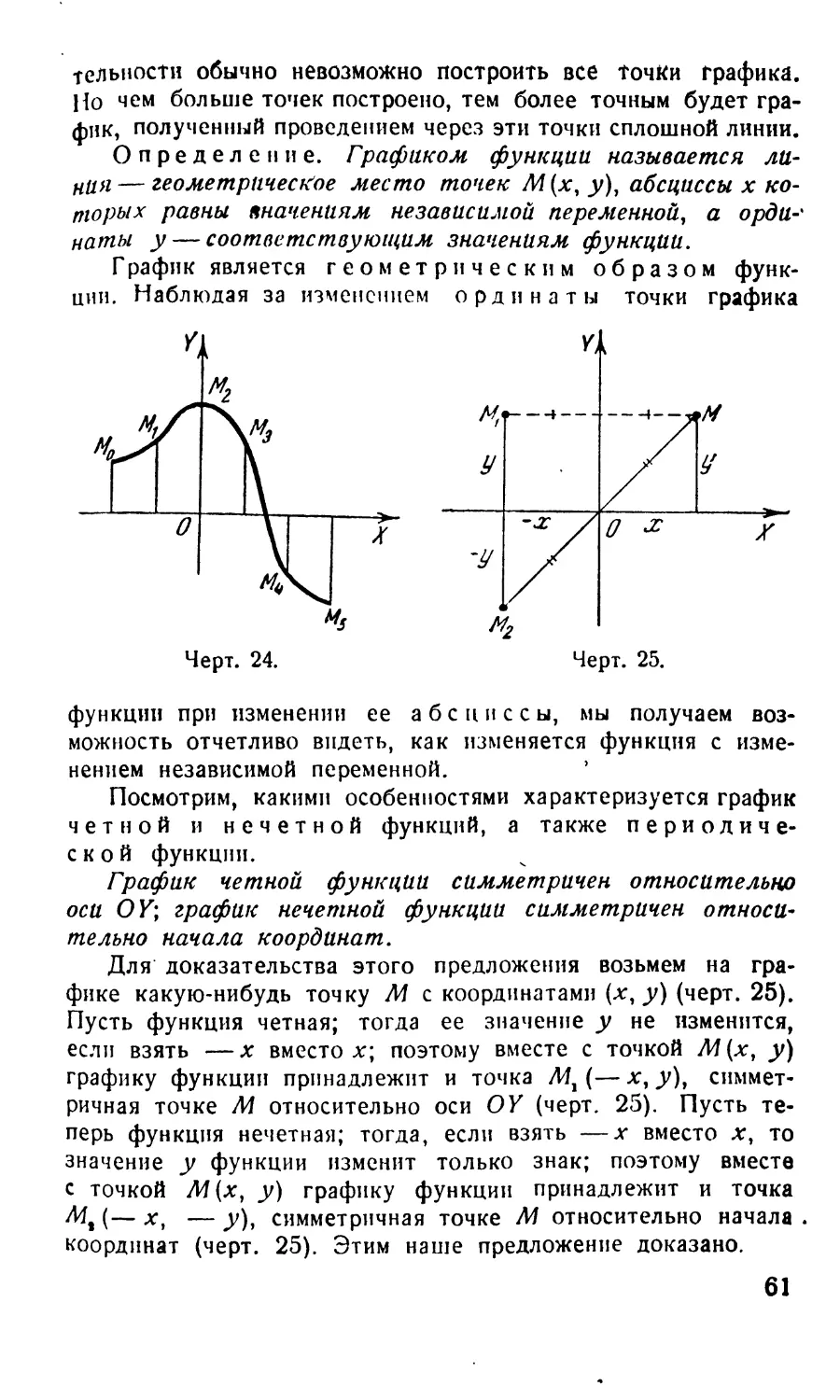
Определение. Если функция не меняет своего зна-
чения при изменении знака у любого значения своего аргу-
мента, то она называется четной функцией', если же зна-
чение функции меняет только свой знак при изменении знака
у любого значения аргумента, то она называется нечетной
функцией.
Формулы (27) — (29) показывают, что cos a — четная функ-
ция угла а, а sin a, tga и ctgа — нечетные функции угла а.
Другими примерами четных функций могут служить функ-
ции у/ = х2, у = х* и т. п. аргумента х, а нечетных функ-
ций— функции у = х, у — хъ и т. п. аргумента х.
37
Формулы (27) — (29) позволяют выразить значения тригоно;
метрических функций отрицательных углов через значе»
ния тригонометрических функций положительных углов.
Пример ы.
i/''Т t/’v
sin (— 45°) = — sin 45° ; Cos (—45°)=cos 45°= Г— ;
tg(—45°) =— tg45°=— 1; ctg (—45°)=—ctg 45°=—1.
19. Тригонометрические функции дополнительных углов,
Теорема. Для произвольного угла а существуют со-
отношения:
sin (90° — а) — cos а; cos (90° — а) = sin а. (7]
tg (90° — а) — ctg а; ctg (90° — а) — tg а. (7')
[Углы а и 90°—с/ —дополнительные; см. соотношения
(7) и (7') на стр. 12.]
Доказательство. Справедливость этих соотношений
для любого острого угла была доказана в п. 4, а теперь
мы докажем их для про-
извольного угла.
Если единичный век-
тор ОЕ образует угол а
с первой осью LLX (на
черт. 20 угол а взят
во второй четверти), то со
второй осью Л!Л11 он об-
разует угол $=а — 90°.
Проекция ОЕ2 векто-
ра ОЕ на ось AlAIj равна,
по определению синуса:
ОЕ2 = sin «.
С другой стороны, по фор-
муле проекций (19) та же проекция равна:
ОЕй = 1 • cos (а — 90°) = cos (90° — а)
(косинус не меняется от перемены знака угла).
Сравнивая два последних равенства, получаем вторую фор-
мулу (7):
cos (90° — а) — sin а.
38
Если в л ой формуле вместо угла а взя1ь угол 90°—го
придем к первой формуле (7):
cos а — sin (90° — а).
0з формул (7) вытекают формулы (7'), ч. т. д.
§ 6. Приведение к острому углу
20. Приведение к углу, меньшему 360°. Обратимся к важ-
ной задаче приведения тригонометрических функций к
острому углу, т. е. к задаче выражения тригонометриче-
ских функций любого угла через тригонометрические функ-
ции острого угла.
На Основании формул (20) мы можем сразу привести
тригонометрические функции любого угла к тригонометриче-
ским функциям неотрицательного угла, меньшего
360°. В самом деле, любой угол [5 можно представить так:
^ = //•360°+а, 0<а<360°, /z = 0, ±1, ±2, ... (10)
Формулы же (20) дают:
sin р = sin a, cos = cos а, tg [J = tg а, ctg [J = ctg а.
Пример. 750° — 2 • 360°-j-30°, откуда
sin 750° = sin 30°= |; cos 750° = cos 30° = ; ...
Что же касается специально тангенса и котангенса, то их
на основании формул (21) можно сразу привести и к
углу, меньшему 180°.
Пример.
tg 585° = tg (3 • 180° —45°) = tg 45° = U
21. Формулы приведения.
Определение. Формулами приведения Называются
формулы, выражающие тригонометрические функции углов
90° ± а, 180° +а, 270° ± а, 360° —а
через тригонометрические функции угла а.
Углы 180° -4- а, 360° — а можно считать образованными
откладыванием угла а от первой оси; углы 90°-4-а, 270°-4-а
— откладыванием угла а от второй оси.
Мы уже вывели для произвольных углов а форму-
лы (7):
sin (90° — а) = cos а, cos (90° — а) = sin а. (А)
89
Заменим в этих формулах а на—а и, значит, 90° — а
90°-|~а. Мы получим:
sin (90° Ц- а) = cos (— а) = cos а;
cos (90° -j- а) = sin (— а) — — sin а.
Снова пользуясь произвольностью угла а, заменим здесь а на
90°4»а, а значит, 90°4"ана 180°—а; найдем следующую
пару формул:
sin (180° + а) = sin [90° + (90° + а)] =
= cos (90° а) = — sin а; (BJ
cos (180° + а) = cos [90° ф (90° + а)] =
= — sin (90° -|- а) = — cos а. (Cx)j
Далее: i
sin (270° + а) = sin [90° + (180° + а)] =
— cos (180° -J- а) = — cos а; (В2)
cos (270° + а) = cos [90° + (180°+ а)] =
= — sin (180° -|- а) = sin а. (С2)
Из четырех последних формул, справедливых для любого а,
заменой а на — а получаем следующие четыре
sin (180° — а) = sin а;
cos (180° — а) = — cos а;
sin (270° — а) — — cos а;
cos (270° — а) = — sin а.
Наконец, поскольку значения одноименных
ческих функций углов, отличающихся на 360°,
собой, получаем:
sin (360° — а) = sin (— а) = — sin а;
cos (360° — а) = cos (— а) = cos а.
формулы:
(В3)
(С3)
(В<)
(С.)
тригонометри-
равны между
(В6)
(CJ
Теперь можно легко вывести формулы приведения
генса и котангенса:
. , ПЛО ч sin (90° — a) cos а
tg ( 90° — а) — —\ = -г- — ctg а;
® ' cos (90° — а) sin а & *
. . ПЛО I ч sin (90° + а) cos а
tg( 90 + а) = cos (90о а) = -^Га = - ctg а;
ta(1RO° „ч Sin (180°-а) sin а
tg(180 — _з
для
тан-
tg а;
40
ctg( 90° —a) = ~5^—.=,-^_ = tg«;
ctg ( 90° + a) — tg (g(JO _j_ a) «= 77^-g- = — tg a;
Ctg (180° — я) = ет(}о- -а) - "4g4 = “ c‘g “•
Мы не указываем остальных формул приведения для тан-
генса и коташенса, поскольку значения этих функций не ме-
няются от прибавления к аргументу 180°.
Нет необходимости запоминать каждую формулу приве-
дения в отдельности, потому что они строятся по одному
правилу.
Правило приведения. В левой части каждой фор-
мулы приведения стоит «приводимая» функция (т. е. три-
гонометрическая функция угла ft — 90° Ч- ст, 180°£-а, 270°Ч-а.
360° — с); в правой части формулы стоит одноименная
или сходственная функция угла а, снабженная знаком
или — (знак обыкновенно опускается).
Для углов ft — 180° Ч- о?, 360° — а, образованных откла-
дыванием утла а от первой (горизонтальной) оси, в правой
части стоит одноименная функция; для углов ft —90°Ч-а,
270° Ч- а, образованных откладыванием утла а от второй
(вертикальной) оси, стоит сходственная функция.
Остается указать лишь знак, который нужно брать перед
(.приведенной» функцией (т. е. в правой части формул). Фор-
мулы приведения, верные для всех углов а, верны, в частно-
сти, и для острых углов а. Но если угол а острый, то угол ft
есть угол вполне определенной четверти, что сразу указывает,
какой знак имеет приводимая функция. Этот знак и
ставится перед функцией в правой части
формулы.
Примеры. Составим формулы приведения для:
1) tg (90° a); 2) cos (360°—а) прямо на основании указан-
ного правила.
1) Угол 90° 4- а образован откладыванием угла а от вто-
рой (вертикальной) оси; поэтому в правой части формулы
приведения должна быть сходственная функция, т. е. ctg a
со знаком 4- или —. Если угол а острый, то угол 90° 4“a
есть угол второй четверти и, значит, его тангенс отрицате-
лен; следовательно:
tg(90°4-a) =— ctg a.
Эта формула справедлива для любых углов а.
41
2) Угол 360° — а образован откладыванием угла а от
первой (горизонтальной) оси; поэтому в правой части формулы
приведения должна быть одноименная функция, т. е. cos а
со знаком 4" или — . Если угол а острый, то угол 360° — а
есть угол четвертой четверти, в которой косинус положите-
лен; следовательно:
cos (360° — а) = cos а.
Эта формула также справедлива для любых углов а.
22. Приведение к острому углу. Формулы приведения
позволяют выразить тригонометрические функции произволь-
ного угла через тригонометрические функции острого угла
(или, как говорят, привести к тригонометрическим функциям
острого угла). В самом деле, тригонометрические функции
произвольного угла можно привести к тригонометрическим
функциям неотрицательного угла меньшего 360° (п. 20).
Далее, всякий угол больший 90°, можно представить или
так: 90° а или 180° — (вторая четверть), или так:
180° 4“ « или 270° — (третья четверть), или так: 270° 4~«
или 860° — ах (четвертая четверть), где а и —острые
углы. Наконец, с помощью формул приведения можно вы-
разить тригонометрические функции этого угла через три-
гонометрические функции острого угла а или ах. Таким об-
разом, тригонометрические функции угла [J будут приведены
к функциям острого угла.
Это дает- возможность при помощи таблицы значений
тригонометрических функций острых углов вычислять
значения тригонометрических функций любых углов.
На стр. 14 приведена таблица значений тригонометриче-
ских функций для всех острых углов, выражающихся целым
числом градусов (таблица через 1°).
Примеры.
1) sin 870°= sin (2-360°4- 150°) = sin 150° =
= sin (180° — 30°) = sin 30° = 1.
2) cos 1180°= cos (3 • 360° -f- 100°) = cos 100° =
= cos (90° 4-10°) = — sin 10°.
По таблице находим: sin 10° 0,174. Значит, cos 1180е
«5= —0,174.
42
3) sin (— 850°) = — sin 850° = — sin (2 • 860° -f-130°) —
= — sin 130° = — sin (90° + 40°) =
= — cos 40° — 0,766,
или
sin (— 850°) = sin (— 3 • 360° + 230°) = sin 230° =
«= sin (270° — 40°) = — cos 40°^ —- 0,766.
Задачи к главе 1
I..П роверить, что треугольник с данными сторонами прямоуголь-
ный, и найти значения тригонометрических функций острых углов
а И Р’
(а) а — 3, b z= 4, с = 5;
(Ь) а = 8, £ = 15, с =17.
2. По данным двум сторонам прямоугольного треугольника найти
третью сторону и значения тригонометрических функций острых уг-
лов а и 0:
(а) а = 21, £ = 20; (Ь) а = 24, с=25.
3. Гипотенуза прямоугольного треугольника равна 50 см. Синус
одного из острых углов равен 0,28. Найти катеты.
4. Котангенс одного из острых углов прямоугольного треуголь-
2
ника равен , меньший катет равен 10 см. Найти второй катет.
5. Найти сумму косинусов острых углов прямоугольного тре-
угольника, гипотенуза которого равна 20 см, а периметр равен 45 см.
б. Сумма катетов прямоугольного треугольника равна 12 см,
гипотенуза равна 10 см. Найти произведение синусов острых углов
треугольника.
7а Может ли синус острого угла быть равным:
(а)4; Ф) (с)^-; (Ф (е)а + у?
8» Может ли косинус острого угла быть равным:
т/Т — V2 1/3 1
(а) 0,947; ф) ; (с) И >
9а Найти значение суммы sin а -|~ cos а при следующих значениях
угла «:
(а) 30°; (Ь) 45°; (с) 60°.
10а Найти значение выражения cos 2а — cos а при значении
уТла а, равном 30°.
„ sin (а 4-15°) — sin а
II. Найти значение выражения —-—--------------- при значении
угла а, равном 30°.
12. Найти произведение суммы синусов углов в 60° и 30° на ко-
синус разности этих углов.
43
13. Найти sin 15°. 1
Указание. К треугольнику АВС с углами А = 15° и С=90® ’<
и стороной АВ~ 1 приложить равный ему треугольник ACD и найти
сторону BD, пользуясь теоремой о квадрате стороны, лежащей про-
тив острого угла.
14. Найти cos 15° (см. Указание к предыдущей задаче).
15. Могут ли синус и косинус одного и того же острого угла
быть равными соответственно:
(а) X И ; (Ь) 0,6 и 0,8; (с) -у.. Д и * .
20 20 у £8 У £2
16. Могут ли тангенс и котангенс одного и того же острого
угла быть равными соответственно:
(а) 0,6 и 1|; (b) m4-— и ; (с) /2+ 1 и )Л2 - 1?
' ' 3 т пг -|- 1
17. Найти косинус, тангенс и котангенс острою угла а, если
sin а равен:
(а) ; (Ь) 0,28; (с) -у 1^2 ; (d) — , причем р > 0.
18. Найти синус, косинус и котангенс острого угла а, если tg а
равен:
(a)l; (b) V2; (с) .
.. --cos2 а .
19. Из формулы tg а —------------ выразить cos а через tg а.
20. Проверить справедливость равенства
1___I___1 1
sin2 а "* cos« а sin2 а cos4 а
при следующих значениях угла а: 30°, 45° и 60°. Будет ли это равен-
ство справедливым при любых значениях острого угла а?
21. Проверить справедливость равенства
cos4 а — sin4 а = 1 — 2 sin2 а
при следующих значениях угла а: 30°, 45° и 60°. Можно ли назвать
это равенство тригонометрическим тождеством?
Доказать тождества (задачи 22—29):
22. tg2 а — sin2 а = tg2 a sin2 a.
23. cos2 а 4- 2 sin2 а 4- sin2 а tg2 а = —.
‘ ’ * C0S2 а
24- -т-.----;——г—г-*—г-т-S— = COS2 а.
cos4 а COS2 a sin2 а -|- sin2 а tg2 а
25 __s^n g cos g ____tg2 a 4~ 1
COS a Sin a cos а — sin a tg2 a — 1 *
2g ctg а cos a ___ctg a — cos g
ctg а 4- cos a ctg a cos а *
44
I — t COS* a . .
>7 , — = tg a — ctg a,
sin a cos a 6 6
28- cos1 a (tg a + 2) (2 tg a + 1) — 5 sin a cos a = 2.
29. cos a + Sin a tg a + COS a ctga 4" sln a — -1-г—
* 1 bi, bi cos a r Sin a
Упростить выражения (задачи 30—37):
30. (sin a 4* cos a)2 4~ (sin a — cos a)2.
31. sin4 a -f-2 sin2 a cos2 a 4" COS4 a.
32. sin4 a — cos4 a -|- cos2 a. 33. (tg a 4“ ctg a)2 — (tg a — ctg a)\
34. Sin a COS a (tg a 4- ctg a).
35. ( —--p tg a • ( —!— ~ tg оЛ 36. tg ’ a 4- tg2 a.
\ cos a b J \ cos a /
37, f tgg + ct£g tga - ctga\ . f 1___________1\
\ tga — ctga tg a-|-Ctg a / \ Sin2 a COS2 a /
38. Дано: sin a 4- cos a = 1,2. Найти произведение sin a cos a.
39. Заменить синусом дополнительного угла:
(а) cos 52°; (b) cos 18°; (с) cos (60° — a); (d) cos (a —20°).
40. Заменил* косинусом дополнительного угла:
(а) sin 48°; (b) sin (45° + a); (c) sin (30° - 2a); (d) sin .
41. Заменить тангенсом дополнительного угла:
(а) ctg 72°; (b) ctg (45° + a); (c) ctg (90° - .
42. Заменить котангенсом дополнительного угла:
(а) tg 38°; (b) tg |; (c) tg (30° - 2a); (d) tg^^ .
43. Зная sin 15° и cos 15° (см. задачи 13 и 14), найти sin 75° _
и cos 75°.
44. Проверить справедливость равенств:
(а) sin 35°30' = cos 54°30';
(b) sin (30° — a) = cos (60° 4- «);
(с) cos (2a -f- 14°) = sin (76° — 2a);
(d) cos^y 4* 55°^ = sin ^35° —;
(e) tg(66°- i)=ctg(24° + |).
45. Сумма тангенсов двух дополнительных углов равна 3. Найти
сумму квадратов тангенсов этих углов.
46. Построить на миллиметровой бумаге с помощью транспор-
тира углы в 10°, 20°, 30°, 40° и 45° и измерением соответствующих
отрезков найти значения тригонометрических функций этих углов.
Сравнить с таблицей.
45
47. По таблице значений тригонометрических функций найти:
(a) sin 32°; (Ь) sin 44°; (с) cos 18°; (d) tj>27°; (е) tg 5°;
(f) ctg 12°; (g) ctg 45°..
48. Найти no таблице:
(a) cos 75°; (b) tg 48°; (c) sin 68е;
(d) ctg 81®; (e) cos 67°; (f) sin 60°.
49. По таблице убедиться в том, что с увеличением остроге
угла вдвое его синус увеличивается менее чем вдвое. Взять, напри-
мер, следующие углы: 20°, 35° и 42°.
50. Проверить по таблице справедливость неравенства
sin За < 3 sin а для следующих значений угла а: 14°, 20° и 25°.
51. Проверить по таблице справедливость неравенства
tg + f) < *g » + *g ₽ для следующих значений углов аир:
23° и 15°, 36° и 28°, 19° и 26°.
52. Найти по таблице острый угол а, если:
(a) sin а = 0,559; (b) tg а = 0,424;
(с) cos а — 0,978; (d) ctg а = 2,05;
(е) sin а = 0,616; (f) cos а = 0,777.
53. Найти по таблице острый угол а, если:
(a) tg о = 1,28; (b) ctg а = 1,881; (с) sin а = 0,906;
(d) cos а = 0,94; (е) sin а = 0,707; (f) tga = 0,510;
(g) cos а = 0,191; (h) ctg a = 5,145.
54. Найти по таблице острый угол al), если:
(a) sin a = 0,394; (b) tg a = 0,580; (c) cos a = 0,9;
9
(d) tg a = 2; (e) ctg a = у.
55. Найти по таблице острый угол а, если:
(а) sin а = ]^2 — 1; (b) tg а = V5;
(С) cos а = уу _|_ ] ’ (d) tg«= у-
56. Найти, пользуясь таблицей, значения выражения
ctg8 a — ctg8 a sin8a
V tg8 a — tg8 a cos8 a
при следующих значениях угла а: (а) 32°; (b) 55°.
У Казани е. Предварительно выражение упростить.
х) В задачах 54—55 угол находится по таблице с точностью до ’//•
46
57. Найти, пользуясь таблицей, значения выражения
I ~\/ * + cos а -1Л 1 — cosaV
\ V 1 — cos а V 1 -|- cos a J
при следующих значениях угла а: (а) 45°; (Ь) 48° (см. указание к за-
даче 56).
58. На оси (черт. 21) даны отрезки АВ, CD, EF и КМ.
Найти алгебраическую величину и длину каждого из этих отрез-
ков оси.
м К Е F А ВВС
Ь' '* ' ' ------------------------
Черт. 21.
59. Чему равна сумма алгебраических величин отрезков АВ и
ВА оси ZZj и сумма их длин, если | АВ | = 2?
60. Построить на оси LLr отрезки АВ = Ь, ВС—— 5 и CD— 3.
Найти AD. ___ ___ ____
61. Найти сумму проекций векторов АВ, ВС и CD — трех сто-
рон параллелограмма ABCD — на четвертую сторону AD, если
|Л£>| = с. ___
62. Найти сумму проекций векторов АЁ>, ВС и CD — сторон
ромба ABCD — на диагональ ЛС, если |АС| = d.
63. Углом какой четверти является угол, равный:
(а) 72°; (Ь) 325°; (с) 164°; (d) 200°; (е) 92°; (f) 2689?
64. Если рассматривать только положительные углы, меньшие
чем 360°, то углом какой четверти является угол, равный:
(а) половине угла второй четверти;
(Ь) половине угла третьей четверти;
(с) одной трети угла четвертой четверти;
(d) одной четверти угла четвертой четверти.
65. Найти в градусной мере угол поворота махового колеса,
сделавшего:
7
(а) 4 полных оборота; (Ь) 2 оборота; (с) 3,1 оборота; (d) оборота,
о
66. Найти и построить с помощью транспортира угол
₽ = 360°.«4-a
при следующих значениях п и а:
(а) л = 3, я = 40®; (Ь)л=1, а = 240°; (с) п = 2, а = 30°.
67. Вектор АЁ, занимавший горизонтальное положение, повернулся
вокруг точки А против часовой стрелки на угол р. Построить началь-
ное и конечное положение вектора АВ, если угол р равен: (а) 210°;
(Ь) 765°; (с) 1200°; (d) 540°.
47
60. Две точки А и А, находясь на противоположных концах диа-
метра окружности, начинают одновременно двигаться по окружности
в одном направлении. Точка А каждую минуту описывает дугу в 30°,
точка В — дугу в 45°. Через сколько минут после начала движения
произойдет 1-е, 4-е и л-е совпадение точек?
69* Углом какой четверти является угол, равный:
(а) —60°; (Ь) -240°; (с) - 150°; (d) - 260°.
70. Представить угол р в виде р = 360° • п -f- а, где п — любое
целое число или нуль, а а — неотрицательный угол, меньший 360°, если
Черт. 22.
(а) ₽ = — 180°; (b) f = - 780°; (с) ? = - 1510°;
(d) р = 2000°; (е) р = 1080°; (f) ₽ = — 490°; ’
(g) р = —540°; (h) ₽ = - 1800°; (!) 0 = 350°.
71. Две точки А и В, находящиеся на кон-
цах взаимно перпендикулярных диаметров
окружности (черт. 22), начинают одновременно
двигаться по окружности: точка Л — в поло-
жительном направлении, описывая каждую ми-
нуту дугу в 20°, а точка В — в отрицательном
направлении, описывая каждую минуту дугу
в 10°. Через сколько минут произойдет 1-е,
3-е и л-е совпадение точек?
72. Какое время показывают стрелки часов в моменты их совме-
щения?
73. Найти значения тригонометрических функций угла, равного:
(а) 135°; (Ь) 150°; (с) 225°; (d) 300°; (е) -240°.
74. Найти значения тригонометрических функций угла, равного
(а) 450°; (Ь) 600°;
(с) 840°; (d) -420°;
(е) — 750°; (f) -1110°.
75. Вектор АВ, длина которого равна с, образует с осью LLX
угол а. Найти проекцию этого вектора на данную ось, если:
(а) с = 18, а = 60°; (Ь) с = 23,5, а = 90°;
(с) с = 20, а=135°; (d) с=1,5, а = 180°.
76. Найти длину вектора АВ, зная проекцию а этого вектора на
ось LLX и угол а между вектором и данной осью:
(а) л = 2, а = 30°; (Ь) л = 0,75, а = 0°.
(с)л = —1, а =120°; (фл = —6, «=180°.
77. На прямолинейно движущееся тело действует сила F, образую-
щая с направлением движения угол а. Найти проекцию этой силы на
48
(a) F=8 кГ, a = 45°; (b) F = 28. кГ, a = 135°;
(c)F=10kF, a = 150°; (d) F=\l кГ\ a = 0?
78, С помощью теорем о проекциях доказать, что
cos 144° 4- cos 72° = — -i-.
указание. В правильном пятиугольнике ABCDE спроектиро-
на АЕ замкнутую ломаную FEDCF, где F — середина АЕ.
79. Найти знаки следующих значений три! онометрических функ-
(а) sin 102°, (b) cos 212°; (с) tg 168° (d) ctg 310°; (е) sin 200°;
(f) tg 105°; (g) ctg 220°; (h) cos 160°; (i) tg 350°; (k) ctg 93°.
80. Углом какой четверти является угол,
(а) синус которого положителен, а косинус отрицателен?
(Ь) тангенс которого отрицателен, а косинус положителен?
(с) котангенс которого отрицателен и синус отрицателен?
81. Вычислить:
(а) 3 sin 90° + 2 cos 0° - 3 sin 270°;
(b) 2 cos 270° - J tg 180° + sin 90°;
(c) tg 180° —j sin 270° - A- cos 180°.
82. Найти значения выражения
sin (a 4" 45°) 4- 2 sin (a — 45°) 4~ 4 cos 2a 4" 2 cos (a 4- 135°);
если угол a имеет следующие значения: 45° и 135°.
83. Найти значения выражения
2 sin а 4- cos 2a — 3 sin 3a — 4 cos 6a,
угол a равен: 0°, 30° и 45°.
Упростить выражения (задачи 84—85):
х2 sin* 90° — у2 cos8 0°
' х cos 180° — у sin 270° 4-* xy tg 180° *
85 (a sin 90°)8 - a'b* tg 0° 4- ab2 ctg 90° 4~ (b cos 180°)s
(acos 180°)2 4~ sin 270° cos 180° 4~ sin 270°)a
86. Построить синус и косинус угла, равного:
(а) 110°; (Ь) 255°; (с) 320°;
(d) 210°; (е) - 160°; (f) 530°.
49
87. Построить тангенс и котангенс угла, равного:
(а)—70°; (Ь) 130°; (с) - 20°;
(d) 215°; (е) - 345°; (f) - 870°.
88. Найти все значения yi ла 2, если:
(a) sin з = 0; (b) sin з=1; (с) cosa = 0; d) ctg а = 0.
По данному значению одной тригонометрической функции
найти значения всех остальных функций того же угла (задачи 89-
2
89. sin а = - у , где 270° < а < 360°.
9
90. cos а = jj-, где 0° < а < 90°.
91. tga = — -4-, где 90° < а < 180°.
92. ctga=l, где 180° < а < 270°.
93. cos т. = - 7 , где 180° < а < 270°.
2о
94. ctgа = 2, где 180°<а<36(Г\
95. Выразить все три! онометрические функции угла а через его
тангенс.
3
96. Зная, что sina = —- и cos a > 0, найти значения всех три-
гонометрических функций угла а.
г т ” 1 tg а 7
97. Наити значение выражения ' > если sina“'25 И
90° <а< 180°.
„ о sin а 4- 2 cos а . 1
98. Наити значение выражения -------- --— , если tg a — — .
н COS a — 3 Sin a s 2
tg a
99. Найти значешк выражения ---------—j— , если cos i — — 0,4.
tg a + Ctg з
Доказать тождества (задачи 100 — 103):
IGO. COS а(1 — tg a) (Sin a COS a) = COS4 а — Sill4 a.
{c°s а , sin a 4 .
IO!. л------L-_— I; (tg i 4. ctg а — 1) = sin a -4- cos i.
\ tg а 1 Ctg а / b ' ° 1
IO2. (1 4 tg2 a) (1 -I Ctg2 a) tg2 a - (1 - tg2 a)2 = 4 tg2 a.
IO3. 2 Sin2 a — COS2 a (1g2 a 4" ctg2 a) + (tg a — ctg a)2 = tg2 a — J.
Упростить выражения (задачи 104—108):
104. (a)
tga
IO5. (tg a + Ctg a) (I
IC6. ----------r-
sin a cos a
IO7. }rsiif a(l cig
(b)
1 1 + ctg2 a
cos a)(l — cos a).
- tg2 a)2
tg2 2
44«41 +O
50
Ю8.
Sin8 a COS’ а
V1 — sin2 а (] -j- COS2 а) ]Л1 — cos2 a (1 4~ Sin2 а)
109. Найти:
(a) sin (-30°); (b) tg (- 45°); (с) sin (— 60°); (d) ctg (- 135°).
НО. Найти:
(a) sin (—90°); (Ь) cos(- 180°); (с) ctg (—270°); (d) sin (- 270°).
HI. Пользуясь таблицей, найти:
(a) tg (- 48°); (Ь) cos (- 32°); (с) sin (- 72°); (d) ctg (- 11 %
Пользуясь таблицей, найти значения выражений (задачи 112—Н4):
112. sin2 а-|-sin 2? при а ——13°.
ИЗ. cos3 а -|- 2 ПРИ а~ — 45°.
114. sin (a — 20°) -J- cos (a — 1(Г) при а —0°.
Упростить выражения (задачи 115—118):
Sin (а — ft) — sin (3 — а) tg (2a - Р) - tg (? — 2a)
COS (а — f) -|- COS (J — a) ’ ctg (t3 — 2a) — ctg (2a — f) *
||7e sin2 (a 4-45°)__________||8. cos3 (— a) -f- sin3 (— a)
’ COS (a — 45°) cos (45° — a) * ’ cos a -|- sin (— a)
119. Привести к тригонометрическим функциям положительного
угла, меньшего чем 180°:
(а) tg(— 520°); (b) sin (—710°), (с) cos (—525°);
(d) ctg (— 740°); (е) sin (— 100°); (f) tg (— 130°).
I2O. Найти:
(a) sin 540°; (b) tg 720°; (c) cos 450°; (d) ctg 450°;
(e) cos 900°; (f) sin 810°.
121. Найти:
(a) tg(—900°); (b) sin (—450°); (c) cos (- 630°); (d) ctg (—810°).
122. Пользуясь формулами приведения, найти:
(а) sin 210°; (b) cos 240°; (c)tg315°; (d) cos 570°;
(e) ctg 480°; (f) cos (— 330°); (g) sin (— 225°).
123. Тангенс внешнего угла прямоугольного треугольника, не
смежного с прямым углом, равен k. Найти тангенсы острых углоз
треугольника.
3
124. Косинус одного из смежных углов равен —Найти си-
о
нус второго смежно! о } I ла.
61
*
125. Найти tg (270° — а), если tg а = -=•.
о
126. Найти sin (180° + а)> если cosa = ^| и 0° < а < 90°.
v5
о ।
127. Найти cos (360° — а), если tg а = — и 90° < а < 180°.
7
128. Найти ctg (180° — а), если cosa =и 270° < а < 360°.
129. Привести к тригонометрическим функциям положительнс
угла, меньшего чем 45°:
(a) tg 995°; (b) cos (— 1544°); (с) sin 916°; (d) ctg 400°;
(е) sin 850°; (f) cos 700°; (g) tg (— 385°); (h) sin (—288°);
(i) tg(— 325°); (k) sin (—610°); (1) ctg (—508°), (m) cos 1020
I3O. Пользуясь таблицей, найти следующие .значения тригоно!
трических функций:
(a) cos 520°; (b) tg ( — 148°); (с) sin (— 160°); (d) cos 202е):
(е) ctg 170°; (f) tg (— 147°); (g) cos 870°; (h) sin (— 1000°).
131. Пользуясь таблицей, найти значения выражения
cos а cos 2а -|~ cos За,
если угол а имеет следующие значения: 35°, 69°, 100° и 120°.
132. По таблице найти угол а, если
(a) sina =— 0,515 и 180° < а < с 270°:
(b) sin а = 0,669 и 90° < ' а < С 180°;
(с) tg а =—1,376 и 90° < С а < С 180°;
(d) cos а = 0,407 и 270° < а < С 360°;
(е) tg а = 0,577 и 180° < а < С 270°;
(f) ctg а = — 2,747 и 90° < ' а < С 180°.
133. По таблице найти положительный угол а, меньший чем 36
если:
(a) tg а = 0,344 и sin а > 0;
(b) sin а = 0,616 и cos а < 0;
(с) ctg а = 1,072 и sin а < 0.
134. Построить угол о, если:
Sin а = 1 3 и 90° < [а < 180°;
cosa — — 2 5 и 180° < : а < 270°;
tg а~ — 2 3 и 90° < > < 180°;
ctga = — 2 и Sin а - <0.
52
135. Проверить, что sin а и tg ~ имеют одинаковые внаки прв
л10бых значениях угла а (при которых tg~ существует). Рассмо-
треть отдельно случаи:
0° < а < 180°, 180° < а < 360°,
360° < а < 540° и 540° < а < 720°.
а
136. Проверить, что sin а и cos-j имеют одинаковые енаки при
всех значениях ума а, заключенных между 0° и 360°. Рассмотреть
отдельно случаи: 0° < а < 180° и 180° < а < 360°.
Сохранится ли это свойство при значениях угла а, заключенных
между 360’ и 540°?
Упростить выражения (задачи 137—144):
137.
[sin (180° + а) + cos (90° + а)]’ -[- [cos (360е - а) - sin (270° - а)]’.
tg (90° + g) + ctg (270° ~ ~ tg (180° - а) - Ctg а
tg (180° 4- а) sin (360° - а) [sin(l80° + а) - cos (180° - а)]'
ctg 228° ctg 222° -|- sin 155° cos 245°
ctg 73° ctg 197° + tg 155° ctg 335° ‘
cos* 336° - cos’ 156° + tg 100° tg 350’
,4°' tg’ 72’ + ctg’ 162’
ctg (“ - 90°) (sin <a ~ 270°) - sin <180° ~ °)1
,41' tg (180° + a) [cos (a + 360°) 4- sin (a - 360°)]'
sin’ ( - 212°) cos 302° 4- cos’ ( — 148°)__
,4Z’ sin ( - 82°) cos (—8°) 4- sin 368° sin (—172°)—sin 58° sin 148° ‘
sin’ (a - 180°) - cos3 (270° - a) sin (180° 4- a)
tg® (90° — a) cos’ (a — 270°) sin’ (a - 90°) ’
144 tg (180° - a) ctg’ (a - 180°) - tg’ (a - 360°) tg’ (270° - a)
tg (a - 90 °) [sin’ (a - 270°) 4- sin’ (270° 4- a)J
145. Доказать тождества:
(a) sin (a — 30°) 4- sin (a 4-150°) = 0;
(b) cos (a 100°) = - Sin (170° — a),
146. Показать, что при it целом справедливо равенство
cos (1.180’^4-cos^ • 180°) 4- ... +cos(-^ • 180°) = 0.
ГЛАВА ВТОРАЯ
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
ЧИСЛОВОГО АРГУМЕНТА
§ 7. Тригонометрические функции числового аргументу
и их периодичность
23. Радианное измерение дуг и углов. До сих пор мы
пользовались градусной мерой дуг и углов, в которой за еди-
ницу измерения дуги (угла) принимается часть о кружно-
* ооО
( 1 X \ о
сти часть полного оборота . В теоретических рассуж-
\ uOU J
дениях, однако, предпочтительнее другая система измерения —
так называемая «радианная».
В радианной системе измерения единицей дуги окруж-
ности служит дуга, длина которой равна радиусу окруж-
ности. Такая дуга называется радианом. Радианной мерой
данной дуги называется число радианов, заключенных в этой
дуге. Зто значит, что радианная мера а дуги равна отноше-
нию ее длины I к радиусу R окружности:
а=д- (1)
Радианная мера дуги, соответствующей некоторому
центральному углу, зависит только от этого угла, но не
зависит от радиуса окружности.
В самом деле, длины I и двух дуг, соответствующих
одному и тому же центральному углу, как известно из гео-
метрии, пропорциональны их радиусам R и /?х:
I__I,
R ~ Rl ’
т. с. радианные меры обеих дуг одни ы те же.
54
Из формулы (1) следует:
l = aRt
(2)
т е. длина дуги равна длине радиуса, умноженной на ро
дианную меру дуги; в частности, для дуги единичной ок-
ружности (/? = 1) длина дуги равна ее радианной мере. Вот
9То обстоятельство и делает особенно удобной радианную
систему измерения.
Радианная мера угла равна радианной мере такой дуги,
для которой этот угол является центральным.
Единицей при радианном измерении углов служит, следо-
вательно, центральный угол, соответствующий дуге в один
радиан. Такой угол также называется радианом.
Радианная мера полной окружности или полного оборота
(360°) равна 2п = 6,28... радиана; радианная мера полуок-
ружности или развернутого угла (180°) равна п = 3,14... ра-
диана; для четверти окружности или прямого угла (90°) она
ft < г- <7
равна у=1,э7... радиана и т. д.
Следует запомнить еще радианную меру следующие углов
(дуг):
30° = -^- рад.; 45°=-^- рад.;
60° = 4 рад.; 270° = 3-4 рад.
При измерении углов и дуг радианами наименование еди-
ницы измерения — радиана — обычно опускают. Говорят, на-
К Г,
пример: «угол равен у» вместо «угол равен — радиана»;
«угол равен 1,4» вместо «угол равен 1,4 радиана».
Легко перейти от радианной меры к градусной и обратно.
Так как тг = 3,14159... радиана соответствует 180°, то
1 180 180
1 радиан — — градуса =3^59 градуса о7°17 44 ,8,
1 ft 1 *7 Л “ I 80Д
I градус = радиана 0,0174о радиана; а радианов =-------------
1о0 к
градуса а • 57°17'44",8; £ градусов = радиана =^0,01745 р
радиана.
Аргумент тригонометрических функций (угол или дугу)
можно теперь рассматривать заданным в радианной мере.
Например; sin ~ рад. = sin sin 28°38'52",4,
4 **
63
24. Определение тригонометрических функций числом
вого аргумента. Одна и та же математическая функция мо-
жет выражать зависимости между разными физическими вели-
чинами. Например, квадратичная функция у = х* устанавливает
зависимость между площадью квадрата у и длиной его сто-
роны х. Значит, х выражает длину, а у — площадь. Назва-
ние функции y^-xz — «квадратичная» — указывает на ее
связь с задачей измерения площади квадрата. Однако квад-
ратичная функция появляется и в иных случаях, когда она
выражает зависимость не между длиной и площадью, а между
другими величинами. Например, расстояние у, проходимо^
свободно падающим телом в пустоте, является квадратично#
функцией ^с коэффициентом -yQ времени падения х. Вот!
эта функция: :
Поэтому в математике рассматривают квадратичную функцию
как функцию числовой переменной величины х, которая может
выражать различные физические величины.
Дело обстоит так же и с тригонометрическими функциями.
Сначала они определяются как функции угла, а затем им при-
дается более широкий смысл функций числового аргумента.
Многие вопросы математики, фишки и других наук при-
водят к тригонометрическим функциям, аргументы которых
выражают различные физические величины (длину, время, тем-
пературу и т. п.).
Пусть дано число х. Под значением функции j/ = sinx,
где х — некоторое число, понимают значение синуса угла в
х радианов.
Пример, sin 2,705 = sin 2,705 рад. Так как 2,705 рад.
^155°, то sin 2,705 sin 155°= sin 25° 0,423 (см. таб-
лицу на стр. 14).
Аналогично определяются функции у — cos х, tgx, ctg х
числового аргумента х.
О п р е д е л е и и е. Тригонометрические функции число*
вого аргумента х — это одноименные тригонометрические
функции угла в х радианов.
Дадим теперь в качестве иллюстрации небольшую часть
таблицы значений тригонометрических функций числового ар-
гумента х (с точностью до 0,0001) для значений х, заклю-
ченных между х — 0 и Х-—1.57 , взятых через ОД.
56
X Соответствующее число градусов sin х COS X tgx
0,0 0,00 0,0000 1,0000 0,000
0,1 5,44 0,0998 0,9950 0,103
0,2 11,28 0,1987 0,9801 0,2027
0,3 17,11 0,2955 i 0,9553 i > 0,3093
0,4 22,55 0,3894 ; 0,9211 । | 0,4228
0,5 28,39 0,4794 I 0,8776 ’ 1 0,5463
0,6 34,23 0,5646 i 0,8253 0,6841
0,7 . 40,06 0,6442 1 0,7648 0,8423
0,8 1 45,50 0,7171 i 1 0,6967 1,0296
0,9 51,34 0,7833 | 0,6216 1,2602
1,0 । 57,18 0,8415 j 0,5403 1,5574
1,1 i 63,02 0,8912 1 0,4536 1,9648
1,2 68,45 0,9320 | I 0,3624 2,5722
1,3 74,29 0,9636 0,2675 3,6021
1,4 1 80,13 : 0,9854 0,1700 5,7979
1,5 | 85,57 . 0,9975 0,0707 14,1014
1 ,57 : 89,95 1,0000 0,0008 1255,766
Эта таблица позволяет в некоторой мере судигь о ходе
зменения тригонометрических функций в связи с изменением
ргумента. Читатель, например, обратит внимание на быстрое
эзрастание tgx при приближении х к у =1,5707 . . .
25. Периодичность тригонометрических функций. Харак-
ериым свойством трш онометрических функций является их
е р и о д и ч и о с т ь.
Определение. Функция, вообще, называется перио-
ической, если существует число, отличное от нуля, при-
авление которого к произвольному значению ее аргумента
е меняет значения функции.
Наименьшее положительное число, прибавление кото-
ого к любому значению аргумента не меняет значения
ункции, называется периодом функции1}.
Теорема. Период функций sinx и cos х равен 2п, а
ериод функций tgx и с tgx равен тг.
Доказательство. Полученные раньше (см. стр. 27
33) формулы (20) и (21) гл. 1 можно записать в радианной
’) Иногда всякое число такого рода называют периодом функции,
наименьшее положительное из них — основным периодом.
&
мере так:
sin (х 4“ л • 2п) = sin х; cos (х п * 2тг) — cos х, (3)
^(х + л-тт) r=tgx; ctg(x4~/rn) = ctgx, (4)
где л = 0, ± L ±2, ...
Формула (3) показывает, что от прибавления чисел л-2п
к любому значению аргумента значения функций sin хи cosx
не меняются.
Нам остается показать, что других чисел, обладающих
этим свойством, не существует. В самом деле, пусть таким
свойством для sin х обладает число /г, г. е.
sin (х -j- h) = sin х,
при любом х. Значит, в частности, это равенство справед-
ливо при х = у, т. е. должно быть
sin (/z) = s'n'l= 1;
по формуле приведения (В)гл. 1 (см.стр.40) sin h^ = cos ht
и потому
cos h = 1.
Но косинус может равняться 1, как это мы видели в п. 15,
лишь при /г = /г-2п, ч. т. д.
Пусть, далее,
cos (х 4- h) = cos х
при любом х. Тогда, полагая х = 0, получим:
cos h = cos 0 = 1
и снова заключаем, что Л = л-2п.
Наименьшим положительным числом среди всех чисел вида
л-2тг является число 2тг; значит, оно и служит периодом для
sinx и cosx, что мы и хотели показать.
Аналогично доказывается и вторая часть теоремы. Фор-
мула (4) показывает, что от прибавления чисел /гтг к любому
значению аргумента значения функций tgx и etgx не ме-
няются. Покажем, что других чисел, обладающих этим свой-
ством, не существует. Пусть таким свойством для tgx обла-
58
tg (аг 7г) = tg л:
при любом х, для которого и tgx и tg(x-|-A) существуют.
Значит, в частностй, при х = 0 должно быть
tg h — tg 0 = О,
а это может быть тогда и только тогда, когда А = лп
(см. п. 15). Далее, если ctgx не меняется от прибавления к лю-
бому х некоторого числа А, то не меняется и tgx = ^~j
и, следовательно, как только что было доказано,
h = птх.
Наименьшим положительным числом среди всех чисел вида
zm является число тг; значит, оно и служит периодом для
tgx и ctgx, ч. т. д.
Можно указать и другие числа, прибавление которых к
аргументу не меняет некоторых значений, например си-
нуса; прибавление такого числа к одному значению аргу-
мента не меняет значения синуса, прибавление же к дру-
гому— меняет. Такие числа не являются периодами функции.
Пример, sin 0 = sin тг = О, но уже sin (п ) ==
. 3 . . г.
= sinтг = —1, в то время как sin у = 1; следовательно,
п не есть период функции sinx.
§ 8. Графики тригонометрических функций
26. График функции. Существует простой способ для
наглядного представления заданной функциональной зависи-
мости.
Возьмем две взаимно перпендикулярные оси ОХ и OY
(черт. 23). За ось ОХ на чертеже обычно принимают гори-
зонтальную ось, направленную слева направо,— она называется
осью иксов или осью абсцисс; ось OY—вертикальная — на-
правлена снизу вверх, она называется осью игреков или осью
ординат. Точка О пересечения осей ОХ и OY называется
началом координат. Будем откладывать в выбранном мас-
штабе значения независимой переменной х на оси ОХ, а со-
ответствующие значения у — в том же или другом масштабе
на оси OY. В соответствии с указанными направлениями на
59
осях положительные числа по осй ОХ изображаются отре^
ками, отложенными вправо от точки О, отрицательные числа —|
влево от нее, а по оси OY положительные числа изображав
ются отрезками, отложенными вверх, отрицательные—-вни^
от точки О.
Пусть задана функция у независимой переменной х. Да;
значение х0 и изобразим число х0 от-
резком ОА на оси ОХ (черт. 23),
Соответствующее значениефункции^
изобразим отрезком ОВ на оси OY,
Из концов А и В полученных отрез:
ков проведем прямые, параллельный
осям ОХ и OY\ точка их пересече-
ния Л40 изобразит совместные
значения независимой переменной к
функции. В самом деле, расстояние
X точки МС1 (взятое с соответствующим
знаком) от оси OY является значе-
Черт. 23. нием аргумента (х0), а ее же расстоя-
ние от оси ОХ (также взятое сс
знаком) является значением функции (j/0), соответствующим
значению х0.
Числа х0 и у0, определяющие положение точки /Ио, на-
зываются ее координатами; при этом число х0 называется
абсциссой точки Л40, a — ее ординатой г); записываем этс
так: Л40 (х0, j/0), на первом месте обычно указывается абс-
цисса, а на втором — ордината точки. Вся система осей ОХ
и OY с принятыми на них направлениями и масштабами на-
зывается системой координат.
Вместо откладывания ординаты по оси OY можно восста-
вить перпендикуляр АА10 в точке А к оси ОХ, длина кото-
рого равна абсолютной величине yQ; его направление выби-
раем вверх от оси ОХ, если и вниз от нее, если
Л<0-
Допустим теперь, что нам удалось построить точки, изо-
бражающие совместные значения независимой переменной и
функции для всех возможных значений независимой перемен-
ной. Тогда точки М, отмеченные на плоскости, образуют,
вообще говоря, некоторую кривую линию (черт. 24), которая
называется графиком рассматриваемой функции. В действи-
——►
х) Абсцисса и ордината точки Л10 суть проекции вектора ОЛТ
на оси ОХ и OY (черт. 23).
60
тельности обычно невозможно построить все точки графика.
Цо чем больше точек построено, тем более точным будет гра-
фик, полученный проведением через эти точки сплошной линии.
Определение. Графиком функции называется ли-
ния — геометрическое место точек М (х, у), абсциссы х ко-
торых равны значениям независимой переменной, а орди-'
наты у — соответствующим значениям функции.
График является геометрическим образом функ-
ции. Наблюдая за изменением ординаты точки графика
функции при изменении ее абсциссы, мы получаем воз-
можность отчетливо видеть, как изменяется функция с изме-
нением независимой переменной.
Посмотрим, какими особенностями характеризуется график
четной и нечетной функций, а также периодиче-
ской функции.
График четной функции симметричен относительно
оси OY\ график нечетной функции симметричен относи-
тельно начала координат.
Для доказательства этого предложения возьмем на гра-
фике какую-нибудь точку М с координатами (х, у) (черт. 25).
Пусть функция четная; тогда ее значение у не изменится,
если взять —х вместо х; поэтому вместе с точкой М (х, у)
графику функции принадлежит и точка (— х, у), симмет-
ричная точке М относительно оси OY (черт. 25). Пусть те-
перь функция нечетная; тогда, если взять —х вместо х, то
значение у функции изменит только знак; поэтому вместе
с точкой Л4(х, у) графику функции принадлежит и точка
(— х, — у), симметричная точке М относительно начала
координат (черт. 25). Этим наше предложение доказано.
61
В качестве примеров мы приводим графики четной функ-1
ции у = х* (черт. 26, а) и нечетной функции у = х*]
(черт. 26, б). 1
Черт. 26.
Возьмем теперь график периодической функции
с периодом h и рассмотрим часть этого графика, соответ-
ствующую какому-нибудь отрезку оси независимой переменной
длиною й, например от 0 до Л. Так как значения функции
повторяются при прибавлении h к значениям независимой
62
переменной, то точки графика, абсциссы которых различаются
на Л, имеют равные ординаты. Поэтому передвинув указанную
часть графика (как твердое тело, причем параллельно
оси ОХ) на /г, на 2Л, на ЗЛ и т. д. вправо и влево, получим
весь* график функции (черт. 27).
27. Графики функций sin х и cosx. Укажем весьма про-
стой геометрический способ построения точек графика функ-
ции у = sin х.
Построим единичную окружность с центром в какой-ни-
будь точке оси ОХ (черт. 28). Разделим окружность на
некоторое число равных частей (на чертеже взято 12 частей)
и пронумеруем точки деления последовательно, как показано
на чертеже, цифрами 0, 1, 2, ..., 12. Затем разделим отре-
зок оси ОХ от 0 до 2п на такое же число равных частей
(на 12) и пронумеруем точки деления слева направо цифрами
О, I, II, ..., XII. Тогда точки на оси ОХ и на окружности,
обозначенные одинаковыми номерами, соответствуют друг
другу в том смысле, что отрезок ON оси ОХ изображает
число, равное числу радианов, заключенных в дуге ON ок-
ружности. Например, отрезок оси ОХ от точки О до точки
IV изображает число -к-тг; дуга окружности от 0 до точки 4
и
Отсюда видно, что значение функции y = sinx в точке
IV оси ОХ совпадает со значением синуса дуги 04. Синус
дуги единичной окружности численно равен перпендикуляру,
опущенному из конечной точки дуги на горизонтальный
диаметр (см. стр. 30). Ясно, что точка графика, соответ-
ствующая точке IV, получается в пересечении прямой, про-
веденной через точку 4 окружности параллельно оси ОХ,
63
t перпендикуляром, восставленным к осн ОХ в точке IV. i
Таким способом можно отметить столько точек, принадлежащих 1
графику функции у = sin х, сколько точек деления было '
взято на отрезке от 0 до 2п (и на единичной окружности). •
Соединив найденные точки сплошной плавной линией, мы
получим ту часть графика функции, которая соответствует
v
/
-/
Черт. 29.
изменению независимой переменной от 0 до 2тг. Чем больше
построено точек графика, тем точнее он будет. Так как
sinx—периодическая функция (с периодом, равным 2п), то,
передвинув последовательно уже вычерченную часть графика
параллельно оси ОХ на 2тт, на 4тг, на бтт и т. д. вправо и
влево, мы построим весь график функции (см. п. 26).
Кривая линия, являющаяся графиком функции j/ = sinx,
изображена на черт. 29; эта линия называется синусоидой.
Так как функция у = sin х нечетная, то ее график дол-
жен «быть симметричен относительно начала координат (п. 26).
Это хорошо видно на черт. 29.
График функции j/ = cosx нетрудно получить, имея гра-
фик функции ey = s!nx. При любом х имеем:
/ I я
cos х ~ sm х -f- —
64
;м. формулу (6) п. 21]. Следовательно, йместо значений ко-
^синуса> можно взять значение синуса, увеличив аргумент
на . Значит, графиком функции^/ = cos х служит та же сину-
соида, но передвинутая на ~ влево (черт. 30). В таком по-
ложении синусоида иногда называется косинусоидой (так как
при этом она является графиком функции у = cos х).
Так как функция ^ = cosx четная, то ее график должен
быть симметричен относительно оси OY (п. 26). Это хорошо
видно на черт. 30.
28. Графики функций tgx и ctgx. Подобно тому как
была построена синусоида, может быть построен график
функции y = tgx. Но так как период этой функции равен тг,
то можно ограничиться нахождением точек графика, соответ-
ствующих точкам оси ОХ между 0 и тг, и, следовательно,
рассматривать дуги в границах одной полуокружности.
Построим единичную окружность с центром в какой-
нибудь точке оси ОХ и касательную РРХ к этой окружности
в точке О' (черт. 31).
: А. В.рмагг, Л. Люстарижк
65
Разделим на одинаковое число равных частей верхнюц
полуокружность и отрезок осн ОХ от 0 до п. На черт. 3
взято шесть частей. Точки деления перенумеруем по порядку
как показано на чертеже. •
Для того чтобы найти точку графика, соответствующую
например, точке деления // па осп ОХ, нужно и.? точки [.
восставить перпендикуляр к оси ОХ, выражающий танген
дуги 0'2 полуокружности. Но, как известно, тангенс дуги 0'
изображается отрезком 0'2' оси РР1 (черт. 31). Подобны]
образом отрезок 0'5' оси РРг изображает тангенс дуги 0'1
окружности.
Перенесем эти отрезки параллельно так, чтобы их началу
ные точки попали соответственно в точки //и V оси ОХ\
тогда концы отрезков будут точками графика функция
соответствующими точкам // и V оси ОХ.
Затем таким же образом получим точки графика, соот-
ветствующие другим точкам деления отрезка от 0 до и на
оси ОХ. Заметим, что на графике нет точки, соответствую-
щей точке = Действительно, тангенса дуги O'i
^дуги, равной не существует (радиус, проходящий че-
рез точку 3, параллелен касательной РРг).
Соединив построенные точки, соответствующие точкаы
интервала от 0 до и от ~ до и на осп ОХ, сплошными
линиями, получим ту часть графика, которая соответствует
изменению независимой переменной от 0 до тг. Чем больше
построено точек графика, тем точнее он будет. Сразу заме-;
тим, что график тангенса в интервале от 0 до тг — разрывная;
линия, что хорошо видно на черт. 31.
Так как функция j* = tg.v периодическая (с периодом/
равным п), то, передвинув параллельно оси ОХ последова-'
тельно вычерченную часть графика па тг, 2п, Зтг и т. д/
вправо и влево, мы построим весь график функции (см. п. 26).-
Кривая линия, являющаяся графиком функции
У = tg -V, ’
изображена на черт. 32; эта линия называется тангенсоидой.'
Как видим, тангенсоида состоит из совершенно одинаковых'
и одинаково расположенных о i дельных ветвей, заключенных-
66
и параллельных полосах шириной в тт 1 в полосах от — <’
г. г. 3
ди д-, от у до ^-тг и т. д.
Так как у = tgх — функция нечетая, то ее график сим-
метричен относительно начала координат. На черт. 32 отчет-
ливо видна эта симметрия.
График функции
у — ctg X
можно легко получить из графика функции y = tgx. Дей-
ствительно, из формулы (см. п. 21)
ctg.r= — tg (х-\-
следует, что точку графика функции v = ctgx, соответствую-
щую какой-нибудь абсциссе х, можно найти так: отметить
ючку графика j» = tgx, соответствующую точке оси ОХ,
лежащей на правее х, а затем взять точку, симметричную
с ней относительно оси ОХ.
Поэтому весь график функции y = ctgx получается из
графика функции >’ = tgx сдвигом последнего влево (вдоль
оси ОХ) на и последующего отражения его (перевертыва-
ния) относительно ©си ОХ.
3* 67
На черт. 33 изображена тонкой линией тангенсоида; пунк-
тирной линией — тангенсоида, сдвинутая влево — вдоль оси
ОХ—на жирной линией — график функции v-—ctgx.
Черт. 33.
Так как функция у = ctgx нечетная, то ее график сим-
метричен относительно начала координат, как это и видно
на черт. 33.
§ 9. Изменения тригонометрических функций
29. Характер изменения sinx и cosx. Пользуясь гра-
фиками тригонометрических функций, исследуем изменения
этих функций при изменении независимой переменной. Начнем
с функции j/ = sinx.
Пусть х возрастает от 0 до у (что соответствует воз-
растанию угла от 0° до 90°). По графику (см. черт. 29) видно,
что при этом функция возрастает от 0 до 1 (ордината точки
графика увеличивается от 0 до 1).
При возрастании х от -- до п (что соответствует воз-
растанию угла от 90° до 180°) sin х убывает от 1 до 0. Пусть х
3 ,
возрастает от п до п (что соответствует увеличению угла
от 180° до 270°). Как видно по графику (см. черт. 29), sin х
при этом убывает от 0 до — 1.
68
Наконец, если х возрастает от у тг до 2тг (что соответ-
ствует возрастанию угла от 270° до 360°), sinx возрастает
от -1 ДО °-
В силу своей периодичности функция у = sinx повторяет
свой ход изменения через период, равный 2п.
По графику функции j^ = cosx (см. черт. 30) можно та-
ким же образом выяснить характер изменения cos х. Ниже
приведена таблица, в которой указаны особенности в измене-
нии функций у = sinx и у = cosх.
Функции sin х и cos х могут изменяться только в гра-
ницах от —1 до -|-1.
30. Характер изменения tgx и ctgx. По графику (см.
черт. 32) мы видим, что когда х возрастает от 0 до у ,
функция tgx неограниченно возрастает, начиная’
от 0. По мере приближения х к у значения tg х становятся
все больше и больше и могут превзойти любое, как угодно боль-
шое, положительное число. Точка кривой на участке оси ОХ
от 0 до у круто поднимается вверх, стремясь коснуться пря-
мой /CKt параллельной оси OY, но нигде ее не касается
(как говорят, асимптотически приближается к
прямой К К).
Итак, если х приближается к у , возрастая (угол, воз-
растая, приближается к 90°), то тангенс неограниченно воз-
растает.
69
Пусть, далее, х возрастает от ~ до и. График показы-
вает, что tgx при этом снова возрастает, переходя от как угод-
но больших по абсолютной величине отрицательных значений
к меньшим по абсолютной величине отрицательным значе-
ниям и становится равным нулю при х = п. Если заставить
х приближаться к у, убывая, то тангенс, очевидно, может
сделаться меньше (в алгебраическом смысле) любого как угод-
но большого по абсолютной величине отрицательного числа.
Итак, если х приближается к ~ , убывая (угол, умень-
шаясь, приближается к 90°), то тангенс неограниченно убы-
вает.
Условно говорят, что tg у р&ен бесконечности, и
пишут: . к
tgy = OO.
Эту запись и ее словесное выражение следует понимать только
в том смысле, что если х неограниченно приближается к
у, то tgx по абсолютной величине неограниченно возрастает
(при х возрастающем — будучи положительным, при х убы-
вающем— будучи отрицательным). Знак оо не обозначает
какого-нибудь числа и, как уже упоминалось, значения тан-
генса при х =— (или при х — 90°) не существует.
Заметим, чго в интервале от — ~ до ~ функция y — tgx
возрастает. Так как этот интервал является периодом функ-
ции у — tgx, то tgx возрастает и в интервалах от ~ до
3 3 т:
от —у тт до —-ту- и т. д. Это постоянное возрастание
нарушается только при значениях аргумента zbv»
Ч--^- тт и т. п., при этих значениях тангенса не существует,
и здесь он «перескакивает» от как угодно больших положи-
тельных значений к как угодно большим по абсолютной ве-
личине, но отрицательным значениям.
Функция у = ctg х в противоположность функции _у —tgx
является функцией убывающей для значений аргумента, за-
ключенных между 0 и тг, тг и 2тг, —п и —2п и т. д. Это
постоянное убывание нарушается только тогда, когда х, воз-
растая, переходит через значения 0, + тт, Ч- 2п и т. д.; здесь
70
котангенс «перескакивает» от как угодно больших по абсо-
лютной величине отрицательных значений к как угодно боль-
шим положительным значениям.
Ниже приведена таблица, в которой указаны особенности
в изменении функций y = tgx и y = ctgx:
0 (0°) I четверть гс "2 (90°) II четверть л (180°) III четверть 3 2 ’ (270°) IV четверть 2гс (360°)
tgx 0 возра- стает не суще- ствует возра- стает 0 возра- стает не суще- ствует возра- стает 0
ctg X не суще- ствует убы- вает 0 убы- вает не суще- ствует убы- вает 0 . । убы- вает не суще- ствует
Функции tgx и ctgx могут принимать любые значения.
§ 10. Гармонические колебания
окружности радихса R (ч?рт. 34).
Черт. 34.
31. Простые гармонические колебания» Рассмот им равно-
мерное движение точки по
Пусть точка начинает дви-
гаться из точки Qo окруж-
ности в направлении, про-
тивоположном движению
часовой стрелки, со ско-
ростью п оборотов в се-
кунду, т. е. радианная
мера дуги, пробегаемой
точкой в 1 секунду, равна
2тгл.
Пусть через t секунд
движущаяся точка попа-
дает в точку Q окружно-
сти. Обозначим через
проекцию ОР вектора OQ
на ось и поставим
перед собой задачу выяснить,
вдоль ММ^ при указанном движении точки Q по окружности.
как передвигается точка Р
71
Пусть дуга 4Q0 равна <р0. Дуга AQ равна дуге сло-
женной с дугой Q0Q, описанной точкой за t секунд; но по-
следняя дуга равна 2tW, и, значит,
.4Q = AQq + (TQ = + 2то/,
ИЛИ / AOQ =.с2^п1-\- <р0.
Следовательно,
$ = OP— OQ sin X AOQ = Rsin (w/-ф- cp0), где a)— 2wi. (o)
Полученная формула дает возможность указать положение
точки Р в любой момент времени.
Движение точки Р вдоль диаметра DB, описываемое соот-
ношением (5), называется простым гармоническим колеба-
нием. При этом точка Р описывает отрезок DB то снизу вверх,
то сверху вниз.
Постоянная величина R в формуле (5) называется амплиту-
дой колебания. Она указывает наибольшее отклонение точки
Р от середины О отрезка DB. Это наибольшее отклонение
называют размахом колебания.
Переменную величину 'р = (а/-|-<р0 называют переменной
фазой колебания, а значение ср при t — Q (в начальный мо
мент), т. е. <р0, называют начальной фазой. Величина
у, 2 г.
(£>
называется периодом колебания [это есть период функции
$ = A sin (a)t <р0)]- самом деле, при увеличении t (вре-
мени) на Т значение s не изменяется:
A sin [ю (/ + О + ?<J = Л si" (wZ + ш[ + ^о) =
= A sin (ю/ -|- 2п) — Д sin (ш/ 4- ф0).
В течение промежутка времени Т ючка Р дважды описы-
вает отрезок DB (один раз снизу вверх, другой раз сверху вниз).
Величина, обратная периоду колебания,
1 <0
7 2z ’
называется частотой колебания. Она показывает, сколько
полных колебаний совершает точка в единицу времени
(в 1 секунду).
72
В нашем примере частота колебания проекции Р точки Q
на отрезок DB равна л:
1 __со 2ял____
7 2«=2« Л>
Действительно, из условий задачи ясно, что колеблющаяся
точка Р проходит п раз в секунду через каждую точку
отрезка DB при движении снизу вверх (и п раз при движении
сверху вниз).
Иногда частотой называют величину со. Она показывает,
сколько полных колебаний совершает точка Р в течение 2п
единиц времени (секунды).
Аналогично доказывается, что движение проекции точки Q
на какой-нибудь другой диаметр окружности будет также
простым гармоническим колебанием с теми же амплитудой и
периодом (а следовательно, и частотой), но с другой началь-
ной фазой.
32. График простого гармонического колебания. По-
строим график функции
$ = A sin (о)/ -|- (р0) — A sin
приняв горизонтальную ось за ось значений независимой перемен-
ной /, а вертикальную — за ось значений функции 5 (черт. 35).
Для этого можно употребить тот же геометрический прием,
который был использован при построении обыкновенной сину-
соиды, если на горизонтальной оси разместить значения пере-
менной фазы (р = а)/-|”?о‘
Прежде всего отметим на этой оси те значения /0 и
для которых фаза (р равна 0 и 2тг.
tn = — %- и / —=/и 4-Г.
О ф * (,) (й Ц) и '
73
Отрезок оси между точками /0 и разделим на некоторое
число п равных частей (на черт. 35 взято 12 частей) и обо
значим точки деления последовательно цифрами от 0 до XII.
Возьмем, далее, окружность радиуса А с центром в какой-
нибудь точке горизонтальной оси. Разделим ее также на ii
равных частей и перенумеруем точки деления в направлении,
противоположном движению часовой стрелки, начиная от
точки 0.
Через точки 0, 7, 2, ... окружности проведем горизон-
тальные прямые, а через точки 7, 77, ... оси проведем вер-
тикальные прямые. Точки пересечения соответствующих пря-
мых принадлежат искомому графику. Соединив найденные
точки сплошной плавной линией, получим ту часть графика
функции 5 = A sin ((о/ 4" которая соответствует изменению
независимой переменной i в границах одного периода от /0
до /1 = /0-]-7'. Передвигая затем эту часть вправо и влево
на Г, на 2Г, на ЗГ и т. д., вычертим весь график.
Полученная линия называется деформированной синусоидой.
Задачи к главе II
I. Найти радианную меру дуги окружности, радиус которой равен
12 см, если длина дуги равна:
(а) 4 си; (Ь) 1,2 см', (с) 6 см', (d) 2,4 дм', (е) 0,66 м.
2. Радиус окружности равен 20 см. Найти длину дуги, если ее
радианная мера равна:
(а) 3; (Ь) 2,4; (с) у; (d) 0,28.
3. Найти радианную меру угла, составляющего:
(а) ~ полного оборота; (Ь) 2 полных оборота.
О
4. Найти радианную меру угла, равного:
(а) Г; (Ь) 10°; (с) 135°; (d) 210°.
5. Найти радианную меру угла, равного:
(а) 300°; (Ь) - 45°; (с) - 120°; (d) 750°.
6. Найти градусную меру угла, равного:
, ч к ,,. Зя
(a) pg радианам; (Ь) — радианам,
(с) 4л радианам; (d) радианам.
00
74
7. Найти градусную меру угла, равного:
(а) 0,6; (Ь) 1,7; (с) -2; (d) -2,6; (е) 0,76.
8. Точка движется по окружности радиуса R с угловой скоро-
стью Найти линейную скорость, если:
(a) R= 40 см, <0 = 2 — ; (b) R = 60 см, <о = 4я — .
' ' сек 1 сек
9« Длина дуги сектора вдвое меньше его периметра. Найти ра-
дианную меру угла сектора.
10. Найти в радианной мере углы треугольника, если они отно-
сятся, как 2:3:4.
И. Найти в радианной мере угол правильного пятиугольника.
Упростить выражения (задачи 12—14):
12.
14.
• 1? I . Л
sin - — cos К 4- tg -4-
n . Я . Зя
2sin — sin —
о 2
cos (а — тс) ctg + -J ) sin (4я — а)
3sin (Зя 4~ а) ctg я — а )
sin ------а^ tg(n — а) — ctg (а — я) sin (а — 2я)
cos (а 4" я) c°s (а — я) sin (я 4- а) sin (2я — а) *
15. Найти значения выражения
2sina — 3 cos 2a t
3 sin 2a 4- 2cos a
я я я я
если a имеет следующие значения: -g-, -у, —— и я.
16. Найти значения выражения
Sln^g- -®у+‘И (д + «)
sin I з-4-з ] — tg I j-a )
n я 3
если a имеет следующие значения: 0, , —к и —-у я.
17. Найти значения выражения
я cos a — 1
я ctg a 4- 1 ’
я я я 5я
если а имеет следующие значения:—, -g-, — и
75
18. Пользуясь таблицей, найти с точностью до 0,001 значения
отношения если а имеет следующие значения: 1; 0,5; 0,2 и 0,1.
а
19. Дока зать (геометрически) справедливость неравенств
•in а < a <tg а для любого положительного числа а, меньшего чем ~ .
Указание. Построить центральные углы а и — а и сравнить
длину соответствующей дуги с длиной хорды.
20. Что больше: sin 1 или cos 1?
21. Пользуясь таблицей, найги с точностью до 0,001 ошибку
приближенного равенства tg а я, если а имеет следующие значения:
0,4; 0,3; 0,2.
22. Являются ли периодическими функции:
(а) у = 1 sin х; (Ь) у = х + sin х; (с) у = sin х cos х\
sin х . . ctgx ... n, . ,~
(d)^T+^: ' (t)y = 2tgx+l?
23. Найти периоды функций:
У = i (Ь) у = sin х + tg х; (с) у = sin8 х.
24. Показать, что функции
. . , , .. ч tg х . ч 1 + cos х,
(a)y=sin*х; (b) у = (с) у =
X Л*
... х4- sin х . . sin х 4- tg х
<e> >,c%inx—~tgx
являются четными.
25. Показать, что функции
(а) у = tg8 х; (Ь) у *=х + sin х; (с) у z=z sin х + tg х;
... sin х . . . 1 /n 14- sin 2х
) cos2 х ’ е sin3 х ’ ) tg Зх
являются нечетными.
26. Указать, какие из нижеследующих функций являются чет-
ными, нечетными и какие не являются ни четными, ни нечетными.
(а) у = tgx + ctgx; (b) у = tg х 4- cos х; (с)>' = пЕ4?4:
1 -j— ЫН А*
.. Ji . г. х sin х
(d) у = 1 4- Sin х; (е) у = х2 4-cos X, (f) у = •
1 -г- COS X
27. По графикам функций у —sinx, y = cosx и y = tgx выяс-
нить знаки следующих чисел:
2 / 5 \
(a) sin -х- л; (b) sin I —-г я ) ; (с) sin 5;
О \ т J
(d) cos 2; (е) cos (f) cos 3,2;
(g)tgl,5; (h)tg4,5; (i) tg(- 3,1).
76
г
28. Не производя вычислений, выяснить (по графику), что больше:
(a) sin 0,7 л или sin 0,71 к;
(с) tg 7,2к или tg 7,25 л;
(е) tg2 или tg2^«;
(b) cos 1,6л или cos 1,68л;
или
(f) ctg 6,9л или ctg 7,1л?
29. Не производя вычислений, указать знак разности:
(a) sin ( — 2) — sin ( — 2,1); (b) cos 5,1 — cos 5;
(c) tg (- S) tg (~ S); (d) ctg 0,583 ~ctg o,582;
(e) tg 1,6 — tg 1,5; (Г) ctg 6,3 — ctg 6,2.
30. Проверить, что в границах от 0 до 2л неравенство sin х > —
справедливо при всех значениях независимой переменной х, эаклю-
л 5л „
ценных между числами — и -g- . При каких значениях х в границах
от 0 до 2л справедливо неравенство cos х < -i- ?
31. Построить график функции у = | tg х | и, пользуясь графиком,
л л
указать, при каких значениях х в границах от — у до у справед-
ливо неравенство | tgx | < 1?
32. Построить график функции у = | sin х | и, пользуясь графи-
ком, указать, при каких значениях х в границах от 0 до 2л справед-
т/’'2"
ливо неравенство | sin х | > —— ?
33. При каких значениях х в границах от л до 2л справедливо
неравенство ctg2x > 1?
34. Построить график функции y = secx = ^-^ и по графику
разобрать вопрос о поведении функции. Результаты свести в таблицу.
35. То же для функции у = cosec х = .
36. Точка Р совершает простое гармоническое колебание вдоль
отрезка СС'=16 см. Расстояние $ точки Р от середины отрезка СС'
изменяется в зависимости от изменения времени t по следующему
закону:
О • ( 71 4 I Я
s — 8 sin --г t + -т-
\ 4 6
Определить положение точки Р на отрезке СС' в начале движе-
ния и по прошествии 2, 4, 8 секунд. Через сколько секунд после
начала движения точка Р в первый раз достигнет точки C'f
37. Точка Р совершает простое гармоническое колебание вдоль
отрезка СС; О — середина отрезка СС. Расстояние СС, равное 12 см,
точка Р проходит за 14 секунд. От начальною положения, совпадав-
77
iiiero с серединой отрезка СС', точка Р начала перемещаться по
направлению к точке С'. Составить формулу, выражающую закон
изменения расстояния 5 точки Р от точки О в зависимости от вре-
мени t.
38. Т очка движется равномерно ио окружности, радиус которой
равен 10 см, в направлении, обратном движению часовой стрелки,
делая 2 полных оборота в секунду. Составить формулу, выражающую
закон изменения расстояния проекции точки на вертикальны.! диаметр
от центра окружности, если начальное положение точки совпадало
с правым концом горизонтального диаметра.
39. Найти амплитуду, период и начальную фазу простого i армо-
нического колебания, заданного формулой:
(а) $ = 6 sin 3/ + у ) » (b) ~ sin nt — ;
(с) 5 — 2,5 sin ~ 1 ; (d) 5 = 3 sin 2/;
(е) 5 = 0,2 sin (0,1^4--^ » (0 $ = sin (/ — 2).
40. Построить график простою гармонического колебания в гра-
ницах одного периода:
(а) 5 = 3 sin 2Z;
(b) s = 2slnf-|--|-у
41. Построить график функции:
1 / Х’ '
(a)y = sin2x; (Ь) у = -- sin Д- j;
(с) у — 2,5 sin ( 1,5 х I И) у = 4 sin ( ~ -f- 1);
(е) у — 2 sin (Зх Д 2).
ГЛАВА ТРЕТЬЯ
ПРЕОБРАЗОВАНИЯ ТРИГОНОМЕТРИЧЕСКИХ
ВЫРАЖЕНИЙ
§ И. Формулы сложения и вычитания
33. Обобщение формулы проекций. Для дальнейшего
нам необходимо обобщить формулу проекций [см. формулу (19)
гл. 1 на стр. 26]: a = Ccosa,
которая позволяет вычислить проекцию а век юра на ось,
если известны его длина с и угол а вектора с осью.
Мы докажем, что эта формула остается справедливой, если
вместо длины с вектора взять алгебраическую вели-
чину d этого вектора как отрезка, лежащего на некоторой
оси, а под о понимать угол между э т о й осью и осью
проекции.
Теорема. Проекция а отрезка оси на другую ось
равна алгебраической величине d отрезка, умноженной на
косинус угла а между осями, т. е.
d = d cos а. (1)
Доказательство. Пусть дана ось MVt, образующая
угол а с осью проекций RRX (черт. 36). Рассмотрим как по-
ложительные, так и отрицательные отрезки оси и возь-
мем их проекции на ось RRr.
Алгебраическая величина d положительного отрезка АВ
равна его длине с, т. е. d = c. Этот отрезок, рассматривае-
мый как вектор АВ, образует угол а с осью RRX. Его про-
екция AtBt на эту ось по формуле (19) гл. I равна:
A1^1=fcosa. (2)
Здесь А1В1 — а, с---d и формула (1) доказана.
79
Алгебраическая величина отрицательного отрезка &А
равна — с, т. е. d ——с; из формулы (2) следует:
BiA1 = — с cos а = d cos а.
Черт. 36.
к доказываемой формуле:
а = d cos а,
ч. т. д.
34. Формулы сложения и вычитания для косинуса.
В основе теории тригонометрических функций лежат так на-
зываемые формулы сложения, выражающие значение триго-
нометрической функции суммы двух аргументов через значе-
ния тригонометрических функций аргументов-слагаемых.
Теорема. Для произвольных значений а и р имеет
место следующая формула сложения для косинуса:
cos (а (О — cos а cos [J — sin а sin р, (3)
т. е. косинус суммы равен произведению косинусов минус
произведение синусов слагаемых ').
Доказательство. Через точку О какой-нибудь оси
RRX проведем под углом а другую ось AWlt а под углом [J
к оси через ту же точку О проведем единичный вектор
ОЕ (черт. 37). Таким образом, вектор ОЕ образует угол
«4"? с осью RRX. Через конец Е вектора ОЕ проведем третью
ось РРХ, перпендикулярную к оси. AWj. Ось РРг составляет
*) Это — краткое словесное выражение формулы (3). Для некото-
рых важных формул мы и в последующем даем такие словесные
выражения, которые иногда удобнее запомнить, чем вид самой
формулы.
80
уг)Л о +а с осью Точку пересечения осей РР1 и NNx
обозначим через F.
Выразим проекцию ОЕг единичного вектора ОЕ на ось
RRX двумя способами. С одной стороны, непосредственно
найдем:
ОЕг = 1 • cos (а -]- ji) = cos (а 4“ ?)» (4)
а с другой стороны, рассматривая вектор ОЕ как замыкаю-
щий ломаной, составленной из векторов OF и FE, получим
(см. п. 8):
OEi = OFI-}-FIEi, (4')
причем OF1 есть проекция вектора OF на ось RR^ a F1E1—
проекция на ту же ось вектора FE.
Заметим теперь, что вектор OF можно считать отрезком
оси NN1 с алгебраической величиной d = cos }3, а вектор FE —
отрезком оси РР2 с алгебраической величиной fZ = sinp.
Действительно, единичный вектор ОЕ образует угол jj с осью
которую можно рассматривать в качестве «первой
оси», а ось РРг—в качестве «второй оси», и тогда
проекции вектора ОЕ на эти оси будут равны: ОЛ=соз{5,
(см. п. 12).
В соответствии с формулой (1) будем иметь:
OFX == OF- cos а = cos cos а
и
FlEl = FE- cos f у -L — — sin sin а. (5)
81
Подставляя эти выражения для ОРХ и FlEl в формулу (4*)
и сравнивая с формулой (4), придем к доказываемому равен*
ству (3):
cos (а 3) = cos а соз 3 — sin а sin 3.
Формула (3) справедлива для любых значений аргумента
а и 3, лак как теоремы о проекциях, на которые опиралось
доказательство, были доказаны для любых углов.
Заменив в формуле (3) р на —3, получим формулу
вычитания для косинуса:
cos (а — р) — cos а cos ( — 3) — sin а sin ( — Р) =
cos a cos 8 -J- sin a sin p, (6)
т. e. косинус разности равен произведению косинусов плюс
произведение синусов уменьшаемого и вычитаемого.
35. Формулы сложения и вычитания для синуса. Вы-
ведем сначала формулу сложения для синуса. На
основании формулы (6) имеем:
sin (а + Р) = cos [£—(« + ₽)] =cos =
= cos ~ cos Ji 4~ sin — а) sin 3 =>
t= sin а cos р -|“ cos а sin 3.
Итак,
sin (а 4" Р) = sin a cos р cos a sin р, (7]
т. е. синус суммы равен сумме произведении синуса первой
слагаемого на косинус второго и косинуса первого слагав*
мого на синус emoj ого.
Заменяя в форм;. ie (7) р на —р, получим формул)
вычитан и я для с и и у с а:
sin (а — 3) sin а cos р — cos а sin р, (8]
т. е. синус разности равен разности произведений синусе
уменьшаемого на косинус вычитаемого и косинуса умен*
шнемого на синус вычитаемого.
Формулы (7) и (8) верны для любых значений а и 3.
Пример ы.
1) cos 15°— cos (45° — 30°) = cos 45° cos 30°-[- sin 45° sin 30°=s
-ЛЛ :T?-OTO'3 + I>;
О г,
о 2
2) sin (тт -j- “ sin и cos a cos tt sin a —
— 0-cos a (—1) sin a —— sin a.
Все выведенные раньше формулы приведения
1ВЛяюТся частным случаем формул сложения.
36. Формулы
форм}'л (?) п (3)
Именно:
tg (a + Р)
сложения и вычитания для тангенса. Из
следует формула сложения для тангенса.
__sin (а -|- 0) sin a cos 0 -|- cos a sin 0
COS (a 4" 0) cos a cos 0 — Sin a sin 0 *
Предположим, что и cos a, и cos p отличны от нуля. Разде-
лив числитель и знаменатель дроби, стоящей в правой части,
на cos a cos р, получим:
sin a cos 0 . cos a sin 0 sin a , sin 0
I Qx _cos a cos 0 ’ cos a cos 0_ cos a ‘ cos 0 _
g i r/ cos a cos SJ Sin a sin p j sin a sin 0
COS a COS 0 cos 3 COS 0 COS g COS 0
= tgа 4~ tg ft
I - tg a tg ft •
Приходим к формуле сложения для тангенса:
tg (а 4-3) == Д-а-+ , (9)
Ь \ I Г/ 1 — tg a tg 0 ’ ' '
т. е. тангенс суммы равен сумме тангенсов слагаемых,
деленной на разность между единицей и произведением
этих тангенсов.
Если же cosa = 0 или cos 3 = 0, то не существует tga
или tg-}.
Таким образом, формула (9) справедлива для всех значе-
ний аргументов, за исключением тех, для которых не суще-
ствует хотя бы одна из функций, входящих в формулу.
Заменив в формуле (9) р на —3, получим формулу
вычитания для тангенса:
"0|
т- С. тангенс разности равен разности тангенсов умень-
шаемого и вычитаемого, деленной на сумму единицы и про-
ведении этих тангенсов.
83
Аналогично могут быть выведены формулы сложения
вычитания для котангенса, но они употребляются весьма редж
при необходимости читатель выведет их самостоятельно.
§ 12. Формулы для двойного и половинного аргумента
37. Тригонометрические функции двойного аргумента
Рассмотрим частный случай формул сложения, когда аргуме$
ты-слагаемые равны между собой. Положив в формулах (7|
(3) и (9) р = а, получим: 1
sin 2а = sin а cos а -ф- cos а sin а = 2 sin а cos а, (1!
cos 2а = cos а cos а — sin а sin а = cos2 а — sin* а, (1!
tg2a= tg а + tg а = 2 tg a
® 1 — tg ot tg а 1 — tg2 а * ’
Формулы (11) — (13) выражают тригонометрические фунг
ции двойного аргумента 2а через тригонометрические функця
аргумента а.
Последовательное применение теорем сложения позволяв
выразить тригонометрические функции аргументов За, 4а, 5а,
через тригонометрические функции аргумента а.
Пример.
sin За = sin (2а -|- а) = sin 2а cos а -ф cos 2а sin а =
= 2 sin а cos а cos а -ф (cos2 а — sin2 а) sin а —
— 3 sin а cos2 а — sin* а.
Из сказанного следует, что по значениям тригонсметрич^
скпх функций, например для 1°, можно при помощи форму|
сложения найти значения тригонометрических функций д$
всех углов, выраженных целым числом градусов.
38. Тригонометрические функции половинного арг$|
мента. Выразим тригонометрические функции половинном
(а \ . 1
аргумента ) через тригонометрические функции целопй
аргумента (а). Заменив в формулах (11) и (12) аргумент а нг]
у и, следовательно, 2а на а и переставив правые и левые]
части этих тождеств, получим: а
2 sin у cos у ~ sin а, (14д
cos2 ~—sin2 — cos а. (151
84
I
Добавим еще основное соотношение:
cosi 2 -Г sin2 у = 1. (16)
Почленное сложение тождеств (15) и (16) дает: 2 cos2 y= 1 -4- cos а. (17)
Почленное вычитание тождества (15) из тождества (16) дает: 2 sin2 — = 1 — cos а. (18)
Из тождеств (17) и (18) имеем:
cos ± j/ , (19) sin 4 = ± ]/"J— • (20)
Наконец, почленное деление тождества (14) на тождество (17)
1риводнт к тождеству
a a 2 sin — cos 2 2 SIU a 2cos2-“- 1+c0Sa’
шачит, b 2 1+cosa V '
Аналогично почленным делением тождества (18) на тож-
дество (14) находим:
tg4 = ——— , (22) & 2 sin a ’
i если почленно разделить тождество (20) на тождество (19),
о получим:
. а / 1 —- COS a ZQQX
(23)
В формулах (19), (20) и (23) значения cos ~, sin 4 и
g -,у находятся с помощью извлечения квадратного корня.
1нак перед корнем ставится в зависимости от величины
гл а ; необходимость выбора знака делает формулу (23)
83
менее удобной для отыскания tg-^ , чем формулы (21) и (22;
(если, разумеется, заранее известны значения и cos а и sin а).
Примеры.
«in 225"= - /.
39. Выражение тригонометрических функций через тан-
генс половинного аргумента. Покажем сейчас, что все трв
тонометрические функции аргумента а выражаются через tg-~
рационально, т. е. с помощью одних только четырех
арифметических действий. (Вспомним, что тригонометрические
функции одного и того же аргумента выражаются друг через
друга, как правило, иррационально, с помощью извлечения
корней.)
В самом деле, заменяя в формуле (13) а на получаем:
отсюда
Вывести формулу для sin а можно так:
о , а , а л . а
a 2sinycos’y 2tgy
sin а 2 sin тг cos -тг =-—------
2 2 а 1 . . . а
C0SJ l + tg*y
(2 ® I \ «
потому, что cos—=----и аналогично находим фор-
l+l«T
мулу для cos а:
(• 2 3 \ 1 1 2 а
sinI 2 — \ 1 — tg2 —
1 2 2
I * 1 I £ 2 «
COS8-уу ] + J
86
Выведенные формулы дают нам рациональные выра-
жения sin a, cos а, tga и ctgа через tg~.
Обозначая tgy через получим:
. 2t 1 - Р
sina=rp5) cosa = j—j-^5
, 2/ . 1 -
tga = T—с^а = ~2Г
(24)
§ 18, Преобразования произведений тригонометрических
функций в сумму и обратные преобразования
40. Формулы для произведений синусов и косинусов.
Выведем формулы, выражающие произведения тригоно-
метрических функций через их сумм ы.
Почленным сложением и вычитанием формул
sin (a -j“ Р) = sin a cos р 4“ cos a sin P>
sin (a — p) = sin a cos p — cos a sin p
получим:
sin (a 4~ P) 4“ s*n (a — P) = 2 sin a cos p, (25)
sin (a 4~ P) — sin (a — P) = 2 cos a sin p. (25J
Аналогично из формул
cos (a 4“ p) = cos a cos p —sin a sin p,
cos (a — p) = cos a cos p 4“ s*n a s*n P
путем почленного сложения и вычитания получим:
cos (a 4~ Р) 4“ cos (a — Р) — 2 cos a cos p, (26)
cos (a —"p) — cos (a 4~ p) = 2 sin a sin p. (27)
Переставив правые и левые части формул (25), (26), (27)
и разделив их почленно на 2, приходим к тождествам:
sin a cos р — у [sin (a 4~ р) 4“ sin (a — Р)]> (25')
cos a cos p — у [cos (a 4“ P) 4“ cos (a — P)], (26')
sin a sin p — 4- [cos (a — P) — cos (a 4- p)l. (27')
87
41. Приведение к виду* удобному для логарифмировав
ния. При пользовании таблицами логарифмов и логарифми-
ческой линейкой полезны бывают преобразования сумм*
тригонометрических функций в их произведения, т. е.
преобразования, обратные рассмотренным в п. 40. Положим:
= а — р =У-
Тогда
-=^.
Формулы (25) — (27) примут вид:
sin х sin у = 2 sin cos , (28)
sin х — sin у = 2 cos sin , (29)
cos х cos у — 2 cos Ц^соз — , (30)
n . x4-y . x — у
COSX---COS J/ = — 2sm---Sin ---2Z==a
x= 2 sin sin (31)
(потому что sin —= — sin ^-4" .
Тождества (28) — (31) обычно формулируют так:
Сумма синусов равна удвоенному произведению синуса
полусуммы на косинус полу разности1).
Разность синусов равна удвоенному произведению коси-
нуса полусуммы на синус полу разности.
Сумма косинусов равна удвоенному произведению коси-
нуса полусуммы на косинус полу разности.
Разность косинусов равна удвоенному произведению си-
нуса полусуммы на синус обратной полуразности (обрат-
ной разностью чисел а и b называют b — а).
Найдем аналогичные выражения для суммы тангенсов:
. . _sin х । sin у sin х cos у 4~ cos х sin У
® т ъУ cosх * cosy cosx.cosy
Так как числитель в правой части равен sin(x4-^)» то
tg х 4“ tgy — . (32)
to 1 cos x cos у ' '
x) Более точная формулировка такова: сумма синусов двух аргу-
ментов равна удвоенному произведению синуса полусуммы этих ар-
гументов на косинус их полуразности. Аналогичные замечания отно-
сятся и к дальнейшим кратким словесным формулировкам.
й
Подобным же образом найдем:
. А sin (х — у)
tg X tg У = i.
° cosx cos у
Преобразование суммы тригонометрических функций в их
произведение называется приведением к виду, удобному для
логарифмирования.
Пример.
, , . ~7О , . 1 qo\ 1 /о . 67° 4-13° 67°—13°\
lg (sin 67 -f- sin 13 ) = 1g ( 2 sin-у— cos--
= lg (2 sin 40° • cos 27°) =
= lg 2 -j- lg sin 40° lg cos 27°.
42. Преобразования с помощью вспомогательного ар-
гумента. Познакомимся с особым приемом преобразования
тригонометрических выражений — введением вспомога-
тельного аргумента. Этот прием заключается в том,
что некоторые числа рассматриваются как значения тригоно-
метрических функций вспомогательного аргумента <р.
В качестве примера преобразования такого рода рассмот-
рим преобразование выражения
a sin а 4~ b cos а
к виду, удобному для логарифмирования. Мы подберем такой
аргумент <р и такой положительный множитель р, чтобы было
р cos (р = a, psin<p = Z>.
Для подбора таких р и <р возведем обе части каждого из
последних равенств в квадрат и сложим их после этого по-
членно. Получим:
р2 (cos2 <р 4~ sin2 ?) — 4“
или р* = я24~#2, откуда находим:
р = У с? -[-Ь\
Значит,
a a b Ъ
cos (р = — = г - ; sin (р = — = .
r р + r Р
Из этих равенств можно найти вспомогательный аргумент (р.
Итак,
a sin а b cos а = р cos <р sin а р sin ср cos а =
= р (sin а cos ср 4- cos а sin у) = р sin (а 4~ ¥>)•
89
Пример.
8 sin а 4 cos а — 5 sin (а 0,643),
так как
s = ^/З2 —4а = 5; ein <р = ~ = 0,6; cos<p=~ = 0,8
(из второго или третьего равенства и находим, что у = 0,643,
см. таблицу на стр. 57).
Задачи к главе Ш
I. Найти c(»s 105°, рассматривая угол в 105° как сумму углов
в 60° и 45°.
2. Найти по таблице sin 13°, cos 13°, sin 37° и cos 37°, а затем,
пользуясь формулами сложения и вычитания, найти cos50° и cos 24°.
Найденные результаты сверить с таблицей.
3. Пользуясь формулами сложения и вычитания, доказать следую-
щие формулы приведения:
(a) cos (180° + а) = — cos a; (b) cos (270° — а) = — sin а,
(с) cos (к — а) = — cos а; (d) cos ( у к + о ) = ein з.
_ 1 0 1 я
4. Дано: cos а = —, cos р — - -, причем < а т,
4л ? <2г-
Найти cos (а —|— р) и cos (а — Р).
8 3
5. Дано: slna = — , cos р = 0,96, причем к < а < - г..
0 < Р < -у. Найти sin (а 4" ₽) и sin (а — Р).
6. Синусы двух острых углов треугольника соответственно равны
7 4
25 и -у. Найти косинус третьего угла.
7. Из точки О, взятой внутри треугольника АВС, стороны АВ,
АС и ВС видны под тупыми углами. Зная, чго sin / АОВ~ —~ ,
/3
a cos / ВОС = —~ , найти sin / АОС.
о
8. Найти sin (60° — а), если tg a — и 180° < a 270°.
3 2
9. Найти tg (a 4~ ?) и tg (a — ?)» если tg a = и tg p = -y .
IO. Найти tg (a + ?) и tg (a — P), если tg a = у и ship = 0,28,
причем 0 < p < -у .
12
II. Найти tg (45ю - а), если sin a = — -7 и 18U° а ч. 270°.
90
12. Найти tga, если
а.
1
и
причем
3 3
5 ’ 4
13. Найти sin a, если sin (— оЛ =------и < a < к.
\ 4 ) о 2
14. Дано: sin (a 4~ ?) = sin (a 4-Y) == ^, причем каждое из поло-
жительных чисел a, f и у меньше, чем . Найти sin (Ц — у).
(5. Синусы двух острых углов соответственно равны ;
Доказать, что сумма данных углов равна 45°.
16. Дано: sina —0,8, sin 3 = 0,28, cos’f = —Д.,
1 о
*- < a < к, 0 < J < —, -^- < ? < к. Найти cos (a 4~ ? Y)«
Z 2 2
17. Тангенсы трех острых углов соответственно равны
g
н --д. Доказать, что сумма первых двух углов на 45° превышает
третий угол.
Упростить выражения (задачи 18—28):
18. (а) sin (а 4- 30°) — sin (a — 30°); (b) cos (a 4- 45°) — cos (a — 45°).
sin(a + ^)+ sin(a-p) . , c°s (a + ^) 4-cos (a - ?.)
sin (a 4- ?) — Sin (a — f) ’ ' ' cos (a 4~ f) — COS (a — £) *
2O1 sin (3-H) sin (g-P)
sin a 4~ sin 0
2i. sin 10° cos 50° 4- cos 10° sin 50°.
Зк к , Зк к
22. cos -g- cos g- 4- sin у sin -g-.
23. cos (20° 4~ a) cos (20° — a) 4- sin (20° 4" *) sin (20° — a).
24. cos (36° 4- *) cos (54° 4~ ^) — sin (36° 4- 4 sin (54° 4- <*)•
25. sin (4- — a ) sin ( 4- * ) — cos ( ~ — a I ccs |-t 4~ 1 I •
\ 4 j \4 J \ 4 J \ 4 у
26. sin a 4" sin ? cos (a + ?)•
27 (a) + (b1 tg 2a - tg a
W l-tg2atga ’ V J 1tg 2a tg a ’
28. (a) sin 15° 4- tg 30° cos 15°; (b) cos 20° 4- tg a sin 20°;
(С) sin a 4~ ctg За cos a.
Доказать тождества (задачи 29—36):
Q
29. cos2 a — sin (30° а) sin (30° — a) = -у.
30. cos (a -f- f) cos (i — f) — cos2 a — sin2 (L
31. T—j-----r~n' “ c os 27.
1 4- tg a tg 2i
sin (a 4- p) cos (*--£) + cos (a 4~ 8) sin (i - ft) __
cos (g 4“ ?) C0S (3 — f) —* sin (* + ?) sin — ?) * ~ *
91
за. tg.e + tg.f.
2 cos’ a CCS2 0 5 I S r
34. cos (a -f- f) cos f — cos (a 4- 7) cos 7 =
= sin (a + 7) s,n T “ sIn (a + ?) ®ln P-
35. tg (45° 4~ °) —tga=14-tg(45° + a)tga.
86. tg(a — j) + tg(p-f)+tg(Y-a) =
= tg (a - f) tg ft - Y) tg (Y - a).
37. Косинус суммы двух углов равен 0,3, а косинус их разности
равен 0,8. Найти произведение синусов данных углов.
38. Доказать, что тангенс разности двух дополнительных углов
вдвое меньше разности тангенсов этих углов.
’ 39. Найти по таблице sin 39° и cos 39°, а затем, пользуясь фор-
мулами, найти sin 78° и cos 78°. Найденные результаты сверить
с таблицей.
40. Найти по таблице tg31°, а затем, пользуясь формулами,
найти tg 62° и tg 28°.
41. Найти sin 20°, если sin 10° = а.
.. „ к я
42. Наити cos , если cos = а.
43. Дапо sin а = ~, -где < a < л. Найти sin 2a, cos 2a и tg 2a.
2o 2
44. Выразить cos a через
a
sm T.
4S. Дано: %
46. Дано: tgy=y, tg
. Найти sin a и tg a.
• Найти tg — “)•
47. Дано: sin a — 0,8, cos ? = — y^, причем углы аир тупые.
Найти: (а) sin (a 4- 2{J); (b) cos (2a — 0); (с) tg [2 (a — 0)].
48. Доказать, что sin 2a < 2 sin a, если 0 < a < л.
49. Доказать, что tg 2a > 2 tg a, если 0 < a < .
50. Синус угла, образованного диагональю ромба с его стороной,
равен 0,2. Найти косинусы углов ромба.
51. Косинус угла при основании равнобедренного треугольника
3
равен -у-. Найти косинус угла при вершине треугольника.
52. Выразить tg3a через tga.
53. При каком значении х в границах от 0 до у функция
у = sin х + c°s х принимает наибольшее значение? Найти это наи-
большее значение функции.
Указание. Предварительно доказать тождество
sin х 4- cos х = 1^1 -ф- sin 2х.
54. При каком значении х в границах от 0 до л функция
у = sin х — cos х принимает наибольшее значение?
92
Упростить выражения (задачи 55—65):
55. (а) 2 sin 20° cos 20°;
56. (a) cos2 2a — sin2 2a;
58. cos2 f к —~ ) — sin
(b) sin 10° cos 10°.
(b) cos2 a — 4 sin2 у cos2 у.
tg (45° - a)
1 _ tg2 (45° - a) ‘
/ , a \ Зя — a
(* + t )cos-^—•
(b)
sin -5------a sin -+- a
\ 4 / \ 4 1 /
sin 3a cos a — cos 3a sin a
59.(a) -ln gcusa •
1 — 2 sin* a ’
gg sin 2a cos 2a
2 sin a cos a
82. (a) 2^4-; (b)
1 4" tg2 a
63. (tg a ctg a) sin 2a.
65. (a) 2 sin a cos a (cos2 a —
61. cos'
- tg2a
1
Ctg a — tg a
COS 2a
64.
sin2
(b) cos4 a — 6 cos2 a sin2 a 4- sin4 a.
Проверить справедливость равенств (задачи 66—67):
, ft
1 ^g ЗГ ।
66. (а) sin 15° cos 15° = -г; (b) -= •
l-tg’l
м 1 — tg2 15° 1КЗ . к . п Q
®7- (а) l -f-tg* 15° = —; (Ь) Ctg 8 - tg Т = 2-
Доказать тождества (задачи 68—81);
св „ » . -я sin 4а
68. cos3 a sin a — sin3 a cos a — —— .
4
69 cos2e ___cos a — sin a
1 -|- sin 2a cos a 4~ sin a ‘
4 ( ft । \ i ( ft \ 2 cos 2a 1
7О1ЦбЖб'“Г^wr
71.
1 -|- sin 2a
1 — sin 2a *
„ 1 — cos 2a 4- sin 2a .
72. ------------!------= tg a.
1 + cos 2a + sin 2a g
tg2 45° + a) - 1 , _
74. x r'"i = sin 2a*
tg2(45°4-a)+ 1
_ 1
— cos 2a *
1 — COS a + cos 2a .
73. -----— ----!—;-----= ctg a.
sin 2a — sin a
75. g + *& g _L Sin 2a tg 2a
ctg2 a — tg2 a ’ 2 6
76. sin2 (a + f) + sin2 (.3 - a) -
— 2 sin (a f) sin (? — a) cos 2a = sin2 2a.
93
tg1 a -j- ctg1 a —• 6__
tg* a -j- ctg* a + 2 “
17.
78.
COS 4a.
cos8 a — eqs 3a . sin* a 4~ sln За__з
cos a ”* sin a
9Q . 4тс —3a 2те —3a / к \ 10^ —- 3a
78. sin —g— sin —g-----------H cos I у + a j cos----g----=
— — cos 2a.
80- tg a -|- 2 tg 2a = ctg a — 4 ctg 4a.
Проверить справедливость равенств (задачи 81—82):
81. sin 18° со» 36е = 4-.
4
Укавание. Умножить и разделить левую часть на cos 18°.
82. cos 20° cos 40° cos 80° = -i- (см. Указание к предыдущей
о
вадаче).
83. Найти sin 15°, cos 15° и tg 15°, зная значения тригонометри- •
ческих функций угла в 30°.
84. Пользуясь результатами решения предыдущей задачи, найти
tg 7°30'.
85. Найти tg22°30'.
86. Дано: cos a = , причем 0 < о < у . Найти sin у, cos -у
1 в
" ‘8-2-
4
87. Дано: sin 2a = — -g , причем 90°<a<135°. Найти sin a,
cos a и tga.
88. Дано: tg у = 2,4, причем 0 < a < те. Найти sin у , cos у
. °
и tef
89. Дано: cos 3a = —1-, причем -£• < a < -J-. Найти sin^- ,
о О о 2
3a 3a
cosy a tgy.
90.
91.
формулу tgy
Дано: sin a = , причем 0<a<y. Найти tgy.
Вывести геометрически (непосредственно из треугольника)
sin a
1 -j- cos g‘ ДЛЯ 0СТР0Г0 Угла a-
Указание. В прямоугольном треугольнике провести биссект-
рису острого угла а и воспользоваться теоремой о биссектрисе угла
в треугольнике.
94
43"
92. Доказать, что два значения, которые может принимать tgy
прп данном значении sin а, взаимно обратны. Дать геометрическое
истолкование этого факта.
Упростить выражения (задачи 93—95):
93. (а) ‘ 2 ; (b) 1 + ^1*.
94. (а)
95. (а)
(b) S,n(a-H)_
(>1 +cos(a + £)
cos 12° . cos а
1 - sin 12° ’ ( } 1 - sin а ’
Указание. Заменить cos 12° и sin 12° соответствующим., три-
гонометрическими функциями угла в 102°.
Доказать тождества (задачи 96—100):
96. (а) 2 sin1 — cos о = 1; (Ь) 2 cos1 а — cos 2а = 1.
„ cos 2а /я \ cos 2а . / я
97. (a) iFT- = ctg -----------а (Ь) -г—;-----Г-77- = tg -у -
1 — sin 2a s \ 4 J ' 1 -f- sin 2a 6 \ 4
___ о
98. cos a (cos a — cos f) 4- sin a (sin a — sin 0) = 2 sin1 —•
2 sin a — sin 2a . . a ___ , a . _ . , a ,
99. к—; :———- — tg’ —. IOO. tg — 4~ 2sin2 — ctg a — sin a.
2 sin a 4- sin 2a 6 2 s 2 ' 2 6
101. Дано: cos20° = m. Найти cos 5°.
102. Синус разности двух дополнительных углов равен т. Найти
тангенсы данных углов.
103. Дано: tg . Найти sin a, cos а и tg a.
2 о
.лл t» « sin* t a 1
104. Наити значение выражения ---, если tg —= —.
2 — о COS a 2 2
вЛв U « tg a — Sin a a 2
105. Наити значение выражения --;;, если tg — =
* tga 4-sin a 2 15
106. Выразить sin2a через ctga.
107. Доказать, что синус и косинус одного и того же угла
могут быть оба рациональными тогда и только тогда, когда тангенс
половинного угла есть число рациональное (или не существует).
108. Найти, не пользуясь таблицей, числовые значения выраже-
ний: (а) sin 45° cos 15°; b) sin sin ; (c) cos 75° sin 105°.
95
Пользуясь таблицей и формулами преобразования произ-
ведения функций в сумму, найги числовые значения выражений:
(a) sin 18° sin 22° sin 10°; (b) sin 36° sin 24° sin 48°;
(c) cos 10° cos 20° cos 40°.
Преобразовать произведения функций в суммы (задачи 110-114);
НО. (a) sin (а -ф- £) cos (а — р); (b) sin (л — cos (a -|- f).
III. (a) sin (60° 4-a) sin (60° — a); (b) sin ^-2 4-a sin ^-2 — 7 у •
112. (a) sin a cos 2а; (b) cos a cos За.
H3. sin a sin J cos (a -|- f).
114. sin a sin 2a sin 3a.
H5. Пользуясь формулами преобразования произведения фун -л'ий
в сумму, доказать следующие тождества:
(а) 2 sin 2a sin a cos 3a = cos a;
2 sin _ 1^3
(b) sin (a - 30°) cos (a 4- 30°) ;
(c) sin a — 2 sin --15°^ cos 4~ 15° ~ .
Преобразовать суммы функций в произволения (задачи 116--12]):
116. (а) sin 12° 4- sin 20"; (b) sin 40э — sin 16°;
(c) cos 50° 4- cos 30°; (d) cos 17° — cos 13°;
(e) sin - sin ~ ; (f) cos ~ 4- cos^ .
117. (a) sin 25° 4- cos 55°; (b) cos 22° - sin 66°;
(c) sin — + cos —; (d) sin — cos .
о О и О
7г к
118. (a) tg 10° 4- tg 20°; (b) tg - tg^;
(с) tg 12° - ctg 40"; (d) ctg 15" - ctg 25°.
M9. (a) tg a-|-ctg a; (b) cos a — sin a.
I2O. (a) sin 16° 4~ sin 24° 4- sin 40°; (b) sin a 4- sin 2т 4 sin 3a.
Указан и e. Воспользоваться формулой sin 2i~2 sin a <*os a.
121. (a) cos 16° sin 56° 4' sin 50°;
(b) cos (54° -|-з)4 cos(18°— a) 4- sin (36° 4~ 2л).
Привести к виду, удобному для логарифмирования (задачи
122—128):
, к sin 19° — sin 37° .. . cos a 4- sina
U cos 65° — cos 47° ’ J cos a — sin a *
l23. (4^ + 1Ц; (b) 4 +
tg a — tg p tg a — ctg i
96
COS ( 2a — ~ ) — COS ( 2a 4" •?• )
124. (a) cos a----X-----1Z--------V------LZ;
2 cos a
... sin a 4~ sin 3 a sin a
sin 4a sin 2a *
/к COS 3a—cos 5a cos 2a — cos 4a
125. (a) ’—5—j----=------------—;-г-;
cos 3a 4" cos 5a cos 2a 4~ cos 4a
.. sin (a 4~ ft) — sin a cos (<* 4~ ft) 4~ c°s ?
sin (a 4“ ft) 4" sin a cos (a "h ft) — cos a ’
126. (a)
tg 2a 4- tg 2?
sin 2a 4- sin 2} ’
|O7 COS a 4~ 2 COS 2a 4~ cos 3a _ sin 2a 4~ sin 4a — sin 6a
sin a 4- 2 Sin 2a 4- sin 3a " tg a 4- tg 2a — tg 3a
Проверить справедливость равенств (задачи 129—130):
129. (а) sin 10° 4- sin 50° — cos 20° = 0;
(b) cos 85° 4“ cos 35° — cos 25° = 0.
cos 20° — cos 50°______sin 80° — sin 70° .
Э cos 31 ° 4“ sin 110 sin 29° — sin 196 ’
, sin 22° 4- sin 8°__ sin 12° — sin 2°
(b) sirT30° “ cos 70° - cos 80° ’
Доказать тождества (задачи 131—133):
«а. /ч cos 2a — cos 4a . o .
131. (a) -------—;----— = tg 3 a tg a;
v ' COS 2a 4- cos 4a 6 5
. 3a
tg —
sin 2a 4~ sin a 2 sin 2a 4~ sin 6a ,
' ) sin 2a — sin a . a ’ cos 2a 4- COS 6a *
tg-2
182 sln а + sin ? _ sin (a + ft) sin (a — ft)
‘ a -|~ ft , а — ji — 2 COS ft
tg-p + ctg-2-!
133 cos a + cos 3a “ s'n __ ctg 2a
cos a — COS 3a — sin 4a , /к , a \
tg (z+2)
Привести к виду, удобному для логарифмирования (задачи
134—142):
134. (а) 1 + cos 2а; (b) 1 - cos у.
I3S. (а) 1 + cos 20°; (b) 1 - sin 32°.
136. (а) 1 4- sin у; (b) 1 — sin у .
137, j ~~ cos 2.3 . |38, 1.~ ?|П .а
i -{-cos 2a 1 4- sin a 4
4 А. Вермант, Л. Люстерник
97
143.
144.
845.
I4S.
847.
148.
139. (a) 1 -f- sin a -|- cos a; (b) 1 -|~ sin a — cos a.
140. 1 — cos 3л cos 2a 4- sin 3a sin 2л.
141. (sin 2a 4- sin 4a)2 (cos 2a 4“ COS 4a)8.
142. cos2 a — sin2 2a.
Указание. Воспользоваться формулами
, 1 — cos 2a „ 14 - cos 2a
Siu2 a ------------ и cos a =--------------- .
Доказать тождества (задачи 143—148):
2 sin a — sin 3a 4~ sin ,Г)3 2 cos 2a
COS a — 2 cos 2a -I- cos 3a , a
1 fa —
* 2
Y 2 — COS a — sin a_____ ( a г \
sin a — cos a k 2 8 J '
( a V / ; I • 7 V
( COS a 4“ COS — I sill a 4' Sin — )
sin 2a — sin a 4
a
• о COS --
Sin 2a COS a 2 a
1 4- cos 2a 1 4- cos a ~ a “ 4 •
1 4“ cos -
Q
COS2 a 4- COS2 (60° -j- a) 4" COS2 (60 э — a) = — .
C;'s2 a — 2 cos a cos £ COS (a 4~ ?) 4~ COS2 (a + ?) — sin2 f.
Введением вспо.могательного угла привести к виду, удобному для
логарифмирования (задачи 149—155):
!49. (а) 1 - tg a; (b) / 3 + tg a.
150. (а) V 2 + 2 cos a; (b) V 3 — 2 sin a.
151. (a) 1-4 sin2 a; (b) 3 - tg2 2a.
152. (a) sin a — У 3 cos a; (b) 3 COS a + У 3 sin a.
153. (a) 7 cos a 4~ 24 sin a; (b) 5 cos a — 12 sin a.
154. p2 — q2 sin2 a, | p | < | q |. 855. p2 sin2 a — q2 cos2 a.
Для каждой из нижеследующих функций (задачи 156—160) найти’
1) значение независимой переменной в границах от 0 до при
котором функция принимает наибольшее значение, и
2) соответствующее наибольшее значение функции (по табл i :<?)’
856. (а) у = sin 2х 4- cos 2%: (b) у = sin 3?; — cos Зх.
157. (а) у = sin х 4~ Y 3 cos х; (Ь) у — Y 3 -in 2х — cos 2х.
158. (а) у = 3 sin 2х 4~ 4 cos 2х; (Ь)у =9 sin R — 40 cos Зх.
159. (а) у — sin х 2 cos х; (b) у = 4 sin 2х — cos 2ю
I6O. у = sin ( 4- 2х ) cos ( ~ — 2х ) .
\ 3 J \ 6 j
ГЛАВА ЧЕТВЕРТАЯ
ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ.
ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ
§ 14. Обратные тригонометрические функции
43 . Определения и общий вид для значений обратных
тригонометрических функций. Во многих задачах встречается
необходимость находить не только значения тригонометриче-
ских функций по данному углу пли дуге, но и, обратно,
угол паи дугу по заданному значению какой-нибудь тригоно-
метрической функции.
Пусть, например, синус некоторого аргуменia а (угла или
дуги) равен а:
sin а = а.
Отсюда следует, что аргумент, синус которого есть а, равен
а (раз аргументом является угол или дуга, то а выражено
в радианах). Вместо такого словесного утверждения упог
требляют запись:
а = Arcsin а
(произносят: а равно арксинус а). Приставка Аге (со-
кращение от Arcus — дуга) неотделима от обозначения sin и
вместе с ним образует символ, указывающий величину а, си-
нус которого равен числу а, стоящему за символом Arcsin.
Подобным образом вводятся:
Arccos а (арккосинус <?),
Arctg а (а р к т а н гене л),
ArccLg а (а р к к о т а и г е н с а).
Запись Arccosа указывает величину аргумента (угла или
дуги), косинус которого равен а\ запись Arctg а — величину
аргумента (угла или душ), тангенс которою равен а\ запись
4* А. Бермант, Я. Люстерник 99
Arcctg a— величину аргумента (угла или дуги), котангенс ко-
торого равен а. Относительно этих обозначений следует сде-
лать те же замечания, которые были сделаны относительно
обозначения Arcsin а.
Каждому (возможному) значению а соответствуют значе-
ния Arcsin a, Arccosa, Arctga, Arcctg а, которые мы, следо-
вательно, можем рассматривать как функции аргумента а.
Эти функции называются обратными тригонометрическими
функциями. Функции же sin a, cos а, tga, ctg а иногда на-
зывают прямыми тригонометрическими функциями.
Функции Arcsin а и Arccosa имеют смысл, только если
|а|^1, ибо значения синуса и косинуса любого угла по
абсолютной величине не могут быть больше единицы. Что
касается функций Arctg а и Arcctg а, то они имеют смысл
при любом а.
Выявим сейчас одну важную особенность обратных три го
нометрических функций: любому возможному значению аргу-
мента соответствует много значений данной обратной
тригонометрической функции. Эта особенность называется
многозначностью. (Прямые же тригонометрические функции
однозначны, каждому значению аргумента соответствует лишь
одно значение функции.)
Мы обнаружим многозначность, находя для каждой об-
ратной тригонометрической функции в отдельности общий вид
ее значений, соответствующих данному значению аргумента.
Арксинус. Пусть известно, что
Arcsin a = a.
Это значит, по определению, что sin a = а. Но тогда
в силу периодичности и sin (a -|- k- 2тг) = а, где k— произ-
вольное целое число. Отсюда сразу следует:
Arcsin а = а k- 2тг = a 2Атг. (1J
Кроме того, в согласии с формулами приведения (п. 21)
sin a = sin (п — о.) = а.
Поэтому
Arcsin а = п — a
и в силу периодичности
Arcsin л = п — a -1- k • 2тг = — a-]- (2k 1) п. (12)
Мы видим, что если известен один угол а, синус которого
равен данному числу а, то всякий угол одного из двух ви-
100
дов a-j-2Zm и —a —1) тг имеет синус, равный тому
же числу а. Два выражения а-(-2/гтг и —а (2k 4- 1) тт
можно заменить одним, если заметить, что в первом из них
множителем при тт служит произвольное четное число, а
во втором — произвольное нечетное число. Очевидно, вы-
ражение (— 1)ла4~шь где п — любое целое число, соеди-
няет в себе оба предыдущих выражения (1J и (12). Именно,
при п четном оно обращается в первое из них, а при п не-
четном— во второе.
Таким образом:
Arcsin а — ( — Ifa 4~AZTT> U)
где a — какой-нибудь угол, синус которого равен а,
а п — целое число (положительное или отрицательное) или
нуль. Правая часть формулы (1) дает нам общий вид
углов (дуг), имеющих данный синус.
Пример. Так как sin— у, то
Arcsin ~ = ( — 1 )п -g- 4“ лтг.
Арккосинус. Если известно, что
Arccos a — а,
т. е. что cos а = а, то и cos (а 4” п' 2п) — а> а значит,
Arccos а = а 4~ 2шт.
Далее, в силу четности косинуса (п. 18)
cos (— a) = cos a = a,
и поэтому
Arccos a = — a 4“ 2шт.
Итак, если a — какой-нибудь угол, косинус которого ра-
вен данному числу а, то всякий угол одного из двух видов
а4~2шт и —а 4г- 2/ztt имеет косинус, равный тому же числу а.
Таким образом:
Arccos a = Ц- а 4~ 2лгтт, (2)
|де a — какой-нибудь угол, косинус которого равен а,
а п — целое число (положительное или отрицательное) или
нуль. Правая часть формулы (2) дает нам общий вид
углов (дуг), имеющих данный косинус.
4**
101
Пример. Так как cos — — , то
Arccos — = -1- у -у- 2/гтг.
Арктангенс. Пусть известно, что
Arctg я = а.
Значит, tga = a и в сиду периодичности tg (а-|-/ш) = а.
Поэтому наряд}’ со значением, равным a, Arctg а равен также
любому углу (дуге) вида a-ф-ятг. Таким образом:
Arctg а = a -1- шт, (3)
где a — какой-нибудь угол, тангенс которого равен а,
а п — целое число (положительное или отрицательное) или
нуль. Правая часть формулы (3) дает нам общий вид уг-
лов (дуг), имеющих данный тангенс.
Пример. Так как tgy-= 1, то
Arctg 1 = у -j- /гп,
А р к к о т а н г е н с. Пусть известно, что
Arcctg а= а.
Таким же образом, как и в случае арктангенса, убеждаемся,
что
A rcctg а = а //тт, (4)
где a — какой-нибудь угол, кота hi енс которого равен а,
а п — целое число (положительное или отрицательное) или
нуль. Правая часть формулы (4) дает нам общий вид уг-
лов (дуг), им ею пт их данный котангенс.
Пример. Так как ctgy = Jz 3, то
Arcctg / 3 = у шт.
44. Главные значения обратных тригонометрических
функций. Для того чтобы найти все значения обратной три-
гонометрической функции, достаточно знать только одно
ее значение (п. 43). Другие ее значения получаются тогда
по формулам (1) — (4).
1U2
Рассмотрим каждую из обратных тригонометрических функ-
ций в отдельности.
I. Arcsin а. Среди всех значений Arcsin а особо выделим
то, которое заключено между — и у. Оно называется
главным значением Arcsin я и обозначается так: arcsin а.
Так как при увеличении угла or — у до у синус увели-
чивается от—1 до -j- 1, то каждому значению fl, заключен-
ному между—1 и 1, соответствует один угол, заключен-
ный между—у и у, синус которою равен данному
значению а. (Это наглядно показано в п. 46, где рассматри-
вается график арксинуса.)
Покажем, как найти arcsin а по данному значению аргу-
мента а, |а|^1. Пусть а—число положительное или нуль;
тогда в первой четверти, т. е. между 0 и у, существует
единственный угол а, для которого sin а —а. Это а и будет
искомым главным значением Arcsin а, т. е.
arcsin а = а.
Для отыскания а можно использовать (в обратном направле-
нии) таблицу натуральных значений синуса, составленную для
углов первой четверти.
Пусть теперь а — число отрицательное; тогда —а —число
положительное, и мы можем написать, что
arcsin (— а) = а,
[де 0 а сс ~ ; отсюда — а = bin а и, в силу нечетности
синуса, sin (—а)=А. Так как —а заключено между 0 и
— у, то —а и является искомым главным значением Arcsin а:
arcsin а = — а.
Главное значение urcs л а есть наименьшее по абсолют-
ной величине значение Arcsin fl при любом а, | а | 1.
Это значение особенно просто находится по таблице зна-
чений синуса для острых углов. Этим и объясняется назва-
ние: главное значение.
В соответствии с формулой (1) имеем:
Arcsin а — ( — 1 )п arcsin а /иг.
103
Пример. Найдем Arcsin)—. Так как arcsin= Л
у 2 / 2 о
к 1 \ / 1 \ к
потому что sm -£- = -у ) , то arcsin i-2 j =-6” и ’ значит»
11. Arccos а. Среди всех значений Arccos а особо выде-
ляется то, которое заключено между 0 и тт. Оно называется
главным значением Arccos а и обозначается так: arccos а.
Так как при увеличении угла от 0 до тт косинус умень-
шается от 1 до — 1, то каждому значению а, заключенному
между —1 и 1, соответствует один уюл, заключенный между
О и тт, косинус которого равен данному значению а. (Это
ясно показано в п. 47, где рассматривается график арккосинуса.)
Покажем, как найти arccos а по данному значению аргу-
мента а, |а|^1. Пусть а — число положительное пли нуль;
тогда в первой четверти, т. е. между 0 и у, существует
единственный угол а, для которою cos а = а. Это а и будет
искомым главным значением, т. е.
arccos а = а.
Для отыскания а можно использовать (в обратном направле-
нии) таблицу натуральных значений косинуса, составленную
для углов первой четверти.
Пусть теперь а — число отрицаюльнос; тогда —а — число
положительное, и мы можем найти arccos (—а} —а, где
О а у ; отсюда —а ~~ cos а. Ввиду того, что косинус
не является нечетной функцией, мы ге можем поступить как
в случае арксинуса. Воспользуемся здесь формулой приведе-
ния: cos (и — а) =— cosa = — (—а) —- а. Так как а заклю-
м к К
чено между 0 и -у , то тт — а заключено между и и и,
следовательно, п — а является искомым главным значением
Arccos а\
arccos а — и—а.
Ясно, что для Arccos а нельзя выбрать главное значение
заключенным между------и Т (анал0Г11Ч,ю слУчаю Arcsinа),
ибо тогда не существовало бы главного значения Arccos я
при отрицательном а. Приведенное же определение главного
104
потому
значения Arccos а позволяет найти его, причем единственным
образом, при любом а, | а | 1.
Главное значение arc cos а есть наименьшее положитель-
ное значение Arccos л при любом а,
Это значение особенно просто находится по таблице зна-
чений косинуса для острых углов. Этим и объясняется наз-
вание: главное значение.
В соответствии с формулой (2) имеем:
Arccos а — arccos а 2/zrr.
Пример. Найдем Arccos (—). Так как arccos
\ 2 J 2 о
что cos =
о
и, значит,
/ 1 \ о ( 2 \
Arccos — -тг = zb т п 2яп = I ± v 4- 2/z ) тг.
II I. Arctg а. Главным значением Arctg а (а — произволь-
ное число) называется то его значение, которое заключено
между — у и оно обозначается так: arctg а.
ял
Так как при увеличении угла от — до у тангенс
увеличивается, принимая любое (отрицательное, нулевое,
положительное) значение, то каждому значению а соответ*
.. г. п
ci вует один угол, заключенный между — у и , тангенс кото-
рого равен данному значению а.(Это мы с большой отчетливостью
увидим в п. 48, где будет рассмотрен график арктангенса.)
Отыскание arctgа по данному значению аргумента а в таб-
лицах совершенно аналогично отысканию arcsina.
Главное значение arctg а есть наименьшее по абсолютной,
величине значение Arctgа при любом а.
Это значение особенно просто находится по таблице зна-
чений тангенса для острых углов.
В соответствии с формулой (3) имеем:
Arctg а = arctg а пъ.
Пример. Найдем Arctg (—1). Так как arctg
, то arctg (—1) = — ~ и, значит,
Arctg (— 1) = — 4- ли = (— | 4-л)п.
^потому что tg ~
103
IV. Arcctg л. Главным значением Arcctgа (а — произ*
вольное число) называется то его значение, которое заклю,
чено между 0 и и; оно обозначается так: arcctg а.
Так как при увеличении угла от 0 до и котангенс умень-
шается, принимая любое (положительное, нулевое, отрица-
тельное) значение, то каждому значению а соответствует один
угол, заключенный между 0 и и, котангенс которого равен
данному значению а. (Это отчетливо будет видно в п. 49,
где рассматривается график арккотангенса.)
Отыскание arcctgа по данному значению аргумента а со-
вершенно аналогично отысканию arccos а.
Главное значение arcctg а есть наименьшее положитель-
ное значение Arcctg а при любом а.
Это значение особенно просто находится по таблице зна-
чений котангенса для острых углов.
В соответствии с формулой (4) имеем:
Arcctg а = arcctg а /иг.
Пример. Найдем Arcctg (—1). Так как arcctg 1— ~
(потому что ctg= 1 ) , то arcctg(—1) = тг — ~ = и,
значит,
Arcctg (— 1) = -у п ,/тт — ("4- “г п )тт-
§ 15. Изменения обратных тригонометрических функций.
45. Общее понятие обратной функции. Прежде чем об-
ратиться к изучению характера изменения обратных тригоно-
метрических функций, обратимся к общему понятию обратной
функции.
Пусть дана функциональная зависимость между двумя пе-
ременными величинами х и у. Обычно выбор одной из них
в качестве независимой переменной (аргумент) может быть
сделан вполне произвольно, по нашему усмотрению. Если,
скажем, х выбрана аргументом (независимой переменной), то
функцией будет у; обратно: если в силу каких-нибудь сооб-
ражений целесообразнее счшать аргументом у (т. е. выбирав
значения у по нашему усмотрению), то функцией (зависимой
переменной) будет х.
Однако у как функция х выражается, вообще говоря,
иначе, чем х как функция у. Эти две функции называются
106
обратными. Разъясним понятие взаимной обратности
двух функций на примере.
Пусть х и у находятся между собой в такой зависимости,
что значение у получается из соответствующего значения'чг
возведением последнего в квадрат. Такую зависимость можно
выразить равенством
У = х\ (5)
Здесь у—функция, явно представленная через аргумент х.
Ту же самую зависимость можно выразить, очевидно, и
таким равенством:
x = ±J'/V- (6)
Это только другая запись предыдущего равенства. Считая
здесь у независимой переменной, замечаем, что х как функ-
ция выражается через свой аргумент (у) иначе, чем у как
функция своего аргумента (х). Первая функция (у = х2) оп-
ределяется тем, что для получения ее значения нужно значе-
ние независимой переменной возвести в квадрат; вторая
же функция (x = zbl7 у) определяется тем, что для получе-
ния ее значения нужно из значения независимой переменной
извлечь квадратный корень. Две функции, из ко-
торых одна есть квадрат аргумента, а вторая — корень квад-
ратный из аргумента, и являются взаимно обратными.
Обозначим независимую переменную в равенстве (6), как
обычно принято, через х, а функцию — через у (т. е. в ра-
венстве х = У поменяем местами х и у). Тогда мы бу-
дем иметь два таких выражения для наших взаимно обратных
функций:
у = х2 и y — zhVx.
График одной из взаимно обратных функций легко полу-
чить по графику другой. Покажем это на рассмотренном при-
мере. Графиком функции у — х2 служит, как мы знаем, па-
рабола (жирная линия на черт. 38). Она же является графиком
функции х = ]/у 6i6o последнее равенство только своим
видом отличается от равенства у — х2). Но если заменить у
на х, а х на у, то мы получим функцию у = -г- V х, график
которой в той же системе осей должен быть, очевидно, так
расположен относительно осп OJV, как график функции
г =: -ф-у относительно оси ОУ. Таким образом, сразу на-
ходим график функции у = -4- ф х (тонкая линия на черт. 38).
107
Легко видеть, что он может быть вычерчен по графику функции
у — х2 при помощи простого перегибания чертежа по бис-
сектрисе PQ первого и третьего углов между осями ОХ и ОУ.
Такой автоматический способ вычерчивания графика об-
ратной функции является вполне общим. В одной и той же
системе осей графики двух
А любых взаимно обратных
к / функций (с одинаково, обозна-
/ / ченными аргументами) совмеща-
/ // ются между собой, если чер-
!/ теж перегнуть по биссек-
трисе первого и третьего
/7 / углов между осями.
----------------------Рассмотрим теперь, как ог-
/---------------------ражается на графике функции
свойство ее однозначности.
Р Если каждому значению х со-
Черт. 38. ответствует одно значение у,
то прямая, перпендикулярная к
оси ОХ, может пересекать график функции не больше
чем в одной точке. В случае же многозначности
функции прямая, перпендикулярная к оси ОХ, может пересе-
кать график больше чем в одной точке.
Так, например, функция у — х2— однозначная и каждая
прямая, перпендикулярная к оси ОХ, пересекает параболу —
график функции — только в одной точке. Функция же
у — -к ]/х (обратная первой) — двузначная (каждому поло-
жительному значению х соответствуют два значения у: одно
положительное, другое отрицательное) и прямая, перпенди-
кулярная к оси ОХ, не пересекает график функции у = х.
если она расположена левее оси ОУ, или пересекает его в
двух точках М и М (черт. 38), если она расположена пра-
вее оси ОУ: одна из этих точек находится над осью ОХ.
другая — под осью ОХ.
Из этого примера видно, что функция, обратная данной
однозначной функции, может быть и многозначной.
Подойдем теперь с изложенной сейчас общей точки зре
ния к обратным тригонометрическим функциям.
46. Функция y = Arcsinx и ее график. Пусть дана три
тонометрическая функция
у — sin х.
Так как, по определению, у есть значение синуса угла (дуги)
108
в х радианов, то (см. п. 43)
х — Arcsin
Рассматривая х как функцию у, мы приходим к функции,
обратной функции у = sin х, т. е. именно
нометрической функции арксинус. Меняя
местами х и у, получаем запись функции
арксинус в обычном виде, когда аргумент
и функция обозначены так же, как и в пря-
мой функции:
у = Arcsin х.
Функцией Arcsin х называется функ-
ция, обратная функции sinx.
В равенстве у — Arcsin х переменные х
и у могут выражать разнообразные вели-
чины. Так, у (значение функции) может
выражать и длину, и время, и темпера-
туру и т. д. То же самое относится и к
другим обратным тригонометрическим функ-
циям, которые мы изучаем ниже. Но чи-
сленное значение у мы определяем как
радианную меру угла, синус которого ра-
вен х. График функции у — Arcsin х
легко получить из графика функции
у = sinx посредством приема, указанного
в п. 45.
Перегнув черт. 29 (см. стр. 64) по
биссектрисе первого и третьего углов между
осями, получим график арксинуса, которым
будет синусоида, «навертывающаяся» на
эсь OY (черт. 39) так же, как первона-
(альная синусоида —график синуса — «на-
вертывалась» на ось ОХ.
Из черт. 39 видно, что прямая, пер-
пендикулярная к осп ОХ, или вовсе не
имеет с графиком
лбщих точек, или имеет с ним бесчисленное множество общих
точек. Это указывает на многозначность функции у = Arcsin х.
Ординаты у точек пересечения графика с прямой и будут
значениями арксинуса, соответствующими тому значению аргу-
мента, которое равно абсциссе х.
Выделим на графике функции у = Arcsin х такую его
наибольшую часть, чтобы прямая, перпендикулярная к
109
оси ОХ и проходящая через любую точку отрезка о г
до 4"Н — 1<х<1), пересекала ее в одной и толыс^
в одной точке. Это можно сделать по-разному. Например^
частью графика, удовлетворяющей поставленному условию^
является дуга /И1Л42 (черт. 39). Такой частью может быть
также дуга М2УИ3 и т. п. Каждая такая дуга служит графи-
ком некоторой однозначной функции (ибо каждому значению
х на отрезке от —1 до -ф-1 соответствует одно значение
функции).
Из всех возможных частей графика арксинуса, обладающих
указанным свойством, остановимся на Эта часть ближе
находится к оси ОХ, чем любая другая часть (А42А48 и т. д.).
Линия и является графиком главного значения
Arcsin х, т. е. графиком функции у = arcsin х.
Главное значение арксинуса у= arcsin.к является одно-
значной функцией х(—1 ^х^1), причем если х^>0, то
и arcsin х^> О, если х = 0, то и arcsin х — 0, если х<^0,
то и arcsin х<^0. Возрастание функции у = arcsin х
графически проявляется в том, что точка, двигаясь слева
направо вдоль линии поднимается.
Заме!им сще; что у = arcsin х — функция нечетная'.
arcsin (— х) = — arcsin х.
47. Функция у = Arccos х и ее график. Возьмем теперь
тригонометрическую функцию
у = cos х.
По определению, у есть значение косинуса угла (дуги) в х
радианов. Значит (см. п. 43),
х = Arccos у.
Считая х функцией, а у аргументом, приходим к функции,
обратной! функции j'=cosx, т. е. к обратной тригонометри-
ческой фхнкцни арккосинус. Меняя х и у местами, получим*
у = Arccos х.
Функцией Arccos х называется функция, обратная функ-
ции cos г
Значениями функции *V = Arccost являются числа, изме-
ряющие (обязательно в рздиа-чюй мере) унты (дуги), косинус
которых равен данному чнел) х.
110
Перегибая черт. 30 (см. стр. 64) по биссектрисе первого
и третьего углов между осями, получим график функции
у —Arccos х (черт. 40).
Прямая, перпендикулярная к оси ОХ,
пли вовсе не имеет общих точек с гра-
фиком арккосинуса, или имеет с ним
бесчисленное множество общих точек, в
чем графически и выражается много-
значность функции у = Arccos х.
Выделим на графике функции
v = Arccos х такую его наиболь-
шую часть, чтобы прямая, перпенди-
кулярная к оси ОХ и проходящая через
л ю бу ю точку отрезка от — 1 до 1
(— 1 1), пересекала ее в одной
и только в одной точке. Такими ча-
стями могут быть дуги
Л/2Л/3 и т. п. (черт. 40). Каждая из
этих дуг служит графиком некоторой
однозначной функции (ибо каждому
значению х на отрезке от —1 до-J-1
соответствует одно значение функции).
Среди этих дуг две, а именно:
и расположены к оси ОХ
ближе других; выберем, однако, дугу
учитывая, что ординаты всех ее
точек положительны.
Линия и является графиком
главного значения Arccosx, т. е. гра-
фиком функции у =• arccos х.
Главное значение арккосинуса у =
= arccos х является однозначной функ-
цией х (—причем положи-
тельной для каждого х. Убывание функции у = arccos .х
графически выражается в том, что точка графика, передвигаясь
слева направо, опускается.
48. Функция у = Arctgx и ее график. Пусть дана три-
гонометрическая функция
у = tg X.
По определению, у есть значение тангенса угла (дуги) в х
радианов. Значит (см. п. 41),
х= Arclgj.
Ill
Считая х функцией от у, получаем функцию, обратную
функции у = tg л*, т. е. обратную тригонометрическую функ-
цию арктангенс. Меняя х и у местами, придем к функции
У — Arctg х.
Функцией Arctg х называется функция, обратная функ-
ции tgx.
Значениями функции у — Arctgх являются числа, измеря-
ющие (обязательно в радианной мере) углы (дуги), тангенс
которых равен данному чис-
лу х.
Если черт. 32 (см. cip,
67) перегнуть по биссек-
трисе первого и третьего
углов между осями, то мы
получим график функции
у = Arctgx (черт. 41).
Всякая прямая, перпен-
дикулярная к оси ОХ, пе-
ресекает график Arctgx в
бесчисленном множестве то-
чек, в чем графически и
выражается многозначность
функции у = Arctg х.
График функции
у = Arctg х
Черт. 41.
(черт. 41) состоит из отдель-
ных ветвей Л41Л12, М8М4 и т. п., каждая из которых служит
графиком некоторой однозначной функции (ибо каждому
значению х соответствует одно значение функции).
Выделим ветвь она расположена б л и ж е к оси ОХ,
чем другие ветви (ЛГ3Л44 в т. д.). Линия и является
графиком главного значения Arctgx, т. е. графиком функции
у = arctgx.
Главное значение арктангенса у = arctgx является одно-
значной функцией х, причем если х^>0, то arctg х> 0, если
х = 0, то и arctg х = 0, если х 0, то и arctg х<^0. Воз-
растание функции у = arctg х ясно видно из графика (черт. 41)
Функция у — arctgx нечетная'. %
arctg (— х) = — arctgx.
112
49. Функция у = Arcctg х и ее график. Наконец, возь-
мем функцию
у = Ctg X.
По определению, у есть значение котангенса угла (дуги)
в х радианов. Поэтому (см. п. 43)
х = Arcctg у.
Рассматривая х как функцию у, мы приходим к функции,
обратной функции у — ctg х, т. е. к обратной тригонометри-
ческой функции арккотангенс. Меняя х и у местами, полу-
чим функцию:
у = Arcctg х.
Функцией Arcctg х назы-
вается функция, обратная
функции etgx.
Перегибая ' черт. 33 (см.
стр. 68) по биссектрисе
первого и третьего углов
между осями, получим гра-
фик функции v = Arcctg х
(черт. 42).
Всякая прямая, перпен-
дикулярная к оси OzV, пере-
секает график функции
Arcctgл: в бесчисленном мно-
жестве точек, в чем графически
выражается многозначность
функции у = Arcctgх.
График функции у = Arcctg х (черт. 42) состоит из от-
дельных ветвей Л43Л74 и т. п., каждая из которых слу-
жит графиком некоторой однозначной функции (ибо каждому
значению х соответствует одно значение функции).
Среди этих ветвей две, а именно: ММ2 и Л43Л44, распо-
ложены к оси ОХ ближе других; мы выберем Afj/W2, так
как ординаты ее точек положительные. Линия MjM* и
является графиком главного значения Arcctg х, т. е. графиком
функции у — arcctgл*.
Главное значение арккотангенса у — arcctg х является одно-
значной функцией х, причем положительной для каждого х.
Убывание ф\ нккии у = arcctg х очень ясно обнаруживае гея
из графика (черт. 42).
ИЗ
§ 16. Преобразования обратных тригонометрических
функций
50. Простейшие преобразования. Рассмотрим некоторые
простейшие соотношения между тригонометрическими и обрат-
ными тригонометрическими функциями.
1) Возьмем выражение sin (arcsin х). Обозначим его черезу;
у = sin (arcsin х).
Отсюда
arcsin х = arcsinу
и, значит, у = х.
Итак,
sin (arcsin х)=®х.
Этот результат делается совершенно понятным, если вни-
мательно присмотреться к выражению в левой части. Дейст-
вительно, оно представляет синус некоторого угла, именно
равного arcsin х, т. е. такого, синус которого равен х. В са-
мой этой фразе заключен ответ.
Точно так же
cos (arccos х) = х, tg (arctg х) = х, ctg (arcctg х) = х.
Равенства sin (arcsin х) — х и cos (arccos х) = х имеют
смысл лишь при | х | 1.
2) Преобразуем выражение sin (arccos х). Применяя извест-
ную формулу, получим:
sin (агесс, х) = Y1 — [cos (arccos х)]1,
в силу предыдущего, cos (arccos х) = х и, значит,
sin (arccos х) = У 1 — х1.
Точно так же
cos (arcsin х) = ]/1 — х*.
Без особых объяснений должны быть понятны равенства:
tg(arcCtgx) = cliIi?zn?7) = 7,
ctg (arctg =4.
3) Возьмем выражение Arcsin (sinx). Обозначим его через у',
у = Arcsin (sin х).
114
Отсюда
sin х = sin^
и, значит, имеется такое значение у, которое равно х. Общим
же ответом, как мы знаем, будет:
Arcsin (sin х) = (— 1 )л • х-j-лтт (п = 0} 4И, 44 2,...).
Точно так же
Arccos (cos х) = Чп х 4- 2/гтс; Arctg (tg х) = х 4~ пщ
Arcctg(ctgх) — х4~лтт (л = 0, 1, i2, ...).
4) Если в выражении Arcsin (cos х) заменить cos х через
, / я \
sn\ 2----/’ Т0 МЫ’ очевидно’ получим:
Arcsin (cos х) = (—1)п ^4—xj 4~ZZTT (л = 0, ± 1> ±;2,. • •).
Точно так же
Arccos (sinх) = + ---(л = 0, + 1, 4^2).
5) В качестве очень интересного примера возьмем функцию,
рассмотренную великим русским математиком П. Л. Чебы-
шевым (1821—1894): cos (п arccos х), где п— целое неотри-
цательное число. Докажем, что эта функция есть многочлен
п-й, степени относительно х, коэффициентом которого при
старшей степени х, т. е. при хп, служит число 2П“1.
При л=1, п = 2 это очевидно:
cos (arccos х) = х,
cos (2arccos х) = 2 cos2 (arccos х) — 1 = 2х* — 1.
Применим теперь метод полной математической индукции.
Предположим, что наше утверждение справедливо до какого-
нибудь п включительно; докажем, что при этом оно имеет
место и для л —|—1. Так как (п. 41)
cos (п 1) 0 + cos (п — 1) 0 = 2 cos л0 cos О,
то
cos (л 4~ 1) 0 = 2 cos ^0 cos 0 — cos (л — 1)0.
Положим здесь 0 = arccos х; тогда
cos [(л -j- 1) arccos х] =
= 2cos (arccos х) cos (л arccos х) — cos [(п — 1) arccos х] =
= 2х cos (л arccos х) — cos [(л — 1) arccos х].
115
В силу сделанного допущения имеем:
cos (п arccos х) — 2п~'хп а1хп~1
cos [(л — l)arccosx] = 2п~2хп~* -)-•••
Поэтому
cos [(л -j- П arccosx] — 2Z7xn + 1 -ф- 2д1хг/-|-. . .—(2п~2хп~1 -ф-...).
Отсюда видно, что cos [(я J- 1) arccos х] действительно
есть многочлен степени п ф- 1, причем коэффициентом при
х"м служит число 2п, что и требовалось доказать. Ввиду
того, что это предложение справедливо, для /г=1 и п = 2>
оно справедливо, по доказанному, для любого п.
Многочлены cos (п arccos х) обладают целым рядом заме-
чательных свойств, изучаемых в высшей математике. Эти
многочлены, разделенные на 2П“\ называются многочленами
Чебышева,
Многочленами Чебышева 2-го рода называются функции
------sin (/z arccos х), которые являются, как это дока-
1-л'2
зывается аналогично предыдущему, многочленами относительно х
степени п—1.
61. Дальнейшие преобразования. Естественно, что фор-
мулы, связывающие между собой тригонометрические функции,
приводят к формулам, связывающим между собой обратные
1ригонометричсские функции.
1) Докажем, что
arcsin х arccos х = ф .
Положим arcsin х = a, arccos х = $. Отсюда x = sina,
xe=cos^ и, следовательно,
sin а = cos {$ = sin — f).
По условию
Из последних неравенств следует, чго
Таким образом, имеем равенство синусов от двух углов, ле-
жащих в первой положительной или в первой отрицательной
четверти. Но это равенство может иметь место только в том
116
случае, если сами )глы равны:
откуда
или
arcsin х -ф- arccos х = ~ .
Справедливость этого равенства также легко усмотреть
по графикам функций у = arcsin ,v и у — arccos х.
2) Точно так же
arctg х -ф- arcctg х — ~ .
3) Найдем формулу для суммы арксинусов:
arcsin х -ф- arcsinj/.
Положим а = arcsin х, = arcsinj/. Тогда х = sin а, у — sin [J.
Возьмем синус суммы:
sin (а -ф- н) = sin а cos [i cos а sin [J.
Подставляя сюда вместо sin a, cos [5, cos а, sin 0 их выра-
жения через х и у, получим:
sin (а 4- = х К1 —У2 4“У "К 1 —х*-
Перед корнями берем знак плюс, так как в первой поло-
жительной и в первой отрицательной четверти косинус поло-
жителен (ведь рассматриваются главные значения!).
Значит,
а 4- р = arcsin х -ф- arcsin =
=arcsin (х У1 —у2 4-У V 1 — лг2),
если «4“? (так же» как и а 11 в отдельности) удовлетво-
ряют неравенствам
2 а 4 р 2 •
Если а 4“^ выходит за эти границы, то нужно принять
в расчет другие (неглавные) значения арксинуса. (Заметим,
что при наших условиях aвсегда удовлетворяет нера-
венствам — тт а 4~ л.)
117
4) В частности, при х—у ^если—~ arcsin х < -~
нахеДям:
2 arcsin х = arcsin (2х К1 — х1).
Подобным же образом читатель сам может вывести фор.
мулу для суммы арккосинусов.
5) Преобразуем сумму арктангенсов:
arctgx-]- arctg у.
Положим a =sarctgx, [5 = arctgу. Тогда x = tga, j, = tg£.
Возьмем тангенс суммы:
= tga + tg? __ х + у
1 _ tg a tg Р 1 — ху ’
Если сумма a-J-jJ (так же, как и а и [J в отдельности)
я . я
заключена между — — и ф , то
a + ₽ = arctg х + arctgу = arctg *
В том случае, когда а-[-[5 выходит за указанные границы,
необходимо обратиться к другим (неглавным) значениям арк-
тангенса. (При наших условиях сумма всегда заклю-
чена между —пип.)
6) В частности, при х=у ^если —< arctg х «С
находим:
2 arctg х = arctg .
7) Меняя в формуле для суммы арктангенсов у на —у,
получим:
arctg х — arctgу = arctg
при условии, что
— < arctg х — arctgу < -J ,
— j< arctgx <j, — j <arctgj < j.
П»
8) Для иллюстрации применения выведенных формул при-™
ведем оДИй интересный Пример. Вычислим значение гараяеения
4 arctg | —arctg jL.
Так как arctg arctg ^д, то эта разность положительна.
Покажем, что она меньше -£•. Действительно,
. . 1 . 1 Л . 1 1
4 arctg-5-— arctg 23Q < 4 arctg у < 4 • у,
гак как в первой четверти дуга меньше своего тангенса. Но
в свою очередь 1>57; таким образом, для преобра-
зования данной разности можно воспользоваться выведенными
здесь формулами.
Прежде всего преобразуем первый член:
2-1
4 arctg у = 2 ( 2 arctg 1) = 2 arctg--ду2 = 2 arctg 1.
Снова применяя формулу удвоенного арктангенса, получим:
А . 1 ,12 .120
4 arctg у=arctg----гур = arctg .
Итак,
А . 1 ,1 .120 ,1
4 arctg у- arctg = arctg - arctg .
Воспользовавшись формулой для разности арктангенсов, най-
дем:
120____1_
. 120 t 1 , 119 239 , 1 «
arct« ПЭ ~ arctg 239 = arctg , . l20~ = arctg 1 = 4 *
1 + 119 239
Окончательно приходим к любопытному результату:
. , 1 t 1 к
4 arctg у-arctg 2зэ = у.
11?
По образцу примеров этого параграфа следует решать
и другие задачи, связанные с преобразованием обратны* три-
гонометрических функций.
§ 17. Тригонометрические уравнения
52. Определение. Тригонометрическим уравнением назы-
вается равенство, содержащее неизвестную величину только
под знаком тригонометрических функций и справедливое
лшиь при некоторых определенных значениях неизвестной.
Последние называются корнями уравнения. Иными словами,
корнями тригонометрического уравнения являются значения
неизвестной величины, которые удовлетворяют уравне-
нию. В отличие от тригонометрических уравнений три-
гонометрические тождества удовлетворяются при всех
значениях переменных величин, стоящих под знаками тригоно-
метрических функций, для которых эти функции имеют смысл.
Решить тригонометрическое уравнение значит найти
все его корни.
Мы будем рассматривать лишь некоторые простые типы
тригонометрических уравнений. Решение их обычно сводится
к отысканию значения одной какой-нибудь тригонометриче-
ской функции, аргументом которой служит выражение, содер-
жащее неизвестную величину. По значению тригонометриче-
ской функции можно найти (посредством обратной тригоно-
метрической функции) и значение ее аргумента.
Пусть, например, в результате преобразований мы полу-
чили следующее, равносильное заданному, простейшее три-
гонометрическое уравнение:
sin (ах b) — с, где | с | 1. (7)
Оно решается сразу. Имеем:
ах -|- b = Arcsin с = (— 1 )п arcsin с -}- пи
(л = 0, ±1, ±2, ...),
откуда
х = -1-Г— Ъ (— 1)" arcsin г —I— тгтг!
a L 1 ' 7 1 J (8)
(л = 0, ±1, ±2, ...).
Правая часть выражения (8) заключает в себе все корни
уравнения (7). Придавая п значения 0, -1- 1, -т- 2Т по-
лучим частные значения неизвестного х: х0, х. х.., . , ,
120
Отсюда видно, что исходное уравнение имеет бесчислен-
ное множество корней. Если же |г|^>1, то решение
уравнения невозможно: оно вовсе не имеет корней.
Обычно тригонометрическое уравнение или вовсе не имеет
корней, или имеет их бесчисленное множество. (В противо-
положность этому алгебраические уравнения с одним неиз-
вестным имеют лишь конечное число корней.)
Что касается методов, при помощи которых данное три-
гонометрическое уравнение приводится к уравнению простей-
шего вида, то они состоят в преобразованиях уравнения в
равносильное. Наряду с этим используются тригонометриче-
ские тождества. Если в процессе решения уравнения про-
изводятся преобразования, которые могут приводить к новым
корням, как, например, возведение обеих частей уравнения
в квадрат, то необходимо учесть, какие новые, посторонние
заданному уравнению корни появляются в результате этих
преобразований.
53. Примеры уравнений.
Пример 1. Решить уравнение
2 cos х -f- 1 = 0.
Здесь сразу имеем:
1
cos х — — ;
отсюда находим:
7 1 \ 2
х — + arccos ( — у ) + 2/гтг = zhy тг + 2/иг
(л = 0, ± 1, ±2, ...),
Пример 2 (пример на приведение к одному a fP
гумен ту). Решить уравнение
sin 2х = sin2 х.
Заменяя sin 2х через 2 sin х cos х, получим:
sin х (2 cos х — sin х) = 0.
Приравняв нулю каждый из двух множителей левой части,
придем к двум уравнениям:
sinx = 0 и 2 cos х — sinx = 0.
Первое даег:
г —//п (п --- 0, - г: 1, 2, . . .). 9)
121
Второе после деления на cos х дает:
tgx = 2,
откуда
х —arctg2 4- «п 1,11 -L ли (^ = 0, -k 1, ±2, ...) (10)
(см. таблицу на стр. 57).
Формулы (9) и (10) и указывают корни исходного урав-
нения. В данном случае деление на cosх не приводит к
потере корней, так как значения х, обращающие cos х в нуль,
не являются корнями исходного уравнения.
Пример 3 (пример на приведение к одной функ-
ции). Решить уравнение
a sin2 х -J- b sin х cos х -j~ с cos2 х 0.
а) Рассмотрим сначала случай, когда оу-0. Для того
чтобы заданное уравнение привести к уравнению, содержа-
щему одну тригонометрическую функцию, разделим обе части
на cos2 х (мы не потеряем при этом корней данного уравнения,
так как при cosx = 0 левая часть не обращается в нуль).
Получим уравнение
а х + *8 х + с ~
Решая его относительно tgx, найдем:
. — b + — Ьас
tg X = ------4г------ .
s 2а
Отсюда видно, что условием возможности решения перво-
начального уравнения является неравенство:
Ь2 4 ас.
Если оно выполнено, то
xe=arctg (---— ------I (^ = 0, 4; 1, ±2,. .
б) Пусть теперь а = 0. Тогда уравнение имеет вид:
cos х (b sin х -]- £ cos х) — 0.
Приравняв нулю каждый ih твух множителей левой части,
получим два уравнения:
cos х — 0; b sin х -! с cos х = 0.
122
из них дает:
х = + -£4-2от (л = 0, ±1,±2,
Что касается второго, то при £=^=0, деля на cosx (корни
уравнения cosx = 0 уже учтены), находим:
откуда
х —— arctg у 4-пк (п — 0, 4- 1, 4-2, ...).
При £ = 0 мы приходим к прежним корням уравнения
cos х = 0.
Пример 4. Решить уравнение
sin2 х ctg 2х = 0.
Заданное уравнение распадается на два уравнения:
sin2x = 0 и ctg2x = 0.
Корни первого из этих уравнений (х = пк) нельзя, однако,
считать корнями исходного уравнения, так как ctg2x при
х = лгп не существует. Корни же второго уравнения, именно:
х = т + («=0,±1,±2,
и являются искомыми корнями заданного уравнения.
Пример 5 (пример равенства двух одноимен-
ных тригонометрических функций). Решить
уравнение
sin 5х = sin 4х.
Перенося sin 4х в левую часть и применив формулу для
разности синусов, получим:
п , х 9 п
2 sin -9 cos у х = 0.
Следовательно, имеем два уравнении:
х 9
sin--0-—-0 и cosх = 0.
Далее находим:
'2 ',тт' 2 V — I + 2лП*
123
и окончательно:
x = 2ст, х = -4- ~ А лтг (п = О, 4z 1, 4г 2, .,.).
Пример 6 (пример на введение вспомогател^
но го аргумента; см. п. 42). Решить уравнение
a sin х -\-b cos х с = 0.
Полагая
р = ]/а2-|-^2, siirp = y, cos у — у ,
получим:
a sin х -j- b cos х = р sin (х <?)•
Таким образом, наше уравнение принимает вид:
р sin (х -\-с—0,
или
sin (х 4~ <р) = —~,
т. е. вид, указанный в п. 52. Мы видим, что уравнение
имеет корни, если j р, т. е. если с2^аа4-^*.
В и. 54 будет изложен один общий метод, с помощыа
которого также может быть решено рассматриваемое урав-
нение.
Пример 7. Решить уравнение
sin х 4" cos х == а.
Это уравнение является частным случаем уравнения преды-
дущего примера, но решить его можно проще.
Заменив cos х через sin —х) и используя формулу
для суммы синусов, получим:
sin V 4 - Sin -ту----X j — 2 Sin -J- COS X - -- j- J =
- ~ 2 cos f х —• 4 — У 2 cos f х —
2 \ 4 / \ /
Таким образом: У2 cos^x j) ~а
и, следовательно, ! 7 \ а СОЗ X 1 ---- . \ 41 ] г
124
Очевидно, что полученное
ния лишь
при т.
Н У 2
условие выполнено, то
х — -у- arccos 2/ztt
4 — I
уравнение может иметь реше-
е. при | а | ]/2 . Если это
(/z~0, ±1, ±2,. ..).
Пример 8. Решить уравнение
sin тх______cos тх
sin х ‘ cos х
(И)
После перенесения всех членов этою уравнения в левую
часть и приведения к общему знаменателю получим:
sin тх cos х — cos тх sin х_
sin х cos х
Числитель представляет собой синус разности аргументов тх
и х, следовательно, окончательно приходим к уравнению
sin (тх — х) sin [(/и — 1) х] Q
sin х cos х sin x cos x ' ' '
Дробь может быть равна нулю только при условии, что
числитель равен нулю, если одновременно не обращается в
нуль и знаменатель. Поэтому найдем прежде всего, при ка-
ких значениях х обращается в нуль знаменатель уравнения (12).
Пусть sinx cos х = 0 или sin 2х = 0, отсюда 2х = лп,
г. е. х=у (/г = 0, ±1, ±2,...). Теперь следует решить
уравнение sin [(m—1) х] = 0. Все корни этого уравнения, за
исключением значений х, кратных у, будут удовлетворять за-
данному уравнению (И).
Решая уравнение sin [(т — 1) х] = 0, находим (т — 1) х =z
_-пк, откуда
х =——гК или х = ——। v (л = 0, +1, ±2,...).
т — 1 т — 1 2
Исследуя это решение, сразу исключаем т—\\ в этом слу-
чае уравнение (11) обращается в тождество:
sin х cos х
sin х cos x
При /п = 2 и /п = 3 получаем:
х = 2// • и х = п • у ;
125
все эти значения х кратны — и, следовательно, корнями
уравнения (12) быть не могут, ибо обращают в нуль и числи-
тель и знаменатель.
Таким образом, уравнение (И) при т — 2, т = 3 со-
всем не имеет решений.
Наконец, если т отлично от 1, 2 и 3, то все решения
уравнения (11) заключены в формуле
2п я
X =----“ . -тт ,
т — 1 2 ’
где п может принимать значения 1, + 2,..., кроме тех,
-г Л 2л тг
которые обращают дробь в целое число. Например,
при т — 4 х = где п — любое целое положительное
О
или отрицательное число, но не кратное числу 3.
54. Один общий метод. Укажем общий метод, позво-
ляющий решать рациональные тригонометрические уравне-
ния. Так называются уравнения, у которых одна часть есть
нуль, а другая часть представляет собой рациональное выра-
жение относительно тригонометрических функций от одного
и того же аргумента (см. п. 39); в простейшем случае этим
аргументом служит неизвестная величина х.
Как известно (ср. формулы (24) на стр. 87), все три-
гонометрические функции от х рационально выражаются
через tg-j , а именно:
2/ 1 —/2 . 2t /1Q.
slnx=Tqr?> cosx=TqrF’
где
. X *
Если в данное рациональное тригонометрическое уравне-
ние подставить вместо тригонометрических функций от х их
выражения через /, то получим рациональное уравнение отно-
сительно /, из которого и найдем неизвестную величину i.
Зная f = tg-^- , мы найдем и х.
Пример. Решить уравнение
a sin х b cos х -j- с = 0 (14)
126
(ср. пример 6 п. 53). Заменяя в уравнении (14) sin х и cosx
выражениями через /, находим:
откуда
(с 2at -j- (с + Ь) = 0. (15)
Мы получили квадратное уравнение относительно t при усло-
вии, что Ь^с. Решая его, найдем:
. — a )Лга — са + д1
\ с — Ь
Отсюда снова видно, что неравенство а2-\-Ь2^с2 является
условием возможности решения первоначального уравнения.
Если это условие выполнено, то
/ __а — с2 -4- \
x = 2^arctg (п=0, ± 1, ± 2,...).
Если же Ь — с, то уравнение (14) следует решать непо-
средственно, так как квадратное уравнение (15) обращается
в линейное, что сопровождается потерей корня.
Тогда из уравнения (14) имеем:
a sin х 4" ^ (1 cos х) =
т. е.
2а sin у cos 4“ cos2 = 0»
откуда
cos’ i (a tg у b ) = 0
и, значит,
х п . х b
cosr-=0, tg7=--.
Находим:
х = (2п + 1) я, х = 2(— arctg 4“
(л = 0,±1,±2,...).
Вторая из этих серий корней получается и из решения
линейного уравнения, в которое обращается квадратное урав-
нение (15), при Ь = с, а первая серия корней при этом ока-
зывается потерянной.
Вообще при подстановке в тригонометрическое уравнение
t вместо tg у можно потерять корни х = (2ппри
127
атих значениях tg — не существует. Поэтому, решая урав-
нение этим приемом, нужно проверить, не являются ли ука-
занные значения корнями уравнения.
Решение уравнений по изложенному общему ме году не всегда
является наиболее простым. Часто какой-нибудь прием, спе-
циально приспособленный для данного уравнения, спорее
приводит к цели, чем общий метод. Поэтому нужно стре-
миться искать специальный, наиболее короткий, простой и
изящный прием для решения уравнения.
Если более удобный специальный прием не удается найти,
следует обратиться к общему методу.
Задачи к главе IV
Выразить с помощью символов обратных тригонометрических
функций угол (дугу) а из следующих равенств (задачи 1—3):
I. (a) sin 2 а _ 0,7; (b) cos
2. о
(с) tg За = 3; (d) ctg Л- = А-.
2. (a) sin ( а 4~ ) = 0,1; (b) c^s ( 2а — ) z=z 0,85;
\ о j у 1 и j
(с) tg |; (d) ctg (2а — I) = Г"2.
3. (a) sin moi = a\ (b) cos pna + #) = c\ (c) tg -J- — 7^ = r.
Найти общий вид углов, имеющих данное значение тригонометри-
ческой функции (задачи 4—6):
У'з- 1
4. (a) Sin а = ’ (b) Sin а = 1; (с) Sin а = — ; (d) sin а = 0.
5. (a) cosa~0; (b) cos а =-у;
У 2
(c) cos а =-----— ; (d) COS а = — 1.
6. (a) tg а — — 1; (b) ctg a — 1; (c) tg a = — У 3J (d) ctg а = 0.
Пользуясь общими формулами, найти значения следующих обрат-
ных тригонометрических функций (задачи 7—9):
7. (a) Arcsin (-; (b) Arcsin ~~ ; (с) Arcsin ( — 1).
/ 1 \ у
8- (a) Arccos ( —- j ; ф) Arccos O-J (с) Arccos 1.
128
6. (a) Arctg 0; (b) Arcctg (-Q- J (c) Arctg У 3.
\ о /
У 2
10. Найти все значения Arcsin—^— , заключенные между числами
— 2я и 4я.
* II. Найти все значения Arccos заключенные между чис-
лами 0 и 6я.
12. Найти все значения Arctg ( - У 3), заключенные между чис-
лами — 2я и 2я.
13. Найти все значения Arcctg (— 1), заключенные между числами
— я и к.
Указать, для каких значений х имеет смысл каждая из следую-
щих функций (задачи 14—15):
14. (a) Arcsin ; (b) Arcsin 4х; (с) Arcsin znx, где т > 0.
о
15. (a) Arcsin (2х — 1); (b) Arcsin (1 — Зх); (с) Arcsin- .
16. Выразить х через у:
(а) у = Arccos 2х;
(с) у = — Arccos у ,
(е) у = ~ — 2 Arcsin х;
(g) у = 1 — 4 Arcctg у;
(Ь) у = Arccos х -f- я;
(d) у — Arccos х;
о
.. я — Arctg х .
(0 у=----------
, X — 1
(h) у = -g - arcsin —4—
17. Найти значения функции у = arcsin х, если х имеет следующие
V2
значения: —1;-----; 0; —1.
18. Пользуясь таблицами, найти с точностью до 0,001 значения
ж . 2* + 3
функции у = arcsin —, если х имеет следующие значения:
-3; — 2; -1; 0; 1.
19. Пользуясь таблицами, найти с точностью до 0,001 значения
функции у = arctg х + arcctg Зх, если х имеет следующие значения:
0,1; L; 1;---------0,5; —1.
3 / 3
20. Найти значения функции у — arccos х — arctg 2х, если х
Л 1 • Уъ
имеет следующие значения: 0; —----------— •
21. Выразить углы прямоугольного треугольника через его ги-
потенузу с и площадь S.
129
82. Выразить периметр сектора через его радиус R и радиус г
вписанной в него окружности.
те. По графику функции у — arcsin х найти значения аргумента
, 1 1 1 ’
при которых функция имеет следующие значения: ~; — у; 1;—1,5.
Результаты сверить с таблицей.
24. Построить на одном чертеже графики функций у — arccos х
х
и у = arccos у ; выяснить по чертежу, при каком значении аргумента
разность
arccos 2----arccos х
будет наибольшей, наименьшей, равна нулю.
25. Найти наибольшее и наименьшее значения функции у —
1 /т
с=х arcsin х в границах изменения х от до ——.
26. Найти наибольшее и наименьшее значения функции
у — arccos х -J- х2
в 1 раиицах изменения х от — у до нуля
27. Пользуясь графиками функций у = arcsin х и у = arccos х,
найти знак каждой из разностей:
(a) arccos 0,7 — arccos 0,5;
(b) arccos —— arccos
\ 5 j
3\ .
4 / ’
(c) arcsin (У' 2 — 1) — arcsin (V 5 — 2);
(ft
sin -j2
28. He производя вычислений, найти знак каждого из отношений:
arcsin 0,85 — arcsin 0,8 .
3 arccos 0,85 — arccos 0,8’
, к — 2 arcsin 0,9 .
it — 2 arccos (—0,1) ’
arcsin (— 0,4)
--------------A
arccos 0.6 — -x-
О
29. Указать, какие из нижеследующих функций являю«сч чет-
ными, какие нечетными и какие не являются ни четными, ни нечет-
ными:
(а) у = arcsin х + 2 arctg х; (Ь) у = arccos х + arctg х;
/1Ч arctgx
(cl) у = — ----------х arc sm х.
. . arcsin х .
с) у <=---------,
7 aj ccos х
130
Доказать тождества (задачи 30—32):
30. (a) sin (arcsin х)^=х; (b) arccos (cos х) = х, еслиО^х^я;
(с) arctg х + arcctg х=~.
X 1
31. (a) tg (arcsin х) = ; (b)cos (aictg х)~
X
32. (a) arctgx = aicsin -у==
V 1
l/- 1 _ у2
если х 0; (с) arccos х = arctg X---------
(b) arcsin х = arccos V1 -- х*,
Вычислить (задачи 33—35);
33. (a) sin (arccos ;
(b) sin I arccos
35. (a) cos [arctg ( — У 3)]; (b) sin (arctg 2).
Проверить справедливость следующих равенств (задачи 36 — 37):
, к ,15 8 ,4 . 3
36. (a) arcsin-у = arccos у *, (b) arcsin у = arctg —.
/ 7 \ 7
37. (a) arcsin ( — 55 ) = — arctg
/КЧ f 9 А 1 40
(b) arccos —--г ) ж=тс — arcsin 7-г.
\ 41 / 41
Вычислить (задачи 38—45):
38. (a) arcsin sin — у)] ’ (Ь) arcsin ^sin~:J ,
(с) arcsin (cos 1); (d) arctg (tg 2).
(36 \
— cos у к J ;
(c) arccos £sin ; (d) arcctg (tg 0,7 л).
(3 5 A /1 \
arcsin у — arccos -y 1 . 41. tg ( arctg —— arcctg 5 1.
42. sin (arctg —arcsin-pQ . 43. tg [2 aictg ( — -0] .
/ 1 3 \
44. cos I 2 arctg — arccos у I.
45. sin [2 f arcsin 1C5 _ aiccos 1 ♦
131
Проверить справедливость следующих равенств (задачи 46—
ж Л , 2 .1 тс ... . 1 । .4 3
4в. (a) arctg у 4- arctg у — -у; (b) arcctg 4- arcctg -j- = у я.
. 1 , .1 ,16
47. 2 arctg у 4- arctg у = arctg yg.
48. arcsin
7.1 7
“г "2 arccos = arccos
Доказать тождества (задачи 49—51):
49. 2 arccos j/^*g= arccos x.
50. arecos (2x2 — 1) = arccos x, если x^O.
51. 2 arctg x + arcsin
2x
если xbl.
Убедиться в том, что указанные справа числа являются корнями
соответствующего уравнения (задачи 52-~54).
52. cos х + cos 5х = 1; у , — у .
„ Л о тс л Зл
53. sin 2х з= cos Зх; — , , р} •
54. tg кх =е 2 cos1 кх; т, 4 •
Л 4 4
55. Можно ли считать число л корнем уравнения у х
59. Можно ли считать число корнем уравнения
cos 2х tg ^х + == О?
57. Показать, что уравнения
sin1 2х — sin1 х =з у и sin 8х sin х ви -i-
равпосильны.
59. Можно ли считать равносильными уравнения
tg* (1 — 2cosx) (2 +sin х) = 0 и tgх (2sinх) = О?
59. Можно ли считать равносильными уравнения
(1 4-2 sin Зх) tg х = 0 и (1 4-2sln3x)y^=0?
132
60. Доказать, что уравнения
tg х -|- 2 ctg х = 3 и 2 ctg2 х — 3 ctgx 4-1 = О
равносильны.
61. Показать, что все корни уравнения sinx~O являются кор-
нями уравнения sin5x = 0. можно ли считать эти уравнения равно-
сильными?
Решить уравнения (задачи 62—79): *
62. 2 sin х — 1 = 0. 63. 2 cos х -f- Y 2 = 0.
64. 3 tg(x + 15°) — У Т=0. 65. cos + 1=0.
66. ctg^x + -2-) + +"3 = 0. 67. ctg5x = 0.
68. tgyX-l=0. 69. 2sin^-±2._|_i=o.
70. УЗ" tg(3x+18°) + 3 = 0, 71. 4sln*4x —3 = 0.
72. 2 sin2 x — 3 sin x 4~ 1 — 0. 73. tg® 3x = 2 tg 3x.
” c+I+)+3'18(2-+)-4 = °'
75. 4 cos2 x + sin x = 1. 76. tg x Д- 5 ctg x = 6.
77. 2 ctg 3x -J- tg 3x -j- 3 = 0.
78. m tg x + n ctg x — 2. При каком соотношении между величи-
нами т и п существует решение уравнения?
79. a sin2 х 4~ cos2 х = с. При каком соотношении между вели-
чинами а, b и с существует решение уравнения?
80. Су мма двух равных высот равнобедренного треугольника равна
третьей высоте. Найти углы треугольника.
81. Синусы углов прямоугольного треугольника составляют гео-
метрическую прогрессию. Найти углы треугольника.
82. В прямоугольном треугольнике высота, опущенная на гипо-
тенузу, равна разности проекций катетов на гипотенузу. Найти углы
треугольника.
Решить уравнения (задачи 83—99):
83. sin х (1 Д-2 cos х) = 0. 84. sin 2х cos Зх = 0.
86. cos 5х (1 4~ cos 2х) = 0. 87. ctg х — cos х = 1 — sin х.
88. 1 + sin х cos Зх sin х 4~ cos Зх = 0.
89. — — 2 — tgx. 90. sin Зх ctg х = 0.
1 4- sin х b &
91. sin 3x = cos 3x. 92. sin2 3x = 3 cos2 3x.
93. 5 cos x 4" 2 sin x = 5 cos x cos 2x 4- 2 sin x cos 2x.
94. sin x tg x 4- cos x ctg x = sin x 4“ cos x.
95. sin2 x 4- ^in x cos x 4~ 4 cos2 x — 0.
96. 3 sin2 x — 7 sin x cos x -j- 6 cos2 x = 1.
б А. Бсрмант. Л. Люстерник
133
sin x 4~ 2 cos x _ 3
9 " sinX — 2cosx
gg 2 sin2 x — 4 cos2 x_____
sin2 x + 3 sin x cos x + 6 cos2 x
89. ~a-s-n-a X C — = 1. При каком соотношении между ве-
Z?2 sin2 х 4- a cos2 х r
личинами а и b существует решение уравнения?
1ОО» Дан угол ЛЮ Л —60°. На его стороне ОЛ1 взята произволь-
ная точка Л, а на стороне ON точка В так, что 0А — 20В. Под ка-
ким углом к стороне ON следует провести внутри данного угла по-
лупрямую OL, чтобы она была равноудалена от точек А и В?
101. Однородный стержень АВ согнут в точке С под прямым
углом так, что АС=4 см \\BC-1Q см, и подвешен в точке С на
нити. Найти угол между стороной АС и горизонтом при равновесии
стержня.
Решить уравнения (задачи 102—121):
102. sin Зх cos х = cos Зх sin х.
103. cos 7х cos Зх — cos 4х.
104. sin у — х cos 2х 4- sin (2х — г.) sin х = 0.
. Зя — х /я о \ /о ч Зя 4- X
105. sin —— cos ^2— Зх j = cos (Зх — я) cos ——
106. tg х tg Зх — = 1. 107. sin х cos х — ~.
У"2
108. sin (34° 4- х)- sin (56° — х) — —j- .
109- cos4 х — sin4 х — 1.
НО. cos8 (х + 30°) - sin8 (x + 30°) = — -Ь.
114. 2 cos 2x ~ 7 sin x.
116. 2 sin2 x 4- sin2 2x — 2.
118. sin 4x = 2 cos2 x — 1.
113. 1 — tg2 x = 2 tg x tg 2x.
115. sin 2x 4~ V 2 sin x = 0.
in. —cos 2*. = 0.
COS X — sin X
119. sin x cos x cos 2x =— ,
8
120. ctgx — tg x = tg 2x. 12!. 2-sin4 = 2cos-£.
Указан и e. Воспользоваться форм\ лой ctg 1П 3—.
1 J ь 2 1 — cos a
134
122. В квадрат вписан другой квадрат. Один из острых углов
между сторонами квадратов равен а. При каком значении угла з
2
площадь вписанного квадрата составит -л- площади другого квад-
и
рата?
123. В равнобедренном треугольнике через вершину угла при
основании и центр описанной окружности проведена прямая. Отно-
шение т отрезка этой прямой, заключенного внутри треугольника,
к его боковой стороне равно 1,2. Найти углы треугольника. Ис-
следовать задачу: указать, в каких границах должна заключаться
величина т.
Решить уравнения (задачи 124—156):
124. sin 2х = sin Зх.
125. cos (2х 4" 15°) = cos (4х — 15°).
126. tg(| + 30°j=tg (2x4-60°).
128. tg — х^ = ctg 4~ Зх^ .
129. sin2x =— sin Л. ISO. tg 3x-|-ctgy — 0.
1
131. sin 3x + —2~ Sin 2x = у cos 2x. 132. cos x — sin x — 1.
133. cos (2x 4-15°) J-cos (2x — 15°) = -^-.
£
134. sin x -f- cos x = 2 V 2 sin x cos x.
135. sin 3x cos x — sin 7x cos 5x.
136. 2 cos (x 4" 20°)ccs x — cos 40°.
137. sin ^2x 4~ pg) cos ^2x —^-) =—.
138. sin (x 4-15°) sin (x — 30°) = sin (50° -f- x) cos (85° — x).
139. cos 7x 4~ cos x = cos 4x. 148. tg x 4~ tg 2x = sin 3x cos x.
141. cos 8x cos Sx — V 3 cos x.
142. 1 — cos 2x — 4 sin x. 143. sin 2x 4~ 2 sin x = sin .
144. sin x 4~ sin 2x 4- sin 3x = 0.
145. cos x -j- cos 2x — cos 3x — 1.
146. tg x 4- tg 2x = tg 3x.
147. 1 + cos 2x 4- sin x — 2 cos2 —-.
648. sin2 (x -p 10°) — sin2 x = sin 20°,
135
149. sin* x 4- sfa12x -|- sin13x = .
ISO. cos1 x + cos12x + cos13x = 1.
151. sin12x-|-sin1 4x = ~ . 152. К 3 cos x 4-sin x = iKT
&
155. 4 sin x 4- 3 cos x = 2. Решить двумя способами* введением
вспомогательного угла и подстановкой z = tg .
154. sin Зх 4- 2 cos Зх = 1,
155. 5 cos (2x4-18°)- 12 sin (2x4-18°) =13.
156. (4 sin x — 5 cos x)1 — 13 (4 sin x — 5 cos x) 4- 42 = 0.
157. Найти углы ромба, если отношение его периметра к сумме
я 3
диагоналей равно у.
158. Пусть т — отношение периметра прямоугольного треуголь-
ника к радиусу вписанной окружности. Найти углы треугольника npi(
m = 12. Исследовать задачу: указать, в каком треугольнике величина т
принимает наименьшее значение, и найти это наименьшее значениел
Существует ли прямоугольный треугольник, у которого периметр"
в 10 раз больше радиуса вписанной окружности?
ГЛАВА ПЯТАЯ
ЭЛЕМЕНТЫ ТЕОРИИ ТРЕУГОЛЬНИКА
И РЕШЕНИЕ ТРЕУГОЛЬНИКОВ
§ 18. Основные зависимости между элементами
треугольника
55. Постановка вопроса. Основными элементами тре-
угольника называются три его стороны и три его угла. К не-
основным причисляются другие его элементы, как то: высоты,
биссектрисы, медианы, периметр, площадь и т. п.
Решить треугольник — это значит по известным эле-
ментам треугольника при помощи вычислений найти все
основные его элементы.
Задачи решения треугольников возникают в связи с раз-
личными вопросами при измерениях на местности, в навига-
ции, в строительном деле и т. д. Исторически именно за-
дачи решения треугольников и привели к созданию тригоно-
метрии.
Конечно, решить треугольник можно только тогда, когда
известные элементы треугольника вполне его определяют.
Например, треугольник можно решить, если известны длины
трех его сторон, но треугольник нельзя решить, если даны
величины трех его углов, потому что три угла определяют
бесконечно много треугольников, подобных между собой.
Из геометрии известно, что три основных элемента (из
которых, по крайней мере, один линейный, т. е. сторона)
определяют, вообще говоря, единственный треугольник. (Как
выполняется при этом решение треугольника, будет показано
ниже.) Отсюда следует, что шесть основных элементов
треугольника должны быть связаны тремя независимыми
соотношениями, позволяющими по трем заданным эле-
ментам *1ийти остальные три, т. е. решить треугольник.
137
Введем прежде всего три наиболее важных и практически
употребительных соотношения между основными,
элементами треугольника.
В дальнейшем везде углы треугольника обозначаются
через а, у, противолежащие им стороны соответственно
через а, Ь, с, площадь треугольника через S, полупериметр
через р (^р = д + + , радиусы описанной и вписанной
окружности соответственно через R и г.
56. Зависимость между углами треугольника. Одной из
зависимостей между основными элементами треугольника
является зависимость между его углами. Именно: сумма
углов треугольника всегда равна тт (180°):
а + £-Н = тт (=180°). - (1)
Благодаря этой зависимости между углами тригонометри-
ческие функции углов треугольника также оказываются свя-
занными между собой. Например:
sin а = sin [тт — $ у)] = sin (£ у);
cos а = cos [тт — $ -ф- у)] — — cos $ -ф- у)
и т. д.
Из того, что
< = 90°>.
следует:
а
SIH у
2 Г ? I Y \1 . / ? । Y
cos -2 = cos [у — (Д + у = Sln ( у Ту
и т. д.
57. Теоремы синусов и косинусов. Приведем две важные
в теории треугольника теоремы, дающие две употребительные
при решении треугольников формулы.
1) Теорема синусов. Во всяком треугольнике сто*
роны относятся между собой, как синусы противолежа*
щих углов, т. е.
а __sin а ' b __sin . а __sin а
с sin у ’ с sin 7 ’ b sin р
138
Переставляя члены этих пропорций, получим:
а b с
(3)
sin a sin sin у *
Таким образом, теорему синусов можно высказать и так:
Во всяком треугольнике стороны пропорциональны сину-
сам противолежащих углов.
Дока зательство. Рассмотрим угол а треугольника АВС
(черт. 43). Опишем около треугольника окружность и из вер-
шины В проведем диаметр BD этой окружности. В зависимо-
сти от того, будет ли угол а острый или тупой, мы будем
иметь либо случай I, либо случай II, изображенные на
черт. 43. Точку D соединим с вершиной С. Получим прямо-
угольный треугольник BCD. Поэтому
где 5 — угол при вершине D, R—радиус описанной окруж-
ности. В первом случае S = a, так как оба угла а и 5 опи-
раются на дугу СВ; следовательно, sin 3 = sin а. Во втором
случае —71, так как ® и а— противоположные углы
четырехугольника ABDC, вписанного в окружность; значит,
опять sin 5 = sin (и — а) = sin а. Итак,
sin 3 sin а
Таким же образом докажем, что
= и —— = 2/?.
sin р sm 7
Следовательно,
sin з sin р sin у
139
Этим теорема синусов доказана, а также выяснено, что общее
значение отношений (3) равно диаметру окружности, опи-
санной около треугольника.
На основании равенств (4) получаем:
a = 2/?sina, Z? = 2/?sin^, £=2/?siny,
т. е. сторона треугольника равна диаметру описанной
окружности, умноженному на синус противолежащего угла.
2) Теорема косинусов. Квадрат стороны тре-
угольника равен сумме квадратов двух других его сторон
без удвоенного произведения этих сторон на косинус угла
между ними (т. е. на косинус угла, противолежащего вы-
числяемой стороне):
а2 — Ь2 -|- с2 — 2bc cos a, (5J
b2 = a2 4- с2 — 2ас cos , (5J
с2 = а2 -|- Ь2 — 2ab cos у. (58)
Доказательство. Докажем справедливость форму-
лы (5J. В случае острого угла а (черт. 44, а) имеем:
a2 = b2 + c2 — 2c-AD,
но
AD = b cos a,
и мы получаем формулу (5J.
а) б)
Черт. 44.
В случае тупого угла а (черт. 44, б) имеем:
а?— Ь2с2-\-2c-AD у
но
AD = b cos (и — а) — — b cos а
и снова получаем то же равенство (5Х):
а2 = Ь2-{-с2-\-2с( — b cos a) — b2-\-c2 — 2Ьс cos a.
140
В случае прямого угла а имеем cos а = О, и равенство (5Х)
при этом выражает теорему Пифагора.
Аналогично доказываются формулы (5г) и (58).
Теорема косинусов объединяет три геометрические теоремы:
теорему Пифагора, теорему о квадрате стороны, лежащей
против острого угла, и теорему о квадрате стороны, лежащей
против тупого угла треугольника.
§ 19. Другие зависимости между элементами треугольника
58. Теорема тангенсов. Преобразование формулы (2),
выражающей теорему синусов, дает возможность получить
формулу, иногда удобную при вычислениях.
Теорема тангенсов. Отношение суммы двух сто-
рон треугольника к их разности равно отношению тан-
генса полусуммы противолежащих углов к тангенсу их
полуразности, т. е.
tg а 4- » _ 8 2 a — b . a — g ’ tg-v tg ““ fr 4- c = 8 2 b — c g — 7 ’ tgl+^ c 4- а _ 8 2 c — a . 7 — a ‘ ‘8 — (6,) (6.) (6,)
Доказательство. Из формулы (2):
а sin а
Т sin £
образуем производные пропорции:
а 4-^ sin а 4-sing .
If k sin g *
g — b _ sin а — sin g
b ‘ sin g
Деля по частям первое равенство на второе, получим:
а 4- Ь___________________sin а 4* sin f
а — b sin а — sin f *
141
Применим формулы лля суммы и разности синусов:
а-\~Ь
а — b
2sin —~ cos
О’ а - Р а "j" ?
2 sin —cos —2
. a -f- р а — р
sin —- cos —2^"
a -j- Р . а — р
cos—sin —2^
а р а — р
2 ctg~2“ ’
или
ч. т. д.
Тем же способом можно получить два других соотношения
теоремы тангенсов:
tg — -
fr + c 8 2
tgl+?
c-f-a_ g____2
c — a , Y — a *
tg^y-
59. Зависимости между площадью, периметром и дру-
гими элементами треугольника.
Теорема 1. Площадь треугольника равна половине
произведения двух его сторон на синус угла между ними,
именно:
S = yfosina. (7)
Доказательство. Из вершины С треугольника АВС
проведем высоту CD (см. черт. 44). Эта высота равна b sin a.
Так как площадь треугольника равна полупроизведению осно-
вания с на эту высоту, то мы и приходим к формуле (7).
Теорема 2. Радиус окружности, описанной около
треугольника, равен частному от деления произведения
его сторон на учетверенную площадь:
D___abc
К~ 4S ’
142
Доказательство. Так как
[см, п. 57, формулу (4)], а из формулы (7) следует, что
2S
sina = v- ,
be ’
то
О —
— 4S *
Теорема 3. Радиус окружности, вписанной в тре-
угольник, равен частному от деления его площади на по лу-
пе риметр'.
Г = -. (9)
Р
Доказательство. Впишем окружность в треуголь-
ник АВС (черт. 45) и соединим ее центр О с вершинами
треугольника и с точками касания О, В, F. Тогда
пл. Л ВС = пл. АОВ -|- пл. ВОС-j-пл. СОА =
сг । аг । Ьг а 4- b 4- с
= 2 + 2 +-2 = Г “^2 = ГР>
т. е. S = rp или
S
г = — ,
Р
ч. т. д.
Пользуясь известной из геометрии формулой Герои а,
получим:
r__Vp(p-a)<P-b)ip-c)__ р/(р — а)(р — Ь) (р - с)
143
Заметим, что величины р— а, р — Ь, р — с всегда
положительны. В самом деле, например,
а 4- £ 4- с & 4- с — а
Р~а= ,
а эта величина всегда положительна, так как сумма любых
двух сторон треугольника больше третьей его стороны.
Теорема 4. Тангенс половины угла треугольника равен
частному от деления радиуса вписанной окружности на
разность между полупериметром и стороной, противоле-
жащей углу'.
. а г . р г . у г
tg2=/^:
Доказательство. Из треугольника AOD (черт. 45)
имеем:
(")
(АО — биссектриса угла А). Найдем AD. Так как
AD-\-DB-[-BE-\-EC-^CF^EA = 2p
и
AE = AD, DB — BE, CE = CF
как отрезки касательных, проведенных из одной точки, toj
AD-\-BE-\~EC=p. '
Отсюда
AD —а = р,
т. е.
AD = p — а.
Таким образом, формула (11) получает вид:
(,2>)
и аналогично:
('У
ч. Т. Д.
144
Заменяя в формулах (12) г его выражением из формулы (10),
придем к формулам:
ц(13)
- V р(р — а) ' ' 1 ’
см
'Н=/'5<^ сз.)
§ 20. Логарифмы тригонометрических функций
60. Таблица логарифмов тригонометрических функций.
Выведенные в пп. 56—59 соотношения применяются для ре-
шения треугольников. При этом приходится иметь дело с
выражениями, содержащими тригонометрические функции.
Находить численные значения этих выражений можно или с
помощью таблиц натуральных значений тригоно-
метрических функций (см. стр. 14), или с помощью таблиц
логарифмов тригонометрических функций.
В последних таблицах по данному значению острого угла а
даются значения lg sin a, lg cos а, lg tg a, Igctga.
Пусть, например,
4 = 753 cos 27°.
По таблице (см. стр. 14) находим cos 27° ^0,891 и, значит,
А 753-0,891 671.
В подобных вычислениях часто бывает удобным пользо-
ваться логарифмами, потому что они позволяют заменять
действие умножения действием сложения. В данном случае
по таблицам логарифмов чисел находим:
1gЛ 1g 7534- 1g0,891 2,8768 + 1,9499 = 2,8267;
отсюда, с помощью тех же таблиц получаем А 671. Здесь
мы для отыскания lg cos 27° сначала нашли из таблиц нату-
ральных значений cos 27°, а затем из таблицы логарифмов
чисел — его логарифм.
Таблицы же логарифмов тригонометрических
функций дают возможность избежать двукратного обраще-
ния к таблицам и получить сразу нужное нам значение (во
взятом примере lg cos 27°).
Как и в обычных таблицах логарифмов, мантиссы (т. е.
дробные части) логарифмов тригонометрических функций
143
всегда даются положительными, а характеристики (т. е.
целые части) логарифмов могут быть и отрицательными (в послед-
нем случае знак «минус» обычно пишут над характеристикой).
Например: lg cos 27°=Т,9499= — 1 -[-0,9499=--0,0501.
Напомним, что логарифмы чисел, меньших единицы, отрица-
тельны, а больших единицы — положительны. Поэтому lg sin а
и lg cos а для 0 а <С 90° отрицательны; lg tg а для 0 < а < 45°,
a lgctg а для 45° < а <90° отрицательны; lg tga для
45° а <^90°, a lg ctg а для 0<^а<^45° положительны.
Наибольшее распространение имеют четырехзначные и пя-
тизначные таблицы логарифмов тригонометрических функций.
Для особо точных вычислений, например в астрономии, поль-
зуются семизначными и десятизначными таблицами.
Мы здесь ориентируемся на четырехзначные таблицы Брадиса.
Углы а, для которых приведены в таблице значения
lg sin a, lg cos а, Igtga и Igctga, даются через определенный
промежуток, который называется шагом таблицы. В таблиц
цах Брадиса этот шаг равен б минутам. (Значения lg sin
и Igtga для углов а, меньших 14°, и Igtga для углов^
больших 65°, даны через минуту, ввиду того что для этиж
углов указанные функции очень быстро меняются.)
Вейлу зависимости sin (90° — a) = cos а и tg(90°—a)=ctg^
таблицы логарифмов синусов и тангенсов служат и для наЗ
хождения логарифмов соответственно косинусов и котангенсов-»
Для отыскания логарифма какой-нибудь функции угла а,*
отсутствующего в таблицах Брадиса (например, lg sin 20°20')r
ищем в таблице значение логарифма той же функции от
угла а0, ближайшего к а (в нашем примере таким углом
будет угол в 20° 18'). Угол а получается путем прибавления
к а0 или вычитания из «0 некоторого //; поскольку шаг таб-
лицы равен б минутам, h не превосходит 3 минут. В той же
строке, где находится значение логарифма функции для угла а0,
указана поправка d для А=Г, /.’ = 2', h = 3'. Прибавление
или вычитание этой поправки из значения логарифма функции
угла а0 и дает значение логарифма функции угла а.
Важно заметить, что при возрастании острого угла a
функции sin а и tga возрастают, а cos а и ctga убывают.
Значит, при возрасгании острого утла а функции lg sin a
и Igtga возрастают, а lg cos а и Igctga убывают. В силу
этого для отыскания lg sin а и Igtga нужно к lg sin a0 и
lgtga0 прибавить d, если h прибавляется к a0, и
вычесть из них d, если h вычитается из а0; наоборот,
для отыскания lg cos а и Igctga нужно из lg cos a0 и lgctgaa
146
вычесть d, если h прибавляется к а0, и прибавить
к ним d, если h вычитается из а0/
Точно так же можно пользоваться и четырехзначными «на-
туральными» таблицами.
Пример 1. Найти lgsin20°20'.
Имеем:
а = 20°20', ао = 2О°18'; Л = 2', d = 0,0007.
По таблицам находим:
lg sin 20° 18' = 1,5402
+ 2' 4-7
lg sin 20°20' = 1,5409
Пример 2. Найти lg cos 30°32'.
Имеем:
а = 30°32', ао = ЗО°ЗО'; Л = 2', d = 0,0001.
По таблицам находим:
lg cos 30°30' = 1,9353
+ 2' —1
lg cos30°32' =4,9352
Таблицы логарифмов тригонометрических функций могут
быть также использованы для отыскания острого угла а по
заданному значению одной из функций lg sin a, lg cos а,
lgtg а и Igctga. Ход выкладок обратен тому, который был
указан для отыскания значений этих функций по заданному
углу. Поясним его на числовых примерах.
Пример 3. Найти а, если lgtga = 0,2221.
В таблице значений функции lgtga нет числа 0,2221.
Ищем ближайшее к нему значение этой функции, помещенное в
таблице; это есть число 0,2229 = lg tg 59°6'; значит, а0 = 59°6'.
Заданное число 0,2221 получается из 0,2229 вычитанием
0,0008. В таблице поправок (в той же строке) мы видим,
что поправка d = 0,0009, ближайшая к 0,0008, соответствует
Л = 3\ Так как поправка d вычитается, то /г = 3' должна
тоже вычитаться.
Имеем:
lg tg a = 0,2221
lg tg 59°6'= 0,2229
-3' —8
a = 59°3'
Пример 4. Найти a, если lg cos a = 1,9377.
147
Имеем:
lg cos a = 1,9377
lgcos30° = 1,9375
-3' 4-2
a = 29°57'
скую («счетную») линейку. Она
/
Совершенно аналогично находятся значения тригонометри-
ческих функций по значению острого угла и, наоборот, зна-
чение острого угла по значению тригонометрических функций,,
если пользоваться таблицами натуральных значений тригоно-
метрических функций.
61. Применения логарифмической линейки в тригоно-
метрических вычислениях. В практических расчетах часто
вместо логарифмических таблиц употребляют логарифмиче-
используется также и в
тригонометрических вы-
числениях. Прежде чем
разъяснить принципы это-'
го применения логариф-'
мпческой линейки, кос-,
немея важного понятий
функционально^
шкалы. 1
Функциональной шка$
лой для заданной функ^
ции называется ось,
точки которой отмечен#
числами так: числом к
отмечена такая точка
оси, что отрезок Ох
(О — начало) в избранном масштабе равен значению функ-
ции для значения аргумента, равного х.
Логарифмическая линейка наряду со шкалой для функции
1gх (логарифмическая шкала — сокращенно Л-ш кала)
содержит шкалы для функций lgsin a (S-шкала) и lgtga.
(7-шкала), причем a выражен в градусах. Начало О А-шкалы
отмечено числом 1 (1g 1=0); начало S-шкалы — числом
90(Igsin90°=0); начало О2 Т-шкалы — числом 45(lgtg45°=0).
На черт. 4G приведены А-, S- и Т'-шкалы с общей масштаб-
ной единицей и общим положительным направлением (слева
направо). На обычной логарифмической линейке в качестве
масштабной единицы служит отрезок длиной 25 см\ £-шкалн
,---------------£-----
0,1 1
,---------------Д-----5^
М 90
,ф °2 г г
5,6 45
Черт. 46.
148
расположены на корпусе и на движке линейки, 5- и 7-шкалы —
на оборотной стороне движка.
На черт. 46 А-, 5- и 7-шкалы изображены в своем
исходном положении: их начала О, Ог и О2 лежат друг
против друга (т. е. на общем перпендикуляре к этим шка-
лам). Если против отметки а A-шкалы лежат отметки а 5-шкалы
и 7-шкалы, то \ga = lg sin а= lg tg т. e. a = sin a = tg[k
Для того чтобы найти с помощью логарифмической ли-
нейки произведение b — «sin а, нужно (черт. 47, а) передви-
нуть 5-шкалу так, чтобы ее начало легло против отметки/?
/.-шкалы. Тогда против отметки а 5-шкалы находится отметка/?
Ь _ 1д ь а lg? 0,
"Г Г*
ig sin а
а)
_________igb________a iga О
1^*— igb-Lga —►-! /
:________/?, 5
ь-t* igsinfi- igsma
б)
Черт. 47.
A-шкалы. В самом деле, в таком положении lg/? = lga-f-
lg sin a, т. e. lg b — lg (a sin a) и, значит, /? = «sina.
Для того чтобы найти частное а = , надо (черт. 47, а)
передвинуть 5-шкалу гак, чюбы ее отметка а легла против
отметки b A-шкалы. Тогда против Ог — начала 5-шкалы (от-
метки 90°) найдем на A-шкале отметку а.
Аналогично, пользуясь Т'-шкалой, находят выражения
b — atg$, a = ~j. Заметим, что логарифмическая линейка
имеет лишь часть 7-шкалы, расположенную левее начала О2
(отметки 45°) и соответствующую острым углам меньшим 45°.
Если же 45°<£<90°. то tg= {^90° - ?)’ где °<90° —
— j}<^45°, и умножение и деление на tg^ заменяются соот-
ветственно делением и умножением на tg(90°—13).
На расстоянии 1 влево от начала О A-шкалы находится
на ней точка с отметкой 0,1 (1g 0,1 =—1); на 5- и 7-шкалах
ей соответствуют точки с отметками 5,6 (sin 5°,6=^0,1;
tg 5°,6 =^0,1). Для всех углов а, меньших 5°,6, можно считать
с точностью, которая допустима при расчетах с помощью
логарифмической линейки, что sin a = tga. В самом деле,
sin з
tga =-----•, а cos а для указанных углов достаточно близок
° cos а
149
к единице: 0,995 < cos а < 1. Части 5- и Т-шкал, лежащие
левее их отметок 5°,6, практически совпадают. Эга общая
часть обеих шкал называется 5Г-шкалой; ее исходное поло-
жение на логарифмической линейке (также на оборотной сто-
роне движка) приведено на черт. 46. Она сдвинута относи-
тельно 5- и Г-шкал на 1 вправо).
Заметим, что если отметки а и J S- (или Л) шкалы нахо-
дятся против отметок а и b A-шкалы (черт. 47,6), то имеем:
b sin 8 / b tg 8
— = или — =
a sin а \ a tg а
х В самом деле, так как отрезки наших шкал между соот-
ветствующими отметками равны между собой, а отрезок на
A-шкале равен lg b — lga = lg~ и на 5-шкале (или Т-шкале)
равен lg sin fl — Igsina = lg-^~ ^или lg то
i b « sin p 7 , b i tg
lg — = lg -г—L или lg — = lg ,
b a 6 sin a \ a tga/
§ 21. Решение треугольников
62. Решение прямоугольных треугольников. Задача ре-
шения треугольника значительно упрощается в случае прямо-
угольного треугольника. В этом случае один из углов — пря-
мой, у=хк90° и, значит, а-|-р = 90о, а соотношения между эле-
ментами треугольника имеют особенно простой вид [см. фор-
мулы (1) — (4) главы I]. Поскольку один элемент — угол у —
заранее известен, для решения прямоугольного треуголь-
ника необходимо задание двух элементов, из которых по
меньшей мере один — линейный. При вычислениях можно
пользоваться как таблицами натуральных значений, так и
«логарифмическими» таблицами или логарифмической линей-
кой. Числовые примеры будем здесь решать с помощью
«логарифмических» таблиц.
Рассмотрим четыре основных случая решения прямоуголь-
ных треугольников, указав в каждом из них одно из возмож-
ных решений.
Случай I. Дана гипотенуза с и угол а.
Имеем:
£=90° — а, а — с sin a, Z? = 6’cosa.
150
Для проверки результатов можно прибегнуть или к любому
из соотношений (1) — (4) главы I, не использованному в дан-
ном подсчете, или, например, к теореме Пифагора. Подставляя
в контрольное соотношение заданные и вычисленные элементы
треугольника, проверяют, получается или не получается чис-
ленное тождество.
Пример 1. с= 12,783; а = 23°177".
Поскольку таблицы Брадиса четырехзначные, округлим зна-
чения с до четырех значащих цифр, положив с= 12,78; точно
так же при пользовании этими таблицами угол а округлим
до целого числа минут: а = 23®17'. Находим:
3^90° — 23° 17' = 66°43\
Имеем:
lgo = lgc-г Igsin a, lgb = lgc + lgcos a.
Находим:
. lg£=l,1065
* lg sin a = 1,5969
lg a = 6,7034
Отсюда
a = 5,047.
Далее находим:
. lgc=l,1065
’ lg cos a= 1,9632
lg#= 1,0697
откуда
b= 11,74.
Для контроля здесь можно воспользоваться формулой
b = atg$ пли lg# = Ig^ + lgtgji.
Имеем:
। lg а = 0,7034
। lg tg = 0,3662
’ lg^= 1,069б
Раньше было найдено: 1g#=1,0697. Мы имеем хорошее
совпадение.
Случай П. Дан катет а и угол а или
Имеем:
^ = 90° — а или a =90° — # = atg[J, с =
151
Случай 1П. Даны катет а а гипотенуза с.
Имеем:
sina = — , £ = c'cosa, 3 = 90° — сс.
с г
Пример 2. <2 = 23,15; £ = 31,81.
Вычисления будем вести снова с помощью «логарифмиче-
ских» таблиц. Имеем:
lg sin a = lg a — lg c. lg b _. lg c -j- lg cos a.
Находим:
— lg c = 2,4975
4- lg а = 1,3645
fg sin a = 1,8620
Отсюда
a = 46°42';
£ = 90° —46°42' = 43°18'.
Далее,
, lgc= 1,5025
‘ lg cos a = 1,8362
lg^= 1,3387
откуда
b = 21,81.
В качестве контрольной используем формулу
а = b tg а или lg а = lg b -ф- lg tg a.
Имеем:
lg £= 1,3387
lg tg a = 0,0258
lg a = 1,3645
что совпадает с табличным значением lg a.
Случай IV. Ланы катеты а й Ь.
Имеем:
tga = ~; с = -?—\ 8 = 90°—а.
» b Sin а ’ г
63. Решение косоугольных треугольников. Основными
случаями в решении треугольников называют случаи, когда
по заданным трем основным элементам (из которых по
меньшей мере один линейный) находят остальные три ос-
н о в н ы х элемента.
Таких основных случаев может быть четыре, именно слу-.
чаи, когда заданы: 1) сторона и два угла; 2) две стороны и
152
угол, лежащий между ними; 3) две стороны и угол, лежащий
против одной из них; 4) три стороны.
Решение косоугольного треугольника упрощается, если
известно, что он равнобедренный; при этом высота, опущен-
ная на основание, разбивает треугольник на два равных пря-
моугольных треугольника, и задача сводится к решению пря-
моугольного треугольника.
Неосновные случаи в решении треугольников мы специ-
ально рассматривать не будем.
Для отыскания трех неизвестных основных элементов со-
ставляют три уравнения. В качестве одного из них берут
соотношение (1):
« + ?+Т = 180°.
в качестве двух других — два из соотношений между основ-
ными элементами треугольника, выведенных в пп. 57—59
(теоремы синусов, косинусов, тангенсов и др.). Для контроля
прибегают к соотношению, не использованному при решении.
Решение треугольника иногда оказывается невозможным.
Например, нельзя решить треугольник, если заданы стороны
20, 10, 5 (так как каждая сторона треугольника должна быть
меньше суммы двух других сторон) или если заданы стороны
а = 20, b — 10 и угол [5=100°, лежащий против стороны b
(так как против меньшей стороны b не может лежать тупой
угол).
Случай 1. Дана сторона и два угла, например, а, а и. [5.
Имеем:
у = 180° — а —
По теореме синусов:
Задача всегда имеет решение и всегда только одно.
Пример, а = 20, а = 69°, {5 = 82°.
Получаем:
у = 180° — 69° — 82° = 29°.
По таблицам натуральных значений тригонометрических функ-
ций находим:
sin а — 0,934; sin fl = 0,990; sin у = 0,485.
153
Следовательно,
b »sin 8 = • 0,990 = 21,4 • 0,990 = 21,2;
sin a r 0,934 1
с = -2-sinY = 21,4-0,485= 10,4.
Sin а * ’ ’ ’
Для контроля возьмем, например, теорему косинусов:
с1 = а2 -|- Ь* — 2ab cos у. Имеем:
108,2 400449,4 —2*20*21,2*0,875 107,4.
Этот же пример решаем с помощью таблиц логарифмо!
тригонометрических функций. Имеем:
lg b = (1g а — lg sin а) + lg sin 0,
lgc = (\ga — lg sin a) -|- lg sin y.
Находим;
lg a = 1,3010
— Igsin a = 0,0299
• lg a — lg sin a — 1,3309
‘ lg sin fl = 1,9958
lg£= 1,3267
откуда
£ = 21,21.
Далее,
। lg a — lg sin a = 1,3309
lg sin у = 1,6855
lgr = 1,0164
откуда
c= 10,39.
В качестве контрольной здесь удобней использовать фор-
мулу тангенсов:
taX±l
8___2
а —с . в —у *
т. в.
0 + с) tg Х^Х= (а — с) tg Х±Х,
откуда
tefc + ^ + lgtg^-y^lg(в — С)4-lg tgX±I.
154
Находим:
а с — 30,39; а — с = 9,61;
а-=^- — 20°; tgM^ = ctg-L = ctg41°.
Z А А
Получаем:
1g (а 4- с) = 1,4827 1g (а — с) = 0,9828
~lgtg?-=^ = I,5611 lg ctg 1 = 0,0607
= 1,0438 =1,0435
1,0438 = 1,0435.
Случай IL Даны две стороны и угол между ними, на-
пример, а, # ft у.
Сторону с можно найти по теореме косинусов:
с* = а1 & — 2ab cos у.
Угол а также найдем на основании теоремы косинусов из
формулы
Наконец,
0=180° —а—у.
Если для решения треугольника пользоваться «логариф-
мическими» таблицами или логарифмической линейкой, то
углы а и 0 удобнее находить, применяя формулу тангенсов:
tgl+l ctg £
a + b___ s 2 _
a — b . a — p a — В *
tg-2^ tg-yJ!
а — 8 a — 8 a -I— 8 ( Л Л у \
Отсюда находим —у1; по —у1 и —= 90°—-у! нахо-
дим а и 0. Сторону с вычисляем по теореме синусов:
__a sin 7
С sin a ’
Задача всегда имеет решение и притом только одно.
Для контроля здесь удобно воспользоваться также теоре-
мой синусов:
a sin a
b sin p •
155
Случай III. Даны две стороны а угол против одной из
них, например, а, b и а.
Из теоремы синусов следует:
sin р = -^- sin а. (14)
Определив [}, найдем:
у = 180° — а —
Тогда с можно вычислить также по теореме синусов:
a sin y
С = —;--1 .
sm а
В отличие от предыдущих случаев задача не всегда имеет
решение, а если и имеет, то не всегда единственное.
Произведем исследование задачи, оставив
без рассмотрения случай равнобедренного треугольника а — Ь,
о котором уже говорилось выше. Рассмотрим отдельно слу-
чаи а b и а < Ь.
1) а^> b (данный угол а лежит против большей из
данных сторон).
При этом -^-<4 и в силу формулы (14) sin р < sin а^1,
т. е. sin 1, и задача нахождения разрешима. Так как
[J — угол треугольника, то найденному значению sin могут
соответствовать два значения угла ji: один. острый, другой
тупой. Но поскольку (3 лежит против меньшей стороны Ь, то
угол $ должен быть острым.
Итак, в случае а^> b задача имеет решение и притом
только одно.
2) а <^Ь (данный угол а лежит против меньшей из
данных сторон).
При этом, если угол а тупой или прямой, то задача
не имеет решения, так как ни тупой, ни прямой угол
не может лежать против меньшей стороны. Если а — острый
уюл, то имеются три возможности:
а) — sin а >* 1 (т. е. а <2 b sin а); тогда sin 3 = — sin а Ъ> 1
и, как видно, задача не имеет решения.
б) у sin а = 1 (т. е. a = £sina); тогда sin t3 = 1, и pe-
in е н и е е д явственное — прямоугольный треугольник.
136
в) ~ sin a < 1 (т. е. а b sin а); тогда sin < 1; данному
значению sin £ соответствуют два угла jk один острый, другой
тупой, и задача имеет два решения.
Результаты исследования могут быть записаны в виде
схемы:
a > b a < b
a >90° a < 90°
a < b sin a a — b sin a a > b sin a
Одно Нет Нет Одно Два
решение решения решения решение решения
Когда задача имеет решение, в качестве контрольной можно
использовать формулу тангенсов.
Пример. а = 20,21; £=15,76; а=100°3' (а> Ь).
Имеем:
lg sin = lg b -f- lg sin a — lg a.
Находим:
— lg a = 2,6944
lg b= 1,1976
lg sin a = 1,9933
lg sin£ = T,8853—
откуда
[J = 50°9' или £ = 180° — 50°9' = 129°5 1'.
Второе из этих значений должно быть отброшено, так как угол,
лежащий против меньшей стороны Ь, не может быть тупым.
Далее,
у = 180° — a — р = 180° — 100°3' — 50°9' = 29°48'.
Теперь имеем:
____________________________a sin 7
С Sin a ’
1g с = 1g а lg sin у — lg sin a.
Находим:
— lg sin a = 0,0067
4- lg a = 1,3056
lg sin y = 1,6963
lg <?= 1,0086
157
откуда
с = 10,20.
Контроль:
lg(a —0)-|-lgtg^^ = lg(a 4-b) + lg tg,
и так как
a-]- b — 35,97; a — b = 4,45;
L±1 = 75°6', a-^ = 24°57',
то имеем:
lg (a — t>) = 0,6484 lg (a-(-/>)= 1,5560
IgtgMp.— 0,5750 lg tg = 1,6667
= 1,2234 — 1,2237
1,2234 == 1,2237.
Случай IV. Даны стороны a, b, с. Угол a можно вы-
числить или согласно теореме косинусов:
или по формуле (130:
t «=_£_ = _J_ 1/ (p-a)(p-b)(p-c) 1б
® 2 р — а р ~ а V р * ' '
Точно так же можно вычислить, например, угол [5, а затем
п угол у по формуле
у—180° —а-—
Первый метод [по формуле (15)] удобнее при пользовании
таблицами натуральных значений тригонометрических функций,
второй [по формуле (16)] — при пользовании таблицами лога-
рифмов тригонометрических функций или логарифмической
линейкой.
Из геометрических соображений очевидно, что задача
имеет решение и притом только одно, если каждая сторона
меньше суммы двух других сторон. Это же заключение можно
вывести и из формул (15) и (16).
В качестве контрольной можно прибегнуть, например,
к любой из формул (15) и (16), не использованной при ре-
шении задачи.
158
земной поверхности и углы
Черт. 48.
64. Измерения линий и углов на местности. Во многих
задачах практического характера оказывается необходимым
знать расстояния между точками
между линиями на ней. Непо-
средственное измерение этих
расстояний и углов часто
бывает затруднительным, а
иногда и невозможным. Реше-
ние треугольников позволяет
найти расстояние между двумя
точками, не производя не-
посредственного измерения,
а измеряя лишь углы и рас-
стояния между доступными точ-
ками, не слишком отдаленными
друг от друга. Измерение углов
на местности выполняется про-
ще, чем измерение расстояний.
Оно производится с помощью
так называемых угломерных
приборов (например, теодо-
литов; черт. 48).
Зрительная труба теодолита
способна вращаться как в го-
ризонтальной, так и в верти-
кальной плоскости. Благодаря этому
теодолит позволяет нахо-
дить угол между горизонтальными проекциями направлений на
две точки, а также «угловое возвышение» точки, т. е. угол
между направлением на точку и
его горизонтальной проекцией.
Приведем несколько при-
меров вычисления расстояний с
помощью решения треуголь-
ников.
Задача 1. Вычисление
расстояния от доступной
точки до недоступной.
Пусть точка А доступна, а
Черт. 49. точка В недоступна (черт. 49).
Для отыскания расстояния АВ
выбирают доступную точку С, из которой видны А и В. Измеряют
расстояние СА и углы САВ=а и АСВ — ^. Решая треугольник
АВС по стороне АС и двум углам « и у, находят сторону АВ.
159
Задача 2. Вычисление расстояния между недоступ-
ными точками»
Пусть А и В — дъе недоступные точки (черт. 50). Выби-
рают две доступные точки С и D, из которых видны А и В,
д Измеряют расстояние CD и
углы ADC=a, BDC = $t
ACD = <(, BCD = $.
Решая треугольник ACD по
стороне CD и углам ADC=a
и ACD = y и треугольник BCD
8 по стороне CD и углам BDC— [J
и BCD — Ъ, находят стороны
АС и ВС. Решая треуголь-
ник АВС по двум сторо-
нам АС и ВС и углу меж-
ду ними (/ АСВ = / BCD —
— /ACD = 5 — у), находят искомое расстояние.
Задача 3. Вычисление высоты предмета.
Пусть С—недоступная точка, D — ее горизонтальная
проекция, А и В — две доступные точки в горизонтальной
плоскости, из которых видна точка С (черт. 51).
С
Черт. 51.
В
Находят (как в предыдущей задаче) расстояние АС из
треугольника АВС. Далее измеряют угол а = /_CAD между
АС и AD (AD — проекция АС}. Отрезок DC находят из
прямоугольного треугольника ADC по гипотенузе АС и углу а.
Задача 4. Вычисление расстояния между двумя да-
лекими точками А и В (способ т р и а н г у л я ц и и).
Соединяют точки А и В сетью треугольников ААгА2,
АгАгАг, Д2,Д3Д4, . . Ап_1АпВ (черт. 52). Вершины тре-
угольников выбирают так, чтобы из каждой вершины тре-
угольника были видны две другие, а первый треугольник
ААгА2 выбирают так, чтобы сторона АА1 (или АА2} была
160
доступна непосредственному измерению. Измерив эту сторону
и углы X и ^AvAA2, находят, как в задаче 2, из
треугольника ААгА2 стороны АА2 и Далее, точно таким
же образом, зная сторону АХА2 треугольника АгА2А8 и изме-
рив его углы, вычисляют другие его стороны. Так последо-
вательно находят, измеряя в дальнейшем лишь углы, стороны
всех наших треугольников. Далее рассматривают вспомога-
тельные треугольники А42Д8, ЛЛ3Д4, ЛЛ4Л5, . . ААпВ.
В треугольнике ЛЛ2Л3 по найденным сторонам АА2, Л8Л3
и X ЛЛ2Л3 = У ЛЛ2Л4 X находят сторону ААа и
^АА3А2\ аналогично, в треугольнике ЛЛ3Л4 по сторонам АА3,
Д8Л4 и / ЛЛ8Л4 = / ДЛ3Л2 -|- / Л2Л3Л4 находят сторону АА4
и / ЛЛ4Л3 и т. д. Последовательно решая так один за дру-
гим все вспомогательные треугольники, находят в конце кон-
цов сторону АВ последнего из этих треугольников (на
черт. 52 — треугольника ААЬВ).
Задачи к главе V
I. Упростить выражения:
(a) sin a cos ? + cos з sin (b) cos ~ cos у — sin у sin у.
1 4 я
2. Найти cos а, если cos 3 = — и sin 7 = , причем 7 > ~ .
о О 2
3. Найти tg 7, если tg a = 2 и tg f = 3.
Доказать тождества (задачи 4—7):
_ a В v
4. sin a 4- sin p 4- sin 7 = cos — cos у cos .
5. cos 3 4- cos £ — cos r = 4 cos cos sin 4- — 1.
222
6. tg a 4- tg f + tg t = tg 3 tg ₽ tg t.
161
7. ctg 5 ctg ? + ctg a ctg у ctg ? ctg у = 1.
8. Углы остроугольного треугольника связаны соотношением
. . а . 0 у
sin я = 4 sin у sin у cos у .
Доказать, что трех , эльник равнобедренный.
9. Углы треугольника связаны соотношением
cos я -j- cos р = sin у.
Доказать, что треугольник прямоугольный.
10. Углы треугольника связаны соотношением
sin а = 2 sin р cos у.
Доказать, что треугольник равнобедренный.
II. Два угла треугольника относятся, как 1:2, а противолежащие
им стороны, как 1:J^3. Найти углы треугольника.
12. Пользуясь теоремой синусов, доказать теорему о биссектрисе
внутреннего угла треугольника.
13. Найти сумму косинусов углов треугольника, стороны которого
к 3
образуют геометрическую прогрессию со знаменателем, равным у .
14. Стороны треугольника связаны соотношением
а2 — (Ь — с)2_
Ьс ~~
Найти а.
15. Пользуясь теоремами косинусов и синусов, доказать тождество .
sin* я -|- sin2f — sin2 у = 2 sin а sin р cos 7.
Указание. Выразить cos у через стороны треугольника и в по-
лученной дроби стороны заменить синусами противолежащих им углов. -
16. Из системы соотношений
a b с , 0 ,
—.— —----г — —— и 1 4- 3 -4- т — ~
sin a sin р sin у
вывести алгебраически теорему косинусов.
17. Доказать, что в прямоугольном треугольнике отношение суммы
катетов к их разности равно котангенсу полуразности острых углов.
18. Геометрическими построениями доказать теорему тангенсов.
Указание. В треугольнике АВС отложить на стороне ВС (до-
пуская, что а > с) и на ее продолжении отрезки DB — ВЕ = с, соеди-
нить точки D и Е с вершиной Л, провести DF \\ АЕ и рассмотреть
подобные треугольники АЕС и DFC.
19. Дано: Ь~ 40, с =15, я = 60°. Найти S.
20. Треугольный участок земли АВС был обмерен так называемым
полярным способом. Из точки О, выбранной внутри участка, были
измерены расстояния СМ = 28,и, ОВ=43л< и ОС =50 .и и углы
АОВ= 152° и ВОС— 94°. Найти площадь участка.
21. В круг радиуса R вписана трапеция. Одно основание совпа-
дает с диаметром круга, а другое — стягивает дугу я. Найти площадь
трапеции.
162
22. Выразить площадь параллелограмма через его стороны т и п
и острый \тол между его диагоналями.
Указание Выразить стороны параллелограмма через его диа-
гонали и угол Ср.
23. Указать знак числа:
(a) lg sin 72°; (b) lg tg 38°; (c) lg cos 15°;
(d) lg ctg 10°; (e)lgtg78°; (f) Igsin8°; (g) lgtg65°.
24. Указать знак числа:
(a) Igsin j; (b) Igcosl; (c)lgtgji (d) Igctgy! (e)lgtgl,4.
25. Указать знак разности:
(a) lg sin 41° — lg sin 40°; (b) lg tg 1 — lg tg 0,9;
(c) lg cos 10° — lg cos 9°; (d) lg sin — lg sin ;
(e) lg ctg — lg ct£ уд I (0 lg cos 0,5 — lg cos 0,4.
Упростить выражения (задачи 26—28).
26. (a) lg sin a — lg cos a; (b) lg tg a -f- lg ctg a.
27. lg (1 4- tg2a) 4- 2 lg cos a. 28. lg sin я + lg cos a 4- lg 2.
Пользуясь таблицей логарифмов тригонометрических функций,
найти (задачи 29—30):
29. (а) lg sin 22°30<; (b) lg cos 18° 12'; (с) lg tg 38°18'; (d) lg ctg 10°36'.
30. (a) lg cos 52°24'; (b) lg sin 63°; (c) lg tg 51°48'; (d) lg ctg 81°42'.
Пользуясь таблицей логарифмов тригонометрических функций,
найти острый угол а, если (задачи 31—32):
31. (a) lg tg а = 1,6300; (b) lg cos a = 1,9487;
(с) lg cos a = 1,9808; (d) lg sin a = 2,9614;
(e) lg tg a = 3,9952; (f) lg ctg a — 0,7741.
32. (a) Igctga =1,3200; (b) lg cos a = 1,6510;
(c) lg tg a = 0,0106; (d) lg tg a = 1,0008;
(e) lg sin a = 1,9974; (f) lg ctg a = 1,5727.
Найти по таблице (задачи 33—34):
33. (a) lg tg 32°25'; (b) lg sin 57°10'; (c) lg tg 12°14';
(d) lg tg 45°8'; (e) lg sin 30°40'; (f) lg sin 5°4';
(g) lg sin 81 °52'; (h) lg tg 88°46'.
34. (a) Igcos52°H'; (b) lgcos64°26'; (c) Igctgll°2';
(d) lgctg74°15', (e) Igcos8r58'; (f) lgcosl5°5';
(g) lg ctg84°41'.
163
Найти по таблице острый угол л, если (задачи 35—36):
35. (a) lg sin а = 1,1542; (b) lg sin 1,8344;
(с) lg tg а = 1,0437; (d) lg tg a = 1,0437;
(e) lg tg a = 1,9946; (f) lg sin a = 1,3000;
(g) lg tg 'i — 0,5000; (h) lg sin i — T ,6983.
86. (a) lg cos а = 1,2525; (b) lg cos a = 1,0346;
(c) lg cos a — 2,6869; (d) lg ctg a = 0,1245;
(e) lg ctg a = 1,0022; (f) lg cos a — 1,0400;
(g) lg cos a = 1,8793; (h) lg ctg a = 1,1245.
Пользуясь таблицей логарифмов чисел и таблицей логарифмов
тригонометрических функций, вычислить следующие выражения (за-
дачи 37—40):
„ 13,56 sin 12°43'
cos 36°18'
/sin 41=20' -ctg 13°28'
39,
sin235°10'.tg354°18'
2,3-cos 62° 14'
sin216°17'-cos51°41'
40. ----------
0,0046 ./tg 33° 12'
Привести выражения к виду, удобному для логарифмирования, и
найти с помощью таблиц значения" ------- -----------4 ‘------
COS а — CCS 2а
COS а 4- cos 2а
sin а Sin 2а -|- sin За
У tg 72=2'
ЭТИХ
выражений (задачи 41—44):
при a = 12°22';
(b)
42.
43.
при a = 24°8'.
при a = 31 ° 15'.
44.
sin 2a
tg * + tg (45° 4- a)
tg a — tg (45° — a)
/1 — COS a f \ 4- cos a
1 4" cos a V 1 —cosanPH
cos a — 2 Sin 3a — COS 5a
Sin a — 2 cos 3a — sin 5a
при
a=112°34'.
2 = 54°27'.
41- (a)
Пользуясь таблицами, найти острый
45’(а) sina=^TF; (ЬП^ 0,03
46. tgа = /cos 12е 17'-5,212 sin 7° 18'.
угол
cos 17°15'
a, если (задачи 45—50):
47. cos a =
cos 12C8' 4~ cos 15° 14'
sin 58°4Г 4- sin 31°19' ‘
tg — tg io
48> ‘8з= ..г
50. (a) cos a — lg tg 61 = 18'; (b) sin a = lg ctg 20=10'.
49. (a) ctg a = у: (b) sin a = у .
164
С помощью логарифмических таблиц решить прямоугольный тре-
угольник по следующим данным (задачи 51—56):
51. с = 42,43, d = 31°44'. 52. с = 761, а = 80°6'.
53. а =184,3, а = 28°48'. 54. Ь = 49,41, а = 59°44'.
55. а=166,1 с=187,3. 56. а = 476,5 6= 1489.
57. Решить прямоугольный треугольник, зная его угол а = 32*18'
и биссектрису этого угла I = 0,423.
58. Из некоторой точки, лежащей в одной горизонтальной пло-
скости с основанием башни, верхушка башни видна под углом а = 35*14'
к горизонту. Приблизившись к основанию башни так, что расстояние
до основания башни уменьшилось на tZ= 12 лг, наблюдатель видит
верхушку башни под углом f = 48° 11'. Найти высоту башни.
59. Сумма т двух неравных высот равнобедренного треугольника
равна 40,2, угол а при основании равен 52°14'. Найти боковую сторону.
60. Меньшая диагональ прямоугольной трапеции равна большему
основанию, площадь трапеции 5 = 28,5 си2, острый угол я = 58°38'.
Найти стороны трапеции. При каких значениях угла л задача имеет
решение?
Пользуясь таблицами натуральных значений тригонометрических
функций или логарифмической линейкой, решить треугольник поданной
стороне и двум данным углам (задачи 61—64):
61. а = 18, a =z 42°, f = 62°. 62. 6 = 3, а = 51°, 7 = 58°.
63. с = 20, ₽ = 124°, 7 = 31°. 64.6 = 32, а = 36°, f = 42°.
Пользуясь таблицей логарифмов, решить треугольник по данной
стороне и двум данным углам (задачи 65—68):
65. с = 444,8 а=11°11', у = 57°37'.
66. а = 6,738, f = 20°20', 7=12°28'.
67. 6 = 0,731, а = 28°14', т=109°32'.
68. 6 = 479,4, а = 20°3', f = 102°38'.
69. Две силы действуют под углом в 75° друг к другу. Рав-
нодействующая делит этот угол в отношении 2:3. Найти вели-
чину равнодействующей, если меньшая из составляющих сил рав-
на 2,6 кГ.
70. Чтобы определить расстояние от данной точки А до недо-
ступной точки В, измерили базис АС = 40,4 м и углы ZMC=57°38'
и АС В =63° 14'. Найти АВ.
Пользуясь таблицами натуральных значений тригонометрических
функций или логарифмической линейкой, решить треугольник по дан-
ным двум сторонам и углу, заключенному между ними (задачи 71—74):
71. а = 22, с = 26, f = 78°. 72. 6 = 5, с = 10, а = 102°.
73. а = 0,8, с = 0,6 ₽ = 50°. 74. а = 4, 6 = 5, 7 = 60°.
6 А. Верман!, Л. Литерник
165
Пользуясь таблицей логарифмов, решить треугольник по данный
двум сторонам и углу, заключенному между ними (задачи 75—78):
75. 0 = 49,37, £? = 26,44, Т = 47°18'.
78. 0 = 283,4, Ь = 268,5, т = б3°38'.
77. 0 = 9,768, с = 2, р = 26"26'.
78. с = 0,024, /7 = 0,015, а=19°1Г.
79. На материальную точку действуют две силы: р — 42,74 кГ
и 7 = 34,08 кГ, образующие между собой угол я = 64с24'. Найти
равнодействующую этих сил и углы, которые образует равнодей-
ствующая с данными силами.
80. В треугольнике ЛВС известны сторона /7=16, угол а=122°
и биссектриса /= 10, проведенная через вершину А. Найти две другие
стороны треугольника АВС.
Пользуясь таблицами натуральных значений тригонометрических
функций или логарифмической линейкой, решить треугольник по
данным двум сторонам и углу, противолежащему одной из них (за-
дачи 81—88):
81. 0=12, с =15, 7 = 39°.
83. с = 0,12, £7 = 0,24, ?=44°.
85. /7=18, 0=14, а = 50с24'.
87. с= 1,5, £7 = 2,4, т = 28°30'.
82. /7 = 3,5, 0 = 4,2, а = 70°.
84.0 = 10, /7 = 6,6, ? = 41°18\
36. с = 32, /7 = 20, f = 47°36'.
88. /7 = 0,8, 0 = 0,7, а =19°.
Пользуясь таблицей логарифмов, решить треугольник по данным
двум сторонам и углу, противолежащему одной из них (задачи
89—96):
89. 0 = 86,42, с = 73,46, т = 49° 19'.
90. /7 = 223,5, с = 327,9, 7 = 116°20i
91. /7 = 32,49, с = 52,39, р = 27°49'.
92. 0 = 67,31, с = 111, з = 37°20'.
93. /7 = 4,587, с = 5,632, f = 20° 14'.
94. 0 = 23,62, с = 45,63, а = 36°43'.
95. 0 = 0,5715, b = 0,467, 0 = 19°18'.
96. 0= 15,8 /7= 17,9, а = 21с17'.
97. Хорда, стягивающая дугу сегмента в 280°, равна 9,6 слг.
В каком отношении разделит дугу сегмента точка па окружности,
отстоящая от одного из концов хорды па 10 слг?
98. Основания трапеции равны 27 и 9 слг, а одна из диагоналей
равна 24 см и образует с боковой стороной угол в 108°. Найти вто-
рую диагональ.
Пользуясь таблицами натуральных значений тригонометрических
функций или логарифмическом линейкой, решить треугольник по трем
данным сторонам (задачи 99—102):
99. 0 = 40, /7 = 19, с = 41. IOO. 0 = 1,5, /7 = 2,5, с = 1,8.
(01. а = 6Д = 3.с = ЗГа (02. а — /10, b — 4, c = V~2.
166
Пользуясь таблицей логарифмов, решить треугольник по трем
данным сторонам (задачи 103—106):
103. а = 24,57, Ъ = 24,74, с = 10,05.
104. а = 125,3, Ь= 176,2, с = 91,2.
105. а = 10,03, b = 9,44, с= 15,07.
106. а = 0,2243, b = 0,2469, с = 0,3126.
107. Длина минутной стрелки часов равна 60 мм, а длина часо-
вой 54 мм. Через сколько времени после полудня расстояние между
концами стрелок впервые будет равно 90 мм?
108. Стороны треугольника равны 12, 15 и 18 см. Найти угол
между медианой и биссектрисой, проведенными к большей стороне.
109. Сторона треугольника, равная 33 см, разделена на три рав-
ные части. Прямые, соединяющие точки деления с вершиной проти-
волежащего угла, делят его на три угла. Найти эти углы, зная, что
углы, прилежащие к данной стороне, равны 44° и 54°6'.
НО. Две противоположные стороны четырехугольника, описан-
ного около круга, равны 7 и 12 см, а два противоположных угла
равны 36°52' и 78с28'. Найти две другие стороны четырехугольника.
III. Острый угол ромба равен а. Под каким углом его сторона
видна из середины противоположной стороны? В каком ромбе этот
угол принимает наибольшее значение?
112. Для определения расстояния между двумя взаимно невиди-
мыми точками С и D была провешена на местности прямая DN и на
этой прямой выбраны две точки А и В, из которых видна точка С.
Затем измерены расстояния DA = 836 м и 4^ = 513 м и углы
Л)4С = 54С16' и DBC—^^З'. Найти CD.
113. Чтобы определить расстояние между двумя недоступными
точками А и В, измерили базис CD~ 245 м и углы ACD =. 32°14',
ЯС£)=48°23', 4DC = 62°7' и ££>С=81°17'. Найти АВ.
114. На берегу моря из двух пунктов А и В, отстоящих друг от
друга на расстоянии d = 2,9 км, наблюдают за пароходом, движу-
щимся равномерно и прямолинейно. В некоторый момент времени
пароход был виден из пункта А под углом а— 102°5' к направле-
нию АВ, а из пункта В— под углом р = 51°12' к направлению ВА.
Через 10 минут углы изменились и стали соответственно равными
а =84° 16' и р — 74°34'. Найти скорость парохода.
115. Тр игонометрические знаки А, В и С образуют на местности
равносторонний треугольник со стороной а — 2,5 км. Вычислить рас-
стояния от пункта Л4, расположенного внутри угла АВС, до тригоно-
метрических знаков, если из точки М сторона АВ видна под углом
а = 22°12', сторона ВС — под углом р = 10с28'.
Указание. Применить теорему синусов к треугольникам АВМ
и ВСМ и найти угол ВСМ.
6
СВОДКА ВАЖНЫХ ФОРМУЛ
А. Соотношения между тригонометриче-
скими функциями одного аргумента:
sin2 x-4-cos2x = 1. cosecx = -J— .
1 sin X
tgx sinx cosx ’ ctgx = 1 tgx •
cosx 1 V
ctgx sin x ’ sin2 x = 1 +ctg2x •
_ 1 1
QPC V COSZ X '—~
COSX • 1 + tg‘x •
В. Формулы приведения:
cos( — x) = cosx.
tg( — X) — — tgx.
ctg( —x) = —tgx.
sin (2/ztt 4- x) = sin x,
cos (2nn 4- x) = cos x.
tg(«n4-x) = tgx.
ctg (nit 4- x) = ctg X.
(K \
у— X j = cosx.
sin (тг— x) = sinx.
sin (тг 4“ x) — — Sln x-
sin ^y тг 4"x) = “ cos x-
sin (2тг — x) = — sin x.
cos ^y — x^ = sinx.
cos у + x ) = — sin x.
cos (n — x) = — cos X.
COS (тг 4“ X) = — cos x-
COSl yTT —X 1 = — sin X.
cos^yir 4"x) = sin x.
cos (2tt — x) = cos X.
. (It \ .
— ^J=ctgx.
168
(•5’ + x) = — ctgx-
tg(n —x) = —tgx.
tg (тг —|— x) == tg x.
. /3 \
tg I yn—x l=ctgx.
tg I yir-|-xj = —ctgx.
tg(2n —x) = —tgx.
ctg(y — Jf) = tgx.
ctg(y+x) = —tgx.
ctg(n—x) = — ctgx.
ctg (n-|-x) = ctgx.
ctg(|n-x) = tgx.
ctg(yiT4-x)= —tgx.
ctg (2n—x) = — ctg x.
С. Преобразования тригонометрических
функций:
sin (x -j-j/) = sinxcosj/ cosxsinу.
sin (x—y) = sinx cos у — cos x siny.
cos (x +>) = cos x cos у — sin x sin y.
cos (x —y) = cos x cos у 4- sin x sin y.
__ tgx + tgy
1 — tgxtgy •
tg(*— У)
tgx —tgj
l + tgxtgy •
sin 2x = 2sin x cos x.
cos 2x = cos2 x — sin2 x.
. x , -в Л1—cosx
siny = ±y —2—.
X , n f 14-cosx
cosy=±y —y—.
x___ sinx
g 2 1 -|- cos x ’
. x 1 — cosx
tg 2" sinx *
X____I -| Л1—cosx
14-cosx-
2tSy
sin x --------.
t + tg’y
t-tg’y
COS X =------- .
1 + tg‘y
tg(-^H-J)
. _ 2tgx
tg 2x =,—f-j— .
1 — tg* x
2tgy
tg* =-----4
l-tg‘-J
sinxsin_y = y[ cos (x—y) — cos (x -j)].
sin x cos у = у [sin (x 4~_y) sin (x —_y)].
COS X cos у = у [cos (x y) cos (x —_y)].
169
sin x-|- siny = 2 sin Х--£ У cos —g ? .
sin x — sin у= 2 cos —'t’-^ sin
COS X-f-COSJ/ = 2COS * COS—y„
n . x-f-y . x — у
COS X — cosу — — 2 sin Sin ~-yz
tg*4-tgj=
sin (X + y)
COS X cos у
tg*---tgy =
sin (x — y)
cos x cos у
D. Обратные тригонометрические функции*
Aresia x «к (— 1)" arcsin x 4~ от,
— ~ arcsin x < “, zz = O, zb h ±2* •••<
Arccos x s=x zb arccos x 4- 2/m,
0 arccos x it, n = 0, zb h ±2, ...
Arctg x — arctg x 4- or,
— 4 arctgx , n = 0, ±1, zb 2, ...
Arcctg x = arcctg x 4~ от,
0 arcctg x тг, n = 0, + 1, ±2, ...
sin (arcsin x) = x. cos (arccos x) = x.
tg (arctg x) — x. ctg (arctg x) = x.
sin (arccos x) = cos (arcsin x) = )/rl —x2.
tg (arcctg x) = ctg (arctg x) = ~ •
л
। к
arcsin x -f- arccos x = у .
arctg x 4- arcctg x = у .
arcsin x4- arcsinу = arcsin (x]/l —J't4“J' V1 —
— -у arcsin x 4- arcsinу ~ .
It L
arctg x 4- arctg у = arctg |Xj~,
— у < arctg x arctg j < .
17Q
Е. Соотношения между элементами тре-
угольника (a, fi, у— углы, а, с—соответственно
противолежащие стороны, S — площадь, 2р — периметр,
R и г — радиусы соответственно описанной и вписанной
окружностей):
CL Ь С л г-,
-— = -г— = -— = 2R теорема синусов,
sin a sinp sin? r J
a2 = b2 -|- c2 — 2bc cos a;
b2 — a2 -j- c2 — 2ac cos (5;
c2 = a2 b2 — 2ab cos у
теорема косинусов.
a-\-b
a — b
b + c
b — c
c-f-a
теорема тангенсов
S = be sin a = у ас sin = у ab sin y,
~ abc S
*=4$’ r=7-
.a r ,8 r . t r
tg~2 p—a' g 2* p — b"' tg2" p — c'
± i /(p-b)(p — c). £ i /~(p-a)(p — c).
2— V P(p-a) ’ Ig 2 V P(p-b) •
8 2 V P(P-c) *
ОТВЕТЫ
К главе I
3. 14 и 48 см, 4. 25 см. S. 1,25. 6. 0,22. 7. (с) да; (d) нет*,
(е) нет. 8. (Ь) да; (с) нет; (d) нет. 9. (а) - ; (Ь) У У. 10.
и. ^(^2- 1). 12. 3+4У'У И.
I4_/2+7s = m!g±n. и „„ а>„ „ >>0.
4 Q Q
16. (с) да. 17. (a) eosa = -^-, tga = —; (b) cos а = 0,96, ctga = 3-=-;
и 4 I
(c) COS а = Д'» tg a = 2 У 2 ; (d) cos a = , tg a — ? ~ ,
' 3 • q & q* — p* .
, 10/4* 2V"5 /4 .
ctg а = —---— . 18. (a) sin а = —, cos a = —=— (c) sin а = -T-, -y ,
s p 5 5 v л4+1
9/7* 1
C0S3 = ^t_^ . 19. . 30. 2. 31. 1. 32. sin8 a. 33. 4. 34. 1.
a‘+l /l+tg8a
35. 1. 36. 37. -4. 38. 0,22. 39. (c) sin(30° +a).
19ПО _l_ a
40. (d) cos 2 4b (b) tg(45°-a). 42. (c) ctg (60° + 2a). 45.7,
55. (a) 24°; (b) 66°; (c) 66°; (d) 39°. 56. (a) 2,56; (b) 0,49. 57. (a) 4;
(b) 3,24. 59. О и 4. 60. 2. 61. c. 62. 63. (d) III четверти;
(e) II четверти. 64. (b) II четверти; (d) I четверти. 65. (c) 1116°.
68. Через 12 мин., 1 час 24 мин. и 12 (2л— 1) мин. 69. (с) III чет-
верти. 70. (с) п = — 5, а = 290°. 71. Через 3 мин., 27 мин. и
3(4л — 3) мин. 72. п час. -д мин., где л = 0, 1, 2, ...» 10.
У о" Уз"
73. (a) sinl35® = -~—; (b) cos 150° == —2L_±; (С) tg225° = 1;
(4) «tg 300° = - . 74. (b) sin 600° = - ; (d) tg (- 420°) = -/3;
in
(f) 75. (а) $ (Ъ) 0; (с) -10 V2; (4) - 1Д
А
(b) 0,75; (с) 2; (d) 6. 77. (а) 4/Г; (с)-5/У
1 и 2. О». —8,
- (х + у). 89. а-Ь. 88. (а) 180° п; (d) 90’4-180° п,
79. (а)
79. (а) положительный. 81. (а) 8; (b) 1; (с) 1. 82.
2 ’
где
90.
, 40
Slna = ^,
z*z2, ... 89. cos a
, 9
91.
92.
94.
93.
2
sin a = eqs a == -
, 1
sin a =-----т-зж ,
V 5
4 . 3
cos 3 > tg a =3-----y. 97,
(a) zt sin a; (b) + cos a. IO9. tg a. IO6. 4.
1. ИО. (а) - 1; (d) 1.
113. 0. 114. 0,643.
118. 1 + sin a cos a.
(e) ‘ - * —
(c)
96.
104.
108.
b) 0,848.
116. — tg’(2a — ₽).
(d) ctg 160°. 120.
122. (а) -1; (b)
1. 109. (а) -1; (d)
112. - 0,387.
117. 1.
(а) 0;
_2.
2 ’
= L3-’ =
. 3 4
Sin a = , COS a = — -3-.
5 0
, 24 ♦ о 3
sina = ~25' 18в5ж3Т-
sin a a i - ^8°.
95.
17
ЗГ
98. -5.
107.
-и (0 1.
- и (Ф
121.
2
99. 0,84.
± (sin a -f- cos «).
III. (a) - 1,111;
IIS. tg (a — P).
119. (a) tg20°;
(b) -1; (d)_0.
(=> -V-;
и ‘ «24. I- ’25. 126.-11
«53 65
(a) — ctg 5°; (c) — sin 16°; (e) cos 40°;
cos 20°; (1) ctg 32°. I3O. (a) -0,940;
(g) 123.-Л
127. -J°. 128. 2. <29.
(f) cos 20°; (h) cos 18°; (к)
(с) —0,342; (h) 0,985. 131. 0,902, - 1,276, —^0,613 и 0. 132. (а) 211°;
(b) 138°; (с) 126°; (d) 294°; (е) 210°; (f) 160°. 133. (а) 19°; (b) 142°;
(с) 223°. 137. 4. 138. ° + c-°-s.а). 139. 4-cos’25°. 140.1 tg218°.
' ' sin8 a 2 2 *
141. —1. 142. cos 32°-sin 32°. 143. tg’a. 144. o * . .
• 2 cos*a
К главе II
I. (a) y; (e) 5,5. 2. (d)5,6 cm. 8. (a) 4. (a) (d) J.
5. (b) —6. (a) 18°; (b) - 135°; (d) 5°. 7. (b) 97°24'; (d) - 148°59';
(e) 43°35'. 8. (a) 80 см^сек. 9. 2. IO. j, у и II. y. 12. 1,5.
cose <, । , Z3" 3/2-2 12 4-5/3
IS. 14. — (sin a 4-cos a). IS.---j^-, -----i---, -y—.
173
12-5/3 3
ЙГ ’ 2
16. - (7 4 V 3), -1, 4/.3 -7, _|.
U7-~2 , -l.-L^ + 2. 18.
2 (г, V 3 + 1) 2 (я + 1) ’•
0,023; 0,009; 0,003. 22. (а) да; (Ь) нет; (d) да.
(с) я. 26. (а) нечетная; (с) четная; (d) ни четная, ни
Зд -6
,7‘ б-2я/Т’
0,994; 0,998. 21.
23. (a) 2r; (Ь) 2г:,
нечетная. 27. (а) положительный; (с) отрицательный; (е) положитель-
ный; (i) положительный. 28. (a) sin 0,7т: > sin 0,71 л; (с) tg 7,25л > tg 7,2л;
(f) ctg 7,1л > ctg 6,9л. 29. (а) отрицательный; (Ь) положительный;
. ч о __ л 5л л я «.м. ft
(е) отрицательный. 30. у < х < у • —^- < х < у < х <
33. и < х < 2ir. 36. ОР=4,
44 4 44
4 Y 3,-4 и 4 см\ через 1 у сек. 37. 5 = 6 sin t. 38. s = 10 sin 4л/.
39. (а) Л = 6, 7 = ^, ? = (Ь) А= ’ 7 = 2,
О О Z Ч
(с) Л=г0,2, Г = 20, ? = (Г) Л== 1, Г = 2л, ? = —2. 4L (Ь) См.
черт. 53.
Черт. 53.
К главе III
I. ^J-(l-/3). 4. 1 (2 /30 - 1) и -1 (2/30+1).
_ 297 87 _ 44 5 КЗ 1
’ ~425 И -425- 6' -125- 7> ~9— 8- ~ Jo [4 V 3 ~ 3>-
« 25 5 38 2 f| 7 а — 1 У2 9
9- 19 И ЗУ’ ‘°- 41 И Л’ "• "И- ,2’ ^+1- ,3* ^Г(2 + Т 5)‘
14. а /ПЛУ2 -ъУ\—аг. 16.^, «8. (a) cosa; (b) — V2sina.
оэ
19. (а) (b) — ctg a ctg р. 20. sin з —sin?. 21. . 22.
23. cos fa. 24. — sin 2а. 25. 0. 26. sin (a + ?) cos ?. 27. (a) tg 3a;
/б . cos (20J — a) cos 2a 1
(b) tga. 28. (a) —; (b) , (c) —37.
\1\
_ 336 527
625’ 625 И
( 4/2(1 — n2)
1 — bn2 + n4'
0,92 и - 0,92. 51,
336
527*
«I
,._±
41. 2a /1 — a1. 42. 2a’ - 1. 43.
44. 1 —2sin2-^-. 45. ~ -fty -ij,-- и
116 253 2016 вл
47,(a)-§45; (b)~ 325’ (C>3713- 30
3 tg a — tg3a к
52. 53. При —; наиоольшее значение функции
равно /2. 54. При х = —. 55. (Ь) —
57. (а) tg 6a; (b) —1>—* • 58. cos a.
60. tga sin a. 61. sin2a. 62. p) sin 2a; (b)
. 56. (a) cos 4a; (b) cos 2a.
59. (a)^; (b)£!s2a.
cos 2a. 63. 2. 64. —-_____
_________ sin 2a
<b> cos 4i. 83. = 1^1=1).
2
I/2 + /3 ^m-'3+l) _ v-s 84. rS^V3 + /2-2
2 4 _
85. VT-1. 88. >?, !СВ.К1.87.ЦА, —2,
4 4/5 5
ee 2/13 3/13 2 ee /6 /3
88. —v. 89. —тт— . —ft— , V 2. 90. V а, если a 1,
1 о IO о о О
и —— , если a^l. 93. (а) z± sin ~; (b)ztzcosa.
а 4
94. (а) tg a;
(b) tg (y+f) • 95. (a) tg51°. 101. И2+/2(1+>п) 2
102. ,, 103. “. 1 m 1 — m 29 Ш4.4.
IOS. — 106. 2 ctga— 108. (a) l^A+J. 225 14- ctg2 a 4 <ь,П^П;
(C) -t-. 109. (a) 0,02; ib) 0,177; (c) 0,709. 110. z 4 sin 2a 4- sin 23 (a) J ;
/U1 sin 2a —sin 2? Ilt t x 2 cos 2a 4-1 (b) 2 III. (a) ... 2 cos 2a — 1 (Ь) 4 ' *
ил /С Sin 3a — sin a cos 4a 4- cos 2a И2. (a) ; 2 •
ИЗ cos 2a-f-COS 2? — cos [2 (a 4-fl)] — 1 sin 2asin 4a — sin 6a
4 • • 4 •
116. (a) 2 sin 16° cos 4°; (d) — 2 sin 15° sin 2°; (f) 2cos^cos^.
Зтс T* 1
117. (a) cos 5°; (d) 2cos^sin^. H8. (a) ;
. ( • Sin 38° • (V sin l0°
1 ' 7x 1: ’• (c) cos 12° cos 59” td' ЛпТ5“51л25э'’
2 cos cos
175
lie. (a) (b) Vi cos (a-f--|). 180. (a) 4 sin 20’cos 12* cos 8°;
(b) 4 sin у cos a cos у. 121. (a) 4 cos 25° sin 53° cos 96°;
(b) 4 aos(18* + a) sin (и* + eos (18* - -j) . 122. (a) ;
(b) tg (Л-|-а). 123. (a) (b)---Ц-.
* \ 4 1 / v ' sin (a — f) ' 7 cos 2a
•лл / к 1ЛГ (к i \ ... 2 sin a . . tga sin a
124. а У 2 cos -j- + a ; (b) 125- (a) —
v ' \ 4 ’ J sin 4 a v ’ cos 4a cos 3a
/Ы 2ctg(a~l~ 2~) |26 cos(s + P) sin2a
” sin (l ’ * cos 2a cos 2₽ cos (a — f) ’ 5 ’
127. ctg 2a. 128. — 4 cos a cos 2a cos 3a. 134. (b) 2 sin* .
135. (b) 2 sin* 29°. 136. (a) 2 cos’ 2-=-?; (b)2sin*” ~*3a .137. tg’a.
138. tg’f-J-y). 138. (a) 2/2 cos | cos (4-4):
(b) 2 1^2 sin у cos « |cm 1 К |тг 140. 2 * 4 * * sin* у
141. 4 cos2 a. 142. cos a cos 3a. VTsm (i-.) <» sosV 7
2 sin I -я—p al / \ / \
<b>—,so- (а) Mr4)C0S(H);
(b)4cos(-|-+y)sin(^--y). 151. (a) 4 sin (-|-4-a) sin (-1-a);
4 sinf-^-4- 2зЛ sin (— 2a j . .
W —U «,.*2.-----------------L <"> 2 « (" -1)
(b) 2 /3 cos (a - . 153. (a) 25 sin (a + 0,284); (b) 13 sin (0,395— a).
154. (a) </’sin (0 — a) sin $-|-a), где sinf = £. 155. (p*4-?*)X
X sin (a + ?) sin (a - ₽), где 801? = -^=^= и cos ? = -?. J’ u :.
Ур’ + д’ Ур’ + ?*
156. (а) 1) 2) /2; (b) 1)-J, 2) /z 157. (a) 1) £, 2) 2;
(b) l)v- 2) 2. 158. (a) 1)0,322, 2)5; (b) 1)0,97, 2)41. 159. (a) 1) 0,506,
2) /5; (b) 1) 1,82, 2) /17. I6O. 1)^, 2) L
17«
К главе IV
I. (Ь) а = 2 Arccos -i-. 2. (а) а = Arcsin 0,1 —. 3. (с) а =
О о
=/> (Arctg л + </). 4. (а) а = ял + (—1)я у! (Ь)а = 2ял + у;
(d) a = ял. 5. (Ь) а = 2ял -1; d) е = я (2л + 1). 6. (Ь) а = 1 -|- хл;
(с) а=—-^-4-ял. 7. (а) ял — (—1У2; (Ь) ял + (— 1)" •£-.
О От
в о 2я . . л л /t 4 2я , 7к 5it п Зк
8. (а) 2ял :± у; (с) 2™. 9. (Ь) у-|-кл. IО. — у , у»
9гс lift |. 2к 4к 8я Юк 14к 16к 4к к 2к
4 и 4 • • "З ’ 3“’ Т ’ Т’ Т’ Т’ -У’ -Т ’ У
и V • *• “ 7 и 7- <а) — 3 х «S 3; (Ь) —т < Ж 4-1
0 4 4 4 4
1 1 2
(с) — — х ~. 15. (а) 0 х 1; (Ь) 0 х у; (с) — 1 х «с 3.
16. (a)x = -i-cosy; (b) х = — cosy; (c)x = 2siny; (d) xs=cos3y;
(h)x=l-4sinfy--l). 17. -1,-1, 0, у и у. 18. -0,848;
— 0,253; 0,253; 0,848; 1,571. 19. 1,379; 1,107; 1,107; 2,094; 2,090;
плок AA к 11к 7к 1 .45 к 1 . 4S
2,035. 20. 21. у arcsinи у -у arcsin^
22. 2R (1 + arcsin ^7) • 2*- При х= 1, 0 и - 1. 25.
и j^. 26. - и 1. 27. (а) отрицательный; (Ь) отрицательный;
(с) положительный; (d) отрицательный. 28. (а) отрицательный; (Ь) отри-
цательный; (с) отрицательный. 29. (а) нечетная; (Ь) ни четная, ни не-
4 12.1
четная; (d) четная. 33. (а)-4г-; (Ь) 34. (а) 1; (Ъ) -г. 35. (а) тг-;
2 О 0 2
(Ь) Ц^-. 38.(а)-4; (Ь)-^-; (с) ЦА (d)2-x. 89. (а) 0;
О I О Z
№> «£;(1)0Л. 41.
48.^1. 55. Нельзя. 62. «л + (- If 4 | = И0" п 4- (- If 30°].
о! о
64. 15°+180° л. 66. 51=-? +«л.
1 о
68. [= 67°30' + 270°л]. 69. 4ял -(—1)"^-1.
о 2 о
70. 60°л - 26°. 71. ™ st jl [= 45°л * 15°].
72. у(4л+1)[=90°(4л+1)] и ял+(-1)я у [= 180°л + (— 1)л 30°].
177
73. ^[=60’л] и + 0,369 [=60° л 4-21°9'].
О о
74. 2ял + ^ [= 360°л + 135°] и 2г.п +0,296 [=360°л + 16’56’].
75. ±(4n + l)[=90°(4n+l)], м - (- 1)л 0,848 [=180°«—(—1)" 48°35'].
76. + ял [= 45° + 180°л] и 1,373 + т [= 78°41'+ 180°л].
77. -£+4 « I = -15° + 60°л] и -0,369 + = -21’9' + 60°л].
• 12 О о
Г, ^1. л 4 I — 1 — тп
78. Решение уравнения возможно, если шл ^1;х=Arctg----------,
2 2
если т 0 и п Ф 0; х =; Arctg —, если zz=O; х = Arctg—,
/~ I) с
если т = 0. 79. + Arcsin у & ; решение уравнения
возможно, если а^Ъ и а^с^Ь или Ь^с^а\ при а = £ = с
уравнение обращается в тождество. 80. 75°31' и 28°58'. 81. 38° 10' и
51’50'. 82. 58° 17' и 31°43'. 83. ял и 2ял ± . 84. и 4 (2л + 1),
О 2, v
85. у;, (6л +1) и -g- + -jj-. 86. уд (2л + 1) и (2л + 1). 87. -у + 2ял
и 4 + ™- 88> 4(2л+ О и -4+2пл- ••.2«я±:4.‘
90. 4<Зл-1) и А(2„+1).91. 92. + 8®-™ и
О Z 1Z О У о
. б | 0Ж Я I Я/2 — Я .
— arctgy + яп. 94. —+ у. 95. — — 4-1Г72 и — arctg 4ял.
я 5
96. у + ™ и arctg у + ®7. arctg 4 4- кп. 98. arctg 5 -|- ял
и — arctg 2 + ял. 99. zt Arctg , если л + 6>0 и а Ь;
при а = b уравнение обращается в тождество. IOO. 40°54'. IOI. 9’5'.
102. п. 103. ^и^. 104. 4<2л+1)- «08.
106. J + Jg. 107. ~ + (- 1)" Д . 108. 90°л + (- 1)" 22°30' - 34°.
109. ял. 110. 180°л i60’ - 30°. III. ^-(- 1)л — — Л,
2 ' '8-10
112. ял +-^-. ИЗ. i ^-+ггл. 114. ял+ (—1)" arcsin 4-. 115. ял
о о 4
и 2ял-^. 116. |(2л + 1) и + 117. ля-£.
118. |(2л+1) и |/> + (-l)»i 119. ^ + (-1)»
120. zt arctg1^2 + nr.. 121. 4ял и 4 arctg ^-+4ял. 122.15’или 75°.
Л
178
i23. 48°35' и 82°50'; 4 <m^V2. 124. 4 (2л +1) и 2wt
125. 60°л и 180°л 15". 126. 120°л - 20°. 127. гсл - у и у+-§ •
128. 4" + т§- ,29" ¥ и Т(2"+1)- «3°-<2я-Ь’)-
Z 1 и UO 1 и
131. я(2п + 1)- + 132. 2ял-4 и 2ял.
133. 180°л * 37°,5. 134. 2яп4--^ « ,35. ™ и ^(2л+ 1).
138. 180°л — 60° и 180°л + 40°. 137. £ п -4- ,88- 90°л - 10°.
2 9
139. 4<2л-|-1) и ^*4- ,40> Т- ,4h у(2й+1) и
О О г? О Z
к ил вjbо г» л 2л я » » Л р. 2л
-=- zt 25 • >42. ял. "43. 2лл и 4лл z± -к- - 144. — п и 2лл ±z .
/ О £л О
145. «л и 4(2л+!). 146. 147. 2ггл, 4 + 2™ и Т + ™
О о 2 4 •
148. 180°л + 45° и 180°п + 35°. 149. (2л 4-1)
О
Л
и лл±:
150. £(2«4-1) и 4(2л-Н). 151. (2л4-1) и
н и о и
it 2 3
152. 2кл и -у4-2пл. 153. itn-|-(—l)"arcsin-g- — arcsin-5-
[= 180° 4-( — 1)”23°34'— 36°52'] или 2пл - 2 arctg 0,117
[=360°л - 13°18'] и 2пл4-2 arctg 1,717[=360°п-|- 119°34']. 154.^ +
О
4-4-(-1)” arcsin^ — 4- arcsin^p[=60°л4-(—1)”8°51' — 21°8'].
155. 180’л — 42°42'. 156. кл 4-(—1)” arcsin -4=-4-arcsin-р=-.
/41 /41
[== 180°л 4-(—1)л69°34'4-51°21']. 157. 51°4' и J28°56'.
158. 36°52' и 53°8'. Наименьшее значение, равное 2 (3 2 1^2), вели-
чина tn принимает в равнобедренном треугольнике. Нет, не суще-
ствует.
К главе V
I. (a) sin г, (b) sin Х-. 2. 3 У2 . 3. 1. II. 30°, 60° и 90°.
2 1Э
13. 60°. 19. 150/Т 20. ^4- га. 21. 2/?»cos4X
о4оо О 2
X cos*^45° — 22. 1 л* — /л* | tg ср. 23. (а) отрицательный; (Ь) от-
рицательный; (с) отрицательный; (d) положительный; е) положитель-
ный; 24. (Ь) отрицательный; (е) положительный; 25. (а) положитель-
ный; (с) отрицательный; (е) отрицательный. 26. (Ь) 0. 28. lg sin 2я.
29. (а) I, 5828; (с) Т, 8975. 30. (а) I, 7854; (d) I, 1640. 31. (а) 23°6';
179
S.) 5’15", (•) 34'; (1) 9’33'. 32. (a) 78°12'; (b) 63’24'; (c) 45°42'; (f) 69°30'.
3. (a) I, 8028; (b) I, 9244; (d) 0,0020; (f) 2,9460. 34. (a) 1,7876;
(c) 0,7100; (f) I, 9848; (g) 2,9688. 3S. (a) 8°12'; (b) 43°5'; (c) 84°50';
(d) 6’19'. 36. (b) 83’47'; (e) 84’16" (g) 40°46'. 37. 3,703. 38. 0,8341.
39. 2,332. 40. 131. 41. (a) 0,03636; (b) 2,825. 42. 12,96. 43. 0,8312.
44. -0,008277. 45. (a) 47° 12'; (b) 88’12'. 46, 73’39'. 47. 66’39',
48. 20’54'. 49. (a) 32’29'; (b) 51’46'. 50. (a) 74’50'; (b) 25’47'.
51. a = 22,31; b = 36,08; 0 = 58’16'. 52. a = 749,8; b = 130,8;
0 = 9’54'. 53. * = 335,2; c — 382,5; 0 = 61’12'. 54. a = 84,66;
c = 98,03; 0 = 30’16'. 55. * = 86,48; a = 62’30'; 0 = 27’30’. 56. c =
= 1563; a = 17’45'; 0 = 72’15" 57. a = 0,2568; * = 0,4063; c = 0,4806;
0 = 57’42'. 58. 23,02. 59. 22,86. 60. Основания: 6,631 см и 3,038 си;
боковые стороны: 6,902 см и 5,894 см. Задача имеет решение при
a >45°. 61. * = 23,8; с = 26,1 и т = 76°. 62. а = 2,47; с = 2,69;
0 = 71°. 63. а= 16,4; * = 32,2; а = 25°. 64. а = 28,1; с = 46,8;
7=102°. 65. а—102,2; * = 491,1; 0=111’12'. 66. *=4,321;
с = 2,685; а= 147’12'. 67. а = 0,5144;с= 1,025;0 = 42’14'. 68. а =
= 168,5; с = 413,6; 7 = 57’19'. 69. 5,02 кГ. 70. 42 м. 71. * = 30,4;
a = 45’6'; 7 = 56’54'. 72. а = 12,1; 0 = 23’54’; 7 = 54’6'. 73. * =
= 0,619; a = 82’4'; 7 = 47’56'. 74. с = 4,58; а = 49°6'; 0 = 70’54'.
75. с = 36,96; а= 100’59'; 0 = 31’43'. 76. с = 291,2; а = 60’40';
0 = 55’42'. 77. * = 8,028; а= 147’12'; 7 = 6’22'. 78. а = 0,011;
0 = 26’37'; 7=134’12'. 79. 65,15 к Г, 36’16' и 28’8'. 80. 39,86 и 29.
81. * = 22,3; а = 30°14" 0=110’46'. 82. с = 3,81; 0 = 51’34"
у = 58’26'. 83. а = 0,311; а = 115’40'; 7 = 20’20'. 84. с = 7,51; а = 90°;
7 = 48’42'. 85. с, = 13,4; с2 = 9,6; 0, =82’12'; 0 =97’48" 7, = 47’24';
7 = 31’48'. 86. Задача не имеет решения. 8<. а. = 1,14; а. = 3,08;
а, = 21’16'; а,= 101’44'; 0,= 130’14" 02 = 49’46'. 88. с. = 1,41;
с, = 0,1; 0.=21’5О" 02= 158’10" Tl= 139^1 О'; 72 = 2’50'. 89.*,=
= 89,56; *. = 23,09; а. = 63’6'; а. = 116’54'; 0, = 67’35'; 0, = 13^47'.
90. а=160,5; а = 26°1'; 0 = 37’39'. 91. а.=67,73; а. = 24,91;
а,=103’24'; а.=20’58'; 7,=48°47'; 72=131’13'. 92. *=88,24; 0=52’40"
7=90°. 93. а1 = 9,44; а2= 1,133; а, = 134’38" а, =4’54'; 7,=25’8';
7, = 154’52'. 94. Задача не имеет решения. 95. с, = 0,9663;
с. = 0,1121; а. = 23’51'; а2= 156’9'; Т1 =136’51'; 7, = 4’33'. 96. с.=
= 31,09; с, = 2,278; 0. = 24’17'; 02 = 155’43", 7. = 134’26" 7, = 3°.
97. 3:7 (прибл.). 98. 14 см. 99. а=73°30" 0 = 27’6" 7 = 79’24'.
IOO. а = 36’27" 0 = 98’5" 7 = 45’28'. IOI. а = 90’; 3 = 30°; 7 = 60°.
IO2. а = 45°; 0=116’34'; 7=18’26'. 103. а = 77’18'; 0 = 79’12"
7 = 23’30'. 104. а = 42°36" 0 = 107’54" 7 = 29’30'. IO5. а = 40°44"
0 = 37’52" 7=101’24'. IO6. а = 45’24" 0 = 51’38" 7 = 82’58'.
IO7. Приблизительно через 19 мин. 108. 5’6'. IO9. 28’5" 32°; 21’49'.
3
110. 13,3 см и 5,7 см. 111. cos = - ——:. Угол р принимает
У 25-16 cos2a
наибольшее значение в квадрате. 112. 981 м. 113. 122 м,
114. 20 км/час, 115. 4,620 км\ 6,067 км и 3,723 км.
Цена