Author: Переломова Н.В. Тагиева М.М.
Tags: свойства и структура молекулярных систем физика
Year: 1982
Text
Н. В.ПЕРЕЛОМОВА, М. М. ТАГИЕВА
ЗАДАЧНИК
по
кристаллофизике
ИЗДАНИЕ ВТОРОЕ, ПЕРЕРАБОТАННОЕ
Под редакцией М. П. ШЛСКОЛЬСКОЙ
Допущено Министерством
высшего и среднего специального образования СССР
в качестве учебного пособия
для студентов высших учебных заведений
X Tfcrz tT'is;.;
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОИ ЛИТЕРАТУРЫ
1 882
22.37
П 27
УДК 539.2
ПЕРЕЛОМОВА Н. В., ТАГИЕВА М. М. Задачник по кристалло-
физике: Учебное пособне/Под ред. М. П. Шаскольской.— 2-е изд.,
перераб.— М.: Наука. Главная редакция физико-математической
литературы. 1982.— 288 с.
Задачник содержит более 350 оригинальных задач по основным
разделам кристаллофизики, которые дают возможность уяснить
физический смысл различных коэффициентов, характеризующих
свойства кристаллов, оценить их величину и анизотропию, а также
выбрать оптимальные значения коэффициентов в зависимости от
конкретных условии практического применения кристаллов. В за-
дачник включены также краткие теоретические сведения и спра-
вочные данные, облегчающие решение задач и дающие наглядное
представление о порядках реальных крпсталлофпзпческпх харак-
теристик. Настоящее издание дополнено задачами по свойствам
кристаллов, получивших применение в новейших приборах элект-
ронной техники (пьезорезпстпвные свойства, нелинейные оптиче-
ские свойства и др.).
Рис. 98. Табл. 15. Библ. 14 назв.
1704060000 —110 7- 82
П 053(02)-82
(^'.Издательство «Наука».
^Главная редакция
физико-математической
литературы, 198?
ОГЛАВЛЕНИЕ
ОТ РЕДАКТОРА ..... . 4
ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ................... 5
ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ................. 5
СПИСОК ОБОЗНАЧЕНИЙ 7
§ 1. МАТРИЧНОЕ ПРЕДСТАВЛЕНИЕ СИММЕТРИЧЕСКИХ ОПЕ-
РАЦИЙ И КЛАССОВ СИММЕТРИИ .... . 9
§ 2. ПРИНЦИП СИММЕТРИИ В КРИСТАЛЛОФИЗИКЕ. СИММЕТ-
РИЯ ФИЗИЧЕСКИХ ЯВЛЕНИЙ И СВОЙСТВ КРИСТАЛЛОВ 18
§ 3. ФИЗИЧЕСКИЕ СВОЙСТВА КРИСТАЛЛОВ, ОПИСЫВАЕМЫЕ
ТЕНЗОРОМ ПЕРВОГО РАНГА .......................33
§ 4. ФИЗИЧЕСКИЕ СВОЙСТВА КРИСТАЛЛОВ, ОПИСЫВАЕМЫЕ
ТЕНЗОРОМ ВТОРОГО РАНГА - 44
§ 5. НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ В КРИСТАЛЛАХ. АНАЛИЗ
НАПРЯЖЕННОГО СОСТОЯНИЯ . 6g
§ 6. ПЬЕЗОЭЛЕКТРИЧЕСКИЕ СВОЙСТВА КРИСТАЛЛОВ , §5
§ 7. УПРУГИЕ СВОЙСТВА КРИСТАЛЛОВ. ЗАКОН ГУКА . . jpg
§ 8. ПЬЕЗОРЕЗИСТИВНЫЙ (ТЕНЗОРЕЗИСТИВНЫЙ) ЭФФЕКТ
В ПОЛУПРОВОДНИКОВЫХ КРИСТАЛЛАХ...............133
§ 9. ОПТИЧЕСКИЕ СВОЙСТВА КРИСТАЛЛОВ . ... 150
§ 10. ПЬЕЗООПТИЧЕСКИЕ СВОЙСТВА КРИСТАЛЛОВ . . . 170
§11. ЭЛЕКТРООПТИЧЕСКИЕ СВОЙСТВА КРИСТАЛЛОВ . 181
§ 12. ГЕНЕРАЦИЯ ОПТИЧЕСКИХ ГАРМОНИК ..... 210
§ 13. ТЕРМОДИНАМИКА КРИСТАЛЛОВ .... 227
ответы ........................................ 246
ПРИЛОЖЕНИЕ ........ . . 250
ЛИТЕРАТУРА . ................... 286
УКАЗАТЕЛЬ ТАБЛИЦ, ПОМЕЩЕННЫХ В ПРИЛОЖЕНИИ . . 287
ОТ РЕДАКТОРА
Предлагаемый задачник в свое время, т. е. при пер-
вом издании в 1972 г., был вообще первым сборником
задач по кристаллофизике не только в отечественной, но
и в мировой литературе. И хотя за последнее десятиле-
тие в связи с бурно расширяющимся развитием кристал-
лофизики и ее практических применений в новой техни-
ке появился ряд сборников задач, но практическая на-
правленность данного сборника, предназначенного для
углубленного изучения Курса и развития практических
навыков у слушателей курсов кристаллофизики и физи-
ческой кристаллографии в вузах, остается единственной.
Задачник прошел проверку временем и строгое испытав
ние на занятиях по курсу физической кристаллографии
в Московском институте стали и сплавов (МИСиС) и во
многих других вузах. В нем учтены замечания студентов
за ряд лет, а также опыт не только редактора и авторов,
но и остальных преподавателей кафедры кристаллогра-
фии МИСиС.
Как авторы, так и редактор будут весьма благодарны
за любые критические замечания и указания.
М. П. Шасколъская
ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
За время, истекшее с момента выхода первого изда-
ния, чрезвычайно расширилась сфера применения крис-
таллов в технике. В связи с этим оказалось необходимым
ввести в Задачник новые разделы: «Пьезорезистивный
эффект в полупроводниковых кристаллах», «Пьезоопти-
ческие свойства кристаллов», «Электрооптические свойст-
ва кристаллов», написанные Н. В. Переломовой, и «Опти-
ческие свойства кристаллов», «Генерация оптических гар-
моник», «Термодинамика кристаллов», написанпые
М. М. Тагпевой. Кроме того, существенной переработке
подверглись многие разделы первого издания и приложе-
ния; составлено большое число новых задач, посвящен-
ных расчету физических свойств кристаллов, применяе-
мых в оптике, акустике, акустоэлектронике, тензометрии,
нелинейной оптике. Поскольку данные для решения мно-
гих задач взяты из журнальных статей, в которых, как
правило, используется система единиц СГС, эта же си-
стема сохранена в ряде задач. Читатель при необходимо-
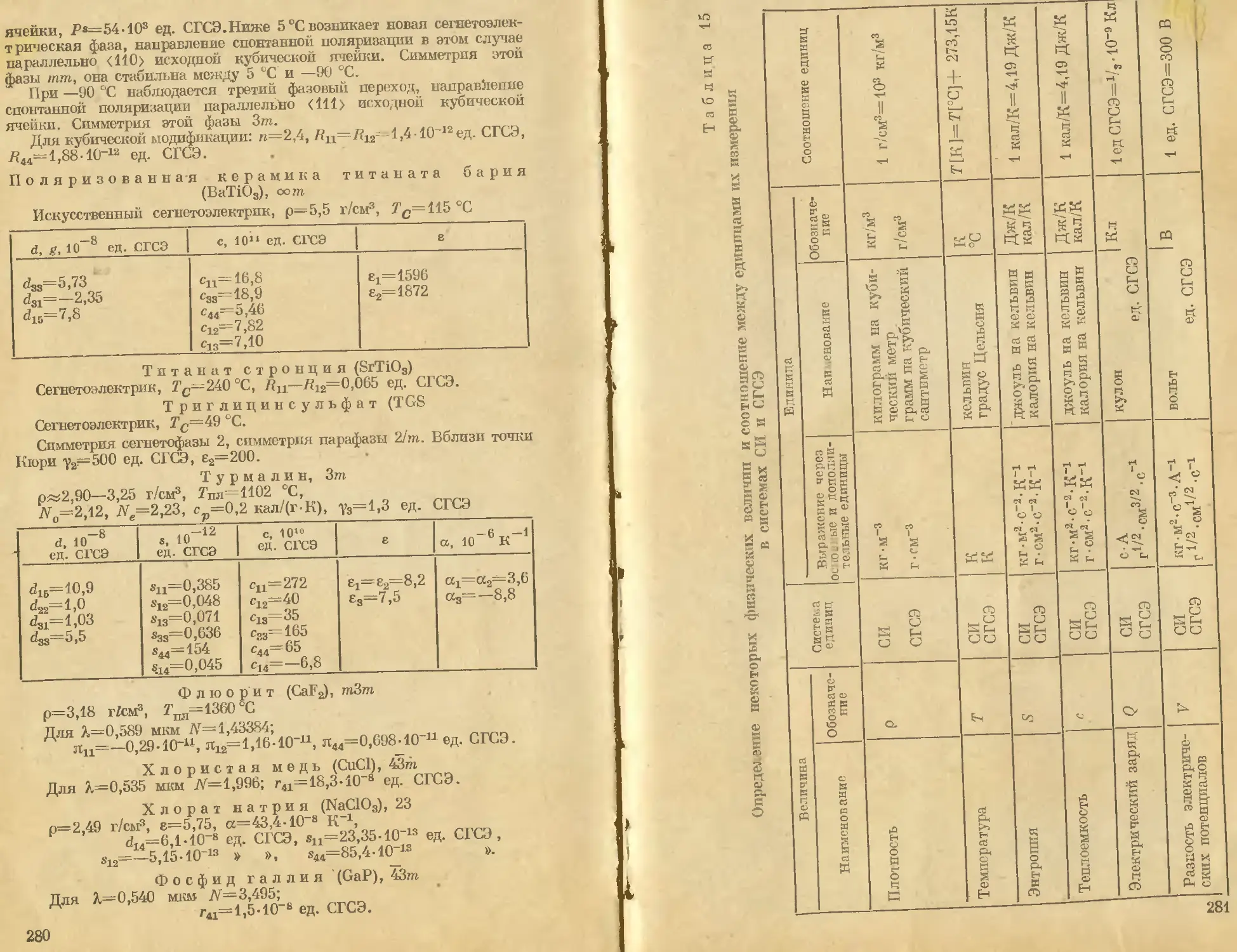
сти может перейти к системе СИ, используя табл. 15.
«Задачник» рассчитан на студентов и аспирантов ву-
зов и втузов, а также инженерно-технических работников,
занимающихся практическим применением кристаллов.
> Авторы
ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
Последние годы характеризуются быстрым развитием
кристаллофизики и все расширяющимся применением
монокристаллов в различных областях техники.
Анизотропные свойства кристаллов, представлявшие
ранее узко специальный интерес,— пироэлектрические,
5
пьезоэлектрические, электрооптические свойства и т. д.—
в настоящее время широко используются в новейших об-
ластях радиотехники, электроники, оптики, акустики.
В связи с этим появилась необходимость создания ме-
тодики преподавания кристаллографии и кристаллофи-
зики будущим инженерам.
Широкий общий курс технической кристаллографии
и кристаллофизики для инженерных специальностей впер-
вые в Советском Союзе был разработан в 1963 г. на»
кафедре кристаллографии факультета полупроводниковые
материалов и приборов Московского института стали и
сплавов. Предлагаемый задачник является частью мето-
дической работы кафедры кристаллографии по постанов-
ке этого курса. В данную работу вошли задачи, которые
в течение ряда лет прошли неоднократную проверку на
практических занятиях, проводимых авторами задачника
и другими преподавателями кафедры кристаллографии,
которые также внесли некоторый вклад в уточнение фор-
мулировок и отбор задач, разработанных авторами.
Авторы выражают глубокую благодарность профес-
сору М. II. Шаскольской, чьи обширные знания и педа-
гогический опыт явились основой для написания данной
книги. М. П. Шаскольской принадлежат идеи мпогих
задач.
Авторы с глубокой признательностью отмечают боль-
шой вклад в данную работу доцента МГУ Ю. И. Сироти-
на, чьи семинары, проводимые на кафедре кристаллогра-
фии МИСиС, послужили решающим стимулом для
написания настоящего задачника. Авторы благодарят
доктора химических наук И. С. Реза за ряд полезных
замечапий и советов.
Задачи составлены авторами па оспове учебной ли-
тературы, специальных монографий и журнальных ста-
тей. Большинство задач составлено авторами и печата-
ется впервые. Авторы будут весьма благодарны за любые
замечания об их работе.
И. Б. Переломова,
М. М. Тагиева
СПИСОК ОБОЗНАЧЕНИЙ
Обозначения классов точечных групп симметрии см. табл. 1
Обозначения элементов симметрии см. табл. 2.
X, Y, Z — оси кристаллографической системы координат
X], Х2, Х3 — оси кристаллофпзической системы координат
(Ci3)—матрица преобразования кристаллофивической си-
стемы координат (матрица косинусов)
р — плотность
Е — вектор напряженности электрического поля
II — вектор напряженности магнитного поля
D — вектор электрической индукции
Р — вектор электрической полярпзованности (поляриза-
ции)
j — вектор плотности электрического тока
[ei3] — тензор диэлектрической проницаемости
[т]г3] — тензор диэлектрической непроницаемости или по-
ляризационных констант
[х«3] — тензор коэффициентов поляризуемости
[pij] — тензор удельного сопротивления
[сц3] — тензор удельной проводимости
[гг3] — тензор малых деформаций
[<йг3] — тензор малых вращений
[t{3] — тензор механических напряжений
[а;,] — тензор коэффициентов теплового расширения
[М3] — тензор коэффициентов теплопроводности
No, Ne — показатели преломления обыкновенной и необыкно-
венной волп для одноосных кристаллов
Ng, Nm, Np — или ni, п2, пз — показатели преломления двуосных
кристаллов вдоль главных осей
Г г
п2— показатели преломления для произвольного на-
правления распространения света
[si3s(] — тензор коэффициентов упругой податливости
[cj3bz] — тензор коэффициентов упругой жесткости
— тензор пьезомодулей
7
[П<3*;] — тепзор пьезорезистивных коэффициентов
[л,;,-*;] — тензор пьезооптических коэффициентов
[p»j*z] — тензор упругооптических коэффициентов
[nrj*] — тензор электрооптических коэффициентов
[%<,•*] — тензор нелинейной поляризуемости или квадратич-
ной восприимчивости
Yt— пироэлектрические коэффициенты
с — теплоемкость
Тпп — температура плавления
Тс — температура сегнетоэлектрического фазового пере-
хода (температура Кюри)
§ 1. МАТРИЧНОЕ ПРЕДСТАВЛЕНИЕ
СИММЕТРИЧЕСКИХ ОПЕРАЦИЙ И КЛАССОВ
СИММЕТРИИ
Специфические особенности кристаллов связаны с сим-
метрией и анизотропией кристаллической среды.
Симметрия кристаллического пространства определяет-
ся как свойство такого пространства совмещаться с са-
мим собой путем некоторых преобразований, называемых
операциями симметрии.
Различаются два типа таких преобразований: опера-
ции симметрии I рода (повороты) и операции симметрии
II рода (зеркальные отражения). Операция I рода преоб-
разуют правую систему координат, связанную с кристал-
лом, в правую, левую — в левую, а операции II рода при-
водят к замене правой координатной системы на левую
(и наоборот).
Возможные сочетания симметрических операций кри-
сталлических многогранников образуют 32 точечные груп-
пы или 32 класса симметрии. Точечными эти группы на-
зываются потому, что входящие в них симметрические
преобразования оставляют неподвижной хотя бы одну
точку кристаллического пространства (начало координат).
В табл. 1 (см. в конце книги) приведены обозначения
32 классов симметрии; в табл. 2 даны обозначения эле-
ментов симметрии на стереографической проекции.
Стандартные кристаллографические и кристаллофи-
зические координатные системы. Для однозначного опи-
сания направлений и плоскостей кристаллов служат кри-
сталлографические координатные оси X, Y, Z; стандарт-
ные правила их выбора приведены в табл. 3. Для опи-
сания физических свойств кристаллов, а также для
аналитического представления их точечных групп симмет-
рии в кристаллах выбираются ортогональные кристалло-
физические оси Xi, Х2, Х3; стандартные правила ориен-
тировки этих осей относительно кристаллографических
9
приведены в табл. 4 и 5. Кристаллографические и кристал-
лофизические координатные системы всегда выбираются
правыми, а углы между положительными направлениями
соответствующих кристаллографических и кристаллофп-
зических осей меньшими 90°. Положительному направ-
лению кристаллографической оси отвечает положительное
направление соответствующей кристаллофизической оси.
Для кубической, тетрагональной и ромбической сингоний
направления осей в кристаллофпзической и в кристалло-
графической системах координат совпадают.
Матричное представление операций симметрии. Опе-
рации симметрии могут быть описаны аналитически как
операции преобразования координатных осей. Точку про-
странства, остающуюся неподвижной при всех симмет-
рических операциях точечной группы, примем за начало
ортогональной кристаллофпзической системы координат
Xt, Х2, X,. Любая симметрическая операция кристалло-
графического класса переведет оси Xt, Х2, X, в новые
положения А\, Х2, Х3 (см. рис. 1.1—1.3).
Углы между новыми (Xlt Х2, Х3) и старыми (Х\, Хг, Х3)
осями определяются таблицей направляющих косинусов:
Оси х. X, А’з
Сп С12 Gs
Х2 Gi С22 Gis
X' 3 ^81 с32 С33
Первый индекс при символе C(j (i, j •= 1, 2, 3) относит-
ся к новым осям, второй — к старым. Так, например,
Сгз — косинус угла между осями Х2 и А 3.
Таким образом, любому симметрическому преобразо-
ванию можно поставить в соответствие свою матрицу на-
правляющих косинусов С(}, т. е. записать его в матричном
представлении. Угол поворота считается положитель-
ным, если при наблюдении из положительного конца оси
в направлении к началу координат поворот от старой оси
к новой происходит против часовой стрелки.
Девять коэффициентов С(} не являются независимыми.
Поскольку каждая строка матрицы (Су) представляет со-
бой направляющие косинусы штрихованной оси коорди-
10
6./={
иат по отношению к петптрпхованпым осям Хл, Х2, Х3, то
= 1 при i = j. (1.1)
Так как каждая пара строк матрицы (С„) является
направляющими косинусами двух взаимно перпендику-
лярных направлений, то
Са.Сл = 0 при i =# j. (1.2)
Уравнения (1.1) и (1.2) называются соотношениями
ортогональности и могут быть кратко записаны в виде
CikCjf, — 6ij,
где — символ Кронекера, определяемый следующим
образом:
1 при i— /,
О при г#=/.
Для преобразований I рода, при которых правая си-
стема координат остается правой, левая — левой, опре-
делитель матрицы направляющих косинусов ICJ равен
+ 1. Для преобразований II рода IС„\ = —1.
Кристаллографические группы (классы симметрии).
Множество операций симметрии идеального кристалличе-
ского многогранника, т. е. мпожество преобразований,
в результате действия которых этот многогранник совме-
щается с собой, образует его точечную группу симметрии
или класс симметрии, являющийся математической груп-
пой, т. е. подчиняющийся следующим постулатам:
1. Произведение двух симметрических операций А и
В, входящих в группу симметрии, эквивалентно сим-
метрической операции С, входящей в ту же группу:
АВ = С.
Произведению симметрических преобразований отно-
сительно системы осей, жестко связанных с кристаллом;
отвечает произведение соответствующих матриц (в смыс-
ле обычного матричного умножения).
Результат двух последовательных симметрических пре-,
образований может зависеть от порядка проведения опе-
раций, поэтому необходимо следить за порядком записи
соответствующих матриц.
2. Умножение операций ассоциативно:
(АВ)С — А(ВС).
3. Среди операций симметрии существует такая опе-
рация отождествления Е, что АЕ — ЕА = А для любой'
И
из операций группы. Операция Е в этом случае называ-
ется единичной.
Для симметрических преобразований единичной опе-
рацией является поворот на 360° вокруг произвольного
направления в кристалле — ось сим'метрии первого по-
рядка.
4. Для каждой операции А существует обратная опе-
рация А~', входящая в группу симметрии и удовлетво-
ряющая соотношению
АА~* = А~'А = Е.
Например, если А — поворот на угол ср по часовой
стрелке, то А~1 — такой же поворот против часовой
стрелки.
Совокупность матриц (Су), построенная для всех не-
эквивалентных *) симметрических операций, входящих
в конкретную точечную группу симметрии, называется
матричным представлением этой группы, а число неэкви-
валентных операций, образующих группу симметрии, на-
зывается порядком группы.
Если некоторая операция преобразует кристаллический
многогранник в себя, то он будет преобразовываться в
себя и при повторениях этой операции. Результат по-
следовательных повторений операций симметрии обозна-
чается как степень этой операции. Нацример, 61, 62, 63
означает поворот вокруг оси вращения на 60°, 120° и
180°. Таким образом, в группу вместе с любо11 операцией
входят и все возможные ее степени.
Группы, порождаемые одним элементом симметрии,
т. е. состоящие из степеней одной-единственной операции,
называются циклическими и обозначаются символами
порождающих их элементов симметрии: 1, 2, 3, 4, 6, 1, 2
(= т), 3, 4, 6. Некоторая система операций симметрии,
входящих в данную группу, называется системой обра-
зующих (генераторов), если эти операции при перемно-
жении всеми способами дают все операции, входящие
в эту группу.
*) Симметрические операции считаются эквивалентными, ес-
ли они приводят к одной и той же перегруппировке частей фигу-
ры. Например, эквивалентными являются операция поворота на
60° по часовой стрелке и операция поворота на 300° против часо-
вой стрелки.
12
Примеры решения задач
1.1. Записать матричное представление всех опера-
ций симметрии, входящих в точечную группу ттт.
Решение. В точечную группу симметрии ттт входят во-
семь операций симметрии: три отражения в координатных плос-
костях симметрии, три поворота на 180° вокруг координатных
Рпс. 1.1. Преобразование кри-
сталлофизических осей коор-
динат плоскостью симметрии,
перпендикулярной оси Х3.
Рпс. 1.2. Преобразование кри
сталлофизических осей коор-
динат осью симметрии второ-
го порядка, совпадающей с
осью Х3.
осей, а также поворот на 360° и инверсия в точке 0. Систему ко-
ординатных осей, получаемую из исходной действием операций
симметрии, обозначим через Ху, Х2, Х3.
Матричное представление операции отражения в плоскости
Х\Х2 (или, сокращенно, т _1_ Х3) (рис. 1.1) запишется в виде
/1 0 0\
С-. (т _!_ Х3) = 0 1 0
\0 0 — 1 /
Аналогично для (m_LX2) и (m_LXi) получим выражения
/1 0 0\
Су (т _L Х2) = 0 - 1 0 ,
\0 0 1/
/—1 0 0\
Cj.(m_LX1)= 010.
\ 0 0 1/
Определитель |С^(т _!_ Х<) | =— 1, следовательно, операция
отражения в плоскости симметрии есть операция II рода.
13
Матричное представление операции поворота на 180е вокруг,
оси Х3(Х3, 180°; рис. 1.2) запишется в виде
/-1 0 0\
Cii (*з>180’) = о-ю.
\ 0 0 1/
Аналогично для (Х2, 180°) и (Хь 180') будем иметь
/— 1 о 0\ /1 0 0\
С{.(Х,180°) = 0 1 0 , С-. (Хг 180°) = 0 - 1 0.
1 \ 0 0 — 1/ \0 0 — 1/
Матрица поворота на 360° вокруг любого направления в кристал-
ле, например вокруг оси Х3(Х3, 360°), имеет вид
Съ.(Х3,360°) =
1 О 0\
0 10 1
0 0 1/
Рис. 1.3. Преобразование
кристаллофизических осей
координат центром инвер-
сии.
так же как и определитель
| Ci j (Xit 360°) |, равен 1, т. е. сим-
метрические операции поворота
на 180 и 360° являются операция-
ми I рода.
И наконец, матричное пред-
ставление операции инверсии (1)
(рис. 1.3):
/—1 0 0\
Ci;(l)= 0-1 0.
_ \ 0 0-1/
| Ci j (1) | = — 1, т. е. это операция
II рода.
1.2. Найти матричное пред-
ставление и порядок груп-
пы симметрии низкотемпера-
турной модификации квар-
ца *).
Решение. В соответствии с правилами выбора кристалло-
физических осей (см. табл. 4 и 5) оси Xf, Х3, Х3 точечной груп-
пы симметрии 32 ориентируются, как показано на рис. 1.4.
Матрицы, соответствующие операциям поворота вокруг оси Х3
на углы 120, 240 и 360° (повороты на эти углы содержит ось сим-
метрии третьего порядка), т. е. повороты 3’, З2, З3, записываются
*) Все сведения о кристаллах, необходимые для решения за-
дач, см. в табл. 14, с. 272.
14
следующим образом:
/1 о 0\
Q, (X, 360") =010.
\0 О 1/
Матрицы операций поворота на 180° вокруг осей второго по-
рядка имеют вид
/1 0 0\
СЪ-(2Иг) = Г-"1 ° ’
\0 0—1/
Ci‘ (2 под углом 60° к Хх) =
(—1/2 - Д/3/2 0\
— /3/2 1/2 0 ,
0 0 -iy
C4j (2 под углом 30° к Х^ =
(—1/2 1/3 /2 0\
1/3 /2 1/2 0 ].
0 0 — 1J
Рис. 1.4. Выбор кристалло-
физических осей для точеч-
ной группы симметрии 32.
Шесть неэквивалентных матриц (С,3), соответствующих раз-
личным операциям симметрии, входящим в группу 32, являются
матричным' представлением этой группы симметрии. Порядок
группы равен шести.
1.3. Известна теорема Эйлера: равнодействующей
двух пересекающихся Осей симметрии является третья
ось симметрии, проходящая через точку пересечения пер-
вых двух. Пользуясь матричным представлением элемен-
тов симметрии, проиллюстрировать теорему Эйлера на
примере класса 422.
Решение. За исходные элементы симметрии примем ось
четвертого порядка и одну ось второго порядка, перпендикуляр-
ную к ней. Согласно правилам выбора кристаллофизической сис-
темы координат ось Х3 направляем по оси четвертого порядка,
15
ось Xi — по оси второго порядка, ось Х2 выбираем из условия ор-
тогональности координатной системы (рис. 1.4).
Запишем матрицу, соответствующую повороту па 90° вокруг
оси Х3:
/ 0 1 0\
(*3> 90’) =-Ю0.
\ 0 0 1/
Матрица, соответствующая повороту на 180° вокруг оси Xi,
имеет вид
/1 0 0\
Ci5 (X,, 180е) = 0 - 1 0 .
\0 0 — 1 /
Пусть (С„(Х3, 90°))= A, (Cis(Xh 180°))= В. Воспользовав-
Рис. 1.5. Преобразование
осей координат осью сим-
метрии второго порядка, со-
ставляющей угол 45° с ко-
ординатными осями Хд и Х2.
расположатся четыре оси 2.
шись первым свойством группы
(АВ —С), найдем матричное пред-
ставление элемента С;
/ 0 1 0\ /1 0 0\
с.. = — 1 0 0 0 - 1 о =
\ оо 1До о—1/
/0—1 0\
= —1 о о .
\ 0 0—1/
Очевидно,. элемент С — это такая
симметрическая операция, которая
переводит ось X, в —Х2, ось Х2 в
•—Xj, а ось Х3 в —Х3.
Таким элементом симметрии яв-
ляется ось второго порядка, распо-
лагающаяся под углом 45° к осям
Xi и Х2 и проходящая перпендику-
лярно оси Х3 (рис. 1.5). Аналогично, беря поочередно произведе-
ния всех матриц, соответствующих поворотам па 90, 180, 270 и
360° вокруг оси Х3, на матрицу, соответствующую повороту на
180° вокруг оси Xi (2|[Xi), получим, что перпендикулярно оси 4
Задачи
1.4. Записать матрицу преобразования системы коор-
динат плоскостью симметрии, проходящей через ось Х3
и располагающейся под произвольным углом ф к оси X,.
16
1.5. Найти матрицу преобразования системы коорди-
нат осью симметрии второго порядка, лежащей в коорди-
натной плоскости XiX2 и располагающейся под произ-
вольным углом ф к оси Х2.
1.6. Кристалл поворачивают на 90° с последующим
отражением в центре инверсии, затем поворачивают на
180° вокруг направления, перпендикулярного оси перво-
го поворота. Найти матричное представление операции
симметрии, которая приводит к тому же результату.
1.7. Кристалл поворачивают на 120° против часовой
стрелки, затем отражают в центре инверсии. Найти мат-
ричное представление операции симметрии, которая при-
водит к тому же результату. В группу какого элемента
симметрии входит эта операция? * ’
1.8. Используя матричное представление элементов
симметрии, найти такую операцию симметрии, действие
которой давало бы тот же результат, что и действие двух
осей второго порядка, пересекающихся под углом 90°.
1.9. Найти матричное представление операции сим-
метрии, действие которой дает тот же результат, что и
действие осей второго порядка, расположенных под углом
60° друг к другу. В группу какого элемента симметрии
входит эта операция?
1.10. Найти матричное представление и порядок то-
чечной группы симметрии дигидрофосфата калия (KDP)
для стандартного и нестандартного dm2) выбора кристал-
лофизических осей координат.
1.11. Найти матричное представление точечной груп-
пы симметрии 622.
1.12. Найти матричное представление и порядок груп-
пы 6.
1.13. Найти матричное представление группы 2/т в
установках 2НХ2 и 2IIXS.
1.14. Пользуясь матричным представлением операций
симметрии, проверить справедливость теоремы Эйлера на
примере точечной группы 222.
1.15. Используя матричное представление операций
симметрии, проверить справедливость теоремы: сочетание
оси четного порядка и перпендикулярной ей плоскости
симметрии дает центр симметрии.
1.16. Убедиться в справедливости теоремы Эйлера на
примере осей второго порядка, располагающихся под уг-
лом 45° друг к другу.
1.17. Каков порядок следующих групп симметрии:
тт, 222, 4mm, 422?
2 Н. В. Переломова, M. М. Тагиева 17
1.18. Записать систему генераторов для группы 4/mmm.
1.19. На примере точечной группы симметрии 2/т
проверить, выполняются ли все групповые аксиомы.
1.20. Перечислить циклические кристаллографические-
группы четвертого порядка.
1.21. Какими матрицами описываются инверсионные
повороты вокруг оси на 90°? на 120°?
1.22. Каков порядок циклических групп 3 и 3?
1.23. Какие матрицы отвечают оси симметрии третьего
порядка, равнопаклонной к осям Xt, Х2, Х3?
1.24. Пользуясь матричным представлением операций
симметрии, доказать эквивалентность поворота на 180° с
последующей инверсией и отражения в плоскости, пер-
пендикулярной оси поворота.
1.25. Записать матричное представление операции
отражения в координатной и диагональной плоскости
симметрии в кристаллах класса 4тт.
1.26. Перечислить циклические группы второго по-
рядка.
1.27. Записать матричное представление операции сим-
метрии З1 и обратной ей.
1.28. Какая матрица отвечает плоскости симметрии,
проходящей через биссектрису внутреннего угла между
координатными плоскостями и X2OX-J
§ 2. ПРИНЦИП СИММЕТРИИ В КРИСТАЛЛОФИЗИКЕ.
СИММЕТРИЯ ФИЗИЧЕСКИХ ЯВЛЕНИЙ И СВОЙСТВ
КРИСТАЛЛОВ
Принцип Неймана. Симметрия физических свойств
кристалла *) связана с его точечной группой симметрии.
Эта связь устанавливается фундаментальным законом
кристаллофизики, сформулированным в работах Неймана
и Миннигероде и известным в литературе по кристалло-
физике под названием принципа Неймана'.
Группа симметрии любого физического свойства
кристалла включает в себя точечную группу симметрии
кристалла.
Это означает, что группа симметрии кристалла либо
совпадает с группой симметрии его физического свойства,
либо является подгруппой последней.
*) Под симметрией физического свойства кристалла понима-
ется симметрия тензорной поверхности, с помощью которой опи-
сывается это свойство (см. § 4).
18
В соответствии с принципом Неймана физическое
свойство кристалла должно иметь все те элементы симмет-
рии, которыми обладает кристалл. Среди групп симмет-
рии, описывающих физические свойства кристаллов,
имеются группы, содержащие оси бесконечного порядка.
Такие группы симметрии называются предельными (груп-
пами Кюри).
Предельные точечные группы симметрии. Предельные
группы симметрии легко запоминаются по геометриче-
ским фигурам (рис. 2.1). С помощью предельных групп
Рис. 2.1. Фигуры, иллюстпирующие предельные группы симмет-
рии. Стрелками на рисунках указаны направления вращения или
закручивания фигур.
симметрии можно охарактеризовать также и симметрию
текстур, являющихся поликристаллическими агрегатами,
в которых расположение кристалликов упорядочено.
2* 19
жение чистого
Рис. 2.2. Схема-
тическое изо-
бражение век-
торов напря-
женности
электрического
(слева) и маг-
нитного (спра-
ва) полей.
Например, симметрия искусственных пьезоэлектриков —
керамики титаната бария и текстуры сегнетовой соли ха-
рактеризуются соответственно группами °°т и °°2.
Некоторыми из предельных групп симметрии можно
описывать симметрию физических воздействий. Напри-
мер, симметрию постоянного однородного электрического
поля можно охарактеризовать группой °°т, постоянного
однородного магнитного поля — группой °°/т, одноосное
растягивающее или сжимающее механическое напряже-
ние — группой симметрии °°/ттт, механическое напря-
сдвига — группой ттт, всестороннее сжа-
тие — группой Явление вращения
плоскости поляризации может быть оха-
рактеризовано предельной группой °000.
В соответствии с различием в симмет-
рии напряженность однородных магнит-
ного и электрического полей графически
должны изображаться так, как показа-
но на рис. 2.2.
Из принципа Неймана также следует,
что определенными физическими свойст-
вами кристалл может обладать'лишь тог-
да, когда точечная группа симметрии кри-
сталла является подгруппой точечной
группы симметрии рассматриваемого фи-
зического свойства.
Принцип Кюри. Если на кристалл накладывается фи-
зическое воздействие, обладающее определенной сим-
метрией, то симметрия такого кристалла, находящегося
в поле воздействия, изменяется и может быть определена
при помощи принципа суперпозиции симметрий, назы-
ваемого принципом Кюри.
Когда несколько различных явлений природы накла-
дываются друг на друга, образуя одну систему, диссим-
метрии *) их складываются. В результате остаются лишь
те элементы симметрии, которые являются общими для
каждого явления, взятого в отдельности.
При этом предполагается, что все элементы симмет-
рии взаимодействующих явлений пересекаются в одной
точке. Это означает, что кристалл, находящийся под влия-
нием внешнего воздействия, будет обладать теми эле-
ментами симметрии, которые являются общими для
*) Под диссимметрией, по А. В. Шубникову, следует донимать
отсутствие элементов симметрии-
20
кристалла в отсутствие воздействия и для воздействия
в отсутствие кристалла.
Для выяснения симметрии результирующего явления
важна не только симметрия взаимодействующих явлений,
но и взаимное расположение их элементов симметрии.
При решении такого рода задач удобно пользоваться
стереографическими проекциями точечных групп сим-
метрии кристаллов.
Для иллюстрации принципа Кюри интересно рассмот-
реть вопрос об ограничениях, накладываемых симметри-
ей кристаллов на возможность существования в них пи-
роэлектрического эффекта, пьезоэлектрического эффекта
и явления поляризации во внешнем электрическом поле
(см. §§ 3, 4. и 6). Составим таблицу.
Эффект Уравнение Старшие группы симметрии кристал- лов и тек- стур ДО воздей- ствия Симметрия воздей- ствия Симметрия кристал- лов, обнаруживаю- щих аффект
Пироэлектри- ческий эффект у^Т 1 сот oooojn 10 полярных классов. Кри- сталл сам обеспе- чивает диссим- метрию, необхо- димую для суще- ствования век- тора Р
Пьезоэлектри- ческий эффект Pi=dijktjk оо 2, ОО tn, 43т, Ът.2 ттт 20 нецентросим- метричных клас- сов. Диссиммет- рия кристалла должна уничто- жить центросим- метричность воз- действия
Поляризация во внешнем поле ьД х~ II w аГ оооот оот 32 точечные груп- пы симметрии. Необходимая по- лярная симмет- рия обеспечи- вается диссиммет- рией воздействия
21
Как видно из таблицы, при наложении различных
физических полей, обладающих также и различной сим-
метрией, реакция кристалла может оказаться одинаковой.
Пол призов апный кристалл, согласно принципу Ней-
мана, должен иметь симметрию одного из 10 полярных
классов, так как эти классы имеют единичное полярное
направление, вдоль которого располагается вектор Р.
В кристаллах может наблюдаться поляризация, если
в результате наложения симметрии воздействия на сим-
метрию кристалла, согласно принципу Кюри, останется
симметрия одного из 10 полярных классов, причем неваж-
но, будет ли это достигнуто за счет симметрии кристалла
при самой высокой симметрии воздействия (пироэлектри-
ческий зффект) или, наоборот, за счет полярной сим-
метрии воздействия, когда поляризация может наблю-
даться в кристалле любой симметрии и даже в изотроп-
ном теле.
Примеры решения задач
2.1. Известно, что кристаллы кварца являются пьезо-
электрическими, т. е. поляризуются под действием меха-
нических напряжений. Применяя принцип Кюри и прин-
цип Неймана, ответить на следующие вопросы:
а) Какие из ориентированных кварцевых пластинок:
пластинки, перпендикулярные оси 3 пли оси 2, следует
выбрать в качестве чувствительных элементов пьезоэлект-
рических датчиков одноосного давления?
б) Можно ли кристаллы кварца использовать в ка-
честве датчиков гидростатического давления?
Решение. Кристаллы кварца принадлежат к классу 32.
а) Поляризация кристаллов под действием одноосного сжатия
возникает в том случае, если при этом в кристалле появляется
единичное направление, являющееся в то же самое время и по-
лярным*). В классе 32 ось третьего порядка является единичным,
но не полярным направлением из-за присутствия перпендикуляр-
ных этой оси осей второго порядка.
Действуя на кристалл кварца сжатием, обладающим группой
симметрии оо/пггат вдоль оси третьего порядка, что условно
*) Единичным (особым) направлением называется такое на-
правление, которое не может быть повторено элементами сим-
метрии кристалла. Полярное направление—это такое направле-
'ние в кристалле, два конца которого не могут быть совмещены
никакими элементами симметрии данного класса.
23
можно записать в виде
32 П oo/mmm,
Из
где П — знак, обозначающий пересечение (или произведение)
групп, мы получаем, что симметрия кристалла в этом случае не
изменяется:
32 П оо/ттт = 32.
Из
Следовательно, сжимая кварцевую пластинку, вырезанную так,
что ее рабочие грани перпендикулярны оси 3 (пластинку 2-среза;
рис. 2.3), мы не обнаружим эф-
фекта поляризации.
Попробуем сжать кристалл
кварца вдоль одной из осей 2:
32 fl оо/ттт = 2.
II»
В этом случае из всех поляр-
ных направлений кристалла, рас-
полагающихся в плоскости, пер-
пендикулярной оси 3, выделяется
одно. Теперь оно оказывается
единичным и полярным; следова-
тельно, вдоль него и располагает-
ся вектор пьезоэлектрической по-
ляризации.
Очевидно, для получения пьезоэлектрического эффекта при
действии одноосного сжатия кварцевую пластинку следует выре-
зать так, чтобы ее рабочие грани были перпендикулярны одной
из осей 2 (например, пластинка Х-среза, рис. 2.3).
б) В качестве датчиков гидростатического давления, симмет-
рия которого характеризуется группой оооот, могут использовать-
ся только те кристаллы, которые обладают единичным полярным-
направлением в отсутствие воздействия. Поэтому для этой цели
кристаллы кварца не годятся.
2.2. Для исследования физических свойств кристал-
лов сегнетовой соли при температуре выше 24 °C были
изготовлены пластинки Х-, Y-, Z- (рис. 2.3) и £-срезов
(рис. 2.4). Будут ли эти пластинки поляризоваться при
действии одпоосного сжатия перпендикулярно их торцам?
Решение. Кристаллы сегнетовой соли при температуре вы-
ше 24 °C принадлежат к классу 222, для которого все направления,
лежащие в координатных плоскостях, не являются полярными.
Сжатие пластинок Х-, У- и Z-срезов (см. рис. 2.3) перпенди-
кулярно их торцам означает, что механическое напряжение с сим-
23
Рис. 2.4. Пластинка /-среза.
метрией oolmmm поочередно действует вдоль кристаллографиче-
ских направлений [100], [010] и [001]. Применяя принцип Кюри,
получаем, что при действии одноосного механического напряже-
ния вдоль указанных направлений симметрия кристалла не по-
нижается.
Следовательно, в соответствии с принципом Неймана такие
пластинки не могут поляризоваться при действии одноосного сжи-
мающего напряжения, приложен-
ного перпендикулярно к их
торцам.
При действии сжимающего
напряжения на пластинку /.-сре-
за, одинаково наклоненную к осям
симметрии второго порядка, сим-
метрия кристалла понижается до
класса 1; у кристалла появляет-
ся выделенное полярное направ-
ление, совпадающее с направле-
лением действия напряжения,
вдоль которого может распола-
гаться вектор пьезоэлектрической
поляризации.
Такая пластинка может поляризоваться при сжатии, действу-
ющем перпендикулярно ее рабочим граням, что и подтверждается
экспериментально.
2.3. К кубическому кристаллу с симметрией тЗт при-
ложили одноосное напряжение растяжения. Какой сим-
метрией будет обладать кристалл, если напряжение при-
кладывается вдоль направлений: а) [001], б) [1111,
в) [110], г) [ТгЛгО]?
Решение, а) По условию задачи растягивающее усилие,
симметрия которого oolmmm, приложили к кристаллу с симмет-
рией тЗт вдоль направления [001], совпадающего с осью чет-
вертого порядка. В рассматриваемом случае взаимодействуют по-
ле одноосного напряжения с симметрией oolmmm и кристалл
с симметрией тЗт.
Применяя принцип суперпозиции симметрии, получим, что
группа симметрии результирующего явления (в данном случае
симметрия кристалла) должна содержать ось четвертого порядка,
четыре плоскости, проходящие через нее, и одну перпендикуляр-
ную к ней плоскость, центр инверсии и четыре оси второго по-
рядка. Симметрия кристалла должна быть 4/итт, т. е. тетраго-
нальной (рпс. 2.5). '
б) Растяжение вдоль направления [111], совпадающего с осью
третьего порядка, приводит к тому, что кристалл сохраняет ось
24
третьего порядка, вдоль которой производится растяжение, три
плоскости симметрии, центр инверсии и три оси второго порядка.
тЗт II осиЛ 4/ттт
Рис. 2,5. Изменение симметрии кристалла класса тЗт при дейст-
вии одноосного напряжения вдоль [001].
Рис. 2.6. Изменение симметрии кристалла класса тЗт при дейст-
вии одноосного напряжения вдоль [111].
Иначе говоря, при таком способе наложения напряжения мы
получаем тригональный кристалл с симметрией ромбоэдра—Зт
(рис. 2.6).
25
Рис. 2.7. Изменение симметрии кристалла класса тЗт ири дей-
ствии одноосного напряжения вдоль [110].
ПроИЗЬОЛЬНО
Ь плоскости
Рис. 2.8. Изменение симметрии кристалла класса тЗт ири дейст-
вии одноосного напряжения вдоль Г/гАО].
26
в) При растяжении кубического кристалла с симметрией т2т
вдоль одной из осей второго порядка у кристалла остается только
совокупность элементов симметрии ттт, характерная для ром-
бических кристаллов (рис. 2.7).
г) Наконец, прикладывая растягивающее усилие по направле-
нию [/ifcO], т. е. произвольным образом в одной из плоскостей сим-
метрии, например ио направлению АВ, получаем, что в этом слу-
чае кристалл будет обладать симметрией 2/т (при таком наложе-
нии напряжений кристалл становится моноклинным) (рис. 2.8).
2.4. Из сфалерита изготовлена пластинка Z-среза
(см. рис. 2.3).
Будет ли такая пластинка поляризоваться при дейст-
вии: а) напряжения одноосного сжатия, приложенного к
ее рабочим граням? б) напряжения чистого сдвига, дейст-
вующего в плоскости рабочих граней и характеризующе-
гося группой симметрии ттт?
Решение, а) Сжатие сфалеритовой пластинки Z-среза оз-
начает, что одноосное механическое напряжение, характеризую-
щееся группой симметрии оо/ттт, действует на кристалл с сим-
метрией 43m в направлении [001]. Это приводит к понижению
симметрии кристалла до класса 42т. Поскольку в этом случае не
появляется выделенных полярных направлений, то ие может воз-
никнуть и пьезоэлектрическая поляризация.
б) Действие напряжения чистого сдвига, характеризующегося
группой симметрии т тт, понижает симметрию кристалла до клас-
са 2, в котором ось второго порядка является особенным полярным
направлением. В этом случае сфалеритоваа пластинка Z-среза мо-
жет обнаруживать пьезоэлектрический эффект, что и наблюдает-
ся на опыте.
2.5. Монокристаллический кубик каменной соли по-
мещают в однородное постоянное электрическое поле та-
ким образом, что направление вектора напряженности
поля Е поочередно совпадает со следующими кристалло-
графическими направлениями: а) [001], б) [111],
в) [110], г) [ЛЛО].
Как изменится оптическая индикатриса кристалла в
каждом из перечисленных случаев *)?
Решение, а) Симметрия электрического поля оо т. Если
направление вектора напряженности электрического поля совпа-
дает с кристаллографическим направлением [001], т. е. поле
*) Оптическая индикатриса может быть трехосным эллипсо-
идом, эллипсоидом вращения или сферой (см. § 9).
27
Рис. 2.9. Изменение симметрии кристалла класса тЗт при нало-
жении электрического поля вдоль [001].'
Рис. 2.10. Изменение симметрии кристалла класса тЗт при нало-
жении электрического поля вдоль [111].
Рис. 2.11. Изменение симметрии кристалла класса тЗт при нало-
жении электрического поля вдоль [110].
Рис. 2.12. Изменение симметрии кристалла класса тЗт при нало-
жении электрического поля вдоль [МО].
28
прикладывается в направлении оси четвертого порядка, то, согласно
принципу суперпозиции симметрий, симметрия кубического кри-
сталла тЗт понижается до тетрагональной, imm (рис. 2.9).
б) Если поле направлено вдоль [111], т. е. в направлении оси
симметрии третьего порядка, симметрия кристалла понижается
до тригональной, Зт (рис. 2.10).- В отсутствие электрического по-
ля оптическая индикатриса кубического кристалла является сфе-
рой, и двойного лучепреломления в таком кристалле пет.
При наложении электрического поля на кристалл в первом
п втором случаях оптическая индикатриса его деформируется,
превращаясь из сферы в эллипсоид вращения. В кристалле возни-
кает двойное лучепреломление — кристалл становится оптически
одноосным.
в) При наложении электрического поля вдоль направления
[110] ,т. е. вдоль оси симметрии второго порядка, симметрия кри-
сталла понижается до ромбической, тт (рис. 2.11).
г) Если же поле накладывается в^оль направлений типа [Л.А-0],
т. е. по произвольному направлению, по лежащему в плоскости
симметрии, то кристалл становится моноклинным с симметрией т
(рис. 2.12).
В последних двух случаях оптическая индикатриса кристалла
превращается в трехосный эллипсоид, т. е. кристалл становится
оптически двуосным.
Задачи
2.6. Для исследования физических свойств сфалерита
приготовили две ориентированные пластинки. Одна из
них вырезана перпендикулярно направлению [100], вто-
рая— перпендикулярно [111]. Какой из этих пластинок
следует воспользоваться для обнаружения пьезоэлектри-
ческого эффекта при действии одноосного сжатия перпен-
дикулярно к их рабочим граням?
2.7. Кристалл кварца растянули: а) вдоль направле-
ния [0001], б) вдоль направления [1010]. В каком из ука-
занных случаев в кристалле может наблюдаться измене-
ние поляризации при нагревании?
2.8. К кристаллу KDP (дигидрофосфат калия) при-
кладывают электрическое поле вдоль направлений:
а) [ООН; б) [110]; в) [010]. Найти симметрию кристалла,
находящегося в поле, для каждого из указанных направ-
лений электрического поля.
2.9. Возможно ли наложением одноосного механиче-
ского напряжения в направлении [110] превратить
29
кристалл с исходной симметрией 432 в кристалл с поляр- >
ной группой симметрии? Можно ли такое превращение
осуществить наложением электрического поля вдоль этого i
же направления?
2.10. Определить все возможные изменения в точеч-
ной группе симметрии сегнетоэлектрического кристалла*),
принадлежащего к классу 22i2, если в кристалле совер-
шается сегнетоэлектрический переход. Рассмотреть сле-
дующие направления, вдоль которых предположительно
может располагаться вектор спонтанной поляризации:
а) [100], б) [010], в) [001], г) [МО], д) Lhkl],
2.11. Кристалл с симметрией mm2 поместили в элект-
рическое поле таким образом, что направление поля сов-
пало с направлением [001], затем с направлением [010].
Найти симметрию кристалла в поле в том и другом
случаях.
2.12. Вдоль каких кристаллографических направлений
одноосное растяжение пе приводит к изменению сим-
метрии кристаллов средней категории?
2.13. В каких классах симметрии и вдоль каких на-
правлений наложение электрического поля Е не вызыва-
ет изменения симметрии кристаллов?
2.14. Вдоль каких кристаллографических направлений
нужно растянуть гексагональный кристалл с симмет-
рией б/mmm, чтобы его симметрия понизилась: а) до ром-
бической, б) до моноклинной? ,
2.15. К кристаллу с симметрией 6 приложили элект-
рическое поле вдоль направлений: а) [0001], б) [1010].
Определить симметрию кристалла в поле.
2.16. Найти кристаллографические направления, по
которым следует приложить электрическое поле к кри-
сталлу с симметрией 6т2, чтобы его симметрия понизи-
лась: а) до тригональной Зт, б) до ромбической mm2,
в) до моноклинной т.
2.17. Определить симметрию кристалла в поле одно-
осного механического напряжения, приложенного вдоль
кристаллографических направлений: а) [100], б) [110],
в) [111], г) [МО], д) Ihkl], если его симметрия в нена-
пряженном состоянии 432.
2.18. Кристаллы какой симметрии обнаруживают
пьезоэлектрический эффект при всестороннем сжатии?
*) Под симметрией кристалла в сегнетоэлектрической фазе
здесь подразумевается симметрия домена — см. § 3, с. 36.
30
2.19. К кристаллу с симметрией 23 приложено элект-
рическое поле вдоль направлений: а) [100], б) [111],
в) [110], г) [ЛАЮ], д) [hkk], е) Ihkl], Найти симметрию
кристалла в поле для каждого из указанных способов на-
ложения поля.
2.20. Для каких классов симметрии средней катего-
рии приложение электрического поля в направлении оси
высшего порядка приводит к изменению симметрии опти-
ческой индикатрисы?
2.21. Вдоль каких кристаллографических направле-
ний нужно приложить электрическое поле к кристаллу
с симметрией 622, чтобы симметрия кристалла понизи-
лась до моноклинной? Перечислить все кристаллографи-
ческие направления, наложение поля Е вдоль которых
приводит к тому же результату.
2.22. К кристаллу с симметрией 432 приложили элект-
рическое поле вдоль кристаллографических направлений,
указанных в задаче 2.19. Определить- симметрию кристал-
ла в поле.
2.23. Определить симметрию монокристалла сфалери-
та при наложении электрического поля вдоль направле-
ний, перечисленные в задаче 2.19.
2.24. Пластипка из ниобата лития помещена в элект-
рическое поле таким образом, что направление вектора
напряженности поля Е _совпало а) с кристаллографиче-
ским направлением [1010], б) с направлением [1120].
Найти симметрию кристалла в поле. Перечислить ряд
кристаллографических направлений, вдоль которых при
наложении поля Е результат будет одинаковым для обо-
их случаев.
2.25. Определить симметрию кристалла, подвергнуто-
го одноосному механическому растяжению в направлени-
ях, указанных в задаче 2.19, если симметрия кристалла
в ненапряженном состоянии 23.
2.26. Найти все возможные изменения в точечной
группе симметрии сегнетоэлектрического кристалла, при-
надлежащего к классу 2/т, если в кристалле совершается
сегнетоэлектрический фазовый переход. Рассмотреть сле-
дующие кристаллографические направления, по которым
предположительно может располагаться вектор спонтан-
ной поляризации: а) [100], б) [010], в) [001], г) [ЛА.О].
2.27. Определить симметрию монокристалла титаната
бария, в котором совершается сегнетоэлектрический фа-
зовый переход, если вектор спонтанной поляризации рас-
31
полагается: а) вдоль направления [1001, б) вдоль направ-
ления [111].
2.28. Какую симметрию приобретает кристалл поц-
действпем одноосного механического растяжения по на-
правлениям, указанным в задаче 2.19, если его симметрия
в ненапряженном состоянии m3? Рассмотреть случай дей-
ствия одноосного растяжения на кристалл с симметрией
Зт вдоль направлений, указанных в задаче 2.24.
2.29. Симметрия граней кристаллов укладывается в
следующие десять классов: 1, 2, 3, 4, 6, т, тт, Зт, imm,
6mm.
При измерении микротвердости кристалла ставится
отпечаток четырехгранной алмазной пирамиды на его
грани. При этом симметрия 4mm накладывается на сим-
метрию грани Пользуясь принципом Кюри, Определить
симметрию, которую может приобретать отпечаток при
вдавливании алмазной пирамиды в случае различных по
симметрии граней.
2.30. Какую симметрию приобретает однородная не-
прерывная изотропная среда (например, расплав): а) в
электрическом поле, б) в магнитном поле?
2.31. Можно ли использовать пластинки ADP, ориен-
тированные по плоскостям (100), (НО) и (001), для по-
лучения поляризации в направлении приложенного пер-
пендикулярно их рабочим граням одноосного механиче-
ского напряжения?
2.32 *). Возможна ли монодоменизация сегнетоэлект-
рика посредством приложения механического напряже-
ния? Каким по характеру (одноосное растяжение, чистый
сдвиг, всестороннее сжатие) должно быть напряжение?
Играет ли роль ориентировка приложенного напряжения
относительно направления спонтанной поляризации?
2.33. Как с точки зрения принципа Кюри объяснить
сохранение макроскопической симметрии сегнетоэлектри-
ческого кристалла, соответствующей точечной группе его
параэлектрической фазы при охлаждении его ниже тем-
пературы Кюри?
Указание. Под макросимметрпей сегнетоэлектри-
ческого кристалла подразумевается симметрия его домен-
ной упаковки.
2.34. Как с использованием симметрийных закономер-
ностей объяснить обязательную поляризацию диэлектри-
') При решении задач 2.32—2.35 см. § 3.
32
ческих кристаллов во внешнем электрическом поле не-
зависимо от их симметрии?
2.35. Изменяется ли макроскопическая симметрия
кристалла ВаТЮ3 при фазовых переходах от тетрагональ-
ной к тригональной и ромбической сегнетоэлектрическим
модификациям?
2.36. Можно ли изменить оптическую индикатрису
кристалла, помещая его в магнитное поле?
2.37. К кристаллу с симметрией Зтп приложили маг-
нитное поле в направлениях: .а) [0001], б) [1010]. Опре-
делить симметрию кристалла в магнитном поле.»
2.38. Определить симметрию кристалла в магнитном
поле, приложенном в направлениях, указанных в задаче
2.37, если кристалл принадлежит к точечной группе 6.
§ 3. ФИЗИЧЕСКИЕ СВОЙСТВА КРИСТАЛЛОВ, ОПИСЫВАЕМЫЕ
ТЕНЗОРОМ ПЕРВОГО РАНГА
Пироэлектрический эффект. Диэлектрические кристал-
лы, которые в отсутствие внешнего электрического поля
имеют отличный от нуля вектор спонтанной поляризации
во всей области температур их существования, называют-
ся пироэлектриками.
Кристаллы, у которых направление вектора спонтан-
ной поляризации не может быть изменено наложением
внешнего электрического поля даже при напряжениях,
близких к величине пробойного напряжения, называются
собственно пироэлектрическими кристаллами. К таким
кристаллам относятся турмалин, сульфат лития, винно-
кислый калий и др.
Благодаря наличию спонтанной поляризации на про-
тивоположных гранях пластинки, вырезанной из пиро-
электрического кристалла, находятся связанные заряды.
Их плотность о зависит от величины и направления век-
тора спонтанной поляризации относительно граней пла-
стинки *!):
Ст = (Ps. п) = = |Р I cos а, (3.1)
где и — единичный вектор нормали к грани пластинки,
а — угол между векторами Ps и п (рис. 3.1).
*) В реальных кристаллах о =/= |Р'| из-за компенсации по-
верхностных зарядов за счет собственной проводимости кри-
сталлов.
3 Н. в. Переломова, М. М. Тагисва 33
Рис. 3.1. Связь плотности по-
верхностного заряда о со спон-
танной поляризацией Р8.
Максимальная плотность зарядов будет наблюдаться
на гранях пластинки, вырезанной перпендикулярно на-
правлению спонтанной поляризации. Однако обнаружить
разность потенциалов, возникающую между противопо-
ложными гранями пластинки, не удается из-за того, что
связанные заряды оказываются компенсированными заря-
дами из воздуха, а также из-
за отличной от пуля прово-
димости пироэлектрических
кристаллов.
При однородном измене-
нии температуры пироэлект-
риков изменяется и величина
их спонтанной поляризации.
Эффект изменения спонтан-
ной поляризации кристаллов,
связанный с однородным из-
менением их температуры,
называется пироэлектрическим эффектом {пироэффектом,}.
При условии, что происходит небольшое изменение
температуры ЛТ, одинаковое во всех точках кристалла
(однородный нагрев), изменение вектора спонтанной по-
ляризации ДР1 пропорционально изменению температуры,
т. е.
ДР’ == уДГ или ^Psi = (3.2)
где у (у1, 72, 7з) — вектор пироэлектрических коэффици-
ентов (или просто пироэлектрический коэффициент:), ана-
литически определяемый как
= dP\/dT. (3.3)
Пироэлектрический коэффициент у считается положи-
тельным, если возрастание температуры приводит к уве-
личению спонтанной поляризации кристалла.
Ограничения, налагаемые симметрией кристалла. Век-
тор электрической поляризации Р' благодаря своей соб-
ственнрй симметрии °°7?г может располагаться в кристал-
ле только вдоль единичного полярного направления. По-
этому, в соответствии с принципом Неймана, пироэффект
могут обнаруживать кристаллы, принадлежащие к одно-
му из 10 полярных классов симметрии: 1, 2, 3, 4, 6, т,
mm, Зт, hmm, бтт, являющихся подгруппами группы
°°т. Кроме того, пироэлектрический эффект может на-
блюдаться в текстурах с симметрией °° и °°т.
34
Расположение векторов Ps и у в кристалле определяет-
ся его симметрией. В тех из десяти полярных классов, в
которых имеется только одно единичное полярное направ-
ление, указанные векторы располагаются строго вдоль
этого направления. Так как в этих классах симметрии
обычно с единичным полярным направлением совмещает-
ся координатная ось Х3, то и векторы Р! и у оказывают-
ся направленными вдоль A's и имеют отличную от нуля
компоненту только по этой координатной осп. Так, в кри-
сталле турмалина, имеющего симметрию Зт, единичным
полярным направлением является направление оси сим-
метрии 3. Следовательно, вдоль этой оси располагаются
вектор спонтанной поляризации Р’ и вектор у. В кристал-
лофизической системе координат ось симметрии 3 сов-
падает с координатной осью Х3; вектор у направлен вдоль
Х3, а его компоненты = у2 = 0; =/= 0, т. е. у имеет
только одну отличную от нуля компоненту.
Если кристалл имеет множество единичных полярных
направлений (классы 1 и т), то направление векторов
Р“ и f оказывается не предопределенным симметрией кри-
сталла. В принципе эти векторы могут располагаться по
любому из единичных полярных направлений. А так как
в этом случае и выбор системы координат допускает не-
которую свободу, то поэтому в классе симметрии 1 вектор
Y может иметь три отличные от пуля компоненты; в клас-
се т — две, пулевой будет компонента по координатной
осп, перпендикулярной плоскости симметрии т.
Электрокалорическпй эффект. Из термодинамических
соображений следует существование эффекта, обратного
пироэлектрическому. Этот эффект заключается в измене-
нии температуры пироэлектрика при действии на него
электрического поля и цосит название электрокалориче-
ского эффекта. Уравнение электрокалорпческого эффекта
A7’ = qAE, (3.4)
где электрокалорическпй коэффициент q = dT/dK. Он
связан с пироэлектрическим коэффициентом у соотноше-
нием
где рис — соответственно плотность и теплоемкость кри-
сталла, J — механический эквивалент тепла (вывод фор-
мулы (3.5) см. в задаче 3.3).
3* 35
Подставляя значение q из (3.5) в уравнение (3.4), по-
лучаем следующее соотношение, описывающее электрока-
лорический эффект:
ду = де, (3.6)
pcj ’ ' '
из которого следует, что в случае, когда коэффициент у
положителен, а вектор напряженности электрического по-
ля Е совпадает с направлением Р, коэффициент q отри-
цателен (т. е, в этом случае увеличение поляризации кри-
сталла за счет приложенного поля приводит к пониже-
нию его температуры).
Сегнетоэлектрические кристаллы. Сегнетоэлектриче-
ские кристаллы или сегнетоэлектрики представляют собой
подгруппу пироэлектриков и обладают рядом особых
свойств, присущих только этой группе кристаллов. Глав-
ное отличие сегнетоэлектриков от собственно пироэлект-
рических кристаллов состоит в том, что в них направле-
ние спонтанной поляризации может быть изменено при-
ложением внешнего электрического поля.
Сегнетоэлектрики при определенной температуре, на-
зываемой температурой Кюри или точкой Кюри, испыты-
вают фазовое превращение, связанное с изменением их
структуры. Выше точки Кюри спонтанная поляризация,
отсутствует — кристалл находится в параэлектрической
фазе. Симметрия кристалла в парафазе неполярна. При
Температуре ниже точки Кюри возникает спонтанная по-
ляризация, симметрия кристалла понижается до поляр-
ной, т. е. до симметрии одного из десяти полярных клас-
сов. Изменение симметрии при фазовом переходе обуслов-
лено изменением формы элементарной ячейки спонтанной
деформацией.
Из принципа Неймана следует, что группа симметрии
кристаллов в сегнетофазе должна быть подгруппой груп-
пы симметрии параэлектрической фазы кристалла, причем
это будет общая наивысшая подгруппа предельной группы
симметрии °°т, описывающей спонтанную поляризацию,
и точечной группы симметрии кристалла при определен-
ном расположении элементов симметрии этих групп.
Ниже точки Кюри направление спонтанной поляриза-
ции не одинаково по всему объему кристалла. Обычно
кристалл оказывается разбит на макроскопические обла-
сти — домены, в которых векторы спонтанной поляриза-
ции антппараллельны или спонтанная поляризация рас-
полагается по кристаллографически эквивалентным на-
36
правлениям так, что полидоменный кристалл сохраняет
симметрию параэлектрической фазы*). Отдельный домен,
так же как и монодоменный кристалл данного сегнето-
электрика, будет иметь полярную группу симметрии.
Таким образом, разбиение на домены возвращает сег-
нетоэлектрический кристалл к симметрии его параэлек-
трической фазы. Поэтому его макроскопические свойства
(пьезоэлектрические, оптические, механические и другие)
определяются симметрией параэлектрической фазы.
Примеры решения задач
3.1. Какое изменение температуры можно измерить,
используя пироэлектрический приемник, состоящий из
турмалиновой пластинки толщиной 1 мм и милливольт-
метра чувствительностью 10_3 В/деление? Как наилучшим
способом вырезать пластинку для этих целей? Какой ве-
личиной можно охарактеризовать чувствительность та-
кого пироэлектрического приемника? Во сколько раз
увеличилась бы чувствительность приемника, если бы
вместо турмалиновой пластинки использовать пластинку
сульфата лития той же толщины, вырезанную перпенди-
кулярно полярной оси?
Решение. Единственный пироэлектрический коэффициент
турмалина 73 связан с полярным направлением кристалла, т. е.
с осью 3. Согласно уравнению (3.1) наивыгодпейшим образом
ориентировать турмалиновую пластинку —• значит вырезать ее
перпендикулярно оси 3, т. е. вдоль плоскости (0001). Изменение
температуры, которое может «почувствовать» такая пластинка,
можно найти из уравнения (3.2), которое в этом случае запишет-
ся так:
ДР3 = -|>3ДГ. (3. 7)
Очевидно, что ДР8=|До|, ДР = LQjC « 10-3 В/деление, Д<2 =
= Да5, С = где S — площадь пластины, d — ее толщина,
Д<2 — суммарный заряд, возникающий при изменении температу-
ры, С — емкость кристаллического конденсатора. Из (3.7) найдем,
что минимальное изменение температуры, которое можно измерить
при использовании милливольтметра и турмалиновой пластинки
*) Здесь и в дальнейшем,, когда речь идет о полидоменном
кристалле, имеется в виду разбиение сегнетоэлектрика на домены,
приводящее к деполяризации кристалла, т. е. к полной взаимной
компенсации спонтанной поляризации доменов с различной ори-
ентацией векторов Ps.
37
толщиной в 1 мм, равно
е „„ДР-8,85 10“12
Д7’ = ——-----—-----------« 10“ 5К •
d-y.
Чувствительность приемника пироэлектрического напряжения
может быть охарактеризована отношением
ДР А Уг
- А 6ii ’
Рис. 3.2. Взаимное располо-
жение полярного направле-
ния и штрихованной систе-
мы координат.
где А —постоянная величина, равная Л/(8,85-10_ 12); 7,- и е,,- — зна-
чения пироэлектрического коэффициента и диэлектрической про-
ницаемости вдоль полярной осп Xt.
Используя значения е<,- и 7,- для тур-
малина и сульфата лития*), полу-
чаем, что чувствительность прием-
ника с пластинкой сульфата лития
приблизительно в 27 раз выше, чем
с турмалиновой пластинкой.
3.2. Найти уравнение указа-
тельной **) поверхности пиро-
электрического эффекта. Какова
симметрия этой поверхности?
Решение. Пусть в координат-
ной системе Xi, Х2, Х3 вдоль поляр-
ного направления ОА пироэлектри-
ческий эффект определяется вектором A(At, А2, А3) (рис. 3.2).
Выберем произвольное направление и совместим с ним ось Х3
повой координатной системы. Тогда по этому направлению пиро-
электрический эффект будет определяться компонентой А3, для
которой имеем
А? = х2 + х2 4- аг|. (3.8)
Выразим Ag через компоненты исходного вектора
A(Ai, Л2, Аз);
Аз = ^зт^г + £32^2 + ^зз^з’ (3-9)
*) Для сульфата лития, как и для всех кристаллов класса 2,
полярной осью в стандартной установке является ось Х2.
**) Указательная поверхность физического свойства кристал-
ла — это поверхность, радиус-вектор которой в каждом направле-
нии числепно равен величине, характеризующей свойство в этом
направлении.
38
Проведем через начало координат перпендикулярно вектору А
плоскость Р Проекция вектора А на ось X' (Лд) положительна
для точек (xi, х2, xs), лежащих «выше» плоскости Р и отрица-
тельна для точек (zb х2, xs), лежащих «ниже» плоскости Р. Тогда
коэффициенты (см. (3.9))
£31 ± XJA3' ^32 — XJA& ^33 ~ — Хз/Аз’
где знак «+» соответствует точкам над плоскостью Р, а «—» —
точкам под плоскостью Р.
Следовательно,
/ 2
Аз = ± (Ми VUW
(3.10)
Приравнивая (3.8) и (3.10), получим
Х1 + Х1 + хз xiAi + хгАг + хзАз (3.11)
для точек А3 (х^ х%, хд), лежащих «выше» плоскости Р, и уравне-
ние
Х1 + Х1 + Х3 = ~ Х1А1 ~ Х2А2 “ Х3А3
для точек Л3 (хг, х^, х^, лежащих «ниже» плоскости Р.
Уравнение (3.11) преобразуется к виду
(3.12)
а (3.12) — к виду
СД \2 / Д \2 ( Л \2 Д2 л2 л2
*1 + +(Х2 + +(*3 + —Г+-Т-+~Г- (3-W)
Этими уравнениями определяются две сферы, соприкасающиеся
в начале координат, причем центр сферы, определенной уравне-
нием (3.13), лежит в точке 4-А/2, а центр сферы, определенной
уравнением (3.14), —в точке —А/2 (рис. 3.3).
Фигура, изображенная на рис. 3.3, имеет симметрию <х>/ттт,
если учитывать только ее форму. Если же учесть и знаки зарядов
(здесь их символизируют цвета черный и белый), то между двумя
сферами имеется плоскость антисимметрии.
39
схэГТ]
Рис. 3.3. Указательная
поверхность пироэлект-
рического эффекта.
Операции антисимметрии состоят пз операций обыкновенной
симметрии в сочетании с операцией перемены знака фигуры. Фи-
зический смысл перемены знака фигуры может быть различным:
перемена знака заряда (плюс — минус), перемена цвета (черный —
белый), перемена знака деформации (растяжение — сжатие) и т. п.
Введенное академиком А. В. Шубниковым понятие антисиммет-
рии *) применяется в кристаллофизике для описания векторных
и тензорных поверхностей, для объяс-
нения магнитных свойств кристаллов
и т. д. Операции антисимметрии обо-
значаются символом соответствующей
операции симметрии с чертой внизу.
В этих символах антисимметрия
указательной поверхности пироэлектри-
ческого эффекта определяется как
oo/mm.
3.3. Определить симметрию мо-
нодомениого кристалла титаната
бария в сегнетофазе, если его сим-
метрия в парафазе тЗт, а вектор
спонтанной поляризации распола-
гается: а) вдоль направления
[100], б) вдоль направления [111],
г) вдоль направления [110].
Р е ш е и и е. Если в кристалле воз-
никает спонтанная поляризация, имеющая собственную симмет-
рию ост, то симметрия монодомепного кристалла в сегнетофазе бу-
дет общей наивысшей подгруппой группы симметрии кристалла в
парафазе и группы ост. Для перечисленных в условии задачи на-
правлений Р« это будут группы: a) 4mm (см. рис. 2.9), б) 3m
(см. рис. 2.10), в) тт (см. рис. 2.11).
3.4. В интервале комнатных температур (22—24 °C)
требуется проконтролировать точность поддержания по-
стоянной температуры или измерить малое изменение ее.
Какой кристалл: турмалин или сегнетову соль, приме-
нить для этой цели? Каким прибором воспользо-
ваться: баллистическим гальванометром или милливольт-
метром?
Решение. Предложенные температуры близки к верхней
точке Кюри сегнетовой соли. Поэтому соответствующий пиро-
электрический коэффициент будет велик: = 200 ед. СГСЭ. Но
*) А. В. Шубников. Симметрия и антисимметрия конечных
фигур,— М.: Изд-во АН СССР, 1951.
40
и диэлектрическая проницаемость 6] достигнет максимального
значения ei = 1000.
Для пластинки Х-среза сегнетовой соли, согласно (3.2),
ЬР[ = 200ДГ ед. СГСЭ.
Так как Е = Р/х, а е = 1 + 4лх, то
Для пластинки Z-среза турмалина
12,8-1,2
ДР’ = 1,2ДГ, Е„ = ----7-Е--ДР = 2,00ДГ.
а з /,о
Очевидно, что при большом значении '(i у сегнетоэлектрика
разность потенциалов между противоположными гранями пластин-
ки оказывается примерно той же, что и у линейного диэлектри-
ка — турмалина, имеющего небольшой пироэлектрический коэф-
фициент. Но величина заряда па грани, пропорциональная ДР®,
у сегнетовой соли почти в 200 раз больше, чем у турмалина. По-
этому для цели, поставленной в задаче, целесообразно использовать
пластинку сегнетовой соли и баллистический гальванометр.
3.5. Выдержит ли пластинка из кристалла триглицин-
сульфата (TGC) резкое понижение температуры от точки
Кюри 49 °C до 39 °C? Электрическую прочность кристалла
принять равной 40 кВ/см.
Решение. Симметрия кристалла TGC в парафазе 2/т, в
сегпетофазе 2. Направление оси 2 принимается за направление
координатной оси Х2. Поэтому уравнение пироэлектрического эф-
фекта будет иметь вид
ДР’ = у2ДР.
Принимаем для у? вблизи точки Кюри среднее значение, равное
500 ед. СГСЭ. Тогда
ДР® = 500-10 = 5-10s ед. СГСЭ.
Напряженность соответствующего электрического поля
4л-ДР 12,8-5-103 й
Е =------—— =-------25----= 2600 еД- сгсэ » 10 В/см.
Она превышает электрическую прочность кристалла. Кристалл
будет разрушен.
3.6. На сколько градусов и в область каких темпера-
тур можно «сдвинуть» точку фазового перехода кристал-
лов дигидрофосфата калия (KDP) за счет электрокало-
рического эффекта, помещая их при температуре фазового
41
перехода Тя = —150 °C в электрическое поле напряжен-
ностью 20 кВ/см, приложенное таким образом, что на-
правление вектора Е: а) совпадает с направлением Р‘;
б) противоположно направлению Р'? (с = 0,1 кал/(г-К),
Тз = 5000 ед. СГСЭ.)
Решение. Значение единственного электрокалорического
коэффициента кристаллов KDP в сегнетоэлектрической фазе на-
ходится согласно соотношению (3.5);
V т
— —5— = — 0,06 ед. СГСЭ.
3 Рс/
Изменение температуры, вызванное наложением электрического
поля, равно
АГ = <7зА2? = — 4 К.
Таким образом, ноле напряженностью 20 кВ/см, совпадающее
с направлением спонтанной поляризации вблизи точки Кюри,
будет охлаждать кристалл за счет электрокалорического эффекта
приблизительно на 4 К; это означает, что такое поле в состоянии
«сдвинуть» точку Кюри KDP в сторону более высоких температур
на 4 К.
Если же это ноле приложить в направлении, обратном на-
правлению Р, кристалл нагреется на 4 К и точка Кюри в этом
случае сдвинется в область более низких температур на эту же
величину.
Задачи
3.7. Вычислить изменение температуры пластппки из
кристалла KDP за счет спонтанного электрокалорическо-
го эффекта.
3.8. Найти плотность поверхностных зарядов, возни-
кающих на противоположных гранях турмалиновой пла-
стинки при однородном нагревании ее па 30 К, если пла-
стинка вырезана .так, что:
а) нормаль к пластинке параллельна оси симметрии 3;
б) угол между нормалью к пластинке и осью 3 состав-
ляет 60°;
в) нормаль к пластинке перпендикулярна к оси 3.
3.9. Какое изменение температуры можно измерить,
используя пластинку из сульфата лития толщиной 1 мм
и милливольтметр чувствительностью 10-3 В/деление. Как
наилучшим способом вырезать пластинку для этих целей?
3.10. Определить напряженность электрического по-
ля, приложенного к кристаллу турмалина вдоль на-
42
правления [00011, которая вызвала бы такую же поляри-
зацию, как и однородное изменение температуры кристал-
ла на 10 К.
3.11. Какую разность потенциалов приобретает пла-
стинка виннокислого калия размером 1 X 1 X 0,1 см3, вы-
резанная перпендикулярно осн 2, при однородном нагре-
вании ее па 10 К. Какой заряд появляется па ее гранях?
3.12. Как сдвинется температура точек Кюри сегнето-
вой соли, если кристалл помещен в электрическое поле
напряженностей 1000 В/см? Поле приложено в направле-
нии электрической оси кристалла.
3.13. Вычислить величину пироэлектрического коэф-
фициента титаната бария вблизи его верхней точки Кюри,
если известно, что спонтанный электрокалорическпй эф-
фект приводит к сдвигу точки Кюри примерно на 1 К.
3.14. Какое напряжение генерируется между обклад-
ками конденсатора, представляющего собой турмалиновую
пластинку Z-среза толщиной 1 мм, при охлаждении ее
от 50 °C до комнатной температуры?
3.15. В кристаллах каких классов симметрии вектор
спонтанной поляризации пироэлектрика при изменении
температуры может изменять не только свою величину,
но и направление?
3.16. Оценить изменение температуры турмалиновой
пластинки, если ее поместить в электрическое поле на-
пряженностью 20 кВ/см.
j/3.171 Какой заряд можно снять с противоположных
граМи пластинки кристалла сульфата лития размером
1,2 X 2 X 0,2 см3, вырезанной под углом 60° к оси 2, при
ее нагревании на 40 К?
3.18. Используя принцип Неймана, определить нену-
левые компоненты векторного свойства кристалла, отно-
сящегося к классу 6mm.
3.19. Будут ли обнаруживать пироэлектрический эф-
фект кристаллы: а) кварца, б) арсенида галлия, в) кри-
сталлы ADP в параэлектрической фазе?
3.20. Может ли обнаруживать пироэлектрический эф-
фект сегнетоэлектрический кристалл, разбитый на до-
мены?
3.21. Какие электрические заряды появляются па про-
тивоположных гранях турмалиновой пластинки толщиной
0,1 см площадью 1 см2, вырезанной перпендикулярно на-
правлению [00011, при однородном нагревании на 10 К?
Какова разность потенциалов между ее противоположны-
ми гранями?
43
3.22. Оценить изменение температуры пластинки
У-среза толщиной 0,1 см из сульфата лития в поле 300 В.
3.23. К пластинке Z-среза кристалла KDP размерами
1 X 1 X 0,1 см3 в области фазового перехода приложили
электрическое поле 10 кВ/см. Считая q3 = — 0,6 ед. СГСЭ,
найти изменение температуры пластинки за счет элек-
трокалорического эффекта.
§ 4. ФИЗИЧЕСКИЕ СВОЙСТВА КРИСТАЛЛОВ, ОПИСЫВАЕМЫЕ
ТЕНЗОРОМ ВТОРОГО РАНГА
Тензором второго ранга в кристаллах описываются
диэлектрические и магнитные проницаемости и восприим-
чивости, удельная проводимость и удельное сопротивле-
ние, теплопроводность, тепловое расширение, пьезокалори-
ческий эффект и др. Так, например, закон Ома для изо-
тропной среды записывается в виде
j = оЕ,
где векторы j — плотность тока и Е — напряженность по-
ля параллельны, а удельная проводимость о задается од-
ним числом. В кристаллах же величина удельной прово-
димости зависит от направления. При этом в общем слу-‘
чае каждая компонента вектора плотности тока линейно
зависит от всех трех компонент вектора напряженности
поля,.
Если выбрана ортогональная система координат, то
дифференциальный закон Ома для кристаллов в общем
случае записывается в виде системы трех уравнений:
Ji = ОцЕ1 -Ь О12Е2 “Ь ЩзЕ3,
]г — CiziEi + U22E2 “Ь
js — О31Е1 + U32E2 "Ь c3JEs-
Используя правило суммирования Эйнштейна, можно
предыдущие уравнения записать в виде
ji = CijEj (i, j = 1, 2, 3). (4.1)
Суммирование производится по повторяющемуся индек-
су, Значения коэффициентов пропорциональности в
уравнениях (4.1) определяют удельную проводимость кри-
сталла. Таким образом, в отличие от изотропных тел,
в кристалле для определения удельной проводимости тре-
44
буется задание пе одного числа, а
ти чисел:
G
в общем случае девя-
«и
12
kwl =
<4i
«31
22
32
«13
«23
«33
G
G
Конкретные значения коэффициентов on, o2z> Озз и т. д.
зависят от выбора системы координат, связанной с кри-
сталлом. При переходе от координатной системы Xt, Х2,
Х3 к новой системе Хг, Х2, Х3 величины коэффициентов
оо изменяются по закопу
(Ту = CikCjiOhi,
где (Ту— коэффициенты в новой системе ХЪХ2,Х3,
оы — коэффициенты в старой системе Х1ч Х2, Х3, Са,
Сл — направляющие косинусы, определяющие положения
осей Х15 Х2, Х3 относительно осей Х„ Хг, Х3.
Величины, которые определяются девятью числами,
зависящими от выбора системы координат, и преобразу-
ются при переходе к другой системе по закону (4.2), пред-
ставляют собой тензор второго ранга.
Старые коэффициенты могут быть выражены через
новые при помощи соотношения
(Ту = CkiCijCthb (4.2а)
Явления прохождения тока через кристаллическую
среду, теплового расширения и теплопроводности, пьезо-
калорический эффект, состоящий в изменении температу-
ры кристалла под действием механических напряжений,
описываются соответственно следующими уравнениями:
ji = Гу = СХуАУ,
Qi ~ dx- ’ ~ ^^У^У,
где — коэффициенты теплового расширения, д{ — ком-
поненты вектора теплового потока, ?.« — коэффициенты
теплопроводности, га — компоненты тензора механических
деформаций, ti} — компоненты тензора напряжений.
Удельная проводимость, диэлектрическая проницае-
мость и восприимчивость, удельная теплопроводность и
тепловое расширение, магнитная проницаемость и воспри-
имчивость описываются симметричными тензорами второ-
го ранга, а это означает, что для них справедливы
45
соотношения
o.j = Oji, Eij — Eji и т. д., (4.3)
которые сокращают число независимых компонент ука-
занных тензоров до шести.
Характеристическая поверхность симметричного тен-
зора второго ранга. Для наглядного представления рас-
сматриваемых свойств кристаллов, характера их анизо-
тропии и связи с симметрией кристалла пользуются гео-
метрической интерпретацией тензоров второго ранга по-
верхностями второго порядка. Если в общем уравнении
поверхности второго порядка
^22^2 8g3Xg Ч- ^12'>'Г^2 ^*21^2^1 Ч~
4“ ‘^ГЗ'Н^'З Ч~ ^31^3^1 Ч~ ^23^2^3 Ч~ ^32^3^2 ~ (^•'^)
в качестве коэффициентов взять компоненты симметрич-
ного тензора второго ранга (5,, = 5д), то получим по-
верхность, называемую характеристической поверхностью
тензора второго ранга.
Так, характеристическая поверхность удельной прово-
димости кристалла в общем .случае описывается уравне-
нием
<Ти^ 4- <т22Ж2 + + 2сг32аг3ж2 + 2tr13Xj,a:3 + 2/O^Xg = 1.
Главные оси симметричного тензора второго ранга. По-
верхности второго порядка, для которых Stj = 8ц, облада-
ют так называемыми главными осями — тремя взаимно
перпендикулярными направлениями, при выборе которых
за координатные оси общее уравнение поверхности (4.4)
принимает наиболее простой вид:
*$11^1 4~ ^22Х2 4“ &33Х3 — 1. (^-5)
Если величины Хп, 822, 833 положительны, то поверх-
ность (4.5) представляет собой эллипсоид; если два коэф-
фициента положительны, а один отрицателен, поверхность
(4.5) является однополостным гиперболоидом. Если один
коэффициент положителен, а два отрицательны, поверх-
ность (4.5) представляет собой двухполостный гипербо-
лоид.
Уравнение характеристической поверхности удельной
проводимости, записанное в главных осях, имеет вид
4~ <722-^2 “1“ ^33Х3 ~
46
Величины оь о2, Оз называются главными компонентами
тензора удельной проводимости или, сокращенно, главны-
ми удельными проводимостями кристалла.
В главной системе координат уравнения (4.1) также
становятся более простыми:
71 = О11?1, /г = 02^2, /з = Оз^<з.
Если электрическое поле приложено в направлении глав-
ке 'координатной оси то Е2 — Е3 = 0; тогда /2 — /з “ О
и j параллельно Е.
Те же рассуждения справедливы по отношению к ко-
ординатным осям Х2 и Х3. Поэтому можно сказать, что
главные оси в кристалле — это те направления, вдоль
которых вектор воздействия и вектор реакции совпадают
по направлению для случая, когда явление представляет
собой вектор-векторпое взаимодействие.
При рассмотрении влияния симметрии кристалла на
вид тензора второго ранга особенно удобно использовать
запись тензоров второго ранга и уравнений соответству-
ющих характеристических поверхностей в главной систе-
ме координат.
Величина, характеризующая свойство в заданном на-
правлении. Кристаллы анизотропны, т. е. их свойства
различны в зависимости от направления. В общем случае,
если кристалл подвергается векторному воздействию, на-
пример помещается в электрическое поле, направленно
тока в нем не совпадает с направлением поля. Поэтому
величину, характеризующую свойство в кристалле по ка-
кому-либо направлению, в данном случае удельную про-
водимость, определяют как параллельную Е компоненту
плотности тока j№, деленную на Е. Если приложено еди-
ничное поле, то удельная проводимость численно рав-
на /и.
Если известен тензор, определяющий физическое свой-
ство кристалла в выбранной системе координат, например
тензор диэлектрической проницаемости [ец], то величина
диэлектрической проницаемости по любому направлению
47
п в кристалле вычисляется с помощью соотношения
Е71 EjjZZjAZjj
(4.6)
где ni? rtj — компоненты единичного вектора и (паправля-
ющие косинусы заданного направления!).
Геометрические свойства характеристической поверх-
ности. Величина радиуса-вектора характеристической по-
Рис. 4.1. Характеристиче-
ская поверхность тензора
удельной проводимости.
верхности г в каком-лиоо на-
правлении связана с величи-
ной, характеризующей соот-
ветствующее свойство в этом
же направлении, например о,
соотношением (рис. 4.1)
г = 1/Уо, или о = 1/г2. (4.7)
Если рассматриваемое
свойство входит в уравнение
вектор-векторного взаимодей-
ствия (векторное воздействие,
векторная реакция), как это имеет место в законе Ома,
то характеристическая поверхность свойства дает возмож-
ность определить направление вектора реакции по на
правлению вектора воздействия и наоборот.
Если j{ = (УцЕ5, то на-
правление j для заданного
Е можно найти, построив
параллельный полю Е ра-
диус-вектор ОР характери-
стической поверхности и
затем восставив перпенди-
куляр к плоскости, каса-
тельной к характеристи-
ческой поверхности в
точке Р (рис. 4.2).
Влияние симметрии кри-
сталла на его свойства,
описываемые тензорами
второго ранга. Симметрия
кристалла накладывает
Рис. 4.2. Определение с помощью
характеристической поверхности
направления вектора реакции по
направлению вектора воздейст-
вия.
существенные ограничения на число независимых ком-
понент тензора второго ранга. Ориентация характеристи-
ческой поверхности относительно элементов симметрии
кристалла определяется согласно принципу Неймана, как
указано в таблице на с. 49.
48
Классификация кристаллов по оптическим свойствам Сингония X арактеризую- щая симметрия Вид характе- ристической поверхности и ее ориентация Число независи- мых компонент тензора Тензор, при- веденный к осям приня- той ориента- ции
Изотропная среда 1 Кубическая Четыре оси 3 Сфера 1
'S 0 01 OSO oos
Одноосные кристаллы Тетраго- нальная Одна ось 4 Поверх- ность вра- щения во- круг глав- ной оси симметрии Х3 (Z) 2
Гексаго- нальная Одна ось 6 ~S1 0 O’ 0 0 0 0 s3
Триго- нальная Одна ось 3
Двуосные кристаллы Ромбиче- ская Три взаимно перпендику- лярные оси 2. Осей высшего порядка нет Поверх- ность вто- рого поряд- ка с осями х2, хэ, параллель- ными осям 2: X, Y, Z 3 Г 0 0 0 S2 0 0 0 s3
Моно- клинная Одна ось 2 или одна пло- скость т Поверх- ность второ- го порядка с одной осью Х2, парал- лельной оси 2 или перпен- дикулярной плоскости т 4 5ц 0 .Sls 0 5'22 0 .513 0 S33_
Триклин- ная Центр сим- метрии или от- сутствие сим- метрии Поверх- ность второ- го порядка. Положение относитель- но кристал- лографиче- ских осей не определено 6 1 1 CO CO CO pH <N CO Co Co СЧ <N CO pH « СЧ co Co Co pH СЧ CO to co%"
4 Н В. Переломова, М. М. Тагиева
49
Уравнение характеристической поверхности содержит
столько же независимых коэффициентов, сколько компо-
нент имеет соответствующий тензор, и симметрия поверх-
ности совпадает с симметрией физического свойства.
Измерения на ориентированных образцах. На практи-
ке соотношением (4.6) широко пользуются для вычисле-
ния величин, характеризующих физические свойства ори-
ентированных образцов, а также для обратной задачи —
по данным измерений на ориентированных образцах
составить тензор, описывающий физическое свойство кри-
сталла. При обозначении «среза» имеется в виду направ-
ление нормали к главным («рабочим») граням пластинки
или бруска в кристаллофизической спстеме координат.
Так, например, Х-, Y- и Z-срезы — это пластинки или
бруски, у которых нормали к рабочим граням соответ-
ственно параллельны осям X, Y, Z (см. рис. 2.3). Рабочи-
ми гранями называют обычно грани, к которым прикла-
дывается внешнее воздействие: электрическое поле, меха-
ническое напряжение и др.
Для характеристики ориентировки косых срезов ныне
приняты следующие обозначения: XYs/a, YZsb/a/y,
XYsbl/a/y/fi и т. д. Первые две буквы обозначают кри-
сталлофизические оси *), вдоль которых первоначально
направлены толщина s и длина I (Ь — ширина) кристал-
лических срезов; последующие буквы, если они имеются,
показывают, какое из ребер среза служит осью поворота;
а, Р, у, принимающие в конкретных случаях численные
значения, поставленные после букв I, b, s через косую
черту, обозначают углы последовательных поворотов, при-
чем поворот вокруг толщины кристаллического среза s
обозначается а, вокруг длины Z — вокруг ширины Ъ — у.
Углы измеряются в градусах и минутах. Поворот против
часовой стрелки считается положительным.
Некоторые срезы показаны па рис. 4.3. При исследо-
вании свойств косых срезов, связанных c новыми осями
Хх, Х2, Х3 (штрихованные оси направляются по реб-
рам бруска или пластинки), используются соотношения
(4.2) и (4.6). Очевидно, каждый из коэффициентов в осях
Хх, Х2, Х3 будет -являться линейной комбинацией глав-
пых коэффициентов. И, наоборот, для получения глав-
*) В принятых обозначениях косых срезов ортогональные кри-
стал'лофизические оси Xh Х2, Х3 обозначаются X, Y, Z. При этом
не следует смешивать их с кристаллографическими осями коор-
динат, которые могут быть не ортогональны.
50
ных коэффициентов часто практически удобнее проводить
измерения свойств па косых срезах кристалла и от по-
лученных данных перейти к требуемым величинам путем
вычислений.
Пусть Х„ Х2, Х3 — оси, жестко связанные с моноклин-
ным кристаллом в стандартной установке; Х2, Х3 —
ортогональные осп, связанные с ориентированным образ-
цом, причем ось Х3 совпадает с направлением, вдоль ко-
торого измеряется величина диэлектрической проницаемо-
сти кристалла (рис. 4.4). В этом случае в осях Хт, Х2, Х3
она обозначается как е33. С другой стороны, измеряемая
величина £33, согласно уравнению (4.6), выражается через
Рис. 4.3. Примеры различно ориентиро-
ванных кристаллических пластинок-
срезов: а) ХУ//+45°; 6) ХУ/>/-|-45";
в) УУЛ/+45°; г) PZsfc/+457+45°.
компоненты тен-
зора [е„] в стан-
дартной установ-
ке. Измеряя зна-
чения е33 для об-
разцов четырех
различных ориен-
Рис. 4.4. Кристалли-
ческая пластинка
произвольной ориен-
тации.
таций, мы получаем четыре уравнения, связывающие не-
зависимые компоненты тензора [е4Д моноклинного кри-
сталла. Решая их, получаем компоненты тензора ди-
электрической проницаемости в координатной системе
X,, Х2, Х3. Таким образом, измерения на ориентирован-
ных образцах дают возможность определить все компо-
ненты тензора [е<3], как и любого тензора второго ранга,
4*
51
описывающего физические свойства кристаллов в стан-
дартной установке.
Указательные поверхности. Для практических целей
весьма удобными оказываются указательные поверхности
физических свойств кристаллов, позволяющие наглядно
изобразить их симметрию и анизотропию. Так, например,
указательная поверхность тензора диэлектрической про-
ницаемости [е„] описывается уравнением г(п) = ко-
торое означает, что указательную поверхность образуют
концы радиусов-векторов г, в выбранном масштабе равные
диэлектрической проницаемости вдоль рассматриваемого
направления.
Если все собственные значения тензора второго ранга,
описывающего какое-либо физическое свойство кристалла,
положительны, то расстояние г любой точки указательной
поверхности тоже положительно. Если же среди собствен-
ных значений имеются отрицательные, то для некоторых
направлений г также будет отрицательно. В этом случае
части поверхности, соответствующие отрицательным зна-
чениям г, строят так же, как обычные положительные
части поверхности, но окрашивают их в черный цвет,
в отличие от положительных, белых частей поверхности
(см. рис. 3.3 и 4.6).
Обратные тензоры. Для расчета величин, характеризу-
ющих физические свойства кристаллов, иногда бывает не-
обходимо по известным компонентам тензора, описываю-
щего какое-либо физическое свойство кристаллов, найти
компоненты обратного ему тензора. Например, зпая тен-
зор удельной проводимости кристалла, компоненты кото-
рого входят в уравнение
ji = О.Л,
пайти тензор удельного сопротивления, компоненты кото-
рого входят в уравнение
Et = РоЬ.
В общем случае компоненты тензора [p?j] по отдельности
не являются просто обратными величинами соответствую-
щих компонент тензора [ov,], а находятся из соотношения
(-
Oii = --------
52
где Д° — определитель вида
П11 °12 °13
° 12 °22 °23
С13 °23 Ст33
Дч. — минор, полученный из него зачеркиванием i-й
строки и ;-го столбца. Из уравнения (4.8) очевидно, что
тензор имеет обратный себе только в том случае, если
все его три главные значения отличны от нуля.
Примеры решения задач
4.1. Найти величину и направление вектора плотности
тока (в координатной системе Хг, Х3), возникающего
в кристаллической пластинке площадью 5 и толщиной
d( l'S > d) под действием внешнего поля Е, равного
150 В/см и приложенного в направлении (У2/2, V2/2, 0),
если удельная проводимость кристалла (в 10-7 Ом-1 • см-1)
в этой координатной системе описывается тензором
1*7111 •—
9 — 2 8
— 2 16 0
8 0 25.
Решение. Компоненты вектора Е (Z?b Е2, Es):
Et = 150-V2/2 В/см, Е2 = 150-У2/2 В/см, Е3 = 0;
Zi = oiA + ni2r2 + oi3S3 =
1/2' l/T
= — — 2- 10~7-150 — = 7,4-10-5 А/см2,
J2 = °S,1E1 + С22Е2 + °2ЧЙ’з =
1/2" 1/2”
= — 2-10~7-150 + 16-10-7-150 = 14,7-10“5 А/см2,
!3 ~ °31Е1 + °32^2 + °33Е3 ~
, 1/2
= 8-10~7-150 — = 8,461О-5 А/см,
Л
I j|₽ 18,5-10-5 А/см2.
Направление вектора j определяется углами а, р и у, которые он
составляет с осями координат. Углы а, р и у находятся из соот-
ношений
cos а = cos В = —2-, cos у = . /3 .
ИГ lil т 111
53
cos a = 0,398, a = 66°,
cos ₽ = 0,797, p = 37°,
cos y = 0,452, у = 63°.
4.2. Тензором какого вида описывается линейное рас-
ширение сульфата лития в ортогональной системе коорди-
нат Хх, Xz, Х3, если: а) ось симметрии 2HXS; б) ось сим-
метрии 211Х2?
Решение. Для кристаллов класса 2 операция поворота на
180° вокруг оси 2 является тождественным преобразованием. Мат-
рицы направляющих косинусов, соответствующие этому преобра-
зованию, имеют вид
/—1 о 0\ / — 1 о 0\
С-(X , 180е) = 0-10, ci5 (X , 180°) = I 01 0
\ 0 0 1/ \ о О -1/
Воспользовавшись законом преобразования компонент тен-
зора второго ранга и вышеприведенными операторами поворота,
получаем для случая 2 || Х3
«и = а,ц,
«22 = «22,
G.33 = Пзз,
«21 = ССц,
«зз = —Сгз,
«31 = —Изь
В результате поворота величины a23 = as2 и а и = а31 пере-
шли в антиравные. Но условия симметрического преобразования
требуют, чтобы эти величины сохранили свои прежние значения,
а это выполняется в единственном случае, когда они равны нулю.
Таким образом, тепловое расширение сульфата лития в орто-
гональной координатной системе, ось Х3 которой совпадает с осью
симметрии 2, определяется тензором вида
О' OL 0 '
11 12
«12 «22 0
0 0 «33
Аналогичным образом можно показать, что в установке (2 II Х2)
тензор теплового расширения имеет вид
«и о «13
0 К22 0
«13 ° «33
54
4.3. Тензор удельной проводимости,
10~’ Ом-1 • м-1, кристалла имеет вид
выраженной в
25
О
О
О О
7 — 3 Уз
— з Уз 13
В каких направлениях относительно системы коорди-
нат, в которой тензор [а,,] имеет приведенный в задаче
вид, направление вектора плотности тока будет совпадать
с направлением приложенного электрического поля?
Решение. Математически решение задачи состоит в на-
хождении собственных значений и собственных векторов данного
тензора, т. е. в приведении его к главным осям. Главные оси
тензора обладают тем свойством, что в точках их пересечения
с характеристической поверхностью нормаль к поверхности п
—О
параллельна радиусу-вектору ОР (см. рис. 4.2). Обозначим через
Р точку характеристической поверхности, заданной уравнением
OijXiXj = 1, через Ai— компоненты вектора ОР. В соответствий
с только что указанным свойством радиус-вектор ОгьДл паралле-
лен нормали к поверхности в точке Р. Из условия того, что ради-
ус-вектор и нормаль должны быть параллельны, следует пропор-
циональность их соответствующих компонент, т. е.
OikAk — 7.Л,,
где X — константа.
Последнее соотношение представляет собой систему трех
однородных линейных уравнений в переменных At (i = 1, 2, 3),
которые могут быть записаны в виде
о,kAk — = 0 или (c{h — = О,
гДе — символ Кронекера.
Развернем эти уравнения:
(он — X)4i + СцАг + СцАз = О,
O21Д i 4" (й22— Х)Лг -|- ЩзДз = О,
ОзИ 1 4- ОзгДг 4" (Озз — Х)4з = 0.
Эта однородная система служит для определения At, А2 и А3. При
зтом ищется отличное от нуля (нетривиальное) решение этой
системы.
Как известно, однородная система имеет нетривиальное ре-
шение только в том случае, если определитель ее равен нулю, т. е.
ст — X О,/ о, „ 1
11 12 13
°22 — °23 = о,
°81 °32 °33
55
что кратко записывается в виде
| Gift X§jft | = О*
Это кубическое уравнение называется вековым уравнением тен-
зора.
Три его корня X], Х2, Х3 дают три возможных значения, при
которых приведенная выше система уравнений имеет отличное
от нуля решение. Каждый из корней определяет направление, в
котором радиус-вектор поверхности второго порядка параллелен
одной из главных осей.
Вековое уравнение для нашего случая имеет вид
(25 - X) [(7 - X) (13 - X) - 27] = О,
или
X2 —20Х + 64 = 0.
Находим
Х2, з = 10 ± flOO-64 = 10 ± 6, X, = 25, Х2 = 16, Х3 = 4.
Таким образом, значения диагональных компонент тензора
проводимости в главных осях равны (в Ом-1-м-1)
oj = 25 • IO"7, о2 = 16 • IO-7, Оз = 4 . ю-7.
Найдем теперь направления главных осей тензора а,-; относи-
тельно исходной системы координат. Пусть А{1\ А^2\ А<3> —
векторы, направленные по главным осям. Обозначим через Л^\
компоненты вектора А(1\ Для нахождения этих ком-
понент подставим в систему линейных уравнений значение X =
= 25 и вместо Ль Л2, А3 значения Л^х), Л^\ Л^:
25Л<Х) + 0-Л<х) + О-Л^ = 25Л<Х),
о-л<х) + 7Л<1) — з Узл^) = 25Л^\
О-Л*» — 3 Узл<1} + 13Л<Х) = 25Л<Х>.
Отсюда получаем: Л^ — любое, Л^ и Л^ равные нулю.
Чтобы найти направляющие косинусы главной оси тензора, соот-
ветствующей значению Xi, относительно исходных осей тензора,
вектор А^ нужно пронормировать; в нашем случае это дает
Л*1’ = + 1, А™ = Л<х> = 0.
L А о -
Поступая аналогичным образом со значениями Х2 и Х3, по-
лучаем, что
Л^ = 0, Л<2> = 1/2, 42) = -УЗ/2,
Л<3> = 0, Л<®> = Уз/2, Л<3>=1/2.
56
Таким образом, таблица направляющих косинусов, задающая
ориентацию главных осей тензора [<ц3] относительно исходных
осей, имеет вид
Оси Хг ха Л’,
%; 1 0 0
Х2 0 +1/2 —/3/2
Хз 0 /3/2 1/2
4.4. Измерение коэффициентов диэлектрической про-
ницаемости резорцина проводилось на трех различно
Рис. 4.5. Ориентация кристаллических пластинок-срезов, исполь-
зуемых в задаче 4.4.
ориентированных пластинках, показанных на рис. 4.5.
Результаты измерений приведены в таблице.
Номер среза (см. рис, 4.5) S, см2 1, см _1» С. 10 Ф
1 3,305 0,179 5,25
2 0,784 0,255 0,92
3 2,672 0,196 3,92
Каковы главные диэлектрические проницаемости ре-
зорцина?
Решение. Диэлектрические свойства кристаллов класса тт
характеризуются тремя главными значениями диэлектрической
проницаемости: 81, е2 и е3. Обозначим через Xf, Х2, Х3 оси кристал-
лофизической системы координат, связанные с кристаллом в стан-
I *
57
дартной установке, а через Xf, Х2, Х3 — ортогональные оси, свя-
занные с образцом. Если металлизуются грани образца, парал-
лельные плоскости Х±Х2, то, измеряя емкость и размеры получив-
шегося кристаллического конденсатора, можно вычислить вели-
чину диэлектрической проницаемости е33 в направлении оси Xs,
совпадающей с направлением нормали п к пластинке.
Поскольку компоненты тензора [е, J связаны с измеряемыми
величинами едз соотношением типа
то измерения па ориентированных образцах позволяют опреде-
лить все компоненты тензора в кристаллофизической системе ко-
ординат Xi, Х2, А'3.
При этом значения е33 находятся из измерений емкости ука-
занных пластинок С = e3g-5/(4nt), откуда е33 = faitC/S (t — тол-
щина, S — площадь пластинок). Очевидно, из измерений емко-
сти первой пластинки (пластинки Z-среза) сразу можно получить
значение
ез = 3,22.
Ориентация нормали ко -второй пластинке относительно кри-
сталлофизических осей (см. рис. 45) определяется как
пх - 0, п2 — —sin <р, ’м3 = cos <р, <р = 35°,
а ее диэлектрическая проницаемость
Езз = е2 si°2 S’ + ез cos2 Езз = 3’39-
Соответственно для третьей пластинки
и = — cos ф, п2 = 0, ns = sin <р, <р = 30°,
езз = eicos f + ез Sln S’-
Полагая в последних уравнениях е3 = 3,22 и решая эти уравне-
ния относительно и е2, получаем
ei = 3,26, е2 = 3,74
4.5. Для моноклинного кристалла было найдено, что
величина коэффициента теплового расширения вдоль на-
правления [0101, являющегося осью симметрии второго
порядка, составляет 41 10~6 К-1. Следующие измерения
были сделаны в плоскости (010). При этом оказалось, что
величина коэффициента теплового расширения по двум
взаимно перпендикулярным направлениям в плоскости
(010) равна 32 10-6 и 15 10—6 К-1, а вдоль направления,
58
составляющего угол в 45° с указанными направлениями,
составила 16 • 10_® К-1. Определить коэффициенты тензо-
ра [оц,] в стандартной установке, а также значения его
главных коэффициентов.
Решение. В моноклинных кристаллах одна из главных
осей тензора (в стандартной установке — ось Х2) совпадает с на-
правлением [010], являющимся либо осью симметрии 2, либо
нормалью к плоскости симметрии. Две остальные главные оси
тензора относительно этого направления могут иметь различные
ориентации, ввиду чего тензор [ai3] такого кристалла содержит
четыре независимых компоненты. Совместим с направлением [010]
ось Х2, взаимно перпендикулярные направления, лежащие в пло-
скости (010), вдоль которых были получены величины теплового
расширения 32 • 10-Е и 15- 10“6 К-1, совместим соответственно с
осями Xs и X]. При таком выборе системы координат
ап = 15 • 10-6 К-1, аа = 41 10~6 К-1, ass = 32 IO"6 K~i,
а коэффициент теплового расширения вдоль направления, состав-
ляющего угол в 45° с осями Х3 и Хг, найдется из соотношения
а„ == ацгцп! = ’/2 (“и + азз + 2а13).
Отсюда а13 = —7,5 • 10-6 К-1.
Следовательно, тензор теплового расширения этого кристалла
в системе координат Хь Х2, Х3, выраженный в 10“6 К-1, имеет вид
[%] =
15
0
— 7,5
0 —7,5’
41 0
0 32
Найдем главные коэффициенты теплового расширения по ме-
тоду, приведенному в задаче 4.3. Они равны щ = 34,8 • 10-6 К-1,
02 = 41 - 10~6 К”1, а3 = 12,2 10-6 К-'1.
Перейдя к главным осям, мы уменьшим число компонент
тензора до трех, но в этом случае необходимо указывать доба-
вочную константу (угол поворота вокруг оси Х2), задающую
ориентацию осей Xj,X2,X3, в которых тензор [«;_,] имеет диаго-
нальный вид, относительно осей Xlt Х2, Х3.
4.6. Измерение коэффициентов теплового расширения
триклинного кристалла проводилось на образце, имеющем
форму куба. При этом были сделаны измерения этих
коэффициентов вдоль ребер куба и трех его объемных
диагоналей. Показать, как по данным измерений могут
быть вычислены компоненты тензора теплового расши-
рения.
59
Решение. Тепловое расширение триклинных кристаллов
в общем случае характеризуется тензором вида
“12 “22 “23
“13 “гЗ “зз
Симметрия триклинных кристаллов не налагает никаких
ограничений на ориентацию характеристической поверхности тен-
зора второго ранга, и ориентация главных осей тензора коэффи-
циентов теплового расширения в кристалле заранее неизвестна.
Поэтому выбираем оси Хц Х* Х3 произвольным образом, напри-
мер совмещаем их с ребрами куба.
В этом случае направляющие косинусы указанных в условии
задачи направлений, вдоль которых измерялись коэффициенты
теплового расширения, будут следующими:
(1, 0, 0), (0, 1, 0), (0, 0, 1), (1/уз, i/уз, 1/УЗ),
(-1/А i/А i/уз?, (1/уз; i/уз; -1/узТ.
Обозначим величины коэффициентов теплового расширения,
измеренные вдоль перечисленных направлений, соответственно
через а^1’, а(2), а(3>, а<4), а(5), а(6). В выбранной координатной
системе, связанной с ребрами куба,
а<1) = “11’ “<2) = “22’ “<3) = “зз-
Используя уравнения типа ап — ацПгП}, гДе ап — коэффици-
енты теплового расширения в направлении и, получаем
а<4> = Т (“и + а22 + “зз + 2“12 + 2“гз + 2а31)’
а<Б> = Т (“11 + “22 + “33 ~ 2“12 + 2а23 ~ 2“з1)-
а<«> = Т (“11 + а22 + “зз + 2“12 ~ 2“гз 2а31)’
Преобразуем эти уравнения к виду
а<«- 1 Т (“11 + “22 + “зз) = 2 Т (“12 + “2з+“з1)’
а<«- Т(а11+“22 + “зз) = 2 3 (““12 + “23 - “з1
Т(а11+а2г + “зз) = 2 3 (“12“ “23 ~“31)-
60
Отсюда находим
~ 4 “зХ = (“(Б) + а<6)) - 4 (“xi+ Ю22 + “зз)>
1 3
кзх = ~2 (ахх + а22 + азз) - Т (а(Б) + а(6))-
Аналогично
3 1
«23 = Т (а<4) + а15)) ~ Т (“Х1 + «22 + «ЗЗ) >
3 1
“12 = Т (“<4) + а(б))~ Т (“Х1 + “22 + “ЗЗ)'
Таким образом определим все независимые компоненты тензора
теплового расширения триклинного кристалла в системе коор-
динат Xh Х2, Хз, связанной с ребрами образца, вырезанного в
форме куба.
Разумеется, осп Xi, Х2, Хз не являются главными для тензо-
ра [“.«Я- В системе своих главных осей Хг, Х%, Х3 тензор [а..]
имеет лишь три главных коэффициента расширения: аг, а2а3.
Но для полного описания теплового расширения кристалла нуж-
но знать не только абсолютные значения коэффициентов тепло-
вого расширения вдоль главных осей X , Х2, Х3, но и ориентацию
этих осей по отношению к фиксированным осям Xlt Х2, Х3. Оче-
видно, для этого нужно задать еще три величины, характеризую-
щие ориентацию осей X],Xi,X3 относительно осей Хь Х2, Х2.
4.7. Как следует ориентировать кальцитовую пластин-
ку, чтобы при нагревании она не изменяла своей тол-
щины?
Решение. Кальцит относится к тригональной сингонии и
ого тепловое расширение характеризуется тремя главными коэф-
фициентами ап, а22, ссзз, при этом ап = аи = —5,6 • 10-6 К-1, а33 =
= 25 10~6 К-1. Поэтому тепловое расширение этого кристалла
для каких-то направлений обязательно будет иметь нулевые зна-
чения. Согласно принципу Неймана симметрия указательной по-
верхности теплового расширения кальцита оо т, поэтому вокруг
оси третьего порядка имеется целый конус направлений, вдоль
которых расширение отсутствует.
Ориентировка пластинки определяется положением нормали
к ее поверхности п относительно кристаллофизической системы
координат. Совместим ось Х3 с единичным вектором п нормали
к пластинке. Тогда значение теплового расширения в направле-
нии толщины пластинки ап = аа3. По условию задачи пластинка
не должна деформироваться в направлении толщины, а это озна-
чает, что а„ = а3з = 0.
61
Рис. 4.6. Указатель-
ная поверхность ко-
эффициента теплово-
го расширения каль-
Согласно (4.6)
j азз = % + Ф22 + пз«зз = «и (И1 + ”2) + Фвз
Учитывая, что п® -f- п| 4- = 1, получаем
I азз = «11 (1 - п1) + Ъз'13 = «11 + («33 - «11) п3-
Очевидно, а33 = 0 при «3 = au/(au ~ а33). пз — это косинус ут-
ла, составляемого нормалью п к пластинке с осью симметрии
третьего порядка кальцита. В данном случае этой величине п3 со-
ответствует угол, равный 64°43'. Следова-
тельно, кальцитовая пластинка с пулевым
тепловым расширением должна быть вы-
резана так, чтобы нормаль к пей составля-
ла с осью третьего порядка угол, равный
64°43'.
Указательная поверхность для тепло-
вого расширения является двухполостпой
поверхностью вращения вокруг оси Х3. Ее
сечение изображено на рис. 4.6.
Задачи
4.8. Показать, что свойства, опи-
сываемые тензором второго ранга,
присущи кристаллам любой сим-
натной плоскостью метрии.
-У1-У3. 4.9. Как должен выглядеть тен-
зор коэффициентов теплового рас-
ширения кристалла в главных осях, чтобы кристалл об-
ладал направлениями нулевого расширения?
4.10. Найти величину коэффициента теплового расши-
рения в направлении нормали к плоскости симметрии в
кристалле KDP.
4.11. Найти величину удельного сопротивления кварца
в направлении биссектрисы угла между осями симметрии
третьего и второго порядков и в направлении биссектрисы
угла между осями симметрии второго порядка. Объяснить
полученный результат.
4.12. Найти величину относительной диэлектрической
проницаемости сегнетовой соли в направлениях биссект-
рис углов между каждой из пар осей симметрии второго
порядка *).
*) Во всех задачах § 4 имеется в виду кристалл сегнетовой
соли в сегнетофазе, свойства которого приведены в табл. 14.
62
*1 4.13. Найти величину удельного сопротивления кри-
сталла в направлении (1/Т'З, 1/Т'З, 1/Т'З) относительно си-
стемы координат, в которой удельная проводимость
(в 10-7 Ом-1 • см-1') этого кристалла описывается тензором
вида
-25 0 0 -
О 7 — З^Т •
- О -3^3 13
4.14. Определить угол между направлением электриче-
ского поля и тока в кристалле кварца, если поле прило-
жено к рабочим граням пластины 45° У-среза.
4.15. В плоский конденсатор вставлена пластипка из
гипса площадью 1 X 2,5 см2 и толщиной 0,4 см, вырезан-
ная таким образом, что нормаль к ее поверхности состав-
ляет с кристаллофизическими осями углы:
^X,ON == 90°, ^X2ON = 30°, ^X3ON = 60°.
Найти емкость такого конденсатора.
4.16. Вычислить суммарный заряд, возникающий па
поверхности пластинки из кристалла арагонита размером
2 X 4 X 0,2 см3, вырезанной перпендикулярно направле-
нию (1/V2, 0, 1/V2), если нластипка помещена в электри-
ческое поле напряженностью 400 В/см. Направление по-
ля совпадает с направлением нормали к пластинке.
4.17. Определить тензор диэлектрической проницаемо-
сти кварца:
а) в системе координат, повернутой относительно кри-
сталлофизической системы па угол 30° вокруг оси X, по
часовой стрелке;
б) в системе координат, повернутой вокруг осп Xi
кристаллофизической системы па угол 30° против часовой
стрелки;
в!) в системе координат, повернутой вокруг оси Х3
кристаллофизической системы координат на угол 60° по
и против часовой стрелки.
Объяснить полученные результаты.
4.18. Тензор относительной диэлектрической проницае-
мости некоторого кристалла с симметрией 42?К в кристал-
лофизической системе координат имеет вид
Еу —
’89
0
. 0]
о
89
0
О'
о
173 _
63
Как будет выглядеть этот тензор в системе координат,
связанной с исходной поворотом на угол 45° вокруг оси
Х3, т. е. во второй кристаллофизической установке?
4,19. Найти выражение для энергии поляризованного
ромбического кристалла, если электрическое поле прило-
жено в направлениях: а) [100], б) [0101.
4.20. Как следует вырезать пластинку из моноклинно-
1го кристалла, обладающую наименьшей величиной тепло-
вого расширения, если тепловое расширение (10-6 К“9
этого кристалла в системе ортогональных осей Хъ Х2, Х3
описывается тензором вида
10 — 5 О'
— 5 20 0 ?
0 0 80
• 4.21. Как ориентировать пластинку из кальцита, чтобы
| коэффициент теплового расширения в направлении ее тол-
щины был равен 15 10-6 К-’?
4.22. В каких направлениях кристаллы графита не
I испытывают расширения при нагревании?
4.23. Диэлектрическая проницаемость моноклинного
кристалла в ортогональной системе координат Хи Х2, Х3
1 задается тензором вида
'10 5 0‘
5 20 0 .
. 0 0 30
Как следует вырезать кристаллическую пластинку
фиксированных размеров, обладающую наибольшей ем-
костью?
4.24. Определить ориентацию главных осей тензора
теплового расширения моноклинного кристалла относи-
тельно ортогональных осей Хи Х2, Х3, в которых тепло-
вое расширение кристалла (в 10~6 К-1) описывается тен-
зором вида
Г 15 0 —7,5'
0 41 0 .
L—7,5 0 32
4.25. Какой должна быть точность ориентации пласти-
нок кристалла рутила Х-среза, Z-среза и 45° У-среза,
| чтобы их диэлектрическая проницаемость отличалась от
расчетной не более чем на 2%?
4.26. Как изменится температура кварцевой пластин-
। кп, ориентированной так, как представлено па рис. 4.3, б,
64
при кратковременном воздействии на нее силы, десяти-
кратно превышающей ее вес? Размеры пластинки 1 X 3 X
X 10 мм3. Рассмотреть три случая приложения силы к
каждой паре взаимно параллельных граней.
4.27. Кристаллическая пластинка L-среза сегнетовой
соли помещена в электрическое поле напряженностью
200 В/см. Определить плотность зарядов, возникающих на
ее боковых гранях. Решить задачу с учетом и без учета
электрической проводимости кристалла.
4.28. В кристаллах каких классов симметрии направ-
ления главных осей тензоров, описывающих различные
свойства кристаллов ([еч], [а«], [а«] и другие), совпада-
ют? не совпадают?
4.29. В кристаллах каких классов симметрии нагрева-
ние приводит к изменению направлений главных осей
тензора диэлектрической проницаемости?
4.30. В кристаллах каких классов симметрии, совпада-
ют паправления главных осей тензоров удельной прово-
димости и удельного сопротивления?
4.31. Вывести уравнение указательной поверхности ди-
электрической проницаемости триклинного кристалла.
4.32. Пластинка сегнетовой соли вырезана так, что нор-
маль к ней составляет с осями координат углы 30, 70 и
08,6°. Найти коэффициент теплового расширения пла-
стинки.
4.33. Определить теплопроводность кварцевой пластин-
ки, вырезанной параллельно естественной грани ромбо-
эдра (10111), если угол между нормалью к пластинке и
осью Х3 составляет 52°.
4.34. Пластинка толщиной 4 мм вырезана из монокри-
сталлического висмута так, что нормаль к пластинке со-
ставляет с осью третьего порядка угол, равный 30°. Най-
ти плотность тока, протекающего через такую пластинку,
если к ее рабочим граням приложено электрическое на-
пряжение 1 В.
4.35. Из монокристаллического висмута вырезан стер-
жень диаметром 1 см таким образом, что ось стержня со-
ставляет с осью третьего порядка угол 30°. Разность по-
тенциалов вдоль длины стержня поддерживается постоян-
ной и равной 1 В/см. Найти максимальное значение раз-
ности потенциалов между двумя диаметрально противопо-
ложными точками сечения, перпендикулярного осп
стержня.
5 Н. В. Переломова, M. М. Тагиева
65
§ 5. НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ В КРИСТАЛЛАХ. АНАЛИЗ
НАПРЯЖЕННОГО СОСТОЯНИЯ
Состояние однородного напряжения в некоторой точке
сплошной однородной среды может быть представлено де-
вятью компонентами тензора напряжении в произвольно
выбранной системе координат
*11
*21
*31
*12
*22
*32
*13
*23
*33
Здесь приняты следующие обозначения напряжений:
первый индекс компоненты тензора напряжений относит-
Рис. 5.1. Физический смысл
компонент тензора напряже-
ний.
ся к направлению силы,
второй — к направлению
нормали к площадке, на
которую действует сила
(рис. 5.1). Например, на-
пряжение t32 означает ком-
поненту силы в направле-
нии оси Х3, действующей
на единичную площадку,
перпендикулярную оси Х2.
Очевидно, t{{, т. е. диаго-
нальные, или так называ-
емые нормальные, компо-
ненты тензора напряже-
ний являются растягива-
ющими (сжимающими)
напряжениями в направ-
лении координатных осей; ti} (i f) — сдвиговые, или ка-
сательные, напряжения, лежащие в плоскости тех площа-
док, па которые они действуют. Из условия статического
равновесия моментов относительно координатных осей
Xt, Х2 и A’s вытекает равенство педиагональных компо-
нент тензора [£„]:
?12 --- ^21> ^23 = ^32, ^31 -------- tl
(5.1)
Отсюда следует, что напряженное состояние полностью
описывается шестью независимыми компонентами тензора
напряжений: тремя нормальными tn, t22 и t33 и тремя
касательными tl2, ti3 и t23.
Можно показать, что соотношения (5.1) остаются спра-
ведливыми даже в тех случаях, когда напряжение неодно-
родно, когда тело пе находится в статическом равновесии
66
и когда присутствуют объемные силы, но отсутствуют
объемные моменты.
Знаки напряжений. Нормальные и касательные напря-
жения считаются положительными, когда они действуют
в направлениях; указанных па рис. 5.1. Отсюда следует,
что нормальные напряжения, соответствующие напряже-
ниям растяжения, являются положительными. Однако при
рассмотрении пьезоэлектрического и пьезооптического эф-
фектов принято обратное правило знаков: здесь положи-
тельными считаются напряжения сжатия.
Главные оси тензора напряжений и поверхность нап-
ряжений. Тензор напряжений симметричен и может быть
приведен к главным осям:
' t 0 0 "
О О
° 0 t3
где Л, i2, t3 — так
называемые главные напряжения.
Рис. 5.2. Определение направ-
ления результирующей силы,
передаваемой через площадку
65, с помощью характеристиче-
ского эллипсоида напряжений.
Рис. 5.3. Напряжения, дейст-
вующие на площадку произ-
вольной ориентации: tT — пол-
ное напряжение, — каса-
тельное напряжение, tn — нор-
мальное напряжение.
Главные оси тензора напряжений замечательны тем,
что на площадках, перпендикулярных к ним, компоненты
касательного напряжения отсутствуют.
Характеристическая поверхность второго порядка, со-
ответствующая тензору [Jyl, называется поверхностью на-
пряжений. Ее уравнение имеет вид
tiPCiXj = 1
(5.2)
67
5*
или при переходе к главным осям
+ ^2-г2 + ^зхз — !•
Поскольку каждое из напряжений ti, t2, t3 может быть
I как положительным, так и отрицательным, поверхность
.напряжений может быть действительным или мнимым
эллипсоидом или гиперболоидом. Направление результи-
рующей силы P6S, действующей па элемент поверхности
6S, может быть найдено с помощью свойства радиуса-век
тора и нормали к поверхности напряжений (рис. 5.2).
Длина вектора г определяет нормальное напряжение t„,
действующее на элемент поверхности 6S, показанный на
рис. 5.2, а именно
tn = 1/г2.
Полное, нормальное, касательное, среднее и эффектив-
ное напряжения. При решении практических задач часто
оказывается необходимым определять следующие вели-
чины:
а) Полное напряжение tr, действующее на площадку
с нормалью п (рис. 5.3):
(5.3)
где
tri tijTlj.
б) Нормальное напряжение tn, действующее на пло-
щадку с той же нормалью:
tn = tijiiinj. (5.4)
в) Касательное напряжение tt в плоскости той же пло-
щадки:
= (5.5)
г) Максимальное касательное напряжение <™ах, дейст-
вующее в плоскости XiX2:
>i°“~ К~Г‘”)’.+(5-6>
Аналогичные соотношения справедливы для напряже-
ний i™ux, действующих в плоскостях Х^ и Х2Х3.
д) Среднее напряжение tm:
U = 1/3(/n + Z22 + ^). (5.7)
68
е) Эффективное пли обобщенное напряжение:
t2 = 4 W11 - + (^22 - *33)2 + (*33 - *il)2] +
+ 3 (ij2 + i|3 + t^. (5.8)
Тензор напряжений как пример полевого тензора. Тен-
зор напряжений близок по смыслу к силе, приложенной
к кристаллу. Поэтому тензор напряжений не зависит от
симметрии кристалла. Этот
для кристаллов, но и для
изотропных тел, находя-
щихся в напряженном со-
стоянии. Такой тензор на-
зывается полевым, в отли-
чие от материальных тен-
зоров, которые описывают
физические свойства кри-
сталла и связаны с его
симметрией.
Анализ деформаций.
Для деформированного те-
ла существенны не абсо-
лютные смещения, а сме-
щения его точек отпоси-
тензор имеет смысл не только
Рис. 5.4. Смещение точек тела при
деформации.
тельно друг друга.
Чтобы описать деформацию тела, свяжем с ним пря-
моугольную систему координат XiX2Xs.
Пусть при деформировании положение начала коорди-
нат не изменяется, а все прочие точки получают некото-
рые смещения. Если точка А (рис. 5.4) займет положе-
ние А', а точка В, отстоящая от А на расстоянии Вх,
займет положение В', то точки А и В получат смещения,
выражаемые векторами иА и и® соответственно.
Вектор и называется вектором смещения; щ — — хг),
где i = 1, 2, 3; xt — координаты точки тела до деформа-
ции, Xi — ее координаты после деформации.
Так как при деформациях существенно смещение то-
чек тела относительно друг друга, необходимо рассматри-
вать вектор Ди = и® — пА, представляющий собой прира-
щение смещений точек, первоначально отстоящих друг от
друга на расстоянии Лх.
Если и, = Xi — Xi постоянно для всех i и для всех то-
чек тела, то Дп = 0 и деформации тела отсутствуют, т. е.
имеет место перенос тела параллельно самому себе. При
69
деформациях смещения для различных точек будут раз-
личны.
Однородными деформациями называются деформации,
при которых компоненты вектора смещения являются ли-
нейными функциями координат:
щ = e^Xi + е12х2 + е13ж3,
u2 = ez-iXi + е22х2 + е23ха, (5.9)
и2 = ~h е32х2 В е22х2.
Значения еи не зависят от величины смещения.
Для приращения смещений в случае однородной де-
формации можно записать
Дщ = e^AXi + е12Дх2 + е13Дж3,
Дп2 = е21 Дх, + е22Дл:2 + е23Дл;3, (5.10)
Дп3 = e31Az! + е32Дх2 + е33Дж3.
Выражения (5.10) определяют вектор-векторное взаи-
модействие, а девять величин etj = dujdxj представляет
собой тензор второго ранга:
[Ojl —
е11
е21
631
ei2
е22
е32
егз
в23
езз
(5.11)
Тензор [еу1 носит название тензора малых смещений.
В общем случае этот тензор несимметричен. Он всегда
может быть представлен в виде суммы симметричного и
антисимметричного тензоров:
еи = Гц + оу, (5.12)
где
Гц = V2(ea + ел) = Гц, (5.13)
Очевидно, тензор [гД является симметричным. Тензор
[соу] антисимметричен:
со« = V2(ey — ел) = —coji. (5.14)
Он описывает вращение тела как целого вокруг непод-
вижной оси без смещения его точек относительно друг
друга.
Тензор [rj представляет собой собственно тензор де-
формаций.
Относительное изменение объема тела
А В/В == г‘ц = Гл В г22 + г33. (о. 1а)
70
Диагональные компоненты тензора [ry] — ru, r22, г33 — яв-
ляются деформациями сжатия или растяжения элементов
единичной длины вдоль осей координат (рис. 5.5). Не-
диагональйые компоненты — rs2, r3l, rl2 — определяют
сдвиговые деформации. При этом, например, величина
2г32 равна изменению угла между двумя элементами, рас-
положенными до деформации параллельно осям Х3 и Х2
(рис. 5.6). Аналогичный смысл имеют компоненты г13 и г12.
Рис. 5.5. Деформация куба еди-
ничных размеров с ребрами, па-
раллельными главным осям де-
формации.
Рис. 5.6. Поворот отрезков,
параллельных осям коорди-
нат, при деформациях
сдвига.
Знаки деформаций. Положительными принято считать
деформации растяжения. Сдвиговые деформации счита-
ются положительными в том случае, если в процессе де-
формации происходит уменьшение угла между линейны-
ми элементами, выделенными в недеформированном теле
параллельно положительным направлениям соответству-
ющих координатных осей. Например, деформация 2г32
считается положительной, если угол между линейными
элементами, параллельными положительным направле-
ниям осей Х2 и Х3, уменьшается (рис. 5.6).
Главные осп и характеристическая поверхность тен-
зора деформаций. Тензор деформаций является симмет-
ричным тензором. Его можно привести к главным осям:
Гх 0 О'
о Г О
О 0 г3
Это означает, что при любых деформациях тела можно
выбрать такую систему координат, в которой деформация
71
Если деформация
Рис. 5.7. Определение на-
правления смещения точки
с помощью характеристи-
ческой поверхности дефор-
маций.
тела может быть представлена только сжатиями и растя-
жениями по трем взаимно перпендикулярным направле-
ниям, без сдвигов.
Деформация может быть представлена характеристи-
ческой поверхностью деформаций, уравнение которой за-
писывается в виде
r^Xj — 1. (5.16)
Эта поверхность может быть как действительным, так и
мнимым эллипсоидом или гиперболоидом.
является однородной, то смещение
за счет деформации определя-
ется как *
пг = гвж5. (5.17)
Направление вектора и и зна-
чение г для любого заданного
направления 1 могут быть най-
дены с помощью свойства радиу-
са-вектора и нормали к поверх-
ности деформаций (рис. 5.7).
Удлинение в произвольном на-
правлении 1 выражается в виде
Г=ГцЦ}. (5.18)
Эллипсоид деформаций. Для наглядного представле-
ния деформации тела удобно пользоваться так называе-
мым эллипсоидом деформаций. Это — поверхность, в кото-
рую перепде.т сфера единичного радиуса, выделенная в
недеформпрованном теле, после деформации этого тела.
Уравнение сферы единичного радиуса
#1 У У жз = 1-
Зафиксируем радиус-вектор Ох этой сферы. Его коор-
динаты (ж,, хг, хг). После деформации тела, описываемой
тензором
' гг 0 0 "
° г2 °
° ° г3
этот радиус-вектор превращается в вектор Ох' с коорди-
/ * / • >
патами х^, #2, ,т3 (рис. 5.8). Компоненты вектора Ох'
72
связаны с компонентами вектора Ох уравнениями
х[ = ^1(1 + '1)» х'г — (1 + гг), = я3 (1 + г3).
....
Если выразить из этих уравнений значения компо-
нент вектора Ох и подставить их в уравнение сферы еди-
ничного радиуса, то получим выражение
*1
(1+гх)2
2______।________3
(1 + г2)2 (1 + г3)2
(5.19)
распределение де-
Это и будет уравнение эллипсоида деформаций. Эллипсо-
ид деформаций наглядно показывает
формаций в теле: например,
направления наибольших, наи-
меньших и т. п. деформаций.
Тензор деформаций и прин-
цип Неймана. Деформации, опи-
сывающие реакцию кристалла
на внешнее воздействие, не яв-
ляются его физическим свой-
ством. В силу этого тензор де-
формаций, подобно тензору на-
пряжений, не подчиняется
принципу Неймана.
Исключение составля!от де-
формации, вызванные измене-
нием температуры (тепловое
расширение) кристаллов.
Тепловое расширение. При однородном изменении тем-
пературы кристалла на величину ДУ кристалл испытыва-
ет однородную деформацию, описываемую уравнением
Рис.
5.8. Деформация сфе-
ры единичного радиуса.
гц = ацкТ,
(5.20)
где ац — коэффициенты теплового расширения, являющие-
ся компонентами симметричного тензора второго ранга.
Существуют три главных коэффициента теплового рас-
ширения — сц, az, as, и соответствующие им главные на-
правления, деформация вдоль которых может быть най-
дена из соотношений
Г1 = аЛУ, г2 = а2ДУ, г3 = а3ДУ,
где сц, а2, «3 — главные коэффициенты расширения.
73
Примеры решения задач
5.1. К кристаллической пластинке L-среза ADP (см.
рис. 2.4) приложили одноосное механическое напряже-
ние сжатия t в направлении нормали к ее рабочим гра-
ням. Как будет выглядеть тензор напряжений в кристал-
лофизической системе координат?
Решение. Направление сжатия п (щ, и2, п3) совместим с
осью Х3 новой штрихованной системы координат, связанной с реб-
рами пластинки £-среза. В этом случае тецзор, характеризующий
напряженное состояние кристаллической пластинки в штрихован-
ных осях, запишется в виде
О о -
О О
О *зз-
0 0 О'
0 0 о
О О — t
где *зз = - t.
Чтобы перейти к кристаллофизической системе координат,
нужпо воспользоваться законом преобразования компонент тензо-
ра второго ранга (4.2а)
*ij ~ C3iC3j*33 — ПгП3 ( *)•
Тогда
*11 = “ П1*’ *33 = “ К1*’
*12 = *21 = ~ «Л*’ *13 = *31 = - ИЛ*>
*23 = *32 = “ К2В3*-
Напряженное , состояние кристалла в кристаллофизической
системе координат имеет вид
П1
пл
пл
К1,г2
П1
П2П3
П1П3
'г2'г3
П1
(^ *)
Таким образом, одноосное напряжение, задаваемое произ-
вольным направлением n (щ, п2, Пз) относительно кристаллофп-
зической системы координат, в этой системе представляется тен-
зором напряжений общего впда, имеющим как нормальные, так
и сдвиговые компоненты.
5.2. Напряженное состояние кристалла кварца в
кристаллофизической системе координат задается следую-
щим образом:
tn = 10 Н/смг, 122 = 20 Н/см2, t33 == 30 Н/см2, tl2 = —5 Н/см2.
74
Определить: а) величину экстремальных нормальных
напряжений; б) ориентацию плоскости, испытывающей
максимальное п минимальное нормальные напряжения.
Решение, а) Очевидно указанное напряженное состоя-
ние (в Н/см2) задается тензором
'10—5 0"
— 5 20 0 .
_ 0 0 30.
Для нахождения экстремальных значении нормальных на-
пряжений необходимо определить главные напряжения, т. е.
привести тензор к главным осям. Одно из главных напряжений
определяется сразу же по виду данного тензора, а именно
«з = 30 Н/см2.
Определим главные напряжения tr и t2:
I 10 — t — 5 I
1-5 20 — 11 ~ °’
t? — 30f + 17,5 = 0, t!, 2 .= 15 ± 7,1.
Отсюда
ft = 22,1 Н/см2, «2 = 7,9 Н/см2.
Следовательно, максимальная величина нормального напряжения,
испытываемого кристаллом, равна 30 Н/см2, минимальная величи-
на нормального напряжения равна 7,9 Н/см2.
б) Чтобы ответить па второй вопрос задачи, надо найти на-
правляющие косинусы главных напряжений относительно исход-
ных крпсталлофизпческих осей; воспользовавшись для этой цели
методом, описанным в задаче 4.3, получаем
n(/> = 0,925, п™ = — 0,384, = 0,
и<2> = 0,384, п<2) = 0,925, и(32) = 0,
= п(з) = о, к<з) = !.
Таким образом, максимальное нормальное напряжение, рав-
ное 30 Н/см2, испытывает плоскость, нормаль к которой имеет
направляющие косинусы (0, 0, 1). Минимальное нормальное на-
пряжение, равное 7,9 Н/см2, испытывает плоскость, нормаль к ко-
торой имеет направляющие косинусы (0,384; 0,925; 0).
5.3. Приложение электрического поля к рабочим гра-
ням кристаллической пластинки Х-среза сегнетовой соли
(см. рис. 2.3) вызывает в такой пластинке деформацию
сдвига в плоскости Х2Х3. Как следует направить ребра
пластинки Х-среза, чтобы указанное состояние деформа-
55
ций представляло собой деформации сжатия — растяже-
ния в направлении ее ребер?
Решение. Очевидно, деформированное состояние пластин-
ки Х-среза в системе осей, связанных с ее ребрами, описывается
тензором
гО 0 0 т
0 0
ДО •
L° Г23 0 J
Деформации растяжения и сжатия представляют собой диа-
гональные компоненты тензора [г^,], поэтому для их пахождепия
тензор деформаций следует привести к главным осям.
Приведение к главным осям заданного тензора осуществляет-
ся поворотом на 45° вокруг оси Хд при этом тензор [г,,-] прини-
мает вид
'О О О’
Or 0 ,
.0 0 —г.
где |г| = |г23|.
Следовательно, для получения деформаций сжатия — растя-
жения с помощью пластинки Х-среза сегнетовой солп при при-
ложении электрического поля к ее рабочим граням, такая пла-
стинка должна быть вырезапа так, чтобы ее ребра составляли с
осями Х2 и Х3 углы, равные 45°. Такие пластинки называются
45° Х-срезами.
5.4. При упругой деформации кристаллического об-
разца, имеющего форму куба размером 1X1X1 см3, его
точки испытывают следующие смещения:
ut = (4^! + Зж2 — 5ж3) - 10~4 см,
и2 = (7xt — 13ж2 + 4ж3) - 10-4 см,
и3 — (9^1 — 2ж2-+ 4ж3) 10’4 см.
Найти изменение углов между ребрамп куба и изме-
нение его объема при деформации.
Решение. Тензор малых смещении, тензор деформаций
и тензор вращений соответственно равны
76
Изменение углов между ребрами куба единичных размеров
характеризуется недиагональными значениями компонент тензо-
ра rij, т. е. компонентами ri2, г23, г13. Угол между ребрами, па-
раллельными осям Xi и Х2, будет равен 112л — 2ri2. Изменение
этого угла равно величине 2 г ^2.
Изменения углов между ребрами, параллельными осям Xj и
Х2, Xi и Х3, Х2 и Хз до деформации, соответственно равны
2г12 = 3,42', 2г13 = 1,2', 2г23 = 0,68'.
Лу/. .'Гц
Относительное изменение объема AV/F найдется как сумма
диагональных компонент тензора [ri3], т. е. оно равно —5 • 10~4.
5.5. Состояние упругой деформации кристалла задает-
ся в виде:
Определить вид характеристической поверхности де-
формаций, а также поверхность, в которую переходит
сфера единичного радпуса после деформаций, определя-
емых данными тензорами.
Решение, а) Тензор деформаций приведен к главным осям
деформации, следовательно, уравнение соответствующей ему ха-
рактеристической поверхности деформаций имеет вид
0,001.^2 — 0,004^2 + 0,008ж| = 1.
Эта поверхность деформаций является однополостным гиперболо-
идом. Выделим в недеформированном кристалле сферу единично-
го радиуса. Ее уравнение запишется в виде
4 + 4 + 4 = 1-
Текущие координаты новой поверхности, получившейся из сферы
после деформации, найдутся из соотношений
4 = *1 + 4 = *2 + w2- 4 = Х3 + “з-
Так как И; = TijXj, ТО Щ — Г1Я], и2 = r2X2, US = Г3Х3,
4 = Х1 (4+'г1)’ '4 = х2 (! + гг)’ 4 = хз (! + '•?)•
Уравнение поверхности, получившейся после деформации сфе-
ры, имеет вид
/2 /2
OW (l + r2)2 + (l + r3)a==1-
77
Для нашего случая
X 3*^ 'г
_____а____ + л +____h_____= 1.
(1 + 0,001)2__________________________(1 — 0,004)2_(1 — 0,008)2
Очевидно, что выделенная в недеформированном кристалле
сфера • после деформации превратилась в трехосный эллипсоид
с полуосями 1,001; 0,996 и 0,992.
б) Уравнение характеристической поверхности деформаций в
этом случае имеет вид 0,0001к2-}-0,001к2 = 1 или ж2 + Юж2 == 104>
т. е. поверхность деформаций имеет форму цилиндра с элли"ти-
ческим сечением.
Выделим в недеформированном кристалле единичную сферу
^ + ^ + ^ = 1.
После деформации единичная сфера превращается в по-
верхность
>2 л2 ,2
к. г, х
----± ' -= —L — = 1
(1.0001)2-----(1,001)2 П 1
которая представляет собой трехосный эллипсоид с полуосями
1,0001; 1,001 и 1.
5.6. Чтобы найти коэффициенты теплового расшире-
ния кристаллов этилендиаминтартрата (EDT), были сдела-
ны измерения коэффициента теплового расширения а.
в четырех различных направлениях.
Параллельно направлению [010], являющемуся осью симметрии второго порядка 20,3 -10~8 К"1
В двух взаимно перпендикулярных направле- ниях, лежащих в плоскости (010); п(Ч пт 80-IO”6 К-1 0
В направлении п(3), лежащем в плоскости (010) и составляющем угол 45° с направлениями nW и п(2) 8-10-8К-х
Определить коэффициенты, характеризующие линейное
расширение кристаллов EDT при нагревании, а также
значения наибольшего и наименьшего коэффициентов
теплового расширения. Какое предварительное заключение
можно сделать о поведении кристаллов EDT в условиях
неравномерного нагрева?
78
Р е ш е й и е. Тепловое расширение кристаллов класса z ха-
рактеризуется четырьмя коэффициентами (см. задачу 42). Выбе-
рем координатные оси: ось Х2 совместим с направлением [010],
оси Х3 и Xi в плоскости (010). Одно из направлений в плоскости
(010), скажем то, вдоль которого величина теплового расширения
оказалась равной 80 • 10-6 К-1, обозначим через Х2, а направление,
соответствующее нулевой величине теплового расширения,—
через X,.
Тогда в выбранной системе координат
ап = 0, а22 = 20,03-10-6 К-1, а33 = 80- 10~е К-*.
Чтобы найти коэффициент Щз, используем величину теплово-
го расширения, измеренную вдоль направления, составляющего
угол 45° с направлениями осей Xi и Х3.
Обозначим это направление через 1: тогда его направляющие
косинусы относительно осей Xi, Х2 и Хз равны 1/}2, 0 и 1/У2, и
тепловое расширение в направлении I найдется из уравнения а( =
= которое в нашем случае принимает вид
az = '/а (ац + Изз + 2<Х]3).
Подставляя в последнее соотношение значения а/, ац й азз,
получаем
8.10-6 = i/2(80 + 2ctIS) - IO"6 К-1;
отсюда
а13 = -32-Ю-6 К"1.
Следовательно, коэффициенты, характеризующие тепловое
расширение кристаллов EDT в выбранной координатной системе
Xi, Х2, Хз, равны (в IO-6 ц-1)
ап = 0, «22 = 20,03, «зз = 80, ais=—32.
Для определения наибольшего и наименьшего коэффициентов
необходимо найти значения главных коэффициентов ab а2 и а3
(в IO-6 к~!), т. е: привести тензор
' 0 0 —32'
0 20,03 0
32 0 80.
к главным осям. Очевидно, ось Х2 является главной осью данного
тензора; отсюда а2=20,03-10~6 К-1.
Значения коэффициентов aj и а3 определяются методом, опи-
санным в задаче 4.3. Таким образом, главные коэффициенты теп-
лового расширения кристаллов EDT равны (в 10“6 К-1)
aj = 91,2 (наибольший), а2 — 20,03, а3 = —11,2 (наименьший).
79
Значения коэффициентов теплового расширения EDT свиде-
тельствуют о необычном характере теплового расширения этого
кристалла: в одном направлении кристалл имеет очень высокий
положительный коэффициент линейного расширения (91,2-10-6),
а в перпендикулярном направленпп — небольшой отрицательный
коэффициент (—11,2-‘10~6). Ввиду этого кристалл оказывается
хрупким в условиях резкого не-
% равномерного нагрева и охлажде-
3 ния, что затрудняет его исполь-
зование.
Рис. 5.9. Углы между гранями
(100) и (110), (001) и (011)
кристаллов арагонита.
5.7. Параметры ячейки
арагонита
а : b : с = 0,6224 : 1: 0,7206.
При нагревании от 0 до
100 °C угол <р между гранями
(100) и (110) уменьшается
па 1,14', а угол у между гра-
нями (001) и (011) возраста-
ет на 2,84" (рис. 5.9). Коэф-
фициент объемного расши-
рения этого кристалла равен
62,0 • 10~6 К-1. Вычислить
три главных коэффициента
теплового расширения.
Решение. Тепловое расши-
рение кристаллов арагонита опи-
сывается тремя главными коэф-
фициентами линейного расшире-
ния аь аз и а3, а коэффициент
объемного расширения р находит-
ся как сумма коэффициентов ли-
нейного расширения, т. е. р =
= И] + аг + аз. При однородном
нагревании на температуру ДГ
кристалл испытывает однородную
деформацию, описываемую уравнением rjj = a,jA7’. Выразим из-
менение углов между заданными кристаллографическими плоско-*
стями через параметры ячейки и коэффициенты линейного расши-
рения арагонита. Запишем:
tg <р — ajb, tg f = с/Ъ.
При возрастании температуры кристалла на AZ параметры его
ячейки изменяются. Обозначим штрихованными буквами значе-
|80
ния параметров ячейки и углов между указанными плоскостями
кристалла при пзмененпи его температуры па ДГ; тогда
а,' = а (1 + аДГ), Ъ' = Ь (1 + а2Д7’), с' = с (1 + а5Д 7’).
Углы между плоскостями (100) и (110), (001) и (ОН) также
изменяются, п их величина может быть найдена пз следующих
соотношений;
а' (1 + 04ДГ) а (1 + а^Т)
tg ф - — р + b - + tg <р -
= [1 + Д7 (Kj—a2)]tg ф.
С другой стороны,
1
ф' = ф + Дф, tg ф' = tg (ф + Дф) = tg ф +-2— ДФ-
COS ф
Приравнивая правые части уравнений для tg ф\ получаем
ДГ (а — а ) = —7---1----Дф.
41 sin ф cos ф
„ . а а2 + Ь2 Д<р
Поскольку sin ф =-----====- то а. — а =----------------!—
gaa + 62' ab М
Аналогичным образом, если положить tg 7 = с/Ь,
с’ G + %Д7’) с
tg? = — =-(1— а-дгр =[1+А7’(%-«2)]‘ёТ.
Отсюда
4 _2 I
(a3 “ aa) ДГ = ----•-------ДТ-
' sin у cos у Ъс
Итак, мы получили следующие соотношения:
₽ = а, + а2 + а3,
2 । ,2 2 _L г2
(«1 - сх2) Д7 = Дф, (а3 - а2) Д7 = J—— Ду.
С/»-'
Учитывая, что а: b : с = 0,6224 : 1 : 0,7206, Дф = —1,14', Ду = 2,84",
Р = 62-10-6 К-1, и разрешая систему приведенных выше уравне-
ний относительно ai, a2 и аз, получаем
й! = ад-Ю-вК-1, a2 = 17,3-10-6К-', а3 = 34,7-10-6К"1.
Задачи
5.8. Напряженное состояние (в Н/см2) кристалличе-
ской пластинки L-среза сегнетовой соли (см. рис. 2.4)
в кристаллофпзической системе координат задается
6 Н. В. Переломова, М. М. Тагиева 81
тензором
’50 0 О'
О 50 О
О 0 75
Определить величину полного, нормального и каса-
тельного напряжений, действующих на пластинку.
5.9. Напряженное состояние (в 102 Н/см2) кристалли-
ческого образца задается тензором
2 2 0"
2 2 0
0 0 9
Найти систему координат, в которой данное напряжен-
ное состояние можно рассматривать только как систему
сжатий и растяжений.
5.10. Напряженное состояние кристалла задается тен-
зором вида
0 0 *зз
Найти нормальное и касательное напряжения,, дейст-
вующие на плоскость, нормаль к которой лежит в пло-
скости XfX2 и образует угол а с осью Хл.
5.11. Общее напряженное состояние в точке кристал-
лического образца задается следующими компонентами
тензора напряжений (в Н/м2):
tu = 50, t22 — 0, t33 = —30, Лг = 50,
t23 = —75, t3l = 80.
Определить величину главных, нормальных и каса-
тельных напряжений.
5.12. При распиливании кристаллов сфалерита на об-
разцы в них возникли напряжения (в Н/м2), описывае-
мые тензором
—10 — 60 О’
— 60 —100 0 .
0 0—100
Найти величину среднего давления, а также величину
максимального касательного напряжения, испытываемо-
го кристаллическими образцами.
82
Д^.13. При малой деформации тела каждая его точка
испытывает малые смещения:
ut — (8a?i + Зж2 — 5;г3) • Ю~5 см,
и2 = (7.Z, + За-2 + 4.г3) • 10~5 см,
и3 — (xt — 8х> + х3) 10-5 см.
Определить тензор деформации тела [г„] и тензор враще-
ний [®„]. Найти объемное расширение тела.
5.14. При малой упругой деформации кристаллическо-
го образца, имеющего форму куба размером 1X1X1 см3,
его точки испытывают смещения:
щ = (4х, + Зж2 — 5^3) • 10-4 см,
и2 = (1х1 — 13ж2 + 4а:3) • 10-4 см,
и3 — (9а;, — 2аг2 + 4ж3) 10-4 см.
Найти изменение углов между ребрами образца и изме-
нение его объема при деформации.
5.15. Тензор упругой деформации кристалла задается
в виде
' 8 — 1
1 Л 6
— 5 О
— 11
О
2
-10’6-
Определить тензор деформаций [гу], тензор вращений
[цю], а также значения главных деформаций.
Л4.16. Кристалл деформирован так, что его деформация
описывается тензором
8 О
О 12
— 4 О
— 4'
О -10“6.
2.
Найти такие три взаимно перпендикулярных направления
в кристалле, которые и после деформации оставались бы
взаимно перпендикулярными.
5.17. В результате обратного пьезоэлектрического эф-
фекта кристаллический образец, представляющий собой
пластинку L-среза сегнетовой соли (см. рис. 2.4), испыты-
вает относительную деформацию растяжения по толщине,
равную 0,005. Как представить деформацию образца в
кристаллофизической системе координат?
5.18. Кубик каменной соли, ориентированный своими
ребрами вдоль направлений типа [100], испытывает
плоскую деформацию так, что относительное удлинение
вдоль ребра [100] составляет 4 10“вдоль ребра [010] —
6* 83
12 • 10~5. Найти относительное удлинение в направле-
ниях [111], [121].
5.19. Плоскопараллельная пластинка, вырезанная из
триклинного кристалла, при нагревании на Л 7’ дефор-
мируется таким образом, что точка А переходит в точку
В (рис. 5.10). Выразить угол АОВ через коэффициенты
теплового расширения.
5.20. Определить вид поверхности, в которую перехо-
дит сфера единичного радиуса, выделенная в ромбическом
кристалле при нагревании его на Д1.
5.21. Найти коэффициенты теплового расширения
гексагонального кристалла, если известен объемный ко-
X эффициент расширения и
изменение отношения его
параметров da при нагре-
-------------------- вании.
-----------______________ 5.22. Прямоугольный кри-
А / сталлический брусок 10 X
# / X 4 X 2 см3 растянут силой
X / 10 Н, приложенной вдоль его
-------------------------Хг длины. Длина бруска при
.----------------------этом увеличилась на 22мкм,
Рис. 5.10. Тепловое расшире- ,а ширина и толщина сокра-
ние плоскопараллельной пла- тнлись на 4 и 1 мкм соот-
стинки.
ветственно.
Определить компоненты тензоров напряжения и де-
формации, предполагая, что ребра бруска длиной 10, 4
и 2 см соответственно параллельны осям Х1г Х2, Х3.
5.23. Прямоугольный изотропный брусок 8X3X2 см3
поместили в жидкость под гидростатическим давлением
1000 Н/см2, при этом объем бруска уменьшился на 1 мм3.
Найти компоненты тензоров напряжения и деформации.
5.24. Кристаллический образец размерами 5X5X2 см3
сжат силой 10 Н, приложенной к граням размерами
5X2 см2, и растянут таким же усилием, действующим
на две другие грани размерами 5X2 см2. Найти компо-
ненты тензора напряжения в системе координат XtX2X:t,
считая, что оси Х2, Х3 параллельны ребрам длиной
5, 5, 2 см соответственно.
Определить компоненты тензора деформации, если
размер образца вдоль осп Xt уменьшился на 2 мкм,
а вдоль оси Х2 увеличился на 2 мкм.
5.25. Гексагональный кристалл в форме тригональной
призмы высотой 5 см и боковыми гранями шириной 1 см
подвергается гидростатическому давлению 10 000 Н/см2,
84
в результате высота призмы увеличивается на 5 мкм,
а ширина боковых граней уменьшается на 1 мкм. Опре-
делить компоненты тензоров напряжения и деформации,
приняв боковое ребро призмы за ось Х3, а одно из ребер
основания за ось Xi.
§ 6. ПЬЕЗОЭЛЕКТРИЧЕСКИЕ СВОЙСТВА КРИСТАЛЛОВ
Прямой пьезоэлектрический эффект. Прямой пьезо-
электрический эффект включает в себя группу явлений,
в которых механические напряжения или деформации вы-
зывают в кристаллах прямо пропорциональную указан-
ным величинам электрическую поляризацию (электриче-
ское поле). При этом механические и электрические вели-
чины оказываются линейно связанными друг с другом.
Прямой пьезоэлектрический эффект описывают уравне-
ния четырех типов:
Р l dtfhtaki (6.1)
Pi = eljkrjk, (6.2)
Ег = -gijktik, (6.3)
Ei = —hijhrjh (i, 7, к = 1, 2, 3), (6.4)
где Pi и Ei — соответственно компоненты вектора элект-
рической поляризации и вектора напряженности электри-
ческого поля, и rik — соответственно компоненты тен-
зора механических напряжений и тензора деформаций,
dift, gift, hijh — пьезоэлектрические коэффициенты,
образующие тензор третьего ранга. Это означает, что при
переходе из координатной системы Х^.,Х3 в систему
Хг Х2 Х:, пьезоэлектрические коэффициенты,. например
коэффициенты dtih, преобразуются по закону
dqlm === CqiCljCmk^iik* (6.5)
Коэффициенты dijk обычно называются пьезоэлектриче-
скими модулями.
Число независимых пьезомодулей. Матричные обозна-
чения. Число компонент тензора третьего ранга равно
двадцати семи, но в силу симметричности тензоров меха-
нических напряжений и деформаций (см. § 5)
ti} = iji, ri} = rjt (6.6)
тензоры пьезоэлектрических коэффициентов оказываются
85
симметричными относительно перестановок последних
двух индексов, т. е. выполняются соотношения
duk^dikj. (6.7)
Это уменьшает число независимых пьезоэлектрических
коэффициентов до 18 и дает возможность записывать
уравнения пьезоэлектрического эффекта в более короткой
матричной форме. Для этой цели вводится один индекс
вместо двух для компонент тензора напряжений:
*и Z12 V *6
t t
12 22 23 .— 6 2 4
t - t „ t t Г t
_ 13 23 г33_ 5 4 3 J
а также для компонент тензора деформаций:
Г, 1 г„ 1 г
Г Г т 11 12 13 1 1 2 6 2 1 5
Г г г 12 22 23 — 2 Гв га 2 Г4
Г Г Г 13 23 33 1 1
ж* w* г. — г.
_ 2 ° 2 4 3
Уравнения прямого пьезоэффекта в матричной записи
принимают вид
Р, = duti, (6.8)
Pi = eurh (6.9)
Ei — —gutl, (6.10)
E^-hur, (i = l, 2, 3; Z= 1, 2, ..., 6). (6.11)
Коэффициенты da, ea, gu, hit образуют матрицы, состоя-
щие из трех строк и шести столбцов.
Пьезоэлектрические коэффициенты в тензорных и мат-
ричных обозначениях связаны определенными соотноше-
ниями, например для пьезомодулей d:
dijk = din, когда п = 1, 2, 3, i = 1, 2, 3;
(6.12)
2di]h = din, когда n = 4, 5, 6, i = 1, 2, 3.
Следует иметь в виду, что при-решении задач, требую-
щем перехода от одной системы координат к другой, нуж-
но пользоваться не матричной, а тензорной записью.
Требования, налагаемые сим» етрией кристаллов. Сим-
метрия кристаллов накладывает ограничения на сущест-
вование пьезоэлектрического эффекта и на вид матрицы
пьезомодулей. Центросимметричные кристаллы не могут
86
быть пьезоэлектриками. Вид (^)-матрицы нецептросим-
метричпых кристаллов, ие относящихся к тригональной
и гексагональной системе, может быть получен с по-
мощью метода прямой проверки (метода Фуми). Этот ме-
тод основан на том, что компоненты тензора третьего
ранга при переходе к новой системе координат преобра-
зуются аналогично произведению трех координат произ-
вольной точки, а именно:
X^XjX^ = С ^iCjm(J^nXiXmXn. (6.13)
Так, например, если кристалл обладает осью симметрии 2,
параллельной оси Х3, то преобразование осей координат
происходит следующим образом:
Х2-+-Хг, х3-+х'3
Г t 9
и координат точки хг-^>—хг, х2->— х2, х3-+х3 или в
более компактной записи:
1 -> -1, 2 -> -2, 3 -> 3.
Для этого случая d122 преобразуется так:
^122 ~* ^122» (6.14)
поскольку х±х2 — хгх2 . Но так как ось второго поряд-
ка, параллельная оси Х3, является операцией симметрии,
то пьезомодуль d122 при таком преобразовании координат
должен оставаться тем же, т. е.
d122 = dj22. (6.15)
Соотношения (6.14) и (6.15) могут одновременно вы-
полняться в единственном случае, когда d122= d122 = О'.
Следовательно, для кристалла, обладающего осью сим-
метрии 2, параллельной оси Х3, пьезомодуль d122 равен
пулю.
Проделывая подобную операцию с каждым из восем-
надцати независимых пьезомодулей, можно найти вид
матрицы пьезомодулей для всех классов симметрии, кроме
классов тригональной и гексагональной сингоний, для
которых при нахождении пьеаомодулей в новой системе
координат Х{, X', X'3t связанной с исходной операцией
симметрии, необходимо применять аналитический метод,
т. е. пользоваться соотношением (6.5) и далее соотноше-
ниями типа (6.15).
Формы матриц (di3) для различных кристаллографиче-
ских классов приведены в табл. 6. Матрицы коэффициен-
87
тов gii совпадают с приведенными в табл. 6 матрицами
коэффициентов di3. Для некоторых классов симметрии
имеется отличие в форме матриц коэффициентов ец и
от приведенных матриц коэффициентов Я При переходе
от двузначных индексов к трехзначным для коэффициен-
тов е и h в формулах, аналогичных (6.12), множители 1/2
отсутствуют. Формы матриц (ей) и отличных от мат-
риц (Др, приведены в табл. 7.
Обратный пьезоэлектрический эффект. Обратный пье-
зоэлектрический эффект является термодинамическим
следствием прямого пьезоэффекта.
Обратный пьезоэффект описывается уравнениями
г} = (1цЕ{, (6.16)
r} = gijPi, _ (6.17)
tj — —ецЕц (6.18)
t} = (6.19)
где d, g, h, e с индексами — уже введенные ранее пьезо-
электрические коэффициенты (см. уравнения (6.1)—(6.4)
или (6.8)—(6.11)).
Принципиальные возможности применения пьезоэлект-
рических кристаллов и различные пьезоэлектрические
коэффициенты Целый ряд приборов: микрофон, динамо-
метр, виброметр, сейсмограф, звукосниматель, излуча-
тель ультразвука и т. д., используют пьезоэлектрический
кристалл в качестве электромеханического преобразова-
теля энергии. Режим работы, а следовательно, и пьезо-
электрические коэффициенты, характеризующие чувстви-
тельность соответствующего прибора, оказываются раз-
личными.
Так, в приборах для измерения малых деформаций
электрическими методами (пьезоэлектрический сейсмо-
граф, пьезоэлектрический звукосниматель и др.) пьезо-
электрический кристалл работает в режиме прямого пье-
зоэффекта (уравнения (6.2) и (6.4)) и должен иметь
возможно большие коэффициенты h и е. В приборах,
преобразующих электрические колебания в механические,
например в излучателях ультразвука, кристалл работает
в режиме обратного пьезоэффекта (уравнение (6.16)) и
должен иметь большие пьезомодули d.
Если кристалл имеет какой-либо из пьезоэлектриче-
ских коэффициентов существенно больший, чем другие,
то целесообразно использовать этот кристалл в соответ-
ствующем режиме.
88
Пьезоэлектрические коэффициенты d, g, h н e не яв-
ляются независимыми и могут быть вычислены, если из-
вестны коэффициенты какого-либо типа с использованием
соотношений, следующих из уравнений пьезоэффекта, по-
ляризации диэлектрика во внешнем поле и закона Гука*)
~ Smil =
Для применения пьезоэлектрических кристаллов, по-
мимо эффективности преобразования, большое значение
имеют другие свойства кристаллов: механическая и элект-
рическая прочность, устойчивость к воздействию влаж-
ности, стабильность диэлектрических свойств, устойчи-
вость свойств по отношению к изменению температуры.
Коэффициент электромеханической связи. Важней-
шей характеристикой пьезоэлектрического кристалла как
электромеханического преобразователя энергии является
коэффициент электромеханической связи
к2 = UmJUan, (6.20)
где иал — электрическая энергия, подаваемая на крис-
талл, Кмех — снимаемая с кристалла механическая энергия.
Если происходит преобразование энергии, связанное
с i-ii компонентой электрического поля и j-й компонентой
деформации, то коэффициент электромеханической связи
выражается следующим соотношением:
к = (6.21)
i/Xr
|/ 4л 33
где — пьезоэлектрические модули, которыми описыва-
ется пьезоэлектрическое возбуждение, — диэлектриче-
ские проницаемости механически свободного кристалла,
s - — действующие коэффициенты упругой податливости,
измеренные при постоянном электрическом поле **).
Коэффициенты электромеханической связи характери-
зуют эффект преобразования мощности в пьезоэлектри-
ках, с их помощью Можно непосредственно сравнивать
*) См. § 7.
**) Для пьезоэлектрических кристаллов, особенно сегнето-
электрических, диэлектрические проницаемости механически сво-
бодного и механически зажатого кристалла различаются. То же
относится и к упругим податливостям, измеренным в условиях по-
стоянства поля Е или индукции D.
89
пьезоэлектрические материалы, у которых диэлектриче-
ские проницаемости и упругие постоянные существенно
различны по порядку величины.
Зависимость пьезоэлектрических свойств кристалличе-
ской пластинки от ее ориентации относительно кристал-
лофизических осей. Каждый пьезомодуль имеет опреде-
ленный физический смысл и численную величину только
в рассматриваемой системе координат, связанной с крис-
таллом. Если эта система является кристаллофизической,
то пьезомодули называются основными.
В кристаллофизической системе координат в зависи-
мости от симметрии кристалла некоторые пьезомодули
обращаются в нуль (см. табл. 6).
С другой стороны, часто бывает возможно найти но-
вую систему координат Xlt Х2, Х3, относительно кото-
рой какой-либо пьезомодуль, отличный от нуля в кристал-
лофизической системе координат, в этой новой системе
обращается в нуль. Одновременно могут появиться новые
пьезомодули, которые имели нулевые значения в кристал-
лофизических осях.
Отсюда следует, что характер свойств кристаллической
пластинки зависит от ее ориентации по отношению к кри-
сталлофизическим осям. Вырезая пластинки, определен-
ным образом ориентированные по отношению к кристал-
лофизическим осям, можно добиться появления новых
пьезоэлектрических эффектов, которых нет в прямых сре-
зах, и наоборот, надлежащим выбором среза некоторые
эффекты можно устранить.
Указательная поверхность продольного пьезоэлектри-
ческого эффекта. Тензор пьезомодулей dijh не может быть
полностью представлен единственной характеристической
Поверхностью. Поэтому рассматриваются лишь частные
случаи, имеющие значение для практического примене-
ния пьезоэффекта.
Особый интерес представляют поверхности продольно-
го пьезоэффекта. Радиусы-векторы таких поверхностей
пропорциональны плотности заряда, возникающего на по-
верхности, перпендикулярной к растягивающему или
сжимающему усилию tn, действующему вдоль радиуса-
вектора, с которым совмещена ось Xj вспомогательной
системы координат (рис. 6.1). Поскольку
|ог| = |Р1| и Рг = di
очевидно, радиусы-векторы поверхностей продольного
90
пьезоэффекта пропорцпопалкпы du. Ввиду того, Что
Гц =
Рис. 6.1. Схема, поясня-
ющая продольный пьезо-
электрический эффект.
эта поверхность изображает также деформацию, возни-
кающую в направлении приложенного поля.
Пьезоэлектрические текстуры. В современной пьезо-
технике широкое применение нашли искусственные пье-
зоэлектрики, так называемые пьезоэлектрические тексту-
ры (керамики), возможность су-
ществования пьезоэлектрического
эффекта в которых была пред-
сказана А. В. Шубниковым.
Пьезоэлектрическая текстура
(керамика) представляет собой по-
ликристаллический агрегат, состо-
ящий из сегнетоэлектрических
кристаллов малого размера, век-
торы спонтанной поляризации ко-
торых ориентированы внешним
полем и после снятия поля сохра-
няют свое направление (поляри-
зованные керамики). Направление
ся для пьезоэлектрической керамики осью бесконечного
порядка. Наличие пьезоэлектрических свойств следует
ожидать в керамиках с симметрией °° т, °° 2
т. е. в нецентросимметричных средах.
Матрица пьезоэлектрических коэффициентов тексту-
ры с симметрией оо/оо состоит только из нулевых компо-
поляризации являет-
Л оо/оо,
' пепт.
Текстуры, принадлежащие к группам симметрии °°,
оо т, оо 2, имеют отличные от нуля пьезоэлектрические
коэффициенты: матрицы коэффициентов d, g, е и h для
текстур не различаются.
Формы матриц kdij) для пьезоэлектрических текстур
"приведены в табл. 8.
Расчет параметров пьезоэлектрических текстур произ-
водится при помощи уравнений прямого и обратного
пьезоэлектрического эффекта, где d, g, е и h — пьезоэлект-
рические коэффициенты соответствующей текстуры
в кристаллофизической системе координат, ось X, ко-
торой совмещается с осью симметрии бесконечного по-
рядка.
Пьезоэлектрические текстуры имеют по сравнению с
монокристаллами ряд преимуществ. Так, например, пу-
тем несложных технологических приемов (шлифовки,
91
прессования, литья) можно придать керамическому пье-
зоэлементу любую необходимую форму — плоской плас-
тинки, сферической пли цилиндрической оболочки, и т. п.
Создавая различны^ направления искусственной поляри-
зации — продольное, поперечное, радиальное и т. д., а за-
тем различные направления поляризации на различных
участках одного и того же пьезоэлемента, получаем воз-
можпость неограниченного варьирования конструктивных
форм керамических пьезоэлементов.
Колебания пьезоэлектрических вибраторов. Если на
противоположные грани пластинки, вырезанной опреде-
ленным образом из
нести электроды и
Рис. 6.2. Эквивалент-
ная схема пьезоэлект-
рического вибратора.
пьезоэлектрического кристалла, на-
лриложпть к ним переменную раз-
ность потенциалов, то вследствие об-
ратного пьезоэффекта в такой пла-
стинке возникнут механические ко-
лебания. Амплитуда этих колебаний
достигнет максимума в том случае,
если частота подводимого перемен-
ного напряжения совпадет с соб-
ственной частотой механических ко-
лебаний пластинки.
Колеблющаяся кристаллическая
пластинка' с электродами называет-
ся пьезоэлектрическим вибратором.
Пьезоэлектрический вибратор эквивалентен колеба-
тельному контуру, состоящему из последовательно вклю-
ченных сопротивления В, индуктивности L и емкости Ci
в одной ветви цепи и емкости С2 в параллельной ветви
(рис. 6.2).
В современной технике приборы — резонаторы, исполь-
зующие пьезоэлектрический вибратор как колебательный
контур с высокой добротностью, применяются для стаби-
лизации частоты радиотехнических устройств, особенно
в технике связи и службе времени.
Вибратор как колебательный контур обладает двумя
резонансными частотами: fR — частотой последовательно-
го резонанса или резонанса токов (при Z = 0, где Z —
комплексное сопротивление вибратора) и fA — частотой
параллельного резонанса или резонанса напряжений
(при Z = °°); fR—называется частотой резонанса, fA-
частотой антирезонанса. Они определяются размерами,
плотностью, упругими, диэлектрическими и пьезоэлект-
рическими свойствами пластинки. Эти частоты свя-
заны с коэффициентом электромеханической связи
92
соотношением
fA ~~ Ir _ 4 fca
/в n 1 —fc2'
(6.22)
Отсюда к = —
где Л/ = fA — fn- Следовательно, из-
мерения fA и /в позволяют определить коэффициент элек-
тромеханической связи, который, согласно соотношению
(6.21), в свою очередь связан с упругими, пьезоэлектриче-
скими и диэлектрическими параметрами кристалла.
Колебания в кристаллических вибраторах классифи
цируются по типу деформаций и по размерам пьезоэлект-
рического элемента, определяющим резонансную частоту.
Простейшими типами колебаний пьезоэлектрических виб-
раторов являются колебания брусков по длине (продоль-
ные колебания) п сдвиговые колебания пластинок по
толщине. Если вибратор, имеющий форму стержня, со-
вершает колебания в направлении своей длины, то соб-
ственные частоты резонанса для пего определяются соот-
ношением
где п — номер гармоники, I — длина стержня, »ц— зна-
чение коэффициента упругой податливости в направле-
нии длины стержня, р — плотность. Вибратор, совершаю-
щий колебания сдвига по толщине, обычно представляет
собой круглую или квадратную пластинку, толщина ко-
торой мала по сравнению с диаметром или длиной ребра.
Собственная частота резонанса такой пластинки
(в-24)
где d — толщина пластинки, с66 — упругая жесткость,
определяющая деформацию сдвига по толщине плас-
тины *).
Так как все физические величины, определяющие ре-
зонансную частоту вибратора, зависят от температуры,
будет изменяться с температурой и сама резонансная
частота. Для количественной характеристики этого изме-
нения вводится так называемый температурный коэффп-
') О коэффициентах s,,- и с,, см. § 7.
93
Циент частоты fT, определяемый следующим образом;
Тт № fR
Для конкретного вида колебаний выражение для /г
может быть получено дифференцированием по темпера-
туре выражения для fR. Так, для бруска произвольной
ориентации, совершающего колебания по длине, выраже-
ние для /т имеет вид
ds,
fT 4 2~P 2"
ijkm Till
sijkm
где ац — коэффициенты теплового расширения кристалла,
Р — температурный коэффициент плотности, определяе-
мый через главные коэффициенты теплового расширения:
Р — — («и + «22 + «зз), к — компоненты единичного векто-
ра в направлении длины вибратора, sijkm — упругие по-
датливости кристалла.
Измерения резонансных и антпрезонансных частот
ориентированных брусков и пластин используются для
определения пьезоэлектрических и упругих коэффициен-
тов пьезоэлектрических кристаллов. Для этого необходимо
возбудить в кристалле колебания возможно более про-
стого вида п измерить резонансные и антирезонансные
частоты и емкость кристалла на низких частотах*). Из-
мерениями /в и [л кристаллических пластинок, в которых
возбуждаются продольные колебания, можно пользовать-
ся для определения всех диэлектрических, пьезоэлектри-
ческих и упругих постоянных, за исключением сдвиговых
упругих постоянных, для определения которых обычно
пользуются колебаниями сдвига вдоль грани или колеба-
ниями сдвига по толщине кристаллической пластинки.
Примеры решения задач
6.1. Найти вид матрицы пьезомодулей для сегнето-
вой соли **).
Решение. Для решения задачи воспользуемся методом пря-
мой проверки. Рассмотрим сначала ось симметрии 2, совпадаю-
*) Диэлектрическая проницаемость, измеренная на низких
частотах, оказывается выше, чем измеренная на высоких частотах.
Особенно велика разница для сегнетоэлектрических кристаллов.
*,*) В задачах, посвященных пьезоэффекту в сегнетовой соли,
имеется в виду кристалл в сегнетоэлектрической фазе, в полидо-
менном состоянии.
94
щук» с осью Хз кристаллофизпческой системы координат. Ось 2 Ц Х3
преобразует координатные оси следующим образом: X, -> —
Х2->—Х2, Х3-+Х3 или, в краткой записи: 1->—1, 2-5—2, 3->3.
Будем все модули поочередно преобразовывать согласно (6.5).
Если знак модуля при этом изменится на обратный, то соответ-
ствующий модуль равен пулю, если же знак остается неизменным,
то модуль остается в матрице пьезомодулей. Очевидно, сохраня-
ются только те модули d{?, которые имеют в индексах либо одну,
либо три цифры 3. Поэтому
din— о, d]i2 = 0, dlls =7^ 0, <?211 = О, ^212 = О, С?213 #= О, Й]23 О,
d]33 — О,, <?222 = 0, 6^233 = 0, <?223 =7^ О, С?331 = О, ^323 = 0, dsn О,
й312 ¥= 0, <?122 — 0, d322 0, йззз ¥= 0, или в матричных обозначениях:
О 0 0 d.„ d„ 0 \
14 15 \
0 0 0 d24d25 0
^31 ^32 ЧзЗ 0 ^зеу
Далее возьмем следующую ось 2, совпадающую с Х2. Эта ось
симметрии преобразует координатные осп следующим образом:
X'-+-Xi, Х2->Х2, Хз-> —Хз;
1-> —1, 2->2, 3->-3.
Из оставшихся восьми пьезомодулей сохраняются лишь те,
которые имеют в индексах либо одну, либо три цифры 2, т. е.
пьезомодули
dj32 = ^123(^14), d2si — d2is(d2s), d32i — d3i2(dsg).
Рассматривать действие третьей оси второго порядка, совпа-
дающей с Xi, не имеет смысла: по теореме Эйлера она является
порожденным элементом симметрии и ее действие сводится к дей-
ствию уже рассмотренных осей 2 || Х3 и 2 || Х2.
В окончательном виде матрица пьезомодулей кристаллов клас-
са симметрии 222 имеет вид
г0 0 о я О о \
0 0 0 0 d„t. 0 I
0 0 0 0 О d,e /
< Зо/
6.2. Охарактеризовать продольный пьезоэлектрический
эффект в кристаллах сегнетовой соли, ответив на сле-
дующие вопросы:
а) Каким уравнением описывается продольный пьезо-
электрический эффект пластинки произвольной ориен-
тации?
б) Есть ли такие направления, в которых' этот эффект
отсутствует?
95
в) Как ориентированы относительно кристаллофизи-
ческих осей пластинки, обладающие максимальным про-
дольным пьезоэлектрическим эффектом?
Решение, а) Рассмотрим пластинку с нормалью n(ni, п2, п3),
произвольно ориентированную относительно кристаппофизических
осей, и растянем (или сожмем) пластинку вдоль направления ее
нормали. Чтобы найти величину продольного пьезоэлектрического
эффекта, т. е. плотность зарядов, возникающих на поверхности
пластинки, перпендикулярной направлению растяжения, восполь-
зуемся уравнением прямого пьезоэлектрического эффекта (6.1).
При этом тензор пьезомодулей и тензор напряжений должны быть
выражены в одной и той же координатной системе. Можно свя-
зать систему координат с направлением растяжения (сжатия) —
в этой системе тензор напряжений будет иметь самый простой
вид, но отличными от нуля могут быть все 18 компонент матри-
цы пьезомодулей. Поэтому нет смысла связывать систему коорди-
нат с этим направлением. Проведем решение в кристаллофизиче-
ской системе координат, в которой матрица пьезомодулей задается
и имеет наиболее простой вид. Одноосное растяжение (сжатие) в
произвольном направлении n(ni, п2, п3) представляется в кристал-
лофизической системе координат тензором, компоненты которого
находятся из соотношения ijk = tnjnh', отсюда
Ы =
П1 п1п2 ПЛ
П1П2 П2 П3П2
П1П3 П2П3 П1 -
Продольный пьезоэлектрический эффект определяется компонен-
той поляризации, параллельной направлению растяжения (сжа-
тия), т. е.
Р|| = РгШ.
Учитывая, что Pi = daktjk, получаем Рц = dijktmnjiik.
Для сегнетовой соли отличными от нуля являются пьезо-
модули
<?14 = Зфгз, ^25 = 2ф>31, д3в = 2Й321-
В соответствии с этим продольный пьезоэлектрический эф-
фект пластинки сегнетовой соли, ориентация которой задается
направлением ее нормали п, относительно кристаллофизической
системы координат описывается уравнением
P|i = n1n2ns(2di23 + 2<?231 + 2d32i)t = -}- d23 + <?33)Z.
б) Исходя из выражения для Рц, можно заключить, что для
всех направлений, лежащих в координатных плоскостях, продоль-
ного пьезоэффекта нет.
96
в) Максимальным продольным пьезоэлектрическим эффектом
обладают кристаллические пластинки, нормаль к которым состав-
ляет равные углы с крпсталлофизическими осями. Такие пластин-
ки (/.-срезы, см. рпс. 2.4) широко применяются для практических
целей.
6.3. Как следует направить ребра пластинки /-среза
ADP (см. рис. 2.3), чтобы она поляризовалась при дейст-
вии па нее только нормаль-
ных напряжений, прило-
женных в направлениях,
параллельных ее ребрам?
Решение. Из вида мат-
рицы пьезомодулей класса
симметрии 42m следует, что
пластинка 2-среза будет поля-
ризована (Рз ф 0) только в
том случае, если ее напряжен-
ное состояние описывается
тензором
Г° f6°i
/6 0 0 .
.0 О 0.
Рис. 6.3. 45°Х-, 45° У- и 45°Z-
срезы.
Приведем указанный тензор напряжений к главным осям
Xj,X2,X3 и найдем ориентацию главных осей относительно по-
ходных. Искомые направления ребер пластинки Z-среза и будут
являться направлениями главных осей тензора напряжений.
Приведение заданного тензора к главным осям осуществляет-
ся поворотом исходных осей тензора вокруг оси Х3 на 45° по часо-
вой стрелке. При этом тензор напряжений принимает вид
t 0 0"
0 t о .
. 0 0 0,
Следовательно, чтобы кристаллическая пластинка Z-среза ADP
поляризовалась при действии па нее нормальных напряжений, ее
следует вырезать так, как это показано на рис. 6.3. Такие пластин-
ки называются 45°Z-cpe3aMn.
6.4. Для определения пьезомодулей поляризованной
керамики титаната бария из нее изготовили образец в
виде куба и подействовали напряжением сжатия t в на-
правлении оси поляризации керамики. Затем этот же
образец был подвергнут действию гидростатического сжа-
тия р.
Н. В. Переломова, М. М. Тагиева 97
На каких гранях куба при таких испытаниях возни-
кают электрические заряды? Какие пьезомодули керами-
ки титаната бария могут быть определены по результа-
там этих испытаний?
Решение. Поскольку ось Х3 кристаллофизической системы
координат керамики совпадает с направлением-поляризации, то ее
напряженное состояние будет описываться тензором
гО О
О О
О о
0 1
о
Гидростатическое сжатие задается тензором вида
•—р О О'
О -р О
О 0 — р.
следовательно, Ч = t2 = t3 = — р. И одноосное сжатие в указан-
ном направлении, и гидростатическое сжатие вызывают поляриза-
Пластинки свгнетобой.
Рис. 6.4. Схема устройства
пьезоэлектрического приемни-
ка звука.
цию керамики в направлении ее
полярной оси; в первом случае
Р3 = йзз(—13), во втором Ps =
= (2d31 -f- d33) (—р). Таким обра-
зом, по результатам эксперимен-
тов могут быть определены два
из трех пезависимьтх пьезомоду-
лей керамики титаната бария;
<2з1 и d33.
6.5. Пьезоэлектрический
приемник звука состоит из
мембраны, на внутренней
стороне которой набирается
столбик из тонких кристал-
лических пластинок. Между пластинками прокладывают-
ся электроды из тонкой металлической фольги (рис. 6.4).
Какие из пластинок сегнетовой соли — 45° Х-среза или
45° У-среза — обладают большей чувствительностью в ка-
честве приемников?
Решение. Чувствительность приемника может быть опре-
делена как отношение электрического напряжения, возникшего
под действием данного механического напряжения (давления зву-
ковой волны), к величине этого механического напряжения, т. е.
как V/t.
98
Звуковые колебания, воздействующие на пластинки сегнетовой
соли, имеют частоты, значительно меньшие резонансных частот,
поэтому в данном случае можно воспользоваться уравнением (6.10)
Ei = —giltl,
которое для пластппки 45°А-среза запишется в виде
Ei = —giti,
где ti — механическое напряжение, действующее по направлению
длины пластинки, проходящей под углом 45° к кристаллофизиче-
ским осям Х2 и А3 (см. рис. 6.3); gi — эффективный пьезоэлектриг
ческий коэффициент, ответственный за возбуждение пластинки
45°Х-среза. Он может быть вычислен из соотношения gi = liljlkgak,
где gijk — пьезоэлектрические коэффициенты сегнетовой соли,
а Ц — направляющие косинусы длины пластинки относительно
кристаллофизических осей.
Величина напряженности электрического поля, возбужденного
механическим напряжением i, равна
Et = V!d = — gtti = 31,5 10-8 • h ед. СГСЭ,
где ti — давление в дин/см2, d — толщина пластинки в см, V —
электрическое напряжение, возникающее между рабочими гранями
пластинки сегнетовой соли 45°А-среза в ед. СГСЭ. Отсюда
V = —dgiti = dgiti.
В этом случае чувствительность приемника, определяемая от-
ношением V/ti, равна dgi. Следовательно, чувствительность пропор-
циональна пьезоэлектрическому коэффициенту g,. Если мембрана
’состоит из п последовательно соединенных пластин-приемников,
то ее чувствительность будет в п раз больше.
Пьезоэлектрические коэффициенты gi для 45°А- и 45°У-срезов
соответственно равны
gi = 'Izgu = 3,15-10-7 ед. СГСЭ, gt = 72g25 = — 9,5-Ю-7 ед. СГСЭ,
откуда следует, что gt для 45°А-среза втрое меньше, чем для 45°У-
среза. Поэтому пластинка 45°У-среза при том же давлении будет
возбуждать электрическое напряжение в разомкнутой цепи при-
мерно втрое большее, чем пластинка 45°А-среза, а следовательно,
чувствительность пластинок 45°У-среза втрое больше, чем чувст-
вительность пластинок 45°А-среза сегнетовой соли. Пластинки
45° У-среза употребляются как в приемниках звука, так и в каче-
стве датчиков гидростатических давлений.
6.6. Какой из продольно колеблющихся вибраторов,
применяемых в качестве излучателей ультразвука: 45° X-
или 45°У-срез сегнетовой соли (см. рис. 6.3), обладает
7* 99
большим коэффициентом электромеханической связи?
Какой частоты колебания можно получить с помощью
таких излучателей длиной 20 мм? На каких волнах дол-
жен работать генератор, чтобы возбудить колебания пла-
стинок указанных срезов?
Решение. Система координат, связанная с ребрами вибра-
тора, представляющего собой 45°Х-срез, относительно кристалло-
физической системы координат кристалла сегнетовой соли зада-
ется следующей таблицей косинусов:
Оси X, Xt
%; 1 0 0
*2 0 cos 45° sin 45°
х'3 0 —sin 45° cos 45°
Уравнение пьезоэлектрического возбуждения 45°Х-среза
r2 = t?j Е и коэффициент электромеханической связи для того
же среза
к = J12 V^^22 >
где <?'2 — пьезоэлектрический модуль, s22 — коэффициент упругой
податливости в направлении длины вибратора. Согласно (6.5)
^12 = ^122 = ^li^2j^2h^ijh ~ % (^11^22^23^123 +
+ ^12^23^21^231 + С 13^21^22^312) =
= 2 cos 45” sin 45” t?12s = х/гй14 = 5,75 • 10“6 ед. СГСЭ.
Согласно (7.2а)
622 = S2222 = ^2i^2j^2k^2lSijkl = ^22S22 + ^23S33
+ 2C222C3V23 + = (со® «”)\2 + (sin 45”)S33 +
+ 2 (cos 45” sin 45") s23 +(sin 45” cos 45 )2s44 = 1/4 (s22 +
+ s33 + 2s23 + sa) = 3,17 ’ 10-12 см2/дпн-
Отсюда
fc = 5,75 • 10~® ' 3’- • 10U = 0,524 « 52%.
45 x ) 480
Резонансная частота 45°Х-среза найдется из соотношения
100
Зная резонансную частоту кристаллической пластинки, легко оп-
ределить длину волны, на которой должен работать генератор,
чтобы возбудить колебания пластинки 45°Х-среза. В случае ре-
зонанса частота колебаний /и равна частоте колебаний электриче-
ского тока, т. е. /в =/эл = с/Хэл, где с = 3-108 м/с, Хэл — длина
волны электрических колебаний. Отсюда волновой коэффициент
Хэл// — 145 при I = 20 мм, Хэл = 2,9-103 мм.
Аналогично для вибратора, представляющего собой 45е У-срез
сегнетовой соли, получаем таблицу косинусов.
Оси х, хг Хз
%; cos 45° 0 —sin 45°
*2 0 1 0
х'3 sin 45° 0 cos 45°
Как следует из расчетов,
r' = d'E к 1= 80-10~8ед.СГСЭ,
3 °,23с2’ 45 г О2з|/ СТ' ' 23 2
V e2S33
s33 = *Z4 (su + s33 + s55.+ 2sls) = 9,275 • 10~12 см2/дин,
*45 'У = 27%, /д = 118^кГц, = 254
(при I = 20 мм, /л = 50 кГц, Хэл = 5,08-103 мм).
Вибраторы из сегнетовой соли, представляющие собой 45°Х- и
45°У-срезы, обладают довольно большими значениями коэффици-
ентов электромеханической связи. Но для изготовления излуча-
телей ультразвука кристаллы сегнетовой соли мало пригодны
вследствие низкой механической прочности. В прпемппках же
ультразвука благодаря высоким пьезоэлектрическим коэффициен-
там они могут применяться.
Вибраторы, колеблющиеся по длине, обычно используются для
возбуждения ультразвуковых колебаний в диапазоне 20—200 кГц.
К недостаткам вибраторов, колеблющихся по длине, следует от-
нести относительно небольшую площадь излучающей поверхности
(торцы вибратора), которая не может быть увеличена произволь-
но. На высоких частотах целесообразнее использовать вибраторы,
колеблющиеся по толщине.
6.7. Определение пьезомодулей кристаллов кварца
динамическим методом па основных частотах проводи-
лось на брусках двух различных ориентаций (рис. 6.5).
101
Результаты измерений для этих брусков приведены
в таблице.
Ориентация среза Длина брус- ка. мм 7Д. кГц кГц Диэлектрическ ая проницаемость сво- бодного кристалла t Е
Х-срез 29,99 89,215 89,535 4,49
30°Х-срез 32,26 79,96 80,067 4,49
Рассчитать значения пьезомодулей по результатам
эксперимента.
Решение. Уравнение пьезоэлектрического возбуждения
кварцевого стержня Х-среза: r2 = daEi.
Пьезоэлектрический коэффициент di2, ответственный за воз-
буждение Х-среза, может быть рассчитан из соотношения (6.21)
di2 = к Vег4/4л-
если известен коэффициент электромеханической связи бруска,
а также значение упругой податливости в направлении длины бру-
ска, совпадающей с осью Х2. Коэффициент электромеханической
Рис. 6.5. Ориентировка брусков, используемых для определения
пьезомодулей кварца динамическим методом.
связи, согласно (6.22), равен '/глД'Л///я, где Д/ = /х—/«= 0,32 кГц;
отсюда Л = 0,0935.
Согласно (6.23) основная резонансная частота продольно ко-
леблющегося бруска Х-среза, удлиненного в направлении оси Х2,
fn = l/(2/|'ps22). Отсюда может быть найден коэффициент s22:
1
^~4Z2p/2R‘
Подставляя в последнее выражение длину бруска I (в см), зпаче-
102
ние резонансной частоты fR (в Гц) и плотность кварца (в г/см3),
получаем
«22 = 131,6-10“14 см2/дин.
Для кристаллов кварца sn = S22 и |di2| = |йц|. Подставляя значе-
ния к, s22 и диэлектрическую проницаемость ei свободного кри-
сталла в выражение для dJ2, находим
|dI2| = |d„| =6,45-10-8 ед. СГСЭ.
Направление длины бруска, который использовался для опреде-
ления независимого пьезомодуля кварца du, выбиралось под уг-
лом 30° к оси Х2 (см. рис. 6.5). Ориентация осей Xf, Х2, Xg, связан-
ных с ребрами этого бруска, относительно кристаллофизических
осей кварца задается следующей таблицей.
Оси Х1 X, X.
Х1 1 0 0
Х2 0 /3/2 1/2
Хз 0 -1/2 /3/2
Уравнение пьезоэлектрического возбуждения такого стержня:
г2 = <2Ei’
где d12— действующий пьезоэлектрический модуль, ответственный
за возбуждение колебаний бруска. Выразим й12 через основные
пьезомодули кварца:
^12 = ^122 = С/ЛДй = + ^11^22^122 +
+ 2CuC22C23d123 -(- 2С12С23С21^213 + 2С12СиС22<?212 =
з i/з" з д/т
= Т d12 + -^ d14 = - Т dll + -^ Й14 = “ °’7Ч1 + °’43Ч4-
d12 = FKeiS22/4"’
где к' — коэффициент электромеханической связи второго бруска,
равный VstcVA/Z/h, «22 — значение упругой податливости данного
бруска, равное l/(4Z2p/|j).
Подставляя в последние соотношения значения fR, XfR, дли-
ну бруска I, а также р, находим
к' = 0,0577, s'2=139,6 • 10-14см2/дин.
103
Отсюда
d' = 0,577 1 /~4,49 ' 139’6 ' 10 14 = 4,06 • 10~8 ед. СГСЭ.
у 12,56
Подставляя полученные значения dlt и г?12 в выражение d12 =
= —0,75йц + 0,434d14 и зная, что du = —cZ|2, получаем
dI4 = 1,7-10-» ед. СГСЭ.
Задачи
6.8. Будет ли обнаруживать пьезоэлектрический эф-
фект полидомениый кристалл сегнетовой соли? полидо-
мепный кристалл титаната бария?
( 6.9. Пользуясь методом Фуми, пайти вид матрицы
пьезомодулей кристаллов класса 42m. Какой вид приоб-
ретает матрица (с?,Д в координатной системе Хг Х2 Х3,
повернутой па 45° вокруг оси 4 против часовой стрелки?
6.10. Определить число независимых пьезомодулей для
керамики титаната бария (класс симметрии °°т).
Указание. Для решения этой задачи следует рас-
смотреть не все восемнадцать пьезомодулей, а лишь те
пьезомодулп, которые составляют матрицу (гД) для клас-
са симметрии, скажем, 6mm (см. табл. 6), поскольку те
пьезомодулп, которые обращаются в нуль в классе 6mm,
будут нулями и в классе симметрии °°т.
6.11. Найти вид матрицы пьезомодулей для текстуры
сегнетовой соли (класс симметрии °°2).
Указание. Для решения задачи следует восполь-
зоваться матрицей пьезомодулей класса 222 (см. табл. 6).
6.12. Показать, что кристаллы, относящиеся к классу
4, обладают осью симметрии бесконечного порядка в от-
ношении пьезоэлектрических свойств. Назвать классы
симметрии, кристаллы которых обладают таким же свой-
ством.
6.13. Показать, что для классов симметрии 422 и 622
не существует продольного пьезоэлектрического эффекта
пи в одном направлении.
% 6.14. К рабочим граням пластинок Х-, Y- и Z-срезов
(см. рпс. 2.3) сегнетовой соли приложили электрическое
поле напряженностью Е. Какие деформации испытывают
такие пластинки?
6.15. Кристаллы турмалина, сульфата лития, а также
калия виннокислого относятся к- полярным классам сим-
метрии и могут быть использованы в качестве датчиков
104
статического или низкочастотного гидростатического дав-
ления. Какой из перечисленных кристаллов обладает наи-
большей чувствительностью к гидростатическому дав-
лению?
6.16. Записать уравнение продольного пьезоэлект-
рического эффекта в кристаллах кварца и хлората нат-
рия. Вдоль каких направлений невозможен продольный
пьезоэлектрический эффект в этих кристаллах?
6.17. Кварцевый параллелепипед с ребрами а, Ь, с,
параллельными соответственно кристаллофизическим
осям Xt, Х2, Х3, подвергается действию силы F, направ-
ленной поочередно вдоль его ребер. Найти выражение
для величины зарядов, возникающих на гранях парал-
лелепипеда.
6.18. К пластине Z-среза турмалина в направлении
[0001] прикладывается напряжение 101 Н/смг. Между
какими гранями пластины возникнет разность потенциа-
лов? Определить ее величину.
6.19. Определить относительные деформации ребер
пластинки сегнетовой соли 45° Х-среза (см. рис. 6.3),
если к ее рабочим граням приложено постоянное элект-
рическое поле напряженностью 103 В/см. Можно ли ис-
пользовать этот срез для получения продольных колеба-
ний по толщине?
6.20. Как нужно вырезать пластинку из сфалерита,
чтобы получить максимальную плотность заряда па ее
рабочих гранях, если приложено одноосное растягиваю-
щее усилие t перпендикулярно к поверхности пластинки?
6.21. К кубику дпгидрофосфата аммония, ориентиро-
ванному своими ребрами вдоль кристаллофизических
осей, приложили по направлению его плоской диагонали
электрическое поле £ = 2000 В/см. Определить величину
и характер деформаций, испытываемых кубиком.
6.22. Какие абсолютные смещения испытывает край
кварцевой пластинки Х-среза (см. рис. 2.3) размерами:
Xi = 0,1 см, х2 = 5 см, если к электродам, нанесенным
на ее рабочие грани, приложено напряжение 3 кВ?
6.23. Определить характер деформаций, испытываемых
кварцевыми пластинками Х-, Y- и Z-срезов (см. рис. 2.3)
при обратном пьезоэлектрическом эффекте, если электро-
ды наносятся на их рабочие грани. Какие типы колеба-
ний могут быть возбуждены в этих пластинках при ис-
пользовании переменного электрического поля?
6.24. Определить относительные деформации ребер
45°Z-cpesa сегнетовой соли (см. рпс. 6.3), . вызываемые
105
приложением электрического поля папряжепнос1ью
10s В/см (электроды нанесены на рабочие грани).
6.25. Записать уравнение и найти пьезомодуль, харак-
теризующий пьезоэлектрическое возбуждение «вращае-
мого» кварцевого бруска Х-среза, т. е. бруска, длина
которого располагается под произвольным углом ср к оси
Х2 (рис. 6.6). Рассмотреть случаи ф = 0° и (р = 90°.
6.26. Записать уравнение для поверхности продольно-
го пьезоэлектрического эффекта кварца. Используя по-
лярные координаты, построить сечение этой поверхности
х координатной плоскостью
Рис. 6.6. Ориентировка бру-
сков, вращаемых X- и Y-
срезов кварца.
XtX2 и определить симмет-
рию полученного сечения.
6.27. Постоянное одноос-
ное напряжение t приложе-
но к кристаллу кварца в на-
правлении, перпендикуляр-
ном к оси третьего порядка.
Показать, что если направ-
ление t поворачивается во-
круг оси третьего порядка,
то вектор пьезоэлектрической
поляризациц, оставаясь по-
стоянным по величине-, так-
же будет поворачиваться вокруг оси третьего порядка,
но вдвое быстрее и в противоположном направлении.
6.28. Как должна быть ориентирована пластинка сфа-
лерита, чтобы опа испытывала максимально возможную
деформацию в направлении приложенного электрического
поля?
6.29. В каком направлении по отношению к оси °°
следует растянуть пластинку пьезоэлектрической тексту-
ры с симметрией <»2, чтобы получить максимальную
плотность зарядов на ее торцах?
6.30. Плотность зарядов, возникающих па противопо-
ложных гранях турмалиновой пластинки Z-среза, исполь-
зуемой в качестве датчика гидростатических давлений,
равна 2,5 • 10~s Кл/см2. Определить величину гидростати-
ческого давления, измеряемого такой пластинкой.
6.31. Прямоугольный параллелепипед с ребрами а, Ъ
и с из текстуры с симметрией °°2 изготовлен так, что ось
оо текстуры задается произвольным направлением
n(?2,, п2, щ) относительно его ребер. Параллелепипед рас-
тянут вдоль ребра усилием t. Найти выражение для вели-
чины зарядов, возникающих на гранях параллелепипеда.
106
6.32. Пластинка из кристалла резорцина Z-среза раз-
мерами 10 X 10 X 1 мм3 деформирована так, что одна из
граней, перпендикулярная короткому ребру, испытала
смещение 10~3 мм. Какова разность потенциалов между
рабочими гранями пластинки? Вычислить величину за-
ряда на ее рабочих гранях.
6.33. Каково направление максимального продольного
пьезоэффекта в кристалле KDP?
6.34. Определить величину угла моноклинности сегне-
товой соли в сегнетоэлектрической фазе, возникающего
за счет спонтанной деформации при фазовом переходе
(Ps = 0,2 • IO"6 Кл/см2).
6.35. Определить величину коэффициента электроме-
ханической связи Z-среза кристалла CdS для трех воз-
можных типов колебаний бруска этого среза.
6.36. Вычислить величину абсолютного смещения края
пластинки Z-среза кристалла CdS при приложении к' ее
рабочим граням напряжения 3 • 103 В/см. Толщина плас-
тинки 10-2 мм.
6.37. Какими пьезомодулями определяется пьезоэлект-
рическое возбуждение 45°У-среза кристалла CdS?
6.38. Как должна быть ориентирована пластинка крис-
талла CdS относительно кристаллофпзических осей, чтобы
приложение переменного электрического поля к ее рабо-
чим граням вызывало деформации сдвига по ее толщине?
6.39. Рассчитать значение коэффициентов электроме-
ханической связи 45°Х-среза бруска сегнетовой соли,
а также ее L-среза (см. рис. 2.3 и 2.4) в параэлектриче-
ской фазе.
6.40. Определить величину коэффициента электроме-
ханической связи 45° Z-среза ADP, а также А-среза
ADP (см. рис. 2.3 и 2.4).
6.41. Пластинка из сфалерита вырезана так, что ее
рабочие грани перпендикулярны направлению [110]. Ка-
ким пьезомодулем определяются деформации сдвига по
толщине такой пластинки, если электрическое поле при-
ложено к ее рабочим граням?
6.42. Кристаллический образец хлората натрия имеет
форму куба, причем направления его ребер совпадают с
направлениями <100>. Найти выражение для плотности
зарядов, возникающих на гранях образца при его растя-
жении усилием t в направлениях а) [1001, б) [110],
в) [111].
6.43. Какой следует взять срез кристалла EDT (эти-
лендиамиитартрата), чтобы при наложении электрическо-
107
го поля на рабочие грани он испытывал как деформации
растяжения или сжатия, так и деформацию сдвига?
6.44. Какой должна быть толщина вибратора, пред-
ставляющего собой кварцевую пластинку Х-среза (см.
рис. 2.3), колеблющегося по толщине и настроенного па
Излучение частот 30 МГц? Можно ли с помощью такой
пластинки получить колебания с частотой 3000 МГц?
Какой толщины должна быть турмалиновая пластинка
Z-среза (см. рис. 2.3), настроенная на излучение колеба-
ний такого же типа и частоты?
6.45. Рассчитать коэффициенты электромеханической
связи пластинок, указанных в предыдущей задаче.
6.46. Для измерения пьезомодулей поляризованной ке-
рамики титаната бария образец, имеющий форму куби-
ка размером 1X1X1- см3 (рис. 6.7, а), сжали силой
800 Н в направлении оси Х3, являющейся направлением
Рис. 6.7. Ориентировка образцов, используемых для определения
пьезомодулей керамики титаната бария.
поляризации, затем в направлении оси X, тем же усили-
ем. При этом величина заряда, возникающего на грани,
перпендикулярной оси Х3, в первом случае' равнялась
14,8 • 10~8 Кл, во втором случае величина заряда обрат-
ного знака составила 6,15 • 10~8 Кл. Определение третье-
го независимого пьезомодуля производилось па образце
тех же размеров, ориентированном так, как это показано
на рис. 6.7, б; при действии на грань АВ усилием 800 Н
величина заряда, возникающего на грани АВ, составила
10,3 • 10-8 Кл.
Определить значения пьезомодулей поляризованной
керамики титаната бария.
' 108
6.47. Измерение резонансной и антирезонанспой час-
тоты сфалеритовой пластинки, представляющей собой
45°У-срез (см. рис. 6.3), дало следующие значения:
= 117 кГц, /А = 117,146 кГц.
Рассчитать величину пьезомодуля сфалерита.
6.48. Снонтаппая поляризация собственно пироэлект-
рических кристаллов может быть оценена по величине
пьезоэлектрической поляризации, обусловленной гидро-
статическим сжатием (растяжением), а также по величи-
не ее изменения за счет линейных размеров кристалла.
Найти соотношения, позволяющие оценить величину спон-
танной поляризации для кристаллов турмалина и суль-
фата лития.
6.49. Какие деформации будут испытывать кварцевые
бруски, ориентированные так, как показано па рис. 6-8,
Рис. 6.8. Ориентировка кварцевых брусков, используемых для
возбуждения колебаний с неоднородными деформациями.
при приложении к их боковым граням перемепного элект-
рического поля? К каждой паре боковых граней бруски
прикладывается поле противоположного знака.
6.50. Является ли пьезоэлектриком кристалл KDP в
параэлектрической фазе? в сегнетоэлектрической фазе?
Наблюдается ли отличие в пьезосвойствах этих фаз кри-
сталла KDP?
6.51. Определить коэффициент электромеханической
связи Х-среза кварца для трех типов колебаний бруска
этот цреза.
Qi. 52.^Определить коэффициент электромеханической
связи У-среза кварца для двух возможных типов коле-
баний пластины этого среза.
§ 7. УПРУГИЕ СВОЙСТВА КРИСТАЛЛОВ. ЗАКОН ГУКА
Под действием механических напряжений кристаллы
испытывают деформации. Если величина напряжения ни-
же предельного значения, называемого пределом упруго-
сти, деформация является обратимой.
109
При достаточно малых напряжениях деформация про-
порциональна величине приложенного напряжения. Если
к кристаллу приложено произвольное однородное напря-
жение [iwJ, возникающая однородная деформация такова,
что каждая ее компонента гу линейно связана со всеми
компонентами тензора напряжений, т. е.
= (i,/, fc, Z = 1, 2, 3). (7.1)
Выражение (7.1) представляет собой закон Гука в обоб-
щенной форме. Здесь sijW — коэффициенты упругой подат-
ливости кристалла. Всего имеется 81 коэффициент
Закон Гука может быть записан также в виде
tii (7.2)
где ciftI — коэффициенты упругой жесткости кристалла.
Коэффициенты siM и cift( образуют тензоры четвертого
ранга. Это означав?, что при переходе от координатной
системы Хг, Х3 к Хг, Х2, Х3 коэффициенты sijfj
(cw) преобразуются в smnop (ст?гор) по закону
$mnop — ('mi^'nj^'okCplSijki, (7.2а)
где Cmi, C„j, Cok, Cpi — направляющие косинусы, задаю-
щие ориентацию осей Хг, Х2, Х3 относительно осей Xt,
Х2. Х3. Каждый коэффициент sijU (с(}Ы) имеет определен-
ный смысл и численную величину для данной системы
координат, связанной с кристаллом. Если эта система сов-
падает с кристаллофизической координатной системой, то
коэффициенты называются основными.
В силу симметричности тензора деформации и тензора
напряжений компоненты тензора и Сцы симметричны
относительно индексов i и /, к и I, т. е.
Sijkl Sjikh (7.3)
Sijhl ~ Sijlki Ciikl = Cijlki (7.4)
Соотношения (7.3) и (7.4) уменьшают число независи-
мых компонент SiiU и ciiu до 36. Благодаря симметрично-
сти 8цЫ и cijhl по первым двум и последним двум индексам
можно использовать матричные обозначенйя, введенные
в § 6. В этих обозначениях уравнения (7.1) и (7.2) запи-
сываются в более краткой форме:
П = Sutj (i, ] = 1, 2, 3, 4, 5, 6),
' (7 tn
к = с^ (i, / = 1, 2, 3, 4, 5, 6).
110
Введение матричной записи приводит к уменьшению
числа слагаемых в правой части уравнения (7.1), но вы-
зывает необходимость вводить множители 2 и 4 по сле-
дующему правилу:
sw = s,„n, когда тип равны 1, 2 или 3,
2sij7i( = smn, когда т или п равны 4, 5 или 6, (7.6)
4«<)М = smn, когда т и п равны 4, 5 пли 6.
Энергия деформированного кристалла. Работа на еди-
ницу объема, произведенная при малом изменении де-
формации кристалла, выражается формулой dW =
Когда это изменение деформации является изотерми-
ческим и обратимым, dW можно приравнять возрастанию
свободной энергии йф, т. е.
с/ф = dW = ttdrt. (7.7)
Если выполняется закон Гука, то уравнение (7.7)
принимает вид
йф = ci}rsdrf,
следовательно,
Йф/ЙГ,- = СцГу.
Дифференцируя обе части уравнения по г,-, получаем
д / <?ф \__________________
Cii‘
Но, так как ф есть функция только состояния тела, опре-
деляемого компонентами деформации, то порядок диффе-
ренцирования не существен, поэтому
® Cj,. (7.3)
Диалогично
Sij Sjf, (7.8а)
Благодаря симметричности матриц (ci3) и (s„) число
независимых жесткостей и податливостей уменьшается
еще больше: от 36 до 21.
Интегрируя соотношение (7.7), получаем, что отнесен-
ная к единице объема кристалла работа, необходимая для
создания деформации г,, так называемая энергия дефор-
мации, равна
V2СуГ^.
(7.86)
ill
Требования, налагаемые симметрией. Вследствие сим-
метрии кристалла число независимых коэффициентов s{}
и с,3 уменьшается.
Вид матриц упругих податливостей можно получить
с помощью метода прямой проверки, который позволяет
определить число независимых коэффициентов для всех
классов, исключая классы тригональной и гексагональной
сингоний. Для тригональной и гексагональной сингоний
необходимо применять аналитический метод.
Вид матриц (si3) и (с,3) для различных кристаллогра-
фических классов, а также для пьезоэлектрических тек-
стур, приведен в табл. 9.
Соотношения, связывающие коэффициенты s,3 и с,3.
Константы упругой податливости si3 и константы упругой
жесткости ci3 связаны следующим соотношением:
(-l)WAc..
(7.9)
где Ас — определитель, составленный из коэффициентов
упругих жесткостей:
Си 12 13 14 15 16
С12 С22 С23 С24 С25 С26
С13 С23 сзз С34 С35 сзв
С14 С24 С34 С44 С45 f46
С15 С25 %5 С45 С55 С56
С16 С26 С36 С46 С56 С66
Асй — минор, получающийся из этого определителя за-
черкиванием i-й строки и /-го столбца. Аналогично
(-
г*.. =. ----------------------—
гз да
(7.9а)
Модуль Юнга, модуль сдвига и коэффициент Пуассона.
При описании упругих свойств как изотропных, так и
анизотропных сред часто используются следующие по-
стоянные.
Модуль Юнга Е, характеризующий упругие свойства
среды по какому-либо направлению, определяется отно-
шением механического напряжения по этому направле-
нию к величине деформации в этом же направлении.
Коэффициент Пуассона о определяется как отношение
деформации поперечного сжатия к деформации продоль-
ного растяжения, вызванных механическим напряжением.
12
Модуль сдвига ц определяется как отношение напря-
жения сдвига к деформации сдвига.
Для изотропных тел из перечисленных констант толь-
ко две являются независимыми. Для описания упругих
свойств изотропных тел часто используются постоянные
К и ц, называемые константами Ламэ', при этом постоян-
ные ц, /., £ и v связаны следующими соотношениями:
р Р (ЗА, + 2|i) лгу.
T+V ’ (7Л0)
?. ллх
H = W)- <7-12>
Если упругие свойства изотропных тел характеризо-
вать матрицей (si3) (табл. 9), то
sn = 1/Е, sl2 = ~v/E, 2(sn — s12) = 1/ц, си = 2ц + Л,
ci2 = X. . (7.13)
В случае анизотропных сред модуль Юнга в произ-
вольном направлении Х3:
Е = 1/433, (7.14)
где ^зйзз= а Сз3, (Xi направляю-
щие косинусы оси Х3 относительно кристаллофизиче-
ской системы координат, 8уы — основные коэффициенты,
отнесенные к кристаллофизической системе координат.
Для всех кристаллографических классов, включая ку-
бические, величина модуля Юнга зависит от направления.
Коэффициент Пуассопа в случае анизотропных сред
равен
Ш = shh/skk (7.15)
и является мерой бокового сжатия, параллельного Хк, ко-
торое сопровождается растяжением, параллельным Хк.
Указательные поверхности упругих коэффициентов.
Поскольку упругие свойства кристаллов нельзя пол-
ностью представить одной поверхностью, указательную
поверхность строят обычно для какого-либо упругого
коэффициента. Такая поверхность наглядно демонстри-
рует изменения этого коэффициента в зависимости о г
направления в кристалле.
Практически важной является поверхность, изобра-
жающая изменение модуля Юнга с направлением. Ради-
8 Н. В. Переломова, М. М. Тагиева 113
ус-вектор этой поверхности пропорционален величине мо-
дуля Юнга по направлению радиуса-вектора.
Объемная и линейная сжимаемость кристаллов. Объем-
ной сжимаемостью называется относительное уменьше-
ние объема кристалла под действием единичного гидро-
статического давления. Тензор напряжения всесторонне-
го, или гидростатического, сжатия
[М =
.0
— р
о
~ 0'
о
— р.
или thl = — р8м,
о
о
где Ъы — символ Кронекера.
Деформации, вызываемые гидростатическим сжатием,
ra = = -psijkk, (7.16)
объемное сжатие Д — Д V/V = г и = —psiikh, где V — объем
кристалла. Следовательно, объемная сжимаемость равна
—-7"=SiiAfe. (7.17)
Линейная сжимаемость р есть относительное умень-
шение длины некоторого отрезка в кристалле при дей-
ствии на кристалл единичного гидростатического дав-
ления.
Относительное изменение длины отрезка в произволь-
ном направлении и (и,, п2, «з) записывается в виде 1\рг{п,.
Поскольку это изменение вызывается действием гидроста-
тического давления р, то г^п{п} = — Отсюда
линейная сжимаемость
(7.18)
Примеры решения задач
7.1. Определить вид матрицы упругих коэффициентов
Stj класса симметрии 222, к которому относятся кристаллы'
сегнетовой соли.
Решение. Для нахождения независимых коэффициентов
упругой податливости s,j сегнетовой соли следует применить ме-
тод прямой проверки. Поскольку коэффициенты st} симметричны
относительно перестановок индексов i и / (sfj = sj4), можно опу-
стить нижнюю половину матрицы (s,j), т. е, рассматривать
114
коэффициенты
®11 ®12 ®13 ®14 ®15 ®16
®22 ®23 ®24 ®25 ®26
®33 ®34 ®35 S36
®44 ®45 S46
®55 ®66
®66
Выпишем таблицу индексов, соответствующую верхней пра-
вой половине матрицы (sjj):
11 12 13 14 15 16
22 23 24 25 26
33 34 35 36
44 45 46
55 56
66
Симметрия точечной группы 222 полностью определяется двумя
осями второго порядка, совпадающими с кристаллофизическими
осями Хз и Xf (или любой другой парой осей симметрии 2), третья
ось порождается наличием двух предыдущих осей.
Рассмотрим сначала действие осп 2, параллельной Х3. Такое
преобразование можно записать следующим образом:
*!-*-*;. ^2->-4 Х3^%3
или, более компактно,
1 ——1, 2- — 2, 3 — 3.
При четырехмндексном обозначении пары индексов преобра-
зуются по правилу
11 — 11, 22 — 22, 33 — 33,
23 —— 23, 31 —— 31, 12—12.
Соответственно при двухиндексном обозначении, используе-
мом для матричной записи, преобразования индексов имеют вид.
1 — 1, 2 — 2, 3 — 3,
4 —— 4, 5 —— 5, 6 — 6.
Тогда таблица индексов преобразуется так:
11 12 13 —14 —15 16
22 23 — 24 — 25 26
33 — 34 — 35 36
44 45 — 46
55 — 56
66
8*
115
Сравнивая эту таблицу компонента за компонентой с перво-
начальной таблицей и учитывая, что коэффициенты s,,- при та-
ком преобразовании должны переходить сами в себя, получаем
следующий вид матрицы:
' S11 S12 S13 0 0 S16
S22 S23 0 0 S26
S33 0 0 S36
S44 S45 0
S55 0
Рассмотрим действие оси 2, параллельной кристаллофизиче-
скоп оси X,:
1->1, 2-^ — 2, 3-> —3.
Пары индексов преобразуются по правилу
11-+11, 22->-22, 33->-33,
23—>-23, 31-> — 31, 12^ — 12
или, прп двухипдекспом обозначении:
1->-1, 2->2, 3->-3,
4->-4, Гн- —5, 6->- —6.
Очевидно, теперь в пуль будут обращаться те коэффициенты
s,j, которые имеют в индексах одну цифру 5 или 6, т. е. все sis
и все sig.
В соответствии с этим получаем следующую матрицу коэффи-
цисптов Sij для сегнетовой соли:
S11 S12 S13 0 0 0
S22 S23 0 0 0
s33 ° 0 0
s„ 0 0 •
44
S55
S66
Матрица содержит девять независимых коэффициентов s;j.
7.2. Кристалл кварца подвергли однооспому сжа-
тию t: а) вдоль направления [2110], б) вдоль направле-
ния [0001]. Найти характер упругих деформаций, испы-
тываемых кристаллом.
Решение. Согласно правилам выбора кристаллофизических
осей в кристаллах класса 32 ось Х| направляется по оси 2, ось
Х3 — по осп 3 (см, табл. 4).
116
Чтобы найти характер деформаций, испытываемых кварцем
при сжатии вдоль указанных направлений, надо воспользоваться
законом Гука (7.5).
При сжатии кварца вдоль направления [2110], т. е. вдоль оси
2, совпадающей с осью у тензора механических напряжений
отличной от нуля является единственная компонента а при
сжатии вдоль направления [0001] — компонента t3. В соответ-
ствии с видом матрицы коэффициентов упругой податливости (см.
табл. 9) получаем при сжатии по [2110], т. е. вдоль оси сле-
дующие деформации:
Г’Е == Г3 = Si3t],
т. е. деформации сжатия (растяжения) вдоль кристаллофпзиче-
ских осей (знак деформаций будет зависеть от знака коэффици-
ентов упругой податливости), а также r4 = s14tb т. е. деформацию
сдвига в плоскости Х2Х3. Для кварца sn >0, si2 < 0, s13 < 0,
поэтому кварц будет испытывать деформацию растяжения вдоль
оси Xt и деформацию сжатия вдоль осей Х2 и А3.
При сжатии вдоль направления [0001], совпадающего с осью
симметрии 3:
Г1 = г2 = sl3^3, г3 = s33i3,
т. е. получим деформацию сжатия вдоль осей А, и Х2 (так как
«1з < 0) и деформацию растяжения вдоль осп А'3 (так как
sss > 0).
7.3. а) Найти направления, отвечающие максималь-
ным значениям модуля Юнга для кубических кристаллов,
а также направления, соответствующие минимальным
значениям этой величины, принимая (su — sl2 — VzSiJX).
б) Охарактеризовать указательную поверхность моду-
ля Юнга.
в) Как выглядят сечения этой поверхности плоско-
стями типа {111}?
Решение, а) Величина, обратная модулю Юнга, в пластип-
ке произвольной ориентации задается, согласно (7.2а) и (7.14),
выражением
S33 ~ S3333 = Зг^'ззС3^3lSijkl ИЛП s3333 = ninjnknlSijkl’
где Csi, С31, Сзк, C3l — направляющие косинусы интересующего
нас направления п (щ, п2, ns), stju— коэффициенты упругой
податливости кубических кристаллов.
В кристаллофизической системе координат матрица упругих
коэффициентов (я;,) для всех классов кубической спнгонпп имеет
117
вид (см. табл. 9)
S11 S12 0 0 0
S12 S11 S12 0 0 0
Sij S12 0 S12 0 S11 0 0 s44 0 0 0 0
0 0 0 0 s44 0
0 0 0 0 0 s44
Запишем коэффициенты упругой податливости, отличные от пу-
ля, в тензорном обозначении'
Sl'lll = s2222 = S3333, S1122 = «2233 = -51133» s2323 = s3131 = S2121.
Подставляя в выражение для s3333 отличные от нуля коэффициен-
ты упругой податливости и переходя к матричным обозначениям,
получаем
s33 = sn (^31 + ^32 + С33) + (s44 + 2®1г) х
х зг^зз + зз^зг + ^зг^зг)"
Проделаем некоторые упрощения:
z>4 ____z-»2 (л _ z^2 _ /^2 \ _ /^'2 _ z>2 z’2 __ z^2 z~»2
Ь31 ^31 v1 Ь32 ^33/ °31 u31v32 31U33’
z^4 ___ z-»2 (л _ f2 ___ r>2 \ _ z-»2 _ z^2 r2 _ z-»2 z-<2
t/32“t'32V G31 ''33/ “ V32 С32Ь31 Ь32С33’
И, наконец,
z>4 ___ ^-2 Л __ r>2 ___ ^-2 \ _ ^2 ____ z^2 z--2 _ r2 (2
G33 — '-'33 '-'31 ' '-'32/ ^ '-'3.3 L'31b33 ,33C32'
Подставив выражения для c|p cj2 и c|3 в предыдущее урав-
нение, получаем
®зз = sii 2sn (^зг^зз + ^зз^31 “Ь ^зг^зг) ~Ь
“Ь (S44 2®1г) (^32^33 + ^33^31 "Ь ^31^32) =
= S11 2 (Sll S12 ^/2S44) (^31^32 -J- £32^33 "Ь ^31^33)
или
4 = S11 - 2 (sil - S12 ~ 1/2s44) + П1П3 + П1П1)
Следовательно, модуль Юнга для кубических кристаллов зависит
от направления и является функцией величины
”1,г2 + п2пз + "1гез-
б) Найдем максимум этой величины, используя метод неоп-
ределенных множителей Лагранжа. Составим функцию
/ = -j- n2snl — X (n| -j- -j- п23 — 1).
118
Дифференцируя ее по в,, п| и Пд и прправйивая производные пу-
лю, получим ^2 = '4 + “1 - * = °- —~ — Но ф- п? — X = 0, 3'1 ^ = ^ + 4~х = 0-
Решая эту систему уравнений, получаем
п2 + пз = ,гз + "! = П2 + п1 =
Отсюда следует, что = н? = п? = 1/3,
1 1 1
wi=±_W’ ге* = ±уГ’ ^=±W.
Таким образом, имеется восемь направлений, соответствую-
щих максимальному зпаченпю величины ф- ф- п^п*:
1 1 1
ууил.-п. уу(-1.-1.1), W(i,-i,-D,
-^(1.-1.!), ^(-l.-l.-l).
Это означает, что если величина зц — s12 — V4S44 положитель-
на, как это имеет место для всех кубических кристаллов (исклю-
чение составляют кристаллы молибдена), то наибольшее значение
модуля Юга соответствует направлениям типа <111>.
Очевидно, наименьшее значение модуля Юнга соответствует на-
правлениям типа <100>, для которых величина п^п|ф- п^ф-
обращается в нуль. Исходя из вышесказанного, делаем вывод, что
указательная поверхность модуля Юнга будет иметь форму куба
со скругленными углами и углублениями в центрах граней.
в) Найдем вид сечепия этой поверхности плоскостью (111).
Пусть единичный вектор п(щ, пг, и3) перпендикулярен направ-
лению [111]. Это означает, что nt ф-п2 ф- «з = 0, т. е. п3 =
= —(щ + '’2). Но + ”2 + = 1; отсюда
п1 + ,г2 + ("1 + ге2)2 = 2,г1 + 2п2 + 2л1,г2 =1’
пли
П1 + П2 + П1П2 = 1/2’
119
С учетом этого равенства преобразуем выражение п^и| -[ +
н ">!•
п1п1 + п1п1 + ngni = п1п1 + (П1 + п1) (1 — — П®) =
= + п[ + n-l — (га® + га®) = nf -|- п* + пгп2 — 1/4 = 1/4.
Таким образом, величина модуля Юнга в плоскости, перпен-
дикулярной направлению [111], не зависит от направления, а се-
чения указательной поверхности модуля Юпга, перпендикуляр-
ные направлениям < 111>,— окружности.
7.4. а) Какие из упругих коэффициентов кубических
кристаллов могут быть определены по результатам изме-
рений величины продольной деформации, а также вели-
чины объемного сжатия AV/V кристаллических образцов,
испытывающих напряжение одноосного сжатия t в на-
правлении типа <100>?
б) Зависит ли величина объемного сжатия кубиче-
ских кристаллов от направления действия одноосного
механического напряжения?
Решение, а) Если одноосное механическое напряжение
действует на кубический кристалл в направлении [100], это озна-
чает, что в кристаллофизической системе координат только одна
компонента тензора напряжения — Ц отлична от нуля. Поэтому
по результатам измерений величины продольной деформации гь
согласно (7.5), может быть определен коэффициент sli=ri/tl.
Величина объемного сжатия ДЕ/Е = гц в этом случае равна
(2si2 + sn) (— р), следовательно, по результатам ее измерения
можно определить коэффициент «12.
б) Зададим одноосное напряжение t по произвольному отно-
сительно кристаллофпзической системы координат направлению
п(гаь п2, Пз).
Направим вдоль п ось Хд повой штрихованной системы коор-
динат, тогда напряженное состояние в повой системе координат
будет описываться тензором
ООО
Найдем вид тензора напряжений в кристаллофпзической систе-
ме координат, воспользовавшись законом преобразования компо-
нент тепзора второго ранга при переходе из новой координатной
системы в старую: t.. = Для нашего случая
= С3»С3?33 ’ пгп^
120
Определим изменение объема кубического кристалла под дей-
ствием одноосного растяжения в произвольном направлении Так
как ДГ/У = Гц = Гц + Г22 + Гзз, причем
Г11 ~ 4 (sllllRi + ®1122П2 + ®1133Пз)’
г22 ~ f (S221ini S2222n2 "Ь ®223з”з)’
Г33 = * (S3311"l + ®3322П1 + S3333R1)>
где t = tga, или в матричном обозначении
ri = t(S114+S12nI + S13Rl)’
r2 = i(f2iniTV2 + ®23R32)’
Г3= 4S31R? + S32"1+S33RI)’
и учитывая, что для кубических кристаллов
$ц = $22 = $33i «12 = «13 = «231
получаем
др
Т = Г1'+ Г2 + r3 = 4 + ®12w2 + S12nl + S12R1 +
+ ®11П2 + S12ni + Vl +^12n2 + S11WD-
Так как -}- n£ + ng = 1, to —- = t 2«ia)- Таким образом,
изменение объема кубического кристалла под действием одиооспого
напряжения не зависит от направления растяжеппя.
7.5. Определение величин коэффициентов упругой
податливости кристаллов кварца проводилось путем из-
мерения резонансных частот на шести различно ориенти-
рованных образцах, показанных на рис. 7.1.
Результаты измерений приведены в таблице.
Ориентация среза (см. рис. 7.1) Вид колебаний Размеры по направлению колебаний, мм Резонансная частота, кГц
Х-срез 30° Х-срез —30° Х-срез 60° Х-срез У-срез » Сжатие—растяжение по длине То же » » » » Сдвиг по грани Сдвиг по толщине 30,04 32,18 20 20,05 1,6 1,05 89,215 80,52 168,5 150 1453 1825
121
Пользуясь приведенными экспериментальными дан-
ными, рассчитать значения всех независимых коэффици-
ентов упругой податливости кварца.
Решение. Для кристаллов кварца, относящихся к клас-
су 32, определению подлежат шесть независимых коэффициентов
упругой податливости (см. табл. 9):
«II, «12, S13, S33, S44 И «14.
Величина «и, для кварца равная «22, определяется непосредственно
из данных для Х-среза. Уравнение пьезоэлектрического возбужде-
ния этого среза r2—d,2Ei, поэтому резонансная частота продоль-
Рис. 7.1. Ориентировка образцов, используемых в задаче 7.5.
ных колебаний Х-среза, удлиненного в направлении оси Х2, задает-
ся отношением /в = l/(2Zy'ps22); отсюда
« - 1
22 4/^Z2p •
Подставляя в это выражение значение длины Х-среза (в см),
резонансной частоты (в Гц) и плотности кварца (в г/см3),
получаем
«22 = 131 10~14 см2/дин = «и.
122
Для длинных и тонких образцов «вращаемых» Х-срезов, тол-
щина которых направлена вдоль оси Хь а длина принята за на-
правление Х2, уравнение пьезоэлектрического возбуждения запи-
сывается в виде r2 = с/12й’1> гДе г2’ ^12 — деформация и пьезомо-
дуль соответственно в направлении длины образцов «вращаемых»
Х-срезов.
Таблица направляющих косинусов осей, связанных с ребрами
этих срезов, относительно кристаллофизических осей имеет вид
Оси xt х2 X,
х; 1 0 0
*2 0 COS ф sin ф
х'3 0 —sin ф COS ф
Здесь <р = 30° для 30°Х-среза; <р = —30° для — 30°Х-среза; <р =
= 60° для 60°Х-среза. Для этих срезов
4 = S2222 = C2iC2iC2hC2lSijM = S11 <₽+ S33 +
+ 2sJ4 cos3<p sing) +(2«13 + s'44) sin2tp cos2q>.
(Для 30°Х-среза sin <p = Vs, cos <p = 1'3/2.)
Поскольку образцы указанных ориентаций совершают колеба-
ния сжатия — растяжения в направлении длины, являющейся
осью Х', то = 1/(4/д(ар). Для 30сХ - среза s22 = 139,6х
X 10-14см2/дин; для —30° X -среза s^2 = 84-10-14см2/дин; для
60° X - среза s22 = 104,5-Ю-14 см2/дин.
Вычитая из выражения для s22(—зо°) ВЬ1Ражсппс для «22(зос)’
получаем
S22(-30°) S22(30°) =
Отсюда
sl4 = 42,6 • 10-14 см2/дин.
Для получения величин остальных коэффициентов упругой
податливости кварца определялись модули сдвига, которые в свою
очередь рассчитывались по известным разонансным частотам
123
колебаний сдвига по толщине и вдоль грани образцов У-среза.
При приложении поля к рабочим граням образцов У-среза (Е\ =
=/?3 = О, Е2 =/= 0) возникают деформации двух типов rs(z-13) и
ГбСПг)- Обе деформации являются деформациями сдвига, причем
деформация rs, ответственная за деформирование кристаллической
пластинки в плоскости Х1Х3, называется деформацией сдвига
вдоль грани, а деформация г6, ответственная за деформирование
в плоскости Х1-У2, называется деформацией сдвига по толщине',
оба типа этих колебаний легко возбуждаются.
Вычитая из удвоенного выражения для «22(60°) выражение
Для 4(зо ') п $22(-зо‘) получаем
2$22(60°) ~ $22(30°) — $22(-30 ) — $11 + $33 “ $14’
отсюда
$33 = 2®22(60‘) ~~ 1®22(—30°) + $22(30°)] + $11 + $14 =
= 98,6-10-14 см2/дип.
Найдем теперь 2si3 + s44, вычитая из выражения для ®22(зо°) сла~
гаемые, содержащие уже определенные нами коэффициенты
«И, «33, «141
2$13 + $44 = (^^$22(30°) ~~ 9$11 ~ $33 6Д/3 SJ3).
Подставляя чпелепные значения величин «22(зо°)’ su» «33 и si3’
получаем
2«I3 + «44 — 167,3 • 10~14 см2/дпп.
По величине резонансной частоты колебаний сдвига по тол-
щине образца У-среза можно рассчитать коэффициент упругой
жесткости с66; по величине резонансной частоты колебаний сдвига
вдоль грани — коэффициент с44:
— iff, (d2) Р = 39-Ю10 дин/см2;
$55 = $44 = р = 57,1 -1°10 дип/см2.
Чтобы от коэффициентов ctj перейти к коэффициентам вц,
нужно использовать соотношения (7.0а), связывающие эти коэф-
фициенты.
Найдем связь коэффициентов с44 и с№ с коэффициентами s,j:
___________$11 ~ $12 _ $11 ~ $12
$44 s /, _ _ х _ 2s 2 ’ $66 2
$44 V 11 $12) "14
___________^41_______________
2$44 ($11 — $12) ~ 2$14
124
Отсюда
Подставляя в последние выражения значения измеренных
величин, получаем (в см2/дин)
«м = 199,3 • IO”14, sn — sJ2..= 145,6 • IO-14, s12 = —14 - 10-|4j
Зная S44, коэффициент sls найдем из соотношения
2si3 + s44 = 167,3 • 10-14 см2/дин.
Отсюда sI3 = —16 10"14 см2/дип.
Таким образом, по шести измерениям резонансных частот
различно ориентированных кристаллических образцов кварца
определяются шесть независимых коэффициентов «;;.
su = 131 • 10-14, SJ2 = —14-IO-14, s13 = —16 • 10-14,
s33 = 98,6 Ю-14, «и = -42,6- 10“14, «44=199,3 • 10~14.
7.6. Измерение коэффициентов упругой податливости
сфалерита производилось при комнатной температуре
Рис. 7.2. Ориентпровка образцов, используемых в задаче 7.6.
динамический методом па трех различно ориентированных
брусках Z-среза, представленных на рис. 7.2. Электроды
наносились на их рабочие грани. Усредненные результа-
ты измерений сведены в таблицу па с. 126.
Пользуясь приведенными данными, рассчитать значе-
ния коэффициентов упругой податливости сфалерита*). * s
*) Поскольку измерения проводились динамическим методом,
то в результате получены упругие коэффициенты, измеренные в
адиабатических условиях при постоянном электрическом поле
sijkl (см. § 13).
125
Ориентация среза <рис. 7.2) Размеры, мм Вид колеба- ний Резонансная /'и антире- 2г зонансная / . А частота, кГц Относитель- ная диэлек- трическая проницае- мость свобод- ного кристал- ла
1 t d
22,5°/-срез 20 2,7 1,0 Продоль- ные колеба- ния на ос- новной ча- стоте /л=101,7 /
45°/-срез 20 2,7 1,0 То же /д=117 fA = 117,146 8,37
0°/-срез 30 6,0 1,0 Колебания сдвига вдоль грани на ос- новной ча- стоте /л =279
Решение. Кристаллы сфалерита (точечная группа симмет-
рии 43тга) характеризуются тремя коэффициентами упругой по-
датливости: sin «12 и «44. Все указанные коэффициенты могут быть
измерены па трех различно ориентированных брусках.
Как видно из рис. 7.2, все три бруска вырезаются перпенди-
кулярно к оси Хз — одной из трех эквивалентных кристаллофи-
зических осей, являющихся инверсионными осями симметрии чет-
вертого порядка. Длины двух первых брусков, называемых «вра-
щаемыми» /-срезами, взяты большими по сравнению с их шири-
ной и толщиной. Так как кристалл сфалерита является пьезо-
электриком, приложение переменного электрического поля к ра-
бочим граням таких брусков возбуждает в них колебания сжа-
тия — растяжения в направлении их длины, которая выбирается
в качестве оси X... В этом случае коэффициентом: упругости ука-
занных пластинок будет величина «и. Согласно (6.23) резонанс-
ная частота продольных колебаний на основной частоте
_ 1
~ 21
поэтому из измерений резонансных частот таких брусков непо-
средственно определяются коэффициенты «п. Ориентация осей
Х1,Х2, Xg, связанных с ребрами брусков «вращаемых» /-срезов,
относительно кристаллофизических осей сфалерита, задается
126
следующей таблицей направляющих косипусов:
Оси Xt х3
х/ cos ср sin ф 0
х2' —sin ср COS ф 0
Х3' 0 0 1
Коэффициент упругой податливости sn в направлении дли-
ны брусков «вращаемых» Z-срезов может быть найден из урав-
нения (7.2а), которое для нашего случая имеет вид
= «И (С0®4 Ф + Sh‘4 + (2«12 + Sit) Sin2 Ф COS2 ф.
Коэффициент s44 определяется с помощью пластинки 0°/-cpe-
за, длина которой значительно больше ее ширины. В такой пла-
стинке возбуждаются колебания сдвига вдоль грани (так назы-
ваемые контурные колебания). Резонансная частота колебаний
сдвига вдоль грани определяется соотношением
где t — ширина пластинки.
Для кубических кристаллов сее — с44 = l/s44; отсюда
1
~ №)2Р ’
Пользуясь приведенными соотношениями, а также экспери-
ментальными и табличными данными, можно рассчитать все уп-
ругие постоянные сфалерита.
Из соотношения для резонансных частот продольно колеблю-
щихся брусков «вращаемых» /-срезов найдем значения s 5
, 1
Отсюда
«11(22,5°) = 14>73 ’ 10~13 см2/дин,
Sll(45°) = 11,08 ’ 10-13 см2/дин-
С другой стороны,
«11 = «11 (С°84 Ф + sin<l Ф) + (2«12 + «44) sin^ COg2 Ф;
для 22,5°/-среза sin <р = 0,3827, cos ф = 0,9239, = 0,75su ф-
127
+ 0,125 (2sJ2 + S44); для 45 Z-среза sin <p = cos <p = 0,7071, sn =
= 0,5su 0,25(2si2+ s44).
Решая эти уравнения относительно sn и 2si2 + s44, находим
S11 = 2sil(22,5°) ~ Sll(45°) “= 18’42 • 10-13£М2/дПН,
2s!2 + S44 = 8s11(45°) 4s11(22,5°)’
Величина sti Определяется из данных для 0°7-среза:
s = ------------------------= 21,7 • IO-13 см®/дин.
(2 0,6 279 • 103)2 • 4,102
Далее найдем
= (7,56 — 21,7) • Ю-13 =
12 2
Таким образом, коэффициенты упругой податливости сфале-
рита равны (в ед. СГСЭ)
щ = 18,42 1СГ13, sI2 =—7,07 • 10~13, s44 = 21,7 10“13.
Задачи
7.7. На какие группы аналогичных по физическому
смыслу компонент можно разделить матрицу упругих по-
датливостей (sa) триклинных кристаллов?
7.8. Пользуясь табл. 9, ответить на вопросы:
а) Кристаллы с какой симметрией будут испытывать
сдвиговые деформации под действием всестороннего сжа-
тия?
б) Можно ли всесторонним сжатием изменить только
форму кристаллического образца без изменения его
объема?
7.9. Пользуясь методом прямой проверки, показать,
что матрица (sfi) для кристаллов группы KDP имеет
шесть независимых компонент.
7.10. К кристаллу хлората натрия вдоль одной пз осей
второго порядка приложили напряжение сжатия, равное
1500 Н/см2.
Определить относительную деформацию, которую ис-
пытывает кристалл вдоль направлений типа [111].
7.11. Кристалл хлората натрия подвергнут действию
одноосного растягивающего усилия 104 Н/см2 в произ-
вольном направлении.'
На сколько градусов нужно нагреть этот кристалл,
чтобы относительное изменение объема было таким же,
128
как в случае деформации кристалла под действием ука-
занного одноосного растяжения?
7.12. В результате обратного пьезоэлектрического эф-
фекта пластинка А-среза ADP (см. рпс. 2.4) испытывает
относительную деформацию сжатия по толщине, равную
6 • 10~3. Охарактеризовать напряженное состояние пла-
стинки в кристаллофнзической системе координат.
7.13. Рассчитать объемную сжимаемость кристаллов
турмалина и сегнетовой соли; сравнить эти величины.
7.14. Определить модуль Юнга в направлении кри-
сталлофизических осей Xi п Xs, а также в направлении
длины бруска, представляющего собой 45° Z-срез ADP
(см. рис. 6.3).
7.15. ) Найти уравнение указательной поверхности ко-
эффициента «зз (величины, обратной модулю Юпга) для
кристаллов кварца. Как выглядит сечепие этой поверхно-
сти плоскостью Х,Х2?
7.16. Записать уравнение указательной поверхности
коэффициента sS3 (величины, обратной модулю Юнга) для
кристаллов вюрцита. Что можно сказать о симметрии
этой поверхности?
7.17. Кварцевая пластинка Х-среза (см. рпс. 2.3) раз-
мером 1X 1 X 0,3 см3 сжимается силой 800 Н. Найти
работу, произведенную при деформировании, если сила
приложена к рабочим граням пластинки.
7.18. Из кристалла кварца вырезан кубик с ребрами,
равными 1 см. Кубик подвергнут всестороннему сжатию
напряжением 500 Н/см2. Каково изменение внутренней
энергии деформированного кубика?
7.19. Найти энергию деформации монокристаллическо-
го кубика кремния, подвергнутого действию одноосного
сжатия по направлению, задаваемому относительно кри-
сталлофизической системы координат направляющими ко-
синусами (0,705; 0,705; 0). Напряжение сжатия 400 Н/см2.
7.20. Показать, что величина, обратная сжимаемости,
для кубических кристаллов связана с коэффициентами
упругой жесткости соотношением
1 _ С11 + 2cia
Р 3
7.21. Показать, что для кристаллов с симметрией
4/ттт выполняется соотношение си — с12 — l/(sn — s12).
7.22. Показать, что для кубических кристаллов коэф-
фициент упругой жесткости clt связан с коэффициентами
Н. В. Передо нова, М. M. Тагиева 129
упругой податливости sn п s12 соотношением
„ *11 +*12
11 (sn ~ sia) (®и + 2sia)
7.23. Какие из коэффициентов упругой податливости
могут быть определены при измерении объемного сжатия
AP7V и продольной деформации образца вюрцита, испы-
тывающего напряжения сжатия в направлении [00011?
7.24. К кристаллическому образцу сфалерита при-
ложили напряжения сжатия 2,0 103 Н/см2 в направлении
[100]; при этом величина продольной относительной де-
формации оказалась равной 1,7 10 4. Затем образец под-
вергли действию гидростатического давления, равного
2 -104 Н/см2; при этом относительное уменьшение объема
образца составило 2,6 • 10"3. Какие коэффициенты si3 мо-
гут быть найдены по результатам эксперимента?
7.25. Для получения упругих характеристик поляри-
зованной керамики титаната бария из нее изготовили два.
образца в виде удлиненных параллелепипедов с квадрат-
ным сечением (рис. 7.3). Осью поляризованной керамики
Рис. 7.3. Ориентировка ооразцов, используемых в задаче 7.25.
в обоих случаях являлась ось Х3, а одноосное напряжение
сжатия действовало по нормали к квадратному сечению
образцов. Какие коэффициенты, характеризующие упру-
гие свойства керамики, могут быть получены по резуль-
татам измерения продольной деформации и объемного
сжатия образцов?
7.26. Какие упругие коэффициенты кварца можно оп-
ределить, нагружая по длине стержень, вырезанный, как
на рис. 7.3 слева,, и измеряя деформации его ребер?
130
7.27. Измерение коэффициентов, необходимых для ха-
рактеристики упругих свойств кубического кристалла,
проводилось с помощью измерения резонансных частот
трех различно ориентированных образцов, представлен-
ных на рис. 7.2.
Усредненные результаты измерений сведены в таб-
лицу.
Ориентация среза Размеры, мм Вид колебаний Резонансная частота, кГц
1 t d
22,5° Z-срез 20,1 2,69 1 Продольные коле- бания на основной частоте 95,976
45° Z-срез 20,38 2,7 1,01 То же 89,205
0° Z-срез 29,9 6,02 1,01 Колебания сдвига вдоль грани на ос- новной частоте 180,398
Определить, какие коэффициенты могут быть получе-
ны по результатам измерений, и рассчитать их значения.
7.28. Показать, что относительное изменение объема
AV/V кубического кристалла при одноосном растяжении
не зависит от направления растяжеция.
7.29. Показать, что в отношении упругих свойств пло-
скость (0001) в кристаллах класса бтт является пло-
скостью упругой изотропии.
7.30. Показать, что кристаллы гексагональной синго-
нии обладают осью симметрии бесконечного порядка в
«отношении упругих свойств.
7.31. Показать, что в отношении упругих свойств ось
•симметрии 2 эквивалентна перпендикулярной к ней пло-
скости симметрии.
7.32. Определить максимальные значения допустимых
.упругих деформаций сжатия для кристалла КС1, если его
•предал упругости при одноосн,ом сжатип в направлении
if 100] составляет 800 Н/см2.
7.33. Определить допустимые значения электрических
•полей, используемых для возбуждения пьезопреобразова-
теля из кристалла KDP, если предел механической проч-
ности этого кристалла 120 Н/см2. Рассмотреть £-срез.
9* 131
7.34. Определить напряжения, испытываемые пластин-
|кой 45° Z-среза сегнетовой соли (см. рис. 6.3), если к ее
рабочим граням прикладывается электрическое поле на-
пряженностью 103 В/см.
7.35. Какие из коэффициентов упругой податливости
кристаллов ADP могут быть получены при измерении
резонансных частот продольно колеблющихся брусков
j 22,5° Х-, 45° X- и 67,5° Х-срезов?
7.36. Монокристаллический образец кремния сжали уси-
лием 1,5 • 107 Н/м2 в направлении [100], при этом
величина продольной деформации оказалась равной
1,13 • 10-4. Затем образец подвергли действию гидростати-
ческого давления, равного 107 Н/м2, при этом относитель-
ное изменение объема образца составило 1,1 • 10_3. Какие
коэффициенты 8Й могут быть найдены по этим измере-
ниям?
7.37. Определить деформации, испытываемые образ-
цами поляризованной керамики титаната бария, ориента-
ция которых показана на рис. 6.7, при действии на них
напряжений, указанных в задаче 6.46.
7.38. Вывести выражение для температурного коэф-
фициента частоты /т кубических кристаллов. На основе
анализа этого выражения ответить па вопрос: в каких
случаях в кубических пьезоэлектриках возможны срезы
с нулевым коэффициентом /т*)?
7.39. Вычислить температурный коэффициент частоты
/т кварцевого бруска Х-среза, колеблющегося по длине.
7.40. Определить относительное изменение частоты
кварцевого бруска Х-срёза при нагревании его до 60 °C.
Длина бруска 15 мм.
7.41. Каковы допустимые изменения температуры
кварцевого вибратора Х-среза, колеблющегося по длине,
если относительное изменение его частоты А/// не долж-
но превышать 10 4.
7.42. Кварцевый брусок Х-среза ориентирован так, что
нормаль к его рабочей грани лежит в координатной пло-
скости Х,Х3 и составляет с осью X, угол 5°. Определить
температурный коэффициент частоты /т такого вибра-
тора.
7.43. Для вибратора, описанного в предыдущей задаче,
определить относительное изменение частоты в темпера-
турном интервале —60 — +60 °C.
*) Для решения задач 7.38- 7.43 см. § 6.
132
ПЬЕЗОРЕЗИСТИВТТЫП (ТЕНЗОРЕЗИСТИВИЫП) ЭФФЕКТ
Z В ПОЛУПРОВОДНИКОВЫХ КРИСТАЛЛАХ
Пьезорезистивный эффект заключается в изменении
величины удельного электрического сопротивления кри-
сталла, обусловленном действием на него механических
напряжений. Большая часть кристаллов обладает этим
эффектом в той или ипой степени. Особенно велик этот
эффект в полупроводниковых кристаллах.
В отсутствие механических напряжений закон Ома
для кристаллов имеет вид
/?. = р.ф
(8.1)
где Ei и jt — компоненты векторов напряженности элек-
трического поля и плотности тока; р,г — компоненты тен-
зора удельного сопротивления в отсутствие механических
Напряжений.
При действии на кристалл механических напряжений
величина его удельного сопротивления изменяется и за-
кон Ома в этом случае принимает вид
Ei = (pu + Дри)д. (8.2)
В случае малых механических напряжений добавка
Дря к тензору удельного сопротивления линейно зависит
от напряжения, т; е.
Др./ P-Umn^mn (8*8)
Ритк — коэффициенты, образующие тензор четвертого
ранга.
Соотношение (8.2) принимает теперь вид
Ei (р,7 Р
Обычно пьезорезистивные свойства кристаллов характе-
ризуются тензором пьезорезистивных коэффициентов
ПЫтоп, которые связаны с коэффициентами Рцтп соотно-
шением
Pilmn ~ РНгПытп, (8-4)
при этом уравнение пьезорезистивного эффекта прини-
мает вид
Ei ' — Pife (5bl Пыпт^тп)
(8-5)
133
У кристаллов кубической сингонии, к которой относится
большинство полупроводниковых кристаллов, применяе-
о о®
мых в качестве тензорезисторов, р»ь = р о^ и
= р (йы + (8.6)
Другой аспект пьезорезистивного эффекта — зависимость
удельного сопротивления кристаллов от деформации гре,
характеризуется уравнением
Et — Pik f^klpg^pg) jb ($-0
Компоненты тензора эласторезистивпых коэффициентов
mklpg связаны с компонентами тензора пьезорезистивных
коэффициентов соотношениями
W-Mpg = ^klpg^pgnint (8.8)
в которых стпре — коэффициенты упругой жесткости,
Spgmn коэффициенты упругой податливости.
Матричные обозначения. В соответствии с симметрич-
ностью тензоров IpJ, [tmn] и [rPg] компоненты тензоров
пьезорезистивных и эласторезистивпых коэффициентов
симметричны по первым двум и по вторым двум индек-
сам:
llftz»nn Пмнт П/^nin. (8.9)
Эти тензоры можно записать с двумя индексами ПЛц,
которые принято связывать с ПЫт„ соотношением
I Щг?пп (А, — 1, ..., 6; р. = 1, 2, 3),
l2TIftfmn(l= 1, ...,6;ц= 4,5,6), (Л)
а т>л, с mklpg соотношением
mKv = mh,pg (А, = 1, ..., 6; v = 1, ..., 6). (8.11)
Симметрия кристалла и число независимых пь^зоре-
зпстивных коэффициентов. В силу симметрии коэффици-
ентов npv и по индексам ц и v число независимых
коэффициентов в общем случае равно 36. Учет симмет-
рии кристалла уменьшает это число. Вид матриц пьезо-
резистивных коэффициентов для кристаллов, относящихся
к различным кристаллографическим классам, а также зна-
чения пьезорезистивных коэффициентов различных полу-
проводниковых кристаллов приведены в табл. 10 и 14.
134
Продольный, поперечный и сдвиговый пьезорезистив-
ные эффекты. Пусть на кристалл, обладающий пьезоре-
зистивным эффектом, действует одноосное механическое
напряжение.
Если направления тока и электрического поля совпа-
дают с направлением действия механического напряже-
ния (рпс. 8.1, а), то изменение сопротивления кристалла
в этом случае называется продольным пьезорезистивным
эффектом.
Если же направления тока и поля перпендикулярны
направлению механического напряжения (рис. 8.1, б),
то такой пьезорезистивный эффект называется попереч-
ным. Так, например,
для одноосного напря-
жения, действующего
вдоль оси Xi, коэффи-
циент Пп описывает
продольный эффект, ко-
эффициенты П12 и
П13 — поперечные эф-
фекты.
Изменение сопротив-
ления кристалла, обус-
ловленное действием
сдвиговых напряжений,
называется сдвиговым
пьезорезистивным эф-
фектом. Сдвиговые ко-
эффициенты П14, П24,
П34. описывают измене-
ние сопротивления, выз-
ванное действием на-
пряжения сдвига i4 для
случая, если направле-
ния электрического по-
ля и тока совпадают;
коэффициент П44 описы-
вает изменение сопро-
тивления, обусловлен-
ное действием того же
напряжения t4 в слу-
чае, если поле направ-
Рис. 8.1. Схематическое изображение
продольного и поперечного пьезо-
резистивных эффектов.
лено вдоль оси Х2 и плотность тока — вдоль оси Х3.
Зависимость величины пьезорезистивного эффекта от
направления. В большинстве случаев максимальное зпа-
135
Рис. 8.2. Полупроводнико-
вый тензодатчик, работаю-
щий в режиме продольного
эффекта.
чение величины продольного, поперечного или сдвигового
пьезорезистивного эффекта не связано с направлением
кристаллофизпческих осей. Для нахождения направлений,
соответствующих экстремальным значениям пьезорезис-
тивных коэффициентов, следует воспользоваться законом
их преобразования
Пщп — CimCjnChpCigTImnpg (8.12)
и исследовать это выражение на экстремум. Здесь Cim,
Ст, ChP, Ctg — направляющие косинусы, задающие ориен-
тацию осей Х2, Х3 относительно кристаллофизпческих
осей, с которыми связаны коэффициенты Птпрв.
Датчики, работающие в ре-
жиме продольного, поперечного
и сдвигового пьезорезистивно-
го эффекта. Монокристалличес-
ские датчики этого типа пред-
ставляют собой тонкие ориенти-
рованные стержни или бруски,
длина которых совпадает с на-
правлением максимального зна-
чения продольного пьезорезис-
тивпого коэффициента для дан-
ного кристалла (рис. 8.2). Пред-
положим, что образец, длина
которого п совпадает с направ-
лением Xv подвергается действию механических напря-
жений. В этом случае при ]2 = /з = О
£1 = Д (1 + п;х) р. (8.13)
Поскольку Е± = Д (р + Ар), то
Ар/р = П^Х или Ар/р = nntu, (8.14)
где IIu— значение продольного ньезорезистивпого коэф-
фициента в направлении п. Из (8.14) следует, что коэф-
фициент II п можно назвать коэффициентом чувствитель-
ности по напряжению (Пп = Ap/pi).
Одной из важнейших характеристик рассматриваемых
датчиков является коэффициент тензочувстеительности К,
определяемый следующим образом:
£ = (8.15)
где \R/R н г — изменение сопротивления и деформация
в направлении длины датчика.
136
Из (8.15) следует, что коэффициент К характеризует
чувствительность датчика по деформации.
Учитывая закон Гука, получаем, что
где in—напряжение, действующее в направлении длины
датчика n; sn и Еп— значения коэффициента упругой
податливости и модуля Юнга в направлении длины дат-
чика.
Для кристаллов кубической сингонии
«п = su — 2(su — s12 + V2s44) (n?n| + n23nl + п|п1). (8.16)
Благодаря тому, что для полупроводниковых кристал-
лов коэффициент П14 =И= 0, они
для измерения напряжений
сдвига и крутящих моментов.
На использовании попе-
речного и сдвигового эффек-
тов основаны датчики, позво-
ляющие определять дефор-
мации, испытываемые сво-
бодной поверхностью. Схема-
тическое изображение тако-
го датчика показано на
рис. 8.3. Для полного опреде-
ления деформаций необходи-
мо сделать три измерения:
измерить сопротивление в
двух перпендикулярных на-
правлениях (например,вдоль
Х',и Х0
тока пет, и величину
могут быть использованы
Рве. 8.3. Тензодатчик, с по-
мощью которого измеряет-
ся сумма напряжений, дей-
ствующих в плоскости.
при условии, что в поперечных направлениях
Vjl-L при /2 = 0. Очевидно, по
результатам этих трех измерений могут быть определены
деформации в двух перпендикулярных направлениях и
сдвиговая деформация в плоскости, касательной к по-
верхности.
Примеры решения задач
8.1. Для измерения относительных деформаций, испы-
тываемых различными конструкциями, обычно использу-
ются германиевые или кремниевые датчики, представляю-
щие собой тонкие ориентированные стержни, работающие
137
в режиме продольного пьезорезистивного эффекта. Каким
выражением определяется величина продольного пьезоре-
зистивного эффекта указанных датчиков произвольной
ориентации? Как следует ориентировать стержни герма-
ниевых датчиков р- и тг-типа и кремниевых датчиков
лг-типа для получения максимального продольного
эффекта?
Решение. Пусть n(nb п2, п3)—направление длины датчи-
ка. Совместим ось с направлением п, в этом случае согласно
(8.12) продольный пьезорезистивный эффект будет описываться
коэффициентом
П„ — = ПП11= ~ nininhnl^ijhl-
Подставляя в это выражение коэффициенты П.ом, отличные
от нуля, для класса тЗт, к которому относятся кристаллы гер-
мания и кремния, получаем
ПП = ("J + П2 + Пз) П11 + 2 (П12 + П44) + П1П1 + •
где П44 = 2Пгз23 = 2П313, = 2П1212. Возводя выражение nf -|- п* +
+ «3= 1 в квадрат, имеем
п1 + п2 + пз = 1 “ 2 (nin2 + пзп1 + Фз)’
Учитывая это, выражение для Пп можно записать в виде
Пц *= 2 (Пц П12 П44) (я,п2 + п3пг -f- п3п2) =
= П11 ~ 2ПА (П1П2 + П3П1 +
где Пл = Пи — П12 — П44.
Чтобы найти область изменения коэффициента ПИ1 достаточно
найти предел изменения величины -|- ф- п^п^, изменя-
ющейся от 0 до Vs. Таким образом, Пп меняется от Пц до
Пп — 2/3ПЛ. Экстремальному значению ПХ1 = Пи соответствуют
три направления <100), экстремальному значению11х1=П11—2/3Пд
соответствуют восемь направлений. Максимальные и минималь-
ные значения Пп зависят от знака величин Пц и Пл. Макси-
мальные значения коэффициента Пп для германиевых датчиков
р- и n-типа соответствуют направлениям <111>, для кремниевых
датчиков п-типа— направлениям <100> (см. табл. 14).
Таким образом, германиевые датчики п- и д-типа следует
ориентировать вдоль направлений <111>, кремниевые п-типа —
вдоль <100>.
138
8.2. Как изменится сопротивление нитевидного крем-
ниевого тензодатчика п-типа, размерами 6X1X1 мм,
ориентированного в направлении [100], работающего в
режиме продольного эффекта, при деформации 0,05%:
а) за счет изменения удельного сопротивления, б) за
счет изменения его геометрических размеров?
Определить коэффициент тензочувствителыюсти и вы-
ходной сигнал, получаемый при деформации 0,05%, если
величина постоянного тока, текущего через датчик, рав-
на 5А.
Решение, а) Для полупроводникового тензодатчика, пред-
ставляющего собой тонкий стержень, ориентированный в направ-
лении [100], все напряжения, кроме продольного напряжения Ц,
равны нулю. Деформации, соответствующие этому напряжению,
равны
И = «ц4ь г2 = Ssjti; Гз = «3it|.
Поскольку датчик используется в режиме продольного эффекта,
то /г = 7з = 0; Е2 = Е3 = 0 и согласно (8.6)
Ei/p — /1(1 + Пий) =71(1 + ПцГ1/®ц).
Относительное изменение удельного сопротивления датчика
равно Др/р = ПпЦ = (Пц/su) И.
Для n-типа кремния р = 11,7 Ом • см, Пц = 102,2 • 10~|2см2/дин,
sji = 0,768 10-12 см2/дип и в случае относительной деформации
п = 5- 10~4, ДК/7? = Др/р = 665 • 10-3 = 0,665.
б) Относительное изменение сопротивления тензодатчика,
обусловленное изменением его размеров, равно
s2i+41А
sn /
Первый член в скобках появляется как следствие увеличения
длины образца, член (s2i + S3i)/sii возникает вследствие измене-
ния площади поперечного сечения:
0,428\
1 + о76§ + ' Ю =10,008.
Изменение общего сопротивления нитевидного тензодатчика,
ориентированного вдоль [100], равно
&R/R = (1 — 2s12/sn + nu)rj = гр
Как следует из результатов расчета для тонких кремниевых
тензодатчиков, изменение сопротивления датчика в основном (в
Данном случае на 99%) обусловлено изменением его удельного
ДЯ /
Я -д
1.39
сопротивления. Этот же результат справедлив и для остальных
полупроводниковых тензодатчиков этого типа.
Коэффициент тензочувствительности тензодатчика
к = = 1 + п + — ~п -L« - 1зз.
/?г 1‘ sn »
Выходной сигнал при деформации 5 10~4 равен
| V | = /АЛ = lit ЛР = ip 4-г.» 2,3 В.
р 5 su
8.3. Найти выражение, позволяющее рассчитать ве-
личину поперечного пьезорезистивного эффекта в полу-
проводниковых кристаллах, относящихся к классам т'бт
и 4.3m, в произвольном направлении. Онределить экстре-
мальные значения коэффициентов поперечного пьезо-
резистивного эффекта и соответствующие им экстремаль-
ные направления.
Решение. Поперечный пьезорезистивный эффект опреде-
ляется коэффициентами Пг-д где i =# j, i, j = 1, 2, 3.
В случае, если механическое напряжение действует вдоль
оси Х2, а векторы плотности тока и поля направлены по оси Хь
такой эффект описывается коэффициентом П12. Рассмотрим слу-
чай, когда одноосное механическое напряжение действует в на-
правлении п(пь п2, и3) || Х", а ток и поле имеют направление
1(1ь h, k) II Х[. Тогда
<2 = п;122 = = Пп {пЩ + пЩ + +
+ п12 № + + "V2 + *Х) +
+ 2П44 (n2W3Z21 3 + "iVA + VVA)’
Для упрощения выражения для П12 используем условие ортого-
нальности векторов и и 1, возведенное в квадрат:
("A+^A + Vs)^ °-
ИЛИ
niZl + R2Z2 + n3Z3 + 2 (”ira2ZlZ2 + ni"3ZlZ3 + "2n3Z2Z3) = 0
и го, что векторы n и 1 являются единичными:
(ni + + и|) (г1 + + ZD = !•
Учитывая эти соотношении, приходпм к следующему выражению
дли п'2; —х
Пп = Пи + Пл (^+^+41)’
140
где Па = ГГц — П12— П14. Экстремальные значения П12 определя-
ются величиной + пз^з> мипимальное значение кото-
рой, очевидно, равно нулю. Это соответствует следующим направ-
лениям пи1:
II 1 п 1
(1, 0, 0) (0, 12, 13) (0, n2, n3) (1, 0, 0)
(0, 1, 0) (Zj, 0, Zg) или (и1, 0, п3) (0, 1, 0)
(0, 0, Г) (Zr Z2, f)) (nr и2, 0) (0, 0, 1).
Для нахождения максимального значения величины n2l2 -f-
+ n2lz пз1з воспользуемся методом неопределенных множите-
лей Лагранжа. Составим функцию f
j = n2l2 + njl2 + n|Z| - Z, (n* + + n23 - 1) -
- \ Or + % + *1 - 1) - 1 + n2Z2 + n3l3).
Дифференцируя f по nt и lt и приравнивая производные ну-
лю, получаем
-g- = 2niZ|-2Z1Hi-ZZi = 0,
^- = 2гЛ?-2Х^-Хпг=0.
Умножая dfldrii на и,-, df/dlt на Z, и сравнивая полученные
выражении, находим n? = Z?, или щ = ± Ц. Выражение n1Z1 +
+ ”sZ2 -f- n3ls = 0 теперь принимает вид
+• «j + п2 ± пз = 0.
Выбор всех положительных пли всех отрицательных знаков
У пъ >’2, пз не удовлетворяет условию нормировки вектора и. Рас-
смотрим какую-либо из шести оставшихся комбинаций знаков,
например п2—п|-|-п?=0. Вычитая это равенство из условия
нормировки вектора п, получаем = 1/2; ng = + l/”l/2. При
этом
п —(П , + —1 nA 1 = (щ, ± -4=-, «А
\ 1 1/2 7 1/2 ’ Sj’
nlll + П2г2 + П113 = И1 + 1/4 + П3-
С учетом условия и® -j- п2 = 1/2 находим, что максимальное зна-
чение коэффициента П12 соответствует направлениям типа
n(l/V2, 1/У2, 0), 1(1/1’2, — 1/}'2, 0) (всего шесть таких направлений)
и равно —‘/г. Таким образом, коэффициент поперечного эффекта
141
меняется от Hi2 до П12+’/2(Щ1— П]2—П44), а его максимальное
и минимальное значения зависят от знака (Пи —Пв— П44).
8.4. Для определения пьезорезпстпвных коэффициен-
тов монокристаллов теллурида свинца (класс тЗт) р-ти-
па проводимости с концентрацией 1 -ь 3 • 1018 см~3 были
изготовлены образцы сечением 10-2 см2. Ориентировка
образцов и схема эксперимента представлены на рис. 8.1.
При сжатии образцов усилием 9,8 II величина удельного
сопротивления первого (рис. 8.1, а), второго (рис. 8.1, б)
п третьего (рис. 8.1, в) образцов, измеренного при посто-
янном токе, уменьшалась на 0,24, 0,15 и 1,27% соответ-*
ственно. Рассчитать значения пьезорезпстпвных коэф-
фициентов кристаллов р-РЬТе.
Решение: Как видно из рис. 8.1, в случае первого и треть-
его образцов используется продольный эффект (направления поля
и тока совпадают с направлением механического напряжения), в
случае второго образца — поперечный эффект (направления поля
и тока перпендикулярны направлению напряжения).
Пьезорезистивные свойства теллурида свинца описываются
тремя независимыми коэффициентами Иц, П|2, П44, а удельное
сопротивление является скалярной величиной. Для первого образ-
ца (рис. 8.1, с) Ц = — t, i2 = f3 = 0; /1=7; ;2 = /3 = 0; Ei = Е;
Z?2 = 0, и уравнение пьезорезистпвного эффекта записывается в
виде
Ei/h — р(1 + Пц«1) = р + Др; Др/р = ПцЦ.
Отсюда
п ( ДР/Р) _ (- Др/р) _ 24 -10-4 _ 2/
П11~ — t — (-F/S) ~ 10е.Юа -2'4'10 см/дин.
Для второго образца (рис. 8.1, б) Ц = —t, f2 = t3 = 0, J2 = J.
/! = /3 = 0, E2 — E, E\ = E3 = 0, п уравнение пьезорезистпвного
эффекта принимает вид
®2 АР
Д = Р (1 + П12Г1)> (Г” —
'2 г
II = —= 15-10~12 см2/дин.
Для третьего образца (рис. 8,1, в) уравнение пьезорезистпвного
эффекта записывается в виде
Ei/ji = р(1 + П;й),
где /—направление длины образца, задаваемое направляющими
косинусами (1/у*2, 1/у'2, 0).
142
В этом случае согласно (8.12) П( = Ч2(Пц + П12.+ П44),
ДР _ i_ Пц + П12 + П44
р_ 2 *
Пн + П12 + П44 =
_ g —Л?!?)- __ 254-10~12 см2/дин,
Отсюда П« = 215 10 12 см2/дпп.
8.5. Для измерения сдвиговых напряжений, а также
крутящих моментов могут быть использованы полупровод-
никовые датчики, работающие в режиме сдвигового пьезо-
резистивного эффекта. Найти выражение, позволяющее
рассчитать величину этого эффекта для полупроводнико-
вых кристаллов классов тЗт, 43m в произвольном на-
правлении. Определить экстремальные значения этой ве-'
личины и направления, соответствующие ее экстремаль-
ным значениям.
Решение. Сдвиговый пьезорезистивпый эффект описыва-
ется коэффициентом типа Ilf, (г = 1, 2, 3, / = 4, 5, 6 и г, j = 4, 5, 6).
Если направления электрического поля и тока совпадают, то
сдвиговое напряжение, например tt, влияет на сопротивление по-
лупроводника через Пи, П24, II34. С другой стороны, то же самое
сдвиговое напряжение f4 влияет на отношение поля к плотности
тока, направленных вдоль оси Х2, через коэффициент П44. По-
скольку для полупроводниковых кристаллов класса тЗт, 43т
все коэффициенты первого типа (Пн, П24, П34) равны нулю, то
пьезорезистивный эффект в таких кристаллах определяется от-
личными от нуля и равными коэффициентами
П44 = П55 = Пес.
Таким образом, величина сдвигового пьезорезистпвного эффекта
в кристаллах указанных классов в произвольном направлении
определяется значением коэффициента П44 вдоль этого направ-
ления.
Рассмотрим случай, когда механическое напряжение сдвига
*<(*23^32) определяется направлениями Х^ ||п п^, п3) и
(^i’ ^а, *3), напряженность поля направлена по оси Х2, плот-
ность тока по оси Х3. Тогда
%П44 = П2323 = —
= П2323 + П112 + +
+ 2П2323 (VsVs + Ш + П1П21112) +
+ П1Ш (П!г1 + ге2г2 + n3Zl) - 2П1122 (пЬг + Фг + пзГз) -
143
^2323 {П111 "Ь n2J2 + П1Ч) —^2323 + (^1111 2^2323 ^Цй) X
X ("ft + "ft + "ft) = 14П44 + ПА ("ft + "ft + "ft).
П44 = П44 + 2ПЛ ("ft + + ^Ч)-
Находя экстремальные значения коэффициента П44 (см. задачу
8.3), получаем, что первое экстремальное значение, равное П44,
соответствует значениям п типа (1, 0, 0) и значениям 1 типа
(О, Zj, 1з), а также значениям 1 типа (1,0,0) и значениям п типа
(О, п2, п3).
Второе экстремальное значение коэффициента П44, равное
П44 + Пд = Пц — П12, соответствует направлениям п типа (1/7'2,
1/У2, 0) и направлениям 1 типа (1/У2, —1/У2, 0).
Таким образом, коэффициенты П44 в зависимости от направле-
ния приложенного сдвигового напряжения меняются в пределах от
Пц до Пц — П12, а минимальное и максимальное значения П44
для различных кристаллов зависят от величины и знаков пьезо-
резистивных коэффициентов.
8.6. В последнее время широкое распространение по-
лучил способ производства полупроводниковых тензодат-
чиков из германиевой дендритной ленты, выращиваемой
на специальных затравках в направлении [211]. Основным
достоинством этого способа является простота технологи-
ческого процесса, состоящего в разрезании ленты на эле-
менты и присоединении к ним проводов. Рассчитать
коэффициент чувствительности тензодатчиков, изготовлен-
ных из дендритной ленты германия с тг-типом проводи-
мости, работающих в режиме продольного пьезорезистив-
ного эффекта, предназначенных: а) для измерения дефор-
маций, б) для измерения напряжений, и сравнить ее с
чувствительностью таких же тензодатчиков, вырезанных
в направлении [111].
Решение, а) Коэффициент тензочувствительности тензо-
датчика, предназначенного для измерения деформаций в режиме
продольного пьезорезистивного эффекта, определяется как
ЛЯ „ „
К- Rr ~П1Е1'
где П( и Ei соответственно значения пьезорезистивного коэффици-
ента и модуля Юнга в направлении длины тензодатчика.
Для тензодатчика и дендритной ленты 11| [211] (h = 2/У6,
12 = 13 = 1/У6), а значения II; и Ei находятся соответственно из
144
соотношений (8.12) и (8.17);
П1 = П[гп] = Пи + (П4« + П12 ~ Пп)= ~ 73'8 ’ Ю-12см2/дин,
Е1 = ^[811] = su - Vg (Su - S18 - Vs Sit) =1>37 • Ю12днн/см2,
К = П[2н]Я[2п] = —101.
15) Коэффициент чувствительности тензодатчика, предназна-
ченного для измерения напряжения, равен величине пьезорези-
стивного коэффициента вдоль оси датчика, т. е.
П[2п] = —73,8 • 10-12 см2/дин.
Для германиевого датчика n-типа, вырезанного в направле-
нии [111]:
П(1и] = '/зПц + 2/з(П|2 — П44) = —9,684 • 10-s см2/дин.
Сравнивая эти коэффициенты, получаем, что коэффициенты
чувствительности датчиков напряжений и деформаций из денд-
ритной ленты германия n-типа в 1, 3 п в 1,75 раз меньше, чем
чувствительность датчиков, вырезанных в направлении [111].
8.7. Для измерения продольной деформации, испыты-
ваемой элементами конструкций самолета, использовался
кремниевый датчик p-типа размерами 6 X 0,5 X 1 мм3,
Рис. 8.4. Схема включения кремниевого датчика для измерения
продольной деформации различных конструкций.
ориентированный в направлении 1111], который включался
в электрическую схему, обеспечивающую постоянный ток
через него, равный 0,02 А, и включалось противонапря-
жепие через холостой датчик (рис. 8.4). Какой деформа-
ции подвергался испытываемый элемент конструкции,
если выходпой сигнал составил 0,63 В?
Решение. Если в процессе измерения используется схема,
приведенная па рпс. 8.4, то в отсутствие деформации активного
датчика выполняется условие ItRi = I2R2, т. е. ЕВых = 0. При де-
формации активного датчика сопротивление его изменяется на
величину ДЛ1 и в этом случае
Рвых = 71 (Л, + АЛ,) — 75Лг = 71 (Л i -{- ДЛ1) — 71Л i = 71ДЛь
Ю н. в. Переломова, М. M. Тагиева 145
Таким образом, сигнал, получаемый при деформации датчика,
прямо пропорционален величине изменения его сопротивления.
Согласно (8.15) ДЯ1 = ЯгК[111] = р-£гП1111]£[111]. Отсюда
/ 1 \-1
г ~~ ^вых s П[Ш]^[ш]у
Значении пьезорезистивного коэффициента и модули Юнга в на-
правлении [111] находятся соответственно из соотношений (8.12)
и (8.17) и для кремния p-типа равны Ппн] = 83,53 • 10~12 см2/дин,
E[i и j — 1,88 • 10“12 дин/см2, г = 2,06 • 10-4.
8.8. Тензометр из германия с n-типом проводимости,
измеряющий сумму главных напряжений в плоскости,
показан на рис. 8.5.
Плоскость датчика ориентирована по (111), и ток про-
пускается в направлении, перпендикулярном плоскости.
Рис. 8.5. Германиевый тен-
зометр для измерения сум-
мы главных напряжений,
действующих в плоскости.
Какова величина измеренных напряжений, если относи-
тельное изменение сопротивления датчика состави-
ло 0,12%.
Решение. Если ток и напряженность электрического поля
в датчике имеют направление п, изменение сопротивления дат-
чика, вызванное действием напряжений [£*/], определяется соот-
ношением Д7?/7? = ni/ijUijkiikb Для нашего случая п = (1/УЗ, lf/3,
~д~ — 1/з (Илы + + n33ft{ -f- 2П12/г -f-
+ 2n23ftl + 2n31ftl) = 1/Snu + f2 + t3) +
+ 2/зП12 + *2 + *3) + 2/зПи (t4 + tB+te).
Поскольку напряжения лежат в плоскости пластинки, то =
= 0. Следовательно, Дц + + tj3 == 0, т. е.
^12 4" ^13 — •—fn
^21 + tn = —tn
t3l + ^32 = —^33
te + fs — —ti>
ИЛИ -f- £4 ~ —t2i
h + it — —fs>
146
откуда
2 (<е + ts + h) = — (ti + t2 + is)
Подставляя значение + fs + te в выражение для AR/Й, полу-
чаем Ай/й — */з(Пц + 2П12— П44) (ti + t2 + t3).
Обозначим главные напряжения, действующие в плоскости
пластинки, через ta и ft. Поскольку tt + t2 + t3 — след тензора
напряжений, испытываемых пластинкой, то он равен сумме соб-
ственных значений тензора, т. е. ta + tt>.
Для германия и-типа Пц + 2П]2 — П44 = 123,2 • 10-12 см2 дин и
ЗАЙ „е
fa + *ь - R (П + 2П — ПЛ «3-10 Па.
\ 11 1 12 44/
8.9. Одним из практических применений полупровод-
никовых тензодатчиков является измерение давления.
Какой из полупроводниковых кристаллов: р = Ge, р —
=> РЬТе или р = InSb обладает наибольшей чувствитель-
ностью в качестве индикатора гидростатического дав-
ления?
Решение. Коэффициент чувствительности полупроводнико-
вого датчика гидростатического давления, основанного на пьезо-
резистивном эффекте, определяется как отношение изменения
сопротивления образца AR/Й, вызванного действием гидростати-
ческого давления, к величине этого давления, т. е.
nP“JH^i--(nn + 2nis).
Следовательно, коэффициент чувствительности в 10-12 см2/дин
для p-Ge — 2,7, для р-РЬТе — 115, для p-InSb — 300. Таким образом,
коэффициент чувствительности датчика давлений из р-InSb в три
раза больше, чем датчика из р-РЬТе, и в 100 раз больше, чем из
p-Ge.
Задачи
8.10. Насколько изменится сопротивление кристалличе-
ского образца антимонида индия, подвергнутого действию
гидростатического давления 107 Па?
8.11. Для измерения главных напряжений, действую-
щих в плоскости, использовался кремниевый тензометр
n-тппа, такой как на рис. 8.5. Ток пропускается в на-
правлении, перпендикулярном плоскости датчика, ориен-
тированной по (100).
Какова сумма измеряемых напряжений, если измене-
ние сопротивления датчика составило 0,11%?
ю* 147
8.12. Определить чувствительность кремниевого^тензо-
датчика р-тппа, предназначенного для измерения напря-
жений, вырезанного в направлении [111], работающего
в режиме: продольного пьезорезистпвного эффекта и
поперечного эффекта, наблюдаемого в направлении
[110].
8.13. Какая относительная деформация может быть
измерена с помощью полупроводникового датчика с коэф-
фициентом тензочувствительности 50, сопротивлением
100 Ом, если напряжение тепловых шумов для такого дат-
чика VT ~ 1,3 • 10~9 В, а напряжение сигнала должно в
10 раз превышать напряжение шума?
Ток через датчик принять равным 0,01 А.
8.14. Определение пьезорезистивных коэффициентов
монокристаллов германия n-типа с сопротивлением
9,9 • 10-2 Ом проводилось па трех образцах разме-
рами 6X1X1 мм3. Ориентировка образцов и схематиче-
ское изображение эксперимента показаны на рис. 8.1.
При действии одноосного сжимающего напряжения, рав-
ного 102 Па, сопротивление 1-го (рис. 8.1, а), 2-го
(рис. 8.1, б) и 3-го (рис. 8.1, в) образцов увеличилось со-
ответственно на 0,279, 0,279 и 4,37 Ом.
Какими пьезорезистивными коэффициентами характе-
ризуются эти монокристаллы?
8.15. Сравнить величину выходного сигнала, получае-
мого от металлического и полупроводникового датчиков,
работающих при деформации 0,05%, в схеме, показанной
на рис. 8.4, если ток через датчики равнялся 20 мА. Для
металлического датчика коэффициент тензочувствитель-
ности К = 2, R — 120 Ом. Для полупроводникового датчи-
ка, изготовленного из германия n-типа, ориентированно-
го в направлении [111], R = 350 Ом.
8.16. Изменение сопротивления полупроводникового
датчика гидростатического давления из антимонида ин-
дия p-типа размером 1,6 X 1 X 0,8 мм3 составило 3,24 Ом.
Какова величина измеренного давления?
8.17. Во сколько раз чувствительность длинного тон-
кого датчика напряжения из кремния p-типа, ориенти-
рованного в направлении [111], больше чувствительности
датчиков из того же материала, ориентированных в на-
правлении [100] и [110].
8.18. Каковы пределы изменения величины коэффици-
ента, определяющего сдвиговый пьезорезистивный эффект,
в кристаллах германия и кремния с p-типом проводимо-
сти?
148
8.19. В области измерительной техники и анализа де-
формаций до обнаружения пьезорезистпвного эффекта в
полупроводниковых кристаллах широко использовались
металлические тензодатчики, коэффициент тензочувстви-
тельпости которых лежал в пределах от 2 до 4. Рассчи-
тать, в каких пределах изменяется коэффициент тензо-
чувствительности датчиков деформаций из кремния и
германия p-типа, основанных на использовании продоль-
ного эффекта и сравнить его с коэффициентом тензочув-
ствительностп металлических датчиков.
8.20. Какими эласторезистпвными коэффициентами ха-
рактеризуются кристаллы кремния?
8.21. Какое механическое напряжение может быть из-
мерено с помощью тонкого кремниевого тензодатчика
р-тппа, ориентированного в направлении [111], если на-
пряжение сигнала, превышающее в 10 раз напряжение
тепловых шумов, для такого датчика, равно 1,3 • 10_3 В?
Сопротивление датчика 100 Ом, ток через датчик
10 мА.
8.22. Тонкий германиевый датчик p-типа, ориентиро-
ванный в направлении [111], и металлический датчик ра-
ботают при деформации 8 • 10-4 в схеме, показанной на
рис. 8.4. Рассчитать величину выходного сигнала для обо-
их датчиков, если их сопротивление равно 25 Ом, ток
равен 20 мА, чувствительность металлического датчика
равна 2.
8.23. В процессе прочностных испытаний для измере-
ния деформаций одной из деталей самолета на нее на-
клеивался нитевидный кремниевый тензодатчик р-тппа,
ориентированный в направлении [111], размерами 15 X
XIX 0,5 мм3. Какие деформации испытала деталь, если
максимальное изменение сопротивления тензодатчика со-
ставило 2,44 Ом.
8.24. Для измерения давления в высокотемпературной
среде использовался кремниевый датчик n-типа. Рассчи-
тать величину давления в среде, если изменение сопро-
тивления датчика составило 0,09 %.
8.25. Каковы пределы изменений коэффициента чув-
ствительности проволочных кремниевых датчиков п-типа,
соответствующие экстремальным значениям пьезорези-
стивного коэффициента?
8.26. Какие из пьезорезпстпвных коэффициентов ру-
тила (класс симметрии 4/mmm) могут быть определены
при помощи эксперимента, схематически изображенного
на рис. 8.1?
149
§ 9. ОПТИЧЕСКИЕ СВОЙСТВА КРИСТАЛЛОВ
Главная особенность распространения света в кри-
сталлах по сравнению с изотропными средами заключа-
ется в существовании в них явления двойного преломления:
в общем случае по какому-либо направлению в кри-
сталле распространяются две световые волпы, поляризо-
ванные во взаимно перпендикулярных плоскостях и име-
ющие разные скорости, а следовательно, различные пока-
затели преломления. Причина этого — диэлектрическая
анизотропия кристаллов. Показатель преломления света
п = Гер, = c/v, где е — относительная диэлектрическая
проницаемость, р — магнитная проницаемость, с и v —
скорости света в вакууме и среде. Для прозрачной не-
проводящей среды па оптических частотах можно поло-
жить jt ~ 1, тогда п ~ Ге.
У изотропных сред диэлектрическая проницаемость и,
следовательно, показатель преломления не зависят от на-
правления: D = еЕ, векторы D и Е коллинеарны. Для ани-
зотропных сред Di = EijEj, где е,3 — компоненты тензора
второго ранга. В общем случае векторы И и Е не совпа-
дают по направлению.
Все особенности распространения света в кристаллах
следуют из решения уравнений Максвелла с учетом ма-
териального уравнения, приведенного выше: Di = е13Е3- или
уравнения
_ Ек = (9.1)
Векторы D, Н и m взаимно ортогональны. Иначе го-
воря, векторы D и II лежат в плоскости волнового фрон-
та, перпендикулярной т, т. е. световая волна по-
перечна.
Векторы Н и Е также ортогональны, но вектор Е не
параллелен D, а лежит в плоскости, перпендикулярной
волновому фронту и составляет с ним некоторый угол
(рис. 9.1).
Используя уравнения Максвелла и материальное урав-
нение в форме Ei = тр3О3, можно получить систему урав-
нений, позволяющую для различных направлений распро-
странения света в кристалле, задаваемых вектором т,
определить коэффициенты преломления и направления
векторов D, если известна диэлектрическая непроницае-
мость кристалла т]д.
Для плоской световой волпы, распространяющейся в
направлении т, из уравнений Максвелла следует соот-
150
ношение между векторами га, Ё и D:
n2mX (тХЕ) = —D.
Раскрывая двойное векторное произведение и учитывая
взаимную ориентацию векторов Е, D и ш, получаем
E-m(mE) = —2D. (9.2)
Слева в (9.2) стоит компонента вектора Е, лежащая
в плоскости волнового фронта,
раллельпая D (рис. 9.1). Урав-
нение (9.2) с учетом (9.1) мож-
но записать в координатной
форме:
(Пи — Dj = ~Dh.
п
(9-3)
Получим систему трех урав-
нений относительно неизвест-
ных компонент вектора D (Z?t,
D2, D3), которая имеет нетри-
виальное решение при некото-
ром значении п, определяемом
т. е. компонента Е, па-
Рис. 9.1. Взаимное располо-
жение векторов D, Е, Н, m
и s при распространении
света в анизотропной среде.
из условия совместности урав-
нений (9.3) — равенства нулю
определителя этой системы.
Таким образом, из уравне-
ний (9.3) можно определить
как показатели преломления световых воли п, так и на-
правление вектора D относительно системы координат,
в которой задан тензор [т]ч].
Рассмотрим (9.3) в системе координат XtXzX3, выбран-
ной так, что ось Х3 параллельна ш, а оси Xt и Х2 лежат
в плоскости волнового фронта. В такой системе координат
вектор m имеет компоненты (0, 0, т3) и уравнения (9.3)
принимают вид
(т]и — n~2)Di + t]12D2 = О,
T]i2^t + (т]22 — n~2)D2 = 0.
Собственные значения двумерного тензора
411 ’’п
'412 ^22
(9.4)
151
могут быть найдены из условия
4ц ~ [г]1а = 0
412 422~п~2
(см. решение задачи 4.3):
^(М) = х/2 (Ли + Л22) ± V(Ли — Л22)2 + (2Л1г)2-
Таким образом, в направлении m распространяются две
волны, имеющие показатели преломления и(1) и и(2), вы-
ражаемые через компоненты тензора тр3- в выбранной на-
ми системе координат XiX2Xs. Скорости этих волн
П(1) = с/Ир), 17(2) = С,/И(2).
Ясно, что с изменением направления m изменяются
и(1) и и(2), р(1) и 17(2), так как при новом направлении ш,
а значит, в новой системе координат компоненты тензора
тр3- того же кристалла будут иметь иное значение.
Каждому собственному значению и-2 соответствует
собственный вектор D. Найдем собственный вектор D*1’
для волны, распространяющейся со скоростью г?(1):
(т]и — и(12) Di1) + — 0, + (Л22 — = 0.
(9.5)
Если координатные оси X, и Х2 выбраны так, что
т]12 = 0 и т]и > т]22, из уравнений (9.5) будет следовать
параллельность вектора D(1) координатной оси X,, так
как D(1) будет иметь отличной от нуля только компоненту
Рх^.Для волны с индукцией D(1) показатель преломления
и(1) = 1/Утщ. Вектор D(2) из тех же соображений окажет-
ся параллельным Х2, a n(2) = 1/Ущ?..
Таким образом, задача нахождения показателей пре-
ломления и направления векторов индукции D(I) и D<2)
двух волн, распространяющихся в направлении т, сво-
дится к приведению к главным осям двумерного тензора
для координатной плоскости XtX2, совпадающей с пло-
скостью волнового фронта (см. задачу 4.3).
Все сказанное выше приобретает геометрическую на-
глядность при использовании характеристической поверх-
ности тензора диэлектрической непроницаемости [цц],
называемой оптической индикатрисой (рис. 9.2).
Уравнение оптической индикатрисы:
riijXfZj = 1. (9.6)
152
Эта поверхность представляет собой эллипсоид, обла-
дающий следующим важным свойством. Если построить
центральное сечение, перпендикулярное волновой норма-
ли ш, то оно будет эллипсом. Показатели преломления
двух волн, распространяющихся в направлении in, п(1)
и тг(2) определяются длинами полуосей (ОА и ОБ) этого
Рис. 9.2. Построение оптической индикатрисы кристалла.
эллипса, а направления этих полуосей являются соответ-
ственно направлениями колебаний векторов D(1) и D(2)
для каждой из двух волн.
В кристаллах низшей категории тензор второго ран-
га, характеризующий свойство кристалла (в данном слу-
чае тензор диэлектрической непроницаемости [цД), име-
ет три независимых компоненты, в кристаллах средней
категории — две и в кристаллах высшей' категории — од-
ну. Соответственно оптическая индикатриса для кристал-
лов низшей категории представляет собой трехосный
эллипсоид *i):
Л11ж1 + ^22Х2 + Лзз^З = 1»
или «
I Х2 | Ж3 _ л
П1 п2 "з
где и, = п2 = 1/Уг]2г; п3 = 1/Vriss — так называемые
главные показатели преломления кристалла.
Для кристаллов средней категории т]и = т]22, оптиче-
ская индикатриса — эллипсоид вращения:
Л11 Czi 4~ + Нззжз ==Д,
*) Поверхность + ‘Ч22а:2 + ^зз^з = ~ эллипсоид, а не
какая-либо другая поверхность второго порядка, потому что
Чн, 1122, т)зз величины существенно положительные.
153
НЛП
Для кристаллов высшей категории оптическая инди-
катриса — сфера:
У)п (,xi Ч" х2 "V ж3) = 1,
или
Если какое-либо сечение оптической индикатрисы — круг,
это означает, что в направлении, перпендикулярном это-
му сечению, распространяются волны, имеющие одинако-
вую фазовую скорость и одинаковые показатели прелом-
ления, а направления колебаний вектора D для них не
определены. В этом направлении распространяется фак-
тически одна волна со скоростью, определяемой радиусом
Рис. 9.3. Оптическая индикатриса двухосного кристалла.
кругового сечения индикатрисы, т. е. двойное лучепре-
ломление отсутствует. Такое направление называется оп-
тической осью кристалла или бинормалью.
У трехосного эллипсоида два круговых сеченпя, ра-
диус которых равен средней по величине полуоси эллип-
соида (рис. 9.3). Следовательно, кристаллы низшей кате-
гории имеют две оптические оси и называются оптически
двухосными. Для них принято следующее обозначение по-
казателей преломления: Ne — наибольший, Np — наимень-
ший, Nm — средний. Свет, распространяющейся вдоль оп-
154
тических осей, имеет показатель преломления Nm. Опти-
ческие оси лежат в плоскости эллипсоида, определяемой
его полуосями Ne и 7VP; эта плоскость называется пло-
скостью оптических осей. Острый угол между оптически-
ми осями называется углом
ется 2V (рис. 9.4).
оптических осей и обознача-
Рпс. 9.4. Оптическая индикатриса
двухосного кристалла с указани-
ем угла между оптическими
осями.
дпкатриса одноосного
кристалла.
Эллипсоид вращения имеет одно центральное круговое
сечение, перпендикулярное его оси симметрии бесконеч-
ного порядка. Направление этой оси и есть оптическая
ось кристалла. Таким образом, у кристаллов средней ка-
тегории одна оптическая ось, они называются оптически
одноосными. Направление оптической оси совпадает с
осью симметрии высшего порядка кристалла. Все другие
центральные сечения эллипсоида вращения обязательно
имеют одну полуось, равную радиусу кругового сечения
(рис. 9.5). Другая полуось изменяет свою длину от ра-
диуса кругового сечения до длины полуоси эллипсоида
вращения в направлении осп симметрии бесконечного по-
рядка. Это означает, что в одноосном кристалле одна
световая волна имеет один и тот же показатель прелом-
ления независимо от направления распространения. Та-
кая волна носит название обыкновенной, и ее коэффи-
циент преломления обозначается No. Для другой волны
показатель преломления зависит от направления и изме-
няется от значения No до значения Ne. Она называется
необыкновенной.
155
Одноосные кристаллы условно разделяют на оптически
положительные, если Ne > No, и оптически отрицательные,
если No > Ne. Величина Ди — Ne — No называется двупре-
ломлением кристалла и является одной из главных его
оптических характеристик.
У кубических кристаллов оптическая индикатриса —
сфера. Любое ее центральное сечение — круг. Поэтому
в кубических кристаллах по любому направлению распро-
страняется одна волпа, показатель преломления которой
N не зависит от направления и равен радиусу сферы.
В отношении распространения света кубические кристал-
лы ведут себя, как изотропные тела.
У двухосных кристаллов для каждой из двух волн
показатель преломления зависит от направления, и, сле-
довательно, обе волпы являются необыкновенными. Двух-
осный кристалл считается положительным, если Ne — Nm >
>Ng — Np, т. е. Ng служит биссектрисой острого угла 2V.
Оптически отрицательны двухосные кристаллы, у кото-
рых биссектрисой острого угла является Np.
Диэлектрическая анизо-
тропия кристаллов, помимо
двойного лучепреломления,
приводит к еще одной важ-
ной особенности оптических
явлений в кристаллах: в об-
щем случае направление вол-
новой нормали, т. е. направ-
ление распространения вол-
нового фронта или фазы ко-
лебаний, не совпадает с на-
правлением светового луча,
т. е. направлением распрост-
ранения энергии световой
волпы. Соответственно разли-
чаются фазовая и волновая
скорости, а также показатели преломления для волны
и луча.
Действительно, распространенпе энергии электромаг-
нитной волны определяется вектором Пойнтинга
S = Д-ЕхН.
Так как Н располагается в плоскости волнового фронта,
а Е не лежит в этой плоскости, то векторное произведе-
ние этих векторов, S, не совпадает с т, а лежит в пло-
скости векторов I) и Е (рис. 9.6). Так как в направле-
156
Рис. 9.6. Взаимное расположе-
ние вектора волновой норма-
ли m световой волны и двух
векторов s(1) и s(2> лучей,
соответствующих световой
волне.
нии m распространяются две волны с D(1) и D<2), то им
будут соответствовать два луча S(1) и S(2), составляющие
с m углы а и [3.
Эти углы равны углам между векторами D и Е и мо-
гут быть определены по формулам
D<1>E(1) „ D<2)E(2)
COS а = ;—7—п—7777, COS |Э = ;—77777-;——
/d<i>||e<1)| |d(2)||e(2)|
Соответственно скорость распространения световой энер-
гии в направлении одного из лучей и — v/cos а. Можно
ввести величину q — ulc, обратную показателю преломле-
ния для луча и связанную с показателем преломления
волпы п соотношением
1
q =-------•
1 п cos а
Аналогично определяется q для второго луча, имеющего
волновую нормаль ш.
Примеры решения задач
9.1. Определить угол менаду волновой нормалью и лу-
чом для световой волны, распространяющейся в направ-
лении т(пг„ т2, т3), если тензор диэлектрической непро-
ницаемости кристалла имеет вид
i]1 0 0 '
О т]2 О
О 0 г]3
Схема решения задачи. Графическое решение этой задачи с
помощью оптической индикатрисы состоит из следующих этапов:
а) построения сечения оптической индикатрисы, перпендику-
лярного направлению in;
б) определения длины и направления полуосей эллипса, по-
лучившегося в сечении.
Длины полуосей дадут значения показателей преломлепия
двух волп и П(2), направления полуосей — направления век-
торов D<*> и D<2> этих волн (рис. 9.7).
Дальнейшее решение не требует использования оптической
индикатрисы.
Уравнение Et = щД); для каждого из векторов D(i> позволит
определить направление соответствующих векторов Е<’> и Е<2>.
Для каждой из волп, распространяющихся вдоль го с разной
скоростью, будет свой угол между вектором D и Е и соответ-
157
Рис. 9.7. Оптическая инди-
катриса и взаимное распо-
ложение векторов Е<*>,
и Е<2>, D<2) для волн,
распространяющихся в на-
правлении in.
сительно системы к
ственно два направления распространения светового луча s(1>
и s(2>.
Аналитическое решение этой задачи проводится по топ же
схеме.
а) Для построения сечения индикатрисы, перпендикулярного
ш, выберем систему' координат X 1Х,1ХЯ такую, что Хг парал-
лельна ш, Х2 и Х3 выбираются пз условия ортогональности и
сохранения правой системы коордипат.
б) Определяется матрица пере-
хода от XjX2X3 к х'х'х'.
в) В новой системе координат
Z
находится и сечение эллипсои-
да, перпендикулярноеX р уравне-
ние которого записывается через
компоненты двумерного тензора;
^22 ^23
^23 ^33
который приводится к главным
осям, т. е. находятся его главные
значения а через них по-
казатели преломления двух волн и
направления полуосей, т. е. на-
правления векторов D<*> и D<2> отно-
XjXgXg.
г) Далее определяются векторы Е<*), Е<2>:
АО) = .£)(!) £<2) = D(2)
д) Угол между лучом и волновой нормалью <р равен углу
между векторами Е и D, поэтому
E(OD(i)
cos *Р1 — | Е(1> | |Ю(1)| •
Аналогично вычисляется <р2.
Решение, а) Найдем орты у(1>, у<2>, у<3> системы коор-
динат X1X2Xg. По условию выбора системы Х^Х^Хд у<*> =
= (mi, т2, т3); у<2> выбирается ортогональным у<*>; у(3)—из
условия ортогональности к у(1) и у<2>. Итак:
у(1) = (m,, т2, т3},
у<2> = (1, 0, 0) + руО,
у<3> = (0, 1, 0) + щу<») + р2у<2>,
158
где g, gi, g2 — числовые множители, определяемые из условий
у(1)у(2> = 0; у(!)у(3) _ 0; у(2)у(3) = q. для у(2) находим g:
у(2)у(1) = ИЦ + gy< = 0
т1 __
Н — — у(1)у(1) — т1
Для у<3> находим gi и g2:
y(3)y(i) _ m2+ giy(,)y(1) + g2y(2)y(1> = 0,
ОТ2
— у(1)у(1) “ т2’
у(3)у(2) _ _mim2 + giy(1Jy(2) + g2y(2)y(2),
т1т2 т1т2
^2 = y(2)y(2) = 1 — m2'
Таким образом:
у<4 = (mi; m2; m3),
y(2) _ _ m2. _ _ mLm2),
/ m?m2m2\
y(3> = - тгт2 + тгт2; 1 - - ——2; - .
После нормировки к единице каждого из векторов у<’) получаем
у<*) = (ть т2, тг),
б) Соответственно матрица перехода от ХуХяХз к
Определитель этой матрицы равен —1. Значит, преобразование с
помощью матрицы Сц переводит правую систему координат в ле-
159
вую. Для сохранения знака системы
цию координатных осей п А’.., а
следования второй и третьей строк
/ = 1 — rn%, окончательно получим
Х1Х^Х3 поменяем нумера-
значит, изменим порядок
матрицы Cij. Обозначая
П?1 0 П>2 тз 1 тз f
mjn 1 2 т1тз
I / f
в) Преобразуем тензор
закону д' = CihC^hl.
[ц,,] к новой системе координат по
Получим
т гп
2 3
2,2,2
"!1П1+т?1а+т|д3 -у? n2 f
"'3 .
т т? т
- "'ЛУЗ ,, + "ЧУ.) ,,
/2 2 /2 3
т?т% тЪп^
,2
Двумерный тензор
т т т
m m in
т ~т
т~т?
Обозначим для краткости
а b
b с
и приведем к главным осям следующим образом (см. задачу 4.3):
I а — X b 1 X2 —- X (я -|- с) ас — Ь —
I Ь с - X | = °’ А1 2 = V2 [(« + с) ± /(а _ с)2 + 4Ь2].
Заметим, что Х( = п^, где —показатель преломления одной
из волн, распространяющихся вдоль т, Х2 = п^, где — пока-
затель преломления другой волны.
160
Показатели преломления п выражаются через глав-
ные значения диэлектрической непроницаемости кристалла rji,
т]2 и 1]з и направляющие косинусы направления распространения
волны, т. е. через компоненты вектора т.
Для нахождения направлений собственных векторов d(1> и d<2>
двумерного тензора используем условия:
= Z/.D, = z/{2),
adl1) + bc№ = X.dl1 , bcfcp + cc& = Z.dJ.1),
о A «3 л о 1 О
(“ “ \) 41’ + bd™ = 0, bd™ + (c - % ) d™ = 0,
Ь C-I
из которых получаем ”^у= —-----------—или -= —--------------1-.
Пусть -^у = —--------—— и = 1, тогда d_ = —----------------~.
а — Л- d 2 а — V
« 1 1
Окончательно получаем вектор d(*>:
d(i) = (о,---------------_________ =- л
(° — с) + У (а _ С)2 _р ’ J-
Вектор d<2> может быть найден из условия ортогональности векто-
ров d(1), d(2), m:
d(2)= f 0,1,—--------;--- - =-
(« — с) + ]Л (a — c)2-f-4fc2 )'
г) Далее, зная направления векторов D<*> и D<2> световых
волн, находим в системе координат Ху, Х2, Х3:
Е™ = и' £'<2> = t)'..Z)<2)
г '4 3 г '43
д) Окончательно
E(1)D(1) E(2)D(2)
C°S ф1 = |Е<Х>| iDd»! : C°S ф2 = | Е<2> | |D(S)| ’
9.2. Определить угол между волновой нормалью m
и направлением луча s для световой волны, распростра-
няющейся в кристалле LiNbO3 в направлении, состав-
ляющем угол 30° с оптической осью кристалла.
Решение. На рис. 9.8 представлено сечение оптической
индикатрисы кристалла координатной плоскостью XjX3. Решение
проводится для направления гп, лежащего в этой плоскости. Так
как в отношении оптических свойств ось симметрии 3 является
осью бесконечного порядка, полученный результат будет спра-
11 Н В Переломова, М. М. Тагиева 161
ведлив для всех направлений, получающихся из m вращением
вокруг Хз и образующих непрерывный конус направлений.
Для решения задачи воспользуемся результатами задачи 9.1.
Из рис. 9.8 видно, что m = m(sin0, 0, cos 6). Матрица перехода
от ХхХ2Х3 к Х'х'х':
(sin 0 0 cos 0 \
О 1 О I.
cos 0 0 — sin 0 /
Тензор г].^ в системе координат
[%•] =
sin20ii1 + cos20t]3 0 sin 0 cos Gr^ — cos 0 sin 0ц3
0 rjj 0
sin 0 cos 0ц1 — cos 0 sin 0т)3 0 cos20r]1 |- sin20i]
Используя результаты задачи 9.1, получаем d<!) = (0, 0, 1).
Рис. 9.8. Сечение
оптической инди-
катрисы кристал-
ла координатной
плоскостью Х{Х3.
Пусть [Dfl) | = 1, тогда Е(|> имеет компоненты:
Е= (sin 0 cos 0ц1 — cos 0 sin 0ца),
4Х) = О,
== (cos20 т^-f- sin201]3).
Далее определяем угол ер:
Е(1) D(1) cos20 Ц1-4-
<₽1 | Е(1) | | D(1) | (sin20 cos20 г]2 + cos20 sin20 ц2 4-
________4~ sin20 т)з_________
+ cos40 ц2 + sin40 ц4)1/2
cos20 + sin20 T]3
|ц2 (cos40 sin20 cos2©) + r)| (sin40 + sin20 cos20) j1'2
162
Для LiNbO3 (t]i = 0,023; щ, = 0,030; 6 = 30е):
cos <pi = 0,992, ф! = 6°.
Аналогично для d<2> = (0, 1, 0) имеем Е<2> = (0, щ7)2, 0).
Отсюда: векторы Е(2) и D(2) коллпйеарпы: cos ф2 = 1, <р2 = 0.
Таким образом, для волны с плоскостью колебаний, совпадаю-
щей с плоскостью чертежа, т. е. для необыкновенной волпы, на-
правления m и s пе совпадают и составляют угол <р. Для волпы
с плоскостью колебаний, перпендикулярной плоскости чертежа,
т. е. для обыкновенной волны <р = 0 и m||s. Для оптически двух-
осного кристалла обе волны необыкновенные и оба угла да и <р2
отличались бы от пуля и друг от друга.
9.3. Определить двупреломление пластины £-среза
сегнетовой соли. Определить толщину пластины, создаю-
щей разность хода в половину длины волны для света с
X = 0,63 мкм.
Решение. Двупреломленпем какой-либо кристаллической
пластинки называется разница показателей преломления двух
волн ni и п2, распространяющихся в направлении нормали к
пластинке: Ап = ид — п2.
Для сегнетовой соли главные диэлектрические непроницаемо-
сти: щ - = 1/е, = 0,4462, т)2 = 1/е2 = 0,4704, т)3 = 1/е3 = 0,4505. Так
как двупреломление определяется для /.-среза, то вектор волновой
нормали имеет следующие компоненты:
m(V]/3; I/УЗ^ 1/УЗ).
Для дальнейшего решения воспользуемся данными задачи 9.1:
-2 = (а + f) + V (а — с)2 + 4Ь2
1 2
—2 __ (а + с) (а — с)2 -|- 4Ь2
2 2-------------;
где а, Ъ, с — компоненты двумерного тензора 3. В данном
случае двумерный тензор имеет вид
г 0 460 — 0,005'
[—0,005 0,365]*
Подставляя в формулы для п\ п п2 значения а, Ь, с, опреде-
лим их величину и двупреломление = 0,181.
Если двупреломление пластинки Ап, то разность хода, при-
обретаемая световыми волнами при прохождении пластинки тол-
щиной d,
Г = Ап • d.
Для нашего случая Г — Х/2 = ’/2 -63-10 6 см. Поэтому требуе-
мая толщина пластинки d = 16,5 • 10-6 см.
163
9.4. Определить угол преломления г необыкновенной
волны в кристалле кальцита для света, падающего на
пластинку под углом 30°. Пластинка вырезана так, что
оптическая ось составляет с нормалью к пластинке угол
15° и лежит в плоскости падения света.
Решение. Решить эту задачу можно с помощью построе-
ния Гюйгенса. Мы воспользуемся законом сохранения импульса
световой волны при ее преломлении. Волновой вектор к волны
представляет собой пмпульс соответствующего фотона и должен
Рис. 9.9. Сечение оптической
индикатрисы кристалла пло-
скостью падения.
сохраняться при преломлении.
Поэтому компонента к, парал-
лельна границе двух сред, непре-
рывна па этой границе.
Для определения угла г
(рис. 9.9) проведем окружность с
центром в точке падения Р ради-
уса к], где kt— волновой вектор
падающей волны, и с центром в
этой же точке проведем эллипс,
который является геометрическим
местом точек концов волновых
векторов для раличных направ-
лений распространения света в
кристалле. Для нахождения на-
правления преломленной волны
продолжим направление падающей волны до пересечения с ок-
ружностью, затем через точку пересечения проведем перпендику-
ляр к границе раздела сред.
Линия, соединяющая точку Р с точкой пересечения перпен-
дикуляра с эллипсом, даст направление преломленной волны.
Действительно, оба волновых вектора к, и к2 при таком построе-
нии будут иметь одинаковую составляющую в направлении’ по-
верхности кристалла.
г, , со
Заметим, что так как к =------пт, то построенный нами эл-
с
липе можно рассматривать как сечение оптической индикатрисы
плоскостью падения света, повернутое относительно перпендику-
ляра к плоскости падения на 90°. Запишем уравнение сечения
этой поверхности в ее главных осях:
V1 +Vl = 1'
Преобразуем систему координат так, чтобы ось _ Xs расположилась
параллельно поверхности . кристалла. Это преобразование со-
ответствует повороту координатных осей на угол а, составляе-
164
мый оптической осью кристалла с нормалью к поверхности
пластинки.
Соответствующая матрица перехода С„3:
(10 0 \
0 cos а — sin а I
I
0 sin a cos а J _
В повой системе координат рассматриваемое сечение индикатри-
сы будет иметь уравнение
(cos2a т)2 + sin2a т]2) ж'2 Д- (sin2a i]2 + cos2a т]2) х'3 -f-
+ (112 — ч|)з1п2аяфг'= 1. (9.7)
Из рис. 9.9 следует, что ctgr = х2/х3, sin i — x3. Подставляя по-
следнее в (9.7), получим
(sin2a т)| + cos2a т]2) ctg2r -f- (т)| — T]|) sin 2a ctg r -|-
+ (cos2a T)g + sin2a tj2) — l/sin2i = 0, (9.8)
ctgr =
(т)2~TJ2) sin 2a+ j/^2 sin2a/sin2i-(-Tjg cos2a/sin2i —Т]21)з
2 (sin2a Tjg-|-cos2a T)g)
Для преломления света пластинкой кальцита при условиях,
указанных в задаче, получаем
ctg г = 2,764, г = 19°7'. ** -
9.5. Определить интенсивность света, прошедшего че-
рез систему: поляризатор — кристалл — анализатор
(рис. 9.10), если плоскости колебаний в анализаторе и
поляризаторе составляют угол 7, а плоскости колебаний
в кристалле составляют углы а и р с соответствующими
плоскостями поляризатора и анализатора.
При каком взаимном расположении поляризатора,
анализатора и кристалла интенсивность прошедшего света
будет максимальной? минимальной?
Решение: На рис. 9.10 представлено сечение оптической
индикатрисы поверхностью кристаллической пластинки, перпен-
дикулярной падающей волне, прошедшей поляризатор, I и II — на-
правления полуосей этого сечения, а следовательно, направления
колебаний в кристалле.
Пусть П] и п2 — показатели преломления для волн с направ-
лением колебаний I и II соответственно. Проходя через пластинку
165
толщиной d, две волны приобретут разность фаз
2л
= "2)-
Интенсивность света, прошедшего через анализатор,
7= (Ш[)I 2 * *+ (ОЛ2)2 —2(ОЛ|)(Л42) cos гр,
Рис. 9.10. Схема, поясняю-
щая расчет интенсивности
света, прошедшего через
систему поляризатор — кри-
сталл — анализатор.
где О А! и ОА2 — амплитуды прошедших волн могут быть выра-
жены через амплитуду света, прошедшего через поляризатор ОР
и амплитуды света в кристалле ОМ\ и ОМ2.
Обозначим интенсивность про-
шедшего через поляризатор света 10.
Тогда ОР = у/(|, ОМ< = "]//о cos а,
ОМ2 = у/о sin а, О A j = |'7О cos а cos ,В,
ОА2 = У/о sin а sin [J.
Подстановка этих выражений в
формулу для I дает
/= 10 cos2 у-Т/о sin 2ci sin 2fJ sin2(<p/2).
В скрещенных ппколях 1 = Io X
X sin 2а sin2 (<р/2). В этом случае
максимальная интенсивность света
паблюдается при толщине кристал-
ла, обеспечивающей разность фаз
<р = л/2. При повороте кристалла на
360° вокруг направления нормали
к пластинке четыре раза будет на-
и четыре раза полпое просветление.
блюдаться полпое погасание
Если <р = л, при любом положении пластипкп (т. е. при любом
значении угла а) будет наблюдаться полное отсутствие освещен-
ности экрана.
При параллельном положении анализатора и поляризатора
I = Io sin2 2а sin2 (<jp/2).
Положению максимального просветления пластинки в скрещен-
ных николях будет соответствовать погасание в параллельных.
Задачи
9.6. Определить двупреломление кварцевой пластипки,
вырезанной параллельно оптической оси кристалла. Оп-
ределить разность фаз между обыкновенной и необыкно-
венной волной для света /. — 5,9 • 10~5 см, если толщина
пластинки 0,1 мм.
166
9.7. Каково двупреломление кварца в направлении
нормали к грани ромбоэдра? Грань ромбоэдра (1011) со-
ставляет с гранью призмы (1010) угол 142°.
9.8. Определить оптический знак ромбического кри-
сталла, если величина двупреломленпя для пластинки
Х-среза 0,019 и для пластины Y-среза 0,036.
9.9. Какой толщины должна быть пластинка кальци-
та, выколотая по плоскости спайности (1011), чтобы она
давала разность хода Г = 1000 нм?
9.10. Как ориентировать пластинку из гипса, чтобы
при наименьшей толщине она давала наибольшую раз-
ность хода? При какой толщине пластинка может слу-
жить пластинкой в «1/4 волны» для света с 7. =
= 5,46 10 5 см?
9.11. Какова должна быть толщина пластинки Х-среза
кальцита, чтобы с ее помощью можно было скомпенси-
ровать естественное двупреломлеппе иластппки йодата
лития толщиной 1 мм, вырезанной под углом 28,9° к
оси Х3? Используется свет с IX = 0,43 мкм.
9.12. Какая картина будет наблюдаться па экране,
если на пути узкого неполярпзоваиного луча поместить
последовательно две одинаковые пластинки кальцита, вы-
колотые по спайности? Обе пластинки ориентированы
друг относительно друга так, что их оптические осп па-
раллельны. Вторая пластинка повернута вокруг нормали
к ней относительно первоначального положения па 45,
90 и 180°.
9.13. Определить угол между направлением волновой
нормали и лучом для необыкновенной волпы при распро-
странении ее под углом 30° к оптической осп в кристал-
ле турмалина.
9.14. Определить величину «сноса луча»*) при рас-
пространении света в направлении синхронизма в кри-
сталле KDP, если толщина пластинки 8 мм, направление
синхронизма составляет с осью 4 угол 49°.
9.15. Определить угол максимального разведения обык-
новенной и необыкновенной волны в кристалле кальцита.
Какому направлению в кристалле соответствует этот слу-
чай?
9.16. Сравнить величины максимального двупрелом-
ленпя и максимального разведения обыкновенной и не-
ооыкновенной волн в кристаллах кварца, кальцита и ру-
тила.
*) О «сносе луча» см. § 12.
167
9.17. При какой ориентации пластинки относительно
оптической оси в оптически одноосном кристалле прелом-
ленный необыкновенный луч лежит в одной плоскости с
падающим лучом и нормалью к поверхности, т. е. лежит
в плоскости падения? Не лежит в плоскости падения?
9.18. Пластинка кальцпта выколота по спайности. Ка-
кая картина будет наблюдаться па экране за пластинкой
при падении на нее узкого пучка неполяризованного све-
та? Что можно видеть при повороте пластинки вокруг
нормали к ее поверхности? Ответить на вопрос с помощью
построения Гюйгенса.
9.19. Определить расстояние на экране между двумя
лучами, образующимися после прохождения света через
пластинку кальцита толщиной 2 мм, выколотую по спай-
ности. Решить задачу расчетным путем.
9.20. Определить интенсивность света, прошедшего че-
рез систему поляризатор — кристалл — анализатор, если
поляризатор и анализатор скрещены, а пластинка, выре-
занная из кристалла KDP параллельно оптической оси,
ориентирована так, что ее оптическая ось составляет
угол 45° с направлением колебаний в поляризаторе. Тол-
щина пластинки 5 мм, ?. = 0,54 мкм *).
9.21. При каком положении пластинки (см. условие
предыдущей задачи) интенсивность прошедшего света бу-
дет максимальной?
9.22. При какой толщине пластинки, вырезанной из
кристалла турмалина параллельно ее оптической осп, ин-
тенсивность света (X = 0,43 мкм), прошедшего через си-
стему поляризатор — кристалл — анализатор, не будет за-
висеть от угла поворота пластинки вокруг направления,
перпендикулярного ее поверхности?
9.23. Интенсивность света уменьшается при прохож-
дении через поляризатор и анализатор, расположенные
так, что плоскости колебаний в них составляют угол ср.
Найти величину относительной ошибки определения
интенсивности света за счет неточности в измерении угла
между поляризатором и анализатором Дф.
9.24. Определить отношение интенсивностей обыкно-
венного и необыкновенного лучей, прошедших последова-
тельно через две кальцитовые пластинки одинаковой тол-
щины, выколотые по плоскости спайности, если они по-
вернуты друт относительно друга на угол 90°.
*) В задачах 9.20—9.25 поглощением света в кристалле пре-
небречь.
168
9.25 Определить интенсивность света (А = 0,546 мкм),
прошедшего через систему поляризатор — кристалл —
анализатор, если поляризатор и анализатор скрещены,
а кристалл представляет собой кубик из сегнетовой соли,
вырезанный так, что его ребра параллельны осям сим-
метрии 2, а длина ребра равна 1 см. Рассмотреть случаи,
когда свет падает на грань куба, совпадающую с пло-
скостью оптических осей, и грань куба, перпендикуляр-
ную биссектрисе угла между оптическими осями. Принять
интенсивность падающего света равной 10.
9.26. Узкий луч света падает под скользящим углом
на пластинку из кристалла сульфата аммония, вырезан-
ную параллельно оптической оси. Обыкновенный п не-
обыкновенный лучи (.No = 1,525, Ne — 1,479) по выходе из
пластинки смещены на 1,75 мм. Определить толщину пла-
стинки.
9.27. Показать, что если пластинка из одноосного кри-
сталла вырезана так, что оптическая ось кристалла пер-
пендикулярна преломляющей поверхности, преломленные
лучи и оптическая ось лежат в одной плоскости.
9.28. Чем различается характер разведения лучей в
призмах Волластона и Рошона (рис. 9.11)?
Рис. 9.11. Призмы Рошона (а) и Волластона (б). Стрелками
указаны направления оптических осей.
9.29. Призма Волластона вырезана из кальцита. Пре-
ломляющий угол призмы 15°. Определить угол разведе-
ния лучей этой призмой.
9.30. Рассчитать преломляющий угол призмы Рошона,
если опа дает разведенпе лучей на 5°.
9.31. Какой угол разведения лучей дает призма Вол-
ластона при преломляющем угле призмы 30° ?
9.32. Определить максимальный угол между лучом и
волновой нормалью в кристалле ниобата лития.
9.33. Топкая пластинка из кальцита, вырезанная па-
раллельно оптической осп, помещается между скрещен-
169
ными поляризатором и анализатором. Пластинка может
поворачиваться вокруг нормали к своей поверхности. При
каком положении пластинки интенсивность света, про-
шедшего через систему, будет максимальной?
9.34. При какой толщине пластинки белый свет, про-
шедший через систему (см. условие предыдущей задачи),
будет красным? Что будет наблюдаться при вращении
поляризатора и анализатора как целого?
9.35. Вычислить толщину пластинок из кальцита и
кварца, которые могут служить пластинками Х/4 для
красного, зеленого и фиолетового света. (Дисперсией све-
та пренебречь.)
9.36. Рассчитать точно необходимую толщину пластин-
ки Х/2 из кальцита для X = 889 нм с тем, чтобы ее тол-
щина была не менее 1 мм.
9.37. Какая разница в картине, наблюдаемой при вра-
щении слюдяной монокристаллической пластинки, поме-
щенной между анализатором и поляризатором (см. зада-
чу 9.5), и вращении слюдяных беспорядочно ориентиро-
ванных друг относительно друга пластинок, образующих
стопу с толщиной, равной толщине монокристаллической
пластинки?
9.38. Почему тонкая двупреломляющая пластинка в
скрещенных николях при освещении белым светом при-
обретает цветную окраску?
9.39. Определить оптический знак двухосного кристал-
ла, если для него Ns — Nm — 0,036, Ne — Np = 0,019.
§ 10. ПЬЕЗООПТИЧЁСКИЕ СВОЙСТВА КРИСТАЛЛОВ
Пъезооптический эффект (явление фотоупругости) со-
стоит в изменении оптических свойств кристаллов в ре-
зультате влияния внешних статических или переменных
механических напряжений и описывается как изменение
их оптической индикатрисы.
При наложении поля механических напряжений изме-
няется форма и ориентировка оптической индикатрисы
и в общем случае ее новые главные оси не будут совпа-
дать с исходными главными осями. В произвольной систе-
ме координат XiX2X3, имеющей общее начало с главной
(кристаллофпзической) системой координат, уравнение оп-
тической индикатрисы общего вида можно записать как
'11гЧ "Ь '*122‘С2 Чз3*3 2т]23.Г2.Г3 ^]13Х1Х3 “Ь 2l]12'4'^2 =
(10.1)
170
Изменения диэлектрических непроницаемостей Дт]ц (поля-
ризационных констант*)), обусловленные приложением
механических напряжений, равны
Дпу = (1°-2)
При этом изменения компонент тензора диэлектрической
непроницаемости (с точностью до членов первого порядка)
оказываются пропорциональными механическим напря-
жениям
Дщ., = лда1ы. (10.3)
Изменение тензора диэлектрической непроницаемости
можно выразить п через деформации:
Дтрз = РамГы- (10.4)
Эффект изменения оптической индикатрисы кристалла,
обусловленный возникновением деформаций, называется
упругооптическим. Коэффициенты л,да и piM образуют
тензор четвертого ранга и называются соответственно
пъезооптическими и упругооптическими постоянными.
В силу того, что Дтр, = Дцц п tki = tth (в отсутствие
объемных моментов), лда = ляы = л,,1(! = njaft.
Матричные обозначения. Переходя к матричной запи-
си, уравнения (10.3) и (10.4) можно записать в виде
Дт]т Лщп^п, '(10.5)
где лга„ = л,да, когда п = 1, 2 пли 3, лтп = 2лда, когда
п = 4, 5 или 6,
Al)m = /Wn, (10.6)
ртп — безразмерные упругооптические коэффициенты,
причем pmn = piM для всех т и п. В общем случае л,„„ =£
Лпт, Р-тп Рпт. Коэффициенты пьезооптические и уп-
ругооптические связаны следующими соотношениями:
Pmn ^mr^rnf Лтп Ртг^гп) (10./ )
где Ст — коэффициенты упругой жесткости, srn — коэф-
фициенты упругой податливости.
Формы матриц (л„) и (//,/) Для кристаллов различных
кристаллографических классов приведены в табл. 11.
Поскольку упругооптические и пьезооптические коэф-
фициенты являются компонентами тензора четного ранга,
эти эффекты наблюдаются в кристаллах любой симметрии.
*) В литературе, посвященной рассмотрению пьезооптическо-
го, упругооптического и электрпческого эффекта, коэффициенты
тензора диэлектрической непроницаемости принято называть по-
ляризационными константами.
171
Для решения задач уравнения (10.5) и (10.6) удобно
записывать в виде таблицы типа
«1 ^Я ^Я t.
ДД1 Л11 Л12 Я13 Я14 Л16 Л1в
П21 •^22 л2Э л24 Лзб л2в
АДз Л 31 ^32 л33 Л34 эт35 л36
Дтц п41 Л42 Л 43 л44 Л45 П46
A’ls П61 ЛБ2 Л53 Л34 Л55 Лье
АД6 Л61 Л 62 Я63 Я64 Л6Б Лев
Продольный и поперечный пьезооптические эффекты.
Для практических применений наибольшее значение име-
ют продольный и поперечный эффекты. Продольный пьезо-
оптический эффект — это эффект искусственного дву-
преломления, наблюдаемый в том же направлении, в ко-
тором приложено одноосное механическое напряжение
(механическое напряжение и свет направлены по одной
оси) (рис. 10.1, а).
Рис. 10.1. Схематическое изображение продольного (а) и попе-
речного (б) пьезооптических эффектов.
Поперечный пьезооптический эффект — это эффект,
наблюдаемый в направлении, перпендикулярном направ-
лению действия одноосного механического напряжения
(рис. 10.1, б).
Примеры решения задач
10.1. На образец каменной соли в виде кубика 1 X 1 X
X 1 см3, выколотый по плоскостям спайности (100), дей-
ствует механическое напряжение в направлении оси чет-
вертого порядка. Определить величину этого напряжения,
если разность хода обыкновенного и необыкновенного лу-
172
чей с длиной волны 5890 А, измеренная в направлении
[100], оказалась равной 10,2 • 10-5 см.
.Решение. -Симметрия каменной соли тЗт (см. табл. 14),
следовательно, в отсутствие механических напряжений оптиче-
ская индикатриса такого кубика представляет собой сферу
Tl0(xi + ^ + ^) = 1,
где ’1О = 1/По-
Так как одноосное растяжение кубика производится по на-
правлению [100], тензор механических напряжений имеет един-
ственную компоненту t\ = t. Соответствующие изменения компо-
нент тензора диэлектрической непроницаемости:
Дщ — Jinf, Дц2 = Лт]з = nJ2i, Дц4 = Дц5 = Дце = 0.
Уравнение измененной оптической индикатрисы принимает вид
(’1о + Д111) Х1 + (^0 + Дт)2) *2 + (’Jo + Дг12) 4=1’
или
+ М + ^) = 1-
Так как щ = tjs = це = 0, то осп этой оптической индикатрисы
совпадают с кристаллофизическими осями Xt, Х2 и Х3, т. е. при
растяжении в направлении [100] оси оптической индикатрисы
каменной соли только деформируются, по не изменяют своего
положения.
Найдем значения трех главных показателей преломления:
1_________1___________1_________1________
П1 ~ V ~ /’lo + ~ V1 + Д’li/’Jo ~
1 л _ i Дт1л = 1 _ 1 Ani в
~ фЧ \ 2 / /?0 2 п0 /т;
=- 4- - 4 ^п*-
Аналогично
«2 П3= NO~1/2Xon12t-
Гакпм образом, оптическая индикатриса каменной соли при рас-
тяжении кристалла вдоль [100] становится эллипсоидом враще-
ния, и кубик каменной соли ведет себя как одноосный кристалл.
Этот же результат может быть получен и из принципа Кюри
(см. задачу 2.3).
Величина двупреломления световых лучей, распространя-
ющихся вдоль направления [010], выражается соотношением
Дп = П1 - п3 = - */,Л* (лп - л18) t.
173
Отсюда
AnJ Ю,2 • 10“° -1 „ ,
t =-----------------= п--------ч----------г;-— 5 10‘Па.
'ЛХ (Л - Л ) d V2 (1,51)8 • 1,21 • 10-11 • 1
10.2. Германиевый фотоупругий модулятор на дву-
преломлении, применяемый для модуляции излучения
инфракрасного диапазона, ориентируется таким образом,
что одноосное механическое напряжение действует в на-
правлении [111]. Найти величину максимального искус-
ственного двупреломления, индуцируемого приложением
механического напряжения в направлении [111]. В ре-
жиме продольного или поперечного эффекта должен ра-
ботать такой модулятор? 1
Решение. Уравнение оптической индикатрисы ненапря-
женного кристалла класса т’Зт имеет вид
11 (4 + ж2 + ж1) =1-
Одноосное механическое напряжение в направлении [111] в
кристаллофизической координатной системе задается тензором
вида
Г/ t t ~
_L t t t .
3 J t t _
Изменения поляризационных констант, согласно (10.5), равны
Aili = Ац2 = Ai]s = 1/з(лц + 2л12), Ац4 = Ац5 = Ац6 = '/з^м.
Уравнение оптической индикатрисы в исходной системе коорди-.
пат принимает вид
[11 + 1/3 (лп + 2л12)^] (4 + 4 + +
+ 14Я44 (*1*2 + *А + *2*з) = !’
и тензор поляризационных констант в этом случае выглядит так:
~ с Ь Ъ ~
b с b .
Ъ с _
где
с = ц + '/з^ (^Гц + 2л12), Ъ =
Находя главные значения тензора [Цо], получаем ip == ц2 =
= с — Ь, = с + 2Ь, а направления соответствующие
главным значениям тензора [ц,/], определяются векторами
174
Следовательно, направление оси Хд совпадает с направле-
нием действия механического напряжения.
Чтобы найти значения показателей преломления напряжен-
ного кристалла, необходимо привести уравнение его оптической
индикатрисы к главным осям х', х', X';
pl + г/3 (лц + 2я1а - л44) «] + <2) +
+ П + V3 (Я11 + 2я12 + 2я44) Ч = 1 >
Коэффициенты преломления в направлении главных осей
Х4, Х2, Х3 соответственно равны
< = «г = ~ (лц + 2л1а + 2зт44),
пз = No ~ (nii + 2л1г - п44) •
Величина максимального двупреломления, индуцируемого
приложением одноосного механического напряжения, действую-
щего в направлении [111], равна
П1 - П3 = - 1/Л>44*-
В режиме продольного эффекта, когда механическое напря-
жение и свет направлены по [111], такой модулятор работать не
будет, так как п± = п^, и величина искусственного двупре-
ломления в этом случае равна ну-
лю. Модулятор будет работать толь-
ко в режиме поперечного эффекта.
10.3. Для создания дефлек-
торов — устройств, управляю-
щих направлением распростра-
нения света, может быть ис-
пользован эффект изменения
угла полного внутреннего отра-
жения в кристаллах, наблюдае-
мый при действии на них меха-
нического напряжения (элект-
рического поля), действующего
перпендикулярно плоскости па-
дения.
На рис. 10.2 приведена
ориентация поворачивающей
Рис. 10.2. Ориентация по-
ворачивающей призмы с
управляемым углом полно-
го внутреннего отражения.
призмы с управляемым углом полного внутреннего от-
ражения. В этом случае линейно поляризованный луч
света, направление колебаний которого лежит в плоскости
падения света, за счет пьезооптического или электрооп-
175
тического эффекта отклоняется от направления невозму,
щепного луча на угол ф, равный Vj/V® (ДЦц — Ац22),
где Ацп и Аг|22 — изменения поляризационных констант,
обусловленные действием
механического напряжения
(электрического поля). Рассчитать значение
можно получить с помощью
NaCl для светового сигнала с
отклоняющей
к = 0,589
которое
призмы
мк при
из
действии
механического напряжения, равного 107 Н/м2.
Решение. Как следует из рис. 10.2, падающий свет на-
правлен вдоль оси .Хр отраженный свет — вдоль
осиое механическое напряжение — вдоль осп Хд-
Ориентация координатной системы ХхХ2Х
оси Х2, одно-
относительно
кристаллофизических
осей X1X2X3
задается следующей
матрицей
направляющих косинусов:
X, х. х3
х'1 1 0 0
0 1//2 1//2
Х3 0 -i/V^ 1/1/2 .
Согласно (10.5) Дц^ = Поскольку одноосное механи-
ческое напряжение действует вдоль оси Хд, то единственной ком-
понентой тензора отличной от нуля, является
компонента
^зз' Следовательно, Д^ц я11зз^зз> Д^22 ^ггзз^зз1
Я1133 Я2233 ^2i^2j^3h^3inijfil’
здесь л,3ы — пьезооптические коэффициенты в кристаллофизиче-
ской системе координат, Сц — элементы приведенной выше матри-
цы косинусов. Учитывая отличные от нуля коэффициенты для
класса с симметрией тЗт, к которому относятся кристаллы NaCl,
получаем-:
Л1133
1122 + Л113з) ~ ”12'
Л2233 Х/-1 (Я2222 + Я2233 + ”"3333 ^Я232з) 2”12 2^)
Полагая £зд == t, получаем
Д<1 = ”12«' Дт>22 = Va (Лп + Л12 - Л44)
’р = Х/2^ (Д<1 - Д<2) = - V^O (”11 - ”12 - Л44У = 2Л'-
176
10.4. Для исследования пьезооптических свойств
кристаллов RDP (класс симметрии 42m) использовалась
кристаллическая пластинка 45° Z-среза (рис. 11.5), удли-
ненная в направлении [110].
Пластинка подвергалась действию растягивающего
напряжения в направлении [110] и одновременно дейст-
вию напряжения сжатия в направлении [110]. При рас-
пространении света длиной волны 0,535 мкм в направ-
лении [ООП разность хода, равная V2, достигалась при
напряжении 0,776 'кг/см2. Какой из пьезооптических
коэффициентов можно определить, пользуясь результа-
тами эксперимента? Рассчитать величину этого коэф-
фициента, если толщина пластинки равнялась 10 мм и
для света сХ = 0,535 мкм, N„ = 1,509?
Решение. В системе осей, связанных с ребрами 45°2-среза,
напряженное состояние кристаллической пластинки запишется в
виде
't оо-
0 — t о .
-0 0 0.
В кристаллофизической системе координат данное напряженное
состояние, очевидно, будет описываться тензором вида
'0 t 0‘
t 0 0
0 0 0’
содержащем только компоненты сдвига, обозначаемые в матрич-
ной записи как t^.
Уравнение оптической индикатрисы ненапряженного кристал-
ла имеет вид
41 (4 + х1) + 4^ = К
где
^=1/^, П3=1М-
Изменение поляризационных констант, обусловленное дей-
ствием механического напряжения г6, согласно (10.5) равно Дц6 =
~ ?W, и уравнение оптической индикатрисы в этом случае записы
вается дз виде
4Х + 4) + VI + 2пвв1хЛ = L
Изменение преломляющих свойств определяется сечением
оптической индикатрисы, перпендикулярным направлению рас-
№ Н. В. Переломова, М. М. Тагиева 177
пространения света. Поскольку свет распространяется в направле
нии [001], уравнение этого сечения
’ll (*i + 4) + 2nwtxix2 =
записанное в его главных осях, имеет вид
(’ll + W ) х1 + (’ll - W) Х22 = 1
Отсюда легко могут быть найдены значения новых коэффициен-
тов преломления RDP:
< = Хо + - VAef-
Величина индуцированного двупреломления находится как раз-
ность новых коэффициентов преломления
Дп = п' - и' = N^t.
Разность хода Z/2 достигалась при t « 104 Па, т. е.
X/2 = •/VoITceiA./2d-
Следовательно, пользуясь данными эксперимента, можно опреде-
лить пьезооптическии коэффициент л66, величина которого равна
=-----А--- 10,5 - «““Па-1
68 2n3f <7
10.5. На кристаллический образец ADP действует
одноосное механическое напряжение в направлении^
[100]. Найти выражения, позволяющие оценить величину!
показателей преломления напряженного кристалла.
Решение. Оптическая индикатриса ненапряженного кри-
сталла представляет собой эллипсоид вращения, уравнение кото-
рого имеет вид
’ll (*i + *2) + ЪХ1 = !•
На кристалл действует одноосное механическое напряжение
в направлении [100], являющемся осью Xt кристаллофизической
системы координат, поэтому у тензора механических напряжений
отличной от пуля является единственная компонента 1]. Согласно
(10.5) и в соответствии с видом матрицы (лц) для кристаллов с
симметрией 42 m изменения поляризационных констант в этом
случае равпы
Д1]1 = Лц#, Дт)2 = Л12<, Дт]з = Л13«,
а уравнение оптической индикатрисы принимает вид
(’ll + я1?) 4 + (’ll + л12(1) <+ (’Is + л1з'1) Х1 = к
178
Из этого уравнения видно, что одноосное механическое на-
пряжение, действующее в направлении [100], вызывает лишь
деформацию оптической индикатрисы в направлении главных
осей.
Поскольку поворот отсутствует, то значения новых главных
показателей могут быть определены непосредственно из послед-
него уравнения:
< = = No -
пз = N»~ 1у/гл1з*1^о‘
Задачи
10.6. Исходя только из соображений симметрии, по-
казать, что для кристаллов, относящихся к классам 23 и
m3, пьезооптический коэффициент л12 не равен коэф-
фициенту Л13.
10.7. Кристалл сфалерита сжат в направлении [110].
Как изменилась его оптическая индикатриса? Связано ли
направление растяжения с направлением осей оптической
индикатрисы кристалла?
10.8. Будет ли наблюдаться продольный пьезооптице-
ский эффект в выколотом по плоскостям спайности {100}
кубике каменной соли при действии механического напря-
жения вдоль направлений типа <100>? Будет ли наблю-
даться поперечный эффект?
10.9. Назвать классы симметрии кристаллов, оптиче-
ские индикатрисы которых испытывают не только де-
формации своих осей, но и поворачиваются на не-
который угол при действии на них гидростатических
давлений.
10.10. В пластинке флюорита толщиной 1 см, выре-
занной перпендикулярно направлению [111], наблюдали
поперечный пьезооптический эффект. При этом разность
хода, равная 7./2, для монохроматического света с длиной
волны 0,590 мкм достигалась при сжатии пластинки на-
пряжением 3,2 кг/см2. Найти значение пьезооптического
коэффициента, который может быть рассчитан по данным
эксперимента.
10.11. Какое механическое напряжение растяжения
необходимо приложить к пластинке 45° Z-среза ADP тол-
щиной 5 мм в направлении [110], прикладывая одновре-
менно равное по величине напряжение сжатия в направ-
лении [110], чтобы при распространении монохроматиче-
12* 179
ского света с длиной волны 0,534 мкм по направлению
[001] такая пластинка давала разность хода л/4? При-
нять для Х = 0,535 мкм значение No равным 1,525.
10.12. Определить величину двупреломления кристал-
лов алюмокалиевых квасцов в направлениях [010] и [001],
индуцированного приложением одноосного механического
напряжения, направленного по [100].
10.13. На кристаллический образец ADP действует
одноосное механическое напряжение t в направлении
[100]. Найти выражения, позволяющие оценить величину
показателей преломления напряженного кристалла.
10.14. Будет ли наблюдаться продольный пьезоопти-
ческий эффект в пластинке Z-среза KDP (рис. 2.3)? По-
перечный пьезооптический эффект?
10.15. Фотоупругий модулятор, используемый в узко-
полосных системах (например, в светодальномерах), ра-
ботающий в режиме поперечного эффекта, представляет
собой пластинку железо-иттриевого граната толщиной
3 мм, нормаль к которой совпадает с направлением [111].
Рассчитать величину управляющего механического напря-
жения, необходимую для создания полуволновой разно-
сти хода для светового сигнала с л = 1,15 мк.
10.16. Кристаллический кварцевый кубик с ребрами,
параллельными кристаллофизическим осям, сжимался
г направлении оси А\. Какие из пьезооптических коэф-
фициентов кварца могут быть получены по результа-
там эксперимента, в процессе которого измерялось изме-
нение показателей преломления в направлении ребер та-
кого кубика?
10.17. Фотоупругий модулятор, представляющий собой
монокристаллическую корундовую (класс симметрии Зт)
пластинку Z-среза (см. рис. 2.3) размерами 1X 1 X
X 0,3 см3, работает в режиме поперечного эффекта. Какие
деформации по толщине необходимо возбудить в такой
пластинке, чтобы при распространении светового сигна-
ла с X = 0,63 мкм в направлении оси Xt получалась раз-
ность хода, равная 7/2?
Значение коэффициента р13 принять равным 0,08, No =
= 1,765, Ne = 1,759.
10.18. Какие деформации по толщине необходимо соз-
дать в квадратной пластинке Z-среза ниобата лития раз-
мерами 1 X 1 X 0,3 см3, чтобы при прохождении света в
направлении [0001] она давала разность хода, равную 7/2,
для света с длиной волны 0,63 мкм?
180
10.19. Какой величины должно быть сдвиговое напря-
жение tiz, чтобы при распространении света с л =
= 0,535 мкм по направлению [001] получить разность хо-
да Х/2 в образцах единичных размеров ADP и DKDP?
§ 11. ЭЛЕКТРООПТИЧЕСКИЕ СВОЙСТВА КРИСТАЛЛОВ
Линейный электрооптический эффект. Линейным элек-
трооптическим эффектом называется изменение показа-
телей преломления среды, пропорциональное величине
приложенного постоянного или переменного электрическо-
го поля. Важным свойством линейного электрооптического
эффекта является его малая инерционность, позволяющая
осуществлять модуляцию света до частот в десятки гига-
герц. Кроме того, из-за линейной зависимости между по-
казателем преломления и электрическим полем нелиней-
ные искажения при модуляции относительно невелики.
При аналитическом описании электрооптического эффек-
та рассматривается связь между изменением поляризаци-
онных констант и электрическим полем:
= rtihEh, (11.1)
где rijh — коэффициенты, образующие полярный тензор
третьего ранга, называемый тензором линейного электро-
оптического эффекта. При рассмотрении спонтанного элек-
трооптического эффекта в сегнетоэлектриках уравнение
(11.1) записывается в виде
Дцъ = тъЛ, (11.2)
где mijh — коэффициенты, аналогичные rijh.
Электрооптические свойства сегнетоэлектриков суще-
ственно зависят от того, электрически закорочен
(Е = const) или разомкнут (D = const) кристалл в процес-
се измерений. Из уравнений (11.1) и (11.2) видно, что ко-
эффициенты rijh определяются в условиях постоянства
напряженности электрического поля, а коэффициент mljh—
в условиях постоянства электрической индукции.
Матричные обозначения. В силу симметричности тен-
зора поляризационных констант уравнения >(11.1) и (11.2)
могут быть записаны в матричных обозначениях:
Дц„ = rnlEh (11.3)
Дт)п = m„iPt. (11.4)
181
При замене г<л(шол) па ги;(тя,) множители 2 и 1/2 не по-
являются.
Для решения задач уравнения (11.3) удобно записы-
вать в виде таблицы:
£.
Дщ 'll '12 '13
Ад2 Г21 '22 Г23
Ад3 '.31 '.32 Г33
АТ)4 Г41 '42 г43
Ат|5 '.31 '.52 'бЗ
Аде Г61 'б2 'бЗ
Требования, налагаемые симметрией. В общем случае
имеются 18 независимых коэффициентов г„;. Благодаря
симметрии кристалла это число уменьшается точно так
же, как в случае пьезоэлектрических модулей. Формы
матриц совпадают с формами транспонированных пьезо-
электрических матриц с точностью до постоянных множи-
телей и приведены в табл. 12. Линейный электрооптиче-
ский эффект, как и любой эффект, описываемый поляр-
ным тензором третьего ранга, невозможен в центросим-
метричных кристаллах.
Первичный и вторичный электрооптические эффекты.
Линейный электрооптический эффект возможен лишь в
нецентросимметричных кристаллах, т. е. в тех же кри-
сталлах, в которых может наблюдаться пьезоэлектриче-
ский эффект. Поэтому, если кристалл механически свобо-
ден (напряжения равны нулю), то вследствие обратного
пьезоэлектрического эффекта электрическое поле будет
вызывать деформации, которые в свою очередь, согласно
уравнению (10.4), приведут к изменению показателей
преломления в результате упругооптического эффекта.
Таким образом, в статических или низкочастотных элек-
трических полях, когда кристалл может свободно дефор-
мироваться, наблюдается суммарный эффект. Изменение
поляризационных констант, вызванное наложением элек-
трического поля и не связанное с обратным пьезоэлектри-
ческим эффектом >(через упругооптический эффект), назы-
вают первичным («истинным») электрооптическим эф-
фектом. Иными словами, «истинный» линейный электро-
оптический эффект является результатом только прямого
воздействия электрического поля на диэлектрик. Очевид-
но, первичный («истинный») электрооптический эффект
182
наблюдается в кристаллах с запрещенной деформацией,
т. е. в механических «зажатых» кристаллах. Условие ме-
ханического зажатия кристалла осуществляется при на-
блюдении электрооптического эффекта в высокочастотном
электрическом поле, частота которого значительно превы-
шает частоту собственных колебаний кристалла. Вторич-
ным или «ложным» линейным электрооптическим эффек-
том называется изменение поляризационных констант,
обусловленное обратным пьезоэлектрическим эффектом
(через упругооптический эффект). Связь между обоими
эффектами описывается следующим уравнением:
ЛЦц “ CiptEji = 4~ PijlrrPlm = (Pijk Eht
(11.5)
отсюда
f'ijh = Cjjfi 4~Pijlm^hlm, (11.6)
где r*jk—коэффициент первичного («истинного») элек-
трооптического эффекта, Раш — упругооптические коэф-
фициенты, dhim — пьезоэлектрические модули.
Аналогичным образом
АЦу = ф Pijlmghlm) Ph, (11-7)
где m*jk — коэффициенты первичного («истинного») элек-
трооптического эффекта, g^m — пьезоэлектрические кон-
станты. !
Квадратичный электрооптический эффект (эффект
Керра). Приложение электрического поля Е может вы-
звать в кристаллах как линейные (пропорциональные Е),
так и квадратичные (пропорциональные Е2) эффекты.
Изменения поляризационных констант, обусловленные
приложением поля к электрооптической среде с точностью
до членов второго порядка малости, могут быть найдены
из соотношения
Дца сohEk ЕцшЕьЕц.
Здесь члены ГцкЕк характеризуют линейный электрооп-
тический эффект, члены RiMEkEt — квадратичный эффект.
Таким образом, изменения поляризационных констант,
обусловленные квадратичным электрооптическим эффек-
том, могут быть найдены из уравнений
Дцу = ВцыЕ^Е^ (11.8)
Изменения поляризационных констант, вызванные воз-
никновением (или изменением) спонтанной поляризации
183
Р' в сегнетоэлектриках за счет квадратичного электрооп-
тического эффекта, находятся из уравнений
(11.9)
Коэффициенты квадратичного электрооптического эф-
фекта являются компонентами тензора четвертого
ранга и аналогично коэффициентами электрострикции
симметричными как по паре индексов i и /, так и по паре
индексов I и к, т. е.
Pijkl — Pjttki (11.10)
но не перестановочны по парам индексов:
(11.11)
Если ввести следующие обозначения:
Е^Е*, Е2Е, = Е1 Е3Е3 = Е*, Е,Е3,Е3Е2 = Е*,
ЕаЕ1г ЕуЕ3 = Е5, EyE^i Е&Ег — Е6, (11.12)
то уравнения (11.8) и (11.9) могут быть записаны в мат-
ричной форме
Дт]г = (11.13)
Дтц = Л/УР-. (11.14)
Для проведения конкретных расчетов уравнения
(11.13) удобно записывать в более развернутом виде:
Е1 4 Ез Е24 Е5 F2 Е6
Лщ Ли Л12 Л is ли Л16 Ей
Дт]2 Л21 Л 22 Л2з Л24 Л25 Егв
ЛЦз Л81 ^32 Езз л84 Л зб Л зв
Лщ л41 Л42 Л4з л44 Л4б Л4в
A'le Л61 Л62 Л бз Лб4 Л66 Лбв
ЛПб Я61 jR62 Л оз Л64 Лез Лев
Аналогично записывается уравнение (11.14). Матрицы
коэффициентов (Ец) и (Л/ъ) целиком совпадают с матри-
цами коэффициентов электрострикции (С?ч) и (Яу).
Квадратичный электрооптический эффект наблюдает-
ся в кристаллах любой симметрии, а также в изотропных
средах.
Первичный и вторичный квадратичные электрооптиче-
ские эффекты. Первичный («истинный») квадратичный
электрооптический эффект состоит в изменении поляриза-
184
пионных констант, пропорциональных квадрату прило-
женного поля (поляризации) только за счет этого поля
(поляризации).
«Ложный» квадратичный электрооптический эффект
состоит в изменении поляризационных констант, пропор-
циональных квадрату электрического поля (поляризации),
обусловленных деформацией кристалла за счет электро-
стрикции.
Изменения поляризационных констант, обусловленные
как «истинным», так и «ложным» эффектом, находятся из
соотношений
= R-ijk lE^Ei PijmnPmm (11.15)
= ElijklPhPl 4“ Pijmn fmm (11.16)
которые могут быть записаны в виде
= 4" Pijmn^nmkl) E^Ei, (11.17)
- PijmnQmnk^ PhPli (11.18)
где Mijki — коэффициенты «истинного» квадратич-
ного электрооптического эффекта, рвтп — упрутооптиче-
ские коэффициенты; LmrM, Qmn» — электрострикционные
коэффициенты. Сравнивая уравнения (11.8) и (11.9) с
уравнениями (11.17) и (11.18), получаём, что
E-ijh.1 ~ -}- PijmnEmnhl: (11.19)
Elijhl — М ijhl 4" PiimnQmnhl- (11.20)
При практически достижимых электрических полях имеет
место следующее соотношение 1 > rVhE > RijwEhEi, т. е.
квадратичный эффект дает малые добавки по сравнению
с линейным изменением поляризационных констант. Од-
нако в кристаллах центросимметричных классов и в изо-
тропных телах, в частности, в жидкостях, для которых
rtjk = 0, квадратичный эффект играет основную роль.
Примеры решения задач
11.1. Быстродействующий электрооптический световой
затвор, применяемый для получения последовательности
импульсов и увеличения пиковой мощности излучения оп-
тических квантовых генераторов, представляет собой пла-
стинку Z-среза KDP, помещенную между скрещенными
поляризаторами (рис. 11.1). На рабочие грани пластинки
185
нанесены токопроводящие электроды. Какое напряжение
необходимо приложить к затвору для его полного откры-
тия в случае светового сигнала с ?. = 0,546 мкм? Какова
величина напряжения для
Рис. 11.1. Схематическое изобра-
жение электрооптического свето-
вого затвора.
лической пластинке (в данном
Ди — величина двупреломления,
аналогичного затвора, пред-
ставляющего собой плас-
тинку Z-среза DKDP?
Решение. Для полного
открытия затвора к кристал-
лической пластинке нужно
приложить напряжение, необ-
ходимое для получения разно-
сти хода в 2-/2, так называе-
мое полуволновое напряжение
V>,/2, величина которого может
быть найдена из соотноше-
ния Дп • d = 2-/2, где d — путь
светового сигнала в кристал-
случае толщина пластинки),
индуцированного приложением
напряжения. Матрица коэффициентов линейного электрооптиче-
ского эффекта для класса симметрии 42m имеет три компонен-
ты, отличные от нуля: r4i, г52 = r4i, г63 (см. табл. 14). В отсут-
ствие поля уравнение оптической индикатрисы записывается
в виде
’ll (4 + + VI =
где г1| = 1 *1з = 1 /^е’ I'1'0’ — соответственно показатели
преломления обыкновенной и необыкновенной волпы. Поле Е
приложено к граням пластинки Z-среза, следовательно, fcj =Е2 =
= 0, Е3=|Е|. Отсюда, согласно (11.3), Др6 = = resE3 и урав-
нение оптической индикатрисы в систем исходных осей X,, Х2, Хз,
принимает вид
’ll (4 + жг) + ^Зх3 + 2гвзЕМ = 1 •
Поскольку свет распространяется в направлении оси Х3, зна-
чения показателей преломления равны ^величине полуосей сече-
ния оптической индикатрисы, перпендикулярной осп Х3. Если
рассматривать сечение индикатрисы координатной плоскостью
Х|Х2, получим эллипс. Полуоси этого эллипса не совпадают с
кристаллофизическими осями X] и Х2. Уравнение (х® /А’„ +
+ 2г63ж1а:2Е'3= 1 эллипса симметрично относительно перестанов-
ки координатных осей Х( и Х2, следовательно, можно сделать вы-
вод о том, что полуоси эллипса составляют с исходными кристал-
1186
дофизическпми осями координат Х1 и Х2 углы, равные 45°
(рис. 11.2). Этот результат может Сыть получен также из рас-
смотрения принципа Кюри. В отсутствие электрического поля
главные оси кристалла с симметрией 42m совпадают с осями 2.
При паложеппи поля Е вдоль [001] мы получаем кристалл с
метрпей mm2, одна из осей которого
совпадает с осью Х3, а оси Х* и Х2 сов- 1
падают с направлениями нормалей к пло-
скостям т, располагающимся под углом
45° по отношению к главным осям Xt и
кристалла в отсутствие поля. Вычислим
новые главные показатели преломления
кристалла п' и пх>. Для этого приведем
1 о
сим-
уравнепие эллипса к главным осям: а ж л
-1 Рис. 11.2. Поворот
(1 \ ,о осей оптической ип-
д.2 + г6з^в I Xi“ + дпкатрисы _крпстал-
0 ' лов класса 42m при
(1 \ , наложении поля.
— Г63^3 ) ^2 = 1 •
О /
Очевидно, новые коэффициенты преломления будут иметь
значения
1________1
'2 Д’2 Г63 .1’
отсюда
1 *
/2
,г_ во
1 + ГвЗ^З^о
где г63Е ЛГр — величина малая, поэтому, используя известное
/ 1
соотношение, справедливое для случая малых а: 1/ -------st 1 —
' 1 + а
1
— -g- получаем
П1 = No - l/2reSE3n0’ П2 == No +
Следовательно, в рассматриваемом случае мы имеем двуосный
кристалл с главными показателями преломления
В1 = О V2ГвзЕ3^о’ П2 = + V2ГвЗЕ3Ео' пз ~ Е О'
187
188
Величина двупреломления для света, распространяющегося в
пластинке Z среза перпендикулярно к ее граням, равна
Дп — п' — п. = г EJV3.
Z j. и о о о
Световой сигнал проходит в кристалле путь d, следовательно
гвз^з^о^ = ^2- Для = 0.540 мкм имеем: г63 = 30-10~8 ед. СГСЭ,
No = 1,51152; отсюда V>./2 = 7,9 кВ.
Аналогичным образом для светового затвора, представляю-
щего собой кристаллическую пластинку Z-среза DKDP, имеем
V,/2 = 3,4 кВ.
11.2. В устройствах, обеспечивающих как низкочастот-
ную, так и высокочастотную модуляцию света (порядка
10—109 Гц), в качестве модулирующих элементов приме-
няются кристаллические пластинки ADP. Рассчитать
значения управляющих напряжений V>./2 (X = 0,516 мк)
для модулятора, представляющего собой пластинку Z-сре-
за ADP, работающую в режиме продольного электроопти-
ческого эффекта, для случаев: а) низкочастотной моду-
ляции, б) CB'L модуляции.
Решение. Величина двупреломления пластинки Z-среза
ADP, индуцированного приложением электрического поля к ее
рабочим граням, равна re3E3N° (см. задачу 11.1), а разность хо-
да, соответствующая Z/2, равна re3P?./2-%> отсюда Vy2~ ~—мз-"'
2гбз"о
Если к кристаллической пластинке приложено низкочастотное
электрическое поле (частота поля значительно меньше резонанс-
ной частоты пластинки), то коэффициент г63 определяет в дан-
ном случае электрооптические свойства пластинки и является
суммой коэффициентов первичного и вторичного эффектов; он
равен 25 • 10~8 ед. СГСЭ. Полуволновое напряжение Рхуг для
пластинки Z-среза ADP, используемой в качестве низкочастотного
модулятора, равно 9,2 кВ. При частотах, превышающих резонанс-
ные частоты, электрооптические элементы работают в режиме
пьезоэлектрического зажатия; модуляция в этом случае обуслов-
лена только первичным («истинным») электрооптическим эффек-
том и электрооптические свойства пластинки Z-среза определяются
коэффициентом г*3.
* Согласно (11.6) Г63 = г;з + B66d36 = r*3 + n66ceed36. Отсюда
%з = гвз лввсвв^зв‘...........
Следовательно, для пластинки Z-среза ADP, используемой
для СВЧ модуляции света, у* = 13д кв.
\
11.3. Известно, что высокочастотная модуляция света
может быть осуществлена при использовании квадратич-
ного электрооптического эффекта на кристаллах пиоба-
та-танталата калия (KTN) в их кубической модифика-
ции— класс тЗт (поскольку квадратичный эффект в кри-
сталлах перовскитов безынерционен до частот 200 ГГц).
В режиме продольного или поперечного квадратичного
электрооптического эффекта должен работать высоко-
частотный модулятор из KTN, представляющий собой
пластину Z-среза (см. рис. 2.3).
Решение. Используем матрицу коэффициентов электрооп-
тического эффекта из табл. 13.
Уравнение оптической индикатрисы в отсутствие поля:
т] (я® -f- х® я®) = 1. При наложении электрического поля по на-
правлению [100] (Е1! = Е, Е2 = Е3 = 0) согласно (11.13):
= -Вц-Ер = Д^з — -^12^1
и уравнение оптической индикатрисы принимает вид
(п + яп4) 4+0» +(4 + 4) = *•
Здесь т] — поляризационная константа в отсутствие поля. Как
видно из последнего уравнения, под действием поля кристалл
KTN становится оптически одпооспым с оптической осью, совпа-
дающей с направлением поля. При этом главные оси оптических
индикатрис кристалла до и после наложения поля совпадают.
Найдем новые главные показатели преломления:
_?_______1______« „ ' +
12 ~ 2 ~' м2 Ж 7’1]1 м2
Пу пх' •” о JVO
Аналогично
Поскольку п2 = п3, то при использовании продольного электрооп-
тического эффекта двупреломление пластинки Х-среза будет ну-
левым. Пластинка Х-среза, как и пластинки Y- и Z-срезов, будет
работать только в режиме поперечного квадратичного электрооп-
тического эффекта, когда направление поля и направление рас-
пространения света взаимно перпендикулярны.
11.4. Принцип действия кристаллического дефлектора
с управляемым углом отражения описан в задаче 10.3.
189
На рпс. 11.3 приведена схема поворачивающей призмы
из хлористой меди (класс симметрии 43m) и указаны на-
правления падающего и отраженного света, а также на-
правление действия электрического поля. В какое управ-
ляющее поле необходимо поместить поворачивающую
призму из CuCl, чтобы выходящий пз призмы световой
сигнал с X = 0,535 мкм отклонился от направления не-
возмущенного сигнала на угол ф = 20°? Каким должно
Рис. 11.3. Ориентация повора-
чивающей призмы из хлори-
стой меди.
Рис. 11.4. Схематическое изо-
бражение дефлектора полного
внутреннего отражения.
быть управляющее поле для такого же откчонения сигна-
ла, если использовать рефлектор многократного внутрен-
него отражения (рис. 11.4) с числом отражений 103, если
выходящий сигнал отклоняется таким дефлектором на
угол 6 = фт, где т — число внутренних отражений, ф —
угол отклонения за счет одного отражения?
Решение. Как следует пз рис. 11.3, падающий свет на-
правлен вдоль оси Xj, электрическое поле — вдоль оси Х3. Ори-
ентация координатной системы Х]Х2Х3 относительно кристал-
лофизических осей XtX2X3 задается следующей матрицей направ-
ляющих косинусов:
х2 х,
х; 1/1/2 1/1/2 0
*2 -1/1/2 1/V2 0
хз 0 0 1
Согласно (112) Дт]^. = Поскольку электрическое поле
действует в направлении оси Х3, то единственной компонентой
190
поля, отличной от нуля, будет компонента Е3=|Е|. Следе на-
тельно,
АДм = '1'13£з’ ATjgg = г'223Е'3.
Поскольку коэффициенты являются компонентами поляр-
ного тензора третьего ранга, то
г113 = Г223 = ^2i^23^3krijk’
где rijt — отличные от нуля электрооптические коэффициенты,
отнесенные к кристаллофизической системе координат, С(,-— эле-
менты приведенной выше матрицы направляющих косинусов.
Для класса симметрии 43m в крпсталлофизической системе
координат отличными от нуля являются коэффициенты гц, 'и,
гзе, причем
Г14 = Г25 = Г36,
Г113 ~ ^11^12^33Г123 + ^12^11^33Г213 ~ Г123 — Г63‘
Аналогично
»• — С С С1 г —г- С1 (' ( г == •— г = •— т*
' 223 21 22 33 123 ‘ v22 21 33 123 123 63
Поскольку ф = ^огвз^’ получаем Е’=1,2-106 В/см.
Для дефлектора с числом отклонений 103 Е = 1,2 103 В/см.
Таким образом, применение дефлектора многократного внутрен-
него отражения (рис. 11.4) позволяет снизить величину поля до
обычпо достижимых полей (103 — 104 В/см).
11.5. Какой выигрыш по модулирующему напряжению
можно получить, используя в качестве модулирующего
элемента образец 45°Я-среза ADP
размером 3 X 3 X 100 мм3 (Z =
= 100 мм), работающий в режиме
поперечного электрооптического
эффекта (рпс. 11.5), по сравне-
нию с таким же модулятором,
работающим на продольном эф-
фекте?
Решение. Как видно из рис. 11.5,
Ej = Ег = 0, Е3 = |С|, и уравнение оп-
тической индикатрисы кристалла АПР
в этом случае принимает вид
’11 + 2re3E3V1 = 1.
Kai: показано в задаче 11.1, главные оси оптической индикатрисы
связаны с исходными осями Х1Х2^з поворотом на 45°
Рис. 11.5. Модулирую-
щий элемент 45°2-среза.
191
вокруг оси Х3 (рис. 11.2). Таким образом, направление [НО],
являющееся направлением распространения светового сигнала, в
этом случае является одной из главных осей оптической инди-
катрисы — осью X*. Сечепие' эллипсоида показателей преломле-
ния плоскостью Хг = 0 дает эллипс:
(г11+гбз£)а:г2 + г13а:зг = 1-
Отсюда следует, что
п' = No О - 2ЛГогвз£’) > П'з = Ne’
а компоненты света, поляризованные по осям Х2 и Х3(Х3), рас-
пространяются со скоростями
"2 = АД1 — T 7V°r63£J’ гз = N~e'
Полная разность фаз между компонентами света, поляризован-
ными вдоль осей Х2 и Хд, равна
2 л I
F = ~ (7Ve-2V0)+-^3_
2jx
— (Ne — No) обусловлены естественной ани-
Л
при этом слагаемые
зотропией кристалла, лЛГрГвз£'1/Л —приложением электрического
поля. Полуволновое напряжение, соответствующее изменению раз-
ности фаз па л, в данном случае равно
Т^/2 1^гв3
Сравнивая эту величину с полуволновым напряжением модули-
рующего элемента па продольном эффекте (см, задачу 11.1), по-
лучаем, что Fx/2 модулятора на поперечном эффекте в l/2d раз
(для кристаллов ADP в 17 раз) меньше, чем Л\ц модулятора на
продольном эффекте. Кроме выигрыша по модулирующему на-
пряжению, преимущества поперечного электрооптического эффек-
та состоят и в упрощении конструкции электродов, так как от-
падает необходимость в пропускании света через электроды.
11.6. Экспериментальное измерение угла поворота
оптической индикатрисы кристалла (домена) сегнетовой
соли *), обусловленное спонтанным электрооптическим эф-
*) Угол поворота оптической индикатрисы экспериментально
определяется из измерений угла между положениями погасания
смежных доменов в пластинке Х-среза. -
192
фектом, а также спонтанной поляризации Р'Н [ 1001
дали соответственно значения 0,8° и 7,5 102 ед. СГСЭ.
Какой из электрооптических коэффициентов сегне-
товой соли можно определить по результатам экспери-
мента? Рассчитать его значение, полагая, что показатели
преломления п2 и п3 изменяются несущественно. Оценить
соотношение между «истинным» п «ложным» эффектами.
Решеви е. Уравнение оптической индикатрисы сегнетовой
соли в параэлектрической фазе имеет вид
’l 1Х1 ‘ = К
где
Изменение поляризационных констант, обусловленное нали-
чием спонтанной поляризации Р® II [100] (Р| = |Р®|, Р2 = Р3 =
= 0) в соответствии с видом матрицы (тп,^) для кристаллов с
симметрией 2, согласно (11.4), равно
Дт]4 = т41Р[ = тп41Р®.
Уравнение оптической индикатрисы в этом случае принимает вид
V1 + т]2х| + т]34 + 2т41Р8х2.т3 = 1.
Из уравнения видно, что оптическая индикатриса в сегнетоэлект-
рической фазе является повернутой вокруг оси X, на некоторый
угол а. Задача нахождения угла а сводится к задаче нахождения
собственных векторов матрицы вида
1/7/2 т^р!
1 „I
Собственные значения этой матрицы равны
1 -f- Ьп^Р**
Учитывая малость величины т4|Р', получаем
II а 1 № 1 II + S го ъ с» ьз 1 S 1 ЬЛ, W го 1
1 1 Л2 2 пх' 3 II 1 S (л to лн 1 а со to 1 1 н-
13 н. В. Псреломова, M. М. Тагиева
193
Подставляя в матрицу значения Z, и Л2, находим соответ-
ствующие им главные направления:
т4гЧ+(А-^*'»г=0-
\”2 / \пз /
Значение tga задается соотношением
1/«2-1/^
(т41Н-«.
Поскольку угол а мал, то
tg a « a «----11-----,
1/n? — 1/nl
Л о
следовательно, по результатам эксперимента можно определить
коэффициент т41. Подставляя в выражение для m4l значения
a, Ps при О °C, а также значения п2 п п3 (см. приложение), полу-
чаем величину т41 = 0,22 • 4 10~7 ед. СГСЭ. Соотношение между
«истинным» и «ложным» эффектами можпо оцепить, пользуясь
соотношением (11.7), которое для нашего случая принимает вид
т41 = т41 + рие 14.
Для кристаллов сегнетовой соли gI4 = 6,7 • 10 7 ед. СГСЭ,
Р44 = 8,95 • 10 *3 ед. СГСЭ, Рц£14 = 0,6 • 10~8 ед. СГСЭ, откуда сле-
дует, что «ложным» эффект в сегнетовой соли составляет 27%
«истинного».
11.7. На рис. 11.6 изображена конструкция модулиру-
ющей ячейки, состоящая из 2V кристаллических пластинок
Электроды Кристаллические
пластинки
Рис. 11.6. Принципиальная схема модулирующей ячейки.
Z-среза KDP, разделенных электродами со знакочередую-
щимися электрическими полями. Как должны быть ориен-
тированы эти пластинки, чтобы разность фаз, создаваемая
двумя последовательно стоящими пластинками, равнялась
194
сумме отдельных разностей? Какова величина полувол-
нового напряжения такой ячейки с десятью пластинками
(7V = Ю), если ячейка служит для низкочастотной моду-
ляции света с Л = 0,546 мкм? Каким должно быть полу-
волновое напряжение для случая, когда модулирующий
элемент состоит из одной пластинки Z-среза KDP?
Решение. Как следует из рис. 11.6, модулирующие эле-
менты, представляющие собой кристаллические пластинки Z-сре-
за KDP, используются в режиме продольного электрооптического
эффекта. Следовательно, величина двупреломлепия, индуцирован-
ного приложением электрического поля, направленного по [001],
для светового сигнала, распространяющегося в этом же направ-
лении, равна re3N°E (см. задачу 11.1), а соответствующая раз-
ность фаз (фазовая задержка) светового сигнала при прохожде-
нии пути d (толщина пластинки) равна
2^JV3Ed = ^N3oV.
Значит, при продольном эффекте разность фаз (соответственно глу-
бина модуляции) зависит от напряжения на кристаллической
пластинке и не зависит от ее толщины. Поэтому модулирующий
элемент может быть вырезан в виде тонкой пластинки. Если
взять набор таких пластинок и к каждой из них приложить одно
и то же напряжение V, суммарная разность фаз Г между орто-
гонально поляризованными компонентами светового луча при на-
ложении поля будет равна ЛТ, где N— число пластинок. Если
на кристалл KDP действует поле в направлении [001], то
< = Лго (1 + 1/а^гвзЕ), п' = No (1 - resE)
(см. задачу 11.1). Это означает, что скорость компоненты света,
поляризованной по осп Xv равная С/Л'о (1 + мень-
ше, чем скорость компоненты света, поляризованной по оси X
и равной c/Nc (1 — 1/8^гез/?). Сдвиг фаз Г > 0. При смене
знака поля
< = С1 “ < = No О + 1/^огезЕ).
В этом случае компонента света, поляризованная по оси Хг,
опережает компоненту, поляризованную по оси Х2 и Г < 0.
Очевидно, что для того чтобы разность фаз, создаваемая двумя
последовательно стоящими пластинками KDP, равнялась сумме
разностей хода, приобретаемых световым сигналом в каждой из
пластинок, каждая последующая пластипка должна быть повер-
нута на 90“ вокруг осп X.' относительно предыдущей. Величина
Управляющего напряжения Рх/2 для одной модулирующей пла-
стинки в случае низкочастотной модуляции для светового сигнала
13*
195
с /, = 0,546 мкм рассчитывается из соотношения
Ъ./2 = 1/М « 7’9 КР"
Следовательно, величина управляющего напряжения для моду
лпрующей ячейки пз десяти пластинок « 0,79 кВ.
Рис. 11.7. Элемент, работа-
ющий в режиме поперечно-
го электрооптического эф-
фекта.
11.8. Перспективными кристаллами для целей
электрооптической модуляции света являются сегнето-
электрические перовскиты, обладающие экстремально
низким значением управляющего напряжения. Како-
ва величина управляющего напряжения W2 модулятора,
представляющего собой обра-
зец тапталата-ниобата калия
(KTN) размером 1X1X1 см3,
работающего при комнатной
температуре в режиме попе-
речного электрооптического эф-
фекта (рпс. 11.7) для светового
сигнала с /. = 0,633 мкм?
Решение. Для кристаллов
класса imm (см. табл. 12) имеется
пять коэффициентов гтп, причем
Cis = г23, г42 = г6|. Как следует из
рис. 11.7, электрическое поле направлено вдоль кристаллофизиче-
ской оси Х3, т. е. Et = Е2 = 0, Е3 = | Е |, и уравнение оптической
индикатрисы кристалла запишется в виде
(^1 + г13£3) *1 + (*11 + Г!3Ез) Х1 + (*13 + гзз£з) Х1 =
где = 1/N%, дз = 1/lVg. Из этого уравнения находим выраже-
ние для новых главных показателей преломления (см. задачу
111):
ni = < = No + "з =7Ve+1/2A>33Eg.
При распространении света в направлении [010], т. е. в на-
правлении оси Х2, разность фаз между компонентами света, по-
ляризованными параллельно и перпендикулярно оси Х3, равна
2л л . „ „ , I
г = — - Ne) г + Т (л>зз - ^гз) Г
Первый член выражеппя для Г обусловлен естественной ани-
зотропией кристалла, второй — приложенным электрическим по-
лем Е = Vid, где d— толщина кристалла в направлении поля,
Т'— напряжение, подаваемое па кристалл. Модулирующее па-
196
пряжение, соответствующее изменению Г на л в случае образца
единичных размеров (I = d) для света СЛ — 0.633 мкм, равно
К ----5— = 107 В-
Л/2 ргЗ — дгЗ
"еЗЗ Vo'13
11.9. Рассчитать величину управляющего напряжения
Рх/г Для светового затвора, представляющего собой пла-
стинку У-среза ппрониобата кальция размерами 5Х5Х
X 20 мм3, используемую в режиме поперечного электро-
оптического эффекта, если световой сигнал с X = 0,546 мкм
распространяется в направлении [100].
Решение. Кристаллы пиропиобата кальция относятся к
классу 2 и являются оптически двухосными (см. табл. 14).
Уравнение оптической индикатрисы кристалла, записанное в
кристаллофизической системе координат, в отсутствие поля имеет
впд
Vi + M + V^1-
При наложении электрического поля в направлении осп Х2 (Ei =
= Е3 = О, Е2 — | Е |) уравнение оптической индикатрисы прини
мает вид
(711 + Г12Е) + (^2 + Г22Е) Х2 + (% + Г32Е) 4 + V'Vs = 1 ‘
Учитывая только линейные по полю члены, получаем следую-
щие выражения для новых коэффициентов преломления:
n'i = ni - г12П1г12Е' п2=п2- ll2nlr22E' из = из -
При прохождении света в направлении осп Xi существенна
разность показателей преломления п2 — п3. Поскольку свет про-
ходйт путь I, то при наложении поля вдоль осп Х2 возникает
разность фаз
Г=Г* + т(П2Г22~,гз',32)£/’
2л
где Г*=-- — (п2-из)/.
Величина управляющего напряжения У, соответствующая до-
полнительной разностп фаз, равной л, найдется пз соотношения
11.10. Исследование квадратичного электрооптического
эффекта в кристаллах KDP проводилось па образцах раз
мерами 1X1X1 см3. Значения управляющих напряже-
197
ний, необходимых для получения полуволновой разности
хода для света с X = 0,540 мкм, соответствующих опре-
деленным направлениям поля и прохождения света, при-
ведены в таблице.
Направление поля Направление про- хождения света Управляющее напряжение V . вВ/см
а) [001] [010] 13,2
б) [110] [001] 42,4
Какие пз коэффициентов или их комбинаций
(табл. 13) могут быть рассчитаны по этим данным? Ка-
ковы пх значения?
Решение, а) Электрическое поле, приложенное вдоль оси
А'з кристаллофизической системы координат (Х31| [001]), приводит
к тому, что уравнение оптической индикатрисы, до наложения
поля имевшее вид
(4+^)i]1 + i]3^ = i,
превращается в уравнение вида
(^i+(4+О+(%+д3Л) = 1-
Отсюда находим значения новых показателей преломления:
< = < = NO - W^E* n3^Ne- 1/а^3Л33Е3\
Таким образом, при распространении света вдоль [010] вели-
чина двупреломления задается соотношением п пд = (No —
- + v2 (Л17?зз - ^Хз) El =(*о - Ne) + а величи-
на двупреломления, индуцированного приложением поля, равна
1/2C7VeX3-7Vo^3)^ = 1/A4
Следовательно, измеряя величину управляющего напряжения
Рл/2, можно определить коэффициент По, который оказывается
равным 3,4 • 10-18 ед. CGSE.
б) Если электрическое поле приложено по [110], то Ei—E2^=
ф 0, Е3 = 0, отсюда Е[Е2 = Е2Е2 = Е,Е2 ф 0, в матричных обо-
значениях Е* = =И= 0, и оптическая индикатриса кри-
сталлов KDP в этом случае принимает вид
(’h Н Л+К++
+1Ъ + Д31 (£1 + ^)] *3 + = 1 •
198
Ifpn распространении света по [001] величина двупреломления
задается разностью —п2. Значения и п2 для нашего слу-
чая равны
”1 = (ЛП + - WZ
< = Л'о - (*и + *12) S2 +
^'-^ = *ОЧХ-
Следовательно, пользуясь приведенными в таблице на с. 198
данными, можно определить следующие величины:
Лп = ^Ч3-^/?13иЛ6в.
11.11. В кристаллах титаната бария вблизи точки
Кюри (120 °C) наблюдалось резкое уменьшение показателя
преломления в направлении сегнетоэлектрической оси
[0011 от значения 2,42 в кубической модификации до зна-
чения 2,38 в тетрагональной модификации; при этом
значения показателей преломления в направлениях [1001
и [010] практически не изменялись. Оценить значения
коэффициента, характеризующего наблюдаемый спонтан-
ный электрооптический эффект, а также долю «истинно-
го» и «ложного» эффектов.
Решение. Кристаллы титаната бария в параэлектрической
модификации относятся к классу тЗт (см. табл. 14) и не могут
испытывать линейного электрооптического эффекта. Следователь-
но, спонтанный электрооптический эффект в BaTiO3, в точке
Кюри является квадратичным.
Уравнение оптической индикатрисы кристаллов титапата ба-
рия в параэлектрической модификации имеет вид т] (я2 -]-
+ = !
Возникновение спонтанной поляризации Ps в направлении
[001] (Р® = | Ps |, Р‘ = Р2 = 0), согласно (11.14) и в соответ-
ствии с видом матрицы (Л/;;) для кристаллов класса тЗт, при-
водит к следующему изменению коэффициентов диэлектрических
непронпцаемостей Атр, Ащ, Ащ, определяющих изменение показа-
телей преломления в направлениях [100], [010] и [001] соответ-
ственно:
А= Дщ = М12 (Ps)2. Д% = М33 (Ps)2 = Л/ '(Ps)2.
Поскольку показателя преломления в направлениях [100] и [010]
практически не изменяются, то уравнение оптической индикатри-
сы запишется в виде
п (4 + + [п + м33 (Р8)2] = 1-
199
Отсюда получаем:
"1 = ”2 =
,/ = -1 - = — 6 - ДМГ)2Л
]Л’1 + А/33(Р8)2 Уч\ 211 /
"з = "3 -т4у3з (ps>2-
Принимая в точке Кюри п' = 2,38, пд = 2,42, Р* = | Ps |
= 54 • 103 ед. СГСЭ, получим, что Л/33 = 1,88 • 10“12 ед. СГСЭ. Со-
гласно (11.20) Л/33 = Л/*а -р PsmQmS, где М*3 — коэффициент
«истинного» квадратичного электрооптического эффекта, величи-
на PimQms — электрострикцпопная поправка к этому коэффициен-
ту, характеризующая долю «ложного» эффекта. Поскольку 4>12 ~
= С>з = —0,53 10_ 12 ед. СГСЭ (см. табл. 14), значения коэффи-
циентов Р3от порядка 0,1 ед. СГСЭ и поправка P^mQ-mz оценивается
как 10~14 ед. СГСЭ, то М*3 « 1,87 • 10—12 ед. СГСЭ. Следовательно,
в кристаллах титаната бария в точке Кюри имеет место спонтан-
ный квадратичный электрооптический эффект, на 99% являющий
ся «истинным» эффектом.
11.12. Поворачивающая призма кристаллического деф-
лектора, принцип действия которого состоит в изменении
угла полпого внутреннего отражения при действии элект-
рических полей, показана па рис. 11.3.
В какое управляющее поле необходимо поместить та-
кую призму из титаната бария кубической модификации,
чтобы выходящий из призмы луч мог отклониться от
направления невозмущенного луча на 30'?
Решение. Возможность управления направлением светового
луча с помощью отклоняющей призмы из титаната бария кубиче-
ской модификации, помещенной в электрическом поле, обусловле-
на квадратичным электрооптическим эффектом.
Если направление падающего света считать направлением оси
Х±, направление отраженного света — направлением оси Х2, на-
правление действия электрического поля — направлением оси Х3,
то ориентация этих осей относительно кристаллофизических осей
Х^ХгХз будет задаваться следующей матрицей косинусов:
1 X, xt А’з
х; 1/1/2 1/1/2 0
А -1/]/2 1'1/2 0
А 0 0 1
200
Поскольку £1 = £2 = О; Е3 = |Е|, то согласно (118) измене-
ния поляризационных констант, входящих в выражение для Д0ОТр
найдутся из следующих соотношений:
А1]ц = ^1133^3 Л1133£ ’ ^22 = ^2233^ ’
где #пзз 11 Й2233 — коэффициенты квадратичного электроопти-
ческого эффекта в координатной системе Х±Х2Х3. Поскольку
коэффициенты Rijki являются компонентами тензора четвертого
ранга, то
й1133 = Д2233 = C2iC2j^3/iC3//;yhI’
где Ct) — элементы матрицы косинусов; Rijki — коэффициенты
квадратичного электрооптического эффекта в крпсталлофизиче-
скоп системе координат. Учитывая вид матрицы (Rij) для кри-
сталлов с симметрией т'Ат, получаем, что
Д1133 = (^11.22 + й113з) — 1 2 (Л12 + й1з)'
Для кристаллов кубической сингонии Д|2 = Аз (см. приложе-
ние), отсюда Я113д = /?1122,
^2233 ~ ^2 (^11 + ^12 ^41)*
Следовательно,
де = 1/2п3 (Д< - ArQ — 1 X (ЙЦ - Я12-Я44) Е2- Е ъ 0,3 кВ.
Задачи
11.13. Как использовать электрооптический эффект на
пластине Z-среза кристалла KDP для поворота плоскости
поляризации света на 9(Г?
11.14. Как должна быть ориентирована пластина из
кристалла LiNbO3 для использования в целях, указанных
в задаче 11.13?
11.15. При каком электрическом напряжении плоскость
поляризации света, падающего на пластину Z-среза кри-
сталла ADP, поворачивается на 90°? (Использовать ре-
зультаты решения задачи 11.13).
11.16. Используя таблицы матриц электрооптических
коэффициентов (см. табл. 13), ответить на вопросы:
а) В кристаллах какой симметрии приложение электри-
ческого поля вдоль оси Х3 приводит только к изменению
величины главных коэффициентов преломления кристал-
ла без изменения формы оптической индикатрисы кри-
сталла? Возможно ли в кристаллах этих классов симмет-
рии изменить форму оптической индикатрисы приложе-
нием поля по другим направлениям?
201
б) В кристаллах какой симметрии приложение элек-
трического поля вдоль осп Хз приводит к изменению фор-
мы оптической индикатрисы кристалла без изменения
направлений главных осей оптической индикатрисы?
в) В кристаллах какой симметрии изменяется как ве-
личина главных коэффициентов преломления, так и нап-
равления главпых осей оптической индикатрисы?
11.17. К монокристаллическому образцу фосфида гал-
лия в направлении [111] прикладывается электрическое
поле. Будет ли наблюдаться в этом случае продольный
электрооптический эффект? Поперечный эффект?
11.18. В кристаллах каких тетрагональных классог
симметрии электрическое поле любого направления (в том
числе и £Н[001]) приводит к изменению симметрии опти-
ческой ппдикатрисы?
11.19. Высокие оптические качества кварца позволяют
применять его в модуляторах, несмотря на малость его
электрооптического эффекта. Возможно ли использовать
кварцевые пластинки Z-среза для целей модуляции на ос-
нове линейного электрооптического эффекта?
11.20. Какие пз одпоосных кристаллов не будут изме-
нять своих оптических свойств в линейном приближении
при внесении их в электри-
ческое поле, направленное по
осп высшего порядка?
11.21. На рис. 11.8 пред-
ставлены зависимости эффек-
тивного электрооптического
коэффициента г3 = гвзпо кри-
сталлов KDP и DKDP от'
температуры, измеренные в
статическом режиме на дли-
не волны 0,535 мкм. Во
сколько раз можно было бы
Рис. 11.8. Зависимость эффек-
тивного электрооптического
коэффициента кристаллов KDP
и DKDP от температуры.
снизить управляющее напря-
жение модуляторов из KDP
и DKDP (представляющих
собой пластинки 45°£-срсзов,
работающие в режиме по-
перечного электрооптического эффекта) осуществляя мо-
дуляцию при температурах, близких к точке Кюри, по
сравнению со значениями V\/2, необходимыми для моду-
ляции при компатной температуре?
С какими трудностями сопряжено осуществление мо-
дуляции при температурах, близких к Тс?
202
11.22. Найти выражения, позволяющие рассчитать ве-
личину спонтанного двупреломления кристалла (домена)
KDP, в точке Кюри (7’с), индуцированного возникнове-
нием вектора спонтанной поляризации Р8, располагающе-
гося по направлению [ООН для света, распространяюще-
гося в направлениях [1001, [010] и 10011.
11.23. Какой из электрооптических коэффициентов
танталата лития можно определить, измеряя величину
полуволнового напряжения, прикладываемого к пластин-
ке Z-среза, если в пластинке наблюдается продольный
электрооптический эффект?
11.24. В модуляторах инфракрасного диапазона прак-
тическое применение находят монокристаллы арсепида
галлия, легированные примесями Cr, Fe. Рассчитать вели-
чину разности фаз, которая может быть получена с по-
мощью монокристаллической пластинки арсепида галлия
при использовании поперечного электрооптического эф-
фекта, если величина напряженности электрического по-
ля, направленного по [1101, равна 104 В/см, а длина про-
хождения светового сигнала с А = 1,25 мкм, распростра-
няющегося в направлении [110], составила 20 мм.
11.25. Кристаллы грпнокита CdS, прозрачные в инфра-
красном диапазоне, могут использоваться для создания
модуляторов в этом диапазоне. Какое управляющее нап-
ряжение необходимо приложить к модулирующему эле-
менту из гринокита, представляющего пластипку Z-среза,
используемую в режиме продольного электрооптического
эффекта для светового сигнала с А = 0,515 мкм?
11.26. Какой толщины должна быть пластинка арсени-
да галлия, рабочие грани которой перпендикулярны на
правлению [1101, если при наблюдении поперечного элек-
трооптического эффекта в направлении [110] разность
хода А/4 для света с А = 0,546 мкм должна достигаться
при напряженности поля, равной 5,25 кВ/см?
11.27. В качестве чувствительного элемента установки,
предназначенной для измерения статических напряжений,
использовалась пластинка Z-среза ADP, работающая в ре-
жиме продольного электрооптического эффекта. Какова
величина измеряемого напряжения, если для получения
полного потемнения при А = 0,546 мкм в центре ин-
терференционной картины анализатор был повернут
па 30°?
11.28. Для наблюдения электрооптического эффекта в
кварцевой пластинке Х-среза толщиной 0,5 см на ее ра-
бочие грани подавалось напряжение, равное 30 кВ. Оха-
203
рактеризовать изменение оптических свойств такой плас-
тинки и оценить величину угла, па который поворачива-
ются оси оптической индикатрисы при наложении поля.
11.29. ] Iри исследовании свойств кристаллов титаната
бария в тетрагональной модификации было обнаружено,
что изменению поляризации в 24 • 103 ед. СГСЭ соот-
ветствует изменение показателей преломления, равное
—0,03. Оцепить значение электрооптического коэффициен-
та, которое может быть получено по результатам этого
эксперимента.
11.30. Кристаллическая пластинка Х-среза сегнетовой
соли помещается в электрическое поле напряженности Е.
Найти значения новых показателей преломления, а также
угол, на который поворачивается оптическая индикатриса
при наложении поля.
11.31. Какой толщины должна быть пластинка Z-сре-
за KDP, используемая в качестве светового затвора для
скоростной киносъемки, чтобы при приложении электри-
ческого поля Е = 10 кВ/см к ее противоположным гра-
ням пластинка давала разность хода ?./4 для света с Z =
= 0,540 мкм при его распространении вдоль направления
[ООН?
11.32. Измерение продольного электрооптического
эффекта механически свободной пластинки Z-среза KDP
дало значение коэффициента г63 = 30 10-3 ед. СГСЭ.
Оценить значение этого коэффициента для случая исполь-
зования такой пластипки в переменном поле высокой
частоты (в предположении, что частота поля и толщина
пластинки выбраны так, что резонанс не возникает).
11.33. Какой из электрооптических коэффициентов
кварца можно определить, используя ориентированный об-
разец Х-среза и измеряя величину управляющего напря-
жения Р\/2 для светового сигнала с определенной длиной
волны, распространяющегося в направлении оптической
оси?
11.34. К рабочим граням пластинки сфалерита, ориен-
тированным перпендикулярно направлению [111], прило-
жено электрическое поле Е. Какими показателями пре-
ломления характеризуются оптические свойства такой пла-
стинки? Каким соотношением характеризуется величина
фазовой задержки светового сигнала, поляризованного
вдоль [111], распространяющегося в направлении, пер-
пендикулярном направлению [111]?
11.35. При исследовании электрооптических свойств
кристаллов KTN при температуре Т = Тс для света с
204
% = 0,633 мкм измерялось изменение показателя прелом-
ления Д/г в направлении [0101, вызванное наложением
электрического поля вдоль [ 1001; при напряженности
поля, равной 104 В/см, изменение показателя пре-
ломления Ди оказалось равным 6 • 10~4. Какой из электро-
оптических коэффициентов может быть определен по этим
данным? Какова его величина?
11.36. Два образца единичных размеров кристаллов
KDP и DKDP помещают в электрическое поле таким об-
разом, что поле совпадает с направлением [001], а свет
распространяется в направлении [110]. Какую разность
потенциалов следует приложить в том и другом случаях,
чтобы каждая из пластинок давала разность хода Х/2 для
X = 0,535 мкм?
11.37. Рассчитать величину фазовой задержки свето-
вого сигнала с X = 0,633 мкм, которую можно получить
с помощью пластинки Z-среза танталата лития, исполь-
зуемой в режиме продольного эффекта, если к электродам,
нанесенным на ее рабочие грани, подается напряже-
ние 30 кВ.
11.38. Какой толщины должна быть пластинка арсени-
да галлия, ориентированная таким образом, что ее нор-
маль совпадает с направлением
[111], чтобы при приложении к
ее рабочим граням поля напря-
женностью 103 В/см для света с
X = 1,25 мкм она работала как
пластинка «в Х/4»?
11.39. Оцепить величину угла,
на который поворачивается опти-
ческая индикатриса кристаллов
KDP при наложении электриче-
ского поля напряженностью
10' В/см по направлению [100].
11.40. На монокристалличес-
ком образце арсенида галлия, орп-
Рис. 11.9. Ориентация
элемента арсенида гал-
лия, работающего в ре-
жимс поперечного элект-
рооптического эффекта.
оптированного так, как это показано на рис. 11.9, наблю-
дают поперечный электрооптический эффект (поле Е при-
ложено вдоль [110], свет распространяется вдоль [110]).
Каковы значения главных коэффициентов преломле-
ния арсенида галлия в ноле? Какова разность фаз для
света, поляризованного вдоль [001], индуцированная при-
ложением поля?
11.41. Возможно ли осуществление модуляции света па
основе использования продольного квадратичного электро-
205
оптического эффекта в кристаллах кубических перовски-
тов в направлениях:
а) [100], [0101, б) [1101?
11.42. *). Как изменяется оптическая индикатриса кри-
сталлов, относящихся к классам 23 и m3 при наложении
электрического поля по направлениям типа <100> за счет
квадратичного электрооптического эффекта?
11.43 *). Вдоль каких кристаллографических направ-
лений следует приложить электрическое поле к кристал-
лам средних сингоний, чтобы симметрия их оптических
индикатрис не понизилась за счет квадратичного элек-
трооптического эффекта?
11.44. *). Как изменятся оптические свойства кварце-
вых пластинок X- и Z-среза при приложении электриче-
ского поля, вектор напряженности которого совпадает с
направлением толщины пластинок, за счет квадратичного
электрооптического эффекта?
11.45. *). Возможно ли наблюдение продольного линей-
ного и квадратичного электрооптического эффекта в кри-
сталлах турмалина по направлению [00011?
11.46 *). Как изменятся оптические свойства кристал-
лов каменной соли и сфалерита при наложении электри-
ческого поля вдоль направлений типа < 100> за счет: а) ли-
нейного электрооптического эффекта; б) квадратичного
электрооптического эффекта?
11.47. При экспериментальном исследовании квадра-
тичного электрооптического эффекта в нецентросиммет-
ричных кристаллах важно отделить его от линейного.
Вдоль каких из кристаллографических направлений:
[1001, [010] или [ООН в кристаллах класса 2 можно на-
блюдать чистый продольный квадратичный электроопти-
ческий эффект?
11.48. Исследование квадратичного электрооптического
эффекта в кристаллах KDP проводилось па образцах раз-
мерами 1X1X1 см3. Значения управляющих напряже-
ний, необходимых для получения полуволновой разности
хода для света с ). = 0,540 мкм и соответствующих опре-
деленным направлениям поля и прохождения света, при-
ведены в таблице на с. 207.
Какие из коэффициентов /i'„- (или их комбинаций) мо-
гут быть рассчитаны по этим данным?
♦) При рритенпи задач 11.42—11.46 воспользоваться принпипом
Кюри, учитывая, что произведение ЕьЕс обладает симметрией
оо/тт.
206
Направление поля Направление про- хождения света Управляющее напряжение Ух/2. кВ/см
[100] [010] 20
[0101 [ооп 24,6
11.49. Рассчитать величину управляющего напряже-
ния Рх/2 модулятора из ADP размером 1X1X1 см3, рабо-
тающего в режиме поперечного квадратичного электрооп-
тического эффекта (поле направлено вдоль [110], свет
вдоль 1001]), для светового сигнала с Х = 0,540 мкм. Во
сколько раз управляющее напряжение указанного моду-
лятора на квадратичном электрооптическом эффекте боль-
ше величины управляющего напряжения модулятора из
АВР, основанного на продольном линейном электроопти-
ческом эффекте в направлении [001]?
Рис. 11.11. Схема эксперимента
для определения коэффициента
квадратичного электрооптическо-
го эффекта.
Рис. 11.10. Отклоняющая
призма дефлектора.
11.50. Одной из важнейших технических характери-
стик дефлекторов оптпческего излучения, применяемых в
системах оптической связи, является разрешающая спо-
собность N, характеризуемая числом разрешаемых све-
товых элементов. Оценить максимальную разрешаю-
щую способность дефлектора с отклоняющей призмой из
KTN (нпобата-танталата калия) с длиной основания 1 см,
помещенную в электрическое ноле напряженностью
104 В/см (рпс. 11.10), работающую в интервале темпера-
тур 20—30 СС для светового сигнала с ).= 0,633 мкм.
Примечание. Максимальное значение 7Vmax харак-
теризуется соотношением: Armax — -г-кп,гце I — длина ос-
Л
207
новация призм, л — длина волны светового сигнала, Ап —
изменение показателя преломления.
11.51. Какой из коэффициентов квадратичного электро-
оптического эффекта кристаллов ADP можно определить
по результатам эксперимента, схематически изображенно-
го на рис. 11.11, если величина Их/2 для образца с разме-
рами 1X1X1 см3 составила 52 кВ.
11.52. Рассчитать величину управляющего напряже-
ния Р\/2 для высокочастотного модулятора, представляю-
щего собой пластинку Z-среза ниобата-танталата калия
(KTN) толщиной 1 мм, длиной 10 мм, работающую в ре-
жиме поперечного квадратичного электрооптического эф-
фекта при «комнатной температуре.
11.53. Рассчитать величину двупреломления, индуци-
рованного наложением электрического поля по направле-
нию [010] для случая распространения света по [100] для.
кристаллов трпглицинсульфата (TGC): а) в параэлектри-
ческой модификации, б) в сегнетоэлектрической модифи-
кации.
11.54. Кубические монокристаллы титаната стронция
SrTiOs могут оказаться практически важными для постро-
ения широкоаппертурных модуляционных устройств, ра-
ботающих при низких температурах. Рассчитать величи-
ну управляющего напряжения Px/2 модулятора из SrTiO3,
представляющего собой пластинку Z-среза, удлиненную в
направлении [010] с размерами I = 2,5 см, d = 0,3 см.
Пластинка используется в режиме поперечного квад-
ратичного электрооптического эффекта (поле приложено
вдоль [ООН, световой сигнал распространяется вдоль
11001), если значение PV2 для образца единичных раз-
меров при температуре —100 °C составило 6,5 кВ/см.
11.55. В кристаллах триглиципсульфата наблюдался
продольный электрооптический эффект в направлении
[010]. Рассчитать величину двупреломления, индуцирован-
ного наложением поля.
11.56. Можно ли наблюдать продольный квадратичный
электрооптический эффект в кристаллах с симметрией
422 в направлениях: [1001, [010] и [ООП?
11.57. В простейших системах для сканирования све-
тового луча используется призма из электрооптического
кристалла, помещенная в электрическое поле (рис. 11.10).
При изменении показателя преломления призмы меня-
ется направление преломленного луча. Рассчитать изме-
нение показателя преломления призмы из титаната ба-
рия, которая помещена в электрическое поле напряжен-
208
постыо 104 В/см и используется для статического откло-
нения светового сигнала с 7. = 0,633 мкм в температурном
интервале 130—140 °C.
11.58. Па рис. 11.12 дана зависимость спонтанного
двупреломления кристаллов титаната бария, обусловлен-
ного возникновением спонтанной поляризации Р”Н [001]
в точке Кюри, от квадрата спонтанной поляризации.
Рис. 11.12. Зависимость
спонтанного двуирелом-
ления кристаллов BaTiO3
от квадрата спонтанной
поляризации.
Рис. 11.13. Зависимость
спонтанного двупреломле-
ния кристаллов сегнетовой
соли от квадрата спонтан
ной поляризации.
Какой из коэффициентов квадратичного электрооптиче-
ского эффекта (или их комбинаций) может быть рассчи-
тан по этим данным? Каково его значение?
11.59. Результаты экспериментального исследования
квадратичного электрооптического эффекта па ориенти
рованпых образцах единичных размеров кристаллов RDP
на длине волны света X = 0,540 мкм приведены в таблице.
Направление поля Направление про- хождения света Управляющее напряжение V. /о, кВ/см A Z
[110] [ООН 32
[010] [001] 24,9
Рассчитать значения коэффициентов (или их ком-
бинации), которые могут быть получены по результатам
эксперимента.
11.60. На рис. 11.13 приведены зависимости спонтан-
ного двупреломления кристаллов сегнетовой соли, изме-
ренного в направлениях [100], [010] и [001], в зависи-
Н. в. Переломова, М. М Тагиева 209
мости от квадрата спонтанной поляризации (P'll [100]).
Какие из коэффициентов квадратичного электрооптиче-
ского эффекта (или^их комбинаций) могут быть опреде-
лены по этим данным? Каковы их значения?
§ 12. ГЕНЕРАЦИЯ ОПТИЧЕСКИХ ГАРМОНИК.
Основные законы кристаллооптики для света срав-
нительно малой интенсивности следуют из решений урав-
нений Максвелла в предположении линейности кристалли-
ческой среды в отношении диэлектрических свойств.
Используемое в § 9 материальное уравнение Д ~
представляет собой линейную зависимость D от Е, из
которой вытекает линейная зависимость поляризации
кристалла Р от Е : Д = ХуД, где Ху — компонента тен-
зора поляризуемости среды, связанная с «у соотношением
Xjj = 1--Величины ву и Ху считались независимы-
ми от величины поля.
При сильных взаимодействиях, когда напряженность
внешнего поля велика, линейного приближения оказы-
вается недостаточно и для правильного описания взаимо-
действия сильного поля с диэлектриком следует учесть
квадратичные по полю члены материального уравнения.
Так как нас интересуют оптические явления, вытекаю-
щие из диэлектрической нелинейности кристаллов, а так-
же учитывая, что в роли «внешнего» поля может высту-
пать электрическое поле самой световой волпы, введем
в рассмотрение частоты электрического поля и поляри-
зации.
Рассмотрим поляризацию, возникающую под дейст-
вием полей E(®J и Е(®2). Используя разложение Р по
степеням Е(<щ) и Е(<о2) и полагая Р = Ро в начальный
момент времени, когда Е((о,) и Е(<в2) равны нулю, по-
лучим
дР. дР,
Pi (®) = Poi + дЕ. Д (®i) + Е* (®2) +
а2Р.
+ '8E~fij8Eh (Ш1) Ej Е* (“1) +
д2Р.г d'Pi
+ й^ЭЕ^ Ek (“2) + сД (сог)
ХД(И1) Д(<о2). (12-1)
210
В уравнении (12.1) первые производные являются
поляризуемостями х,, и описывают распространение света
в линейном приближении, когда частота возникающей
поляризации равна частоте электрического поля.
Вторые производные — нелинейная поляризуемость
пли квадратичная восприимчивость х,-д((о, fih, <о2) — пред-
ставляют собой компоненты тензора третьего ранга, ко-
торые есть функции частот coj, со2 и генерируемой часто-
ты со. Физический смысл компонент тензора %ift следует
из уравнения для нелинейной составляющей поляриза-
ции, квадратично зависящей от поля:
Р,((о) = <т>1, co2)£?(®i)£\(®2). (12.2)
Введем соотношения между частотами со, <r>i и со2 для
нелинейных членов разложения (12.1). Пусть в любой
фиксированной точке кристалла поля Е(<щ) и Е(со2) из-
меняются со временем по гармоническому закону:
= Eoj cos (со4), Eh(a2) = E,.h cos (co2i + ф),
где ср — сдвиг фаз в данной точке.
Так как
Ej (®i) (®г) =
= ~ EojEoh {COS [(«! — С02) t — ф] -j- COS [(ffli + со2) t + ф]},
то поляризация, квадратично зависящая от поля, имеет
либо разностную (иц — со2), либо суммарную (со, + со2
частоту, и тензор [ХчД®> соъ со2)] отличен от нуля лишь
в двух случаях, когда
ХчЪ = М2,
или
Хш = Х«л(®1 + «2, со,, <о2)-
Если через кристалл пропускается свет высокой интен-
сивности и частоты со, т. е. учитывается нелинейная по-
ляризуемость среды, возникающая под действием элект-
рического поля самого светового луча, то
Х<л = Х«^°, ®), Х«ь = 'Хи(2со, “)-
Таким образом, в этом случае учет диэлектрической не-
линейности приводит к появлению постоянной составля-
ющей поляризации и генерации второй гармоники основ-
ной частоты (ГВГ). Далее из всех явлений преобразова-
М* 211
ния частоты света с помощью нелинейной среды будет
рассматриваться только ГВГ.
Возникновение света удвоенной частоты можно пред-
ставить с помощью следующей схемы (рис. 12.1). Па-
дающая волна Е((о), распространяющаяся со скоростью
vt = c/n-i, возбуждает волну поляризации Р(2ы), распрост-
раняющуюся с той же скоростью щ. Поляризация Р(2ы)
I-------Л Г,
I
i
Р(7.ы)| vf
I
Е(2ы) i vz
-----------I-------
Р(7.Ы)। vz
Рис. 12.1. Схема, поясняющая
возникновение второй гармоники.
приводит к появлению све-
товой волны удвоенной
частоты Е(2ы), распрост-
раняющейся с другой ско-
ростью п2 = с/п2, так как
среда обладает дисперсией,
п,(щ) =/= п2(2со).
Световая волна Е(2со)
имеет достаточную интен-
сивность по выходе из
кристалла, если• квадра-
тичная поляризация будет
усиливать проходящую че-
частоты, т. е. при интер-
рез эту точку волну основной
ферепции волн Е(щ) и Е(2ю).
Интерференция излучения с частотами со и 2 с» воз-
можна, если щ = v2. Это требование равнозначно требо-
ванию равенства показателя преломления для частот со
и 2со: щ(со) = /г,(2со) или, отбрасывая индексы,
п(со) = и(2со). (12.3)
Условие равенства показателей преломления волн
основной частоты и ее второй гармоники (ВГ) носит на-
звание условия волнового синхронизма. Оно может выпол-
няться лишь в некоторых кристаллах в определенных на-
правлениях, называемых направлениями синхронизма.
Действительно, в изотропном теле условие п(со) = п(2со)
невыполнимо, так как в области нормальной дисперсии
п возрастает с частотой. В области аномальной дисперсии
выполнение условия синхронизма возможно только для
частот, близких к частоте резонансного поглощения. Так
как в этой области частот велико поглощение света, то
получить ВГ достаточной интенсивности в изотропных
телах невозможно.
В двупреломляющих кристаллах показатели преломле-
ния зависят от направления. Поэтому даже в области
нормальной дисперсии для двух волн, распространяю-
щихся по одному направлению, выполнение условия
212
синхронизма возможно. На рис. 12.2, а представлены
поверхности показателей преломления для волн с часто-
той и и 2<о для оптически положительного одноосного
кристалла. Ясно, что в направлениях, составляющих угол
0 с оптической осью кристалла, поверхности для пе(2ы)
и по(со) пересекаются. Это означает, что в указанных
Рис. 12.2. Сечения поверхностей показателей преломления одно-
осных кристаллов для оптически положительного и оптиче-
ски отрицательного кристаллов. Направление синхронизма со-
ставляет угол 0 с оптической осью.
стрелкой направлениях условие синхронизма выполни
ется для обыкновенного луча основной частоты и необык-
новенного луча ВГ. Рис. 12.3 демонстрирует случай
невыполнимости условия синхронизма в кристалле с
высокой дисперсией при сравнительно невысокой
анизотропии.
Рпс. 12.3. Сечение поверх-
ностей показателей прелом-
ления оптически положи-
тельного кристалла, не име-
ющего направлений синхро-
низма.
При практическом использовании кристаллов для ГВГ
важно получать максимальную интенсивность ВГ, кото-
рая реализуется в направлении синхронизма, а также
знать, какие отклонения от условий синхронизма на нее
влияют.
213
Для определения интенсивности ВГ рассмотрим урав-
нения Максвелла с учетом нелинейной поляризации:
rotH--±^, (12.4а)
м1Е = 7-“ <12«>
Z?i = 4-(12.4b)
В материальном уравнении (12.4в) добавка 4лР< явля-
ется только нелинейной частью поляризации, e„Ej — ли-
нейная часть индукции Dt.
Так как интенсивность света выражается через ампли-
туду Ео световой волпы, определим амплитуду волпы ВГ
через амплитуду волны основной частоты. Для этого
решим систему (12.4) для поля удвоенной частоты 2oi,
учитывая при расчете нелинейную добавку Р.
Преобразуем уравнения Максвелла (12.4), продиф-
ференцировав по времени (12.4а) и взяв ротор от пра-
вой и левой частей уравнения (12.46):
д . TJ 1 52D , , r 1 , д и
— rot И —-------5-, rot rot Е —— rot —H.
dt c . c dt
Раскрыв rot rot E и подставив из второго уравненпя в
первое выражение для rot И, получим
V2E = —-^5-. (12.5)
с dt?
Для одномерного случая распространения света вдоль
оси Х3 уравнение (12.5) примет вид
<92Е __ 1 д2Р
дх1 с2 dt2 ’
или, используя (12.4в):
<72Е е а2Е , 4л <?2Р
dx$ с dt с dt
Пусть волна основной частоты
Ет = E0i(x3) exp [—i(oif — ktx3)],
волна второй гармоники
Ег = ЕМ exp [—i(2cof — Zst»s)],
214
волна поляризации частоты 2о
Рг = уЕ01{х3') exp [—i(2co£ — Тс^з)].
Если условие синхронизма не выполняется, то 2Zct =/= кг.
Обозначим 2к1 — кг — кк и будем рассматривать Д/с как
меру отклонения от условия синхронизма.
Определим производные всех величин, входящих в
(12.6), и подставим их в это уравнение:
2—— ik2 exp [— i (2a>t — k2x3) ] =
dx3
= (^з) exP [— * (2ю — 2/сгж3)].
c
Умножим обе части уравнения на i и разделим на
exp [—i(2cot — /с2^3)] :
(*з) ехР (М'*») dx3. (12.7)
0хз с fc2
Получим уравнение относительно амплитуды волны вто-
рой гармоники Е02Ы. Интегрирование (12.7) по коорди-
нате х3 в предположении малой зависимости амплитуды
основной частоты Е01(х3) от координаты х3 даст амплиту-
ду волны ВГ в точке с координатой L:
L
ЕОг (L) = i ехР (iEkx3} dx3.
с \ J
Далее интенсивность света
найдена по формуле
о
удвоенной частоты может быть
СП ....
где Е и Е* — комплексно сопряженные амплитуды све-
товой волпы.
Для второй гармоники
L L
Г, Г.* / 8лсо2 Vr „* С iAfeXg , f -1ДЙХ3
ЕогЕй2 I % I j е dx3 J е dx3.
' 2 ' о о
Воспользовавшись формулой Эйлера: е’х = cos х + i sin х
и выражая Е01Е01 через интенсивность света основ-
ной частоты, а также учитывая, что к2 = 2лп2/Х2, kt =
= 2ЛП/ХЦ — ki/2, получим для интенсивности 12 ВГ
215
выражение
64л5 2? .,^2/sin (Д/сЛ/2)\2
c«j/i2 Xj \ ДЛД/2 j
(12.8)
где п, показатель преломления света основной часто-
ты, т. е. тг(со), тг2 = тг(2со); — длина волны основной
частоты, х — нелинейная восприимчивость среды.
Из формулы (12.8) следует, что интенсивность ВГ
пропорциональна квадрату интенсивности излучения ос-
новной частоты. Функция 1 является периодической функ-
цией NkLI2, изменяясь по длине кристалла как
sin (Д/с£/2)\2
ДАЦ/2 /• Если Д/с =А 0, она достигает первого мак-
симума при L = л/Д/с. Эта длина кристалла называется
когерентной длиной LKor.
Выразим £ког через показатели преломления и
тг(2со). Если первичная волна и ее вторая гармоника
имеют общую волновую нормаль т, то
Д/с = ^[тг(2со)-7г(ы)] = |^Дп. (12.9)
Следовательно,
j- зтс
К0Г = &
(для кристаллов £кпг является весьма малой величиной).
Так, например, у кварца для излучения неодимового ла-
зера (А, = 1,06 мкм) Дтг = 10“2 и LK0T = 13 мкм. Ясно, что
при Д/с =/= 0 максимальный сигнал, который можно по-
лучить в кристалле, будет равен сигналу, генерируемому
на одной когерентной длине кристалла, независимо от
его полной длины.
При невыполнении условия синхронизма даже при
когерентной длине кристалла интенсивность ВГ весьма
мала.
При выполнении условия синхронизма из (12.8) сле-
дует пропорциональность интенсивности ВГ квадрату
длины кристалла. Генерируемый сигнал будет значитель-
ным. Но в этом случае ограничение на использование
кристаллов большой длины накладывает так называемый
«снос луча». Явление «сноса луча» при распространении
света в направлении синхронизма, не совпадающего с
одной из полуосей оптической индикатрисы, в оптически
одноосном кристалле заключается в отклонении светового
луча, соответствующего необыкновенной волне, от направ-
ления ее волновой нормали и от направления обыкновен-
ного луча. Возникает снос энергии необыкновенного луча
216
относительно обыкновенною, и реальная длина эффектив-
ного взаимодействия оказывается меньше длины кристал-
ла, причем тем меньше, чем больше угол между лучом
и волновой нормалью для необыкновенного луча. Поэтому
наиболее эффективным является преобразование при так
называемом 90-градусном синхронизме, когда 0 = 90°.
Для достижения 90-градусного синхронизма можно ис-
пользовать температурную зависимость показателей пре-
ломления па основной и удвоенных частотах, а также за-
висимость этих величин от состава кристалла.
Для характеристики диэлектрической нелинейности
кристаллов на оптических частотах используются коэф-
фициенты квадратичной восприимчивости и коэффи-
циенты нелинейности di№. В научной литературе приме-
няются коэффициенты квадратичной восприимчивости,
связывающие комплексную поляризуемость с комплекс-
ным электрическим полем:
Л(2со) =х^(ы)£Дй). (12.10)
В экспериментальных работах используют коэффициенты
нелинейности, связывающие действительные значения по-
ляризации и электрического поля:
{Л(2<о)} = йЖ(со)){Ек(ы)}. (12.11)
Учитывая, что Г* (2со) — х/2 {Г} е 3, Е (и) =
1 / —ikx»
= 1/2{jb}e , для волны, распространяющейся вдоль
оси Х3, можно показать, что
— ^гХУь- (12.12)
В таблицах для нелинейных оптических материалов обыч-
но приводятся значения компонент тензора diih. Заметим,
что нелинейные оптические эффекты, в частности ГВГ,
наблюдаются только в нецентросимметричных кристаллах,
а форма матриц diik в этих кристаллах совпадает с фор-
мой матриц пьезомодулей.
Для случая ГВГ соотношение (12.11) может быть рас-
писано в матричной форме следующим образом:
pi
Р2
рз
dll d12 d13
d2l d22 d23
^31 d32 d33
dlt d15 ^16
^24 d25 d26
d3t d33 d3S
El
E2E3
E!E3
E!E2
217
где Pj, Р2, Рз — компоненты нелинейной поляризации
Р(2ш), Е2, Е3 — компоненты электрического поля све-
товой волны основной частоты Е(со).
Для конкретной световой волны, распространяющейся
в направлении т, совпадающем, например, с направле-
нием синхронизма кристалла, направления компонент
Pi и Ei относительно кристаллофизпческих осей определе-
ны, и может быть проведено суммирование в соответствии
с (12.11) для матрицы определяемой симметрией дан-
ного кристалла. В результате суммирования получается
коэффициент йЭфф, связывающий конкретные поляриза-
цию и электрическое поле:
{Р(2со)} = й;1фф{Е(ш)}2.
Далее, Д,фф для рассматриваемого взаимодействия может
быть использовано для расчета интенсивности ВГ по фор-
муле (12.8) с учетом соотношения (12.12).
Примеры решения задач
12.1. Определить эффективный коэффициент нелиней-
ности Д,фф для взаимодействий различного типа в направ-
лениях, составляющих угол 6 с оптической осью, для
кристаллов с симметрией 42тп.
Чему равен в кристалле KDP для взаимодействия
оо ->• е, т. е. для ГВГ?
Решение. Из рассмотрения рис. 12.2, а следует, что усло-
вия синхронизма при ГВГ в оптически положительных одноос-
ных кристаллах выполняются для необыкновенной волпы падаю-
щего излучения и обыкновенной волны ВГ. Сокращенно такое
взаимодействие обозначается ее —> о. Для оптически отрицатель-
ных кристаллов ситуация противоположна, т. е. реализуется взаи-
модействие оо —> е. Условие синхронизма можно выполнить и в
том случае, когда падающее излучение является суперпозицией
обыкновенной и необыкновенной волн. Синхронными оказываются
взаимодействия двух — обыкновенной и необыкновенной — падаю-
щих волп с обыкновенной волной ВГ в положительном кристалле:
ое —»- о и необыкновенной в отрицательном: ое —> е.
Рассмотрим общий случай получения йЭфф для кристалла с
симметрией 42т, не ограничиваясь определенным оптическим зна-
ком кристалла.
Уравнение (12.11) связывает нелинейную часть поляриза-
ции с напряженностью электрического поля волп основной ча-
стоты:
Pi(2co) = dijkEj(b))Ek (и),
218
где d.ijh для класса 42 та имеет вид
/0 0 0 Й14 0 0 '
1 ° 0 0 0 ^14 0
\0 0 0 0 0 ^36
По определению йЭфф = {Р(2ы)}/{Е(со)}2 и может быть вычислен
для кристалла данного класса симметрии как функция направле-
ния распространения световых волн основной и удвоенной ча-
стот.
Для вычисления йЭфф воспользуемся уравнением (12.11) и
рис. 12.4, на котором представлено взаимное расположение век-
торов ш, Е°(со) и Ее(со) для падающих волн и Рс (2со) и Pf(2w)
для волны БГ в крпсталлофизической системе координат. Оптиче-
ская ось кристалла и вектор m лежат в главной плоскости кри-
сталла, определяемой этими двумя направлениями и составляю-
щей'с осью Xt угол ср; Е‘ (со) лежит в этой же плоскости: Е°(со)
перпендикулярна т, лежит в плоскости XiX2 и составляет с Xt
угол (90° — ср),
Рис. 12.4. К выводу выражения для йафф кристалла KDP. При
построении предполагается, что вектор Е<е> перпендикулярен
вектору волновой нормали т, так как угол между D(e) и Е<е>
мал.
Выпишем компоненты нелинейной поляризации Р,(2ы) с ис-
пользованием тензорной, а не матричной записи коэффициентов
diikt
Р1 = а12аЕ2Ез+с1132Е°зЕ1
= +^да-
219
В матричной записи, учитывая, что dI4 — d2i, получаем
Л = ^(^з + ВД).
р2 = (ВД + Р3 = азе (е°& + Е°&}.
Найдем компоненты Е° и Ес по осям координат:
= Е° sin ср, Е® = Ее cos 0 cos ср,
Е° = — Е° cos ср, Е® = Ее cos 0 sin <р,
Е° = О, Ее3 = — Ее sin 0.
Соответственно для компонент нелинейной поляризации получим
Р1 = ^(Е0 cos <Р Ее sin 0) == с1^Е°Ее sin 0 cos ср,
Eg = — dliE°Ee sin cp, sin 0,
E3 = — ds6E°Ee (sin2 cp cos 0 — cos2 cp cos 0) =
= — d9(iE°Ee cos0 cos'2 <p.
Далее, для нахождения йзфф пужпо определить проекции компо-
нент вектора Р(2со) на направления векторов Е°(со), Ее(со), т. е.
значения Р,‘(2<о), P°(2cd).
Из рпс. 12.4 следует, что Ре(2оо) лежит в главной плоскости
кристалла и может быть выражен следующим образом:
Ре = ое + oh, ое = оа -f- ob, oa = PIcoscp, ob = Р2 sin ср,
Г,. 2 = P,i cos ip + Р2 sin ср,
ое = Р[, 2 cos 0 = (Р, cos ср + Р2 sin ср) cos 0,
oh = —Р3 sin 0,
Ре — d3ePvEe cos 0 sin 0 cos 2<p + EeE°c/I4(sin2 cp cos 0 sin 0 —
— cos2 cp sin 0 cos 0) = —(du + dS6) cos 2<p cos 0 sin 0 (E°Ee), (12.13)
P° = og + of = Pi sin cp + P2 cos cp = d,4 (cos cp sin cp sin 0 +
+ sin cp cos cp sin 0) = di4 sin 0 sin 2<p(E°Ec). (12.14)
Из (12.13) n (12.14) следует, что для взаимодействия ое—>-е
йэФФ = — (dI4 + d36) cos 2<р cos 0 sin 0;
для ое —> о
<ЕфФ = di4sin 0 sin 2ср.
Вычислим далее йэФф для взаимодействия оо —>- е в кристал-
ле KDP. Для этого случая
Pi = О, Р2 = 0, Р3 = — с?36 sin ср cos 0 (Е°)2,
ое = Pi, 2 cos 0=0; Ре = ос + oh =
= 0 — Р3 sin 0 = — d3e sin ср cos ср sin 0 (Е°)2.
220
Следовательно, йэфф = — d36 sin 0 sin 2q? будет иметь максимальное
значение при <р = л/4 и 0 = 41°, т. е. в направлении син-
хронизма.
Для 7. = 1,06 мкм; d36 = 1,04 • 10-9 см/динЧ Поэтому йЭфф =
—1,04 10-9 • 0,65 = 0,67 10-9 см/динЧ
12.2. Определить угол синхронизма кристалла KDP
для Л = 0,694 мкм, если для Л = 0,694 мкм No = 1,51;
Ne = 1,47, для Л = 0,347 мкм No — 1,54; Ne = 1,49.
Решение. Симметрия кристалла KDP 42m; No > Ne — кри-
сталл одпоосный отрицательный. Следовательно, в нем возможно
синхронное взаимодействие оо —> е. Для одноосных отрицатель-
ных кристаллов условие синхронизма выполняется, если главные
показатели преломления на соответствующих частотах подчиняют-
ся соотношению (см. рис. 12.2, б):
Л\, (<и) > Xf(2co).
В данном случае действительно 1,51 > 1,49. Значит, в кристалле
есть направление, вдоль которого выполняется условие синхро-
низма. Найдем это направление, исходя из следующих сообра
/Кении.
Для синхронного взаимодействия оо —> е в направлении
синхронизма должны быть равными показатели преломления
обыкновенной волпы основной частоты и показатель преломления
необыкновенной волны удвоенной частоты и® (2ы):
1VO (со) н®(2ы).
(12.15)
Так как показатель преломления необыкновенной волны зависит
от направления ее волновой норма-
ли, выразим в® как функцию уг-
ла 6 между волновой нормалью m
и оптической осью кристалла, совпа-
дающей с кристаллофизической
осью Х3 (рис. 12.5). Значение и® мо-
жет быть найдено как радиус-вектор
оптической индикатрисы г, лежащий
в одной плоскости с волновой нор-
малью и перпендикулярный ей.
С оптической осью г будет состав-
лять угол 90° — 0. Поскольку опти-
Рис. 12.5. Рисунок, поясня-
ющий вывод выражения
(12.18) для кристалла KDP.
ческая индикатриса одноосных кри
сталлов обладает осью симметрии бесконечного порядка, совпада
ющей с координатной осью Х3, вектор г и нормаль к пластинке
ш можно расположить в координатной плоскости Х2Х3; вектор г
будет иметь координаты (О, г2, г3).
221
Запишем уравнение сечения индикатрисы координатной пло-
скостью Х2Х3:
х2 х2
—— J- —— = 1
Я2
(12.16)
Так как (90° — 6) —угол, составляемый г с осью Х3, то
х2 = г sin (90° — 6) = г cos 6, х2 = г cos (90° — 6) = г sin 0.
Подставим х2 и х3 в уравнение (12.16):
г 2 2П COS 0 г2 sin2 0
Отсюда 2 Л’2 + 1 TV2 Л,2Л’2
1 — cos2 0 sin" 0 TV2 cos2 0 + TV2 sin2 0 '
Следовательно, или TV2 Л’2 (TV2 cos2 We 0-f-lV2sin2o)1/2 ’
(п®) 2 = No 2 cos20 + Ne 2sin20.
(12.17)
Подставим выражение для п® в (12.15) и, учитывая, что п® бе-
рется для частоты 2со, получим Л'~2(и) = Л'“2(2и) cos2 0 +
+ N~2 (2со) sin2 0. Решаем это уравнение относительно sin 0:
sin 0 —
Г N~2 (со) - 7У~2 (2со) _
V N~2 (2со) - N~2 (2со) ’
(12.18)
Подставляем в (12.18) значения показателей преломления для кри-
сталла KDP: sin 0 = 0,76. Отсюда 0 = 50°.
12.3. Определить плотность мощности ВГ, получаемой
с помощью кристалла KDP при плотности мощности све-
та основной частоты 109 Вт/см2, длине волпы X =
= 0,694 мкм и длине кристалла 0,5 см.
Решение. Для расчета воспользуемся данными предыду-
щей задачи и формулой для плотности мощности ВГ, выраженной
в Вт/см2:
_ 52>2 ^ффЛ2^2 (ю) / sin (AfcL/2)
“ TV2 (со) Ne (2со) X2 (со) АА-2,/2 J *
(12.19)
222
Заметим, что формула (12.19) может быть получена из (12.8) вы-
бором соответствующих единиц измерений.
Так как рассматривается срез кристалла KDP, соответствую-
щий направлению синхронизма, множитель в скобках в (12.19)
полагается равным единице.
Тогда
52,2- 0,67 -109-0,5* 2 * * * * *-1018
Р(2“)= 1,512-1,49.0,б942-10-8
= 0,3-109 Вт/см2.
12.4. Определить, как изменится плотность мощности
второй гармоники при отклонении падающей волпы от
направления синхронизма 0с на угол ДО при взаимодей-
ствии оо е (имеющем место, например, в кристал-
ле KDP).
Решение. Основой решения является формула (12.8).
В этой формуле зависимыми от угла 0 являются множители йафф
sin (AkL/2) \2
AkL/2 J
обозначим А:
Для краткости множитель, стоящий перед ци-
Р (2со) = Лй2фф
/ sin (ДАД/2) у
\ MrL/2 I '
Для решения задачи исследуем, как изменяется с изменением
п / sin (ДАД/2) \2 а а
угла 0 множитель ------- —— I, равный единице при 0 = 0С.
\ Д/гь/2 /
Для преобразования оо —»- е, имеющего место в KDP,
2 со г а 1
Д/с = —— [и® (2со) — Дгс (со) ] =
__2ыГ ^О(2со)/Уе(2со) 1
с l (7V2(2co) cos20 + 7V2(2co)sin20)1/2
(12.20)
Если 0 = 0с, то ДА = 0.
Дифференцированием (12.20) найдем ДА, соответствующее
углу, отличающемуся от 0С на Д0:
ДА =-----(со) —;--------- —;---------- sin (20„) Д0.
с > 7V2(2Q) дг2 (2со) с>
Далее определим изменение Р(2со) в зависимостп от Д0: ДР2о(Д0).
Для этого разложим в ряд sin2(AAL/2) в окрестности ДА = 0.
223
1 3
Известно, что sin х = х — —jp х . Тогда:
2
3!
(2
1-^Г*2
р2й(е+де)=Л1/|фф(0 + д0) 1-_2-
т2 2
L со
4
1 _ 1
Л’2 (2<о) Л'2 (2<о)
sin2 (2%) ДО2
ЛР2<0 = *>(%) -/J2&1(Oc + AO),
ДР __ (6с + Д6) -'Wc) 1
2(0 ---------------------
L2
3 4~
<о2ЛГ®(<о) / 1 1
72 ^(2ш) “ TV2(2w)
2
sii)2 (20с)ДОг.
Задачи
12.5. При каком соотношении между Ne(.a>), NAa) и
A>.(2(i>), jV<,(2(o) возможно синхронное взаимодействие в
оптически положительных одноосных кристаллах? в оп-
тически отрицательных одноосных кристаллах?
12.6. Возможно ли синхронное взаимодействие в крис-
талле селенида кадмия (симметрия бтт) для лазера на
IAG : Nd3+ (X = 1,06 мкм) и СО2-лазера (Л =10,6 мкм)?
Для этого кристалла дисперсионные зависимости имеют
вид
N2 = 4,2243 + -/-’76-2- Д
X2 - 0,227
3,12Х2
X2 — 3380’
Л'2 = 4,2009 + 4’8875Х2
X2 - 0,2171
3,6461X2
X2 — 3629 ‘
12.7. Возможно ли синхронное взаимодействие в крис-
талле прустита Ag3AsS3 (симметрия Зт) для излучения
СО2-лазера, если дисперсионные зависимости для этого
кристалла имеют вид
N2 = 9,220 + 2 °’4454 + —1733
X2-0,1264 1000 —X2
N2 = 7,007 + -^Ь-3230 + 660
X2 —0,1192 1000 —X2
224
с
12.8. Возможно ли синхронное взаимодействий в
кристалле кварца на длине волны К = 0,347 мкм?
12.9. Определить температуру 90-градусного синхро-
низма в кристалле ниобата лития определенного стехио-
метрического состава для X — 1,064 мкм, если дисперсион-
ные и температурные зависимости показателей преломле-
ния для кристалла этого состава имеют вид
N2 = 4,9130 +
0,1173+ 1,65-10~8-712
X2 — (0,212 + 2,7 • 10~8 • У2)2
N2e = 4,5567 + 2,605-10-7-У2 +
0,097 + 2,7-10" 8-У2
+ X2 — (0,201 + 5,4-«Г8 - У2)2
2,78- 10-2-Х2,
2,24-ю-2. Г.
12.10. Показать, что в классе симметрии 422 й0фф для
взаимодействия ее-* о не зависит от угла <р, составляемо-
го главной плоскостью кристалла с координатной плос-
костью XiXi.
12.11. Показать, что в классе симметрии 3 йэфф при
взаимодействии оо е равен сумме йэфф для классов
6 и 6.
*12.12 . Показать, что для класса Зт йвфф для взаимо-
действия оо -* е равен сумме йзфф классов 6т2 и 6mm.
12.13. Для каких кристаллографических направлений
в пиобате лития йэфф для взаимодействия оо -* е зависит
только от коэффициента d3i? Будет ли в этом направле-
нии преобразование света основной частоты во ВГ более
или менее эффективным, чем в других возможных
в кристалле направлениях синхронизма?
12.14. Показать, что для кристаллов классов сим-
метрии 622 и 422 для взаимодействия оо -* е й8фф = 0.
12.15. Определить угол синхронизма для кристалла
киновари HgS для X = 5,3 мкм, если его показатели пре-
ломления
для X = 5,3 мкм 7Vd = 2,83, Ne ’= 3,15,
для X = 10,6 мкм No = 2,60, Ne = 2,85.
12.16. Определить мощность ВГ СО2-лазера, генерируе-
мой с помощью кристалла киновари длиной 0,8 см при
плотности мощности падающего излучения 107 Вт/см2.
12.17. Определить когерентную длину кристалла квар-
ца при генерации ВГ в направлениях, составляющих
углы 30 и 90° с оптической осью кристалла.
15 н. В. Переломова, М. М. Тагиева
225
12.18. Какова плотность мощности ВГ, получаемой с
помощью кристалла кварца в направлениях, указанных
в предыдущей задаче?
Плотность мощности падающего излучения 109 Вт/см2,
длина кристалла ^авна когерентной длине кристалла в
соответствующем направлении.
12.19. Определить когерентную длину кристалла KDP
в направлениях, отличающихся от направления синхро-
низма, определяемого углом 0, на 5°, т. е. (6 +5е) и
(0-5°).
12.20. Как изменится плотность мощности ВГ, полу-
чаемой на кристалле ниобата лития, при отклонении от
угла синхронизма на 5, 10 и 15° для X —1,06 мкм и со-
става кристалла, допускающего 90-градусный синхронизм.
Использовать данные задачи 12.9.
12.21. Определить угол синхронизма для кристалла
селенида галлия для Л. = 10,6 мкм, если его коэффициен-
ты преломления
No = 2,81, Ne = 2,44 для к = 10,6 мкм;
No = 2,83, Ne = 2,46 для X = 0,53 мкм.
12.22. При каких углах синхронизма «снос луча» не
накладывает ограничений на реальную длину синхрон-
ного взаимодействия при Д7с = 0?
12.23. Определить плотность мощности ВГ в кристал-
ле ниобата лития при 90-градусном синхронизме, если
длина кристалла L = 1 см, X = 1,06 мкм, мощность пада-
ющего излучения 5 105 Вт и площадь поперечного сече-
ния пучка 5=1 см2. Как изменится плотность мощности
ВГ при уменьшении площади сечения пучка до 0,01 см2
при той же его мощности?
12.24. Рассчитать, при какой мощности падающей
волны мощность ВГ составит 50 и 90% от мощности па-
дающей волны для кристалла ниобата лития при 90-гра-
дусном синхронизме. Длина кристалла L = 1 см, X =
= 1,06 мкм, площадь поперечного сечения пучка S =
=> 0,01 см2.
12.25. Рассчитать реальную длину взаимодействия с
учетом сноса луча в кристалле KDP при распростране-
нии волны основной частоты в направлении синхронизма
0 = 41° при диаметре падающего пучка d — 1 мм.
12.26. Выполнить задание предыдущей задачи при
d ~ 1 см.
12.27. Определить угол между волновой нормалью и
лучом в направлении синхронизма для кристалла кино-
226
вари при 1 = 10,6 мкм. Какова длина взаимодействия
при d = 1 см?
12.28. Определить, как изменится мощность ВГ при
уменьшении диаметра пучка от 1 до 0,1 см в кристал-
ле KDP, учитывая влияние диаметра пучка на длину
синхронного взаимодействия. Свет распространяется в на-
правлении синхронизма 0 = 49°, мощность падающего из-
лучения 10s Вт.
§ 13. ТЕРМОДИНАМИКА КРИСТАЛЛОВ
Линейные эффекты. Состояние диэлектрического
кристалла как термодинамической системы определяется
следующими величинами: механическими напряжениями
tij и деформациями r(j, напряженностью электрического
поля Et и индукцией Df (или поляризацией Р{), темпера-
турой Т и энтропией S.
Энтропию, электрическую индукцию и деформации
принято считать обобщенными термодинамическими ко-
ординатами, а температуру, напряженность электрическо-
го поля, механические напряжения — обобщенными сила-
ми. Однако в обычных экспериментах проще изменять
температуру, напряженность электрического поля, меха-
нические напряжения и количественно определять изме-
нения этих величин, рассматривая их в качестве неза-
висимых переменных. Изменение энтропии, электрической
индукции, деформаций непосредственно регулировать
трудно. Вообще, в качестве независимых переменных
можно выбрать любую тройку величин, характеризующих
механическое, электрическое и тепловое состояние крис-
талла. Тогда остальные величины будут функциями вы-
бранных независимых переменных.
Независимых переменных для однозначной характе-
ристики состояния кристалла должно быть задано десять:
шесть компонент тензора механических напряжений (или
деформаций), три компоненты вектора электрического
поля (или электрической индукции), температура (или
энтропия),
Из первого начала термодинамики следует, что су-
ществует единственная функция выбранных десяти не-
зависимых переменных, приращение которой есть полный
дифференциал.
Каждому конкретному выбору независимых перемен-
ных соответствует определенная термодинамическая
функция.
15* 227
Рассмотрим два из всех возможных вариантов выбора
независимых переменных
1) rtj — Et, Т),
Dt — D^itj, Et, D,
S = Sktij, Et, T).
и их функций:
2) tij = Dt, S),
Ei = Dt, S),
T = T(rt}, D{, S).
Первая форма записи наиболее естественна для реаль-
но проводимых экспериментов. Вторая форма записи яв-
ляется основной для сегнетоэлектрических кристаллов,
для которых спонтанно возникающую при фазовом пере-
ходе электрическую поляризацию (индукцию) и деформа-
цию удобно считать независимыми переменными.
В первом случае термодинамическим потенциалом от-
носительно независимых переменных tn, Е.:, Т является
функция Гиббса
dG — —rijdtfj — DrndEm — S dT.
Разложим выражения для гы, Dm и S в ряд Тейлора
в окрестности некоторой произвольной ТОЧКИ ^feZ, -Em, То),
т. е. некоторого начального состояния кристалла, ограни-
чиваясь членами разложения первого порядка:
dS (дв\ / д2С \ (. .о
~ dt “ I dT ]0 I дТ dt ' 11 11
\ 11 / о
228
(Дифференцирование производится по одной переменной
при фиксированных значениях остальных переменных.)
Таким образом, получаем систему из десяти уравне-
ний: шесть уравнений для определения деформаций гц,
три — для индукции Dm и одно — для энтропии.
Далее, в качестве начального состояния, выбираем
механически ненапряженное состояние = 0 при отсут-
ствии электрического поля Е°== 0. Таким образом, отлич-
на от нуля только начальная температура кристалла Т =
= Та. Условимся считать в начальном состоянии кристалл
недеформированным и неполяризованным:
dG'
SEm
= 0 и
о
8G ___ л
~дТ) ~ °o>
т. е. будем считать Тв началом отсчета температурных
деформаций и пироэлектрической поляризации. Обозна-
чим 2"—7’0 = Д71 и 5 — So = AS.
Тогда систему уравнений (13.1) можно записать в виде
( d2G \ f ( d2G \ / д2С .т
ri}~ VW/' WEJom ’
(13.1a)
( d2G . ( d2G / d2G \
m~ \<>EMokl VEmdEJol VEmdTh ’
(13.16)
“=- (А)л - (^).A7-' <131b)
Рассмотрим все имеющиеся в уравнениях коэффици-
енты:
I 8iG — I — Е'т
\dtiidthl/o \dthl/o llM
— коэффициент упругой податливости, измеренный при
постоянных электрическом поле и температуре;
/ d2G _ р'-у лт
229
— пьезоэлектрический коэффициент, измеренный при по-
стоянной температуре;
_ I d*G
dt-.dT I 57 I гз
\ гз /о \ /о
— коэффициент теплового расширения, измеренный при
постоянных механическом напряжении и электрическом
поле;
( й2С _ (dDm\ _ у
V>Emdthl}0 [ethl)0 а^1
— пьезоэлектрический коэффициент;
( 82G \ _ (8D™\ _ t.T
k*vJ0 k t>Ei k Eml
— диэлектрическую проницаемость, измеренную при по-
стоянных механических напряжениях и температуре;
( d2G \ = \ = t
\ОЕтдТ ).о \дт } Ут
— пироэлектрический коэффициент, измеренный при по-
стоянных механических напряжениях;
( d2G \ Т (dS\ 8Q __ ’
k^Jo VMo dtki~ahl
— коэффициент термоупругих напряжений;
( d*G ) т — I 88 \ Т = dQ = '
\8TMJO \дЕЛ> 8Ет
— коэффициент, определяющий электрокалорический эф-
фект;
(s2g\ т t,E
—2 7 = с ’ — темплоемкость, измеренная при по-
\^7’ /о
стоянных механических напряжениях и электрических
полях.
Здесь и далее условия измерения коэффициентов будут
обозначаться верхними индексами.
Так как dG является полным дифференциалом, то зна-
чение второй производной функции G не зависит от по-
рядка дифференцирования и между перечисленными вы-
ше коэффициентами существует следующая связь:
8Ет 6tij ’
230
следовательно,
8S
Ут
dmij — ^miji
8D
~~дТ ~ НЕ и У™ ~ Т '
m
dri;
8S
8Т — 8t.. и Т ‘
Умножим уравнение (13.1в) на Т\
ES-T = АС =
/ д2С
~ “ ^7 8tki
ГП. I 8 G ] ГП Г,
. м \8T8Em]/Em
д2С
8Т2
тьт.
Тогда окончательно уравнения (13.1а, б, в) можно за-
писать так:
rH = 4- drmjEm + ai’j ЕТ,
Dm = ZmlEi + Ут^Т, (13.2)
де = TahTtkl + T.y\nEm + pcE-fA7\
Эта система уравнений описывает совокупность элект-
рических, механических и тепловых явлений, наблюдае-
мых при изменении механических напряжений, электриче-
ского поля и температуры диэлектрического кристалла:
деформацию под действием механических напряжений и
изменения температуры, прямой и обратный пьезоэффект,
поляризацию диэлектрика во внешнем поле, пироэлектри-
ческий эффект и т. д.
Для второго варианта выбора независимых перемен-
ных и их функций аналогично предыдущему разложим
функции в ряд Тейлора с использованием внутренней
энергии U и получим систему уравнений:
1ц = сц'&и — — Pi-DAQ,
Ег = - hf^r^ + v^Dm - gTi’DEQ, (13.3)
AT = - TpEsrij _ Tg^sDm +
pc
Заметим, что коэффициентам p{j и принято при-
писывать знак минус.
Эта система уравнений в отличие от (13.2) определяет
электрические, механические и тепловые явления в крп-
231
сталлах, возникающие при изменении деформаций, элект-
рической индукции и энтропии.
Аналогичные уравнения могут быть представлены для
любого из возможных выборов независимых переменных
и их функций.
Эффекты второго порядка. Выше были рассмотрены
уравнения, которые учитывали механические напряжения
и электрическое поле в кристаллах, зависящие от дефор-
мации и индукции линейно. То же относилось к зависи-
мости деформаций и индукции от механических напряже-
ний и электрического поля.
Если же не ограничиться первыми членами в разло-
жении в ряд величин гц, Д и 8 или ti}, Т и Д, а учесть
следующие нелинейные члены разложения, то можно опи-
сать ряд новых физических явлений, наблюдаемых в кри-
сталлах и называемых эффектами второго порядка. Эти
эффекты особенно сильно проявляются и представ-
ляют практический интерес в сегнетоэлектриках.
В эффектах второго порядка роль тепловых явлений
незначительна, поэтому далее будем рассматривать в каче-
стве независимых переменных только механические напря-
жения и индукцию, а их функциями — деформации и
электрическое поле, полагая условия измерения изотерми-
ческими. Для адиабатических условий рассмотрение ана-
логично.
С учетом членов второго порядка малости в разложе-
нии в ряд Тейлора и при тех же начальных условиях, что
и в уравнениях (13.3), механические напряжения и элект-
рическое поле могут быть выражены следующим образом:
/ dt..\n / Qt.. \?
Мм М<М
“b "2Г \ dr dr / rtarP1 + 2 ( dr dD ) rklDm -f-
M L \ OrMOrpq /О V OrhlOLm /0
/ d2t.. \
+ \ dDmbDn LDmDn ’
(13.4)
drkldrpg /
Pkl^pq 4“
0
/ d2E^ \ I d2Em \
+ 2hrM+ ]D^ •
\ /0 \ 01JqalJp /0
232
Б этих уравнениях
(dtiAD V /ЙДт\Д / дЕт V
[drhi J ’ \6Чп/ — ) и /
— известные коэффициенты упругой жесткости с^ы, пье-
зоэлектрические коэффициенты h,nij и коэффициенты ди
электрической непроницаемости цт„.
Далее обозначим:
( — f d*U — ( '^Еп _ <)nTD
\ drijdDn) \ дгмдгца£>п / \ дгмвга) drij ~
( о\ \ D
8гря
( &2tkl — ( д*и — ( d^En =
\ dDn0Dq ) \ 8rkldDndDq )\ drhldDq /
dhM _ _ 9n
™q 8rkl lPMW1'
( 8 Em 8rimq r,r
\8DqdDv )- SDp “
Физический смысл введенных коэффициентов Mnhnj,
ijhlpqi Phlnq^ fmqp ясен. Так коэффициенты MnUij, образую-
щие тензор пятого ранга, определяют изменение пьезо-
электрических коэффициентов в зависимости от деформа-
ций Гц, коэффициенты pktnq — изменение тех же пьезо-
коэффициентов в зависимости от индукции Dq или изме-
нение диэлектрической непроницаемости цпд в зависимо-
сти от деформаций rhl и т. д.
Теперь уравнения (13.4) можно записать так:
^hl ^klijPij hnhlDn ~Т NijkipqYijTpq -ф
4“ 4" Pklme^m^ei (13.4a)
= ^‘mklPkl T" ?]mnDn "T MmpqklPpqPkl “Ф
+ PhlmnruDn + fmnqDq
ИЛИ
^kl = 4“ Nijhlpq^pq "4“ nklij^n) 4“
+ (— ^nkl Ч- PhlTnrtPin} J (13.5)
^vti — ( 4“ MrnpqklTpq) ^kl 4“
4-Gimn 4“ PklmuPhl 4“ fmnqDq) Dn-
233
Выражение, стоящее в скобках перед rtj, представляет
собой упругую жесткость с поправками за счет отличных
ОТ нуля деформаций N?jhlpqrpq и индукции MnUijDn
(после свертывания по индексам pq и п — это тензор чет-
вертого ранга). Выражение, стоящее в скобках перед Dn,
есть пьезоэлектрический коэффициент с учетом поправки
за счет отличной от нуля электрической индукции:
PklmnDm*
Выражение, стоящее в скобках перед гы, представляет
пьезоэлектрический коэффициент с поправкой за счет де-
формаций MmpqhiJ'pq- Во второй скобке последнего урав-
нения — диэлектрическая непроницаемость с поправками
за счет деформации рытпгы и индукции fmnqDq.
Окончательно уравнения (13.5) можно записать в сле-
дующем виде:
~ “Ь ACft/jj) Oj (^nkZ “Ь ^Inhl} Dn,
Ет = ^kl (Цтпп “Ь A2T]mn) Dn,
Рассмотрим подробнее поправки к диэлектрической не-
проницаемости кристалла Л1Цтп и AzT]™»:
АхЦтп = fmnqDq, (13.6)
АгЦтп ~ PklmnTkb (13.7)
Уравнение (13.6) — уравнение электрооптического эф-
фекта, называемого линейным в том смысле, что измене-
ние диэлектрической непроницаемости кристалла в (13.6)
является линейной функцией индукции. Однако эта линей-
ная зависимость возникает вследствие нелинейной связи
обобщенных координат, т. е. нелинейности зависимости
Е от D, что выражается через зависимость диэлектриче-
ских свойств, в данном случае т]„ от величины электриче-
ского воздействия D.
Вообще, термодинамическая теория для электроопти-
ческого эффекта предлагает четыре различных системы
уравнений и четыре типа электрооптических коэффициен-
тов в зависимости от того, является ли внешнее воздей-
ствие индукцией D или электрическим полем Е и харак-
теризуются ли диэлектрические свойства кристалла тен-
зорами еа, а1з- (Е( = а,цР}) или (Р1 = х«Е3):
АЦтпп = fmnqDq, pijkEk, (13 g)
Aa^ 6mlqPg, AXjnn
234
Все эти уравнения и электрооптические коэффициен-
ты равноправны и могут быть использованы для описания
электрооптического эффекта в зависимости от конкретных
физических условий. Но наиболее употребительными яв-
ляются не указанные выше коэффициенты, a rVk, фигури-
рующие в уравнении (см. § 11, формула (11.1)):
Д Цтп = гтпгЛЕк. (13.9)
Именно это уравнение легче всего интерпретировать,
используя геометрическое представление об изменении
оптической индикатрисы под действием приложенного
внешнего электрического поля.
Вторая поправка к диэлектрической непроницаемости,
описываемая уравнением (13.7), представляет собой уп-
ругооптпческий эффект, заключающийся в изменении
оптических свойств кристалла под действием механиче-
ских деформаций.
Наконец, если рассмотреть члены третьего порядка
малости в уравнениях (13.1) и (13.3), можно получить
квадратичный электрооптический эффект:
й'т ( 77трдьЕPQ^^kl 1”
"Н (Pmn Phlmn^'kl fmnqEq В FщпдрЕ)qT)p)7)n,
77m + (emn ~B fimnqEq “B EmnpqEqEp)En.
В этих уравнениях последние слагаемые в скобках
Fmnq-pDqDf и KmnrqEqEp учитывают квадратичную зависи-
мость диэлектрических свойств (т]ч и е„) от индукции D
и поля Е соответственно:
Дт]ц = FijfJDjfii, Лг,,,- = K(jUEhEi.
Уравнения (13.10) — две из четырех возможных форм
записи квадратичного электрооптического эффекта, Fijki
и КцЫ — коэффициенты квадратичного электрооптического
эффекта. Так как они образуют тензор четвертого ранга,
наблюдаться этот эффект может в кристаллах любой
симметрии.
Однако удобнее наблюдать его в центросимметричных
кристаллах, в которых отсутствует линейный эффект, ко-
торый обычно значительно больше квадратичного.
Форма матриц коэффициентов квадратичного электро-
оптического эффекта для различных классов симметрии
тождественна форме матриц упругих коэффициентов
SUM И Cfju.
(13.10)
235
Назовем еще один эффект второго порядка, имеющий
практическое значение,— это электрострикция. Она состо-
ит в деформации кристалла, пропорциональной второй
степени напряженности электрического поля:
Cji GijT,-.nE Т..Е yL.
Из уравнения электрострикции следует, что знак дефор-
мации не изменяется при изменении направления поля
на противоположное.
Для электрострикции в зависимости от условий наблю-
дения можно записать еще три уравнения:
Гу QijmnPщЕ'пч tij GyjmnPmPnj EijmnEmEn*
Электрострикционные коэффициенты 7?ymn, Qa-mn, Gilmn,
Hiimn не являются независимыми.
Электрострикция наблюдается в кристаллах любой
симметрии. Вид матриц электрострикционных коэффици-
ентов совпадает с видом матриц упругооптических коэф-
фициентов.
Связь между коэффициентами, измеренными при раз-
личных условиях. Из сказанного выше следует, что зна-
чения коэффициентов, описывающих механические,
электрические и тепловые, а также пьезо- и пироэлектри-
ческие свойства кристаллов, зависят от условий их изме-
рения.’ Так, механические свойства зависят от тепловых
и электрических условий наблюдения, электрические — от
механических и тепловых, теплоемкость — от механиче-
ских и т. д.
Выделим наиболее важные условия измерения.
Тепловые условия:
1. Т = const (изотермические измерения). Это условие
реализуется при медленно протекающих процессах, когда
кристалл во время испытаний находится в тепловом рав-
новесии с окружающей средой. Соответствующие испыта-
ния кристалла называются статическими.
2. S = const (адиабатические измерения). Это условие
реализуется при быстро протекающих процессах, при ко-
торых невозможен обмен теплом между отдельными час-
тями кристалла или кристаллом и окружающей средой.
Соответствующие испытания называются динамическими
и осуществляются при упругих колебаниях кристалла на
частотах выше его собственной частоты колебаний.
Электрические условия:
1. Е = const (электрически свободный кристалл). В
этом случае вся поверхность кристалла должна находиться
236
под одним потенциалом. Для этого электроды, нанесен-
ные на кристаллическую пластину, должны быть замкну-
ты, т. е. замкнута внешняя цепь кристалла.
2. D — const (электрически «зажатый» кристалл). Та-
кое условие трудно осуществить экспериментально. Ближе
всего к нему наблюдение кристалла при разомкнутой его
внешней цепи.
Механические условия:
1. £ц = const (механически свободный кристалл). Это
условие осуществляется тогда, когда кристалл свободно
деформируется под воздействием внешних сил, что воз-
можно при статических испытаниях.
2. гц = const (механически «зажатый» кристалл). Для
реализации этого условия необходимо, чтобы кристалл
был окружен со всех сторон средой с бесконечно большой
жесткостью. Практически условие Гу = const можно осу-
ществить при динамических испытаниях на высоких час-
тотах, когда деформации кристалла не успевают следовать
за изменением внешних сил.
Примеры решения задач
13.1. Рассчитать долю первичного и вторичного пиро-
электрического эффекта для кристаллов нитрита бария.
Решение. Пироэлектрические кристаллы в силу своей по-
лярной симметрии и отсутствия центра инверсии являются также
и пьезоэлектрическими кристаллами. Поэтому при наблюдении
на опыте пироэлектрической поляризации при однородном на-
гревании кристалла неизбежно будет наблюдаться и пьезоэлектри-
ческий эффект, вызванный тепловой деформацией кристалла.
Если кристалл механически зажат, т. е. не может деформировать-
ся, пьезоэлектрический эффект будет вызван механическими на-
пряжениями, возникающими при нагревании в зажатом кри-
сталле.
Следовательно, наблюдаемый на опыте пироэлектрический
эффект, кроме «истинного» пироэффекта, т. е. непосредственного
влияния изменения температуры на поляризацию, включает в
себя «ложный» пироэффект — пьезоэффект, вызванный тепловой
деформацией кристалла. Если обозначить коэффициент «истин-
ного» пироэффекта у', а коэффициент «ложного» пироэффекта 7",
то 7 = Y + 7" (см. § 3).
Рассчитать долю первичного и вторичного пироэффекта в
общем эффекте позволяет следующее термодинамическое рас-
смотрение этого явления. Будем считать независимыми перемен-
237
нымп, характеризующими состояние кристалла, следующие вели-
чины: Е — напряженность внешнего электрического поля, rft(__
деформации, испытываемые кристаллом, Т — температуру кри-
сталла.
Величины: D — электрическая индукция, t13- — механические
напряжения, 5 — энтропия, будут представлять собой функции
величин Е, rht и Т\
Di = Df T), tij = ^ij(Em, Bfez, 7), jS* = S (Emi TftZ, T).
Рассмотрим зависимость вектора индукции D от температуры
прп условии отсутствия внешнего электрического поля (Е = 0).
Поскольку О, = eoEi + Р,-. то прп Е = О
f 8D. \ _ /”ар; \
\ 8Т Jt,E \ 8Т )t,E
Так как Di = D,{(T, rkt) и rki = гм(^ь 7), то можно записать:
(13.11)
Если измерения проводятся при постоянном внешнем давлении,
то dt{j = 0 и
(13.12)
Подставляя в выражение (13.11) drkl из соотношения (13.12),
получаем
8Di дтм
d'kl 8Т
ат.
(13.13)
Выражение, стоящее в скобках, представляет собой коэффи-
циент суммарного пироэлектрического эффекта. Слагаемое Т. =
fdD.X
= ( gy / определяет величину первичного («истинного») пиро-
„ dD* дгм
эффекта; величина yi=~g^' характеризует вторичный
(«ложный») пироэффект, обусловленный пьезоэффектом прп теп-
ловом расширении кристалла.
5г., dD. 9D. 9t_._ р
Поскольку —= ahl, ---------— — -----I----Z22- =
ЙР дГм gtmn дГы гтптпк1,
где Kki—коэффициенты теплового расширения, dimn—пьезомоду-
ли, стпм — упругие жесткости кристалла, измеренные при постоян-
238
ном электрическом поле, то коэффициент вторичного пироэлект-
рического эффекта может быть записан в виде
Vi = dimncmnklakr
В правую часть выражения (13.14) входят величины, непо-
средствепно измеряемые па опыте. Поэтому коэффициент мо-
жет быть вычислен, а следовательно, если известен коэффициент
7,-, можно оценить долю первичного и вторичного пироэлектриче-
ского эффекта.
Для кристаллов нитрита бария, имеющих один пироэлектри-
ческий коэффициент Т3 = выражение (13.11) приобретает
вид
Уз =
где аь — коэффициенты теплового расширения, d33 — пьезоэлект-
рические модули, стоящие в третьей строке матрицы (d<3), c3-ft-—
упругие жесткости кристалла.
Для нитрита бария отличными от нуля являются следующие
коэффициенты d3j (см табл 6): dai, = d3i, dss.
Учитывая это, а также вид матриц (aft) и (c3ft) (см. табл. 6
и 9) для нитрита бария, мы получаем следующее выражение
Для у":
?3 = d3jCjkah = Й31 (С1Л ^12а2 С13аз) +
+ d32 (С21а1 + С22И2 + С23“3) + Й33 (С31“1 + «32% + СА)‘
Или, учитывая, что сп = с22, ci3 = с23, «1 = ц2, получаем
?з = 2d3i [ (сп ~Ь с1г) а1 с1заз1 + 2йззсз1а1 + d33c33a3'
Подставляя значения коэффициентов d3j-, c3fl и ак из табл. 14,
получаем у" = 0,72 ед. СГСЭ. Поскольку коэффициент полного
пироэффекта равен — 8 ед. СГСЭ, то вклад вторичного пироэффек-
та в общий при комнатной температуре составляет приблизитель-
но 9%. Основная доля (около 90%) пироэффекта в кристаллах
нитрита бария обусловлена первичным («истинным») пироэф-
фектом.
13.2. Определить, как связаны между собой коэффи-
циенты упругой податливости, измеренные в изотермиче-
ских и адиабатических условиях.
Решение. Для решения задачи воспользуемся уравнениями,
связывающими механические и тепловые характеристики состояния
239
кристалла, пренебрегая электрическими явлениями:
dr4=|^2i| dthl + (^Jp\ dT, (13.15)
\ dtM / \ dT 1
f dS \T [ OS V
\ rib / \ /
Полагаем условия измерения адиабатическими, т. е. S =
= const и dS = O в (13.16). Тогда выражаем dT из (13.16) и под-
ставляем в (13.15)
_ l^JL Г ЫдТУ(д8/а^)Та^
dri} \ dtM ) dtM‘ (dS/dT)*
(13.17)
Учитывая, что для данного выбора независимых переменны*,
и их функций приращение соответствующей термодинамической
функции dG есть полный дифференциал, получим
_ ( д2° \_____I дггз V______( dR \Т
\atijdT ) \дТ] \dtyj'
Полученные соотношения подставляем в (13.19):
Используя введенные ранее обозначения, получаем
sijhl ~ siikl ~ aijahl —р-
13.3. Определить вид матрицы упругоэлектрических
коэффициентов для класса симметрии 32.
Решение. Используя уравнение (13.4а), для изменения
коэффициентов упругой жесткости в зависимости от электриче-
ской индукции кристалла можно записать:
Дс|-Зы = MnijhiDn- (13.18)
Выражение (13.18) можно рассматривать как уравнение упруго-
электрического эффекта. Если внешним воздействием является
электрическое поле, то
ACijM = SmijklRm*
Компоненты тензора gmijta связаны с Мп,цм через коэффициенты
диэлектрической проницаемости.
Для кристалла класса 32 генераторами группы могут быть
выбраны операции поворота вокруг оси 2, параллельной Xi, и по-
ворота на 120° вокруг оси 3, параллельной А'з- Последователь-
240
ность действия указанных генераторов не имеет значения, поэто-
му целесообразно сначала рассмотреть действие преобразования
осью 2, допускающего использование метода Фуми (см. §§ 6, 7):
С2||Х1
1.0 0\
0—1 о
О 0—1/
Затем уже можно рассмотреть действие поворота
/—1/2 —1/3/2 0\
Сзцх3 = 1 ]/з/2 -1/2 0 ’
\ 0 0 1/
требующее применения метода прямой проверки,
системы уравнений
gpqrst рт^qi^sh^" '
В результате для класса 32 получим три матрицы:
вокруг' оси 3:
т. е. решения
*111 (*111 “Ь *122) *113 *114 0 0
*122 ~ *113 *124 0 0
0 *134 0 0
*144 0 0
*144 (*124 ~ *144
2 (^щ + *122'
0 0 0 0 — g124 -j- 3g122
о о о — g114 — (3glu + g122)
0 ° ~ *134 ~~ 2*из
О *144 *114 *124
О О
о
-0 0 0 0 g316 О -
О О о - gsl5 о
ООО о
° ° -*315 ’
о о
' _ о _
с помощью которых удобно представлять тензор пятого ранга в
матричном обозначении: gimft, gain и, Л', Z, q, i, j — индексы,
получающиеся при свертывании двух пар индексов, относящихся
к упругим коэффициентам, и пробегающие значения от 1 до 6.
Для наглядности влияние электрического поля па упругость
кристалла класса 32 удобно представить в виде таблицы, которая
приведена па с. 242.
16 и. в. Переломова, М, М. Тагиева
241
felirb^izz)^ —(3flll+gl22)^2 —2g113E2 (<?114 (£124 £114)^1 C66 “(£111+£112)®
—2g315E3
242
13.4. Значения коэффициентов линейного электрооп-
тического эффекта г22 и rS3 кристаллов ниобата лития,
измеренные в электрическом поле, частота которого пре-
вышала собственные частоты колебаний образца, равны
г*2 = 0,1 - 10“в ед. СГСЭ, г*3 = 0,9 ед. СГСЭ.
Вычислить значения соответствующих коэффициентов,
характеризующих электрооптические свойства ниобата
лития в статических и низкочастотных полях. Какой из
приведенных коэффициентов будет наиболее сильно за-
висеть от частоты?
Решение. Приведенные значения электрооптических коэф-
фициентов характеризуют «истинный» электрооптический эффект,
поскольку они измерены на частотах, превышающих собственные
частоты колебаний образцов. В этом случае кристалл механиче-
ски «зажат», так как его деформации не успевают следовать за
колебаниями внешнего электрического поля. Значения электроопти-
ческих коэффициентов г22 и г33, характеризующие свойства нио-
бата лития в низкочастотных и статических полях, больше на
величину вклада упругооптического эффекта, поскольку в этом
случае кристалл, являясь механически «свободным», деформиру-
ется, а деформация в свою очередь вызывает дополнительное из-
менение поляризационных констант. Уравнение (11.6) позволяет
рассчитывать значения интересующих нас коэффициентов.
Матрицы коэффициентов di7- и Рц, необходимые для расчета
коэффициентов г22 и г33 для кристаллов с симметрией 3m, к ко-
торым относится ниобат лития, представлены в табл. 6 и 11.
Согласно (116) и в соответствии с видом матриц dtj и до-
получаем
Г222 Г222 ^2211^211 ' ^2222^222 + ^2223^223
или в матричном обозначении
Г22 + (?12 — ?11) d21 ~ Р1/15 = °’194 ’ 10-6 еД- СГСЭ.
Таким образом, коэффициент г^, характеризующий электро-
оптические свойства ниобата лития в низкочастотном или стати-
ческом поле, в два раза больше, чем коэффициент г*2, характе-
ризующий указанные свойства в высокочастотном электрическом
поле. Найдем значение г33:
гзз “ гзз + Рзз^дз = 0,0004 • 10 6 ед. СГСЭ.
Отсюда следует, что коэффициент г33 будет отличаться от
коэффициента г33 на 0,4%.
Очевидно, что из коэффициентов г22 и г33 наиболее сильно от
частоты будет зависеть коэффициент г33.
16* 243
Задачи
13.5. Какие явления наблюдаются при однородном и
неоднородном нагревании кристаллов с симметрией 3, 32
и m3?
13.6. Какие физические явления возможны только в
кристаллах 10 полярных классов симметрии?
13.7. Какие физические явления с учетом явлений вто-
рого порядка возможны при помещении в однородное
электрическое поле кристаллов с симметрией ттп и 23?
13.8. В табл. 14 даны коэффициенты упругой податли-
т
востп кварца, измеренные в изотермических условиях, s^.
Воспользовавшись данными этой таблицы, рассчитать зна-
чения адиабатических коэффициентов упругих податли-
востей кварца Sy.
13.9. Как связаны между собой компоненты тензора
диэлектрической проницаемости, измеренные на механи-
чески свободном еу и механически зажатом еу кристал-
лах? Для кристаллов каких классов симметрии они разли-
чаются? Для каких равны?
13.10. Как связаны между собой компоненты тензора
диэлектрической проницаемости, измеренные в изотерми-
ческих еу и адиабатических еу условиях? Для кристал-
лов каких классов симметрии они различаются? Для ка-
ких равны?
13.11. Определить относительное изменение емкости
конденсатора, представляющего собой пластину Х-среза
сегнетовой соли, при работе его на частотах ниже и выше
собственной резонансной частоты колебаний пластины
(емкость механически свободного и механически зажато-
го кристалла).
13.12. Изменится ли емкость слюдяного конденсатора
при переходе от работы на низких частотах переменного
тока к высоким частотам?
13.13. Можно ли для расчета резонансных частот пье-
зоэлектрических вибраторов использовать значения коэф-
фициентов упругой податливости, полученных по измере-
ниям скоростей звука в кристалле?
13.14. Показать, что для кристаллов кубической сим-
метрии адиабатический коэффициент упругой податливо-
S Т '
сти S44 равен изотермическому s44.
13.15. Определить соотношения, связывающие адиаба-
тические и изотермические пьезомодули. Отличаются ли
244
эти коэффициенты для кристаллов: а) ниобата лития,
б) кварца, в) KDP?
13.16. Как изменится температура кварцевой пласти-
ны, ориентированной, как показано на рис. 4.3, б, при
кратковременном воздействии на нее силы, десятикратно
превышающей ее силу тяжести? Размеры пластины 1 X
X 3 X 10 мм3. Рассмотреть три случая приложения силы
к каждой паре взаимно параллельных граней.
13.17. Определить вид матрицы упругоэлектрических
коэффициентов для класса симметрии 42m.
13.18. Определить вид матрицы упругоэлектрических
коэффициентов для класса симметрии Зт.
13.19. Как изменится резонансная частота колебаний
пьезоэлектрического вибратора, представляющего собой
брусок Х-среза кварца длиной 10 мм и совершающего ко-
лебания сжатия — растяжения по длине, если его поме-
стить в постоянное электрическое поле 105 В/см, прило-
женное в направлении оси 2?
13.20. Рассчитать относительное изменение резонанс
ной частоты пьезоэлектрического вибратора, представля-
ющего собой пластину У-среза кварца, совершающего
колебания сдвига по толщине, при приложении постоян-
ного электрического поля 5 • 105 В/м в направлении
оси Х\.
13.21. Как изменится модуль Юнга ниобата лития в
направлении оси 3, если к кристаллу приложено постоян-
ное электрическое поле 106 В/м в направлении, составля-
ющем с кристаллофизическими осями равные углы?
13.22. Найти и построить сечение указательной поверх-
ности коэффициента с33 ниобата лития координатной пло-
скостью Х1Х2, если кристалл помещен в электрическое
поле, направленное по биссектрисе угла между осями
X, и Х2.
13.23. Какое поле надо приложить к Z-срезу кварца,
чтобы получить электрострикционную деформацию г33,
равную пьезоэлектрической деформации г14 Х-среза в по-
ле Е = 105 В/см. Для кварца Д33 = 0,3 • 10-12 ед. СГСЭ.
ОТВЕТЫ
§ 3
3.8. а) о = 36 ед. СГСЭ; б) о = 18 ед. СГСЭ; в) о = 0.
3.9. ДГ = 5,7 10-7 К. Пластинка должна быть вырезана перпенди-
кулярно оси 2. 3.10. — 750 В/см. 3.11. 3,2 • 103 В. 3.14. Нижняя
точка Кюри сместится на 1,4 К в сторону более высоких темпера-
тур, если поле Е будет совпадать по направлению с Р‘. Если Е бу-
дет противоположно Ps, то нижняя точка Кюри сместится на ту же
величину в сторону низких температур. 3.13. 7 ~ 6 • 104 ед. СГСЭ
3.14. 156 В. 3.15. В классах 1 и т. 3.16. \Т = 3 - 10~4 К. 3.17. Q =
= 4,8 • 10“7 Кл. 3.21. Q = 5- 10~9 Кл, V = 1200 В. 3.22. ДГ = 5Х
X 10~5 К. 3.23. ДГ = 10-6 К. 3.24. ДГ = —0,2 К.
§ 4
4.10. 3,6 • Ю^К-1. 4.11. 200 10й Ом • см; 100 - IQi4 Ом • см.
4.12. 246; 245; 11. 4.13. 1,7 • 106 Ом • см. 4.14. 0°. 415. 1,4 • 10~|2Ф.
4.16. 1,4 • 10-5 Кл. 4.17. а) и б) У £
о
4,52
-0,04
'4,5
0
о
ЕИ
о
— 0,04 , в) не изменится.
4,57.
4.20. Вырезать пластинку перпендикулярно п (0,92; 0,33; 0).
4.21. 34°52'. 4.22. В направлениях, составляющих угол 86°50' с осью
высшего порядка. 4.23. Вырезать пластинку перпендикулярно
[001]. 4.24. Главные оси тензора [а«3] связаны с исходными осями
поворотом вокруг оси Хг на 20,7° против часовой стрелки. 4.25.
Для Х-среза 2°, для 45° У-среза 57'. 4.26. ДГ, = 2,3 • 10~3 К; Д72 =
= 4,0 • 10~3 К. 4.27. 3,3 10-3 Кл/см2. 4.32. 0,628 • ICr7 К-1. 4.33. 20,8 X
X 10-3 кал/(К • см с). 4.35. 0,096 В.
§ 5
5.9. Искомая координатная система связана с исходными ося-
ми тензора поворотом на 45° вокруг оси Хз против часовой
стрелки.
5.10. t =t cos2 a -j- sin2 а + t sin 2a;
tt = 1(E22 - tu) sin 2a + t12 cos 2a.
5.11. t, » №,3 Н/см2; t2 = « 58,8 Н/см2; t3 = —1380 Н/см2. 5.12.
Pep = 700 Н/см2; tt m»x = 75 Н/см2.
246 /
5.13.
- 8
5
— 2
ч
5—21 ГО
3—2 -10“6; toj. = 12
—L2 ij [_3
— 2
О
— 6
• 10”6;
6
О
ЛV!V = 12 10-5.
5.16. щ (0,8945; 0; —0,4470); п2(0, 1, 0); п3(0,4470; 0; 0,8945).
5.18. 5,33 • 10-5; 8,67 • 10"*. 5.19. ф = 2Д7' | а?3 + “23 . 5.22. t„ =
= 1250 Н/см2, гц = 2,2 10—*, г22 = —10~4, г33= —0,5 • 10—». 5.23.
tn = t22 = <33 = 9,81 * 103 н/см2; tj2 = t23 = t3i = 0; rlr = r22 = r33;
/*12 == r23 = /*3i = 0. 5.24. tn = 1 Н/см2, t22 = 1 Н/см2, t33 = 0, t^2 =
= <23 = <3l = 0; ru — —0, 4- IO-4, ги = 0,4 • 10-4, r33 = rl2 = газ —
= r31 = 0. 5.25. tn = <22 == <33 == 104 H/CM2, t|2 = <23 — <31 = 0, r33 =
= 10-4, Гц = —10-4.
§ 6
6.16. Для кварца P ц = zij (n2— 3n2) dn<; продольный эф-
фект невозможен в направлении [0001]. Для хлората натрия
Ри = 3n.1n2n3d14t; продольный эффект невозможен в направлениях,
лежащих в координатных плоскостях, т. е. в направлениях типа
[МО]. 6.17. Q = Fd{l; Q =—FdtiXbla-, Q = 6.18^5,5 ед. СГСЭ.
6.19. г'=-1,9-10“ Б; г' = —г2. 6.20. п(УЗ/3; УЗ/З; V3/3). 6.21. г4 =
= г6 = —7,5 • 10-6. 6.22. Az, = —6,7 10"7 см; Дх2 = 3,38 • 10“5 см.
6.24. Относительные деформации ребер в плоскости рабочих гра-
ней 5,83 • 10~7. 6.25. d'l2 = — cos2 ф -f- d14 sin <pcos ф; при ф = 0°
d'2=—du; при <p=90° d'12 = 0. 6.26. r=n1 (n2—3n|) dn. 6.28. Еди-
ничный вектор нормали к пластинке в кристаллофпзической си-
стеме координат должен задаваться компонентами nl = n2 = n3 =
= 0,5774. 6.29. Под углом 45°. 6.30. 1,01 10« Н/см2. 6.31. Qi =
= dltn2n3tbc; Q2 = dl4nin3tac; Qs = 0. 6.32. Q = 1,4 • 10-5 Кл, V =
— 45 В. 6.33. п(УЗ/3, У3/3, УЗ/З). 6.34. Угол моноклинности 90°2".
6.35. А = 3%. 6.36. Смещение края пластинки примерно равно
IO-® мкм. 6.40. к = 22%—для 45°2-среза и к = 32 % для В-среза.
6.41. d14. 6.42. а) На всех гранях о = 0; б) на грани, перпен-
дикулярной направлению [001], а — dltt/2, на остальных о = 0;
в) на всех гранях о = dItt/3. 6.43. У-срез. 6.44. 0,27 см. 6.45.
/с = 10%; к = 9%. 6.46. d33 = 5,63 • 10~6, d31 = —2,35 • 10-6,
dl5 = 7,8 • 10-6 ед. СГСЭ. 6.47. d14 = 9,52 1Q-8 ед. СГСЭ. 6.48. Р‘ =
2 (й„. -] - й,)
= 7—- ДФ—для турмалина; Р — -———__ р— для
33 “11 “12 S22 S11 S33 ZS13
сульфата лития. 6.51.1%; 1%; 0,3%. 6.52. 0,3%; 1,3%.
^21 ~Ь ^22 ^23
§ 7
7.10. 1,82 10~4. 7.11. Ha 4 K. 7.12. t( = t2 = 180 Н/см2; <3 =
= 146 Н/см2; <4 = <5 = 17,3 Н/см2; <6 = 12 Н/см2. 7.13. 1,026 X
X 10-8 см2/дин; 2,67 IO-12 см2/дин. 7.14. 5.52 • 1011 дин/см2; 2,08 X
X 10” дин/см2; 1,95 • 10” дин/см2. 7.15.s'3 = ЦЕ = (1 —
— cos2 03)2 + (s44 + 2si3) cos 63(1 — cos2 03) + s33 cos4 63+ 2si4 X
X cos 02cos 03(3cos2 0! — cos2 02), где 0t, 02 и 03 — углы, состав-
247
ляемые произвольным направлением Х3 с кристаллофизическими
осями. 7.16. s '3 = su sin4 6 + S33 cos4 6 + (s44 + 2sI3) sin2 6 cos2 6,
где 0 — угол между произвольным направлением А3 и осью выс-
шего порядка. 7.17. 1200 эрг. 7.18. 3320 эрг. 7.23. s33 и si3. 7.25. sI3
«зз- 7.26. s13, з33. 7.27. sn = 2,34 • IO-12, sI2 = -0,515 • 10~12, stt ~
=8,54 • 10-12 (в см2/дпп). 7.33. 1,5 кВ/см. 7.34. 1,2 • 103 Н/м2. 7.35.
«12, «13. 7.39. —3,7 • 10-° К-1; 7.41. Д7' = 0,27 К. 7.42. fr = 1,9 X
X 105 к-*.
§ 8
8.10. Ha 3%. 8.11. 19,6 • 104 Па. 8.12. —80 • IO"12 см2/дпн и
42,4 • IO"12 см2/дин. 8.13. 2,6 • IO-10. 8.14. Цп = —4,7 - 10~12 см2/дин
П12 = —5 • 10-12 см2/дин, П44 = —137,9 10~i2 см2/дин. 8.15. 0,002 В-
0,525 В. 8.16. Р « 9,8 • 10е Па. 8.17. в 14 раз; в 1,3 раза. 8.18. Для
р — Ge: 96,7 • 10-12 см2/дин П44 —0,5 • 10~12 см2/дин. 8.19. Для
р — Ge: 144 К > 8,58; для р — Si: 66,02 > К > —3,78. 8.21.
« 14 Па. 8.22. 0,3 В; 6,4 • 10"4 В. 8.25.133 13.
§ 9
9.6. Дп = 0,009; Д<р = 0,24 рад. 9.7. Дп = 0,006. 9.8. Кристалл
оптически отрицателен. 9.9. 0,011 мм. 9.10. 0,014 мм. 9.11. 1,53 мм
9.13. 1,03°. 9.14. 0,48 мм. 9.15. 3,06°. 9.16. 0,17°, 3,06°, 2,07°. 9.19.
0,203 мм. 9.20. /До = 0,616. 9.22. 4,5 • 10~3 мм. 9.24. Отношение ин-
тенсивностей равпо 1; 9.25. 1/10 = 0,029 sin2 а, 1/10 = 0,094 sin2 а.
9.29. 5,3°. 9.30. 13,5°. 9.31. 11,4°. 9.32. 3,4°. 9.36. 1,003 мм.
§ 10
10.7. При действии напряжения сжатия на кристалл сфалери-
та его оптическая индикатриса деформируется таким образом, что
из сферы превращается в трехосный эллипсоид, при этом одна из
осей оптической индикатрисы параллельна направлению действия
напряжения сжатия. 10.8. Продольный эффект равен нулю, попе-
речный равен */2 (л11 — ^12)' Ю-9 Классы, относящиеся к три-
клинной и моноклинной сингонии. 10.10. я44 = 0,706 • 10-11 см2/дин.
10.11. « 8,8 кг/см2. 10.12. В[010] = -1/2 ;уЗ(Я11 _ t. B[wiJ =
=г/2 (лп - л12) t. 10.13. п ,= N- /уз. n , =jV() _ V Лз.
2 х2 &
п , = N— 10.16. лн, Л12, «31. 10.18. 1,65 • 10-4. 10.19.
х3 u 2
8,8 кг/см2 для ADP; 22,8 кг/см2 для DKDP.
§ 11
11.18. 4, 42m. 11.19. Невозможно. 11.20. Кристаллы с симметрией
422, 32, 622, 3m и 6т2. 11.21. В 660 раз для KDP и в 500 раз для
DKDP. 11.22. Р' (n|m33 -n>23), Р’
-Ф13). ^оо1] = 1/з^(^'П23-Ф1з)- 1123- Из- П-26. 0,2 см.
11.27. 12,3 кВ. 11.28. ~ 16'. 11.29. т33 = 1,87 • 10“7 ед. СГСЭ.
11.30. пх> = "р
1 = 1 ... Г41Д1 . 1 = 1 _ Г11Д1
П , „2 1 1 ’ П , га2 1 1
Хс 2 d '
248
11.31. ~ 0,4 см. 11.32. ~ 27,8 • 10~8 ед. СГСЭ. 11.34. п , = п , =
Х1
1 1 2л
'=7V° + 2 У 3 ЛГоГ41£; V =7V0 ~ 2 У 3 ^г41Б; г = y^X7Vor4i£’L
11.35. г42 = 24 - 10-в ед. СГСЭ. 11.36. Г)./2 = 15,6 кВ для KDP,
Гг/2 = 6,7 кВ для DKDP. 11.37 0,34л. 11.39. ~ 13'. 11.47. По на-
правлению [010]. 11.48. ^е^з1 — = 1,35-10-13см2.В~2,
Лг3 (Т?12— 7?11)=0,89-10-13см2-В-2. 11.49. Г>./2 модулятора на осно-
ве квадратичного электрооптического эффекта в шесть раз больше,
чем модулятора на основе линейного электрооптического эффек-
та. 11.50. 7Vmax=100. 11.51. Т?66 = 0,20 • 10-13 см2 В-2. 11.53.
a) 1/2(\anI-jR22nDZ?i; б) 1/2(r32"3-r22n|)E2 +
-Д22п1)’£2- 11.54. 3,9 кВ. 11.55. 1/2(^S2-nI-^12-nfX + An(J),
где Дп,, — двупреяомление, обусловленное поворотом оптической
индикатрисы. 11.56. Продольный квадратичный электрооптический
эффект возможно наблюдать в направлениях [100] и [010]. 11.57.
~ 6 10-3. 11.58. — М12 = 1,67 • 10-12 СГСЭ.
11.59.7У3/?вв=0,5-10-13см2-В“2, -^0(^12"-Д11)= 0,87-10~13см2- В'2.
11.60. V2 (и|-Л/31—п3-М21)=5 10_пед. СГСЭ;
—п3Л/ )=12-10—11ед.СГСЭ;1/2(л3Л/ —п3Л/ )=11-10—11ед.СГСЭ.
§ 12
12.9. 44 °C. 12.15. 0 = 21°. 12.16. 1,8-106 Вт/см2. 12.17. Для
0 = 30° £ког = 52,5 мкм. 12.18. Для 0 = 30° Р2Ш = 1,46 • 10 Втусм2,
для 0 = 90° Р2Ш = 0. 12.19. Для 0+5° £ког = 35,5 мкм, для 0 — 5°
£ког = 49,3 мкм. 12.20. Мощность ВГ уменьшается соответственно
в 2,6 IO-4, 8,4 • IO-6 и 8,7 - КГ7 раз. 12.21. 0 = 11,5°. 12.25. 37,5 мм.
12.26. 53 мм. 12.28. Мощность ВГ уменьшится в 100 раз.
§ 13
13.8. s^n, 10-13сд. СГСЭ: = 12,77; s® =9,73; s® = - 1,81;
s® = — 1,23; s® = 19,98; s® = 29,16; s®.= 4,52.13.11. Емкость кон-
Id ’ 44 ’ ob ' 14 '
денсатора на высокой частоте меньше, чем на низкой в 2 раза.
13.16. ДТ, = 2,33 • 10-з к, ДТг = 4 • 10“3 К. 13.19. А/// = 1,3 10~s.
13.20. Д/// = 2 • IO"6.
ПРИЛОЖЕНИЕ
Таблица 1
Обозначения 32 классов симметрии
Сингония Обозначения
интернацио- нальные по Шенфлису формула симмет- рии
Триклинная J_ 1 С, ci C
Моноклинная 2 т 21т Сг с* C2h L3 P l2pc
Ромбическая 222 mm2 ттт ta nt, tc М № 3l2 L22P 3L23PC
Т етрагональная 4 Мт 422 4mm 4/znmm Г 42m С. cth »i С tv D th Si D2d Li LJ>C LtiL2 L^P L^L25PC Lit L^2L22P
Тригональная 3 3 32 3m 3m C3 c„. 3г D3 C3v D3d L3 LSC LS3L2 L33P L£L23PC
Г ексагопаль- ная 6 6/m 622 6/mmm 3 6m2 cs Cgh D6 c6v Deh C3h D3h Le ЦРС LeGL2 L^P T66£27PCjF L3P L23L2iP 6 6 : m 6:2 6- m m • 6 : m 3 : m m-3: m
Кубическая 23 T 4ЛзЗ£/2 3/2
m3 Th 4£33L23PC 6/2
432 0 iLz3Li&L2 3/4
43zra Td 4LS3L16P 3/4
тЗт Oh iL^LtG^QPC 6/4
250
Таблица 2
Обозначения элементов симметрии на стереографической
проекции
Элемент симметрии Символ на стереограмме Интерна- циональ- ный сим- вол
Центр симметрии Символа нет т
Зеркальная пло- скость Сплошная прямая или дуга окруж- ности т
Поворотные оси
Ось первого по- рядка Символа нет 1
Ось второго по- рядка ф 2
Ось третьего по- рядка 3
Ось четвертого по- рядка в 4
Ось шестого по- рядка Инверсионные оси 6
Ось первого по- рядка—центр сим- Символа нет т
метрии
Ось второго по- рядка = зеркаль- ная плоскость, пер- пендикулярная оси Сплошная прямая или дуга окруж- ности 2(=т)
Ось третьего по- рядка 3
Ось четвертого по- рядка ф 4
Ось шестого по- рядка $ 6(=ЗЛп)
251
Таблица 3
Правила установки кристаллов по сингониям
г чес
сшъчлриь
< 2:3,б.Б~оси
симметрии
Обозначения.
Ромбическая
2,т
V >
~.р-у-дв‘
Тригсвальная
игерсаготльюя
6,6,3,3 „
af¥co .
а=р-до°
у-ШГ
Тетрагс ильная
б б
а-р~-у .
Таблица 4
Элсмепты симметрии и правила выбора осей
в 32 кристаллографических классах
(Символы центросимметричпых классов заключены в рамку)
|252
Продолжение табл. 4
Ромбическая сингония
Тетрагональная сингония
253
Продолжение табл. 4
Гексагональная сингония
254
Окончание табл. 4
Кубическая сингония
Таблица 5
Правила выбора кристаллофизических осей
! Сингония хг х, Xi
Триклинная [001] В плоскости, г ной к напра te рпендикуляр- влению [001] В плоскости
Моноклинная [001] [010] (100)
Ромбическая [001] [010] [100]
Тетрагональная Тригональная и [001] [010] [100]
гексагональная [0001] [0110] [2110]
Кубическая [001] [010] [100]
255
Таблица 6
Форма матриц пьезомодулей (Яц) и пьезоэлектрических
коэффициентов
Центросимметричные классы: все модули равны нулю.
Нецентросимметричные классы:
Триклинная сингония
Класс 1
(du d12 d13 d]5 dj0\
^21 ^22 ^23 ^24 ^25 ^26 I
^31 ^33 ^34 ^35 ^38'(18)
Моноклинная сингония
Класс 2, 2 [| X2 (обычная ориентация) Класс 2, 2 || Х3
/О 0 0 d14 0 dle \ ( 0 0 0 di4 dj6 0 \
I ^21 ^22 ^23 О d23 О I I 0 0 0 d24 d25 0 1
\О О О d34 О ф,в / (8) \ d31 d32 d33 О О d3e / (8)
Класс т, т_1_Х2 (обычная ориентация) Класс т, т_1_Х3
/ dj4 dj2 dj3 0 dj5 О \ /dJ1 d12 d13 О 0 dle\
I 0 О О ^24 ^2в I I ^21 ^22 d23 0 0 d261
\“31 ^32 d33 О d.(5 О /(10) \ О О О dg4 d35 О /(io)
Ромбическая сингония
Класс 222
Класс mm2
О О О d14 О О \
О О О О d23 О
О О О О О d3c / (з)
/О О О О d15 О\
О О О d24 О О
\ ^31 ^32 ^зз ООО ' (5)
О О
О О
^31 ^31
Тетрагональная сингония
Класс 4 Класс 4
О d]4 d]5 О \ / О О О dj4 d15 О \
О ^14 О I IOOO —d15 d14 О I
^зз ООО /(4) \ d3^ d31 ООО d3e / (4)
Класс 422 Класс imm
О 0 dj4 О (JV / О О О 0 dia 0 \
ООО — d]4cl 0 0 0 ^0 01
ООО 0 ш 1) \ d31 <^4 d33 О 0 0/(3)
Класс 42?п, 2 || Xt (обычная ориентация)
/О О 0 dj4 О 0 \
О О О 0 dj4 О
\0 О О О 0 d3e /(2)
256
Тригональная сингония
Класс 3
Класс 32
( ^11—О d. 4 dir.—2d22 \ / dji d-ц О d44 О О X
I -d22 d^ О d15 ^d14 2du | (OOOO -d14 -2d,41
V d31 d3J d33 О О О /(6) \ О О О О О О /(2)
Класс Зт, т_1_Х1 (обычная Класс Зт, т_1_Х2
ориентация)
(ОООО djg —2d22 X /” ^11 ^11 О Q ^15 Q X
-d22 d22 0 d15 О О О О 0 d15 0 -2du
d34 d31 d33 0 0 0 )(4) \ dgj йз4 d33 ООО/ (4)
Гексагональная сингония
Класс 6 Класс бтт
О О 0 d14 d15 0 X ( О О О О <?1Б 0 X
О О 0 d16 —d14 О I I О О 0 d15 О О
d34 d34 ^зз ООО /(4) \ d34 d31 d33 ООО / (з)
Класс 622 Класс 6
О О 0 d14 О 0 \ / d11 — dll О О 0 —2dss \
0 0 0 0 —d14 0 —<^2 d22 О О 0 —2du
0 0 0 0 0 0 /(г) \ 0 0 000 0 /(2)
Класс 6тп2,
(обычная ориентация)
Класс 6m2, mJ_X2
О 0 0 0 0 —2d22 \ / du —du ООО О X
—d22 d2S О О О О 10 000 0—2du
О 0 0 0 0 0 /(1) \ О 0 0 0 0 0 /(1)
Кубическая сингония
Класс 432 Класс 43m и класс 23
/ООООООХ / О О 0 d14 О 0\
оооооо) 0 0 0 0 <^4 О I
\000000/(о) \000 0 0 d14 /(1)
17 Н В. Переломова, М. М, Тагиева
257
Таблица 7
Форма матриц пьезоэлектрических коэффициентов (hij) и (ву)
для кристаллов, имеющих эти матрицы, отличные от матриц
(dii) “ (^,)
Класс 3 Класс 32
^11 б ^'14 ^15 ^22 \ f ^11 ^11 9 ^14 Г 0 \
^22 ^22 0 ^'15 ^14 ^11 j 10 0 0 0 foj4 I
Л31 hsl Лдз 0 0 0 /(в) \ 0 0 0 0 0 0 /(2)
Класс 6 Класс 3m, mj_ Ху
(/in —Лп ООО —h2i \ / 0 0 0 0 h15 —h22 \
—^22 ^22 000 —71ц I I * ^22 ^22 Tljg О 9
О 0 0 0 0 0 /(з) \ h31 h31 h33 ООО /(4)
Класс 6т2
(АгХ1 -—hlt 0 0 0 0 \
О 0 0 0 0 /гп
О 0 0 0 0 0 /(1)
Таблица 8
Форма матриц пьезомодулей (d,,) для некоторых
пьезоэлектрических текстур
Группа оо Группа oom
0 0 0 dlh 0 \ /0 0 0 0 d15 0 \
0 0 0 J15 —d14 0 j О о мг О О О
^31 ^31 $33 0 0 0/ (4) \ d31 б?31 d33 0 0 0/ (3)
Группа оо2
О 0 0 dJ4 0 0 \
0 0 0 0 —d14 О
0 0 0 0 0 0 /(1)
Таблица 9
Форма матриц упругих податливостей (ву) и упругих
жесткостей (Су)
Триклинная синг oji и я
Оба класса
S11 «12 «13 «14 «15 «16' ell «12 «13 «14 «15 «16
«12 s22 «23 «24 «25 «26 c12 c22 «23 «24 «25 «26
«13 s23 «33 «34 «35 «36 c13 «23 «3 3 «34 «35 «36
«14 s24 «34 «44 «45 «46 «14 ^24 «34 «44 «45 «46
S16 «25 «35 «45 «55 «56 c15 c25 «35 «45 «55 «56
I «16 «25 «36 «46 «56 «66 (21) , c16 «26 «3 6 «46 «56 «66
(21)
258
Моноклинная СИНГОНИЯ
Все классы, 2 || Х2 (обычная ориентация)
«11 «12 «13 0 «15 ' в е11 «12 «13 0 с 16 0
«12 «22 «23 0 «25 0 с 12 «22 «23 0 с 25 0
«13 «23 «33 0 «35 0 «13 «23 «33 0 с 35 0
0 0 0 «44 0 «46 0 0 0 С 44 0 '46
«15 «25 «35 0 «55 0 С L5 «25 «35 0 С 55 0
0 0 0 «46 0 «66 (13) 0 0 с 46 0 С 66 . (18)
Ромбическая сингония
Все классы
«11 «12 «13 0 0 0 С1 «12 «13 0 0 0
«12 «22 «23 0 0 0 «1 «22 «23 0 0 0
«13 «23 «33 0 0 0 «1 «23 «33 0 0 0
0 0 0 «44 0 0 0 0 0 «44 0 0
О— 0 - 0 0 «55 0 X- 0 0 0 0 «55 0
0 0 0 0 0 «66 . (») 1 0 0 0 0 0 «66 (8)
Т е тр агональная с и н г о н и я
классы 4, 4, 4/т
«11 «12 «13 0 0 « L6 € и «12 «13 0 0 с 16
«12 «11 «13 0 0 —« в С 12 «11 «13 0 0 —с 1в
«13 «13 «33 0 0 0 С 13 «13 «33 0 0 0
0 0 «44 0 0 0 0 0 «44 0 0
0 0 0 «44 0 0 0 0 0 «44 0
, «16 «1« 0 0 0 «66 (7) «16 «1в 0 0 «66 (7)
Классы 4mm, 42m, 422 4/mmm
«11 «12 «13 0 0 0 «11 «12 «1 0 0 )
«12 «11 «13 0 0 0 с 12 «11 «13 0 0 )
«13 «13 «33 0 0 0 с 13 «13 «33 0 0 )
0 0 0 «44 0 0 ООО «44 0 )
0 0 0 0 «44 0 ООО 0 «4< 0
, 0 0 0 0 0 «66 J (в) L ООО 0 0 «66 (в)
Тригональная сингония
Классы 3, 3
«11 «13 «13 «14 «25 0
«12 «И «13 —«14 «25 0
«13 «13 «33 0 0 0
«14 «14 0 «44 0 2«25
«25 «25 0 0 «44 2«14
0 0 0 2«25 2«14 2 («ц з1а) (7)
17*
259
«11 «12 «13 <44 «2Б 0
«12 «11 «13 «14 «2Б 0
«13 «13 «S3 0 0 0
«14 —«14 0 «44- 0 «ЗБ
«ЗБ «ЗБ 0 0 «44 «14
0 0 0 «ЗБ «14 1/г(с11 «12) (7)
Классы 32, 3m, 3m
«11 «12 «12 «и «13 «13 * «14 ~«14 0 0 0 0
«13 «13 «33 0 0 0
«14 «14 0 «44 0 0
0 0 0 0 «44 2«14
0 0 0 0 2«14 2(«хх «12) (6)
«11 «12 «13 «14 0 0
«12 «11 «13 " —«14 0 0
<43 «13 «33 0 0 0
«14 «14 0 «44 0 0
0 0 0 0 «44 «14
0 0 0 0 «14 г( 41*—«1 г). (6)
Г е к с а г она льная сингония
Все классы
«11 «12 «13 0 0 0
«12 «11 «13 0 0 0
«13 «13 «33 0 0 0
0 0 0 «44 0 0
0 0 0 0 *44 •0 (5)
0 0 0 0 0 2(«ц «12)
«11 «12 «13 0 0 0
«12 «11 «13 0 0 0
«13 «13 «33 0 0 0
0 0 0 «44 0 0
0 0 0 0 «44 0
0 0 0 0 0 Уs(«il «12) , (6)
Однородные непрерывные среды (текстуры), описываемые группами оо т, оо, oo/wt, со/ттт оо2
«11- «12 «13 0 0 0
. «12 «11 «в 0 0 0
«1з «is «зз 6 0 0
0 0 0 з44 0 0
0 0 0 0 з44 0
0 0 0 0 0 2(sxx—sx2) (б)
«и «12 «1з 0 0 0
«12 «ц «1з 0 0 0
«13 «13 «зз 0 0 0
0 0 0 с44 0 0
0 0 0 0 с44 0
0 0 0 0 0 1/2(схх сХ2)
Изотропная среда
«11 «12 «12 0 0 0 )
й12 S11 s12 0 0 0
S12 s12 S11 ООО
0 0 0 2(sxl—s]2) 0 0
0 0 0 ° 2(sxx—sX2) 0 (2)
0 0 0 0 0 2(sxx—sX2)
«11 «12 <42 0 0 0
«12 «11 «12 0 0 0
«12 «12 «11 0 0 0
0 0 0 cx2) 0 0
0 0 0 O' V2(Cxx-C12) 0
1000 0 0 V2(CXX-CX2) (2)
Таблица 10
Форма матриц пьезорезистивных коэффициентов
Кубическая сингония
Все классы
Триклинная сингония
Оба класса
«11 «12 «12 0 0 0 «11 «12- «12 0 0 0
«12 «11 «12 0 0 0 «12 «11 «12 0 0 0
«12 «12 «11 0 0 0 «12 «12 «11 0 0 0
0 0 0 «44 0 0 0 0 0 «44 0 0
0 0 0 0 «44 0 0 0 0 0 «44 0
0 0 0 0 0 «44 (3) 0 0 0 0 0 «44 (3)
Пц ПХ2 Пхз ПХ4 ,П16 Пхв
П21 П22 П23 П24 П26 П26
П31 П32 П33 П34 п86 пзв
П4Х П42 П43 П44 П46 п4в
пБ2 П63 П61 П6Б П66
( Пег Ног Пез Пв4 П66 пвв
260
(36)
261
Моноклинная сингония
Все классы
Ось 21| Х3
Ось 2II Х3
Пм п13 о п1Б о
П2х П22 П23 О П2Б о
П31 П32 П33 О ПЗБ о
о о о п44 о п4Б
Пб1 ПБ2 Пьа О Пбб О
Щх Пва Пвз П64 О П66
(20)
Пи П12 П13 0 0 Пхв
П2Х П22 П23 О О П26
П31 п32 П3з о о пзв
ООО П44П4Б о
ООО ПБ4ПББ о
П.Х Пв2 Пвз 0 0 Пев
(20)
Ромбическая сингония
Все классы
П1Х П„ П13 ООО
П21 П22 П23 ООО
П31 П32 П33 ООО
О О О П44 О О
о о, о о ПББ о
0 0 0 0 0 пм J{12)
Тетрагональная сингония
Классы 4, 4, 4/т
Классы 4тт, 42т, 422, 4/ттт
(Пц П12 Пхз 0
пХ2 Пц Пхз 0
П31 п31 П33 0
0 0 0 П44
0 0 0 -П46
П6Х —Пвх 0 0
О
О
О
П46
П44
О
111в
-П1в
О
о
о
Пи
п12
П31
О
О
Пев j(xo) 0
П12 П13 О
Пц П13 О
П31 П33 О
О о п44
ООО
ООО
о
о
о
о
П44
о
0.
о
о
пвв j(7)
о
о
Тригональная сингония
Классы 3, 3
Пхх Пх2 Пхз П14 —П2Б 2Пв2
п12 Пхх Пхз -п14 п2Б —2Пв2
Пзх П31 П33 0 0 0
п41- -п„ 0 П44 П4Б 2ПБ2
П2Б пБ2 0 -П4Б П44 -2П41
Пв2 ПБ2 0 П2Б П14 (Пц п12)
(12)
Классы Зт, 32, Зт
Пхх П12 Пхз Пхх 0 0
Пх2 Пи Пхз —п14 0 0
Пзх Пдх П33 0 0 0
П41 -п41 0 П44 0 0
0 0 0 0 П44 2П4х
О О О О П14 (Пхх-Пхз) (8)
262
Гексагональная сингония
Классы 6, 6, 6/т
Пи П1а П13
П12 Пи П18
П31 п81 П33
ООО
ООО
П61 —Пв1 о
О О —2Пв1
О 0 2Пв1
ООО
п44 п46 о
п46 п44 о
О 0 (Пхх—Пх2)
(Я)
Классы 6т2 6mm, 622, 6/ттт
Пхх П12 Пхз 0 0 0
п12 Пи Пхз 0 0 0
п31 Пзх П33 0 0 0
0 0 0 П44 0 0
0 0 0 0 П44 0
0 0 0 0 0 (Пхх—Щ2) (в)
Кубическая сингония
Классы 23, m3 Классы 43m, 432, тЗт
Пхх Пхз П42 0 0 0 Пх2 П13 П4х ПХ2 Пхз Пц 0 0 0 0 0 0 0 0 0 п44 О 0 0 0 0 0 0 0 0 0 П44 0 0 п44 (4) Пхх П12 П12 0 Пхз Пхх п12 0 П4з П12 ПХх 0 0 0 0 п44 0 0 0 0 0 0 0 0 0 0 ' 0 0 0 0 0 0 П44 0 0 П44 1(8)
Изотропная среда
Пхх п12 п12 0 0 0
П12 Пи п12 0 0 0
п12 п12 Пхх 0 0 0
0 0 0 Пхх—П12 0 0
0 0 0 0 Пхх Пх2 0
0 0 0 0 0 Пхх—Пх2 (2)
Таблица 11
Форма матриц пьезооптических коэффициентов
и упругооптических коэффициентов (phl)
Триклинная сингония
Оба класса
Пхх ЯХ2 Пхз Я14 Лхб ЯХ6 Pit Pia Р13 Ри Ри Pie
Л 21 л 22 Л23 я24 Л2Б Л26 Pai Р22 Раз Pat Раз Рав
Л31 Л 32 я33 Л34 ЯЗБ Я36 Р31 Р32 Рзз Рза Рзз Рзз
Л41 Л42 Л 43 Л44 Я46 Л4в Pai Раа Р43 Раа Раз Рав
Л6х Л Б2 л 53 Л 64 Лб6 Я5в Ры Рза Рзз Рза Рзз Рзз
яех Л б2 Лвз Л 64 ЛвБ Лее . (36) Рп Р 32 Рез Г 64 Рез Рве
(86)
263
Моноклинная сингония
Все классы
Ось 2 || Х2 (обычная ориентация)
Л11 Я12 ЯаЗ 0 я15 0 Р11 Р12 Р13 0 Р15 0
Л 21 Я22 Я 23 0 л25 0 Р21 Р22 РзЗ 0 Рзз 0
Л31 Я32 ^зз 0 ^ЗВ 0 Рз1 Рз2 Рзз 0 Рзз 0
0 0 0 яаа 0 л4е 0 0 0 Ри 0 Рае
Я51 •^32 Я53 0 ЯВВ 0 Рва РВ2 Рзз 0 Рзз 0
о 0 0 ^еа 0 яее . (20) „ 0 0 0 Рб4 0 Рзз (20)
Ось 2 || Х3
Лц Л42 Л13 0 0 яае Рп Р12 Р13 0 0 Рае
Л21 Л22 Л23 0 0 я26 Рз\ Р22 Ргз 0 0 Ргз
Л31 я32 Л33 0 0 Я36 Рз1 Рз2 Рзз 0 0 Рзв
0 0 0 л44 Я4В 0 0 0 0 Pit Рав 0
0 0 0 я54 Я5В 0 0 0 0 Psi Рзз 0
Яеа я62 Л63 0 0 я66 , (20) Pei Рб2 Рез 0 0 Рзв ' (20)
Ромбическая сингония
Все классы
Ли Л42 яаз 0 0 0 Р11 Р12 Раз 0 0 0
Л21 Я22 Л23 0 0 0 Р21 Р22 Ргз 0 0 0
яза Я32 я33 0 0 0 Рз1 Рзз Рзз 0 0 0
0 0 0 л44 0 0 0 0 0 Раа 0 0
0 0 0 0 ЯВВ 0 0 0 0 0 Рзз 0
1 0 0 0 0 0 яее (12) 0 0 0 0 0 Рзз (12)
Тетрагональная сингония
Классы 4,4 и 4/т
Лц л42 Л13 0 0 яае
л42 Лц Л13 0 0 - -Л1в
Я31 л31 язз 0 0 0
0 0 0 Л 44 Я4В 0
0 0 0 ~~П45 яаа 0
яеа яеа 0 0 0 яее (10)
Раа Р12 Раз 0 0 Рае
Р12 Р11 Раз 0 0 - ~Р13
Рза Рза Рзз 0 0 0
0 0 0 Раа Рав 0
0 fl 0 Раз Раа 0
р31 Р31 0 0 0 Рее (10)
264
Лц
"12
"si
О
О
О
"12
Лц
"si
О
О
о
"is ООО
"is ООО
"зз О О О
О л44 О О
0 О л44 О
О О О лвв
Классы 4mm, 42m, 422 и 4/mmm
(7)
Ри Ри Pis О О
/'12 Ри Р13 О О
Psi Psi Рзз О О
0 о О Pii О
О О О О р44
о О о о о
Тригональная сингония
О
О
О
О
О
Рвв
J(7)
Классы 3 и 3
"и Л 12 "13 "14 п25 2ftg2
"12 Л 11 "13 п23 2 3^62
"з1 Л 31 "зз О О О
"11 —Л 41 О л4< "45 2 л 52
"52 Л 52 О "45 "44 2 л44
( "б2 Л 32 О П23 "14 "11—л12 (12)
Ри Р12 P1S Р1А ^~Р25 Рв2
Р12 Ри Р13 ~ ~Ри 'Рзз 2/'зг
Psi Psi Рзз О О О
Ри ~ -Ри О Ри Ри РЗЗ
PS2 PS2 О - 'Ри Ра Ри
РВ2 Рв2 О Рзз Ри *!djPu—Ри) '(12)
Классы 3m, 32 и 3m
Лц "12 "si "41 О а П12 "13 "11 "13 "з1 "зз —"41 О О О О О "14 О —л14 О О О "44 О 0 "44 0 "14 О О О О 2"4j Лц Л12 (8)
Ри Р12 Р13 /'14 О О
Р12 Ри Pis — "Ри О О
Psi Psi Рзз О О О
Ри — Ри О Ри О О
С О О О Ри •Р41
с О О О Ри a (/'ll—Ри) (8)
Гек сагональ пая с и н г о ния
Классы 6 6 и 6/т
Лц "12 "13 ' О О 2"в2
"12 "11 "13 О О 2лв2
"з! "si "зз О О О
О О О "44 "45 О
О О О - ~"45 "44 О
~"в2 "в2 О О О "11—"12 . (8)
265
Яц л12 л21 П13 Л11 Л12 Я12 Л21 лп ООО ООО ООО п18 Л12 Ли Л^ лм ям л1а ли ООО ООО ООО л л л Pit Pis Pis 0 0 'Рва Р12 Р11 Р13 0 0 —рва Psi Psi Рзз О О О ООО рц pib 0 ООО — р4Б pti О . Рез Рез 0 0 0 VafPu Р12) (8) Классы 6m2, 6mm, 622 и 6/mmm Я!1 л12 л„ О О О ^12 ^13 О О О яз! Я31 ^зз ОО 0 ООО л44 0 0 0 0 0 0 л44 0 0 0 0 0 0 ли—л12 J(6) Р11 Р12 Pis 0 0 0 Р12 Р11 Pis 0 0 0 Psi Psi Рзз 0 0 0 ООО р44 0 0 0 0 0 0 р44 0 0 0 0 0 0 х/2(рц—р12) ](б) Кубическая сингония Классы 23 и m3 ООО р14 р1а рц 0 0 0 ооо Pig рц р1а ооо ООО р4а Р21 Р11 ООО л44 0 0 000 р44 0 0 0 л44 0 0 0 0 0 р44 0 о 0 л44 )(4) о 0 0 0 0 р44 )(4) Классы 43m, 432 и тЗт ООО рц р12 Рц ООО ООО Р12 Рп Ри 0 00 ООО р12 Pia Pii ООО л44 0 0 000 р44 0 0 0 л44 0 0 0 0 0 р44 0 о о «44 *(3) о 0 0 0 0 Р44 /(3) Изотропная среда Л42 ^12 000 12 ^11 ^12 000 is ^12 ^11 000 ООО ли—я12 0 0 ) 0 0 0 ^11—^12 о ООО 0 0 ли—л1а /(2)
266
Р11 Р12 Р12 0 0 0
Р12 Р11 Р12 0 0 0
Р12 Р12 Р11 0 0 0
0 0 0 2(Р11 Р12) 0 0
0 0 0 0 1^з(Ри—Р12) 0
0 0 0 0 0 г(Р11—Р12) (2)
Таблица 12
Форма матриц коэффициентов линейного электрооптического
эффекта (rftI)
Триклинная сингония
гц Г12 г г13
Г21 г22 г23
Г31 г32 г33
га ria г43
r6i г 62 ГБЗ
rei Г62 res 1(18)
Моноклинная сингония
Класс 2
2||Х2 2||Х3
, п о п .
0 г12 0 0 0 г13
0 г22 0 0 0 г23
0 г32 0 0 0 г33
г« 0 г43 Г41 г42 0
0 г52 0 ГБ1 ГБ2 0
r6i 0 г63 (8) 0 0 г63 (8)
Класс 71
mJ_X2 т±Х3
гн 0 г13 Г11 г12 0
r2i 0 г23 Г21 г22 0 <•
Гз1 0 г33 Г31 г32 0
0 Г 42 0 0 0 Г43
• Г61 0 г53 0 0 ГБЗ
0 г62 0 (10) ГП 0 0 (10)
Р о м б и ч е с к а я сингония
Класс 222 Класс mm2
ООО 0 0 г13
ООО 0 0 г23
ООО 0 0 г33
г41 0 0 0 г42 0
0 г52 0 г51 0 0
0 г63 (3) ООО (5)
267
Тетрагональная сингония
Класс 4 Класс 4
О о w О о W
О О W О О 1 W
0 0 г33 ООО
ra rsi 0 гй rsi 0
Г51 —ГЙ 0 Г51 Г41 0
0 0 ) (4) О о а W (4)
Класс 422
Класс 4mm
0 0 0 о 0 ri3
ООО о о г13
ООО 0 0 г33
ГЦ о 0 о Г81 0
0 — ги о г51 0 0
0 0 0 (1) о о о (3)
Класс 42m, 21|
О
О
О
г«
О
. о
О
О
о
о
Ги
О
О
О
о
о
о
гвз
(2)
Тригональная сингония
Класс 3 Класс 32
ги г2г г13 гх1 0 0 1
ги rS2 г13 —Гц 0 0
0 0 г88 ООО
ги ги 0 о о
Г51 Г41 0 0 — Ги о
2г22 2г ц 0 (6) О 1 г- о (2)
Класс 3m, mJ_X1 Класс Зт, mJ_X2
6 г22 Г13 Г11 0 г13
0 г22 г13 —ги 0 г13
О о о? W 0 0 г88
0 Г51 0 0 г61 0
rBi 0 0 «Л* м О О
—2г2а 0 0 (4) 0 —тц 0 (4)
268
Гексагональная сингония
Класс 6 Класс 6mm
0 0 г13 0 0 г13 0 0 г33 Г41 Г51 0 Г51 —Г41 0 0 0 г43 0 0 г13 0 0 г33 0 г51 0 7*51 0 0
0 0 0 (4) Класс 622 0 0 0 ООО ООО гц 0 0 0 — rii о ООО )<1) ООО Класс 6 Г11 —г22 —Г£1 "7*22 0 0 0 0 0 0 2г22 2г11 (3) 0 ' 0 0 0 0 0 Н2)
Г Jiacc 6m2, mA.Xi 0 —г^з 0 0 r12 0 ООО ООО ООО Класс 6т2 t*ii 0 —Гц 0 0 0 0 0 0 0 mJ_X2 0 ' 0 0 0 0
—2т 12 0 0 /(1) Кубическая Класс 432 К ООО ООО ООО ООО ООО 0 0 0 )(С) о —Гц сингония ласс 43m и кл ООО ООО ООО 7*41 0 0 0 г41 0 0 0 г41 0 )(1) асе 23 (1) Таблица 13
Форма матриц коэффициентов квадратичного электрооптического эффекта <Rtj) Триклинная сингония
Оба класса
Лц /?12 7?1з Т?14 7?16 7?16
^21 ^22 ^23 ^24 ^25 ^26
Rgl -^’32 /?33 Т?з4 Я35 /?36
0*41 ^42 ^43 Иц Л45 Яде
Rgl и и ньз 7?54 Т?55 Я56
.R»l Н*а 7?и R*t Rm
(36)
269
Моноклинная сингония
Все классы
Ян
Я 21
Яз1
О
ЯЕ1
о
я12
Я 22
Я 32
о
Я 62
о
2II X.
Я13
Ягз
Я33
О
Я 53
О
2>
0
О
о
Я<4
о
Я 64
Х2Л_т
Яц
Я25
Язь
О
Ябб
О
о '
о
о
Я46
о
Ябв •
(20)
2 || Х3, X3J_,„
Яц Я12 7?|3 О 0 7?16
Я21 Я22 Я23 0 0 Т?26
Я31 Язг 7?33 О 0 7?36
° ° о я44 /?4В о
° 0 о я64 НВ5 о
Яе1 Я62 Я63 0 0 7?66
(20)
Ромбическая сингония
Все классы
Яц Я12 Яц
Я21 Я 22 Я23
Я31 Я32 7?33
ООО
ООО
(ооо
ООО
ООО
ООО
я44 о о
О Я6е о
О О /?66
(12)
Тетрагональная сингония
Классы 4, 4, 4/т Классы 4mm, 42m, 422 4/m mm
(Яи Я42 Я13 0 0 Rle • Яц Я12 Яц 0 0 0
Я12 Яц Я13 0 0 -7?16 Я12 Яц Яц 0 0 0
Я31 Я31 Я33 ООО Я31 Я31 Я33 0 0 0
0 0 0 Я44 я4С 0 0 0 0 /?44 0 0
0 0 0 Я4Й Я44 0 0 0 0 0 я44 0
яе1 -Яв1 0 о о /?66 J (10) 0 0 0 0 0 Яее 1 (7)
Тригональная сингония
Классы 3 3
Яц Я12 Я43 Яц —Я2б 2Я2в
Яц Яц я13 - ~я14 Я 25 -2Я2в
Яз1 Я31 Я33 0 0 0
Я 4J -Я41 0 Я44 Я45 2ЯЕ2
Я52 ЯЕ2 0 - “Я4В я44 2Я41
Я 62 Я62 0 Я26 я14 (Яц—я12), (12)
Классы Зт, Зт, 32
Яц Я)2 Я13 Я14 0 0
Я12 Яц Я1з —я14 0 0
Я31 Я31 Язз 0 0 0
Я4ь —я44 0 я44 0 0
0 0 0 0 Я44 2Я41
i 0 0 0 0 Яц (Яц—Я/2)1 (8)
270
Гексагональнан сингония
Классы 6, 6, б/т
Fin Fils Fiis 0 0 2«ei
Fiis Иц Fiis 0 0 —2«si
Fisi Fiat Fiss 0 0 0
0 0 0 «44 Fiis 0
0 0 0 —Fits tin U
—Fiei Figi 0 0 0 (Fin—«12). (8)
Классы 6т2, бтт, 622, б!ттт
Fin «12 «13 0 0 0
^12 Fin /?1з 0 0 0
Fisi «31 Figs 0 0 О
О О О Д44 О о
О О О О Л44 о
.0 0 0 0 0 (Яц-Я12)
(6)
Кубическая сингония
Классы 23, m3
Класы 43т, 432, тЗт
Fin Fiis «13 0 0 0 «11 Fiis «12 0 0 0 '
His Fin Fin 0 0 0 Fiis Fin Fiis 0 0 0
Fiis Fiis «11 0 0 0 «12 Fiis Fin 0 0 0
0 0 0 «44 0 0 0 0 0 «44 0 0
0 0 0 0 «44 0 0 0 0 0 Fin 0
0 0 0 0 0 Fill (4) . 0 0 0 0 0 Fin (3)
Текстуры со, оо/т
«11 Fiis Fiis 0 0 2«62
«12 R11 Fiis 0 0 - 27?62
«31 Fisi Fiss 0 0 0
0 0 0 Fin Fits 0
0 0 0 ' Fii6 Fin 0
. —Fits Figs 0 0 0 (Fin Fila),
(8)
Текстуры оо»т, оо/2
Fin «12 «13 0 0 0
Fiis «и «13 0 0 0
Fisi «31 «33 0 0 0
0 0 0 «44 0 0
0 0 0 0 ^44 0
О О О О 0 (7?и-7?12) (6)
271
Изотропная среда
Ни н» 0 0 0
//12 Ян 0 0 0
//12 //12 Ян 0 0 0
0 0 0 (Ян—Я]2)
0 0 0 0 (//11 -Я12) 0
. 0 0 0 0 о (//и—//12). (2)
, Таблица 14
Некоторые справочные данные о кристаллах, необходимые
для решения задач *)
Вещества в таблице расположены в алфавитном порядке по наи-
более употребительным названиям.
Если нет специальной оговорки, то приведены значения физи-
ческих констант кристаллов, измеренные при комнатной температуре.
Дигидрофосфат аммония (ADP, NH4H2PO4), 42m
р= 1,803 г/см3;
для Л -0,546 мкм No= 1,52662, А е= 1,48072
d, 10 8 ед. СГСЭ а. 10-12 ед. СГСЭ с, 1011 ед. СГСЭ е а, 10 6 К 1
d14=5,27 йзв=—145 su=l,82 s33=4,35 з44= 11,53 «вв=16,46 s12=0,19 «13=—1,18 Сц=6,17 с33=3,28 *с44=0,85 сбб=^»Ь9 с12=0,72 см=1,19 w 11 • II t-л 05 J £н * in — а1=а2=30,1 «з=4,1
Антимонид индия (InSb), 43m
р=5,75 г/см3, 7’пл=523 °C
— 12 s, 10 ед. СГСЭ с, 1011 ед. СГСЭ П, 10 18 ед. СГСЭ р. Ом-см
зи=2,42 sla=—0,855 s44=3,3 । си=6,72 с12=3,07- с44=3,02 ааа tc Н* II II II gl 1 0,54
Арагонит (СаСО3), ттт
р=2,6 г/см3,
а1=35-10"« К-1,
е1=9,8,
Тпл=129 °C
а2=17-10“6 К’1,
е2=7,7,
а3=10-10-6 К’1,
Е3=6,6.
*) Там, где не указаны условия измерения коэффициентов, следует
считать их измеренными при условии механической свободы и постоянства
температуры.
272
Арсенид галлия (GaAs), 43m
р=5,316 г/см3, 7ПЛ=1238 °C;
для Z=10,6 мкм /7=3,08, г41=4,8 10-8 ед. СГСЭ;
для Z=1,52mkm А=3,42, г41=3,6-10~8 ед. СГСЭ
. ,=12,64-10~12 ед. СГСЭ, с11=1,19-101<> ед. СГСЭ [1],
« .=18,60-10-12 » », с44=0,54-1010 » »,
s42=4,23-10*12 » », с12=0,59-1010 » ».
Виннокислый калий (С4Н4Ов), 2
р= 1,988 г/см3, р2=—4,9 ед. СГСЭ
d, 10 8 ед. СГСЭ —12 s, 10 ед. СГСЭ e a, 10 6 К 1
d14=-25,0 d16=-|-6j5 ^2i=—2,2 ^22— 8,5 d23=—10,4 d25=—22,5 d34=-|-29,4 </36=—66,0 «и=-|-2,24 «35=4-3,86 «12=—0,08 «34=-j-0,90 «13=—1,64 s44= + ll,90 «15=—0,64 s46=0,57 522=-l_ 3,3/ «55=8,15 s23=—1,05 «66= 10,41 «35=—0,57 II II II II © © 5я C75 0^00 JS Я Я й Я et w n н II II II II м о °° во о о
Вюрцит
(см. сернистый цинк)
Герм аний (Ge), тЗт
р=5,327 г/см3, 7’пл=936 °C
s, 10 12ед. СГСЭ с, 1011 ед. СГСЭ 1 9 П.., 10 ед. СГСЭ гз р, Ом-см
n-Ge p-Ge n-Ge p-Ge
«11=0,979 «12= —0,267 «44= 1,497 С11=13,114 Ci2=4,924 с44= 6,816 ааа £ N Н II II II 1 1 л ь* СЛ -<1 й© о 1 СО СЗ II II II w W 2 аве 9,9 1,1
Гипс (СаСО3), ттт
N = 1,532, А =1,527, А’ =1,522
Б "I Р
Гринокит
(см. сульфид кадмия)
Графит (С), 6/ттт
р=2,21 г/см3, Т^ЗвОО—3900 °C
а1=а2=—1,5-10“е К-1, аз=+28,2.10~в К-1
Железо-иттриевый гранат (YgFe6O12, YIG), m3m
р=5,17 г/см8;
для Z=l,15 мкм N—2,22
Ри=0,025, р1а=0,073, £„=0,041.
IS Н, В, Переломова, М, М, Тагиева 273
Иодат Лития (LiIO3),6
р=4,5 г/см3, Гпл=420°С;
для Х= 1,06 мкм 7Vo= 1,86, 7Ve=l,72
Этилендиаминтартр а'т (EDT) (СвН14Н2Ов) ,2
р= 1,538 г/см3
—4 d, 10 ед. СГСЭ », 10 —12 ед. СГСЭ a, 10 6 К 1
dii=—30,4 su=3,34 $25—15,0 a4=0
die=—36,6 —0,3 s33=10,8 a2-20,3
d21=30,3- s13=—3,0 ^25——2,65 a3=80,0
d22=6,6 »i6= 1Д s44=19,1 a5=—32
d23=—34 s22=3,65 s46=0,38
d25=—53,8 s23~ 1’8 «55=11>6
<13!=—50,9 «66=19,1
c/ge~ 55,1
Кальцит (исландский шпат) (СаС03), Зт
р—2,64-2,8 г/см3, 7^=1339 °C при давлении порядка 102,5 атм.
Обладает спайностью по плоскостям, параллельным граням ромбо-
эдра (1011). Нормаль к граням ромбоэдра составляет с осью 3 угол,
равный 44°.
Для Х=0,589 мкм ДГО=1,658, 7Ve=l,486;
а1=а2=_5,6-10-6 К"1, а3=+2510-в К"1.
Калий хлористый (КС1), тЗт
р=1,98 г/см», ГПЛ=776°С,
с11=3,98-10ц ед. СГСЭ, ац=2,62-10~12 ед. СГСЭ,
с44=0,62-10Ч » » s44=16,0-10-12 » »
с12=0,62-10ц » » «12=—0,35-10 12 » »
Каменная соль (NaCl), тЗт
р=2,2 г/см3, Т’пл=804°С;
для Х=0,589 мкм N=l,51
ли=+0,25-10-Н’ед. СГСЭ, 7?u=+2,7-10-12 ед. СГСЭ,
1,46-1011 » », /?12=—1,35-10~1а » » ,
л14=— 0,85-10-и » », 7?44=+0,9-10-12 » » .
Кварц (SiO2)
Симметрия низкотемпературной модификации 32, симметрия вы-
сокотемпературной модификации 622.
р=2,648 г/см3, 7,пл=1700”С.
Для X,—0,589 мкм 7УО= 1,544, Ne—1,553;
для %=0,53 мкм Д1О=1,5468, 7Уе=1,5559;
274
для Х=1,06 мкм Лго=1,5340, Лге=1,5428;
ер=О,177 кал-г"1- К"1,
р1=р2=200 1014 Ом-см, р3=1-1014 Ом-см.
Для Х=О,546 мкм гп=0,59- 10-8 ед. СГСЭ, г41=1,4-10~8 ед. СГСЭ;
х=1,2-10-8 ед. СГСЭ (для Х=1,06 мкм).
d, 10 8 ед. СГСЭ в, 10 14 ед. СГСЭ с, 10"' ед. СГСЭ е а, ю 6 к 1
dlt=—6,76 dj[4=“h2,56 зи= 127,9 s12=—15,35 s,3=—11,0 л14= -44,6 $33=95,6 $44=197,8 see=286,5 сп=86,05 с12=4,85 с13= 10,45 с14= 18,25 е38= Ю7,1 с44=58,65 св6=40,5 е1=с2=4,5 е3=4,6 а1=<х2=13,4 а3=7,8
Температурные коэффициенты упругих податливостей кварца, при 25 °C
[1+^у(7’-7’о)+^Jr-То) ].
ij т(1), ю6 °с 1 т(2), Ю9 °с 1
11 15,5 85,3
33 140 247
12 —1370 21 385
13 —166 —718
44 210 262
66 —145 —85
14 134 93
Квасцы алюмокалиевые (KA1[SO4]2-12H2O), m3
л11=3,7-1О-ч ед. СГСЭ, л13=8,5-10-и ед. СГСЭ,
л12=9,1-1(Г11 » » , л14=—0,65-10-11 » » .
Дигидрофосфат калия (KDP), КН2РО4, 42m
Сегнетоэлектрик, Тс=—151 °C. В точке Кюри Р’=104 ед. СГСЭ;
Симметрия сегнетофазы mm; е3=7-104,у3=5000ед. СГСЭ, р=2,338 г/см3,
Гпл=254 °C, ср=0,1 кал-г-i-K-1. '
Для Х=0,546 мкм No =1,511, /Уе=1,469; г41=+25-10~8 ед. СГСЭ,
гвя=—30-Ю-8 ед. СГСЭ.
Для /.=0,535 мкм л6в=0,5-10-12 ед. СГСЭ, У14=0,59-10-8ед. СГСЭ,
Хзв=0,62.10-8 ед. СГСЭ.
18* * 275
Дейтерированный дигидрофосфат калия (DKDP),
КН2РО4, 42m
Для 1=0,546 мкм №О=1,47, №,=1,51
d, 10 8 ед. СГСЭ в. 10 12 ед. СГСЭ c, 10’“ ед. СГСЭ e a, 10 6 K-l
dri=4,2 d3e=69,6 su=l,65 s12=—0,4 s13=— 0,75 s33=2,0 s41=7,9 see=16,6 c11=86,8 «12=40,2 c13=47,6 c23=85,7 c44=12,7 cee=6,0 e1=e2=4,6 8g—21,8 a1=a2=36 a3=41,l
Киноварь (HgS), 32
Для 1=0,694 мкм, №„=2,83, №,=3,15;
Для 1=1,06 мкм №о=2,70, №,=2,99;
ДЛЯ 1=10,6 мкм №„=2,60, №,=2,87;
Для 1=10,6 мкм Xii=2,4-10-’ ед. СГСЭ,
Корунд (см. рубин)
Кремний (Si), m3m
р=2,328 г/см3, Тпл= 1410 °C, ср=0,181 кал/(г-К), 8=12
S, 10 12 ед. СГСЭ с, 10’* ед. СГСЭ —12 П.., 10 ед. СГСЭ г} р, Ом-см
n-Sl • P-SI n-Sl p-Si
sr С х—< 1 СО М О О * 1Л < 1 о? си=16,57 с42=6,39 с44=7,96 Пй=—102,2 П12=58,4 П44=—13,6 Пц=6,5 ni2=-l,l II4j=138,1 11,7 78
Н и о б а т-т а н т а л а т калия (KTN, KTaNbi— ЯО3)
Сегнетоэлектрик, 7^= 10 °C; ниже Тс — симметрия 4mm,
выше Тс — тЗт.
Для 1=0,633 мкм №О=2,318, №,=2,277 (в тетрагональной фазе)
Ли—Л12=9,67-10~м ед. СГСЭ.
Ниобат лития (LiNbO3), 3m
Сегнетоэлектрик, Тс= 1160 °C, Гпл=1253 °C, р=4,7’г/см3, ei=8j=
=99,5, е3=38,5.
Для 1=0,1060 мкм №О=2,2336, №,=2,1567;
для 1=0,5300 мкм №О=2,3225, .№,=2,3212.
гм=0,1-10~* ед. СГСЭ, еи=204-101° ед. СГСЭ,
276
r13=0,25-10-s ед. СГСЭ, c33=242,1010 ед. СГСЭ,
r33=0,9-10-8 » » , см=60-1010 » » ,
r61=0,9-10-8 „> » , c66=73-1010 » » ,
7.22=3,8-10-8, Хз1=6,ыо-и, Хзз=49,8-10-8 ед. СГСЭ.
ётп^ Ю’22 H-i-B-i-мЗ,
£111= 6,23, £241= 2,46, gi3i=—9,48,
1>’з41=—2,89, £141=15,14; £44i=—21,00,
£221=0,38, £i63=1,14.
d22=0,63-10-e ед. СГСЭ, d3i=—0,33-10"’ ед. СГСЭ,
</15=2,04-10“в » » , d33=l,6-10-4 » » .
Для Z=0,6>300 мкм Лго=2,20
p3i=0,178, />13=0,092, />з3=0,088,
/>41=0,155, />11=0,036, рм=0,072.
Нитрит бария (Ba(NO2)2-H2O), 6
ai=a2=16-10“e К" , «3=76-10-8 К-1, у8=—8 ед. СГСЭ
d3i=5,3-Ю-8 ед. СГСЭ, d33=5,l-IO’8 ед. СГСЭ,
<-11=0,525-1012 » » , с83=0,3-1012 » » ,
<>12=2,5-10“ » » , С1з=0,15-1012 » » .
Дигидрофосфат рубидия (RDP, RbH2PO4), 42m
Для 7=0,547 мкм Ао=1,609, Ае=1,479; лвв=10,5-10-12
Резорцин (СвН4(0Н),), mm2
р=1,272 г/см3, 7пл~100оС
d, 10 8 ед. СГСЭ s, 10 12ед. СГСЭ с, 101» ед. СГСЭ е
<115=53,9 «11=19 «11=10,3 61=3,51
<131=—12,4 «22=10,6 С22~ 14,4 ^=4,14
</33=16,8 s3g=15 сзз=12,9 е3=3,54
</24=55,3 «44=30,7 «44=3,3
^32” 12,8 «бв=23 «бб=4А
«вз= 25 сбв~4»0
512=—4 С12“9,2
513=—3,4 «18=7,4
«23=—8,8 с23=6,9
Рубин (а-А12О3), Зт
(Рубином называют кристаллы корунда а-А12О3, окрашенные в
красный цвет примесью Сг.)
р=3,98 г/см3, 7^=2030 °C.
Для Х=0,5890 мкм А,=1,768, А,=1,759
277
—12 з, 10 ед. СГСЭ c, 1011 ед. СГСЭ e a, 10 6 К 1
s11=0,2353 s33=0,2170 s44=0,6940 s12=—0,0716 s13=—0,0364 s14=—0,0489 cu=49,68 c33=49,81 c44= 14,74 c12= 16,36 c13=ll,09 c14=—2,35 e1=e2=8,6 e3= 10,55 <Xi=aa=5,0 a3=6,66
Рутил (TiO2), 4! ттт
p=4,26 г/см8, 7nJ =1820 °C, 4=86, e3=170.
Для /.=0,630 мкм ^=2,600, ^=2,890.
Сегнетова соль (NaKC4H40e-4H20)
Сегне оэлектрик имеет две точки Кюри — 18 °C и 24 °C. Симметрия
сегнетофазы 2, симметрия парафазы 222. Вблизи верхней точки Кюри
Т!=200 ед. СГСЭ.
р=1,77 г/см3, 2^=55 °C
Для /.=0,546 мкм ^=1,4954,^=1,4920, 7Vp=l,4900;
Ря=7,5-10а ед. СГСЭ, £14=6,7-10~7 ед. СГСЭ,
Р44=8,9-1О-3 » », т41=0,224-10“7 »„ »
d, g, io 8 ед. СГСЭ s, 10 12 ед. С.ГСЭ с, IO10 ед. СГСЭ e a, 10 6 К 1
d14=1150 su=5,2 сц=40 eJ=480 a!=58,3
d№=—160 $12= 2,1 Cj2=—30 62=12 c&2— 35,5
^36~ 35 Sjg— 2,0 c13 63=10 a3=—136,1
£14=31 522~ ^22= 50 6j=220
g25=-170 523= —^’3 c23~ e2=11
gse=44 5зз=3,2 C33~ 63=9,8
s44=20 c44=10
$55==32 СБ5=3
see=10 ^6=10
Сернистый цинк (ZnS)
Сфалерит, 43т (кубическая модификация ZnS)
р=4,102 г/см®, для Х=0,546 мкм Аг=2,37, е=8,37,
<114=9,54-10“8 ед. СГСЭ, su= 18,39-10~13 ед. СГСЭ,
s12=—7,07-Ю-12 ед. СГСЭ, s44=21,69-10-13 ед. СГСЭ,
г41=5,0-10~8 ед. СГСЭ (для Х=0,546 мкм).
Вюрцит бтт (гексагональная модификация ZnS)
йц=8,6-10~8 ед. СГСЭ.
Сульфид кадмия (CdS), 6mm
р=4,82 г/см3, 2^=1500 °C при давлении 100 атм.
Для Х=0,5150 мкм 7VO=2,743, 1^=2,726
г1Я=3,3-10~3, гзя=7,2-10~8, ги=11,1-10“8 ед. СГСЭ
278
d, 10 8 ед. СГСЭ з, 10-12 ед. СГСЭ с, 1011 ед. СГСЭ 8 а, 10 6 К 1
d3i=-l,7 d33 3,4 «ы=2,22 «12=—0,87 Sj3——0,80 «33“^,19 «44=7,0 сц=8,1 с12=4,9 Ci3=4,8 С 44= 1,43 СО оГ (1 - с«О со II II to* to5 ai=a2=5,0 сх3— 3,5
Сульфат лития (LijSC^-HjO)^
р=2,06 г/см5, уа=ЗО ед. СГСЭ
d, 10 8 ед. СГСЭ 10-12 ед. СГСЭ е
d14=14,0 sn=2,39 «12=—0,95 е‘=5,6
d16=12,5 «22=2,13 «1з=- 0,5 eJ,=6,5
d21=ll,6 «зз“2,31 «23=0,36 4=10,3
d22=45,0 (^23— ~~5 ,5 d25=16,5 d34=26,4 d3e=10,0 s4i=3,69 «65—4,1 e« «о <f5 а о» ел ел II II II II II о р I р фч фч о "-Ч О СП - е‘=0,07
Танталат лития (LiTaO3), Зт
Сегнетоэлектрик, Тс=630 °C
р=7,58 г/см3, у3=75 ед. СГСЭ, ст3=10-11 Ом’1-см-1, е3=80.
Для Х=0,6330 мкм АГО=2,176, Ne= 2,180
г13=21-10’8 ед. СГСЭ, г33=90,8-10’8 ед. СГСЭ,
г31=60-10’8 » » , г22=3-10 6 » » .
Теллурид свинца (РЬТе), тЗт
р=8,16 г/см3, Гпл=917 °C
з, io’12 ед. СГСЭ П, 10 12 ед. СГСЭ р. Ом-см
з Концентрация ~ 3 • 101*см
п-РЬТе р-РЬТе p-PbTei р-РЬТе
su=0,947 «ia= —0,073 «44=7,63 д Я Я » м II II II 1 8 g Кч О а я1 Я1 £ ьз м II II II фч со СО О СП 1-3 1—3
Титанат бария (BaTiO3)
р=5,9 г/см3, Гпл=1625 °C
Выше 120 °C имеет симметрию тЗт, ниже 120 °C — сегнетоэлект-
рик. Между 120 °C и 5 °C стабильна тетрагональная фаза с симмет-
рией 4mm. Направление Р1 параллельно < 100> исходной кубической
279
ячейки, Р‘=54-103 ед. СГСЭ.Ниже 5 °C возникает новая сегнетоэлек-
трическая фаза, направление спонтанной поляризации в этом случае
параллельно <110> исходной кубической ячейки. Симметрия этой
фазы шт, она стабильна между 5 СС и —90 °C.
При —90 °C наблюдается третий фазовый переход, направление
спонтанной поляризации параллельно <111> исходной кубической
ячейки. Симметрия этой фазы Зт.
Для кубической модификации: п=2,4, /<ц=/<12 -1,4-10-12ед. СГСЭ,
/?44=1,88-10-12 ед. СГСЭ.
Поляризованная керамика титаната бария
(BaTiOs), оот
Искусственный сегнетоэлектрик, р=5,5 г/см3, Гс=115 °C
d, g, 10 8 ед. СГСЭ с, 10” ед. СГСЭ е
й ” сч со in 1 II II II «МЛ «мн "С си=16,8 с33=18,9 с44=5,46 с42—7,82 С13=7,10 П оо ьо м II II 1-ж ОО Си со ге о
Титанат стронция (SrTiOs)
Сегнетоэлектрик, 7'с=240 °C, Нг1—/Д2=0,065 ед. СГСЭ.
Триглицин сульфат (TGS
Сегнетоэлектрик, Тс=49 °C.
Симметрия сегнетофазы 2, симметрия парафазы 2/т. Вблизи точки
Кюри у2=500 ед. СГСЭ, е2=200.
Турмалин, Зт
р«2,90—3,25 г/см3, 7'пл=И02 °C,
ХО=2,12, A<e=2,23, с„=0,2 кал/(г-К), у3=1,3 ед. СГСЭ
а, ю 8 ед. СГСЭ , л—12 з, 10 ед. СГСЭ с, 10” ед. СГСЭ е а, 10 6 К 1
d16=10,9 d22=l,0 Э31=1,ОЗ <233—5,5 зп=0,385 з12=0,048 з13=0,071 Ззз= 0,636 s44=154 s14=0,045 сп=272 с12=40 С13=35 с33=165 с44=65 С14= 6,8 со" II 0? I'- ll Н Я w со aj=a2=3,6 а3=—8,8
Флюорит (CaF2), тЗт
р=3,18 г/см3, 2^=1360 °C
Для Х=0,589 мкм Лг= 1,43384;
ли=— 0,29.10-и, л12=1,16-10’и, л44=0,698-10~и ед. СГСЭ.
Хлористая медь (CuCl), 43m
Для /.=0,535 мкм ./V=l,996; г41=18,3-10-8 ед. СГСЭ.
Хлорат натрия (NaClO3), 23
р=2,49 г/сы3, е=5,75, а=43,4-10-8 К-1,
d14=6,l-10“8 ед. СГСЭ, з11=23,35-10“13 ед. СГСЭ,
з12=—5,15-Ю’13 » », s44=85,4-10 13 ».
Фосфид галлия (GaP), 43m
Для /.=0,540 мкм N= 3,495;
г41=1,5-10-8 ед. СГСЭ.
280
Соотношение единиц 1 г/см3=10® кг/м3 7’[К]=Т[°С]+ 273,15К 1 кал/К=4,19 Дж/К 1 кал/К=4,19 Дж/К ч Й OS 1 О СО II О о и п: о т—’ 1 ед. СГСЭ=300 В |
Единица Обозначе- ние кг/м3 г/см3 >—< о Дж/К кал /К Дж/К кал/К | Кл m
Наи .снование килограмм на куби- ческий метр грамм па кубический сантиметр кельвин градус Цельсия джоуль на кельвин калория на кельвин джоуль на кельвин калория на кельвин кулон ед. СГСЭ ВОЛЬТ ед. СГСЭ
Выражение через ос io_ ые и дополни- тельные единицы КГ'М-3 Г • см-3 7* Г ЙЙ ед eq О О еч ет S 3 о И Ен ЙК СД eq о'о S g Я е СМ со 3 о о ’"L ет о
Система единиц СИ СГСЭ СИ СГСЭ СИ сгсэ си сгсэ си сгсэ СИ сгсэ
। Величина 1 Обозначе- ние О. Е- СО о
Наименование Плотность Температура Энтропия Теплоемкость Электрический заряд Разность электриче- ских потенциалов
281
оо Продолжение табл. 15
Величина Система единиц Единица Соотношение единиц
Наименование Обозначе- ние Выражение через ос- новные и дополни- тельные единицы Наименование Обозначе- ние
Сила F си СГСЭ кг-м-с~2 г•см с"2 НЬЮТОН дина н дин 1 дин=10“? Н
Смещение при дефор- мации и СИ СГСЭ м см метр сантиметр м см 1 см=10*3 м
Напряженность электрического поля Е СИ СГСЭ кг-м-с“3-А-1 г1/2-см“1/2-с~1 вольт на метр ед. СГСЭ В/м 1 ед. СГСЭ=3-104 В/м
Электрическое сме- щение (индукция) D СИ СГСЭ м~2-с-А 1/2 -1/2 „-1 1 • см • с кулон на квадратный метр ед. СГСЭ Кл/м3 1 ед. СГСЭ= 1 =£Гз-10’5 Кл/м
Электрическая поля- ризованность Р СИ СГСЭ м-2’С-А г1/2 -см~^2 -с-1 кулон на квадратный метр ед. СГСЭ Кл/м2 1 ед. СГСЭ= =Z7-q-Ws Кл/м2 4 л -3
Пироэлектрические коэффициенты Vi СИ СГСЭ м“2-с-А-К-1 г1/2 -см-1^2-с-1К~1 кулон на квадратный метр на кельвин | ед. СГСЭ Кл/(м2’К) 1 ед. СГСЭ= 1 -4л.3 -Ю-вКл/(м3.К)
Электрокалорические коэффициенты <?1 СИ СГСЭ кг-1-м-1-с3-А-К г-1/2-см1/2-с-К кельнпн-мотр на вольт| ед. СГСЭ К-м/В 4 ед. СГСЭ= =1/з-Ю-4К-м/В
.—"tf" —к» 11 ' *чГ
Продолжение табл. 15
N5 00 се Величина Система единиц Единица Соотношение единиц
Наименование Обозначе- ние Выражение через ос- новные и дополни- тельные единицы Наименование Обозначе- ние
Механическое напря- жение си СГСЭ кг'М-1-с_3 г-см-1-с'3 пьютон на квадрат- ный метр дина на квадратный сантиметр Н/м2 дин/см2 1 дин/см2=0,1 Н/м2
Механические дефор- мации rii СИ СГСЭ — — — 1
Коэффициенты тепло- вого расширения “и СИ СГСЭ К"1 к-1 Кельвин в минус пер- вой степени К-1 1
Диэлектрическая про- ницаемость siJ СИ СГСЭ кг-1.м_3.с4- А2 фарад на метр ед. СГСЭ Ф/м 1 ед. СГСЭ= =7-Ц-.1О-» Ф/м 4л-9
Диэлектрическая не- проницаемость СИ СГСЭ кг.м3-с~4.А-3 метр на фарад ед. СГСЭ | м/Ф 1 ед. СГСЭ= =36л-108 м/Ф
Магнитная проницае- емость СИ СГСЭ кг м с-2 А-2 см-2-с2 генри на метр ед. СГСЭ | Гн/м 1 ед. СГСЭ= =1/в-10_5 Гн/м
Удельная электриче- ская проводимость СИ СГСЭ кг^.м-^с’-А2 с-1 сименс на метр ед. СГСЭ | См/м 1 ед. СГСЭ= =1/в- Ю-’См/м
Величина Система единиц Единица Соотношение единиц
Наименование Обозначе- ние Выражение через ос- новные и дополни- тельные единицы Наименование Обозначе- ние
Удельное электриче- ское сопротивление Pij си СГСЭ кг-м3-с"3-А"2 С ом-метр ед. СГСЭ ОМ'М 1 ед. СГСЭ= = 9-109 ОМ'М
dijh СИ СГСЭ кг-1-м-1-с3-А г-1/2 •см1''2 -с кулон на ньютон ед. СГСЭ Кл/Н 1 ед. СГСЭ= = 10"4Кл/Н
Пьезоэлектрические коэффициенты eijn &ijh ^ijk СИ СГСЭ СИ СГСЭ СИ СГСЭ 7 7 V ° « м Г1' 1 < Я” 1 < Я - ® о я ° ” й “ c\j о a c i 1 « I СнС? Я Ь S А И кулон на квадратный метр ед. СГСЭ квадратный метр на кулон ед. СГСЭ ньютон на кулон ед. СГСЭ Кл/м2 м2/Кл Н/Кл 1 ед. СГСЭ= =1/3-10-5Кл/м2 1 ед. СГСЭ= = 3'10Б м2/Кл 1 ед. СГСЭ= = 3-104 Н/Кл ।
Коэффициенты линей- ного электрооптиче- ского эффекта rijk СИ СГСЭ м2-с-1'А-1 г-1/2 -см1/2-с квадратный метр на кулон ед. СГСЭ м2/Кл 1 ед. СГСЭ= = 3.105 м2/Кл
Нелинейная диэлек- трическая восприим- чивость СИ СГСЭ кг-м-с'3-А-1 Г1/2 -см- 1/2-с-1 квадратный мот'р на вольт ед. СГСЭ м2/В ед. СГСЭ=1/3м2/В
Окончание табл. 15
Величина Система единиц Единица Соотношение единиц
Наименование Обозначе- ние Выражение через ос- новные и дополни- тельные единицы Наименование Обозначе- ние
Коэффициенты упру- гой податливости sijkl ей СГСЭ КГ-1.М-С2 г-1-см-с2 квадратный метр на ньютон квадратный санти- метр на дину м2/Н см2/дин 1 см2/дин=10 м2/Н
Коэффициенты упру- гой жесткости cijkl СИ СГСЭ КГ.М-1.С-2 г-см-1-с-2 ньютон на квадрат- ный метр дина на квадратный сантиметр Н/м2 дин/см2. 1 дин/см2=0,1 Н/м2
Коэффициенты пьезо- оптического эффекта nijkl СИ СГСЭ КГ^-М-С2 Г-1-см-с2 квадратный метр на пьютон ед. СГСЭ м2/Н 1 ед. СГСЭ=10 м2/Н
Коэффициенты упру- гооптического эф- фекта РЦМ СИ СГСЭ — — — —
Коэффициенты пьезо- резистивного эффекта о э СИ СГСЭ кг-м4.с-4-А-4 г-1 • см • с"4 килограмм-метр в седьмой на кулон в четвертой ед. СГСЭ кг-м’/Кл4 1 ед. СГСЭ= =81-IO19-кг-м’/Кл4
ЛИТЕРАТУРА
1. Дж. Пай. Физические свойства кристаллов.— М.: Мир, 1967.
2. Ю. И. Сиротин, М. П. Шаскольская. Основы кристаллофизики.—
М.: Наука, 1979.
3. М. П. Шаскольская. Кристаллография.— М.: Высшая школа,
1976.
4. Ф. Цернике, Дж. Мидвинтер. Прикладная нелинейная оптика.—
М.: Мир, 1976.
5. Е. М. Воронкова, Б. Н. Гречушников, Г. II. Дистлер, И. П. Пет-
ров. Оптические материалы для инфракрасной техники.— М.:
Наука, 1965.
6. И. С. Желудев. Физика кристаллических диэлектриков.— М.:
Наука, 1968.
7. Е. Р. Мустель, В. Н. Парыгин. Методы модуляции и сканиро-
вания света.— М.: Наука, 1970.
8. А. В. Шубников. Избранные труды по кристаллографии.— М.:
Наука, 1970.
9. А. С. Сонин, А. С. Василевская. Электрооптические кристал-
лы.— М.: Атомиздат, 1973.
10. Landolt — Bernstein. Zahlenwerte und Functionen aus Naturwis-
senschaften und Technic, Neue Serie, Grupp III. B. 1, V. 1.: Sprin-
ger-Verlag, 1966.
11. А. В. пТубников. Оптическая кристаллография.— Изд-во АН
СССР, 1950.
12. У. Мэзон. Пьезоэлектрические кристаллы и их применение в
ультраакустике.— М.: ИЛ, 1952.
13. Современная кристаллография/Под ред. Б. К. Вайнштейна,
А. А. Чернова, Л. А. Шувалова, т. 4.— М.: Наука, 1981.
14. Акустические кристаллы/Под ред. М. П. Шаскольской,— М.:
Наука, 1982.
УКАЗАТЕЛЬ ТАБЛИЦ, ПОМЕЩЕННЫХ В ПРИЛОЖЕНИИ
1. Обозначения 32 классов симметрии....................250
2. Обозначения элементов симметрии на стереографической
проекции.................'.................. . . 251
3. Правила установки кристаллов ио сингониям .... 252
4. Элементы симметрии и правила выбора осей в 32 кристал-
лографических классах..................................252
5. Правила выбора кристаллофизических осей .... 255
6. Форма матриц пьезомодулей (</,;) и пьезоэлектрических
коэффициентов (gij)....................................256
7. Форма матриц пьезоэлектрических коэффициентов (Л,-3)
и (ei3) для кристаллов, имеющих эти матрицы, отличные
от матриц (й;,-) и (g<j)......................... ... 258
8. Форма матриц пьезомодулей для текстур...............258
9. Форма матриц упругих податливостей (я3) и упругих
жесткостей (c,j) . ................. 258
10. Форма матриц пьезорезистивных коэффициентов (П,3) 261
11. Форма матриц пьезооптических (Пн) и упругооптических
коэффициентов (рк).....................................263
12. Форма матриц коэффициентов линейного электрооптиче-
ского эффекта (о,,)....................................267
13. Форма матриц коэффициентов квадратичного электрооп-
тического эффекта (7?i3).............................. 269
14. Некоторые справочные данные о кристаллах, необходи-
мые для решения задач..................................272
15. Определение некоторых физических величин и соотноше-
ние между единицами их измерения в системах Си и СГСЭ 281
Наталья Владиславовна Переломова
Марианна Мамедовна Тагиееа
ЗАДАЧНИК ПО КРИСТАЛЛОФИЗИКЕ
Оформление художника В. Я- Батищева.
Редакторы Д. А. Миртова, Н. А. Михалина.
Технический редактор С. Я. Шкляр.
Корректоры О. А. Сигал, Е. Я. Строева.
ПБ № 11479
Сдано в набор 15.01.82. Подписано-к печати 23.07.82.
Т-11160. Формат 84х108‘/з2. Бумага тип. J4 3. Обыкно-
венная гарнитура. Высокая печать. Условп. печ. л
15,12. Уч.-изд. л. 15,62. Тираж 7500 зкз. Заказ № 29.
Цена 80 коп.
Издательство «Наука»
Главная редакция физико-математической литературы
117071, Москва, В-71, Ленинский проспект, 15
4-я типография издательства «Наука»
630077, Новосибирск, 77, Станиславского, 25