Author: Левин Д.М. Стефан Д. Кребиль Т.С. Беренсон М.Л.
Tags: компьютерные технологии социальная (общая) психология историческая психология личность психология семьи, быта, воспитания детей менеджмент бизнес
ISBN: 5-8459-0607-5
Year: 2005
Статистика для менеджеров с использованием
Microsoft* Excel
ЧЕТВЕРТОЕ ИЗДАНИЕ
ЛЕВИН СТЕФАН
КРЕБИЛЬ БЕРЕНСОН
PEARSON
Прилагается компакт-диск с программным обеспечением
rrnticc Hall
www prenhall com/le vine
www.wrlliamspublishing.com
Статистика для менеджеров с использованием Microsoft* Excel
Четвертое издание
Statistics for
Managers
Using Microsoft® Excel
Fourth Edition
David M. Levine
Bernard M. Baruch College, Zicklin School of
Business, City University of New York
David Stephan
Bernard M. Baruch College, Zicklin School of
Business, City University of New York
Timothy C. Krehbiel
Miami University, Richard T. Farmer School of Business Administration
Mark Berenson
Department of Information and Decision Sciences, School of Business, Montclair State University
PEARSON
1 111,11 “-Ч.
Prentice Hall
Prentice Hall
Upper Saddle River, New Jersey 07458
Статистика для менеджеров
с использованием Microsoft® Excel
Четвертое издание
Дэвид М. Левин
Колледж Бернарда М. Баруха, Школа бизнеса Зиклина, Городской университет Нью-Йорка
Дэвид Стефан
Колледж Бернарда М. БарухасШкола бизнеса Зиклина, Городской университет Нью-Йорка
Тимоти С. Кребиль
Университет Майами, Школа делового администрирования Ричарда Т. Фармера
МаркЛ. Беренсон
Факультет информатики и теории принятия решений, Школа бизнеса, Государственный университет Монклер
К4
ВИЛЬЯМС
Москва Санкт-Петербург • Киев 2005
ББК 88.5
С78
УДК 681.3.07
Издательский дом “Вильямс”
Зав. редакцией С. Н. Тригуб
Перевод с английского и редакция канд. физ.-мат. наук Д. А. Клюшина
По общим вопросам обращайтесь в Издательский дом “Вильямс” по адресу: info@williamspublishing.com, http://www.williamspublishing.com
Левин, Дэвид М., Стефан, Дэвид, Кребиль, Тимоти С., Беренсон, Марк Л.
С78 Статистика для менеджеров с использованием Microsoft Excel, 4-е изд. : Пер. с англ. — М. : Издательский дом “Вильямс”, 2004. — 1312 с. : ил. — Парал. тит. англ.
ISBN 5-8459-0607-5 (рус.)
Книга представляет собой вводный курс бизнес-статистики. В ней рассмотрены практически все традиционные темы, касающиеся анализа данных, — от описательных статистик до регрессионного анализа и карт контроля. Особую ценность книге придает множество примеров, почерпнутых из практики, а также компакт-диск с большим количеством приложений, иллюстрирующих методы статистического анализа данных с помощью программы Microsoft Excel.
Книга предназначена для студентов, изучающих основы менеджмента, преподавателей бизнес-школ, а также менеджеров, желающих повысить качество своей работы.
ББК 88.5
Все названия программных продуктов являются зарегистрированными торговыми марками соответствующих фирм.
Никакая часть настоящего издания ни в каких целях не может быть воспроизведена в какой бы то ни было форме и какими бы то ни было средствами, будь то электронные или механические, включая фотокопирование и запись на магнитный носитель, если на это нет письменного разрешения издательства Prentice Hall, Inc.
Authorized translation from the English language edition published by Prentice Hall, Copyright ©2005,2002, 1999, 1997
All rights reserved. No part of this book may be reproduced or transmitted in any form or by any means, electronic or mechanical, including photocopying, recording or by any information storage retrieval system, without permission from the Publisher.
Russian language edition was published by Williams Publishing House according to the Agreement with R&I Enterprises International, Copyright © 2005
ISBN 5-8459-0607-5 (рус.) © Издательский дом “Вильямс”, 2005
ISBN 0-13-107389-3 (англ.) © Pearson Education, Inc., 2005
Оглавление
Предисловие 25
1 Введение и сбор данных 33
2 Представление данных в виде таблиц и диаграмм 97
3 Описательные статистики 177
4 Основы теории вероятностей 251
5 Дискретные распределения 293
б Нормальное и другие непрерывные распределения 345
7 Построение доверительных интервалов 447
8 Основы проверки гипотез: одновыборочные критерии 519
9 Двухвыборочные критерии 579
10 Дисперсионный анализ 641
11 Критерий "хи-квадрат" и непараметрические критерии 707
12 Простая линейная регрессия 791
13 Введение в множественную регрессию 873
14 Построение моделей множественной регрессии 937
15 Анализ временных рядов 983
16 Принятие решений 1075
17 Статистические методы управления качеством
и производительностью труда 1113
Ответы на избранные вопросы 1169
Приложение А Некоторые правила алгебры и арифметики 1217
Приложение Б Правила суммирования 1219
Приложение В Статистические обозначения и греческий алфавит 1223
Приложение Г Обзор компакт-диска 1225
Приложение Д Таблицы 1235
Приложение Е Установка и настройка программы Microsoft Excel 1285
Приложение Ж Дополнительные сведения о программе PHStat 1289
Приложение 3 Подготовка отчетов и презентаций с помощью пакета Microsoft Office 1293
Предметный указатель 1305
Содержание
Предисловие 25
1. Введение и сбор данных зз
1.1. Что такое статистика 34
1.2. Развитие статистики и информационных технологий 35
1.3. Программа Microsoft Excel: решение проблемы или новая
проблема? 36
1.4. Обучение коммерческой статистике 37
1.5. Обучение статистике с помощью программы Microsoft Excel 38
1.6. Наиболее эффективное использование программы
Microsoft Excel 38
1.7. Обучение статистике по учебнику 39
1.8. Зачем нужны данные 41
1.9. Идентификация источников данных 42
1.10. Методы выборочного исследования 43
Простая случайная выборка 45
Систематическая выборка 48
Стратифицированная выборка 49
Кластерная выборка 49
Упражнения к разделу 1.10 50
1.11. Типы данных 52
Шкалы измерений 53
Упражнения к разделу 1.11 54
1.12. Оценка достоверности результатов исследования 57
Ошибки статистических исследований 57
Этические проблемы 60
Упражнения к разделу 1.12 60
Резюме 61
Основные понятия 63
Упражнения к главе 1 63
Применение Web 69
Дополнительная литература 70
Букварь Excel 71
ЕР.1. Введение в Microsoft Excel 72
ЕР.2. Пользовательский интерфейс программы Microsoft Excel 72
ЕР.2.1. Основные операции с мышью 72
ЕР.2.2. Открытие окна приложения Microsoft Excel 73
ЕР.2.3. Стандартные свойства меню и диалоговых окон программы Microsoft Excel 75
ЕР.2.4. Исправление ошибок 77
ЕР.2.5. Использование справочной системы 77
ЕР.2.6. Получение контекстных подсказок 79
ЕР.З. Основные операции над рабочими книгами 81
ЕР.3.1. Открытие рабочих книг 81
ЕР.3.2. Сохранение рабочих книг 82
ЕР.3.3. Вывод рабочих книг на печать 82
ЕР.3.4. Использование области задач для открытия рабочих книг (версии Excel 2002 и 2003) 84
ЕРЛ. Основные операции над рабочими листами 85
ЕРЛ. 1. Использование рабочих листов программы Microsoft Excel 85
ЕР.4.2. Формулы 85
ЕР.4.3. Оформление рабочего листа 86
ЕР.5. Более сложные операции с рабочими листами 87
ЕР.5.1. Копирование ячеек и формул на одном листе 87
ЕР.5.2. Копирование формул с одного листа на другой 87
ЕР.5.3. Копирование и переименование рабочих листов 88
ЕР.6. Применение мастера диаграмм 89
ЕР.7. Применение мастера сводных таблиц 91
ЕР.8. Использование надстроек 93
Основные понятия 95
2. Представление данных в виде таблиц и диаграмм 97
Введение 98
2.1. Организация числовых данных 98
Упорядоченный массив 99
Диаграмма “ствол и листья” 100
Упражнения к разделу 2.1 102
2.2. Представление числовых данных в виде таблиц и диаграмм 105
Распределение частот 105
Выбор количества групп 105
Вычисление интервала группирования 105
Вычисление границ групп 105
Субъективность при выборе границ групп 106
Распределение относительных частот и процентное распределение 107
Функция распределения 108
Гистограмма 111
Полигон 111
Полигон интегральных процентов (кривая распределения) 113
Упражнения к разделу 2.2 115
2.3. Изображение двумерных числовых данных 118
Упражнения к разделу 2.3 120
2.4. Представление категорийных данных в виде таблиц и диаграмм 124
Сводная таблица 124
Линейчатая диаграмма 125
Круговая диаграмма 125
Диаграмма Парето 126
Упражнения к разделу 2.4 130
2.5. Представление двумерных категорийных данных в виде таблиц и графиков 134
Таблица сопряженности признаков 134
Параллельная линейчатая диаграмма 136
Упражнения к разделу 2.5 138
2.6. Искусство графического представления данных 141
Принципы графического представления данных 142
Упражнения к разделу 2.6 145
Резюме 147
Основные понятия 148
Упражнения к главе 2 149
Разбор конкретной ситуации — газета Springville Herald 164
Применение Web 164
Справочник Excel. ГЛАВА 2 165
ЕН.2.1. Корректировка распределения частот, построенного с помощью процедуры Analysis ToolPak Histogram 165
ЕН.2.2. Вычисление распределения частот с помощью функции ЧАСТОТА 165
ЕН.2.3. Корректировка гистограмм 167
ЕН.2.4. Построение гистограмм по готовым таблицам частот 168
ЕН.2.5. Построение полигонов с помощью средства Мастер диаграмм 169
ЕН.2.6. Перемещение осей диаграмм 171
ЕН.2.7. Создание таблиц для категорийных данных • 171
ЕН.2.8. Создание линейчатых и круговых диаграмм для категорийных данных 172
ЕН.2.9. Создание диаграммы Парето с помощью средства Мастер диаграмм 173
ЕН.2.10. Создание таблиц для двумерных категорийных данных 175
Дополнительная литература 176
3. Описательные статистики 177
Введение 178
3.1. Исследование числовых данных и их свойств 178
3.2. Определение среднего значения, вариации
и формы распределения 179
Медиана 183
Форма распределения 196
Упражнения к разделу 3.2 199
3.3. Вычисление описательных статистик
для генеральной совокупности 205
Математическое ожидание 206
Дисперсия и стандартное отклонение генеральной совокупности 206
Эмпирическое правило 208
Правило Бьенамэ-Чебышева 209
Упражнения к разделу 3.3 210
3.4. Анализ данных 213
Пять базовых показателей 213
Блочная диаграмма 214
Упражнения к разделу 3.4 218
3.5. Ковариация и коэффициент корреляции 221
Упражнения к разделу 3.5 227
3.6. Ловушки, связанные с описательными статистиками,
и этические проблемы 229
Этические проблемы 230
3.7. Вычисление количественных показателей
на основе распределения частот 230
Приближенное вычисление среднего арифметического и стандартного отклонения 231
Упражнения к разделу 3.7 232
Резюме 235
Основные понятия 236
Упражнения к главе 3 236
Разбор конкретной ситуации — газета The Springville Herald 247
Применение Web 247
Справочник по Excel. Глава 3 248
ЕН .3.1. Создание точечных масштабированных диаграмм 248
ЕН.3.2. Вычисление квартилей 249
Дополнительная литература 250
4. Основы теории вероятностей 251
Введение 252
4.1. Основные понятия теории вероятностей 253
Выборочное пространство и события 254
Таблица сопряженности признаков 254
Безусловная вероятность 255
Вероятность совместных событий 256
Общее правило сложения вероятностей 257
Правило сложения вероятностей взаимоисключающих событий 258
Правило сложения вероятностей исчерпывающих событий 259
Упражнения к разделу 4.1 260
4.2. Условная вероятность 265
Дерево решений 267
Статистическая независимость 269
Правило умножения вероятностей 270
Упражнения к разделу 4.2 272
4.3. Теорема Байеса 276
Упражнения к разделу 4.3 279
4.4. Этические проблемы и вероятность 281
Упражнения к разделу 4.4 281
4.5. Правила счета 281
Упражнения к разделу 4.5 283
Резюме 285
Основные понятия 285
Упражнения к главе 4 286
Применение Web 290
Справочник по Excel. Глава 4 291
ЕН.4.1. Применение оператора конкатенации 291
Дополнительная литература 291
5. Дискретные распределения 293
5.1. Распределение дискретной случайной величины 294
Математическое ожидание дискретной случайной величины 295
Дисперсия и стандартное отклонение дискретной случайной величины 296
Упражнения к разделу 5.1 297
5.2. Ковариация и ее применение в финансовом деле 300
Ковариация 300
Математическое ожидание, дисперсия и стандартное отклонение суммы двух случайных величин 301
Ожидаемая доходность и риск портфельных инвестиций 302
Упражнения к разделу 5.2 303
5.3. Биномиальное распределение 307
Свойства биномиального распределения 312
Упражнения к разделу 5.3 314
5.4. Гипергеометрическое распределение 316
Упражнения к разделу 5.4 319
5.5. Распределение Пуассона 320
Упражнения к разделу 5.5 324
5.6. Аппроксимация биномиального распределения
с помощью распределения Пуассона 326
Упражнения к разделу 5.6 328
Резюме 330
Основные понятия 330
Упражнения к главе 5 330
Разбор конкретной ситуации — газета Springville Herald 336
Применение Web 337
Справочник по Excel. Глава 5 338
ЕН.5.1. Вычисление ожидаемой доходности и риска портфельных инвестиций 338
ЕН.5.2. Вычисление биномиальных вероятностей 339
ЕН.5.3. Вычисление гипергеометрического распределения 340
ЕН.5.4. Вычисление распределения Пуассона 341
ЕН.5.5. Построение гистограмм для дискретных распределений 342
Дополнительная литература 344
6. Нормальное и другие непрерывные распределения 345
Введение 346
6.1. Нормальное распределение 347
Упражнения к разделу 6.1 364
6.2. Проверка гипотезы о нормальном распределении 368
Оценка свойств 368
Построение графика нормального распределения 369
Упражнения к разделу 6.2 376
6.3. Равномерное распределение 379
Упражнения к разделу 6.3 380
6.4. Экспоненциальное распределение 382
Упражнения к разделу 6.4 383
6.5. Введение в выборочные распределения 385
6.6. Выборочное распределение средних значений 386
Несмещенные свойства арифметического среднего 386
Стандартная ошибка среднего 388
Выборки из нормально распределенных генеральных совокупностей 389 Выборки из генеральных совокупностей, распределения которых отличаются от нормального 393
Упражнения к разделу 6.6 398
6.7. Выборочное распределение долей 402
Упражнения к разделу 6.7 403
6.8. Аппроксимация биномиального и пуассоновского
распределений с помощью нормального распределения 407
Поправка на непрерывность распределения 407
Аппроксимация биномиального распределения 408
Аппроксимация распределения Пуассона 410
Упражнения к разделу 6.8 411
6.9. Выборки из конечных генеральных совокупностей 413
Упражнения к разделу 6.11 415
6.10. Применение стандартизованного нормального распределения 416
Преобразование данных 416
Использование таблиц нормального распределения 417
Вычислений вероятностей, соответствующих заданным значениям 420
Вычисление значений, соответствующих заданным вероятностям 424
Резюме 428
Основные понятия 428
Упражнения к разделу 6 429
Разбор конкретной ситуации — газета Springville Herald 437
Применение Web 437
Применение Web 438
Справочник по Excel, глава 6 439
ЕН.6.1. Вычисление вероятностей нормального распределения 439
ЕН.6.2. Построение графика нормального распределения 440
ЕН.6.3. Вычисление вероятностей экспоненциального распределения 443
ЕН.6.4. Генерирование случайных выборок 443
ЕН .6.5. Построение гистограмм для вычисленных выборочных средних 444
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА 445
7. Построение доверительных интервалов 447
Введение 448
7.1. Построение доверительного интервала для математического ожидания генеральной совокупности при известном стандартном отклонении 449
Упражнения к разделу 7.1 454
7.2. Построение доверительного интервала для математического ожидания генеральной совокупности при неизвестной дисперсии 456
Распределение Стьюдента 456
Степени свободы 458
Доверительный интервал 458
Упражнения к разделу 7.2 463
7.3. Построение доверительного интервала для доли признака
в генеральной совокупности 466
Упражнения к разделу 7.3 469
7.4. Определение объема выборки 471
Определение объема выборки для оценки математического ожидания 471
Определение объема выборки для оценки доли признака в генеральной совокупности 474
Упражнения к разделу 7.4 477
7.5. Применение доверительных интервалов в аудиторском деле 480
Оценка суммы элементов генеральной совокупности 481
Оценка разности 483
Односторонняя оценка доли нарушений установленных правил 487
Упражнения к разделу 7.5 488
7.6. Доверительные интервалы и этические проблемы 490
7.7. Вычисление оценок и объема выборок, извлеченных из конечной генеральной совокупности 491
Оценка математического ожидания 491
Оценка доли признака 492
Определение объема выборки 493
Упражнения к разделу 7.7 496
Резюме 498
Основные понятия 498
Упражнения к главе 7 499
Разбор конкретной ситуации — газета Springville Herald 507
Применение Web 510
Справочник по Excel. Глава 7 511
ЕН.7.1. Вычисление доверительного интервала для математического ожидания при известном стандартном отклонении ст 511
ЕН.7.2. Вычисление доверительного интервала для математического ожидания при неизвестном стандартном отклонении ст 512
ЕН.7.3. Вычисление доверительного интервала для доли признака в генеральной совокупности 512
ЕН.7.4. Определение объема выборки для математического ожидания генеральной совокупности 513
ЕН.7.5. Определение объема выборки для оценки доли признака в генеральной совокупности 514
ЕН.7.6. Вычисление доверительного интервала, содержащего общую сумму элементов генеральной совокупности 515
ЕН.7.7. Вычисление доверительного интервала, содержащего полную разность генеральной совокупности 516
Дополнительная литература 518
8. Основы проверки гипотез: одновыборочные критерии 519
Введение 520
8.1. Проверка гипотез 520
Нулевая и альтернативная гипотеза 520
Критическое значение тестовой статистики 522
Области отклонения и принятия гипотез 522
Риски, возникающие при проверке гипотез 523
Упражнения к разделу 8.1 525
8.2. Использование Z-критерия для проверки гипотезы о математическом ожидании при известном стандартном отклонении 526
Проверка гипотез с помощью критического значения 527
Проверка гипотез по наблюдаемому уровню значимости 529
Связь между построением доверительных интервалов и проверкой гипотез 532
Упражнения к разделу 8.2 533
8.3. Односторонние критерии 535
Применение критического значения 535
Применение наблюдаемого уровня значимости 537
Упражнения к разделу 8.3 538
8.4. Использование t-критерия для проверки гипотезы о математическом ожидании при неизвестном стандартном отклонении 540
Упражнения к разделу 8.4 547
8.5. Применение Z-критерия для проверки гипотезы о доле признака в генеральной совокупности 551
Упражнения к разделу 8.5 554
8.6. Потенциальные проблемы и этические вопросы, связанные с проверкой гипотез 556
Метод сбора данных — рандомизация 557
Добросовестность респондентов 557
Вид критерия — двусторонний или односторонний 557
Выбор уровня значимости 557
Подтасовка данных 558
Очистка и отбрасывание данных 558
Документирование результатов 558
Статистическая значимость и практическая ценность 558
8.7. Мощность критерия 559
Упражнения к разделу 8.7 565
Резюме 566
Основные понятия 567
Упражнения к главе 8 568
Разбор конкретной ситуации— газета Springville Herald 573
Применение Web 573
Справочник по Excel. Глава 8 574
ЕН.8.1. Использование Z-критерия проверки гипотез о математическом ожидании при известном стандартном отклонении 574
ЕН.8.2. Использование t-критерия для проверки гипотез о математическом ожидании при неизвестном стандартном отклонении 575
ЕН.8.3. Применение Z-критерия для проверки гипотез о доле признака в генеральной совокупности 577
Дополнительная литература 578
9. Двухвыборочные критерии 579
Введение 580
9.1. Сравнение двух независимых выборок: критерии для оценки разности между двумя математическими ожиданиями 580
Использование Z-критерия для оценки разности между двумя математическими ожиданиями 580
Применение t-критерия для оценки разности между математическими ожиданиями с помощью суммарной дисперсии 581
Доверительный интервал для разности между математическими ожиданиями 588
Использование t-критерия для оценки разности между двумя математическими ожиданиями с помощью раздельной дисперсии 588
Упражнения к разделу 9.1 590
9.2. Сравнение двух зависимых выборок: критерии для оценки разности между двумя математическими ожиданиями 595
Доверительный интервал, содержащий разность между двумя математическими ожиданиями 601
Упражнения к разделу 9.2 601
9.3. Использование Z-критерия для оценки разности между двумя долями признака 604
Доверительный интервал, содержащий разность между долями успехов в двух независимых группах 608
Упражнения к разделу 9.3 609
9.4. Использование F-критерия для оценки разности между двумя дисперсиями 611
Вычисление нижнего критического значения 613
Упражнения к разделу 9.4 618
Резюме 622
Основные понятия 623
Упражнения к главе 9 623
Разбор конкретной ситуации — газета Springville Herald 631
Применение Web 632
Справочник по Excel. Глава 9 633
ЕН.9.1. Применение t-критерия, использующего суммарную дисперсию для проверки гипотез о разности между двумя математическими ожиданиями 633
ЕН.9.2. Сгруппированные и разгруппированные данные 635
ЕН.9.3. Применение Z-критерия для проверки гипотез о разности между двумя долями 636
ЕН.9.4. Использование F-критерия для проверки гипотез о разности между дисперсиями 638
Дополнительная литература 640
10. Дисперсионный анализ 615
Введение 642
10.1. Полностью рандомизированный эксперимент: однофакторный дисперсионный анализ 642
Использование F-критерия для оценки разностей между несколькими математическими ожиданиями 643
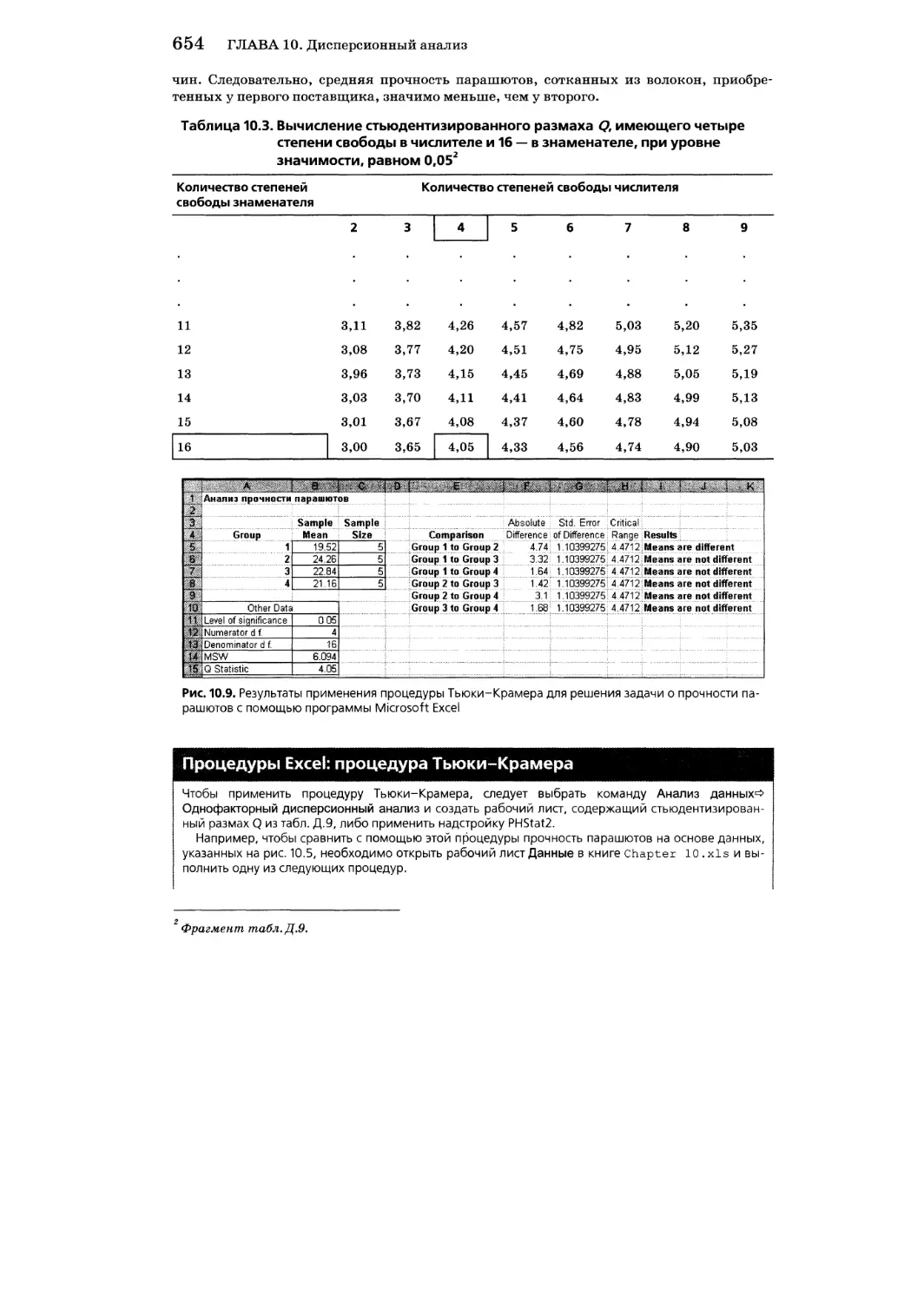
Множественное сравнение: процедура Тыоки-Крамера 652
Необходимые условия однофакторного дисперсионного анализа 655
Критерий Левенэ для проверки однородности дисперсии 656
Упражнения к разделу 10.1 658
10.2. Двухфакторный дисперсионный анализ 664
Оценка факторов и эффектов взаимодействия 664
Интерпретация эффектов взаимодействия 672
Множественные сравнения 675
Упражнения к разделу 10.2 676
10.3. Блочный рандомизированный эксперимент 681
Критерии для оценки эффектов условий факторного эксперимента и блоков 682
Множественные сравнения: процедура Тьюки 688
Упражнения к разделу 10.3 689
Резюме 693
Основные понятия 693
Упражнения к главе 10 694
Разбор конкретной ситуации — газета Springville Herald 700
Применение Web 702
Справочник по Excel. Глава 10 703
ЕН. 10.1. Процедура Тьюки-Крамера 703
ЕН. 10.2. Вычисление разностей между наблюдениями и медианами 705
Дополнительная литература 706
11. Критерий "хи-квадрат" и непараметрические критерии 707
Введение 708
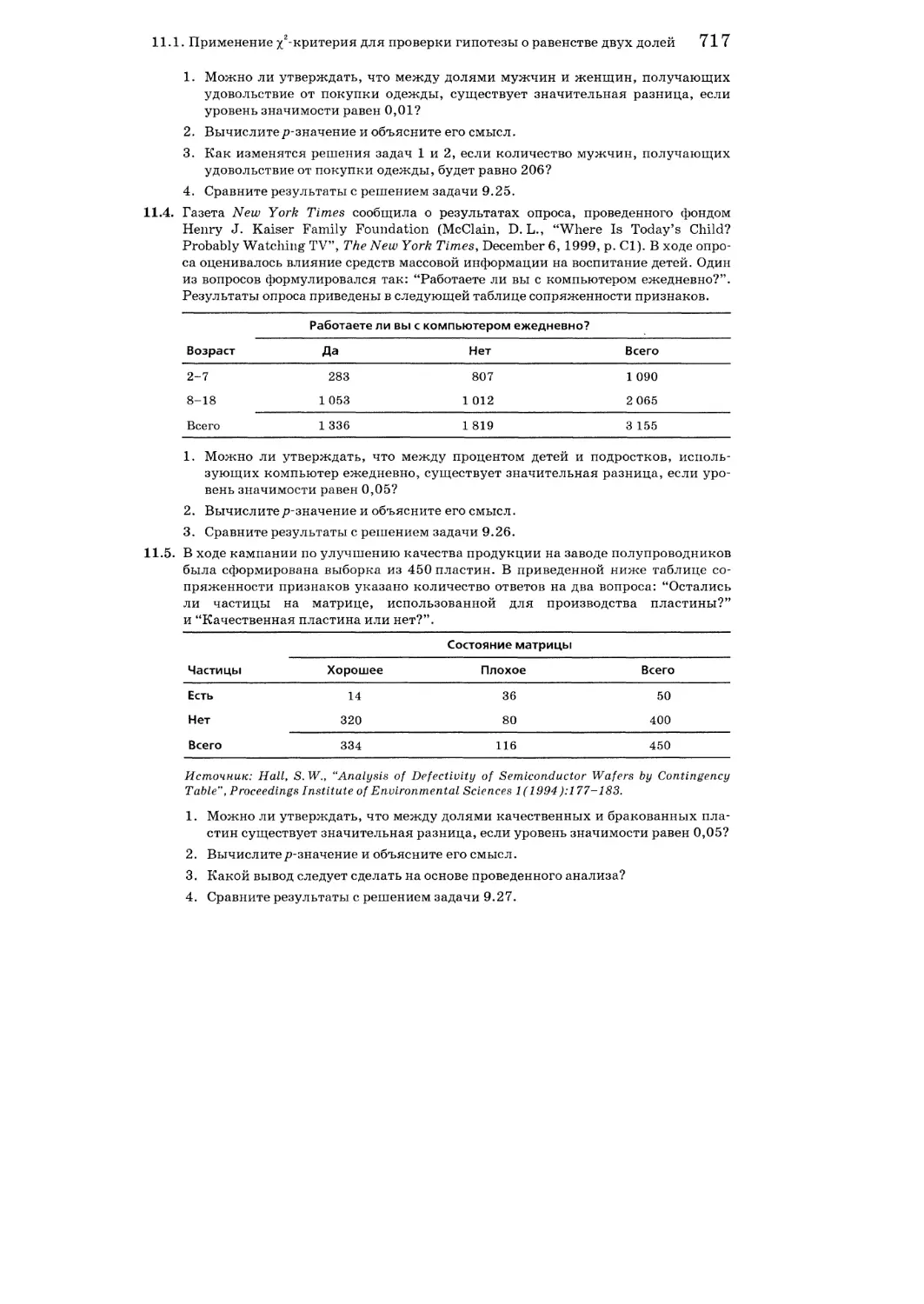
11.1. Применение %2-критерия для проверки гипотезы о равенстве двух долей 708
Упражнения к разделу 11.1 716
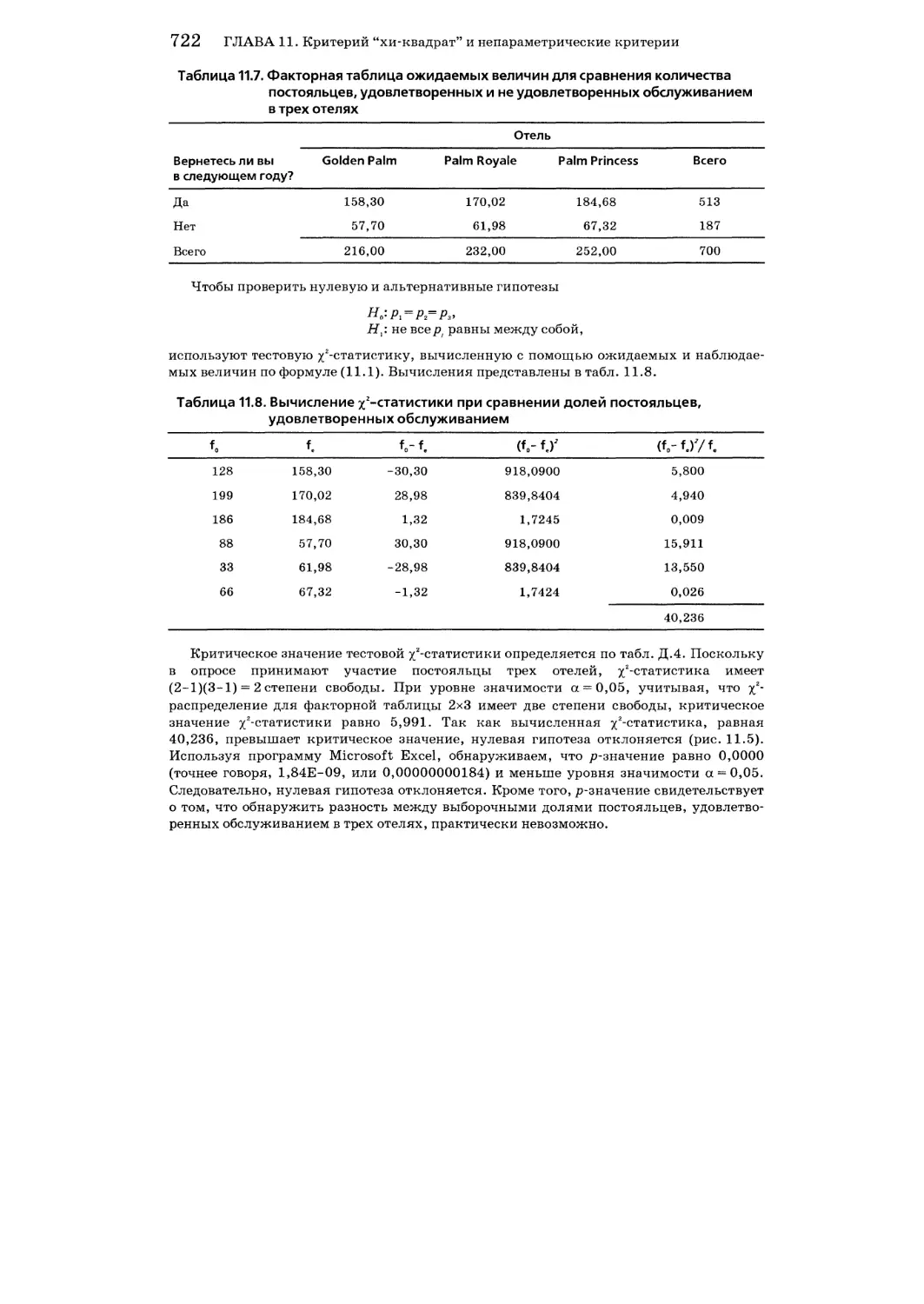
11.2. Применение %2-критерия для проверки гипотезы о равенстве нескольких долей 719
Упражнения к разделу 11.2 727
11.3. Применение %2-критерия независимости 730
Упражнения к разделу! 1.3 736
11.4. Ранговый критерий Уилкоксона: непараметрический метод для проверки гипотезы о разности между двумя медианами 739
Упражнения к разделу 11.4 744
11.5. Ранговый критерий Крускала—Уоллиса: непараметрический метод для полностью рандомизированного эксперимента 748
Упражнения к разделу 11.5 753
11.6. Критерий “хи-квадрат” для дисперсий 755
Упражнения к разделу 11.6 760
11.7. Критерий согласия “хи-квадрат” 763
Использование %2-критерия согласия для распределения Пуассона 763
Применение %2-критерия согласия для нормального распределения 765
Упражнения к разделу 11.7 768
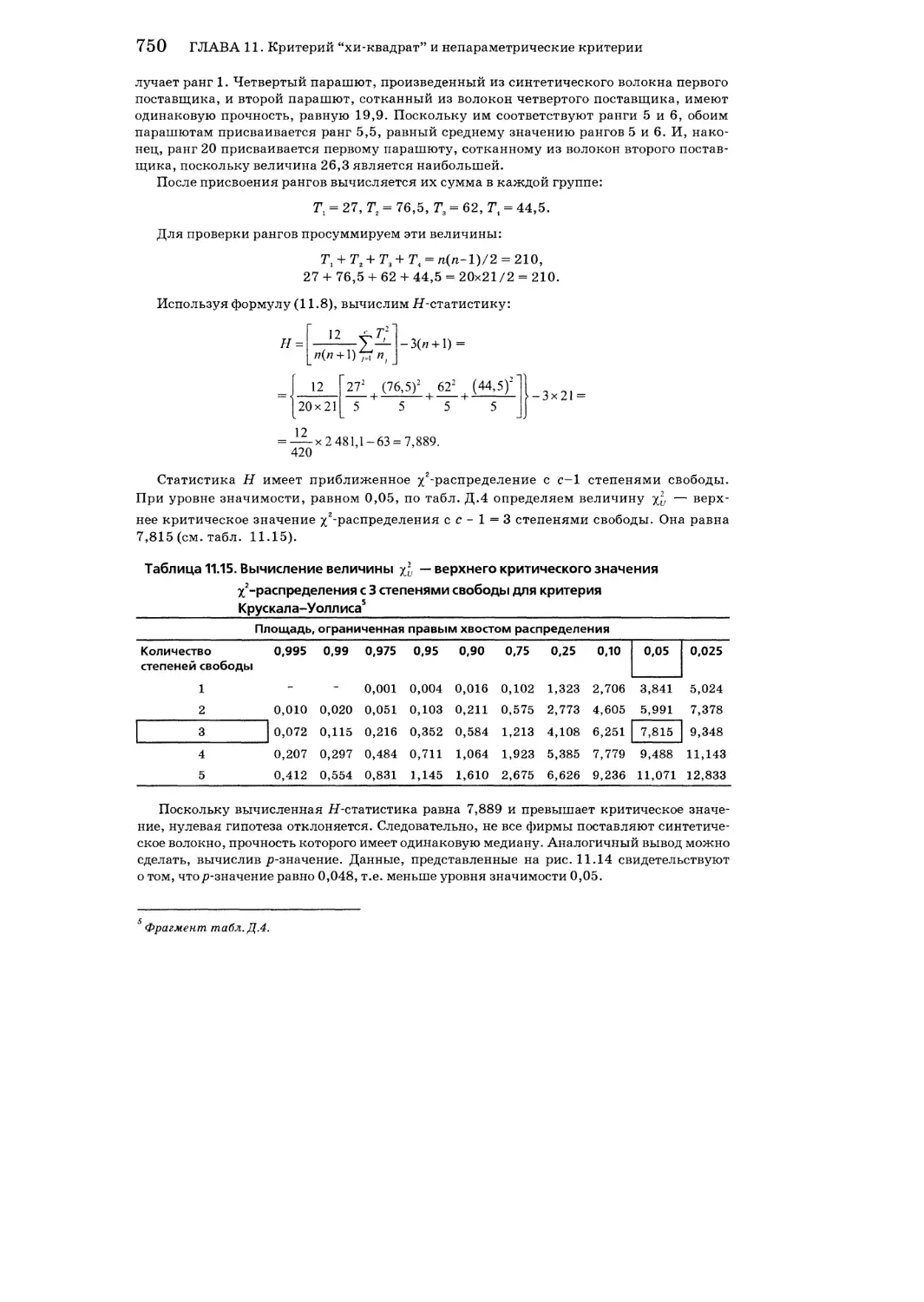
Резюме 770
Основные понятия 770
Упражнения к главе 11 770
Разбор конкретной ситуации — газета Springville Herald 777
Применение Web 779
Справочник по Excel. Глава 11 780
ЕН. 11.1. Применение %2-критерия для оценки разности между двумя долями 780
ЕН.11.2. Применение %2-критерия для оценки разностей между с долями 782
ЕН.11.3. Применение процедуры Мараскуило 783
ЕН. 11.4. Применение %2-критерия независимости 784
ЕН. 11.5. Ранговый критерий Уилкоксона для проверки гипотезы о разности между двумя медианами 786
ЕН. 11.6. Критерий Крускала-Уоллиса для проверки гипотезы о разностях между несколькими медианами 788
Дополнительная литература 790
12. Простая линейная регрессия 791
Введение 792
12.1. Виды регрессионных моделей 793
12.2. Вывод уравнения простой линейной регрессии 795
Метод наименьших квадратов 796
Прогнозирование в регрессионном анализе: интерполяция и экстраполяция 800
Упражнения к разделу 12.2 802
12.3. Оценки изменчивости 806
Вычисление сумм квадратов 806
Коэффициент смешанной корреляции 808
Среднеквадратичная ошибка оценки 809
Упражнения к разделу 12.3 810
12.4. Предположения 811
12.5. Анализ остатков 812
Оценка пригодности эмпирической модели 812
Проверка условий 815
Упражнения к разделу 12.5 817
12.6. Измерение автокорреляции: статистика Дурбина—Уотсона 818
Распознавание автокорреляции с помощью графика остатков 819
Статистика Дурбина-Уотсона 820
Упражнения к разделу 12.6 823
12.7. Проверка гипотез о наклоне и коэффициенте корреляции 827
Применение t-критерия для наклона 827
Применение F-критерия для наклона 828
Доверительный интервал, содержащий наклон 0, 830
Использование t-критерия для коэффициента корреляции 831
Упражнения к разделу 12.7 831
12.8. Оценка математического ожидания и предсказание индивидуальных значений 836
Построение доверительного интервала 836
Вычисление доверительного интервала для предсказанного значения 837
Упражнения к разделу 12.8 840
12.9. Подводные камни и этические проблемы, связанные с применением регрессии 841
12.10. Вычисления, связанные с простой линейной регрессией 845
Вычисление сдвига Ьо и наклона Ьх 845
Вычисление оценок вариации 847
Вычисление среднеквадратичной ошибки наклона 848
Резюме 850
Основные понятия 852
Упражнения к главе 12 852
Разбор конкретной ситуации — газета Springville Herald 865
Применение Web 866
Справочник по Excel. Глава 12 867
ЕН.12.1. Выполнение простого линейного регрессионного анализа 867
ЕН. 12.2. Добавление линии регрессии на диаграмму разброса 867
ЕН. 12.3. Модификация диаграмм разброса и графиков остатков 868
ЕН. 12.4. Вычисление статистики Дурбина-Уотсона 870
ЕН. 12.5. Вычисление доверительных интервалов
для математического ожидания и предсказанного значения отклика 870
Дополнительная литература 872
13. Введение в множественную регрессию 873
Введение 874
13.1. Модель множественной регрессии 874
Интерпретация регрессионных коэффициентов 875
Предсказание значений зависимой переменной Y 878
Коэффициент множественной смешанной корреляции 879
Упражнения к разделу 13.1 882
13.2. Анализ остатков для модели множественной регрессии 886
Упражнения к разделу 13.2 890
13.3. Проверка значимости модели множественной регрессии 890
Упражнения к разделу 13.3 892
13.4. Статистические выводы о генеральной совокупности коэффициентов регрессии 893
Проверка гипотез 894
Доверительные интервалы 895
Упражнения к разделу 13.4 896
13.5. Оценка значимости поясняющих переменных в модели множественной регрессии 898
Коэффициент частной смешанной корреляции 903
Упражнения к разделу 13.5 905
13.6. Регрессионные модели с фиктивной переменной и эффекты взаимодействия 907
Эффект взаимодействия 910
Упражнения к разделу 13.6 917
Резюме 926
Основные понятия 926
Упражнения к главе 13 926
Разбор конкретной ситуации — газета Springville Herald 931
Применение Web 931
Справочник по Excel. Глава 13 932
ЕН. 13.1. Вычисление коэффициентов множественной регрессии 932
ЕН. 13.2. Построение доверительных интервалов для математического ожидания и предсказанного значения отклика 932
ЕН. 13.3. Построение диаграммы разброса остатков по предсказанным значениям отклика 935
ЕН. 13.4. Вычисление коэффициентов частной смешанной корреляции 935
Дополнительная литература 936
14. Построение моделей множественной регрессии 937
14.1. Модель квадратичной регрессии 938
Вычисление коэффициентов регрессии и предсказание отклика 939
Проверка значимости квадратичной модели 942
Оценка квадратичного эффекта 943
Вычисление коэффициента множественной смешанной корреляции 946
Упражнения к разделу 14.1 946
14.2. Преобразование данных в регрессионных моделях 949
Извлечение квадратного корня 949
Логарифмическое преобразование 951
Упражнения к разделу 14.2 954
14.3. Коллинеарность 956
Упражнения к разделу 14.3 957
14.4. Построение модели 958
Пошаговый подход к построению регрессионной модели 960
Метод выбора наилучшего подмножества 962
Упражнения к разделу 14.4 970
14.5. Ловушки и этические проблемы, связанные со множественной регрессией 972
Ловушки множественной регрессии 972
Этические вопросы 972
Резюме 972
Основные понятия 974
Упражнения к главе 14 974
Разбор конкретной ситуации — корпорация Mountain States Potato 980
Применение Web 981
Дополнительная литература 981
15. Анализ временных рядов 983
Введение 984
15.1. Прогнозирование в бизнесе 984
15.2. Компоненты классической мультипликативной модели временных рядов 985
15.3. Сглаживание годовых временных рядов 988
Скользящие средние 989
Экспоненциальное сглаживание 992
Упражнения к разделу 15.3 996
15.4. Вычисление трендов с помощью метода наименьших квадратов и прогнозирование 999
Модель линейного тренда 999
Модель квадратичного тренда 1002
Модель экспоненциального тренда 1004
Выбор модели на основе разностей первого и второго порядка, а также относительных разностей 1011
Упражнения к разделу 15.4 1014
15.5. Вычисление тренда с помощью авторегрессии и прогнозирование 1019
Упражнения к разделу 15.5 1031
15.6. Выбор адекватной модели прогнозирования 1032
Анализ остатков 1033
Измерение абсолютной и среднеквадратичной остаточных погрешностей 1033
Принцип экономии 1034
Сравнение четырех методов прогнозирования 1034
Упражнения к разделу 15.6 1037
15.7. Прогнозирование временных рядов на основе сезонных данных 1038
Прогнозирование месячных и временных рядов с помощью метода наименьших квадратов 1040
Упражнения к разделу 15.7 1045
15.8. Индексы 1049
Индекс цен 1049
Невзвешенные составные индексы цен 1051
Взвешенные составные индексы цен 1052
Некоторые популярные индексы цен 1054
Упражнения к разделу 15.8 1055
15.9. Ловушки, связанные с анализом временных рядов 1060
Резюме 1060
Основные понятия 1060
Упражнения к главе 15 1062
Разбор конкретной ситуации — газета Springville Herald 1069
Применение Web 1069
Справочник по Excel. Глава 15 1070
ЕН. 15.1. Создание графиков скользящих средних 1070
ЕН.15.2. Создание графиков экспоненциального сглаживания 1070
ЕН. 15.3. Создание диаграмм разброса для трендов, построенных методом наименьших квадратов 1071
ЕН.15.4. Логарифмическое преобразование 1072
ЕН. 15.5. Создание диаграмм разброса с экспоненциальным трендом 1072
ЕН.15.6. Создание графиков для авторегрессионных моделей 1073
Дополнительная литература 1074
16. Принятие решений 1075
Введение 1076
16.1. Таблица выигрышей и дерево решений 1077
Упражнения к разделу 16.1 1082
16.2. Критерии принятия решений 1083
Ожидаемая прибыль 1083
Ожидаемый размер упущенной выгоды 1085
Отношение “доходность/риск” 1087
Упражнения к разделу 16.2 1090
16.3. Принятие решений на основе выборочной информации 1096
Упражнения к разделу 16.3 1099
16.4. Полезность 1101
Упражнения к разделу 16.4 1102
Резюме 1102
Основные понятия 1103
Упражнения к главе 16 1104
Применение Web 1108
Справочник по Excel. Глава 16 1109
ЕН. 16.1. Анализ упущенной выгоды 1109
ЕН. 16.2. Применение критериев принятия решений на основе таблицы выигрышей 1110
Дополнительная литература 1112
17. Статистические методы управления качеством и производительностью труда 1113
Введение 1114
17.1. Полный контроль качества 1115
17.2. Метод Six Sigma® 1118
17.3. Контрольные карты 1119
17.4. Процентные контрольные карты 1121
Упражнения к разделу 17.4 1127
17.5. Эксперимент с красными шарами: вариация процесса 1129
Упражнения к разделу 17.5 1132
17.6. Контрольные карты для размаха и среднего значения 1132
Контрольная карта для размаха: Я-карта 1132
Контрольная X -карта 1135
Упражнения к разделу 17.6 1138
17.7. Характеристики процесса 1143
Удовлетворение клиентов и допускаемые пределы 1143
Показатели мощности 1145
Показатели CPL, CPU и С,А 1146
Упражнения к разделу 17.7 1148
Резюме 1149
Основные понятия 1150
Упражнения к главе 17 1150
Разбор конкретной ситуации — компания Harnswell Sewing Machine Company 1155
Разбор конкретной ситуации — газета Springville Herald 1159
Справочник по Excel. Глава 17 1162
ЕН. 17.1. Вычисление контрольных границ и координат точек нар-карте 1162
ЕН.17.2. Созданиер-карт 1163
ЕН. 17.3. Построение R- и X -карт 1165
ЕН. 17.4. Создание R- и X -карт 1167
Дополнительная литература 1167
Ответы на избранные вопросы 1169
Глава 1 1169
Глава 2 1171
Глава 3 1174
Глава 4 1179
Глава 5 1180
Глава 6 1182
Глава 7 1184
Глава 8 1186
Глава 9 1189
Глава 10 1193
Глава 11 1195
Глава 12 1198
Глава 13 1202
Глава 14 1207
Глава 15 1211
Глава 16 1214
Глава 17 1215
Приложение А. Некоторые правила алгебры и арифметики 1217
А.1. Правила выполнения арифметических операций 1217
А.2. Правила возведения в степень и извлечения корня 1217
А.З. Правила вычисления логарифмов 1218
Десятичный логарифм 1218
Натуральный логарифм 1218
Приложение Б. Правила суммирования 1219
Задача 1222
Дополнительная литература 1222
Приложение В. Статистические обозначения и греческий алфавит 1223
В.1. Статистические обозначения 1223
В.2. Греческий алфавит 1223
Приложение Г. Обзор компакт-диска 1225
Файлы, содержащиеся в каталоге Excel 1226
Приложение Д. Таблицы 1235
Приложение Е. Установка и настройка программы
Microsoft Excel 1285
Е.1. Введение
1285
Е.2. Необходимые условия инсталляции 1285
Е.З. Общие параметры 1286
Е.4. Настройка интерфейса 1286
Е.5. Установки печати 1287
Приложение Ж. Дополнительные сведения о программе PHStat 1289
Ж.1. Введение 1289
Ж.2. Установка программы Phstat2 1289
Ж.З. Запуск инсталляции программы Phstat2 1290
Ж.4. Применение программы Phstat2 1290
Ж.5. Подготовка данных для анализа с помощью программы Phstat2 1291
Ж.6. Чего не может программа Phstat2 1291
Ж.7. Дополнительная информация 1291
Приложение 3. Подготовка отчетов и презентаций с помощью пакета Microsoft Office 1293
3.1. Работа с пакетом Microsoft Office: обмен данными между программами Microsoft Excel и Microsoft Word 1293
3.2. Применение пакета Microsoft Office: использование таблиц и диаграмм, созданных программой Microsoft Excel, для презентаций Microsoft Powerpoint 1295
3.3. Использование пакета Microsoft Office: сохранение рабочих листов в виде Web-страницы для браузера Internet Explorer 1298
3.4. Применение пакета Microsoft Office: извлечение форматированных табличных данных из World Wide Web с помощью браузера 1301
3.5. Применение пакета Microsoft Office: извлечение данных
из World Wide Web с помощью браузера 1302
Предметный указатель 1305
Предисловие
Принципы обучения
Многие годы читая вводный курс статистики, мы постоянно стремились улучшить стиль преподавания. Наши подходы к изложению вводного курса коммерческой статистики оттачивались в ходе активных дискуссий на конференциях “Эффективность преподавания статистики в школах бизнеса” (“Making Statistics More Effective in Schools of Business”), проводимых Институтом поддержки принятия решений (Decision Science Institute) и Американской статистической ассоциацией (American Statistical Association), а также в процессе обучения различных групп студентов в больших университетах. В итоге нашу точку зрения можно изложить в виде следующих принципов.
1. Преподавание статистики необходимо сопровождать примерами из практики, особенно если статистика не является основной специализацией студентов. Область применения статистики при обучении студентов школ бизнеса должна включать в себя различные коммерческие приложения, в частности, бухгалтерское дело, экономическую и финансовую науку, информационные системы, менеджмент, а также маркетинг. Любая тема должна иллюстрироваться приложениями хотя бы в одной из указанных областей бизнеса.
2. Практически все студенты, изучающие вводный курс коммерческой статистики, специализируются в иных областях знаний. Вводный курс должен фокусировать их внимание на основополагающих принципах, которые могут оказаться полезными при овладении другими науками.
3. Изложение любой темы вводного курса статистики непременно должно сопровождаться применением электронных таблиц и/или статистического программного обеспечения, поскольку они, как правило, являются частью рабочего места руководителя. Осознавая этот факт, мы должны привести наши подходы к преподаванию коммерческой статистики в соответствие с требованиями практики.
4. Учебники, в которых описывается применение программного обеспечения, должны содержать подробные инструкции, облегчающие студентам освоение программ. Однако программное обеспечение не должно быть доминирующей темой.
5. При изложении любой темы основное внимание следует уделять ее применению в конкретной сфере бизнеса, интерпретации результатов, формулировке и оценке гипотез, а также обсуждению действий, которые необходимо предпринять, если предположения не выполняются. Эти вопросы особенно важны при изучении регрессии, а также методов прогнозирования и проверки гипотез. Несмотря на то что некоторые вычисления требуют пояснений, описание вычислительных процедур должно быть минимальным.
6. Примеры, рассматриваемые на занятиях, и домашние задания должны иметь практический смысл и основываться на реальных данных. Студенты обязаны овладеть приемами работы с наборами данных любого объема и легко переходить от статистических вычислений к интерпретации результатов для принятия решений.
7. В рамках вводного курса следует избегать излишней концентрации внимания на одном из разделов (например, на проверке гипотез). Напротив, необходимо как можно шире осветить различные темы статистики. Это поможет студентам избежать распространенной ошибки, когда за деревьями не видят леса.
Изменения, внесенные в новое издание
В четвертое издание книги внесено много новшеств.
• Изменен порядок изложения тем в главах, посвященных методам проверки гипотез. Теперь все критерии, связанные с нормальным и t-распределениями, рассматриваются до описания F-критерия для проверки гипотез о разности между двумя дисперсиями. Сам F-критерий описывается в конце главы 9, “Двухвыборочные критерии”. Кроме того, описание непараметрических критериев выделено в отдельную главу 11, “Критерий “хи-квадрат” и непараметрические критерии”. Преобразование этих глав позволяет преподавателям рассмотреть критерии, связанные с нормальным и t-распределениями, в рамках одной темы, не нарушая логической последовательности.
• Сведения о программе Excel излагаются так, что теперь ее можно использовать как совместно с надстройкой PHStat2, так и независимо от нее. В новом издании результаты применения программы Excel рассматриваются внутри главы, что позволяет использовать их для интерпретации решений, подавляющее большинство которых получено без помощи надстроек. Упрощены инструкции и описание диалоговых окон программы Excel. Теперь они ясно демонстрируют, как выполнить статистический анализ, используя программу Excel как совместно с надстройкой PHStat2, так и независимо от нее. Таким образом, четвертое издание книги представляет собой вводный курс коммерческой статистики, предоставляющий читателям выбор: применять программу Excel с надстройками или без них.
• В книгу включены сотни новых реалистичных примеров и упражнений, использующих данные из журналов Wall Street Journal, USA Today, Consumer Reports, а также из других источников.
• Обновлена надстройка PHStat2. Теперь к учебнику прилагается программа PHStat2 version 2.5— новейшая версия надстройки для программы Microsoft Excel, разработанная компанией Prentice Hall. Эта версия надстройки позволяет работать с новыми средствами обеспечения безопасности, предусмотренными в пакете Microsoft Office, и применять множественную регрессию, когда значения независимых переменных расположены в несмежных столбцах. Кроме того, улучшены средства изображения диаграмм “ствол и листья” и блочных диаграмм, включены Z-критерий для проверки гипотезы о разности между математическими ожиданиями, критерий Левина для проверки гипотезы об однородности дисперсии, а также процедура Мараскуило (Marascuilo) для множественного сравнения долей признака. Версия 2.5 полностью поддерживается на обновленном Web-сайте www. prenhall. com/phstat.
• Перестроены и переписаны разделы “Справочника по Excel”. Теперь эти разделы позволяют не прибегать к помощи надстройки PHStat2. Кроме того, они предоставляют читателям возможность анализировать устройство рабочих листов, создаваемых надстройкой PHStat2. Разделы “Справочника по Excel” по-прежнему расположены в конце глав и содержат детальную информацию, необходимую для создания рабочих листов, выполняющих статистический анализ с помощью программы Microsoft Excel.
• Применение сети Web. В книге появились новые разделы под названием “Применение Web”. Они посвящены статистическому анализу данных и проверке правдивости информации. В этих разделах студентам предлагается посетить Web-сайты компаний, упомянутых в сценариях “Применение статистики”. Эти сценарии излагаются в начале каждой главы. В отличие от традиционных задач, содержащих лишь необходимые данные, на Web-сайтах, как и в реальной жизни, часто содержится противоречивая либо избыточная информация. Задачи, описанные в разделах “Применение Web”, должны развивать у студентов критический образ мышления. Для того чтобы вызвать интерес у читателей, некоторые задачи формулируются в шутливой форме. Примеры из этих разделов идеально подходят для выполнения групповых проектов и всестороннего обсуждения на семинарах.
• В приложении “Подготовка отчетов и презентаций с помощью пакета Microsoft Office” описываются способы внедрения результатов, полученных с помощью программы Microsoft Excel, в документы, подготовленные текстовым процессором Microsoft Word. Кроме того, в этом приложении описываются способы подготовки презентаций с помощью программы Microsoft PowerPoint, а также применение браузера Internet Explorer и программы Microsoft Excel для извлечения данных из World Wide Web.
• Некоторые темы изложены более полно. В текст включены новые темы, например, метод Six Sigma®, критерий Левина для проверки гипотезы об однородности дисперсии, а также описание равномерного распределения. Кроме того, в книгу добавлены новые разделы, посвященные вычислению распределений частот, правилам счета, аппроксимации биномиального распределения с помощью распределения Пуассона, аппроксимации нормального распределения с помощью биномиального и пуассоновского распределения, применению таблицы стандартизованного нормального распределения, мощности критерия, блочным рандомизированным экспериментам, /2-критерию для дисперсии и /2-критерию согласия.
• Увеличено количество примеров, посвященных управлению газетой Springville Herald. Теперь эти примеры описаны в 13 главах.
Особенности
Мы продолжили традиции, заложенные в предыдущих изданиях. Отметим некоторые особенности.
• Деловые сценарии “Применение статистики”. Каждая глава начинается с примера, демонстрирующего применение статистики в конкретной области бизнеса — бухгалтерском деле, менеджменте или маркетинге. Этот сценарий анализируется на протяжении всей главы и образует основу для описания прикладных аспектов статистических понятий.
• Основное внимание уделяется анализу данных и интерпретации результатов, полученных с помощью программного обеспечения. Мы считаем, что применение статистического программного обеспечения, в частности программы Microsoft Excel, является неотъемлемой частью обучения статистике. В связи с этим основное внимание в книге уделяется анализу данных и интерпретации результатов, полученных с помощью программы Microsoft Excel, а сам процесс вычислений остается в тени. Например, в главе 2 основное внимание уделяется интерпретации различных диаграмм, а не способам их создания. При описании методов проверки гипотез в главах 8-11 вычисление p-значений, связанное со сложными вычислениями, сопровождается многочисленными иллюстрациями. Кроме того, рассматривая простую линейную регрессию в главе 12, мы предполагали, что читатели применяют программу
Microsoft Excel, поэтому основное внимание уделили интерпретации результатов, а не вычислительным процедурам (которые описаны в отдельном разделе.)
• Надстройка PHStat2l расширяет функциональные возможности программы Microsoft Excel и позволяет читателю выбирать пункты низкоуровневых меню и заполнять поля рабочих листов, предназначенных для статистического анализа. В сочетании с собственной надстройкой Microsoft Excel — программой Data Analysis ToolPak — программа PHStat2 позволяет освоить практически все статистические методы, относящиеся к вводному курсу статистики.
• Педагогические приемы, к которым относятся активный, разговорный стиль изложения; врезки, выделяющие важные понятия; врезки, содержащие пронумерованные формулы; примеры, иллюстрирующие основные понятия; врезки, содержащие предположения, необходимые для применения статистических методов; резюме, сопровождающие каждую главу; разделение задач на две категории — “Изучение основ” и “Применение понятий”, а также предметные указатели в конце каждой главы, позволяют читателям легче освоить вводный курс статистики.
• В конце книги приведены ответы на большинство задач, имеющих четные номера.
• Упражнения, связанные с написанием отчетов, позволяют читателям применить результаты статистического анализа в деловых приложениях, а также освоить приемы работы с пакетом Microsoft Office, в частности, вставку таблиц и диаграмм, созданных программой Microsoft Excel, в документы, подготовленные с помощью текстового процессора Microsoft Word, и презентации, оформленные с помощью программы Microsoft PowerPoint.
• Упражнения, связанные с применением Интернет, размещенные на Web-сайте www.prenhall.com/levine, позволяют студентам исследовать источники данных, доступные в сети World Wide Web.
• В конце каждой главы рассматриваются практические ситуации и групповые проекты. В большинстве глав исследуются ситуации, связанные с работой газеты The Springville Herald. Групповые проекты, в основном, относятся к изучению функционирования взаимных фондов.
• Программа Visual Exploration, распространяемая на прилагаемом компакт-диске, позволяет студентам исследовать важные понятия статистики в интерактивном режиме. В частности, с ее помощью можно изучать описательную статистику, понятие о вероятности, свойства нормального распределения и регрессионный анализ. Например, изучая описательную статистику, студент может наблюдать влияние, которое изменение данных оказывает на математическое ожидание, медиану и стандартное отклонение. Осваивая понятие о вероятности, студенты могут исследовать влияние объема выборки на распределение вероятности. Рассматривая нормальное распределение, они могут воочию убедиться, как изменения математического ожидания и стандартного отклонения влияют на площадь фигур, ограниченных нормальной кривой. В регрессионном анализе студенты могут исследовать влияние наклона и длины отрезка, отсекаемого линией регрессии на координатной оси, на точность приближения.
‘Особенности работы надстройки PHStat2 с локализованными версиями программы Excel описаны в приложении Ж в разделе Ж.7, “Дополнительная информация ”. — Прим. ред.
Изменения в содержании четвертого издания
• Глава 1 содержит совершенно новые разделы 1.1-1.7. Раздел “Типы данных” теперь следует за разделом “Методы выборочного обследования”.
• Раздел “Букварь Excel” переписан и перестроен.
• Глава 2 содержит обновленные данные, касающиеся работы взаимных фондов за период с 1997 по 2001 гг., а также пример, связанный с применением сети Web.
• Глава 3 содержит обновленные данные, касающиеся работы взаимных фондов за период с 1997 по 2001 гг., а также пример, связанный с применением сети Web. Кроме того, раздел “Анализ данных” теперь является разделом 3.4. Пример, иллюстрирующий понятие ковариации, теперь включен в раздел 3.5. В главу также добавлен раздел, посвященный вычислению количественных показателей на основе распределения частот.
• В главу 4 включен раздел, описывающий применение сети Web, а также раздел, в котором рассматриваются правила счета.
• Глава 5 содержит раздел, посвященный применению сети Web, а также раздел “Аппроксимация биномиального распределения с помощью распределения Пуассона”.
• В главу 6 включен раздел, в котором описано равномерное распределение, а также разделы “Применение стандартизованного нормального распределения” и “Аппроксимация биномиального и пуассоновского распределений с помощью нормального распределения”.
• Глава 7 содержит раздел, посвященный применению сети Web.
• В главу 8 включен раздел, посвященный вопросам управления газетой The Springville Herald, раздел, связанный с применением сети Web, а также раздел “Мощность критерия”.
• Глава 9 переделана так, что двухвыборочные критерии для проверки гипотез о математическом ожидании и долях признака теперь предшествуют описанию F-критерия для проверки гипотез о разности между дисперсиями. Ранговый критерий Уилкоксона перенесен в главу 11. Кроме того, глава содержит новый раздел, посвященный применению сети Web.
• В главу 10 добавлен раздел, описывающий применение сети Web. Помимо этого, в главе рассматривается критерий Левина для проверки однородности дисперсий и блочный рандомизированный эксперимент. Критерий Крускала-Уоллиса перемещен в главу 11.
• В главе 11 теперь описываются /2-критерии и непараметрические критерии. Она содержит раздел, связанный с применением сети Web, а также описание рангового критерия Уилкоксона, критерия Крускала-Уоллиса, /2-критерия для проверки гипотезы о дисперсии и /2-критерия согласия.
• В главе 12 упрощены вычисления, связанные с решением примера и рассмотрено применение сети Web.
• Глава 13 представляет собой введение в множественную регрессию и содержит раздел, посвященный фиктивным переменным. Расширено изложение вопросов, связанных с взаимодействием между членами регрессии. Кроме того, в главу включены разделы, посвященные управлению газетой The Springville Herald и применению сети Web.
• Глава 14 теперь называется “Построение моделей множественной регрессии” и включает в себя раздел, посвященный применению сети Web.
• В главе 15 обновлены все примеры, а также включены разделы, посвященные индексам и применению сети Web.
• Глава 16 содержит раздел, посвященный применению сети Web.
• В главе 17 более точно излагается история теории качества, включены раздел о методе Six Sigma® и примеры, содержащие исходные данные для построения контрольных карт размаха и среднего значения.
Материалы, размещенные в сети World Wide Web
Книге посвящена Web-страница www. prenhall. com/levine. Этот сайт полезен как преподавателям, так и студентам. На нем, в частности, представлены следующие материалы.
• Ссылки на другие сайты, предоставляющие данные для статистических курсов.
• Советы студентам.
• Образцы экзаменационных билетов.
• Новые упражнения, использующие современные данные.
• Упражнения, связанные с Интернет-приложениями.
Программе PHStat2 посвящен Web-сайт www. prenhall. com/phstat.
Индексная страница для материалов, необходимых для решения задач, связанных с применением сети Web и включенных в книгу, расположена по адресу www .prenhall. сот/Springville.
Благодарности
Мы крайне признательны многим организациям и компаниям, позволившим нам использовать их данные для разработки задач и примеров, вошедших в книгу. Мы хотели бы высказать благодарность газете The New York Times, Совету потребителей (издателю журнала Consumer Reports), инвестиционному агенству Mergent's (издателю справочника Mergent’s Handbook of Common Stocks), а также компании CEEPress.
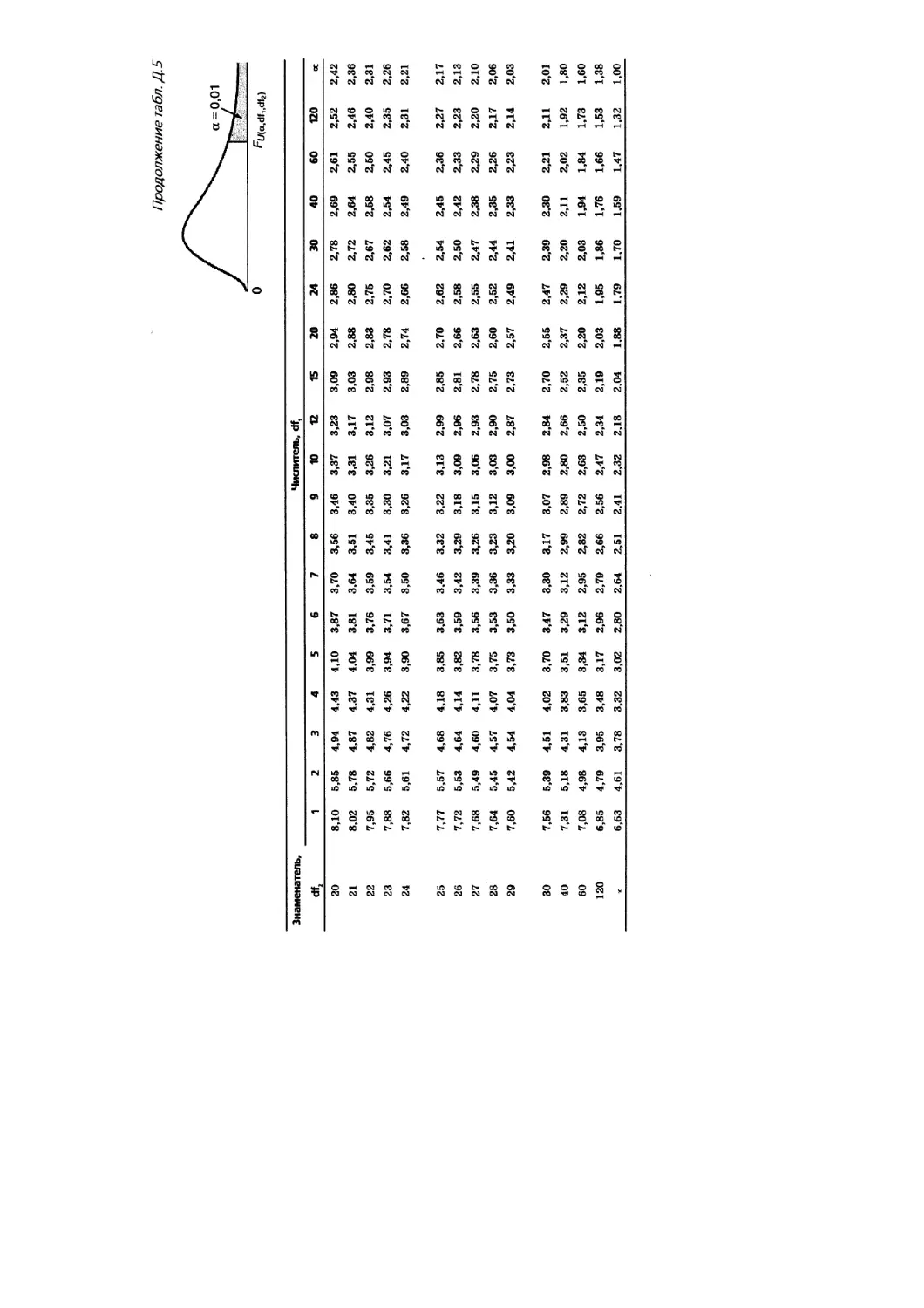
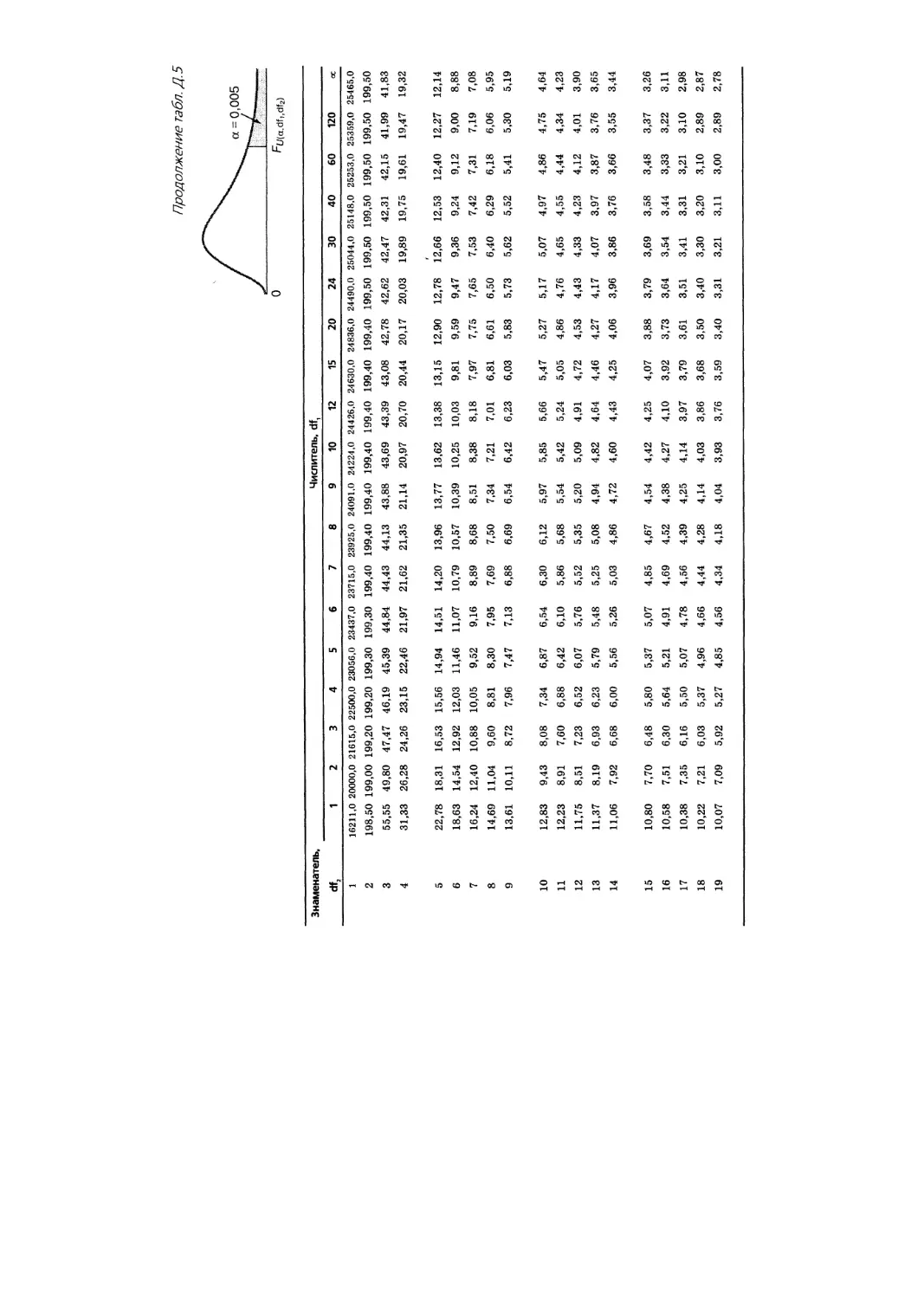
Кроме того, мы благодарны компаниям Biometrika Trustees, American Cyanimid Company и Rand Corporation, Американскому обществу тестирования и материалов (The American Society for Testing and Materials) за таблицы, которые оно любезно разрешило опубликовать в приложении Д, а также Американской статистической ассоциации (The American Statistical Assiciation) за разрешение опубликовать диаграммы из журнала American Statistician. В заключение мы выражаем благодарность профессорам Джорджу Джонсону (George A. Johnson) и Джоанне Токль (Joanne Tokle) из университета штата Айдахо (Idaho State University), а также Эду Конну (Ed Conn) из компании Mountain States Potato Company за их любезное разрешение использовать часть их работы, выполненной по заказу компании Mountain States Potato Company, при описании примера в главе 14.
Мы также выражаем благодарность Джону Аффиско (John Affisco) из университета Хофстра (Hofstra University), Энн Брэндвайн (Ann Brandwein) из колледжа Баруха (Bernard М. Baruch College — CUNY), Терри Далтон (Terry Dalton) из Университета Денвера (University of Denver), Сарву Девараджу (Sarv Devaraj) из университета Нотр-Дам (University of Notre Dame), Бен Леву (Ben Lev) из университета Мичигана (University of Michigan-Dierborn), Кипу Пирклю (Kip Pirkle) из университета Вашингтона и Ли (Washington and Lee University), Руперту Родду (Rupert Rhodd) из Атлантического университета Флориды (Florida Atlantic University), Уильяму Стюарту (William G. Stewart)
из Мэрилендского университета (University of Maryland), а также Эбенге Юсипу (Ebenge Usip) из Янгстоунского государственного университета (Youngstown State University) за их комментарии, позволившие улучшить книгу.
Отдельную благодарность авторы выражают Тому Такеру (Tom Tucker), Дебби Клэр (Debbie Clair), Керри Лимперт Томассо (Kerri Limpert Tomasso), Синтии Реган (Cynthia Regan), Эрике Руснак (Erika Rusnak), Дауну Стэплтону (Dawn Stapelton), Нэнси Уэлчер (Nancy Welcher) и Блейру Брауну (Blair Brown) из редакции, отдела маркетинга, производственного отдела и технической редакции издательства Prentice Hall. Мы хотели бы поблагодарить нашего консультанта по статистике Роберта Брукера (Robert Brooker) из университета Гэннона (Gannon University), выполнившего тщательную проверку нашей работы, Эрику Руснак, проверившую корректуру, Джулию Кеннеди (Julie Kennedy), перепечатавшую рукопись, и Нэнси Уэлан (Nancy Whelan) из компании UG/GGS Information Services, Inc., сверставшую книгу.
Заключительные замечания
Мы прошли долгий путь, стремясь сделать книгу ясной и исправить все ошибки. Если у вас есть предложения, позволяющие сделать ее понятнее, или вы нашли какие-либо ошибки, пожалуйста, напишите по адресам David_Levine@BARUCH.CUNY.EDU, DavidMLevine@msn.com или KREHBITC@MUOHIO. EDU. За информацией, касающейся программы PHStat2, обращайтесь к приложению Ж или на сайт, размещенный по адресу www.prenhall.com/phstat.
Дэвид M. Левин (David М. Levine)
Дэвид Стефан (David Stephan)
Тимоти Кребиль (Timothy С. Krehbiel) Марк Л. Беренсон (Mark L. Berenson)
ОТ ИЗДАТЕЛЬСТВА
Вы, читатель этой книги, и есть главный ее критик и комментатор. Мы ценим ваш(1 мнение и хотим знать, что было сделано нами правильно, что можно было сделать луч< ше и что еще вы хотели бы увидеть изданным нами. Нам интересно услышать и любы( другие замечания, которые вам хотелось бы высказать в наш адрес.
Мы ждем ваших комментариев и надеемся на них. Вы можете прислать нам бумажно или электронное письмо, либо просто посетить наш Web-сервер и оставить свои замечание там. Одним словом, любым удобным для вас способом дайте нам знать, нравится или не вам эта книга, а также выскажите свое мнение о том, как сделать наши книги более инте ресными для вас.
Посылая письмо или сообщение, не забудьте указать название книги и ее авторов а также ваш обратный адрес. Мы внимательно ознакомимся с вашим мнением и обязательн учтем его при отборе и подготовке к изданию последующих книг. Наши координаты:
E-mail: info@williamspublishing. com
WWW: http: //www.williamspublishing.com
Информация для писем из:
России: 115419, Москва, а/я 783
Украины: 03150, Киев, а/я 152
Глава 1
Введение и сбор данных
ПРИМЕНЕНИЕ СТАТИСТИКИ: компания Good Tunes — часть I
1.1. ЧТО ТАКОЕ СТАТИСТИКА
1.2. РАЗВИТИЕ СТАТИСТИКИ И ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ
1.3. ПРОГРАММА MICROSOFT EXCEL: РЕШЕНИЕ ПРОБЛЕМЫ ИЛИ НОВАЯ ПРОБЛЕМА?
1.4. ОБУЧЕНИЕ КОММЕРЧЕСКОЙ СТАТИСТИКЕ
1.5. ОБУЧЕНИЕ СТАТИСТИКЕ С ПОМОЩЬЮ ПРОГРАММЫ MICROSOFT EXCEL
1.6. НАИБОЛЕЕ ЭФФЕКТИВНОЕ ИСПОЛЬЗОВАНИЕ ПРОГРАММЫ MICROSOFT EXCEL
1.7. ОБУЧЕНИЕ СТАТИСТИКЕ ПО УЧЕБНИКУ
Применение статистики: компания Good Tunes — часть II
1.8. ЗАЧЕМ НУЖНЫ ДАННЫЕ
1.9. ИДЕНТИФИКАЦИЯ ИСТОЧНИКОВ
ДАННЫХ
1.10. МЕТОДЫ ВЫБОРОЧНОГО ИССЛЕДОВАНИЯ
Простая случайная выборка Систематическая выборка Стратифицированная выборка Кластерная выборка
1.11. ТИПЫ ДАННЫХ
1.12. ОЦЕНКА ДОСТОВЕРНОСТИ РЕЗУЛЬТАТОВ ИССЛЕДОВАНИЯ
ЧЕМУ ДОЛЖЕН НАУЧИТЬСЯ СТУДЕНТ
• Понимать, как статистика используется в бизнесе
• Идентифицировать источники данных
• Различать разные методы выборочного исследования
• Различать шкалы измерений
ПРИМЕНЕНИЕ СТАТИСТИКИ
Компания Good Tunes — часть I
Частная компания Good Tunes, осуществляющая розничную продажу высококачественного стереофонического оборудования и другой электронной бытовой аппаратуры через Интернет, стремится расширить свой бизнес. Чтобы получить необходимую финансовую поддержку, компания должна взять ссуду в местных банках. Менедже-’ ры компании решили создать электронную презентацию, описывающую их бизнес и состояние i дел. Эта презентация должна убедить банкиров предоставить компании необходимую ссуду. Представьте себе, что вас привлекли к подготовке демонстрации слайдов. Какие факты следует включить в доклад? Как их оформить?
1.1. ЧТО ТАКОЕ СТАТИСТИКА
Для успешного бизнеса необходимо постоянно собирать и генерировать данные, отражающие текущее состояние дел. Чтобы принять обоснованное решение, эти данные следует преобразовывать в информацию. В настоящее время существует много способов извлечь информацию из собранных фактов с помощью методов статистики — отрасли математики, изучающей методы обработки и анализа данных.
Статистика разделяется на две ветви, каждая из которых находит широкое применение в бизнесе. Описательная статистика (descriptive statistics) сосредоточивает внимание на сборе, резюмировании и характеризации совокупностей данных. Статистика вывода (inferential statistics) оценивает характеристики совокупностей данных и выявляет скрытые закономерности.
Описательная статистика возникла благодаря тому, что крупные политические и социальные организации нуждались в средствах учета. Например, с 1790 г. Соединенные Штаты Америки каждые десять лет проводят перепись населения, собирая и обрабатывая данные о своих гражданах. За время, прошедшее с тех пор, Бюро переписи населения США (U.S. Census Bureau) стало одной из авторитетных организаций, уточняющих методы описательной статистики.
В основе статистики вывода лежит теория вероятностей. Предметом статистики вывода являются выборки (samples), т.е. части полных совокупностей данных, называемых генеральными совокупностями (population, or universe). Методы статистического вывода используют выборочные данные для вычисления суммарных количественных показателей (summary measures), т.е. статистик (statistics), позволяющих оценивать параметры (parameters) всей генеральной совокупности.
Выборка
Выборка — это часть генеральной совокупности, извлекаемая для анализа.
Генеральная совокупность
Генеральная совокупность — это множество всех рассматриваемых объектов.
Статистика
Статистикой называется суммарный количественный показатель, вычисленный по выборке и позволяющий оценить характеристику всей генеральной совокупности.
Параметр
Параметр — это суммарный количественный показатель, характеризующий всю генеральную совокупность.
В настоящее время статистические методы применяются в самых разнообразных сферах бизнеса. В бухгалтерском учете статистические методы используются для извлечения и анализа выборок данных, подвергающихся аудиторской проверке, а также для определения затрат при исчислении себестоимости. В финансовом деле статистика позволяет принять правильное решение при выборе объектов капиталовложения и отслеживать финансовые показатели, изменяющиеся с течением времени. Менеджеры используют статистические методы для улучшения качества производимой продукции или предоставляемых услуг. В маркетинге статистика позволяет оценить долю клиентов, предпочитающих один вид продукции другому, выяснить причины этого явления, а также определить, какая из рекламных стратегий увеличивает сбыт продукции.
1.2. РАЗВИТИЕ СТАТИСТИКИ И ИНФОРМАЦИОННЫХ
ТЕХНОЛОГИЙ
На протяжении последнего столетия статистика играла важную роль в стимулировании развития информационных технологий. В свою очередь, новые информационные технологии способствовали расцвету статистики. В начале 20-го века постоянно увеличивающийся объем ручной работы при обработке данных, полученных в ходе переписи населения, непосредственно привел к созданию табуляторов — предшественников современных компьютерных систем. Такие статистики, как Пирсон (Pearson), Фишер (Fisher), Госсе (Gosset), Нейман (Neyman), Вальд (Wald) и Тьюки (Tukey), разработали новые статистические методы анализа больших совокупностей данных, для сбора которых требовалось все больше денег, времени и усилий. По мере развития компьютерных систем стали появляться программы, облегчающие вычисления и статистическую обработку данных. В свою очередь, первые компьютерные программы способствовали расширению сферы статистических приложений в бизнесе. По мере развития информационных технологий статистические методы становились все сложнее и сложнее.
В настоящее время, при упоминании розничных торговых компаний, инвестирующих средства в “систему управления взаимоотношениями с клиентами” (customer-relationship management system), или производителей товаров, занимающихся “информационной проходкой” (data mining), чтобы выяснить предпочтения заказчиков, следует понимать, что все это было бы невозможно сделать без статистических методов. Поскольку для таких приложений требуются специальные программы, уже многие годы в бизнесе используются статистические пакеты (statistical packages), позволяющие автоматизировать рутинные вычисления и обработку данных. Стандартные наборы статистических программ, к которым относится продукция компаний Minitab, SAS® и SPSS®, раньше были доступны лишь вычислительным центрам крупных корпораций. Однако увеличение мощности персональных компьютеров и появление компьютерных сетей позволили создать статистические пакеты, которые можно использовать совместно с текстовыми процессорами, электронными таблицами и браузерами.
1.3. ПРОГРАММА MICROSOFT EXCEL: РЕШЕНИЕ ПРОБЛЕМЫ
ИЛИ НОВАЯ ПРОБЛЕМА?
Высокая стоимость аренды статистических пакетов и обучения персонала вынудили некоторых менеджеров искать более дешевую альтернативу. Многие из них нашли выход в применении графических и статистических функций программы Microsoft Excel. Перечислим привлекательные черты этой программы.
• Она уже стала неотъемлемой частью рабочего места менеджера, поэтому отпадают затраты на дополнительное программное обеспечение.
• Многие пользователи в той или иной степени знакомы с ней.
• Программа проста как для обучения, так и для применения.
• Графические и статистические функции программы Excel оперируют с теми же рабочими листами, которые пользователи применяют для хранения данных.
• Некоторые графические функции программы Excel создают более ясное визуальное представление данных, чем многие статистические пакеты.
Несмотря на все эти действительно превосходные качества программы Microsoft Excel, многие менеджеры полагают, что точность и полнота статистических результатов не относятся к ее достоинствам. К сожалению, некоторые исследователи обнаружили, что отдельные статистические функции программы Microsoft Excel содержат ошибки и могут привести к некорректным результатам, особенно если набор данных очень велик или обладает необычными статистическими свойствами [7]. Впрочем, при вычислении описательных статистик применение программы Microsoft Excel даже к небольшим наборам данных тоже может привести к нестандартным результатам. (Пример, связанный с построением гистограмм, описан в главе 2.) Очевидно, что при использовании этой программы необходимо проявлять осторожность как при подготовке данных, так и при их анализе. Перевешивают ли достоинства программы Excel ее недостатки? Ответ на это вопрос до сих пор не найден.
Помимо проблем с точностью вычислений, программа Microsoft Excel обладает еще одним недостатком, присущим всем программам, предназначенным для простых пользователей (включая некоторые статистические пакеты для персональных компьютеров) — она не предотвращает ошибок! Например, каждый день многие пользователи используют Мастер диаграмм (описанный в разделе ЕР.6) для создания диаграмм, которые в разделе 2.6 названы “графическим хламом”. Пользователи, создающие такие диаграммы, демонстрируют свое умение работать с программой Microsoft Excel, но не владеют ею как статистическим инструментом.
Используя программу Microsoft Excel для статистического анализа, пользователь должен не только делать правильный выбор метода, но и хорошо знать условия его применения. Только глубокое понимание статистических понятий, связанных с решаемой задачей, может предотвратить некорректный анализ или другую широко распространенную ошибку, когда менеджеры принимают слишком простые решения, полагаясь лишь на некоторые легко вычисляемые статистики. Кроме того, для правильного применения программы необходимо знать ограничения, которые на нее налагаются, например, учитывать ее недостатки, упомянутые выше. Освоение программы Microsoft Excel нельзя сводить исключительно к заучиванию комбинаций клавиш и команд меню. Это всего лишь механика программы. Она ничего не стоит, если пользователь не знает статистики.
1.4. ОБУЧЕНИЕ КОММЕРЧЕСКОЙ СТАТИСТИКЕ
Основная цель книги — помочь читателям овладеть коммерческой статистикой, т.е. научиться успешно применять статистические методы в процессе принятия решений. Это означает следующее.
• Умение правильно представлять данные и коммерческую информацию.
• Умение делать выводы о крупной генеральной совокупности на основе информации о выборке.
• Умение совершенствовать процессы управления и производства.
• Умение правильно прогнозировать тенденции развития бизнеса.
Какой способ обучения коммерческой статистике наиболее эффективен? До сих пор этот вопрос остается предметом многочисленных дискуссий.
Как указано в разделе 1.2, компьютерные программы, предназначенные для статистического анализа, существенно повлияли на применение статистических методов в бизнесе. Как только они появились, преподаватели статистики начали спорить, следует ли перестраивать процесс обучения, который ранее ориентировался на ручные вычисления и применение калькуляторов. Некоторые преподаватели считали, что такие уроки позволяют студентам лучше усваивать азы статистики, в то же время другие обращали внимание на новые возможности, которые открылись с появлением статистических программ.
Эти споры продолжаются до сих пор. Обе стороны выдвигают веские аргументы, стремясь к одной цели — определить, как применение статистических программ влияет на освоение статистических понятий. В нашей книге мы выбрали “золотую середину”: наряду с интенсивным применением программы Microsoft Excel для иллюстрации статистических методов решения коммерческих задач, в тексте изложены вычислительные основы ключевых статистических процедур. Более того, решения задач, полученные с помощью программы Microsoft Excel, позволяют читателям лучше разобраться в вычислительных тонкостях статистических процедур, даже если эти нюансы не являются основной темой конкретной главы. Студенты и их преподаватели могут одновременно рассматривать как применение статистических методов в бизнесе, так и их вычислительные аспекты.
Поскольку практические примеры позволяют студентам лучше понять излагаемый материал, каждая глава начинается со сценария “Применение статистики” (как, например, сценарий “Компания Good Tunes — часть П”). В этих сценариях формулируется некая коммерческая проблема, при решении которой статистические методы превращают исходные данные в полезную информацию, необходимую для принятия правильного решения. Вопросы, поднимаемые в сценарии, требуют применения статистических методов, рассматриваемых в последующих разделах главы. Обдумывая эти вопросы, читатель поймет, как менеджеры используют статистические методы для решения поставленных перед ними задач, улучшая качество своей продукции и услуг.
В сценарии “Компания Good Tunes — часть I” вопрос, что включить в презентацию, не менее важен, чем сам способ представления фактов. Вполне вероятно, что банкиры потребуют информацию о финансовом положении компании. А какие еще данные стоило бы собрать и продемонстрировать для того, чтобы получить ссуду? (Ответ на этот вопрос содержится в сценарии “Компания Good Tunes — часть II”.) Разумеется, проведя презентацию, менеджеры компании вправе надеяться, что банк примет правильное решение. Иначе говоря, предполагается, что банкиры также владеют методами статистического вывода и способны прийти к правильному решению!
1.5. ОБУЧЕНИЕ СТАТИСТИКЕ С ПОМОЩЬЮ ПРОГРАММЫ MICROSOFT EXCEL
Как показано в разделе 1.2, развитие статистики на протяжении последнего столетия привело к более широкому использованию компьютерных программ, автоматизирующих обработку данных и статистический анализ. Если бы в книге рассматривались только статистические понятия и не описывалось применение компьютерных программ, генерирующих статистическую информацию, образование читателей было бы неполным.
Идеальная программа, описываемая в учебнике по коммерческой статистике, должна иметь широкое распространение в деловом мире, быть легкой в использовании и достаточно простой для обучения, а также всегда генерировать точную статистическую информацию. К сожалению, такой программы не существует до сих пор! Вместо нее в книге используется программа Microsoft Excel. Несмотря на недостатки, упомянутые в разделе 1.3, эта программа предоставляет превосходные возможности для изложения вводного курса статистики и для демонстрации применения статистических методов в процессе принятия деловых решений.
Разумеется, все, что говорилось о программе Microsoft Excel ранее, остается в силе, поэтому примеры тщательно подобраны так, чтобы минимизировать или совсем исключить влияние ее статистических недостатков. Применяя программу Microsoft Excel к любому из наборов данных, приведенных в книге, читатель может быть уверен, что он придет к правильному статистическому выводу. (Правда, это утверждение может оказаться неверным в отношении других наборов данных, поэтому, как сказано в разделе 1.3, при работе с программой Microsoft Excel следует иметь в виду возможные проблемы, связанные с точностью вычислений.)
1.6. НАИБОЛЕЕ ЭФФЕКТИВНОЕ ИСПОЛЬЗОВАНИЕ ПРОГРАММЫ MICROSOFT EXCEL
Программа Microsoft Excel используется в книге для того, чтобы помочь читателям овладеть коммерческой статистикой. Преподаватели статистики снова разошлись во мнениях о том, как лучше всего применять эту программу в процессе обучения. Некоторые преподаватели считают, что программу Microsoft Excel следует применять лишь для иллюстрации приложений статистики. Другие считают, что студенты могут использовать эту программу в качестве основного инструмента статистического анализа, надеясь, что разработчики внесут в нее необходимые уточнения и расширят ее возможности.
Эти споры означают, что не существует единого оптимального способа применения программы Microsoft Excel, который подошел бы всем студентам при овладении любым вводным курсом коммерческой статистики. На практике применение программы Microsoft Excel зависит от многих дополнительных факторов: подготовки и опыта преподавателя, технологического уровня, а также от качества технической поддержки и длительности курса обучения. Исходя из этого, преподаватель может использовать как один из двух подходов, так и их комбинацию.
По этим причинам в текст книги включены разделы “Стратегии Excel”, содержащие краткие описания конкретных статистических процедур программы Microsoft Excel и детальные инструкции, предназначенные как тем читателям, кто хочет использовать программу с максимальным удобством, так и тем, кто хочет вникнуть в технические детали. Книга предоставляет студентам и преподавателям возможность гибко использовать программу Microsoft Excel в процессе обучения. Даже если читатели выберут какой-то один подход, представление об альтернативном подходе лишь упрочит их знания о программе Microsoft Excel.
Стремясь помочь студентам и преподавателям максимально эффективно использовать программу Microsoft Excel, авторы предусмотрели следующие возможности.
• Многочисленные примеры рабочих листов и диаграмм, созданных с помощью программы Microsoft Excel. Эти примеры представлены как рисунки в основном тексте и как листы в рабочих книгах, сопровождающих каждую главу. Читатель может увидеть, как применять программу Excel, даже если у него нет времени получить свои собственные результаты при освоении конкретного статистического метода.
• Полная интеграция с надстройкой PHStat2, разработанной компанией Prentice Hall для программы Microsoft Excel. Применение надстройки PHStat2 позволяет минимизировать трудоемкие и подверженные ошибкам процедуры, выполняемые программой Microsoft Excel, а также получить более удобный инструмент статистического анализа, не углубляясь в технические детали, связанные с функционированием программы Microsoft Excel. (Руководство пользователя надстройки PHStat2 изложено в приложении Ж.)
• Удобные шаблоны рабочих листов и книги макросов для некоторых статистических методов. Эти рабочие листы и книги позволяют читателям получить результаты, которые трудно вычислить с помощью программы Microsoft Excel. Применение этих шаблонов и книг позволяет воспользоваться преимуществами технологии PHStat2, не инсталлируя эту надстройку и не применяя другие макросы.
• Разделы “Справочник по Excel”, подробно описывающие процедуры создания рабочих листов для применения статистических методов или анализа результатов, полученных с помощью стандартных команд программы Microsoft Excel. Эти разделы особенно полезны читателям, интересующимся техническими подробностями работы программ Microsoft Excel и PHStat2.
• Приложение “Подготовка отчетов и презентаций с помощью пакета Microsoft Office” описывает способы внедрения результатов, полученных с помощью программы Microsoft Excel, в документы, созданные текстовым процессором Microsoft Word, и презентации, подготовленные с помощью программы Microsoft PowerPoint, а также способы извлечения данных из сети World Wide Web для дальнейшей обработки программой Microsoft Excel.
Поскольку оба подхода требуют знания основ работы с операционной системой Microsoft Windows и программой Microsoft Excel, в книгу включен раздел “Букварь Excel”. В нем изложены элементарные сведения о программе Microsoft Excel, для овладения которыми не требуется никакого предварительного опыта. Прежде чем перейти к этому разделу, рассмотрим структурную схему всей книги и введем некоторые из основных понятий статистики.
1.7. ОБУЧЕНИЕ СТАТИСТИКЕ ПО УЧЕБНИКУ
Чтобы помочь читателям овладеть коммерческой статистикой, перед учебником поставлены четыре задачи, перечисленные в разделе 1.4. На рис. 1.1 представлена структурная схема, демонстрирующая связи между главами. В оставшейся части главы излагаются методы сбора, представления и описания данных. Этой же теме посвящены главы 2 и 3. В главах 4-6 рассмотрены основные понятия теории вероятностей, а также биномиальное, нормальное и другие распределения. В главах 7-11 читатели научатся делать выводы о крупных генеральных совокупностях на основе информации о выборках. Главы 12-15 посвящены методам регрессии, моделям множественной регрессии и прогнозированию на основе временных рядов. В главе 17 излагаются методы улучшения процессов производства и управления.
ПРИМЕНЕНИЕ СТАТИСТИКИ
Компания Good Tunes — часть II
Владельцы компании Good Tunes решили включить в презентацию данные о мнении своих клиентов. Для этого они попросили клиентов заполнить и отправить в адрес компании анкету, сопровождающую каждый заказ. Анкета содержала следующие пункты.
Укажите количество дней, прошедших с момента заказа товара до момента его получения.
Сколько денег (в долларах) вы планируете потратить на приобретение стереофонического оборудования и другой электронной бытовой аппаратуры на протяжении следующих 12 месяцев?
Как вы оцениваете качество обслуживания вашего последнего заказа?
□ Намного лучше ожидаемого
□ Лучше ожидаемого
□ Соответствует ожиданиям
□ Хуже ожидаемого
□ Намного хуже ожидаемого
Оцените, пожалуйста, качество стереофонического оборудования, приобретенного вами в нашей компании.
□ Намного лучше ожидаемого
□ Лучше ожидаемого
□ Соответствует ожиданиям
□ Хуже ожидаемого
□ Намного хуже ожидаемого
Хотели бы вы приобрести еще какие-нибудь товары в нашей компании в течение следующих 12 месяцев? Да Нет
Представьте себе, что вас попросили проанализировать результаты опроса. Какие данные могут быть собраны в результате данного опроса? Какую информацию можно извлечь из этих данных после завершения опроса? Каким образом компания Good Tunes может использовать эту информацию, чтобы улучшить обслуживание своих клиентов? Как использовать эту информацию для повышения шансов получить ссуду в банке? Какие еще вопросы вы предложили бы включить в анкету?
Принятие рациональных решений
Выводы о генеральной совокупности, основанные на инфор- '" ’’ мации о выборках
Как улучшить w Надежное
процессы прогнозирование
Представление и описание информации
Введение и сбор данных (глава 1)
Основы теории вероятностей (глава 4)
Г
Статистические приложения в управлении качеством и производительностью труда (глава 17)
Простая линейная регрессия и корреляция (глава 12)
! — I
Таблицы и диаграммы (глава 2)
Дискретные распределения вероятностей (глава 5)
Принятие решений (глава 16)
Описательная статистика (глава 3)
Построение моделей множественной регрессии (глава 14)
Множественная регрессия (глава 13)
Анализ временных рядов и индексы (глава 15)
Непрерывные и выборочные распределения (глава 6)
Доверительные интервалы (глава 7)
Проверка гипотез (главы 8-11)
Рис. 1.1. Структурная схема книги
1.8. ЗАЧЕМ НУЖНЫ ДАННЫЕ
Для принятия верного решения необходима информация. Перечислим ситуации, в которых необходимо анализировать данные.
• Специалисту по маркетингу нужно оценить свойства товаров, чтобы отличить их друг от друга.
• Производителю лекарств необходимо оценить эффективность нового лекарства по сравнению с существующими.
• Технолог хочет регулярно контролировать процесс производства, чтобы качество продукции соответствовало стандартам компании.
• Аудитору необходимо отследить финансовые транзакции компании, чтобы выяснить, соответствуют ли они общепринятым принципам бухгалтерского учета.
• Финансовому аналитику нужно определить, какие компании и в каких отраслях промышленности будут ускоренно развиваться в период экономического восстановления.
• Студент хочет получить данные о любимых рок-группах, чтобы удовлетворить свое любопытство.
Для сбора данных существуют шесть основных причин, перечисленных во врезке 1.1.
ВРЕЗКА 1.1. ЗАЧЕМ НУЖНЫ ДАННЫЕ
• Для обзора.
• Для изучения.
• Для оценки качества предоставляемых услуг или производственного процесса.
• Для проверки соответствия продукции принятым стандартам.
• Для выработки альтернативных решений.
• Для удовлетворения любопытства.
Сценарий “Компания Good Tunes — часть П”, описывающий опрос клиентов для оценки степени их удовлетворенности работой компании Good Tunes, иллюстрирует причины 1, 3, 4 и 5. Например, компания Good Tunes накапливает информацию, полученную в ходе опроса, для дальнейшего анализа качества предоставляемых услуг, оценки соответствия стандартам и выработки возможного альтернативного решения. Помимо прочего, эту информацию можно использовать для получения банковской ссуды.
1.9. ИДЕНТИФИКАЦИЯ ИСТОЧНИКОВ ДАННЫХ
Исключительную роль в статистическом анализе играет правильный выбор источников данных. Если данные подобраны предвзято, противоречивы или просто неверны, даже самый сложный статистический метод не сможет компенсировать их недостатки.
ВРЕЗКА 1.2. ОСНОВНЫЕ СПОСОБЫ ПОЛУЧЕНИЯ ДАННЫХ
• Изучение правительственных, промышленных или других источников.
• Эксперимент.
• Опрос.
• Наблюдение.
Источники данных разделяются на первичные (primary) и вторичные (secondary). Источник называется первичным, если его данные непосредственно используются для анализа. Если же некто собирает данные для последующей передачи, он становится вторичным источником.
Организации и люди, публикующие собранные данные, как правило, используют первичные источники, а другие потребители этой информации применяют их в качестве вторичных источников. Например, в США основой системы сбора и накопления данных для общественных и личных нужд является правительство. Бюро статистики труда (Bureau of Labor Statistics) отвечает за сбор информации о занятости населения, а также за сбор данных, публикуемых в ежемесячнике Consumer Price Index (“Индекс потребительских цен”). В свою очередь, Бюро переписи населения (Bureau of the Cen-cus) осуществляет разнообразные опросы, касающиеся жителей, жилищного строительства и промышленности.
Исследователи рынка также распространяют данные о состоянии промышленности или отдельных сегментов рынка. Например, инвестиционное агентство Mergent's предоставляет компаниям данные о финансовом состоянии других компаний. Ин-
формационные синдикаты, такие как А. С. Nielsen, снабжают своих клиентов информацией, позволяющей сравнивать качество их продукции с качеством продукции конкурентов. Еще одним источником являются ежедневные газеты, наполненные числовой информацией, касающейся биржевых цен и погодных условий, а также спортивной статистикой.
Как показано во врезке 1.2, вторым важным источником данных является эксперимент. В эксперименте все испытания проводятся под строгим контролем. Например, исследуя эффективность моющих средств, экспериментаторы определяют, какое из них лучше очищает грязную одежду, стирая ее, а не спрашивают у клиентов их мнение о том или ином порошке. Планирование эксперимента довольно сложная тема и не является предметом нашей книги, поскольку оно затрагивает сложные статистические проблемы. Однако, чтобы дать читателям представление о них, в главах 9 и 10 приводятся основные понятия, связанные с планированием эксперимента.
Третьим важным источником данных является опрос. В ходе опроса респонденты абсолютно свободны. Их просят ответить на ряд вопросов, касающихся их мнений, предпочтений, поведения и других особенностей. Затем ответы редактируются, шифруются и табулируются для дальнейшего анализа.
Четвертый важный метод получения данных основан на наблюдении. Исследователи непосредственно наблюдают некое явление, обычно протекающее в естественных условиях. Большинство знаний о животном мире получено именно этим путем. Кроме того, наблюдения широко используются в социологии и бизнесе. Например, весьма популярным способом маркетинговых исследований является наблюдение за фокус-группой (focus-group), которое позволяет извлечь информацию из ответов на вопросы, допускающие разные толкования. В ходе этих исследований арбитр контролирует ход дискуссии, а все участники отвечают на заданные вопросы. Существуют более сложные способы получения информации и поиска консенсуса, учитывающие динамику поведения коллектива, а также инструменты прикладной психологии, например, мозговой штурм, метод экспертных оценок и метод номинальных групп. Методы наблюдений также используются с целью повышения эффективности коллективной работы, а также для улучшения качества продукции и услуг.
1.10. МЕТОДЫ ВЫБОРОЧНОГО ИССЛЕДОВАНИЯ
Как указывалось в разделе 1.1, выборка — это часть генеральной совокупности, извлеченная для анализа. Вместо осуществления полной переписи, статистические процедуры выборочного исследования концентрируют внимание на сборе информации о малой репрезентативной группе, взятой из большой генеральной совокупности. Выборка, полученная в результате этих процедур, содержит информацию, которую можно использовать для оценки свойств всей генеральной совокупности.
Процедура выбора начинается с определения основы (frame), представляющей собой полное или частичное перечисление объектов, содержащихся в генеральной совокупности. Основой могут служить источники данных, например, списки населения, каталоги или карты. Затем из основы извлекаются выборки. Если основа является неадекватной, например, вследствие того, что лица или объекты, принадлежащие генеральной совокупности, выбраны неправильно, то выборки будут неточными и тенденциозными. Выбор разных основных совокупностей для получения данных может привести к противоположным результатам, как показано ниже.
ПРИМЕР 1.1. ПРОТИВОПОЛОЖНЫЕ ВЫВОДЫ
В одной из газет, издающихся в пригороде Нью-Йорка, в 1988 году появился следующий заголовок: “Завершена перепись населения: правда ли, что графство Саффолк более густо населено, чем Нассау? Между компанией LILCO и Бюро переписи существуют разногласия.” (Newsday, 25 апреля 1988 года). Основываясь на данных, полученных в ходе переписи, органы исполнительной власти графства Саффолк убеждены, что численность их населения превосходит количество жителей Нассау, а власти Нассау уверены в обратном. Кто из них прав?
РЕШЕНИЕ. Разница между двумя оценками объясняется тем, что Бюро переписи населения и компания LILCO (Long Island Lighting Company) использовали разные основные совокупности и оценивали численность населения, руководствуясь разными критериями. Бюро переписи населения использовало уровни рождаемости и смертности, а также скорость миграции населения, взяв за основу декларации о подоходном налоге. Кроме того, оно применило демографическую формулу, учитывающую уменьшение среднего количества жильцов, проживающих в отдельном жилище, за последние несколько лет. В свою очередь, компания LILCO использовала показатели счетчиков электроэнергии и газа, площадь строений и множитель, оценивающий среднее количество жильцов в отдельном жилище.
Как показано во врезке 1.3, выборочное исследование необходимо по трем причинам.
ВРЕЗКА 1.3. ВЫБОРОЧНОЕ ИССЛЕДОВАНИЕ
• Выборочное исследование занимает меньше времени, чем исследование всей генеральной совокупности.
• Выборочное исследование дешевле, чем исследование всей генеральной совокупности.
• Выборочное исследование проще и практичнее, чем полное исследование.
Как показано на рис. 1.2, существует два вида выборок: детерминированные и вероятностные.
Разновидности выборок
Детерминированные выборки
Не вполне Выборка Порция Непрезентативная случайная по группам данных выборка выборка
Вероятностные выборки
Случайная простая выборка
Система- Стратифици- Кластерная
тическая рованная выборка
выборка выборка
Рис. 1.2. Разновидности выборок
Детерминированная выборка
Детерминированная выборка (nonprobability sample) состоит из элементов, включенных в нее без учета вероятности их появления.
Поскольку детерминированные выборки содержат элементы без учета вероятности их появления, причем в некоторых случаях респонденты участвуют в опросах по собственной инициативе, к ним нельзя применить теорию, разработанную для вероятностных выборок. Типичным примером детерминированных выборок являются нерепрезентативные выборки (convenience samples). Объекты включаются в такие выборки на основе соображений простоты, дешевизны или удобства отбора. Например, многие компании проводят опросы, предоставляя посетителям их Web-страниц возможность заполнить анкету и переслать ее через Интернет. Такие анкеты позволяют собрать большое количество информации за короткий промежуток времени, однако выборки состоят из ответов пользователей World Wide Web, которые принимают участие в опросе по собственной инициативе. Во многих ситуациях единственным видом доступных выборок являются не вполне случайные выборки (judgment samples). В этом случае крайне важным для получения осмысленных результатов становится мнение эксперта в предметной области опроса. Групповые выборки (quota samples) и порции данных (chunks of data) представляют собой еще один пример детерминированных выборок. Они подробно описаны в работах, посвященных методам выборочного исследования [1, 2].
Детерминированные выборки, например, нерепрезентативные, обладают некоторыми преимуществами, в частности, их можно легко и быстро создавать, не расходуя больших средств. С другой стороны, у них есть два важных недостатка — низкая точность, являющаяся следствием тенденциозности, и ограниченность результатов. Преимущества детерминированных выборок не компенсируют их недостатки. Следовательно, детерминированные выборки следует применять лишь для грубых и недорогих оценок, предназначенных для удовлетворения любопытства, либо в качестве учебного или пилотного проекта, который подлежит дальнейшему уточнению.
Вероятностная выборка
Вероятностная выборка (probability sample) состоит из элементов, вероятность появления которых известна заранее.
Вероятностные выборки следует применять всегда, когда это возможно, поскольку лишь они позволяют сделать корректные статистические выводы о генеральной совокупности. На практике получить истинно вероятностную выборку очень трудно или просто невозможно. Однако для создания вероятностной выборки необходимо следовать правилам и учитывать любую возможную тенденциозность. Существует четыре вида вероятностных выборок: простая случайная (simple random), систематическая (systematic), стратифицированная (stratified) и кластер (cluster). Каждой из этих выборок соответствует свой метод выбора, который характеризуется собственной стоимостью, точностью и сложностью. Рассмотрим каждую из разновидностей вероятностных выборок.
Простая случайная выборка
Вероятность выбора элементов простой случайной выборки (simple random sample) из основы совпадает с вероятностью выбора любого другого элемента. Кроме того, вероятность извлечения из основной совокупности любых выборок фиксированного объема является постоянной для данного объема. Простой случайный выбор представляет собой элементарную процедуру, на основе которой создаются более сложные методы выбора.
В рамках простого случайного выбора (simple random sampling) символом п обычно обозначают объем выборки, а символом N— объем основы. Каждый элемент основы нумеруется числами от 1 до N. Вероятность выбрать любой конкретный элемент основы при первом извлечении равна 1/2V.
Существует два основных способа извлечения выборок: с возвращением и без него.
Выбор с возвращением (sampling with replacement) означает, что выбранный элемент возвращается в основу, причем вероятность его повторного извлечения остается постоянной. Представьте себе урну, в которой находятся 100 визитных карточек. Допустим, что при выборе первого элемента мы извлекли визитную карточку Джуди Крэйвен (Judy Craven). Отметим этот факт в своих записях и вернем карточку в урну. Перемешаем карточки, а затем извлечем из урны вторую визитку. При втором испытании вероятность извлечь визитную карточку Джуди Крэйвен остается равной 1/N. Процесс продолжается до тех пор, пока не будет достигнут желаемый объем выборки п. Однако часто более предпочтительным является способ, при котором выборки не содержат повторяющихся элементов.
Выбор без возвращения (sampling without replacement) означает, что после извлечения элемент не возвращается в основу и, следовательно, не может быть выбран вновь. При первом извлечении элемента вероятность его выбора из основы равна 1/N. Однако, в отличие от выбора с возвращением, вероятность выбора элемента, не извлеченного при первом испытании, равна 1/(А-1). Процесс продолжается до тех пор, пока не будет достигнут желаемый объем выборки п.
Независимо от выбранной схемы выбора (с возвращением или без), такой подход имеет один существенный недостаток — он зависит от тщательности перемешивания элементов и случайности их выбора. Поэтому метод урн (“fishbowl method”) считается не вполне приемлемым. Желательно применять более простой и научно обоснованный метод выбора элементов.
Один из таких методов основан на таблице случайных чисел (см. табл. Д.1 в приложении Д), состоящей из последовательности цифр, сгенерированных случайным образом [12]. Поскольку при записи чисел используются 10 цифр (0, 1, ..., 9), все цифры являются равновероятными. Вероятность их появления равна 1/10. Следовательно, если сгенерировать последовательность, состоящую из 800 цифр, цифра 0, как и любая другая цифра, встретится приблизительно 80 раз. Обычно, прежде чем применить таблицу случайных чисел на практике, исследователи проверяют их случайность. Таким образом, табл.Д.1 удовлетворяет критерию случайности. Поскольку каждая цифра или последовательность цифр, приведенных в этой таблице, являются случайными, эту таблицу можно читать как по строкам, так и по столбцам. Для удобства применения цифры в таблице сгруппированы.
Для того чтобы использовать такую таблицу вместо урны, необходимо сначала присвоить элементам основы соответствующий числовой код. Затем следует извлечь из таблицы случайную выборку цифр и выбрать из урны элемент, код которого совпадает с извлеченным случайным числом. Чтобы лучше освоить принципы случайного выбора, проиллюстрируем его примером.
ПРИМЕР 1.2. ПРОСТОЙ СЛУЧАЙНЫЙ ВЫБОР, ОСНОВАННЫЙ НА ТАБЛИЦЕ СЛУЧАЙНЫХ ЧИСЕЛ
Некая компания оплачивает своим сотрудникам стоматологическую помощь и желает оценить свои затраты. Для этого необходимо извлечь из генеральной совокупности, состоящей из 800 постоянных сотрудников, случайную выборку, объем которой равен 32. Компания предполагает, что не каждый сотрудник захочет добровольно принять участие в опросе, поэтому завышает объем выборки, чтобы в случае отказа в ней осталось хотя бы 32 человека. Предполагая, что в опросе примут участие 8 сотрудников из каждых 10 (т.е. 80% персонала), можно утверждать, что для создания выборки, состоящей из 32 сотрудников, необходимо опросить как минимум 40. Следовательно, анкету следует распространить среди 40 сотрудников, произвольным образом выбирая их личные дела. Как организовать простой случайный выбор?
РЕШЕНИЕ. Чтобы составить случайную выборку, применим таблицу случайных чисел. Основа представляет собой список имен и учетных номеров всех 800 сотрудников. Таким образом, основа является точным и полным перечислением всех элементов генеральной совокупности. Поскольку ее объем (800) задается трехзначным числом, код, присвоенный каждому сотруднику, также должен состоять из трех цифр, чтобы вероятность выбора любого постоянного сотрудника была одинаковой. Первому постоянному сотруднику присваивается код 001, второму — 002 и так далее, пока не будет достигнут код 800, присвоенный последнему сотруднику. Поскольку число N = 800 представляет собой максимально возможный код, все остальные трехзначные последовательности цифр (от 801 до 999, а также 000) игнорируются.
Для того чтобы извлечь простую случайную выборку, выберем из таблицы случайных чисел стартовую точку. Достаточно просто закрыть глаза и наугад ткнуть в таблицу ручкой. Допустим, что в качестве стартовой точки выбрана 6-я строка и 5-й столбец в табл. 1.1 (приведен фрагмент табл. Д.1). Хотя эту таблицу можно читать в любом направлении, мы примем естественный порядок — будем извлекать по три цифры слева направо без пропусков.
Таблица 1.1. Применение таблицы случайных чисел
Столбцы
Строка 00000 12345 00001 67890 11111 12345 11112 67890 22222 12345 22223 67890 33333 12345 33334 67890
01 49280 88924 35779 00283 81163 07275 89863 02348
02 61870 41657 07468 08612 98083 97349 20775 45091
03 43898 65923 25078 86129 78496 97653 91550 08078
04 62993 93912 30454 84598 56095 20664 12872 64647
Стартовая точка 05 33850 58555 51438 85507 71865 79488 76783 31708
(строка 06, 06 97340 03364 88472 04334 63919 36394 11095 92470
столбец 05) 07 70543 29776 10087 10072 55980 64688 68239 20461
08 89382 93809 00796 95945 34101 81277 66090 88872
09 37818 72142 67140 50785 22380 16703 53362 44940
10 60430 22834 14130 96593 23298 56203 92671 15925
11 82975 66158 84731 19436 55790 69229 28661 13675
12 39087 71938 40355 54324 08401 26299 49420 59208
13 55700 24586 93247 32596 11865 63397 44251 43189
14 14756 23997 78643 75912 83832 32768 18928 57070
15 32166 53251 70654 92827 63491 04233 33825 69662
16 23236 73751 31888 81718 06546 83246 47651 04877
17 45794 26926 15130 82455 78305 55058 52551 47182
18 09893 20505 14225 68514 46427 56788 96297 78822
19 54382 74598 91499 14523 68479 27686 46162 83554
20 94750 89923 37089 20048 80336 94598 26940 36858
21 70297 34135 53140 33340 42050 82341 44104 82949
22 85157 47954 32979 26575 57600 40881 12250 73742
Окончание табл. 7.7
Столбцы
Строка 00000 12345 00001 67890 11111 12345 11112 67890 22222 12345 22223 67890 33333 12345 33334 67890
23 11100 02340 12860 74697 96644 89439 28707 25815
24 36871 50775 30592 57143 17381 68856 25853 35041
25 23913 48357 63308 16090 51690 54607 72407 55538
Источник: табл. Д.1, приведенная в приложении Д, взята из справочника The Rand Corporation, A Million Random Digits with 100,000 Normal Deviates (Glencoe, IL; The Free Press, 1995).
Сотрудник, имеющий код 003, является первым элементом выборки (строка 06, столбцы 05-07), второй сотрудник имеет код 364 (строка 06, столбцы 08-10), а третий — 884. Поскольку в компании работает 800 сотрудников, этот код отбрасывается. В качестве элементов с 3-го по 10-й выбираются сотрудники с кодами 720, 433, 463, 363, 109, 592, 470 и 705 соответственно.
Выбор продолжается до тех пор, пока не будет сформирована выборка, состоящая из 40 постоянных сотрудников. Если в этом процессе обнаружится одна и та же трехзначная комбинация цифр, соответствующий сотрудник включается в выборку, если принята схема выбора с возвращением, в противном случае этот код игнорируется.
Систематическая выборка
При формировании систематической выборки N элементов, образующих основу, разбиваются на А групп, имеющих объем и. Иначе говоря,
п
Число k округляется до ближайшего целого числа. Чтобы получить систематическую выборку, ее первый элемент нужно случайным образом выбрать из первых k элементов первой группы, взятой из основы. Остальные элементы образуются путем выбора каждого А-го элемента всей основы.
Если основа состоит из списка пронумерованных чеков, квитанций или счетов либо списка членов клуба, студентов и т.п., систематическую выборку легче и проще получить с помощью простого случайного выбора. В этих ситуациях систематическая выборка является удобным механизмом для получения желаемых данных.
Если систематическая выборка, состоящая из 40 элементов, должна быть образована из генеральной совокупности, в которую входят 800 сотрудников, основу необходимо разделить на 20 групп (800/40=20). Среди первых 20 кодов следует выбрать случайное число, а затем включить в выборку каждый 20-й элемент основы. Например, если в качестве первого случайного числа выбран код 008, следующими элементами должны стать сотрудники с номерами 028, 048, 068, 088, 108, ..., 768 и 788.
Несмотря на свою простоту, методы простого случайного и систематического выбора обычно менее эффективны, чем остальные, более сложные методы получения вероятностных выборок. Это значит, что данные, полученные с помощью простого или систематического выбора, не всегда хорошо отражают свойства всей генеральной совокупности. Хотя метод простого выбора теоретически позволяет правильно оценить свойства генеральной совокупности, в каждом конкретном случае невозможно определить, является ли та или иная выборка репрезентативной.
Систематические выборки чаще бывают более неадекватными и нерепрезентативными, чем выборки, сформированные путем простого случайного выбора. Если в основе существует определенная структура, может возникнуть систематическая ошибка. Для решения потенциальной проблемы неадекватности специфических групп, входящих в выборку, применяется либо метод стратифицированного выбора либо метод кластерного выбора.
Стратифицированная выборка
При формировании стратифицированной выборки N элементов генеральной совокупности или основы разделяются на отдельные подмножества, или страты (strata), обладающие общими свойствами. Затем к каждому подмножеству применяется простой случайный выбор, и его результаты объединяются в одно целое. Этот метод выбора более эффективен, чем методы простого или систематического выбора, поскольку он обеспечивает большую репрезентативность выборки. Точность оценки параметров генеральной совокупности гарантируется однородностью элементов, принадлежащих одному подмножеству.
ПРИМЕР 1.3. ИЗВЛЕЧЕНИЕ СТРАТИФИЦИРОВАННОЙ ВЫБОРКИ
Некая компания оплачивает своим сотрудникам стоматологическую помощь и желает оценить свои затраты. Для этого необходимо извлечь из генеральной совокупности, состоящей из 800 постоянных сотрудников, случайную выборку, включающую в себя 32 человека. Компания предполагает, что в опросе примет участие 80% персонала, поэтому необходимо опросить как минимум 40 человек. Как извлечь стратифицированную выборку?
РЕШЕНИЕ. Основа представляет собой список имен и учетных номеров всех 800 сотрудников. Поскольку 25% постоянных сотрудников относится к управляющему персоналу, сначала необходимо разделить основу на две страты: подмножество, состоящее из 200 менеджеров, и подмножество, включающее в себя 600 остальных сотрудников. Поскольку первая страта состоит из 200 менеджеров, код каждого менеджера задается трехзначным числом от 001 до 200. Аналогично, поскольку вторая страта состоит из 600 сотрудников, каждому из них призваивается трехзначный код от 001 до 600.
Для того чтобы создать стратифицированную выборку, необходимо выбрать из первой страты 25% выборки, а остальные 75% извлечь из второй страты. Следовательно, достаточно дважды применить простой случайный выбор элементов из каждой страты, выбирая разные стартовые точки в табл. 1.1. Возникнут две простые случайные выборки. Первая из них состоит из 10 сотрудников, извлеченных из первой страты, а вторая — из 30 сотрудников, принадлежащих второй страте. Выборка, полученная в результате этой процедуры, будет правильно отображать структуру компании.
Кластерная выборка
Для образования кластерной выборки основа, состоящая из N элементов, разбивается на несколько кластеров так, чтобы каждый кластер отражал свойства всей генеральной совокупности. Затем осуществляется простой случайный выбор кластеров, в которых изучаются все элементы. Кластеры естественным образом получаются при статистическом анализе округов, избирательных участков, городов, районов или семей.
Метод кластерного выбора может оказаться менее дорогостоящим, чем метод простого случайного выбора, особенно если генеральная совокупность распределена по широкому географическому региону. Однако метод кластерного анализа в целом менее эффективен, чем методы простого случайного и систематического выбора, и для получения более точной оценки свойств генеральной совокупности приходится значительно увеличивать объем выборки.
Подробное описание методов систематического, стратифицированного и кластерного выбора приводится в работах [1, 2].
УПРАЖНЕНИЯ К РАЗДЕЛУ It
Изучение основ
1.1. Какой код следует присвоить следующим элементам генеральной совокупности, состоящей из А = 902 элементов?
1. Первому элементу.
2. Сороковому элементу.
3. Последнему элементу.
1.2. Предположим, что объем генеральной совокупности равен А = 902. Докажите, что, если стартовая точка находится в пятой строке таблицы случайных чисел (табл. Д.1), для формирования выборки, состоящей из п = 60 элементов, путем выбора без повторения достаточно шести строк.
1.3. Предположим, что объем генеральной совокупности равен А = 93, а стартовая точка находится в 29-й строке таблицы случайных чисел (табл. Д.1), причем чтение цифр производится вдоль строки. Сформируйте выборку, состоящую из п = 15 элементов, пользуясь указанным ниже методом.
1. Выбор без возвращения.
2. Выбор с возвращением.
Применение понятий
1.4. Объясните, почему при изучении результатов личного собеседования с участниками (без помощи почты или телефона) метод простого случайного выбора менее эффективен, чем остальные методы.
1.5. Допустим, нам необходимо создать случайную выборку объема 1 из генеральной совокупности, состоящей из трех элементов (А, В и С). Правило формирования выборки таково: бросаем монету; если выпал орел, выбираем элемент А, если решка, бросаем монету еще раз. Если снова выпал орел, выбираем элемент В, в противном случае выбираем элемент С. Объясните, почему выборка, полученная таким образом, не является простой случайной выборкой.
1.6. Допустим, что генеральная совокупность состоит из четырех элементов (А, В, С и D). Нам необходимо сформировать случайную выборку объема 2, пользуясь следующим правилом. Бросаем монету: если выпал орел, выбираем элементы А и В, если решка, выбираем элементы С и D. Хотя эта выборка является случайной, она не является простой случайной выборкой. Объясните почему. (Если вы решили задачу 1.5, сравните процедуры, описанные в этих задачах.)
1.7. Ректор колледжа, в котором учатся А = 4000 студентов, поручил секретарю провести опрос студентов и выяснить, довольны ли они своей жизнью в студенческом городке. В следующей таблице приведено распределение студентов в соответствии с полом и курсами.
Курсы
Пол 1 2 3 4 Сумма
Жен. 700 520 500 480 2200
Муж. 560 460 400 380 1800
Сумма 1 260 980 900 860 4000
Секретарь должен образовать вероятностную выборку, имеющую объем п = 200, и распространить полученные результаты на всю генеральную совокупность.
1. Если в качестве основы секретарь может использовать личные дела всех студентов, упорядоченные в алфавитном порядке, подумайте, какой тип выборки можно создать.
2. В чем проявляется преимущество простого случайного выбора при решении задачи 1?
3. В чем проявляется преимущество систематического выбора при решении задачи 1?
4. Какой тип выборки следует создать, если в качестве основы секретарь может использовать личные дела всех студентов, упорядоченные в алфавитном порядке на восьми листах в соответствии с полом и курсом, как показано в вышеприведенной таблице?
5. Допустим, что каждый из зарегистрированных 4000 студентов живет в одном из 20 общежитий. Каждое общежитие имеет четыре этажа, на каждом этаже расположены 50 коек. Следовательно, в каждом общежитии может жить 200 студентов. Администрация колледжа стремится собрать студентов одного пола и учащихся на одном курсе на отдельных этажах каждого общежития. Какой тип выборки следует создать, если у секретаря есть возможность описать основу, состоящую из студентов, распределенных по общежитиям и этажам?
1.8. В журнале учета продаж хранятся счета, пронумерованные числами от 0001 до 5000.
1. Допустим, что стартовая точка находится в табл. Д.1 на пересечении строки 16 и столбца 1, а чтение выполняется в горизонтальном направлении. Сформируйте простую случайную выборку, состоящую из 50 счетов.
2. Создайте систематическую выборку, состоящую из 50 счетов. Используйте случайное число, находящееся в табл. Д.1 на пересечении строки 16 и столбцов 5-7.
3. Совпадают ли выборки, полученные при решении задач 1 и 2? Обоснуйте свой ответ.
1.9. Допустим, что 5 000 счетов разделены на 4 подмножества. В первом подмножестве содержатся 50 счетов, во втором — 500, в третьем — 1 000, в четвертом — 3 450. Следует выбрать 500 счетов.
1. Какой метод выбора следует предпочесть? Почему?
2. Объясните, как использовать метод выбора, определенный при решении задачи 1.
3. Почему для решения задачи 1 не годится простой случайный выбор?
1.11. ТИПЫ ДАННЫХ
Результатом опросов являются случайные величины (random variables). Эти данные изменяются от объекта к объекту (от респондента к респонденту), поскольку двух абсолютно одинаковых объектов не существует. Как показано на рис. 1.3, существуют две разновидности случайных переменных, значения которых образуют наборы данных: категорийные и числовые.
Разновидности данных
Разновидности вопросов Ответы
Категорийные
Дискретные
Владеете ли Вы в настоящее время да q
какими-либо акциями или облигациями?
Нет □
Числовые
Сколько журналов Вы выписываете?
Непрерывные
Каков Ваш рост?
Штук
Дюймов
Рис. 1.3. Разновидности данных
Категорийные случайные величины (categorical random variables) возникают в результате категорических ответов на заданные вопросы, скажем, “да” или “нет”. Например, ответить на вопрос “Владеете ли Вы в настоящее время какими-либо акциями или облигациями?” можно лишь положительно или отрицательно. Другим примером подобных данных являются ответы на вопрос о качестве услуг, предоставляемых компанией Good Tunes: “Хотели бы Вы приобрести еще какие-нибудь товары в нашей компании в течение следующих 12 месяцев?”. Категорийные переменные могут иметь не только два возможных значения. Например, существуют несколько вариантов ответа на вопрос: “В какой день недели вы предпочитаете обедать в ресторане?”.
Числовые случайные величины (numerical random variables) являются ответами на вопросы о каком-либо измерении, например, о росте опрашиваемого. Кроме того, в ответ на вопросы “Сколько денег (в долларах) Вы планируете потратить на приобретение стереофонического оборудования на протяжении следующих 12 месяцев?” или “Сколько журналов Вы выписываете?” опрашиваемый также должен указать конкретное число. Существуют две разновидности числовых переменных: дискретные и непрерывные.
Дискретные случайные величины (discrete random variables) используются для ответа на вопрос, требующий подсчета. Например, в ответ на вопрос “Сколько журналов Вы выписываете?” опрашиваемый должен указать дискретное значение, т.е. конечное целое число. Можно совсем не выписывать журналов (ответ равен нулю) или выписывать один, два и более журналов.
Непрерывная случайная величина (continuous random variables) возникает как ответ на вопрос, требующий измерения. Типичным примером такой величины является рост опрашиваемого, который может изменяться в определенном интервале и измеряться с заданной точностью. Например, ваш рост может равняться 67, 6?74, 677/а2 или 67э8/250 дюйма в зависимости от точности проведенных измерений.
Теоретически не существует двух людей, имеющих одинаковый рост, поскольку, чем точнее проводятся измерения, тем выше вероятность обнаружить различие между полученными величинами. Однако большинство измерительных приборов не настолько совершенны, чтобы выявлять небольшие различия между измеренными величинами. Поэтому в большинстве случаев результаты эксперимента или опроса содержат взаимосвязанные наблюдения, даже если случайная величина на самом деле является непрерывной.
Шкалы измерений
Данные можно классифицировать по шкалам (scales), или уровням измерений. Существуют четыре общепризнанных шкалы измерений: номинальная (nominal), порядковая (ordinal), интервальная (interval) и шкала отношений (ratio scale).
Номинальная и порядковая шкалы. Данные, представляющие собой значения категорийных переменных, измеряются либо по номинальной, либо по порядковой шкале. Номинальная шкала (рис. 1.4) классифицирует данные по разным неупорядоченным категориям. Например, ответ на вопрос “Планируете ли Вы приобретать стереофоническое оборудование на протяжении следующих 12 месяцев?” является номинальной переменной. Аналогично номинальными переменными являются ответы на вопросы о любимых напитках, а также о политической или половой принадлежности. Номинальное шкалирование является слабейшей формой измерения, поскольку исследователи не дифференцируют результаты, принадлежащие одной и той же категории, и не устанавливают отношение порядка между категориями.
Категорийная переменная
Есть ли у вас персональный компьютер?
Категории
Да □ НетП
Прибыльными □ Стабильными □ Другими □ НикакимиП
Какая компания является вашим ... „ , г—1 гп п гп
Интернет-провайдером? Microsoft Network □ АОШ Другая □
Рис. 1.4. Примеры номинальных шкал
Порядковая шкала классифицирует данные по разным упорядоченным категориям. Например, ответ на вопрос “Как Вы оцениваете качество обслуживания Вашего последнего заказа?” представляет собой порядковую переменную, поскольку ее значения ранжируются по’ степени удовлетворенности клиентов: намного лучше ожидаемого, лучше ожидаемого, соответствует ожиданиям, хуже ожидаемого, намного хуже ожидаемого. На рис. 1.5 приведены другие примеры порядковых переменных.
Категорийная переменная
Упорядоченные категории
Названия студенческих групп Оценка продукции
(Низшая-высшая)
Первый курс Второй курс Третий курс Четвертый курс
Очень плохо Плохо Удовлетворительно Хорошо Очень хорошо
Преподавательские должностиПрофессор Доцент Ассистент Преподаватель
Рейтинг облигаций
Оценки студентов
AAA АА а ВВВ ВВ В ССС ОС с DDD DD D
Рис. 1.5. Примеры порядковых шкал
Порядковая шкала представляет собой более точную форму измерений, поскольку между ответами, отнесенными к разным категориям, устанавливается отношение порядка. Несмотря на это, порядковое шкалирование является разновидностью относительно менее точных измерений, поскольку данные, относящиеся к одной и той же категории по-прежнему не дифференцируются. При порядковых измерениях у исследователей нет разумных инструментов, позволяющих дать количественную оценку ответов. Известно лишь, какая категория “больше”, “лучше” или “предпочтительнее”, но
неизвестно насколько.
А В С D F
Интервальные шкалы и шкалы отношений. Интервальная шкала (рис. 1.6) представляет собой порядковую шкалу, в которой разности между измерениями выражаются ненулевым числом. Например, температура воздуха, равная 67 °F, на 2 °F теплее, чем 65 °F. Кроме того, разность между температурами, равными 74 °F и 76 °F, также равна 2 °F. Следовательно, указанные разности сохраняют смысл для любых измерений.
Числовая переменная
Температура (по Цельсию или Фаренгейту) Стандартизованная экзаменационная оценка Высота (в дюймах или сантиметрах) Вес (в фунтах или килограммах) Возраст (в годах или днях)
Зарплата (в долларах США или японских йенах)
Уровень измерений
Интервальная шкала Интервальная шкала Шкала отношений Шкала отношений Шкала отношений Шкала отношений
Рис. 1.6. Примеры интервальных шкал и шкал отношений
Шкала отношений — это упорядоченная шкала, в которой разности между измерениями (высоты, веса, возраста или зарплаты) могут равняться нулю. Например, сумма денег (в долларах США), которую клиент планирует потратить на приобретение стереофонического оборудования на протяжении следующих 12 месяцев, представляет собой переменную, измеренную по шкале отношений. Кроме того, шкала отношений может содержать рост человека, равный 76 дюймам, который вдвое превышает рост другого человека, равный 38 дюймам. Температура представляет собой более сложный случай: шкалы Фаренгейта и Цельсия являются интервальными, но их нельзя назвать шкалами отношений, поскольку нулевая температура — это условная величина, а не реальная. Нельзя сказать, что температура воздуха, равная 76 °F, вдвое теплее, чем температура, равная 38 °F. Однако, в отличие от шкал Фаренгейта и Цельсия, шкала Кельвина является шкалой отношений, поскольку включает в себя не условный, а абсолютный нуль.
Значения числовых переменных, как правило, измеряются либо по интервальной шкале, либо по шкале отношений. Эти шкалы образуют высший уровень измерения. Они точнее, чем порядковая шкала, поскольку позволяют определить, не только, какая из наблюдаемых величин больше другой, но и насколько.
УПРАЖНЕНИЯ К РАЗДЕЛУ 1.1
Изучение основ
1.10. Предположим, что в кафе продаются три разновидности напитков — лимонад, чай и кофе.
1. Объясните, почему тип напитка является примером категорийных данных.
2. Объясните, почему тип напитка являются переменной, измеренной по номинальной шкале.
1.11. Допустим, что безалкогольные напитки продаются в кафе в трех разных емкостях — маленькой, средней и большой. Объясните, почему объем емкости является категорийной величиной.
1.12. Предположим, что вы измерили время загрузки МРЗ-файла через Интернет.
1. Объясните, почему время загрузки является числовой величиной.
2. Объясните, почему время загрузки является переменной, измеренной по шкале отношений.
Применение понятий
1.13. Какие случайные величины приведены ниже — категорийные или числовые? Если переменная является числовой, определите ее разновидность (дискретная или непрерывная). Определите уровень измерения.
1. Количество телефонов в жилище.
2. Наиболее распространенный тип телефона.
3. Количество междугородных разговоров за месяц.
4. Продолжительность (в минутах) наиболее долгого междугородного телефонного разговора за последний месяц.
5. Наиболее распространенный цвет телефона.
6. Ежемесячная оплата (в долларах и центах) за междугородные телефонные разговоры.
7. Владение сотовым телефоном.
8. Количество местных телефонных разговоров за месяц.
9. Продолжительность (в минутах) наиболее долгого местного телефонного разговора за последний месяц.
10. Подключена ли телефонная линия к компьютерному модему?
11. Имеется ли факс?
1.14. Предположим, что от студентов, посещавших книжный магазин в студенческом городке на протяжении первой недели занятий, получена следующая информация.
1. Количество денег, потраченных на книги.
2. Количество приобретенных книг.
3. Количество времени, проведенного в магазине.
4. Академическая специализация студента.
5. Пол.
6. Владение персональным компьютером.
7. Владение DVD-плейером.
8. Количество курсов, посещаемых студентом в текущем семестре.
9. Покупал ли студент в книжном магазине какие-либо предметы одежды?
10. Способ оплаты покупки.
Определите, какие пункты опроса соответствуют категорийным переменным, а какие — числовым. Укажите уровень измерения.
1.15. Определите, какие пункты соответствуют категорийным случайным переменным, а какие— числовым. Если переменная является числовой, определите ее тип — дискретная или непрерывная. Укажите уровень измерения.
1. Название Интернет-провайдера.
2. Ежемесячная оплата услуг Интернет-провайдера.
3. Еженедельный объем времени, проведенного в Интернет.
4. Основная цель блуждания в Интернет.
5. Количество писем, получаемых по электронной почте за неделю.
6. Ежемесячная оплата телефонных услуг.
7. Количество покупок, сделанных через Интернет, за месяц.
8. Сумма, потраченная на оплату покупок, сделанных через Интернет, за месяц.
9. Оснащен ли компьютер записывающим компакт-приводом?
1.16. Определите, какие пункты соответствуют категорийным случайным переменным, а какие — числовым. Если переменная является числовой, определите ее тип — дискретная или непрерывная. Укажите уровень измерения.
1. Количество денег, потраченных на приобретение одежды в прошлом месяце.
2. Количество предметов зимней одежды.
3. Излюбленный универмаг.
4. Количество времени, затраченного на приобретение одежды в прошлом месяце.
5. Излюбленное время посещения магазинов одежды (рабочие дни, вечера или выходные).
6. Количество имеющихся пар зимних перчаток.
7. Основной вид транспорта, использованного для посещения магазинов одежды.
1.17. Предположим, что в своем запросе на кредит под залог дома в банке Metro County Savings and Loan Association Роберт Кеелер указал следующую информацию.
1. Место жительства: Стоуни Брук, Нью-Йорк.
2. Вид жилья: отдельный семейный дом.
3. Дата рождения: 9 апреля 1962 года.
4. Ежемесячные платежи: 1 427 долл.
5. Занятие: газетный репортер/корреспондент.
6. Работодатель: Daily newspaper.
7. Рабочий стаж: 14 лет.
8. Количество мест работы за последний год: 1.
9. Ежегодный совокупный доход семьи за счет зарплаты: 66 000 долл.
10. Другие источники дохода: 26 000 долл.
11. Семейное положение: женат.
12. Количество детей: 2.
13. Запрашиваемый заем: 120 000 долл.
14. Срок займа: 30 лет.
15. Другие займы: автомобиль.
16. Объем остальных займов: 8 000 долл.
Классифицируйте ответы по типам данных.
1.18. Доход является одной из наиболее распространенных величин, включаемых в различные опросы. Иногда вопрос о доходе формулируется так: “Каков Ваш доход (в тысячах долларов)?”. В других опросах вопрос звучит иначе: “Поставьте крестик в кружочек, соответствующий Вашему уровню доходов”. Этот вопрос сопровождается несколькими вариантами ответов.
1. Укажите, по каким шкалам измеряется переменная в каждом из двух опросов: номинальной, порядковой, интервальной или шкале отношений.
2. Объясните, почему в первом случае ответ можно интерпретировать как дискретную или непрерывную величину.
3. Какой из этих вариантов вопроса вы выбрали бы для своего опроса? Почему?
4. Какой из этих вариантов вопроса дает отвечающему больше свободы при выборе ответа? Почему?
1.19. Если два студента набрали на экзамене по 90 баллов, как объяснить, что эта величина является непрерывной?
1.20. Допустим, что руководитель маркетингового исследования в большой сети универмагов желает провести опрос пассажиров метро, чтобы определить, сколько времени работающая женщина тратит на покупки предметов одежды ежемесячно.
1. Опишите исследуемую генеральную совокупность и выборку из нее. Укажите, тип данных, которые можно собрать в ходе такого опроса.
2. Разработайте примерный вариант анкеты, необходимой для получения информации, определенной при ответе на задачу 1. Анкета должна содержать три вопроса для получения категорийных данных и три вопроса для определения числовых переменных.
1.12. ОЦЕНКА ДОСТОВЕРНОСТИ РЕЗУЛЬТАТОВ ИССЛЕДОВАНИЯ
Современные газеты, радио, телевидение, а также Интернет заполнены результатами различных социологических исследований или опросов. Совершенно очевидно, что с развитием информационных технологий таких исследований становится все больше. Не все из них можно признать правильными и осмысленными.
Чтобы результаты исследования были объективными, следует придирчиво проверять их достоверность. Во-первых, необходимо точно определить цель опроса и понять, зачем и для кого он проводится. Опрос общественного мнения, предназначенный для удовлетворения чьего-то любопытства, нельзя рассматривать всерьез. Его результаты ничего не объясняют. К таким опросам следует относиться скептически, поскольку их результаты бесполезны.
Определив цель исследования, следует выяснить, какие выборки положены в его основу: вероятностные или детерминированные (см. раздел 1.10). Напомним, что достоверные статистические выводы о генеральной совокупности можно сделать лишь с помощью вероятностных выборок. Исследования, основанные на детерминированных выборках, могут содержать систематические ошибки, лишающие результаты какого-либо смысла.
СКАНДАЛ, ВЫЗВАННЫЙ ИСПОЛЬЗОВАНИЕМ ДЕТЕРМИНИРОВАННОЙ ВЫБОРКИ
В 1948 году социологи пророчили победу на выборах президента США Томасу Девею (Thomas Е. Devey), тогдашнему губернатору штата Нью-Йорк, а не президенту Гарри Трумену (Harry S. Truman). Газета Chicago Tribune была настолько уверена в этом, что поспешила оповестить о результатах выборов, не дождавшись окончательного подсчета голосов.
Сконфуженные журналисты и незадачливые социологи вынуждены были долго оправдываться. Почему результаты исследований оказались настолько далеки от истины? Разбираясь в причинах неудачи, социологи выяснили, что виной всему оказалась детерминированная выборка [9]. В результате организации, прогнозирующие исход будущих выборов на основе опросов общественного мнения, стали применять только вероятностные выборки.
Ошибки статистических исследований
Даже если в основу статистических исследований положены вероятностные выборочные методы, ошибки не исключены. Как показано во врезке 1.4, существуют четыре категории ошибок. Хорошее статистическое исследование должно исключить или хотя бы минимизировать эти ошибки, даже ценой дополнительных затрат.
ВРЕЗКА 1.4. ОШИБКИ СТАТИСТИЧЕСКИХ ИССЛЕДОВАНИЙ
• Ошибка, связанная с охватом исследования (систематическая ошибка выбора).
• Ошибка, связанная с отсутствием ответов.
• Ошибка выборочного исследования.
• Ошибка измерения.
Ошибка, связанная с охватом исследования. Ключевым моментом при формировании выборки является выбор адекватной основы или списка всех элементов, из которых должна состоять выборка. Ошибка, связанная с охватом исследования (coverage error), возникает, если из основы исключаются определенные группы элементов, которые вследствие этого не могут быть включены в выборку. В результате возникает систематическая ошибка выбора (selection bias). Если список объектов, подлежащих исследованию, не адекватно отражает содержание генеральной совокупности, все характеристики, вычисленные на основе любых случайных выборок, будут присущи лишь основной совокупности, а не всей генеральной совокупности.
Ошибка, связанная с отказами от ответов. Не все люди охотно принимают участие в социологических опросах. Как правило, люди из высших и низших слоев общества реже отвечают на вопросы анкет, чем люди среднего класса. Систематическая ошибка, связанная с отказами от ответов (nonresponse bias), возникает, если некоторые участники анкетирования отказываются отвечать на вопросы. Поскольку обычно нет никаких причин считать, что лица, отказавшиеся отвечать на вопросы анкеты, ничем не отличаются от тех, кто согласился принять участие в опросе, крайне важно повторить опрос отказавшихся через некоторое время. Следует предпринять несколько таких попыток либо по почте, либо по телефону, чтобы убедиться, что опрашиваемый человек не изменил своего мнения. Чтобы итог опроса оказался достоверным, результаты, полученные в ходе первого анкетирования, следует связать с результатами последующих попыток опроса [1].
Форма опроса влияет на количество полученных ответов. Персональный или телефонный опрос обычно характеризуются более высоким количеством ответов, чем опрос по почте, правда, такие способы анкетирования оказываются дороже. Ниже приведен широко известный пример, иллюстрирующий ошибку охвата и ошибку, связанную с отказом отвечать на вопросы.
ОШИБКА ОХВАТА И ОШИБКА, СВЯЗАННАЯ С ОТКАЗОМ ОТВЕЧАТЬ НА ВОПРОСЫ
В 1936 году журнал Literary Digest предсказал, что губернатор штата Канзас Альф Лэндон (Alf Landon) получит на президентских выборах 57% голосов и намного опередит действующего президента Франклина Д. Рузвельта (Franklin D. Roosevelt). Однако Лэндон с треском проиграл, получив лишь 38% голосов. Такой большой ошибки в прогнозах еще не бывало. В результате журнал потерял доверие читателей и в конце концов обанкротился.
На первый взгляд, социологический опрос, проведенный журналом, выглядел вполне достоверно. В нем приняли участие 2,4 миллиона респондентов из 10 миллионов приглашенных. Что же стало причиной неверного прогноза? На этот вопрос есть два ответа: ошибка охвата и ошибка, связанная с отказами респондентов.
Чтобы понять значение ошибки охвата в этом опросе, необходимо дать историческую справку. В 1936 году в США свирепствовала Великая депрессия. Проигнорировав этот факт, журнал составил основную совокупность респондентов по телефонным книгам, спискам членов различных клубов, списку подписчиков журнала и данным о регистрации автомобилей [3]. В результате в опросе приняли участие, в основном, состоятельные люди, а остальные избиратели, которые не могли позволить себе телефон, <
членство в клубе, подписку на журнал и автомобиль, остались за рамками опроса. В итоге оценка количества голосов, которые могли быть поданы на Лэндона, хорошо отражала мнение участников опроса, а не намерения населения США в целом.
Второй причиной неверных выводов является ошибка, связанная с огромным количеством людей, отказавшихся принять участие в опросе. Количество ответов не пре- ; вышает 24%. Этого совершенно недостаточно для точной оценки параметров генеральной совокупности, если не предположить, что 7,6 млн. чел., отказавшихся участвовать в опросе, ничем не отличаются от остальных. И все же, по сравнению с ошибкой охвата, проблема отказа является вторичной. Даже если бы все 10 мил- ; лионов зарегистрированных участников опроса ответили бы на вопросы анкеты, это не компенсировало бы тот факт, что основная совокупность респондентов сильно отличалась от генеральной совокупности в целом.
Ошибка выборочного исследования. Существуют три причины, по которым выборочное исследование предпочтительнее полного — целесообразность, относительная дешевизна и эффективность. Однако элементы выборки случайны. В результате возникает ошибка выборочного исследования (sampling error), отражающая неоднородность генеральной совокупности. Она зависит от вероятности того, что отдельные элементы будут включены в конкретные выборки.
Читая результаты социологических опросов в газетах и журналах, вы можете обнаружить в них утверждения о величине ошибки или точности исследования. Например, “отклонение результатов опроса от истинного значения не превышает 4% ”. Эта величина и является ошибкой выборочного исследования. Ее можно уменьшить за счет увеличения объема выборки, хотя это приведет к дополнительным затратам.
Ошибка измерения. Продуманные анкеты должны добывать полезную информацию. Однако сформулировать это требование легче, чем выполнить.
Человек, у которого есть часы, всегда знает точное время.
Человек, у которого две пары часов, всегда сомневается в их показаниях.
Человек, у которого десять пар часов, знает, как трудно точно измерить время.
Ошибка измерения
Ошибка измерения (measurement error) отражает неточности в записанных ответах, возникающие вследствие неверно сформулированных вопросов, влияния опрашивающего или ошибки отвечающего.
К сожалению, процесс измерения часто считают удобным, но не очень нужным аспектом опроса. В результате вместо точных ответов организаторы опроса получают приблизительные.
В работах по статистике большое внимание уделяется ошибкам измерения, возникшим вследствие неправильной формулировки вопросов [4]. Вопрос должен быть понятным и не допускающим неоднозначного толкования. Форма вопроса должна быть нейтральной. Наводящих вопросов следует избегать.
Ошибка измерения может возникнуть по трем причинам: неоднозначная трактовка вопроса, эффект ореола (halo effect) и ошибка респондента. Рассмотрим пример неоднозначной формулировки вопроса. Несколько лет назад Министерство труда США сообщило, что уровень безработицы в США на протяжении последних десяти лет был определен неточно, поскольку для его оценки использовались неверные анкеты, разработанные в Службе опроса населения (Current Population Survey). В частности, формулировки вопросов приводили к значительной недооценке доли женщин среди рабочих
и служащих. Поскольку оценка уровня безработицы тесно связана с программами социальной помощи, например, с системами компенсаций для безработных, социологам из государственных органов было предписано уточнить анкеты.
Эффект ореола возникает, когда респондент хочет понравиться интервьюеру. Этот вид ошибки можно минимизировать, проведя обучение лиц, занимающихся опросом.
Ошибка респондента является следствием чрезмерного усердия или, наоборот, небрежности респондента. Есть два способа минимизации этих ошибок: 1) тщательное изучение данных и повторное обращение к респонденту, давшему неаккуратный ответ, и 2) внедрение программы случайно выбранных повторных обращений к респондентам для повышения надежности полученных ответов.
Этические проблемы
Ошибки, возникающие при проведении статистических исследований, могут породить этические проблемы, связанные с вольным или невольным исключением из опроса определенных групп респондентов. Если это происходит преднамеренно, возникает ошибка охвата. Она приводит к искажению основной совокупности и появлению систематических ошибок в результатах опроса, соответствующих интересам спонсора.
Аналогичная ситуация складывается, если анкета содержит формулировки вопросов, неприемлемые для определенных групп населения. Это приводит к их отказу от участия в опросе и возникновению ошибки, связанной с отказом от ответа.
Ошибка выборки может вызвать этические проблемы, только если результаты опросов интерпретируются без учета объема выборки. Это позволяет заказчикам произвольно толковать смысл результатов. Этические проблемы, связанные с ошибками измерения, возникают в ситуациях трех видов.
1. Заказчик может преднамеренно сформулировать наводящие вопросы, которые навязывают респондентам желательные ответы.
2. Манеры или тон, которым интервьюер задает вопросы, могут вызвать эффект ореола либо подсказать желательные ответы.
3. Респондент, презирающий социологические опросы, может преднамеренно вводить интервьюера в заблуждение.
Кроме того, этические проблемы могут возникать, когда суждения о всей генеральной совокупности выносятся на основании информации о неслучайной выборке. В таких случаях необходимо ясно указывать на примененный способ выбора и понимать, что полученные результаты нельзя обобщать на всю генеральную совокупность.
УПРАЖНЕНИЯ К РАЗДЕЛУ 1.12
Применение понятий
1.21. “Результаты опроса свидетельствуют, что мужчины охотнее женщин делают покупки через Интернет.” Какую информацию следует потребовать, прежде чем согласиться с приведенным утверждением?
1.22. Выборка, состоящая из п = 300 элементов, получена путем простого случайного выбора. Она образована на основе списка, в котором перечислены N = 5000 сотрудников компании, чтобы оценить степень их удовлетворенности своей работой. 1. Приведите пример возможной ошибки охвата.
2. Приведите пример возможной ошибки, связанной с отказом отвечать на вопросы.
3. Приведите пример возможной ошибки выборочного исследования.
4. Приведите пример возможной ошибки измерения.
1.23. Согласно результатам опроса 1 000 подписчиков компании AOL (Harry Berkowitz, “Screen Name Loyalty”, Newsday, December 1, 2002, A42) 92% клиентов “не желают менять свои электронные адреса”. Компания назвала это явление основной причиной постоянства своих клиентов. Какую информацию следует потребовать, прежде чем согласиться с приведенным утверждением?
1.24. Компания Forrester Research Inc. (Michael Totty, “The Masses Have Arrived”, Wall Street Journal, January 27, 2003, R8) провела опрос клиентов, совершивших покупки с помощью Интернет. Выяснилось, что среди покупателей, использующих Интернет не более года, 39% имели высшее образование, 57% оказались женщинами, а средний объем покупок, сделанных опрошенными клиентами, составил 52 300 долл. Какую информацию следует потребовать, прежде чем согласиться с приведенным утверждением?
1.25. Согласно опросу 1 004 взрослых водителей, проведенному компанией Maritz (“Snapshots”, USA Today, October 23, 2002), 45% опрошенных позволяют себе есть или пить за рулем, а 36% иногда разговаривают по мобильному телефону. Какую информацию следует потребовать, прежде чем согласиться с приведенным утверждением?
1.26. Опрос, проведенный компанией Carrier Builder, показал, что некоторые рабочие дольше, чем обычно, восстанавливают свои профессиональные навыки после отпуска (“Snapshots”, USA Today, July 18, 2001). Оказалось, что 19% респондентов немедленно входят в рабочий ритм, 40% адаптируются к работе в течение одного дня, 34% несколько дней приходят в себя, а 7% заявили, что для восстановления профессиональных навыков им требуется не меньше недели. Какую информацию следует потребовать, прежде чем согласиться с приведенным утверждением?
1.27. Согласно опросу, проведенному социологической службой Opinion Research Corporation для компании Cingular Wireless 67% американцев раздражают звонки мобильных телефонов в общественных местах (“Snapshots”, USA Today, August 13, 2001). Какую информацию следует потребовать, прежде чем согласиться с приведенным утверждением? Как использовать эту информацию?
1.28. Журнал The Wall Street Journal сообщил, что среди американцев, загружающих музыкальные файлы из Интернет, подавляющее большинство пользуются бесплатными источниками (“Low on the Charts”, May 7, 2002, Al). В частности, 91% респондентов заявили, что они используют исключительно бесплатные источники, 1% опрошенных сообщили, что используют только платные источники, а 7% участников опроса сказали, что загружают файлы из источников обоих видов. Эти результаты были получены в ходе опроса, проведенного компанией eMarketer в течение февраля 2002 г. Какую информацию следует потребовать, прежде чем согласиться с приведенным утверждением?
РЕЗЮМЕ
Как следует из структурной схемы, в главе описаны основные понятия статистики и рассмотрены методы сбора данных. Ознакомившись с различными видами данных и способами извлечения случайных выборок, мы обсудили некоторые аспекты, связанные с проверкой достоверности результатов опроса.
В разделе “Применение, статистики” описан сценарий опроса, проведенного компанией Good Tunes. Читатели должны убедиться, что первые два вопроса анкеты предполагают числовые ответы, а последние три — категорийные. Кроме того, ответы на первый вопрос (количество дней) подразумевают дискретные числовые данные, а на второй (количество денег) — непрерывные. Собрав данные, их следует организовать для последующего анализа. В следующих двух главах мы рассмотрим способы представления статистических данных в виде таблиц и диаграмм, методы предварительного анализа данных, а также опишем числовые характеристики, применяемые при их анализе и интерпретации.
Структурная схема главы 1
ОСНОВНЫЕ ПОНЯТИЯ
Выбор
без возвращения, 46
с возвращением, 46
Выборка
вероятностная, 45
детерминированная, 44
кластерная, 49
систематическая, 48
стратифицированная, 49
Источник данных
вторичный, 42
Ошибка
выбора систематическая, 58
выборки, 59
измерения,59
связанная с отказами от ответов, 58 связанная с охватом
исследования, 58
Случайная величина, 52
дискретная, 52
категорийная, 52
непрерывная, 52
числовая, 52
Совокупность
основная, 43
Статистический пакет, 35
Страта, 49
Таблица случайных чисел, 46
Фокус-группа, 43
Проверка знаний
1.29. В чем заключается разница между выборкой и генеральной совокупностью?
1.30. В чем состоит различие между статистикой и параметром?
1.31. Чем описательная статистика отличается от статистики вывода?
1.32. Чем категорийные переменные отличаются от числовых?
1.33. В чем заключается различие между дискретными и непрерывными числовыми данными?
1.34. Укажите различия между номинальной и порядковой шкалами.
1.35. Укажите различия между интервальными шкалами и шкалами отношений.
1.36. Для чего собираются данные?
1.37. В чем заключаются различия между детерминированным и случайным выбором?
1.38. Какие потенциальные проблемы могут возникнуть при использовании урновой модели для формирования простой случайной выборки?
1.39. В чем заключается разница между выбором с возвращением и выбором без возвращения?
1.40. Чем простая случайная выборка отличается от систематической?
1.41. В чем состоит отличие стратифицированной выборки от систематической?
1.42. Чем стратифицированные выборки отличаются от кластерных?
1.43. Чем отличаются четыре потенциальных источника ошибок, возникающих при проведении опросов для формирования вероятностных выборок?
Применение понятий
1.44. В электронной библиотеке Data and Story Library (lib.stat.cmu.edu/DASL) хранятся файлы с данными и сюжетами, иллюстрирующими применение основных статистических методов. Каждый набор данных связан с одним или не-
сколькими сюжетами, которые классифицированы по методам и предмету исследований. Зайдите на этот сайт и прочитайте сценарий, а затем опишите, как применить статистические методы в выбранной вами предметной области.
1.45. Зайдите на официальный сайт компании Microsoft (www. microsof t. com/ office/excel). Объясните, чем программа Excel может быть полезной для статистических исследований.
1.46. Организация Гэллапа (The Gallup organization) хранит результаты недавних выборов на Web-сайте www.gallup.com. Зайдите на этот сайт и щелкните на гиперссылках Business и Economy. Там приведены результаты различных опросов.
1. Приведите пример категорийной случайной величины, использованной в этих опросах.
2. Приведите пример числовой случайной величины, использованной в этих опросах.
3. Сформулируйте три вопроса, которые можно было бы включить в анкету.
1.47. Web-сайт Бюро переписи населения США (www.census.gov) содержит ссылки на разные типы данных. На нем хранится разнообразная информация о населении, экономике, географии и другие данные. Зайдите на этот сайт и найдите описание опроса домовладельцев (American Housing Survey) в разделе People.
1. Кратко опишите опрос домовладельцев.
2. Каков объем выборки? Какой метод выбора применен?
3. Приведите пример категорийной случайной величины, использованной в этих опросах.
4. Приведите пример числовой случайной величины, использованной в этих опросах.
5. Укажите, в каких областях бизнеса могут пригодиться результаты опроса домовладельцев. Обоснуйте свой ответ.
6. Откройте страницу, посвященную бизнесу, и найдите раздел, в котором хранятся данные о промышленности. Опишите ежегодный опрос производителей (Annual Survey of Manufacturers).
7. Каков объем выборки? Какой метод выбора применен?
8. Приведите пример категорийной случайной величины, использованной в этих опросах.
9. Приведите пример числовой случайной величины, использованной в этих опросах.
10. Укажите, в каких областях бизнеса могут пригодиться результаты ежегодного опроса производителей.
1.48. При изучении политических пристрастий населения чаще всего применяется телефонный опрос. Исследователи из компании Harris Black International Ltd. считают, что опрос с помощью Интернет дешевле, быстрее и обеспечивает более высокое количество ответов, чем телефонный опрос. Критики сомневаются в научной обоснованности такого подхода (Wall Street Journal, April 13, 1999). Несмотря на сильную критику, опросы с помощью Интернет становятся все более популярными. Что вы знаете об этом?
1.49. В исследовании Раеша Мирани (Rajesh Mirani) и Альберта Ледерера (Albert Lederer) (“An Instrument for Assessing the Organizational Benefits of IS Projects”, Decision Sciences, Vol. 29, 1998, pp. 803-838) обсуждаются способы оценки до-
ходности информационных проектов (IS projects). Исследователи разослали 936 анкет случайно выбранным членам большой национальной организации, состоящей из специалистов по информационным системам. Было получено 200 корректных ответов. Количество полученных ответов равно 21% от общего количество разосланных анкет. Из 200 ответов 190 касались недавно завершенных проектов. Средний размер бюджета этих проектов равен 3,8 млн. долл. Диапазон изменения размера бюджета колеблется от 4 000 долл, до 100 млн. долл. В 45% из 190 присланных ответов указывалось, что для начала проекта требовалось согласие главного администратора организации.
1. Какой источник данных использовался для этого опроса?
2. Назовите категорийную случайную величину, примененную в опросе?
3. Назовите числовую случайную величину, примененную в опросе?
4. Обсудите метод выбора, примененный в этом исследовании.
5. Какие типы ошибок могли возникнуть в этом исследовании?
1.50. В опросе, проведенном компанией Taylor Nelson Sofres Intersearch (“Snapshots”, USA Today, February 3, 2002, Al), приняли участие 703 респондента. Ниже приведено распределение ответов на вопрос, как респонденты нашли свое последнее место работы.
Категория %
При личном или сетевом общении 61
Через газету 16
Путем обхода компаний 9
С помощью Web-сайтов, публикующих новости 5
С помощью специализированных сайтов в Интернет 4
Через биржу труда/агента 2
С помощью школы 1
1. Опишите генеральную совокупность респондентов, принявших участие в опросе.
2. Постройте основу данного опроса.
3. Опишите способ выбора, который можно было бы применить в данном опросе.
4. Какой переменной является ответ на вопрос: “Как Вы нашли свое последнее место работы?” — категорийной или числовой?
5. Шестьдесят один процент респондентов заявили, что нашли свое последнее место работы путем личного или сетевого общения. Чем является это число — параметром или статистикой?
1.51. В ходе опроса компаний, занимающихся электронной оптовой торговлей, их попросили указать, какой количественный показатель они используют для измерения успеха своих сайтов (Michael Totty, “So much information”, Wall Street Journal, December 9, 2002, p. R.4).
1. Опишите генеральную совокупность респондентов, принявших участие в опросе.
2. Постройте основу данного опроса.
3. Опишите способ выбора, который можно было бы применить в данном опросе.
4. Какой переменной является ответ на вопрос: “Используете ли Вы объем сетевого трафика для оценки успешности сайта?” — категорийной или числовой?
5. Почему ответ на вопрос “Используете ли Вы продолжительность сетевого соединения для оценки успешности сайта?” является категорийной, а не числовой переменной?
1.52. В ходе судебного процесса под председательством федерального судьи было рассмотрено ходатайство, обвинявшее город Цинциннати, штат Огайо (Cincinnati, Ohio) в дискриминации афроамериканцев. Для завершения тяжбы судья провел опрос, который должен был ответить на вопрос, улучшились ли отношения между полицией Цинциннати и афроамериканской общиной. В опросе приняли участие 1 020 полицейских. Анкета сопровождалась письмом, в котором шеф полиции и президент Общества полицейских просили потенциальных респондентов принять участие в опросе. Респонденты либо возвращали бумажный вариант анкеты, либо заполняли интерактивную анкету в Интернет. К ужасу организаторов опроса, были заполнены только 158 анкет (“Few Cops Fill Out Survey”, The Cincinnati Enquirer, August 22, 2001, B3).
1. Какому виду ошибки исследователи должны уделить особое внимание?
2. Какие меры должны предпринять исследователи для того, чтобы решить возникшую проблему?
3. Что следовало сделать иначе?
1.53. Согласно результатам опроса, проведенного компанией International Communications Research для банка Capital One Financial, 24% подростков в возрасте от 13 до 19 лет владеют мобильными телефонами, а 10% имеют пейджер (“USA Snapshots”, USA Today, August 16, 2001, Al).
1. Какую дополнительную информацию необходимо потребовать, прежде чем делать выводы о результатах опроса?
2. Предположим, что вам необходимо организовать аналогичный опрос в другом географическом регионе. Опишите генеральную совокупность, исследуемую в вашем опросе.
3. Объясните, как минимизировать ошибку охвата в описанном опросе.
4. Объясните, как минимизировать ошибку, связанную с отказом от участия в опросе.
5. Объясните, как минимизировать ошибку выборочного исследования в этом опросе.
6. Объясните, как минимизировать ошибку измерений, связанную с отказом от участия в опросе.
1.54. Согласно результатам опроса, проведенного Сарой Бет Эстес (Sarah Beth Estes), профессором социологии университета Цинциннати, и Дженнифер Гласс (Jennifer Glass), профессором социологии Университета штата Айова, женщины, работающие по свободному графику, могут терять в зарплате. В опросе приняли участие 300 женщин, имеющих детей, вернувшихся на работу и выбравших либо свободный график либо работу на дому. Оказалось, что зарплата этих женщин возросла на величину, которая от 16% до 26% меньше, чем прирост зарплаты их коллег. (“Study: Face Time Can Affect Mom’s Raises”, The Cincinnati Enquirer, August 28, 2001, Al.)
1. Какую дополнительную информацию необходимо потребовать, прежде чем делать выводы о результатах опроса?
2. Предположим, что вам необходимо организовать аналогичный опрос в другом географическом регионе. Опишите генеральную совокупность и основу, исследуемые в вашем опросе, а также применяемый метод выбора.
1.55. В исследовании, опубликованном Министерством транспорта США (U.S. Department of Transportation), указывается, что у 27% транспортных средств, предназначенных для перевозки пассажиров, по меньшей мере в одной шине давление воздуха недостаточно. Это утверждение основано на исследовании 11 530 пассажирских транспортных средств, останавливавшихся на заправочных станциях США (“Many Drivers Risk Blowouts”, The Cincinnati Enquirer, August 30, 2001, Al).
1. Опишите генеральную совокупность и основу, исследуемые в данном опросе, а также применяемый метод выбора.
2. Что такое 27% —параметр или статистика?
1.56. Согласно исследованию Национальной ассоциации колледжей и работодателей (National Association of Colleges and Employers (NACE)) студенты имеют мрачные перспективы найти работу (Stephanie Armour, “Job Market Bleak for Grads”, USA Today, May 2, 2002). В 2001-2002 гг. работодатели собираются нанять на 36% меньше выпускников, чем в 2000-2001 гг. Более 20% студентов назвали недостаток опыта основной причиной, препятствующей успешному поиску работы, еще 20% считают, что корни всех бед лежат в экономической плоскости. В статье также утверждается, что начальные зарплаты сейчас меньше, чем были в предыдущие годы.
1. Какую дополнительную информацию необходимо потребовать, прежде чем делать выводы о результатах опроса?
2. Приведите пример категорийной переменной, исследованной в данном опросе.
3. Приведите пример числовой переменной, исследованной в данном опросе. Укажите уровень ее измерения.
4. Пятая часть студентов считает, что главной причиной безработицы среди выпускников является экономическое положение страны. Что это — параметр или статистика? Обоснуйте свой ответ
5. Предположим, что вам необходимо организовать аналогичный опрос. Какой метод выбора вы бы применили и почему?
1.57. Менеджер отдела обслуживания клиентов в компании, производящей бытовые электронные товары, хотел бы знать, удовлетворены ли покупатели качеством DVD-плейеров, приобретенных ими на протяжении последних 12 месяцев. Используя гарантийные талоны, предъявленные после продажи, менеджер спланировал опрос.
1. Опишите генеральную совокупность, исследованную в ходе данного опроса.
2. Опишите основу.
3. Чем основа отличается от генеральной совокупности? Как эти отличия влияют на результат опроса?
4. Сформулируйте три категорийных вопроса, которые можно было бы включить в анкету.
5. Сформулируйте три числовых вопроса, которые можно было бы включить в анкету.
6. Как образовать простую случайную выборку гарантийных талонов?
7. Допустим, что менеджер желает создать выборку гарантийных талонов для каждого типа DVD-плейера. Как это сделать?
1.58. Для прогнозирования исхода выборов применяются опросы общественного мнения. Результаты таких опросов обычно публикуются в газетах и комментируются по телевидению в течение нескольких недель или месяцев до выборов.
1. Какую генеральную совокупность обычно пытаются описать при прогнозировании исхода выборов президента США?
2. Как получить простую случайную выборку из генеральной совокупности?
3. Какие проблемы могут возникнуть при выборочном исследовании, если вам известно, как на самом деле проводится опрос?
1.59. В каждом номере широко известного и популярного отеля есть анкета, приведенная ниже. Ее цель — оценить степень удовлетворенности гостя.
Хорошо ли мы Вас обслужили? Отлично Хорошо Удовлетворительно Плохо
Размещение
Портье
Комната
Чистота
Ресторан
1. Считаете ли вы, что указанные степени удовлетворенности являются исчерпывающими? Обоснуйте свой ответ.
2. Следует ли в дополнение к двум категориям “отлично” и “хорошо” добавить категорию “очень плохо”? Обоснуйте свой ответ.
3. К какому виду услуг отнести самообслуживание? Можно ли включить их в анкету на некоторое время (неделю или месяц)? Обоснуйте свой ответ.
4. Какой вопрос вы добавили бы в анкету?
5. Какой категорийный вопрос вы добавили бы в анкету?
6. Какой числовой вопрос вы добавили бы в анкету?
1.60. Производитель корма для кошек запланировал опрос домовладельцев по всей стране, чтобы учесть покупательские привычки хозяев, имеющих кошек. В анкете есть следующие вопросы.
А. Где вы обычно покупаете корм для кошек?
Б. Какой корм для кошек вы приобретаете: сухой или консервированный?
В. Сколько кошек живет в вашем доме?
Г. Какой породы ваша кошка?
1. Опишите генеральную совокупность.
2. Определите основу.
3. Укажите и обоснуйте метод выбора.
4. Определите вид ответа на каждый из указанных выше вопросов: категорийный или числовой.
5. Сформулируйте пять категорийных вопросов для указанного опроса.
6. Сформулируйте пять числовых вопросов для указанного опроса.
Применение Интернет
1.61. Зайдите на Web-сайт www. prenhall. com/levine .
Щелкните на ссылке Chapter 1, а затем — на ссылке Internet Exercises.
ПРИМЕНЕНИЕ WEB
Как правило, статистические методы используются как для того, чтобы сообщить важную информацию, так и для внутренних целей. К сожалению, очень часто люди неправильно применяют эти методы.
• Менеджер по продажам с помощью “легкой в использовании” программы построения диаграмм выбирает неправильный вид диаграммы, искажающий реальные связи между данными.
• Редактор ежегодного отчета приводит диаграмму доходов, в которой ось Y укорочена. Это создает ложное впечатление о резком возрастании доходов.
• Аналитик вычисляет бессмысленную статистику, описывающую набор категорийных данных, используя методы, предназначенные для числовых данных.
Несмотря на то что в большинстве случаев такие ошибки являются непреднамеренными, опытный менеджер должен их распознавать. Основная цель раздела “Применение Web” — научить читателей распознавать типичные ошибки, связанные с применением статистических методов, и устранять их.
В разделе “Применение Web” мы просим читателей зайти на Web-сайт компании, описанной в сценарии “Применение статистики”, или на Web-сайт, посвященный исследованию работы газеты Springville Herald, издаваемой в маленьком городке. Мы просим читателей сравнить данные, содержащиеся в деловой документации компании с рекламными заявлениями. Как и во многих реальных ситуациях, в отличие от традиционных учебных задач, на Web-сайте содержится либо неполная, либо противоречивая информация. Для решения задачи выявленные противоречия необходимо устранить.
Чтобы помочь читателю освоить материал, в начале каждого раздела “Применение Web” излагается цель и краткое содержание сценария. Читатель должен зайти на указанный Web-сайт или Web-страницу. Там он обнаружит список вопросов, которые помогут ему исследовать Web-сайт. Если читатель захочет, он может сам изучить требуемый Web-сайт, соединившись с Web-страницей Springville Chamber of Commerce по адресу www .prenhall. com/Springville.
В большинстве глав раздел “Применение Web” ставит перед читателями типичные задачи, стоящие перед руководством газеты Springville Herald, для решения которых необходимо применять статистические методы.
Итак, зайдите на Web-сайт розничной торговой компании Good Tunes (www. prenhall. com/Springville/Good_Tunes. htm), упомянутой в сценарии “Применение статистики”. Напомним, что частная компания Good Tunes нуждается в финансовых средствах. Поскольку менеджеры компании заинтересованы представить ее как бурно развивающийся бизнес, ничего удивительного, что сайт содержит заявление: “Наши дела идут хорошо, как никогда!” (Our best sales year ever).
Это заявление является гиперссылкой, щелкнув на которой, читатель откроет страницу, содержащую деловую информацию о компании. Соответствует ли эта информация рекламному заявлению? Содержит ли она все необходимые таблицы, диаграммы и ссылки на источники данных? Для иллюстрации объемов продаж компания Good Tunes использует категории “два года тому назад” и “последние двенадцать месяцев”. Все ли правильно на этой Web-странице? Конечно, нет!.
Во-первых, обратите внимание на то, что шкала объемов продаж не размечена, поэтому выяснить реальный объем продаж невозможно. Как читатели узнают в разделе 2.6, такие диаграммы называются графическим хламом и никогда не должны применяться.
Второй важный вопрос — в каких единицах измерения выражен объем продаж? Использование символов создает впечатление, что объем продаж выражается через еди-
ницы проданного товара. Если это правда, то необходимо выяснить, хорошо ли эти данные отражают реальное положение дел. Возможно, объем продаж, выраженный в долларах, является более точным индикатором?
Метки диаграмм также вызывают недоумение. Выражение “последние двенадцать месяцев” двусмысленно — в этот период могут включаться месяцы текущего года, а также месяцы, относящиеся к прошедшему году. Поскольку компания была основана в 1997 г., почему компания не обосновала выражение “хорошо, как никогда” (“best sales year ever”) диаграммами, иллюстрирующими объем продаж в каждом году, прошедшем после 1997г.?
Скрывает ли компания Good Tunes важную информацию или ее менеджеры просто не разбираются в статистике? В любом случае они неправильно представили чрезвычайно важную информацию.
В последующих разделах “Применение Web” читатели должны будут самостоятельно провести такой анализ, используя в качестве путеводителя вопросы, перечисленные на Web-странице. Не все задачи будут такими простыми, как рассмотренная выше. В некоторых ситуациях читатель должен будет применить довольно сложные методы статистики.
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
1. Cochran, W. G., Sampling Techniques, 3rd ed. (New York: Wiley, 1977).
2. Deming, W. E., Sample Design in Business Research (New York: Wiley, 1960).
3. Gallup, G.H., The Sophisticated Poll-Watcher's Guide (Princeton, NJ: Princeton Opinion Press, 1972).
4. Goleman, D., “Pollsters Enlist Psychologist in Quest for Unbiased Results”, The New York Times, September 7, 1993, Cl and Cll.
5. Kendall, M. G., and R. L. Plackett, eds., Studies in the History of Statistics and Probability, vol. 2 (London: Charles W. Griffin, 1997).
6. Kirk, R. E., ed., Statistical Issues: A Reader for the Behavioral Sciences (Monterey, CA: Brooks/Cole, 1972).
7. McCullough, B. D., and B. Wilson, “On the Accuracy of Statistical Procedures in Microsoft Excel 97”, Computational Statistics and Data Analysis, 31 (1999), 27-37.
8. Microsoft Excel 2002 (Redmond, WA: Microsoft Corporation, 2001).
9. Mosteller, F. et al., The Pre-Election Polls of 1948 (New York: Social Science Research Council, 1949).
10. Pearson, E. S., ed., The History of Statistics in the Seventeenth and Eighteenth Centuries (New York: Macmillan, 1978).
11. Pearson, E. S., and M. G. Kendall, eds., Studies in the History of Statistics and Probability (Darien, CT: Hafner, 1970).
12. The Rand Corporation, A Million Random Digits with 100,000 Normal Deviates (New York: The Free Press, 1955).
13. Walker, H. M., Studies in the History of the Statistical Method (Baltimore: Williams & Wilkins, 1929).
14. Wattenberg, В. E., ed., Statistical History of the United States: From Colonial Times to the Present (New York: Basic Books, 1976).
Букварь Exce
ЕРЛ. ВВЕДЕНИЕ В MICROSOFT EXCEL
Описываются основные приемы работы с программами под управлением операционной системы Windows. Никакого предварительного опыта не требуется.
ЕР.2. ПОЛЬЗОВАТЕЛЬСКИЙ ИНТЕРФЕЙС ПРОГРАММЫ MICROSOFT EXCEL
Описываются основные понятия и процедуры, необходимые для успешной работы с программой Excel.
ЕР.З. ОСНОВНЫЕ ОПЕРАЦИИ НАД РАБОЧИМИ КНИГАМИ
Рассматриваются операции открытия, сохранения и печати рабочих книг.
ЕРД. ОСНОВНЫЕ ОПЕРАЦИИ НАД РАБОЧИМИ ЛИСТАМИ
Читатели узнают, как заполнять ячейки рабочего листа и редактировать его оформление.
ЕР.5. БОЛЕЕ СЛОЖНЫЕ ОПЕРАЦИИ С РАБОЧИМИ ЛИСТАМИ
Обсуждаются команды и процедуры, необходимые для создания, изменения или копирования рабочих листов.
ЕР.6. ПРИМЕНЕНИЕ МАСТЕРА ДИАГРАММ
Описываются основы работы с Мастером диаграмм.
ЕР.7. ПРИМЕНЕНИЕ МАСТЕРА СВОДНЫХ
ТАБЛИЦ
Рассматриваются основы работы с Мастером сводных таблиц.
ЕР.8. ИСПОЛЬЗОВАНИЕ НАДСТРОЕК
Читатели узнают, что такое надстройки и как они используются в программе Microsoft Excel.
В разделе рассматриваются основные понятия и приемы работы с программой Microsoft Excel. Читатели могут выбирать темы из этого раздела, руководствуясь своим опытом. Как минимум, им следует ознакомиться с терминами, которые используются в дальнейшем.
ЕР.1. ВВЕДЕНИЕ В MICROSOFT EXCEL
Программа Microsoft Excel является частью пакета Microsoft Office для персональных компьютеров. Несмотря на то что программа Microsoft Excel не предназначена специально для статистического анализа, в ней содержатся основные статистические функции, а также надстройка Пакет анализа (Data Analysis ToolPak). Кроме того, в программе Microsoft Excel предусмотрены мастера (wizards) — специальные наборы диалоговых окон, заполняя которые пользователь может создавать диаграммы и сводные таблицы для статистического анализа. Чтобы компенсировать недостаток статистических процедур и упростить работу с программой Excel, к книге прилагается надстройка PHStat2, разработанная компанией Prentice Hall.
Работая с программой Microsoft Excel, пользователи создают, открывают и сохраняют файлы, называемые рабочими книгами (workbooks). Рабочие книги состоят из рабочих листов (worksheets), содержащих исходные данные, результаты анализа, а также промежуточные вычисления. Рабочий лист представляет собой массив, состоящий из столбцов и строк. Столбцы обозначаются буквами, а строки — цифрами. Пересечение столбца и строки образует ячейку (cell). Следует иметь в виду, что надстройки Analysis ToolPak и PHStat2 автоматически создают рабочие листы, содержащие результаты анализа, добавляя их в рабочую книгу.
Программа Microsoft Excel получила чрезвычайно широкое распространение. По этой причине она представляет собой весьма удобный инструмент для обучения статистике. Однако читатель должен иметь в виду проблемы с точностью, указанные в разделе 1.5. В сочетании с надстройкой PHStat2 статистические процедуры программы Microsoft Excel охватывают практически все темы, изложенные в книге. Прежде чем перейти к применению этих программ, следует ознакомиться с инструкциями, приведенными в приложении Ж и файле readme . txt, расположенном на компакт-диске.
ЕР.2. ПОЛЬЗОВАТЕЛЬСКИЙ ИНТЕРФЕЙС ПРОГРАММЫ
MICROSOFT EXCEL
ЕР.2.1. Основные операции с мышью
Основным средством, предназначенным для выбора пиктограмм и команд меню, является координатно-указательное устройство, например, мышь. Перемещение координатно-указательного устройства приводит к перемещению по экрану графического изображения — так называемого курсора мыши (mouse pointer). Как правило, мыши имеют две кнопки — основную и вспомогательную. Для того чтобы выполнить одну из четырех основных операций с мышью, необходимо установить курсор мыши на требуемый объект, а затем нажать и отпустить одну из этих клавиш (см. врезку ЕР.1).
ВРЕЗКА ЕР.1. ОСНОВНЫЕ ОПЕРАЦИИ С МЫШЬЮ
Щелчок. Переместите курсор мыши на объект и нажмите основную кнопку. Как правило, в таких случаях используют слово “выберите объект”, “выполните команду” или “снимите выделение”, “сбросьте флажок”. Например, “выполните команду PHStat в меню Excel” или “сбросьте флажок Формулы”.
Перетаскивание. Переместите курсор мыши на объект и нажмите основную кнопку мыши. Удерживая ее, переместите курсор мыши по экрану, а затем отпустите. Как правило, эта операция используется для перетаскивания объектов в новое положение или для выделения нескольких объектов одновременно.
Двойной щелчок. Переместите курсор мыши на объект и дважды щелкните основной кнопкой с очень небольшим интервалом.
Щелчок правой кнопкой. Переместите курсор мыши на объект и щелкните вспомогательной кнопкой.
Замечание: упражнения для работы с мышью содержатся в рабочей книге Mousing Practice. xls, = расположенной в каталоге Instructional Files на компакт-диске.
По умолчанию основной клавишей считается левая клавиша мыши, а вспомогательной — правая, однако операционная система Windows позволяет изменить эти настройки.
ЕР.2.2. Открытие окна приложения Microsoft Excel
Запустить программу Miscosoft Excel на рабочем столе можно тремя способами (см. врезку ЕР.2).
ВРЕЗКА ЕР.2. МЕТОДЫ ЗАПУСКА ПРОГРАММ В ОПЕРАЦИОННОЙ СИСТЕМЕ MICROSOFT WINDOWS
Щелчок на пиктограмме. Дважды щелкните на пиктограмме программы, находящейся на рабочем столе (в некоторых версиях Windows достаточно простого щелчка).
Выполнение команды меню Пуск. Нажмите клавишу Windows (или щелкните на кнопке Пуск) и выполните команду Программы или Все программы. Выберите пункт Microsoft Excel в появившемся списке команд меню.
Щелчок на пиктограмме файла. Дважды щелкните на пиктограмме файла, связанного с программой Microsoft Excel. Например, если щелкнуть на пиктограмме рабочей книги, откроется не только окно приложения программы Microsoft Excel, но и сама рабочая книга.
При запуске программы Microsoft Excel открывается окно приложения (Excel application window). Оно представляет собой ограниченную область экрана, размеры которой можно изменять. Окно приложения содержит строку заголовка (title bar), которая идентифицирует открытую рабочую книгу, системные кнопки (system buttons), расположенные в правом верхнем углу окна, строку меню (menu bar), содержащую команды программы Excel, панели инструментов (toolbars), состоящие из пиктограмм, связанных с командами меню, а также рабочую область (worksheet area), состоящую из строк, столбцов и ячеек, в которые вводятся данные. Основные компоненты окна приложения программы Microsoft Excel 2002 приведены на рис. ЕР.1 и во врезке ЕР.З. (Для того чтобы настроить окно приложения своей программы Microsoft Excel так, как показано на рис. ЕР.1, обратитесь к приложению Е.)
Строка меню
Кнопки изменения размеров и закрытия окна
Стандартная
инструментов
Панель" инструментов форматирования
Рис. ЕР.1. Окно приложения Microsoft Excel 2002
ВРЕЗКА ЕР.З. ОСНОВНЫЕ КОМПОНЕНТЫ ОКНА ПРИЛОЖЕНИЯ ПРОГРАММЫ MICROSOFT EXCEL
Системные кнопки минимизации, восстановления и закрытия окна соответственно сворачивают, изменяют размер и закрывают рабочее окно программы Microsoft Excel.
Строка меню представляет собой горизонтальный список слов, обозначающих выбор команд.
Стандартная панель инструментов содержит пиктограммы, позволяющие выбрать команды для работы с файлами, включая основные операции с рабочими книгами, рассмотренные в разделе ЕР.З.
Панель инструментов форматирования содержит пиктограммы, позволяющие выбрать основные команды форматирования (подробности описаны в разделе ЕР.4.3).
Строка формул отображает название активной ячейки (см. раздел ЕРЛ) и ее содержимое.
Рабочая область содержит открытую рабочую книгу или книги. Обычно пользователи работают с одной рабочей книгой, но существует возможность работать с несколькими книгами одновременно, переключаясь между ними с помощью меню системы Windows.
Ярлычки листов идентифицируют названия отдельных рабочих листов. Щелкая на ярлычке, можно выбрать конкретный лист и сделать его активным. Кроме того, дважды щелкнув на ярлычке, можно изменить название рабочего листа.
Полосы прокрутки позволяют отображать фрагменты рабочего листа, выходящего за пределы экрана (например, строку 100 или столбец Т на рис. ЕР.1).
ЕР.2.3. Стандартные свойства меню и диалоговых окон программы Microsoft Excel
Основными средствами, предназначенными для выбора команд, являются выпадающие (pull-down) меню программы Microsoft Excel и контекстные (shortcut) меню, появляющиеся при щелчке правой кнопкой. Основные свойства стандартных меню показаны на рис. ЕР.2.
Пиктограммы стандартной панели инструментов
Троеточие
Рис. ЕР.2. Меню Файл программы Microsoft Excel
комбинации
Ускоряющие клавиши
Маркеры подменю
Как показано на рис. ЕРЛ, относительно меню приняты следующие соглашения.
• Горячие клавиши (accelerator keys), предназначенные для выбора определенной команды, подчеркнуты.
• Для выделения пунктов меню, выбор которых сопровождается открытием диалогового окна, используется многоточие (ellipsis).
• Чтобы выделить пункты меню, выбор которых сопровождается открытием подменю, используется треугольный маркер (triangular marker).
• Некоторые пункты меню содержат пиктограммы стандартной панели инструментов (toolbar button).
• Некоторые пункты меню сопровождаются комбинацией быстрых клавиш (keyboard shortcut), позволяющей выполнить соответствующую команду.
Выбор некоторых команд меню непосредственно приводит к выполнению определенной процедуры, однако чаще всего в ответ открывается диалоговое окно, позволяющее вводить данные и выводить сообщения. Типичным примером являются диалоговые окна Открытие документа и Печать, предусмотренные в программе Microsoft Excel 2002 (рис. ЕР.З). Стандартные элементы диалоговых окон перечислены во врезке ЕРЛ.
Список
Открытие документа
Папка:
Mutual
Рабочий стол
Принтер
Печать
Мои последние документы/
Мои документы
Раскрывающиеся списки
J 4Х
23 ’ Сервис
Canon LBP-800
v [ Свойства.., j
Окно редактирования [найти принтер... | со счетчиком 1--------------
Мой компьютер
Имя файла:
Мое сетевое окружение
Тип файлов: ! все файлы
Печатать
О страницы
Имя: Состояние: Свободен Тип: Canon LBP-8OO
Порт: LPT1:
Заметки:
Вывести
по:
[Просмотр I
выделенные листы
Переключатели
Копии
чать в файл
О выбеленный диапазон О всю книгу
Число копий:
Флажок
. по копиям
fl [ Отмена ]
Кнопка ОК Кнопка Отмена
Рис. ЕР.З. Диалоговые окна Открытие документа и Печать программы Microsoft Excel 2002
Как показано на панелях А и Б рис. ЕР.5, в программе Microsoft Excel предусмотрены следующие стандартные элементы диалогового окна.
ВРЕЗКА ЕРД. СТАНДАРТНЫЕ ЭЛЕМЕНТЫ ДИАЛОГОВЫХ ОКОН
Окно раскрывающегося списка позволяет выбрать пункт из списка, появляющегося при нажатии кнопки, помеченной треугольным маркером и расположенной на правой стороне окна.
Окно списка содержит перечень элементов, например, файлов или папок, подлежащих выбору. Если список слишком велик и не помещается в окне, необходимо щелкнуть на кнопке прокрутки (scroll button) или ползунке (slider).
Окно редактирования позволяет вводить и редактировать данные. Как правило, окна редактирования используются в сочетании с раскрывающимися списками или кнопками счетчика (spinner buttons), облегчающими ввод данных. (Нажатие кнопки счетчика увеличивает или уменьшает числовое значение, указанное в окне редактирования.)
Переключатели (option buttons) позволяют выбрать один из нескольких взаимоисключающих вариантов. Установка одного из переключателей автоматически приводит к сбрасыванию остальных переключателей. Таким образом, в каждый момент времени можно установить только один из нескольких переключателей.
Флажки (check boxes) позволяют выбрать несколько вариантов. В отличие от переключателей, несколько флажков можно устанавливать одновременно. Если флажок был установлен ранее, повторный щелчок сбрасывает его.
Кнопка OK (OK button) заставляет программу Microsoft Excel выполнить операцию, предусмотренную в открытом диалоговом окне, с учетом введенных данных, выбранных переключателей и установленных флажков. Эта кнопка может иметь другую метку. Например, диалоговое окно Открытие документа, показанное на рис. ЕР.З, содержит кнопку Открыть (на панели А), а диалоговое окно Сохранение документа — кнопку Сохранить.
Кнопка Отмена закрывает диалоговое окно и отменяет выполнение операции. В большинстве случаев щелчок на кнопке Отмена эквивалентен щелчку на кнопке Закрыть панели инструментов.
Кнопка, помеченная знаком вопроса, выводит на экран контекстное окно, содержащее справку о выбранном объекте (см. раздел ЕР.2.5). Как правило, диалоговые окна содержат кнопку Справка, выполняющую аналогичные функции.
ЕР.2.4. Исправление ошибок
Если пользователь ошибся, выполнив команду меню или щелкнув на кнопке, последнее действие можно отменить, выполнив команду Отменить из меню Правка. Если пользователь ошибся при вводе данных, ошибку можно исправить тремя способами.
• Нажать клавишу <ESC>, отменив последний ввод.
• Нажать клавишу <BACKSPACE>, стирая символы по одному справа налево, начиная с текущего положения курсора.
• Нажать клавишу <Del>, стирая символы по одному слева направо, начиная с текущего положения курсора.
Если ошибка сделана в середине введенного числа или слова, поместите курсор мыши перед ошибочным символом, удалите его и наберите правильный текст. Выполнение команды Отменить меню Правка отменяет не только последнее действие, но и стирает введенный текст. Если после исправления ошибки пользователь передумал, он может восстановить исходное положение, выполнив команду Повторить меню Правка.
КАК ОБОЗНАЧАЮТСЯ ПОСЛЕДОВАТЕЛЬНО ВЫПОЛНЯЕМЫЕ КОМАНДЫ
Если инструкция требует последовательно выполнить несколько команд, пункты соответствующих меню разделяются символом ct>. Например, фраза “выполните команду Отменить из меню Правка” в дальнейшем будет записываться так: “выполните команду Правка^Отменить”. •
ЕР.2.5. Использование справочной системы
Работая с программой Microsoft Excel, пользователь может обратиться либо к ее справочной системе, либо вызвать контекстную подсказку. Для того чтобы получить полную информацию о программе Microsoft Excel, ее меню, функциях или других объектах, выполните команду CnpaBKa^CnpaBKaWicrosoft Excel. В зависимости от настроек будет запущен либо браузер справочной системы Microsoft Excel (см. рис. ЕРЛ), либо Помощник — комический мультипликационный персонаж (см. рис. ЕР.5) .
В программе Microsoft Excel 2003 браузер справочной системы является частью панели задач.
Рис. ЕР.4. Браузер справочной системы программы Microsoft Excel
Рис. ЕР.5. Помощник программы Microsoft Excel
Дизайн браузера программы Microsoft Excel зависит от конкретной версии. Браузер позволяет выполнять поиск по ключевому слову или фразе, перечисленным в алфавитном порядке. Для того чтобы выполнить поиск справки с помощью браузера программы Microsoft Excel, выполните следующие действия.
ЕР.2. Пользовательский интерфейс программы Microsoft Excel
79
1. Щелкните на корешке вкладки Указатель.
2. Наберите в окне редактирования 1. Введите ключевые слова интересующее вас слово или фразу. Щелкните на кнопке Найти.
3. Выберите интересующие вас элементы (или элементы) из списка, появляющегося на левой панели. Текст справки появится на правой панели.
Правая панель может содержать гиперссылки, щелкнув на которых, пользователь может получить дополнительную справочную информацию. Чтобы получить новую справку, щелкните на кнопке Очистить и повторите п. 1 и 2. Вместо выполнения п. 1 пользователь может просто выбрать элемент списка 2. Или выберите ключевые слова.
Если на экране появился Помощник, последовательность действий практически не изменяется. Нужно лишь набрать имя интересующей вас команды, функции или объекта, а затем щелкнуть на кнопке Найти. Поскольку выбор тем у Помощника меньше, чем в общей справочной системе, и, кроме того, он может отвлекать внимание, многие предпочитают работать с браузером. Для того чтобы отключить функцию Помощника, следует выполнить такие действия.
1. Щелкнуть на Помощнике правой кнопкой мыши.
2. Выполнить команду Параметры в появившемся контекстном меню.
3. Находясь в диалоговом окне Помощник, сбросить флажок Использовать помощника.
4. Щелкнуть на кнопке ОК.
С этого момента Помощник будет скрыт, пока пользователь не выполнит команду Справкам Показать помощника.
ЗАМЕЧАНИЯ ДЛЯ ПОЛЬЗОВАТЕЛЕЙ ПРОГРАММЫ MICROSOFT EXCEL 97
Дизайн браузера справочной системы Microsoft Excel 97 отличается от дизайна браузера справочной системы Microsoft Excel 2002, показанного на рис. ЕРЛ. В старом ; браузере для получения справки достаточно было щелкнуть на корешке вкладки
Указатель. Для того чтобы избавиться от Помощника, достаточно было выполнить команду Справка^Содержание и указатель.
ЕР.2.6. Получение контекстных подсказок
Большинство объектов, создаваемых программой Microsoft Excel на экране, сопровождаются всплывающими подсказками или сообщениями “Что это такое?”.
Подсказки (tool tips) представляют собой контекстные всплывающие справки об элементах рабочего окна программы Excel или других объектах, например, диаграммах. Для вызова подсказки следует поместить курсор мыши на интересующий вас объект и немного подождать, пока не появится всплывающее сообщение. Например, на рис. ЕР. 11 приведена подсказка об оси гистограммы.
Рис. ЕР.6. Подсказка об оси гистограммы
Подсказка “Что это такое?” представляет собой контекстное сообщение об элементе рабочего окна программы Excel. Чтобы вызвать эту подсказку, сначала следует выполнить команду Справкам Что это такое?. После этого курсор мыши изменит свою форму (рис. ЕР.7, верхний экран). Теперь курсор мыши следует переместить на интересующий вас объект и щелкнуть левой кнопкой мыши. В результате на экране появится справка об указанном элементе (см. рис. ЕР.7, нижний экран). Чтобы удалить справку с экрана, достаточно щелкнуть в любом месте экрана. (Многие диалоговые
окна содержат кнопку, помеченную знаком вопроса. Ее также можно использовать для
получения справки о содержании диалогового окна.)
Е2 Microsoft Excel - Книга!
Файл Правка Вид Вставка Форцат Сервис Данные Окно £праека i Л ? х Ъ .ъ юох
- ю - ж к ч г « -к ЦП ч? с % от» „
. —f".-----------------------------„.Объединить и поместить б центре I-.- -
В С D Е -----------------------------------F----:---------------FT1 i
’ - В X
Anal С,г
D
J
2
3
4
5
6
7
8
9
10
11'
12
13
14
'15'
16
17
18
19
20
21'
22
23
24
'25
26
27
28
29
30
31
32
33
3.4
14 4 ► Н\лист1/Пнст2/ЛистЗ/
Панель А
Файл Правка Вид Вставка Формат Сервис Данные Окно £правкв
□ й а а ав * ч» г, • <? « г • @ и » и л •«* - о.
Arial Cvr
Al
2 3
4
5 .
6 ’
7 8
9 ' ю‘
11 12
13 14
15 16
17 18 •
19 20
21
’10 ’ ж к ч к ® з §g ® « % ООО tdg ® ’ Ъ ’ Д. ’ ,
ft--------------— Объединить и поместить в центре I---------- — —------
в ... „с. ... d...... е . ; —г—g----------ft1 ' ;т" Z j Г. к Л271
файл Правка Вид Вставка Формат Сервис Данные Окно Справка
□ & й е a v # -т *-<’•*• < z ’ ® 14 В 10С% ’ СЗ -
& & _ * & - д,
”н : i ! Т
С4
1 А
4
5
6
7
8
9
10
$ Объединить и поместить в центре
j Объединение двух или нескольких выделенных смежных ячеек в одну Конечная ячейка будет содержать данные только из левой верхней ячейки исходного диапазона, которые будут расположены по центру объединенной ячейки Ссылкой на объединенную ячейку является адрес верхней левой ячейки исходного диапазона.
11
в
Панель Б
Рис. ЕР.7. Форма курсора мыши в справке "Что это такое?" (панель А) и сообщение о кнопке
Объединить и поместить в центре (панель Б)
ЕР.З. ОСНОВНЫЕ ОПЕРАЦИИ НАД РАБОЧИМИ КНИГАМИ
В этом разделе рассматриваются операции и диалоговые окна, предусмотренные в программе Microsoft Excel 2002. (Если вы используете другую версию программы Microsoft Excel, некоторые детали могут отличаться, однако основные операции, описанные в данном разделе, выполняются аналогично.)
ЕР.3.1. Открытие рабочих книг
Для того чтобы открыть рабочую книгу Microsoft Excel, необходимо выбрать команду ФайлФОткрыть.... В открывшемся диалоговом окне Открытие документа (рис. ЕР.З) следует выполнить такие операции.
1. Выбрать требуемый каталог в раскрывающемся списке Папка.
2. Если это необходимо, выбрать соответствующее значение из раскрывающегося списка Тип файлов. По умолчанию в раскрывающемся списке выводятся имена всех файлов, создаваемых программой Microsoft Excel, что соответствует опции Все файлы Microsoft Excel. Для того чтобы отобразить в окне все текстовые файлы, следует выбрать опцию Текстовые файлы. Для того чтобы отобразить все без исключения файлы, необходимо выбрать опцию Все файлы.
3. Если это необходимо, изменить представление списка файлов, щелкнув на соответствующей кнопке выбора формата (кнопка Представление).
4. Выбрать файл из раскрывающегося списка. Если файла нет, нужно проверить, правильно ли вы выполнили п. 1 и 3.
5. Щелкнуть на кнопке ОК.
Открыв рабочую книгу, прежде чем начать работу, проверьте ее содержимое.
ЕР.3.2. Сохранение рабочих книг
Чтобы в дальнейшем иметь возможность работать с рабочей книгой, ее необходимо сохранить. Для этого следует выполнить команду Файл ^Сохранить как.... В появившемся диалоговом окне Сохранение документа выполните следующие действия (рис. ЕР.8).
1. Выберите в раскрывающемся списке Папка каталог, в котором вы желаете сохранить файл.
2. Выберите нужное значение в раскрывающемся списке Тип файла. По умолчанию предлагается тип Книга Microsoft Excel. Однако при сохранении данных, предназначенных для других программ, оказываются полезными опции Текстовые файлы (с разделителями табуляции) и CSV (разделители — запятые).
3. Введите имя сохраняемого файла в окне редактирования Имя файла.
4. Щелкните на кнопке Сохранить.
Рис. ЕР.8. Диалоговое окно Сохранение документа
; При открытии рабочей книги непосредственно с прилагаемого компакт-диска программа Microsoft Excel автоматически сопровождает ее меткой “только для чтения”. Такую книгу можно сохранить только под другим именем, воспользовавшись командой Файл ^Сохранить как....
ЕР.3.3. Вывод рабочих книг на печать
Результаты расчетов не обязательно рассматривать на экране компьютера — их можно вывести на печать. Для того чтобы распечатать рабочий лист, выберите его, а затем выполните команду Файл^Предварительный просмотр (рис. ЕР.9). Если предварительный вариант листа содержит ошибки или выглядит не так, как вам хотелось, щелкните на
кнопке Закрыть, внесите необходимые изменения и снова выполните команду Файл1^ Предварительный просмотр. Затем щелкните на кнопке Печать в окне Предварительный просмотр или, если окно просмотра закрыто, выполните команду Файл ^Печать....
Рис. ЕР.9. Диалоговое окно Предварительный просмотр
Выполните в диалоговом окне Печать (см. рис. ЕР.З) следующие действия.
1. Выберите принтер в раскрывающемся списке Имя.
2. Установите переключатель Печатать в положение Все.
3. Установите переключатель Вывести на печать в положение Выделенные листы. (Не следует устанавливать переключатель в положение Всю книгу, если вы хотите распечатать отдельный лист.)
4. Выберите количество копий в списке Число копий.
5. Щелкните на кнопке ОК.
После завершения печати внимательно просмотрите распечатку. Большинство ошибок, связанных с печатью, вызывается неправильно выбранными опциями в диалоговом окне Свойства. Исправьте их, прежде чем выполнять вторую попытку печати. Макет распечатки можно настроить с помощью команды Файл^Параметры страницы... (либо щелкнув на кнопке Страница в окне Предварительный просмотр). Например, для того чтобы распечатать рабочий лист в виде разграфленной таблицы с размеченными строками и столбцами (т.е. так, как она выглядит на экране), следует выполнить команду Параметры страницы. Затем, находясь в диалоговом окне Параметры страницы,
необходимо щелкнуть на корешке вкладки Лист, установить флажки Сетка и Заголовки строки столбцов в группе флажков Печать и щелкнуть на кнопке ОК (см. рис. ЕР. 10). (Подробная информация об этом диалоговом окне представлена в приложении Ж.)
Рис. ЕР.10. Диалоговое окно Параметры страницы
ЕР.3.4. Использование области задач для открытия рабочих книг (версии Excel 2002 и 2003)
Рис. ЕР.11. Область задач программы Microsoft Excel
Начиная с версии Microsoft Excel 2002, для того чтобы открыть рабочую книгу и выполнить другие операции, пользователь может использовать область задач (task рапе). На рис. ЕР. 11 продемонстрирована область задач, представляющая собой окно, свободно перемещающееся поверх рабочей области. Для того чтобы запустить надстройку PHStat2, достаточно щелкнуть на синей гиперссылке PHStat2. Если пользователь желает открыть диалоговое окно Открытие документа, описанное в разделе ЕР.3.1, можно щелкнуть на гиперссылке Другие книги. Поскольку область задач не добавляет новых функциональных возможностей и лишь усложняет работу с рабочей областью, многие пользователи отключают ее. Для этого необходимо либо щелкнуть на кнопке закрытия окна на строке заголовка или выполнить команду ВидФОбласть задач. Для того чтобы предотвратить появление области задач, перед тем как скрыть ее, пользователь должен сбросить флажок Показывать при запуске (как показано на рис. ЕР. 11).
ЕР.4. ОСНОВНЫЕ ОПЕРАЦИИ НАД РАБОЧИМИ ЛИСТАМИ
ЕР.4.1. Использование рабочих листов программы Microsoft Excel
Как указывалось в разделе ЕР.1, при работе с программой Microsoft Excel пользователь вводит данные в рабочие листы, состоящие из именованных столбцов и оцифрованных строк, пересечение которых образует ячейку. Обычно значения отдельных переменных вводятся в отдельном столбце, причем первая ячейка резервируется для метки. Несмотря на то что рабочий лист содержит много столбцов и строк и, следовательно, может хранить значения многих переменных, разные наборы данных следует хранить на разных рабочих листах.
Для перемещения курсора ячейки (cell pointer) по рабочему листу используется клавиша <ТаЬ> или мышь. Для ссылки на конкретную ячейку необходимо использовать следующую форму записи: ИмяЛиста!СтолбецСтрока. Например, имя Данные ! А2 относится к ячейке, расположенной на листе Данные на пересечении столбца А и строки 2. Для того чтобы сослаться на диапазон ячеек (cell range), состоящий из нескольких ячеек, следует использовать запись: ИмяЛиста!ВерхняяЛевая Ячей-ка:ПраваяНижняяЯчейка. Например, запись Данные! А2: В11 обозначает 20 ячеек, расположенных в строках 2 -11 и столбцах А и В на листе Данные.
Каждый рабочий лист имеет свое имя. По умолчанию программа Microsoft Excel именует рабочие листы последовательно: Лист1, Лист2 и т.д. Однако лучше присваивать рабочим листам осмысленные имена, например, рабочий лист, содержащий данные, следует называть Данные, а лист, содержащий результаты вычислений, логично назвать Вычисления. Для того чтобы переименовать рабочий лист, необходимо дважды щелкнуть на его ярлычке (sheet tab), набрать новое имя и нажать клавишу <Enter>.
ЕР.4.2. Формулы
Для выполнения вычислений пользователь может набирать формулы — инструкции, манипулирующие с данными рабочего листа. Формулы всегда начинаются символом = (равенство) и могут содержать арифметические операции.
В простых формулах используются символы +, *, / и л, обозначающие операции
сложения, вычитания, умножения, деления и возведения в степень соответственно. Например, формула ^Данные!В2+Данные!ВЗ+Данные!В4+Данные!В5 складывает величины, хранящиеся в ячейках В2, ВЗ, В4 и В5 на рабочем листе Данные. Результат этого выражения записывается в ячейку, содержащую формулу. Кроме простых арифметических операций, формулы могут использовать функции. Например, предыдущую формулу можно переписать в виде формулы =СУММ(Данные!В2:В5), использующей функцию СУММ. Если формула использует только данные, хранящиеся на текущем листе, указывать название рабочего листа не обязательно.
Для того чтобы различать ячейки, расположенные в одинаковых строках и столбцах ’ на одинаковых листах, но в разных рабочих книгах, используется обозначение [РабочаяКнига]ИмяЛиста!СтолбецСтрока. Например, обозначение ’ [Глава 1] Данные * ! А1 относится к левой верхней ячейке рабочего листа Данные в рабочей книге Глава 1.
Формулы позволяют находить общие решения и заново вычислять результаты, если исходные данные изменились. Некоторые процедуры программы Microsoft Excel и надстройка PHStat2 автоматически добавляют формулы в рабочие листы. Для того чтобы отобразить их на экране, необходимо выполнить команду Сервис^Параметры..., а затем, находясь в диалоговом окне Параметры, установить флажок Формулы в группе Параметры окна и щелкнуть на кнопке ОК. (Для того чтобы восстановить исходное положение, следует сбросить флажок Формулы.)
Если для создания своего рабочего листа вы используете шаблоны из раздела “Справочник по Excel”, необходимо отображать формулы в ячейках для проверки правильности вычислений.
ЕР.4.3. Оформление рабочего листа
В программе Microsoft Excel предусмотрено очень много возможностей для улучшения внешнего вида рабочих листов. Многие операции форматирования изображаются пиктограммами на панели форматирования (formatting toolbar). Кроме того, их можно выполнить, выбрав пункт меню Формат^Ячейки... и установив параметры в диалоговом окне Формат ячеек. Панель форматирования показана на рис. ЕР. 12.
, >» «К»
Рис. ЕР.12. Панель инструментов форматирования
ВРЕЗКА ЕР.5. ОПЕРАЦИИ ФОРМАТИРОВАНИЯ
• Чтобы выделить содержимое ячейки полужирным шрифтом, выберите ячейку (или диапазон ячеек), содержащую значения, подлежащие выделению, и щелк- ; ните на кнопке Пол ужйрный пане л и инструментов форматирования.
• Чтобы выровнять содержимое ячейки по центру, выберите ячейку (или диапазон ячеек), содержащую значения, подлежащие выделению, и щелкните на кнопке По центру панели инструментов форматирования. (Выравнивание по левому и правому краю, а также по ширине осуществляется аналогично, путем выбора соответствующих пиктограмм.)
• Чтобы выровнять по центру диапазона ячейку, содержащую его заголовок, выделите ячейки, расположенные над диапазоном (включая заголовок), и щелкните на кнопке Объединить и поместить в центре.
• Чтобы отобразить на экране все содержимое столбца, выберите форматируемый столбец, щелкнув на его заголовке, а затем выполните команду Формат^ Столбец1^Автоподбор ширины.
• Чтобы вывести числовые данные в виде процентов, выберите диапазон ячеек, содержащих числовые величины, подлежащие выводу, и щелкните на кнопке Процентный формат, расположенной на панели инструментов форматирования.
; • Чтобы выровнять десятичное представление в последовательности числовых величин, выберите диапазон ячеек, содержащих числовые величины, подлежащий : выравниванию, и щелкните на кнопке Увеличить разрядность или Уменьшить разрядность.
• Чтобы изменить цвет фона, выберите соответствующий диапазон ячеек и щелкните на кнопке Цвет заливки. В диалоговом окне Цвет заливки (рис. ЕРЛЗ) пользователь ; должен выбрать новый цвет фона. (В большинстве таблиц, представленных в книге, ячейки, в которые можно вводить данные, окрашены в светло-бирюзовый цвет, а ячейки, содержащие результаты, — в светло-желтый. Эти цвета являются пятым ; и третьим в последней строке палитры цветов заливки соответственно.)
• Чтобы изменить обрамление ячейки, выберите соответствующий диапазон ячеек и щелкните на кнопке Границы, открывающей список возможных вариантов обрамления (рис. ЕР. 14). (Таблицы, приведенные в книге, используют разнообразные варианты обрамления ячеек, включая стили Внешние границы, Нет границы и Нижняя граница.)
_ I I
~ Ш □ □
Нарисовать границы.,.
Рис. ЕРЛЗ. Диалоговое окно Цвет заливки
Рис. ЕР.14. Диалоговое окно Границы
ЕР.5. БОЛЕЕ СЛОЖНЫЕ ОПЕРАЦИИ С РАБОЧИМИ ЛИСТАМИ
ЕР.5.1. Копирование ячеек и формул на одном листе
Довольно часто для выполнения дополнительных вычислений необходимо добавлять формулы в ячейки всего столбца или строки. Вместо того чтобы многократно вводить формулы в каждую ячейку, можно просто скопировать их.
Обычно для копирования содержимого одной ячейки в другую достаточно выделить исходную ячейку и выбрать команду Правкам Копировать. Затем следует выделить ячейку, в которую выполняется копирование, и выбрать команду Правка^Вставить. Если копируемая ячейка содержит формулы, результат зависит от того, правильно ли введены ссылки на ячейки. Если ссылки на ячейки имеют вид БукваНомер, например, А1, или любую из форм, указанных в разделе ЕР.4.1, они называются относительными (relative references) и при копировании будут адаптированы к новому адресу. Например, формула =А2+В2, находящаяся в ячейке С2, при копировании в ячейку СЗ будет изменена на формулу =АЗ+ВЗ, чтобы учесть ее новое местоположение. Аналогично формула =СУММ (Al: А4), записанная в ячейке А5, будучи скопированной в ячейку В5, преобразуется в формулу =СУММ (В1: В4) .
Если пользователь хочет отменить автоматическую настройку формул, ссылки на ячейки следует сделать абсолютными (absolute reference). Например, формула =$А$2+$В$2 всегда будет суммировать содержимое ячеек, находящихся в первом и втором столбцах, независимо от того, куда она будет скопирована. Обратите внимание на знак доллара. В данном контексте этот символ имеет совершенно иной смысл — он просто предотвращает модификацию формулы при копировании в новое место. Программа Microsoft Excel допускает смешение относительных и абсолютных ссылок в одной формуле. Например, допустим, что в ячейке С2 хранится формула =А2/$В$10, которая копируется в ячейку СЗ. В этом случае она будет заменена формулой =АЗ/$В$10. Такой способ записи часто позволяет упростить реализацию формул и применять их в любых таблицах.
ЕР.5.2. Копирование формул с одного листа на другой
Используя команды Правка^ Копировать и Правкам Вставить, формулы можно копировать с одного листа на другой. В этих случаях следует убедиться, что все ссылки, использованные в формулах, являются абсолютными, например, Данные ! $А$1: $А$12.
Если при копировании формулы необходимо передать лишь ее результат, можно применить два способа. Первый способ применяется, если копируется содержимое только одной или нескольких ячеек. В этом случае можно использовать формулу вида =ИмяЛистаИсточника!ИмяЯчейки. Например, если вы собираетесь скопировать формулу, хранящуюся в ячейке В10 на листе Результаты, в ячейку А5 на листе Итоги, чтобы отобразить ее результат, введите в ячейку А5 на листе Итоги формулу ^Результаты! В10, а исходную формулу не копируйте.
Второй способ применяется, когда необходимо скопировать большой диапазон ячеек. Для этого сначала на первом листе следует выделить исходный диапазон ячеек и выполнить команду Правка^Копировать. Затем на втором рабочем листе необходимо выделить диапазон ячеек, в которые будут скопированы формулы, и выполнить команду ПравкаФСпециальная вставка.... Находясь в диалоговом окне Специальная вставка (рис. ЕР.15), нужно установить переключатель Вставить в положение Значения и форматы чисел и щелкнуть на кнопке ОК. В этом случае вставка выполняется так, что при дальнейшем изменении исходных данных повторять процедуру копирования не обязательно.
Специальная вставка
Вставить ® все О формулы О значения О Форматы О примечания
Операция ©нет
О сложить О вычесть
О условия на значения
О без рамки
О ширины столбцов
О формулы и форматы чисел
О значения и форматы чисел
О умножить
О разделить
0 пропускать пустые ячейки □ транспонировать
f Вставить связь
ОК
Отмена |
Рис. ЕР.15. Диалоговое окно Специальная вставка
ОБМЕН ДАННЫМИ МЕЖДУ ДОКУМЕНТАМИ ПАКЕТА MICROSOFT OFFICE
Процедуры обмена данными между программой Microsoft Excel и документами, созданными разными компонентами пакета Microsoft Excel, описаны в разделах 3.1 и 3.2 приложения 3.
ЕР.5.3. Копирование и переименование рабочих листов
Если рабочий лист должен быть оформлен в разных стилях или один из вариантов листа должен быть представлен в режиме просмотра формул, а в другом варианте должны отображаться лишь их результаты, возникает необходимость скопировать такой лист целиком. Чтобы скопировать рабочий лист, нужно сначала его выбрать, щелкнув на ярлычке. Затем следует выполнить команду Правка*^Переместить/ Скопировать лист.... В открывшемся диалоговом окне Переместить или Скопировать следует выполнить такие действия (см. рис. ЕР. 16).
1. Установить флажок Создавать копию.
2. Выбрать опцию (новая книга) из списка Переместить выбранные листы в книгу, если лист должен быть скопирован в новую книгу (см. рис. ЕР. 16). Если лист копируется в текущую книгу, необходимо указать относительное положение копии в списке Перед листом.
3. Щелкнуть на кнопке ОК.
Программа Microsoft Excel присваивает копии имя исходного листа, добавляя номер, заключенный в скобки. Например, копия листа Вычисления называется Вычисления (2). Намного полезнее присвоить копии более осмысленное имя, например, Форматированные результаты. Для того чтобы сделать это, воспользуйтесь процедурой, описанной в разделе ЕР.4.1.
Рис. ЕР.16. Диалоговое окно
Переместить или скопировать
ЕР.6. ПРИМЕНЕНИЕ МАСТЕРА ДИАГРАММ
Мастера (wizards) представляют собой набор взаимосвязанных диалоговых окон, облегчающих процесс создания различных объектов, например, диаграмм или сводных таблиц. Чтобы создать объект, в каждом из этих окон пользователь должен вводить информацию и делать выбор, переходя от одного окна к другому, щелкая на кнопке Далее>, а в последнем окне— на кнопке Готово. Прекратить работу мастера можно в любой момент, щелкнув на кнопке Отмена. Кроме того, можно вернуться на предыдущий этап создания объекта, щелкнув на кнопке Назад.
Мастер диаграмм позволяет создавать диаграммы, переходя от одного окна к другому и выбирая различные варианты. Для запуска мастера следует выполнить команду ВставитьФДиаграмма..., Процесс создания состоит из четырех этапов, каждому из которых соответствует собственное диалоговое окно (рис. ЕР. 17).
1. Выберите тип диаграммы в первом диалоговом окне.
2. На втором этапе укажите диапазон ячеек во вкладке Диапазон данных. При необходимости щелкните на корешке вкладки Ряд, а затем выберите пункт раскрывающегося списка Ряд.
3. Выберите и укажите параметры диаграммы в третьем диалоговом окне (см. врезку ЕР.6).
4. Если вы хотите поместить диаграмму на новом листе, находясь на четвертом этапе, установите переключатель Поместить диаграмму на листе в положение Отдельном, в противном случае установите переключатель в положение Имеющемся. Более предпочтительным является первый вариант.
Мастер диаграмм (шаг 1 из 4): тип диаграммы
Е®’
i Стандартные > Нестандартные i
Тип:
Е Линейчатая График
! <3 Круговая
|__Точечная
: С областями
: ф Кольцевая
: Лепестковая
Поверхность
•; Пузырьковая
Мастер диаграмм (шаг 3
Вид:
Оси
пароме гры диаграммы
Мастер диаграмм (шаг 2 из 4): источник данных диа..
Диапазон данных ; Ряд
Е®
Подписи данных
Заголовки
Таблица данных
Линии сетки Легенда
Название диаграммы:
| Ось X (категорий):
10000-1-
900D -
| Ось Y (значений):
woo
---I |ВРШ|
ХЕ
Мастер диаграмм (шаг 4 из 4): размещение диаграммы
Е®5
Поместить диаграмму на листе:
Г Отмен
О отдельном: .Диаграмма!
© имеющемся: ИШ
[ Отмена ] [ < Назад ]
[готово ]
Рис. ЕР.17. Окна Мастера диаграмм в программе Microsoft Excel 2002
\ ВРЕЗКА ЕР.6. ВЫБОР ОПТИМАЛЬНЫХ ПАРАМЕТРОВ ДИАГРАММ
; Чтобы не применять установки, принятые по умолчанию, необходимо самостоятель-
; но выбрать нужные параметры диаграммы, руководствуясь следующими инструк-
; днями (рис. ЕР.18).
\ ♦ Щелкните на корешке вкладки Заголовки и введите соответствующие названия.
; • Щелкните на корешке вкладки Оси, а затем установите флажки Ось X (категорий) и Ось Y (значений). Кроме этого, следует установить переключатель ОсьХ • (категорий) в положение Автоматическая.
j • Щелкните на корешке вкладки Линии сетки и сбросьте все флажки, относящиеся к осям X и Y.
; • Щелкните на корешке вкладки Легенда и сбросьте флажок Добавить легенду.
• Щелкните на корешке вкладки Подписи данных й сбросьте все флажки.
• Если Мастер диаграмм содержит вкладку Таблица данных, щелкните на ее корешке и сбросьте флажок Таблица данных.
Обратите внимание на то, что некоторые инструкций предписывают пользователю снимать флажки и изменять параметры, автоматически установленные программой Microsoft Excel. В противном случае диаграммы могут содержать ошибки. Если все же диаграмма оказалась неверной, щелкните на ней правой кнопкой мыши и выполните команду Параметры диаграммы... из всплывающего меню. В этом случае вы вернетесь на этап 3.
Мастер диаграмм (шаг 3 из 4): параметры диаграммы
Рис. ЕР.18. Третье диалоговое окно Мастера диаграмм в программе Microsoft Excel 2002
ЕР.7. ПРИМЕНЕНИЕ МАСТЕРА СВОДНЫХ ТАБЛИЦ
Мастер сводных таблиц и диаграмм позволяет создавать интерактивные сводные таблицы, которые автоматически изменяются при модификации исходных данных. В книге мы применяем его для построения однофакторных и двухфакторных таблиц распределения частот (one-way and two-way frequency distribution tables) для категорийных данных (см. главу 2). Однако следует иметь в виду, что сводные таблицы можно использовать для динамического исследования данных, удаляя или добавляя переменные в интерактивном режиме.
Для того чтобы подробнее ознакомиться с приемами динамического исследования данных с помощью сводных таблиц, откройте рабочую книгу Exploring PivotTables .xls, находящуюся на компакт-диске в каталоге Instructional Files.
Для запуска мастера в программе Microsoft Excel 2002 и более поздних версиях следует выбрать команду Данные^Сводная таблица...2. Затем необходимо выполнить следующие действия.
В программе Microsoft Excel 97 четырехэтапное построение сводной таблицы начинается с выполнения команды Данные ^Сводная таблица....
1. В первом диалоговом окне (см. рис. ЕР. 19) выберите источник исходных данных для сводной таблицы и вид отчета, который должен быть создан. (В нашей книге в качестве источника таблицы всегда указывается Список или база данных Microsoft Excel, а в качестве вида создаваемого отчета выбирается Сводная таблица.)
2. Во втором окне выберите диапазон ячеек, содержащий исходные данные. (Первая строка содержит названия переменных.)
3. В третьем окне щелкните на кнопках Макет... и Параметры... (для установки вида и параметров таблицы) и выберите местоположение новой сводной таблицы (как правило, на новом листе).
Щелкая мышью на кнопке Макет..., пользователь выводит на экран диалоговое окно Мастер сводных таблиц и диаграмм - макет. Находясь на этом диалоговом окне, необходимо перетащить метки с названиями переменных (частично закрытых на рис. ЕР.20) в шаблон сводной таблицы, содержащий страницу, строку, столбец и область данных. (Область страницы в нашей книге не используется.) Некоторые пользователи находят эту процедуру довольно запутанной и предпочитают использовать для построения одно-и двухфакторных таблиц и диаграмм процедуры надстройки PHStat2 (см. главу 2).
Щелкнув мышью на кнопке Параметры..., пользователь открывает диалоговое окно Параметры сводной таблицы. Для решения большинства задач, приведенных в книге, достаточно ввести в окно редактирования Имя некое разумное название таблицы, в окно Для пустых ячеек отображать ввести число 0, а остальные настройки оставить неизменными, как показано на рис. ЕР.20.
шаг 1 из 3
Укажите диапазон, содержащий исходные данные. Диапазон: Н
Создать таблицу на основе данных, находящихся:
О 80 енешнен источнике данных
О в нескольких диапазонах консолидации
Вид создавав»
О сводна: О сведи®
Для создания таблицы нажмите кнопку Тотово".
Поместить таблицу в:
©^OBbtHJMCTj
О существующий лист
Мастер сводных таблиц и диаграмм шаг 2 из 3
Мастер сводных таблиц и диаграмм - шаг 3 из 3
| Макет... ]| Параметры... ] [ Отмена ] | < Назад ]
| Готово ]
Рис. ЕР.19. Окна Мастера сводных таблиц и диаграмм в программе Microsoft Excel 2002
1ена
Параметры сводной таблицы
Имя:
Формат
0 общая сумма по столбцам 0 общая сумма по строкам 0 автоформат
I I включать скрытые значения 0 объединять ячейки заголовков 0 сохранять форматирование 0 повторять подписи на каждой странице печати
макет страницы:
вниз, затем поперек
число полей в столбце:
I I для ошибок отображать:
0 для пустых ячеек отображать:
0 печать заголовков
О
Данные
Источник:
0 сохранить данные вместе с таблицей
0 развертывание разрешено
□ обновить при открытии
Внешние данные:
J [ Отмена ]
Рис ЕР.2О. Окна Макет (частично закрытое) и Параметры
ЕР.8. ИСПОЛЬЗОВАНИЕ НАДСТРОЕК
Надстройки (adds-in) — это вспомогательные программы, расширяющие функциональные возможности Microsoft Excel. Компания Microsoft предлагает большое количество надстроек, в частности, программу Пакет анализа для пакета Microsoft Office. Кроме того, существует широкий выбор надстроек, предоставляемых независимыми производителями, например, программа PHStat2, разработанная компанией Prentice Hall.
Как правило, надстройка модифицирует строку меню программы Microsoft Excel, добавляя новое меню или новый пункт. Например, надстройка Пакет анализа вставляет в меню Сервис новый пункт Анализ данных... (рис. ЕР.21), предоставляющий пользователю возможность выполнить статистический анализ данных, который было бы очень трудно сделать самостоятельно. В свою очередь, надстройка PHStat2 вставляет в меню программы Excel новый пункт PHStat (рис. ЕР.22), содержащий большое количество статистических функций, расширяющих возможности надстройки Пакет анализа и упрощающих ее процедуры.
Поскольку надстройки представляют собой особую разновидность рабочей книги, их можно открывать с помощью процедуры Файл^Открыть..., как и любую другую рабочую книгу. Однако их можно “инсталлировать” так, чтобы они автоматически открывались при каждом запуске программы Microsoft Excel. Для того чтобы инсталлировать надстройку, сначала следует выполнить команду Сервис^Надстройки..., а затем, нахо
дясь в диалоговом окне Надстройки (рис. ЕР.23), установить соответствующий флажок в списке Доступные надстройки. (Предполагается, что на компьютерах читателей надстройка Пакет анализа открывается автоматически, а надстройка PHStat2 — вручную.)
Анализ данных
Инструменты анализа
| Двухфакторный дисперсионный анализ с повторениями j Двухфакторный дисперсионный анализ без повторений £ Корреляция
!Ковариация
| Описательная статистика
I Экспоненциальное сглаживание
i Двухвыборочный F-тест для дисперсии
| Анализ Фурье
iГистограмма__
[ Отмена )
[ Справка ]
Рис. ЕР.21. Диалоговое окно Анализ данных
&W j йсно Справка ~
Data Preparation ►
Descriptive Statistics ►
| Decision-Making ►
Probability & Prob. Distributions ►
A Sampling ►
Confidence Intervals ►
Sample Size ►
? One-Sample Tests ►
i Two-Sample Tests ►
1 Multiple-Sample Tests ►
J Control Charts ►
Regression ►
J Utilities ►
j About PHStat...
~ Help for PHStat
Рис. EP.22. Меню PHStat
Рис. EP.23. Диалоговое окно Надстройки
Безопасность j
Й.^рв^ безопасгости ;; Надежные издатели
I О Очень высокая. Разрешается запуск только макросов, установленных в ; | надежных расположениях. Все остальные подписанные и i;
। неподписанные макросы отключаются. t
! О Высокая. Разрешается запуск только подписанных макросов из !
I надежных источников. Неподписанные макросы отключаются !
] автоматически.
\ (*) Средняя. Решение о запуске потенциально опасных макросов j
j принимается пользователем. i
s О Низкая (не рекомендуется). Защита от потенциально опасных макросов I I отсутствует. Используйте этот режим только при наличии антивирусных | ! программ и после проверки на безопасность всех открываемых с
j документов. i
I {
Рис. ЕР.24. Диалоговое окно Безопасность
Открытие надстроек контролируется системой безопасности Microsoft Excel. Если вы пользуетесь программой Microsoft Excel 2000 версии SR-1 и выше, чтобы безопасно пользоваться надстройкой PHStat2, сначала необходимо выполнить команду Сервис^ Макрос^ Безопасность... и установить флажок Средняя во вкладке Уровень безопасности в окне Безопасность (рис. ЕР.24). Это не создает никакой угрозы для операционной системы, но предоставляет пользователю полный контроль над макросами. (Советуем никогда не снижать уровень безопасности до низкого, несмотря на то, что он также позволяет открывать надстройки наподобие PHStat2.)
Установив средний уровень безопасности и открыв надстройку PHStat2, вы получите предупреждение об опасности выполнить макрокоманду, зараженную вирусом (рис. ЕР.25). Чтобы продолжить открытие надстройки, следует щелкнуть на кнопке Не отключать макросы, разрешающей выполнять корректные макросы.
Предупреждение системы безопасности
"C:\Program Files\PHStat2 version 2.5\PHStat2.xla” содержит макросы
Макросы могут содержать вирусы. Безопаснее отключить макросы, но если они необходимы, то часть функциональности может быть утеряна.
[ Отключить макросы [“не^отключатьМакросы | {" подробности ]
Рис. ЕР.25. Предупреждение о макровирусах в программе Microsoft Excel 2002 (в других версиях предупреждение выглядит аналогично)
ОСНОВНЫЕ понятия
Автоформат, 86
Выделение, 86
Выравнивание, 86
Горячая клавиша, 75
Заливка, 86
Кнопка
системная, 74
счетчика, 76
Комбинация быстрых клавиш, 75
Курсор мыши, 72
Мастер, 89
диаграмм, 89
сводных таблиц, 91
Многоточие, 75
Надстройка, 93
Обрамление, 86
Окно
диалоговое, 75
редактирования, 76
списка, 76
Панель инструментов стандартная, 74 форматирования, 74
Переключатель, 76
Пиктограмма, 75
Полоса прокрутки, 74
Процентный формат, 86
Разрядность, 86
Список
раскрывающийся, 76
Ссылка
абсолютная, 87 относительная, 87
Строка
меню, 74
формул, 74
Треугольный маркер, 75
Флажок опции, 76
Формула, 85
Ярлык листа, 74
Глава 2
Представление данных в виде таблиц и диаграмм
ПРИМЕНЕНИЕ СТАТИСТИКИ: сравнение эффективности взаимных фондов
2.1. ОРГАНИЗАЦИЯ ЧИСЛОВЫХ ДАННЫХ
Упорядоченный массив Процедуры Excel: создание упорядоченных массивов Диаграмма “ствол и листья” Процедуры Excel: построение диаграмм “ствол и листья”
2.2. ПРЕДСТАВЛЕНИЕ ЧИСЛОВЫХ ДАННЫХ В ВИДЕ ТАБЛИЦ И ДИАГРАММ
Распределение частот
Определение количества групп Разбиение на интервалы группирования Определение границ интервалов группирования
Субъективность при определении границ интервалов группирования
Распределение относительных частот и процентное распределение Функция распределения Процедуры Excel: вычисление распределения частот для числовых данных Гистограмма Полигон
Полигон интегральных процентов (кривая распределения)
Процедуры Excel: построение гистограмм и полигонов для числовых данных
2.3. ИЗОБРАЖЕНИЕ ДВУМЕРНЫХ ЧИСЛОВЫХ ДАННЫХ
Процедуры Excel: построение диаграмм разброса
2.4. ПРЕДСТАВЛЕНИЕ КАТЕГОРИЙНЫХ ДАННЫХ В ВИДЕ ТАБЛИЦ
И ДИАГРАММ
Сводная таблица
Линейчатая диаграмма
Круговая диаграмма
Диаграмма Парето
Процедуры Excel: создание таблиц и диаграмм для категорийных данных
2.5. ПРЕДСТАВЛЕНИЕ ДВУМЕРНЫХ КАТЕГОРИЙНЫХ ДАННЫХ В ВИДЕ ТАБЛИЦ И ГРАФИКОВ
Таблица сопряженности признаков Параллельная линейчатая диаграмма Процедуры Excel: создание таблиц и диаграмм для двумерных категорийных данных
2.6. ИСКУССТВО ГРАФИЧЕСКОГО ПРЕДСТАВЛЕНИЯ ДАННЫХ
Принципы графического представления данных
СПРАВОЧНИК EXCEL. ГЛАВА 2
ЧЕМУ ДОЛЖЕН НАУЧИТЬСЯ СТУДЕНТ
• Организовывать числовые данные.
• Создавать таблицы и диаграммы для числовых и категорийных
• Понимать принципы правильного графического представления
|||||||И^
ПРИМЕНЕНИЕ СТАТИСТИКИ
Сравнение эффективности взаимных фондов
В последние годы вклады во взаимные фонды составили миллиарды долларов. В следующих двух главах мы проанализируем работу взаимных фондов, владеющих портфелем ценных бумаг. Приобретая акции (долю) взаимного фонда, инвестор вступает во владение всеми акциями компаний, принадлежащими фонду. В нашем сценарии мы сыграем роль финансового советника, выбирающего фонд, в который следует вкладывать средства. Взаимные фонды преследуют разные цели. Обычно капитал фонда складывается из акций схожих компаний. Например, фонды могут специализироваться на акциях крупных, средних или мелких
компаний. Кроме того, взаимные фонды различаются по степени риска, связанного с ценными бумагами, которыми они владеют. В соответствии с этим критерием они
разделяются на фонды с очень высоким, высоким, средним, низким и очень низким
уровнями риска.
Финансовый советник должен порекомендовать клиенту наилучшее капиталовложение. Для этого сначала необходимо сравнить эффективность взаимных фондов из разных категорий. Являются ли фонды, ориентированные на быстрый рост капитала (growth funds), более эффективными, чем фонды, ориентированные на медленный рост (value funds)? Можно ли утверждать, что изменчивость доходности фондов первого типа больше, чем у фондов второго типа? Как использовать таблицы и диаграммы для анализа эффективности различных фондов?
ВВЕДЕНИЕ
Как правило, если исходный набор данных состоит из 20 и более записей, необходимо создавать соответствующую таблицу или диаграмму, позволяющие выявить важную информацию. В данной главе таблицы и диаграммы используются для эффективной реализации двух ключевых аспектов принятия решений — анализа данных и последующей интерпретации.
2.1. ОРГАНИЗАЦИЯ ЧИСЛОВЫХ ДАННЫХ
Mutual Funds.XLS
Для того чтобы ответить на вопросы, поставленные в сценарии, необходимо проанализировать последние данные об эффективности взаимных фондов. Для этого на компакт-диске приведены данные о 259 фондах.
Проанализируем годовые показатели фондов разного типа за последние 5 лет. В рабочей книге Mutual Funds .xls содержатся данные о фондах, ориентированных на быстрый и медленный рост капитала соответственно. Фонды, ориентированные на быстрый рост капитала, владеют акциями, отношение рыночной цены которых к чистой прибыли в расчете на одну акцию (отношение Р/Е (price-to-earning ratio)) превышает среднее значение Р/Е у аналогичных компаний. Фонды, ориентированные на медленный рост капи-
тала, владеют акциями, отношение Р/Е которых меньше, чем среднее отношение Р/Е у аналогичных компаний. Сравнив годовые показатели доходности фондов из этих групп, легко ответить на вопрос “Какие фонды эффективнее: ориентированные на быстрый рост капитала или на медленный?”. В рабочей книге Mutual Funds, xls приведены данные о 158 фондах, ориентированных на быстрый рост капитала, и 101 фонде, ориентированном на медленный рост капитала. Годовые показатели относятся к периоду с 1 апреля 1997 по 31 декабря 2001 года. Этот период характеризуется очень сильными колебаниями доходности взаимных фондов. (Полное описание рабочей книги Mutual Funds . xls приведено в приложении Г.)
Чем больше анализируемых данных, тем труднее сконцентрировать внимание на их основных характеристиках. Чтобы лучше воспринять информацию, содержащуюся в наборе данных, их необходимо правильно организовать. Для этого используют либо упорядоченный массив, либо диаграмму “ствол и листья”.
Упорядоченный массив
Упорядоченный массив (ordered array) состоит из последовательности данных, расположенных по возрастанию. Например, табл. 2.1 содержит показатели о пятилетней среднегодовой доходности 158 фондов, ориентированных на быстрый рост капитала. Упорядоченные массивы позволяют сразу определить минимальное и максимальное значения, типичные величины, а также диапазон, которому принадлежит основная масса значений.
Таблица 2.1. Упорядоченный массив, содержащий данные о пятилетней среднегодовой доходности 158 фондов, ориентированных на быстрый рост капитала, за период с 1 января 1997 до 31 декабря 2001 г.
Mutual Funds.XLS
-6,1 -2,8 -1,2 -0,7 0,5 1,8 1,9 2,5 2,8 3,3
3,5 3,8 3,8 4,0 4,2 4,3 4,5 4,6 5,0 5,1
5,2 5,4 5,5 5,8 5,9 6,0 6,2 6,3 6,5 6,5
7,0 7,1 7,1 7,2 7,2 7,3 7,5 7,6 7,6 7,8
7,8 7,8 7,9 8,1 8,1 8,2 8,3 8,3 8,4 8,5
8,5 8,5 8,6 8,8 8,8 8,8 9,0 9,0 9,1 9,1
9,1 9,2 9,3 9,3 9,5 9,5 9,5 9,5 9,6 9,6
9,7 9,8 9,9 9,9 9,9 9,9 10,1 10,1 10,1 10,1
10,2 10,3 10,3 10,4 10,5 10,5 10,5 10,5 10,5 10,5
10,6 10,7 10,7 10,8 10,9 11,0 11,0 11,1 11,1 11,1
11,2 11,2 11,3 11,3 11,3 11,3 11,4 11,5 11,5 11,5
11,6 11,7 11,7 11,9 11,9 12,2 12,2 12,3 12,3 12,4
12,5 12,7 12,9 12,9 12,9 13,0 13,1 13,2 13,4 13,4
13,7 13,7 13,9 14,1 14,7 14,8 14,9 15,0 15,7 15,8
15,8 16,0 16,9 17,0 17,0 17,6 17,8 18,1 18,1 18,2
18,5 18,5 18,7 18,9 21,4 22,0 22,9 26,3
Как видим, наименьший уровень пяти летней среднегодовой доходности равен -6,1% в год, а наивысший достигает 26,3%. Кроме того, среднегодовые показатели большинства фондов колеблются в диапазоне от 5 до 15%. Прежде чем создавать сводные таблицы и диаграммы или вычислять средние значения показателей (см. главу 3), данные можно представить в виде диаграммы “ствол и листья” [9,10].
Процедуры Excel: создание упорядоченных массивов
Для упорядочения содержимого рабочей таблицы или диапазона ячеек следует выбрать команду Данные^Сортировка.... Например, чтобы создать упорядоченный массив, соответствующий табл. 2.1, необходимо открыть файл Growth Funds Sample. xls и сделать следующее.
1. Выбрать пункт меню ДанныеФСортировка....
2. В диалоговом окне Сортировка диапазона выполнить такие действия.
2.1. Выбрать столбец Пятилетняя доходность в раскрывающемся списке.
2.2. Установить переключатель Сортировать по в положение По возрастанию.
2.3. Установить переключатель Идентифицировать поля по в положение По обозначениям столбцов листа.
2.4. Щелкнуть на кнопке ОК.
Сортировка диапазона
Сортировать по
i Пятилетняя доход! vj ® по возрастанию .......... ' О по убываникз
Затем по
i v l ® по возрастанию
....... О по убыванию
В последнюю очередь., по
® по возрастанию
.............. Q по убыванию
Идентифицировать диапазон данных по
<$) подписям (первая строка диапазона)
О обозначениям столбцов листа
[ Параметры., j | .QK. [ Отмена ]
Можно просто перетащить курсор мыши через диапазон ячеек, содержащих данные о пятилетней доходности фондов (11:1159), а затем скопировать и вставить этот диапазон (см. раздел ЕР.5.1) в новый рабочий лист.
Диаграмма "ствол и листья"
Диаграмма “ствол и листья” (stem-and-leaf display) представляет собой инструмент для организации набора данных и анализа их распределения. Данные в диаграмме “ствол и листья” распределены в соответствии с первыми цифрами, или стволами, и замыкающими цифрами, или листьями. В диаграмме “ствол и листья” число 10,9 (соответствующее пятилетней среднегодовой доходности, равной 10,9%) состоит из ствола 10 и листа 9.
На рис. 2.1 показана диаграмма “ствол и листья”, отображающая пятилетнюю доходность 158 фондов, ориентированных на быстрый рост капитала. Первые два столбца цифр образуют ствол, содержащий ведущие цифры чисел. Листья, или замыкающие цифры, расположены справа.
Анализируя рис. 2.1, можно сделать некоторые выводы относительно среднегодовой доходности фондов за последние пять лет.
1. Наименьший уровень пятилетней среднегодовой доходности равен -6,1%.
2. Наивысший уровень пятилетней среднегодовой доходности равен 26,3%.
3. Уровни доходности 158 фондов, ориентированных на быстрый рост капитала, колеблются между наименьшим и наивысшим значениями, причем наибольшая концентрация доходности наблюдается в интервале от 1,8 до 18,9%. Количество фондов, доходность которых близка к наибольшей или наименьшей, невелико.
4. Только четыре взаимных фонда приносят убытки. В то же время лишь у четырех взаимных фондов среднегодовая доходность превышает 20%.
А
2
3 I
4
5
6
7 В
9
10
________________________В
Диаграмма "ствол и листья"
Шаг
-6
-5
4
-3
-2
11
12
13
14
15
16
J7
18
19
20
21
22
23
24
-0 6
2 3
4 5
6
8 9
io и 12
8
'2
5
89
58 3588 02358 0124589 02355 0112235668889 1123345556888 00111233555566789999 0111233455555567789 00111223333455567799 2233457999
Рис. 2.1. Диаграмма "ствол и листья", содержащая показатели пятилетней доходности 158 фондов, ориентированных на быстрый рост капитала (построена с помощью программы Microsoft Excel)
Процедуры Excel: построение диаграмм "ствол и листья"
Для создания диаграммы "ствол и листья" сначала необходимо упорядочить данные, а затем записать их в двух смежных столбцах, представляющих ствол и листья. Эту задачу можно решить как с помощью надстройки PHStat2, так и самостоятельно. Однако следует иметь в виду, что процедура создания листьев диаграммы трудоемка и подвержена ошибкам.
Например, для того чтобы создать диаграмму "ствол и листья", представленную на рис. 2.1, необходимо открыть файл Growth Funds Sample.xls на рабочем листе Данные, а затем выполнить одну из следующих процедур.
Применение Excel в сочетании с надстройкой PHStatZ
Для создания диаграммы "ствол и листья" следует выполнить команду PHStatZDescriptive Statistics1^ Stem-and-Leaf Display... (PHStat ^Описательная статистика^ Диаграмма “ствол и листья”...) и следующие инструкции.
1. Выполнить команду PHStatZDescriptive Statistics1^ Stem-and-Leaf Display....
2. В диалоговом окне Stem-and-Leaf Display необходимо сделать следующее.
2.1. Ввести в окне редактирования Variable Cell Range (Входной диапазон) диапазон и: 1159.
2.2. Установить флажок First cell contains label (Метка в первой ячейке).
2.3. Установить переключатель Stem Unit (Шаг) в положение Autocalculate stem unit (Автоматическое вычисление шага).
Siem and Leaf Display [X|
i Variable Cell Range: ...*""| ,
j R First cell contains label
Stem Unit
j <* Autocalculate stem unit !
! C* Set stem unit as: |" ' ''
Output Options _________ ,
I Title: | Диаграмма "ствол и листья" I
j P Summary Statistics I
Help | ILZoTJI Cancel |
2.4. Ввести заголовок структуры в окне редактирования Title (Заголовок).
2.5. Щелкнуть на кнопке ОК.
Для того чтобы включить в таблицу пятерку базовых показателей, описанных в главе 3, установите флажок Summary Statistics (Базовые показатели).
Применение Excel
Скопируйте диапазон ячеек, содержащий данные, которые подлежат сортировке, в столбец А на новом рабочем листе. Выполните команду Данные^Сортировка.... Запишите в столбец в листья, вычисленные вручную. Все числа в столбце в должны начинаться с апострофа, чтобы программа Microsoft Excel не перепутала их со строкой цифр, образующих очень длинное число. Замените числа в столбце а соответствующими значениями, образующими ствол, и удалите дубликаты.
Mutual Funds.XLS. Диаграмма, аналогичная приведенной на рис. 2.1, содержится на рабо-~ чем листе Рис2.1 в рабочей книге Chapter 2.xls.
Проиллюстрируем процедуру построения диаграммы “ствол и листья” следующим примером.
ПРИМЕР 2.1. ПОСТРОЕНИЕ ДИАГРАММЫ “СТВОЛ И ЛИСТЬЯ"
Ниже приведены суммы, которые 15 студентов тратят на завтрак в ресторане быстрого обслуживания.
5,35 4,75 4,30 5,47 4,85 6,62 3,54 4,87 6,26 5,48 7,27 8,45 6,05 4,76 5,91
Постройте диаграмму “ствол и листья”.
РЕШЕНИЕ. Сначала следует упорядочить значения по возрастанию, а затем использовать в качестве ствола единицы, а в качестве листьев — десятичные части, округленные до десятых долей.
3 5
4
5
6
7
83998
4559
631
3
Изучение основ
2.1. Создайте упорядоченный массив из приведенных ниже п = 7 экзаменационных оценок по бухгалтерскому учету.
68 94 63 75 71 88 64
2.2. Создайте диаграмму “ствол и листья” из приведенных ниже п= 7 экзаменационных оценок по финансовому делу.
80 54 69 98 93 53 74
2.3. Создайте упорядоченный массив из приведенных ниже п = 7 экзаменационных оценок по маркетингу.
88 78 78 73 91 78 85
2.4. Создайте упорядоченный массив из диаграммы “ствол и листья”, содержащей экзаменационные оценки по информатике.
5
6
7
8
9
0
446
19
2
Применение понятий
2.5. Ниже приведена диаграмма “ствол и листья”, содержащая данные об объеме продаж бензина. Ее листьями являются десятки. Выборка состоит из 25 автомобилей, обслуживающихся конкретной автозаправочной станцией в г. Нью-Джерси Торнпарк (New Jersey Turnpark).
9 147
10 02238
11 125566777
12 223489
13 02
1. Создайте упорядоченный массив, содержащий указанные данные.
2. Какой способ представления данных более информативен? Обоснуйте свой ответ.
3. Какой объем бензина автомобилисты покупают чаще всего?
4. Наблюдается ли концентрация объемов проданного бензина в центре распределения?
5. Является ли выборка, состоящая из 25 элементов, репрезентативной? Обоснуйте свой ответ.
2.6. Файл ft^PE.XLS содержит случайную выборку, состоящую из 30 акций, проданных на Нью-Йоркской фондовой бирже. Для каждой акции указаны ее аббревиатура и отношение рыночной цены к чистой прибыли в расчете на одну акцию, опубликованные в журнале The Wall Street Journal 2 января 2003 года. Отношение рыночной цены акции компании к ее чистой прибыли в расчете на одну акцию, называемое также отношением Р/Е (price-to-earning ratio), является результатом деления ее цены на момент закрытия торгов на прибыль, начисленную на каждую акцию компании в течение последних четырех кварталов. Акции со сверхвысоким отношением Р/Е называются переоцененными. В то же время акции с необычно низким отношением Р/Е часто называются недооцененными.
1. Создайте упорядоченный массив, содержащий указанные данные.
2. Постройте диаграмму “ствол и листья”, содержащую указанные данные.
3. Какой способ представления данных более информативен? Обоснуйте свой ответ.
4. Не кажется ли вам, что недооцененных акций больше, чем переоцененных? Обоснуйте свой ответ.
5. Используя листинг акций, публикуемый в журналах The Wall Street Journal и USA Today, или другие источники, создайте свою собственную случайную выборку, состоящую из 30 элементов, и сравните с выборкой, приведенной выше.
6. Используя листинг акций, публикуемый в журналах The Wall Street Journal и USA Today, или другие источники, создайте свою собственную случайную выборку, состоящую из акций 30 компаний, котируемых на бирже NASDAQ, и сравните ее с выборкой, составленной из акций, котируемых на Нью-Йоркской фондовой бирже.
2.7. Данные, приведенные ниже, содержат количество чеков, возвращенных 23 банками своим вкладчикам ввиду отсутствия средств на счете. (Минимальный размер вклада не должен быть ниже 100 долл.) ^BANKCOSTl. XLS.
26 28 20 20 21 22 25 25 18 25 15 20
18 20 25 25 22 30 30 30 15 20 29
Источник: справочник “The New Face of Banking” Copyright ©2000, изданный компанией Consumers Union of U.S. Ink., Yonkers, NY. Данные цитируются no журналу Consumer Reports, июнь 2000 с разрешения компании Consumers Union of U. S. Ink., Yonkers, NY 10703-1057.
1. Создайте упорядоченный массив, содержащий указанные данные.
2. Постройте диаграмму “ствол и листья”, содержащую указанные данные.
3. Какой способ представления данных более информативен? Обоснуйте свой ответ.
4. Определите значение, вокруг которого концентрируется распределение количества возвращенных чеков. Обоснуйте свой ответ.
2.8. Данные, приведенные ниже, содержат величину ежемесячной платы за услуги (в долларах), взимаемой 26 банками со своих клиентов, если сумма на счету клиента не превышает установленного минимума, равного 1 500 долл. ^BANKCOST2. XLS.
12 85566 10 10 97 10 7750 10 69 12 05 10 8559
Источник данных: справочник “The New Face of Banking" Copyrlgh © 2000, изданный компанией Consumers Union of U. S. Ink., Yonkers, NY. Данные цитируются no журналу Consumer Reports, июнь 2000 с разрешения компании Consumers Union of U. S. Ink., Yonkers, NY 10703-1057.
1. Создайте упорядоченный массив, содержащий указанные данные.
2. Постройте диаграмму “ствол и листья”, содержащую указанные данные.
3. Какой способ представления данных более информативен? Обоснуйте свой ответ.
4. Определите значение, вокруг которого концентрируется распределение ежемесячной оплаты банковских услуг. Обоснуйте свой ответ.
2.9. Данные, приведенные ниже, содержат количество калорий, получаемых потребителями гамбургеров и куриного мяса в сети ресторанов быстрого питания. CfFASTFOOD.XLS.
Гамбургеры
19 31 34 35 39 39 43
Куриное мясо
7 9 15 16 16 18 22 25 27 33 39
Источник: справочник “Быстрая закуска?” © 2001, изданный компанией Consumers Union of U. S. Ink., Yonkers, NY. Цитируется no журналу Consumer Reports, март 2001, 46, c разрешения компании Consumers Union of U. S. Ink., Yonkers, NY 10703-1057.
Отдельно для гамбургеров и куриного мяса выполните следующие задания.
1. Создайте упорядоченный массив, содержащий указанные данные.
2. Постройте диаграмму “ствол и листья”, содержащую указанные данные.
3. Какой способ представления данных более информативен? Обоснуйте свой ответ.
4. Сравните гамбургеры и куриное мясо по количеству калорий. Какой вывод напрашивается?
2.2. ПРЕДСТАВЛЕНИЕ ЧИСЛОВЫХ ДАННЫХ В ВИДЕ ТАБЛИЦ
И ДИАГРАММ
Распределение частот
При увеличении объема выборки ни упорядоченный массив, ни диаграмма “ствол и листья” уже не позволяют легко представлять, анализировать и интерпретировать результаты. Для больших наборов данных следует создавать сводные таблицы, распределяя данные по группам (или категориям). Такой способ представления данных называется распределением частот.
Распределение частот (frequency distribution) представляет собой сводную таблицу, в которой данные распределены по группам или категориям.
Если данные сгруппированы в виде распределения частот, процесс их анализа и интерпретации становится более управляемым и осмысленным. При распределении частот следует внимательно выбирать интервал группирования (class interval), или размах (width) групп, а также вычислять границы, (boundaries) каждой группы, не допуская их перекрытия.
Выбор количества групп
Количество групп, выбранных для группировки данных, непосредственно зависит от объема исходной выборки. Чем больше элементов содержит выборка, тем больше групп можно создать. Однако, как правило, распределение частот должно содержать не менее 5 и не более 15 групп. Если групп слишком мало или слишком много, новую информацию получить довольно сложно.
Вычисление интервала группирования
Каждая группа, образующая распределение частот, должна иметь одинаковый размах. Чтобы определить ширину интервала группирования (width of class interval), диапазон изменения данных делят на заданное количество групп.
ВЫЧИСЛЕНИЕ ШИРИНЫ ИНТЕРВАЛА ГРУППИРОВАНИЯ
... Диапазон /о
Ширина интервала группирования =-—---------- (2.1)
Количество групп
Поскольку в нашем примере имеются данные лишь о 158 фондах, достаточно создать восемь групп. Диапазон значений, содержащихся в табл. 2.1, вычисляется по формуле 26,3-(-6,1) = 32,4. С учетом формулы (2.1) ширина интервала группирования вычисляется следующим образом.
32 4 Ширина интервала группирования = —= 4,05.
8
Для удобства эта величина округляется до 5,0.
Вычисление границ групп
Для вычисления распределения частот необходимо так определить границы групп (class boundaries), чтобы они не пересекались. Перекрытие групп не допускается.
Поскольку размах каждой группы, построенной на основе данных о пятилетней среднегодовой доходности фондов, равен 5,0%, границы групп должны быть установлены так, чтобы учесть все данные. По возможности эти границы должны быть достаточно наглядными. Например, величины из первой группы должны изменяться в диапазоне от -10,0 до -5,0% и так далее, пока не будут сформированы 8 неперекрываю-щихся групп, ширина каждого из которых равна 5,0%. Результат этой процедуры приведен в табл. 2.2.
Таблица 2.2. Распределение частот для пятилетней среднегодовой доходности 158 фондов, ориентированных на быстрый рост капитала
Пятилетняя среднегодовая доходность Количество фондов
от -10,0 До -5,0 1
от -5,0 До 0,0 3
от 0,0 До 5,0 14
от 5,0 ДО 10,0 58
от 10,0 ДО 15,0 61
от 15,0 ДО 20,0 17
от 20,0 ДО 25,0 3
от 25,0 До 30,0 1
Итого 158
Главным преимуществом этой таблицы является возможность легко вычислять основные характеристики данных. Например, табл. 2.2 демонстрирует, что приближенный диапазон среднегодовой доходности 158 фондов, ориентированных на быстрый рост капитала, ограничен числами -10,0 и 30,0%, причем показатели в основном группируются в диапазоне от 5,0 до 15,0%.
С другой стороны, эта сводная таблица имеет недостаток: по ней невозможно определить, как распределены индивидуальные данные внутри групп. Например, доходность трех фондов из представленных в табл. 2.2 изменяется в диапазоне от 20,0 до 25,0%, но определить, вокруг какого значения они сконцентрированы (20 или 25%), невозможно. Для представления средней доходности этих трех фондов выбирается срединная точка (22,5%). Срединной точкой (midpoint) интервала, границами которой являются величины -10,0 и -5,0%, является значение -7,5%. (Срединные точки остальных интервалов равны -2,5, 2,5, 7,5, 12,5, 17,5, 22,5 и 27,5% соответственно.)
Субъективность при выборе границ групп
Выбор границ групп при вычислении распределения частот является весьма субъективным. Если наборы данных невелики, одинаковый выбор границ групп для разных выборок может привести к разным результатам. Например, если при вычислении распределения частот для показателей пятилетней среднегодовой доходности ширину интервалов группирования установить равной 4,0, а не 5,0% (как в табл. 2.2), возникнет смещение распределения. Особенно сильно этот эффект проявляется при работе с малыми выборками.
Смещение распределения возникает не только в результате изменения границ групп. Например, ширину интервала группирования можно оставить равной 5,0%, изменив границы первой и последней групп. Эта манипуляция также приводит к смещению распределения, особенно, если объем выборки невелик. К счастью, по мере увеличения объема выборки этот эффект становится менее выраженным.
Распределение относительных частот и процентное распределение
Для более углубленного анализа распределения частот можно построить либо распределение относительных частот (долей) либо процентное распределение. Выбор распределения зависит от того, с какими данными желает работать пользователь: с долями или процентами. В табл. 2.3 приведены оба вида распределения.
Таблица 2.3. Распределение относительных частот и процентное распределение для пятилетней среднегодовой доходности 158 фондов, ориентированных на быстрый рост капитала
Пятилетняя среднегодовая доходность Доля фондов Процент фондов
от -10,0 ДО -5,0 0,006 0,6
от -5,0 ДО 0,0 0,019 1,9
от 0,0 ДО 5,0 0,089 8,9
от 5,0 ДО 10,0 0,367 36,7
от 10,0 До 15,0 0,386 38,6
от 15,0 До 20,0 0,108 10,8
от 20,0 До 25,0 0,019 1,9
от 25,0 ДО 30,0 0,006 0,6
Итого 1,000 100,0
Источник: данные взяты из табл. 2.2.
Распределение относительных частот (relative frequency distribution) вычисляется путем деления количества элементов каждой группы, образующей распределение частот (см. табл. 2.2), на общее количество наблюдений. Процентное распределение (percentage distribution) вычисляется путем умножения каждой относительной частоты, или доли, на 100,0. Таким образом, доля фондов, ориентированных на быстрый рост капитала, среднегодовая доходность которых изменяется от 10,0 до 15,0% , равна 0,386, а процент — 38,6.
Как правило, работать с долями или процентами удобнее, чем с количеством элементов в группе. Распределение относительных частот, как и процентное распределение, позволяет сравнивать даже наборы данных, имеющие разные объемы.
Чтобы проиллюстрировать это утверждение, вспомним сценарий, описанный в начале главы. В нем требовалось сравнить среднегодовые показатели доходности фондов, ориентированных на быстрый и медленный рост капитала соответственно. В табл. 2.4 показано распределение относительных частот и процентное распределение пятилетней среднегодовой доходности 101 фонда, ориентированного на медленный рост капитала. Обратите внимание на то, что при построении распределения относительных частот мы стремились по возможности сохранить разбиение выборки на группы, принятое в табл. 2.3 для фондов, ориентированных на быстрый рост капитала.
Таблица 2.4. Распределение относительных частот и процентное распределение для пятилетней среднегодовой доходности 101 фонда, ориентированного на медленный рост капитала
Среднегодовая относительная доходность Доля фондов Процент фондов
от -10,0 До -5,0 0 0,0
от -5,0 До 0,0 0 0,0
от 0,0 До 5,0 3 3,0
Окончание табл. 2.4
Среднегодовая относительная доходность Доля фондов Процент фондов
от 5,0 ДО 10,0 34 33,7
от 10,0 ДО 15,0 41 40,6
от 15,0 ДО 20,0 20 19,8
от 20,0 ДО 25,0 2 2,0
от 25,0 ДО 30,0 1 1,0
Итого 101 100,0*
* Результаты немного отличаются от 100,0 за счет округления.
Процентные распределения, приведенные в табл. 2.3 и 2.4, позволяют сравнивать среднегодовые показатели доходности фондов, ориентированных на быстрый и медленный рост капитала соответственно. Значительные различия распределений, присущих этим показателям, проявляются следующим образом.
1. Среднегодовой показатель доходности 10,8% фондов, ориентированных на быстрый рост капитала, колеблется в диапазоне от -5,0 до 5,0%. В то же время процентная доля фондов, ориентированных на медленный рост капитала, в этом диапазоне доходности равна 3,0% .
2. Только 10,8% фондов, ориентированных на быстрый рост капитала, имеют среднегодовую доходность от 15 до 20%. Процентная доля фондов, ориентированных на медленный рост капитала, в этом диапазоне доходности равна 19,8% .
Функция распределения
Для табулирования данных часто оказывается полезной таблица интегральных процентов, которую также называют распределением интегральных процентов (cumulative percentage distribution). Функция распределения и связанный с нею полигон позволяют обнаружить информацию, которая ускользает от распределения частот.
Пример 2.2 демонстрирует способ вычисления распределения интегральных процентов на основе процентного распределения среднегодовых показателей доходности 158 фондов, ориентированных на быстрый рост капитала.
ПРИМЕР 2.2. ВЫЧИСЛЕНИЕ РАСПРЕДЕЛЕНИЯ ИНТЕГРАЛЬНЫХ ПРОЦЕНТОВ
Построить распределение интегральных процентов, используя данные, приведенные в табл. 2.3 и 2.4.
РЕШЕНИЕ. Из табл. 2.5 следует, что ни один фонд, ориентированный на быстрый рост капитала, не имеет доходности меньше -10,0%, среднегодовые показатели доходности 0,6% фондов не превышают -5,0% и т.д. В итоге приходим к выводу, что 100,0% фондов имеют пятилетнюю среднегодовую доходность ниже 30,0%.
Таблица 2.5. Распределение интегральных процентов
Пятилетняя среднегодовая Процент фондов Процент фондов, доходность которых
доходность, % в группе не превышает верхней границы группы
от -10,0 ДО -5,0 0,6 0,0
от -5,0 До 0,0 1,9 0,6
от 0,0 ДО 5,0 8,9 2,5 = 0,6+1,9
от 5,0 ДО 10,0 36,7 11,4 = 0,6+1,9 + 8,9
от 10,0 До 15,0 38,6 48,1 = 0,6+ 1,9 + 8,9 + 36,7 ‘
от 15,0 ДО 20,0 10,8 86,7 = 0,6 + 1,9 + 8,9 + 36,7 + 38,6
от 20,0 ДО 25,0 1,9 97,5 = 0,6 + 1,9 + 8,9 + 36,7 + 38,6 + 10,8
от 25,0 ДО 30,0 0,6 99,4 = 0,6 + 1,9 + 8,9 + 36,7 + 38,6 + 10,8 + 1,9
от 30,0 ДО 35,0 0,0 100,0 = 0,6 + 1,9 + 8,9 + 36,7 + 38,6 + 10,8 +
+1,9+ 0,6
В табл. 2.6 приведены распределения интегральных процентов для среднегодовых показателей доходности 158 фондов, ориентированных на быстрый рост капитала, и 101 фонда, ориентированного на медленный рост капитала.
Таблица 2.6. Распределение интегральных процентов для пятилетней среднегодовой доходности 101 фонда, ориентированного на медленный рост капитала, и 158 фондов, ориентированных на быстрый рост капитала*
Пятилетняя среднегодовая доходность Процентная доля фондов, ориентированных на быстрый рост, не превышающая указанной величины Процентная доля фондов ориентированных на медленный рост, не превышающая указанной величины
-10,0 0,0 0,0
-5,0 6,0 0,0
0,0 2,5 0,0
5,0 11,4 3,0
10,0 48,1 36,7
15,0 86,7 77,3
20,0 97,5 97,1
25,0 99,4 99.1
30,0 100,0 100,0
'Данные взяты из табл. 2.3 и 2.4.
Из данных, приведенных в табл. 2.6, следует, что в основном пятилетняя среднегодовая доходность фондов, ориентированных на быстрый рост капитала, меньше, чем у фондов, ориентированных на медленный рост капитала. В частности, 48,1% фондов, ориентированных на быстрый рост капитала, имеют показатели доходности, не превышающие 10%. Соответствующая доля фондов, ориентированных на медленный рост капитала, равна 36,7%.
Процедуры Excel: вычисление распределения частот для числовых данных
Для вычисления распределения частот можно воспользоваться командой Сервис^Анализ данных^ Гистограмма. Поскольку эта процедура содержит несколько ошибок, результаты придется скорректировать. В качестве альтернативы можно использовать надстройку PHStat2, которая автоматически исправляет эти ошибки.
Одна из сложностей состоит в том, что программа Micrisoft Excel использует "карманы", представляющие собой группы, образованные из упорядоченного массива верхних границ групп, записанных в "диапазоне карманов". Для того чтобы представить границы групп в виде "от а до Ь', как в табл. 2.2, в диапазон карманов следует записать числа, ненамного меньше величины/). Например, для интервала "от 5,0 до 10,0" в качестве верхней границы следует указать 9,99. Для интервала "от -10,0 до -5,0" верхнюю границу необходимо задать равной -5,01.
Например, для вычисления распределения частот, представленного в табл. 2.2, необходимо открыть рабочую книгу Growth Funds Sample.xls на листе Пятилетняя_доходность и следовать инструкциям, приведенным ниже. (Величины, порождающие распределение частот, представленное в табл. 2.2, уже записаны на рабочем листе Пятилетняя^доходность в столбце с.)
Применение Excel в сочетании с надстройкой PHStatZ
Для вычисления распределения частот на основе данных, записанных на рабочем листе Пятилетняя_доходность, выполните такие действия.
1. Выберите PH Stat ^Descriptive Statistics1^ Frequency Distribution... (РН51аЮОписательная статистика^ Распределение частот...).
2. В диалоговом окне Frequency Distribution сделайте следующее (см. иллюстрацию.).
2.1. Введите в окне редактирования Variable Cel Range (Входной интервал) диапазон В1 :В159.
2.2. Введите в окне редактирования Bins Cell Range (Интервал карманов) диапазон cl: СЮ.
2.3. Установите флажок First cell contains label (Первая ячейка содержит метку).
2.4. Установите переключатель Input Options (Параметры вывода) в положение Single Group Variable (Отдельная группа).
2.5. Введите заголовок структуры в окне редактирования Title (Заголовок).
2.6. Щелкните на кнопке ОК.
Frequency Distribution fx]
Data
Variable Cell Range:
Bins Cell Range:
|B1:B159 -I
[cncio
First cell in each range contains label
Input Options
<• Single Group Variable
Multiple Groups - Unstacksd
Multiple Groups - Stacked
Output Options
Title: [распределение частот
Help | IL ЗЖ....Д| Cancel |
Применение Excel
Распределение частот можно построить с помощью процедуры создания гистограмм надстройки Пакет анализа. Для этого следует выполнить команду Сервис^Анализ данных..., а затем выбрать из списка Инструменты анализа, расположенного в окне Анализ данных, пункт Гистограмма и щелкнуть на кнопке ОК. В диалоговом окне Гистограмма нужно ввести ссылки В1:В159 в окне редактирования Входной интервал и С1:С1О в окне редактирования Интервал карманов, затем установить переключатель Параметры вывода в положение Новый рабочий лист и щелкнуть на кнопке ОК. Для того чтобы исправить ошибки, порождаемые процедурой построения гистограмм программы Excel, выполните инструкции, приведенные в разделе ЕН.2.1. (Кроме того, в разделе ЕН.2.1 описан шаблон рабочего листа, допускающего динамическое обновление частот при изменении исходных данных.)
I 4U Chapter 2.XLS. Распределение частот, аналогичное приведенной в табл. 2.2, содержится на | * рабочем листе Табл2.2 в рабочей книге Chapter 2.xls.
Гистограмма
Следуя принципу “лучше один раз увидеть, чем сто раз услышать”, для анализа статистических данных часто используют графические изображения, а не таблицы. Одна из разновидностей таких графических изображений называется гистограммой (histogram). С ее помощью описываются числовые данные, сгруппированные по частоте, относительной частоте или процентной доле.
Гистограмма — это диаграмма, на которой изображены столбики, границы которых совпадают с границами групп.
При построении гистограмм исследуемая случайная величина откладывается по горизонтальной оси (т.е. вдоль осиХ), а количество элементов в соответствующих группах, их относительная частота или процентная доля — по вертикальной (т.е. вдоль оси У).
На рис. 2.2 изображена гистограмма, построенная на основе данных о пятилетней среднегодовой доходности 158 фондов, ориентированных на быстрый рост капитала. Обратите внимание на высокую концентрацию фондов в диапазоне от 5 до 15% и более низкую концентрацию в других группах.
Рис. 2.2. Гистограмма, построенная с помощью программы Microsoft Excel на основе пятилетней среднегодовой доходности фондов, ориентированных на быстрый рост капитала
При сравнении нескольких наборов данных бывает довольно сложно создавать диаграммы “ствол и листья” и гистограммы. Например, иногда трудно правильно интерпретировать разницу между высотами соответствующих столбцов разных гистограмм. В этих ситуациях более предпочтительными оказываются полигоны, построенные по относительным частотам или процентным долям.
Полигон
Как и при построении гистограмм, величина исследуемой переменной откладывается вдоль горизонтальной оси. По вертикальной оси откладывается количество элементов в каждой группе, их относительная доля или процент.
Процентный полигон (percentage polygon) представляет собой график, построенный путем соединения средних точек, соответствующих процентной доле каждой группы.
На рис. 2.3 показан процентный полигон, построенный с помощью программы Microsoft Excel на основе пятилетней среднегодовой доходности 158 фондов, ориентированных на быстрый рост капитала, и 101 фонда, ориентированного на медленный рост капитала. Различия между двумя распределениями, обнаруженные ранее при анализе табл. 2.3 и 2.4, теперь видны четче. Хотя показатели доходности фондов, ориентированных на быстрый и медленный рост капитала соответственно, сосредоточены, в основном, в интервале от 5 до 15%, бросается в глаза большое количество фондов, ориентированных на медленный рост капитала, доходность которых колеблется в интервале от 15 до 20%. В отличие от них, распределение показателей фондов, ориентированных на быстрый рост капитала, характеризуется большим разбросом.
Рис. 2.3. Процентные полигоны, построенные с помощью программы Microsoft Excel на основе пятилетней среднегодовой доходности фондов, ориентированных на быстрый и медленный рост капитала
Построение полигона. Обратите внимание на то, что полигон, изображенный на рис. 2.3, построен по срединным точкам интервалов разбиения. Возьмем, к примеру, точку на осиХ, соответствующую уровню доходности 17,5% . Этой точке соответствует 19,8% фондов, ориентированных на медленный рост капитала, среднегодовой показатель доходности которых колеблется в диапазоне от 15 до 20%. Кроме того, этой точке соответствует число 10,8%, равное процентной доле фондов, ориентированных на быстрый роста капитала, среднегодовой показатель доходности которых колеблется в том же диапазоне. Заметьте также, что при построении полигона или гистограммы ось У должна начинаться в начале координат (т.е. с нуля), чтобы избежать неверной интерпретации результатов. В то же время ось X не обязана начинаться с нуля. По эстетическим причинам начало оси X выбирают так, чтобы гистограмма или полигон охватывали все данные.
Полигон интегральных процентов (кривая распределения)
Полигон интегральных процентов (cumulative percentage polygon), или кривая распределения (ogive), является графическим изображением распределения суммарных процентов (cumulative percentage distribution). При построении полигона интегральных процентов исследуемая величина откладывается вдоль оси X, а интегральные проценты — вдоль оси У.
Чтобы построить интересующий нас полигон интегральных процентов по табл. 2.6, отложим по оси X пятилетнюю среднегодовую доходность фондов, а вдоль оси У — интегральные проценты (из столбца “меньше чем”).
На рис. 2.4 изображены полигоны интегральных процентов, построенные с помощью программы Microsoft Excel на основе пятилетней среднегодовой доходности 158 фондов, ориентированных на быстрый рост капитала, и 101 фонда, ориентированного на медленный рост капитала. На оси X отложены нижние границы групп. Анализ рис. 2.4 показывает, что среднегодовая доходность 48,1% фондов, ориентированных на быстрый рост капитала, не превышает 10%, в то время как доля фондов, ориентированных на медленный рост капитала, в этом интервале равна 36,7%. Обратите внимание на то, что в интервале до 20,0% кривая распределения среднегодовой доходности фондов, ориентированных на быстрый рост капитала, расположена слева от кривой распределения доходности фондов, ориентированных на медленный рост капитала. В то же время количество фондов, ориентированных на быстрый и медленный рост капитала, доходность которых не превышает 20,0%, приблизительно одинаково.
Рис. 2.4. Полигоны интегральных процентов, построенные с помощью программы Microsoft Excel на основе пятилетней среднегодовой доходности фондов, ориентированных на быстрый и медленный рост капитала
Процедура Excel: создание гистограмм и полигонов для числовых данных
Для создания гистограмм, полигонов и распределения частот можно воспользоваться процедурой Сервиса Анализ данных... => Гистограмма и Мастером диаграмм. Поскольку эта процедура содержит несколько ошибок, результаты придется скорректировать. В качестве альтернативы можно использовать надстройку PHStat2, которая автоматически исправляет эти ошибки. Кроме того, надстройка PHStat2 позволяет построить полигон для разных групп за один шаг. (Для того чтобы понять разницу между группами и "карманами", обратитесь к предыдущей врезке "Процедура Excel".) Например, для того чтобы создать гистограммы и полигоны для среднегодовой доходности фондов, ориентированных на быстрый и медленный рост капитала соответственно, как показано на рис. 2.2-2.4, следует открыть рабочую книгу Chapter2.xls на рабочем листе Сравнительные_данные и выполнить следующие действия.
Применение Excel в сочетании с надстройкой PHStat2
Для построения гистограмм и полигонов необходимо применить процедуру PHStat*=>Descriptive Statistics*^Hystogram & Polygons... (PHStat=>Описательная статистика^Гистограммы&Полигоны...). Для этого следует выполнить такие действия.
1. Выполнить команду PHStat=>Descriptive Statistics*^ Hystogram & Polygons....
2. В диалоговом окне Hystogram & Polygons (на рисунке справа) сделать следующее.
2.1. Ввести в окне редактирования Variable Cell Range (Входной интервал) диапазон А1 :В159.
2.2. Ввести в окне редактирования Bins Cell Range (Интервал карманов) диапазон Cl: СЮ.
2.3. Ввести в окне редактирования Midpoints Cell Range (Интервал средних точек) диапазон DI :D9.
2.4. Установить флажок First cell contains label (Первая ячейка содержит метку).
2.5. Установить переключатель Multiple Groups (Несколько групп) в положение Unstacked (Разгруппированы).
2.6. Ввести заголовок структуры в окне редактирования Title (Заголовок).
Histogram ft Polygons
2.7. Установить флажок Hystogram (Гистограмма).
Data - - -
Variable Cell Range;
Bins Cell Range:
Midpoints Cell Range:
P First cell in each range contains label
Input Options
C Single Group Variable :
<* Multiple Groups - Unstacked
C Multiple Groups - Stacked
Output Options
Title: |взаимные фонды
P Histogram
Г Frequency Polygon
P Percentage Polygon
P Cumulative Percentage Polygon (Ogive)
Help j |* 71 Cancel J
2.8. Установить флажки Percentage Polygon (Процентный полигон) и Cumulative Percentage Polygon (Ogive) (Полигон интегральных процентов (Кривая распределения)).
2.9. Щелкнуть на кнопке ОК.
Применение Excel
Построение гистограмм. Гистограммы и полигоны для среднегодовой доходности фондов, ориентированных на быстрый рост капитала, можно построить с помощью процедуры построения гистограмм надстройки Пакет анализа и Мастера диаграмм. Для этого следует выполнить команду Сервис*^Анализ данных..., а затем выбрать из списка Инструменты анализа, расположенного в окне Анализ данных, пункт Гистограмма и щелкнуть на кнопке ОК. В открывшемся диалоговом окне Гистограмма нужно ввести в окне редактирования Входной интервал диапазон ссылок Al: А159, а в окне редактирования Интервал карманов - диапазон ссылок cl: СЮ. Затем необходимо установить переключатель Параметры вывода в положение Новый рабочий лист и щелкнуть на кнопке ОК. Чтобы создать гистограмму и полигон для среднегодовой доходности фондов, ориентированных на медленный рост капитала, следует повторить описанные выше действия, введя в окне редактирования Входной интервал диапазон ссылок Bl: В102.
В заключение, для того чтобы исправить ошибки, внесенные процедурой программы Excel при построении распределения частот и полигона, необходимо выполнить инструкции, приведенные в разделе ЕН.2.3. Замечание: если таблица распределения частот уже построена, следуйте инструкциям из раздела ЕН.2.4.
Построение полигонов. Для построения полигонов частот, процентов или интегральных процентов следует выполнить инструкции по работе с Мастером диаграмм, приведенные в разделе ЕН.2.5.
#4 Chapter 2.XLS. Гистограммы и полигоны, приведенные на рис. 2.2, 2.3 и 2.4, содержатся на " рабочих листах Рис2.2, Рис2.3 и Рис2.4 в рабочей книге chapter 2 . xls.
И1И
Изучение основ
2.10. Предположим, что значения, содержащиеся в наборе данных, изменяются в диапазоне от 11,6 до 97,8.
1. Укажите границы девяти групп, в которые можно объединить эти данные.
2. Укажите ширину выбранных интервалов.
3. Укажите срединную точку каждого интервала.
2.11. При анализе распределения частот, вычисленного на основе выборки, состоящей из оценок, полученных 50 абитуриентами на вступительных экзаменах, обнаружилось, что ни один из абитуриентов не получил меньше 450 баллов. Границы интервалов группирования равны 450, 500, 550, ..., 750. Допустим, что оценки двух абитуриентов лежат в интервале от 450 до 500, а 16 абитуриентов получили оценки от 500 до 550. Вычислите следующие показатели.
1. Процентная доля абитуриентов, получивших меньше 500 баллов.
2. Процентная доля абитуриентов, получивших меньше 550 баллов.
3. Процентная доля абитуриентов, получивших больше 500 и меньше 550 баллов.
4. Количество абитуриентов, получивших больше 500 и меньше 550 баллов.
5. Количество абитуриентов, получивших меньше 750 баллов.
Применение понятий
Задачи 2.12-2.16 можно решить вручную или с помощью программы Microsoft Excel.
2.12. Данные, представленные ниже, описывают стоимость потребления электричества на протяжении июля 2003 года в 50 случайно выбранных двухквартирных домах в большом городе.
^UTILITY. XLS
Затраты на оплату услуг электрокомпании (в долларах)
96 171 202 178 147 102 153 197 127 87
157 185 90 116 172 111 148 213 130 165
141 149 206 175 123 128 144 168 109 167
95 163 150 154 130 143 187 166 139 149
108 119 183 151 114 135 191 137 129 158
1. Постройте распределение частот:
а) по 5 интервалам группирования;
б) по б интервалам группирования;
в) по 7 интервалам группирования.
Подсказка. Чтобы определить границы групп, сначала следует построить либо диаграмму “ствол и листья” либо упорядоченный массив.
2. Постройте распределение частот по 7 интервалам группирования с границами 99 долл., 119 долл, и т.д.
3. Постройте распределение процентных долей по распределению частот, построенному в п. 2.
4. Постройте процентную гистограмму.
5. Постройте процентный полигон.
6. Постройте распределение накопленных частот.
7. Постройте распределение интегральных процентов.
8. Нарисуйте кривую распределения (полигон интегральных процентов).
9. Вокруг какого значения концентрируется плата за услуги энергетических компаний?
10. Какой график лучше всего отражает характеристики распределения платы за услуги энергетических компаний? Обоснуйте свой ответ.
2.13. Приведенный ниже упорядоченный массив содержит данные о длительности эксплуатации (в часах) сорока 100-ваттных лампочек, произведенных компанией А, и сорока 100-ваттных лампочек, произведенных компанией Б.
ftfBULBS.XLS
Компания А Компания Б
684 697 720 773 821 819 836 888 897 903
831 835 848 852 852 907 912 918 942 943
859 860 868 870 876 952 959 962 986 992
893 899 905 909 911 994 1 004 1 005 1 007 1 015
922 924 926 926 938 1016 1 018 1 020 1 022 1 034
939 943 946 954 971 1 038 1 072 1 077 1 077 1 082
972 977 984 1 005 1 014 1096 1 100 1 113 1 113 1 116
1 016 1 041 1052 1 080 1093 1 153 1 154 1 174 1 188 1 230
1. Постройте распределение частот для каждого набора данных используя ширину интервалов группирования, равную 100 ч:
а) компания А: от 650 до 750, от 750 до 850 и т.д.;
б) компания Б: от 750 до 850, от 850 до 950 и т.д.
2. Установите ширину интервала группирования равной 50, чтобы границами интервала были значения 650, 700, 750 и т.д. Прокомментируйте новые результаты.
3. Постройте процентное распределение на основе распределения частот, полученного при решении задачи 1.
4. Постройте две разные процентные гистограммы.
5. Совместите два процентных полигона.
6. Постройте распределение накопленных частот.
7. Постройте распределение интегральных процентов.
8. Постройте кривые распределения.
9. Какие лампочки работают дольше — производства компании А или Б? Обоснуйте свой ответ.
2.14. Ниже представлена диаграмма “ствол и листья”, описывающая распределение объемов продажи бензина (в качестве листьев используются десятки). Выборка состоит из 25 автомобилей, обслуживающихся конкретной автозаправочной станцией в г. Нью-Джерси Торнпарк.
9
10
11
12
13
147
02238 135566777
223489
02
1. Постройте распределение частот и процентных долей.
2. Постройте распределение накопленных частот и интегральных процентов.
3. Постройте процентную гистограмму.
4. Постройте процентный полигон.
5. Постройте кривую распределения.
6. Вокруг какого значения концентрируется основной объем продаж?
2.15. Приведенные ниже данные характеризуют объем лимонада в 50 двухлитровых бутылках. Результаты измерений представлены в виде неупорядоченного массива. ^DRINK.XLS
2,109 2,086 2,066 2,075 2,065 2,057 2,052 2,044 2,036 2,038
2,031 2,029 2,025 2,029 2,023 2,020 2,015 2,014 2,013 2,014
2,012 2,012 2,012 2,010 2,005 2,003 1,999 1,996 1,997 1,992
1,994 1,986 1,984 1,981 1,973 1,975 1,971 1,969 1,966 1,967
1,963 1,957 1,951 1,951 1,947 1,941 1,941 1,938 1,908 1,894
1. Постройте диаграмму “ствол и листья”.
2. Постройте распределение накопленных частот и интегральных процентов.
3. Постройте процентную гистограмму.
4. Постройте процентный полигон.
5. Постройте кривую распределения.
6. Постройте полигон накопленных частот.
7. Вокруг какого значения концентрируется основной объем лимонада в двухлитровых бутылках?
8. Можно ли на основе этих данных предсказать объем жидкости в следующей бутылке? Почему?
2.16. Пресс разрезает куски стали на части, которые в дальнейшем используются в качестве каркаса переднего сиденья автомобиля. Для разрезания стали используется алмазная пила. Автомобильная компания постановила, что отклонение размеров
каркаса от эталона не должно превышать 0,005 дюйма. В файле ^STEEL.XLS приведены отклонения от эталона размеров 100 заготовок, измеренных с помощью лазерных приборов. Например, величина -0,002 означает, что заготовка короче эталона на 0,002 дюйма.
1. Постройте распределение накопленных частот и процентных долей.
2. Постройте процентную гистограмму.
3. Постройте процентный полигон.
4. Постройте кривую распределения.
5. Соответствует ли работа пресса стандартам, установленным автомобильной компанией? Обоснуйте свой ответ.
2.17. В файле ^ENERGY. XLS приведены данные о потреблении электроэнергии на душу населения (в кВт/ч) в каждом из 50 штатов, а также в округе Колумбия в прошлом году.
1. Постройте распределение накопленных частот и процентных долей.
2. Постройте процентную гистограмму.
3. Постройте процентный полигон.
4. Постройте распределение интегральных процентов.
5. Постройте полигон интегральных процентов.
6. Вокруг какого значения концентрируется удельное потребление электроэнергии?
7. Какой график лучше остальных характеризует распределение удельного потребления электроэнергии? Обоснуйте свой ответ.
2.3. ИЗОБРАЖЕНИЕ ДВУМЕРНЫХ ЧИСЛОВЫХ ДАННЫХ
В разделе 2.2 мы рассмотрели гистограммы, полигоны, кривые распределений и полигоны накопленных частот, представляющие собой удобные графические инструменты для анализа числовых данных, например, среднегодовых показателей доходности фондов за пять лет. В этом разделе мы проиллюстрируем способ исследования двумерных числовых величин — диаграмму разброса (scatter diagram). (В программе Excel эта диаграмма называется точечной, а в научной литературе — корреляционной. — Прим, ред.) Такие диаграммы оказываются полезными в разных областях деловой активности. Например, специалисты по маркетингу с помощью таких диаграмм могут исследовать эффективность рекламной компании, сравнивая объемы недельных продаж и расходы на рекламу, а менеджеры по кадрам — изучать систему оплаты труда в компании, сравнивая трудовой стаж сотрудников и их текущую зарплату.
Продемонстрируем диаграмму разброса, построенную для сравнения пятилетней среднегодовой доходности фондов и доходности в 2001 году. На оси У отложим среднегодовую доходность каждого взаимного фонда за пять лет, а на оси X — в 2001 году (рис. 2.5).
Несмотря на большой разброс доходности фондов, между их показателями за пять лет и 2001 год существует возрастающая (положительная) зависимость. Иначе говоря, фонды, имевшие высокий уровень доходности в течение пяти лет, продолжали приносить высокую прибыль и в 2001 году. Возможны также варианты, когда одна из переменных, входящих в пару, убывает, в то время как другая возрастает. Такая зависимость называется убывающей (отрицательной). Диаграммы разброса будут рассмотрены в главе 3 при изучении коэффициента корреляции, а также в главах 12 и 13 при описании регрессионного анализа.
Рис. 2.5. Диаграмма разброса, построенная с помощью программы Microsoft Excel на основе пятилетней среднегодовой доходности фондов и доходности фондов в 2001 году
Процедура Excel: создание диаграмм разброса
Для создания диаграммы разброса применяется Мастер диаграмм. Например, чтобы построить диаграмму разброса, изображенную на рис. 2.5, необходимо открыть лист Данные в рабочей книге Mutual Funds.xls, выполнить команду Вставка^Диаграмма... и следовать приведенным ниже инструкциям.
1. На первом шаге диалога сделать следующее (см. иллюстрацию).
1.1. Щелкнуть на корешке вкладки Стандартные, а затем выбрать пункт Точечная в раскрывающемся списке Тип.
1.2. Выбрать первую (верхнюю) диаграмму, сопровождающуюся описанием: "Точечная диаграмма позволяет сравнить пары значений", а затем щелкнуть на кнопке Далее>.
2. На втором шаге диалога выполнить такие действия.
2.1. Щелкнуть на корешке вкладки Диапазон данных, а затем ввести в окне редактирования Диапазон ссылки на ячейки Данные !G1:G26O, II: 1260. (Указывая диапазон ячеек, убедитесь, не забудьте поставить запятую.)
2.2. Установить переключатель Ряды в положение В столбцах и щелкнуть на кнопке Далее>.
3. На третьем шаге диалога выполнить следующее.
3.1. Щелкнуть на корешке вкладки Заголовки. Ввести в окне редактирования Название диаграммы Строку Диаграмма разброса, В окне редактирования ОсьХ- строку Доходность в 2001 г., а в окне редактирования Ось Y-строку Пятилетняя доходность.
3.2. По очереди щелкнуть на корешках вкладок Оси, Линии сетки, Легенда и Подписи данных. Установить флажки и переключатели, как показано в разделе ЕР.6.2.
3.3. Щелкнуть на кнопке Далее>.
4. На четвертом шаге диалога установите переключатель Поместить диаграмму на листе в положение Отдельном и щелкните на кнопке Готово.
Оси диаграммы разброса, построенной по описанному выше алгоритму, проходят прямо через точки данных, а не так, как показано на рис. 2.5. Для того чтобы переместить оси, обратитесь к инструкциям, приведенным в разделе ЕН.2.6.
Обратите внимание на то, что Мастер диаграмм по умолчанию считает, что переменная X находится в первом столбце диапазона. Если данные на вашем листе расположены иначе, поменяйте столбцы местами.
Chapter 2.XLS. Диаграмма разброса, приведенная на рис. 2.5, содержится на рабочем ж листе Рис2.5 в рабочей книге Chapter 2 . xls.
УПРАЖНЕНИЯ К РАЗДЕЛУ 2,3
Изучение основ
2.18. Ниже приведена выборка, содержащая 11 пар.
X 7 5 8 3 6 10 12 4 9 15 18
У 21 15 24 9 18 30 36 12 27 45 54
1. Постройте диаграмму разброса.
2. Существует ли зависимость между величинами X и У? Обоснуйте свой ответ.
2.19. Приведенные ниже данные представляют собой объемы ежегодных продаж (в миллионах долларов) за 11-летний период (1992-2002).
Годы 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001 2002
Объем 13,0 17,0 19,0 20,0 20,5 20,5 20,5 20,0 19,0 17,0 13,0
1. Постройте диаграмму разброса, в которой на оси X отложены года.
2. Изменяются ли объемы продаж с течением времени? Объясните свой ответ.
Применение понятий
Рекомендуем решать задачи 2.20-2.26 с помощью программы Microsoft Excel.
2.20. В файле ^REFRIGERATOR.XLS содержатся приблизительные розничные цены (в долларах) и стоимость электроэнергии (в долларах), затрачиваемой морозильниками.
Источник: справочник “Refrigerators” Copyright 2002 by Consumer Union of U.S., Inc. Цитируется no журналу Consumer Reports, August 2002, 26, с разрешения организации Consumer Union of U. S„ Inc., Yonkers, NY 10703-1057.
1. Постройте диаграмму разброса, у которой по оси X отложена стоимость энергии, а по оси У — розничная цена.
2. Существует ли зависимость между розничной ценой морозильника и стоимостью электроэнергии? Если существует, то какая: положительная или отрицательная?
3. Можно ли утверждать, что более дорогой морозильник эффективнее использует электроэнергию? Следует ли это из приведенных данных?
2.21. В файле ©SECURITY. XLS содержатся данные о производительности металлоискателей в аэропортах в 1998-1999 гг. и количестве нарушений правил безопасности на миллион пассажиров.
Город Производительность Нарушения
Сент-Луис 416 11,9
Атланта 375 7,3
Хьюстон 237 10,6
Бостон 207 22,9
Чикаго 200 6,5
Денвер 193 15,2
Даллас 156 18,2
Балтимор 155 21,7
Сиэтл/Такома 140 31,5
Сан-Франциско 110 20,7
Орландо 100 9,9
Вашингтон 90 14,8
Лос-Анжелес 88 25,1
Детройт 79 13,5
Сан-Хуан 70 10,3
Майами 64 13,1
Нью-Йорк — аэропорт им. Кеннеди 53 30,1
Вашингтон — аэропорт им. Рейгана 47 31,8
Гонолулу 37 14,9
Источник: Alan В. Krueger, “A Small Dose of Common Sense Would Help Congress Break the Gridlock over Airport Security”, The New York Times, November 15,2001, C 2.
1. Постройте диаграмму разброса, у которой по оси X отложена производительность металлоискателей, а по оси У — количество нарушений.
2. Существует ли зависимость между производительностью металлоискателей и количеством нарушений?
2.22. В файле ©CELLPHONE.XLS хранятся данные о длительности разговоров по мобильным телефонам (в часах) и емкость батареек (в мА/ч).
Длительность разговоров Емкость батареек Длительность разговоров Емкость батареек
4,50 800 1,50 450
4,00 1 500 2,25 900
3,00 1 300 2,25 900
2,00 1550 3,25 900
2,75 900 2,25 700
1,75 875 2,25 800
1,75 750 2,50 800
2,25 1 100 2,25 900
1,75 850 2,00 900
Источник: справочник “Service Shortcomings”, Copyright © 2002 by Consumers Union of U.S., Inc. Цитируется no журналу Consumer Reports February 2002, 25 с разрешения организации Consumer Union of U. S., Inc., Yonkers, NY 10703-1057.
1. Постройте диаграмму разброса, у которой по оси X отложена емкость батареек, а по оси Y — продолжительность разговоров по мобильному телефону.
2. Существует ли зависимость между емкостью батареек и продолжительностью телефонных разговоров по мобильному телефону?
3. Естественно предположить, что разговоры по мобильному телефону, имеющему большую емкость батареек, должны быть более продолжительными. Подтверждается ли это предположение реальными данными?
2.23. В файле €)BATTERIES2. XLS записаны цены и данные о силе пускового тока для холодного запуска двигателя, обеспечиваемого автомобильными аккумуляторами. Источник: справочник “Leading the Charge”, Copyright 2001 by Consumers Union of U. S., Inc. Цитируется no журналу Consumer Reports October 2001, 25 с разрешения организации Consumer Union of U. S., Inc., Yonkers, NY 10703-1057.
1. Постройте диаграмму разброса, у которой по оси X отложена сила пускового тока, а по оси Y — цены аккумуляторов.
2. Существует ли зависимость между силой пускового тока и ценой аккумулятора?
3. Естественно предположить, что аккумуляторы, обеспечивающие большую силу пускового тока, должны быть дороже. Подтверждается ли это предположение реальными данными?
2.24. Компания S&P 500 Index пытается отследить тенденции фондового рынка, наблюдая за стоимостью акций 500 крупных корпораций. Файл данных ftsTOCK02 . XLS содержит еженедельные данные о стоимости акций трех компаний на момент закрытия торгов на бирже на протяжении 2002 года. В файле хранятся значения следующих переменных.
WEEK — даты последних дней недели.
S&P— средняя стоимость акций компаний, входящих в список S&P Index, на момент закрытия торгов за неделю.
SEARS — средняя стоимость акций компаний Sears, Roebuck и Company на момент закрытия торгов за неделю.
TARGET — средняя стоимость акций компании Target Corporation на момент закрытия торгов за неделю.
SARA LEE — средняя стоимость акций компании Sara Lee Corporation на момент закрытия торгов за неделю.
Источник данных: www. £inance. yahoo. сот/?и.
1. Постройте диаграмму разброса, у которой по оси Y отложены значения переменной S & Р, а по оси X — значения переменной WEEK.
2. Прокомментируйте диаграмму разброса.
3. Постройте диаграмму разброса, у которой по оси Y отложены значения переменной SEARS, а по оси X — значения переменной WEEK.
4. Прокомментируйте диаграмму разброса, построенную при решении задачи 3. Сравните выводы с результатами, полученными при выполнении задания 2.
5. Постройте диаграмму разброса, у которой по оси У отложены значения переменной TARGET, а по оси X — значения переменной WEEK.
6. Прокомментируйте диаграмму разброса, построенную при решении задачи 5. Сравните выводы с результатами, полученными при выполнении задания 2.
7. Постройте диаграмму разброса, у которой по оси У отложены значения переменной SARA LEE, а по оси X — значения переменной WEEK.
8. Прокомментируйте диаграмму разброса, построенную при решении задачи 7. Сравните выводы с результатами, полученными при выполнении задания 2.
9. Кратко изложите ваши выводы.
2.25. Бюро статистики труда (U. S. Bureau of Labor Statistics) собирает данные о рабочей силе. В приведенной ниже таблице содержатся данные об уровне сезонной безработицы в США за период с 1997 по 2002 годы.
^lUERATE.XLS
Уровень сезонной безработицы (%)
Месяц 1997 1998 1999 2000 2001 2002
Январь 5,3 4,7 4,3 4,0 4,2 5,6
Февраль 5,3 4,6 4,4 4,1 4,2 5,6
Март 5,2 4,7 4,2 4,0 4,3 5,7
Апрель 5,0 4,3 4,3 4,0 4,5 5,9
Май 4,9 4,4 4,2 4,1 4,4 5,8
Июнь 5,0 4,5 4,3 4,0 4,5 5,8
Июль 4,8 4,5 4,3 4,0 4,5 5,8
Август 4,8 4,5 4,2 4,1 4,9 5,8
Сентябрь 4,9 4,5 4,2 3,9 4,9 5,7
Октябрь 4,7 4,5 4,1 3,9 5,4 5,8
Ноябрь 4,6 4,4 4,1 4,0 5,6 5,9
Декабрь 4,7 4,4 4,1 4,0 5,8 6,0
Источник:www.fedstats.gov.
1. Постройте диаграмму разброса, у которой по оси Y отложены уровни сезонной безработицы в США, а по оси X — месяцы в последовательном порядке.
2. Прокомментируйте диаграмму разброса.
2.26. Приведенные ниже данные характеризуют объем лимонада в 50 двухлитровых бутылках. Результаты измерений представлены в виде неупорядоченного массива. ftDRINK.XLS
2,109 2,086 2,066 2,075 2,065 2,057 2,052 2,044 2,036 2,038
2,031 2,029 2,025 2,029 2,023 2,020 2,015 2,014 2,013 2,014
2,012 2,012 2,012 2,010 2,005 2,003 1,999 1,996 1,997 1,992
1,994 1,986 1,984 1,981 1,973 1,975 1,971 1,969 1,966 1,967
1,963 1,957 1,951 1,951 1,947 1,941 1,941 1,938 1,908 1,894
1. Постройте диаграмму разброса, у которой по оси X отложены последовательные номера бутылок (от 1 до 50), а на оси Y — объем содержащегося в них лимонада.
2. Существует ли зависимость между этими величинами?
3. Какой ответ вы бы дали, если бы вас попросили предсказать объем жидкости в следующей бутылке?
4. Сравните свой ответ на вопрос 3 с ответом к задаче 2.15.8. Какой из этих прогнозов ближе к действительности? Почему?
2.4. ПРЕДСТАВЛЕНИЕ КАТЕГОРИЙНЫХ ДАННЫХ В ВИДЕ ТАБЛИЦ И ДИАГРАММ
До сих пор таблицы и диаграммы применялись для представления числовых данных. Однако часто данные носят не числовой, а категориальный характер. В этом и следующем разделах изучаются способы организации и представления категорийных данных в виде таблиц и диаграмм.
Вернемся к анализу доходности взаимных фондов. Кроме среднегодовой доходности фондов, рабочий лист Данные содержит информацию о риске, связанном с инвестированием в эти фонды. Взаимные фонды могут иметь очень низкий, низкий, средний, высокий и очень высокий риск. При работе с категорийными переменными данные сначала заносятся в сводную таблицу, а затем графически представляются в виде гистограмм, круговых диаграмм или диаграмм Парето (Pareto).
Сводная таблица
По внешнему виду сводная таблица (summary table) для категорийных данных напоминает распределение частот для числовых данных. Чтобы проиллюстрировать процесс ее построения, рассмотрим данные о классификации взаимных фондов по уровню риска. Оказывается, из 259 изученных фондов 6 имеют очень низкий риск, 76 — низкий, 82 — средний риск, 80 — высокий и 15 — очень высокий. Эта информация представлена в табл. 2.7.
Таблица 2.7. Суммарная таблица, содержащая частоты и процентные доли 259 взаимных фондов
Уровень риска Количество фондов Процентная доля фондов
Очень низкий 6 2,32
Низкий 76 29,34
Средний 82 31,66
Высокий 80 30,89
Очень высокий 15 5,79
Всего: 259 100,00
Линейчатая диаграмма
Информацию, содержащуюся в табл. 2.7, можно представить в виде линейчатой диаграммы (рис. 2.6), в которой каждая категория элементов изображается в виде столбца. Высота столбца равна частоте или процентной доле элементов выборки, относящихся к данной категории. На рис. 2.6 показано, что линейчатая диаграмма (bar chart) позволяет непосредственно сравнивать количество фондов, имеющих разный уровень риска. Как видим, 82 фонда имеют средний уровень риска, а 80 фондов — высокий.
Рис. 2.6. Линейчатая диаграмма, отображающая уровень риска фондов (построена с помощью программы Microsoft Excel)
Круговая диаграмма
Существует еще один весьма популярный способ отображения информации, содержащейся в сводной таблице, — круговая диаграмма (pie chart). На рис. 2.7 показана круговая диаграмма, отображающая распределение риска инвестиций на основе данных, представленных в табл. 2.7.
Рис. 2.7. Круговая диаграмма, отображающая уровень риска фондов (построена с помощью программы Microsoft Excel)
При построении круговых диаграмм используется тот факт, что угол окружности равен 360°. Круг разделяется на секторы, углы которых соответствуют процентным долям каждой категории. Например, на рис. 2.7 показан сектор, соответствующий доле взаимных фондов с низким риском, которая равна 29,34%. При построении круговой диаграммы величина 360° умножается на 0,2934. В результате образуется сектор, угол которого равен 105,6°. Как видим, круговая диаграмма позволяет отразить долю каждой категории в общем “пироге”. Обратите внимание на то, что фонды со средним уровнем риска составляют более 30% от общего количества фондов.
Цель графического представления данных — точность и ясность. Например, рис. 2.6 и 2.7 отображают одинаковую информацию. Какой из двух видов диаграмм предпочесть — дело вкуса [1-3, 6, 7]. В частности, некоторые исследования [3] показывают, что люди труднее воспринимают круговые диаграммы. Оказывается, человеку намного проще интерпретировать разницу между высотами столбцов в линейчатых диаграммах, чем углы секторов в круговых диаграммах. Обратите внимание на то, что по рис. 2.7 нелегко определить, какая из категорий фондов больше — с низким, средним или высоким уровнем риска. В то же время по линейчатой диаграмме легко определить, что доля фондов со средним уровнем риска больше, чем доли фондов с высоким и низким уровнями риска.
С другой стороны, круговые диаграммы четко демонстрируют, что сумма долей всех категорий равна 100,0%. Таким образом, выбор диаграммы является субъективным и часто зависит от предпочтений пользователя. Если необходимо сравнивать доли двух категорий, лучше применять линейчатые диаграммы. Если важно продемонстрировать величину доли отдельной категории в общем “пироге”, лучше использовать круговые диаграммы.
Диаграмма Парето
Существует более информативный способ графического изображения категорийных данных — диаграмма Парето. Она особенно полезна, если количество категорий слишком велико. Диаграмма Парето (Pareto disgram) — это особая разновидность вертикальной линейчатой диаграммы, в которой категории приводятся в порядке убывания их частот одновременно с полигоном накопленных частот. Это позволяет выделить наи
более важные категории из большого количества малозначимых групп. Диаграмма Парето получила широкое распространение при анализе производственных процессов и контроле качества (глава 17).
Обратимся к рис. 2.6, на котором изображены процентные доли фондов с разными уровнями риска. Диаграмма Парето упорядочивает эти доли в порядке убывания. На рис. 2.8 показана диаграмма Парето, построенная с помощью программы Microsoft Excel. Анализируя высоту столбцов, легко видеть, что доля фондов со средним уровнем риска составляет 32%. Полигон накопленных частот показывает, что 62,55% фондов имеют средний или высокий уровень риска.
Рис. 2.8. Диаграмма Парето, отображающая специфику фондов (построена с помощью программы Microsoft Excel)
Вдоль левой вертикальной оси диаграммы Парето откладываются частоты или процентные доли, а вдоль правой — накопленные частоты (снизу вверх). По горизонтальной оси указываются категории. Столбцы располагаются на одинаковом расстоянии друг от друга и имеют одинаковую ширину. Точки полигона накопленных частот для каждой категории находятся в центре соответствующего столбца. При изучении диаграмм Парето внимание фокусируется на двух моментах: разности между высотами смежных столбцов и накопленных частотах смежных категорий.
Диаграмма Парето представляет собой весьма полезный инструмент для представления категорийных данных, особенно если количество категорий велико. Продемонстрируем ее преимущества с помощью следующего примера из области управления производством.
ПРИМЕР 2.3. ПРИМЕНЕНИЕ ДИАГРАММЫ ПАРЕТО ДЛЯ УЛУЧШЕНИЯ ПРОЦЕССА ПРОИЗВОДСТВА
Данные, приведенные ниже, получены в литейной компании, занимающейся производством пластмассовых деталей для компьютерных клавиатур, стиральных машин, автомобилей и телевизоров. В табл. 2.8 указаны частоты дефектов компьютерных клавиатур, обнаруженных в течение трех месяцев.
Таблица 2.8. Суммарная таблица, содержащая частоты дефектов компьютерных клавиатур, обнаруженных в течение трех месяцев
Дефект Количество Процентная доля
Черное пятно 413 6,53
Повреждение 1 039 16,43
Впрыскивание 258 4,08
Отпечаток опоры 834 13,19
Царапины 442 6,99
Брызги 275 4,35
Серебряная полоска 413 6,13
Отпечаток формы 371 5,87
След пульверизатора 292 4,62
Деформация 1 987 31,42
Всего: 6 324 100,00*
* Вследствие округлений результат отличается от 100,0.
Источник: Acharya, U. Н., and С. Mahech “Winning Back the Customers Confidence: A Case Study on the Application of Design of Experiments to an Injection-Molding Process”, Quality Engineering, 11,1999, pp. 357-363.
Для построения диаграммы Парето сводная таблица (табл. 2.9) организуется не в алфавитном порядке, а в порядке убывания частоты дефекта. Кроме того, в нее включены накопленные процентные доли.
Таблица 2.9. Упорядоченная суммарная таблица, содержащая данные о дефектах компьютерных клавиатур, обнаруженных в течение трех месяцев
Дефект Количество Процентная доля Накопленная процентная доля
Деформация 1 987 31,42 31,42
Повреждение 1 039 16,43 47,85
Отпечаток опоры 834 13,19 61,04
Царапины 442 6,99 68,03
Черное пятно 413 6,53 74,56
Серебряная полоска 413 6,13 81,09
Отпечаток формы 371 5,87 86,96
След пульверизатора 292 4,62 91,58
Брызги 275 4,35 95,93
Впрыскивание 258 4,08 100,00
Всего: 6 324 100,00*
'Вследствие округлений результат отличается от 100,0.
Как следует из табл. 2.9, основной причиной дефектов является деформация (31,42% всех обнаруженных дефектов), за ней следуют повреждения (16,43%) и отпечаток опоры (13,19%). Две наиболее распространенные разновидности дефектов (деформация и повреждение) составляют 47,85% всех дефектов, три категории — деформация, повреждение и отпечаток опоры — являются причиной 61,04% случаев брака и т.д. Результаты, приведенные в табл. 2.9, изображены на рис. 2.9 в виде диаграммы Парето.
Рис. 2.9. Диаграмма Парето, отображающая данные о дефектах клавиатуры (построена с помощью программы Microsoft Excel)
Для большей наглядности диаграмма Парето содержит не только столбцы, но и график полигона накопленных частот. Анализируя кривую полигона, проходящую через срединные точки интервалов, легко обнаружить, что первые три категории дефектов являются причинами 61,04% всего брака. Поскольку все категории в диаграмме Парето приводятся в порядке убывания их частот, исследователь сразу выявляет основные причины брака и их вклад в общее количество дефектов.
Если количество категорий велико, иногда приходится объединять некоторые из них в новые категории под названием Другая или Смешанная. В этих ситуациях столбец, соответствующий этой категории, размещается справа от остальных.
Процедуры Excel: создание таблиц и диаграмм по категорийным данным
Сводную таблицу для категорийных данных можно создать с помощью Мастера сводных таблиц и диаграмм (см. раздел ЕР.7). На основе этой таблицы, используя Мастер диаграмм, можно создать линейчатую и круговую диаграммы, а также диаграмму Парето. Надстройка PHStat2 позволяет выполнить эти процедуры за один шаг.
Например, чтобы построить сводную таблицу, аналогичную табл. 2.7, линейчатую и круговую диаграммы, а также диаграмму Парето, изображенные на рис. 2.6-2.8, следует открыть лист Данные рабочей книги Mutual Funds. xls и применить одну из двух процедур.
Применение Excel в сочетании с надстройкой PHStat2
Для того чтобы создать сводную таблицу и диаграммы на отдельных листах, необходимо выполнить такие действия.
1. Выполнить команду PHStat^Descriptive Statistics^One-Way Tables & Charts... (PHStat^OnncaTenbHaa статистикам Сводные таблицы & Диаграммы...).
2. В диалоговом окне One-Way Tables & Charts сделать следующее.
2.1. Установить переключатель Type of Data (Тип данных) в положение Raw Categorical Data (Исходные категорийные данные).
2.2. Ввести в окне редактирования Raw Data Cell Range (Входной интервал) диапазон К1 :К2 6О.
2.3. Ввести в окне редактирования Title (Заголовок) название диаграммы.
2.4. Установить флажок First cell contains label (Первая ячейка содержит метку).
2.5. Установить флажки Ваг Chart (Линейчатая диаграмма), Pie Chart (Круговая диаграмма) и Pareto Diagram (Диаграмма Парето).
2.6. Щелкнуть на кнопке ОК.
Процедура One-Way Tables & Charts позволяет также создавать диаграммы по частотным таблицам, таким как табл. 2.9. Для этого сначала необходимо перенести таблицу (вместе с заголовками столбцов) на новый лист. Затем следует установить переключатель Type of Data в положение Table of Frequencies (Таблица частот) и ввести диапазон ячеек таблицы в окне редактирования Freq. Table Cell Range (Установка переключателя Type of Data в положение Table of Frequencies приводит к замене метки "Raw Data Cell Range" на метку "Freq. Table Cell Range".)
Применение Excel
Построение сводной таблицы. Сводную таблицу можно построить с помощью Мастера сводных таблиц и диаграмм, руководствуясь инструкциями, приведенными в разделе ЕН2.7.
Построение диаграмм. Линейчатую и круговую диаграмму, а также диаграмму Парето можно построить с помощью Мастера диаграмм, следуя инструкциям из раздела ЕН2.8 и ЕН2.9.
4U chapter 2.XLS. Сводная таблица и диаграммы, приведенные выше, содержатся на рабочих ж листах Табл2.7, Рис2.6, Рис2.7 и Рис2.8 в рабочей книге Chapter 2.xls.
УПРАЖНЕНИЯ К РАЗДЕЛУ 2.4
Изучение основ
2.27. Некая категорийная переменная распределена на три группы частот.
Категория Частота
А 13
В 28
С 9
1. Вычислите процентную долю каждой категории.
2. Постройте линейчатую диаграмму.
3. Постройте круговую диаграмму.
4. Постройте диаграмму Парето.
2.28. Некая категорийная переменная распределена на четыре группы частот.
Категория Процентная доля Категория Процентная доля
А 12 С 35
В 29 D 24
1. Постройте линейчатую диаграмму.
2. Постройте круговую диаграмму.
3. Постройте диаграмму Парето.
Применение понятий
2.29. Системный аналитик зарегистрировал основные причины краха компьютерной сети в течение шести месяцев.
Причины краха Частота
Нарушение физического контакта 1
Сбой источников питания 3
Сбой программного обеспечения сервера 29
Сбой аппаратного обеспечения сервера 2
Переполнение памяти сервера 32
Недостаточная ширина полосы пропускания 1
1. Постройте диаграмму Парето.
2. Определите основные и второстепенные причины краха компьютерной сети.
2.30. Объем электронных переводов с кредитных карточек, выполненных американцами в 2000 г., превысил 50 млрд. долл. (Byron Acohido, “Microsoft, Banks Battle to Control Your e-info”, USA Today, August 13, 2001, 1B-2B). Эти транзакции распределились следующим образом.
Кредитная карта Объем (млрд, долл.) Процентная доля
American Express 8,04 15,6
Discover 1,97 3,8
Master Card 15,57 30,2
Visa 25,96 50,4
1. Постройте линейчатую диаграмму.
2. Постройте круговую диаграмму.
3. Постройте диаграмму Парето.
4. Какая из диаграмм предпочтительнее? Почему?
2.31. Компания RHI Management Resources провела опрос 1 400 руководящих финансистов. На вопрос: “Какое влияние оказывает ссудный процент на решение о приобретении чего-либо?” 672 респондента ответили: “Никакого”, 700 — “Значительное”, а 28 руководителей затруднились с ответом. (“USA Today Snapshots”, USA Today, August 27, 2001, Al.)
1. Постройте таблицу частот и сводную таблицу.
2. Постройте линейчатую диаграмму.
3. Постройте круговую диаграмму.
4. Какая из диаграмм предпочтительнее? Почему?
2.32. Ниже приведены результаты опроса, проведенного сайтом Monster.com 21-24 мая 2001 г. Пользователей Интернет попросили ответить на вопрос: “Готовы ли вы поменять место жительства, получив более выгодную работу?”. Каждый респондент должен был выбрать только один из вариантов ответа.
Ответ Частота
Да, если работа стоит этого 8 183
Да, но только если я мечтал об этой работе 2 772
Нет, мне и так хорошо 792
Нет, ни в коем случае 1 452
Источник: цитируется по журналу USA Today, June 26, 2001, Al.
1. Постройте сводную таблицу.
2. Постройте линейчатую диаграмму.
3. Постройте круговую диаграмму.
4. Какая из диаграмм предпочтительнее? Почему?
2.33. В статье, опубликованной в журнале USA Today (Peter McMahon, “Green Power Gets Second Wind”, USA Today, August 16, 2001, ЗА), обсуждается возрождение в США интереса к энергии ветра. В следующей таблице приведено распределение источников энергии в США.
Источник Процентная доля
Уголь 51,8
Гидроэлектроэнергия 7,3
Природный газ 15,7
Атомная энергия 19,8
Нефть 2,9
Ветер 0,1
Другие источники 2,4
Источник: Министерство энергетики США.
1. Постройте диаграмму Парето.
2. Какой процент электроэнергии производится за счет угля, атомной энергии и природного газа?
3. Постройте круговую диаграмму.
4. Какая из диаграмм предпочтительнее? Почему?
2.34. В ходе опроса 150 менеджеров попросили указать основные ошибки, которые допускают соискатели работы в ходе собеседования. Ответы респондентов приведены ниже (USA Today Snapshots, November 19, 2001).
Причина Процентная доля
Отсутствие знаний о компании 44
Слабое представление о дальнейшей карьере 23
Слабый энтузиазм 16
Бегающий взгляд 5
Недостаточный опыт работы 3
Другие причины 9
1. Постройте линейчатую диаграмму.
2. Постройте круговую диаграмму.
3. Постройте диаграмму Парето.
4. Какая из диаграмм предпочтительнее? Почему?
5. Если бы вы были соискателем работы, какой ошибки вам следует опасаться больше остальных?
2.35. В следующей таблице приведена информация о среднем объеме потребления воды на семью в пригородном районе на протяжении последнего лета.
Цель потребления воды Количество галлонов в день
Ванна и душ 99
Мытье посуды 13
Питье и приготовление пищи 11
Стирка 33
Орошение газонов 150
Туалет 88
Другие цели 20
Всего: 414
1. Постройте диаграмму Парето.
2. Если бы водопроводная компания разрабатывала план сокращения потребления воды, какие причины следовало бы изучить более внимательно?
2.36. В крупной городской больнице был проведен опрос 210 пациентов. Их попросили оценить качество лечения и ухода за больными на протяжении июня. Ниже приводится список, в котором подытожены 384 жалобы.
Жалоба Количество
Раздражают другие пациенты и посетители 13
Медперсонал несвоевременно реагирует на вызовы 71
Неадекватные ответы на вопросы 38
Задержка анализов 34
Шум 28
Плохое качество пищи 117
Невежливость персонала 62
Другие жалобы 21
Всего: 384
1. Постройте диаграмму Парето.
2. Если бы руководство больницы захотело сократить количество жалоб, на что следовало бы обратить внимание прежде всего?
2.5. ПРЕДСТАВЛЕНИЕ ДВУМЕРНЫХ КАТЕГОРИЙНЫХ ДАННЫХ
В ВИДЕ ТАБЛИЦ И ГРАФИКОВ
Довольно часто необходимо анализировать пары категорийных переменных. В данном разделе описываются таблица сопряженности признаков и параллельные линейчатые диаграммы.
Таблица сопряженности признаков
Чтобы можно было одновременно анализировать две категорийные переменные, образующие пару, используются таблицы перекрестной классификации с двумя входами (cross-classification table), или таблицы сопряжености признаков. (Их также называют факторными таблицами. — Прим, ред.) Например, может возникнуть вопрос: существует ли зависимость между уровнем риска и платой, взимаемой фондами за осуществление продаж своих акций? Информация о 259 фондах, необходимая для ответа на этот вопрос, приведена в табл. 2.10.
Таблица 2.10. Таблица сопряженности признаков, содержащая данные об уровне риска и плате, взимаемой фондами за осуществление продаж своих акций
Уровень риска (%)
Плата Очень высокий Высокий Средний Низкий Очень низкий Всего
Да 4 35 23 31 2 95
Нет 11 45 59 45 4 164
Всего 15 80 82 76 6 259
Таблица сопряженности признаков содержит данные о 259 фондах, распределенные по 10 ячейкам. Например, первый из перечисленных фондов (компания Amro Montag & Colwell Growth I) классифицирован как фонд со средним уровнем риска, не взи-
мающий плату за продажу своих акций (взаимный фонд, акции которого продаются без брокерской комиссии). Эта пара значений соответствует ячейке, образованной пересечением второй строки и третьего столбца таблицы. Остальные 258 фондов исследуются аналогично.
Чтобы выявить любую возможную зависимость между специализацией фонда и прейскурантом его комиссионных сборов, эти результаты сначала преобразуют в процентные доли, используя три следующие совокупные величины (табл. 2.11-2.13).
1. Общая сумма (259 взаимных фондов).
2. Сумма по строкам (фонды, взимающие плату за продажу своих акций, и фонды без брокерской комиссии).
3. Сумма по столбцам (пять уровней риска).
Таблица 2.11. Таблица сопряженности признаков, содержащая процентные доли, подсчитанные на основе общей суммы
Уровень риска (процент от общей суммы)
Плата Очень высокий Высокий Средний Низкий Очень низкий Всего
Да 1,54 13,51 8,88 11,97 0,77 36,68*
Нет 4,25 17,37 22,78 17,37 1,54 63,32
Всего 5,79 30,89* 31,66 29,34 2,32* 100,00
"Учитывается влияние округления.
Таблица 2.12. Таблица сопряженности признаков, содержащая процентные доли, подсчитанные на основе суммы по строкам
Уровень риска (процент от суммы по строкам)
Плата Очень высокий Высокий Средний Низкий Очень низкий Всего
Да 4,21 36,84 24,21 32,63 2,11 100,00
Нет 6,71 27,44 35,98 27,44 2,44 100,00*
Всего 5,79 30,89 31,66 29,34 2,32 100,00
"Вследствие округлений результат отличается от 100,0.
Таблица 2.13. Таблица сопряженности признаков, содержащая процентные доли, подсчитанные на основе суммы по столбцам
Уровень риска (процент от суммы по столбцам)
Плата Очень высокий Высокий Средний Низкий Очень низкий Всего
Да 26,67 43,75 28,05 40,79 33,33 36,68
Нет 73,33 56,25 71,95 59,21 66,67 63,32
Всего 100,00 100,00 100,00 100,00 100,00 100,00
Из табл. 2.11 следует, что 30,89% взаимных фондов имеют высокий уровень риска, 63,32% не взимают брокерскую комиссию, причем 17,37% фондов с высоким уровнем риска также не взимают плату за продажу своих акций. В табл. 2.12 показано, что 36,84% взаимных фондов, взимающих брокерскую комиссию, имеют высокий риск, а 2,11% — очень низкий. Из табл. 2.13 следует, что 43,75% фондов имеют высокий уровень риска и лишь 28,05% фондов со средним уровнем риска взимают брокерскую комиссию. Эти таблицы позволяют сделать важный вывод: фонды с высоким и низким уровнями риска, как правило, взимают плату за продажу своих акций, а фонды со средним и очень высоким уровнями риска — нет.
Параллельная линейчатая диаграмма
Для визуализации двумерных категорийных данных часто строят параллельную линейчатую диаграмму (side-by-side bar chart). На рис. 2.10 показана диаграмма, построенная на основе данных, содержащихся в табл. 2.10, с помощью программы Microsoft Excel. Она позволяет сравнивать пять категорий взаимных фондов, классифицируя их по уровню риска. Выводы, к которым приводит анализ рис. 2.10, полностью совпадают с выводами, сделанными на основе табл. 2.11-2.13: фонды с высоким и низким уровнями риска, как правило, взимают плату за продажу своих акций, а фонды со средним и очень высоким уровнями риска — нет.
Рис. 2.10. Параллельная линейчатая диаграмма, отображающая данные о специализации фонда и взимании брокерской комиссии (построена с помощью программы Microsoft Excel)
Процедуры Excel: создание таблицы сопряженности признаков и диаграмм по категорийным данным
Чтобы создать таблицу сопряженности признаков для двумерных категорийных данных, можно воспользоваться Мастером сводных таблиц и диаграмм и Мастером диаграмм. Надстройка PHStat2 позволяет выполнить эту процедуру за один шаг. (Если таблица сопряженности признаков уже построена, следуйте инструкциям по созданию параллельных диаграмм с помощью программы Microsoft Excel.)
Для того чтобы создать таблицу сопряженности признаков, аналогичную табл. 2.10, необходимо открыть лист Данные в рабочей книге Mutual Funds.xls и выполнить такие действия.
Применение Excel в сочетании с надстройкой PHStat2
1. Выполнить команду PHStatd>Descriptive Statisticsd>Two-Way
Tables & Charts... (PHStat4>Описательная статистика^ Двухфакторные таблицы & Диаграммы...).
2. В диалоговом окне Two-Way Tables & Charts (см. иллюстрацию) сделать следующее.
2.1. Ввести в окне редактирования Row Variable Cell Range (Входной интервал) диапазон К1 :К2 6О.
2.2. Ввести в окне редактирования Column Variable Cell Range (Интервал переменной в столбце) диапазон Е1 :Е260.
2.3. Установить флажок First cell contains label (Первая ячейка содержит метку).
2.4. Ввести в диалоговом окне Title заголовок таблицы.
Two Way Tables & Charts fx]
Data ................................
Row Variable Cell Range: [Й1:K260 - j
Column Variable Cell Range: ?E 1:E260 _ 1
P First cell in each range contains label
Output Options
Title: {риск и комиссия
P Side-by-Side Bar Chart
Help
| OK |
2.5. Сбросить флажок Side-by-Side Bar Chart (Параллельная линейчатая диаграмма).
2.6. Щелкнуть на кнопке ОК.
Для разбиения данных на категории при построении параллельных линейчатых диаграмм надстройка PHStat2 (как и Мастер сводных таблиц и диаграмм) использует переменную, значения которой записаны в строке. Например, для создания диаграммы, изображенной на рис. 2.10, диапазон К1 :К2 6О должен быть записан в строке, однако построенная по таким данным таблица сопряженности признаков окажется транспонированной. Для того чтобы привести таблицу к исходному виду, диапазоны данных следует поменять местами.
Применение Excel
Создание таблицы сопряженности признаков. Для создания таблицы сопряженности признаков примените Мастер сводных таблиц и диаграмм, следуя инструкциям, приведенным в разделе ЕН2.10. Если таблица сопряженности признаков уже построена, следует применить Мастер диаграмм. Щелкните на таблице правой кнопкой мыши и выберите в контекстном меню команду Сводная диаграмма. Щелкните правой кнопкой мыши на фоне вновь сгенерированной диаграммы и выберите в контекстном меню команду Тип диаграммы. Находясь в диалоговом окне Тип диаграммы, выполните действия, перечисленные ниже (п.1) и щелкните на кнопке ОК. В заключение щелкните правой кнопкой мыши на раскрывающемся списке Комиссионный сбор (или Риск) и выберите в контекстном меню команду Скрыть кнопки полей сводной диаграммы, чтобы не загромождать рисунок.
Если таблица сопряженности признаков отличается от сводной, или вы пользуетесь программой Microsoft Excel 97, предыдущие инструкции бесполезны. Откройте вашу таблицу сопряженности признаков и вызовите Мастер диаграмм. Например, для того чтобы создать параллельную линейчатую диаграмму, аналогичную рис. 2.10, откройте рабочий лист Сводная_таблица, созданный на предыдущем этапе (или рабочий лист Таблица 2.10 в рабочей книге Chapter 2 .xls), выполните команду Вставка ^Диаграмма... и заполните поля в диалоговых окнах Мастера диаграмм.
На первом этапе следует выполнить такие действия.
1.1. Щелкнуть на корешке вкладки Стандартные и выбрать пункт Линейчатая в раскрывающемся списке Тип.
1.2. Выбрать первый тип диаграммы на панели Вид, сопровождающейся пояснением: "Линейчатая диаграмма отображает значения различных категорий". Щелкнуть на кнопке Далее>.
На втором этапе следует выполнить такие действия.
2.1. Щелкнуть на корешке вкладки Диапазон данных. Ввести в окне редактирования Диапазон ссылки A4:D9.
2.2. Установить переключатель Ряды в положение В строках и щелкнуть на кнопке Далее>.
На третьем этапе следует выполнить следующее.
3.1. Щелкнуть на корешке вкладки Заголовки. Ввести в окне редактирования Название диаграммы заголовок Параллельная линейчатая диаграмма, в окне редактирования Ось X (категорий) — строку Уровень риска, а в окне редактирования Ось Y (значений) — строку Брокерская комиссия, %.
3.2. Щелкнуть по очереди на корешках вкладок Оси, Линии сетки и Таблица данных и установить флажки и переключатели в соответствии с указаниями, приведенными в разделе ЕР.б.
3.3. Установить флажок Добавить легенду и щелкнуть на кнопке Далее>.
На четвертом этапе следует установить переключатель Поместить диаграмму на отдельном листе, указать информативное название листа, не совпадающее с другими, и щелкнуть на кнопке Готово.
Chapter 2 .XLS. Таблица сопряженности признаков и параллельная линейчатая диаграмма, приведенные выше, содержатся на рабочих листах Таблица 2.10 и Рис. 2.10 в рабочей книге Chapter 2.xls.
УПРАЖНЕНИЯ К РАЗДЕЛУ 2.5
Изучение основ
2.37. Ниже приведены данные, состоящие из альтернативных ответов на два вопроса, полученных в ходе опроса 40 студентов, изучающих бизнес в колледже: “Укажите ваш пол” (мужской — М, женский — Ж) и “Укажите вашу специализацию” (бухгалтерский учет — Б, компьютерные информационные системы — К, торговля — Т).
Пол М м м /iv М /IV Ж м /IV М
Специальность Б к к т Б к Б Б к К
Пол птл /1V м м м М /iv лтл /IV М ж ПТЛ /IV
Специальность Б Б Б т К т Б Б Б к
Пол М м м м «\тл /IV м ПТЛ /IV лтл /IV м м
Специальность К к Б Б т т к Б Б Б
Пол ж м М м м /tv м ПТЛ /IV М м
Специальность к к Б Б Б Б к к Б к
1. Составьте таблицу сопряженности признаков, в которой две строки представляют категорию пола, а три столбца — академические специализации.
2. Составьте таблицу сопряженности признаков, используя процентные доли категорий по отношению к общему количеству студентов (40).
3. Составьте таблицу сопряженности признаков, используя процентные доли категорий по отношению к сумме по строкам.
4. Составьте таблицу сопряженности признаков, используя процентные доли категорий по отношению к сумме по столбцам.
5. Используя решение задачи 1, постройте параллельную линейчатую диаграмму пола, основываясь на данных о специализации студентов.
2.38. Основываясь на двухфакторной таблице, приведенной ниже, постройте параллельную линейчатую диаграмму, позволяющую сравнить значения А и Б для каждой из трех категорий, отложенных по вертикальной оси.
1 2 3 Всего
А 20 40 40 100
Б 80 80 40 200
Применение понятий
2.39. Результаты контроля продукции производственной компании позволили выявить дефекты в партии, состоящей из 450 плат. В приведенной ниже таблице содержатся ответы на два вопроса: “Найдены ли частицы на матрице?” и “Качественная плата или нет?”.
Состояние матрицы
Качество платы Нет частиц Есть частицы Всего
Хорошее 320 14 334
Плохое 80 36 116
Всего 400 50 450
Источник: Hall, S. W. “Analysis of Detectivity of Semiconductor Wafers by Contingency Table”, Proceedings Institute of Environmental Sciences, 1 (1994 ):177-183.
1. Постройте общую таблицу процентных долей.
2. Постройте таблицу процентных долей по строкам.
3. Постройте таблицу процентных долей по столбцам.
4. Постройте параллельную линейчатую диаграмму качества плат на основе данных о качестве матрицы.
5. К каким выводам приводит этот анализ?
2.40. Объем розничных продаж в США в апреле 2002 года оказался немного больше, чем в апреле 2001 года. Компании, практикующие оптовые скидки, такие как Wal-Mart, Costco, Target и Dollar General, увеличили объемы продаж на 9% и более. Однако в швейной промышленности сложилась более пестрая картина (Ann Zimmerman, “Retail Sales Grow Modestly”, Wall Street Journal, May 10, 2002, B4). В следующей таблице приведены объемы продаж (в млн. долл.) ведущих швейных компаний за период с апреля 2001 г. по апрель 2002 г.
Общий объем продаж, млн. долл.
Швейная компания Апрель 2001 Апрель 2002
Gap 1 159,0 962,0
TJX 781,7 899,0
Limited 596,5 620,4
Kohl’s 544,9 678,9
Nordstrom 402,6 418,3
Talbots 139,9 130.1
AnnTaylor 114,2 124,8
Источник: цитируется по журналу Wall Street Journal.
1. Постройте общую таблицу процентных долей.
2. Постройте параллельную линейчатую диаграмму.
3. Как изменились объемы продаж в швейной промышленности за период с апреля 2001 г. по апрель 2002 г.?
2.41. Международная сеть гостиниц, включающая в себя компании Mariott International и Holiday Inn Resorts, бурно развивается в юго-восточной Азии и на островах Тихого океана. Увеличение количества гостиниц в этом регионе продолжалось и в 2002 году, несмотря на падение уровня заполняемости и доходности в расчете на номер (Zach Coleman, “Hotel Groups Bolster Presence in Asia”, Wall Street Journal, May 8, 2002, D10). В приведенной ниже таблице указаны уровень заполняемости и доходность в расчете на номер для гостиниц в пяти азиатских городах в 2000 и 2001 гг.
Доходность в расчете на номер, долл. Уровень заполняемости, %
Город 2000 2001 2000 2001
Токио, Япония 132,63 116,98 80,9 78,9
Гонконг, Китай 112,89 103,29 82,6 73,2
Шанхай, Китай 53,44 58,25 69,7 69,2
Пекин, Китай 49,57 48,53 73,5 73,0
Бангкок, Таиланд 45,63 44,95 67,8 65,8
Источник: цитируется по журналу Wall Street Journal.
1. Постройте общую таблицу процентных долей для доходности в расчете на номер.
2. Постройте общую таблицу процентных долей для уровня заполняемости гостиниц.
3. Какие выводы можно сделать на основе анализа этих диаграмм?
2.42. Каждый день в крупной больнице выполняется несколько сотен анализов. Уровень некачественных анализов, которые необходимо повторить, постоянен и равен приблизительно 4%. Стремясь снизить уровень брака, директор лаборатории решил изучить записи об анализах, проведенных в лаборатории за неделю, и распределить их по исполнителям. В результате получилась следующая таблица.
Смена
Качество лабораторного анализа День Вечер Всего
Неудовлетворительное 16 24 40
Удовлетворительное 654 306 960
Всего 670 330 1 000
1. Постройте таблицу процентных долей по строкам.
2. Постройте таблицу процентных долей по столбцам.
3. Постройте общую таблицу процентных долей.
4. Какая таблица — общая, по строкам или по столбцам — более информативна? Почему?
5. К каким выводам может прийти директор лаборатории?
2.43. Сберегательный банк в течение месяца проводит опрос клиентов о степени их удовлетворенности работой и качеством обслуживания. Результаты опроса 200 клиентов приведены ниже.
Вид услуг Количество удовлетворенных клиентов Количество недовольных клиентов
Время ожидания в очереди 123 65
Работа банкомата 73 7
Консультирование по инвестициям 43 6
Обслуживание дорожных чеков 25 11
Хранилище 24 5
Обслуживание счетов 46 4
Примечание. Поскольку клиенты не могут воспользоваться всеми услугами одновременно, количество ответов в каждой строке разное.
1. Постройте таблицу процентных долей по строкам.
2. Постройте таблицу процентных долей по столбцам.
3. Постройте общую таблицу процентных долей.
4. Какая таблица — общая, по строкам или по столбцам — более информативна? Почему?
5. Постройте параллельную линейчатую диаграмму, характеризующую степень удовлетворенности клиентов банка каждым видом услуг.
6. Одинаково ли довольны клиенты всеми видами услуг? Какие услуги требуют дополнительного внимания? Обоснуйте свой ответ.
2.6. ИСКУССТВО ГРАФИЧЕСКОГО ПРЕДСТАВЛЕНИЯ ДАННЫХ
Наиболее простыми и эффективными способами представления статистических данных являются графические изображения. Хороший рисунок позволяет сразу выявить основные закономерности, скрытые в массиве информации. Для улучшения анализа данных необходимы ясные и точные таблицы и графики. Излишние украшения и вычурность лишь мешают [4, 6-8].
В последние годы широкое распространение электронных таблиц и графических пакетов привело к интенсивному использованию рисунков для иллюстрации статистических данных. Несмотря на то что графические изображения довольно часто приносят пользу, злоупотребление графикой создает впечатление, что единственной целью статистики является наукообразный обман.
Принципы графического представления данных
Вероятно, одним из наиболее известных пропагандистов правильного представления данных с помощью графических средств является Эдвард Р. Тафт (Edward R. Tufte) [6-8]. В данном разделе мы кратко изложим его идеи.
Во врезке 2.1 перечислены основные свойства графических данных.
ВРЕЗКА 2.1. СВОЙСТВА ГРАФИЧЕСКИХ ДАННЫХ
Идеальная диаграмма должна обладать следующими основными свойствами.
• Иллюстрировать данные.
• Концентрировать внимание на существе графического изображения, а не на способе его создания.
• Предотвращать искажения.
• Облегчать сравнение данных.
• Быть наглядной.
• Быть тесно связанной со статистическими и словесными описаниями изображения.
В работе [6] Тафт сформулировал пять принципов графического представления данных (врезка 2.2).
ВРЕЗКА 2.2. ПРИНЦИПЫ ГРАФИЧЕСКОГО ПРЕДСТАВЛЕНИЯ ДАННЫХ
• Графическое представление данных должно отражать суть дела, статистические свойства данных и быть хорошо продуманным.
• Графическое представление данных должно просто, ясно и эффективно представлять сложные идеи.
• Графическое представление данных должно порождать у наблюдателя наибольшее количество идей за минимальный промежуток времени.
• Графическое представление данных всегда многомерно.
• Графическое представление данных должно отображать истинный смысл данных.
Существует несколько способов оценки качества графического представления данных. Одним из них является вычисление информативности рисунка на основе доли чернил, затраченных на иллюстрацию данных.
ИНФОРМАТИВНОСТЬ РИСУНКА
Информативность рисунка равна доле чернил, затраченных на иллюстрацию данных, в общем объеме чернил, затраченных на весь рисунок. Цель этого показателя — не допустить излишеств.
. Объем чернил, затраченных на иллюстрацию данных
Информативность =------------3— ---------------— -------- (2.2)
Общий объем затраченных чернил
Цель этого отношения — максимизировать долю чернил, затраченных на иллюстрацию данных. Не следует перегружать рисунок элементами, не имеющими отношения к делу. Например, это часто относится к линиям сетки на графике. Такие элементы называются графическим хламом (chartjunk).
Графический хлам — это декоративные украшения, не имеющие отношения к данным или являющиеся их излишними уточнениями.
Графический хлам часто представляет собой самостоятельное графическое изображение, фокусирующее внимание на способе его создания, а не на данных.
При создании рисунка нельзя искажать данные. График считается верным, если он полностью соответствует исходным данным. Количество искажений, которые вносятся графиком, называются фактором лжи (lie factor).
Фактор лжи — это отношение величины эффекта, изображенного на графике, к величине эффекта исходной выборки.
Любое изменение, показанное на графике, должно соответствовать изменениям, существующим в исходных данных. Довольно часто при построении графика этим правилом пренебрегают. Это приводит к искажениям и несоответствиям между графическим изображением и данными.
Чтобы лучше разобраться с этими принципами, рассмотрим несколько примеров, которые нарушают правила построения графических изображений.
На рис. 2.11 представлена иллюстрация к статье в журнале The Time, посвященной возрастающему экспорту австралийского вина в США. На ней, в частности, показан бокал, символизирующий 6,77 млн. галлонов вина, поставленного из Австралии в США в 1997 году. Обратите внимание на то, что объем вина в этом бокале должен почти в два раза превышать объем вина в предыдущем бокале, соответствующем 2,67 млн. галлонов, а тот, в свою очередь, должен содержать в два раза больше вина, чем первый бокал. На самом деле этот не так. Отчасти это объясняется тем, что иллюстраторы использовали трехмерный элемент рисунка вместо двухмерного. Такие иллюстрации могут привлекать внимание, но все же правильнее было бы использовать двухмерную диаграмму или график.
Кроме того, если на рисунке не указано начало координат, набор данных оказывается искаженным. В качестве примера обратимся к рис. 2.12, приведенному в той же статье. У этого рисунка есть несколько недостатков. Во-первых, на оси X не отложено ни одного значения. Поскольку рис. 2.12 представляет собой график, изображающий рост площадей, занятых виноградниками в винной промышленности с течением времени, на оси X следовало бы отметить годы. Вместо этого, годы (в правильном порядке) указаны рядом с объемами площадей. Во-вторых, точки изображены неверно. Это более серьезная ошибка. Точка, соответствующая 135 326 акрам в 1949-1950 г., изображена выше, чем точка, соответствующая 150 300 акрам в 1969-1970 г.! Кроме того, разница между
1979-1980 и 1997-1998 г. должна в три раза превышать разницу между 1979-1980 и 1969-1970 г., а на рисунке эта пропорция нарушена. В-третьих, интервалы времени на оси X изображены неверно. Точка, соответствующая 1979-1980 г., намного ближе к точке, соответствующей 1989-1990 г., чем к точке, изображающей площадь виноградников в 1969-1970 г.
Мы пьем все больше вина...
Объем экспорта австралийского вина в США (млн. галлонов)
1989 1992 1995 1997
Рис. 2.11. Неверная иллюстрация объема экспорта австралийского вина в США (млн. галлонов)
Рис. 2.12. Неверная иллюстрация площади, занятой виноградниками в винодельческой промышленности. Источник: S. Watterson "Liquid Gold - Australians are Changing the World of Wine. Even the French Seem Grateful", Time, November 22,1999, p. 68, 69
В журналах и газетах часто печатают рисунки, содержащие излишнюю информацию. Например, рис. 2.13 иллюстрирует рынок газированных безалкогольных напитков в 1999 году. Хотя в целом рисунок правильно отображает разницу между долями рынка, занятыми разными напитками, он содержит массу ненужных деталей. Количество чернил, затраченных на изображение пены, рвущейся из бутылок, намного превышает разумную величину. Гораздо лучше было бы изобразить эти данные в виде круговой диаграммы.
Кока-кола по-прежнему шипит громче всех <
Coke Classic Наиболее распространенные газированные «
20% безалкогольные напитки, заполнившие |
Рис. 2.13. Изображение долей рынка, занятого газированными безалкогольными напитками в 1999 году. Источник: Carey, А.В., and S. Ward "Coke still has most fizz", USA Today, May 10, 2000, p. 1B
Подведем итоги. Каждый из нас поглощает огромный объем информации из газет и журналов. Поскольку большая ее часть представляет собой ненужный хлам, необходимо научиться отбрасывать лишнее. Следует также помнить, что иногда графики захламляются по невежеству, а иногда — чтобы ввести читателей в заблуждение. Следовательно, очень важно сохранять скептический настрой.
Как указывает Тафт [6], первое, что приходит в голову людям, рассматривающим иллюстрации статистических данных, — “неправда”. Слишком часто графики искажают реальные данные, затрудняя читателям поиск истины. При выборе способа изображения статистических данных — таблиц или рисунков — возникает много этических проблем. Необходимо одинаково честно изображать как хорошие, так и плохие результаты. Делая устный или письменный доклад, необходимо излагать информацию честно, объективно и нейтрально. Следует различать неудачную и нечестную презентацию. Критерий, с помощью которого это можно сделать, — намерения докладчика. Очень часто искажения и излишества при иллюстрации статистических данных возникают в результате невежества. Однако бывает, что под этим скрывается стремление обмануть читателей и слушателей.
УПРАЖНЕНИЯ К РАЗДЕЛУ 2.6
Изучение основ
2.44. Студенческий проект. Принесите в класс диаграмму, опубликованную в газете или журнале, которая изображает числовые данные и которую вы считаете неверной. Объясните, почему вы полагаете, что эта диаграмма искажает реальные данные.
2.45. Студенческий проект. Принесите в класс диаграмму, опубликованную в газете или журнале, которая изображает категорийные данные и которую вы считаете неверной. Объясните, почему вы полагаете, что эта диаграмма искажает реальные данные.
2.46. Студенческий проект. Принесите в класс диаграмму, опубликованную в газете или журнале, которую вы считаете излишне громоздкой. Объясните, почему вы полагаете, что эта диаграмма неудачна.
2.47. Разукрашенная диаграмма, приведенная ниже, опубликована в журнале USA Today. Она иллюстрирует снижение количества смертей от попадания молнии в США.
Источник: USA Today, November 12, 2002.
1. Укажите хотя бы одно преимущество этой диаграммы.
2. Укажите хотя бы один недостаток этой диаграммы.
3. Перерисуйте диаграмму, используя принципы графического представления данных.
2.48. Диаграмма, приведенная ниже, опубликована в журнале USA Today. Она иллюстрирует относительную величину департаментов полиции в основных городах США.
; Количество полицейских на душу населения
I Среди 50 городов США количество полицейских в расчете на s i 10000 жителей является наибольшим в следующих городах.
Источник: USA Today, February, 2000.
1. Укажите особенности этой диаграммы, которые нарушают принципы графического представления данных.
2. Перерисуйте эту диаграмму в соответствии с принципами графического представления данных.
2.49. Разукрашенная диаграмма, приведенная ниже, опубликована в журнале USA Today. В ней показаны источники электроэнергии в США.
Уголь — основной источник электроэнергии
60 Источники электроэнергии в США: I
Источник: USA Today, January 30, 2002.
1. Укажите хотя бы одно преимущество этой диаграммы.
2. Укажите хотя бы один недостаток этой диаграммы.
3. Перерисуйте диаграмму, используя принципы графического представления данных.
2.50. В статье, опубликованной в газете The New York Times (Donna Rosato, New York Times, September 15, 2002, 7), сообщается о том, что профессор Денна Берджес (Deanna Oxender Burgess) из университета Галф-Кост штата Флорида (Florida Gulf Coast University) исследовала ежегодные отчеты корпораций. Она заметила, что даже небольшое искажение диаграммы оказывает заметное влияние на впечатление читателей. Статья ссылается на отчет, содержащий объемы годовых продаж компании Zale Corporation. Зайдите в World Wide Web или в библиотеку и проанализируйте ежегодный отчет какой-нибудь корпорации. Укажите хотя бы одну диаграмму, которую вы считаете неудачной, и расскажите, как ее улучшить. Объясните, почему вы считаете свой вариант диаграммы более точным, чем исходный.
РЕЗЮМЕ
Как следует из схемы, приведенной ниже, эта глава посвящена средствам представления данных. Чтобы сделать выводы о деятельности взаимных фондов, описанных в сценарии “Применение статистики”, мы использовали различные таблицы и диаграммы. Теперь, представив данные в виде таблицы или диаграммы, мы должны вычислить и проинтерпретировать их количественные характеристики. Этому посвящена глава 3.
Числовые г“——
Тип данных <
Категорийные
Количество >, переменных -
Диаграмма разброса
Г истограмма
Сводная таблица
Количество переменных
2
Г
1
"ПС
Упорядоченный, \ Диаграмма массив . “ствол и листья
Круговая диаграмма
Линейчатая диаграмма
Диаграмма Парето
Распределение' частот
Полигон
Функция • распределения
Таблица сопряженности признаков
Параллельная линейчатая диаграмма
Г
Кривая распределения
Структурная схема главы 2
ОСНОВНЫЕ ПОНЯТИЯ
Гистограмма, 111
Графический хлам, 143
Графическое представление
данных, 142
Диаграмма
круговая, 125
линейчатая, 125
параллельная, 136
Парето, 126
Диаграмма, 100
Интервал группирования, 105
Информативность рисунка, 142
Класс, 105
Кривая распределения, 113
Полигон
накопленных частот, 113
процентный, 112
Распределение
накопленных процентов, 108; 113
относительных частот, 107
процентное, 107
частот, 105
Таблица
перекрестной классификации с
двумя входами, 134
сводная, 124
сопряженности признаков, 134
факторная, 134
Упорядоченный массив, 99
Фактор лжи, 143
УПРАЖНЕНИЯ К ГЛАВЕ i'/L J \
Проверка знаний
2.51. Почему собранные данные необходимо организовать?
2.52. Чем отличаются друг от друга упорядоченный массив и диаграмма “ствол и листья”?
2.53. Чем отличаются друг от друга гистограммы и полигоны?
2.54. Чем так полезен полигон интегральных процентов?
2.55. Зачем нужны распределение частот и сводная таблица процентных долей?
2.56. В чем заключаются преимущества и недостатки линейчатой диаграммы, круговой диаграммы и диаграммы Парето?
2.57. Сравните между собой линейчатую диаграмму для категорийных данных и гистограмму, построенную по числовым данным.
2.58. Какой из приведенных ниже способов графического представления данных больше других похож на диаграмму Парето — диаграмма “ствол и листья”, гистограмма, полигон, кривая распределения, линейчатая диаграмма или круговая диаграмма? Обоснуйте свой ответ.
2.59. Почему говорят, что основным преимуществом диаграммы Парето является возможность отделить важные данные от второстепенных?
2.60. Какой вид процентного распределения больше других подходит для интерпретации результатов перекрестного анализа двумерных категорийных величин?
2.61. Какие этические проблемы возникают, если данные представлены в виде таблиц или диаграмм?
Применение понятий
Рекомендуем решать задачи 2.62-2.80 с помощью программы Microsoft Excel.
2.62. Один из основных критериев качества услуг, предоставляемых любой организацией, — скорость, с которой она реагирует на жалобы клиентов. Один из больших универмагов, торгующих фурнитурой и коврами, за последние годы значительно расширился. В частности, отдел ковровых покрытий, в котором прежде работали 2 человека, теперь состоит из руководителя, измерителя и 15 продавцов. На протяжении последнего года компания получила 50 жалоб на работу этого отдела. Ниже приведены данные о количестве дней, прошедших со дня получения жалобы до принятия решения.
© FURNITURE.XLS
54 5 35 137 31 27 152 2 123 81 74 27 11
19 126 110 110 29 61 35 94 31 26 5 12 4
165 32 29 28 29 26 25 1 14 13 13 10 5
27 4 52 30 22 36 26 20 23 33 68
1. Вычислите распределение частот и процентное распределение.
2. Постройте гистограмму.
3. Постройте процентный полигон.
4. Постройте распределение интегральных процентов.
5. Постройте кривую распределения (распределение интегральных процентов).
6. Значительно ли варьируется время принятия решения? Обоснуйте свой ответ.
7. Какова средняя продолжительность ожидания ответа на жалобу?
2.63. В рабочей книге ^PI'ZZA.XLS содержатся данные о 36 порциях пиццы: стоимость в долларах, количество калорий и количество жира в граммах (SFat) для трех категорий продуктов: сырной пиццы из пиццерии (тип 1), сырной пиццы из супермаркета (тип 2) и острой пиццы из супермаркета (тип 3).
Источник: “Frozen Pizza on the Rize”, Copyright © 2002 by Consumers Union of U. S. Adapted from Consumer Reports, January 2002, p. 40-41. Публикуется с разрешения компании Consumer Union of U. S., Inc., Yonkers, NY 10703-1057.
1. Для каждой из трех числовых переменных (стоимость, количество калорий и жирность) создайте упорядоченный массив и диаграмму “ствол и листья”.
2. В зависимости от разновидности пиццы (сырная или острая) для каждой из трех числовых переменных (стоимость, количество калорий и жирность) создайте упорядоченный массив и диаграмму “ствол и листья”.
3. Вычислите распределение частот и процентное распределение для стоимости, калорий и жирности.
4. Вычислите распределение накопленных процентов для стоимости, калорий и жирности.
5. Постройте процентный полигон для стоимости, калорий и жирности.
6. Постройте кривую распределения (полигон накопленных процентов) для стоимости, калорий и жирности.
7. Постройте точечную диаграмму для стоимости и калорийности, стоимости и жирности, а также калорийности и жирности.
8. Какие выводы можно сделать о стоимости, калорийности и жирности каждой из разновидностей пиццы?
2.64. В одной из статей, опубликованных в журнале Quality Engineering, исследуется вязкость (т.е. величина сопротивления потоку) химических веществ из разных партий. Допустим, что стандартная вязкость должна колебаться в интервале от 13 до 18. В файле ^CHEMICAL. XLS приведены данные о 120 партиях.
Источник: D. S. Holmes, and Mergen А. Е., “Parabolic Control Limits for the Exponentially Weighted Moving Average Control Charts", Quality Engineerong, 4(1992): p. 487-495.
1. Создайте упорядоченный массив.
2. Вычислите распределение частот и процентное распределение.
3. Постройте процентную гистограмму.
4. Сколько партий соответствует спецификациям компании?
2.65. Исследования, проведенные компаниями, производящими рубероидную кровельную плитку в Бостоне и Вермонте, показали, что основным фактором, влияющим на оценку качества продукции, является ее вес. Более того, вес продукции отражает количество материала, затраченного на ее производство, и, следовательно, играет важную роль в формировании себестоимости. На последнем этапе плитка пакуется, а затем размещается на деревянных стеллажах (как правило, на поддоне помещается 16 плиток). После заполнения стеллажа регистрируется его вес. В соответствии со стандартами вес стеллажа в бостонском отделении компании колеблется в интервале от 3 050 до 3 260 фунтов. В вермонтском отделении компании вес стеллажа варьируется от 3 600 до 3 800 фунтов. Файл ftfpALLET.XLS содержит данные о весе (в фунтах) 368 стеллажей, заполненных плитками, произведенными в бостонском отделении компании, и 330 стеллажей, загруженных в Вермонте.
1. Вычислите распределение частот для веса стеллажей, загруженных в Бостоне, используя интервалы группирования с границами 3 015, 3 050, 3 085, 3 120, 3 155, 3 190, 3 260 и 3 295.
2. Вычислите процентное распределение на основе распределения частот, полученного при решении задачи 1.
3. Постройте процентную гистограмму на основе процентного распределения, полученного при решении задачи 2.
4. Проанализируйте распределение веса стеллажей, произведенных в бостонском отделении компании. Определите процент стеллажей, не соответствующих стандартам.
5. Вычислите распределение частот для веса стеллажей, загруженных в Вермонте, используя интервалы группирования с границами 3 550, 3 600, 3 650, 3 700, 3 750, 3 800, 3 850 и 3 900.
6. Вычислите процентное распределение на основе распределения частот, полученного при решении задачи 5.
7. Постройте процентную гистограмму на основе процентного распределения, полученного при решении задачи 6.
8. Проанализируйте распределение веса стеллажей, произведенных в вермонтском отделении компании. Определите процент стеллажей, не соответствующих стандартам.
2.66. Может ли раздача сувениров повысить посещаемость матчей Высшей бейсбольной лиги (Major League Baseball)? В статье, опубликованной в журнале Sports Marketing Quarterly, исследуется эффективность рекламных акций (Boyd, Т. С. and Krehbiel, Т. С. “Promotion Timing in Major League Baseball Attendance”, Sports Marketing Quarterly, 12 (March 2003)). Файл данных ^ROYALS. XLS содержит следующую информацию о посещении матчей с участием команды Kansas City Royals в 2002 году.
ИГРА — матчи в соответствии с расписанием;
ПОСЕЩАЕМОСТЬ — количество зрителей на матче.
РЕКЛАМА — (Да — рекламная акция проводилась, Нет — рекламная акция не проводилась).
1. Постройте гистограмму посещаемости. Проинтерпретируйте ее.
2. Постройте процентный полигон посещаемости. Проинтерпретируйте его.
3. Какой вид графика более предпочтителен? Обоснуйте свой выбор.
4. Постройте график двух процентных полигонов посещаемости — для 43 игр, сопровождаемых рекламной акцией, и 37 игр без рекламы. Сравните два распределения посещаемости.
2.67. В файле данных fttpROTEIN.XLS записаны содержание жира и холестерола в популярных белковых продуктах (в мясе домашних животных и рыбе).
Источник: Министерство сельского хозяйства США.
Выполните следующие задания, используя эти показатели.
1. Постройте диаграмму “ствол и листья”.
2. Вычислите распределение частот и процентное распределение.
3. Постройте процентную гистограмму.
4. Постройте процентный полигон.
5. Вычислите распределение интегральных процентов.
6. Постройте полигон интегральных процентов.
7. Какие выводы можно сделать на основе этого анализа?
2.68. Допустим, что нам необходимо провести сравнительное исследование характеристик 2002 различных моделей автомобилей. При сравнении учитываются следующие показатели: количество лошадиных сил, пробег в милях на галлон топлива, длина, ширина, радиус поворота, вес и грузоподъемность машины. ^>AUTO2002.XLS.
Источник: "The 2002 Cars", Copyright ©2002 by Consumers Union of U. S. Приводится no журналу Consumer Reports, April 2002, p. 22-71, с разрешения компании Consumer Union of U. S., Inc., Yonkers, NY 10703-1057.
Выполните следующие задания, используя эти показатели.
1. Постройте диаграмму “ствол и листья”.
2. Вычислите распределение частот и процентное распределение.
3. Постройте процентную гистограмму.
4. Постройте процентный полигон.
5. Вычислите распределение интегральных процентов.
6. Постройте полигон интегральных процентов.
7. Какие выводы можно сделать на основе этого анализа?
8. Допустим, нам необходимо сравнить автомобили с передним приводом и автомобили с задним приводом. Выполните задания 1-7 для каждой из этих групп и опишите различия между ними.
9. Постройте таблицу сопряженности признаков для перекрестного сравнения машин по типу привода (передний и задний) и типу топлива.
10. Постройте параллельную линейчатую диаграмму по типу привода (передний и задний) и типу топлива.
11. Существует ли зависимость между типом привода (передний или задний) и типом топлива?
2.69. В файле ^STATES.XLS приведены данные, собранные в ходе переписи населения США в 2000 г.: время проезда до места работы (мин.), процент домов с восемью или более комнатами, средний доход семьи и процент домовладельцев, у которых оплата стоимости дома превосходит 30% их дохода.
1. Вычислите распределение частот и процентное распределение.
2. Постройте процентную гистограмму.
3. Постройте процентный полигон.
4. Постройте кривую распределения.
5. Постройте распределение интегральных процентов.
6. Постройте полигон интегральных процентов.
7. Какой вид графика более предпочтителен? Обоснуйте свой выбор.
8. Какие выводы можно сделать на основе анализа указанных четырех переменных?
2.70. Экономика бейсбола порождает противоречия между владельцами клубов, которые утверждают, что они теряют деньги, игроками, утверждающими, что владельцы
клубов получают прибыль, и болельщиками, жалующимися на высокую стоимость билетов и абонентской платы за просмотр игр по кабельному телевидению. Кроме данных об игровой статистике команд в сезоне 2001 года, файл ФвВ2001. XLS содержит данные о стоимости билетов, членства в фан-клубе, абонементов, абонементов местного телевидения, радио и кабельного телевидения, доходах от всех остальных операций, компенсациях и премиях игрокам, национальных и локальных расходах и доходах от бейсбольных операций. Для каждой из перечисленных переменных выполните следующие задания.
1. Вычислите распределение частот и процентное распределение.
2. Постройте процентную гистограмму.
3. Постройте процентный полигон.
4. Постройте кривую распределения.
5. Постройте распределение интегральных процентов.
6. Постройте процентный полигон.
7. Какой вид графика более предпочтителен? Обоснуйте свой выбор.
8. Постройте диаграмму разброса, отложив на оси У количество побед, а на оси X — доходы.
9. Какие выводы можно сделать на основе анализа диаграммы разброса?
10. Какие выводы можно сделать на основе анализа указанных переменных?
2.71. Файл ^AIRCLEANER.XLS содержит данные о цене, стоимости годового потребления энергии и годовой эксплуатации кондиционера.
1. Постройте диаграмму разброса, отложив на оси У цену кондиционера, а на оси X — стоимость электроэнергии.
2. Постройте диаграмму разброса, отложив на оси У цену кондиционера, а на оси X — стоимость его эксплуатации.
3. Существует ли взаимосвязь между стоимостью потребляемой электроэнергии и стоимостью кондиционера?
Источник: “Portable Room Air Cleaners”, Copyright © 2002 by Consumers Union of U. S. Приводится no журналу Consumer Reports, February 2002, 47, с разрешения компании Consumer Union of U. S., Inc., Yonkers, NY 10703-1057.
2.72. Файл ^PRINTERS . XLS содержит данные о цене принтера, скорости и цене печати текста, продолжительности и стоимости печати фотографии на разных принтерах.
1. Постройте диаграмму разброса, отложив на оси У цену принтера, а на оси X — скорость печати текста.
2. Постройте диаграмму разброса, отложив на оси У цену принтера, а на оси X — стоимость печати текста.
3. Постройте диаграмму разброса, отложив на оси У цену принтера, а на оси X — продолжительность печати фотографии.
4. Постройте диаграмму разброса, отложив на оси У цену принтера, а на оси X — стоимость печати фотографии.
5. Можно ли использовать указанные переменные для предсказания цены принтера? Обоснуйте свой ответ.
Источник: “Printers”, Copyright ©2002 by Consumers Union of U. S. Приводится no журналу Consumer Reports, March 2002, 51, с разрешения компании Consumer Union of U. S., Inc., Yonkers, NY 10703-105 7.
2.73. Бразилия является вторым по величине потребителем кофе в мире. В отличие от основных рынков жарки и продажи кофе, на котором доминируют горстка компаний, в Бразилии функционируют около 2 000 маленьких компаний, занимающихся жаркой кофе. Компания Sara Lee Corporation стала лидером розничных продаж кофе в Бразилии, поглотив несколько бразильских компаний (Miriam Jordan, “Sara Lee Wants to Percolate through All of Brasil”, Wall Street Journal, May 8, 2002, A14). В следующей таблице приведены объемы закупок кофе семью странами — основными потребителями кофе.
Потребление кофе на основных рынках в 2000 г.
Страна Объем потребления (млн. мешков по 60 кг)
США 18,6
Бразилия 12,8
Германия 9,2
Япония 6,7
Франция 5,4
Нидерланды 1,8
Финляндия 0,9
Источник: цитируется по журналу The Wall Street Journal.
Лидирующие торговые марки кофе в Бразилии
Страна Доля на рынке, %
Sara Lee 27,6
Nescafe 6,1
Tres Coracoes 4,8
Melitta 4,0
Все остальные 57,5
Источник: цитируется no журналу The Wall Street Journal.
1. Постройте график объемов потребления кофе основными странами-потребителями. Какой тип графика предпочтительнее? Обоснуйте свой ответ.
2. Постройте диаграмму, иллюстрирующую распределение долей на рынке потребления кофе. Какой тип графика предпочтительнее? Обоснуйте свой ответ.
2.74. Приведенные ниже данные иллюстрируют распределение разведанных запасов нефти по разным географическим регионам.
Страна или регион Разведанные запасы нефти (млрд, баррелей)
Северная Америка 54,8
Мексика 28,3
США 21,8
Канада 4,7
Центральная и Южная Америка 95,2
Страна или регион Разведанные запасы нефти (млрд, баррелей)
Венесуэла 76,9
Бразилия 8,1
Другие страны Центральной 10,2
и Южной Америки
Западная Европа 17,2
Норвегия 9,5
Великобритания 5,0
Другие страны Западной Европы 2,7
Африка 74,9
Ливия 29,5
Нигерия 22,5
Алжир 9,2
Ангола 5,4
Другие страны Африки 8,3
Ближний Восток 683,6
Саудовская Аравия 259,2
Ирак 112,5
Объединенные Арабские Эмираты 97,8
Кувейт 94,0
Иран 89,7
Катар 13,2
Оман 5,5
Другие страны Ближнего Востока 11,7
Дальний Восток и Океания 44,0
Китай 24,0
Индонезия 5,0
Индия 4,7
Другие страны Дальнего Востока 10,3
и Океании
Восточная Европа и бывший СССР 59,0
Россия 48,6
Казахстан 5,4
Другие страны Восточной Европы 5,0
и бывшего СССР
Источник: Министерство энергетики США.
1. Постройте линейчатую диаграмму для стран.
2. Постройте круговую диаграмму для стран.
3. Постройте диаграмму Парето для стран.
4. Постройте линейчатую диаграмму для регионов.
5. Постройте круговую диаграмму для регионов.
6. Постройте диаграмму Парето для регионов.
7. Какой вид графика более предпочтителен? Обоснуйте свой выбор.
8. Какие выводы можно сделать на основе анализа приведенных данных?
2.75. Анализируя последствия террористической атаки на США 11 сентября 2001 года, исследователи из Национального центра статистики здравоохранения сосредоточились на разработке методов выявления и классификации жертв терроризма (Е. Weinstein, “Tracking Terror’s Rising Toll”, Wall Street Journal, January 25, 2002, A13). В приведенных ниже таблицах указано количество смертей жертв терроризма в США за период с 1990 по 2001 гг. и количество смертей в США в целом в 2000 г. от разных причин.
Причина
Грипп и пневм
Год Количество смертей жертв терроризма
1990 0
1991 0
1992 0
1993 6
1994 1
1995 169
1996 2
1997 0
1998 1
1999 3
2000 0
2001 2 717
Причина Причины смерти в США (тыс.)
Пожар 3,3
Утопление 3,3
Алкогольное отравление 18,5
Болезнь Альцгеймера 49,0
Огнестрельное ранение 10,4
Ранение холодным оружием 5,7
Астма 4,4
Рак 551,8
Инсульт и сопутствующие заболевания 166,0
Эмфизема 16,9
Диабет 68,7
Сердечно-сосудистые заболевания 710,0
Падение с высоты 12,0
СПИД 14,4
Причина Причины смерти в США (тыс.)
Грипп и пневмония 67,0
Несчастный случай на производстве 5,3
Дорожно-транспортное происшествие 41,8
Самоубийство 28,3
Наркотическая зависимость 15,9
Источник: Федеральное бюро криминальной статистики, Национальный центр статистики здравоохранения, Национальное управление безопасности дорожного движения, Министерство обороны.
1. Постройте диаграмму разброса, где на оси Y отложено количество смертей от терроризма, а на оси X — годы.
2. Существует ли какая либо зависимость между количеством смертей от терроризма и годами?
Проанализируйте причины смертей в США и выполните следующие задания.
3. Постройте линейчатую диаграмму.
4. Постройте круговую диаграмму.
5. Постройте диаграмму Парето.
6. Какой вид графика более предпочтителен? Обоснуйте свой выбор.
7. Какие выводы можно сделать на основе анализа приведенных данных?
2.76. В статье, опубликованной в журнале The Wall Street Journal, компания Forrester Research Inc. заявила, что 19% всех пользователей Интернет принимают участие в сетевых играх. Предложения принять участие в таких играх резко увеличивают трафик сайта, а следовательно, и его популярность. Это дает компаниям возможность повышать цены на рекламные объявления, размещаемые в Интернет. В следующей таблице перечислены восемь ведущих компаний, предлагающих сетевые игры, согласно данным компании PC Data Inc. по состоянию на март 2000 г.
Сайт Количество пользователей (тыс.) Доля аудитории, %
freelotto.com 12 901 19,1
AOLGames .com 9 416 13,9
uproar.com 8 821 13,1
webstakes.com 7 499 ИД
iwin.com 7 410 11,0
speedyclick.com 6 628 9,8
shockwave.com 5 582 8,3
prizecentral .com 4 899 7,3
Источник: Dean Takahashi, “Don't Shoot”, Wall Street Journal, April 1 7, 2000, R53.
1. Постройте линейчатую диаграмму для количества пользователей.
2. Постройте круговую диаграмму для распределения долей аудитории.
3. Сравните построенные диаграммы. Какая из них предпочтительнее? Почему?
2.77. Владелец ресторана европейской кухни заинтересовался особенностями заказов, принимаемых на выходные. Он стал записывать количество заказов на различные виды блюд. В результате возникла следующая таблица.
Блюдо Количество заказов
Говядина 187
Курица 103
Утка 25
Рыба 122
Спагетти 63
Моллюски 74
Телятина 26
1. Постройте по этим данным линейчатую диаграмму.
2. Постройте по этим данным диаграмму Парето.
3. Постройте по этим данным круговую диаграмму.
4. Какая диаграмма предпочтительнее: Парето или круговая? Почему?
5. Кратко изложите свои выводы.
Предположим, что владельца ресторана интересует также, заказывают ли посетители десерт. Он решил фиксировать информацию о поле посетителя и том, заказывал ли он говядину. Результаты этих исследований приведены ниже.
Пол
Заказ десерта Мужской Женский Всего
Да 96 40 136
Нет 224 240 464
Всего 320 280 600
Заказ говядины
Заказ десерта Да Нет Всего
Да 71 65 136
Нет 116 348 464
Всего 187 413 600
Для каждой из этих таблиц перекрестной классификации выполните следующие задания.
1. Постройте таблицу процентов по строкам.
2. Постройте таблицу процентов по столбцам.
3. Постройте общую таблицу процентов.
4. Какая таблица наиболее информативна (по столбцам, по строкам или общая) для исследования зависимости между полом посетителя и заказом говядины? Обоснуйте свой ответ.
5. Изложите свои выводы относительно заказов десерта.
2.78. Компания AT&T является лидером по доходам и количеству частных клиентов среди компаний, обеспечивающих междугородную телефонную связь в США. В январе 2002 года компания Verizon занимала четвертое место вслед за компа-
ниями AT&T, MCI и Sprint. Используя агрессивную маркетинговую стратегию, компания Verizon обошла компанию Sprint в третьем квартале 2002 года.
Компания междугородной телефонной связи Доля частных клиентов (%) Доля доходов на рынке (%)
AT&T 33,8 33,0
MCI 15,8 19,4
Verizon 10,6 5,9
Sprint 8,3 9,1
VarTec 6,3 3,7
Другие 25,2 28,9
Источник: цитируется по статье S. Backover, “Verizon Tops Sprint in Long-distance”, иsatoday. com, January 8, 2003.
1. Постройте круговые диаграммы распределения рынка частных клиентов и доходов.
2. Постройте параллельную линейчатую диаграмму для этих данных.
3. Какой вид диаграммы более информативен? Почему?
4. Какие выводы можно сделать о распределении рынка частных клиентов и доходов?
2.79. В статье, опубликованной в журнале The New York Times (William McNulty and Hugh K. Truslow, “How It Looked Inside the Booth”, The New York Times, November 6, 2002), приведены следующие данные о методе регистрации голосов избирателей в 1980, 2000 и 2002 гг. Для каждого метода указаны доля счетчиков, использовавших метод, и количество избирателей, зарегистрированных с его помощью.
Доля счетчиков, применяющих метод
Метод 1980 2000 2002
Перфокарта 18,5 18,5 15,5
Рычажная машина 36,7 14,4 10,6
Бюллетени 40,7 11,9 10,5
Сканирование 0,8 41,5 43,0
Электронное голосование 0,2 9,3 16,3
Смешанный 3,1 4,4 4,1
Доля избирателей, зарегистрированных с помощью метода
Метод 1980 2000 2002
Перфокарта 31,7 31,4 22,6
Рычажная машина 42,9 17,4 15,5
Бюллетени 10,5 1,5 1,3
Сканирование 2,1 30,8 31,8
Электронное голосование 0,7 12,2 19,6
Смешанный 12,0 6,7 9,3
1. Постройте для каждого года круговые диаграммы распределения доли счетчиков, использовавших методы подсчета голосов, и доли голосов, зарегистрированных с помощью этих методов.
2. Постройте для каждого года параллельные линейчатые диаграммы распределения доли счетчиков, использовавших методы подсчета голосов, и доли голосов, зарегистрированных с помощью этих методов.
3. Какой вид диаграммы более информативен? Почему?
4. Какие выводы можно сделать о распределении рынка частных клиентов и доходов?
2.80. Летом 2000 г. возросшее количество гарантийных рекламаций на шины компании Firestone, проданные вместе с автомобилями Ford SUV, вынудило обе компании отозвать свою продукцию. Анализ рекламаций позволил определить, какие именно модели следует отозвать. В следующей таблице приведены данные о распределении 2 504 поступивших гарантийных рекламаций по маркам шин.
Марка Количество рекламаций
23575R15 2 030
311050R15 137
30950R15 82
23570R16 81
331250R15 58
25570R16 54
Другие 62
Источник: Simison, R.L., “Ford Steps Up Recall Without Firestone”, The Wall Street Journal, August 14, 2000, p. A3.
2030 гарантийных рекламаций на шины марки 23575R15 относились к моделям АТХ и Wilderness. Ниже перечислены виды дорожно-транспортных происшествий, связанных с этими моделями.
Происшествие Количество рекламаций на модель АТХ Количество рекламаций на модель Wilderness
Отслоение протектора 1 365 59
Разрыв шины 77 41
Прочие 422 66
Всего: 1 864 166
Источник: Simison, R. L., “Ford Steps Up Recall Without Firestone”, The Wall Street
Journal, August 14, 2000, p. A3.
1. Постройте диаграмму Парето на основе распределения количества гарантийных рекламаций по маркам шин. Какая марка вызвала наибольшее количество рекламаций?
2. Постройте круговую диаграмму, иллюстрирующую долю каждой исследованной модели в распределении гарантийных рекламаций: АТХ и Wilderness. Дайте свою интерпретацию диаграммы.
3. Постройте диаграмму Парето на основе распределения количества дорожно-транспортных происшествий, связанных с моделью АТХ. Можно ли утверждать, что эта модель чаще всего провоцирует определенный вид происшествий?
4. Постройте диаграмму Парето на основе распределения количества дорожно-транспортных происшествий, связанных с моделью Wilderness? Можно ли утверждать, что эта модель чаще всего провоцирует определенный вид происшествий?
5. Кратко изложите выводы, к которым вы пришли.
2.81. Классная работа. Задайте каждому студенту вопрос: “Какую газированную воду вы любите?”. Запишите результаты опроса в сводную таблицу.
1. Переведите результаты опроса в процентные доли и постройте диаграмму Парето.
2. Проанализируйте полученные результаты.
2.82. Классная работа. Попросите студентов указать свой пол (мужской, женский) и статус занятости (да, нет). Запишите результаты опроса в сводную таблицу.
1. Постройте таблицу процентного распределения по столбцам или строкам.
2. К каким выводам вы пришли?
3. Какие другие переменные следовало бы изменить, чтобы уточнить информацию о занятости студентов?
Отчеты
2.83. На основе результатов, полученных при решении задачи 2.65, оцените, насколько вес стеллажей соответствует стандартам компании, и напишите отчет. Вставьте в отчет таблицы и диаграммы, построенные с помощью программы Microsoft Excel.
2.84. На основе результатов, полученных при решении задачи 2.80, оцените распределение количества гарантийных рекламаций по моделям шин компании Firestone и напишите отчет. Вставьте в отчет таблицы и диаграммы, построенные с помощью программы Microsoft Excel.
Применение Интернет
2.85. Зайдите на сайт www. prenhall. com/levine. Выберите ссылку Chapter 2 и щелкните на ссылке Internet exercises.
ГРУППОВОЙ ПРОЕКТ
ТР.2.1.Файл данных ^MUTUAL FUNDS.XLS содержит информацию о 13 переменных, характеризующих 259 взаимных фондов.
Фонд — название взаимного фонда.
Вид — вид акций, принадлежащих взаимному фонду: малые, средние и крупные компании.
Цель — цель фонда (быстрый или медленный рост капитала).
Активы — в млн. долл.
Комиссия — да или нет.
Издержки — издержки, понесенные взаимным фондом (в процентах от среднего объема чистых активов).
Доходность 2 001 — доходность за двенадцать месяцев 2001 г.
Трехлетняя доходность — среднегодовая доходность за период с 1999 по 2001 гг.
Пятилетняя доходность — среднегодовая доходность за период с 1997 по 2001 гг.
Оборачиваемость — уровень торговой активности фонда: очень низкий, низкий, средний, высокий, очень высокий.
Риск — уровень риска: очень низкий, низкий, средний, высокий, очень высокий.
Лучший квартал — квартал с наивысшей доходностью за период с 1997 по 2001 гг.
Худший квартал — квартал с наименьшей доходностью за период с 1997 по 2001 гг.
1. Создайте упорядоченный массив и диаграмму “ствол и листья”, содержащие издержки всех 259 фондов.
2. Выделите взаимные фонды, не взимающие брокерскую комиссию. Создайте упорядоченный массив и диаграмму “ствол и листья”, содержащие издержки этих фондов.
3. Выделите взаимные фонды, взимающие брокерскую комиссию. Создайте упорядоченный массив и диаграмму “ствол и листья”, содержащие издержки этих фондов.
4. Проанализируйте распределение издержек. Сравните распределение издержек у фондов, взимающих и не взимающих брокерскую комиссию.
Выполните следующие действия для переменной Доходность 2001.
5. Создайте упорядоченный массив и диаграмму “ствол и листья” для всех 259 фондов.
6. Какова процентная доля фондов, имеющих положительный доход? Какова процентная доля фондов, доход которых превышает 10% ?
7. Создайте упорядоченный массив и диаграмму “ствол и листья” для взаимных фондов, не взимающих брокерскую комиссию.
8. Какова процентная доля фондов, не взимающих брокерскую комиссию и имеющих положительный доход? Какова процентная доля фондов, не взимающих брокерскую комиссию, доход которых превышает 10% ?
9. Создайте упорядоченный массив и диаграмму “ствол и листья” для взаимных фондов, взимающих брокерскую комиссию.
10. Какова процентная доля фондов, взимающих брокерскую комиссию и имеющих положительный доход? Какова процентная доля фондов, взимающих брокерскую комиссию, доход которых превышает 10% ?
11. Проанализируйте распределение доходов взаимных фондов в 2001 г. Сравните распределение доходов у фондов, взимающих и не взимающих брокерскую комиссию.
12. Повторите задания 5-11 для переменной Трехлетняя доходность.
ТР.2.2.Файл данных ^MUTUAL FUNDS.XLS содержит информацию о 13 переменных, характеризующих 259 взаимных фондов.
1. Постройте процентную гистограмму значений переменной Доходность 2001, используя данные о 46 взаимных фондах, специализирующихся на компаниях среднего размера.
2. Какова процентная доля фондов, специализирующихся на компаниях среднего размера и имеющих положительный доход? Какова процентная доля фондов, специализирующихся на компаниях среднего размера, доход которых превышает 10% ?
3. Постройте процентную гистограмму значений переменной Доходность 2001, используя данные о 42 взаимных фондах, специализирующихся на небольших компаниях.
4. Какова процентная доля фондов, специализирующихся на небольших компаниях и имеющих положительный доход? Какова процентная доля фондов, специализирующихся на небольших компаниях, доход которых превышает 10% ?
5. Сравните доходы взаимных фондов, специализирующихся на акциях средних и небольших компаний.
6. Повторите задания 1-5 для переменной Трехлетняя доходность.
ТР.2.3.Файл данных ^MUTUAL FUNDS.XLS содержит информацию о 259 взаимных фондах, распределенных по уровням оборачиваемости (очень низкий, низкий, средний, высокий и очень высокий).
1. Постройте линейчатую диаграмму, иллюстрирующую уровень оборачиваемости акций, принадлежащих взаимным фондам.
2. Постройте круговую диаграмму иллюстрирующую уровень оборачиваемости акций, принадлежащих взаимным фондам.
3. Какая диаграмма предпочтительнее? Почему?
4. Используя данные из файла ^MUTUAL FUNDS.XLS, заполните следующую таблицу сопряженности признаков.
Вид фонда
Уровень оборачиваемости Малые Средние Крупные Всего компании компании компании
Очень низкий
Низкий
Средний
Высокий
Очень высокий
Всего
5. Не кажется ли вам, что доля фондов с высоким уровнем оборачиваемости среди фондов определенной специализации непропорционально мала? Если да, объясните причину.
6. Постройте параллельную линейчатую диаграмму.
Доходы от размещения рекламных объявлений являются важной статьей дохода любой газеты. Для того чтобы увеличить доходы и минимизировать количество дорогостоящих ошибок, руководство газеты The Springville Herald создало специальную группу специалистов для повышения качества работы с клиентами в отделе рекламы. Зайдите на Web-страницу www. prenhall. com/HeraldCase/Ad_Errors . htm, просмотрите данные, собранные этой группой, и выделите среди них особенно важные показатели, характеризующие качество работы отдела рекламы. Постройте для этих данных диаграммы, которые иллюстрируют их наилучшим образом, и обоснуйте свой выбор. Укажите, какую еще информацию об ошибках в рекламных объявлениях следует собрать. Предложите свои пути повышения качества работы отдела рекламы.
ПРИМЕНЕНИЕ WEB
В сценарии “Применение статистики” мы предложили вам сыграть роль финансового аналитика и собрать информацию, позволяющую сделать правильный выбор при инвестировании средств. Источниками этой информации могут быть брокерские фирмы и консультанты по инвестициям. Примените свои знания о таблицах и диаграммах для того чтобы оценить обоснованность прогнозов и заявлений компании StockTout Investing Service.
Посетите Web-сайт компании StockTout Investing Service (www.prenhall.com/ Springville/StockTout. htm). Проанализируйте рекламные заявления и сопровождающих их данные, а затем ответьте на следующие вопросы.
1. Как способ представления данных на Web-сайте компании StockTout Investing Service влияет на ваше восприятие их бизнеса?
2. Является ли утверждение о том, что большинство инвесторов, руководствующихся советами консультантов из компании StockTout Investing Service, получают прибыль, честным? Если вы считаете это заявление нечестным, предложите свой способ представления данных, который вы считаете правильным и точным.
3. “Большая восьмерка” взаимных фондов, принадлежащих компании Stock-Tout Investing Service, входит в число взаимных фондов, упомянутых в файле ^MUTUAL FUNDS2002.XLS. Какие еще данные следовало бы включить в таблицу Большая Восьмерка? Как эти данные могут изменить ваше восприятие заявлений компании?
4. Компания StockTout Investing Service гордится тем, что “Большая восьмерка” фондов увеличила рыночную цену своих акций за последние пять лет. Стоит ли этим гордиться? Объясните свой ответ.
СПРАВОЧНИК EXCEL ГЛАВА 2
ЕН.2.1. Корректировка распределения частот, построенного с помощью процедуры Analysis ToolPak Histogram
Процедура Анализ данных...1^Гистограмма ошибочно создает в распределении частот дополнительную группу “Еще”. Например, если следовать инструкциям, приведенным во врезке “Процедуры Excel: вычисление распределения частот для числовых данных”, распределение частот будет похоже на распределение, показанное на рис. ЕН.2.1.
А О. в L _
1 <Карманы Частота Интегральный % ;
-10 01 0 0 00%
3 -5 01 1 0 63%
4 ’ -0 01 3 2,53%
41. 4,99 14 11,39%
jl- 9,99 58 48,10%
L 14 99 61 86,71%
30 19,99 17 97.47%
24 99 3 99,37%
29,99 1 100.00%
11 'Ещ е О' 100.00%
Рис. ЕН.2.1. Распределение частот, созданное процедурой Гистограмма
Чтобы исключить группу “Еще”, сначала необходимо вручную добавить ее значение к предыдущей группе и установить интегральный процент, равный 100%. (Обратите внимание на то, что на рис. ЕН.2.1 частота группы “Еще” равна 0, поэтому описанные выше действия не повлияют на значения, находящиеся в 10-й строке.) Затем следует выбрать ячейки, содержащие строку “Еще” (ячейки All:СИ на рис. ЕН.2.1), и выполнить команду ПравкаФУдалить.... В диалоговом окне Удалить необходимо установить переключатель Удаление ячеек в положение Ячейки, со сдвигом вверх и щелкнуть на кнопке ОК.
Чтобы улучшить внешний вид рабочего листа, выделите ячейку в строке 1 и выполните команду Вставка ^Строки, чтобы вставить строку над заголовком. Выровняйте ширину столбцов, чтобы они полностью вмещали в себя заголовки. Чтобы добавить столбец частот, выберите столбец С и выполните команду Вставка^Столбцы. Находясь в новом столбце С, введите в ячейку СЗ формулу =ВЗ/СУММ (В:В) и скопируйте ее в остальные ячейки столбца, Для чисел, записываемых в ячейки этого столбца, следует выбрать процентный формат. В ячейку С2 запишите заглавие столбца — Проценты. В столбце Е укажите срединные точки и заголовки, как показано в табл. ЕН.2.1.
ЕН.2.2. Вычисление распределения частот с помощью функции ЧАСТОТА
Распределение частот можно вычислить альтернативным способом. Для этого необходимо создать новый лист, ячейки которого используют функцию ЧАСТОТА. Такой рабочий лист позволяет динамически изменять частоты при модификации исходных данных.
Например, в табл. ЕН.2.1 показана схема рабочего листа Частоты, содержащего данные, записанные на листе Данные рабочей книги Growth Funds Sample . xls. Этот рабочий лист содержит данные о пяти летней доходности взаимных фондов. Функция Частота имеет следующий формат: ЧАСТОТА(лшсспв данных; массив интервалов), где первый параметр задает диапазон анализируемых данных, а второй — диапазон ячеек, содержащих упорядоченные верхние границы интервалов.
Таблица ЕН.2.1. Схема листа Частоты
А В С D В
1 Распределение частот пятилетнего среднегодового дохода
2 Карманы Частота Проценты Интегральные проценты Срединные точки
JliiiJI -10,01 =ЧАСТОТА('Пятилетняя_доходность'!В1:В158;АЗ:А11) = ВЗ/В$13 =СЗ —
lllilll -5,01 =ЧАСТОТА('Пятилетняя_доходность’!В1:В158;АЗ:А11) = В4/В$13 = D3+C4 -7,5
5 -0,01 =ЧАСТОТА('Пятилетняя_доходность'!В1:В158;АЗ:А11) =В5/В$13 =D4+C5 -2,5
6 4,99 =ЧАСТОТА('Пятилетняя_доходность'!В1:В158;АЗ:А11) =В6/В$13 =D5+C6 2,5
7 9,99 =ЧАСТОТА('Пятилетняя_доходность’!В1:В158;АЗ:А11) = В7/В$13 =D6+C7 7.5
8 14,99 =ЧАСТОТА(’Пятилетняя_доходность'!В1:В158;АЗ:А11) = В8/В$13 = D7+C8 12,5
9 19,99 =ЧАСТОТА('Пятилетняя_доходность'!В1:В158;АЗ:А11) =В9/В$13 =D8+C9 17,5
10 24,99 =ЧАСТОТА(’Пятилетняя_доходность'!В1:В158;АЗ:А11) = В10/В$13 =D9+C10 22,5
11 29,99 =ЧАСТОТА('Пятилетняя_доходность'!В1:В158;АЗ:А11) =В11/В$13 =D10+C11 27,5
12
13 Всего: =СУММ(ВЗ:В11)
Поскольку функция ЧАСТОТА предназначена для работы с массивами, при вводе формул в ячейки ВЗ : Bl 1 выполните следующую процедуру.
1. Выберите диапазон ячеек ВЗ : Bl 1.
2. Напечатайте формулу =ЧАСТОТА(’Пятилетняя_доходность’!В1:В158,АЗ:All), не нажимая клавиши <Enter> или <ТаЪ>.
3. Нажмите <Ctrl+Shift+Enter>.
ЕН.23. Корректировка гистограмм
Для того чтобы скорректировать гистограмму, построенную процедурой Анализ данных... ^Гистограмма, сначала необходимо выполнить инструкции, приведенные в разделе ЕН.2.1, и исправить распределение частот. Гистограмма, построенная процедурой Анализ данных... ^Гистограмма, может содержать ошибки: между столбцами гистограммы зияют пробелы; карманы помечены верхними границами групп, а не срединными точками, максимальное значение на вспомогательной оси Y превышает 100%, заголовок и ось X сопровождаются нежелательными метками (рис. ЕН.2.2). Кроме того, в дальнейшем может возникнуть потребность удалить из рисунка график полигона интегральных процентов или изменить подписи оси X.
Гистограмма
Частота
-*- Интегральный %
Рис. ЕН.2.2. Ошибочный рабочий лист, созданный с помощью процедуры
Г истограмма
Чтобы исправить ошибки, необходимо выполнить следующие действия.
• Чтобы удалить пробелы между столбцами, щелкните правой кнопкой мыши на одном из столбцов гистограммы. (Если курсор мыши установлен на столбце, на экране появится подсказка, начинающаяся словами "Ряд "Частота".) Выберите в контекстном меню команду Формат рядов данных.... В диалоговом окне Формат ряда данных щелкните на корешке вкладки Параметры, а затем сделайте значение Ширина зазора равным нулю. Щелкните на кнопке ОК.
• Чтобы изменить метки карманов, введите в столбце Е срединные точки (если столбец Е занят, введите срединные точки в первом свободном стобце). Щелкните правой кнопкой мыши на закрашенном фоне гистограммы. (Если курсор мыши
установлен правильно, на экране появится подсказка “Область построения диаграммы”.) Выберите в контекстном меню команду Исходные данные.... В диалоговом окне Исходные данные щелкните на корешке вкладки Ряд и введите в окне редактирования Подписи оси X формулу, идентифицирующую диапазон ячеек, содержащий частоты, в формате ИмяЛистаЩиапазонЯчеек. Удалите текст, введенный в окне редактирования Подписи второй оси X, и щелкните на кнопке ОК. Например, для изменения меток карманов, содержащихся в диапазоне ячеек ЕЗ : El 1 рабочего листа Частоты, в окне редактирования Подписи оси X необходимо ввести формулу =Частоты! ЕЗ : Е11.
• Чтобы изменить масштаб вторичной оси Y, щелкните правой кнопкой мыши, установив курсор на дополнительную (правую) ось Y. (Если курсор мыши установлен правильно, на экране появится подсказка “Дополнительная ось значений”.) Выберите в контекстном меню команду Формат оси.... Замените единицей величину в окне редактирования Максимальное значение во вкладке Шкала в диалоговом окне Формат оси и щелкните на кнопке ОК.
• Чтобы изменить подпись оси X, щелкните на подписи (вокруг нее появится ореол), введите в строке формул текст новой подписи и нажмите клавишу <Enter>.
• Чтобы удалить график полигона интегральных процентов, щелкните на нем правой кнопкой мыши. (Если курсор мыши установлен правильно, на экране появится подсказка "Ряд "Интегральный процент".) Выберите в контекстном меню команду Очистить.
ЕН.2.4. Построение гистограмм по готовым таблицам частот
Для построения гистограмм по таблице распределения частот можно воспользоваться Мастером диаграмм. Например, чтобы построить гистограмму, соответствующую шаблону, приведенному в табл. ЕН.2.1, откройте созданный вами рабочий лист Частоты (или рабочий лист Частоты в файле Chapter 2.xls), выполните команду Вставка^ Диаграмма... и следуйте инструкциям.
1. На первом этапе диалога (см. рис. ниже) выполните такие действия.
1.1. Щелкните на корешке вкладки Стандартные и выберите в списке диаграмм пункт Гистограмма.
1.2. Выберите первый вариант гистограммы (“Обычная”). Щелкните на кнопке Далее>.
2. На втором этапе диалога выполните следующие действия.
2.1. Щелкните на корешке вкладки Диапазон данных. Введите в окне редактирования Диапазон ссылки ВЗ:В11 и установите переключатель Ряды в положение В столбцах.
2.2. Щелкните на корешке вкладки Ряды. Введите в окне редактирования Подписи оси X формулу, идентифицирующую диапазон ячеек, содержащий частоты, в формате ИмяЛистаЩиапазонЯчеек и щелкните на кнопке Далее. Если вы используете шаблон рабочего листа Частоты, формула будет иметь вид =Частоты!ЕЗ : Е11.
3. На третьем этапе диалога выполните такие действия.
3.1. Щелкните на корешке вкладки Заголовки. Введите в окне редактирования Название диаграммы строку Гистограмма, в окне редактирования
Ось X (категорий) — строку Срединные точки, а в окне редактирования Ось Y (значений) — строку Частота.
3.2. Щелкните по очереди на корешках вкладок Оси, Линии сетки, Подписи данных и Таблицы данных и установите флажки и переключатели так, как описано в разделе ЕР.6.
3.3. Щелкните на кнопке Далее>.
4. На четвертом этапе диалога установите переключатель в положение Поместить диаграмму на листе в положение Отдельном и щелкните на кнопке Готово.
Мастер диаграмм (шаг 1 из 4): тип диаграммы
Стандартные > Нестандартные s
[Гистограмма
> Тип:
Ml_______________
г Линейчатая
|/>: Г рафик
i! ф Круговая
:[ Точечная
i; С областями
; : Кольцевая
:; Лепестковая
& Поверхность
: i •• Пузырьковая
Вид:
Обычная гистограмма отображает Значения различных категорий.
[ Просмотр результата ] [ Отмена ]
Чтобы удалить зазоры между столбцами диаграммы, достаточно щелкнуть правой кнопкой мыши, установив курсор на одном из столбцов. (Если курсор мыши установлен правильно, на экране появится подсказка, начинающаяся словами “Ряд 1”.) Выберите команду Формат рядов данных... в контекстном меню. В диалоговом окне Формат ряда данных щелкните на корешке вкладки Параметры, замените величину, указанную в окне редактирования Ширина зазора, нулем и щелкните на кнопке ОК.
ЕН.2.5. Построение полигонов с помощью средства Мастер диаграмм
Мастер диаграмм позволяет строить полигоны, используя распределение частот. Чтобы построить полигон на основе распределения частот, следует выбрать на рабочем листе Частоты любую ячейку в строке 3, выполнить команду Вставка^Строки и ввести нули в ячейки ВЗ, СЗ, D3, В13 и С13. (Это позволит правильно задать координаты начальной и конечной точки полигона на оси X.) На этом этапе строки 3-13 должны выглядеть так, как показано на рис. ЕН.2.3 (таблица распределения частот, модифицированная для построения полигона на основе данных из рабочего листа Данные из рабочей книги Growth Funds Sample.xls).
А | в ; С I D |
1 Распределение частот для фондов быстрого роста
2 Карманы Частота Процент ' Интегральный % Срединные точки
_з 0 0 0
V -10,01 0 0,00% ,00% —
V -5,01; 1! 0,63% .63% -7.5
'б -0,0 V 3 1.90% 2,53% -2,5
7 4.99 14 8,86% 11,39% 2,5
8 9,99 58 36,71% 48,10% 7,5
9 14,99 61 38,61% 86,71 %: 12,5
10' 19,99 17 10,76% 97,47%: 17,5
11 24,99: 3 1,90%: 99,37% 22,5
12 29,99: 1. 0,63% 100,00% 27,5
Рис. ЕН.2.3. Таблица распределения частот, модифицированная для построения полигона
Чтобы построить полигон, откройте рабочий лист, содержащий таблицу распределения частот, выполните команду ВставкаФДиаграмма... и следуйте инструкциям.
1. На первом этапе диалога выполните такие действия.
1.1. Щелкните на корешке вкладки Стандартные и выберите в списке диаграмм пункт График.
1.2. Выберите первый вариант графика во втором ряду (“График с маркерами, помечающими точки данных”). Щелкните на кнопке Далее>.
2. На втором этапе диалога выполните следующие действия.
2.1. Щелкните на корешке вкладки Диапазон данных. Введите в окне редактирования Диапазон ссылки на соответствующие ячейки и установите переключатель Ряды в положение В столбцах. Для построения распределения частот введите диапазон ВЗ:В13, а для построения полигона— диапазон СЗ:С13. Для построения интегрального полигона следует ввести диапазон D3 : D12.
2.2. Щелкните на корешке вкладки Ряды. Если вы хотите построить распределение частот или процентный полигон, введите в окне редактирования Подписи оси X формулу, идентифицирующую диапазон ячеек, содержащий частоты, в формате ИмяЛистаЩиапазонЯчеек и щелкните на кнопке Далее>. Если вы применяете шаблон рабочего листа Частоты, то при создании гистограммы и процентного полигона следует ввести формулу =Частоты! ЕЗ : Е13, а при создании полигона интегральных процентов — формулу =Частоты'.ЕЗ :Е12.
3. На третьем этапе диалога выполните следующие действия.
3.1. Щелкните на корешке вкладки Заголовки. Введите соответствующие названия в окнах редактирования Название диаграммы, Ось X (категорий) и Ось Y (значений).
3.2. Щелкните по очереди на корешках вкладок Оси, Линии сетки, Подписи данных и Таблицы данных и установите флажки и переключатели так, как описано в разделе ЕР.6.
3.3. Щелкните на корешках вкладок Легенда и установите флажок Добавить легенду, а затем щелкните на кнопке Далее>.
4. На четвертом шаге диалога установите переключатель Поместить диаграмму на листе в положение Отдельном, присвойте листу информативное название и щелкните на кнопке Готово.
Чтобы построить диаграммы, изображенные на рис. 2.3 и 2.4, можно добавить дополнительные ряды данных. Для этого достаточно открыть лист, содержащий диаграмму, и выполнить команду Диаграмма^Добавить данные... в меню программы Excel. Введите в диалоговом окне Новые данные новый диапазон ячеек в формате ИмяЛистаЩиапазонЯчеек и щелкните на кнопке ОК. Если на экране появится диалоговое окно Специальная вставка, установите переключатель Добавить значения как в положение Новые ряды, а переключатель Значения (Y) — в положение В столбцах. Затем щелкните на кнопке ОК.
ЕН.2.6. Перемещение осей диаграмм
Когда Мастер диаграмм создает диаграмму разброса на основе данных, содержащих отрицательные числа, оси X и У проходят прямо через точки, а не по сторонам диаграммы, как на рис. 2.5. Для того чтобы переместить оси диаграммы, необходимо открыть ее и выполнить следующие действия.
Чтобы изменить положение осиХ, выделите на диаграмме ось Y. (Если курсор мыши установлен правильно, на экране появится подсказка “Ось Y (значений)”.) Щелкните на оси У правой кнопкой мыши и выполните команду Формат оси... во всплывающем меню. Находясь в диалоговом окне Формат оси, щелкните на корешке вкладки Шкала и введите в диалоговое окно Ось X (категорий) пересекает в значении число, указанное в окне Минимальное значение. (При ввода числа соответствующий флажок автоматически сбрасывается.) Щелкните на кнопке ОК.
Чтобы изменить положение оси У, выделите на диаграмме ось X. (Если курсор мыши установлен правильно, на экране появится подсказка “Ось X (категорий)”.) Щелкните на осиХ правой кнопкой мыши и выполните команду Формат оси... во всплывающем меню. Находясь в диалоговом окне Формат оси, щелкните на корешке вкладки Шкала и введите в диалоговое окно Ось Y (значений) пересекает в значении число, указанное в окне Минимальное значение. (При ввода числа соответствующий флажок автоматически сбрасывается.) Щелкните на кнопке ОК.
ЕН.2.7. Создание таблиц для категорийных данных
Для создания сводных таблиц категорийных данных применяется Мастер сводных таблиц и диаграмм программы Microsoft Excel, уже упоминавшийся в разделе ЕР.7. Например, чтобы создать таблицу, аналогичную табл. 2.7, необходимо открыть рабочую книгу Mutual Funds .xls на листе Данные, выбрать в меню Excel пункт ДанныеФ Сводная таблица..., а затем выполнить следующие действия.
1. На первом этапе диалога установите переключатель Создать таблицу на основе данных, находящихся: в положение В списке или базе данных Microsoft Excel, а переключатель Вид создаваемого отчета — в положение Сводная таблица. Затем щелкните на кнопке Далее>.
2. На втором этапе диалога в окне редактирования Диапазон введите ссылки на ячейки KI: К2 60, а затем щелкните на кнопке Далее>.
3. На третьем этапе диалога выполните следующие действия.
3.1. Установите переключатель Поместить таблицу в положение В новый лист и щелкните на кнопке Макет.
3.2. Находясь в диалоговом окне Макет, перетащите кнопку поля Риск, находящегося справа, в область Строка и в область Данные. Когда кнопка будет скопирована во второй раз, ее метка в поле Данные станет называться Количество по полю Риск. Щелкните на кнопке ОК.
3.3. Щелкните на кнопке ОК диалогового окна Макет и вернитесь в диалоговое окно Мастер сводных таблиц и диаграмм — шаг 3 из 3.
3.4. Щелкните на кнопке Параметры. В диалоговом окне Параметры введите в окне редактирования Имя информативное название таблицы, установите флажок Для пустых ячеек отображать и введите в соответствующее окно редактирование число 0. Затем щелкните на кнопке ОК и вернитесь в диалоговое окно Мастер сводных таблиц и диаграмм — шаг 3 из 3.
3.5. Щелкните на кнопке Готово.
4. Закройте плавающую инструментальную панель Сводные таблицы, присвойте новому листу осмысленное название, например Сводная_таблица, введите заголовок в его первую строку. В результате должна получиться сводная таблица, изображенная на рис. ЕН.2.4.
А
С
1 Риск взаимных фондов __________________________
3 ; Количество, по полю Риск
4 {Риск ~7F
5 ^средний
6 jвысокий
7 ।низкий
8
9
очень высокий очень низкий
10 Общий итог
Итог 82
80 76 ..
;___е
259
Процент
31.66%
30,89%
29,34%
5,79%
2,32%
Рис. ЕН.2.4. Сводная таблица
Для вставки столбца, содержащего проценты, введите в ячейку С4 заголовок “Проценты”, а в ячейку С5 — формулу =В5/В$10. Скопируйте эту формулу во все ячейки, включая ячейку С9, и установите для отображения чисел в диапазоне С5 :С9 процентный формат. В результате таблица примет вид, изображенный на рис. ЕН.2.4.
ЕН.2.8. Создание линейчатых и круговых диаграмм для категорийных данных
Для создания диаграмм категорийных данных на основе сводной таблицы применяется Мастер диаграмм программы Microsoft Excel. Например, чтобы построить линейчатую или круговую диаграмму по сводной таблице, созданной в предыдущем разделе (рис. ЕН.2.4), откройте рабочий лист, содержащий сводную таблицу (или рабочий листТабл2.7 в рабочей книге Chapter 2 . xls) и выделите любую ячейку вне таблицы, например, ячейку D1. Затем выполните команду Вставка^Диаграмма... и следуйте инструкциям, приведенным ниже.
1. На первом этапе диалога щелкните на корешке вкладки Стандартные.
1.1. Если вы собираетесь построить линейчатую диаграмму, выберите из списка Тип пункт Линейчатая, а на панели Вид— первый вариант, которому соответствует пояснение “Линейчатая диаграмма отображает значения различных категорий”. Затем щелкните на кнопке Далее>.
1.2. Если вы собираетесь построить круговую диаграмму, выберите из списка Тип пункт Круговая, а на панели Вид — первый вариант, которому соответствует пояснение “Круговая диаграмма. Отображает вклад каждого значения в общую сумму”. Затем щелкните на кнопке Далее>.
2. На втором этапе диалога щелкните на корешке вкладки Диапазон данных и введите в окне редактирования Диапазон ссылки на ячейки АЗ: В9, установите переключатель Ряды в положение В столбцах, если эта группа доступна, и щелкните на кнопке Далее>.
3. На третьем этапе щелкните на корешке вкладки Заголовки. Введите в окна редактирования Название диаграммы, Ось X (категорий), Ось Y (значений) соответствующие заголовки.
3.1. При создании линейчатой диаграммы щелкните по очереди на корешках вкладок Оси, Линии сетки, Легенда и Таблица данных и установите флажки и переключатели в соответствии с указаниями, приведенными в разделе ЕР.6. Затем щелкните на кнопке Далее>.
3.2. При создании круговой диаграммы щелкните на корешках вкладок Легенда и сбросьте флажок Добавить легенду. Затем щелкните на корешке вкладки Подписи данных и установите флажок Включить в подписи доли (если вы используете программы Microsoft Excel 97 или 2000). Если вы используете программу Microsoft Excel 2002, установите флажки Имена категорий и Проценты. Щелкните на кнопке Далее>.
4. На четвертом этапе диалога установите переключатель Поместить диаграмму на листе в положение Отдельном, присвойте новому листу осмысленное название и щелкните на кнопке Готово.
Находясь на новом листе, щелкните правой кнопкой мыши на раскрывающемся списке Риск и выполните команду Скрыть кнопки полей сводной диаграммы. (Если вы пользуетесь программой Microsoft Excel 1997, этот пункт следует пропустить.)
ЕН.2.9. Создание диаграммы Парето с помощью средства
Мастер диаграмм
Для создания диаграммы Парето применяется Мастер диаграмм программы Microsoft Excel. В отличие от линейчатых и круговых диаграмм, перед созданием диаграммы Парето исходный рабочий лист необходимо модифицировать, добавив в него столбец, содержащий интегральные проценты. Например, чтобы создать диаграмму Парето на основе сводной таблицы, следуя инструкциям из раздела ЕН.2.7, нужно открыть рабочую книгу, содержащую таблицу (или рабочий лист РисЕН.2.4 в рабочей книге Chapter 2 . xls). Если в сводной таблице нет столбца, содержащего интегральные проценты, его необходимо добавить, следуя инструкциям из раздела ЕН.2.7. Затем в ячейку D4 нужно ввести заголовок Интегральные проценты, в ячейку D5 — формулу =С5, а в ячейку D6 — формулу =D5+C6. Затем необходимо скопировать последнюю формулу в ячейки столбца D вплоть до ячейки D9, форматируя ячейки по мере необходимости. Теперь нужно изменить порядок следования ячеек в сводной таблице, руководствуясь инструкциями, приведенными ниже.
1. Щелкните правой кнопкой мыши на ячейке А4 и выберите пункт Параметры поля во всплывающем контекстном меню. (Если вы работаете с программой Microsoft Excel 97, выберите пункт Поле.)
2. Находясь в диалоговом окне Вычисление поля сводной таблицы, щелкните на кнопке Дополнительно.
3. В открывшемся диалоговом окне Дополнительные параметры поля сводной таблицы (рис. ЕН.2.5) установите переключатель По убыванию в группе Параметры сортировки, а в списке С помощью поля выберите пункт Количество по полю Риск. Щелкните на кнопке ОК.
4. Чтобы вернуться на рабочий лист, находясь в диалоговом окне Вычисление поля сводной таблицы, щелкните на кнопке ОК. Данные, содержащиеся в таблице, будут упорядочены по убыванию.
шолнительные параметры поля сводной таблицы [1Х~|
Вычисление поля сводной табл и
Параметры поля сводной таблицы
Имя: j Risk
Итоги
(*) автоматические
О другие
Сумма Количество Среднее Максимум Минимум Произведение
□(Отображать пустые элементы:
Параметры сортировки Двтоотображение лучшей десятки
О вручную (разрешается перетаскивание)
О по возрастанию ,
®|по убыванию; ............... отображать:
с помощью полд: с помощью поля:
Risk V:
[ ОК ] | Отмена ]
Рис. ЕН.2.5. Диалоговые окна Параметры поля и Дополнительные параметры поля сводной таблицы
Поскольку изменение порядка следования ячеек может повлиять на другие диаграммы, перед построением диаграммы Парето рабочий лист рекомендуется скопировать, следуя инструкциям из раздела ЕР.5.3, а саму процедуру построения выполнять, находясь на скопированном листе.
После предварительной сортировки для построения диаграммы Парето вызывается Мастер диаграмм. Например, чтобы создать диаграмму Парето на основе упорядоченной сводной таблицы, откройте рабочую книгу, содержащую эту таблицу (или рабочий лист Риск в рабочей книге Chapter 2.xls). Теперь выберите Вставка^Диаграмма... и следуйте инструкциям.
1. На первом этапе диалога щелкните на корешке вкладки Нестандартные. Установите переключатель Вывести в положение Встроенные, а затем выберите пункт График)Гистограмма 2 в списке Тип. Щелкните на кнопке Далее>.
2. На втором этапе диалога выполните следующие действия.
2.1. Щелкните на корешке вкладки Диапазон данных, введите в окне редактирования Диапазон ссылки на ячейки с4 : D9, установите переключатель Ряды в положение В столбцах, если эта группа доступна, и щелкните на кнопке Далее>.
2.2. Щелкните на корешке вкладки Ряды. Введите формулу, =Риск IА5:А9 в окне редактирования Подписи оси X. Окно редактирования Вторая ось X (категорий) должно оставаться пустым.
2.3. Щелкните на кнопке Далее>.
3. На третьем этапе выполните такие действия.
3.1. Щелкните на корешке вкладки Заголовки. Введите в окне редактирования Название диаграммы строку Диаграмма Парето для риска, в окне редактирован Ось X (категорий) — строку Уровень риска, а в окне редактирования Ось Y (значений) — строку Проценты.
3.2. Щелкните по очереди на корешках вкладок Оси, Линии сетки, Легенда и Таблица данных и установите флажки и переключатели в соответствии с указаниями, приведенными в разделе ЕР.6. Затем щелкните на кнопке Далее>.
4. На четвертом этапе диалога установите переключатель Поместить диаграмму на листе в положение Отдельном, присвойте новому листу осмысленное название, например, “Диаграмма_Парето” и щелкните на кнопке Готово.
Как и в разделе ЕН.2.3, максимальное значение на вспомогательной оси Y следует установить равным 1. Для этого необходимо щелкнуть правой кнопкой мыши на дополнительной (правой) оси Y, выбрать пункт Формат оси..., щелкнуть на корешке вкладки Шкала, а затем изменить число в окне редактирования Максимальное значение и щелкнуть на кнопке ОК.
ЕН.2.10. Создание таблиц для двумерных категорийных данных
Для создания таблицы сопряженности признаков, описывающей двумерные категорийные данные, применяется Мастер сводных таблиц и диаграмм программы Microsoft Excel. Например, чтобы создать сводную таблицу, аналогичную табл. 2.10, откройте рабочую книгу Mutual Funds.xls на листе Данные, выберите пункт меню Данные^ Сводная таблица... и выполните следующие действия.
1. На первом этапе диалога установите переключатель в положение Создать таблицу на основе данных, находящихся: в списке или базе данных Microsoft Excel, а переключатель Вид создаваемого отчета — в положение Сводная таблица. Затем щелкните на кнопке Далее>.
2. На втором этапе диалога в окне редактирования Диапазон введите ссылки на ячейки Al: К2 60, а затем щелкните на кнопке Далее>.
3. На третьем этапе диалога выполните следующие действия.
3.1. Установите переключатель Новый лист и щелкните на кнопке Макет.
3.2. Находясь в диалоговом окне Макет, перетащите кнопку поля Риск, находящегося справа, в область Строка. Затем перетащите поле Комиссия в область Столбец, а поле Название — в область Данные. Метка в поле Данные станет называться Количество по полю Название.
3.3. Щелкните на кнопке ОК диалогового окна Макет и вернитесь в диалоговое окно Мастер сводных таблиц и диаграмм — шаг 3 из 3.
3.4. Щелкните на кнопке Параметры. В диалоговом окне Параметры введите в поле Имя информативное название таблицы, установите флажки Для пустых ячеек отображать и введите в соответствующем окне редактирование число 0. Затем щелкните на кнопке ОК и вернитесь в диалоговое окно Мастер сводных таблиц и диаграмм — шаг 3 из 3.
3.5. Щелкните на кнопке Готово.
4. Закройте плавающую инструментальную панель Сводные таблицы, присвойте новому листу осмысленное название, например Сводная_таблица, и введите заголовок в его первую строку. В результате должна получиться сводная таблица, изображенная на рис. ЕН.2.6.
j A j В j 0 _1 ^Сводная таблица для риска и комиссии ‘ 2 | \ D j
3_^Количество по полю Фонд Комиссия
4 (Риск [▼ Да Нет Общий итог
5 !ВЫСОКИЙ 6 ^низкий 7 !очень высокий 8 Щчень низкий 9 ^средний 35 45 31 45 4 11 2 4 23 59 80 76 15 6 82
10 Юбщий итог 95 164 259
Рис. ЕН.2.6. Таблица сопряженности признаков, содержащая данные об уровне риска и сборе брокерской комиссии
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
1. Cleveland, W. S., “Graphs in Scientific Publication”, The American Statistician 38 (November 1984): 261-269.
2. Cleveland, W. S., “Graphical Methods for Data Presentation: Full Scale Breaks, Dot Charts, and Multibased Loggings”, The American Statistician 38 (November 1984): 270-280.
3. Cleveland, W. S., and R. McGill, “Graphical Perception: Theory, Experimentation, and Application to the Development of Graphical Methods”, Journal of the American Statistical Association 79 (September 1984): 531-554.
4. Huff, D., How to Lie with Statistics (New York: Norton, 1954).
5. Microsoft Excel 2002 (Redmond, WA: Microsoft Corporation, 2001).
6. Tufte, E. R., The Visual Display of Quantitative Information, 2nd ed. (Cheshire, CT: Graphics Press, 2002).
7. Tufte, E. R., Envisioning Information (Cheshire, CT: Graphics Press, 1990).
8. Tufte, E. R., Visual Explanations (Cheshire, CT: Graphics Press, 1997).
9. Tukey, J., Exploratory Data Analysis (Reading, MA: Addison-Wesley, 1977).
10. Velleman, P. E., and D. C.Hoaglin, Applications, Basics, and Computing of Exploratory Data Analysis (Boston, MA: Duxbury Press, 1981).
11. Wainer, H., “How to Display Data Badly”, The American Statistician 38 (May 1984): 137-147.
12. Wainer, H., Visual Revelations: Graphical Tales of Fate and Deception from Napoleon Bonaparte to Ross Perot (New York: Copernicus/Springer-Verlag, 1997).
Глава 3
Описательные статистики
ПРИМЕНЕНИЕ СТАТИСТИКИ: сравнение эффективности взаимных фондов
3.1. ИССЛЕДОВАНИЕ ЧИСЛОВЫХ ДАННЫХ И ИХ СВОЙСТВ
3.2. ОПРЕДЕЛЕНИЕ СРЕДНЕГО ЗНАЧЕНИЯ, ВАРИАЦИИ И ФОРМЫ РАСПРЕДЕЛЕНИЯ
Арифметическое среднее
Процедуры Excel: создание точечных масштабированных диаграмм
Медиана
Мода
Квартили
Геометрическое среднее
Процедуры Excel: вычисление распределения частот для числовых данных
Размах
Межквартильный размах
Дисперсия и стандартное отклонение
Коэффициент вариации
Visual Explorations: исследование описательных статистик
Форма распределения
Вычисление описательных статистик с помощью программы Microsoft Excel Процедуры Excel: вычисление описательных статистик
3.3. ВЫЧИСЛЕНИЕ ОПИСАТЕЛЬНЫХ СТАТИСТИК ДЛЯ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ
Математическое ожидание
Дисперсия и стандартное отклонение генеральной совокупности Эмпирическое правило Правило Чебышева-Бьенаме
3.4. АНАЛИЗ ДАННЫХ
Пятерка базовых показателей
Блочная диаграмма Процедуры Excel: создание блочных диаграмм
3.5. КОВАРИАЦИЯ И КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ
Процедуры Excel: вычисление коэффициента корреляции
3.6. ЛОВУШКИ, СВЯЗАННЫЕ
С ОПИСАТЕЛЬНЫМИ СТАТИСТИКАМИ, И ЭТИЧЕСКИЕ ПРОБЛЕМЫ
3.7. ВЫЧИСЛЕНИЕ КОЛИЧЕСТВЕННЫХ ПОКАЗАТЕЛЕЙ НА ОСНОВЕ РАСПРЕДЕЛЕНИЯ ЧАСТОТ
Приближенное вычисление среднего арифметического и стандартного отклонения
СПРАВОЧНИК ПО EXCEL. ГЛАВА 3
ЧЕМУ ДОЛЖЕН НАУЧИТЬСЯ СТУДЕНТ
• Определять среднее значение, дисперсию и форму распределения числовых данных.
• Создавать и интерпретировать блочные диаграммы.
• Вычислять описательные статистики.
• Вычислять и интерпретировать коэффициент корреляции.
ПРИМЕНЕНИЕ СТАТИСТИКИ
Сравнение эффективности взаимных фондов
Вернемся к исследованию взаимных фондов, рассмотренных в главе 2. Предположим, что вы — консультант по финансовым вопросам и должны посоветовать своим клиентам, в какой из взаимных фондов следует вкладывать деньги. В главе 2 мы уже показали, как представить данные в виде таблиц и диаграмм. Однако, изучая числовую информацию, например, среднегодовые показатели доходности за последние пять лет, мы должны не только представить данные и понять, что они означают, но и вычислить их основные характеристики, а затем проанализировать их. Какова средняя доход-какие средние показатели доходности за по
следние пять лет имеют взаимные фонды с очень низким, низким, средним, высоким и очень высоким уровнем риска? Насколько изменчива доходность этих фондов? Можно ли утверждать, что разброс доходности фондов с высоким уровнем риска выше, чем у фондов со средним и низким уровнем риска? Как использовать эту информацию для принятия правильного решения?
ВВЕДЕНИЕ
Способы представления числовых и категорийных данных в виде таблиц и диаграмм являются существенной, но не основной частью анализа данных. Ведущая роль принадлежит методам исследования числовых данных и их свойств. Сначала мы рассмотрим способы определения среднего значения (central tendency), вариации (variation) и формы (shape) распределения генеральной совокупности. Затем изучим методы анализа данных, в частности, способы вычисления описательных статистик, характеризующих выборки и генеральные совокупности. Переходя к анализу двумерных данных, мы рассмотрим коэффициент корреляции (correlation), позволяющий измерить степень зависимости между двумя переменными. В заключении обсуждаются различные ловушки, которые подстерегают исследователей при вычислении основных числовых характеристик, а также некоторые этические проблемы.
3.1. ИССЛЕДОВАНИЕ ЧИСЛОВЫХ ДАННЫХ И ИХ СВОЙСТВ
Выбор инвестиционной стратегии должен начинаться с анализа среднегодовой доходности фондов за пять последних лет, прошедших до 31 декабря 2001 года. Целесообразно сравнить доходность фондов, имеющих разную степень риска. Для начала исследуем доходность 15 фондов с очень высоким уровнем риска. Можно предположить, что доходность этих фондов очень переменчива, однако превышает показатели других фондов. Среднегодовая доходность фондов с очень высоким уровнем риска за последние пять лет приведена на рис. 3.1.
A j В
Фонд Пятилетняя
2 jAmer. Century GiftTrust Inv.
3 AXP Stategy Aggressive A
4 Berger Small Company Growth Inv
5 Consulting Group Small Cap Growth
6 Fidelity Aggressive Growth
7 Invesco Growth Inv
8 Janus Enterprise
9 Janus Venture
10 John Hancock Small Cap Growth A VViWiS Wiid Cap Equity Tr. В
12 PBHG Growth
Putnam OTC Emerging Growth A
14 I RS Emerging Growth A
15 Rydex OTC Inv
16 Van Kampen Aggressive Growth A ;
-2.8 5.5
8.3 4.3
5.9 -0,7
6.5 9,8
73 9.6 -1.2 -6,1 18,5 13,1
12,9
Рис. 3.1. Среднегодовая доходность фондов с очень высоким уровнем риска за последние ПЯТЬ лет ^MUTUAL FUNDS . XLS
Какие выводы можно сделать на основе полученных данных? Упорядочим 15 фондов с очень высоким уровнем риска в порядке возрастания их доходности.
-6,1 -2,8 -1,2 -0,7 4,3 5,5 5,9 6,5 7,6 8,3 9,6 9,8 12,9 13,1 18,5
Проанализировав эту выборку, мы можем сформулировать следующие выводы.
1. Взаимные фонды имеют разную доходность.
2. Доходность взаимных фондов с очень высоким уровнем риска за последние пять лет колеблется от -6,1 до 18,5.
3. Только один взаимный фонд имеет чрезвычайно высокую пятилетнюю доходность — фонд RS Emerging Growth А (18,5%).
Число 18,5 можно считать выбросом (outlier), или экстремальным значением. Как консультант по финансовым вопросам, вы обязаны заинтересоваться причинами таких необычно высоких показателей. Сравнение характеристик фонда, имеющего чрезвычайно высокие доходы, с остальными фондами, приносящими средний доход, поможет разработать более эффективную инвестиционную стратегию. Однако более глубокие выводы можно сделать, лишь обладая полной информацией о финансовом положении фондов. Чтобы понять причины, определяющие доходность основной массы фондов, необходимо определить основные характеристики существующей числовой информации: среднее значение, вариацию и форму распределения.
3.2. ОПРЕДЕЛЕНИЕ СРЕДНЕГО ЗНАЧЕНИЯ, ВАРИАЦИИ И ФОРМЫ РАСПРЕДЕЛЕНИЯ
В большинстве случаев данные концентрируются вокруг некоей центральной точки. Таким образом, чтобы описать любой набор данных, достаточно указать некое типичное значение. Эту величину называют средним значением (central tendency, or location). В этом разделе рассматриваются три числовые характеристики, которые используются для оценки среднего значения распределения: среднее арифметическое (arithmetic mean), медиана (median) и мода (mode).
Среднее арифметическое
Среднее арифметическое (часто называемое просто средним) — наиболее распространенная оценка среднего значения распределения. Она является результатом деления суммы всех наблюдаемых числовых величин на их количество.
Для выборки, состоящей из чисел Х2, ..., Хп, выборочное среднее (обозначаемое символом X ) равно
- _Х{+Х2+... +Хп А —------------- .
П
Чтобы упростить формулы, сумма элементов выборки обозначается как1
V.V.
Иначе говоря,
уХ' = х} + х2 + ...+хп.
ВЫБОРОЧНОЕ СРЕДНЕЕ t*.
Х = ^--, (3.1)
и
где X — выборочное среднее, п — объем выборки, X, — i-й элемент выборки,
—сумма всех элементов выборки.
Рассмотрим вычисление среднего арифметического значения пятилетней среднегодовой доходности 15 взаимных фондов с очень высоким уровнем риска.
Фонд Доходность
Amer. Century GiftTrust Inv. Х\ =-2,8
AXP Strategy Aggressive A X2 = 5,5
Berger Small Company Growth Inv X3 = 8,3
Consulting Group Small Cap Growth A>4,3
Fidelity Aggressive Growth X5 = 5,9
Invesco Growth Inv Xfi = -0,7
Janus Enterprise XT = 6,5
Janus Venture X8=9,8
John Hancock Small Cap Growth A X9=7,6
MS Mid Cap Equity Tr. В x;0=9,6
PBHG Growth Xn = -1,2
Putnam OTC Emerging Growth A ^=-6,1
1 Обозначения суммы обсуждаются в приложении Б.
Фонд
RS Emerging Growth А
Rydex ОТС Inv
Van Kampen Aggressive Growth A
Доходность
X13 = 18,5
X14=13,l
X15 = 12,9
Выборочное среднее вычисляется следующим образом.
15
_ -2,8 + 5,5 + ...+ 12,9
п
91,2
-— = 6,08.
15
Итак, среднее значение годовой доходности взаимных фондов с очень высоким уровнем риска равно 6,08. Это хороший доход, особенно по сравнению с 3-4% дохода, который получили вкладчики банков или кредитных союзов за тот же период времени. Кроме того, на точечной масштабированной диаграмме (dot scale diagram), приведенной на рис. 3.2, видно, что восемь фондов имеют доходность выше, а семь — ниже среднего значения. Как видим, среднее арифметическое играет роль точки равновесия (balancing point), так что фонды с низкими доходами уравновешивают фонды с высокими доходами. В вычислении среднего задействованы все элементы выборки (Хт, Х2, ..., Х15). Ни одна из других оценок среднего значения распределения не обладает этим свойством.
Фонды с очень высоким риском
Рис. 3.2. Точечная масштабированная диаграмма среднегодовой доходности 15 взаимных фондов с очень высоким уровнем риска, построенная с помощью программы Microsoft Excel
КОГДА СЛЕДУЕТ ВЫЧИСЛЯТЬ СРЕДНЕЕ АРИФМЕТИЧЕСКОЕ
Поскольку среднее арифметическое зависит от всех элементов выборки, наличие ; экстремальных значений значительно влияет на результат. В таких ситуациях среднее арифметическое может исказить смысл числовых данных. Следовательно, описывая набор данных, содержащий экстремальные значения, необходимо указывать медиану либо среднее арифметическое и медиану.
Чтобы продемонстрировать влияние выбросов на вычисление среднего значения распределения, удалим из выборки доходность фонда RS Emerging Growth А.2
ПРИМЕР 3.1. ВЫЧИСЛЕНИЕ СРЕДНЕГО АРИФМЕТИЧЕСКОГО ПОСЛЕ УДАЛЕНИЯ ВЫБРОСА
РЕШЕНИЕ. Выборочное среднее доходности 14 фондов вычисляется следующим образом.
п
- _ _ -2,8 + 5,5 + 8,3...+ 12,9
.А —-----—----------------------.
п 14
После удаления показателей фонда RS Emerging Growth А среднее арифметическое уменьшается с 6,08 до 5,19. Эти результаты отражены на новой точечной масштабированной диаграмме (рис. 3.3).
Фонды с очень высоким риском
Рис. 3.3. Точечная масштабированная диаграмма среднегодовой доходности 14 взаимных фондов с высоким уровнем риска, построенная с помощью программы Microsoft Excel
Процедуры Excel: создание точечных масштабированных диаграмм
Для создания точечной диаграммы можно применить процедуру надстройки PHStat2 или вручную настроить рабочий лист, содержащийся в рабочей книге Chapter 3.xls. (В программе Microsoft Excel не предусмотрена процедура автоматического создания точечной масштабированной диаграммы.) Например, чтобы построить точечную диаграмму, изображенную на рис. 3.2, нужно открыть рабочую книгу Chapter 3.xls и выполнить одну из следующих процедур.
Чтобы исследовать влияние выброса на среднее арифметическое значение или медиану, зайдите в раздел Visual Explorations на компакт-диске и выберите пункт Descriptive Statistics (Описательная статистика).
Применение Excel в сочетании с надстройкой PHStatZ
Для того чтобы создать точечную масштабированную диаграмму на новом рабочем листе, содержащем копию исходных данных, следует выполнить процедуру Dot Scale Diagram надстройки PHStat2, руководствуясь инструкциями, приведенными ниже.
1. Выбрать команду PHStat^Descriptive Statistics* 1^Dot Scale Diagram... (PHStatZОписательная статистика^Точечная диаграмма...).
2. В диалоговом окне Dot Scale Diagram выполнить следующее.
2.1. Ввести в окне редактирования Variable Cell Range (Входной интервал) диапазон и: 116.
2.2. Установить флажок First cell contains label (Первая ячейка содержит метку).
2.3. Ввести название диаграммы в окне редактирования
Title (Заголовок).
2.4. Щелкнуть на кнопке ОК.
Эта процедура размещает точечную масштабированную диаграмму на новом рабочем листе. Изменяя данные, записанные в столбце А, можно наблюдать изменения, происходящие на диаграмме.
Применение Excel
Откройте рабочую книгу Chapter 3 на листе Точечная_диаграмма и следуйте инструкциям, приведенным в разделе ЕН3.1.
Chapter 3.xls
Диаграмма, изображенная на рис. 3.2, содержится в рабочей книге Chapter 3. xls на листе Рис3.1.
Медиана
Медиана (median) представляет собой срединное значение упорядоченного массива чисел. Если массив не содержит повторяющихся чисел, то половина его элементов окажется меньше, а половина — больше медианы. Если выборка содержит экстремальные значения, для оценки среднего значения лучше использовать не среднее арифметическое, а медиану.
Чтобы вычислить медиану выборки, ее сначала необходимо упорядочить.
МЕДИАНА
Медианой называется число, разделяющее выборку пополам: 50% элементов меньше медианы, а 50% — больше.
п +1
Медиана =----и элемент упорядоченного массива. (3.2)
Формула (3.2) неоднозначна. Ее результат зависит от четности или нечетности числа п.
т-1 - « + 1
1. Если выборка содержит нечетное количество элементов, медиана равна —-—му элементу.
2. Если выборка содержит четное количество элементов, медиана лежит между двумя средними элементами выборки и равна среднему арифметическому, вычисленному по этим двум элементам.
Чтобы вычислить медиану выборки, содержащей данные о доходности 15 взаимных фондов с очень высокий уровнем риска, сначала необходимо упорядочить исходные данные.
-6,1 -2,8 -1,2 -0,7 4,3 5,5 5,9 6,5 7,6 8,3 9,6 9,8 12,9 13,1 18,5
т
Медиана = 6,5 г
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
В соответствии с правилом 1, относящимся к выборкам, содержащим нечетное количество элементов, позигция медианы вычисляется по формуле
к + 1 15 + 1 _ ----=-----= о.
2 2
Таким образом, медиана равна 6,5. Это означает, что доходность одной половины фондов с очень высоким уровнем риска не превышает 6,5, а доходность второй половины — превышает ее. Обратите внимание на то, что медиана, равная 6,5, ненамного больше среднего значения, равного 6,08.
ПРИМЕР 3.2. ВЫЧИСЛЕНИЕ МЕДИАНЫ ВЫБОРКИ, СОДЕРЖАЩЕЙ ЧЕТНОЕ КОЛИЧЕСТВО ЭЛЕМЕНТОВ
В выборке, содержащей данные о взаимных фондах, упоминаются шесть фондов с очень низким уровнем риска. Вычислите медиану их среднегодовой доходности за последние пять лет.
РЕШЕНИЕ. Упорядоченный массив теперь выглядит так .
11 12 12,1 12,3 15,1 18,2
Упорядоченные наблюдения: 12 3? 456
Медиана = 12,2
Согласно правилу 2, относящемуся к вычислению медианы выборки, содержащей четное количество элементов, позиция медианы задается формулой
/7 + 1 _ 6 + 1 5
2 “ 2 ” ’
Следовательно, медиана равна среднему значению, вычисленному по третьему и четвертому элементам, т.е. 12,2.
Мода
Мода (mode) — это число, которое чаще других встречается в выборке. В отличие от среднего арифметического, выбросы на моду не влияют. Моду используют исключительно для иллюстрации, поскольку она сильнее зависит от конкретной выборки, чем другие оценки среднего значения. Для непрерывно распределенных случайных величин, например, для показателей среднегодовой доходности взаимных фондов, мода иногда вообще не существует. Поскольку эти показатели могут принимать самые разные значения, повторяющиеся величины встречаются крайне редко. Продемонстрируем вычисление моды на следующем примере.
ПРИМЕР 3.3. ВЫЧИСЛЕНИЕ МОДЫ
Системный администратор, руководящий работой корпоративной сети, подсчитывает количество сбоев сервера, происходящих за день. В следующей таблице приведены данные его наблюдений за последние две недели.
1303 26 274023 3 6 3
Вычислите моду этой выборки .
РЕШЕНИЕ. Упорядочим массив.
00122333334 6 7 26
Чаще всего в этой выборке повторяется число 3. Следовательно, мода равна 3. Таким образом, системный администратор может утверждать, что, как правило, сервер сбоит 3 раза в день. Обратите внимание на то, что мода этой выборки равна 3, а среднее выборочное значение равно 4,5. Число 26 является выбросом, поэтому для оценки среднего количества сбоев за день следует пользоваться медианой или модой, а не средним арифметическим значением.
Приведем пример, в котором ни одно значение не повторяется дважды, т.е. выборка не имеет моды.
ПРИМЕР 3.4. ВЫБОРКА, НЕ ИМЕЮЩАЯ МОДЫ
Вычислите моду выборки, содержащей данные о среднегодовой доходности 15 взаимных фондов с очень высоким уровнем риска.
РЕШЕНИЕ. Упорядочим массив.
-6,1 -2,8 -1,2 -0,7 4,3 5,5 5,9 6,5 7,6 8,3 9,6 9,8 12,9 13,1 18,5
Эта выборка не имеет моды, поскольку ни одно из значений не повторяется дважды.
Квартили
Квартили (quartiles) — это показатели, которые чаще всего используются для оценки распределения данных при описании свойств больших числовых выборок. В то время как медиана разделяет упорядоченный массив пополам (50% элементов массива меньше медианы и 50% — больше), квартили разбивают упорядоченный набор данных на четыре части.
Квартили3 вычисляются по формулам (3.3) и (3.4).
ПЕРВЫЙ КВАРТИЛЬ, Q
Первый квартиль Qx — это число, разделяющее выборку на две части: 25% элементов меньше, а 75% — больше первого квартиля.
„ "+l А /О ОХ
=—-—и элемент упорядоченного массива. (о.о)
Величины Q,, медиана и Q3 являются 25-м, 50-м и 75-м перцентилем соответственно. Формулы (3.2)-(3.4) можно переписать в терминах перцентилей: (рхЮО)-й перцентиль = п+1)-му на-
блюдению.
ТРЕТИЙ КВАРТИЛЬ, Q3
Третий квартиль Q3 — это число, разделяющее выборку на две части: 75% элементов меньше, а 25% — больше третьего квартиля.
_ 3(/7 +.1) элемент упорядоченного массива. (3.4)
4
Для вычисления квартилей применяются следующие правила.
1. Если индекс квартиля задается целым числом, значением квартиля считается элемент выборки с указанным индексом.
2. Если индекс квартиля задается величиной, представляющей собой среднее значение, вычисленное по двум целым числам, квартиль равен среднему арифметическому, вычисленному по элементам, индексы которых равны этим двум числам.
3. Если индекс квартиля задается числом, которое не является целым и не кратно 1/2, он просто округляется до ближайшего целого. Квартилем считается элемент с указанным индексом.
Вычислим квартили выборки, содержащей данные о среднегодовой доходности 15 взаимных фондов с очень высоким уровнем риска. Упорядоченный массив имеет следующий вид.
-6,1 -2,8 -1,2 -0,7 4,3 5,5 5,9 6,5 7,6 8,3 9,6 9,8 12,9 13,1 18,5
Следовательно,
к + 1 „
Q. -----и элемент упорядоченного массива,
4
15 + 1 л индекс квартиля = —-— = 4 .
Таким образом, согласно правилу 1 первый квартиль является четвертым элементом упорядоченного массива.
£,=-0,7.
Это означает, что доходность 25% фондов с очень высоким уровнем риска не превышает -0,7%. Кроме того,
п 3(и + 1) .
Q3 =-------и элемент упорядоченного массива,
3(15 + 1)
индекс квартиля =-------= 12.
Таким образом, по правилу 1 третий квартиль является двенадцатым элементом упорядоченного массива.
Q3 = 9,8.
Среднее геометрическое
В отличие от среднего арифметического среднее геометрическое (geometric mean) и среднее геометрическое значение нормы прибыли (geometric rate of return) позволяют оценить степень изменения переменной с течением времени. Среднее геометрическое определяется формулой (3.5).
СРЕДНЕЕ ГЕОМЕТРИЧЕСКОЕ
Среднее геометрическое — это корень n-й степени из произведения п величин. %с=(Х,хХ2х...хХ„)Х. (3.5)
Среднее геометрическое значение нормы прибыли определяется формулой (3.6).
СРЕДНЕЕ ГЕОМЕТРИЧЕСКОЕ ЗНАЧЕНИЕ НОРМЫ ПРИБЫЛИ =[(1 + л|)х(1 + /г,)х...х(1 + л„)]^-1, (3.6)
где R — норма прибыли за i-й период времени.
Проиллюстрируем эти числовые характеристики следующим примером. Предположим, что объем вложенных средств в исходный момент времени равен 100 000 долл. К концу первого года он падает до уровня 50 000 долл., а к концу второго года восстанавливается до исходной отметки 100 000 долл. Норма прибыли этой инвестиции за двухлетний период равна 0, поскольку первоначальный и финальный объем средств равны между собой. Однако среднее арифметическое годовых норм прибыли равно
-0,50 + 1,00 п ------------= 0,25 , или 25%,
2
поскольку норма прибыли за первый год равна
D 50 000-10 000 к_0/
R. --------------= -0,50 , или -50%,
100 000
а за второй год —
_ 100 000-50 000
R, =--------------= 1,00 , или 100% .
100 000
В то же время, среднее геометрическое значение нормы прибыли за два года в соответствии с формулой (3.6) равно
Re =[(1+Р1)х (1+Я2)]1/2-1 =[(1-0,5)х (1+1)]1 г-1 = [0,5x2,0]В * * * 12-1 = 1-1 = 0.
Таким образом, среднее геометрическое точнее отражает изменение (точнее, отсутствие изменений) объема инвестиций за двухлетний период, чем среднее арифметическое.
Второе важное свойство числовых данных — их вариация, характеризующая степень дисперсии (dispersion) данных. Две разные выборки могут отличаться как средними значениями, так и вариациями. Однако, как показано на рис. 3.4 и 3.5, две выборки могут иметь одинаковые вариации, но разные средние значения, либо одинако-
вые средние значения и совершенно разные вариации. Данные, которым соответствует полигон Б на рис. 3.5, изменяются намного меньше, чем данные, по которым построен полигон А.
Рис. 3.4. Два симметричных распределения колоколообразной формы с одинаковым разбросом и разными средними значениями
Рис. 3.5. Два симметричных распределения колоколообразной формы с одинаковыми средними значениями и разным разбросом
Существует пять оценок вариации данных: размах (range), межквартильный размах (interquartile range), дисперсия (variance), стандартное отклонение (standard deviation) и коэффициент вариации (coefficient of variation).
Размах
Размахом (range) называется разность между наибольшим и наименьшим элементами выборки.
РАЗМАХ
Размах — это разность между наибольшим и наименьшим элементами выборки.
Размах = Хтах - Хтт. (3.7)
Размах выборки, содержащей данные о среднегодовой доходности 15 взаимных фондов с очень высоким уровнем риска, можно вычислить, используя следующий упорядоченный массив.
-6,1 -2,8 -1,2 -0,7 4,3 5,5 5,9 6,5 7,6 8,3 9,6 9,8 12,9 13,1 18,5
Используя формулу (3.7), получаем, что размах равен 38,16 - 28,39 = 24,6. Это значит, что разница между наибольшей и наименьшей среднегодовой доходностью фондов с очень высоким уровнем риска равна 24,6% .
Размах позволяет измерить общий разброс (total spread) данных. Хотя размах выборки является весьма простой оценкой общего разброса данных, его слабость заключается в том, что он никак не учитывает, как именно распределены данные между минимальным и максимальным элементами. Этот эффект хорошо прослеживается на рис. 3.7, который иллюстрирует выборки, имеющие одинаковый размах. Шкала В демонстрирует, что если выборка содержит хотя бы одно экстремальное значение, размах выборки оказывается весьма неточной оценкой разброса данных.
о
7 8 9
Шкала А
Шкала Б
11 12
13
13
7 8 9 10 11
Шкала В
Рис. 3.6. Сравнение трех выборок, имеющих одинаковый размах
Межквартильный размах
Межквартильный, или средний, размах (interquartile range, or midspread) — это разность между третьим и первым квартилями выборки.
МЕЖКВАРТИЛЬНЫЙ РАЗМАХ
Межквартильный размах — это разность между третьим и первым квартилями выборки.
Межквартильный размах = Q3 - Qx. (3.8)
L . ______ ... , ___ _____________ ____________ _
Эта величина позволяет оценить разброс 50% элементов и не учитывать влияние экстремальных элементов. Межквартильный размах выборки, содержащей данные о среднегодовой доходности 15 взаимных фондов с очень высоким уровнем риска, можно вычислить, используя следующий упорядоченный массив.
-6,1 -2,8 -1,2 -0,7 4,3 5,5 5,9 6,5 7,6 8,3 9,6 9,8 12,9 13,1 18,5
Используя вычисленные ранее значения Q± и Q3, а также формулу (3.8), получаем следующий результат.
Межквартильный размах = Q3 - Qx = 9,8 - (-0,7) = 10,5.
Эта величина характеризует размах половины выборки, содержащей данные о среднегодовой доходности 15 взаимных фондов с высоким уровнем риска. Интервал, ограниченный числами 9,8 и -0,7, часто называют средней половиной.
Следует отметить, что величины Qx и Q3, а значит, и межквартильный размах, не зависят от наличия выбросов, поскольку при их вычислении не учитывается ни одна величина, которая была бы меньше Qx или больше Q3. Суммарные количественные характеристики, такие как медиана, первый и третий квартили, а также межквартильный размах, на которые не влияют выбросы, называются устойчивыми показателями (resistant measures).
Дисперсия и стандартное отклонение
Хотя размах и межквартильный размах позволяют оценить общий и средний разброс выборки соответственно, ни одна из этих оценок не учитывает, как именно распределены данные. Дисперсия и стандартное отклонение лишены этого недостатка. Эти показатели позволяют оценить степень колебания данных вокруг среднего значения. Выборочная дисперсия является приближением среднего арифметического, вычисленного на основе квадратов разностей между каждым элементом выборки и выборочным средним.
Для выборки Хх, Х2, ..., Хп выборочная дисперсия (обозначаемая символом S2) задается следующей формулой.
(X,-y)2+(X;-X)2 + ... + (X„-Z);
п — \
ВЫБОРОЧНАЯ ДИСПЕРСИЯ
Выборочная дисперсия — это сумма квадратов разностей между элементами выборки и выборочным средним, деленная на величину, равную объему выборки минус один.
S'= —--------, (3.9)
/7-1
где X — арифметическое среднее, п — объем выборки, X, — i-й элемент выборки X,
-X)" — сумма квадратов разностей между элементами выборки и выборочным /=1
средним.
Если бы знаменатель был равен п, а не п-1, мы получили бы среднее арифметическое квадратов разностей между элементами выборки и выборочным средним. Однако в этом случае выборочная дисперсия S2 не обладала бы свойствами, необходимыми в теории статистических выводов, которую мы рассмотрим в главе 6. При увеличении объема выборки различие между оценками, полученными при делении на п и п-1, становится все меньше.
Наиболее практичной и широко распространенной оценкой разброса данных является стандартное выборочное отклонение (sample standard deviation). Этот показатель обозначается символом S и равен квадратному корню из выборочной дисперсии.
СТАНДАРТНОЕ ВЫБОРОЧНОЕ ОТКЛОНЕНИЕ
Стандартное выборочное отклонение — квадратный корень из суммы квадратов разностей между элементами выборки и выборочным средним, деленной на величину, равную объему выборки минус один.
(3.10)
Рассмотрим этапы вычисления выборочной дисперсии и стандартного выборочного отклонения (врезка 3.1).
ВРЕЗКА 3.1. ВЫЧИСЛЕНИЕ ПОКАЗАТЕЛЕЙ S2 MS
Чтобы вычислить выборочную дисперсию, следует выполнись следующее.
; • Вычислить разность между каждым элементом выборки и выборочным средним.
• Возвести каждую разность в квадрат.
• Сложить все разности, возведенные в квадрат.
♦ Поделить результат на п~1.
Чтобы вычислить показатель S, т.е. стандартное выборочное отклонение, необхо- ; димо извлечь квадратный корень из выборочной дисперсии.
Чтобы вычислить выборочную дисперсию и стандартное выборочное отклонение доходности взаимных фондов с очень высоким уровнем риска, следует применить описанный выше алгоритм к данным, приведенным на рис. 3.8. (Выборочное среднее показателей доходности фондов с очень высоким уровнем риска вычислено ранее и равно 6,08.)
X {Xj-X) (Х,-Х)2
A J В I
1 Фонд Xi Пятилетняя доходность /С 1 XBar / D (Xi-XBai) / ! (Xi-Xbai)A2
2 Amer. Century GiftTrust Inv. -2,8 6,08 -8,88 78,854
3 AXP Stategy Aggressive A 5,6 6,08 -0,58 0,336
4 Berger Small Company Growth Inv 8,3 6,08 2,22 4,928
5 j Consulting Group Small Cap Growth 4,3 6,08 -1,78 3,168
6 {Fidelity Aggressive Growth 5,9 6,08 -0,18 0,032.
7 jlnvesco Growth Inv -0,7 6,08 -6,78 45,968
8 iJanus Enterprise 6,5 6,08 0,42 0,176
э : iJanus Venture 9.8 6,08 3,72 13,838
10 jJohn Hancock Small Cap Growth A 7,6 6,08 1,52 2,310
11 IMS Mid Cap Equity Tr. В 9.6 6,08 3,52 12,390
12 IPBHG Growth -1,2 6,08 -7,28 52,998
131 Putnam OTC Emerging Growth A -6,1 6,08 -12,18 148,352
14 RS Emerging Growth A 18,5 6,08 12,42 154,256
"is1 Rydex OTC Inv 13,1 6,08 7,02 49,280
16 Van Kampen Aggressive Growth A 12,9 6,08 6,82 46,512
Суммы: 0,00 613,404
£ (Х-х> £ (х,-х)2 /=1 /=1
Рис. 3.7. Вычисление выборочной дисперсии и стандартного выборочного отклонения среднегодовых показателей доходности фондов с очень высоким уровнем риска за последние пять лет
В соответствии с формулой (3.9) выборочная дисперсия равна
.2 (—2,8-6,08)2+(5,5-6,08)!+... + (12,9-6,08)2 613,404
э —----------= ------------------------------------= -------= 4 3, б 14о.
п-1 15-1 14
Формула (3.10) позволяет вычислить стандартное выборочное отклонение.
S = y/S2 = ----j----- ^/43,8146 = 6,62.
В ходе этих вычислений разность между каждым элементом выборки и выборочным средним возводится в квадрат. Следовательно, ни выборочная дисперсия, ни стандартное выборочное отклонение не могут быть отрицательными. Единственная ситуация, в которой показатели S2 и S могут быть нулевыми, — если все элементы выборки равны между собой. В этом совершенно невероятном случае размах и межквартильный размах также равны нулю.
Числовые данные по своей природе изменчивы. Любая переменная может принимать множество разных значений. Например, разные взаимные фонды имеют разные показатели доходности и убытков. Вследствие изменчивости числовых данных очень важно изучать не только оценки среднего значения, которые по своей природе являются суммарными, но и оценки дисперсии, характеризующие разброс данных.
ИНТЕРПРЕТАЦИЯ ДИСПЕРСИИ И СТАНДАРТНОГО ОТКЛОНЕНИЯ
Дисперсия и стандартное отклонение позволяют оценить разброс данных вокруг среднего значения, иначе говоря, определить, сколько элементов выборки меньше среднего, а сколько — больше. Дисперсия обладает некоторыми ценными математическими свойствами. Однако ее величина представляет собой квадрат единицы измерения — квадратный процент, квадратный доллар, квадратный дюйм и т.п. Следовательно, естественной оценкой дисперсии является стандартное отклонение, которое выражается в обычных единицах измерений — процентах дохода, долларах или : дюймах.
Стандартное отклонение позволяет оценить величину колебаний элементов выборки вокруг среднего значения. Практически во всех ситуациях основное количество наблюдаемых величин лежит в интервале плюс-минус одно стандартное отклонение от среднего значения. Следовательно, зная среднее арифметическое элементов выборки и стандартное выборочное отклонение, можно определить интервал, которому принадлежит основная масса данных.
ЧТО ОЗНАЧАЕТ СТАНДАРТНОЕ ОТКЛОНЕНИЕ
Стандартное отклонение доходности 15 взаимных фондов с очень высоким уровнем риска равно 6,62. Это значит, что доходность основной массы фондов отличается от среднего значения не более чем на 6,62% (т.е. колеблется в интервале от X - S = -’0,54 : до X + S = 12,70). Фактически в этом интервале лежит пятилетняя среднегодовая до- . ходность 53,3% (8 из 15) фондов.
Обратите внимание на то, что квадраты разностей суммируются следующим образом:
ш-*)2
7=1
В процессе суммирования элементы выборки, лежащие дальше от среднего значения, приобретают больший вес, чем элементы, лежащие ближе. Соответствующие значения квадратов разностей приведены в последнем столбце на рис. 3.8. Обратите внимание на то, что тринадцатое значение Х13 = 18,5 соответствует фонду RS Emerging Growth А, доходность которого дальше всех отклоняется от среднего значения, равного 6,08. При возведении в квадрат это значение вносит в суммы S2 и S наибольший вклад. Кроме того, сумма квадратов всех разностей в четвертом столбце равна 0 (если не учитывать ошибки округления).
£(х,-х)=о.
/=1
Это свойство является основной причиной того, что для оценки среднего значения распределения чаще всего используется среднее арифметическое значение.
Свойства размаха, межквартильного размаха, дисперсии и стандартного отклонения изложены во врезке 3.2.
ВРЕЗКА 3.2. ХАРАКТЕРИСТИКИ ИЗМЕНЧИВОСТИ ДАННЫХ
• Чем больший разброс имеют данные, тем больше их размах, межквартильный размах, дисперсия и стандартное отклонение.
• Чем более концентрированы, или однородны, данные, тем меньше их размах, межквартильный размах, дисперсия и стандартное отклонение.
• Если все элементы выборки равны между собой (т.е. разброс отсутствует), межквартильный размах, дисперсия и стандартное отклонение равны нулю.
• Ни одна из оценок изменчивости данных (размах, межквартильный размах, дисперсия и стандартное отклонение) не может быть отрицательной.
Пример 3.5 иллюстрирует изменение стандартных выборочных отклонений.
ПРИМЕР 3.5. СРАВНЕНИЕ СТАНДАРТНЫХ ОТКЛОНЕНИЙ
Сравните разброс доходности фондов с очень низким, низким, средним, высоким и очень высоким уровнями риска, вычислив среднее отклонение для каждой из этих категорий.
РЕШЕНИЕ. Стандартные отклонения, вычисленные с помощью программы Microsoft Excel, приведены ниже.
Очень низкий риск: 8 = 2,700.
Низкий риск: 8 = 3,583.
Средний риск: 8 = 4,179.
Высокий риск: 8 = 4,543.
Очень высокий риск: 8 = 6,620.
Разброс доходности фондов с очень высоким и высоким уровнями риска превышает разброс доходности фондов со средним уровнем риска. В свою очередь, разброс доходности фондов со средним уровнем риска превышает разброс доходности фондов с низким и очень низким уровнями риска. Показатели доходности фондов с низким уровнем риска более плотно концентрируются вокруг своего среднего значения, чем показатели фондов с высоким уровнем риска. Иначе говоря, инвесторы фондов с высоким уровнем риска имеют больше шансов получить доход меньше среднего значения. С другой стороны, велика вероятность того, что эти инвесторы получат чрезвычайно высокий доход.
VISUAL EXPLORATIONS: исследование описательных статистик
Для исследования описательных статистик следует применить процедуру Descriptive Statistics из программы Visual Explorations. Эта процедура создает точечную диаграмму, изображенную на рисунке. Она иллюстрирует данные о доходности 15 взаимных фондов с очень высоким уровнем риска.
Чтобы выполнить эту процедуру, сделайте следующее.
1. Откройте рабочую книгу макросов Visual Explorations .xla.
2. Выберите команду Visual Exploration^Descriptive Statistics (Visual Ехр1ога^опФОписательная статистика).
3. Изучите инструкции и щелкните на кнопке ОК в открывшемся диалоговом окне.
4. Измените данные в диапазоне ячеек А2: А1 б и оцените изменения, происшедшие со статистиками.
Попробуйте, например, изменить максимальное выборочное значение 18,5 на 85 и определите новые значения среднего и медианы.
Коэффициент вариации
В отличие от предыдущих оценок разброса, коэффициент вариации (coefficient of variation) является относительной оценкой (relative measure). Он всегда измеряется в процентах, а не в единицах измерения исходных данных.
Коэффициент вариации, обозначаемый символами CV, измеряет рассеивание данных относительно среднего значения.
КОЭФФИЦИЕНТ ВАРИАЦИИ
Коэффициент вариации равен стандартному отклонению, деленному на среднее арифметическое и умноженному на 100% .
СГ = -£х100% , (3.11)
где S — стандартное выборочное отклонение, X — выборочное среднее.
Коэффициент вариации доходности фондов с очень низким, низким, средним, высоким и очень высоким уровнями риска вычисляется следующим образом. Сначала вычисляются средние арифметические и стандартные отклонения доходности в каждой категории.
Очень низкий риск: X = 13,45 8 = 2,70.
Низкий риск: X = 12,234 8 = 3,583.
Средний риск: X =11,209 8 = 4,179.
Высокий риск: X = 9,547 8 = 4,543.
Очень высокий риск: X = 6,08 8 = 6,62.
Следуя формуле (3.11), получаем:
V 2 70
Очень низкий риск: CV = — х 100% = —-—х 100% - 20,07%.
X 13,45
Низкий риск: CV = Jtx 100% - 3’583 * _ 29 29%.
X 12,234
V 4 179
Средний риск: CV = -= х 100% = х 100% - 37,28%.
Высокий риск: CV = -£гх 100% = 4,543 х 100% = 47,58%.
X 9,547
Очень высокий риск: CV = х 100% = х 100% = 108,88%.
X 6,08
Как видим, чем выше риск, тем больше относительный разброс доходности вокруг среднего значения. Обратите внимание на то, что фонды с низким и средним уровнями риска имеют более высокую среднюю доходность и меньший коэффициент вариации, чем фонды с высоким уровнем риска. Это означает, что эффективность фондов со средним уровнем риска выше, чем эффективность фондов с высоким уровнем риска.
Коэффициент вариации позволяет также сравнить две выборки, элементы которых выражаются в разных единицах измерения.
ПРИМЕР 3.6. СРАВНЕНИЕ ДВУХ КОЭФФИЦИЕНТОВ ВАРИАЦИИ, КОГДА ПЕРЕМЕННЫЕ ВЫРАЖАЮТСЯ В РАЗНЫХ ЕДИНИЦАХ ИЗМЕРЕНИЯ
Управляющий службы доставки корреспонденции намеревается обновить парк грузовиков. При погрузке пакетов следует учитывать два вида ограничений: вес (в фунтах) и объем (в кубических футах) каждого пакета.
Предположим, что в выборке, содержащей 200 пакетов, средний вес равен 26,0 фунтов, стандартное отклонение веса— 3,9 фунтов, средний объем пакета — 8,8 кубических футов, а стандартное отклонение объема — 2,2 кубических фута. Как сравнить разброс веса и объема пакетов?
РЕШЕНИЕ. Поскольку единицы измерения веса и объема отличаются друг от друга, управляющий должен сравнить относительный разброс этих величин. Коэффициент 3 9
вариации веса равен CVW = ——х 100% = 15,0%, а коэффициент вариации объема — 26,0
2 2
СГГ =---х 100% = 25,0% . Таким образом, относительный разброс объема пакетов на-
8,8
много больше относительного разброса их веса.
Форма распределения
Третье важное свойство выборки — форма ее распределения. Это распределение может быть симметричным (symmetrical) или асимметричным (asymmetrical).
Чтобы описать форму распределения, необходимо вычислить его среднее значение и медиану. Если эти два показателя совпадают, переменная считается симметрично распределенной (zero-skewed). Если среднее значение переменной больше медианы, ее распределение имеет положительную асимметрию (right-skewed). Если медиана больше среднего значения, распределение переменной имеет отрицательную асимметрию (left-skewed).
Положительная асимметрия возникает, когда среднее значение увеличивается до необычайно высоких значений. Отрицательная асимметрия возникает, когда среднее значение уменьшается до необычайно малых значений. Переменная является симметрично распределенной, если она не принимает никаких экстремальных значений ни в одном из направлений, так что большие и малые значения переменной уравновешивают друг друга.
Три вида распределений, описанных выше, изображены на рис. 3.8.
Шкала А Распределение с отрицательной асимметрией
Шкала Б
Симметричное распределение
Шкала В Распределение с положительной асимметрией
Рис. 3.8. Сравнение разных видов распределения
Данные, изображенные на панели А, имеют отрицательную асимметрию. На этом рисунке виден длинный хвост и перекос влево, вызванные наличием необычно малых значений. Эти крайне малые величины смещают среднее значение влево, и оно становится меньше медианы.
Данные, изображенные на панели Б, распределены симметрично. Левая и правая половины распределения являются своими зеркальными отражениями. Большие и малые величины уравновешивают друг друга, а среднее значение и медиана равны между собой.
Данные, изображенные на панели В, имеют положительную асимметрию. На этом рисунке виден длинный хвост и перекос вправо, вызванные наличием необычайно высоких значений. Эти слишком большие величины смещают среднее значение вправо, и оно становится больше медианы.
Показатели доходности 15 взаимных фондов с очень высоким уровнем риска приведены на точечной масштабированной диаграмме, показанной на рис. 3.2. Что можно сказать о виде распределения этих данных? Среднее значение равно 6,08, а медиана равна 6,50. Следовательно, поскольку среднее значение меньше медианы, распределение имеет отрицательную асимметрию.
Вычисление описательных статистик с помощью программы Microsoft Excel
Результаты вычисления количественных показателей распределения, полученные с помощью программы Microsoft Excel, приведены на рис. 3.9.
А I В I с „I 0 . Е F |
1 Описательные статистики для фондов с разным уровнем риска
2 Очень низкий Низкий Средний Высокий: Очень высокий
3 | 4 {Среднее 13.45 12.23421 11,20854 9.786585 8.185714286
5 Стандартная ошибка 1.103554862 0.411009 0.46148 0.525165 1,449733731
6 Медиана 12.2 11.75 10,55 9,5 9,6
' 7 ' Мода ‘Ж.Д 9.4 10,5 9,9 РНД
8^ Стандартное отклонение 2.703146315 3,583092 4.178877 4,755575 6.64351456
9 Дисперсия выборки 7.307 12 83855 17.46301 22.6155 44.13628571
10{Эксцесс 1.118103304 1,411879 1,478965 0,260427 -0.177778136
11 . Асимметричность 1.36586422 1,017377 0,965596 0,541774 -0,564394602
^Интервал 7.2 18.4 23,5 22.4 24,6
JJJ Минимум 11 6,6 2.8 0,5 -6.1
14 IМаксимум 18.2 25 26.3 22.9 18,5
15{Сумма 80.7 929,8 919.1 802,5 171,9
~16{Счет 6 76 82 82 21
17!Наибольший(1) 18.2 25 26.3 22,9 18,5
18 ]Наименыиий(1) 11 6.6 2.8 0.5 ^,1
Рис. 3.9. Описательные статистики пятилетней среднегодовой доходности фондов с очень низким, низким, средним, высоким и очень высоким уровнями риска, вычисленные с помощью программы Microsoft Excel
Обратите внимание на то, что программа Microsoft Excel вычисляет арифметическое среднее, медиану, моду, стандартное отклонение, дисперсию, размах, минимум, максимум и объем выборки, т.е. все статистики, рассмотренные в главе. Кроме того, программа Excel вычисляет стандартную ошибку, эксцесс и асимметричность. Стандартная ошибка (standard error) равна стандартному отклонению, деленному на квадратный корень объема выборки (эта характеристика рассматривается в главе 6). Асимметричность (skewness) характеризует отклонение от симметричности распределения и является функцией, зависящей от куба разностей между элементами выборки и средним значением. Эксцесс (kurtosis) представляет собой меру относительной концентрации данных вокруг среднего значения по сравнению с хвостами распределения и зависит от разностей между элементами выборки и средним значением, возведенных в четвертую степень. Эти показатели в книге не рассматриваются [2].
Анализ рис. 3.9 ясно демонстрирует различия между описательными статистиками доходности фондов с разными уровнями риска. Наибольшей среднегодовой доходности достигли фонды с низким уровнем риска, в то же время фонды с высоким уровнем риска имеют наименьшую доходность. Средняя пяти летняя доходность фондов с очень низким уровнем риска равна 13,45%, а медиана — 12,2% . Средняя пяти летняя доходность фондов с низким уровнем риска равна 12,234%, а медиана— 11,75%. Средняя пятилетняя доходность фондов со средним уровнем риска равна 11,209%, а медиана — 10,55%. Средняя пятилетняя доходность фондов с высоким уровнем риска равна 9,547%, а медиана— 9,4%. Средняя пятилетняя доходность фондов с очень высоким уровнем риска равна 6,08%, а медиана — 6,5% .
Аналогичные закономерности справедливы и для медиан. Например, пяти летняя среднегодовая доходность 50% взаимных фондов с низким уровнем риска не превышает 11,75%, пятилетняя среднегодовая доходность 50% взаимных фондов со средним уровнем риска не превышает 10,55%, а пятилетняя среднегодовая доходность 50% взаимных фондов с высоким уровнем риска не превышает 9,4%. Суммируя сказанное, можно утверждать: чем меньше уровень риска, тем меньше колебания доходности в соответствующей группе фондов. Стандартное отклонение среднегодовой доходности в группе фондов с очень низким уровнем риска равно 2,7, с низким уровнем риска — 3,583, со средним уровнем риска — 4,179, с высоким уровнем риска — 4,543 и с очень высоким уровнем риска — 6,62.
Процедуры Excel: вычисление описательных статистик
Для вычисления описательных статистик можно применить процедуру Анализ данных или статистические функции программы Excel. (Надстройка PHStat2 не предусматривает отдельной процедуры для вычисления описательных статистик, хотя некоторые процедуры, в частности, Stem-and-Leaf Display и Dot Scale Diagram также создают таблицы описательных статистик.)
Для того чтобы вычислить описательные статистики, характеризующие распределение пятилетней среднегодовой доходности взаимных фондов, следует открыть рабочую книгу Chapter 3.xls на листе ОВРФонды и выполнить одну из следующих процедур.
Вычисление описательных статистик. Выполните команду Анализ данных...^Описательная статистика и следуйте инструкциям, приведенным ниже.
1. Выберите команду Сервис^Анализ данных..., а затем — пункт Описательная статистика в списке Инструменты анализа. Щелкните на кнопке ОК.
2. В диалоговом окне Описательная статистика (см. иллюстрацию) выполните следующее.
2.1. Введите в окне редактирования Входной интервал диапазон 11:116.
2.2. Установите переключатель Группирование в положение По столбцам.
2.3. Установите флажок Метки в первой строке.
2.4. Установите переключатель Параметры вывода в положение Новый рабочий лист и введите имя листа, например Описательная статистика.
2.5. Установите флажок Итоговая статистика.
2.6. Установите флажки К-ый наименьший и К-ый наибольший, оставив неизменными значения, указанные в соответствующих окнах редактирования (1). Это позволит вычислить наименьший и наибольший элементы выборки.
2.7. Щелкните на кнопке ОК.
Эта процедура размещает на новом листе вычисленные описательные статистики, в частности, арифметическое среднее, медиану, моду, стандартное отклонение, выборочную дисперсию, максимальный и минимальный элементы, а также объем выборки. Кроме того, в этой таблице содержится стандартная ошибка, которую мы рассмотрим в главе б, а также показатель асимметрии, характеризующий вид распределения, и эксцесс (kurtosis) - показатель относительной концентрации значений в центре распределения по сравнению с ее хвостами [2].
Вычисление индивидуальных статистик. Для оценки среднего значения, вариации и формы распределения данных, содержащихся в заданном диапазоне ячеек, можно воспользоваться функциями, вызов которых имеет вид ®у\\К}\У1Я(диапазон ячеек)'.
срзнач (среднее арифметическое) мин мах
счёт (объем выборки) медиана мода
СТАНДОТКДОН (стандартное отклонение) дисп (дисперсия) скос
Например, чтобы вычислить среднее арифметическое значение пятилетней среднегодовой доходности 15 фондов с очень высоким уровнем риска, необходимо ввести в любую свободную ячейку любого листа рабочей книги Chapter 3.xls формулу =СРЗНАЧ (ОВРФонды! 12 :116). Если требуется вычислить первый и третий квартили, можно воспользоваться инструкциями, приведенными в разделе ЕН.3.2, избегая применения функции квартиль, которая для некоторых наборов данных вычисляет неправильные результаты.
Для вычисления стандартного отклонения и дисперсии генеральной совокупности предназначены функции стандотклонп и диспр со2012ответственно (см. раздел 3.3).
Chapter 3.xls
Таблица, изображенная на рис. 3.9, содержится в рабочей книге Chapter 3.xls на листе
РисЗ.9.
УПРАЖНЕНИЯ К РАЗДЕЛУ 3.2
Изучение основ
3.1. Ниже приведена выборка чисел, имеющая объем п = 5:
7 4 9 8 2
1. Вычислите выборочное среднее, медиану и моду.
2. Вычислите размах, межквартильный размах, выборочную дисперсию, стандартное отклонение и коэффициент вариации.
3. Опишите форму распределения этих данных.
3.2. Ниже приведена выборка чисел, имеющая объем п = 6:
7 4 9 7 3 12
1. Вычислите выборочное среднее, медиану и моду.
2. Вычислите размах, межквартильный размах, выборочную дисперсию, стандартное отклонение и коэффициент вариации.
3. Опишите форму распределения этих данных.
3.3. Ниже приведена выборка чисел, имеющая объем п = 7:
12 7 4 9 0 7 3
1. Вычислите выборочное среднее, медиану и моду.
2. Вычислите размах, межквартильный размах, выборочную дисперсию, стандартное отклонение и коэффициент вариации.
3. Опишите форму распределения этих данных.
3.4. Ниже приведена выборка чисел, имеющая объем п = 5: 7-5-879
1. Вычислите выборочное среднее, медиану и моду.
2. Вычислите размах, межквартильный размах, выборочную дисперсию, стандартное отклонение и коэффициент вариации.
3. Опишите форму распределения этих данных.
3.5. Ниже приведены две выборки чисел, имеющие объем п = 7:
Выборка 1: 10 232425
Выборка 2: 20 12 13 12 14 12 15
1. Для каждой выборки вычислите выборочное среднее, медиану и моду.
2. Сравните результаты и сформулируйте выводы.
3. Попарно сравните первые, вторые и последующие элементы каждой выборки. Кратко изложите ваши выводы, учитывая результаты, полученные при решении задачи 2.
4. Вычислите размах, межквартильный размах, выборочную дисперсию, стандартное отклонение и коэффициент вариации каждой выборки.
5. Опишите форму распределения данных в каждой из выборок.
6. Сравните результаты решения задач 4 и 5. Сформулируйте выводы.
7. Используя результаты решения задач 1-5, укажите свойства среднего значения, дисперсии и распределения данных, содержащихся в каждой из выборок.
3.6. Предположим, что норма прибыли конкретной акции за последние два года принимала значения 10 и 30%. Вычислите среднее геометрическое значение нормы прибыли. (Замечание', норма прибыли, равная 10%, записывается как 0,10, а 30% — записывается как 0,30.)
Применение понятий
Задачи 3.7-3.19 можно решать вручную либо с помощью программы Microsoft Excel.
3.7. Управляющий шинным заводом желает сравнить реальный внутренний диаметр двух сортов шин, каждый из которых должен быть равным 575 мм. Для оценки были выбраны по пять шин каждого сорта. Результаты измерения их внутренних диаметров, упорядоченные по возрастанию, приведены ниже.
Сорт X Сорт Y
568 570 575 578 584 573 574 575 577 578
1. Для каждого сорта шин вычислите выборочное среднее, медиану и моду.
2. Какой сорт шин имеет более высокое качество? Почему?
3. Каким был бы ваш ответ, если бы последним элементом выборки Y было число 588, а не 578? Обоснуйте свой ответ.
3.8. Следующая таблица содержит данные о жирности гамбургеров и куриного мяса, продаваемых в сети закусочных, FAST FOOD. XLS.
Гамбургеры
19 31 34 35 39 39 43
Куриное мясо
7 9 15 16 16 18 22 25 27 33 39
Источник: “Quick Bites”. Copyright © 2001 by Consumers Union of U. S. Inc. Цитируется no журналу Consumer Reports, March 2001, 46, с разрешения организации Consumer Union U. S., Inc., Yonkers, NY 10703-1057.
Для каждого из наборов данных выполните следующее задание.
1. Вычислите выборочное среднее, медиану, а также первый и третий квартили.
2. Вычислите выборочную дисперсию, стандартное отклонение, размах, межквартильный размах и коэффициент вариации.
3. Опишите форму распределения этих данных. Если данные смещены, объясните причину.
4. Что можно сказать о жирности гамбургеров и куриного мяса на основании проделанного анализа?
3.9. Средняя цена дома в США в 2001 году возросла до 147 500 долл., т.е. на 6% по сравнению с 2000 годом. Медиана цены дома увеличилась больше, чем медиана семейного дохода, поэтому для многих семей собственный дом оказался недостижимой мечтой. (Barbara Hagenbaugh, “Homes Too Expensive for Many”, www.usatoday.com, May 5, 2002.)
1. Как вы думаете, почему автор ссылается на медиану цены, а не на среднюю цену?
2. Опишите форму распределения семейного дохода. Опишите отношение между средним значением и медианой.
3.10. Файл данных filpE.XLS содержит случайную выборку показателей, характеризующих 30 акций, котируемых на Нью-Йоркской фондовой бирже. Для каждой из акций указана ее аббревиатура и отношение Р/Е (отношение рыночной цены акции компании к ее чистой прибыли в расчете на одну акцию), опубликованные 2 января 2003 года в журнале The Wall Street Journal. Отношение Р/Е вычисляется путем деления цены акции на момент закрытия торгов на прибыль, начисленную на каждую акцию компании в течение последних четырех кварталов. Акции со сверхвысоким отношением Р/Е называются переоцененными. В то же время акции с необычайно низким отношением Р/Е часто называются недооцененными.
1. Вычислите среднее арифметическое, медиану, моду, размах, дисперсию и стандартное отклонение отношения Р/Е.
2. Дайте интерпретацию среднего значения и разброса показателей Р/Е.
3. Используя текущий список акций, опубликованных в журналах The Wall Street Journal, USA Today или других источниках, создайте свою собственную случайную выборку из 30 показателей Р/Е и сравните ваши результаты с решениями задач 1 и 2.
4. Используя текущий список акций, опубликованных в журналах The Wall Street Journal, USA Today или других источниках, создайте свою собственную случайную выборку из 30 показателей Р/Е, характеризующих акции, котирующиеся на фондовой бирже NASDAQ, и сравните ваши результаты с решениями задач 1 и 2.
3.11. Из-за сокращения бюджетных субсидий в 2002-2003 учебном году многие государственные университеты в США повысили плату за обучение. (Mary Beth Маг-klein, “Public Universities Raise Tuition, Fees— and Ire”, USA Today, August 8, 2002, 1A~2A). ftcOLLEGECOST.XLS.
Университет Изменение платы за обучение, долл.
Университет штата Калифорния, г. Беркли 1 589
Университет штата Джорджия, г. Афины 593
Университет штата Иллинойс, г. Урбана-Шампань 1 223
Университет штата Канзас, г. Манхэттен 869
Университет Майна, г. Ороно 423
Университет Миссисипи, г. Оксфорд 1 720
Университет Нью-Хэмпшира, г. Дурхэм 708
Университет штата Огайо, г. Колумбус 1 425
Университет Южной Каролины, г. Колумбия 922
Университет штата Юта, г. Логан 308
1. Вычислите выборочное среднее, медиану, а также первый и третий квартили.
2. Вычислите выборочную дисперсию, стандартное отклонение, размах, межквартильный размах и коэффициент вариации.
3. Опишите форму распределения этих данных. Если данные смещены, объясните причину.
4. Сравните изменение платы за обучение в 2001-2002 и 2002-2003 учебных годах.
3.12. Некая компания разрабатывает программное обеспечение для управления сетями на основе повторного использования программного обеспечения. Иначе говоря, компания не разрабатывает новые проекты с нуля, а вместо этого на протяжении 10 лет поддерживает базу данных, в которой хранятся записи о повторно используемых компонентах, общий объем которых достигает 2 000 000 строк кода. Восемь аналитиков компании получили задание оценить степень повторного использования компонентов при разработке нового программного обеспечения. В следующей таблице приведены процентные доли повторно используемого кода в новом программном обеспечении, ft REUSE. XLS.
50 62,5 37,5 75,0 45,0 47,5 15,0 25,0
Источник: Rothenberger, М.А., and К. J. Dooley, “A Performance Measure for Software Reuse Projects”, Decision Sciences, 30 (Fall 1999): p. 1131-1153.
1. Вычислите среднее арифметическое, медиану и моду.
2. Вычислите размах, дисперсию и стандартное отклонение.
3. Дайте интерпретацию суммарных показателей, вычисленных при выполнении заданий 1 и 2.
3.13. Компания, производящая батарейки для ручных фонариков, создала выборку из 13 батареек, произведенных за смену, и подвергла их испытанию на длитель-
ность работы. Ниже приведено количество часов, которые проработала каждая батарейка до момента отказа.
^BATTERIES. XLS
342 426 317 545 264 451 1049 631 512 266 492 562 298
1. Вычислите среднее арифметическое, медиану и моду. Проанализируйте распределение времени работы батареек до момента отказа. Какой способ оценки средней длительности работы лучше, а какой хуже? Почему?
2. Как использовать эту информацию на производстве? Обоснуйте свой ответ.
3. Вычислите размах, дисперсию и стандартное отклонение.
4. Для многих распределений размах приблизительно равен шести стандартным отклонениям. Подтверждается ли это правило в данном случае? Если нет, попробуйте объяснить, почему.
5. Что бы вы посоветовали руководству завода, если бы оно захотело указать в рекламе, что их батарейки работают “не менее 400 часов”? (Замечание: на этот вопрос не существует правильного ответа — все зависит от толкования этого утверждения.)
6. Предположим, что первое значение равно 1 342, а не 342. Повторите упражнение 1 с новыми данными. Прокомментируйте новые результаты.
7. Выполните упражнения 3-5, заменив первое значение числом 1 342. Прокомментируйте новые результаты.
8. Каково распределение данных, если первое значение равно 342?
9. Каково распределение данных, если первое значение равно 1 342?
3.14. Филиал банка, расположенный в промышленном районе города, стремится повысить качество обслуживания клиентов во время обеда, с 12:00 до 13:00. На протяжении недели сотрудники записывали время ожидания клиентов, стоящих в очереди в течение обеденного перерыва (количество минут, прошедших от момента, когда клиент переступил порог филиала, до момента его обслуживания). Для оценки эффективности обслуживания создана выборка, содержащая данные о времени ожидания 15 клиентов.
^Ibanki.xls
4,21 5,55 3,02 5,13 4,77 2,34 3,54 3,20 4,50 6,10 0,38 5,12 6,46 6,19 3,79
1. Вычислите среднее арифметическое, медиану, первый и третий квартиль.
2. Вычислите дисперсию, стандартное отклонение, размах, межквартильный размах и коэффициент вариации.
3. Является ли распределение данных асимметричным? Если да, почему?
4. Когда клиент приходит в банк во время обеденного перерыва, он обычно спрашивает менеджера, сколько времени ему придется стоять в очереди. Менеджер отвечает: “Почти наверняка, не больше 5 минут”. Прав ли менеджер?
5. Допустим, что менеджер хотел бы гарантировать определенный уровень обслуживания клиентов в течение обеденного перерыва. Несвоевременное обслуживание клиента может компенсироваться небольшим вознаграждением за терпение или другим подарком. Как выбрать оптимальный предел времени, после которого клиенту полагается компенсация? Обоснуйте свой ответ.
3.15. Предположим, что другой филиал банка, расположенный в жилом районе города, стремится повысить качество обслуживания клиентов в конце недели: с 17:00 до 19:00 в пятницу. На протяжении недели сотрудники записывали время ожидания клиентов, стоящих в очереди в указанные часы (количество минут, прошедших от момента, когда клиент переступил порог филиала, до момента его обслуживания). Для оценки эффективности обслуживания создана выборка, содержащая данные о времени ожидания 15 клиентов.
ftBANK2.XLS
9,66 5,90 8,02 5,79 8,73 3,82 8,01 8,35 10,496,68 5,64 4,08 6,17 9,91 5,47
1. Вычислите среднее арифметическое, медиану, первый и третий квартиль.
2. Вычислите дисперсию, стандартное отклонение, размах, межквартильный размах и коэффициент вариации.
3. Является ли распределение данных асимметричным? Если да, почему?
4. Когда клиент приходит в банк вечером в пятницу, он обычно спрашивает менеджера, сколько времени ему придется стоять в очереди. Менеджер отвечает: “Почти наверняка, не больше 5 минут”. Прав ли менеджер?
5. Допустим, что менеджер хотел бы гарантировать определенный уровень обслуживания клиентов в вечерние часы в пятницу. Несвоевременное обслуживание клиента может компенсироваться небольшим вознаграждением за терпение или другим подарком. Как выбрать оптимальный предел времени, после которого клиенту полагается компенсация? Обоснуйте свой ответ.
6. Чем отличаются задачи 3.13 и 3.14?
3.16. Рыночная цена акций компании Microsoft Corporation в ноябре 2002 года возросла на 7,88% , а в декабре — упала на 10,3% .
1. Вычислите среднее арифметическое значение нормы прибыли.
2. Вычислите среднее геометрическое значение нормы прибыли.
3. Объясните разницу между этими результатами.
3.17. В 2000-2002 гг. стоимость акций сильно колебалась. В следующей таблице приведены индексы Dow Jones Industrial Index, Standard & Poor 500, Russell 2000 и Wilshire 5000 за этот период. STOCKRETURN . XLS.
Год DJIA SP500 RusselZOOO Wilshire5000
2002 -15,01 -22,1 -21,58 -20,90
2001 -5,44 -11,9 -1,03 -10,97
2000 -6,20 -9,1 -3,02 -10,89
1. Вычислите среднее геометрическое DJIA. значение нормы прибыли для индекса
2. Вычислите среднее геометрическое SP500. значение нормы прибыли для индекса
3. Вычислите среднее геометрическое Russel2000. значение нормы прибыли для индекса
4. Вычислите среднее геометрическое значение нормы прибыли для индекса
Wilshire5000.
5. Какую информацию можно извлечь, анализируя среднее геометрическое значение нормы прибыли для этих четырех индексов?
6. Сравните результаты решения задачи 5 с решением задач 3.18.4 и 3.19.4.
3.18. В 2000-2002 гг. доходность инвестиций сильно колебалась. В следующей таблице приведена общая доходность годовых и тридцатимесячных депозитных сертификатов, а также депозитных сертификатов денежного рынка за этот период. ^BANKRETURN. XLS.
Год Один год 30 месяцев Денежный рынок
2002 1,98 2,74 1,02
2001 3,60 3,97 1,73
2000 5,46 5,64 2,09
1. Вычислите среднее геометрическое значение нормы прибыли для годовых депозитных сертификатов.
2. Вычислите среднее геометрическое значение нормы прибыли для тридцатимесячных депозитных сертификатов.
3. Вычислите среднее геометрическое значение нормы прибыли для депозитных сертификатов денежного рынка.
4. Какую информацию можно извлечь, анализируя среднее геометрическое значение нормы прибыли для этих депозитных сертификатов?
5. Сравните результаты решения задачи 4 с решением задач 3.17.5 и 3.19.4.
3.19. В 2000-2002 гг. доходность инвестиций сильно колебалась. В следующей таблице приведена общая доходность платины, золота и серебра за этот период. ^METALRETURN . XLS.
Год Платина Золото Серебро
2002 24,5 24,5 5,5
2001 -21,3 1,2 -3,0
2000 -23,3 1,8 -5,9
1. Вычислите среднее геометрическое значение нормы прибыли для платины.
2. Вычислите среднее геометрическое значение нормы прибыли для золота.
3. Вычислите среднее геометрическое значение нормы прибыли для серебра.
4. Какую информацию можно извлечь, анализируя среднее геометрическое значение нормы прибыли для драгоценных металлов?
5. Сравните результаты решения задачи 4 с решением задач 3.17.5 и 3.18.4.
3.3. ВЫЧИСЛЕНИЕ ОПИСАТЕЛЬНЫХ СТАТИСТИК
ДЛЯ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ •
Среднее значение, разброс и форма распределения, рассмотренные в разделе 3.2, представляют собой характеристики, определяемые по выборке. Однако, если набор данных содержит числовые измерения всей генеральной совокупности, можно вычислить ее параметры. К числу таких параметров относятся математическое ожидание
(population mean), а также дисперсия (population variance) и стандартное отклонение генеральной совокупности (population standard deviation).
В табл. 3.1 приведены названия и пятилетняя среднегодовая доходность крупнейших облигационных фондов США. Эти данные представляют собой информацию о всей исследуемой генеральной совокупности таких фондов.
Таблица 3.1. Среднегодовая доходность пяти крупнейших облигационных фондов за пять лет, предшествующих 31 декабря 2002 года ^LARGEST BONDS.XLS
Фонд Среднегодовая доходность фонда за последние пять лет, %
Vanguard GNMA 7,3
Vanguard Total Bond Market Index 7,1
Franklin California Tax-Free Income 5,2
Bond Fund of America A 5,4
Vanguard Short-Term Corporate 6,2
Математическое ожидание
Математическое ожидание (population mean) обозначается греческой буквой р.
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ
Математическое ожидание равно сумме всех значений генеральной совокупности, деленной на объем генеральной совокупности N.
,v
м = (3.12)
гдер— математическое ожидание, X.— п-е наблюдение переменной X, —
/=1
сумма всех значений генеральной совокупности.
Для того чтобы вычислить среднюю доходность крупнейших облигационных фондов, образующих генеральную совокупность, представленную в табл. 3.1, применим формулу (3.12).
7,3 + 7,1 + 5,2+ 5,4 + 6,2 _ 31,2
Таким образом, пятилетняя среднегодовая доходность этих облигационных фондов равна 6,24%.
Дисперсия и стандартное отклонение генеральной совокупности
Дисперсия генеральной совокупности (population variance) обозначается символом о2.
ДИСПЕРСИЯ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ
Дисперсия генеральной совокупности равна сумме квадратов разностей между элементами генеральной совокупности и математическим ожиданием, деленной на объем генеральной совокупности.
Ж-И)2
<г=^—-------. (3.13)
где ц — математическое ожидание, X — п-е наблюдение переменной X, ^(Х; - —
/=1
сумма квадратов разностей между элементами генеральной совокупности и математическим ожиданием.
Стандартное отклонение генеральной совокупности (population standard deviation) равно квадратному корню, извлеченному из дисперсии генеральной совокупности. Оно обозначается греческой буквой ст.
СТАНДАРТНОЕ ОТКЛОНЕНИЕ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ
|ж-м)2
— (3-14)
Обратите внимание на то, что формулы для дисперсии и стандартного отклонения генеральной совокупности отличаются от формул для вычисления выборочной дисперсии и стандартного отклонения. При вычислении выборочных статистик S2 и S знаменатель дроби равен п-1 (см. формулы (3.9) и (3.10)), а при вычислении параметров о2 и <т — объему генеральной совокупности N.
Для вычисления дисперсии генеральной совокупности, представленной в табл. 3.2, воспользуемся формулой (3.13).
.1 (7,3-6,24)2 +(7,1-6,24)2 +(5,2-6,24)2 +(5,4-6,24)2 +(6,2-6,24)2
а " к ~ 5 ”
= = 0,7304
5
Таким образом, дисперсия доходности равна 0,7304 квадратных процентов. Поскольку дисперсия представляет собой величину измерения, возведенную в квадрат, ее трудно интерпретировать. Намного проще истолковать стандартное отклонение генеральной совокупности, обратив внимание на то, что формула (3.14) представляет собой квадратный корень, извлеченный из дисперсии.
Ж-и)2 ,_________
и = \И------= >/0,7304 = 0,8546 .
\ N
Следовательно, как правило, пятилетняя среднегодовая доходность колеблется вокруг среднего значения, равного 6,24% , на расстоянии, не превосходящем 0,8546% .
Эмпирическое правило
В большинстве ситуаций крупная доля наблюдений концентрируется вокруг медианы, образуя кластер. В наборах данных, имеющих положительную асимметрию, этот кластер расположен левее (т.е. ниже) математического ожидания, а в наборах, имеющих отрицательную асимметрию, этот кластер расположен правее (т.е. выше) математического ожидания. У симметричных данных математическое ожидание и медиана совпадают, а наблюдения концентрируются вокруг математического ожидания, формируя колоколообразное распределение. Если распределение не имеет ярко выраженной асимметрии, а данные концентрируются вокруг некоего центра тяжести, для оценки изменчивости можно применять эмпирическое правило (empirical rule).
Эмпирическое правило гласит: если данные имеют колоколообразное распределение, то приблизительно 68% наблюдений отстоят от математического ожидания не более чем на одно стандартное отклонение, приблизительно 95% наблюдений отстоят от математического ожидания не более чем на два стандартных отклонения и 99% наблюдений отстоят от математического ожидания не более чем на три стандартных отклонения.
Таким образом, стандартное отклонение, представляющее собой оценку среднего колебания вокруг математического ожидания, помогает понять, как распределены наблюдения, и идентифицировать выбросы. Из эмпирического правила следует, что для колоколообразных распределений лишь одно значение из двадцати отличается от математического ожидания больше, чем на два стандартных отклонения. Следовательно, значения, лежащие за пределами интервала р±2с, можно считать выбросами. Кроме того, только три из 1 000 наблюдений отличаются от математического ожидания больше чем на три стандартных отклонения. Таким образом, значения, лежащие за пределами интервала р ± Зо практически всегда являются выбросами. Для распределений, имеющих сильную асимметрию или не имеющих колоколообразной формы, можно применять эмпирическое правило Бьенамэ-Чебышева (Bienayme-Chebyshev), рассмотренное ниже.
ПРИМЕР 3.7. ПРИМЕНЕНИЕ ЭМПИРИЧЕСКОГО ПРАВИЛА
Известно, что средний вес 12-унциевой банки кока-колы равен 12,06 унций, а стандартное отклонение равно 0,02 унции. Кроме того, известно, что распределение генеральной совокупности имеет колоколообразную форму. Опишите распределение веса. Велика ли вероятность того, что банка содержит меньше 12 унций кока-колы?
РЕШЕНИЕ.
р ± с = 12,06 ± 0,02 = (12,04; 12,08),
р ± 2сг = 12,06 ± 2x0,02 - (12,02; 12,10),
р ± Зег = 12,06 ± 3x0,02 = (12,00; 12,12).
Применяя эмпирическое правило, получаем, что приблизительно 68% банок кока-колы имеют вес от 12,04 до 12,08 унций, приблизительно 95% банок содержит от 12,02 до 12,10 унций кока-колы, а вес приблизительно 99,7% банок колеблется от 12,00 до 12,12 унций. Таким образом, вероятность того, что банка содержит меньше 12 унций кока-колы, весьма невелика.
Правило Бьенамэ-Чебышева
Более ста лет назад математики Бьенамэ и Чебышев [1] независимо друг от друга открыли полезное свойство стандартного отклонения. Они обнаружили, что для любого набора данных, независимо от формы распределения, процент наблюдений, лежащих на расстоянии не превышающем k стандартных отклонений от математического ожидания, не меньше
(1-1//г2) х 100%.
Рассмотрим случай k = 2. Правило Бьенамэ-Чебышева гласит, что как минимум (1—(1 /2)2) х 100% = 75% наблюдений должно лежать в интервале ц ± 2сг. Это правило справедливо для любого k, превышающего единицу.
Правило Бьенамэ-Чебышева. По крайней мере 3/4, или 75%, всех наблюдений из любого набора данных содержится в интервале р±2сг, по крайней мере 8/9, или 88,89%, наблюдений содержится в интервале р ± Зег, и как минимум 15/16, или
93,75% , наблюдений содержится в интервале р ± 4сг.
Правило Бьенамэ-Чебышева носит весьма общий характер и справедливо для распределений любого вида. Оно указывает минимальное количество наблюдений, расстояние от которых до математического ожидания не превышает заданной величины. Однако, если распределение имеет колоколообразную форму, эмпирическое правило более точно оценивает концентрацию данных вокруг математического ожидания. Эти два правила сформулированы в табл. 3.2.
Таблица 3.2. Сколько данных лежит вокруг математического ожидания
Процент наблюдений, попадающих в интервал
Интервал Правило Бьенамэ-Чебышева Эмпирическое правило
(р-ст, р + ст) Как минимум 0% Приблизительно 68%
(ц - 2ст, ц + 2ст) Как минимум 75% Приблизительно 95%
(ц - Зст, ц + Зст) Как минимум 88,89% Приблизительно 99,7%
ПРИМЕР 3.8. ПРИМЕНЕНИЕ ПРАВИЛА БЬЕНАМЭ-ЧЕБЫШЕВА
В примере 3.7 было известно, что математическое ожидание генеральной совокупности 12-унциевых банок кока-колы равно 12,06 унций, а стандартное отклонение — 0,02 унции. Однако нам неизвестна форма распределения веса банок кока-колы. Опишите это распределение. Велика ли вероятность того, что банка содержит меньше 12 унций кока-колы?
РЕШЕНИЕ.
ц±ст= 12,06 ±0,02 = (12,04; 12,08),
р±2о = 12,06 ±2x0,02 = (12,02; 12,10), ц± Зст =12,06 ±3x0,02 = (12,00; 12,12).
Поскольку форма распределения нам неизвестна, мы не можем использовать эмпирическое правило. Применяя вместо него правило Бьенамэ-Чебышева, мы не можем сказать ничего определенного об интервале (12,04, 12,08). Мы можем лишь утверждать, что в интервале (12,02, 12,10) лежат не менее 75% банок, а в интервале (12,00, 12,12)— не менее 88,89%. Таким образом, количество банок, содержащих меньше 12 унций кока-колы, лежит в пределах от 0 до 11,11% . и
УПРАЖНЕНИЯ К РАЗДЕЛУ 3.3
Изучение основ
3.20. Ниже приведена генеральная совокупность, имеющая объем N = 10: 75 11 8362198
1. Вычислите математическое ожидание.
2. Вычислите стандартное отклонение генеральной совокупности.
3.21. Ниже приведена генеральная совокупность, имеющая объем N = 10: 756664863
1. Вычислите математическое ожидание.
2. Вычислите стандартное отклонение генеральной совокупности.
Применение понятий
Задачи 3.22-3.27 можно решать вручную либо с помощью программы Microsoft Excel
3.22. Ниже приведены данные об уплате квартального налога с оборота (тыс. долл.), представленные 50 компаниями в налоговую инспекцию поселка Фейр-Лейк за период, завершающийся в конце марта 2003 г. ^ТАХ. XLS.
10,3 11,1 9,6 9,0 14,5
13,0 6,7 11,0 8,4 10,3
13,0 11,2 7,3 5,3 12,5
8,0 11,8 8,7 10,6 9,5
ИД 10,2 11,1 9,9 9,8
11,6 15,1 12,5 6,5 7,5
10,0 12,9 9,2 10,0 12,8
12,5 9,3 10,4 12,7 10,5
9,3 11,5 10,7 11,6 7,8
10,5 7,6 10,1 8,9 8,6
1. Представьте данные в виде упорядоченного массива или диаграммы “ствол-и-листья”.
2. Вычислите математическое ожидание.
3. Вычислите дисперсию и стандартное отклонение генеральной совокупности.
4. Сколько компаний платят налог с оборота, который отличается от среднего не более чем на одно стандартное отклонение?
5. Сколько компаний платят налог с оборота, который отличается от среднего не более чем на два стандартных отклонения?
6. Сколько компаний платят налог с оборота, который отличается от среднего не более чем на три стандартных отклонения?
7. Не удивил ли вас ответ на вопрос 4? (Подсказка: сравните ваши ответы с результатами, полученными по эмпирическому правилу.)
3.23. Рассмотрим генеральную совокупность, состоящую из 1 024 взаимных фондов, инвестирующих средства преимущественно в крупные компании. Известно, что математическое ожидание р среднегодовой доходности этих фондов равно 8,20%, а стандартное отклонение ст— 2,75%. Предположим также, что среднегодовая доходность фондов колеблется в пределах от -2,0% до 17,1%, а первый, Qu и третий, Q3, квартили равны 5,5 и 10,5 соответственно.
1. Применяя эмпирическое правило, определите, сколько фондов имеют доходность, отличающуюся от средней не более чем на одно стандартное отклонение.
2. Применяя эмпирическое правило, определите, сколько фондов имеют доходность, отличающуюся от средней не более чем на два стандартных отклонения.
3. Применяя правило Бьенамэ-Чебышева, определите, сколько фондов имеют доходность, отличающуюся от средней не более чем на одно стандартное отклонение.
4. Применяя правило Бьенамэ-Чебышева, определите, сколько фондов имеют доходность, отличающуюся от средней не более чем на два стандартных отклонения.
5. Применяя правило Бьенамэ-Чебышева, определите, сколько фондов имеют доходность, отличающуюся от средней не более чем на три стандартных отклонения.
6. Применяя правило Бьенамэ-Чебышева, определите, между какими величинами колеблется доходность 93,75% фондов.
3.24. В таблице приведены данные о 52-недельной доходности пяти крупнейших облигационных фондов ^LARGEST BONDS 1 YR.XLS.
Фонд Годовая доходность, %
Pimco Inst TotRet 9,5
Vanguard GNMA 8,6
Vanguard TotBoard 8,1
Pimco Admin TotRet 9,3
Frank Temp CA 5,7
Источник: цитируется по журналу Wall Street Journal, February 27, 2003.
1. Вычислите математическое ожидание для генеральной совокупности, состоящей из пяти крупнейших облигационных фондов. Дайте интерпретацию этого параметра.
2. Вычислите дисперсию и стандартное отклонение генеральной совокупности, состоящей из пяти крупнейших облигационных фондов. Дайте интерпретацию этих параметров.
3. Сильно ли колеблется доходность облигационных взаимных фондов?
3.25. В файле ^ENERGY .XLS приведены данные о потреблении электроэнергии (кВт/ч) на душу населения для каждого из 50 штатов и округа Колумбия за прошлый год.
1. Представьте данные в виде диаграммы “ствол-и-листья”, гистограммы или процентного полигона.
2. Вычислите математическое ожидание.
3. Вычислите дисперсию и стандартное отклонение генеральной совокупности.
4. В скольких штатах среднедушевое потребление электроэнергии отличается от среднего не более чем на одно стандартное отклонение, на два стандартных отклонения и на три стандартных отклонения?
5. Не удивил ли вас ответ на вопрос 4? (Подсказка', сравните ваши ответы с результатами, полученными по эмпирическому правилу.)
6. Удалите из генеральной совокупности округ Колумбия и повторите задания 1-5. Как изменились результаты?
3.26. В таблице приведены данные о 52-недельной доходности десяти крупнейших акционерных фондов за период, истекший 26 февраля 2003 года.
^BIGSTOCKFUNDS.XLS.
Фонд Годовая доходность, %
Vanguard 500 -24,1
Fidelity Magellan -24,3
American ICAA -17,6
American WshA -19,8
American GrwthA -21,6
Fidelity Contrafd -13,9
Fidelity Gwthlnc -20,9
American Eupac -17,1
American PerA -20,0
American Funds CI A: Income Fund of America -6,6
Источник: цитируется по журналу Wall Street Journal, February 27, 2003.
1. Вычислите математическое ожидание для генеральной совокупности, состоящей из десяти крупнейших акционерных фондов. Дайте интерпретацию этого параметра.
2. Вычислите дисперсию и стандартное отклонение генеральной совокупности, состоящей из десяти крупнейших облигационных фондов. Дайте интерпретацию этих параметров.
3. Примените эмпирическое правило или правило Бьенамэ-Чебышева и объясните вариацию данных.
4. Содержатся ли выбросы в представленном наборе данных?
5. Сравните результаты решения задач 1 и 2 с результатами, полученными для пяти облигационных фондов (табл. 3.1). Какие фонды получают более высокий средний годовой доход? Доходность каких фондов колеблется сильнее?
3.27. Насколько велики компании, учитываемые в промышленном индексе Доу-Джонса? Сильно ли колеблется их размер? Для того чтобы ответить на эти вопросы, можно вычислить величину их рыночной капитализации. Эта величина равна общей рыночной стоимости всех акций компании (т.е. равна произведению количества всех акций на текущую рыночную стоимость одной акции). Данные, представленные в файле ft^DOW CAPITAL.XLS, характеризуют рыночную капитализацию 30 компаний, учитываемых в промышленном индексе Доу-Джонса (www . money. cnn . com, 27 февраля 2003 года).
1. Вычислите математическое ожидание для генеральной совокупности. Дайте интерпретацию этого параметра.
2. Вычислите дисперсию и стандартное отклонение генеральной совокупности. Дайте интерпретацию этих параметров.
3. Примените эмпирическое правило или правило Бьенамэ-Чебышева и объясните вариацию данных.
4. Содержатся ли выбросы в представленном наборе данных? Обоснуйте свой ответ.
3.4. АНАЛИЗ ДАННЫХ
Основные характеристики (среднее значение, разброс и форма распределения) позволяют описать свойства данных и перейти к более глубоким исследованиям. Довольно часто для анализа данных применяется подход, основанный на пятерке базовых показателей и построении блочной диаграммы [3, 4].
Пять базовых показателей
Пятерка базовых показателей (five-number summary), обеспечивающих наиболее точную оценку вида распределения, состоит из следующих характеристик:
X.., Q., медиана, Q3, Х>илх.
Если данные распределены совершенно симметрично, между пятью базовыми показателями наблюдаются зависимости, приведенные во врезке 3.3.
ВРЕЗКА 3.3. ПРИМЕНЕНИЕ ПЯТИ БАЗОВЫХ ПОКАЗАТЕЛЕЙ ДЛЯ ОЦЕНКИ СИММЕТРИЧНОСТИ РАСПРЕДЕЛЕНИЯ
• Расстояние от Хш.в до медианы равно расстоянию от медианы до Х>пвх.
• Расстояние от Xmin до равно расстоянию от Qs до Х|пах.
• Расстояние от QT до медианы равно расстоянию от медианы до Q3.
Зависимости, которые возникают между элементами пятерки показателей, когда данные распределены несимметрично, описаны во врезке 3.4.
ВРЕЗКА 3.4. ПРИМЕНЕНИЕ ПЯТИ БАЗОВЫХ ПОКАЗАТЕЛЕЙ ДЛЯ ОЦЕНКИ АСИММЕТРИЧНОСТИ РАСПРЕДЕЛЕНИЯ
• Если распределение имеет положительную асимметрию, расстояние от ХиП1 до медианы меньше расстояния от медианы до Х1пах.
• Если распределение имеет положительную асимметрию, расстояние от Q3 до Хпяк больше, чем от Xjniii до Q1.
♦ Если распределение имеет отрицательную асимметрию, расстояние от Хт.и до медианы больше расстояния от медианы до Xi(wx.
• Если распределение имеет отрицательную асимметрию, расстояние от Q3 до Хтпх меньше, чем от Хиш до Q,.
Пятерка базовых показателей, характеризующих распределение доходности 15 взаимных фондов с очень высоким уровнем риска, содержит вычисленные ранее значения: медиана = 6,5, первый квартиль =-0,7, третий квартиль = 9,8. Кроме того, наименьший показатель доходности равен -6,1, а наибольший — 18,5. Следовательно, пять базовых показателей имеют следующий вид:
-6,1 -0,7 6,5 9,8 18,5
Применим их для оценки симметричности распределения. Расстояние от медианы до Xinax (18,5 - 6,5 = 12) приблизительно равно расстоянию от Xmin до медианы (6,5 - (-6,1) = = 12,6). Однако расстояние от Q3 до Хтах (18,5 - 9,8 = 8,7) превышает расстояние от Хшш до Qj (-0,7 - (-6,1) = 5,4). Следовательно, распределение пяти летней среднегодовой доходности фондов с очень высоким уровнем риска имеет слабую положительную асимметрию.
Блочная диаграмма
Блочная диаграмма (box-and-whisker diagram) представляет собой удобное средство для изображения пяти базовых показателей. На рис. 3.10 приведена блочная диаграмма, иллюстрирующая показатели среднегодовой доходности 15 фондов с очень высоким уровнем риска.
Рис. 3.10. Блочная диаграмма, иллюстрирующая показатели среднегодовой доходности 15 фондов с очень высоким уровнем риска
Вертикальная линия, проведенная внутри прямоугольника, отмечает медиану. Левая сторона прямоугольника соответствует первому квартилю, Qlt а правая сторона — третьему квартилю, Q3. Таким образом, прямоугольник содержит средние 50% элементов выборки. Младшие 25% данных изображаются в виде линии (так называемый ус), соединяющей левую сторону прямоугольника с наименьшим выборочным значением Х,^. Следовательно, старшим 25% данных соответствует линия, соединяющая правую сторону прямоугольника с наибольшим выборочным значением Хтах.
ИНТЕРПРЕТАЦИЯ БЛОЧНОЙ ДИАГРАММЫ
Блочная диаграмма, представленная на рис. 3.10, демонстрирует, что показатели среднегодовой доходности 15 фондов с очень высоким уровнем риска имеют практически симметричное распределение, поскольку расстояние между медианой и наибольшим значением приблизительно равно расстоянию между наименьшим значением и медианой. Однако другие характеристики распределения указывают на несимметричность. Правый ус диаграммы длиннее левого, поскольку выборка содержит выброс, равный 18,5, а медиана расположена ближе к правой стороне диаграммы, чем к левой.
На рис. 3.11 изображены четыре типа распределений, а также соответствующие им блочные диаграммы и полигоны.
Колоколообразное распределение
Панель Б Распределение с отрицательной асимметрией
Панель В Распределение с положительной асимметрией
Панель Г
Прямоугольное распределение
Рис. 3.11. Четыре гипотетических распределения, исследованных с помощью блочной диаграммы и соответствующих полигонов. Область, расположенная под каждым полигоном, разбита квартилями, входящими в пятерку базовых показателей
Если данные распределены совершенно симметрично, как показано на рис. 3.10, панели А и Г, среднее выборочное значение и медиана совпадают. Кроме того, длина левого уса равна длине правого, а линия медианы проходит через середину прямоугольника.
Если распределение данных имеет отрицательную асимметрию, как показано на рис. 3.11, панель Б, среднее выборочное значение смещается вдоль левого хвоста. Отрицательная асимметрия проявляется в виде высокой концентрации данных в правой половине шкалы. При этом 75% всех данных расположены между левой стороной прямоугольника (первый квартиль, и концом правого уса (наибольшее выборочное значение, Хшах). Следовательно, вдоль длинного левого уса распределены всего 25% данных. Это свидетельствует о сильной асимметрии распределения.
Если распределение данных имеет положительную асимметрию, как показано на рис. 3.11, панель В, пик распределения смещается влево. Теперь 75% всех данных расположены между началом левого уса (наименьшее выборочное значение, Хшп) и правой стороной прямоугольника (третий квартиль, Q3). Остальные 25% данных распределены вдоль длинного правого уса.
С помощью программы Microsoft Excel можно одновременно создавать несколько параллельных блочных диаграмм. На рис. 3.12 показаны блочные диаграммы, иллюстрирующие показатели среднегодовой доходности фондов с очень низким, низким, средним, высоким и очень высоким уровнями риска.
Рис. 3.12. Блочные диаграммы, иллюстрирующие показатели среднегодовой доходности фондов с очень низким, низким, средним, высоким и очень высоким уровнями риска (построены с помощью программы Microsoft Excel)
Изображение нескольких диаграмм на одном рисунке намного облегчает анализ и сравнение данных. Доходность всех фондов, кроме фондов с очень высоким уровнем риска, имеет положительную асимметрию. Как и следовало ожидать, фонды с очень высоким уровнем риска характеризуются большим разбросом доходности, о чем свидетельствуют более вытянутый прямоугольник и длинные усы. Доходность фондов с очень низким и низким уровнями риска имеет наименьший разброс. Кроме того, медиана и квартили доходов взаимных фондов, избегающих риска (т.е. имеющих очень низкий, низкий и средний уровень риска) являются наибольшими, а у рискованных фондов (с высоким и очень высоким уровнем риска) — наименьшими. Итак, данные, относящиеся к периоду 1997-2001 гг. свидетельствуют: чем меньше риск, тем выше эффективность фонда.
Процедуры Excel: создание блочных диаграмм
Чтобы создать блочную диаграмму, можно воспользоваться одним из двух способов. Если исходные данные не подвергались предварительной обработке, можно применить специальную процедуру надстройки PHStat2. Если же на основе данных уже были вычислены пять базовых показателей, их можно занести на лист Блочная^диаграмма рабочей книги Chapter 3.xls и создать диаграмму самостоятельно.
В программе Microsoft Excel не предусмотрена процедура автоматического построения блочной диаграммы по исходным данным. Кроме того, соответствующая процедура надстройки PHStat2 и рабочий лист Блочная_диаграмма используют тонкие свойства программы Microsoft Excel, которые изначально предназначались для решения других задач.
Существует два способа построить блочную диаграмму, изображенную на рис. 3.10.
Применение Excel в сочетании с надстройкой PHStat2
Чтобы создать на новом рабочем листе блочную диаграмму и таблицу, содержащую пять базовых показателей, можно выполнить процедуру Box-and-Wisker Plot надстройки PHStat2. Для этого следует открыть лист ОВРФонды рабочей книги Chapter 3. xls и выполнить следующие инструкции.
1. Выбрать команду РНStatч>Descriptive Statistics^ Box-and-Whisker Plot... (PHStat^OnncaTenbHbie статистики ^Блочная диаграмма...).
2. В диалоговом окне Box-and-Whisker Plot сделать следующее (см. иллюстрацию).
2.1. Ввести в окне редактирования Raw Data Cell Range (Диапазон исходных данных) диапазон 11:116.
2.2. Установить переключатель Input Options (Параметры ввода) в положение Single Group Variable (Отдельная группа).
2.3. Ввести в окне редактирования Title (Заголовок) название диаграммы.
2.4. Щелкнуть на кнопке ОК.
Box-and-Whisker Plot {5<|
Data
Raw Data Cell Range: [иТпб
P First cell contains label
Input Options
<* Single Group Variable
C Multiple Groups - Unstacked
C Multiple Groups - Stacked
Output Options -..............
Title: [фонды с очень высоким уровнем риска
Г~ Five-Number Summary
___Не|р I Canc![
С помощью этой процедуры можно также построить блочную диаграмму для данных, содержащих несколько групп. Например, чтобы создать диаграмму, изображенную на рис. 3.12, необходимо открыть рабочую книгу Chapter 3. xls на листе Данные и следовать инструкциям, приведенным ниже.
1. Выполнить команду PHStat4>Descriptive Statistics^Box-and-Whisker Plot....
2. Находясь в диалоговом окне Box-and-Whisker Plot, сделать следующее.
2.1. Ввести в окне редактирования Raw Data Cell Range диапазон II: 12 60.
2.2. Установить переключатель Input Options в положение Multiple Group - Stacked (Сгруппированные данные).
2.3. В доступное окно Grouping Variable Range (Диапазон сгруппированных данных) ввести ссылки К1 :К2 60.
2.4. Ввести в окне редактирования Title (Заголовок) название диаграммы.
2.5. Щелкнуть" на кнопке ОК.
Применение Excel
Если пять базовых показателей уже вычислены, откройте лист Блочная_диаграмма в рабочей книге Chapter 3.xls. Этот рабочий лист содержит демонстрационные данные (пять базовых показателей для пятилетней среднегодовой доходности взаимных фондов с очень высоким уровнем риска), позволяющие создать блочную диаграмму. Введите свои пять базовых показателей в закрашенные ячейки В2 :В6.
Если блочную диаграмму нужно поместить на отдельном рабочем листе, щелкните правой кнопкой мыши на фоне диаграммы и выберите в появившемся контекстном меню команду Размещение.... Затем, находясь в диалоговом окне Размещение диаграммы, необходимо установить переключатель Поместить диаграмму на листе в положение Отдельном, ввести информативное название диаграммы и щелкнуть на клавише ОК.
Chapter 3.xls
Диаграммы, изображенные на рис. 3.10 и 3.12, содержатся в рабочей книге Chapter 3 .xls на листах РисЗ.Ю и Рис3.12.
УПРАЖНЕНИЯ К РАЗДЕЛУ 3.4
Изучение основ
3.28. Ниже приведена выборка чисел, имеющая объем п = 5:
7 4 9 8 2
1. Вычислите пять базовых показателей.
2. Постройте блочную диаграмму и опишите форму распределения этих данных.
3. Сравните результаты с решением задачи 3.1.3.
3.29. Ниже приведена выборка чисел, имеющая объем п = 6:
7 4 9 7 3 12
1. Вычислите пять базовых показателей.
2. Постройте блочную диаграмму и опишите форму распределения этих данных.
3. Сравните результаты с решением задачи 3.2.3.
3.30. Ниже приведена выборка чисел, имеющая объем п = 7:
12 7 4 9 0 7 3
1. Вычислите пять базовых показателей.
2. Постройте блочную диаграмму и опишите форму распределения этих данных.
3. Сравните результаты с решением задачи 3.3.3.
3.31. Ниже приведена выборка чисел, имеющая объем п = 5:
7-5-8 79
1. Вычислите пять базовых показателей.
2. Постройте блочную диаграмму и опишите форму распределения этих данных.
3. Сравните результаты с решением задачи 3.4.3.
Применение понятий
Задачи 3.32-3.38 можно решать вручную или с помощью программы Microsoft Excel.
3.32. Компания, производящая батарейки для ручных фонариков, создала выборку из 13 батареек, произведенных за смену, и подвергла их испытанию на длительность работы. Ниже приведено количество часов, которые проработала каждая батарейка до момента отказа. ^BATTERIES. XLS.
342 426 317 545 264 451 1049 631 512 266 492 562 298
1. Вычислите пять базовых показателей.
2. Постройте блочную диаграмму и опишите форму распределения этих данных.
3. Сравните результаты с решением задачи 3.13.8.
3.33. Файл данных ftpE.XLS содержит случайную выборку показателей, характеризующих 30 акций, котируемых на Нью-Йоркской фондовой бирже. Для каждой акции указана ее аббревиатура и отношение Р/Е (отношение рыночной цены акции компании к ее чистой прибыли в расчете на одну акцию), опубликованные 2 января 2003 года в журнале The Wall Street Journal. Отношение Р/Е вычисляется путем деления цены акции на момент закрытия торгов на прибыль, начисленную на каждую акцию компании в течение последних четырех кварталов.
Акции со сверхвысоким отношением Р/Е называются переоцененными, а акции с необычно низким отношением Р/Е — недооцененными.
1. Вычислите пять базовых показателей.
2. Постройте блочную диаграмму и опишите вид распределения этих данных.
3.34. Данные, приведенные в файле BANKCOST 1. XLS, содержат количество чеков, возвращенных 23 банками своим вкладчикам ввиду отсутствия средств на счете. (Минимальный размер вклада не должен быть ниже 100 долл.) Файл BANKCOST2 . XLS содержит величину ежемесячной платы за услуги (в долларах), взимаемых 26 банками со своих клиентов, если величина счета клиента не превышает установленного минимума, равного 1 500 долл.
Возвращенные чеки
ft^BANKCOSTl.XLS
26 28 20 20 21 22 25 25 18 25 15 20
18 20 25 25 22 30 30 30 15 20 29
Ежемесячная оплата
OBANKC0ST2 .XLS
12 85566 10 10 97 10 7750 10 69 12 05 10 8559
Источник данных: справочник “The New Face of Banking” Copyrigh © 2000, изданный компанией Consumers Union of U. S. Ink., Yonkers, NY. Адаптирован с разрешения журнала Consumer Reports, июнь 2000.
1. Вычислите пять базовых показателей, характеризующих количество чеков, возвращенных 23 банками своим вкладчикам ввиду отсутствия средств на счете.
2. Постройте блочную диаграмму и опишите форму распределения сумм возвращенных чеков.
3. Вычислите пять базовых показателей, характеризующих величину ежемесячной платы за услуги.
4. Постройте блочную диаграмму и опишите форму распределения ежемесячной оплаты.
5. Сравните результаты, полученные при решении задач 1 и 2, с решениями задач 3 и 4.
3.35. Данные, приведенные ниже, содержат величину калорий, получаемых потребителями гамбургеров и куриного мяса в сети ресторанов быстрого питания. Ofastfood.xls
Гамбургеры
19 31 34 35 39 39 43
Куриное мясо
7 9 15 16 16 18 22 25 27 33 39
Источник данных: “Quick Bites?" © 2001 by Consumers Union of U. S. Ink., Yonkers, NY. Цитируется no журналу Consumer Reports, March 2001, 46 с разрешения организации Consumers Union of U. S. Ink., Yonkers, NY 10703-1057.
1. Вычислите пять базовых показателей, характеризующих количество калорий, получаемых потребителями гамбургеров.
2. Постройте блочную диаграмму и опишите форму распределения калорийности гамбургеров.
3. Вычислите пять базовых показателей, характеризующих количество калорий, получаемых потребителями куриного мяса.
4. Постройте блочную диаграмму и опишите форму распределения калорийности куриного мяса.
5. Сравните результаты, полученные при решении задач 1 и 2, с решениями задач 3 и 4. Укажите различия и сходство между распределениями количества калорий в гамбургерах и курином мясе.
3.36. Из-за сокращения бюджетных субсидий в 2002-2003 учебном году многие государственные университеты в США повысили плату за обучение. (Mary Beth Маг-klein, “Public Universities Raise Tuition, Fees — and Ire”, USA Today, August 8, 2002, 1A-2A.) Изменение платы за обучение, проживание в общежитии и питание по сравнению с 2001-2002 гг. приведено в файле ^COLLEGECOST. XLS.
Университет Изменение платы за обучение, долл.
Университет штата Калифорния, г. Беркли 1 589
Университет штата Джорджия, г. Афины 593
Университет штата Иллинойс, г. Урбана-Шампань 1 223
Университет штата Канзас, г. Манхэттен 869
Университет Майна, г. Ороно 423
Университет Миссисипи, г. Оксфорд 1 720
Университет Нью-Хэмпшира, г. Дурхэм 708
Университет штата Огайо, г. Колумбус 1 425
Университет Южной Каролины, г. Колумбия 922
Университет штата Юта, г. Логан 308
1. Вычислите пять базовых показателей, характеризующих распределение изменения платы за учебу.
2. Постройте блочную диаграмму и опишите форму распределения этих данных.
3.37. Некая компания разрабатывает программное обеспечение для управления сетями на основе повторного использования программного обеспечения. Иначе говоря, компания не разрабатывает новые проекты с нуля, а вместо этого на протяжении 10 лет поддерживает базу данных, в которой хранятся записи о повторно используемых компонентах, общий объем которых достигает 2 000 000 строк кода. Восемь аналитиков компании получили задание оценить степень повторного использования компонентов при разработке нового программного обеспечения. В следующей таблице приведены процентные доли повторно используемого кода в новом программном обеспечении. ^REUSE. XLS.
50 62,5 37,5 75,0 45,0 47,5 15,0 25,0
Источник: Rothenberger, М.А., and К. J. Dooley, “A Performance Measure for Software Reuse Projects”, Decision Sciences, 30 (Fall 1999): p. 1131-1153.
1. Вычислите пять базовых показателей, характеризующих распределение процентных долей повторно используемого кода.
2. Постройте блочную диаграмму и опишите форму распределения этих данных.
3.38. Филиал банка, расположенный в промышленном районе города, стремится повысить качество обслуживания клиентов во время обеда, с 12:00 до 13:00. На протяжении недели сотрудники записывали время ожидания клиентов, стоящих в очереди в течение обеденного перерыва (количество минут, прошедших от момента, когда клиент переступил порог филиала, до момента его обслуживания). Для оценки эффективности обслуживания создана выборка, содержащая данные о времени ожидания 15 клиентов.
^BANKl .XLS
4,21 5,55 3,02 5,13 4,77 2,34 3,54 3,20 4,50 6,10 0,38 5,12 6,46 6,19 3,79
Допустим, что другой филиал банка, расположенный в жилом районе города, стремится повысить качество обслуживания клиентов в конце недели: с 17:00 до 19:00 в пятницу. На протяжении недели сотрудники записывали время ожидания клиентов, стоящих в очереди в указанные часы (количество минут, прошедших от момента, когда клиент переступил порог филиала, до момента его обслуживания). Для оценки эффективности обслуживания создана выборка, содержащая данные о времени ожидания 15 клиентов.
^BANK2 .XLS
9,66 5,90 8,02 5,79 8,73 3,82 8,01 8,35 10,496,68 5,64 4,08 6,17 9,91 5,47
1. Вычислите пять базовых показателей, характеризующих распределение времени ожидания клиентов филиала, расположенного в промышленном районе.
2. Постройте блочную диаграмму и опишите форму распределения этих данных, характеризующих работу филиала в промышленном районе.
3. Вычислите пять базовых показателей, характеризующих распределение времени ожидания клиентов филиала, расположенного в жилом районе.
4. Постройте блочную диаграмму и опишите форму распределения этих данных, характеризующих работу филиала в жилом районе.
5. Сравните результаты, полученные при решении задач 1 и 2, с решениями задач 3 и 4. Укажите различия и сходство между распределениями времени ожидания клиентов в филиалах банка.
3.5. КОВАРИАЦИЯ И КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ
В разделе 2.5 рассмотрены диаграммы разброса, иллюстрирующие двумерные числовые данные. Теперь мы изучим два количественных показателя, характеризующих силу зависимости между двумя переменными — ковариацию и коэффициент корреляции. Ковариация (covariance) оценивает силу линейной зависимости между двумя числовыми переменными X и У.
ВЫБОРОЧНАЯ КОВАРИАЦИЯ
cov(%,y) = -s!-----. (3.15)
Проиллюстрируем вычисление ковариации следующим примером.
ПРИМЕР 3.9. ВЫЧИСЛЕНИЕ ВЫБОРОЧНОЙ КОВАРИАЦИИ
Рассмотрим пятилетнюю среднегодовую доходность и долю затрат в фондах с очень низким уровнем риска, представленные в табл. 3.3.
Таблица 3.3. Пятилетняя среднегодовая доходность и доля затрат взаимных фондов с очень низким уровнем риска
Пятилетняя доходность Доля затрат
11,0 0,59
18,2 1,09
15,1 1,00
12,3 0,81
12,0 0,80
12,1 0,78
На рис. 3.13 приведены результаты расчетов, выполненных с помощью программы Microsoft Excel.
А I В I С IDI | Е | F I
1 Пятилетняя доходность Издержки (X-XBarj(Y-YBar)
2 11.0 0,59 0,62475
18.2 1,09 1.16375 Результаты
4 15 1 1.00 0,25575 XBai 13,45
5 12,3 0,81 0,04025 YBar 0,845
6 [ 12,0 0,80 0,06525 Cov 0,4475
7 12,1 0.78 0,08775
8 Сумма: 2,23750
Рис. 3.13. Вычисления ковариации между пятилетней среднегодовой доходностью и долей затрат, выполненные программой Microsoft Excel
Применяя формулу (3.15), получаем
9 947S cov(X,У) == 0,4475.
Будучи мерой линейной зависимости между двумя переменными, ковариация имеет крупный недостаток — она не позволяет оценить относительную силу зависимости. Для того чтобы точнее оценить эту величину, необходимо вычислить коэффициент корреляции.
Относительная сила зависимости, или связи, между двумя переменными, образующими двумерную выборку, измеряется коэффициентом корреляции (coefficient of correlation), изменяющимся от -1 для идеальной обратной зависимости до +1 для идеальной прямой зависимости. Коэффициент корреляции обозначается греческой буквой р. Линейность корреляции (perfect correlation) означает, что все точки, изображенные на диаграмме разброса, лежат на прямой. На рис. 3.14 показаны три вида корреляции между двумя переменными.
Рис. 3.14. Три вида зависимости между двумя переменными
На рис. 3.14, панель А, изображена обратная линейная зависимость между переменными X и У. Таким образом, коэффициент корреляции р равен -1, т.е., когда переменная X возрастает, переменная У убывает. На панели Б показана ситуация, в которой между переменными X и У нет корреляции. В этом случае коэффициент корреляции р равен 0, и, когда переменная X возрастает, переменная У не проявляет никакой определенной тенденции: она ни убывает, ни возрастает. На панели В изображена линейная прямая зависимость между переменными X и У. Таким образом, коэффициент корреляции р равен +1, и, когда переменная X возрастает, переменная У также возрастает.
При анализе выборок, содержащих двумерные данные, вычисляется выборочный коэффициент корреляции, который обозначается буквой г. В реальных ситуациях коэффициент корреляции редко принимает точные значения -1, 0 и +1. На рис. 3.15 приведены шесть диаграмм разброса и соответствующие коэффициенты корреляции г между 100 значениями переменных X и У.
На панели А показана ситуация, в которой выборочный коэффициент корреляции г равен -0,9. Прослеживается четко выраженная тенденция: небольшим значениям переменной X соответствуют очень большие значения переменной У, и, наоборот, большим значениям переменной X соответствуют малые значения переменной У. Однако данные не лежат на одной прямой, поэтому зависимость между ними нельзя назвать линейной. На панели Б приведены данные, выборочный коэффициент корреляции между которыми равен -0,6. Небольшим значениям переменной X соответствуют большие значения переменной У. Обратите внимание на то, что зависимость между переменными X и У нельзя назвать линейной, как на панели А, и корреляция между ними уже не так велика. Коэффициент корреляции между переменными X и У, изображенными на панели В, равен -0,3. Прослеживается слабая тенденция, согласно которой большим значениям переменной У, в основном, соответствуют малые значения переменной У. Панели Г-Е иллюстрируют положительную корреляцию между данными — малым значениям переменной X соответствуют большие значения переменной У.
Обсуждая рис. 3.15, мы употребляли термин тенденция, поскольку между переменными X и У нет причинно-следственных связей. Наличие корреляции не означает наличия причинно-следственных связей между переменными X и У, т.е. изменение значения одной из переменных не обязательно приводит к изменению значения другой. Сильная корреляция может быть случайной и объясняться третьей переменной, оставшейся за рамками анализа. В таких ситуациях необходимо проводить дополнительное исследование. Таким образом, можно утверждать, что причинно-следственные связи порождают корреляцию, но корреляция не означает наличия причинно-следственных связей.
Корреляционная диаграмма для г=-0,9 Корреляционная диаграмма для г=-0,6
Панель А * Панель Б
Корреляционная диаграмма для г=-0,3 Корреляционная диаграмма для г=0,3
Панель В х Панель Г
Корреляционная диаграмма для г=0,6 Корреляционная диаграмма для г=0,9
Рис. 3.15. Шесть диаграмм разброса и соответствующие коэффициенты корреляции, полученные с помощью программы Microsoft Excel
ВЫБОРОЧНЫЙ КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ
где
В сценарии “Применение статистики”, изложенном в начале главы, собрано несколько числовых переменных, характеризующих все взаимные фонды. На рис. 3.16 приведены доходность в 2001 г. и пятилетняя среднегодовая доходность 15 взаимных фондов с очень высоким уровнем риска.
Фонд Доходность 2001 (X) Пятилетняя доходность (Y)
Amer. Century GiftTrust Inv. -35,4 -2,8:
AXP Stategy Aggressive A -32,9 5.5
Berger Small Company Growth Inv -33,8 8.3
Consulting Group Small Cap Growth -13,3 4,3
Fidelity Aggressive Growth -47,3 5,9
Invesco Growth Inv -49,1: -0,7.
Janus Enterprise -39,9: 6,5
Janus Venture -11,9: 9,8.
John Hancock Small Cap Growth A -14,2. 7.6
MS Mid Cap Equity Tr В -39,4 i 9,6 =
PBHG Growth -34,5. -1.2.
Putnam OTC Emerging Growth A -46,1 -6,1'
RS Emerging Growth A -27,3' 18,5^
Rydex OTC Inv -34,7 13,1
Van Kampen Aggressive Growth A -39 7 12.9
Рис. 3.16. Доходность в 2001 г. и пятилетняя среднегодовая доходность взаимных фондов с очень высоким уровнем риска
| А В i С I 0 I ... .е. | F ! G j L2L1
! У,-
j(Доходность (Доходность
1 | 2001) за 5 лет) (X, - ХСредГ (У, -УСредГ IX, -ХСред) (У, -УСред)
2 1 -35.4 -2.8 4,41 78.85 18,65 Итог -X
JF| -32.9 5,5 0.16 0,34 -0,23 ХСред -33,30" А
4 1 -33.8 8.3 0,25 4,93 -1.11 УСред 6,08- -Y
5 i -13.3 4.3 400.00 3,17 -35.60 г 0.3265
6 I 47,3 5.9 196.00 0,03 2.52
7 j 49.1 -0,7 249,64 45,97 107.12
8 j -39,9 6.5 43,56 0,18 -2.77
9 i -11,9 9.8 457,96 13,84 79,61
10~ -14,2 7.6 364,81 2,31 29,03
11'~ -39,4 9.6 37.21 12,39 -21.47
12 j -34,5 -1,2 1,44 53,00 8,74
131 46,1 -6.1 163.84 148,35 155,90
141 27.3 18,5 36.00 154,26 74.52
lTi -34,7 13,1 1.96 49,28 -9.83
16 i -39,7 12,9 40.96 46,51 43,65
17 I Суммы: , 1998.2 613,40 361.43
18 ! Квадратные корни: / 44,70 24,77 \
/ п \ X)(YrY)
Е(х,-х)2 /=1 /=1 у)2 /=1
Рис. 3.17. Вычисление коэффициента корреляции между доходностью фондов в 2001 г. и на протяжении пяти лет с помощью программы Microsoft Excel
Данные, приведенные на рис. 3.16, изображены на диаграмме разброса, изображенной на рис. 2.5. Вычисления коэффициента корреляции между доходностью фондов в 2001 г. и на протяжении пяти лет показаны на рис. 3.17.
Используя результаты, приведеные на рис. 3.17 и формулу (3.16, а), получаем
г =
361,43^^ = 0 326461
71998,27613,404
Аналогично, применяя формулу (3.16, б), получаем
,._с°у(ХГ)
S^Sy
cov(XX) = 361,43 = 25,816428, v 7 15-1
/1 QQR ? v = =11,946906,
V 15-1
= 1613,404 = 6 6192575
У 15-1
Следовательно,
25,816428
= 0,326461.
11,946906x6,6192575
Между доходностью 15 взаимных фондов с очень высоким уровнем риска в 2001 году и за последние пять лет существует положительная корреляция. Взаимные фонды, имевшие более высокую доходность в 2001 году, также имели более высокую доходность в течение последних пяти лет, и, наоборот, фонды, имевшую невысокую доходность в 2001 году, не приносили высоких дивидендов уже пять лет. Эта зависимость до-
вольно слаба, поскольку выборочный коэффициент корреляции г = 0,326 близок к +0. Иначе говоря, взаимные фонды, бывшие прибыльными в 1999 году, остались в числе лучших и в первом квартале 2000 года. Более того, нельзя утверждать, что фонды, имевшие высокую доходность в течение последних пяти лет, принесут в 2001 году высокую прибыль. Можно лишь констатировать наличие тенденции, характерной для данной выборки. Как всегда, прошлые успехи инвестиционных фондов не гарантируют будущих прибылей.
Итак, коэффициент корреляции свидетельствует о линейной зависимости, или связи, между двумя переменными. Чем ближе коэффициент корреляции к -1 или +1, тем сильнее линейная зависимость между двумя переменными. Знак коэффициента корреляции определяет характер зависимости: прямая (чем больше значение переменной X, тем больше значение переменной У) и обратная (чем больше значение переменной X, тем меньше значение переменной У). Сильная корреляция не является причинно-следственной зависимостью. Она лишь свидетельствует о наличии тенденции, характерной для данной выборки.
Процедуры Excel: создание блочных диаграмм
Чтобы вычислить коэффициент корреляции, можно воспользоваться функцией коррел, вызов которой выглядит следующим образом: коррел {диапазон переменной X, диапазон переменной Y). Для того чтобы увидеть, как применяется эта функция, откройте рабочую книгу Chapter 3.xls на листе Рис3.17. Формула для вычисления коэффициента корреляции г имеет вид =коррел(А2:А16;В2:В16) и записана в ячейке G5.
УПРАЖНЕНИЯ К РАЗДЕЛУ 3.5 ГрСП X-
Изучение основ
3.39. Ниже приведена выборка чисел, имеющая объем п = 11.
X 7 5 8 3 6 10 12 4 9 15 18
У 21 15 24 9 18 30 36 12 27 45 54
1. Вычислите выборочный коэффициент корреляции г.
2. Насколько сильна зависимость между переменными X и У? Обоснуйте свой ответ.
Применение понятий
Задачи 3.40-3.45 можно решать вручную или с помощью программы Microsoft Excel.
3.40. С 1990 по 1990 год биржа NASDAQ демонстрировала впечатляющий рост. Аналитики Джордж Андерс (George Anders) и Скотт Турм (Scott Turm) считают, что этот рост стимулировался значительным увеличением объемов инвестиций в компьютерные и другие технологии в США. Фактически информационные технологии составляют около четверти объема всех инвестиций в США. (“ The Rocket Under the Tech Boom: Big Spending by Basic Industries”, The Wall Street Journal, March 30,1999.)
1. Определите вид зависимости между темпами роста биржи NASDAQ и объемом инвестиций в информационные технологии на протяжении 1990-х годов: отрицательная или положительная корреляция? Обоснуйте свой ответ.
2. Создайте диаграмму разброса, иллюстрирующую зависимость между годовой доходностью 20 компаний, акции которых котируются на бирже NASDAQ, и объемом инвестиций в информационные технологии на протяжении 1990-х годов.
3.41. Компания Baltimore Gas & Electric Company обнаружила, что необычно холодная погода, установившаяся в первые три месяца 1999 года, подняла чистый доход до 86,2 млн. долл, по сравнению с 80,2 млн. долл, в первом квартале 1998 года. (“Cold Weather Boost Earnings 7,5% in 1st Period”, The Wall Street Journal, April 19, 1999.)
1. Существует ли корреляция между чистым доходом компании Baltimore Gas & Electric Company и температурой за указанный период? Обоснуйте свой ответ.
2. Как инвесторы могут использовать эту информацию?
3. Можно ли распространить выводы, полученные при решении задачи 2 на акции любой компании, торгующей природными ресурсами, или это характерно лишь для компании Baltimore Gas & Electric Company?
3.42. В файле ^REFRIGERATOR. XLS содержатся данные о розничной цене и годовой стоимости электроэнергии для десяти разновидностей морозильных установок.
1. Вычислите коэффициент корреляции г.
2. Насколько сильна зависимость между ценой и стоимостью электроэнергии, затрачиваемой морозильными установками? Обоснуйте свой ответ.
3.43. В файле ^SECURITY. XLS содержатся данные о производительности металлоискателей в аэропортах в 1998-1999 гг. и количестве нарушений правил безопасности на миллион пассажиров.
Город Производительность Нарушения
Сент-Луис 416 11,9
Атланта 375 7,3
Хьюстон 237 10,6
Бостон 207 22,9
Чикаго 200 6,5
Денвер 193 15,2
Даллас 156 18,2
Балтимор 155 21,7
Сиэтл/Такома 140 31,5
Сан-Франциско 110 20,7
Орландо 100 9,9
Вашингтон 90 14,8
Лос-Анджелес 88 25,1
Детройт 79 13,5
Сан-Хуан 70 10,3
Майами 64 13,1
Нью-Йорк — аэропорт им. Кеннеди 53 30,1
Вашингтон — аэропорт им. Рейгана 47 31,8
Гонолулу 37 14,9
Источник: Alan В. Krueger, “A Small Dose of Common Sense Would Help Congress Break the Gridlock over Airport Security”, The New York Times, November 15,2001, C2.
1. Вычислите коэффициент корреляции г.
2. Насколько сильна зависимость между производительностью и количеством выявленных нарушений? Обоснуйте свой ответ.
3.44. В файле ftcELLPHONE.XLS хранятся данные о длительности разговоров по мобильным телефонам (ч) и емкость батареек (мА/ч).
Длительность разговоров Емкость батареек Длительность разговоров Емкость батареек
4,50 800 1,50 450
4,00 1 500 2,25 900
3,00 1 300 2,25 900
2,00 1 550 3,25 900
2,75 900 2,25 700
1,75 875 2,25 800
1,75 750 2,50 800
2,25 1 100 2,25 900
1,75 850 2,00 900
Источник: справочник “Service Shortcomings”, Copyright © 2002 by Consumers Union of U. S., Inc. Цитируется no журналу Consumer Reports February 2002, 25 с разрешения организации Consumer Union of U. S., Inc., Yonkers, NY 10703-1057.
1. Вычислите коэффициент корреляции г.
2. Насколько сильна зависимость между длительностью разговоров и емкостью батареек?
3. Можно ли на основании этих данных утверждать, что владельцы более емких батареек разговаривают дольше?
3.45. В файле ©BATTERIES2 . XLS записаны цены и данные о силе пускового тока для холодного запуска двигателя, обеспечиваемого автомобильными аккумуляторами. Источник: справочник “Leading the Charge”, Copyright 2001 by Consumers Union of U.S., Inc. Цитируется no журналу Consumer Reports October 2001, 25 с разрешения организации Consumer Union of U. S., Inc., Yonkers, NY 10703-1057.
1. Вычислите коэффициент корреляции г.
2. Существует ли зависимость между силой пускового тока и ценой аккумулятора?
3. Естественно предположить, что аккумуляторы, обеспечивающие большую силу пускового тока, должны иметь более высокую цену. Подтверждается ли это предположение реальными данными?
3.6. ЛОВУШКИ, СВЯЗАННЫЕ С ОПИСАТЕЛЬНЫМИ СТАТИСТИКАМИ, И ЭТИЧЕСКИЕ ПРОБЛЕМЫ
В этой главе мы узнали, как описать набор данных с помощью различных статистик, оценивающих его среднее значение, разброс и вид распределения. Следующим этапом является анализ и интерпретация данных. Ранее мы изучали объективные
свойства данных, а теперь переходим к их субъективной трактовке. Исследователя подстерегают две ошибки: неверно выбранный предмет анализа и неправильная интерпретация результатов.
Анализ доходности 15 взаимных фондов с очень высоким уровнем риска является вполне беспристрастным. Он привел к совершенно объективным выводам: все взаимные фонды имеют разную доходность, разброс доходности фондов колеблется от -6,1 до 18,5, а средняя доходность равна 6,08. Объективность анализа данных обеспечивается правильным выбором суммарных количественных показателей распределения. В главе рассмотрено несколько способов оценки среднего значения и разброса данных, указаны их преимущества и недостатки. Как же выбрать правильную статистику, обеспечивающую объективный и беспристрастный анализ? Если распределение данных имеет небольшую асимметрию, следует ли выбирать медиану, а не среднее арифметическое? Какой показатель более точно характеризует разброс данных: стандартное отклонение или размах? Следует ли констатировать положительную асимметрию распределения?
С другой стороны, интерпретация данных является субъективным процессом. Разные люди приходят к разным выводам, истолковывая одни и те же результаты. У каждого своя точка зрения. Кто-то считает суммарные показатели среднегодовой доходности 15 фондов с очень высоким уровнем риска хорошими и вполне доволен полученным доходом. Другим может показаться, что эти фонды имеют слишком низкую доходность. Таким образом, субъективность следует компенсировать честностью, нейтральностью и ясностью выводов.
Этические проблемы
S Анализ данных неразрывно связан с этическими вопросами. Следует критически относиться к информации, распространяемой газетами, радио, телевидением и World Wide Web. Со временем вы научитесь скептически относиться не только к результатам, но и к целям, предмету и объективности исследований. Лучше всего об этом сказал известный британский политик Бенджамин Дизраэли (Benjamin Disraeli): “Существуют три вида лжи: ложь, наглая ложь и статистика” (“There are three kinds of lies: lies, damned lies and statistics”).
Как уже указывалось в разделе 1.12, этические проблемы возникают при выборе результатов, которые следует привести в отчете. Следует публиковать как положительные, так и отрицательные результаты. Кроме того, делая доклад или письменный отчет, результаты необходимо излагать честно, нейтрально и объективно. Следует различать неудачную и нечестную презентации. Для этого необходимо определить, каковы были намерения докладчика. Иногда важную информацию докладчик пропускает по невежеству, а иногда — умышленно (например, если он применяет среднее арифметическое для оценки среднего значения явно асимметричных данных, чтобы получить желаемый результат). Нечестно также замалчивать результаты, которые не соответствуют точке зрения исследователя.
3.7. ВЫЧИСЛЕНИЕ КОЛИЧЕСТВЕННЫХ ПОКАЗАТЕЛЕЙ НА ОСНОВЕ
РАСПРЕДЕЛЕНИЯ ЧАСТОТ
Если исходные данные недоступны, единственным источником информации становится распределение частот. В таких ситуациях можно вычислить приближенные значения количественных показателей распределения, таких как среднее арифметическое и стандартное отклонение.
Приближенное вычисление среднего арифметического и стандартного отклонения
Если выборочные данные представлены в виде распределения частот, приближенное значение среднего арифметического можно вычислить, предполагая, что все значения внутри каждого класса сосредоточены в средней точке класса.
ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ СРЕДНЕГО АРИФМЕТИЧЕСКОГО НА ОСНОВЕ РАСПРЕДЕЛЕНИЯ ЧАСТОТ
Х = -^---, (3.17)
п
где X — выборочное среднее, п — количество наблюдений, или объем выборки, с — объем классов в распределении частот, mj — средняя точка у-го класса, ft — частота, соответствующая у'-му классу.
Для вычисления стандартного отклонения по распределению частот также предполагается, что все значения внутри каждого класса сосредоточены в средней точке класса.
ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ СТАНДАРТНОГО ОТКЛОНЕНИЯ НА ОСНОВЕ РАСПРЕДЕЛЕНИЯ ЧАСТОТ
S = №----------. (3.18)
1 л-1
Проиллюстрируем использование этих формул следующим примером.
ПРИМЕР 3.9. ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ СРЕДНЕГО АРИФМЕТИЧЕСКОГО И СТАНДАРТНОГО ОТКЛОНЕНИЯ НА ОСНОВЕ РАСПРЕДЕЛЕНИЯ ЧАСТОТ
Рассмотрим распределение частот 5-летней доходности 158 инвестиционных взаимных фондов, представленное в табл. 3.4 .
Таблица 3.4. Распределение частот 5-летней доходности 158 инвестиционных взаимных фондов
5-летняя доходность Количество фондов
от -10,0 До -5,0 1
от -5,0 До 0,0 3
от 0,0 До 5,0 14
от 5,0 До 10,0 58
от 10,0 До 15,0 61
от 15,0 До 20,0 17
от 20,0 До 25,0 3
от 25,0 ДО 30,0 1
Всего 158
РЕШЕНИЕ. Для этих данных получаем следующие количественные показатели.
5-летняя доходность т. от/ тгХ (от, -X/ (от,.-А-)^.
от -10,0 ДО -5,0 1 -7,5 -7,5 -17,69 312,9361 312,9361
от -5,0 ДО 0,0 3 -2,5 -7,5 -12,69 161,0361 483,1083
от 0,0 ДО 5,0 14 2,5 35,0 -7,69 59,1361 827,9054
от 5,0 До 10,0 58 7,5 435,0 -2,69 7,2361 419,6938
от 10,0 ДО 15,0 61 12,5 762,5 2,31 5,3361 325,5021
от 15,0 ДО 20,0 17 17,5 297,5 7,31 53,4361 908,4137
от 20,0 ДО 25,0 3 22,5 67,5 12,31 151,5361 454,6083
от 25,0 ДО 30,0 1 27,5 27,5 17,31 299,6361 299,6361
Всего 158 1 610,0 4 031,8038
Используя формулы (3.17) и (3.18), вычислим среднее арифметическое и стандартное отклонение.
Lv, х = -^ и 1610,0 158 10,19,
С - А /4 031,8038 _g _
п -1 1 158-1
УПРАЖНЕНИЯ К РАЗДЕЛУ 3.7
Изучение основ
3.46. Рассмотрим следующее распределение частот при п — 100.
Классы Частота
от 0 ДО 10 10
от 10 ДО 20 20
от 20 ДО 30 40
от 30 До 40 20
от 40 ДО 50 10
100
1. Вычислите среднее арифметическое.
2. Вычислите стандартное отклонение.
3.47. Рассмотрим следующее распределение частот при п = 100.
Классы Частота
от 0 До 10 45
от 10 ДО 20 25
от 20 ДО 30 15
от 30 ДО 40 15
от 40 ДО 50 5
100
1. Вычислите среднее арифметическое.
2. Вычислите стандартное отклонение.
Применение понятий
3.48. Оптовая фирма, торгующая электроприборами, решила проанализировать счета, полученные на протяжении двух последовательных месяцев. Для этого были сформированы две независимые выборки, каждая из которых содержала 50 счетов, полученных в определенном месяце. Результаты анализа приведены в следующей таблице.
Сумма, долл. Частота в марте Частота в апреле
от 0 ДО 2 000 6 10
от 2 000 ДО 4 000 13 14
от 4 000 ДО 6 000 17 13
от 6 000 До 8 000 10 10
от 8 000 ДО 10 000 4 0
от 10 000 ДО 12 000 0 3
50 50
1. Вычислите среднее арифметическое для каждого месяца.
2. Вычислите стандартное отклонение для каждого месяца.
3. Существенна ли разница между средними суммами счетов и их стандартными отклонениями в марте и апреле? Обоснуйте свой ответ.
3.49. В следующей таблице приведены интегральная функция распределения и распределение интегральных процентов длины тормозного пути автомобиля (в футах) при скорости 80 миль в час для двух выборок, одна из которых содержит 25 автомобилей, произведенных в США, а другая состоит из 72 иностранных моделей, импортированных в прошлом году.
Интегральная функция распределения и распределение интегральных процентов тормозного пути автомобиля (в футах) при скорости 80 миль в час для американских и иностранных моделей*
Длина тормозного пути, футы Американские автомобили Иностранные автомобили
Количество Процент Количество Процент
210 0 0,0 0 0,0
220 1 4,0 1 1,4
230 2 8,0 4 5,6
240 3 12,0 19 26,4
250 4 16,0 32 44,4
260 8 32,0 54 75,0
270 11 44,0 61 84,7
280 17 68,0 68 94,4
290 21 84,0 68 94,4
300 23 92,0 70 97,2
310 25 100,0 71 98,6
320 25 100,0 72 100,0
‘Приведены проценты автомобилей, тормозной путь которых не превышает указанной величины.
Выполните следующие вычисления для американских и иностранных автомобилей.
1. Постройте распределение частот для каждой из групп.
2. Используя результаты задачи 1, найдите приближенное среднее арифметическое значение длины тормозного пути.
3. Используя результаты задачи 1, найдите приближенное стандартное отклонение длины тормозного пути.
4. Используя результаты задач 2 и 3, определите, различаются ли длины тормозного пути у американских и иностранных автомобилей. Обоснуйте свой ответ.
3.50. В следующей таблице приведены распределения возраста сотрудников в двух разных подразделениях одного издательства.
Возраст, лет Частота А Частота Б
от 20 До 30 8 15
от 30 До 40 17 32
от 40 ДО 50 11 20
от 50 До 60 8 4
от 60 До 70 2 0
Резюме 235
1. Вычислите среднее арифметическое для каждого подразделения.
2. Вычислите стандартное отклонение для каждого подразделения.
3. Используя результаты задач 1 и 2, определите, на сколько различаются распределения возраста в указанных подразделениях. Обоснуйте свой ответ.
Характеристики числовых данных
Разброс
Вид < распределения
'вреднее значение распределения
Корреляция
Среднее
Медиана
Мода
Геометрическое среднее
РЕЗЮМЕ
Размах
* Межквартильный размах
Дисперсия
Стандартное отклонение
Коэффициент вариации
Пять базовых показателей
Блочная диаграмма
Структурная схема главы 3
Итак, мы закончили изучать главу, посвященную описательным статистикам. В этой и двух предыдущих главах рассматривался предмет описательной статистики: методы сбора, представления и анализа данных. Мы проанализировали доходность взаимных фондов, научились представлять данные в виде таблиц и диаграмм. Мы оценили свойства, характеризующие эффективность работы фондов, — среднее значение, вариацию, форму распределения, — используя математическое ожидание, медиану, квартили, размах, стандартное отклонение и коэффициент корреляции. Детальный
анализ пяти категорий фондов, имеющих разный уровень риска, позволил определить, что взаимные фонды с очень низким уровнем риска характеризуются наименьшей изменчивостью доходности, и в этом смысле действительно являются наиболее надежными. Взаимные фонды с очень низким уровнем риска имеют наибольшую медиану доходности, за ними следуют фонды с низким и средним уровнем риска, а наименьшая медиана доходности характерна для фондов с высоким и очень высоким уровнем риска. Таким образом, инвесторы, вкладывающие средства в фонды с большим разбросом доходности, имеют шанс получить большую прибыль.
В следующей главе мы изучим основы теории вероятностей, чтобы перейти от описательной статистики к статистическим выводам.
ОСНОВНЫЕ ПОНЯТИЯ
Среднее, 179
арифметическое, 180
Асимметрия
отрицательная, 196
положительная, 196
Базовые показатели, 213
Диаграмма
блочная, 214
точечная, 182
Дисперсия, 187
выборочная, 190
генеральной совокупности, 206
Квартиль,185
первый, 185
третий, 186
Коэффициент
вариации, 194
корреляции, 222
Математическое ожидание, 206
Медиана, 183
Мода, 184
Размах, 188
межквартильный, 189
средний, 189
Распределение
асимметричное, 196
симметричное, 196
Среднее
выборочное, 180
геометрическое, 186
Стандартное отклонение
выборочное, 190
генеральной совокупности, 207
Тенденция, 223
УПРАЖНЕНИЯ К ГЛАВЕ 3
Проверка знаний
3.51. Перечислите свойства, которыми обладают наборы числовых данных.
3.52. Что называется средним значением распределения?
3.53. Чем отличаются математическое ожидание, медиана и мода? Укажите их преимущества и недостатки.
3.54. В чем заключается различие между оценками центрального среднего и нецентрального среднего?
3.55. Что означает разброс данных?
3.56. Чем отличаются разные оценки разброса, например, размах, межквартильный размах, дисперсия, стандартное отклонение и коэффициент корреляции? Укажите их преимущества и недостатки.
3.57. Как эмпирическое правило помогает описать концентрацию и распределение числовых данных?
3.58. Что описывает вид распределения?
3.59. Чем отличаются среднее арифметическое и среднее геометрическое?
Применение понятий
Задачи 3.60-3.68 можно решать как вручную, так и с помощью программы Microsoft Excel. Для решения задач 3.69-3.76 и 3.79 рекомендуется применить программу Microsoft Excel.
3.60. Одним из показателей качества процесса упаковки чая является вес отдельного пакетика. Если пакетик чая неполон, возникают две проблемы. Во-первых, потребитель чая может не получить требуемой крепости заварки. Во-вторых, компанию могут привлечь к ответственности за нарушение правил маркировки. В данном примере на упаковке указывается номинальный средний вес чая в пакетике: 5,5 г. Если реальный средний вес чая в пакетике превышает указанное значение, компания несет дополнительные убытки. Точно засыпать в пакетик 5,5 г невозможно, поскольку температура и влажность воздуха на чайной фабрике постоянно изменяются, а это влияет на вес чая. Кроме того, скорость работы упаковочной машины чрезвычайно высока (170 пакетиков в минуту). В следующей таблице приведен вес в граммах 50 пакетиков чая, заполненных в течение часа конкретной упаковочной машиной. ^TEABAGS . XLS.
5,65 5,44 5,42 5,40 5,53 5,34 5,54 5,45 5,52 5,41
5,57 5,40 5,53 5,54 5,55 5,62 5,56 5,46 5,44 5,51
5,47 5,40 5,47 5,61 5,53 5,32 5,67 5,29 5,49 5,55
5,77 5,57 5,42 5,58 5,58 5,50 5,32 5,50 5,53 5,58
5,61 5,45 5,44 5,25 5,56 5,63 5,50 5,57 5,67 5,36
1. Вычислите среднее арифметическое и медиану.
2. Вычислите первый и третий квартили.
3. Вычислите размах, межквартильный размах, выборочную дисперсию, стандартное отклонение и коэффициент вариации.
4. Дайте интерпретацию разных оценок среднего значения в контексте данного примера. Почему чайную фабрику должен интересовать именно средний вес пакетика?
5. Дайте интерпретацию разных оценок разброса в контексте данного примера. Почему чайную фабрику должен интересовать разброс веса?
6. Постройте блочную диаграмму.
7. Являются ли эти данные асимметричными? Если да, определите вид асимметрии.
8. Соответствует ли реальный вес упаковок номинальному?
9. Какие изменения в процесс упаковки чая вы бы внесли?
3.61. В штате Нью-Йорк сберегательным банкам разрешено осуществлять страхование жизни. В процедуру оформления страховки входят изучение запроса, проверка медицинской информации, возможные дополнительные медицинские исследования и проверка информации, поступившей из полиции. Чтобы страхование жизни было прибыльным для банка, необходимо ускорить оформление страховки. Банк создал выборку, в которой указано время, затраченное на оформление 27 страховок в течение одного месяца. ^INSURANCE . XLS.
73 19 16 64 28 28 31 90 60 56 31 56 22 18
45 48 17 17 17 91 92 63 50 51 69 16 17
1. Вычислите среднее арифметическое и медиану.
2. Вычислите первый и третий квартили.
3. Вычислите размах, межквартильный размах, выборочную дисперсию, стандартное отклонение и коэффициент вариации.
4. Постройте блочную диаграмму.
5. Являются ли эти данные асимметричными? Если да, определите вид асимметрии.
6. Какова средняя продолжительность оформления страховки?
3.62. Один из основных критериев качества услуг, предоставляемых любой организацией, — скорость, с которой она реагирует на жалобы клиентов. Крупный универмаг, торгующий фурнитурой и коврами, за последние годы значительно расширился. В частности, отдел ковровых покрытий, в котором прежде работали 2 человека, теперь состоит из руководителя, измерителя и 15 продавцов. На протяжении последнего года компания получила 50 жалоб на работу этого отдела. Ниже приведены данные о количестве дней, прошедших со дня получения жалобы до принятия решения. ^FURNITURE . XLS.
54 5 35 137 31 27 152 2 123 81 74 27
11 19 126 110 110 29 61 35 94 31 26 5
239 4 165 32 29 28 29 26 25 1 14 13
12
13 10 5 27 4 52 30 22 36 26 20 23
33 68
1. Вычислите среднее арифметическое и медиану.
2. Вычислите первый и третий квартили.
3. Вычислите размах, межквартильный размах, выборочную дисперсию, стандартное отклонение и коэффициент вариации.
4. Постройте блочную диаграмму.
5. Являются ли эти данные асимметричными? Если да, определите вид асимметрии.
6. Какова средняя продолжительность ответа на жалобу?
3.63. Может ли раздача сувениров повысить посещаемость матчей Высшей бейсбольной лиги (Major League Baseball)? В статье, опубликованной в журнале Sports Marketing Quarterly, исследуется эффективность рекламных акций (Boyd, Т. С. and Krehbiel, Т. С. “Promotion Timing in Major League Baseball Attendance”, Sports Marketing Quarterly, 12 (March 2003). Файл данных ^ROYALS. XLS содержит следующую информацию о посещении матчей с участием команды Kansas City Royals в 2002 году.
ИГРА — матчи в соответствии с расписанием.
ПОСЕЩАЕМОСТЬ — количество зрителей на матче.
РЕКЛАМА — (Да — рекламная акция проводилась, Нет — рекламная акция не проводилась).
1. Вычислите среднее арифметическое и медиану для 43 игр, сопровождавшихся рекламными мероприятиями, и 37 игр, проходивших без рекламной кампании.
2. Вычислите пять базовых показателей для 43 игр, сопровождавшихся рекламными мероприятиями, и 37 игр, проходивших без рекламной кампании.
3. Постройте две блочные диаграммы — для 43 игр, сопровождавшихся рекламными мероприятиями, и для 37 игр, проходивших без рекламной кампании.
4. Оцените эффективность рекламной кампании команды Royals в сезоне 2000 года.
3.64. Промышленная компания на Среднем Западе производит стальные корпуса для электротехнического оборудования. Основным компонентом корпуса является прямоугольный профиль, который создается из 14-дюймового рулона стальной полосы с помощью 250-тонного пресса. Основным параметром корпуса является расстояние между боковыми сторонами профиля, допускающее установку электротехнического оборудования. Это расстояние не должно быть меньше 8,31 дюйма и больше 8,61 дюйма. В таблице приведены данные о 49 профилях. ftTROUGH. XLS.
8,312 8,343 8,317 8,383 8,348 8,410 8,351 8,373 8,481 8,422
8,476 8,382 8,484 8,403 8,414 8,419 8,385 8,465 8,498 8,447
8,436 8,413 8,489 8,414 8,481 8,415 8,479 8,429 8,458 8,462
8,460 8,444 8,429 8,460 8,412 8,420 8,410 8,405 8,323 8,420
8,396 8,447 8,405 8,439 8,411 8,427 8,420 8,498 8,409
1. Вычислите выборочное среднее, медиану, размах и стандартное отклонение ширины корпуса. Прокомментируйте полученные результаты.
2. Вычислите пять основных показателей.
3. Постройте блочную диаграмму и опишите вид распределения.
4. Много ли корпусов, произведенных компанией, соответствуют требованиям стандарта?
3.65. Промышленная компания на Среднем Западе, о которой шла речь в задаче 3.59, производит также электрические изоляторы. Если во время работы изолятор выходит из строя, происходит короткое замыкание. Чтобы проверить прочность изолятора, компания проводит испытания, в ходе которых определяется максимальная сила, необходимая для разрушения изолятора. Сила измеряется в фунтах нагрузки, приводящей к разрушению изолятора. В таблице приведены результаты 30 экспериментов. ftpORCE . XLS.
1 870 1 728 1 656 1 610 1 634 1 784 1 522 1 696 1 592 1 662
1 866 1 764 1 734 1 662 1 734 1 774 1 550 1 756 1 762 1 866
1 820 1 744 1 788 1 688 1 810 1 752 1 680 1 810 1 652 1 736
1. Вычислите выборочное среднее, медиану, размах и стандартное отклонение прочности.
2. Дайте интерпретацию оценок среднего значения и изменчивости прочности.
3. Вычислите пять основных показателей.
4. Постройте блочную диаграмму и опишите вид распределения.
5. К каким выводам вы пришли, если учесть, что компания требует, чтобы изоляторы выдерживали нагрузку не менее 1 500 фунтов?
3.66. Клиенты и телефонная компания обеспокоены нарушениями телефонной связи. Причины этих нарушений разделяются на две группы: повреждения на телефонной станции и на линии. Ниже приведены данные о 20 повреждениях телефонной связи и длительности ремонта (в минутах) на двух телефонных станциях, ftPHONE. XLS.
Длительность ремонта (мин.) на телефонной станции I
1,48 1,75 0,78 2,85 0,52 1,60 4,15 3,97 1,48 3,10
1,02 0,53 0,93 1,60 0,80 1,05 6,32 3,93 5,45 0,97
Длительность ремонта (мин.) на телефонной станции II
7,55 3,75 0,10 1,10 0,60 0,52 3,30 2,10 0,58 4,02
3,75 0,65 1,92 0,60 1,53 4,23 0,08 1,48 1,65 0,72
1. Вычислите среднее арифметическое и медиану каждой выборки.
2. Вычислите первый и третий квартили каждой выборки.
3. Определите размах, межквартильный размах, дисперсию, стандартное отклонение и коэффициент вариации каждой выборки.
4. Постройте блочные диаграммы выборок.
5. Являются ли эти данные асимметричными? Если да, определите вид асимметрии.
6. Отличается ли длительность ремонта на двух телефонных станциях? Обоснуйте свой ответ.
7. К каким выводам вы бы пришли, если бы первое значение во второй таблице вместо 7,55 было равным 27,55?
3.67. Во многих технологических процессах существует так называемый период незавершенного производства (work-in-process— WIP). В типографии периодом незавершенного производства называют интервал времени, в течение которого отпечатанные листы фальцуют, комплектуют, склеивают, обрезают и переплетают. В следующей таблице приведена длительность производства 20 книг, напечатанных в двух типографиях. (Длительность производства измеряется в днях, прошедших с момента завершения печати книги и до упаковки в картонные коробки.) . XLS.
Типография A
5,62 5,29 16,25 10,92 11,46 21,62 8,45 8,58 5,41 11,42
11,62 7,29 7,50 7,96 4,42 10,50 7,58 9,29 7,54 8,92
Типография Б
9,54 11,46 16,62 12,62 25,75 15,41 14,29 13,13 13,71 10,04
5,75 12,46 9,17 13,21 6,00 2,33 14,25 5,37 6,25 9,71
1. Вычислите среднее арифметическое и медиану каждой выборки.
2. Вычислите первый и третий квартили каждой выборки.
3. Определите размах, межквартильный размах, дисперсию, стандартное отклонение и коэффициент вариации каждой выборки.
4. Постройте блочные диаграммы выборок.
5. Являются ли эти данные асимметричными? Если да, определите вид асимметрии.
6. Отличается ли длительность производства в этих типографиях? Обоснуйте свой ответ.
3.68. В файле ФCEREALS. XLS содержатся данные о стоимости в центах за унцию, а также о количестве калорий, клетчатки и сахара в 33 разных сортах кукурузных хлопьев. Источник: Copyright 1999 by Consumers Union of U.S., Inc. Цитируется no журналу Consumer Reports, October 1999, p. 33, 34 с разрешения компании Consumers Union of U. S., Inc., Yonkers, N.Y. 10703-1057.
1. Вычислите среднее арифметическое и медиану каждой переменной.
2. Вычислите первый и третий квартили каждой переменной.
3. Определите размах, межквартильный размах, дисперсию, стандартное отклонение и коэффициент вариации каждой переменной.
4. Постройте блочные диаграммы выборок.
5. Являются ли эти данные асимметричными? Если да, определите вид асимметрии.
6. К каким выводам вы пришли?
3.69. В файле ftpETFOOD2 . XLS содержатся данные о стоимости, а также о количестве белка и жира в 97 сортах сухого и консервированного корма для кошек и собак. Источник: Copyright 1998 by Consumers Union of U.S., Inc. Цитируется no журналу Consumer Reports, February 1998, p. 18, 19 с разрешения компании Consumers Union of U'. S., Inc., Yonkers, N.Y. 10703-1057.
1. Вычислите среднее арифметическое и медиану каждого показателя в зависимости от разновидности корма (сухой или консервированный) и вида животного (кошка или собака).
2. Вычислите первый и третий квартили каждой переменной в зависимости от разновидности корма (сухой или консервированный) и вида животного (кошка или собака).
3. Определите размах, межквартильный размах, дисперсию, стандартное отклонение и коэффициент вариации каждой переменной в зависимости от разновидности корма (сухой или консервированный) и вида животного (кошка или собака).
4. Постройте блочные диаграммы каждого показателя в зависимости от разновидности корма (сухой или консервированный) и вида животного (кошка или собака).
5. Являются ли эти данные асимметричными? Если да, определите вид асимметрии.
6. К каким выводам вы пришли?
3.70. Производитель рубероидной кровельной плитки на заводах в Бостоне и Вермонте предоставляет своим клиентам 20-летнюю гарантию. Для того чтобы убедиться в том, что плитки прослужат указанный срок, на заводах проводят ускоренное испытание на долговечность. В ходе этого эксперимента плитка на протяжении нескольких минут подвергается интенсивному воздействию, эквивалентному воздействию, которому плитка подвергалась бы в обычных условиях в течение 20 лет. В частности, плитку несколько минут очень энергично скребут щетками, а затем взвешивают гранулы, которые отскакивают от плиток (в граммах). Чем меыпе гранул образуется в ходе эксперимента, тем долговечнее плитка. Для того чтобы прослужить весь гарантийный срок, плитка не должна потерять больше 0,8 г. В файле ftGRANULE. XLS содержатся данные о выборке, состоящей из 170 измерений, проведенных на заводе в Бостоне, и 140 измерений, осуществленных на заводе в Вермонте.
1. Вычислите пять базовых показателей для плиток, произведенных на заводе в Бостоне.
2. Вычислите пять базовых показателей для плиток, произведенных на заводе в Вермонте.
3. Постройте блочные диаграммы для каждой выборки и опишите форму распределения.
4. Прокомментируйте способность плиток терять не более 0,8 г гранул.
3.71. В файле ©STATES.XLS приведены данные, собранные в ходе переписи населения США в 2000 г.: время проезда до места работы (мин.), процент домов с восемью или более комнатами, медиана семейного дохода и процент домовладельцев, у которых оплата стоимости дома превосходит 30% их дохода.
1. Вычислите среднее арифметическое и медиану каждой переменной.
2. Вычислите первый и третий квартили каждой переменной.
3. Определите размах, межквартильный размах, дисперсию, стандартное отклонение и коэффициент вариации каждой переменной.
4. Постройте блочную диаграмму.
5. Являются ли эти данные асимметричными? Если да, определите вид асимметрии.
6. Какие выводы можно сделать о времени проезда до места работы (мин.), проценте домов с восемью или более комнатами, медиане семейного дохода и проценте домовладельцев, у которых оплата стоимости дома превосходит 30% их дохода?
3.72. Экономика бейсбола порождает противоречия между владельцами клубов, которые утверждают, что они теряют деньги, игроками, утверждающими, что владельцы клубов получают прибыль, и болельщиками, жалующимися на высокую стоимость билетов и абонентской платы за просмотр игр по кабельному телевидению. Кроме данных об игровой статистике команд в сезоне 2001 года, файл ^ВВ2001.XLS содержит данные о стоимости билетов, стоимости членства в фан-клубе, стоимости абонементов, стоимости абонементов локального телевидения, радио и кабельного телевидения, доходах от всех остальных операций, компенсациях и премиях игрокам, национальных и локальных расходах и доходах от бейсбольных операций. Для каждой из перечисленных переменных выполните следующие задания.
1. Вычислите среднее арифметическое и медиану.
2. Вычислите первый и третий квартили.
3. Определите размах, межквартильный размах, дисперсию, стандартное отклонение и коэффициент вариации.
4. Постройте блочную диаграмму.
5. Являются ли эти данные асимметричными? Если да, определите вид асимметрии.
6. Вычислите корреляцию между количеством побед и суммой компенсаций и премий, полученных игроками. Насколько сильна зависимость между этими двумя переменными?
7. Какие выводы можно сделать о доходах от продажи абонементов локального телевидения, радио и кабельного телевидения; доходах от всех остальных операций; сумме компенсации и премий игрокам; национальных и локальных расходах и доходах от бейсбольных операций?
3.73. Файл ^AIRCLEANERS. XLS содержит данные о цене, стоимости потребляемой электроэнергии и стоимости годового обслуживания комнатного кондиционера. Источник: “Portable Room Air Cleaner”. Copyright © 2002 by Consumers Union of U. S„ Inc. Цитируется no журналу Consumer Reports, February 2002, 47 с разрешения компании Consumers Union of U.S., Inc., Yonkers, N.Y. 10703-1057.
1. Вычислите коэффициент корреляции между ценой и стоимостью потребляемой электроэнергии.
2. Вычислите коэффициент корреляции между ценой и стоимостью фильтра.
3. Какие выводы можно сделать о зависимости между стоимостью потребления электроэнергии и стоимостью фильтра?
3.74. Файл WPRINTERS . XLS содержит данные о цене, скорости и стоимости печати текста, скорости и стоимости печати цветной фотографии для разных принтеров.
1. Вычислите коэффициент корреляции между ценой и скоростью печати текста.
2. Вычислите коэффициент корреляции между ценой и стоимостью печати текста.
3. Вычислите коэффициент корреляции между ценой и скоростью печати цветной фотографии.
4. Вычислите коэффициент корреляции между ценой и стоимостью печати цветной фотографии.
5. Следует ли рассмотреть другие переменные, чтобы оценить стоимость принтера? Обоснуйте свой ответ.
3.75. Допустим, что нам необходимо провести сравнительное исследование характеристик различных моделей автомобилей 2002 года. При сравнении учитываются следующие показатели: количество лошадиных сил, пробег в милях на галлон топлива, длина, ширина, радиус поворота, вес и грузоподъемность машины. ^AUT02002 . XLS.
Источник: “The 2002 Cars”, Copyright © 2002 by Consumers Union of U. S. Приводится no журналу Consumer Reports, April 2002, p. 22-71, с разрешения компании Consumer Union of U. S., Inc., Yonkers, NY 10703-1057.
1. Вычислите среднее арифметическое и медиану каждой переменной.
2. Вычислите первый и третий квартили каждой переменной.
3. Определите размах, межквартильный размах, дисперсию, стандартное отклонение и коэффициент вариации каждой переменной.
4. Постройте блочные диаграммы выборок.
5. Являются ли эти данные асимметричными? Если да, определите вид асимметрии.
6. К каким выводам вы пришли?
7. Предположим, нам необходимо сравнить спортивные и обычные автомобили. Проведите исследование этих групп. В чем заключаются различия между этими моделями?
3.76. Компания Zagat публикует рейтинги ресторанов, расположенных в разных городах США. В файле ^RESTRATE. XLS содержатся оценки качества пищи, оформления блюд, уровня обслуживания и стоимость обеда для одного человека в 50 ресторанах Нью-Йорк Сити и 50 ресторанах Лонг-Айленда.
Источник: цитируется по изданиям Zagat Survey “2002 New York City Restraunts” и Zagat Survey 2002 Long Island Restraunts.
1. Вычислите среднее арифметическое и медиану каждого показателя для двух групп ресторанов.
2. Вычислите первый и третий квартили каждого показателя для двух групп ресторанов.
3. Определите размах, межквартильный размах, дисперсию, стандартное отклонение и коэффициент вариации каждого показателя для двух групп ресторанов.
3.77.
4. Постройте блочные диаграммы выборок каждого показателя для двух групп ресторанов.
5. Являются ли эти данные асимметричными? Если да, определите вид асимметрии.
6. К каким выводам вы пришли? Существуют ли различия между ресторанами Нью-Йорк Сити и Лонг-Айленда?
В качестве примера неправильного применения статистики рассмотрим статью Гленна Крэмона (Glenn Kramon) (“Coaxing the Standford Elephant to Dance”, The New York Times Sunday Business Section, November 11, 1990). В ней утверждается, что стоимость обслуживания в Стэнфордском медицинском центре (Stanford Medical Center) была поднята из-за того, что он чаще других принимал неимущих и более сложных пациентов. Чтобы доказать этот тезис, в статье была помещена диаграмма, изображающая средние затраты трех госпиталей (ЭльКамино, Секвойя и Стэнфорд) в 1989-1990 годах на три вида медицинских процедур (аортокоронарное шунтирование, роды без осложнений и протезирование тазобедренного сустава). Представьте себе, что вы работаете в медицинском центре. Ваш главный администратор знает, что вы только что прослушали курс статистики, и вызывает вас для беседы. Она сообщает вам, что упомянутая статья подверглась критике со стороны одного из членов регионального совета администраторов, который считает приведенную в ней диаграмму совершенно бессмысленной, и просит вас высказать свое мнение. Что вы ответите?
Данные по госпиталю Стэнфорд получены путем усреднения затрат на все виды операций.
Данные по госпиталю Секвойя представляют собой средние 50% всех затрат на каждую из операций.
Стэнфордский медицинский центр, госпиталь Эль-Камино и госпиталь Секвойя.
3.78. Представьте себе, что вместе с группой однокурсников вы готовитесь к сдаче экзамена по статистике. Один из ваших сокурсников для представления суммарных показателей, таблиц и диаграмм желает применить программу Microsoft Excel. Данные, предложенные преподавателем, разделяются на числовые и категорийные. Ваш друг приходит к вам распечатать свой отчет и восклицает: “Я вычислил все — математические ожидания, медианы, стандартные отклонения. Я построил диаграммы “ствол и листья”, а также блочные и круговые диаграммы для всех переменных. Однако некоторые из них выглядят странно — например, диаграммы “ствол и листья” и блочные диаграммы для пола и специализации, а также круговые диаграммы для распределения баллов и роста.
Кроме того, я не понимаю, почему профессор Кребиль (Krehbiel) говорит, что для некоторых переменных невозможно вычислить количественные показатели — я же их вычислил! Вот посмотри, средний рост равен 68,23, средний балл — 2,76, математическое ожидание для пола — 1,5, а математическое ожидание для специализации — 4,33”. Что вы скажете на это?
Отчеты
3.79. В файле ^BEER.XLS приведены данные об упаковках, содержащих шесть 12-унциевых бутылок пива 69 сортов. В их число входят цена, количество калорий в 12 жидких унциях, процентное содержание алкоголя в 12 жидких унциях, вид пива (светлое, эль, импортное легкое, обычное, ледяное, легкое, безалкогольное), а также страны производства (США или другие).
Напишите отчет, содержащий полное описание каждой переменной — цены, количества калорий и содержания алкоголя, — независимо от вида пива и страны производства. Затем выполните аналогичное исследование каждой числовой переменной, учитывая вид пива — светлое, эль, импортное легкое, обычное, ледяное, легкое, безалкогольное. После этого выполните аналогичное исследование каждой числовой переменной, учитывая страну производства. Включите в отчет все необходимые таблицы, диаграммы и количественные показатели, полученные в ходе исследования.
Источник: “Beers”, Copyright © 1996 by Consumers Union of U. S. Inc., Yonkers, N.Y. Цитируется с разрешения журнала Consumer Reports, June, 1996.
Применение Интернет
3.80. Зайдите на сайт www. prenhall. сот/levins. Выберите ссылку Chapter 3 и щелкните на ссылке Internet exercises.
—'—
‘ V ГРУППОВОЙ ПРОЕКТ
ТР.3.1. Файл данных Cl MUTUAL FUNDS.XLS содержит информацию о 13 переменных, характеризующих 259 взаимных фондов.
Фонд — название взаимного фонда.
Вид — вид акций, принадлежащих взаимному фонду: малые, средние и крупные компании.
Цель — цель фонда (быстрый или медленный рост капитала).
Активы — в млн. долл.
Комиссия — да или нет.
Издержки — издержки, понесенные взаимным фондом (в процентах от среднего объема чистых активов).
Доходность 2 001 — доходность за двенадцать месяцев 2001 г.
Трехлетняя доходность — среднегодовая доходность за период с 1999 по 2001 гг.
Пятилетняя доходность — среднегодовая доходность за период с 1997 по 2001 гг.
Оборачиваемость — уровень торговой активности фонда: очень низкий, низкий, средний, высокий, очень высокий.
Риск — уровень риска: очень низкий, низкий, средний, высокий, очень высокий.
Лучший квартал — квартал с наивысшей доходностью за период с 1997 по 2001 гг.
Худший квартал — квартал с наименьшей доходностью за период с 1997 по 2001 гг.
Проанализируйте издержки и вычислите следующие статистики.
1. Среднее.
2. Медиана.
3. Размах.
4. Дисперсия.
5. Стандартное отклонение.
6. Коэффициент вариации.
7. Первый квартиль,
8. Третий квартиль, Q3.
9. Межквартильный размах.
ТР.3.2. Изучите данные о взаимных фондах, приведенные в задаче ТР.3.1. Файл MF2000.XLS содержит информацию о взимании фондами брокерской комиссии. ^MUTUAL FUNDS . XLS.
1. Постройте таблицу, содержащую среднее арифметическое, медиану, размах и стандартное отклонение доходности фондов, не взимающих брокерскую комиссию, в 2001 году.
2. Вычислите пять базовых показателей и постройте блочную диаграмму для доходности фондов, не взимающих брокерскую комиссию, в 2001 году.
3. Постройте таблицу, содержащую среднее арифметическое, медиану, размах и стандартное отклонение доходности фондов, взимающих брокерскую комиссию, в 2001 году.
4. Вычислите пять базовых показателей и постройте блочную диаграмму для доходности фондов, взимающих брокерскую комиссию, в 2001 году.
5. Повторите упражнения 1-4 для трехлетней доходности.
6. Напишите краткий отчет.
ТР.3.3. Изучите данные о взаимных фондах, приведенные в задаче ТР.3.1. Оцените эффективность фондов, ориентированных на быстрый и медленный рост капитала соответственно. ^MUTUAL FUNDS . XLS.
1. Постройте таблицу, содержащую среднее арифметическое, медиану, размах и стандартное отклонение доходности фондов, ориентированных на быстрый и медленный рост капитала соответственно в 2001 году.
2. Постройте блочные диаграммы для доходности указанных фондов в 2001 году.
3. Повторите упражнения 1-2 для трехлетней доходности фондов.
4. Напишите краткий отчет.
ТР.3.4. Изучите данные о взаимных фондах, приведенные в задаче ТР.3.1. Оцените доходность фондов, специализирующихся на акциях малых, средних и крупных компаний, в 2001 году. ^MUTUAL FUNDS . XLS.
1. Вычислите среднее и медиану. Прокомментируйте результаты.
2. Определите размах, дисперсию и стандартное отклонение. Дайте их интерпретацию.
3. Вычислите пять основных показателей. Прокомментируйте результаты.
4. Вычислите коэффициент вариации. Прокомментируйте результат.
5. Постройте блочную диаграмму. Прокомментируйте ее.
6. Повторите упражнения 1-6 для трехлетней доходности.
7. Напишите краткий отчет.
РАЗБОР КОНКРЕТНОЙ СИТУАЦИИ А ГАЗЕТА THE SPRINGVILLE HERALD
Для какой переменной, упомянутой в разделе “Разбор конкретной ситуации — газета The Springville Herald” (глава 2), следовало бы вычислить описательные статистики?
1. Вычислите описательные статистики, а затем постройте диаграмму “ствол-и-листья” и блочную диаграмму.
2. Подумайте, какая диаграмма дополнила бы полученные результаты, и постройте ее. Какую новую информацию можно извлечь из этой диаграммы?
Изложите ваши выводы в отчете.
ПРИМЕНЕНИЕ WEB
Примените ваши знания об описательных статистиках для решения задачи, поставленной в главе 2.
Посетите Web-сайт компании StockTout Investing Service (www.prenhall.com/ Springville/StockTout. htm). Еще раз проанализируйте рекламные заявления и сопровождающие их данные, а затем ответьте на следующие вопросы.
1. Можно ли вычислить описательные статистики для переменных, приведенных на сайте? Соответствуют ли эти статистики рекламным заявлениям компании? Как они влияют на ваше восприятие данных о компании?
2. Оцените методы, которые компания StockTout Investing Service применила в своем обзоре (www.prenhall.com/Springville/ST_Survey.htm). Что следовало бы сделать иначе?
3. Обратите внимание на то, что последний вопрос в обзоре допускает несколько вариантов ответа. Какие факторы могли бы ограничить количество этих вариантов?
СПРАВОЧНИК ПО EXCEL. ГЛАВА 3
ЕН.3.1. Создание точечных масштабированных диаграмм
Откройте рабочий лист Точечная_диаграмма в рабочей книге Chapter 3 .xls. Этот лист (рис. ЕН.3.1) содержит несколько наборов формул, реализованных ранее, сфор-матированную заранее диаграмму, в которой ось Y невидима, а также восемь наборов данных — Values, Mean, Median, 1st Quartile, 3rd Quartile, +/- 1 Std. Dev., + /- 2 Std. Dev.,+/- 3 Std. Dev. Скопировав данные в столбец А, немного изменив формулы в столбце В и отредактировав диапазоны ячеек, связанные с рядом Values, вы можете приспособить этот лист для работы с любыми данными.
корреляция(р = -1)
Панель В Положительная прямолинейная корреляция(р = +1)
Панель Б Отсутствие корреляции (Р = 0)
Рис. ЕН.3.1. Рабочий лист Точечная_диаграмма
Чтобы создать точечную диаграмму, откройте рабочий лист Точечная_Диаграмма в рабочей книге Chapter 3.xls. В столбце А содержатся семь чисел, предназначенных для демонстрации. В столбце В измените формулы, используемые для вычисления координат Y каждой точки. Для того чтобы подсчитать частоту числа из столбца А в указанном диапазоне, эти формулы используют функцию СЧЕТЕСЛИ. Это число меньше 1 и используется как масштабирующий множитель при вычислении координат У. Если число встречается только один раз, координата равна 1. Если число входит в набор несколько раз, координата его будет равна 1+(количество вхождений числа минус один, умноженное на 0,025). Например, если в наборе содержится три идентичных значения, равных 4,00, то координата числа будет равна 1,05 (т.е. 1+(3-1)*0,025).
Для данных, содержащихся в первом столбце (ячейка А2), формула, записанная в ячейке В2 выглядит следующим образом: = (СЧЕТЕСЛИ (диапазон ячеек в столбце А; $А2) -1) *0,025+1. Вторая и последующие формулы используют еще один вызов функции СЧЕТЕСЛИ, чтобы точки на точечной диаграмме не сливались. Эти формулы имеют следующий вид: =(СЧЕТЕСЛИ(диапазон ячеек; текущая ячейка)-1)*0,025+1 -(СЧЕТЕСЛИ(диапазон предшествующих ячеек; текущая ячейка)*0,025).
Модификация формул в столбце В. Выберите столбец В и выполните команду Правка^Заменить.... Находясь в открытом диалоговом окне Заменить, введите в окне редактирования Найти диапазон $А$2:$А$8, а в окне редактирования Заменить паевой диапазон, используя абсолютные ссылки. Затем щелкните на кнопке Заменить все. Например, если требуется скопировать 15 чисел из одного столбца листа ОВРФонды рабочей книги Chapter 3.xls, введите в окне редактирования Заменить на диапазон $А$2:$А$16 (см. иллюстрацию). Если на экране появится диалоговое окно, сообщающее о внесенных изменениях, щелкните на кнопке ОК.
Выберите ячейку ВЗ еще раз и скопируйте измененную формулу во все нижележа щие ячейки этого столбца, пока не закончится диапазон исходных данных.
Редактирование диапазонов, связанных с рядом Values. Щелкните правой кнопкой мыши на серой области точечной диаграммы и выберите команду Исходные данные.... Щелкните на корешке вкладки Ряд и выберите пункт Values из раскрывающегося списка Ряд (см. иллюстрацию). Отредактируйте содержимое окон редактирования Значения X и Значения У, введя свои диапазоны ячеек вместе с именем рабочего листа. Щелкните на кнопке ОК. Например, если требуется скопировать один из столбцов рабочего листа ОВРФонды, измените формулу в окне редактирования Значения X на следующую: = ’ Точечная_диаграмма ’ ! А2 : А16, а формулу в окне редактирования Значения У — на такую: = ’ Точечная_диаграмма ’ ! В2 : В16.
Исходные данные [? |fx]
C2EZ31 о™ена ]
ЕН.3.2. Вычисление квартилей
Хотя программа Microsoft Excel содержит функцию КВАРТИЛЬ, позволяющую вычислять квартили выборок, этой функцией пользоваться не следует, поскольку она возвращает неверные результаты при вычислении первого и третьего квартилей. Вместо этого следует воспользоваться табл. ЕН.3.1.
Реализуя этот шаблон, сначала замените шесть вхождений переменной Диапазон своим диапазоном в формате РабочийЛист! ДиапазонЯчеек. Введите все формулы, не разрывая строки (в табл. ЕН.3.1 некоторые формулы занимают несколько строк). Фра
зы “Применяем правило 2” и “средние ранги” должны быть взяты в двойные кавычки. Обратите внимание также на то, что формулы в ячейках ВЗ, В4, В7, В8 и В9 содержат пары закрывающих скобок, а в ячейках С4,С5,С9иС10 — пары двойных кавычек.
Если вам не хочется использовать этот шаблон, откройте рабочий лист Точечная —Диаграмма в файле Chapter 3.xls и переместите диаграмму так, чтобы увидеть диапазон F2 :112. (Ячейка G2 на этом рабочем листе соответствует ячейке А1 в табл. ЕН.3.1.)
Таблица ЕН.3.1. Шаблон рабочего листа для вычисления первого и третьего квартилей
iiBllllliBieiilllll В
1 Вычисление квартилей
2 Исходный ранг первого квартиля =(СЧЕТ(Диапазон)+1)/4
3 =ЕСЛИ(В2=ЦЕЛОЕ(В2); "Применяем правило 1"; ЕСЛИ(В2=ОКРУГЛВВЕРХ(В2;0,5); "Применяем правило 2"; "Применяем правило 3"))
4 = ЕСЛИ(ВЗ="Применяем правило 2"; "средние ранги:"; "используем ранг:") = ЕСЛИ(ВЗ="Применяем правило 2"; ОКРУГЛВНИЗ(В2;1); ОКРУГЛ(В2;0)) =ЕСЛИ(ВЗ="Применяем правило 2"; 0КРУГЛВВЕРХ(В2;1);"")
5 =ЕСЛИ(ВЗ="Применяем правило 2"; "средние ранги:"; "используем ранг:") =НАИМЕНЬШИЙ(Диапазон;В4) =ЕСЛИ(ВЗ="Применяем правило 2"; НАИМЕНЬШИЙ(Диапазон; С4);"")
6 Первый квартиль = ЕСЛИ(ВЗ="Применяем правило 2"; (В5+С5)/2;В5)
7 Исходный ранг третьего квартиля =(3*(СЧЁТ(Диапазон)+1))/4
'Л =ЕСЛИ(В7=ЦЕЛОЕ(В7); "Применяем правило 1"; ЕСЛИ(В7=ОКРУГЛВВЕРХ(В7;0,5); "Применяем правило 2"; "Применяем правило 3"))
9 =ЕСЛИ(В8="Применяем правило 2"; "средние ранги:"; "используем ранг:") =ЕСЛИ(В8="Применяем правило 2"; ОКРУГЛВНИЗ(В7;1); ОКРУГЛ(В7;0)) =(ЕСЛИ(В8="Применяем правило 2"; 0КРУГЛВВЕРХ(В7;1);"")
10 = ЕСЛИ(В8="Применяем правило 2"; "средние ранги:"; "используем ранг:") ==НАИМЕНЬШИЙ(Диапазон;В9) =(ЕСЛИ(В8="Применяем правило 2"; НАИМЕНЬШИЙ(Диапазон; С9);"")
11 Третий квартиль =ЕСЛИ(В8="Применяем правило 2"; (В10+С10)/2;В10)
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
1. Kendall, М. G., and A. Stuart, The Advanced Theory of Statistics, vol.l (London: Charles W. Griffin, 1958).
2. Microsoft Excel 2002 (Redmond, WA: Microsoft Corporation, 1999).
3. Tukey, J., Exploratory Data Analysis (Reading, MA: Addison-Wesley, 1977).
4. Velleman, P. E., and D. C. Hoaglin, Applications, Basics, and Computing of Exploratory Data Analysis (Boston, MA: Duxbury Press, 1981).
Глава 4
Основы теории вероятностей
ПРИМЕНЕНИЕ СТАТИСТИКИ: компания Consumer Electronics
4.1. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ
ВЕРОЯТНОСТЕЙ
Выборочное пространство и события Таблица сопряженности признаков Безусловная вероятность
Вероятность безусловных событий
Правило сложения вероятностей для взаимоисключающих событий
Правило сложения вероятностей для исчерпывающих событий
Процедуры Excel: вычисление безусловных вероятностей
4.2. УСЛОВНАЯ ВЕРОЯТНОСТЬ
Вычисление условных вероятностей
Деревья решений
Статистическая независимость
Правило умножения вероятностей
4.3. ТЕОРЕМА БАЙЕСА
Процедуры Excel: применение теоремы
Байеса
4.4. ЭТИЧЕСКИЕ ПРОБЛЕМЫ
И ВЕРОЯТНОСТЬ
4.5. ПРАВИЛА СЧЕТА
СПРАВОЧНИК ПО EXCEL. ГЛАВА 4
ЧЕМУ ДОЛЖЕН НАУЧИТЬСЯ СТУДЕНТ
• Овладеть основными понятиями теорий вероятностей.
• Понимать смысл условной вероятности.
• Применять теорему Байеса для уточнения вероятностей.
ПРИМЕНЕНИЕ СТАТИСТИКИ
Компания Consumer Electronics
Представьте себе, что вы — менеджер по маркетингу в компании, производящей бытовую электронную аппаратуру. Ваша задача — провести опрос и узнать, сколько семей из 1000 собираются приобрести телевизор с широким экраном (31 дюйм и выше по диагонали) в течение ближайших 12 месяцев. Исследования такого рода называются изучением намерений. Через 12 месяцев вам придется снова опросить те же самые семьи, чтобы узнать, приобрели они телевизор или нет. Кроме того, в семьях, купивших телевизор, необходимо уточнить, купили ли они телевизор с высоким разрешением экрана
(HDTV), а также узнать, не приобрели ли они в течение этих 12 месяцев DVD-плейер и довольны ли они своей покупкой. Необходимо ответить на следующие вопросы.
Какова вероятность того, что семья собирается приобрести широкоэкранный телевизор в следующем году?
Какова вероятность того, что эта семья действительно купит широкоэкранный телевизор в следующем году?
Какова вероятность того, что семья, собирающаяся приобрести широкоэкранный телевизор в следующем году, действительно купит его?
Какова вероятность того, что семья купит широкоэкранный телевизор в следующем году, если она планировала сделать это?
Как влияет информация о планах семьи на вероятность покупки телевизора?
Какова вероятность того, что семья купит телевизор с высоким разрешением экрана, если известно, что она приобрела широкоэкранный телевизор?
Какова вероятность того, что семья в следующем году купит не только широкоэкранный телевизор, но и DVD-плейер?
Какова вероятность того, что семья, купившая широкоэкранный телевизор в следующем году, останется довольной покупкой?
Ответы на эти вопросы помогут разработать правильную маркетинговую стратегию. Например, следует ли в ходе маркетинговой кампании уделить особое внимание семьям, выразившим желание купить телевизор с большим экраном? Легко ли уговорить людей, купивших широкоэкранный телевизор, приобрести телевизор с высоким разрешением экрана и/или DVD-плейер?
ВВЕДЕНИЕ
Предыдущие главы были посвящены методам сбора данных, способам построения таблиц и диаграмм, а также исследованию описательных статистик. В данной главе излагаются основы теории вероятностей, позволяющей распространять результаты, полученные при изучении выборок, на всю генеральную совокупность. Мы рассмотрим три подхода к определению вероятности различных событий: априорную классическую
вероятность, эмпирическую классическую вероятность и субъективную вероятность. Кроме того, будут введены разные типы вероятностей, а также описаны способы уточнения вероятности на основе новой информации. Затем мы изучим понятия распределения вероятностей, математического ожидания, биномиальное и гипергеометрическое распределение, а также распределение Пуассона.
4.1. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Что означает слово “вероятность”? Вероятность (probability) — это возможность наступления некоторого события. Можно говорить о вероятности того, что из колоды карт будет вынута карта черной масти, что человек предпочтет один продукт другому или что новый продукт, появившийся на рынке, будет пользоваться спросом. В каждом из этих вариантов вероятность является числовой величиной, лежащей в интервале от 0 до 1 включительно. Вероятность события, которое никогда не может произойти (невозможное событие), равна 0, а вероятность события, которое происходит постоянно (достоверное событие), равна 1.
Существует три подхода к предмету теории вероятностей: априорная классическая вероятность, эмпирическая классическая вероятность и субъективная вероятность. В рамках априорного классического подхода вероятность события оценивается на основе априорной информации. В простейшем случае, когда все исходы испытаний равновероятны, их вероятность определяется в соответствии с формулой (4.1).
ВЕРОЯТНОСТЬ СОБЫТИЯ
%
Вероятность события (4-1)
где X — количество испытаний, в которых произошло событие, Т — общее количество испытаний.
Что означает эта вероятность? Например, в стандартной колоде игральных карт есть 26 карт красной и 26 карт черной масти. Предположим, что после извлечения карта возвращается в колоду. Означает ли это, что из двух извлеченных карт одна обязательно окажется черной масти? Нет, поскольку никто не может предсказать исходы нескольких последовательных испытаний. Однако, если продолжать испытания достаточно долго, количество карт черной масти, извлеченных из колоды, будет приблизительно равно 0,50.
В предыдущем примере количество успешных испытаний и общее количество испытаний известно заранее. В рамках эмпирического классического подхода вероятность по-прежнему лежит в интервале от 0 до 1 и является результатом деления количества успешных исходов на общее количество испытаний, но вероятность вычисляется на основе наблюдаемой информации, а не априорной. В качестве примера можно привести количество семей, действительно купивших телевизор, количество избирателей, предпочитающих отдельного политика, или количество школьников, принятых на временную работу.
Третий подход к определению вероятностей — субъективный. В двух предыдущих случаях вероятность вычислялась совершенно объективно на основе априорной или апостериорной информации. Субъективная вероятность представляет собой шанс, который приписывается событию конкретным человеком. Другой человек может иначе оценивать шансы этого события. Оценки субъективной вероятности различных событий, как правило, основываются на личном опыте, общественном мнении и анализе конкретной ситуации. Субъективная вероятность особенно полезна в ситуациях, когда эмпирическую вероятность события вычислить невозможно.
Выборочное пространство и события
Основным понятием теории вероятностей является событие (event). Чтобы лучше понять смысл этого термина, вернемся к сценарию, изложенному в начале главы. В табл. 4.1 приведены результаты опроса 1000 семей, в которых отражены как их намерения, так и реальные покупки.
Таблица 4.1. Поведение покупателей широкоэкранных телевизоров
Планировалась ли покупка? Да Совершена ли покупка?
Нет Всего
Да 200 50 250
Нет 100 650 750
Всего 300 700 1000
Событие (event) — это любой возможный результат случайного эксперимента.
Элементарное событие (simple event) — это событие, которое можно описать одной характеристикой.
Совокупность всех элементарных событий называется выборочным пространством (sample space) или пространством исходов.
В данном примере пространство элементарных событий состоит из 1 000 семей. Элементарные события, принадлежащие выборочному пространству, классифицируются в зависимости от разновидности исхода. Например, если нас интересуют планы семей, события формулируются так: “покупка планируется” и “покупка не планируется”. Таким образом, способ, которым разбивается выборочное пространство, зависит от вида оцениваемой вероятности.
Во врезках даны определения двух важных понятий: дополнения и совместного события. Так, в табл. 4.1 дополнением события “покупка планируется” является событие “покупка не планируется”. Кроме того, событие “покупка планируется и покупка совершена” является совместным, поскольку оно состоит из двух элементарных событий — “покупка планируется” и “покупка совершена”.
Дополнением (complement) события А называются все события, которые не являются частью события А. Дополнение события А обозначается символом А'.
Совместное событие (joint event) — это событие, которое имеет несколько характеристик.
Таблица сопряженности признаков
Существует несколько способов изучения выборочного пространства. Мы рассмотрим метод, основанный на таблице перекрестной классификации (table of crossclassification), частным случаем которой является табл. 4.1. Эту таблицу также называют таблицей сопряженности признаков (contingency table) или факторной (см. раздел 2.5). Числа, указанные в ячейках таблицы, получены в результате разделения вы-
боронного пространства, состоящего из 1 000 семей, на семьи, планировавшие покупку и действительно купившие широкоэкранный телевизор, и семьи, не планировавшие и не сделавшие этого. Так, например, 200 семей планировали покупки и осуществили свои намерения.
Безусловная вероятность
До сих пор мы рассматривали определения терминов и разбиение выборочного пространства. Теперь, чтобы ответить на некоторые вопросы, поставленные в сценарии, мы сформулируем несколько правил, позволяющих вычислить вероятности событий.
Прежде всего, вероятность должна лежать в интервале от 0 до 1. Вероятность невозможного события равна 0, а достоверного — 1. Вероятность элементарного события А называется безусловной (simple probability) и обозначается как Р(А). Например, безусловной является вероятность события “покупка планируется”.
Для того чтобы вычислить вероятность этого события, следует применить формулу (4.1)
. количество семей, планирующих покупку 250 Л
Р(покупка планируется) =------------------------------=-----= 0,25.
общее количество семей 1 000
Таким образом, вероятность того, что отдельная семья планирует покупку широкоэкранного телевизора, равна 0,25 (25%).
Эта вероятность называется безусловной (marginal probability), поскольку общее количество успешных исходов (т.е. количество семей, планирующих покупку) можно просто извлечь из соответствующей ячейки таблицы сопряженности признаков (например, табл. 4.1). Рассмотрим еще один пример вычисления безусловной вероятности.
ПРИМЕР 4.1. ВЫЧИСЛЕНИЕ ВЕРОЯТНОСТИ ТОГО, ЧТО ПРИОБРЕТЕННЫЙ ТЕЛЕВИЗОР ИМЕЕТ ВЫСОКОЕ РАЗРЕШЕНИЕ ЭКРАНА
Исследователи попросили 300 семей, купивших широкоэкранный телевизор, ответить на дополнительные вопросы. В табл. 4.2 указано, сколько из них купило телевизоры с высоким разрешением экрана и DVD-плейеры.
Таблица 4.2. Поведение покупателей DVD-плейеров и широкоэкранных телевизоров с высоким разрешением экрана (HDTV-телевизоров)
Куплен DVD-плейер
Куплен HDTV Да Нет Всего
Да 38 42 80
Нет 70 150 220
Всего 108 192 300
Определите вероятность того, что случайно выбранная семья, купившая широкоэкранный телевизор, купила телевизор с высоким разрешением (HDTV-телевизор).
РЕШЕНИЕ. Введем несколько обозначений.
А — семья купила HDTV-телевизор В — семья купила DVD-плейер
А' — семья не купила HDTV-телевизор В' — семья не купила DVD-плейер
количество семей, купивших HDTV-телевизор 80
Р(А} = --------------------------------------= ——• = 0,26 /.
общее количество семей, купивших телевизор 300
Следовательно, вероятность того, что случайно выбранная семья, купившая широкоэкранный телевизор, приобрела HDTV-телевизор, равна 0,267 (26,7%).
Вероятность совместных событий
В то время как безусловная вероятность относится к элементарным исходам, вероятность совместного события вычисляется в ситуациях, когда происходит несколько событий. Допустим, семья планирует и действительно приобретает широкоэкранный телевизор.
Напомним, что совместное событие состоит из одновременных элементарных событий. В табл. 4.1 указано количество семей, которые планировали купить и действительно купили широкоэкранный телевизор. Поскольку эта группа состоит из 200 семей, вероятность события “покупка планировалась и осуществилась” вычисляется по следующей формуле.
Р(покупка планировалась и осуществилась} —
_ количество семей, планировавших покупку и осуществивших ее _ 200 _ общее количество семей 1 000
Решение получено.
Рассмотрим еще один пример вычисления вероятности совместного события.
ПРИМЕР 4.2. ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ СОВМЕСТНОГО СОБЫТИЯ, СОСТОЯЩЕГО В ТОМ, ЧТО СЕМЬЯ КУПИТ HDTV-ТЕЛЕВИЗОР И DVD-ПЛЕЙЕР
В табл. 4.2 указано, сколько семей купило телевизоры с высоким разрешением экрана или DVD-плейеры. Определите вероятность того, что случайно выбранная семья приобрела широкоэкранный HDTV-телевизор и DVD-плейер одновременно.
РЕШЕНИЕ. Используя формулу (4.1), получаем
Р(куплен HDTV-телевизор и DVD-плейер} =
количество семей, кутивших HDTV-телевизор и DVD-плейер _ 38 _qj27 общее количество семей, купивших широкоэкранный телевизор 300
Следовательно, вероятность того, что случайно выбранная семья приобрела широкоэкранный HDTV-телевизор и DVD-плейер, равна 0,127 (12,7%).
С помощью понятия вероятности совместного события можно иначе определить без условную вероятность элементарного исхода. Допустим, событие В состоит из дву^ взаимоисключающих событий — В} и В2. Тогда вероятность исхода А можно вычислит как сумму вероятности событий “А и В/’ и “А и В2”.
БЕЗУСЛОВНАЯ ВЕРОЯТНОСТЬ ЭЛЕМЕНТАРНОГО СОБЫТИЯ
Р(А) = Р(А и В,) + Р(Аи В2) + ... + Р(А и BJ, (4.2]
где события В;, В2, ..., Вк являются взаимоисключающими и исчерпывающими.
Два события называются взаимоисключающими (mutually exclusive), если они не могут происходить одновременно. Множество событий называется исчерпывающим (collectively exhaustive), если обязательно происходит хотя бы одно из них.
Например, события “человек является мужчиной” и “человек является женщиной” являются взаимоисключающими и исчерпывающими. Эти события никогда не происходят одновременно, и в то же время человек всегда является либо мужчиной, либо женщиной.
Применим формулу (4.2) для вычисления вероятности события “покупка планировалась”.
Р(покупка планировалась} =
_ количество семей, планировавших покупку’ и осуществивших ее общее количество семей
количество семей, планировавших покупку’ и не осуществивших ее общее количество семей
_ 200 ! 50 250 Q 25
” 1000 1 000 ” 1000 ” ’
Этот результат можно было бы получить, просто сложив количество семей, планировавших покупку, и поделив его на общее количество семей.
Общее правило сложения вероятностей
Зная вероятности события А и события “А и В”, можно вычислить вероятность события “А или В”. В формулу для вычисления вероятности этого события входят вероятности событий А, В и “А и В”.
Как определить вероятность того, что семья планировала покупку или совершила ее? Событие “покупка либо планировалась, либо совершена” охватывает все семьи, которые планировали покупку, и все семьи, совершившие ее. Для ответа на этот вопрос придется проверить каждую ячейку таблицы сопряженности признаков (табл. 4.1). Ячейка, соответствующая событию “покупка планировалась, но не совершена”, относится к событию “покупка планировалась”, поскольку учитывает семьи, которые действительно планировали приобрести широкоформатный телевизор. Ячейка, соответствующая событию “покупка не планировалась, но была совершена”, относится к событию “покупка совершена”, поскольку учитывает семьи, которые действительно приобрели широкоформатный телевизор. Ячейка, соответствующая событию “покупка планировалась и совершена”, удовлетворяет обоим условиям. Таким образом, вероятность того, что семья либо планировала, либо приобрела широкоформатный телевизор, вычисляется по следующей формуле.
Р(семъя. либо планировала, либо приобрела широкоформатный телевизор} =
= Р(семъя планировала, но не приобрела широкоформатный телевизор} + + Р (семья не планировала, но приобрела широкоформатный телевизор} + + Р(семья планировала и приобрела широкоформатный телевизор}
Вычисление вероятности события “А или В" подчиняется общей формуле сложения вероятностей.
ОБЩЕЕ ПРАВИЛО СЛОЖЕНИЯ ВЕРОЯТНОСТЕЙ
Вероятность события “А или В” равна вероятности события А плюс вероятность события В минус вероятность события “А и В".
Р(А или В) = Р(А) + Р(В) -Р(АиВ) (4.3)
Применяя общее правило сложения вероятностей к предыдущему примеру, получим следующее.
Р(семья либо планировала, либо приобрела широкоформатный телевизор) —
= Р (семья планировала, но не приобрела широкоформатный телевизор) +
+ Р (семья не планировала, но приобрела широкоформатный телевизор) +
+ Р (семья планировала и приобрела широкоформатный телевизор)
_ 250 t 300 200 350 Q 25
1000 1000 1 000 ~ 1 000 ~ ’
Для вычисления вероятности события “А или В" необходимо сначала сложить вероятности событий А и В, а затем вычесть из суммы вероятность события “А и В", чтобы не учитывать вероятности событий А и В дважды. Продемонстрируем это правило на примере табл. 4.1. Если количество исходов “покупка планировалась” сложить с количеством исходов “покупка совершена”, совместное событие “покупка планировалась и действительно совершена” будет учтено дважды. Следовательно, чтобы получить правильный результат, вероятность совместного события следует вычесть.
Рассмотрим еще один пример, демонстрирующий правило сложения вероятностей.
ПРИМЕР 4.3. ПРИМЕНЕНИЕ ПРАВИЛА СЛОЖЕНИЯ ВЕРОЯТНОСТЕЙ
ДЛЯ ВЫЧИСЛЕНИЯ ВЕРОЯТНОСТИ ТОГО, ЧТО ОТДЕЛЬНАЯ СЕМЬЯ КУПИТ ШИРОКОЭКРАННЫЙ ТЕЛЕВИЗОР
В табл. 4.2 указано, сколько семей купило телевизоры с высоким разрешением экрана или DVD-плейеры. Определите вероятность того, что случайно выбранная семья, купившая широкоэкранный телевизор, приобрела HDTV-телевизор или DVD-плейер.
РЕШЕНИЕ. Используя формулу (4.3), получаем
Р(куплен HDTV-телевизор или DVD-плейер) — Р(семъя купила HDTV-телевизор) +
+ Р(семъя купила DVD-плейер) - Р(семъя купила HDTV-телевизор и DVD-плейер) =
80 108 38 150 лсл
=---+--------=----= 0,50.
300 300 300 300
Следовательно, вероятность того, что случайно выбранная семья, купившая широкоэкранный телевизор, приобрела HDTV-телевизор или DVD-плейер, равна 0,5 (50%).
Правило сложения вероятностей взаимоисключающих событий
В некоторых ситуациях вероятность совместного события вычитать необязательно, поскольку она равна нулю.
ПРИМЕР 4.4. ПРИМЕНЕНИЕ ПРАВИЛА СЛОЖЕНИЯ ВЕРОЯТНОСТЕЙ ВЗАИМОИСКЛЮЧАЮЩИХ СОБЫТИЙ
Попросим 300 семей, купивших широкоформатный телевизор, ответить, где они совершили покупку. Результаты опроса помещены в табл. 4.3.
Таблица 4.3. Сводная таблица покупок
Место покупки Количество респондентов
В магазине 183
По Интернет 87
По почте 30
Какова вероятность того, что случайно выбранная семья, купившая широкоэкранный телевизор, заказала его через Интернет или по почте?
РЕШЕНИЕ.
Р(телевизор заказан через Интернет или по почте) =
= Р(телевизор заказан через Интернет) + Р(телевизор заказан по почте) -Р(телевизор заказан через Интернет и по почте)
=JL+21__L=HZ=0,39.
300 300 300 300
Следовательно, вероятность того, что случайно выбранная семья, купившая широкоэкранный телевизор, заказала его через Интернет или по почте, равна 0,39 (39%).
Совершенно очевидно, что клиент не может совершать заказы одновременно через Интернет и по почте. Следовательно, вероятность совместного события равна нулю. Реальная покупка может быть совершена только одним способом, иначе клиенту придется платить дважды. Как указывалось ранее, события, которые не могут происходить одновременно, называются взаимоисключающими.
ПРАВИЛО СЛОЖЕНИЯ ВЕРОЯТНОСТЕЙ ВЗАИМОИСКЛЮЧАЮЩИХ СОБЫТИЙ
Если события А и В являются взаимоисключающими, вероятность события “А или В” равна вероятности события А плюс вероятность события В.
Р(А или В) = Р(А) 4- Р(В) (4.4)
Правило сложения вероятностей исчерпывающих событий
Рассмотрим правило для исчерпывающих событий на конкретном примере.
ПРИМЕР 4.5. ПРИМЕНЕНИЕ ДОПОЛНИТЕЛЬНОГО ПРАВИЛА СЛОЖЕНИЯ ВЕРОЯТНОСТЕЙ ИСЧЕРПЫВАЮЩИХ СОБЫТИЙ
В табл. 4.2 указано, сколько семей купило телевизоры с высоким разрешением экрана или DVD-плейеры. Определите вероятность того, что случайно выбранная семья, купившая широкоэкранный телевизор, приобрела DVD-плейер или не приобрела его.
РЕШЕНИЕ. Используя формулу (4.4), получаем
Р(И¥Т)-плейер либо куплен, либо нет) = Р(семья купила DVD-плейер) +
। п/ nvn - Ч 108 192 300
+ Р(семья не купила DVD-плеиер) =-h--------= 1,0 .
300 300 300
Следовательно, вероятность того, что случайно выбранная семья, купившая широкоэкранный телевизор, купила или не купила DVD-плейер, равна 1,0 (100%), поскольку эти два события являются взаимоисключающими.
Для вычисления безусловных вероятностей следует заполнить выборочное пространство на листе Вероятности в рабочей книге Chapter 4 .xls и применить арифметические формулы. С помощью надстройки PHStat2 можно создать копию этого рабочего листа.
Например, чтобы вычислить вероятности событий по табл. 4.2, нужно открыть рабочий лист Вероятности в рабочей книге Chapter 4.xls или выполнить команду PHStat* 1^Probability & Prob. Distribution^Simple & Joint Probabilities (PHStat^Вероятности & Распределения^Безусловные & Совместные вероятности). Затем необходимо выполнить следующие действия.
Метки таблицы пространства исходов
1. Ввести заголовок Покупка hdtv (событие А} в ячейку А5.
2. Ввести заголовок HDTV-Да (событие А) ячейку В5.
3. Ввести заголовок HDTV-Нет (событие А2) в ячейку вб.
4. Ввести заголовок Покупка DVD (событие В) в ячейку СЗ.
5. Ввести заголовок DVD-Да (событие В) в ячейку С4.
б. Ввести заголовок DVD-Нет (событие Вг) в ячейку D4.
Заполнение таблицы пространства исходов
1. Ввести в ячейку С5 число 3 8 (событие HDTV-Да И DVD-Да).
2. Ввести в ячейку С6 число 7 0 (событие HDTV-Нет и DVD-Да).
3. Ввести В ячейку D5 ЧИСЛО 42 (событие HDTV-Да И DVD-Нет).
4. Ввести в ячейку D6 число 150 (событие hdtv-Hgt и dvd-Hgt).
Оператор конкатенации, использованный в некоторых формулах при формировании меток, описан в разделе ЕН.4.1.
Chapter 4.xls
Изучение основ
4.1. Подбрасываются две монеты.
1. Приведите пример элементарного события.
2. Приведите пример совместного события.
4.2. В урне находятся 12 красных шаров и 8 белых. Из урны извлекается один шар.
1. Приведите пример элементарного события.
2. Какое событие является дополнительным по отношению к красному шару?
4.3. Дана следующая таблица сопряженности признаков.
В В’
А 10 20
А* 20 40
Какова вероятность следующих событий?
1. Событие А.
2. Событие В.
3. Событие А'.
4. Событие “А и В”.
5. Событие “А и В'”.
6. Событие “А' и В’”.
7. Событие “А' или В’”.
$. Событие “А или В’”.
9. Событие “А'или В’”.
4.4. Дана следующая таблица сопряженности признаков.
В В’
А 10 30
А' 25 35
Какова вероятность следующих событий?
1. Событие А.
2. Событие В.
3. Событие А'.
4. Событие “А и В”.
5. Событие “А и В'”.
6. Событие “А’и В'”.
7. Событие “А ил и В”.
8. Событие‘А или В’”.
9. Событие‘А’или В’”.
Применение понятий
4.5. Для каждого из указанных ниже испытаний укажите вид вычисляемой вероятности: классическая априорная, классическая эмпирическая или субъективная.
1. При следующем подбрасывании идеальная монета упадет орлом вверх.
2. В следующий раз сборная Италии станет чемпионом мира по футболу.
3. Сумма очков на двух игральных кубиках будет равной 7.
4. Поезд опоздает на 10 минут.
5. На следующих президентских выборах в США победят республиканцы.
4.6. Для каждой из перечисленных ниже ситуаций укажите, какие события являются взаимоисключающими и/или исчерпывающими. Если события не являются
взаимоисключающими и/или исчерпывающими, либо переформулируйте задачу, чтобы они стали таковыми, либо объясните, почему это невозможно.
1. Избиратели в США регистрируются как республиканцы или демократы.
2. Респонденты классифицируются по странам, в которых собраны их автомобили: США, Европа, Япония и др.
3. В ходе опроса был задан вопрос: “Где вы сейчас живете: а) в квартире или б) в собственном доме?”.
4. Товар классифицируется как бракованный или качественный.
5. В ходе опроса был задан вопрос: “Собираетесь ли вы покупать новый автомобиль в течение следующих шести месяцев? Да или нет?”.
4.7. Вероятность каждого из перечисленных ниже событий равна нулю. Объясните почему. Укажите причины, из-за которых событие стало невозможным.
1. Избиратели в США могут быть и республиканцами и демократами одновременно.
2. Товар может бракованным и качественным одновременно.
3. Дом, в котором все комнаты расположены на одном этаже, может иметь комнаты, расположенные на разных этажах.
4.8. Результаты контроля продукции производственной компании позволили выявить дефекты в партии, состоящей из 450 плат. В приведенной ниже таблице содержатся ответы на два вопроса: “Найдены ли частицы на матрице?” и “Качественная плата или нет?”.
Состояние матрицы
Качество платы Нет частиц Есть частицы Всего
Хорошее 320 14 334
Плохое 80 36 116
Всего 400 50 450
Источник: Hall, S. ТУ. “Analysis of Detectivity of Semiconductor Wafers by Contingency Table”, Proceedings Institute of Environmental Sciences, 1 (1994):177-183.
1. Приведите пример элементарного события.
2. Приведите пример совместного события.
3. Какое событие является дополнительным по отношению к событию “плата является качественной”?
4. Почему событие “плата является качественной” и событие “обнаружены частицы на матрице” являются совместными?
Какова вероятность следующих событий, если платы выбираются случайно?
5. Плата отпечатана с матрицы, содержащей частицы.
6. Плата является дефектной.
7. Плата является дефектной и отпечатана с матрицы, не содержащей частиц.
8. Плата является качественной и отпечатана с матрицы, не содержащей частиц.
9. Плата является качественной или отпечатана с матрицы, не содержащей частиц.
10. Плата является дефектной и отпечатана с матрицы, содержащей частицы.
11. Объясните разницу между результатами решения задач 8 и 9.
4.9. Недавно в США было проведено анкетирование, призванное выяснить, каким образом домовладельцы добираются на работу (“How People Get То Work”, USA Today Snapshots, February 25, 2003, 1A). Предположим, что в опросе приняли участие 1 000 домовладельцев и 1 000 арендаторов. Результаты опроса приведены в следующей таблице.
Добираетесь ли вы на работу на автомобиле? Домовладельцы Арендаторы Всего
Да 824 681 1 505
Нет 176 319 595
Всего 1 000 1 000 2 000
1. Приведите пример элементарного события.
2. Приведите пример совместного события.
3. Какое событие является дополнительным по отношению к ответу “добираюсь на работу на автомобиле”?
4. Почему события “добираюсь на работу на автомобиле” и “являюсь домовладельцем” совместны?
Предположим, что респондент выбирается случайно. Какова вероятность следующих событий?
5. Респондент добирается на работу на автомобиле.
6. Респондент является домовладельцем.
7. Респондент добирается на работу на автомобиле и респондент является домовладельцем.
8. Респондент добирается на работу не на автомобиле и респондент является арендатором.
9. Респондент добирается на работу на автомобиле или респондент является домовладельцем.
10. Респондент добирается на работу не на автомобиле или респондент является арендатором.
11. Объясните разницу между ответами на вопросы 7 и 9.
4.10. Можно ли утверждать, что крупные компании реже предлагают фондовые опционы членам правления, чем малые и средние компании? Опрос, проведенный компанией Segal Company of New York, позволил определить, что среди 189 крупных компаний, входящих в выборку, 40 предлагали фондовые опционы членам своих правлений в рамках безналичного компенсационного пакета. В то же время среди 180 малых и средних компаний 43 компании предлагали фондовые опционы членам своих правлений в рамках безналичного компенсационного пакета. (Kemba J. Dunham, “The Jungle: Focus on Recruitment, Pay and Getting Ahead”, Wall Street Journal, August 21, 2001, B6.)
1. Создайте таблицу сопряженности признаков, имеющую размер 2x2, и оцените вероятности разных событий.
2. Приведите пример элементарного события.
3. Приведите пример совместного события.
4. Какое событие является дополнительным по отношению к ответу “компания предлагает фоновый опцион членам своего правления”?
5. Почему события “крупная компания” и “компания предлагает фоновый опцион членам своего правления” являются совместными?
Вычислите вероятность следующих событий для случайно выбранной компании.
6. Компания явдяется крупной.
7. Компания предлагает фондовые опционы членам своего правления.
8. Компания является крупной и предлагает фондовые опционы членам своего правления.
9. Компания является средней или малой и предлагает фондовые опционы членам своего правления.
10. Компания является крупной или предлагает фондовые опционы членам своего правления.
11. Компания является средней или малой или предлагает фондовые опционы членам своего правления.
12. Объясните разницу между ответами на вопросы 8 и 10.
4.11. Можно ли утверждать, что белые рабочие чаще заявляют о несправедливости своего увольнения? Опрос, проведенный Барри Гольдманом (“White Fight: A Researcher Finds Whites Are More Likely to Claim Bias”, Wall Street Journal, Work Week, April 10, 2001, Al) показал, что из 56 уволенных белых рабочих 29 заявили, что это несправедливо. В то же время из 407 уволенных черных рабочих о несправедливости заявили 126.
1. Создайте таблицу сопряженности признаков, имеющую размер 2x2, и оцените вероятности разных событий.
2. Приведите пример элементарного события.
3. Приведите пример совместного события.
4. Какое событие является дополнительным по отношению к ответу “рабочий заявил о несправедливом увольнении”?
5. Почему события “рабочий является белым” и “рабочий заявил о несправедливом увольнении” являются совместными?
Вычислите вероятность следующих событий для случайно выбранного рабочего.
6. Он— белый.
7. Он считает свое увольнение несправедливым.
8. Он — белый и считает свое увольнение несправедливым.
9. Он — черный и не считает свое увольнение несправедливым.
10. Он — белый или считает свое увольнение несправедливым.
11. Он — черный или считает свое увольнение несправедливым.
12. Объясните разницу между ответами на вопросы 8 и 10.
4.12. В ходе опроса было опрошено 500 пассажиров метрополитена. Помимо прочего, в анкете был вопрос: “Любите ли вы покупать одежду?”. Из 240 мужчин 136 ответили “Да”. Из 260 женщин 224 ответили “Да”.
1. Создайте таблицу сопряженности признаков, имеющую размер 2x2, и оцените вероятности разных событий.
2. Приведите пример элементарного события.
3. Приведите пример совместного события.
4. Какое событие является дополнительным по отношению к ответу “люблю покупать одежду”?
Вычислите вероятность следующих событий для случайно выбранного респондента.
5. Он — мужчина.
6. Он любит покупать одежду.
7. Она — женщина и любит покупать одежду.
8. Он — мужчина и не любит покупать одежду.
9. Респондент — женщина или любит покупать одежду.
10. Респондент — мужчина или женщина.
4.13. Каждый год создается рейтинговый лист, оценивающий поведение автомобилей на протяжении первых 90 дней после покупки. Предположим, что автомобили разделены на две категории: требует ли автомобиль гарантийного ремонта (да или нет), и в какой стране он был собран (США или нет). На основе этих данных была вычислена вероятность того, что новый автомобиль потребует гарантийного ремонта, — 0,04, вероятность того, что автомобиль собран в США, — 0,60, а также вероятность того, что новый автомобиль, собранный в США, потребует гарантийного ремонта, — 0,025.
1. Создайте таблицу сопряженности признаков, имеющую размер 2x2, и оцените вероятности разных событий.
2. Приведите пример элементарного события.
3. Приведите пример совместного события.
4. Какое событие является дополнительным по отношению к ответу “автомобиль произведен в США”?
Вычислите вероятность следующих событий для случайно выбранного автомобиля.
5. Автомобиль требует гарантийного ремонта.
6. Автомобиль не произведен в США.
7. Автомобиль требует гарантийного ремонта и произведен в США.
8. Автомобиль не требует гарантийного ремонта и не произведен в США.
9. Автомобиль требует гарантийного ремонта или произведен в США.
10. Автомобиль требует гарантийного ремонта или произведен не в США.
11. Автомобиль требует или не требует гарантийного ремонта.
4.2. УСЛОВНАЯ ВЕРОЯТНОСТЬ
В рассмотренных выше примерах вычислялись вероятности элементарных событий. Возникает вопрос: как определить вероятность события, если известна некая информация о событиях, происшедших до него?
Вероятность события А, при вычислении которого учитывается информация о событии В, называется условной (conditional probability) и обозначается как Р(А\В).
УСЛОВНАЯ ВЕРОЯТНОСТЬ
Вероятность события А при условии, что наступило событие В, равна вероятности события “А и В”, деленной на вероятность события В.
Р(А\В)=Р^ив^. (4.5, а)
Вероятность события В при условии, что наступило событие А, равна вероятности события “А и В”, деленной на вероятность события А.
Р(В|Л) = ^^. (4.5,6)
Здесь использованы следующие обозначения: Р(АиВ) — вероятность события “А и В”, Р(А) — вероятность события А, Р(В) — вероятность события В.
Вместо формул (4.5, а) и (4.5, б) при вычислении условной вероятности можно воспользоваться таблицей сопряженности признаков. Вернемся к сценарию, изложенному в начале главы, и предположим, что нам стало известно, будто некая семья собирается купить широкоэкранный телевизор. Какова вероятность того, что эта семья действительно купит такой телевизор? В данном случае нам необходимо вычислить условную вероятность Р(покупка совершена\покупка планировалась}. Поскольку нам известно, что семья планирует покупку, выборочное пространство состоит не из всех 1 000 семей, а только из тех, которые планируют покупку широкоэкранного телевизора. Из 250 таких семей 200 действительно купили этот телевизор (см. табл. 4.1). Следовательно, вероятность того, что семья действительно купит широкоэкранный телевизор, если она это запланировала, можно вычислить по следующей формуле.
Р(покупка совершена\покупка планировалась} =
_ количество семей, планировавших и купивших широкоэкранный телевизор _ 200
----------------------------------------------------------------------= 0, о0
количество семей, планировавших купить широкоэкранный телевизор 250
Этот же результат дает формула (4.5, б):
Р(А и В) Р(В\А) = —-----
1 Р(А)
где событие А заключается в том, что семья планирует покупку широкоформатного телевизора, а событие В — в том, что она его действительно купит. Подставляя в формулу реальные данные, получаем следующий ответ.
200/1 000
250/1 000
Р(покупка совершена\покупка планировалась} =
ПРИМЕР 4.6. ВЫЧИСЛЕНИЕ УСЛОВНОЙ ВЕРОЯТНОСТИ ТОГО, ЧТО ОТДЕЛЬНАЯ СЕМЬЯ КУПИТ DVD-ПЛЕЙЕР, ЕСЛИ ОНА КУПИЛА ШИРОКОЭКРАННЫЙ ТЕЛЕВИЗОР С ВЫСОКИМ РАЗРЕШЕНИЕМ ЭКРАНА
В табл. 4.2 указано, сколько семей купило телевизоры с высоким разрешением экрана или DVD-плейеры. Определите вероятность того, что случайно выбранная семья приобретет DVD-плейер, если она уже купила широкоэкранный HDTV-телевизор.
РЕШЕНИЕ. Поскольку заранее известно, что семья купила широкоэкранный телевизор, выборочное пространство сужается до 80 семей. Из этих 80 семей 38 купили DVD-плейер. Следовательно, вероятность того, что семья купит DVD-плейер, при условии, что она уже купила широкоэкранный телевизор, вычисляется по следующей формуле.
Р (семья купит ВРВ-плейер\семъя купила HDTV-телевизор} =
_ количество семей, купивших HDTV -телевизор и DVD-плейер _ 38 $
количество семей, купивших HDTV-телевизор 80
Используя формулу (4.5, а), получаем следующий ответ.
Р(Л|В) = Р(ЛиВ'> = 2Ж = 0,475,
где событие А заключается в том, что семья купит DVD-плейер, а событие В — в том, что она уже купила широкоэкранный телевизор с высоким разрешением экрана.
Следовательно, если семья купила широкоэкранный HDTV-телевизор, шансы, что она купит еще и DVD-плейер, равны 47,5%. Обратите внимание на то, что безусловная вероятность покупки DVD-плейера в данном примере равна 108/300=0,36, или 36%. Таким образом, вероятность покупки DVD-плейера семьей, которая купила HDTV-телевизор, выше, чем вероятность покупки DVD-плейера семьей, которая купила обычный широкоэкранный телевизор.
Дерево решений
В табл. 4.1 семьи разделены на четыре категории: планировавшие покупку широкоэкранного телевизора и не планировавшие, а также купившие такой телевизор и не купившие. Аналогичную классификацию можно выполнить с помощью дерева решений (decision tree) (рис. 4.1).
Дерево, изображенное на рис. 4.1, имеет две ветви, соответствующие семьям, которые планировали приобрести широкоэкранный телевизор, и семьям, которые не делали этого. Каждая из этих ветвей разделяется на две дополнительные ветви, соответствующие семьям, купившим и не купившим широкоэкранный телевизор. Вероятности, записанные на концах двух основных ветвей, являются безусловными вероятностями событий АиА'. Вероятности, записанные на концах четырех дополнительных ветвей, являются условными вероятностями каждой комбинации событий А и В. Условные вероятности вычисляются путем деления совместной вероятности событий на соответствующую безусловную вероятность каждого из них.
Рис. 4.1. Дерево решения при покупке широкоэкранного телевизора
Например, чтобы вычислить вероятность того, что семья купит широкоэкранный телевизор, если она запланировала сделать это, следует определить вероятность события “покупка запланирована и совершена”, а затем поделить его на вероятность события “покупка запланирована”. Перемещаясь по дереву решения, изображенному на рис. 4.1, получаем следующий ответ.
200/
Р(покупка совершена\покупка запланирована) = ,--=----= 0,80.
/юоо 250
Таким образом, задача решена.
ПРИМЕР 4.7. ПОСТРОЕНИЕ ДЕРЕВА РЕШЕНИЯ ДЛЯ СЕМЕЙ, КУПИВШИХ ШИРОКОЭКРАННЫЙ ТЕЛЕВИЗОР
Постройте дерево решений, используя данные, приведенные в табл. 4.2. Определите вероятность того, что случайно выбранная семья приобретет DVD-плейер, если она уже купила широкоэкранный HDTV-телевизор.
РЕШЕНИЕ. Используя формулу (4.5, а), получаем следующий ответ.
Р(В\ А) = Р(АиВ} = УЖ = о 475 %0
где событие А заключается в том, что семья купила широкоэкранный телевизор с высоким разрешением экрана, а событие В — в том, что она купит DVD-плейер.
Дерево решений для семей, купивших и DVD-плейер, и HDTV-телевизор, изображено на рис. 4.2.
Рис. 4.2. Дерево решения при покупке HDTV-телевизора и DVD-плейера
Задача решена.
Статистическая независимость
В примере с покупкой широкоэкранного телевизора вероятность того, что случайно выбранная семья приобрела широкоэкранный телевизор при условии, что она планировала это сделать, равна 200/250 = 0,80. Напомним, что безусловная вероятность того, что случайно выбранная семья приобрела широкоэкранный телевизор, равна 300/1000 = 0,30. Отсюда следует несколько важных выводов. Априорная информация о том, что семья планировала покупку, влияет на вероятность самой покупки. Иначе говоря, эти два события зависят друг от друга. В противоположность этому примеру, существуют статистически независимые события, вероятности которых не зависят друг от друга.
СТАТИСТИЧЕСКАЯ НЕЗАВИСИМОСТЬ
Р(А|В) = Р(А), (4.6) j
где Р(А|В) — вероятность события А при условии, что произошло событие В, Р(А) — безусловная вероятность события А.
Обратите внимание на то, что события А и В являются статистически независимыми друг от друга тогда и только тогда, когда Р(А|В)= Р(А). Если в таблице сопряженности признаков, имеющей размер 2x2, это условие выполняется хотя бы для одной комбинации событий А и В, оно будет справедливым и для любой другой комбинации.1 В нашем примере события “покупка запланирована” и “покупка совершена” не являются статистически независимыми, поскольку информация об одном событии влияет на вероятность другого. Рассмотрим пример, в котором показано, как проверить статистическую независимость двух событий.
В таблице сопряженности признаков, состоящей из г столбцов и q строк, это правило следует проверить на (г-1)(с-1) разных комбинациях событий А и В.
ПРИМЕР 4.8. РАСПОЗНАВАНИЕ СТАТИСТИЧЕСКОЙ НЕЗАВИСИМОСТИ
Спросим у 300 семей, купивших широкоформатный телевизор, довольны ли они своей покупкой.
Таблица 4.4. Данные, характеризующие степень удовлетворенности покупателей широкоэкранных телевизоров
Удовлетворены ли вы покупкой?
Тип телевизора Да Нет Всего
HDTV 64 16 80
Другой 176 44 220
Всего 240 60 300
Определите, связаны ли между собой степень удовлетворенности покупкой и тип телевизора.
РЕШЕНИЕ. Судя по этим данным,
6У 64
Р{покупатель удовлетворен\куплен HDTV -телевизор ) = - — - 0,80.
’/300 80
В то же время,
240 Р(покупателъ удовлетворен} = = 0,80.
Следовательно, вероятность того, что покупатель удовлетворен покупкой, и того, что семья купила HDTV-телевизор, равны между собой, и эти события являются статистически независимыми, поскольку никак не связаны между собой.
Правило умножения вероятностей
Формула для вычисления условной вероятности позволяет определить вероятность совместного события “А и В”. Разрешив формулу (4.5, а),
Р(А\В) =
Р(АиВ) Р(В)
относительно совместной вероятности Р(Аи В), получаем общее.правило умножения вероятностей.
ПРАВИЛО УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ
Вероятность события “А и В” равна вероятности события А при условии, что наступило событие В, умноженной на вероятность события В.
Р(А иВ) = Р(А\В) Р(В). (4.7)
ПРИМЕР 4.9. ПРИМЕНЕНИЕ ПРАВИЛА УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ
Рассмотрим 80 семей, купивших широкоэкранный HDTV-телевизор. В табл. 4.4 указано, что 64 семьи удовлетворены покупкой и 16 — нет. Предположим, что среди них случайным образом выбираются две семьи. Определите вероятность, что оба покупателя окажутся довольными.
РЕШЕНИЕ. Используя формулу (4.7), получаем:
Р(АиВ) = Р(А\В)Р(В),
где событие А заключается в том, что вторая семья удовлетворена своей покупкой, а событие В — в том, что первая семья удовлетворена своей покупкой.
Вероятность того, что первая семья удовлетворена своей покупкой, равна 64/80. Однако вероятность того, что вторая семья также удовлетворена своей покупкой, зависит от ответа первой семьи. Если первая семья после опроса не возвращается в выборку (выбор без возвращения), количество респондентов снижается до 79. Если первая семья оказалась удовлетворенной своей покупкой, вероятность того, что вторая семья также будет довольна, равна 63/79, поскольку в выборке осталось только 63 семьи, удовлетворенные своим приобретением. Таким образом, подставляя в формулу (4.7) конкретные данные, получим следующий ответ:
Р(А иВ) = (63/79)(64/80)=0,6380.
Следовательно, вероятность того, что обе семьи довольны своими покупками, равна 63,80%. и
ПРИМЕР 4.10. ПРИМЕНЕНИЕ ПРАВИЛА УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ ПРИ ВЫБОРЕ С ВОЗВРАЩЕНИЕМ
Предположим, что после опроса первая семья возвращается в выборку. Определите вероятность того, что обе семьи окажутся довольными своей покупкой.
РЕШЕНИЕ. В данном примере вероятность того, что первая семья удовлетворена своей покупкой, как и прежде, равна 64/80, поскольку в выборке из 80 семей находятся 64 семьи, довольные своим приобретением. Следовательно,
Р(А иВ) = Р(А|В)Р(В)=(64/80)(64/80)=0,64.
Таким образом, вероятность того, что обе семьи довольны своими покупками, равна 64,0%.
Пример 4.10 показывает, что выбор второй семьи не зависит от выбора первой. Таким образом, заменяя в формуле (4.7) условную вероятность Р(А|В) вероятностью Р(А), мы получаем формулу умножения вероятностей независимых событий.
ПРАВИЛО УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ НЕЗАВИСИМЫХ СОБЫТИЙ
Если события А и В являются статистически независимыми, вероятность события “А и В” равна вероятности события А, умноженной на вероятность события В.
Р(А и В) = Р(А)Р(В). (4.8)
Если это правило выполняется для событий А и В, значит, они являются статистически независимыми. Таким образом, существуют два способа определить статистиче--скую независимость двух событий.
1. События А и В являются статистически независимыми друг от друга тогда и только тогда, когда Р(А|В)=Р(А).
2. События А и В являются статистически независимыми друг от друга тогда и только тогда, когда Р(А и В) = Р(А)Р(В).
Если в таблице сопряженности признаков, имеющей размер 2x2, одно из этих условий выполняется хотя бы для одной комбинации событий А и В, оно будет справедливым и для любой другой комбинации.2
Теперь можно модифицировать формулу (4.2) для вычисления безусловной вероятности элементарного события А:
Р(А) = Р(А u Bt) + Р(А и В2) + ... + Р(А u Вк),
где события В,, В2, ..., Вк являются взаимоисключающими и исчерпывающими.
БЕЗУСЛОВНАЯ ВЕРОЯТНОСТЬ ЭЛЕМЕНТАРНОГО СОБЫТИЯ
Р(А) = Р(А|В1)Р(В1) + Р(А|В2)Р(В2) + ... + P(A|BJP(BJ, (4.9)
где события В,, В2, ..., Вк являются взаимоисключающими и исчерпывающими.
Проиллюстрируем применение этой формулы на примере табл. 4.1. Используя формулу (4.9), получаем:
Р(А) = P(A|BJ Р(В.) + Р(А|В2) Р(В2),
где Р(А) — вероятность того, что покупка планировалась, P(BJ — вероятность того, что покупка совершена, Р(В2) — вероятность того, что покупка не совершена.
п/ 200 300 50 700 200 50 250 А
300 1 000 700 1 000 1 000 1 000 1 000
УПРАЖНЕНИЯ К РАЗДЕЛУ 4,2
Изучение основ
4.14. Дана следующая таблица сопряженности признаков.
В В*
А 10 20
А' 20 40
1. Чему равна вероятность Р(А|В)?
2. Чему равна вероятность Р(А|В’)?
3. Чему равна вероятность Р(А'|В*)?
4. Являются ли события А и В статистически независимыми?
2
В таблице сопряженности признаков, состоящей из г столбцов и q строк, это правило следует проверить на (г-1 )(с~1) разных комбинациях событий А и В.
4.15. Дана следующая таблица сопряженности признаков.
В В’
А 10 30
А' 25 35
1. Чему равна вероятность Р(А\В)?
2. Чему равна вероятность Р(А\В')?
3. Чему равна вероятность Р(А'\В')?
4. Являются ли события А и В статистически независимыми?
4.16. Найдите условную вероятность Р(А\В), если Р(АиВ) = 0,4 и Р(В) = 0,8.
4.17. Найдите вероятность Р(АпВ), если Р(А) — 0,7, Р(В) = 0,6, причем события АиВ являются статистически независимыми.
4.18. Определите, являются ли события А и В статистически независимыми, если Р(А) = 0,3, Р(В) = 0,4, аР(АиВ) = 0,2.
Применение понятий
4.19. Результаты контроля продукции производственной компании позволили выявить дефекты в партии, состоящей из 450 плат. В приведенной ниже таблице содержатся ответы на два вопроса: “Найдены ли частицы на матрице?” и “Качественная плата или нет?”.
Состояние матрицы
Качество платы Нет частиц Есть частицы Всего
Хорошее 320 14 334
Плохое 80 36 116
Всего 400 50 450
Источник: Hall, S. W. “Analysis of Defectivity of Semiconductor Wafers by Contingency Table”, Proceedings Institute of Environmental Sciences, 1 (1994 ):177-183.
1. Предположим, нам известно, что плата является дефектной. Какова вероятность, что она отпечатана на матрице, имеющей частицы?
2. Предположим, нам известно, что плата является качественной. Какова вероятность, что она отпечатана на матрице, имеющей частицы?
3. Являются ли события “качественная плата” и “матрица не имеет частиц” статистически независимыми? Обоснуйте свой ответ.
4.20. Недавно в США было проведено анкетирование, призванное выяснить, каким образом домовладельцы добираются на работу (“How People Get То Work”, USA Today Snapshots, February 25, 2003, 1A). Предположим, что в опросе приняли участие 1 000 домовладельцев и 1 000 арендаторов. Результаты опроса приведены в следующей таблице.
Добираетесь ли вы на работу на автомобиле? Домовладельцы Арендаторы Всего
Да 824 681 1 505
Нет 176 319 595
Всего 1 000 1000 2 000
1. Предположим, что респондент добирается на работу на автомобиле. Какова вероятность, что он является домовладельцем?
2. Предположим, что респондент является домовладельцем? Какова вероятность, что он добирается на работу на автомобиле?
3. Объясните разницу между ответами на вопросы 1 и 2?
4. Являются ли события “респондент добирается на работу на автомобиле” и “респондент является домовладельцем” статистически независимыми?
4.21. Можно ли утверждать, что крупные компании реже предлагают фондовые опционы членам правления, чем малые и средние компании? Опрос, проведенный компанией Segal Company of New York, выяснил, что среди 189 крупных компаний, входящих в выборку, 40 предлагали фондовые опционы членам своих правлений в рамках безналичного компенсационного пакета. В то же время среди 180 малых и средних компаний 43 компании предлагали фондовые опционы членам своих правлений в рамках безналичного компенсационного пакета. (Kemba J. Dunham, “The Jungle: Focus on Recruitment, Pay and Getting Ahead”, Wall Street Journal, August 21, 2001, B6.)
1. Предположим, что компания является крупной. Какова вероятность, что она предлагает членам своего правления фондовые опционы?
2. Предположим, что компания является малой или средней. Какова вероятность, что она предлагает членам своего правления фондовые опционы?
3. Являются ли размер компании и предложение фондового опциона статистически независимыми событиями?
4.22. Можно ли утверждать, что белые рабочие чаще заявляют о несправедливости своего увольнения? Опрос, проведенный Барри Гольдманом (“White Fight: A Researcher Finds Whites Are More Likely to Claim Bias”, Wall Street Journal, Work Week, April 10, 2001, Al) показал, что из 56 уволенных белых рабочих 29 заявили, что это несправедливо. В то же время из 407 уволенных черных рабочих о несправедливости заявили 126.
1. Предположим, что уволенный рабочий является белым. Какова вероятность, что он заявит о несправедливости?
2. Предположим, что уволенный рабочий заявил о несправедливости. Какова вероятность, что он является белым?
3. Объясните разницу между ответами на вопросы 1 и 2.
4. Являются ли события “уволенный рабочий — белый” и “уволенный рабочий заявил о несправедливости” статистически независимыми?
4.23. В ходе опроса было опрошено 500 пассажиров метрополитена. Помимо прочего, в анкете был вопрос: “Любите ли вы покупать одежду?”. Результаты опроса приведены в следующей таблице сопряженности признаков.
Любит покупать одежду Пол
Мужской Женский Всего
Да 136 224 360
Нет 104 36 140
Всего 240 260 500
1. Предположим, что случайно выбранный респондент оказался женщиной. Какова вероятность, что она не любит приобретать одежду?
2. Предположим, что случайно выбранный респондент любит приобретать одежду? Какова вероятность, что он — мужчина?
3. Являются ли отношение к покупке одежды и пол статистически независимыми?
4.24. Каждый год создается рейтинговый лист, оценивающий поведение автомобилей на протяжении первых 90 дней после покупки. Предположим, что автомобили разделены на две категории: требует ли автомобиль гарантийного ремонта (да или нет), и в какой стране он был собран (США или нет). На основе этих данных была вычислена вероятность того, что новый автомобиль потребует гарантийного ремонта, — 0,04, вероятность того, что автомобиль собран в США, — 0,60, а также вероятность того, что новый автомобиль, собранный в США, потребует гарантийного ремонта, — 0,025.
1. Предположим, что компания базируется в США. Какова вероятность, что автомобилю потребуется гарантийный ремонт?
2. Предположим, что автомобиль произведен компанией, базирующейся вне США. Какова вероятность, что автомобилю потребуется гарантийный ремонт?
3. Являются ли гарантийный ремонт и место расположения автомобильной компании статистически независимыми?
4.25. Допустим, некий студент предполагает, что вероятность получить отличную оценку на экзамене по статистике равна 0,6, а по психологии — 0,8. Какова вероятность того, что студент получит отличную оценку по обоим предметам, если эти события статистически независимы? Приведите разумные причины, почему эти события не могут быть статистически независимыми, даже если преподаватели этих предметов не имеют возможности обмениваться мнениями о студентах.
4.26. Предположим, что в игре используется стандартная колода карт. В нее входят четыре масти (черви, бубны, трефы и пики), каждая из которых состоит из 13 карт (туз, 2, 3, 4, 5, 6, 7, 8, 9, 10, валет, дама и король). Всего в колоде — 52 карты. Допустим, что из тщательно перетасованной полной колоды извлекаются две карты без возвращения.
1. Какова вероятность, что обе карты окажутся дамами?
2. Какова вероятность, что первая карта будет десяткой, а вторая — пятеркой или шестеркой?
3. Как изменится ответ на вопрос 1, если карты извлекаются с возвращением?
4. В игре “очко” фигуры (валет, дама, король) оцениваются десятью баллами, а туз— одним или 11. Все остальные карты оцениваются по номиналу. “Очко” достигается, если игрок набирает 21 баллов. Какова вероятность набрать “очко”?
4.27. В коробке с девятью перчатками для гольфа лежат две левых перчатки и семь правых.
1. Предположим, что из коробки извлекаются две перчатки без возвращения. Какова вероятность, что обе извлеченные перчатки окажутся правыми?
2. Предположим, что из коробки извлекаются две перчатки без возвращения. Какова вероятность, что одна из них окажется правой, а вторая — левой?
3. Предположим, что из коробки извлекаются три перчатки с возвращением. Какова вероятность, что все извлеченные перчатки окажутся левыми?
4. Как изменится ответ на вопросы 1 и 2, если перчатки извлекаются с возвращением?
4.3. ТЕОРЕМА БАЙЕСА
Условная вероятность события учитывает информацию о том, что произошло некое другое событие. Этот подход можно использовать как для уточнения вероятности с учетом вновь поступившей информации, так и для вычисления вероятности, что наблюдаемый эффект является следствием некоей конкретной причины. Процедура уточнения этих вероятностей называется теоремой Байеса (Bayes’ theorem). Впервые она была разработана Реверендом Томасом Байесом (Reverend Thomas Bayes) в 18 веке [1].
Предположим, что компания, упомянутая в сценарии, исследует рынок сбыта новой модели телевизора. В прошлом 40% телевизоров, созданных компанией, пользовались успехом, а 60% моделей признания не получили. Прежде чем объявить о выпуске новой модели, специалисты по маркетингу тщательно исследуют рынок и фиксируют спрос. В прошлом успех 80% моделей, получивших признание, прогнозировался заранее, в то же время 30% благоприятных прогнозов оказались неверными. Для новой модели отдел маркетинга дал благоприятный прогноз. Какова вероятность того, что новая модель телевизора будет пользоваться спросом?
Теорему Байеса можно вывести из определений условной вероятности (4.5, а) и (4.5, б). Чтобы вычислить вероятность Р(В|А), применим формулу (4.5,6).
1 Р(А)
Подставляя вместо Р(А) формулу (4.9), получаем теорему Байеса.
ТЕОРЕМА БАЙЕСА
Р(В[А} =______________Р(А\В.)Р(В,)______________
' Р(Л|5|)Р(В,) + Р(^|В,)Р(В:;) + ... + Р(Л|В1)Р(В1) ’
где события В2, ..., Вк являются взаимоисключающими и исчерпывающими.
Введем следующие обозначения: событие S — “телевизор пользуется спросом”, событие S' — “телевизор не пользуется спросом”, событие F — “благоприятный прогноз”, событие F'— “неблагоприятный прогноз”. Допустим, что P(S) = 0,40, Р(8’) = 0,60, P(F\S) = 0,80, P(F\S') = 0,30. Применяя формулу (4.10), получаем:
P(S| F) = —-------------------=-------°'80*0-40----= °-32 = = 0,64.
' 1 7 P(F|5)P(5) + P(F|S')P(5') 0,80x0,40 + 0,30x0,60 0,32 + 0,18 0,50
Вероятность спроса на новую модель телевизора при условии благоприятного прогноза равна 0,64. Таким образом, вероятность отсутствия спроса при условии благоприятного прогноза равна 1-0,64=0,36. Процесс вычислений представлен в виде табл. 4.5 и на рис. 4.3.
Таблица 4.5. Вычисления по формуле Байеса для оценки вероятности спроса
Событие Sj Априорная вероятность P(SJ Условная Совместная Уточненная вероятность P(Ss|F) вероятность вероятность P(F|S,) P(F|S,)P(S,)
S — спрос есть 0,40 0,80 0,32 0,32/0,50 = 0,64 = P(S|P)
<S' — спроса нет 0,60 0,30 0,18 0,18/0,50 = 0,36 = P(S'\F) 0,50
Рис. 4.3. Дерево решения при исследовании спроса на новую модель телевизора
ПРИМЕР 4.11. ПРИМЕНЕНИЕ ТЕОРЕМЫ БАЙЕСА ДЛЯ МЕДИЦИНСКОЙ ДИАГНОСТИКИ
Вероятность того, что человек страдает от определенного заболевания, равна 0,03. Медицинский тест позволяет проверить, так ли это. Если человек действительно болен, вероятность точного диагноза (утверждающего, что человек болен, когда он действительно болен) равна 0,9. Если человек здоров, вероятность ложноположительного диагноза (утверждающего, что человек болен, когда он здоров) равна 0,02. Допустим, что медицинский тест дал положительный результат. Какова вероятность того, что человек действительно болен? Какова вероятность точного диагноза?
РЕШЕНИЕ. Введем следующие обозначения: событие D — “человек болен”, событие D' — “человек здоров”, событие Т — “диагноз положительный”, событие Т' — “диагноз отрицательный”. Допустим, что P(Z>) = 0,03, P(D') = 0,97, P(T\D) = 0,90, P(T\D') = 0,02. Применяя формулу (4.10), получаем:
Р№)=__________£И£И£)___________=
' 1 ’ Р(Т|£>)Р(П) + Р(Г|£>')Р(Г>')
= 0,90x0,03 = 0,0270 = 0,0270 _ 5g2
”0,90x0,03 + 0,02x0,97 " 0,0270 + 0,0194 " 0,0464 “ ’
Вероятность того, что при положительном диагнозе человек действительно болен, равна 0,582. Процесс вычислений представлен в виде табл. 4.6.
Таблица 4.6. Вычисления по формуле Байеса для оценки точности медицинского диагноза
Событие Dj Априорная вероятность P(D.) Условная вероятность РСПО,) Совместная вероятность P(T|D,)P(D,J Уточненная вероятность P(DJT)
D — болен 0,03 0,90 0,0270 0,0270/0,0464 = 0,582 = P(D\T)
D’ — здоров 0,97 0,02 0,0194 0,0194/0,0464 = 0,418 = P(D'\T)
0,0494
иТ) = Р(Г1О)Р(О)
= (0,90) (0,03) = 0,0270
P(Dj = 0,97
и7) = Р(Т|О')Р(О')
(0,02) (0,97) = 0,0194
иГ) = Р(Г|О/)Р(£Г)
(0,98) (0,97) = 0,$$0^' I
Т£)иГ) = Р(Г|О)Р(О)
(0,10) (0,03) = 0,0030
Рис. 4.4. Дерево решения при оценке точности медицинского диагноза
Обратите внимание на то, что знаменатель формулы Байеса равен вероятности положительного диагноза, т.е. 0,0464.
И|^МйМ1в1в^И1ЙМвИйМ11вЙвВ1И!|ЛИИ11111в
Для вычислений, связанных с применением теоремы Байеса, следует открыть рабочий лист Байес в книге Chapter 4.xls. Шаблон этого рабочего листа приведен ниже.
А В ' С ' " & "EV-
1 Вычисления по формуле Байеса
2
3 Вероятности
4 Событие Априорная Условная Совместная Уточненная
5 S =В5*С5 =D5/$D$7
йШ S’ =В6*С6 =D6/$D$7
Hi Всего: =D5+D6
Откройте рабочий лист Байес и замените демонстрационные данные в ячейках В5 : С6 своими вероятностями. В частности, для того чтобы создать табл. 4.5, введите в ячейку В5 число 0,4, в ячейку вб - число 0,6, в ячейку С5 — число 0,8, а в ячейку сб - число о, 3.
Chapter 4.xls
Изучение основ
4.28. Дано: Р(В) = 0,05, Р(А\В) = 0,80, Р(В') = 0,95 и Р(А\В') = 0,40. Найдите Р(В|А).
4.29. Дано: Р(В) = 0,30, Р(А|В) = 0,60, Р(В’) = 0,70 и Р(А\В') = 0,50. Найдите Р(В|А).
Применение понятий
4.30. Вернемся к примеру 4.11. Предположим теперь, что вероятность положительного диагноза равна не 0,02, а 0,01.
1. Какова вероятность того, что человек действительно болен, если медицинский тест дает положительный результат (означающий, что человек болен)?
2. Какова вероятность того, что человек действительно здоров, если медицинский тест дает негативный результат (утверждающий, что человек здоров)?
4.31. Рекламное агентство изучило предпочтения женатых мужчин и замужних женщин, смотрящих телевизор в лучшее эфирное время. В результате выяснилось, что мужья смотрят телевизор 60% времени. Кроме того, оказалось, что, когда мужья смотрят телевизор, 40% времени жены смотрят телевизор вместе с ними. Если муж не смотрит телевизор, жены смотрят телевизор 30% времени. Определите вероятности следующих событий.
1. Когда жена смотрит телевизор, муж тоже смотрит его.
2. Жена смотрит телевизор в лучшее эфирное время.
4.32. Компания Olive Construction желает выяснить, следует ли подавать заявку на строительство нового торгового центра. В прошлом ее основной конкурент — компания Base Construction — выигрывала конкурсы в 70% случаев. Если компания Base Construction не подаст заявку на получение подряда, вероятность то-
го, что он достанется компании Olive Construction, равна 0,50. Если же компания Base Construction подаст заявку, вероятность того, что он достанется компании Olive Construction, равна 0,25.
1. Предположим, что компания Olive Construction выиграла конкурс. Какова вероятность того, что компания Base Construction не подавала заявки?
2. Какова вероятность того, что компания Olive Construction выиграет конкурс?
4.33. Уволенные рабочие, ставшие предпринимателями, поскольку не смогли найти новую работу в другой компании, называются предпринимателями поневоле (entrepreneurs by necessity). Журнал The Wall Street Journal сообщает, что предприниматели поневоле реже становятся крупными бизнесменами, чем предприниматели по призванию (entrepreneurs by choice). (Jeff Bailey, “Desire — More Than Need — Builds a Business”, Wall Street Journal, May 21, 2001, B4). В статье утверждается, что 89% предпринимателей в США являются предпринимателями по призванию, а 11% — поневоле. Только 2% предпринимателей поневоле планируют нанять больше 20 сотрудников на протяжении следующих пяти лет, в то время как доля предпринимателей по призванию, планирующих нанять более 20 сотрудников в течение следующих пяти лет, равна 14% .
1. Предположим, что случайно выбранный предприниматель планирует нанять в течение следующих пяти лет более 20 сотрудников. Какова вероятность того, что он — предприниматель по призванию?
2. Как вы думаете, почему предприниматели по призванию больше склонны к расширению своего бизнеса?
4.34. Редактор издательства пытается решить, стоит ли печатать предложенный учебник по бизнес-статистике. Опыт подсказывает ему, что в 10% случаев такие учебники пользуются огромным спросом, в 20% случаев — умеренным, в 40% случаев они окупаются и в 30% случаев приносят убытки. Однако, прежде чем принять решение, редакция рецензирует книгу. В прошлом положительную предварительную рецензию получили 99% учебников, пользовавшихся огромным спросом, 70% учебников, имевших умеренный успех, 40% окупившихся учебников и 20% убыточных.
1. Предположим, что предложенная книга получила положительный отзыв. Оцените вероятности прибыли и убытков.
2. Сколько учебников получило положительные отзывы?
4.35. Облигации муниципального займа подразделяются на три категории: А, В и С. Предположим, что в прошлом году из всех облигаций муниципальных займов, выпущенных в США, 70% имели рейтинг А, 20% — рейтинг В и 10% — рейтинг С. Из облигаций муниципального займа, имевших рейтинг А, 50% были выпущены в городах, 40% — в пригородах и 10% — в промышленных районах. Из облигаций муниципального займа, имевших рейтинг В, 60% были выпущены в городах, 20% — в пригородах и 20% — в промышленных районах. Из облигаций муниципального займа, имевших рейтинг С, 90% были выпущены в городах, 5% — в пригородах и 5% — в промышленных районах.
1. Предположим, что облигации муниципального займа были выпущены в городе. Какова вероятность того, что они получат рейтинг А?
2. Какова доля облигаций муниципальных займов, выпущенных в пригородах?
4.4. ЭТИЧЕСКИЕ ПРОБЛЕМЫ И ВЕРОЯТНОСТЬ
В Когда в ходе рекламной кампании используются аргументы, апеллирующие к понятию вероятности, возникают этические проблемы. К сожалению, большинство населения слабо понимает смысл любых математических концепций [3] и неправильно интерпретирует понятие вероятности. В некоторых ситуациях неправильная интерпретация является непреднамеренной, но в других случаях рекламное агентство может нарочно вводить потенциальных клиентов в заблуждение.
Рассмотрим один из типичных примеров неэтичного применения теории вероятностей — государственную лотерею, для выигрыша в которой необходимо угадать заданное количество номеров (например, 6) из большого списка номеров (например, 54). Хотя большинство участников лотереи слабо верят в выигрыш, они даже не представляют, насколько мала вероятность угадать 6, 5 или 4 номеров из 54.
Учитывая это, рекламный девиз “Мы не остановимся, пока все не станут миллионерами” следует признать совершенно ложным. Разумеется, пока лотерея приносит государству миллионы долларов в виде налогов, оно никогда не остановится, однако осчастливить всех играющих оно никогда не сможет.
Другой пример потенциально неэтичных применений теории вероятностей — обещание инвестиционных фондов принести 20% прибыли с 90%-ной вероятностью. В этом случае фонд должен: 1) разъяснить, как он вычислил эту вероятность, 2) сформулировать результат в другом виде (например, 9 шансов из 10) и 3) объяснить, что произойдет с остальными 10% инвестиций, которые не принесут 20% прибыли (будут ли они потеряны вообще?).
Изучение основ
4.36. Сформулируйте этически правильный рекламный девиз государственной лотереи.
4.37. Напишите этически правильное рекламное объявление для инвестиционного фонда, который обещает 20% дохода.
4.5. ПРАВИЛА СЧЕТА
Вероятность интересующего нас исхода равна количеству вариантов, в которых возникает данный исход, деленному на общее количество исходов. Из-за большого количества возможностей во многих ситуациях трудно перечислить все варианты исходов. В таких случаях вместо списка исходов следует применять правила счета. В данном разделе мы рассмотрим пять разных правил счета.
Предположим, что мы 10 раз подбрасываем монету. Каково количество разных возможных исходов (последовательностей “орла” и “решки”)?
ПЕРВОЕ ПРАВИЛО СЧЕТА
Если в п испытаниях могут возникнуть k взаимоисключающих и исчерпывающих событий, то количество возможных исходов равно
(4.11)
Если монета подбрасывается 10 раз, то из формулы (4.11) следует, что общее количество исходов равно 210= 1 024. Если игральный кубик, имеющий шесть сторон, выбрасывается два раза, то из формулы (4.11) следует, что общее количество разных исходов равно 62 = 36.
Второе правило счета обобщает первое и допускает ситуации, когда количество возможных исходов изменяется от испытания к испытанию. Допустим, государственная инспекция по контролю за транспортными средствами заинтересовалась, сколько автомобильных номеров можно составить из трех букв и трех цифр. Каждая из букв порождает 26 исходов, а каждая из цифр —10 исходов.
ВТОРОЕ ПРАВИЛО СЧЕТА
Если первое испытание порождает kx событий, второе — k2 событий, ..., а п-е испытание — kn событий, то общее количество возможных исходов равно
k,k2...kn (4.12)
Таким образом, используя формулу (4.12), мы можем вычислить количество автомобильных номеров, которые можно составить из трех букв и трех цифр: 26x26x26x10x10x10 = 17 576 000. Рассмотрим другой пример. Предположим, что ресторанное меню предусматривает обед с фиксированной ценой, состоящий из закуски, главного блюда, напитка и десерта, причем посетитель имеет право выбрать пять видов закуски, десять главных блюд, три вида напитков и шесть десертных блюд. Используя формулу (4.12), получаем, что общее количество возможных меню равно 5x10x3x6 — 900.
Третье правило счета позволяет вычислить количество способов, которыми можно упорядочить заданный набор объектов. Предположим, нам нужно расставить на книжной полке шесть книг. Сколько существует способов расстановки? Для начала следует понять, что на первом месте может стоять любая из шести книг. Как только первая позиция занята, на вторую позицию остается только пять кандидатов. Продолжим эту процедуру, пока все места не окажутся занятыми.
ТРЕТЬЕ ПРАВИЛО СЧЕТА
Количество способов, которыми можно упорядочить заданный набор объектов равно и! = их(п-1)х ... xl, (4.13)
где величина п\ называется факториалом, причем 0! = 1 и 1! = 1 по определению.
Количество способов, которыми можно упорядочить шесть книг, равно
п\ = 6! = 6х5х4хЗх2х1 = 720.
Во многих задачах необходимо знать количество способов, которыми можно упорядочить подмножество, принадлежащее определенной группе объектов. Каждый вариант упорядочения называется перестановкой (permutation). Для примера изменим постановку предыдущей задачи. Предположим, что на полке помещаются только четыре книги. Сколько существует способов расставить книги на полке, если общее количество книг равно шести?
ЧЕТВЕРТОЕ ПРАВИЛО СЧЕТА
Перестановки-, количество способов упорядочить X объектов, извлеченных из совокупности, состоящей п объектов, равно
Следовательно, по формуле (4.14) получаем, что общее количество вариантов упорядочения четырех книг, выбранных среди шести книг, равно
п\ 6! 6! 6х5х4хЗх2х1
------- = ----- — — = — 360. (п-Х)\ (6-4)! 2! 2x1
В заключение рассмотрим ситуации, в которых порядок следования объектов не важен, а учитывается лишь количество вариантов извлечения X объектов из совокупности, состоящей из п объектов. Это правило называется правилом сочетаний (combinations).
ПЯТОЕ ПРАВИЛО СЧЕТА
Сочетания: количество способов извлечения X объектов из совокупности, состоящей п объектов, равно
(4.15)
Сравнивая это правило с предыдущим, легко обнаружить, что они отличаются лишь множителем X! в знаменателе. Обратите внимание на то, что в формуле (4.14) все перестановки отличаются друг от друга. В формуле (4.15) порядок следования X объектов не важен, значит, X! перестановок не отличаются друг от друга. Таким образом, по формуле (4.15) общее количество комбинаций четырех книг, извлеченных из совокупности, состоящей из шести книг, равно
- п- - 6! _ 6! _ 6х5х4хЗх2х1 _ $
х ~ Х’(и-Х)! ~ 4!(б-4)! “ 4!2! ~ 4x3x2xlx2xl ”
УПРАЖНЕНИЯ К РАЗДЕЛУ 4.5
Применение понятий
4.38. Предположим, что экзаменационный билет состоит из десяти вопросов с тремя вариантами ответа. Сколько существует вариантов ответов?
4.39. Замок банковского сейфа состоит из трех цифровых дисков, в каждом из которых предусмотрено 30 позиций. Для того чтобы открыть запертый сейф, каждый из дисков должен быть установлен в правильную позицию.
1. Сколько разных комбинаций имеет такой замок?
2. Какова вероятность, что мы откроем сейф, случайно угадав правильную комбинацию?
3. Объясните, почему количество комбинаций замка не вычисляется по формуле (4.15)?
4.40. Ответьте на следующие вопросы.
1. Сколько исходов имеет эксперимент, в ходе которого монета подбрасывается семь раз?
2. Сколько исходов имеет эксперимент, в ходе которого игральный кубик подбрасывается семь раз?
3. Чем отличаются ответы на вопросы 1 и 2?
4.41. Некая марка женских джинсов имеет семь разных размеров, три разных цвета и три разных стиля. Предположим, что менеджер магазина хочет иметь по одной паре джинсов каждого типа. Сколько джинсов ему нужно заказать?
4.42. Сколько разных слов, состоящих из букв Е, L, О и V, можно составить, используя каждую букву только один раз?
4.43. В Западном дивизионе Национальной лиги выступают пять команд: Аризона, Лос-Анджелес, Сан-Франциско, Сан-Диего и Колорадо. Сколько существует вариантов расстановки этих команд в турнирной таблице? Уверены ли вы, что все эти расстановки одинаково вероятны? Обоснуйте свой ответ.
4.44. Вернитесь в задаче 4.59 и определите, сколько существует разных вариантов расстановки этих команд в первых четырех позициях турнирной таблицы?
4.45. На шести грядках садовник может посадить помидоры, баклажаны, перец, огурцы, фасоль и салат-латук. Каждый вид овощей должен занимать только одну грядку. Сколько существует способов размещения овощей на огороде, состоящем из шести грядок?
4.46. Для выигрыша в “тройке” на ипподромном тотализаторе необходимо, чтобы в девятом заезде три лошади пришли в указанном игроком порядке. Предположим, что для участия в девятом заезде заявлено 12 лошадей. Сколько вариантов исходов существует в этой игре?
4.47. Для выигрыша в “дубле” на ипподромном тотализаторе необходимо, чтобы в заезде две лошади, указанные игроком, пришли первыми, причем порядок не важен. Предположим, что для участия в заезде заявлено 8 лошадей. Сколько вариантов исходов существует в этой игре?
4.48. Студент раздумывает, как разместить шесть книг в своем портфеле. К сожалению, в портфель помещаются только четыре книги. Сколько вариантов выбора книг имеет студент, если их порядок не важен?
4.49. В ежедневной лотерее из 100 номеров извлекаются два выигрышных номера. Сколько выигрышных комбинаций существует в этой лотерее?
4.50. Список книг, рекомендованных для изучения в курсе менеджмента, состоит из 20 пунктов. Сколько существует способов извлечь три книги из этого списка?
Вероятность
Теорема Байеса
bewffisw- -' - --V Ж гпамйЬг
Структурная схема главы 4
РЕЗЮМЕ
В главе продемонстрированы понятия вероятности, условной вероятности и теорема Байеса. В следующей главе будут рассмотрены описаны основные свойства широко рас-
пространенных дискретных распределений -геометрического. Вероятность, 253 безусловная, 255 совместного события, 256 условная, 266 Выборочное пространство, 254 Дерево решений, 267 Дополнение, 254 Подход априорный, 253 субъективный, 253 эмпирический, 253 Правило сложения вероятностей, 258 - биномиального, пуассоновского и гипер- сложения вероятностей взаимоисключающих событий, 258 сложения вероятностей исчерпывающих событий, 259 умножения вероятностей, 270 независимых событий, 271 Событие достоверное, 253 невозможное, 253 совместное, 254 элементарное, 254 События
взаимоисключающие, 257
исчерпывающие, 257
Статистическая назависимость, 269
Таблица
перекрестной классификации, 254
сопряженности признаков, 254
факторная, 254
Теорема Байеса, 276
УПРАЖНЕНИЙ К ГЛАВЕ <
Изучение основ
4.51. Чем отличаются друг от друга априорная классическая, эмпирическая классическая и субъективная вероятности?
4.52. В чем заключается разница между элементарным и совместным событиями?
4.53. Как вычислить вероятность события “А или В” с помощью правила сложения вероятностей?
4.54. В чем заключается разница между взаимоисключающими и исчерпывающими событиями?
4.55. Какая связь существует между понятиями условной вероятности и статистической независимости?
4.56. Чем различаются правила умножения вероятностей зависимых и независимых событий?
4.57. Как уточнить вероятность на основе вновь поступившей информации с помощью теоремы Байеса?
Применение понятий
4.58. Компания по производству безалкогольных напитков ведет учет количества бракованных бутылок, заполненных разливочно-укупорочными машинами. В соответствии с этими данными вероятность того, что бутылка заполнена Машиной I и оказалась бракованной, равна 0,01. Для Машины II эта вероятность равна 0,025. Половина всех бутылок заполняется Машиной I, а другая — Машиной II.
1. Приведите пример элементарного события.
2. Приведите пример совместного события.
3. Какова вероятность того, что наугад выбранная заполненная бутылка окажется бракованной?
4. Какова вероятность того, что наугад выбранная бутылка окажется заполненной Машиной II?
5. Какова вероятность того, что наугад выбранная бутылка окажется заполненной Машиной I и не бракованной?
6. Какова вероятность того, что наугад выбранная бутылка окажется заполненной Машиной II и не бракованной?
7. Какова вероятность того, что наугад выбранная бутылка окажется заполненной Машиной I или не бракованной?
8. Какова вероятность того, что наугад выбранная бутылка, заполненная Машиной I, окажется бракованной?
9. Какова вероятность того, что наугад выбранная бракованная бутылка заполнена Машиной I?
10. Объясните разницу между ответами на вопросы 8 и 9.
(Подсказка: заполните таблицу сопряженности признаков 2x2.)
4.59. Недавно проведенный опрос был посвящен выяснению того, что сотрудники считают наиболее важным для успешной работы (“Snapshot”, USA Today, May 15, 2000). В опросе приняли участие 500 мужчин и 500 женщин. Его результаты указаны в следующей таблице.
фактор успеха Мужчины (%) Женщины (%)
Хорошие отношения с начальником 63 77
Современное оборудование 59 69
Достаточные ресурсы 55 74
Удобное расположение офиса 48 60
Гибкий график работы 40 53
Возможность работать дома 21 34
(Подсказка: заполните таблицу сопряженности признаков 2x2.)
1. Какова вероятность того, что наугад выбранный респондент считает наиболее важным фактором успеха хорошие отношения с начальником?
2. Какова вероятность того, что наугад выбранный респондент считает наиболее важным фактором успеха удобное расположение офиса?
3. Какова вероятность того, что наугад выбранный респондент окажется мужчиной и считает наиболее важным фактором успеха хорошие отношения с начальником?
4. Какова вероятность того, что наугад выбранный респондент окажется женщиной и считает наиболее важным фактором успеха гибкий график работы?
5. Какова вероятность того, что наугад выбранный респондент, считающий наиболее важным фактором успеха хорошие отношения с начальником, окажется мужчиной?
6. Существует ли статистическая связь между полом и факторами успеха? Обоснуйте свой ответ.
4.60. Недавно проведенный опрос был посвящен оценке позитивного влияния технологии (“Snapshot”, USA Today, October 22, 2001). Опрос проводился в два этапа. Допустим, что в 1998 и 2001 гг. в нем приняли участие по 500 респондентов. Доля людей, позитивно оценивающих влияние технологии, приведена ниже.
Выгоды 1998 2001
Увеличивается объем профессиональных знаний 54% 87%
Увеличивается производительность труда 66% 80%
Улучшается связь с клиентами и заказчиками 42% 80%
Ослабляется производственный стресс 26% 54%
(Подсказка: заполните таблицу сопряженности признаков 2x2.)
Предположим, что респондент выбирается наугад. Вычислите вероятность следующих событий.
1. Респондент считает, что технология увеличивает его профессиональные знания.
2. Респондент считает, что технология улучшает связь с клиентами и заказчиками.
3. Респондент считает, что технология улучшает связь с клиентами и заказчиками, и принял участие в опросе 2001 года.
4. Респондент считает, что технология ослабляет производственный стресс, и принял участие в опросе 1998 года.
5. Можно ли утверждать, что оценки выгод, доставляемых технологией, и год опроса являются статистически независимыми? Обоснуйте свой ответ.
4.61. Владелец ресторана европейской кухни заинтересовался особенностями заказов, принимаемых на выходные. Он стал записывать количество заказов на различные виды блюд. Предположим, что владельца ресторана интересует также, заказывают ли посетители десерт. Он решил записывать значения еще двух переменных: пол посетителя и заказывал ли он говядину. Результаты этих исследований приведены ниже.
Пол
Заказ десерта Мужской Женский Всего
Да 96 40 136
Нет 224 240 464
Всего 320 280 600
Заказ говядины
Заказ десерта Да Нет Всего
Да 71 65 136
Нет 116 348 464
Всего 187 413 600
1. Какова вероятность того, что первый же клиент закажет десерт?
2. Какова вероятность того, что первый клиент не закажет говядину?
3. Какова вероятность того, что первый клиент закажет десерт или говядину?
4. Какова вероятность того, что первый клиент окажется женщиной и не закажет десерт?
5. Какова вероятность того, что первый клиент закажет десерт и говядину?
6. Какова вероятность того, что первый клиент окажется женщиной или не закажет десерт?
7. Предположим, что первый клиент, у которого официант принял заказ, оказался женщиной. Какова вероятность того, что она не закажет десерт?
8. Предположим, первый же клиент заказал говядину. Какова вероятность, что он закажет и десерт?
9. Являются ли пол клиента и заказ десерта статистически независимыми?
10. Являются ли заказ десерта и заказ говядины статистически независимыми?
4.62. Более 80% пользователей обычно удаляют непрошеные коммерческие предложения, получаемые по электронной почте (так называемый спам), не читая. В то же время некоторые пользователи читают спам и даже приобретают вещи, которые там предлагаются. Многие компании пользуются таким приемом из-за того, что он чрезвычайно дешев. Компания Movies Unlimited из Филадельфии, занимающаяся электронной торговлей видеокассетами и DVD-дисками, достигла успеха именно благодаря рассылаемому ею спаму. Эд Вайс (Edd Weiss), генеральный менеджер компании, считает, что их сообщения читают от 15% до 20% получателей. Более того, более 15% прочитавших рекламные объявления компании делают заказ (Stacy Forster, “E-Marketers Look to Polish Spam’s Rusty Image”, Wall Street Journal, May 22, 2002, D2).
1. Воспользуйтесь оценкой мистера Вайса, утверждающего, что сообщения его компании читают 15% адресатов, и вычислите вероятность того, что получатель прочитает рекламу и сделает заказ.
2. Компания Movies Unlimited хранит в своей базе 175 000 электронных адресов. Предположим, что сообщения рассылаются по всем адресам. Сколько клиентов прочитают его и сделают заказ?
3. Допустим, вероятность того, что адресат прочитает рекламное сообщение, равна 0,15. Какова вероятность, что получатель, прочитавший его, сделает заказ?
4. Как изменится ответ на вопрос 2, если вероятность того, что получатель прочитает рекламное сообщение равно 0,20?
4.63. В феврале 2002 года курс аргентинского песо по отношению к американскому доллару упал на 70%. Эта девальвация резко подняла цены на импортные продукты. Согласно результатам опроса, проведенного компанией AC Nielsen в апреле 2002 года, 68% заказчиков в Аргентине стали покупать меньше товаров, чем до девальвации, 24% покупают столько же, а 8% стали покупать больше. Коме того, появилась тенденция покупать более дешевые вещи, причем 88% респондентов указали, что они изменили свои предпочтения. (Michelle Wallin, “Argentines Hone Art of Shopping in a Crisis”, Wall Street Journal, May 28, 2002, A15). Предположим, что результаты опроса выглядят следующим образом.
Количество приобретаемых товаров
Торговые марки Меньше Столько же Больше Всего
Не изменились 10 14 24 48
Изменились 262 82 8 352
Всего 272 96 32 400
(Подсказка: заполните таблицу сопряженности признаков 2x2.)
Предположим, что респондент выбирается наугад. Вычислите вероятность следующих событий.
1. Респондент приобретает меньше товаров, чем раньше.
2. Респондент приобретает столько же товаров.
3. Респондент приобретает столько же товаров или больше.
4. Респондент приобретает меньше товаров, чем раньше, причем предпочитает другие торговые марки.
5. Респондент приобретает столько же товаров, что и раньше, предпочитая те же самые торговые марки.
Будем считать, что потребитель изменил свои предпочтения. Вычислите вероятности следующих событий.
6. Респондент приобретает меньше товаров, чем раньше.
7. Респондент приобретает столько же товаров.
8. Респондент приобретает столько же товаров или больше.
9. Сравните ответы на вопросы 1-3 и 6-8.
4.64. Считается, что спортивные автомобили, фургоны и пикапы чаще переворачиваются во время аварий. В 1997 году переворотами автомобилей сопровождалось 24% дорожно-транспортных происшествий. В 15,8% из них участвовали спортивные автомобили, фургоны и пикапы. В 5,6% всех дорожно-транспортных происшествий, в которых участвовали спортивные автомобили, фургоны и пикапы, переворотов не было. Введем следующие определения: событие А— до-
рожно-транспортное происшествие, в котором участвовали спортивные автомобили, фургоны и пикапы, В — дорожно-транспортное происшествие, сопровождаемое переворотом автомобилей (Mathews, A. W., “Ford Ranger, Chevy Tracker Tilt in Test”, The Wall Street Journal, July 14, 1999, p. A2).
1. Примените теорему Байеса и найдите вероятность аварии, связанной с переворотом автомобиля, если известно, что в ней принимал участие спортивный автомобиль, фургон или пикап.
2. Сравните результат, полученный при решении задачи 1, с вероятностью дорожно-транспортных происшествий, в ходе которых переворачивались автомобили. Объясните, почему считается, что спортивные автомобили, фургоны и пикапы чаще переворачиваются во время аварий.
4.65. Метод обнаружения специфических антител или антигенов с помощью иммобилизованного на антигене или антителе фермента (enzyme-linked immunosorbent assays — ELISA) является наиболее распространенным способом диагностики СПИДа. Положительный результат этого теста означает, что человек болен СПИДом. Тест ELISA обладает высокой чувствительностью (позволяет обнаружить инфекцию) и специфичностью (позволяет констатировать отсутствие инфекции). (Более подробную информацию можно найти на Web-странице HIVInsite.ucsf.edu/.) Допустим, вероятность, что человек болен СПИДом, равна 0,015. Если человек действительно болен, вероятность, что тест ELISA даст положительный результат, равна 0,995. Если человек здоров, вероятность того, что тест ELISA даст положительный результат, равна 0,01. Предположим, что тест ELISA дал положительный результат. Примените теорему Байеса и определите вероятность того, что человек действительно болен.
Применение Интернет
4.66. Зайдите на сайт www.prenhall.com/levine. Выберите ссылку Chapter 4 и щелкните на кнопке Internet exercises.
ПРИМЕНЕНИЕ WEB
Примените свои знания о таблицах сопряженности признаков и вероятностях для того, чтобы оценить обоснованность прогнозов и заявлений компании StockTout Investing Service.
Посетите Web-сайт компании StockTout Guaranteed Investment Package Web (www. prenhall.com/Springville/ST_Guaranteed.htm). Проанализируйте рекламные заявления и сопровождающие их данные, а затем ответьте на следующие вопросы.
1. Насколько точно вычислена вероятность успеха инвестиций компании StockTout Guaranteed Investment Package Web? В чем заключается ошибочность рекламных заявлений компании? Какова вероятность того, что годовая доходность инвестиций превышает 15% ?
2. В чем заключается ошибочность рекламного заявления, утверждающего, что вероятность успеха равна 7% ? Используя таблицу на Web-странице “Winning Probabilities” (ST_Guaranteed3.htm), вычислите правильную вероятность для каждой группы инвесторов.
3. Существуют ли какие-либо способы вычисления вероятностей успеха, которые можно было бы применить для оценки инвестиционной деятельности? Обоснуйте свой ответ.
СПРАВОЧНИК ПО EXCEL. ГЛАВА 4
ЕН.4.1. Применение оператора конкатенации
Откроем рабочий лист Вероятности в книге Chapter 4 .xls, использующий оператор Excel & для формирования меток выборочного пространства событий. Некоторые из этих формул приведены в табл. ЕН.4.1.
Таблица ЕН.4.1. фрагмент рабочего листа Вероятности
A
9 Безусловные вероятности
10 = "₽("& B5 &")"
11 = ”₽(”& B6 &")"
12 = "₽("&С4 &")"
13 = "₽("& D4&")"
14
15 Совместные вероятности
16 = "₽("& В5 &" и "& С4 &*’)"
17 = Р( & В5 &" и & D4 & ')
18 ="Р("& В6 &" и "& С4 &")"
lllll ="Р("& В5 &" и "& D4 &")"
Формулы в ячейках А10:А13 содержат по две пары двойных кавычек и по два оператора конкатенации. Это позволяет присоединить к метке вероятности “Р (” метку события из выборочного пространства (этот фрагмент в табл. ЕН.4.1 не показан). Например, если бы ячейка В5 содержала метку HDTV-Да, то формула в ячейке А10 должна была бы вывести на экран метку Р (HDTV-Да). Формулы в диапазоне ячеек С16:С19 (и ячейки С22 : С25, не показанные в таблице) используют два набора операторов конкатенации, что позволяет сформировать метки, используя метки значений из двух других ячеек. Например, если ячейка С4 содержит метку DVD-Да, то формула, записанная в ячейке Аб, должна вывести на экран метку Р (HDTV-Да и DVD-Да) .
В табл. ЕН.4.1 иллюстрируется тот факт, что формулы в программе Excel могут применяться не только для математических вычислений, но и для других целей.
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
1. Kirk, R. L., ed., Statistical Issues: A Reader for the Behavioral Sciences (Belmont, CA: Wadsworth, 1972).
2. Microsoft Excel 2002 (Redmond, WA: Microsoft Corporation, 2001).
3. Paulos, J. A., Innumeracy (New York: Hill and Wang, 1988).
Глава 5
Дискретные распределения
ПРИМЕНЕНИЕ СТАТИСТИКИ: автоматизированная бухгалтерская система компании Saxon Home Improvement
5.1. РАСПРЕДЕЛЕНИЕ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
Математическое ожидание дискретной случайной величины
Дисперсия и стандартное отклонение дискретной случайной величины Процедуры Excel: вычисление математического ожидания дискретной случайной величины
5.2. КОВАРИАЦИЯ И ЕЕ ПРИМЕНЕНИЕ В ФИНАНСОВОМ ДЕЛЕ
Ковариация
Математическое ожидание, дисперсия и стандартное отклонение суммы двух случайных величин
Ожидаемая доходность и риск портфельных инвестиций
Процедуры Excel: вычисление ожидаемой доходности и риска портфельных инвестиций
5.3. БИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
Биномиальное распределение
Процедуры Excel: вычисление биномиального распределения
5.4. ГИПЕРГЕОМЕТРИЧЕСКОЕ
РАСПРЕДЕЛЕНИЕ
Процедуры Excel: вычисление гипергеометрического распределения
5.5. РАСПРЕДЕЛЕНИЕ ПУАССОНА
Процедуры Excel: вычисление распределения Пуассона
5.6. АППРОКСИМАЦИЯ БИНОМИАЛЬНОГО РАСПРЕДЕЛЕНИЯ С ПОМОЩЬЮ РАСПРЕДЕЛЕНИЯ ПУАССОНА
СПРАВОЧНИК ПО EXCEL ГЛАВА 5
ЧЕМУ ДОЛЖЕН НАУЧИТЬСЯ СТУДЕНТ
• Знать свойства распределений.
• Вычислять математическое ожидание и дисперсию дискретной случайной величины.
• Вычислять коэффициент ковариации и уметь применять его в финансовом деле.
• Уметь вычислять биномиальное, гипергеометрическое и пуассоновское распределение и применять их для решения практических задач.
ПРИМЕНЕНИЕ СТАТИСТИКИ
Автоматизированная бухгалтерская система компании Saxon
Информационная система состоит из нескольких взаимосвязанных подсистем, предназначенных для совместного накапливания, обработки, хранения, преобразования и распространения информации, используемой для планирования, принятия решений и управления. Бухгалтерская информационная система (БИС) является подсистемой, предназначенной для обмена финансовой информацией между подразделениями компании и ее партнерами [5]. Компьютерная БИС обеспечивает непрерывный аудит бухгалтерской информации. Например, для того чтобы сделать заказ, клиенты компании Saxon Home Improvement Company могут воспользоваться интерактивной электронной формой и послать
ее в компанию. Затем информационная система проверяет, нет ли в заказах ошибок, а также неполной или недостоверной информации. Любой заказ, вызывающий сомнения, помечается и включается в ежедневный отчет об исключительных ситуациях. Данные, собранные компанией, свидетельствуют, что вероятность ошибок в заказах равна 0,10. Компания хотела бы знать, какова вероятность обнаружить определенное количество ошибочных заказов в заданной выборке. Например, предположим, что клиенты заполнили четыре электронных формы. Какова вероятность, что все заказы окажутся безошибочными? Как вычислить эту вероятность?
Home Improvement Company
$saxQ.n Нэте hrnp/ovement
s Ноте > Online Store > Shopping Cart
. Listed below are the items you have added to your shopping : cart Please review, then select a Checkout Option below to i purchase your items
< Want to retneve a previous shopping list or order? Click here to Petneve Shoopinu ust Would you ike to save the items i in your cart as a shopping list? Click here to Save Showing iUSL
bJ - - ' * Subtotal $104 94
i СЬготеспй
Chrome Adiufflitte $1497 , " ' SEUSLSbSShead
* CC2601
. Gamma
*14.97 Remove
$84.00 Remove
asafeJdwjwra swoo ij
5.1. РАСПРЕДЕЛЕНИЕ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
Как указывалось в разделе 1.12, исход испытания может представлять собой числовую переменную. В свою очередь, числовые переменные разделяются на дискретные и непрерывные. Дискретные переменные характерны для перечислений и подсчета, а непрерывные — для измерений. В оставшейся части главы мы рассмотрим несколько наиболее распространенных распределений, описывающих дискретные случайные величины.
Распределение дискретной случайной величины — это исчерпывающий список всех возможных значений случайной переменной, где каждому исходу поставлена в соответствие его вероятность.
Например, в табл. 5.1 приведено распределение количества ипотечных займов, выданных в течение недели местным филиалом банка. Поскольку в таблице приведены все возможные исходы, сумма их вероятностей равна 1.
Таблица 5.1. Распределение количества ипотечных займов, выданных за неделю
Количество ипотечных займов, выданных за неделю Вероятность
0 0,10
1 0,10
2 0,20
3 0,30
4 0,15
5 0,10
6 0,05
Графическое изображение распределения количества ипотечных займов, одобренных в течение недели, приведено на рис. 5.1.
Рис. 5.1. Распределение количества ипотечных займов, одобренных в течение недели
Математическое ожидание дискретной случайной величины
Математическим ожиданием р (expected value) дискретной случайной величины X называется среднее значение ее распределения. Эта величина равна сумме произведений всех значений случайной величины X на соответствующие вероятности .
Математическое ожидание ц дискретной случайной величины X — это взвешенное среднее (weighted value) всех возможных исходов, где в качестве весов служат вероятности каждого исхода.
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
р = £(%) = £% £(.¥,), (5.1)
1=1
где X' — i-e значение дискретной случайной величины X, Р(Х,) — вероятность /-го значения дискретной случайной величины X.
Математическое ожидание количества ипотечных займов, выданных за неделю, вычисляется по следующей формуле.
М = £(Х) = £^Ж) =
1=1
— 0x0,01+1x0,1+2x0,2+3x0,3+3x0,15+5x0,1+6x0,05 =
= 0 + 0,1 + 0,4 + 0,9 + 0,6 + 0,5 + 0,3 = 2,8.
Обратите внимание на то, что математическое ожидание количества ипотечных займов, выданных за неделю, выражается числом, которое не имеет буквального смысла, поскольку количество займов может измеряться только целыми числами. Математическое ожидание количества ипотечных займов, выданных за неделю, представляет собой среднее значение этой величины.
Дисперсия и стандартное отклонение дискретной случайной величины
Дисперсия о2 (variance) дискретной случайной величины X представляет собой взвешенное среднее квадратов разностей между всеми ее возможными значениями и математическим ожиданием. В качестве весов служат вероятности соответствующих исходов. Дисперсия равна сумме произведений квадратов разностей (X, - Е(Х))г на соответствующие вероятности Р(Х).
ДИСПЕРСИЯ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
а2 = ^Х,-Е(Х)]2Р(Х,), (5.2)
где X, — i-e значение дискретной случайной величины X, Р(Х,) — вероятность i-ro значения дискретной случайной величины X.
Стандартное отклонение о дискретной случайной величины задается формулой (5.3).
СТАНДАРТНОЕ ОТКЛОНЕНИЕ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
° = j£,(x.-£(*))2 ?(*,) (5.3)
Дисперсия и стандартное отклонение количества ипотечных займов, выданных за неделю, вычисляются по следующим формулам.
<г=£(Х,-Е(Х))2Р(Х,) =
= (О-2,8)2хО,1О+(1-2,8)2хО,1+(2-2,8)2хО,2О+(3-2,8)2хО,3+(4-2,8)2хО,15+ +(5-2,8)2х0,10 + (6-2,8)2х0,05 =
= 0,784 + 0,324 + 0,128 + 0,012 + 0,216 + 0,484 + 0,512 = 2,46.
о= Vo7 = у/^46 = 1,57.
Таким образом, математическое ожидание распределения количества ипотечных займов, выданных за неделю, равно 2,8, дисперсия равна 2,46, а стандартное отклонение — 1,57.
Процедуры Excel: вычисление математического ожидания дискретной случайной величины < - >
Для вычисления математического ожидания, дисперсии и стандартного отклонения дискретной случайной величины следует применить шаблон рабочего листа, приведенный ниже. Он предназначен для демонстрации данных о недельном количестве выданных ипотечных займов, приведенных в табл. 5.1. Введя новые значения дискретной случайной величины, этот лист можно использовать для решения других задач. Для этого следует либо уменьшить количество строк (если количество возможных значений переменной меньше семи), либо скопировать формулу из ячейки СЮ в ячейки, расположенные ниже (если количество возможных значений переменной больше семи).
Чтобы реализовать этот шаблон, откройте рабочий лист Дискретная_величина в файле Chapter 5.xls, а затем настройте его при необходимости. Обратите внимание на то, что для вычисления математического ожидания и дисперсии в ячейках Н4 и Н5 используется функция сумм, а для вычисления стандартного отклонения в ячейке нб используется функция корень (корень квадратный) .
С Е F G j|||j|j||BM||||l
1 Распределение дискретной случайной величины
2
3 X Р(Х) Х*Р(Х) [Х-Е(Х)]Л2 (Х-Е(Х)]Л2*Р(Х) Статистики
4 0 0,1 =А4*В4 = (А4-$Н$4)Л2 =D4*B4 Математическое ожидание =СУММ(С:С)
5 1 0,1 =А5*В5 =(А5-$Н$4)Л2 = D5*B5 Дисперсия =СУММ(Е:Е)
6 2 0,2 =Аб*Вб =(Аб-$Н$4)л2 = D6*B6 Стандартное отклонение =К0РЕНЬ(Н5)
7 3 0,3 =А7*В7 = (А7-$Н$4)Л2 = D7*B7
8 4 0,15 =А8*В8 =(А8-$Н$4)Л2 =D8*B8
9 5 0,1 =А9*В9 =(А9-$Н$4)Л2 =D9*B9
10 6 0,05 =А10*В1 0 = (А10-$Н$4)л2 =D10*B10
УПРАЖНЕНИЯ К РАЗ/
Изучение основ
5.1. Даны следующие распределения дискретных случайных величин.
Распределение А Распределение Б
X PW X PW
0 0,50 0 0,05
1 0,20 1 0,10
2 0,15 2 0,15
3 0,10 3 0,20
4 0,05 4 0,50
1. Вычислите математическое ожидание каждого распределения.
2. Вычислите стандартное отклонение каждого распределения.
3. Сравните результаты, полученные для распределений А и Б.
5.2. Даны следующие распределения дискретных случайных величин.
Распределение В Распределение Г
X PW X PW
0 0,20 0 0,10
1 0,20 1 0,20
2 0,20 2 0,40
3 0,20 3 0,20
4 0,20 4 0,10
1. Вычислите математическое ожидание каждого распределения.
2. Вычислите стандартное отклонение каждого распределения.
3. Сравните результаты, полученные для распределений А и Б.
Применение понятий
5.3. Используя записи о ежедневном количестве проданных машин в течение последние
500 рабочих дней, менеджер компании Konig Motors создал следующую таблицу.
Количество проданных автомобилей Частота
0 40
1 100
2 142
3 66
4 36
5 30
6 26
7 20
8 16
9 14
10 8
11 2
Всего 500
1. Постройте распределение ежедневного количества проданных автомобилей.
2. Вычислите математическое ожидание распределения.
3. Вычислите стандартное отклонение распределения.
Вычислите вероятности следующих событий.
4. Продано меньше четырех автомобилей.
5. Продано не более четырех автомобилей.
6. Продано не менее четырех автомобилей.
7. Продано четыре автомобиля.
8. Продано более четырех автомобилей.
5.4. В следующей таблице приведено распределение количества дорожно-транспортных происшествий в течение дня в небольшом городе.
Количество происшествий, X PW
0 0,10
1 0,20
2 0,45
3 0,15
4 0,05
5 0,05
1. Вычислите математическое ожидание количества дорожно-транспортных происшествий.
2. Вычислите стандартное отклонение.
5.5. Менеджер крупной компьютерной сети определил распределение количества сбоев в течение дня.
Количество происшествий, X PW
0 0,32
1 0,35
2 0,18
3 0,08
4 0,04
5 0,02
6 0,01 ‘
1. Вычислите математическое ожидание количества сбоев за день.
2. Вычислите стандартное отклонение.
5.6. В азартной игре “Больше-меньше семи” выбрасывается пара игральных кубиков. Результат игры определяется по сумме выпавших очков. Например, игрок может поставить 1 доллар на то, что сумма очков будет меньше 7, т.е. 2, 3, 4, 5 или 6. Если сумма очков будет равна или больше семи, игрок проигрывает 1 доллар, а если меньше — выигрывает. Аналогично игрок может поставить 1 доллар на то, что сумма очков будет больше 7, т.е. 8, 9, 10, 11 или 12. Если сумма очков будет равна или больше 7, игрок выигрывает 1 доллар, а если меньше — проигрывает. Игрок может поставить 1 доллар на то, что сумма очков будет равна 7. Если сумма выпавших очков окажется равной 7, он выиграет 4 доллара, в противном случае он потеряет 1 доллар.
1. Постройте распределение вероятностей, учитывающее все возможные исходы, сумма очков которых меньше 7.
2. Постройте распределение вероятностей, учитывающее все возможные исходы, сумма очков которых больше 7.
3. Постройте распределение вероятностей, учитывающее все возможные исходы, сумма очков которых равна 7.
4. Докажите, что ожидаемый выигрыш (или проигрыш) игрока постоянен и не зависит от сделанной ставки.
5.2. КОВАРИАЦИЯ И ЕЕ ПРИМЕНЕНИЕ В ФИНАНСОВОМ ДЕЛЕ
Выше мы рассмотрели понятия математического ожидания, дисперсии и стандартного отклонения дискретной случайной величины. В данном разделе вводится понятие ковариации между двумя переменными и его применение для управления портфелем активов. Эта задача вызывает большой интерес у финансовых аналитиков.
Ковариация
Ковариация пху (covariance) между двумя дискретными случайными величинами X и У определяется формулой (5.4).
КОВАРИАЦИЯ
<^xl=ft(X,-E(X))(Y,-E(Y))P(X,Y,), (5.4)
/=1
где X, — i-e значение дискретной случайной величины X, Р(Х) — вероятность i-ro значения дискретной случайной величины X, У — i-e значение дискретной случайной величины У, Р(У) — вероятность i-ro значения дискретной случайной величины У, Р(ХУ) — вероятность i-ro значения дискретной случайной величины X и i-ro значения дискретной случайной величины У, i = 1, 2, ..., А.
Проиллюстрируем понятие ковариации следующим примером. Представьте, что вам предстоит сделать одну из двух альтернативных инвестиций. Первая инвестиция представляет собой вложение средств во взаимный фонд, владеющий различными акциями, определяющими индекс Доу-Джонса (Dow Jones Industrial Average). Назовем его фондом Доу-Джонса. Вторая инвестиция — приобретение акций взаимного фонда, приносящих наибольшую доходность во время экономического спада. Присвоим ему название фонд экономического спада. Вы оцениваете доходность каждой инвестиции (прибыль на 1000 долл.) для каждого из трех возможных вариантов состояния эконо-' мики, имеющих определенную вероятность, и заполняете табл. 5.2.
Таблица 5.2. Прогнозируемая прибыль от каждой инвестиции для каждого из трех возможных вариантов состояния экономики
Инвестиция
PfXYj) Состояние экономики Фонд Доу-Джонса, долл. Фонд экономического спада, долл.
0,2 Экономический спад -100 +200
0,5 Стабильная экономика + 100 +50
0,3 Экономический рост +250 -100
Математическое ожидание и стандартное отклонение доходности каждой инвестиции, а также ковариация между их показателями доходности вычисляются следующим образом.
Введем следующие обозначения: X— доходность фонда Доу-Джонса, У— доходность фонда экономического спада.
Е(Х) = щ = -100x0,2 + 100x0,5 + 250x0,3 = 105 долл.,
Е(У) = = 200x0,2 + 50x0,5 + (-100) х0,3 = 35 долл.,
Var(X) = о; = (-100-105)2х0,2 + (100-105)2х0,5 + (250-105)2х0,3 - 14,725,
стх = 121,35 долл.,
Var(Y) = а- = (200-35)2х0,2 + (50-35)2х0,5 + (-100-35)2х0,3 = 11,025,
оу = 105,00 долл-,
пАГ = (-100-105)(200-35)х0,2 + (1ОО-1О5)(5О-35)хО,5+(25О-1О5)(-1ОО-35)хО,3 =
= -6 765 - 37,5 - 5 872,5 = -12 675.
Таким образом, математическое ожидание доходности фонда Доу-Джонса выше, чем у фонда экономического спада. Однако стандартное отклонение фонда Доу-Джонса также превышает стандартное отклонение фонда экономического спада, что говорит о более высокой степени риска. Ковариация между показателями доходности обоих фондов, равная -12 675, свидетельствует о сильной обратной зависимости. Иначе говоря, доходность обоих фондов изменяется в противоположных направлениях. Если доходность одного из фондов возрастает, доходность другого снижается.
Математическое ожидание, дисперсия и стандартное отклонение суммы двух случайных величин
Вычислив ковариацию между двумя случайными переменными X и У, можно определить математическое ожидание, дисперсию и стандартное отклонение их суммы.
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ СУММЫ ДВУХ СЛУЧАЙНЫХ ВЕЛИЧИН
Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий каждой величины.
E(X+Y) = Е(Х) + Е(У). (5.5)
ДИСПЕРСИЯ СУММЫ ДВУХ СЛУЧАЙНЫХ ВЕЛИЧИН
Дисперсия суммы двух случайных величин равна сумме дисперсий каждой величины и удвоенной ковариации между ними.
Vai-(X + Y) = oy+r = aj. +Q,, +2алу . (5.6)
Стандартное отклонение равно квадратному корню из дисперсии.
СТАНДАРТНОЕ ОТКЛОНЕНИЕ СУММЫ ДВУХ СЛУЧАЙНЫХ ВЕЛИЧИН
Стл-.r • (5.7)
Проиллюстрируем вычисление математического ожидания, дисперсии и стандартного отклонения суммы двух случайных величин на примере двух инвестиционных фондов, описанных выше. Обозначим через X — доходность фонда Доу-Джонса, а через У— доходность фонда экономического спада.
E(X+Y) = Е(Х) + Е(У) = 105 + 35 = 140,
+г = °х + <*У + 2стАУ = 14 725 +11 025 + 2 X (-12 675) = 400 ,
= 20 долл.
Математическое ожидание суммы прибылей фонда Доу-Джонса и фонда экономического спада равно 140 долл., а стандартное отклонение равно 20 долл. Обратите внимание на то, что стандартное отклонение суммы прибылей, которые могут быть получены в результате двух инвестиций, намного меньше, чем стандартное отклонение доход-
ности каждой инвестиции в отдельности. Это объясняется большой отрицательной ковариацией, существующей между показателями доходности этих фондов.
Ожидаемая доходность и риск портфельных инвестиций
Ковариация, математическое ожидание и стандартное отклонение суммы двух случайных величин позволяют оценить доходность и риск портфельных инвестиций (portfolio). Диверсифицируя свои вклады, инвесторы приобретают разные ценные бумаги, стремясь получить максимум прибыли при минимальном риске [1, 2]. При исследовании доходности портфелей ценных бумаг каждому пакету акций присваивают определенный вес. Это позволяет оценить ожидаемую доходность портфеля акций (portfolio expected return) и его риск (portfolio risk).
ОЖИДАЕМАЯ ДОХОДНОСТЬ ПОРТФЕЛЯ ЦЕННЫХ БУМАГ
Ожидаемая доходность портфеля ценных бумаг, состоящего из двух пакетов акций, определяется следующей формулой.
Е(Р) = wE(X) + (l-w)E(Y), (5.8)
где Е(Р) — ожидаемая доходность портфеля, Е(Х) — ожидаемая доходность пакета акций X, E(Y) — ожидаемая доходность пакета акций У, w — доля пакета акций X в портфеле ценных бумаг, (1-гд) — доля пакета акций У в портфеле ценных бумаг.
РИСК ПОРТФЕЛЯ ЦЕННЫХ БУМАГ
Op = +(1-и')‘сГу + 2w( 1 -w). (5.9)
В предыдущем примере мы оценили математическое ожидание и стандартное отклонение инвестиций в фонд Доу-Джонса и фонд экономического спада, а также ковариацию между ними. Допустим, что портфель активов состоит из пакетов акций двух фондов стоимостью по 500 долл, каждый. Вычислим ожидаемую доходность и риск такого портфеля акций, используя формулы (5.8) и (5.9): и; = 0,50, Е(Х) = 105 долл., £(У) = 35 долл., о2 = 14 725 , о; = 11 025 , оху = -12 675 .
Е(Р) = 0,5x105 + (1 - 0,5) х35 = 70 долл.,
Ор = ^(0,5)2 х 14 725 + (1 - 0,5)2 х 11 025 + 2 х 0,5 х (1 - 0,5) х (-12 675) = VTOO = 10 долл.
Таким образом, ожидаемая доходность портфеля составляет 70 долл, на каждую тысячу вложенных долларов (доходность равна 7%), а риск портфельных инвестиций равен 10 долл. Обратите внимание на то, что такой небольшой риск объясняется большой отрицательной ковариацией между двумя инвестициями. То, что инвестиции приносят максимальную прибыль в разных экономических ситуациях, позволяет минимизировать общий риск.
Процедуры Excel: вычисление ожидаемой доходности и риска портфельных инвестиций
Для вычисления ожидаемой доходности и риска портфеля ценных бумаг можно воспользоваться функцией суммпроизв. Надстройка PHStat2 позволяет решить эту задачу за один шаг.
Например, провести анализ данных, представленных в табл. 5.2, можно двумя способами.
Применение Excel в сочетании с надстройкой PHStat2
Для вычисления ожидаемой доходности и риска портфеля ценных бумаг следует применить процедуру PHStat1^ Decision Making ^Covariance and Portfolio Analysis... (PHStat1^ Принятие решений^ Ковариация и анализ портфельных инвестиций...) и выполнить следующие инструкции.
1. Выбрать команду PH Stat Decision Making^Covariance and Portfolio Analysis...
2. В диалоговом окне Covariance and Portfolio Management (см. иллюстрацию) сделать следующее.
2.1. Ввести в окне редактирования Number of Outcomes (Количество исходов) число 3.
2.2. Ввести в окне редактирования Title (Заголовок) соответствующее название.
2.3. Установить флажок Portfolio Management Analysis (Анализ портфельных инвестиций).
Covariance and Portfolio Management
Data -
Number of Outcomes: |з
Output Options
Title: {Анализ инвестиций
Im* Portfolio Management Analysis
Help | |LZ9iLZj| Cancel |
i
2.4. Щелкнуть на кнопке OK.
3. В новом листе, созданном программой PHStat, выполнить следующее.
3.1. Ввести в ячейки В4 : D6 вероятности и ожидаемую прибыль каждой инвестиции, указанные в табл. 5.2. В ячейки В4, В5 и Вб ввести числа 0,2, 0,5 и 0,3 соответственно. В ячейки С4, С5 и сб ввести числа -100, 100 и 250 соответственно. В ячейки D4, D5 и D6 ввести числа 200, 50 и-100 соответственно.
3.2. Ввести в ячейку В8 вес инвестиции.
Применение Excel
Для самостоятельной реализации рабочего листа, вычисляющего ожидаемую доходность и риск портфеля ценных бумаг, следуйте инструкциям из раздела ЕН.5.1.
Chapter 5.xls
ж Результаты анализа портфельных инвестиций на основе данных из табл. 5.2 записаны на листе Портфельные_инвестиции в рабочей книге chapter 5.
УПРАЖНЕНИЯ К РАЗДЕЛУ 5.2
Изучение основ
5.7. Даны следующие распределения дискретных случайных величин X и У.
X Y
0,4 100 200
0,6 200 100
Вычислите следующие величины.
1. Е(Х).
2. Е(У).
3.
4.
5. Qxy.
6. E(X+Y).
5.8. Даны такие распределения дискретных случайных величин X и У.
PfW X Y
0,2 -100 50
0,4 50 30
0,3 200 20
0,1 300 20
Вычислите следующие величины.
1. Е(Х).
2. E(Y).
3. сгх.
4. сгг.
5. сХУ.
6. Е(Х+У).
7. сух у.
5.9. Предположим, что портфель инвестиций состоит из акций двух фондов: X и У, причем Е(Х) = 50 долл., E(Y) = 100 долл., aj -9 000, с=15 000, султ=7 500. Акции фонда X составляют 40% портфеля.
1. Вычислите ожидаемую доходность.
2. Вычислите риск портфельных активов.
Применение понятий t
5.10. В примере, рассмотренном нами в тексте, портфель состоял из одинакового количества акций фонда Доу-Джонса и фонда экономического спада.
1. Вычислите ожидаемую доходность и риск портфельных активов, если акции фонда Доу-Джонса составляют 30% портфеля, а акции фонда экономического спада — 70%.
2. Вычислите ожидаемую доходность и риск портфельных активов, если акции фонда Доу-Джонса составляют 70% портфеля, а акции фонда экономического спада — 30%.
3. Какая из инвестиционных стратегий эффективнее— 30, 50 или 70% акций фонда Доу-Джонса? Почему?
5.11. Попробуем разработать инвестиционную стратегию для двух пакетов акций. Ожидаемая доходность каждой акции на 1 000 вложенных долларов приведена в таблице.
Вероятность Доходность
Акция X Акция Y
0,1 -100 50
0,3 0 150
0,3 80 -20
0,3 150 -100
1. Вычислите ожидаемую доходность акции X.
2. Вычислите ожидаемую доходность акции У.
3. Вычислите стандартное отклонение доходности акции X.
4. Вычислите стандартное отклонение доходности акции У.
5. Вычислите ковариацию между показателями доходности акций X и У.
6. Какие акции следует приобрести: X или У? Обоснуйте свою рекомендацию.
Предположим, нам необходимо сформировать портфель ценных бумаг, состоящий из акций X и У. Вычислите ожидаемую доходность и риск портфельных активов для разных пропорций пакета акций X.
7. 0,10.
8. 0,30.
9. 0,50.
10. 0,70.
11. 0,90.
*
12. Используя результаты, полученные при решении задач 7-11, сформируйте свой портфель акций. Объясните свой выбор.
5.12. Разработайте инвестиционную стратегию для двух пакетов акций. Ожидаемая доходность каждой акции на 1 000 вложенных долларов приведена в таблице.
Вероятность Доходность
Акция X Акция Y
0,1 -50 -100
0,3 20 50
0,4 100 130
0,2 150 200
1. Вычислите ожидаемую доходность акции X.
2. Вычислите ожидаемую доходность акции У.
3. Вычислите стандартное отклонение доходности акции X.
4. Вычислите стандартное отклонение доходности акции Y.
5. Вычислите ковариацию между показателями доходности акций X и Y.
6. Какие акции следует приобрести: X или У? Обоснуйте свою рекомендацию.
Предположим, нам необходимо сформировать портфель ценных бумаг, состоящий из акций X и У. Вычислите ожидаемую доходность и риск портфельных активов для разных пропорций пакета акций X.
7. 0,10.
8. 0,30.
9. 0,50.
10. 0,70.
11. 0,90.
12. Используя результаты, полученные при решении задач 7-11, сформируйте портфель акций. Объясните свой выбор.
5.13. Разработайте инвестиционную стратегию для двух пакетов, состоящих из промышленных облигаций и обычных акций. Ожидаемый доход на 1 000 вложенных долларов, который может принести каждая ценная бумага в разных экономических ситуациях, приведен в таблице.
Вероятность Состояние экономики Промышленные облигации, долл. Обычные акции, долл.
0,10 Спад -30 -150
0,15 Застой 50 -20
0,35 Медленный рост 90 120
0,30 Средний рост 100 160
0,10 Бурный рост 110 250
1. Вычислите ожидаемую доходность промышленных облигаций.
2. Вычислите ожидаемую доходность обычных акций.
3. Вычислите стандартное отклонение доходности промышленных облигаций.
4. Вычислите стандартное отклонение доходности обычных акций.
5. Вычислите ковариацию между показателями доходности промышленных облигаций и обычных акций.
6. Какие ценные бумаги следует приобрести: промышленные облигации или обычные акции? Обоснуйте свою рекомендацию.
Предположим, нам необходимо сформировать портфель ценных бумаг, состоящий из промышленных облигаций и обычных акций. Вычислите ожидаемую доходность и риск портфельных активов для разных пропорций пакета промышленных облигаций.
7. 0,10.
8. 0,30.
9. 0,50.
10. 0,70.
11. 0,90.
12. Используя результаты, полученные при решении задач 7-11, сформируйте портфель ценных бумаг. Объясните свой выбор.
5.3. БИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
В следующих трех разделах мы рассмотрим математические модели случайных событий.
Математическая модель — это математическое выражение, представляющее случайную величину. Для дискретных случайных величин это математическое выражение известно под названием функция распределения (probability distribution function).
Если задача позволяет явно записать математическое выражение, представляющее случайную величину, можно вычислить точную вероятность любого ее значения. В этом случае можно вычислить и перечислить все значения функции распределения. В деловых, социологических и медицинских приложениях встречаются разнообразные распределения случайных величин. Одним из наиболее полезных распределений является биномиальное.
Биномиальное распределение (binomial distribution) — это функция распределения дискретной случайной величины, встречающаяся во многих приложениях. Ее основные свойства перечислены во врезке 5.1.
ВРЕЗКА 5.1. СВОЙСТВА БИНОМИАЛЬНОГО РАСПРЕДЕЛЕНИЯ
Биномиальное распределение используется для моделирования ситуаций, характеризующихся следующими особенностями.
, • Выборка состоит из фиксированного числа элементов п, представляющих собой • исходы некоего испытания.
• Каждый элемент выборки принадлежит одной из двух взаимоисключающих ка- : тегорий, исчерпывающих все выборочное пространство. Как правило, эти две категории называют успех и неудача,
• Вероятность успеха р является постоянной. Следовательно, вероятность неудачи равна 1-р.
• Исход (т.е. удача или неудача) любого испытания не зависит от результата другого испытания. Чтобы гарантировать независимость исходов, элементы выборки, как правило, получают с помощью двух разных методов. Каждый элемент выборки случайным образом извлекается из бесконечной генеральной совокупности без возвращения или из конечной генеральной совокупности с возвращением.
Биномиальное распределение используется для оценки количества успехов в выборке, состоящей из п наблюдений. Вернемся к сценарию, изложенному в начале раздела. Под успехом в бухгалтерской информационной системе будем понимать ошибку при заполнении формы, а все остальные исходы будем считать неудачей. Напомним, что нас интересует количество ошибочных заказов в заданной выборке.
Какие исходы мы можем наблюдать? Если выборка состоит из четырех заказов, ошибочными могут оказаться один, два, три или все четыре, кроме того, все они могут оказаться правильно заполненными. Может ли случайная величина, описывающая количество неправильно заполненных форм, принимать какое-либо иное значение? Это невозможно, поскольку количество неправильно заполненных форм не может превышать объем выборки п или быть отрицательным. Таким образом, случайная величина, подчиняющаяся биномиальному закону распределения, принимает значения от 0 до п.
Допустим, что в выборке из четырех заказов наблюдаются следующие исходы.
Первый заказ Второй заказ Третий заказ Четвертый заказ
Ошибочный Ошибочный Правильный Ошибочный
Какова вероятность обнаружить три ошибочных заказа в выборке, состоящей из четырех заказов, причем в указанной последовательности? Поскольку предварительные исследования показали, что вероятность ошибки при заполнении формы равна 0,10, вероятности указанных выше исходов вычисляются следующим образом.
Первый заказ Второй заказ Третий заказ Четвертый заказ
р = 0,10 р = 0,10 1-р —0,90 р = 0,10
Поскольку исходы не зависят друг от друга, вероятность указанной последовательности исходов равна
рр(1-р)р = Р3(1~Р) = рЧ 1-р) = (0,10)3(0,90)1 = 0,0009.
Если же необходимо вычислить количество вариантов выбора X объектов из выборки, содержащей п элементов, следует воспользоваться формулой (5.10).
СОЧЕТАНИЯ
Количество вариантов выбора X объектов из выборки, содержащей п элементов, определяется по формуле
где п\ = п(п - 1)...2х1 — факториал числа и, причем 0! = 1 и 1! = 1.
Это выражение часто обозначают как I . Таким образом, если п = 4 и X ~ 3, количество последовательностей, состоящих из трех элементов, извлеченных из выборки, объем которой равен 4, определяется по следующей формуле:
(п ) п\ 4! 4х 3 х 2 х1
-------------------=----------= 4 .
Х\(п~Х)\ 31(4-3)! 3x2xlxl
Рассмотрим вероятности каждой последовательности.
Последовательность 1 = ошибочный, ошибочный, ошибочный, правильный ppp(l-p) = р3(1-р) = 0,0009.
Последовательность 2 = ошибочный, ошибочный, правильный, ошибочный.
рр(1-р)р = р3( 1~р) = 0,0009.
Последовательность 3 = ошибочный, правильный, ошибочный, ошибочный. р(1-р)рр = р3( 1-р) = 0,0009.
Последовательность 4 = правильный, ошибочный, ошибочный, ошибочный. (1-р) ррр = р3(1-р) = 0,0009.
Следовательно, вероятность обнаружить три ошибочных заказа вычисляется следующим образом.
(Количество возможных последовательностей) х х (вероятность конкретной последовательности) = = 4x0,0009 = 0,0036.
Аналогично можно вычислить вероятность того, что среди четырех заказов окажутся один или два ошибочных, а также вероятность того, что все заказы ошибочны или все верны. Однако при увеличении объема выборки п определить вероятность конкретной последовательности исходов становится труднее. В этом случае следует применить соответствующую математическую модель, описывающую биномиальное распределение количества вариантов выбора X объектов из выборки, содержащей п элементов.
БИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
где Р(Х) — вероятность X успехов при заданных объеме выборки п и вероятности успеха р, X = 0, 1, 2, ..., п.
Обратите внимание на то, что формула (5.11) представляет собой формализацию интуитивных выводов. Случайная величина X, подчиняющаяся биномиальному распределению, может принимать любое целое значение в диапазоне от 0 до п. Произведение рх(1~р)"' представляет собой вероятность конкретной последовательности, состоящей и!
из X успехов в выборке, объем которой равен п. Величина определяет коли-
чество возможных комбинаций, состоящих из X успехов в п испытаниях. Следовательно, при заданном количестве испытаний п и вероятности успеха р вероятность последовательности, состоящей из X успехов, равна
Р(Х) = (количество возможных последовательностей) х х(вероятность конкретной последовательности) =
Рассмотрим пример, иллюстрирующий применение формулы (5.11).
ПРИМЕР 5.1. ВЫЧИСЛЕНИЕ Р(Х= 3) ПРИ УСЛОВИИ, ЧТО л= 4 и р= 0,1
Допустим, что вероятность неверно заполнить форму равна 0,1. Какова вероятность того, что среди четырех заполненных форм три окажутся ошибочными?
РЕШЕНИЕ. Используя формулу (5.11), получаем, что вероятность обнаружить три ошибочных заказа в выборке, состоящей из четырех заказов, равна
4> , 4 ^^з^-з/0’0 °”0’0 , 41 , ==———(0,1)70,9) =4x0,1x0,1x0,1x0,9 = 0,0036. 3!(4-3)Г 7 v ’
ПРИМЕР 5.2. ВЫЧИСЛЕНИЕ /\Х> 3) ПРИ УСЛОВИИ, ЧТО п= 4 и р = 0,1
Допустим, что вероятность неверно заполнить форму равна 0,1. Какова вероятность того, что среди четырех заполненных форм не менее трех окажутся ошибочными?
РЕШЕНИЕ. Как показано в примере 5.1, вероятность того, что среди четырех заполненных форм три окажутся ошибочными, равна 0,0036. Чтобы вычислить вероятность того, что среди четырех заполненных форм не менее трех будут неправильно заполнены, необходимо сложить вероятность того, что среди четырех заполненных форм три окажутся ошибочными, и вероятность того, что среди четырех заполненных форм все окажутся ошибочными. Вероятность второго события равна
Р<Х=4>=;П(^(О,,)4(1-О’1)4
41 . ,,
= —(0,1) (0,9) = 1 х 0,1 х 0,1 х 0,1 х 0,1 = 0,0001
Таким образом, вероятность того, что среди четырех заполненных форм не менее трех окажутся ошибочными, равна
Р(Х> 3) = Р(Х = 3) + Р(Х = 4) = 0,0036 + 0,0001 = 0,0037.
Следовательно, шансы, что среди четырех заполненных форм найдутся не менее трех ошибочных, равны 0,37% . и
ПРИМЕР 5.3. ВЫЧИСЛЕНИЕ Р(Х< 3) ПРИ УСЛОВИИ, ЧТО п = 4 и р = 0,1
Допустим, что вероятность неверно заполнить форму равна 0,1. Какова вероятность того, что среди четырех заполненных форм менее трех окажутся ошибочными?
РЕШЕНИЕ. Вероятность этого события равна
Р{Х < 3) = Р(Х = 0) + Р(Х = 1) + Р{Х = 2).
Используя формулу (5.11), вычислим каждую из этих вероятностей.
^ = 0> = 0!(441о)-(0’1)”(1-0’1)4" = 0’6561 ’ /,(А' = 1) = 1!(4411),(0’1)'(1 <'=0,29.6, Р(Х = Ъ = 2!(44-2)!(0’1)’(1 °’0’ = 0’0486 ’
Следовательно, Р(Х < 3) = 0,6561+0,2916+0,0486 = 0,9963.
Вероятность Р(Х < 3) можно вычислить иначе. Для этого воспользуемся тем, что со-
бытие X < ' 3 является дополнительным по отношению к событию Х> 3. Тогда Р(Х< 3) = 1- Р(Х> 3) = 1 - 0,0037 = 0,9963.
По мере увеличения объема выборки п вычисления, аналогичные проведенным в примере 5.3, становятся затруднительными. Чтобы избегать этих сложностей, многие биномиальные вероятности табулируют заранее (табл. Д.6). Некоторые из этих вероятностей приведены в табл. 5.3. В табл. Д.6 приведены вероятности того, что при заданных параметрах пир биномиальная случайная величина X принимает значения 0, 1, 2, ..., п. Например, чтобы получить вероятность, что X = 2 при п = 4 ир = 0,1, следует извлечь из таблицы число, стоящее на пересечении строки Х = 2 и столбцар = 0,1.
Таблица 5.3. Биномиальная вероятность при п= 4f Х= 2 и р= 0,1
п X 0,01 0,02 0,10
4 0 0,9606 0,9224 0,6561
1 0,0388 0,0753 0,2916
2 0,0006 0,0023 0,0486
3 0,0000 0,0000 0,0036
4 0,0000 0,0000 0,0001
Биномиальное распределение можно вычислить с помощью программы Microsoft Excel. На рис. 5.2 показано биномиальное распределение при п = 4 и р = 0,1, вычисленное с помощью программы Microsoft Excel.
TT A7 Гв ;
1 Биномиальное распределение У-’з ‘
4 ! 5*
7
8 Ji JT; Гоф 'if '\2\
13 14 '151
16 "17-
18
_____________Data Sample size__
Probability of success
Statistics
Mean_____________
Variance__________
Standard deviation
0.1
0.4
0.36
0.6
2 3
Binomial Probabilities Table X 0
Р(Х) Р(<=Х) Р(<Х) Р(>Х) Р(>°Х)
0.6561 0.6561 0 0.3439 1
0.2916 0.9477 0.6561 0.0523 0.3439
0.0486 0.9963 0.9477 0.0037 0.0523
0.0036 0.9999 0.9963 1Е-04 0.0037
0.0001 1 0.9999 0 1Е-04
4
Рис. 5.2. Биномиальное распределение при n — 4 и р = 0,1, вычисленное с помощью программы Microsoft Excel
Процедуры Excel: вычисление биномиальных вероятностей
Для вычисления биномиальных вероятностей можно воспользоваться функцией биномрасп либо применить процедуру надстройки PHStat2.
Например, чтобы вычислить биномиальные вероятности, приведенные на рис. 5.2, можно применить одну из следующих процедур. |
Применение Excel в сочетании с надстройкой PHStat2
Для вычисления биномиального распределения необходимо выполнить такие действия.
1.
2.
Выбрать команду PHStat1^Probability & Prob. Distributions1^ Binomial... (PHStat1^Вероятность & Распределения=> Биномиальное...).
В диалоговом окне Binomial Probability Distribution (см. иллюстрацию) сделать следующее.
2.1. Ввести в окне редактирования Sample Size (Объем выборки) число 4.
2.2. Ввести в окне редактирования Probability of Success (Вероятность успеха) число 0.11.
2.3. Ввести в окне редактирования Outcomes From (Минимальное количество успехов) число 0, а в окне Outcomes То (Максимальное количество успехов) -ЧИСЛО 4.
Binomial Probability Distribution
Data ..............
Sample Size: h
Probability of Success: jo.l
Outcomes From: |0 To: j4
Output Options
Title: |Биномиальное распределение
P Cumulative Probabilities
Г" Histogram
Help j |rZ'^Z.'j| „Cancel I
2.4. Ввести в окне редактирования Title (Заголовок) соответствующее название.
2.5. Установить флажок Cumulative Probabilities (Интегральные вероятности) и сбросить флажок Histogram (Гистограмма).
2.6. Щелкнуть на кнопке ОК.
Применение Excel
Для того чтобы самостоятельно реализовать рабочий лист, вычисляющий биномиальные вероятности, следуйте инструкциям из раздела ЕН.5.2. Для того чтобы построить гистограмму по данным, записанным на рабочем листе, следуйте инструкциям ЕН.5.5.
е Chapter 5.xls
Таблица и гистограмма, построенные на основе биномиальных вероятностей, приведенные на рис. 5.2 и 5.3, содержатся в рабочей книге chapter 5 на листах Рис5.2 и Рисб.З.
Свойства биномиального распределения
Биномиальное распределение зависит от параметров пир.
Форма распределения. Биномиальное распределение может быть как симметричным, так и асимметричным. Еслир = 0,05, биномиальное распределение является симметричным независимо от величины параметра п. Однако, если р^0,05, распределение становится асимметричным. Чем ближе значение параметра р к 0,05 и чем больше объем выборки п, тем слабее выражена асимметрия распределения. Таким образом, распределение количества неправильно заполненных форм смещено вправо, поскольку р = 0,01. На рис. 5.3 изображена гистограмма биномиального распределения при п = 4 ир = 0,01.
Математическое ожидание. Математическое ожидание биномиального распределения равно произведению параметров пир.
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ БИНОМИАЛЬНОГО РАСПРЕДЕЛЕНИЯ
Математическое ожидание биномиального распределения равно произведению объема выборки п на вероятность успеха р:
ц = Е(Х) = пр. (5.12)
Напомним, что в дробные числа диалоговых окнах надстройки PHStat2 необходимо вводить либо в американском стандарте (т.е. с десятичной точкой), либо в научном формате (например, 1Е-01). — Прим.ред.
Рис. 5.3. Гистограмма биномиального распределения при п = 4 и р = 0,1, построенная’с помощью программы Microsoft Excel
Интуитивно ясно, что формула (5.12) имеет определенный смысл. В среднем, при достаточно долгой серии испытаний в выборке, состоящей из четырех заказов, может оказаться ц = Е(Х) = 4 х 0,1 = 0,4 неправильно заполненных форм.
Стандартное отклонение. Стандартное отклонение биномиального распределения вычисляется по формуле (5.13).
СТАНДАРТНОЕ ОТКЛОНЕНИЕ БИНОМИАЛЬНОГО РАСПРЕДЕЛЕНИЯ
а = фЪг(Х) = yjnp(l-p).
(5.13)
Например, стандартное отклонение количества неверно заполненных форм в бухгалтерской информационной системе равно
о = 74x0,1x0,9 = 0,60.
Этот же результат мы получили с помощью формулы (5.13), которая носит более общий характер.
Биномиальное распределение — весьма интересный пример распределения дискретной случайной величины. Как мы убедились, оно оказалось довольно полезным при исследовании особенностей информационной бухгалтерской системы. Однако еще более важную роль биномиальное распределение играет в теории статистических выводов и при проверке гипотез, которые будут рассмотрены в главах 7 и 8.
УПРАЖНЕНИЯ К РАЗДЕЛУ 5.3
Изучение основ
5.14. Вычислите следующие вероятности
1. Р(Х= 0), если п = 4ир = 0,12.
2. Р(Х = 9), если п = 10ир = 0,40.
3. Р(Х = 8), если п = 10 ир = 0,50.
4. Р(Х = 5), если п = 6 ир = 0,83.
5. Р(Х = 9), если п = 10 ир = 0,90.
5.15. Вычислите математическое ожидание и стандартное отклонение случайной величины X, подчиняющейся биномиальному закону распределения.
1. Если п = 4 ир = 0,10.
2. Если п = 4 ир = 0,40.
3. Если п = 5 ир = 0,80.
4. Если п = 3 ир = 0,50.
Применение понятий
5.16. Считается, что уменьшение и увеличение цены акции в течение операционного дня являются равновероятными случайными событиями. Какова вероятность того, что цена акции на момент закрытия торгов будет повышаться в течение пяти дней подряд?
5.17. Ставка комиссионного вознаграждения, выплачиваемая коммерческими авиалиниями агентам бюро путешествий, на протяжении нескольких лет неуклонно уменьшается. Для того чтобы увеличить прибыль, многие бюро путешествий стали вводить наценки на билеты, как правило, от 10 до 15 долл. Согласно данным Американского общества транспортных агентств по продаже билетов, около 90% агентов бюро путешествий ввели наценки на авиационные билеты (Kortney Stringer, “American Air Fees for Travel Agents to be Cut Again”, Wall Street Journal, August 20, 2001, B2).
1. Можно ли назвать величину 90%, указанную Американским обществом транспортных агентств по продаже билетов, априорной классической, эмпирической или субъективной вероятностью?
2. Предположим, Что мы сформировали случайную выборку, состоящую из 10 бюро путешествий, а количество бюро, практикующих наценки на билеты, является биномиальной случайной величиной. Чему равно математическое ожидание и стандартное отклонение этого распределения?
3. Какие предположения должны выполняться при решении задачи 2?
Для выборки, состоящей из 10 бюро путешествий, вычислите вероятности следующих событий.
4. Ни одно бюро не вводило наценки на билеты.
5. Наценки на билеты ввело только одно бюро.
6. Наценки на билеты ввели только два бюро.
7. Наценки на билеты ввели не более двух бюро.
8. Наценки на билеты ввели не менее трех бюро.
5.18. Телевизионные каналы каждую осень организуют новые шоу. Для того чтобы заинтересовать ими свою аудиторию, они все лето проводят массированную рекламную кампанию, а затем — опрос, чтобы определить, сколько телезрителей уже знают о предстоящей премьере. Как свидетельствуют опросы, осенью 2001 г. 68% зрителей в возрасте от 18 до 49 лет слышали о новом сериале “Преступный умысел” (Criminal Intent), в то время как о шоу “Тайны Шварца” (Inside Schwartz) знали только 24%. (Joe Flint, “Viewers Awareness of of New Shows Rises”, Wall Street Journal, August 20, 2001, B7.)
1. Что значит “знали”? Дайте точное определение этого слова.
2. Можно ли назвать величины 68 и 24%, указанные телеканалами, априорной классической, эмпирической или субъективной вероятностью?
Предположим, что мы сформировали случайную выборку, состоящую из 20 телезрителей в возрасте от 18 до 49 лет. Вычислите вероятности следующих событий, используя программу Microsoft Excel.
3. О сериале “Преступный умысел” знают меньше пяти телезрителей.
4. О сериале “Преступный умысел” знают не меньше 10 телезрителей.
5. О сериале “Преступный умысел” знают не меньше 15 телезрителей.
6. О сериале “Преступный умысел” знают все 20 телезрителей.
7. Чему равно ожидаемое количество телезрителей, знающих о премьере сериала “Преступный умысел”, в выборке, состоящей из 20 человек?
5.19. Одним из важнейших показателей качества услуг, предоставляемых телефонной компанией, является скорость, с которой она восстанавливает телефонную связь. Предположим, что вероятность восстановления телефонной связи в тот же день равна 0,7. Допустим, что в течение дня уже возникло 5 повреждений телефонной линии. 1. Какова вероятность того, что все повреждения будут исправлены в течение дня?
2. Какова вероятность того, что в течение дня будут исправлены хотя бы три повреждения?
3. Какова вероятность того, что в течение дня будет исправлено меньше двух повреждений?
4. Какие условия должны выполняться при вычислении вероятностей в задачах 1-3?
5. Чему равны математическое ожидание и стандартное отклонение распределения вероятности восстановления связи в течение дня?
6. Как изменятся ответы на вопросы 1-3 и 5, если вероятность восстановления связи в течение дня равна 0,80?
7. Сравните ответы на вопросы 1-3 и 6.
5.20. Некий студент сдает тест, в котором на каждый вопрос предлагается выбрать один из четырех вариантов ответа. Предположим, студент не знает ни одного правильного ответа и решает отвечать случайным образом. Для этого он кладет в шапку четыре жребия, помеченных буквами А, В, С и D. Затем при ответе на вопрос он вынимает жребий, отмечает соответствующий ответ и возвращает жребий обратно. Экзамен состоит из пяти вопросов.
1. Какова вероятность того, что студент правильно ответит на все поставленные вопросы?
2. Какова вероятность того, что студент правильно ответит по крайней мере на четыре вопроса?
3. Какова вероятность того, что студент ни на один вопрос не ответит правильно?
4. Какова вероятность того, что студент правильно ответит не более чем на два вопроса?
, 5. Какие условия должны выполняться при вычислении вероятностей в зада-
чах 1-4?
6. Чему равно математическое ожидание и стандартное отклонение количества правильных ответов?
7. Предположим, что экзамен состоит из 50 вопросов, предполагающих несколько вариантов ответа. Для сдачи экзамена достаточно ответить хотя бы на 30 вопросов. Какова вероятность того, что студент сдаст экзамен, руководствуясь выбранной им стратегией? (Вычислите эту вероятность, используя программу Microsoft Excel.)
5.21. Когда клиент заполняет бланк заказа в компании Rudy’s On-Line Office Supplies, компьютерная бухгалтерская система автоматически проверяет, не превысил ли он верхний предел кредита. Недавние исследования показали, что вероятность превышения верхнего предела кредита равна 0,05. Допустим, что в течение дня в систему поступило 20 заказов. Предположим также, что количество клиентов, превысивших верхний предел кредита, подчиняется биномиальному закону распределения.
1. Чему равно математическое ожидание и стандартное отклонение количества клиентов, превысивших верхний предел кредита?
2. Какова вероятность, что ни один клиент не превысит предел кредита?
3. Какова вероятность, что предел кредита превысит только один клиент?
4. Какова вероятность, что предел кредита превысят два и более клиентов?
5.4. ГИПЕРГЕОМЕТРИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ
Гипергеометрическое распределение, как и биномиальное, позволяет оценить количество успехов в серии из п испытаний. Разница между ними заключается лишь в способе получения исходных данных. В биномиальной модели данные выбираются либо из конечной генеральной совокупности с возвращением либо из бесконечной генеральной совокупности без возвращения. В гипергеометрической модели данные извлекаются только из конечной генеральной совокупности без возвращения. Таким образом, в то время как в биномиальной модели вероятность успеха р остается постоянной, а испытания не зависят друг от друга, в гипергеометрической модели эти условия не выполняются. Наоборот, в гипергеометрической модели каждый исход зависит от предыдущих исходов.
Гипергеометрическое распределение, описывающее вероятность X успехов при заданных параметрах n, N и А, задается формулой (5.14).
ГИПЕРГЕОМЕТРИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ
(5.14)
где Р(Х) — вероятность X успехов при заданных п, N и А, п — объем выборки, N — объем генеральной совокупности, А — количество успешных исходов в генеральной совокупности, N-A — количество неудачных исходов в генеральной совокупности, X — количество успехов в выборке, N -X — количество неудачных исходов в выборке.
Количество успехов X в выборке не может превосходить количество успехов А в генеральной совокупности либо объем выборки п. Таким образом, диапазон значений, которые может принимать случайная величина, подчиняющаяся гипергеометрическому распределению, ограничен либо объемом выборки (как и диапазон биномиальной переменной), либо объемом генеральной совокупности.
Математическое ожидание гипергеометрического распределения вычисляется по формуле (5.15).
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ ГИПЕРГЕОМЕТРИЧЕСКОГО РАСПРЕДЕЛЕНИЯ
ц = ЕС¥) = ^. (5.15)
Стандартное отклонение гипергеометрического распределения вычисляется по формуле (5.16).
СТАНДАРТНОЕ ОТКЛОНЕНИЕ ГИПЕРГЕОМЕТРИЧЕСКОГО РАСПРЕДЕЛЕНИЯ
(5.16)
V N2 VX-1
Выражение
In - п V W-1
называется поправочным коэффициентом конечной генеральной совокупности (finite population correction factor). Он необходим, поскольку элементы выборки извлекаются из конечной генеральной совокупности.
Проиллюстрируем применение гипергеометрического распределения следующим примером. Предположим, что некая организация пытается создать группу из 8 человек, обладающих определенными знаниями о производственном процессе. В организации работают 30 сотрудников, обладающих необходимыми знаниями, причем 10 из них работают в конструкторском бюро. Какова вероятность того, что в группу попадут два сотрудника из конструкторского бюро, если членов группы выбирают случайно? Объем генеральной совокупности в этой задаче равен N = 30, объем выборки п = 8, а количество успехов А = 10.
Используя формулу (5.14), получаем
p0Y20A 10! ; 20!
Р(Х = 2) = ЦЛ11 = ^*6^ = 0.298,
8 J 8’22!
Таким образом, вероятность того, что в группу попадут два сотрудника из конструкторского бюро, равна 0,298 (или 29,8%).
При увеличении генеральной совокупности и объема выборки вычисления гипергеометрического распределения становятся все более утомительными. Однако гипергеометрическое распределение можно вычислить с помощью программы Microsoft Excel, как показано на рис. 5.4.
! А В 1 С
1 Типергеоиетрическое распределение
2 '_________________________________
3 ________________Data________
4 Sample size_______________________
5 No. of successes in population____
6 Population size 7
8 Hypergeometric Probabilities Table
9
'10
11
12 13 14’
15'
16’
17
is
8 10
30
X. 0 1 2 3 4 5 6
m.....
0.021523 0.132447 0.298005 0.317872 0.173836 0.049083 0.006817
0.00041 7.69Е-06
8
Рис. 5.4. Гипергеометрическое распределение при N = 30, А = 10 и п = 8, вычисленное с помощью программы Microsoft Excel
Процедуры Excel: вычисление гипергеометрических вероятностей
Для вычисления гипергеометрических вероятностей можно воспользоваться функцией гипергеомет или процедурой надстройки PHStat2.
Например, чтобы вычислить гипергеометрические вероятности, приведенные на рис. 5.4, необходимо выполнить одну из следующих процедур.
Применение Excel в сочетании с надстройкой PHStat2
Для вычисления гипергеометрического распределения необходимо применить процедуру Hypergeometric надстройки PHStat2, создающую новый рабочий лист, и выполнить следующие инструкции.
1. Выбрать команду PHStatn>Probability & Prob.Distributions^ Hypergeometric... (PHStat^*Вероятность & РаспределенияФ Г ипергеометрическое...).
2. В диалоговом окне Hypergeometric Probability Distribution (см. иллюстрацию) сделать следующее.
2.1. Ввести в окне редактирования Sample Size (Объем выборки) число 8.
2.2. Ввести в окне редактирования No. of Success in Population (Количество успехов в генеральной совокупности) число 10.
2.3. Ввести в окне редактирования Population Size (Объем генеральной совокупности) число 30.
2.4. Ввести в окне редактирования Title (Заголовок) соответствующее название.
2.5. Щелкнуть на кнопке ОК.
Применение Excel
Для того чтобы самостоятельно создать рабочий лист, вычисляющий гипергеометрические вероятности, следуйте инструкциям из раздела ЕН.5.3. Для того чтобы создать гистограмму на основе данных, содержащихся на рабочем листе, следуйте инструкциям из раздела ЕН.5.5.
Chapter 5.xls
Гипергеометрические вероятности содержатся на листе Рис5.4 в рабочей книге Chapter 5.
УПРАЖНЕНИЯ К РАЗДЕЛУ 5.4
Изучение основ
5.22. Вычислите следующие вероятности.
1. Р(Х = 3), если тг = 4, N = 10иА = 5.
2. PCX’= 1), если тг = 4, А = 6 и А = 3.
3. Р(Х = 0), если тг = 5, А = 12 и А = 3.
4. Р(Х = 3), если п = 3, W = 10иА = 3.
5.23. Вычислите математическое ожидание и стандартное отклонение каждого из гипергеометрических распределений, указанных в задачах 5.22.1-5.22.4.
Применение понятий
5.24. Аудитор налогового управления выбрал 6 деклараций о доходах, полученных от лиц, обладающих конкретной профессией. Если среди них окажется не менее двух нарушителей, проверке подвергается вся генеральная совокупность, состоящая из 100 деклараций о доходах.
1. Какова вероятность, что проверке подвергнется вся генеральная совокупность, если истинное количество нарушителей равно 25?
2. Какова вероятность, что проверке подвергнется вся генеральная совокупность, если истинное количество нарушителей равно 30?
3. Какова вероятность, что проверке подвергнется вся генеральная совокупность, если истинное количество нарушителей равно 5?
4. Какова вероятность, что проверке подвергнется вся генеральная совокупность, если истинное количество нарушителей равно 10?
5. Как эти вероятности зависят от истинного количества нарушителей?
5.25. Декан школы бизнеса формирует исполнительный комитет, состоящий из 5 членов. В школе работают 40 преподавателей, 8 из них преподают бухгалтерский учет. Члены исполнительного комитета выбираются случайно.
1. Какова вероятность того, что в комитет не войдет ни один преподаватель бухгалтерского учета?
2. Какова вероятность того, что в комитет войдет хотя бы один преподаватель бухгалтерского учета?
3. Какова вероятность того, что в комитет войдет не больше одного преподавателя бухгалтерского учета?
4. Как изменятся ответ на вопрос 1, если исполнительный комитет состоит из 7 членов?
5.26. В инвентарной ведомости перечислены 48 автомобилей, проданных местным дилерам, причем в 12 из них установлены бракованные радиоприемники. Предположим, что некий дилер получил 8 автомобилей.
1. Какова вероятность того, что все 8 автомобилей оборудованы бракованными радиоприемниками?
2. Какова вероятность того, что все 8 автомобилей оборудованы исправными радиоприемниками?
3. Какова вероятность того, что бракованный радиоприемник установлен только в одном автомобиле?
4. Как изменятся ответы на вопросы 1-3, если дилер получил 6 автомобилей?
5.27. В государственной лотерее для выигрыша необходимо угадать 6 номеров из 54.
1. Какова вероятность того, что среди 6 наугад выбранных номеров все окажутся выигрышными?
2. Какова вероятность того, что среди 6 наугад выбранных номеров 5 номеров окажутся выигрышными?
3. Какова вероятность того, что среди 6 наугад выбранных номеров 4 номера окажутся выигрышными?
4. Какова вероятность того, что среди 6 наугад выбранных номеров 3 номера окажутся выигрышными?
5. Какова вероятность того, что среди 6 наугад выбранных номеров не окажется ни одного выигрышного?
6. Как изменятся ответы на вопросы 1-5, если для выигрыша необходимо угадать 6 номеров из 40?
5.28. В партии из 15 жестких дисков обнаружено 5 дефектных. Предположим, что проверке подвергаются 4 диска.
1. Какова вероятность того, что среди них окажется только один дефектный?
2. Какова вероятность того, что среди них окажется по крайней мере один дефектный?
3. Какова вероятность того, что среди них окажется не более двух дефектных?
4. Каково ожидаемое среднее количество бракованных изделий в выборке из 4 дисков?
5.5. РАСПРЕДЕЛЕНИЕ ПУАССОНА
Во многих практически важных приложениях большую роль играет распределение Пуассона. Многие из числовых дискретных величин являются реализациями пуассоновского процесса, свойства которого описаны во врезке 5.2.
ВРЕЗКА 5.2. ПУАССОНОВСКИЙ ПРОЦЕСС
Пуассоновский процесс (Poisson process) возникает в ситуациях, обладающих следующими свойствами.
• Нас интересует, сколько раз происходит некое событие в заданной области возможных исходов случайного эксперимента. Область возможных исходов (area of opportunity) может представлять собой интервал времени, отрезок, поверхность и т. п.
• Вероятность данного события одинакова для всех областей возможных исходов.
• Количество событий, происходящих в одной области возможных исходов, не зависит от количества событий, происходящих в других областях.
• Вероятность того, что в одной и той же области возможных исходов данное событие происходит больше одного раза, стремится к нулю по мере уменьшения области возможных исходов.
Чтобы глубже понять смысл пуассоновского процесса, предположим, что мы исследуем количество клиентов, посещающих отделение банка, расположенное в центральном деловом районе, во время ленча, т.е. с 12 до 13 часов. Предположим, требуется определить количество клиентов, приходящих за одну минуту. Обладает ли эта ситуация особенностями, перечисленными во врезке 5.2? Во-первых, событие, которое нас интересует, представляет собой приход клиента, а область возможных исходов — одноминутный интервал. Сколько клиентов придет в банк за минуту — ни одного, один, два или больше? Во-вторых, разумно предположить, что вероятность прихода клиента на протяжении минуты одинакова для всех одноминутных интервалов. В-третьих, приход одного клиента в течение любого одноминутного интервала не зависит от прихода любого другого клиента в течение любого другого одноминутного интервала. И, наконец, вероятность того, что в банк придет больше одного клиента стремится к нулю, если временной интервал стремится к нулю, например, становится меньше 0,01 с. Итак, количество клиентов, приходящих в банк во время ленча в течение одной минуты, описывается распределением Пуассона.
Распределение Пуассона имеет один параметр, обозначаемый символом X (греческая буква “лямбда”). Этим параметром является среднее количество успешных испытаний в заданной области возможных исходов. Дисперсия распределения Пуассона также равна X., а его стандартное отклонение равно . Количество успешных испытаний X пуассоновской случайной величины изменяется от 0 до бесконечности.
Распределение Пуассона описывается формулой (5.17).
РАСПРЕДЕЛЕНИЕ ПУАССОНА
= (5-17)
гдеР(Х) — вероятность X успешных испытаний, X — ожидаемое количество успехов, е— основание натурального логарифма, равное 2,71828, X— количество успехов в единицу времени.
Вернемся к нашему примеру. Допустим, что в течение обеденного перерыва в среднем в банк приходят три клиента в минуту. Какова вероятность того, что в данную минуту в банк придут два клиента? А чему равна вероятность того, что в банк придут более двух клиентов?
Применим формулу (5.17) с параметром X = 3. Тогда вероятность того, что в течение данной минуты в банк придут два клиента, равна
еГзо(3,О)‘ 9
Р( X = 2) -----=---------------------= 0,2240
2! (2,71828) х 2
Вероятность того, что в банк придут более двух клиентов, равна
Р(X > 2) = Р{X = 3) + Р(Х = 4) +... + Р(Х = оо) .
Поскольку сумма всех вероятностей должна быть равной 1, члены ряда, стоящего в правой части формулы, представляют собой вероятность дополнения к событию X < 2. Иначе говоря, сумма этого ряда равна 1- Р(Х < 2). Таким образом,
Р(Х> 2) = 1-Р(Х<2) = 1-[Р(Х = 0) + Р(Х = 1)+Р(Х = 2)].
Теперь, используя формулу (5.17), получаем ответ:
Р(Х>2) = 1-
е~3()(3,0)(,1 Г е~зо(3,О)‘ °! J + [ 1!
е~зо(3,О)2 2!
= 1 - [0,0498 + 0,1494 + 0,2240] = 1 - 0,4232 = 0,5768.
Таким образом, вероятность того, что в банк в течение минуты придут не больше двух клиентов, равна 0,4232 (или приблизительно 42,3%). Следовательно, вероятность того, что в банк в течение минуты придут больше двух клиентов, равна 0,5768 (или приблизительно 57,7%).
Такие вычисления могут показаться утомительными, особенно если параметр X достаточно велик. Чтобы избежать сложных вычислений, многие пуассоновские вероятности можно найти непосредственно в табл. Д.7, часть которой приведена в табл. 5.4. Вероятность того, что в заданную минуту в банк придут два клиента, если в среднем в банк приходят три клиента в минута, находится в табл. 5.4 на пересечении строки X ~ 2 и столбца X = 3. Таким образом, она равна 0,2240.
Таблица 5.4. Пуассоновская вероятность при X = 3
Я
X 2.1 2.2 3.0
0 0,1125 0,1108 0,0498
1 0,2572 0,2438 0,1494
2 0,2700 0,2681 0,2240
3 0,1890 0,1966 0,2240
4 0,0992 0,1082 0,1680
5 0,0417 0,0476 0,1008
6 0,0146 0,0174 0,0504
7 0,0044 0,0055 0,0216
8 0,0011 0,0015 0,0081
9 0,0003 0,0004 0,0027
10 0,0001 0,0001 0,0008
11 0,0000 0,0000 0,0002
12 0,0000 0,0000 0,0001
Пуассоновские вероятности, приведенные в табл. Д.7, можно вычислить с помощью программы Microsoft Excel. На рис. 5.5 приведен рабочий лист программы Microsoft Excel, содержащий пуассоновские вероятности, вычисленные при условии, что Х=3.
А В c D 1 . F J . A . •
1 2 Распределение Пуассона
А Data
4 Average/Expected number of successes:! 3
Poisson Probabilities Table
7 X P(X) P(<°X) P(<X) P(>X) P(>=X)
в 0 0.049787 0.049787 0.000000 0.950213 1.000000
9 1 0.149361 0.199148 0.049787 0.800852 0.950213
10 2 0.224042 0.423190 0.199148 0.576810 0.800852
11 3 0.224042 0.647232 0.423190 0.352768 0.576810
12 4 0.168031 0.815263 0.647232 0.184737 0.352768
5 0.100819 0.916082 0.815263 0.083918 0.184737
14 6 0.050409 0.966491 0.916082 0.033509 0.083918
15 7 0.021604 0.988095 0.966491 0.011905 0.033509
16 8 0.008102 0.996197 0.988095 0.003803 0.011905
17 9 0.002701 0.998898 0.996197 0.001102 0.003803
18 10 0.000810 0.999708 0.998898 0.000292 0.001102
19 11 0.000221 0.999929 0.999708 0.000071 0.000292
20" 12 0.000055 0.999984 0.999929 0.000016 0.000071
21 13 0.000013 0.999997 0.999984 0.000003 0.000016
22! 14 0.000003 0.999999 0.999997 0.000001 0.000003
23 15 0.000001 1.000000 0.999999 0.000000 0Л00001
24 | 16 0.000000 1.000000 1.000000 0.000000 0.000000
25 17 0.000000 1.000000 1.000000 0.000000 0.000000
26 18 0.000000 1.000000 1.000000 0.000000 0.000000
27 19 0.000000 1.000000 1.000000 0.000000 0.000000
.28’ 20 0.000000 1.000000 1.000000 0.000000 0.000000
Рис. 5.5. Пуассоновские вероятности при Х=3, вычисленные с помощью программы Microsoft Excel
Процедуры Excel: вычисление пуассоновских вероятностей
Для вычисления пуассоновских вероятностей можно воспользоваться функцией пуассон или процедурой Poisson надстройки PHStat2.
Например, чтобы вычислить биномиальные вероятности, приведенные на рис. 5.5, можно воспользоваться одним из следующих способов.
Применение Excel в сочетании с надстройкой PHStat2
Для вычисления пуассоновского распределения с помощью процедуры Poisson надстройки PHStat2, создающей новый рабочий лист, необходимо выполнить следующие инструкции.
1. Выбрать команду PHStat=> Probability & Prob. Distributions^ Poisson... (PHStat=>Вероятность & Распределения^ Распределение Пуассона...).
2. В диалоговом окне Poisson Probability Distribution (см. иллюстрацию) сделать следующее.
2.1. Ввести в окне редактирования Average/Expected No. of Successes (Среднее/Ожидаемое количество успехов) число 3.
2.2. Ввести в окне редактирования Title (Заголовок) соответствующее название.
Poisson Probability Distribution
Data ' '' ____
Average/Expected No. of Successes: [з*
Output Options
Title: распределение Пуассона ;
57 Cumulative Probabilities
f~ Histogram >
Help | |i, OK., J Cancel J
2.3. Установить флажок Cumulative Probabilities (Интегральные вероятности).
2.4. Щелкнуть на кнопке ОК.
Применение Excel
Для того чтобы самостоятельно создать рабочий лист, вычисляющий пуассоновские вероятности, следуйте инструкциям из раздела ЕН.5.4. Для того чтобы создать гистограмму на основе созданного рабочего листа, следуйте инструкциям из раздела ЕН.5.5.
Chapter 5.xls
" Пуассоновские вероятности, приведенные на рис. 5.5, содержатся в рабочей книге Chapter 5 на листе Рис5.5.
Изучение основ
5.29. Вычислите следующие пуассоновские вероятности.
1. Р(Х = 2), если л = 2,5.
2. Р(Х = 8), если А. = 8,0.
3. Р(Х = 1), если А. = 0,5.
4. Р(Х = 0), если А. = 3,7.
5. Р(Х = 7), если А. = 4,4.
5.30. Вычислите следующие пуассоновские вероятности.
1. Р(Х > 2), если X = 2,0.
2. Р(Х > 3), если А. = 8,0.
3. Р(Х < 1), если А. = 0,5.
4. Р(Х > 1), если А. = 4,0.
5. Р(Х <3), если к = 5,0.
Применение понятий
5.31. Компания J. D. Power & Associates вычисляет и публикует различные статистические данные, касающиеся качества автомобилей. Используемый ею индекс качества представляет собой результат деления количества обнаруженных изъянов на количество проданных новых автомобилей. Среди моделей 2002 года марка Lexus занимала первое место. Ее индекс качества равен 0,85. Корейская модель KIA занимает последнее место, имея индекс качества, равный 2,67. (Gregory L. White and Northiko Shirouzu, “What’s in a Car-Quality Score?” Wall Street Journal, May 30, 2002, D6.) Введем случайную переменную X, равную индексу качества только что проданного автомобиля Lexus.
1. Какие предположения необходимо сделать, чтобы случайная переменная X имела распределение Пуассона? Разумны ли эти предположения?
Предположим, что вы приобрели автомобиль Lexus 2002 года выпуска. Вычислите вероятности следующих событий.
2. Автомобиль не имеет ни одного изъяна.
3. Автомобиль имеет только один изъян.
4. Автомобиль имеет только два изъяна.
5. Автомобиль имеет не более двух изъянов.
6. Автомобиль имеет не менее трех изъянов.
7. Дайте определение слова “изъян”. Почему это определение имеет такое значение для интерпретации индекса качества?
8. Повторите решение задач 1-6 для модели KIA2002. Сравните полученные результаты с ответами для модели Lexus.
5.32. Представьте себе, что каждый покупатель с 9:00 до 21:00 может зарегистрировать свою жалобу на продукцию вашей компании по бесплатному телефонному номеру. Опыт показывает, что в среднем за час поступает 0,4 жалоб.
1. Какие предположения необходимо сделать, чтобы случайная переменная X, описывающая количество жалоб, поступающих в течение часа, имела распределение Пуассона?
Предположим, что ситуация соответствует требованиям, выдвигаемым к пуассоновскому процессу. Вычислите вероятность того, что в течение часа произойдут следующие события.
2. Не поступит ни одного звонка.
3. Поступит только один звонок.
4. Поступит только два звонка.
5. Поступит не менее трех звонков.
6. Какое максимальное количество звонков поступает в течение часа в 99,99% случаев?
5.33. Допустим, что количество сбоев в локальной компьютерной сети, возникающих в течение дня, подчиняется пуассоновскому закону. Среднее количество сбоев, возникающих в течение дня, равно 2,4. Вычислите вероятности следующих событий.
1. В течение дня в сети не возникнет ни одного сбоя.
2. В течение дня в сети возникнет только один сбой.
3. В течение дня в сети возникнет не менее двух сбоев.
4. В течение дня в сети возникнет не более трех сбоев.
5.34. Инспектор по контролю качества в компании Marilin's Cookies проверил партию свежего шоколадного печенья. Если печенье качественное, то среднее количество кусочков шоколада в нем должно быть равным 6,0.
1. Какова вероятность того, что в произвольном печенье содержится меньше пяти кусочков шоколада?
2. Какова вероятность того, что в произвольном печенье содержится ровно пять кусочков шоколада?
3. Какова вероятность того, что в произвольном печенье содержится не менее пяти кусочков шоколада?
4. Какова вероятность того, что в произвольном печенье содержится четыре или пять кусочков шоколада?
5. Как изменятся ответы на вопросы 1-3, если среднее количество кусочков шоколада в печенье равно 5,0?
5.35. Вернемся к задаче 5.34. Сколько штук печенья должен проверить инспектор по качеству, если партия состоит из 100 штук, а количество кусочков шоколада в печенье должно быть не меньше четырех?
5.36. В аэропорту небольшого городка от пассажиров одной широко известной авиакомпании ежедневно поступает 9 жалоб на потерю багажа. Вычислите вероятности следующих событий.
1. В течение дня поступит меньше трех жалоб.
2. В течение дня поступит три жалобы.
3. В течение дня поступит не менее трех жалоб.
4. В течение дня поступит более трех жалоб.
5.37. Опыт подсказывает, что количество повреждений в рулоне бумаги второго сорта подчиняется закону Пуассона, причем среднее количество повреждений равно 1 в расчете на 5 футов бумаги (т.е. 0,2 единицы брака на один фут). Вычислите вероятности следующих событий.
1. В рулоне длиной 1 фут будет обнаружено не менее двух повреждений.
2. В рулоне длиной 12 футов будет обнаружено по крайней мере одно повреждение.
3. В рулоне длиной 50 футов будет обнаружено от 5 до 15 (включительно) повреждений.
5.6. АППРОКСИМАЦИЯ БИНОМИАЛЬНОГО РАСПРЕДЕЛЕНИЯ С ПОМОЩЬЮ РАСПРЕДЕЛЕНИЯ ПУАССОНА
Если число п велико, а число р — мало, биномиальное распределение можно аппроксимировать с помощью распределения Пуассона. Чем больше число п и меньше числор, тем выше точность аппроксимации. Для аппроксимации биномиального распределения используется следующая модель Пуассона.
АППРОКСИМАЦИЯ БИНОМИАЛЬНОГО РАСПРЕДЕЛЕНИЯ С ПОМОЩЬЮ РАСПРЕДЕЛЕНИЯ ПУАССОНА
Р{Х} = е , (5.18)
где Р(Х) — вероятность X успехов при заданных параметрах п и р, п — объем выборки, р — истинная вероятность успеха, е — константа Эйлера, приближенно равная 2,71828, X — количество успехов в выборке (X = 0, 1, 2, ..., п).
Теоретически случайная величина, имеющая распределение Пуассона, принимает значения от 0 до со . Однако в тех ситуациях, когда распределение Пуассона применяется для приближения биномиального распределения, пуассоновская случайная величина — количество успехов среди п наблюдений — не может превышать число п. Из формулы (5.18) следует, что с увеличением числа п и уменьшением числар вероятность обнаружить большое количество успехов уменьшается и стремится к нулю.
Как указывалось ранее, математическое ожидание р и дисперсия а2 распределения Пуассона равны X. Следовательно, при аппроксимации биномиального распределения с помощью распределения Пуассона для приближения математического ожидания следует применять формулу (5.19).
ПРИБЛИЖЕНИЕ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ БИНОМИАЛЬНОГО РАСПРЕДЕЛЕНИЯ
ц = Е(х) = X = пр. (5.19)
Для аппроксимации стандартного отклонения используется формула (5.20).
АППРОКСИМАЦИЯ СТАНДАРТНОГО ОТКЛОНЕНИЯ БИНОМИАЛЬНОГО РАСПРЕДЕЛЕНИЯ
(5.20)
Обратите внимание на то, что стандартное отклонение, вычисленное по формуле (5.20), стремится к стандартному отклонению в биномиальной модели (формула (5.13)), когда вероятность успехар стремится к нулю, и, соответственно, вероятность неудачи 1-р стремится к единице.
Предположим, что 8% шин, произведенных на некотором заводе, являются бракованными. Чтобы проиллюстрировать применение распределения Пуассона для аппроксимации биномиального распределения, вычислим вероятность обнаружить одну дефектную шину в выборке, состоящей из 20 шин. Применим формулу (5.18).
Р( X=1) s g~3W8x20x0’08==О,323О.
Вместо формулы можно использовать таблицу распределения Пуассона (табл. Д.7). Для вычисления искомой вероятности необходимо знать параметр X и заданное количество успехов X. Поскольку в рассмотренном выше примере X = 1,6, аХ = 1, применяя табл. Д.7, получаем следующий результат.
Р(Х=1) = 0,3230.
Процедура поиска числа Р(Х = 1) по заданным параметрам X и X продемонстрирована в табл. 5.5, представляющей собой фрагмент табл. Д.7.
Таблица 5.5. Вычисление пуассоновской вероятности
X
X 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0
0 0,3329 0,3012 0,2725 0,2466 0,2231 0,2019 0,1827 0,1653 0,1496 0,1353
1 0,3662 0,3614 0,3543 0,3452 0,3347 0,3230 0,3106 0,2975 0,2842 0,2707
2 0,2014 0,2169 0,2303 0,2417 0,2510 0,2584 0,2640 0,2678 0,2700 0,2707
3 0,0738 0,0867 0,0998 0,1128 0,1255 0,1378 0,1496 0,1607 0,1710 0,1804
4 0,0203 0,0260 0,0324 0,0395 0,0471 0,0551 0,0636 0,0723 0,0812 0,0902
Источник: фрагмент табл. Д.7.
Если бы мы могли вычислить истинное биномиальное распределение, а не его приближение, то получили бы следующий результат.
р(Х = 1) = j х 0,08 х (0,92)19 =0,3282.
Однако эти вычисления довольно утомительны. Очевидно, что тот же самый ответ мы получили бы, воспользовавшись табл. Д.6 или программой Microsoft Excel для непосредственного вычисления биномиальной вероятности при п = 20, р = 0,08 и Х= 1. В этом случае применение распределения Пуассона становится излишним.
На рис. 5.6 показан процесс решения задачи о вероятности обнаружить дефектную шину в выборке, состоящей из 20 шин, с помощью биномиального распределения (панель А) и распределения Пуассона (панель Б). Поскольку результаты очень схожи, можно утверждать, что распределение Пуассона позволяет правильно вычислять биномиальные вероятности, когдар больше 0,08.
= А В liiii D 9ЯЛ
1 Распределение Пуа ссона
2 ,
3 . Data
4 ; Average/Expected number of successes:! 3
5 '
6 'Poisson Probabilities Table
7 i X Р(Х) Р(<=Х) Р(<Х) Р(>Х) Р(>“Х)
a ! 0 0.049787 0.049787 0.000000 0.950213 1.000000
9~1 1 0.149361 0.199148 0.049787 0.800852 0.950213
10: 2 0.224042 0.423190 0.199148 0.576810 0.800852
_iv 3 0.224042 0.647232 0.423190 0.352768 0.576810
12; 4 0.168031 0.815263 0.647232 0.184737 0.352768
J3~ 5 0.100819 0.916082 0.815263 0.083918 0.184737
14 s 6 0.050409 0.966491 0.916082 0.033509 0.083918
7 0.021604 0.988095 0.966491 0.011905 0.033509
16" 8 0.008102 0.996197 0.988095 0.003803 0.011905
"17 9 0.002701 0.998898 0.996197 0.001102 0.003803
10 0.000810 0.999708 0.998898 0.000292 0.001102
19! 11 0.000221 0.999929 0.999708 0.000071 0.000292
201 12 0.000055 0.999984 0.999929 0.000016 0.000071
21 I 13 0.000013 0.999997 0.999984 0.000003 0.000016
22j 14 0.000003 0.999999 0.999997 0.000001 0.000003
23' 15 0.000001 1.000000 0.999999 0.000000 0.000001
24l 16 0.000000 1.000000 1.000000 0.000000 0.000000
25 17 0.000000 1.000000 1.000000 0.000000 0.000000
26 18 0.000000 1.000000 1.000000 0.000000 0.000000
27 19 0.000000 1.000000 1.000000 0.000000 0.000000
28'. 20 0.000000 1.000000 1.000000 0.000000 0.000000
Рис. 5.6. Биномиальное распределение и его аппроксимация с помощью распределения Пуассона
Изучение основ
5.38. В каких ситуациях для аппроксимации биномиального распределения следует применять распределение Пуассона?
5.39. Чему равны математическое ожидание и дисперсия распределения Пуассона, использованного для аппроксимации биномиального распределения, при заданных параметрах пар!
5.40. Вычислите биномиальные вероятности, перечисленные ниже, используя распределение Пуассона при п = 100 и р = 0,01.
1. Р(Х = 0).
2. Р(Х=1).
3. Р(Х = 2).
4. Р(Х<2).
5. Р(Х>2).
5.41. Вычислите биномиальные вероятности, перечисленные ниже, используя распределение Пуассона при п = 50 ир = 0,004.
1. Р(Х = 0).
2. Р(Х=1).
3. Р(Х==2).
4. Р(Х<2).
5. Р(Х>2).
Применение понятий
5.42. Опыт показывает, что 1% счетов за телефонные переговоры, посланных домовладельцам, оказываются неверными. Вычислите вероятность того, что в выборке, состоящей из 20 счетов, по крайней мере один счет окажется неверным.
5.43. Компания, производящая компьютеры, осуществляет выборочный контроль поступающих микросхем. Получив крупную партию, компания случайным образом выбирает 800 микросхем. Если в выборке обнаруживается не более трех бракованных микросхем, остальные микросхемы не проверяются, и партия принимается. Если в выборке обнаруживается больше трех бракованных микросхем, каждая из оставшихся микросхем проверяется самым тщательным образом. Предположим, что истинная доля бракованных микросхем в поступившей партии равна 0,001. Какова вероятность, что партия будет принята?
5.44. В течение последнего месяца некая компания продала 10 000 новых наручных часов. Как подсказывает опыт, вероятность того, что в течение гарантийного срока новым часам потребуется ремонт, равна 0,002. Вычислите вероятности следующих событий.
1. В течение гарантийного срока ремонт не понадобится ни одним часам.
2. В течение гарантийного срока ремонт понадобится не более чем 5 часам.
3. В течение гарантийного срока ремонт понадобится не более чем 10 часам.
4. В течение гарантийного срока ремонт понадобится не более чем 20 часам.
Дискретные распределения вероятностей
Математическое
Дисперсия
Ковариация
Фиксировано ли количество наблюдений л, . Нет Распределение представляющих > . Пуассона
собой успех или
неудачу? _
Да
Биномиальное : распределение
Да
Является ли вероятность успеха постоянной величиной для всех испытаний?
Нет
Гипергеометрическое распределение
Структурная схема главы 5
РЕЗЮМЕ
В главе описаны математическое ожидание, ковариация и ее применение. Кроме того, рассмотрены основные свойства широко распространенных дискретных распределений — биномиального, гипергеометрического и пуассоновского. В сценарии, описывающем функционирование автоматизированной бухгалтерской системы в компании Saxon Home Improvements Company, продемонстрировано практическое применение биномиального распределения. В следующей главе мы перейдем к изучению непрерывных распределений и, в частности, рассмотрим весьма важное нормальное распределение.
ОСНОВНЫЕ понятия
Дисперсия
дискретной случайной величины, 296
суммы двух случайных величин, 301
Ковариация, 300
Математическое ожидание
дискретной случайной величины, 295
суммы двух случайных величин, 301
Портфельные инвестиции, 302
ожидаемая доходность, 302
риск, 302
Пуассоновский процесс, 320
Распределение
биномиальное, 307
гипергеометрическое, 316
дискретное, 294
Пуассона, 320
Сочетания, 308
Стандартное отклонение
дискретной случайной величины, 296
суммы двух случайных величин, 301
Изучение основ
5.45. Сформулируйте определение математического ожидания случайной величины.
5.46. Перечислите свойства биномиального распределения.
5.47. Перечислите свойства распределения Пуассона. Чем они отличаются от свойств биномиального распределения?
5.48. При каких условиях вместо биномиального распределения можно использовать гипергеометрическое?
5.49. Как оценить риск портфельных инвестиций с помощью ковариации?
Применение понятий
5.50. Страхование событий позволяет организаторам спортивных и развлекательных мероприятий защищать себя от финансовых потерь в случае непредвиденных обстоятельств, в частности, землетрясения. Например, каждую весну в Цинциннати проводится городской праздник. Весна в Цинциннати, как правило, дождлива, и вероятность того, что за выходные дни выпадет более 4 дюймов осадков, равна 0,25. В газете Cincinnati Enquirer (Knippenberg, J., “Chicken Pox Means 3 Dog Night Remedy”, Cincinnati Enquirer, May 28, 1997, p. El) были опубликованы детали страхового полиса, заключенного городским советом. В частности, городской совет получит страховку на сумму 100 000 долл., если за время фестиваля выпадет более дюйма осадков. Стоимость страхового полиса равна 6 500 долл.
1. Считаете ли вы правильной указанную сумму страхового полиса? (Подсказка: вычислите ожидаемую прибыль страховой компании.)
2. Допустим, что сумма страхового полиса вычислена правильно. Выгодна ли эта сделка городскому совету?
5.51. Телефонный звонок, обрабатываемый автоматической системой, стоит компаниям в среднем 0,45 долл. В то же время, затраты на телефонный звонок, переадресованный живому оператору, в среднем равны 5,50 долл. Однако большое количество клиентов не желают общаться с автоответчиками и бросают трубку, услышав “Для связи с торговым представителем нажмите кнопку 0”. Согласно данным Центра по удерживанию клиентов (Center for Client Retention) 40% всех клиентов, позвонивших в автоматическую службу ответов, желают при малейшей возможности связаться с живым оператором (Jane Spencer, “In Search of the Operator”, Wall Street Journal, May 8, 2002, DI).
Предположим, что с автоматической системой ответов независимо друг от друга связались 10 абонентов. Вычислите следующие вероятности.
1. Никто из них не пожелает автоматически связаться с живым оператором.
2. Только один из них пожелает автоматически связаться с живым оператором.
3. Только два из них пожелают автоматически связаться с живым оператором.
4. Не более двух из них пожелают автоматически связаться с живым оператором.
5. Все десять пожелают автоматически связаться с живым оператором.
6. Считаете ли вы, что число 40%, указанное в статье, относится к рассматриваемой автоматической системе ответов, если все 10 клиентов пожелали автоматически связаться с живым оператором?
5.52. Компании, выпускающие кредитные карточки, увеличивают свои доходы, поднимая платеж, взыскиваемый с заемщика за опоздание при перечислении средств на погашение ссуды. По данным компании CardWeb.com этот платеж является третьим и последним средством, с помощью которого компании могут извлечь прибыль. Первыми двумя являются процентные платежи и оплата, поступающая от торговых компаний, принимающих кредитные карточки. Более того, за последний год 58% всех клиентов, пользующихся кредитными карточками, платили пеню за опоздание (Ron Lieber, “Credit-Card Firms Collect Record Levels of Late Fees”, Wall Street Journal, May 21, 2002, DI).
Предположим, что мы сформировали случайную выборку, состоящую из 20 клиентов, пользующихся кредитными карточками.
1. Никто из них не платил пеню за опоздание.
2. Не более пяти клиентов платили пеню за опоздание.
3. Не более десяти клиентов платили пеню за опоздание.
4. Более пяти клиентов платили пеню за опоздание.
5. Какие предположения должны выполняться при решении задач 1-4?
5.53. Почтовая служба Priority Mail является альтернативой коммерческой экспресс-почте США наподобие Federal Express. Статья, опубликованная в журнале The Wall Street, содержит несколько интересных сведений о результатах сравнения скорости доставки корреспонденции с меткой Priority Mail и наиболее дешевых заказных бандеролей первого класса, предназначенных для доставки в течение трех дней (Rick Brooks, “New Data Reveal ‘Priority Mail’ Is Slower Than a Stamp”, Wall Street Journal, May 29, 2002, DI). Сравнение показало, что заказные бандероли доставлялись с опозданием в 19% случаев, а отправления с меткой Priority Mail — в 33% случаев. Обратите внимание на то, что в момент опубликования статьи отправка заказной корреспонденции стоила как минимум 0,34 долл., в то время как отправление с меткой Priority Mail стоило не менее 3,50 долл.
Предположим, что 10 заказных бандеролей первого класса в течение трех дней должны быть доставлены в 10 разных адресов.
1. Какова вероятность, что все бандероли будут доставлены в течение трех дней?
2. Какова вероятность, что только одна бандероль будет доставлена с опозданием?
3. Какова вероятность, что не менее двух бандеролей будут доставлены с опозданием?
4. Чему равны математическое ожидание и стандартное отклонение распределения анализируемой случайной величины?
5. Повторите решение задач 1-4 для отправлений с меткой Priority Mail.
5.54. Реклама кино постоянно увеличивается. Обычно она длится от 60 до 90 с. Становясь все более длинной и экстравагантной реклама стремится охватить все более широкие слои населения. Неудивительно, что запоминаемость кинорекламы превышает запоминаемость телевизионной рекламы. По данным опроса, проведенного подразделением ComQUEST компании ВВМ Bureau of Mesurement в Торонто, вероятность, что зритель запомнит кинорекламу, равна 0,74, в то время как вероятность, что телезритель запомнит 30-секундную рекламу, равна 0,37 (Hate Hendley, “Cinema Advertizing Comes of Age”, Marketing Magazine, May 6, 2002,16).
1. Можно ли назвать величину 0,74, указанную компанией ВВМ Bureau of Mesurement, априорной классической, эмпирической или субъективной вероятностью?
2. Предположим, что мы выбрали 10 случайных кинозрителей. Рассмотрим случайную переменную, характеризующую количество зрителей, запомнивших рекламу. Какие предположения должны выполняться для того, чтобы эта случайная величина имела биномиальное распределение?
3. Предположим, что количество кинозрителей, запомнивших рекламу, имеет биномиальное распределение. Чему равно математическое ожидание и стандартное отклонение этого распределения?
4. Предположим, что в задаче 3 ни один кинозритель не запомнил рекламы. Какой вывод можно сделать о числе 0,74, приведенном в статье?
Допустим, что выборка содержит 10 зрителей. Вычислите вероятность следующих событий.
5. Ни один зритель не запомнит рекламу.
6. Рекламу запомнит только один зритель.
7. Рекламу запомнят только два зрителя.
8. Все десять зрителей запомнят рекламу.
9. Рекламу запомнят больше половины зрителей.
10. Рекламу запомнят не менее восьми зрителей.
11. Повторите решения задач 5-10 для телевизионной рекламы, считая, что вероятность запомнить телерекламу равна 0,37.
5.55. Исследование, проведенное компанией Council for Marketing and Opinion Research (CMOR), базирующейся в Цинциннати, показало, что 1 628 взрослых граждан США из 3 700 опрошенных отказываются участвовать в телефонных опросах (Steve Jarvis, “CMOR Finds Survey Refusal Rate Still Rising”, Marketing News, February 4, 2002, 4). Предположим, что выборка состоит из 10 случайно отобранных взрослых граждан США, которым предложили принять участие в телефонном опросе. Вычислите вероятности следующих событий, используя данные компании CMOR.
1. От участия в телефонном опросе откажутся все десять человек.
2. От участия в телефонном опросе откажутся пять человек.
3. От участия в телефонном опросе откажутся не меньше пяти человек.
4. От участия в телефонном опросе откажутся менее пяти человек.
5. Менее пяти человек согласятся принять участие в телефонном опросе.
6. Чему равно ожидаемое количество людей, отказывающихся принимать участие в телефонных опросах? В чем заключается практическое значение этой величины?
5.56. Для электронной коммерции недостаточно, чтобы клиент просто посетил Web-страницу. Необходимо еще убедить его потратить деньги на покупку. Эксперты компании Andersen Consulting считают, что 88% покупателей в Интернет отказались от оплаты своих корзинок товаров и не завершили транзакцию (Rebecca Quick, “The Lesson Learned”, Wall Street Journal, April 17, 2000, p. R6). Рассмотрим выборку, состоящую из 20 покупателей, посетивших Web-страницу электронного магазина. Будем считать, что вероятность отказа от оплаты в последний момент равна 0,88, а их количество распределено по биномиальному закону. 1. Чему равно математическое ожидание данного биномиального распределения? 2. Чему равно стандартное отклонение данного биномиального распределения?
3. Какова вероятность того, что все 20 клиентов откажутся от завершения транзакции?
4. Какова вероятность того, что не менее 18 клиентов откажутся от завершения транзакции?
5. Какова вероятность того, что не менее 15 клиентов откажутся от завершения транзакции?
6. Допустим, Web-страница настолько хороша, что только 70% клиентов отказываются от завершения транзакции. Как изменятся ответы на вопросы 1-5?
5.57. Для того чтобы измерить аудиторию радиослушателей, компания Arbitron рассылает анкеты случайно выбранным домовладельцам на 283 рынках США. Респондентам раздают дневники и просят указывать радиостанции, которые они прослушивают. Как только дневник заполнен, респонденты возвращают его в компанию Arbitron и получают вознаграждение за свое участие (как правило, 10 долл.). В статье указывается, что в 2002 году респонденты вернули рекордно низкое за последние 20 лет количество дневников— всего 32,6% (К. Bachman, “Consumers: Respond, S.V.P.”, Mediaweek, January 6, 2003, 5). Допустим, что на конкретном рынке случайно отобраны 100 респондентов.
1. Какие предположения должны выполняться для того, чтобы количество возвращенных дневников являлось случайной величиной, имеющей биномиальное распределение?
2. Чему равно математическое ожидание данного биномиального распределения?
3. Чему равно стандартное отклонение данного биномиального распределения? 4. Чему равна вероятность того, что респонденты вернут не более 30 дневников? 5. Чему равна вероятность того, что респонденты вернут не более 25 дневников? 6. Чему равна вероятность того, что респонденты вернут больше 40 дневников? 7. Чему равна вероятность того, что респонденты вернут от 30 до 35 дневников? 8. Предположим, что компания Arbitron увеличит оплату респондентам так, что уровень ответов возрастет до 40% . Как изменятся ответы на вопросы 1-7?
Примечание: для решения задач 4-8 примените программу Microsoft Excel.
5.58. Многие люди прослушивают образцы музыкальной продукции, загружая ее через Интернет. Покупают ли они после этого компакт-диски? Маркетинговое исследование, проведенное компанией Yankelovich Partners, показало, что 66% всех потребителей, слушавших песни в Интернет, купили по крайней мере один компакт-диск (Mathews, A. W., “Music Samplers on Web Buy CDs in Stores”, The Wall Street Journal, June 15, 2000, p. АЗ). Рассмотрим случайную выборку, состоящую из 20 пользователей Интернет, прослушавших некую песню. Допустим, что количество клиентов, купивших компакт-диск после прослушивания в Интернет, распределено по биномиальному закону.
1. Чему равно ожидаемое количество потребителей, слушавших песни в Интернет и купивших после этого по крайней мере один компакт-диск?
2. Чему равно стандартное отклонение количества потребителей, слушавших песни в Интернет и купивших после этого по крайней мере один компакт-диск?
3. Какова вероятность того, что не меньше 15 пользователей, слушавших песни в Интернет, купят после этого по крайней мере один компакт-диск?
4. Какова вероятность того, что не меньше 10 пользователей, слушавших песни в Интернет, купят после этого по крайней мере один компакт-диск?
5.59. С 1872 по 2000 гг. стоимость акций за год возрастала в 74% случаев (Mark Hulbert, “The Stock Market Must Rise in 2002? Think Again”, The New York Times, December 6, 2001, Business, 6). Используя эту информацию и предполагая, что случайная величина имеет биномиальное распределение, определите вероятность следующих событий.
1. Стоимость акций увеличится в следующем году.
2. Стоимость акций увеличится через два года.
3. Стоимость акций будет увеличиваться четыре года из следующих пяти.
4. Стоимость акций не будет расти в течение пяти лет.
5. Какие условия в рассматриваемой задаче не позволяют считать случайную величину биномиальной?
5.60. Ложной корреляцией называется кажущаяся зависимость между переменными, которые на самом деле зависимыми не являются, или мнимая зависимость между переменными, которая не может быть измерена. Например, ярким примером ложной корреляции является зависимость между победителем Национальной лиги по американскому футболу и индексом Доу-Джонса. Этот индикатор показывает, что если в чемпионате победит команда из Национальной футбольной конференции, то индекс Доу-Джонса в этом году вырастет. Если же чемпионом станет команда из Американской футбольной конференции, то индекс Доу-Джонса упадет. На протяжении 36-летнего периода с 1967 по 2002 гг. этот индикатор давал правильные ответы в 30 случаях из 36. Если предположить, что этот индикатор является случайной величиной, можно ожидать, что в половине случаев он будет давать правильные прогнозы.
1. Используя программу Microsoft Excel, вычислите вероятность того, что этот индикатор дает правильный прогноз в 30 и более случаях из 36.
2. Что можно сказать о полезности этого индикатора?
5.61. Лотерея Mega Millions является одной из самых популярных игр в США. В этой лотерее принимают участие штаты Джорджия, Иллинойс, Мэриленд, Массачусетс, Нью-Джерси, Огайо и Вирджиния. Правила этой лотереи приведены ниже (“Win Megamoney Playing Ohio’s Biggest Jackpot Game”, Ohio Lottery Headquarters, 2002).
Правила.
• Выберите пять чисел и дополнительное число Mega Ball в диапазоне от 1 до 52.
• Каждая ставка равна 1 долл.
Призы.
• Если с выигрышными номерами совпали все выбранные пять чисел и число Mega Ball, вы получаете джекпот (как минимум, 10 000 000 долл.).
• Если с выигрышными номерами совпали только пять выбранных чисел, выигрыш составляет 175 000 долл.
• Если с выигрышными номерами совпали только четыре выбранных числа и число Mega Ball, выигрыш составляет 5 000 долл.
• Если с выигрышными номерами совпали только четыре выбранных числа, выигрыш составляет 150 долл.
• Если с выигрышными номерами совпали только три выбранных числа и номер Mega Ball, выигрыш составляет 150 долл.
• Если с выигрышными номерами совпали только два выбранных числа и номер Mega Ball, выигрыш составляет 10 долл.
• Если с выигрышными номерами совпали только три выбранных числа, выигрыш составляет 7 долл.
• Если с выигрышными номерами совпали только одно выбранное число и номер Mega Ball, выигрыш составляет 3 долл.
• Если с выигрышными номерами совпал только номер Mega Ball, выигрыш составляет 2 долл.
Вычислите вероятности следующих событий.
1. Джекпот.
2. Выигрыш 175 000 долл. (Для этого необходимо, чтобы выигрышными были пять выбранных номеров, а номер Mega Ball не учитывается.)
3. Выигрыш 5 000 долл.
4. Выигрыш 150 долл.
5. Выигрыш 10 долл.
6. Выигрыш 7 долл.
7. Выигрыш 3 долл.
8. Выигрыш 2 долл.
9. Проигрыш.
10. Во всех буклетах, распространяемых вместе с лотерейными билетами, указываются вероятности выигрышей, но не вероятность проигрыша. В штате Огайо лотерея проводится под девизом “Играйте ответственно. Чудеса случаются— вы будете довольны”. Считаете ли вы девиз и информацию, распространяемую в буклетах, этичными?
5.62. Объем продажи мячей для гольфа в мире в 2000 году достиг 1,3 млрд. долл. Одне из причин такого большого количества проданных мячей заключается в том, чтс во время обхода 18 лунок игроки в среднем теряют 4,5 мяча (James Р. Sterbe “Does Your Golf Ball Beep, Tick, Perform Some Special Trick?”, Wall Street Journal, June 15, 2000, p. Al). Допустим, что количество мячей для гольфа, по терянных во время игры, распределено по закону Пуассона.
1. Какие условия должны выполняться, чтобы количество мячей для гольфа, потерянных во время игры, было распределено по закону Пуассона?
2. Какова вероятность того, что во время игры ни один мяч не будет потерян?
3. Какова вероятность того, что во время игры будет потерян только один мяч?
4. Какова вероятность того, что во время игры будут потеряны два мяча?
5. Какова вероятность того, что во время игры будут потеряны три мяча?
6. Какова вероятность того, что во время игры будут потеряны четыре мяча?
7. Какова вероятность того, что во время игры будут потеряны пять мячей?
8. Какова вероятность того, что во время игры будут потеряны не более пяти мячей?
9. Какова вероятность того, что во время игры будут потеряны не менее шести мячей?
5.63. Исследование Web-страниц компаний, входящих в список Fortune 500, показало, что среднее количество недействительных ссылок на одной странице равно 0,4, переднее количество грамматических ошибок равно 0,16 (Nabil Tamimi, Murii Rajan and Rose Sebastianella, “Benchmarking the Home Pages of ‘Fortune’ 500 Companies”, Quality Progress, July, 2000). Будем считать, что эти величины распределены по закону Пуассона.
1. Какова вероятность того, что на Web-странице нет ни одной недействительной ссылки?
2. Какова вероятность того, что на Web-странице есть одна недействительная ссылка?
3. Какова вероятность того, что на Web-странице есть не менее двух недействительных ссылок?
4. Какова вероятность того, что на Web-странице содержится не менее пяти недействительных ссылок?
5. Какова вероятность того, что на Web-странице нет ни одной грамматической ошибки?
6. Какова вероятность того, что на Web-странице есть одна грамматическая ошибка?
7. Какова вероятность того, что Web-страница содержит не менее двух грамматических ошибок?
8. Какова вероятность того, что Web-страница содержит не менее десяти грамматических ошибок?
Применение Интернет
5.64. Зайдите на сайт www. prenhall. com/levine. Выберите ссылку Chapter 5 и щелкните на кнопке Internet exercises.
РАЗБОР КОНКРЕТНОЙ СИТУАЦИИ-ГАЗЕТА SPRINGVILLE HERALD -
Отдел маркетинга газеты Springville Herald разрабатывает новую стратегию, направленную на увеличение количества подписчиков. Для этого он планирует агрессивную рекламную кампанию, включающую в себя бесплатную рассылку корреспонденции, купоны подписки со скидкой и телефонные уговоры. Одним из важных моментов, влияющих на количество подписчиков, является время утренней доставки газеты.
После нескольких рабочих совещаний команда менеджеров решила, что необходимо добиться гарантированной доставки газеты в установленное время. Опросив потенциальных подписчиков, администрация решила, что газету следует доставлять в 7 часов утра. Кроме того, если номер газеты доставлен несвоевременно, подписчик может за него не платить.
Теперь необходимо выяснить, какой процент подписчиков согласен на такие условия. Ал Лесли (Al Leslie), руководитель исследовательской группы, предложил оценить своевременность доставки газеты, используя данные, которыми владеет отдел доставки. Ян Шапиро (Jan Shapiro) напомнил, что подписчиков попросили указать, в какое время они хотели бы получать газету. Эти данные помещены на Web-страницу газеты (см. страницу Circulation_Data.htm в каталоге HeraldCase, расположенном на компакт-диске, или зайдите на Web-сайт www .prenhall. com/HeraldCase/Circulation_data . htm).
УПРАЖНЕНИЯ
Изучите данные и предложите разумное время доставки (с точностью до 15 минут).
SH.5.1.B течение дня наугад выбираются 50 подписчиков. Определите вероятность следующих событий.
1. Бесплатный номер получат не более трех подписчиков.
2. Бесплатный номер получат от двух до четырех подписчиков.
3. Бесплатный номер получат не менее пяти подписчиков.
SH.5.2. Предположим, количество подписчиков, получающих газету не вовремя, удалось сократить до 2% . В течение дня наугад выбираются 50 подписчиков. Определите вероятность следующих событий.
1. Бесплатный номер получат не более трех подписчиков.
2. Бесплатный номер получат от двух до четырех подписчиков.
3. Бесплатный номер получат не менее пяти подписчиков.
ПРИМЕНЕНИЕ WEB
Используйте свои знания о ковариации и ее применении в финансовом деле для того, чтобы оценить обоснованность прогнозов и заявлений компании StockTout Bulls and Bears.
Посетите Web-сайт компании StockTout Bulls and Bears (www.prenhall.com/ Springville/ST_BullsandBears .htm). Проанализируйте рекламные заявления и сопровождающие их данные, а затем ответьте на следующие вопросы.
1. Правильную ли информацию предоставляют фонды Happy Bull и Worried Bear?
2. Какие субъективные данные влияют на анализ доходности фондов? Можно ли обвинить компанию StockTout в обмане?
3. Данные свидетельствуют о том, что доходность фонда Worried Bear превышает доходность фонда Happy Bull. Означает ли это, что приобретать акции фонда Happy Bull не следует?
4. Какой инвестиционной стратегии следует придерживаться, если вы хотите минимизировать риск?
СПРАВОЧНИК ПО EXCEL ГЛАВА 5
ЕН.5.1. Вычисление ожидаемой доходности и риска портфельных инвестиций
Создадим рабочий лист, использующий для вычисления ожидаемой доходности ириска портфельных инвестиций функцию СУММПРОИЗВ. Вызов этой функции имеет следующий вид:
СУММПРОИЗВ(лшоэ/штель; множимое)
Здесь параметр множитель представляет собой диапазон ячеек, содержащий вероятности, а параметр множимое — диапазон ячеек, содержащий значения случайной величины.
Например, в табл. ЕН.5.1 и ЕН.5.2 продемонстрирован рабочий лист Портфельные_ инвестиции, соответствующий данным, приведенным в табл. 5.2. Введите в ячейку В25 формулу, не разрывая строку, а строки от 1 до 9 в столбцах от Е до I оставьте пустыми.
Таблица ЕН.5.1. Фрагмент рабочего листа Портфельные_инвестиции (столбцы A—D)
А В С D
1 Анализ доходности инвестиций
2
3 Вероятности и прибыль Р X Y
4 0,2 -100 200
5 0,5 100 50
6 0,3 250 -100
7
8 Вес, приписанный значениям X 0,5
9
10 Статистические показатели
11 Е(Х) =СУММПРОИЗВ(В4:В6;С4:С6)
12 E(Y) = СУММПРОИЗВ(В4:В6;04:06)
13 Дисперсия (X) = СУММПРОИЗВ(В4:В6;С13:С15)
14 Стандартное отклонение (X) =К0РЕНЬ(В13)
ЗЙ Дисперсия (Y) =СУММПРОИЗВ(В4:В6;Н13:Н15)
16 Стандартное отклонение (Y) =К0РЕНЬ(В15)
17 Ковариация(ХУ) = СУММПРОИЗВ(В4:В6;113:115)
18 Дисперсия(Х+У) =В13+В15+2*В17
19 Стандартное отклонение(Х+У) =К0РЕНЬ(В18)
20
21 Управление портфельными инвестициями
22 Вес, приписанный значениям X =В8
23 Вес, приписанный значениям Y =1-В22
24 Ожидаемая доходность портфеля =В22* В11 + В23 * В12
25 Риск портфельных инвестиций =КОРЕНЬ(В22Л2*В13+В23Л2*В15+2*В22*В23*В17)
Таблица ЕН.5.2. Фрагмент рабочего листа Портфельные_инвестиции (ячейки
ЕЮ: 115 заполнены, остальные ячейки в столбцах от Е до I — пусты)
Е F 6 Н ' ' \ 1
10 Область вычислений
11 Для дисперсии и стандартного отклонения: Для ковариации:
1111 X-mu Y-mu (X-mu)A2 (Y-mu)A2 (X-mu)(Y-mu)
13 =С4-$В$11 =D4-$B$12 = Е13Л2 = F13A2 =E13*F13
14 =С5-$В$11 =D5-$B$12 =Е14Л2 =F14A2 =F14*F14
15 =Сб-$В$11 =D6-$B$12 =Е15Л2 =F15A2 =E15*F15
Этот рабочий лист можно адаптировать для вычисления вероятностей, зависящих от нескольких условий.
Если в задаче всего два условия, следует открыть таблицу и выполнить следующие действия.
1. Выделить диапазон Е15 :115, а затем выбрать команду Правка^Удалить....
2. Выделить строку 5 (щелкнуть на метке 5, находящейся на левой границе рабочего листа).
3. Выполнить команду Правка ^Удалить....
Если в задаче сформулировано больше трех условий, следует открыть таблицу и выполнить следующие действия.
1. Выделить строку 5 (щелкнуть на метке 5, находящейся на левой границе рабочего листа).
2. Выбрать команду Правка^Вставить столько раз, сколько необходимо для вычисления вероятности дополнительных возможностей.
3. Выделить диапазон Е15 :115 и скопировать его в дополнительные строки рабочего листа, расположенные ниже. (Например, если в задаче есть две дополнительные возможности, содержимое диапазона следует скопировать в строки 16 и 17.)
ЕН.5.2. Вычисление биномиальных вероятностей
Создадим рабочий лист, использующий для вычисления биномиального распределения функцию БИНОМРАСП.-Вызов этой функции имеет следующий вид:
БИНОМРАСП(Х; n; р\ cumulative)
Здесь параметр X — количество успехов, п — объем выборки, р — вероятность успеха, cumulative — величина, принимающая значение ИСТИНА или ЛОЖЬ (в первом случае вычисляется вероятность не менее X событий, а во втором — вероятность точно X событий).
Например, в табл. ЕН.5.3 и ЕН.5.4 продемонстрирован рабочий лист Биномиальное_ распределение, соответствующий данным, приведенным на рис. 5.2. При реализации этого шаблона в ячейки А5 и А10 необходимо ввести метки, а формулы в ячейках С14 : D18 набирать, не разрывая строки. (В табл. ЕН.5.4 эти формулы разбиты на несколько строк.) Для того чтобы вычислить вероятности, сначала введите формулы в ячейки С14 : G14, а затем скопируйте их в ячейки, расположенные ниже, вплоть до строки 18. (Ячейки Cl: Gl 1 должны оставаться пустыми, поэтому в таблице не приводятся.)
Таблица ЕН.5.3. Фрагмент рабочего листа Биномиальное_распределение (ячейки А1-В10)
А
1 Биномиальные вероятности
шяш
Данные
4 Объем выборки 4
5 Вероятность успеха 0,1
jiiiiiiiiiii
Статистики
8 Математическое ожидание =В4*В5
9 Дисперсия =В8*(1-В5)
10 Стандартное отклонение = К0РЕНЬ(В9)
Таблица ЕН.5.4. Фрагмент рабочего листа Биномиальные_вероятности (ячейки A12-G18)
А в iiliilM Е F G
12 Таблица биномиальных вероятностей
13 X Р(Х) Р«=Х) Р«Х) pox) po=x)
14 0 = БИНОМРАСП (В14;$В$4; $В$5; ЛОЖЬ) - БИНОМРАСП (В14;$В$4; $В$5, ИСТИНА) =D14-C14 =1-D14 =1-E14
15 1 =БИНОМРАСП (В15;$В$4; $В$5; ЛОЖЬ) = БИНОМРАСП (В15;$В$4; $В$5; ИСТИНА) =D15-C15 =1-D15 =1-E15
16 2 = БИНОМРАСП (В16;$В$4; $В$5; ЛОЖЬ) =БИНОМРАСП (В16;$В$4; $В$5; ИСТИНА) =D16-C16 =1-D16 =1-E16
17 3 = БИНОМРАСП (В17;$В$4; $В$5; ЛОЖЬ) =БИНОМРАСП (В17;$В$4; $В$Б; ИСТИНА) =D17-CI7 =1-D17 =1-E17
18 4 ^БИНОМРАСП (В18;$В$4; $В$5; ЛОЖЬ) =БИНОМРАСП (В18;$В$4; $В$5, ИСТИНА) = D18-C18 =1-D18 =1-E18
Этот рабочий лист можно адаптировать для вычисления биномиальных вероятностей при других объемах выборок. Для этого необходимо скопировать формулы в дополнительные строки или удалить строки начиная с 18-й, если объем выборки меньше 4.
ЕН.5.3. Вычисление гипергеометрического распределения
Создадим рабочий лист, использующий для вычисления гипергеометрического распределения функцию ГИПЕРГЕОМЕТ. Вызов этой функции имеет следующий вид:
ГИПЕРГЕОМЕТ(Х; п; A; N)
Здесь параметр X — количество успехов, п — объем выборки, А — количество успехов в генеральной совокупности, N — объем генеральной совокупности.
Например, в табл. ЕН.5.5 продемонстрирован рабочий лист Гипергеометрическое_ распределение, соответствующий данным, приведенным на рис. 5.4. Для того чтобы вычислить вероятности, сначала введите формулу в ячейку СЮ, а затем скопируйте ее в ячейки, расположенные ниже, вплоть до строки 18. (Строки С12:С16 в таблице не приводятся.)
Таблица ЕН.5.5. Рабочий лист Гипергеометрическое_распределение
А В С
1 Гипергеометрические вероятности
2
3 Данные
4 Объем выборки 8
5 Количество успехов в генеральной совокупности 10
6 Объем генеральной совокупности 30
7
8 Таблица гипергеометрических таблиц
9 X Р(Х)
10 0 =ГИПЕРГЕОМЕТ(ВЮ;$В$4;$В$5;$В$б)
11 1 =ТИПЕРГЕОМЕТ(В11;$В$4;$В$5;$В$6)
...
17 7 =ГИПЕРГЕОМЕТ(В17;$В$4;$В$5;$В$6)
18 8 =ГИПЕРГЕОМЕТ(В18;$В$4;$В$5;$В$6)
Этот рабочий лист можно адаптировать для вычисления гипергеометрического распределения при другом количестве успехов. Для этого необходимо вставить в таблицу новые строки и скопировать в них содержимое строки 18, либо, наоборот, удалить ненужные строки.
ЕН.5.4. Вычисление распределения Пуассона
Создадим рабочий лист, использующий для вычисления распределения Пуассона функцию ПУАССОН. Вызов этой функции имеет следующий вид:
ПУАССОН(Х; lambda:, cumulative)
Здесь параметр X — количество успехов, lambda — ожидаемое количество успехов, cumulative — величина, принимающая значение ИСТИНА или ЛОЖЬ (в первом случае вычисляется вероятность не менее X событий, а во втором — вероятность точно X событий).
Например, в табл. ЕН.5.6 продемонстрирован рабочий лист Распределение_Пуассона, соответствующий данным, приведенным на рис. 5.5. Для того чтобы вычислить вероятности, сначала введите формулы в столбцы С и D, используя как относительные, так и абсолютные ссылки, как показано в таблице. (Хотя эти формулы занимают несколько строк, в реальном листе их нельзя разрывать.) Затем введите формулы в ячейки С8 : G8 и скопируйте их в ячейки, расположенные ниже, вплоть до строки 2 3. (Строки от 10 до 21 в табл. ЕН.5.6 не приводятся.)
Таблица ЕН.5.6. Рабочий лист Распределение_Пуассона
А В £ \
1 Пуассоновские вероятности
2
3 Данные
4 Среднее/ожидаемое количество успехов 3
5
ill Таблица пуассоновских вероятностей
7 X Р(Х) Р«=Х) Р«Х) POX) PO=X)
8 > 0 ^ПУАССОН (В8;$Е$4; ЛОЖЬ) = ПУАССОН (В8;$Е$4; ИСТИНА) =D8-C8 =1-D8 =1-E8
9 1 =ПУАССОН (В9;$Е$4; ЛОЖЬ) = ПУАССОН (В9;$Е$4; ИСТИНА) =D9-C9 =1-D9 =1-E9
•м
22 14 = ПУАССОН (В22;$Е$4; ЛОЖЬ) = ПУАССОН (В22;$Е$4; ИСТИНА) =D22-C22 =1-D22 =1-E22
23 15 = ПУАССОН (В23,$Е$4; ЛОЖЬ) =ПУАССОН (В23;$Е$4; ИСТИНА) =D23-C23 =1-D23 =1-E23
Обратите внимание на то, что в данном примере количество успехов произвольно ограничено числом 15, а среднее количество успехов равно 3. Этот рабочий лист можно адаптировать для вычисления распределения Пуассона для другого количества успехов. Для этого достаточно скопировать содержимое строки 23 в дополнительные строки таблицы или удалить лишние строки. (Внешний вид таблицы можно изменить, управляя форматом чисел, как показано во врезке ЕР.5)
ЕН.5.5. Построение гистограмм для дискретных распределений
Чтобы создать гистограмму для дискретного распределения, следует применить Мастер диаграмм к каждому из приведенных выше рабочих листов Биномиальное_распределение, Гипергеометрическое_распределение и Биномиальное_распределение. Откройте соответствующий рабочий лист, выполните команду ВставкаФДиаграмма... и следуйте инструкциям, приведенным ниже.
1. На первом этапе диалога сделайте следующее.
1.1. Щелкните на корешке закладки Стандартные и выберите в раскрывающемся списке пункт Гистограмма.
1.2. Выберите первый вариант гистограммы, описанный как “Обычная гистограмма отображает значения различных категорий”, и щелкните на кнопке Далее>.
2. На втором этапе диалога сделайте следующее.
2.1. Щелкните на корешке закладки Диапазон данных. Введите в окне редактирования Диапазон ссылки на ячейки, указанные в табл. ЕН.5.7 и установите переключатель Ряды в положение В столбцах.
2.2. Щелкните на корешке закладки Ряды. Введите в окно редактирования Подписи оси X соответствующую формулу из табл. ЕН.5.7. Обратите внимание на то, что формула должна иметь форму ИмяЛистаЩиапазонЯчеек.
2.3. Щелкните на кнопке Далее>.
3. На третьем этапе диалога сделайте следующее.
3.1. Щелкните на корешке закладки Заголовки. Введите в окне редактирования Название диаграммы строку Количество успехов (X) — в окне редактирования Ось X (категорий) и строку Р(х) — в окне редактирования Ось Y (значений).
3.2. Щелкните по очереди на корешках вкладок Оси, Линии сетки, Легенда, Подписи данных и Таблица данных и сделайте необходимые установки, руководствуясь указаниями, приведенными во врезке ЕР.6.
3.3. Щелкните на кнопке Далее>.
4. На четвертом этапе диалога сделайте следующее.
4.1. Установите переключатель Поместить диаграмму на листе в положение Отдельном и введите информативное и уникальное имя листа в соответствующем окне редактирования.
4.2. Щелкните на кнопке Готово.
Поскольку данное распределение является дискретным, столбцы гистограмм должны выглядеть, как пики. Для этого можно уменьшить ширину столбцов, выполнив следующие действия.
1. Щелкните правой кнопкой мыши на столбце гистограммы. (При правильном положении курсора мыши на экране появится надпись, начинающаяся словом “Ряд”.)
2. Выберите во всплывающем контекстном меню команду Формат рядов данных....
3. В диалоговом окне Формат ряда данных щелкните на корешке вкладки Параметры и введите в окне редактирования Ширина зазора число 500, а затем щелкните на кнопке ОК.
Таблица ЕН.5.7. Диапазоны и формулы, которые вводятся на втором этапе диалога при построении гистограмм для рабочих листов Биномиальноераспределение, Гипергеометрическое_распределение и Распределение_Пуассона
Рабочий лист Диапазон Формула в окне Ось X (категорий)
Биномиальноераспределение С4:С18 =Биномиал ьное_распредел ение!В 14: В18
Гипергеометрическое_распределение С10:С18 =Гипергеометрическое_распределение!В 10: В18
Распределение_Пуассона С8:С23 =Распределение_Пуассона!В8:В23
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
1. Bernstein, Р. L., Against the Gods: The Remarkable Story of Risk (New York: Wiley, 1996).
2. Emery, D. R., and J. D. Finnerty, Corporate Financial Management, 3nd ed. (Upper Saddle River, NJ: Prentice Hall, 2004).
3. Kirk, R. L., Statistical Issues: A Reader for the Behavioral Sciences (Belmont, CA: Wadsworth, 1972).
4. Levine, D. M., P. Ramsey, and R. Smidt, Applied Statistics for Engineers and Scientists using Microsoft Excel and Minitab (Upper Saddle River, NJ: Prentice Hall, 2001).
5. Mescove, S. A., M. G. Simkin, and A. Barganoff, Core Concepts of Accounting Information Systems, 7th ed. (New York: Wiley, 2001).
6. Microsoft Excel 2002 (Redmond, WA: Microsoft Corporation, 2001).
непрерывные распределения
ПРИМЕНЕНИЕ СТАТИСТИКИ: время загрузки Web-страницы
6.1. НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
Visual Explorations: исследование свойств нормального распределения
Процедуры Excel: вычисление нормальных вероятностей
6.2. ПРОВЕРКА ГИПОТЕЗЫ О
НОРМАЛЬНОМ РАСПРЕДЕЛЕНИИ
Оценка свойств
Построение графика нормального распре-
деления
Процедуры Excel: построение графиков нормального распределения
6.3. РАВНОМЕРНОЕ РАСПРЕДЕЛЕНИЕ
6.4. ЭКСПОНЕНЦИАЛЬНОЕ
РАСПРЕДЕЛЕНИЕ
Процедуры Excel: вычисление экспоненциальных вероятностей
ПРИМЕНЕНИЕ СТАТИСТИКИ: процесс расфасовки кукурузных хлопьев
6.5. ВВЕДЕНИЕ В ВЫБОРОЧНЫЕ РАСПРЕДЕЛЕНИЯ
6.6. ВЫБОРОЧНОЕ РАСПРЕДЕЛЕНИЕ СРЕДНИХ ЗНАЧЕНИЙ
Несмещенность среднего арифметического
Стандартная ошибка среднего
Выборки из нормально распределенных генеральных совокупностей
Выборки из генеральных совокупностей, распределения которых отличаются от нормального
Visual Explorations: исследование выборочных распределений
Распределения
Процедуры Excel: генерирование модельных выборочных распределений
6.7. ВЫБОРОЧНОЕ РАСПРЕДЕЛЕНИЕ ДОЛЕЙ
6.8. АППРОКСИМАЦИЯ
БИНОМИАЛЬНОГО И ПУАССОНОВСКОГО РАСПРЕДЕЛЕНИЙ С ПОМОЩЬЮ НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ
Поправка на непрерывность распределения Аппроксимация биномиального распределения
Аппроксимация распределения Пуассона
6.9. ВЫБОРКИ ИЗ КОНЕЧНЫХ ГЕНЕРАЛЬНЫХ СОВОКУПНОСТЕЙ
6.10. ПРИМЕНЕНИЕ СТАНДАРТИЗОВАННОГО НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ
Преобразование данных
Использование таблиц нормального распределения
Вычисление вероятностей, соответствующих заданным значениям
Вычисление значений, соответствующих заданным вероятностям
СПРАВОЧНИК ПО EXCEL. ГЛАВА б
ЧЕМУ ДОЛЖЕН НАУЧИТЬСЯ СТУДЕНТ
• Вычислять нормальные вероятности.
• Применять график нормального распределения для исследования выборки.
• Вычислять равномерные вероятности.
• Вычислять экспоненциальные вероятности.
• Знать свойства выборочных распределений.
• Вычислять вероятности, связанные с выборочным средним и выборочной долей признака.
ПРИМЕНЕНИЕ СТАТИСТИКИ
Время загрузки Web-страницы
Представьте себе, что вы разрабатываете Web-сайт для компании On Campus!, специализирующейся на электронной коммерции в студенческом городке. Компания стремится привлечь новых клиентов с помощью интересного Web-сайта, который должен очень быстро загружаться. Время загрузки зависит от конструкции Web-сайта и текущего трафика. Допустим, что для измерения скорости загрузки используется домашний персональный компьютер. Исследования показали, что среднее время загрузки равно 7 с, а его стандартное отклонение — 2 с. Приблизительно две трети измерений колеблются в диапазоне от 5 до 9 с, причем 95% всех измерений лежат в интервале от 3 до 11 с. Иначе говоря, распределение продолжительности загрузки можно изобразить с помощью колоколообразной кривой, а основная масса измерений лежит в окрестности 7 с. Как использовать эту информацию для ответа на следующие вопросы: “Как часто время загрузки превышает 10 с? В каком интервале колеблются 99% измерений? Как изменятся эти показатели, если иначе сконструировать Web-страницу?”.
ВВЕДЕНИЕ
Числовые случайные величины могут быть либо дискретными, либо непрерывными. Дискретные случайные величины (т.е. величины, возникающие в результате подсчета событий) рассмотрены в главе 5, а в этой главе мы изучим непрерывные случайные величины, которые возникают в результате измерений, результатом которых может являться любая величина, принадлежащая числовой оси или интервалу. Примером такой случайной величины может служить вес какой-нибудь коробки, время загрузки Web-страницы, расходы на рекламу, доходы от продажи, время обслуживания клиента и время между двумя приходами клиентов в банк.
Математическое выражение, описывающее распределение значений непрерывной случайной величины, называется плотностью непрерывного распределения вероятностей (continuous probability density function). На рис. 6.1 изображены графики трех плотностей непрерывных распределений, рассматриваемых в главе. На панели А представлена плотность нормального распределения. Эта функция является симметричной и колоколообразной. Следовательно, большинство значений такой случайной величины концентрируется вокруг математического ожидания, которое совпадает с медианой. Несмотря на то что нормально распределенная случайная величина может принимать любые числовые значения, вероятность очень больших положительных или отрицательных значений крайне мала. На панели Б изображена плотность равномерного распределения. Значения случайной величины, равномерно распределенной на интервале от а до &, равновероятны. Иногда это распределение называют прямоугольным. Оно является симметричным, и, следовательно, его математическое ожидание равно медиане. На панели В показана плотность экспоненциального распределения. Это распределение имеет ярко выраженную положительную асимметрию, и, следовательно, его математическое ожидание больше медианы. Экспоненциально распределенные случайные величины изменяются от нуля до плюс бесконечности, однако очень большие значения крайне мало вероятны.
Панель А
Нормальное распределение
Панель Б Панель В
Равномерное распределение Экспоненциальное распределение
Рис. 6.1. Три непрерывных распределения
6.1. НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
В этой главе описывается одно из наиболее важных распределений в статистике — нормальное распределение (normal distribution), которое иногда называют гауссовым (Gaussian distribution). Плотность этого распределения изображена на рис. 6.1. Можно вычислить вероятность того, что нормально распределенная случайная величина лежит в заданном интервале. Однако вероятность того, что она принимает наперед заданное значение, равна нулю. Это отличает непрерывные случайные величины (измеряемые) от дискретных (подсчитываемых). Например, время измеряется, а не подсчитывается. Следовательно, можно вычислить вероятность того, что Web-страница будет загружаться от 7 до 10 с. Сужая заданный интервал, можно вычислить вероятность того, что она будет загружаться от 8 до 9 с. Кроме того, можно вычислить вероятность того, что она будет загружаться от 8,99 до 9,01 с. Однако вероятность того, что Web-страница будет загружаться ровно 8 с, равна нулю.
Определение вероятностей или вычисление математического ожидания и стандартного отклонения непрерывной случайной величины требует знания интегрального исчисления и выходит за рамки нашей книги. Несмотря на это, нормальное распределение является настолько важным, что в приложении Д мы привели табл. Д.2, позволяющую избежать сложных математических вычислений. Важность нормального распределения в статистике обусловлена тремя причинами.
1. Оно описывает (точно или приблизительно) распределение многих непрерывных случайных величин.
2. С помощью нормального распределения можно аппроксимировать разнообразные дискретные распределения (см. раздел 6.8).
3. Нормальное распределение лежит в основе классической теории статистических выводов (classical statistical inference), поскольку оно тесно связано с центральной предельной теоремой (central limit theorem) (см. раздел 6.6).
Основные свойства нормального распределения перечислены во врезке 6.1.
ВРЕЗКА 6.1. СВОЙСТВА НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ
Нормальное распределение обладает четырьмя основными свойствами.
• Имеет колоколообразную (а значит, симметричную) форму.
• Его математическое ожидание, медиана и мода совпадают друг с другом.
• Основная масса нормально распределенных значений лежит в интервале, длина которого равна 4/3 стандартного отклонения. Это значит, что межквартильный
размах находится в интервале от 2/3 стандартного отклонения левее среднего значения до 2/3 стандартного отклонения правее среднего значения.
• Значения нормально распределенной случайной величины лежат на всей числовой оси (-оо < А < +оо )«
На практике многие случайные величины являются лишь приближенно нормальными. Иначе говоря, их свойства лишь аппроксимируют теоретические свойства нормального распределения, перечисленные во врезке 6.1. Рассмотрим в качестве примера табл. 6.1.
Таблица 6.1. Толщина 10 000 медных дисков
Толщина (дюймы) Относительная частота
<0,0180 48/10 000=0,0048
0,0180 <0,0182 122/10 000=0,0122
0,0182 < 0,0184 325/10 000=0,0325
0,0184 <0,0186 695/10 000=0,0695
0,0186 < 0,0188 1 198/10 000=0,1198
0,0188 < 0,0190 1 664/10 000=0,1164
0,0190 < 0,0192 1 896/10 000=0,1896
0,0192 <0,0194 1 664/10 000=0,1664
0,0194 < 0,0196 1 198/10 000=0,1198
0,0196 < 0,0198 695/10 000=0,0695
0,0198 < 0,0200 325/10 000=0,0325
>0,0202 48/10 000=0,0048
Всего: 1,0000
В табл. 6.1 перечислены результаты измерения толщины 10 000 медных дисков, произведенных некоей компанией. Толщина представляет собой непрерывную случайную величину, распределение которой аппроксимируется нормальным. Основная масса значений этой величины лежит в интервале от 0,0190 до 0,0192 дюймов и распределена симметрично относительно этого интервала, формируя колоколообразную кривую. Как следует из таблицы, разбиение числовой прямой на интервалы образует группы взаимоисключающих и исчерпывающих событий, сумма вероятностей которых равна единице. Таким образом, распределение вероятностей можно интерпретировать как распределение относительных частот (см. раздел 2.2), соответствующих средним точкам интервалов (за исключением бесконечных интервалов).
На рис. 6.2 изображена гистограмма относительных частот и полигон распределения толщины 10 000 медных дисков. Как видим, первые три условия нормального распределения выполняются, а четвертое — нет. Толщина диска не может быть отрицательной или равной нулю. Из табл. 6.1 следует, что из 10 000 медных дисков только 48 толще 0,0202 дюйма и такое же количество дисков тоньше 0,0180 дюйма. Таким образом, вероятность случайно выбрать слишком толстый или слишком тонкий диск равна 0,0048+0,0048=0,0096, т.е. меньше 1 из 100.
Рис. 6.2. Гистограмма относительных частот и полигон распределения ширины 10 000 медных дисков
Плотность распределения вероятностей обозначается /(X). Плотность нормального распределения вычисляется по формуле (6.1).
ПЛОТНОСТЬ НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ
/(X) = -J=3~} , (6.1)
\/2л:су
где е— математическая константа, приближенно равная 2,71828, л— математическая константа, приближенно равная 3,14159, ц— математическое ожидание генеральной совокупности, ст — стандартное отклонение генеральной совокупности, X — произвольное значение непрерывной случайной величины, -оо < X < +оо .
Поскольку величины сил являются математическими константами, плотность нормального распределения зависит только от двух параметров — математического ожидания ц и стандартного отклонения су. Как показано на рис. 6.3, разным комбинациям этих параметров соответствуют разные плотности нормального распределения. Распределения А и Б имеют одинаковое математическое ожидание ц, но разные стандартные отклонения. С другой стороны, распределения А и В имеют одинаковое стандартное отклонение су, но разные математические ожидания. Кроме того, распределения БиВ имеют разные математические ожидания и стандартные отклонения.
К сожалению, вычислить математическое выражение, заданное формулой (6.1), довольно сложно. Чтобы упростить задачу, значения плотности нормального распределения, как правило, табулируют. Поскольку количество возможных комбинаций параметров ц и су бесконечно, для вычислений понадобилось бы бесконечное количество таблиц. Однако, если нормировать (standardize) данные, все распределения можно свести к одной таблице (табл. Д.2). Используя формулу преобразования (transformation formula), любую нормально распределенную случайную величину X можно преобразовать в нормированную нормально распределенную случайную величину Z.
Рис. 6.3. Три разных нормальных распределения, соответствующих разным комбинациям параметров //и ст
ФОРМУЛА ПРЕОБРАЗОВАНИЯ
Величина Z равна разности между величиной X и математическим ожиданием генеральной совокупности ц, деленной на стандартное отклонение ст
2 = ^. (6.2)
СТ
Математическое ожидание стандартизованного нормального распределения (standardized normal distribution) равно нулю, а стандартное отклонение — единице.
Плотность стандартизованного нормального распределения можно получить, под ставив формулу (6.2) в формулу (6.1).
ПЛОТНОСТЬ СТАНДАРТИЗОВАННОГО НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ
1 — Z2
/Р0 = ^=е2 . (6.3)
Таким образом, любое множество нормально распределенных величин можно преобразовать в стандартизованную форму, а затем определить искомую вероятность по таблице кумулятивного стандартизованного нормального распределения, например, по табл. Д.21.
Проиллюстрируем процедуру нормирования на примере рассмотренного ранее сценария. Напомним, что время загрузки Web-страницы распределено нормально, причем его математическое ожидание равно ц = 7 с, а стандартное отклонение — ст = 2 с.
Как показывает рис. 6.4, каждому значению переменной X соответствует нормированное значение Z, полученное с помощью формулы преобразования (6.2). Следовательно, время загрузки, равное 9 с, на одну стандартную единицу превышает математическое ожидание:
В тексте используется табл. Д.2, представляющая собой таблицу кумулятивного стандартизованного нормального распределения. При необходимости читатели могут воспользоваться табл. Д.12, являющейся таблицей стандартизованного нормального распределения (см. раздел 6.10 ).
а время загрузки (1 с) на три стандартные единицы (стандартных отклонения) меньше математического ожидания:
Таким образом, стандартное отклонение становится единицей измерения. Иначе говоря, время загрузки, равное 9 с, на 2 с (т.е. на одно стандартное отклонение) превышает математическое ожидание, а время, равное 1 с, на 6 с (т.е на три стандартных отклонения) меньше математического ожидания.
Рис. 6.4. Преобразование шкал для Web-сайта компании On Campus!
Допустим теперь, что среднее время загрузки другого Web-сайта равно 4 с, а стандартное отклонение — 1с. Соответствующее распределение изображено на рис. 6.5.
Сравнивая новые результаты с данными, характеризующими время загрузки Web-сайта компании On Campus!, легко обнаружить, что время загрузки, равное 5 с, на одно стандартное отклонение меньше среднего времени загрузки:
а время загрузки, равное 1 с, на три стандартных отклонения меньше математического ожидания:
На рис. 6.4 и 6.5 показаны полигоны относительных частот, соответствующие времени загрузки двух Web-сайтов. Поскольку результаты измерений образуют полную генеральную совокупность, сумма вероятностей, т.е. площадь фигуры, лежащей под кривой, должна быть равной единице.
Рис. 6.5. Преобразование шкал
Предположим, нам необходимо определить вероятность того, что время загрузки Web-сайта компании On Campus! меньше 9 с. Поскольку это время на одно стандартное отклонение превышает математическое ожидание, следует найти вероятность того, что время загрузки не превышает величины, равной математическому ожиданию плюс одно стандартное отклонение. В табл. Д.2 приведены кумулятивные вероятности, т.е. площади фигур, ограниченных стандартизованной гауссовой кривой и лежащих левее величины X. По отношению к формуле (6.2) эти вероятности представляют собой площади фигур, ограниченных стандартизованной гауссовой кривой и лежащих левее нормированной величины Z. Чтобы правильно применить табл. Д.2, следует иметь в виду, что величину Z необходимо записывать с двумя цифрами после десятичной запятой. Таким образом, в нашем примере величину Z следует записать как 4-1,00. Чтобы найти вероятность, соответствующую значению Z = 4-1,00, необходимо просмотреть столбец Z в табл. Д.2 и найти строку, соответствующую первым двум цифрам величины Z. Так, числу 1,0 соответствует 10-я строка. Теперь, перемещаясь по этой строке, необходимо найти ее пересечение со столбцом, соответствующим сотым долям величины Z. В нашем примере сотая доля значения 1,00 равна 0, следовательно, искомая вероятность записана на пересечении десятой строки и первого столбца. Как показано в табл. 6.2, эта вероятность равна 0,8413. Таким образом, как показано на рис. 6.6, шансы, что Web-сайт загрузится меньше, чем за 9 с, равны 84,13%.
Таблица 6.2. Площадь фигуры, ограниченной кривой нормального распределения2
Z 0.00 0,01 0,02 0,03 0,04 0,05 0,06 0,07 0,08 0,09
0,0 0,5000 0,5040 0,5080 0,5120 0,5160 0,5199 0,5239 0,5279 0,5319 0,5359
0,1 0,5358 0,5438 0,5478 0,5517 0,5557 0,5596 0,5636 0,5675 0,5714 0,5753
0,2 0,5793 0,5832 0,5871 0,5910 0,5948 0,5987 0,6026 0,6064 0,6103 0,6141
0,3 0,6179 0,6217 0,6255 0,6293 0,6331 0,6368 0,6406 0,6443 0,6480 0,6517
0,4 0,6554 0,6591 0,6628 0,6664 0,6700 0,6736 0,6772 0,6808 0,6844 0,6879
0,5 0,6915 0,6950 0,6985 0,7019 0,7054 0,7088 0,7123 0,7157 0,7190 0,7224
0,6 0,7257 0,7291 0,7324 0,7357 0,7389 0,7422 0,7454 0,7486 0,7518 0,7549
0,7 0,7580 0,7612 0,7642 0,7673 0,7704 0,7734 0,7764 0,7794 0,7823 0,7852
0,8 0,7881 0,7910 0,7939 0,7967 0,7995 0,8023 0,8051 0,8078 0,8106 0,8133
0,9 0,8159 0,8186 0,8212 0,8238 0,8264 0,8289 0,8315 0,8340 0,8365 0,8389
1,0 0,8413 0,8438 0,8461 0,8485 0,8508 0,8531 0,8554 0,8577 0,8599 0,8621
Рис. б.б. Площадь фигуры, ограниченной интегральной кривой стандартизованного нормального распределения
С другой стороны, рис. 6.5 свидетельствует, что время загрузки другой Web-страницы, равное 5 с, на одно стандартное отклонение превышает математическое ожидание, т.е. 4 с. Следовательно, вероятность того, что Web-страница загрузится быстрее, чем за 5 с, равна 0,8413. Эти данные представлены на рис. 6.7, из которого следует, что вероятность того, что время загрузки второй Web-страницы не превысит 5 с, равна вероятности того, что время загрузки Web-страницы On Campus! не превысит 9 с.
С помощью табл. Е.2 можно решать многие задачи, связанные с нормальным распределением. Рассмотрим несколько примеров.
ПРИМЕР 6.1. ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ Р(Х> 9)
Определите вероятность того, что время загрузки Web-страницы On Campus! Превысит 9 с.
РЕШЕНИЕ. Вероятность того, что время загрузки не превысит 9 с, равна 0,8413, следовательно, искомая вероятность равна 1-0,8413=0,1587. Процесс решения проиллюстрирован на рис. 6.8.и
Рис. 6.7. Преобразование шкал для площадей фигур, ограниченных интегральными кривыми двух нормальных распределений
ПРИМЕР 6.2. ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ Р(7 < Х< 9)
Определите вероятность того, что время загрузки Web-страницы On Campus! лежит в интервале от 7 до 9 с.
РЕШЕНИЕ. Вероятность того, что время загрузки не превысит 9 с, равна 0,8413. Чтобы найти ответ, необходимо определить вероятность того, что загрузка продлится больше 7 с, и вычесть ее из вероятности, что загрузка будет длиться не более 9 с. Процесс решения проиллюстрирован на рис. 6.9.
Поскольку математическое ожидание и медиана нормального распределения совпадают между собой, вероятность того, что загрузка продлится больше 7 с, равна 0,5. Это следует из формулы:
7-7 Z = —— = 0,00. 2
Используя табл. Д.2, определяем, что площадь фигуры, ограниченной нормальной кривой и значением Z = 0,00, равна 0,05. Следовательно, площадь фигуры, лежащей под нормальной кривой между значениями Z = 0,00 и Z=l,00, равна 0,8413-0,5000 = 0,3413.
Рис. 6.9. Определение вероятности Р(7 < X < 9)
ПРИМЕР 6.3. ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ Р(Х< 7 или Х> 9)
Определите вероятность того, что время загрузки Web-страницы On Campus! меньше 7 или больше 9 с.
РЕШЕНИЕ. Поскольку вероятность того, что время загрузки лежит в интервале от 7 до 9 с, равна 0,3413, то вероятность противоположного события равна 1 -0,3413 = 0,6587 (см. рис. 6.9).
Впрочем, эту задачу можно решить иначе. Для этого необходимо определить вероятности Р(Х < 7) и Р(Х > 9), а затем сложить их. Это решение иллюстрируется на рис. 6.10.
Поскольку математическое ожидание и медиана нормального распределения совпадают между собой, вероятность того, что загрузка продлится больше 7 с, равна 0,5. Из примера 6.1 следует, что вероятность Р(Х > 9) равна 0,1587. Следовательно, вероятность того, что время загрузки меньше 7 или больше 9 с, равна 0,5000 + 0,1587 = 0,6587.
Рис. 6.10. Определение вероятности Р(Х<7) или Р(Х>9)
Пример 6.4. ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ Р(5 < Х< 9)
Определите вероятность того, что время загрузки лежит в интервале от 5 до 9 с.
РЕШЕНИЕ. Как показано на рис. 6.11, границы интересующего нас интервала находятся по разные стороны от математического ожидания. Поскольку формула преобразования (6.2) позволяет вычислить лишь вероятность того, что случайная величина меньше определенного значения, необходимо выполнить следующее.
1. Вычислить вероятность Р(Х < 9).
2. Вычислить вероятность Р(Х < 5).
3. Вычесть меньший результат из большего.
Первый этап вычислений мы уже выполнили: вероятность того, что время загрузки не превысит 9 с, равна 0,8413. Чтобы определить вероятность того, что загрузка продлится меньше 5 с, необходимо вычислить значение Z:
5-7
Z=^—- = -1,00.
2
Обратимся к табл. Д.2. Величине Z= -1,00 соответствует вероятность 0,1587. Следовательно, вероятность того, что время загрузки лежит в интервале от 5 до 9 с, равна 0,8413 - 0,1587 = 0,6826 (рис. 6.11).
Площадь = 0,1587, поскольку Суммарная площадь = 0,8413, поскольку
Рис. 6.11. Определение вероятности Р(5 < X < 9)
Полученный результат довольно важен3. Для любого нормального распределения вероятность того, что случайно выбранное число лежит в окрестности математического ожидания на расстоянии, не превышающем одно стандартное отклонение, равно 0,6826. Анализ рис. 6.12 показывает, что в окрестности математического ожидания на расстоянии, не превышающем двух стандартных отклонений, лежит чуть более 95% нормально распределенных величин. Это значит, что 95,44% всех результатов измерений времени загрузки Web-страницы находятся в интервале от 3 до 11 с. На рис. 6.13 показано, что в окрестности математического ожидания на расстоянии, не превышающем трех стандартных отклонений, расположено 99,7% всех нормально распределенных величин. Следовательно, 99,73% результатов измерений времени загрузки Web-страницы лежат в интервале от 1 до 13 с. Таким образом, весьма маловероятно (0,0027, или 27 шансов из 10 000), что время загрузки Web-страницы будет меньше 1 с или больше 13 с. Вот почему на практике считают, что интервал длиной бст, центром которого является математическое ожидание, содержит практически все значения нормально распределенной случайной величины.
Площадь фигуры, расположенной под кривой, равна 0,0228, поскольку
Площадь фигуры, расположенной под кривой, равна 0,9772, поскольку
-3,00 -2,00 -1,00
13 Шкала переменной X
+1,00 +2,00 +3,00 Шкала переменной Z
Рис. 6.12. Определение вероятности Р(3 < X < 11)
Площадь фигуры, расположенной под кривой, равна 0,00135, поскольку
Площадь фигуры, расположенной под кривой, равна 0,99865, поскольку
Z = - - =-3,00 о /
Z = х И =+3,00 о /
13 Шкала переменной X
-3,00 -2,00 -1,00
+1,00 +2,00 +3,00 Шкала переменной Z
Рис. 6.13. Определение вероятности Р(1 < X < 13)
3 Эмпирическое правило, сформулированное в разделе 3.3, относится к нормальным распределе-
ниям. Чем ближе распределение данных к нормальному, тем точнее эмпирическое правило. Если же распределение данных радикально отличается от нормального, эмпирическое правило становится неверным.
ПРИМЕР 6.5. ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ Р(Х< 3.5)
Определите вероятность того, что время загрузки меньше 3,5 с.
РЕШЕНИЕ. Чтобы определить вероятность этого события, необходимо вычислить область закрашенной фигуры на рис. 6.14.
Для этого сначала следует вычислить значение переменной Z:
Z = ^L^= 3,5 ~7 =-1,75. о 2
Найдем в табл. Д.2 величину Z= -1,75. Соответствующая вероятность лежит на пересечении строк Z=-l,7 и столбца 0,05 (см. табл. 6.3). Следовательно, вероятность того, что время загрузки меньше 3,5 с, равна 0,0401.
Таблица 6.3. Суммарная площадь фигуры, ограниченной нормальной кривой4
Z 0,00 0,01 0,02 0,03 0,04 0,05 0,06
-1,7 0,0446 0,0436 0,0427 0,0418 0,0409 0,0401 0,0392
-1,6 0,0548 0,0537 0,0526 0,0516 0,0505 0,0495 0,0485
0,07 0,08 0,09
0,0384 0,0375 0,0367
0,0475 0,0465 0,0455
Visual Explorations: исследовании© нормального распределения
Чтобы увидеть, как математическое ожидание и стандартное отклонение влияют на площадь фигуры, ограниченной гауссовой кривой, следует применить процедуру Normal Distribution из книги макросов Visual Explorations in Statistics. Для этого необходимо открыть книгу макросов visual Explorations ,xla и выбрать команду Visual Explorations Normal Distribution (Visual Explorations Нормальное распределение). Эта процедура создает гауссову кривую, соответствующую описанному выше сценарию, и выводит на экран панель, позволяющую изменять форму кривой и площадь закрашенной фигуры (см. иллюстрацию).
Чтобы изменить математическое ожидание, стандартное отклонение и величину X, следует воспользоваться кнопками счетчика. Кроме того, пользователь может установить переключатель X Axis Labels (Метки оси X) в положение Z Values (Значения Z). В этом случае на оси Xбудут отложены соответствующие метки.
4
Normal Distribution fxj
Arithmetic Mean: [~7
Probability of X<= j~5000
X Axis Labels
: X Values r Z Values
Чтобы удалить все значения, следует щелкнуть на кнопке Reset (Сброс). Подробную информацию пользователь может получить, щелкнув на кнопке Help (Справка). Чтобы завершить работу, можно щелкнуть на кнопке Finish (Готово).
Std. Deviation:
X Value:
Reset
| Finish
В примерах 6.1-6.5 мы вычислили вероятности, связанные с разными значениями измеренной величины. Примеры 6.6 и 6.7 посвящены обратной задаче: как определить значение переменной, соответствующей заданной вероятности?
ПРИМЕР 6.6. НАЙТИ ЗНАЧЕНИЕ ПЕРЕМЕННОЙ X, СООТВЕТСТВУЮЩЕЙ ИНТЕГРАЛЬНОЙ ВЕРОЯТНОСТИ, РАВНОЙ 0,1
Сколько секунд длится загрузка Web-страницы в 10% случаев?
РЕШЕНИЕ. Поскольку в задаче предполагается, что в 10% случаев Web-страница загружается не более чем за X с, площадь фигуры, ограниченной гауссовой кривой и прямой X, равна 0,1000. Используя табл. Д.2, найдем ячейку, соответствующую указанной вероятности. Ближайшей является ячейка, содержащая вероятность 0,1003 (табл. 6.4).
Таблица 6.4. Определение значения переменной Z, соответствующего заданной суммарной площади фигуры, ограниченной нормальной кривой (0,10)5
Z 0,00 0,01 0,02 0,03 0,04 0,05 0,06 0,07 0,08 0,09
-1,5 0,0668 0,0655 0,0643 0,0630 0,0618 0,0606 0,0594 0,0582 0,0571 0,0559
-1,4 0,0808 0,0793 0,0778 0,0764 0,0749 0,0735 0,0721 0,0708 0,0694 0,0681
-1,3 0,0968 0,0951 0,0934 0,0918 0,0901 0,0885 0,0869 0,0853 0,0838 0,0823
-1,2 0,1151 0,1131 0,1112 0,1093 0,1075 0,1056 0,0138 0,1020 0,1003 0,0985
Строка, в которой расположена эта ячейка, соответствует значению-1,2, а столбец — значению 0,08. Таким образом, Z = -1,28 (рис. 6.15).
Рис. 6.15. Определение значения Z, соответствующей величине X
Зная значение переменной Z, можно применить формулу преобразования (6.2):
а
Отсюда следует, что
Ип = Х-ц,
X = ц + Zo.
Следовательно,
Х=7-1,28x2 = 4,44с.
Таким образом, в 10% случаев Web-страница будет загружаться быстрее 4,44 с.
ОПРЕДЕЛЕНИЕ ЗНАЧЕНИЯ ПЕРЕМЕННОЙ X, СООТВЕТСТВУЮЩЕГО ЗАДАННОЙ ВЕРОЯТНОСТИ
Величина X равна сумме математического ожидания генеральной совокупности ц и произведения величины Z на стандартное отклонение с.
X = p + Zo. (6.4)
Чтобы вычислить значение переменной X, соответствующее заданной вероятности, необходимо следовать указаниям, перечисленным во врезке 6.2.
ВРЕЗКА 6.2. ВЫЧИСЛЕНИЕ ЗНАЧЕНИЯ ПЕРЕМЕННОЙ X СООТВЕТСТВУЮЩЕГО ЗАДАННОЙ ВЕРОЯТНОСТИ
• Нарисовать гауссову кривую и отложить на ней математические ожидания по шкале переменных X и Z.
• Вычислить суммарную площадь фигуры, ограниченной нормальной кривой и лежащей слева от прямой X.
• Закрасить интересующую нас область.
• Используя табл. Д.2, определить величину Z, соответствующую суммарной пло- : щади области, ограниченной нормальной кривой и лежащей слева от прямой X.
• С помощью формулы (6.4) вычислить значение переменной X.
X = ц + Za.
ПРИМЕР 6.7. НАЙТИ НИЖНЮЮ И ВЕРХНЮЮ ГРАНИЦЫ ИНТЕРВАЛА, СОДЕРЖАЩЕГО 95% ВСЕХ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЯ ВРЕМЕНИ ЗАГРУЗКИ WEB-СТРАНИЦЫ
Определите нижнюю и верхнюю границы интервала с центром в математическом ожидании нормального распределения, который содержит 95% значений случайной величины.
РЕШЕНИЕ. Сначала определим нижнюю границу а затем — верхнюю границу Ха. Поскольку 95% всех значений расположены между этими границами, причем величины XL и Хи размещены симметрично относительно математического ожидания, слева от этого интервала оказываются 2,5% величин (рис. 6.16).
Рис. 6.16. Определение величины Z, соответствующей значению Хи
Хотя значение XL неизвестно, мы можем вычислить стандартизованную величину Z, поскольку площадь фигуры, ограниченной нормальной кривой, известна и равна 0,0250. Найдем это значение в табл. Д.2. Фрагмент этой таблицы приведен ниже.
Таблица 6.5. Определение значения переменной Z, соответствующего суммарной площади фигуры, равной 0,025б
Z 0,00 0,01 0,02 0,03 0,04 0,05 0,06 0,07 0,08 0,09
-2,0 0,0228 0,0222 0,0217 0,0212 0,0207 0,0202 0,0197 0,0192 0,0188 0,0183
-1,9 0,0287 0,0281 0,0274 0,0268 0,0262 0,0256 0,0250 0,0244 0,0239 0,0233
-1.8 0,0359 0,0351 0,0344 0,0336 0,0329 0,0232 0,0314 0,0307 0,0301 0,0294
Строка, в которой расположена искомая ячейка, соответствует значению -1,9, а столбец — значению 0,06. Таким образом, Z = -1,96.
Теперь можно вычислить значение X из уравнения (6.4).
X - ц + Zct = 7 - 1,96 х 2 = 7 - 3,92 = 3,08 с.
Для того чтобы найти величину Хи, следует учесть, что только 2,5% Web-страниц загружаются дольше Ху секунд и 97,5% Web-страниц загружаются быстрее Хи секунд. Используя симметричность нормального распределения (рис. 6.17), приходим к выводу, что искомая величина Z равна +1,96 (поскольку эта величина лежит справа от нуля на стандартизованной шкале). Эту величину можно также извлечь из табл. 6.6, поскольку 97,5% площади фигуры, ограниченной нормальной кривой, лежит левее значения Z = +1,96.
Таблица 6.6. Определение значения переменной Z, соответствующего суммарной площади фигуры, равной 0,9757
Z 0,00 0,01 0,02 0,03 0,04 0,05 0,06 0,07 0,08 0,09
+1,8 0,9641 0,9649 0,9656 0,9664 0,9671 0,9678 0,9686 0,9693 0,9699 0,9706
+1,9 0,9713 0,9719 0,9726 0,9732 0,9738 0,9744 0,9750 0,9756 0,9761 0,9767
+2,0 0,9772 0,9778 0,9783 0,9788 0,9793 0,9798 0,9803 0,9808 0,9812 0,9817
Рис. 6.17. Вычисление нормальных вероятностей с помощью программы Microsoft Excel
Теперь можно вычислить значение X из уравнения (6.4).
X = ц + Zo = 7 + 1,96 х 2 = 7 + 3,92 = 10,92 с.
Таким образом, 95% результатов измерения времени загрузки Web-страницы, лежат в интервале от 3,08 до 10,92 с.
Нормальное распределение можно вычислить с помощью программы Microsoft Excel. Рабочие листы, соответствующие примерам 6.1, 6.2, 6.3, 6.5 и 6.6, приведены на рис. 6.18.
А. 9 , i
1 Нормальное распределение
2
3 Common Data__________________
4 Mean 7
5 Standard Deviation ~2
_6_____________________
7 Probability for X <=
“8 X Value 3.5
9 Z Value________________-1.75
10 P(X<=3.5) 0.0400591
11"______________________________
12 Probability for X > ТЭНХ Value 9
14 IZ Value 1
Probability for a Range
From X Value 7
To X Value 9
Z Value for 7 0
Z Value for 9 1
P(X<=7) 0.5000
P(X<=9) 0.8413
P(7<=X<=9) 0.3413
15 P(X>9) ’16
17 Probability for X<3.5 or X >9
16 P(X<3.5 or X >9) | 0.1987
Find X and Z Given Cum. Pctaqe.
Cumulative Percentage 10.00%
Z Value -1.281552
X Value 4.436896
Рис. 6.18. Вычисление нормального распределения с помощью программы Microsoft Excel
Процедуры Excel: вычисление нормальных вероятностей
Для вычисления нормальных вероятностей применяются функции нормализация, нормстрасп, нормстобр и нормобр. Кроме того, эти вероятности можно вычислить с помощью надстройки PHStat2.
Например, чтобы вычислить вероятности, как показано на рис. 6.18, можно воспользоваться одной из следующих стратегий.
Применение Excel в сочетании с надстройкой PHStat2
Для вычисления нормальных вероятностей на новом рабочем листе можно применить процедуру Normal надстройки PHStat2. Для этого необходимо выполнить следующие действия .
1. Выбрать команду PHStat1^Probability &Prob.
Distributions^ Normal... (PHStat1^ Вероятность & Распределения^ Нормальное...).
2. В диалоговом окне Normal Probability Distribution (см. иллюстрацию) сделать следующее.
2.1. Ввести в окне редактирования Mean (Математическое ожидание) число 7.
2.2. Ввести в окне редактирования Standard Deviation (Стандартное отклонение) число 2.
2.3. Установить флажок Probability for: Х<= (Вероятность для:Х<=) и ввести в соответствующем окне редактирования число 3.5 (пример 6.5).
2.4. Установить флажок Probability for: Х> (Вероятность для:Х>) и ввести в соответствующем окне редактирования число 9 (примеры 6.1 и 6.3).
Normal Probability Distribution
Data
Mean: [7*
Standard Deviation: j2
Input Options
P Probability for: X <= |з.5~
P Probability for: X > [9 ;
I** Probability for range: 17 <=X<= [9
IS* X for Cumulative Percentage: [To %
Output Options
Title: (нормальное распределение
Help j | jl Cancel |
2.5. Установить флажок Probability for range (Вероятность для интервала) и ввести в соответствующих окнах редактирования числа 7 и 9 (пример 6.2).
2.6. Установить флажок X for Cumulative Percentage (X для интегральных процентов) и ввести в соответствующем окне редактирования число 10.
2.7. Ввести в окне редактирования Title соответствующий заголовок.
2.8. Щелкнуть на кнопке ОК.
Применение Excel
Для самостоятельного создания рабочего листа, вычисляющего нормальные вероятности, можно воспользоваться функциями НОРМАЛИЗАЦИЯ, нормрасп, нормстобр и нормобр, следуя инструкциям из раздела ЕН.6.1.
Chapter 6.xls
Данные, на основе которых вычисляются нормальные вероятности, приведенные на рис. 6.18, содержатся в рабочей книге Chapter 6 . xls на листе Рис6.18.
УПРАЖНЕНИЯ К РАЗДЕЛУ 6.
Изучение основ
6.1. Рассмотрим стандартизованное нормальное распределение (математическое ожидание равно 0, а стандартное отклонение — 1 (см. табл. Д.2)).
1. Чему равна вероятность P(Z < 1,57)?
2. Чему равна вероятность P(Z > 1,84)?
3. Чему равна вероятность Р(1,57 < Z < 1,84)?
4. Чему равна вероятность P(Z < 1,57 или Z > 1,84)?
5. Чему равна вероятность Р(-1,57 < Z < 1,84)?
6. Чему равна вероятность P{Z < -1,57 или Z > 1,84)?
7. Чему равна величина Z, если 50% всех значений превышают Z?
8. Чему равна величина Z, если только 2,5% всех значений превышают Z?
9. Между какими значениями переменной Z (симметрично распределенной относительно математического ожидания) лежат 68,26% всех ее возможных значений?
6.2. Рассмотрим стандартизованное нормальное распределение (математическое ожидание равно 0, а стандартное отклонение— 1 (см. табл. Д.2)). Вычислите следующие вероятности.
1. P(Z > +1,34).
2. P(Z<+1,17).
3. Р(0 < Z <+1,17).
4. P(Z<-1,17).
5. P(-l,17 < Z<+1,34).
6. P(-l,17 < Z <-0,50).
6.3. Рассмотрим стандартизованное нормальное распределение (математическое ожидание равно 0, а стандартное отклонение — 1 (см. табл. Д.2)). Вычислите вероятности следующих событий.
1. Величина Z больше+1,08.
2. Величина Z больше-0,21.
3. Величина Z больше математического ожидания и меньше +1,08.
4. Величина Z меньше математического ожидания или больше +1,08.
5. Величина Z больше -0,21 и меньше математического ожидания.
6. Величина Z меньше -0,21 или больше математического ожидания.
7. Величина Z больше -0,21 и меньше +1,08.
8. Величина Z меньше -0,21 или больше +1,08.
6.4. Рассмотрим стандартизованное нормальное распределение (математическое ожидание равно 0, а стандартное отклонение — 1 (см. табл. Д.2)). Вычислите следующие вероятности.
1. P(Z> +1,08).
2. P(Z< -0,21).
3. P(-l,96 < Z <-0,21).
4. P(-l,96 < Z <+1,08).
5. P(+l,08 < Z < +1,96).
6. Чему равна величина Z, если выполняются следующие условия?
7. Половина всех возможных значений меньше этой величины.
8. Только 15,87% всех возможных значений меньше этой величины
9. Только 15,87% всех возможных значений больше этой величины.
6.5. Рассмотрим нормальное распределение, математическое ожидание которого равно 100, а стандартное отклонение — 10.
Вычислите следующие вероятности.
1. Р(Х>75).
2. Р(Х<70).
3. Р(Х>112).
4. Р(75<Х<85).
5. Р(Х < 80 или X > 110).
6. Какое число X превышает 10% всех возможных значений?
7. Между какими двумя числами (симметрично расположенными относительно математического ожидания) лежат 80% всех возможных значений?
8. Какое число X меньше 70% всех возможных значений?
6.6. Рассмотрим нормальное распределение, математическое ожидание которого равно 50, а стандартное отклонение — 4.
Вычислите следующие вероятности.
1. Р(Х > 43).
2. Р(Х<42).
3. Р(Х>57,5).
4. Р(42<Х<48).
5. Р(Х < 40 или X > 55).
6. Какое число X превышает 5% всех возможных значений?
7. Между какими двумя числами (симметрично расположенными относительно математического ожидания) лежат 60% всех возможных значений?
8. Какое число X меньше 85% всех возможных значений?
Применение понятий
6.7. На протяжении 2001 года 61,3% семей в США покупали зерна кофе, затратив на это в среднем 36,16 долл. (“Annual Product Preference Study”, Progressive Grocer, May 1, 2002, 31). Исследуйте годовые расходы на покупку зерен кофе, предполагая, что эти расходы имеют нормальное распределение, у которого математическое ожидание равно 36,16 долл., а стандартное отклонение — 10,00 долл.
1. Какова вероятность того, что американская семья затратит на покупку зерен кофе меньше 25,00 долл.?
2. Какова вероятность того, что американская семья затратит на покупку зерен кофе больше 50,00 долл.?
3. Какова вероятность того, что американская семья затратит на покупку зерен кофе больше 57,00 долл.?
4. Какова доля семей, затрачивающих на покупку кофе от 30,00 до 40,00 долл.?
5. Меньше какой суммы затрачивают на покупку зерен кофе 99% американских семей?
6. Больше какой суммы затрачивают на покупку зерен кофе 80% американских семей?
7. Обоснованно ли предположение, что распределение расходов на покупку зерен кофе является приближенно нормальным?
6.8. Транспортная компания Toby's Trucking Company определила, что расстояние, пройденное грузовиком за год, распределено по нормальному закону. Его математическое ожидание равно 50,0 тыс. миль, а стандартное отклонение — 12,0 тыс. миль.
1. Какая доля грузовиков проходит за год от 34,0 до 50,0 тыс. миль?
2. Какова вероятность того, что наугад выбранный грузовик прошел за год от 34,0 до 38,0 тыс. миль?
3. Какая доля грузовиков проходит за год меньше 30,0 или больше 60,0 тыс. миль?
4. Сколько из 1 000 грузовиков, принадлежащих парку компании, проходят за год от 30,0 до 60,0 тыс. миль?
5. Сколько миль проходят за год по крайней мере 80% грузовиков?
6. Как изменятся ответы на вопросы 1-5, если стандартное отклонение равно 10,0 тыс. миль?
6.9. Предельная нагрузка, которую выдерживают пластиковые пакеты, является нормально распределенной случайной величиной. Ее математическое ожидание равно 5 фунтам на квадратный дюйм, а стандартное отклонение — 1,5 фунта на квадратный дюйм.
1. Какая доля пакетов выдерживает максимальную нагрузку не больше 3,17 фунта на квадратный дюйм?
2. Какая доля пакетов выдерживает максимальную нагрузку не меньше 3,6 фунта на квадратный дюйм?
3. Какая доля пакетов выдерживает максимальную нагрузку от 5 до 5,5 фунта на квадратный дюйм?
4. Какая доля пакетов выдерживает максимальную нагрузку от 3,2 до 4,2 фунта на квадратный дюйм?
5. Между какими двумя величинами (симметрично расположенными относительно математического ожидания) распределены 95% всех возможных значений максимальной нагрузки?
6. Как изменятся ответы на вопросы 1-5, если стандартное отклонение равно 1,0 фунт на квадратный дюйм?
6.10. Оценки, полученные студентами на экзамене по статистике, являются нормально распределенными случайными величинами. Математическое ожидание этого распределения равно 73, а стандартное отклонение — 8.
1. Какова вероятность получить на экзамене меньше 91 баллов?
2. Какова доля студентов, получивших на экзамене от 65 до 89 баллов?
3. Какова доля студентов, получивших на экзамене от 81 до 89 баллов?
4. Укажите сумму баллов, которую превысили только 5% студентов.
5. Предположим, что оценки, поставленные профессором, распределены по нормальному закону (т.е. высшую оценку получит только 10% студентов). Сравните вероятность получить больше 81 балла на экзамене по статистике и вероятность получить больше 68 баллов на другом экзамене, оценки которого также распределены как нормальная случайная величина с математическим ожиданием, равным 62, и стандартным отклонением, равным 3. Обоснуйте свой ответ.
6.11. Статистический анализ 1 000 междугородных телефонных разговоров в офисе корпорации Bricks and Clicks Computer Corporation показал, что их продолжительность является нормально распределенной случайной величиной. Математическое ожидание этого распределения равно 240 с, а стандартное отклонение — 40 с.
1. Какова доля разговоров, длящихся менее 180 с?
2. Какова вероятность того, что продолжительность наугад выбранного разговора окажется больше 180 и меньше 300 с?
3. Сколько разговоров длятся меньше 180 или больше 300 с?
4. Сколько разговоров длятся больше 110 и меньше 180 с?
5. Какова продолжительность разговора, если известно, что более короткими оказались лишь 1 % разговоров?
6.12. Web-сайт Unisys.com является одним из наиболее популярных коммерческих сайтов, ориентированных на осуществление операций и поддержку отношений между компаниями, а не между компаниями и клиентами (business-to-business Web site). В статье, опубликованной в журнале Wall Street Journal (“Reality Bytes”, February 28, 2000, B6), утверждается, что деловые партнеры, посещающие сайт Unisys.com, проводят там в среднем 65,7 мин. Предположим, что продолжительность посещения сайта Unisys.com является нормально распределенной случайной величиной. Ее математическое ожидание равно 65,7 мин., а стандартное отклонение — 15 мин.
1. Какова вероятность того, что случайно выбранное посещение сайта длилось более 90 мин.?
2. Какова вероятность того, что случайно выбранное посещение сайта длилось от 60 до 90 мин.?
3. Меньше какой величины длились 20% посещений сайта?
4. Между какими значениями (симметрично расположенными относительно математического ожидания) заключена продолжительность 90% посещений?
5. Насколько естественным является предположение, что продолжительность посещения сайта является нормально распределенной случайной величиной?
6.13. На производстве многое зависит от точности подгонки деталей, например, оси должны входить в отверстия клапанов. Предположим, проектировщики предусмотрели ось диаметром 22,000 мм, а на практике ее диаметр колеблется от 21,900 до 22,010 мм. Допустим, что диаметр оси является нормально распределенной случайной величиной с математическим ожиданием, равным 22,002 мм, и стандартным отклонением, равным 0,005 мм.
1. Какова доля осей, диаметр которых больше 21,90 и меньше 22,00 мм?
2. Какова вероятность выбрать ось, удовлетворяющую техническим требованиям?
3. Каков диаметр оси, если известно, что меньший диаметр имеют только 2% осей?
4. Как изменятся ответы на вопросы 1-3, если стандартное отклонение диаметра оси равно 0,004 мм?
6.2. ПРОВЕРКА ГИПОТЕЗЫ О НОРМАЛЬНОМ РАСПРЕДЕЛЕНИИ
В разделе 6.1 мы обсудили свойства нормального распределения. Рассмотрим теперь весьма важную практическую проблему. Насколько естественным является предположение о том, что конкретные данные представляют собой значения нормально распределенной случайной величины?
Следует иметь в виду, что не все непрерывные случайные величины являются нормально распределенными. Довольно часто наблюдаемая случайная величина не является даже приближенно нормально распределенной.
Таким образом, остается открытым следующий вопрос: как определить, что конкретный набор данных является приближенно нормально распределенным, и к нему можно применять методы, описанные в разделе 6.1? Для ответа на этот вопрос используется один из следующих исследовательских методов.
1. Сравнение характеристик набора данных со свойствами соответствующего нормального распределения.
2. Построение графика нормального распределения.
Оценка свойств
В разделе 6.1 указывалось, что нормальное распределение является симметричным и колоколообразным, так что все характеристики его среднего значения — математическое ожидание, мода и медиана — совпадают друг с другом. Межквартильный размах нормального распределения равен 1,33 стандартного отклонения. Нормальное распределение является непрерывным, причем нормально распределенная случайная величина принимает произвольные значения, лежащие на всей числовой оси.
На практике характеристики набора данных могут немного отличаться от теоретических, либо потому, что случайная величина является лишь приближенно нормальной, либо потому, что ее реальные свойства отличаются от предполагаемых. В таких ситуациях кривая распределения оказывается не совсем симметричной и колоколообразной. Оценки математического ожидания могут слегка отличаться от теоретических, а межквартильный размах может не быть равным 1,33 стандартного отклонения. Кроме того, на практике диапазон изменения данных не может быть бесконечным — на самом деле он ограничен шестью стандартными отклонениями.
Многие непрерывные случайные величины не являются ни точно, ни приближенно нормальными. Свойства таких величин довольно сильно отличаются от четырех свойств нормального распределения. Для того чтобы проверить, является ли данная случайная величина нормально распределенной, следует выполнить действия, перечисленные во врезке 6.3.
ВРЕЗКА 6.3. ПРОВЕРКА ГИПОТЕЗЫ О НОРМАЛЬНОМ РАСПРЕДЕЛЕНИИ
• Построить диаграммы и оценить их внешний вид. Для малых и средних наборов данных следует построить диаграмму “ствол и листья” и блочную диаграмму. Для больших наборов данных необходимо построить гистограмму или полигон.
• Вычислить описательные статистики и сравнить их с теоретическими свойствами • нормального распределения. Вычислить моду и медиану. Определить, совпадают . они или нет. Вычислить межквартильный размах и стандартное отклонение. Проверить, равен ли межквартильный размах 1,33 стандартного отклонения. Определить диапазон изменения переменной. Проверить, аппроксимируется ли он ; шестью стандартными отклонениями.
• Оценить распределение данных. Проверить, лежат ли две трети наблюдений в окрест? ности среднего значения на расстоянии не более одного стандартного отклонения. Проверить, лежат ли 4/5 наблюдений в окрестности среднего значения на расстоянии не более 1,28 стандартного отклонения. Проверить, лежат ли 19/20 наблюдений в окрестности среднего значения на расстоянии не более 2 стандартных отклонений.
Построение графика нормального распределения
Второй подход к проверке гипотезы о нормальном распределении использует график. В разделе 3.2 для оценки смещения распределения были введены квартили. Кроме квартилей, для оценки нормальности распределения можно вычислять децили (разбивающие диапазон изменения данных на десятые доли) и процентили (разбивающие диапазон изменения данных на сотые доли).
График нормального распределения (normal probability plot) — двумерный график, на вертикальной оси которого отложены наблюдаемые данные, а на горизонтальной оси — соответствующие квантили стандартизованного нормального распределения.
Если точки, соответствующие наблюдаемым данным, лежат на графике нормального распределения близко к прямой, проведенной из левого нижнего угла в правый верхний угол, значит, данные распределены приближенно нормально. С другой стороны, если эти точки отклоняются от проведенной линии, распределение данных отличается от нормального.
Чтобы построить и применить график нормального распределения, необходимо выполнить действия, перечисленные во врезке 6.4.
ВРЕЗКА 6.4. ПОСТРОЕНИЕ ГРАФИКА НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ
Чтобы построить график нормального распределения, необходимо выполнить следующее.
• Упорядочить набор данных по возрастанию.
• Вычислить квантили стандартизованного нормального распределения.
• Изобразить указанные пары точек на графике, откладывая на вертикальной оси i значения наблюдаемых данных, а на горизонтальной оси — соответствующие квантили стандартизованного нормального распределения.
♦ Оценить вероятность того, что анализируемая случайная величина является хотя бы приближенно нормальной, основываясь на отклонении точек от прямой линии, проведенной из нижнего левого угла в правый верхний угол графика.
Создание массива упорядоченных данных. Поскольку исходные данные обычно записываются в произвольном порядке, их следует упорядочить по возрастанию. Это позволит вычислить соответствующие квантили стандартизованного нормального распределения.
• Первый квантиль стандартизованного нормального распределения Ql представляет собой стандартизованную нормально распределенную величину Z, которой соответствует площадь фигуры, лежащей под кривой плотности вероятностей, равная 1/(п+1).
• Второй квантиль стандартизованного нормального распределения Q2 представляет собой стандартизованную нормально распределенную величину Z, которой соответствует площадь фигуры, лежащей под кривой плотности вероятностей, равная 2/(п+1).
• /-й квантиль стандартизованного нормального распределения Q представляет собой стандартизованную нормально распределенную величину Z, которой соответствует площадь фигуры, лежащей под кривой плотности вероятностей, равная i/(n+l).
• А-й квантиль стандартизованного нормального распределения Qn представляет собой стандартизованную нормально распределенную величину Z, которой соответствует площадь фигуры, лежащей под кривой плотности вероятностей, равная п/(тг+1).
Вычисление квантилей стандартизованного нормального распределения. Математическое ожидание стандартизованного нормального распределения равно 0, а стандартное отклонение— 1. Поскольку это распределение симметрично, его медиана также равна 0. Следовательно, квантили стандартизованного нормального распределения, не превышающие медианы, являются отрицательными, а превышающие медиану — положительными. Квантили этого распределения вычисляются с помощью обратного преобразования нормально распределенных данных (inverse normal scores transformation).
Это преобразование применяется к набору данных, содержащему п значений случайной величины, имеющей стандартизованное нормальное распределение. В результате вычисляются квантили стандартизованного нормального распределения Q., упорядоченные по возрастанию. Поскольку это распределение симметрично, первый квантиль является отрицательным, а последний — положительным.
Обратное преобразование нормально распределенных данных. Площади фигур, ограниченных гауссовой кривой и прямыми, соответствующими значениям случайной величины Z, имеющей стандартизованное нормальное распределение, приведены в табл. Д.2. Следовательно, чтобы найти i-ю стандартизованную нормально распределенную случайную величину в упорядоченном наборе, содержащем п наблюдений, необходимо найти в табл. Д.2 величину Z, соответствующую площади, равной i/(n+l). Проиллюстрируем эту процедуру следующим примером.
ПРИМЕР 6.8. ВЫЧИСЛЕНИЕ КВАНТИЛЕЙ СТАНДАРТИЗОВАННОГО НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ
Допустим, что нам необходимо найти 1-, 2- и 10-й квантиль в выборке, состоящей из 19 наблюдений.
РЕШЕНИЕ. Первый квантиль Qt является величиной Z, которая отсекает от фигуры, ограниченной гауссовой кривой, область, площадь которой равна
Эта область показана на рис. 6.19. Из табл. Д.2 следует, что квантиль Qt находится между числами -1,65 и-1,64. Поскольку значения стандартизованных нормальных величин обычно приводятся с двумя десятичными знаками, выберем число -1,65.
Рис. 6.19. Определение величины Z, соответствующей значению XL
Найдем это значение в табл. Д.2. Фрагмент этой таблицы приведен ниже.
Таблица 6.7. Определение величины Z, соответствующей суммарной площади фигуры, равной 0,05s
Z 0,00 0,01 0,02 0,03 0,04 0,05 0,06 0,07 0,08 0,09
-1,9 0,0287 0,0281 0,0274 0,0268 0,0262 0,0256 0,0250 0,0244 0,0239 0,0233
-1,8 0,0359 0,0351 0,0344 0,0336 0,0329 0,0322 0,0314 0,0307 0,0301 0,0294
-1,7 0,0446 0,0436 0,0427 0,0418 0,0409 0,0401 0,0392 0,0384 0,0375 0,0367
-1,6 0,0548 0,0537 0,0526 0,0516 0,0505 0,0495 0,0485 0,0475 0,0465 0,0455
Второй квантиль Q2 является величиной Z, которая отсекает от фигуры, ограниченной гауссовой кривой, область, площадь которой равна
2 2
----=------= 0,10.
и + 1 19 + 1
Из табл. Д.2 следует, что квантиль Q2 находится между числами -1,29 и -1,28, причем ближе к -1,28. Следовательно, в качестве второго квантиля выбирается число -1,28.
Аналогично десятый квантиль Q;o является величиной Z, которая отсекает от фигуры, ограниченной гауссовой кривой, область, площадь которой равна
10 = -^- = 0,50.
п + 1 19 + 1
Поскольку это значение является медианой, десятый квантиль равен 0,00.и
5 Фрагмент табл. Д.2.
В табл. 6.8 приведен упорядоченный массив оценок, полученных студентами при сдаче четырех тестов (разделы I-IV) по финансовому делу. Кроме того, в табл. 6.8 содержатся значения стандартизованной нормально распределенной случайной величины, полученной с помощью обратного преобразования. Графики распределений для каждого из четырех тестов изображены на рис. 6.20.
Таблица 6.8. Упорядоченный массив оценок, полученных студентами при сдаче четырех тестов (разделы I-IV) по финансовому делу, и соответствующие значения стандартизованной нормально распределенной случайной величины
1 Колоколообразн ое нормальное распределение II Распределение с отрицательной асимметрией III Распределение с положительной асимметрией IV Равномерное распределение Q.
48 47 47 38 -1,65
52 54 48 41 -1,28
55 58 50 44 -1,04
57 61 51 47 -0,84
58 64 52 50 -0,67
60 66 53 53 -0,52
61 68 53 56 -0,39
62 71 54 59 -0,25
64 73 55 62 -0,13
65 74 56 65 0,00
66 75 57 68 0,13
68 76 59 71 0,25
69 77 62 74 0,39
70 77 64 77 0,52
72 78 66 80 0,67
73 79 69 83 0,84
75 80 72 86 1,04
78 82 76 89 1,28
82 83 83 92 1,65
Рис. 6.20. Графики распределений для каждого из четырех тестов
График на рис. 6.20, панель А, свидетельствует, что наблюдаемые точки лежат очень близко к прямой линии, поэтому можно считать, что оценки, полученные студентами при сдаче первого теста, распределены практически нормально. (Обратите внимание на соответствующие полигон и блочную диаграмму, изображенные на рис. 3.11, панель А.)
С другой стороны, на рис. 6.20, панель Б, точки значительно отклоняются от прямой линии. Значения случайной переменной сначала возрастают довольно резко, а затем их рост становится умеренным. Этот рисунок соответствует распределению с отрицательной асимметрией, о чем свидетельствует более длинный левый хвост распределения. (Обратите внимание на соответствующие полигон и блочную диаграмму, изображенные на рис. 3.11, панель Б.)
На рис. 6.20, панель В, наблюдается противоположная картина. Значения случайной переменной сначала возрастают довольно медленно, а затем их рост становится более заметным. Этот рисунок соответствует распределению с положительной асимметрией, о чем свидетельствует более длинный правый хвост распределения. (Обратите внимание на соответствующие полигон и блочную диаграмму, изображенные на рис. 3.11, панель В.)
На рис. 6.20, панель Г, изображен симметричный график, средняя часть которого почти линейна. Значения случайной переменной сначала довольно медленно возрастают, затем их рост прекращается, а в третьей части — ускоряется. Этот рисунок не совпадает ни с панелью В, ни с панелью В. Это распределение не имеет хвостов. Следовательно, оно является равномерным (или прямоугольным). (Обратите внимание на соответствующие полигон и блочную диаграмму, изображенные на рис. 3.11, панель Г.)
Проверив гипотезу о нормальности распределения экзаменационных оценок, перейдем к анализу распределения доходности взаимных фондов, рассмотренной в главе 3.
А C D E
1 Блочная диаграмма для пятилетней доходности >
3_ Five number Summary 4 Minimum -6.1 First Quartile 8.2 6 "Median 10.5 >2 Third Quartile 13 _8_ 4 Maximum 26.3
Панель А
Блочная диаграмма для пятилетней доходности
о
5
10
15
20
Пятилетняя доходность
Панель Б
Рис. 6.21. Суммарные характеристики (панель А) и блочная диаграмма (панель Б) распределения пятилетней среднегодовой доходности 259 взаимных фондов
Анализируя рис. 6.21, приходим к выводу, что разность между медианой и максимальным значением намного превышает разность между медианой и минимальным значением, а левый ус блочной диаграммы ненамного короче правого. Эти наблюдения хорошо согласуются с графиком распределения, изображенным на рис. 6.22. На нем хорошо видно, что большинство показателей годовой доходности взаимных фондов лежат на прямой линии. Исключение составляют несколько экстремальных точек в верхней части графика. Таким образом, данное распределение обладает положительной правой асимметрией.
Рис. 6.22. График нормального распределения пятилетней среднегодовой доходности 259 взаимных фондов, построенный с помощью программы Microsoft Excel
Процедуры Excel: построение графика нормального распределения
Для построения графика нормального распределения применяется функция нормстобр и Мастер диаграмм. Надстройка PHStat2 может выполнить эту задачу за одни шаг.
Например, чтобы построить график нормального распределения пятилетней среднегодовой доходности 259 взаимных фондов, необходимо открыть рабочую книгу Mutual Funds . xls на листе Данные и следовать инструкциям.
Применение Excel в сочетании с надстройкой PHStat2
Для построения графика нормального распределения следует применить процедуру PHStatM Probability & Prob. Distributions^Normal Probability Plot... (PHStat^Вероятность & Распределениям График нормального распределения...). Для этого необходимо выполнить следующие действия .
1. Выбрать команду PHStatMProbability &
Prob. Distributions^Normal Probability Plot.
2. В диалоговом окне Normal Probability Plot (см. иллюстрацию) сделать следующее.
2.1. Ввести в окне редактирования Variable Cell Range (Входной интервал) диапазон 11:12 60.
2.2. Установить флажок First cell contains label (Первая ячейка содержит метку).
2.3. Ввести в окне редактирования Title соответствующий заголовок.
2.4. Щелкнуть на кнопке ОК.
Эта процедура сначала создает рабочий лист График, содержащий таблицу категории, накопленные частоты, значения стандартизованной нормальной величины Z, а также исходные показатели доходности, а затем использует этот лист для построения графика нормального распределения.
Применение Excel
Инструкции по созданию рабочего листа, предназначенного для построения графика нормального распределения с помощью функции нормстобр и Мастера диаграмм, содержатся в разделе ЕН.б.2.
Chapter: 6.xls
График нормального распределения, приведенный на рис. 6.22, содержится в рабочей книге Chapter б . xls на листе Рис6.22.
УПРАЖНЕНИЯ К РАЗДЕЛУ 6.2
Изучение основ
6.14. Докажите, что для выборки, содержащей 19 значений некоей случайной величины, 18-й квантиль стандартизованной нормально распределенной случайной величины, полученный с помощью обратного преобразования нормального распределения, равен +1,28, а 19-й------Ы,65.
6.15. Докажите, что для выборки, содержащей 39 значений некоей случайной величины, наименьший и наибольший квантили стандартизованной нормально распределенной случайной величины, полученные с помощью обратного преобразования нормального распределения, равны -1,96 и +1,96 соответственно, а средний (т.е. 20-й) квантиль равен 0,00.
6.16. Применяя обратное преобразование нормального распределения к выборке из шести наблюдений, перечислите шесть ожидаемых вероятностей, соответствующих площадям фигур, отсекаемых гауссовой кривой и случайной величиной, имеющей стандартизованное нормальное распределение.
Применение понятий
Задачи 6.16-6.19 можно решать как вручную, так и с помощью программы Microsoft Excel. Задачи 6.20-6.23 специально предназначены для решения с помощью программы Microsoft Excel.
6.17. Из раздела объявлений газеты Cincinnati Enquirer извлечена выборка, состоящая из 24 объявлений о сдаче в аренду немеблированных квартир с двумя спальнями. В таблице ^APARTMENT. XLS приведены данные о стоимости месячной аренды этих квартир (Cincinnati Enquirer, June 23, 2002).
Стоимость месячной аренды 24 квартир с двумя спальнями
735 499 490 475 800 675
550 475 575 575 530 790
510 500 800 485 975 690
475 535 599 700 670 625
Являются ли эти данные значениями нормально распределенной случайной величины? Ответьте на этот вопрос, выполнив следующие задания.
1. Сравните характеристики фактического набора данных с теоретическими свойствами нормального распределения.
6.18. Клиенты и телефонная компания обеспокоены нарушениями телефонной связи. Причины этих нарушений разделяются на две группы: повреждения на телефонной станции и на линии. Ниже приведены данные о 20 повреждениях телефонной связи и длительности ремонта (в минутах). ^PHONE .XLS.
Длительность ремонта повреждений на телефонной станции I (мин.)
1,48 1,75 0,78 2,85 0,52 1,60 4,15 3,97 1,48 3,10
1,02 0,53 0,93 1,60 0,80 1,05 6,32 3,93 5,45 0,97
Длительность ремонта повреждений на телефонной станции II (мин.)
7,55 3,75 0,10 1,10 0,60 0,52 3,30 2,10 0,58 4,02
3,75 0,65 1,92 0,60 1,53 4,23 0,08 1,48 1,65 0,72
Являются ли эти данные значениями нормально распределенной случайной величины? Ответьте на этот вопрос, выполнив следующие задания.
1. Сравните характеристики фактического набора данных с теоретическими свойствами нормального распределения.
2. Постройте график нормального распределения.
6.19. Во многих технологических процессах существует так называемый “период незавершенного производства” (work-in-process — WIP). В типографии периодом незавершенного производства называют интервал времени, в течение которого отпечатанные листы книги фальцуют, комплектуют, склеивают, обрезают и переплетают. В следующей таблице приведена длительность производства 20 книг, напечатанных в двух типографиях. (Длительность производства измеряется в днях, прошедших с момента завершения печати и до упаковки книг в картонные коробки.) WIP . XLS.
Типография А
15,62 5,29 16,25 10,92 11,46 21,62 8,45 8,58 5,41 11,42
11,62 7,29 17,50 17,96 14,42 10,50 7,58 9,29 7,54 18,92
Типография Б
9,54 11,46 16,62 12,62 25,75 15,41 14,29 13,13 13,71 10,04
5,75 12,46 19,17 13,21 16,00 12,33 14,25 15,37 16,25 19,71
Являются ли эти данные значениями нормально распределенной случайной величины? Ответьте на этот вопрос, выполнив следующие задания.
1. Сравните характеристики фактического набора данных с теоретическими свойствами нормального распределения.
2. Постройте график нормального распределения.
6.20. Сводный индекс NASDAQ 4 марта 2003 года снизился приблизительно на 1%. В файле Wnet-CHG . XLS записаны величины изменения курса 50 акций, учитываемых индексом NASDAQ, выраженные в долларах.
Являются ли эти данные значениями нормально распределенной случайной величины? Ответьте на этот вопрос, выполнив следующие задания.
1. Сравните характеристики фактического набора данных с теоретическими свойствами нормального распределения.
2. Постройте график нормального распределения.
6.21. Одной из операций, выполняемых прессом, является нарезка стали на части, ис которых в дальнейшем будут изготовлены передние автомобильные сиденья. Сталь разрезается алмазной пилой. Длина заготовок для сидений должна отличаться от стандартной не более чем на 0,005 дюйма. В файле ^STEEL. XLS записаны данные о 100 заготовках. Они представляют собой разности между фактической и номинальной длинами заготовок, измеренные с помощью лазерной установки.
Являются ли эти данные значениями нормально распределенной случайной величины? Ответьте на этот вопрос, выполнив следующие задания.
1. Сравните характеристики фактического набора данных с теоретическими свойствами нормального распределения.
2. Постройте график нормального распределения.
6.22. При производстве резиновых прокладок исходную массу сначала перемешивают, а затем нарезают на ленты. После этого резина загружается в литейные машины и разливается по формам. Веса (в граммах) резиновых прокладок приведены в файле ^RUBBER. XLS.
Источник: Pearn, W. L., and К. S. Chen, “Practical Implementation of the Process Capability Index Cpk”, Quality Engineering (1997) 9:p. 721-737.
Являются ли эти данные значениями нормально распределенной случайной величины?
1. Сравните характеристики фактического набора данных с теоретическими свойствами нормального распределения.
2. Постройте график нормального распределения.
6.23. В таблице приведена стоимость электроэнергии (в долларах), потребленной в 50 случайно выбранных двухквартирных домах на протяжении июля 2002 года. Futility, xls.
96 171 202 178 147 102 153 197 127 82
157 185 90 116 172 111 148 213 130 163
141 149 206 175 123 128 144 168 109 167
95 163 150 154 130 143 187 166 139 149
108 119 183 151 114 135 191 137 129 158
Являются ли эти данные значениями нормально распределенной случайной величины?
1. Сравните характеристики фактического набора данных с теоретическими свойствами нормального распределения.
2. Постройте график нормального распределения.
6.3. РАВНОМЕРНОЕ РАСПРЕДЕЛЕНИЕ
Случайная величина имеет равномерное распределение, если вероятность того, что она принимает любое значение в интервале, ограниченном минимальным числом а и максимальным числом Ь, постоянна. Поскольку график плотности этого распределения имеет вид прямоугольника, равномерное распределение иногда называют прямоугольным (см. панель Б на рис. 6.1). Функция плотности равномерного распределения задается формулой (6.5).
ПЛОТНОСТЬ РАВНОМЕРНОГО РАСПРЕДЕЛЕНИЯ
/(X) ={!/(%) =
(6.5)
Ь-а
О в противном случае, где а — минимальное значение переменной X, b — максимальное значение переменной X.
Математическое ожидание равномерного распределения вычисляется по формуле (6.6).
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ РАВНОМЕРНОГО РАСПРЕДЕЛЕНИЯ
а + Ь
(6.6)
Дисперсия и стандартное отклонение равномерного распределения вычисляются по формулам (6.7, а) и (6.7, б) соответственно.
ДИСПЕРСИЯ РАВНОМЕРНОГО РАСПРЕДЕЛЕНИЯ
12
(6.7, а)
СТАНДАРТНОЕ ОТКЛОНЕНИЕ РАВНОМЕРНОГО РАСПРЕДЕЛЕНИЯ
1(Ь-а)2
N 12
* (6.7,6)
Чаще всего равномерное распределение используется для выбора случайных чисел. При осуществлении простого случайного выбора (см. раздел 1.10) предполагается, что каждое число извлекается из генеральной совокупности, равномерно распределенной в интервале от О до 1. Вычислим вероятность извлечь случайное число, превышающее 0,10 и меньше 0,30.
График функции плотности равномерного распределения для а = 0 и b = 1 изображен на рис. 6.23. Общая площадь прямоугольника, ограниченного этой функцией, равна единице. Следовательно, этот график удовлетворяет требованию, согласно которому, площадь фигуры, ограниченной графиком плотности любого распределения, должна равняться единице. Площадь прямоугольника, заключенная между числами 0,10 и 0,30, равна произведению длин его сторон, т.е. 0,2 х 1 = 0,2. Итак,
Р(0,10 < X < 0,30) = 0,2 х 1 = 0,2.
0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0
Рис. 6.23. График функции плотности равномерного распределения для а = 0 и b = 1
| fM
I
I 1,0 j
I i
J_____I_____________I____I____I____L____I___L
0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0
Рис. 6.24. Вычисление вероятности P(0,10 < X < 0,30) для равномерного распределения при а = 0 и b = 1
Из формул (6.6) и (6.7) следует, что математическое ожидание, дисперсия и стандартное отклонение равномерного распределения при а = 0 и b = 1 вычисляются еле дующим образом.
а + h 0 + 1
Ц =------=-----= 0,5,
2 2
о2 = = --------— = — = 0,0833,
12 12 12
а = ^/0,0833 = 0,2887.
Итак, математическое ожидание равно 0,5, а стандартное отклонение 0,2887.
УПРАЖНЕНИЯ К РАЗДЕЛУ 63
Изучение основ
6.24. Предположим, что из генеральной совокупности, равномерно распределенной между а = 0 и b = 10, извлекаются случайные числа. Вычислите вероятности следующих событий.
1. Вычислите вероятность извлечь число, которое больше 5 и меньше 7.
2. Вычислите вероятность извлечь число, которое больше 2 и меньше 3.
3. Чему равно математическое ожидание?
4. Чему равно стандартное отклонение?
Применение понятий
6.25. Предположим, что время между двумя последовательными приходами клиентов в отделение банка в первой половине дня равномерно распределено в интервале от 0 до 120 с.
1. Вычислите вероятность того, что время между двумя приходами меньше 20 с.
2. Вычислите вероятность того, что время между двумя приходами больше 10 и меньше 30 с.
3. Вычислите вероятность того, что время между двумя приходами больше 35 с.
4. Чему равно математическое ожидание времени между двумя последовательными приходами клиентов?
5. Чему равно стандартное отклонение времени между двумя последовательными приходами клиентов?
6.26. На некоей атомной электростанции, расположенной на берегу океана, для охлаждения реактора используется морская вода. Нагретая вода возвращается обратно в океан. Предположим, что повышение температуры равномерно распределено в интервале от 10 до 25 °C.
1. Вычислите вероятность того, что температура воды поднимется меньше, чем на 20 °C .
2. Вычислите вероятность того, что температура воды поднимется больше, чем на 20, но меньше чем на 22 °C .
3. Предположим, что повышение температуры более чем на 18"С представляет потенциальную опасность для прилегающей акватории. Какова вероятность, что в любой момент времени температура воды повышена до опасных пределов?
4. Чему равно математическое ожидание повышения температуры воды?
5. Чему равно стандартное отклонение повышения температуры воды?
6.27. Предположим, что моменты отказов устройства для контроля за чистотой воздуха равномерно распределены в течение суток.
1. В зависимости от времени года светлое время суток может наступать не ранее 5:55 и заканчиваться не позднее 19:38. Какова вероятность того, что отказ оборудования устройства произойдет в течение светлого времени суток?
2. Допустим, что с 22:00 до 5:00 устройство переходит в режим пониженного энергопотребления. Какова вероятность того, что отказ произойдет в указанный период времени?
3. Предположим, что в состав устройства входит процессор, каждый час осуществляющий проверку работоспособности оборудования. Какова вероятность того, что отказ будет обнаружен не позднее, чем через 10 мин.?
4. Предположим, что в состав устройства входит процессор, каждый час осуществляющий проверку работоспособности оборудования. Какова вероятность того, что отказ будет обнаружен не раньше, чем через 40 мин.?
6.28. Допустим, что время соединения между клиентами кольцевой локальной сети распределено равномерно в интервале от 0 до 2 с.
1. Вычислите вероятность того, что время соединения меньше 0,6 с.
2. Вычислите вероятность того, что время соединения больше 0,4 с, но меньше 1,6 с.
3. Вычислите вероятность того, что время соединения больше 1,8 с.
4. Вычислите вероятность того, что время соединения больше 2 с.
5. Чему равно математическое ожидание времени соединения между клиентами?
6. Чему равно стандартное отклонение времени соединения между клиентами?
6.4. ЭКСПОНЕНЦИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
В разделе изучается экспоненциальное распределение (exponential distribution). Оно является непрерывным, имеет положительную асимметрию и изменяется от нуля до плюс бесконечности (см. рис. 6.1). Экспоненциальное распределение оказывается весьма полезным в деловых приложениях, особенно при моделировании производства и систем массового обслуживания. Оно широко используется в теории расписаний (очередей) для моделирования промежутков времени между двумя запросами, которые могут представлять собой приход клиента в банк или ресторан быстрого обслуживания, поступление пациента в больницу, а также посещение Web-сайта.
Экспоненциальное распределение зависит только от одного параметр^который обозначается буквой X и представляет собой среднее количество запросов, поступающих в систему за единицу времени. Величина 1 /X равна среднему промежутку времени, прошедшего между двумя последовательными запросами. Например, если в систему в среднем поступает 4 запроса в минуту, т.е. X = 4, то среднее время, прошедшее между двумя последовательными запросами, равно 1/Х = 0,25 мин., или 15 с. Вероятность того, что следующий запрос поступит раньше, чем через X единиц времени, определяется по формуле (6.8).
ЭКСПОНЕНЦИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
Р(вре.мя поступления запроса < X) = 1 - е~^ , (6.8)
где е — математическая константа, приближенно равная 2,71828, X — среднее количество запросов, поступающих в систему за единицу времени, X— произвольное значение непрерывной величины, 0 < X < оо .
Проиллюстрируем применение экспоненциального распределения следующим примером. Допустим, что в отделение банка приходят 20 клиентов в час. Предположим, что в банк уже пришел один клиент. Какова вероятность того, что следующий клиент придет в течение 6 мин. (т.е. 0,1 ч)?
В данном случае X = 20, а X = 0,1. Используя формулу (6.8), получаем:
Р(время прибытия < 0,1) = 1 - е~20х0,1 = 1 - е~2 = 1 - 0,1353 = 0,8647 .
Таким образом, вероятность, что следующий клиент придет в течение 6 мин., равна 0,8647, т.е. 86,47%.
Экспоненциальное распределение можно вычислить с помощью программы Microsoft Excel (рис. 6.25).
Рис. 6.25. Вычисление экспоненциального распределения с помощью программы Microsoft Excel
Процедуры Excel: вычисление экспоненциального распределения
Для создания рабочего листа, вычисляющего экспоненциальное распределение, следует воспользоваться функцией экспрасп. Надстройка PHStat2 создает такой лист автоматически.
Например, чтобы вычислить вероятности, приведенные на рис. 6.25, можно применить следующие процедуры.
Применение Excel в сочетании с надстройкой PHStat2
Для создания нового рабочего листа, вычисляющего экспоненциальное распределение, можно применить процедуру PHStat^Probability & Prob. Distributions^Exponential... (PHStat^ Вероятность & Распределения ^Экспоненциальное...), следуя инструкциям, приведенным ниже.
1. Выбрать пункт PHStat^Probability & Prob. Distributions^ Exponential....
2. В диалоговом окне Exponential Probability Distribution (см. иллюстрацию) сделать следующее.
2.1. Ввести в окне редактирования Mean per unit (lambda) (Среднее количество событий за единицу времени (лямбда)) число 20.
2.2. Ввести в окне редактирования X Value (Значение X) число 0.1.
2.3. Ввести в окне редактирования Title соответствующий заголовок.
2.4. Щелкнуть на кнопке ОК.
Применение Excel
Для создания рабочего листа, вычисляющего экспоненциальное распределение, воспользуйтесь указаниями, приведенными в разделе ЕН.6.3.
4^ Chapter 6.xls
Данные, на основе которых вычисляются экспоненциальные распределения, приведенные на рис. 6.25, содержатся в рабочей книге Chapter 6 на листе Рис6.25.
УПРАЖНЕНИЯ К РАЗДЕЛУ 6.4
Изучение основ
6.29. Рассмотрим экспоненциальное распределение при Z = 10. Вычислите вероятности следующих событий.
1. Время ожидания меньше X = 0,1.
2. Время ожидания больше X = 0,1.
3. Время ожидания больше X = 0,1 и меньше X = 0,2.
4. Время ожидания меньше X = 0,1 или больше X = 0,2.
6.30. Рассмотрим экспоненциальное распределение при Z = 30. Вычислите вероятности следующих событий.
1. Время ожидания меньше X = 0,1.
2. Время ожидания больше X = 0,1.
3. Время ожидания больше X = 0,1 и меньше X — 0,2.
4. Время ожидания меньше X = 0,1 или больше X = 0,2.
6.31. Рассмотрим экспоненциальное распределение при X = 20. Вычислите вероятности следующих событий.
1. Время ожидания меньше X = 0,4.
2. Время ожидания больше X = 0,4.
3. Время ожидания больше X = 0,4 и меньше X = 0,5.
4. Время ожидания меньше X = 0,4 или больше X = 0,5.
Применение понятий
6.32. С 5 до 6 вечера через контрольно-пропускной пункт, расположенный при въезде на мост, проезжают 50 автомобилей в минуту. Допустим, на мост уже въехал один автомобиль.
1. Какова вероятность, что следующий автомобиль въедет на мост в течение следующих 3 с (0,05 мин.)?
2. Какова вероятность, что следующий автомобиль въедет на мост в течение следующей секунды (0,0167 мин.)?
3. Как изменятся ответы на вопросы 1 и 2, если через мост проезжают 60 авто-' мобилей в минуту?
4. Как изменятся ответы на вопросы 1 и 2, если через мост проезжают 30 автомобилей в минуту?
6.33. К окошку ресторана быстрого обслуживания в часы ленча подходят в среднем два клиента в минуту. Допустим, к окошку уже подошел один клиент.
1. Какова вероятность, что в течение следующей минуты придет еще один клиент?
2. Какова вероятность, что следующий клиент придет в течение 5 мин.?
3. Во время обеда поток клиентов снижается и равен одному клиенту в минуту. Как изменятся ответы на вопросы 1 и 2?
6.34. В справочную систему крупной компьютерной компании поступают 15 телефонных звонков в минуту.
1. Какова вероятность, что следующий телефонный звонок поступит в течение 3 мин. (0,05 ч)?
2. Какова вероятность, что следующий телефонный звонок поступит в течение 15 мин. (0,25 ч)?
3. Допустим, что компания обновила свои программы, и теперь количество телефонных звонков, поступающих в ее справочную систему, увеличилось до 25 в минуту. Как изменятся ответы на вопросы 1 и 2?
6.35. В среднем на автомобильном заводе за 10 дней происходит один несчастный случай.
1. Какова вероятность, что следующий несчастный случай произойдет в течение 10 дней?
2. Какова вероятность, что следующий несчастный случай произойдет в течение 5 дней?
3. Какова вероятность, что следующий несчастный случай произойдет завтра?
6.36. В среднем на электростанции за 20 дней происходит один сбой.
1. Какова вероятность, что следующий сбой произойдет в течение 14 дней?
2. Какова вероятность, что в ближайшие 21 день сбоев не будет?
3. Какова вероятность, что сбой произойдет в ближайшую неделю?
6.37. В течение уик-энда на контрольно-пропускной пункт гольф-клуба приходят 8 игроков в час. Допустим, что в клуб уже пришел один игрок.
1. Какова вероятность, что следующий игрок придет в течение ближайших 15 мин. (0,25 ч)?
2. Какова вероятность, что следующий игрок придет в течение ближайших 3 мин. (0,05 ч)?
3. Допустим, что в пятницу в гольф-клуб приходят 15 игроков в час. Как изменятся ответы на вопросы 1 и 2?
ПРИМЕНЕНИЕ СТАТИСТИКИ
Процесс расфасовки кукурузных хлопьев
На заводе компании Oxford Cereal Company за 8-часовую смену заполняются тысячи коробок с кукурузными хлопьями. Представьте себе, что вы — управляющий этого завода и отвечаете за процесс расфасовки кукурузных хлопьев по коробкам. Предполагается, что коробка содержит в среднем 368 г хлопьев. Поскольку процедура заполнения коробки выполняется очень быстро, вес некоторых коробок может отклоняться от номинального. Если процесс осуществляется неправильно, это отклонение становится слишком боль
шим. Каждую коробку взвесить невозможно, поэтому для взвешивания создается
определенная выборка коробок и вычисляется их средний вес X . Необходимо оценить вероятность того, что выборочный средний вес можно считать средним весом коробки во всей генеральной совокупности, математическое ожидание которой равно 368 г. Основываясь на этих результатах, можно оценить качество упаковки и принять соответствующие меры.
6.5. ВВЕДЕНИЕ В ВЫБОРОЧНЫЕ РАСПРЕДЕЛЕНИЯ
Основной целью анализа данных являются статистические выводы, т.е. применение выборочных показателей для оценки параметров генеральной совокупности. Статистические выводы относятся к генеральным совокупностям, а не к выборкам из них. Например, социологи изучают результаты выборочных обследований только для того, чтобы оценить шансы кандидатов получить голоса из всей генеральной совокупности избирателей в целом. Аналогично менеджера компании Oxford Cereal Company выборочные показатели интересуют лишь потому, что они позволяют сделать выводы о среднем весе коробок во всей генеральной совокупности. Выборочное среднее, полученное при обследовании конкретной выборки, само по себе интереса не представляет.
На практике из генеральной совокупности извлекается выборка заранее установленного объема. Элементы, принадлежащие данной выборке, выбираются случайным образом, например, с помощью датчика или таблицы случайных чисел (см. раздел 1.10 и табл. Д.1).
Гипотетически, чтобы по выборочным характеристикам сделать вывод о параметрах генеральной совокупности, необходимо оценить все возможные выборки. Распределения выборочных параметров называют выборочными.
6.6. ВЫБОРОЧНОЕ РАСПРЕДЕЛЕНИЕ СРЕДНИХ ЗНАЧЕНИЙ
В главе 3 мы рассмотрели несколько оценок математического ожидания распределения. Чаще всего для этого используется арифметическое среднее. Это наилучшая оценка математического ожидания, если распределение является нормальным.
Несмещенные свойства арифметического среднего
Арифметическое среднее называется несмещенным (unbiased), поскольку среднее значение всех выборочных средних (при заданном объеме выборки п) равно математическому ожиданию генеральной совокупности. Продемонстрируем это свойство на следующем примере. Предположим, что генеральная совокупность машинисток в секретариате компании состоит из четырех сотрудниц. Каждую из них попросили напечатать один и тот же текст. Количество опечаток, сделанных каждой машинисткой, приведено в табл. 6.9.
Таблица 6.9. Количество опечаток, сделанных каждой из четырех машинисток
Машинистка Количество опечаток
Энн Х1 = 3
Кэт Х2=2
Карла Х3= 1
Ширли Х4=4
Распределение ошибок приведено на рис. 6.26.
Рис. 6.26. Количество ошибок, сделанных четырьмя машинистками
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ
Математическим ожиданием генеральной совокупности называется сумма всех значений совокупности, деленная на ее объем:
где ц — математическое ожидание генеральной совокупности, N — объем генераль-V
ной совокупности, X,— i-й элемент генеральной совокупности, — сумма всех /=1
элементов генеральной совокупности.
СТАНДАРТНОЕ ОТКЛОНЕНИЕ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ
Стандартным отклонением генеральной совокупности называется корень квадрат-
ный из ее дисперсии:
(6.10)
Таким образом, для данных, приведенных в табл. 6.9, имеем:
3 + 2 +1 + 4
ц =---------= 2,5 опечатки.
4
1(3 - 2,5)2 + (2 - 2,5)2 + (1 - 2,5)2 + (4 - 2,5)2
о = 4 ---------------------------------------= 1,12 опечатки.
V 4
Если из этой генеральной совокупности необходимо извлечь без возвращения выборку, состоящую из двух машинисток, возникает 16 вариантов выбора (Nm= 42=16). Эти варианты приведены в табл. 6.10. Если усреднить все 16 средних значений, мы получим величину , равную математическому ожиданию генеральной совокупности ц, т.е. числу 2,5.
Таблица 6.10. Все 16 вариантов выбора двух машинисток из четырех с возвращением
Выборка Машинистки Количество опечаток Среднее значение
1 Энн, Энн 3, 3 и со
2 Энн, Кэт 3, 2 X, = 2,5
3 Энн, Карла 3, 1 Х3 = 2
4 Энн, Ширли 3, 4 Х4 = 3,5
5 Кэт, Энн 2, 3 Х5 = 2,5
6 Кэт, Кэт 2, 2 А = 2
7 Кэт, Карла 2, 1 Х7 = 1,5
8 Кэт, Ширли 2, 4 У8 = 3
Окончание табл. 6.10
Выборка Машинистки Количество опечаток Среднее значение
9 Карла, Энн 1, з Х9 = 2
10 Карла, Кэт 1, 2 Х10=1,5
11 Карла, Карла 1, 1 Хн=1
12 Карла, Ширли 1, 4 %12 = 2,5
13 Ширли, Энн 4, 3 %13 = 3,5
14 Ширли, Кэт 4, 2 *14 = 3
15 Ширли, Карла 4, 1 Х15 = 2,5
16 Ширли, Ширли 4, 4 *16 = 4
Мл.=2,5
Итак, среднее значение всех выборочных средних ц- равно математическому ожиданию генеральной совокупности. Следовательно, хотя нам неизвестно, насколько хорошо конкретное выборочное среднее аппроксимирует математическое ожидание генеральной совокупности, среднее значение всех выборочных средних совпадает со математическим ожиданием генеральной совокупности.
Стандартная ошибка среднего
На рис. 6.27 приведено выборочное распределение среднего количества ошибок, сделанных машинистками, образующих все 16 возможных выборок, полученных путем случайного выбора с возвращением. Как видим, колебание выборочных средних вокруг математического ожидания генеральной совокупности меньше, чем колебание исходных данных. Этот факт непосредственно следует из закона больших чисел (law of large number). Исходная генеральная совокупность может содержать числа, которые являются как очень большими, так и очень маленькими. Однако, если экстремальное значение попадет в выборку, ее влияние на среднее значение будет ослаблено, поскольку оно будет просуммировано со всеми остальными элементами выборки. При увеличении объема выборки влияние экстремальных значений ослабевает, поскольку в усреднении принимает участие все большее количество элементов.
Рис. 6.27. Выборочное распределение среднего количества ошибок, сделанных двумя машинистками
Диапазон изменения выборочных средних описывается их стандартным отклонением. Эта величина называется стандартной ошибкой среднего (standard error of the mean) и обозначается как q- .
СТАНДАРТНАЯ ОШИБКА СРЕДНЕГО ПРИ ВЫБОРЕ БЕЗ ВОЗВРАЩЕНИЯ
Стандартная ошибка среднего су- равна стандартному отклонению генеральной совокупности о, деленному на квадратный корень из объема выборки п:
<зх=-^=. (6.11)
Следовательно, при возрастании объема выборки п стандартная ошибка среднего уменьшается со скоростью, пропорциональной квадратному корню из п. Мы еще вернемся к исследованию этого соотношения между стандартной ошибкой среднего и объемом выборки в главе 7.
Кроме того, формулу (6.11) можно применять для аппроксимации стандартной ошибки среднего, если выборки извлекаются из генеральной совокупности без возвращения при условии, что каждая выборка содержит не более 5% элементов всей генеральной совокупности. Проиллюстрируем это свойство следующим примером. (Вариант, когда объем выборки, извлеченной из генеральной совокупности без возвращения, содержит более 5% элементов, рассмотрен в разделе 6.9.)
ПРИМЕР 6.9. ВЫЧИСЛЕНИЕ СТАНДАРТНОЙ ОШИБКИ СРЕДНЕГО
Вернемся к сценарию, описанному в начале раздела. Если из нескольких тысяч коробок случайным образом извлекается без возвращения выборка из 25 коробок, в нее попадет не более 5% элементов всей генеральной совокупности. Вычислите стандартную ошибку среднего, если стандартное отклонение веса коробки равно 15 г.
РЕШЕНИЕ. Применяя формулу (6.11) для п = 25и о =15, получаем стандартную ошибку среднего:
у 15
и V25 5
Обратите внимание на то, что изменчивость выборочных средних намного меньше, чем изменчивость исходных данных (т.е. о- - 3 намного меньше, чем о = 15).
Выборки из нормально распределенных генеральных совокупностей
Введя понятие выборочных распределений и дав определение стандартной ошибки среднего, мы можем ответить на вопрос, как распределены выборочные средние X . Можно доказать, что если выборки извлекаются с возвращением из нормально распределенной генеральной совокупности, математическое ожидание которого равно щ а стандартное отклонение — о, то выборочное распределение средних (sampling distribution of the mean) также является нормальным при любом объеме выборок п, причем ц - = ц , а стандартная ошибка— .
В наиболее простом варианте, когда объем каждой выборки равен единице, каждое среднее значение равно единственному элементу выборки.
Следовательно, если генеральная совокупность является нормально распределенной, причем ее математическое ожидание равно ц, а стандартное отклонение — ст, то выборочное распределение средних также является нормальным при п = 1, причем ц- = ц , а стандартная ошибка стх, = ст/л/1 =ст . Обратите внимание на то, что при увеличении объема выборок выборочное распределение средних остается нормальным, причем ц _ = ц . Однакс увеличение объема выборки приводит к уменьшению стандартной ошибки среднего, поэтому чем больше становится выборка, тем ближе становятся выборочные средние к математическому ожиданию генеральной совокупности. В этом можно убедиться, проанализировав рис. 6.28. На нем изображены выборочные распределения среднего, построенные по 500 выборкам с объемами п = 1, 2, 4, 8, 16 и 32, случайным образом извлеченным иг нормально распределенной генеральной совокупности. Полигоны, изображенные на рис. 6.28, свидетельствуют от том, что выборочное распределение средних является лишь приближенно нормальным.9 Однако по мере возрастания объема выборок выборочные средние становятся ближе к математическому ожиданию генеральной совокупности.
Чтобы глубже разобраться в понятии выборочного распределения, вернемся к сценарию, описанному в начале раздела. Предположим, что упаковочная машина, заполняющая 368-граммовые коробки (т.е. коробки, вмещающие 13 унций), настроена так, что количество кукурузных хлопьев, засыпанных в мешки, распределено нормально, причем среднее значение распределения равно 368 г. Измерения показали, что стандартное отклонение веса коробок равно 15 г.
Допустим, что из многих тысяч коробок, заполненных за день, наугад выбираются 25 коробок и вычисляется их средний вес. Следует ли ожидать, что выборочный средний вес окажется равным 368 г? А может быть, он будет равен 200 г или 365 г?
Выборка является миниатюрной моделью генеральной совокупности, поэтому если исходная генеральная совокупность распределена нормально, выборка из нее должна быть приближенно нормальной. Следовательно, если математическое ожидание генеральной совокупности равно 368 г, выборочное среднее также должно быть близким к 368 г.
Продолжая наши рассуждения, зададимся вопросом, как вычислить вероятность того, что выборочное среднее, полученное для выборки объемом п = 25, окажется меньше 365 г. Из свойств нормального распределения следует, что площадь, отсекаемая каждым значением случайной величины X от фигуры, ограниченной гауссовой кривой, можно вычислить, преобразовав стандартизованную нормальную случайную величину Z и определив соответствующее значение по таблице нормального распределения (табл. Д.2).
z = ^. ст
В примерах, рассмотренных в разделе 6.1, мы проанализировали, как отдельные значения X колеблются вокруг среднего. Теперь этими значениями являются средние значения X , и мы можем оценить вероятность того, что выборочное среднее, полученное для выборки объемом п = 25, окажется меньше 365 г. Подставляя в приведенную выше формулу величину X вместо X, величину вместо ц и величину ст? вместо ст, получаем формулу (6.12).
Учтите, что из бесконечной генеральной совокупности извлечено лишь 500 выборок, поэтому полученное распределение в принципе не может быть абсолютно нормальным.
Рис. 6.28. Выборочные распределения средних, построенные по 500 выборкам с объемами п = 1, 2, 4, 8, 16 и 32, извлеченным из нормально распределенной генеральной совокупности
ОПРЕДЕЛЕНИЕ ВЕЛИЧИНЫ гДЛЯ ВЫБОРОЧНОГО РАСПРЕДЕЛЕНИЯ СРЕДНИХ
Величина Z равна разности между выборочным средним X и математическим ожиданием генеральной совокупности ц, деленной на стандартную ошибку среднего.
Z =
(6.12)
Обратите внимание на то, что благодаря несмещенности величина pv всегда равна ц. Таким образом, значение величины Z, соответствующее вероятности того, что выборочное среднее, полученное для выборки объемом п = 25, окажется меньше 365 г, равна
2 = £^ = 365-368 = -3
15 3
V25
В табл. Д.2 значению Z= -1,0 соответствует площадь 0,1587. Следовательно, выборочное среднее 15,87% всех возможных выборок, имеющих объем п = 25, не превосходит 365 г. Это не значит, что вес 15,87% элементов выборок не превосходит 365 г. Долю таких элементов можно вычислить по следующей формуле.
г = £-ц = 365-368 = -3 а 15 3
В табл. Д.2 значению Z= -0,02 соответствует площадь 0,4207. Следовательно, в каждой выборке, имеющей объем п = 25, вес 42,07% коробок не превосходит 365 г. Это можно объяснить тем, что каждая выборка состоит из 25 разных значений, некоторые из которых велики, а некоторые — малы. Процедура усреднения ослабляет влияние отдельных элементов, особенно при увеличении объема выборки. Таким образом, вероятность того, что выборочное среднее, вычисленное по выборке, состоящей из 25 коробок, будет значительно отличаться от математического ожидания генеральной совокупности, меньше вероятности, что вес отдельных элементов значительно отличается от этого значения.
ПРИМЕР 6.10. ВЛИЯНИЕ ОБЪЕМА ВЫБОРКИ п НА СТАНДАРТНОЕ ОТКЛОНЕНИЕ ВЫБОРОЧНОГО СРЕДНЕГО с -
Увеличим объем выборки с 25 до 100. Как изменится стандартное отклонение выборочного среднего?
РЕШЕНИЕ. Если п = 100, то
ст 15 15
(5 у = —'= = —,= =-= 1,5.
лМ >/100 10
Обратите внимание на то, что четырехкратное увеличение объема выборки приводит к уменьшению стандартного отклонения выборочного среднего вдвое — с 3 г до 1,5 г. Это значит, что, извлекая из генеральной совокупности выборки большего объема, мы обнаружим меньшую изменчивость выборочного среднего.
ПРИМЕР 6.11. ВЛИЯНИЕ ОБЪЕМА ВЫБОРКИ л НА КОНЦЕНТРАЦИЮ СРЕДНИХ ЗНАЧЕНИЙ В ВЫБОРОЧНОМ РАСПРЕДЕЛЕНИИ
Увеличим объем выборки с 25 до 100. Как изменится вероятность того, что выборочное среднее, полученное для выборки объемом п = 25, окажется меньше 365 г?
РЕШЕНИЕ. Используя формулу (6.12), получаем:
z = = 365-368 = -3
а. 15 1,5
л/loo
В табл. Д.2 значению Z = -2,00 соответствует площадь 0,0228. Следовательно, в каждой выборке, имеющей объем п = 100, вес 2,28% мешков не превосходит 365 г. Напомним, что для выборок, имеющих объем п = 25, эта вероятность была равна 15,87%.
Иногда необходимо найти интервал, в котором лежит фиксированная часть элементов выборки или выборочных средних. Как и в разделе 6.1, в этом случае необходимо вычислить расстояние от математического ожидания генеральной совокупности, которому соответствует заданная площадь фигуры, ограниченной гауссовой кривой. Воспользуемся формулой (6.12).
а
Следовательно, величину X можно вычислить по формуле (6.13).
ОПРЕДЕЛЕНИЕ X
X = \x + Z-^=. (6.13)
Проиллюстрируем применение этой формулы следующим примером.
ПРИМЕР 6.12. ОПРЕДЕЛЕНИЕ ИНТЕРВАЛА, СОДЕРЖАЩЕГО ЗАДАННУЮ ЧАСТЬ ВЫБОРОЧНЫХ СРЕДНИХ
Найдите интервал, в котором лежат 95% всех выборочных средних, вычисленных по выборкам, состоящим из 25 коробок с кукурузными хлопьями.
РЕШЕНИЕ. Интервал, содержащий 95% всех выборочных средних, вычисленных по выборкам, имеющим объем п = 25, делится на две равные части. Первая часть лежит слева от математического ожидания генеральной совокупности, а вторая — справа. Значение величины Z, соответствующей площади 0,0250, равно -1,96, а значение величины Z, соответствующей суммарной площади 0,975, равно +1,96 (см. табл. Д.2). Нижняя и верхняя границы величины X определяются по формуле (6.13).
X, = 368 + (-1,96)4^= = 368 - 5,88 = 362,12,
' 7а/25
Хи = 368 +1,96-IL = 368 + 5,88 = 373,88.
725
Следовательно, 95% всех выборочных средних, вычисленных по выборкам, имеющим объем п = 25, лежат в интервале от 362,12 г до 373,88 г.
Выборки из генеральных совокупностей, распределения которых отличаются от нормального
До сих пор мы рассматривали выборочное распределение средних для нормально распределенной генеральной совокупности. Однако во многих ситуациях распределение генеральной совокупности либо неизвестно, либо заведомо отличается от нормального. Таким образом, следует рассмотреть выборочное распределение средних для генеральной совокупности, распределение которой отличается от нормального. Этот анализ приводит нас к основной теореме статистики — центральной предельной теореме.
Центральная предельная теорема (central limit theorem) утверждает, что при достаточно большом объеме выборок выборочное распределение средних можно аппроксимировать нормальным распределением. Это свойство не зависит от вида распределения генеральной совокупности.
Какой объем выборок следует считать “достаточно большим”? Этот вопрос изучался во многих статистических исследованиях. Как правило, для подавляющего большинства генеральных совокупностей выборочное распределение средних становится приближенно нормальным при п = 30. Однако, если известно, что распределение генеральной совокупности является колоколообразным, эту теорему можно применять и для меньшего объема выборок. Если же распределение генеральной совокупности обладает сильной асимметрией или имеет несколько мод, объем выборок следует увеличить.
Применение центральной предельной теоремы к различным генеральным совокупностям проиллюстрировано на рис. 6.29.
На рис. 6.29, панель А, показано выборочное распределение средних, построенное для генеральной совокупности, имеющей нормальное распределение. Как указывалось выше, если генеральная совокупность является нормально распределенной, выборочное распределение средних также является нормальным, независимо от объема выборок. При увеличении объема выборок изменчивость выборочных средних уменьшается. Поскольку выборочное среднее является несмещенной оценкой, среднее выборочных средних всегда совпадает с математическим ожиданием генеральной совокупности.
На рис. 6.29, панель Б, показано выборочное распределение средних, построенное для генеральной совокупности, имеющей равномерное распределение. При п = 2 центральная предельная теорема остается справедливой. При п = 5 выборочное распределение средних является приближенно нормальным. При п = 30 выборочное распределение средних становится практически нормальным. В общем, чем больше объем выборки, тем ближе выборочное распределение средних к нормальному. В любом случае среднее выборочных средних всегда совпадает с математическим ожиданием генеральной совокупности, а его изменчивость при увеличении объема выборок уменьшается.
На рис. 6.29, панель В, показано выборочное распределение средних, построенное для генеральной совокупности, имеющей экспоненциальное распределение. Это распределение имеет ярко выраженную положительную асимметрию. При п = 2 асимметрия выборочного распределения средних сохраняется, но выражена слабее. При п = 5 выборочное распределение средних становится почти симметричным со слабой положительной асимметрией. При п = 30 выборочное распределение средних становится приближенно нормальным. В любом случае среднее выборочных средних всегда совпадает с математическим ожиданием генеральной совокупности, а его изменчивость при увеличении объема выборок уменьшается.
Свойства выборочного распределения средних перечислены во врезке 6.5.
ВРЕЗКА 6.5. СВОЙСТВА ВЫБОРОЧНОГО РАСПРЕДЕЛЕНИЯ СРЕДНИХ
• Если объем выборок превышает 30, выборочное распределение средних для большинства генеральных совокупностей является приближенно нормальным.
• Если генеральная совокупность распределена симметрично, выборочное распределение средних становится приближенно нормальным уже при п = 15.
• Если генеральная совокупность является нормально распределенной, выборочное^ распределение средних является нормальным при любом объеме выборок.
Г енеральная совокупность
Генеральная совокупность
Значениях
Значения X
Панель А
Нормальное распределение
Панель Б Панель В
Равномерное распределение Экспоненциальное распределение
Рис. 6.29. Выборочное распределение средних для разных генеральных совокупностей при объемах выборок п = 2, 5 и 30
Visual Explorations: исследование выборочного распределения средних
Чтобы продемонстрировать распределение частот сумм очков, выпадающих на двух игральных кубиках, следует применить процедуру Two Dice Probability (Вероятность для двух кубиков) приложения Visual Explorations in Statistics. Для этого необходимо открыть книгу макросов visual Explorations. xla и выбрать команду Visual Exploration^ Two Dice Probability. Эта процедура создает рабочий лист, содержащий пустую таблицу распределения частот, гистограмму и всплывающую панель (см. иллюстрацию).
визад-г:,-».
ЧлпЬег of throws ICT per tally' '
U A А ’
Ж Ч Е Я :
s Формат Серак £анныг PHStat Qkho VisuaExpforations Справка
/ - ’i.a s ’ в <ioo% ’ e|
I % 000 38 48; 3* : ill - о ’ A ’ I
_ x
| Finish |
Е
F I. G : H
D
J
2
3
4
5
6
7
8 ’9
10
11
12 '13
14
15
16
17
Twos Threes Fours Fives Sixes Sevens Eights Nines Tens Elevens Twelves
0 0 О о о о о о о о о
Frequency Table
0 7 -
0 6 -
0 5 -
04 -
0 3 -
02 -
0 1 -
0 --
Twos Threes Fours Fives Sixes Sevens Eights Nines Tens Elevens Twelves
0 9 -
20
21
J
и 4
Чтобы заполнить таблицу распределения частот, следует щелкнуть на кнопке Tally (Счет), имитирующей серию испытаний и подсчет очков. В качестве альтернативы можно воспользоваться также кнопками счетчика, установив количество испытаний.
Подробную информацию пользователь может получить, щелкнув на кнопке Help (Справка). Чтобы завершить работу программы, щелкните на кнопке Finish (Готово).
Процедуры Excel: генерирование выборочного распределения средних
Чтобы создать рабочий лист, моделирующий выборочные распределения, следует воспользоваться процедурой СервисФАнализ данных... => Генератор случайных чисел, а затем добавить формулы, вычисляющие выборочные средние и другие показатели. После этого для создания гистограммы следует вызвать процедуру Сервис^Анализ данных...^Гистограмма. Надстройка PHStat2 выполняет эту процедуру автоматически.
Например, чтобы смоделировать выборочное распределение для равномерно распределенной генеральной совокупности, используя 100 выборок объема 30, необходимо открыть новый рабочий лист и выполнить следующие действия.
Применение Excel в сочетании с надстройкой PHStatZ
Если вы хотите создать рабочий лист, генерирующий выборочное распределение, необходимо сделать следующее.
1. Выбрать команду PHStatoSamplingoSampling Distributions Simulation.... (PHStat^ Выборг Моделирование выборочных распределений...).
2. В диалоговом окне Sampling Distributions Simulation (см. иллюстрацию) сделать следующее.
2.1. Ввести в окне редактирования Number of Samples (Количество выборок) число 100.
2.2. Ввести в окне редактирования Sample Size (Объем выборок) число 30.
2.3. Установить переключатель Distribution Options (Параметры распределения) в положение Uniform (Равномерное).
2.4. Ввести в окне редактирования Title соответствующий заголовок.
2.5. Установить флажок Histogram (Гистограмма).
2.6. Щелкнуть на кнопке ОК.
Sampling Distributions Simulation
- Data - ----
: Number of Samples: [Too
i Sample Size:
; - - Distribution Options - -...........
15 Uniform
II
!; Standardized Normal
C Discrete
>- Output Options - - —
; Title: [сгенерированное выборочное распределение i ! P Histogram
Help | |i OK.„.„„J| Cancel J
Чтобы построить выборочное распределение средних по 100 выборкам объема 30, извлеченным из стандартизованной нормально распределенной генеральной совокупности, необходимо в п. 2.2 установить переключатель Distribution Options (Параметры распределения) в положение Standardized Normal (Стандартизованное нормальное распределение). Для генерирования распределения выборочных средних по дискретно распределенной генеральной совокупности следует установить переключатель Distribution Options (Параметры распределения) в положение Discrete (Дискретное), открыть рабочий лист, содержащий таблицу величин /и Р(Х), и указать диапазон ячеек в окне редактирования X and Р(Х) Values Cell Range.
Применение Excel
Для моделирования выборочного распределения необходимо выполнить следующие действия.
Создание рабочего листа, содержащего несколько выборок. Для создания рабочего листа, содержащего в диапазоне Al :CV30 несколько случайных выборок, полученных с помощью процедуры Генератор случайных чисел, следуйте инструкциям из раздела ЕН.6.4. Создавая новый рабочий лист, модифицируйте его так, чтобы он вычислял выборочные средние и общее среднее. Для вы-
числения выборочных средних введите в ячейку А31 метку Выборочные средние:, в ячейку А32 - формулу =срзнач (А1 :А30), а затем скопируйте эту формулу во все 100 столбцов вплоть до ячейки CV32. Для вычисления общего среднего введите в ячейку АЗЗ метку Общее среднее:, а в ячейку А34 - формулу =СРЗНАЧ (32 : 32 ) .
При решении задач, в которых требуется генерировать несколько выборок, извлеченных из генеральной совокупности, имеющей стандартизованное нормальное или дискретное распределение, нужно дополнительно вычислять стандартную ошибку среднего. Для этого необходимо ввести в ячей-куКУЬ метку Стандартная ошибка среднего, а в ячейку 6 — формулу =СТАНДОТКЛОН(32:32). Создание гистограммы. Для создания гистограммы на основе выборочных средних, содержащихся в рабочем листе, следуйте инструкциям, приведенным в разделе ЕН.6.5.
А| Chapter 6.xls
Выборки и гистограмма распределения выборочных средних для равномерно распределенной генеральной совокупности содержатся в рабочей книге Chapter 6.xls на листах МБР и МВРГистограмма.
УПРАЖНЕНИЯ К РАЗДЕЛУ 6.6
Изучение основ
6.38. Рассмотрим выборку, имеющую объем п = 25, извлеченную из нормально распределенной генеральной совокупности, математическое ожидание которой равно 100, а стандартное отклонение — 10.
1. Вычислите вероятность того, что X < 95 .
2. Вычислите вероятность того, что 95 < X < 97,5 .
3. Вычислите вероятность того, что X >102,2 .
4. Вычислите вероятность того, что 99 < X <101.
5. Какому значению X соответствует вероятность Р(Х > X), равная 65% ?
6. Как изменятся ответы на вопросы 1-5, если объем выборки п = 16?
6.39. Рассмотрим выборку, имеющую объем п = 100, извлеченную из нормально распределенной генеральной совокупности, математическое ожидание которой равно 50, а стандартное отклонение — 5.
1. Вычислите вероятность того, что X < 47 .
2. Вычислите вероятность того, что 47 < X < 49,5 .
3. Вычислите вероятность того, что X > 51,1 .
4. Вычислите вероятность того, что 49 < X < 51 .
5. Какому значению X соответствует вероятность Р(Х > X), равная 35% ?
6. Как изменятся ответы на вопросы 1-5, если объем выборки п = 25?
Применение понятий
6.40. Для каждого из трех распределений, приведенных ниже, укажите тип распределения выборочных средних при п = 25.
1. Расходы на командировки в течение года.
2. Количество прогулов в 2003 году, совершенных сотрудниками крупной компании.
3. Объем годовых продаж бензина (в галлонах) на автозаправочной станции, расположенной в небольшом городке.
6.41. Ниже приведено количество прогулов (дней за год), совершенных шестью сотрудниками небольшой компании.
1 3 6 7 7 12
1. Извлеките из этой генеральной совокупности все возможные выборки, состоящие из двух сотрудников, применяя выбор без возвращения, и постройте распределение выборочных средних. Вычислите среднее арифметическоеt всех выборочных средних, а также математическое ожидание генеральной1 совокупности. Равны ли они между собой? Как называется это свойство?
2. Повторите упражнение 1, извлекая выборки, состоящие из 3 сотрудников.
3. Сравните распределения выборочных средних, построенные при решении задач 1 и 2. Какое распределение характеризуется меньшей изменчивостью? Почему?
4. Предположим, что при извлечении выборок применяется выбор с возвращением. Выполните упражнения 1-3. Какое распределение характеризуется меньшей изменчивостью? Почему?
6.42. Диаметры шариков для настольного тенниса, произведенных на большой фабрике, имеют приближенно нормальное распределение. Математическое ожидание этого распределения равно 1,30 дюймов, а стандартное отклонение — 0,04 дюйма.
1. Какова вероятность того, что диаметр случайно выбранного шарика меньше 1,28 дюйма?
2. Какова вероятность того, что диаметр случайно выбранного шарика лежит в интервале от 1,31 до 1,33 дюйма?
3. Между какими двумя значениями (симметрично расположенными относительно математического ожидания) лежат 60% диаметров шариков?
4. Чему равны математическое ожидание генеральной совокупности и стандартная ошибка среднего, вычисленные по большому количеству выборок, состоящих из 16 шариков?
5. Как распределены выборочные средние, вычисленные по большому количеству выборок, состоящих из 16 шариков?
6. Какая доля выборочных средних, вычисленных по большому количеству выборок, состоящих из 16 шариков, меньше 1,28 дюйма?
7. Какая доля выборочных средних, вычисленных по большому количеству выборок, состоящих из 16 шариков, лежит в интервале от 1,31 до 1,33 дюйма?
8. Между какими двумя значениями (симметрично расположенными относительно математического ожидания) лежат 60% выборочных средних?
9. Сравните ответы на задачи 1 и 6, а также 2 и 7. Объясните результаты сравнения.
10. Объясните разницу между ответами на вопросы 3 и 8.
11. Что более вероятно — диаметр отдельного шарика превысит 1,34 дюйма, выборочное среднее, подсчитанное по выборке, состоящей из 4 шариков, окажется больше 1,32, или выборочное среднее, подсчитанное по выборке, состоящей из 16 шариков, окажется больше 1,31? Обоснуйте свой ответ.
6.43. Биржевой сектор промышленных материалов в течение первого полугодия 2000 года имел очень плохие показатели. Средняя стоимость акции в этом секторе упала на 27% (“Business Bulletin”, The Wall Street Journal, July 20, 2000, p. Al). Предположим, что доходность акций распределена по нормальному закону, причем математическое ожидание равно -27%, а стандартное отклонение равно 15%.
1. Какова вероятность того, что доходность акции, наугад выбранной из этой генеральной совокупности, лежит в интервале от -32 до -22% ?
2. Какова вероятность того, что доходность акции, наугад выбранной из этой генеральной совокупности, лежит в интервале от -37 до -17% ?
3. Какова вероятность того, что доходность акции, наугад выбранной из этой генеральной совокупности, лежит в интервале от -47 до -7% ?
4. Какова вероятность того, что акция, наугад выбранная из этой генеральной совокупности, окупится, т.е. ее доходность равна 0,0% ?
5. Какая доля выборочных средних, вычисленных по большому количеству выборок, состоящих из 10 акций, лежит в интервале от -32 до -22% ?
6. Какая доля выборочных средних, вычисленных по большому количеству выборок, состоящих из 10 акций, лежит в интервале от -37 до -17% ?
7. Какая доля выборочных средних, вычисленных по большому количеству выборок, состоящих из 10 акций, лежит в интервале от -47 до -7% ?
8. Какая доля выборочных средних, вычисленных по большому количеству выборок, состоящих из 10 акций, равна 0,0%, т.е. выборка акций является самоокупаемой?
9. Сравните ответы на вопросы 1 и 5, 2 и 6, 3 и 7, а также 4 и 8. Объясните результаты сравнения.
6.44. Время, которое пользователи проводят, пользуясь электронной почтой, распределено по нормальному закону. Его математическое ожидание равно 8 мин., а стандартное отклонение — 2 мин.
1. Какая доля выборочных средних, вычисленных по большому количеству выборок, состоящих из 25 сеансов работы с электронной почтой, лежит в интервале от 7,8 до 8,2 с?
2. Какая доля выборочных средних, вычисленных по большому количеству выборок, состоящих из 25 сеансов работы с электронной почтой, лежит в интервале от 7,5 до 8 с?
3. Какая доля выборочных средних, вычисленных по большому количеству выборок, состоящих из 100 сеансов работы с электронной почтой, лежит в интервале от 7,8 до 8,2 с?
4. Объясните разницу между ответами на вопросы 1 и 3.
5. Какое событие более вероятно — продолжительность определенного сеанса работы с электронной почтой превышает Имин., выборочное среднее, вычисленное по большому количеству выборок, состоящему из 25 сеансов, превысит 9 мин. или выборочное среднее, вычисленное по большому количеству выборок, состоящему из 100 сеансов, превысит 8,6 мин.? Обоснуйте свой ответ.
6.45. Время, которое служащий банка затрачивает на одного клиента, распределено по нормальному закону. Его математическое ожидание равно 3,10 мин., а стандартное отклонение — 0,40 мин. Предположим, из генеральной совокупности извлечена выборка, состоящая из 16 клиентов.
1. Какова вероятность, что среднее время, которое затрачивается на обслуживание клиента, не меньше 3 мин.?
2. Допустим, вероятность того, что выборочное среднее, подсчитанное по выборке, состоящей из 16 клиентов, не превосходит некую продолжительность обслуживания, равна 85% . Вычислите эту величину.
3. Какие условия следует наложить на распределение генеральной совокупно- сти при решении задач 1 и 2? s
4. Допустим, вероятность того, что выборочное среднее, подсчитанное по выборке, состоящей из 64 клиентов, не превосходит некую продолжительность обслуживания, равна 85% . Вычислите эту величину.
5. Какие условия следует наложить на распределение генеральной совокупности при решении задачи 5?
6. Какое событие более вероятно— отдельный клиент обслуживается быстрее 2 мин., выборочное среднее, подсчитанное по выборке, состоящей из 16 клиентов, превышает 3,4 мин. или выборочное среднее, подсчитанное по выборке, состоящей из 64 клиентов, не превышает 2,9 мин.? Обоснуйте свой ответ.
6.46. Как сообщила газета New York Times (Laurie J. Flinn, “Tax Surfing”, The New York Times, March 25, 2002, CIO), среднее время загрузки домашней страницы Web-сайта www.irs.com, принадлежащего компании Internal Revenue Service, равно 0,8 с. Допустим, что время загрузки имеет нормальное распределение со стандартным отклонением, равным 0,2 с. Кроме того, предположим, что из генеральной совокупности извлекается выборка из 30 загрузок.
1. Какая доля выборочных средних не превышает 0,75 с?
2. Какая доля выборочных средних лежит в интервале от 0,70 до 0,90 с?
3. Между какими двумя значениями (симметрично расположенными относительно математического ожидания) лежат 80% выборочных средних?
4. Какую величину не превышают 90% всех выборочных средних?
В той же статье сообщалось, что среднее время загрузки домашней страницы Web-сайта www.hrblock.com, принадлежащего компании H&R Block, равно 2,5 с. Допустим, что время загрузки имеет нормальное распределение со стандартным отклонением, равным 0,5 с. Кроме того, предположим, что из генеральной совокупности извлекается выборка из 30 загрузок.
5. Какая доля выборочных средних не превышает 2,75 с?
6. Какая доля выборочных средних лежит в интервале от 2,70 до 2,90 с?
7. Между какими двумя значениями (симметрично расположенными относительно математического ожидания) лежат 80% выборочных средних?
8. Какую величину не превышают 90% всех выборочных средних?
9. Какие условия следует наложить на распределение генеральной совокупности при решении задач 1-8?
6.47. По данным Бюро переписи населения США, средний доход американской семьи в 2000 г. был равен 57 045 долл., а медиана дохода была равной 42 148 долл. (U.S. Census Bureau, “Money Income in the United States: 2000”, www. census . gov, September 2001). Изменчивость семейного дохода довольна велика, поскольку 10-й персентиль приближенно равен 10 600 долл., а 90-й персентиль— 111 600 долл., вто время как стандартное отклонение приближенно равно 25 000 долл. Предположим, что из генеральной совокупности семей извлекается случайная выборка, состоящая из 225 семей.
1. Какая доля выборочных средних не превышает 55 000 долл.?
2. Какая доля выборочных средних превышает 60 000 долл.?
3. Какая доля выборочных средних превышает 111 600 долл.?
4. Почему вероятность, вычисленная в задаче 3, настолько меньше 0,10, хотя 10% семей имеют доход, превышающий 111 600 долл.?
5. Можно ли применять для решения задач 1-3 метод, описанный в главе, если объем извлекаемых выборок равен 20?
6.48. Несмотря на то что первый квартал 2002 г. с деловой точки зрения оказался довольно мрачным, доля взаимных фондов, инвестировавших средства в золотодобывающие компании, возросла на 35,2% (“Stock Funds Perk Up in the First Quarter”, www.usatoday.com, April 4, 2002). Предположим, что распределение доходности взаимных фондов, инвестировавших средства в золотодобывающие компании в первом квартале 2002 года, является симметричным относительно значения 35,2%, причем его стандартное отклонение равно 20% . Допустим, что из генеральной совокупности таких взаимных фондов извлечены выборки, состоящие из 16 фондов.
1. Вычислите вероятность того, что выборочное среднее доходности не превышает 25%.
2. Вычислите вероятность того, что выборочное среднее доходности превышает 40%.
3. Вычислите вероятность того, что выборочное среднее доходности больше 25% и меньше 45% .
4. Между какими двумя значениями (симметрично расположенными относительно математического ожидания) лежат 80% выборочных средних?
5. Между какими двумя значениями (симметрично расположенными относительно математического ожидания) лежат 90% выборочных средних?
6. Между какими двумя значениями (симметрично расположенными относительно математического ожидания) лежат 95% выборочных средних?
6.7. ВЫБОРОЧНОЕ РАСПРЕДЕЛЕНИЕ ДОЛЕЙ
При анализе категорийных данных, принимающих одно из двух значений — мужчина или женщина, любит или не любит и т.д., — результаты часто обозначают единицами (да) и нулями (нет). Среднее значение, вычисленное по выборке, состоящей из п таких элементов, равно количеству единиц, деленному на п. Например, из пяти респондентов три человека предпочитают торговую марку А, а двое — торговую марку Б. Следовательно, выборка состоит из трех единиц и двух нулей. Суммируя элементы выборки и деля сумму на пять, получаем, что доля поклонников торговой марки А в данной выборке равна 0,60. Таким образом, для категорийных данных выборочное среднее нулей и единиц представляет собой выборочную долю рь некоторой характеристики, которой обладают элементы выборки.
ВЫБОРОЧНАЯ ДОЛЯ ПРИЗНАКА
X количество объектов, имеюгцих указанную характеристику , ..
А = — =---------------------------:--------------------• (6.14)
п размер выборки
Выборочная доля признака рк имеет особое свойство: она принимает значения от 0 до 1. Если все элементы выборки обладают одинаковыми характеристиками, то каждому из них присваивается единица, а выборочная доля признака также становится равной единице. Если только половина элементов выборки обладает интересующим нас свойством, им приписываются единицы, а остальные обозначаются нулями. В этом случае выборочная доля признака ps равна 0,5. Если ни один элемент выборки не обладает интересующим нас свойством, им приписываются нули. В этом случае выборочная доля признакаps равна нулю.
В то время как выборочное среднее является несмещенной оценкой математического ожидания генеральной совокупности ц, статистика ре является несмещенной оценкой доли признака р в генеральной совокупности. По аналогии с распределением выборочных средних можно ввести стандартную ошибку доли признака.
СТАНДАРТНАЯ ОШИБКА ДОЛИ ПРИЗНАКА
V п
Если выборка извлекается из конечной генеральной совокупности без возвращения, выборочное распределение доли признака подчиняется биномиальному закону (см. раздел 5.3). Однако, если значения пр и п(1-р) больше 4 (см. раздел 6.8), это распределение можно аппроксимировать нормальным. При статистическом анализе долей признака объем выборки играет очень важную роль [1]. Следовательно, во многих ситуациях для оценки выборочного распределения доли признака можно использовать нормальное распределение. Таким образом, в формуле (6.12) величину X можно заменить величи-1р(1-р) „ а
ноирй, величину р — величиной ц, а величину , --— — величиной -=.
V п у/п
РАЗНОСТЬ МЕЖДУ ВЫБОРОЧНОЙ ДОЛЕЙ ПРИЗНАКА И ДОЛЕЙ ПРИЗНАКА В ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ
Z= ,Р' ~Р—. (6.16)
рв-р)
N п
Проиллюстрируем выборочное распределение доли признака следующим примером. Предположим, что менеджер местного отделения банка выяснил, что 40% всех вкладчиков имеют в банке несколько счетов. Если создать выборку из 200 вкладчиков, то можно вычислить вероятность того, что выборочная доля вкладчиков, имеющих несколько счетов, не превосходит 0,30.
Поскольку пр = 200x0,40 = 80 > 5 и п(1-р) = 200x0,60 = 120 > 5, выборочное распределение доли вкладчиков практически совпадает с нормальным. Применим формулу (6.16):
рх-р 0,30-0,40 -0,10 -0,10 ? 89
1р(1-р) ~ /0,40x0,60 ~ /0,24 ~ 0,0346 ~ N и V 200 V 200
В табл. Д.2 значению Z = -2,89 соответствует площадь 0,0019. Следовательно, вероятность того, что доля вкладчиков, имеющих несколько счетов, не превосходит 0,30, равна 0,0019, т.е. крайне маловероятна. Это значит, что если истинная доля таких вкладчиков в генеральной совокупности равна 0,40, их доля в 1/5 одного процента выборок, состоящих из 200 вкладчиков, окажется меньше 0,30.
УПРАЖНЕНИЯ К РАЗДЕЛУ 67
Изучение основ
6.49. В случайной выборке, состоящей из 64 человек, 48 классифицированы как “успешные”. Предположим, что доля успехов в генеральной совокупности равна 0,70.
1. Вычислите выборочную долю успехов ps.
2. Вычислите стандартную ошибку этой выборочной доли.
6.50. Для телефонного опроса случайным образом выбраны 50 семей. Им задали вопрос: “Имеете ли вы DVD-плейер?”. Пятнадцать человек ответили “Да” и 35 — “Нет”. Предположим, что доля признака в генеральной совокупности равна 0,40.
1. Вычислите выборочную долюрх владельцев DVD-плейеров.
2. Вычислите стандартную ошибку этой выборочной доли.
6.51. Ниже приведены необработанные результаты опроса 40 студентов (Y — да, N — нет). Им задавали вопрос: “Владеете ли вы какими-либо акциями?”.
NNYNNYNYNYNNYNYYNNNY
NYNNNNYNNYYNNNYNNYNN
Предположим, что доля признака в генеральной совокупности равна 0,30.
1. Вычислите выборочную долюрк студентов, владеющих акциями.
2. Вычислите стандартную ошибку этой выборочной доли.
Применение понятий
6.52. Для выявления предпочтений избирателей социологи провели выборочный опрос. Предположим, что на предстоящих выборах выдвинуты два кандидата. Фаворитом считается кандидат, набравший 55% голосов избирателей, принявших участие в опросе. Выборка состоит из 100 наугад выбранных избирателей.
1. Какова вероятность того, что кандидат станет фаворитом опроса, если на самом деле за него собираются голосовать 50,1% избирателей?
2. Какова вероятность того, что кандидат станет фаворитом опроса, если на самом деле за него собираются голосовать 60% избирателей?
3. Какова вероятность того, что кандидат станет фаворитом опроса, если на самом деле за него собираются голосовать 49% избирателей (т.е. фактически оь проиграет выборы)?
4. Увеличим объем выборки до 400. Как изменятся ответы на вопросы 1-3/ Обоснуйте свой ответ.
6.53. В ходе маркетингового эксперимента студентов просят попробовать два безалкогольных напитка и определить их марку. Случайные выборки состоят из 200 наугад выбранных студентов. Предполагается, что студентам не известен ни один из напитков. (Подсказка', если человек никогда не пробовал ни один из напитков, значит, он делает выбор наугад.)
1. Какова доля выборок, в которых количество правильных ответов колеблется между 50 и 60% ?
2. Между какими двумя процентными долями правильных ответов в генеральной совокупности (симметрично расположенными относительно математического ожидания) лежат 90% выборочных процентных долей правильных ответов?
3. Какова вероятность, что процент правильных ответов в выборке больше 65% ?
4. Какое из следующих событий наиболее вероятно — в выборке, состоящей из 200 студентов, фиксируется более 60% правильных ответов, или в выборке, состоящей из 1 000 студентов, фиксируется более 50% ответов? Обоснуйте свой ответ.
6.54. Приблизительно 5% семей в США обладают капиталом, объем которого превышает один млн. долл. Однако 30% из 31 000 сотрудников компании Microsoft также являются миллионерами (Wetlanfer, S., “Who Want$ to Manage a Millionaire?” Harvard Business Review, July-August, 2000, p. 53-60). Предположим, что выборки состоят из 100 случайно выбранных сотрудников Microsoft.
1. Какова доля выборок, в которых количество миллионеров колеблется между 25 и 35% ?
2. Какова доля выборок, в которых количество миллионеров колеблется между 20 и 40% ?
3. Какова доля выборок, в которых количество миллионеров превышает 40% ?
4. Как изменятся ответы на вопросы 1-3, если объемы выборок равны 50?
6.55. Приблизительно 58,3% из 222 900 семей в городке Монтгомери-Каунти выписывают воскресный выпуск газеты Dayton Daily News (Hudson, E.D., “Market Profile: Dayton, Ohio”, Media Week, July 17, 2000, p. 16-24). Предположим, что выборки состоят из 200 случайно выбранных семей, проживающих в Монтгомери-Каунти.
1. Какова доля выборок, в которых количество подписчиков газеты Dayton Daily News колеблется между 55 и 60% ?
2. Какова доля выборок, в которых количество подписчиков газеты Dayton Daily News колеблется между 50 и 65% ?
3. Какова доля выборок, в которых количество подписчиков газеты Dayton Daily News не превышает 45% ?
4. Как изменятся ответы на вопросы 1-3, если объемы выборок равны 100?
6.56. Приблизительно 19% населения США слушают радиопередачи в Интернет (Gardyn, R., “High Frequency”, American Demographics, July, 2000, p. 32-36). Предположим, что выборки состоят из 200 случайно выбранных людей.
1. Какова доля выборок, в которых количество радиослушателей колеблется между 14 и 24% ?
2. Какова доля выборок, в которых количество радиослушателей колеблется между 9 и 29% ?
3. Какова доля выборок, в которых количество радиослушателей превышает 30% ?
4. Как изменятся ответы на вопросы 1-3, если объемы выборок равны 100?
6.57. Интерактивное обслуживание клиентов является ключевым пунктом электронной розничной торговли. По данным компании WSJ Market Data Group, приблизительно 37,5% посетителей сайта www. priceline . com пользуются интерактивными услугами (“Reality Bytes”, The Wall Street Journal, June 5, 2000, p. C2). Предположим, что выборки состоят из 200 случайно выбранных клиентов.
1. Какова доля выборок, в которых количество потребителей интерактивных услуг колеблется между 35 и 40% ?
2. Между какими двумя процентными долями потребителей интерактивных услуг в генеральной совокупности (симметрично расположенными относительно математического ожидания) лежат 90% выборочных процентных долей?
3. Между какими двумя процентными долями потребителей интерактивных услуг в генеральной совокупности (симметрично расположенными относительно математического ожидания) лежат 95% выборочных процентных долей?
6.58. По данным Национальной ассоциации владельцев ресторанов, в 20% ресторанов высокого класса использование мобильных телефонов запрещено (“Business Bulletin”, The Wall Street Journal, June 1, 2000, p. Al). Предположим, что выборки состоят из 100 случайно выбранных ресторанов.
1. Какова доля выборок, в которых количество ресторанов, где мобильные телефоны запрещены, колеблется между 15 и 25% ?
2. Между какими двумя процентными долями ресторанов, где мобильные телефоны запрещены (симметрично расположенными относительно математического ожидания) лежат 90% выборочных процентных долей таких ресторанов?
3. Между какими двумя процентными долями ресторанов, где мобильные телефоны запрещены (симметрично расположенными относительно математического ожидания) лежат 95% выборочных процентных долей таких ресторанов?
6.59. Около 13% студентов колледжей в США весной 2000 года заказали книги через Интернет (Abramson, R., “Textbook Sellers Get an Education”, The Industry Standard, July 10-17, 2000, p. 96). Предположим, что выборки состоят из 400 случайно выбранных студентов.
1. Какова доля выборок, в которых количество студентов, заказавших книги через Интернет, колеблется между 10 и 15% ?
2. Допустим, что в отдельной выборке, состоящей из 400 студентов, количество студентов, заказавших книги через Интернет, равно 18% . Как это согласуется с тем, что количество студентов, заказавших книги через Интернет, во всей генеральной совокупности равно 13% ? Обоснуйте свой ответ.
3. Допустим, что в отдельной выборке, состоящей из 100 студентов, количество студентов, заказавших книги через Интернет, превышает 18%. Как это согласуется с тем, что количество студентов, заказавших книги через Интернет, во всей генеральной совокупности равно 13% ? Обоснуйте свой ответ.
6.60. Компания International Revenue Service (IRS) прекратила осуществлять случайные аудиты в 1988 году. Вместо этого компания IRS проводит аудит доходности сомнительных фирм с помощью сложной и весьма секретной компьютерной системы DFS (Discriminant Function System). Стремясь уменьшить количество безрезультатных аудитов (т.е. аудитов, не выявляющих налоговые недоимки), компания IRS проводит аудит лишь тех компаний, которые система DFS считает подозрительными. С годами доля безрезультатных аудитов возросла и в настоящее время равна приблизительно 0,25 (Tom Herman, “Unhappy Returns: IRS Moves to Bring Back Random Audits”, Wall Street Journal, June 20, 2002, Al). Предположим, что из генеральной совокупности аудитов извлекаются случайные выборки, состоящие из 100 аудитов.
1. Какова доля выборок, в которых количество безрезультатных аудитов колеблется между 24 и 26% ?
2. Какова доля выборок, в которых количество безрезультатных аудитов колеблется между 20 и 30% ?
3. Какова доля выборок, в которых количество безрезультатных аудитов превышает 30% ?
Компания IRS сообщила, что планирует вообще отказаться от случайных аудитов в 2002 году. Допустим, что из генеральной совокупности извлекаются случайные выборки, состоящие из 200 совершенно случайных аудитов, причем только 10% всех зарегистрированных доходов должны быть обложены дополнительными налогами.
4. Какова доля выборок, в которых количество безрезультатных аудитов колеблется между 89 и 91% ?
5. Какова доля выборок, в которых количество безрезультатных аудитов колеблется между 85 и 95% ?
6. Какова доля выборок, в которых количество безрезультатных аудитов превышает 95% ?
6.8. АППРОКСИМАЦИЯ БИНОМИАЛЬНОГО И ПУАССОНОВСКОГО РАСПРЕДЕЛЕНИЙ С ПОМОЩЬЮ НОРМАЛЬНОГО
РАСПРЕДЕЛЕНИЯ
В предыдущих главах мы изучали свойства нормального распределения. Рассмотрим теперь, как с его помощью аппроксимировать биномиальное и пуассоновское распределение.
Поправка на непрерывность распределения
Существуют две причины, по которым необходимо делать поправку на непрерывность распределения.
Во-первых, напомним, что дискретная случайная величина может принимать лишь фиксированные значения, в то время как непрерывная случайная величина может принимать любые значения на числовой прямой или в интервале. Следовательно, используя нормальное распределение для аппроксимации биномиального или пуассоновского распределения, для того чтобы достичь хорошего приближения, мы должны делать поправку на непрерывность.
Во-вторых, вероятность того, что непрерывно распределенная случайная величина (в том числе, имеющая нормальное распределение) принимает конкретное значение, равна нулю. С другой стороны, когда нормальное распределение применяется для аппроксимации биномиального, поправка на непрерывность позволяет приближенно вычислить вероятность того, что дискретная случайная величина принимает конкретное значение.
В качестве примера рассмотрим эксперимент, в котором 10 раз подбрасывается идеальная монета и подсчитывается количество выпавших “орлов”. Предположим, требуется вычислить вероятность того, что “орлы” выпадут ровно четыре раза. В то время как дискретная случайная величина может принимать только фиксированное значение (например, четыре), непрерывная случайная величина, аппроксимирующая дискретную, может принимать любые значения, лежащие в его окрестности (см. рисунок ниже).
3 4 5 \
j 2,5 3,5 4,5 5,5 |
Для того чтобы сделать поправку на непрерывность, необходимо прибавить 0,5 к фиксированному значению дискретной величины X или вычесть это число из него. Следовательно, чтобы аппроксимировать вероятность того, что “орел” выпадет ровно четыре раза (т.е. X = 4), необходимо вычислить площадь фигуры, лежащей под кривой нормального распределения между значениями X = 3,5 и X = 4,5. Если нам требуется вычислить вероятность того, что орлы выпадут не менее четырех раз, нужно определить площадь фигуры, лежащей под нормальной кривой справа от точки X = 3,5, поскольку число 3,5 является в данном случае нижней границей непрерывной случайной величины X. Аналогично, для того чтобы вычислить вероятность того, что орлы выпадут не более четырех раз, следует определить площадь фигуры, лежащей под нормальной кривой слева от точки X = 4,5, поскольку число 4,5 в данном случае является верхней границей непрерывной случайной величины X.
При аппроксимации дискретных распределений с помощью нормального точное употребление слов играет очень важную роль. Для того чтобы приближенно вычислить вероятность того, что при десятикратном подбрасывании монеты выпадет меньше че-
тырех орлов, необходимо определить площадь фигуры, лежащей под нормальной кривой слева от точки X = 3,5. Для того чтобы приближенно вычислить вероятность того, что при десятикратном подбрасывании монеты выпадет больше четырех орлов, необходимо определить площадь фигуры, лежащей под нормальной кривой справа от точки Х = 4,5. Для того чтобы приближенно вычислить вероятность того, что при десятикратном подбрасывании монеты выпадет от 4 до 7 орлов, необходимо определить площадь фигуры, лежащей под нормальной кривой между точками X = 3,5 и X = 7,5.
Аппроксимация биномиального распределения
В разделе 5.3 показано, что биномиальное распределение является симметричным (как и нормальное), если р = 0,5. Если р^0,5, биномиальное распределение становится несимметричным. Однако, чем ближе параметр р к числу 0,5 и чем больше количество выборочных наблюдений п, тем более симметричным становится биномиальное распределение.
С другой стороны, по мере увеличения объема выборки процесс вычисления точных вероятностей успеха по формуле (5.11) становится все более сложным. К счастью, при увеличении объема выборки для аппроксимации точных вероятностей успеха можно использовать нормальное распределение.
Как правило, нормальное распределение можно применять, когда числа пр и п(1-р) больше пяти. Напомним, что математическое ожидание биномиального распределения равно
а стандартное отклонение —
с^у/пр^-р) .
Подставив эти величины в формулу преобразования (6.2)
z = ^, а
получим
z = х~пр .
yjnp^-p)
Следовательно, при достаточно больших значениях п случайная величина Z будет иметь приближенное нормальное распределение.
Итак, для того чтобы аппроксимировать вероятности, соответствующие значениям дискретной случайной величины X, можно применять формулу (6.17).
АППРОКСИМАЦИЯ БИНОМИАЛЬНОГО РАСПРЕДЕЛЕНИЯ С ПОМОЩЬЮ НОРМАЛЬНОГО
Za Х‘~пр , (6.17)
фгр(\-р)
где р = пр — математическое ожидание биномиального распределения, о = yjnpfl - р) — стандартное отклонение биномиального распределения, Ха — количество успехов, скорректированное по дискретной величине X, т.е. Ха = X - 0,5 или Ха = X + 0,5.
ПРИМЕР 6.13. АППРОКСИМАЦИЯ БИНОМИАЛЬНОГО РАСПРЕДЕЛЕНИЯ С ПОМОЩЬЮ НОРМАЛЬНОГО
Предположим, что из крупной партии шин, содержащей 8% бракованной продукции, случайным образом выбраны п = 1 600 шин одинакового типа. Какова вероятность того, что в этой выборке обнаружатся не более 150 дефектных шин?
РЕШЕНИЕ. Поскольку пр = 1 600 х 0,08 = 128 и п(1-р) = 1 600 х 0,92 = 1 472 больше пяти, для аппроксимации биномиального распределения можно применять нормальное распределение.
Zz Х„-пр 150,5-128 22,5 _ ,,
у]пр(1-р) л/1600х0>08х0'92 10'85
Здесь число Ха = 150,5 является скорректированным количеством успехов, а величина Z = +2,07.
Используя табл. Д.2, находим, что площадь фигуры, лежащей под нормальной кривой слева от точки Z = +2,07, равна 0,9808 (рис. 6.30).
Рис. 6.30. Аппроксимация биномиального распределения
Если бы мы применили биномиальное распределение, то вычислить вероятность того, что выборка содержит не более 150 дефектных шин, было бы довольно трудно.
Р(Х< 150) = Р(Х = 0) + Р(Х = 1) + ... +Р(Х = 150) = 1 600 |(0,08)л'(0,92.
/=1 у X )
Для того чтобы осознать, сколько сил и времени экономит применение нормального распределения вместо биномиального, представьте себе, что вам необходимо вычислить 151 слагаемых, входящих в формулу (5.11).
600](0,08)a (0,92)'“-v =р 60°](0,08)'’(0,92Г +
(0,08)' (0,92)'+... + 5q0](0.08)IS0 (0,92)' 45“
Вычисление приближенной вероятности по конкретному значению. Предположим, требуется вычислить вероятность того, что в выборке будет обнаружено ровно 150 бракованных шин. Поправка на непрерывность означает, что вероятность обнаружить 150 бракованных шин равна площади фигуры, лежащей под нормальной кривой между точками 149,5 и 150,5. Следовательно, используя формулу (6.17), получаем
Za .50,5-128 =^ = +207
71600x0,08x0,92 10,85
и
zs 149,5-128 =ai = +l,98.
71600x0,08x0,92 10,85
В табл. Д.2 находим, что площадь фигуры, лежащей под нормальной кривой слева от точки Х= 150,5 (Z = +2,07), равна 0,9808, а площадь фигуры, лежащей под нормальной кривой слева от точки Х= 149,5 (Z = +l,98), равна 0,9761. Следовательно, приближенная вероятность того, что выборка содержит 150 бракованных шин, равна разности между этими двумя площадями, т.е. числу 0,0047.
Аппроксимация распределения Пуассона
Пуассоновское распределение можно аппроксимировать нормальным, если параметр X — ожидаемое количество успехов — больше или равно пяти. Поскольку математическое ожидание и дисперсия распределения Пуассона совпадают
ц = ст2 = X, стандартное отклонение равно
ст = 7?ё.
Подставляя эти величины в формулу преобразования (6.2), получаем
а ~ лД ’
Следовательно, при достаточно больших значениях X случайная величина Z будет иметь приближенно нормальное распределение.
Таким образом, для того чтобы вычислить приближенную вероятность, соответствующую значениям пуассоновской случайной величины X, можно применять формулу (6.18).
АППРОКСИМАЦИЯ РАСПРЕДЕЛЕНИЯ ПУАССОНА С ПОМОЩЬЮ НОРМАЛЬНОГО
где X — математическое ожидание распределения Пуассона, или ожидаемое количество успехов, ст = 7?ё — стандартное отклонение распределения Пуассона, Ха — количество успехов, скорректированное по дискретной величинеX, т.е. Ха = Х-0,5 илиХ, = Х + 0,5.
ПРИМЕР 6.14. АППРОКСИМАЦИЯ РАСПРЕДЕЛЕНИЯ ПУАССОНА С ПОМОЩЬЮ НОРМАЛЬНОГО
Предположим, что на некоем автомобильном заводе среднее количество остановок работы вследствие проблем с оборудованием равно 12,0. Чему равна приближенная вероятность того, что в указанный день будет не более 15 остановок работы из-за проблем с оборудованием?
РЕШЕНИЕ. Используя формулу (6.18), получаем
Zsi-X = 1515-12;0 =
Здесь Ха — скорректированное количество успехов, равное 15,5. Следовательно, приближенная вероятность того, что величина X не превосходит заданное значение, равна вероятности того, что случайная величинаZ не превосходит +1,01. В табл. Д.2 находим, что площадь фигуры, лежащей под нормальной кривой слева от точки Z = +l,01, равна 0,8438. Следовательно, приближенная вероятность того, что в указанный день будет не более 15 остановок работы из-за проблем с оборудованием, равно 0,8438. Эта величина хорошо согласуется с истинной пуассоновской вероятностью, равной 0,8445.и
УПРАЖНЕНИЯИРАЗДЕЛУ 6Л
Изучение основ
6.61. Почему необходимо делать поправку на непрерывность?
6.62. В каких ситуациях биномиальное распределение можно аппроксимировать нормальным?
6.63. В каких ситуациях распределение Пуассона можно аппроксимировать нормальным?
Применение понятий
6.64. Рассмотрим эксперимент, в котором идеальная монета подбрасывается 10 раз и фиксируется количество выпавших “орлов”. Используя формулу (5.11), табл. Д.6 или программу Microsoft Excel, определите вероятность следующих событий.
1. Выпало четыре орла.
2. Выпало не менее четырех орлов.
3. Выпало не более четырех орлов.
4. Выпало меньше четырех орлов.
5. Выпало больше четырех орлов.
6. Выпало от 4 до 7 орлов.
7. Примените нормальное распределение для вычисления биномиальных вероятностей в задачах 1-6.
8. Сравните результаты решения задач 1-6 и 7. Обеспечивает ли нормальное распределение хорошую аппроксимацию биномиального распределения в задаче 7?
6.65. На международных авиалиниях авиакомпания предлагает три варианта десерта — мороженое, пирожок с апельсиновым вареньем и шоколадное пирожное. Опыт показывает, что все десерты пользуются одинаковой популярностью.
1. Предположим, что из генеральной совокупности извлечена случайная выборка, состоящая из четырех пассажиров. Какова вероятность того, что по крайней мере двое из них выберут на десерт мороженое?
2. Предположим, что из генеральной совокупности извлечена случайная выборка, состоящая из 21 пассажира. Какова приближенная вероятность того, что по крайней мере двое из них выберут на десерт мороженое?
6.66. Опыт показывает, что 40% всех клиентов компании Miller’s Automotive Service Station оплачивают свои покупки кредитными карточками. Предположим, что случайная выборка содержит трех клиентов. Вычислите вероятность следующих событий.
1. Ни один из клиентов не оплатит покупку кредитной карточкой.
2. Два клиента оплатят покупку кредитной карточкой.
3. По крайней мере два клиента оплатят покупку кредитной карточкой.
4. Не больше двух клиентов оплатят покупку кредитной карточкой.
Предположим, что из генеральной совокупности извлечена случайная выборка, состоящая из 200 клиентов. Вычислите приближенную вероятность следующих событий.
5. По крайней мере 75 клиентов оплатят покупку кредитной карточкой.
6. Не более 70 клиентов оплатят покупку кредитной карточкой.
7. От 70 до 75 клиентов, включительно, оплатят покупку кредитной карточкой.
6.67. С 8 до 9 утра в очередь к лифту в вестибюле крупного офисного здания в среднем становятся 10 человек в минуту.
1. Какова вероятность того, что на протяжении произвольно выбранной минуты в очереди стоят не более четырех человек?
2. Какова приближенная вероятность того, что на протяжении произвольно выбранной минуты в очереди стоят не более четырех человек?
3. Сравните результаты решения задач 1 и 2.
6.68. Количество автомобилей, подъезжающих к билетной кассе на мосту за минуту, имеет распределение Пуассона с математическим ожиданием 2,5. Вычислите вероятность следующих событий.
1. За минуту к билетной кассе не подъедет ни одного автомобиля.
2. За минуту к билетной кассе не подъедет больше двух автомобилей.
Предположим, что за десять минут к билетной кассе на мосту подъезжает 25 автомобилей в минуту. Вычислите приближенную вероятность следующих событий.
3. За 10 минут к билетной кассе подъедут не более 20 автомобилей.
4. За 10 минут к билетной кассе подъедут не менее 20, но не более 30 автомобилей.
6.69. За полчаса на мойку компании Kenny's Car Wash прибывают девять автомобилей.
1. Какова вероятность того, что за произвольно выбранный получасовой интервал на мойку прибудет не менее трех автомобилей?
2. Какова приближенная вероятность того, что за произвольно выбранный получасовой интервал на мойку прибудет не менее трех автомобилей?
* 3. Сравните результаты решения задач 1 и 2.
6.70. Предположим, что за день в пункт проката возвращается семь бракованных видеокассет.
1. Какова (точная) вероятность того, что сегодня в пункт проката будет возвращено две видеокассеты?
2. Какова (точная) вероятность того, что сегодня в пункт проката будет возвращено не более двух видеокассет?
3. Какие предположения о распределении вероятностей были сделаны в задачах 1 и 2? Обоснуйте свой ответ.
4. Вычислите приближенные вероятности событий, упомянутых в задачах 1 и 2. Обсудите отличия между ответами.
6.9. ВЫБОРКИ ИЗ КОНЕЧНЫХ ГЕНЕРАЛЬНЫХ СОВОКУПНОСТЕЙ
Центральная предельная теорема, а также формулы для вычисления стандартной ошибки среднего и стандартной ошибки доли признака основаны на предположении, что выборки извлекаются из генеральной совокупности с возвращением. Однако практически во всех статистических исследованиях выборки извлекаются из генеральных совокупностей конечного объема N без возвращения. Если объем выборок п достаточно велик по сравнению с объемом генеральной совокупности N (т.е. выборка содержит более 5% элементов генеральной совокупности), так что n/N > 0,05, то при вычислении стандартной ошибки среднего и стандартной ошибки доли признака следует учитывать поправочный коэффициент для конечной генеральной совокупности (fpc — finite population correction factor). Эта поправка вычисляется по формуле (6.19).
ПОПРАВОЧНЫЙ КОЭФФИЦИЕНТ ДЛЯ КОНЕЧНОЙ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ
= (6.19)
где п — объем выборки, a N — объем генеральной совокупности.
Таким образом, формулы для вычисления стандартной ошибки среднего и стандартной ошибки доли признака принимают следующий вид.
СТАНДАРТНАЯ ОШИБКА СРЕДНЕГО ДЛЯ КОНЕЧНОЙ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ
_ о lN-f?
* N-l *
(6.20)
СТАНДАРТНАЯ ОШИБКА ДОЛИ ПРИЗНАКА ДЛЯ КОНЕЧНОЙ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ
Ip(i-p) /^-/7
л v п NN-1 '
Анализ формулы для вычисления поправочного коэффициента для конечной генеральной совокупности (6.19) показывает, что ее числитель всегда меньше знаменателя, поскольку число п всегда больше единицы. Следовательно, поправочный коэффициент для конечной генеральной совокупности меньше единицы. Поскольку этот коэффициент умножается на стандартную ошибку, скорректированная стандартная ошибка уменьшается. Таким образом, с учетом поправочного коэффициента для конечной генеральной совокупности мы получаем более точные оценки.
Проиллюстрируем применение поправочного коэффициента следующими примерами.
ПРИМЕР 6.15. ПРИМЕНЕНИЕ ПОПРАВОЧНОГО КОЭФФИЦИЕНТА ДЛЯ КОНЕЧНОЙ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ ПРИ ОЦЕНКЕ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ
В задаче о расфасовке кукурузных хлопьев, рассмотренной в разделе 6.6, из генеральной совокупности упаковок извлекалась выборка, состоящая из 25 коробок. Допустим, что за день фабрика заполняет 2 000 коробок, которые образуют всю генеральную совокупность. Используя поправочный коэффициент для конечной генеральной совокупности, определите вероятность извлечь выборку, среднее выборочное которой меньше 365 г.
РЕШЕНИЕ. Используя формулу (6.20) при о=15,п = 25иА=2 ООО, получаем
ст ,7V-Л Op = —f=J----
И 2000-25 =
/25 V 2000-1
Вероятность извлечь выборку, выборочное среднее которой лежит между 365 и 368 г, вычисляется следующим образом.
= —•£ = —— = -1,01 . ст 2,982 л/л
Из табл. Д.2 следует, что площадь области, ограниченной нормальной кривой и соответствующей весу коробки, не превышающему 365 г, равна 0,1562.
Очевидно, что в данном примере учет поправочного коэффициента для конечной генеральной совокупности очень мало влияет на стандартную ошибку среднего и площадь области, ограниченной нормальной кривой, поскольку объем выборки (т.е., п = 25) составляет только 1,25% от всей генеральной совокупности (т.е., N = 2 000).
ПРИМЕР 6.16. ПРИМЕНЕНИЕ ПОПРАВОЧНОГО КОЭФФИЦИЕНТА ДЛЯ КОНЕЧНОЙ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ ПРИ ОЦЕНКЕ ДОЛИ ПРИЗНАКА
Вернемся к задаче о нескольких банковских счетах. Предположим, что банк обслуживает 1 000 клиентов, причем 400 из них имеют больше одного счета. Используя поправочный коэффициент для конечной генеральной совокупности, определите вероятность извлечь выборку, состоящую из 200 клиентов, в которой доля клиентов, имеющих несколько банковских счетов меньше 0,30.
РЕШЕНИЕ. Используя формулу (6.21) при п = 200, получаем
_ p(l-p) N-n _ /0,40x0,60 /1000-200 л V п N N-1 ~
200 V 1000-1
1,0012 V0,801 = 0,0346 х 0,895 = 0,031
Итак, стандартная ошибка выборочной доли признака равна 0,031. Следовательно,
z = 0,30-0,40_3>23
0,031
Из табл. Д.2 следует, что площадь области, ограниченной нормальной кривой слева от величины р, = 0,30, равна 0,00062. В данном примере учет поправочного коэффициента для конечной генеральной совокупности оказал умеренное влияние на стандартную ошибку доли признака и площадь области, ограниченной нормальной кривой, поскольку объем выборки составляет 20% от всей генеральной совокупности (т.е., n/N = 0,20).
УПРАЖНЕНИЯ К РАЗДЕЛУ 6.9 - '
Изучение основ
6.71. Предположим, что N = 80 и п = 10, причем выборка получена путем извлечения без возвращения. Вычислите поправочный коэффициент для конечной генеральной совокупности.
6.72. Какой из следующих поправочных коэффициентов для конечной генеральной совокупности сильнее уменьшает стандартную ошибку — вычисленный для выборки, состоящей из 100 элементов, извлеченных без возвращения из генеральной совокупности, состоящей из 400 элементов, или вычисленный для выборки, состоящей из 200 элементов, извлеченных без возвращения из генеральной совокупности, состоящей из 900 элементов? Аргументируйте свой ответ.
6.73. Допустим, что N = 60 и п = 20, причем выборка получена путем извлечения с возвращением. Следует ли применять поправочный коэффициент для конечной генеральной совокупности? Аргументируйте свой ответ.
Применение понятий
6.74. Предполагается, что диаметр шариков для настольного тенниса, произведенных на крупной фабрике, имеет приближенное нормальное распределение с математическим ожиданием, равным 1,30 дюйма, и стандартным отклонением, равным 0,04 дюйма. Допустим, что из генеральной совокупности, состоящей из 200 шариков, извлекаются без возвращения случайные выборки, состоящие из 16 шариков. Какая доля выборочных средних лежит в интервале от 1,31 до 1,33 дюйма?
6.75. Количество времени, которое служащий банка затрачивает на обслуживание одного клиента, образует генеральную совокупность с математическим ожиданием ц = 3,10 мин. и стандартным отклонением, равным ст = 0,40 мин. Предположим, что из генеральной совокупности, состоящей из 500 клиентов, извлекается случайная выборка, состоящая из 16 клиентов.
1. Чему равна вероятность того, что в среднем на обслуживание одного клиента уходит больше трех минут?
2. Вычислите количество времени, затрачиваемое в среднем на одного клиента, если вероятность того, что выборочное среднее не превышает его, равна 85%.
6.76. Опыт показывает, что 10% крупных партий запчастей является браком. Предположим, что из партии, состоящей из 5 000 деталей, извлекаются без возвращения случайные выборки, состоящие из 400 деталей.
1. Какая доля выборок содержит от 9 до 10% брака?
2. Какая доля выборок содержит меньше 8% брака?
6.77. Опыт показывает, что 93% ночных почтовых отправлений доставляется до 10:30 следующего утра. Предположим, что из 10 000 почтовых отправлений, извлекаются без возвращения случайные выборки, объем которых равен 500.
1. Какая доля выборок содержит от 93 до 95% почтовых отправлений, доставленных вовремя?
2. Какая доля выборок содержит больше 95% почтовых отправлений, доставленных вовремя?
6.10. ПРИМЕНЕНИЕ СТАНДАРТИЗОВАННОГО НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ
Любой набор нормально распределенных случайных величин можно преобразовать в стандартизованный вид и вычислить искомые вероятности, пользуясь таблицей стандартизованного нормального распределения.
Для того чтобы продемонстрировать применение формулы преобразования (6.2) и поиск вероятностей в таблице стандартизованного нормального распределения (табл. Д. 12), рассмотрим Следующую задачу.
Предположим, что некий консультант на автомобильном заводе исследовал время, которое работники конвейера тратят на сборку определенной части автомобиля после индивидуального курса обучения. Консультант выяснил, что это время является нормально распределенным, причем его математическое ожидание р. равно 75 с, а стандартное отклонение о — 6 с.
Преобразование данных
На рис. 6.31 показано, что каждому измерению X соответствует стандартизованная величина Z, полученная с помощью формулы преобразования (6.2). Кроме того, из рис. 6.31 следует, что справа от среднего значения время сборки, равное 81 с, эквивалентно одной стандартизованной единице (т.е. одному стандартному отклонению), поскольку
В то же время, слева от среднего значения время сборки, равное 57 с, эквивалентно трем стандартным единицам (т.е. трем стандартным отклонениям), так как
z = ^ = _3.
6
Таким образом, стандартное отклонение становится единицей измерения. Иначе говоря, время, равное 81 с, на 6 с (т.е. на одно стандартное отклонение) больше, чем среднее время сборки, равное 75 с, а время, равное 57 с, на 18 с (т.е. на три стандартных отклонения) меньше среднего времени.
Рис. 6.31. Преобразование шкал
Предположим теперь, что консультант провел аналогичное исследование на другом автомобильном заводе, на котором работники обучаются по коллективной программе. Допустим, консультант выяснил, что время, затрачиваемое работниками на сборку,
имеет нормальное распределение, его математическое ожидание ц равно 60 с, а стандартное отклонение— 3 с. Эти данные изображены на рис. 6.32. Сравнение результатов, достигнутых работниками, прошедшими индивидуальное и коллективное обучение, показывает, что на заводе с коллективной формой обучения работников время сборки, равное 57 с, соответствует только одному стандартному отклонению влево от математического ожидания, поскольку
Z = ^ = -l.
3
Обратите внимание на то, что время сборки, равное 63 с, соответствует одному стандартному отклонению от среднего времени сборки, поскольку
63-60
Z =-------+1,
3
а время сборки, равное 51 с, равно трем стандартным отклонениям от среднего времени сборки, поскольку
Z = ^ = -3.
3
-3 -2 -1 0 +1 +2 +3 Z
J J
Рис. 6.32. Разные преобразования шкал
Использование таблиц нормального распределения
Колоколообразные кривые, представленные на рис. 6.31 и 6.32, изображают полигоны относительных частот для нормальных распределений. Эти полигоны характеризуют время сборки (в секундах), затрачиваемое всеми работниками, прошедшими обучение по индивидуальным и коллективной программам. Поскольку время сборки, затрачиваемое каждым работником, известно, данные относятся ко всей генеральной со-
вокупности работников отдельного завода. Следовательно, вероятности, или доли площади, ограниченной всей кривой, должны равняться единице. Таким образом, площадь, ограниченная кривой и двумя моментами времени, представляет собой только часть всей возможной площади.
Предположим, консультант стремится определить вероятность того, что случайно выбранный работник завода, прошедший индивидуальное обучение, затратит на выполнение задания от 75 до 81 с. Иначе говоря, какова вероятность того, что время, затраченное случайно выбранным работником, на одно стандартное отклонение больше математического ожидания? Ответ можно найти с помощью табл. Д.12.
В табл. Д.12 представлены вероятности, равные площадям фигур, ограниченных нормальной кривой, математическим ожиданием р и конкретным значением X. Используя формулу (6.2), можно убедиться, что это соответствует вероятностям, равным площадям фигур, ограниченных стандартизованной нормальной кривой, математическим ожиданием и преобразованными значениями Z. В таблице перечислены только положительные значения Z, поскольку для симметричных распределений площадь фигуры, ограниченной кривой распределения, математическим ожиданием и заданным значением+Z (т.е. вправо от математического ожидания отсчитываются Z стандартных отклонений), равна площади фигуры, ограниченной кривой распределения, математическим ожиданием и значением-Z (т.е. влево от математического ожидания отсчитываются Z стандартных отклонений).
Используя табл. Д.12, следует иметь в виду, что все значения Z должны быть записаны с двумя цифрами после десятичной запятой. Иначе говоря, искомая величина Z должна иметь вид +1,00. Чтобы определить вероятность, или площадь фигуры, ограниченной кривой распределения, математическим ожиданием и величиной Z = +1,00, необходимо просмотреть столбец таблицы Д.12, соответствующий сотым долям величины Z, пока не обнаружится число, стоящее на пересечении со строкой, соответствующей десятым долям числа Z. Следовательно, мы должны остановиться на строке Z = 1,0. Таким образом, искомая вероятность находится в ячейке, образованной пересечением строки Z= 1,0 и столбца Z = 0,00, как показано в табл. 6.11, представляющей собой фрагмент табл. Д.12. Эта вероятность равна 0,3413. Как показано на рис. 6.33, существуют 34,13 шансов из 100, что случайно выбранный работник завода, прошедший индивидуальную подготовку, затратит на сборку от 75 до 81 с.
Таблица 6.11. Вычисление площади, ограниченной нормальной кривой10
X 0,00 0,01 0,02 0,03 0,04 0,05 0,06 0,07 0,08 0,09
0,0 0,0000 0,0040 0,0080 0,0120 0,0160 0,0199 0,0239 0,0279 0,0319 0,0359
0,1 0,0398 0,0438 0,0478 0,0517 0,0557 0,0596 0,0636 0,0675 0,0714 0.0753
0,2 0,0793 0,0832 0,0871 0,0910 0,0948 0,0987 0,1026 0,1064 0,1103 0,1141
0,3 0,1179 0,1217 0,1255 0,1293 0,1331 0,1368 0,1406 0,1443 0,1480 0,1517
0,4 0,1554 0,1591 0,1628 0,1664 0,1700 0,1736 0,1772 0,1808 0,1844 0,1879
0,5 0,1915 0,1950 0,1985 0,2019 0,2054 0,2088 0,2123 0,2157 0,2190 0,2224
0,6 0,2257 0,2291 0,2324 0,2357 0,2389 0,2422 0,2454 0,2486 0,2518 0,2549
0,7 0,2580 0,2612 0,2642 0,2673 0,2704 0,2734 0,2764 0,2794 0,2823 0,2852
0,8 0,2881 0,2910 0,2939 0,2967 0,2995 0,3023 0,3051 0,3078 0,3106 0,3133
0,9 0,3159 0,3186 0,3112 0,3238 0,3264 0,3289 0,3315 0,3340 0,3365 0,3389
1,0 0,3413 0,3438 0,3461 0,3485 0,3508 0,3531 0,3554 0,3577 0,3599 0,3621
1,1 0,3643 0,3665 0,3686 0,3708 0,3729 0,3749 0,3770 0,3790 0,3810 0,3830
-3,00 -2,00 -1,00 0 +1,00 +2,00 +3,00 Шкала Z
Рис. 6.33. Определение площади фигуры, ограниченной кривой стандартизованного нормального распределения, математическим ожиданием и величиной Z
С другой стороны, как показано на рис. 6.32, на заводе, работники которого проходят коллективное обучение, время сборки, равное 63 с, на одно стандартное отклонение превышает среднее время, равное 60 с. Следовательно, вероятность того, что случайно выбранный работник, прошедший коллективное обучение, затратит на сборку от 60 до 63 с, равна 0,3413. Эти результаты представлены на рис. 6.34. Как видим, независимо от математического ожидания р. и стандартного отклонения о нормально распределенные данные можно преобразовать с помощью формулы (6.12) в стандартизованную шкалу и определить площадь фигуры, лежащей под кривой. Анализ рис. 6.34 показывает, что вероятность того, что случайно выбранный работник, прошедший коллективное обучение, затратит на сборку от 60 до 63 с, равна вероятности того, что случайно выбранный работник, прошедший индивидуальное обучение, затратит на сборку от 75 до 81 с.
Рис. 6.34. Преобразование шкал, соответствующих двум областям, ограниченным нормальными кривыми
Освоив табл. Д.12 и формулу (6.2), мы можем решать разнообразные задачи, связанные с нормальным распределением. Для иллюстрации предположим, что консультант поставил в своем исследовании следующие вопросы, касающиеся работников, прошедших индивидуальную подготовку.
1. Какова вероятность того, что случайно выбранный работник затратит на сборку от 75 до 81 с?
2. Какова вероятность того, что случайно выбранный работник затратит на сборку от 69 до 81 с?
3. Какова вероятность того, что случайно выбранный работник затратит на сборку меньше 62 с?
4. Какова вероятность того, что случайно выбранный работник затратит на сборку от 62 до 69 с?
5. Сколько секунд пройдет, прежде чем 50% работников завода выполнят свое задание?
6. Сколько секунд пройдет, прежде чем 10% работников завода выполнят свое задание?
7. Каково межквартильное расстояние (в секундах) для времени сборки?
Вычислений вероятностей, соответствующих заданным значениям
Напомним, что время, которое затрачивают на сборку автомобиля работники, прошедшие индивидуальную подготовку, имеет нормальное распределение, математическое ожидание, ц которого равно 75 с, а стандартное отклонение — 6 с. Эта информация позволяет ответить на вопросы 1-4.
Задача!: найти Р(Х<75 или Х>81). Как вычислить вероятность того, что случайно выбранный работник затратит на сборку меньше 75 или больше 81с? До сих пор мы отвечали на вопрос: “какова вероятность того, что случайно выбранный работник затратит на сборку от 75 до 81 с?”. Из рис. 6.33 следует, что искомая вероятность представляет собой вероятность дополнения: 1-0,3413 = 0,6587.
Однако существует и другой способ решения этой задачи. Для этого достаточно отдельно найти вероятность того, что случайно выбранный работник затратит на сборку менее 75 с, и вероятность того, что случайно выбранный работник затратит на сборку больше 81 с. Затем необходимо применить правило сложения вероятностей взаимоисключающих событий (формула (4.4)). Процесс решения этой задачи изображен на рис. 6.35.
-3,00 -2,00 1,00 О +1,00 +2,00 +3,00 UlicanaZ
Рис. 6.35. Вычисление Р(Х < 75 или X > 81)
Поскольку теоретически у нормально распределенных данных математическое ожидание и медиана совпадают, приходим к выводу, что 50% рабочих способны выполнить сборку быстрее 75 с. Для того чтобы доказать это, применим формулу (6.2).
/ = £-ц = 75-75 = 0 00.
СТ 6
Используя табл. Д.12, легко определить, что площадь фигуры, лежащей под кривой нормального распределения между математическим ожиданием и величиной Z = 0,0, равна 0,0000. Следовательно, площадь фигуры, лежащей под кривой нормального распределения левее величины Z=0,0, равна 0,5000-0,0000 = 0,5000. (Как показано на рис. 6.35, эта фигура простирается от величины Z до -оо ).
Теперь необходимо определить вероятность того, что случайно выбранный работник затратит на сборку больше 81 с. Однако формула (6.2) позволяет вычислить лишь площадь фигуры, лежащей между математическим ожиданием и величиной Z, а не от Z до оо . Следовательно, необходимо вычислить площадь фигуры, лежащей между математическим ожиданием и величиной Z, а затем вычесть это число из 0,5000. Это и будет искомым ответом. Поскольку нам известно, что площадь фигуры, лежащей между математическим ожиданием и величиной Z=+l,00, равна 0,3413, приходим к выводу, что площадь фигуры, лежащей между Z=+l,00 и Z = +оо, равна 0,5000-0,3413 = 0,1587. Следовательно, вероятность того, что случайно выбранный работник затратит за сборку от 75 до 81 с, равна 0,5000+0,1587 = 0,6587.
Задача 2: найти Р(69<Х <81). Предположим, нас интересует вероятность того, что случайно выбранный работник затратит на сборку от 69 до 81 с, т.е. Р(69< X < 81). Из рис. 6.36 следует, что одна из интересующих нас величин больше математического ожидания, равного 75 с, а другая — меньше. Поскольку преобразование, заданное формулой (6.2), позволяет найти лишь вероятность, что величина X лежит между математическим ожиданием и заданным, решение задачи необходимо разбить на три этапа.
1. Определяем вероятность Р(ц <Х < 81).
2. Определяем вероятность Р(ц < X < 69).
3. Суммируем два взаимоисключающих результата.
Рис. 6.36. Вычисление Р(б9 <Х <81)
Например, представим себе, что мы уже выполнили первый шаг, и площадь фигуры, лежащей под кривой нормального распределения между 75 и 81 с, равна 0,3413. Для того чтобы найти площадь фигуры, лежащей под кривой нормального распределения между 69 и 75 с (шаг 2), необходимо вычислить
СТ 6
В табл. Д. 12 предусмотрены только положительные величины Z. Вследствие симметрии площадь фигуры, лежащей между математическим ожиданием и величиной Z = -l,00, равна площади фигуры, лежащей между математическим ожиданием и ве-
личиной Z=+1,OO. Отбрасывая знак “минус”, ищем в табл. Д.12 величину Z = +l,00 и находим вероятность, равную 0,3413. Следовательно, вероятность того, что случайно выбранный работник затратит на сборку от 69 до 81 с, равна 0,3413+0,3413 = 0,6826 (шаг 3). Этот результат представлен на рис. 6.36.
Полученный результат довольно важен. Как видим, для любого нормального распределения вероятность того, что случайная величина лежит на расстоянии одного стандартного отклонения от математического ожидания, равна 0,6826.
На заводе, применяющем индивидуальное обучение, примерно две трети рабочих (68,26%) тратят на сборку среднее время плюс-минус одно стандартное отклонение. Более того, как следует из рис. 6.37, примерно 19 из 20 работников (95,44%) тратят на сборку среднее время плюс-минус два стандартных отклонения (т.е. от 63 до 87 с), и, наконец, практически все рабочие (99,73%) могут выполнить задание, затратив среднее время плюс-минус три стандартных отклонения (т.е. от 57 до 93 с).
57 63 69 75 81 87 93 Шкалах
-3,00 -2,00 -1,00 0 +1,00 +2,00 +3,00 Шкала Z
Рис. 6.37. Вычисление Р(63 <Х <87)
57 63 69 75 81 87 93 Шкалах
-3,00 -2,00 -1,00 0 +1,00 +2,00 +3,00 Шкала Z
Рис. 6.38. Вычисление Р(57 <Х <93)
Как следует из рис. 6.38, практически невероятно (Р = 0,0027, или 27 рабочих из 10 000), что случайно выбранный рабочий будет настолько ловким или медлительным, что выполнит задание быстрее 57 с или медленнее 93 с. Таким образом, совершенно очевидно, почему число 6о (т.е. плюс-минус три стандартных отклонения от математического ожидания) часто используется на практике для приближенного вычисления размаха нормально распределенных данных. (“Правило Зо” выполняется не только для нормального, но и для всех одномодальных распределений. — Прим.ред.)
Задача 3: найти Р(Х < 62). Для того чтобы вычислить вероятность того, что случайно выбранный рабочий сможет собрать деталь быстрее 62 с, необходимо проанализировать закрашенную область на рис. 6.39. Формула (6.2) позволяет найти лишь площадь фигуры, лежащей под кривой стандартизованного нормального распределения между математическим ожиданием и величиной Z, а не между Z и -оо . Следовательно, необходимо вычислить вероятность того, что случайная величина лежит между математическим ожиданием и величиной Z, а затем вычислить результат из числа 0,5000.
Рис. 6.39. Вычисление Р(Х < 62)
Для того чтобы вычислить площадь фигуры, лежащей под кривой стандартизованного нормального распределения между 62 с и математическим ожиданием, необходимо найти
Z- _ 62-75 _-13 _ -2,17 .
а 6 6
Отбрасывая знак “минус”, находим в табл. Д.12 величину Z= 2,17, разложенную на
два числа: в строке Z = 2,1 и столбце Z = 0,07, как показано в табл. 6.12.
Таблица 6.12. Вычисление площади. ограниченной нормальной кривой11
X 0,00 0,01 0,02 0,03 0,04 0,05 0,06 0,07 0,08 0,09
0,0 0,0000 0,0040 0,0080 0,0120 0,0160 0,0199 0,0239 0,0279 0,0319 0,0359
0,1 0,0398 0,0438 0,0478 0,0517 0,0557 0,0596 0,0636 0,0675 0,0714 0,0753
0,2 0,0793 0,0832 0,0871 0,0910 0,0948 0,0987 0,1026 0,1064 0,1103 0,1141
0,3 0,1179 0,1217 0,1255 0,1293 0,1331 0,1368 0,1406 0,1443 0,1480 0,1517
0,4 0,1554 0,1591 0,1628 0,1664 0,1700 0,1736 0,1772 0,1808 0,1844 0,1879
2,0 0,4772 0,4778 0,4783 0,4788 0,4793 0,4798 0,4803 0,4808 0,4812 0,4817
2,1 0,4821 0,4826 0,4830 0,4834 0,4838 0,4842 0,4846 0,4850 0,4854 0,4857
2,2 0,4861 0,4864 0,4868 0,4871 0,4875 0,4878 0,4881 0,4884 0,4887 0,4890
2,3 0,4893 0,4896 0,4898 0,4901 0,4904 0,4906 0,4909 0,4911 0,4913 0,4916
2,4 0,4918 0,4920 0,4922 0,4925 0,4927 0,4929 0,4931 0,4932 0,4934 0,4936
Задача 3: найти Р(62 < X < 69). В последнем примере, иллюстрирующем вычисление вероятностей с помощью стандартизованного нормального распределения, необходимо определить вероятность того, что случайно выбранный работник затратит на сборку от 62 до 69 с. Поскольку обе эти величины меньше математического ожидания, из рис. 6.40 следует, что искомая вероятность меньше 0,5000. Формула (6.2) позволяет
найти лишь площадь фигуры, лежащей под кривой стандартизованного нормального распределения между математическим ожиданием и величиной Z, поэтому задачу придется разбить на три этапа.
1. Определяем вероятность Р(62 < X < ц).
2. Определяем вероятность Р(69 < X < ц).
3. Вычитаем меньшую вероятность из большей.
-3,00 -2,00 -1,00 0 +1,00 +2,00 +3,00 Шкалаг
-2,17
Рис. 6.40. Вычисление Р(62 < X < 69)
Мы уже выполнили этапы 1 и 2, решая задачи 3 и 2 соответственно. Площадь фигуры, лежащей между 62 с и математическим ожиданием, равна 0,4850, а площадь фигуры, лежащей между 69 с и математическим ожиданием, — 0,3413. Вычитая меньшую площадь из большей, находим вероятность того, что случайно выбранный работник затратит на сборку от 62 до 69 с. Эта вероятность равна 0,1437.
Р(62 < X < 69) = Р(62 < X < 75) - Р(69 < X < 75) = 0,4850 - 0,3413 = 0,1437.
Вычисление значений, соответствующих заданным вероятностям
В предыдущих примерах, связанных с нормально распределенными данными, мы вычисляли вероятности по заданным величинам. Предположим теперь, что нам требуется определить значения случайных величин, соответствующих известным вероятностям. В качестве примера рассмотрим задачи 5-7.
Задача 5. Для того чтобы определить, сколько секунд понадобится 50% работникам завода на сборку детали, рассмотрим рис. 6.41. Это время соответствует медиане, а у всех симметричных распределений математическое ожидание и медиана совпадают. Следовательно, медиана равна 75 с.
Рис. 6.41. Вычисление X
Задача 6. Для того чтобы определить, сколько секунд пройдет, пока 10% работников завода соберут деталь, рассмотрим рис. 6.42. Поскольку ожидается, что 10% работников выполнят задание быстрее X с, остальные 90% работников затратят больше X с. Из рис. 6.42 следует, что эти 90% можно разбить на две части — работники, затрачивающие на сборку меньше среднего времени (50% работников) и больше среднего времени, но меньше X с (40% работников). Поскольку величина X нам неизвестна, можно определить соответствующее стандартизованное значение Z, так как площадь, лежащая под кривой стандартизованного нормального распределения между числами 0 и Z, должна быть равной 0,4000. Используя табл. Д.12, найдем вероятность 0,4000. Как показано в табл. 6.13, ближайшее значение равно 0,3997.
Рис. 6.42. Определение величины Z, соответствующей заданной величине X
Таблица 6.13. Определение величины Z, соответствующей заданной площади фигуры, лежащей под кривой стандартизованного нормального распределения12
X 0,00 0,01 0,02 0,03 0,04 0,05 0,06 0,07 0,08 0,09
0,0 0,0000 0,0040 0,0080 0,0120 0,0160 0,0199 0,0239 0,0279 0,0319 0,0359
0,1 0,0398 0,0438 0,0478 0,0517 0,0557 0,0596 0,0636 0,0675 0,0714 0,0753
0,2 0,0793 0,0832 0,0871 0,0910 0,0948 0,0987 0,1026 0,1064 0,1103 0,1141
0,3 0,1179 0,1217 0,1255 0,1293 0,1331 0,1368 0,1406 0,1443 0,1480 0,1517
0,4 0,1554 0,1591 0,1628 0,1664 0,1700 0,1736 0,1772 0,1808 0,1844 0,1879
1,0 0,3413 0,3438 0,3461 0,3485 0,3508 0,3531 0,3554 0,3577 0,3599 0,3621
1,1 0,3643 0,3665 0,3686 0,3708 0,3729 0,3749 0,3770 0,3790 0,3810 0,3830
1,2 0,3849 0,3869 0,3888 0,3907 0,3925 0,3944 0,3962 0,3980 0,3997 0,4015
1,3 0,4032 0,4049 0,4066 0,4082 0,4099 0,4115 0,4131 0,4147 0,4162 0,4177
1,4 0,4192 0,4207 0,4222 0,4236 0,4251 0,4265 0,4279 0,4292 0,4306 0,4319
12
Перемещаясь от найденной величины по строке, находим соответствующее значение 1,2. Аналогично, перемещаясь по столбцу, находим величину 0,08. Следовательно, 2=1,28. Однако, как показывает рис. 6.42, величина Z может быть отрицательной (2=-1,28), поскольку она меньше стандартизированного математического ожидания, равного нулю.
Определив значение 2, применим формулу (6.12).
7_^-Ц X/ — •
о Следовательно,
Х = ц + 2о. (6.22)
Подставим конкретные значения.
X = 75 + (-1,28)х6 = 67,32 с.
Итак, 10% работников затратят на сборку меньше 67,32 с.
Алгоритм определения величины 2, соответствующей заданной вероятности, состоит из следующих этапов.
1. Рассмотреть кривую нормального распределения и определить математические ожидания на шкалах X и 2.
2. Разбить соответствующую половину нормальной кривой на две части — от искомой величины X до математического ожидания и от искомой величины X до бесконечности.
3. Заштриховать интересующую нас область.
4. Используя табл. Д.12, определить величину 2, соответствующую площади фигуры, лежащей под нормальной кривой между искомой величиной X и математическим ожиданием ц.
5. Используя формулу (6.22), находим величину X = ц + 2су.
Задача 7. Чтобы определить межквартильное расстояние, сначала необходимо найти величину X, соответствующую первому квартилю и величину X, соответствующую третьему квартилю Q3. Затем первую величину нужно вычесть из второй.
Для того чтобы найти величину X, соответствующую первому квартилю Qr, следует определить время (в секундах), которое 25% работников тратят на сборку детали (см. рис. 6.43).
Рис. 6.43. Вычисление Q,
Несмотря на то что величина нам неизвестна, можно определить соответствующее стандартизованное значение Z, поскольку площадь фигуры, лежащей под кривой стандартизованного нормального распределения между 0 и величиной Z, должна быть равной 0,2500. Используя табл. 6.14, найдем значение, ближайшее к 0,2500. Оно равно 0,2486.
Таблица 6.14. Вычисление площади, ограниченной нормальной кривой13
X 0,00 0,01 0,02 0,03 0,04 0,05 0,06 0,07 0,08 0,09
0,0 0,0000 0,0040 0,0080 0,0120 0,0160 0,0199 0,0239 0,0279 0,0319 0,0359
0,1 0,0398 0,0438 0,0478 0,0517 0,0557 0,0596 0,0636 0,0675 0,0714 0,0753
0,2 0,0793 0,0832 0,0871 0,0910 0,0948 0,0987 0,1026 0,1064 0,1103 0,1141
0,3 0,1179 0,1217 0,1255 0,1293 0,1331 0,1368 0,1406 0,1443 0,1480 0,1517
0,4 0,1554 0,1591 0,1628 0,1664 0,1700 0,1736 0,1772 0,1808 0,1844 0,1879
0,5 0,1915 0,1950 0,1985 0,2019 0,2054 0,2088 0,2123 0,2157 0,2190 0,2224
0,6 0,2257 0,2291 0,2324 0,2357 0,2389 0,2422 0,2454 0,2486 0,2518 0,2549
0,7 0,2580 0,2612 0,2642 0,2673 0,2704 0,2734 0,2764 0,2794 0,2823 0,2852
0,8 0,2881 0,2910 0,2939 0,2967 0,2995 0,3023 0,3051 0,3078 0,3106 0,3133
0,9 0,3159 0,3186 0,3112 0,3238 0,3264 0,3289 0,3315 0,3340 0,3365 0,3389
1,0 0,3413 0,3438 0,3461 0,3485 0,3508 0,3531 0,3554 0,3577 0,3599 0,3621
1,1 0,3643 0,3665 0,3686 0,3708 0,3729 0,3749 0,3770 0,3790 0,3810 0,3830
Перемещаясь от найденной величины по строке, находим соответствующее значение 0,6. Аналогично, перемещаясь по столбцу, находим величину 0,07. Следовательно, 2 = 0,67. Однако, как показывает рис. 6.44, величина Z может быть отрицательной (2 =-0,67), поскольку она меньше стандартизованного математического ожидания, равного нулю.
Определив значение 2, применим формулу (6.13). Следовательно,
Q1=X = p + 2o= 75 + (-0,67)х6 = 75-4 = 71с.
Чтобы определить третий квартиль, необходимо найти время (в секундах), за которое 75% работников успеют выполнить сборку (а 25% работников — нет). Решение задачи изображено на рис. 6.44.
Рис. 6.44. Вычисление Q3
Вследствие симметричности нормального распределения искомая величина Z должна быть равной +0,67 (поскольку эта величина лежит правее стандартизованного математического ожидания, равного нулю). Итак, применяя формулу (6.13), получаем
Q3 = X = р + Zo = 75 + (+0,67)х6 = 75 + 4 = 79 с.
Межквартильный размах распределения равен
Q3-Q1 = 79-71 = 8c.
РЕЗЮМЕ
В этой главе мы применили нормальное распределение для исследования продолжительности загрузки Web-страницы. Как показано на структурной схеме, мы рассмотрели также равномерное и экспоненциальное распределение, а также научились строить график нормального распределения.
В главе введено понятие выборочного распределения выборочных средних и долей признака. Мы узнали, что выборочное среднее является несмещенной оценкой математического ожидания генеральной совокупности, а выборочная доля признака является несмещенной оценкой доли признака в генеральной совокупности. Помимо этого, с помощью центральной предельной теоремы мы продемонстрировали важность нормального распределения. Выборочные распределения лежат в основе теории статистического вывода, основной целью которого является извлечение информации из выборочных наблюдений и ее применение для оценки свойств всей генеральной совокупности. Например, вычисление выборочных средних весов коробок с кукурузными хлопьями на заводе компании Oxford Cereal Company позволяет сделать вывод о среднем весе коробок во всей генеральной совокупности. Теперь можно оценить вероятность того, что средний вес коробки в генеральной совокупности равен 368 г.
В следующих пяти главах мы рассмотрим методы построения доверительных интервалов и проверки гипотез, широко применяемые в теории статистических выводов.
ОСНОВНЫЕ ПОНЯТИЯ
График нормального распределения, 369
Закон больших чисел, 388
Квантиль стандартизованного нормального распределения, 370 Математическое ожидание, 387; 430
Обратное преобразование, 370
Оценка
несмещенная, 386
Плотность
нормального распределения, 349
стандартизованного нормального распределения, 350
Распределение
выборочное, 386
выборочной доли, 403
нормальное, 347
равномерное, 379
стандартизованное нормальное, 350
экспоненциальное, 382
Стандартная ошибка
доли признака, 402
среднего, 389
Стандартное отклонение
генеральной совокупности, 387
Формула преобразования, 350
Центральная предельная теорема, 394
Является ли распределение нет вероятностей • непрерывным?
См. главу 5
Имеет ли распределение нет вероятностей колоколообразную форму?
Да f
Нормальное Выборочные
. распределение распределения
Uewv Ss^es-и-
Является ли распределение Нет Экспоненциальное вероятностей распределение
симметри- ?
чным? : ”-*’*--*
Да J
Равномерное распределение
Да .
График нормального j распределения
Г~———™г—-----------------1
Центральная
Несмещенность Определение предельная
; J теорема
Выборочное Выборочное
распределение распределение
Приложения
Структурная схема главы 6
УПРАЖНЕНИЯ К РАЗДЕЛУ 6
Проверка знаний
6.78. Почему табл. Д.2 вполне достаточно для вычисления вероятностей нормального распределения ?
6.79. Как вычислить площадь фигуры, ограниченной нормальной кривой и двумя величинами?
6.80. Как определить значение X, соответствующее заданному процентилю нормального распределения?
6.81. Почему при построении графика нормального распределения его необходимо преобразовать в стандартизованное нормальное распределение?
6.82. Перечислите свойства нормального распределения.
6.83. Как с помощью графика нормального распределения распознать нормально распределенные данные?
6.84. При каких условиях можно применять экспоненциальное распределение?
6.85. Почему выборочное среднее является несмещенной оценкой математического ожидания генеральной совокупности?
6.86. Почему стандартная ошибка среднего уменьшается при увеличении объема выборок?
6.87. Почему распределение выборочных средних при достаточно больших объемах выборки является нормальным независимо от распределения генеральной совокупности?
6.88. Объясните, почему менеджер должен стремиться оценить параметры генеральной совокупности, а не описывать свойства конкретной выборки.
6.89. В чем заключается разница между распределением вероятностей и выборочным распределением?
6.90. При каких условиях распределение выборочной доли признака подчиняется нормальному закону?
Применение понятий
6.91. В промышленных швейных машинах используются шарикоподшипники, имеющие диаметр 0,75 дюйма. Спецификация допускает колебания диаметра в пределах от 0,74 до 0,76 дюйма. Опыт показывает, что диаметр шарикоподшипника является случайной величиной, имеющей нормальное распределение, математическое ожидание которого равно 0,753 дюйма, а стандартное отклонение — 0,004 дюйма.
1. Какова вероятность того, что диаметр шарикоподшипника находится между номинальным значением и математическим ожиданием?
2. Какова вероятность того, что диаметр шарикоподшипника находится между нижней допустимой границей и математическим ожиданием?
3. Какова вероятность того, что диаметр шарикоподшипника превышает верхнее допустимое значение?
4. Какова вероятность того, что диаметр шарикоподшипника меньше нижнего допустимого значения?
5. Выше какого значения находятся диаметры 93% всех шарикоподшипников? Предположим, что из генеральной совокупности извлекается выборка, состоящая из 25 шарикоподшипников. Вычислите вероятности следующих событий.
6. Выборочное среднее лежит между номинальным значением и математическим ожиданием генеральной совокупности, равным 0,753 дюйма.
7. Выборочное среднее лежит между нижним допустимым значением и номинальным.
8. Выборочное среднее превышает верхнее допустимое значение.
9. Выборочное среднее меньше нижнего допустимого значения.
10. Выше какого значения лежат 93% выборочных средних?
6.92. Объем жидкости в бутылках, содержащих безалкогольный напиток, является нормально распределенной случайной величиной. Математическое ожидание этого распределения равно 2,0 л, а стандартное отклонение— 0,05 л. Бутылки, содержащие меньше 95% номинального объема (1,90 л), могут стать предметом судебных разбирательств, а бутылки, содержащие более 2,10 л, опасны при открывании.
1. Какова доля бутылок, содержащих от 1,90 до 2,0 л?
2. Какова доля бутылок, содержащих от 1,90 до 2,10 л?
3. Какова доля бутылок, содержащих до 1,90 л?
4. Какова доля бутылок, содержащих меньше 1,90 или больше 2,10 л?
5. Какова доля бутылок, содержащих больше 2,10 л?
6. Какова доля бутылок, содержащих от 2,05 до 2,10 л?
7. В 99% бутылок содержится не меньше определенного объема жидкости. Чему равен этот объем?
8. Между какими двумя величинами (симметрично расположенными относительно математического ожидания) находятся объемы 99% бутылок?
9. Объясните разницу между ответами на вопросы 7 и 8.
10. Допустим, что производители напитков настроили разливочную машину так, что средний объем стал равным 2,02 л. Как изменятся ответы на вопросы 1-9?
Предположим, что из генеральной совокупности извлекается выборка, состоящая из 25 бутылок. Вычислите вероятности следующих событий.
11. Выборочное среднее больше 1,99 и меньше 2,0 л.
12. Выборочное среднее больше 1,99 и меньше 2,01 л.
13. Выборочное среднее меньше 1,98 л.
14. Выборочное среднее меньше 1,98 или меньше 2,02 л.
15. Выборочное среднее больше 2,01 л.
16. Выборочное среднее больше 2,01 и меньше 2,03 л.
17. Выше какого значения лежат 99% выборочных средних?
18. Между какими двумя величинами (симметрично расположенными относительно математического ожидания) находятся объемы 99% бутылок?
19. Объясните разницу между ответами на вопросы 17 и 18.
6.93. Производитель апельсинового сока покупает апельсины, которые выращиваются на одной крупной плантации. Объем сока, выжимаемого из одного апельсина, представляет собой нормально распределенную случайную величину. Математическое ожидание этого распределения равно 4,70 унции, а стандартное отклонение — 0,40 унции.
1. Какова вероятность, что случайно выбранный апельсин содержит от 4,70 до 5,00 унции сока?
2. Какова вероятность, что случайно выбранный апельсин содержит от 5,00 до 5,50 унции сока?
3. В 77% апельсинов содержится не меньше определенного объема жидкости. Чему равен этот объем?
4. Между какими двумя величинами (симметрично расположенными относительно математического ожидания) находятся объемы сока в 80% апельсинов?
Допустим, что выборка содержит 25 апельсинов.
5. Какова вероятность, что выборочное среднее не превышает 4,60 унции?
6. Между какими двумя величинами (симметрично расположенными относительно математического ожидания) находятся средние значения 70% выборок?
7. В 77% выборок среднее значение не превышает определенной величины. Чему равен этот объем?
6.94. По данным журнала Investment Digest (“Diversification and the Risk/Reward Relationship”, Winter 1994, 1-3), средняя годовая доходность обычных акций за период с 1926 по 1992 годы равна 12,4%, а стандартное отклонение— 20,6%. За этот же период средняя доходность облигаций правительственного займа равна 5,2%, а стандартное отклонение — 8,6%. В статье утверждается, что распределения обеих случайных величин являются колоколообразными и симметричными. Предположим, что распределения этих величин являются нормальными.
1. Какова вероятность, что доходность случайно выбранной акции больше нуля?
2. Какова вероятность, что доходность случайно выбранной акции меньше нуля?
3. Какова вероятность, что доходность случайно выбранной акции больше 10,0% ?
4. Какова вероятность, что доходность случайно выбранной акции больше 20,0% ?
5. Какова вероятность, что доходность случайно выбранной акции больше 30,0% ?
6. Какова вероятность, что доходность случайно выбранной акции меньше -10,0% ?
7. Оцените вероятности этих событий для долговременных правительственных облигаций.
8. Объясните разницу между результатами, полученными для акций и облигаций.
6.95. На протяжении первого полугодия 2002 года фондовый рынок был довольно изменчивым, и подавляющее большинство основных индексов снизилось. К июню 2002 года индекс S&P 500 уменьшился на 12,3%, а составной индекс NASDAQ — на 23%. Рынок акций взаимных фондов в США был более стабильным и его потери не превысили 10% (Mara der Hovanesian, “Active Managers Flex Their Muscles”, Business Week, July, 2002, 127-128). Предположим, что доходности взаимных фондов на протяжении этого периода имели нормальное распределение, математическое ожидание которого равно -10,0%, а стандартное отклонение равно 8,0%.
1. Какова вероятность, что доходность случайно выбранного взаимного фонда упала не меньше, чем на 18% ?
2. Какова вероятность, что доходность случайно выбранного взаимного фонда упала не меньше, чем на 25% ?
3. Какова вероятность, что доходность случайно выбранного взаимного фонда повысилась?
4. Какова вероятность, что доходность случайно выбранного взаимного фонда повысилась как минимум на 10% ?
5. Определите значение, которое превышает доходность 80% взаимных фондов.
6. Определите значение, которое не превышает доходность 90% взаимных фондов.
7. Между какими двумя величинами (симметрично расположенными относительно математического ожидания) находятся доходности 95% взаимных фондов?
6.96. По сообщению газеты The New York Times (Laurie J. Flynn, “Tax Surfing”, The New York Times, March 25, 2002, CIO), средняя продолжительность загрузки Web-страницы компании Internal Revenue Service www.irs.gov была равна 0,8c. Допустим, что продолжительность загрузки имеет нормальное распределение, стандартное отклонение которого равно 0,2 с. Вычислите вероятность следующих событий.
1. Какова вероятность, что продолжительность загрузки окажется меньше 1 с?
2. Какова вероятность, что продолжительность загрузки окажется больше 0,5 и меньше 1,5 с?
3. Какова вероятность, что продолжительность загрузки окажется больше 0,5 с?
4. Определите значение, которое не превышает продолжительность 99% загрузок.
5. Между какими двумя величинами (симметрично расположенными относительно математического ожидания) находится продолжительность 95% загрузок?
В той же статье сообщалось, что среднее время загрузки домашней страницы Web-сайта www. hrblock. com, принадлежащего компании H&R Block, равно 2,5 с. Допустим, что время загрузки имеет нормальное распределение со стандартным отклонением, равным 0,5 с. Вычислите вероятность следующих событий.
6. Какова вероятность, что продолжительность загрузки окажется меньше 1 с?
7. Какова вероятность, что продолжительность загрузки окажется больше 0,5 и меньше 1,5 с?
8. Какова вероятность, что продолжительность загрузки окажется больше 0,5 с?
9. Определите значение, которое не превышает продолжительность 99% загрузок.
10. Между какими двумя величинами (симметрично расположенными относительно математического ожидания) находится продолжительность 95% загрузок?
11. Сравните результаты, полученные для Web-сайтов компаний IRS и H&R Block.
6.97. Количество взаимных фондов, инвестировавших средства в телекоммуникационные компании, уменьшилось на 18,4% (“Stock Funds Perk Up in the First Quater”, www.usatoday.com, April 4, 2002). Предположим, что распределение доходности взаимных фондов, инвестировавших средства в телекоммуникационные компании в первом квартале 2002 года, является симметричным относительно значения -18,4%, причем его стандартное отклонение равно 20%. Допустим, что из генеральной совокупности таких взаимных фондов извлечены выборки, состоящие из 25 фондов, специализирующихся на телекоммуникационных компаниях.
1. Какова вероятность, что выборочное среднее меньше -20,0% ?
2. Какова вероятность, что выборочное среднее меньше -25,0% ?
3. Какова вероятность, что выборочное среднее больше 0,0% ?
4. Определите значение, которое не превышает выборочное среднее доходности 80% взаимных фондов, специализирующихся на телекоммуникационных компаниях.
5. Определите значение, которое не превышает выборочное среднее доходности 90% взаимных фондов, специализирующихся на телекоммуникационных компаниях.
6. Можно ли применить методы, описанные в главе, для анализа данных, если выборка состоит из четырех фондов?
6.98. Телевизионная реклама замороженной пиццы DiGiorno является одной из наиболее интересных и привлекательных. В статье, опубликованной в журнале USA Today, утверждается, что эта реклама очень понравилась 20% зрителей (Theresa Howard, “DiGiorno Campaign Delivers Major Sales”, www. usatoday. com, April 1, 2002). Предположим, что из генеральной совокупности извлекаются выборки, состоящие из 400 телезрителей.
1. Какова доля выборок, в которых от 18 до 22% телезрителей считают рекламу компании DiGiorno весьма привлекательной?
2. Какова доля выборок, в которых от 16 до 24% телезрителей считают рекламу компании DiGiorno весьма привлекательной?
3. Какова доля выборок, в которых от 14 до 26% телезрителей считают рекламу компании DiGiorno весьма привлекательной?
4. Какова доля выборок, в которых от 12 до 28% телезрителей считают рекламу компании DiGiorno весьма привлекательной?
6.99. Классная работа. По данным Бартона Малкиеля (Burton G. Malkiel), колебания цен акций на момент закрытия торгов представляют собой случайное блуждание, иначе говоря, цены акций на момент закрытия торгов в разные дни не зависят друг от друга, изменяясь случайным образом. Бартон Малкиель утверждает, что эти случайные величины имеют приближенно нормальное распределение.
Чтобы проверить эту теорию, воспользуйтесь либо газетой, либо Интернет, выбрав одну компанию, акции которой котируются на Нью-Йоркской фондовой бирже, одну компанию, акции которой котируются на Американской фондовой бирже, и одну компанию, акции которой котируются “по всей стране” (например, на бирже NASDAQ).
• Записывайте цены акций этих компаний на момент закрытия торгов в течение шести последовательных недель (чтобы получить по 30 наблюдений для каждой компании).
• Записывайте изменения цены акций этих компаний на момент закрытия торгов в течение шести последовательных недель (чтобы получить по 30 наблюдений для каждой компании).
1. Для каждого из полученных наборов данных постройте диаграмму “ствол и листья”, гистограмму, полигон и блочную диаграмму, чтобы убедиться в том, что данные распределены по приближенно нормальному закону.
2. Проверьте, выполняются ли теоретические свойства нормального распределения для каждого из полученных наборов данных.
3. Проверьте, являются ли данные из полученных наборов нормально распределенными, построив график нормального распределения.
4. Объясните результаты, полученные при выполнении заданий 1-3.
5. Обратите внимание на то, что теория случайных блужданий относится лишь к колебаниям цен акций на момент закрытия торгов, а не к самим ценам.
6. Используя результат, полученный при выполнении задания 4, определите вид трех распределений, построенных на основании набора цен акций на момент закрытия торгов и набора колебаний этих цен. Можно ли утверждать, что эти распределения являются приближенно нормальными?
6.100. Классная работа. Таблица случайных чисел представляет собой набор равномерно распределенных чисел, поскольку все цифры в ней являются равновероятными. Выберите в таблице случайных чисел (табл. Д.1) строку, соответствующую порядковому номеру месяца, в который вы родились, а затем выбирайте из нее по одной цифре. Сначала создайте выборки, имеющие объемы п = 2, п = 5ип=10. Для каждой из них вычислите выборочное среднее. Пусть каждый студент создаст по пять выборок указанных объемов и построит распределение выборочных средних. Как распределены эти величины?
6.101. Классная работа. Подбросьте монету десять раз и запишите, сколько раз выпал орел. Если каждый студент повторит этот эксперимент пять раз, можно построить распределение частот. Проверьте, является ли оно нормальным.
6.102. Классная работа. В следующей таблице приведено количество автомобилей, ожидающих своей очереди на мойке.
Количество автомобилей Вероятность
0 0,25
1 0,40
2 0,20
3 0,10
4 0,04
5 0,01
Для извлечения выборок из этой генеральной совокупности можно воспользоваться таблицей случайных чисел.
• Выберите в таблице случайных чисел (см. табл. Д.1) строку, соответствующую порядковому номеру месяца, в котором вы родились.
• Выберите двузначное случайное число.
• Если выбранное число больше 0 и меньше 24, длина очереди равна 0; если выбранное число больше 25 и меньше 64, длина очереди равна 1; если выбранное число больше 65 и меньше 84, длина очереди равна 2; если выбранное число больше 85 и меньше 94, длина очереди равна 3; если выбранное число больше 95 и меньше 98, длина очереди равна 4, если выбранное число равно 99, длина очереди равна 5.
Извлеките из генеральной совокупности очередей выборки, имеющие объемы д = 2, д = 5ид = 10. Для каждой из них вычислите выборочное среднее. Например, если выборка содержит числа 18 и 46, ей соответствуют длины очереди 0 и 1, следовательно, средняя длина очереди равна 0,5. Пусть каждый студент создаст по пять выборок указанных объемов и построит распределение выборочных средних. Как распределены эти величины?
6.103. Классная работа. С помощью таблицы случайных чисел можно моделировать выбор из урны разноцветных шаров.
• Выберите в таблице случайных чисел (см. табл. Д.1) строку, соответствующую порядковому номеру месяца, в котором вы родились.
• Выберите однозначное случайное число.
• Если выбранное число больше 0 и меньше 6, будем считать, что из урны извлечен белый шар; если выбранное число равно 7, 8 или 9, будем считать, что из урны извлечен черный шар.
Извлеките из генеральной совокупности выборки, имеющие объемы д = 10, п = 25 и д = 30. Для каждой из них вычислите количество белых шаров. Пусть каждый студент создаст по пять выборок указанных объемов и построит выборочное распределение процентных долей белых шаров. Как распределены эти величины?
6.104. Классная работа. Предположим, что в задаче 6.103 в п. 3 применяется следующее правило.
• Если выбранное число больше 0 и меньше 8, будем считать, что из урны извлечен белый шар; если выбранное число равно 9, будем считать, что из урны извлечен черный шар.
Сравните решение этой задачи с решением задачи 6.103.
Применение Интернет
6.105. Зайдите на сайт www.prenhall. com/levine. Выберите ссылку Chapter 6 и щелкните на ссылке Internet exercises.
ГРУППОВОЙ ПРОЕКТ
ТР.6.1. Файл данных ^MUTUAL FUNDS . XLS содержит информацию о 13 переменных, характеризующих 259 взаимных фондов.
Фонд — название взаимного фонда.
Вид — вид акций, принадлежащих взаимному фонду: малые, средние и крупные компании.
Цель — цель фонда (быстрый или медленный рост капитала).
Активы — В млн. долл.
Комиссия — да или нет.
Издержки — издержки, понесенные взаимным фондом (в процентах от среднего объема чистых активов).
Доходность 2001 —доходность за двенадцать месяцев 2001 г.
Трехлетняя доходность — среднегодовая доходность за период с 1999 по 2001 гг.
Пятилетняя доходность — среднегодовая доходность за период с 1997 по 2001 гг.
Оборачиваемость — уровень торговой активности фонда: очень низкий, низкий, средний, высокий, очень высокий.
Риск — уровень риска: очень низкий, низкий, средний, высокий, очень высокий.
Лучший квартал — квартал с наивысшей доходностью за период с 1997 по 2001 гг.
Худший квартал — квартал с наименьшей доходностью за период с 1997 по 2001 гг.
Рассмотрите распределение трех случайных величин: Издержки, Доходность 2 001 и Трехлетняя доходность. Проверьте вид распределения этих величин, сравнив их характеристики с теоретическими свойствами нормального распределения и построив график нормального распределения.
РАЗБОР конкретной СИТУАЦИИ -ГАЗЕТА SPRINGVILLEHERALD
Производственный отдел газеты Springville Herald предпринимает усилия для улучшения качества печати. Для начала он решил проверить четкость печатного шрифта и стал ежедневно проверять насыщенность типографской краски. Номинальная величина насыщенности равна 1,0. Оказалось, что данные, собранные за несколько лет, имеют нормальное распределение с математическим ожиданием, равным 1,005 и стандартным отклонением, равным 0,10.
Каждый день наугад выбирается произвольный фрагмент газеты, а затем измеряется насыщенность его шрифта. Насыщенность считается приемлемой, если ее величина колеблется в интервале от 0,95 до 1,05.
УПРАЖНЕНИЯ
Предположим, что за последние несколько лет распределение насыщенности не изменилось. Определите вероятность следующих событий.
1. Насыщенность не превышает 1,0.
2. Насыщенность больше 0,95 и меньше 1,0.
3. Насыщенность больше 1,0 и меньше 1,05.
4. Насыщенность меньше 0,95 или больше 1,05.
Предположим, производственный отдел стремится уменьшить вероятность того, что насыщенность краски окажется меньше 0,95 или больше 1,05. Что выбрать в качестве цели: чтобы насыщенность краски не превышала 1,0 или чтобы стандартное отклонение уменьшилось до 0,075? Обоснуйте свой ответ.
Предположим, что производственный отдел выбирает не один, а 25 случайных фрагментов текста. Считая, что на протяжении нескольких лет распределение насыщенности остается неизменным, определите вероятности следующих событий.
1. Средняя насыщенность не превышает 1,0.
2. Средняя насыщенность больше 0,95 и меньше 1,0.
3. Средняя насыщенность больше 1,00 и меньше 1,05.
4. Средняя насыщенность меньше 0,95 или больше 1,05.
5. Допустим, что средняя насыщенность, определенная по 25 наугад выбранным фрагментам текста, равна 0,952. Что можно сказать о насыщенности всей газеты? Обоснуйте свое утверждение.
ПРИМЕНЕНИЕ WEB
Примените свои знания о нормальном распределении и оцените данные о продолжительности загрузки Web-страницы компании On Campus!.
Для того чтобы заинтересовать потенциальных рекламодателей, руководство компании On Campus! решило оценить время, на которое посетители задерживаются на Web-сайте (этот показатель называется “липкостью” (stickiness)). Отдел маркетинга собрал соответствующие данные, заявил, что они имеют нормальное распределение, и сделал некоторые умозаключения. Эти данные и выводы изложены в отчете, размещенном на Web-странице www.prenhall. com/Springville/OC_MarketingSurvey.htm). Проанализируйте этот отчет и ответьте на следующие вопросы.
1. Имеют ли собранные данные нормальное распределение?
2. Оцените обоснованность выводов, сделанных отделом маркетинга компании On Campus!. Какие из них правильны, а какие — нет?
3. Допустим, что компании On Campus! удалось увеличить среднее время посещения своей Web-страницы до 5 мин. Как изменится распределение вероятностей?
ПРИМЕНЕНИЕ WEB
Примените свои знания о выборочных распределениях и оцените данные о расфасовке кукурузных хлопьев на заводе компании Oxford Cereals.
Организация потребителей, уверенных, что компания Oxford Cereal мошенничает (сокращенно — ОПУЧКОСМ), убеждена, что реальный вес коробок с кукурузными хлопьями меньше, чем номинальный. Посетите Web-страницу ОПУЧКОСМ (www .prenhall. сот/ Springville/CerealCheaters . htm) и проверьте эти заявления.
1. Корректны ли методы, которыми ОПУЧКОСМ собирала данные?
2. Предположим, что члены ОПУЧКОСМ сформировали две случайные выборки, состоящие из пяти коробок (по одной выборке на каждую разновидность кукурузных хлопьев). Для каждой выборки выполните следующие задания.
2.1. Вычислите выборочное среднее.
2.2. Вычислите процент всех выборок (для каждой разновидности), выборочное среднее которых меньше, чем вычисленное в п. 2.1, предполагая, что стандартное отклонение равно 15 г.
2.3. Вычислите процент всех коробок, вес которых меньше, чем выборочное среднее, вычисленное в п. 2.1, предполагая, что стандартное отклонение равно 15 г.
3. Позволяют ли полученные результаты сделать какие-нибудь выводы о процессе расфасовки кукурузных хлопьев двух разновидностей? Если да, то какие?
4. Представитель компании Oxford Cereals потребовал от ОПУЧОСМ закрыть Web-страницу, на которой обсуждался недовес в коробках с кукурузными хлопьями. Обосновано ли это требование? Аргументируйте свой ответ.
5. Можно ли обнаружить мошенничество, пользуясь методами, изложенными в главе? Обоснуйте свой ответ.
СПРАВОЧНИК ПО EXCEL. ГЛАВА 6
ЕН.6.1. Вычисление вероятностей нормального распределения
Реализуем рабочий лист, использующий для вычисления вероятностей нормального распределения функции НОРМАЛИЗАЦИЯ, НОРМРАСП, НОРМСТОБР и НОРМОБР. Вызовы этих функций имеют следующий вид.
НОРМАЛИЗАЦИЯ {X; математическое_ожидание; стандартное—Отклонение),
НОРМРАСП (X; математическое_ожидание', стандартное-Отклонение', ИСТИНА), где параметр X задает интересующую нас величину X, а параметры математическое—ожидание и стандартное—отклонение — математическое ожидание и стандартное отклонение нормального распределения.
НОРМСТОБР {вероятность) ,
где параметр вероятность представляет собой площадь, ограниченную кривой и расположенную слева от величины X.
НОРМОБР {вероятность; математическое_ожидание; стандартное отклонение), где параметр вероятность представляет собой площадь, ограниченную кривой и расположенную слева от величины X, а параметры математическое—ожидание и стандартное отклонение задаются функцией НОРМРАСП.
Функция НОРМАЛИЗАЦИЯ возвращает величину Z, соответствующую заданному значению X, математическому ожиданию и стандартному отклонению. Функция НОРМРАСП вычисляет площадь, ограниченную гауссовой кривой и величиной X. Функция НОРМСТОБР возвращает обратное значение стандартизованного нормального распределения. Функция НОРМОБР вычисляет величину X, соответствующую заданной вероятности, математическому ожиданию и стандартному отклонению.
В табл. ЕН.6.1 и ЕН.6.2 продемонстрирован шаблон рабочего листа Нормальное_ распределение, вычисляющего вероятности нормального распределения, рассмотренные в примерах 6.1, 6.2, 6.5 и 6.6. Реализуя этот шаблон, учтите, что формулы в ячейках А18 и D13 должны набираться в одной строке, а столбец С должен оставаться пустым. Кроме того, обратите внимание на то, что А10, А15, А17, А18, D11 и D12 содержат по две пары двойных кавычек, а формула в ячейке D13 — три пары двойных кавычек. Для того чтобы вычислить вероятность, которая должна быть неотрицательной, в ячейке Е13 использована функция ABS, возвращающая абсолютную величину.
Таблица ЕН.6.1. Шаблон рабочего листа Нормальное_распределение (столбцы А и в)
А у-. "" z ; в у,
1 Нормальное распределение
: 2 "
3 Общие данные
4 Математическое ожидание 7
5 Стандартное отклонение 2
6
7 Вероятность того, что Х<=
8 Значение X 3,5
9 Значение Z =НОРМАЛИЗАЦИЯ(В8;В4;В5)
10 ="Р(Х <=" & В8 &")" =НОРМРАСП(В8;В4;В5;ИСТИНА)
11
Окончание табл. ЕН. 6.1
А В
12 Вероятность того, что Х>
ill Значение X 9
14 Значение Z =НОРМАЛИЗАЦИЯ(В13;В4;В5)
15 ="Р(Х >" & В13 &")" =1-НОРМРАСП(В13;В4;В5;ИСТИНА)
16
17 ="Вероятность того, что Х< "&В8&" или Х>" &В13
18 ="Р(Х <" & В8 & " или X >" & В13 = В10+В15
Таблица ЕН.6.2. Диапазон D6: Е18 из шаблона рабочего листа
Нормальное_распределение (диапазон D1 :Е5 пуст)
D
6 Вероятность того, что A<= X <=B
7 Значение А 7
8 Значение В 9
jjlillil ="3начение Z для" &Е7 =НОРМАЛИЗАЦИЯ(Е7;В4;В5)
ill ="3начение Z для" &Е8 = НОРМАЛИЗАЦИЯ(Е8;В4;В5)
iiiil ="Р(Х <=" & Е7 & ")" = НОРМРАСП(Е7;В4;В5;ИСТИНА)
||Н| ="Р(Х<=" & Е8 & ")" = НОРМРАСП(Е8;В4;В5;ИСТИНА)
||1|| ="Р(" & Е7 & "<=Х <=" &Е8&")" =ABS(E12-E11)
Вычисление величин X и Z по заданной интегральной вероятности
11111 Интегральная вероятность 0,1
lliji Значение Z = Н0РМСТ0БР(Е16)
lijill Значение X =НОРМОБР(Е16;В4;В5)
Этот рабочий лист можно настроить для решения аналогичных задач. Например, если вам не нужно вычислять вероятность того, что величина X лежит в заданном диапазоне, выберите сначала диапазон ячеек D6:Е13, а затем — команду Правка^Удалить..,. В диалоговом окне Удалить установите переключатель Удалить ячейки со сдвигом влево и щелкните на кнопке ОК.
ЕН.6.2. Построение графика нормального распределения
Для построения графика нормального распределения необходимо реализовать рабочий лист, использующий функцию НОРМДИСТ.
В табл. ЕН.6.3 приведен шаблон рабочего листа ГрафикНормРасп, в котором содержатся данные о пятилетней среднегодовой доходности 259 взаимных фондов. Скопируйте в столбец D данные, записанные на листе Данные в рабочей книге MUTUAL FUNDS.XLS в диапазоне 11:12 60. Затем отсортируйте их в порядке возрастания, используя команду Данные^Сортировка.
Таблица ЕН.6.3. Шаблон рабочего листа ГрафикНормРасп (три первые и три последние строки)
А В С D
1 Номер Доля Значение Z Доходность
2 1 =А2/А260 =Н0РМСТ0БР(В2) -6,1
3 2 =АЗ/А260 =НОРМСТОБР(ВЗ) -2,8
4 3 =А4/А260 =Н0РМСТ0БР(В4) -1,2
...
258 258 =А258/А260 =НОРМСТОБР(В258) 22,9
259 259 =А259/А260 =НОРМСТОБР(В259) 25,0
260 260 =А260/А260 =НОРМСТОБР(В260) 26,3
Процедуру ввода порядковых номеров фондов можно облегчить следующим образом.
1. Введите в ячейку А2 число 1, а затем выделите ее снова.
2. Выберите Правка^Заполнить...1^Прогрессия....
Расположение О по строкам 0 по столбцам □ Автоматическое определение шага Тип 0 арифметическая О геометрическая О даты О автозаполнение
Шаг: 1 Предельное значение: 1 259
Е2О L Отмена ]
3. В диалоговом окне Прогрессия (см. рисунок) установите переключатель Расположение в положение По столбцам, а переключатель Тип — в положение Арифметическая. Затем введите в окне редактирования Предельное значение число 25 9 и щелкните на кнопке ОК. Программа Microsoft Excel автоматически заполнит диапазон АЗ:А2 60 числами от 2 до 259.
Чтобы простроить график нормального распределения, создайте рабочий лист ГрафикНормРасп и вызовите Мастер диаграмм. Затем откройте рабочий лист, выберите команду Вставка ^Диаграмма... и следуйте инструкциям.
1. На первом этапе диалога выполните следующее.
1.1. Щелкните на корешке вкладки Стандартные и выберите пункт Точечная в раскрывающемся списке Тип.
1.2. Выберите первую диаграмму во втором ряду, сопровождающуюся описанием: Точечная диаграмма позволяет сравнить пары значений. Щелкните на кнопке Далее>.
2. На втором этапе диалога выполните следующее.
2.1. Щелкните на корешке вкладки Диапазон данных. Введите в окне редактирования Диапазон ссылки на ячейки С1: D2 б 0.
2.2. Установите флажок В столбцах в группе Ряды и щелкните на кнопке Далее>.
3. На третьем этапе диалога выполните такие действия.
3.1. Щелкните на корешке вкладки Заголовки. Введите в окне редактирования Название диаграммы заголовок диаграммы, в окне редактирования Ось X (категорий) — строку Значение Z, а в окне редактирования Ось Y (значений) — строку Среднегодовая доходность.
3.2. По очереди щелкните на корешках вкладок Оси, Линии сетки и Подписи данных. Установите флажки и переключатели, как показано во врезке ЕР.6. Щелкните на корешке вкладки Легенда и установите флажок Добавить легенду.
3.3. Щелкните на кнопке Далее>.
4. На четвертом этапе диалога сделайте следующее.
4.1. Установите переключатель Поместить диаграмму на листе в положение Отдельном и введите в диалоговом листе, расположенном справа от переключателя, строку График нормального распределения.
4.2. Щелкните на кнопке Готово.
На графике, построенном с помощью Мастера диаграмм, оси координат могут быть изображены неверно (в зависимости от версии программы Microsoft Excel Прим, ред.). Чтобы разместить ось Y вдоль левой стороны графика, а ось X — вдоль нижней стороны графика, необходимо выполнить следующие действия.
1. Установить курсор на ось X и щелкнуть правой кнопкой. (Если курсор мыши установлен правильно, на экране появится подсказка Ось X (категорий).)
2. Во всплывающем меню выбрать команду Формат оси.
3. В диалоговом окне Формат оси (см. рис.) щелкнуть на корешке вкладки Шкала, ввести число -Зв окне редактирования Ось Y (значение) пересекает в значении и щелкнуть на кнопке ОК.
Исправленный график должен выглядеть так, как показано на рис. 6.22.
Для того чтобы построить график нормального распределения на основе других наборов данных, шаблон рабочего листа ГрафикНормРасп следует настроить, добавив но-
вые или удалив лишние строки, а также изменив знаменатель в столбце В. (Этот числитель должен на единицу превышать объем выборки.) Перемещая ось Y, введите в окне Ось Y (значение) пересекает в значении число, равное минимальному значению переменной X.
ЕН.6.3. Вычисление вероятностей экспоненциального распределения
Для вычисления вероятностей экспоненциального распределения следует реализовать рабочий лист, использующий функцию ЭКСПРАСП. Вызов этой функции имеет следующий вид:
ЭКСПРАСП (X; математическое ожидание; ИСТИНА), где параметр X задает интересующую нас величину X, параметр математическое ^ожидание — математическое ожидание X экспоненциального распределения.
В табл. ЕН.6.4 продемонстрирован шаблон рабочего листа Экспоненциальное_ распределение, содержащий данные о количестве клиентов, воспользовавшихся услугами банкомата.
Таблица ЕН.6.4. Шаблон рабочего листа Экспоненциальное_распределение
В
1 Экспоненциальное распределение
2
3 Данные
4 Математическое ожидание 20
5 Значение X 0,1
И111
,111 Результаты
а РК=Х) =ЭКСПРАСП(В5;В4;ИСТИНА)
ЕН.6.4. Генерирование случайных выборок
Для генерирования нескольких выборок используется процедура Сервис^Анализ данных...^Генерация случайных чисел. Например, чтобы сгенерировать 100 выборок, состоящих из 30 чисел, извлеченных из генеральной совокупности, равномерно распределенной на интервале от 0 до 1, необходимо открыть рабочий лист и выполнить следующие действия.
1. Выбрать команду Сервис^Анализ данных. В диалоговом окне Анализ данных в списке Инструменты анализа выбрать пункт Генерация случайных чисел.
2. В диалоговом окне Генерация случайных чисел (см. рисунок) выполнить следующее.
2.1. Ввести число 100 в окне редактирования Число переменных.
2.2. Ввести число 30 в окне редактирования Число случайных чисел.
2.3. Выбрать пункт Равномерное в раскрывающемся списке Распределение.
2.4. В разделе Параметры ввести числа 0 и 1 в соответствующих окнах редактирования.
2.5. Установить переключатель Параметры выводы в положение Новый рабочий лист и ввести название листа.
2.6. Щелкнуть на кнопке ОК.
Чтобы сгенерировать несколько выборок стандартизованного нормального распределения, в п. 2.3 в списке Распределение выберите пункт Нормальное и введите в окнах редактирования Среднее и Стандартное отклонение параметры 0 и 1 соответственно.
Эту процедуру можно применять и для генерирования выборок из дискретной генеральной совокупности. Для этого необходимо открыть рабочий лист, содержащий величины X и Р(Х), например, рабочий лист Дискретные_данные в книге Chapter 6.xls, выбрать пункт Дискретное в раскрывающемся списке Распределение, а затем ввести диапазон А2.-В7 в окне редактирования Входной интервал значений и вероятностей.
ЕН.6.5. Построение гистограмм для вычисленных выборочных средних
Для построения гистограммы выборочных средних используется процедура Сервис^ Анализ данных... ^Гистограмма. Для этого необходимо открыть рабочий лист, содержащий вычисленные выборочные средние, и выполнить следующие действия.
1. Выбрать команду Сервис^Анализ данных.... В диалоговом окне Анализ данных в списке Инструменты анализа выбрать пункт Гистограмма. Щелкнуть на кнопке ОК.
2. В диалоговом окне Гистограмма выполнить следующее.
2.1. Ввести в окне редактирования Входной интервал диапазон АЗ 2 : CV32.
2.2. Не вводить никаких данных в окне редактирования Интервал карманов.
2.3. Установить переключатель Параметры вывода в положение Новый рабочий лист и ввести название листа.
2.4. Установить флажок Вывод графика.
2.5. Щелкнуть на кнопке ОК.
Г истограмма |х]
Входные данные
Входной интервал:
Интервал карманов:
□ Метки
С°О) | Отмена ]
[ Справка ]
Параметры вывода
О Выходной интервал: i 7s
{•) Новый рабочий лист: : ГистограммаВыборочн
О Новая рабочая книга
□ Парето (отсортированная гистограмма)
□ Интегральный процент
0 Вывод графика
Для исправления созданного рабочего листа воспользуйтесь указаниями, приведенными в разделах ЕН.2.1 и ЕН.2.3. После этого рабочий лист будет выглядеть так, как показано на рис. ЕН.6.1.
г, А_________1____В____‘ ’ С j О___________!__Е_____I F < ,,.G J, Н
1 [Карманы Частота
2 : 0.017914 1
3 0.115635 12
4 0 213356 11
XI 0.311075 10
6 • 0 4087S5 6
Т‘ 0.506516 15
81 0.604236 10
"э ” 0 701956 8
761 0 799677 7
7Г 0.897397 20
12
Гистограмма
о о о о о о
Карманы
Рис. ЕН.6.1. Выборочное распределение и гистограмма выборочных средних
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
1. Cochran, W. G., Sampling Techniques, 3rd ed. (New York: Wiley, 1977).
2. Gunter, B., “Q-Q Plots”, Quality Progress ( February 1994), 81-86.
3. Levine, D. M., P. Ramsey, and R. Smidt, Applied Statistics for Engineers and Scientists Using Microsoft Excel and Minitab (Upper Saddle River, NJ: Prentice Hall, 2001).
4. Marascuilo, L. A., and M. McSweeney, Nonparametric and Distribution-Free Methods for the Social Sciences (Monterey, CA Brooks/Cole, 1977).
5. Microsoft Excel 2002 (Redmond, WA: Microsoft Corporation, 2001).
6. Ramsey, P. P., and P. H. Ramsey, “Simple Tests for Normality in Small Samples”, Journal of Quality Technology 22(1990): 299-309.
7. Sievers, G. L., “Probability Plotting”, In Encyclopedia of Statistical Sciences, vol. 7, edited by S. Kotz and N. L. Johnson (New York: Wiley, 1986), 232-237.
Глава 7
Построение доверительных интервалов
ПРИМЕНЕНИЕ СТАТИСТИКИ: аудиторская проверка накладных в компании Saxon Home Improvement Company
7.1. ПОСТРОЕНИЕ ДОВЕРИТЕЛЬНОГО ИНТЕРВАЛА ДЛЯ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ ПРИ ИЗВЕСТНОМ СТАНДАРТНОМ ОТКЛОНЕНИИ
Процедуры Excel: построение доверительного интервала для математического ожидания генеральной совокупности при известном стандартном отклонении
7.2. ПОСТРОЕНИЕ ДОВЕРИТЕЛЬНОГО ИНТЕРВАЛА ДЛЯ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ ПРИ НЕИЗВЕСТНОЙ ДИСПЕРСИИ
Распределение Стьюдента
Степени свободы
Доверительный интервал
Процедуры Excel: построение доверительного интервала для математического ожидания генеральной совокупности при неизвестном стандартном отклонении
7.3. ПОСТРОЕНИЕ ДОВЕРИТЕЛЬНОГО ИНТЕРВАЛА ДЛЯ ДОЛИ ПРИЗНАКА В ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ
Процедуры Excel: построение доверительного интервала для доли признака в генеральной совокупности
7.4. ОПРЕДЕЛЕНИЕ ОБЪЕМА ВЫБОРКИ
Определение объема выборки для оценки математического ожидания
Процедуры Excel: определение объема выборки для оценки математического ожидания
Определение объема выборки для оценки доли признака в генеральной совокупности Процедуры Excel: определение объема выборки для оценки доли признака в генеральной совокупности
7.5. ПРИМЕНЕНИЕ ДОВЕРИТЕЛЬНЫХ ИНТЕРВАЛОВ В АУДИТОРСКОМ ДЕЛЕ
Оценка общей суммы элементов генеральной совокупности
Процедуры Excel: построение доверительного интервала для общей суммы генеральной совокупности
Оценка разности
Процедуры Excel: построение доверительного интервала для полной разност и генеральной совокупности
Односторонняя оценка доли нарушений установленных правил
7.6. ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ
И ЭТИЧЕСКИЕ ПРОБЛЕМЫ
7.7. ВЫЧИСЛЕНИЕ ОЦЕНОК И ОБЪЕМА ВЫБОРОК, ИЗВЛЕЧЕННЫХ ИЗ КОНЕЧНОЙ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ
Оценка математического ожидания
Оценка доли признака
Определение объема выборки
Процедуры Excel: вычисление поправочного коэффициента для конечной генеральной совокупности
СПРАВОЧНИК ПО EXCEL. ГЛАВА 7
ЧЕМУ ДОЛЖЕН НАУЧИТЬСЯ СТУДЕНТ
• Строить доверительные интервалы для математического ожидания и доли признака.
• Определять объем выборки, необходимый для построения доверительного интервала, содержащего математическое ожидание или долю признака.
• Применять доверительные интервалы в аудиторском деле.
ПРИМЕНЕНИЕ СТАТИСТИКИ
Аудиторская проверка накладных в компании Saxon Home Improvement Company
Компания Saxon Home Improvement Company — крупный дистрибьютор санитарнотехнического оборудования в пригороде одного из городов на северо-западе США. Представьте себе, что вы работаете бухгалтером этой компании и отвечаете за точность записей в информационной системе. Разумеется, оценить точность регистрации документов можно путем тотальной проверки всех записей. Однако этот путь слишком долог и дорог. Чтобы оценить точность всей генеральной совокупности записей, достаточно извлечь из нее относительно небольшую выборку. Поэтому в конце каждого месяца аудиторы извлекают из ин-
формационной системы выборку накладных и выполняют следующие процедуры.
• Вычисляют среднюю сумму, указанную в накладных за месяц.
• Подсчитывают общую сумму, указанную в накладных за месяц.
• Вычисляют все разности между суммами, указанными в накладных, и суммами, занесенными в информационную систему.
• Определяют, как часто встречаются ошибки, нарушающие систему отчетности, принятую в компании. К этим ошибкам относятся: отгрузка партии товара без складских расписок, неправильно указанные номера накладных и ошибочная \ отгрузка товара.
Насколько точна информация, полученная на основе анализа выборки, и как ее использовать? Достаточно ли велик объем выборки для того, чтобы делать обоснованные выводы?
ВВЕДЕНИЕ
В теории статистического вывода для оценки характеристик генеральной совокупности используются выборочные параметры. В этой главе мы рассмотрим статистические процедуры, позволяющие оценить математическое ожидание и долю признака в генеральной совокупности.
В статистике существует два вида оценок: точечные и интервальные. Точечная оценка (point estimate) представляет собой отдельную выборочную статистику, которая используется для оценки параметра генеральной совокупности. Например, выборочное среднее X — это точечная оценка математического ожидания генеральной совокупности, а выборочная дисперсия S2 — точечная оценка дисперсии генеральной совокупности о2. В разделе 6.6 показано, что выборочное среднее является несмещенной оценкой математического ожидания генеральной совокупности. Хотя на практике, как правило, используется только одна выборка, можно показать, что среднее всех выборочных средних равно математическому ожиданию генеральной совокупности ц.1 При оценке
Аналогично, чтобы выборочная дисперсия S2 стала несмещенной оценкой дисперсии генеральной совокупности а, знаменатель выборочной дисперсии следует положить равным п-1, а не п. Иначе говоря, дисперсия генеральной совокупности является средним значением всевозможных выборочных дисперсий.
параметров генеральной совокупности следует иметь в виду, что выборочные статистики, такие как X , зависят от конкретных выборок. Чтобы учесть этот факт, для получения интервальной оценки (interval estimate) математического ожидания генеральной совокупности анализируют распределение выборочных средних (см. раздел 6.6). Построенный интервал характеризуется определенным доверительным уровнем, который представляет собой вероятность того, что истинный параметр генеральной совокупности оценен правильно. Аналогичные доверительные интервалы можно применять для оценки доли признака р и основной распределенной массы генеральной совокупности. Например, можно построить доверительный интервал, которому с вероятностью, равной 95%, принадлежит средняя сумма, указанная в накладных компании Saxon Home Improvement Company за последний месяц.
В этой главе мы покажем, как определить объем выборки, чтобы гарантировать заданные свойства доверительного интервала, а также обсудим несколько важных аудиторских процедур.
7.1. ПОСТРОЕНИЕ ДОВЕРИТЕЛЬНОГО ИНТЕРВАЛА
ДЛЯ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ ПРИ ИЗВЕСТНОМ СТАНДАРТНОМ ОТКЛОНЕНИИ
В разделе 6.6 мы применили информацию о распределении и центральную предельную теорему, чтобы вычислить процентную долю выборочных средних, лежащих в окрестности математического ожидания генеральной совокупности на расстоянии, не превышающем заданное. Например, в примере, посвященном анализу веса коробок с кукурузными хлопьями, 95% всех выборочных средних лежат в интервале от 362,12 до 373,88%. Это утверждение получено с помощью дедукции (deductive reasoning), поскольку свойства выборки определялись на основе данных о генеральной совокупности. Однако теперь нам необходимо применить противоположный способ рассуждения — индуктивный (inductive reasoning), так как в теории статистического вывода, наоборот, свойства генеральной совокупности определяются на основе параметров отдельной выборки. На практике математическое ожидание генеральной совокупности, как правило, не известно и должно быть оценено. Вернемся к примеру с коробками. Допустим теперь, что математическое ожидание генеральной совокупности р не известно, а истинное стандартное отклонение генеральной совокупности су равно 15 г. Тогда в формулах для определения границ интервала ц ± 1,96 су/V? математическое ожидание генеральной совокупности ц следует заменить выборочным средним X . Следовательно, для оценки неизвестного математического ожидания генеральной совокупности можно применить интервал X ±1,96сгД/п . На практике, как правило, из генеральной совокупности извлекают выборку фиксированного объема п и вычисляют выборочное среднее X . Однако, чтобы понять смысл интервальной оценки, необходимо рассмотреть гипотетическое множество всех возможных выборок данного объема.
Допустим, например, что математическое ожидание генеральной совокупности ц равно 368 г. Предположим, что из генеральной совокупности коробок извлекается выборка, состоящая из 25 коробок, средний вес которых равен 362,3 г. Интервал, предложенный для оценки математического ожидания ц, имеет границы: 362,3± 1,96x15/^2? , т.е. 362,3±5,88. Таким образом,
356,42 <ц< 368,18.
Поскольку математическое ожидание генеральной совокупности р равно 368, оно попадает в этот интервал, и, следовательно, данная выборка позволяет правильно ее оценить (рис. 7.1).
Рис. 7.1. Доверительные интервальные оценки математического ожидания генеральной совокупности, полученные по пяти разным выборкам объема п = 25, извлеченным из генеральной совокупности с параметрами //=368 и ст= 15
Продолжим анализ нашего гипотетического примера. Допустим, что выборочное среднее некоей выборки объема п = 25, равно 369,5. Доверительный интервал, построенный по этой выборке, имеет границы, равные 369,5 ± 1,96 х 15/>/25 , т.е. 369,5±5,88. Таким образом,
363,62 <ц< 375,38.
Поскольку математическое ожидание генеральной совокупности ц равно 368, оно попадает в этот интервал, и, следовательно, данная оценка является правильной.
Возникает впечатление, что выборки, имеющие объем п = 25, всегда приводят к правильным оценкам математического ожидания генеральной совокупности ц. Чтобы опровергнуть это, рассмотрим третий гипотетический пример. Допустим, что средний вес коробок равен 360 г. Интервал, предложенный для оценки математического ожиданйя ц, имеет границы: 360 ± 1,96x15/725 , т.е. 360 ± 5,88. Таким образом, в данном случае
354,12 <ц< 365,88.
Эта оценка неверна, поскольку математическое ожидание генеральной совокупности ц равно 368 и не попадает в этот интервал (см. рис. 7.1). Таким образом, для некоторых выборок эта оценка верна, а для некоторых — нет. Кроме того, на практике, как правило, из генеральной совокупности извлекается только одна выборка. Следовательно, поскольку математическое ожидание генеральной совокупности ц не известно, невозможно сказать, верна полученная интервальная оценка или нет.
Чтобы разрешить эту дилемму, необходимо определить долю выборок, позволяющих правильно оценить математическое ожидание генеральной совокупности ц. Для этого следует исследовать еще две гипотетические выборки, средние значения которых равны 362,12 и 373,88 г соответственно.
Если X =362,12 , мы получаем интервал 362,12 ±1,96x15/>/25 , т.е. 362,12 ±5,88. Это приводит к оценке
356,24 <ц< 368,00.
Поскольку математическое ожидание генеральной совокупности ц, равное 368, является верхней границей интервала, эта оценка верна.
Если ^ = 373,88 , мы получаем интервал 373,88 ±1,96x15/^25 , т.е. 373,88 ±5,88. Это приводит к оценке
368,00 < ц < 379,76.
Поскольку математическое ожидание генеральной совокупности ц, равное 368, является нижней границей интервала, эта оценка верна.
Таким образом, если выборочное среднее изменяется в диапазоне от 362,12 до 373,88 г, математическое ожидание генеральной совокупности лежит где-то внутри этого соответствующего доверительного интервала. Вероятность того, что это значение лежит в интервале с границами 362,12 и 373,88, равна 95% (см. раздел 6.6). Следовательно, 95% средних значений всех выборок, имеющих объем п = 25, позволяют правильно оценить математическое ожидание генеральной совокупности, а 5% — нет.
Интервальная оценка, доверительный уровень которой равен 95% , интерпретируется следующим образом: если из генеральной совокупности извлечь все выборки, имеющие объем п, и вычислить их выборочные средние, то 95% доверительных интервалов, построенных на их основе, будут содержать математическое ожидание генеральной совокупности, а 5% — нет.
На практике, как правило, из генеральной совокупности извлекается только одна выборка, а математическое ожидание генеральной совокупности р не известно. По этой причине невозможно гарантировать, что некий конкретный доверительный интервал содержит величину ц. Можно лишь утверждать, что вероятность этого события равна 95%.
В некоторых ситуациях желательно иметь более высокий доверительный уровень, а следовательно, точность оценки величины ц (например, 99%). Но иногда можно ограничиться и менее точной оценкой (например, 90%).
Как правило, доверительный уровень (level of confidence) обозначают следующим образом: (1-а)х100%, где величина а представляет собой площадь, ограниченную хвостом распределения, выходящим за пределы доверительного интервала. (Величину а называют уровнем значимости доверительного интервала. Кроме того, в качестве синонима для доверительного уровня иногда употребляется выражение “доверительная вероятность”. — Прим, ред.) Площади, ограниченные как левым, так и правым хвостами распределения, выходящими за пределы доверительного интервала, равны а/2.
ПОСТРОЕНИЕ ДОВЕРИТЕЛЬНОГО ИНТЕРВАЛА ДЛЯ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ ПРИ ИЗВЕСТНОМ СТАНДАРТНОМ ОТКЛОНЕНИИ
x±z-Z=,
у]П
или
X-Z-^=<p<X + Z-^= , (7.1)
yjn
где Z — значение стандартизованной нормально распределенной случайной величины, соответствующее интегральной вероятности, равной 1-а/2, ст— стандартное отклонение генеральной совокупности.
Величина Z, выбранная для построения доверительного интервала, называется критическим значением (critical value) распределения. Чтобы построить интервал, имеющий 95% -ный доверительный уровень, необходимо выбрать а = 0,05. Половина площади симметричной фигуры, ограниченной концами доверительного интервала и кривой стандартизованного нормального распределения, равна 0,95/2=0,4750. Величина Z, соответствующая площади 0,4750, равна 1,96, поскольку площадь фигуры, ограниченной правым хвостом распределения, равна 0,025, а суммарная площадь фигуры, лежащей левее значения Z = 1,96, равна 0,975.
Каждому доверительному уровню 1 - а соответствует свое критическое значение. Например, доверительному уровню, равному 95%, соответствует Z = ±l,96 (рис. 7.2). Если требуется построить интервал, доверительный уровень которого равен 99%, следует выбрать ос = 0,01. В этом случае величина Z приближенно равна 2,58, поскольку площадь, ограниченная правым хвостом распределения, выходящим за пределы доверительного интервала, равна 0,005, а суммарная площадь фигуры, лежащей левее значения Z, равна 0,995 (рис. 7.3).
Рис. 7.2. Гауссова кривая для определения критического значения Z, соответствующего доверительному уровню, равному 95%
Рис. 7.3. Гауссова кривая для определения критического значения Z, соответствующего доверительному уровню, равному 99%
Возникает вопрос, почему бы не построить интервал, доверительный уровень которого был бы очень близок к 100%. Это нецелесообразно, поскольку такой доверительный интервал оказался бы слишком широким, а оценка математического ожидания — слишком неточной. Разумеется, вероятность того, что математическое ожидание лежит в этом интервале, очень высока, однако для принятия решения этот факт практически бесполезен. В разделе 7.4 мы более подробно обсудим способы достижения компромисса между шириной интервала и доверительным уровнем.
ПРИМЕР 7.1. ОЦЕНКА СРЕДНЕЙ ДЛИНЫ ЛИСТА БУМАГИ С ДОВЕРИТЕЛЬНЫМ УРОВНЕМ, РАВНЫМ 95%
При производстве бумаги средняя длина листа должна быть равной 11 дюймам, а ее стандартное отклонение — 0,02 дюйма. Периодически из произведенной продукции, чтобы оценить ее качество, извлекаются выборки. Допустим, выборка состоит из 100 листов, а ее выборочное среднее — 10,998 дюйма. Постройте интервал, содержащий математическое ожидание генеральной совокупности, доверительный уровень которого равен 95%.
РЕШЕНИЕ. Подставим в формулу (7.1) величину Z = 1,96, соответствующую доверительному уровню, равному 95%.
X ± < 10,998 ± 1,96-^В = 10,998 ± 0,00392 .
Jn VI00
10,99408 <м< 11,00192.
Таким образом, вероятность того, что математическое ожидание генеральной совокупности лежит в интервале от 10,99408 до 11,00192, равна 95%. Поскольку номинальная длина бумаги — 11 дюймов, она попадает в построенный интервал. Следовательно, производственный процесс выполняется правильно.
ПРИМЕР 7.2. ОЦЕНКА СРЕДНЕЙ ДЛИНЫ ЛИСТА БУМАГИ С ДОВЕРИТЕЛЬНЫМ УРОВНЕМ, РАВНЫМ 99%
Постройте интервал, содержащий математическое ожидание генеральной совокупности листов бумаги, доверительный уровень которого равен 99% .
РЕШЕНИЕ. Подставим в формулу (7.1) величину Z = 2,58, соответствующую доверительному уровню, равному 99%.
X±Z-^=< 10,998±2,58-^21 = 10,998±0,00516 .
<Jn VI00
10,99284 <ц< 11,00316.
Поскольку номинальная длина бумаги попадает в построенный интервал, можно сделать вывод, что производственный процесс выполняется правильно.
для математического ожидания генеральной совокупности при известном стандартном отклонении , ^.1, т -
a A Z " > { /Д» ЧУ ' А > А < A. t Ч V « \ ?> *
Чтобы построить доверительный интервал для математического ожидания генеральной совокупности по известному стандартному отклонению, можно воспользоваться функцией доверит или применить надстройку PHStat2.
Например, чтобы построить доверительный интервал для средней длины листа бумаги в примере 7.1, необходимо воспользоваться одной из следующих процедур.
Применение Excel в сочетании с надстройкой PHStatZ
Чтобы построить доверительный интервал для математического ожидания генеральной совокупности по известному стандартному отклонению, следует применить процедуру PHStat^Confidence Intervals^ Estimate for the Mean, sigma known... (PHStat^Доверительные интервалы^Оценка математического ожидания, стандартное отклонение известно...).
1. Выбрать команду PHStat^Confidence Intervals ^Estimate for the Mean, sigma known.
2. В диалоговом окне Estimate for the Mean, sigma known (см. иллюстрацию) сделать следующее.
2.1. Ввести в окне редактирования Population Standard Deviation (Стандартное отклонение генеральной совокупности) число 0.02.
2.2. Ввести в окне редактирования Confidence Level (Доверительный уровень) число 95.
2.3. Установить переключатель Input Options (Параметры ввода) в положение Sample Statistics Known (Выборочные статистики известны) и ввести в окне редактирования Sample Size (Объем выборки) число 100, а в окне редактирования Sample Mean (Выборочное среднее) - число 10.998.
2.4. Ввести в окне редактирования Title соответствующий заголовок.
2.5. Щелкнуть на кнопке ОК.
Estimate for the Mean, sigma known |X:
Data - -
Population Standard Deviation: (oToz
Confidence Level: [95" %
Input Options - • .............
(* Sample Statistics Known
Sample Size: [100
Sample Mean: [To. 998
Sample Statistics Unknown
; Output Options -
: Г” Finite Population Correction
Help I |QTZ]| Cancel
Если выборочное среднее неизвестно, в п. 2.3 следует установить переключатель Input Options в положение Sample Statistics Unknown (Выборочные статистики неизвестны), а в окне редактирования Sample Cell Range (Диапазон ячеек, содержащий выборку) ввести диапазон ячеек, в которых записаны элементы выборки.
Применение Excel
Инструкции, позволяющие самостоятельно создать рабочий лист, вычисляющий доверительный интервал для математического ожидания генеральной совокупности по известному стандартному отклонению, содержатся в разделе ЕН.7.1.
Chapter 7.xls
Данные, на основе которых вычисляется доверительный интервал, содержащий среднюю длину листа бумаги по известному стандартному отклонению (пример 7.1), хранятся в рабочей книге chapter 7 . xls на листе Пример?.1.
УПРАЖНЕНИЯ К РАЗДЕЛУ 7.1
Изучение основ
7.1. Предположим, что X = 85, о = 8 и и = 64. Постройте 95%-ный доверительный интервал для математического ожидания генеральной совокупности.
7.2. Предположим, что Х = 125,ст = 24итг = 36. Постройте 99% -ный доверительный интервал для математического ожидания генеральной совокупности.
7.3. По данным специалиста по маркетингу, вероятность того, что средний объем продаж колеблется между 170 000 и 200 000 долл., равна 95%. Объясните смысл этого утверждения.
7.4. Почему в примере 7.1 невозможно добиться 100% -ного доверительного уровня?
7.5. Правда ли, что 95% всех выборочных средних, вычисленных в примере 7.1, лежат в интервале от 10,99408 до 11,00192 дюймов? Обоснуйте свой ответ.
7.6. Правда ли, что существуют выборочные средние, вычисленные в примере 7.1, не лежащие между числами 10,99408 и 11,00192 дюймов? Обоснуйте свой ответ.
Применение понятий
7.7. Менеджер магазина стройматериалов хочет оценить фактический объем краски, содержащейся в галлонных банках известной компании. Известно, что стандартное отклонение объема краски равно 0,02 галлона. Менеджер выбрал 50 банок. Выборочный средний объем равен 0,995 галлона.
1. Постройте интервал, содержащий математическое ожидание генеральной совокупности, доверительный уровень которого равен 99% .
2. Основываясь на решении задачи 1, определите, стоит ли менеджеру жаловаться на завод-производитель и почему.
3. Можно ли утверждать, что объем краски в банке подчиняется нормальному закону распределения? Объясните свой ответ.
4. Объясните, почему объем краски, равный 0,98 галлона, считается допустимым, хотя он не попадает в построенный вами доверительный интервал.
5. Допустим, что доверительный уровень интервала должен быть равен 95%. Как изменятся ответы на вопросы 1 и 2?
7.8. Менеджер из отдела контроля за качеством продукции на заводе, производящем электрические лампочки, желает оценить среднюю продолжительность работы лампочек из крупной партии. Номинальное стандартное отклонение равно 100 ч. Для контроля выбрана партия, состоящая из 64 лампочек, средняя продолжительность работы которых равна 350 ч.
1. Постройте интервал, содержащий математическое ожидание генеральной совокупности, доверительный уровень которого равен 95% .
2. Можно ли утверждать, что средняя продолжительность работы лампочек из анализируемой партии не меньше 400 ч? Обоснуйте свой ответ.
3. Можно ли утверждать, что продолжительность работы лампочек подчиняется нормальному закону распределения? Объясните сцой ответ.
4. Объясните, почему продолжительность работы лампочки, равная 320 ч, считается допустимой, хотя она не попадает в построенный вами доверительный интервал.
5. Допустим, что стандартное отклонение продолжительности работы лампочек равно 80 ч. Как изменятся ответы на вопросы 1 и 2?
7.9. Отдел технического контроля на заводе, производящем газированные напитки, желает выяснить фактический объем жидкости, содержащейся в двухлитровых бутылках. Известно, что стандартное отклонение объема жидкости в двухлитровой бутылке равно 0,05 л. Менеджер выбрал 100 двухлитровых бутылок. Выборочный средний объем составил 1,99 л.
1. Постройте интервал, содержащий математическое ожидание генеральной совокупности, доверительный уровень которого равен 95% .
2. Можно ли утверждать, что объем жидкости в бутылках подчиняется нормальному закону распределения? Объясните свой ответ.
3. Объясните, почему объем жидкости, равный 2,02 л, считается допустимым, хотя он не попадает в построенный вами доверительный интервал.
4. Предположим, что выборочное среднее равно 1,97 л. Как изменится ответ на вопрос 1?
7.2. ПОСТРОЕНИЕ ДОВЕРИТЕЛЬНОГО ИНТЕРВАЛА ДЛЯ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ ПРИ НЕИЗВЕСТНОЙ ДИСПЕРСИИ
На практике как математическое значение генеральной совокупности, так и его стандартное отклонение часто бывают неизвестными. Следовательно, необходимо построить доверительный интервал, содержащий математическое значение генеральной совокупности, используя лишь выборочные статистики X и S.
Распределение Стьюдента
В начале 20-го века статистик Уильям С. Госсет (William S. Gosset), сотрудник ирландского отделения пивоваренной компании Guinness [3], заинтересовался проблемой оценки математического ожидания при неизвестном стандартном отклонении. Поскольку компания Guinness запрещала своим сотрудникам публиковать работы под собственными именами, Госсет взял псевдоним Стпъюдент. По этой причине распределение, предложенное Госсетом, называется t-распределением Стьюдента (Student's t distribution).
Если случайная величина X является нормально распределенной, то следующая статистика имеет t-распределение си-1 степенями свободы:
Обратите внимание на то, что это выражение почти совпадает с формулой (6.12), только вместо величины ст в нем стоит выборочное стандартное отклонение S. Понятие степени свободы обсуждается далее.
Внешне распределение Стьюдента очень напоминает стандартизованное нормальное распределение. Оба распределения имеют колоколообразную форму и являются симметричными. Однако хвосты t-распределения “тяжелее” (т.е. ограничивают большую площадь), а площадь фигуры в центре определения меньше, чем у стандартизованного нормального распределения (рис. 7.4). Это происходит потому, что стандартное отклонение о не известно, а вместо него используется его выборочная оценка S. Неопределенность значения о порождает большую изменчивость переменной t по сравнению с величиной Z.
Рис. 7.4. Стандартизованное нормальное распределение и t-распределение Стьюдента с пятью степенями свободы
Однако при увеличении количества степеней свободы t-распределение становится все ближе к стандартизованному нормальному распределению. Это происходит потому, что при увеличении объема выборки оценка S становится все точнее. При объеме выборки, равном 120 и более, величина S довольно точно аппроксимирует стандартное отклонение о, так что разница между t-распределением и стандартизованным нормальным отклонением становится минимальной. По этой причине, если объем выборки превышает 120, многие статистики вместо величины t используют переменную Z.
ПРОВЕРКА ПРЕДПОЛОЖЕНИЙ
Напомним, что t-распределение основано на предположении, что изучаемая случайная величинах является нормально распределенной. Однако на практике t-распределение = можно применять для оценки неизвестного математического ожидания генеральной совокупности при неизвестном стандартном отклонении при достаточно большом объеме выборки и не слишком асимметричном распределении. При работе с небольшими выборками эти условия уже не выполняются автоматически, поэтому их следует проверять. Для этого необходимо строить гистограмму, диаграмму “ствол и листья”, блочную диаграмму или график нормального распределения.
Критические значения для t-распределения с соответствующими степенями свободы можно найти в табл. Д.З. В заголовке каждого столбца этой таблицы указана площадь фигуры, ограниченной хвостом t-распределения (поскольку для переменной t указаны только положительные значения, эта площадь ограничена правым хвостом распределения). В заголовке каждой строки указано количество степеней свободы. Например, в табл. 7.1 показано, как найти площадь фигуры, ограниченной t-распределением, имеющим 99 степеней свободы, и соответствующим значением переменной t, если необходимо построить интервал, доверительный уровень которого равен 95%. Этот доверительный уровень означает, что площадь каждой фигуры, ограниченной хвостами t-распределения, равна 0,025. Найдем пересечение столбца, соответствующего величине 0,025, и строки, соответствующей 99 степеням свободы. В этой ячейке записано критическое значение, равное 1,9842. Поскольку t-распределение является симметричным и его математическое ожидание равно 0, площади, ограниченной правым хвостом, соответствует величина +1,9842, а площади, ограниченной левым хвостом, соответствует величина -1,9842. Величина 1,9842 означает следующее: вероятность того, что величина t превосходит +1,9842, равна 0,025, т.е. 2,5% (рис. 7.5).
Таблица 7.1.2 Определение площади фигуры, ограниченной ^-распределением, имеющим 99 степеней свободы, и соответствующим значением переменной t
Площади фигуры, ограниченной правым хвостом t-распределения
Степени свободы 0,25 0,10 0,05 0,025 0,01 0,005
1 1,0000 3,0777 6,3138 12,7062 31,8207 63,6574
2 0,8165 1,8856 2,9200 4,3027 6,9646 9,9248
3 0,7649 1,6477 2,3534 3,1824 4,5407 5,8409
4 0,7407 1,5332 2,1318 2,7764 3,7469 4,6041
5 0,7267 1,4759 2,0150 2,5706 3,3649 4,0322
96 0,6771 1,2904 1,6609 1,9850 2,3658 2,6280
97 0,6770 1,2903 1,6607 1,9847 2,3654 2,6275
98 0,6770 1,2902 1,6606 1,9845 2,3650 2,6269
99 0,6770 1,2902 1,6604 1,9842 2,3646 2,6264
100 0,6770 1,2901 1,6602 1,9840 2,3642 2,6259
2
Фрагмент табл. Д.З.
Рис. 7.5. Распределение Стьюдента с 99 степенями свободы
Степени свободы
Напомним, что для вычисления выборочной дисперсии S2 необходимо вычислить величину
Ёк.-Ч-/=1
Таким образом, для вычисления выборочной дисперсии необходимо знать X . Следовательно, мы можем варьировать лишь п-1 выборочных значений. Это означает, что величина обладает п-1 степенями свободы.
Допустим, например, что выборка состоит из 5 чисел, а ее выборочное среднее равно 20. Сколько разных значений необходимо знать для того, чтобы однозначно определить остальные? Если п = 5 и X = 20, то
£х,=100, /=i
поскольку
-tx, = X.
П ,=1
Таким образом, если известны четыре величины, пятое значение уже не свободно, поскольку сумма должна быть равна 100. Например, если нам известны величины 18, 24, 19 и 16, пятая величина должна быть равной 23, поскольку сумма равна 100.
Доверительный интервал
Рассмотрим формулу для вычисления интервала, содержащего математическое ожидание при неизвестном стандартном отклонении с вероятностью (1-а)х100% .
ПОСТРОЕНИЕ ДОВЕРИТЕЛЬНОГО ИНТЕРВАЛА ДЛЯ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ ПРИ НЕИЗВЕСТНОМ СТАНДАРТНОМ ОТКЛОНЕНИИ
или
+ (7.2)
yjn yjn
где tn j — критическое значение /-распределения с п-1 степенями свободы, соответствующее площади, ограниченной правым хвостом и равной а/2.
Чтобы проиллюстрировать применение этой формулы, вернемся к задаче об аудиторской проверке в компании Saxon Home Improvement Company. Предположим, что из информационной системы извлечена выборка, состоящая из 100 накладных, заполненных в течение последнего месяца. Допустим, что выборочное среднее равно 110,27долл., а выборочное стандартное отклонение — 28,95 долл. Если компания желает построить интервал, имеющий доверительный уровень, равный 95%, критическое значение t-распределения равно 1,9842 (см. табл. 7.1). Используя формулу (7.2), получаем:
— V 28 95
X ± tn j -= = 110,27 ± 1,9842-5==- = 110,27 ± 5,74 ,
4^ Лоо
104,53 <ц< 116,01.
На рис. 7.6 продемонстрировано вычисление доверительного интервала, содержащего среднюю сумму накладных, с помощью программы Microsoft Excel.
“J А J £. В i 1 Средняя сунна накладных 3;
3 Data
4 Sample Standard Deviation 28.95
5 Sample Mean 110.27
6 Sample Size 100
7 Confidence Level 95%
e . .
9 . Intermediate Calculations
10 ‘Standard Error of the Mean 2.895
11 Degrees of Freedom 99
12 ,t value 1.984217306
13 ’interval Half Width 5.744309101
,u; :
151 Confidence Interval
16 Interval Lower Limit 104.53
17 'Interval Upper Limit 116.01
Рис. 7.6. Вычисление доверительного интервала, содержащего среднюю сумму накладных, с помощью программы Microsoft Excel
Таким образом, вероятность того, что средняя сумма накладных находится в интервале от 104,53 до 116,01, равна 95%. Это значит, что если мы извлечем из информационной системы все возможные выборки, состоящие из 100 накладных (что практически невозможно), 95% доверительных интервалов будут содержать математическое ожидание генеральной совокупности. Корректность этих доверительных интервалов зависит от того, насколько распределение генеральной совокупности близко к нормальному. Поскольку объем выборки довольно велик (и = 100), предположение о нормальном распределении вполне правдоподобно, а полученная оценка математического ожидания довольно надежна. Таким образом, применение £-распределения вполне оправданно. На практике корректность доверительного интервала необходимо проверить, сравнив со средней суммой накладных, введенных в информационную систему. Если обнаружится расхождение, следует продолжить исследование.
Процедуры Excel: построение доверительного интервала для математического ожидания генеральной совокупности при неизвестном стандартном отклонении
Чтобы построить доверительный интервал для математического ожидания генеральной совокупности при неизвестном стандартном отклонении, можно воспользоваться функцией стьюдраспобр или надстройкой PHStat2.
Например, чтобы построить доверительный интервал для средней суммы накладных в компании Saxon Home Improvement Company, необходимо выполнить одну из следующих процедур.
Применение Excel в сочетании с надстройкой PHStat2
Чтобы построить доверительный интервал для математического ожидания генеральной совокупности при неизвестном стандартном отклонении, следует применить процедуру PHStat1^Confidence Intervals ^Estimate for the Mean, sigma unknown... (PHStat1^ Доверительные интервалы^Оценка математического ожидания, стандартное отклонение неизвестно...).
1. Выбрать PHStaWConfidence Intervals^Estimate for the Mean, sigma unknown....
2. В диалоговом окне Estimate for the Mean, sigma unknown (см. иллюстрацию) сделать следующее.
2.1. Ввести в окне редактирования Confidence Level (Доверительный уровень) число 95.
2.2. Установить переключатель Input Options (Параметры ввода) в положение Sample Statistics Known (Выборочные статистики известны) и ввести в окне редактирования Sample Size (Объем выборки) число 10 0, в окне редактирования Sample Mean (Выборочное среднее) - число 110.27, а в окне редактирования Sample Std. Deviation — число 28.95.
2.3. Ввести в окне редактирования Title соответствующий заголовок.
2.4. Щелкнуть на кнопке ОК.
Estimate for the Mean, sigjma unknown [X]
Data
Confidence Level: (95 %
Input Options
Sample Statistics Known
Sample Size: 1100
Sample Mean: 1110.27
Sample Std. Deviation: 128.95
i' Sample Statistics Unknown
Output Options .......
Title: ^Средняя сумма накладных
Г* Finite Population Correction
Help ! 11 OK Cancel j
Если выборочное среднее и выборочное стандартное отклонение не известны, в п. 2.2 следует установить переключатель Input Options в положение Sample Statistics Unknown (Выборочные статистики неизвестны), а в окне редактирования Sample Cell Range (Диапазон ячеек, содержащий выборку) ввести диапазон ячеек, в которых записаны элементы выборки.
Применение Excel
Для того чтобы самостоятельно создать рабочий лист, вычисляющий доверительный интервал для математического ожидания генеральной совокупности при неизвестном стандартном отклонении, следуйте инструкциям, приведенным в разделе ЕН.7.2.
Лл Chapter 7.xls
Данные, на основе которых вычисляется доверительный интервал, содержащий среднюю сумму накладных, хранятся в рабочей книге Chapter 7 . xls на листе Рис7.6.
ПРИМЕР 7.3. ОЦЕНКА СРЕДНЕЙ ВЕЛИЧИНЫ СИЛЫ РАЗРУШЕНИЯ ИЗОЛЯТОРА
Некая промышленная компания на Среднем Западе производит электрические изоляторы. Если во время работы изолятор выходит из строя, происходит короткое замыкание. Чтобы проверить прочность изолятора, компания проводит испытания, в ходе которых определяется максимальная сила, необходимая для разрушения изолятора. Сила измеряется в фунтах нагрузки, приводящей к разрушению изолятора. В табл. 7.2 приведены результаты 30 экспериментов.
Таблица 7.2. Сила (в фунтах), необходимая для разрушения изолятора
1 870 1 728 1 656 1610 1634 1 784 1 522 1696 1 592 1 662
1 866 1 764 1 734 1 662 1 734 1 774 1 550 1 756 1 762 1 866
1 820 1 744 1 788 1 688 1 810 1 752 1 680 1 810 1 652 1 736
Постройте интервал, содержащий математическое ожидание генеральной совокупности величин силы, необходимой для разрушения изолятора, доверительный уровень которого равен 95%.
РЕШЕНИЕ. Как показано на рис. 7.7, выборочное среднее равно X =1 723,4 фунта, а выборочное стандартное отклонение равно S = 89,55 фунта.
Рис. 7.7. Вычисление доверительного интервала для средней величины силы, необходимой для разрушения изолятора, с помощью программы Microsoft Excel
Чтобы вычислить нижнюю и верхнюю границы доверительного интервала с помощью формулы (7.2), необходимо определить критическое значение ^-распределения с 29 степенями свободы для площади, равной 0,025. Как следует из табл. Д.З, критическое значение t2a = 2,0452.
Итак, х =1 723,4, S = 89,55, п = 30 и t29 = 2,0452. Следовательно,
X ± tn. 4= = 1723,4 ± 2,0452= 1 723,4 ± 33,44 . л/30
1 689,96 <ц<1 756,84.
Таким образом, вероятность того, что средняя величина силы разрушения изолятора находится в интервале от 1 689,96 до 1 756,84, равна 95%. Корректность этих доверительных интервалов зависит от того, насколько распределение генеральной совокупности близко к нормальному. Напомним, что требование о большом объеме выборки можно ослабить. Таким образом, если объем выборки равен 30, предположение о нормальном распределении остается правдоподобным, даже если распределение силы разрушения слегка асимметрично. График нормального распределения, изображенный на рис. 7.8, и блочная диаграмма, представленная на рис. 7.9, свидетельствуют о том, что распределение силы разрушения имеет легкую асимметрию, следовательно, для решения задачи можно применять ^-распределение.
Рис. 7.8. График нормального распределения для средней величины силы, необходимой для разрушения изолятора, построенный с помощью программы Microsoft Excel
Прочность изоляторов
1500 1550 1600 1650 1700 1750 1800 1850 1900
Рис. 7.9. Блочная диаграмма для средней величины силы, необходимой для разрушения изолятора, построенная с помощью программы Microsoft Excel
УП₽АЖНЕЙЙЯК₽АЗДЕЯУ13.
Изучение основ
7.10. Определите критическое значение t при следующих данных.
1. 1-а = 0,95,п = 10.
2. 1-а = 0,99, тг = 10.
3. 1-а = 0,95, п = 32.
4. 1-а = 0,95, тг = 65.
5. 1-а = 0,90, тг = 16.
7.11. Предположим, что X = 15,S = 24, тг = 36, и генеральная совокупность является нормально распределенной. Постройте интервал, содержащий математическое ожидание генеральной совокупности, доверительный уровень которого равен 95%.
7.12. Предположим, что X =50, S = 15, тг = 16, и генеральная совокупность является нормально распределенной. Постройте интервал, содержащий математическое ожидание генеральной совокупности, доверительный уровень которого равен 99%.
7.13. По каждой из выборок, приведенных ниже, постройте интервал, содержащий математическое ожидание генеральной совокупности, доверительный уровень которого равен 95%, предполагая, что генеральная совокупность имеет нормальное распределение.
Выборка 1:11118888
Выборка 2:12345678
Объясните, почему эти выборки имеют разный доверительный интервал, хотя их средние значения и размах совпадают.
7.14. Постройте интервал, содержащий математическое ожидание генеральной совокупности, доверительный уровень которого равен 95%, для выборки {1, 2, 3, 4, 5, 6, 20}. Замените 20 на 7 и снова постройте доверительный интервал. Используя этот пример, продемонстрируйте влияние выброса (т.е. экстремального значения) на доверительный интервал.
Применение понятий
Задачи, 7.15-7.19 можно решать как вручную, так и с помощью программы, Microsoft Excel. Задачи 7.20 и 7.21 рекомендуется решать с помощью программы Microsoft Excel.
7.15. Министерство транспорта США потребовало от производителей автомобильных шин опубликовать данные о боковинах шин, чтобы информировать покупателей о качестве товара. Одним из основных показателей качества шины является износоустойчивость протектора. Этот показатель является относительным. В качестве эталона выбирается шина, у которой показатель износоустойчивости равен числу 100. Таким образом, шина с показателем износоустойчивости, равным 200, в среднем прослужит вдвое больше, чем эталон. Общество потребителей желает оценить реальный показатель износоустойчивости шин, произведенных некоей широко известной компанией. Производитель утверждает, что показатель износоустойчивости его шин равен 200. Выборочное среднее, вычисленное по случайной выборке, состоящей из 18 шин, равно 195,3, а выборочное стандартное отклонение — 21,4.
1. Предположим, что генеральная совокупность показателей износоустойчивости шин имеет нормальное распределение. Постройте интервал, содержащий математическое ожидание этой генеральной совокупности, доверительный уровень которого равен 95% .
2. Стоит ли обществу потребителей обвинять компанию в сокрытии информации об износоустойчивости ее шин? Обоснуйте свой ответ.
3. Объясните, почему показатель износоустойчивости шины, равный 210, не является экстремальным значением, хотя он и не попадает в доверительный интервал, построенный при решении задачи 1.
7.16. Магазин канцтоваров желает оценить среднюю стоимость поздравительных открыток, хранящихся на складе. Выборочное среднее, вычисленное по случайной выборке, состоящей из 20 поздравительных открыток, равно 1,67 долл., а выборочное стандартное отклонение — 0,32 долл.
1. Предположим, что генеральная совокупность цен имеет нормальное распределение. Постройте интервал, содержащий математическое ожидание этой генеральной совокупности, доверительный уровень которого равен 95% .
2. Может ли ответ на вопрос 1 помочь владельцу магазина оценить среднюю стоимость товаров, хранящихся на его складе?
7.17. Один из основных критериев качества услуг, предоставляемых любой организацией, — скорость, с которой она реагирует на жалобы клиентов. Крупный универмаг, торгующий фурнитурой и коврами, за последние годы значительно расширился. В частности, отдел ковровых покрытий, в котором прежде работали 2 человека, теперь состоит из руководителя, измерителя и 15 продавцов. На протяжении последнего года компания получила 50 жалоб на работу этого отдела. Ниже приведены данные о количестве дней, прошедших со дня получения жалобы до принятия решения, ft) FURNITURE . XLS.
54 5 35 137 31 27 152 2 123 81 74 27
11 19 126 110 110 29 61 35 94 31 26 5
12 4 165 32 29 28 29 26 25 1 14 13
13 10 5 27 4 52 30 22 36 26 20 23
33 68
1. Постройте интервал, содержащий математическое ожидание этой генеральной совокупности, доверительный уровень которого равен 95% .
2. Какие предположения должны выполняться при решении задачи 1?
3. Можно ли утверждать, что предположения, сформулированные в задаче 2, серьезно нарушаются? Аргументируйте свой ответ.
4. Как ответ на вопрос 3 влияет на оценку корректности доверительного интервала, построенного в задаче 1?
7.18. В штате Нью-Йорк сберегательным банкам разрешено осуществлять страхование жизни. В процедуру оформления страховки входят изучение запроса, проверка медицинской информации, дополнительные медицинские исследования и проверка информации, поступившей из полиции. Чтобы страхование жизни было прибыльным для банка, необходимо ускорить оформление страховки. Банк создал выборку, в которой указано время, затраченное на оформление 27 страховок в течение одного месяца, t#INSURANCE . XLS.
73 19 16 64 28 28 31 90 60 56 31 56 22 18
45 48 17 17 17 91 92 63 50 51 69 16 17
1. Постройте 95%-ный доверительный интервал, содержащий среднее время оформления страховки.
2. Какие предположения должны выполняться при решении задачи 1?
3. Можно ли утверждать, что предположения, сформулированные в задаче 2, серьезно нарушаются? Аргументируйте свой ответ.
4. Сравните выводы, полученные при решении задачи 1, с результатами решения задачи 3.56.
7.19. Стоимость номера в гостинице и проката автомобилей в разных городах различается. В таблице представлены данные о 20 городах, опубликованные компанией Dow Jones Travel Index по состоянию на 2-4 июня 2002 года. ^TRAVEL. XLS.
Город Г остиница Прокат автомобиля
Сиэтл 176 45
Сан-Франциско 178 42
Лос-Анджелес 223 36
Феникс 124 38
Денвер 139 38
Миннеаполис 167 53
Чикаго 257 51
Сент-Луис 159 53
Даллас 167 46
Хьюстон 180 48
Детройт 141 53
Кливленд 145 40
Новый Орлеан 142 49
Питсбург 148 49
Атланта 173 46
Бостон 243 46
Нью-Йорк 273 69
Вашингтон 262 47
Орландо 133 40
Майами 116 39
Источник: “Travel”, The Wall Street Journal, 7 июня, 2002.
1. Постройте интервал, содержащий среднюю стоимость номера в гостинице, доверительный уровень которого равен 95% .
2. Постройте интервал, содержащий среднюю стоимость проката автомобиля, доверительный уровень которого равен 95% .
3. Какие ограничения следует наложить на распределение интересующих нас генеральных совокупностей при решении задач 1 и 2?
4. Выполняются ли предположения, необходимые для решения задач 1 и 2? Аргументируйте свой ответ.
7.20. Пресс разрезает куски стали на части, которые в дальнейшем используются в качестве каркаса переднего сиденья автомобиля. Для разрезания стали используется алмазная пила. Автомобильная компания постановила, что отклонение объемов каркаса от эталона не должно превышать 0,005 дюйма. В файле ftsTEEL.XLS при-
ведены отклонения от эталона объемов 100 заготовок, измеренных с помощью лазерных приборов. Например, величина -0,002 означает, что заготовка короче эталона на 0,002 дюйма.
1. Постройте 95%-ный доверительный интервал, содержащий среднюю разность между фактическим и эталонным объемом каркаса.
2. Можно ли утверждать, что предположения, необходимые для решения задачи 1, не выполняются? Аргументируйте свой ответ.
3. Сравните выводы, полученные при решении задачи 1, с результатами решения задачи 2.16.
7.21. В одной из статей, опубликованных в журнале Quality Engineering, исследуется вязкость (т.е. величина сопротивления потоку) химического вещества из разных партий. В файле ^CHEMICAL. XLS приведены данные о 120 партиях.
Источник: D. S. Holmes, and Mergen А. Е., “Parabolic Control Limits for the Exponentially Weighted Moving Average Control Charts”, Quality Engineering, 4(1992 ): p. 487-495.
1. Постройте 99%-ный доверительный интервал, содержащий среднюю вязкость вещества.
2. Какие ограничения следует наложить на распределение интересующей нас генеральной совокупности при решении задачи 1?
3. Можно ли утверждать, что предположения, необходимые для решения задачи 1, не выполняются? Аргументируйте свой ответ.
4. Сравните выводы, полученные при решении задачи 1, с результатами решения задачи 2.64.
7.3. ПОСТРОЕНИЕ ДОВЕРИТЕЛЬНОГО ИНТЕРВАЛА ДЛЯ ДОЛИ ПРИЗНАКА В ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ
В этом разделе понятие доверительного интервала распространяется на категорийные данные. Это позволяет оценить долю признака в генеральной совокупности р с помощью выборочной доли рк = Х/п. Как указывалось в разделе 6.7, если величины пр и п(1-р) превышают число 5, биномиальное распределение можно аппроксимировать нормальным. Следовательно, для оценки доли признака в генеральной совокупности р можно построить интервал, доверительный уровень которого равен (1-а)х100% .
ПОСТРОЕНИЕ ДОВЕРИТЕЛЬНОГО ИНТЕРВАЛА ДЛЯ ДОЛИ ПРИЗНАКА В ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ
, 7
ps ± z j— --,
V п
или
a_zJMzA)<p<a + zMza). (7.3)
V п \ п
где pt — выборочная доля признака, равная Х/п, т.е. количеству успехов, деленному на объем выборки, р — доля признака в генеральной совокупности, Z — критическое значение стандартизованного нормального распределения, п — объем выборки.
Чтобы продемонстрировать применение этой формулы, вернемся к задаче об аудиторской проверке в компании Saxon Home Improvement Company. Требуется определить частоту ошибок, нарушающих правила, установленные компанией. Для этого можно построить 95%-доверительный интервал, содержащий долю ошибочных накладных в генеральной совокупности всех накладных компании Saxon Home Improvement Company. Предположим, что из информационной системы извлечена выборка, состоящая из 100 накладных, заполненных в течение последнего месяца. Допустим, что 10 из этих накладных составлены с ошибками. Таким образом, р = 10/100 = 0,10. Доверительному уровню 95% соответствует критическое значение Z = 1,96.
Л±г^0-л)=
V п N 100
= 0,10 ± 1,96 х 0,03 = 0,10 ± 0,0588 .
0,0412 <р <0,1588.
Таким образом, вероятность того, что от 4,12 до 15,88% накладных содержат ошибки, равна 95%. На рис. 7.10 продемонстрировано вычисление доверительного интервала, содержащего долю ошибок в генеральной совокупности накладных, с помощью программы Microsoft Excel.
„ .А .. • В 1 Доля ошибочных накладных 2;
3 Data
4 Sample Size 100
5 Number of Successes 10
6 'Confidence Level 95%
7 ; ।
В Intermediate Calculations
9 -Sample Proportion 0.1
10 Z Value -1.95996279
11 ' Standard Error of the Proportion 0.03
12 .Interval Half Width 0.058798884
_13; : j
14 Confidence Interval
15 Interval Lower Limit 0.041201116
16 ! Interval Upper Limit 0.158798884|
Рис. 7.10. Вычисление доверительного интервала, содержащего долю ошибок в генеральной совокупности накладных, с помощью программы Microsoft Excel
Процедуры Excel: построение доверительного интервала для доли признака в генеральной совокупности
Чтобы построить доверительный интервал для доли признака в генеральной совокупности, можно воспользоваться функцией нормстобр или надстройкой PHStat2.
Например, чтобы построить доверительный интервал, показанный на рис. 7.10, необходимо выполнить одну из следующих процедур.
Применение Excel в сочетании с надстройкой PHStat2
Чтобы построить доверительный интервал для доли признака в генеральной совокупности при неизвестном стандартном отклонении, следует применить процедуру PHStat^Confidence Intervals1^ Estimate for the Proportion... (PHStat1^ Доверительные интервалы^Оценка доли...). Для этого необходимо выполнить инструкции, приведенные ниже.
1. Выбрать команду PHStat1^Confidence Intervals1^Estimate for the Proportion....
2. В диалоговом окне Estimate for the Proportion (см. иллюстрацию) сделать следующее.
2.1. Ввести в окне редактирования Sample Size (Объем выборки) число 10 0.
2.2. Ввести в окне редактирования Number of Success (Количество успехов) число 10.
2.3. Ввести в окне редактирования Confidence Level (Доверительный интервал) число 95.
2.4. Ввести в окне редактирования Title соответствующий заголовок.
Estimate for the Proportion
Data
Sample Size: '100
Number of Successes: 110
Confidence Level: i95 %
Output Options
Title: 1Долч ошибочных накладных
Г' Finite Population Correction
Help i OK j Cancel
I 2.5. Щелкнуть на кнопке OK. j
[ Применение Excel
I Для того чтобы самостоятельно создать рабочий лист, вычисляющий доверительный интервал для j | доли признака в генеральной совокупности при неизвестном стандартном отклонении, следуйте I
I инструкциям, приведенным в разделе ЕН.7.3. \
\ Chapter 7.xls i
j Данные, на основе которых вычисляется доверительный интервал, показанный на рис. 7.10, !
! содержатся в рабочей книге Chapter 7. xls на листе Рис7.10. j
ПРИМЕР 7.4. ОЦЕНКА ДОЛИ БРАКОВАННЫХ ЭКЗЕМПЛЯРОВ ГАЗЕТЫ
Редактор крупной газеты желает оценить среднегодовую долю бракованных экземпляров в тираже. Бракованными считаются экземпляры, содержащие пятна, нарушение нумерации страниц, пропуски и дубликаты страниц. Для этого он создал выборку, состоящую из 200 экземпляров. В данной выборке 35 экземпляров оказались бракованными. Постройте интервал, содержащий долю брака с 90% -ным доверительным уровнем.
РЕШЕНИЕ. Доверительный интервал вычисляется следующим образом. Доверительному уровню 90% соответствует критическое значение Z = 1,645.
ps = 35/200 = 0,175,
р ± zJ-s^~Ps^ = 0,175 ± 1,645, Г’175* 0,825 = 0,175 ± 1,645 х 0,0269 = 0,175 ± 0,0442 ,
V п У 200
0,1308 <р < 0,2192.
Таким образом, вероятность того, что от 13,08 до 21,92% экземпляров окажутся бракованными, равна 90%.
ПРОВЕРКА ПРЕДПОЛОЖЕНИЙ
В примере 7.4 количество успехов и неудач относительно велико, поэтому биномиальное распределение можно аппроксимировать нормальным. Однако, если объем выборки невелик или количество успехов мало, следует использовать биномиальное, а не нормальное распределение [1, 6]. Таблицы, содержащие точные доверительные интервалы для разных объемов выборок и долей успеха, созданы Фишером и Йейтсом (Fisher and Yates) [2].
Для заданного объема выборки доверительный интервал, содержащий долю признака в генеральной совокупности, кажется более широким, чем для непрерывной случайной величины. Это объясняется тем, что измерения непрерывной случайной величины содержат больше информации, чем измерения категорийных данных. Иначе говоря, категорийные данные, принимающие лишь два значения, содержат недостаточно информации для оценки параметров их распределения.
УПРАЖНЕНИЯ К РАЗДЕЛУ 7.3
Изучение основ
7.22. Вычислите 95%-ный доверительный интервал, содержащий долю признака в генеральной совокупности, если п = 200, а X = 50.
7.23. Вычислите 99% -ный доверительный интервал, содержащий долю признака в генеральной совокупности, если п = 400, а X = 25.
Применение понятий
7.24. Телефонной компании необходимо оценить количество владельцев телефонных номеров, желающих установить дополнительную телефонную линию по сниженной цене. Для этого была создана случайная выборка, состоящая из 500 клиентов. Оказалось, что 135 владельцев телефонных номеров согласны оплатить эту услугу.
1. Постройте интервал, содержащий долю владельцев телефонных номеров, желающих установить дополнительную телефонную линию, доверительный уровень которого равен 99% .
2. Какие выводы может сделать менеджер телефонной компании, анализируя результаты решения задачи 1?
7.25. В статье, недавно опубликованной в журнале Wall Street Journal, утверждается, что женщины начинают новое дело, стремясь к свободе и независимости, а не из-за денег (“Work Week”, Wall Street Journal, June 8, 1999, p. Al). В опросе участвовали 763 женщины, основавшие новые компании, 229 из них ответили, что начали новое дело, стремясь к большей свободе. Только 99 женщин заявили, что занимаются бизнесом, чтобы заработать больше денег.
1. Постройте интервал с 90%-ным доверительным уровнем, содержащий долю женщин, которые начали новое дело, стремясь к свободе и независимости.
2. Постройте интервал с 90%-ным доверительным уровнем, содержащий долю женщин, которые начали новое дело, желая заработать больше денег.
7.26. Исследование, проведенное организацией Randstad North America, показало, что только 41% из 1110 американских рабочих считают, что их начальники относятся к ним лояльно (Carlos Tejada, “Work Week”, Wall Street Journal, May 29, 2002, B10).
1. Постройте 95%-ный доверительный интервал, содержащий долю рабочих, считающих, что их начальники относятся к ним лояльно.
2. Постройте 90%-ный доверительный интервал, содержащий долю рабочих, считающих, что их начальники относятся к ним лояльно.
3. Какой из этих интервалов шире? Аргументируйте свой ответ.
7.27. В ходе исследования, проведенного журналом Reader's Digest (“Testing Honesty Around the World”, USA Today, May 1, 2001, 1A), в разных странах мира были “потеряны” 1 100 кошельков, в которых лежали 50 долл, и записка с фамилией и телефонным номером “хозяина”. В 484 случаях люди, нашедшие кошелек, не вернули его “хозяину”. Постройте 95%-ный доверительный интервал для доли “потерянных” кошельков, возвращенных “владельцам”.
7.28. Опрос автомобилистов, использующих мобильные телефоны, показал, что 46% респондентов сбились с пути, а 10% заявили, что знают случаи, когда люди попадали в аварию, разговаривая по мобильному телефону (“Drivers Using Cell Phones Have Problems”, USA Today, May 16, 2001, 1A). Предположим, что в исследовании приняли участие 500 респондентов.
1. Постройте 95%-ный доверительный интервал, содержащий долю автомобилистов, которые сбились с пути, разговаривая по мобильному телефону.
2. Постройте 95%-ный доверительный интервал, содержащий долю автомобилистов, знающих о случаях, когда люди попадали в аварию, разговаривая по мобильному телефону.
7.29. Компания Walker Information, Inc. спросила у 2 800 американских рабочих, испытывают ли они чувство неловкости, сообщая руководству о плохой работе своих коллег. В 1 456 случаях респонденты ответили утвердительно, а 1 344 рабочих ответили отрицательно (“Work Week”, Wall Street Journal, September 4, 2001, Al).
1. Постройте 95%-ный доверительный интервал, содержащий долю американских рабочих, которые испытывают чувство неловкости, сообщая руководству о плохой работе своих коллег.
2. Постройте 99%-ный доверительный интервал, содержащий долю американских рабочих, которые испытывают чувство неловкости, сообщая руководству о плохой работе своих коллег.
3. Уверены ли вы, что более половины американских рабочих испытывают чувство неловкости, сообщая руководству о плохой работе своих коллег?
4. В статье утверждается также, что в 1999 году 34% всех американских рабочих не испытывали чувства неловкости, сообщая руководству о плохой работе своих коллег. Уверены ли вы, что этот процент значимо увеличился с 1999 по 2001 гг.?
7.30. Клиническое подразделение компании Estee Lauder Cosmetics провело в Северной Америке опрос работающих женщин. Из 1 000 опрошенных женщин 55% полагают, что компании должны резервировать место работы для женщин, находящихся в декретном отпуске, на срок до 6 месяцев, а остальные 45% считают, что этот срок должен превышать 6 месяцев (“Work Week”, Wall Street Journal, September 11, 2001, Al).
1. Постройте 95%-ный доверительный интервал, содержащий долю североамериканских женщин, полагающих, что компании должны резервировать место работы для женщин, находящихся в декретном отпуске, на срок более 6 месяцев.
2. Дайте интерпретацию доверительного интервала, построенного при решении задачи 1.
7.31. На протяжении июня и июля 2001 года комиссия Европейского Союза провела опрос 6 543 взрослых европейцев. Среди опрошенных 56% заявили, что введение единой европейской вылюты будет способствовать экономическому росту, а 73% точно знали дату ее введения (1 января 2002 года) (“Retail Cheating Seen as Likely”, Marketing News, September 24, 2001, 42).
1. Постройте 95%-ный доверительный интервал, содержащий долю взрослых европейцев, уверенных, что введение единой европейской вылюты будет способствовать экономическому росту.
2. Постройте 95%-ный доверительный интервал, содержащий долю взрослых европейцев, знающих точную дату введения единой европейской валюты.
7.4. ОПРЕДЕЛЕНИЕ ОБЪЕМА ВЫБОРКИ
В каждом из рассмотренных примеров мы заранее фиксировали объем выборки, не учитывая ширину доверительного интервала. В реальных задачах определить объем выборки довольно сложно. Это зависит от наличия финансовых ресурсов, времени и легкости создания выборки. Если нам необходимо оценить среднюю сумму накладных или долю ошибочных накладных в информационной системе компании Saxon Home Improvement Company, сначала следует выяснить, насколько точной должна быть оценка. Иначе говоря, следует задать ошибку выборочного исследования, допускаемую при оценке каждого из параметров. Кроме того, необходимо заранее определить доверительный уровень оценки истинного параметра генеральной совокупности.
Определение объема выборки для оценки математического ожидания
Чтобы определить объем выборки, необходимый для оценки математического ожидания генеральной совокупности, следует учесть величину ошибки выборочного исследования и доверительный уровень. Кроме того, необходима дополнительная информация о величине стандартного отклонения.
Для того чтобы вывести формулу, позволяющую вычислить объем выборки, напомним формулу (7.1):
X±Z-^, у/п
где Z — критическое значение случайной величины, имеющей стандартизированное нормальное распределение.
Величина, добавляемая и вычитаемая из X , равна половине длины интервала. Она определяет меру неточности оценки, возникающей вследствие ошибки выборочного исследования, которая обозначается символом е и вычисляется по формуле
e = Z-S=-.
Дп
Следовательно, объем выборки п определяется по такой формуле.
ОПРЕДЕЛЕНИЕ ОБЪЕМА ВЫБОРКИ ДЛЯ ОЦЕНКИ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ
Объем выборки равен произведению квадрата величины Z на дисперсию о2, деленному на квадрат ошибки выборочного исследования е:
Таким образом, для определения объема выборки необходимо знать три параметра.
1. Требуемый доверительный уровень, который влияет на величину Z, являющуюся критическим значением стандартизованного нормального распределения.3
2. Приемлемую ошибку выборочного исследования е;
3. Стандартное отклонение о.
Для определения размера выборки используется величина Z, а не t, поскольку для вычисления критического значения t размер выборки необходимо знать заранее. В большинстве случаев размеры выборки позволяют хорошо аппроксимировать t-распределение стандартизованным нормальным распределением.
На практике вычислить эти величины непросто. Как определить доверительный уровень и ошибку выборочного исследования? Обычно ответить на этот вопрос могут лишь эксперты в предметной области (т.е. люди, понимающие смысл оцениваемых величин). Как правило, доверительный уровень равен 95% (в этом случае Z = 1,96). Если требуется поднять доверительный уровень, обычно выбирают величину, равную 99%. Если можно ограничиться более низким доверительным уровнем, выбирают 90%. Определяя ошибку выборочного исследования, не стоит думать о ее величине (в принципе, любая ошибка нежелательна). Следует задать такую ошибку, чтобы полученные результаты допускали разумную интерпретацию.
Кроме доверительного уровня и ошибки выборочного исследования, необходимо знать стандартное отклонение генеральной совокупности. К сожалению, этот параметр почти никогда не известен. В некоторых случаях стандартное отклонение генеральной совокупности можно оценить на основе предшествующих исследований. В других ситуациях опытный эксперт может учесть размах выборки и распределение случайной переменной. Например, если генеральная совокупность имеет нормальное распределение, ее размах приближенно равен 6о (т.е. ±3о в окрестности математического ожидания). Следовательно, стандартное отклонение приближенно равно одной шестой части диапазона. Если величину о невозможно оценить таким способом, необходимо выполнить пилотный проект и вычислить стандартное отклонение по результатам.
Чтобы продемонстрировать применение этого подхода, вернемся к задаче об аудиторской проверке в компании Saxon Home Improvement Company. Предположим, что из информационной системы извлечена выборка, состоящая из 100 накладных, заполненных в течение последнего месяца. Компания желает построить интервал, содержащий математическое ожидание генеральной совокупности, доверительный уровень которого равен 95% . Как был определен объем выборки? Следует ли его уточнить?
Допустим, что после консультаций с экспертами, работающими в компании, статистики установили допустимую ошибку выборочного исследования равной ±5 долл., а доверительный уровень — 95%. Результаты предшествующих исследований свидетельствуют, что стандартное отклонение генеральной совокупности приближенно равно 25 долл. Таким образом, е = 5, о = 25 и Z=l,96 (что соответствует 95%-ному доверительному уровню). По формуле (7.4) получаем:
Z2c2 _ (1,96)2252
= 96,04.
Следовательно, п = 97, поскольку дробные результаты, как правило, округляют с избытком до ближайшего целого. Таким образом, объем выборки, равный 100, был выбран удачно и вполне соответствует требованиям, выдвинутым компанией. Однако, если стандартное отклонение равно 28,95, доверительный интервал оказывается немного шире, чем требуется. Пример вычисления объема выборки с помощью программы Microsoft Excel приведен на рис. 7.11.
Рис. 7.11. Вычисление объема выборки при построении доверительного интервала для математического ожидания генеральной совокупности накладных с помощью программы Microsoft Excel
Процедуры Excel: определение объема выборки при оценке математического ожидания генеральной совокупности
Чтобы определить объем выборки, необходимой для построения доверительного интервала, со-j держащего математическое ожидание генеральной совокупности, можно воспользоваться функ-| цией нормстобр или надстройкой PHStat2.
| Например, чтобы определить объем выборки для оценки средней суммы накладных компании I Saxon Home Improvement Company, необходимо выполнить одну из следующих процедур.
Применение Excel в сочетании с надстройкой PHStat2
Чтобы определить объем выборки, необходимой для построения доверительного интервала, содержащего математическое ожидание генеральной совокупности, следует применить процедуру PHStat4>Sample Size4>Determination for the Mean... (PHStat1^Объем выборки1^Определение математического ожидания...).
1. Выбрать PHStat4>Sample Size ^Determination for the Mean....
2. В диалоговом окне Sample Size Determination for the Mean Estimate (Определение объема выборки для оценки математического ожидания) (см. иллюстрацию) сделать следующее.
2.1. Ввести в окне редактирования Population Standard Deviation (Стандартное отклонение генеральной совокупности) число 2 5.
2.2. Ввести в окне редактирования Sampling Error (Ошибка выборочного исследования) число 5.
2.3. Ввести в окне редактирования Confidence Level (Доверительный уровень) число 95.
Sample Size Determination for the M... fx]
Data
Population Standard Deviation: s 25
Sampling Error: j5
Confidence Level: :95 %
Output Options
Title: j Средняя сумма накладных Г' Finite Population Correction
2.4. Ввести в окне редактирования Title соответствующий заголовок.
2.5. Щелкнуть на кнопке ОК.
Применение Excel
Для того чтобы самостоятельно создать рабочий лист, определяющий объем выборки, необходимый для вычисления доверительного интервала, содержащего математическое ожидание генеральной совокупности, следуйте инструкциям, приведенным в разделе ЕН.7.4.
Chapter 7.xls
Данные, на основе которых определяется объем выборки, необходимый для вычисления доверительного интервала, содержащего математическое ожидание генеральной совокупности накладных, содержатся в рабочей книге chapter 7 . xls на листе Рис7.11.
ПРИМЕР 7.5. ОПРЕДЕЛЕНИЕ ОБЪЕМА ВЫБОРКИ ДЛЯ ОЦЕНКИ СРЕДНЕГО
Вернемся к примеру 7.3. Предположим, что нам необходимо оценить среднюю силу разрушения изолятора с точностью +25 фунтов и построить 95% -ный доверительный интервал для этой величины. Данные, полученные в предыдущем исследовании, свидетельствуют, что стандартное отклонение равно 100 фунтов. Определите требуемый объем выборки.
РЕШЕНИЕ. Итак, е = 25, о = 100, а доверительный уровень равен 95% (т.е. Z = 1,96). n = (1,96)400^ 6 7-
е2 25
Таким образом, п = 62. Напомним, что дробные результаты, как правило, округляют с избытком до ближайшего целого.
Обратите внимание на то, что при указанных данных объем выборки равен 62, а не 30, как было установлено в примере 7.3. Кроме того, величина стандартного отклонения определена на основе прошлогодних наблюдений. Если реальное стандартное отклонение значительно отличается от этой величины, ошибка выборочного исследования окажется совершенно иной.
Определение объема выборки для оценки доли признака в генеральной совокупности
Выше мы рассмотрели способ определения объема выборки для оценки математического ожидания генеральной совокупности. Предположим теперь, что мы проводим аудиторскую проверку в компании Saxon Home Improvement Company. Нам необходимо определить долю накладных, не соответствующих правилам, принятым компанией. Сколько накладных следует извлечь из информационной системы, чтобы построенный интервал имел заданный доверительный уровень? Для ответа на этот вопрос применим тот же подход, что и при определении объема выборки для оценки математического ожидания.
Напомним, что ошибка выборочного исследования определяется по формуле:
При оценке доли признака величину о следует заменить на величину ^р(1 - р) . Таким образом, формула для ошибки выборочного исследования принимает следующий вид:
e = z Hzrt N п
Выражая п через остальные величины, получаем следующую формулу.
ОПРЕДЕЛЕНИЕ ОБЪЕМА ВЫБОРКИ ДЛЯ ОЦЕНКИ ДОЛИ ПРИЗНАКА
Объем выборки равен произведению квадрата величины Z на р(1-р), деленному на квадрат ошибки выборочного исследования е:
n = Z2^. (7.5)
е~
Таким образом, для определения объема выборки необходимо знать три параметра.
1. Требуемый доверительный уровень, по которому определяется величина Z.
2. Допустимую ошибку выборочного исследования е.
3. Истинную долю успеховр.
На практике вычислить эти величины нелегко. Если известен доверительный уровень, можно вычислить критическое значение стандартизованного нормального распределения Z. Ошибка выборочного исследования е определяет точность, с которой оценивается доля успехов в генеральной совокупности. Третий параметр — доля успехов в генеральной совокупности р — это именно тот параметр, который нам необходимо оценить. Итак, как оценить диапазон изменения величины р по его выборочным значениям?
Существуют два способа. Во-первых, во многих ситуациях для оценки величины р можно использовать результаты предыдущих исследований. Во-вторых, если данные
о предыдущих исследованиях недоступны, можно попытаться оценить параметр р так, чтобы исключить недооценку объема выборки. Обратите внимание на то, что в формуле (7.5) величина р(1-р) стоит в числителе. Следовательно, необходимо найти максимальное значение этой величины. Очевидно, что оно достигается при р = 0,5. Перечислим некоторые значения произведения р(1-р).
Еслир = 0,9, тор(1-р) = 0,9 х 0,1 = 0,09.
Еслир = 0,7, тор(1-р) = 0,7 х 0,3 = 0,21.
Еслир = 0,5, тор(1~р) = 0,5 х 0,5 = 0,25.
Еслир = 0,3, тор(1~р) = 0,3 х 0,7 = 0,21.
Еслир = 0,1, тор(1-р) = 0,1 х 0,9 = 0,09.
Таким образом, если доля признака в генеральной совокупности р заранее неизвестна, для определения объема выборки следует задать р = 0,5. В этом случае объем выборки будет переоценен, что приведет к дополнительным затратам на ее создание. Если истинная доля успехов в генеральной совокупности сильно отличается от 0,5, доверительный интервал окажется значительно i/же, чем требовалось. Оценка параметра р в этом случае будет весьма точной, однако за это придется заплатить дополнительными временными и финансовыми ресурсами.
Вернемся к задаче об аудиторской проверке в компании Saxon Home Improvement Company. Предположим, аудитор желает построить интервал, содержащий долю ошибочных накладных, доверительный уровень которого равен 95%. Допустимая точность равна ±0,07. Результаты предыдущих проверок свидетельствуют, что доля ошибочных накладных не превышает 0,15. Таким образом, е = 0,07, р = 0,15 и Z = 1,96 (что соответствует 95% -ному доверительному уровню). По формуле (7.5) получаем:
п = Z2P(\-p} = (1,96)2х 0,15x0,85 = %
ег (0,07)2
Следовательно, п = 100, поскольку дробные результаты, как правило, округляют с избытком до ближайшего целого. Таким образом, объем выборки, равный 100, был выбран совершенно правильно и вполне соответствует требованиям, выдвинутым компанией. Однако, если стандартное отклонение равно 0,10, доверительный интервал оказывается немного уже, чем требуется. Пример вычисления объема выборки с помощью программ PHStat и Microsoft Excel приведен на рис. 7.12.
0.15
0.07
95%
Для доли ошибочных накладных
2 ___________________________.
Data
4 ; Estimate of True Proportion__
5 jSampling Error________________
6 ] Confidence Level_____________
7 J______________________________
_________Intermediate Calculations
9 7 Value
10 j Calculated Sample Size
'l\________________________
12j_________________Result
JSjSample Size Needed
-1.95996279
99 95620435
100
Рис. 7.12. Вычисление объема выборки при построении доверительного интервала, содержащего долю признака в генеральной совокупности накладных, с помощью программы Microsoft Excel
Процедуры Excel: определение объема выборки при оценке доли признака в генеральной совокупности
Чтобы определить объем выборки, необходимой для построения доверительного интервала, содержащего долю признака в генеральной совокупности, можно воспользоваться функцией НОРМСТОБР или надстройкой PHStat2.
Например, чтобы определить объем выборки для оценки доли ошибочных накладных, как показано на рис. 7.12, необходимо выполнить одну из следующих процедур.
Применение Excel в сочетании с надстройкой PHStat2
Чтобы определить объем выборки, необходимой для построения доверительного интервала, содержащего долю признака в генеральной совокупности, следует применить процедуру PHStat^Sample Size4>Determination for the Proportion... (PHStat4>Объем выборки^Определение для доли признака...).
1. Выбрать PHStat4>Sample Size4>Determination for the Proportion....
2. В диалоговом окне Sample Size Determination for the Proportion (Определение объема выборки для оценки доли признака) (см. иллюстрацию) сделать следующее.
2.1. Ввести в окне редактирования Estimate of True Proportion (Оценка истинной доли) число 0.15.
2.2. Ввести в окне редактирования Sampling Error (Ошибка выборочного исследования) число 0.07,
2.3. Ввести в окне редактирования Confidence Level (Доверительный уровень) число 95.
2.4. Ввести в окне редактирования Title соответствующий заголовок.
2.5. Щелкнуть на кнопке ОК.
Sample Size Determination for the P... [x]
Data ....
Estimate of True Proportion: [cTTs
Sampling Error: |o,O7
Confidence Level: [95 %
Output Options........................
Title: |Доля ошибочных накладных
Г~ Finite Population Correction
Help | |i OK ~j] Cancel j
Применение Excel
Для того чтобы самостоятельно создать рабочий лист, определяющий объем выборки, необходимый для вычисления доверительного интервала, содержащего долю признака в генеральной совокупности, следуйте инструкциям, приведенным в разделе ЕН.7.5.
Chapter 7.xls
Данные, на основе которых определяется объем выборки для вычислений, показанных на рис. 7.12, содержатся в рабочей книге chapter 7 . xls на листе Рис7.12.
ПРИМЕР 7.6. ОПРЕДЕЛЕНИЕ ОБЪЕМА ВЫБОРКИ ДЛЯ ОЦЕНКИ ДОЛИ ПРИЗНАКА В ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ
Редактор крупной газеты, упомянутой в примере 7.4, желает построить интервал, содержащий долю брака с 90%-ным доверительным уровнем. Допустимая ошибка выборочной проверки равна ±0,05. Кроме того, редактору неизвестны результаты предшествующих проверок. Определите необходимый объем выборки.
РЕШЕНИЕ. Поскольку никаких данных о предыдущих проверках нет, примем р = 0,50. Кроме того, е = 0,05, а доверительный уровень равен 90% (т.е. Z = 1,645).
;; J1.645)2 х0,50x0,50 __2?06
(0,05)2
Таким образом, и = 271. Итак, чтобы построить интервал, содержащий долю брака с 90% -ным доверительным уровнем при допустимой ошибке выборочного исследования, равной ±0,05, выборка должна содержать 271 экземпляр газеты.
'L лЧ^>ж '4s‘ <£ -±± ц^З
Изучение основ
7.32. Вычислите объем выборки, необходимой для построения интервала, содержащего математическое ожидание генеральной совокупности с 95%-ным доверительным уровнем, если допустимая ошибка выборочного исследования равна ±5, а стандартное отклонение — 15.
7.33. Вычислите объем выборки, необходимой для построения интервала, содержащего математическое ожидание генеральной совокупности с 99% -ным доверительным уровнем, если допустимая ошибка выборочного исследования равна ±20, а стандартное отклонение — 100.
7.34. Вычислите объем выборки, необходимой для построения интервала, содержащего долю признака в генеральной совокупности с 99%-ным доверительным уровнем, если допустимая ошибка выборочного исследования равна ±0,04.
7.35. Вычислите объем выборки, необходимой для построения интервала, содержащего долю признака в генеральной совокупности с 99%-ным доверительным уровнем, если допустимая ошибка выборочного исследования равна ±0,04, а предыдущие исследования показали, что приблизительное значение параметрар равно 0,40.
Применение понятий
7.36. В крупной компании планируется опрос сотрудников. Цель опроса— выяснить среднегодовую величину расходов на медицинские услуги. Администрация компании желает построить 95%-ный доверительный интервал, содержащий математическое ожидание генеральной совокупности с точностью ±50 долл. Предварительный опрос показал, что стандартное отклонение приближенно равно 400 долл.
1. Определите необходимый объем выборки.
2. Предположим, что администрация компании решила повысить точность прогноза до ±25 долл. Определите необходимый объем выборки.
7.37. Директор магазина стройматериалов желает оценить средний объем краски, содержащейся в банке, емкостью один галлон с точностью ±0,004. Для этого он собирается построить 95%-ный доверительный интервал, предполагая, что стандартное отклонение равно 0,02 галлона. Определите необходимый объем выборки.
7.38. Инспектор по контролю за качеством продукции желает оценить среднюю продолжительность работы электрических лампочек с точностью ±20 . Для этого он собирается построить 95%-ный доверительный интервал, предполагая, что стандартное отклонение равно 100 ч. Определите необходимый объем выборки.
7.39. Метролог компании, производящей безалкогольные напитки, желает оценить средний объем жидкости в двухлитровых бутылках с точностью ±0,01 л. Для этого он собирается построить 95%-ный доверительный интервал, предполагая, что стандартное отклонение равно 0,05 л. Определите объем выборки.
7.40. Общество защиты прав потребителей желает оценить среднюю сумму, затраченную обычной семьей на оплату электричества за июль. Предварительные исследования, проведенные в других городах, показали, что стандартное отклонение равно 25 долл. Допустимая точность оценки равна ±5 долл. Необходимо построить 99%-ный доверительный интервал, содержащий среднюю сумму затрат на электричество.
1. Определите необходимый объем выборки.
2. Предположим, что доверительный уровень равен 95%. Определите необходимый объем выборки.
7.41. Рекламное агентство, заключившее договор с местной радиостудией, желает оценить среднее время, которое слушатели ежедневно проводят перед радиоприемником. Предварительные исследования показали, что стандартное отклонение равно 45 мин.
1. Определите объем выборки, если допустимая точность оценки равна ±5 мин., а доверительный уровень — 90%.
2. Предположим, что доверительный уровень равен 99%. Определите необходимый объем выборки.
7.42. Компания, поставляющая газ, желает оценить среднее время ожидания своих потребителей. Определите необходимый объем выборки, если допустимая точность оценки равна ±5 дней, доверительный уровень — 95% , а стандартное отклонение равно 20 дней.
7.43. Файл ©NYSE.XLS содержит случайную выборку, состоящую из стоимости 18 акций, котируемых на Нью-Йоркской фондовой бирже по состоянию на 4 марта 2003 года.
1. Постройте 95%-ный доверительный интервал, содержащий математическое ожидание этой генеральной совокупности.
2. Какой объем должна иметь выборка, если доверительный уровень равен 95% , а допустимая точность — ±20 000 акций?
3. Сравните ваши оценки с реальными данными. Обоснуйте свои рассуждения.
7.44. Социологическая служба желает оценить долю избирателей, собирающихся проголосовать на предстоящих президентских выборах за представителя демократической партии. Необходимо построить 90%-ный доверительный интервал с точностью ±0,04.
1. Определите необходимый объем выборки.
2. Предположим, что доверительный уровень равен 95%. Определите необходимый объем выборки.
3. Предположим, что доверительный уровень равен 95%, а точность— ±0,03. Определите необходимый объем выборки.
4. Объясните, как объем выборки зависит от доверительного уровня и ошибки выборочного исследования. Аргументируйте свой ответ.
7.45. В 2001 г. 45% семей в США приобретали бакалейные товары в ближайших лавках, а 29% семей — в оптовых магазинах (“68th Annual Report of the Grocery Industry”, Progressive Grocer, April 2002, 29).
1. Определите объем выборки, необходимый для оценки доли американских семей, приобретающих бакалейные товары в ближайших лавках, если точность выборочного исследования равна ±0,02, а доверительный уровень — 95%.
2. Определите объем выборки, необходимый для оценки доли американских семей, приобретающих бакалейные товары в оптовых магазинах, если точность выборочного исследования равна ±0,02, а доверительный уровень — 95%.
3. Сравните результаты решения задач 1 и 2. Объясните разницу между ними.
4. Предположим, вы планируете дальнейшие исследования. Можно ли использовать одну и ту же выборку, задавая респондентам оба вопроса одновременно, или следует сформировать две отдельные выборки? Аргументируйте свой ответ.
5. Как сформировать выборки для исследования в задаче 4?
7.46. Сколько людей, живущих в США, планируют свой отпуск с помощью Интернет? Согласно опросу, проведенному компанией American Express, доля таких людей составляет 35% (A. R. Carey and К. Carter, “Snapshots”, USA Today, January 14, 2003, 1A). Предположим, что вы планируете свое исследование.
1. Определите объем выборки, необходимый для оценки доли американцев, планирующих свой отпуск с помощью Интернет, если точность выборочного исследования равна ±0,04, а доверительный уровень — 95% .
2. Определите объем выборки, необходимый для оценки доли американцев, планирующих свой отпуск с помощью Интернет, если точность выборочного исследования равна ±0,04, а доверительный уровень — 99% .
3. Определите объем выборки, необходимый для оценки доли американцев, планирующих свой отпуск с помощью Интернет, если точность выборочного исследования равна ±0,02, а доверительный уровень — 95% .
4. Определите объем выборки, необходимый для оценки доли американцев, планирующих свой отпуск с помощью Интернет, если точность выборочного исследования равна ±0,02, а доверительный уровень — 99% .
5. Объясните, как изменение ошибки выборочного исследования и доверительного уровня влияют на требуемый объем выборки.
7.47. Мешают ли звонки мобильных телефонов во время презентации деловых проектов? В ходе опроса 326 бизнесменов ответили “Да” и только 23 ответили “Нет”. (“You say”, Presentations: Technology and Techniques for Effective Communication, January 2003, 18.)
1. Постройте 95%-ный доверительный интервал для доли бизнесменов, считающих, что звонки мобильных телефонов мешают презентации деловых проектов.
2. Дайте интерпретацию доверительного интервала, построенного при решении задачи 1.
3. Предположим, что вы планируете собственное исследование. Определите объем выборки, необходимый для оценки доли бизнесменов, считающих, что звонки мобильных телефонов мешают презентации деловых проектов, если точность выборочного исследования равна ±0,04, а доверительный уровень — 95%.
4. Предположим, что вы планируете собственное исследование. Определите объем выборки, необходимый для оценки доли бизнесменов, считающих, что звонки мобильных телефонов мешают презентации деловых проектов, если точность выборочного исследования равна ±0,04, а доверительный уровень — 99%.
5. Предположим, что вы планируете собственное исследование. Определите объем выборки, необходимый для оценки доли бизнесменов, считающих, что звонки мобильных телефонов мешают презентации деловых проектов, если точность выборочного исследования равна ±0,02, а доверительный уровень — 95%.
6. Предположим, что вы планируете собственное исследование. Определите объем выборки, необходимый для оценки доли бизнесменов, считающих, что звонки мобильных телефонов мешают презентации деловых проектов, если точность выборочного исследования равна ±0,02, а доверительный уровень — 99%.
7. Объясните, как изменение ошибки выборочного исследования и доверительного уровня влияют на требуемый объем выборки.
8. Сравните свои выводы о влиянии ошибки выборочного исследования и доверительного уровня на требуемый объем выборки с решением задачи 7.46.
7.48. Исследование, проведенное Федеральной резервной системой США, показало, что 52% из 4 449 семей в 2001 году владели акциями либо непосредственно, либо через взаимные фонды. (Barbara Hagenbaugh, “Nation’s Wealth Disparity Widens”, USA Today, January 22, 2003, 1A.)
1. Постройте 95%-ный доверительный интервал для доли семей, владевших акциями в 2001 году.
2. Дайте интерпретацию доверительного интервала, построенного при решении задачи 1.
3. Предположим, что вы планируете собственное исследование. Определите объем выборки, необходимый для оценки доли семей, владеющих акциями, если точность выборочного исследования равна ±0,01, а доверительный уровень — 95%.
7.49. Исследование, проведенное фондом At-A-Glance Communications, показало, что 434 из 611 опрошенных клерков отвечают на полученное электронное письмо в течение одного или двух часов (D. Haralson and S. Ward, “You Have Mail”, USA Today, May 7, 2002, 1A.)
1. Постройте 95% -ный доверительный интервал для доли клерков, отвечающих на полученное электронное письмо в течение одного или двух часов
2. Дайте интерпретацию доверительного интервала, построенного при решении задачи 1.
3. Предположим, что вы планируете собственное исследование. Определите объем выборки, необходимый для оценки доли клерков, отвечающих на полученное электронное письмо в течение одного или двух часов, если точность выборочного исследования равна ±0,01, а доверительный уровень — 95% .
7.5. ПРИМЕНЕНИЕ ДОВЕРИТЕЛЬНЫХ ИНТЕРВАЛОВ
В АУДИТОРСКОМ ДЕЛЕ
Описывая доверительные интервалы, мы сосредоточили внимание на математическом ожидании и доле признака в генеральной совокупности. Эти средства статистического анализа нашли весьма широкое применение в аудиторском деле.
Аудит — это сбор и оценка информации, позволяющей оценить состояние экономического объекта, например, компании, акционерного общества, корпорации или правительственного агентства. Цель аудита — оценить, насколько деятельность проверяемого объекта соответствует установленным критериям.
Во врезке 7.1 перечислены шесть основных преимуществ выборочного исследования, применяемого при аудите.
ВРЕЗКА 7.1. ПРЕИМУЩЕСТВА АУДИТОРСКОГО ОБСЛЕДОВАНИЯ
• Результаты выборочного исследования объективны и обоснованны. Поскольку определение объема выборки основано на точно сформулированных статистических принципах, результаты аудиторской проверки можно защищать в суде.
• Метод выборочного исследования позволяет заранее определить объем выборки.
• Метод позволяет оценить ошибку выборочного исследования.
• Этот подход можно применять для более точной оценки параметров, поскольку исследование большой генеральной совокупности может занять много времени и даже сопровождаться значительными ошибками нестатистического характера.
• Метод выборочного исследования могут применять сразу несколько аудиторов. Поскольку этот метод является научно обоснованным, можно считать, что в параллельной проверке принимает участие один аудитор.
• Метод выборочного исследования позволяет объективно оценить результаты проверки, поскольку его точность известна заранее.
Оценка суммы элементов генеральной совокупности
В аудиторском деле часто приходится оценивать сумму элементов генеральной совокупности. Она определяется по следующей формуле.
ОЦЕНКА СУММЫ ЭЛЕМЕНТОВ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ
Точечная оценка суммы элементов генеральной совокупности равна объему генеральной совокупности N, умноженному на выборочное среднее X:
Суммам NX. (7.6)
Границы доверительного интервала, содержащего сумму элементов генеральной совокупности, определяются по формуле (7.7).
ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ, СОДЕРЖАЩИЙ СУММУ ЭЛЕМЕНТОВ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ
+ (7.7)
Чтобы продемонстрировать применение этой формулы, вернемся к задаче об аудиторской проверке в компании Saxon Home Improvement Company. Предположим, что для вычисления общей суммы накладных из информационной системы извлечены 100 записей, сделанных за последний месяц. Вся генеральная совокупность состоит из 5 000 накладных. Итак, N = 5 000, п = 100, X =110,27, S = 28,95, доверительный уровень равен 95%, a t99 = 1,9842.
Сумма = 5 000 х 110,27 = 551 350.
Таким образом, границы доверительного интервала равны:
NX ± JV(z„ , = 551350 ± 1,9842 х 5 000 /5 000-J_00 =
' ’J714N-1 -ЛОО V 5000-1
= 551 350 ± 28 721,295 х 0,99005.
522 914 < Сумма элементов генеральной совокупности < 579 786.
Следовательно, вероятность того, что сумма элементов генеральной совокупности не меньше 522 914 и не больше 579 786, равна 95%. На рис. 7.13 продемонстрировано вычисление доверительного интервала, содержащего общую сумму генеральной совокупности накладных, с помощью программы Microsoft Excel.
В
А . I.
1_ Общая cyuua накладных 2 i........ ................ 1.....
3____________________Data
4 Population Size
5 j Sample Mean ______
6 .Sample Size
7 Sample Standard Deviation_
В 1 Confidence Level ______
9*.,__________________________:
10_________Intermediate Calculations
11 Population Total________
. 12FPC Factor_____________
13 Standard Error of the Total 14 Degrees of Freedom______
15 il Value________________
16 Interval Half Width_____
17 ' 18'____________________
19 Interval Lower Limit 20 i Interval Upper Limit
5000
110.27
100
28.95
95%
551350.00 0.990048503 14330.95209
_________99
1.984217306
28435 72
Confidence Interval_________
522914.28
579785.72
Рис. 7.13. Вычисление доверительного интервала, содержащего общую сумму генеральной совокупности накладных, с помощью программы Microsoft Excel
Процедуры Excel: построение доверительного интервала для общей суммы генеральной совокупности
Чтобы построить доверительный интервал для общей суммы генеральной совокупности при неизвестном стандартном отклонении, можно воспользоваться функцией стьюдраспобр или надстройкой PHStat2.
Например, чтобы построить доверительный интервал для общей суммы накладных компании Saxon Home Improvement Company, показанный на рис. 7.13, необходимо открыть новый рабочий лист и выполнить одну из следующих процедур.
Применение Excel в сочетании с надстройкой Excel
Чтобы построить доверительный интервал для общей суммы генеральной совокупности, следует применить процедуру PH Stat ^Confidence Intervals^Estimate for the Population Total... (PHStat^ Доверительные интервалы^Оценка общей суммы генеральной совокупности...).
1. Выбрать PHStat^>Confidence Intervals^Estimate for the Population Total....
2. В диалоговом окне Estimate for the Population Total (cm. иллюстрацию) сделать следующее.
2.1. Ввести в окне редактирования Population Size (Объем выборки) число 5000.
2.2. Ввести в окне редактирования Confidence Level (Доверительный интервал) число 95.
2.3. Установить переключатель Input Options (Параметры выборки) в положение Sample Statistics Known (Выборочные статистики известны) и ввести в окне редактирования Sample Size (Объем выборки) число 100, в окне редактирования Sample
Mean (Выборочное среднее) - число 110.27, а в окне редактирования Sample Std. Deviation (Выборочное стандартное отклонение) - число 28.95.
Estimate for the Population Total fXj
Data
Population Size: |5000
Confidence Level: (95 % I
Input Options - - - - - - '
Sample Statistics Known
Sample Size: [100
Sample Mean: [110.27 ।.
Sample Standard Deviation: |28.95
Sample Statistics Unknown
Output Options -
Title: j Общая сумма накладных
Heto j |Г’7^.13| Cancel j
2.4. Ввести в окне редактирования Title соответствующий заголовок.
2.5. Щелкнуть на кнопке ОК.
Если выборочное среднее и выборочное стандартное отклонение не известны, в п. 2.2 следует установить переключатель Input Options (Параметры ввода) в положение Sample Statistics Unknown (Выборочные статистики известны), а в окне редактирования Sample Cell Range (Диапазон ячеек, содержащий выборку) ввести диапазон ячеек, в которых записаны элементы выборки.
Применение Excel
Для того чтобы самостоятельно создать рабочий лист, вычисляющий доверительный интервал, содержащий общую сумму элементов генеральной совокупности, следуйте инструкциям, приведенным в разделе ЕН.7.6.
4^ Chapter 7.xls
' Данные, на основе которых вычисляется доверительный интервал, содержащий общую сумму накладных, как показано на 7.13, хранятся в рабочей книге chapter 7 на листе Рис7.13.
ПРИМЕР 7.7. ПОСТРОЕНИЕ ДОВЕРИТЕЛЬНОГО ИНТЕРВАЛА, СОДЕРЖАЩЕГО ОБЩУЮ СУММУ ЭЛЕМЕНТОВ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ
Предположим, что в распоряжении аудитора оказалась генеральная совокупность чеков. Он желает оценить их общую сумму. Для этого аудитор извлекает из генеральной совокупности 50 чеков и вычисляет выборочное среднее и стандартное отклонение.
Выборочное среднее X = 1 076,39.
Стандартное отклонение S = 273,62 долл.
Необходимо построить 95% -ный доверительный интервал, содержащий общую сумму чеков.
РЕШЕНИЕ. Используя формулу (7.6), получим точечную оценку общей суммы чеков.
NX = 1 000 х 1 076,39 = 1 076 390.
Далее, по формуле (7.7) вычисляем границы 95%-ного доверительного интервала, содержащего общую сумму чеков.
NX ± N(t,, =1 000 х1 076,39 ± 1,000 х 2,0096-^Ь^ |1000~?°. =
v 17ЛИ-1 V100 V 1000-1
= 1 076 390 ± 77 762,902 х 0,97517 = 1 076 390 ± 75 832.
1 000 558 < Общая сумма чеков < 1 152 222.
Следовательно, вероятность того, что сумма элементов генеральной совокупности не меньше 1 000 558 и не больше 1 152 222, равна 95%.
Оценка разности
Оценка разности (difference estimation) применяется тогда, когда аудитор считает, что в анализируемой генеральной совокупности содержатся ошибки, которые необходимо оценить на основе выборочных данных. Для этого выполняются следующие процедуры.
1. Определяется необходимый объем выборки.
2. Вычисляются разности между величинами, обнаруженными в ходе аудита, и номинальными величинами. Обратите внимание на то, что разность Д равна нулю, если обнаруженная величина правильна; является положительной величиной, если обнаруженная величина больше номинальной; и отрицательной — если обнаруженная величина меньше номинальной.
3. Вычисляется средняя выборочная разность D, которая является результатом деления суммы разностей на объем выборки.
СРЕДНЯЯ РАЗНОСТЬ
(7.8)
где Д = обнаруженная величина - номинальная величина.
4. Вычисляется стандартное отклонение разностей SD. Элементам выборки, не являющимся ошибками, соответствуют нулевые разности.
СТАНДАРТНОЕ ОТКЛОНЕНИЕ РАЗНОСТЕЙ
1=1
(7.9)
5. Вычисляются границы доверительного интервала, содержащего сумму разностей элементов генеральной совокупности.
ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ, СОДЕРЖАЩИЙ ПОЛНУЮ РАЗНОСТЬ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ
(7.10)
Продемонстрируем применение этой формулы на примере аудиторской проверки в компании Saxon Home Improvement Company. Предположим, что компания желает построить 95% -ный доверительный интервал, содержащий полную разность между фактическими суммами, указанными в накладных, и суммами, занесенными в информационную систему. В выборку, состоящую из 100 записей, входят 12 накладных, не соответствующих действительности. Перечислим эти разности, выраженные в долларах.
PLUMBINV.XLS
9,3 7,47 17,32 8,30 5,21 10,80 6,22 5,63 4,97 7,43 2,99 4,63
В остальных 88 накладных ошибок нет, следовательно, их разности равны нулю. Итак,
- 9о
D = —----=----= 0,90,
п 100
i-1
1(9,03 - 0,9)2 + (7,47 - 0,9)2 +... + (0 - 0,9)2 _ 2
100-1 “ ’
Таким образом, границы доверительного интервала, содержащего полную разность генеральной совокупности, состоящей из 5 000 накладных, вычисляются по формуле (7.10):
5 000 x 0,90 ±1,9842 x 5 000^22 /5°00 100 = 450012702,91 , л/100 V 5000-1
1 797,09 < Полная разность < 7 202,91.
Следовательно, вероятность того, что полная разность генеральной совокупности накладных не меньше 1 797,09 и не больше 7 202,91, равна 95%. На рис. 7.14 показано, как вычисляется доверительный интервал, содержащий полную разность генеральной совокупности накладных, с помощью программы Microsoft Excel.
“ А 1 в I С . P : Е~[
1 Полная разность между фактическими и зарегистрированными накладными
2
3__________________Data
4 Population Size______
Sample Size__________
Confidence Level
5 6 7 ё
9
5000
100 95%
Intermediate Calculations
) Sum of Differences________________
10 Average Difference in Sample
11 Total Difference_________________
12 Standard Deviation of Differences
13 FPC Factor_______________________
14 Standard Error of the Total Diff.
15 Degrees of Freedom_______________
16 t Value__________________________
17 Interval Half Width______________
10
_______90
______0.9
4500 2 751797 0.990049 1362 206 _______99
1 984217 2702 913'
______________Calculations Area
For standard deviation of differences.
Number of Differences Not = 0 12
Number of Differences = 0 88
SS for Differences Not = 0 678.3864
SS for Differences = 0 71.28
Sum of Squares 749.6664
Variance of Differences 7 572388
Confidence Interval
19 _______________________
20 .Interval Lower Limit
21 Interval Upper Limit
1797.09
7202.91
Рис. 7.14. Вычисление доверительного интервала, содержащего полную разность генеральной совокупности накладных, с помощью программы Microsoft Excel
Процедуры Excel: построение доверительного интервала для полной разности генеральной совокупности
Чтобы построить доверительный интервал для общей суммы генеральной совокупности при неизвестном стандартном отклонении, можно воспользоваться функцией стьюдраспобр или надстройкой PHStat2.
Например, чтобы построить доверительный интервал, показанный на рис. 7.14, необходимо открыть рабочий лист Данные в книге Chapter 7 .xls и выполнить одну из следующих процедур.
Применение Excel в сочетании с надстройкой PHStat2
Чтобы построить доверительный интервал для полной разности генеральной совокупности, следует применить процедуру PHStat^Confidence Intervals^Estimate for the Total Difference... (PHStat1^ Доверительные интервалы^Оценка полной разности...), придерживаясь инструкций, приведенных ниже.
1. Выбрать PHStat^Confidence Intervals^Estimate for the Total Difference....
2. В диалоговом окне Estimate for the Total Difference (см. иллюстрацию) сделать следующее.
2.1. Ввести в окне редактирования Sample Size (Объем выборки) число 100.
2.2. Ввести в окне редактирования Population Size (Объем генеральной совокупности) число 5000.
2.3. Ввести в окне редактирования Confidence Level (Доверительные уровень) число 95.
2.4. Ввести в окне редактирования Differences Cell Range (Диапазон ячеек, содержащий разности) диапазон Al: А13 и установить флажок First cell contains table (Первая ячейка содержит метку).
Estimate for the Total Difference
- Data
Sample Size: |100
Population Size: ]5000
Confidence Level: Гэ5 %
Differences Cell Range: {A1: A13 .
P First cell contains label
Output Options ........
Title: {Полная разность накладных
Help | | EZ Ж""" 11 Cancel j
2.5. Ввести в окне редактирования Title соответствующий заголовок.
2.6. Щелкнуть на кнопке ОК.
Применение Excel
Для того чтобы самостоятельно создать рабочий лист, вычисляющий доверительный интервал для полной разности элементов генеральной совокупности, следуйте инструкциям, приведенным в разделе ЕН.7.7.
4^ Chapter 7.xls
Данные, на основе которых вычисляется доверительный интервал, содержащий полную разность, как показано на рис. 7.14, хранится в рабочей книге Chapter 7 на листе Рис7.14.
В рассмотренном ранее примере все 12 разностей были положительными, поскольку общая сумма накладных превышала сумму, записанную в базе данных. Разумеется, ошибки могут быть не только положительными, но и отрицательными. Проиллюстрируем это с помощью следующего примера.
ПРИМЕР 7.8. ОЦЕНКА ПОЛНОЙ РАЗНОСТИ
Вернемся к примеру 7.7. Предположим, что в выборке, состоящей из 100 записей, обнаружены 14 накладных, содержащих ошибки. Перечислим их разности, выраженные в долларах.
DIFFTEST.XLS
75,41 38,97 108,54 -37,18 62,75 118,32 -88,84
127,74 55,42 39,03 29,41 47,99 28,73 84,05
Необходимо построить 95%-ный доверительный интервал, содержащий полную разность генеральной совокупности, состоящей из 1 000 накладных.
РЕШЕНИЕ.
п
690,34
50
-13,8068
JtT ' _ (75,41-13,8068)2 +(38,97-13,8068)2 +...+ (0-13,8068)2
О л — \ — 4 I — 3 / ,4 X /
° V л-1 V 50-1
Затем по формуле (7.10) вычисляем границы 95%-ного доверительного интервала, содержащего полную разность.
1 000 X 13,8068 ± 1,000 X 2,0096 --ff I—00 ~ 50 = 13 806,8 ± 10 372,4 . V50 V Ю00-1
3 434,40 < Полная разность < 24 179,20.
Следовательно, вероятность того, что полная разность генеральной совокупности не меньше 3 434,40 и не больше 24 179,20, равна 95% .
Односторонняя оценка доли нарушений установленных правил
Организации часто используют механизмы внутреннего контроля, чтобы убедиться в том, что сотрудники следуют правилам, принятым в компании. Например, администрация компании Saxon Home Improvement Company настаивает, чтобы товары не отгружались со склада без заверенной складской расписки. В ходе ежемесячной проверки ревизоры попытались определить долю продукции, отправленной со склада без соответствующих документов. Такое явление мы будем называть нарушением правил. Чтобы оценить их количество, ревизоры извлекают из генеральной совокупности накладных выборку и подсчитывают количество нарушений. Затем аудиторы сравнивают результаты с предельно допустимым уровнем нарушений, принятым в компании. Этот уровень представляет собой максимальную долю нарушений, которую компания считает приемлемой. При оценке количества нарушений обычно применяют односторонний доверительный интервал (one-sided confidence interval). Иначе говоря, ревизоры вычисляют только верхнюю границу доверительного интервала, содержащего долю нарушений.
ОДНОСТОРОННИЙ ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ, СОДЕРЖАЩИЙ ДОЛЮ ПРИЗНАКА В ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ
„ ^ п(1—и) N —п
Верхняя граница = д + Z. —-—J------, (7.11)
V п \ N -1
где Z— критическое значение стандартизованного нормального распределения, соответствующее интегральной вероятности, равной 1-а.
Если предельно допустимый уровень нарушений выше верхней границы этого интервала, ревизоры считают, что деятельность компании не выходит за пределы установленных норм. В противном случае аудиторы фиксируют систематическое нарушение установленных правил. Аудиторы могут потребовать увеличить объем выборок. Предположим, что ежемесячная проверка коснулась 400 накладных, извлеченных из генеральной совокупности, состоящей из 10 000 накладных. Среди проверенных накладных оказалось 20 неправильных. Предельно допустимый уровень нарушений, принятый в компании, равен 6%. Постройте односторонний 95% -ный доверительный интервал.
Итак,рк = 20/400 = 0,05, aZ = 1,645. Используя формулу (7.11), получаем:
п \р (\-р ) \N - п л |0,05(1-0,05) 110 000-400
' \ п NN-1 N 400 V Ю000-1
= 0,05 + 1,645x0,0109x0,98 = 0,05 + 0,0175 = 0,0675.
Итак, верхняя граница доверительного интервала равна 6,76%. Поскольку предельно допустимый уровень нарушений равен 6%, следует зафиксировать существенное нарушение правил компании и потребовать для проверки более крупную выборку.
ПРИМЕР 7.9. ОЦЕНКА УРОВНЯ НАРУШЕНИЙ
Работники крупной фирмы, производящей электронную бытовую аппаратуру, подписывают около одного миллиона чеков в год. В соответствии с правилами, принятыми в компании, любой чек становится действительным только после того, как будет подписан бухгалтером. Компания считает приемлемыми не более 4% нарушений. Предположим, что в ходе проверки выяснилось, что в выборке, состоящей из 400 чеков, восемь оказались недействительными. Какой вывод должен сделать аудитор?
РЕШЕНИЕ. Следует построить 95%-ный доверительный интервал, содержащий долю нарушений, и сравнить его верхнюю границу с предельно допустимым уровнем ошибок.
В данном случаеps = 8/400 = 0,02, a Z = 1,645. Используя формулу (7.11), получаем:
D 7 IpM-pJ п /0,02(1-0,02) /1000000-400
Верхняя граница = р+ Z. —----.-----= 0,02 +1,645./---------- /-----------=
V п \ NN 400 У 1000000-1
= 0,02 + 1,645x0,007x0,9998 = 0,02 + 0,0115 = 0,0315.
Итак, верхняя граница доверительного интервала равна 3,15% . Поскольку предельно допустимый уровень нарушений равен 4%, следует признать, что правила компании не нарушены. Иначе говоря, аудитор на 95% уверен, что количество нарушений не превышает 4% .
УПРАЖНЕНИЯ К РАЗДЕЛУ Z5
Изучение основ
7.50. Из генеральной совокупности, состоящей из 500 элементов, извлекается выборка, объем которой равен 25. Выборочное среднее равно 25,7, а выборочное стандартное распределение — 7,8. Постройте 99%-ный доверительный интервал, содержащий общую сумму элементов генеральной совокупности.
7.51. Из генеральной совокупности, состоящей из 10 000 элементов, извлечена выборка, объем которой равен 200. Среди них 10 элементов оказались ошибочными. fthTEMERR.XLS.
13,76 42,87 34,65 11,09 14,54
22,87 25,52 9,81 10,03 15,49
Постройте 99% -ный доверительный интервал, содержащий полную разность генеральной совокупности.
7.52. Предположим, что ря = 0,04, п = 300, а А = 5000. Вычислите верхнюю границу одностороннего доверительного интервала, содержащего долю признака р с заданной вероятностью.
1. 90%.
2. 95%.
Применение понятий
7.53. Магазин канцелярских принадлежностей желает оценить общую стоимость 300 поздравительных открыток, хранящихся на складе. Выборочное среднее, вычисленное по случайной выборке, состоящей из 20 поздравительных открыток, равно 1,67 долл., а выборочное стандартное отклонение— 0,32 долл. Постройте интервал, содержащий общую стоимость поздравительных открыток, доверительный уровень которого равен 95% .
7.54. В крупной компании работают 3 000 сотрудников. Администрация этой компании решила провести опрос и выяснить среднегодовую величину расходов на медицинские услуги. Для этого из генеральной совокупности сотрудников извлечена выборка, объем которой равен 10.
ftDENTAL.XLS
110 362 246 85 510 208 173 425 316 179
Постройте 90%-ный доверительный интервал, содержащий общую сумму, затраченную сотрудниками компании на медицинские услуги.
7.55. Подразделение крупной складской сети проводит ежемесячную инвентаризацию товаров. Выяснилось, что на момент проверки на складе хранилось 1 546 предметов. Для проверки из них были случайным образом выбраны 50 предметов и вычислены средняя стоимость X =252,28 и стандартное отклонение S — 93,67. Постройте 95%-ный доверительный интервал, содержащий общую сумму товаров, хранящихся на складе.
7.56. Клиенты оптовых магазинов одежды часто получают скидки на приобретаемые ими товары. Из генеральной совокупности, состоящей из 4 000 накладных, извлечена случайная выборка, содержащая 150 элементов. Оказалось, что в 13 случаях клиенты не получили скидок, которые им полагались. Объемы скидок, не полученных покупателями, перечислены в таблице. ^DISCOUNT. XLS.
6,45 15,32 97,36 230,63 104,18 84,92 132,76
66,12 26,55 129,43 88,32 47,81 89,01
Постройте 99%-ный доверительный интервал, содержащий общую сумму скидок, не полученных клиентами.
7.57. Econe Dresses — небольшая компания, производящая женскую одежду для продажи через сеть специальных магазинов. В инвентарной ведомости этой компании хранятся 1 200 записей, внесенных по принципу FIFO — “первой внесена, первой удалена”. Известно, что около 15% записей являются неверными. В ходе проверки из генеральной совокупности инвентарных записей извлечена выборка, содержащая 120 элементов. Разница между реальной и фиктивной ценой каждого товара приведена в таблице. ^FIFO. XLS.
Номер образца Фактическая стоимость Фиктивная стоимость
5 261 240
9 87 105
17 201 276
18 121 110
28 315 298
Номер образца Фактическая стоимость Фиктивная стоимость
35 411 356
43 249 211
51 216 305
60 21 210
73 140 152
86 129 112
95 340 216
96 341 402
107 135 97
119 228 220
Постройте 95%-ный доверительный интервал, содержащий полную разность между фактической и фиктивной ценами.
7.58. Компания Tom and Brent's Alpline Outfitters проводит ежегодный аудит своей финансовой отчетности. В соответствии с правилами, принятыми в компании, любой чек становится действительным только после того, как будет подписан бухгалтером. Компания считает приемлемыми не более 4% нарушений. В ходе проверки из генеральной совокупности, состоящей из 10 000 записей, были извлечены 300 чеков, среди которых 11 оказались недействительными.
1. Постройте 95%-ный односторонний доверительный интервал, содержащий долю нарушений в финансовой отчетности.
2. Какой вывод должен сделать аудитор?
7.59. Компания Rhonda’s Online Fashion Accessories требует, чтобы на каждую партию товара заполнялся гарантийный талон. Фирма допускает не более 5% нарушений. В ходе проверки из генеральной совокупности, состоящей из 5 000 талонов, были извлечены 500 талонов, среди которых 12 оказались недействительными .
1. Постройте 95%-ный односторонний доверительный интервал, содержащий долю нарушений.
2. Какой вывод должен сделать аудитор?
7.6. ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ И ЭТИЧЕСКИЕ ПРОБЛЕМЫ
При выборочном исследовании генеральной совокупности и формулировании ста-| тистических выводов часто возникают этические проблемы. Основная из них — как согласуются доверительные интервалы и точечные оценки выборочных статистик. Публикация точечных оценок без указания соответствующих доверительных интервалов (как правило, имеющих 95%-ный доверительный уровень) и объема выборки, на основе которых они получены, может породить недоразумения. Это может создать у пользователя впечатление, что точечная оценка — именно то, что ему необходимо, чтобы предсказать свойства всей генеральной совокупности. Таким образом, необходимо понимать, что в любых исследованиях во главу угла должны быть поставлены не точечные, а интервальные оценки. Кроме того, особое внимание следует уделять правильному выбору объемов выборки.
Чаще всего объектами статистических манипуляций становятся результаты социологических опросов населения по тем или иным политическим проблемам. При этом результаты опроса выносят на первые страницы газет, а ошибку выборочного исследования и методологию статистического анализа печатают где-нибудь в середине. Чтобы доказать обоснованность полученных точечных оценок, необходимо указывать объем выборки, на основе которой они получены, границы доверительного интервала и его уровень значимости.
7.7. ВЫЧИСЛЕНИЕ ОЦЕНОК И ОБЪЕМА ВЫБОРОК, ИЗВЛЕЧЕННЫХ ИЗ КОНЕЧНОЙ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ
Оценка математического ожидания
В разделе 6.9 поправочный коэффициент для конечной генеральной совокупности (fpc) использовался для уменьшения стандартной ошибки в - n)/(N . При вычислении доверительных интервалов для оценок параметров генеральной совокупности поправочный коэффициент применяется в ситуациях, когда выборки извлекаются без возвращения. Таким образом, доверительный интервал для математического ожидания, имеющий доверительный уровень, равный (1-а)х100%, вычисляется по формуле (7.12).
ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ ДЛЯ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ КОНЕЧНОЙ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ (ст НЕИЗВЕСТНА)
Чтобы проиллюстрировать применение поправочного коэффициента для конечной генеральной совокупности, вернемся к задаче о вычислении доверительного интервала для средней суммы накладных в компании Saxon Home Impovement Company, рассмотренной в разделе 7.2. Предположим, что за месяц в компании выписываются 5 000 накладных, причем X =110,27долл., S = 28,95 долл., N = 5 000, и = 100, а = 0.05, £ад= 1,9842. По формуле (7.12) получаем следующие результаты.
110,27 ± 1,9842-^2 = 100,27 ± 5,744 х 0,99 = 110,27 ± 5,69 .
Лооу 5 000-1
104,58 < ц < 115,96.
Результаты решения этой задачи с помощью программы PHStat представлены на рис. 7.15.
Поскольку в данной задаче выборка представляет собой очень маленькую часть генеральной совокупности, поправочный коэффициент почти не влияет на ширину доверительного интервала. Для того чтобы проверить влияние поправочного коэффициента на ширину доверительного интервала, когда объем выборки превышает 5% генеральной совокупности, рассмотрим следующий пример.
А . В 1 Средняя cyuua накладных | 2; i
3 Data
4 Sample Standard Deviation 28.95
5 .Sample Mean 110.27
6 Sample Size 100
7 Confidence Level 95%
. 6
9 Intermediate Calculations
10 Standard Error of the Mean 2 895
11 Degrees of Freedom 99
12 f Value 1.984217306
13 Interval Half Width 5 744309101
14
15 Confidence Interval
16 Interval Lower Limit 104.53
17 Interval Upper Limit 116.01
18 19 ‘(
20 Finite Populations
21 .Population Size 5000
22 ,FPC Factor 0 990048503
23 interval Half Width 5 687144629
24 jinterval Lower Limit 104.58
25 [Interval Upper Limit 115.961
Рис. 7.15. Оценка доверительного интервала для средней суммы накладных компании Saxon Home Impovement Company с учетом поправочного коэффициента для конечной генеральной совокупности
ПРИМЕР 7.10. ОЦЕНКА СРЕДНЕГОДОВОГО ПОТРЕБЛЕНИЯ ТОПЛИВА
В примере 7.3 из генеральной совокупности была извлечена выборка, состоящая из 30 изоляторов. Допустим, что вся генеральная совокупность состоит из 300 изоляторов. Постройте 95%-ный доверительный интервал для математического ожидания генеральной совокупности.
РЕШЕНИЕ. Поскольку X =1 723,4 галлонов, S = 89,55, п = 30, N = 300 и t29 = 2,0452 (для доверительного уровня, равного 95%), с учетом поправочного коэффициента для конечной генеральной совокупности получаем следующие результаты.
X ± t . = 1723,4 ± 2,0452^^- Ц2°~30 = 1 723,4 ± 33,44 х 0,9503 = 1 723 ± 31,776 .
ТЗО V 300-1
1 691,62 < ц < 1 755,18.
Объем выборки в этой задаче равен 10% объема генеральной совокупности, поэтому поправочный коэффициент оказывает небольшое влияние на ширину доверительного интервала.
Оценка доли признака
При выборе без возвращения доверительный интервал для доли признака, имеющий доверительный уровень, равный (1-а)х100% , вычисляется по формуле (7.13).
ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ ДЛЯ ДОЛИ ПРИЗНАКА В КОНЕЧНОЙ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ
+ Z \N~n
N п NN-1 '
Чтобы проиллюстрировать применение поправочного коэффициента при вычислении доверительного интервала для доли признака в конечной генеральной совокупности, вновь вернемся к задаче о накладных в компании Saxon Home Impovement Company, рассмотренной в разделе 7.3. Исходные данные таковы: N = 5 000, п = 100, ps = 10/100 = 0,10, а = 0,05, Z = 1,96. По формуле (7.13) получаем следующие результаты.
±z |р.(1-а) о 10±1 96 /0,10*0,90 /5 000-100.
V п NN-1 ’ ’ N 100 V 5 000-1
= 0,10 ± 1,96 х 0.03 х 0,99 = 0,10 ± 0,0582
0,0418 <р < 0,1582.
В рассмотренной задаче выборка представляет собой очень маленькую часть генеральной совокупности, поэтому поправочный коэффициент почти не влияет на ширину доверительного интервала.
Определение объема выборки
Поправочный коэффициент можно также применять для определения объема выборки, извлеченной из конечной генеральной совокупности без возвращения. Например, при оценке математического ожидания выборочная ошибка вычисляется по следующей формуле.
При оценке доли признака ошибка выборочного исследования равна
Ip(l-p) iN-n
е = ZA— --J-----.
N п U-1
Чтобы вычислить объем выборки для оценки математического ожидания или доли признака, применяются формулы (7.4) и (7.5):
Z2o2 Z2/?(l-/>)
«о =—— И ио =--------- ,
е~ е~
где п0 — объем выборки без учета поправочного коэффициента для конечной генеральной совокупности. Применение поправочного коэффициента приводит к следующей формуле.
ОПРЕДЕЛЕНИЕ ОБЪЕМА ВЫБОРКИ С УЧЕТОМ ПОПРАВОЧНОГО КОЭФФИЦИЕНТА ДЛЯ КОНЕЧНОЙ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ
п =--------
по + (tf-l)
(7.14)
При решении задачи о компании Saxon Home Impovement Company оказалось, что для оценки средней суммы накладных необходима выборка, состоящая из 97 накладных, а для оценки доли ошибочных накладных необходима выборка, состоящая из 100 записей. Используя формулу (7.14) для оценки математического ожидания при N = 5 000, е = 5 долл., S = 25 долл, и Z = 1,96 (для доверительного уровня, равного 95%), получаем следующие результаты.
96,04x5 000 п. _ п =----------------- 94,25.
96,04 +(5 000-1)
Таким образом, п = 95.
Применение формулы (7.14) для оценки доли признака при N = 5 000, е = 0,07, р = 0,15 и Z = 1,96 (для доверительного уровня, равного 95%), получаем следующие результаты.
„ = ^96х5М0 =
99,96 +(5 000-1)
Таким образом, п = 99.
Итак, для того чтобы правильно вычислить обе оценки необходимо выбрать наибольший из двух объемов, т.е. 99. Результаты вычислений, полученных с помощью программы PHStat, представлены на рис. 7.16.
[ А В ' 1 Объем выборки для оценки среднего X
3 Data
4 Population Standard Deviation 25
r 5 .Sampling Error 5
6 Confidence Level 95%
X
; 8 I Intermediate Calculations
»Z Value -1.95996279
10 i Calculated Sample Size 96.0363532
.!!!
12! Result
13-Sample Size Needed ?7
. it :
16 । Finite Populations
17 ; Population Size 5000
18 Sample Size with FPC 94 24501274
19 Sample Size Needed 951
Рис. 7.16. Оценка доверительного интервала для средней суммы накладных компании Saxon Home Impovement Company с учетом поправочного коэффициента для конечной генеральной совокупности
Процедуры Excel: вычисление поправочного коэффициента для конечной генеральной совокупности
Чтобы вычислить поправочный коэффициент для конечной генеральной совокупности и требуемый объем выборки, необходимо добавить новые формулы в рабочие листы, описанные в главе. Надстройка PHStat2 позволяет учесть поправку автоматически.
Применение Excel в сочетании с PHStatZ
Установите флажок Finite Population Correction (Поправочный коэффициент для конечной генеральной совокупности) и введите объем генеральной совокупности в окне редактирования Population Size (Объем генеральной совокупности). Эти действия следует выполнить, находясь в диалоговых окна процедур PHStat, предназначенных для вычислоения доверительных интервалов и определения объема выборки.
Применение Excel
Чтобы вычислить поправочный коэффициент для конечных генеральных совокупностей при оценке доверительных интервалов и определении объема выборок, введите дополнительные формулы в рабочие листы, описанные в табл.ЕН.7.1-ЕН.7.4. Изменения, которые необходимо внести в рабочие листы, предназначенные для вычисления доверительных интервалов для математического ожидания при известном стандартном отклонении, математического ожидания при неизвестном стандартном отклонении и доли признака, а также для определения объема выборки при оценке математического ожидания и доли признака соответственно, представлены в табл. 7.3-7.6.
Таблица 7.3. Дополнения к табл. ЕН.7.1 при вычислении доверительного интервала
для математического ожидания (о известна)
А ,i ’" ' В , -
иИ Конечные генеральные совокупности
IIIII Объем генеральной совокупности 5000
21 Поправочный коэффициент = КОРЕНЬ((В20-В6)/(В20-1))
1111 Половина ширины интервала =В12*В21
111 Нижняя доверительная граница =В5-В22
24 Верхняя доверительная граница =В5+В22
Таблица 7.4. Дополнения к табл. ЕН.7.2 при вычислении доверительного интервала для математического ожидания (о неизвестна)
20 Конечные генеральные совокупности
21 Объем генеральной совокупности 5000
22 Поправочный коэффициент = КОРЕНЬ((В21-Вб)/(В21-1))
23 Половина ширины интервала = В13*В22
24 Нижняя доверительная граница = В5-В23
25 Верхняя доверительная граница =В5+В23
Таблица 7.5. Дополнения к табл. ЕН.7.3 при вычислении доверительного интервала для доли признака
А . / - , В
20 Конечные генеральные совокупности
21 Объем генеральной совокупности 5000
22 Поправочный коэффициент =КОРЕНЬ((В20-В4)/(В20-1))
23 Половина ширина интервала =В12*В21
24 Нижняя доверительная граница =В9-В22
25 Верхняя доверительная граница = В9+В22
Таблица 7.6. Дополнения к табл. ЕН.7.4 и ЕН.7.5 при вычислении объема выборки для оценки математического ожидания и доли признака
А В
16 Конечные генеральные совокупности
17 Объем генеральной совокупности 5000
18 Объем выборки с учетом поправочного коэффициента =(В10-В17)/(В10+В17-1)
Ц||| Необходимый объем выборки =ОКРУГЛВВЕРХ(В18;0)
УУЙРАЙНВДИЯ1СРАЗДЕЛУ?^ %
Изучение основ
7.60. Предположим, что X =75, 8 = 24, п = 36 и А = 200, причем выборка получена путем извлечения без возвращения. Постройте 95%-ный доверительный интервал для математического ожидания ц конечной генеральной совокупности.
7.61. Допустим, что объем генеральной совокупности равен 1 000, а стандартное отклонение равно 20. Какой объем выборки необходим, если выбор осуществляется без возвращения, доверительный уровень равен 95%, а выборочная ошибка равна ±5.
Применение понятий
7.62. Инспектор отдела технического контроля на фабрике, производящей электрические лампочки, желает оценить среднюю продолжительность работы лампочек из крупной партии. Стандартное отклонение этой величины известно и равно 100 часов. Предположим, что партия состоит из 2 000 электрических лампочек, а выбор выполняется без возвращения.
1. Постройте 95%-ный доверительный интервал для средней продолжительности работы лампочек из указанной партии, если средняя продолжительность работы 50 лампочек, принадлежащих выборке, извлеченной из партии, равно 350 часов.
2. Определите объем выборки, необходимый для оценки средней продолжительности работы лампочек, если стандартное отклонение равно ±20 часов, а доверительный уровень равен 95%.
3. Как изменятся ответы к задачам 1 и 2, если партия состоит из 1 000 лампочек?
7.63. Крупная компания планирует провести статистическое исследование, чтобы определить средний годовой объем средств, затрачиваемых семьями сотрудников на медицинское обслуживание. Администрация желает гарантировать 95% -ный доверительный уровень оценки, допуская выборочную ошибку, равную ±50 долл. Предварительный опрос показал, что стандартное отклонение равно 400 долл. Какой объем выборки следует установить, если в компании работают 3 000 сотрудников, а извлечение выборки производится без возвращения?
7.64. Управляющий банка, обслуживающего 1 000 жителей маленького городка, желает оценить долю клиентов, имеющих несколько счетов.
1. Постройте 90%-ный доверительный интервал для доли вкладчиков, имеющих несколько счетов, если банк сформировал выборку из 100 клиентов, используя выбор без возвращения и оказалось, что 30 из них имеют несколько счетов.
2. Управляющий банка желает построить 90%-ный доверительный интервал, содержащий долю вкладчиков, имеющих несколько счетов, установив выборочную ошибку равной ±0,05. Какой объем выборки следуют установить, если извлечение выборки производится без возвращения?
3. Как изменятся ответы к задачам 1 и 2, если банк обслуживает 2 000 вкладчиков?
7.65. Дилер автомобильной компании желает оценить долю клиентов, продолжающих ездить на автомобилях, приобретенных пять лет назад. Записи о продажах указывают, что генеральная совокупность состоит из 4 000 клиентов.
1. Постройте 95%-ный доверительный интервал для доли клиентов, продолжающих ездить на автомобилях, приобретенных пять лет назад, если дилер сформировал выборку из 200 клиентов, используя выбор без возвращения и оказалось, что 82 из них продолжают ездить на старых автомобилях.
2. Какой объем выборки необходим для оценки истинной доли клиентов, клиентов, продолжающих ездить на автомобилях, приобретенных пять лет назад, если доверительный уровень равен 95%, а выборочная ошибка равна ±0,025?
3. Как изменятся ответы к задачам 1 и 2, если количество клиентов равно 6 000?
7.66. Отдел технического контроля крупной компании решил оценить реальный объем безалкогольных напитков, разлитых в двухлитровые бутылки на местом заводе. Генеральная совокупность состоит из 2 000 бутылок. Завод проинформировал компанию, что стандартное отклонение объема жидкости, разлитой в двухлитровые бутылки, равно 0,05 л.
1. Постройте 95% -ный доверительный интервал для среднего объема напитка в каждой бутылке, если в выборке, состоящей из 100 двухлитровых бутылок, извлеченной без возвращения, средний объем напитка в бутылке оказался равным 1,99.
2. Определите объем выборки, необходимый для оценки математического ожидания генеральной совокупности, если доверительный уровень равен 95%, а выборочная ошибка равна ±0,01 л.
3. Как изменятся ответы к задачам 1 и 2, если генеральная совокупность состоит из 1 000 бутылок?
7.67. Магазин канцелярских принадлежностей желает оценить среднюю розничную цену поздравительных открыток. Генеральная совокупность состоит из 300 открыток.
1. Постройте 95%-ный доверительный интервал для средней розничной цены поздравительных открыток, если в выборке, состоящей из 20 открыток, извлеченной без возвращения, средняя цена оказалась равной 1,67 долл., а стандартное отклонение равно 0,32 долл.
2. Как изменится ответ к задаче 1, если генеральная совокупность состоит из 500 открыток?
Оценка
Этические Точечная
{проблемы I оценка
Интервальная оценка
Г- .. ,
Определение ; объема выборки
Математическое ожидание
шиш
Доля признака
Доверительный } интервал ?
Доля признака
Применение в аудиторском
Математическое ожидание
да Стандартное “8ей*явв отклонение -известна?
Нет
...
Полная сумма ; Оценка разности . Односторонний
Применяется । Z-статистика WMW М «ам
Применяется f-статистика
Структурная схема главы 7
РЕЗЮМЕ
Как показано на структурной схеме главы, мы рассмотрели методы построения доверительных интервалов, содержащих параметры генеральной совокупности, а также способ определения объема выборки, необходимого для достижения заданного доверительного уровня. Мы поняли, как на основе небольшой выборки накладных оценить общую стоимость товаров, отгруженных компанией Saxon Home Improvement Company, и долю неверно заполненных накладных. В следующих четырех главах мы рассмотрим методы проверки гипотез о параметрах генеральной совокупности.
ОСНОВНЫЕ ПОНЯТИЯ
Аудит, 480
Доверительный интервал для доли признака, 466 односторонний, 487 для математического ожидания при известном стандартном отклонении, 451
при неизвестном стандартном отклонении, 458
для общей суммы, 481
для полной разности, 484
односторонний, 487
Доверительный уровень, 451
Критическое значение, 452
Объем выборки
для оценки доли признака, 474
для оценки среднего, 471
Оценка
интервальная,449
точечная, 448
общей суммы, 481
Ошибка выборочного обследования, 471
Распределение
стандартизованное нормальное, 456
Стьюдента, 456
Средняя разность, 484
Стандартное отклонение разностей, 484
'^'З^З-ЗЗ^
Проверка знаний
7.68. Почему невозможно построить 100%-ный доверительный интервал, позволяющий оценить параметры генеральной совокупности?
7.69. Когда для построения доверительного интервала можно применять ^распределение?
7.70. Почему при фиксированном объеме выборки п повышение доверительного уровня приводит к расширению доверительного интервала, что в свою очередь снижает точность оценки?
7.71. При каких условиях можно использовать односторонний, а не двусторонний интервал?
7.72. Когда следует оценивать общую сумму элементов генеральной совокупности, а не ее математическое ожидание?
7.73. Чем оценка разностей отличается от оценки математического ожидания?
Задачи к резюме
Задачи 7.74—7.88 можно решать без применения программы Microsoft Excel. Задачи 7.89—7.94 рекомендуется решать с помощью программы Microsoft Excel.
7.74. Журнал Redbook регулярно проводит социологические опросы с помощью своего Web-сайта (Kravetz, S., “Work Week”, Wall Street Journal, April 13, 1999, Al). Посетителям сайта предлагается заполнить электронную анкету. В ходе одного из опросов 665 женщин спросили, что бы они предпочли: четырехдневные выходные или увеличение заработной платы на 20%. Первый вариант выбрали 412 женщин.
1. Назовите генеральную совокупность, из которой извлечена данная выборка респондентов.
2. Можно ли данную выборку считать случайной?
3. Можно ли считать корректными статистические выводы, полученные в результате этого опроса?
4. Как организовать статистически корректный опрос читателей журнала Redbookl Какой объем выборки необходим, чтобы оценить долю женщин, предпочитающих четырехдневные выходные, в генеральной совокупности читателей журнала Redbook с точностью ±0,02 и доверительным уровнем 95% ?
7.75. В настоящее время компании стали затрачивать гораздо больше времени на исследование кандидатур, претендующих за вакантные должности. В результате выяснилось, что многие кандидаты искажают сведения о себе. Исследование, проведенное компанией Automatic Data Processing, выявило неточности в 44% проверенных резюме. К сожалению, в статье не указан объем выборки, на основе которой сделаны эти выводы (Stephanie Armour, “Security Checks Worry Workers”, USA Today, June 19, 2002, Bl).
1. Допустим, что выборка состояла из 500 резюме. Постройте 95%-ный доверительный интервал для доли резюме, содержащих неточности.
2. Можно ли на основании решения задачи 1 утверждать, что половина всех кандидатов допускают неточности, излагая сведения о себе?
3. Допустим, что выборка состояла из 200 резюме. Постройте 95% -ный доверительный интервал для доли резюме, содержащих неточности.
4. Можно ли на основании решения задачи 2 утверждать, что половина всех кандидатов допускают неточности, излагая сведения о себе?
5. Опишите влияние, которое оказывает объем выборки на решения задач 1-3.
6. Изложите возникающие этические проблемы, если объем выборки не указан.
7.76. Журнал, посвященный маркетингу, провел опрос продавцов, допустивших искажения отчетности и совершивших другие неэтичные поступки (D. Haralson and Q. Tian, “Cheating Hearts”, USA Today, February 15, 2001, 1A). Выяснилось, что в 58% случаев продавцы искажали отчетность, в 50% случаев — подрабатывали на стороне в рабочее время, в 22% случаев — оформляли посещение стрип-тиз-баров как посещение ресторанов и в 19% случаев давали клиентам “откат”. Предположим, что в опросе приняло участие 200 менеджеров.
1. Постройте 95%-ный доверительный интервал, содержащий долю менеджеров, допустивших искажение отчетности.
2. Постройте 95%-ный доверительный интервал, содержащий долю менеджеров, подрабатывавших на стороне в рабочее время.
3. Постройте 95%-ный доверительный интервал, содержащий долю менеджеров, оформлявших посещение стриптиз-баров как посещение ресторанов.
4. Постройте 95%-ный доверительный интервал, содержащий долю менеджеров, дававших клиентам “откат”.
5. Определите объем выборки, необходимый для оценки доли менеджеров, подрабатывавших на стороне в рабочее время, если точность выборочного исследования равна ±0,02, а доверительный уровень равен 95% .
6. Можно ли утверждать, что 58% всех менеджеров, искажают отчетность? Аргументируйте свой ответ.
7.77. Компания Starwood Hotels провела опрос 401 руководителей верхнего звена, играющих в гольф (Del Jones, “Many CEOs Bend the Rules (of Golf)”, USA Today, June 26, 2002). Результаты опроса приведены ниже.
• 329 менеджеров жульничают, играя в гольф.
• 329 менеджеров ненавидят тех, кто жульничает, играя в гольф.
• 289 менеджеров считают, что поведение игроков на поле и в бизнесе одинаково.
• 80 игроков в гольф готовы поддаться клиенту ради выгодной сделки.
• 40 прикидываются больными, чтобы сыграть в гольф.
Постройте 95%-ный доверительный интервал, содержащий долю менеджеров для каждого пункта анкеты. Какие выводы можно сделать на основе этой информации?
7.78. Специалисты по маркетингу, работающие в компании, производящей электронные бытовые приборы, желают изучить привычки телезрителей в небольшом городке. Для этого они создали случайную выборку, состоящую из 40 человек. Каждого респондента попросили сделать подробные записи о телепередачах, которые он просмотрел в течение недели. Среднее время просмотра телепередач оказалось равным X =15,3 ч, а стандартное отклонение — S = 3,8 ч. Кроме того, 27 телезрителей смотрели вечерние новости хотя бы по выходным.
1. Постройте 95%-ный доверительный интервал, содержащий среднюю продолжительность просмотра телепередач за неделю.
2. Постройте 95%-ный доверительный интервал, содержащий долю телезрителей, смотрящих вечерние новости хотя бы по выходным.
3. Предположим, что данный опрос проводится в другом городе. Какую выборку следует создать, чтобы построить 95%-ный доверительный интервал, содержащий среднюю продолжительность просмотра телепередач с точностью ±2 ч, если стандартное отклонение равно 5 ч?
4. Предположим, что данный опрос проводится в другом городе. Какую выборку следует создать, чтобы построить 95%-ный доверительный интервал, содержащий долю телезрителей, смотрящих вечерние новости по крайней мере по выходным, с точностью ±0,035 ч, если стандартное отклонение неизвестно?
5. Какой объем должна иметь выборка в задачах 3 и 4, если опросы проводятся одновременно?
7.79. Советник по торговле недвижимостью, работающий в органах местного самоуправления, изучает характеристики одноквартирных домов. Для этого он создал случайную выборку, состоящую из 70 домов и вычислил следующие параметры.
• Отапливаемая площадь дома (кв. фут.): X = 1 759, S = 380.
• 42 дома подключены к центральной системе отопления.
1. Постройте 95%-ный доверительный интервал, содержащий среднюю отапливаемую площадь.
2. Постройте 95%-ный доверительный интервал, содержащий долю домов, подключенных к центральной системе отопления.
7.80. Начальник отдела кадров крупной корпорации желает оценить количество рабочих дней, пропущенных за год религиозными сотрудниками. Для этого он создал случайную выборку, состоящую из 25 религиозных сотрудников, и вычислил следующие параметры.
• Отсутствие на рабочем месте: X = 9,7 дня, 8 = 4,0 дня.
• 12 религиозных сотрудников отсутствовали на работе более 10 дней.
1. Постройте 95%-ный доверительный интервал, содержащий среднее время отсутствия на рабочем месте религиозных сотрудников.
2. Постройте 95%-ный доверительный интервал, содержащий долю религиозных сотрудников, отсутствовавших на работе более 10 дней.
Предположим, что начальник отдела кадров пожелал провести опрос в другом подразделении.
3. Какой объем выборки он должен установить, чтобы оценить среднее время отсутствия на рабочем месте религиозных сотрудников с 95%-ным доверительным уровнем и точностью ±1,5 дней, если стандартное отклонение равно 4,5 дня?
4. Какой объем выборки он должен установить, чтобы оценить долю религиозных сотрудников, отсутствовавших на работе более 10дней с 90%-ным доверительным уровнем и точностью ±0,075 дня, если стандартное отклонение неизвестно?
5. Какой объем должна иметь выборка в задачах 3 и 4, если опросы проводятся одновременно?
7.81. Начальник отдела маркетинга универмага Dotty's желает оценить количество денег, потраченных женщинами на приобретение косметики в течение года. Для этого он создал выборку владельцев кредитных карточек и разослал им анкеты. В результате анкетирования должны быть вычислены следующие показатели.
• Количество денег, потраченных женщинами на приобретение косметики в течение года.
• Доля женщин, приобретающих косметику в универмаге Dotty's.
1. Какой объем выборки следует зафиксировать, чтобы оценить среднее количество денег, потраченных женщинами на приобретение косметики в течение года с 99%-ным доверительным уровнем и точностью ±5 долл., если стандартное отклонение равно 18 долл, (по данным предыдущих опросов)?
2. Какой объем выборки следует зафиксировать, чтобы оценить долю женщин, приобретающих косметику в универмаге Dotty’s с 90%-ным доверительным уровнем и точностью ±0,045?
3. Какой объем должна иметь выборка в задачах 2 и 3, если опросы проводятся одновременно?
7.82. Менеджер книжного магазина, расположенного в районе студенческого городка, желает оценить предпочтения своих клиентов. Его интересуют два показателя: объем денег, потраченных отдельным клиентом на покупки, и популярность видеокассет с учебными материалами. В частности, менеджера интересуют, покупают ли студенты видеокассеты с лекциями по конкретным предметам, например по статистике, бухучету и т.п., а также с материалами, предназначенными для подготовки к выпускным экзаменам, например, GMAT, GRE или LSAT. Для этого он создал случайную выборку, состоящую из 70 человек, и получил следующую информацию.
• Объем потраченных денег: X = 28,52 долл., S = 11,39 долл.
• Среди опрошенных клиентов оказалось 28 покупателей, предпочитающих кассеты с учебными материалами.
1. Постройте 95%-ный доверительный интервал, содержащий среднее количество денег, потраченных клиентами.
2. Постройте 90%-ный доверительный интервал, содержащий долю клиентов, предпочитающих видеокассеты с учебными материалами.
Предположим, что менеджер решил провести опрос в магазине, расположенном в другом студенческом городке.
3. Какой объем выборки он должен установить, чтобы оценить среднее количество потраченных клиентами денег с 95%-ным доверительным уровнем и точностью ±2 долл., если стандартное отклонение равно 10 долл.?
4. Какой объем выборки он должен установить, чтобы оценить среднее количество потраченных клиентами денег с 90% -ным доверительным уровнем и точностью ±0,04 долл., если стандартное отклонение равно 10 долл.?
5. Какой объем должна иметь выборка в задачах 3 и 4, если опросы проводятся одновременно?
7.83. Менеджер зоомагазина желает оценить предпочтения своих клиентов. Его интересуют два показателя: объем денег, потраченных отдельным клиентом на покупки, и количество животных, принадлежащих ему: одна собака, один кот или несколько собак и/или кошек. Для этого он создал случайную выборку, состоящую из 70 человек, и получил следующую информацию.
• Объем потраченных денег: X = 21,34 долл., 8 = 9,22 долл.
• 37 клиентов имеют только собаку.
• 26 клиентов имеют только кошку.
• 7 клиентов имеют несколько собак и/или кошек.
1. Постройте 95%-ный доверительный интервал, содержащий среднее количество денег, потраченных клиентами.
2. Постройте 90%-ный доверительный интервал, содержащий долю клиентов, имеющих только одного кота.
Предположим, что менеджер решил провести опрос в другом зоомагазине.
3. Какой объем выборки он должен установить, чтобы оценить среднее количество потраченных клиентами денег с 95%-ным доверительным уровнем и точностью ±1,5 долл., если стандартное отклонение равно 10 долл.?
4. Какой объем выборки он должен установить, чтобы оценить долю клиентов, имеющих только одного кота, с 90%-ным доверительным уровнем и точностью ±0,045 долл.?
5. Какой объем должна иметь выборка в задачах 3 и 4, если опросы проводятся одновременно?
7.84. Владелец ресторана европейской кухни желает знать вкусы своих клиентов. В частности, его интересуют два показателя: объем денег, потраченных отдельным клиентом на покупки, и заказывают ли они десерт. Для этого он создал случайную выборку, состоящую из 60 человек, и получил следующую информацию.
• Объем потраченных денег: X = 38,54 долл., S = 7,26 долл.
• 18 клиентов заказали десерт.
1. Постройте 95%-ный доверительный интервал, содержащий среднее количество денег, затрачиваемых клиентами ресторана.
2. Постройте 90%-ный доверительный интервал, содержащий долю клиентов, заказывающих десерт.
Предположим, что конкурент решил провести опрос в своем ресторане (независимо от результатов первого опроса).
3. Какой объем выборки он должен установить, чтобы оценить среднее количество затрачиваемых клиентами денег с 95% -ным доверительным уровнем и точностью ±1,5 долл., если стандартное отклонение равно 8 долл.?
4. Какой объем выборки он должен установить, чтобы оценить долю клиентов, заказывающих десерт, с 90%-ным доверительным уровнем и точностью ±0,04 долл.?
5. Какой объем должна иметь выборка в задачах 3 и 4, если опросы проводятся одновременно?
7.85. Представителя крупной сети магазинов, торгующих промышленным оборудованием, заинтересовали характеристики новой продукции под названием Ice Melt. Производители утверждают, что их порошок позволяет растапливать лед даже при температуре ниже 0° по Фаренгейту (-17° по Цельсию. — Прим.ред.). Сеть магазинов приобрела большую партию 5-фунтовых упаковок с порошком. Менеджер желает построить 95%-ный доверительный интервал, содержащий долю продукции Ice Melt, соответствующей рекламным обещаниям, с точностью ±0,05.
1. Сколько упаковок порошка следует проверить?
Какие предположения о доле признака необходимо принять? (Такая проверка называется разрушающей, иначе говоря, после тестирования продукция выходит из строя и не пригодна к продаже.)
Предположим, что для тестирования отобраны 50 упаковок, причем 42 из них оказались пригодными к употреблению.
2. Постройте 95%-ный доверительный интервал, содержащий долю качественной продукции.
3. Стоит ли покупать новый порошок?
7.86. В компании проводится аудиторская проверка. Предположим, что для анализа из генеральной совокупности, состоящей из 1 000 документов, отобраны 50. Оказалось, что семь из них не соответствуют правилам, принятым в компании.
1. Постройте 90%-ный односторонний доверительный интервал, содержащий долю документов, не соответствующих правилам.
2. Допустим, что приемлемый уровень ошибок равен 0,15. Какой вывод должен сделать аудитор?
7.87. Аудитору правительственного агентства поручено оценить, правильно ли осуществляется компенсация оплаты визитов к врачу по программе Medicare. Аудиторской проверке подвергаются все компенсации, выплаченные в определенном районе в течение месяца. Генеральная совокупность состоит из 25 056 визитов к врачу. Аудитор желает оценить общий объем компенсаций, выплаченных в течение месяца. Кроме того, он хочет построить 95% -ный доверительный интервал, содержащий средний объем компенсации с точностью ±5 долл. Основываясь на прошлом опыте, аудитор считает, что стандартное отклонение равно 30 долл.
1. Какой объем должна иметь выборка?
Предположим, что аудит проводится на основе выборки, определенной в задаче!. Обнаружилось 12 случаев неправильно оплаченной компенсации, причем X = 93,70 долл., S = 34,55 долл. Разности между правильными и неправильными суммами компенсации приведены в таблице. ^MEDICARE . XLS.
17 25 14 -10 20 40 35 30 28 22 15 5
2. Постройте 90%-ный односторонний доверительный интервал, содержащий долю неправильных компенсаций.
3. Постройте 95%-ный доверительный интервал, содержащий среднюю сумму компенсации.
4. Постройте 95%-ный доверительный интервал, содержащий общую сумму компенсации.
5. Постройте 95%-ный доверительный интервал, содержащий полную разность между правильными и неправильными компенсациями.
7.88. Крупный склад компьютерной техники проводит ежемесячную инвентаризацию. Аудитор желает оценить среднюю стоимость компьютеров, хранящихся на складе. Для этого он хочет построить 99%-ный доверительный интервал, содержащий среднюю стоимость компьютеров с точностью ±200 долл. Основываясь на прошлом опыте, аудитор считает, что стандартное отклонение равно 400 долл.
1. Какой объем должна иметь выборка?
Предположим, что аудит проводится на основе выборки, определенной в задаче 1. Оказалось, что X = 3 054,13 долл., S = 384,62 долл.
2. Постройте 99%-ный доверительный интервал, содержащий общую стоимость 258 компьютеров, хранящихся на складе.
7.89. Одним из показателей качества процесса упаковки чая является вес отдельного пакетика. Если пакетик чая неполон, возникают две проблемы. Во-первых, потребитель чая может не получить требуемой крепости заварки. Во-вторых, компанию могут привлечь к ответственности за нарушение правил маркировки. В данном примере на упаковке указывается номинальный средний вес чая в пакетике: 5,5 г. Если реальный средний вес чая в пакетике превышает указанное значение, компания несет дополнительные убытки. Точно засыпать в пакетик
5,5 г невозможно, поскольку температура и влажность воздуха на чайной фабрике постоянно изменяются, а это влияет на плотность чая. Кроме того, скорость работы упаковочной машины чрезвычайно высока (170 пакетиков в минуту). В следующей таблице приведен вес в граммах 50 пакетиков чая, заполненных в течение часа конкретной упаковочной машиной. ©TEABAGS . XLS.
5,65 5,44 5,42 5,40 5,53 5,34 5,54 5,45 5,52 5,41
5,57 5,40 5,53 5,54 5,55 5,62 5,56 5,46 5,44 5,51
5,47 5,40 5,47 5,61 5,53 5,32 5,67 5,29 5,49 5,55
5,77 5,57 5,42 5,58 5,58 5,50 5,32 5,50 5,53 5,58
5,61 5,45 5,44 5,25 5,56 5,63 5,50 5,57 5,67 5,36
1. Постройте 99%-ный доверительный интервал, содержащий средний вес пакетиков с чаем.
2. Соответствует ли средний вес пакета требованиям стандарта?
7.90. Промышленная компания на Среднем Западе производит стальные корпуса для электротехнического оборудования. Основным компонентом корпуса является прямоугольный профиль, который создается из 14-дюймового рулона стальной полосы с помощью 250-тонного пресса. Основным параметром корпуса является расстояние между боковыми сторонами профиля, допускающее установку электротехнического оборудования. В таблице приведены данные о 49 профилях. ©TROUGH. XLS.
8,312 8,343 8,317 8,383 8,348 8,410 8,351 8,373 8,481 8,422
8,476 8,382 8,484 8,403 8,414 8,419 8,385 8,465 8,498 8,447
8,436 8,413 8,489 8,414 8,481 8,415 8,479 8,429 8,458 8,462
8,460 8,444 8,429 8,460 8,412 8,420 8,410 8,405 8,323 8,420
8,396 8,447 8,405 8,439 8,411 8,427 8,420 8,498 8,409
1. Постройте 95%-ный доверительный интервал, содержащий среднее расстояние между боковыми сторонами профиля.
2. Дайте интерпретацию этого интервала.
7.91. Исследования, проведенные компаниями, производящими рубероидную кровельную плитку в Бостоне и Вермонте, показали, что основным фактором, влияющим на оценку качества продукции, является ее вес. На последнем этапе плитка пакуется, а затем размещается на деревянных стеллажах (как правило, на поддоне помещается 16 плиток). После заполнения стеллажа регистрируется его вес. Файл ©PALLET.XLS содержит данные о весе (в фунтах) 368 стеллажей, заполненных плитками, произведенными в Бостоне, и 330 стеллажей, загруженных плитками, сделанными в Вермонте.
1. Постройте 95% -ный доверительный интервал, содержащий средний вес плиток, произведенных на заводе в Бостоне.
2. Постройте 95% -ный доверительный интервал, содержащий средний вес плиток, произведенных на заводе в Вермонте.
3. Выполняются ли предположения, необходимые для решения задач 1 и 2?
4. Какие выводы о среднем весе плиток, произведенных в Бостоне и Вермонте, можно сделать на основании решения задач 1-3?
7.92. Производитель рубероидной кровельной плитки на заводах в Бостоне и Вермонте предоставляет своим клиентам 20-летнюю гарантию. Для того чтобы убедиться в том, что плитки прослужат указанный срок, на заводах проводят ускоренное испытание на долговечность. В ходе этого эксперимента плитка на протяжении несколь-
ких минут подвергается интенсивному воздействию, эквивалентному воздействию, которому плитка подвергалась бы в обычных условиях в течение 20 лет. В частности, плитку несколько минут очень энергично скребут щетками, а затем взвешивают гранулы, которые отскакивают от плиток (в граммах). Чем меньше гранул образуется в ходе эксперимента, тем долговечнее плитка. Для того чтобы прослужить весь гарантийный срок, плитка не должна потерять больше 0,8 г. В файле ftGRANULE. XLS содержатся данные о выборке, состоящей из 170 измерений, проведенных на заводе в Бостоне, и 140 измерениях, осуществленных на заводе в Вермонте.
1. Постройте 95%-ный доверительный интервал, содержащий средний вес гранул, потерянных кровельными плитками, произведенными на заводе в Бостоне.
2. Постройте 95%-ный доверительный интервал, содержащий средний вес гранул, потерянных кровельными плитками, произведенными на заводе в Вермонте.
3. Выполняются ли предположения, необходимые для решения задач 1 и 2?
4. Какие выводы о среднем весе гранул, потерянных кровельными плитками, произведенными в Бостоне и Вермонте, можно сделать на основании решения задач 1-3?
7.93. Компания Zagat публикует рейтинги ресторанов, расположенных в разных городах США. В файле ftRESTRATE. XLS содержатся оценки качества пищи, оформления блюд, уровня обслуживания и стоимость обеда для одного человека в 50 ресторанах Нью-Йорк Сити и 50 ресторанах Лонг-Айленда.
Источник: цитируется по изданиям Zagat Survey “2002 New York City Restraunts” и Zagat Survey “2000 long Island Restraunts”.
Выполните следующие задания для ресторанов Нью-Йорк Сити и Лонг-Айленда отдельно.
1. Постройте 95% -ные доверительные интервалы, содержащие оценки качества пищи, оформления блюд, уровня обслуживания и стоимость обеда для одного человека.
2. Какие выводы можно сделать о ресторанах Нью-Йорк Сити и Лонг-Айленда на основе результатов, полученных при решении задачи 1?
Отчеты
7.94. Напишите отчет, содержащий результаты решения задачи 7.82 (расстояния между боковыми сторонами стального профиля). Вычислите статистические показатели с помощью программы Microsoft Excel и вставьте их в отчет, созданный с помощью пакета Microsoft Office, руководствуясь инструкциями из приложения 3.
Применение Интернет
7.95. Зайдите на сайт www. prenhall. com/levine. Выберите ссылку Chapter 7 и щелкните на ссылке Internet exercises.
ГРУППОВОЙ ПРОЕКТ
ТР.7.1.Вернитесь к заданию ТР.2.1. Получите интервальные оценки статистических показателей, характеризующих генеральную совокупность взаимных фондов с очень низким, низким, средним, высоким и очень высоким уровнями риска. Изложите полученные оценки в письменном отчете и доложите на семинаре. ftMUTUAL FUNDS.XLS.
РАЗБОР КОНКРЕТНОЙ СИТУАЦИИ -ГАЗЕТА SPRINGVILLE HERALD
Отдел маркетинга газеты Springville Herald ищет способы увеличить общее количество подписчиков газеты и удержать подписчиков, согласившихся участвовать в эксперименте. Лорен Альфонсо (Lauren Alfonso), менеджер по продажам, предложила провести опрос, чтобы выяснить привычки читателей, предпочитающих не подписывать газету, а покупать ее в киосках. После продолжительной дискуссии было решено включить в анкету следующие вопросы.
Вы или члены вашей семьи когда-нибудь покупали газету Springville Herald*?
1. Да.
2. Нет (опрос прекращается).
Выписываете ли вы газету Springville Herald*?
1. Да.
2. Нет (переходим к вопросу 4).
Когда вы получаете газету Springville Herald*?
1. С понедельника по субботу.
2. Только в воскресенье.
3. Каждый день (переходим к вопросу 9).
Как часто вы получаете газету Springville Herald с понедельника по субботу?
1. Каждый день.
2. Почти каждый день.
3. Редко.
Часто ли вы покупаете газету Springville Herald по воскресеньям?
1. Каждое воскресенье.
2. 2-3 раза в месяц.
3. Раз в месяц.
Где вы предпочитаете покупать газету Springville Herald*?
1. В бакалейных лавках.
2. В кондитерских магазинах.
3. В торговом автомате.
4. В супермаркете.
5. В другом месте.
Согласились бы вы подписаться на газету Springville Herald с испытательным сроком по сниженной цене?
1. Да.
2. Нет (переходим к вопросу 9).
В данный момент экземпляр газеты Springville Herald стоит 50 центов — с понедельника по субботу и 1 доллар 50 центов — в воскресенье. Суммарная стоимость газеты за
неделю — 4 доллара 50 центов. Какую цену вы готовы заплатить, чтобы получать газету в течение 90 дней?
Читаете ли вы еще какую-либо ежедневную газету, кроме Springville Herald*}
1. Да.
2. Нет.
В качестве поощрения постоянные подписчики (выписывающие газету в течение 6 месяцев на сумму более 100 долларов) получают дисконтную карточку для посещения некоторых ресторанов в г. Спрингвилль. Хотите ли вы получить такую карточку?
1. Да.
2. Нет.
Для телефонного опроса была создана случайная выборка, состоящая из 500 местных жителей. Телефонный номер генерировался с помощью случайных цифр. При этом первые три цифры фиксировались, а последние четыре — выбирались случайным образом. В опросе принимали участие только телефонные номера, зарегистрированные в г. Спрингвилль.
Из 500 опрошенных жителей 94 респондента отказались принимать участие в анкетировании, не стали отвечать на повторный звонок, имели несуществующий номер или снимали квартиру. Результаты представлены в таблице.
Семьи, покупающие газету Springville Herald Частота
Да 352
Нет 54
Семьи, выписывающие газету Springville Herald Частота
Да 136
Нет 216
Разновидность подписки Частота
С понедельника по субботу 18
Только по воскресеньям 25
Каждый день 93
Поведение покупателей, не являющихся подписчиками (понедельник-суббота) Частота
Покупают каждый день 78
Покупают почти каждый день 95
Покупают редко 43
Поведение покупателей, не являющихся подписчиками (воскресенье) Частота
Покупают каждое воскресенье 138
Покупают 2-3 раза в месяц 54
Покупают 1 раз в месяц 24
Место покупки Частота
Бакалейная лавка 74
Кондитерский магазин 95
Торговый автомат 21
Супермаркет 13
Другое 13
Согласны подписаться на испытательный период Частота
Да 46
Нет 170
Суммы, которые респонденты согласны платить (в неделю) за подписку в течение 90-дневного испытательного срока.
OsH7 .XLS
4,15 3,60 4,10 3,60 3,60 3,60 4,40
3,15 4,00 3,75 4,00 3,25 3,75 3,30
3,75 3,65 4,00 4,10 3,90 3,50 3,75
3,00 3,40 4,00 3,80 3,50 4,10 4,25
3,50 3,90 3,95 4,30 4,20 3,50 3,75
3,30 3,85 3,20 4,40 3,80 3,40 3,50
2,85 3,75 3,80 3,90
Читают другие ежедневные газеты Частота
Да 138
Нет 214
Хотели бы получить дисконтные карточки для постоянных подписчиков Частота
Да 66
Нет 286
УПРАЖНЕНИЯ
Некоторые сотрудники отдела маркетинга заинтересовались методом выбора телефонных номеров респондентов с помощью случайных чисел, использованным для опроса. Подготовьте отчет, в котором исследованы следующие вопросы.
1. Преимущества и недостатки метода случайных чисел.
2. Опишите возможные альтернативы, укажите их преимущества и недостатки.
Проанализируйте результаты опроса жителей г. Спрингвилль. Напишите отчет, содержащий выводы маркетингового исследования.
ПРИМЕНЕНИЕ WEB
Примените свои знания о доверительных интервалах и оцените данные о деятельности компании OnCampus!, упомянутые в главе 6.
Помимо всего прочего, компания OnCampus! предоставляет посетителям своего Web-сайта возможность воспользоваться системой электронной торговли OnCampus! Life-Styles. Для обеспечения электронной системы обработки платежей компания OnCampus! заключила соглашения со следующими фирмами.
• PayAFriend (PAF): система электронной обработки платежей, в которой безопасность обеспечивается предварительной регистрацией всех клиентов и компаний, без применения кредитных карточек.
• Continental Banking Company (Cobanco): провайдер услуг по электронной обработке платежей, позволяющих клиентам компании OnCampus! оплачивать товары общепризнанными кредитными карточками, выпускаемыми финансовыми организациями.
Чтобы снизить стоимость системы, руководство компании OnCampus! решило отказаться от услуг одного из партнеров, обеспечивающих обработку электронных платежей. Однако Вирджиния Даффи (Virginia Duffy) из отдела продаж заподозрила, что две формы оплаты пользуются у клиентов неодинаковой популярностью, что влияет на их покупательскую активность. Чтобы проверить свои подозрения, она решила вычислить следующие статистики.
1. Доля клиентов, пользующихся услугами компании PAF, и доля клиентов, использующих кредитные карточки.
2. Средний объем продаж при оплате через компанию PAF и средний объем продаж при оплате с помощью кредитных карточек.
Помогите мисс Даффи провести анализ на основе случайной выборки, состоящей из 50 транзакций. Собранные данные хранятся в файле по адресу www.prenhall.com/ Springville/OnCampus_PymtSample. htm. Подведите итоги своих исследований и ответьте, подтверждается ли гипотеза мисс Даффи. Достаточно ли велика выборка, созданная мисс Даффи для проведения корректного анализа, если ошибка выборочного исследования не превышает 3 долл.?
СПРАВОЧНИК ПО EXCEL. ГЛАВА 7
ЕН.7.1. Вычисление доверительного интервала для математического ожидания при известном стандартном отклонении о
Чтобы вычислить доверительный интервал для математического ожидания при известном стандартном отклонении су, создадим рабочий лист, использующий функцию ДОВЕРИТ. Вызов этой функции выглядит следующим образом.
ДОВЕРИТ (1 -доверительный уровень', стандартное^отклонение', объем_выборки). Шаблон этого рабочего листа, соответствующий примеру 7.1, приведен в табл. ЕН.7.1. Для вычисления нижней и верхней доверительной границы ширина доверительного интервала, возвращаемая функцией ДОВЕРИТ, делится пополам и прибавляется к выборочному среднему. На листе также продемонстрированы вычисления стандартной ошибки и величины Z.
Таблица ЕН.7.1. Шаблон рабочего листа Доверительный интервал
А
1 Вычисление доверительного интервала, содержащего среднюю длину листа
2
3 Данные
4 Выборочное стандартное отклонение 0,02
5 Выборочное среднее 10,998
6 Объем выборки 100
7 Доверительный уровень 0,95
3 Промежуточные вычисления
10 Стандартная ошибка среднего =В4/КОРЕНЬ(В6)
11 Величина Z = НОРМСТОБР((1-В7)/2)
12 Половина доверительного интервала =ДОВЕРИТ(1-В7;В4;В6)
13
14 Доверительный интервал
15 Нижняя доверительная граница =В5-В12
16 Верхняя доверительная граница =В5+В12
При реализации этого шаблона ячейку В7 следует отформатировать так, чтобы величина 0,95 была представлена как 95% (см. врезку ЕР.5). В этом случае величина 0,95 будет представлена как 95%. Если при решении аналогичной задачи выборочное среднее не известно и подлежит вычислению, необходимо заменить формулу в ячейке В5 формулой =СРЗНАЧ (диапазон) .
ЕН.7.2. Вычисление доверительного интервала для математического ожидания при неизвестном стандартном отклонении о
Чтобы вычислить доверительный интервал для математического ожидания при неизвестном стандартном отклонении су, создадим рабочий лист, использующий функцию СТЬЮДРАСПОБР. Вызов этой функции выглядит следующим образом.
СТЬЮДРАСПОБР (1-доверительный уровень; степени_свободы).
Шаблон этого рабочего листа, соответствующий рис. 7.6, приведен в табл. ЕН.7.2. Для вычисления половины доверительного интервала, содержащего математическое ожидание, ^-значение распределения Стьюдента, возвращаемое функцией СТЬЮДРАСПОБР, умножается на стандартную ошибку среднего и делится пополам.
Таблица ЕН.7.2. Шаблон рабочего листа Доверительный_интервал
В
1 Вычисление доверительного интервала, содержащего среднюю сумму накладных
2
3 Данные
4 Выборочное стандартное отклонение 28,95
5 Выборочное среднее 110,27
6 Объем выборки 100
7 Доверительный уровень 0,95
8
9 Промежуточные вычисления
10 Стандартная ошибка среднего = В4/КОРЕНЬ(В6)
liiiil Степени свободы =В6-1
,|® Г-значение =СТЬЮДРАСП0БР(1-В7;В11)
13 Половина доверительного интервала =В12*В10
14
15 Доверительный интервал
16 Нижняя доверительная граница = В5-В13
17 Верхняя доверительная граница = В5+В13
При реализации этого шаблона ячейку В7 следует отформатировать так, чтобы величина 0,95 была представлена как 95% (см. врезку ЕР.5). Если при решении аналогичной задачи выборочное среднее не известно и подлежит вычислению, необходимо заменить формулу в ячейке В5 формулой, использующей функцию =СРЗНАЧ (диапазон).
ЕН.7.3. Вычисление доверительного интервала для доли признака в генеральной совокупности
Создадим рабочий лист, использующий для вычисления доверительного интервала, содержащего долю признака в генеральной совокупности, функцию НОРМСТОБР, вызов которой имеет вид НОРМСТОБР (вероятноетъ), где аргумент вероятность представляет собой площадь фигуры, ограниченной кривой стандартизованного нормального распределения и лежащей левее числа X.
Шаблон рабочего листа, соответствующий рис. 7.10, приведен в табл. ЕН.7.3. Для вычисления половины доверительного интервала, содержащего долю признака, значение Z, возвращаемое функцией НОРМСТОБР, умножается на стандартную ошибку среднего и делится пополам. Затем эта половина вычитается и добавляется к выборочному среднему. Чтобы половина доверительного интервала всегда была положительной, в ячейке В12 использована функция ABS.
Таблица ЕН.7.3. Шаблон рабочего листа Доверительный_интервал
В
1 Вычисление доверительного интервала, содержащего долю признака
2
3 Данные
4 Объем выборки 100
5 Количество успехов 10
6 Доверительный уровень 0,95
7
8 Промежуточные вычисления
9 Выборочная доля признака =В5/В4
10 Величина Z = НОРМСТОБР((1-В6)/2)
11 Стандартная ошибка доли признака = КОРЕНЬ(В9*(1-В9)/В4)
12 Половина доверительного интервала =ABS(B10*B11)
13
14 Доверительный интервал
15 Нижняя доверительная граница = В9-В12
16 Верхняя доверительная граница =В9+В12
При реализации этого шаблона ячейку В6 следует отформатировать так, чтобы величина 0,95 была представлена как 95% (см. врезку ЕР.5).
ЕН.7.4. Определение объема выборки для математического ожидания генеральной совокупности
Создадим рабочий лист, использующий функцию НОРМСТОБР для определения объема выборки, необходимой для вычисления доверительного интервала, содержащего математическое ожидание генеральной совокупности. Вызов этой функции имеет вид НОРМСТОБР (вероятность), где аргумент вероятность представляет собой площадь фигуры, ограниченной кривой стандартизованного нормального распределения и лежащей левее числа X.
Шаблон рабочего листа, соответствующий рис. 7.11, приведен в табл. ЕН.7.4. Для вычисления объема выборки, необходимой для вычисления доверительного интервала, содержащего среднюю сумму накладных, используется значение Z, возвращаемое функцией НОРМСТОБР. Объем выборки округляется с помощью функции ОКРУГЛВВЕРХ.
Таблица ЕН.7.4. Шаблон рабочего листа Объемвыборки
: . А ' • \ 1 ; ; - в '' '
ЙЙ Вычисление объема выборки, необходимой для оценки средней суммы накладных
111
3 Данные
lii Стандартное отклонение 25
iji Выборочная ошибка 5
о Доверительный уровень 0,95
7
Промежуточные вычисления
1111 Величина Z =НОРМСТОБР((1-В6)/2)
10 Вычисленный объем выборки =((В9*В4)/В5)Л2
1111
12 Результаты
13 Необходимый объем выборки =ОКРУГЛВВЕРХ(В10;0)
При реализации этого шаблона ячейку В б следует отформатировать так, чтобы величина 0,95 была представлена как 95% (см. врезку ЕР.5).
ЕН.7.5. Определение объема выборки для оценки доли признака в генеральной совокупности
Создадим рабочий лист, использующий функцию НОРМСТОБР для определения объема выборки, которая необходима для вычисления доверительного интервала, содержащего долю признака в генеральной совокупности. Вызов этой функции имеет вид НОРМСТОБР (вероятность) , где аргумент вероятность представляет собой площадь фигуры, ограниченной кривой стандартизованного нормального распределения и лежащей левее числа X.
Шаблон рабочего листа, соответствующий рис. 7.12, приведен в табл. ЕН.7.5. Для определения объема выборки, необходимой для вычисления доверительного интервала, содержащего долю ошибочных накладных, используется значение Z, возвращаемое функцией НОРМСТОБР. Объем выборки округляется с помощью функции ОКРУГЛВВЕРХ.
Таблица ЕН.7.5. Шаблон рабочего листа Объем выборки
А ./ ''
1 Вычисление объема выборки, необходимой для оценки доли ошибочных накладных
lii
3 Данные
4 Оценка истинной доли признака 0,15
IIIII Выборочная ошибка 0,07
|ЦИ| Доверительный уровень 0,95
lljjl
Окончание табл. ЕН. 7.5
111! Промежуточные вычисления
11111 Величина Z =НОРМСТОБР((1-В6)/12)
iiil Вычисленный объем выборки = (В9Л2*В4*(1-В4)/В5)Л2
fill
IHI Результаты
13 Необходимый объем выборки =ОКРУГЛВВЕРХ(В10;0)
При реализации этого шаблона ячейку В б следует отформатировать так, чтобы величина 0,95 была представлена как 95% (см. врезку ЕР.5).
ЕН.7.6. Вычисление доверительного интервала, содержащего общую сумму элементов генеральной совокупности
Создадим рабочий лист, использующий для вычисления доверительного интервала, который содержит общую сумму элементов генеральной совокупности, функцию СТЬЮДРАСПОБР. Вызов этой функции выглядит следующим образом.
СТЬЮДРАСПОБР (X-доверительный уровень; степени_свободы).
Шаблон рабочего листа, соответствующий рис. 7.13, приведен в табл. ЕН.7.6. Для вычисления половины доверительного интервала, содержащего общую сумму элементов генеральной совокупности, i-значение распределения Стьюдента, которое возвращается функцией СТЬЮДРАСПОБР, умножается на стандартную ошибку среднего. Затем полученная величина вычитается из выборочного среднего и добавляется к нему.
Таблица ЕН.7.6. Шаблон рабочего листа Доверительный_интервал
А
1 Вычисление доверительного интервала, содержащего общую сумму накладных
г
3 Данные
4 Объем генеральной совокупности 5000
' 5 ' Выборочное среднее 110,27
б Объем выборки 100
7 Выборочное стандартное отклонение 28,95
8 Доверительный уровень 0,95
S
10 Промежуточные вычисления
11 Сумма элементов генеральной совокупности =В4*В5
12 Множитель =КОРЕНЬ((В4-В6)/(В4-1))
13 Стандартная ошибка общей суммы = (В4*В7*В12)/КОРЕНЬ(В6)
14 Степени свободы =Вб-1
15 Лзначение =СТЬЮДРАСПОБР(1-В8;В14)
16 Половина доверительного интервала =В15*В13
17
Окончание табл. ЕН. 7.6
А В
18 Доверительный интервал
19 Нижняя доверительная граница =В11-В16
20 Верхняя доверительная граница =В11+В16
При реализации этого шаблона ячейку В8 следует отформатировать так, чтобы величина 0,95 была представлена как 95% (см. врезку ЕР.5). Если при решении аналогичной задачи выборочное среднее и выборочное стандартное отклонение не известны и подлежат вычислению, необходимо заменить формулы в ячейках В5 и В7 формулами =СРЗНАЧ {диапазон) и =СТАНДОТКЛОН {диапазон) соответственно.
ЕН.7.7. Вычисление доверительного интервала, содержащего полную разность генеральной совокупности
Создадим два рабочих листа, предназначенных для вычисления доверительного интервала, содержащего общую сумму разностей элементов генеральной совокупности. В табл. ЕН.7.7-ЕН.7.9 приведены шаблоны двух рабочих листов, предназначенных для оценки общей суммы разностей между правильными и неправильными суммами накладных, как показано на рис. 7.14.
Таблица ЕН.7.7. Изменения рабочего листа Разности
В
1 Разности (D-Dbar)A2
2 9,03 = (А2-Оценка!$В$10)л2
3 7,47 = (АЗ-Оценка!$В$Ю)л2
4 17,32 = (А4-Оценка!$В$Ю)л2
...
ilill 7,43 = (А11-Оценка!$В$Ю)л2
12 2,99 = (А12-Оценка!$В$Ю)л2
13 4,63 = (А13-Оценка!$В$10)л2
В табл. ЕН.7.7 приведены формулы, которые необходимо добавить в рабочий лист Разности, находящийся в книге Chapter 7.XLS. Эти формулы вычисляют квадраты разностей между ошибками и средней выборочной разностью, которая отдельно вычисляется в ячейке В10 на втором рабочем листе. Под ошибкой подразумевается разность между правильной и неправильной суммами накладной. В свою очередь, формулы, записанные в ячейках Е11 и Е13 на рабочем листе Оценка (см. табл. ЕН.7.8), вычисляют количество ненулевых разностей и суммы их квадратов соответственно. Остальные ячейки в табл. ЕН.7.8 предназначены для вычисления стандартного отклонения разностей, записанного в ячейке В12 на листе Оценка (см. табл. ЕН.7.9).
Таблица ЕН.7.8. Шаблон рабочего листа Оценка (диапазон D9 :Е16)
С . ' ' , ' ' • •
9 Область вычислений
Illi Для стандартного отклонения разностей
11 Количество ненулевых разностей =СЧ ЕТ( Разности! А: А)
12 Количество нулевых разностей =В5-Е11
13 Сумма квадратов ненулевых разностей =СУММ(Разности!В:В)
14 Сумма квадратов нулевых разностей =Е12*(-В1О)Л2
15 Сумма квадратов =Е13+Е14
16 Дисперсия разностей =Е15/В15
Таблица ЕН.7.9. Шаблон рабочего листа Оценка (столбцы А и в, столбец С пуст)
А ' в
1 Вычисление доверительного интервала, содержащего общую сумму накладных
2
3 Данные
4 Объем генеральной совокупности 5000
5 Выборочное среднее 100
6 Доверительный уровень 0,95
7
8 Промежуточные вычисления
9 Сумма разностей =СУММ(Разности!А:А)
10 Средняя выборочная разность =В9/В5
11 Полная разность =В4*В10
12 Стандартное отклонение разностей =К0РЕНЬ(Е16)
13 Множитель =КОРЕНЬ((В4-В5)/(В4-1))
14 Стандартная ошибка полной разности = (В4*В12*В13)/КОРЕНЬ(В5)
15 Степени свободы =В5-1
16 /-значение =СТЬЮДРАСПОБР(1-В6;В15)
17 Половина доверительного интервала = В16*В14
18
19 Доверительный интервал
20 Нижняя доверительная граница =В11-В17
21 Верхняя доверительная граница =В11+В17
Второй шаблон предназначен для вычисления половины длины доверительного интервала. Результат вычислений записывается в ячейку В17 и представляет собой произведение t-значения, возвращаемого функцией СТЬЮДРАСПОБР {1-доверительный_уровенъ', спгепени_свободы) и стандартной ошибки полной разности. Добавляя и вычитая полученную величину из полной разности, мы получаем верхнюю и нижнюю границы доверительного интервала.
Реализуя шаблон, представленный в табл. ЕН.7.7, введите формулу в ячейку В2 и скопируйте ее во всей ячейки этого столбца вплоть до строки 13. При реализации шаблона, представленного в табл. ЕН.7.9, отформатируйте ячейку В6 так, чтобы величина 0,95 была представлена как 95% (см. врезку ЕР.5). Для решения аналогичных задач измените первый шаблон, введя в столбце А новые разности. Если в новой задаче больше 12 разностей, скопируйте формулу из ячейки В13 в ячейки, лежащие ниже. Если в новой задаче меньше 12 разностей, удалите лишние строки.
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
1. Cochran, W. G., Sampling Techniques, 3rd ed. (New York: Wiley, 1977).
2. Fisher, R. A., and F. Yates, Statistical Tables for Biological, Agricultural and Medical Research, 5th ed. (Edinburgh, Scotland: Oliver & Boyd, 1957).
3. Kirk, R. E., ed., Statistical Issues: A Reader for the Behavioral Sciences (Belmont, CA: Wadsworth, 1972).
4. Lasen, R. L., and M. L. Marx, An Introduction to Mathematical Statistics and Its Applications, 2nd ed. (Englewood Cliffs, NJ: Prentice Hill, 1986).
5. Microsoft Excel 2002 (Redmond, WA: Microsoft Corporation, 2001).
6. Snedekor, G. W., and W. G. Cochran, Statistical Methods, 7th ed. (Ames, IA: Iowa State University Press, 1980).
Глава 8
Основы проверки гипотез: одновыборочные критерии
ПРИМЕНЕНИЕ СТАТИСТИКИ: процесс расфасовки кукурузных хлопьев
8.1. ПРОВЕРКА ГИПОТЕЗ
Нулевая и альтернативная гипотезы Критическое значение тестовой статистики
Области отклонения и принятия гипотез Риски, возникающие при проверке гипотез
8.2. ИСПОЛЬЗОВАНИЕ Z-КРИТЕРИЯ
ДЛЯ ПРОВЕРКИ ГИПОТЕЗЫ
О МАТЕМАТИЧЕСКОМ ОЖИДАНИИ ПРИ ИЗВЕСТНОМ СТАНДАРТНОМ ОТКЛОНЕНИИ
Проверка гипотез с помощью критического значения
Проверка гипотез по наблюдаемому уровню значимости
Процедуры Excel: проверка гипотезы о математическом ожидании при известном стандартном отклонении с помощью Z-критерия Связь между построением доверительных интервалов и проверкой гипотез
8.3. ОДНОСТОРОННИЕ КРИТЕРИИ
Применение критического значения
Применение наблюдаемого уровня значимости
8.4. ИСПОЛЬЗОВАНИЕ t-КРИТЕРИЯ
ДЛЯ ПРОВЕРКИ ГИПОТЕЗЫ
О МАТЕМАТИЧЕСКОМ ОЖИДАНИИ ПРИ НЕИЗВЕСТНОМ СТАНДАРТНОМ ОТКЛОНЕНИИ
Процедуры Excel: проверка гипотезы о математическом ожидании при неизвестном стандартном отклонении с помощью t-критерия
8.5. ПРИМЕНЕНИЕ Z-КРИТЕРИЯ
ДЛЯ ПРОВЕРКИ ГИПОТЕЗЫ О ДОЛЕ ПРИЗНАКА В ГЕНЕРАЛЬНОЙ
СОВОКУПНОСТИ
Процедуры Excel: проверка гипотезы о доле признака с помощью Z-критерия
8.6. ПОТЕНЦИАЛЬНЫЕ ПРОБЛЕМЫ
И ЭТИЧЕСКИЕ ВОПРОСЫ, СВЯЗАННЫЕ С ПРОВЕРКОЙ ГИПОТЕЗ
8.7. МОЩНОСТЬ КРИТЕРИЯ
СПРАВОЧНИК ПО EXCEL. ГЛАВА 8
ЧЕМУ ДОЛЖЕН НАУЧИТЬСЯ СТУДЕНТ
• Овладеть основами теории проверки гипотез.
• Применять полученные знания для проверки гипотез о математическом ожидании или доле признака.
• Проверять условия, необходимые для применения каждой процедуры проверки гипотез, и понимать последствия нарушения этих условий.
• Избегать ловушек, связанных с проверкой гипотез.
• Понимать этические проблемы, связанные с проверкой гипотез.
ПРИМЕНЕНИЕ СТАТИСТИКИ
Процесс расфасовки кукурузных хлопьев
Вернемся к сценарию, описанному в главе 6. Напомним, что, будучи управляющим компании Oxford Cereal Company, вы отвечаете за процесс расфасовки кукурузных хлопьев по коробкам. Необходимо убедиться, что конвейер работает нормально, и каждая коробка содержит в среднем 368 г зерна. Для этого вы извлекаете из генеральной совокупности 25 коробок, взвешиваете их и оцениваете отклонение реального веса от номинального. Коробки из этой выборки могут содержать либо слишком мало, либо слишком много хлопьев. В этом случае следует остановить производство и определить причину неполадок. Анализируя
разности между реальным весом и номинальным, необходимо решить, равно ли математическое ожидание генеральной совокупности 368 г или нет. Если равно, процесс расфасовки не требует вмешательства, если нет — следует остановить конвейер.
ВВЕДЕНИЕ
В главе 6 изложена концепция выборочных распределений, которая применяется в главе 7 для построения доверительных интервалов. В данной главе основное внимание уделяется методам проверки гипотез, которые представляют собой часть теории статистического вывода, использующую информацию, содержащуюся в выборке. Мы последовательно рассмотрим процесс оценки параметров генеральной совокупности, анализируя разности между результатами наблюдений (выборочными статистиками) и ожидаемыми результатами. Например, равен ли средний вес коробок в выборке, извлеченной из генеральной совокупности коробок, упакованных на заводе компании Oxford Cereal Company, среднему весу всей совокупности коробок, т.е. 368 г? Можно ли утверждать, что средний вес всех коробок не равен 368 г, если выборочное среднее значительно отличается от 368 г?
8.1. ПРОВЕРКА ГИПОТЕЗ
Нулевая и альтернативная гипотеза
Проверка гипотез (hypothesis testing) обычно начинается с некоего утверждения, касающегося конкретного параметра генеральной совокупности. Например, при статистическом анализе описанного выше процесса расфасовки кукурузных хлопьев естественно предположить, что конвейер работает нормально, и, следовательно, средний вес коробок равен 368 г.
Гипотеза о том, что параметр генеральной совокупности равен ожидаемому, называется нулевой (null hypothesis). Обычная гипотеза, как правило, предполагает некий статус-кво и обозначается как Но. В нашем примере нулевая гипотеза заключается в том, что заполнение коробок осуществляется правильно и средний вес коробок равен 368 г. Сформулируем это следующим образом:
Н0:ц = 368.
Несмотря на то что нам доступна только информация об отдельной выборке, нулевая гипотеза относится к параметру всей генеральной совокупности, потому что нас интересует процесс расфасовки в целом, а для его оценки используется выборочная статистика. В результате статистического анализа мы можем прийти к выводу, что нулевая гипотеза неверна. Следовательно, необходимо сформулировать ее альтернативу, т.е. гипотезу, которая считается истинной, если нулевая гипотеза оказывается ложной.
Альтернативная гипотеза (alternative hypothesis) противоположна нулевой гипотезе Но:
Нх: ц ф 368.
Иными словами, альтернативная гипотеза является отрицанием нулевой. Она оказывается истинной, если существуют статистические данные, свидетельствующие о том, что нулевая гипотеза неверна. Если в нашем примере выяснится, что средний вес коробок в выборке значительно отличается от 368 г, нулевая гипотеза отклоняется, и используется альтернативная гипотеза. В этом случае производство следует остановить и предпринять необходимые действия, направленные на устранение неполадок. Если нулевая гипотеза не отвергается, следует признать, что процесс расфасовки протекает правильно и никакие действия предпринимать не надо. Обратите внимание на то, что во втором сценарии мы не доказываем, что процесс расфасовки выполняется правильно, просто мы не в состоянии доказать обратное и поэтому должны верить (хотя и бездоказательно) в справедливость нулевой гипотезы.
Если выборочная статистика свидетельствует в пользу альтернативной гипотезы, нулевая гипотеза отклоняется. В этом и заключается проверка гипотез (hypothesis-testing methodology). Однако отказ отклонить нулевую гипотезу не означает, что она является истинной. Доказать, что нулевая гипотеза верна, в принципе невозможно, поскольку при ее проверке используется выборка, а не вся генеральная совокупность. Следовательно, отказ отвергнуть нулевую гипотезу означает лишь, что для ее отклонения нет оснований. Свойства нулевой и альтернативной гипотез приведены во врезке 8.1.
ВРЕЗКА 8.1. НУЛЕВАЯ И АЛЬТЕРНАТИВНАЯ ГИПОТЕЗЫ
Нулевая и альтернативная гипотезы обладают следующими свойствами.
♦ Нулевая гипотеза Но отражает статус-кво или текущее положение дел.
: • Альтернативная гипотеза Н, является отрицанием нулевой гипотезы и представляет собой исследовательское предположение или особое умозаключение, которое требуется доказать.
• Если нулевая гипотеза отвергается, альтернативная гипотеза считается истинной.
• Если нулевая гипотеза не отвергается, альтернативная гипотеза считается недоказанной. Однако недоказанность альтернативной гипотезы не означает, что нулевая гипотеза является истинной.
• Нулевая гипотеза Н„ всегда формулируется относительно конкретного значения параметра генеральной совокупности (например, математического ожидания ц), а не выборочной статистики (например, выборочного среднего х )•
• Нулевая гипотеза всегда содержит утверждение о равенстве параметра генеральной совокупности заранее заданному значению (например, Но: ц = 368).
• Альтернативная гипотеза никогда не содержит утверждения о равенстве параметра генеральной совокупности заранее заданному значению (например, Нх: ц * 368).
Критическое значение тестовой статистики
Опишем проверку гипотез на конкретном примере. В сценарии, касающемся компании Oxford Cereal Company, нулевая гипотеза означает, что средний вес коробок равен 368 г (т.е. параметр генеральной совокупности ц равен номинальному). Из генеральной совокупности извлекается выборка, каждая коробка из этой выборки взвешивается, и вычисляется их средний вес. Эта статистика является оценкой соответствующего параметра генеральной совокупности, из которой извлечена выборка. Даже если нулевая гипотеза на самом деле истинна, из-за изменчивости выборочное среднее не может в точности совпадать со средним значением генеральной совокупности. Однако в этом случае можно ожидать, что выборочное среднее будет мало отличаться от математического ожидания генеральной совокупности. Например, если средний выборочный вес коробок равен 367,9, естественно заключить, что математическое ожидание генеральной совокупности очень близко к номинальному (т.е. ц = 368 г). Интуиция подсказывает, что выборка, среднее значение которой равно 367,9, извлечена из генеральной совокупности, математическое ожидание которой равно 368 г.
С другой стороны, если между выборочной статистикой и параметром генеральной совокупности наблюдаются значительные различия, естественно отклонить нулевую гипотезу. Например, если средний выборочный вес коробок равен 320 г, можно прийти к выводу, что математическое ожидание генеральной совокупности не равно номинальному (т.е. ц 368 г). Следовательно, логично предположить, что математическое ожидание генеральной совокупности не равно 368 г. В любом случае статистический вывод основывается на предположении, что случайные выборки являются репрезентативными и правильно представляют свойства генеральной совокупности, из которых они извлечены.
К сожалению, процесс принятия решения на практике не так прост. Он существенно зависит от субъективного восприятия понятий “большое отклонение” и “небольшое отклонение”. Проверка гипотез позволяет формализовать эти понятия и оценить вероятность того, что нулевая гипотеза является истинной. Для этого сначала вычисляется выборочная статистика (например, выборочное среднее), а затем — статистика, положенная в основу критерия, которая, как правило, обладает стандартизованным нормальным или t-распределением.
Области отклонения и принятия гипотез1
Распределение статистики, положенной в основу критерия, разделяется на две части — область отклонения гипотезы (region of rejection) (иногда называемую критической областью (critical region)) и область принятия гипотезы (region of nonrejection) (рис. 8.1).
Если тестовая статистика попадает в область принятия гипотезы, нулевую гипотезу отклонить нельзя. В примере, связанном с наполнением коробок, выяснилось, что у менеджера нет основания считать, будто средний вес не равен 368 г. Если тестовая статистика попадает в критическую область, нулевая гипотеза отклоняется. В этом случае менеджер полагает, что средний вес всех коробок не равен 368 г.
В критическую область попадают лишь те значения тестовой статистики, при которых нулевая гипотеза неверна. Следовательно, если некое значение тестовой статистики попадает в критическую область, нулевую гипотезу следует отклонить.
Напомним, что принятие гипотезы означает лишь, что ее не удалось опровергнуть. По этой причине авторы используют более строгий термин “region of nonrejection'’, который для краткости мы перевели как “область принятия гипотезы ”. — Прим. ред’.
Рис. 8.1. Области принятия и отклонения гипотез
При проверке гипотез прежде всего следует определить критическое значение (critical value) тестовой статистики. Это число отделяет область принятия гипотезы от области отклонения гипотезы и зависит от размера критической области. Размер критической области непосредственно связан с величиной риска, возникающего, когда параметр генеральной совокупности оценивается по выборочным данным.
Риски, возникающие при проверке гипотез
При оценке параметра генеральной совокупности по выборочным значениям существует риск прийти к неверным выводам. При проверке гипотез возможны два типа ошибок: 1- и 2-го рода.
В нашем сценарии ошибка 1-го рода возникает, когда менеджер считает, что средний вес всех коробок не равен 368 г, в то время как на самом деле он равен 368 г. С другой стороны, если менеджер придет к выводу, что вес коробок равен 368 г, в то время как на самом деле он не равен 368 г, возникнет ошибка 2-го рода.
Ошибка 1-го рода (type I error) возникает, когда отклоняется истинная нулевая гипотеза Но. Ее вероятность обозначается буквой а.
Ошибка 2-го рода (type II error) возникает, когда не отклоняется ложная нулевая гипотеза Но. Ее вероятность обозначается буквой р.
Уровень значимости (а). Вероятность сделать ошибку 1-го рода обозначается буквой а и называется уровнем значимости (level of significance) статистического критерия. Эта вероятность определяет уровень риска, возникающего при отклонении истинной гипотезы. Поскольку уровень значимости задается заранее, он находится под полным контролем лица, выполняющего проверку. Как правило, уровни значимости равны 0,01, 0,05 и 0,1. Уровень риска зависит от стоимости ошибки 1-го рода. По уровню значимости а можно вычислить размер критической области, а значит, и критическое значение статистики, положенной в основу критерия.
Доверительная вероятность. Вероятность события, противоположного ошибке 1-го рода, называется доверительной вероятностью (confidence coefficient) и равна 1 -а. Умножив ее на 100%, можно вычислить доверительный уровень, рассмотренный в разделе 7.1.
Доверительная вероятность 1-а равна вероятности принять истинную нулевую гипотезу Но. Доверительный уровень (confidence level) критерия равен (1-а)х100%.
В терминах теории проверки гипотез доверительная вероятность представляет собой вероятность прийти к выводу, что проверяемое значение параметра является достоверным, когда это на самом деле так. В нашем примере доверительная вероятность равна вероятности принять гипотезу, что средний вес коробок равен 368 г, если он действительно равен этому числу.
Уровень риска (р). Вероятность ошибки 2-го рода обозначается буквой р. В отличие от ошибки 1-го рода, которая зависит от уровня значимости а, вероятность ошибки 2-го рода зависит от разности между гипотетическим параметром и фактической выборочной статистикой. Поскольку большую разность легче заметить, чем маленькую, при большой разности вероятность ошибки 2-го рода мала. Например, если математическое ожидание генеральной совокупности (неизвестное нам) равно 320 г, вероятность того, что оно мало отклоняется от 368 г, весьма невелика. С другой стороны, если разность между выборочной статистикой и гипотетическим параметром генеральной совокупности мала, вероятность ошибки 2-го рода становится большой. Следовательно, если математическое ожидание генеральной совокупности равно 367 г, вероятность того, что оно мало отклоняется от 368 г, довольно высока (и вы можете сделать ошибку 2-го рода).
Мощность критерия. Вероятность противоположного события равна 1—J3 и называется мощностью статистического критерия (power of a statistical test). В нашем сценарии мощность критерия равна вероятности прийти к выводу, что средний вес коробок не равен 368 г, когда он действительно не равен этому числу.
Мощность критерия 1-£ равна вероятности отклонить ложную нулевую гипотезу Но.
Риски, возникающие при принятии решений: точный баланс. В табл. 8.1 показаны два возможных решения (принять или отклонить нулевую гипотезу Но) при проверке гипотез. Как видим, решение может оказаться правильным либо стать причиной ошибки 1т или 2-го рода2.
Таблица 8.1. Проверка гипотез и принятие решения
Фактическая ситуация
Статистическое решение Гипотеза Но верна Гипотеза Но неверна
Гипотеза Ноне отклоняется Правильное решение Доверительная вероятность равна 1-сс Ошибка 2-го рода Вероятность ошибки 2-го рода равна £
Гипотеза Но отклоняется Ошибка 1-го рода Вероятность ошибки 1-го рода равна а Правильное решение Мощность критерия равна 1-р
Ошибку I-го рода можно уменьшить, увеличив объем выборки. Более крупные объемы выборки позволяют снизить отклонение выборочных статистик от оцениваемых параметров генеральной совокупности. При заданной ошибке 1-го рода а увеличение объема выборки приводит к уменьшению величины £ и, следовательно, к возрастанию мощности критерия. Однако объем выборки нельзя увеличивать бесконечно. Таким образом, необ-
Запомнить соответствие между вероятностями и типами ошибок легко, если учесть, что а— первая буква греческого алфавита и обозначает вероятность ошибки 1-города, a ft— вторая буква греческого алфавита и обозначает вероятность ошибки 2-города.
ходимо найти компромисс между ошибками двух видов. Поскольку в нашем распоряжении находится лишь вероятность ошибки 1-го рода, следует уменьшить ее величину. Например, если при проверке гипотез ошибка 1-го рода приводит к крайне нежелательным последствиям, необходимо выбрать ос = 0,01, а не ос = 0,05. Однако при уменьшении величины а увеличивается величина [3, следовательно, снижение вероятности ошибки 1-го рода сопровождается увеличением вероятности ошибки 2-го рода. С другой стороны, уменьшая вероятность [3, мы увеличиваем вероятность а. Следовательно, если необходимо избежать ошибки 2-го рода, можно выбрать а = 0,05 или ос = 0,1, а не ос = 0,01.
В нашем сценарии ошибка 1-го рода означает, что менеджер считает процесс заполнения коробок неправильным, в то время как на самом деле он выполняется верно. Ошибка 2-го рода означает, что менеджер считает процесс верным, хотя он выполняется неправильно. Выбор конкретных значений ос и {3 зависит от конкретной стоимости последствий, вызываемых ошибками 1- и 2-го рода. Например, если процесс заполнения коробок очень трудно перестроить, прежде чем останавливать конвейер, необходимо быть в этом совершенно уверенным. Для этого следует сделать ошибку 1-го рода как можно более маленькой. С другой стороны, если отклонение фактического веса коробок от номинального нельзя допускать ни в коем случае, следует минимизировать ошибку 2-го рода.
Изучение основ
8-1- Какая гипотеза обозначается символом Но?
8.2. Какая гипотеза обозначается символом
8.3. Каким символом обозначается ошибка 1-го рода?
8.4. Каким символом обозначается ошибка 2-го рода?
8.5. Как называется величина, равная 1-0?
8.6. Как называется величина, равная а?
8.7. Как называется величина, равная [3?
8.8. Как связаны мощность и вероятность ошибки 2-го рода?
8.9. Чему равна вероятность отклонить истинную нулевую гипотезу?
8.10. Чему равна вероятность не отклонить ложную нулевую гипотезу?
8.11. Как изменится величина [3 при фиксированном объеме выборки, если величина а уменьшается с 0,1 до 0,05?
8.12. Увеличивается ли величина 0 при нулевой гипотезе Нп: ц=100, альтернативной гипотезе Н,: цтЧОО и фиксированном объеме выборки н, если фактическое значение ц равно 90, а не 75?
Применение понятий
8.13. В США обвиняемый считается невиновным, пока его виновность не доказана судом. Нулевая гипотеза Н1} заключается в том, что обвиняемый невиновен, а альтернативная гипотеза Н, состоит в том, что обвиняемый виновен. Жюри присяжных может вынести два решения: заключить обвиняемого под стражу (т.е. отклонить нулевую гипотезу) или освободить его (т.е. не отклонить нулевую гипотезу). Объясните, в чем заключается риск, возникающий при ошибках 1- и 2-го рода.
8.14. Предположим, что обвиняемый из упражнения 8.13 считается виновным, пока его невиновность не доказана. Сформулируйте нулевую и альтернативную гипотезы. Объясните, в чем заключается риск, возникающий при ошибках 1- и 2-го рода.
8.15. Управление по санитарному надзору за качеством пищевых продуктов и медикаментов в США несет ответственность за качество новых лекарств. Многие группы потребителей считают, что процесс апробации лекарств слишком упрощен и на рынке появляется очень много некачественных лекарств (Sharpe, R., “FDA Tries to Find Right Balance on Drug Approvals”, The Wall Street Journal, April 20, 1999, A24). С другой стороны, большое количество промышленных лоббистов стремятся ускорить процедуру проверки лекарств, чтобы фармацевтические компании быстрее получали разрешение на их продажу. Нулевая гипотеза заключается в том, что новое лекарство является опасным, а альтернативная гипотеза состоит в том, что оно совершенно безопасно.
1. Объясните, в чем заключается риск, возникающий при ошибках 1- и 2-го рода.
2. Ошибку какого типа стремятся избежать потребители? Обоснуйте свой ответ.
3. Ошибку какого типа стремятся избежать промышленные лоббисты? Обоснуйте свой ответ.
4. Как уменьшить вероятности ошибок 1- и 2-го рода?
8.16. Студенты и преподаватели не довольны расписанием занятий, поэтому секретарь университета решил учесть время, необходимое для перехода из одной аудитории в другую. Секретарь полагает, что 20 мин. перерыва между занятиями вполне достаточно. Сформулируйте нулевую и альтернативную гипотезы.
8.17. Менеджер местного отделения крупного банка полагает, что за последние годы банк стал намного лучше обслуживать клиентов, и что средняя сумма, которую вкладчики извлекают из банкомата, не превышает 140 долл. Сформулируйте нулевую и альтернативную гипотезы.
8.2. ИСПОЛЬЗОВАНИЕ Z-КРИТЕРИЯ ДЛЯ ПРОВЕРКИ ГИПОТЕЗЫ О МАТЕМАТИЧЕСКОМ ОЖИДАНИИ ПРИ ИЗВЕСТНОМ СТАНДАРТНОМ ОТКЛОНЕНИИ
Напомним, что менеджер компании Oxford Cereal Company должен оценить качество заполнения коробок. Для этого необходимо убедиться, что конвейер работает правильно и средний вес коробок равен 368 г. Для этого из генеральной совокупности извлекается выборка, состоящая из 25 коробок. Затем каждая из них взвешивается, и вычисляется отклонение реального веса от номинального. Нулевая и альтернативная гипотезы формулируются так:
Но: ц = 368, Нх: ц*368.
Если стандартное отклонение о известно, выборочное распределение средних подчиняется нормальному закону. Это позволяет сформулировать Z-критерий3.
Выборочное распределение является нормально распределенным, если вся генеральная совокупность является нормально распределенной и/или размер выборки достаточно велик. Детали изложены в разделе 5.5.
ИСПОЛЬЗОВАНИЕ Z-КРИТЕРИЯ ДЛЯ ПРОВЕРКИ ГИПОТЕЗЫ О МАТЕМАТИЧЕСКОМ ОЖИДАНИИ ПРИ ИЗВЕСТНОМ СТАНДАРТНОМ ОТКЛОНЕНИИ
о
(8.1)
Числитель формулы (8.1) представляет собой отклонение выборочного среднего от математического ожидания генеральной совокупности. Знаменатель равен стандартному отклонению о, деленному на корень квадратный из объема выборки п. Таким образом, статистика Z выражает разность между X и ц, выраженную в единицах стандартного отклонения.
Проверка гипотез с помощью критического значения
Если уровень значимости равен 0,05, то размер критической области также равен 0,05. Следовательно, можно определить критическое значение нормального распределения, выраженное через стандартизованную Z-статистику. Поскольку критическая область разделена на две части (так называемый двусторонний критерий (two-tail test)), число 0,05 также следует разделить на два. Таким образом, площадь критической области, ограниченной хвостом гауссовой кривой и нижним критическим значением, равна 0,025. Соответственно, площадь области, ограниченной гауссовой кривой и верхним критическим значением, равна 0,975. По табл. Д.2, содержащей значения стандартизованного нормального распределения, легко определить критические значения, разделяющие области принятия и отклонения гипотезы. Они равны -1,96 и +1,96. Эта ситуация проиллюстрирована на рис. 8.2. Следовательно, если средний вес коробки действительно равен 368 г, как утверждает нулевая гипотеза Но, Z-статистика имеет стандартизованное нормальное распределение с центром в точке 0 (что соответствует условию X =368). Если значение статистики Z меньше -1,96 или больше +1,96, величина X настолько далека от р = 368, что гипотезу Но нельзя признать истинной.
Рис. 8.2. Области принятия и отклонения гипотезы о математическом ожидании при известном стандартном отклонении и уровне значимости, равном 0,05
Следовательно, решающее правило выглядит следующим образом:
если£> +1,96 или£< -1,96, гипотеза Но отклоняется; в противном случае она не отклоняется.
Допустим, что средний вес коробок, содержащихся в выборке из 25 коробок, равен 372,5, а стандартное отклонение равно 15 г. Используя формулу (8.1), получаем:
z = %ZH=37215-368 =
о 15_
55
п
Поскольку Z = +l,50, а -1,96 < +1,50 < +1,96, гипотезу Но отклонять нельзя (рис. 8.3). Таким образом, следует признать, что средний вес коробок равен 368 г. Чтобы учесть ошибку 2-го рода, результат необходимо сформулировать так: “Гипотеза о том, что средний вес коробок отличается от 368 г, не имеет достаточных подтверждений”.
Рис. 8.3. Проверка гипотезы о математическом ожидании при известном стандартном отклонении и уровне значимости, равном 0,05
Проверка гипотезы о математическом ожидании при известном стандартном отклонении выполняется следующим образом (врезка 8.2).
ВРЕЗКА 8.2. ЭТАПЫ ПРОВЕРКИ ГИПОТЕЗЫ
• Формулируется нулевая гипотеза На о параметрах генеральной совокупности. В задаче о расфасовке кукурузных хлопьев нулевая гипотеза Но выглядит так: р = 368.
• Формулируется альтернативная гипотеза Нг о параметрах генеральной совокупности. В задаче расфасовке кукурузных хлопьев нулевая гипотеза Нп выглядит так: 368.
• Выбирается уровень значимости а. Его конкретная величина определяется относительной важностью риска, вызванного ошибками 1- и 2-го рода. В нашем примере а=0,05.
• Определяется объем выборки и, зависящий от величины риска, вызванного ошибками 1- и 2-го рода (т.е. величин а и 0), а также от затрат, необходимых для ее формирования. В нашем примере объем случайной выборки равен 25.
• Выбирается требуемый статистический метод и соответствующая статистика, положенная в основу критерия. Поскольку в нашем примере стандартное отклонение известно заранее, для проверки критерия применяется Z-статистика,
• Устанавливаются критические значения, разделяющие плоскость на области отклонения и принятия гипотезы. В нашем примере критическими значениями являются числа -1,96 и +1,96, поскольку статистика Z имеет стандартизованное нормальное распределение.
• По выборке вычисляется значение статистики, положенной в основу критерия. В нашем примере - =372,5, поэтому Z = +1,50.
• Определяется область, в которую попадает вычисленное значение статистики, положенной в основу критерия. Для этого статистика сравнивается с критическими значениями. В нашем примере Z = +l,50, следовательно, вычисленное значение лежит в области принятия гипотезы, поскольку -1,96 < +1,50 < +1,96.
• Принимается статистическое решение. Если статистика, положенная в основу критерия, попадает в область принятия гипотезы, нулевую гипотезу Нп отклонять нельзя. В противном случае нулевая гипотеза отклоняется. В нашем примере нулевая гипотеза не была отвергнута.
• Формулируется статистическое решение, учитывающее специфику задачи. В нашем примере гипотеза о том, что средний вес коробок отличается от 368 г, не имеет достаточных подтверждений.
Проверка гипотез по наблюдаемому уровню значимости
В последние годы все большую популярность приобретают критерии проверки гипотез по наблюдаемому уровню значимости (observed level of significance), который часто называют p-значением (p-value). Эта величина соответствует минимальной вероятности того, что нулевая гипотеза Но будет отклонена на основе анализа исходного набора данных. Правило отклонения гипотезы Но в этом случае выглядит так.
1. Если p-значение больше или равно а, нулевая гипотеза не отклоняется.
2. Если p-значение меньше а, нулевая гипотеза отклоняется.
Наблюдаемый уровень значимости, или p-значение, представляет собой вероятность того, что тестовая статистика лежит в области отклонения гипотезы при условии, что нулевая гипотеза Но верна.
Проиллюстрируем этот подход на примере нашего сценария. Мы по-прежнему хотим знать, равен ли средний вес коробок 368 г. Получив значение Z = +1,50, мы не можем отклонить гипотезу Но, поскольку -1,96 < +1,50 < +1,96.
Применим подход, использующий уровень значимости. Для применения двустороннего критерия необходимо найти вероятность того, что статистика Z отстоит от центра стандартизованного нормального распределения не менее, чем на 1,5 стандартных отклонения. Иначе говоря, следует вычислить вероятность того, что статистика Z больше +1,50 или меньше, чем -1,50. По табл. Д.2 легко определить вероятность того, что статистика Z меньше -1,50. Она равна 0,0668. Вероятность того, что статистика Z меньше +1,50, равна 0,9332. Следовательно, вероятность того, что статистика Z больше +1,50, равна 0,0668. Таким образом, уровень значимости двустороннего критерия равен 0,0668+0,0668 = 0,1336 (рис. 8.4). Следовательно, вероятность того, что тестовая статистика лежит в области отклонения гипотезы, равна 0,1336. Поскольку эта величина больше, чем заданная ошибка 1-го рода а, нулевую гипотезу отклонять нельзя.
Рис. 8.4. Вычисление наблюдаемого уровня значимости двустороннего критерия
Если статистика, лежащая в основе критерия, не имеет нормального распределения, вычислить p-значение очень трудно. По этой причине в статистическом программном обеспечении, например, в программе Microsoft Excel, предусмотрены специальные процедуры для вычисления p-значений. Применение Z-критерия с помощью программы Microsoft Excel продемонстрировано на рис. 8.5.
4. '2
Проверка гипотезы о среднем весе коробок
Data
Null Hypothesis 368
Level of Significance 0.05
Population Standard Deviation 15
Sample Size 25
Sample Mean 372.5
Intermediate Calculations
Standard Error of the Mean 3
Z Test Statistic 1.5
Two-Tail Test
Lower Critical Value -1.959962787
Upper Critical Value 1.959962787
p-Value 0.133614458
Do not reject the null hypothesis
Рис. 8.5. Применение Z-критерия с помощью программы Microsoft Excel
Этапы проверки гипотезы по уровню значимости приведены во врезке 8.3.
ВРЕЗКА 8.3. ЭТАПЫ ПРОВЕРКИ ГИПОТЕЗЫ ПО УРОВНЮ ЗНАЧИМОСТИ
1. -Формулируется нулевая гипотеза Но.
2. Формулируется альтернативная гипотеза
3. Выбирается уровень значимости а.
4. Определяется объем выборки и.
: 5. Выбирается требуемый статистический метод и соответствующая тестовая статистика.
. 6. По выборке вычисляется значение тестовой статистики.
7. По вычисленной статистике определяется p-значение. Для этого выполняются следующие действия.
7.1. Изображается график распределения, соответствующий нулевой гипотезе.
7.2. На горизонтальной оси откладывается тестовая статистика.
7.3. Закрашивается область, соответствующая альтернативной гипотезе.
• Наблюдаемый уровень значимости р сравнивается с величиной а»
• Принимается статистическое решение. Если p-значение больше или равно а, нулевая гипотеза не отклоняется. Если p-значение меньше а, нулевая гипотеза отклоняется.
8. Формулируется статистическое решение, учитывающее специфику задачи.
Процедуры Excel: проверка гипотезы о математическом ожидании при известном стандартном отклонении с помощью Z-критерия
Чтобы создать рабочий лист, предназначенный для проверки гипотезы о математическом ожидании генеральной совокупности при известном стандартном отклонении с помощью Z-критерия, МОЖНО воспользоваться функциями НОРМРАСП И НОРМСТОБР.
Например, чтобы проверить с помощью Z-критерия гипотезу о среднем весе коробок, как показано на рис. 8.5, необходимо выполнить одну из следующих процедур.
Применение Excel в сочетании с надстройкой PHStat2
Чтобы проверить гипотезу о математическом ожидании генеральной совокупности при известном стандартном отклонении с помощью Z-критерия, следует применить процедуру PHStat^One-Sample Tests^Z-test for the Mean, sigma known... (PHStatoОдновыборочные критерии^ Z-критерий для математического ожидания, стандартное отклонение известно...) и выполнить следующие действия.
1. Выбрать команду PHStat^One-Sample Tests^Z-test for the Mean, sigma known.
2. В диалоговом окне Z-test for the Mean, sigma known (см. иллюстрацию) сделать следующее.
2.1. Ввести в окне редактирования Null Hypothesis (Нулевая гипотеза) число 3 68.
2.2. Ввести в окне редактирования Level of Significance (Уровень значимости) число 0.05.
2.3. Ввести в окне редактирования Population Standard Deviation (Стандартное отклонение генеральной совокупности) число 15.
2.4. Установить переключатель Sample Statistics Options (Параметры выборочных статистик) в положение Sample Statistics Known (Выборочные статистики известны) и ввести в окне редактирования Sample Size (Объем выборки) число 25, а в окне редактирования Sample Mean (Выборочное среднее) - число 372.5.
2.5. Установить переключатель Test Options (Параметры критерия) в положение Two-Tailed Test (Двусторонний критерий).
2.6. Ввести в окне редактирования Title соответствующий заголовок.
2.7. Щелкнуть на кнопке ОК.
Z Test for the Mean, sigma known
Data ...................-...............
Null Hypothesis: [зб8
Level of Significance: [o.O5
Population Standard Deviation: [15 Sample Statistics Options G Sample Statistics Known
Sample Size: |z5
Sample Mean: |з72?5~”
C‘ Sample Statistics Unknown
- Test Options
Two-Tail Test
Upper-Tail Test
Lower-Tail Test
Output Options.........................
Title: [проверка гипотезы о среднем весе
Help I lEZgOl Cancel
Если выборочное среднее неизвестно, в п. 2.3 следует установить переключатель Sample Statistics Options в положение Sample Statistics Unknown (Выборочные статистики неизвестны), а в окне редактирования Sample Cell Range (Диапазон ячеек, содержащий выборку) ввести диапазон ячеек, в которых записаны элементы выборки.
Для односторонних критериев (см. раздел 8.3) переключатель Test Options вместо положения Two-Tailed Test в п. 2.5 следует установить в положение Upper-Tail Test (Ограниченный сверху критерий) или Lower-Tail Test (Ограниченный снизу критерий).
Применение Excel
Чтобы самостоятельно создать рабочий лист, выполняющий проверку гипотезы о математическом ожидании при известном стандартном отклонении с помощью Z-критерия, следуйте инструкциям, изложенным в разделе ЕН.8.1.
Chapter 8.xls
Данные, на основе которых выполняется проверка гипотезы о среднем весе коробок, заполненных на заводе компании Oxford Cereal Company, при известном стандартном отклонении с помощью Z-критерия, содержатся в рабочей книге chapter 8. xls на листе Рис8.5.
Связь между построением доверительных интервалов и проверкой гипотез
В этой главе и главе 7 рассмотрены две основные задачи теории статистического вывода: построение доверительного интервала и проверка гипотез. Несмотря на то что они используют одни и те же понятия, эти задачи имеют разный смысл. В главе 7 доверительные интервалы используются для оценки параметров генеральной совокупности, в то время как проверка гипотез касается конкретных значений этих параметров. В данной главе проверка гипотез применяется для принятия решений, касающихся конкретных значений параметров генеральной совокупности. Однако правильная интерпретация доверительного интервала также может свидетельствовать о том, что исследуемый параметр меньше, больше заданного значения или равен ему. Более того, доверительный интервал является интервальной оценкой исследуемого параметра генеральной совокупности. Наблюдаемый уровень значимости позволяет еще глубже понять преимущества проверки гипотез.
Например, в данном разделе мы проверили гипотезу о том, что средний вес коробок, заполненных на заводе компании Oxford Cereal Company, отличается от 368 г. Для этого мы использовали формулу (8.1):
о у[п
Вместо проверки этой гипотезы, можно было бы построить доверительный интервал, содержащий величину ц. Если гипотетическая величина ц = 368 попадает в доверительный интервал, нулевая гипотеза не отклоняется, поскольку величина 368 не является чем-то необычным. С другой стороны, если гипотетическая величина не попадает в доверительный интервал, нулевая гипотеза отклоняется, поскольку величина 368 теперь является экстремальной. Для вычисления доверительного интервала, содержащего величину ц, требуются следующие данные:
п = 25, X =372,5 г, о = 15 г (установлено компанией).
Если доверительный уровень равен 95% (что соответствует уровню значимости, равному 0,05, т.е. а = 0,05), имеем:
X±Z-^ = 372,5±1,96^ = 372,5±5,88 .
Jn л/25
Следовательно,
366,62 < ц < 378,38.
Поскольку гипотетическое значение 368 попадает в данный доверительный интервал, нулевая гипотеза не отклоняется. У нас нет достаточных оснований утверждать, что средний вес коробок отличается от 368 г. К такому же решению мы пришли, используя методы проверки гипотез.
УПРАЖНЕНИЯ К РАЗДЕЛУ 8.2
Изучение основ
8.18. Предположим, что уровень значимости двустороннего критерия равен 0,05. Какой вывод можно сделать, если Z = +2,21?
8.19. Предположим, что уровень значимости двустороннего критерия равен 0,10. Какое решающее правило следует сформулировать для отклонения гипотезы о том, что математическое ожидание генеральной совокупности равно 500?
8.20. Предположим, что уровень значимости двустороннего критерия равен 0,10. Какое решающее правило следует сформулировать для отклонения гипотезы о том, что математическое ожидание генеральной совокупности равно 12,5?
8.21. Как изменится решающее правило, сформулированное в задаче 8.20, если Z = -2,61?
8.22. Чему равно значениер в двустороннем критерии, если Z = +2,00?
8.23. Какое статистическое решение следует принять в задаче 8.22 при проверке нулевой гипотезы при уровне значимости, равном 0,10?
8.24. Чему равно значениер в двустороннем критерии, если Z = -1,38?
8.25. Какое статистическое решение следует принять в задаче 8.24 при проверке нулевой гипотезы при уровне значимости, равном 0,10?
Применение понятий
8.26. Директор швейной фабрики желает определить, соответствует ли ткань, произведенная на новом станке, заданным техническим требованиям. В частности, ткань должна иметь прочность 70 фунтов на кв. дюйм при стандартном отклонении 3,5 фунта. Анализ выборки, состоящей из 49 отрезов ткани, показал, что средняя прочность ткани равна 69,1.
1. Сформулируйте нулевую и альтернативную гипотезы.
2. Есть ли основания утверждать, что новый станок не соответствует техническим требованиям? (Уровень значимости равен 0,05.)
3. Вычислите p-значение и дайте его интерпретацию.
4. Как изменится ответ на вопрос 2, если стандартное отклонение равно 1,75 фунта?
5. Как изменится ответ на вопрос 2, если выборка состоит из 69 отрезов ткани, а стандартное отклонение — 3,5 фунта?
8.27. Менеджер магазина, торгующего красками, хочет проверить, равен ли средний объем краски, содержащейся в галлонных банках известной компании, одному галлону. Известно, что стандартное отклонение объема краски равно 0,02 галлона. Менеджер выбрал 50 банок. Выборочный средний объем равен 0,995 галлона.
1. Сформулируйте нулевую и альтернативную гипотезы.
2. Есть ли основания утверждать, что средний объем краски не равен одному галлону? (Уровень значимости равен 0,01.)
3. Вычислите p-значение и дайте его интерпретацию.
4. Постройте 99%-ный доверительный интервал, содержащий средний объем краски.
5. Сравните ответы на вопросы 2 и 4. Какие выводы напрашиваются?
8.28. Менеджер из отдела контроля за качеством продукции на заводе, производящем электрические лампочки, желает проверить, равна ли средняя продолжительность работы лампочек из крупной партии 375 ч. Номинальное стандартное отклонение равно 100 ч. Для контроля выбрана партия, состоящая из 64 лампочек, средняя продолжительность работы которых равна 350 ч.
1. Сформулируйте нулевую и альтернативную гипотезы.
2. Есть ли основания утверждать, что средняя продолжительность работы лампочек не равна 375 ч? (Уровень значимости равен 0,05.)
3. Вычислите p-значение и дайте его интерпретацию.
4. Постройте интервал, содержащий математическое ожидание генеральной совокупности, доверительный уровень которого равен 95%.
5. Сравните ответы на вопросы 2 и 4. Какие выводы напрашиваются?
8.29. Отдел технического контроля на заводе, производящем газированные напитки, желает выяснить, равен ли средний объем жидкости, содержащейся в двухлитровых бутылках, номинальному объему. Известно, что стандартное отклонение объема жидкости в двухлитровой бутылке равно 0,05 л. Менеджер выбрал 100 двухлитровых бутылок. Выборочный средний объем составил 1,99 л.
1. Сформулируйте нулевую и альтернативную гипотезы.
2. Есть ли основания утверждать, что средний объем жидкости в бутылках не равен 2 л? (Уровень значимости равен 0,05.)
3. Вычислите p-значение и дайте его интерпретацию.
4. Постройте интервал, содержащий математическое ожидание генеральной совокупности, доверительный уровень которого равен 95% .
5. Сравните ответы на вопросы 2 и 4. Какие выводы напрашиваются?
8.30. Производитель соусов использует для заполнения бутылок конвейерный разливочный автомат. В соответствии с техническими требованиями в каждой бутылке должно содержаться 8 унций соуса. Стандартное отклонение количества соуса в бутылке равно 0,15 унции. Периодически из произведенной продукции выбираются 50 бутылок. Если среднее количество соуса в бутылке отличается от 8 унций, конвейер останавливается. Допустим, что выборочное среднее равно 7,983.
1. Сформулируйте нулевую и альтернативную гипотезы.
2. Есть ли основания утверждать, что среднее количество соуса в бутылках не равно 8 унциям? (Уровень значимости равен 0,05.)
3. Вычислите p-значение и дайте его интерпретацию.
4. Как изменится ответ на вопрос 2, если стандартное отклонение равно 0,05 унции?
5. Как изменится ответ на вопрос 2, если выборочное среднее равно 7,952 унции, а стандартное отклонение равно 0,15 унции?
8.31. Банкоматы должны содержать достаточное количество денег, чтобы удовлетворить запросы клиентов на протяжении выходных. Однако, если банкомат содержит избыточное количество денег, банк теряет прибыль. Допустим, что в конкретном отделении банка среднее количество денег, извлекаемых клиентами из банкомата, равно 160 долл., причем стандартное отклонение равно 30 долл.
1. Сформулируйте нулевую и альтернативную гипотезы.
2. Предположим, что для анализа из генеральной совокупности извлечена выборка, состоящая из 36 транзакций. Выборочное среднее оказалось равным 172 долл. Есть ли основания утверждать, что среднее количество денег, снятых клиентами, не равно 160 долл.? (Уровень значимости равен 0,05.)
3. Вычислите p-значение и дайте его интерпретацию.
4. Как изменится ответ на вопрос 2, если уровень значимости равен 0,01?
5. Как изменится ответ на вопрос 2, если стандартное отклонение равно 24 долл.?
8.3. ОДНОСТОРОННИЕ КРИТЕРИИ
До сих пор нулевая гипотеза предполагала равенство исследуемого параметра генеральной совокупности заданному значению. Например, мы проверили, равен ли средний вес коробок 368 г. Альтернативная гипотеза (Н^. 368) распадается на две: сред-
ний вес коробок может быть меньше или больше 368 г. По этой причине область отклонения гипотезы разделяется на две части, которые соответствуют двум хвостам распределения выборочных средних.
Однако в некоторых ситуациях альтернативная гипотеза формулируется конкретнее и предполагает, что параметр генеральной совокупности строго больше заданного значения (или меньше). Рассмотрим один из таких примеров. Допустим, что компания, производящая сыр, желает проверить качество поставляемого молока. В частности, ее интересует, не подмешивает ли поставщик воду в молоко. Как известно, добавление воды снижает температуру замерзания молока, которая равна -0,545 °C. Стандартное отклонение температуры замерзания молока равно 0,008 °C. Поскольку компанию интересует, не стала ли температура замерзания молока меньше номинальной, область отклонения гипотезы теперь ограничена лишь левым хвостом распределения.
Применение критического значения
В данном примере нулевая и альтернативная гипотезы формулируются так:
Шаги 1 и 2. Но: ц > -0,545 °C,
Н/. ц< -0,545 °C.
Обратите внимание на то, что наша цель — доказать альтернативную гипотезу. Если нулевая гипотеза отклоняется, значит, у нас есть веские доказательства того, что температура замерзания молока меньше естественной. Если нулевая гипотеза не отклоняется, значит, у нас нет достаточных доказательств, чтобы утверждать, будто температура замерзания молока меньше естественной.
Шаг 3. а = 0,05.
Шаг 4. п = 25.
Шаг 5. Для проверки гипотезы применяется Z-критерий, поскольку стандартное отклонение температуры замерзания молока известно.
Шаг 6. Область отклонения гипотезы целиком ограничена левым хвостом распределения выборочных средних, поскольку мы хотим отклонить нулевую гипотезу Но, только если выборочное среднее значительно меньше -0,545 °C. Когда область отклонения гипотезы ограничена только одним хвостом распределения, критерий называется односторонним (one-tail test) или направленным (directional test). Если альтернативная гипотеза содержит знак “меньше”, критическое значение тестовой статистики Z должно быть отрицательным. Поскольку вся область отклонения гипотезы ограничена левым хвостом стандартизованного нормального распределения и его площадь превышает 0,05, то площадь,
ограниченная кривой и критическим значением тестовой статистики должна быть равной 0,05, как показано в табл. 8.2 и на рис. 8.6. Таким образом, критическое значение тестовой статистики Z равно -1,645, т.е. арифметическому среднему чисел -1,64 и -1,65.
Таблица 8.2. Вычисление критического значения Z-статистики, имеющей стандартизованное нормальное распределение и положенной в основу одностороннего критерия с уровнем значимости а = 0,054
Фактическая ситуация
Z 0,00 0,01 0,02 0,03 0,04 0,05 0,06 0,07 0,08 0,09
-1,8 0,0359 0,0351 0,0344 0,0336 0,0329 0,0322 0,0314 0,0307 0,0301 0,0294
-1,7 0,0446 0,0436 0,0427 0,0418 0,0409 0,0401 0,0392 0,0384 0,0375 0,0367
-1,6 0,0548 0,0537 0,0526 0,0516 0,0505 0,0495 0,0485 0,0475 0,0465 0,0455
Рис. 8.6. Односторонний критерий для проверки гипотезы о математическом ожидании генеральной совокупности при известном стандартном отклонении и уровне значимости, равном 0,05
Решающее правило выглядит следующим образом:
если2 < -1,645, гипотеза Но отклоняется; в противном случае она не отклоняется.
Шаг 7. Допустим, что из партии молока выбраны 25 бидонов. Выборочная средняя температура замерзания равна -0,550 °C, а стандартное отклонение равно 15 г. Используя формулу (8.1), получаем:
п = 25, X = -0,550 °C, о = 0,008 °C,
_-0,550-(-0,545) а 0,008 ’
V25
Шаг 8. Поскольку Z= -3,125 < -1,645, гипотеза Но отклоняется, так как тестовая статистика лежит в области отклонения гипотезы (рис. 8.6).
Шаг 9. Гипотеза Но отклоняется.
Шаг 10. Таким образом, средняя температура замерзания молока оказалось меньше -0,545°С. Молоко сильно разбавлено, и компания должна провести тщательное расследование этого факта.
4
Фрагмент табл. Д.2.
Применение наблюдаемого уровня значимости
Применим для решения рассмотренной выше задачи наблюдаемый уровень значимости.
Шаги 1-5. Совпадают с алгоритмом, использующим критические значения.
Шаг 6. Z = -3,125 (см. шаг 7 предыдущего алгоритма).
Шаг 7. Альтернативная гипотеза определяет критическую область, целиком ограниченную левым хвостом выборочного распределения Z-статистики, положенной в основу критерия, следовательно, для вычисления p-значения необходимо вычислить вероятность того, что Z < -3,125. Из табл. Д.2 следует, что вероятность этого события равна 0,0009 (рис. 8.7).
Шаг 8. Вычисленное p-значение меньше уровня значимости а = 0,05.
Шаг 9. Нулевая гипотеза Но отклоняется.
Шаг 10. Таким образом, средняя температура замерзания молока оказалось меньше -0,545°С. Молоко сильно разбавлено, и компания должна провести тщательное расследование этого факта.
Более того, p-значение, равное 0,0009, является вероятностью того, что выборочное среднее не превосходит -0,550 °C, если истинная средняя температура замерзания во всей генеральной совокупности бидонов равна -0,545 °C. Поскольку эта вероятность весьма мала, гипотетическое значение -0,545 °C следует считать неправдоподобным. Результаты расчетов, полученные с помощью программы Microsoft Excel, продемонстрированы на рис. 8.8.
Рис. 8.7. Вычисление p-значения для одностороннего критерия
.А ... I . в „I... Проверка гипотезы о средней весе коробок
3 Data
4 Null Hypothesis ц= 368
5 Level of Significance 0.05
В Population Standard Deviation 15
7 Sample Size 25
е Sample Mean 372.5
9
Intermediate Calculations
'11 Standard Error of the Mean 3
12 Z Test Statistic 1.5
13
14 Two-Tail Test
15 Lower Critical Value -1.959962787
16 Upper Critical Value 1.959962787
p -Value 0.133614458
Do not reject the null hypothesis
Рис. 8.8. Проверка гипотезы о средней температуре замерзания молока с помощью программы Microsoft Excel
Чтобы выполнить проверку с помощью одностороннего критерия, сначала необходимо сформулировать нулевую и альтернативную гипотезы (врезка 8.4).
ВРЕЗКА 8.4. НУЛЕВАЯ И АЛЬТЕРНАТИВНАЯ ГИПОТЕЗЫ ДЛЯ ОДНОСТОРОННЕГО КРИТЕРИЯ
• Нулевая гипотеза Нй отражает статус-кво или текущее положение дел.
• Альтернативная гипотеза Н, является отрицанием нулевой гипотезы и представляет собой исследовательское предположение или особое умозаключение, которое требуется доказать.
• Если нулевая гипотеза отвергается, альтернативная гипотеза считается истинной.
• Если нулевая гипотеза не отвергается, альтернативная гипотеза считается недо- : казанной. Однако недоказанность альтернативной гипотезы не означает, что нулевая гипотеза является истинной.
• Нулевая гипотеза Нп всегда формулируется относительно конкретного значения параметра генеральной совокупности (например, математического ожидания ц), а не выборочной статистики (например, выборочного среднего % ).
• Нулевая гипотеза всегда содержит утверждение о равенстве параметра генеральной совокупности заранее заданному значению (например, : ц > -0,545 °C).
• Альтернативная гипотеза никогда не содержит утверждения о равенстве параметра генеральной совокупности заранее заданному значению (например, Н1: ц < -0,545°C).
УПРАЖНЕНИЯ К РАЗДЕЛУ 8.3
Изучение основ
8.32. Чему равно верхнее критическое значение Z-статистики, положенной в основу одностороннего критерия с уровнем значимости, равным 0,01?
8.33. Какое статистическое решение следует принять, если в задаче 8.32 вычисленное значение Z-статистики равно 2,39?
8.34. Чему равно нижнее критическое значение Z-статистики, положенной в основу одностороннего критерия с уровнем значимости, равным 0,01?
8.35. Какое статистическое решение следует принять, если в задаче 8.34 вычисленное значение Z-статистики равно -1,15?
8.36. Предположим, что односторонний критерий отклоняет гипотезу, только если вычисленное значение статистики попадает в область, ограниченную правым хвостом. Вычисленное значение Z-статистики равно +2,00. Чему равно р-значение?
8.37. Какое статистическое решение следует принять, если в задаче 8.36 уровень значимости равен 0,05?
8.38. Предположим, что односторонний критерий отклоняет гипотезу, только если вычисленное значение статистики попадает в область, ограниченную левым хвостом. Вычисленное значение Z-статистики равно -1,38. Чему равнор-значение?
8.39. Какое статистическое решение следует принять, если в задаче 8.38 уровень значимости равен 0,01?
8.40. Предположим, что односторонний критерий отклоняет гипотезу, только если вычисленное значение статистики попадает в область, ограниченную левым хвостом. Вычисленное значение Z-статистики равно 4-1,38. Чему равнор-значение?
8.41. Какое статистическое решение следует принять, если в задаче 8.40 уровень значимости равен 0,01?
Применение понятий
8.42. Компания Glen Valley Steel Company производит стальные стержни. Если процесс производства осуществляется нормально, средняя длина стержней не меньше 2,8 фута, а стандартное отклонение равно 0,20 фута (это значение установлено техническими требованиями). Более длинные стержни могут быть использованы для других целей либо укорочены, а более короткие выбрасываются в отходы. Из партии произведенной продукции извлекается случайная выборка, состоящая из 25 стержней. Средняя длина стержней в выборке равна 2,73 фута. Компания желает определить, соответствует ли продукция стандарту.
1. Сформулируйте нулевую и альтернативную гипотезы.
2. Допустим, что компания применяет критерий с уровнем значимости, равным 0,05. Какое решение следует принять, если для проверки гипотезы вычисляется критическое значение?
3. Допустим, что компания применяет критерий с уровнем значимости, равным 0,05. Какое решение следует принять, если для проверки гипотезы вычисляется р-значение?
4. Дайте интерпретацию p-значения в данной задаче.
5. Сравните решения задач 2 и 3.
8.43. Директор швейной фабрики желает определить, соответствует ли ткань, произведенная на новом станке, заданным техническим требованиям. В частности, ткань должна иметь прочность не меньше 70 фунтов на кв. дюйм при стандартном отклонении 3,5 фунта. Анализ выборки, состоящей из 49 отрезов ткани, показал, что средняя прочность ткани равна 69,1 фунта.
1. Сформулируйте нулевую и альтернативную гипотезы.
2. Есть ли основания утверждать, что новый станок не соответствует техническим требованиям, если для проверки гипотезы вычисляется критическое значение? (Уровень значимости равен 0,05.)
3. Есть ли основания утверждать, что новый станок не соответствует техническим требованиям, если для проверки гипотезы вычисляется р-значение? (Уровень значимости равен 0,05.)
4. Дайте интерпретациюр-значения в этой задаче.
5. Сравните решения задач 2 и 3?
6. Повторите решение задач 1-5, если средняя прочность ткани в выборке, состоящей из 49 отрезов, равна 70,4 фунта.
8.44. Производитель соусов использует для заполнения бутылок конвейерный разливочный автомат. В соответствии с техническими требованиями в каждой бутылке должно содержаться 8 унций соуса. Стандартное отклонение количества соуса в бутылке равно 0,15 унции. Периодически из произведенной продукции выбираются 50 бутылок. Если среднее количество соуса в бутылке меньше 8 унций, конвейер останавливается. Допустим, что выборочное среднее равно 7,983.
1. Сформулируйте нулевую и альтернативную гипотезы.
2. Есть ли основания утверждать, что среднее количество соуса в бутылках меньше 8 унций, если для проверки гипотезы вычисляется критическое значение? (Уровень значимости равен 0,05.)
3. Есть ли основания утверждать, что среднее количество соуса в бутылках меньше 8 унций, если для проверки гипотезы вычисляется р-значение? (Уровень значимости равен 0,05.)
4. Дайте интерпретацию p-значения в этой задаче.
5. Сравните решения задач 2 и 3.
8.45. Банкоматы должны содержать достаточное количество денег, чтобы удовлетворить запросы клиентов на протяжении выходных. Однако, если банкомат содержит избыточное количество денег, банк теряет прибыль. Допустим, что в конкретном отделении банка среднее количество денег, извлекаемых клиентами из банкомата, равно 160 долл., причем стандартное отклонение равно 30 долл. Предположим, что для анализа из генеральной совокупности извлечена выборка, состоящая из 36 транзакций. Выборочное среднее оказалось равным 172 долл.
1. Есть ли основания утверждать, что среднее количество денег, снятых клиентами, больше 160 долл., если для проверки гипотезы вычисляется критическое значение? (Уровень значимости равен 0,05.)
2. Есть ли основания утверждать, что среднее количество денег, снятых клиентами, больше 160 долл., если для проверки гипотезы вычисляется p-значение? (Уровень значимости равен 0,05.)
3. Дайте интерпретацию p-значения в этой задаче.
4. Сравните решения задач 2 и 3.
8.4. ИСПОЛЬЗОВАНИЕ f-КРИТЕРИЯ ДЛЯ ПРОВЕРКИ ГИПОТЕЗЫ О МАТЕМАТИЧЕСКОМ ОЖИДАНИИ ПРИ НЕИЗВЕСТНОМ СТАНДАРТНОМ ОТКЛОНЕНИИ
В большинстве ситуаций, касающихся числовых данных, стандартное отклонение ст неизвестно. Однако эту величину можно оценить, вычислив выборочное стандартное отклонение S. Если генеральная совокупность является нормально распределенной, выборочное среднее обладает /-распределением с п-1 степенями свободы. Это дает возможность сформулировать /-критерий для оценки разности между выборочным средним X и математическим ожиданием генеральной совокупности ц.
ИСПОЛЬЗОВАНИЕ f-КРИТЕРИЯ ДЛЯ ПРОВЕРКИ ГИПОТЕЗЫ О МАТЕМАТИЧЕСКОМ ОЖИДАНИИ ПРИ ИЗВЕСТНОМ СТАНДАРТНОМ ОТКЛОНЕНИИ
где тестовая статистика t имеет /-распределение с п-1 степенями свободы.
Чтобы проиллюстрировать применение /-критерия, вернемся к задаче об аудиторской проверке в компании Saxon Home Improvement Company. Для проверки аудитор извлекает из информационной системы выборку накладных, заполненных в течение
последнего месяца. Средняя сумма накладных за последние пять лет равна 120 долл. Аудитор должен оценить, изменилась ли сумма накладных. Иначе говоря, в ходе проверки гипотезы требуется доказать, что средняя сумма накладных увеличивается или уменьшается.
Применение критического значения. Для проверки гипотезы с помощью двустороннего критерия применяется алгоритм, приведенный во врезке 8.2.
Шаги 1 и 2. Формулируем нулевую и альтернативную гипотезы.
Ио: ц = 120 долл., Нх: р 120 долл.
Обратите внимание на то, что предметом доказательства является альтернативная гипотеза. Если нулевая гипотеза отклоняется, значит, у нас есть веские доказательства того, что средняя сумма накладных отличается от 120 долл. Если нулевая гипотеза не отклоняется, значит, у нас нет достаточных доказательств, чтобы утверждать, будто средняя сумма накладных отличается от 120 долл.
Шаг 3. Полагаем а = 0,05.
Шаг 4. Из генеральной совокупности накладных извлекается случайная выборка, состоящая из п = 12 накладных.
Шаг 5. Поскольку предполагается, что генеральная совокупность является нормально распределенной и стандартное отклонение известно, применяется Z-критерий.
Шаг 6. При фиксированном объеме выборки п тестовая статистика t имеет ^-распределение с п-1 степенями свободы. Если заданный уровень значимости а равен 0,05, критические значения ^-распределения с 12—1=11 степенями свободы можно найти в табл. Д.З, как показано на рис. 8.9. Фрагмент табл. Д.З приведен в табл. 8.3. Поскольку альтернативная гипотеза И1:ц^120 долл, является ненаправленной (nondirectional), область отклонения гипотезы в Z-критерии разделяется на две части, ограниченные левым и правым хвостами Z-распределения. Площадь каждой из областей равна 0,025.
t -2,2010 0 +2,2010 t L.
It i г
Область Область принятия Область отклонения гипотезы отклонения
гипотезы
гипотезы
Критическое $120 Критическое X
значение значение
Рис. 8.9. Проверка гипотезы о математическом ожидании при неизвестном стандартном отклонении, уровне значимости, равном 0,05, и 11 степенях свободы
Таблица 8.3. Вычисление критического значения f-статистики для интегральной площади, равной 0,025, при 11 степенях свободы5
Площади, ограниченные правым хвостом распределения
Степени свободы 0,25 0,10 0,05 0,025 0,01 0,005
1 1,0000 3,0777 6,3138 12,7062 31,8207 63,6574
2 0,8165 1,8856 2,9200 4,3027 6,9646 9,9248
3 0,7649 1,6377 2,3534 3,1824 4,5407 5,8409
4 0,7407 1,5332 2,1318 2,7764 3,7469 4,6041
5 0,7267 1,4759 2,0150 2,5706 3,3649 4,0322
6 0,7176 1,4398 1,9432 2,4469 3,1427 3,7074
7 0,7111 1,4149 1,8946 2,3646 2,9980 3,4995
8 0,7064 1,3968 1,8595 2,3060 2,8965 3,3554
9 0,7027 1,3830 1,8331 2,2622 2,8214 3,2498
10 0,6998 1,3722 1,8125 2,2281 2,7638 3,1693
11 0,6974 1,3634 1,7959 2,2010 2,7181 3,1058
По табл. Д.З определяем, что критическое значение равно ±2,2010. Решающее правило таково:
если t < -^=-2,2010 или t > Zu=+2,2010, нулевая гипотеза отклоняется, в противном случае она не отклоняется.
Шаг 7. Ниже приведены данные о суммах (в долларах) из выборки, состоящей из 12 накладных.
INVOICES.XLS
108,98 152,22 111,45 110,59 127,46 107,26 93,32 91,97 111,56 75,71 128,58 135,11
Результаты вычислений, связанных с аудиторской проверкой компании Saxon Home Improvement Company, приведены на рис. 8.10.
п
X = —---= 112,85 долл.,
п
S = —--------= 20,80 долл.
п — \
В соответствии с формулой (8.2) ^-статистика равна:
J-ц _ 112,85-120 = 5 20,80
4п -jn
5 Фрагмент табл. Д.З.
___J------ . a . . ..-.I___________
1 Проверка гипотезы о средней сунне накладных
э —
4 Null Hypothesis
5 Level of Significance
6 'Sample Size________
7 Sample Mean_______________
8 -Sample Standard Deviation
JO ________________________
11 -Standard Error of the Mean Degrees of Freedom
13 - t Test Statistic
“14
Data ..
120 0.05 __________12 112.8508333 20.7979918
Intermediate Calculations
6.003863082
__________11
-1.19076111
15 'IB' "l7
IB "19
Two-Tail Test
Lower Critical Value Upper Critical Value p-Value_____________________________________
Do not reject the null hypothesis
-2.200986273 2.200986273 0.258809315
Рис. 8.10. Результаты применения одновыборочного t-критерия для проверки гипотезы о средней сумме накладных, полученные с помощью программы Microsoft Excel
Шаг 8. Поскольку -2,201 < t = -1,19 < 2,201, тестовая статистика попадает в область принятия гипотезы (см. рис. 8.9).
Шаг 9. Гипотеза Ноне отклоняется.
Шаг 10. Аудитор не имеет оснований утверждать, что средняя сумма накладных за последний месяц значительно отличается от 120 долл.
Подход, основанный на вычислении p-значения. Применим подход, основанный на вычислении наблюдаемого уровня значимости (р-значения).
Шаги 1-5. Совпадают с алгоритмом, использующим критические значения.
Шаг 6.t = -1,19 (см. шаг 7 алгоритма, использующего критические значения).
Шаг 7. Программа Microsoft Excel позволяет вычислять p-значение. Например, как показывают результаты аудиторской проверки, продемонстрированные на рис. 8.10, p-значение для двустороннего критерия равно 0,26.
Шаг 8. Наблюдаемый уровень значимостир = 0,26 больше уровня значимости а = 0,05.
Шаг 9. Гипотеза Но не отклоняется.
Шаг 10. Аудитор не имеет оснований утверждать, что средняя сумма накладных отличается от 120 долл. Более того, p-значение означает, что, если бы нулевая гипотеза была верной, вероятность того, что выборочное среднее 12 накладных отличается от 120 долл, на величину не меньше 7,5 долл., равна 0,26. Иначе говоря, если математическое ожидание генеральной совокупности накладных действительно равно 120 долл., то в 26% случаев наблюдаемое выборочное среднее меньше 112,85 или больше 127,15 долл.
Обратите внимание на то, что в рассмотренном примере нельзя утверждать, что в 26% случаев нулевая гипотеза верна. Эта неправильная интерпретация р-значения свидетельствует о недостаточном знании статистики. Помните, что p-значение является условной вероятностью, вычисляемой в предположении, что нулевая гипотеза верна. В общем, можно утверждать следующее. Если нулевая гипотеза верна, то шанс обнаружить выборку, которая противоречит нулевой гипотезе, равенр х 100% .
Одновыборочный t-критерий применяется в тех ситуациях, когда стандартное отклонение генеральной совокупности о неизвестно и оценивается с помощью выборочного стандартного отклонения S. Этот критерий является классической параметрической процедурой. Он сопровождается большим количеством строгих ограничений, гарантирующих корректность полученных результатов. Эти ограничения перечислены ниже.
ОГРАНИЧЕНИЯ, НАЛАГАЕМЫЕ НА ПРИМЕНЕНИЕ ОДНОВЫБОРОЧНОГО Г-КРИТЕРИЯ
Предполагается, что выборка принадлежит нормально распределенной генеральной совокупности. На практике, если выборка достаточно велика, а распределение не слишком асимметрично, t-распределение хорошо аппроксимирует выборочное распределение средних, когда s неизвестно.
Процедуры Excel: проверка гипотезы о математическом ожидании при неизвестном стандартном отклонении с помощью ^-критерия
Чтобы создать рабочий лист, предназначенный для проверки гипотезы о математическом ожидании генеральной совокупности при неизвестном стандартном отклонении с помощью ^критерия, можно воспользоваться функциями стьюдрасп и стьюдраспобр или надстройкой PHStat2.
Например, чтобы проверить с помощью t-критерия гипотезу о средней сумме накладных, как показано на рис. 8.10, необходимо выполнить одну из следующих процедур.
Применение Excel в сочетании с надстройкой PHStat2
Чтобы проверить гипотезу о математическом ожидании генеральной совокупности при неизвестном стандартном отклонении с помощью t-критерия, следует применить процедуру PHStat1^One-Sample Tests^t-test for the Mean, sigma unknown... (РН31а^Одновыборочные критерии1^t-критерий для математического ожидания, стандартное отклонение неизвестно...).
1. Выбрать команду PHStat^One-Sample Tests^t-test for the Mean, sigma unknown.
2. В диалоговом окне t-test for the Mean, sigma unknown (см. иллюстрацию) сделать следующее.
2.1. Ввести в окне редактирования Null Hypothesis (Нулевая гипотеза) число 120.
2.2. Ввести в окне редактирования Level of Significance (Уровень значимости) число о. 05.
2.3. Установить переключатель Sample Statistics Options (Параметры выборочных статистик) в положение Sample Statistics Unknown (Выборочные статистики неизвестны). Ввести в окне редактирования Sample Range Cell (Диапазон ячеек, содержащий выборку) диапазон ячеек А1 :А13 и установить флажок First cell contains label (Первая ячейка содержит метку).
2.4. Установить переключатель Test Options (Параметры критерия) в положение Two-Tailed Test (Двусторонний критерий).
2.5. Ввести в окне редактирования Title соответствующий заголовок.
2.6. Щелкнуть на кнопке ОК.
t Test for the Mean, sigma unknown
Data - -
Null Hypothesis:
Level of Significance;
Sample Statistics Options
Г Sample Statistics Known
i* Sample Statistics Unknown Sample Cell Range: |A1:A13 _-j
M First cell contains label
Test Options
»• Two-Tail Testi
Г Upper-Tail Test
Г' Lower-Tail Test
Output Options
Title: |Проверка гипотезы о средней сумме
Help j | OK Cancel |
Если объем выборки, выборочное среднее и стандартное отклонение известны, в п. 2.3 следует установить переключатель Sample Statistics Options в положение Sample Statistics Known (Выборочные статистики известны) и ввести значения в соответствующих окнах редактирования. Для односторонних критериев в п. 2.4 переключатель Test Options вместо положения Two-Tailed Test необходимо установить в положение Upper-Tail Test (Ограниченный сверху критерий) или Lower-Tail Test (Ограниченный снизу критерий).
Применение Excel I
Чтобы самостоятельно создать рабочий лист, выполняющий проверку гипотезы о математическом ожидании при известном стандартном отклонении с помощью Лкритерия, следуйте инструкциям, изложенным в разделе ЕН.8.2.
Chapter 8.xls
* Данные, на основе которых выполняется проверка гипотезы о средней сумме накладных при неизвестном стандартном отклонении с помощью Лкритерия, содержатся в рабочей книге Chapter 8 . xls на листе Рис8.10.
Условия, налагаемые на применение одновыборочного ^-критерия, можно проверить с помощью программы Microsoft Excel. Как показано в разделе 5.2, предположение о нормальности распределения можно проверить несколькими способами. Чтобы убедиться, насколько точно выборочные данные соответствуют теоретическим свойствам нормального распределения, можно воспользоваться методами описательной статистики, а также средствами графического анализа (гистограммой, диаграммой “ствол и листья”, блочной диаграммой и графиком нормального распределения).
На рис. 8.11-8.13 приведены описательные статистики, график нормального распределения и блочная диаграмма, полученные с помощью программы Microsoft Excel на основе данных о накладных.
Суммы накладных
, 1. !______
‘З Среднее 112,8508333
4 J Стандартная ошибка 6,003863082
_5 .Медиана 111,02
_6*Мода #Н/Д
Стандартное отклонение 20,7979918
8 [Дисперсия выборки
9 IЭксцесс 15' 1Т 1'2
Асимметричность Интервал Минимум
13 Максимум Сумма Счет
14
15
16 [Наибольший(1)
17 j Наименьший(1)
432,5564629 0,172707598 0,13363802
76,51
75,71
152,22
1354,21
12
152,22
75,71
Рис. 8.11. Описательные статистики, полученные с помощью программы Microsoft Excel на основе данных о накладных
Г рафик нормального распределения для суммы накладных
-2 -1.5 -1 -0.5 0 0.5 1 1.5 2
Z-значение
Рис. 8.12. График нормального распределения, построенный с помощью программы Microsoft Excel на основе данных о накладных
Блочная диаграмма для суммы накладных
70 80 90 100 110 120 130 140 150 160
Рис. 8.13. Блочная диаграмма, построенная с помощью программы Microsoft Excel на основе данных о накладных
Поскольку среднее значение очень близко к медиане, а точки на графике нормального распределения возрастают, колеблясь вокруг прямой линии, нет оснований говорить, что генеральная совокупность сумм накладных не является нормально распределенной. Таким образом, аудиторскую проверку следует признать корректной.
Одновыборочный t-критерий является устойчивым (robust). Его мощность не снижается, если кривая распределения, из которой извлечена выборка, отличается от нормальной, особенно если объем выборки достаточно велик (в этом случае для t-статистики справедлива центральная предельная теорема). Однако некорректное применение t-статистики может привести к ошибочным выводам. Если объем выборки п невелик (меньше 30) и распределение генеральной совокупности не является даже приближенно нормальным, следует применять непараметрические (nonparametrical) процедуры проверки гипотез [1, 2].
УПРАЖНЕНИЯ К РАЗДЕЛУ 8.4
Изучение основ
8.46. Предположим, что из нормально распределенной генеральной совокупности извлечена выборка, объем которой п = 16, выборочное среднее X = 56, а выборочное стандартное отклонение S' = 12. Чему равно значение t-статистики при проверке нулевой гипотезы, заключающейся в том, что ц = 50?
8.47. Сколько степеней свободы имеет t-статистика, положенная в основу одновыборочного t-критерия в задаче 8.46?
8.48. Чему равно критическое значение t-статистики, положенной в основу одновыборочного t-критерия с уровнем значимости, равным 0,05, в задачах 8.46-8.47 если альтернативная гипотеза заключается в следующем?
1. р*50.
2. ц> 50.
8.49. Какой статистический вывод следует сделать в задачах 8.46-8.48, если альтернативная гипотеза заключается в следующем?
1. ц^50.
2. ц> 50.
8.50. Можно ли применять t-критерий для проверки нулевой гипотезы Нп, заключающейся в том, что ц = 60, если выборка имеет объем п = 16 и извлечена из генеральной совокупности с распределением, имеющим отрицательную асимметрию? Выборочное среднее равно X = 65, а выборочное стандартное отклонение S = 21. Обоснуйте свой ответ.
8.51. Можно ли применять t-критерий для проверки нулевой гипотезы Н„, заключающейся в том, что ц = 60, если выборка имеет объем п = 160 и извлечена из генеральной совокупности с распределением, имеющим отрицательную асимметрию? Выборочное среднее равно X = 65, а выборочное стандартное отклонение S = 21. Обоснуйте свой ответ.
Применение понятий
Задачи 8.52-8.54 можно решить вручную или с помощью программы Microsoft Excel. Задачи 8.55-8.61 следует решать с помощью программы Microsoft Excel.
8.52. Консультант крупного университета сообщает родителям абитуриентов стоимость учебников, необходимых в течение семестра. Выборочное среднее, подсчитанное для 100 студентов, равно 315,40 долл., а стандартное отклонение — 43,20 долл.
1. Можно ли утверждать, что математическое ожидание генеральной совокупности больше 300 долл., если уровень значимости равен 0,01?
2. Как изменится ответ на вопрос 1, если стандартное отклонение равно 75 долл., а уровень значимости — 0,05?
3. Как изменится ответ на вопрос 1, если выборочное среднее равно 305,11 долл., а стандартное отклонение — 43,20 долл.?
8.53. Компания, производящая батарейки для ручных фонариков, создала выборку из 13 батареек, произведенных за смену, и подвергла их испытанию на длительность работы. Ниже приведено количество часов, которые проработала каждая батарейка до момента отказа.
^BATTERIES .XLS
342 426 317 545 264 451 1049 631 512 266 492 562 298
1. Можно ли утверждать, что средняя продолжительность работы батареек больше 400 ч (уровень значимости равен 0,05)?
2. Вычислите p-значение и дайте его интерпретацию.
3. Можно ли заявлять в рекламном объявлении, что “батарейки работают не менее 400 ч”?
4. Допустим, что первое значение в выборке равно 1 342, а не 342. Решите задачи 1-3 при новых данных. Сравните результаты.
8.54. В недавно опубликованной статье (Nanci Hellmich, “Supermarket Guru’ Has a Simple Mantra”, USA Today, June 19, 2002, 7D) утверждалось, что средняя продолжительность пребывания в супермаркете равна 22 мин. Предположим, что для проверки этого утверждения из генеральной совокупности извлечена выборка, состоящая из 50 покупателей местного супермаркета. Средняя выборочная продолжительность пребывания в супермаркете оказалась равной 25,36 мин., а стандартное отклонение — 7,24 мин. Можно ли утверждать, что средняя продолжительность пребывания в местном супермаркете отличается от 22 мин., если уровень значимости равен 0,01?
8.55. Приведенные ниже данные характеризуют объем лимонада в 50 двухлитровых бутылках. Результаты измерений представлены в виде неупорядоченного массива. fi^DRINK.XLS
2,109 2,086 2,066 2,075 2,065 2,057 2,052 2,044 2,036 2,038
2,031 2,029 2,025 2,029 2,023 2,020 2,015 2,014 2,013 2,014
2,012 2,012 2,012 2,010 2,005 2,003 1,999 1,996 1,997 1,992
1,994 1,986 1,984 1,981 1,973 1,975 1,971 1,969 1,966 1,967
1,963 1,957 1,951 1,951 1,947 1,941 1,941 1,938 1,908 1,894
1. Можно ли утверждать, что средний объем жидкости в бутылках отличается от 2 литров (уровень значимости равен 0,05)?
2. Вычислите /7-значение и дайте его интерпретацию.
3. Какие предположения о среднем объеме жидкости в бутылках следует принять в задаче 1?
4. Проверьте предположение, сформулированное в задаче 3, используя средства графического анализа. Корректны ли результаты, полученные при решении задачи 1? Объясните свой ответ.
5. Упорядочьте числа, указанные в таблице. Какое распределение имеет генеральная совокупность, из которой извлечена эта выборка? Корректны ли результаты, полученные при решении задачи 1?
8.56. Один из основных критериев качества услуг, предоставляемых любой организацией, — скорость, с которой она реагирует на жалобы клиентов. Крупный универмаг, торгующий фурнитурой и коврами, за последние годы значительно расширился. В частности, отдел ковровых покрытий, в котором прежде работали два человека, теперь состоит из руководителя, измерителя и 15 продавцов. На протяжении последнего года компания получила 50 жалоб на работу этого отдела. Ниже приведены данные о количестве дней, прошедших со дня получения жалобы до принятия решения. ftFURNITURE .XLS.
54 5 35 137 31 27 152 2 123 81 74 27
11 19 126 110 110 29 61 35 94 31 26 5
12 4 165 32 29 28 29 26 25 1 14 13
13 10 5 27 4 52 30 22 36 26 20 23
33 68
1. Начальник отдела утверждает, что средняя продолжительность рассмотрения жалобы не превышает 20 дней. Можно ли утверждать, что это утверждение не соответствует действительности, если уровень значимости равен 0,05 (иначе говоря, средний срок рассмотрения жалоб превышает 20 дней)?
2. Какие ограничения должны быть наложены на распределение генеральной совокупности в задаче 1?
3. Можно ли утверждать, что ограничения, наложенные в задаче 2, серьезно нарушаются? Аргументируйте свой ответ.
4. Как влияет ответ на вопрос 3 на корректность результатов, полученных при решении задачи 1?
8.57. В одной из статей, опубликованных в журнале Quality Engineering, исследуется вязкость (т.е. величина сопротивления потоку) химического вещества из разных партий. В файле ft CHEMICAL. XLS приведены данные о 120 партиях.
Источник: D. S. Holmes, and Mergen А. Е., “Parabolic Control Limits for the Exponentially Weighted Moving Average Control Charts”, Quality Engineerong, 4( 1992): p. 487-495.
1. Предыдущие исследования показывают, что средняя вязкость равна 15,5. Можно ли утверждать, что средняя вязкость изменилась, если уровень значимости равен 0,01?
2. Какие ограничения должны быть наложены на распределение генеральной совокупности в задаче 1?
3. Можно ли утверждать, что ограничения, наложенные в задаче 2, серьезно нарушаются? Аргументируйте свой ответ.
4. Сравните выводы, полученные при решении задачи 1, с результатами решения задачи 2.64.
8.58. В штате Нью-Йорк сберегательным банкам разрешено осуществлять страхование жизни. В процедуру оформления страховки входят изучение запроса, проверка медицинской информации, возможные дополнительные медицинские исследования и проверка информации, поступившей из полиции. Чтобы страхование жизни было прибыльным для банка, необходимо ускорить оформление страховки. Банк создал выборку, в которой указано время, затраченное на оформление 27 страховок в течение одного месяца, ft INSURANCE .XLS.
73 19 16 64 28 28 31 90 60 56 31 56 22 18
45 48 17 17 17 91 92 63 50 51 69 16 17
1. Предыдущие исследования показывают, что средний срок оформления заявки равен 45 дней. Можно ли утверждать, что средний срок оформления изменился, если уровень значимости равен 0,05?
2. Какие ограничения должны быть наложены на распределение генеральной совокупности в задаче 1?
3. Можно ли утверждать, что ограничения, наложенные в задаче 2, серъезно нарушаются? Аргументируйте свой ответ.
4. Сравните выводы, полученные при решении задачи 1, с результатами решения задачи 3.56.
8.59. На автомобильном заводе стальные заготовки разрезаются на куски, из которых впоследствии изготавливаются передние сиденья автомобилей. Заготовки разрезаются с помощью алмазной пилы. Отклонение от эталона не должно превышать 0,005 дюйма. В файле ftsTEEL. XLS приведены отклонения от эталона размеров 100 заготовок, измеренных с помощью лазерных приборов. Например, величина -0,002 означает, что заготовка короче эталона на 0,002 дюйма.
1. Можно ли утверждать, что среднее отклонение от эталона не равно 0,0 дюйма (уровень значимости равен 0,05)?
2. Какие ограничения должны быть наложены на распределение генеральной совокупности в задаче 1?
3. Можно ли утверждать, что ограничения, наложенные в задаче 2, серъезно нарушаются? Аргументируйте свой ответ.
4. Проверьте выполнение предположений, необходимых для решения задачи 3, с помощью графических средств. Адекватны ли результаты, полученные при решении задачи 1? Аргументируйте свой ответ.
8.60. Одним из показателей качества процесса упаковки чая является вес отдельного пакетика (см. задачу 3.55). В файле ftTEABAGS . XLS приведен вес 50 пакетиков чая.
1. Можно ли утверждать, что средний вес пакетика не равен 5,5 г (уровень значимости равен 0,01)?
2. Постройте 99%-ный доверительный интервал для среднего веса пакетика в генеральной совокупности. Дайте его интерпретацию.
3. Сравните решения задач 1 и 2.
8.61. В файле ftcHANGE. XLS приведены колебания стоимости акций 30 взаимных фондов (Wall Street Journal, March 7, 2003). Для каждого фонда в столбце “Изменение” указана разница между стоимостью акций 6 и 7 марта 2003 года.
1. Можно ли утверждать, что средний курс акций отличается от курса, зарегистрированного 6 марта 2003 года (уровень значимости равен 0,05)?
2. Какие предположения следует сделать при решении задачи 1?
3. Вычислите p-значение и дайте его интерпретацию.
8.5. ПРИМЕНЕНИЕ Z-КРИТЕРИЯ ДЛЯ ПРОВЕРКИ ГИПОТЕЗЫ О ДОЛЕ ПРИЗНАКА В ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ
В некоторых ситуациях необходимо оценить долю признака р в генеральной совокупности, а не математическое ожидание. Из генеральной совокупности можно извлечь случайную выборку, вычислить долю признака в выборке ps = Х/п (sample proportion) и сравнить ее с гипотетическим значением параметра р.
Если количество успехов X и количество неудач п-Х больше пяти, выборочное распределение доли хорошо аппроксимируется стандартизованным нормальным распределением. Чтобы оценить разность между фактической долей признака ps и гипотетическим параметром р, применяется критерий для проверки гипотезы о доле признака (test for the proportion).
КРИТЕРИЙ ДЛЯ ПРОВЕРКИ ГИПОТЕЗЫ О ДОЛЕ ПРИЗНАКА В ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ
Z=-P~P , (8.3)
рО-р)
N и
X количество успехов „ .
где pv = — =-------------= наблюдаемая доля успехов , р — гипотетическая доля
п размер выборки
успехов в генеральной совокупности. Z-статистика аппроксимируется стандартизованным нормальным распределением.
Статистику, положенную в основу Z-критерия, можно записать следующим образом.
КРИТЕРИЙ ДЛЯ ПРОВЕРКИ ГИПОТЕЗЫ О ДОЛЕ ПРИЗНАКА, ИСПОЛЬЗУЮЩИЙ КОЛИЧЕСТВО УСПЕХОВ
Z = .Х"пр . (8.4)
у]пр(\-р)
В качестве иллюстрации рассмотрим результаты опроса, опубликованные недавно в журнале Wall Street Journal. В ходе исследования оценивалось количество мужчин и женщин, владеющих надомным бизнесом. В опросе приняли участие 899 респондентов, в том числе 369 женщин. (De Lisser, Е., and D. Morse, “More Men Work at Home Than Women, Study Shows”, The Wall Street Journal, May 18, 1999, p. B2.)
Нулевая и альтернативная гипотезы формулируются следующим образом:
Но: р = 0,50 (доля женщин, владеющих надомным бизнесом, равна 0,5), р Ф 0,50 (доля женщин, владеющих надомным бизнесом, не равна 0,5).
Применение критического значения. Поскольку нас интересует, равна ли доля женщин, владеющих надомным бизнесом, числу 0,5, следует применить двусторонний критерий. Если уровень значимости равен 0,05, области отклонения принятия гипотезы определяются так, как показано на рис. 8.14. Решающее правило формулируется следующим образом:
если Z > +1,96 или Z < -1,96, гипотеза Но отклоняется;
в противном случае она принимается.
Рис. 8.14. Двусторонний критерий для проверки гипотезы о доле признака с уровнем значимости, равным 0,05
Поскольку среди 899 владельцев надомного бизнеса оказалось 369 женщин, имеем: 369 р= —= 0,41046.
s 899
Используя формулу (8.3), получаем:
р-р 0,41046-0,50 -0,08954 г „
р(1-р) 0,50(1-0,50) 0,0167
N п У 899
Тот же самый результат можно получить, применяя формулу (8.4).
z Х-пр 369-899x0,50 _ -80,5 _ 5 3?
~ y/npfl-p) ”7^00x0,50x0,50 " 14,99 “
Поскольку -5,37 < -1,96, нулевую гипотезу следует отклонить. Таким образом, есть основания утверждать, что доля женщин среди владельцев надомного бизнеса не равна 0,50. Результаты этой проверки приведены на рис. 8.15.
А В Проверка гипотезы о доле женщин среди 1 владельцев надомного бизнеса ”2
3 Data
4 Hull Hypothesis р= 0.5
5 Level of Significance 0.05
6 Humber of Successes 369
7 Sample Size 899
В .
9 Intermediate Calculations
1D -Sample Proportion 0 410456062
11 'Standard Error 0 016675934
12 Z Test Statistic -5.369650635
13
14 Two-Tail Test
15 Lower Critical Value -1.959962787
16 Upper Critical value 1.959962787
17 p-Value 7.9064E-08
10 Reject the null hypothesis
Рис. 8.15. Результаты проверки гипотезы о доле женщин среди владельцев надомного бизнеса с помощью программы Microsoft Excel
Применение p-значения. Существует альтернативный подход к проверке гипотез о доле признака в генеральной совокупности. Он основан на вычислении р-значения. Поскольку мы применяем двусторонний критерий, в котором критическая область разделена на две части, ограниченные левым и правым хвостами распределения, необходимо вычислить площадь области, расположенной левее -5,37 и правее +5,37. На рис. 8.15 показано, что эта вероятность равна 0,000000079064 (т.е. 7,9064Е-08). Поскольку эта величина меньше уровня значимости (а = 0,05), нулевая гипотеза отклоняется. Чрезвычайно малоер-значение означает, что выборочная доля признака, равная 0,41046, если истинная доля равна 0,5, весьма маловероятна.
Процедуры Excel: проверка гипотезы о доле признака с помощью Z-критерия
Чтобы создать рабочий лист, предназначенный для проверки гипотезы о доле признака в генеральной совокупности с помощью Z-критерия, можно воспользоваться функциями НОРМРАСП И НОРМРАСПОБР.
Например, чтобы проверить с помощью Z-критерия гипотезу о доле женщин среди владельцев надомного бизнеса, как показано на рис. 8.15, необходимо выполнить одну из следующих процедур.
Применение Excel в сочетании с надстройкой PHStat2
Чтобы проверить гипотезу о доле признака с помощью /критерия, следует применить процедуру PHStat^One-Sample Tests^Z-test for the Proportion... (PHStat^OflHOBbi6opo4Hbie критерии^ Z-критерий для доли признака...) и выполнить следующие действия.
1. Выбрать команду PHStati=>One-Sample Tests^Z-test for the Proportion.
2. В диалоговом окне Z-test for the Proportion (см. иллюстрацию) сделать следующее.
2.1. Ввести в окне редактирования Null Hypothesis (Нулевая гипотеза) число 0.5.
2.2. Ввести в окне редактирования Level of Significance (Уровень значимости) число 0.05.
2.3. Ввести в окне редактирования Number of Successes (Количество успехов) число 369.
2.4. Ввести в окне редактирования Sample Size (Объем выборки) число 8 99.
2.5. Установить переключатель Test Options (Параметры критерия) в положение Two-Tailed Test (Двусторонний критерий).
Z Test for the Proportion
Data
Null Hypothesis: 10.5
Level of Significance: 10.05
Number of Successes: |зб9
Sample Size: 1899
Test Options
<• Two-Tail Test
C Upper-Tail Test
Lower-Tail Test
Output Options
Title: iПроверка гипотезы о доле женщин
Cancel |
i*J I I
2.6. Ввести в окне редактирования Title соответствующий заголовок.
2.7. Щелкнуть на кнопке ОК.
Для односторонних критериев в п. 2.5 переключатель Test Options необходимо установить в положение Upper-Tail Test (Ограниченный сверху критерий) или Lower-Tail Test (Ограниченный снизу критерий).
Применение Excel
Чтобы самостоятельно создать рабочий лист, выполняющий проверку гипотезы о доле признака с помощью /критерия, следуйте инструкциям, изложенным в разделе ЕН.8.3.
Chapter 8.xls
Данные, на основе которых выполняется проверка гипотезы о доле женщин среди владельцев надомного бизнеса с помощью /критерия, содержатся в рабочей книге Chapter 8.xls на листе Рис8.15.
Изучение основ
8.62. Предположим, что в выборке, состоящей из 400 элементов, 88 оказались бракованными. Какова доля бракованных элементов в выборке?
8.63. Допустим, нулевая гипотеза в задаче 8.62 заключается в том, что выборка содержит 20% бракованных элементов. Чему равна Z-статистика, положенная в основу критерия?
8.64. Вернемся к задачам 8.62 и 8.63. Рассмотрите нулевую гипотезу Нп:р = 0,20 и двустороннюю альтернативную гипотезу Н^.р^ 0,20 при уровне значимости, равном 0,05. Какой вывод следует сделать?
Применение понятий
8.65. В статье, опубликованной в журнале Wall Street Journal (Carlos Tejada, “Work Week”, Wall Street Journal, July 25, 2000, Al), утверждается, что более половины всех американцев предпочитают получить 100 долларов вместо дополнительного выходного дня. Этот вывод основан на исследовании, проведенном компанией American Express Incentive Services, в ходе которого 593 из 1 040 респондентов заявили, что предпочитают деньги дополнительному отдыху.
1. Можно ли утверждать, что более половины всех американцев предпочитают получить 100 долларов вместо дополнительного выходного дня, если уровень значимости равен 0,05?
2. Вычислите p-значение и дайте его интерпретацию.
8.66. В ходе общенационального опроса, проведенного организацией Peter D. Hart Research Associates, 44% (или 357 человека) из 811 опрошенных владельцев персональных компьютеров указали, что считают защиту информации об их кредитных карточках основным препятствием для развития электронной торговли. Кроме того, 72% (584 человека) готовы приобрести более безопасный компьютер, если бы это стало возможным. На вопрос, сколько они готовы заплатить за дополнительную безопасность, 57% (462 человека) указали, что доплатили бы более 75 долл. (“Hart Poll Finds 72% of PC Owners Would Purchase a More Secure Computer if Available”, Business Wire, Washington D.C., September 11, 2001).
1. Проверьте нулевую гипотезу о том, что 50% всех владельцев персональных компьютеров в США считают защиту информации об их кредитных карточках основной проблемой. Альтернативная гипотеза утверждает, что доля таких респондентов не равна 50%. Уровень значимости равен 0,05.
2. Вычислите p-значение и дайте его интерпретацию р-значения.
3. Можно ли утверждать, что более половины всех владельцев персональных компьютеров в США готовы доплатить более 75 долл, за дополнительную безопасность своих компьютеров?
4. Вычислитеp-значение и дайте его интерпретацию р-значения.
5. Можно ли утверждать, что более 55% всех владельцев персональных компьютеров в США готовы доплатить более 75 долл, за дополнительную безопасность своих компьютеров?
6. Вычислитеp-значение и дайте его интерпретацию р-значения.
8.67. Для того чтобы хранить и обрабатывать огромные массивы данных, многие компании затрачивают крупные средства на увеличение емкости хранилищ. Однако
на фоне экономического спада, наступившего в экономике США, многие компании не в состоянии нести дополнительные расходы. В июле 2001 г. выяснилось, что 38% опрошенных компаний не стали тратить средства на расширение своих хранилищ данных из-за экономического спада. Объем выборки не указывался (Jeff Mead, “The Real Cost of Storage”, eWEEK, October 1, 2001, 40).
1. Предположим, что приведенные выше результаты получены в ходе опроса 50 компаний. Можно ли утверждать, что менее половины компаний не стали тратить средства на расширение своих хранилищ данных из-за экономического спада, если уровень значимости равен 0,01?
2. Вычислитер-значение и дайте его интерпретацию.
3. Предположим, что приведенные выше результаты получены в ходе опроса 100 компаний. Можно ли утверждать, что менее половины компаний не стали тратить средства на расширение своих хранилищ данных из-за экономического спада, если уровень значимости равен 0,01?
4. Вычислитер-значение и дайте его интерпретацию.
5. Сравните решения задач 1 и 2 с решениями задач 3 и 4. Объясните, как объем выборки влияет на уровень значимости.
6. Какие этические проблемы возникают из-за того, что в отчете не указан объем выборки?
8.68. Одной из основных задач, стоящих перед электронными торговцами, является способность превращать посетителей Web-сайтов в покупателей (М. Totty, “Making the Sale”, Wall Street Journal, September 24, 2001, R6). Эта способность измеряется показателем, который равен проценту посетителей, купивших что-либо. В статье утверждалось, что этот показатель для сайта llbean.com равен 10,1%, а для сайта vistoriasecret.com— 8,2%. Допустим, что каждый из этих сайтов был реконструирован, чтобы повысить процент покупателей. Предположим, что для каждого сайта была отобрана случайная выборка, состоящая из 200 посетителей, причем покупки сделали 24 посетителя сайта llbean.com и 25 посетителей сайта vistoriasecret. com .
1. Можно ли утверждать, что процент покупателей сайта llbean.com увеличился, если уровень значимости равен 0,05?
2. Можно ли утверждать, что процент покупателей сайта vistoriasecret. com увеличился, если уровень значимости равен 0,05?
8.69. Все больше работающих женщин откладывают материнство на будущее, считая, что это может помешать их карьере. До сих пор многие женщины основное время уделяют восхождению по карьерной лестнице, а детей считают обузой. Опрос 187 участников конференции “Самая деловая женщина”, организованного журналом Fortune Magazine, показал, что 133 участника имели по крайней мере одного ребенка (Carol Hymowitz, “Women Plotting Mix of Work and Family Won’t Find Perfect Plan”, Wall Street Journal, June 11, 2002, Bl). Предположим, что группа из 187 женщин представляет собой случайную выборку из генеральной совокупности всех деловых женщин, достигших успеха.
1. Чему равна выборочная доля деловых женщин, имеющих детей?
2. Можно ли утверждать, что более половины деловых женщин, добившихся успеха не имеют детей, если уровень значимости равен 0,05?
3. Можно ли утверждать, что более половины деловых женщин, добившихся успеха, имеют детей, если уровень значимости равен 0,05?
4. Можно ли утверждать, что более двух третей деловых женщин, добившихся успеха, имеют детей, если уровень значимости равен 0,05?
5. Выполняются ли условия, налагаемые на выборку? Аргументируйте свой ответ.
8.70. Весной 2002 года фирма Office Depot начала самую крупную рекламную кампанию в своей истории. В ее основу была положена серия телевизионных рекламных роликов, в которых снялись известные эстрадные артисты и спортсмены, включая бывшего тренера NHL Билла Парселса (Bill Parcells), супермодель Кэти Айрленд (Kathy Ireland) и олимпийскую чемпионку по фигурному катанию Тару Липински (Tara Lipinski). Руководство компании испытывало смешанные чувства от успеха своих звездных рекламных роликов. Ключевой мерой успеха телевизионных роликов является доля зрителей, которым они “очень понравились”. Социологическая служба Harris Ad Research Service провела опрос 1 189 взрослых зрителей, видевших ролики, и выяснила, что 18% зрителей считают ролики очень привлекательными. По данным организации Harris, доля телезрителей, которым нравится смотреть рекламные ролики, равна 22% (Theresa Howard, “Stars Don’t Mean Hits for Ads”, www. usatoday. com, April 22, 2002).
1. Существуют ли основания утверждать, что рекламная кампания фирмы Home Depot оказалась менее успешной, чем обычно, т.е. доля зрителей, которым понравились рекламные ролики компании Home Depot, меньше 22%, если уровень значимости равен 0,01?
2. Вычислите p-значение и объясните его смысл.
8.71. В ходе недавнего опроса интервьюеры попросили 400 жителей США в возрасте от 35 до 64 лет, имеющих высшее образование и годовой доход выше 100 000 долл., ответить, согласны ли они с утверждением: “Правительство должно больше контролировать частный бизнес”. Пятьдесят два процентов респондентов согласились с этим утверждением (“USA Today Snapshots”, USA Today, July 16, 2002, Bl). Вычислите p-значение и проверьте, есть ли основания утверждать, что более половины жителей США в возрасте от 35 до 64 лет, имеющих высшее образование и годовой доход выше 100 000 долл, согласны с тем, что правительство должно больше контролировать частный бизнес.
8.6. ПОТЕНЦИАЛЬНЫЕ ПРОБЛЕМЫ И ЭТИЧЕСКИЕ ВОПРОСЫ, СВЯЗАННЫЕ С ПРОВЕРКОЙ ГИПОТЕЗ
Итак, мы рассмотрели основные принципы проверки гипотез. Она используется Г / i для анализа разности между выборочными оценками (т.е. статистиками) и ха-’--рактеристиками генеральной совокупности (т.е. параметрами). Кроме того, мы
можем оценивать вероятность ошибок 1- и 2-го рода.
На некоторые вопросы необходимо ответить еще на этапе планирования. Для этого следует обратиться к профессиональному статистику. Однако часто это происходит слишком поздно, когда данные уже собраны. Единственное, что может сделать профессионал в этой ситуации, — посоветовать подходящую процедуру обработки данных. Остается лишь надеяться, что плохое планирование опроса не приведет к существенным искажениям результатов, хотя это является большой натяжкой. Корректное исследование невозможно без хорошего планирования. Чтобы избежать искажения результатов опроса, необходимо с самого начала придерживаться правильной стратегии.
ВРЕЗКА 8.5. ВОПРОСЫ, НА КОТОРЫЕ НЕОБХОДИМО ОТВЕТИТЬ ПРИ ПЛАНИРОВАНИИ ПРОВЕРКИ ГИПОТЕЗ
• Какова цель опроса, исследования или эксперимента? Можно ли сформулировать ее в виде нулевой и альтернативной гипотез?
• Какой вид критерия следует выбрать: дву- или односторонний?
• Можно ли извлечь случайную выборку из интересующей нас генеральной совокупности?
• Какие измерения можно выполнить на основе выборки? Какие показатели получаются в результате измерений: числовые или категорийные?
• Какой уровень значимости следует выбрать?
• Достаточно ли велик объем выборки, чтобы достичь желаемой мощности критерия при заданном уровне значимости?
• Какую процедуру выбора следует применить при формировании выборки и почему?
• Какие выводы можно сделать на основе проверки гипотез и как интерпретировать результаты?
Следует различать некорректную методологию и неэтичное поведение, которое, как правило, выражается в нечестном манипулировании процедурой проверки гипотез. Этические проблемы возникают на всех этапах проверки гипотез: при сборе данных, при проведении опроса, при выборе критерия и уровня значимости, при подтасовке, очистке и отбрасывании данных, а также при документировании результатов.
Метод сбора данных — рандомизация
Чтобы избежать возможного искажения результатов, необходимо применять правильный метод сбора данных. Для получения осмысленных результатов выборку следует формировать случайным образом, а в ходе эксперимента использовать процедуру рандомизации. Респондентов нельзя отбирать целенаправленно или по их собственному желанию. Пренебрежение рандомизацией может привести к серьезному искажению результатов и обесценить весь опрос.
Добросовестность респондентов
Этические нормы требуют, чтобы респонденты были проинформированы о цели исследования и потенциальных последствиях опроса. Кроме того, респондент должен быть добросовестным и честно отвечать на вопросы.
Вид критерия — двусторонний или односторонний
Как правило, односторонние критерии обладают более высокой мощностью, чем двусторонние. С другой стороны, если исследователей интересует лишь величина отклонения от нулевой гипотезы, а не ее знак, более приемлемым является двусторонний критерий. Например, если предыдущие исследования или теоретические рассуждения показали, что отклонение от нулевой гипотезы имеет определенный знак, можно применять односторонний критерий.
Выбор уровня значимости
В хорошо продуманном исследовании уровень значимости устанавливают до сбора данных. Его нельзя изменять задним числом, стремясь достичь желаемого результата. Это привело бы к подтасовке данных. Таким образом, формулируя выводы, полученные в результате проверки гипотезы, всегда необходимо указывать/>-значение.
Подтасовка данных
Никогда не следует подтасовывать данные (data snooping). Ни в коем случае нельзя сначала проверить гипотезу, проанализировать результат, а затем выбрать вид критерия и/или уровень значимости. Эти этапы выполняют заранее, еще до сбора данных. Иначе выводы исследования потеряют смысл. Нулевая и альтернативная гипотезы, а также уровень значимости должны быть установлены с самого начала.
Очистка и отбрасывание данных
Очистка данных не является подтасовкой. При редактировании, кодировании и переписывании ответов на вопросы исследователи могут обнаружить экстремальные или необычные данные. Если проверка гипотез касается числовых данных, необходимо построить диаграмму “ствол и листья” и блочную диаграмму. Это позволит очистить данные и отбросить экстремальные значения, которые лишь искажают истинную картину. Кроме того, предварительный анализ полученных данных должен сопровождаться проверкой предположения о распределении генеральной совокупности.
Процесс очистки данных поднимает важные этические вопросы. Следует ли вообще исключать некие данные из исследования? Разумеется, да, если выяснится, что измерения проводились некорректно. Иногда у исследователей нет выбора — например, респондент может отказаться от дальнейшего участия в опросе, не закончив отвечать на вопросы. В хорошо продуманном исследовании статистик должен заранее сформулировать правила отбрасывания данных.
Документирование результатов
В любом исследовании необходимо честно документировать как положительные, так и отрицательные результаты, чтобы последователи не повторяли ваших ошибок. Нельзя публиковать лишь результаты, обладающие статистической значимостью, игнорируя результаты, не имеющие достаточных подтверждений. Если исследователь не имеет достаточных оснований отклонить нулевую гипотезу, он должен понимать, что это не является доказательством ее истинности. Это лишь означает, что у вас нет достаточной информации, чтобы опровергнуть нулевую гипотезу при данном объеме выборки.
Статистическая значимость и практическая ценность
Исследователь, принимающий решение на основе проверки гипотезы, должен ясно различать статистическую значимость и практическую ценность результата в контексте конкретной прикладной области. Иногда очень большой объем выборки, необходимый для достижения статистически значимого результата, сводит на нет его практическую ценность. Например, предположим, что перед проведением общенациональной рекламной кампании по телевидению считалось, что доля людей, признающих некую торговую марку, равна 0,30. После завершения кампании выяснилось, что рекламируемую торговую марку признают 6 168 респондентов из 20 000. Односторонний критерий показывает, что эта доля теперь превышает 0,30 с уровнем значимости р, равным 0,0047, и можно вполне обоснованно утверждать, что доля потребителей, признающих данную торговую марку, увеличилась. Значит ли это, что рекламная кампания была успешной? Результаты проверки гипотез свидетельствуют, что признание торговой марки выросло на статистически значимую величину, но можно ли считать это увеличение значимым с практической точки зрения? Обратите внимание на то, что доля потребителей, признающих указанную торговую марку, равна 6 168/20 000 = 0,3084, или 30,84%. Это величина превышает гипотетическое значение, равное 30%, меньше чем на 1%. Привели ли крупные затраты на телевизионную рекламу к существенному росту популярности торговой марки? Учитывая большой объем затраченных средств и незначительный прирост популярности,
рекламную кампанию следует признать неудачной. С другой стороны, если доля поклонников рекламируемой торговой марки увеличилась бы на 20%, рекламную кампанию пришлось бы назвать успешной.
Подводя итоги, следует отметить, что главным аспектом в обсуждении проверки гипотез является намерение. Необходимо различать неправильный анализ данных и нечестное поведение, которое проявляется в целенаправленном формировании выборки, манипулировании респондентами, подтасовке данных, выборе подходящего критерия (дву- или одностороннего), подгонке уровня значимости, игнорировании фактов, противоречащих желательной гипотезе, и замалчивании неудобных данных.
8.7. МОЩНОСТЬ КРИТЕРИЯ
Обсуждая критерии для проверки гипотез, мы определили два вида риска, возникающего при принятии решений о параметрах генеральной совокупности на основе выборочного анализа. Как указывалось в разделе 8.1, величина а представляет собой вероятность того, что будет отклонена истинная нулевая гипотеза, которая не должна быть отвергнута, а величина р является вероятностью того, что не будет отвергнута ложная нулевая гипотеза, которую следовало отклонить. Мощность критерия, равная величине 1-р, характеризует чувствительность статистического критерия — вероятность отклонить ложную нулевую гипотезу, которая должна быть отвергнута. Мощность статистического критерия зависит от того, насколько значительно истинное математическое ожидание генеральной совокупности отличается от гипотетического (принятого в гипотезе Но), уровня значимости ос и объема выборки. Если истинное и гипотетическое математические ожидания существенно отличаются друг от друга, мощность критерия будет выше, а если разность между истинным и гипотетическим математическим ожиданием мала, мощность критерия снижается. Чем выше уровень значимости а, тем легче отвергнуть гипотезу Но, и, следовательно, выше мощность критерия. Чем больше объем выборки, тем точнее оценки и легче обнаружить разность между истинными и гипотетическими параметрами. Это также увеличивает мощность критерия.
В данном разделе понятие мощности статистического критерия иллюстрируется задачей о расфасовке кукурузных хлопьев. Предположим, что процесс расфасовки подвергается периодическим проверкам, проводимым местным обществом по защите прав потребителей. Цель этих проверок — обнаружить недовес, т.е. выявить коробки, содержащие меньше 368 г кукурузных хлопьев. Таким образом, проверяющие стремятся найти свидетельства, что средний вес коробок меньше 368 г. В этой ситуации нулевая и альтернативная гипотезы формулируются следующим образом.
Но: ц > 368 (расфасовка выполняется правильно),
Ну: ц < 368 (расфасовка выполняется неправильно).
Проверяющий должен учесть, что стандартное отклонение веса коробки <т равно 15 г. Следовательно, можно применить Z-критерий. Если уровень значимости а равен 0,05, а случайная выборка состоит из 25 коробок, то значение X, позволяющее отклонить нулевую гипотезу, можно определить по формуле (8.1), в которой вместо X подставляется величина XL .
z = Az_H, а л/н
Поскольку этот критерий является односторонним, а его уровень значимости равен 0,05, то по табл. Д.2 (см. рис. 8.16) получаем, что величина Z на 1,645 стандартных отклонений меньше гипотетического математического ожидания, т.е.£ = -1,65.
Следовательно,
XL = 368 + (-1,645)-^= = 368 “ 4’935 = 363,065.
Решающее правило одностороннего критерия таково:
Гипотеза Но отклоняется, если X <363,065, в противном случае гипотеза Но не отклоняется.
Рис. 8.16. Определение нижнего критического значения одностороннего Z-критерия для проверки гипотезы о математическом ожидании генеральной совокупности при уровне значимости, равном 0,05
Решающее правило устанавливает, что, если выборочное среднее, вычисленное для случайной выборки, состоящей из 25 коробок, меньше 363,065 г, нулевая гипотеза отклоняется, и проверяющий приходит к выводу, что процесс расфасовки осуществляется неправильно. Мощность критерия измеряет вероятность прийти к выводу, что процесс выполняется неверно, на основе анализа величин, отличающихся от истинного математического ожидания генеральной совокупности.
Предположим, требуется определить вероятность отклонить нулевую гипотезу при условии, что истинный средний вес в генеральной совокупности коробок равен 360 г. На основе решающего правила необходимо определить площадь фигуры, лежащей под нормальной кривой слева от точки 363,065. На основе центральной предельной теоремы и предположения о нормальности распределения веса в генеральной совокупности коробок можно допустить, что выборочное распределение является нормальным. Следовательно, площадь фигуры, лежащей под нормальной кривой слева от точки 363,065, можно выразить в единицах стандартного отклонения, так как мы вычисляем вероятности отклонить нулевую гипотезу при условии, что истинный средний вес в генеральной совокупности коробок равен 360,00 г. Используя формулу (8.1), получаем.
z_x~^
а
4п
где Pi — истинное математическое ожидание генеральной совокупности. Следовательно,
363,065-360
V25
По табл. Д.2 определяем, что P(Z < +1,02) = 0,8461. Это и есть мощность критерия, равная площади фигуры, лежащей под нормальной кривой слева от точки 363,065 (рис. 8.17). Вероятность |3 того, что нулевая гипотеза (ц = 368) будет отклонена, равна 1 - 0,8461 = 0,1539. Следовательно, вероятность ошибки 2-го рода равна 0,1539.
Рис. 8.17. Определение мощности критерия и вероятности ошибки 2-го рода при условии, что 360 г
Определив мощность критерия при условии, что истинное математическое ожидание генеральной совокупности равно 360 г, мы можем вычислить мощность критерия при любом другом значении ц. Например, какова мощность критерия, если истинное математическое ожидание генеральной совокупности равно 352 г? Предположим, что стандартное отклонение, объем выборки и уровень значимости остаются неизменными. Тогда решающее правило принимает следующий вид.
Гипотеза Но отклоняется, если X <363,065, в противном случае гипотеза Но не отклоняется.
Поскольку мы проверяем гипотезу о математическом ожидании, снова применим формулу (8.1).
Z^X~^.
Если истинный средний вес генеральной совокупности коробок равен 352 г (см. рис. 8.18), то
7 363,065-352 , _ Z =-----g------= 3,69.
V25
По табл. Д.2 определяем, что P(Z < +3,69) = 0,99989. Это и есть мощность критерия, равная площади фигуры, лежащей под нормальной кривой слева от точки 363,065 (см. рис. 8.18). Таким образом, вероятность ошибки 2-го рода равна 0,00011.
Рис. 8.18. Определение мощности критерия и вероятности ошибки 2-го рода при условии, что 11,= 352 г
В двух рассмотренных выше примерах мощность критерия была довольно высокой, а вероятность ошибки 2-го рода, наоборот, небольшой. В следующем примере мощность критерия вычисляется при условии, что средний вес генеральной совокупности коробок равен 367 г. Это значение очень близко к гипотетическому математическому ожиданию, равному 368 г.
Вновь применим формулу (8.1).
z .
о
Если математическое ожидание генеральной совокупности равно 367 г (см. рис. 8.19), то
363,065-367 _
15 " ’
л/25
По табл. Д.2 определяем, что P(Z < -1,31) = 0,0951. Поскольку в данном примере область отклонения гипотезы лежит в левой части распределения, мощность критерия равна 0,0951, а вероятность совершить ошибку 2-го рода — 0,9049.
+3,69 Z
Рис. 8.19. Определение мощности критерия и вероятности ошибки 2-го рода при условии, что ц,= 367 г
На рис. 8.20 показана мощность критерия для разных значений щ (включая три рассмотренные выше задачи). Этот график называется кривой мощности (power curve). Вычисления, проведенные для всех трех задач, суммированы на рис. 8.21.
Возможные истинные значения (г)
Рис. 8.20. Кривая мощности критерия для проверки гипотезы о среднем весе коробки кукурузных хлопьев при альтернативной гипотезе Н; ц < 368 г
Анализ рис. 8.21 показывает, что мощность рассмотренного одностороннего критерия резко возрастает (и стремится к 100%) по мере того, как истинное математическое ожидание генеральной совокупности удаляется от гипотетического математического ожидания, равного 368 г. Очевидно, что для данного одностороннего критерия, чем меньше истинное значение щ по сравнению с гипотетическим, тем больше вероятность обнаружить это отличие6. С другой стороны, если истинное значение щ близко к 368 г, мощность критерия снижается, поскольку он не может эффективно распознавать маленькие отличия между истинным и гипотетическим математическими ожиданиями.
Анализируя рис. 8.21, можно обнаружить резкие различия между мощностями критерия, соответствующими разным значениям истинного математического ожидания. Как оказано на панелях А и Б, если истинное математическое ожидание генеральной совокупности незначительно отличается от 368 г, вероятность отклонить нулевую гипотезу невелика. Однако, как только истинное математическое ожидание значительно отклоняется от гипотетического, мощность критерия резко возрастает и стремится к максимуму, равному единице (или 100%).
В ситуациях, относящихся к односторонним критериям, когда истинное среднее превышает гипотетическое среднее, наблюдается противоположная зависимость. Чем больше истинное среднее д, по сравнению с гипотетическим средним, тем выше мощность. С другой стороны, для двусторонних критериев, чем больше расстояние между истинным и гипотетическим средними, тем выше мощность критерия.
Область отклонения гипотезы Область принятия гипотезы
Панель А X = 363,065
Дано: а = 0,05, о = 15, л = 25
Односторонний критерий р1 = 368 (нулевая гипотеза является истинной)
X, = 368 - (1,645) -4^ = 363,065
<25
Решающее правило: если X < 363,065 гипотеза Но отклоняется; в противном случае она не отклоняется
Панель Б
Дано: а = 0,05, о = 15, п = 25
Односторонний критерий
Но: р = 368
р1 = 367 (истинное математическое ожидание равно 367 г) . Х-р1 _363,065-367, о 3
У п
Мощность = 0,0951
Р = 0,9049
Мощность = 0,0951
Панель В
367
X
Дано: а = 0,05, о = 15, л = 25
Односторонний критерий
Но: р = 368
Дано: а = 0,05, о = 15, л = 25
Односторонний критерий
Но: р = 368
Р! = 352 (истинное математическое ожидание равно 352 г)
_ 363,065-352 _ |369
° 3 Мощность = 0,99989
<л
3 = 0,00011
Мощность = 0,99989
352
Х= 363,065
Область отклонения гипотезы Область принятия гипотезы
Рис. 8.21. Вычисление мощности статистических критериев при разных значениях истинного математического ожидания генеральной совокупности
При вычислении мощности одностороннего статистического критерия мы полагали, что уровень значимости равен 0,05, а выборка состоит из 25 коробок. Учитывая это, можно определить эффект, который оказывают на мощность критерия перечисленные ниже параметры, варьируя их по одному.
• Тип статистического критерия — односторонний или двусторонний.
• Уровень значимости а.
• Объем выборки п.
Оставляя эти упражнения в качестве самостоятельной работы (задачи 8.95-8.101), сформулируем три основных вывода, касающихся мощности критерия.
ВРЕЗКА 8.6. МОЩНОСТЬ КРИТЕРИЯ
Три основных вывода, относящихся к мощности критерия.
• Односторонний критерий имеет более высокую мощность, чем двусторонний. Его следует применять, когда требуется определить направление альтернативной гипотезы.
• Поскольку вероятность ошибки 1-го рода (а) и вероятность ошибки 2-го рода (£) противоположны, причем ошибка 2-го рода является параметром, дополнительным к мощности критерия 1-р, мощность критерия прямо зависит от параметра а. Повышение уровня значимости а увеличивает мощность критерия, а снижение уровня значимости уменьшает ее.
• С увеличением объема выборки п мощность критерия повышается, а с уменыпе- . нием — снижается.
УПРАЖНЕНИЯ К РАЗДЕЛУ
Применение понятий
8.72. Торговый автомат газированной воды выдает по крайней мере 7 унций напитка на стакан при стандартном отклонении, равном 0,2 унции. Статистик, исследующий качество работы автомата, сформировал случайную выборку, содержащую 16 полных стаканов напитка. Вероятность ошибки 1-го рода принята равной а = 0,05. Необходимо вычислить вероятность ошибки 2-го рода (р) при следующих истинных математических ожиданиях генеральной совокупности.
1. 6,9 унции на стакан.
2. 6,8 унции на стакан.
8.73. Вернемся к задаче 8.72. Предположим, что статистик установил уровень значимости а равным 0,01. Вычислите мощность критерия и вероятность ошибки 2-го рода (Р) при следующих истинных математических ожиданиях генеральной совокупности.
1. 6,9 унции на стакан.
2. 6,8 унции на стакан.
3. Сравните результаты решения задач 1 и 2, а также задачи 8.72. Какой вывод можно сделать?
8.74. Вернемся к задаче 8.72. Предположим, что статистик сформировал случайную выборку, состоящую из 25 стаканов, а уровень значимости а установил равным 0,05. Вычислите мощность критерия и вероятность ошибки 2-го рода (р) при следующих истинных математических ожиданиях генеральной совокупности.
1. 6,9 унции на стакан.
2. 6,8 унции на стакан.
3. Сравните результаты решения задач 1 и 2, а также задачи 8.72. Какой вывод можно сделать?
8.75. Шины, произведенные на заводе, должны выдерживать не меньше 25 000 миль пробега. Опыт показывает, что стандартное отклонение пробега равно 3 500 миль. Начальник производства должен остановить процесс, если окажется, что шины не выдерживают больше 25 000 миль пробега. Предположим, что для разрушающей проверки случайным образом отобраны 100 шин, а уровень значимости а установлен равным 0,05. Вычислите мощность критерия и вероятность ошибки 2-го рода (р) при следующих истинных математических ожиданиях генеральной совокупности.
1. 24 000 миль.
2. 24 900 миль.
8.76. Вернемся к задаче 8.75. Предположим, что начальник производства установил уровень значимости а равным 0,01. Вычислите мощность критерия и вероятность ошибки 2-го рода (р) при следующих истинных математических ожиданиях генеральной совокупности.
1. 24 000 миль.
2. 24 900 миль.
3. Сравните результаты решения задач 1 и 2, а также задачи 8.75. Какой вывод можно сделать?
8.77. Вернемся к задаче 8.75. Предположим, что начальник производства случайным образом выбрал 25 шин и установил уровень значимости а равным 0,05. Вычислите мощность критерия и вероятность ошибки 2-го рода (Р) при следующих истинных математических ожиданиях генеральной совокупности.
1. 24 000 миль.
2. 24 900 миль.
3. Сравните результаты решения задач 1 и 2, а также задачи 8.75. Какой вывод можно сделать?
8.78. Вернемся к задаче 8.75. Предположим, что начальник производства должен остановить процесс, если окажется, что средний пробег шин отличается от 25 000 миль (как в большую, так и в меньшую сторону). Для проверки случайным образом выбраны 100 шин. Уровень значимости а установлен равным 0,05. Вычислите мощность критерия и вероятность ошибки 2-го рода (р) при следующих истинных математических ожиданиях генеральной совокупности.
1. 24 000 миль.
2. 24 900 миль.
3. Сравните результаты решения задач 1 и 2, а также задачи 8.75. Какой вывод можно сделать?
РЕЗЮМЕ
Как показано на структурной схеме главы, мы рассмотрели основные принципы проверки гипотез. В частности, изложены Z- и £-критерии проверки гипотез о математическом ожидании генеральной совокупности, а также Z-критерии для проверки гипотез о доле признака в генеральной совокупности. Кроме того, в главе рассмотрен ряд важных практических примеров. Следующие три главы развивают начатую тему.
Введение в проверку гипотез
Категорийные
. Числовые данные
Вид данных ।
Z-тест для доли признака
Нет
Да
Известно ли стандартное отклонение?
t- критерий
Z-критерий
Структурная схема главы 8
ОСНОВНЫЕ понятия
р-значение, 529
i-критерий для математического ожидания при неизвестном а, 540
Z-критерий для математического
ожидания при известном ст, 526
Z-критерий для проверки гипотезы о доле признака, 551
Вероятность
доверительная, 523
ошибки 1-го рода, 523
ошибки 2-го рода, 523
Гипотеза
альтернативная, 521
нулевая, 520
Критерий
двусторонний, 527
для проверки гипотезы о доле признака в генеральной совокупности, 551
направленный, 535
односторонний, 535
устойчивый, 547
Критическое значение, 523
Мощность критерия, 524
Отбрасывание данных, 558
Очистка данных, 558
Ошибка
1-го рода, 523
2-го рода, 523
Подтасовка данных, 558
Проверка гипотез, 520
Рандомизация, 557
Уровень
доверительный, 523
значимости, 523
наблюдаемый, 529
риска, 524
УПРАЖНЕНИЯК ГЛАВЕ I
Проверка знаний
8.79. Чем нулевая гипотеза отличается от альтернативной?
8.80. Чем ошибка 1-го рода отличается от ошибки 2-го рода?
8.81. Что называется мощностью критерия?
8.82. Чем односторонний критерий отличается от двустороннего?
8.83. Что называетсяр-значением?
8.84. Как проверить гипотезу о математическом ожидании генеральной совокупности с помощью доверительного интервала?
8.85. Перечислите этапы проверки гипотез.
8.86. Какие этические проблемы связаны с проверкой гипотез?
8.87. На какие вопросы необходимо ответить, планируя эксперимент или опрос для проверки гипотезы?
Применение понятий
Задачи 8.88-8.93 можно решать вручную или с помощью программы Microsoft Excel. Задачи 8.94-8.100 рекомендуется решать с помощью программы Microsoft Excel.
8.88. В статье, опубликованной в журнале Marketing News, утверждается, что при сравнении двух видов продукции компании часто занижают уровень значимости (Semon, Т. Т., “Consider a Statistical Insignificance Test”, Marketing News, February 1, 1999). Иначе говоря, в статье рекомендуется устанавливать уровень значимости больше 0,05. В частности, в статье повторяется проверка гипотезы о доле потребителей, предпочитающих покупать товар 1, а не товар 2. Нулевая гипотеза заключается в том, что доля покупателей, предпочитающих товар 1, равна 0,5. Наблюдаемый уровень значимости критерия (p-значение) равен 0,22. В статье предполагается, что в некоторых случаях существуют достаточные основания, чтобы отклонить нулевую гипотезу.
1. Сформулируйте нулевую и альтернативную гипотезы.
2. Опишите риски, связанные с ошибками 1- и 2-го рода.
3. К каким последствиям приведет отклонение нулевой гипотезы, если p-значение равно 0,22?
4. Почему в статье рекомендуется повысить уровень значимости?
5. Как бы вы поступили в этой ситуации?
6. Как вы ответите на вопрос 5, если p-значение равно 0,12? А если оно равно 0,06?
8.89. Компания La Quinta Inns разработала компьютерную модель, позволяющую оценивать прибыльность земельных участков, на которых предполагается строить новые гостиницы (Kines, S.E., and J. A. Fitzsimmon, “Selecting Profitable Hotel Sites at La Quinta Motor Inns”, Interfaces, 20, March-April 1990: 12-20). Если компьютерная модель прогнозирует большую прибыль, компания La Quinta покупает предложенный участок и строит на нем новый отель. Если программа прогнозирует небольшую или умеренную прибыль, компания отказывается от приобретения участка. Работу этой модели можно описать в терминах проверки гипотез. Нулевая гипотеза заключается в том, что предложенный земельный участок является убыточным. Альтернативная гипотеза состоит в том, что земельный участок принесет прибыль.
1. В чем заключается риск, связанный с ошибкой 1-го рода?
2. В чем заключается риск, связанный с ошибкой 2-го рода?
3. Какой тип ошибки наиболее опасен для компании La Quinta Motos Inns? Обоснуйте свой ответ.
4. Как изменение критерия, в соответствии с которым нулевая гипотеза отклоняется, влияет на вероятность ошибок 1- и 2-го рода?
8.90. В 1999 г. Главное бухгалтерское управление выяснило, что около трети из 23,4 млн. пенсионеров в возрасте от 65 лет и старше пользуются медицинскими страховками по программе Medicare, в той или иной степени оплачиваемыми работодателями (Carlos Tejada, “Work Week”, Wall Street Journal, June 26, 2002, B5). В статье предполагается, что доля этих пенсионеров возросла. Предположим, что в результате нового исследования выяснилось, что среди 500 случайно выбранных пенсионеров старше 65 лет 185 респондентов пользуются медицинскими льготами, предоставляемыми работодателями.
1. Можно ли утверждать, что доля пенсионеров старше 65 лет, пользующихся льготами, выросла, если уровень значимости равен 0,01?
2. Вычислите p-значение и дайте его интерпретацию.
8.91. Владелец автозаправочной станции желает знать предпочтения своих клиентов. Для этого на протяжении конкретной недели он создал выборку, состоящую из 60 автомобилистов, и вычислил следующие показатели.
• Объем купленного топлива: X =11,3 галлона, S = 3,1 галлона.
• Высококачественный бензин купили 11 автомобилистов.
1. Существуют ли основания утверждать, что средний объем купленного топлива не равен 10 галлонам, если уровень значимости равен 0,05?
2. Вычислите p-значение в задаче 1.
3. Существуют ли основания утверждать, что высококачественный бензин покупают меньше 20% автомобилистов, если уровень значимости равен 0,05?
4. Как изменится ответ на вопрос 1, если выборочное среднее равно 10,3 галлона?
5. Как изменится ответ на вопрос 3, если высококачественный бензин приобрели 7 автомобилистов?
8.92. Аудитору правительственного агентства поручено оценить, правильно ли осуществляется компенсация оплаты визитов к врачу по программе Medicare. Аудиторской проверке подвергаются все компенсации, выплаченные в определенном районе в течение месяца. Для проведения аудиторской проверки из генеральной совокупности извлечены 75 документов. Выборка характеризуется следующими показателями.
• Количество неправильно оплаченных компенсаций — 12.
• Средний размер компенсаций: X = 93,7 долл., S = 34,55 долл.
1. Существуют ли основания утверждать, что средний размер компенсации меньше 100 долл., если уровень значимости равен 0,05?
2. Существуют ли основания утверждать, что доля неверно оплаченных компенсаций больше 0,10, если уровень значимости равен 0,05?
3. При каких допущениях верен ответ на вопрос 1?
4. Как изменится ответ на вопрос 1, если выборочное среднее равно 90 долл.?
5. Как изменится вопрос на ответ 2, если в выборке оказалось 15 неправильно оплаченных компенсаций?
8.93. Филиал банка, расположенный в промышленном районе города, стремится повысить качество обслуживания клиентов во время обеда, с 12:00 до 13:00. На протяжении недели сотрудники записывали время ожидания клиентов, стоящих в очереди в течение обеденного перерыва (количество минут, прошедших от момента, когда клиент переступил порог филиала, до момента его обслуживания). Для оценки эффективности обслуживания создана выборка, содержащая данные о времени ожидания 15 клиентов.
ftbanki .xls
4,21 5,55 3,02 5,13 4,77 2,34 3,54 3,20 4,50 6,10 0,38 5,12 6,46 6,19 3,79
1. Существуют ли основания утверждать, что среднее время ожидания не превышает 5 мин., если уровень значимости равен 0,05?
2. При каких допущениях верен ответ на вопрос 1?
3. Оцените сделанные допущения с помощью средств графического анализа.
4. Когда клиент приходит в банк в течение обеденного перерыва, он обычно спрашивает менеджера, сколько времени ему придется стоять в очереди. Менеджер отвечает: “Почти наверняка, не больше 5 минут”. Прав ли менеджер?
8.94. Один из основных критериев качества услуг, предоставляемых любой организацией, — скорость, с которой она реагирует на жалобы клиентов. Один из больших универмагов, торгующих фурнитурой и коврами, за последние годы значительно расширился. В частности, отдел ковровых покрытий, в котором прежде работали два человека, теперь состоит из руководителя, измерителя и 15 продавцов. На протяжении последнего года компания получила 50 жалоб на работу этого отдела. Ниже приведены данные о количестве дней, прошедших со дня получения жалобы до принятия решения.
ftFURNITURE. XLS
54 5 35 137 31 27 152 2 123 81 74 27
11 19 126 110 110 29 61 35 94 31 26 5
12 4 165 32 29 28 29 26 25 1 14 13
13 10 5 27 4 52 30 22 36 26 20 23
33 68
Один из клиентов обратился в магазин с жалобой. Клиента интересует, скоро ли будет решена его проблема, а менеджер отвечает: “Почти наверняка, в течение 20 дней”. Оцените это утверждение.
8.95. В штате Нью-Йорк сберегательным банкам разрешено осуществлять страхование жизни. В процедуру оформления страховки входят изучение запроса, проверка медицинской информации, возможные дополнительные медицинские исследования и проверка информации, поступившей из полиции. Чтобы страхование жизни было прибыльным для банка, необходимо ускорить оформление страховки. Банк создал выборку, в которой указано время, затраченное на оформление 27 страховок в течение одного месяца, ft INSURANCE. XLS.
73 19 16 64 28 28 31 90 60 56 31 56 22 18
45 48 17 17 17 91 92 63 50 51 69 16 17
В банк обращается клиент. Его интересует, как долго будет оформляться страховка, а служащий отвечает: “Около 30 дней”. Оцените это утверждение.
8.96. Промышленная компания на Среднем Западе производит электрические изоляторы. Если во время работы изолятор выходит из строя, происходит короткое замыкание. Чтобы проверить прочность изолятора, компания проводит испытания. Сила, необходимая для разрушения изолятора, измеряется в фунтах. В таблице приведены результаты 30 экспериментов. FORCE. XLS.
1870 1728 1 656 1 610 1 634 1 784 1 522 1 696 1 592 1 662
1 866 1 764 1 734 1 662 1 734 1 774 1 550 1 756 1 762 1 866
1 820 1 744 1 788 1 688 1 810 1 752 1 680 1 810 1 652 1 736
1. Существуют ли основания утверждать, что средняя прочность изоляторов больше 1 500 фунтов, если уровень значимости равен 0,05?
2. При каких допущениях верен ответ на вопрос 1?
3. Оцените сделанные допущения с помощью средств графического анализа.
4. Какой вывод можно сделать о прочности изоляторов?
8.97. Исследования, проведенные компанией, производящей асфальтовую кровельную плитку в Бостоне и Вермонте, показали, что основным фактором, влияющим на оценку качества продукции, является ее объем или влажность. Если клиент обнаруживает в пакете сырую или влажную плитку, он считает ее бракованной. Иногда повышенная влажность плитки приводит к тому, что гранулы, приклеенные к ее поверхности для улучшения текстуры или цвета, отваливаются, ухудшая внешний вид. Компания предпринимает дополнительные меры для контроля влажности плиток. Плитка сначала взвешивается, а затем высушивается. Далее плитка вновь взвешивается, и на основании полученных результатов вычисляется вес жидкости на 100 квадратных футов. Компания стремится, чтобы среднее количество влаги не превышало 0,35 фунтов на 100 квадратных футов. В файле ^MOISTURE . XLS записаны результаты 36 измерений (фунтов на 100 кв. футов), выполненных для плиток, произведенных в Бостоне, и данные 31 измерения, выполненного для продукции завода в Вермонте.
1. Существуют ли основания утверждать, что средняя влажность бостонской плитки меньше 0,35 фунта на 100 кв. футов, если уровень значимости равен 0,05?
2. Дайте интерпретацию p-значения в задаче 1.
3. Существуют ли основания утверждать, что средняя влажность вермонтской плитки меньше 0,35 фунта на 100 кв. футов, если уровень значимости равен 0,05?
4. Дайте интерпретацию p-значения в задаче 3.
5. Оцените допущения, сделанные в задачах 1 и 3, с помощью средств графического анализа.
6. Проверьте предположения, касающиеся распределения влажности плиток, произведенных в Бостоне и Вермонте. Примените графические методы исследования.
8.98. Исследования, проведенные компанией, производящими рубероидную кровельную плитку в Бостоне и Вермонте, показали, что основным фактором, влияющим на оценку качества продукции, является ее вес. На последнем этапе плитка пакуется, а затем размещается на деревянных стеллажах (как правило, на поддоне помещается
16 плиток). После заполнения стеллажа регистрируется его вес. Файл © PALLET. XLS содержит данные о весе (в фунтах) 368 стеллажей, заполненных плитками, произведенными в бостонском отделении компании, и 330 стеллажей, загруженных в Вермонте.
1. Существуют ли основания утверждать, что средний вес стеллажа, заполненного плитками “Бостон”, больше 3 150 фунтов?
2. Дайте интерпретациюр-значения в задаче 1.
3. Существуют ли основания утверждать, что средний вес стеллажа, заполненного плитками “Вермонт”, больше 3 700 фунтов?
4. Дайте интерпретацию р-значения в задаче 3.
5. Можно ли утверждать, что предположения, необходимые для решения задач 1 и 3, серьезно нарушаются?
8.99. Производитель рубероидной кровельной плитки на заводах в Бостоне и Вермонте предоставляет своим клиентам 20-летнюю гарантию. Для того чтобы убедиться в том, что плитки прослужат указанный срок, на заводах проводят ускоренное испытание на долговечность. В ходе этого эксперимента плитка на протяжении нескольких минут подвергается интенсивному воздействию, эквивалентному воздействию, которому плитка подвергалась бы в обычных условиях в течение 20 лет. В частности, плитку несколько минут очень энергично скребут щетками, а затем взвешивают гранулы, которые отскакивают от плиток (в граммах). Чем меыпе гранул образуется в ходе эксперимента, тем долговечнее плитка. Для того чтобы прослужить весь гарантийный срок, плитка не должна потерять больше 0,8 г. В файле ^GRANULE. XLS содержатся данные о выборке, состоящей из 170 измерений, проведенных на заводе в Бостоне, и 140 измерениях, осуществленных на заводе в Вермонте.
1. Существуют ли основания утверждать, что средний вес гранул, утерянных плитками “Бостон”, отличается от 0,50 г?
2. Дайте интерпретацию р-значения в задаче 1.
3. Существуют ли основания утверждать, что средний вес гранул, утерянных плитками “Вермонт”, отличается от 0,50 г?
4. Дайте интерпретациюр-значения в задаче 3.
5. Можно ли утверждать, что предположения, необходимые для решения задач 1 и 3, серьезно нарушаются?
Отчеты
8.100. Напишите отчет, содержащий результаты решения задач 8.97-8.99. Соответствуют ли стандарту влажность, вес и долговечность плиток, произведенных на заводах в Бостоне и Вермонте? Вычислите статистические показатели с помощью программы Microsoft Excel и подготовьте презентацию с помощью программы Power Point.
Применение Интернет
8.101. Зайдите на сайт www.prenhall. com/levine. Выберите ссылку Chapter 8 и щелкните на ссылке Internet exercises.
Продолжая мониторинг качества печати, производственный отдел Springville Herald желает убедиться, что средняя насыщенность печати во всех экземплярах не меньше 0,97 по стандартной шкале, где наибольшее значение равно 1,0. Была сформирована случайная выборка, состоящая из 50 экземпляров ^SH8.XLS, и измерена насыщенность печати. Вычислите выборочные статистики и определите, существуют ли свидетельства, что насыщенность печати меньше 0,97. Напишите отчет, в котором изложите ваши выводы.
Насыщенность печати 50 экземпляров газеты
0,854 1,023 1,005 1,030 1,219 0,977 1,044 0,778 1,122 1,114
1,091 1,086 1,141 0,931 0,723 0,934 1,060 1,047 0,800 0,889
1,012 0,695 0,869 0,734 1,131 0,993 0,762 0,814 1,108 0,805
1,223 1,024 0,884 0,799 0,870 0,898 0,621 0,818 1,113 1,286
1,052 0,678 1,162 0,808 1,012 0,859 0,951 1,112 1,003 0,972
ПРИМЕНЕНИЕ WEB
Примените свои знания о проверке гипотез и оцените качество процесса расфасовки кукурузных хлопьев на заводе компании Oxford Cereals.
Компания Oxford Cereals провела публичный эксперимент и заявила, что успешно опровергла обвинения Организации потребителей, уверенных, что компания Oxford Cereal мошенничает (сокращенно — ОПУЧКОСМ), утверждавшей, что реальный вес коробок с кукурузными хлопьями меньше, чем номинальный. Проанализируйте пресс-релиз компании и сопровождающие документы, размещенные на Web-странице www.prenhall.com/ Springville/OC_WinTrust. htm), и ответьте на следующие вопросы.
1. Являются ли корректными результаты независимой проверки? Аргументируйте свой ответ. Предположим, что вы сами проводите подобный эксперимент. Что бы вы сделали иначе?
2. Подтверждают ли результаты проверки заявление компании Oxford Cereals, что она не обманывает потребителей?
3. Удивляет ли вас заявление компании Oxford Cereals о том, что реальный вес многих коробок превышает 368 г? Верно ли это заявление?
4. Существуют ли условия, при которых результаты публичного эксперимента и утверждения ОПУЧКОСМ одновременно являются правильными? Аргументируйте свой ответ.
СПРАВОЧНИК ПО EXCEL. ГЛАВА 8
ЕН.8.1. Использование Z-критерия проверки гипотез о математическом ожидании при известном стандартном отклонении
Создадим рабочий лист, использующий функции НОРМСТОБР и НОРМРАСП для проверки гипотезы о математическом ожидании при известном стандартном отклонении на основе Z-критерия. Вызовы функций НОРМСТОБР и НОРМСТРАСП выглядят следующим образом.
НОРМСТОБР {вероятность),
НОРМСТРАСП (Z-значение) ,
где параметр вероятность представляет собой площадь области, ограниченной кривой распределения и величиной X, а параметр Z-значение является значением Z-статистики, имеющей стандартизованное нормальное распределение.
Шаблон рабочего листа Z-критерий, соответствующий рис. 8.5, приведен в табл. ЕН.8.1. Здесь для вычисления нижнего и верхнего критических значений применяется функция НОРМСТОБР, а для вычисления р-статистики по критическому значению Z-статистики (ячейка В12), — функция НОРМСТРАСП. Чтобы применить двусторонний критерий, значение, возвращенное функцией НОРМСТРАСП, вычитается из единицы, а результат умножается на 2. Таким образом, в ячейке В17 находится р-значение критерия. Для сравнения p-значения, записанного в ячейке В17, с уровнем значимости, находящимся в ячейке В5, в шаблоне применяется также функция ЕСЛИ в ячейке А18 (см. раздел ЕН.З). В зависимости от результата рабочий лист выводит сообщение об отклонении или принятии гипотезы.
Таблица ЕН.8.1. Шаблон рабочего листа Z-критерий
д »
т Проверка гипотезы о среднем весе коробок с кукурузными хлопьями
2
3 Данные
4 Нулевая гипотеза ц= 368
5 Уровень значимости 0,05
6 Стандартное отклонение генеральной совокупности 15
7 Объем выборки 25
8 Выборочное среднее 372,5
9
10 Промежуточные вычисления
11 Стандартная ошибка среднего = В6/КОРЕНЬ(В7)
1Ш1 Величина Z =(В8-В4)/В11
13
14 Двусторонний критерий
15 Нижняя доверительная граница =НОРМСТОБР(В5/2)
16 Верхняя доверительная граница =НОРМСТОБР(1-В5/2)
17 р-значение =2*(1-НОРМСТРАСП(АВ5(В12))
18 =ЕСЛИ(В17<В5;"Нулевая гипотеза отклоняется"; "Нулевая гипотеза не отклоняется")
Реализация одностороннего критерия приведена в табл. ЕН.8.2.1 и ЕН.8.2.2. Эти таблицы отличаются от табл. ЕН.8.1 лишь строками 14-17. (Строка 18 всегда остается пустой.)
Таблица ЕН.8.2.1. Шаблон рабочего листа Z-критерий для одностороннего критерия
.В .. •. . '
14 Ограниченный снизу критерий
15 Нижнее критическое значение =Н0РМСТ0БР(В5)
16 р-значение =Н0РМСТРАСП(В12)
1 =ЕСЛИ(В1б<В5;"Нулевая гипотеза отклоняется"; "Нулевая гипотеза не отклоняется")
Таблица ЕН.8.2.2. Шаблон рабочего листа Гипотеза для одностороннего критерия
14 Ограниченный сверху критерий
15 Верхнее критическое значение =Н0РМСТ0БР(1-В5)
16 р-значение =1-Н0РМСТРАСП(В12)
17 =ЕСЛИ(В16<В5;"Нулевая гипотеза отклоняется"; "Нулевая гипотеза не отклоняется")
ЕН.8.2. Использование f-критерия для проверки гипотез о математическом ожидании при неизвестном стандартном отклонении
Создадим рабочий лист, использующий функции СТЬЮДРАСПОБР и СТЬЮДРАСП для проверки гипотезы о математическом ожидании при неизвестном стандартном отклонении на основе i-критерия. Вызовы этих функций выглядят следующим образом.
СТЬЮДРАСПОБР {1 -доверительный уровень-, степени_свободы),
СТЬЮДРАСП (ABS(t); степени_свободы; хвосты),
где ABS (£) — абсолютная величина t-статистики, параметр хвосты принимает значение 1 для одностороннего критерия и 2 — для двустороннего.
Шаблон рабочего листа t-критерий, соответствующий рис. 8.10, приведен в табл. ЕН.8.3. Он предназначен для проверки гипотезы о средней сумме накладных компании Saxon Home Improvement Company с помощью i-критерия. Здесь для вычисления нижнего и верхнего критических значений f-статистики применяется функция СТЬЮДРАСПОБР, а для вычисления р-значения, — функция СТЬЮДРАСП. В табл. ЕН.8.3 предполагается, что суммы накладных введены в столбце А рабочего листа Данные. Для вывода на экран сообщения об отклонении или принятии гипотезы в ячейке А18 используется функция ЕСЛИ.
Для вставки в ячейку А4 символа ц следует использовать шрифт Symbol. Реализация одностороннего критерия приведена в табл. ЕН.8.4. Обратите внимание на то, что табл. ЕН.8.5.1 и ЕН.8.5.2 отличаются от табл. ЕН.8.4 только ячейками D15 : Е18. (В ячейке Е17 параметр хвосты функции СТЬЮДРАСП равен единице.) Для вывода на экран сообщения об отклонении или принятии гипотезы в ячейке А18 используется функция ЕСЛИ.
Таблица ЕН.8.3. Шаблон рабочего листа t-критерий
А
1 Проверка гипотезы о средней сумме накладных
2
3 Данные
4 Нулевая гипотеза 120
5 Уровень значимости 0,05
6 Объем выборки =СЧЁТ(Данные!А:А)
7 Выборочное среднее =СРЗНАЧ(Данные!А:А)
8 Выборочное стандартное отклонение =СТАНДОТКЛОН(Данные!А:А)
9
10 Промежуточные вычисления
11 Стандартная ошибка среднего = В8/КОРЕНЬ(В6)
12 Степени свободы =Вб-1
1йв Л статистика =(В7-В4)/В11
14
15 Двусторонний критерий
16 Нижняя доверительная граница = -(СТЬЮДРАСПОБР(В5;В12))
iiill Верхняя доверительная граница =СТЬЮДРАСПОБР(В5;В12)
liili р-значение =СТЬЮДРАСП(АВ$(В13);В12;2)
19 =ЕСЛИ(В18<В5;"Нулевая гипотеза отклоняется"; "Нулевая гипотеза не отклоняется")
Таблица ЕН.8.4. Шаблон рабочего листа t-критерий для одностороннего критерия
;/ '' ' '' f Е * -с . /;?'
15 Область вычислений
16 Для односторонних критериев:
17 Значение СТЬЮДРАСП =СТЬЮДРАСП(АВ5(В13);В12;1)
18 1- СТЬЮДРАСП =1-Е17
Таблица ЕН.8.5.1. Шаблон рабочего листа t-критерий для одностороннего критерия.
ограниченного снизу
15 Ограниченный снизу критерий
16 Нижнее критическое значение =-(СТЬЮДРАСПОБР(2*В5;В12))
17 р-значение = ЕСЛИ(В13<0;Е17;Е18)
18 = ЕСЛИ(В17<В5;"Нулевая гипотеза отклоняется"; "Нулевая гипотеза не отклоняется")
Таблица ЕН.8.5.2. Шаблон рабочего листа t-критерий для одностороннего критерия,
ограниченного сверху
• - • ' ‘Л' - ‘ < А '' '
15 Ограниченный сверху критерий
16 Верхнее критическое значение =(СТЬЮДРАСПОЕ>Р(2*В5;В12))
jljlj р-значение = ЕСЛИ(В13<0;Е18;Е17)
18 = ЕСЛИ(В17<В5;"Нулевая гипотеза отклоняется"; "Нулевая гипотеза не отклоняется")
ЕН.8.3. Применение Z-критерия для проверки гипотез о доле признака в генеральной совокупности
Создадим рабочий лист, использующий функции НОРМСТОБР и НОРМСТРАСП, для проверки гипотезы о доле признака в генеральной совокупности на основе Z-критерия. Вызовы функций НОРМСТОБР и НОРМСТРАСП выглядят следующим образом.
НОРМСТОБР (вероятность) ,
НОРМСТРАСП (Z-значение) ,
где параметр вероятность представляет собой площадь области, ограниченной кривой распределения и величиной X, а параметр Z-значение является значением Z-статистики, имеющей стандартизованное нормальное распределение.
Шаблон рабочего листа Z-критерий, соответствующий рис. 8.15, приведен в табл. ЕН.8.6. Этот шаблон аналогичен рабочим листам, рассмотренным в разделе ЕН.8.1. Здесь для вычисления нижнего и верхнего критических значений применяется функция НОРМСТОБР, а для вычисления р-значения, — функция НОРМСТРАСП. Для сравнения p-значения, записанного в ячейке В17, с уровнем значимости, находящимся в ячейке В5, в шаблоне применяется также функция ЕСЛИ в ячейке А19. В зависимости от результата рабочий лист выводит сообщение об отклонении или принятии гипотезы.
Таблица ЕН.8.6. Шаблон рабочего листа Z-критерий
• ' - 1 А ; ' ' ... В
1 Проверка гипотезы о доле женщин, владеющих надомным бизнесом
2
<..31. ' Данные
4 Нулевая гипотеза р= 0,5
5 Уровень значимости 0,05
6 Количество успехов 369
7 Объем выборки 899
8
9 Промежуточные вычисления
ю Выборочная доля = Вб/В7
11 Стандартная ошибка = КОРЕНЬ(В4*(1-В4)/В7)
12 Величина Z =(В10-В4)/В11
13
Окончание табл. ЕН. 8.6
' ; В „У-, 'б. '
14 Двусторонний критерий
15 Нижняя доверительная граница = НОРМСТОБР(В5/2)
16 Верхняя доверительная граница =НОРМСТОБР(1-В5/2)
17 ^-значение =2*(1-НОРМСТРАСП(АВ5(В12)))
18 =ЕСЛИ(В17<В5;"Нулевая гипотеза отклоняется"; "Нулевая гипотеза не отклоняется")
Реализация одностороннего критерия приведена в табл. ЕН.8.7.1 и ЕН.8.7.2. Эти таблицы отличаются от табл. ЕН.8.6 лишь строками 14-17. (Строка 18 всегда остается пустой.)
Таблица ЕН.8.7.1. Шаблон рабочего листа Z-критерий для одностороннего критерия, ограниченного снизу
А
14 Ограниченный снизу критерий
15 Нижнее критическое значение = Н0РМСТ0БР(В5)
II /7-значение =НОРМСТРАСП(В12)
17 = ЕСЛИ(В1б<В5;"Нулевая гипотеза отклоняется"; "Нулевая гипотеза не отклоняется")
Таблица ЕН.8.7.2. Шаблон рабочего листа Z-критерий для одностороннего критерия,
ограниченного сверху
А : \ , ' В 7 .. .
14 Ограниченный сверху критерий
15 Нижнее критическое значение =Н0РМСТ0БР(1-В5)
16 /7-значение =1-НОРМСТРАСП(В12)
17 =ЕСЛИ(В16<В5;"Нулевая гипотеза отклоняется"; "Нулевая гипотеза не отклоняется")
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
1. Bradley, J. V., Distribution-Free Statistical Tests (Englewood Cliffs, NJ: Prentice Hall, 1968).
2. Daniel, W., Applied Nonparametric Statistics, 2nd ed. (Boston, MA: Houghton Mifflin, 1990).
3. Microsoft Excel 2002 (Redmond, WA: Microsoft Corporation, 2001).
Глава 9
Двухвыборочные критерии
ПРИМЕНЕНИЕ СТАТИСТИКИ: зависит ли объем продаж от вида полок в магазине?
9.1. СРАВНЕНИЕ ДВУХ НЕЗАВИСИМЫХ ВЫБОРОК: КРИТЕРИИ ДЛЯ ОЦЕНКИ РАЗНОСТИ МЕЖДУ ДВУМЯ МАТЕМАТИЧЕСКИМИ ОЖИДАНИЯМИ
Использование Z-критерия для оценки разности между двумя математическими ожиданиями
Применение 2-критерия для оценки разности между двумя математическими ожиданиями с помощью суммарной дисперсии Процедуры Excel: проверка гипотезы о разности математических ожиданий двух генеральных совокупностей на основе исходных выборок с помощью t-критерия, использующего суммарную дисперсию Процедуры Excel: проверка гипотезы о разности математических ожиданий двух генеральных совокупностей на основе сводных данных с помощью t-критерия, использующего суммарную дисперсию Доверительный интервал для разности между математическими ожиданиями Использование 2-критерия для оценки разности между двумя математическими ожиданиями с помощью раздельной дисперсии Процедуры Excel: проверка гипотезы о разности математических ожиданий двух генеральных совокупностей на основе выборок с помощью t-критерия, использующего раздельную дисперсию
9.2. СРАВНЕНИЕ ДВУХ ЗАВИСИМЫХ ВЫБОРОК: КРИТЕРИИ ДЛЯ ОЦЕНКИ РАЗНОСТИ МЕЖДУ ДВУМЯ МАТЕМАТИЧЕСКИМИ ОЖИДАНИЯМИ
Процедуры Excel: проверка гипотезы о разности между математическими ожиданиями двух генеральных совокупностей с помощью t-критерия Доверительный интервал, содержащий разность между двумя математическими ожиданиями
9.3. ИСПОЛЬЗОВАНИЕ Z-КРИТЕРИЯ
ДЛЯ ОЦЕНКИ РАЗНОСТИ МЕЖДУ ДВУМЯ ДОЛЯМИ ПРИЗНАКА
Процедуры Excel: применение Z-критерия для проверки гипотезы о разности между двумя долями признака
Доверительный интервал, содержащий разность между долями успехов в двух независимых группах
9.4. ИСПОЛЬЗОВАНИЕ F-КРИТЕРИЯ
ДЛЯ ОЦЕНКИ РАЗНОСТИ МЕЖДУ ДВУМЯ ДИСПЕРСИЯМИ
Вычисление нижнего критического значения Процедуры Excel: проверка гипотезы о разности между дисперсиями двух генеральных совокупностей на основе исходных выборок с помощью Е-критерия Процедуры Excel: проверка гипотезы о разности между дисперсиями двух генеральных совокупностей на основе сводных данных с помощью Е-критерия
СПРАВОЧНИК ПО EXCEL. ГЛАВА 9
ЧЕМУ ДОЛЖЕН НАУЧИТЬСЯ СТУДЕНТ
• Применять методы проверки гипотез для оценки разности между математическими ожиданиями двух независимых групп,
• Применять методы проверки гипотез для зависимых выборок.
• Применять методы проверки гипотез для оценки разности между двумя долями признака.
• Применять методы проверки гипотез для оценки разности между дисперсиями двух независимых групп.
ПРИМЕНЕНИЕ СТАТИСТИКИ
Зависит ли объем продаж от вида полок в магазине?
Влияет ли вид полок в магазине на объем продаж? Представьте себе, что вы — региональный менеджер по продажам компании BLK Foods и хотите сравнить объемы продаж BLK-колы, выставленной на обычных полках и на специализированных стеллажах. Для этого вы создаете выборку, состоящую из 20 магазинов компании BLK Foods, в которых объявлена полная распродажа товаров. Затем вы случайным образом делите эту выборку пополам: 10 магазинов относите к первой группе, а остальные 10 — ко второй. Менеджеры магазинов из первой группы размещают бутылки с BLK-колой на
| обычных полках среди других прохладительных напитков. В то же время менеджеры ма-I газинов из второй группы должны расположить бутылки с BLK-колой на специализиро-! ванных стеллажах и разместить на них рекламу. Как определить, одинаковы ли объемы ! продаж BLK-колы в магазинах из этих двух групп? Совпадает ли изменчивость объемов I продаж в этих магазинах? Как использовать ответы на эти вопросы, чтобы повысить объ-j емы продаж BLK-колы?
ВВЕДЕНИЕ
Проверка гипотез основана на подтверждающем подходе к анализу данных. В главе 9 рассмотрены широко распространенные процедуры проверки гипотез на основе одной выборки, извлеченной из одной генеральной совокупности. В этой главе описываются процедуры проверки гипотез на основе двух числовых выборок, извлеченных из двух генеральных совокупностей. Например, равны ли средние недельные объемы продаж BLK-колы, размещенной на специализированных стеллажах и на обычных полках?
9.1. СРАВНЕНИЕ ДВУХ НЕЗАВИСИМЫХ ВЫБОРОК: КРИТЕРИИ
ДЛЯ ОЦЕНКИ РАЗНОСТИ МЕЖДУ ДВУМЯ
МАТЕМАТИЧЕСКИМИ ОЖИДАНИЯМИ
Использование Z-критерия для оценки разности между двумя математическими ожиданиями
Предположим, что из первой генеральной совокупности извлекается случайная выборка, имеющая объем пр а из второй — случайная выборка, объем которой равен п2. Требуется проанализировать данные, принадлежащие каждой выборке. Обозначим математическое ожидание первой генеральной совокупности через а стандартное отклонение — через оР Аналогично математическое ожидание второй генеральной совокупности обозначим символом ц2, а стандартное отклонение — о2.
Статистика, положенная в основу критерия для проверки равенства математических ожиданий двух генеральных совокупностей, основана на разности между выборочными средними Ху - Хг. По центральной предельной теореме, сформулированной в разделе 6.6, при достаточно больших объемах выборок эта статистика имеет стандартизованное нормальное распределение. Следовательно, для оценки разности двух математических ожиданий можно сформулировать следующий критерий.
Z-КРИТЕРИЙ ДЛЯ ОЦЕНКИ РАЗНОСТИ МЕЖДУ ДВУМЯ МАТЕМАТИЧЕСКИМИ ОЖИДАНИЯМИ
Д, — и»'- » ~ "* а I
V п\ п1
где Ху — среднее значение выборки из первой генеральной совокупности, щ — математическое ожидание первой генеральной совокупности, с* — дисперсия первой генеральной совокупности, п, — объем выборки, извлеченной из первой генеральной совокупности, Х2 — среднее значение выборки из второй генеральной совокупности, ц2 — математическое ожидание второй генеральной совокупности, ст? — дисперсия второй генеральной совокупности, п2 — объем выборки, извлеченной из второй генеральной совокупности.
Статистика Z имеет стандартизованное нормальное распределение.
Применение ^-критерия для оценки разности между математическими ожиданиями с помощью суммарной дисперсии
В большинстве ситуаций дисперсии и стандартные отклонения двух генеральных совокупностей неизвестны. Единственная информация, доступная исследователю, — выборочные средние, выборочные дисперсии и выборочные стандартные отклонения. Если выборки являются случайными, независимыми и извлечены из нормально распределенных генеральных совокупностей, имеющих одинаковую дисперсию (т.е. Ст]2 = ст?), для проверки гипотезы о значимом различии между математическими ожиданиями двух генеральных совокупностей можно применять t-критерий, использующий суммарную дисперсию.
Нулевая гипотеза состоит в том, что математические ожидания двух независимых генеральных совокупностей не отличаются друг от друга:
Яо: И, - м, или g, - р, - 0.
Альтернативная гипотеза заключается в том, что математические ожидания не совпадают:
Н,:р1#р1или м,-р!*О.
t-КРИТЕРИЙ ДЛЯ ОЦЕНКИ РАЗНОСТИ МЕЖДУ ДВУМЯ МАТЕМАТИЧЕСКИМИ ОЖИДАНИЯМИ С ПОМОЩЬЮ СУММАРНОЙ ДИСПЕРСИИ
Wi.il
V
, (п, -1)52 +(п^ -1)5.2 -
где S' = -—-—-—-— — — суммарная дисперсия, X, — среднее значение выбор-
ки из первой генеральной совокупности, S2 — дисперсия выборки из первой генеральной совокупности, Tij — объем выборки, извлеченной из первой генеральной совокупности, Х2 — среднее значение выборки из второй генеральной совокупности, S; — дисперсия выборки из второй генеральной совокупности, п2 — объем выборки, извлеченной из второй генеральной совокупности.
Статистика t имеет t-распределение Стьюдента с пх+ п2-2 степенями свободы.
Статистика t, зависящая от суммарной дисперсии, имеет t-распределение Стьюдента с п1+/г2-2 степенями свободы. При заданном уровне значимости ос двусторонний критерий отклоняет нулевую гипотезу, если t-статистика больше верхнего критического значения или меньше нижнего критического значения. Критическая область критерия показана на рис. 9.1. Ограниченный сверху критерий отклоняет нулевую гипотезу, если t-статистика больше верхнего критического значения, а ограниченный снизу критерий — если она меньше нижнего критического значения.
Рис. 9.1. Области принятия и отклонения гипотез при использовании двустороннего t-критерия для оценки разности между двумя математическими ожиданиями
Продемонстрируем применение t-критерия, использующего суммарную дисперсию, на примере сценария, описанного в начале главы. В нем требовалось определить, совпадают ли средние объемы продаж BLK-колы, размещенной на обычных полках и специализированных стеллажах. В этой задаче рассматриваются две генеральные совокупности. Первая генеральная совокупность состоит из всевозможных еженедельных объемов продаж BLK-колы, если все супермаркеты компании BLK используют обычные стеллажи. Во вторую генеральную совокупность входят всевозможные еженедельные
объемы продаж BLK-колы, если все супермаркеты компании BLK используют специализированные стеллажи. Результаты проверки приведены в табл. 9.1. ft COLA. XLS.
Таблица 9.1. Сравнение еженедельных продаж BLK-колы, размещенной на разных стеллажах (количество покупок)
Вид стеллажа
Обычный Специализированный
22 34 52 62 30 52 71 76 54 67
40 64 84 56 59 83 66 90 77 84
Нулевая и альтернативная гипотезы формулируются следующим образом:
Ио: илиМ1-ц2 = О.
Нх: щ * ц2 или ц, - ц2 * 0.
Предполагая, что выборки извлечены из нормально распределенных генеральных совокупностей, имеющих одинаковую дисперсию (т.е. g2 = c2), применим t-критерий, использующий суммарную дисперсию. Эта статистика имеет t-распределение, имеющее 10 + 10-2 = 18 степеней свободы. Если уровень значимости двустороннего критерия равен 0,05, критическая область разбивается на две части, каждая из которых соответствует вероятности, равной 0,025. Из табл. Д.З следует, что критические значения t-статистики равны +2,1009 и -2,1009. Как показано на рис. 9.2, решающее правило имеет следующий вид:
если t > t18 = +2,1009 или t < -t18 = -2,1009, нулевая гипотеза Но отклоняется, в противном случае она не отклоняется.
0,95
0,025
0 Область принятия гипотезы
+2,1009 t t18 Область отклонения гипотезы
f -2,1009 Область отклонения гипотезы
Критическое *1 Критическое
значение значение
Рис. 9.2. Области принятия и отклонения гипотез при использовании двустороннего t-критерия для оценки разности между двумя математическими ожиданиями с уровнем значимости, равным 0,05, при 18 степенях свободы
Используя данные, содержащиеся в табл. 9.1, формулу (9.2) и программу Microsoft Excel (см. рис. 9.3), получаем следующие результаты.
, = (х,-х2)-(И1-^)
= (л,-1)^+(П2-1Х = 9x350,6778+9x157,3333 =
(я.-l) + (n,-1) 9 + 9
Обычные стеллажи
Специализированные стеллажи
4 ] Стандартная ошибка ,5 Медиана “>1 Мода
8 9 ’10 ii
Стандартное отклонение Дисперсия выборки Эксцесс Асимметричность Интервал
12 Минимум 13- Максимум Uj Сумма 15J Счет 1бНаибольший(1)
17 Наименьший(1)
50,3 Среднее 72
5,9218 Стандартная ошибка 3,9665
54 Медиана 73,5
#Н/Д Мода #Н/Д
18,7264 Стандартное отклонение 12,5433 350,6778 Дисперсия выборки 157,3333
-0,3573 Эксцесс -0,7408
0,1447 Асимметричность -0,3505
62 Интервал 38
22 Минимум 52
84 Максимум 90
503 Сумма 720
10 Счет 10
84 Наибольший(1) 90
22 Наименьший(1) 52
Панель А
- , « , _
1 Двухвыборочный t-тест с одинаковыми дисперсиями
2______________________________________________________
3________________________________
4 Среднее
5 Дисперсия
6 Наблюдения
7 Объединенная дисперсия
В Гипотетическая разность средних
9 df
10 t-статистика
11 P(T<-t) одностороннее
12 t критическое одностороннее
13 P(T<-t) двухстороннее
14 ,t критическое двухстороннее
Обычные Специализированные стеллажи____________стеллажи________
50,3 72
350,6778 157,3333
10 10
254,0055556 0
18
-3,04455 0,00349 1,73406 0,00697 2,10092
Панель Б
Рис. 9.3. Описательные статистики (панель А) и результаты применения t-критерия (панель Б) для двух разновидностей стеллажей
Следовательно,
(50,3-72,0)-0,0 _ -21,7
/г54,оо5б(—+—1 ^50,801
V <10 10J
Поскольку уровень значимости равен 0,05, нулевая гипотеза отклоняется, так как t = -3,045 < £18 < -2,1009. Наблюдаемый уровень значимости (p-значение), вычисленный с помощью программы Microsoft Excel, равен 0,006975. Иначе говоря, вероятность того, что t> 3,045 или t< -3,045, равна 0,006975. Значит, если математические ожидания обеих генеральных совокупностей на самом деле равны, вероятность обнаружить статистически значимую разность между ними равна 0,006975. Поскольку р-значение
меньше 0,05, у нас есть основания отклонить нулевую гипотезу. Таким образом, можно утверждать, что объем продаж BLK-колы, размещенной на обычных полках, значительно меньше объема продаж BLK-колы, расположенной на специализированных стеллажах.
Процедуры Excel: проверка гипотезы о разн математических ожиданий двух генеральны совокупностей на основе исходных выборок с помощью f-критерия, использующего суммарную дисперси!
Чтобы создать рабочий лист, предназначенный для проверки гипотезы о разности между математическими ожиданиями двух генеральных совокупностей на основе исходных выборок с помощью
/-критерия, использующего суммарную дисперсию, можно воспользоваться функциями стьюдраспобр (см. раздел ЕН.9.1) и стьюдрасп или процедурой Анализ данных...1^ Двухвыборочный t-тест с одинаковыми дисперсиями. В надстройке PHStat2 такая процедура не
предусмотрена.
Например, чтобы проверить с помощью этого критерия гипотезу о равенстве средних объемов ! продаж колы на основе данных, указанных в табл. 9.1, необходимо открыть рабочий лист Данные ! в рабочей книге Chapter 9. xls и выполнить следующие действия. j
1. Выбрать команду Сервис^Анализ данных....
2. В диалоговом окне Анализ данных выбрать пункт Двухвыборочный t-тест с одинаковыми дисперсиями в списке Инструменты анализа и щелкнуть на кнопке ОК.
3. В диалоговом окне Двухвыборочный t-тест с одинаковыми дисперсиями (см. иллюстрацию) сделать следующее.
3.1. Ввести в окне редактирования Интервал переменной 1 диапазон А1 :А11.
Двухвыборочный t-тест с одинаковыми дисперсиями
Входные данные
Интервал переменной Д «А1: А11
Интервал переменной 2: в 1: В11
Гипотетическая средняя разность: 0
0 Метки
Альфа:: 0,05 i
Параметры вывода
О Выходной интервал: >
©Новыйрабочий лист: iСтеллажи
О Новая рабочая книга
| Отмена ] [ ^правка ]
3.2. Ввести в окне редактирования Интервал переменной 2 диапазон В1 :В11.
3.3. Ввести в окне редактирования Гипотетическая средняя разность число 0.
3.4. Установить флажок Метки.
3.5. Ввести в окне редактирования Альфа число 0,05.
З.б. Установить переключатель Параметры вывода в положение Новый рабочий лист и ввести название нового листа.
3.7. Щелкнуть на кнопке ОК.
Рабочий лист, созданный с помощью этой процедуры, не является динамически обновляемым. Следовательно, если данные изменятся, все описанные выше действия необходимо выполнить заново. Для этой процедуры необходимо, чтобы данные для каждой группы располагались в разных столбцах. Такие данные называются разгруппироваными. Для того чтобы обработать сгруппированные данные, следует воспользоваться инструкцией, изложенной в разделе ЕН.9.2.
Chapter 9.xls
Данные, на основе которых выполняется проверка гипотезы о разности между математическими ожиданиями двух генеральных совокупностей на основе исходных выборок с помощью /-критерия, использующего суммарную дисперсию, содержатся в рабочей книге Chapter 9 .xls на листе Рис9.ЗБ.
Процедуры Excel: проверка гипотезы о разности математических ожиданий двух генеральных совокупностей на основе сводных данных с помощью t-критерия, использующего суммарную дисперсию
Чтобы создать рабочий лист, предназначенный для проверки гипотезы о разности между математическими ожиданиями двух генеральных совокупностей на основе сводных данных с помощью 7-критерия, использующего суммарную дисперсию, можно воспользоваться функциями стьюдраспобр и стьюдрасп или надстройкой PHStat2.
Например, чтобы проверить с помощью этого критерия гипотезу о равенстве средних объемов продаж колы на основе сводных данных, представленных на рис. 9.3 (панель 6), необходимо выполнить одну из следующих процедур.
Применение Excel в сочетании с надстройкой PHStatZ
Чтобы проверить гипотезу о разности математических ожиданий двух генеральных совокупностей на основе сводных данных с помощью 7-критерия, использующего суммарную дисперсию, следует применить процедуру PHStatoTwo-sample testsot-Test for Differences in Two Means... (PHStato Двухвыборочные критерииоЬкритерий для разностей между двумя математическими ожиданиями...), воспользовавшись инструкциями, приведенными ниже.
1. Выбрать команду PHStat^Two-sample tests=>t-Test for Differences in Two Means.
2. В диалоговом окне t-Test for Differences in Two Means (cm. иллюстрацию) сделать следующее.
2.1. Ввести в окне редактирования Hypothesized Difference (Гипотетическая разность) число 0.
2.2. Ввести в окне редактирования Level Significance (Уровень значимости) число 0.05.
2.3. В группе окон Population 1 Sample в окне редактирования Sample size (Объем выборки) ввести число 10, в окне редактирования Sample Mean (Выборочное среднее) - число 5 0,3, а в окне редактирования Sample Standard Deviation (Выборочное стандартное отклонение) - число 18.72 6.
2.4. В группе окон Population 2 Sample в окне редактирования Sample size ввести число 10, в окне редактирования Sample Mean — число 72, а в окне редактирования Sample Standard Deviation - число 12.543.
2.5. Установить переключатель Test Options (Параметры критерия) в положение Two-Tailed Test.
2.6. В окне редактирования Title (Заголовок) ввести название нового листа.
2.7. Щелкнуть на кнопке ОК.
t Test for Differences in Two Means
Data - -
Hypothesized Difference: [o
Level of Significance: [o~O5
Population 1 Sample....... - — •-
Sample Size: [10 > i
Sample Mean: fso.3
Sample Standard Deviation: [18,726
Population 2 Sample
Sample Size: flO
Sample Mean: p2
Sample Standard Deviation: [7^543
Test Options
Two-Tail Test
Г Upper-Tail Test
Г Lower-Tail Test
Output Options
Title: [влияние видаГстеллажейТи объёмы ,
Help | [ OK ~~j| Cancel ]
Применение Excel
Чтобы самостоятельно реализовать шаблон рабочего листа, предназначенный для проверки гипотезы о разности между математическими ожиданиями двух генеральных совокупностей на основе сводных данных с помощью 7-критерия, использующего суммарную дисперсию, следуйте инструкциям, приведенным в разделе ЕН.9.1.
Chapter 9.xls
Проверка гипотезы о разности математических ожиданий двух генеральных совокупностей на основе сводных данных, представленных на рис. 9.3 (панель А}, с помощью 7-критерия, использующего суммарную дисперсию, выполняется в рабочей книге chapter 9. xls на листе Анализ.
ПРОВЕРКА ПРЕДПОЛОЖЕНИЙ
При проверке гипотезы о разности математических ожиданий двух генеральных совокупностей с помощью e-критерия предполагается, что обе генеральные совокупности распределены нормально и имеют одинаковую дисперсию. Если объемы выборок достаточно велики, t-критерий, использующий суммарную дисперсию, является устойчивым и мало чувствительным к отклонению от предположения о нормальности генеральных совокупностей. В этих ситуациях t-критерий можно использовать без существенной потери мощности.
С другой стороны, если предположение о нормальном распределении генеральных совокупностей не выполняется, существуют две возможности.
1. Можно использовать непараметрическую процедуру, например, ранговый критерий Уилкоксона (см. раздел 11.4), который не зависит от предположения о нормальности распределения генеральной совокупности.
: 2. К каждой выборке можно применить нормирующее преобразование (normalizing transformation) [5], а затем — t-критерий, использующий суммарную дисперсию.
Для проверки предположения о нормальном распределении каждой генеральной совокупности можно применить блочную диаграмму (рис. 9.4).
Влияние вида стеллажей на объем продаж лимонада
Рис. 9.4. Блочные диаграммы, построенные с помощью программы Microsoft Excel, для двух разновидностей стеллажей
На рис. 9.4 показано, что предположение о нормальном распределении генеральных совокупностей нарушается незначительно, следовательно, применение t-критерия не приведет к серьезным ошибкам.
Доверительный интервал для разности между математическими ожиданиями
Вместо проверки гипотезы о разности между математическими ожиданиями двух генеральных совокупностей (или в дополнение к ней) можно построить доверительный интервал, содержащий среднюю разность.
ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ, СОДЕРЖАЩИЙ РАЗНОСТЬ МЕЖДУ ДВУМЯ МАТЕМАТИЧЕСКИМИ ОЖИДАНИЯМИ
(%,-x2)±t s4- + -1 , (9.3)
У V П2 J
или
(50,3-72) ±2,1009 х
где t 2 — критическое значение t-распределения с nt+ п.-2 степенями свободы для области, ограниченной верхним хвостом распределения, площадь которой равна а/2.
Используя формулу (9.3) и данные, показанные на рис. 9.3, получаем следующий 95% -ный доверительный интервал.
X. = 50,3 , пх = 10, Х2 = 72 , п2 = 10, S2 = 254,0056 , t - 2,1009,
254,0056х| — + — |=-21,7 ±2,1009x7,1275 = -21,7 ±14,97 . <10 ю;
-36,67 <И1-ц2<-6,73.
Вероятность того, что разность объемов продаж колы, находящейся на обычных полках и специализированных стеллажах, лежит в диапазоне от -36,67 до -6,73, равна 95% . Поскольку нуль не лежит в этом интервале, нулевую гипотезу следует отклонить.
Использование f-критерия для оценки разности между двумя математическими ожиданиями с помощью раздельной дисперсии
Поскольку при обсуждении t-критерия, предназначенного для проверки гипотезы о разности между математическими ожиданиями двух генеральных совокупностей, мы предполагали, что дисперсии этих совокупностей одинаковы, выборочные дисперсии были объединены в одну величину — суммарную дисперсию S2 . Однако, если это предположение ошибочно, суммарная дисперсия становится неприемлемой. Для решения этой проблемы Саттерсвейт (Satterthwaite) предложил t-критерий, использующий раздельную дисперсию (separate-variance t test) [5]. В процедуре Саттерсвейта для аппроксимации t-статистики используются две выборочные дисперсии. Эта процедура довольна сложна, поэтому для нее следует применять программу Microsoft Excel. На рис. 9.5 показано, что дисперсия продаж колы, расположенной на двусторонних стеллажах, вдвое превосходит дисперсию продаж колы, выставленной на обычных полках. Таким образом, для проверки гипотезы о равенстве средних объемов продаж следует приме-
нить t-критерий, использующий раздельную дисперсию. Результат применения t-критерия, использующего раздельную дисперсию, полученный с помощью программы Microsoft Excel, для двух разновидностей стеллажей, показан на рис. 9.5.
‘~ - —г- g: - -
1 'Двухвыборочный t-тест с различными дисперсиями
2 ’_________________________________________________________
Обычные Специализированные
3 j____________________________стеллажи_______стеллажи______
4 jСреднее 50Д 72
5*1 Дисперсия 350,6778 157,3333
61 Наблюдения 10 10
7~ Гипотетическая разность средних 0:
~8ldf 16
9 t-статистика -3,04455
ЩР(Т<=1) одностороннее 0,00386
Жш критическое одностороннее 1,74588
W|P(T<=t) двухстороннее 0,00773
Mt критическое двухстороннее________ 2,11990
Рис. 9.5. Результат применения t-критерия, использующего раздельную дисперсию, полученный с помощью программы Microsoft Excel, для двух разновидностей стеллажей
В частности, из рис. 9.5 следует, что t-статистика равна t = -3,04, причемр-значение равно 0,008 < 0,05. Следовательно, результаты применения t-критерия, использующего раздельную дисперсию, практически не отличаются от результатов, полученных с помощью t-критерия, использующего суммарную дисперсию.
Процедуры Excel: проверка гипотезы о разности математических ожиданий двух генеральных совокупностей на основе выборок с помощью Г-критерия, использующего раздельную дисперсию
Чтобы проверить гипотезу о разности математических ожиданий двух генеральных совокупностей на основе выборок с помощью t-критерия, использующего раздельную дисперсию, следует применить процедуру Анализ данных...^> Двухвыборочный t-тест с различными дисперсиями. В надстройке PHStat2 эта процедура не предусмотрена.
Например, чтобы проверить с помощью этого критерия гипотезу о равенстве средних объемов продаж колы на основе данных, указанных в табл. 9.1, необходимо открыть рабочий лист Данные в рабочей книге Chapter 9. xls и выполнить такие действия.
1. Выбрать команду Сервис^Анализ данных....
2. В диалоговом окне Анализ данных выбрать пункт Двухвыборочный Ьтест с различными дисперсиями в списке Инструменты анализа и щелкнуть на кнопке ОК.
3. В диалоговом окне Двухвыборочный t-тест с различными дисперсиями (см. иллюстрацию) сделать следующее.
3.1. Ввести в окне редактирования
Интервал переменной 1 диапазон А1:А11.
Двухвыборочный t-тест с различными дисперсиями [X
Входные данные
Интервал переменной Д | д 1: д 11
Интервал переменной £: ;В Г В11
, Гипотетическая средняя разность: ю
01 Метки &льфа: Д.05 i
Параметры вывода
О Выходной интервал: !................
® Новый рабочий диет: i Стеллажи
О Новая рабочая книга
EZHZJ [ Отмена ] [ ^правка |
3.2. Ввести в окне редактирования Интервал переменной 2 диапазон В1 :В11.
3.3. Ввести в окне редактирования Гипотетическая средняя разность число 0.
3.4. Установить флажок Метки.
3.5. Ввести в окне редактирования Альфа число 0,05.
3.6. Установить переключатель Параметры вывода в положение Новый рабочий лист и ввести название нового листа.
3.7. Щелкнуть на кнопке ОК.
Рабочий лист, созданный с помощью этой процедуры, не является динамически обновляемым. Следовательно, если данные изменятся, все описанные выше действия необходимо выполнить заново. Для этой процедуры необходимо, чтобы данные каждой группы располагались в разных столбцах. Такие данные называются разгруппированными. Для того чтобы обработать сгруппированные данные, следует выполнить инструкции, приведенные в разделе ЕН.9.2.
Chapter 9.xls
Данные, по которым выполняется проверка гипотезы о разности математических ожиданий двух генеральных совокупностей на основе выборок с помощью t-критерия, использующего раздельную дисперсию, содержатся в рабочей книге Chapter 9 . xls на листе Рис9.5.
Обратите внимание на то, что два разных t-критерия привели к одинаковым результатам. Предположение о равенстве дисперсий в этой задаче практически не влияет на результат. Однако в других ситуациях эти критерии могут привести к противоположным выводам. Именно поэтому следует уделять много внимания проверке предположения о равенстве дисперсий и лишь затем выбирать критерий. Эта проблема является весьма важной частью анализа данных. Для ее решения можно применять F-критерий, описанный в разделе 9.4. Это позволит правильно выбрать t-критерий (использующий либо суммарную, либо раздельную дисперсию).
УПРАЖНЕНИЯ К РАЗДЕЛУ ЭЛ
Изучение основ
9.1. Из первой генеральной совокупности, стандартное отклонение которой равно с, = 20, извлечена выборка, имеющая объем п,= 40, а из второй генеральной совокупности, стандартное отклонение которой равно а2=10, извлечена независимая выборка, имеющая объем п2= 50. Чему равна Z-статистика, используемая в критерии для проверки гипотезы о равенстве математических ожиданий двух генеральных совокупностей, если Хх = 72, а Х2 = 66?
9.2. Как изменится решение задачи 9.1, если для проверки нулевой гипотезы Нп: ц, = |щ и альтернативной гипотезы Н,: щ ц2 применяется двусторонний критерий с уровнем значимости а = 0,05?
9.3. Чему равнор-значение в задаче 9.1 при проверке гипотез Но: щ = ц2 и Ht: щ ц2?
9.4. Предположим, имеются две независимые выборки. Объем первой выборки равен п} = 8, выборочное среднее равно Х} = 42, а выборочное стандартное отклонение — Sj = 4. Объем второй выборки равен тг, = 15, выборочное среднее равно Х2=34, а выборочное стандартное отклонение — S2 = 5.
1. Чему равно значение t-статистики, зависящей от суммарной дисперсии, при проверке гипотезы о равенстве математических ожиданий двух генеральных совокупностей, из которых извлечены эти выборки?
2. Сколько степеней свободы имеет эта статистика?
3. Чему равно критическое значение одностороннего критерия с уровнем значимости а = 0,01 при проверке гипотез Но: pt < ц2 и Hr: pt > ц2?
4. Какой статистический вывод следует сделать?
5. Какие предположения о свойствах двух генеральных совокупностей должны выполняться?
6. Постройте 95%-ный доверительный интервал, содержащий разность двух математических ожиданий pt и ц2.
Применение понятий
Задачи 9.5—9.13 можно решать как вручную, так и с помощью программы Microsoft Excel. Задачи 9.14 и 9.15 рекомендуется решать с помощью программы Microsoft Excel.
9.5. Управляющий заводом по производству электрических лампочек желает определить, отличаются ли средние значения продолжительности работы лампочек, произведенных на двух разных машинах. Стандартное отклонение продолжительности работы лампочек, произведенных на первой машине, равно 110 ч, а на второй — 125 ч. Объем выборки, состоящей из лампочек, сделанных на первой машине, равен 25, а выборочная средняя продолжительность их работы — 375 ч. Объем выборки, состоящей из лампочек, сделанных на второй машине, равен 25, а выборочная средняя продолжительность их работы — 362 ч.
1. Существуют ли основания утверждать, что лампочки, произведенные на разных машинах, имеют одинаковую среднюю продолжительность работы, если уровень значимости равен 0,05?
2. Вычислитер-значение и объясните его смысл.
9.6. Начальник отдела снабжения крупного завода решает вопрос о закупке фрезерных станков нового типа. Он считает, что станки следует покупать, если средняя прочность деталей, произведенных на них, выше прочности деталей, сделанных на станках старого типа. Стандартное отклонение прочности деталей, созданных на станках старого типа, равно 10 кг, а на новых станках — 9 кг. Из совокупности деталей, созданных на станках старого типа, извлечена выборка, объем которой равен 100. Ее выборочное среднее равно 65 кг. Выборочное среднее аналогичной выборки, состоящее из 100 деталей, произведенных на станках нового типа, равно 72 кг.
1. Следует ли покупать станки нового типа, если уровень значимости равен 0,01?
2. Вычислитер-значение и объясните его смысл.
9.7. В металлографии чертеж или рисунок гравируется на поверхности твердого металла или камня. Представьте себе эксперимент, в котором сравнивается средняя твердость поверхности стальных плит, используемых в металлографии. Твердость металла измеряется условными единицами. В эксперименте сравниваются два вида поверхностей — необработанная и слегка отполированная наждачной бумагой. Предварительные исследования показывают, что стандартное отклонение твердости равно 10,2 условной единицы для необработанной поверхности и 6,4 — для обработанной наждачной бумагой. Для эксперимента отобрано 40 случайных плит — 20 необработанных и 20 обработанных наждачной бумагой. Выборочная средняя твердость необработанных плит равна 163,4, а обработанных— 156,9. Влияет ли обработка поверхности плиты на ее твердость, если уровень значимости равен 0,05? Иначе говоря, существует ли статистически значимая разница между средней твердостью обработанной и необработанной поверхностей?
1. Следует ли покупать станки нового типа, если уровень значимости равен 0,01?
2. Вычислитер-значение и объясните его смысл.
9.8. По данным опроса, проведенного в октябре 2001 года, клиенты стремятся уменьшить свои долги по кредитным карточкам (Margaret Price, “Credit Debts Get Down to Size”, Newsday, November 25, 2001, F3). Средняя задолженность по кредитной карточке, вычисленная по выборке, состоящей из 1 000 клиентов, в октябре 2000 года, была равна 2 814 долл., а средняя задолженность по кредитной карточке, вычисленная по выборке, состоящей из 1 000 клиентов, в октябре 2001 года, была равна 2 411 долл. Предположим, что выборочное стандартное отклонение в октябре 2000 года было равно 976,93 долл., а в октябре 2000 года — 847,43 долл.
1. Существуют ли основания утверждать, что средняя задолженность по кредитным карточкам в октябре 2001 года меньше, чем в октябре 2000 года, если уровень значимости равен 0,05, а дисперсии генеральных совокупностей предполагаются одинаковыми?
2. Вычислите р-значение и объясните его смысл.
3. Постройте 95%-ный доверительный интервал, содержащий разность между математическими ожиданиями генеральной совокупности задолженностей по кредитным карточкам в октябре 2000 г. и в октябре 2001 г., предполагая, что дисперсии генеральных совокупностей одинаковы.
9.9. Шкала компьютерной фобии (Computer Anxiety Rating Scale — CARS) измеряет индивидуальный уровень тревоги, вызываемой компьютерами. Показатель CARS, равный 20, означает отсутствие тревоги, а 100 — панику. Исследователи университета Майами измерили показатель CARS у 172 студентов. Одной из целей исследования было определить разницу между уровнем тревоги у девушек и юношей.
Юноши Девушки
X 40,26 36,85
s 13,35 9,42
п 100 72
Источник: Travis Broome and Douglas Havelka, “Determinants of Computer Anxiety in Business Students", The Review of Business Information Systems, Spring 2002, 6(2): 9-16.
1. Существуют ли основания утверждать, что средние уровни компьютерной тревоги у обследованных юношей и девушек отличаются друг от друга, если уровень значимости равен 0,05?
2. Вычислитер-значение с помощью программы Microsoft Excel.
3. Какие предположения о двух исследованных генеральных совокупностях должны выполняться, чтобы можно было применять 2-критерий?
9.10. Филиал банка, расположенный в промышленном районе города, стремится повысить качество обслуживания клиентов во время обеда, с 12:00 до 13:00. На протяжении недели сотрудники записывали время ожидания клиентов, стоящих в очереди в течение обеденного перерыва (количество минут, прошедших от момента, когда клиент переступил порог филиала, до момента его обслуживания). Для оценки эффективности обслуживания создана выборка, содержащая данные о времени ожидания 15 клиентов.
^BANKl .XLS
4,21 5,55 3,02 5,13 4,77 2,34 3,54 3,20 4,50 6,10 0,38 5,12 6,46 6,19 3,79
Предположим теперь, что другой филиал банка, расположенный в жилом районе города, стремится повысить качество обслуживания клиентов в конце недели: с 17:00 до 19:00 в пятницу. На протяжении недели сотрудники записывали время ожидания клиентов, стоящих в очереди в указанные часы (количество минут, прошедших от момента, когда клиент переступил порог филиала, до момента его обслуживания). Для оценки эффективности обслуживания создана выборка, содержащая данные о времени ожидания 15 клиентов.
©BANK2.XLS
9,66 5,90 8,02 5,79 8,73 3,82 8,01 8,35 10,49 6,68 5,64 4,08 6,17 9,91 5,47
1. Существуют ли основания утверждать, что оба филиала банка имеют разное среднее время ожидания, если уровень значимости равен 0,05, а дисперсии генеральных совокупностей одинаковы?
2. Вычислитер-значение с помощью программы Microsoft Excel.
3. Какие предположения должны выполняться при решении задачи 1?
4. Постройте 95% -ный доверительный интервал для разности между математическими ожиданиями исследуемого показателя в предположении, что дисперсии генеральных совокупностей одинаковы.
5. Сравните результаты решения задач 1 и 4.
6. Повторите решение задачи 1 в предположении, что дисперсии генеральных совокупностей неодинаковы.
7. Сравните результаты решения задач 1 и 6.
9.11. Клиенты и телефонная компания обеспокоены нарушениями телефонной связи. Причины этих нарушений разделяются на две группы: повреждения на телефонной станции и на линии. Ниже приведены данные о 20 повреждениях телефонной связи и длительности ремонта в двух подразделениях телефонной компании (в минутах). &PHONE. XLS.
Длительность ремонта в подразделении I (мин.)
1,48 1,75 0,78 2,85 0,52 1,60 4,15 3,97 1,48 3,10
1,02 0,53 0,93 1,60 0,80 1,05 6,32 3,93 5,45 0,97
Длительность ремонта в подразделении II (мин.)
7,55 3,75 0,10 1,10 0,60 0,52 3,30 2,10 0,58 4,02
3,75 0,65 1,92 0,60 1,53 4,23 0,08 1,48 1,65 0,72
1. Существуют ли основания утверждать, что длительность ремонта в подразделениях неодинакова, если уровень значимости равен 0,05, а дисперсии генеральных совокупностей совпадают?
2. Вычислитер-значение с помощью программы Microsoft Excel.
3. Какие предположения должны выполняться при решении задачи 1?
4. Постройте 95% -ный доверительный интервал для разности между математическими ожиданиями исследуемого показателя в предположении, что дисперсии генеральных совокупностей одинаковы.
5. Сравните результаты решения задач 1 и 4.
6. Повторите решение задачи 1 в предположении, что дисперсии генеральных совокупностей неодинаковы.
7. Сравните результаты решения задач 1 и 6.
9.12. Агентство недвижимости желает сравнить оцененную стоимость одноквартирных домов в двух поселках округа Нассау-Каунти (Nassau County), штат Нью-Йорк (New York). Статистики, вычисленные по выборкам, состоящим из 60 домов в поселке Фармингдейл (Farmingdale) и 99 домов в поселке Левиттаун (Levittaun) (в тыс. долл.) приведены в таблице.
Фармингдейл Левиттаун
X 191,33 172,34
S 32,60 16,92
п 60 99
1. Существуют ли основания утверждать, что средняя оцененная стоимость домов в поселках Фармингдейл и Левиттаун одинакова, если уровень значимости равен 0,05?
2. Выполняются ли предположения, необходимые для решения задачи 1? Обоснуйте свой ответ.
3. Постройте 95%-ный доверительный интервал, содержащий разность между оцененной стоимостью домов в поселках Фармингдейл и Левиттаун.
9.13. Партии мяса, мясных субпродуктов и другие ингредиенты смешиваются между собой на разных конвейерных линиях фабрики по производству мясных консервов. Несмотря на то что средний вес консервов в банке остается постоянным, администрация фабрики подозревает, что изменчивость веса на линии А больше, чем на линии Б. Ниже приведены данные, полученные в результате обследования выборки 8-унциевых банок.
Линия А Линия Б
X 8,005 7,997
S 0,012 0,005
п 11 16
Существует ли статистически значимая разница между средними весами консервов, произведенных на линиях А и Б, если уровень значимости равен 0,05, а дисперсии весов одинаковы?
9.14. Директор центра обучения сотрудников крупной компании, производящей электронную бытовую аппаратуру, желает сравнить эффективность двух методов подготовки работников конвейера. Для этого он разбил группу, состоящую из 42 недавно нанятых сотрудников, на две случайные подгруппы по 21 человеку. В процессе подготовки сотрудников первой группы использовались индивидуальные, а второй — коллективные программы обучения. Эффективность обучения измерялась количеством секунд, затрачиваемых сотрудником на сборку детали. Результаты приведены в файлеTRAINING.XLS.
1. Существуют ли основания утверждать, что средние эффективности обучения сотрудников по индивидуальным и коллективным программам одинаковы, если уровень значимости равен 0,05, а дисперсии времени сборки равны между собой?
2. Какие предположения должны выполняться при решении задачи 1? Обоснуйте свой ответ.
3. Решите задачу 1, предполагая, что дисперсий двух групп не равны.
4. Сравните решения задач 1 и 3.
5. Постройте 95%-ный доверительный интервал, содержащий разность между средней продолжительностью сборки деталей сотрудниками, прошедшими разные курсы подготовки.
9.15. Неразрушающий контроль — это метод, позволяющий описать свойства компонентов или материалов без изменения их обычного физического состояния. Он позволяет не только оценить свойства материалов, но и классифицировать трещины по размерам, форме, типу и местоположению. Этот метод является наиболее эффективным при обнаружении поверхностных и приповерхностных трещин, а также при описании электрической проводимости материалов. В файле ft) CRACK.XLS содержатся результаты проверки партии бракованных деталей, которые при ручной проверке были классифицированы как целые и треснутые соответственно. Можно ли утверждать, что трещины в деталях, классифицированных как целые, в среднем имеют меньший размер, чем в деталях, признанных треснутыми?
1. Существуют ли основания утверждать, что средний размер трещин в целых образцах меньше, чем в треснутых, если уровень значимости равен 0,05, а дисперсии времени сборки равны между собой?
2. Решите задачу 1, предполагая, что дисперсии двух групп не равны.
3. Сравните решения задач 1 и 3.
9.2. СРАВНЕНИЕ ДВУХ ЗАВИСИМЫХ ВЫБОРОК: КРИТЕРИИ
ДЛЯ ОЦЕНКИ РАЗНОСТИ МЕЖДУ ДВУМЯ МАТЕМАТИЧЕСКИМИ ОЖИДАНИЯМИ
До сих пор мы рассматривали процедуры проверки гипотез о двух независимых генеральных совокупностях на основе извлеченных из них выборок. В этом разделе описывается критерий, позволяющий оценить разность между математическими ожиданиями двух генеральных совокупностей, связанных между собой. Иначе говоря, показатели первой группы зависят от показателей второй. Эта зависимость возникает, поскольку элементы выборок являются парными результатами повторных измерений, выполненных в одном и том же множестве элементов. В этой ситуации интерес представляет разность между величинами, а не сами величины как таковые.
Первый подход к решению задачи о зависимых выборках основывается на попарном сравнении элементов, имеющих определенные свойства. Например, при сравнении результатов двух рекламных кампаний используется объем генеральной совокупности и/или другие экономические и демографические переменные. Исследуя эти переменные, можно измерить эффект двух разных рекламных стратегий.
Второй подход к анализу зависимых выборок использует повторные измерения одних и тех же элементов. Если предположить, что одни и те же элементы при разных воздействиях ведут себя по-разному, следует выявить любые отличия между двумя измерениями одних и тех же элементов. Например, при оценке вкуса некоего продукта каждый элемент выборки подвергается повторным испытаниям одним и тем же дегустатором.
Независимо от подхода к решению задачи, цель исследования двух зависимых выборок — выявить различия между результатами двух измерений, уменьшив влияние изменчивости, присущей элементам выборки.
Для того чтобы определить, существует ли разница между двумя группами, сначала вычисляют разности между отдельными элементами каждой группы, как показано в табл. 9.2. Пусть Ар Х12, ..., Х1л — п наблюдений из одной выборки, аХ21, Х22, ..., Х2л — п наблюдений из второй выборки, соответствующих значениям из первой выборки. Вычислим попарные разности между соответствующими элементами обеих выборок:
А = хп-х21, д = х12-х22,..., А = А,-х2п.
Таблица 9.2. Вычисление разностей между элементами двух зависимых групп
Группа
Наблюдение
1 Аг
2 Х12
Разность
А=АгА1 а=а-а2
/ А А Д=А-А
п Ая D=Xx- х2п
Для оценки средней разности между средними значениями двух зависимых выборок величины А рассматриваются как наблюдения, принадлежащие одной и той же выборке. Если стандартное отклонение разностей известно, применяется Z-статистика, вычисляемая по формуле (9.4)1. Обратите внимание на то, что Z-критерий для оценки разности между математическими ожиданиями на основе выборок из двух зависимых генеральных совокупностей эквивалентен одновыборочному Z-критерию для средней разности (см. формулу (8.1)).
Z-КРИТЕРИЙ ДЛЯ ПРОВЕРКИ ГИПОТЕЗЫ О РАЗНОСТИ МЕЖДУ МАТЕМАТИЧЕСКИМИ ОЖИДАНИЯМИ
Z = , (9.4)
сд у/п
где D = — Yz> , гипотетическое математическое ожидание, crD— стандартное от-fl /-1
клонение генеральной совокупности разностей, п — объем выборки.
Z-статистика имеет стандартизованное нормальное распределение.
Если объем выборки достаточно велик, центральная предельная теорема утверждает, что средняя разность D имеет нормальное распределение.
Как уже упоминалось, в большинстве ситуаций стандартное отклонение генеральной совокупности неизвестно. Единственным параметром, доступным исследователю, являются выборочные статистики, например, выборочное среднее, выборочная дисперсия и выборочное стандартное отклонение.
Если разности предполагаются случайными и независимыми величинами, имеющими нормальное распределение, для оценки разности между математическими ожиданиями зависимых генеральных совокупностей можно применить t-критерий. Для этого следует вычислить t-статистику, имеющую t-распределение с л-1 степенями свободы (см. раздел 8.4).
УСЛОВИЯ, ПРИ КОТОРЫХ МОЖНО ПРИМЕНЯТЬ t-КРИТЕРИЙ
Несмотря на то что генеральная совокупность предполагается нормально распределенной, на практике при достаточно больших объемах выборки и умеренной асимметрии выборочное распределение средней разности р можно аппроксимировать t-распределением.
Чтобы проверить нулевую и альтернативную гипотезы
Яо: = 0, где = цх-ц2,
Но: pD^0,
необходимо вычислить t-статистику по формуле (9.5).
ПРИМЕНЕНИЕ t-КРИТЕРИЯ ДЛЯ ПРОВЕРКИ ГИПОТЕЗЫ О РАЗНОСТИ МЕЖДУ МАТЕМАТИЧЕСКИМИ ОЖИДАНИЯМИ
л/л где D = -^D, , SD = .
По определению t-статистика имеет t-распределение с л-1 степенями свободы.
При заданном уровне значимости а нулевая гипотеза отклоняется, если t-статистика больше верхнего критического значения tn t или меньше нижнего критического значения tnX из t-распределения с л степенями свободы. Иначе говоря, решающее правило выглядит следующим образом:
нулевая гипотеза Но отклоняется, если t > tn х или t < -tn х; в противном случае нулевая гипотеза не отклоняется.
Чтобы продемонстрировать применение t-критерия для оценки разности между двумя математическими ожиданиями, предположим, что некая компания разрабатывает новое программное обеспечение для финансовых расчетов. Поскольку одним из основных критериев качества программного обеспечения является скорость вычислений, разработчики стремятся к тому, чтобы их пакет не уступал по своим возможностям лидерам рынка программ, но превосходил их по скорости расчетов. Если новый пакет окажется эффективным, он будет приводить к тем же результатам, что и другие программы, но за более короткое время. 4
Для оценки программного обеспечения разработчики провели эксперимент, в ходе которого один и тот же набор задач решали как с помощью стандартных программ, так и с помощью нового пакета. Поскольку измерения для каждой конкретной задачи проводились согласованно, для оценки эффективности пакета необходимо сравнить не средние значения двух независимых выборок, а среднюю разность между соответствующими элементами.
Как лучше спланировать эксперимент для сравнения скорости работы нового программного обеспечения с лидером рынка? Один из подходов к решению этой задачи описан в разделе 9.1. В первую выборку входят результаты измерений, полученные при решении финансовых задач с помощью нового пакета программ, а во вторую — с помощью старого. При этом для тестирования разных программ используются разные задачи. Однако, поскольку тестовые задачи могут искусственно завысить или занизить эффективность программ, такой подход нельзя назвать оптимальным. Намного лучше использовать принцип попарных измерений. В этом случае используется один и тот же набор финансовых задач, каждая из которых решается обеими программами. Это позволяет уменьшить изменчивость результатов измерения по сравнению с экспериментом, в котором измерения проводятся для каждого набора задач независимо друг от друга. В данном случае в центре внимания оказываются разности между результатами измерений, полученные при решении одних и тех же задач.
В табл. 9.3 приведены результаты эксперимента, в ходе которого решались 10 задач.
Таблица 9.3. Попарные измерения продолжительности работы двух конкурирующих пакетов при решении финансовых задач (с) ^COMPTIME. XLS
Продолжительность вычислений
Задача Лидер рынка Новый пакет Разность (DJ
С.В. 9,98 9,88 +0,10
T.F. 9,88 9,86 +0,02
М.Н. 9,84 9,75 +0,09
R.K. 9,99 9,80 +0,19
М.О. 9,94 9,87 +0,07
D.S. 9,84 9,84 0,00
S.S. 9,86 9,87 -0,01
с.т. 10,12 9,86 +0,26
к.т. 9,90 9,83 +0,07
S.Z. 9,91 9,86 +0,05
+0,84
Можно ли утверждать, что новое программное обеспечение работает быстрее? Иначе говоря, существуют свидетельства того, что на решение финансовых задач стандартный пакет затрачивает больше времени, чем новый? Нулевая и альтернативная гипотеза формулируются следующим образом:
Но: < 0 (в среднем стандартный пакет работает быстрее, чем новый),
Но: > 0 (в среднем стандартный пакет работает медленнее, чем новый).
Установим уровень значимости а равным 0,05 и предположим, что разности распределены нормально. Это позволяет применить f-критерий для Парных выборок (9.5). Для выборки, состоящей из 10 задач, решающее правило имеет следующий вид:
нулевая гипотеза Но отклоняется, если t > t;) — 1,8331, в противном случае она не отклоняется.
Средняя разность между результатами, полученными в ходе попарных сравнений (табл. 9.3), равна следующей величине:
а стандартное отклонение —
5o=J-^S(5-^)=0’0844-у п - 1
По формуле (9.5) получаем:
£-^=Д084-0 5 0,084
4п Ло
Поскольку значение t = +3,15 лежит в критической области, нулевая гипотеза отклоняется (рис. 9.6). Таким образом, в среднем новый пакет работает быстрее стандартного.
Рис. 9.6. Критическая область одностороннего t-критерия с 5%-ным уровнем значимости и 9 степенями свободы
Как ^-статистику, так и р-значение можно вычислить с помощью программы Microsoft Excel (рис. 9.7). Поскольку р-значение равно 0,006 и меньше а< 0,05, нулевую гипотезу Но следует отклонить. Вычисленноер-значение означает следующее: если на самом деле оба пакета имеют одинаковую среднюю продолжительность работы при решении финансовых задач, то вероятность обнаружить превосходство нового пакета более чем на 0,084 с не превышает 0,006. Поскольку эта величина крайне мала, степень уверенности в нулевой гипотезе весьма невысока, и следует принять альтернативную гипотезу (т.е. стандартный пакет работает медленнее).
„ Av ч — . ' ___„,1ч, Ч. „ .Я ччк ч'™^ , 1 чч! ч
4 .Парный двухвыборочный t-тест для средних
---------L
Лидер Новый
^'Среднее 9,926 9,842
5:Дисперсия 0,0074 0,0016
J5 Наблюдения 10 10
7 .Корреляция Пирсона 0,2798
Qj Гипотетическая разность средних 0
"<Tdf 9
t-статистика 3,14902
jP(T<=t) одностороннее 0,00588
12jt критическое одностороннее 1,83311
13 P(T<=t) двухстороннее 0,01176
-14 Л критическое двухстороннее 2,26216
Рис. 9.7. Результаты применения t-критерия для парных выборок к задаче об эффективности программного обеспечения (получены с помощью программы Microsoft Excel)
математическим!
i - l,
Чтобы проверить гипотезу о разности между математическими ожиданиями двух генеральных совокупностей с помощью Лкритерия, следует применить процедуру Анализ данных...Ч>Парный двухвыборочный t-тест для средних. В надстройке PHStat2 эта процедура не предусмотрена.
Например, чтобы сравнить с помощью этого критерия результаты, приведенные в табл. 9.3, необходимо открыть рабочий лист Обработка_данных в рабочей книге Chapter 9.xls и выполнить такие действия .
1. Выбрать команду Сервис^Анализ данных....
2. В диалоговом окне Анализ данных выбрать пункт Парный двухвыборочный t-тест для средних в списке Инструменты анализа и щелкнуть на кнопке ОК.
3. В диалоговом окне Парный двухвыборочный t-тест для средних (см. иллюстрацию) сделать следующее.
3.1. Ввести в окне редактирования Интервал переменной 1 диапазон А1 :А11.
3.2. Ввести в окне редактирования Интервал переменной 2 диапазон В1 :В11.
Парный двухвмборочный t-тест для средних
Входные данные
Интервал переменной i.: А1:Д11 |Я£)
Интервал переменной21 В1:В11
Сипотетическая средняя разность: о
S Щетки
&льфа:; 0.05 [
Параметры вывода
О Выходной интервал: i я Tfad
0 Новый рабочий диет: Обработка данных
О Новая рабочая $нига
[Отмена ]
[ ^правка j
3.3. Ввести в окне редактирования Гипотетическая средняя разность число 0.
3.4. Установить флажок Метки.
3.5. Ввести в окне редактирования Альфа число 0,05.
3.6. Установить переключатель Параметры вывода в положение Новый рабочий лист и ввести название нового листа.
3.7. Щелкнуть на кнопке ОК.
Рабочий лист, созданный с помощью этой процедуры, не является динамически обновляемым. Следовательно, если данные изменятся, все описанные выше действия необходимо выполнить заново.
Для этой процедуры необходимо, чтобы данные каждой группы располагались в разных столбцах. Такие данные называются разгруппированными. Для того чтобы обработать сгруппированные данные, следует выполнить инструкции, приведенные в разделе ЕН.9.2.
Chapter 9.xls
Данные, по которым выполняется проверка гипотезы о разности между математическими ожиданиями двух генеральных совокупностей с помощью парного двухвыборочного /-критерия, содержатся в рабочей книге chapter 9. xls на листе Рис9.7.
Доверительный интервал, содержащий разность между двумя математическими ожиданиями
Вместо применения парного двухвыборочного t-критерия можно построить доверительный интервал, содержащий разность между математическими ожиданиями двух генеральных совокупностей.
ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ, СОДЕРЖАЩИЙ РАЗНОСТЬ МЕЖДУ МАТЕМАТИЧЕСКИМИ ОЖИДАНИЯМИ ГЕНЕРАЛЬНЫХ СОВОКУПНОСТЕЙ 5±z,A (9.6)
у/И
ИЛИ
В - *,1-\ ^f= < Hd < & + Z»-l •
\Jn yjn
Используя формулу (9.6), получаем следующие величины: D =0,084, SD = 0,0844, п = 10 и t = 2,2622. В этом случае 95% -ный доверительный интервал имеет следующие границы:
0,84 ±0,0604, 0,0236 <цо< 0,1444.
Таким образом, при доверительном уровне 95% средняя разность между результатами измерения эффективности двух пакетов колеблется в интервале от 0,0236 до 0,1444 с. Поскольку нуль не принадлежит этому интервалу, следует сделать вывод, что эффективность нового пакета выше.
УПРАЖНЕНИЯ К РАЗДЕЛУ 9.2
Изучение основ
9.16. Предположим, что результаты эксперимента содержат 20 пар совершенно одинаковых чисел. Сколько степеней свободы имеет соответствующий /-критерий?
9.17. Предположим, что в ходе эксперимента 15 объектов подвергаются определенному воздействию. Измерения производятся до и после воздействия. Сколько степеней свободы имеет соответствующий /-критерий?
Применение понятий
Задачи 9.18-9.22 можно решать как вручную, так и с помощью программы Microsoft Excel. Задачу 9.23 рекомендуется решать с помощью программы Microsoft Excel.
9.18. Командировочные затраты компаний значительно зависят от средней стоимости аренды гостиничного номера и/или проката автомобилей. Остались ли эти цены неизменными с июня 2000 г. по июнь 2002 г.? Данные, приведенные в файле ^TRAVEL2 .XLS, характеризуют обычную стоимость аренды гостиничного номера и проката автомобилей в 20 городах на протяжении двух периодов времени: 22-28 мая 2000 года и 4-9 июня 2002 года, (цитируется по статьям “Travel”, Wall Street Journal, May 26, 2000, W5 и “Travel”, Wall Street Journal, June 7, 2002, W4).
1. Существуют ли основания утверждать, что средняя стоимость аренды гостиничного номера в июне 2002 года изменилась по сравнению с маем 2002 года, если уровень значимости равен 0,05?
2. Какие предположения должны выполняться при решении задачи 1?
3. Вычислитер-значение и объясните его смысл.
4. Постройте 95%-ный доверительный интервал для разности между средней стоимостью гостиничного номера в июне 2002 года и мае 2000 года.
5. Сравните результаты решения задач 1 и 4.
6. Повторите решение задач 1-5 для проката машин.
7. Изложите ваши выводы в кратком отчете.
9.19. Изменились ли средние цены на новые дома с 2001 по 2002 год? Файл ^ZIPCODES .XLS содержит типичные продажные цены домов (в долл.) из случайной выборки, состоящей из 10 районов США, в которых медиана годового дохода равна 40 000 долл. Данные, относящиеся к 2001 году, вычислялись на основании продаж, оформленных на протяжении всего года, а данные, относящиеся к 2002 году, учитывают продажи, оформленные с января по май 2002 года. (Цитируется по журналу Wall Street Journal, June 29, 2002, W10.)
1. Существуют ли основания утверждать, что средняя стоимость нового дома в районах, медиана доходов жителей которого равна 40 000 долл., в 2002 году изменилась по сравнению с 2001 годом, если уровень значимости равен 0,1?
2. Какие предположения должны выполняться при решении задачи 1?
3. Вычислитер-значение и объясните его смысл.
4. Постройте 90%-ный доверительный интервал для разности между средней стоимостью нового дома в 2001 и 2002 гг.
5. Сравните результаты решения задач 1 и 4.
9.20. В промышленности многие переменные, как правило, измеряются разными способами. Данные, записанные в файле ^MEASUREMENT. XLS, закодированы. Он представляют собой записи, собранные в процессе промышленного производства. (М. Leitnaker, “Comparing Measurement Processes: In-Line versus Analytical Measurement”, Quality Engineering, 13, 2000-2001, 293-298.)
1. Существуют ли основания утверждать, что средние результаты промышленных и лабораторных измерений отличаются друг от друга, если уровень значимости равен 0,05?
2. Какие предположения должны выполняться при решении задачи 1?
3. Проверьте с помощью графических методов, выполняются ли предположения, необходимые для решения задачи 1.
4. Вычислитер-значение и объясните его смысл.
5. Постройте 95%-ный доверительный интервал для разности между средними промышленными и лабораторными измерениями.
9.21. Могут ли студенты сэкономить деньги, покупая книги в Интернет-магазине Amazon.com? Чтобы ответить на этот вопрос, в университете Майами весной 2001 года была сформирована случайная выборка, состоящая из 15 учебников. Цены на эти книги в местном книжном магазине и в Интернет-магазине Атаzon.com (с учетом налогов и стоимости доставки) приведены в файле ftTEXTBOOK. XLS.
Учебник Цена в магазине Цена на сайте Amazon. com
Access 2000 Guidebook 52,22 57,34
HTML 4.0 CD with Java Script 52,74 44,47
Designing the Physical Education Curriculum 39,04 41,48
Service Management Operations, Strategy and IT 101,28 73,72
Fundamentals of Real Estate Appraisal 37,45 42,04
Investments 113,41 95,38
Intermediate Financial Management 109,72 119,80
Real Estate Principles 101,28 62,48
The Automobile Age 29,49 32,43
Geographic Information Systems in Ecology 70,07 74,43
Geosystems: An Introduction to Physical Geography 83,87 83,81
Understanding Contemporary Africa 23,21 26,48
Early Childhood Education Today 72,80 73,48
System of Transcendental Idealism (1800) 17,41 20,98
Principles and Labs for Fitness and Wellness 37,72 40,43
1. Существуют ли основания утверждать, что средняя стоимость книг в местном магазине и на Web-сайте Amazon.com отличаются друг от друга, если уровень значимости равен 0,01?
2. Какие предположения должны выполняться при решении задачи 1?
3. Вычислите р-значение и объясните его смысл.
4. Сравните результаты решения задач 1 и 4.
9.22. На протяжении последнего года вице-президент по кадрам крупного медицинского центра проводил ряд мероприятий и лекций, направленных на повышение качества работы персонала. Чтобы оценить эффективность проведенных мероприятий, он сформировал случайную выборку, состоящую из личных дел 35 сотрудников, и записал показатели качества их работы до и после лекций. Результаты этой проверки приведены на рисунках. Проведите анализ и сделайте выводы. Изложите свои соображения в письменном виде, ft PERFORM. XLS.
Разность
i -5,257142857 1,947781698
-5
-10 11,52323192! 132,7848739 1,103030746 0,110341368
61 34 27?
-184! 35!
27
__________-34!
Интервал
Стандартная ошибка Медиана Мода
Стандартное отклонение Дисперсия выборки Эксцесс Асимметричность Интервал
Минимум Максимум Сумма Счет
Наибольший(1) Наименьший^) ;
Панель А
Парный двухвыборочный t-тест для средних
_____________________:................. Др Среднее______________74,54285714
Дисперсия 80,90252101
Наблюдения 35
Корреляция Пирсона -0,134202934
Гипотетическая разность средних 0
df 34
t-статистика -2,699041101
P(T<-t) одностороннее 0,005376171
t критическое одностороннее 1,690923455
P(Tot) двухстороннее 0,010752342
t критическое двухстороннее 2,032243174
После
79,8
37,16470588
35
Панель Б
9.23. В файле ftcONCRETEl.XLS содержатся показатели, характеризующие прочность 40 образцов бетона через 2 и 7 дней после заливки.
Источник: Carrillo-Gamboa, О., and R. F. Gunst, “Measurement-Error-Model Collinearities”, Technometrics, 34, (1992): 454-464.
1. Существуют ли основания утверждать, что средняя прочность бетона через 2 дня после заливки меньше чем через 7 дней, если уровень значимости равен 0,01?
2. Какие предположения должны выполняться при решении задачи 1?
3. Вычислите р-значение и объясните его смысл.
9.3. ИСПОЛЬЗОВАНИЕ Z-КРИТЕРИЯ ДЛЯ ОЦЕНКИ РАЗНОСТИ МЕЖДУ ДВУМЯ ДОЛЯМИ ПРИЗНАКА
Иногда необходимо выполнить анализ различий между двумя генеральными совокупностями, используя категорийные данные. Оценку разности между двумя долями признака в независимых выборках можно осуществить двумя способами. В данном разделе мы рассмотрим процедуру, в которой тестовая Z-статистика аппроксимируется стандартизованным нормальным распределением. В разделе 11.1 описывается процедура, в которой используется тестовая %2-статистика, аппроксимированная %2-распределением с одной степенью свободы. Как мы убедимся, эти два критерия эквивалентны.
Для оценки различий между двумя генеральными совокупностями на основе независимых выборок можно применять Z-критерий. На основе разности между двумя вы-
боронными долями признака Ps - Ps вычисляется Z-статистика, используемая для оценки разности между двумя долями признака в генеральных совокупностях. Если объем выборок достаточно велик, эта тестовая статистика имеет стандартизованное нормальное распределение.
Z-КРИТЕРИЙ ДЛЯ ОЦЕНКИ РАЗНОСТИ МЕЖДУ ДВУМЯ ДОЛЯМИ
(9.7)
где ps — доля успехов в первой выборке, — количество успехов в первой выборке, п1 — объем выборки из первой генеральной совокупности, д — доля успехов в первой генеральной совокупности, ps — доля успехов во второй выборке, Х2 — количество успехов во второй выборке, п2 — объем выборки из второй генеральной совокупности, р —оценка доли успехов в объединенной генеральной совокупности.
При достаточно большом объеме выборок тестовая Z-статистика подчиняется стандартизованному нормальному распределению.
Нулевая гипотеза заключается в том, что доли признака в двух генеральных совокупностях одинаковы. Следовательно, проверку равенства долей признака в двух генеральных совокупностях можно свести к оценке доли признака в объединенной генеральной совокупности. Оценка объединенной доли равна результату деления количества успехов в обеих выборках Х,-1-Х2 на сумму объемов выборок пх+п2.
С помощью Z-критерия можно определить, существуют ли различия между долями успеха в двух группах (двусторонний тест), а также установить, превышает ли доля успехов в одной группе долю успехов в другой (односторонний критерий).
Двусторонний критерий Односторонний критерий Односторонний критерий
Н<,:р,=А Н'„:р,>р2 Н„:р,<р2
Нрр,*рг Н2-.р,<р2 Ht-.pt>p2
Здесь рх — доля успехов в первой генеральной совокупности, р2 — доля успехов во второй генеральной совокупности.
Чтобы проверить нулевую и альтернативные гипотезы
Н^.р,=рг,
Н,-.р^р2,
следует использовать тестовую Z-статистику (9.7)2. При заданном уровне значимости а нулевая гипотеза отклоняется, если вычисленная Z-статистика больше верхнего или меньше нижнего критического значения стандартизованного нормального распределения.
Для того чтобы проиллюстрировать Z-критерий для проверки гипотезы о равенстве двух долей, предположим, вы — менеджер компании Т. С. Resort Properties. На одном из
Если гипотетическая разность равна 0 (т.е. р}~ р2=® > или р- = р2 ), числитель в формуле (9.7) равен ps - pS; .
островов компании Т. С. Resort Properties принадлежат два отеля: Beachcomer и Windsurfer. На вопрос “Планируете ли вы вернуться в наш отель снова?” 163 из 227 постояльцев отеля Beachcomer ответили: “Да”, в то же время 154 из 262 постояльцев отеля Windsurfer на этот вопрос ответили: “Нет”. Можно ли утверждать, что при уровне значимости, равном 0,05, между степенью удовлетворенности постояльцев обоих отелей (вероятностью, что в следующем сезоне они вернутся в отель) значимой разницы нет?
Нулевая и альтернативная гипотезы формулируются следующим образом:
Н0:р=р2 илир1-р2 = 0, Ht: р^рг или/^-/^ + 0.
Поскольку уровень значимости равен 0,05, критические значения равны -1,96 и 4-1,96 (рис. 9.8), а решающее правило имеет следующий вид:
нулевая гипотеза Но отклоняется, если Z < -1,96 или£ < 4-1,96, в противном случае нулевая гипотеза Но не отклоняется.
Рис. 9.8. Проверка гипотезы о разности между двумя долями при уровне значимости, равном 0,05
Вычислим Z-статистику
(а-,-а;)-(л-а) L _ f i п
JpO-t’) — 4- —
V \ J
X. 163 *
где р5- = — = —— = 0,718, pSi = — п, 227 п2
Таким образом, z _ (0,718-0,588)-0
40,648(1-0,648) ^-^у +
154
262
= 0,588,^^^=163-'5-4-=^ = 0,648.
^+/7, 227 + 262 489
(,228x0,0082 00187 °’0432
При уровне значимости, равном 0,05, нулевая гипотеза Но отклоняется, поскольку Z = +3,01> +1,96. Если нулевая гипотеза является истинной, вероятность того, что Z-статистика будет больше +1,96 и меньше -1,96 стандартного отклонения от центра Z-распределения, равна 0,05. Наблюдаемый уровень значимости представляет собой веро
ятность того, что разность между двумя выборочными долями равна 0,00262. (Эта величина определяется по табл. Д.2 или с помощью программы Microsoft Excel (см. рис. 9.9)). Следовательно, если нулевая гипотеза истинна, вероятность того, что Z-статистика меньше -3,01, равна 0,00131. Вероятность того, что Z-статистика больше +3,01, также равна 0,00131, если нулевая гипотеза верна. Таким образом, в двухстороннем критерии р-значение равно 0,00131 + 0,00131 = 0,00262. Поскольку 0,00262 < а = 0,05, нулевая гипотеза отклоняется. Таким образом, можно утверждать, что два отеля значительно различаются по качеству обслуживания. Иначе говоря, доля гостей, планирующих вернуться, в отеле Beachcomer больше, чем в гостинице Windsurfer.
A 1 i,
1 2 Анализ удовлетворенности гостей
,? Data
т Hypothesized Difference 0
Level of Significance 0.05
8 Group 1
’’Г Number of Successes 163
Sample Size 227
9 Group 2
10 Number of Successes 154
11 Sample Size 262
.12.
13 Intermediate Calculations
14 Group 1 Proportion 0.718061674
15 'Group 2 Proportion 0.58778626
16. j Difference in Two Proportions 0.130275414
17 'Average Proportion 0.648261759
IB Z Test Statistic 3.00075353
19 20 21 22
I Two-Tail Test
Lower Critical Value -1.959962707
I Upper Critical Value 1.959962787
23 p-Value 0.002623357
24 • Reject the null hypothesis
Рис. 9.9. Результаты применения Z-критерия для проверки гипотезы о разности между долями удовлетворенных постояльцев при уровне значимости, равном 0,05 (получены с помощью программы Microsoft Excel)
Процедуры Excel: применение Z-критерия для проверки гипотезы о разности между двумя долями признака
Чтобы использовать Z-критерий для проверки гипотезы о разности между двумя долями, необходимо создать рабочий лист, использующий функции нормобр и нормрасп, или надстройку PHStat2.
Например, чтобы сравнить с помощью этого критерия степень удовлетворенности гостей отелей Beachcomer и Windsurfer, необходимо создать новый рабочий лист и выполнить одну из следующих процедур.
Применение Excel в сочетании с надстройкой PHStat2
Чтобы использовать Z-критерий для проверки гипотезы о разности между двумя долями, следует выбрать команду PHStat'+Two-sample tests'+Z Test for Differences in Two Proportions... (PHStat4> Двухвыборочные критерии'+г-критерий для разностей между двумя долями признака...), выполняя инструкции, приведенные ниже.
1. Выбрать команду PHStat^Two-sample tests^Z Test for Differences in Two Proportions....
2. В диалоговом окне Z Test for Differences in Two Proportions (см. иллюстрацию) выполнить следующие действия.
2.1. Ввести в окне редактирования Hypothesized Difference (Гипотетическая разность) число о.
2.2. Ввести в окне редактирования Level of Significance (Уровень значимости) число 0.05.
2.3. Ввести в группе окон Population 1 Sample (Выборка из первой генеральной совокупности) данные о первой выборке: в окне редактирования Number of Success (Количество успехов) - число 163, а в окне редактирования Sample size (Объем выборки) - 227.
2.4. Ввести в группе окон Population 2 Sample (Выборка из второй генеральной совокупности) данные о второй выборке: в окне редактирования Number of Success - число 154, а в окне редактирования Sample size - 2 62.
2.5. Установить флажок Two-Tailed Test (Двусторонний критерий).
Z Test for the Difference in Two Pro...
Data ...............................
Hypothesized Difference: [o
Level of Significance: Jo?O5™
Population 1 Sample ........—-........
; Number of Successes: [163
; : Sample Size: |z27
i Population 2 Sample ..................
: Number of Successes: (154~"
! i Sample Size: [z62
r-Test Options ................
i <• Two-Tail Test
: Г Upper-Tail Test
i C Lower-Tail Test
Output Options - -
j Title: [лйал^^довлетворенности гостей
____Help J |CZqEZ.J| Cancel
2.6. Ввести в окне редактирования Title (Заголовок) название нового листа.
2.7. Щелкнуть на кнопке ОК.
Применение Excel
Чтобы самостоятельно создать рабочий лист, применяющий Z-критерий для проверки гипотезы о разности между двумя долями, следуйте инструкциям, приведенным в разделе ЕН.9.3.
Chapter 9.xls
Данные, на основе которых вычисляется Z-критерий для сравнения двух долей при оценке степени удовлетворенности постояльцев отелей Beachcomer и Windsurfer, содержатся в рабочей книге Chapter 9. xls на листе Рис9.9.
Доверительный интервал, содержащий разность между долями успехов в двух независимых группах
Вместо применения Z-критерия для сравнения двух долей успехов в двух независимых группах, можно построить доверительный интервал, содержащий среднюю разность, вычисленную по формуле (9.8).
ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ, СОДЕРЖАЩИЙ РАЗНОСТЬ МЕЖДУ ДВУМЯ ДОЛЯМИ
U -Ps)±Z
(pS1-a2)-z
(9.8)
Используя данные, представленные на рис. 9.9, имеем:
А, =
163
227
= 0,718, pSi=^ «2
154
262
= 0,588.
Применяя формулу (9.8), получаем
, ,о |0,718(1-0,718) 0,588(1-0,588)
(0,718 - 0,588) ± 1,96. —-+ -----------*------=
v 7 V 227 262
= 0,13±1,96x0,0426 = 0,13±0,0835 .
0,0465 < р-р2< 0,2135
Таким образом, вероятность того, что разность между долями постояльцев отелей Beachcomer и Windsurfer, планирующих вернуться, лежит в интервале от 0,0465 до 0,2135, равна 0,95. Это означает, что доля гостей, отдающих предпочтение отелю Beachcomer, превышает долю постояльцев, которым нравится отель Windsurfer, на величину от 4,65% до 21,35%.
УПРАЖНЕНИЯ К РАЗДЕЛУ 9.3
Изучение основ
9.24. Предположим, что щ = 100, Хг = 45, п2 = 50, Х2= 25.
1. Можно ли утверждать, что между долями успеха в первой и второй выборках существует значительная разница, если уровень значимости равен 0,01?
2. Постройте 99%-ный доверительный интервал, содержащий разность между долями успехов в обеих выборках.
Применение понятий
Задачи 9.25-9.30 можно решать как вручную, так и с помощью программы Microsoft Excel.
9.25. Для исследования потребительского спроса был проведен опрос 500 пассажиров метро. Среди вопросов был и такой: “Получаете ли вы удовольствие от покупки одежды?”. Из 240 мужчин “Да” ответили 136, а из 260 женщин — 224.
1. Можно ли утверждать, что между долями мужчин и женщин, получающих удовольствие от покупки одежды, существует значительная разница, если уровень значимости равен 0,01?
2. Вычислитер-значение и объясните его смысл.
3. Постройте 99%-ный доверительный интервал, содержащий разность между долями мужчин и женщин, получающих удовольствие от покупки одежды.
4. Сравните результаты решения задач 1 и 3.
5. Как изменятся решения задач 1-4, если количество мужчин, получающих удовольствие от покупки одежды, будет равно 206?
9.26. Газета New York Times сообщила о результатах опроса, проведенного фондом Henry J. Kaiser Family Foundation. В ходе опроса оценивалось влияние средств массовой информации на воспитание детей. Один из вопросов формулировался так: “Используете ли вы компьютер ежедневно?”. Из выборки, содержащей 1 090 детей в возрасте от 2 до 7 лет, 283 ребенка пользовалось компьютером каждый день. Среди 2 065 подростков в возрасте от 8 до 18 лет компьютер ежедневно использовали 1 053 человека.
Источник: McClain, D. L., '‘Where Is Today;s Child? Probably Watching TV”, The New York Times, December 6,1999, p. Cl.
1. Можно ли утверждать, что между долями детей и подростков, использующих компьютер ежедневно, существует значительная разница, если уровень значимости равен 0,05?
2. Вычислите р-значение и объясните его смысл.
3. Постройте 99%-ный доверительный интервал, содержащий разность между долями детей и подростков, использующих компьютер ежедневно.
9.27. В ходе кампании по улучшению качества продукции на заводе полупроводников была сформирована выборка из 450 пластин. В приведенной ниже таблице сопряженности признаков указано количество ответов на два вопроса: “Остались ли частицы на матрице, использованной для производства пластины?” и “Качественная пластина или нет?”.
Состояние матрицы
Частицы Хорошее Есть частицы Всего
Есть 14 36 50
Нет 320 80 400
Всего 334 116 450
Источник: Hall, S. W., “Analysis of Detectivity of Semiconductor Wafers by Contingency Table”, Proceedings Institute of Environmental Sciences 1(1994):177-183.
1. Можно ли утверждать, что между долями качественных и бракованных пластин существует значительная разница, если уровень значимости равен 0,05?
2. Вычислитер-значение и объясните его смысл.
3. Постройте 95%-ный доверительный интервал, содержащий разность между долями качественных и бракованных пластин.
4. Какой вывод следует сделать на основе проведенного анализа?
9.28. Можно ли утверждать, что крупные компании реже предлагают фондовые опционы членам правления, чем малые и средние компании? Опрос, проведенный компанией Segal Company of New York, выяснил, что среди 189 крупных компаний, входящих в выборку, 40 предлагали фондовые опционы членам своих правлений в рамках безналичного компенсационного пакета. В то же время среди 180 малых и средних компаний 43 компании предлагали фондовые опционы членам своих правлений в рамках безналичного компенсационного пакета. (Kemba J. Dunham, “The Jungle: Focus on Recruitment, Pay and Getting Ahead”, Wall Street Journal, August 21, 2001, B6.) 1. Можно ли утверждать, что крупные компании реже предлагают фондовые опционы членам правления, чем малые и средние компании, если уровень значимости равен 0,05?
2. Вычислите р-значение и объясните его смысл.
9.29. Можно ли утверждать, что белые рабочие чаще заявляют о несправедливости своего увольнения? Опрос, проведенный Барри Гольдманом (“White Fight: A Researcher Finds Whites Are More Likely to Claim Bias”, Wall Street Journal, Work Week, April 10, 2001, Al), показал, что из 56 уволенных белых рабочих 29 заявили, что это несправедливо. В то же время из 407 уволенных черных рабочих о несправедливости заявили 126.
1. Можно ли утверждать, что белые рабочие чаще заявляют о несправедливости своего увольнения, если уровень значимости равен 0,05?
2. Вычислите р-значение и объясните его смысл.
9.30. В исследовании, проведенном компаниями Ariel Mutual Funds и Charles Schwab Corporation, приняли участие 500 афроамериканцев и 500 белых, чей годовой доход превышал 50 000 долл. Оказалось, что 74% афроамериканцев и 84% белых
владеют акциями (Cheryl Winokur Munk, “Stock-Ownership Race Gap Shinks”, Wall Street Journal, June 13, 2002, Bll).
1. Можно ли утверждать, что существует значимая разница между долями инвесторов среди афроамериканцев и белых, чей доход превышает 50 000 долл., если уровень значимости равен 0,05?
2. Вычислитер-значение и объясните его смысл.
3. Постройте 95%-ный доверительный интервал, содержащий разность между долями инвесторов среди афроамериканцев и белых, чей доход превышает 50 000 долл.
9.4. ИСПОЛЬЗОВАНИЕ /^КРИТЕРИЯ ДЛЯ ОЦЕНКИ РАЗНОСТИ МЕЖДУ ДВУМЯ ДИСПЕРСИЯМИ
Довольно часто возникает необходимость проверить, имеют ли две независимые генеральные совокупности одинаковую дисперсию. Например, это требуется для того, чтобы выбрать правильный t-критерий — использующий суммарную или раздельную дисперсию.
Проверка разности между дисперсиями двух генеральных совокупностей основана на исследовании их отношения. Если каждая генеральная совокупность является нормально распределенной, отношение Sx/Sf подчиняется F-распределению (см. табл. Д.5), получившему свое название в честь знаменитого статистика Р. Фишера (R. A. Fisher). Критическое значение F-распределения зависит от двух множеств степеней свободы. Степени свободы числителя относятся к первой выборке, а степени свободы знаменателя — ко второй. Для проверки равенства двух дисперсий в критерии используется F-статистика, вычисляемая по формуле (9.9).
^СТАТИСТИКА ДЛЯ ПРОВЕРКИ РАВЕНСТВА ДВУХ ДИСПЕРСИЙ
F = ^-, (9.9)
где S2 — дисперсия выборки из первой генеральной совокупности, п1 — объем выборки, извлеченной из первой генеральной совокупности, 52 — дисперсия выборки из первой генеральной совокупности, п2 — объем выборки, извлеченной из второй генеральной совокупности, п-1 — количество степеней свободы числителя, п2-1 — количество степеней свободы знаменателя.
F-статистика имеет F-распределение с п,-1 и п2-1 степенями свободы.
При заданном уровне значимости а нулевая и альтернативная гипотеза выглядят так:
Нх : су2 су2 .
Если F-статистика больше верхнего критического значения или меньше нижнего критического значения из F-распределения с пх - 1 степенями свободы в числителе и п2- 1 степенями свободы в знаменателе, нулевая гипотеза отклоняется. Таким образом, решающее правило выглядит следующим образом:
нулевая гипотеза Но отклоняется, если F > Fv или F < FL;
в противном случае нулевая гипотеза не отклоняется.
Критическая область F-критерия показана на рис. 9.10.
Рис. 9.10. Критическая область двустороннего F-критерия
Продемонстрируем применение Е-критерия на примере сценария, описанного в начале главы. Напомним, что в нем требовалось определить, совпадают ли средние объемы продаж BLK-колы, выставленной на обычных полках и специализированных стеллажах. Чтобы выбрать правильный t-критерий (с суммарной или раздельной дисперсией), необходимо сначала проверить гипотезу о равенстве дисперсий двух генеральных совокупностей. Следовательно, нулевая и альтернативная гипотеза формулируются так:
Яо: су? = а; ,
77, : 07 сц .
Поскольку критерий является двусторонним, критическая область разбивается на две части, ограниченные левым и правым хвостом F-распределения. Если уровень значимости а = 0,05, каждая из этих областей соответствует вероятности, равной 0,025.
Поскольку выборки содержат по 10 магазинов с разными видами полок, в первой и второй группах существуют 10-1 = 9 степеней свободы. Верхнее и нижнее критическое значения F-распределения определяются по табл. Д.5, фрагмент которой приведен в табл. 9.4. Поскольку количество степеней свободы числителя и знаменателя равно 9, верхнее критическое значение следует искать на пересечении девятой строки и девятого столбца. Таким образом, верхнее критическое значение F-распределения равно 4,03.
Таблица 9.4. Определение верхнего и нижнего критического значений A-распределения, числитель и знаменатель которого имеют по 9 степеней свободы, если верхняя часть критической области соответствует вероятности 0,0253
Знаменатель, D.F.2 Числитель, D.F.2
1 2 3 7 8 9
1 647,80 799,50 864,20 948,20 956,70 963,30
2 38,51 39,00 39,17 39,36 39,37 39,39
3 17,44 16,04 15,44 14,62 14,54 14,47
7 8,07 6,54 5,89 4,99 4,90 4,82
8 7,57 6,06 5,42 4,53 4,43 4,36
9 7,21 5,71 5,08 4,20 4,10 4,03
Вычисление нижнего критического значения
Нижнее критическое значение FL, присущее F-распределению с п1 - 1 степенями свободы в числителе и п2- 1 степенями свободы в знаменателе, вычисляется с помощью обратного значения F. , которое равно критическому значению F-распределения с п2 - 1 степенями свободы в числителе и п,- 1 степенями свободы в знаменателе.
ВЫЧИСЛЕНИЕ НИЖНЕГО КРИТИЧЕСКОГО ЗНАЧЕНИЯ ^РАСПРЕДЕЛЕНИЯ
/7=-^-. (9.Ю)
где Еи. — критическое значение F-распределения с п2-1 степенями свободы в числителе и rij-1 степенями свободы в знаменателе.
Поскольку в нашем примере число степеней свободы в числителе и знаменателе равно 9, перестановку производить не обязательно. Следовательно, чтобы вычислить нижнее критическое значение, соответствующее вероятности, равной 0,025, необходимо определить верхнее критическое значение F-распределения с 9 степенями свободы в числителе и знаменателе, а затем найти обратную величину. Как следует из табл. 9.4, верхнее критическое значение равно 4,03. Следовательно,
Таким образом, как показано на рис. 9.11, решающее правило выглядит следующим образом:
нулевая гипотеза Но отклоняется, если F > Fv = 4,03 или F < FL = 0,248, в противном случае нулевая гипотеза не отклоняется.
Рис. 9.11. Критическая область двустороннего F-критерия с уровнем значимости, равным 0,05, и 9 степенями свободы в числителе и знаменателе
Используя формулу (9.9) и данные о продажах колы (см. табл. 9.1), получаем следующее значение F-статистики:
F-SL--223
S22 157,3333 ’
Поскольку Fl = 0,248 < F = 2,23 < Fv = 4,03, у нас нет оснований отклонять нулевую гипотезу. Если необходимо применить подход, основанный на определении р-значения, F-статистику следует вычислять с помощью программы Microsoft Excel (рис. 9.12).
А _ 1 Двухвыборочный F-тест для ди 2 f ' 31 i . В j сперсии Обычные стеллажи С Специализированные стеллажи
4 iСреднее 50.3 72
^Дисперсия 350,6778 157,3333333
6 j Наблюдения 10 10
7 Jdf 9 9
8 jF 2,2289
$ ]P(F<=f) одностороннее 0,1241
10 jF критическое одностороннее 3,1789
Рис. 9.12. Результаты применения F-критерия для решения задачи о продаже колы, выставленной на разных стеллажах
Поскольку р-значение для двустороннего критерия равно 0,248 (удвоенное р-значение для одностороннего критерия, приведенное на рис. 9.12), приходим к выводу, что продажи колы с разных стеллажей обладают практически одинаковой изменчивостью. Итак, ^-критерий для сравнения математических ожиданий двух групп на основе суммарной дисперсии является вполне корректным.
ПРОВЕРКА УСЛОВИЙ
При оценке разности между двумя дисперсиями с помощью F-критерия предполагается, что обе генеральные совокупности имеют нормальное распределение. F-критерий очень чувствителен к нарушению этого условия. Если блочная диаграмма или график нормального распределения демонстрируют значительное отклонение ; от указанного требования, F-критерий применять нельзя. В таких ситуациях следует • применять непараметрические процедуры [1,2].
Процедуры Excel: проверка гипотезы о разности между дисперсиями двух генеральных совокупностей на основе исходных выборок с помощью А-критерия
Чтобы проверить гипотезу о разности дисперсий двух генеральных совокупностей на основе исходных выборок с помощью A-критерия, следует применить процедуру Анализ данныхЧ> Двухвыборочный F-тест для дисперсии. В надстройке PHStat2 эта процедура не предусмотрена, однако, следуя инструкциям из раздела ЕН.9.4, можно самостоятельно создать рабочий лист, предназначенный для проверки гипотезы о разности дисперсий двух генеральных совокупностей на основе выборок с помощью А-критерия, вызывая функции браспобр и ерасп.
Например, чтобы проверить с помощью этого критерия гипотезу о равенстве дисперсий продаж колы на основе данных, указанных в табл. 9.1, необходимо открыть рабочий лист Данные в рабочей книге chapter 9. xls и выполнить такие действия.
1. Выбрать команду Сервис^Анализ данных....
2. В диалоговом окне Анализ данных выбрать пункт Двухвыборочный F-тест для дисперсии в списке Инструменты анализа и щелкнуть на кнопке ОК.
3. В диалоговом окне Двухвыборочный F-тест для дисперсии (см. иллюстрацию) сделать следующее.
3.1. Ввести в окне редактирования Интервал переменной 1 диапазон А1:А11.
3.2. Ввести в окне редактирования
Интервал переменной 2 диапазон В1 :В11.
3.3. Установить флажок Метки.
3.4. Ввести в окне редактирования Альфа число 0,05.
3.5. Установить переключатель Параметры вывода в положение Новый рабочий лист и ввести название нового листа.
З.б. Щелкнуть на кнопке ОК.
Рабочий лист, созданный с помощью этой процедуры, не является динамически обновляемым. Следовательно, если данные изменятся, все описанные выше действия необходимо выполнить заново. Для этой процедуры необходимо, чтобы данные каждой группы располагались в разных столбцах. Такие данные называются разгруппированными. Для того чтобы обработать сгруппированные данные, следует выполнить инструкции, приведенные в разделе ЕН.9.2.
Chapter 9.xls
Данные, по которым выполняется проверка гипотезы о разности между дисперсиями двух генеральных совокупностей на основе выборок с помощью A-критерия, содержатся в рабочей книге Chapter 9.xls на листе Рис9.12.
Процедуры Excel: проверка гипотезы о разности между дисперсиями двух генеральных совокупностей на основе сводных данных с помощью /^критерия
Чтобы проверить гипотезу о разности дисперсий двух генеральных совокупностей на основе сводных данных с помощью A-критерия, следует создать рабочий лист, предназначенный для проверки гипотезы о разности дисперсий двух генеральных совокупностей на основе выборок с помощью A-критерия, вызывая функции граспобр и fpacii.
Например, чтобы проверить с помощью этого критерия гипотезу о равенстве дисперсий продаж колы на основе сводных данных, приведенных на рис. 9.3, панель А необходимо создать новый рабочий лист и выполнить одну из следующих процедур.
Применение Excel в сочетании с надстройкой PHStatZ
Чтобы проверить гипотезу о разности дисперсий двух генеральных совокупностей на основе сводных данных с помощью A-критерия, можно применить процедуру PHStat^Two-sample tests'^ F-Test for Differences in Two Variances... (PHStat1^Двухвыборочные критерии1^F-критерий для разностей между двумя дисперсиями...), следуя инструкциям, приведенным ниже.
1. Выбрать команду PHStat1^ Two-sample tests^F-Test for Differences in Two Variances.
2. В диалоговом окне F-Test for Differences in Two Variances (см. иллюстрацию) сделать следующее.
2.1. Ввести в окне редактирования Level Significance (Уровень значимости) число 0.05.
2.2. Ввести в группе окон Population 1 Sample (Выборка из первой генеральной совокупности) данные о первой выборке; в окне редактирования Sample size (Объем выборки) число 10, а в окне Sample Standard Deviation (Выборочное стандартное отклонение) -ЧИСЛО 18.726.
2.3. Ввести в группе окон Population 2 Sample (Выборка из второй генеральной совокупности) данные о второй выборке: в окне редактирования Sample size (Объем выборки) число 10, а в окне Sample Standard Deviation (Выборочное стандартное отклонение) -число 12.543.
2.4. Установить переключатель Test Options (Параметры критерия) в положение Two-Tailed Test (Двусторонний критерий).
2.5. В окне редактирования Title (Заголовок) ввести название нового листа.
2.6. Щелкнуть на кнопке ОК.
Г Test for Differences in Two Varian... [X)
' .................................................
i Level of Significance: |o.O5"
! Population 1 Sample - -.........- ।
| j Sample Size: |7o j
j; Sample Standard Deviation: I18J26 Г ...................
Population 2 Sample........ ............. ;
; j Sample Size: |7o I
Sample Standard Deviation: [12^543 ‘ ।
Test Options
i Two-Tall Test
f Г1 Upper-Tail Test
j Г Lower-Tail Test
r- Output Option? — - —- j
1 Title: (влияниевида стеллажей на'объёмы' ;
Help j Cancel |
Применение Excel
Чтобы самостоятельно создать рабочий лист, осуществляющий проверку гипотезы о разности дисперсий двух генеральных совокупностей на основе сводных данных с помощью F-критерия, следуйте инструкциям из раздела ЕН.9.3.
Chapter 9.xls
Данные, по которым выполняется проверка гипотезы о разности дисперсий двух генеральных совокупностей на основе сводных данных, представленных на рис. 9.3, панель Д с помощью F-критерия, содержатся в рабочей книге Chapter 9. xls на листе F-критерий.
При выборе разновидности f-критерия, как правило, применяется двусторонний F-критерий. Однако, если исследователя интересует собственно изменчивость данных, можно применять односторонний F-критерий. Таким образом, для сравнения дисперсии двух генеральных совокупностей можно применять как двусторонний, так и односторонний F-критерии. Эти ситуации изображены на рис. 9.13.
/\А/\
О Fl Fu F о Fl F 0 Fu
Панель A Двусторонний тест w «2-«2 г/0. <?1 - а2 Н^. а? *а2
Панель Б Односторонний тест Но: а?>а2 Н1: а? < а2
Панель В Односторонний тест
Н0:а?<°2
Н1: а? > а2
Область отклонения гипотезы
м Область принятия гипотезы
Рис. 9.13. Критические области при проверке гипотез о равенстве дисперсий двух генеральных совокупностей
Довольно часто объемы выборок не равны. В примере 9.1 показано, как поступать в таких ситуациях.
ПРИМЕР 9.1. ВЫЧИСЛЕНИЕ НИЖНЕГО КРИТИЧЕСКОГО УРОВНЯ ДЛЯ ДВУСТОРОННЕГО ^КРИТЕРИЯ
Из нормально распределенной генеральной совокупности извлечена выборка, имеющая объем пх = 8. Дисперсия S* этой выборки равна 56,0. Из второй распределенной генеральной совокупности, независимой от первой, извлечена выборка, имеющая объем п2 = 10. Дисперсия St этой выборки равна 24,0. Проверьте нулевую гипотезу, заключающуюся в том, что дисперсии двух генеральных совокупностей равны между собой, и альтернативную гипотезу, состоящую в том, что между дисперсиями этих генеральных совокупностей нет существенной разницы.
РЕШЕНИЕ. Выполним действия, перечисленные во врезках 8.2 и 8.3.
Шаг 1 и 2.
//о . ст.
Н} : о2 * ст
Шаг 3. а - 0,05.
Шаг 4. nr = 8и п2 = 10.
Шаг 5. Предполагая, что выборки извлечены из независимых нормально распределенных генеральных совокупностей, вычислим F-статистику:
гД.
st
Шаг 6. Используя табл. Д.5, сформулируем следующее решающее правило: нулевая гипотеза отклоняется, если вычисленная F-статистика больше верхнего критического значения Fv или меньше нижнего критического значения FL, присущих F-распределению с пг-1 = 7 степенями свободы в числителе и п2-1 =9 степенями свободы в знаменателе. Поскольку критический уровень а = 0,05 поровну распределен между двумя критическими областями, применим табл. Д.5 для верхней критической области, соответствующей вероятности 0,025, и получим Fv = 4,20 (см. табл. 9.5).
Таблица 9.5. Определение верхнего и нижнего критического значений ^распределения, числитель и знаменатель которого имеют по 7 степеней свободы в числителе и 9 в знаменателе, если верхняя часть критической области соответствует вероятности 0,0254
Знаменатель, D.F.2 Числитель, 1
1 2 3 7 8 9
1 647,80 799,50 864,20 948,20 956,70 963,30
2 38,51 39,00 39,17 39,36 39,37 39,39
3 17,44 16,04 15,44 14,62 14,54 14,47
7 8,07 6,54 5,89 4,99 4,90 4,82
8 7,57 6,06 5,42 4,53 4,43 4,36
9 7,21 5,71 5,08 4,20 4,10 4,03
Решающее правило выглядит так:
нулевая гипотеза Но отклоняется, если F < Fv = 4,20 или F > FL; в противном случае нулевая гипотеза Но не отклоняется.
Нижнее критическое значение FLc 7 степенями свободы в числителе и 9 степенями свободы в знаменателе является величиной, обратной к верхнему критическому значению распределения F. с 9 степенями свободы в числителе и 7 — в знаменателе.
Таким образом, применяя формулу (9.10) и табл. 9.5, получаем:
Г, = — = —!— = 0,207.
4,82
Шаг 7. По формуле (9.9) вычисляем F-статистику:
4 = ^ = 2,33.
S; 24,0
Шаги 8-10. Поскольку F-статистика, равная 2,33, лежит в интервале между Fl = 0,207 и Fo = 4,20, нулевую гипотезу Но отклонять нельзя. Итак, при заданном уровне значимости а = 0,05 между дисперсиями двух независимых генеральных совокупностей нет статистически значимой разницы. Хотя дисперсия одной из генеральных совокупностей в 2,33 раза превышает другую, этот факт может оказаться случайным.
Изучение основ
9.31. Вычислите верхнее и нижнее критические значения F-u и Fl, присущие F-распределению для каждого из следующих двусторонних критериев.
1. « = 0,10,71^16, п2= 21.
2. а = 0,05,/1,= 16, п2= 21.
3. а = 0,02, Tij = 16, п2— 21.
4. а = 0,01,7ij= 16, тг2= 21.
5. Как изменяется ширина области принятия гипотезы при уменьшении уровня значимости?
9.32. Вычислите верхнее критическое значение Fu, присущее F-распределению для каждого из следующих односторонних критериев.
1. а = 0,05,7ij= 16, тг2= 21.
2. а = 0,025, пх= 16, п2= 21.
3. а = 0,01, п,= 16, тг2= 21.
4. « = 0,005,^=16, п= 21.
5. Как изменяется ширина области принятия гипотезы при уменьшении уровня значимости?
9.33. Вычислите нижнее критическое значение Fl, присущее F-распределению для каждого из следующих односторонних критериев.
1. а = 0,05, п1 = 16, п2 = 21.
2. а = 0,025,/1]= 16, п2= 21.
3. а = 0,01, zi]= 16, п2= 21.
4. а = 0,005, 7i]= 16, п2= 21.
5. Как изменяется ширина области принятия гипотезы при уменьшении уровня значимости?
9.34. Две выборки, извлеченные из двух независимых генеральных совокупностей, характеризуются следующими показателями:
71] = 25, S, = 133,7, п2 = 25, S; = 161,9.
Чему равна F-статистика при проверке нулевой гипотезы На: а* = ст2 ?
9.35. Сколько степеней свободы имеют числитель и знаменатель F-статистики в задаче 9.34?
9.36. Чему равны в задачах 9.34 и 9.35 верхнее и нижнее критические значения Fu и Fl, содержащиеся в табл. Д.5, если уровень значимости а равен 0,05, а альтернативная гипотеза заключается в следующем: Я,: ст2 =£ ?
9.37. Какой статистический вывод следует сделать в задачах 9.34 и 9.35?
9.38. Две выборки, извлеченные из двух независимых генеральных совокупностей, имеющих сильную положительную асимметрию, характеризуются следующими показателями:
71] = 16, S,2 = 47,3, тг2 = 13, S; = 36,4.
Можно ли применить F-критерий для проверки нулевой гипотезы Яо: о2 - ст2 ? Обоснуйте свой ответ.
Применение понятий
Задачи, 9.39-9.44 можно решать как вручную, так и с помощью программы, Microsoft Excel.
9.39. Профессор факультета бухучета в бизнес-школе утверждает, что оценки выпускного экзамена, полученные студентами других факультетов, характеризуются большей изменчивостью, чем оценки его студентов. Из списка случайным образом извлечены 13 студентов других факультетов (первая группа) и 10 студентов факультета бухучета (вторая группа). Оценки, полученные ими на выпускном экзамене, характеризуются следующими показателями:
71] = 13, S2 = 210,2, п2 = 10, S~ = 36,5.
1. Существуют ли основания утверждать, что профессор прав, если уровень значимости равен 0,05?
2. Вычислите p-значение, используя программу Microsoft Excel.
3. Какие предположения о генеральных совокупностях должны выполняться при использовании F-критерия?
9.40. Шкала компьютерной фобии (Computer Anxiety Rating Scale — CARS) измеряет индивидуальный уровень тревоги, вызываемой компьютерами. Показатель CARS, равный 20, означает отсутствие тревоги, а 100 — панику. Исследователи университета Майами измерили показатель CARS у 172 студентов. Одной из целей исследования было определить разницу между уровнем тревоги у девушек и юношей.
Юноши Девушки
X 40,26 36,85
S 13,35 9,42
п 100 72
Источник: Travis Broome and Douglas Havelka, “Determinants of Computer Anxiety in Business Students”, The Review of Business Information Systems, Spring 2002, 6(2): 9-16.
1. Существуют ли основания утверждать, что изменчивость уровня компьютерной тревоги у обследованных юношей и девушек отличаются друг от друга, если уровень значимости равен 0,05?
2. Вычислитер-значение с помощью программы Microsoft Excel.
3. Какие предположения о двух исследованных генеральных совокупностях должны выполняться, чтобы можно было применять F-критерий?
4. Используя ответ к задачам 1 и 2, определите, какой t-критерий из раздела 9.1 следует применить для проверки гипотезы о статистически значимой разнице между средними уровнями компьютерной тревоги у мужчин и женщин.
9.41. Филиал банка, расположенный в промышленном районе города, стремится повысить качество обслуживания клиентов во время обеда, с 12:00 до 13:00. На протяжении недели сотрудники записывали время ожидания клиентов, стоящих в очереди в течение обеденного перерыва (количество минут, прошедших от момента, когда клиент переступил порог филиала, до момента его обслуживания). Для оценки эффективности обслуживания создана выборка, содержащая данные о времени ожидания 15 клиентов.
BANK1.XLS
4,21 5,55 3,02 5,13 4,77 2,34 3,54 3,20 4,50 6,10 0,38 5,12 6,46 6,19 3,79
Предположим теперь, что другой филиал банка, расположенный в жилом районе города, стремится повысить качество обслуживания клиентов в конце недели: с 17:00 до 19:00 в пятницу. На протяжении недели сотрудники записывали время ожидания клиентов, стоящих в очереди в указанные часы (количество минут, прошедших от момента, когда клиент переступил порог филиала, до момента его обслуживания). Для оценки эффективности обслуживания создана выборка, содержащая данные о времени ожидания 15 клиентов.
ОBANK2.XLS
9,66 5,90 8,02 5,79 8,73 3,82 8,01 8,35 10,49 6,68 5,64 4,08 6,17 9,91 5,47
1. Существуют ли основания утверждать, что оба филиала банка имеют разную изменчивость времени ожидания, если уровень значимости равен 0,05?
2. Вычислитер-значение и объясните его смысл.
3. Какие предположения должны выполняться при решении задачи 1? Выполняются ли они?
4. Можно ли применять t-критерий, использующий суммарную дисперсию, для сравнения математических ожиданий времени ожидания клиентов в двух подразделениях?
9.42. Клиенты и телефонная компания обеспокоены нарушениями телефонной связи. Причины этих нарушений разделяются на две группы: повреждения на телефонной станции и на линии. Ниже приведены данные о 20 повреждениях теле-
фонной связи и длительности ремонта в двух подразделениях телефонной компании (в минутах). PHONE . XLS.
Длительность ремонта в подразделении 1 (мин.)
1,48 1,75 0,78 2,85 0,52 1,60 4,15 3,97 1,48 3,10
1,02 0,53 0,93 1,60 0,80 1,05 6,32 3,93 5,45 0,97
Длительность ремонта в подразделении II (мин.)
7,55 3,75 0,10 1,10 0,60 0,52 3,30 2,10 0,58 4,02
3,75 0,65 1,92 0,60 1,53 4,23 0,08 1,48 1,65 0,72
1. Существуют ли основания утверждать, что изменчивость длительности ремонта в подразделениях неодинакова, если уровень значимости равен 0,05?
2. Вычислитер-значение и объясните его смысл.
3. Какие предположения должны выполняться при решении задачи 1? Выполняются ли они?
4. Можно ли применять i-критерий, использующий суммарную дисперсию, для сравнения математических ожиданий длительности ремонта в двух подразделениях?
9.43. Директор центра обучения сотрудников крупной компании, производящей электронную бытовую аппаратуру, желает сравнить эффективность двух методов подготовки работников конвейера. Для этого он разбил группу, состоящую из 42 недавно нанятых сотрудников, на две случайные подгруппы по 21 человеку. В процессе подготовки сотрудников первой группы использовались индивидуальные, а второй — коллективные программы обучения. Эффективность обучения измерялась количеством секунд, затрачиваемых сотрудником на сборку детали. Результаты приведены в файле ^TRAINING .XLS.
1. Существуют ли основания утверждать, что дисперсии эффективности обучения сотрудников по индивидуальным и коллективным программам отличаются друг от друга, если уровень значимости равен 0,05?
2. Можно ли применять i-критерий, использующий суммарную дисперсию, для сравнения математических ожиданий эффективности обучения в двух группах?.
9.44. Партии мяса, мясных субпродуктов и другие ингредиенты смешиваются между собой на разных конвейерных линиях фабрики по производству мясных консервов. Несмотря на то что средний вес консервов в банке остается постоянным, администрация фабрики подозревает, что изменчивость веса на линии А больше, чем на линии Б. Ниже приведены данные, полученные в результате обследования выборки 8-унциевых банок.
Линия А Линия Б
X 8,005 7,997
S 0,012 0,005
п 11 16
Существует ли статистически значимая разница между дисперсиями веса консервов, произведенных на линиях А и Б, если уровень значимости равен 0,05, а дисперсии весов одинаковы?
РЕЗЮМЕ
В главе рассмотрены статистические процедуры, широко применяемые при анализе различий между двумя независимыми генеральными совокупностями. Рассмотрена задача о сравнении эффективности двух разных способов торговли, когда товары выставляются на обычных или специализированных стеллажах. Продемонстрировано применение статистических критериев для оценки степени удовлетворенности постояльцев двух отелей. Кроме того, описан критерий, позволяющий сравнивать математические ожидания двух зависимых генеральных совокупностей. Показано, как применять эти критерии при решении практических задач. Подробно рассмотрены ограничения, которые налагаются на генеральные совокупности. Напомним, что значительная часть статистического анализа посвящается проверке предположений, которые должны выполняться при использовании того или иного критерия. Помимо всего прочего, это позволяет правильно выбрать сам критерий проверки гипотез.
Как показано на структурной схеме главы, основное различие между критериями для сравнения двух групп заключается в свойствах генеральных совокупностей: независимы они или взаимозависимы, а также в особенностях исследуемой переменной, числовой или категорийной. Классифицировав критерии по группам, необходимо обратить особое внимание на условия, которые должны выполняться при их применении.
Нет
«I
Двухвыборочные
Категорийные „
I
Z-критерий для
; проверки гипотезы | о разности между. I двумя долями
Среднее значение
О?=
Числовые
Да
Независимые выборки?
Центр
Нет
Изменчивость
F-критерий для проверки гипотезы о
Парный f-критерий
<ф ----------32.
t-критерий, использующий г раздельную дисперсию. jhwwII > * .a%**» vs-
t-критерий, использующий ' суммарную дисперсию -
Структурная схема главы 9
ОСНОВНЫЕ ПОНЯТИЯ
F-распределение, 611 t-распределение, 582; 597
Z-критерий, 604
Выборки
зависимые, 596
независимые, 581
парные, 595
Гипотеза о разности двух дисперсий
F-критерий, 611
Гипотеза о разности математических ожиданий
зависимые группы
t-критерий, 597
Z-критерий, 596
независимые группы t-критерий использующий объединенную дисперсию, 581 использующий раздельную дисперсию, 588 Z-критерий, 581
Доверительный интервал разность математических ожиданий, 588 средняя разность, 601
Непараметрическая процедура, 587
Нормирующее преобразование, 587
Повторные измерения, 595
УПРАЖНЕНИЯ К ГЛАВЕ 9
Проверка знаний
9.45. Какие критерии применяются для проверки гипотез?
9.46. При каких условиях для проверки гипотезы о равенстве математических ожиданий двух независимых генеральных совокупностей можно применять t-критерий, использующий суммарную дисперсию?
9.47. При каких условиях для проверки гипотезы о равенстве дисперсий двух независимых генеральных совокупностей можно применять F-критерий?
9.48. Чем отличаются независимые и зависимые генеральные совокупности?
9.49. Чем отличаются повторные измерения от парных элементов?
9.50. При каких условиях для проверки гипотезы о равенстве математических ожиданий двух зависимых генеральных совокупностей можно применять ^-критерий?
9.51. Укажите сходство и различия между критериями для проверки гипотез о математических ожиданиях двух независимых генеральных совокупностей и доверительным интервалом, содержащим разность между математическим ожиданием.
Применение понятий
Задачи 9.52-9.58 можно решать как вручную, так и с помощью программы Microsoft Excel. Задачи 9.59-9.71 рекомендуется решать с помощью программы Microsoft Excel.
9.52. В исследовании, опубликованном в журнале Journal of Business Strategies, сравнивались цены на музыкальные компакт-диски, установленные виртуальными розничными торговцами, применяющими Интернет, и традиционными физическими продавцами (Lee Zoonky and Sanjay Gosain, “A Longitudinal Price Comparison for Music CDs in Electronic and Brick-and-Mortar Markets: Pricing Strategies in Emergent Electronic Commerce”, Spring 2002, 19(1): 55-72). Прежде чем начинать собирать данные, исследователи тщательно сформулировали несколько рабочих гипотез.
• Разброс цен у виртуальных продавцов меньше, чем у физических продавцов.
• Цены электронного рынка меньше цен физического рынка.
1. Исследуйте первую гипотезу. Сформулируйте нулевую и альтернативную гипотезы в терминах параметров генеральной совокупности. Тщательно определите параметры генеральной совокупности, которые должны быть исследованы.
2. Определите ошибки 1 -го и 2-го рода для гипотез, сформулированных в задаче 1.
3. Какой тип статистических критериев следует применить?
4. Какие условия должны выполняться при проверке гипотез с помощью выбранного вами статистического критерия?
5. Повторите решения задач 1-4 для второй гипотезы.
9.53. Рынок лекарств для домашних животных стремительно растет. Прежде чем новое лекарство появится на рынке, оно должно быть одобрено Управлением по санитарному надзору за качеством пищевых продуктов и медикаментов (Food and Drug Administration). В 1999 г. компания Norvatis попыталась получить одобрение своего нового лекарства — анафранила, снимающего тревогу у собак (Elise Tanouye “The Ow in Bowwow: With Growing Market in Per Drugs, Makers Revamp Clinical Trials”, The Wall Street Journal, April 13, 1999). Как следует из статьи, компании удалось описать симптомы тревоги у собак с помощью чисел и доказать, что новое лекарство имеет статистически значимый эффект.
1. Что означает выражение статистически значимый эффект!
2. Представьте себе эксперимент, в котором собаки, страдающие от приступов тревоги, разделены на две группы. Одной группе давали анафранил, а другой — плацебо (лекарство, не содержащее активных ингредиентов). Как описать симптомы тревоги у собак с помощью чисел? Иначе говоря, определите непрерывную случайную переменную Хх, измеряющую эффективность лекарства, и переменную Хг, измеряющую эффективность плацебо.
3. Сформулируйте нулевую и альтернативную гипотезу.
9.54. В ответ на судебные иски, выдвинутые против табачных компаний, многие производители табачных изделий, например, компания Philip Morris, оплатили телевизионные программы, которые описывали опасность курения для подростков. Была ли успешной эта антитабачная кампания? Возможно, антитабачные мероприятия, профинансированные государством, были более эффективными? В одной из статей (Gordon Fairclough “Philip Morris's Antismoking Campaign Draws Fire”, The Wall Street Journal, April 6, 1999, p. Bl) описан эксперимент, проведенный в Калифорнии, в ходе которого была оценена эффективность анти-табачных кампаний, оплаченных правительством штата и компанией Philip Mossis соответственно. Исследователи продемонстрировали ролики двум группам подростков и оценили их эффективность. Результаты эксперимента показали, что антитабачные ролики, созданные на деньги государства, оказались более эффективными. Однако в статье выдвинуто предположение, что данное исследование было недостаточно статистически надежным, поскольку объемы выборок были слишком малыми, а в эксперименте принимали участие специально отобранные участники, которые считались более склонными к курению.
1. Как исследователи оценивали эффективность?
2. Сформулируйте нулевую и альтернативную гипотезу.
3. Опишите риски, связанные с ошибками 1- и 2-го рода.
4. Какой критерий для проверки гипотез является наиболее подходящим?
5. Что означает выражение статистически надежный!
9.55. Большая компания желает сравнить потребление электроэнергии в одноквартирных домах на протяжении летнего сезона в двух обслуживаемых ею поселках. Выборки состоят из счетов за электроэнергию. Результаты их обработки приведены в таблице.
Поселок А Поселок Б
X 115 долл. 98 долл.
S 30 долл. 18 долл.
п 25 21
Предположим, что уровень значимости равен 0,01 (соответственно, доверительный уровень равен 99%). Для статистического вывода можно применять либо процедуру проверки гипотез, либо доверительный интервал.
1. Оцените среднюю стоимость электроэнергии, потребленной в первом поселке.
2. Существуют ли основания утверждать, что средняя стоимость электроэнергии, потребленной во втором поселке, превышает 80 долл.?
3. Существуют ли основания утверждать, что дисперсии стоимости электроэнергии в двух поселках одинаковы?
4. Существуют ли основания утверждать, что средняя стоимость электроэнергии в первом поселке выше, чем во втором?
5. Вычислите p-значения в задачах 2-4 и опишите их смысл.
6. Оцените разность между средней стоимостью электроэнергии в первом и втором поселках.
7. Какие статистические выводы должен сделать менеджер?
9.56. Системный администратор крупной компании исследует загрузку компьютера в двух подразделениях — исследовательском отделе и бухгалтерии. Исследуемая выборка состоит из пяти заданий, представленных бухгалтерией, и шести заданий, представленных исследовательским отделом, за последнюю неделю. В таблице приведено время выполнения задач (в секундах). ft^ACCRES . XLS.
Отдел Время выполнения задачи (с)
Бухгалтерия 9 3 8 7 12
Исследовательский 4 13 10 9 9 6
Предположим, что уровень значимости равен 0,05 (соответственно, доверительный уровень равен 95%). Для статистического вывода можно применять либо процедуру проверки гипотез, либо доверительный интервал.
1. Оцените среднее время выполнения заданий бухгалтерии.
2. Существуют ли основания утверждать, что среднее время выполнения заданий исследовательского отдела превышает 6 с?
3. Существуют ли основания утверждать, что дисперсии времени выполнения заданий двух отделов одинаковы?
4. Какие предположения должны выполняться в задаче 3?
5. Оцените разность между средней продолжительностью выполнения заданий бухгалтерии и исследовательского отдела.
6. Какие предположения должны выполняться в задаче 5?
7. Вычислитер-значения в задачах 2, 3 и 6. Опишите их смысл.
8. Оцените разность между средней продолжительностью выполнения заданий бухгалтерии и исследовательского отдела.
9. Какие статистические выводы должен сделать системный администратор?
9.57. Профессор, преподающий компьютерные науки, желает оценить время, за которое студент, прослушавший вводный курс, может написать и отладить программу на языке Visual Basic. Результаты случайно выбранных девяти студентов (в минутах) приведены ниже. OvB. XLS.
10 13 9 15 12 13 11 13 12
1. Можно ли утверждать, что среднее время выполнения задания превышает 10 мин., если уровень значимости равен 0,05?
2. Предположим, оказалось, что четвертому студенту для создания программы необходимо не 15, а 51 мин. Решите задачу 1 при новых данных, сохраняя прежний уровень значимости.
3. Профессор сбит с толку неожиданными результатами и пытается определить, чем отличаются решения задач 1 и 2.
4. Через несколько дней профессор пришел к выводу, что проблема полностью решена. Исходное число (15) было правильным, и, следовательно, решение задачи 1 можно опубликовать в специализированном журнале. Теперь необходимо сравнить полученные результаты с результатами группы, состоящей из 11 студентов, прослушавших полный курс. Среднее время, необходимое этим студентам для создания программы, равно 8,5 мин., а стандартное отклонение равно 2 мин. Выполните анализ данных при уровне значимости, равном 0,05.
5. Рецензент статьи пришел к выводу, что в ней необходимо опубликовать р-значение, вычисленное при решении задачи 1. Кроме того, следует решить проблему неравных дисперсий. Опишите постановку этих задач. Вычислите р-значение в задаче 1 и определите, имеет ли какое-либо значение проблема неравных дисперсий для данных исследований.
9.58. В течение последних лет использование мобильных телефонов резко возросло. Результаты опроса (D. Sharp, “Cellphones Reveal Screaming Lack of Courtesy”, USA Today, September 2001, A4) свидетельствуют, что средняя продолжительность разговоров по мобильному телефону в течение месяца равна 372 мин. для мужчин и 275 мин. для женщин. Для традиционных домашних телефонов эти показатели равны 334 мин. и 510 мин. соответственно. Предположим, что в опросе приняли участие 100 мужчин и 100 женщин, причем стандартное отклонение продолжительности телефонных разговоров по мобильному телефону в течение месяца равно 120 мин. для мужчин и 100 мин. для женщин. Аналогичные показатели для домашних телефонов равны 100 мин. и 150 мин. соответственно.
Предположим, что уровень значимости равен 0,05 (соответственно, доверительный уровень равен 95%). Для статистического вывода можно применять либо процедуру проверки гипотез, либо доверительный интервал.
1. Оцените среднюю продолжительность телефонных разговоров по мобильному телефону в течение месяца у мужчин.
2. Оцените среднюю продолжительность телефонных разговоров по традиционному домашнему телефону в течение месяца у женщин.
3. Существует ли статистически значимая разница между средней продолжительностью телефонных разговоров по мобильному телефону в течение месяца у мужчин и женщин?
4. Существует ли статистически значимая разница между средней продолжительностью телефонных разговоров по домашнему телефону в течение месяца у мужчин и женщин?
5. Какие условия должны выполняться при решении задач 3 и 4?
6. Оцените разность между средней продолжительностью телефонных разговоров по мобильному телефону в течение месяца у мужчин и женщин.
7. Оцените разность между средней продолжительностью телефонных разговоров по традиционному домашнему телефону в течение месяца у мужчин и женщин.
8. Существует ли статистически значимая разница между дисперсиями продолжительности телефонных разговоров по мобильному телефону в течение месяца у мужчин и женщин?
9. Существует ли статистически значимая разница между дисперсиями продолжительности телефонных разговоров по традиционному домашнему телефону в течение месяца у мужчин и женщин?
10. Какие условия должны выполняться при решении задач 8 и 9?
11. Какие выводы можно сделать об использовании мобильных и традиционных домашних телефонов мужчинами и женщинами, основываясь на решении задач 1-10?
9.59. Сравните первые и третьи квартили баллов, набранных при сдаче теста SAT, полную стоимость обучения, стоимость проживания в общежитии и питания в столовой, а также общую академическую задолженность в государственных и частных университетах, используя данные, приведенные в файле ftcOLLEGES2002 .XLS.
9.60. Журнал Working Women провел крупное исследование, стремясь определить типичный размер зарплаты у мужчин и женщин в разных отраслях экономики (“Annual Salary Survey”, Working Women, July-August 2001, 44-47). Данные о 114 рабочих местах и размерах оплаты приведены в файле ft SALARIES . XLS.
1. Можно ли утверждать, что средняя зарплата мужчин выше, чем у женщин, если уровень значимости равен 0,01?
2. Вычислитер-значение в задаче 1.
3. Напишите краткий отчет, содержащий результаты объективной проверки гипотезы. Попробуйте объяснить полученные результаты на основе объективных рассуждений и интуитивных догадок.
9.61. Количество страниц, отведенных для рекламы, варьируется от журнала к журналу и от выпуска к выпуску. Во время экономического роста затраты на рекламу и, соответственно, количество страниц, отведенных для рекламных объявлений, увеличиваются. Данные, собранные в файле ftwEEKLIES.XLS, позволяют сравнить количество рекламных страниц в последних выпусках 19 разных журналов с количеством страниц в тех же выпусках тех же журналов, изданных на год раньше (“Magazines”, Mediaweek, September 24, 2001, 48).
1. Можно ли утверждать, что среднее количество рекламных страниц в текущих выпусках отличается от прошлогоднего, если уровень значимости равен 0,05?
2. Вычислите р-значение в задаче 1.
3. Постройте 95% -ный доверительный интервал для разности между средним количеством рекламных страниц в текущих и прошлогодних номерах журналов.
4. Сравните результаты решения задач 1 и 3.
9.62. Продолжительность работы (в часах) 40 стоваттных электрических ламп, произведенных на заводе А, и 40 стоваттных ламп, сделанных на заводе Б, записана в файле fi^BULB .XLS. Выполните анализ разностей между продолжительностью работы электрических ламп в обеих выборках, если уровень значимости равен 0,05.
9.63. Данные, содержащиеся в файле ФPETFOOD2 . XLS, описывают стоимость порции, вес консервов, количество белка в граммах и жирность в граммах 97 разновидностей сухого и консервированного корма для кошек и собак. Выполните анализ разностей между показателями сухого и консервированного корма. Выполните аналогичный анализ для показателей сухого корма для кошек и собак соответственно. Уровень значимости положите равным 0,05.
Источник: публикуется с разрешения компании Consumers Union of U. S., Inc., Yonkers, New York. Consumer Reports, February 1998, pp. 18,19.
9.64. Используя данные, содержащиеся в файле ^AUT02000. XLS, сравните следующие характеристики 2 000 моделей автомобилей: расход топлива в милях на галлон бензина, емкость бензобака, длина, колесная база, ширина, радиус поворота, вес, грузоподъемность, высота передней части машины, высота переднего сиденья, ширина переднего сиденья, высота задней части машины, высота заднего сиденья и ширина заднего сиденья. Сравните эти показатели у автомобилей с передним и задним приводом. Уровень значимости положите равным 0,05.
Источник: “The 2000 Cars”, Copyright ©2000 by Consumers Union of U. S. Приводится no журналу Consumer Reports, April 2000, pp.66-71, с разрешения компании Consumer Union of U. S., Inc., Yonkers, NY.
9.65. Компания Zagat публикует рейтинги ресторанов, расположенных в разных городах США. В файле Wrestrate.XLS содержатся оценки качества пищи, оформления блюд, уровня обслуживания и стоимость обеда для одного человека в 50 ресторанах Нью-Йорк Сити и 50 ресторанах Лонг-Айленда. Сравните показатели этих ресторанов при уровне значимости, равном 0,05.
Источник: цитируется по изданиям Zagat Survey “2000 New York City Restraunts” и Zagat Survey “2000 long Island Restraunts”.
9.66. В файле ^BEER.XLS приведены данные об упаковках, содержащих шесть 12-унциевых бутылок пива 69 сортов. В их число входят цена, количество калорий в 12 жидких унциях, процентное содержание алкоголя в 12 жидких унциях, вид пива (светлое, эль, импортное легкое, обычное, ледяное, легкое, безалкогольное), а также страны производства (США или другие). Сравните показатели этих сортов пива при уровне значимости, равном 0,05.
Источник: “Beers”. Copyright ©1996 by Consumers Union of U.S. inc., Yonkers, N.Y. Цитируется с разрешения журнала Consumer reports, June 1996
9.67. Во многих технологических процессах существует так называемый период незавершенного производства (work-in-process — WIP). В типографии периодом незавершенного производства называют интервал времени, в течение которого отпечатанные листы фальцуют, комплектуют, склеивают, обрезают и переплетают. В следующей таблице приведена длительность производства 20 книг, напечатанных в двух типографиях. (Длительность производства измеряется в днях, прошедших с момента завершения печати книги и до упаковки в картонные коробки.) . XLS.
Типография А
5,62 5,29 16,25 10,92 11,46 21,62 8,45 8,58 5,41 11,42
11,62 7,29 7,50 7,96 4,42 10,50 7,58 9,29 7,54 8,92
Типография Б
9,54 11,46 16,62 12,62 25,75 15,41 14,29 13,13 13,71 10,04
5,75 12,46 9,17 13,21 6,00 2,33 14,25 5,37 6,25 9,71
Выполните анализ разностей между продолжительностью незавершенного производства в двух типографиях при уровне значимости, равном 0,05, и напишите отчет о полученных результатах.
9.68. Может ли раздача сувениров повысить посещаемость матчей Высшей бейсбольной лиги (Major League Baseball)? В статье, опубликованной в журнале Sports Marketing Quarterly, исследуется эффективность рекламных акций (Boyd, Т. С. and Krehbiel, Т. С. “Promotion Timing in Major League Baseball Attendance”, Sports Marketing Quarterly, 12 (March 2003). Файл данных ROYALS. XLS содержит следующую информацию о посещении матчей с участием команды Kansas City Royals в 2002 году.
ИГРА — матчи в соответствии с расписанием;
ПОСЕЩАЕМОСТЬ — количество зрителей на матче.
РЕКЛАМА — (Да — рекламная акция проводилась, Нет — рекламная акция не проводилась).
1. Можно ли утверждать, что между посещаемостью игр, сопровождаемых рекламными кампаниями, и посещаемостью обычных игр существует статистически значимое различие, если уровень значимости равен 0,05?
2. Проверьте гипотезу о равенстве уровней посещаемости игр, сопровождаемых рекламными кампаниями, и обычных игр, если уровень значимости равен 0,05.
3. Напишите краткий отчет о полученных результатах.
9.69. Исследования, проведенные компаниями, производящими рубероидную кровельную плитку в Бостоне и Вермонте, показали, что основным фактором, влияющим на оценку качества продукции, является ее вес. Более того, вес продукции отражает количество материала, затраченного на ее производство, и, следовательно, играет важную роль в формировании себестоимости. На последнем этапе плитка пакуется, а затем размещается на деревянных стеллажах (как правило, на поддоне помещается 16 плиток). После заполнения стеллажа регистрируется его вес. В соответствии со стандартами вес стеллажа в бостонском отделении компании колеблется в интервале от 3 050 до 3 260 фунтов. В вермонтском отделении компании вес стеллажа варьируется от 3 600 до 3 800 фунтов. Файл ttpALLET.XLS содержит данные о весе (в фунтах) 368 стеллажей, заполненных плитками, произведенными в бостонском отделении компании, и 330 стеллажей, загруженных в Вермонте. Выполните анализ разностей между весами плиток, произведенных в Бостоне и Вермонте, если уровень значимости равен 0,05.
9.70. Производитель рубероидной кровельной плитки на заводах в Бостоне и Вермонте предоставляет своим клиентам 20-летнюю гарантию. Для того чтобы убедиться в том, что плитки прослужат указанный срок, на заводах проводят ускоренное испытание на долговечность. В ходе этого эксперимента плитка на протяжении нескольких минут подвергается интенсивному воздействию, эквивалентному воздействию, которому плитка подвергалась бы в обычных условиях в течение 20 лет. В частности,
плитку несколько минут очень энергично скребут щетками, а затем взвешивают гранулы, которые отскакивают от плиток (в граммах). Чем меньше гранул образуется в ходе эксперимента, тем долговечнее плитка. Для того чтобы прослужить весь гарантийный срок, плитка не должна потерять больше 0,8 г. В файле ft GRANULE. XLS содержатся данные о выборке, состоящей из 170 измерений, проведенных на заводе в Бостоне, и 140 измерений, осуществленных на заводе в Вермонте. Выполните анализ разностей между весами гранул, утерянных плитками в ходе испытаний, произведенных в Бостоне и Вермонте, если уровень значимости равен 0,05.
Отчеты
9.71. Напишите отчет о результатах решения задач 9.69 и 9.70, используя средства пакета Microsoft Office.
Применение Интернет
9.72. Зайдите на сайт www.prenhall. com/levine. Выберите ссылку Chapter 9 и щелкните на ссылке Internet exercises.
ГРУППОВОЙ ПРОЕКТ
ТР.9.1. Файл данных ftMUTUAL FUNDS.XLS содержит информацию о 13 переменных, характеризующих 259 взаимных фондов.
Фонд — название взаимного фонда.
Вид — вид акций, принадлежащих взаимному фонду: малые, средние и крупные компании.
Цель — цель фонда (быстрый или медленный рост капитала).
Активы — в млн. долл.
Комиссия — да или нет.
Издержки — издержки, понесенные взаимным фондом (в процентах от среднего объема чистых активов).
Доходность 2001 — доходность за двенадцать месяцев 2001 г.
Трехлетняя доходность — среднегодовая доходность за период с 1999 по 2001 гг.
Пятилетняя доходность — среднегодовая доходность за период с 1997 по 2001 гг. Оборачиваемость — уровень торговой активности фонда: очень низкий, низкий, средний, высокий, очень высокий.
Риск — уровень риска: очень низкий, низкий, средний, высокий, очень высокий. Лучший квартал — квартал с наивысшей доходностью за период с 1997 по 2001 гг. Худший квартал — квартал с наименьшей доходностью за период с 1997 по 2001 гг.
Проанализируйте разности между доходностью в 2001 г., а также трехлетней и пятилетней доходностями взаимных фондов, не взимающих комиссионной платы, и фондов, взимающих брокерскую комиссию при уровне значимости, равном 0,05. Изложите свои выводы в письменном виде. Для создания отчета примените программу Microsoft Excel и другие средства пакета Microsoft Office (в частности, программу для подготовки презентаций PowerPoint).
РАЗБОР КОНКРЕТНОЙ СИТУАЦИИ -ГАЗЕТА 5РЯ/ЛЛ7И/£££#£Л4££> а
Группа, разрабатывающая новую подписную политику, решила проверить, как влияет прямой маркетинг по телефону на количество подписчиков. После нескольких рабочих совещаний, в которых приняли участие как инструкторы, так и непосредственные участники телефонных рекламных акций, было принято решение повысить продолжительность телефонных переговоров с потенциальными подписчиками, поскольку при более продолжительном разговоре вероятность оформления подписки повышается.
Группа решила оценить влияние продолжительности телефонного разговора с потенциальным подписчиком на успех подписной кампании. Все телефонные звонки производились с 17:00 до 19:00 с понедельника по пятницу. Группа измерила продолжительность телефонных звонков, сделанных с 17:00 до 19:00, и сравнила их с длительностью разговоров с 19:00 до 21:00. Это позволило определить, какой период предпочтительнее для телефонных звонков. Группа отобрала 30 женщин, разбив их на две группы по 15 человек. Они знали, что исследователи внимательно следят за их работой, но не знали, какой именно разговор будет прослушан. Звонившие обязаны были вести разговор по заранее разработанному плану, текст читался с листа, однако обращение к потенциальному подписчику было неформальным. (Например: “Привет, это Мэри Джонс из газеты Spingville Herald. Могу я поговорить с Биллом Ричардсом?”.)
Продолжительность телефонных разговоров измерялась в секундах, прошедших от момента, когда абонент ответил на вопрос, до момента, когда он положил трубку. Результаты приведены в табл. SH.9.1. ^SH9 . XLS.
Таблица SH.9.1. Продолжительность телефонных разговоров
Продолжительность разговора Продолжительность разговора
17:00-19:00 19:00-21:00 17:00-19:00 19:00-21:00
41,3 37,1 40,6 40,7
37,5 38,9 33,3 38,0
39,3 42,2 39,6 43,6
37,4 45,7 35,7 43,8
33,6 42,4 31,3 34,9
38,5 39,9 36,8 35,7
32,6 40,9 36,3 47,4
37,3 40,5
УПРАЖНЕНИЯ
Проанализируйте данные, приведенные в табл. SH.9.1. Изложите свои выводы в отчете. Обоснуйте выбор статистического критерия для сравнения двух независимых групп.
Допустим, что вместо исследования, описанного выше, для анализа создана выборка, состоящая лишь из 15 абонентов, каждый из которых за один вечер прослушивался дважды: с 17:00 до 19:00 и с 19:00 до 21:00. Предположим, что в табл. SH.9.1 приведены данные о двух прослушиваниях одних и тех же абонентов. Повторите анализ данных. Изложите свои выводы в письменном отчете.
Какие переменные необходимо проанализировать в следующий раз? Обоснуйте свой ответ.
ПРИМЕНЕНИЕ WEB
Примените свои знания о проверке гипотез и оцените качество процесса расфасовки кукурузных хлопьев на заводе компании Oxford Cereals (см. главы 6 и 8).
После того как компания Oxford Cereals провела публичный эксперимент, Организация потребителей, уверенных, что компания Oxford Cereal мошенничает (сокращенно — ОПУЧКОСМ), продолжала подозревать, что компания жульничает. Организация создала и распространила документ, в котором заявила, что вес коробок с кукурузными хлопьями, расфасованных за заводе № 2 в г. Спрингвилль, постоянно меньше номинального. Проанализируйте этот документ и содержащиеся в нем данные, размещенные на Web-странице www.prenhci.ll.com/Springville/MoreOnCheaters.htm), и ответьте на следующие вопросы.
1. Существует ли статистически значимая разница между средними весами коробок с кукурузными хлопьями, расфасованными на заводах № 1 и2?
2. Проверьте гипотезу ОПУЧКОСМ. Какие выводы можно сделать на основе приведенных данных?
СПРАВОЧНИК ПО EXCEL ГЛАВА 9
ЕН.9.1. Применение f-критерия, использующего суммарную дисперсию для проверки гипотез о разности между двумя математическими ожиданиями
Создадим рабочий лист, применяющий функции СТЬЮДРАСПОБР и СТЬЮДРАСП для проверки гипотезы о разности между двумя математическими ожиданиями на основе t-критерия, использующего суммарную дисперсию. Вызовы этих функций выглядят следующим образом.
СТЬЮДРАСПОБР {1 -доверительный уровень; степени_свободы),
СТЬЮДРАСП (ABS(t); степени-Свободы; хвосты) ,
где ABS (t) — абсолютная величина t-статистики, параметр хвосты принимает значение 1 для одностороннего критерия и 2 — для двустороннего.
Шаблон рабочего листа t-критерий для проверки гипотезы о разности между двумя математическими ожиданиями на основе t-критерия, использующего суммарную дисперсию по данным, содержащимся в табл. 9.1, приведен в табл. ЕН.9.1. Предполагается, что данные о продажах в магазинах, использующих обычные и специализированные стеллажи, содержатся в столбцах А и В рабочего листа Данные. Для вычисления верхнего и нижнего критических значений этот шаблон использует функцию СТЬЮДРАСПОБР, а для вычисления вероятностей — функцию СТЬЮДРАСП. Для вывода на экран сообщения об отклонении или принятии гипотезы в шаблоне применяется функция ЕСЛИ, сравнивающая р-значение, содержащееся в ячейке В2 6, с уровнем значимости, записанным в ячейке В5.
Таблица ЕН.9.1. Шаблон рабочего листа t-критерий
д 1 , ? 1 8
1 Анализ влияния вида полок на объем продаж
2
з Данные
у 4 Гипотетическая разность 0
5 ' ' Уровень значимости 0,05
; 6 Выборка из первой генеральной совокупности
/7с; Объем выборки =СЧЁТ(Данные!А:А)
8 Выборочное среднее =СРЗНАЧ(Данные!А:А)
9 Выборочное стандартное отклонение =СТАНДОТКЛОН(Данные!А:А)
18 Выборка из второй генеральной совокупности
11 Объем выборки =СЧЁТ(Данные!В:В)
12 Выборочное среднее =СРЗНАЧ(Данные!В:В)
13 Выборочное стандартное отклонение =СТАНДОТКЛОН(Данные!В:В)
14
Окончание табл. ЕН. 9.7
' ' ' -S 'v • A
15 Промежуточные вычисления
16 Степени свободы первой выборки = В7-1
17 Степени свободы второй выборки =В11-1
18 Общее количество степеней свободы = В16+В17
19 Суммарная дисперсия = ((В16*В9Л2)+(В17*В13Л2))/В18
20 Разность между математическими ожиданиями = В8-В12
21 Тестовая t-статистика =(В20-В4)/КОРЕНЬ(В19*(1/В7+1/В11))
22
23 Двусторонний критерий
24 Нижнее критическое значение = -(СТЬЮДРАСПОБР(В5;В18))
25 Верхнее критическое значение =СТЬЮДРАСПОБР(В5;В18)
26 р-значение =СТЬЮДРАСП(АВ5(В21);В18;2)
27 =ЕСЛИ(В26<В5;"Нулевая гипотеза отклоняется"; "Нулевая гипотеза не отклоняется")
Если для решения задачи используются сводные данные, вместо формул в ячейки В7:В9иВ11:В13 следует ввести выборочные статистики.
Для применения одностороннего критерия к шаблону добавляются ячейки D23:E26, приведенные в табл. ЕН.9.2, а строки 23-26 зависят от вида критерия, как показано в табл. ЕН.9.3.1 и ЕН.9.3.2.
Таблица ЕН.9.2. Шаблон рабочего листа t-критерий (диапазон D23: Е26 необходим для любого одностороннего f-критерия, а столбец с остается пустым)
Е
IBS Область вычислений
31 Для односторонних критериев:
32 Значение СТЬЮДРАСП =СТЬЮДРАСП(АВ5(В21);В18;1)
33 1 - значение СТЬЮДРАСП 1-Е25
Таблица ЕН.9.3.1. Шаблон рабочего листа t-критерий для одностороннего критерия.
ограниченного снизу
23 Ограниченный снизу критерий
24 Нижнее критическое значение =-(СТЬЮДРАСПОБР(2*В5;В18))
25 р-значение =ЕСЛИ(В21<0;Е25;Е2б)
26 =ЕСЛИ(В25<В5;"Нулевая гипотеза отклоняется"; "Нулевая гипотеза не отклоняется")
Таблица ЕН.9.3.2. Шаблон рабочего листа t-критерий для одностороннего критерия.
ограниченного сверху
t> V-; -. / ;
23 Ограниченный сверху критерий
24 Верхнее критическое значение =-(СТЬЮДРАСПОБР(2*В5;В18))
^-значение =ЕСЛИ(В21<0;Е26;Е25)
26 =ЕСЛИ(В25<В5;"Нулевая гипотеза отклоняется"; "Нулевая гипотеза не отклоняется")
ЕН.9.2. Сгруппированные и разгруппированные данные
Исходные данные о двух или нескольких группах могут храниться в рабочем листе в сгруппированном виде (stacked data), т.е. в одном столбце, примыкающем к столбцу идентификаторов, или разгруппированном виде (unstacked data), когда данные о каждой группе хранятся в разных столбцах. Например, на приведенных ниже иллюстрациях показаны сгруппированные и разгруппированные данные о продажах колы, размещенной на специализированных и обычных стеллажах.
А
1 Группа
2 ;Обычные
3 Обычные
"У Обычные
“'5'
7*
Обычные Обычные Обычные Обычные Обычные Обычные Обычные
"fl..
S Специализированные Специализиро!
Специализиро!
18
званные Специализированные Специализированные Специализированные Специализированные Специализированные
Специализированные Специализированные
Специализированные
Значение, 22' 34 52 62' 30 40 64 84, 56 59 52. 71 76 54 67: 83 66: 90. 77 84'
1
. А. ’ В. _ ..J Обычные Специализированные
22
34
52
62
30
40
64
84
56
59
52
71
76
54
67
83
66
90
77
84
Некоторые статистические процедуры и рабочие листы, предназначенные для обработки данных о нескольких группах, требуют, чтобы данные были представлены в определенном виде. Если исходные данные представлены в другой форме, их следует привести к требуемому формату.
Вместо утомительного переформатирования диапазонов ячеек (см. раздел ЕН.5.1), можно воспользоваться процедурами PHStatSData Preparations Unstack Data... или PHStatsData PreparationSStack Data.... Эти процедуры выводят на экран диалоговые окна, показанные ниже, в которых требуется указать диапазон ячеек, подлежащих группированию или разгруппированию. Для того чтобы разгруппировать данные, необходимо также указать диапазон сгруппированных ячеек (например, Al: А21, как показано на предыдущем рисунке).
.а..1 ILa-J, .I
*1
ЕН.9.3. Применение Z-критерия для проверки гипотез о разности между двумя долями
Создадим рабочий лист, использующий функции НОРМСТОБР и НОРМСТРАСП, для проверки гипотезы о доле признака в генеральной совокупности на основе Z-критерия. Вызовы функций НОРМСТОБР и НОРМСТРАСП выглядят следующим образом.
НОРМСТОБР (вероятность),
НОРМСТРАСП (Z-значение),
где параметр вероятность представляет собой площадь области, ограниченной кривой распределения и величиной X, а параметр Z-значение является значением Z-статистики, имеющей стандартизованное нормальное распределение.
Шаблон рабочего листа Z-критерий для проверки гипотезы о разности между двумя долями признака в генеральной совокупности с помощью Z-критерия на основе данных о степени удовлетворенности постояльцев двух отелей приведен в табл. ЕН.9.4. В этом шаблоне для вычисления верхнего и нижнего критического значения тестовой Z-статистики используется функция НОРМСТОБР, а для вычисления р-значения — функция НОРМСТРАСП. Чтобы вычислить р-значение двустороннего критерия, хранящееся в ячейке В23, результат вычитания из единицы значения функции НОРМСТРАСП умножается на два. Для вывода на экран сообщения об отклонении или принятии гипотезы в шаблоне применяется функция ЕСЛИ, сравнивающая р-значение, содержащееся в ячейке В23, с уровнем значимости, записанным в ячейке В5.
Для применения одностороннего критерия к шаблону добавляются строки 20-23, представленные в табл. ЕН.9.5.1 и ЕН.9.5.2. (В случае применения односторонних критериев строка 19 остается пустой.) В этих строках функции НОРМСТОБР и НОРМСТРАСП используются так же, как и в предыдущих листах.
Таблица ЕН.9.4. Шаблон рабочего листа Z-критерий
Анализ степени удовлетворенности постояльцев
I Данные
1 Гипотетическая разность 0
I Уровень значимости 0,05
j Группа!
| Количество успехов 163
| Объем выборки 227
Окончание табл. ЕН. 9.4
А
9 Группа 2
SMS' Количество успехов 154
11 Объем выборки 262
111111
13 Промежуточные вычисления
и Доля успехов в первой выборке =В7/В8
Swsi- Доля успехов во второй выборке =В10/В11
16 Разность между двумя долями =В14-В15
17 Средняя доля = (В7+В10)/(В8+В11)
18 Тестовая Z-статистика = (В16-В4)/КОРЕНЬ(В17*(1- В17)*(1/В8+1/В11))
19
20 Двусторонний критерий
21 Нижняя доверительная граница = НОРМСТОБР( В5/2)
22 Верхняя доверительная граница = НОРМСТОБР(1-В5/2)
23 /7-значение =2*(1-НОРМСТРАСП(АВ5(В18)))
24 =ЕСЛИ(В23<В5;"Нулевая гипотеза отклоняется"; "Нулевая гипотеза не отклоняется")
Таблица ЕН.9.5.1. Шаблон рабочего листа Z-критерий для одностороннего критерия.
ограниченного снизу
В
20 Ограниченный снизу критерий
21 Нижнее критическое значение = Н0РМСТ0БР(В5)
22 /2-значение = НОРМСТРАСП(В18)
Illi = ЕСЛИ(В22<В5;"Нулевая гипотеза отклоняется"; "Нулевая гипотеза не отклоняется")
Таблица ЕН.9.5.2. Шаблон рабочего листа Гипотеза для одностороннего критерия,
ограниченного сверху
А В ' „
20 Ограниченный сверху критерий
21 Верхнее критическое значение = Н0РМСТ0БР(1-В5)
22 р-значение =1-НОРМСТРАСП(В18)
||||| =ЕСЛИ(В22<В5;"Нулевая гипотеза отклоняется"; "Нулевая гипотеза не отклоняется")
ЕН.9.4. Использование F-критерия для проверки гипотез о разности между дисперсиями
Создадим рабочий лист, применяя функции FPACIIOBP и РРАСПР для проверки гипотезы о разности между дисперсиями двух генеральных совокупностей. Эти функции имеют следующий вид.
ЕРАСПОБР [верхнееp-значение; количество степеней свободы числителя;
количество степеней свободы знаменателя}
ЕРАСПР [тестовая F-статистика; количество степеней свободы числителя;
количество степеней свободы знаменателя}
Верхнее p-значение представляет собой вероятность того, что Е-статистика превышает данную величину.
Шаблон рабочего листа F-критерий для проверки гипотезы о разности между дисперсиями двух генеральных совокупностей, соответствующий данным, содержащимся в табл. 9.1, приведен в табл. ЕН.9.6 и ЕН.9.7. Предполагается, что данные о продажах в магазинах, использующих обычные и специализированные стеллажи, содержатся в столбцах А и В рабочего листа Данные. В ячейке А21 используется функция ИЛИ, имеющая следующий вид:
ИЛИ [значение 1; значение 2}
С ее помощью ^-значение, содержащееся в ячейке В20, сравнивается с величинами а и 1-а. Как и в других шаблонах, для вывода на экран сообщения об отклонении или принятии гипотезы в шаблоне применяется функция ЕСЛИ.
Таблица ЕН.9.6. Шаблон рабочего листа F-критерий (столбцы Айв)
- ' ' ' -
1 Анализ влияния вида стеллажей на объем продаж
2 '
3 Данные
4 Уровень значимости 0,05
5 : : Выборка из первой генеральной совокупности
6 Объем выборки =СЧЁТ(Данные!А:А)
7 Выборочное стандартное отклонение =СТАНДОТКЛ ОН (Данные!А:А)
В' Выборка из второй генеральной совокупности
3 Объем выборки =СЧЁТ(Данные!В:В)
10 Выборочное стандартное отклонение =СТАНДОТКЛОН(Данные!В:В)
'<;1l\
Промежуточные вычисления
13 Тестовая F-статистика =В7Л2/В1ОЛ2
Степени свободы первой выборки = Вб-1
15 Степени свободы второй выборки =В9-1
16
Окончание табл. ЕН. 9.6
А
17 Двусторонний критерий
18 Нижнее критическое значение = ЕРАСПОБР(1-В4/2;В14;В15)
19 Верхнее критическое значение = РРАСПОБР(В4/2;В14;В15)
20 р-значение =ЕСЛИ(В13>1;2*Е17;2*Е18)
21 =ЕСЛИ(ИЛИ(В20<В4;В20>1-В4);"Нулевая гипотеза отклоняется"; "Нулевая гипотеза не отклоняется")
Для применения одностороннего критерия к шаблону добавляются ячейки, приведенные в табл. ЕН.9.7 или табл. ЕН.9.8.1 и табл. ЕН.9.8.2. Строка 21 должна оставаться пустой.
Таблица ЕН.9.7. Шаблон рабочего листа F-критерий (столбцы D и Е, столбец С пуст)
D ' . .. л-".- v V
• Область вычислений
||||| Значение функции РРАСП = РРАСП(В13;В14;В15)
18 1-значение функции FPACn =1-Е17
Таблица ЕН.9.8.1. Шаблон рабочего листа F-критерий для одностороннего критерия.
ограниченного снизу
А ' ' в ' '•
||||1 Ограниченный снизу критерий
Нижнее критическое значение = РРАСПОБ Р( 1 - В4; В14; В15)
19 р-значение = Е18
20 =ЕСЛИ(В19<В4;"Нулевая гипотеза отклоняется"; "Нулевая гипотеза не отклоняется")
Таблица ЕН.9.8.2. Шаблон рабочего листа F-критерий для одностороннего критерия, ограниченного сверху
' : а - < ' - : -, - — в \у
17 Ограниченный сверху критерий
18 Верхнее критическое значение = ЕРАСПОБР(В4;В14;В15)
19 р-значение =Е17
20 =ЕСЛИ(В19<В4;"Нулевая гипотеза отклоняется"; “Нулевая гипотеза не отклоняется")
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
1. Conover, W. J., Practical Nonparametric Statistics, 3nd ed. (New York: Wiley, 2000).
2. Daniel, W., Applied Nonparametric Statistics, 2nd ed. (Boston, MA: Houghton Mifflin, 1990).
3. Microsoft Excel 2002 (Redmond, WA: Microsoft Corporation, 2001).
4. Satterthwhite, F. E., “An Approximate Distribution of Estimates of Variance Components”, Biometrics Bulletin 2 (1946): 110-114.
5. Snedecor, G. W., and W. G. Cochran, Statistical Methods, 7th ed. (Ames, IA: Iowa State University Press, 1980).
6. Winer, B. J. Statistical Principles in Experimental Design, 2nd ed. (New York: McGraw-Hill, 1971).
Глава 10
Дисперсионный анализ
ПРИМЕНЕНИЕ СТАТИСТИКИ: компания Perfect Parachute
10.1. ПОЛНОСТЬЮ РАНДОМИЗИРОВАННЫЙ ЭКСПЕРИМЕНТ: ОДНОФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ
Использование F-критерия для оценки разностей между несколькими математическими ожиданиями Процедуры Excel: однофакторный дисперсионный анализ Множественное сравнение: процедура Тьюки-Крамера Процедуры Excel: процедура Тьюки-Крамера Необходимые условия однофакторного дисперсионного анализа Критерий Левенэ для проверки однородности дисперсии Процедуры Excel: критерий Левенэ для проверки однородности дисперсий
10.2. ДВУХФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ
Оценка факторов и эффектов взаимодействия
Процедуры Excel: двухфакторный дисперсионный анализ
Интерпретация эффектов взаимодействия Множественные сравнения
10.3. БЛОЧНЫЙ РАНДОМИЗИРОВАННЫЙ ЭКСПЕРИМЕНТ
Критерии для оценки эффектов условий факторного эксперимента и блоков
Процедуры Excel: дисперсионный анализ с помощью блочного рандомизированного эксперимента
СПРАВОЧНИК ПО EXCEL. ГЛАВА 10
ЧЕМУ ДОЛЖЕН НАУЧИТЬСЯ СТУДЕНТ
• Понимать принципы разработки экспериментов.
• Применять методы однофакторного дисперсионного анализа для проверки гипотез о разности между математическими ожидания ми нескольких групп данных.
• Уметь разрабатывать план факторного эксперимента и понимать сущность взаимодействия между факторами.
ПРИМЕНЕНИЕ СТАТИСТИКИ
Компания Perfect Parachute
Предположим, что вы — руководитель производства в компании Perfect Parachute (“Идеальный парашют”). Парашюты изготавливаются из синтетических волокон, поставляемых четырьмя разными поставщиками. Совершенно очевидно, что одной из основных характеристик парашюта является его прочность. Вам необходимо убедиться, что все поставляемые волокна обладают одинаковой прочностью. Более того, на фабрике используется два вида ткацких станков: Jetta и Turk. Можно ли утверждать, что парашюты, изготовленные на станке фирмы Jetta, так же прочны, как
и парашюты, произведенные на станках компании Turk? Существует ли разница между прочностью парашютов, сотканных из синтетических волокон разных поставщиков на разных станках? Чтобы ответить на этот вопрос, следует разработать схему эксперимента, в ходе которого измеряется прочность парашютов, сотканных из синтетических волокон разных поставщиков на разных станках. Информация, полученная в ходе этого эксперимента, позволит определить, какой поставщик и какой тип станка обеспечивают наибольшую прочность парашютов.
ВВЕДЕНИЕ
В главе 9 рассмотрены методы проверки гипотез, применяемые для анализа возможных разностей между параметрами двух групп. Однако зачастую необходимо оценить разности между параметрами нескольких групп. Например, может возникнуть необходимость сравнить альтернативные материалы, методы или условия проведения эксперимента на основе заранее установленных критериев.
Данная глава начинается с описания полностью рандомизированного плана эксперимента, в котором рассматривается только один фактор и несколько групп (например, тип шины, рыночная стратегия, марка лекарства или разные поставщики, как в нашем сценарии). Затем описывается факторный план, в котором учитывается несколько факторов, изучаемых в одном эксперименте. Для каждого из этих планов описаны соответствующие процедуры анализа данных. На протяжении всей главы особое внимание уделяется предположениям, которые должны выполняться в каждой процедуре.
10.1. ПОЛНОСТЬЮ РАНДОМИЗИРОВАННЫЙ ЭКСПЕРИМЕНТ:
ОДНОФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ
Многие приложения связаны с экспериментами, в которых рассматривается несколько групп или уровней одного фактора. Некоторые факторы, например, температура обжига керамики, могут иметь несколько числовых уровней (т.е. 300°, 350°, 400° и 450°). Другие факторы, например, местоположение товаров в супермаркете, могут иметь категориальные уровни (например, первый поставщик, второй поставщик, третий поставщик, четвертый поставщик). Однофакторные эксперименты, в ходе которых экспериментальные единицы случайным образом распределяются по группам или уровням фактора, называются полностью рандомизированными (completely randomized designes).
Использование F-критерия для оценки разностей между несколькими математическими ожиданиями
Если числовые измерения фактора в группах являются непрерывными и выполняются некоторые дополнительные условия, для сравнения математических ожиданий нескольких групп применяется дисперсионный анализ (ANOVA — Analysis of Variance). Дисперсионный анализ, использующий полностью рандомизированные планы, называется однофакторной процедурой ANOVA. В некотором смысле термин дисперсионный анализ является неточным, поскольку при этом анализе сравниваются разности между математическими ожиданиями групп, а не между дисперсиями. Однако сравнение математических ожиданий осуществляется именно на основе анализа вариации данных. В процедуре ANOVA полная вариация результатов измерений подразделяется на межгрупповую и внутригрупповую (рис. 10.1). Внутригрупповая вариация (within group variation) объясняется ошибкой эксперимента (experimental error), а межгрупповая (among group variation) — эффектами условий эксперимента (treatment effects). Символ с обозначает количество групп.
Разделение полной вариации SST = SSA + SS W
Межгрупповая вариация (SSA) d.f. =с-1
Внутригрупповая вариация (SSIV) d.f. = п - с
jeSftSV.. g
Рис. 10.1. Разделение полной вариации в полностью рандомизированном эксперименте
Предположим, что с групп извлечено из независимых генеральных совокупностей, имеющих нормальное распределение и одинаковую дисперсию. Нулевая гипотеза заключается в том, что математические ожидания генеральных совокупностей одинаковы.
Но: 1^=^=...=^
Альтернативная гипотеза гласит, что не все математические ожидания одинаковы.
Нх‘. не все ц одинаковы (j=l, 2, ..., с)
На рис. 10.2 продемонстрирована истинная нулевая гипотеза о математических ожиданиях пяти сравниваемых групп при условии, что генеральные совокупности имеют нормальное распределение и одинаковую дисперсию. Пять генеральных совокупностей, связанных с разными уровнями фактора, идентичны. Следовательно, они накладываются одна на другую, имея одинаковые математическое ожидание, вариацию и форму.
Рис. 10.2. Все пять генеральных совокупностей имеют одинаковое математическое ожидание:
Ml= Ц2=
С другой стороны, предположим, что на самом деле нулевая гипотеза является ложной, причем четвертый уровень имеет наибольшее математическое ожидание, первый уровень — меньшее математическое ожидание, а остальные уровни — одинаковые математические ожидания (рис. 10.3). Обратите внимание на то, что за исключением математических ожиданий (ц4> 1А> |х2= |х8 = К) все пять генеральных совокупностей идентичны (т.е. имеют одинаковую изменчивость и форму).
Нб
Рис. 10.3. Наблюдается эффект условий эксперимента: ^4> = Z4
При проверке гипотезы о равенстве математических ожиданий нескольких генеральных совокупностей полная вариация разделяется на две части: межгрупповую вариацию, обусловленную разностями между группами, и внутригрупповую, обусловленную разностями между элементами, принадлежащими одной группе. Полная вариация выражается полной суммой квадратов (sum of squares total — SST). Поскольку нулевая гипотеза заключается в том, что математические ожидания всех с групп равны между собой, полная вариация равна сумме квадратов разностей между отдельными наблюдениями и общим средним X (grand mean), вычисленным по всем выборкам.
ПОЛНАЯ ВАРИАЦИЯ
= (10.1)
где X = — — общее среднее, Xtj — i-e наблюдение в у-й группе или уровне, п —
и /=i ,=1
количество наблюдений в у-й группе, п — общее количество наблюдений во всех группах (т.е. п = пх + п2 + ... + + п), с — количество изучаемых групп или уровней.
Межгрупповая вариация, называемая обычно межгрупповой суммой квадратов (sum of squares among groups — SSA), равна сумме квадратов разностей между выборочным средним каждой группы Xf и общим средним X , умноженных на объем соответствующей группы п.
МЕЖГРУППОВАЯ ВАРИАЦИЯ
S^ = ^7/(Z/-^)2 , (10.2)
где с — количество изучаемых групп или уровней, п — количество наблюдений в у-й группе, X — среднее значение у-й группы, X — общее среднее.
Внутригрупповая вариация, называемая обычно внутригрупповой суммой квадратов (sum of squares withing groups — SSW), равна сумме квадратов разностей между элементами каждой группы и выборочным средним этой группы X .
ВНУТРИГРУППОВАЯ ВАРИАЦИЯ
^ = LS(A’„-^)2, (10.3)
/=1 /=1
где Х„ — i-й элемент у-й группы, X — среднее значение у-й группы.
Поскольку сравнению подвергаются с уровней фактора, межгрупповая сумма квадратов имеет с-1 степеней свободы. Каждый из с уровней обладает п-1 степенями свободы, поэтому внутригрупповая сумма квадратов имеет п-с степеней свободы, и
7=1
Кроме того, общая сумма квадратов имеет п-1 степеней свободы, поскольку каждое наблюдение XtJ сравнивается с общим средним X , вычисленным по всем п наблюдениям.
Если каждую из этих сумм разделить на соответствующее количество степеней свободы, возникнут три вида дисперсии: межгрупповая (mean square among — MSA), внутригрупповая (mean square within — MSW) и полная (mean square total — MST).
СРЕДНИЕ СУММЫ КВАДРАТОВ
SSA MSA = , с -1 lzr,T77 SSW MSW = , n — c MST^. n-1 (10.4, a) (10.4,6) (10.4,e)
Несмотря на то что основное предназначение дисперсионного анализа — сравнить математические ожидания с групп, чтобы выявить эффект условий эксперимента, его название обусловлено тем, что главным инструментом является анализ дисперсий разного типа. Если нулевая гипотеза является истинной, и между математическими ожиданиями с групп нет существенных различий, все три дисперсии — MSA, MSW и MST — являются оценками дисперсии ст2, присущей анализируемым данным. Таким образом, чтобы проверить нулевую гипотезу
Но: ... = щ
и альтернативную гипотезу
Нг: не все ц одинаковы (/=1, 2, ..., с), необходимо вычислить статистику F-критерия, представляющую собой отношение двух дисперсий, MSA и MSW.
ТЕСТОВАЯ F-СТАТИСТИКА В ОДНОФАКТОРНОМ ДИСПЕРСИОННОМ АНАЛИЗЕ
MSA
MSW
(10.5)
Статистика F-критерия подчиняется F-распределению с с-1 степенями свободы в числителе MSA и п-с степенями свободы в знаменателе MSW. При заданном уровне значимости а нулевая гипотеза отклоняется, если вычисленная F-статистика больше верхнего критического значения Fv, присущего F-распределению с с-1 степенями свободы в числителе и п-с степенями свободы в знаменателе (см. табл. Д.5). Таким образом, как показано на рис. 10.4, решающее правило формулируется следующим образом:
нулевая гипотеза Ноотклоняется, если F > Fb; в противном случае она не отклоняется.
Если нулевая гипотеза /Д является истинной, вычисленная F-статистика близка к 1, поскольку ее числитель и знаменатель являются оценками одной и той же величины — дисперсии а2, присущей анализируемым данным. Если нулевая гипотеза Но является ложной (и между математическими ожиданиями разных групп существует значительная разница), вычисленная F-статистика будет намного больше единицы, поскольку ее числитель, MSA, помимо естественной изменчивости данных, оценивает эффект условий эксперимента или разности между группами, в то время как знаменатель MSW оценивает лишь естественную изменчивость данных. Таким образом, процедура ANOVA представляет собой F-критерий, в котором при заданном уровне значимости а нулевая гипотеза отклоняется, если вычисленная F-статистика больше верхнего критического значения Fy, присущего F-распределению с с-1 степенями свободы в числителе и п-с степенями свободы в знаменателе, как показано на рис. 10.4.
гипотезы гипотезы
Рис. 10.4. Критическая область дисперсионного анализа при проверке гипотезы Но
Результаты дисперсионного анализа, как правило, представляются в виде сводной таблицы дисперсионного анализа (табл. 10.1). Ячейки этой таблицы содержат вид величины (межгрупповая, внутригрупповая и полная), количество степеней свободы, суммы квадратов, средние суммы квадратов (т.е. дисперсии) и вычисленную F-статистику. Кроме того, таблица дисперсионного анализа (summary table ANOVA) содержит р-значение (т.е. вероятность того, что F-статистика превышает верхнее критическое значение, соответствующее истинной нулевой гипотезе). Это р-значение позволяет сделать непосредственные выводы об истинности нулевой гипотезы без проверки таблицы F-распределения. Если р-значение меньше выбранного уровня значимости а, нулевая гипотеза отклоняется.
Таблица 10.1. Сводная таблица дисперсионного анализа
Вид величины Количество степеней свободы Суммы квадратов Дисперсии F-статистика
Межгрупповая с-1 SSA MSA=SSA/(c-l) F^MSA/MSW
Внутригрупповая п-с SSW MSW=SSW/(n-c)
Полная п-1 SST
Для иллюстрации однофакторного дисперсионного анализа вернемся к нашему сценарию, изложенному в начале главы. Цель эксперимента — определить, имеют ли парашюты, сотканные из синтетического волокна, полученного от разных поставщиков, одинаковую прочность. В каждой из групп соткано по пять парашютов. Группы разделены по поставщикам— Поставщик!, Поставщик 2, Поставщик 3 и Поставщик 4. Прочность парашютов измеряется с помощью специального устройства, испытывающего ткань на разрыв с двух сторон. Сила, необходимая для разрыва парашюта, измеряется по особой шкале. Чем выше сила разрыва, тем прочнее парашют. Результаты эксперимента (сила разрыва) и некоторые описательные статистики представлены на рис. 10.5.
Анализ рис. 10.5 показывает, что между выборочными средними наблюдается некоторая разница. Средняя прочность волокон, полученных от первого поставщика, равна 19,52, от второго — 24,26, от третьего — 22,84 и от четвертого — 21,16. Можно ли назвать эту разницу статистически значимой?
!
1 ' Поставщик 1 Поставщик 2 Поставщик 3 Поставщик 4
2^ 18,50: 26,30 20,60 25,40
3J 24,00 25,30 25,20 19,90
4 : 17,20 24,00 20,80 22,60
"5? 19,90 21,20 24,70 17,50
.6 .j 18,00 24,50 22,90 20,40
7 iCf )еднее арифметическое 19,52 24,26: 22,84 21,16
8 I Стандартное отклонение 2,69 1,92 2,13 2,98
Рис. 10.5. Показатели прочности парашютов, сотканных из синтетических волокон, полученных от разных поставщиков, а также арифметическое среднее и стандартное отклонение, вычисленные с помощью программы Microsoft Excel ЛPARACHUTE.XLS
Распределение силы разрыва продемонстрировано на диаграмме разброса (рис. 10.6). На ней ясно видны разности как между группами, так и внутри них. Если бы объем каждой группы был больше, для их анализа можно было бы применить диаграмму “ствол и листья”, блочную диаграмму и график нормального распределения.
Диаграмма разброса прочности парашютов
Поставщик
Рис. 10.6. Диаграмма разброса прочности парашютов, сотканных из синтетических волокон, полученных от четырех поставщиков, построенная с помощью программы Microsoft Excel
Нулевая гипотеза утверждает, что между средними показателями прочности нет существенных различий:
Но: F4= ц2 = р3 = ц4.
Альтернативная гипотеза заключается в том, что существует по крайней мере один поставщик, у которого средняя прочность волокон отличается от других:
Н,: не все |1 одинаковы 2, 3, 4).
Чтобы построить сводную таблицу дисперсионного анализа, сначала необходимо вычислить выборочные средние для каждой группы (см. рис. 10.5). Затем нужно найти общее среднее, просуммировав все 20 чисел и разделив их на общее количество наблюдений.
IvVr _ 438>9
11 20
= 21,945
После этого по формулам (10.1)—(10.3) вычисляются суммы квадратов.
SSA = Y», (*, - ^)2 = 5х(19,52-21,945)2 + 5х(24,26-21,945)2 +
+ 5х(22,84-21,945)2 + 5х(21,16-21,945)2 = 63,2855,
= (18,5-19,52)2 + ... + (18-19,52)2+
+ (26,3-24,26)2 + ... + (24,5-24,26)2 +
+ (20,6-22,84)2 + ... + (22,9-22,84)2 + (25,4-21,16)2 + ... +(20,4-21,16)2 = 97,504,
SST = -*) = (18,5-21,945)2+ (24-21,945)2 + ... + (20,4-21,945)2 =
= 160,7895.
Средние значения вычисляются путем деления этих сумм квадратов на соответствующее количество степеней свободы. Поскольку с = 4, а п = 20, получаем следующие значения дисперсии.
^=^1 = 6V855 с-1 4-1
MSW=SSW = 92,504 =6 094
п — с 20 — 4
Таким образом, используя формулу (10.5), можно вычислить F-статистику.
г MSA 21,095 _ . ,
F =------=-------= 3,46 .
MSW 6,094
При заданном уровне значимости ос верхнее критическое значение характерное для F-распределения, определяется по табл. Д.5, фрагмент которой приведен в табл. 10.2. В задаче о прочности парашютов числитель имеет три степени свободы, а знаменатель — 16. Таким образом, при уровне значимости, равном 0,05, верхнее критическое значение F-распределения равно 3,24. Поскольку вычисленная F-статистика, равная 3,46, превышает верхнее критическое значение нулевая гипотеза отклоняется (рис. 10.7).
Таблица 10.2. Определение верхнего критического значения ^-распределения, числитель которого имеет три степени свободы, а знаменатель —16, при уровне значимости, равном 0,051
Знаменатель, D.F.2 Числитель, D.FM
1 2 3 4 5 6 7 8 9
11 4,84 3,98 3,59 3,36 3,20 3,09 3,01 2,95 2,90
12 4,75 3,89 3,49 3,26 3,11 3,00 2,91 2,85 2,80
13 4,67 3,81 3,41 3,18 3,03 2,92 2,83 2,77 2,71
14 4,60 3,74 3,34 3,11 2,96 2,85 2,76 2,70 2,65
15 4,54 3,68 3,29 3,06 2,90 2,79 2,71 2,64 2,59
16 4,49 3,63 3,24 3,01 2,85 2,74 2,66 2,59 2,54
значение
Рис. 10.7. Критическая область дисперсионного анализа при уровне значимости, равном 0,05, если числитель имеет три степени свободы, а знаменатель —16
Сводная таблица дисперсионного анализа и р-значение, вычисленные с помощью программы Microsoft Excel, представлены на рис. 10.8. Таким образом, р-значение, т.е. вероятность того, что при истинной нулевой гипотезе F-статистика не меньше 3,46, равно 0,041. Поскольку эта величина не превышает уровень значимости, нулевая гипотеза отклоняется. Более того, р-значение свидетельствует о том, что вероятность обнаружить такую или большую разность между математическими ожиданиями генеральных совокупностей при условии, что на самом деле они одинаковы, равна 4,1% .
Рис. 10.8. Дисперсионный анализ прочности парашютов, выполненный с помощью программы Microsoft Excel
Подведем итоги. Как следует из рис. 10.5, между четырьмя выборочными средними существует разница. Нулевая гипотеза заключалась в том, что все математические ожидания четырех генеральных совокупностей равны между собой. В этих условиях мера полной изменчивости (т.е. полная вариация SST) прочности всех парашютов вычисляется путем суммирования квадратов разностей между каждым наблюдением и общим средним, равным 22,945. Затем полная вариация разделялась на два компонента (см. рис. 10.1). Первый компонент представлял собой межгрупповую вариацию, а второй — внутригрупповую.
Чем объясняется изменчивость данных? Иначе говоря, почему все наблюдения не одинаковы? Одна из причин заключается в том, что разные фирмы поставляют волокна разной прочности. Это частично объясняет, почему группы имеют разные математические ожидания: чем сильнее эффект условий эксперимента, тем больше разность между математическими ожиданиями групп. Другой причиной изменчивости данных является естественная изменчивость любого процесса, в данном случае — производства парашютов. Даже если бы все волокна приобретались у одного и того же поставщика, их прочность была бы неодинаковой при прочих равных условиях. Поскольку этот эффект проявляется в каждой из групп, он называется внутригрупповой вариацией (SSW).
Разности между выборочными средними называются межгрупповой вариацией (SSA). Часть внутригрупповой вариации, как уже указывалось, объясняется принадлежностью данных разным группам. Однако даже если бы группы были совершенно одинаковыми (т.е. нулевая гипотеза была бы истинной), межгрупповая вариация все равно существовала. Причина этого заключается в естественной изменчивости процесса производства парашютов. Поскольку выборки разные, их выборочные средние отличаются друг от друга. Следовательно, если нулевая гипотеза является истинной, как межгрупповая, так и внутригрупповая изменчивость представляют собой оценку изменчивости генеральной совокупности. Если нулевая гипотеза является ложной, межгрупповая гипотеза будет больше. Именно этот факт лежит в основе F-критерия для сравнения разностей между математическими ожиданиями нескольких групп.
После выполнения однофакторного дисперсионного анализа и обнаружения значительной разницы между фирмами остается неизвестным, какой же из поставщиков существенно отличается от остальных. Нам известно лишь, что математические ожидания генеральных совокупностей не равны. Иначе говоря, по крайней мере одно из математических ожиданий существенно отличается от других. Чтобы определить, какой из поставщиков отличается от других, можно воспользоваться процедурой Тьюки, использующей попарное сравнение между поставщиками. Эта процедура была разработа-
на Джоном Тьюки (John Tukey). Впоследствии он и К. Крамер (С. Y. Cramer) независимо друг от друга модифицировали эту процедуру для ситуаций, в которых объемы выборок отличаются друг от друга [5, 7, 9].
Процедуры Excel: однофакторный дисперсионный анализ
Чтобы выполнить однофакторный дисперсионный анализ, следует применить процедуру Анализ данныхЧ>Однофакторный дисперсионный анализ. В надстройке PHStat2 процедура, выполняющая дисперсионный анализ, не предусмотрена. Кроме того, вследствие сложности вычислений самостоятельно создать рабочий лист для дисперсионного анализа довольно трудно.
Например, чтобы осуществить однофакторный дисперсионный анализ прочности парашютов на основе данных, указанных на рис. 10.5, необходимо открыть рабочий лист Данные в рабочей книге Chapter 10.xls и выполнить такие действия.
1. Выбрать команду СервисЧ>Анализ данных....
2. В диалоговом окне Анализ данных выбрать пункт Однофакторный дисперсионный анализ в списке Инструменты анализа. Щелкнуть на кнопке ОК.
3. В диалоговом окне Однофакторный дисперсионный анализ (см. иллюстрацию) сделать следующее.
3.1. Ввести в окне редактирования
Входной интервал переменной 1 диапазон Al: D6.
3.2. Установить переключатель
Группирование в положение По столбцам.
3.3. Установить флажок Метки в первой строке.
3.4. Ввести в окне редактирования Альфа число 0,05.
3.5. Установить переключатель Параметры вывода в положение Новый рабочий лист и ввести название нового листа.
З.б. Щелкнуть на кнопке ОК.
Рабочий лист, созданный с помощью этой процедуры, не является динамически обновляемым. Следовательно, если данные изменятся, все описанные выше действия необходимо повторить. Для | выполнения этой процедуры необходимо, чтобы данные для каждой группы располагались в раз- ! ных столбцах. Такие данные называются разгруппированными. Для того чтобы обработать сгруппи- \ рованные данные, следует выполнить команду PHStat^Data Preparation^Unstack Data (PHStat4> j
Подготовка данных1^Разгруппировать данные...). \
Chapter 10.xls ['
Данные, на основе которых выполняется однофакторный дисперсионный анализ прочности | парашютов, содержатся в рабочей книге Chapter 10.xls на листе Рис10.8. |
Однофакторный дисперсионный анализ
Входные данные
Входной интервал:
Группирование:
0 Метки в первой строке Альфа: 0,05
Параметры вывода
О Выходной интервал:
Q} Новый рабочий лист:
О Новая рабочая книга
X
Множественное сравнение: процедура Тьюки-Крамера
В нашем сценарии для сравнения прочности парашютов использовался однофакторный дисперсионный анализ. Обнаружив значительные различия между математическими ожиданиями четырех групп, необходимо определить, какие именно группы отличаются друг от друга.
Хотя существует несколько способов решить эту задачу [4, 7, 8], мы опишем лишь процедуру множественного сравнения Тьюки—Крамера (Tukey-Kramer multiple comparison
procedure). Этот метод является примером процедур апостериорного сравнения (post hoc comparison), поскольку проверяемая гипотеза формулируется после анализа данных.
Процедура Тьюки-Крамера позволяет одновременно сравнить все пары групп. На первом этапе вычисляются разности X. - X ., где j ф j , между математическими ожиданиями с(с-1)/2 групп. Критический размах (critical range) процедуры Тьюки-Крамера вычисляется по формуле (10.6).
КРИТИЧЕСКИЙ РАЗМАХ ПРОЦЕДУРЫ ТЬЮКИ-КРАМЕРА
„ „ „ \MSWl 1 1
Критический размах - I----------1-
V 2 I п, п.
(10.6)
где — верхнее критическое значение распределения стьюдентизированного размаха, имеющего с степеней свободы в числителе и п - с степеней свободы в знаменателе.
Если объемы выборок не одинаковы, критический размах вычисляется для каждой пары математических ожиданий отдельно. На последнем этапе каждая из с(с-1)/2 пар математических ожиданий сравнивается с соответствующим критическим размахом. Элементы пары считаются значимо различными, если модуль разности |Ху - Xz.| между ними превышает критический размах.
Применим процедуру Тьюки-Крамера к задаче о прочности парашютов. Поскольку компания, производящая парашюты, имеет четыре поставщика, следует проверить 4(4-1)/2=6 пар поставщиков. Используя данные, приведенные на рис. 10.5, вычислим модуль разности между соответствующими выборочными средними.
1. |а; - А\| = |19,52-24,2б| = 4,74.
2. |J,-J3| = |19,52-22,84| = 3,32.
3. |^-J4| = |19,52-21,1б| = 1,64.
4. |А\-Х3| = |24,26-22,84| = 1,42.
5. |Х2-Х4| = |24,26-21,16| = 3,10.
6. |Х3-Х4|=|22,84-21,1б| = 1,68.
Поскольку все группы имеют одинаковый объем, достаточно вычислить только один критический размах. Для этого по сводной таблице дисперсионного анализа (рис. 10.8) определим величины MSE = 6,094 и и =5. Затем по табл. 10.3 при а = 0,05, с = 4 и п-с = 20-4 = 16 найдем величину Qv — верхнее критическое значение распределения стьюдентизированного размаха, имеющего четыре степени свободы в числителе и 16 степеней свободы в знаменателе. Как следует из таблицы, Qy = 4,05. Таким образом, по формуле (10.6) получаем:
16,094 61 Г)
Критический размах = 4,05 J—-—I — + — I = 4,471.
Поскольку 4,74 >4,471, статистически значимая разница существует между первым и вторым поставщиком. Все остальные пары состоят из практически одинаковых вели-
чин. Следовательно, средняя прочность парашютов, сотканных из волокон, приобретенных у первого поставщика, значимо меньше, чем у второго.
Таблица 10.3. Вычисление стьюдентизированного размаха Q, имеющего четыре степени свободы в числителе и 16 — в знаменателе, при уровне значимости, равном 0,052
Количество степеней свободы знаменателя Количество степеней свободы числителя
2 3 4 5 6 7 8 9
11 3,11 3,82 4,26 4,57 4,82 5,03 5,20 5,35
12 3,08 3,77 4,20 4,51 4,75 4,95 5,12 5,27
13 3,96 3,73 4,15 4,45 4,69 4,88 5,05 5,19
14 3,03 3,70 4,11 4,41 4,64 4,83 4,99 5,13
15 3,01 3,67 4,08 4,37 4,60 4,78 4,94 5,08
16 3,00 3,65 4,05 4,33 4,56 4,74 4,90 5,03
А
1 Анализ прочности парашютов 2
3 4
5
6 '
7
Т
*9
10\_________________
11 Level of significance Numerator d f. Denominator d f.
MSW
15 Q Statistic
_J=__________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________\
Group
1
2
3
4
Sample Sample Mean Size
19.52 5
24.26 5
22.84 5
21.16 5
0 05
_____4
____16
6.094
4.05
Other Data
Comparison
Group 1 to Group 2
Group 1 to Group 3
Group 1 to Group 4
Group 2 to Group 3
Group 2 to Group 4
Group 3 to Group 4
Absolute Difference
4.74
3.32
1.64
1.42
3.1
1.68
Std. Error of Difference
1.10399275
1.10399275
1.10399275
1 10399275
1.10399275
1.10399275
Critical
Range Results
4.4712 Means are different
4.4712 Means are not different 4 4712 Means are not different 4 4712 Means are not different 4.4712 Means are not different 4.4712 Means are not different
Рис. 10.9. Результаты применения процедуры Тьюки-Крамера для решения задачи о прочности парашютов с помощью программы Microsoft Excel
Процедуры Excel: процедура Тьюки-Крамера
Чтобы применить процедуру Тьюки-Крамера, следует выбрать команду Анализ данных^» Однофакторный дисперсионный анализ и создать рабочий лист, содержащий стьюдентизированный размах Q из табл. Д.9, либо применить надстройку PHStat2.
Например, чтобы сравнить с помощью этой процедуры прочность парашютов на основе данных, указанных на рис. 10.5, необходимо открыть рабочий лист Данные в книге Chapter 10 .xls и выполнить одну из следующих процедур.
2
Применение Excel в сочетании с надстройкой PHStat2
Чтобы применить процедуру Тьюки-Крамера, необходимо выбрать команду PHStat^Multiple-sample tests^Tukey-Cramer Procedure (РН81а1Ч>Многовыборочные критерииПроцедура Тьюки-Крамера). Затем нужно следовать таким инструкциям.3
1. Выбрать команду PHStaWMultiple-sample tests4> Т ukey-Cramer Procedure....
2. В диалоговом окне Tukey-Cramer Procedure (см. иллюстрацию) сделать следующее.
2.1. Ввести в окне редактирования Group Data Cell Range (Диапазон ячеек, содержащий группу данных) диапазон Al: D6.
2.2. Установить флажок First cell contains label (Первая ячейка содержит метку).
Tukey-Kramer Procedure
Data
Group Data Cell Range: iAl:D6 _j
V First cells contain label
Output Options
Title: ^Анализ прочности парашютов
Help | j: OK Cancel j
2.3. Ввести в окне редактирования Title (Заголовок) название нового листа.
2.4. Щелкнуть на кнопке ОК.
3. Найти в табл. Д.9 стьюдентизированный размах Q, соответствующий уровню значимости а = 0,05 и количеству степеней свободы, указанным на рабочем листе.
4. Ввести статистику Qв соответствующую ячейку рабочего листа (с помощью диалогового окна).
Рабочий лист, созданный с помощью этой процедуры, не является динамически обновляемым. Следовательно, если данные изменятся, все описанные выше действия необходимо повторить. Для выполнения этой процедуры необходимо, чтобы данные каждой группы располагались в разных столбцах. Такие данные называются разгруппированными. Для того чтобы обработать сгруппированные данные, следует выбрать команду PHStat^Data Preparation^Unstack Data... (PHStat^ Подготовка данных1^Разгруппировать данные...).
Применение Excel
С помощью процедуры Сервис^Анапиз данных...ФОднофакгорный дисперсионный анализ вычислите выборочные средние и объемы выборок из каждой группы, количество степеней свободы внутри каждой I группы и величину MSW. Затем найдите в табл. Д.9 стьюдентизированный размах Q, соответствующий i уровню значимости а = 0,05 и количеству степеней свободы. Создайте рабочий лист, вычисляющий мо- | дуль разностей и критический размах для каждой пары. Шаблоны рабочих листов, реализующих проце- ( дуру Тьюки-Крамера, описаны в разделе "Справочник по Excel" в конце главы. |
Chapter 10.xls !
Данные, на основе которых выполняется процедура Тьюки-Крамера при сравнении прочности парашютов, содержатся в рабочей книге Chapter 10 .xls на листе РисЮ.9.
Необходимые условия однофакторного дисперсионного анализа
При решении задачи о прочности парашютов мы не проверяли, выполняются ли условия, при которых можно использовать однофакторный F-критерий. Как же узнать, можно ли применять однофакторный F-критерий при анализе конкретных экспериментальных данных?
В главах 7 и 8 каждая процедура проверки гипотез применялась лишь при определенных условиях. Кроме того, в этих главах обсуждались последствия нарушения этих условий. Однофакторный F-критерий также можно применять, только если выполняются три основных предположения: экспериментальные данные должны быть случайными и независимыми, иметь нормальное распределение, а их дисперсии должны быть одинаковыми.
3 К сожалению, в некоторых локализованных версиях программы Microsoft Excel процедура Тъю-ки-Крамера блокируется сообщением об ошибке. В качестве альтернативы следует применять шаблон рабочего листа ТьюкиКрамер, описанный в разделе ЕН.10.1. — Прим.ред.
Первое предположение — случайность и независимость данных — должно выполняться всегда, поскольку корректность любого эксперимента зависит от случайности выбора и/или процесса рандомизации. Чтобы избежать искажения результатов, необходимо, чтобы данные извлекались из с генеральных совокупностей случайно и независимо друг от друга. Аналогично данные должны быть случайным образом распределенными по с уровням интересующего нас фактора (экспериментальным группам). Нарушение этих условий может серьезно исказить результаты дисперсионного анализа. Эти проблемы весьма подробно рассматриваются в работах [4, 7].
Второе предположение — нормальность — означает, что данные извлечены из нормально распределенных генеральных совокупностей. Как и для t-критерия, однофакторный дисперсионный анализ на основе F-критерия относительно мало чувствителен к нарушению этого условия. Если распределение не слишком значительно отличается от нормального, уровень значимости F-критерия изменяется мало, особенно если объем выборок достаточно велик. Если же условие о нормальности распределения нарушается серьезно, следует применять непараметрические процедуры дисперсионного анализа (см. раздел 11.5). Предположение о нормальности проверяется путем проверки каждой из с выборок. Как и в разделе 6.2, это предположение оценивается путем сравнения фактических и теоретических величин либо с помощью графика нормального распределения.
Третье предположение — однородность дисперсии — означает, что дисперсии каждой генеральной совокупности равны между собой (т.е. а,2 = сц = ... = а;). Это предположение позволяет решить, разделять или объединять внутригрупповые дисперсии. Если объемы групп совпадают, условие однородности дисперсии слабо влияет на выводы, полученные с помощью F-критерия. Однако, если объемы выборок неодинаковы, нарушение условия о равенстве дисперсий может серьезно исказить результаты дисперсионного анализа. Таким образом, следует стремиться к тому, чтобы объемы выборок были одинаковыми. Одним из методов проверки предположения об однородности дисперсии является критерий Левенэ, описанный ниже.
Если из всех трех условий нарушается лишь условие об однородности дисперсии, можно применять процедуру, аналогичную t-критерию, использующему раздельную дисперсию (см. раздел 9.1). Однако, если предположения о нормальном распределении и однородности дисперсии нарушаются одновременно, необходимо выполнить нормализацию данных и уменьшить разности между дисперсиями [8] или применить непараметрическую процедуру (см. раздел 11.5).
Критерий Левенэ для проверки однородности дисперсии
Несмотря на то что F-критерий относительно устойчив к нарушениям условия о равенстве дисперсий в группах, грубое нарушение этого предположения существенно влияет на уровень значимости и мощность критерия. Возможно, одним из наиболее мощных является критерий Левенэ (Levene) [1, 8]. Для проверки равенства дисперсий с генеральных совокупностей проверим следующие гипотезы:
Но: of =о2 =... = сг ,
Ht: не все ст одинаковы (7=1, 2, ..., с).
Модифицированный критерий Левенэ основан на утверждении, что если изменчивость в группах одинакова, для проверки нулевой гипотезы о равенстве дисперсий можно применить анализ дисперсии абсолютных величин разностей между наблюдениями и медианами групп. Итак, сначала следует вычислить абсолютные величины разностей между наблюдениями и медианами в каждой группе, а затем выполнить однофакторный дисперсионный анализ полученных абсолютных величин разностей. Для иллюстрации критерия Левенэ вернемся к сценарию, изложенному в начале главы. Используя данные, представленные на рис. 10.5, заполним следующую таблицу.
Таблица 10.4. Абсолютные величины разностей между медианами прочности волокон и наблюдениями в каждой группе поставщиков
Поставщик 1 (Медиана = 18,5) Поставщик 2 (Медиана = 24,5) Поставщик 3 (Медиана = 22,9) Поставщик 4 (Медиана = 20,4)
|18,5—18,5| =0,0 |26,3-24,5| =1,8 |20,6-22,9| =2,3 |25,4-20,4| =5,0
|24,5-18,5| =5,5 |25,3-24,5| =0,8 |25,2-22,9| =2,3 |19,9-20,4| =0,5
|17,2-18,5| =1,3 |24,0-24,5| =0,5 |20,8-22,9| =2,1 |22,6-20,4| =2,2
|19,9-18,5| =1,4 |21,2-24,5| =3,3 |24,7-22,9| =1,8 |17,5-20,4| =2,9
|18,0-18,5| =0,5 |24,5-24,5| =0,0 |22,9-22,9| =0,0 |20,4-20,4| =0,0
Результаты вычислений на основе данных из табл. 10.4, полученные с помощью программы Microsoft Excel, приведены на рис. 10.10. Как видим, F = 0,207 < 3,238867 (р-значение = 0,89 > 0,05). Таким образом, гипотеза Но не отклоняется. Между дисперсиями внутри каждой группы поставщиков существенной разницы нет.
А . Б С : D Е < F } G ;
1 ;Анализ прочности парашютов
2J
Э j ИТОГО________________________________________________________
4 Группы__________________Счет Сумма Среднее Дисперсия
5 J Поставщик 1 5 8.7 1.74 4.753
6 j Поставщик 2 5 6.4 1.28 1.707
7 jПоставщик 3 5 8.5 1.7 0.945
8 Поставщик 4 5 10.6 2.12 4.007
9
ioj
1 ^Дисперсионный анализ____________________________________________________
12______Источник вариации________SS______df_____MS_________F_____Р-значение F крит.
13НМежду группами 1.77 3 0.59 0.20679986 0.890188801 3.238866952
14 В н тур и групп 45.648 16 2.853
15:1
16^ Итого 47.418 19
Рис. 10.10. Результаты применения процедуры Тьюки-Крамера для решения задачи о прочности парашютов с помощью программы Microsoft Excel
Процедуры Excel: критерий Левенэ для проверки однородности дисперсий4
Чтобы применить критерий Левенэ, следует создать новый рабочий лист, вычисляющий абсолютные величины разностей между данными и медианой в каждой группе, а затем выбрать команду Сервис^Анализ данных...^Однофакторный дисперсионный анализ, либо применить надстройку PHStat2.
Например, чтобы применить этот критерий к данным о прочности парашютов, приведенным на рис. 10.10, необходимо открыть рабочий лист Данные в книге Chapter 10.xls и выполнить одну ! из следующих процедур.
К сожалению, в некоторых локализованных версиях программы Microsoft Excel критерий Левенэ блокируется сообщением об ошибке. В качестве альтернативы следует применять шаблон рабочего листа КритерийЛевенэ, описанный в разделе ЕН.10.2. — Прим.ред.
Применение Excel в сочетании с надстройкой PHStat2
Чтобы применить критерий Левенэ для проверки однородности дисперсий, необходимо сделать следующее.
1. Выбрать команду PHStat* 1^*Multiple-sample tests=> Levene’s Test (РН81а1Ч>Многовыборочные критерииЧ> Критерий Левенэ).
2. В диалоговом окне Levene’s Test (см. иллюстрацию) выполнить такие действия.
2.1. Ввести в окне редактирования Significance Level (Уровень значимости) число 0.05.
2.2. Ввести в окне редактирования Group Data Cell Range (Диапазон ячеек, содержащий группу данных) диапазон Al: D6.
Data
Level of Significance: (оТо5
Sample Data Cell Range: Jai :D6
I? First cells contain label
Output Options
Title: jАнализ прочности парашютов
Help ] 11...OK....31 Cancel J
2.3. Установить флажок First cell contains label (Первая ячейка содержит метку).
2.4. Ввести в окне редактирования Title (Заголовок) название нового листа.
2.5. Щелкнуть на кнопке ОК.
Применение Excel
Вычисление абсолютных величин разностей между данными и медианами в каждой группе. Чтобы самостоятельно создать рабочий лист, вычисляющий абсолютные величины разностей между данными и медианами в каждой группе, следуйте инструкциям из раздела ЕН.10.2.
Выполнение критерия Левенэ. Откройте рабочий лист КритерийЛевенэ, реализованный в разделе ЕН.10.2, и следуйте инструкциям.
1. Выберите команду Сервис^>Анализ данных....
2. Выберите в раскрывающемся списке Анализ данных пункт Однофакторный дисперсионный анализ и щелкните на кнопке ОК.
3. В диалоговом окне Однофакторный дисперсионный анализ выполните такие действия.
3.1. Введите в окне редактирования Входной интервал диапазон Fl: F16.
3.2. Установите переключатель Группирование в положение По столбцам.
3.3. Установите флажок Метки в первой строке.
3.4. Введите в диалоговом окне Альфа число 0,05.
3.5. Установите переключатель Параметры вывода в положение Новый рабочий лист.
3.6. Щелкните на кнопке ОК.
Chapter 10.xls
Данные, на основе которых выполняется модифицированный критерий Левенэ, содержатся в рабочей книге Chapter 10.xls на листе РисЮ.Ю.
УПРАЖНЕНИЯ К РАЗДЕЛУ 10.1
Изучение основ
10.1. Представьте себе, что данные в однофакторном эксперименте распределены по пяти группам, каждая из которых состоит из семи элементов.
1. Сколько степеней свободы существует при определении межгрупповой вариации?
2. Сколько степеней свободы существует при определении внутригрупповой вариации?
3. Сколько степеней свободы существует при определении полной вариации?
10.2. Рассмотрим эксперимент, описанный в задаче 10.1.
1. Предположим, что SSA = 60, SST = 210. Чему равна величина SSTV?
2. Чему равна величина MSA‘?
3. Чему равна величина MSW?
4. Чему равна F-статистика?
10.3. Рассмотрим эксперимент, описанный в задачах 10.1 и 10.2.
1. Заполните сводную таблицу ANOVA.
2. Чему равно верхнее критическое значение F-pacnpeделения при 5%-ном уровне значимости?
3. Сформулируйте решающее правило для проверки нулевой гипотезы о равенстве математических ожиданий всех пяти генеральных совокупностей.
4. Какой статистический вывод следует сделать?
10.4. Представьте себе, что данные в однофакторном эксперименте распределены по трем группам, каждая из которых состоит из семи элементов.
1. Сколько степеней свободы существует при определении межгрупповой вариации?
2. Сколько степеней свободы существует при определении внутригрупповой вариации?
3. Сколько степеней свободы существует при определении полной вариации?
10.5. Представьте себе, что данные в однофакторном эксперименте распределены по четырем группам, каждая из которых состоит из восьми элементов. Заполните сводную таблицу AN0VA.
Вид величины Количество степеней свободы Суммы квадратов Дисперсии F-статистика
Межгрупповая с-1=? SSA-? MSA=80 F=?
Внутригрупповая п-с=? SSW=560 MSW=?
Полная п-1=?
10.6. Рассмотрим эксперимент, описанный в задаче 10.5.
1. Чему равно верхнее критическое значение F-распределения при 5%-ном уровне значимости?
2. Сформулируйте решающее правило для проверки нулевой гипотезы о равенстве математических ожиданий всех пяти генеральных совокупностей.
3. Какой статистический вывод следует сделать?
4. Сколько степеней свободы в числителе и знаменателе имеет распределение стьюдентизированного размаха в процедуре Тьюки-Крамера?
5. Чему равно верхнее критическое значение распределения стьюдентизированного размаха при 5% -ном уровне значимости?
6. Чему равен критический размах в процедуре Тьюки-Крамера?
Применение понятий
Задачи 10.7—10.14 можно решать как вручную, так и с помощью программы Microsoft Excel.
10.7. Для экспресс-закусочных окно, оборудованное для обслуживания клиентов без выхода из движущегося автомобиля, является источником дополнительного дохода. Закусочные, обеспечивающие самую высокую скорость обслуживания, считаются наиболее привлекательными для клиентов (Ordonez, J. “An Effectiveness Drive: Fast-Food Lanes Are Getting Even Faster”, The Wall Street Journal, May 18, 2000, p. Al, A10). Статистическое исследование показало, что средняя продолжительность обслуживания в закусочных сети Wendy равна 150 с, в сети McDonald's — 167 с, в сети Checkers — 169 с, в сети Burger Kings — 171 с, в сети Long John Silvers — 172 с. Допустим, что из каждой сети отбирается по 20 закусочных и на основе их показателей заполняется сводная таблица ANOVA.
Вид величины Количество степеней свободы Суммы квадратов Дисперсии F-статистика
Межгрупповая 4 6 536 1 634,0 12,51
Внутригрупповая 95 12 407 130,6
1. Можно ли утверждать, что средняя продолжительность обслуживания в закусочных пяти компаний неодинакова, если уровень значимости равен 0,05?
2. Определите, какая сеть закусочных отличается от других по продолжительности обслуживания клиентов, если это возможно.
3. Можно ли определить, какая сеть закусочных обеспечивает самое быстрое обслуживание?
10.8. Журнал The Wall Street Journal в марте 2001 года провел сравнительное исследование акций. В ходе этого эксперимента для отбора перспективных акций, обещающих доход в течение ближайших пяти месяцев, применялись три разных метода. Четыре эксперта и четыре случайных читателя журнала выбрали по четыре акции. Еще четыре акции были отобраны путем жеребьевки. Доходность отобранных акций за период с 20 марта по 31 августа 2001 года (в процентах) приведены в следующей таблице. Индекс Доу-Джонса для акций промышленных компаний за этот период был равен 2,4% . ftfcONTEST2 002 . XLS.
Эксперты Читатели Жребий
+39,5 -31,0 +39,0
-1Д -20,7 +31,9
-4,5 -45,0 +14,1
-8,0 -73,3 +5,4
Источник: Wall Street Journal.
1. Можно ли утверждать, что средняя доходность акций этих трех категорий неодинакова, если уровень значимости равен 0,05?
2. Определите, какая группа акций отличается по средней доходности, если это возможно.
3. Оцените корректность вывода, сформулированного в заголовке статьи.
4. Существует ли статистически значимая разница между дисперсиями доходов акций из трех категорий, если уровень значимости равен 0,05?
10.9. Шкала компьютерной фобии (Computer Anxiety Rating Scale — CARS) измеряет индивидуальный уровень тревоги, вызываемой компьютерами. Показатель CARS, равный 20, означает отсутствие тревоги, а 100 — панику. Исследователи университета Майами измерили показатель CARS у 172 студентов. Одной из целей исследования было определить разницу между уровнем тревоги у девушек и юношей.
Вариация Степени Сумма Средние F
свободы квадратов квадраты
Между старшекурсниками 5 3 172
Среди старшекурсников 166 21 246
Полная вариация 171 24 418
Старшекурсники п Среднее
Маркетинг 19 44,37
Менеджмент 11 43,18
Другие 14 42,21
Финансовое дело 45 41,80
Бухгалтерское дело 36 37,56
Информационные системы 47 42,21
Источник: Travis Broome and Douglas Havelka, “Determinants of Computer Anxiety in Business Students”, The Review of Business Information Systems, Spring 2002,6(2): 9-16.
1. Постройте сводную таблицу дисперсионного анализа.
2. Существует ли статистически значимая разница между средним уровнем тревоги, испытываемой старшекурсниками из разных групп, если уровень значимости равен 0,05?
3. Если результаты решения задачи 1 позволяют, выполните процедуру Тьюки-Крамера и определите, у каких старшекурсников уровень тревоги отличается от среднего.
10.10. Студенты, изучающие статистику, осуществили полностью рандомизированный эксперимент, чтобы проверить прочность мусорных мешков четырех видов. Для этого в мешки по одному добавлялись грузы, вес которых равен одному фунту, пока мешок не разорвется, а результаты записывались в таблицу. В эксперименте были испытаны 40 мешков. Данные о прочности мешков хранятся в файле ^TRASHBAGS . XLS.
1. Существует ли статистически значимая разница между средней прочностью мешков из разных групп, если уровень значимости равен 0,05?
2. Определите, прочность каких мешков отличается от среднего, если это возможно.
3. Существует ли статистически значимая разница между дисперсиями прочности мешков из разных групп, если уровень значимости равен 0,05?
4. Мешки какого вида вы бы купили, а какие — нет?
10.11. В файле ФALLOY. XLS записаны данные о долговечности четырех сплавов.
Сплав
1 2 3 4
999 1 022 1 026 974
1 010 973 1 008 1 015
995 1 023 1 005 1 009
998 1 023 1 007 1 001
1 001 996 981 995
Источник: Р .Wludyka, Р. Nelson, and Р. Silva, “Power Curves for the Analysis of Means for Variances”, Journal of Quality Technology, 33,2001,60-65.
1. Существует ли статистически значимая разница между средней долговечностью разных сплавов, если уровень значимости равен 0,05?
2. Определите, долговечность каких сплавов отличается от средней, если это возможно.
3. Существует ли статистически значимая разница между дисперсиями долговечности разных сплавов, если уровень значимости равен 0,05?
4. Как результат решения задачи 3 влияет на корректность результатов решения задач 1 и 2?
10.12. Компания, производящая шариковые авторучки, наняла рекламное агентство, чтобы организовать общенациональную рекламную кампанию. Для начала директор компании решил исследовать влияние рекламы на восприятие их продукции. Был организован эксперимент, в котором сравнивались пять видов рекламы шариковых авторучек. В рекламе А свойства авторучек были сильно занижены, в рекламе Б — занижены умеренно, в рекламе В — слегка преувеличены, в рекламе Г — сильно преувеличены, и лишь в рекламе Д характеристики ручек описывались объективно. Из крупной фокус-группы была извлечена выборка, в которую были включены 30 респондентов, случайным образом распределенные по пяти группам, соответствующим разным видам рекламы (по шесть человек в группе). Прочитав рекламное объявление и сформировав свое представление о продукции компании, респонденты получали авторучки одного и того же вида, испытывали их и оценивали достоверность рекламных обещаний. Респондентов просили оценить внешний вид, долговечность и качество авторучек по семибалльной шкале. Суммарный рейтинг рекламы, учитывающий баллы по каждому из показателей (внешний вид, долговечность и качество), поставленные каждым из 30 респондентов, приведены в файле ftfPEN. XLS.
1. Существует ли статистически значимая разница между средними рейтингами разных рекламных объявлений, если уровень значимости равен 0,05?
2. Определите, рейтинг какого рекламного объявления отличается от среднего, если это возможно.
3. Существует ли статистически значимая разница между дисперсиями рейтингов разных рекламных объявлений, если уровень значимости равен 0,05?
4. Как результат решения задачи 3 влияет на корректность результатов решения задач 1 и 2?
10.13. Менеджер по розничным продажам в сети супермаркетов желает знать, влияет ли расположение игрушек для домашних животных на объем их продаж. Рассмотрены три вида стеллажей: передние, средние и задние. Для анализа отобраны 18 случайных магазинов, причем для каждого вида стеллажей отобраны по 6 магазинов. Размер витрины и цены на товары во всех магазинах одинаковы. Эксперимент проходил в течение месяца. Объемы продаж (в тыс. долл.) приведены в следующей таблице. ©LOCATE . XLS.
Расположение стеллажей
Впереди В середине Сзади
8,6 3,2 4,6
7,2 2,4 6,0
5,4 2,0 4,0
6,2 1,4 2,8
5,0 1,8 2,2
4,0 1,6 2,8
1. Можно ли утверждать, что средний объем продаж в магазинах, использующих разное положение стеллажей, неодинаков, если уровень значимости равен 0,05?
2. Определите, какая группа магазинов отличается от остальных по среднему объему продаж, если это возможно.
3. Какой вывод можно сделать на основе проведенного анализа? Подробно обоснуйте свою точку зрения.
10.14. Компания, производящая спортивные товары, желает сравнить расстояние, которое пролетают мячи для гольфа, изготовленные по четырем разным технологиям. По каждой технологии было произведено по десять мячей. Затем эти мячи были переданы местному гольф-клубу для испытаний. Порядок следования мячей был случайным. Все 40 мячей были испытаны в течение короткого отрезка времени при одинаковых погодных условиях. Результаты испытания (в ярдах) приведены в таблице.
Технология
1 2 3 4
206,32 203,81 217,08 213,90
226,77 223,85 230,55 231,10
207,94 206,75 221,43 221,28
224,79 223,97 227,95 221,53
206,19 205,68 218,04 229,43
229,75 234,30 231,84 235,45
204,45 204,49 224,13 213,54
228,51 219,50 224,87 228,35
209,65 210,86 211,82 214,51
221,44 233,00 229,49 225,09
1. Можно ли утверждать, что среднее расстояние, которое пролетают мячи для гольфа, произведенные по разным технологиям, неодинаково, если уровень значимости равен 0,05?
2. Если среднее расстояние, которое пролетают мячи для гольфа, произведенные по разным технологиям, неодинаково, примените процедуру Тьюки-Крамера и определите отличающиеся группы.
3. Какие условия должны выполняться при решении задачи 1? Выполняются ли эти условия?
4. Какую технологию следует предпочесть? Обоснуйте свою рекомендацию.
10.2. ДВУХФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ
В разделе 10.1 рассмотрен полностью рандомизированный эксперимент и связанный с ним однофакторный дисперсионный анализ. Теперь мы обсудим двухфакторный дисперсионный анализ, в ходе которого одновременно оцениваются два фактора. Мы рассмотрим лишь ситуации, в которых количество реплик (replicates) в группах, соответствующих определенным уровням (или группам) факторов А и В, одинаково (т.е. выборки имеют одинаковый объем п’). (Двухфакторный дисперсионный анализ для выборок, имеющих разный объем, рассматривается в работах [1, 8].) Многофакторный дисперсионный анализ, в котором количество групп превышает два, изложен в работах [4, 7].
Вследствие сложности вычислений, особенно при большом количестве уровней каждого фактора и реплик, для двухфакторного анализа следует применять либо программу Microsoft Excel, либо специализированное программное обеспечение. Однако для иллюстрации метода мы рассмотрим разложение полной вариации в двухфакторном анализе с одинаковым количеством реплик. Для начала введем следующие обозначения: г — количество уровней фактора А, с — количество уровней фактора В, п — количество величин (реплик) в каждой ячейке, соответствующей конкретным уровням факторов А и В, п — общее количество реплик (где п = гсп), Х11к — значение k-ro наблюдения, соответствующего i-му уровню фактора А и у-му уровню фактора В; X = —VVVXцк — общее среднее, Xt = — У'.'У.Х к — среднее значение, соответст-
вующее Z-му уровню фактора А (г = 1, 2, ...» г), X =—V V — среднее значение, со-
Л гп ,=| х=| '
ответствующее у-му уровню фактора В (;=1, 2, ..., с), Хч =~^Х1/к — среднее значе-п к=\
ние, соответствующее Z-му уровню фактора А и j-му уровню фактора В.
Оценка факторов и эффектов взаимодействия
В двухфакторном эксперименте факторы А и В считаются взаимодействующими, если эффект фактора А зависит от уровня фактора В.5 Напомним, что в полностью рандомизированном плане полная сумма квадратов (SST) подразделяется на межгрупповую сумму квадратов (SSA) и внутригрупповую сумму квадратов (SSW). В двухфакторном эксперименте с одинаковым количеством реплик в каждой ячейке полная вариация (SST) подразделяется на сумму квадратов, соответствующую фактору A (SSA), сумму квадратов, соответствующую фактору В (SSB), сумму квадратов, учитывающую
Аналогично факторы А и В называются взаимодействующими, если эффект фактора В зависит от уровня фактора А.
взаимодействие факторов А и В (SSAB), и сумму квадратов, возникающую вследствие случайной ошибки (SSE). Это разложение полной вариации (SST) продемонстрировано на рис. 10.11.
Рис. 10.11. Разделение полной вариации в двухфакторном эксперименте
Полная сумма квадратов (SST) представляет собой полную вариацию всех наблюдений вокруг общего среднего.
ПОЛНАЯ ВАРИАЦИЯ
,=1 7=1 £=| ' '
(Ю.7)
Сумма квадратов, соответствующая фактору A (SSA), представляет собой сумму квадратов разностей между разными уровнями фактора А и общим средним.
ВАРИАЦИЯ ФАКТОРА А
SSA = сп'^Х, - . (10.8)
Сумма квадратов, соответствующая фактору В (SSA), представляет собой сумму квадратов разностей между разными уровнями фактора В и общим средним.
ВАРИАЦИЯ ФАКТОРА В
SSB = rn'Y^X} -Х^ .
(10.9)
Сумма квадратов, учитывающая взаимодействие между факторами А и В (SSAB), представляет собой эффект взаимодействия между факторами А и В.
ВАРИАЦИЯ ВЗАИМОДЕЙСТВИЯ
SSAB = h'^Y\xii -X, -Xf+x}~ . (10.10)
Сумма квадратов ошибок (SSE) представляет собой сумму квадратов разностей между наблюдениями внутри каждой ячейки и соответствующим средним значением по ячейке.
СЛУЧАЙНАЯ ОШИБКА
SSE = ±tt(X„t-xX /=1 /=1 А=1 (10.11)
Поскольку фактор А имеет г уровней, существует г-1 степеней свободы, связанных с величиной SSA. Аналогично, поскольку фактор В имеет с уровней, существует с-1 степеней свободы, связанных с величиной SSB. Более того, поскольку каждой из гс ячеек соответствует п реплик, существуют 7'с(п’-1) степеней свободы, связанных с величиной SSE. Продолжая этот процесс дальше, можно прийти к выводу, что при вычислении полной вариации существует тг-1 степеней свободы, поскольку каждое наблюдение Х1/к сравнивается с общим средним значением X , учитывающим п наблюдений. Поскольку количество степеней свободы каждого источника вариации в сумме дает полную вариацию, количество степеней свободы, существующих при вычислении компонента взаимодействия (SSAB), получается путем вычитания. Общее количество степеней свободы равно (г-1)(с-1).
Если каждую сумму квадратов разделить на соответствующее количество степеней свободы, получится четыре типа дисперсии: MS A, MSB, MS АВ и MSE.
ВЫЧИСЛЕНИЕ ДИСПЕРСИЙ
MSA^, г -1 (10.12, а)
с -1 (10.12,6)
. _ _ SSAB MS АВ = , (г-1)(с-1) (10.12,в)
SSE MSE - . гс(п' -1) (10.12, г)
В двухфакторном дисперсионном анализе применяются три разных критерия.
1. Для проверки гипотезы об отсутствии эффекта фактора А
Но: ^ =\л2 = ... = ]лг
и альтернативной гипотезы
Н}\ не все ц равны
применяется F-статистика, вычисленная по формуле (10.13).
F-СТАТИСТИКА ДЛЯ ЭФФЕКТА ФАКТОРА А
MSA
MSE ’
(10.13)
При заданном уровне значимости а нулевая гипотеза отклоняется, если
где F,. — верхнее критическое значение F-pacnpe деления, имеющего г-1 степеней свободы в числителе и rc(n’-l) степеней свободы в знаменателе.
2. Для проверки гипотезы об отсутствии эффекта фактора В
К). = И2.=
и альтернативной гипотезы
Н}: не все равны
применяется F-статистика, вычисленная по формуле (10.14).
^-КРИТЕРИЙ ДЛЯ ЭФФЕКТА ФАКТОРА В
MSB
MSE'
(10.14)
При заданном уровне значимости а нулевая гипотеза отклоняется, если
г. MSB F =----> F,,
MSE
где Fv — верхнее критическое значение F-распределения, имеющего с-1 степеней свободы в числителе и rc(n’-l) степеней свободы в знаменателе.
3. Для проверки гипотезы об отсутствии эффекта взаимодействия факторов А и В
Но: взаимодействие факторов А и В равно нулю
и альтернативной гипотезы
взаимодействие факторов А и В не равно нулю
применяется F-статистика, вычисленная по формуле (10.15).
F-КРИТЕРИЙ ДЛЯ ЭФФЕКТА ВЗАИМОДЕЙСТВИЯ ФАКТОРОВ Аул В
MSAB MSE ’
(10.15)
При заданном уровне значимости а нулевая гипотеза отклоняется, если
MSAB F -----> F.
MSE
где Fu— верхнее критическое значение F-распределения, имеющего (г-1)(с-1) степеней свободы в числителе и rc(n’-l) степеней свободы в знаменателе.
Подытожим эту информацию в табл. 10.5.
Таблица 10.5. Дисперсионный анализ в двухфакторном эксперименте
Источник вариации Количество степеней свободы Сумма квадратов Дисперсия F
А г-1 SSA MSA= SSA/(r-l) F-MSA/MSE
В с-1 SSB MSB = SSB/(c-l) F=MSB/MSE
АВ (г-1)(с-1) SSAB MSAB = SSAB/(г- l)(c-l) F^MSAB/MSE
Ошибка rc(n'-l) SSE MSE — SSE / rc(n-1)
Всего п-1 SST
Для иллюстрации двухфакторного дисперсионного анализа вернемся к нашему сценарию. Допустим, что, будучи руководителем производства, вы решили не только сравнить несколько поставщиков синтетических волокон, но и оценить, на каком из станков выпускаются более прочные парашюты: Jetta или Turk. Кроме того, необходимо определить, зависит ли разница между четырьмя поставщиками от типа станков, на которых производятся парашюты. Итак, необходимо разработать план эксперимента, в котором каждому поставщику и типу станка соответствует пять парашютов. Результаты приведены в табл. 10.6.
Таблица 10.6. Прочность парашютов, сотканных на двух типах станков из синтетических волокон, приобретенных у четырех поставщиков ИPARACHUTE2.XLS
Поставщик
Тип станка 1 2 3 4
Jetta 20,6 22,6 27,7 21,5
18,0 24,6 18,6 20,0
19,0 19,6 20,8 21,1
21,3 23,8 25,1 23,9
13,2 27,1 17,7 16,0
Turk 18,5 26,3 20,6 25,4
24,0 25,3 25,2 19,9
17,2 24,0 20,8 22,6
19,9 21,2 24,7 17,5
18,0 24,5 22,9 20,4
На рис. 10.12 показаны результаты двухфакторного дисперсионного анализа данных, приведенных в табл. 10.5. На рис. 10.12 представлены объем выборки, сумма, арифметическое среднее и дисперсия каждой комбинации типа станка и поставщика. В первых двух таблицах приведены результаты дисперсионного анализа для всех типов станка, а в третьей — для каждого поставщика. Кроме того, в сводной таблице дисперсионного анализа идентификатор df обозначает количество степеней свободы, SS — сумму квадратов, MS — среднее квадратичное отклонение, a F — вычисленную F-статистику.
А В С D Е F G
1 Двухвыборочный дисперсионный анализ с повторенияни
2 •
3 ИТОГИ Поставщик 1 Поставщик 2 Поставщик 3 Поставщик 4 Итого
4 Jetta
5 Счет 5 5 5 5 20
6 Сунна 92,1 117,7 109,9 102,5 422.2
7 Среднее 18,42 23,54 21,98 20,5 21,11
8 Дисперсия 10,202 7,568 18,397 8,355 13,12831579
9
10 Turk
11 Счет 5 5 5 5 20
12 Сунна 97,6 121,3 114,2 105,8 438,9
13 Среднее 19,52 24,26 22,84 21,16 21,945
14 Дисперсия 7,237 3,683 4,553 8,903 8,462605263
15
16 Итого
17 Счет 10 10 10 10
18 Сунна 189,7 239 224,1 208,3
19 Среднее 18,97 23,9 22,41 20,83
20 Дисперсия 8,086777778 5,144444444 10,40544444 7,791222222
21
32
23 Дисперсионный анализ
24 Источник вариации SS df MS F Р-значение F крит
25 Выборка 6,97225 1 6,97225 0,809573573 0,374967795 4,149086408
28 Столбцы 134,34875 3 44,78291667 5,199909044 0,004866172 2,901117568
27 Взаинодействие 0,28675 3 0,095583333 0,011098532 0,998364568 2,901117568
28 Внутри 275,592 32 8,61225
29
30 Итого 417,19975 39
Рис. 10.12. Результат двухфакторного дисперсионного анализа прочности парашютов
Чтобы проанализировать эти результаты, сначала следует проверить, существует ли взаимодействие между факторами А (типами станка) и В (поставщиками). Если эффект взаимодействия является значительным, дальнейший анализ ограничивается лишь оценкой этого эффекта. С другой стороны, если эффект взаимодействия (interaction effects) незначителен, необходимо сосредоточиться на главных эффектах (main effects) — потенциальных различиях между типами станков (фактор А) и поставщиками (фактор В).
Чтобы определить наличие эффекта взаимодействия при уровне значимости, равном 0,05, применяется следующее решающее правило: нулевая гипотеза об отсутствии эффекта взаимодействия отклоняется, если вычисленное значение /-статистики больше 2,92, т.е. больше верхнего критического значения /-распределения с тремя степенями свободы в числителе и 32 степенями свободы в знаменателе (рис. 10.13)? Поскольку F = 0,011 < F,. = 2,90, ар-значение равно 0,998 (см. рис. 10.12), гипотеза Но не отклоняется. Следовательно, у нас недостаточно оснований утверждать, что факторы станка и поставщика взаимодействуют друг с другом. Следовательно, необходимо проанализировать главные эффекты.
Критическое значение
Рис. 10.13. Критическая область F-статистики с тремя степенями свободы в числителе и 32 степенями свободы в знаменателе, соответствующая уровню значимости, равному 0,05
При заданном уровне значимости, равном 0,05, в основе проверки разности между двумя станками (фактор А) лежит следующее решающее правило: нулевая гипотеза отклоняется, если вычисленное значение /’-статистики больше 4,17, т.е. больше верхнего критического значения /’-распределения с одной степенью свободы в числителе и 32 степенями свободы в знаменателе (рис. 10.14). Поскольку/ = 0,81 < F;, = 4,17, ар-значение равно 0,375 и больше уровня значимости (см. рис. 10.12), гипотеза/f,, не отклоняется. Следовательно, у нас недостаточно оснований утверждать, что между прочностью парашютов, произведенных на разных станках, существует значимая разница.
При заданном уровне значимости, равном 0,05, в основе проверки разности между поставщиками (фактор В) лежит следующее решающее правило: нулевая гипотеза отклоняется, если вычисленное значение / статистики больше 2,92, т.е. больше верхнего крити-
В табл. Д.5 нет верхнего критического значения F-распределения, имеющего 32 степени свободы в знаменателе. В нем есть лишь верхние критические значения F-распределения, имеющего 30 или 40 степеней свободы в знаменателе. Таким образом, необходимо округлять величину, ближайшую к заданной, или использовать р-значение.
ческого значения F-распределения с тремя степенями свободы в числителе и 32 степенями свободы в знаменателе (рис. 10.13). Поскольку F = 5,20 > Fv = 2,92, а р-значение равно 0,055 и меньше уровня значимости (см. рис. 10.12), гипотеза Но отклоняется. Следовательно, можно утверждать, что между прочностью парашютов, произведенных из волокна, приобретенного у разных поставщиков, существует значимая разница.
Критическое значение
Рис. 10.14. Критическая область F-статистики с одной степенью свободы в числителе и 32 степенями свободы в знаменателе, соответствующая уровню значимости, равному 0,05
Процедуры Excel: двухфактроный дисперсионный анализ
Чтобы выполнить двухфакторный дисперсионный анализ, следует применить процедуру Анализ данныхЧ>Двухфакгорный дисперсионный анализ. В надстройке PHStat2 эта процедура не предусмотрена. Кроме того, поскольку вычисления довольно сложны, самостоятельно создать рабочий лист, выполняющий дисперсионный анализ, нелегко.
Например, чтобы осуществить двухфакторный дисперсионный анализ прочности парашютов на основе данных, приведенных в табл. 10.6, необходимо открыть рабочий лист Станки в рабочей книге Chapter 10.xls и выполнить такие действия.
1. Выбрать команду Сервис^Анализ данных....
2. В диалоговом окне Анализ данных выбрать команду Двухфакгорный дисперсионный анализ с повторениями в списке Инструменты анализа и щелкнуть на кнопке ОК.
3. В диалоговом окне Двухфакгорный дисперсионный анализ с повторениями (см. иллюстрацию) сделать следующее.
3.1. Ввести в окне редактирования Входной интервал диапазон Al: Е11.
3.2. Ввести в окне редактирования Число строк для выборки число 5.
3.3. Ввести в окне редактирования Альфа число 0,05.
3.4. Установить переключатель Параметры вывода в положение Новый рабочий лист и ввести название нового листа.
3.5. Щелкнуть на кнопке ОК.
Рабочий лист, созданный с помощью этой процедуры, не является динамически обновляемым. | Следовательно, если данные изменятся, все описанные выше действия следует повторить. Для вы- j полнения этой процедуры необходимо, чтобы данные каждой группы располагались в разных I столбцах. Такие данные называются разгруппированными. Для того чтобы обработать сгруппиро- | ванные данные, нужно выбрать команду PHStatsData Preparation sUnstack Data (PHStats | Подготовка данны^Разгруппировать данные). |
Ла Chapter 10.xls
Данные, на основе которых выполняется двухфакторный дисперсионный анализ прочности | парашютов, содержатся в рабочей книге Chapter 10 .xls на листе РисЮ.12. I
Интерпретация эффектов взаимодействия
Чтобы лучше разобраться во взаимодействии факторов, следует построить график средних значений в ячейках (т.е. средних значений, соответствующих конкретным уровням факторов), как показано на рис. 10.15. Средние значения по ячейкам для факторов станок—поставщик приведены на рис. 10.12. Из графика средней прочности для каждой комбинации станок-поставщик следует, что две линии, соответствующие разным станкам, проходят почти параллельно друг другу. Это означает, что разности между средними величинами прочности парашютов, произведенных на разных станках, практически одинаковы для всех четырех поставщиков. Иначе говоря, между этими двумя факторами нет связи, что полностью подтверждается F-критерием.
Рис. 10.15. График средних значений прочности парашютов в зависимости от станков и поставщиков, построенный с помощью программы Microsoft Excel
В чем проявляется эффект взаимодействия? В некоторых ситуациях определенные уровни фактора А могут оказаться связанными с конкретными уровнями фактора В. Например, предположим, что некоторые парашюты оказываются более прочными, если они сотканы из определенных волокон на станках Jetta, а другие — если они сотканы из волокон других поставщиков на станках Turk. Если бы это было правдой, линии на рис. 10.15 не были бы параллельными и взаимодействие между факторами было бы статистически значимым. Следовательно, в этих ситуациях разница между станками не будет одинаковой при разных поставщиках. Это усложняет интерпретацию главных
эффектов, поскольку разности, соответствующие одному фактору (например, типу станка), не согласуются с другим фактором (например, поставщиком).
Проиллюстрируем эту ситуацию следующим примером.
ПРИМЕР 10.1. Интерпретация статистически значимых эффектов взаимодействия
Данные, приведенные в табл. 10.7, характеризуют продолжительность работы подшип ников под воздействием двух факторов: автоколебания и нагревания. ^BEARING. XLS .
Таблица 10.7. Продолжительность работы подшипников при автоколебании и нагревании
Нагревание
Автоколебание Слабое Сильное
Слабое 12 26
24 16
Сильное 18 101
28 113
Как влияют автоколебания и нагревание на продолжительность работы подшипников?
РЕШЕНИЕ. Результаты решения приведены на рис. 10.16.
А В i _С । о : Е . F G
ТОДвухфакгорный дисперсионный анализ с повторениями 5
ИТОГИ Слабое нагревание Сильное нагревание Итого
4 Слабое автоколебание - 5 [Счет 2 2 4
6 -Сумма 36 42 78
^Среднее 18 21 19,5
8 -Дисперсия ' g 72 50 43.66666667
10 Сильное автоколебание
11 Счет 2 2 4
12 Сумма 46 214 260;
13 Хреднее 23 107 65
14 ;Дисперсия 50 72 2392,666667
16 Итого Г?; Счет 4 4
18 Сумма 82 256
49а Среднее 20.5 64
Щ)?] Дисперсия И"""'"""" 49: 2506
ш
^^Дисперсионный анализ
24 Источник вариации SS df MS F P-Значение F критическое
25 J Выборка 4140.5 1 4140,5 67,87704918 0,001183615 7,708649719
28] Столбцы 3784,5 Г 3784,5 62,04098361 0,001404462 7,708649719
Взаимодействие 3280.5 1 3280,5 53,77868852 0,001840449 7,708649719
Внутри 244 4 61
“29
30! Итого 11449.5 7
Рис. 10.16. Результаты двухфакторного дисперсионного анализа продолжительности работы подшипников, полученные с помощью программы Microsoft Excel
Обратите внимание на то, что, кроме сводной таблицы дисперсионного анализа, программа Microsoft Excel вычисляет среднее значение для каждой комбинации двух факторов: степени автоколебаний и нагревания, а также среднее значение для каждого уровня факторов. Для того чтобы проанализировать эти результаты, сначала необходимо определить, наблюдается ли статистически значимый эффект взаимодействия факторов автоколебания (фактор А) и нагревания (фактор В). При уровне значимости а = 0,05 нулевую гипотезу об отсутствии эффекта взаимодействия следует отклонить, поскольку р-значение равно 0,0018, т.е. меньше 0,05. Кроме того, F-статистика равна 53,779 и превышает величину 7,71 — верхнее критическое значение F-распределения с одной степенью свободы в числителе и четырьмя степенями свободы в знаменателе.
Значимый эффект взаимодействия между автоколебанием и нагреванием можно проследить на рис. 10.17. Поскольку графики средних значений продолжительности работы подшипников при слабом и сильном нагревании, соответствующие двум степеням автоколебаний, не параллельны, разности между средними значениями продолжительности работы при двух типах автоколебаний и двух степенях нагревания неодинаковы.
Рис. 10.17. График средних значений продолжительности работы подшипников по ячейкам, построенный с помощью программы Microsoft Excel
Наличие эффекта взаимодействия факторов усложняет анализ основных эффектов. Теперь невозможно определить, существует ли статистически значимая разница между средними продолжительностями работы подшипников при слабых и сильных автоколебаниях, поскольку при разных степенях нагревания эта разность неодинакова. Аналогично невозможно определить, существует ли статистически значимая разница между средними продолжительностями работы подшипников при слабом и сильном нагревании, поскольку при разных степенях автоколебаний эта разность неодинакова.
Множественные сравнения
Если эффект взаимодействия факторов не важен, для множественного сравнения нескольких факторов можно применять процедуру Тьюки-Крамера [7, 9].
КРИТИЧЕСКИЙ РАЗМАХ ПРОЦЕДУРЫ ТЬЮКИ-КРАМЕРА ДЛЯ ФАКТОРА А
Критический размах = О1:. /-, (10.16)
V си'
где Qt, — верхнее критическое значение распределения стьюдентизированного размаха, имеющего г степеней свободы в числителе и rc(zi’-l) степеней свободы в знаменателе. Распределение стьюдентизированного размаха приведено в табл. Д.9.
КРИТИЧЕСКИЙ РАЗМАХ ПРОЦЕДУРЫ ТЬЮКИ-КРАМЕРА ДЛЯ ФАКТОРА В
Критический размах = OL J, (10.17)
V гп'
где Q, — верхнее критическое значение распределения стьюдентизированного размаха, имеющего с степеней свободы в числителе и rc(n'-l) степеней свободы в знаменателе. Распределение стьюдентизированного размаха приведено в табл. Д.9.
Применим процедуру Тьюки-Крамера к задаче о прочности парашютов, данные для которой приведены в табл. 10.6. Анализ сводной таблицы дисперсионного анализа, представленной на рис. 10.12, показывает, что статистически значимым является лишь один главный эффект. При уровне значимости, равном 0,05, нет оснований утверждать, что между двумя типами станков (Jetta и Turk) существует значимая разница (фактор А), однако между четырьмя поставщиками (фактор В) эта разница существует. Таким образом, дальнейший анализ должен концентрироваться на разностях между разными поставщиками.
Поскольку компания, производящая парашюты, имеет четыре фирмы-поставщика, следует проверить 4(4-1)/2=6 пар поставщиков. Используя результаты, приведенные на рис. 10.12, вычислим модуль разности между соответствующими средними значениями.
1. |Х, -Х,| = |18,97-23,90| = 4,93.
2. |Х, -Х3| = |18,97-22,41| = 3,44.
3. |А, -%4| = |18,97-20,83| = 1,86.
4. |Х,-Х3| = |23,90-22,41| = 1,49.
5. |Х2-Х4| = |23,90-20,83| = 3,07.
6. |Х,-%4| = |22,41-20,83| = 1,58.
Чтобы вычислить критический размах, обратимся к рис. 10.12. Как видим, MSE = 8,612, г = 2, с = 4 и п = 5. По табл. Д.9 (при а = 0,05, с = 4 и rc(n -1) = 32) определим, что Q( — верхнее критическое значение F-статистики с четырьмя степенями свободы в числителе и 32 степенями свободы в знаменателе — приближенно равно 3,84. Используя формулу (10.7), получаем:
- - о. /8,612 _
Критический размах = 3,84 =3,56.
Поскольку 4,93 > 3,56, статистически значимая разница существует лишь между первым и вторым поставщиком. Как и при однофакторном дисперсионном анализе, приходим к выводу, что средняя прочность парашютов, сотканных из волокон, приобретенных у первого поставщика, значительно ниже, чем у второго.
Изучение основ
10.15. Допустим, что при двухфакторном эксперименте факторы А и В имеют по три уровня. В каждой из девяти ячеек, соответствующих комбинациям уровней факторов А и В, находятся по четыре реплики.
1. Сколько степеней свободы существует при определении вариации фактора А?
2. Сколько степеней свободы существует при определении вариации фактора В?
3. Сколько степеней свободы существует при определении вариации взаимодействия факторов?
4. Сколько степеней свободы существует при определении вариации случайной ошибки?
5. Сколько степеней свободы существует при определении полной вариации?
10.16. Рассмотрим эксперимент, описанный в задаче 10.15.
1. Предположим, что SSA = 120, SSB = 110, SSE = 270 и SST = 540. Чему равна величина SSAB?
2. Чему равна величина MSA?
3. Чему равна величина MSB?
4. Чему равна величина MS АВ?
5. Чему равна величина MSE?
6. Чему равна F-статистика для эффекта взаимодействия?
7. Чему равна J7-статистика для эффекта фактора А?
8. Чему равна F-статистика для эффекта фактора В?
9. Заполните сводную таблицу дисперсионного анализа.
10.17. Рассмотрим эксперимент, описанный в задачах 10.15 и 10.16, при уровне значимости, равном 0,05.
1. Чему равно верхнее критическое значение F-распределения для эффекта фактора А?
2. Чему равно верхнее критическое значение F-распределения для эффекта фактора В?
3. Чему равно верхнее критическое значение F-распределения для эффекта взаимодействия факторов?
4. Сформулируйте решающее правило для проверки нулевой гипотезы о наличии эффекта взаимодействия факторов.
5. Сформулируйте решающее правило для проверки нулевой гипотезы о наличии эффекта фактора А.
6. Сформулируйте решающее правило для проверки нулевой гипотезы о наличии эффекта фактора В.
10.18. Предположим, что при двухфакторном эксперименте фактор А имеет три уровня, а фактор В— пять уровней. В каждой из десяти ячеек, соответствующих комбинациям уровней факторов А и В, находятся по четыре реплики. Допустим, что SSA = 18, SSB = 64, SSE = 60 и SST = 150, а уровень значимости равен 0,01.
1. Чему равна величина SSAB?
2. Заполните сводную таблицу дисперсионного анализа.
3. Чему равно верхнее критическое значение F-распределения для эффекта фактора А?
4. Чему равно верхнее критическое значение F-распределения для эффекта фактора В?
5. Чему равно верхнее критическое значение F-распределения для эффекта взаимодействия факторов?
6. Сформулируйте решающее правило для проверки нулевой гипотезы о наличии эффекта взаимодействия факторов.
7. Сформулируйте решающее правило для проверки нулевой гипотезы о наличии эффекта фактора А.
8. Сформулируйте решающее правило для проверки нулевой гипотезы о наличии эффекта фактора В.
10.19. Заполните сводную таблицу дисперсионного анализа для указанного двухфакторного эксперимента.
Вид величины Количество степеней свободы Суммы квадратов Дисперсии F-статистика
Фактор А г-1 = 2 SSA- ? MSA = 80 F= ?
Фактор В с-1 = ? SSB = 220 MSB= ? F=ll,0
Взаимодействие АВ (г-1)(с-1) = 8 SSAB= ? MSAB = 10 F=?
Ошибка rc(n'-l) = 30 SSE = ? MSE = ?
Всего 71—1 — ? SST= ?
10.20. Рассмотрим эксперимент, описанный в задаче 10.19, при уровне значимости,
равном 0,01.
1. Чему равно верхнее критическое значение F-распределения для эффекта
фактора А?
2. Чему равно верхнее критическое значение F-распределения для эффекта
фактора В?
3. Чему равно верхнее критическое значение Е-распределения для эффекта
взаимодействия факторов?
4. Сформулируйте решающее правило для проверки нулевой гипотезы о наличии эффекта взаимодействия факторов.
5. Сформулируйте решающее правило для проверки нулевой гипотезы о наличии эффекта фактора А.
6. Сформулируйте решающее правило для проверки нулевой гипотезы о наличии эффекта фактора В.
Применение понятий
Задачи 10.21-10.25 можно решать как вручную, так и с помощью программы Microsoft Excel.
10.21. В эксперименте исследуется влияние концентрации проявителя (фактор А) и продолжительности проявки (фактор В) на плотность фотопластинки. Использовались два значения концентрации и две продолжительности проявки. Для каждой комбинации уровней фактора создаются четыре реплики. Результаты эксперимента приведены в таблице (чем выше прочность, тем лучше), ftPHOTO. XLS.
Время проявки (мин.) Время проявки (мин.)
Концентрация 10 14 Концентрация 10 14
проявителя проявителя
1 0 1 2 4 6
5 4 7 7
2 3 6 8
4 2 5 7
1. Существует ли статистически значимый эффект взаимодействия факторов, если уровень значимости равен 0,05?
2. Существует ли статистически значимый эффект концентрации проявителя, если уровень значимости равен 0,05?
3. Существует ли статистически значимый эффект продолжительности проявления, если уровень значимости равен 0,05?
4. Постройте график зависимости средней плотности фотопластинки от времени проявки для каждого значения концентрации проявителя.
5. Как влияет концентрация проявителя и продолжительность проявки на прочность фотопластинки?
10.22. Владелец ресторана, специализирующегося на макаронных блюдах, испытывает сложности при изготовлении спагетти: они не должна быть слишком крахмальными или жесткими. Он решил провести эксперимент и сравнить две разновидности спагетти— американских и итальянских, которые готовятся либо 4, либо 8 минут. В эксперименте измерялся вес спагетти, поскольку в ходе приготовления макароны поглощают влагу. Спагетти, которые более интенсивно поглощают влагу, готовятся быстрее, следовательно, возрастает риск их разварить. В эксперименте использовались заготовки весом 150 г, которые запускались в кастрюлю, содержащую 6 кварт умеренно кипящей несоленой воды. Через заданный интервал времени спагетти извлекались из кастрюли и взвешивались. Результаты (в граммах), соответствующие двум репликам каждой разновидности спагетти и двум способам приготовления (в минутах), приведены таблице, ft PASTA. XLS.
Время приготовления (мин.) Время приготовления (мин.)
Разновидность 4 8 Разновидность 4 8
спагетти спагетти
Американские 265 310 Итальянские 250 300
270 320 245 305
1. Существует ли статистически значимый эффект взаимодействия между разновидностью спагетти и временем их приготовления, если уровень значимости равен 0,05?
2. Существует ли статистически значимый эффект разновидности спагетти, если уровень значимости равен 0,05?
3. Существует ли статистически значимый эффект времени приготовления спагетти, если уровень значимости равен 0,05?
4. Постройте график зависимости среднего веса спагетти от продолжительности их приготовления для каждой разновидности.
5. Как влияет разновидность спагетти и время их приготовления на ее вес?
10.23. Студенты, изучающие статистику, провели факторный эксперимент, в ходе которого измерялось время растворения болеутоляющих таблеток в стакане воды. В эксперименте исследовались два фактора: торговая марка (Equate, Kroger, Alka-Seltzer) и температура воды (теплая или холодная). Продолжительность растворения (в секундах) 24 таблеток приведены таблице. ©PAIN-RELIEF.XLS.
Торговая марка
Вода Equate Kroger Alka-Seltzer
Холодная 85,87 75,98 100,11
78,69 87,66 99,65
76,42 85,71 100,83
74,43 86,31 94,16
Теплая 21,53 24,10 23,80
26,26 25,83 21,29
24,95 26,32 20,82
21,52 22,91 23,21
1. Существует ли статистически значимый эффект взаимодействия между разновидностью таблетки и временем ее растворения, если уровень значимости равен 0,05?
2. Существует ли статистически значимый эффект разновидности таблетки, если уровень значимости равен 0,05?
3. Существует ли статистически значимый эффект температуры воды, если уровень значимости равен 0,05?
4. Постройте график средней продолжительности растворения таблеток для каждой разновидности при двух температурах воды.
5. Объясните результаты решения задач 1 и 3.
10.24. Интегральные микросхемы изготавливаются на кремниевых подложках. Процесс их изготовления является поэтапным. В одном из экспериментов исследовались влияние способов очистки и травления на объем производства. ©YIELD. XLS.
Способ травления
Способ очистки Новый Стандартный
38 34
Новый 1 34 19
38 28
Способ травления
Способ очистки Новый Стандартный
29 20
Новый 2 35 35
34 37
31 29
Стандартный 23 32
38 30
Источник: J. Ramirez and W. Taam, “An autologic Model for Intergrated Circuit Manufacturing”, Journal of Quality Technology, 2000, 32, 254-262.
1. Существует ли статистически значимый эффект взаимодействия между способами очистки и травления кремниевых подложек, если уровень значимости равен 0,05?
2. Существует ли статистически значимое влияние способа очистки на объем производства, если уровень значимости равен 0,05?
3. Существует ли статистически значимое влияние способа травления на объем производства, если уровень значимости равен 0,05?
4. Постройте график среднего объема производства для каждого способа очистки при разных способах травления кремниевых подложек.
5. Объясните результаты решения задач 1-4.
10.25. В одном из экспериментов исследовалась прочность автомобильных шин, зависящая от длины шипов и вида установки. ft^GEAR. XLS.
Установка
Длина шипов Низкая Высокая
18,0 13,5
16,5 8,5
26,0 11,5
Короткие 22,5 16,0
21,5 -4.5
21,0 4,0
30,0 1,0
24,5 9,0
27,5 17,5
19,5 11,5
31,0 10,0
Длинные 27,0 1,0
17,0 14,5
14,0 3,5
18,0 7,5
17,5 6,5
Источник: D.R.Bingham and R.R.Sitter, “Design Issues in Fractional Factorial Split-Plot Experiments,” Journal of Quality Technology, 33,2001, 2-15.
1. Существует ли статистически значимый эффект взаимодействия между установкой шины и длиной шипов, если уровень значимости равен 0,05?
2. Существует ли статистически значимое влияние длины шипов на прочность шины, если уровень значимости равен 0,05?
3. Существует ли статистически значимое влияние вида установки шины на ее прочность, если уровень значимости равен 0,05?
4. Постройте график средней прочности шин для каждого вида шипов при разных видах установки.
5. Объясните результаты решения задач 1-4.
10.3. БЛОЧНЫЙ РАНДОМИЗИРОВАННЫЙ ЭКСПЕРИМЕНТ
В разделе 10.1 рассмотрен F-критерий однофакторного дисперсионного анализа для оценки разностей между математическими ожиданиями с групп. Этот критерий применяется в ситуациях, когда п однородных элементов (так называемых экспериментальных объектов) случайным образом распределяются по с уровням исследуемого фактора (так называемые группы условий факторного эксперимента (treatment groups)). Такие однофакторные эксперименты называются однофакторными или полностью рандомизированными (one-way or completely randomized designs).
Кроме того, в разделе 9.2 описан ^-критерий для оценки разностей между математическими ожиданиями, который используется в ситуациях, связанных с повторяющимися измерениями или согласованными выборками. Этот критерий позволяет оценить различия между условиями проведения двух экспериментов. Предположим, что мы исследуем несколько групп условий или уровней исследуемого фактора. В таких ситуациях совокупности неоднородных объектов или индивидуумов, подлежащих сравнению (или повторным измерениям), называются блоками (blocks). Допустим, мы получили числовые результаты измерений для каждой группы условий и комбинаций блоков.
Эксперименты, в которых используются блоки, называются блочными рандомизированными экспериментами (randomized block designs). Хотя в таких схемах используются как условия, так и блоки, основное внимание уделяется оценке разностей между с разными группами условий. Целью объединения условий в блоки является максимально возможное исключение изменчивости экспериментальной ошибки с тем, чтобы разности между с групп условий проявились как можно отчетливее. Блочные рандомизированные эксперименты часто оказываются более эффективными, чем полностью рандомизированные эксперименты и, следовательно, позволяют получать более точные результаты [1,4, 7 и 8].
Для сравнения полностью рандомизированных и блочных рандомизированных экспериментов вернемся к сценарию, посвященному компании Perfect Parachute Company. Предположим, что в полностью рандомизированном эксперименте используются 12 наблюдений — по одному виду ткани на каждую из 12 смен. Любая изменчивость результатов испытаний становится частью экспериментальной ошибки, и, следовательно, различия между четырьмя поставщиками труднее уловить. Для того чтобы уменьшить экспериментальную ошибку, разработаем блочный рандомизированный эксперимент, в котором исследуются три смены, в течение каждой из которых ткутся четыре парашюта (один парашют — из волокон, полученных от первого поставщика, второй — из волокон, полученных от второго поставщика, и т.д.). Три смены рассматриваются как блоки, а условием факторного эксперимента является поставщик. Преимущество блочного рандомизированного эксперимента заключается в том, что из экспериментальной ошибки исключается изменчивость между тремя сменами. Следовательно, этот эксперимент часто обеспечивает более точные оценки различий между четырьмя поставщиками.
Критерии для оценки эффектов условий факторного эксперимента и блоков
Напомним, что в полностью рандомизированном эксперименте полная вариация (SST) подразделяется на межгрупповую (SSA) и внутригрупповую (SSTT). Внутригрупповая вариация считается экспериментальной ошибкой, а межгрупповая вариация возникает вследствие различий между условиями факторного эксперимента.
Для того чтобы отделить эффект блокировки от экспериментальной ошибки блочного рандомизированного эксперимента, необходимо подразделить внутригрупповую вариацию (SSTT) на межблочную вариацию (SSBL) и случайную ошибку (SSE). Следовательно, как показано на рис. 10.18, в блочном рандомизированном эксперименте полная вариация результатов измерений представляет собой сумму межгрупповой вариации (SSA), межблочной вариации (SSBL) и случайной ошибки (SSE).
Разделение полной вариации SST = SSA + SSBL + SSE
Полная вариация (SST) d.f. =п-1
Случайная вариация (SSE) d.f. = (r-1)(c-1)
Межгрупповая вариация (; d.f. = с-1
^блоковая вариация ( d.f. = г-1
Рис. 10.18. Разделение полной вариации в блочном рандомизированном эксперименте
Для того чтобы разработать процедуру дисперсионного анализа для блочного рандомизированного эксперимента, введем следующие обозначения:
г — количество блоков,
с — количество групп или уровней фактора,
п — общее количество наблюдений (п = гс),
Хч — величина в i-м блоке и /-группе,
— среднее всех величин из i-ro блока,
— среднее всех величин из у-й группы,
^^Ху —общая сумма. 7=1 /=1
Полная вариация, называемая также полной суммой квадратов (SST), представляет собой вариацию между всеми наблюдениями. Величина SST равна сумме квадратов разностей между каждым отдельным наблюдением и общим средним X , вычисленным по всем п наблюдениям.
Межгрупповая вариация, называемая также межгрупповой суммой квадратов (SSA), равна сумме квадратов разностей между выборочным средним каждой группы X f и общим средним значением X , деленным на количество блоков г.
МЕЖГРУППОВАЯ ВАРИАЦИЯ
= (10.19)
где X f — среднее значение по у-й группе.
Межблоковая вариация, называемая также межгрупповой суммой квадратов (SSBL), равна сумме квадратов разностей между средними значениями по каждому блоку X' и общим средним значением X , деленному на количество групп с.
МЕЖБЛОКОВАЯ ВАРИАЦИЯ
SSBL^c^X, (10.20)
где X =-±Х — среднее значение по i-му блоку, с 7^
Чисто случайная вариация или ошибка, также называемая суммой квадратов ошибок (SSE), равна сумме квадратов разностей между всеми наблюдениями после определенного воздействия и средними по блокам и группам.
СЛУЧАЙНАЯ ОШИБКА
Поскольку фактор имеет с уровней, существует с-1 степеней свободы, связанных с межгрупповой суммой квадратов (SSA). Аналогично, поскольку существует г блоков, существует /'-1 степеней свободы, связанных с межблоковой суммой квадратов (SSBL). Более того, общая сумма квадратов (SST) имеет п-1 степеней свободы, поскольку каждое наблюдение Xtj сравнивается с общим средним X , вычисленным по всем п наблюдениям. Поскольку количество степеней свободы каждого источника вариации складывается с количеством степеней свободы полной вариации, количество степеней свободы суммы квадратов ошибок (SSE) получается путем вычитания и алгебраических манипуляций. Это количество степеней свободы равно (г-1)(с-1).
Если каждую компоненту суммы квадратов поделить на соответствующее количество степеней свободы, мы получим три вида дисперсии (MSA, MSBL и MSE), необходимых для формулы (10.22, а-в).
ВЫЧИСЛЕНИЕ СРЕДНЕКВАДРАТИЧЕСКИХ ЗНАЧЕНИЙ
сел MSA = ——, (10.22, а) с-1 = (10.22,6) г-1 SSE MSE = - (10.22,6)
Если выполняются предположения, принятые в дисперсионном анализе, можно применить Е-критерий (10.23), позволяющий проверить нулевую и альтернативную гипотезы о разностях между математическими ожиданиями с генеральных совокупностей.
Но: р, = ц2 = ... — (условия не имеют эффекта), Нг: не все р равны между собой, j = 1, 2, ..., с.
РАНДОМИЗИРОВАННАЯ БЛОЧНАЯ F-СТАТИСТИКА ДЛЯ РАЗНОСТЕЙ МЕЖДУ С МАТЕМАТИЧЕСКИМИ ОЖИДАНИЯМИ
Е-статистика имеет Е-распределение, в котором числитель MSA имеет с-1 степеней свободы, а знаменатель MSE имеет (г-1)(с-1) степеней свободы. При заданном уровне значимости а нулевая гипотеза отклоняется, если вычисленная Е-статистика больше верхнего критического значения Ег, присущего Е-распределению с с-1 и (г-1)(с-1) степенями свободы в числителе и знаменателе (см. табл. Д.5). Итак, решающее правило принимает следующий вид.
Нулевая гипотеза HQ отклоняется, если Е > Е^;
в противном случае гипотеза Но не отклоняется.
Для того чтобы выяснить, дает ли какие-либо преимущества блочный рандомизированный эксперимент, некоторые статистики предлагают применять Е-критерий для проверки блоковых эффектов. Нулевая гипотеза заключается в отсутствии блоковых эффектов
Н°: ц, = р2 = ... = |Д. (блоковые эффекты не наблюдаются), Н/. не все р равны между собой, j = 1, 2, ..., г.
F-СТАТИСТИКА ДЛЯ БЛОКОВЫХ ЭФФЕКТОВ
р MSBL
~ MSE
(10.24)
При заданном уровне значимости а нулевая гипотеза отклоняется, если вычисленная Е-статистика больше верхнего критического значения Fv, присущего Е-распределению с с-1 и (г- 1)(с-1) степенями свободы в числителе и знаменателе (см. табл. Д.5). Итак, решающее правило принимает следующий вид.
Нулевая гипотеза Н1} отклоняется, если F > Fv; в противном случае гипотеза Но не отклоняется.
Некоторые статистики полагают, что этот критерий излишен, поскольку единственной целью блоков является создание более эффективного способа проверки наличия эффектов путем уменьшения экспериментальной ошибки.
В разделе 10.1 результаты дисперсионного анализа представлены в виде сводной таблицы ANOVA.
Таблица 10.8. Сводная таблица дисперсионного анализа для блочного рандомизированного эксперимента
Вид величины Количество степеней свободы Суммы квадратов Дисперсии F-статистика
Межгрупповая с-1 SSA MSA=SSA/(c-l) F^MSA/MSW
Межблоковая г-1 SSBL MSBL=SSBL/(r-l) F=MSBL/MSE
Ошибка (г-Л(с-1) SSE MSE=SSE/(r-l)(c-l)
Полная гс-1 SST
Проиллюстрируем блочный рандомизированный эксперимент следующим примером. Предположим, что сеть ресторанов быстрого питания, имеющая четыре подразделения в определенном географическом регионе, желает оценить качество обслуживания в этих ресторанах. Для этой цели директор нанял шесть экспертов, имеющих разный опыт. Чтобы уменьшить эффект вариации между экспертами, был разработан блочный рандомизированный эксперимент, в которых блоками считались эксперты. В свою очередь, четыре ресторана образовали группы условий факторного эксперимента.
Шесть экспертов в случайном порядке инспектировали каждый из четырех ресторанов. Для оценки использовалась шкала баллов от 0 (низшая оценка) до 100 (высшая оценка). Результаты приведены в табл. 10.9.
Таблица 10.9. Рейтинги четырех ресторанов быстрого питания
Рестораны
Эксперты А Б В Г Всего Средние
1 70 61 82 74 287 71,75
2 77 75 88 76 316 79,00
3 76 67 90 80 313 78,25
4 80 63 96 76 315 78,75
5 84 66 92 84 326 81,50
6 78 68 98 86 330 82,50
Всего 465 400 546 476 1 887
Средние 77,50 66,67 91,00 79,33 78,625
Кроме того, как следует из табл. 10.9,
г = 6, с = 4, п = гс = 24
= 78,625.
Результаты анализа результатов, полученных в рамках блочного рандомизированного эксперимента, приведены на рис. 10.19.
в
F
G
а _
1 Двухфакторный дисперсионный анализ без повторений
2Н______________________________________________
D ‘ Е
3 ИТОГИ Счет Сумма Среднее Дисперсия
4 ;Эксперт 1 4 287 71,75 76,25
5 ^Эксперт 2 4 316 79 36,66666667
6 М Эксперт 3 4 313 78,25 90,91666667
7 ^Эксперт 4 4 315 78,75 184,9166667
8JЭксперт 5 4 326 81,5 121
9 :Эксперт 6 4 330 82,5 161
10
11{Ресторан А 6 465 77,5 21,5
12'Ресторан В б 400 66,66666667 23,46666667
13 Ресторан С 6 546 91 33,2
14{Ресторан D 6 476 79,33333333 23,46666667
15
. »б!
17 Дисперсионный анализ
18 Источник вариации SS df MS F
19!Строки 283,375 5 56,675 3,781835032
20'Столбцы 1787,458333 3 595,8194444 39,75810936
21 {Погрешность 224,7916667 15 14,98611111
22 j
23 {Итого 2295,625 23
Р-значение F крит 0,020455782 2,901295204 2,23345Е-07 3,28738281
Рис. 10.19. Результаты инспекции сети ресторанов быстрого питания, полученные с помощью программы Microsoft Excel
Если установить уровень значимости критерия для проверки гипотезы о существовании различий между подразделениями сети ресторанов равным 0,05, решающее правило примет следующий вид: нулевая гипотеза Но (рх = ц2 = ц3 = ц4) отклоняется, если F > 3,29. Число 3,29 представляет собой верхнее критическое значение F-распределения, имеющего три степени свободы в числителе и 15 степеней свободы в знаменателе (см. рис. 10.20). Поскольку F = 39,758 > Fv = 3,29 (т.е. р = 0,000 < 0,05), мы можем отклонить гипотезу Но и утверждать, что средние рейтинги ресторанов статистически значимо различаются между собой. Чрезвычайно малое значение р означает, что, если бы средние рейтинги четырех подразделений были одинаковыми, вероятность обнаружить разности между их выборочными средними, была бы крайне малой. Итак, нулевая гипотеза практически невероятна. Следовательно, альтернативную гипотезу можно считать корректной.
Область I Область принятия /отклонения гипотезы / гипотезы
Критическое значение
Область / Область принятия /отклонения гипотезы / гипотезы
Критическое значение
Рис. 10.20. Области отклонения и принятия гипотез при изучении сети ресторанов быстрого питания при уровне значимости, равном 0,05, стремя и 15 степенями свободы
Рис. 10.21. Области отклонения и принятия гипотез при изучении сети ресторанов быстрого питания при уровне значимости, равном 0,05, с пятью и 15 степенями свободы
Для проверки эффективности блокировки, можно проверить разность между экспертами. При 5% -м уровне значимости решающее правило можно сформулировать следующим образом: нулевая гипотеза НДщ = ц2 = ... = ц6) отклоняется, если вычисленная
статистика F>2,90. Число 2,90 представляет собой верхнее критическое значение F-распределения, имеющего пять степеней свободы в числителе и 15 степеней свободы в знаменателе (см. рис. 10.21). Поскольку F = 3,782 > Fv = 2,90 (т.е. р = 0,02 < 0,05), мы может отклонить гипотезу Но и утверждать, что средние рейтинги ресторанов статистически значимо различаются между собой. Итак, применение блоков уменьшает экспериментальную ошибку.
Процедуры Excel: дисперсионный анализ с помощью блочного рандомизированного эксперимента
! Чтобы выполнить однофакторный дисперсионный анализ, следует применить процедуру I Анализ данных...^Двухфакторный дисперсионный анализ без повторений. В надстройке PHStat2 I эта процедура не предусмотрена. Кроме того, вследствие сложности вычислений шаблон рабочего листа для этого критерия довольно трудно реализовать вручную.
Например, чтобы осуществить дисперсионный анализ данных, приведенных в табл. 10.9, используя блочный рандомизированный эксперимент, необходимо открыть рабочий лист Рейтинги в рабочей книге Chapter 10.xls и выполнить такие действия.
1. Выбрать команду Сервис^Анализ данных....
2. В диалоговом окне Анализ данных выбрать пункт Двухфакторный дисперсионный анализ без повторений в списке Инструменты анализа. Щелкнуть на кнопке ОК.
3. В диалоговом окне Двухфакторный дисперсионный анализ без повторений (см. иллюстрацию) сделать следующее.
3.1. Ввести в окне редактирования Входной интервал переменной 1 диапазон А1:Е7.
3.2. Установить флажок Метки.
3.3. Ввести в окне редактирования Альфа число 0,05.
3.4. Установить переключатель Параметры вывода в положение Новый рабочий лист и ввести название нового листа.
3.5. Щелкнуть на кнопке ОК.
Двухфанторный дисперсионный анализ без повторений [X|
Входные данные
Входной интервал:
0 Метки
Альфа: io.05
Параметры вывода
О Выходной интервал:
*) Новый рабочий лист: Новая рабочая книга
А1:Е7
: Рейтинги
[Отмена] J Справка J
Рабочий лист, созданный с помощью этой процедуры, не является динамически обновляемым. Следовательно, если данные изменятся, все описанные выше действия необходимо повторить.
Для выполнения этой процедуры необходимо, чтобы данные для каждой группы располагались в разных столбцах. Такие данные называются разгруппированными. Для того чтобы обработать сгруппированные данные, следует выполнить процедуру, описанную в разделе ЕН.9.2.
Кроме обычных ограничений, принятых в однофакторном дисперсионном анализе, необходимо также предположить, что между условиями факторного эксперимента и блоками нет взаимодействия. Иначе говоря, необходимо, чтобы все различия между условиями эксперимента (ресторанами) были согласованы со всеми блоками (отмечались всеми экспертами). Понятие взаимодействия (interaction) обсуждается в разделе 10.2.
После разработки схемы блочного рандомизированного эксперимента и анализа данных о рейтингах ресторанов возникает вопрос: какой эффект оказывает блокирование на дисперсионный анализ? Иначе говоря, получаем ли мы более точные результаты, применяя блокирование при анализе разных групп условий факторного эксперимента? Для того чтобы ответить на этот вопрос, следует вычислить оценку относите ль-
ной эффективности (relative efficiency — RE) блочного рандомизированного эксперимента по сравнению с полностью рандомизированным экспериментом.
Г ОЦЕНКА ОТНОСИТЕЛЬНОЙ ЭФФЕКТИВНОСТИ I
(r-l)MSBL + r(c-\)MSE
I RE = --Ц----—. (10.25)
|(rc-l)MSE j
Используя формулу (10.19), получаем
ПЕ, 5x56,675 + 6x3x14,986 ,
RE =--------------= 1,60.
23x14,986
Это означает, что для получения такой же точности при сравнении средних по группам в рамках однофакторного дисперсионного анализа нам понадобилось бы в 1,6 раза увеличить количество наблюдений в каждой группе.
Множественные сравнения: процедура Тьюки
Как и в полностью рандомизированном эксперименте, отклонив нулевую гипотезу о равенстве всех средних по группам, мы можем определить, какая группа условий значительно отличается от остальных. Для блочного рандомизированного эксперимента такая процедура была разработана Джоном Тьюки (John Tukey) [7-9]. Критический размах в процедуре Тьюки (Tukey procedure) вычисляется по формуле (10.26).
КРИТИЧЕСКИЙ РАЗМАХ
Критический размах = Qu.l--, (10.26)
V г
где статистика Qv представляет собой верхнее критическое значение распределения стьюдентизованного размаха, имеющего с степеней свободы в числителе и (г-1)(с-1) степеней свободы в знаменателе. Величины распределения стьюдентизованного размаха приведены в табл. Д.9.
Каждая из с(с-1)/2 пар средних сравнивается с одним критическим размахом. Пара, например, группа j— группа/' объявляется статистически значимо разными, если модуль разности между выборочными средними |^V/ — ATZ.| превышает критический размах.
Продемонстрируем применение процедуры Тьюки на примере анализа сети ресторанов. Поскольку проверке подвергаются четыре ресторана, в процедуре Тьюки будет выполнено 4(4-1)/2 = 6 попарных сравнений. Из данных, приведенных на рис. 10.19, следует, что модули разностей принимают перечисленные ниже значения.
1. |%,-^2| = |77,50-66,67| = 10,83.
2. ]%,-А\| = |77,50-91,00| = 13,50.
3. |а,-А4| = |77,50-79,33| = 1,83.
4. |%2-А\| = |б6,67-91,00| = 24,33.
5. |%2-^1 = 166,67-79,33] = 12,66.
6. |У3-%4| = |91,00-79,33| = 11,67.
Для того чтобы вычислить критический размах, определим по рис. 10.19 величины MSE = 14,986 и г = 6. По табл. Д.9 (для а = 0,05, с = 4 и (г-1)(с-1) = 15) находим, что величина Qv — верхнее критическое значение тестовой статистики, имеющей четыре степени свободы в числителе и 15 степеней свободы в знаменателе— равна 4,08. Используя формулу (10.26), получаем
критический размах = 4,08
(14,986 6
= 6,448.
Обратите внимание на то, что все попарные разности, за исключением величины
-А4| , превышают критический размах. Следовательно, между всеми ресторанами, за исключением ресторанов А и Г, существуют значительные отличия. Кроме того, подразделение В имеет наивысший рейтинг (т.е. работает лучше остальных), а подразделение Б — наименьший (т.е. работает хуже всех).
Изучение основ
10.26. Предположим, что в блочном рандомизированном эксперименте изучается один фактор, имеющий пять уровней и семь блоков.
1. Сколько степеней свободы существует при определении межгрупповой вариации?
2. Сколько степеней свободы существует при определении межблоковой вариации?
3. Сколько степеней свободы существует при определении случайной вариации, или ошибки?
4. Сколько степеней свободы существует при определении полной вариации?
10.27. Вернемся к задаче 10.26.
1. Чему равна величина SSE, если SSA = 60, SSBL = 75 и SST = 210?
2. Чему равна величина MSA?
3. Чему равна величина MSBL?
4. Чему равна величина MSE7
5. Чему равна тестовая статистика F для оценки разностей между пятью средними?
6. Чему равна тестовая статистика F для оценки блочных эффектов?
10.28. Вернемся к задачам 10.26 и 10.27.
1. Сформируйте и заполните сводную таблицу дисперсионного анализа.
2. Чему равно верхнее критическое значение F-распределения при оценке разностей между пятью средними с уровнем значимости, равным 0,05?
3. Сформулируйте решающее правило для проверки нулевой гипотезы о том, что все пять групп имеют одинаковые средние значения.
4. Какое статистическое решение вы примете?
5. Чему равно верхнее критическое значение ^-распределения при оценке блочных эффектов с уровнем значимости, равным 0,05?
6. Сформулируйте решающее правило для проверки нулевой гипотезы о том, что блочных эффектов нет.
7. Какое статистическое решение вы примете?
10.29. Вернемся к задачам 10.26-10.28.
1. Сколько степеней свободы в числителе и знаменателе имеет распределение стьюдентизованного размаха при выполнении процедуры Тьюки?
2. Чему равно верхнее критическое значение распределение стьюдентизованного размаха при уровне значимости, равном 0,05?
3. Объясните смысл критического размаха в процедуре Тьюки.
10.30. Предположим, что в блочном рандомизированном эксперименте изучаются один фактор, три уровня и семь блоков.
1. Сколько степеней свободы существует при определении межгрупповой вариации?
2. Сколько степеней свободы существует при определении межблоковой вариации?
3. Сколько степеней свободы существует при определении случайной вариации, или ошибки?
4. Сколько степеней свободы существует при определении полной вариации?
10.31. Вернемся к задаче 10.30. Предположим, что величина SSA = 36, а рандомизированная блочная F-статистика равна 6,0.
1. Чему равна величина MSE?
2. Чему равна величина SSE?
3. Чему равна величина SSBL, если F-статистика для оценки блочных эффектов равна 4,0?
4. Чему равна величина SST?
5. Существует ли эффект условий, если уровень значимости равен 0,01?
6. Существует ли эффект блоков, если уровень значимости равен 0,01?
10.32. Ниже приведена неполная сводная таблица дисперсионного анализа блочного рандомизированного эксперимента, имеющего четыре уровня и восемь блоков. Заполните недостающие ячейки.
Вид величины Количество степеней свободы Суммы квадратов Дисперсии F-статистика
Межгрупповая с-1 = ? SSA=~ ? MSA = 80 F = ?
Межблоковая г-1 = ? SSBL = 540 MSBL - 7 F= 5,0
Ошибка (г-1)(с-1) = ? SSE = 7 MSE = ?
Полная гс-1 = ? SST =7
10.33. Вернемся к задаче 10.32.
1. Чему равно верхнее критическое значение F-распределения при оценке разностей между четырьмя средними с уровнем значимости, равным 0,05?
2. Сформулируйте решающее правило для проверки нулевой гипотезы о том, что все четыре группы имеют одинаковые математические ожидания.
3. Какое статистическое решение вы примете?
4. Чему равно верхнее критическое значение F-распределения при оценке блочных эффектов с уровнем значимости, равным 0,05?
5. Сформулируйте решающее правило для проверки нулевой гипотезы о том, что блочных эффектов нет.
6. Какое статистическое решение вы примете?
Применение понятий
Примечание: рекомендуем для решения задач 10.34-10.38 использовать программу Microsoft Excel.
10.34. Девять экспертов были приглашены для дегустации четырех сортов колумбийского кофе. Для того чтобы обеспечить объективность оценки, каждый из девяти дегустаторов испытывал каждый сорт кофе в случайном порядке. Четыре характеристики кофе — вкус, аромат, насыщенность и кислотность — оценивались по 7-балльной шкале (1 — очень плохо, 7 — очень хорошо). Полученные результаты приведены в следующей таблице. ^COFFEE . XLS.
Марка
Эксперт А Б В Г
С.С. 24 26 25 22
S.E. 27 27 26 24
E.G. 19 22 20 16
B.L. 24 27 25 23
С.М. 22 25 22 21
C.N. 26 27 24 24
G.N. 27 26 22 23
R.M. 25 27 24 21
P.V. 22 23 20 19
Проанализируйте данные и определите, существуют ли различия между суммарными рейтингами четырех сортов колумбийского кофе при уровне значимости, равном 0,05. Если различия есть, определите, какой из сортов кофе получил наивысшую оценку. Как вы пришли к такому выводу?
10.35. Группа студентов, изучающих бизнес-статистику, поставила эксперимент, в ходе которого исследовался вопрос: влияет ли марка жевательной резинки на размер шарика, который можно из нее выдуть. Студенты были уверены, что Кайл является экспертом по жевательным резинкам, и поэтому его опыт мог отрицательно повлиять на результаты полностью рандомизированного эксперимента. Итак, чтобы уменьшить межличностную изменчивость, студенты решили применить схему блочного рандомизированного эксперимента, в котором блоками являлись бы они сами. Студент разжевывал два кусочка жевательной резинки определенной марки, а затем выдувал два шарика, пытаясь раздуть их как можно больше. Другой студент измерял максимальные диаметры шариков. В следующей таблице приведены результаты 16 наблюдений (в дюймах). ^BUBBLEGUM. XLS.
Марка жевательной резинки
Студент Bazooka Bubbletape Bubbleyum Bubblicious
Кайл 8,75 9,50 8.50 11,50
Сара 9,50 4,00 8,50 11,00
Лей 9,25 5,50 7,50 7,50
Исаак 9,50 8,50 7,50 7,50
1. Можно ли утверждать, что средние диаметры шариков, полученных из жевательных резинок, различаются между собой?
2. Если возможно, примените процедуру Тьюки и определите, какая из марок жевательных резинок отличается от остальных. (Уровень значимости а установите равным 0,05.)
3. Считаете ли вы, что в данном эксперименте наблюдается значительный блочный эффект? Обоснуйте свой ответ.
4. Считаете ли вы, что Кайл действительно лучше остальных умеет выдувать шарики из жевательных резинок?
10.36. Менеджер крупного агентства по торговле недвижимостью закончил обучение трех вновь нанятых работников методам оценки недвижимости. Для того чтобы оценить эффективность своего метода обучения, менеджер решил определить, существует ли какая-либо разница между оценками недвижимости, выставленными каждым из новых агентов. Менеджер случайным образом выбрал 12 домов и поручил каждому агенту оценить эти дома (в тыс. долл.) Результаты приведены в файле ^REAPERS . XLS.
1. Примените блочный рандомизированный эксперимент и определите, существует ли разница между средними оценками, выставленными тремя агентами.
2. Какие условия должны выполняться, чтобы можно было осуществить такую проверку?
3. К каким выводам пришел менеджер? Эффективен ли его метод обучения агентов. Одинаково ли они оценивают недвижимость? Обоснуйте свой ответ.
10.37. Компания Philips Semiconductors является ведущим европейским производителем интегральных микросхем. Основой для микросхем являются кремниевые подложки, которые предварительно доводят до требуемой толщины. Подложки устанавливают в разных местах шлифовального круга и фиксируют с помощью вакуумной декомпрессии. Одной из целей производственного процесса является уменьшение изменчивости толщины подложки в зависимости от ее места на шлифовальном круге и партии. Были собраны данные о 30 партиях. В каждой партии измерялась толщина подложек, находящихся на позициях 1 и 2 (внешняя часть шлифовального круга), 18 и 19 (середина круга) и 28 (внутренняя часть круга). Результаты приведены в файле ^CIRCUIT . XLS. Выполните полный анализ данных при уровне значимости, равном 0,01, и определите, существуют ли различия между средней толщиной подложек, расположенных на пяти позициях. Если такие различия существуют, укажите, какие позиции отличаются друг от друга. Какой вывод следует сделать?
Источник: К. С. В. Roes and R. J. M. M. Does, “Shewhart-type Charts in Nonstandard Situations,” Technometrics, 37,1995,15-24.
10.38. Данные, приведенные в файле ^CONCRETE2 . XLS, описывают прочность на сжатие (psi — тыс. фунтов на кв. дюйм) 40 образцов бетона, взятых на 2-, 7- и 28-й дни после укладки.
Источник: О. Carillo-Gamboa and R.F.Gunst, “Measurement-Error-Model Collinearities”, Technometrics, 34,1992, 454-464.
1. Можно ли утверждать, что между средней прочностью на сжатие образцов бетона, взятых на 2-, 7- и 28-й дни после укладки, существует значительное различие, если уровень значимости равен 0,05?
2. Если возможно, примените процедуру Тьюки и определите, какой день после укладки значительно отличается от остальных с точки зрения прочности бетона на сжатие. (Уровень значимости ос установите равным 0,05.)
3. Определите относительную эффективность блочного рандомизированного эксперимента по сравнению с однофакторным полностью рандомизированным экспериментом.
РЕЗЮМЕ
В главе описана концепция полностью рандомизированного эксперимента. Приведены различные процедуры анализа эффекта одного и двух факторов. Рассмотрен практический пример, иллюстрирующий применение критериев одно- и двухфакторного дисперсионного анализа. Детально описаны условия выполнения статистических процедур. Напомним, что проверка необходимых условий является неотъемлемой частью статистического анализа и позволяет правильно выбирать критерии. Как показано на структурной схеме, существует несколько подходов к сравнению групп числовых данных на основе экспериментов.
^Критерий Левенэ
Планы
F-критерий для
। однофакторного = дисперсионного анализа
Факторный план
Полностью /рандомизированный Ь' план'
F-критерий для однофакторного дисперсионного анализа
Множественное сравнение
М ножественное сравнение
Структурная схема главы 10
ОСНОВНЫЕ понятия
F-критерий
в однофакторном анализе, 646
для фактора А, 667
для фактора В, 667
для эффекта взаимодействия факторов А и В, 667
Вариация
взаимодействия, 666
внутригрупповая, 643; 645
межгрупповая, 643; 645
полная, 644; 665
фактора А, 665
фактора В, 665
Дисперсионный анализ, 643
двухфакторный, 664
однофакторный, 643
Дисперсия
MSA, 666
MSAB, 666
MSB, 666
MSE, 666
Критерий Левенэ, 656
Критический размах, 653
Множественное сравнение, 675
Общее среднее, 644
Ошибка
случайная, 666
эксперимента, 643
План
полностью рандомизированный, 642
факторный, 642
Процедура
ANOVA
двухфакторная, 664
однофакторная, 643
апостериорного сравнения, 653
множественного сравнения, 653
Тьюки-Крамера, 653
Реплика, 664
Сводная таблица ANOVA, 647
Сумма квадратов
внутригрупповая, 645
межгрупповая, 645
ошибок, 666
полная, 645; 665
соответствующая фактору А, 665
соответствующая фактору В, 665 средняя, 646
учитывающая взаимодействие
между факторами А и В, 665
Фактор, 642
Эксперимент
полностью рандомизированный, 642
факторный, 665
Эффект
взаимодействия, 670
главный, 670
условий эксперимента, 643
Проверка знаний
10.39. Чем межгрупповая дисперсия MSA отличается от внутригрупповой дисперсии MSW?
10.40. В чем заключается разница между полностью рандомизированным и двухфакторным экспериментами?
10.41. Какие условия необходимы для проведения дисперсионного анализа?
10.42. При каких условиях можно применять .F-критерий в однофакторном дисперсионном анализе для оценки разностей между математическими ожиданиями с генеральных совокупностей?
10.43. Когда и как следует применять процедуры множественного сравнения для попарного сопоставления математических ожиданий с генеральных совокупностей?
10.44. В чем заключается разница между однофакторным дисперсионным анализом и критерием Левенэ?
10.45. При каких условиях можно применять F-критерий в двухфакторном дисперсионном анализе для оценки разностей между математическими ожиданиями каждого фактора в факторном эксперименте?
10.46. В чем заключается взаимодействие между факторами в двухфакторном эксперименте?
10.47. Как применить F-критерий в двухфакторном дисперсионном анализе для оценки эффекта взаимодействия между факторами?
Применение понятий
Задачи 10.48-10.53 можно решать как вручную, так и с помощью программы Microsoft Excel.
10.48. Управляющий заводом, производящим бытовую технику, хотел бы определить оптимальную продолжительность работы стиральной машины. Для этого он спланировал эксперимент, в ходе которого учитывалось влияние марки стирального порошка и продолжительности работы стиральной машины на качество стирки. В эксперименте использовались четыре марки стирального порошка (А, В, С и В) и четыре разных цикла стирки (18, 20, 22 и 24 мин.). В 32 стиральные машины загружался одинаковый объем случайно выбранного одинаково загрязненного белья: по две загрузки на каждую из 16 комбинаций факторов. Результаты (вес удаленной грязи в фунтах) представлены в таблице. ^LAUNDRY. XLS.
Продолжительность стирки (мин.)
Марка стирального порошка 18 20 22 24
А 0,11 0,13 0,17 0,17
0,09 0,13 0,19 0,18
В 0,12 0,14 0,17 0,19
0,10 0,15 0,18 0,17
С 0,08 0,16 0,18 0,20
0,09 0,13 0,17 0,16
D 0,11 0,12 0,16 0,15
0,13 0,15 0,17 0,17
1. Существует ли статистически значимый эффект взаимодействия между маркой стирального порошка и продолжительностью стирки, если уровень значимости равен 0,05?
2. Существует ли статистически значимый эффект стирального порошка, если уровень значимости равен 0,05?
3. Существует ли статистически значимый эффект продолжительности стирки, если уровень значимости равен 0,05?
4. Постройте график зависимости среднего объема удаленной грязи (в фунтах) от марки стирального порошка при фиксированной продолжительности стирки.
5. Если возможно, примените процедуру Тьюки и определите различия между марками стирального порошка и продолжительностью стирки.
6. Какую продолжительность стирки можно рекомендовать для данной стиральной машины?
7. Повторите анализ, считая продолжительность стирки единственным фактором. Сравните результаты с решениями задач 1-6.
10.49. Начальник ОТК на ткацкой фабрике хотел бы сравнить влияние мастерства ткачих и марки станка на прочность шерстяной ткани. Для этого ткань была разрезана на квадратные куски со стороной один ярд, которые были случайным образом распределены между группами: по три отреза на каждую из 12 комбинаций (четыре ткачихи и три станка). Результаты приведены в таблице. ФBREAKSTW. XLS.
Станок
Ткачиха 1 2 3
А 115 111 109
115 108 110
119 114 107
В 117 105 110
114 102 113
114 106 114
С 109 100 103
110 103 102
106 101 105
D 112 105 108
115 107 111
111 107 110
1. Существует ли статистически значимый эффект взаимодействия между ткачихами и марками станка, если уровень значимости равен 0,05?
2. Существует ли статистически значимый эффект ткачихи, если уровень значимости равен 0,05?
3. Существует ли статистически значимый эффект марки станка, если уровень значимости равен 0,05?
4. Постройте график зависимости средней прочности (в фунтах) от вида станка для каждой ткачихи.
5. Если возможно, примените процедуру Тьюки и определите различия между ткачихами и марками станка.
6. Влияет ли мастерство ткачихи и марка станка на прочность шерстяной ткани? Обоснуйте свой ответ.
7. Повторите анализ, оставив станки в качестве единственного фактора. Сравните результаты с решениями задач 3, 5 и 6.
10.50. Рассмотрим эксперимент, в ходе которого измеряется прочность пряжи. Эксперимент состоит из двух этапов.
Этап 1. Руководитель производства хотел бы знать, влияет ли давление воздуха (в фунтах на квадратный дюйм) на прочность пряжи. Рассматриваются три уровня давления: 30, 40 и 50 фунтов на квадратный дюйм. Для анализа из одной и той же партии отобраны 18 однородных экземпляров пряжи, которые затем распределяются по уровням давления: по шесть штук на каждый из трех уровней. Результаты приведены в файле ^YARN . XLS.
1. Каким условиям должна удовлетворять дисперсия показателей прочности, соответствующих трем уровням давления?
2. Существует ли статистически значимая разница между средними прочностями пряжи при разном давлении воздуха, если уровень значимости равен 0,05?
3. Если возможно, примените процедуру Тьюки-Крамера и определите, какой уровень давления статистически значимо влияет на прочность пряжи, если уровень значимости равен 0,05.
4. Какой вывод должен сделать руководитель производства?
Этап 2. Предположим, что руководитель производства может измерить не только давление воздуха (в фунтах на квадратный дюйм), но и направление его потока. Следовательно, вместо полностью рандомизированного эксперимента на втором этапе осуществляется двухфакторный эксперимент. Первый фактор — направление потока — имеет два уровня: попутный и встречный. Второй фактор — давление — по-прежнему имеет три уровня: 30, 40 и 50 фунтов на квадратный дюйм. Для анализа из одной и той же партии отобраны 18 однородных экземпляров пряжи, которые затем распределяются по уровням давления: по три экземпляра на каждую комбинацию факторов. Результаты приведены в таблице. ^YARN. XLS.
Давление воздуха (фунты на кв. м.)
Направление потока 30 40 50
25,5 24,8 23,2
Попутный 24,9 23,7 23,7
26,1 24,4 22,7
Давление воздуха (фунты на кв. м.)
Направление потока 30 40 50
24,7 23,6 22,6
Встречный 24,2 23,3 22,8
23,6 21,4 24,9
5. Существует ли статистически значимый эффект взаимодействия между направлением потока и давлением воздуха, если уровень значимости равен 0,05?
6. Существует ли статистически значимый эффект направления потока, если уровень значимости равен 0,05?
7. Существует ли статистически значимый эффект давления воздуха, если уровень значимости равен 0,05?
8. Постройте график зависимости средней прочности пряжи для двух направлений потока при разных давлениях.
9. Если возможно, примените процедуру Тьюки и определите различия между разными величинами давления.
10. Какой вывод можно сделать на основе результатов решения задач 5-8?
11. Сравните результаты решения задач 5-10 с результатами решения задач 1-4.
10.51. Современное программное обеспечение требует все более быстрого доступа к данным. Рассмотрим эксперимент, в ходе которого оценивается влияние размера файла на скорость доступа.
Этап1. Рассматриваются три размера файла: небольшой— 50 000 символов, средний— 75 000 символов и большой— 100 000 символов. В эксперименте оценивались восемь файлов каждого размера. Результаты (в миллисекундах) приведены в файле ^ACCESS . XLS.
1. Каким условиям должна удовлетворять дисперсия скорости доступа, соответствующей трем размерам файла?
2. Существует ли статистически значимая разница между средними скоростями доступа при разных размерах файла, если уровень значимости равен 0,05?
3. Если возможно, примените процедуру Тьюки-Крамера и определите, какой размер файла статистически значимо влияет на скорость доступа, если уровень значимости равен 0,05.
4. Какой вывод можно сделать на основе этих данных?
Этап 2. Предположим, что в эксперименте учитывается не только размер файла, но и размер буфера ввода-вывода. Следовательно, вместо полностью рандомизированного эксперимента на втором этапе осуществляется двухфакторный эксперимент. Первый фактор — размер буфера — имеет два уровня: 20 и 40 Кбайт. Второй фактор — размер файла — по-прежнему имеет три уровня: небольшой, средний и большой. Для анализа скорости доступа выполняются четыре программы (реплики) для каждой комбинации факторов. Результаты приведены в файле ^ACCESS . XLS.
5. Существует ли статистически значимый эффект взаимодействия между размерами файла и буфера, если уровень значимости равен 0,05?
6. Существует ли статистически значимый эффект размера буфера, если уровень значимости равен 0,05?
7. Существует ли статистически значимый эффект размера файла, если уровень значимости равен 0,05?
8. Постройте график зависимости средней скорости доступа от размера буфера при разных размерах файла. Опишите взаимодействие этих факторов и дайте интерпретацию их главных эффектов.
9. Какой вывод можно сделать на основе решений задач 5-8?
10. Сравните результаты решения задач 5-8 с решениями задач 1-4.
10.52. Группа студентов, изучающих статистику, провела эксперимент, в ходе которого измерялось время загрузки компьютеров трех разных типов (MAC, iMAC и Dell). Этап 1. Студенты случайным образом выбирали один компьютер из каждой группы. Они заходили на игровой Web-сайт компании Microsoft и загружали компьютерную игру в баскетбол. Регистрировалось время между щелчком на ссылке и окончанием загрузки. После каждой загрузки файл удалялся, а мусорная корзина очищалась. Порядок 30 загрузок определялся случайным образом. ^COMPUTERS . XLS. Выполните анализ данных, приведенных в таблице.
Компьютер
МАС iMAC Dell
156 160 236
166 165 238
148 184 257
160 192 242
139 197 282
151 172 253
158 189 270
167 179 256
142 200 267
219 193 259
Этап 2. Во втором эксперименте, выполненном группой студентов, в качестве второго фактора исследовался браузер (Netscape Communicator и Interner Explorer). В этом эксперименте использовались только два вида компьютеров: МАС и Dell. Было выполнено по восемь загрузок при каждой из четырех комбинаций факторов. ^COMPUTERS2 . XLS. Выполните анализ данных из следующей таблицы.
Компьютер
Браузер MAC Dell
142 284
132 304
125 273
Netscape Communicator 136 340
127 326
138 301
147 291
143 285
Компьютер
Браузер MAC Dell
198 285
210 292
199 305
Internet Explorer 202 325
196 297
213 301
207 285
201 290
Отчеты
10.53. В файле ^BEER.XLS приведены данные об упаковках, содержащих шесть 12-унциевых бутылок пива 69 сортов. В их число входят цена, количество калорий в 12 жидких унциях, процентное содержание алкоголя в 12 жидких унциях, вид пива (светлое, эль, импортное легкое, обычное, ледяное, легкое, безалкогольное), а также страны производства (США или другие).
Напишите отчет, содержащий полную оценку каждой переменной — цены, количества калорий и содержания алкоголя для каждого вида пива — светлого, эля, импортного легкого, обычного, ледяного, легкого, безалкогольного. После этого выполните аналогичное исследование каждой числовой переменной, учитывая страну производства. Включите в отчет все необходимые таблицы, диаграммы и количественные показатели, полученные в ходе исследования.
Для создания отчетов, предложенных в этом разделе, воспользуйтесь программой Microsoft Excel и другими средствами пакета Microsoft Office (в частности, программой для подготовки презентаций PowerPoint).
Источник: “Beers”. Copyright © 1996 by Consumers Union of U.S. Inc., Yonkers, N.Y. Цитируется с разрешения журнала Consumer reports, June 1996.
Применение Интернет
10.54. Зайдите на сайт www.prenhall.com/levine. Выберите ссылку Chapter 10 и щелкните на ссылке Internet exercises.
* ГРУППОВОЙ ПРОЕКТ
ТР.10.1. Файл данных ^MUTUAL FUNDS . XLS содержит информацию о 13 переменных, характеризующих 259 взаимных фондов.
Фонд — название взаимного фонда.
Вид — вид акций, принадлежащих взаимному фонду: малые, средние и крупные компании.
Цель — цель фонда (быстрый или медленный рост капитала).
Активы — в млн. долл.
Комиссия — да или нет.
Издержки — издержки, понесенные взаимным фондом (в процентах от среднего объема чистых активов).
Доходность 2 001 — доходность за двенадцать месяцев 2001 г.
Трехлетняя доходность — среднегодовая доходность за период с 1999 по 2001 гг.
Пятилетняя доходность — среднегодовая доходность за период с 1997 по 2001 гг.
Оборачиваемость — уровень торговой активности фонда: очень низкий, низкий, средний, высокий, очень высокий.
Риск — уровень риска: очень низкий, низкий, средний, высокий, очень высокий.
Лучший квартал — квартал с наивысшей доходностью за период с 1997 по 2001 гг.
Худший квартал — квартал с наименьшей доходностью за период с 1997 по 2001 гг.
Оцените доходность взаимных фондов, относящихся к разным категориям (малые, средние и крупные компании) в 2001 году, за три года (с 1999 по 2001 г.) и за пять лет (с 1997 по 2001 г.) при уровне значимости, равном 0,05.
Выполните анализ данных при уровне значимости, равном 0,05. Изложите свои выводы в письменном виде. Включите в отчет все необходимые таблицы, диаграммы и количественные показатели, полученные в ходе исследования. Для создания отчета используйте программу Microsoft Excel и другие средства пакета Microsoft Office (в частности, программу для подготовки презентаций PowerPoint).
РАЗБОР КОНКРЕТНОЙ СИТ ГАЗЕТА SPRINGVILLE HERA
Этап 1
Группа, разрабатывающая новую подписную политику, решила проверить, как влияет прямой маркетинг по телефону на количество подписчиков. После нескольких рабочих совещаний, в которых приняли участие как инструкторы, так и непосредственные участники телефонных рекламных акций, было принято решение повысить продолжительность телефонных переговоров с потенциальными подписчиками, поскольку при более продолжительном разговоре вероятность оформления подписки повышается.
Группа решила оценить влияние продолжительности телефонного разговора с потенциальным подписчиком на успех подписной кампании. Оказалось, что телефонные разговоры с 19:00 до 21:00 оказались значительно более продолжительными, чем разговоры с 17:00 до 19:00.
После этого группа решила исследовать влияние разновидности презентации на продолжительность разговора. Для этого была создана случайная группа из 24 женщин, разделенная на три подгруппы по восемь женщин. В каждой подгруппе использовалась структурированная, полуструктурированная и совершенно не структурированная презентация. Все звонки выполнялись с 19:00 до 21:00. Звонившие обязаны были обращаться к потенциальному подписчику неформально. (Например: “Привет, это Мэри Джонс из газеты Spingville Herald. Могу я поговорить с Биллом Ричардсом?”.) Абоненты знали, что исследователи внимательно следят за их работой, но не знали, какой именно разговор будет прослушан. Продолжительность телефонных разговоров измерялась в секундах, прошедших от момента, когда абонент ответил на вопрос, до момента, когда он положил трубку. Результаты приведены в табл. SH.10.1. ftsH10-l .XLS.
Таблица SH.10.1. Продолжительность телефонного разговора (в секундах)
в зависимости от плана презентации
План презентации
Структурированный Полуструктурированный Неструктурированный
38,8 41,8 32,9
42,1 36,4 36,1
45,2 39,1 39,2
34,8 28,7 29,3
48,3 36,4 41,9
37,8 36,1 31,7
41,1 35,8 35,2
43,6 33,7 38,1
УПРАЖНЕНИЯ
Проанализируйте данные, приведенные в табл. SH.10.1. Изложите свои выводы и рекомендации в отчете. В приложении обоснуйте свой выбор статистического критерия для сравнения трех независимых групп.
НЕ ПРОДОЛЖАЙТЕ, ПОКА НЕ ЗАКОНЧИТЕ ПЕРВЫЙ ЭТАП
Этап 2
После анализа данных, представленных в табл. SH.10.1, становится очевидным, что структурированный план презентации позволяет значительно увеличить продолжительность разговора по сравнению с полуструктурированной и неструктурированной презентациями. Группа вновь собралась на совещание и стала искать новые возможности повысить продолжительность телефонных переговоров с потенциальными подписчиками и, следовательно, увеличить количество подписчиков. Оказалось, что структурированный телефонный разговор, проведенный с 19:00 до 21:00, наиболее эффективен. В поисках новых возможностей группа решила оценить два дополнительных фактора, влияющих на продолжительность телефонной презентации.
• Пол абонента: мужской или женский.
• Форма обращения: личная, но формальная (“Добрый вечер! Меня зовут Мэри Джонс. Я работаю в газете Spingville Herald. Могу я поговорить с Биллом Ричардсом?”), личная, но неформальная (“Привет, это Мэри Джонс из газеты Spingville Herald. Могу я поговорить с Биллом Ричардсом?”) или безличная (“Вам звонят из газеты Spingville Herald..”).
В ходе предыдущих исследований эти показатели уже фиксировались — в презентациях участвовали исключительно женщины, причем все они использовали неформальный стиль обращения. Теперь необходимо определить, был ли этот выбор наилучшим.
Для испытания были отобраны 30 абонентов — 15 мужчин и 15 женщин. Они были случайным образом распределены на подгруппы, использовавшие разные стили обращения, так что в каждой из шести подгрупп, соответствовавших разным комбинациям факторов, было по пять абонентов. Стили обращения обозначены следующим образом: PF — личное формальное, PI — личное неформальное, Imp — безличное. Абоненты знали, что исследователи внимательно следят за их работой, но не знали, какой именно разговор будет прослушан. Продолжительность телефонных разговоров измерялась в секундах, прошедших от момента, когда абонент ответил на вопрос, до момента, когда он положил трубку. Результаты приведены в табл. SH.10.2.
Таблица SH.10.2. Продолжительность телефонного разговора (в секундах) в зависимости от пола абонента и формы обращения
Форма обращения
Пол PF Р! Imp
Мужской 45,6 41,7 35,3
49,0 42,8 37,7
41,8 40,0 41,0
35,6 39,6 28,7
43,4 36,0 31,8
Женский 44,1 37,9 43,3
40,8 41,1 40,0
46,9 35,8 43,1
51,8 45,3 39,6
48,5 40,2 33,2
УПРАЖНЕНИЯ
Проанализируйте данные, приведенные в табл. SH.10.2. Оцените главные эффекты каждого фактора и эффект их взаимодействия. Изложите свои выводы и рекомендации в отчете. Сформулируйте свои рекомендации, касающиеся дальнейших экспериментов.
Считаете ли вы, что длительность телефонного разговора — самый информативный результат этот эксперимента? Какие еще переменные следует исследовать? Обоснуйте свой ответ.
ПРИМЕНЕНИЕ WEB
Примените свои знания о дисперсионном анализе и оцените качество процесса расфасовки кукурузных хлопьев на заводе компании Oxford Cereals (см. главы 6,8 и 9).
После заявлений Организации потребителей, уверенных, что компания Oxford Cereal мошенничает (сокращенно — ОПУЧКОСМ), компания Oxford Cereal пожаловалась, что ее противники используют подтасованные данные. Проанализируйте ответ компании, размещенный на Web-странице www. prenhall. com/Springville/OC_SelectiveData . htm), и ответьте на следующие вопросы.
1. Обоснована ли жалоба компании? Аргументируйте свой ответ.
2. Предположим, что выборки, проверенные компанией, были действительно случайными. Выполните соответствующий анализ и сделайте свое заключение.
3. К каким выводам вы пришли? Чью сторону вы приняли бы, если вас пригласили стать экспертом: ОПУЧКОСМ или компании Oxford Cereal? Аргументируйте свой ответ.
СПРАВОЧНИК ПО EXCEL. ГЛАВА 10
ЕН.10.1. Процедура Тьюки-Крамера
Процедура Тьюки-Крамера представляет собой двухэтапный процесс. Сначала нужно выбрать команду Сервис^ Анализ данных..,^>Однофакторный дисперсионный анализ, чтобы вычислить выборочные средние и объемы каждой группы, количество степеней свободы в каждой группе и величину MSW. Затем из табл. Д.9 извлекается значение стьюдентизированной статистики размаха Q и создается рабочий лист, в котором для вычисления моделей разностей и критического размаха применяются обычные функции. Кроме того, на этот рабочий лист выводится сообщение о том, является ли различие между средними каждой пары групп статистически значимым.
В табл. ЕН.10.1-ЕН.10.3 показан шаблон рабочего листа, реализующего процедуру Тьюки-Крамера для сравнения прочности парашютов на основе данных, представленных на рис. 10.5. Предполагается, что процедура Анализ данных...1^Однофакторный дисперсионный анализ генерирует рабочий лист с названием Anova, на пересечении строк 5-8 и столбцов D и В содержащий выборочные средние и объемы каждой группы соответственно, в ячейке С14 — количество степеней свободы внутри групп, а в ячейке D14 — величину MSW. Шаблон также содержит в ячейке В15 стьюдентизированный размах Q (4,05), извлеченный из табл. Д.9 при уровне значимости а, равном 0,05, и заданном количестве степеней свободы. В столбце I с помощью функции ЕСЛИ выполняется сравнение абсолютных величин разностей и критических размахов, а также выводится сообщение о том, отличаются математические ожидания друг от друга или нет.
Таблица ЕН.10.1. Шаблон рабочего листа ТьюкиКрамер (столбцы А-с)
А ' В - ' / C ' .
1 Анализ прочности парашютов
2
3 Выборка Выборка
4 Группа Среднее Объем
5 1 =Anova!D5 =Anova!B5
6 2 =Anova!D6 =Anova!B6
7 3 =Anova!D7 =Anova!B7
8 4 =Anova!D8 =Anova!B8
9
10 Другие данные
11 Уровень значимости 0,05
12 Количество степеней свободы в числителе 4
13 Количество степеней свободы в знаменателе =Anova!C14
14 MSW =Anova!D14
15 Q-стати стика 4,05
Таблица ЕН.10.2. Диапазон ЕЗ: G10 шаблона рабочего листа ТьюкиКрамер (столбец D и строки 1 и 2 в столбцах Е: G пусты)
E F G
Модуль Стандартная ошибка разностей
OSS Сравнение Разность
iiSIfe Группа 1 с группой 2 =ABS(B$5-B6) = KOPEHb((B$14/2)*((1/C$5)+1/C6))
Illi Группа 1 с группой 3 =ABS(B$5-B7) = КОРЕНЬ((В$14/2)*((1/С$5)+1/С7))
Группа 1 с группой 4 =ABS(B$5-B8) = КОРЕНЬ((В$14/2)*((1/С$5Ж/С8))
liijlf Группа 2 с группой 3 =ABS(B$6-B7) = КОРЕН Ь( (В$14/2) *( (1/С$б )Н-1/С7))
IHiil Группа 2 с группой 4 =ABS(B$6-B8) = КОРЕН Ь( (В$14/2) *(( 1 /С$6 )Н-1/С8))
jjil Группа 3 с группой 4 =ABS(B$7-B8) = КОРЕН Ь( (В$14/2 )*(( 1/С$7) 4-1/С8))
Таблица ЕН.10.3. Диапазон НЗ: 15 шаблона рабочего листа ТьюкиКрамер (строки 1 и 2 в столбцах Н и I пусты)
Н
3 Критический
4 размах = ЕСЛИ(В15=""; "Пока статистика Q не содержится в ячейке В15; метод не корректен"; "Результаты")
S =$B$15*G5 = ЕСЛИ(Е5>Н5;"Математические ожидания отличаются значимо "Математические ожидания не отличаются")
6 =$B$15*G6 = ЕСЛИ(Е6>Н6;"Математические ожидания отличаются значимо "Математические ожидания не отличаются")
7 =$B$15*G7 =ЕСПИ(Е7>Н7;"Математические ожидания отличаются значимо "Математические ожидания не отличаются")
8 =$B$15*G8 = ЕСЛИ(Е8>Н8;”Математические ожидания отличаются значимо "Математические ожидания не отличаются")
9 =$B$15*G9 = ЕСЛИ(Е9>Н9;"Математические ожидания отличаются значимо " Математические ожидания не отличаются")
10, =$B$15*G10 =ЕСЛИ(Р10>Н10;" Математические ожидания отличаются значимо "Математические ожидания не отличаются")
Модифицируя формулы, содержащиеся в столбцах от Е до I, и меняя выборочные средние и объемы групп в столбцах А, В и С, этот рабочий лист можно настраивать для решения аналогичных задач. Кроме того, при настройке необходимо изменить ссылки на рабочий лист ANOVA. Модифицируя рабочий лист, помните следующее.
• Извлеките объемы выборок и выборочные средние из столбцов Счет и Среднее в сводной таблице, которая начинается со строки 4.
• Извлеките количество степеней свободы в числителе и знаменателе из строк Степени свободы и Внутри группы таблицы ANOVA.
• Извлеките значение MSW из ячейки Дисперсия и строки Внутри группы таблицы ANOVA.
ЕН.10.2. Вычисление разностей между наблюдениями и медианами
Для применения критерия Левенэ сначала необходимо создать рабочий лист, вычисляющий абсолютные величины разностей между наблюдениями и медианами каждой группы, а затем применить процедуру Сервис^Анализ данных...ФОднофакторный дисперсионный анализ.
В табл. ЕН. 10.4 и ЕН. 10.5 продемонстрирован шаблон рабочего листа КритерийЛевенэ, вычисляющий абсолютные величины разностей между медианами групп и данными о прочности парашютов, представленными на рис. 10.5, с помощью функций МЕДИАНА иАВЗ. Для реализации этого шаблона сначала необходимо открыть рабочий лист Данные в книге Chapter 10.xls, скопировать метки и величины из диапазона Al: D6 в тот же диапазон нового рабочего листа КритерийЛевенэ, ввести в ячейку А8 формулу ^МЕДИАНА (А2 : А 6) и скопировать эту формулу в ячейки строки вплоть до ячейки D8.
Таблица ЕН.10.4. Шаблон рабочего листа КритерийЛевенэ
А С D
1 Поставщик 1 Поставщик 2 Поставщик 3 Поставщик 4
2 18,5 26,3 20,6 25,4
|||||1 24,0 25,3 25,2 19,9
liili 17,2 24,0 20,8 22,6
5 19,9 21,2 24,7 17,5
6 18,0 24,5 22,9 20,4
7
8 = МЕДИАНА(А2:Аб) = МЕДИАНА(В2:Вб) = МЕДИАНА(С2:С6) = MEflHAHA(D2:D6)
Для того чтобы реализовать табл. ЕН.10.5, скопируйте метки из диапазона Al: D1 в диапазон Fl: II. Введите в ячейку F2 формулу =ABS (А2-А$8) и скопируйте ее в ячейки всего диапазона F2 :16.
Таблица ЕН.10.5. Столбцы F: I шаблона рабочего листа КритерийЛевенэ
:1Д|Д G H 1
1 Поставщик 1 Поставщик 2 Поставщик 3 Поставщик 4
IIIII =ABS(A2-A$8) =ABS(B2-B$8) =ABS(C2-C$8) =ABS(D2-D$8)
3 =ABS(A3-A$8) =ABS(B3-B$8) =ABS(C3-C$8) =ABS(D3-D$8)
4 =ABS(A4-A$8) =ABS(B4-B$8) =ABS(C4-C$8) =ABS(D4-D$8)
5 =ABS(A5-A$8) =ABS(B5-B$8) =ABS(C5-C$8) =ABS(D5-D$8)
6 =ABS(A6-A$8) =ABS(B6-B$8) =ABS(C6-C$8) =ABS(D6-D$8)
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
1. Berenson, М. L., D. М. Levine, and М. Goldstein, Intermediate Statistical Methods and Applications: A Computer Package Approach (Englewood Cliffs, NJ: Prentice Hall, 1983).
2. Conover, W. J., Practical Nonparametric Statistics, 3rd ed. (New York: Wiley, 2000).
3. Daniel, W., Applied Nonparametric Statistics, 2nd ed. (Boston, MA: Houghton Mifflin, 1990).
4. Hicks, C. R., and К. V. Turner, Fundamental Concepts in the Design Experiments, 5th ed. (New York: Oxford University Press, 1999).
5. Kramer, C. Y., “Extension of Multiple Range Tests to Group Means with Unequal Numbers of Replications”, Biometrics 12(1956): 307-310.
6. Microsoft Excel 2002 (Redmond, WA: Microsoft Corporation, 2001).
7. Montgomery, D.M., Design and Analysis of Experiments, 5th ed. (New York: John Wiley, 2001).
8. Neter, J., M. H. Kutner, C. Nachtsheim, and W. Wasserman, Applied Linear Statistical Models, 4th ed. (Homewood, IL: Irwin, 1996).
9. Tukey, J. W. “Comparing Individual Means in the Analysis of Variance”, Biometrics 5 (1949): 99-114.
Глава 11
Критерий "хи-квадрат" и непараметрические критерии
ПРИМЕНЕНИЕ СТАТИСТИКИ: обслуживание постояльцев отелей, принадлежащих компании Т. С. Resort Properties
11.1. ПРИМЕНЕНИЕ Х2-КРИТЕРИЯ
ДЛЯ ПРОВЕРКИ ГИПОТЕЗЫ О РАВЕНСТВЕ ДВУХ ДОЛЕЙ
Процедуры Excel: применение -критерия для проверки гипотезы о равенстве двух долей
11.2. ПРИМЕНЕНИЕ %2-КРИТЕРИЯ
ДЛЯ ПРОВЕРКИ ГИПОТЕЗЫ О РАВЕНСТВЕ НЕСКОЛЬКИХ ДОЛЕЙ
Процедуры Excel: применение %-критерия для проверки гипотезы о равенстве нескольких долей
11.3. ПРИМЕНЕНИЕ Х2-КРИТЕРИЯ НЕЗАВИСИМОСТИ
Процедуры Excel: применение ^-критерия для проверки независимости
11.4. РАНГОВЫЙ КРИТЕРИЙ УИЛКОКСОНА: НЕПАРАМЕТРИЧЕСКИЙ МЕТОД
ДЛЯ ПРОВЕРКИ ГИПОТЕЗЫ О РАЗНОСТИ МЕЖДУ ДВУМЯ МЕДИАНАМИ
Процедуры Excel: применение критерия Уилкоксона для проверки гипотезы о разности между медианами двух генеральных совокупностей
11.5. РАНГОВЫЙ КРИТЕРИЙ
КРУСКАЛА-УОЛЛИСА: НЕПАРАМЕТРИЧЕСКИЙ МЕТОД ДЛЯ ПОЛНОСТЬЮ РАНДОМИЗИРОВАННОГО ЭКСПЕРИМЕНТА
Процедуры Excel: применение рангового критерия Крускала-Уоллиса для оценки разностей между несколькими медианами
11.6. КРИТЕРИЙ "ХИ-КВАДРАТ" ДЛЯ ДИСПЕРСИЙ
Проверка предположений %2-критерия для проверки гипотезы о дисперсии или стандартном отклонении
Процедура Excel: применение %-критерия для проверки гипотезы о дисперсии
11.7. КРИТЕРИЙ СОГЛАСИЯ "ХИ-КВАДРАТ"
Использование х2_критерия согласия для распределения Пуассона
Применение %2-критерия согласия для нормального распределения
СПРАВОЧНИК ПО EXCEL. ГЛАВА 11
ЧЕМУ ДОЛЖЕН НАУЧИТЬСЯ СТУДЕНТ
• Применять критерий “хи-квадрат” и знать условия его применения.
• Применять процедуру Мараскуило для оценки разностей между несколькими долями.
• Использовать непараметрические критерии и знать условия их применения.
ПРИМЕНЕНИЕ СТАТИСТИКИ
Обслуживание постояльцев отелей, принадлежащих компании Т. С. Resort Properties
Представьте себе, что вы — менеджер компании Т. С. Resort Properties, владеющей пятью высококлассными отелями, расположенными на двух курортных островах. Если гости удовлетворены обслуживанием, велика вероятность, что они вернутся на следующий год и порекомендуют своим друзьям остановиться именно в вашем отеле. Чтобы оценить качество обслуживания, постояльцев просят заполнить анкету и указать, довольны ли они гостеприимством. Вам необходимо проанализировать данные опроса, определить общую степень удовлетворенности запросов постояльцев, оценить вероятность того, что гости приедут
вновь в следующем году, а также установить причины возможного недовольства некоторых клиентов. Например, на одном из островов компании Т. С. Resort Properties принадлежат отели Beachcomber и Windsurfer. Одинаково ли обслуживание в этих отелях? Если нет, как эту информацию можно использовать для улучшения качества работы компании? Более того, если некоторые постояльцы заявили, что больше к вам не приедут, какие причины они указывают чаще других? Можно ли утверждать, что эти причины касаются лишь конкретной гостиницы и не относятся ко всей компании в целом?
ВВЕДЕНИЕ
В предыдущих трех главах описаны процедуры проверки гипотез о числовых и категорийных данных. В главе 8 описано множество одновыборочных критериев, в главе 9 — несколько двухвыборочных, а в главе 10 изложены основы дисперсионного анализа, позволяющего изучать один или два интересующих нас фактора. В этой главе мы рассмотрим методы проверки гипотез о различиях между долями признака в генеральных совокупностях на основе нескольких независимых выборок, а также изучим критерий “хи-квадрат” (х2-критерий) для проверки независимости двух категорийных переменных. Для иллюстрации применяемых методов используется сценарий, в котором оценивается степень удовлетворенности постояльцев отелей, принадлежащих компании Т. С. Resort Properties.
11.1. ПРИМЕНЕНИЕ Х2-КРИТЕРИЯ ДЛЯ ПРОВЕРКИ ГИПОТЕЗЫ О РАВЕНСТВЕ ДВУХ ДОЛЕЙ
В разделе 9.3 описан Z-критерий для сравнения двух долей. В этом разделе мы рассмотрим способ, основанный на сравнении количества успехов в двух группах , а не их долей в генеральных совокупностях. В этой процедуре тестовая %2-статистика аппрок-
В оригинале авторы используют термин “частота” (frequency). В русскоязычной литературе понятие “частота” является синонимом термина “доля” (proportion). По этой причине мы переводим термин “frequency of successes” как “количество успехов”. — Прим. ред.
симируется ^-распределением с одной степенью свободы. Результат, полученный с помощью /2-критерия, эквивалентен результату применения Z-критерия, описанного в разделе 9.3.
Для сравнения количества успехов в двух независимых группах необходимо заполнить таблицу перекрестной классификации с двумя входами (cross-classification table), содержащую количество успехов и неудач в каждой из групп (см. раздел 2.5). Такую таблицу часто называют таблицей сопряженности признаков или факторной (contingency table). В главе 4 мы использовали ее для определения понятия вероятности.
Проиллюстрируем применение таблицы сопряженности признаков на примере сценария, описанного в начале главы. Предположим, что на одном из островов компании Т. С. Resort Properties принадлежит два отеля (Beachcomber и Windsurfer). На вопрос “Вернетесь ли вы в следующем году?” утвердительно ответили 163 из 227 постояльцев отеля Beachcomber, и 154 из 262 постояльцев отеля Windsurfer. Существует ли статистически значимая разность между степенью удовлетворенности постояльцев отелей (представляющая собой вероятность того, что постояльцы вернутся в следующем году), если уровень значимости равен 0,05?
Представленная ниже табл. 11.1 имеет две строки и два столбца, поэтому она называется факторной таблицей 2x2. Ячейки, образованные пересечением каждой строки и столбца, содержат количество успехов или неудач. Например, табл. 11.2 представляет собой таблицу сопряженности признаков, содержащую данные о степени удовлетворенности постояльцев двух отелей.
Таблица 11.1. Шаблон факторной таблицы 2x2
Столбцы (группы)
Строки 1 2 Всего
Успехи X, х2 X
Неудачи п1-Х1 п2-Х2 п-Х
Всего пг п
Здесь использованы следующие обозначения: Хх — количество успехов в первой группе, Х2 — количество успехов во второй группе, п1-Х1 — количество неудач в первой группе, п2-Х2 — количество неудач во второй группе, X = Хх+Х2 — общее количество успехов, п-Х = (пх-Хх) + (и2-Х2) — общее количество неудач, пх — объем первой выборки, п2 — объем второй выборки, п = пх + п2 — суммарный объем выборок.
В табл. 11.2 есть две строки, в которых указывается количество постояльцев каждого отеля, заявивших о своем желании вернуться в следующем году (успех) или выразивших недовольство (неудача). Ячейки, расположенные в строке “Всего”, содержат общее количество гостей, планирующих вернуться в отель в следующем году, а также общее количество гостей, недовольных обслуживанием. Ячейки, расположенные в столбце “Всего”, содержат общее количество опрошенных постояльцев каждого отеля. Доля постояльцев, планирующих вернуться, вычисляется путем деления количества постояльцев, заявивших об этом, на общее количество опрошенных гостей данного отеля. Затем для сравнения вычисленных долей применяется /2-критерий.
Таблица 11.2. Факторная таблица 2x2 для оценки качества обслуживания постояльцев
Столбцы (группы)
Вернетесь ли вы в следующем году? Beachcomber Windsurfer Всего
Да 163 154 317
Нет 64 108 172
Всего 227 262 489
Чтобы проверить нулевую и альтернативные гипотезы
н,--р,^рг,
используем тестовую /2-статистику (11.1).
КРИТЕРИЙ "ХИ-КВАДРАТ" ДЛЯ СРАВНЕНИЯ ДВУХ ДОЛЕЙ
Тестовая /2-статистика равна сумме квадратов разностей между наблюдаемым и ожидаемым количеством успехов, деленных на ожидаемое количество успехов в каждой ячейке таблицы.
х-’= х (11Л)
no et ем ячейкам Jс
где /0 — наблюдаемое количество успехов или неудач в конкретной ячейке таблицы сопряженности признаков, Д — теоретическое, или ожидаемое, количество успехов или неудач в конкретной ячейке таблицы сопряженности признаков при условии, что нулевая гипотеза является истинной.
Тестовая /-статистика аппроксимируется х2-распределением с одной степенью свободы.
Чтобы вычислить ожидаемое количество успехов или неудач в каждой ячейке таблицы сопряженности признаков, необходимо понимать их смысл. Если нулевая гипотеза является истинной, т.е. доли успехов в двух генеральных совокупностях равны, выборочные доли, вычисленные для каждой из двух групп, могут отличаться друг от друга лишь по случайным причинам, причем обе доли являются оценкой общего параметра генеральной совокупности р. В этой ситуации статистика, объединяющая обе доли в одной общей (средней) оценке параметрар, содержит больше информации, чем каждая из них в отдельности. Эта статистика, обозначаемая символом р , представляет собой общую долю успехов в объединенных группах (т.е. равна общему количеству успехов, деленному на суммарный объем выборок). Ее дополнение, 1- р , представляет собой общую долю неудач в объединенных группах. Используя обозначения, смысл которых описан в табл. 11.1, можно вывести формулу (11.2) для вычисления параметра р .
ВЫЧИСЛЕНИЕ СРЕДНЕЙ ДОЛИ ПРИЗНАКА
_ %. + х А'
р = —— пх + /7, П
(И.2)
Чтобы вычислить ожидаемое количество успехов fp (т.е. содержимое первой строки таблицы сопряженности признаков), необходимо умножить объем выборки на параметр р . Чтобы вычислить ожидаемое количество неудач Д (т.е. содержимое второй строки таблицы сопряженности признаков), необходимо умножить объем выборки на параметр 1- р .
Тестовая статистика, вычисленная по формуле (11.1), аппроксимируется ^-распределением с одной степенью свободы. При заданном уровне значимости а нулевая гипотеза отклоняется, если вычисленная /2-статистика больше xj , верхнего критического значения /^распределения с одной степенью свободы. Таким образом, решающее правило выглядит следующим образом:
гипотеза Нп отклоняется, если (рис. 11.1), в противном случае гипотеза Но не отклоняется.
принятия значение отклонения \
гипотезы гипотезы i
Рис. 11.1. Критическая область /^-критерия для сравнения долей при уровне значимости а
Если нулевая гипотеза является истинной, вычисленная х2_статистика близка к нулю, поскольку квадрат разности между наблюдаемой f0 и ожидаемой Д величинами в каждой ячейке очень мал. С другой стороны, если нулевая гипотеза Нп является ложной и между долями успехов в генеральных совокупностях существует значимая разница, вычисленная х2"статистика должна быть большой. Это объясняется разностью между наблюдаемым и ожидаемым количеством успехов или неудач в каждой ячейке, которая увеличивается при возведении в квадрат. Однако вклады разностей между ожидаемыми и наблюдаемыми величинами в общую х2*статистику могут быть неодинаковыми. Одна и та же фактическая разность между Д и Д может оказать большее влияние на х2-статистику, если в ячейке содержатся результаты небольшого количества наблюдений, чем разность, соответствующая большему количеству наблюдений.
Для того чтобы проиллюстрировать х2*критерий для проверки гипотезы о равенстве двух долей, вернемся к сценарию, описанному в начале главы, результаты которого приведены в табл. 11.2. Нулевая гипотеза (Hai р} = р2) утверждает, что при сравнении качества обслуживания в двух отелях доли постояльцев, планирующих вернуться в следующем году, практически одинаковы. Для оценки параметрар, представляющего собой долю гостей, планирующих вернуться в отель, если нулевая гипотеза является истинной, используется величина р , которая вычисляется по формуле
= ^ + 154=317 = п}+н2 227 + 262 489
Доля гостей, оставшихся недовольными обслуживанием, равна 1-0,6483, т.е. 0,3517. Умножая эти две доли на количество опрошенных постояльцев отеля Beachcomber, получаем ожидаемое количество гостей, планирующих вернуться в следующем сезоне, а также число отдыхающих, которые больше не остановятся в этом отеле. Аналогично вычисляются ожидаемые доли постояльцев отеля Windsurfer.
ПРИМЕР 11.1. ВЫЧИСЛЕНИЕ ОЖИДАЕМОГО КОЛИЧЕСТВА ПОСТОЯЛЬЦЕВ
Вычислите ожидаемое количество постояльцев, соответствующее каждой из четырех ячеек табл. 11.2.
РЕШЕНИЕ
Да — Beachcomber: р = 0,6483, пх = 227, следовательно, Д = 147,16.
Да — Windsurfer: р = 0,6483, п2 = 262, следовательно, Д = 169,84.
Нет — Beachcomber: 1- р = 0,3517, пл = 227, следовательно, fr = 79,84.
Нет — Windsurfer: 1- р = 0,3517, п2 = 262, следовательно, Д = 92,16.
Все ожидаемые величины представлены в табл. 11.3.
Таблица 11.3. Факторная таблица 2x2 для сравнения наблюдаемого (Д) и ожидаемого (Д) количества постояльцев, удовлетворенных и не удовлетворенных обслуживанием
Beachcomber Windsurfer
Вернетесь ли вы в следующем году? К f. f0 Всего
Да 163 147,16 154 169,84 317
Нет 64 79,84 108 92,16 172
Всего 227 227,00 262 262,00 489
Чтобы проверить нулевую и альтернативные гипотезы
Н0:д = р2, используем тестовую /2-статистику, вычисленную с помощью ожидаемых и наблюдаемых величин по формуле (11.1). Вычисления представлены в табл. 11.4.
Таблица 11.4. Вычисление х2-статистики при сравнении долей постояльцев, удовлетворенных обслуживанием
fo (f.- O' (f0-fe)7fe
163 147,16 15,84 250,9056 1,705
154 169,84 -15,84 250,9056 1,477
64 79,84 -15,84 250,9056 3,143
108 92,16 15,84 250,9056 2,723
9,048
Критическое значение тестовой /2-статистики определяется по табл. 11.5.
Таблица 11.5. Поиск критического значения /"-статистики по таблице /2-распределения с одной степенью свободы
Площадь области, ограниченной правым хвостом распределения
Количество степеней свободы 0,995 0,99 0,05 0,025 0,01 0,005
1 3,841 5,024 6,635 7,879
2 0,010 0,020 5,991 7,378 9,210 10,597
3 0,072 0,115 7,815 9,348 11,345 12,838
4 0,207 0,297 9,488 11,143 13,277 14,860
5 0,412 0,554 11,071 12,833 15,086 16,750
В табл. 11.5 представлены некоторые из площадей областей, ограниченных правым хвостом /"-распределения. Если уровень значимости а = 0,05, а /"-распределение для факторной таблицы 2x2 имеет одну степень свободы, критическое значение /2-статистики равно 3,841 (рис. 11.2). Поскольку вычисленное значение //-статистики, равное 9,048, превышает число 3,841, нулевая гипотеза отклоняется.
гипотезы гипотезы
Рис. 11.2. Определение критического значения тестовой /"-статистики с одной степенью свободы при уровне значимости а - 0,05
На рис. 11.3 приведены результаты применения /"-критерия для проверки гипотезы о разности между долями удовлетворенных постояльцев при уровне значимости, равном 0,05, полученные с помощью программы Microsoft Excel на основе данных из табл. 11.2.2 Данные, приведенные на рис. 11.3, содержат ожидаемое количество успехов и неудач, /2-статистику, количество степеней свободы и вычисленное р-значение. При этих данных вычисленная /2-статистика равна 3,841 (p-значение равно 0,0026 < 0,05), поэтому нулевая гипотеза, утверждающая, что между долями постояльцев, удовлетворенных обслуживанием в обоих отелях, нет существенной разницы, должна быть отклонена. Кроме того, p-значение, равное 0,0026, — это вероятность того, что разность между выборочными долями постояльцев, удовлетворенных обслужива-
2 Различия между результатами, приведенными на рис. 11.5 и в табл. 11.4, объясняются округ лением чисел.
нием в отелях Beachcomber и Windsurfer, равна или больше 0,718-0,588 = 0,13, если на самом деле их доли в обеих генеральных совокупностях одинаковы. Таким образом, существуют веские основания утверждать, что между двумя отелями есть статистически значимая разница в обслуживании постояльцев. Исследования, приведенные в табл. 11.2, показывают, что количество гостей, удовлетворенных обслуживанием в отеле Beachcomber, больше количества постояльцев, планирующих снова остановиться в гостинице Windsurfer.
А ; в
..1. ^Анализ удовлетворенности гостей
2
3 Observed Frequencies
4 Hote
5 ! i Собираетесь ли вернуться? Beachcomber
8 I Да 163
7 | Нет 64
8 | Total 227
9.
1Q Expected Frequencies
11 Hote
12 Собираетесь ли вернуться? Beachcomber
13 Да 147.1554
14 Нет 79.8446
15 § Total 227
W
17 i Data
18 iLevel of Siqnificance 0.05
19 Number of Rows 2
20 ^Number of Columns 2
21 iDegrees of Freedom 1
22
23 j Results
24 Critical Value 3.8415
25 Chi-Square Test Statistic 9.0526
26 p -Value 0.0026
27 I Reject the null hypothesis
28
29 j Expected frequency assumption
.30 I is met.
c D ... , E F G
el Calculations
Windsurfer Total fo-fe
154 317 15.84458 -15.8446
108 172 -15.8446 15.84458
262 489
el
Windsurfer Total (fo-fe)A2/fe
169 8446 317 1.706024 1.47812
92 1554 172 3.144243 2.72421
262 489
Рис. 11.3. Результаты х2-критерия для проверки гипотезы о разности между долями удовлетворенных постояльцев при уровне значимости, равном 0,05 (получены с помощью программы Microsoft Excel)
ПРОВЕРКА ПРЕДПОЛОЖЕНИЙ. КАСАЮЩИХСЯ ФАКТОРНОЙ ТАБЛИЦЫ 2x2
Для получения точных результатов на основе данных, приведенных в таблице 2x2, необходимо, чтобы количество успехов или неудач превышало число 5. Если это условие не выполняется, следует применять точный критерий Фишера [1, 2].
Процедуры Excel: применение %г-критерия для проверки гипотезы о равенстве двух долей
Чтобы применить х2-критерий для проверки гипотезы о равенстве двух долей, следует создать рабочий лист, использующий функции Х2ОБР и Х2РАСП, либо применить надстройку PHStat2.
Например, чтобы сравнить с помощью этого критерия степень удовлетворенности гостей отелей Beachcomber и Windsurfer на основе данных, приведенных в табл. 11.2, необходимо выполнить одну из следующих процедур.
Применение Excel в сочетании с надстройкой PHStat
Чтобы применить х2-критерий для проверки гипотезы о равенстве двух долей, следует выбрать команду PHStat^Two-sample tests^Chi-Square Test for Differences in Two Proportions... (PHStat1^ Двухвыборочные критерии^/^-критерий для разностей между двумя долями признака...) и выполнить следующие действия.
1. Выбрать команду PHStat^Two-sample tests^Chi-Square Test for Differences in Two Proportions....
2. В диалоговом окне Chi-Square Test for Differences in Two Proportions (см. иллюстрацию) сделать следующее.
2.1. Ввести в окне редактирования Level of Significance (Уровень значимости) число 0.05.
2.2. Ввести в окне редактирования Title (Заголовок) название нового листа.
Chi-Square Test for Differences in T... [Я]
Data.................- -..........-..... - - -
Level of Significance: Jo.05
Output Options - - ' - - - - ,
Title: |Днализ удовлетворенности гостей
Help j | ...........QK,„. „Л Cancel |
2.3. Щелкнуть на кнопке OK.
3. На вновь созданном рабочем листе сделать следующее.
3.1. Ввести метки строк и столбцов для переменных. Ввести строку Собираетесь ли вы вернуться? в ячейке А5 и строку Отель в ячейке В4.
3.2. Ввести метки строк и столбцов для категорий. Ввести строку Да в ячейке Аб и строку Нет в ячейке А7. В ячейке В5 ввести строку Beachcomber, а в ячейке С5 — Windsurfer. При необходимости можно увеличить ширину столбцов.
3.3. В диапазоне вб:С7 ввести данные из табл. 11.2: в ячейку вб — число 163, в ячейку В7 — 64, в ячейку Сб - 154, в ячейку С7 - 108.
Обратите внимание на то, что перед вводом данных из табл. 11.2 многие ячейки содержат сообщение об ошибке #ДЕЛ/0 !. После ввода данных эти сообщения исчезнут.
Применение Excel
Чтобы самостоятельно создать рабочий лист, применяющий х2-критерий для проверки гипотезы о равенстве двух долей, следуйте инструкциям, приведенным в разделе ЕН.11.1.
Лл Chapter ll.xls
~ Данные, на основе которых применяется х2-критерий для сравнения двух долей при оценке степени удовлетворенности постояльцев отелей Beachcomber и Windsurfer, содержатся в рабочей книге Chapter 11 на листе Рис11.3.
При сравнении процента клиентов, удовлетворенных качеством обслуживания в двух отелях, критерии Z и %2 приводят к одинаковым результатам. Это можно объяснить существованием тесной связи между стандартизованным нормальным распределением и х2-распределением с одной степенью свободы. В этом случае х2-статистика всегда является квадратом Z-статистики. Например, при оценке степени удовлетворенности гостей мы обнаружили, что Z-статистика равна +3,01, а х2-статистика — 9,05. Пренебрегая ошибками округления, легко убедиться, что вторая величина является квадратом первой (т.е. 3,012 = 9,05). Кроме того, сравнивая критические значения обеих статистик при уровне значимости а = 0,05, можно обнаружить, что величина %2 , равная 3,841, является квадратом верхнего критического значения Z-статистики, равного +1,96 (т.е. xf = Z2). Более того, p-значения обоих критериев одинаковы.
Таким образом, можно утверждать, что при проверке нулевой и альтернативной гипотез
критерии Z и %2 являются эквивалентными. Однако, если необходимо не просто обнаружить различия, но и определить, какая доля больше (рх>р2), следует применять Z-критерий с одной критической областью, ограниченной хвостом стандартизованного нормального распределения. В разделе 11.2 описано применение критерия // для сравнения долей признака в нескольких группах. Необходимо отметить, что Z-критерий в этой ситуации применять невозможно.
Изучение основ
11.1. Рассмотрим следующую таблицу сопряженности признаков.
А Б Всего
1 20 30 50
2 30 45 75
Всего 50 75 12£
1. Вычислите ожидаемые величины для каждой ячейки таблицы.
2. Сравните наблюдаемые и ожидаемые величины в каждой ячейке таблицы.
3. Определите /2-статистику. Является ли разность между долями значимой, если уровень значимости а равен 0,05?
11.2. Рассмотрим следующую таблицу сопряженности признаков.
А Б Всего
1 20 30 50
2 30 20 50
Всего 50 50 100
1. Вычислите ожидаемые величины для каждой ячейки таблицы.
2. Определите /2-статистику. Является ли разность между долями значимой, если а = 0,05?
Применение понятий
Задачи 11.3-11.8 можно решать как вручную, так и с помощью программы Microsoft Excel.
11.3. Для исследования потребительского спроса был проведен опрос 500 пассажиров метро. Среди вопросов был и такой: “Получаете ли вы удовольствие от покупки одежды?”. Результаты опроса представлены в следующей таблице сопряженности признаков.
Пол
Получаете ли вы удовольствие от покупки одежды? Мужской Женский Всего
Да 136 224 362
Нет 104 36 140
Всего 240 260 500
1. Можно ли утверждать, что между долями мужчин и женщин, получающих удовольствие от покупки одежды, существует значительная разница, если уровень значимости равен 0,01?
2. Вычислитер-значение и объясните его смысл.
3. Как изменятся решения задач 1 и 2, если количество мужчин, получающих удовольствие от покупки одежды, будет равно 206?
4. Сравните результаты с решением задачи 9.25.
11.4. Газета New York Times сообщила о результатах опроса, проведенного фондом Henry J. Kaiser Family Foundation (McClain, D. L., “Where Is Today’s Child? Probably Watching TV”, The New York Times, December 6, 1999, p. Cl). В ходе опроса оценивалось влияние средств массовой информации на воспитание детей. Один из вопросов формулировался так: “Работаете ли вы с компьютером ежедневно?”. Результаты опроса приведены в следующей таблице сопряженности признаков.
Работаете ли вы с компьютером ежедневно?
Возраст Да Нет Всего
2-7 283 807 1 090
8-18 1053 1012 2 065
Всего 1 336 1 819 3 155
1. Можно ли утверждать, что между процентом детей и подростков, использующих компьютер ежедневно, существует значительная разница, если уровень значимости равен 0,05?
2. Вычислите р-значение и объясните его смысл.
3. Сравните результаты с решением задачи 9.26.
11.5. В ходе кампании по улучшению качества продукции на заводе полупроводников была сформирована выборка из 450 пластин. В приведенной ниже таблице сопряженности признаков указано количество ответов на два вопроса: “Остались ли частицы на матрице, использованной для производства пластины?” и “Качественная пластина или нет?”.
Состояние матрицы
Частицы Хорошее Плохое Всего
Есть 14 36 50
Нет 320 80 400
Всего 334 116 450
Источник: Hall, S. W., “Analysis of Detectivity of Semiconductor Wafers by Contingency Table”, Proceedings Institute of Environmental Sciences 1(1994):177-183.
1. Можно ли утверждать, что между долями качественных и бракованных пластин существует значительная разница, если уровень значимости равен 0,05?
2. Вычислитер-значение и объясните его смысл.
3. Какой вывод следует сделать на основе проведенного анализа?
4. Сравните результаты с решением задачи 9.27.
11.6. В исследовании, проведенном компаниями Ariel Mutual Funds и Charles Schwab Corporation, приняли участие 500 афроамериканцев и 500 белых, чей годовой доход превышал 50 000 долл. Оказалось, что 74% афроамериканцев и 84% белых владеют акциями (Cheryl Winokur Munk, “Stock-Ownership Race Gap Shinks”, Wall Street Journal, June 13, 2002, Bll).
1. Можно ли утверждать, что существует значимая разница между долями инвесторов среди афроамериканцев и белых, чей доход превышает 50 000 долл., если уровень значимости равен 0,05?
2. Вычислите/>-значение и объясните его смысл.
3. Сравните результаты с решением задачи 9.30.
11.7. Многие люди отказываются отвечать на анкеты, полученные по почте. Исследователи из университета Джона Кэррола (John Carrol University) провели исследование, в рамках которого попытались выяснить, можно ли повысить количество ответов, если предупреждать респондентов за неделю до отправки анкеты по почте (Paul R. Murphy and James M. Daley, “Postcard Prenotification in Industrial Surveys: Further Evidence”, Mid American Journal of Business, Spring, 2002, 17(l):51-57). Группа, состоящая из 345 респондентов, живущих в США, была разделена на две подгруппы. Респонденты первой подгруппы были заранее предупреждены о том, что через неделю они получат анкету, в которой содержатся вопросы, касающиеся деятельности агентств по отправке грузов. Члены второй группы получали анкеты без предупреждения. Результаты исследования приведены в следующей таблице.
Группы
Результат С уведомлением Без уведомления Всего
Ответили 39 41 80
Не ответили 142 123 265
Всего 181 164 345
1. Можно ли утверждать, что существует значимая разница между долями ответивших респондентов, если уровень значимости равен 0,05?
2. Вычислите р-значение и объясните его смысл.
11.8. Исследователи предположили, что при покупке одежды покупатели стали меньше обращать внимание на торговую марку. Из 7 500 покупателей одежды 57% респондентов ответили, что логотипы, бирки и торговые марки на одежде в настоящее время не имеют такого значения, как несколько лет назад. В то же время только 10% покупателей указали, что важность торговой марки для них возросла (Shelly Branch, “What’s is a Name? Not Much According to Clothes Shoppers”, Wall Street Journal, July 16, 2002, B4). Кроме того, в ходе опроса исследователи оценили различие в отношении к торговым маркам среди мужчин и женщин. Результаты опроса приведены в следующей таблице.
Важность торговой марки Пол
Мужской Женский Всего
Возросла 450 300 750
Не возросла 3 300 3 450 6 750
Всего 3 750 3 750 7 500
1. Можно ли утверждать, что существует значимая разница между долями мужчин и женщин, считающих что важность торговой марки возросла, если уровень значимости равен 0,05?
2. Вычислите p-значение и объясните его смысл.
11.2. ПРИМЕНЕНИЕ Х2-КРИТЕРИЯ ДЛЯ ПРОВЕРКИ ГИПОТЕЗЫ О РАВЕНСТВЕ НЕСКОЛЬКИХ ДОЛЕЙ
Критерий “хи-квадрат” можно распространить на более общий случай и применять для проверки гипотезы о равенстве нескольких долей признака. Обозначим количество анализируемых независимых генеральных совокупностей буквой с. Теперь таблица сопряженности признаков состоит из двух строк и с столбцов. Чтобы проверить нулевую и альтернативные гипотезы
^п-Р=Р2= ••• = р,
Н/. не всер равны между собой, у = 1,2,..., с, используется тестовая /2-статистика (11.1):
r= s
па вс ем ячейкам J е
где fQ — наблюдаемое количество успехов или неудач в конкретной ячейке факторной таблицы 2хс, fe — теоретическое, или ожидаемое, количество успехов или неудач в конкретной ячейке таблицы сопряженности признаков при условии, что нулевая гипотеза является истинной.
Чтобы вычислить ожидаемое количество успехов или неудач в каждой ячейке таблицы сопряженности признаков, необходимо иметь в виду следующее. Если нулевая гипотеза является истинной и доли успехов во всех с генеральных совокупностях равны, соответствующие выборочные доли могут отличаться друг от друга лишь по случайным причинам, поскольку все доли представляют собой оценки доли признака р в общей генеральной совокупности. В этой ситуации статистика, объединяющая все доли в одной общей (или средней) оценке параметрар, содержит больше информации, чем каждая из них в отдельности. Эта статистика, обозначаемая символом р , представляет собой общую (или среднюю) долю успехов в объединенной выборке.
ВЫЧИСЛЕНИЕ СРЕДНЕЙ ДОЛИ
(И-3)
Чтобы вычислить ожидаемое количество успехов Д в первой строке таблицы сопряженности признаков, необходимо умножить объем каждой выборки на параметр р . Чтобы вычислить ожидаемое количество неудач fe во второй строке таблицы сопряженности признаков, необходимо умножить объем каждой выборки на параметр 1-/? . Тестовая статистика, вычисленная по формуле (11.1), аппроксимируется /-распределением. Количество степеней свободы этого распределения задается величиной (г-1)(с-1), где i— количество строк в факторной таблице, с — количество столбцов в таблице. Для факторной таблицы гхс количество степеней свободы равно (2—1)(с—1) = с-1.
При заданном уровне значимости а нулевая гипотеза отклоняется, если вычисленная /-статистика больше верхнего критического значения / , присущего /-распределению с с-1 степенями свободы. Таким образом, решающее правило выглядит следующим образом:
гипотеза Но отклоняется, если / >/ (рис. 11.4),
в противном случае гипотеза отклоняется.
гипотезы гипотезы
Рис. 11.4. Критическая область /-критерия для сравнения с долей при уровне значимости а
ПРОВЕРКА ПРЕДПОЛОЖЕНИЙ, КАСАЮЩИХСЯ ФАКТОРНОЙ ТАБЛИЦЫ 2хС
Для получения точных результатов на основе данных, приведенных в факторной таблице 2хс, необходимо, чтобы количество успехов или неудач было достаточно большим. Некоторые статистики [4] полагают, что критерий дает точные результаты, если ожидаемые частоты превышают 0,5. Более консервативные исследователи требуют, чтобы не более 20% ячеек таблицы сопряженности признаков содержали ожидаемые величины, которые меньше 5, причем ни одна ячейка не должна содержать ожидаемую величину меньше единицы [3]. Последнее условие нам представляется разумным компромиссом между этими крайностями. Чтобы удовлетворить это условие, категории, содержащие небольшие ожидаемые величины, следует объединить в одну. После этого критерий становится более точным. Если по каким-либо причинам объединение нескольких категорий невозможно, следует применять альтернативные процедуры [2,6].
Для того чтобы проиллюстрировать /2-критерий для проверки гипотезы о равенстве долей в нескольких группах, вернемся к сценарию, описанному в начале главы. Рассмотрим аналогичный опрос, в котором принимают участие постояльцы трех отелей, принадлежащих компании Т. С. Resort Resources. Их ответы приведены в табл. 11.6.
Таблица 11.6. Факторная таблица 2x3 для сравнения количества постояльцев, удовлетворенных и не удовлетворенных обслуживанием
Отель
Вернетесь ли вы в следующем году? Golden Palm Palm Royale Palm Princess Всего
Да 128 199 186 513
Нет 88 33 66 187
Всего 216 232 252 700
Нулевая гипотеза утверждает, что доли клиентов, планирующих вернуться в следующем году, во всех отелях практически одинаковы. Для оценки параметра р, представляющего собой долю гостей, планирующих вернуться в отель, используется величина р , которая вычисляется по формуле (11.3)
_ X, + Х,+... + Х X 128 + 199 + 186 513 Л
р = —•--=-------«_ = — =--------------=---- о, 733 .
п}+п2 + ... + п( п 216 + 232 + 252 700
Доля гостей, оставшихся недовольными обслуживанием, равна 1-0,733, т.е. 0,267. Умножая три доли на количество опрошенных постояльцев в каждом из отелей, получаем ожидаемое количество гостей, планирующих вернуться в следующем сезоне, а также число клиентов, которые больше не остановятся в этом отеле.
ПРИМЕР 11.2. ВЫЧИСЛЕНИЕ ОЖИДАЕМОГО КОЛИЧЕСТВА ПОСТОЯЛЬЦЕВ
Вычислите ожидаемое количество постояльцев, соответствующее каждой из шести ячеек табл. 11.6.
РЕШЕНИЕ.
Да — Golden Palm: р = 0,733, п1 = 216, следовательно, fe= 158,30.
Да — Palm Royale: р = 0,733, п2 = 232, следовательно, Д = 170,02.
Да — Palm Princess: р = 0,733, п3 = 252, следовательно,/; = 184,68.
Нет — Golden Palm: 1- р = 0,267, = 216, следовательно, Д = 57,70.
Нет — Palm Royale: 1- р = 0,267, п2 — 232, следовательно, ff = 61,98.
Нет — Palm Princess: 1- р = 0,267, гр = 252, следовательно, fe = 67,32.
Все ожидаемые величины представлены в табл. 11.7.
Таблица 117. Факторная таблица ожидаемых величин для сравнения количества постояльцев, удовлетворенных и не удовлетворенных обслуживанием в трех отелях
Отель
Вернетесь ли вы в следующем году? Golden Palm Palm Royale Palm Princess Всего
Да 158,30 170,02 184,68 513
Нет 57,70 61,98 67,32 187
Всего 216,00 232,00 252,00 700
Чтобы проверить нулевую и альтернативные гипотезы
Н0:рх = р2=р3,
Н/. не всер, равны между собой, используют тестовую /"-статистику, вычисленную с помощью ожидаемых и наблюдаемых величин по формуле (11.1). Вычисления представлены в табл. 11.8.
Таблица 11.8. Вычисление /"-статистики при сравнении долей постояльцев, удовлетворенных обслуживанием
fo fo-f. (fo-t)2
128 158,30 -30,30 918,0900 5,800
199 170,02 28,98 839,8404 4,940
186 184,68 1,32 1,7245 0,009
88 57,70 30,30 918,0900 15,911
33 61,98 -28,98 839,8404 13,550
66 67,32 -1,32 1,7424 0,026
40,236
Критическое значение тестовой /"-статистики определяется по табл. Д.4. Поскольку в опросе принимают участие постояльцы трех отелей, /"-статистика имеет (2—1)(3—1) = 2 степени свободы. При уровне значимости а = 0,05, учитывая, что /2-распределение для факторной таблицы 2x3 имеет две степени свободы, критическое значение /"-статистики равно 5,991. Так как вычисленная /"-статистика, равная 40,236, превышает критическое значение, нулевая гипотеза отклоняется (рис. 11.5). Используя программу Microsoft Excel, обнаруживаем, что р-значение равно 0,0000 (точнее говоря, 1,84Е-09, или 0,00000000184) и меньше уровня значимости а = 0,05. Следовательно, нулевая гипотеза отклоняется. Кроме того, р-значение свидетельствует о том, что обнаружить разность между выборочными долями постояльцев, удовлетворенных обслуживанием в трех отелях, практически невозможно.
Рис. 11.5. Области принятия и отклонения гипотезы о равенстве трех долей при уровне значимости, равном 0,05, и двух степенях свободы
22
23_.__________________Results
24 {Critical Value____________
25 = Chi-Square Test Statistic 26pValue
5.9915 40.2284 1.83871E-09
________Reject the null hypothesis
Expected frequency assumption is met.
Рис. 11.6. Результаты х2-критерия для проверки гипотезы о равенстве долей удовлетворенных постояльцев трех отелей при уровне значимости, равном 0,05 (получены с помощью программы Microsoft Excel на основе данных, приведенных в табл. 11.6)
Отклоняя нулевую гипотезу при сравнении долей, указанных в факторной таблице 2хс, мы можем утверждать лишь, что доли постояльцев, удовлетворенных обслуживанием в трех отелях, не совпадают. Для того чтобы выяснить, какие доли отличаются от других, необходимо применять иные методы, например процедуру Мараскуило (Marascuilo).
Процедуры Excel: применение х -критерия для проверки гипотезы о равенстве нескольких долей
Чтобы применить %2-критерий для проверки гипотезы о равенстве нескольких долей, следует создать рабочий лист, использующий функции Х20БР и Х2РАСП, а затем создать второй рабочий лист, выполняющий процедуру Мараскуило. Надстройка PHStat2 создает эти рабочие листы автоматически.
Например, чтобы сравнить с помощью этого критерия степень удовлетворенности гостей трех отелей на основе данных, приведенных в табл. 11.6, необходимо создать новый рабочий лист и выполнить одну из следующих процедур.
Применение Excel в сочетании с надстройкой PHStat2
Чтобы применить %2-критерий для проверки гипотезы о равенстве нескольких долей, следует выбрать команду PHStatd> Multiple-sample testsd>Chi-Square Test... (PHStatd> Многовыборочные критерии^ %2-критерий...) и выполнить следующие действия .
Chi-Square Test [ST]
Data ...
Level of Significance: jo.OS
Number of Rows: |2
Number of Columns: h
Output Options
Title: ^Анализ удовлетворенности гостей
Г’ Marascuilo Procedure
HelL, I jl Cancel |
1. Выбрать команду PHStatd> Multiple-sample testsd>Chi-Square Test....
2. В диалоговом окне Chi-Square Test (см. иллюстрацию) сделать следующее.
2.1. Ввести в окне редактирования Level of Significance (Уровень значимости) число 0.05.
2.2. Ввести в окне редактирования Number of Rows (Количество строк) число 2.
2.3. Ввести в окне редактирования Number of Columns (Количество столбцов) число 3.
2.4. Ввести в окне редактирования Title (Заглавие) название нового листа.
2.5. Щелкнуть на кнопке ОК.
3. На вновь созданном рабочем листе сделать следующее.
3.1. Ввести метки строк и столбцов для переменных. Ввести строку Собираетесь ли вы вернуться? в ячейке А5 и строку Отель в ячейке В4.
3.2. Ввести метки строк и столбцов для категорий. Ввести строку Да в ячейке А6 и строку Нет в ячейке А7. В ячейке В5 следует ввести строку Golden Palm, в ячейке С5 - Palm Royale, а в ячейке D5 — Palm Princess. При необходимости можно увеличить ширину столбцов.
3.3. В диапазоне В6: D7 ввести данные из табл. 11.6: в ячейку В6 - число 128, в ячейку В7 - 88, в ячейку сб - 199, в ячейку С7 — 33, в ячейку D6 - 186, в ячейку D7 — 66.
Обратите внимание на то, что перед вводом данных из табл. 11.6 многие ячейки содержат сообщение об ошибке #дел/0 !. После ввода данных эти сообщения исчезнут.
Примечание: для того чтобы выполнить процедуру Мараскуило, установите в диалоговом окне Chi-Square test флажок Marascuilo Procedure.
Применение Excel
Выполнение %2-критерия для проверки гипотезы о равенстве нескольких долей. Для того чтобы самостоятельно создать рабочий лист, выполняющий /-критерий для проверки гипотезы о равенстве нескольких долей, следуйте инструкциям, приведенным в разделе ЕН.11.2.
Выполнение процедуры Мараскуило. Для того чтобы самостоятельно создать рабочий лист, выполняющий процедуру Мараскуило, следуйте инструкциям, приведенным в разделе ЕН.11.3.
Chapter ll.xls
Данные, на основе которых выполняется %2-критерий для проверки гипотезы о равенстве нескольких долей, содержатся в рабочей книге chapter 11 на листе Рис11.6.
Процедура Мараскуило позволяет сравнивать все группы попарно. На первом этапе процедуры вычисляются разности ps - ps (где /V/) между с(с-1)/2 парами долей. Со-
ответствующие критические размахи вычисляются по формуле (11.4).
КРИТИЧЕСКИЙ РАЗМАХ В ПРОЦЕДУРЕ МАРАСКУИЛО
Критический размах =
(И.4)
При общем уровне значимости, равном а, величина представляет собой квадратный корень из верхнего критического значения распределения “хи-квадрат”, имеющего с-1 степеней свободы. Для каждой пары выборочных долей необходимо вычислить отдельный критический размах. На последнем этапе каждая из с(с-1)/2 пар долей сравнивается с соответствующим критическим размахом. Доли, образующие конкретную пару, считаются статистически значимо разными, если абсолютная разность выборочных долей -р5.| превышает критический размах.
Проиллюстрируем процедуру Мараскуило на примере опроса постояльцев трех отелей. Применяя критерий “хи-квадрат”, мы убедились, что между долями постояльцев разных отелей, собирающихся вернуться в следующем году, существует статистически значимая разница. Поскольку в опросе участвуют постояльцы трех отелей, необходимо выполнить 3(3-1)/2 = 3 попарных сравнений и вычислить три критических размаха. По табл. 11.6 определяем, что три выборочных доли равны следующим величинам.
i = — = 0,593
Л?! 216
Ps,
Н-
199
----= 0,858
232
Ps,
^ = 1^ = 0,738. т 252
При общем уровне значимости, равном 0,05, верхнее критическое значение тестовой /-статистики для распределения “хи-квадрат”, имеющего (с-1) = 2 степени свободы определяется по табл. Д.4 и равно 5,991. Итак,
ТхГ = V5."* 1 = 2,448 •
Далее, вычислим три пары абсолютных разностей и соответствующие критические размахи. Если абсолютная разность больше ее критического размаха, то соответствующие доли считаются значимо разными.
Абсолютные разности между долями Критический размах
|л, -а,| 2,448 ) V rij nf
|а, 0,593-0,858| = 0,265 2>44о /0/93х °,407 + °,858x0,142 = V 216 232
|’Л,-ps,| = |0,593-0,738 =0,145 2,448л/°’593х0’407 + °-738х0’262 =0,106 \ 216 252
-р51| =|0,858-0,738| = 0,120 2,44 JWOJ42 + 0,738x0,262 = У 232 252
Результаты выполнения процедуры Мараскуило с помощью программы Microsoft Excel приведены на рис. 11.7.
J. ' • ' ’ A • ..
Д (Процедура Мараскуило
2 .Анализ удовлетворенности гостей в трех отелях
_ 3 ; Level of Significance__
4 jSquare Root of Critical Value-
‘5 ।____________
~6 I
7 jGroup 1
8 ,Group 2
9 'Group 3
io;____________
)i_.___________
12 ; Proportions______
13 H Group 1 - Group 2 I
14 | Group 1 - Group зТ
J5;____________________
16 ]| Group 2 - Group 3 |
Sample Proportions
________0 05
2 447749243
0.592592593
0,857758621
0.738095238
MARASCUILO TABLE
Absolute Differences Critical Range 0.0992355 0.106267888
0.265166028
0.145502646
Significant Significant
0.1196633831 0.088017116] Significant
В
Рис. 11.7. Результаты выполнения процедуры Мараскуило для проверки гипотезы о равенстве долей удовлетворенных постояльцев трех отелей при уровне значимости, равном 0,05 (получены с помощью программы Microsoft Excel на основе данных, приведенных в табл. 11.6)
Как видим, при уровне значимости, равном 0,05, степень удовлетворенности постояльцев отеля Palm Royal (ps = 0,858 ) выше, чем у постояльцев отелей Golden Palm (Ps, =0,593) и Palm Princess (ps =0,738 ). Кроме того, степень удовлетворенности постояльцев отеля Palm Princess выше, чем у постояльцев отеля Golden Palm. Эти результаты должны заставить руководство проанализировать причины таких различий и попытаться определить, почему степень удовлетворенности постояльцев отеля Golden Palm значительно ниже, чем у постояльцев других отелей.
Изучение основ
11.9. Рассмотрите таблицу сопряженности признаков, состоящую из двух строк и пяти столбцов.
1. Определите количество степеней свободы.
2. Вычислите критическое значение при уровне значимости а = 0,05.
3. Определите критическое значение при уровне значимости а = 0,01.
11.10. Рассмотрите следующую таблицу сопряженности признаков.
А Б В Всего
1 10 30 50 90
2 40 45 50 135
Всего 50 75 100 225
1. Вычислите ожидаемые величины для каждой ячейки таблицы.
2. Вычислите /1 2-статистику. Существуют ли значимые различия между долями, если уровень значимости равен 0,05?
3. Если возможно, примените процедуру Мараскуило при уровне значимости, равном а = 0,05 и определите, какие группы значимо отличаются друг от друга.
11.11. Рассмотрите следующую таблицу сопряженности признаков.
А Б В Всего
1 20 30 25 75
2 30 20 25 75
Всего 50 50 50 150
1. Вычислите ожидаемые величины для каждой ячейки таблицы.
2. Определите /2-статистику. Существуют ли значимые различия между долями, если уровень значимости равен 0,05?
Применение понятий
Задачи 11.12-11.16 можно решать как вручную, так и с помощью программы Microsoft Excel.
11.12. Д-р Лоуренс Альтман (Lawrence К. Altman) опубликовал результаты клинических испытаний, в ходе которых сравнивалась эффективность четырех курсов лечения, назначенных случайно выбранным пациентам, перенесшим сердечный приступ (The New York Times, May 1, 1993, p. 7). Обследованию подверглись 40 845 пациентов. Каждому из них был назначен один из четырех курсов лечения. Эффективность лечения оценивалась по количеству неблагоприятных исходов (т.е. количеству смертей или инсультов), последовавших в течение 30 дней лечения. Результаты исследования приведены в таблице.
Курс лечения
Исход А Б В Г Всего
Неблагоприятный 714 785 754 820 3 073
Благоприятный 9 630 9 543 9 042 9 557 37 772
Всего 10 344 10 328 9 796 10 377 40 845
Здесь использованы следующие обозначения: А — ускоренный курс ТРА с внутривенным введением гепарина, Б — комбинированный курс ТРА со стрептокиназой и внутривенным введением гепарина, В — стрептокиназа с подкожным введением гепарина, Г — стрептокиназа с внутривенным введением гепарина.
1. Существует ли значительная разница между долями неблагоприятных исходов каждого из четырех курсов лечения, если уровень значимости равен 0,05?
2. Определите, какие курсы лечения статистически значимо отличаются друг от друга при уровне значимости, равном 0,05.
3. Как эти результаты могут повлиять на политику медицинского страхования, если одна доза ТРА стоит 2 400 долл., а доза стрептокиназы — 240 долл.?
11.13. В ходе опроса пользователей Интернет в США, Австралии и Европе исследователи пытались выяснить, приобретают ли респонденты музыкальные компакт-диски, если перед этим они загрузили их из Интернет (“Net Music Inspires Buying”, USA Today, January 23, 2001, 1A). Выяснилось, что 77% американцев, 78% австралийцев и 54% европейцев, загружавших музыкальные файлы из Интернет, впоследствии покупали и музыкальные компакт-диски. Предположим, что в опросе приняли участие 500 американцев, 250 австралийцев и 500 европейцев.
1. Существует ли значительная разница между долями американцев, австралийцев и европейцев, покупавших музыкальные компакт-диски после загрузки музыкальных файлов из Интернет, если уровень значимости равен 0,05?
2. Вычислитер-значение в задаче 1 и объясните его смысл.
3. Примените процедуру Мараскуило при уровне значимости, равном 0,05, и определите, какие группы отличаются друг от друга. Обсудите полученные результаты.
11.14. Многие люди чаще покупают бакалейные товары по субботам, чем в другие дни недели. Зависит ли выбор дня покупки от возраста покупателя? Рассмотрим данные о возрасте покупателей и днях недели, в которые они предпочитают делать покупки (“Major Shopping by Day”, Progressive Grocer Annual Report, April 30, 2002). В таблице приведены лишь процентные доли, но не указаны объемы выборок.
Основной день покупок Возраст, годы
Младше 35, % 35-54,% Старше 54, %
Суббота 24 28 12
Другой день 76 72 88
Допустим, что в каждой возрастной категории были опрошены по 200 покупателей.
1. Существует ли значительная разница между долями покупателей из разных возрастных групп, если уровень значимости равен 0,05?
2. Вычислитер-значение в задаче 1 и объясните его смысл.
3. Примените процедуру Мараскуило при уровне значимости, равном 0,05, и определите, какие группы отличаются друг от друга. Обсудите полученные результаты.
4. Какие выводы можно сделать на основе результатов решения задач 1 и 2? Как менеджеры бакалейных магазинов могут использовать эту информацию для улучшения маркетинга и повышения объемов продаж? Будьте как можно конкретнее.
5. Как влияет на результаты опроса объем выборок, если для проверки гипотезы о равенстве нескольких долей применяется критерий “хи-квадрат”?
11.15. Министерство здравоохранения и общество защиты прав потребителей расходятся во мнениях о возможности раскрытия медицинских данных о пациентах без их согласия. Административные работники системы здравоохранения полагают, что для открытого обмена информацией между докторами, больницами, фармацевтическими и страховыми компаниями согласия пациентов можно не спрашивать. В ходе телефонного опроса, проведенного организацией Gallup Organization, респондентов попросили ответить, возражают ли они против обмена медицинской информацией между разными компаниями и организациями без согласия пациентов (Laura Landro, “Medical-Privacy Rules Leave Consumers’ Data Vulnerable”, Wall Street Journal, June 6, 2002, D3). Некоторые результаты этого опроса, полученные на основе трех выборок, состоящих их 1 000 респондентов, приведены в следующей таблице
Возражаете ли вы против обмена данными? Организация
Страховые компании Фармацевтические компании Научные работники
Да 820 590 670
Нет 180 410 330
1. Существует ли значительная разница между долями сотрудников из трех разных организаций, возражающих против открытого обмена медицинскими данными без согласия пациентов, если уровень значимости равен 0,05?
2. Примените процедуру Мараскуило при уровне значимости, равном 0,05, и определите, какие группы отличаются друг от друга. Обсудите полученные результаты.
11.16. Дж. Шефер (J. С. Schaefer) путешествовал по разным странам, оценивая уровень обслуживания в отелях. Оказалось, что качество обслуживания постояльцев может изменяться даже в пределах одного города. В следующих таблицах приведены оценки некоторых факторов в трех городах.
1. Портье регистрирует имя постояльца
Гонконг Нью-Йорк Париж
Да 26% 39% 28%
Нет 74% 61% 72%
2. Плата за использование минибара правильно отражается при расчете
Г онконг Нью-Йорк Париж
Да 86% 76% 78%
Нет 14% 24% 22%
3. Чистые ванна и душ
Гонконг Нью-Йорк Париж
Да 81% 76% 79%
Нет 19% 24% 21%
Источник: Templin, N., “Undercover With a Hotel Spy”, The Wall Street Journal, May 12,1999.
Предположим, что в каждом городе оценивалось 100 отелей высшей категории.
1. Существует ли значительная разница между долями отелей в трех городах, регистрировавших имена постояльцев, если уровень значимости равен 0,05?
2. Вычислитер-значение в задаче 1 и объясните его смысл.
3. Существует ли значительная разница между долями отелей в трех городах, в которых правильно учитывалась стоимость минибара, если уровень значимости равен 0,05?
4. Вычислитер-значение в задаче 2 и объясните его смысл.
5. Существует ли значительная разница между долями отелей в трех городах, в которых ванна и душ были чистыми, если уровень значимости равен 0,05?
6. Вычислите р-значение и объясните его смысл.
7. Допустим, что выборка состоит не из 100, а из 200 гостиниц. Повторите решение задач 1-6.
8. Как объем выборки влияет на оценку разностей между с долями?
11.3. ПРИМЕНЕНИЕ Х-КРИТЕРИЯ НЕЗАВИСИМОСТИ
В предыдущем разделе £2-критерий применялся для оценки разностей между несколькими долями признака. Если таблица сопряженности признаков состоит из г строк и с столбцов, /2-критерий можно использовать для проверки независимости двух категорийных величин.
В этом случае нулевая и альтернативная гипотезы 4юрмулируются следующим образом:
Но: две категорийные величины независимы (т.е. между ними нет взаимосвязи),
Нх‘. две категорийные величины зависят друг от друга (т.е. между ними есть взаимосвязь).
Для проверки независимости, как и прежде, применяется тестовая %2-статистика (11.1):
При заданном уровне значимости а нулевая гипотеза отклоняется, если вычисленная /2-статистика больше верхнего критического значения , присущего /2-распределению с (г- 1)(с-1) степенями свободы. Решающее правило выглядит следующим образом:
гипотеза Нп отклоняется, если £2 > (рис. 11.8); в противном случае гипотеза Но не отклоняется.
Рис. 11.8. Критическая область х2-критерия для проверки независимости двух переменных в факторной таблице гхс
Альтернативой /"-критерию для проверки гипотезы о равенстве долей служит /"-критерий независимости. В обоих случаях применяется одна и та же тестовая статистика и одно и то же решающее правило, правда, выводы делаются разные. Так, в задаче о постояльцах двух гостиниц, рассмотренной в разделах 11.1 и 11.2, между процентными долями гостей, планирующих вернуться в гостиницу в следующем сезоне, обнаружилась значимая разница. С другой стороны, можно сделать вывод, что между отелями и вероятностью, что гости в них вернутся, есть тесная зависимость. Несмотря на это, между двумя этими критериями существуют принципиальные различия. Основное различие заключается в схеме формирования выборок.
При проверке гипотезы о равенстве долей рассматривается один фактор, имеющий несколько уровней. Разным уровням соответствуют разные выборки, извлеченные из независимых генеральных совокупностей. Категориальные ответы в каждой из выборок классифицируются по двум категориям — успех и неудача. Цель критерия — сравнить и оценить разности между долями успеха для разных уровней фактора.
В то же время при проверке независимости рассматриваются два фактора, каждый из которых имеет несколько уровней. Из генеральной совокупности извлекается одна выборка, а в ячейки таблицы сопряженности признаков помещаются значения двух категорийных переменных, соответствующие разным уровням факторов.
Для того чтобы проиллюстрировать /"-критерий независимости, предположим, что в ходе опроса постояльцев трех отелей, принадлежащих компании Т. С. Resort Resources, гостей, решивших не возвращаться, просили указать причину. Их ответы приведены в табл. 11.9.
Таблица 11.9. Таблица перекрестной классификации причин недовольства постояльцев
Отель
Причина недовольства Golden Palm Palm Royale Palm Princess Всего
Цена 23 7 37 67
Расположение отеля 39 13 8 60
Неудобные комнаты 13 5 13 31
Другие 13 8 8 29
Всего 88 33 66 187
Результаты, приведенные в табл. 11.9, говорят о том, что 67 постояльцев недовольны ценой, 60— расположением отеля, 31 — комнатами и 29 имеют другие причины для недовольства. Как и в табл. 11.6, в таблице сопряженности признаков учтены ответы 88 постояльцев отеля Golden Palm, 33 гостей отеля Palm Royale и 66 отдыхающих из отеля Palm Princess, не планирующих возвращаться на следующий год. Величины, заполнившие ячейки факторной таблицы 4x3, представляют собой количество ответов гостей, недовольных обслуживанием в зависимости от конкретных причин.
Нулевая и альтернативная гипотезы таковы:
На: между недовольством постояльцев и конкретным фактором нет взаимосвязи, И,: между недовольством постояльцев и конкретным фактором есть взаимосвязь.
Для проверки нулевой гипотезы применяется тестовая %2-статистика (11.1):
где f0 — наблюдаемое количество успехов или неудач в конкретной ячейке факторной таблицы гхс, 4 — теоретическое, или ожидаемое, количество успехов или неудач в конкретной ячейке таблицы сопряженности признаков при условии, что нулевая гипотеза является истинной.
Для вычисления величины Д используется правило, сформулированное в разделе 4.2. Это означает, что если нулевая гипотеза является истинной, для определения совместной вероятности, или ожидаемой доли успехов либо неудач, применяется правило умножения вероятностей независимых событий (4.8). Например, если нулевая гипотеза о независимости верна, вероятность, или ожидаемая доля успехов, соответствующих левой верхней ячейке, вычисляется путем умножения двух вероятностей:
Р(цена и отель Golden Palm) = Р(цена) х Р(отель Golden Palm).
Здесь доля постояльцев, указавших в качестве причины своего недовольства слишком высокую цену, равна 67/187, или 0,3583, а доля всех ответов, поступивших от постояльцев отеля Golden Palm, равна 88/187, или 0,4706. Если нулевая гипотеза верна, а основная причина недовольства гостей и характеристика отеля не связаны между собой, ожидаемая доля, или вероятность Р(цена и отель Golden Palm), окажется равной произведению отдельных вероятностей Р(цена) и Р(отель Golden Palm), т.е. 0,3583 х 0,4706 = 0,1686. Тогда ожидаемая величина fc для каждой ячейки должна быть произведением суммарного объема выборок п на эту вероятность: 187 х 0,1686, т.е. 37,53. Величины f, для оставшихся ячеек факторной таблицы 4x3 вычисляются аналогично (табл. 11.10).
Таблица 11.10. Таблица перекрестной классификации причин недовольства постояльцев
Отель
Причина недовольства Golden Palm Palm Royale Palm Princess Всего
Цена 31,53 11,82 23,65 67
Расположение отеля 28,24 10,59 21,18 60
Неудобные комнаты 14,59 5,47 10,94 31
Другие 13,65 5,12 10,24 29
Всего 88,00 33,00 66,00 187
Более простой способ вычисления ожидаемых величин, не требующих сложных вычислений, основан на формуле (11.5).
ВЫЧИСЛЕНИЕ ОЖИДАЕМЫХ ВЕЛИЧИН
Ожидаемая величина в каждой ячейке представляет собой произведение общей суммы по строке и общей суммы по столбцу, деленное на суммарный объем выборок.
общая сумма по строке х общая сумма по столбцу
------:--------------------------------— , (И.5)
П
где общая сумма по строкам равна сумме всех величин, указанных в строке, общая сумма по столбцу равна сумме всех величин, указанных в столбце, ап — суммарный объем выборок.
Например, для вычисления ожидаемой величины, соответствующей левой верхней ячейке (стоимость проживания в отеле Golden Palm), нужно применить следующую формулу
общая сумма по строке х общая сумма по столбцу _ 67 х 88 _
_ _ ,
Для правой нижней ячейки (другие причины недовольства обслуживанием в отеле Palm Princess) эта величина равна
общая сумма по строке х общая сумма по столбцу _ 29 х 66 _
п 187 ~ ’
Тестовая статистика (11.1) аппроксимируется /-распределением, количество степеней свободы которого равно (г-1)(с-1).
В табл. 11.11 приведена /2-статистика для рассмотренного выше опроса.
Таблица 11.11. Вычисление х2-статистики для причин недовольства, связанных
с конкретным отелем
Ячейка fo f. И (fo-tr
Цена/Golden Palm 23 31,53 -8,53 72,7609 2,308
Цена/Palm Royale 7 11,82 -4,82 23,2324 1,966
Цена/Palm Princess 37 23,65 13,35 178,2225 7,536
Расположение/Golden Palm 39 28,24 10,76 115,7776 4,100
Расположение/Palm Royale 13 10,59 2,41 5,8081 0,548
Расположение/Palm Princess 8 21,18 -13,18 173,7124 8,202
Комнаты/Golden Palm 13 14,59 -1,59 2,5281 0,173
Комнаты/Palm Royale 5 5,47 -0,47 0,2209 0,040
Комнаты/Palm Princess 13 10,94 2,06 4,2436 0,388
Другие/Golden Palm 13 13,65 -0,65 0,4225 0,031
Другие/Palm Royale 8 5,12 2,88 8,2944 1,620
Другие/Palm Princess 8 10,24 -2,24 5,0176 0,490
27,402
Установим уровень значимости а = 0,05. Вычисленная х2~статистика равна 27,402. Поскольку х2~распределение для факторной таблицы 4x3 имеет 6 степеней свободы, критическое значение %2-статистики равно 12,592. Вычисленная х2"статистика превышает критическое значение, следовательно, нулевая гипотеза отклоняется (рис. 11.9). Используя программу Microsoft Excel, обнаруживаем, что р-значение равно 0,000121 < 0,05. Следовательно, нулевая гипотеза о независимости между причиной недовольства и конкретными характеристиками отеля отклоняется. Кроме того, р-значение свидетельствует о том, что обнаружить разность между выборочными долями постояльцев, не удовлетворенных обслуживанием в трех отелях и указавших разные причины, практически невозможно, если причины недовольства постояльцев никак не связаны с характеристиками отеля. Следовательно, между причинами недовольства и характеристиками отелей существует тесная взаимосвязь. Сравнение наблюдаемых и ожидаемых величин (табл. 11.11) показывает, что цена не играет особой роли для постояльцев отеля Golden Palm, а для гостей отеля Palm Princess она кажется слишком высокой. В то же время расположение отеля Golden Palm многие постояльцы сочли неудачным, хотя гости отеля Palm Princess не считают это важным фактором.
Рис. 119. Проверка гипотезы о независимости переменных в опросе недовольных постояльцев отелей при уровне значимости а = 0,05 и шести степенях свободы
ПРОВЕРКА ПРЕДПОЛОЖЕНИЙ, КАСАЮЩИХСЯ ФАКТОРНОЙ ТАБЛИЦЫ ГХ С
Для получения точных результатов на основе данных, приведенных в факторной таблице гхс, необходимо, чтобы количество успехов или неудач было достаточно большим. На нее распространяются правила, сформулированные для факторной таблицы 2хс. Иначе говоря, ни одна ячейка не должна содержать нулей. Чтобы удовлетворить это условие, категории, содержащие нули, следует объединить в одну. Эта процедура позволяет увеличить количество успехов или неудач в ячейках таблицы сопряженности признаков и повысить точность критерия.
I А В . C 1 Перекрестная классификация отелей 2". I D -E , F । Q . }. H 1
3 Observed Frequencies Calculations fo-fe
4 - Hotel
5 Причины недовольства Golden Palm Palm Royale Palm Princess Total
6 1 Цена 23 7 37 67 -8.52941 -4.82353 13.35294 10.76471 2.411765 -13.1765 -1.58824 -0.47059 2.058824 -0.64706 2.882353 -2.23529:
7 Местоположение 39 13 8 60
8 ' Коинаты 13 5 13 31
9 : Другие 13 8 8 29
10' Total 88 33 66 187
11 '
12 : Expected Frequencies (fo-fe)*2/fe
13; Hotel
_ 14 ; Причины недовольства Golden Palm Palm Royale Palm Princess Total
15, Цена 31 5294 11 8235 23 6471 67 2.307397 1.967808 7.540094 4.104044 0.549346 8.198693 1 0.172913 0.040481 0.387413 0.03068 1.623394 0.488168
16 I Местоположение 28 2353 10 5882 21 1765 60
17! Комнаты 14 5882 5 4706 10 9412 31
18J Другие 13 6471 5 1176 10 2353 29
191 Total 88 33 66 187
20‘
21 Data
22 Level of Significance 8.85
23 I Number of Rows 4
24 ’Number of Columns 3
25 Degrees of Freedom 6
26.
27 Results
28 Critical Value 12.5916
29 Chi-Square Test Statistic 27.4184
30 ip -Value 0.00012
31 j Reject the null hypothesis
Рис. 11.10. Результаты применения %2-критерия для проверки гипотезы о независимости четырех переменных в опросе недовольных постояльцев трех отелей при уровне значимости, равном 0,05 (получены с помощью программы Microsoft Excel)
Процедуры Excel: применение %2-критерия независимости
Чтобы применить %2-критерий независимости, достаточно слегка изменить процедуру "Применение /-критерия для проверки гипотезы о равенстве нескольких долей", описанную в разделе 11.2.
Например, чтобы проверить с помощью этого критерия независимость причин неудовлетворенности гостей трех отелей на основе данных, приведенных в табл. 11.10, необходимо создать новый рабочий лист и выполнить одну из следующих процедур.
Применение Excel в сочетании с надстройкой PHStatZ
Чтобы применить /-критерий для проверки гипотезы о независимости случайных переменных, следует выбрать команду PHStat1^Multiple-sample tests^Chi-Square Test... (PHStat1^ Многовыборочные критер и и ^/-критерий...) и выполнить следующие действия.
1. Выбрать команду PHStat4>Multiple-sample tests4>Chi-Square Test....
2. В диалоговом окне Chi-Square Test (см. иллюстрацию) сделать следующее.
2.1. Ввести в окне редактирования Level of Significance (Уровень значимости) число 0.05.
2.2. Ввести в окне редактирования Number of Rows (Количество строк) число 4.
2.3. Ввести в окне редактирования Number of Columns (Количество столбцов) число 3.
Chi-Square Test | Х ]
Data..............
Level of Significance Number of Rows: Number of Columns:
Output Options ..-
Title: | Перекрестная классификация
Г
Help j |i OK J Cancel
2.4. Ввести в окне редактирования Title (Заглавие) название нового листа.
2.5. Щелкнуть на кнопке ОК.
3. На вновь созданном рабочем листе сделать следующее.
3.1. Ввести метки строк и столбцов для переменных. Ввести строку Причина недовольства в ячейке А5 и строку Отель в ячейке В4.
3.2. Ввести метки строк и столбцов для категорий. Ввести строку Цена в ячейку Аб, строку Расположение отеля — в ячейку А7, строку Неудобные комнаты — в ячейку А8, и строку Другие - в ячейку А9. В ячейку В5 следует ввести строку Golden Palm, в ячейку С5 -Palm Royale, а в ячейку D5 — Palm Princess.
3.3. В диапазоне вб: D9 ввести данные из табл. 11.10: в ячейки В6:В9 — числа 23, 39, 13 и 13, в ячейки С6:С9 — числа 7, 13, 5 и 8, в ячейки D6 : D9 - числа 37, 8, 13 и 8 соответственно.
Обратите внимание на то, что перед вводом данных из табл. 11.10 многие ячейки содержат сообщение об ошибке #дел/0 !. После ввода данных эти сообщения исчезнут.
Применение Excel
Для того чтобы самостоятельно создать рабочий лист, использующий /2-критерий для проверки гипотезы о независимости случайных переменных, следуйте инструкциям, приведенным в разделе ЕН.11.4.
Chapter 11. xls
" Данные, на основе которых применяется /-критерий для проверки гипотезы о независимости случайных переменных, содержатся в рабочей книге chapter 11 на листе Рис11.10.
УПРАЖНЕНИЯ К РАЗДЕЛУ 11
Изучение основ
11.17. Рассмотрите таблицу сопряженности признаков, состоящую из трех строк и четырех столбцов. Сколько степеней свободы имеет /-критерий независимости?
11.18. Рассмотрите таблицу сопряженности признаков, состоящую из г строк и с столбцов. Определите верхнее критическое значение /-статистики при следующих данных.
1. а = 0,05, г = 4, с = 5.
2. а = 0,01, г = 4, с = 5.
3. а = 0,01, г = 4, с = 6.
4. а = 0,01, г = 3, с = 6.
5. а = 0,01, г = 6, с = 3.
Применение понятий
11.19. Во время войны во Вьетнаме для призыва солдат в армию применялась лотерея. Числа, обозначающие порядковый номер дня в году, выбирались “случайным образом”. Военнообязанные, день рождения которых имел меньший порядковый номер, призывались в первую очередь, остальные не призывались. В следующих факторных таблицах показано, сколько небольших (1-122), средних (123-244) и больших (245-366) чисел выпадало в каждом квартале года.
Числа Квартал
Январь-март Апрель-июнь Июль-сентябрь Октябрь-декабрь Всего
Небольшие 21 28 35 38 122
Средние 34 22 29 37 122
Большие 36 41 28 17 122
Всего 91 91 92 92 366
1. Можно ли утверждать, что выпавшее число значительно зависит от времени года, если уровень значимости равен 0,05?
2. Можно ли сказать, что эта лотерея была случайной?
3. Как изменились бы ваши ответы, если бы таблица сопряженности признаков имела следующий вид?
Квартал
Числа Январь-март Апрель-июнь Июль-сентябрь Октябрь-декабрь Всего
Небольшие 23 30 32 37 122
Средние 27 30 34 31 122
Большие 41 31 26 24 122
Всего 91 91 92 92 366
L1.20. Крупная корпорация желает знать, существует ли связь между временем, которое сотрудники тратят на дорогу, и уровнем стресса, который они испытывают на работе. В опросе приняли участие 116 работников конвейера.
Уровень стресса
Время в дороге Высокий Умеренный Низкий Всего
До 15 мин. 9 5 18 32
15-45 мин. 17 8 28 53
Более 45 мин. 18 6 7 31
Всего 44 19 53 116
1. Можно ли утверждать, что между временем, которое сотрудники тратят на дорогу, и уровнем стресса, который они испытывают на работе, существует статистически значимая связь, если уровень значимости равен 0,01?
2. Как изменится ваш ответ, если уровень значимости равен 0,01?
11.21. По мере ускорения темпа деловой жизни менеджеры стали стремиться сократить время разработки и запуска маркетинговых кампаний (продолжительность цикла разработки). Опрос, проведенный среди 175 менеджеров по маркетингу в США и Великобритании, показал, что средняя продолжительность цикла разработки маркетинговой кампании равна 2,5 месяца, и лишь в 16% случаев цикл разработки длился менее одного месяца (Dana James, “Picking Up the Pace”, Marketing News, April 1, 2002, 3). Результаты опроса означают, что “дольше” не значит “лучше”. Менеджеры по маркетингу указали, что длительная разработка кампании может оказаться бесцельной, поскольку данные быстро устаревают. С другой стороны, менеджеры считают, что слишком быстрая разработка кампании также может снизить ее эффективность. Построим таблицу перекрестной классификации недавно проведенных маркетинговых кампаний, в которую запишем продолжительность цикла их разработки и эффективность.
Продолжительность цикла
Эффективность Меньше месяца 1-2 месяца 2-4 месяца Больше 4 месяцев Всего
Высокая 15 28 24 6 73
Средняя 9 26 33 19 87
Низкая 5_ 2 3_ 5 15
Всего 29 56 60 30 175
Можно ли утверждать, что между эффективностью и продолжительностью цикла разработки маркетинговой кампании существует статистически значимая связь, если уровень значимости равен 0,05?
11.22. Недавно в журнале USA Today была опубликована статья, в которой исследовалось, когда американцы решают, что они будут есть на обед (“What’s for Dinner”, USA Today, January 10, 2000). Предположим, что в опросе приняли участие 1 000 респондентов, причем учитывалось наличие детей до 18 лет. Таблица сопряженности признаков, содержащая результаты опроса, приведена ниже.
Время принятия решения Тип семьи
Один взрослый (без детей) Один взрослый (с детьми) Несколько взрослых (без детей)
Перед обедом 162 54 154
Днем 73 38 69
Утром 59 58 53
За несколько дней 21 64 45
За день 15 50 45
Всегда ем одно и то же 2 16 2
Не могу сказать 7 6 7
Можно ли утверждать, что между временем решения и типом семьи существует статистически значимая связь, если уровень значимости равен 0,05?
11.23. Недавно в журнале USA Today была опубликована статья, в которой исследовались технологические предпочтения водителей. Предположим, что в опросе приняли участие 1 000 респондентов, владеющих седаном, спортивным автомобилем и грузовиком. Таблица сопряженности признаков, содержащая результаты опроса, приведена ниже.
Предпочтения Тип автомобиля
Седан Спортивный Грузовик
Проигрыватель компакт-дисков 178 58 54
Высококачественная стереосистема 80 54 46
Мобильный телефон 100 8 22
Система глобального позиционирования 70 4 16
Видеоплейер/игровая приставка 68 6 6
Средства доступа к Интернет 24 6 10
Детектор радаров 16 34 20
Не знаю 80 26 14
Можно ли утверждать, что между предпочтениями водителей и типом автомобиля существует статистически значимая связь, если уровень значимости равен 0,05?
11.4. РАНГОВЫЙ КРИТЕРИЙ УИЛКОКСОНА:
НЕПАРАМЕТРИЧЕСКИЙ МЕТОД ДЛЯ ПРОВЕРКИ ГИПОТЕЗЫ О РАЗНОСТИ МЕЖДУ ДВУМЯ МЕДИАНАМИ
В разделе 9.1 изложен метод оценки разности между средними значениями выборок, извлеченных из двух независимых генеральных совокупностей. Если объемы выборок малы или генеральные совокупности не являются нормально распределенными, возникают две альтернативы: 1) можно применить непараметрическую процедуру, не зависящую от предположения о нормальном распределении генеральных совокупностей; 2) можно выполнить предварительную нормализацию данных, а затем применить f-критерий, использующий объединенную дисперсию [6].
В данном разделе рассматривается критерий Уилкоксона, позволяющий оценить разность между медианами двух генеральных совокупностей. Этот критерий является весьма популярной непараметрической процедурой. По своей мощности критерий Уилкоксона мало отличается от f-критериев, использующих раздельную или суммарную дисперсии. В то же время для его использования нет необходимости предполагать, что генеральные совокупности распределены нормально. Кроме того, критерий Уилкоксона можно применять даже тогда, когда исследователю доступны лишь ранговые показатели. Эта ситуация довольно часто встречается в маркетинговых исследованиях, когда отсутствие числовых данных не позволяет применять f-критерии.
Для того чтобы применить критерий Уилкоксона, необходимо заменить наблюдения, содержащиеся в двух выборках, имеющих объемы п1 и п2, их объединенными рангами (если исходные данные не являются рангами изначально). Количество наблюдений в обеих выборках равно пх + п2. Наименьший ранг равен наименьшему из пх + п2 наблюдений, второй ранг равен наименьшему из оставшихся наблюдений и так далее, пока мы не достигнем наибольшего ранга. Если несколько значений являются взаимосвязанными, необходимо заменить каждое из них средними рангами, вычисленными так, будто эти величины не зависят друг от друга.
Для удобства будем считать, что когда объемы выборок не одинаковы, число п1 меньше числа п2. Статистика рангового критерия Уилкоксона Тх равна сумме первых пх рангов. (Если объемы выборок равны, в качестве этой статистики можно взять сумму рангов в любой группе.)
Напомним, что сумма первых п последовательных натуральных чисел равна п(п+1)/2. Следовательно, сумма статистик 7\ и Т2 (вычисленных по остальным п2 наблюдениям), должна быть равной п(п+1)/2.
СУММА СТАТИСТИК УИЛКОКСОНА
Т,+Т2 = П('"~^ ' (11-6)
Проверка гипотезы осуществляется с помощью одностороннего или двустороннего критерия, в зависимости от того, какая гипотеза проверяется: о равенстве двух медиан или о том, что одна медиана больше другой.
Двусторонний критерий Односторонний критерий Односторонний критерий
Н0:М = М2 Но: М.>М2 Н0'М< М2
Н,: М2 Я,: Мх<М2 H;.MV> М2
Здесь — медиана первой генеральной совокупности, а М2 — медиана второй генеральной совокупности. Если объемы обеих выборок не превышают число 10, для определения критических значений статистики одностороннего или двустороннего критерия Т\ применяется табл. Д.8. Для двустороннего критерия при заданном уровне зна-
чимости а нулевая гипотеза отклоняется, если статистика критерия больше верхнего критического значения или меньше нижнего критического значения. Эти ситуации изображены на рис. 11.11 (панельА).
Область отклонения гипотезы
Область принятия гипотезы
Рис. 11.11. Области принятия и отклонения гипотезы в ранговом критерии Уилкоксона
Для одностороннего критерия, альтернативная гипотеза Нх которого заключается в том, что Мх< М2, решающее правило формулируется следующим образом: нулевая гипотеза отклоняется, если статистика Тх не превышает нижнего критического значения (рис. 11.11, панель Б).
Для одностороннего критерия, альтернативная гипотеза Нх которого заключается в том, что Мх> М2, решающее правило формулируется следующим образом: нулевая гипотеза отклоняется, если статистика Тх больше верхнего критического значения или равна ему (рис. 11.11, панель В).
При больших объемах выборок статистика Тх является приближенно нормально распределенной, причем ее математическое ожидание ц7. задается формулой
и, (л + 1)
2
а стандартное отклонение <зт вычисляется как
п.к,(п +1)
О’ 7 —- Л I ~ •
' V 12
Таким образом, стандартизованная Z-статистика критерия имеет следующий вид.
КРИТЕРИЙ УИЛКОКСОНА ДЛЯ БОЛЬШИХ ВЫБОРОК
Z = (11.7)
°т,
где статистика критерия Z имеет приближенное нормальное распределение.
Эту статистику применяют, когда объем выборки выходит за пределы, предусмотренные в табл. Д.8. При заданном уровне значимости а нулевую гипотезу отклоняют, когда вычисленная статистика Z попадает в критическую область.
Вернемся к сценарию, рассмотренному в главе 9, в котором требовалось определить, равны ли средние недельные объемы продаж BLK-колы, выставленной на специализированных стеллажах и на обычных полках. Если у нас нет оснований считать, что выборки извлечены из нормально распределенных генеральных совокупностей, можно применить ранговый критерий Уилкоксона.3 (Соответствующие данные приведены в табл. 11.12.)
Чтобы оценить разность между медианами продаж, необходимо предположить, что обе генеральные совокупности являются одинаково распределенными и различаются лишь медианами.
Поскольку нам неизвестно, какая из медиан окажется больше, нулевую и альтернативную гипотезы следует сформулировать следующим образом:
Но: М=М2, НХ:М^М2.
Для того чтобы применить ранговый критерий Уилкоксона, необходимо вычислить ранги для выборок, состоящих из п, = 10 магазинов с обычными полками и из п2 = 10 магазинов со специализированными стеллажами. Вычисленные ранги приведены в табл. 11.12.
Таблица 11.12. Вычисленные ранги4
Объем продаж
Обычные полки (п=10) Объединенные ранги Специализированные стеллажи (п2=10) Объединенные ранги
22 1,0 52 5,5
34 3,0 71 14,0
52 5,5 76 15,0
62 10,0 54 7,0
30 2,0 67 13,0
40 4,0 83 17,0
64 11,0 66 12,0
84 18,5 90 20,0
56 8,0 77 16,0
59 9,0 84 18,5
На следующем этапе вычисляется статистика Т\, равная сумме рангов, вычисленных по меньшей выборке. Если объемы выборок равны между собой, ранги можно вычислять по любой из выборок, поскольку на окончательный результат это повлиять не может. Предположим, что для вычисления рангов используется выборка магазинов с обычными полками.
7\ = 1 + 3 + 5,5 + 10 + 2 + 4 + 11 + 18,5 + 8 + 9 = 72.
Для проверки ранжирования вычисляется статистика
Т2 = 5,5 + 14 + 15 + 7 + 13 + 17 + 12 + 20 + 16 + 18,5 = 138.
Используя формулу (11.6), вычислим сумму первых я = 20 рангов. Она должна быть равной Тх + Т2.
т, + т\ =
2
72 + 138= 20 х2' =210.
2
Перейдем к проверке гипотезы, заключающейся в том, что между медианами продаж существенной разницы нет. Для этого по табл. Д.8 определим нижнее и верхнее критические значения статистики критерия Тх. Из табл. 11.13, представляющей собой 4
4 Источник: данные взяты из табл. 9.1.
фрагмент табл. Д.8, следует, что при уровне значимости, равном 0,05, критические значения равны 78 и 132. Следовательно, решающее правило выглядит так:
нулевая гипотеза Но отклоняется, если Т} < 78 или Т2 > 132, в противном случае гипотеза Но не отклоняется.
Таблица 11.13. Нижнее и верхнее критические значения для критерия Уилкоксона
при /7, = 10, пг - 10 и а = 0,05
п2 Односторонний критерий Двусторонний критерий 4 5 6 7 8 9 10
0,05 0,10 16;40 24;51 33;63 43;76 54;90 66;105
9 0,025 0,05 14;42 22;53 31;65 40;79 51;93 62;109
0,01 0,02 13,-43 20;55 28;68 37;82 47;97 59;112
0,005 0,01 11;45 18;57 26;70 35;84 45;99 56;115
0,05 0,10 17; 43 26;54 35;67 45;81 56;96 69;111 82;128
10 0,025 0,05 15;45 23;57 32;70 42;84 53;99 65;115 78;132
0,01 0,02 13;47 21;59 29; 73 39;87 49;103 61;119 74;136
0,005 0,01 12;48 19,-61 27;75 37;89 47;105 58;122 71;139
Поскольку = 72 < 78, гипотеза Но отклоняется. Таким образом, между медианами объемов продаж в магазинах, принадлежащих двум выборкам, наблюдается значительная разница. Поскольку сумма рангов, вычисленная по выборке, состоящей из магазинов, торгующих с помощью специализированных стеллажей, выше, чем у магазинов, использующих обычные полки, следует признать, что первая медиана больше второй. Результаты вычислений, выполненных с помощью программы Microsoft Excel (рис. 11.12), свидетельствуют, что р-значение равно 0,013, т.е. меньше, чем уровень значимости а=0,05. Это означает, что если бы медианы продаж были равны между собой, вероятность обнаружить существенную разницу между медианами была 0,013.
В табл. Д.8 представлены нижнее и верхнее критические значения статистики рангового критерия Уилкоксона Т\. Однако в ней предусмотрены лишь малые выборки, для которых n,<10 ипг<10. Если объем одной из выборок превышает 10, следует применять приближенную формулу (11.7). Однако следует иметь в виду, что эту формулу можно применять и для малых выборок. Продемонстрируем эту формулу на конкретном примере, посвященном продажам BLK-колы. Применим формулу (11.7):
Z = L±Zl,
Or
где
,^+l) = 10x2i
т' 2 2
ки,(А7 + 1) /10x10x21
71 V 12 V 12
2 = 7^ =
13,23
Поскольку Z = -2,49 меньше критического значения Z, равного -1,96, нулевая гипотеза отклоняется.
1 Влияние вида полок на объемы продаж :
2 _____..................................
3 ' Data___________________________
4 .Level of Significance | 's’________________________:_________
6 Population 1 Sample
'Sample Size______________________
8 Sum of Ranks____________________
9 ' Population 2 Sample
10 .Sample Size____________________
11 । Sum of Ranks__________________
12 ,
13 Intermediate Calculations
14 |Total Sample Size n
15 71 Test Statistic
16
17
18 Z Test Statistic
19\
3L______________________
21 j Lower Critical Value
22 Upper Critical Value
23 p-value____________________________
24J Reject the null hypothesis
71 Mean__________
Standard Error of 71
0Л5
ю
72
10
138
_________20
_________72
_________105
13.22875656
-2.494565522
Two-Tailed Test_____________
-1.959962787 1.959962787 0.012611171
Рис. 11.12. Статистика рангового критерия Уилкоксона, вычисленная с помощью программы Microsoft Excel
Процедуры Excel: применение критерия Уилкоксона для проверки гипотезы о разности медиан двух генеральных совокупностей
I Чтобы проверить гипотезу о разности медиан двух генеральных совокупностей с помощью рангового критерия Уилкоксона, следует упорядочить исходные данные, вычислить их ранги и создать рабочий лист, использующий соответствующие функции. Надстройка PHStat2 выполняет эту процедуру автоматически.
Например, чтобы проверить с помощью этого критерия гипотезу о равенстве медиан продаж колы на основе данных, указанных в табл. 11.12, необходимо открыть рабочую книгу chapter 11 на листе Продажи и выполнить одну из следующих процедур.
Применение Excel в сочетании с надстройкой PHStat2
Чтобы проверить гипотезу о разности медиан двух генеральных совокупностей с помощью рангового критерия Уилкоксона, следует применить процедуру PHStat^Two-sample tests^Wilcoxon Rank Sum Test... (PHStat^>Двухвыборочные критерии^ Ранговый критерий Уилкоксона...).
1. Выбрать команду PHStat1 2^Two-sample tests Wilcoxon Rank Sum Test....
2. В диалоговом окне Wilcoxon Rank Sum Test (см. иллюстрацию) сделать следующее.
2.1. Ввести в окне редактирования Level Significance (Уровень значимости) число 0.05.
2.2. Ввести в окне редактирования Popula-
te»/? 1 Sample Cell Range (Входной интервал для выборки из первой генеральной совокупности) диапазон Al: All.
2.3. Ввести в окне редактирования Popula-
tion 2 Sample Cell Range (Входной интервал для выборки из второй генеральной совокупности) диапазон В1 :В11.
Wilcoxon Rank Sum Test
.- Data -.....-...........................
; Level of Significance: [o7o5 ~
Population 1 Sample Cell Range: [71:Al 1
Population 2 Sample Cell Range: [bITbi 1
i P First cells in both ranges contain label
: Test Options.................................
f & Two-Tail Test
Upper-Tail Test
! Г* Lower-Tail Test
Output Options
Title: [влияниевида стеллажей на объемы продаж
Help | |i....OK j| Cancel |
2.4. Установить флажок First cells in both ranges contain label (Первые ячейки в обоих диапазонах содержат метки).
2.5. Установить переключатель Test Options (Параметры критерия) в положение Two-Tailed Test (Двусторонний критерий).
2.6. В окне редактирования Title ввести название нового листа.
2.7. Щелкнуть на кнопке ОК.
Для выполнения этой процедуры необходимо, чтобы данные для каждой группы располагались в разных столбцах. Такие данные называются разгруппированными. Если исходные данные сгруппированы, их следует переформатировать, руководствуясь инструкциями из раздела ЕН.9.2.
Применение Excel
Чтобы самостоятельно создать рабочий лист, проверяющий гипотезу о разности медиан двух генеральных совокупностей с помощью рангового критерия Уилкоксона, следуйте инструкциям, изложенным в разделе ЕН.11.5.
Mg Chapter ll.xls
Данные, на основе которых выполняется проверка гипотезы о разности между медианами двух генеральных совокупностей с помощью критерия Уилкоксона, содержатся в рабочей книге Chapter 11. xls на листе Рис11.12.
Изучение основ
11.24 . Используя табл. Д.8, вычислите верхнее и нижнее критические значения тестовой статистики критерия Уилкоксона Т, для каждого из следующих двусторонних критериев.
1. а = 0,10, гу = 6, п2= 8.
2. а = 0,05, п,= 6, п2 = 8.
3. а = 0,01, п}= 6, п2= 8.
4. Как изменяется ширина области принятия гипотезы при уменьшении уровня значимости?
11.25 . Используя табл. Д.8, вычислите верхнее критическое значение тестовой статистики критерия Уилкоксона Тх для каждого из следующих односторонних критериев. 1. а = 0,05, 6, п2 = 8.
2. а = 0,025, пу= 6, п2= 8.
3. а = 0,01, пу= 6, п2= 8.
4. а = 0,005, 6, п2= 8.
5. Как изменяется ширина области принятия гипотезы при уменьшении уровня значимости?
11.26. Используя табл. Д.8, вычислите нижнее критическое значение тестовой статистики критерия Уилкоксона Т\ для каждого из следующих односторонних критериев. 1. а = 0,05, тгх= 6, п2 = 8.
2. а = 0,025, пх= 6, п2= 8.
3. а = 0,01, л,= 6, п2= 8.
4. а = 0,005, п} = 6, п2 = 8.
5. Как изменяется ширина области принятия гипотезы при уменьшении уровня значимости?
11.27. Представлена следующая информация о двух выборках, извлеченных из независимых генеральных совокупностей.
Выборка 1: п,= 7 Ранги: 4 1 8 2 5 10 11
Выборка 2: п2 = 9 Ранги: 7 16 12 9 3 14 13 6 15
Чему равна статистика критерия Уилкоксона Тх при проверке нулевой гипотезы Нп о равенстве медиан двух генеральных совокупностей: = М2?
11.28. Чему равны верхнее и нижнее критические значения тестовой статистики критерия Уилкоксона Тх в задаче 11.27, приведенные в табл. Д.8 при уровне значимости, равном 0,05, если альтернативная гипотеза Н1 заключается в том, что Мх * М2?
11.29. Какой статистический вывод следует сделать в задачах 11.27 и 11.28?
11.30. Представлена следующая информация о двух выборках, извлеченных из двух одинаково распределенных генеральных совокупностей, имеющих значительную правую асимметрию.
Выборка 1: п, = 5 Ранги: 1,1 2,3 2,9 3,6 14,7
Выборка 2: п2= 6 Ранги: 2,8 4,4 4,4 5,2 6,0 18,5
Чему равна статистика критерия Уилкоксона Тх при проверке нулевой гипотезы Нп о равенстве медиан двух генеральных совокупностей: Мх = М2?
1. Замените наблюдаемые данные соответствующими рангами (1 — наименьшее значение, п= пх+ п2=11 — наибольшее).
2. Чему равна статистика критерия Tt?
3. Вычислите статистику Т2, равную сумме рангов, вычисленных по большей выборке.
4. Для проверки точности ранжирования, используя формулу (11.6), покажите, что Тх + Т2 = п(п+1)/2.
11.31. Вычислите нижнее критическое значение статистики одностороннего критерия Уилкоксона Тх в задаче 11.30, если нулевая гипотеза Нп заключается в том, что Мх > М2, а альтернативная гипотеза Нх — в том, что Мх < М2.
11.32. Какой статистический вывод следует сделать в задачах 11.30 и 11.31?
Применение понятий
Задачи 11.33 и 11.34 можно решать как вручную, так и с помощью программы Microsoft Excel. Задачи 11.35-11.38 рекомендуется решать с помощью программы Microsoft Excel.
11.33. Вице-президент по маркетингу недавно нанял на работу 20 лучших выпускников колледжа. Все они должны пройти курс менеджмента. Выпускники случайным образом разделены на две группы по 10 человек. В первой группе применяется обычный метод обучения (Т), а во второй — экспериментальный (Е). Через шесть месяцев вице-президент оценил эффективность обучения каждого работника, присвоив им соответствующее место, начиная с первого (худшего) и заканчивая двадцатым (лучшим). ^TESTRANK. XLS.
Т 1 2 3 5 9 10 12 13 14 15
Е 4 6 7 8 11 16 17 18 19 20
Существуют ли основания утверждать, что эффективность обучения по обеим программам одинакова, если уровень значимости равен 0,05?
11.34. Одна из телевизионных компаний Нью-Йорка решила сравнить работу двух пригородных железных дорог — Long Island Rail Road (LIRR) и New Jersey Transit
(NJT). Для этого телекомпания сформировала две выборки, состоящие из пригородных электропоездов: 10 — для LIRR и 12 — для NJT. В файле ^TRAIN2 .XLS приведены отклонения от графика в минутах: опережение (отрицательные числа) и отставание (положительные числа).
LIRR 5 -1 39 9 12 21 15 52 18 23
NJT 8 4 10 4 12 5 4 9 15 33 14 7
1. Существуют ли основания утверждать, что медианы отклонения от графика в обеих компаниях одинаковы, если уровень значимости равен 0,01?
2. Какие предположения должны выполняться при решении задачи 1?
3. Что можно сказать об отставании от графика в обеих компаниях?
11.35. Директор центра обучения сотрудников крупной компании, производящей электронную бытовую аппаратуру, желает сравнить эффективность двух методов подготовки работников конвейера. Для этого он разбил группу, состоящую из 42 недавно нанятых сотрудников, на две случайные подгруппы по 21 человеку. В процессе подготовки сотрудников из первой группы использовались индивидуальные, а во второй — коллективные программы обучения. Эффективность обучения измерялась количеством секунд, затрачиваемых сотрудником на сборку детали. Результаты приведены в файле ^TRAINING. XLS.
1. Существуют ли основания утверждать, что медианы эффективности обучения сотрудников по индивидуальным и коллективным программам одинаковы, если уровень значимости равен 0,05?
2. Какие предположения должны выполняться при решении задачи 1?
3. Сравните решения задач 1 и 9.13. Объясните разницу между ними.
11.36. Неразрушающий контроль — это метод, позволяющий описать свойства компонентов или материалов без изменения их обычного физического состояния. При этом можно не только оценить свойства материалов, но и классифицировать трещины по размерам, форме, типу и местоположению. Неразрушающий контроль наиболее эффективен при обнаружении поверхностных и приповерхностных трещин, а также при описании электрической проводимости материалов. В приведенной ниже таблице содержатся результаты проверки партии бракованных деталей, которые при ручной проверке были классифицированы как целые и треснутые соответственно. Можно ли утверждать, что трещины в деталях, классифицированных как целые, в среднем имеют меньший размер, чем в деталях, признанных треснутыми? &CRACK. XLS.
Размеры трещин в треснутых и целых деталях
Треснутые детали
0,003 0,004 0,012 0,014 0,021 0,023 0,024 0,030 0,034
0,041 0,041 0,042 0,043 0,045 0,057 0,063 0,074 0,076
Целые детали
0,022 0,026 0,026 0,030 0,031 0,034 0,042 0,043 0,044
0,046 0,046 0,052 0,055 0,058 0,060 0,060 0,070 0,071
0,073 0,073 0,078 0,079 0,079 0,083 0,090 0,095 0,095
0,096 0,100 0,102 0,103 0,105 0,114 0,119 0,120 0,130
0,160 0,306 0,328 0,440
Источник: ОНп, В. D., and Meeker, W. Q., “Applications of Statistical Methods to Nondestructive Evaluation”, Technometrics, 38 (1996): 101.
1. Существуют ли основания утверждать, что медианы размера трещин в целых образцах меньше, чем в треснутых, если уровень значимости равен 0,05?
2. Какие предположения должны выполняться при решении задачи 1?
3. Сравните решения задач 1 и 9.14. Объясните разницу между ними.
11.37. Филиал банка, расположенный в промышленном районе города, стремится повысить качество обслуживания клиентов во время обеда, с 12:00 до 13:00. На протяжении недели сотрудники записывали время ожидания клиентов, стоящих в очереди в течение обеденного перерыва (количество минут, прошедших от момента, когда клиент переступил порог филиала, до момента его обслуживания). Для оценки эффективности обслуживания создана выборка, содержащая данные о времени ожидания 15 клиентов.
^>BANK1.XLS
4,21 5,55 3,02 5,13 4,77 2,34 3,54 3,20 4,50 6,10 0,38 5,12 6,46 6,19 3,79 Предположим теперь, что другой филиал банка, расположенный в жилом районе города, стремится повысить качество обслуживания клиентов в конце недели: с 17:00 до 19:00 в пятницу. На протяжении недели сотрудники записывали время ожидания клиентов, стоящих в очереди в указанные часы (количество минут, прошедших от момента, когда клиент переступил порог филиала, до момента его обслуживания). Для оценки эффективности обслуживания создана выборка, содержащая данные о времени ожидания 15 клиентов.
BANK2.XLS
9,66 5,90 8,02 5,79 8,73 3,82 8,01 8,35 10,49 6,68 5,64 4,08 6,17 9,91 5,47
1. Существуют ли основания утверждать, что оба филиала банка имеют разные медианы ожидания, если уровень значимости равен 0,05?
2. Какие предположения должны выполняться при решении задачи 1?
3. Сравните результаты с решением задачи 9.10.1.
11.38. Клиенты и телефонная компания обеспокоены нарушениями телефонной связи. Причины этих нарушений разделяются на две группы: повреждения на телефонной станции и на линии. Ниже приведены данные о 20 повреждениях телефонной связи и длительности ремонта в двух подразделениях телефонной компании (в минутах). ftpHONE . XLS.
Длительность ремонта в подразделении 1 (мин.)
1,48 1,75 0,78 2,85 0,52 1,60 4,15 3,97 1,48 3,10
1,02 0,53 0,93 1,60 0,80 1,05 6,32 3,93 5,45 0,97
Длительность ремонта в подразделении II (мин.)
7,55 3,75 0,10 1,10 0,60 0,52 3,30 2,10 0,58 4,02
3,75 0,65 1,92 0,60 1,53 4,23 0,08 1,48 1,65 0,72
1. Существуют ли основания утверждать, что медианы длительности ремонта в подразделениях неодинаковы, если уровень значимости равен 0,05?
2. Какие предположения должны выполняться при решении задачи 1?
3. Сравните результаты с решением задачи 9.11.
11.5. РАНГОВЫЙ КРИТЕРИЙ КРУСКАЛА-УОЛЛИСА: НЕПАРАМЕТРИЧЕСКИЙ МЕТОД ДЛЯ ПОЛНОСТЬЮ РАНДОМИЗИРОВАННОГО ЭКСПЕРИМЕНТА
Ранговый критерий Крускала-Уоллиса для оценки разностей между с медианами (с>2) представляет собой обобщение рангового критерия Уилкоксона для двух независимых выборок (см. раздел 10.1). Таким образом, критерий Крускала-Уоллиса является непараметрической альтернативой F-критерию в однофакторном дисперсионном анализе, аналогично тому, как критерий Уилкоксона представляет собой непараметрическую альтернативу ^критерию, использующему суммарную дисперсию при сравнении двух независимых выборок. Если выполняются условия, необходимые для применения F-критерия в однофакторном дисперсионном анализе, критерий Крускала-Уоллиса обладает той же мощностью.
Ранговый критерий Крускала-Уоллиса применяется для проверки гипотезы, что с независимых выборок извлечены из генеральных совокупностей, имеющих одинаковые медианы. Иначе говоря, нулевая и альтернативная гипотезы формулируются следующим образом:
Но: Мг = М2 = ...=Мс1
Нх: не все Mi (j = 1, ..., с) являются одинаковыми.
Для этого необходимо знать ранги, вычисленные по всем выборкам, а с генеральных совокупностей, из которых они извлечены, должны иметь одинаковые изменчивость и вид.
Для того чтобы применить критерий Крускала-Уоллиса, сначала необходимо заменить наблюдения в с выборках их объединенными рангами. При этом первый ранг соответствует наименьшему наблюдению, а ранг п — наибольшему (п = п1 + п2 + ... + nv). Если некоторые значения повторяются, им присваивается среднее значение их рангов.
Критерий Крускала-Уоллиса является альтернативой Е-критерию в однофакторном дисперсионном анализе. Н-статистика, применяемая в критерии Крускала-Уоллиса, аналогична величине SSA— межгрупповой вариации (10.2), по которой вычисляется Е-статистика (10.5). Вместо сравнения средних значений X всех с групп с общим средним
значением X , в критерии Крускала-Уоллиса средние ранги каждой из с групп сравниваются с общим рангом, вычисленным на основе всех п наблюдений. Если существует статистически значимый эффект эксперимента, средние ранги каждой группы будут значительно отличаться друг от друга и от общего ранга. При возведении этих разностей в квадрат Н-статистика увеличивается. С другой стороны, если эффект эксперимента не наблюдается, статистика Н теоретически должна быть равной нулю. Однако на практике вследствие случайных изменений статистика Н будет ненулевой, но достаточно малой.
КРИТЕРИЙ КРУСКАЛА-УОЛЛИСА ДЛЯ РАЗНОСТЕЙ МЕЖДУ ^МЕДИАНАМИ
н =
12 у
п(н +1) /=1 nt
-3(и + 1) ,
(11.8)
где п — общее количество наблюдений в объединенных выборках, п, — количество наблюдений в у-й выборке (j — 1, ..., с), Г — сумма рангов у-й выборки, Г2 — квадрат суммы рангов у-й выборки.
При достаточно большом объеме выборок (больше пяти) Н-статистику можно аппроксимировать ^’Распределением с с-1 степенями свободы. Таком образом, при заданном уровне значимости а решающее правило формулируется так:
гипотеза Но отклоняется, если Н > xl (рис. 11.13); в противном случае гипотеза Но не отклоняется.
Критические значения распределения % содержатся в табл. Д.4.
Рис. 11.13. Критическая область критерия Крускала-Уоллиса
Продемонстрируем критерий Крускала-Уоллиса на примере оценки прочности парашютов в зависимости от поставщика синтетических волокон (сценарий “Применение статистики” в разделе 10.1). Если прочность парашютов не является нормально распределенной случайной величиной, для оценки различий между медианами четырех генеральных совокупностей можно применить непараметрический критерий Крускала-Уоллиса.
Нулевая гипотеза заключается в том, что прочность всех парашютов одинакова:
Но: МХ=М2 = М, = М4.
Альтернативная гипотеза утверждает, что по крайней мере один поставщик отличается от других:
Нх. не все М (/ = 1, 2, 3, 4) являются одинаковыми.
Результаты эксперимента и ранги приведены в табл. 11.14.
Таблица 11.14. Прочность и ранги парашютов, сшитых из синтетической ткани, приобретенной у четырех разных поставщиков ^PARACHUTE. XLS.
Поставщик 1 Поставщик 2 Поставщик 3 Поставщик 4
Прочность Ранг Прочность Ранг Прочность Ранг Прочность Ранг
18,5 4 26,3 20 20,6 8 25,4 19
24,0 13,5 25,3 18 25,2 17 19,9 5,5
17,2 1 24,0 13,5 20,8 9 22,6 11
19,9 5,5 21,2 10 24,7 16 17,5 2
18,0 3 24,5 15 22,9 12 20,4 7
В процессе преобразования 20 показателей прочности в объединенные ранги, как показано в табл. 11.14, выясняется, что третий парашют, произведенный из синтетического волокна первого поставщика, имеет наименьшую прочность, равную 17,2. Он по-
лучает ранг 1. Четвертый парашют, произведенный из синтетического волокна первого поставщика, и второй парашют, сотканный из волокон четвертого поставщика, имеют одинаковую прочность, равную 19,9. Поскольку им соответствуют ранги 5 и 6, обоим парашютам присваивается ранг 5,5, равный среднему значению рангов 5 и 6. И, наконец, ранг 20 присваивается первому парашюту, сотканному из волокон второго поставщика, поскольку величина 26,3 является наибольшей.
После присвоения рангов вычисляется их сумма в каждой группе:
Т\ = 27, Т2 = 76,5, Т3 = 62, 7\ = 44,5.
Для проверки рангов просуммируем эти величины:
Т1 + Т2 + Т3 + Т,= п(п-1)/2 = 210,
27 + 76,5 + 62 + 44,5 = 20x21/2 = 210.
Используя формулу (11.8), вычислим Н-статистику:
12 20x21
X— -3(^ + 1) =
272 (76,5)2 622 (44,5)2
5 + 5 + 5 + 5
-3x21=
= — х2481,1-63 = 7,889.
420
Статистика Н имеет приближенное ^-распределение с с-1 степенями свободы. При уровне значимости, равном 0,05, по табл. Д.4 определяем величину /2 — верхнее критическое значение ^-распределения с с - 1 = 3 степенями свободы. Она равна 7,815 (см. табл. 11.15).
Таблица 11.15. Вычисление величины /2 — верхнего критического значения ^-распределения с 3 степенями свободы для критерия Крускала-Уоллиса5
Площадь, ограниченная правым хвостом распределения
Количество степеней свободы 0,995 0,99 0,975 0,95 0,90 0,75 0,25 0,10 0,05 0,025
1 - - 0,001 0,004 0,016 0,102 1,323 2,706 3,841 5,024
2 0,010 0,020 0,051 0,103 0,211 0,575 2,773 4,605 5,991 7,378
3 0,072 0,115 0,216 0,352 0,584 1,213 4,108 6,251 7,815 9,348
4 0,207 0,297 0,484 0,711 1,064 1,923 5,385 7,779 9,488 11,143
5 0,412 0,554 0,831 1,145 1,610 2,675 6,626 9,236 11,071 12,833
Поскольку вычисленная Н-статистика равна 7,889 и превышает критическое значение, нулевая гипотеза отклоняется. Следовательно, не все фирмы поставляют синтетическое волокно, прочность которого имеет одинаковую медиану. Аналогичный вывод можно сделать, вычислив р-значение. Данные, представленные на рис. 11.14 свидетельствуют о том, чтор-значение равно 0,048, т.е. меньше уровня значимости 0,05.
F . G
0.05
2481 1
____20
4
Group Sample Size Sum of Ranks Mean Ranks
1 5 27 5.4
2 5 76 5 15.3
3 5 62 124
4 5 44 5 89
..............А. _ .....В............. iCL.D :...._Е...
1 । Ан ализ прочности парашютов
33---------------------------------
3 .__________________Data________
4 Level of Significance ~I
6 ,___________Intermediate Calculations
7 Sum of Squared Ranks/Sample Size в .Sum of Sample Sizes_____________
9 {Number of Groups________________
"10_________________________________„
11 I Test Result
12 H Test Statistic 7.8886
13 Critical Value 7.8147
14 p-Value 0.0484
15 j Reject the null hypothesis
Рис. 11.14. Результаты применения критерия Крускала-Уоллиса для оценки разностей между с медианами показателей прочности парашютов, полученные с помощью программы Microsoft Excel
Поскольку нулевая гипотеза отклоняется, приходим к выводу, что фирмы поставляют волокна разной прочности. На следующем этапе необходимо попарно сравнить всех поставщиков и определить, какие из них отличаются друг от друга. Для этого можно применить апостериорную процедуру множественного сравнения, предложенную Дж. Данном (J. J. Dunn) [6].
Для применения критерия Крускала-Уоллиса должны выполняться следующие условия.
ВРЕЗКА 11.1. УСЛОВИЯ ИСПОЛЬЗОВАНИЯ КРИТЕРИЯ КРУСКАЛА-УОЛЛИСА
• Все с выборок случайно и независимо друг от друга извлекаются из соответствующих генеральных совокупностей.
• Анализируемая переменная является непрерывной.
• Наблюдения допускают ранжирование как внутри, так и между группами.
• Все с генеральных совокупностей имеют одинаковую изменчивость.
• Все с генеральных совокупностей имеют одинаковый вид.
Процедура Крускала-Уоллиса имеет меньше ограничений, чем F-критерий. Процедура Крускала-Уоллиса предусматривает ранжирование только по всем выборкам в совокупности. Общее распределение должно быть непрерывным, но его вид значения не имеет. Если эти условия не выполняются, критерий Крускала-Уоллиса по-прежнему можно применять для проверки гипотезы о различиях между с генеральными совокупностями. Альтернативная гипотеза утверждает, что среди с генеральных совокупностей существует хотя бы одна, которая отличается от остальных какой-нибудь характеристикой — либо средним значением, либо видом. С другой стороны, для применения F-критерия переменная должна быть числовой, а с выборок должны извлекаться из нормально распределенных генеральных совокупностей, имеющих одинаковую дисперсию.
В полностью рандомизированных экспериментах, для которых выполняются условия F-критерия, следует применять именно его, а не процедуру Крускала-Уоллиса, поскольку мощность F-критерия в этой ситуации немного выше. С другой стороны, если эти условия не выполняются, более мощным становится критерий Крускала-Уоллиса, и следует предпочесть именно его.
Процедуры Excel: применение рангового критерия Крускала-Уоллиса для оценки разностей между несколькими медианами
Чтобы применить критерий Крускала-Уоллиса для оценки разностей между несколькими медианами, следует упорядочить и ранжировать исходные данные, а затем создать рабочий лист, использующий функции ХИ20БР и ХИ2РАСП. Надстройка PHStat2 выполняет эту процедуру автоматически.
Например, чтобы с помощью этой процедуры сравнить прочность парашютов на основе данных, приведенных в табл. 11.14, необходимо открыть рабочий лист Парашюты в книге chapter 11 и выполнить одну из следующих процедур.
Применение Excel в сочетании с надстройкой PHStat2
Чтобы применить критерий Крускала-Уоллиса для оценки разностей между несколькими медианами, следует выполнить команду PHStat4>Multiple-sample tests^Kruskal-Wallis Rank Test...
(PHStat4>Многовыборочные критерии^Критерий Крускала-Уоллиса...).
1. Выбрать команду PHStat^Multiple-sample tests^ Kruskal-Wallis Rank Test.
2. В диалоговом окне Kruskal-Wallis Rank Test (см. иллюстрацию) сделать следующее.
2.1. Ввести в окне редактирования Level of Significance (Уровень значимости) число 0.05.
2.2. Ввести в окне редактирования Sample Data Cell Range (Диапазон данных, содержащий выборку) диапазон Al: D6.
2.3. Установить флажок First cell contains label (Первая ячейка содержит метку).
Kruskal-Wallis Rank Test
Data
Level of Significance: |o?O5
Sample Data Cell Range: p(l?D6~~~*" - ]
P First cells contain label
Output Options
Title: ^Анализ прочности парашютов
Help I |= OK ,| Cancel j
2.4. Ввести в окне редактирования Title (Заголовок) название нового листа.
2.5. Щелкнуть на кнопке ОК.
Рабочий лист, созданный с помощью этой процедуры, не является динамически обновляемым. Следовательно, если данные изменятся, все описанные выше действия необходимо повторить. Для выполнения этой процедуры нужно, чтобы данные каждой группы располагались в разных столбцах. Такие данные называются разгруппированным. Для того чтобы обработать сгруппированные данные, их необходимо предварительно переформатировать, руководствуясь инструкциями из раздела ЕН.9.2.
Применение Excel
Откройте новый рабочий лист, отсортируйте и ранжируйте исходные данные, создавая столбцы для каждой группы, данных и рангов. Для того чтобы самостоятельно создать рабочий лист, применяющий критерий Крускала-Уоллиса для оценки разностей между медианами прочности парашютов четырех разновидностей, следуйте инструкциям из раздела ЕН.11.б.
Chapter ll.xls
Данные, на основе которых выполняется критерий Крускала-Уоллиса при сравнении четырех медиан прочности парашютов, содержатся в рабочей книге Chapter ll.xls на листе Рис11.14.
УПРАЖНЕНИЯ К^А^ЕЛУ ' -/ ~ ; ' -•> Л
Изучение основ
11.39. Чему равно верхнее критическое значение распределения %2, если для проверки гипотезы о равенстве медиан шести генеральных совокупностей применяется критерий Крускала-Уоллиса?
11.40. Выполните следующие задания, используя результаты решения задачи 11.39.
1. Сформулируйте решающее правило для проверки гипотезы о том, что медианы всех шести генеральных совокупностей одинаковы.
2. Какое решение следует принять, если статистика Н равна 13,77?
Применение понятий
Задачи 11.41-11.44 можно решать как вручную, так и с помощью программы Microsoft Excel. Задачу 11.45 рекомендуется решать с помощью программы Microsoft Excel.
11.41. Психолог решил проверить скорость реакции работников конвейера, прошедших обучение по трем разным программам. Из 25 вновь нанятых работников он сформировал три выборки: в первую он включил 9 рабочих, обучение которых должно проводиться по методу А, во вторую — 8 рабочих, обучающихся по методу Б, и в третью — 8 рабочих, подготовка которых основана на методеВ. После обучения работникам предложили пройти испытание, в ходе которого измерялась скорость их реакции. Результаты эксперимента приведены в файле ftINDPSYCH. XLS (работники распределены по скорости реакции: 1 — самая быстрая, 25 — самая медленная).
Существует ли статистически значимая разница между медианами скорости реакции работников, прошедших подготовку по разным программам, если уровень значимости равен 0,01?
11.42. Руководитель производства в компании, выпускающей бытовую электронную аппаратуру, решил проверить качество батареек нового типа. Для этого партия, состоящая из 20 батареек, была случайным образом разделена на 4 группы (по 5 батареек в каждой). Затем каждая группа батареек испытывала давление одного из уровней — низкое, нормальное, высокое и очень высокое. Измерения в каждой группе производились одновременно. Результаты испытаний (продолжительность работы батареек в часах) приведены в таблице, ftBATFAIL. XLS.
Давление
Низкое Нормальное Высокое Очень высокое
8,0 7,6 6,0 5,1
8,1 8,2 6,3 5,6
9,2 9,8 7,1 5,9
9,4 10,9 7,7 6,7
11,7 12,3 8,9 7,8
По своему опыту руководитель производства знает, что эти данные извлечены из генеральной совокупности, распределение которой не является нормальным. По этой причине он применил непараметрическую процедуру анализа.
1. Существует ли статистически значимая разница между медианами продолжительности работы батареек, подвергавшихся давлению разных уровней, если уровень значимости равен 0,05?
2. Какие гарантии вы дали бы, продавая эти батарейки?
11.43. Менеджер по розничным продажам в сети супермаркетов желает знать, влияет ли размещение игрушек для домашних животных на объем их продаж. Рассмотрены три вида стеллажей: передние, средние и задние. Для анализа отобраны 18 случайных магазинов, причем для каждого вида стеллажей отобраны по 6 магазинов. Размер витрины и цены на товары во всех магазинах одинаковы. Эксперимент проходил в течение месяца. Объемы продаж (в тыс. долл.) приведены в следующей таблице. ^LOCATE. XLS.
Расположение стеллажей
Впереди В середине Сзади
8,6 3,2 4,6
7,2 2,4 6,0
5,4 2,0 4,0
6,2 1,4 2,8
5,0 1,8 2,2
4,0 1,6 2,8
1. Можно ли утверждать, что между медианами объема продаж в магазинах,
использующих разное положение стеллажей, существует статистически зна-
чимая разница l, если уровень значимости равен 0,05?
2. Сравните решение этой задачи с выводом, сделанным в задаче 10.13.
11.44. в файле Malloy . XLS записаны данные о долговечности четырех сплавов.
Сплав
1 2 3 4
999 1022 1026 974
1010 973 1008 1015
995 1023 1005 1009
998 1 023 1 007 1 001
1001 996 981 995
Источник: Р. Wludyka, Р. Nelson, and Р. Silva, “Power Curves for the Analysis of Means for Variances’’, Journal of Quality Technology, 33, 2001,60-65.
1. Существует ли статистически значимая разница между медианами долговечности разных сплавов, если уровень значимости равен 0,05?
2. Сравните результаты с решением задачи 10.11.
11.45. Студенты, изучающие статистику, осуществили полностью рандомизированный эксперимент, чтобы проверить прочность мусорных мешков четырех видов. Для этого в мешки по одному добавлялись грузы, вес которых равен одному фунту, пока мешок не разрывался, а результаты записывались в таблицу. В эксперименте были испытаны 40 мешков. Данные в прочности мешков хранятся в файле ^TRASHBAGS . XLS.
1. Существует ли статистически значимая разница между медианами прочности мешков из разных групп, если уровень значимости равен 0,05?
2. Сравните результаты с решением задачи 10.10.
11.6. КРИТЕРИЙ "ХИ-КВАДРАТ" ДЛЯ ДИСПЕРСИЙ
При анализе числовых данных иногда бывает важно оценить не только их среднее значение, но и изменчивость. Для примера вернемся к задаче о расфасовке кукурузных хлопьев, описанной в разделе 8.2. Предполагалось, что стандартное отклонение ст равно 15 г. Предположим теперь, что нам необходимо определить, отличается ли стандартное отклонение от заданного уровня, равного 15 г.
Пытаясь оценить изменчивость генеральной совокупности, мы должны сначала определить, какой статистический критерий можно использовать, чтобы представить распределение изменчивости выборочных данных. Если случайная переменная имеет нормальное распределение, для ответа на вопрос, равны ли дисперсия или стандартное отклонение заданной величине, применяется тестовая %2-статистика (x2-test statistics).
ИСПОЛЬЗОВАНИЕ ^-КРИТЕРИЯ ДЛЯ ПРОВЕРКИ ГИПОТЕЗЫ О ДИСПЕРСИИ ИЛИ СТАНДАРТНОМ ОТКЛОНЕНИИ
X =“---(11.9)
ст*
где п — объем выборки, S2 — выборочная дисперсия, ст2 — гипотетическая дисперсия генеральной совокупности. Тестовая х2_статистика имеет распределение х2 с п-1 степенями свободы.
Распределение х2(chi-square distribution) имеет положительную асимметрию, форма которой зависит исключительно от количества степеней свободы. Математическое ожидание распределения х2 равно количеству степеней свободы, а дисперсия — удвоенному количеству степеней свободы. В табл. Д.4 приведены площади фигур, ограниченных правым хвостом распределения х2 с разным количеством степеней свободы. Фрагмент этой таблицы приведен в табл. 11.16.
Таблица 11.16. Определение критических значений распределений х2 с 24 степенями свободы6
Площади фигур, ограниченных i правым хвостом
Количество степеней свободы 0,995 0,99 | 0,975 | 0,95 0,90 0,10 0,05 0,025
1 0,001 0,004 0,016 2,706 3,841 5,024
2 0,010 0,020 0,051 0,103 0,211 4,605 5,991 7,378
3 0,072 0,115 0,216 0,352 0,584 6,251 7,815 9,348
23 9,260 10,196 11,689 13,091 14,848 32,007 35,172 38,076
24 9,886 10,856 12,401 13,848 15,659 33,196 36,415 39,364
25 10,520 11,524 13,120 14,611 16,473 34,382 37,652 40,646
Число, указанное в первой ячейке каждого столбца, представляет собой площадь фигуры, ограниченной правым хвостом кривой распределения х2. Например, если распределение х2 имеет 24 степени свободы, то площади, равной 0,025, соответствует кри
тическое значение текстовой х2_статистики, равное 39,364. В то же время площади, равной 0,975 (т.е. площадь фигуры, ограниченной левым хвостом кривой, равна 0,025), соответствует критическое значение текстовой х2-статистики, равное 12,401. Эта ситуация изображена на рис. 11.16. Следовательно, для 24 степеней свободы вероятность того, что тестовая %2-статистика будет равна критическому значению 12,401 или превысит его, равна 0,975. В то же время, вероятность того, что тестовая х2_статистика будет равна критическому значению 12,401 или превысит его, равна 0,025. Таким образом, вероятность того, что тестовая х2_статистика лежит между критическими значениями 12,401 и 39,364, равна 0,95. Следовательно, задав уровень значимости и определив количество степеней свободы, мы можем найти критическое значение тестовой %2-статистики для любого конкретного распределения %2.
отклонения принятия отклонения
гипотезы
гипотезы гипотезы
Рис. 11.15. Определение нижнего и верхнего критических значений распределения / с 24 степенями свободы, соответствующего уровню значимости, равному 0,05, при проверке гипотезы о дисперсии или стандартном отклонении с помощью двустороннего критерия
Вернемся к задаче о расфасовке кукурузных хлопьев. Нас интересует, отличается ли стандартное отклонение от заданной величины, равной 15 г. Следовательно, можно применить двусторонний критерий, а нулевую и альтернативную гипотезы сформулировать следующим образом:
Но: а = 15 г (или ст2 = 225 кв. г), Нг: а ф 15 г (или а2 Ф 225 кв. г).
Если для анализа создана выборка, состоящая из 25 коробок, то нулевая гипотеза отклоняется, если тестовая %2-статистика попадает в область отклонения гипотезы, ограниченную левым или правым хвостами кривой распределения %2 с 25 — 1 = 24 степенями свободы. Эта ситуация изображена на рис. 11.15. Из формулы (8.5) следует, что тестовая %2-статистика попадает в область отклонения гипотезы, ограниченную левым хвостом кривой распределения %2, если выборочное стандартное отклонение S существенно меньше гипотетической величины ст= 15 г. Аналогично тестовая х2_статистика попадает в область отклонения гипотезы, ограниченную правым хвостом кривой распределения %2, если выборочное стандартное отклонение S значительно больше гипотетической величины ст= 15 г. Из табл. 11.16 (представляющей собой фрагмент табл. Д.4) и рис. 11.15 следует, что при уровне значимости, равном 0,05, нижнее и верхнее xt критические значения
равны 12,401 и 39,364 соответственно. Следовательно, решающее правило формулируется следующим образом.
Гипотеза Но отклоняется, если %2 > =39,364 или %2 < %2 = 12,401,
в противном случае гипотеза не отклоняется.
Предположим, что выборочное стандартное отклонение S, вычисленное для выборки, состоящей из 25 коробок, равно 17,7 г. Для того чтобы проверить нулевую гипотезу при уровне значимости, равном 0,05, применим формулу (8.5).
2_(п —1)52 (25-1)х(17,7)2
% - - 152
Обратите внимание на то, что 33,42 — вычисленное значение тестовой %2-статистики — лежит в интервале, ограниченном нижним и верхним критическими значениями, т.е. 12,401 и 39,364. Поскольку, как показано на рис. 11.16, %2 = 12,401 < %2 = 33,42 < %2 = 39,364 (т.е. р = 0,0956 > 0,05), гипотезу Но отклонять нельзя. Следовательно, нет оснований утверждать, что стандартное отклонение генеральной совокупности отличается от 15 г.
Проверка гипотезы о дисперсии веса
2
3 ”
4 I
’ 5 ”l 6
' 7 '
’J?_____________________________________
9 Intermediate Calculations
10 ^Degrees of Freedom
. 11 ] Half Area
12 jChi-Square Statistic_______________
’if_____________________________________
J4___________________Two-Tail Test
15 Lower Critical Value________________
_ 16 Upper Critical Value_______________
17 p-Value_____________________________
___________________Data___________
Null Hypothesis_____________pa2=
Level of Significance____________
Sample Size______________________
Sample Standard Deviation
225
0.05
25
17.7
24 0.025
33 4176
12 4011
39.3641
________________________________0.0956
Do not reject the null hypothesis
Рис. 11.16. Результаты проверки гипотезы о дисперсии процесса расфасовки кукурузных клопьев
Критерий %2 для проверки гипотезы от дисперсии или стандартном отклонении считается классической параметрической процедурой (classical parametric procedure). Для того чтобы его выводы были корректными, необходимо чтобы выполнялись сделанные предположения.
ПРОВЕРКА ПРЕДПОЛОЖЕНИЙ ^-КРИТЕРИЯ ДЛЯ ПРОВЕРКИ ГИПОТЕЗЫ
О ДИСПЕРСИИ ИЛИ СТАНДАРТНОМ ОТКЛОНЕНИИ
При проверке гипотезы о дисперсии генеральной совокупности или стандартном отклонении предполагается, что исходные данные имеют нормальное распределение; * К сожалению, %2-критерий довольно чувствителен к нарушению этих предположений ;
(т.е. этот критерий не является устойчивым). Следовательно, если генеральная совокупность не имеет нормального распределения, особенно, когда объем выборки неве- : лик, точность критерия может значительно снизиться.
Процедура Excel: применение /-критерия для проверки гипотезы о дисперсии
Чтобы применить /-критерий для проверки гипотезы о дисперсии, следует создать рабочий лист, использующий функции ХИ20БР и ХИ2РАСП. Надстройка PHStat2 может создать такой рабочий лист автоматически.
Например, чтобы применить /-критерий для проверки гипотезы о дисперсии процесса расфасовки кукурузных клопьев, как показано на рис. 11.16, необходимо создать новый рабочий лист и применить одну из перечисленных ниже стратегий.
Применение программы Excel вместе с надстройкой PHStatZ
Чтобы применить /-критерий для проверки гипотезы о дисперсии, следует использовать процедуру PHStat^One-sample tests^Chi-Square Test for the Variance (PHStat^Одновыборочные критерииЧ> /-критерий для дисперсии). Для этого необходимо выполнить такие действия.
1. Выбрать команду PHStat^One-sample tests^Chi-Square Test for the Variance....
2. В диалоговом окне Chi-Square Test for the Variance (cm. иллюстрацию) сделать следующее.
2.1. Ввести в окне редактирования Null Hypothesis (Нулевая гипотеза) число 225.
2.2. Ввести в окне редактирования Level of Significance (Уровень значимости) число 0.05.
2.3. Ввести в окне редактирования Sample size (Объем выборки) число 25.
2.4. Ввести в окне редактирования Sample Standard Deviation (Выборочное стандартное отклонение) число 17.7.
2.5. Установить переключатель Test Options (Параметры критерия) в положение Two-Tail Test (Двусторонний критерий).
Chi-Square Test for the Variance fxj
- Data----- -
i Null Hypothesis: [z25
Level of Significance: |0.05
j Sample Size: |25
i Sample Standard Deviation:
- Test Options ...............
i (• Two-Tailed Test
Г Upper-Tail Test
; C Lower-Tail Test
- Output Options
Title: [провёркаТипотёзьГ^
Help ] 11...OlJ...JI Cancel
2.6. Ввести в окне редактирования Title (Заголовок) название нового листа.
2.7. Щелкнуть на кнопке ОК.
Для задач, в которых требуется применение одностороннего критерия, переключатель Test Options следует установить в положение Upper-Tail Test (Ограниченный сверху критерий) или Lower-Tail Test (Ограниченный снизу критерий).
Применение программы Excel
Чтобы применить /-критерий для проверки гипотезы о дисперсии, следует создать рабочий лист, использующий функции ХИ2ОБР и ХИ2РАСП. Эти функции имеют следующий формат: ХИ2ОБР (1-уровень значимости, количество степеней свободы) и ХИ2РАСП(статистика хи-квадрат, количество степеней свободы).
Шаблон рабочего листа Критерий хи-квадрат, применяющего /-критерий для проверки гипотезы о дисперсии процесса расфасовки кукурузных хлопьев, приведен в табл. 11.17. Для вычисления нижнего и верхнего критических значений /-распределения используется функция ХИ2ОБР, а для вычисления р-значения — функция ХИ2РАСП (ячейка В12). Шаблон рабочего листа предусматривает выдачу рекомендации, следует отклонить нулевую гипотезу или нет, применив функцию ЕСЛИ для сравнения p-значения, содержащегося в ячейке В17, с уровнем значимости, записанным в ячейке В5.
При реализации этого шаблона формулы, занимающие в ячейках В17 и А18 три строки, следует вводить в одну строку.
Если для решения задач и требуется применить односторонний критерий, строки 14-17 следует заменить так, как показано в табл. 11.18 или табл. 11.19. (Строка 18 в обоих случаях остается пустой.) Эти шаблоны также используют функции, вызываемые в строках 14-18 из табл. ЕН.8.1, позволяющие отклонить или не отклонить нулевую гипотезу. Как и прежде, при реализации этого шаблона формулу, занимающую в ячейке А17 три строки, следует вводить в одну строку.
Таблица 11.17. Шаблон рабочего листа Критерий хи-квадрат
1 Гипотеза о дисперсии расфасовки
2
3 Данные
4 Нулевая гипотеза оЛ2= 225
5 Уровень значимости 0,05
6 Объем выборки 25
7 Выборочное стандартное отклонение 17,7
8
9 Промежуточные вычисления
10 Количество степеней свободы = В6-1
11 Половина площади = В5/2
12 Статистика =В10 * В7Л2/В4
13
14 Двусторонний критерий
15 Нижнее критическое значение =ХИ20БР(1-В11;ВЮ)
16 Верхнее критическое значение =ХИ20БР(В11;В10)
17 р-значение =ЕСЛ И( В12-В15<0; 1-ХИ2РАСП(В12;В10); ХИ2РАСП(В12;В10))
18 =ЕСПИ(В17 < В5/2; "Нулевая гипотеза отклоняется"; "Нулевая гипотеза не отклоняется")
Таблица 11.18. Шаблон рабочего листа для реализации ограниченного снизу Z-критерия
А В
14 Ограниченный снизу критерий
iiillij! Нижнее критическое значение =ХИ20БР(1-В5;В10)
16 р-значение =1-ХИ2РАСП(В12;В10)
17 = ЕСЛИ(В16 < В5; "Нулевая гипотеза отклоняется"; "Нулевая гипотеза не отклоняется")
Таблица 11.19. Шаблон рабочего листа для реализации ограниченного сверху Z-критерия
14 Ограниченный сверху критерий
1111 Верхнее критическое значение =ХИ2ОБР(В5;ВЮ)
р-значение =ХИ2РАСП(В12;В10)
=ЕСЛИ(В16 < В5; "Нулевая гипотеза отклоняется"; "Нулевая гипотеза не отклоняется")
УПРАЖНЕНИЯ К РАЗД1
Изучение основ
11.46. Определите критическое значение /^распределения при следующих данных.
1. Площадь, ограниченная правым хвостом, равна 0,01, п = 16.
2. Площадь, ограниченная правым хвостом, равна 0,025, п = 11.
3. Площадь, ограниченная правым хвостом, равна 0,05, п = 8.
4. Площадь, ограниченная правым хвостом, равна 0,95, п = 28.
5. Площадь, ограниченная правым хвостом, равна 0,975, п = 21.
6. Площадь, ограниченная правым хвостом, равна 0,99, п = 5.
11.47. Определите критическое значение /^распределения при следующих данных.
1. Площадь, ограниченная левым хвостом, равна 0,01, п = 16.
2. Площадь, ограниченная левым хвостом, равна 0,025, л = 11.
3. Площадь, ограниченная левым хвостом, равна 0,05, п = 8.
4. Площадь, ограниченная левым хвостом, равна 0,95, п = 28.
5. Площадь, ограниченная левым хвостом, равна 0,975, тг = 21.
6. Площадь, ограниченная левым хвостом, равна 0,99, тг = 5.
11.48. Определите верхнее и нижнее критические значения /^распределения при следующих данных.
1. а = 0,01, тг = 26.
2. сс = 0,05, тг = 17.
3. сс = 0,10, гг = 14.
11.49. Предположим, что из нормально распределенной генеральной совокупности извлечена выборка, объем которой равен тг = 16, а выборочное стандартное отклонение равно 8=10. Чему равна /2-статистика, если вы проверяете нулевую гипотезу Н„ о том, что ст = 12?
11.50. Сколько степеней свободы имеет //-статистика в задаче 11.66?
11.51. Найдите в табл. Д.4 критические значения из задач 11.66 и 11.67, если уровень значимости сс равен 0,05, а альтернативная гипотеза Нх состоит в следующем:
1. сг*12.
2. <т< 12.
11.52. Какое статистическое решение следует принять в задачах 11.66, 11.67 и 11.68, если альтернативная гипотеза состоит в следующем:
1. ст* 12.
2. <т< 12.
11.53. Предположим, что из генеральной совокупности, распределение которой имеет сильно выраженную отрицательную асимметрию, а стандартное отклонение S равно 24, извлечена выборка, имеющая объем п = 16. Можно ли применить одновыборочный /"-критерий для проверки нулевой гипотезы Нп: а = 20? Обоснуйте свой ответ.
Применение понятий
Для решения задач 11.54—11.59 рекомендуется использовать программу Microsoft Excel.
11.54. Кондитер должен внимательно следить за температурой, при которой варятся леденцы. Слишком сильное колебание температуры снижает вкусовые качества продукции. Исследование показало, что стандартное отклонение температуры равно 1,2 °F. Предположим, что из партии леденцов извлечены 30 пачек, а стандартное отклонение температуры равно 2,1 °F .
1. Можно ли утверждать, что стандартное отклонение генеральной совокупности температурных показателей процесса значительно превышает 1,2 °F, если уровень значимости равен 0,05?
2. Какие условия должны выполняться для того, чтобы можно было применить этот критерий?
3. Вычислитер-значение в задаче 1 и объясните его смысл.
11.55. Маркетолог компании, торгующей автомобилями, желает провести общенациональный опрос, касающийся ремонта автомобилей. Один из вопросов анкеты сформулирован следующим образом: “Сколько денег вы потратили на ремонт автомобиля в прошлом году?”. Для того чтобы определить необходимый объем выборки, необходимо получить оценку стандартного отклонения. Используя результаты предыдущих исследований и экспертные оценки, маркетолог пришел к выводу, что стандартное отклонение сумм, затрачиваемых на ремонт автомобиля в течение года, равно 200 долл. Предположим, что пилотный опрос 25 случайно выбранных автовладельцев показал, что выборочное стандартное отклонение равно 237,52 долл.
1. Можно ли утверждать, что стандартное отклонение затрат на ремонт генеральной совокупности клиентов значительно отличается от 200 долл., если уровень значимости равен 0,05?
2. Какие условия должны выполняться для того, чтобы можно было применить этот критерий?
3. Вычислите р-значение в задаче 1 и объясните его смысл.
11.56. Менеджер по маркетингу компании местного отделения крупной телефонной компании решил исследовать характеристики клиентов, обслуживаемых его офисом. В частности, он хочет оценить среднемесячные затраты на телефонные переговоры в местной телефонной сети. Для того чтобы определить необходимый объем выборки, следует оценить стандартное отклонение. Руководствуясь результатами предыдущих исследований и экспертными оценками, менеджер пришел к выводу, что стандартное отклонение равно 12 долл. Предположим, что пилотный опрос 15 местных клиентов продемонстрировал, что выборочное стандартное отклонение равно 9,25 долл.
1. Можно ли утверждать, что стандартное отклонение затрат генеральной совокупности клиентов значительно отличается от 12 долл., если уровень значимости равен 0,10?
2. Какие условия должны выполняться для того, чтобы можно было применить этот критерий?
3. Вычислите p-значение в задаче 1 и объясните его смысл.
11.57. Номинальный диаметр коаксиальных волноводов равен 2,5 дюйма. Результаты предыдущих исследований показывают, что стандартное отклонение равно 0,035 дюйма. Для того чтобы уменьшить изменчивость производственного процесса, технологи предложили новый метод. Анализ 25 коаксиальных волноводов, произведенных на основе нового метода, показал, что выборочное стандартное отклонение равно 0,025 дюйма.
1. Можно ли утверждать, что стандартное отклонение диаметра генеральной совокупности коаксиальных волноводов значительно отличается от 0,035 дюйма, если уровень значимости равен 0,05?
2. Какие условия должны выполняться для того, чтобы можно было применить этот критерий?
3. Вычислите p-значение в задаче 1 и объясните его смысл.
11.58. Автомат, упаковывающий изюм без косточек, настроен так, чтобы стандартное отклонение веса изюминок в упаковке было равным 0,25 унции. Желая проверить настройки автомата, начальник производства извлек выборку, состоящую из 30 последовательно отобранных упаковок изюма. Их вес приведен в следующей таблице.
^RAI SINS.XLS
15,2 15,3 15,1 15,7 15,3 15,0 15,1 14,3 14,6 14,5
15,0 15,2 15,4 15,6 15,7 15,4 15,3 14,9 14,8 14,6
14,3 14,4 15,5 15,4 15,2 15,5 15,6 15,1 15,3 15,1
1. Можно ли утверждать, что стандартное отклонение веса генеральной совокупности упаковок значительно отличается от 0,25 унций, если уровень значимости равен 0,05?
2. Какие условия должны выполняться для того, чтобы можно было применить этот критерий?
3. Вычислите p-значение в задаче 1 и объясните его смысл.
11.59. Производитель батареек утверждает, что стандартное отклонение их емкости равно 2,5 А* ч. Независимый эксперт из общества защиты прав потребителей желает проверить правдивость утверждения производителя. Для этого он извлек случайную выборку, содержащую 20 батареек, произведенных недавно. Их вес приведен в следующей таблице.
^AMPHRS .XLS
137,4 140,0 138,8 139,1 144,4 139,2 141,8 137,3 133,5 138,2
141,1 139,7 136,7 136,3 135,6 138,0 140,9 140,6 136,7 134,1
1. Можно ли утверждать, что стандартное отклонение емкости генеральной совокупности батареей значительно отличается от 2,5 А • ч, если уровень значимости равен 0,05?
2. Какие условия должны выполняться, для того чтобы можно было применить этот критерий?
3. Вычислите p-значение в задаче 1 и объясните его смысл.
11.7. КРИТЕРИЙ СОГЛАСИЯ "ХИ-КВАДРАТ"
В данном разделе /^распределение используется для проверки согласованности набора данных с фиксированным распределением вероятностей. В критерии согласия частоты, принадлежащие определенной категории, сравниваются с частотами, которые являются теоретически ожидаемыми, если бы данные действительно имели указанное распределение.
Проверка с помощью критерия согласия %2 выполняется за несколько этапов. Во-первых, определяется конкретное распределение вероятностей, которое сравнивается с исходными данными. Во-вторых, выдвигается гипотеза о параметрах выбранного распределения вероятностей (например, о ее математическом ожидании) или проводится их оценка. В-третьих, на основе теоретического распределения определяется теоретическая вероятность, соответствующая каждой категории. В заключение, для проверки согласованности данных и распределения применяется тестовая /"-статистика (11.10).
Использование х2-критерия согласия для распределения Пуассона
В разделе 5.5 распределение Пуассона использовалось для моделирования количества клиентов, прибывающих в отделение банка в течение минуты. Предположим, что в течение недели фактическое количество клиентов, приходящих в отделение банка в течение минуты, измерялось 200 раз. Результат приведен в табл. 11.20.
Таблица 11.20. Распределение частоты прибытий в минуту во время ленча
Прибытия Частота
0 14
1 31
2 47
3 41
4 29
5 21
6 10
7 5
8 2
200
Для того чтобы определить, имеет ли количество прибытий в минуту распределение Пуассона, формулируются нулевая и альтернативная гипотеза.
На: количество прибытий в минуту подчиняется распределению Пуассона,
Нх: количество прибытий в минуту не подчиняется распределению Пуассона.
Поскольку распределение Пуассона имеет один параметр — математическое ожидание Я, в нулевую и альтернативную гипотезы можно включать либо величину Я, либо ее выборочную оценку.
В нашем примере для оценки среднего количества прибытий клиентов необходимо воспользоваться формулой (3.17). Используя эту формулу и вычисления, приведенные в табл. 11.18, получаем
1 nF
иТГ
^ = 2,90.
200
Для оценки параметра X можно воспользоваться оценкой X . В табл. Д.7 можно найти частоту X успехов (X = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 и более), соответствующую параметру X = 2,9. Умножив пуассоновскую вероятность на объем выборки л, получим теоретическую частоту. Результаты этих вычислений приведены в табл. 11.21.
Таблица 11.21. Вычисление выборочного среднего количества прибытий по распределению частоты прибытий в минуту
Прибытия Частота m,f,
0 14 0
1 31 31
2 47 94
3 41 123
4 29 116
5 21 105
6 10 60
7 5 35
8 2 16
200 580
Таблица 11.22. Фактические и теоретические частоты прибытий в минуту
Прибытия Фактическая частота fo Вероятность Р(Х) для распределения Пуассона при X = 2,9 Теоретическая частота fe = пР(Х)
0 14 0,0550 11,00
1 31 0,1596 31,92
2 47 0,2314 46,28
3 41 0,2237 44,74
4 29 0,1622 32,44
5 21 0,0940 18,80
6 10 0,0455 9,10
7 5 0,0188 3,76
8 2 0,0068 1,36
9 и более 0 0,0030 0,60
Как следует из табл. 11.22, теоретическая частота девяти и более прибытий не превосходит 1,0. Для того чтобы каждая категория содержала частоту, равную 1,0 или большему числу, категорию “9 и более” следует объединить с категорией “8”.
Для применения х2_критерия согласия воспользуемся формулой (11.10).
ПРИМЕНЕНИЕ ^-КРИТЕРИЯ СОГЛАСИЯ
2 (Л Л)
Лд- л 1 ~ г
(11.10)
где f0 — наблюдаемая частота, Д — теоретическая, или ожидаемая частота, k — количество категорий, оставшихся после объединения, р — количество оцениваемых параметров.
Возвращаясь к примеру о клиентах, прибывающих в банк, отметим, что в задаче остается девять категорий (0, 1, 2, 3, 4, 5, 6, 7, 8 или более). Поскольку математическое ожидание распределения Пуассона определяется на основе выборочных данных, количество степеней свободы равно
-р-1 = 9 - 1 - 1 = 7.
Используя уровень значимости, равный 0,05, в табл. Д.4 можно найти критическое значение /2-статистики, имеющей 7 степеней свободы, равное 14,067. Решающее правило формулируется следующим образом.
Гипотеза Нп отклоняется, если х2> 14,067, в противном случае гипотеза Но не отклоняется.
Из табл. 11.23 и оценки х2 = 2,28954 < 14,067 следует, что гипотезу Но отклонять нельзя. Иначе говоря, у нас нет оснований утверждать, что прибытие клиентов в банк подчиняется распределению Пуассона.
Таблица 11.23. Вычисления, связанные с применением х2-критерия согласия для распределения Пуассона
Прибытия fo fo-t (Vfe)2 (fo-V/t
0 14 11,00 3,00 9,0000 0,81818
1 31 31,92 -0,92 0,8464 0,02652
2 47 46,28 0,72 0,5184 0,01120
3 41 44,74 -3,74 13,9876 0,31264
4 29 32,44 -3.44 11,8336 0,36478
5 21 18,80 2,20 4,8400 0,25745
6 10 9,10 0,90 0,8100 0,08901
7 5 3,76 1,24 1,5376 0,40894
8 и более 2 1,36 0,04 0,0016 0,00082
2,28954
Применение ^’-критерия согласия для нормального распределения
В главах 7-10 при проверке гипотез о числовых переменных использовалось предположение о том, что исследуемая генеральная совокупность имеет нормальное распределение. Для проверки этого предположения можно применять графические средства,
например, блочную диаграмму или график нормального распределения. При больших объемах выборок для проверки этих предположений можно использовать ^-критерий согласия для нормального распределения.
Рассмотрим в качестве примера данные о 5-летней доходности 158 инвестиционных фондов, приведенные в табл. 2.2. Предположим, требуется поверить, имеют ли эти данные нормальное распределение. Нулевая и альтернативная гипотезы формулируются следующим образом:
Но: 5-летняя доходность подчиняется нормальному распределению, И,: 5-летняя доходность не подчиняется нормальному распределению.
Нормальное распределение имеет два параметра — математическое ожидание ц и стандартное отклонение <у, которые можно оценить на основе выборочных данных. В данном случае X = 10,149 и S = 4,773. Ширина классов в табл. 2.2 равна 5, а границы классов начинаются от -10,0. Поскольку нормальное распределение является непрерывным, необходимо определить площадь фигур, ограниченных кривой нормального распределения и границами каждого интервала. Кроме того, поскольку нормальное распределение теоретически изменяется от -ос до +оо , необходимо учитывать площадь фигур, выходящих за пределы классов. Итак, площадь, лежащая под нормальной кривой слева от точки -10,0, равна площади фигуры, лежащей под стандартизованной нормальной кривой слева от величины Z, равной
^-10,0-10449
4,773
Анализ табл. Д.2 показывает, что площадь фигуры, лежащей под стандартизованной нормальной кривой слева от величины Z = -4,22, приближенно равна 0,0000.
Для того чтобы вычислить площадь фигуры, лежащей под нормальной кривой между точками -10,0 и -5,0, сначала необходимо вычислить площадь фигуры, лежащей слева от точки -5,0.
г=5,0-Ю,149 =
4,773
По табл. Д.2 легко определить, что площадь фигуры, лежащей под стандартизованной нормальной кривой слева от величины Z = -3,17, приближенно равна 0,00076. Итак, площадь фигуры, лежащей под нормальной кривой между точками -10,0 и -5,0, равна 0,00076 - 0,0000 = 0,00076.
Продолжая вычисления, определим площадь фигуры, лежащей под нормальной кривой между точками -5,0 и 0,0. Для этого сначала определяется площадь фигуры, лежащей слева от точки 0,0.
г = 0,0-10,149
4,773
По табл. Д.2 определяем, что площадь фигуры, лежащей под стандартизованной нормальной кривой слева от величины Z = -2,13, приближенно равна 0,0166. Итак, площадь фигуры, лежащей под нормальной кривой между точками 0,0 и -5,0, равна 0,0166 - 0,00076 = 0,01584.
Аналогично можно вычислить площадь фигуры, ограниченной границами каждого класса. Все результаты вычислений приведены в табл. 11.24.
Таблица 11.24. Площади и ожидаемые частоты для каждого к ласса 5-летней доходности
Классы X х-х Z Площадь в классе "меньше" Площадь в классе f. = пР(Х)
меньше -10,0 -10,0 -20,149 -4,22 0,00000 0,00000 0,00000
от -10,0 до -5,0 -5,0 -15,149 -3,17 0,00076 0,00076 0,12008
от -5,0 до 0,0 0,0 -10,149 -2,13 0,01660 0,01584 2,50272
от 0,0 до 5,0 5,0 -5,149 -1,08 0,14010 0,12350 19,51300
от 5,0 до 10,0 10,0 -0,149 -0,03 0,48800 0,37490 54,96820
от 10,0 до 15,0 15,0 4,851 1,02 0,84610 0,35810 56,57980
от 15,0 до 20,0 20,0 9,851 2,06 0,98030 0,13420 21,20360
от 20,0 до 25,0 25,0 14,851 3,11 0,99906 0,01876 2,96408
от 25,0 до 30,0 30,0 19,851 4,16 1,00000 0,00094 0,14852
больше 30,0 — — +00 1,00000 0,00000 0,00000
Из табл. 11.21 следует, что теоретическая частота, в классах “меньше -10,0”, “от -5,0 до -10,0”, “от 25,0 до 30,0” и “больше 30,0” меньше 1,0. Для того чтобы частоты в каждом классы были равны 1,0 или превышали это число, категории “меньше -10,0” и “от -10,0 до -5,0” объединяются с категорией “от -5,0 до 0,0”, а категории “от 25,0 до 30,0” и “больше 30,0” объединяются с категорией “от 20,0 до 25,0”.
Используем /2-критерий согласия данных с нормальным распределением с помощью формулы (11.10). В нашем примере после объединения остаются шесть классов. Поскольку математическое ожидание и стандартное отклонение оцениваются на основе выборочных данных, количество степеней свободы равно /г-р-1 = 6- 2-1 = 3. Используя уровень значимости, равный 0,05, находим, что критическое значение Х2-статистики, имеющее три степени свободы, равно 7,815. Вычисления, связанные с применением ^-критерия согласия, приведены в табл. 11.25.
Таблица 11.25. Вычисления, связанные с применением %2-критерия согласия для нормального распределения
Классы fo (Vfe)2 (f0-fe)7t
меньше 0,0 4 2,6228 1,3772 1,89668 0,71315
от 0,0 до 5,0 14 19,5130 -5,5130 30,39317 1,55759
от 5,0 до 10,0 58 54,9682 3,0318 9,19181 0,16722
от 10,0 до 15,0 61 56,5798 4,4202 19,53817 0,34532
от 15,0 до 20,0 17 21,2036 -4,2036 17,67025 0,83336
больше 20,0 4 3,1126 0,8874 0,78748 0,25300
3,87963
Из табл. 11.25 и оценки = 3,87963 < 7,815 следует, что гипотезу Но отклонять нельзя. Иначе говоря, у нас нет оснований утверждать, что 5-летняя доходность инвестиционных фондов, ориентированных на быстрый рост, подчиняется нормальному распределению.
УПРАЖНЕНИЯ К РАЗДЕЛУ 11.7
11.60. Системный администратор компьютерной сети на протяжении 500 дней собирал данные о ежедневном количестве сбоев оборудования. Результаты приведены в следующей таблице.
Количество сбоев за день Количество дней
0 1 2 3 4 5 6 160 175 86 41 18 12 8 500
Является ли распределение количества сбоев пуассоновским? (Уровень значимости равен 0,01.)
11.61. Предположим, что в задаче 11.60 уровень значимости равен 0,01. Является ли распределение количества сбоев пуассоновским с математическим ожиданием, равным 1,5 сбоя в день?
11.62. Менеджер ипотечного подразделения крупного банка на протяжении двух лет (104 недель) собирал данные о количестве закладов, оформляемых за неделю. Результаты приведены в следующей таблице.
Количество оформленных закладов Частота
0 13
1 25
2 32
3 17
4 9
5 6
6 1
7 1
104
Является ли распределение количества оформленных закладов пуассоновским? (Уровень значимости равен 0,01.)
11.63. В таблице приведены данные, вычисленные по случайной выборке, состоящей из продолжительности службы 500 автомобильных аккумуляторов (в годах).
Срок службы Частота
от 0 до 1 12
от 1 до 2 94
от 2 до 3 170
от 3 до 4 188
от 4 до 5 28
от 5 до 6 8
500
Для этих данных X = 2,80 и S = 0,97. Уровень значимости равен 0,05. Подчиняется ли срок службы аккумуляторов нормальному распределению?
11.64. В таблице приведены данные, вычисленные по случайной выборке, состоящей из продолжительности 500 междугородных телефонных разговоров.
Продолжительность (в минутах) Частота
от 0 до 5 48
от 5 до 10 84
от 10 до 15 164
от 15 до 20 126
от 20 до 25 50
от 25 до 30 28
500
1. Вычислите математическое ожидание и стандартное отклонение данного распределения частот.
2. Подчиняется ли продолжительность междугородных телефонных разговоров нормальному распределению, если уровень значимости равен 0,05?
Непараметрические Процедуры анализа >м j критерии ^категорийных данный
ех2-критерии
Ранговый критерий Уилкоксона
Критерий . Крускала - Уоллиса
Таблица сопряженности признаков
Критерии согласия
Критерии для оценки дисперсии
%2 -критерии независимости
Виды критериев
Критерии для сравнения долей
Таблицы \ Таблицы , 2x2 2хс f В
. f Таблицы
Количество^ выборок '
'Ч
Три и больше
Z-критерий для проверки гипотезы о равенстве двух долей | (см. раздел 8.6)
X2 -критерий для проверки гипотезы
t Pi =Р2~ “• = РС ♦* . ’ г* ««МММ
Процедура Мараскуило
2
i
-критерий дл| проверки гилоте f Pi=P2 J [ (см. раздел 9.3
X2 -критерий V для проверки : гипотезы р1 = р2
Структурная схема главы 11
РЕЗЮМЕ
Как следует из структурной схемы, в главе рассмотрены разные подходы к анализу категорийных данных. Описаны методы проверки гипотез о категорийных данных, полученных на основе анализа двух независимых выборок, а также нескольких независимых выборок. Показано, как правило умножения вероятностей, сформулированное в разделе 4.2, позволяет выполнить проверку гипотезы о независимости двух категорийных переменных. Описанные методы проиллюстрированы на примере опроса, проведенного среди постояльцев отелей, принадлежащих компании Т. С. Resort Properties. Показано, что доля гостей, планирующих вернуться, в отеле Beachcomber выше, чем в отеле Windsurfer. Кроме того, эти доли отличаются друг от друга и в отелях Golden Palm, Palm Royal и Palm Princess. Определено, что причины недовольства постояльцев связаны с конкретными особенностями отелей. Это позволит руководству компании Т. С. Resort Properties повысить качество обслуживания гостей. Как всегда, анализируются условия, при которых должны применяться статистические критерии.
Кроме критериев “хи-квадрат”, в главе рассмотрены непараметрические процедуры. Описан ранговый критерий Уилкоксона, который используется в ситуациях, когда не выполняются условия применения f-критерия для поверки гипотезы о равенстве математических ожиданий двух независимых групп, а также критерий Крускала-Уоллиса, который является альтернативой однофакторному дисперсионному анализу.
ОСНОВНЫЕ ПОНЯТИЯ
Критерий
Крускала-Уоллиса, 748
Уилкоксона, 748
Критерий хи-квадрат
для проверки независимости, 730
для сравнения двух долей, 710
Ранговый критерий Уилкоксона
для больших выборок, 740
для малых выборок, 739
Таблица
перекрестной классификации, 709
сопряженности признаков, 709
факторная, 709
УПРАЖНЕНИЯ К ГЛАВЕ 11
Проверка знаний
11.65. При каких условиях можно применять Z-критерий для оценки разности между долями признака в двух независимых генеральных совокупностях?
11.66. При каких условиях можно применять х2_критерий для оценки разности между долями признака в двух независимых генеральных совокупностях?
11.67. Какие общие свойства имеют Z- и %2-критерий для оценки разности между долями признака в двух независимых генеральных совокупностях?
11.68. При каких условиях можно применять %2-критерий для оценки разности между долями признака в нескольких независимых генеральных совокупностях?
11.69. При каких условиях можно применять /2-критерий независимости?
11.70. При каких условиях следует применять ранговый критерий Уилкоксона?
11.71. При каких условиях следует применять критерий Крускала-Уоллиса?
Применение понятий
Задачи 11.72-11.81 можно решать как вручную, так и с помощью программы Microsoft Excel.
11.72. Среди студентов первого курса университета Майами в г. Оксфорд, штат Огайо (Miami University in Oxford, Ohio), был проведен опрос. В его ходе исследователи пытались оценить связь между полом студента и ценой приобретенной пиццы. Студентов попросили представить, что они планируют купить большую пиццу с доставкой на дом, и предложили выбор между заказом в компании Pizza Hut по сниженной цене 8,49 долл, (обычная стоимость пиццы в компании Oxford Pizza Hut равна 11,49 долл.) и в другой пиццерии. Результаты опроса приведены в таблице сопряженности признаков.
Пиццерия
Пол Pizza Hut Другая Всего
Женский 4 13 17
Мужской 6 12 18
Всего 10 25 35
В ходе опроса исследователи стремились также оценить наиболее подходящую цену. Результаты приведены в таблице сопряженности признаков.
Цена (долл.)
Пицца 8,49 11,49 14,49 Всего
Pizza Hut 10 5 2 17
Другие 25 23 27 75
Всего 35 28 29 92
1. Можно ли утверждать, что между полом покупателей и выбором пиццерии существует статистически значимая связь, если уровень значимости равен 0,05?
2. Как изменится ответ, если девять юношей выберут компанию Pizza Hut, а остальные девять — другие пиццерии?
3. Можно ли утверждать, что между ценой и выбором пиццерии существует статистически значимая связь, если уровень значимости равен 0,05?
4. Вычислитер-значение в задаче 3 и объясните его смысл.
5. Примените процедуру Мараскуило при уровне значимости, равном 0,05, и определите цены, которые существенно отличаются друг от друга.
11.73. Все больше сотрудников корпораций, совершающих деловые поездки, исследуют Интернет в поисках более дешевых авиабилетов (D. Rosato and S. Khan, “Net Surfing Nets Savings for Business Travelers”, USA Today, March 7, 2000, p. IB, 2B). Недавно были опубликованы результаты опроса 400 менеджеров, планирующих деловые поездки. В таблице перекрестной классификации, приведенной ниже, указано, сколько менеджеров занимались поисками более дешевых авиабилетов в Интернет и сколько из них сделали заказ.
Вы заказали авиабилет через Интернет?
Вы искали авиабилет в Интернет? Да Нет Всего
Да 88 124 212
Нет 20 168 188
Всего 108 292 400
1. Можно ли утверждать, что между ценой авиабилета и количеством заказов существует статистически значимая разница, если уровень значимости равен 0,05?
2. Вычислите p-значение в задаче 1 и объясните его смысл.
11.74. Недавно проведенный опрос был посвящен выяснению того, что сотрудники считают наиболее важным для успешной работы (“USA Today Snapshot”, USA Today, May 15, 2000). В опросе приняли участие 500 мужчин и 500 женщин. Его результаты указаны в следующей таблице.
Фактор успеха Мужчины (%) Женщины (%)
Хорошие отношения с начальником 63 77
Современное оборудование 59 69
Достаточные ресурсы 55 74
Удобное расположение офиса 48 60
Гибкий график работы 40 53
Возможность работать дома 21 34
1. Можно ли утверждать, что женщины и мужчины имеют разные приоритеты, если уровень значимости равен 0,05?
2. Какие выводы можно сделать, основываясь на этих данных?
11.75. В таблице сопряженности признаков приведены результаты недавнего опроса, в котором приняли участие 200 семей, пользующихся электронными банковскими услугами, и 400 семей, не делающих этого (С. Dugas, “Virtual Banks Get Real, Offer Deals to Woo Customers”, USA Today, April 13, 2000, p. 12B).
Услуги Электронные услуги (%) Обычные услуги (%)
Оплата счетов по почте 50 74
Посещение банка 46 72
Услуги банкомата 72 40
Прямое зачисление на депозит 57 40
Звонок в автоматическую справочную систему 32 27
Звонок торговому представителю 14 15
1. Можно ли утверждать, что между долей респондентов, пользующихся электронными услугами, и долей респондентов, не делающих этого, существует значимая связь, если уровень значимости равен 0,05?
2. Какие выводы можно сделать, основываясь на этих данных?
11.76. В октябре 2000 года организация Markle Foundation провела телефонный опрос, посвященный насущным проблемам развития Интернет. В ходе опроса респонденты были разделены на две группы: “обычные пользователи” и “эксперты”. Участники опроса читали утверждения, связанные с работой Интернет, а затем отвечали на вопрос, считают ли они названные проблемы серьезными или нет. Ниже приведены таблицы перекрестной классификации, полученные при обработке ответов, касающихся двух утверждений.
Утверждение 1: “Большинство Web-сайтов размещают на вашем компьютере небольшие файлы, называемые cookies, позволяющие отследить все Web-сайты, которые вы посещали”.
Пользователь Серьезно ли вы относитесь к данному утверждению?
Да Нет Всего
Обычный 67 28 93
Эксперт 46 54 _ 100
Всего 113 82 193
Источник: www.markle. . сот.
Утверждение 2: “Три четверти всех крупных компаний регулярно просматривают электронную почту и следят за тем, какие Web-сайты посещают их сотрудники”.
Пользователь Серьезно ли вы относитесь к данному утверждению?
Да Нет Всего
Обычный 54 42 96
Эксперт 37 63 _ 100
Всего 91 105 196
Источник: www .markle . com.
1. Можно ли утверждать, что между характеристикой пользователя и серьезностью его отношения к первому утверждению существует статистически значимая разница, если уровень значимости равен 0,05?
2. Вычислитер-значение в задаче 1 и объясните его смысл.
3. Можно ли утверждать, что между характеристикой пользователя и серьезностью его отношения ко второму утверждению существует статистически значимая разница, если уровень значимости равен 0,05?
4. Вычислитер-значение в задаче 3 и объясните его смысл.
11.77. Компания, производящая и распространяющая учебные видеокассеты по финансовому делу, обычно рассылает своим потенциальным клиентам демонстрационные кассеты с обзором лекционного курса. Клиенты либо соглашаются приобрести видеокассеты с лекциями, либо возвращают демонстрационные материалы торговым представителям компании. Группа торговых представителей попыталась оценить, насколько возросло количество клиентов, согласившихся приобрести учебные видеокассеты, и обнаружила, что многие клиенты не смогли понять по демонстрационным кассетам, соответствует ли предлагаемый лекционный курс их потребностям. Торговые представители решили провести эксперимент и проверить, увеличится ли объем продаж, если вместо демонстрационных кассет рассылать полный курс лекций. Они выбрали 80 потенциальных покупателей и случайным образом разделили их на две группы по 40 человек. Клиентам из первой группы рассылались демонстрационные кассеты, а клиенты из второй группы получа-
ли полный курс лекций. Затем экспериментаторы записывали, сколько кассет приобрели клиенты из каждой группы и сколько кассет они вернули обратно. Результаты исследования приведены в следующей таблице.
Количество полученных видеокассет
Результат Демонстрационная Полный курс Всего
Куплена 6 14 20
Возвращена 34 26 60
Всего 40 40 80
1. Существует ли статистически значимая разница между долями приобретенных кассет разного типа, если уровень значимости равен 0,05?
2. Какой способ рекламы является более эффективным? Обоснуйте свой ответ.
Торговые представители решили продолжить исследование и оценить эффективность трех разных подходов к рекламе учебных видеокассет: 1) по почте; 2) при личной встрече; 3) по телефону. Для эксперимента были отобраны 300 потенциальных покупателей. Они были случайным образом распределены по трем группам. Результаты эксперимента приведены в таблице.
Вид рекламы
Результат По почте Личная встреча По телефону Всего
Куплена 19 27 14 60
Возвращена 81 73 86 240
Всего 100 100 100 300
3. Существует ли статистически значимая разница между долями приобретенных кассет при разных способах рекламы, если уровень значимости равен 0,05?
4. Примените процедуру Мараскуило при уровне значимости, равном 0,05, и определите, какие способы рекламы приводят к существенно разным объемам продаж.
5. Какая стратегия рекламы является более эффективной? Обоснуйте свой ответ.
11.78. Некая компания планирует провести организационные изменения, предоставив рабочим группам больше самостоятельности. Чтобы оценить отношение работников к предлагаемым новшествам, руководство компании сформировало выборку из 400 сотрудников. Каждого из выбранных сотрудников попросили высказать свое отношение к планам руководства, указав один из трех вариантов ответа: за, все равно или против. Результаты опроса приведены в следующей таблице сопряженности признаков.
Должность Отношение к самоуправляемым командам
За Все равно Против Всего
Временный работник 108 46 71 225
Контролер 18 12 30 60
Руководство среднего звена 35 14 26 75
Высшее руководство 24 7 9 40
Всего 185 79 136 400
1. Существует ли статистически значимая зависимость между отношением к самоуправлению и должностью, если уровень значимости равен 0,05?
В ходе опроса респондентов попросили выразить свое отношение к новой инициативе руководства, в соответствии с которой сотрудникам каждый месяц может предоставляться дополнительный выходной без оплаты. Результаты приведены в следующей таблице.
Должность Отношение к дополнительному выходному
За Все равно Против Всего
Временный работник 135 23 67 225
Контролер 39 7 14 60
Руководство среднего звена 47 6 22 75
Высшее руководство 26 6 8 40
Всего 247 42 111 400
2. Существует ли статистически значимая зависимость между отношением к инициативе руководства и должностью, если уровень значимости равен 0,05?
11.79. Национальная ассоциация производителей кофе (National Coffee Association) каждую зиму проводит опрос 3 300 потребителей в возрасте от 10 лет и старше. В статье, посвященной этому опросу, отмечается, что люди все чаще выбирают безалкогольные напитки, а кофе пьют лишь за завтраком (Drogun, N., “Joe Wakes Up, Smells the Soda”, The Wall Street Journal, June 8, 1999, Bl, B16).
1. Опрос показал, что в 1998 году 49% американцев пили кофе накануне. В 1959 году этот показатель был равен 75%. Допустим, что в 1959 году в опросе приняли участие 2 000 респондентов. Существует ли статистически значимая разница между долями американцев, предпочитающих кофе, в 1959 и 1998 годах, если уровень значимости равен 0,01?
2. Вычислите p-значение в задаче 1 и объясните его смысл.
3. Опрос показал, что 23% американцев в возрасте от 18 до 24 лет пили кофе накануне. Среди людей старше 60 лет этот показатель равен 74% . Допустим, что в опросе приняли участие 300 респондентов в возрасте от 18 до 24 лет и 500 респондентов старше 60 лет. Существует ли статистически значимая разница между долями американцев, предпочитающих кофе, в этих возрастных категориях, если уровень значимости равен 0,01?
4. Вычислите p-значение в задаче 3 и объясните его смысл.
5. Опрос 1998 года показал, что дома за завтраком кофе пили 35% американцев, за ленчем — 4%, а за ужином — 3%. В 1988 году эти показатели равнялись 40, 9 и 7% соответственно. Предположим, что в опросе 1988 года приняли участие 3 300 респондентов. Существует ли статистически значимая разница между долями американцев, употребляющих кофе дома, в опросах 1988 и 1998 годов, если уровень значимости равен 0,01? {Подсказка’, необходимо выполнить анализ отдельно для завтрака, ленча и ужина.)
6. Вычислите p-значение в задаче 5 и объясните его смысл.
11.80. Исследователи университета Майами (Miami University) изучили цели и достижения 349 рабочих команд из разных производственных компаний штата Огайо. В первой таблице команды были разделены на категории в зависимости от целей: стремятся они улучшить состояние окружающей среды или нет, а также на четыре группы в зависимости от вида производства. В следующих трех факторных таблицах приведены результаты, достигнутые рабочими командами, стремящимися уменьшить стоимость продукции.
Производство Цель — улучшить состояние окружающей среды
Да Нет Всего
Ремонтная мастерская или булочная 2 42 44
Рутинное производство 4 57 61
Дискретный процесс 15 147 162
Непрерывный процесс 17 65 82
Всего 38 311 349
Цель — уменьшить цену
Результат Да Нет Всего
Состояние окружающей среды улучшилось 77 52 129
Состояние окружающей среды не улучшилось 91 129 220
Всего 168 181 349
Цель — уменьшить цену
Результат Да Нет Всего
Доход увеличился 70 68 138
Доход не увеличился 98 113 211
Всего 168 181 349
Цель — уменьшить цену
Результат Да Нет Всего
Моральное состояние улучшилось 67 55 122
Моральное состояние не улучшилось 101 126 227
Всего 168 181 349
Источник: М. Hanna, W. Newman, and Р. Johnson, “Linking Operational and Environmental Improvement Thru Employee Involvement”, International Journal of Operations and Production Management 20, (2000 ), 148-165.
1. Существует ли статистически значимая связь между стремлением улучшить состояние окружающей среды и видом производства, если уровень значимости равен 0,05?
2. Вычислитер-значение в задаче 1 и объясните его смысл.
3. Существует ли статистически значимая связь между стремлением улучшить состояние окружающей среды и удешевлением продукции, если уровень значимости равен 0,05?
4. Вычислитер-значение в задаче 3 и объясните его смысл.
5. Существует ли статистически значимая связь между стремлением повысить доходность и удешевлением продукции, если уровень значимости равен 0,05?
6. Вычислитер-значение в задаче 5 и объясните его смысл.
7. Существует ли статистически значимая связь между моральным состоянием сотрудников и удешевлением продукции, если уровень значимости равен 0,05?
8. Вычислите р-значение в задаче 7 и объясните его смысл.
11.81. Используя данные задачи 2.80, в которой рассматривались гарантийные требования к шинам фирмы Firestone, установите, существует ли статистически значимая связь между видом дорожно-транспортного происшествия и типом модели.
Применение Интернет
11.82. Зайдите на сайт www.prenhall.com/levine. Выберите ссылку Chapter 11 и щелкните на ссылке Internet exercises.
ГРУППОВОЙ ПРОЕКТ
ТР.11.1. Файл данных ^MUTUAL FUNDS.XLS содержит информацию о 259 взаимных фондах. Предположим, что в этой выборке перечислены все взаимные фонды, существовавшие в 2002 году. Рассмотрим три категорийные переменные.
Цель — вид акций, принадлежащих взаимному фонду (переоцененные или недооцененные).
Комиссия — взимание брокерской комиссии (да или нет).
Риск — уровень риска (очень низкий, низкий, средний, высокий, очень высокий).
1. Постройте таблицу 2x2, поместив в строке переменную Комиссия, а в столбце — переменную Цель.
2. Существует ли статистически значимая связь между целями взаимных фондов и взиманием брокерской комиссии, если уровень значимости равен 0,05?
3. Постройте таблицу 2x5, поместив в строке переменную Комиссия, а в столбце — переменную Риск.
4. Существует ли статистически значимая связь между степенью риска и взиманием брокерской комиссии, если уровень значимости равен 0,05?
5. Постройте таблицу 5x2, поместив в строке переменную Риск, а в столбце — переменную Цель.
6. Существует ли статистически значимая связь между целями фондов и степенью риска, если уровень значимости равен 0,05?
7. Изложите свои выводы в отчете.
РАЗБОР КОНКРЕТНОЙ СИТУ-ГАЗЕТА SPRINGVILLEHERALL
***** ' * - <*
Этап 1
Группа, разрабатывающая новую подписную политику, пришла к выводу, что количество подписчиков увеличится, если стоимость подписки будет снижена. Группа решила провести эксперимент, чтобы определить величину скидки. Респондентам были предложены три вида скидок, а также подписка без скидки.
1. Подписка без скидок. Подписчики должны платить 4,50 долл, в неделю на протяжении 90-дневного испытательного срока.
2. Умеренная скидка. Подписчики должны платить 4,00 долл, в неделю на протяжении 90-дневного испытательного срока.
3. Значительная скидка. Подписчики должны платить 3,00 долл, в неделю на протяжении 90-дневного испытательного срока.
4. Дисконтная ресторанная карточка. Подписчики газеты получают ресторанную карточку, обеспечивающую скидку 15% при посещении избранных ресторанов в г. Спрингвилль на протяжении испытательного периода.
Каждому респонденту предложили случайно выбранный вид скидки. Для каждого вида скидки на протяжении испытательного периода отслеживалась случайная выборка, состоящая из 100 подписчиков. Результаты приведены в табл. SH.11.1
Таблица. SH.11.1. Количество подписчиков, продолжавших выписывать газету после испытательного периода.
План
Продлена ли Без скидки Умеренная Значительная Ресторанная Всего
подписка? скидка скидка дисконтная карточка
Да 34 37 38 61 170
Нет 66 63 62 39 230
Всего 100 100 100 100 400
УПРАЖНЕНИЯ
Проанализируйте результаты эксперимента. Напишите отчет для отдела исследования рынка и укажите оптимальный вид скидки. Опишите ограничения и предположения, которые должны выполняться при проведении эксперимента. Подготовьте короткое выступление.
ф НЕ ПРОДОЛЖАЙТЕ, ПОКА НЕ ЗАКОНЧИТЕ ПЕРВЫЙ ЭТАП
Этап 2
После анализа данных, представленных в главе 7, стало очевидно, что индивидуальные анкеты не позволяют правильно выбрать стратегию подписки. Чтобы уточнить информацию о состоянии рынка, исследовательская группа заполнила следующую таблицу сопряженности признаков.
Читаете ли вы другие газеты?
Доставка на дом Да Нет Всего
Да 61 75 136
Нет 77 139 216
Всего 138 214 352
Доставка на дом Ресторанная карточка
Да Нет Всего
Да 26 110 136
Нет 40 176 216
Всего 66 286 352
Желаете ли подписаться? Покупка газеты по дням недели
Каждый день Как правило Иногда Всего
Да 29 14 3 46
Нет 49 81 40 170
Всего 78 95 43 216
Желаете ли подписаться? Покупка газеты по воскресеньям
Каждое воскресенье 2-3 раза в месяц Раз в месяц Всего
Да 35 10 1 46
Нет 103 44 23 170
Всего 138 54 24 216
Где покупаете газету? Желаете ли подписаться?
Да Нет Всего
В лавке/гастрономе 12 62 74
В магазине канцтова- 15 80 95
ров/кондитерской
В торговом автомате 10 11 21
В супермаркете 5 8 13
В других местах 4 9 13
Всего 46 170 216
Покупка газеты в течение недели
Покупаете ли газету по воскресеньям? Каждый день Как правило Иногда Всего
Каждое воскресенье 55 65 18 138
2-3 раза в месяц 19 23 12 54
Раз в месяц 4 7 13 24
Всего 78 95 43 216
УПРАЖНЕНИЯ
Проанализируйте данные, приведенные в таблицах сопряженности признаков. Изложите свои выводы и рекомендации в отчете.
ПРИМЕНЕНИЕ WEB
Примените свои знания о методах проверки гипотез о равенстве долей признака для решения следующих задач.
Стремясь улучшить качество обслуживания своих постояльцев, компания Т. С. Resort Properties вступила в конкуренцию с компанией SunLow Resorts, открывшей свои отели на тех же островах. Компания SunLow Resorts заявила, будто опрос 300 случайно выбранных клиентов показал, что 60% респондентов предпочитают их программу отдыха, а не развлечения, предоставляемые компанией Т. С. Resort Properties.
Посетите Web-сайт компании SunLow (www. prenhall. com/Springville/SunLowHome. html) и проверьте результаты опроса.
1. Корректны ли заявления компании SunLow?
2. Какие статистические критерии позволяют сделать выводы, благоприятные для компании Т.С. Resort Properties?
3. Примените статистический критерий, выбранный при решении задачи 2.
Какие данные о клиентах компании Т. С. Resort Properties следует собрать в ходе будущего опроса? Обоснуйте свой ответ.
СПРАВОЧНИК ПО EXCEL. ГЛАВА 11
ЕН.11.1. Применение /-критерия для оценки разности между двумя долями
Применяя /-критерий для оценки разности между двумя долями, необходимо создать рабочий лист, использующий функции ХИ2ОБР и ХИ2РАСП. Вызовы этих функций выглядят следующим образом.
ХИ2ОБР {уровень значимости; степени свободы),
ХИ2РАСП {критическое значение х2; степени свободы).
В табл. ЕН. 11.1-ЕН. 11.3 показан шаблон рабочего листа Хи-квадрат, реализующего Х2-критерий для оценки разности между двумя долями постояльцев отелей Beachcomber и Windsurfer, недовольных качеством обслуживания (см. табл. 11.2). Для вычисления Х2-статистики применяется функция ХИ2РАСП, а не ХИ2ТЕСТ, которая при нулевом p-значении может возвращать ошибочное значение #ЗНАЧ!. Для вычисления критического значения в ячейке В24 применяется функция ХИ2ОБР, а для вычисления наблюдаемого уровня значимости в ячейке В2 6 — функция ХИ2РАСП.
Обратите внимание на то, что ячейки В19 и В2 0 содержат формулы, в которых для определения количества строк и столбцов используется функция СЧЕТЗ, возвращающая количество непустых ячеек в столбце А и строке 5. Несмотря на то что в данном критерии количество строк и столбцов всегда равно двум, эти формулы можно применять и при реализации обобщенного х2-критерия, описанного в следующем разделе.
В ячейке А2 7 с помощью функции ЕСЛИ выполняется сравнение р-значения из ячейки В2 6 с уровнем значимости, записанным в ячейке В18. В зависимости от результата сравнения на экран выводится сообщение, следует отклонять нулевую гипотезу или нет. (В ячейке АЗО функция ЕСЛИ используется для проверки необходимых условий применения критерия: наблюдаемые величины не должны быть меньше пяти.)
Используя шаблон, следует учитывать, что формулы, показанные в двух строках, на реальном листе должны вводиться в одной строке (ячейки А27 и АЗО).
Таблица ЕН.11.1. Диапазон Al: D15 в шаблоне рабочего листа Хи-квадрат (наблюдаемые и ожидаемые величины)
А В С D
1 Степень удовлетворенности постояльцев
2
3 Наблюдаемые величины
4 Отель
5 Собираетесь ли вы вернуться? Beachcomber Windsurfer Всего
"ill? Да 163 154 =СУММ(Вб:Сб)
11111 Нет 64 108 =СУММ(В7:С7)
illll Всего =СУММ(Вб:В7) =СУММ(Сб:С7) =СУММ(В8:С8)
9
10 Ожидаемые величины
Окончание табл. ЕН. 77.7
А В С D
11 =В4
12 =А5 = В5 =С5 Всего
13 =А6 =$D6*B$8/$D$8 =$D6*C$8/$D$8 =СУММ(В13:С13)
14 =А7 =$D7*B$8/$D$8 =$D7*C$8/$D$8 =СУММ(В14:С14)
15 Всего =СУММ(В13:В14) =СУММ(С13:С14) =СУММ(В15:С15)
Таблица ЕН.11.2. Строки 17-30 в шаблоне рабочего листа Гипотеза (строка 16 пуста)
А В
17 Данные
18 Нижнее критическое значение 0,05
19 Количество строк =СЧЁТЗ(А6:А7)
20 Количество столбцов =СЧЁТЗ(В5:С5)
21 Количество степеней свободы =(В19-1) *( В20-1)
22
23 Результаты
24 Критическое значение =ХИ2ОБР(В18; В21)
25 Тестовая статистика =СУММ(Е10:С11)
26 р-значение =ХИ2РАСП(В25; В21)
lilili = ЕСЛИ(В26<В18;"Нулевая гипотеза отклоняется"; "Нулевая гипотеза не отклоняется")
||И||
|||| Условия
30 =ЕСЛИ(ИЛИ(В13<5;С13<5;В14<5;С14<5);" наруша ются"; "выполняются")
Таблица ЕН.11.3. Диапазон F4 : G11 в шаблоне рабочего листа Гипотеза
G
4 Область вычислений
IIIII fo-fe
Я|В =В6-В13 =Сб-С13
!В1ЯВ = В7-В14 =С7-С14
8
9 (fo-fe)A2/fe
ИИ =Е6Л2/С13 =G6'2/C13
11 =Е7Л2/В14 =С7Л2/С14
ЕН.11.2. Применение х2-критерия для оценки разностей между с долями
Применяя ^-критерий для сравнения с долей, необходимо выполнить модификацию рабочего листа Хи-квадрат, описанного в разделе ЕН. 11.1. Например, чтобы создать рабочий лист Хи-квадрат, применяющий %2-критерий для оценки разности между долями постояльцев, недовольных качеством обслуживания в трех отелях (см. табл. 11.6), необходимо реализовать шаблон, показанный в табл. ЕН.11.1-ЕН.11.3, а затем выполнить следующие действия.
1. Вставить столбец в таблицы наблюдаемых и ожидаемых величин. Выделить ячейку С1 и вставить новый пустой столбец С с помощью команды Вставка^Столбцы. Выделить ячейку В8 и скопировать ее содержимое в ячейку С 8. Выделить диапазон В12 : В15 и скопировать его в диапазон С12 : С15.
2. Вставить столбец в область вычислений. Выделить ячейку Н1 (пересечение первой строки и последнего столбца области вычислений) и вставить новый пустой столбец Н с помощью команды Вставка^Столбцы. Выделить диапазон G6:G7 и скопировать его в диапазон Н6:Н7. Выделить диапазон ячеек GIO : G11 и скопируйте его в диапазон Н10 : НИ.
3. Модифицировать формулы, проверяющих условия применения критерия. Выделить ячейку АЗО. Изменить аргументы функции ИЛИ: выражение ИЛИ(В13<5, D13<5, В14<5, D14<5) заменить выражением ИЛИ(В13<1, С13<1, D13<1, В14<1, С14<1, D14<1).
4. Проверить введенные данные. Проверить, согласуются ли все остальные формулы с изменениями, сделанными в предыдущих пунктах. Ввести названия отелей и наблюдаемые величины, содержащиеся в табл. 11.6, в строки рабочего листа, начиная с третьей.
В табл. ЕН. 11.4 продемонстрирован шаблон рабочего листа, полученного после выполнения модификаций. Для решения аналогичных задач, в которых исследуются несколько независимых генеральных совокупностей, следует повторить пункты “Добавление столбца” и внести соответствующие изменения в функцию ИЛИ. (Обратите внимание на то, что при добавлении данных о новых генеральных совокупностях ячейка, выбранная в п. 2, будет отодвигать столбцы, всегда оставаясь на пересечении первой строки и последнего столбца области вычислений.)
Таблица ЕН.11.4. Модифицированный шаблон рабочего листа Хи-квадрат
А ' В ' D E
ШЛ Степень удовлетворенности постояльцев трех отелей
2
3 Наблюдаемые величины
4 Отель
5 Собираетесь ли вы вернуться? Golden Palm Palm Royale Palm Princess Всего
6 Да 128 199 186 =СУММ(В6:О6)
7 Нет 88 33 66 =СУММ(В7:07)
8 Всего =СУММ(В6:В7) =СУММ(С6:С7) =CyMM(D6:D7) =СУММ(В8:Э8)
Окончание табл. ЕН. 77.4
А В " с < : В V
9
10 Ожидаемые величины
1111 = В4
1111 =А5 =В5 =С5 = D5 Всего
13 =А6 =$Е6*В$8/$Е$8 =$Е6*С$8/$Е$8 =$E6*D$8/$E$8 =СУММ(В13:С13)
14 =А7 =$Е7*В$8/$Е$8 =$Е7*С$8/$Е$8 =$E7*D$8/$E$8 =СУММ(В14:С14)
15 Всего =СУММ(В13:В14) =СУММ(С13:С14) =СУММ(С13:С14) =СУММ(В15:С15)
ЕН.11.3. Применение процедуры Мараскуило
Для выполнения процедуры Мараскуило необходимо создать рабочий лист, представляющий собой модификацию рабочего листа, выполняющего %2-критерий для проверки гипотезы о равенстве нескольких долей.
В табл. ЕН. 11.5-ЕН. 11.7 показан шаблон рабочего листа Мараскуило, выполняющего процедуру Мараскуило на основе х2-критерия для оценки разности между тремя долями постояльцев отелей, недовольных качеством обслуживания (см. табл. 11.6). Этот шаблон представляет собой модификацию рабочего листа, применяющего /2-критерий. Он вычисляет квадратный корень критического значения, выборочные доли и критические размахи. Рабочий лист сравнивает абсолютные разности с критическими разма-хами, применяя функцию ЕСЛИ. В зависимости от результата сравнения на экран выводится сообщение, значима разница между долями или нет.
В качестве основы для рабочего листа Мараскуило используется рабочий лист Хи-квадрат, описанный в предыдущем разделе. Переименуйте его в лист МараДанные, а затем откройте новый рабочий лист и реализуйте табл. ЕН.11.5-ЕН.11.7. Для сравнения трех групп в шаблон рабочего листа следует добавить строки 10-15.
Таблица ЕН.11.5. Диапазон Al: В9 в шаблоне рабочего листа Мараскуило
'' " / А
1 Процедура Мараскуило
2 Оценка степени удовлетворенности постояльцев трех отелей
3 Уровень значимости =МараДанные!В18
4 Квадратный корень критического значения = КОРЕНЬ(МараДанные!В24)
5
III Выборочные доли
7 Группа 1 =МараДанные!Вб/МараДанные!В8
8 Группа 2 =МараДанные!С6/МараДанные!С8
9 Группа 3 =МараДанныеЮ6/МараДанныеЮ8
Таблица ЕН.11.6. Диапазон All: С16 в шаблоне рабочего листа Мараскуило (строка 10 пуста)
А В С '
iliiii Таблица Мараскуило
12 Доли Абсолютные разности Критический размах
13 (Группа 1 - Группа 2| =ABS(B7-B8) =В4*КОРЕНЬ(В7*(1-В7)/МараДанные!В8 + В8*(1-В8)/МараДанные!С8)
14 (Группа 1 - Группа 3| =ABS(B7-B9) =В4*КОРЕНЬ(В7*(1-7)/МараДанные!В8+ В9*(1-В9)/МараДанныеЮ8)
15
16 (Группа 2 - Группа 3| =ABS(B8-B9) =В4*КОРЕНЬ(В8*(1-В8)/МараДанные!В8+ В9*(1-В9)/МараДанныеЮ8)
Таблица ЕН.11.7. Столбец Е в рабочем листе Мараскуило
=ЕСЛИ(В13>С13; “Значимо”; “Незначимо”)
14 =ЕСЛИ(В14>С14; “Значимо”; “Не значимо”)
16 =ЕСЛИ(В16>С16; “Значимо”; “Незначимо”)
ЕН.11.4. Применение %1 2 3 4-критерия независимости
Применяя /2-критерий для проверки независимости, необходимо выполнить модификацию рабочего листа, описанного в разделе ЕН. 11.1. Например, чтобы реализовать шаблон рабочего листа Хи-квадрат, использующего %2-критерий для оценки независимости между ответами постояльцев, недовольных качеством обслуживания в трех отелях, и характеристиками отелей (см. табл. 11.9), необходимо применить шаблон, показанный в табл. ЕН.11.1-ЕН.11.3, а затем выполнить следующие действия.
1. Вставить строки в таблицы ожидаемых и наблюдаемых величин. Выделить ячейку А7, затем выбрать команду Вставка ^Столбцы и создать пустую строку 7. Повторить. Новые строки 7 и 8 остаются пустыми. Выделить ячейку А16, выбрать команду Вставкам Столбцы и создать пустую строку 16. Повторить. Новые строки 16 и 17 остаются пустыми.
2. Вставить столбец в таблицы наблюдаемых и ожидаемых величин. Выделить ячейку С1, выбрать команду В ставка ^Столбцы и создать пустой столбец С.
3. Вставить столбец в область вычислений. Выделить ячейку Н1 и вставить новый пустой столбец н с помощью команды Вставка ^Столбцы.
4. Вставить формулы в таблицы наблюдаемых и ожидаемых, а также в область вычиалений. Выделить диапазон Аб:1б и скопировать его содержимое в строку 8. Выделить диапазон А15:115 и скопировать его содержимое в строку 17. Выделить ячейку В10 и скопировать ее содержимое в ячейку С10. Выделить диапазон В14:В19 и скопировать его содержимое в диапазон С14:С19. Выделить диапазон G6: G9 и скопировать его содержимое в диапазон Нб : Н9. Выделить диа-
пазон G15 : G18 и скопировать его содержимое в диапазон Н15 : Н18, игнорируя сообщение об ошибке #ДЕЛ/0 !.
5. Модифицировать формул, проверяющих условия применения критерия. Выделить ячейку А14. Изменить аргументы функции ИЛИ: выражение ИЛИ(В13<5, D13<5, В14<5, D14<5) заменить выражением ИЛИ (Bl5<1, С15<1, D15<1, В16<1, С16<1, D16<1, В17<1, С17<1, D17<1, В18<1, С18<1, D18<1).
6. Проверить введенные данные. Проверить, согласуются ли все остальные формулы с изменениями, сделанными в п. 1-5. Ввести названия отелей и наблюдаемые величины, содержащиеся в табл. 11.9, в строки рабочего листа, начиная с третьей.
В табл. ЕН. 11.8 продемонстрирован шаблон рабочего листа, полученного после выполнения п. 1-6. Для решения аналогичных задач, в которых исследуется несколько независимых генеральных совокупностей, следует повторить п. 1-6 и внести соответствующие изменения в функцию ИЛИ. (Содержимое ячеек А5 и А8 на реальном рабочем листе должно занимать одну строку.)
Таблица ЕН.11.8. Модифицированный шаблон Хи-квадрат (диапазон Al: Е19)
А В С D E
1 Анализ качества обслуживания постояльцев отеля
2
3 Наблюдаемые величины
4 Отель
5 Причина недовольства Golden Palm Palm Royale Palm Princess Всего
6 Цена 23 7 37 =СУММ(В6:Об)
1Я1 Расположение 39 13 8 =СУММ(В7:О7)
8 Неудобные комнаты 13 5 13 =СУММ(В8:08)
ЯП Другие 13 8 8 =СУММ(В9:09)
lliel Всего =СУММ(Вб:В9) =СУММ(Сб:С9) =CyMM(D6:D9) =СУММ(В10Ю10)
IIHII
12 Ожидаемые величины
13 =В4
14 =А5 =В5 =С5 = D5 Всего
15 =Аб =$Е6*В$10/$Е$10 =$Е6*С$10/$Е$10 =$E6*D$10/$E$10 =СУММ(В15:С15)
16 =А7 =$Е7*В$1О/$Е$1О =$Е7*С$1О/$Е$1О =$E7*D$1O/$E$1O =СУММ(В1б:С1б)
17 =А8 =$Е8*В$10/$Е$10 =$Е8*С$10/$Е$10 =$E8*D$10/$E$10 =СУММ(В17:С17)
18 =А9 =$Е9*В$10/$Е$10 =$Е9*С$10/$Е$10 =$E9*D$10/$E$10 =СУММ(В18:С18)
19 Всего =СУММ(В15:В18) =СУММ(С15:С18) =CyMM(D15:D18) =СУММ(В19:С19)
ЕН.11.5. Ранговый критерий Уилкоксона для проверки гипотезы о разности между двумя медианами
Для применения рангового критерия Уилкоксона для проверки гипотезы о разности между двумя медианами сначала необходимо упорядочить и ранжировать исходные выборочные данные, а затем реализовать рабочий лист, использующий соответствующие функции.
Будем предполагать, что упорядоченные значения и ранги обеих выборок хранятся на листе Ранги (аналог листа Sorted в рабочей книге Chapter 11. xls. — Прим, ред.) . Например, при анализе объемов продаж колы, расположенной на полках разного вида, рабочий лист Ранги должен выглядеть так, как показано на иллюстрации.
_____Стеллажи_______Значение Ранг
Обычные 3 Юбычные
Обычные 6 Юбычные
Обычные
Специализированные
22
30
34
40
52
52
2
3
4
55
55
Специализированные Обычные
JD Юбычные И.Юбычные 12'Обычные
1Э{ Специализированные 14 Специализированные 15 Специализированные 16'Специализированные 17 । Специализированные 16'Специализированные 19Юбычные
/20, Специализированные J21J Специализированные
54 7
56' 8
59 9
62 10
64 11
66 12
67 13
71 14
76 15
77 16
83 17
84 18.5
84 18.5
90; 20
Заполнив рабочий лист Ранги, следует создать рабочий лист, применяющий для вычисления объемов выборок и суммы рангов функции СЧЕТЕСЛИ, СУММЕСЛИ, НОРМСТОБР и НОРМСТРАСП. В табл. ЕН.11.9 приведен рабочий лист Уилкоксон, предназначенный для применения рангового критерия Уилкоксона при анализе объемов продаж колы, расположенной на полках разного вида (см. табл. 11.9). Предполагается, что идентификаторы групп (например, “Полки” или “Стеллажи”), выборочные данные и ранги расположены в столбцах А-С рабочего листа Ранги соответственно. Функции СЧЕТЕСЛИ и СУММЕСЛИ имеют следующий вид.
СЧЕТЕСЛИ (диапазон; идентификатор выборки)
СУММЕСЛИ (диапазон; идентификатор выборки; диапазон суммы)
Здесь диапазон содержит подсчитываемые величины, идентификатор выборки представляет собой текст названия соответствующей выборки, а диапазон суммы содержит вычисленную сумму рангов.
Кроме того, в шаблоне рабочего листа используются формулы НОРМСТОБР и НОРМСТРАСП. Вызовы функций НОРМСТОБР и НОРМСТРАСП выглядят следующим образом.
НОРМСТОБР (вероятность),
НОРМСТРАСП (Z-значение),
где параметр вероятность представляет собой площадь области, ограниченной кривой распределения и величиной X, а параметр Z-значение является значением Z-статистики, имеющей стандартизованное нормальное распределение.
Таблица ЕН.11.9. Шаблон рабочего листа Уилкоксон
А / . / л,,в ?- . , ' .
1 Анализ объемов продаж
2
3 Данные
4 Уровень значимости 0,05
5
6 Выборка из первой генеральной совокупности
7 Объем выборки =СЧЁТЕСЛИ(Ранги!А2:А21;"Обычные")
8 Сумма рангов =СУММЕСЛИ(Ранги!А2:А21;"Обычные"; Ранги!С2:С21)
9 Выборка из второй генеральной совокупности
10 Объем выборки =СЧЁТЕСЛИ( Ранги !А2:А21/’Специализированные")
11 Сумма рангов =СУ ММЕСПИ (Ранги !А2:А21;"Специализированные"; Ранги!С2:С21)
12
13 Промежуточные вычисления
14 Общий объем выборки п =В7+В10
15 Статистика Т1 =ЕСЛИ(В7<=В10;В8;В11)
jj||| Среднее значение статистики И = ЕСЛИ(В7<=В10; В7*(В14+1 )/2; В10*(В14+1 )/2)
lllill Стандартная ошибка статистики Т1 =КОРЕНЬ(В7*В10*(В14+1)/12)
18 Z-статистика критерия =(В15-В16)/В17
19
Двусторонний критерий
iilil Нижнее критическое значение = НОРМСТОБР(В4/2)
22 Верхнее критическое значение =НОРМСТОБР(1-В4/2)
Ijllli /^значение =2*(1-НОРМСТРАСП(АВ5(В18)))
24 =ЕСЛИ(В23<В4;"Нулевая гипотеза отклоняется"; "Нулевая гипотеза не отклоняется")
Для задач, требующих применения одностороннего критерия, используются альтернативные варианты, показанные в табл. ЕН. 11.10.1 и ЕН. 11.10.2. (В обоих вариантах строка 2 4 остается пустой.) Для проверки решающего правила эти варианты шаблонов используют Функции НОРМСТОБР и НОРМСТРАСП.
Таблица ЕН.11.10.1. Шаблон рабочего листа Гипотеза для одностороннего критерия
В
20 Ограниченный снизу критерий
21 Нижнее критическое значение = Н0РМСТ0БР(В4)
22 ^-значение = Н0РМСТРАСП(В18)
23 = ЕСЛИ(В22<В4;"Нулевая гипотеза отклоняется"; "Нулевая гипотеза не отклоняется")
Таблица ЕН.11.10.2. Шаблон рабочего листа Гипотеза для одностороннего критерия
А ilBlIlillBeiei
20
21 Ограниченный сверху критерий
||||1|| Верхнее критическое значение = Н0РМСТ0БР(1-В4)
llllll /9-значение =1-Н0РМСТРАСП(В18)
lllill = ЕСЛИ(В22<В4;"Нулевая гипотеза отклоняется"; "Нулевая гипотеза не отклоняется")
ЕН.11.6. Критерий Крускала-Уоллиса для проверки гипотезы о разностях между несколькими медианами
Применяя критерий Крускала-Уоллиса для проверки гипотезы о разностях между несколькими медианами, сначала необходимо упорядочить и ранжировать исходные выборочные данные, а затем реализовать рабочий лист, использующий функции СЧЁТЕСЛИ,СУММЕСЛИ, ХИ2ОБР и ХИ2РАСП.
В табл. ЕН. 11.11 и ЕН. 11.12 продемонстрирован шаблон рабочего листа Крускал-Уоллис, предназначенного для решения задачи о прочности парашютов на основе данных, представленных в табл. 11.13. Этот шаблон предполагает, что значения и ранги четырех выборок размещены в столбцах А и С вместе с обозначениями (Поставщик 1, Поставщик 2, Поставщик 3 и Поставщик 4 соответственно) на рабочем листе Поставщики.
Таблица ЕН.11.11. Шаблон рабочего листа Крускал-Уоллис (диапазон Al: В15)
В
1 Анализ прочности парашютов
2
ilBII Данные
lill Уровень значимости 0,05
5
6 Промежуточные вычисления
7 Сумма квадратов рангов/объем выборки = (G6*F6)+(G7*F7)+(G8*F8)+(G9*F9)
8 Сумма объемов выборок =СУММ(Еб:Е9)
Окончание табл. ЕН. 77.77
9 Количество групп 4
10
11 Результаты проверки
leil Н-статистика =(12/(В8*(В8+1)))*В7-(3*(В8+1))
13 Критическое значение =ХИ2ОБР(В4;В9-1)
iBIl р-значение =ХИ2РАСП(В12;В9-1)
|jK = ЕСЛИ(В14<В4; "Нулевая гипотеза отклоняется"; "Нулевая гипотеза не отклоняется")
Таблица ЕН.11.12. Диапазон D5 :G9 шаблона рабочего листа Крускала-Уоллиса (диапазон DI :G4 пуст)
D Е F G
5 Группа Объем выборки Сумма рангов Средние ранги
6 1 =СЧ ЁТЕСЛ 14( Поставщики! А2:А21;"Поставщик 1") =СУММЕСЛИ(Поставщики!А2:А21; "Поставщик 1"; Поставщики!С2:С21) =F6/E6
7 2 =СЧ ЁТЕСЛ И (Поста вщики! А2:А21;"Поставщик 2") =СУММЕСЛ И (Поставщики !А2:А21; "Поставщик 2"; Поставщики!С2:С21) = F7/E7
8 3 =СЧ ЁТЕСЛ И (Поставщики! А2:А21;"Поставщик 3") =СУММЕСЛИ (Поставщики !А2:А21; "Поставщик 3"; Поставщики!С2:С21) =F8/E8
зшш 4 =СЧ ЁТЕСЛ И( Поставщики! А2:А21;"Поставщик 4") =СУММЕСЛИ(Поставщики!А2:А21; "Поставщик 4"; Поставщики!С2:С21) =F9/E9
Для вычисления объемов выборок и сумм рангов каждой из четырех выборок в шаблоне использованы функции СЧЕТЕСЛИ и СУММЕСЛИ, вызов которых имеет следующий вид.
СЧЕТЕСЛИ {диапазон, идентификатор выборки)
СУММЕСЛИ {диапазон, идентификатор выборки, диапазон суммы)
Здесь диапазон содержит подсчитываемые величины, идентификатор выборки представляет собой текст названия соответствующей выборки, а диапазон суммы содержит вычисленную сумму рангов. Как и во многих других шаблонах, в рабочем листе Крускал-Уоллис для вычисления критического значения £2-распределения и р-значения используются функции ХИ2ОБР и ХИ2 РАСП. Вызовы этих функций выглядят следующим образом.
ХИ2ОБР {уровень значимости', степени свободы),
ХИ2РАСП {критическое значение //; степени свободы).
Применяя этот шаблон, следует помнить, что текст и формулы, набранные в нескольких строках, на реальном листе должны вводиться в одной строке.
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
1. Conover, W. J. Practical Nonparametric Statistics, 3rd ed. (New York, John Wiley, 2000).
2. Daniel, W., Applied Nonparametric Statistics, 2nd ed. (Boston, PWS Kent, 1990).
3. Dixon, W. J., and F. J. Massey, Jr., Introduction to Statistical Analysis, 4th ed. (New York: McGraw-Hill, 1983).
4. Lewontin, R. C., and J. Felsenstein, “Robustness of Homogeneity Tests in 2 x n Tables”, Biometrics 21 (March, 1965): 19-33.
5. Marascuilo, L. A., “Large-Sample Multiple Comparisons”, Psychological Bulletin 65 (1966): 280-290.
6. Marascuilo, L. A., and M. McSweeney, Nonparametric and Distribution-Free Methods for the Social Sciences (Monterey, CA: Brooks/Cole, 1977).
7. Microsoft Excel 2002 (Redmond, WA: Microsoft Corporation, 2001).
Глава 12
Простая линейная регрессия
ПРИМЕНЕНИЕ СТАТИСТИКИ: прогнозирование объема продаж в магазине одежды
12.1. ВИДЫ РЕГРЕССИОННЫХ МОДЕЛЕЙ
12.2. ВЫВОД УРАВНЕНИЯ ПРОСТОЙ ЛИНЕЙНОЙ РЕГРЕССИИ
Метод наименьших квадратов
Visual Explorations: исследование коэффициентов простой линейной регрессии Прогнозирование в регрессионном анализе: интерполяция и экстраполяция Процедуры Excel: простой линейный регрессионный анализ
12.3. ОЦЕНКИ ИЗМЕНЧИВОСТИ
Вычисление сумм квадратов Коэффициент смешанной корреляции Среднеквадратичная ошибка оценки
12.4. ПРЕДПОЛОЖЕНИЯ
12.5. АНАЛИЗ ОСТАТКОВ
Оценка пригодности эмпирической модели Процедуры Excel: вычисление остатков Проверка условий
12.6. ИЗМЕРЕНИЕ АВТОКОРРЕЛЯЦИИ: СТАТИСТИКА ДУРБИНА-УОТСОНА
Распознавание автокорреляции с помощью графика остатков
Статистика Дурбина-Уотсона Процедуры Excel: вычисление статистики Дурбина-Уотсона
12.7. ПРОВЕРКА ГИПОТЕЗ О НАКЛОНЕ И КОЭФФИЦИЕНТЕ КОРРЕЛЯЦИИ
Применение t-критерия для наклона Применение F-критерия для наклона Доверительный интервал, содержащий наклон Pj Использование t-критерия для коэффициента корреляции
12.8. ОЦЕНКА МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ И ПРЕДСКАЗАНИЕ ИНДИВИДУАЛЬНЫХ ЗНАЧЕНИЙ
Построение доверительного интервала для математического ожидания отклика Вычисление доверительного интервала для предсказанного значения отклика Процедуры Excel: построение доверительных интервалов для математического ожидания и предсказанного значения отклика
12.9. ПОДВОДНЫЕ КАМНИ И ЭТИЧЕСКИЕ ПРОБЛЕМЫ, СВЯЗАННЫЕ
С ПРИМЕНЕНИЕМ РЕГРЕССИИ
12.10. ВЫЧИСЛЕНИЯ, СВЯЗАННЫЕ С ПРОСТОЙ ЛИНЕЙНОЙ РЕГРЕССИЕЙ
Вычисление сдвига Ьо и наклона Ъх Вычисление оценок вариации Вычисление среднеквадратичной ошибки наклона
СПРАВОЧНИК ПО EXCEL. ГЛАВА 12
ЧЕМУ ДОЛЖЕН НАУЧИТЬСЯ СТУДЕНТ
• Применять регрессионный анализ для предсказания значений зависимой переменной по значениям независимой*
• Понимать смысл регрессионных коэффициентов д0 и
• Оценивать предположения, которые должны выполняться при регрессионном анализе, и выявлять их нарушения.
• Делать выводы о наклоне и коэффициенте корреляции.
• Оценивать средние значения и предсказывать индивидуальные ве-
личины.
ПРИМЕНЕНИЕ СТАТИСТИКИ
Прогнозирование объема продаж в магазине одежды
Сеть магазинов уцененной одежды Sunflowers на протяжении 25 лет постоянно расширялась. Однако в настоящее время у компании нет систематического подхода к выбору новых торговых точек. Место, в котором компания собирается открыть новый магазин, определяется на основе субъективных соображений. Критериями выбора являются выгодные условия аренды или представления менеджера об идеальном местоположении магазина. Представьте себе, что вы — руководитель отдела специальных проектов и планирования. Вам поручили разработать стратегический план открытия новых магазинов. Этот план должен содержать прогноз годового объема продаж во вновь открываемых магазинах. Вы полагае
те, что торговая площадь непосредственно связана с объемом выручки, и хотите учесть этот факт в процессе принятия решения. Как разработать статистическую модель, позволяющую прогнозировать годовой объем продаж на основе размера нового магазина?
ВВЕДЕНИЕ
В предыдущих главах предметом анализа часто становилась отдельная числовая переменная, например, доходность взаимных фондов, время загрузки Web-страницы или объем потребления безалкогольных напитков. В главе 3 были рассмотрены различные средства статистического описания таких переменных. В главе 7 изложены методы построения доверительных интервалов, содержащих математическое ожидание и основную массу значений числовой переменной, а в главах 8-10 описаны критерии проверки гипотез о математическом ожидании одной группы и разностях между математическими ожиданиями двух и более групп. В данной и следующих двух главах мы рассмотрим методы предсказания значений числовой переменной в зависимости от значений одной или нескольких других числовых переменных.
Как правило, для предсказания значений переменной используется регрессионный анализ (regression analysis). Его цель — разработать статистическую модель, позволяющую предсказывать значения зависимой переменной (dependent variable), или отклика (response), по значениям, по крайней мере одной, независимой, или объясняющей, переменной (independent, or explanatory variable). В данной главе мы рассмотрим простую линейную регрессию (simple linear regression) — статистический метод, позволяющий предсказывать значения зависимой переменной Y по значениям независимой переменной X. В главах 13 и 14 описана модель множественной регрессии, предназначенная для предсказания значений независимой переменной Y по значениям нескольких зависимых переменных (Х19 Х2, ..., Xk) \
Если зависимая переменная является категорийной, необходимо применять логистическую регрессию [4].
12.1. ВИДЫ РЕГРЕССИОННЫХ МОДЕЛЕЙ
В разделе 2.3 для иллюстрации зависимости между переменными X и Y использовалась диаграмма разброса (scatter diagram). На ней значения переменной X откладывались по горизонтальной оси, а значения переменной У — по вертикальной. Зависимость между двумя переменными может быть разной: от самой простой до крайне сложной. Пример простейшей (линейной) зависимости показан на рис. 12.1.
_______1_1 ДУ — приращение переменной Y >
ДХ— приращение переменной X \
I
Рис. 12.1. Положительная линейная зависимость
ПРОСТАЯ ЛИНЕЙНАЯ РЕГРЕССИЯ
У, = р0 + р,Х, + 8,, (12.1)
где Ро — сдвиг (длина отрезка, отсекаемого на координатной оси прямой У), pt — наклон прямой У, 8, — случайная ошибка переменной У в i-м наблюдении.
В этой модели наклон pj (slope) представляет собой количество единиц измерения переменной У, приходящихся на одну единицу измерения переменной X. Эта величина характеризует среднюю величину изменения переменной У (положительного или отрицательного) на заданном отрезке оси X. Сдвиг р0 (У intercept) представляет собой среднее значение переменной У, когда переменная X равна 0. Последний компонент модели 8, является случайной ошибкой переменной У в i-м наблюдении.
Выбор подходящей математической модели зависит от распределения значений переменных X и У на диаграмме разброса. Различные виды зависимости переменных показаны на рис. 12.2 (панели А-Е).
На панели А значения переменной У почти линейно возрастают с увеличением переменной X. Этот рисунок аналогичен рис. 12.3, иллюстрирующему положительную зависимость между размером магазина (в квадратных футах) и годовым объемом продаж.
Панель Б является примером отрицательной линейной зависимости. Если переменная X возрастает, переменная У в целом убывает. Примером этой зависимости является связь между стоимостью конкретного товара и объемом продаж.
На панели В показан набор данных, в котором переменные X и Y практически не зависят друг от друга. Каждому значению переменной X соответствуют как большие, так и малые значения переменной У.
Данные, приведенные на панели Г, демонстрируют криволинейную зависимость между переменными X и У. Значения переменной У возрастают при увеличении переменной X, однако скорость роста после определенных значений переменной X падает. Примером положительной криволинейной зависимости является связь между возрастом и стоимостью обслуживания автомобилей. По мере старения машины стоимость ее обслуживания сначала резко возрастает, однако после определенного уровня стабилизируется.
Положительная линейная зависимость Отрицательная линейная зависимость
Переменные X и Y не зависят друг от друга Положительная криволинейная зависимость
U-образная криволинейная зависимость Отрицательная криволинейная зависимость
l> J KI
Рис. 12.2. Диаграммы разброса, иллюстрирующие разные виды зависимостей
Панель Д демонстрирует параболическую U-образную форму зависимости между переменными X и У. По мере увеличения значений переменной X значения переменной У сначала убывают, а затем возрастают. Примером такой зависимости является связь между количеством ошибок, совершенных за час работы, и количеством отработанных часов. Сначала работник осваивается и делает много ошибок, потом привыкает, и количество ошибок уменьшается, однако после определенного момента он начинает чувствовать усталость, и число ошибок увеличивается.
На панели Е показана экспоненциальная зависимость между переменными X и У. В этом случае переменная У сначала очень быстро убывает при возрастании переменной X, однако скорость этого убывания постепенно падает. Например, стоимость автомобиля при перепродаже экспоненциально зависит от его возраста. Если перепродавать автомобиль в течение первого года, его цена резко падает, однако впоследствии ее падение постепенно замедляется.
Итак, мы кратко рассмотрели основные модели, которые позволяют формализовать зависимости между двумя переменными. Несмотря на то что диаграмма разброса чрезвычайно полезна при выборе математической модели зависимости, существуют более сложные и точные статистические процедуры, позволяющие описать отношения между переменными. В дальнейшем мы будем рассматривать лишь линейную зависимость.
14
Диаграмма разброса
--,------------~--JJCS3-
12 -
10 -
4> 5 to о
5
§
8 -
6 -
4 -
2 -
’:.. ч• ,'ННГЪ .. -ч
о --о
2 3 4 5
Площадь, тыс. кв. футов
6
Рис. 12.3. Диаграмма разброса данных о магазинах сети Sunflower (построена с помощью программы Microsoft Excel)
12.2. ВЫВОД УРАВНЕНИЯ ПРОСТОЙ ЛИНЕЙНОЙ РЕГРЕССИИ
Вернемся к сценарию, изложенному в начале главы. Наша цель — предсказать объем годовых продаж для всех новых магазинов, зная их размеры. Для оценки зависимости между размером магазина (в квадратных футах) и объемом его годовых продаж создадим выборки из 14 магазинов (табл. 12.1).
Таблица 12.1. Площади и годовые объемы продаж 14 магазинов сети Sunflowers
Магазин Площадь (тыс. кв. футов) Объем годовых продаж (тыс. долл.) Магазин Площадь (тыс. кв. футов) Объем годовых продаж (тыс. долл.)
1 1,7 3,7 8 1,1 2,7
2 1,6 3,9 9 3,2 5,5
3 2,8 6,7 10 1,5 2,9
4 5,6 9,5 11 5,2 10,7
5 1,3 3,4 12 4,6 7,6
6 2,2 5,6 13 5,8 11,8
7 1,3 3,7 14 3,0 4,1
Диаграмма разброса этих данных продемонстрирована на рис. 12.3. Анализ рис. 12.3 показывает, что между площадью магазина X и годовым объемом продаж У существует положительная зависимость. Если площадь магазина увеличивается, объем продаж возрастает почти линейно. Таким образом, наиболее подходящей для исследо-
вания является линейная модель. Остается лишь определить, какая из линейных моделей точнее остальных описывает зависимость между анализируемыми переменными.
Метод наименьших квадратов
В предыдущем разделе определена статистическая модель, описывающая связь между двумя переменными — площадью и объемом продаж, — характеризующими сеть магазинов уцененной одежды Sunflowers. Однако данные, представленные в табл. 12.1, получены для случайной выборки магазинов. Если верны некоторые предположения (см. раздел 12.4), в качестве оценки параметров генеральной совокупности 0О и 0! можно использовать сдвиг Ьо и наклон Ьх прямой У. Таким образом, уравнение простой линейной регрессии принимает следующий вид.
ПРОСТАЯ ЛИНЕЙНАЯ РЕГРЕССИЯ
Предсказанное значение переменной У равно сумме сдвига и наклона, умноженного на значение переменной X:
Y^b.+b.X,, (12.2)
где Yt — предсказанное значение переменной У для t-го наблюдения, X, — значение переменной X в i-м наблюдении.
Для того чтобы предсказать значение переменной У, в уравнении (12.2) необходимо определить два коэффициента регрессии (regression coefficients) — сдвиг ba и наклон Ьх прямой У. Вычислив эти параметры, проведем прямую на диаграмме разброса. Затем исследователь может визуально оценить, насколько близка регрессионная прямая к точкам наблюдения.
Простая линейная регрессия позволяет найти прямую линию, максимально приближенную к точкам наблюдения. Критерии соответствия можно задать разными способами. Возможно, проще всего минимизировать разности между фактическими значениями У, и предсказанными значениями Yt . Однако, поскольку эти разности могут быть как положительными, так и отрицательными, следует минимизировать сумму их квадратов.
Поскольку
Y=b() + b,Xi ,
сумма квадратов принимает следующий вид:
£(^)!=£(мм*л));-
1=1 ,=1
Параметры Ъо и Ьх неизвестны. Таким образом, сумма квадратов разностей является функцией, зависящей от сдвига Ъо и наклона Ьх выборки У.
Для того чтобы найти значения параметров bQ и Ьх, минимизирующих сумму квадратов разностей, применяется метод наименьших квадратов (least-squares method). При любых других значениях сдвига bQ и наклона Ьх сумма квадратов разностей между фактическими значениями переменной У и ее наблюдаемыми значениями лишь увеличится.
В книге все вычисления, связанные с реализацией метода наименьших квадратов, проводились с помощью программы Microsoft Excel. Однако, чтобы понять результаты, представленные на рис. 12.4, необходимо изучить раздел 12.10, в котором подробно описан процесс вычислений.
____£
1 (Регрессионный анализ данных о магазинах
2~
3 j Регрессионная статистика
^Множественный R 0,95088
jSjR-квадрат 0,90418
6 IНормированный R-квадрат 0,89619
7 jСтандартная ошибка 0,96638
8 (Наблюдения 14
Л4 SSE SSR SST
10 [Дисперсионный анализ__________________/_________________________________
11"' df \ \s / MS
12 .Регрессия 1 105,74761 / 105,74761
13: Остаток 12 ^11,20668/ 0,93389
~14~j Итого 13 116,95429
р-значение
113,23351 1,82269Е-07
II6 J_____________Ор —-—коэффициенты Стандартная ошибка t-статистика P-значение Нижние 95% Верхние 95%
17'iY-пересечение bx 0,96447 0,52619 1,83293 0,09173 -0,18200 2,11095
18]Площадь, кв фут. ' ------------ 1,66986 0,15693 10,64112 0,00000 1,32795 2,01177
Рис. 12.4. Результаты решения задачи о зависимости между площадями и годовыми объемами продаж в магазинах сети Sunflower (получены с помощью программы Microsoft Excel)
Как следует из рис. 12.4, Ьо = 1,670, а Ьг = 0,964. Таким образом, уравнение линейной регрессии для этих данных имеет следующий вид:
^ = 0,964 + 1,670^, .
Рис. 12.5. Диаграмма разброса и линия регрессии в задаче о выборе магазина, построенные с помощью программы Microsoft Excel
Вычисленный наклон Ьо равен +1,670. Это означает, что при возрастании переменной X на единицу среднее значение переменной У возрастает на 1,67 единиц. Иначе говоря, увеличение площади магазина на один квадратный фут приводит к увеличению годового объема продаж на 1,67 долл. Таким образом, наклон представляет собой долю годового объема продаж, зависящую от размера магазина.
Вычисленный сдвиг Ъ{ равен +0,964 (млн. долл.). Эта величина представляет собой среднее значение переменной У при X = 0. Поскольку площадь магазина не может равняться нулю, сдвиг можно считать долей годового дохода, зависящей от других факторов. Следует отметить, однако, что сдвиг переменной У выходит за пределы диапазона переменной X. Следовательно, к интерпретации параметра Ъх необходимо относиться внимательно. График простой линейной регрессии вместе с наблюдаемыми величинами показан на рис. 12.5.
Visual Explorations: исследование коэффициентов простой линейной регрессии
Для построения линии регрессии с помощью метода наименьших квадратов следует применить процедуру Simple Linear Regression из пакета Visual Exploration in Statistics. Чтобы выполнить эту процедуру, необходимо открыть рабочую книгу макросов visual Explorations .xla и выбрать команду Visual Exploration4>Simple Linear Regression (Visual Exploration^Простая линейная регрессия). Эта процедура создает диаграмму разброса, изображая произвольную линию регрессии (см. первую иллюстрацию).
Изменить положение линии регрессии можно с помощью выбора параметров Ьо и Ьг Для этого на экран выводится панель, содержащая окно с кнопкой счетчика (см. вторую иллюстрацию). Попробуйте провести линию регрессии как можно ближе к точкам наблюдения. Контролируйте точность аппроксимации (sum of squares errors - SSE) как визуально, так и с помощью суммы квадратов разностей (ошибки), выведенной в окне Difference from target SSE (Отклонение от требуемой точности аппроксимации).
Для того чтобы вернуть параметры в начальное положение, достаточно щелкнуть на кнопке Reset (Отмена). Если возникнут проблемы, обратитесь к справочной системе, щелкнув на кнопке Help (Справка). Чтобы увидеть, как выглядит истинная линия регрессии, имеющая минимальное среднеквадратичное отклонение от точек наблюдения, щелкните на кнопке Solution (Решение). Завершая исследование линейной регрессии, щелкните на кнопке Finish (Готово).
Исследование собственныхданных. Для исследования коэффициентов простой линейной регрессии, построенной с помощью метода наименьших квадратов на основе ваших собственных данных, следует открыть рабочую книгу макросов Visual Explorations. xla (если она была закрыта) и выполнить такие действия.
1. Выбрать команду Visual Explorations^Simple Linear Regression, находясь в рабочем листе, содержащем ваши собственные данные.
2. В диалоговом окне Simple Linear Regression сделать следующее (см. иллюстрацию).
2.1. Ввести в диалоговом окне Y Variable Cell Range (Входной интервал Y) диапазон ячеек, содержащий значения переменной Y.
2.2. Ввести в диалоговом окне X Variable Cell Range (Входной интервал X) диапазон ячеек, содержащий значения переменной X.
2.3. Установить флажок First cells in both ranges contain a label (Первые ячейки обоих диапазонов содержат метку).
2.4. Ввести в диалоговом окне Title (Заглавие) название диаграммы.
2.5. Щелкнуть на кнопке ОК.
Эта процедура создает диаграмму разброса, изображая произвольную линию регрессии. Для изменения параметров линии регрессии на экран выводится панель, содержащая окно с кнопкой счетчика. Инструкции по настройке линии регрессии приведены в предыдущем разделе. Для завершения работы щелкните на кнопке Finish (Готово).
Рассмотрим интерпретацию сдвига и наклона простой линейной регрессии.
ПРИМЕР 12.1. ИНТЕРПРЕТАЦИЯ СДВИГА Д И НАКЛОНА Д
Один экономист решил предсказать изменение индекса 500 наиболее активно покупаемых акций на Нью-Йоркской фондовой бирже, публикуемого агентством Standard and Poor, на основе показателей экономики США за 50 лет. В результате он получил следующее уравнение линейной регрессии:
У ~-5,0 + 7Х .
Какой смысл имеют параметры сдвига Ьо и наклона Ьг?
РЕШЕНИЕ. Сдвиг регрессии 60 равен -5,0. Это значит, что если рост экономики США равен нулю, индекс акций за год снизится на 5% . Наклон Ъх равен 7. Следовательно, при увеличении темпов роста экономики на 1% индекс акций возрастает на 7%.
Вернемся к сценарию, изложенному в начале главы. Применим модель линейной регрессии для прогноза объема годовых продаж во всех новых магазинах в зависимости от их размеров.
ПРИМЕР 12.2. ПРЕДСКАЗАНИЕ СРЕДНЕГОДОВОГО ОБЪЕМА ПРОДАЖ В МАГАЗИНАХ ПО ИХ ПЛОЩАДИ
Предположим, что площадь магазина равна 4 000 квадратных футов. Какой его среднегодовой объем продаж?
РЕШЕНИЕ. Подставим значение X = 4 (тыс. кв. футов) в уравнение простой линейной регрессии:
Y, = 0,964 + 1,670Х, = 0,964 + 1,670x4 = 7 644 млн. долл.
Итак, прогнозируемый среднегодовой объем продаж в магазине, площадь которого равна 4 000 кв. футов, составляет 7 644 000 долл.
Прогнозирование в регрессионном анализе: интерполяция и экстраполяция
Применяя регрессионную модель для прогнозирования, необходимо учитывать лишь допустимые значения (relevant range) независимой переменной. В этот диапазон входят все значения переменной X, начиная с минимальной и заканчивая максимальной. Таким образом, предсказывая значение переменной Y при конкретном значении переменной X, исследователь выполняет интерполяцию между значениями переменной X в диапазоне возможных значений. Однако экстраполяция значений за пределы этого интервала невозможна. Например, пытаясь предсказать среднегодовой объем продаж в магазине, зная его площадь (табл. 12.1), мы можем вычислять значение переменной Y лишь для значений X от 1,1 до 5,8 тыс. кв. футов. Следовательно, прогнозировать среднегодовой объем продаж можно лишь для магазинов, площадь которых не выходит за пределы указанного диапазона. Любая попытка экстраполяции означает, что мы предполагаем, будто линейная регрессия сохраняет свой характер за пределами допустимого диапазона.
Процедуры Excel: простой линейный регрессионный анализ
Для того чтобы выполнить простой линейный регрессионный анализ, сначала необходимо построить диаграмму разброса, вызвав Мастер диаграмм программы Microsoft Excel, а затем добавить линию регрессии с помощью процедуры Сервис*=>Анализ данных^Регрессия. Надстройка PHStat2 выполняет эти действия автоматически.
Например, чтобы построить диаграмму разброса и линию регрессии по данным, приведенным в табл. 12.1, необходимо открыть рабочую книгу chapter 12.xls на листе Данные, выбрать команду Вставка^Диаграмма... и выполнить одну из следующих процедур.
Применение Excel в сочетании с надстройкой PHStat2
Для построения диаграммы разброса и вычисления регрессионных статистик можно воспользоваться надстройкой PHStat2, выполняя следующие инструкции .
1. Выбрать команду PHStat^Regression^Simple Linear Regression... (PHStat1^ Регрессиям Простая линейная регрессия...).
2. В диалоговом окне Simple Linear Regression выполнить такие действия (см. иллюстрацию).
2.1. Ввести в диалоговом окне Y Variable Cell Range (Входной интервал Y) диапазон ячеек cl: С15.
2.2. Ввести в диалоговом окне X Variable Cell Range (Входной интервал X) диапазон ячеек Bl: В15.
2.3. Установить флажок First cells in both ranges contain a label (Первые метки обоих интервалов содержит метки).
2.4. Ввести в диалоговом окне Confidence level for regression coefficients (Доверительный уровень для коэффициентов регрессии) число 0.95.
2.5. Установить флажки Regression Statistics Table (Таблица регрессионных статистик) и ANOVA and Coefficients Table (Сводная таблица дисперсионного анализа и коэффициентов).
Simple Linear Regression
Data
> Y Variable Cell Range: IcTiciS _- j
! X Variable Cell Range: |в1:В15 T]
i P First cells in both ranges contain label Confidence level for regression coefficients: 195 %
Regression Tool Output Options
P Regression Statistics Table
P ANOVA and Coefficients Table
Г“ Residuals Table
i Г" Residual Plot
Output Options
Title: | Анализ данных о магазинах
I Р Scatter Diagram
Г Durbin-Watson Statistic
Г* Confidence and Prediction Interval for X = |
Help j |L,lgK..’, j] Cancel j
2.6. Ввести в диалоговом окне Title (Заголовок) название диаграммы.
2.7. Установить флажок Scatter diagram (Диаграмма разброса).
2.8. Щелкнуть на кнопке ОК.
Рабочий лист, создаваемый этой процедурой, не является динамически обновляемым, поэтому при изменении исходных данных необходимо заново выполнить все действия.
Для того чтобы добавить на созданную диаграмму разброса линию регрессии, следуйте инструкциям из раздела ЕН.12.2.
Применение Excel
Чтобы построить диаграмму разброса и выполнить простой линейный регрессионный анализ, следуйте инструкциям, приведенным ниже. Построение диаграммы разброса и вычисление регрессионных коэффициентов не связаны между собой, поэтому эти процедуры можно выполнять независимо друг от друга.
Вычисление регрессионных статистик. Для вычисления простой линейной регрессии на основе данных, приведенных в табл. 12.1, следуйте инструкциям из раздела ЕН.12.1.
Построение диаграммы разброса. Для построения диаграммы разброса необходимо открыть pa- j бочую книгу Chapter 12. xls на листе Данные, выбрать команду Вставка^Диаграмма..., вызывая | Мастер диаграмм программы Microsoft Excel, и следовать инструкциям, приведенным ниже. I
1. На первом этапе диалога выполните такие действия.
1.1. Щелкните на корешке вкладки Стандартные, а затем выберите пункт Точечная в раскрывающемся списке Тип.
1.2. Выберите первую (верхнюю) диаграмму, сопровождающуюся описанием: "Точечная диаграмма позволяет сравнить пары значений.", а затем щелкните на кнопке Далее>.
2. На втором этапе диалога выполните такие действия.
2.1. Щелкните на корешке вкладки Диапазон данных, а затем введите в окне редактирования Диапазон ссылки на ячейки Bl: cl5.
2.2. Установите переключатель Ряды в положение В столбцах и щелкните на кнопке Далее>.
3. На третьем этапе диалога выполните такие действия.
3.1. Щелкните на корешке вкладки Заголовки. Введите в окне редактирования Название диаграммы строку Диаграмма разброса, в окне редактирования Ось X - строку Площадь (тыс. кв. футов), а в окне редактирования Ось Y — строку Годовой объем продаж (млн. долл.).
3.2. По очереди щелкните на корешках вкладок Оси, Линии сетки, Легенда и Подписи данных. Установите флажки и переключатели, как показано в разделе ЕР.6.
3.3. Щелкните на кнопке Далее>.
4. На четвертом этапе диалога установите переключатель Поместить диаграмму на листе в положение Отдельном и щелкните на кнопке Готово.
Обратите внимание на то, что Мастер диаграмм всегда предполагает, что первый столбец в диапазоне данных содержит значения переменной %(как в предыдущем примере). Во многих рабочих листах с данными для регрессионного анализа в первом столбце содержатся значения переменной X В этих ситуациях необходимо переместить значения переменной Y в столбец, следующий после переменной X, и лишь затем выполнять инструкции 1-4. Если значения переменной /могут быть отрицательными, Мастер диаграмм проведет ось Х(с метками) через точку У= 0, а не внизу диаграммы. Если вам необходимо переместить ось % и соответствующие метки в нижнюю часть диаграммы, следуйте инструкциям, указанным в разделе ЕН.12.3.
Добавление линии регрессии. Для того чтобы добавить на диаграмму разброса линию регрессии, следуйте инструкциям, приведенным в разделе ЕН.12.2.
Содержимое компакт-диска
г Диаграмма разброса, показанная на рис. 12.3, и результаты регрессионного анализа данных, приведенных в табл. 12.1, содержатся в рабочей книге Chapter 12.xls на листах Рис12.3, Рис12.4 и Рис12.5.
Изучение основ
12.1. Предположим, что, выполнив регрессионный анализ, мы получили следующее уравнение простой линейной регрессии:
^ = 2 + 5^ .
1. Дайте интерпретацию сдвига Ьо.
2. Дайте интерпретацию наклона
3. Предскажите среднее значение переменной Y при X = 3.
Предположим, что переменная X изменяется от 2 до 25. Можно ли предсказать значение переменной Y, если переменная X принимает одно из следующих значений?
4. 3.
5. -3.
6. 0.
7. 24.
8. 26.
12.2. Предположим, что, выполнив регрессионный анализ, мы получили следующее уравнение простой линейной регрессии:
Y, = 16-0,5У,.
1. Дайте интерпретацию сдвига Ьо.
2. Дайте интерпретацию наклона Ь,.
3. Предскажите среднее значение переменной У при X = 6.
Применение понятий
Задачу 12.3 можно решать как вручную, так и с помощью программы Microsoft Excel. Задачи 12.4-12.8 рекомендуется решать с помощью программы Microsoft Excel.
12.3. Менеджер по маркетингу в компании, владеющей крупной сетью супермаркетов, желает оценить влияние расстояния между полками на объем продаж корма для домашних животных. Для анализа создана случайная выборка, состоящая из 12 одинаковых магазинов. ^PETFOOD. XLS.
Магазин Расстояние между полками, X (Футы) Еженедельный объем продаж, Y (тыс. долл.)
1 5 0,16
2 5 0,22
3 5 0,14
4 10 0,19
5 10 0,24
6 10 0,26
7 15 0,23
8 15 0,27
9 15 0,28
10 20 0,26
11 20 0,29
12 20 0,31
1. Постройте диаграмму разброса.
2. Вычислите коэффициенты простой линейной регрессии bQ и Ьо, пользуясь методом наименьших квадратов.
3. Дайте интерпретацию наклона Ьх.
4. Предскажите средний еженедельный объем продаж (в сотнях долларов) в магазине, в котором расстояние между полками составляет 8 футов.
5. Предположим, что в магазине №12 объем продаж равен 0,26 тыс. долл. Повторите упражнения 1-4 с новыми данными и сравните результаты с предыдущими.
6. На каком расстоянии вы рекомендуете устанавливать полки? Обоснуйте свой ответ.
12.4. В каждом агентстве по перевозке грузов внутри города обычно есть опытный менеджер, умеющий предсказывать количество рабочего времени, необходимого для завершения всей работы. В прошлом такой подход оправдывал себя, однако в настоящее время существуют более точные методы предсказания количества требуемого рабочего времени в зависимости от объема перевозимых грузов. Для разработки такого метода в файле ^MOVING. XLS собраны данные о 36 перевозках, которые свидетельствуют о том, что затраты на переезд составляют несущественную долю всего рабочего времени.
1. Постройте диаграмму разброса.
2. Вычислите коэффициенты простой линейной регрессии Ьп и Ь,, пользуясь методом наименьших квадратов.
3. Дайте интерпретацию наклона Ьх.
4. Предскажите количество рабочего времени, требуемого для перевозки 500 куб. футов груза.
5. Какие факторы, кроме объема груза, влияют на затраты рабочего времени?
12.5. Менеджер крупной сети почтовых отделений полагает, что между общим весом корреспонденции и количеством заказов существует связь. Он хотел бы предсказать количество заказов, зная общий вес корреспонденции. Для анализа создана случайная выборка, состоящая из 25 почтовых пакетов, вес которых изменялся от 200 до 700 фунтов. ^MAIL . XLS.
Вес корреспонденции (фунты) Количество заказов (тысячи) Вес корреспонденции (фунты) Количество заказов (тысячи)
216 6,1 432 13,6
283 9,1 409 12,8
237 7,2 553 16,5
203 7,5 572 17,1
259 6,9 506 15,0
374 11,5 528 16,2
342 10,3 501 15,8
301 9,5 628 19,0
365 9,2 677 19,4
384 10,6 602 19,1
404 12,5 630 18,0
426 12,9 652 20,2
482 14,5
1. Постройте диаграмму разброса.
2. Вычислите коэффициенты простой линейной регрессии Ьо и пользуясь методом наименьших квадратов.
3. Дайте интерпретацию наклона Ьг.
4. Предскажите среднее количество заказов (в тысячах), если вес корреспонденции — 500 фунтов.
12.6. Компания, имеющая права на распространение видеокассет с предварительными версиями кинофильмов, хотела бы иметь возможность оценивать возможное количество заказов. Для анализа предоставлены данные о 30 фильмах, в которых указаны объемы кассовых сборов (млн. долл.) и количество проданных видеокассет (тыс. шт.). C^MOVIE . XLS.
1. Постройте диаграмму разброса.
2. Вычислите коэффициенты простой линейной регрессии Ьп и пользуясь методом наименьших квадратов.
3. Запишите уравнение простой линейной регрессии.
4. Дайте интерпретацию сдвига Ьо и наклона д,.
5. Предскажите среднее количество заказов на фильм, если его кассовый сбор равен 20 млн. долл.
6. Какие еще факторы могут повлиять на количество заказов? Обоснуйте свой ответ.
12.7. Агент компании, занимающейся торговлей недвижимостью, хотел бы иметь возможность предсказывать месячную стоимость аренды апартаментов в зависимости от их полезной площади. Для анализа были отобраны 25 апартаментов в определенном районе. Данные о них приведены в следующей таблице. ^RENT. XLS.
Апартаменты Месячная рента (долл.) Площадь (кв. футы) Апартаменты Месячная рента (долл.) Площадь (кв. футы)
1 950 850 14 1 800 1 369
2 1 600 1 450 15 1 400 1 175
3 1 200 1 085 16 1 450 1 225
4 1 500 1 232 17 1 100 1 245
5 950 718 18 1 700 1 259
6 1 700 1 485 19 1 200 1 150
7 1 650 1 136 20 1 150 896
8 935 726 21 1 600 1 361
9 875 700 22 1 650 1 040
10 1 150 956 23 1 200 755
11 1 400 1 100 24 800 1 000
12 1 650 1 285 25 1 750 1 200
13 2 300 1 985
1. Постройте диаграмму разброса.
2. Вычислите коэффициенты простой линейной регрессии Ьо и пользуясь методом наименьших квадратов.
3. Запишите уравнение простой линейной регрессии.
4. Дайте интерпретацию сдвига Ьо и наклона
5. Предскажите месячную стоимость аренды апартаментов, площадь которых равна 1000 кв. футов.
6. Почему эту модель нельзя применить для предсказания месячной стоимости аренды апартаментов, площадь которых равна 500 кв. футов?
7. Представьте себе, что ваши друзья Джим и Дженифер планируют подписать договор аренды апартаментов в указанном районе. У них есть два варианта: апартаменты площадью 1 000 кв. футов за 1 275 долл, в месяц и апартаменты площадью 1 200 кв. футов за 1 425 долл, в месяц. Какой совет вы бы дали своим друзьям? Почему?
12.8. В файле ^HARDNESS . XLS содержатся данные о твердости и прочности 35 образцов прессованного алюминия. Считается, что твердость, измеренную в единицах по Роквеллу (Rockwell Е), можно использовать для предсказания прочности, измеренной в тысячах фунтов на квадратный дюйм.
1. Постройте диаграмму разброса.
2. Вычислите коэффициенты простой линейной регрессии Ьо и bv пользуясь методом наименьших квадратов.
3. Дайте интерпретацию наклона Ъх.
4. Предскажите среднюю прочность прессованного алюминия, если его твердость — 30 единиц по Роквеллу.
12.3. ОЦЕНКИ ИЗМЕНЧИВОСТИ
Вычисление сумм квадратов
Для того чтобы предсказать значение зависимой переменной по значениям независимой переменной в рамках избранной статистической модели, необходимо оценить изменчивость. Существует несколько способов оценки изменчивости. Первый способ использует общую сумму квадратов (total sum of squares — SST), позволяющую оценить колебания значений У вокруг среднего значения У . В регрессионном анализе полная вариация, представляющая собой полную сумму квадратов, разделяется на объяснимую вариацию, или сумму квадратов регрессии (regression sum of squares — SS.R, or explained variation), и необъяснимую вариацию (unexplained variation), или сумму квадратов ошибок (error sum of squares — SSE). Объяснимая вариация характеризует взаимосвязь между переменными X и У, а необъяснимая зависит от других факторов (рис. 12.6).
Рис. 12.6. Оценки изменчивости в модели регрессии
Сумма квадратов регрессии (SSR) представляет собой сумму квадратов разностей между Y( (предсказанным значением переменной У) и У (средним значением переменной Y). Сумма квадратов ошибок (SSE) является частью вариации переменной У, которую невозможно описать с помощью регрессионной модели. Эта величина зависит от разностей между наблюдаемыми и предсказанными значениями.
ОЦЕНКИ ИЗМЕНЧИВОСТИ В РЕГРЕССИОННОЙ МОДЕЛИ
Полная сумма квадратов (SST) равна сумме квадратов регрессии плюс сумма квадратов ошибок:
SST = SSR + SSE. (12.3)
ПОЛНАЯ СУММА КВАДРАТОВ
Полная сумма квадратов (SST) равна сумме квадратов разностей между наблюдаемыми значениями переменной У и ее средним значением:
ssT = ^{Y-y)~ • (12.4)
СУММА КВАДРАТОВ РЕГРЕССИИ
Сумма квадратов регрессии (SSR) равна сумме квадратов разностей между предсказанными значениями переменной У и ее средним значением:
55Я = £(};-г)2 . (12.5)
СУММА КВАДРАТОВ ОШИБОК
Сумма квадратов ошибок (SSE) равна сумме квадратов разностей между наблюдаемыми и предсказанными значениями переменной У:
= . (12.6)
Суммы квадратов, вычисленные с помощью программы Microsoft Excel при решении задачи о сети магазинов Sunflowers, представлены на рис. 12.7.
SSR
10 Дисперсионный анализ \
11 L MS F Значимость F
12 Регрессия 1 ' 105,74761 105,74761 113,23351 1.82269Е-07
13 Остаток 12 11,20668 \ 0,93389
14 Итого 13 „ 116,95429 Х
SST
SSE
Рис. 12.7. Суммы квадратов, вычисленные с помощью программы Microsoft Excel при решении задачи о сети магазинов Sunflowers
Как видим,
SSR = 105,7476, SSE = 11,2067, SST =116,9543.
Кроме того, по формуле (12.3)
SST = SSR + SSE,
116,9543 = 105,7476 + 11,2067.
Полная сумма квадратов разностей равна 116,9543. Эта величина состоит из суммы квадратов регрессии (SSR), равной 105,7476, и суммы квадратов ошибок (SSE), равной 11,2067.
НАУЧНЫЙ ФОРМАТ
Обратите внимание на то, что в некоторых версиях программы Excel величина SSR представляется в так называемом научном формате. Этот формат применяется для • представления очень маленьких или очень больших числовых величин. Число, • стоящее после буквы Е, задает количество позиций, на которое следует перенести десятичную точку: влево — если это число отрицательное, вправо — если положительное. Например, запись 3,7431Е+02 означает, что десятичную точку следует перенести на две позиции вправо, т.е. число равно 374,31. Запись 3,7431Е-02 означает, что десятичную точку необходимо перенести на две позиции влево, т.е. число равно 0,037431. Учтите, что при записи чисел в научном формате количество значащих цифр, как правило, уменьшается, и числа могут округляться.
Коэффициент смешанной корреляции
Величины SRR, SSE и SST не имеют очевидной интерпретации. Однако отношение суммы квадратов регрессии (SSR) к полной сумме квадратов (SST) представляет собой оценку полезности регрессионного уравнения. Это отношение называется коэффициентом смешанной корреляции г2. (Иногда используется термин “коэффициент детерминации” (coefficient of determination). — Прим, ред.)
КОЭФФИЦИЕНТ СМЕШАННОЙ КОРРЕЛЯЦИИ
Коэффициент смешанной корреляции равен результату деления суммы квадратов регрессии на полную сумму квадратов:
_ сумма квадратов регрессии _ SSR (12 7)
полная сумма квадратов SST
Коэффициент смешанной корреляции оценивает долю вариации переменной У, которая объясняется независимой переменной X в регрессионной модели. В задаче о сети магазинов Sunflowers SSR = 105,7476, SSE = 11,2067 и SST = 116,9543. Следовательно,
105,7476
116,9543
= 0,904.
Таким образом, 90,4% вариации годового объема продаж объясняется изменчивостью площади магазинов, измеренной в квадратных футах. Данная величина г2 свидетельствует о сильной положительной линейной взаимосвязи между двумя переменными, поскольку применение регрессионной модели снижает изменчивость прогнозируемых годовых объемов продаж на 90,4%. Только 9,6% изменчивости годовых объемов продаж в выборке магазинов объясняются другими факторами, не учтенными в регрессионной модели.
Коэффициент смешанной корреляции в задаче о сети магазинов Sunflowers представлен на рис. 12.8.
3 _______Регрессионная статистика_________
4 МножественныйiR 0,95088
5 R-квадрат 0,90418
6 ;Нормированный R-квадрат 0.89619
7 |Стандартная ошибка 0,96638
8 (Наблюдения Syx 14
Рис. 12.8. Коэффициент смешанной корреляции, вычисленный с помощью программы Microsoft Excel при решении задачи о сети магазинов Sunflowers
Среднеквадратичная ошибка оценки
Хотя метод наименьших квадратов позволяет вычислить линию, минимизирующую отклонение от наблюдаемых значений, наличие суммы квадратов ошибок (SSE) свидетельствует о том, что линейная регрессия не дает абсолютной точности прогноза, если, конечно, точки наблюдения не лежат на регрессионной прямой. Однако ожидать этого так же неестественно, как предполагать, что все выборочные значения точно равны их среднему арифметическому. Следовательно, необходима статистика, которая позволила бы оценить отклонение предсказанных значений переменной Y от ее реальных значений, аналогично тому, как стандартное отклонение, введенное в главе 3, позволяет оценить колебание данных вокруг их средней величины. Стандартное отклонение наблюдаемых значений переменной Y от.ее регрессионной прямой называется среднеквадратичной ошибкой оценки (standard error of the estimate).
Отклонение реальных данных от регрессионной прямой в задаче о сети магазинов Sunflowers показано на рис. 12.5.
СРЕДНЕКВАДРАТИЧНАЯ ОШИБКА ОЦЕНКИ
(12.8)
где У — фактическое значение переменной У при заданном значении Xt, Yt — предсказанное значение переменной У при заданном значении SSE — сумма квадратов ошибок.
Поскольку SSE = 11,2067, по формуле (12.8) получаем:
/11,2067
N 14-2
= 0,9664.
Таким образом, среднеквадратичная ошибка оценки равна 0,9664 млн. долл, (т.е. 966 400 долл.), что соответствует величине, указанной на рис. 12.8. Среднеквадратичная ошибка оценки характеризует отклонение реальных данных от линии регрессии. Она измеряется в тех же единицах, что и переменная У. По смыслу среднеквадратичная ошибка очень похожа на стандартное отклонение. В то время как стандартное отклонение характеризует разброс данных вокруг их среднего значения, среднеквадратичная ошибка позволяет оценить колебание точек наблюдения вокруг регрессионной прямой. Как следует из рис. 12.7 и 12.8, среднеквадратичная ошибка оценки позволяет обнаружить статистически значимую зависимость, существующую между двумя переменными, и предсказать значения переменной У.
УПРАЖНЕНИЯ К РАЗДЕЛУ 12.:
Изучение основ
12.9. Какой вывод можно сделать, если коэффициент смешанной корреляции г2 равен 0,80?
12.10. Предположим, что SSjR -- 36, a SSE = 4. Вычислите величину SST и коэффициент смешанной корреляции г2. Объясните их смысл.
12.11. Предположим, что SSjR — 66, a SST = 88. Вычислите коэффициент смешанной корреляции г2 и объясните его смысл.
12.12. Допустим, что SSE = 10, а SST = 30. Вычислите коэффициент смешанной корреляции г2 и объясните его смысл.
12.13. Почему величина SST не может быть равной 110, если SSjR = 120?
Применение понятий
Задачу 12.14 можно решать как вручную, так и с помощью программы Microsoft Excel. Задачи 12.15-12.19 рекомендуется решать с помощью программы Microsoft Excel.
12.14. Менеджер по маркетингу в компании, владеющей крупной сетью супермаркетов, желает предсказать недельный объем продаж, зная расстояния между стеллажами. Воспользуйтесь результатами решения задачи 12.3, полученными с помощью программы Microsoft Excel. PETFOOD. XLS.
1. Вычислите коэффициент смешанной корреляции г2 и объясните его смысл.
2. Вычислите среднеквадратичную ошибку оценки.
3. Помогает ли данная регрессионная модель правильно предсказать недельный объем продаж?
12.15. Менеджер агентства по внутригородским грузовым перевозкам желает предсказать затраты рабочего времени, основываясь на данных об объеме грузов. Воспользуйтесь результатами решения задачи 12.4, полученными с помощью программы Microsoft Excel. ^MOVING. XLS.
1. Вычислите коэффициент смешанной корреляции г2 и объясните его смысл.
2. Вычислите среднеквадратичную ошибку оценки.
3. Помогает ли данная регрессионная модель правильно предсказать затраты рабочего времени?
12.16. Менеджер сети почтовых отделений желает предсказать количество заказов, используя вес корреспонденции. Воспользуйтесь результатами решения задачи 12.5, полученными с помощью программы Microsoft Excel. &MAIL. XLS.
1. Вычислите коэффициент смешанной корреляции г2 и объясните его смысл.
2. Вычислите среднеквадратичную ошибку оценки.
3. Помогает ли данная регрессионная модель правильно предсказать недельный объем продаж?
12.17. Менеджер компании, поставляющей видеокассеты, желает предсказать объем продаж, используя данные об объеме кассовых сборов, принесенных кинофильмами. Воспользуйтесь результатами решения задачи 12.6, полученными с помощью программы Microsoft Excel. ^MOVIES. XLS.
1. Вычислите коэффициент смешанной корреляции г2 и объясните его смысл.
2. Вычислите среднеквадратичную ошибку оценки.
3. Помогает ли данная регрессионная модель правильно предсказать объем продаж?
12.18. Агент по продаже недвижимости желает предсказать размер месячной аренды апартаментов по их площади. Воспользуйтесь результатами решения задачи 12.7, полученными с помощью программы Microsoft Excel. ^RENT . XLS.
1. Вычислите коэффициент смешанной корреляции г2 и объясните его смысл.
2. Вычислите среднеквадратичную ошибку оценки.
3. Помогает ли данная регрессионная модель правильно предсказать величину стоимость месячной аренды?
12.19. В задаче 12.8 для предсказания прочности образцов из алюминия использовались данные о его твердости. Воспользуйтесь результатами решения этой задачи, полученными с помощью программы Microsoft Excel. ^HARDNESS. XLS.
1. Вычислите коэффициент смешанной корреляции г2 и объясните его смысл.
2. Вычислите среднеквадратичную ошибку оценки.
3. Помогает ли данная регрессионная модель правильно предсказать прочность алюминиевого образца?
12.4. ПРЕДПОЛОЖЕНИЯ
Обсуждая методы проверки гипотез и дисперсионного анализа, мы не раз подчеркивали важность условий, которые должны обеспечивать корректность сделанных выводов. Поскольку и регрессионный, и дисперсионный анализ используют линейную модель, условия их применения приблизительно одинаковы [6].
ВРЕЗКА 12.1. УСЛОВИЯ ПРИМЕНЕНИЯ РЕГРЕССИОННОГО АНАЛИЗА
• Ошибка должна иметь нормальное распределение.
• Вариация данных вокруг линии регрессии должна быть постоянной (свойство го-москедастичности).
• Ошибки должны быть независимыми.
Первое предположение, о нормальном распределении ошибок (normality), требует, чтобы при каждом значении переменной X ошибки линейной регрессии имели нормальное распределение (рис. 12.9). Как и t- и F-критерий дисперсионного анализа, регрессионный анализ довольно устойчив к нарушениям этого условия. Если распределение ошибок относительно линии регрессии при каждом значении X не слишком сильно отличается от нормального, выводы относительно линии регрессии и коэффициентов регрессии изменяются незначительно.
Второе условие, гомоскедастичность (homoscedasticity), заключается в том, что вариация данных вокруг линии регрессии должна быть постоянной при любом значении переменной X. Это означает, что величина ошибки как при малых, так и при больших значениях переменной X должна изменяться в одном и том же интервале (рис. 12.9). Свойство гомоскедастичности очень важно для метода наименьших квадратов, с помощью которого определяются коэффициенты регрессии. Если это условие нарушается, следует применять либо преобразование данных, либо метод наименьших квадратов с весами [6].
Третье предположение, о независимости ошибок (independence of errors), заключается в том, что ошибки регрессии не должны зависеть от значения переменной X. Это условие особенно важно, если данные собираются на протяжении определенного отрезка времени. В этих ситуациях ошибки, присущие конкретному отрезку времени, часто коррелируют с ошибками, характерными для предыдущего периода.
Рис. 12.9. Предположения о регрессии
12.5. АНАЛИЗ ОСТАТКОВ
В предыдущем разделе при решении задачи о сети магазинов Sunflowers мы использовали модель линейной регрессии. Рассмотрим теперь анализ ошибок (residual analysis) — графический метод, позволяющий оценить точность регрессионной модели. Кроме того, с его помощью можно обнаружить потенциальные нарушения условий применения регрессионного анализа.
Оценка пригодности эмпирической модели
Остаток (residual), или оценка ошибки е, представляет собой разность между наблюдаемым (Y, ) и предсказанным (Yt ) значениями зависимой переменной при заданном значении X, .
ОСТАТОК
Остаток, или оценка ошибки е(, представляет собой разность между наблюдаемым (У) и предсказанным (Y, ) значениями зависимой переменной при заданном значении X:
е, = Yt-Y.. (12.9)
Для оценки пригодности эмпирической модели регрессии остатки откладываются по вертикальной оси, а значения Xt — по горизонтальной. Если эмпирическая модель пригодна, график не должен иметь ярко выраженной закономерности. Если же модель регрессии не пригодна, на рисунке проявится зависимость между значениями X, и остатками е. Рассмотрим примеры.
Панель А иллюстрирует возрастание переменной У при увеличении переменной X. Однако зависимость между этими переменными носит нелинейный характер, поскольку скорость возрастания переменной У падает при увеличении переменной X. Таким образом, для аппроксимации зависимости между этими переменными криволинейная или квадратичная модели подойдут больше, чем модель простой линейной регрессии. Особенно ярко квадратичная зависимость между величинами X.t и е. проявляется на панели Б. Графическое изображение остатков позволяет отфильтровать или удалить линейную зависимость между переменными X и У и выявить недостаточную точность модели простой
линейной регрессии. Таким образом, в данной ситуации вместо простой линейной модели должна применяться квадратичная модель, обладающая более высокой точностью. (Подробное обсуждение квадратичных моделей содержится в разделе 14.1.)
Рис. 12.10. Исследование эмпирической модели простой линейной регрессии
Вернемся к задаче о сети магазинов Sunflowers и посмотрим, хорошо ли подходит простая линейная регрессия для ее решения. Соответствующие данные приведены на рис. 12.12.
22 ВЫВОД ОСТАТКА 23
24 Наблюдение Предсказанные годовые продажи Остатки
25 1 3,803239598 -0,103239598
26 2 3,636253367 0,263746633
2L 3 5,640088147 1,059911853
28 4 10,31570263 -0,815702635
29 5 3,135294672 0,264705328
30 6 4,638170757 0,961829243
31 7 3,135294672 0,564705328
32. 8 2,801322208 -0,101322208
33 9 6,308033074 -0,808033074
34 10 3,469267135 -0,569267135
35 11 9,647757708 1,052242292
36 12 8,645840318 -1,045840318
37 13 10,6496751 1,150324902
38; 14 5,974060611 -1,874060611
Рис. 12.11. Остатки, вычисленные с помощью программы Microsoft Excel при решении задачи о сети магазинов Sunflowers
Построим график, откладывая на вертикальной оси остатки, а на горизонтальной — независимую переменную.
Обратите внимание на то, что, несмотря на большой разброс остатков, между ними и значениями X, нет ярко выраженной зависимости. Остатки одинаково часто принимают как положительные, так и отрицательные значения. Это позволяет сделать вывод, что модель линейной регрессии пригодна для решения задачи о сети магазинов Sunflowers.
Г рафик остатков для площади магазина
Площадь, кв. футов
Рис. 12.12. Диаграмма, построенная с помощью программы Microsoft Excel при решении задачи о сети магазинов Sunflowers
Процедуры Excel: вычисление остатков
Для того чтобы построить график остатков, необходимо модифицировать процедуру простого линейного регрессионного анализа.
Например, чтобы выполнить простой линейный регрессионный анализ по данным, приведенным в табл. 12.1, необходимо открыть рабочую книгу chapter 12.xls на листе Данные и выполнить одну из следующих процедур.
Применение Excel в сочетании с надстройкой PHStat2
Выполните процедуру Excel "Простой линейный регрессионный анализ", описанную в разделе 12.2, установив в группе Вывод регрессионных статистик флажки Regression Statistics Table (Таблица регрессионных статистик), ANOVA and Coefficients Table (Сводная таблица дисперсионного анализа и коэффициентов), Residual Table (Таблица остатков) и Residual Plot (График остатков), как показано на иллюстрации.
Применение Excel
Выполните инструкции, приведенные в разделе ЕН.12.1, установив флажки Остатки и График остатков в диалоговом окне Регрессия, как показано на иллюстрации. При необходимости график остатков можно модифицировать, следуя инструкциям из раздела ЕН.12.3.
I Simple Linear Regression
Data
Y Variable Cell Range: [ci?C 15 T]
X Variable Cell Range: (вГв15~" J
P First cells in both ranges contain label
Confidence level For regression coefficients: [95 %
Regression Tool Output Options -
P Regression Statistics Table
P ANOVA and Coefficients Table
P Residuals Table
P Residual Plot
Output Options
Title; [Анализ данных о магазинах
Р Scatter Diagram
Г Durbin-Watson Statistic
Г* Confidence and Prediction Interval for X » |
Help j |Г'".ОК......]| Cancel
Регрессия
Входные данные g-----
Входной интервал Y: C1:C15 fo]
........................ [ Отмена j
Вводной интервал X: В1: В15 fo|
0 Метки О Константа - ноль J
0 Уровень надежности: : 95 : %
Параметры вывода
О Выходной интервал: ! Ass
Новый рабочий лист: s Анализ данных
О Новая рабочая книга
Остатки.......................
0 Остатки 0 График остатков
0 Стандартизованные остатки 0 График подбора
Нормальная вероятность
0 График нормальной вероятности
Проверка условий
Гомоскедастичность. График остатков позволяет оценить гомоскедастичность ошибок. На рис. 12.12 нет особых различий между ошибками, соответствующими разным значениям Xt . Следовательно, вариации ошибок при разных значениях X. приблизительно одинаковы.
Рассмотрим гипотетическую ситуацию, в которой это условие не выполняется (рис. 12.13). На этом рисунке изображен эффект веера (fanning effect): при возрастании значений X ошибки увеличиваются. Таким образом, изменчивость значений У при разных значениях является непостоянной.
Рис. 12.13. Нарушение условия гомоскедастичности
Нормальность. Чтобы проверить предположение о нормальном распределении ошибок, построим гистограмму распределения частот (см. раздел 2.2). Распределение частот, вычисленное при решении задачи о сети магазинов Sunflowers, приведено в табл. 12.2 (для построения гистограммы данных недостаточно), а график нормального распределения — на рис. 12.14.
Таблица 12.2. Распределение частот, вычисленное по 14 остаткам при решении задачи о сети магазинов Sunflowers
Остатки Частота
-2,25 < е < <-1,75 1
-1,75< е - < -1,25 0
-1,25 < е < < -0,75 3
-0,75 < е < < -0,25 1
-0,25 < е ’ < +0,25 2
+0,25 < е < <+0,75 3
+0,75 < е < <+1,25 4
Всего 14
График нормального распределения для остатков
Значение Z
Рис. 12.14. График остатков, построенный с помощью программы Microsoft Excel при решении задачи о сети магазинов Sunflowers
Без построения гистограммы, диаграммы “ствол и листья”, блочной диаграммы или графика проверить предположение о нормальном распределении ошибок очень трудно. Данные, изображенные на рис. 12.14, не слишком сильно отличаются от нормального распределения. Устойчивость регрессионного анализа и небольшой объем выборки позволяют утверждать, что условие о нормальном распределении ошибок нарушается незначительно.
Независимость. Предположение о независимости ошибок также проверяется с помощью графика остатков. Данные, собранные на протяжении некоторого периода времени, иногда демонстрируют эффект автокорреляции (autocorrelation) между последовательными наблюдениями. В таких ситуациях остатки зависят от значений предыдущих остатков. Подобная связь между остатками нарушает предположение о независи-
мости ошибок. Эффект автокорреляции хорошо выявляется на графике. Кроме того, его можно измерить с помощью процедуры Дурбина-Уотсона (Durbin-Watson), рассмотренной в разделе 12.6. Например, данные о размерах магазинов и объемах продаж собирались в течение одного и того же периода времени. Следовательно, гипотезу об их независимости проверять не имеет смысла.
УПРАЖНЕНИЯ К РАЗДЕЛУ 12.5
Изучение основ
12.20. Проанализируйте таблицу значений переменной X и остатков, а также соответствующий график.
СD Е F G „ Н
1 2 3 4
1?... 2D 21;
X Остатки 1 0,70
2 41,78
3 1,03
4 0,33
5 2,39
6 -0,67
7 0,16
8 1,65
9 -1,19
10 0,84
11 0,29
12 -1,28
13 1,21
14 41,37
15 1,02
16 -0,16
17 1,42
18 -0,71
19 -0,63
20 0,67
График остатков
0 5 10 15 20 25
Существует ли какая-нибудь закономерность на этом графике? Обоснуйте свой ответ.
12.21. Проанализируйте таблицу значений переменной X и остатков, а также соответствующий график.
А ; В X Остатки
С D Е F G Н
-..~_S_U-i__12___±X—Г--
9 10
11
12 13 и
16
17* Ж
19
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
0,70 1,58 1,03 0,33 -0,39 -0,67 -0,56 -0,65 -1,19 -0,84 -0,29 -1,28 -0,21 -0,37 0,22 -0,16 0,82
Г рафик остатков
0 5 10 15 20
Существует ли какая-нибудь закономерность на этом графике? Обоснуйте свой ответ.
Применение понятий
Задачи 12.22-12.27рекомендуется решать с помощью программы Microsoft Excel.
12.22. Менеджер по маркетингу в компании, владеющей крупной сетью супермаркетов, желает предсказать недельный объем продаж, зная расстояния между стеллажами. Выполните анализ остатков на основе данных, приведенных в задаче 12.3. ^PETFOOD . XLS. .
1. Оцените точность эмпирической модели.
2. Какие условия применения регрессии оказались серьезно нарушенными?
12.23. Менеджер агентства по внутригородской перевозке грузов желает предсказать затраты рабочего времени, основываясь на данных об объеме груза. Выполните анализ остатков на основе данных, приведенных в задаче 12.4. ^MOVING. XLS.
1. Оцените точность эмпирической модели.
2. Какие условия применения регрессии оказались серьезно нарушенными?
12.24. Менеджер сети почтовых отделений желает предсказать количество заказов, используя вес корреспонденции. Выполните анализ остатков на основе данных, приведенных в задаче 12.5. ^MAIL.XLS.
1. Оцените точность эмпирической модели.
2. Какие условия применения регрессии оказались серьезно нарушенными?
12.25. Менеджер компании, поставляющей видеокассеты, желает предсказать объем продаж, используя данные об объеме кассовых сборов, принесенных кинофильмами. Выполните анализ остатков на основе данных, приведенных в задаче 12.6. CiMOVIES . XLS.
1. Оцените точность эмпирической модели.
2. Какие условия применения регрессии оказались серьезно нарушенными?
12.26. Агент по продаже недвижимости желает предсказать величину месячной аренды апартаментов по их площади. Выполните анализ остатков на основе данных, приведенных в задаче 12.7. ^RENT .XLS.
1. Оцените точность эмпирической модели.
2. Какие условия применения регрессии оказались серьезно нарушенными?
12.27. В задаче 12.8 для предсказания прочности образцов из алюминия использовались данные о его твердости. Выполните анализ остатков. ^HARDNESS. XLS.
1. Оцените точность эмпирической модели.
2. Какие условия применения регрессии оказались серьезно нарушенными?
12.6. ИЗМЕРЕНИЕ АВТОКОРРЕЛЯЦИИ: СТАТИСТИКА ДУРБИНА-УОТСОНА
Одним из основных предположений о регрессионной модели является гипотеза о независимости ее ошибок. Если данные собираются в течение определенного отрезка времени, это условие часто Нарушается, поскольку остаток в определенный момент времени может оказаться приблизительно равным предыдущим остаткам. Такое поведение остатков называется автокорреляцией (autocorrelation). Если набор данных обладает свойством автокорреляции, корректность регрессионной модели становится весьма сомнительной.
Распознавание автокорреляции с помощью графика остатков
Как указывалось в разделе 12.5, для выявления автокорреляции необходимо упорядочить остатки по времени и построить их график. Если данные обладают положительной автокорреляцией, на графике возникнут кластеры остатков, имеющие одинаковый знак. В случае отрицательной автокорреляции остатки будут скачкообразно принимать то положительные, то отрицательные значения. Этот вид автокорреляции очень редко встречается в регрессионном анализе, поэтому мы рассмотрим лишь положительную автокорреляцию. Проиллюстрируем ее следующим примером.
Предположим, что менеджер магазина, доставляющего товары на дом, пытается предсказать объем продаж по количеству клиентов, совершивших покупки в течение 15 недель. Поскольку данные собирались на протяжении 15 последовательных недель в одном и том же магазине, необходимо определить, наблюдается ли эффект автокорреляции. Данные представлены в табл. 12.3. ^CUSTSALE. XLS.
Таблица 12.3. Количество клиентов и объемы продаж за 15 недель
Неделя Количество клиентов Объем продаж (тыс. долл.) Неделя Количество клиентов Объем продаж (тыс. долл.)
1 794 9,33 9 880 12,07
2 799 8,26 10 905 12,55
3 837 7,48 11 886 11,92
4 855 9,08 12 843 10,27
5 845 9,83 13 904 11,80
6 844 10,09 14 950 12,15
7 863 11,01 15 841 9,64
8 875 11,49
». . . . А 1 в ,С L В . Е . F . . _е...
^Регрессионный анализ данных об объеме продаж '2J 3 Регрессионная статистика
4 ; Множественный R 5gi R-квадрат (^Нормированный R-квадрат /^Стандартная ошибка 8 (Наблюдения 0.810829997 0.657445284 0.631094922 0.936036681 15
9J 10 Дисперсионный анализ .11: df SS MS F Значимость F
12 регрессия 13; Остаток 14i Итого 1 13 14 21.86043264 11.39014069 33.25057333 21.86043264 24.95014171 0.876164669 0.000245105
15*
16 Коэффициенты Стандартная ошибка t-статистика Р-Значение Нижние 96% Верхние 95%
17j ^-пересечение , -16.0321936 5.310167093 -3.019150493 0.009868641 -27.50410993 -4.560277262
18 (Клиенты X , 0030760228 0.006158189 4 995011683 0 000245105 0.017456271 0.044064185
bo''' bf
Рис. 12.15. Результаты решения задачи, полученные с помощью программы Microsoft Excel
Анализ рис. 12.15 показывает, что г2 = 0,657. Это значит, что 65,6% вариации объемов продаж объясняется изменчивостью количества клиентов. Кроме того, сдвиг &0 переменной У равен -16,032, а наклон — 0,03076. Однако, прежде чем применять эту модель, необходимо выполнить анализ остатков. Поскольку данные собирались на протяжении 15 последовательных недель, их следует отобразить на графике в том же порядке (рис. 12.16).
Зависимость остатков от времени
Рис. 12.16. График остатков, построенный с помощью программы Microsoft Excel
Анализ рис. 12.16 показывает, что остатки циклически колеблются вверх и вниз. Эта цикличность является явным признаком автокорреляции. Следовательно, гипотезу от независимости остатков следует отклонить.
Статистика Дурбина-Уотсона
Автокорреляцию можно выявить и измерить с помощью статистики Дурбина-Уотсона (Durbin-Watson statistic). Эта статистика оценивает корреляцию между соседними остатками.
СТАТИСТИКА ДУРБИНА-УОТСОНА
D = ^—„-----, (12.10)
ZX
/=1
где е — остаток, соответствующий i-му периоду времени.
Чтобы лучше понять статистику Дурбина-Уотсона, рассмотрим ее составные части.
Числитель ~ e'-i )2 пРеДставляет собой сумму квадратов разностей между соседними ос-i=2
татками, начиная со второго и заканчивая n-м наблюдением. Знаменатель является i=i
суммой квадратов остатков. Если между соседними остатками существует положительная
автокорреляция, значение D будет близким к нулю. Если остатки не коррелируют между собой, значение D стремится к 2. (При отрицательной автокорреляции статистика D колеблется в диапазоне от 2 до 4.) Применение программы Microsoft Excel (рис. 12.17) показывает, что в нашей задаче D = 0,833.
..4 . ....А
1 Вычисления статистики Дурбина-Уотсона
2 '
4
Sum of Squared Difference of Residuals : 10.05752
Sum of Squared Residuals 11.39014
Durbin-Watson Statistic
| 0.883001
Рис. 12.17. Статистика Дурбина-Уотсона, вычисленная с помощью программы Microsoft Excel
Основной вопрос заключается в следующем — какое значение статистики Дурбина-Уотсона следует считать достаточно малым, чтобы сделать вывод о существовании положительной автокорреляции? Ответ зависит от того, насколько сильно статистика D зависит от количества наблюдений п и количества независимых переменных в модели k (для простой линейной регрессии k = 1); табл. 12.4 является фрагментом табл. Д.10.
Таблица 12.4. Критические значения статистики Дурбина-Уотсона
а = 0,05
к=1 к=2 к=3 k=4 k=5
п dL d0 dL du dL du dL du dL du
15 1,08 1,36 0,95 1,54 0,82 1,75 0,69 1,97 0,56 2,21
16 1,10 1,37 0,98 1,54 0,86 1,73 0,74 1,93 0,62 2,15
17 1,13 1,38 1,02 1,54 0,90 1,71 0,78 1,90 0,67 2,10
18 1,16 1,39 1,05 1,53 0,93 1,69 0,82 1,87 0,71 2,06
Как следует из табл. 12.4, каждой комбинации величин а (уровень значимости), п (объем выборки) и k (количество независимых переменных в модели) соответствуют два значения статистики. Первое значение, dL, представляет собой нижнее критическое значение статистики Дурбина-Уотсона. Если величина D меньше dL, между остатками существует положительная автокорреляция. В этой ситуации метод наименьших квадратов применять нельзя и следует прибегнуть к альтернативным способам [6]. Второе значение, dv, представляет собой верхнее критическое значение статистики Дурбина-Уотсона. Если величина D больше dv, между остатками не существует положительной автокорреляции. Если же значение D лежит в интервале от dL до dv, никаких определенных выводов сделать нельзя.
Таким образом, в задаче об объеме продаж в магазине, доставляющем товары на дом, существуют одна независимая переменная (k = 1) и 15 наблюдений (п = 15), dL = 1,08 и dv = 1,36. Поскольку D = 0,883 < 1,08, между остатками существует положительная автокорреляция, метод наименьших квадратов применять нельзя.
Процедуры Excel: вычисление статистики Дурбина-Уотсона
Для вычисления статистики Дурбина-Уотсона сначала необходимо выполнить простой линейный регрессионный анализ с помощью процедуры СервисЧ>Анализ данных1^Регрессия, а затем создать новый рабочий лист, использующий функции суммквразн и суммкв. Надстройка PHStat2 позволяет сделать это автоматически.
Например, чтобы вычислить статистику Дурбина-Уотсона для данных, приведенных в табл. 12.3, необходимо открыть рабочую книгу chapter 12.xls на листе Продажи и выполнить одну из следующих процедур.
Применение Excel в сочетании с надстройкой PHStat2
Статистику Дурбина-Уотсона можно вычислить с помощью процедуры PHStat^Regression^Simple Linear Regression... (PHStat1^Регрессия^Простая линейная регрессия...), выполняя такие инструкции.
1. Выбрать команду PHStat^ Regression ^Simple Linear Regression....
2. В диалоговом окне Simple Linear Regression сделать следующее (см. иллюстрацию).
2.1. Ввести в диалоговом окне Y Variable Cell Range (Входной интервал Y) диапазон ячеек С1:С16.
2.2. Ввести в диалоговом окне X Variable Cell Range (Входной интервал X) диапазон ячеекв1:В1б.
2.3. Установить флажок First cells in both ranges contain a label (Первые ячейки обоих диапазонов содержит метку).
2.4. Ввести в диалоговом окне Confidence level for regression coefficients (Доверительный уровень для коэффициентов регрессии) число 0.95.
2.5. Установить флажки Regression Statistics Table (Таблица регрессионных статистик) и ANOVA and Coefficients Table (Таблица дисперсионного анализа и коэффициентов).
2.6. Ввести в диалоговом окне Title (Заголовок) название диаграммы.
2.7. Установить флажок Durbin-Watson Statistic (Статистика Дурбина-Уотсона).
2.8. Щелкнуть на кнопке ОК.
Эта процедура создает два рабочих листа, один из которых содержит коэффициенты линейной регрессии и другие статистики, а другой - статистику Дурбина-Уотсона.
Рабочий лист, содержащий параметры простой линейной регрессии, не обновляется динамически, поэтому после изменения исходных данных всю процедуру придется повторить.
Применение Excel
Чтобы самостоятельно создать рабочий лист для вычисления статистики Дурбина-Уотсона, следуйте инструкциям из раздела ЕН.12.4.
4U Chapter 12.xls
Вычисления статистики Дурбина-Уотсона продемонстрированы на листе Рис12.17 в рабочей книге Chapter 12.xls.
УПРАЖНЕНИЯ К РАЗДЕЛУ 12.6
Изучение основ
12.28. В следующей таблице приведены остатки для набора данных, собранных в течение 10 последовательных интервалов времени.
Период времени Остаток Период времени Остаток
1 -5 6 +1
2 -4 7 +3
3 -3 8 +3
4 -2 9 +4
5 -1 10 +5
1. Постройте график зависимости остатков от времени. Какие выводы можно сделать на его основе?
2. Вычислите статистику Дурбина-Уотсона.
3. Можно ли утверждать, что между остатками существует автокорреляция?
12.29. В следующей таблице приведены остатки для набора данных, собранных в течение 15 последовательных интервалов времени.
Период времени Остаток Период времени Остаток
1 +4 9 +6
2 -6 10 -3
3 -1 11 +1
4 -5 12 +3
5 +2 13 0
6 +5 14 -4
7 -2 15 -7
8 + 7
1. Постройте график зависимости остатков от времени. Какие выводы можно сделать на его основе?
2. Вычислите статистику Дурбина-Уотсона.
3. Можно ли утверждать, что между остатками существует автокорреляция?
Применение понятий
12.30. Менеджер по маркетингу в компании, владеющей крупной сетью супермаркетов, желает предсказать недельный объем продаж, зная расстояния между стеллажами. Выполните анализ остатков на основе данных, приведенных в задаче 12.3. ©PETFOOD.XLS.
1. Нужно ли вычислять статистику Дурбина-Уотсона? Обоснуйте свой ответ.
2. При каких условиях необходимо вычислять статистику Дурбина-Уотсона, прежде чем применять метод наименьших квадратов?
12.31. Владелец одноквартирного дома в одном из пригородов на северо-западе США хотел бы создать модель для прогнозирования объемов потребления электричества (освещение, вентилятор, отопление, бытовые приборы и т.д.) в зависимости от температуры воздуха на улице (в градусах по Фаренгейту). Для этого он собрал данные об объемах потребленного электричества и температуре на протяжении 24 месяцев. ^ELECUSE . XLS.
1. Постройте диаграмму разброса.
2. Предположим, что между переменными существует линейная зависимость. Примените метод наименьших квадратов и вычислите коэффициенты регрессии и bv
3. Объясните смысл наклона bv
4. Предскажите объем потребленной электроэнергии, если средняя температура воздуха равна 50 градусов по Фаренгейту.
5. Вычислите коэффициент смешанной корреляции т* и объясните его смысл.
6. Вычислите среднеквадратичную ошибку оценки.
7. Постройте график зависимости остатков от средней температуры воздуха.
8. Постройте график зависимости остатков от времени.
9. Вычислите статистику Дурбина-Уотсона. Существует ли автокорреляция между остатками, если уровень значимости равен 0,05?
10. Можно ли применять модель линейной регрессии?
12.32. Компания, торгующая компьютерами и периферийными устройствами, имеет централизованный склад. Менеджер магазина хотел бы оценить процесс перевозок товаров со склада в магазины, изучив факторы, влияющие на его стоимость. В настоящее время, независимо от объема заказа, в него закладывается небольшая стоимость, связанная с его обработкой. Для предсказания стоимости перевозок в зависимости от количества заказов менеджер собрал данные о последних 24 месяцах. ^WARECOST . XLS.
Месяц Стоимость перевозок (тыс. долл.) Количество заказов
1 52,95 4 015
2 71,66 3 806
3 85,58 5 309
4 63,69 4 262
5 72,81 4 296
6 68,44 4 097
7 52,46 3 213
8 70,77 4 809
9 82,03 5 237
10 74,39 4 732
11 70,84 4 413
12 54,08 2 921
13 62,98 3 977
Месяц Стоимость перевозок (тыс. долл.) Количество заказов
14 72,30 4 428
15 58,99 3 964
16 79,38 4 582
17 94,44 5 582
18 59,74 3 450
19 90,50 5 079
20 93,24 5 735
21 69,33 4 269
22 53,71 3 708
23 89,18 5 387
24 66,80 4 161
1. Постройте диаграмму разброса.
2. Предположим, что между переменными существует линейная зависимость. Примените метод наименьших квадратов и вычислите коэффициенты регрессии Ьа и
3. Объясните смысл наклона
4. Предскажите объем перевозок, если среднее количество заказов равно 4 500.
5. Вычислите коэффициент смешанной корреляции г2 и объясните его смысл.
6. Вычислите среднеквадратичную ошибку оценки.
7. Постройте график зависимости остатков от среднего количества заказов.
8. Постройте график зависимости остатков от времени.
9. Вычислите статистику Дурбина-Уотсона. Существует ли автокорреляция между остатками, если уровень значимости равен 0,05?
10. Можно ли применять модель линейной регрессии?
12.33. Свежеприготовленная порция кофе “эспрессо” состоит из трех компонентов: “сердцевины”, “тела” и сливок. В раздельном состоянии эти компоненты держатся от 10 до 20 с. Именно в этот промежуток времени порцию кофе “эспрессо” можно использовать для приготовления кофе со взбитыми сливками или другой разновидности кофейного напитка. Если опоздать, кофе станет чрезвычайно горьким и кислым, что испортит вкус напитка. Следовательно, чем дольше компоненты кофе “эспрессо” сохраняются в раздельном виде, тем больше времени имеет бармен для приготовления напитка. Менеджер кофейни предположил, что чем плотнее гуща, использованная для приготовления кофе, тем дольше компоненты не смешиваются друг с другом. Для проверки этой гипотезы был проведен эксперимент, в результате которого получены 24 наблюдения. Независимая переменная “плотность” представляла собой расстояние между гущей и верхом кофеварки (чем больше это расстояние, тем плотнее гуща). Зависимая переменная “время” измеряла продолжительность интервала, в течение которого компоненты не смешивались друг с другом. ^ESPRESSO .XLS.
Порция Плотность, дюймы Время, с Порция Плотность, дюймы Время, с
1 0,20 14 13 0,50 18
2 0,50 14 14 0,50 13
3 0,50 18 15 0,35 19
4 0,20 16 16 0,35 19
5 0,20 16 17 0,20 17
6 0,50 13 18 0,20 18
7 0,20 12 19 0,20 15
8 0,35 15 20 0,20 16
9 0,50 9 21 0,35 18
10 0,35 15 22 0,35 16
11 0,50 11 23 0,35 14
12 0,50 16 24 0,35 16
1. Запишите уравнение простой линейной регрессии, в которой “время” является зависимой, а “плотность” — независимой переменной.
2. Объясните смысл наклона Ъх.
3. Постройте график зависимости остатков от номера эксперимента. Существует ли какая-либо закономерность в их распределении?
4. Вычислите статистику Дурбина-Уотсона. Существует ли автокорреляция между остатками, если уровень значимости равен 0,05?
12.34. Владелец магазинов, торгующих мороженым, хотел бы знать, как температура воздуха влияет на объем продаж в течение летнего сезона. Для исследования он в течение 21 дня подряд заполнял таблицу, хранящуюся в файле ICECREAM.XLS. (Определите зависимую и независимую переменные.)
1. Постройте диаграмму разброса.
2. Предположим, что между переменными существует линейная зависимость. Примените метод наименьших квадратов и вычислите коэффициенты регрессии fe0 и fej.
3. Объясните смысл наклона Ьх.
4t. Предскажите объем продаж, если средняя температура воздуха равна 83 °F.
5. Вычислите коэффициент смешанной корреляции г2 и объясните его смысл.
6. Вычислите среднеквадратичную ошибку оценки.
7. Постройте график зависимости остатков от средней температуры воздуха.
8. Постройте график зависимости остатков от времени.
9. Вычислите статистику Дурбина-Уотсона. Существует ли автокорреляция между остатками, если уровень значимости равен 0,05?
10. Можно ли применять модель линейной регрессии?
11. Предположим, что объем продаж в 21-й день был равен 1,75 тыс. долл. Повторите решение задач 1-10 и сравните полученные результаты.
12.7. ПРОВЕРКА ГИПОТЕЗ О НАКЛОНЕ И КОЭФФИЦИЕНТЕ КОРРЕЛЯЦИИ
В разделах 12.1-12.3 регрессия применялась исключительно для прогнозирования. Для определения коэффициентов регрессии и предсказания значения переменной У при заданной величине переменной X использовался метод наименьших квадратов. Кроме того, мы рассмотрели среднеквадратичную ошибку оценки и коэффициент смешанной корреляции.
Если анализ остатков, рассмотренный в разделе 12.5, подтверждает, что условия применимости метода наименьших квадратов не нарушаются, и модель простой линейной регрессии является адекватной, на основе выборочных данных можно утверждать, что между переменными в генеральной совокупности существует линейная зависимость.
Применение t-критерия для наклона
Проверяя, равен ли наклон генеральной совокупности рг нулю, можно определить, существует ли статистически значимая зависимость между переменными X и У. Если эта гипотеза отклоняется, можно утверждать, что между переменными X и Y существует линейная зависимость. Нулевая и альтернативная гипотезы формулируются следующим образом:
Но: Pi = 0 (нет линейной зависимости), Нт: Pj ф 0 (есть линейная зависимость).
Тестовая статистика вычисляется по формуле (12.11).
ПРОВЕРКА ГИПОТЕЗЫ О НАКЛОНЕ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ ₽, С ПОМОЩЬЮ f-КРИТЕРИЯ
По определению t-статистика равна разности между выборочным наклоном и гипотетическим значением наклона генеральной совокупности, деленной на среднеквадратичную ошибку оценки наклона:
(12.11)
f _ &.-Р, g п _ 2
где Sb< = ~т== > SSX = “ х) , а тестовая статистика t имеет t-распределение с п-2
степенями свободы.
Проверим, существует ли статистически значимая зависимость между размером магазина и годовым объемом продаж при а = 0,05. Рассмотрим результаты применения t-критерия, полученные с помощью программы Microsoft Excel (рис. 12.18).2
16 Коэффициенты Стандартная ошибка !-статистикаР-Значение Нижние 95% Верхние 95%
17 Y-пересечение 0.96447 0.52619 1 83293 0 09173 -0,18200 2.11095
18 Площадь 1.66986 0.15693 10,64112ч 0,00000 1,32795 2,01177
t-статистика для pi
Рис. 12.18. Результаты применения t-критерия, полученные с помощью программы Microsoft Excel
Более тювробтле въ1,ч.и,сленл1я, связанные с t-критерием, рассматриваются в разделе 12,10.
Как видим,
Ь, = +1,670, п = 14, = 0,157.
Следовательно,
/ = V1 = 1^ =
Sh 0,157
На рис. 12.18 значение ^-статистики находится в столбце под названием t Stat. Поскольку t = 10,64 > 2,1788 (рис. 12.19), нулевая гипотеза Но отклоняется. С другой стороны, р-значение приближенно равно нулю, поэтому гипотеза Но снова отклоняется. Тот факт, чтор-значение почти равно нулю, означает, что если бы между размерами магазинов и годовым объемом продаж не существовало реальной линейной зависимости, обнаружить ее с помощью линейной регрессии было бы практически невозможно. Следовательно, между средним годовым объемом продаж в магазинах и их размером существует статистически значимая линейная зависимость.
\ -2,1788
Область
0 +2,1788 t f12
Область
Область
отклонения принятия отклонения
гипотезы гипотезы гипотезы
Критическое значение
Критическое значение
Рис. 12.19. Проверка гипотезы о наклоне генеральной совокупности при уровне значимости, равном 0,05, и 12 степенях свободы
Применение ^-критерия для наклона
Альтернативным подходом к проверке гипотез о наклоне простой линейной регрессии является использование F-критерия. Напомним, что F-критерий применяется для проверки отношения между двумя дисперсиями. При проверке гипотезы о наклоне мерой случайных ошибок является дисперсия ошибки (сумма квадратов ошибок, деленная на количество степеней свободы), поэтому F-критерий использует отношение дисперсии, объясняемой регрессией (т.е. величины SSR, деленной на количество независимых переменных /г), к дисперсии ошибок (MSE = ).
ПРОВЕРКА ГИПОТЕЗЫ О НАКЛОНЕ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ 0, С ПОМОЩЬЮ F-КРИТЕРИЯ
По определению F-статистика равна среднему квадрату отклонений, обусловленных регрессией (MSR), деленному на дисперсию ошибки (MSE)
MSR
MSE ’
(12.12)
SSR SSE
где MSR =---, MSE =------, k — количество независимых переменных в регресси-
к п-к-\
онной модели. Тестовая статистика F имеет F-распределение с k и п-k—l степенями свободы.
При заданном уровне значимости а решающее правило формулируется так:
если F > Fut нулевая гипотеза отклоняется; в противном случае она не отклоняется.
Результаты, оформленные в виде сводной таблицы дисперсионного анализа, приведены в табл.12.5.
Таблица 12.5. Таблица дисперсионного анализа для проверки гипотезы о статистической значимости коэффициента регрессии
Источник Количество степеней свободы df Сумма квадратов Среднеквадратичное значение F
Регрессия k SSR MSR^ к r^MSR ~ MSE
Ошибка n—k—1 SSE MSE = SSE п-к-1
Всего п-1 SST
Таблицу ANOVA можно заполнить с помощью программы Microsoft Excel, как показано на рис. 12.20.
MSR
10 {Дисперсионный анализ /
11 i df SS MS / F Значимость F
12 {Регрессия 1 105.74761 105.74761- ''113.23351 1.82269E-07
13 {Остаток 12 11.20668 0.93389 >
14 iИтого 13 116,95429
MSE
Рис. 12.20. Решение задачи о сети магазином Sunflowers с помощью F-критерия, полученное с помощью программы Microsoft Excel
Как видим, вычисленная F-статистика равна 113,23, а р-значение не превосходит 0,001 (р-значение, вычисленное с помощью программы Microsoft Excel, равно 0,000000182).
Если уровень значимости равен 0,05, пользуясь табл. Д.5, легко определить критическое значение F-распределения с одной и 12 степенями свободы. Как показано на рис. 12.21, оно равно 4,75. Поскольку F = 113,23 > 4,75, причем р-значение равно 0,000000182 < 0,05, нулевая гипотеза Но отклоняется, т.е. размер магазина тесно свя-
зан с его годовым объемом продаж. Обратите внимание на то, что р-значение для F-критерия, представленное на рис. 12.20, идентично p-значению для t-критерия, показанному на рис. 12.18 (F = 113,23 = t2 = (10,64)2).
Рис. 12.21. Проверка гипотезы о наклоне генеральной совокупности при уровне значимости, равном 0,05, с одной и 12 степенями свободы
Доверительный интервал, содержащий наклон р,
Для проверки гипотезы о существовании линейной зависимости между переменными можно построить доверительный интервал, содержащий наклон 0Р и убедиться, что гипотетическое значение Р,= 0 принадлежит этому интервалу.
ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ ДЛЯ НАКЛОНА 0,
Центром доверительного интервала, содержащего наклон 0Р является выборочный наклон Ьг, а его границами — величины,
Как показано на рис. 12.18,
bt = +1,670, п = 14, = 0,157.
Из табл. Д.З следует, что t12 = 2,1788. Следовательно,
Ьх ± tn_2Shi = +1,670 ± 2,1788 х 0,157 = +1,670 ± 0,342,
+ 1,328 < 0J <+2,012.
Таким образом, наклон генеральной совокупности с вероятностью 0,95 лежит в интервале от +1,328 до +2,012 (т.е. от 1 328 000 до 2 012 000 долл.). Поскольку эти величины больше нуля, между годовым объемом продаж и площадью магазина существует статистически значимая линейная зависимость. Если бы доверительный интервал содержал нуль, между переменными не было бы зависимости. Кроме того, доверительный интервал означает, что каждое увеличение площади магазина на 1 000 кв. футов приводит к увеличению среднего объема продаж на величину от 1 328 000 до 2 012 000 долларов.
Использование ^-критерия для коэффициента корреляции
В разделе 3.5 был введен коэффициент корреляции г (correlation coefficient), представляющий собой меру зависимости между двумя числовыми переменными. С его помощью можно установить, существует ли между двумя переменными статистически значимая связь. Обозначим коэффициент корреляции между генеральными совокупностями обеих переменных символом р. Нулевая и альтернативная гипотезы формулируются следующим образом:
Н„: р = 0 (нет корреляции),
Нх: р ф 0 (есть корреляция).
ПРОВЕРКА СУЩЕСТВОВАНИЯ КОРРЕЛЯЦИИ
1= Г~Р , (12.14)
/1 - г2
V п - 2 где
г = +\[р , если Ь, > О, г = -Vr2", если Ь, < 0.
Тестовая статистика t имеет t-распределение с п-2 степенями свободы,
В задаче о сети магазинов Sunflowers г = 0,904, а Ьг= 4-1,6’70 (см. рис. 12.4). Поскольку > 0, коэффициент корреляции между объемом годовых продаж и размером магазина равен г = ч-^/0,904 = +0,951. Проверим нулевую гипотезу, утверждающую, что между этими переменными нет корреляции, используя t-статистику.
/-О 0,951-0 1ПГЛ
/ = = .... = 10,64.
/1-7-2 1-0,9512
V77-2 V 14-2
При уровне значимости а = 0,05 нулевую гипотезу следует отклонить, поскольку t = 10,64>2,1788. Таким образом, можно утверждать, что между объемом годовых продаж и размером магазина существует статистически значимая связь (см. рис. 12.18).
При обсуждении выводов, касающихся наклона генеральной совокупности, доверительные интервалы и критерии для проверки гипотез являются взаимозаменяемыми инструментами. Однако вычисление доверительного интервала, содержащего коэффициент корреляции, оказывается более сложным делом, поскольку вид выборочного распределения статистики г зависит от истинного коэффициента корреляции. Подробное обсуждение методов построения доверительных интервалов для коэффициента корреляции содержится в работе [6].
УПРАЖНЕНИЯ К РАЗДЕЛУ 7 ; 7 • - '
Изучение основ
12.35. Допустим, что нулевая гипотеза утверждает, будто между переменными X и Y нет статистически значимой зависимости. Объем выборки п — 18, ^=4-4,5, Sh =1,5.
1. Чему равна тестовая t-статистика?
2. Чему равны критические значения при уровне значимости а = 0,05?
3. Какое статистическое решение следует принять, руководствуясь решениями задач 1 и 2?
4. Постройте 95%-ный доверительный интервал, содержащий наклон генеральной совокупности
12.36. Допустим, что нулевая гипотеза утверждает, будто между переменными X и У нет статистически значимой зависимости. Объем выборки п = 20, SSB = 60, SSE = 40.
1. Чему равна тестовая f-статистика?
2. Чему равны критические значения при уровне значимости а = 0,05?
3. Какое статистическое решение следует принять, руководствуясь решениями задач 1 и 2?
4. Вычислите коэффициент корреляции по величине Г2, считая, что коэффициент ф меньше нуля.
5. Существует ли статистически значимая корреляция между переменными X и У, если уровень значимости равен 0,05?
Применение понятий
Задачи 12.37-12.39 можно решать как вручную, так и с помощью программы Microsoft Excel. Задачи 12.40-12.48 рекомендуется решать с помощью программы Microsoft Excel.
12.37. Менеджер по маркетингу в компании, владеющей крупной сетью супермаркетов, желает предсказать недельный объем продаж, зная расстояния между стеллажами. Воспользуйтесь результатами, полученными при решении задачи 12.3. ^PETFOOD. XLS.
1. Существует ли линейная зависимость между недельным объемом продаж и расстоянием между стеллажами, если уровень значимости равен 0,05?
2. Постройте 95%-ный доверительный интервал, содержащий наклон генеральной совокупности
12.38. Изменчивость биржевого рынка часто измеряют с помощью коэффициента р. Для этого используют модель простой линейной регрессии, считая зависимой переменной процентное изменение курсов анализируемых акций, а независимой — процентное изменение рыночного индекса. В качестве рыночного индекса, как правило, применяется фондовый индекс 500 наиболее активно покупаемых акций на Нью-Йоркской фондовой бирже, публикуемый агентством Standard and Poor (S&P 500). Например, если требуется оценить изменчивость курсов акций компании IBM, применяется следующая рыночная модель:
{Процентное изменение курсов акций компании IBM за неделю) =
= Ро + Р.х(процентное изменение индекса S&P 500 за неделю) + 8.
Регрессионная оценка наклона &„ полученная с помощью метода наименьших квадратов, является оценкой величины р для компании IBM. Обратите внимание на то, что курс акций, для которых коэффициент р равен единице, подчиняется общей рыночной тенденции. Если коэффициент р для каких-либо акций равен 1,5, то скорость роста их стоимости на 50% превышает среднюю скорость роста курса акций на рынке. Если же коэффициент р для каких-либо акций равен 0,6, то скорость роста их курса составляет лишь 60% от рыночного. Акции с отрицательным коэффициентом Р подчиняются противоположной тенденции. В следующей таблице приведены коэффициенты р для некоторых широко распространенных акций.
Компания Коэффициент fl
Procter and Gamble 0,626
Ford Motor Company 1,074
IBM 1,132
LSI Logic 1,705
1. Объясните смысл коэффициента |3 для каждой из четырех компаний.
2. Как инвесторы могут использовать этот коэффициент для правильного вложения средств?
12.39. Некоторые взаимные фонды поддерживают свою доходность на одном уровне с определенным индексом ценных бумаг, например, S&P 500, NASDAQ или Russel 2000. Такие фонды называются индексными. Следовательно, коэффициент fl для акций этих фондов должен быть близок к +1,0. Для оценки изменчивости курсов акций таких фондов применяется следующая рыночная модель:
(Процентное изменение курсов акций индексного фонда за неделю) =
= Ьо + 1,0х(процентное изменение индекса за неделю).
Индексные фонды с высокой степенью риска стремятся усилить эффект от изменения основных индексов. Статья, опубликованная в журнале Mutual Funds (Lynn O'Shaughnessy, “Reach for Higher Returns”, Mutual Funds, July 1999, 44-49), описывает некоторые приобретения и потери, связанные с такими фондами. В ней также приведены данные о некоторых рискованных индексных фондах.
Название (аббревиатура) Описание фонда
Potomac Small Cap Plus (POSCX) 125% от величины индекса Russel 2000
Rydex “Inv” Nova (RYNVX) 150% от величины индекса S&P 500
ProFund UltraOTC “Inv” (UOPIX) 200% индекса NASDAQ
Таким образом, рыночные модели этих фондов выглядят следующим образом:
(Процентное изменение курсов акций фонда POSCX за неделю) = = Ьо + 1,25*(процентное изменение индекса Russel 2000 за неделю) (Процентное изменение курсов акций фонда RYNVX за неделю) = = b0 + 1,50х(процентное изменение индекса S&P 500 за неделю) (Процентное изменение курсов акций фонда UOPIX за неделю) = = Ъо + 2,0х(процентное изменение индекса NASDAQ за неделю)
Таким образом, если индекс Russel 2000 за анализируемый период времени вырос на 10%, курс акций рискованного взаимного фонда увеличится приблизительно на 12,5%. С другой стороны, если индекс Russel 2000 уменьшится на 20%, фонд POSCX потеряет приблизительно 25% .
1. Рассмотрим рискованный взаимный фонд ProFund UltraBull “Inv” (ULPIX), курс акций которого изменяется в два раза сильнее, чем индекс S&P 500. Как выглядит его рыночная модель?
2. Как изменится курс акций фонда ULPIX, если индекс S&P за год вырос на 30% ?
3. Как изменится курс акций фонда ULPIX, если индекс S&P за год уменьшился на 35% ?
4. Каких инвесторов может привлечь рыночная стратегия рискованных индексных фондов? Какие инвесторы избегают покупать акции таких фондов?
12.40. Менеджер агентства по внутригородским грузовым перевозкам желает предсказать затраты рабочего времени, основываясь на данных об объеме груза. Воспользуйтесь результатами, полученными при решении задачи 12.4. ^MOVING. XLS.
1. Существует ли линейная зависимость между объемом груза и количеством рабочих часов, если уровень значимости равен 0,05?
2. Постройте 95%-ный доверительный интервал, содержащий наклон генеральной совокупности
12.41. Менеджер сети почтовых отделений желает предсказать количество заказов, используя вес корреспонденции. Воспользуйтесь результатами, полученными при решении задачи 12.5. ^MAIL. XLS .
1. Существует ли линейная зависимость между количеством заказов и весом корреспонденции, если уровень значимости равен 0,05?
2. Постройте 95%-ный доверительный интервал, содержащий наклон генеральной совокупности
12.42. Менеджер компании, поставляющей видеокассеты, желает предсказать объем продаж, используя данные об объеме кассовых сборов. Воспользуйтесь результатами, полученными при решении задачи 12.6. ^MOVIES . XLS.
1. Существует ли линейная зависимость между объемом продаж видеокассет и кассовыми сборами фильма, если уровень значимости равен 0,05?
2. Постройте 95%-ный доверительный интервал, содержащий наклон генеральной совокупности
12.43. Агент по продаже недвижимости желает предсказать размер месячной аренды апартаментов по их площади. Воспользуйтесь результатами, полученными при решении задачи 12.7. ^IRENT . XLS.
1. Существует ли линейная зависимость между стоимостью месячной аренды и площадью апартаментов, если уровень значимости равен 0,05?
2. Постройте 95%-ный доверительный интервал, содержащий наклон генеральной совокупности р,.
12.44. Для предсказания прочности образцов из алюминия используются данные о его твердости. Воспользуйтесь результатами, полученными при решении задачи 12.8. ^HARDNESS . XLS.
1. Существует ли линейная зависимость между прочностью и твердостью образцов алюминия, если уровень значимости равен 0,05?
2. Постройте 95%-ный доверительный интервал, содержащий наклон генеральной совокупности
12.45. В файле ^REFRIGERATOR.XLS приведены приблизительная розничная цена и стоимость потребляемой электроэнергии за год для 10 морозильников среднего размера.
Источник данных: справочник “Cold Storage” Copyright 1999 by Consumer Union of U. S., Inc. Цитируется no журналу Consumer Reports, февраль 1999, p. 49 с разрешения компании Consumer Union of U. S., Inc., Yonkers, NY.
1. Вычислите коэффициент корреляции г.
2. Существует ли статистически значимая зависимость между розничной ценой морозильника и стоимостью потребляемой электроэнергии за год, если уровень значимости равен 0,05?
12.46. В файле INSECURITY . XLS содержатся данные о производительности металлоискателей в аэропортах в 1998-1999 гг. и количестве нарушений правил безопасности на миллион пассажиров.
Источник: Alan В. Krueger, “A Small Dose of Common Sense Would Help Congress Break the Gridlock over Airport Security”, The New York Times, November 15,2001, C2.
1. Вычислите коэффициент корреляции г.
2. Существует ли статистически значимая линейная зависимость между производительностью металлоискателей и количеством выявленных нарушений, если уровень значимости равен 0,05?
3. Какие выводы можно сделать о зависимости между производительностью металлоискателей и количеством выявленных нарушений?
12.47. В файле llcELLPHONE.XLS хранятся данные о длительности разговоров по мобильным телефонам (ч) и емкость батареек (мА/ч).
Длительность разговоров Емкость батареек Длительность разговоров Емкость батареек
4,50 800 1,50 450
4,00 1 500 2,25 900
3,00 1 300 2,25 900
2,00 1 550 3,25 900
2,75 900 2,25 700
1,75 875 2,25 800
1,75 750 2,50 800
2,25 1 100 2,25 900
1,75 850 2,00 900
Источник: справочник “Service Shortcomings”, Copyright © 2002 by Consumers Union of U.S., Inc. Цитируется no журналу Consumer Reports, February 2002, 25 с разрешения организации Consumer Union of U. S., Inc., Yonkers, NY 10703-1057.
1. Вычислите коэффициент корреляции г.
2. Существует ли статистически значимая линейная зависимость между длительностью разговоров и емкостью батареек, если уровень значимости равен 0,05?
3. Какие выводы можно сделать о зависимости между длительностью разговоров и емкостью батареек?
4. Можно ли на основании этих данных утверждать, что владельцы более емких батареек разговаривают дольше?
12.48. В файле INbatteRIES2 .XLS записаны цены и данные о силе пускового тока для холодного запуска двигателя, обеспечиваемого автомобильными аккумуляторами. Источник: справочник “Leading the Charge”, Copyright 2001 by Consumers Union of U. S., Inc. Цитируется no журналу Consumer Reports, October 2001, 25 с разрешения организации Consumer Union of U. S., Inc., Yonkers, NY 10703-1057.
1. Вычислите коэффициент корреляции г.
2. Существует ли статистически значимая линейная зависимость между силой пускового тока и ценой аккумулятора, если уровень значимости равен 0,05?
3. Какие выводы можно сделать о зависимости между силой пускового тока и ценой аккумулятора?
4. Естественно предположить, что аккумуляторы, обеспечивающие большую силу пускового тока, должны иметь более высокую цену. Подтверждается ли это предположение реальными данными?
12.8. ОЦЕНКА МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ
И ПРЕДСКАЗАНИЕ ИНДИВИДУАЛЬНЫХ ЗНАЧЕНИЙ
В этом разделе рассматриваются методы оценки математического ожидания отклика Y и предсказания индивидуальных значений Y при заданных значениях переменной X.
Построение доверительного интервала
В примере 12.2 регрессионное уравнение позволило предсказать значение переменной Y при заданном значении переменной X. В задаче о выборе места для торговой точки средний годовой объем продаж в магазине площадью 4 000 кв. футов был равен 7,644 млн. долл. Однако эта оценка математического ожидания генеральной совокупности является точечной (point estimate). В главе 7 для оценки математического ожидания генеральной совокупности была предложена концепция доверительного интервала. Аналогично можно ввести понятие доверительного интервала для математического ожидания отклика (confidence interval estimate for the mean responce) при заданном значении переменной X.
ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ ДЛЯ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ ОТКЛИКА Y
Р> |л..д; 2 Y, + , (12.15)
1 (х, -х)'
где ht= — + --— , Yt = b{)- Ь.Х, — предсказанное значение переменной У при
п SSX
X = X', SYX — среднеквадратичная ошибка, п — объем выборки, X, — заданное значение переменной X, Цг|г=л. — математическое ожидание переменной У при Х = Х,, SSX = ±(X,-X)2 .
Анализ формулы (12.15) показывает, что ширина доверительного интервала зависит от нескольких факторов. При заданном уровне значимости возрастание амплитуды колебаний вокруг линии регрессии, измеренное с помощью среднеквадратичной ошибки, приводит к увеличению ширины интервала. С другой стороны, как и следовало ожидать, увеличение объема выборки сопровождается сужением интервала. Кроме того, ширина интервала изменяется в зависимости от значений Xt . Если значение переменной У предсказывается для величин X, близких к среднему значению X , доверительный интервал оказывается t/же, чем при прогнозировании отклика для значений, далеких от среднего.
Допустим, что, выбирая место для магазина, мы хотим построить 95%-ный доверительный интервал для среднего годового объема продаж во всех магазинах, площадь которых равна 4 000 кв. футов.
Y, = 0,964 + 1,670Х, = 0,964 + 1,670x4 = 7,644 млн. долл.
Кроме того,
X = 2,9214 , SYX = 0,9664, SSX = ^Jx, - х)2 = 37,9236 . /=1
По табл. Д.З находим, что t12 = 2,1788. Следовательно, границы доверительного ин тервала равны
Y,±‘„-:Srx^,
где
получаем
= 7,644 ±0,673.
= 7,644 ± 2,1788 х 0,9664 — + ...2,9214.L
у!4 37,9236
Таким образом,
6,971 < цг|л=4 <8,317.
Следовательно, средний годовой объем продаж во всех магазинах, площадь которых равна 4 000 кв. футов, с 95% -ной вероятностью лежит в интервале от 6,971 до 8,317 млн. долл.
Вычисление доверительного интервала для предсказанного значения
Кроме доверительного интервала для математического ожидания отклика при заданном значении переменной X, часто необходимо знать доверительный интервал для предсказанного значения. Несмотря на то что формула для вычисления такого доверительного интервала очень похожа на формулу (12.15), этот интервал содержит предсказанное значение, а не оценку параметра. Интервал для предсказанного отклика Yx=x (prediction interval for an individual responce) при конкретном значении переменной X, определяется по формуле (12.16).
ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ ДЛЯ ПРЕДСКАЗАННОГО ЗНАЧЕНИЯ ОТКЛИКА Yf
Y, ~t^Snл/ПТ < Yx.x < Y, + , (12.16)
1 (x. -x)“
где ht = — + 2-— , Yt = b0 + bxX, — предсказанное значение переменной Y при X = X(,
n SSX
SYX— среднеквадратичная ошибка, n— объем выборки, X,— заданное значение переменной X, Yx=x — предсказанное значение переменной У при X = Х„ SSX = ^(Х, - Х)’ .
Предположим, что, выбирая место для торговой точки, мы хотим построить 95%-ный доверительный интервал для предсказанного годового объема продаж в магазине, площадь которого равна 4 000 кв. футов.
Y, = 0,964 + 1,670Х, = 0,964 + 1,670 х 4 = 7,644 млн. долл.
Кроме того,
X = 2,9214 , = 0,9664, SSX = - Х^ = 37,9236 .
По табл. Д.З находим, что tl2 = 2,1788. Поскольку границы доверительного интервала равны
? — h-2^YX лД + К » где
Z=1
получаем
I i (X'-X)2 I i (4-2,9214?
Y±t„ xJl + - + ^-----— = 7,644 ±2,1788x0,9664.11 + —+ --------->- = 7,644 ± 2,210.
N n SSX \ 14 37,9236
Таким образом,
5,433 < Yx^ <9,854.
Следовательно, предсказанный годовой объем продаж в магазине, площадь которого равна 4000кв. футов, с 95%-ной вероятностью лежит в интервале от 5,433 до 9,854 млн. долл. Доверительные интервалы для математического ожидания отклика и его предсказанного значения при выборе места для магазина из сети Sunflowers, полученные с помощью программы Microsoft Excel, представлены на рис. 12.22. Как видим, доверительный интервал для предсказанного значения отклика намного шире, чем доверительный интервал для его математического ожидания. Это объясняется тем, что изменчивость при прогнозировании индивидуальных значений намного больше, чем при оценке математического ожидания.
г А
1 Анализ данных о магазинах 2 ____________ .
'3 I Data
4 iX Value 4
5 ‘Confidence Level 95%
7 I Intermediate Calculations
8 Sample Size 14
9 Degrees of Freedom 12
10t Value 2,178813
ft! Sample Mean 2,921429
12 Sum of Squared Difference 37,92357
13, Standard Error of the Estimate 0,95638
14 Ih Statistic 0,102104
15 ' Predicted Y (YHat) 7,643923
1b:
17; For Average Y
18 interval Half Width 0,672804
19 < Confidence Interval Lower Limit 6,971119
20; Confidence Interval Upper Limit 8,316727
211
22 : For tadMdual Response ¥
23] Interval Half Width 2,210441
24 ; Prediction Interval Lower Limit 5,433482
25 I Prediction Interval Upper Limit 9,854364
Рис. 12.22. Доверительные интервалы для математического ожидания отклика и его предсказанного значения при выборе места для магазина из сети Sunflowers, полученные с помощью программы Microsoft Excel
Процедуры Excel: построение доверительных интервалов для математического ожидания и предсказанного значения отклика
Для построения доверительных интервалов, содержащих математическое ожидание и предсказанное значение отклика соответственно, следует создать рабочий лист, использующий функции СТЬЮДРАСПОБР и тенденция. Надстройка PHStat2 выполняет эту процедуру автоматически.
Например, чтобы построить доверительные интервалы для математического ожидания и предсказанного годового объема продаж при выборе места для магазина Sunflowers по данным, приведенным в табл. 12.1, необходимо открыть рабочую книгу chapter 12.xls на листе Данные и выполнить одну из следующих процедур.
Применение Excel в сочетании с надстройкой PHStat2
Для построения доверительных интервалов, содержащих математическое ожидание и предсказанное значение отклика соответственно, можно воспользоваться процедурой PHStat^Redgression^ Simple Linear Regression... (РН51а'=>Регрессия'=>Простая линейная регрессия...), следуя приведенным ниже инструкциям.
1. Выбрать команду PHStat^Regression^Simple Linear Regression....
2. В диалоговом окне Simple Linear Regression сделать следующее (см. иллюстрацию).
2.1. Ввести в диалоговом окне Y Variable Cell Range (Входной интервал Y) диапазон ячеек С1:С15.
2.2. Ввести в диалоговом окне X Variable Cell Range (Входной интервал X) диапазон ячеек Bl: В15.
2.3. Установить флажок First cells in both ranges contain a label (Первые ячейки обоих диапазонов содержат метку).
2.4. Ввести в диалоговом окне Confidence level for regression coefficients (Доверительный уровень для коэффициентов регрессии) число 0.95.
2.5. Установить флажки Regression Statistics Table (Таблица регрессионных статистик) и ANOVA and Coefficients Table (Таблица дисперсионного анализа и коэффициентов).
Simple Linear Regression fx]
Data' --- -- -
Y Variable CeM Range: f C1: C16 Z]
X Variable Cell Range: [вквГГ __j
P First cells in both ranges contain label
Confidence level for regression coefficients: [95*”%
Regression Tool Output Options - - — - -P Regression Statistics Table
P ANOVA and Coefficients Table !
Г Residuals Table
Г" Residual Plot
Output Options -
Title: [Анализ данныхэ магазинах
Г“ Scatter Diagram
I Durbin-Watson Statistic
P Confidence and Prediction Interval for X = pF Confidence level for interval estimates: [95”%
Help j |l OK ' j| Cancel |
2.6. Ввести в диалоговом окне Title (Заголовок) название диаграммы.
2.7. Установить флажок Confidence and Prediction Interval for X = (Доверительный интервал и интервал предсказания для переменной X) и ввести число 4000 в соответствующем диалоговом окне. Ввести число 95 в диалоговом окне Confidence level for interval estimates (Доверительный уровень оценок).
2.8. Щелкнуть на кнопке ОК.
Применение Excel
Для того чтобы самостоятельно создать рабочий лист, вычисляющий границы доверительных интервалов, содержащих математическое ожидание и предсказанное значение отклика соответственно, следуйте инструкциям, приведенным в разделе ЕН.12.5.
Жд Chapter 12.xls
Доверительные интервалы для математического ожидания и предсказанного годового объема продаж при выборе места для магазина Sunflowers, построенные по данным, представленным в табл. 12.1, приведены на рабочем листе Рис12.22 в книге chapter 12.xls.
УПРАЖНЕНИЯ К РАЗДЕЛУ 12.8
Изучение основ
12.49. По выборке, содержащей 20 наблюдений, построено уравнение линейной регрессии Yt = 5 + ЗХ, . Кроме того,
8ух=1,0, Х = 2, £(Х,.-Х)2 =20.
1. Постройте 95%-ный доверительный интервал, содержащий математическое ожидание генеральной совокупности откликов при X = 2.
2. Постройте 95%-ный доверительный интервал, содержащий значение отклика при X = 2.
12.50. По выборке, содержащей 20 наблюдений, построено уравнение линейной регрессии Yt = 5 + ЗХ,. Кроме того,
Srx = l,0, Х = 2, £(Х,-Х)2 =20. /=1
1. Постройте 95%-ный доверительный интервал, содержащий математическое ожидание генеральной совокупности откликов при X = 4.
2. Постройте 95%-ный доверительный интервал, содержащий значение отклика при X = 4.
3. Сравните решения задач 12.49.1 и 12.49.2. Какой из интервалов шире? Почему?
Применение понятий
Задачи 12.51-12.56 рекомендуется решать с помощью программы Microsoft Excel.
12.51. Менеджер по маркетингу в компании, владеющей крупной сетью супермаркетов, желает предсказать недельный объем продаж, зная расстояния между стеллажами. Воспользуйтесь результатами, полученными при решении задачи 12.3. ftpETFOOD.XLS.
1. Постройте 95%-ный доверительный интервал, содержащий средний объем продаж во всех магазинах, если расстояние между стеллажами — 8 футов.
2. Постройте 95%-ный доверительный интервал, содержащий объем продаж в магазине, расстояние между стеллажами которого — 8 футов.
3. Объясните разницу между построенными доверительными интервалами.
12.52. Менеджер агентства по внутригородским грузовым перевозкам желает предсказать затраты рабочего времени, основываясь на данных об объеме груза. Воспользуйтесь результатами, полученными при решении задачи 12.4. ^MOVING. XLS.
1. Постройте 95%-ный доверительный интервал, содержащий среднее количество рабочих часов, затраченных на перевозку грузов объемом 500 куб. футов.
2. Постройте 95%-ный доверительный интервал, содержащий количество рабочих часов, затраченных на перевозку конкретного груза объемом 500 куб. футов.
3. Объясните разницу между построенными доверительными интервалами.
12.53. Менеджер сети почтовых отделений желает предсказать количество заказов, используя вес корреспонденции. Воспользуйтесь результатами, полученными при решении задачи 12.5. ^MAIL. XLS.
1. Постройте 95%-ный доверительный интервал, содержащий среднее количество заказов, если вес корреспонденции — 500 фунтов.
2. Постройте 95% -ный доверительный интервал, содержащий количество заказов в корреспонденции, вес которой — 500 фунтов.
3. Объясните разницу между построенными доверительными интервалами.
12.54. Менеджер компании, поставляющей видеокассеты, желает предсказать объем продаж, используя данные об объеме кассовых сборов. Воспользуйтесь результатами, полученными при решении задачи 12.6. ^MOVIES . XLS.
1. Постройте 95%-ный доверительный интервал, содержащий среднее количество проданных видеокассет с фильмами, кассовые сборы которых равны 10 млн. долл.
2. Постройте 95%-ный доверительный интервал, содержащий количество проданных видеокассет с фильмом, кассовые сборы которого равны 10 млн. долл.
3. Объясните разницу между построенными доверительными интервалами.
12.55. Агент по продаже недвижимости желает предсказать размер месячной аренды апартаментов по их площади. Воспользуйтесь результатами, полученными при решении задачи 12.7. ft>RENT . XLS.
1. Постройте 95%-ный доверительный интервал, содержащий среднюю стоимость месячной аренды для всех апартаментов, площадь которых равна 1000 кв. футов.
2. Постройте 95%-ный доверительный интервал, содержащий стоимость месячной аренды апартаментов, площадь которых равна 1000 кв. футов.
3. Объясните разницу между построенными доверительными интервалами.
12.56. Для предсказания прочности образцов из алюминия используются данные о его твердости. Воспользуйтесь результатами, полученными при решении задачи 12.8. ^HARDNESS . XLS.
1. Постройте 95%-ный доверительный интервал, содержащий среднюю прочность образцов, твердость которых равна 30 единиц по Роквеллу.
2. Постройте 95%-ный доверительный интервал, содержащий прочность образца, твердость которого равна 30 единиц по Роквеллу.
3. Объясните разницу между построенными доверительными интервалами.
12.9. ПОДВОДНЫЕ КАМНИ И ЭТИЧЕСКИЕ ПРОБЛЕМЫ, СВЯЗАННЫЕ С ПРИМЕНЕНИЕМ РЕГРЕССИИ
Во врезке перечислены некоторые трудности, связанные с регрессионным анализом.
ВРЕЗКА 12.2. ЛОВУШКИ РЕГРЕССИОННОГО АНАЛИЗА
• Игнорирование условий применимости метода наименьших квадратов.
• Ошибочная оценка условий применимости метода наименьших квадратов.
• Неправильный выбор альтернативных методов при нарушении условий применимости метода наименьших квадратов.
• Применение регрессионного анализа без глубоких знаний о предмете исследования.
• Экстраполяция регрессии за пределы диапазона изменения объясняющей пере-менной.
• Путаница между статистической и причинно-следственной зависимостями.
Широкое распространение электронных таблиц и программного обеспечения для статистических расчетов ликвидировало вычислительные проблемы, препятствовавшие применению регрессионного анализа. Однако это привело к тому, что регрессионный анализ стали применять пользователи, не обладающие достаточной квалификацией и знаниями. Откуда пользователям знать об альтернативных методах, если многие из них вообще не имеют ни малейшего понятия об условиях применимости метода наименьших квадратов и не умеют проверять их выполнение?
Исследователь не должен увлекаться перемалыванием чисел — вычислением сдвига, наклона и коэффициента смешанной корреляции. Ему нужны более глубокие знания. Проиллюстрируем это классическим примером, взятым из учебников.
Анскомб (Anscombe) [1] показал, что все четыре набора данных, приведенных в табл. 12.6, имеют одни и те же параметры регрессии:
Y = 3,0 +0,5Х, ,
SyA. = 1,237, Sh< =0,118, №=0,667,
SSR— объясненная вариация = =27,51,
1-1 v
SSE — необъясненная вариация = ^^-^) =13,76,
/=1 4
SST — полная вариация = ^(У - Г)" = 41,27.
Таблица 12.6. Четыре набора искусственных данных
Набор А Набор Б Набор В Набор Г
X, У, X, У, X, Y. X У,
10 8,04 10 9,14 10 7,46 8 6,58
14 9,96 14 8,10 14 8,84 8 5,76
5 5,68 5 4,74 5 5,73 8 7,71
8 6,95 8 8,14 8 6,77 8 8,84
9 8,81 9 8,77 9 7,11 8 8,47
12 10,84 12 9,13 12 8,15 8 7,04
4 4,26 4 3,10 4 5,39 8 5,25
7 4,82 7 7,26 7 6,42 19 12,50
11 8,33 11 9,26 11 7,81 8 5,56
13 7,58 13 8,74 13 12,74 8 7,91
6 7,24 6 6,13 6 6,08 8 6,89
Источник: Anscombe, F. J., “Graphs in Statistical Analysis’’, American Statistician, 27 (1973): 17-21.
Итак, с точки зрения регрессионного анализа все эти наборы данных совершенно идентичны. Если бы анализ был на этом закончен, мы потеряли бы много полезной информации. Об этом свидетельствуют диаграммы разброса (рис. 12.23) и графики остатков (рис. 12.24), построенные для этих наборов данных.
Рис. 12.23. Диаграммы разброса для четырех наборов данных
Диаграммы разброса и графики остатков свидетельствуют о том, что эти данные отливаются друг от друга. Единственный набор, распределенный вдоль прямой линии, — набор А. График остатков, вычисленных по набору А, не имеет никакой закономерности. Этого нельзя сказать о наборах Б, В и Г. График разброса, построенный по набору Б, демонстрирует ярко выраженную квадратичную модель (см. раздел 12.6). Этот вывод подтверждается графиком остатков, имеющим параболическую форму. Диаграмма разброса и график остатков показывают, что набор данных В содержит выброс. В этой ситуации необходимо исключить выброс из набора данных и повторить анализ. Метод, позволяющий обнаруживать и исключать выбросы из наблюдений, называется анализом влияния [6]. После исключения выброса результат повторной оценки модели может оказаться совершенно иным. Диаграмма разброса, построенная по данным из набора Г, иллюстрирует необычную ситуацию, в которой эмпирическая модель значительно зависит от отдельного отклика (Х8 = 19, У8 = 12,50). Такие регрессионные модели необходимо вычислять особенно тщательно.
Итак, графики остатков являются крайне необходимым инструментом регрессионного анализа и должны быть его неотъемлемой частью. Без них регрессионный анализ не заслуживает доверия.
Остаток +2 г
Р1 -
Р2
Остаток +4 г
+3 -
+2 -
Р1
Р2
Р2
+3
-J X 20
Остаток +2г
10 15
Панель А
5 10 15
Панель В
+2
Р2
Рис. 12.24. Графики остатков для четырех наборов данных
10
Панель Г
Остаток +4
Р11-
10 15
Панель Б
I X 20
о
О
5
ВРЕЗКА 12.3. КАК ИЗБЕЖАТЬ ПОДВОДНЫХ КАМНЕЙ ПРИ РЕГРЕССИОННОМ АНАЛИЗЕ
• Анализ возможной взаимосвязи между переменными X и У всегда начинайте с построения диаграммы разброса.
• Прежде чем интерпретировать результаты регрессионного анализа, проверяйте условия его применимости.
• Постройте график зависимости остатков от независимой переменной. Это позволит определить, насколько эмпирическая модель соответствует результатам наблюдения, и обнаружить нарушение условия гомоскедастичности.
• Для проверки предположения о нормальном распределении ошибок используйте гистограммы, диаграммы “ствол и листья”, блочные диаграммы и графики нормального распределения.
• Если условия применимости метода наименьших квадратов не выполняются, используйте альтернативные методы (например, модели квадратичной или множественной регрессии).
♦ Если условия применимости метода наименьших квадратов выполняются, необходимо проверить гипотезу о статистической значимости коэффициентов регрессии и построить доверительные интервалы, содержащие математическое ожидание и предсказанное значение отклика.
• Избегайте предсказывать значения зависимой переменной за пределами диапазона изменения независимой переменной.
• Имейте в виду, что статистические зависимости не всегда являются причинно-следственными. Помните, что корреляция между переменными не означает наличия причинно-следственной зависимости между ними.
12.10. ВЫЧИСЛЕНИЯ, СВЯЗАННЫЕ С ПРОСТОЙ ЛИНЕЙНОЙ РЕГРЕССИЕЙ
Описывая модель простой линейной регрессии, мы в основном ссылались на результаты, полученные с помощью программы Microsoft Excel. В данном разделе рассматривается процесс вычисления статистик, полученных для простой линейной регрессии.
Вычисление сдвига Ьо и наклона Ь,
Чтобы вычислить регрессионные коэффициенты Ьо и Ьх с помощью метода наименьших квадратов, необходимо решить следующую систему уравнений.
СУММА КВАДРАТОВ ОШИБОК
ж = £(г-у): = ДгЧМ/’ЛК • (12.17)
Значения Ьп и Ъг, минимизирующие выражение (12.17), вычисляются по формулам (12.18) и (12.19).
ФОРМУЛА ДЛЯ НАКЛОНА Д
, SSXY Ь\ — ,
1 SSX
(12.18)
где
SSXY = “X)(Y> ~Y) = XX'Y‘~ —
SSX^X-Xf^X':
п
ФОРМУЛА ДЛЯ СДВИГА Д b^Y-bJ,
(12.19)
Y = ^— п
п
Как показывает анализ формул (12.18) и (12.19), для вычисления регрессионных параметров Ъо и Ьг необходимо знать пять величин: п — объем выборки, ^\Х, — сумму Z=1
п п
значений переменной X, — сумму значений переменной У, — сумму квад-/=1 i=i
ратов значений переменной X и — сумму попарных произведений значений X
i=i
и У,. В задаче о сети магазином Sunflowers для того, чтобы предсказать годовой объем продаж, использовалась площадь магазинов. Значения сумм, необходимых для вычисления параметров Ьо и Ъх при решении этой задачи, приведены на рис. 12.25.
। А В С ; D : Е I F
1 Магазин Площадь (X) Годовые продажи (Y) ХА2 YA2 XY
2 ' 1 1.7 3,7 2,89 13,69. 6,29
3 2 1.6 3,9 2,56 15,21 6,24
4 3 2.8 6.7 7,84 44,89. 18,76
5 . 4 5,6 9.5 31,36 90,25 53,2
6 : 5 1.3 3,4. 1,69 11,56 4,42
7 ’ 6; 2,2 5,6. 4,84 31,36 12,32
0J 7 1,3' 3,7 1,69 13,69 4,81
9 8 1,1 2,7 1,21 7,29 2,97
‘To- 9: 3,2 5,5 10,24 30,25 17,6
тг 10 1.5 2,9 2,25 8,41 4,35
12 11. 5.2 10,7 27,04 114,49 55,64
13 12' 4.6 7,6 21,16 57,76 34,96
14 13 5.8 11,8 33,64 139,24 68,44
15 ( 14 3 4.1 9 16,81 12,3
16 .Всего' 40,9 81,8 157,4 594,9 302,3
Рис. 12.25. Вычисления, выполненные программой Microsoft Excel при решении задачи о сети магазином Sunflowers
Используя формулы (12.18) и (12.19), получим значения параметров Ьо и bt.
SSXY , 1 SSX п п ЕтЕг
SSXY = £(X, - X)(Y, - Y) = Yxiyi ~ =
i=l i=l Z2
= 302,3-40,9x81,8 = 302,3 - 238,97285 = 63,32715.
14
55Х = £(Л-,-Х):=2^:-
п
40 9'
= 157,41----— = 157,41 -119,48642 = 37,92358 .
14
Итак,
63,32715
Л = ————— — Lbbyab 37,92358
ba = Y-bxX ,
где
Y = -=^ = — = 5,842857 , п 14
L— = 2212 = 2,92143 .
и 14
Следовательно,
Ь = 5,842857 - 1,66986 х 2,92143 = 0,964478.
Вычисление оценок вариации
Оценки вариации вычисляются по следующим формулам.
ФОРМУЛА ДЛЯ SSE
SSE = Y(,r.-^ (12.22)
1=1 i=l 1=1 /=1
Используя данные, приведенные на рис. 12.25, получаем:
ОТ = (т; - Y)2 = =
7=1 7=1 и
= 594,9 - = 594,9 - 477,94571 = 116,95429 .
14
" , " fol
SSR = £ £ - У = Ь^У, + =
7 = 1 7 = 1 7=1 П
= 0,964478 х 81,8 +1,66986 х 302,3 - = 105,74726 .
14
SSE = ±(У ~ Г/ = tX~-b{)±Y, - b}±X,Y =
= 594,9 - 0,994478x81,8 - 1,66986x302,3 = 11,20703.
Вычисление среднеквадратичной ошибки наклона
В разделе 12.7 среднеквадратичная ошибка наклона применялась для проверки гипотезы о существовании зависимости между переменными X и У. Формула для вычисления этой ошибки имеет следующий вид:
где
" _ " I ' I дл д2
SSX = У(Х, - X)2 = У X2 --------4- = 157,41---= 37,92358 .
п 14
Следовательно,
О 9663^ = ' V37,92358
Продемонстрируем вычисления, связанные с линейной регрессией, следующим примером.
ПРИМЕР 12.3. ВЫЧИСЛЕНИЕ ПАРАМЕТРОВ Ь„, b„ SST, SSR, SSEW R2
В табл. 12.6 приведены четыре набора данных. Набор А состоит из следующих чисел.
Набор А
X, У
10 8,04
14 9,96
5 5,68
8 6,95
9 8,81
12 10,84
Набор А
X, У,
4 4,26
7 4,82
11 8,33
13 7,58
6 7,24
Вычислите параметры b0, bi9 SST, SSR, SSE, т*, rnSYX.
РЕШЕНИЕ. Необходимо вычислить шесть величин: п — объем выборки, ]ГХг. — ;=1
сумму значений переменной X, ^Yt — сумму значений переменной У, ^Х2 — М п
сумму квадратов значений переменной X, — сумму квадратов значений пере-i=i п
менной У и ^ХД — сумму попарных произведений значений X и Yt. Эти величины, i=i
вычисленные с помощью программы Microsoft Excel, приведены в табл. 12.7.
Таблица 12.7. Параметры, вычисленные с помощью программы Microsoft Excel
A В С I D _ E . F
.1 X Y XA2 YA2 XY
2 10 3.7 100 13,69 37
3 14 3,9 196 15,21 54,6
4 5 6.7 25 44,89 33,5
"s' 8 9,5 64 90,25 76
6 9 3.4 81 11,56 30,6
7 12 5.6 144 31,36 67,2
8 4 3,7 16 13,69 14,8
9 7 2.7 49 7,29 18,9
10 11 5.5 121 30,25 60,5
11 13 2,9 169 8,41 37,7
”12 6 10,7 36 114,49 64,2
13 14 Всего: 99 58,3 1001 381,09 495
Используя формулы (12.18) и (12.19), получим значения параметров Ьо и
L SSXY
~, SSX
п п
YxXY.
ssxy = - y)(i; - г) = Yxiyi ~~—— =
99 x 82 51
= 797,6------- = 797,6-742,59 = 55,01.
11
„ [±х.
SSX = - X)2 = —
/=1 7=1 п
= 1001-----= 1001-891 = 110..
11
Итак,
55,01 НО
= 0,50009.
b{) = Y-b}X,
где
= 7,5009,
82,51
11
Следовательно,
6П= 7,5009 - 0,50009 х 9,0 = 3,00009.
Итак, получаем (н
,ш = I =/_1,-----— =
,=1 Zi' п
= 660,1727- 82,51 = 660,1727-618,9 = 41,2727. 11
ss/? = £(s:-r =*„£}:+/>,=
7=1 7=1 1=1 П
= 3,00009 х 82,51 + 0,50009 х 797,6 - =27,51.
И
SSE^±[Y-Y^±Yi^-b.±Y-h[±XY^
1 = 1 7=1 7 = 1 7=1
= 660,1727-3,00009 х 82,51 - 0,5 0009 х 797,6 = 13,76.
РЕЗЮМЕ
Как показано на структурной схеме, в главе описаны модель простой линейной регрессии, условия ее применимости и способы проверки этих условий. Рассмотрен ^-критерий для проверки статистической значимости наклона регрессии. Для предсказания значений зависимой переменной использована регрессионная модель. Рассмотрен пример, связанный с выбором места для торговой точки, в котором исследуется зависимость годового объема продаж от площади магазина. Полученная информация позволяет точнее выбрать место для магазина и предсказать его годовой объем продаж. В главе 13 будет продолжено обсуждение регрессионного анализа, а также рассмотрены разные модели множественной регрессии.
Простая линейная ррегрессия и корреляи
Регрессия Предназна- $ Корреляция чение
эд наименьших квадратов
Коэффициент
» корреляции^^
ма разброса
простой ре
График Данные
; зависимости Да собирались
। остатков последова-
| от времени % тельно?
Вычисление
Чет
Проверка гипотезы Но;
Анализ остатков
Наблю-
Альтернативные Jia дается ли v Нет методы . <тг,п’ автокор-.реляция?'1'
Модель нет
Да,...
— адекватна'
Проверка гипотезы Но:
Л" J
Имеет
Нет ли модель «Д статистиче значи-
Структурная схема главы 12
ОСНОВНЫЕ ПОНЯТИЯ
F-критерий для наклона, 828 t-критерий
для коэффициента корреляции, 831
для наклона, 827
Автокорреляция, 816
Вариация
необъяснимая, 806
объяснимая,806
полная, 806
Гомоскедастичность, 811
Диаграмма разброса, 793
Доверительный интервал
для математического ожидания отклика, 836
для предсказанного значения отклика, 837
Коэффициент
регрессии, 796
смешанной корреляции, 808
Наклон, 793
Остаток, 812
Отклик,792
Переменная
зависимая, 792
независимая, 792
объясняющая, 792
Регрессия
множественная, 792
простая линейная, 792
Сдвиг, 793
Среднеквадратическая ошибка, 809
Статистика Дурбина-Уотсона, 820
Сумма квадратов
ошибок, 806
полная, 806
регрессии, 806
УПРАЖНЕНИЯ К ГЛАВЕ 12
Проверка знаний
12.57. Объясните смысл сдвига и наклона в регрессионной модели.
12.58. Объясните смысл коэффициента смешанной корреляции.
12.59. В каком случае необъяснимая вариация, или сумма квадратов ошибок, равна нулю?
12.60. В каком случае объяснимая вариация, или сумма квадратов регрессии, равна нулю?
12.61. Почему анализ остатков должен быть неотъемлемой частью регрессионного анализа?
12.62. При каких условиях можно выполнять регрессионный анализ и как его проверить?
12.63. Дайте определение статистики Дурбина-Уотсона.
12.64. При каких условиях необходимо вычислять статистику Дурбина-Уотсона? Обоснуйте свой ответ.
12.65. Чем доверительный интервал для среднего отклика и. отличается от довери-
тельного интервала для предсказанного отклика Yx=x ?
Применение понятий
Задачи 12.66-12.82 рекомендуется решать с помощью программы Microsoft Excel.
12.66. Менеджер компании, производящей безалкогольные напитки, хотел бы минимизировать расходы на перевозку товара потребителям. Часть затрат непосредственно зависит от времени поездки, а другая часть — от времени, затраченного на выгрузку контейнеров. В конкретном районе менеджер отобрал 20 потребителей, а затем зарегистрировал время доставки и количество доставленных контейнеров. ^DELIVERY. XLS.
Потребитель Количество контейнеров Время доставки (мин.)
1 52 32,1
2 64 34,8
3 73 36,2
4 85 37,8
5 95 37,8
6 103 39,7
7 116 38,5
8 121 41,9
9 143 44,2
10 157 47,1
11 161 43,0
12 184 49,4
) 13 202 57,2
14 218 56,8
15 243 60,6
16 254 61,2
17 267 58,2
18 275 63,1
19 287 65,6
20 298 67,3
Постройте модель, позволяющую предсказать время доставки по количеству заказанных контейнеров.
1. Постройте диаграмму разброса.
2. Предположим, что между переменными существует линейная зависимость. Примените метод наименьших квадратов и вычислите коэффициенты регрессии Ъп и Ъх.
3. Запишите уравнение простой линейной регрессии.
4. Объясните смысл наклона Ъх и сдвига Ьо.
5. Предскажите время доставки, если потребитель заказал 150 контейнеров.
6. Можно ли применить эту модель к потребителю, заказавшему 500 контейнеров? Почему?
7. Вычислите коэффициент смешанной корреляции г2 и объясните его смысл.
8. Вычислите коэффициент корреляции.
9. Вычислите среднеквадратичную ошибку оценки.
10. Выполните анализ остатков. Подчиняются ли они какой-либо закономерности? Обоснуйте свой ответ.
11. Существует ли линейная зависимость между временем доставки и количеством заказанных контейнеров, если уровень значимости равен 0,05?
12. Постройте 95% -ный доверительный интервал для среднего времени доставки товара потребителям, заказавшим 150 контейнеров.
13. Постройте 95%-ный доверительный интервал для времени доставки товара потребителю, заказавшему 150 контейнеров.
14. Постройте 95%-ный доверительный интервал для наклона генеральной совокупности откликов.
15. Объясните, как результаты решения задач 1-14 помогают оптимизировать доставку товара потребителям.
12.67. Брокерская контора хотела бы иметь возможность предсказывать количество сделок, совершаемых за один день. В качестве объясняющей переменной было выбрано количество телефонных звонков, поступающих от клиентов. Данные, собранные в течение 35 дней, приведены в файле TRADES . XLS.
1. Постройте диаграмму разброса.
2. Предположим, что между переменными существует линейная зависимость. Примените метод наименьших квадратов и вычислите коэффициенты регрессии bQ и Ьх.
3. Запишите уравнение простой линейной регрессии.
4. Объясните смысл наклона Ьх и сдвига Ьо.
5. Предскажите количество сделок, если в контору за день поступило 2 000 звонков.
6. Можно ли применить эту модель для прогноза количества сделок, если за день в контору поступило 500 звонков? Почему?
7. Вычислите коэффициент смешанной корреляции г2 и объясните его смысл.
8. Вычислите коэффициент корреляции.
9. Вычислите среднеквадратичную ошибку оценки.
10. Постройте график зависимости остатков от времени. Подчиняются ли они какой-либо закономерности? Обоснуйте свой ответ.
11. Вычислите статистику Дурбина-Уотсона.
12. Можно ли считать регрессионную модель адекватной? Обоснуйте свой ответ.
13. Существует ли линейная зависимость между количеством входящих звонков и количеством сделок, если уровень значимости равен 0,05?
14. Постройте 95%-ный доверительный интервал для среднего количества сделок в день, если в контору ежедневно поступает 2 000 звонков.
15. Постройте 95%-ный доверительный интервал для количества сделок в день, когда в контору поступило 2 000 звонков.
16. Постройте 95%-ный доверительный интервал для наклона генеральной совокупности откликов.
17. Следует ли менеджерам брокерской конторы расширить возможности для приема телефонных звонков или увеличить нагрузку на небольшое количество брокеров? Обоснуйте свои рекомендации.
12.68. Постройте линейную модель, позволяющую предсказать продажную цену дома по его оценочной стоимости. В файле ^HOUSEl.XLS приведены данные о 30 недавно проданных одноквартирных домах в небольшом городке на западе США (оценочная стоимость устанавливается один раз в год).
1. Постройте диаграмму разброса.
2. Предположим, что между переменными существует линейная зависимость. Примените метод наименьших квадратов и вычислите коэффициенты регрессии Ьо и bt.
3. Запишите уравнение простой линейной регрессии.
4. Объясните смысл наклона Ьг и сдвига bQ.
5. Предскажите продажную стоимость домов, оценочная стоимость которых равна 70 000 тыс. долл.
6. Вычислите среднеквадратичную ошибку оценки.
7. Вычислите коэффициент смешанной корреляции г* и объясните его смысл.
8. Вычислите коэффициент корреляции.
9. Выполните анализ остатков и оцените адекватность модели.
10. Постройте 95%-ный доверительный интервал для средней продажной стоимости домов, если их оценочная стоимость равна 70 000 тыс. долл.
11. Постройте 95%-ный доверительный интервал для продажной стоимости дома, оценочная стоимость которого равна 70 000 тыс. долл.
12. Постройте 95%-ный доверительный интервал для наклона генеральной совокупности откликов.
L2.69. Постройте линейную модель, позволяющую предсказать оценочную цену дома по его отапливаемой площади. В таблице приведены данные о 15 одноквартирных домах в небольшом городке на Среднем Западе. Оценочная стоимость (в тыс. долл.) и отапливаемая площадь (в кв. футах) приведены в таблице. ^HOUSE2 . XLS.
Дом Оценочная стоимость (тыс. долл.) Отапливаемая площадь (кв. футы)
1 84,4 2,00
2 77,4 1,71
3 75,7 1,45
4 85,9 1,76
5 79,1 1,93
6 70,4 1,20
7 75,8 1,55
8 85,9 1,93
9 78,5 1,59
10 79,2 1,50
11 86,7 1,90
12 79,3 1,39
13 74,5 1,54
14 83,8 1,89
15 76,8 1,59
(Подсказка: сначала определите независимую и зависимую переменные.)
1. Постройте диаграмму разброса. Предполагая, что между переменными существует линейная зависимость, примените метод наименьших квадратов и вычислите коэффициенты регрессии Ьо и Ь,.
2. Объясните смысл наклона и сдвига Ьо.
3. Предскажите оценочную стоимость домов, отапливаемая площадь которых равна 1 750 кв. футов.
4. Вычислите среднеквадратичную ошибку оценки.
5. Вычислите коэффициент смешанной корреляции г* и объясните его смысл.
Вычислите коэффициент корреляции.
7. Выполните анализ остатков и оцените адекватность модели.
8. Существует ли линейная зависимость между оценочной стоимостью домов и их отапливаемыми площадями, если уровень значимости равен 0,05?
9. Постройте 95%-ный доверительный интервал для средней оценочной стоимости домов, если их отапливаемая площадь равна 1 750 тыс. кв. футов.
10. Постройте 95%-ный доверительный интервал для оценочной стоимости дома, если его отапливаемая площадь равна 1 750 тыс. кв. футов.
11. Постройте 95%-ный доверительный интервал для наклона генеральной совокупности откликов.
12. Предположим, что оценочная стоимость четвертого дома равна 79,7 тыс. долл. Повторите решение задач 1-11 и сравните новые результаты со старыми.
12.70. Директор крупной школы бизнеса хотел бы предсказать показатели студентов (grade point index — GPI) по баллам, набранным ими при сдаче выпускного теста (Graduate Management Aptitude Test — GMAT). В таблице приведены данные о 20 студентах, прослушавших двухгодичный курс по избранной программе. ^GPIGMAT .XLS.
Наблюдение GMAT GPI Наблюдение GMAT GPI
1 688 3,72 11 567 3,07
2 647 3,44 12 542 2,86
3 652 3,21 13 551 2,91
4 608 3,29 14 573 2,79
5 680 3,91 15 536 3,00
6 617 3,28 16 639 3,55
7 557 3,02 17 619 3,47
8 599 3,13 18 694 3,60
9 616 3,45 19 718 3,88
10 594 3,33 20 759 3,76
(Подсказка: сначала определите независимую и зависимую переменные.)
1. Постройте диаграмму разброса. Предполагая, что между переменными существует линейная зависимость, примените метод наименьших квадратов и вычислите коэффициенты регрессии д0 и
2. Объясните смысл наклона и сдвига Ьо.
3. Предскажите оценку GPI для студента, получившего 600 баллов при сдаче теста GMAT.
4. Вычислите среднеквадратичную ошибку оценки.
5. Вычислите коэффициент смешанной корреляции г1 2 3 4 5 и объясните его смысл.
6. Вычислите коэффициент корреляции.
7. Выполните анализ остатков и оцените адекватность модели.
8. Существует ли линейная зависимость между оценками GPI и GMAT, если уровень значимости равен 0,05?
9. Постройте 95%-ный доверительный интервал для средней оценки GPI, если оценка GMAT равна 600.
10. Постройте 95%-ный доверительный интервал для оценки GPI, если при сдаче теста GMAT студент набрал 600 баллов.
11. Постройте 95%-ный доверительный интервал для наклона генеральной совокупности откликов.
12. Предположим, что данные о 19- и 20-м студентах были введены неправильно. Балл GPI у 19-го студента равен 3,76, а у 20-го — 3,88. Повторите решение задач 1-11 и сравните новые результаты со старыми.
12.71. Менеджер отдела снабжения крупной банковской организации хотел бы создать модель, позволяющую предсказывать объем времени, необходимый для обработки заказов. В файле INVOICE . XLS приведены данные, собранные в течение 30 дней. Подсказка: определите сначала независимую и зависимую переменные.
1. Постройте диаграмму разброса.
2. Предполагая, что между переменными существует линейная зависимость, примените метод наименьших квадратов и вычислите коэффициенты регрессии Ьо и Ьг.
3. Объясните смысл наклона Ь1 и сдвига д0.
4. Предскажите количество времени, необходимое для обработки 150 заказов.
5. Вычислите среднеквадратичную ошибку оценки.
6. Вычислите коэффициент смешанной корреляции г2 и объясните его смысл.
7. Вычислите коэффициент корреляции.
8. Постройте графики зависимости остатков от количества заказов и от времени.
9. Оцените адекватность линейной модели.
10. Вычислите статистику Дурбина-Уотсона и определите, наблюдается ли автокорреляция в данных, если уровень значимости равен 0,05.
11. Какие выводы о корректности линейной модели можно сделать на основе результатов, полученных при решении задач 8-10?
12. Существует ли линейная зависимость между количеством обработанных заказов и временем, затраченным на их обработку, если уровень значимости равен 0,05?
13. Постройте 95%-ный доверительный интервал для среднего объема времени, затрачиваемого на обработку 150 заказов.
14. Постройте 95%-ный доверительный интервал для объема времени, затрачиваемого на обработку 150 заказов в определенный день.
12.72. 28 января 1986 года на борту космического челнока “Челенджер” погибло семь астронавтов. Перед запуском инженеры компании Morton Triokoi (производителя ракетных двигателей) оценили степень риска, связанную с низкой температурой воздуха, и предложили отложить запуск ракеты. Их аргументы были отвергнуты, и космический корабль трагически погиб. При расследовании обстоятельств трагедии эксперты пришли к выводу, что причиной катастрофы стала утечка топлива
через уплотнительное кольцо, треснувшее вследствие низкой температуры воздуха. В таблице приведены данные о температуре воздуха и степени риска, связанной с повреждением уплотнительного кольца. Йо-RING. XLS.
Номер запуска Температура воздуха (°F) Степень повреждения уплотнительного кольца
1 66 0
2 70 4
3 69 0
5 68 0
6 67 0
7 72 0
8 73 0
9 70 0
41-В 57 4
41-С 63 2
41-D 70 4
41-G 78 0
51-А 67 0
51-В 75 0
51-С 53 11
51-D 67 0
51-F 81 0
51-G 70 0
51-1 67 0
51-J 79 0
61-А 75 4
61-В 76 0
61-С 58 4
Примечание’, данные о четвертом запуске пропущены, поскольку степень повреждения уплотнительного кольца не измерялась.
Основной источник: Report of the Presidental Commission on the Space Shuttle Challenger Accident, Washington, DC, 1986, Vol. II, ppHl-H3, and Volume IV, p.664; Post Challenger Evaluation of Space Shuttle Risk Assessment and Management, Washington, DC, 1988, pp. 135,136. Вспомогательный источник: Tufte, E. R., Visual and Statistical Thinking: Displays of Evidence for Making Decisions (Cheshire, CT: Graphics Press, 1997).
1. Постройте диаграмму разброса для семи запусков, при которых повреждалось уплотнительное кольцо (степень риска не равна нулю). Что можно сказать о зависимости между температурой воздуха и степенью повреждения уплотнительного кольца?
2. Постройте диаграмму разброса для всех 23 запусков.
3. Объясните различия между зависимостями, полученными при решении задач 1 и 2.
4. Почему построенную модель нельзя применять для предсказания степени повреждения при температуре воздуха, равной 31 °F (температура воздуха во время запуска космического корабля “Челенджер”)?
5. Несмотря на то что предположение о линейной зависимости между температурой воздуха и степенью повреждения уплотнительного кольца не реализуется, постройте модель простой линейной регрессии для предсказания степени риска.
6. Проведите прямую линию, аппроксимирующую данные, изображенные на диаграмме разброса.
7. Является ли прямая линия подходящей моделью для аппроксимации этих данных? Обоснуйте свой ответ.
8. Выполните анализ остатков. К каким выводам вы пришли?
12.73. Бретт Трумен (Brett Trueman), профессор школы бизнеса в университете штата Калифорния в Беркли (University of California at Berkeley), изучает зависимость между доходами Интернет-компаний и количеством посетителей их Web-сайтов. Результаты его исследований для 10 крупнейших Интернет-компаний приведены в файле ^PAGEVIEW. XLS.
Источник: Krantz, М., “Net Investors Follow Stats”, USA Today, January 20,2000, p. LB.
В качестве зависимой переменной выберите валовую прибыль (млн. долл.), а в качестве независимой — количество посетителей Web-страниц (тыс. в месяц).
1. Постройте диаграмму разброса и объясните ее смысл.
2. Предполагая, что между переменными существует линейная зависимость, примените метод наименьших квадратов и вычислите коэффициенты регрессии Ьо и
3. Объясните смысл наклона Ьу и сдвига Ьо.
4. Постройте 95%-ный доверительный интервал для наклона генеральной совокупности откликов и объясните его смысл.
5. Вычислите и объясните коэффициент смешанной корреляции.
6. Вычислите и объясните среднеквадратичную ошибку оценки.
7. Есть ли выбросы в исходных данных? Если да, установите соответствующую компанию и опишите полученные результаты.
8. Удалите из таблицы данные о компании Amazon.com и повторите регрессионный анализ. Как это влияет на статистические выводы?
12.74. Во время осеннего сбора урожая в США на фермах продается большое количество тыквенных семечек. Часто вместо взвешивания их засыпают в бочонки. На вопрос “Почему вы это делаете?” фермеры отвечают: “Я могу сказать, сколько семечек в бочонке”. Чтобы определить, правду ли они говорят, были взвешены 23 бочонка семечек. C^PUMPKIN. XLS.
Длина окружности бочонка, см Вес, г Длина окружности бочонка, см Вес, г
50 1 200 57 2 000
55 2 000 66 2 500
54 1 500 82 4 600
52 1 700 83 4 600
37 500 70 3 100
52 1 000 34 600
53 1 500 51 1 500
47 1 400 50 1 500
51 1 500 49 1 600
63 2 500 60 2 300
53 500 59 2 100
43 1 000
1. Постройте диаграмму разброса.
2. Предполагая, что между переменными существует линейная зависимость, примените метод наименьших квадратов и вычислите коэффициенты регрессии Ьо и bj.
3. Объясните смысл наклона Ьх и сдвига Ъо.
4. Предскажите среднее количество семечек в бочонке, длина окружности которого равна 60 см.
5. Правильно ли делают фермеры, продавая семечки в бочонках, а не на вес? Обоснуйте свой ответ.
6. Вычислите коэффициент смешанной корреляции г2 и объясните его смысл.
7. Вычислите среднеквадратичную ошибку оценки.
8. Выполните анализ остатков и оцените адекватность линейной модели.
9. Существует ли линейная зависимость между количеством семечек и длиной окружности бочонка?
10. Постройте 95%-ный доверительный интервал для наклона генеральной совокупности откликов.
11. Постройте 95%-ный доверительный интервал для среднего количества семечек в бочонке, длина окружности которого равна 60 см.
12. Постройте 95%-ный доверительный интервал для количества семечек в бочонке диаметром 60 см.
12.75. Крейзи Дейв (Crazy Dave), популярный бейсбольный обозреватель, изучил статистические показатели разных команд на протяжении сезона 2002 года. Он хотел бы предсказать количество побед, одержанных командами в течение сезона. Для этого он решил использовать среднее количество очков (earned team average — ERA), набранных командой за сезон. В файле ^ВВ2000. XLS содержатся дацные о 30 ведущих командах.
Подсказка: определите сначала независимую и зависимую переменные.
1. Постройте диаграмму разброса.
2. Предполагая, что между переменными существует линейная зависимость, примените метод наименьших квадратов и вычислите коэффициенты регрессии Ьо и Ь}.
3. Объясните смысл наклона и сдвига Ьп.
4. Предскажите количество побед, одержанных командой, показатель ERA которой равен 4,50.
5. Вычислите среднеквадратичную ошибку оценки.
6. Вычислите коэффициент смешанной корреляции г1 и объясните его смысл.
7. Вычислите коэффициент корреляции.
8. Выполните анализ остатков и оцените адекватность модели.
9. Существует ли линейная зависимость между количеством побед и показателем ERA, если уровень значимости равен 0,05?
10. Постройте 95% -ный доверительный интервал для среднего количества побед у команды с показателем ERA, равным 4,50.
11. Постройте 95% -ный доверительный интервал для количества побед у команды с показателем ERA, равным 4,50.
12. Постройте 95%-ный доверительный интервал для наклона генеральной совокупности откликов.
13. Предположим, что указанные 30 команд исчерпывают всю генеральную совокупность. Чтобы статистические выводы были корректными, выборка должна быть случайной. К какой генеральной совокупности относятся сделанные статистические выводы?
14. Какие еще независимые переменные стоит включить в модель?
12.76. Компания Zagat публикует рейтинги ресторанов, расположенных в разных городах США. В файле RESTRATE. XLS содержатся оценки качества пищи, оформления блюд, уровня обслуживания и стоимость обеда для одного человека в 50 ресторанах Нью-Йорк Сити и 50 ресторанах Лонг-Айленда. ^RESTRATE. XLS.
Источник: цитируется по изданиям Zagat Survey “2002 New York City Restraunts” и Zagat Survey “2001 -2002, Long Island Restraunts”.
1. Постройте диаграмму разброса.
2. Предполагая, что между переменными существует линейная зависимость, примените метод наименьших квадратов и вычислите коэффициенты регрессии Ьо и Ъг.
3. Объясните смысл наклона и сдвига Ьо.
4. Предскажите стоимость обеда в ресторане, рейтинг которого равен 50.
5. Вычислите среднеквадратичную ошибку оценки.
6. Вычислите коэффициент смешанной корреляции г2 и объясните его смысл.
7. Вычислите коэффициент корреляции.
8. Выполните анализ остатков и оцените адекватность модели.
9. Существует ли линейная зависимость между стоимостью обеда и рейтингом ресторана, если уровень значимости равен 0,05?
10. Постройте 95% -ный доверительный интервал для средней стоимости обеда в ресторане, рейтинг которого равен 50.
11. Постройте 95% -ный доверительный интервал для стоимости обеда в ресторане, рейтинг которого равен 50.
12. Постройте 95%-ный доверительный интервал для наклона генеральной совокупности откликов.
13. Можно ли на основе рейтинга точно предсказать стоимость обеда в ресторане? Обоснуйте свой ответ.
12.77. Можно ли на основе демографической информации предсказать объем продаж в магазинах спортивных товаров? В файле SPORTING.XLS содержатся ежемесячные объемы продаж в 38 случайно выбранных магазинах, принадлежащих крупной национальной франчайзинговой сети. Следовательно, все магазины имеют одинаковый размер и торгуют одинаковыми товарами. Округ, в котором магазины приносят наибольший доход, называется потребительской базой. Для каждого из 38 магазинов приводится демографическая информация о потребителях. Данные вполне реальны, однако компания не желает обнародовать свое название. В набор входят следующие переменные.
Продажи — данные за последний месяц (в долларах).
Возраст — средний возраст потребительской базы.
Среднее — процентная доля покупателей, имеющих среднее образование.
Высшее — процентная доля покупателей, имеющих высшее образование.
Прирост — ежегодный прирост потребительской базы за последние 10 лет.
Доход — средний доход семьи, входящей в потребительскую базу (в долларах). ^SPORTING.XLS
1. Постройте диаграмму разброса, считая, что зависимой переменной является объем продаж, а независимой — средний доход семьи.
2. Предполагая, что между переменными существует линейная зависимость, примените метод наименьших квадратов и вычислите коэффициенты регрессии Ьо и
3. Объясните смысл наклона Ьг и сдвига Ъо.
4. Вычислите среднеквадратичную ошибку оценки.
5. Вычислите коэффициент смешанной корреляции г2 и объясните его смысл.
6. Вычислите коэффициент корреляции г и объясните его смысл.
7. Выполните анализ остатков и оцените адекватность модели.
8. Существует ли линейная зависимость между переменными, если уровень значимости равен 0,05?
9. Постройте 95%-ный доверительный интервал для наклона генеральной совокупности откликов и объясните его смысл.
10. Повторите решение задач 1-9, считая независимой переменной средний возраст покупателей.
11. Повторите решение задач 1-9, считая независимой переменной количество покупателей, имеющих среднее образование.
12. Повторите решение задач 1-9, считая независимой переменной количество покупателей, имеющих высшее образование.
13. Повторите решение задач 1-9, считая независимой переменной ежегодный прирост потребительской базы.
14. Какая из этих моделей точнее?
15. Напишите краткий отчет о своем исследовании.
12.78. Каждый год ученики 9-х классов на юго-западе штата Огайо должны проходить тестирование. В файле SCHOOLS.XLS приведены результаты тестирования в 47 школьных округах на юго-западе штата Огайо в 1994-1995 годах. В этот набор входят следующие переменные.
Округ — название школьного округа.
Процент — процентная доля учеников, успешно прошедших тестирование.
Посещаемость — средняя посещаемость уроков.
Зарплата — средняя зарплата учителей (в долларах).
Расходы — расходы на одного ученика (в долларах). , ^SCHOOLS.XLS
Источник: Skertic, М., “School Spending Doesn't Add Upp”, Cincinnatti Enquirer, October 22,1995,p.Al.
1. Постройте диаграмму разброса, считая, что зависимой переменной является процентная доля учеников, успешно прошедших тестирование, а независимой — средняя посещаемость уроков. Объясните смысл диаграммы.
2. Предполагая, что между переменными существует линейная зависимость, примените метод наименьших квадратов и вычислите коэффициенты регрессии Ьп и Ь,.
3. Объясните смысл наклона Ьг и сдвига Ьо.
4. Вычислите среднеквадратичную ошибку оценки.
5. Вычислите коэффициент смешанной корреляции т* и объясните его смысл.
6. Вычислите коэффициент корреляции г и объясните его смысл.
7. Выполните анализ остатков и оцените адекватность модели.
8. Существует ли линейная зависимость между переменными, если уровень значимости равен 0,05?
9. Постройте 95%-ный доверительный интервал для наклона генеральной совокупности откликов и объясните его смысл.
10. Повторите решение задач 1-9, считая независимой переменной среднюю зарплату учителей.
11. Повторите решение задач 1-9, считая независимой переменной среднее количество затрат.
12. Какая из этих моделей является наиболее точной?
13. Напишите краткий отчет о своем исследовании.
12.79. Вернемся к обсуждению показателя 0 и рыночных моделей, упомянутых в задачах 12.38 и 12.39. Файл SP500.XLS содержит данные, которые регистрировались каждую неделю с 14 мая 2002 года по 14 мая 2003 года. Недельные колебания индекса S&P 500 и курсов акций шести избранных компаний представляют собой процентное изменение по отношению к курсу акций на предыдущей неделе, зафиксированному на момент закрытия последних торгов. В файле содержатся значения следующих переменных.
Неделя — текущая неделя.
S Р 5 О О — недельное колебание индекса S&P 500.
IAL— недельное колебание биржевой стоимости акций компании International Aluminium.
SEARS — недельное колебание биржевой стоимости акций компании SEARS. BancONE — недельное колебание биржевой стоимости акций корпорации Вап-cONE из штата Огайо.
GM — недельное колебание биржевой стоимости акций компании GM. CtSP500.XLS
Источник: Yahoo. сот, Мау 15, 2003.
1. Оцените рыночную модель для компании IAL. (Подсказка: в качестве независимой переменной используйте колебания индекса S&P 500, а в качестве зависимой — колебания курса акций компании IAL.)
2. Объясните смысл показателя Р для компании IAL.
3. Повторите решение задач 1 и 2 для компании Sears.
4. Повторите решение задач 1 и 2 для корпорации BancONE.
5. Повторите решение задач 1 и 2 для компании General Motors.
6. Кратко изложите свои выводы.
12.80. Файл RETURNS.XLS содержит данные о курсах акций четырех компаний, собранных на протяжении 54 последовательных недель, предшествовавших 14 мая 2003 года. В файле содержатся значения следующих переменных.
Неделя — дата закрытия торгов.
GM — курс акций компании General Motors.
Ford — курс акций компании Ford.
IAL — курс акций компании International Aluminium.
MS FT — курс акций компании Microsoft Corporation.
^RETURNS .XLS
Источник: Yahoo. com, Мау 15, 2003.
1. Вычислите коэффициент корреляции г для каждой из шести пар компаний.
2. Объясните смысл вычисленного коэффициента корреляции г.
3. Целесообразно ли включать в портфель инвестиций только акции компаний, связанных между собой сильной положительной корреляцией? Обоснуйте свой ответ.
12.81. Коррелируют ли между собой ежедневная доходность фондового рынка и процент учетной ставки? Файл BONDRATE . XLS содержит данные об учетной ставке и величине показателя Доу-Джонса для 60 последовательных рабочих дней, предшествующий 14 мая 2003 года. В файле содержатся значения следующих переменных.
Дата — текущая дата.
10-летние облигации— изменение учетной ставки 10-летних облигаций Министерства финансов США (процентное изменение по отношению к величине учетной ставки на момент закрытия предыдущих торгов).
DJIA — изменение показателя Доу-Джонса (процентное изменение по отношению к величине показателя на момент закрытия предыдущих торгов).
^BONDRATE . XLS
Источник: Yahoo. сот, Мау 15,2003.
1. Вычислите коэффициент корреляции г между переменными DJIA и 10-летние облигации.
2. Существует ли линейная зависимость между этими переменными, если уровень значимости равен 0,05? Обоснуйте свой ответ.
3. Существует ли линейная зависимость между этими переменными, если уровень значимости равен 0,01? Обоснуйте свой ответ.
4. Объясните, почему эти переменные коррелируют друг с другом.
Отчеты
12.82. В задаче 12.77 мы разработали регрессионные модели для предсказания ежемесячных объемов продаж в магазинах спортивных товаров. Напишите отчет о своих исследованиях. Дополните свой отчет диаграммами и другой статистической информацией. Для создания и вставки таблиц и диаграмм используйте программу Microsoft Excel и пакет Microsoft Office. Подготовьте презентацию с помощью программы Power Point. S PORT I NG. XLS.
Применение Интернет
12.83. Зайдите на сайт www.prenhall.com/levine. Выберите ссылку Chapter 12 и щелкните на ссылке Internet exercises.
Для того чтобы реализовать корпоративную стратегию, направленную на увеличение числа подписчиков, отделы маркетинга и доставки должны тесно сотрудничать друг с другом. Их цель — обеспечить бесперебойную доставку газеты временным подписчикам. Очень важно, чтобы как можно больше временных подписчиков по истечении испытательного срока стали постоянными читателями газеты. Для этого необходимо избежать неприятных моментов, которые чаще всего возникают в течение первой недели испытательного срока.
В частности, крайне необходимо, чтобы отдел маркетинга как можно точнее предсказывал количество подписчиков в следующем месяце. Для этого объединенная группа менеджеров отделов маркетинга и доставки решила разработать более эффективный метод прогноза. Ранее группа, состоящая из трех менеджеров анализировала данные, собранные в течение предыдущих 2-х или 3-х месяцев, и делала прогноз количества новых подписчиков. Теперь руководство газеты решило нанять Лорен Холл (Lauren Hall) — специалиста по количественным методам прогноза — и поручить ей проанализировать показатели, влияющие на количество новых подписчиков.
Предсказания в течение последнего года были особенно неточными, поскольку основное внимание группы было сосредоточено на развитии прямого телефонного маркетинга, а прогнозы никого не интересовали. В частности, в прошлом месяце общая продолжительность звонков составила всего 1 055 часов, так как участники опроса всю первую неделю осваивали формальный и стандартный стиль общения с респондентами. Тогда Лорен предположила, что необходимые данные можно получить в архиве, подняв документы за последние два года. Ее особенно заинтересовало, сколько новых подписчиков появлялось у газеты в каждом месяце и сколько часов было затрачено на прямой телефонный маркетинг. Эти данные приведены в файле f^SH12 . XLS.
УПРАЖНЕНИЯ
Какие критические замечания можно сделать по поводу метода предсказания количества новых подписчиков, которым редакция пользовалась в прошлом?
Какие факторы, кроме количества часов, затраченных на прямой телефонный маркетинг, могут влиять на количество новых подписчиков? Обоснуйте свой ответ.
Выполните следующие задания.
SH.12.3.1. Проанализируйте данные и разработайте статистическую модель, позволяющую предсказывать среднее количество новых подписчиков в следующем месяце в зависимости от времени, затраченного на прямой телефонный маркетинг. Напишите отчет, содержащий полное описание модели.
SH. 12.3.2. Допустим, что в следующем месяце на прямой телефонный маркетинг будет потрачено 1 200 часов. Предскажите среднее количество новых подписчиков, которые появятся в следующем месяце. Укажите, какие условия должны выполняться при прогнозировании. Выполняются ли они в данном случае? Обоснуйте свой ответ.
SH.12.3.3. Какая опасность кроется в прогнозировании количества новых подписчиков, если в следующем месяце на прямой телефонный маркетинг планируется затратить 2 000 ч? Объясните свой ответ.
ПРИМЕНЕНИЕ WEB
Примените свои знания о простой линейной регрессии при выборе оптимального места для магазина сети Sunflowers.
Агент по лизингу из корпорации Triangle Management предложил компании Sunflowers на выбор несколько мест для открытия магазина в пассажах, приносящих повышенный чистый доход. Хотя площади этих магазинов несколько меньше, чем средняя площадь магазинов в сети Sunflowers, агент утверждает, что повышенный чистый доход окружающих магазинов являются верным индикатором прибыли. В подтверждение своих слов, агент предоставил выборку, состоящую из 14 магазинов Sunflowers.
Проанализируйте предложение агента и сопутствующие документы, посетив Web-сайт компании Triangle Management (www.prenhall.com/Springville/Triangle_ Sunflower . html), и ответьте на следующие вопросы.
1. Следует ли использовать средний чистый доход для предсказания объемов продаж в магазинах Sunflowers на основе выборки, содержащей информацию о 14 магазинах?
2. Следует ли принять предложение агента по лизингу? Обоснуйте свой ответ.
3. Не следует ли пренебречь средним чистым доходом окружающих магазинов при выборе нового места? Обоснуйте свой ответ.
4. Существуют ли другие факторы, не упомянутые агентом по лизингу, но влияющие на принятие решения при выборе места для магазина?
СПРАВОЧНИК ПО EXCEL ГЛАВА 12
ЕН.12.1. Выполнение простого линейного регрессионного анализа
Для вычисления коэффициентов простой линейной регрессии, построенной с помощью метода наименьших квадратов, следует применить процедуру Анализ данных^ Регрессия. Например, чтобы вычислить коэффициенты простой линейной регрессии для данных, приведенных в табл. 12.1, необходимо открыть рабочую книгу Chapter 12 . xls на листе Данные и выполнить следующие процедуры.
1. Выбрать команду PHStat^Regression^Simple Linear Regression... (PHStat^ Регрессия ^Простая линейная регрессия...).
2. В диалоговом окне Simple Linear Regression выполнить такие действия (см. иллюстрацию).
2.1. Ввести в диалоговом окне Входной интервал Y диапазон ячеек cl: С15.
2.2. Ввести в диалоговом окне Входной интервал X диапазон ячеек Bl: В15.
2.3. Установить флажок Метки.
2.4. Ввести в диалоговом окне Уровень надежности число 0.95.
2.5. Установить переключатель Параметры вывода в положение Новый рабочий лист.
2.6. Щелкнуть на кнопке ОК.
Регрессия
X
Входные данные
Входной интервал Y:
Входной интервал X;
0 Метки
0 йювень надежности:
Параметры вывода
О Выходной интервал:
® Новый рабочий лист: О Новая рабочая книга Остатки □ Остатки П Стандартизованные о<
Нормальная вероятность
0 Г рафик нормальной вероятности
•С1:С15
'61:615
[ Отмена ]
0 Константа - ноль |95
: Анализ данных
Q График остатков 0 График подбора
[ Справка ]
ЕН.12.2. Добавление линии регрессии на диаграмму разброса
Для того чтобы добавить на диаграмму разброса линию регрессии, необходимо выделить созданную диаграмму и выполнить такие действия.
1. Выбрать команду Диаграмма^Добавить линию тренда... (опция Диаграмма появляется в линейке меню программы Microsoft Excel, только если пользователь выделил диаграмму).
2. В диалоговом окне Линия тренда сделать следующее.
2.1. Щелкнуть на корешке вкладки Тип и выбрать в списке Построение линии тренда (аппроксимация и сглаживание) пункт Линейная (см. первую иллюстрацию).
2.2. Щелкнуть на корешке вкладки Параметры. Установить переключатель Название аппроксимирующей (сглаженной) кривой в положение Автоматическое. Установить флажки Показывать уравнение на диаграмме и Поместить на диаграмме величину достоверности аппроксимации (RA2) (см. вторую иллюстрацию).
2.3. Щелкнуть на кнопке ОК.
ЕН.12.3. Модификация диаграмм разброса и графиков остатков
Ограничения, связанные с использованием Мастера диаграмм и процедуры Сервис^Анализ данных^Регрессия, иногда приводят к тому, что внешний вид диаграмм разброса и графиков остатков оставляет желать лучшего. Чтобы преодолеть эти ограничения и улучшить внешний вид диаграмм, необходимо выполнять следующие инструкции.
Преобразование внедренной диаграммы в лист диаграммы. Если диаграмма представляет собой объект, внедренный в рабочий лист, ее можно преобразовать в лист диаграммы, т.е. создать новый рабочий лист, содержащий данную диаграмму. Для этого необходимо выделить нужную диаграмму и выполнить следующие действия.
1. Выбрать команду Диаграмма^Размещение....
2. В диалоговом окне Размещение диаграммы установить переключатель Поместить диаграмму на листе в положение Отдельном, ввести в окне редактирования название нового листа диаграммы и щелкнуть на кнопке ОК.
Перемещение оси X в низ диаграммы. Если переменная У на диаграмме разброса или графике остатков может принимать отрицательные значения, программа Microsoft Excel проведет ось X через точку У = 0, возможно, скрыв некоторые точки графика. Чтобы переместить ось X вниз, необходимо выделить диаграмму и выполнить следующие действия.
1. Выделить ось У. Если курсор мыши установлен точно, на экране появится подсказка “Ось Y (значений) ” (см. фрагмент на иллюстрации).
2. Выбрать во всплывающем меню команду Формат оси....
3. Находясь в диалоговом окне Формат оси, щелкнуть на корешке Шкала и ввести в окне редактирования Ось X (категорий) пересекает в значении число, указанное в окне редактирования Минимальное значение. Как только вы введете это значение, соответствующий флажок будет сброшен автоматически.
4. Необязательная операция. Изменить минимальное и максимальное значения переменной У.
5. Щелкнуть на кнопке ОК.
Формат оси
Вид ! Шкала ; Шрифт Число Выравнивание
| Шкала по оси X (категорий)
i Авто
j Н минимальное значение: i -2.5
0 максимальное значение: :1.5
! 0 цена основных делений: :0.5
0 ценз промежуточных леленнй: j D, J
! П Ось Y (значений)
j пересекает в значении: -2,5
J Цена деления Нет v
| 0 логарифмическая шкала
j О обратный порядок значений
) Q пересечение с осью Y (значений) в максимальном значении
ЕН.12.4. Вычисление статистики Дурбина-Уотсона
Для вычисления статистики Дурбина-Уотсона сначала необходимо выполнить простой линейный регрессионный анализ, а затем реализовать шаблон рабочего листа, использующего функции СУММКВРАЗН и СУММКВ. Вызовы этих функций выглядят следующим образом.
СУММКВРАЗН (диапазон первой переменной; диапазон второй переменной), СУММКВ (диапазон переменной).
Например, в табл. ЕН. 12.1 показан шаблон рабочего листа для вычисления статистики Дурбина-Уотсона на основе данных, приведенных в табл. 12.3. Этот лист вычисляет значения е, и е(1 и суммирует квадраты все остатков с помощью функций СУММКВРАЗН и СУММКВ соответственно. Предполагается, что остатки находятся в диапазоне ячеек С25 : С3 9 на рабочем листе SLR. (При вычислении простой линейной регрессии процедуры PHStat^Regression^Simple Linear Regression... и Сервис^Анализ данных... ^Регрессия должны размещать результаты вычислений в указанном диапазоне ячеек на соответствующем рабочем листе.)
Таблица ЕН.12.1. Шаблон рабочего листа Дурбин-Уотсон
А 8
Вычисление статистики Дурбина-Уотсона
||Я|
jJIBI Сумма квадратов разностей остатков =CyMMKBPA3H(SLR!C26:C39;SLR!C25:C38)
4 Сумма квадратов остатков =CyMMKB(SLR!C25:C39)
5
6 Статистика Дурбина-Уотсона =ВЗ/В4
ЕН.12.5. Вычисление доверительных интервалов для математического ожидания и предсказанного значения отклика
Зная величину среднеквадратичной ошибки Syx, можно создать рабочий лист, использующий для вычисления доверительных интервалов для среднего и предсказанного отклика функции СТЬЮДРАСПОБР и ТЕНДЕНЦИЯ. Их вызовы имеют следующий вид.
СТЬЮДРАСПОБР (1 -доверительный уровены, степени свободы),
ТЕНДЕНЦИЯ (диапазон ячеек для переменой Y; значение переменной X) .
В табл. ЕН. 12.2 показан шаблон рабочего листа, реализующий вычисления доверительных интервалов для математического ожидания и предсказанного значения отклика при решении задачи о сети магазинов Sunflowers. Для вычисления t-статистики используется функция СТЬЮДРАСПОБР, а для вычисления среднего значения переменной У при заданном значении переменной X — функция ТЕНДЕНЦИЯ. Предполагается, что данные из табл. 12.1 находятся в столбцах А-С на листе Данные, столбец!) содержит квадраты разностей между значениями переменной X и ее средним значением. Кроме того, предполагается, что среднеквадратичная ошибка оценки Syx находится в ячейке В7 на листе SLR. (Процедура Simple Linear Regression надстройки PHStat2 и стандартная процедура Регрессия программы Microsoft Excel, помещают среднеквадратичную ошибку оценки именно в эту ячейку.)
Таблица ЕН.12.2. Шаблон рабочего листа Интервалы
1 Доверительный интервал
2
3 Данные
4 Значение переменной X 4
5 Доверительный уровень 0,95
6
7 Промежуточные вычисления
8 Объем выборки =СЧЕТ(Данные!В:В)
9 Количество степеней свободы = В8-2
10 Л статистика =СТЬЮДРАСПОБР(1-В5;В9)
11 Выборочное среднее =СРЗНАЧ(Данные!В:В)
12 Сумма квадратов разностей =СУММА(Данные!0:0)
13 Среднеквадратичная ошибка =SLR!B7
14 Л-статистика =1/В8+(В4-В11)Л2/В12
15 Среднее предсказанное значение ( ¥ ) =ТЕНДЕНЦИЯ(Данные!С2:С15;Данные!В2:В15;В4)
|1Ц
17 Для математического ожидания отклика
18 Половина ширины интервала = ВЮ*В13*КОРЕНЬ(В14)
Нижняя граница интервала =В15-В18
20 Верхняя граница интервала =В15+В18
21
22 Для предсказанного значения отклика
23 Половина ширины интервала =В10*В13*КОРЕНЬ(1+В14)
24 Нижняя граница интервала = В15-В23
25 Верхняя граница интервала =В15+В23
При реализации этого шаблона сначала необходимо создать рабочий лист Интервалы, а затем добавить столбец D в рабочий лист Данные, руководствуясь указанными инструкциями. Не следует обращать внимание на сообщения об ошибке #ДЕЛ/0?, поскольку при изменении рабочего листа Данные они исчезнут. Для этого достаточно щелкнуть на корешке листа Данные, ввести в ячейку D1 заголовок (Х-ХВаг) л2, а в ячейку D2 — формулу = (В2-Интервалы! $В$11) л2и скопировать ее в ячейки вплоть до строки 15.
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
1. Anscombe, F. J., “Graphs in Statistical Analysis”, The American Statistician 27 (1973): 17-21.
2. Hoaglin, D. C., and R. Welsch, “The Hat Matrix in Regression and ANOVA”, The American Statistician 32(1978): 17-22.
3. Hocking, R. R., “Developments in Linear Regression Methodology: 1959-1982”, Technometrics 25(1983): 219-250.
4. Hosmer, D. W., and S. Lemeshow, Applied Logistic Regression, 2nd ed. (New York: Wiley, 2001).
5. Microsoft Excel 2002 (Redmond, WA: Microsoft Corporation, 2001).
6. Neter, J., M. H. Kutner, C. J. Nachsheim, and W. Wasserman, Applied Linear Statistical Models, 4th ed. (Homewood, IL: Irwin, 1996).
Глава 13
Введение в множественную регрессию
ПРИМЕНЕНИЕ СТАТИСТИКИ: прогнозирование объема продаж батончиков OmniPower
13.1. МОДЕЛЬ МНОЖЕСТВЕННОЙ РЕГРЕССИИ
Интерпретация регрессионных коэффициентов
Предсказание значений зависимой переменной У
Коэффициент множественной смешанной корреляции
Процедуры Excel: вычисление коэффициентов множественной регрессии
13.2. АНАЛИЗ ОСТАТКОВ ДЛЯ МОДЕЛИ МНОЖЕСТВЕННОЙ РЕГРЕССИИ
Процедура Excel: анализ остатков
13.3. ПРОВЕРКА ЗНАЧИМОСТИ МОДЕЛИ МНОЖЕСТВЕННОЙ РЕГРЕССИИ
13.4. СТАТИСТИЧЕСКИЕ ВЫВОДЫ О ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ КОЭФФИЦИЕНТОВ РЕГРЕССИИ
Проверка гипотез
Доверительные интервалы
13.5. ОЦЕНКА ЗНАЧИМОСТИ ПОЯСНЯЮЩИХ ПЕРЕМЕННЫХ В МОДЕЛИ МНОЖЕСТВЕННОЙ РЕГРЕССИИ
Коэффициент частной смешанной корреляции
Процедуры Excel: вычисление коэффициентов частной смешанной корреляции
13.6. РЕГРЕССИОННЫЕ МОДЕЛИ С ФИКТИВНОЙ ПЕРЕМЕННОЙ И ЭФФЕКТЫ ВЗАИМОДЕЙСТВИЯ
Эффект взаимодействия
Процедуры Excel: создание фиктивных переменных и учет эффектов взаимодействия
СПРАВОЧНИК ПО EXCEL ГЛАВА 13
ЧЕМУ ДОЛЖЕН НАУЧИТЬСЯ СТУДЕНТ
• Разрабатывать модели множественной регрессии.
• Интерпретировать регрессионные коэффициенты.
• Идентифицировать независимые переменные, которые следует включать в регрессионную модель.
• Определять наиболее важные независимые переменные, влияющие на значение зависимой переменной.
• Использовать категорийные переменные в регрессионных моделях.
ПРИМЕНЕНИЕ СТАТИСТИКИ
Прогнозирование объемов продаж компании OmniPower
Представьте себе, что вы — менеджер по маркетингу в крупной национальной сети бакалейных магазинов. В последние годы на рынке появились питательные батончики, содержащие большое количество жиров, углеводов и калорий. Они позволяют быстро восстановить запасы энергии, потраченной бегунами, альпинистами и другими спортсменами на изнурительных тренировках и соревнованиях. За последние годы объем продаж питательных батончиков резко вырос, и руководство компании OmniPower пришло к выводу, что этот сегмент рынка весьма перспективен. Прежде чем предлагать новый вид батончика на общенациональном рынке, компания хотела бы оценить
влияние его стоимости и рекламных затрат на объем продаж. Для маркетингового исследования были отобраны 34 магазина. Вам необходимо создать регрессионную
модель, позволяющую проанализировать данные, полученные в ходе исследования. Можно ли применить для этого модель простой линейной регрессии, рассмотренную в главе 12? Как ее следует изменить?
ВВЕДЕНИЕ
Рассматривая простую регрессию в главе 12, мы сосредоточили внимание на модели, в которой для предсказания значения зависимой переменной, или отклика У, использовалась лишь одна независимая, или объясняющая, переменная X. Однако во многих случаях можно разработать более точную модель, если учесть не одну, а несколько объясняющих переменных. По этой причине мы рассмотрим в этой главе модели множественной регрессии (multiple regression), в которых для предсказания значения зависимой переменной используется несколько независимых переменных.
13.1. МОДЕЛЬ МНОЖЕСТВЕННОЙ РЕГРЕССИИ
Для маркетингового исследования в компании OmniPower была создана выборка, состоящая из 34 магазинов с приблизительно одинаковыми объемами продаж. Рассмотрим две независимые переменные— цена батончика OmniPower в центах (Хх) и месячный бюджет рекламной компании, проводимой в магазине, выраженный в долларах (Х2). В этот бюджет входят расходы на оформление вывесок и витрин, а также на раздачу купонов и бесплатных образцов. Зависимая переменная У представляет собой количество батончиков OmniPower, проданных за месяц. Результаты представлены в табл. 13.1.
Таблица 13.1. Месячный объем продаж батончиков OmniPower, их цена и расходы на рекламу
Магазин Объем продаж Цена Расходы на рекламу Магазин Объем продаж Цена Расходы на рекламу
1 4 141 59 200 18 2 730 79 400
2 3 842 59 200 19 2 618 79 400
3 3 056 59 200 20 4 421 79 400
4 3 519 59 200 21 4 113 79 600
5 4 226 59 400 22 3 746 79 600
6 4 630 59 400 23 3 532 79 600
7 3 507 59 400 24 3 825 79 600
8 3 754 59 400 25 1 096 99 200
9 5 000 59 600 26 761 99 200
10 5 210 59 600 27 2 088 99 200
11 4011 59 600 28 820 99 200
12 5 015 59 600 29 2 114 99 400
13 1 916 79 200 30 1 882 99 400
14 675 79 200 31 2 159 99 400
15 3 636 79 200 32 1 602 99 400
16 3 224 79 200 33 3 354 99 600
17 2 295 79 400 34 2 927 99 600
Интерпретация регрессионных коэффициентов
Если в задаче исследуются несколько объясняющих переменных, модель простой линейной регрессии можно расширить, предполагая, что между откликом и каждой из независимых переменных существует линейная зависимость. Например, при наличии k объясняющих переменных модель множественной линейной регрессии принимает вид (13.1).
МОДЕЛЬ МНОЖЕСТВЕННОЙ РЕГРЕССИИ С ^НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ
У. = Ро + РЛь + РЛ2. +Рз^3, + ... +РХ + (13.1)
где р0 — сдвиг, р, — наклон прямой У, зависящей от переменной если переменные Х2, Х3, ..., Хк являются константами, Р2— наклон прямой У, зависящей от переменной Х2, если переменные Хх, Х3, ..., Хк являются константами, ..., р*— наклон прямой У, зависящей от переменной Хк1 если переменные X,, Х2, Х3, ..., Хк х являются константами, е, — случайная ошибка переменной У в i-м наблюдении.
В частности, модель множественной регрессии с двумя объясняющими переменными выглядит следующим образом.
МОДЕЛЬ МНОЖЕСТВЕННОЙ РЕГРЕССИИ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ
+ + (13.2)
где рп — сдвиг, р, — наклон прямой У, зависящей от переменной Хр если переменная Х2 является константой, р2 — наклон прямой У, зависящей от переменной Х2, если переменная Xj является константой, е — случайная ошибка переменной У в i-м наблюдении.
Сравним эту модель множественной линейной регрессии и модель простой линейной регрессии (12.1).
У = рп + р,Х + е, .
В модели простой линейной регрессии наклон р! представляет собой изменение среднего значения переменной У при изменении значения переменной X на единицу и не учитывает влияние других факторов. В модели множественной регрессии с двумя независимыми переменными (13.2) наклон pj представляет собой изменение среднего значения переменной У при изменении значения переменной X, на единицу с учетом влияния переменной Х2. Эта величина называется коэффициентом чистой регрессии (net regression coefficient)1.
Как и в модели простой линейной регрессии, выборочные регрессионные коэффициенты Ь„, и Ъ2 представляют собой оценки параметров соответствующей генеральной совокупности р0, pj и р2.
УРАВНЕНИЕ МНОЖЕСТВЕННОЙ РЕГРЕССИИ
С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ
\=Ь{} + Ь.ХЬ+Ь2Х2,. (13.3)
Для вычисления коэффициентов регрессии используется метод наименьших квадратов. Фрагмент вычислений, выполненных программой Microsoft Excel при решении задачи об объемах продаж в компании OmniPower, показан на рис. 13.1.
Как видим,
Ьо = 5 837,52, Ьг = -53,2173, Ь2 = 3,1631.
Следовательно,
= 5837,52-53,2173Х„+3,6131Х2,,
где Y — предсказанный объем продаж питательных батончиков OmniPower в t-м магазине, Х1( — цена батончика (в центах) в i-м магазине, Хь — ежемесячные затраты на рекламу в t-M магазине (в долларах).
Выборочный наклон Ъо равен 5 837,52 и является оценкой среднего количества батончиков OmniPower, проданных за месяц при нулевой цене и отсутствии затрат на рекламу. Поскольку эти условия лишены смысла, в данной ситуации величина наклона Ъо не имеет разумной интерпретации.
1 Коэффициент чистой регрессии иногда называют коэффициентом частной регрессии (partial regression coefficient).
А 1 Анализ продаж батончиков OmniPower ± В С D Е F G
3 j Регрессионная статистика
4 Множественный R 5 R-квадрат б Нормированный R-квадрат 7 Стандартная ошибка 8 Наблюдения 9 10 Дисперсионный анализ _11 ; 12 Регрессия 13 Остаток 14 Итого 15 0,870475 0,757726 0,742095 638,06529 34 df 2 31 33 SS 39472730,77 12620946,67 52093677,44 MS 19736365,387 407127,312 F 48,47713433 Значимость F 2,86258Е-10
1Б Коэффициенты Стандартная ошибка t-статистика Р-значение Нижние 95% Верхние 95%
17 Y-пересечение 18 Цена 19 Реклама 5837,5208 -53,21734 3,61306 628,150 6,85222 0,68522 9,29319 -7,76644 5,27283 1,79101Е-10 9,20016Е-09 9,82196 Е 4)6 4556,39921 -67,19254 2,21554 7118,64230 -39,24213 5,01058
Рис. 13.1. фрагмент вычислений, выполненных программой Microsoft Excel при решении задачи о продажах батончика OmniPower
Выборочный наклон Ы равен -53,2173. Это значит, что при заданном ежемесячном объеме затрат на рекламу увеличение цены батончика на один цент приведет к снижению ожидаемого объема продаж на 53,2173 шт. Аналогично выборочный наклон Ъ2, равный 3,6131, означает, что при фиксированной цене увеличение ежемесячных рекламных затрат на один доллар сопровождается увеличением ожидаемого объема продаж батончиков на 3,6131 шт. Эти оценки позволяют лучше понять влияние цены и рекламы на объем продаж. Например, при фиксированном объеме затрат на рекламу уменьшение цены батончика на 10 центов увеличит объем продаж на 532,173 шт., а при фиксированной цене батончика увеличение рекламных затрат на 100 долл, увеличит объем продаж на 361,31 шт.
ИНТЕРПРЕТАЦИЯ НАКЛОНОВ В МОДЕЛИ МНОЖЕСТВЕННОЙ РЕГРЕССИИ
Коэффициенты в модели множественной регрессии называются коэффициентами чистой регрессии. Они оценивают среднее изменение отклика У при изменении величины X на единицу, если все остальные объясняющие переменные “заморожены”. Например, в задаче о батончиках OmniPower магазин с фиксированным объемом рекламных затрат за месяц продаст на 53,22 батончика меньше, если увеличит их стоимость на один цент. Возможна еще одна интерпретация этих коэффициентов. Представьте себе одинаковые магазины с одинаковым объемом затрат на рекламу. При уменьшении цены батончика на один цент объем продаж в этих магазинах упа-: дёт на 53,22 батончика.
Рассмотрим теперь два магазина, в которых батончики стоят одинаково, но затраты на рекламу отличаются. При увеличении этих затрат на один доллар объем продаж в этих магазинах увеличится на 3,61 шт. Как видим, разумная интерпретация наклонов возможна лишь при определенных ограничениях, наложенных на объясняющие переменные.
Предсказание значений зависимой переменной Y
Выяснив, что накопленные данные позволяют использовать модель множественной регрессии, мы можем прогнозировать ежемесячный объем продаж батончиков OmniPower и построить доверительные интервалы для среднего и предсказанного объемов продаж.
Для того чтобы предсказать средний ежемесячный объем продаж батончиков От-niPower по цене 79 центов в магазине, расходующем на рекламу 400 долл, в месяц, следует применить уравнение множественной регрессии
Y, =5 837,52-53,2173А„ +3,6131А2,,
подставив значения Xlt = 79 и X2i = 400. Получаем следующий результат.
Y =5 837,53-53,2173x79 + 3,6131x400 = 3 078,57.
Следовательно, ожидаемый объем продаж в магазинах, торгующих батончиками OmniPower по цене 79 центов и расходующих на рекламу 400 долл, в месяц, равен 3 078,57 шт.
Вычислив величину У и оценив остатки (см. раздел 13.2), можно построить доверительные интервалы, содержащие математическое ожидание и предсказанное значение отклика. В разделе 12.8 мы рассмотрели эту процедуру в рамках модели простой линейной регрессии. Однако построение аналогичных оценок для модели множественной регрессии сопряжено с большими вычислительными трудностями. В качестве примера на рис. 13.2 приведены доверительные интервалы, содержащие математическое ожидание и предсказанное значение отклика в задаче о продажах батончика и OmniPower.
0.012054
0.000149
1.49Е-05
-0.00941
-0.00053
1.12E-06
1.15E-06
0.000115
1.12E-06
'14
'15
16.
17 'XG times Inverse of XX ‘is:
19'.[X'G times Inverse of XX] times XG ; 0.029762
,20 ;t Statistic________________________2.039515
21* Predicted Y (YHat)_________________3078.574
22'__________________________________
23 ,
24 Interval Half Width_______
25 Confidence Interval Lower Limit
26 Confidence Interval Upper Limit
27
28 ]
29 Interval Half Width______
30 : Prediction Interval Lower Limit
31 Prediction Interval Upper Limit
For Average Predicted Y (YHat)
224.5031
2854.071
3303.077
For Individual Response Y__________
1320.567 1758.008 4399.141
Рис. 13.2. Доверительные интервалы, содержащие математическое ожидание и предсказанное значение отклика в задаче о продажах батончика и OmniPower
При указанных выше условиях 95%-ный доверительный интервал для среднего объема продаж батончика OmniPower простирается от 2 854,07 до 3 303,08 шт. Соответственно, 95% -ный доверительный интервал для предсказанного объема продаж в конкретном магазине ограничен 1 758,000 и 4 399,14 шт.
Коэффициент множественной смешанной корреляции
Напомним, что модель регрессии позволяет вычислить коэффициент смешанной корреляции г2. Поскольку в модели множественной регрессии существуют по крайней мере две объясняющие переменные, коэффициент множественной смешанной корреляции (coefficient of multiple determination) представляет собой долю вариации переменной Y, объясняемой заданным набором объясняющих переменных (в качестве синонима используется также термин — множественный коэффициент детерминации. — Прим.ред). Например, коэффициент множественной смешанной корреляции в модели с двумя объясняющими переменными вычисляется по следующей формуле.
КОЭФФИЦИЕНТ МНОЖЕСТВЕННОЙ СМЕШАННОЙ КОРРЕЛЯЦИИ
Коэффициент множественной смешанной корреляции представляет собой сумму квадратов регрессии (SSR), деленную на полную сумму квадратов (SST).
В задаче о продажах батончика OmniPower SSR = 39 472 730,77, SST = 52 093 677,44 и k = 2. Таким образом,
, SSR 39 472 730,77 л
---------------------- 0,7577.
SST 52 093 677,44
Это означает, что 75,77% вариации объемов продаж объясняется изменениями цен и колебаниями объемов затрат на рекламу.
Однако, работая с моделями множественной регрессии, некоторые статистики полагают, что следует вычислять скорректированный коэффициент т* (adjusted Г1), чтобы учесть влияние как объясняющих переменных, так и объема выборки. Это особенно важно при сравнении нескольких регрессионных моделей, предназначенных для предсказания значения одной и той же зависимой переменной при разных наборах объясняющих переменных.
СКОРРЕКТИРОВАННЫЙ КОЭФФИЦИЕНТ МНОЖЕСТВЕННОЙ СМЕШАННОЙ КОРРЕЛЯЦИИ
(13.5)
где k — это количество объясняющих переменных в уравнении регрессии.
В задаче о продажах батончиков OmniPower д;12 =0,7577 , п = 34, a k = 2. Следова-
тельно,
34-1
34-2-1
33 (1-0,7577) —
= 1-0,2579 = 0,7421
- 1 (1 ГУ 12 к )
Таким образом, 74,21% вариации объемов продаж объясняется изменениями цен и колебаниями объемов затрат на рекламу, а также выбранным количеством объясняющих переменных и объемов выборки.
Й^цедуры^хсе1:вычисление %' %
множественнрйрегрессии
__________________________________________________________________________________________________________1
Чтобы вычислить коэффициенты множественной регрессии и построить доверительный интервал для математического ожидания и предсказанного значения отклика, следует воспользоваться процедурой Сервис^Анализ данных... ^Регрессия, а затем создать рабочий лист, используя функции стьюдраспобр и некоторые другие. Надстройка PHStat2 позволяет выполнить эти действия авто
матически.
Например, чтобы вычислить коэффициенты множественной регрессии для данных, приведенных в табл. 13.1, необходимо открыть рабочую книгу Chapter 13.xls на листе Данные и выполнить одну из следующих процедур.
Применение Excel в сочетании с надстройкой PHStat2
Для вычисления коэффициентов множественной регрессии следует применить процедуру PHStat^Regression^Multiple Regression... (PHStat^Регрессия^Множественная регрессия...), ру-। ководствуясь инструкциями, приведенными ниже.
1.
2.
Выбрать команду PHStat^Regression^Multiple Regression....
В диалоговом окне Multiple Regression сделать следующее (см. иллюстрацию).
2.1. Ввести в диалоговом окне Y Variable Cell Range (Диапазон ячеек переменной Y) диапазон ячеек А1 :А35.
2.2. Ввести в диалоговом окне X Variable Cell Range (Диапазон ячеек переменной X) диапазон ячеек В1 :С35.
2.3. Установить флажок First cells in both ranges contain a label (Первые ячейки обоих диапазонов содержат метки).
2.4. Ввести в диалоговом окне Confidence level for regression coefficients (Доверительный уровень для коэффициентов регрессии) число 0.95.
2.5. Установить флажки Regression Statistics Table (Таблица регрессионных статистик) и ANOVA and Coefficients Table (Сводная таблица дисперсионного анализа и коэффициентов регрессии).
Multiple Regression |Х|
Data ;
V Variable Cell Range: |a1:A35 Z\ \
X Variables Cell Range: |b1:C35 _j I
P First cells in both ranges contain label i
Confidence level for regression coefficients: :95 %
Regression Tool Output Options !
P ANOVA and Coefficients Table
Г* Residuals Table
Г ” Residual Plots j
Output Options - i
Title: [Анализ продаж батончиков OmniPower j
Г" Durbin-Watson Statistic j
Г~ Coefficients of Partial Determination {
Г Variance Inflationary Factor (VIF) j
V/ Confidence Interval Estimate & Prediction Interval |
Confidence level for interval estimates: |?5 % ।
Help j | OK Cancel [ [
2.6. Ввести в диалоговом окне Title (Заголовок) название диаграммы.
2.7. Установить флажки Confidence Interval Estimate & Prediction Interval (Доверительные интервалы для математического ожидания и предсказанного значения отклика) и ввести в диалоговом окне Confidence level for interval estimates (Доверительный уровень интервальных оценок) число 95.
2.8. Щелкнуть на кнопке ОК.
Для завершения анализа введите в столбец в значения каждой из объясняющих переменных и вычислите границы доверительных интервалов для математического ожидания и предсказанного значения отклика.
Рабочий лист, созданный с помощью этой процедуры, не является динамически обновляемым. Следовательно, если данные изменятся, все описанные выше действия следует повторить.
Применение Excel
Построение модели множественной регрессии. Для вычисления коэффициентов множественной регрессии следуйте инструкциям из раздела ЕН.13.1.
Вычисление доверительных интервалов для математического ожидания и предсказанного значения отклика. Для того чтобы самостоятельно создать рабочий лист, вычисляющий границы доверительных интервалов для математического ожидания и предсказанного значения отклика, следуйте инструкциям из раздела ЕН.13.2.
Жй Chapter 13.xls
результаты множественной регрессии и доверительные интервалы, содержащие математическое ожидание и предсказанные объемы продаж батончика OmniPower, содержатся на листах Рис13.1 и Рис13.2 в рабочей книге chapter 13.
УПРАЖНЕНИЯ К РАЗДЕЛУ 13.1
Изучение основ
13.1. Предположим, что, выполнив регрессионный анализ, мы получили следующее уравнение множественной регрессии:
Y, = 10 + 5Х1; + ЗХ21,
а коэффициент множественной смешанной корреляции равен
г;12 =0,60.
1. Какой смысл имеют наклоны множественной регрессии?
2. Какой смысл имеет сдвиг регрессии?
3. Какой смысл имеет коэффициент множественной смешанной корреляции ГуЛ2 ?
13.2. Предположим, что, выполнив регрессионный анализ, мы получили следующее уравнение множественной регрессии:
i;=50-2X„ + 7X2, ,
а коэффициент множественной смешанной корреляции равен
Гу 12 =0,40 .
1. Какой смысл имеют наклоны регрессии?
2. Какой смысл имеет сдвиг регрессии?
3. Какой смысл имеет коэффициент множественной смешанной корреляции гу212 ?
Применение понятий
13.3. Аналитик по маркетингу в крупной компании, производящей обувь, разрабатывает новую модель кроссовок. Необходимо определить, какие факторы могут повлиять на длительность эксплуатации этой обуви. Аналитик выбрал две переменные: Хг (АМОРТИЗАЦИЯ) — степень амортизации и Хг (ИЗНОС) — износостойкость. В качестве зависимой переменной Y (ВРЕМЯ) аналитик выбрал длину временного интервала, на протяжении которого обувь способна выдерживать повторяющиеся нагрузки. Для тестирования была создана случайная выборка, содержащая 15 пар кроссовок разных типов. Частичные результаты вычислений, выполненных программой Microsoft Excel, приведены в следующих таблицах.
ДМ9И4 d.f. SS MS F Уровень значимости F-статистики
Регрессия 2 12,61020 6,30510 97,69 0,0001
Остатки 12 0,77453 0,06454
Всего 14 13,38473
Переменная Коэффициенты Среднеквадрат ичная ошибка t-статистика р-значение
Сдвиг -0,02686 0,06905 -0,39 0,7034
Амортизация 0,79116 0,06295 12,57 0,0000
Износ 0,60484 0,07174 8,43 0,0000
1. Предположим, что переменная У линейно зависит от каждой из независимых переменных. Постройте уравнение множественной регрессии.
2. Какой смысл имеют наклоны множественной регрессии?
3. Вычислите коэффициент множественной смешанной корреляции г}1 212 и объясните его смысл.
4. Вычислите скорректированный коэффициент т*.
13.4. Эйлин М. Ван Эйкен (Eileen М. Van Aken) и Брайан М. Клейнер (Brian М. Kleiner), профессоры Вирджинского политехнического института (Virginia Polytechnic Inti-tute) и Государственного университета Вирджинии (Virginia State University), исследовали факторы, влияющие на работу рабочих групп (“Determinants of Effectiveness for Cross Functional Organizational Design Teams”, Quality Management Journal 4 (1997): 51-79). Ученые изучили 34 независимые переменные, например, опыт, различия, частота встреч и ясность целей. Для каждой из рассмотренных групп в результате опросов были определены значения переменных: от 1 до 100, где 100 — наивысший рейтинг. Зависимая переменная, т.е. эффективность группы, также измерялась величиной от 1 до 100, где 100 — наивысшая оценка. Было изучено несколько регрессионных моделей.
Модель 1
Эффективность = 0П + 0, (опыт) + е, г- =0,68 ™1'Р
Модель 2
Эффективность = 0П + 0, (ясность целей) + £, г2 =0,78
Модель 3
Эффективность = 0П + 0, (опыт) + 0, (ясность целей) + £, г2 =0,97
1. Объясните смысл скорректированного коэффициента г2 для каждой из моделей.
2. Какая из этих моделей точнее?
13.5. Компания, торгующая персональными компьютерами и периферийными устройствами по каталогу, имеет центральный склад. Менеджер магазина хотел бы оценить процесс перевозок товаров со склада в магазины, изучив факторы, влияющие на его стоимость. В настоящее время, независимо от размера заказа, в него закладывается небольшая стоимость, связанная с обработкой. Для предсказания стоимости перевозок в зависимости от количества заказов и объема продаж менеджер собрал данные за последние 24 месяца, ft WARECOST . XLS.
1. Постройте модель множественной регрессии.
2. Какой смысл имеют наклоны множественной регрессии в этой задаче?
3. Объясните, почему регрессионный коэффициент 50 в этой задаче не имеет практического смысла.
4. Предскажите среднюю стоимость ежемесячных перевозок, если объем продаж равен 400 000 долл., а количество заказов — 4 500.
5. Постройте 95%-ный доверительный интервал для средней стоимости ежемесячных перевозок, если объем продаж равен 400 000 долл., а количество заказов — 4 500.
6. Постройте 95%-ный доверительный интервал для стоимости ежемесячных перевозок на складе, объем продаж которого равен 400 000 долл., а количество заказов — 4 500.
7. Вычислите коэффициент множественной смешанной корреляции гД, и объясните его смысл.
8. Вычислите скорректированный коэффициент г2.
13.6. Организация потребителей хотела бы разработать модель, позволяющую предсказывать расход топлива на милю пути по количеству лошадиных сил и весу автомобиля. Для исследования была создана случайная выборка, состоящая из 50 автомобилей. Результаты приведены в файле ^AUTO. XLS.
1. Постройте модель множественной регрессии.
2. Какой смысл имеют наклоны множественной регрессии в этой задаче?
3. Объясните, почему регрессионный коэффициент Ьо в этой задаче не имеет практического смысла.
4. Предскажите средний расход топлива на милю пути, если мощность автомобиля равна 60 л.с., а вес — 2 000 фунтов.
5. Постройте 95%-ный доверительный интервал для среднего расхода топлива на милю пути у автомобилей, мощность которых равна 60 л.с., а вес — 2 000 фунтов.
6. Постройте 95%-ный доверительный интервал для расхода топлива на милю пути у автомобиля, мощность которого равна 60 л.с., а вес — 2 000 фунтов.
7. Вычислите коэффициент множественной смешанной корреляции гг212 и объясните его смысл.
8. Вычислите скорректированный коэффициент г2.
13.7. Большая компания, производящая товары широкого спроса, желает измерить эффективность рекламных кампаний разного типа. В частности, рассмотрены два типа рекламных кампаний: по радио и телевидению, а также в газетах (включая расходы на дисконтные купоны). Для исследования были отобраны 22 города с приблизительно одинаковым населением. Расходы на рекламу в каждом городе различны. Объемы продаж (в тысячах долларов), а также расходы на рекламу приведены в следующей таблице. fi^ADRADTV. XLS.
Месяц Объем продаж (тыс. долл.) Расходы на рекламу на радио и ТВ (тыс. долл.) Расходы на рекламу в газетах (тыс. долл.)
1 973 0 40
2 1 119 0 40
3 875 25 25
4 625 25 25
5 910 30 30
6 971 30 30
7 931 35 35
8 1 177 35 35
9 882 40 25
10 982 40 25
11 1 628 45 45
12 1 577 45 45
13 1 044 50 0
14 914 50 0
15 1 329 55 25
16 1 330 55 25
17 1 405 60 30
18 1 436 60 30
19 1 521 65 35
20 1 741 65 35
21 1 866 70 40
22 1 717 70 40
1. Постройте уравнение множественной регрессии.
2. Какой смысл имеют наклоны множественной регрессии в этой задаче?
3. Объясните, почему коэффициент Ьо в этой задаче не имеет практического смысла.
4. Предскажите средний объем продаж в городе, где на рекламу по радио и телевидению, а также в газетах расходуется по 20 000 долл.
5. Постройте 95%-ный доверительный интервал, содержащий средний объем продаж в городах, где на рекламу по радио и телевидению, а также в газетах расходуется по 20 000 долл.
6. Постройте 95%-ный доверительный интервал, содержащий объем продаж в городе, где на рекламу по радио и телевидению, а также в газетах расходуется по 20 000 долл.
7. Вычислите коэффициент множественной смешанной корреляции гг212 и объясните его смысл.
8. Вычислите скорректированный коэффициент г*.
13.8. Директор телевизионной станции хочет изучить проблему “простоя” (“standby hours”), который оплачивается сотрудникам даже тогда, когда они ничего не делают. В модель входят следующие переменные: У — общее количество часов простоя за неделю, X, — общее количество человеко-часов в рабочей неделе, проведенных в офисе (продолжительность работы в офисе), Х2 — общее количество часов, отработанных сотрудниками вне центральной станции (часы, проведенные на выезде). Результаты, собранные на протяжении 26 недель, приведены ниже. ^STANDBY. XLS.
1. Постройте уравнение множественной регрессии.
2. Какой смысл имеют наклоны множественной регрессии в этой задаче?
3. Объясните, почему коэффициент Ьо в этой задаче не имеет практического смысла.
4. Предскажите объем простоя за неделю, если сотрудники отработали 310 часов в офисе и 400 часов провели на выезде.
5. Постройте 95%-ный доверительный интервал, содержащий средний объем простоя за неделю, если сотрудники отработали 310 часов в офисе и 400 часов провели на выезде.
6. Постройте 95%-ный доверительный интервал, содержащий объем простоя за конкретную неделю, если сотрудники отработали 310 часов в офисе и 400 часов провели на выезде.
7. Вычислите коэффициент множественной смешанной корреляции г}212 и объясните его смысл.
8. Вычислите скорректированный коэффициент г2.
13.2. АНАЛИЗ ОСТАТКОВ ДЛЯ МОДЕЛИ МНОЖЕСТВЕННОЙ РЕГРЕССИИ
В разделе 12.5 анализ остатков позволил определить, можно ли применять модель простой линейной регрессии к имеющимся данным. Особый интерес этот вопрос представляет при множественной регрессии с двумя объясняющими переменными.
ВРЕЗКА 13.1. АНАЛИЗ ОСТАТКОВ МНОЖЕСТВЕННОЙ РЕГРЕССИИ
• Распределение остатков по у.
• Распределение остатков по Х!;.
• Распределение остатков по Х21.
• Распределение остатков по времени.
Первый график позволяет проанализировать распределение остатков в зависимости от предсказанных значений Yt . Если величина остатков не постоянна, значит, условие линейной зависимости переменной У от обеих объясняющих переменных нарушается (рис. 12.13), и/или необходимо выполнить преобразование этой переменной. Второй
и третий график демонстрируют зависимость остатков от объясняющих переменных. Эти графики могут выявить квадратичный эффект. В этой ситуации необходимо добавить в модель множественной регрессии квадрат объясняющей переменной. Четвертый график применяется для проверки независимости данных, собранных в течение определенного времени. Как и в разделе 12.6, для выявления положительной автокорреляции между остатками можно вычислить статистику Дурбина-Уотсона.
Построение графика остатков предусмотрено практически в каждом статистическом пакете и в программах для работы с электронными таблицами. В частности, на рис. 13.3 показаны графики остатков, вычисленные программой Microsoft Excel при решении задачи о продажах батончиков OmniPower. Обратите внимание на то, что на рис. 13.3 не видно никакой зависимости остатков ни от объясняющих переменных, ни от предсказанных значений зависимой переменной. Следовательно, модель множественной линейной регрессии можно применять для решения задачи о продажах батончиков OmniPower.
1500
юоо -
500 -
остатков от предсказанного значения Y
№
I-° -500 -
-1000
-1500 -
-2000 -I-----------------н-
О 1000
зам
2000 3000 4000
Предсказанное значение Y
5000
6000
Панель А
1500 т
Зависимость остатков от цены
юоо -
500 -
о -500 -
-1000
-1500
-2000 -I-----------------1------------------1------------------1------------------1------------------Ь-
0 20 40 60 80 100
—i
120
1500 т
1000
500
-500
-1000
1500
-2000 о
Цена
Панель Б
Зависимость остатков от затрат на рекламу
Я
100
200
500
600
700
300 400
Затраты на рекламу
и О
о -
1
I
I
Панель В
Рис. 13.3. Графики остатков, вычисленные программой Microsoft Excel при решении задачи о продажах батончиков OmniPower; панель А — зависимость остатков от цены, панель Б— зависимость остатков от расходов на рекламу, панель В— зависимость остатков от предсказанных значений переменной Y
Процедура Excel: анализ остатков
Для того чтобы построить график остатков на отдельном рабочем листе, необходимо модифицировать процедуру построения модели множественной регрессии.
Например, чтобы построить график остатков для данных, приведенных в табл. 13.1, необходимо открыть рабочую книгу chapter 13. xls на листе Данные и выполнить одну из следующих процедур.
Применение Excel в сочетании с надстройкой PHStat2
Выполните инструкции, содержащиеся в разделе "Применение Excel в сочетании с надстройкой PHStat2" во врезке "Процедура Excel: вычисление коэффициентов множественной регрессии", и на последнем этапе установите все четыре флажка в группе Regression Tool Output Options (Параметры вывода регрессионных статистик): Regression Statistics Table (Таблица регрессионных статистик), ANOVA and Coefficient Table (Сводная таблица дисперсионного анализа и коэффициентов), Residual Table (Таблица остатков) и Residual Plot (График остатков), как показано на иллюстрации. Инструкции, позволяющие построить график зависимости остатков от зависимой переменной Y, приведены в разделе ЕН.13.3. Их следует выполнять после процедуры надстройки PHStat2.
Применение Excel
Multiple Regression
Data
Y Variable Cell Range: ? A1: A35
X Variables Cell Range: [вкС35*
P First cells in both ranges contain label
Confidence level for regression coefficients: 195 %
Regression Tool Output Options
P Regression Statistics Table
I? ANOVA and Coefficients Table
Tv* Residuals Table
P' Residual Plots
Output Options
Title: |Анализ продаж батончиков OmniPower
i Durbin-Watson Statistic
Г” Coefficients of Partial Determination
Г* Variance Inflationary Factor (VIF)
w? Confidence Interval Estimate & Prediction Interval
Confidence level for interval estimates: s 95 %
Help j | OK.. ..... j| Cancel
Выполните инструкции, содержащиеся в разделе ЕН.13.1, установив флажки Остатки и Г рафик остатков в диалоговом окне Регрессия, как показано на иллюстрации. Затем, если нужно, модифицируйте график остатков, руководствуясь указаниями, помещенными в разделе ЕН.12.3.
Инструкции, позволяющие построить график зависимости остатков от зависимой переменной Y, приведены в разделе ЕН.13.3. Их следует выполнять после процедуры Сервис=>Анализ данных... => Регрессия.
Регрессия
Входные данные
Входной интервал Y:
Входной интервал X:
[3 Метки
0 Уровень надежности:
Параметры вывода
О Выходной интервал: ф Новый рабочий лист: О Новая рабочая книга Остатки 0 Остатки
П Стандартизованные остатки
А1:А35
В1:С35
I I Константа - ноль 95 %
I Анализ продаж
0 График остатков
□ Г рафик подбора
[ Отмена ]
[ Справка ]
Нормальная вероятность
□ Г рафик нормальной вероятности
УПРАЖНЕНИЯК РАЗДЕЛУ 13.2
Применение понятий
Задачи 13.9-13.12 можно решать с помощью программы Microsoft Excel.
13.9. В задаче 13.5 для предсказания стоимости перевозок используется объем продаж и количество заказов. ^WARECOST. XLS.
1. Выполните анализ остатков и оцените адекватность выбранной модели.
2. Постройте график распределения остатков по месяцам. Наблюдается ли какая-либо закономерность? Объясните свой ответ.
3. Вычислите статистику Дурбина-Уотсона.
4. Наблюдается ли положительная автокорреляция между остатками, если уровень значимости равен 0,05?
13.10. В задаче 13.6 для предсказания расхода топлива на милю пути использовалось количество лошадиных сил и вес автомобиля. Выполните анализ остатков и оцените адекватность выбранной модели. ft^AUTO. XLS.
13.11. В задаче 13.7 для предсказания объема продаж использовались затраты на рекламу по радио и телевидению, а также в газетах. Выполните анализ остатков и оцените адекватность выбранной модели. ^ADRADTV. XLS.
13.12. В задаче 13.8 для предсказания общего количества часов простоя за неделю использовалось общее количество человеко-часов в рабочей неделе (продолжительность работы в офисе) и общее количество часов, отработанных сотрудниками вне центральной станции (часы, проведенные на выезде). ft)STANDBY. XLS.
1. Выполните анализ остатков и оцените адекватность выбранной модели.
2. Постройте график распределения остатков по неделям. Наблюдается ли какая-либо закономерность? Объясните свой ответ.
3. Вычислите статистику Дурбина-Уотсона.
4. Наблюдается ли положительная автокорреляция между остатками, если уровень значимости равен 0,05?
13.3. ПРОВЕРКА ЗНАЧИМОСТИ МОДЕЛИ МНОЖЕСТВЕННОЙ РЕГРЕССИИ
Убедившись с помощью анализа остатков, что модель линейной множественной регрессии является адекватной, можно определить, существует ли статистически значимая взаимосвязь между зависимой переменной и набором объясняющих переменных. Поскольку в модель входит несколько объясняющих переменных, нулевая и альтернативная гипотезы формулируются следующим образом.
Но: pL = Р2 = ... = Рк = 0 Между откликом и объясняющими перемен-
ными нет линейной зависимости.
Н1: существует по крайней мере Между откликом и хотя бы одной объясняющей одно значение р, 0 переменной существует линейная зависимость.
Для проверки нулевой гипотезы применяется F-критерий.
ПРИМЕНЕНИЕ F-КРИТЕРИЯ ДЛЯ МОДЕЛИ МНОЖЕСТВЕННОЙ РЕГРЕССИИ
Тестовая F-статистика равна среднему квадрату, обусловленному регрессией (MSR), деленному на дисперсию ошибок (MSE)
F=^-, (13.6)
MSE
где F— тестовая статистика, имеющая F-распределение с k и п-k-l степенями свободы, k — количество независимых переменных в регрессионной модели.
Решающее правило выглядит следующим образом:
при уровне значимости а нулевая гипотеза Но отклоняется, если F > FV(kJ в противном случае гипотеза Но не отклоняется.
Таблица 13.2. Сводная таблица дисперсионного анализа для проверки гипотезы о статистической значимости коэффициентов множественной регрессии
Источник Количество степеней свободы df Сумма квадратов Среднеквадратичное значение (дисперсия) F
Регрессия k SSR MSR=^ к F =MSR MSE
Ошибка n-k-1 SSE MSE SSE
п-к -1
Всего п-1 SST
Сводная таблица дисперсионного анализа, заполненная с помощью программы Microsoft Excel при решении задачи о продажах батончиков OmniPower, показана на рис. 13.1.
Если уровень значимости равен 0,05, пользуясь табл. Д.5, легко определить, что критическое значение F-распределения с двумя и 31 степенями свободы равно 3,32 (рис. 13.4). Как показано на рис. 13.1, F-статистика равна 48,48 > Fv = 3,32, ар-значение равно 0,000 < 0,05. Следовательно, нулевая гипотеза Но отклоняется, и объем продаж линейно связан хотя бы с одной из объясняющих переменных (ценой и/или затратами на рекламу).
Рис. 13.4. Проверка гипотезы о значимости коэффициентов регрессии при уровне значимости, равном 0,05, с двумя и 31 степенями свободы
УПРАЖНЕНИЯ К РАЗДЕЛУ 1
Изучение основ
13.13. Рассмотрим сводную таблицу дисперсионного анализа для модели множественной регрессии с двумя независимыми переменными
Источник Количество степеней Сумма Среднеквадратичное F
свободы df квадратов значение
Регрессия 2 60
Ошибка 18 120
Всего 20 180
1. Вычислите средний квадрат, объясненный регрессией (MSR), и дисперсию ошибок (MSE).
2. Вычислите тестовую F-статистику.
3. Определите, существует ли статистически значимая зависимость между переменной Y и двумя независимыми переменными при уровне значимости, равном 0,05.
13.14. Рассмотрим сводную таблицу дисперсионного анализа для модели множественной регрессии с двумя независимыми переменными
Источник Количество степеней свободы df Сумма квадратов Среднеквадратичное значение F
Регрессия 2 30
Ошибка 10 120
Всего 12 150
1. Вычислите средний квадрат, объясненный регрессией (MSR), и дисперсию ошибок (MSE).
2. Вычислите тестовую F-статистику.
3. Определите, существует ли статистически значимая зависимость между переменной Y и двумя независимыми переменными при уровне значимости, равном 0,05.
Применение понятий
13.15. В задаче 13.3 для предсказания длительности эксплуатации нового вида кроссовок используются степень амортизации и уровень износостойкости. Результаты приведены в сводной таблице дисперсионного анализа.
Источник Количество степеней свободы df Сумма квадратов Среднеквадратичное значение F р-значение
Регрессия 2 12,61020 6,30510 97,69 0,0001
Ошибка 12 10,77453 0,06454
Всего 14 13,38473
1. Определите, существует ли статистически значимая зависимость между переменной Y и двумя независимыми переменными при уровне значимости, равном 0,05.
2. Объясните смысл р-значения.
13.16. В задаче 13.5 для предсказания стоимости перевозок используются объем продаж и количество заказов. Постройте сводную таблицу дисперсионного анализа с помощью программы Microsoft Excel. ^WARECOST . XLS.
1. Определите, существует ли статистически значимая зависимость между переменной Y (стоимостью перевозок) и двумя независимыми переменными (объемом продаж и количеством заказов) при уровне значимости, равном 0,05.
2. Объясните смысл р-значения.
13.17. В задаче 13.6 для предсказания расхода топлива на милю пути использовалось количество лошадиных сил и вес автомобиля. Постройте сводную таблицу дисперсионного анализа с помощью программы Microsoft Excel. ^AUTO . XLS.
1. Определите, существует ли статистически значимая зависимость между переменной У (расходом топлива на милю пути) и двумя независимыми переменными (количеством лошадиных сил и весом автомобиля) при уровне значимости, равном 0,05.
2. Объясните смысл р-значения.
13.18. В задаче 13.7 для предсказания объема продаж использовались затраты на рекламы по радио и телевидению, а также в газетах. Постройте сводную таблицу дисперсионного анализа с помощью программы Microsoft Excel. ft^ADRADTV. XLS.
1. Определите, существует ли статистически значимая зависимость между переменной У (объемом продаж) и двумя независимыми переменными (затратами на рекламу по радио и телевидению, а также в газетах) при уровне значимости, равном 0,05.
2. Объясните смысл р-значения.
13.19. В задаче 13.8 для предсказания общего количества часов простоя за неделю использовались общее количество человеко-часов в рабочей неделе (продолжительность работы в офисе) и общее количество часов, отработанных сотрудниками вне центральной станции (часы, проведенные на выезде). Постройте сводную таблицу дисперсионного анализа с помощью программы Microsoft Excel. ^STANDBY.XLS.
1. Определите, существует ли статистически значимая зависимость между переменной У (величиной простоя) и двумя независимыми переменными (продолжительностью работы в офисе и временем, проведенным на выезде) при уровне значимости, равном 0,05.
2. Объясните смысл р-значения.
13.4. СТАТИСТИЧЕСКИЕ ВЫВОДЫ О ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ КОЭФФИЦИЕНТОВ РЕГРЕССИИ
В разделе 12.7, чтобы выявить статистически значимую зависимость между переменными X и У в модели простой линейной регрессии, была выполнена проверка гипотезы о наклоне. Кроме того, для оценки наклона генеральной совокупности был построен доверительный интервал.
Проверка гипотез
Для проверки гипотезы, утверждающей, что наклон генеральной совокупности р] в модели простой линейной регрессии равен нулю, используется формула
Ее можно распространить на модель множественной регрессии.
ПРОВЕРКА ГИПОТЕЗЫ О НАКЛОНЕ В МОДЕЛИ МНОЖЕСТВЕННОЙ РЕГРЕССИИ
где b — наклон переменной по отношению к переменной У, если все остальные объясняющие переменные являются константами, Sh — среднеквадратичная ошибка регрессионного коэффициента b, t — тестовая статистика, имеющая /-распределение с n-k-1 степенями свободы, k — количество объясняющих переменных в уравнении регрессии, р, — гипотетический наклон генеральной совокупности откликов /-й относительно переменной, когда все остальные переменные фиксированы.
В частности, на рис. 13.1 показаны результаты применения /-критерия для каждой из независимых переменных, включенных в регрессионную модель.
Таким образом, если необходимо определить, оказывает ли переменная Х2 (затраты на рекламу) существенное влияние на объем продаж при фиксированной цене батончика OmniPower, формулируются нулевая и альтернативная гипотезы:
Я„:Р„= О, Н,:₽2*0.
В соответствии с формулой (13.7) получаем:
6,-р, 3,6131-0 / = = —-------= 5,27.
\ 0,6852
Если уровень значимости равен 0,05, по табл. Д.З определяем, что критическими значениями /-распределения с 31 степенями свободы являются числа -2,0395 и +2,0395 (рис. 13.5).
Как показано на рис. 13.5, р-значение равно 0,00000982 (или 9,82Е-06 в научном формате). На основании одного из неравенств / = 5,27 > 2,0395 или р = 0,00000982 < 0,05 нулевая гипотеза Но отклоняется. Следовательно, при фиксированной цене батончика между переменной Х2 (затраты на рекламу) и объемом продаж существует статистически значимая зависимость. Кроме того, р-значение указывает, что если бы между затратами на рекламу и объемами продаж не было линейной зависимости, вероятность обнаружить ее была бы равной 0,00000982. Таким образом, существует чрезвычайно малая вероятность отвергнуть нулевую гипотезу, если между затратами на рекламу и объемами продаж нет линейной зависимости.
Рассмотрим пример, в котором проверяется гипотеза о значимости коэффициента р,, представляющего собой наклон объемов продаж, зависящих от цены.
Рис. 13.5. Проверка гипотезы о значимости коэффициентов регрессии при уровне значимости, равном 0,05, с 31 степенью свободы
ПРИМЕР 13.1. ПРОВЕРКА ГИПОТЕЗЫ О ЗНАЧИМОСТИ НАКЛОНА ОБЪЕМОВ ПРОДАЖ, ЗАВИСЯЩИХ ОТ ЦЕНЫ
Можно ли утверждать, что наклон продаж, зависящих от цены, равен нулю, если уровень значимости равен 0,05?
РЕШЕНИЕ. Как показано на рис. 13.1, t = -7,766 < -2,0395 (критическое значение при а = 0,05), а p-значение равно 0,0000000092 < 0,05. Следовательно, при фиксированных затратах на рекламу Х2 между ценой и объемом продаж существует статистически значимая зависимость.
Как видим, проверка значимости конкретных коэффициентов регрессии фактически представляет собой проверку гипотезы о значимости конкретной переменной, включенной в регрессионную модель наряду с другими. Следовательно, /-критерий для проверки гипотезы о значимости регрессионного коэффициента эквивалентен проверке гипотезы о влиянии каждой из объясняющих переменных.
Доверительные интервалы
Вместо проверки гипотезы о наклоне генеральной совокупности можно оценить значение этого наклона. В модели множественной регрессии для построения доверительного интервала используется формула (13.8).
ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ ДЛЯ НАКЛОНА
ь, ±tMSti. (13.8)
Воспользуемся этой формулой для того, чтобы построить 95% -ный доверительный интервал, содержащий наклон генеральной совокупности 0, (влияние цены Х} на объем продаж У при фиксированном объеме затрат на рекламу Х2). По формуле (13.8) получаем:
^1 — ’
Поскольку критическое значение ^-статистики при 95%-ном доверительном уровне и 31 степени свободы равно 2,0395 (см. табл. Д.З), получаем следующие величины:
-53,2173 ± 2,0395 х 6,8522,
-53,2173 ±13,9752,
-67,1925 < Pj <-39,2421.
Таким образом, учитывая эффект затрат на рекламу, можно утверждать, что при увеличении цены батончика на один цент объем продаж уменьшается на величину, которая колеблется от 39,2 до 67,2 шт. Существует 95%-ная вероятность, что этот интервал правильно оценивает зависимость между двумя переменными.
Поскольку данный доверительный интервал не содержит нуля, можно утверждать, что регрессионный коэффициент имеет статистически значимое влияние на объем продаж.
ПРИМЕР 13.2. ПОСТРОЕНИЕ ДОВЕРИТЕЛЬНОГО ИНТЕРВАЛА, СОДЕРЖАЩЕГО НАКЛОН ОБЪЕМА ПРОДАЖ, ЗАВИСЯЩЕГО ОТ ЗАТРАТ НА РЕКЛАМУ
Постройте 95%-ный доверительный интервал, содержащий наклон генеральной совокупности объемов продаж, зависящих от затрат на рекламу.
РЕШЕНИЕ. Как указано в табл. Д.З, критическое значение ^-статистики при а = 0,05 и 31 степени свободы равно 2,0395. Используя формулу (13.8), получаем следующие величины:
3,6131 ±2,0395x0,6852,
3,6131 ±1,3975,
2,2156 < р2 < 5,0106.
Таким образом, учитывая влияние цены, можно утверждать, что при увеличении рекламных затрат на один доллар объем продаж увеличивается на величину, которая колеблется от 2,2 до 5 шт. Существует 95%-ная вероятность, что этот интервал правильно оценивает зависимость между двумя переменными. Поскольку данный доверительный интервал не содержит нуля, можно утверждать, что регрессионный коэффициент р2 имеет статистически значимое влияние на объем продаж.
Изучение основ
13.20. Рассмотрим модель множественной регрессии, характеризующуюся следующими параметрами:
п = 25, Ъ. = 10, Shi = 2, Sh = 8.
1. Какая из переменных имеет наибольший наклон, измеренный в единицах ^-статистики?
2. Постройте 95%-ный доверительный интервал, содержащий наклон генеральной совокупности
3. Существует ли статистически значимая зависимость между переменной У и каждой из объясняющих переменных при уровне значимости, равном 0,05? Укажите, какую из независимых переменных следует включить в модель регрессии.
13.21. Рассмотрим модель множественной регрессии, характеризующуюся следующими параметрами:
п = 20, ^ = 4,^ = 3, = 1,2, =0,8.
1. Какая из переменных имеет наибольший наклон, измеренный в единицах /-статистики?
2. Постройте 95%-ный доверительный интервал, содержащий наклон генеральной совокупности
3. Существует ли статистически значимая зависимость между переменной У и каждой из объясняющих переменных при уровне значимости, равном 0,05? Укажите, какую из независимых переменных следует включить в модель регрессии.
Применение понятий
13.22. В задаче 13.3 для предсказания длительности эксплуатации нового вида кроссовок используются степень амортизации и уровень износостойкости, измеренные у 15 пар кроссовок. Результаты приведены в таблице.
Переменная Коэффициенты Среднеквадратичная ошибка t-статистика р-значение
Сдвиг -0,02686 0,06905 -0,39
Амортизация 0,79116 0,06295 12,57 0,0000
Износ 0,60484 0,07174 8,43 0,0000
1. Постройте 95%-ный доверительный интервал, содержащий наклон генеральной совокупности откликов, зависящих от степени уровня износостойкости и степени амортизации.
2. Существует ли статистически значимая зависимость между переменной У и каждой из объясняющих переменных при уровне значимости, равном 0,05? Укажите, какую из независимых переменных следует включить в модель регрессии.
13.23. В задаче 13.5 для предсказания стоимости перевозок используется объем продаж и количество заказов. Решите эту задачу с помощью программы Microsoft Excel. ^WARECOST. XLS.
1. Постройте 95%-ный доверительный интервал, содержащий наклон генеральной совокупности откликов, зависящих от объема продаж и количества заказов.
2. Существует ли статистически значимая зависимость между переменной У и каждой из объясняющих переменных при уровне значимости, равном 0,05? Укажите, какую из независимых переменных следует включить в модель регрессии.
13.24. В задаче 13.6 для предсказания расхода топлива на милю пути использовалось количество лошадиных сил и вес автомобиля. Решите эту задачу с помощью программы Microsoft Excel. ^AUTO. XLS.
1. Постройте 95%-ный доверительный интервал, содержащий наклон генеральной совокупности откликов, зависящих от количества лошадиных сил и веса автомобиля.
2. Существует ли статистически значимая зависимость между переменной У и каждой из объясняющих переменных при уровне значимости, равном 0,05? Укажите, какую из независимых переменных следует включить в модель регрессии.
13.25. В задаче 13.7 для предсказания объема продаж использовались затраты на рекламу по радио и телевидению, а также в газетах. Решите эту задачу с помощью программы Microsoft Excel. ^ADRADTV. XLS.
1. Постройте 95%-ный доверительный интервал, содержащий наклон генеральной совокупности откликов, зависящих от уровня затрат на рекламу по радио и телевидению, а также в газетах.
2. Существует ли статистически значимая зависимость между переменной У и каждой из объясняющих переменных при уровне значимости, равном 0,05? Укажите, какую из независимых переменных следует включить в модель регрессии.
13.26. В задаче 13.8 для предсказания общего количества часов простоя за неделю использовалось общее количество человеко-часов в рабочей неделе (продолжительность работы в офисе) и общее количество часов, отработанных сотрудниками вне центральной станции (часы, проведенные на выезде). Решите задачу с помощью программы Microsoft Excel. О STANDBY .XLS.
1. Постройте 95%-ный доверительный интервал, содержащий наклон генеральной совокупности откликов, зависящих от количества часов, проведенных на телевизионной станции и на выезде.
2. Существует ли статистически значимая зависимость между переменной У и каждой из объясняющих переменных при уровне значимости, равном 0,05? Укажите, какую из независимых переменных следует включить в модель регрессии.
13.5. ОЦЕНКА ЗНАЧИМОСТИ ПОЯСНЯЮЩИХ ПЕРЕМЕННЫХ В МОДЕЛИ МНОЖЕСТВЕННОЙ РЕГРЕССИИ
В модель множественной регрессии следует включать только те объясняющие переменные, которые позволяют точно предсказать значение зависимой переменной. Если какая-либо из объясняющих переменных не соответствует этому требованию, ее нужно удалить из модели.
В качестве альтернативного метода, позволяющего оценить вклад объясняющей переменной, как правило, применяется частный F-критерий (partial F-test criterion). Он заключается в оценке изменения суммы квадратов регрессии после включения в модель очередной переменной. Новая переменная включается в модель лишь тогда, когда это приводит к значительному увеличению точности предсказания.
Для того чтобы применить частный F-критерий для решения задачи о продажах батончика OmniPower, необходимо оценить вклад переменной Х2 (затраты на рекламу) после включения в модель переменной Хх (цена батончика).
Если в модель входят несколько поясняющих переменных, вклад объясняющей переменной х можно определить, исключив ее из модели и оценив сумму квадратов регрессии (SSB), вычисленную по оставшимся переменным. Для этого применяется формула (13.9).
ОЦЕНКА ВКЛАДА НЕЗАВИСИМОЙ ПЕРЕМЕННОЙ В РЕГРЕССИОННУЮ МОДЕЛЬ
SSR(X> |<?се переменные, кроме X;) = (13 9)
= SSR(ece переменные, включая XSSR(ece переменные, кроме X
Если в модель входят две переменные, вклад каждой из них определяется по формулам (13.10, а) и (13.10, б).
ОЦЕНКА ВКЛАДА ПЕРЕМЕННОЙ X ПРИ УСЛОВИИ, ЧТО В МОДЕЛЬ ВКЛЮЧЕНА ПЕРЕМЕННАЯ Х2
SSR(Xx | Х2) = SS^X, и Х2) - SSR(X2). (13.10, а)
ОЦЕНКА ВКЛАДА ПЕРЕМЕННОЙ Х2 ПРИ УСЛОВИИ, ЧТО В МОДЕЛЬ ВКЛЮЧЕНА ПЕРЕМЕННАЯ \
SSR(X21XJ = 88Д(Х, и Х2) - SSR(Xl). (13.10, б)
Величины SSjR(X2) и SSR(Xx) соответственно представляют собой суммы квадратов регрессии, вычисленных только по одной из объясняемых переменных Х2 (затраты на рекламу) и X, (цена батончика). Результаты, полученные с помощью программы Microsoft Excel, представлены на рис. 13.6 и 13.7.
Таблица 13.3. Таблица ANOVA, содержащая суммы квадратов регрессии для оценки вклада переменной Хл
Источник Количество степеней Сумма квадратов Среднеквадратичное F свободы df значение
Регрессия 2 39 472 730,77 19 736 365,39
J X, 1 Jll J14 915 814,101 24556916,67 60,32 [1J [24 556 916,67]
Ошибка 31 12 620 946,67 407 127,31
Всего 33 52 093 677,44
Нулевая и альтернативная гипотезы о вкладе переменной Хх формулируются следующим образом:
На — включение переменной Хх не приводит к значительному увеличению точности модели, в которой учитывается переменная Х2;
— включение переменной Х} приводит к значительному увеличению точности модели, в которой учтена переменная Х2.
Статистика, положенная в основу частного F-критерия, вычисляется по формуле (13.11).
Итак,
SSjR(X2) = 14 915 814,10.
Как показано на рис. 13.1, SSRfXpi Х2) = 39 472 730,77. Следовательно, по формуле (13.10, а) получаем:
SSB(XJX2) = SSB(XL иХ2) - SSR(X2) = 39 472 730,77 - 14 915 814,1 = 25 556 916,67.
А 1 IОбъемы продаж и затраты на рекламу 2 В С D Е F G
3 Регрессионная статистика 4 Множественный R 5 jR-квадрат 6/Нормированный R-квадрат 7 Стандартная ошибка 8 i Наблюдения а 0,535095 0,286327 0,264024 1077,872084 34
10 Дисперсионный анализ 11 . 12 Регрессия 134 Остаток 14 jИтого 15 df 1 32 33 SS 14915814,102 37177863,339 52093677,441 MS 14915814,102 1161808.229 F 12,83844762 Значимость F 0,0011115
16 Коэффициенты Стандартная ошибка t-статистика Р-Значение Нижние 95% Верхние 95%
17 Y-пересечение 18 Реклама 1496,01613 4,12806 483,978853 1,152100 3,09107747 3,58307795 0,00411111 0,001111494 510,1843006 1,7813154 2481,847958 6,474814
19/ 201 2^ 22
Рис. 13.6. Коэффициенты модели простой линейной регрессии, учитывающей объем продаж и затраты на рекламу SSR(X2) (получены с помощью программы Microsoft Excel)
' A ' В ’ ~ ' С “ D ! Ё F ' G
1 Обьеиы продаж и цены
r2ij...................... г_______________1................... '.'''''' ..............
3 ________Регрессионная статистика_________
<4 Множественный R 0,735146
$ R-квадрат 0,540440
jEr Нормированный R-квадрат 0,526078:
7 Стандартная ошибка 864,945650
6 Наблюдения 34
9 .(
10 Дисперсионный анализ_________________________________________________________________________________
11 ______________________________iff_________________SS________:____MS________ F Значимость F
12 Регрессия 1 28153486,15 28153486,15 37,63176099 7.35855Е-07
13 (Остаток 32 23940191,29 748130,98
14 Итого_________________________________33___________52093677,44________________________________________
15!__________________________________________________________________________________________________________________
16_________________________Коэффициенты Стандартная ошибка t-статистика P-Значение Нижние 95% Верхние 95%
17 ^пересечение 7512,34798 734,6188701 10,22618434 1,30793Е-11 6015,97958 9008,716388
18 Цена -56,71384 9,2451043 -6,13447316 7,35855Е-07 -75,54549 -37,882199
Рис. 13.7. Коэффициенты модели простой линейной регрессии, учитывающей объем продаж и цену батончика SSR(X,) (получены с помощью программы Microsoft Excel)
СТАТИСТИКА, ПОЛОЖЕННАЯ В ОСНОВУ ЧАСТНОГО /^КРИТЕРИЯ ДЛЯ ОЦЕНКИ ВКЛАДА НЕЗАВИСИМОЙ ПЕРЕМЕННОЙ
SSR(Xt |<?се переменные, кроме X
F_ . (13.11)
По определению ^-статистика имеет ^-распределение с одной и п-k-l степенями свободы.
Используя формулу (13.11) и результаты, приведенные в табл. 13.3, получаем:
24 556 916,67 = 2
407127,31
Если уровень значимости равен 0,05, по табл. Д.5 определяем, что критическим значением F-распределения с одной и 31 степенями свободы является число 4,17 (см. рис. 13.8).
Рис. 13.8. Проверка гипотезы о значимости коэффициентов регрессии при уровне значимости, равном 0,05, с одной и 31 степенями свободы
Поскольку вычисленное значение F-статистики больше критического (60,32 > 4,17), гипотеза Но отклоняется, следовательно, учет переменной Хх (цены) значительно улучшает модель регрессии, в которую уже включена переменная Х2 (затраты на рекламу).
Для того чтобы оценить влияние переменной Х2 (затраты на рекламу) на модель, в которую уже включена переменная Х1 (цена), обратим внимание на то, что
SSJ?(Xl иХ2) = 39 472 730,77.
Кроме того, на рис. 13.7 показано, что
88К(ХГ) = 28 153 486,15.
Следовательно, по формуле (13.10, б) получаем:
SSR(X. IX,) = SSR(X, и Х2) - SSR(Xj = 39 472 730,77-28 153 486,15 = 11 319 244,62. Таким образом, для того чтобы определить, имеет ли переменная Хг значительное влияние на модель, учитывающую переменную Хх, необходимо разделить сумму квадратов регрессии на две части, как показано в табл. 13.4.
Таблица 13.4. Сводная таблица дисперсионного анализа, содержащая суммы квадратов регрессии для оценки вклада переменной Х2
Источник Количество степеней Сумма квадратов Среднеквадратичное F свободы df значение
Регрессия 2 39 472 730,77 19 736 365,39
f -V, 1 (11 (28 153 486,151 11 319 244,62 27,80
[1J [11 319 244,62]
Ошибка 31 12 620 946,67 407 127,31
Всего 33 52 093 677,44
Нулевая и альтернативная гипотезы о вкладе переменной Х2 формулируются следующим образом:
Но — включение переменной Х2 не приводит к значительному увеличению точности модели, в которой учтена переменная Х2;
Н1 — включение переменной Х2 приводит к значительному увеличению точности модели, в которой учитывается переменная Xt.
Используя формулу (13.11) и результаты, приведенные в табл. 13.4, получаем:
Если уровень значимости равен 0,05, по табл. Д.5 определяем, что критическим значением F-распределения с одной и 31 степенями свободы является число 4,17.
Поскольку вычисленное значение F-статистики больше критического (27,80 > 4,17), гипотеза Нп отклоняется, следовательно, учет переменной Х2 (затраты на рекламу) значительно улучшает модель регрессии, в которую уже включена переменная Xj (цена).
Итак, включение каждой из переменных повышает точность модели. Следовательно, в модель множественной регрессии необходимо включить обе переменные: и цену, и затраты на рекламу.
Рассмотрим, как связаны между собой величина t-статистики, вычисленная по формуле (13.7), и значение частной F-статистики, заданной формулой (13.11). Значения t-статистики равны -7,77 и +5,27, а соответствующие значения F-статистики — 60,32 и 27,80.
ВЗАИМОСВЯЗЬ МЕЖДУ t- И /^СТАТИСТИКОЙ
(13-12)
где а — количество степеней свободы.
Коэффициент частной смешанной корреляции
В разделе 13.1 был рассмотрен коэффициент множественной смешанной корреляции ГуП, позволяющий оценить долю вариации переменной У, объясняемой изменениями двух объясняющих переменных. Изучив влияние каждой из объясняющих переменных на модель множественной регрессии, можно вычислить коэффициент частной смешанной корреляции (г,2 2 и г}221). Эти коэффициенты оценивают долю вариации зависимой переменной, объясняемую каждой из независимых переменных, при условии, что остальные переменные “заморожены”. Коэффициенты частной смешанной
корреляции для модели множественной регрессии с двумя независимыми переменными определяются по формуле (13.13). (Эти величины также называют коэффициентами частной детерминации (coefficients of partial determination). — Прим, ped.)
(13.13, а)
(13.13,6)
КОЭФФИЦИЕНТЫ ЧАСТНОЙ СМЕШАННОЙ КОРРЕЛЯЦИИ ДЛЯ МОДЕЛИ МНОЖЕСТВЕННОЙ РЕГРЕССИИ, СОДЕРЖАЩЕЙ ДВЕ НЕЗАВИСИМЫЕ ПЕРЕМЕННЫЕ
, SSR(Xt\X,)
’п ~ ~ SST - SSR(X} и Х2) + SSR(X} |Х2) ’
2 SSR(X2\X})
Гу2' “ SST - SSR(X} и Х2) + SSR(X2 |Х,) ’
где SSR(X1 |Х2) — сумма квадратов, объясняемая переменной Х1 при условии, что в модель включена переменная Х2, SST— полная сумма квадратов, SSRIX^X^— сумма квадратов регрессии, объясняемая переменными X, и Х2, SSR(X21 X,) — сумма квадратов, объясняемая переменной Х2 при условии, что в модель включена переменная Хг
Для оценки значимости каждой из объясняющих переменных для создания модели, содержащей k переменных, используется формула (13.14).
КОЭФФИЦИЕНТЫ ЧАСТНОЙ СМЕШАННОЙ КОРРЕЛЯЦИИ ДЛЯ МОДЕЛИ МНОЖЕСТВЕННОЙ РЕГРЕССИИ, СОДЕРЖАЩЕЙ ^НЕЗАВИСИМЫХ ПЕРЕМЕННЫХ
(«с е переменные, кроме j-h)
SSR(X ^переменные, кроме j -и) • (13.14)
SST — SSR( переменные, включая j -ю) + SSR(Xj | переменные, кроме j — й)
В задаче о продаже батончиков OmniPower коэффициенты частной смешанной корреляции равны следующим величинам:
______________24 556 916^______________= 0,6605
52 093 677,44-39 472 730,77 + 24 556 916,67
11319 244,62
52 093 677,44 - 39 472 730,77 + 11319 244,62
= 0,4728.
Коэффициент частной смешанной корреляции ГуХ2 между переменными У и X, при постоянном значении переменной Х2 означает, что при фиксированном объеме затрат на рекламу 66,05% вариации объема продаж батончиков OmniPower можно объяснить изменением цены. Коэффициент частной смешанной корреляции г52,, между переменными Y и Х2 при постоянном значении переменной X, означает, что при фиксированной цене 47,28% вариации объема продаж батончиков OmniPower можно объяснить изменением затрат на рекламу.
Процедуры Excel: вычисление коэффициентов частной смешанной корреляции
Для вычисления коэффициентов частной смешанной корреляции в модели множественной регрессии, содержащей две переменные, необходимо модифицировать процедуру, рассмотренную во врезке "Процедуры Excel: вычисление коэффициентов множественной регрессии".
Например, чтобы вычислить коэффициенты частной смешанной корреляции для модели множественной регрессии, построенной на основе данных, приведенных в табл. 13.1, необходимо открыть рабочую книгу Chapter 13. xls на листе Данные и выполнить одну из следующих процедур.
Применение Excel в сочетании с надстройкой PHStat2
Чтобы вычислить коэффициенты частной смешанной корреляции для модели множественной регрессии, необходимо выполнить все инструкции, приведенные во врезке "Процедуры Excel: вычисление коэффициентов множественной регрессии", установив в п. 2.5 флажок Coefficients of Partial Determination (Коэффициенты частной смешанной корреляции) (см. иллюстрацию).
Применение Excel
Инструкции, позволяющие самостоятельно создать рабочий лист, вычисляющий коэффициенты частной смешанной корреляции для модели множественной регрессии, приведены в разделе ЕН.13.4.
Multiple Regression fx~|
Data
Y Variable Cell Range: [a1 : A35 7]
X Variables Cell Range: [в 1: C35 -j '
f? First cells in both ranges contain label
Confidence level for regression coefficients: [95 %
Regression Tool Output Options .................
P Regression Statistics Table
P ANOVA and Coefficients Table
Г“ Residuals Table
Г“ Residual Plots
Output Options
Title: | Анализ продаж батончиков OmniPower
1“ Durbin-Watson Statistic
P Coefficients of Partial Determination
Г Variance Inflationary Factor (VIF)
P Confidence Interval Estimate & Prediction Interval Confidence level for interval estimates: [95 %
Help| |lZ.ZZ[J| Cancel |
УПРАЖНЕНИЯ К РАЗДЕЛУ 13.5
Изучение основ
13.27. Рассмотрим сводную таблицу дисперсионного анализа для модели множественной регрессии с двумя независимыми переменными
Источник Количество степеней свободы df Сумма квадратов Среднеквадратичное значение F
Регрессия 2 60
Ошибка 18 120
Всего 20 180
SSRfXJ = 45, SSR(X2) = 25.
1. Существует ли статистически значимая зависимость между переменной У и двумя независимыми переменными при уровне значимости, равном 0,05?
2. Вычислите коэффициенты частной смешанной корреляции гУ12 и г?2Л .
13.28. Рассмотрим сводную таблицу дисперсионного анализа для модели множественной регрессии с двумя независимыми переменными.
Источник Количество степеней свободы df Сумма квадратов Среднеквадратичное значение F
Регрессия 2 30
Ошибка 10 120
Всего 12 150
SSRtfQ = 20, SSR(X2) = 15.
1. Существует ли статистически значимая зависимость между переменной У и двумя независимыми переменными при уровне значимости, равном 0,05?
2. Вычислите коэффициенты частной смешанной корреляции г,2 , и гД ].
Применение понятий
Задачи 13.29-13.32 можно решать с помощью программы Microsoft Excel.
13.29. В задаче 13.5 для предсказания стоимости перевозок используются объем продаж и количество заказов. Решите эту задачу с помощью программы Microsoft Excel. t^WARECOST. XLS.
1. Существует ли статистически значимая зависимость между переменной У и каждой из объясняющих переменных при уровне значимости, равном 0,05? Укажите, какую из независимых переменных следует включить в модель регрессии.
2. Вычислите коэффициенты частной смешанной корреляции г}\2 и ^.Объясните их смысл.
13.30. В задаче 13.6 для предсказания расхода топлива на милю пути использовалось количество лошадиных сил и вес автомобиля. Решите эту задачу с помощью программы Microsoft Excel. О AUTO. XLS.
1. Существует ли статистически значимая зависимость между переменной У и каждой из объясняющих переменных при уровне значимости, равном 0,05? Укажите, какую из независимых переменных следует включить в модель регрессии.
2. Вычислите коэффициенты частной смешанной корреляции г?212 и гг221. Объясните их смысл.
13.31. В задаче 13.7 для предсказания объема продаж использовались затраты на рекламу по радио и телевидению, а также в газетах. Решите эту задачу с помощью программы Microsoft Excel. ^ADRADTV. XLS.
1. Существует ли статистически значимая зависимость между переменной У и каждой из объясняющих переменных при уровне значимости, равном 0,05? Укажите, какую из независимых переменных следует включить в модель регрессии.
2. Вычислите коэффициенты частной смешанной корреляции г}2|2 и г}221. Объясните их смысл.
13.32. В задаче 13.8 для предсказания общего количества часов простоя за неделю использовалось общее количество человеко-часов в рабочей неделе (продолжительность работы в офисе) и общее количество часов, отработанных сотрудниками вне центральной станции (часы, проведенные на выезде). Решите задачу с помощью программы Microsoft Excel. Cl STANDBY. XLS.
1. Существует ли статистически значимая зависимость между переменной Y и каждой из объясняющих переменных при уровне значимости, равном 0,05? Укажите, какую из независимых переменных следует включить в модель регрессии.
2. Вычислите коэффициенты частной смешанной корреляции гУ|, и г2,,. Объясните их смысл.
13.6. РЕГРЕССИОННЫЕ МОДЕЛИ С ФИКТИВНОЙ ПЕРЕМЕННОЙ
И ЭФФЕКТЫ ВЗАИМОДЕЙСТВИЯ
Обсуждая модели множественной регрессии, мы предполагали, что каждая независимая переменная является числовой. Однако во многих ситуациях в модель необходимо включать категорийные переменные. Например, в задаче о продажах батончиков OmniPower для предсказания среднемесячного объема продаж использовались цена и затраты на рекламу. Кроме этих числовых переменных, можно попытаться учесть в модели расположение товара внутри магазина (например, на витрине или нет).
Для того чтобы учесть в регрессионной модели категорийные переменные, следует включить в нее фиктивные переменные (dummy variables). Например, если некая категорийная объясняющая переменная имеет две категории, для их представления достаточно одной фиктивной переменной Xd:
Xd = 0, если наблюдение принадлежит первой категории,
Xd = 1, если наблюдение принадлежит второй категории.
Для иллюстрации фиктивных переменных рассмотрим модель для предсказания средней оценочной стоимости недвижимости на основе выборки, состоящей из 15 домов. В качестве объясняющих переменных выберем жилую площадь дома (тыс. кв. футов) и наличие камина. Результаты приведены в табл. 13.5. Фиктивная переменная Х2 (наличие камина) определена следующим образом:
Хг = 0, если камина в доме нет,
Х2 = 1, если в доме есть камин.
Таблица 13.5. Оценочная стоимость, предсказанная по жилой площади и наличию камина ^HOUSES. xls
Дом Оценочная стоимость (тыс. долл.) Жилая площадь (тыс. кв. футов) Наличие камина
1 84,4 2,00 Да
2 77,4 . 1,71 Нет
3 75,7 1,45 Нет
4 85,9 1,76 Да
5 79,1 1,93 Нет
6 70,4 1,20 Да
7 75,8 1,55 Да
8 85,9 1,93 Да
9 78,5 1,59 Да
10 79,2 1,50 Да
Окончание табл. 13.5
Дом Оценочная стоимость (тыс. долл.) Жилая площадь (тыс. кв. футов) Наличие камина
11 86,7 1,90 Да
12 79,3 1,39 Да
13 74,5 1,54 Нет
14 83,8 1,89 Да
15 76,8 1,59 Нет
Предположим, что наклон оценочной стоимости, зависящей от жилой площади, одинаков у домов, имеющих камин и не имеющих его. Тогда модель множественной регрессии выглядит следующим образом:
где У, — оценочная стоимость i-ro дома, измеренная в тысячах долларов, |30 — сдвиг отклика, Хь— жилая площадь i-ro дома, измеренная в тыс. кв. футов, — наклон оценочной стоимости, зависящей от жилой площади дома при постоянном значении фиктивной переменной, Х2; — фиктивная переменная, означающая наличие или отсутствие камина, р2 — эффект увеличения оценочной стоимости дома в зависимости от наличия камина при постоянной величине жилой площади, 8, — случайная ошибка оценочной стоимости i-ro дома.
Результаты вычислений, проведенных по этой модели, представлены на рис. 13.9.
Как видим, уравнение регрессии выглядит следующим образом:
Yt = 50,09 +16,186Х„ + 3,853X,.
Для домов, не имеющих камина, это уравнение сводится к следующему:
Yt = 50,09 +16,186ХЬ , поскольку Х2 = 0 .
Для домов, имеющих камин, уравнение регрессии преобразуется так:
= 53,943 +16,186ХЬ , поскольку Х2 = 1 .
В этой модели коэффициенты регрессии интерпретируются следующим образом.
1. Если фиктивная переменная имеет постоянное значение, увеличение жилой площади на 1 000 кв. футов приводит к увеличению предсказанной средней оценочной стоимости на 16,186 тыс. долл.
2. Если жилая площадь постоянна, наличие камина увеличивает среднюю оценочную стоимость дома на 3,853 тыс. долл.
Обратите внимание на рис. 13.9. Как видим, i-статистика, соответствующая жилой площади, равна 6,29, ар-значение почти равно нулю. В то же время i-статистика, соответствующая фиктивной переменной, равна 3,10, а р-значение равно 0,009. Таким образом, каждая из этих двух переменных вносит существенный вклад в модель, если уровень значимости равен 0,01. Кроме того, коэффициент множественной смешанной корреляции означает, что 81,1% вариации оценочной стоимости объясняется изменчивостью жилой площади дома и наличием камина.
А 1 Анализ оценочной стоимости В С D 1... .. Е .. ' * F G
2 . 3 Регрессионная статистика 4 Множественный R 0,90059 5 R-квадрат 0,81106 6 Нормированный R-квадрат 0,77957 7_ Стандартная ошибка 2,26260 8 Наблюдения 15 9_ 10 Дисперсионный анализ 11 df 12 Регрессия 2 13 Остаток 12 14 Итого 14 15 SS 263,70391 61,43209 325,136 MS 131,85196 5,11934 F 25,75565 Значимость F 4.54968Е-05
16 Коэффициенты Стандартная ошибка t-статистика Р-Значение Нижние 95% Верхние 95%
17 Y-пересечение 50,09049 4,351658 11,510668 7.67943Е-08 40,60904 59,57194
18 Площадь 16,18583 2,574442 6,287124 4Д2437Е-05 10,57661 21,79506
19 Камин 3,85298 1,241223 3,104183 0,00912 1 14859 6,55737
Рис. 13.9. Результаты, полученные с помощью программы Microsoft Excel, для регрессионной модели, учитывающей жилую площадь и наличие камина
ПРИМЕР 13.3. ИЗУЧЕНИЕ РЕГРЕССИОННОЙ МОДЕЛИ, СОДЕРЖАЩЕЙ ТРЕХУРОВНЕВУЮ КАТЕГОРИЙНУЮ ПЕРЕМЕННУЮ
Постройте модель множественной регрессии, в которой зависимой переменной является объем продаж, а независимыми — форма упаковки и цена товара.
РЕШЕНИЕ. Для представления трехуровневой категорийной переменной необходимы две фиктивные переменные.
Хь = 1, если в i-м наблюдении использовалась упаковка А, и 0 — в противном случае. X2i = 1, если в i-м наблюдении использовалась упаковка Б, иО — в противном случае.
Обратите внимание на то, что если в i-м наблюдении использовалась упаковка А, то Xlt = 1 и Х21 = 0, если использовалась упаковка Б — Хь = 0 и Х21 = 1, и если использовалась упаковка В — Xlt = X2i = 0. Третья независимая переменная обозначает цену.
XSi = цена товара в i-м наблюдении.
Итак, для решения задачи следует применить следующую регрессионную модель.
у =р0 + рль + РА Ж + е.,
где У; — объем продаж в i-м наблюдении, [Зп — сдвиг отклика, — разность между средним объемом продаж товара в упаковке А и средним объемом продаж товара в упаковке Б при одинаковой цене, р2 — разность между средним объемом продаж товара в упаковке Б и средним объемом продаж товара в упаковке В при одинаковой цене, рз — наклон продаж при переменной цене и постоянных значениях остальных переменных, е, — случайная ошибка отклика в i-м наблюдении.
Эффект взаимодействия
Во всех регрессионных моделях, рассмотренных выше, считалось, что влияние отклика на объясняющую переменную является статистически независимым от влияния отклика на другие объясняющие переменные. Если это условие не выполняется, возникает взаимодействие (interaction) между зависимыми переменными. Например, вполне вероятно, что реклама оказывает большое влияние на объем продаж товаров, имеющих низкую цену. Однако, если цена товара слишком высока, увеличение расходов на рекламу не может существенно повысить объем продаж. В этом случае наблюдается взаимодействие между ценой товара и затратами на его рекламу. Иначе говоря, нельзя делать общих утверждений о зависимости объема продаж от затрат на рекламу. Влияние рекламных расходов на объем продаж зависит от цены. Это влияние учитывается в модели множественной регрессии с помощью эффекта взаимодействия (interaction effect). Для иллюстрации этого понятия вернемся к задаче о стоимости домов.
В разработанной нами регрессионной модели предполагалось, что влияние размера дома на его стоимость не зависит от того, есть ли в доме камин. Иначе говоря, считалось, что наклон оценочной стоимости, зависящей от жилой площади дома, одинаков у домов, имеющих камин и не имеющих его. Если эти наклоны отличаются друг от друга, между размером дома и наличием камина существует взаимодействие.
Проверка гипотезы о равенстве наклонов сводится к оценке вклада, который вносит в модель регрессии произведение объясняющей переменной X, и фиктивной переменной Х2. Если этот вклад является статистически значимым, исходную модель регрессии применять нельзя. Используя данные, приведенные в табл. 13.5, получаем:
X3 = X,xX2.
Результаты регрессионного анализа, включающего переменные Х„ Х2 и Х3, приведены на рис. 13.10.
| А J в с D | Е F G
1 ’Анализ оценочной стоимости ВЙ ;
- 3 I Регрессионная статистика
4 'Множественный R ЩШ-квадрат ^^Нормированный R-квадрат 7 ;Стандартная ошибка 6 jНаблюдения 9 Г 0,91791 0,84255 0,79961 2,15727 15
10iДисперсионный анализ
И; df SS MS F Значимость F
12 {Регрессия 13 - Остаток 14’Итого 3 11 14 273,94410 51,19190 325,136 91,31470 4,65381 19,62150 0,00010
15 i
16' Коэффициенты Стандартная ошибка t-статистика Р-Значение Нижние 95% Верхние 95%
J7 ^-пересечение 18 Площадь J9 Камин 20 Площадь±Камин 62,95218 8,36242 -11,84036 9,51800 9,61218 5,81730 10,64550 6,41647 6,54921 1,43751 -1,11224 1,48337 4,13993Е-05 0,17841 0,28975 0,16605 41,79591 4,44137 -35,27097 4,60456 84,10845 21,16621 11,59024 23,64056
Рис. 13.10. Результаты, полученные с помощью программы Microsoft Excel для регрессионной модели, учитывающей жилую площадь, наличие камина и их взаимодействие
Для того чтобы проверить нулевую гипотезу Но: Р3 = 0 и альтернативную гипотезу Нг: рз* 0, используя результаты, приведенные на рис. 13.10, обратим внимание на то, что t-статистика, соответствующая эффекту взаимодействия переменных, равна 1,48. Поскольку p-значение равно 0,166 >0,05, нулевая гипотеза не отклоняется. Следовательно, взаимодействие переменных не имеет существенного влияния на модель регрессии, учитывающую жилую площадь и наличие камина.
В регрессионную модель могут входить несколько числовых объясняющих переменных. Пример 13.4 иллюстрирует регрессионную модель, содержащую две числовые переменные и одну категорийную.
ПРИМЕР 13.4. ИЗУЧЕНИЕ РЕГРЕССИОННОЙ МОДЕЛИ, СОДЕРЖАЩЕЙ ФИКТИВНУЮ ПЕРЕМЕННУЮ
Менеджер агентства недвижимости желает предсказать объем топлива, потребляемого для отопления дома, в зависимости от температуры воздуха Xi и высоты чердака Х2 . Допустим теперь, что выборка состоит из 15 домов, в которых 1-, 4-, 6-, 7-, 8-, 10- и 12-й дома представляют собой усадьбы. Постройте регрессионную модель, использующую переменные Хр Х2 и Х3 (фиктивную переменную, обозначающую стиль дома: усадьба или нет).
РЕШЕНИЕ. Фиктивная переменная, обозначающая стиль дома, определяется следующим образом:
Х3 = 0, если дом не является усадьбой,
Х3 = 1, если дом представляет собой усадьбу.
Предполагая, что наклоны отклика, зависящего от каждой из числовых объясняющих переменных, одинаковы для усадьбы и других домов, получаем следующую регрессионную модель.
Y = р0 + Р.Х,, + Р2Х2, +РЛ >
где У — ежемесячный объем потребления топлива в i-м доме, измеренный в галлонах, рп — сдвиг отклика, Pj — наклон отклика, зависящий от температуры воздуха при постоянных значениях остальных переменных, Р2 — наклон отклика, зависящий от высоты чердака при постоянных значениях остальных переменных, Р3 — “эффект усадьбы” при постоянных значениях остальных переменных, е, — случайная ошибка отклика для i-ro дома.
Результаты вычислений, проведенных по этой модели, представлены на рис. 13.11. Как видим, уравнение регрессии выглядит следующим образом:
Yt = 592,5401 - 5,525 lXlt -21,3761X2l - 38,9727Х3, .
Для домов, не являющихся усадьбой, это уравнение сводится к следующему:
V 592,5401-5,525 IX,, -21,3761Х2, , поскольку Х3 = 0.
Для усадьбы уравнение регрессии преобразуется так:
Yt= 553,5674- 5,5251Х„ -21,376IX,,, поскольку Х3 = 1.
i а в _.с о . 1 Е F .
_J ^Анализ потребления топлива о”’
3_t Регрессионная статистика 4 'Множественный R 0,99421 5 R-квадрат 0,98845 _Б Нормированный R-квадрат 0,98529 7 Стандартная ошибка 15,74894 8 Наблюдения 15 Ct
10 Дисперсионный анализ jl 12 Регрессия 13 Остаток 14 Итого 15 df 3 11 14 SS 233406,90935 2728,31998 236135,22933 MS 77802,30312 248,02909 F 313,68217 Значимость F 6,21548Е-11
16 Коэффициенты Стандартная ошибка t-статистика Р-Значение Нижние 95% Верхние 95%
17 ’Y-пересечение 18_‘Температура 19iЧердак 20 Усадьба 592,54012 -5,52510 -21,37613 -38,97267 14,33698 0,20443 1,44802 8,35844 41,32948 -27,02670 -14,76232 4,66267 2,02317Е-13 2,07188Е-11 1,34816ЕД8 0,00069 560,98461 -5,97505 -24,56320 -57,36947 624,09562 -5,07515 -18,18906 -20,57586
Рис. 13.11. Результаты, полученные с помощью программы Microsoft Excel, для регрессионной модели, учитывающей температуру воздуха, высоту чердака и стиль дома
Кроме того, отметим следующие факты.
1. Если высота чердака и стиль являются постоянными величинами, увеличение температуры на 1 °F приводит к увеличению предсказанного расхода топлива на 5,5251 галлонов.
2. Если температура воздуха и стиль являются постоянными величинами, увеличение высоты чердака на один дюйм приводит к уменьшению среднего расхода топлива на 21,376 галлонов.
3. Коэффициент Ьа оценивает изменение расхода топлива в усадьбе (Х3 — 1) по сравнению с другими домами (Х3 = 0). Таким образом, если температура воздуха и высота чердака постоянны, в усадьбе ежемесячные расходы мазута на 38,973 галлона меньше, чем в других домах.
Обратите внимание на рис. 13.11. Как видим, три £-статистики, соответствующие температуре, высоте чердака и стилю дома равны -27,03, -14,76 и -4,66 соответственно. Кроме того, соответствующие p-значения чрезвычайно малы и не превышают 0,001. Таким образом, каждая из трех объясняющих переменных вносит значительный вклад в модель. Кроме того, коэффициент множественной смешанной корреляции означает, что 98,8% вариации расходов топлива объясняется изменчивостью температуры, высоты чердака и стиля дома.
Прежде чем выполнять множественный регрессионный анализ данных в примере 13.4, необходимо убедиться, что наклоны отклика, зависящего от каждой из числовых объясняющих переменных, одинаковы для усадьбы и других домов. Продемонстрируем эту процедуру на следующем примере.
ПРИМЕР 13.5. ИЗУЧЕНИЕ РЕГРЕССИОННОЙ МОДЕЛИ, СОДЕРЖАЩЕЙ НЕСКОЛЬКО ЭФФЕКТОВ ВЗАИМОДЕЙСТВИЯ
Определите, имеют ли эффекты взаимодействия статистически значимое влияние на точность регрессионной модели, построенной на основе данных из примера 13.4.
РЕШЕНИЕ. Для оценки возможных взаимодействий вычисляются три эффекта взаимодействия. Пусть Х4 = Х4 х Х2, Х5 = X, х Х3 и Х6 = Х2 х Х3. В этом случае регрессионная модель принимает следующий вид.
У = Ро + р,Х1( + Р2Х2, +Р3Х3, +Р4Х4, +р5Х5, +РЛ, + е,
где Х4 — температура воздуха, Х2 — высота чердака, Х3 — стиль дома, X, — взаимодействие температуры и высоты чердака, Х5 — взаимодействие температуры и стиля, Хв — взаимодействие между высотой чердака и стилем дома.
Для того чтобы проверить гипотезу о том, что учет трех эффектов взаимодействия значительно повышает точность регрессионной модели, применяется модифицированный частный F-критерий. Нулевая и альтернативная гипотезы формулируются следующим образом.
Но: Р4 = Р5 =Р6 = 0 Между переменными Хр Х2 и Х3 нет взаимодействия.
Н4: Р4 Ф 0 и/или Р5 Ф 0 и/или Р6 * 0 Между переменными Х4 и Х2 и/или Х1 и Х2 и/или Х2 и Х3 есть взаимодействие.
Используя результаты, приведенные на рис. 13.12, приходим к выводу, что
SSR(X}, Х2, Х3, Х4, Х5, Хв) = 234 510,58.
J А 1 'Анализ потребления топлива ’ 5"*! . в. .С 'Di Е F G
3 i Регрессионная статистика
4 ^Множественный R 5. iR-kb адрат _ 6JНормированный R-квадрат _7 Стандартная ошибка 8 Наблюдения 0,99655 0,99312 0,98796 14,25065 15
9_. 10 Дисперсионный анализ
11 1 df SS MS F Значимость F
12 Регрессия 13_ Остаток 14 Итого 6 8 14 234510,58185 1624,64749 236135,22933 39085,09697 203,08094 192,46069 3,32423Е-08
15^
16 Коэффициенты Стандартная ошибка t-статистика P-Значение Нижние 95% Верхние 95%
l7 Y-пересечение Температура Чердак 20 jСтиль 21 Температура * Чердак ,22 Температура * Усадьба 23 !Чердак " Усадьба 642,88670 -6,92627 27,88251 -84,60882 0,17021 0,65957 4,98698 26,70590 0,75311 3,58011 29,99556 0,08863 0,46168 3,51368 24,07283 -9,19687 -7,78818 2,82071 1,92039 1,42862 1,41930 9,45284Е-09 1,58014Е-05 5,29456Е-05 0,02247 0,09106 0,19097 0,19358 581,30273 -8,66295 36,13826 -153,77875 -0,03418 -0,40507 3,11559 704,47066 -5,18959 19,62677 15,43889 0,37460 1,72420 13,08955
Рис. 13.12. Результаты, полученные с помощью программы Microsoft Excel, для регрессионной модели, учитывающей температуру воздуха X,, высоту чердака Х2, стиль дома Х3, взаимодействие температуры и высоты чердака Х4, взаимодействие температуры и стиля Х5, а также взаимодействие высоты чердака и стиля Х6
Эта величина имеет шесть степеней свободы. Из рис. 13.11 следует, что величина SSR(Xlf Х2, Х3) равна 233 406,91 и имеет три степени свободы. Таким образом,
SSR(Xiy Х2, Х3, Х4, Х5, Х6) - SSR(Xlf Х2, Х3) = 234 510,58 - 233 406,91 = 1 103,67,
а разность между количеством их степеней свободы равна 6-3, т.е. 3.
Для того чтобы проверить нулевую гипотезу о вкладе объясняющих переменных в модель регрессии, применим частный F-критерий (13.11), описанный в разделе 13.6.1
F = [SSRkX^X^X^X^X^-SSRkX^X^ = 1103,67/3 = 1 81 MSE{Xx,X2,X3,X„X5,X^ 203,08
Поскольку при уровне значимости, равном 0,05, статистика F=l,81< 4,26 (F-статистика с тремя и восемью степенями свободы), приходим к выводу, что ни один из эффектов взаимодействия между объясняющими и фиктивной переменными не является статистически значимым. Если бы нулевая гипотеза была отклонена, необходимо было бы проанализировать каждый эффект взаимодействия отдельно для того, чтобы определить, сколько эффектов следует включить в модель.
Процедуры Excel: создание фиктивных эффектов взаимодействия
Чтобы создать фиктивные переменные и учесть эффекты взаимодействия, следует добавить в рабочий лист, содержащий исходные данные, столбцы с формулами. Эти столбцы можно рассматривать как часть входного интервала переменной Х(см. диалоговое окно X Variable Cell Range в процедуре Multiple Regression надстройки PHStat2 или Входной интервал X в процедуре Сервис^ Анализ данных... ^Регрессия).
Создание фиктивных переменных. Для превращения категорийной переменной в фиктивную, принимающую значения 0 и 1, следует выбрать команду Правка^Заменить.... Например, чтобы категорийная переменная, обозначающая в табл. 13.5 наличие камина, стала фиктивной переменной, у которой нуль означает отсутствие камина, а единица — его наличие, необходимо открыть рабочую книгу House3.xls на листе Данные и выполнить следующие действия.
1. Скопировать диапазон Cl:С16 в ячейку D1. Это позволит выполнить верификацию, предусмотренную в п. 7.
2. Выделить диапазон ячеек С2 : С16, содержащих значения категорийной переменной Да и Нет.
3. Выбрать команду Правкам Заменить....
4. В диалоговом окне Найти и заменить (см. первую иллюстрацию) сделать следующее.
4.1. Ввести в окне редактирования Найти слово Да, а в окне редактирования Заменить на — цифру 1.
4.2. Щелкнуть на кнопке Заменить все. Если появится окно сообщения, требующее подтверждения замены, щелкнуть на кнопке ОК.
Как правило, если в модель входят несколько переменных и исследователь пытается решить, стоит ли включать в нее дополнительные независимые переменные, то числитель F-статистики представляет собой разность между величинами SSR (все независимые переменные ) и SSR (первоначальный набор переменных), деленную на количество дополнительных независимых переменных.
5. Оставляя диапазон С2 cl 6 выделенным, снова выбрать команду Правка^Заменить....
6. Оказавшись в диалоговом окне Найти и заменить, сделать следующее.
6.1. Ввести в окне редактирования Найти слово Нет, а в окне редактирования Заменить на -цифру 0.
6.2. Щелкнуть на кнопке Заменить все.
7. Проверить, что всем значениям Да в столбце с соответствуют единицы в столбце D, а всем значениям Нет - нули.
8. Выделить столбец D и выбрать команду Правка ^Удалить.... В результате будет создан рабочий лист, содержащий три столбца (см. вторую иллюстрацию).
Учет эффектов взаимодействия. Чтобы учесть эффект взаимодействия, необходимо вставить в новый столбец формулы - ячейка!*ячейка2. В таблице показано, как изменить рабочий лист Данные так, чтобы он содержал формулы, учитывающие взаимодействие между размером дома и наличие камина.
С D
1 Оценочная стоимость Жилая площадь Наличие камина РазмерхНаличие камина
2 84,4 2,00 1 = В2*С2
3 77,4 1,71 0 =ВЗ*СЗ
4 75,7 1,45 0 =В4*С4
5 85,9 1,76 1 =В5*С5
6 79,1 1,93 0 =В6*С6
i|l|||| 70,4 1,20 1 =В7*С7
8 75,8 1,55 1 =В8*С8
9 85,9 1,93 1 =В9*С9
10 78,5 1,59 1 = В10*С10
11 79,2 1,50 1 = В11*С11
Illi 86,7 1,90 1 = В12*С12
1Й88В 79,3 1,39 1 = В13*С13
14 74,5 1,54 0 = В14*С14
15 83,8 1,89 1 = В15*С15
16 76,8 1,59 0 = В16*С16
Изучение основ
13.33. Предположим, что X, — числовая переменная, а Х2 — фиктивная. Рассмотрим уравнение регрессии для выборки, имеющей объем п = 20:
У = 6 + 4ХЬ+2Х2,.
1. Объясните смысл наклона отклика по отношению к переменной Хх.
2. Объясните смысл наклона отклика по отношению к переменной Х2.
3. Предположим, что Z-статистика, вычисленная при проверке гипотезы о вкладе переменной Х2, равна 3,27, а уровень значимости — 0,05. Можно ли утверждать, что переменная Х2 значительно повышает точность модели?
Применение понятий
Задачи 13.34 можно решать вручную. Задачи 13.35-13.44 можно решать с помощью программы Microsoft Excel.
13.34. Декан экономического факультета в крупном университете хочет разработать модель регрессии, чтобы предсказать среднюю экзаменационную оценку студентов, специализирующихся на бухгалтерском учете. Он включил в модель количество баллов, набранных студентом при сдаче теста SAT, а также категорийную переменную, принимающую значение 1, если оценка студента по статистике превышает уровень В, и 0 — в противном случае.
1. Опишите этапы построения этой модели. Какие модели необходимо проверить и оценить?
2. Какой вывод можно сделать, если регрессионный коэффициент, соответствующий категорийной переменной, равен +0,30?
13.35. Менеджер по маркетингу в компании, владеющей крупной сетью супермаркетов, желает оценить влияние расстояния между полками, а также их местоположения на объем продаж корма для домашних животных. Для анализа создана случайная выборка, состоящая из 12 приблизительно одинаковых магазинов. ^PETFOOD. XLS.
Магазин Расстояние между полками, X (футы) Местоположение Еженедельный объем продаж, Y (тыс. долл.)
1 5 Сзади 0,16
2 5 Впереди 0,22
3 5 Сзади 0,14
4 10 Сзади 0,19
5 10 Сзади 0,24
6 10 Впереди 0,26
7 15 Сзади 0,23
8 15 Сзади 0,27
9 15 Впереди 0,28
10 20 Сзади 0,26
11 20 Сзади 0,29
12 20 Впереди 0,31
1. Сформулируйте уравнение множественной регрессии.
2. Объясните смысл наклонов отклика в этой модели.
3. Предскажите среднее значение ежемесячных продаж корма в магазине, внутри которого стеллажи расположены на расстоянии 8 футов друг от друга в глубине торгового зала. Постройте 95%-ные доверительные интервалы для математического ожидания и предсказанного значения отклика.
4. Выполните анализ остатков и оцените адекватность модели.
5. Существует ли статистически значимая зависимость между объемом продаж и двумя объясняющими переменными при уровне значимости, равном 0,05?
6. Являются ли объясняющие переменные статистически значимыми при уровне значимости, равном 0,05? Какую модель регрессии следует применить для решения задачи?
7. Постройте 95%-ный доверительный интервал, содержащий наклон объема продаж относительно расстояния между стеллажами и их расположения внутри торгового зала.
8. Сравните наклон, вычисленный при решении задачи 2, с наклоном простой линейной регрессии в задаче 12.3. Объясните разницу между этими результатами.
9. Объясните смысл коэффициента множественной смешанной корреляции /у12.
10. Вычислите скорректированный коэффициент г2.
11. Сравните коэффициент г?п с коэффициентом г, вычисленным при решении задачи 12.4.1.
12. Вычислите коэффициент частной множественной корреляции и объясните его смысл.
13. Какое предположение о наклоне отклика следует сделать при решении этой задачи?
14. Включите в модель эффект взаимодействия, установив уровень значимости равным 0,05. Вносит ли этот эффект статистически значимый вклад в построенную модель регрессии?
15. Используя результаты решения задач 6 и 14, определите, какая модель точнее. Обоснуйте свой ответ.
13.36. Агентство по торговле недвижимостью в одном из пригородов хотело бы изучить взаимосвязь между количеством комнат в одноквартирном доме и его продажной ценой. Исследование проводилось в двух разных районах: на востоке и на западе. Для анализа были отобраны 20 домов. Результаты приведены в файле ^NEIGHBOR. XLS.
1. Сформулируйте уравнение множественной регрессии.
2. Объясните смысл наклонов отклика в этой модели.
3. Предскажите среднее значение продажной цены дома, состоящего из девяти комнат и расположенного в восточном районе. Постройте 95%-ные доверительные интервалы для математического ожидания и предсказанного значения отклика.
4. Выполните анализ остатков и оцените адекватность модели.
5. Существует ли статистически значимая зависимость между продажной ценой и двумя объясняющими переменными при уровне значимости, равном 0,05?
6. Являются ли объясняющие переменные статистически значимыми при уровне значимости, равном 0,05? Какую модель регрессии следует применить для решения задачи?
7. Постройте 95%-ный доверительный интервал, содержащий наклон продажной цены дома по отношению к количеству комнат, а также по отношению к расположению в городе.
8. Объясните смысл коэффициента множественной смешанной корреляции.
9. Вычислите скорректированный коэффициент г2.
10. Вычислите коэффициент частной множественной корреляции и объясните его смысл.
11. Какое предположение о наклоне отклика следует сделать при решении этой задачи?
12. Включите в модель эффект взаимодействия, установив уровень значимости равным 0,05. Вносит ли этот эффект статистически значимый вклад в построенную модель регрессии?
13. Используя результаты решения задач б и 12, определите, какая модель точнее. Обоснуйте свой ответ.
13.37. Файл ^COLLEGES2 0 02 . XLS содержит данные о 80 колледжах и университетах, в частности, стоимость обучения в течение года (тыс. долл.), среднее количество баллов, набранных студентами при сдаче теста на проверку умственных способностей (Scholastic Aptitude Test — SAT), а также вид заведения — государственное (0) или частное (1). Разработайте модель для предсказания стоимости годового обучения по результатам тестирования и виду заведения.
1. Сформулируйте уравнение множественной регрессии.
2. Объясните смысл наклонов отклика в этой модели.
3. Предскажите среднюю стоимость годового обучения в государственном учебном заведении, студенты которого набрали при сдаче теста SAT в среднем 1 000 баллов.
4. Выполните анализ остатков и оцените адекватность модели.
5. Существует ли статистически значимая зависимость между стоимостью обучения и двумя объясняющими переменными (умственными способностями студентов и формой собственности учебного заведения) при уровне значимости, равном 0,05?
6. Являются ли объясняющие переменные статистически значимыми при уровне значимости, равном 0,05? Какую модель регрессии следует применить для решения задачи?
7. Постройте 95%-ный доверительный интервал, содержащий наклон стоимости годового обучения по отношению к количеству баллов, набранных студентами при сдаче теста SAT, а также по отношению к форме собственности учебного заведения.
8. Объясните смысл коэффициента множественной смешанной корреляции.
9. Вычислите скорректированный коэффициент г2.
10. Вычислите коэффициент частной множественной корреляции и объясните его смысл.
11. Какое предположение о наклоне отклика следует сделать при решении этой задачи?
12. Включите в модель эффект взаимодействия, установив уровень значимости равным 0,05. Вносит ли этот эффект статистически значимый вклад в построенную модель регрессии?
13. Используя результаты решения задач 6 и 12, определите, какая модель точнее. Обоснуйте свой ответ.
13.38. В горном деле скважины в породе часто делают с помощью бурового долота. По мере углубления скважины к буровому долоту добавляются новые стержни. Как правило, чем глубже становится скважина, тем медленнее происходит бурение. Это объясняется несколькими факторами, в частности, массой стержней. Ключевой вопрос заключается в следующем: какое бурение происходит быстрее — сухое или мокрое. При сухом бурении в скважину нагнетается сжатый воздух, выталкивающий буровой шлам и управляющий молотом. При мокром бурении вместо воздуха в скважину нагнетается вода. В файле ft^DRILL.XLS содержатся результаты измерения скорости бурения на каждые 5 футов (в минутах), глубина (в футах), а также вид бурения — сухое или мокрое. Постройте модель регрессии, предназначенную для предсказания времени бурения по глубине скважины и виду бурения (сухое или мокрое).
Источник: Penner, R., and D. G. Watts, “Mining Information”, The American Statistician 45 (1991): 4-9.
1. Сформулируйте уравнение множественной регрессии.
2. Объясните смысл наклонов отклика в этой модели.
3. Предскажите среднюю продолжительность сухого бурения скважины глубиной 100 футов. Постройте 95%-ный доверительный интервал для математического ожидания и предсказанного значения отклика.
4. Выполните анализ остатков и оцените адекватность модели.
5. Существует ли статистически значимая зависимость между продолжительностью бурения и двумя объясняющими переменными (глубиной скважины и видом бурения) при уровне значимости, равном 0,05?
6. Являются ли объясняющие переменные статистически значимыми при уровне значимости, равном 0,05? Какую модель регрессии следует применить для решения задачи?
7. Постройте 95%-ный доверительный интервал, содержащий наклон продолжительности бурения по отношению к глубине скважины, а также по отношению к виду бурения.
8. Объясните смысл коэффициента множественной смешанной корреляции.
9. Вычислите скорректированный коэффициент г1.
10. Вычислите коэффициент частной множественной корреляции и объясните его смысл.
11. Какое предположение о наклоне отклика следует сделать при решении этой задачи?
12. Включите в модель эффект взаимодействия, установив уровень значимости равным 0,05. Вносит ли этот эффект статистически значимый вклад в построенную модель регрессии?
13. Используя результаты решения задач 6 и 12, определите, какая модель точнее. Обоснуйте свой ответ.
13.39. Компания Zagat публикует рейтинги ресторанов, расположенных в разных городах США. В файле ft0RESTRATE.XLS содержатся оценки качества пищи, оформления блюд, уровня обслуживания и стоимость обеда для одного человека в 50 ресторанах Нью-Йорк Сити (Xd = 0) и 50 ресторанах Лонг-Айленда (Xd=l). Постройте регрессионную модель, позволяющую предсказать стоимость обеда для одного человека с учетом суммы рейтингов за качество блюд, оформление, уровень обслуживания и расположение ресторана (Нью-Йорк Сити или Лонг-Айленд).
Источник: цитируется по изданиям Zagat Survey “2000 New York City Restraunts” и Zagat Survey “2000 long Island Restraunts”.
1. Сформулируйте уравнение множественной регрессии.
2. Объясните смысл наклонов отклика в этой модели.
3. Предскажите среднюю стоимость обеда в ресторане, имеющем рейтинг, равный 60, и расположенном в Нью-Йорк Сити. Постройте 95%-ный доверительный интервал для предсказанного и среднего значений отклика.
4. Выполните анализ остатков и оцените адекватность модели.
5. Существует ли статистически значимая зависимость между стоимостью обеда в ресторане и двумя объясняющими переменными (рейтингом и расположением) при уровне значимости, равном 0,05?
6. Являются ли объясняющие переменные статистически значимыми при уровне значимости, равном 0,05? Какую модель регрессии следует применить для решения задачи?
7. Постройте 95%-ный доверительный интервал, содержащий наклон стоимости обеда по отношению к рейтингу и расположению.
8. Сравните наклон, вычисленный при решении задачи 2, с наклоном простой линейной регрессии в задаче 12.76. Объясните разницу между этими результатами.
9. Объясните смысл коэффициента множественной смешанной корреляции /-Д,.
10. Вычислите скорректированный коэффициент г2.
11. Сравните коэффициент с коэффициентом г*, вычисленным при решении задачи 12.76.6.
12. Вычислите коэффициент частной множественной корреляции и объясните его смысл.
13. Какое предположение о наклоне отклика следует сделать при решении этой задачи?
14. Включите в модель эффект взаимодействия, установив уровень значимости равным 0,05. Вносит ли этот эффект статистически значимый вклад в построенную модель регрессии?
15. Используя результаты решения задач 6 и 14, определите, какая модель точнее. Обоснуйте свой ответ.
13.40. В задаче 13.5 для предсказания стоимости перевозок используются объем продаж и количество заказов. Постройте регрессионную модель, учитывающую взаимодействие между объемом продаж и количеством заказов.
1. Определите, имеет ли взаимодействие между объемом продаж и количеством заказов существенное влияние на стоимость перевозок при уровне значимости, равном 0,05.
2. Какую модель регрессии следует применить для решения задачи 13.5?
13.41. В задаче 13.6 для предсказания расхода топлива на милю пути использовалось количество лошадиных сил и вес автомобиля. Постройте регрессионную модель, учитывающую взаимодействие между мощностью двигателя и весом автомобиля.
1. Определите, имеет ли взаимодействие между мощностью двигателя и весом автомобиля существенное влияние на расход топлива при уровне значимости, равном 0,05.
2. Какую модель регрессии следует применить для решения задачи 13.6?
13.42. В задаче 13.7 для предсказания объема продаж использовались затраты на рекламу по радио и телевидению, а также в газетах. Постройте регрессионную модель, учитывающую взаимодействие между затратами на рекламу на радио и телевидении и затратами на рекламу в газетах.
1. Определите, имеет ли взаимодействие между затратами на рекламу на радио и телевидении и затратами на рекламу в газетах, существенное влияние на объем продаж при уровне значимости, равном 0,05.
2. Какую модель регрессии следует применить для решения задачи 13.7?
13.43. В задаче 13.8 для предсказания общего количества часов простоя за неделю использовались общее количество человеко-часов в рабочей неделе (продолжительность работы в офисе) и общее количество часов, отработанных сотрудниками вне центральной станции (часы, проведенные на выезде). Постройте регрессионную модель, учитывающую взаимодействие между этими показателями.
1. Определите, имеет ли взаимодействие между общим количеством человекочасов в рабочей неделе (продолжительность работы в офисе) и общим количеством часов, отработанных сотрудниками вне центральной станции (часы, проведенные на выезде), существенное влияние на общее количество часов простоя за неделю при уровне значимости, равном 0,05.
2. Какую модель регрессии следует применить для решения задачи 13.8?
13.44. Директор учебного центра в крупной страховой компании желает сравнить три разных метода обучения новых страховщиков: традиционный, с помощью компакт-дисков и с помощью Интернет. Он разделил 30 учеников на три случайных группы по 10 человек в каждой. Перед началом обучения каждый ученик сдал экзамен, в ходе которого измерялись его значения по математике и компьютерным наукам. В конце обучения ученики сдали тот же самый экзамен, ftUNDERWRITING. XLS.
Вступительный экзамен Выпускной экзамен Метод
94 14 Традиционный
96 19 Традиционный
98 17 Традиционный
100 38 Традиционный
102 40 Традиционный
105 26 Традиционный
109 41 Традиционный
110 28 Традиционный
111 36 Традиционный
130 66 Традиционный
80 38 Компакт-диск
84 34 Компакт-диск
90 43 Компакт-диск
97 43 Компакт-диск
97 61 Компакт-диск
112 63 Компакт-диск
115 93 Компакт-диск
118 74 Компакт-диск
120 76 Компакт-диск
Вступительный экзамен Выпускной экзамен Метод
120 79 Компакт-диск
92 55 Интернет
96 53 Интернет
99 55 Интернет
101 52 Интернет
102 35 Интернет
104 46 Интернет
107 57 Интернет
110 55 Интернет
111 42 Интернет
118 81 Интернет
Разработайте модель множественной регрессии для предсказания оценок, полученных на выпускном экзамене, на основе информации об оценках, полученных на вступительном экзамене и разновидности метода обучения.
1. Сформулируйте уравнение множественной регрессии.
2. Объясните смысл наклонов отклика в этой модели.
3. Предскажите среднюю оценку на выпускном экзамене для ученика, набравшего на вступительном экзамене 100 баллов и прошедшего обучение с помощью Интернет.
4. Выполните анализ остатков и оцените адекватность модели.
5. Существует ли статистически значимая зависимость между оценками, полученными на выпускном экзамене и двумя объясняющими переменными (оценками, полученными на вступительном экзамене и разновидностью обучения) при уровне значимости, равном 0,05?
6. Являются ли объясняющие переменные статистически значимыми при уровне значимости, равном 0,05? Какую модель регрессии следует применить для решения задачи?
7. Постройте 95%-ный доверительный интервал, содержащий наклон генеральной совокупности оценок на выпускном экзамене по отношению к каждой из поясняющих переменных.
8. Объясните смысл коэффициента множественной смешанной корреляции г}2]23 .
9. Вычислите скорректированный коэффициент г2.
10. Вычислите коэффициент частной множественной корреляции и объясните его смысл.
11. Какое предположение о наклоне отклика следует сделать при решении этой задачи?
12. Включите в модель эффект взаимодействия, установив уровень значимости равным 0,05. Вносит ли этот эффект статистически значимый вклад в построенную модель регрессии?
13. Используя результаты решения задач 6 и 12, определите, какая модель точнее. Обоснуйте свой ответ.
Множественная регрессия
Является ли зависимая Нет Логистическая
переменная j. регрессия
числовой? |
Подгонка
Ф» выбранной -<•
; модели
Содержит j
ли модель фик- ^Определить, являются ли
тивные переменные Да эффекты взаимодействия и/или эффекты / I статистически значимыми
взаимодей- ; ...
ствия? .
I Нет
Анализ остатков
Выпол-н няются ли
УСЛОВИЯ ПрИ-менения регрессии?
* Да
Проверить значимость модели Но:
К- ₽1 - ₽2= = 0k “О
"Г -
Является ли модель |_|ет
статистичес^ значимой?
1 Да
Проверка статистической значимости отдельных I переменных
I
Применение модели для предсказания f и оценки
р-—4^
Оценка Оценка „
коэффициентов величины Предсказание
п ОТКЛИКЗ г ।
3/ > Пух 1
Структурная схема главы 13
РЕЗЮМЕ
В этой главе показано, как менеджер по маркетингу может применять множественный линейный анализ для предсказания объема продаж, зависящего от цены и затрат на рекламу. Рассмотрены различные модели множественной регрессии, включая квадратичные модели, модели с фиктивными переменными и модели с эффектами взаимодействия.
ОСНОВНЫЕ понятия
Коэффициент множественной смешанной корреляции, 879
Коэффициент частной корреляции, 903
Коэффициент чистой регрессии, 876
Скорректированный коэффициент г 880
Частный F-критерий, 898
Эффект взаимодействия, 910
УПРАЖНЕНИЯ К ГЛАВЕ 13
Проверка знаний
13.45. Как различаются интерпретации коэффициентов в моделях множественной и линейной регрессии?
13.46. Чем проверка значимости полной регрессионной модели отличается от проверки значимости вклада каждой из независимых переменных в модель множественной регрессии?
13.47. Чем коэффициенты частной смешанной корреляции отличаются от коэффициентов множественной смешанной корреляции?
13.48. Зачем нужны фиктивные переменные? Как они используются?
13.49. Как проверить, одинаковы ли наклоны отклика по отношению к каждой из независимых переменных при всех значениях фиктивной переменной?
13.50. Когда следует включать фиктивную переменную в регрессионную модель?
13.51. Каким условиям должен удовлетворять наклон отклика У по отношению к числовой переменной X при включении фиктивной переменной в регрессионную модель?
Применение понятий
13.52. Создайте регрессионную модель для предсказания продажной цены дома по его оценочной стоимости и периоду, в течение которого он был выставлен на продажу. Для этого используется выборка, состоящая из 30 недавно проданных одноквартирных домов в небольшом городке на западе США (оценочная стоимость устанавливается один раз в год). ^HOUSEl. XLS.
1. Постройте модель множественной регрессии.
2. Какой смысл имеют наклоны множественной регрессии в этой задаче?
3. Предскажите среднюю продажную цену дома, если его оценочная стоимость равна 70 000 долл., и он был выставлен на торги в течение 12 месяцев.
4. Выполните анализ остатков. Определите адекватность построенной модели.
5. Существует ли статистически значимая зависимость между продажной ценой дома и двумя объясняющими переменными (оценочной стоимостью и временем продажи) при уровне значимости, равном 0,05?
6. Вычислите p-значение в задаче 5 и объясните его смысл.
7. Вычислите коэффициент множественной смешанной корреляции и объясните его смысл.
8. Вычислите скорректированный коэффициент г2.
9. Вносит ли каждая из независимых переменных статистически значимый вклад в построенную модель регрессии, если уровень значимости равен 0,05? Какую модель регрессии следует предпочесть при решении поставленной задачи?
10. Вычислитер-значение в задаче 9 и объясните его смысл.
11. Постройте 95%-ный доверительный интервал, содержащий наклон генеральной совокупности продажных цен по отношению к оценочной стоимости.
12. Вычислите коэффициенты частной смешанной корреляции.
13.53. Измерить высоту красного дерева, произрастающего в Калифорнии, очень трудно, поскольку она достигает 300 футов. Однако исследователи догадались, что высота красного дерева зависит от его диаметра и толщины коры на уровне груди. Высота, диаметр и толщина коры, измеренные у 21 дерева, приведены в файле ^REDWOOD . XLS
1. Постройте модель множественной регрессии.
2. Какой смысл имеют наклоны множественной регрессии в этой задаче?
3. Предскажите среднюю высоту красного дерева, если его диаметр на уровне груди равен 25 дюймов, а толщина коры достигает 2 дюймов.
4. Вычислите коэффициент множественной смешанной корреляции гД2 и объясните его смысл.
5. Выполните анализ остатков. Определите адекватность построенной модели.
6. Постройте 95%-ный доверительный интервал, содержащий наклон высоты по отношению к диаметру и толщине коры на уровне груди.
7. Вносит ли каждая из независимых переменных статистически значимый вклад в построенную модель регрессии, если уровень значимости равен 0,05? Укажите независимые переменные, которые следует включить в модель регрессии.
8. Постройте 95%-ные доверительные интервалы для средней и предсказанной высоты дерева, диаметр которого на уровне груди равен 25 дюймам, а толщина коры достигает двух дюймов.
9. Вычислите коэффициенты частной смешанной корреляции гг" , и /у, ( .
13.54. Постройте модель для предсказания средней оценочной стоимости недвижимости (тыс. долл.) на основе выборки, состоящей из 15 домов. В качестве объясняющих переменных выберите жилую площадь (тыс. кв. футов) и возраст дома (лет). Данные обследования приведены в таблице. WHOUSE2 . XLS
Дом Оценочная стоимость (тыс. долл.) Жилая площадь (тыс. кв. футов) Возраст (лет)
1 84,4 2,00 3,42
2 77,4 1,71 11,50
3 75,7 1,45 8,33
4 85,9 1,76 0,00
5 79,1 1,93 7,42
6 70,4 1,20 32,00
7 75,8 1,55 16,00
8 85,9 1,93 2,00
9 78,5 1,59 1,75
10 79,2 1,50 2,75
Дом Оценочная стоимость (тыс. долл.) Жилая площадь (тыс. кв. футов) Возраст (лет)
11 86,7 1,90 0,00
12 79,3 1,39 0,00
13 74,5 1,54 12,58
14 83,8 1,89 2,75
15 76,8 1,59 7,17
1. Постройте модель множественной регрессии.
2. Какой смысл имеют наклоны множественной регрессии в этой задаче?
3. Предскажите среднюю оценочную стоимость 10-лётнего дома, если жилая площадь равна 1 750 кв. футов.
4. Выполните анализ остатков и оцените адекватность модели.
5. Существует ли статистически значимая взаимосвязь между оценочной стоимостью и двумя независимыми переменными (жилой площади и возраста), если уровень значимости равен 0,05?
6. Вычислите p-значение в задаче 5 и объясните его смысл.
7. Вычислите коэффициент множественной смешанной корреляции и объясните его смысл.
8. Вычислите скорректированный коэффициент г3.
9. Вносит ли каждая из независимых переменных статистически значимый вклад в построенную модель регрессии, если уровень значимости равен 0,05? Укажите независимые переменные, которые следует включить в модель регрессии.
10. Вычислите p-значение в задаче 9 и объясните его смысл.
11. Постройте 95%-ный доверительный интервал, содержащий наклон оценочной стоимости по отношению к жилой площади. Как интерпретация наклона отличается от наклона в задаче 12.69?
12. Вычислите коэффициенты частной смешанной корреляции г}\2 и /;221.
13. Одно из агентств по торговле недвижимостью однажды заявило, что оценочная стоимость дома не зависит от его возраста. Согласны ли вы с этим утверждением? Обоснуйте свой ответ.
13.55. Файл W COLLEGES2002S содержит данные о 80 колледжах и университетах, в частности, стоимость обучения в течение года (тыс. долл.), среднее количество баллов, набранных студентами при сдаче теста на проверку умственных способностей (Scholastic Aptitude Test — SAT), а также стоимость проживания в общежитии. Разработайте модель для предсказания стоимости годового обучения по этим переменным.
1. Сформулируйте уравнение множественной регрессии.
2. Объясните смысл наклонов отклика в этой модели.
3. Предскажите среднюю стоимость годового обучения в государственном учебном заведении, студенты которого набрали при сдаче теста SAT в среднем 1 000 баллов, а на проживание в общежитии тратят 5 000 долларов.
4. Выполните анализ остатков и оцените адекватность модели.
5. Существует ли статистически значимая зависимость между стоимостью обучения и двумя объясняющими переменными (умственными способностями студентов и затратами на проживание в общежитии) при уровне значимости, равном 0,05?
6. Вычислитер-значение в задаче 5 и объясните его смысл.
7. Объясните смысл коэффициента множественной смешанной корреляции.
8. Вычислите скорректированный коэффициент г*.
9. Являются ли объясняющие переменные статистически значимыми при уровне значимости, равном 0,05? Какую модель регрессии следует применить для решения задачи?
10. Вычислитер-значение в задаче 9 и объясните его смысл.
11. Постройте 95%-ный доверительный интервал, содержащий наклон стоимости годового обучения по отношению к количеству баллов, набранных студентами при сдаче теста SAT, а также по отношению к стоимости обучения в течение года.
12. Вычислите коэффициенты частной множественной корреляции г212 и /-22! и объясните их смысл.
13. Объясните, почему наклон стоимости годового обучения по отношению к затратам на проживание в общежитии значительно отличается от 1,0.
14. Какие еще факторы, не включенные в модель, могут оказывать значительное влияние на стоимость годового обучения?
13.56. Файл ^AUT02002 .XLS содержит данные о 121 модели автомобилей, выпущенных в 2002 году. В нем содержатся данные о пробеге автомобиля на галлон топлива, а также о весе (в фунтах) и длине (в дюймах) каждой модели. Постройте оптимальную регрессионную модель, позволяющую предсказать пробег автомобиля на галлон топлива в зависимости от веса и длины автомобиля.
1. Сформулируйте уравнение множественной регрессии.
2. Объясните смысл наклонов отклика в этой модели.
3. Предскажите средний расход топлива на милю пути у автомобиля длиной 195 дюймов и весом 3 000 фунтов.
4. Выполните анализ остатков и оцените адекватность модели.
5. Существует ли статистически значимая зависимость между расходом топлива на милю пути и двумя объясняющими переменными (длиной и весом автомобиля) при уровне значимости, равном 0,05?
6. Вычислитер-значение в задаче 5 и объясните его смысл.
7. Объясните смысл коэффициента множественной смешанной корреляции.
8. Вычислите скорректированный коэффициент г*.
9. Являются ли объясняющие переменные статистически значимыми при уровне значимости, равном 0,05? Какую модель регрессии следует применить для решения задачи?
10. Вычислитер-значение в задаче 9 и объясните его смысл.
11. Постройте 95%-ный доверительный интервал, содержащий наклон расхода топлива на милю пути по отношению к длине и весу автомобиля.
12. Вычислите коэффициенты частной множественной корреляции гу212 и г22] и объясните их смысл.
13.57. Крейзи Дейв (Crazy Dave), популярный бейсбольный обозреватель, изучил статистические показатели разных команд на протяжении сезона 2002 года. Он хотел бы предсказать количество побед, одержанных командами в течение сезона. Для этого он решил использовать среднее количество очков (earned team average — ERA), набранных командой за сезон, и количество очков, набранных в се-
зоне 2002 года. Эти данные записаны в файле ft^BB20 02 . XLS. Постройте регрессионную модель, позволяющую предсказать количество побед по показателю ERA и количеству очков, набранных в 2000 году.
1. Сформулируйте уравнение множественной регрессии.
2. Объясните смысл наклонов отклика в этой модели.
3. Предскажите среднее количество побед у команды, набравшей 750 очков, если показатель ERA равен 4,50.
4. Выполните анализ остатков и оцените адекватность модели.
5. Существует ли статистически значимая зависимость между количеством побед и двумя объясняющими переменными (показателем ERA и количеством очков) при уровне значимости, равном 0,05?
6. Вычислитер-значейие в задаче 5 и объясните его смысл.
7. Объясните смысл коэффициента множественной смешанной корреляции.
8. Вычислите скорректированный коэффициент г2.
9. Являются ли объясняющие переменные статистически значимыми при уровне значимости, равном 0,05? Какую модель регрессии следует применить для решения задачи?
10. Вычислите p-значение в задаче 9 и объясните его смысл.
11. Постройте 95%-ный доверительный интервал, содержащий наклон отклика по отношению к показателю ERA.
12. Вычислите коэффициенты частной множественной корреляции г}2!2 и г,22] и объясните их смысл.
13. Какой из показателей позволяет точнее предсказать количество побед — ERA или количество очков?
13.58. Предположим, что для предсказания количества побед, одержанных командами в течение сезона, Крейзи Дейв решил учесть объясняющую переменную, обозначающую конкретную лигу (Американскую или Национальную). Воспользуйтесь программой Microsoft Excel. €IbB2002 . XLS.
1. Сформулируйте уравнение множественной регрессии.
2. Объясните смысл наклонов отклика в этой модели.
3. Предскажите среднее количество побед у команды, набравшей 750 очков в Американской лиге, если показатель ERA равен 4,50. Постройте 95%-ные доверительные интервалы для среднего и предсказанного количества задач.
4. Выполните анализ остатков и оцените адекватность модели.
5. Существует ли статистически значимая зависимость между количеством побед и двумя объясняющими переменными (показателем ERA и лигой) при уровне значимости, равном 0,05?
6. Являются ли объясняющие переменные статистически значимыми при уровне значимости, равном 0,05? Какую модель регрессии следует применить для решения задачи?
7. Постройте 95%-ные доверительные интервалы, содержащие наклоны отклика по отношению к показателю ERA и разновидности лиги.
8. Объясните смысл коэффициента множественной смешанной корреляции.
9. Вычислите скорректированный коэффициент А
10. Вычислите коэффициенты частной множественной корреляции гг212 и г}221 и объясните их смысл.
11. Какие предположения о наклоне количества побед по отношению к показателю ERA должны выполняться в этой задаче?
12. Включите в модель эффект взаимодействия, если уровень значимости равен 0,05. Определите, имеет ли он статистическую значимость для модели.
13. Какую модель следует предпочесть?
Применение Интернет
13.59. Зайдите на сайт www. prenhall. com/levine. Выберите ссылку Chapter 13 и щелкните на ссылке Internet exercises.
РАЗБОР КОНКРЕТНОЙ СИТУ ГАЗЕТА SPRINGVILLE HERAL
'.......................;......................"
I
Продолжая изучать процесс подписки, отдел маркетинга решил выяснить, как влияет на количество подписчиков форма презентации (формальная или неформальная), а также количество часов, затраченных на телефонный маркетинг. Данные, необходимые для решения этой задачи, находятся на Web-сайте http://www. prenhall. com/HeraldCase/Ef f ectsData. htm, а также в файле EffectsData.htm в каталоге HeraldCase на компакт-диске.^SHl3 . XLS.
Проанализируйте эти данные и разработайте статистическую модель, позволяющую прогнозировать количество новых подписчиков за неделю на основе информации о количестве часов, затраченных на телефонный маркетинг, и форме презентации. Напишите детальный отчет.
ПРИМЕНЕНИЕ WEB
Примените свои знания о моделях множественной регрессии для прогнозирования объема продаж батончиков OmniPower.
Чтобы организовать пробный маркетинг в сети бакалейных магазинов, отдел маркетинга компании OmniFoods организовал специальную группу. Изучив данные о 34 магазинах, группа заявила, что росту продаж способствуют как специализированные витрины, так и торговые автоматы.
Проанализируйте заявления группы и предоставленные ею данные, размещенные на Web-сайте www . prenhall. com/Springville/Omni_ISPGMemo . html), и ответьте на следующие вопросы.
1. Подтверждают ли данные заявления группы? Выполните их статистический анализ и оцените зависимость между объемом продаж, с одной стороны, и наличием специализированных витрин и торговых автоматов, с другой стороны.
2. Представьте себя на месте торгового советника компании OmniFood. Стали бы вы рекомендовать устанавливать специализированные витрины и торговые автоматы для продажи батончиков OmniPower?
3. Какие дополнительные данные нужны, чтобы точнее оценить эффективность маркетинга батончиков OmniPower?
СПРАВОЧНИК ПО EXCEL. ГЛАВА 13
ЕН.13.1. Вычисление коэффициентов множественной регрессии
Чтобы вычислить коэффициенты множественной регрессии, следует воспользоваться процедурой Сервиса Анализ данных... ^Регрессия.
Например, чтобы вычислить коэффициенты множественной регрессии для данных, приведенных в табл. 13.1, необходимо открыть рабочую книгу Chapter 13.xls на листе Данные и выполнить одну из следующих инструкций.
1. Выбрать команду Сервис^Анализ данных... Ф Регрессия.
2. Выбрать в раскрывающемся списке Анализ данных пункт Регрессия и щелкнуть на кнопке ОК.
3. Находясь в диалоговом окне Регрессия, выполнить такие действия.
3.1. В окне редактирования Входной интервал Y ввести диапазон ячеек А1: АЗ5.
3.2. В окне редактирования Входной интервал X ввести диапазон ячеек Bl: С35.
3.3. Установить флажок Метки.
3.4. Ввести в диалоговом окне Уровень надежности число 0,95.
3.5. Установить переключатель Параметры вывода в положение Новый рабочий лист.
3.6. Щелкнуть на кнопке ОК.
Регрессия
Входные данные
Входной интервал V:
Входной интервал X:
0 Метки
0 Уровень надежности:
О Константа - ноль [95 |%
[ Отмена |
[ ^правка j
Параметры вывода
О Выходной интервал:
® Новый рабочий лист: ;Анализ пр°Лаж •
О Новая рабочая книга
Остатки
j | Остатки j I График остатков
□ Стандартизованные остатки О Г рафик подбора
Нормальная вероятность
j | Г рафик нормальной вероятности
Рабочий лист, созданный с помощью этой процедуры, не является динамически обновляемым. Следовательно, если данные изменятся, все описанные выше действия следует повторить.
ЕН.13.2. Построение доверительных интервалов для математического ожидания и предсказанного значения отклика
Для построения доверительных интервалов, содержащих математическое ожидание и предсказанное значение отклика, следует создать рабочий лист, использующий функцию СТЬЮДРАСПОБР, а также матричные функции ТРАСП, МУМНОЖ и МОБР.
В табл. ЕН.13.1 и ЕН.13.2 показан шаблон рабочего листа Интервалы, в котором построены доверительные интервалы, содержащие средний и предсказанный объем про
даж батончиков OmniPower по данным, приведенным в табл. 13.1. Предполагается, что на листе ХМатрица в диапазоне А2:А35 записаны значения отклика, а в диапазоне В2:С35— объясняющие переменные. Кроме того, необходимо создать рабочий лист, содержащий статистики множественной регрессии, вычисленные в результате выполнения инструкций из раздела ЕН. 13.1.
Полное описание вычислений, предусмотренных в этом шаблоне, выходит за рамки нашей книги. Отметим лишь, что функции ТРАНСП и МУМНОЖ имеют следующий формат:
ТРАНСП {диапазон ячеек} ,
МУМНОЖ {диапазон ячеек 1; диапазон ячеек 2), МОБР {диапазон ячеек) .
Первая функция транспонирует столбцы рабочего листа ХМатрица в строки, вторая — перемножает матрицы, а третья возвращает обратную матрицу. Кроме этих функций, в шаблоне используется функция СТЬЮДРАСПОБР, вызов которой выглядит следующим образом.
СТЬЮДРАСПОБР {1-доверительный уровень', степени свободы).
Таблица ЕН.13.1. Шаблон рабочего листа Интервалы (столбцы А и в)
А , . В - ;
1 Доверительные интервалы
2
3 Данные
4 Доверительный уровень 0,95
5 1
6 Цена 79
7 Затраты на рекламу 400
8
9 ХТХ = МУМНОЖ(ТРАНСП(ХМатрица!А2:С35);ХМатрица!А2:С35)
10 = МУМНОЖ(ТРАНСП(ХМатрица!А2:С35);ХМатрица!А2:С35)
11 = МУМНОЖ(ТРАНСП(ХМатрица!А2:С35);ХМатрица!А2:С35)
12
13 Обратная матрица ХТХ =M0BP(B9:D11)
14 = M0BP(B9:D11)
15 =M0BP(B9:D11)
16
17 XTG умножить на ХТХ =МУМНОЖ(ТРАНСП(В5:В7);В13:015)
18
19 [XTG умножить на ХТХ] умножить на XG = МУМНОЖ(В17:017;В5:В7)
20 Л стати стика =СТЬЮРАСПОБР(1-В4);МР!В13)
Окончание табл. ЕН. 13.1
А
21 Предсказанное значение Y =МУМНОЖ(ТРАНСП(В5:В7);МР!В17:В19)
22
23 Доверительный интервал для математического ожидания Y
24 Половина интервала = B20*KOPEHb(B19)*MR!B7
25 Нижняя граница интервала = В21-В29
26 Верхняя граница интервала = В21+В29
27
28 Доверительный интервал для предсказанного значения Y
29 Половина интервала = В20* KOPEHb(1+B19)*MR!B7
30 Нижняя граница интервала = В21-В29
31 Верхняя граница интервала = В21+В29
Таблица ЕН.13.2. Шаблон рабочего листа Интервалы (столбцы chd, строки 1-8 пустые)
С D ~
ЙВЙ11 = МУМНОЖ(ТРАНСП(ХМатрица!А2:С35); ХМатрица!А2:С35) = МУМНОЖ(ТРАНСП(ХМатрица!А2:С35); ХМатрица!А2:С35)
10 =МУМНОЖ(ТРАНСП(ХМатрица!А2:С35); ХМатрица!А2:С35) = МУМНОЖ(ТРАНСП(ХМатрица!А2:С35); Хматрица!А2:С35)
11 =МУМНОЖ(ТРАНСП(ХМатрица!А2:С35); ХМатрица!А2:С35) = МУМНОЖ(ТРАНСП(ХМатрица!А2:С35); ХМатрица!А2:С35)
12
13 = M0BP(B9:D11) =M0BP(B9:D11)
14 = M0BP(B9:D11) =M0BP(B9:D11)
15 = M0BP(B9:D11) =M0BP(B9:D11)
16
17 =МУМНОЖ(ТРАНСП(В5:В7); B13.D15) = МУМНОЖ(ТРАНСП(В5:В7); B13:D15)
Перед реализацией этого шаблона необходимо создать рабочий лист ХМатрица и выполнить множественный регрессионный анализ. Для согласования результатов с шаблоном Интервалы рабочий лист, созданный процедурой Множественная регрессия, необходимо назвать MR.
Формулы в диапазонах В9 : Dll, В13 : D15 и В17 : D17 вводятся следующим образом.
1. Выделите диапазон.
2. Наберите формулу.
3. Удерживая клавиши <Ctrl> и <Shift>, нажмите на клавишу <Enter>.
ЕН.13.3. Построение диаграммы разброса остатков по предсказанным значениям отклика
Чтобы построить диаграмму разброса остатков по предсказанным значениям отклика необходимо выполнить анализ остатков и вызвать Мастер диаграмм.
Например, чтобы построить диаграмму разброса остатков по предсказанным объемам продаж батончиков OmniPower, необходмо открыть рабочий лист, содержащий статистики множественной регрессии и остатки, выбрать команду Вставка1^Диаграмма... и вступить в диалог с Мастером диаграмм.
1. На первом шаге диалога сделать следующее (см. иллюстрацию).
1.1. Щелкнуть на корешке вкладки Стандартные, а затем выбрать пункт Точечная в раскрывающемся списке Тип.
1.2. Выбрать первую (верхнюю) диаграмму, сопровождающуюся описанием: “Точечная диаграмма позволяет сравнить пары значений”, а затем щелкнуть на кнопке Далее>.
2. На втором шаге диалога выполнить такие действия.
2.1. Щелкнуть на корешке вкладки Диапазон данных, а затем ввести в окне редактирования Диапазон ссылки на ячейки С2 б : С5 9.
2.2. Установить переключатель Ряды в положение В столбцах и щелкнуть на кнопке Далее>.
3. На третьем шаге диалога выполнить следующее.
3.1. Щелкнуть на корешке вкладки Заголовки. Ввести в окне редактирования Название диаграммы строку Зависимость остатков от предсказанных значений, в окне редактирования Ось X — строку Предсказанные значения, а в окне редактирования Ось У — строку Остатки.
3.2. По очереди щелкнуть на корешках вкладок Оси, Линии сетки, Легенда и Подписи данных. Установить флажки и переключатели, как показано в разделе ЕР.6.2.
3.3. Щелкнуть на кнопке Далее>.
4. На четвертом шаге диалога установите переключатель Поместить диаграмму на листе в положение Отдельном и щелкните на кнопке Готово.
ЕН.13.4. Вычисление коэффициентов частной смешанной корреляции
Для вычисления коэффициентов частной смешанной корреляции в модели множественной регрессии, содержащей две независимые переменные, следует реализовать шаблон рабочего листа, использующий простые арифметические формулы.
В табл. ЕН. 13.3 показан шаблон рабочего листа Частная_корреляция, предназначенного для вычисления коэффициентов частной смешанной корреляции в модели множественной регрессии, позволяющей предсказать объем продаж батончиков OmniPower по данным, приведенным в табл. 13.1. Предполагается, что рабочие листы MR (полная модель регрессии), NOTX1 (модель регрессии, из которой исключена цена) и NOTX2 (модель регрессии, из которой исключены затраты на рекламу) содержат сумму квадратов регрессии в ячейке С12. Кроме того, полная сумма квадратов содержится в ячейке С14 на листе MR. Это условие должно выполняться как при использовании процедуры PHStat^Regression^Multiple Regression..., так и при выборе Сервис^Анализ данных...^ Регрессия.
Таблица ЕН.13.3. Шаблон рабочего листа Частная_корреляция
A В c D
1 Анализ объемов продаж батончиков OmniPower
2 Коэффициенты частной смешанной корреляции
IBII
4 Промежуточные вычисления
5 SSR(X1,X2) = MR!C12
6 SST = MR!C14
7 SSR(X2) =N0TX1!C12 SSR(X1|X2) = B5-B7
8 SSR(XI) = NOTX2!C12 SSR(X2|X1) = B5-B8
9
10 Коэффициенты
11 r2 Y1.2 = D7/(B6-B5+D7)
llililj г 2 Y2.1 = D8/(B6-B5+D8)
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
1. Hocking, R. R., “Developments in Linear Regression Methodology: 1959-1982,” Technometrics 25(1983): 219-250.
2. Hosmer, D. W., and S. Lemeshow, Applied Logistic Regression, 2nd ed. (New York: Wiley, 2001).
3. Microsoft Excel 2002 (Redmond, WA: Microsoft Corporation, 2001).
4. Neter, J., M. H. Kutner, C. J. Nachsheim, and W. Wasserman, Applied Linear Statistical Models, 4th ed. (Homewood, IL: Irwin, 1996).
Глава 14
Построение моделей множественной регрессии
ПРИМЕНЕНИЕ СТАТИСТИКИ: прогнозирование продолжительности простоя художников, входящих в профсоюз
14.1. МОДЕЛЬ КВАДРАТИЧНОЙ РЕГРЕССИИ
Вычисление коэффициентов регрессии и предсказание отклика
Проверка значимости квадратичной модели
Оценка квадратичного эффекта Процедура Excel: учет квадратичного члена в регрессионной модели
Вычисление коэффициента множественной смешанной корреляции
14.2. ПРЕОБРАЗОВАНИЕ ДАННЫХ В РЕГРЕССИОННЫХ МОДЕЛЯХ
Извлечение квадратного корня Логарифмическое преобразование Процедуры Excel: преобразования переменных
Процедуры Excel: вычисление коэффициентов инфляции
14.3. КОЛЛИНЕАРНОСТЬ
14.4. ПОСТРОЕНИЕ МОДЕЛИ
Пошаговый подход к построению регрессионной модели
Процедура Excel: выполнение пошаговой регрессии
Метод выбора наилучшего подмножества Процедура Excel: метод выбора наилучшего подмножества
14.5. ЛОВУШКИ И ЭТИЧЕСКИЕ ПРОБЛЕМЫ, СВЯЗАННЫЕ СО МНОЖЕСТВЕННОЙ РЕГРЕССИЕЙ
Ловушки множественной регрессии Этические вопросы
ЧЕМУ ДОЛЖЕН НАУЧИТЬСЯ СТУДЕНТ
• Применять модели квадратичной регрессии.
• Применять преобразования переменных в регрессионных моделях.
• Измерять корреляцию между независимыми переменными.
• Создавать регрессионные модели с помощью шаговой регрессии или метода выбора наилучшего подмножества.
• Избегать ловушек при создании моделей множественной регрессии.
ПРИМЕНЕНИЕ СТАТИСТИКИ
Прогнозирование продолжительности простоя художников, входящих в профсоюз
Представьте себе, что вы — директор телевизионной станции и стремитесь сократить производственные расходы. В частности, художники, входящие в профсоюз, получают почасовую оплату, даже когда они ничего не делают. Эти часы называют часами простоя. Считается, что общее количество часов простоя за неделю зависит от общего количества времени, проведенного в офисе, общего количества часов, проведенных на выезде, времени, затраченного на озвучивание, и общей продолжительности работы. Постройте модель множественной регрессии, позволяющую наиболее точно предсказать количество
часов простоя. Она позволит выявить причины возникающих простоев и уменьшить их количество в будущем. Как построить наиболее подходящую модель? С чего начать?
14.1. МОДЕЛЬ КВАДРАТИЧНОЙ РЕГРЕССИИ
Исследуя модели простой и множественной регрессии, мы предполагали, что зависимость между откликом Y и каждой из объясняющих переменных является линейной. Однако существуют и другие виды взаимосвязи. Одной из наиболее распространенных нелинейных взаимосвязей между двумя переменными является квадратичная зависимость (рис. 12.2, панели В-Д). Для ее анализа предназначена модель квадратичной регрессии.
МОДЕЛЬ КВАДРАТИЧНОЙ РЕГРЕССИИ *]
(14.1)
где р0 — сдвиг, Pj — коэффициент линейного эффекта, Р2 — коэффициент квадратичного эффекта, е, — случайная ошибка переменной Y в i-м наблюдении.
Модель квадратичной регрессии (quadratic regression model) похожа на модель множественной регрессии с двумя переменными (13.2), за исключением того, что вторая объясняющая переменная является квадратом первой.
Как и в модели множественной регрессии, выборочные коэффициенты регрессии Ьо, Ъ{ и Ъ2 представляют собой оценки параметров генеральной совокупности р0, и Р2. Таким образом, можно сформулировать следующую квадратичную модель с одной объясняющей переменной Хг и зависимой переменной У.
УРАВНЕНИЕ КВАДРАТИЧНОЙ РЕГРЕССИИ
Yt =Ь„+Ь'ХЪ +Ь2Х*. (14.2)
В уравнении (14.2) коэффициент Ьо является сдвигом, коэффициент Ъг оценивает линейный эффект, а коэффициент Ъ2 — квадратичный эффект.
Вычисление коэффициентов регрессии и предсказание отклика
Проиллюстрируем применение квадратичной модели на примере эксперимента, в котором изучается влияние зольной пыли на прочность бетона. Для этого была создана выборка, состоящая из 18 образцов 28-дневного бетона, прочность которого равна 4 000 фунтов на дюйм. Объем зольной пыли колебался от 0 до 60%. Уровень значимости равен 0,05. Результаты эксперимента приведены в файле ft FLYASH. XLS.
Таблица 14.1. Прочность 28-дневного бетона и содержание зольной пыли в 18 образцах. ftpLYASH. XLS.
Объем зольной пыли (%) Прочность (фунты на дюйм) Объем зольной пыли (%) Прочность (фунты на дюйм)
0 4 779 40 5 995
0 4 706 40 5 628
0 4 350 40 5 897
20 5 189 50 5 746
20 5 140 50 5 719
20 4 976 50 5 782
30 5 110 60 4 895
30 5 685 60 5 030
30 5 618 60 4 648
Для того чтобы выбрать наиболее подходящую модель, описывающую зависимость прочности бетона от процента зольной пыли, построим диаграмму разброса, изображенную на рис. 14.1. Как видим, при возрастании процента зольной пыли прочность бетона увеличивается, достигает максимума при содержании зольной пыли, равном 40% , а затем уменьшается. Итак, квадратичная модель точнее описывает исследуемую зависимость, чем линейная.
Значения трех коэффициентов регрессии (&0, Ъх и &2) можно вычислить с помощью программы Microsoft Excel (рис. 14.2).
Как видим,
Ьо = 4 486,361, Ь, - 63,005, Ь2 = -0,876.
Следовательно, уравнение квадратичной регрессии имеет следующий вид:
Y, = 4 486,361 + 63,005А; - 0,876%,;,
где Yt — предсказанная прочность i-ro образца, Х1: — содержание зольной пыли в i-M образце.
Диаграмма разброса зольности и прочности
0 10 20 30 40 50 60 70
Зольность, %
Рис. 14.1. Диаграмма разброса содержания зольной пыли (ось X) и прочности бетона (ось Y), построенная с помощью программы Microsoft Excel
A i В : .с I О I Е i F ! G
1 ^Анализ прочности бетона
2'1 ......................!.............j............. !.............. Г ....22.
3 Регрессионная статистика;
4 ; Множественный R 0 80527
5 j R-квадрат 0,64847
6 i Нормированный R-квадрат 0.60160
/^Стандартная ошибка 312,11291
8 ; Наблюдения_____________________18
9 J
10 Дисперсионный анализ
11 j df SS MS F Значимость F
12 регрессия 2 2695473.49 1347736.745 13.83508 0.00039
^Остаток 15 1461217.0 1 97414.46735
’ 14"Итого______________________ 17_______________4156690,5______________
15;____________________________________;____________________;___________.___________;_________________
16 1_____________________КоэффициентыСтандартная ошибка 1-статистика P-значение Нижние 95% Верхние 95%
”17 ^-пересечение 4486.36111 174,75315 25 67256 8.2474Е-14 4113.88337 4858 83886
181 Зольность, % 63.00524 12.37255 5.09234 0.00013 36.63377 89.37671
191Зольность *2-0.87647 0.19661 -4,45784 0 00046 -1 29554 -045740
Рис. 14.2. Результаты, полученные с помощью программы Microsoft Excel при решении задачи о прочности бетона
Для того чтобы продемонстрировать соответствие построенной модели исходным данным, на рис. 14.3 приведен график квадратичной зависимости прочности бетона от содержания зольной пыли.
Рис. 14.3. Диаграмма разброса содержания зольной пыли (ось X) и прочности бетона (ось Y), а также график квадратичной зависимости, построенные с помощью программы Microsoft Excel
Коэффициент Ьо, представляющий собой предсказанную среднюю прочность бетона при нулевом содержании зольной пыли, представляет собой сдвиг отклика и равен 4 461,361. Чтобы объяснить смысл коэффициентов Ь1 и Ь2, следует обратить внимание на рис. 14.3. Как видим, при увеличении содержания зольной пыли прочность бетона сначала увеличивается, а затем уменьшается. Этот эффект можно продемонстрировать, предсказав среднюю прочность бетона при содержании зольной пыли, равном 20, 40 и 60% . Используя квадратичную модель
Yt = 4 486,361 + 63,005Xh - 0,876JT2,
получаем следующие результаты.
Если Хи = 20,
4 486,3 61 + 63,005 х 20 - 0,876 х 202 = 5 395,9.
Если Хи = 40,
Yt = 4 486,361 + 63,005 х 40 - 0,876 х 402 = 5 604,2.
Если Х1( = 60,
Yt = 4 486,361 + 63,005 х 60 - 0,876 х 602 = 5 111,4.
Таким образом, прочность бетона при содержании зольной пыли, равном 40%, на 208,3 фунтов на кв. дюйм превышает прочность бетона при 20%-ном содержании зольной пыли. В свою очередь, прочность бетона при содержании зольной пыли, равном 60%, на 492,8 фунтов на кв. дюйм меньше, чем прочность бетона при 40%-ном содержании зольной пыли.
Проверка значимости квадратичной модели
Убедившись, что квадратичная модель адекватна исходным данным, можно проверить, существует ли статистически значимая зависимость между прочностью бетона Y и содержанием зольной пыли X. Нулевая и альтернативная гипотезы формулируются следующим образом.
Но: = Р2 = 0 Между откликом У и объясняющей переменной нет зави-
симости.
Н} : Pj * 0 и/или р! * 0 Между откликом У и объясняющей переменной X, есть зависимость.
Нулевую гипотезу можно проверить с помощью F-критерия (13.6):
MSR
MSE '
Как показано на рис. 14.2,
^ 1347736,75
97 414,47
Если уровень значимости равен 0,05, по табл. Д.5 получаем, что критическое значение F-распределения, имеющего две и 15 степеней свободы, равно 3,68 (рис. 14.4).
Область Критическое Область \ принятия значение отклонения j гипотезы гипотезы !
Рис. 14.4. Проверка гипотезы о существовании зависимости между откликом и объясняющей переменной, если уровень значимости равен 0,05, а F-распределение имеет две степени свободы в числителе и 15 — в знаменателе
Поскольку F= 13,84 > 3,68 и р = 0,00039 < 0,05, нулевая гипотеза Нп отклоняется. Таким образом, между прочностью бетона и содержанием зольной пыли существует статистически значимая зависимость.
Оценка квадратичного эффекта
Регрессионная модель, описывающая зависимость между двумя переменными, должна быть не только как можно более точной, но и максимально простой. Следовательно, необходимо проверить, существуют ли статистически значимые различия между квадратичной моделью
К = Р<, + РЛ, + РХ +£, и линейной моделью
у, = Ро + РЛп + е.
Напомним, что для оценки вклада каждой поясняющей переменной используется t-критерий. Среднеквадратичная ошибка каждого коэффициента регрессии и соответствующие значения t-статистики приведены на рис. 14.5. Чтобы проверить значимость квадратичного эффекта, сформулируем следующую нулевую и альтернативную гипотезы:
Нп — включение квадратичного эффекта не приводит к значительному увеличению точности модели (02 = 0),
— включение квадратичного эффекта значительно повышает точность модели (МО).
Для вычисления t-статистики воспользуемся уравнением (13.7):
-0,8765-0
/ = -2-L2- =-Z-----= -4 46 .
S, 0,1966
Если уровень значимости равен 0,05, по табл. Д.З получаем, что критические значения t-распределения, имеющего15 степеней свободы, равны -2,1315 и +2,1315 (рис. 14.5).
Область Критическое Область Критическое Область
отклонения значение принятия значение отклонения; гипотезы гипотезы гипотезы \
Рис. 14.5. Проверка гипотезы о значимом вкладе квадратичного эффекта, если уровень значимости равен 0,05, a t-распределение имеет 15 степеней свободы
Поскольку t = -4,46 < -2,1315, и, кроме того, р = 0,00046 < 0,05, нулевая гипотеза Но отклоняется. Следовательно, квадратичный эффект значительно повышает точность предсказания по сравнению с линейной моделью, описывающей зависимость между прочностью бетона и содержанием зольной пыли.
дедура Excel: учет квадратичного члена грессйонноймрделиД •; I:
Чтобы включить в модель квадратичной регрессии вторую поясняющую переменную, достаточно вставить в новый столбец формулу = ячейкал2.
Например, для того чтобы учесть квадратичный эффект в регрессионной модели, описывающей потребление топлива при обогреве домов, необходимо открыть рабочий лист Отопление в книге Chapter 14.xls, вставить в ячейку D1 формулу -Чердакл2, а затем вставить в ячейки D2:D16 формулу =С2Л2. После этого следует выполнить множественный регрессионный анализ данных, содержащихся в диапазоне ячеек Bl: D16.
ПРИМЕР 14.1. ИЗУЧЕНИЕ КВАДРАТИЧНОГО ЭФФЕКТА В МОДЕЛИ МНОЖЕСТВЕННОЙ РЕГРЕССИИ
Аналитик из агентства по продаже недвижимости хотел бы изучить влияние температуры воздуха и высоты чердака на количество топлива, израсходованного на отопление в течение заданного месяца. Для исследования сформирована выборка, состоящая из 15 одноквартирных домов, в которых измерено потребление топлива в течение января. Данные записаны в файле HTNGOIL. XLS. Для анализа выбрана модель множественной регрессии с двумя объясняющими переменными. Результаты, полученные с помощью программы Microsoft Excel, приведены на рис. 14.6. ^HTNGOIL . XLS.
Результаты анализа остатков (не приведенные на рисунке) свидетельствуют о наличии квадратичного эффекта. Постройте модель множественной регрессии, включающую в себя квадратичный член, учитывающий высоту чердака. Существует ли статистически значимый квадратичный эффект, объясняемый высотой чердака, если уровень значимости равен 0,05?
РЕШЕНИЕ. Используя программу Microsoft Excel, получаем следующие результаты. Уравнение множественной регрессии имеет следующий вид:
Y = 624,5864-5,3626-44,5868Х?; + 1,8667Х;,.
Чтобы проверить значимость квадратичного эффекта, сформулируем следующую нулевую и альтернативную гипотезы:
Но — включение квадратичного эффекта не приводит к значительному увеличению точности модели (|33 = 0);
Н1 — включение квадратичного эффекта значительно повышает точность модели (р3 ф 0).
Как следует из рис. 14.7, t = 1,661 <2,201. Кроме того,р = 0,1249 >0,05. Таким образом, нулевую гипотезу отклонять нельзя. Следовательно, квадратичный эффект, учитывающий высоту чердака, не приводит к значительному увеличению точности модели. Чтобы сохранить простоту модели, необходимо ограничиться моделью множественной линейной регрессии, построенной на рис. 14.6:
Yt = 562,151 - 5,43658Xh - 20,0123 ,.
А 1 .Анализ потребления топлива 2 В С .0 Е F G
3 Регрессионная статистика 4 Множественный R 0,98265 5 R-квадрат 0,96561 6 Нормированный R-квадрат 0,95988 7 Стандартная ошибка 26,01378 8 Наблюдения 15 9 . 10 Дисперсионный анализ и; dt 12Регрессия 2 13 Остаток 12 14 Итого 14 15 • SS 228014,62632 8120,60302 236135,22933 MS 114007,31316 676,71692 F 168,47120 Значимость F 1,65411Е-09
16 Коэффициенты Стандартная ошибка t-статистика Р-значение Нижние 95%> Верхние 95%
17 Y-пересечение 562,15101 21,09310 26,65094 4.77868Е-12 516,19308 608,10893
18J Температура 19 Чердак -5,43658 .20,01232 0,33622 2,34251 -16,16990 8,54313 1,64178Е89 1,90731Е-06 -6.16913 25,11620 4,70403 -14,90844
Рис. 14.6. Результаты регрессионного анализа потребления топлива, полученные с помощью программы Microsoft Excel
А В С. D Е G
1 2 3 4 5 6 7 *8 Квадратичный эффект для высоты чердака 1 Регрессионная статистика Множественный R i R-квадрат формированный R-квадрат Стандартная ошибка Наблюдения 0,98616 0,97251 0,96501 24,29378 15
9 10 Дисперсионный анализ
11 _ ’ df SS MS F Значимость F
12 j Регрессия 13 ’Остаток 14’Итого «. 3 11 14 229643,2 6492,1 236135,2 76547,72149 590,1877159 129,70063 7,26403Е89
16 Коэффициенты Стандартная ошибка t-статистика Р-значение Нижние 95% Верхние 95%
17 j Y-пересечение 18 ^Температура 19]Чердак 20 ЧердакА2 624,58642 -5,36260 44,58679 1,86670 42,43515952 0,31713 14,95469 1,12376 14,71860664 -16,90988 -2,98146 1,66113 1,39085Е 88 3,20817Е89 0,01249 0,12489 531,18722 -6,06060 -77,50185 8,60667 717,98562 4,66461 11,67172 4,34007
Рис. 14.7. Результаты регрессионного анализа потребления топлива, полученные с помощью программы Microsoft Excel, с учетом квадратичного эффекта, объясняемого высотой чердака
Вычисление коэффициента множественной смешанной корреляции
Коэффициент множественной смешанной корреляции г}?12 (см. раздел 13.1) в модели множественной регрессии позволяет оценить долю вариации переменной У, объясняемой изменениями двух объясняющих переменных. В квадратичном регрессионном анализе влияния содержания золы на прочность бетона этот коэффициент задается формулой:
, SSR
Гу.
>.!. SST
На рис. 14.2 показано, что
SSR = 2 695 473,5 и SST =4 156 690,5.
Таким образом,
2 557? 2 695 473,5 . ,
г..=-----=--------= 0,6485.
” SST 4156 690,5
Эта величина означает, что 64,85% вариации прочности бетона можно объяснить квадратичной зависимостью между прочностью бетона и содержанием зольной пыли. Кроме коэффициента частной смешанной корреляции, можно вычислить скорректированный коэффициент ГуП, учитывающий количество объясняющих переменных и степеней свободы. В квадратичной регрессионной модели учитываются две независимые переменные (k — 2): объясняющая переменная Xj и ее квадрат X* . Следовательно, используя формулу (14.5), получаем:
Г- = (1 -г.?,,)- = 1-(1-0,6485)—= 1-0,3984 = 0,6016.
УПРАЖНЕНИЯ К РАЗДЕЛУ 14.1
Изучение основ
14.1. Рассмотрим уравнение квадратичной регрессии для выборки, имеющей объем л = 25:
}>5Щ, + 1,5^.
1. Предскажите среднее значение переменной У, если Х1 = 2.
2. Предположим, что f-статистика, соответствующая квадратичному коэффициенту, равна 2,35. Можно ли утверждать, что квадратичная модель точнее линейной, если уровень значимости равен 0,05?
3. Предположим, что t-статистика, соответствующая квадратичному коэффициенту, равна 1,17. Можно ли утверждать, что квадратичная модель точнее линейной, если уровень значимости равен 0,05?
4. Предположим, что коэффициент регрессии, соответствующий линейному эффекту, равен -3,0. Предскажите среднее значение переменной У, если Xt = 2.
Применение понятий
Задачи 14.2-14.5 рекомендуется решать с помощью программы Microsoft Excel.
14.2. Аналитик нефтедобывающей компании решил разработать модель, позволяющую предсказывать количество миль, которое преодолевают автомобили, затратив один галлон топлива. В качестве объясняющей переменой аналитик выбрал скорость автомобиля. В ходе эксперимента тестовый автомобиль ехал с разными скоростями: от 10 до 75 миль в час. Результаты испытаний приведены в файле ^SPEED.XLS.
Предположим, что между скоростью и пробегом автомобиля существует квадратичная зависимость. Выполните следующие задания, применяя программу Microsoft Excel.
1. Постройте диаграмму разброса скоростей и пробега.
2. Сформулируйте уравнение квадратичной регрессии.
3. Предскажите средний пробег автомобилей на один галлон топлива, если их скорость равна 55 миль в час.
4. Выполните анализ остатков и оцените адекватность построенной модели.
5. Существует ли статистически значимая квадратичная зависимость между пробегом и скоростью при уровне значимости, равном 0,05?
6. Можно ли утверждать, что квадратичная модель точнее линейной, если уровень значимости равен 0,05?
7. Объясните смысл коэффициента множественной смешанной корреляции.
8. Вычислите скорректированный коэффициент т*.
14.3. Предположим, что отдел маркетинга в большой сети супермаркетов желает изучить эластичность цены одноразовых бритв, т.е. влияние цены на объем продаж. Для исследования отобраны 15 магазинов с приблизительно одинаковым товарооборотом и размещением товаров (магазины самообслуживания). Выборка разбита на три случайные подгруппы, содержащие по пять магазинов. В каждой подгруппе установлена своя цена: 79, 99 и 119 центов за упаковку одноразовых бритв соответственно. Количество упаковок, проданных за неделю, а также установленная цена в каждом из магазинов приведены в файле WdiSPRAZ .XLS.
Объемы продаж Цена (центы) Объемы продаж Цена(центы)
142 79 115 99
151 79 126 99
163 79 77 119
168 79 86 119
176 79 95 119
91 99 100 119
100 99 106 119
107 99
Предположим, что между ценой и объемом продаж существует квадратичная зависимость. Выполните следующие задания, применяя программу Microsoft Excel.
1. Постройте диаграмму разброса цены и объема продаж.
2. Сформулируйте уравнение квадратичной регрессии.
3. Предскажите средний объем продаж одноразовых бритв, если их цена равна 79 центов.
4. Выполните анализ остатков и оцените адекватность построенной модели.
5. Существует ли статистически значимая квадратичная зависимость между ценой и объемом продаж при уровне значимости, равном 0,05?
6. Можно ли утверждать, что квадратичная модель точнее линейной, если уровень значимости равен 0,05?
7. Объясните смысл коэффициента множественной смешанной корреляции.
8. Вычислите скорректированный коэффициент г.
14.4. Агроном решил оценить влияние количества внесенных удобрений (фунтов на 1 000 кв. футов) на урожай томатов (в фунтах), используя модель квадратичной регрессии. Для исследования были выбраны шесть уровней: 0, 20, 40, 60, 80 и 100 фунтов удобрения на 1 000 кв. футов. Эти уровни были случайным образом распределены по участкам. Результаты приведены в таблице. ^TOMYLD2 . XLS.
Участок Количество удобрений Урожай Участок Количество удобрений Урожай
1 0 6 7 60 46
2 0 0 8 60 50
3 20 19 9 80 48
4 20 24 10 80 54
5 40 32 11 100 52
6 40 38 12 100 58
Предположим, что между количеством удобрений и урожайностью существует квадратичная зависимость. Выполните следующие задания, применяя программу Microsoft Excel.
1. Постройте диаграмму разброса объемов удобрения и урожайности.
2. Выведите уравнение квадратичной регрессии.
3. Предскажите среднюю урожайность помидоров, если объем внесенных удобрений равен 70 фунтам на кв. фут.
4. Выполните анализ остатков и оцените адекватность построенной модели.
5. Существует ли статистически значимая квадратичная зависимость между количеством внесенных удобрений и урожайностью помидоров при уровне значимости, равном 0,05?
6. Чему равнор-значение в задаче 5? Объясните его смысл.
7. Существует ли значимый квадратичный эффект, если уровень значимости равен 0,05?
8. Чему равнор-значение в задаче 7? Объясните его смысл.
9. Объясните смысл коэффициента множественной смешанной корреляции.
10. Вычислите скорректированный коэффициент г*.
14.5. Аудитор из органов самоуправления округа желает разработать модель, позволяющую предсказывать размер муниципального налога по среднему возрасту одноквартирных домов. Для этого была создана выборка, состоящая из 19 домов. Результаты приведены в файле TAXES .XLS.
Предположим, что между размером муниципального налога и возрастом дома существует квадратичная зависимость. Выполните следующие задания, применяя программу Microsoft Excel.
1. Постройте диаграмму разброса возрастов и размеров налога.
2. Выведите уравнение квадратичной регрессии.
3. Предскажите средний размер налога, если возраст дома равен 20 годам.
4. Выполните анализ остатков и оцените адекватность построенной модели.
5. Существует ли статистически значимая квадратичная зависимость между размером налога и возрастом дома при уровне значимости, равном 0,05?
6. Чему равнор-значение в задаче 5? Объясните его смысл.
7. Существует ли значимый квадратичный эффект, если уровень значимости равен 0,05?
8. Чему равнор-значение в задаче 7? Объясните его смысл.
9. Объясните смысл коэффициента множественной смешанной корреляции.
10. Вычислите скорректированный коэффициент т*.
14.2. ПРЕОБРАЗОВАНИЕ ДАННЫХ В РЕГРЕССИОННЫХ МОДЕЛЯХ
Итак, мы рассмотрели модель множественной линейной регрессии, модель квадратичной регрессии и модель с фиктивной переменной. Теперь перейдем к изучению регрессионных моделей, в которых независимая переменная X, зависимая переменная Y или обе переменные подвергаются преобразованиям, чтобы преодолеть ограничения, наложенные на модель, либо для ее линеаризации. К наиболее распространенным преобразованиям относятся извлечение квадратного корня или логарифмирование.1
Извлечение квадратного корня
Для преодоления ограничений, связанных со свойством гомоскедастичности, а также для превращения нелинейной модели в линейную часто применяется извлечение квадратного корня (square-root transformation). Если из объясняющей переменной извлекается квадратный корень, регрессионная модель принимает следующий вид.
РЕГРЕССИОННАЯ МОДЕЛЬ, ЗАВИСЯЩАЯ ОТ КВАДРАТНОГО КОРНЯ
(14.3)
Рассмотрим пример, иллюстрирующий извлечение квадратного корня из объясняющей переменной.
1 Более подробную информацию о логарифмах можно найти в приложении А.
ПРИМЕР 14.2. ИЗВЛЕЧЕНИЕ КВАДРАТНОГО КОРНЯ ИЗ ОБЪЯСНЯЮЩЕЙ ПЕРЕМЕННОЙ
Извлеките квадратный корень из переменной X и постройте диаграмму разброса по следующим данным .
Y X
42,7 1
50,4 1
69,1 2
79,8 2
90,0 3
100,4 3
104,7 4
112,3 4
113,6 5
123,9 5
РЕШЕНИЕ. На рис. 14.8 приведены диаграммы разброса до (панель А) и после преоб разования объясняющей переменной (панель Б).
Диаграмма разброса переменных X и Y
0 1 2 3 4 5 6
X
Панель А
Диаграмма разброса квадратного корня от X и переменной Y
Панель Б
Рис. 14.8. Диаграммы разброса до (панель А) и после преобразования объясняющей переменной (панель Б)
Обратите внимание на то, что извлечение квадратного корня превратило нелинейную зависимость в линейную.
Логарифмическое преобразование
Когда нарушается условие гомоскедастичности, кроме извлечения квадратного корня, часто применяется логарифмическое преобразование (logarithm transformation). Оно также позволяет превратить нелинейную модель в линейную.
ИСХОДНАЯ МУЛЬТИПЛИКАТИВНАЯ МОДЕЛЬ
(14.4)
Применяя логарифмирование по основанию 10 к зависимой и объясняющей переменным модели (14.4), можно превратить ее в линейную модель (14.5).
ПРЕОБРАЗОВАННАЯ МУЛЬТИПЛИКАТИВНАЯ МОДЕЛЬ
iog}; = iog(pX^^,) =
= log р„ + log X*; + logXj + loge, = (14.5)
= logp„ + p, log Xu + p, log X2, + loge,.
Таким образом, модель (14.5) относительно логарифмических переменных является линейной. Аналогично можно преобразовать экспоненциальную модель (14.6), применив к зависимой и объясняющим переменным натуральный логарифм.
ИСХОДНАЯ ЭКСПОНЕНЦИАЛЬНАЯ МОДЕЛЬ
(14.6)
Преобразованная модель выглядит следующим образом.
ПРЕОБРАЗОВАННАЯ ЭКСПОНЕНЦИАЛЬНАЯ МОДЕЛЬ
ln^ =
= lne₽"+P|V|^' + ln£, = . (14.7)
=р() + A'; z + рэ X-,t + In £;
ПРИМЕР 14.3. ЛОГАРИФМИРОВАНИЕ МОДЕЛИ
Примените преобразование натурального логарифма к переменным, приведенным в таблице, и постройте диаграмму разброса.
Y X
0,7 1
0,5 1
1,6 2
1,8 2
4,2 3
4,8 3
12,9 4
11,5 4
32,1 5
33,9 5
РЕШЕНИЕ. На рис. 14.9 приведены диаграммы разброса до (панель А) и после преобразования зависимой и объясняющей переменных (панель Б). Обратите внимание на то, что логарифмирование превратило нелинейную зависимость в линейную.
Диаграмма разброса переменных X и Y
40 -
35 -
30 -
25 -
> 20 -
15 -
10 -
5 0
Панель А
Диаграмма разброса
Панель Б
Рис. 14.9. Диаграммы разброса до (панель А) и после преобразования зависимой и объясняющей переменных (панель Б)
Процедуры Excel: преобразования переменных< +
Чтобы выполнить преобразования переменных, необходимо добавить в рабочий лист формулы = ФУНКЦИЯ(ячейка). В качестве функций можно выбрать одну из перечисленных в таблице.
Преобразование Функция
Квадратный корень КОРЕНЬ()
Десятичный логарифм LOG()
Натуральный логарифм LN()
Например, для извлечения квадратного корня из данных, приведенных в таблице, можно воспользоваться следующим шаблоном рабочего листа.
А ,/ ' С , ;
• 1 ' ' Y X КОРЕНЬ(Х)
' г, 42,7 1 = К0РЕНЬ(В2)
з 50,4 1 = КОРЕНЬ(ВЗ)
10 113,6 5 = КОРЕНЬ(ВЮ)
’ 11 123,9 5 = К0РЕНЬ(В11)
Изучение основ
14.6. Рассмотрим следующее уравнение регрессии:
In Yt = 3,07 + 0,9 In Хх, +1,41 In Х2, .
1. Предскажите значение переменной Y при Хг = 8,5 и Х2 = 5,2.
2. Объясните смысл наклона отклика по отношению к объясняющим переменным.
14.7. Рассмотрим следующее уравнение регрессии:
In ^=4,62 + 0,5^4-0,7^.
1. Предскажите значение переменной Y при Х} = 8,5 и Х2 = 5,2.
2. Объясните смысл наклона отклика по отношению к объясняющим переменным.
Применение понятий
14.8. Извлеките квадратный корень из объясняющей переменной в задаче 14.2. ^SPEED.XLS.
1. Сформулируйте уравнение множественной регрессии.
2. Предскажите средний пробег автомобилей на один галлон топлива, если их скорость равна 55 миль в час.
3. Выполните анализ остатков и оцените адекватность построенной модели.
4. Существует ли статистически значимая зависимость в виде квадратного корня между пробегом и скоростью при уровне значимости, равном 0,05?
5. Объясните смысл коэфсрициента множественной смешанной корреляции Л
6. Вычислите скорректированный коэффициент г2.
7. Сравните решения задач 14.2. Какую модель следует предпочесть? Почему?
14.9. Примените преобразование натурального логарифма к отклику и объясняющей переменной в задаче 14.2. ^SPEED. XLS.
1. Сформулируйте уравнение множественной регрессии.
2. Предскажите средний пробег автомобилей на один галлон топлива, если их скорость равна 55 миль в час.
3. Выполните анализ остатков и оцените адекватность построенной модели.
4. Существует ли статистически значимая логарифмическая зависимость корня между пробегом и скоростью при уровне значимости, равном 0,05?
5. Объясните смысл коэффициента множественной смешанной корреляции г2.
6. Вычислите скорректированный коэффициент г2.
7. Сравните решения задач 14.2 и 14.8. Какую модель следует предпочесть? Почему?
14.10. Примените преобразование натурального логарифма к отклику и объясняющей переменной в задаче 14.4. ^TOMYLD2 . XLS.
1. Сформулируйте уравнение множественной регрессии.
2. Предскажите среднюю урожайность помидоров, если объем внесенных удобрений равен 55 фунтам на 1 000 кв. футов.
3. Выполните анализ остатков и оцените адекватность построенной модели.
4. Существует ли статистически значимая логарифмическая зависимость между пробегом и скоростью при уровне значимости, равном 0,05?
5. Объясните смысл коэффициента множественной смешанной корреляции т*.
6. Вычислите скорректированный коэффициент г2.
7. Сравните полученные решения с решениями задачи 14.4. Какую модель следует предпочесть? Почему?
14.11. Извлеките квадратный корень из объясняющей переменной в задаче 14.4. ©TOMYLD2 . XLS.
1. Сформулируйте уравнение множественной регрессии.
2. Предскажите среднюю урожайность помидоров, если объем внесенных удобрений равен 55 фунтам на 1 000 кв. футов.
3. Выполните анализ остатков и оцените адекватность построенной модели.
4. Существует ли статистически значимая зависимость в виде квадратного корня между урожайностью и объемом внесенных удобрений при уровне значимости, равном 0,05?
5. Объясните смысл коэффициента множественной смешанной корреляции г2.
6. Вычислите скорректированный коэффициент г2.
7. Сравните решения задач 14.4 и 14.10. Какую модель следует предпочесть? Почему?
143. КОЛЛИНЕАРНОСТЬ
Применение модели множественной регрессии сопряжено с весьма важной проблемой — возможной коллинеарностью (collinearity) объясняющих переменных. Коллинеарными называют объясняющие переменные, значительно коррелирующие друг с другом. В этих ситуациях переменные не добавляют новой информации, поэтому их влияние на отклик трудно оценить. Это может привести к явной неустойчивости регрессионных коэффициентов, соответствующих коллинеарным переменным.
Оценить коллинеарность можно, вычислив коэффициент инфляции (variance inflationary factor — VIF) для каждой объясняющей переменной.
КОЭФФИЦИЕНТ ИНФЛЯЦИИ
VIF=—L-г, (14.8)
' 1-А;
где R^ — коэффициент множественной смешанной корреляции объясняющей переменной X со всеми другими объясняющими переменными.
Если модель содержит только две объясняющие переменные, величина R^ представляет собой коэффициент смешанной корреляции между переменными Хх и Хг. Он может совпадать с величиной R; — коэффициентом смешанной корреляции между переменными Х2 и Хг. Если в модели содержатся три объясняющие переменные, то величина R^, где j = 1, 2, 3, представляет собой коэффициент множественной смешанной корреляции между переменной X и двумя другими объясняющими переменными.
Если объясняющие переменные не коррелируют друг с другом, коэффициент VIF равен 1. Если объясняющие переменные сильно коррелируют друг с другом, коэффициент VIFj может быть больше 10. Маркварт (Marquart) [2] предположил, что если коэффициент VIFt больше 10, между переменной Х] и другими объясняющими переменными существует очень сильная корреляция. Однако другие статистики [5] придерживаются более консервативных критериев и полагают, что при значениях VIF больше пяти следует применять альтернативные методы.
Модель множественной регрессии, в которой существуют большие коэффициенты инфляции, следует применять с крайней осторожностью. Эти модели позволяют предсказывать значения зависимой переменной только в том случае, если значения независимых переменных, подставляемые в модель, хорошо согласуются с данными, содержащимися в исходном наборе данных. Эти модели нельзя применять для экстраполяции отклика на значения независимых переменных, не содержащихся в исходной выборке. Кроме того, коэффициенты таких моделей не поддаются интерпретации, поскольку независимые переменные содержат перекрывающуюся информацию, а их индивидуальный вклад невозможно вычислить точно. Для решения этой проблемы следует исключить из регрессионной модели переменную, имеющую наибольший коэффициент инфляции. Довольно часто после этой операции сокращенная модель уже не содержит коллинеарных переменных. Если в модели необходимо учесть все независимые переменные, следует применять методы, описанные в работах [2] и [4]. Коллинеарность обсуждается далее в разделе 14.4.
Если вернуться к задаче о продажах батончиков OmniPower, рассмотренной в разделе 13.1, окажется, что коэффициент корреляции между двумя объясняющими переменными (ценой и затратами на рекламу) равен -0,0968. Вычислим коэффициент инфляции этих переменных.
VIE = VIF, =------------ = 1,009 .
‘ 1-(-0,0968)"
Таким образом, объясняющие переменные в задаче о продажах батончиков OmniPower не коллинеарны.
Процедуры Excel: вычисление коэффициентов инфляции
Чтобы вычислить коэффициент инфляции 1//Адля каждой объясняющей переменной, необходимо выполнить процедуру "Вычисление коэффициентов множественной регрессии" для каждой комбинации объясняющих переменных, а затем в каждый рабочий лист вставить соответствующую формулу. Надстройка PHStat2 решает эту задачу автоматически.
Применение Excel в сочетании с надстройкой PHStat2
Следует выполнить все пункты процедуры "Вычисление коэффициентов множественной регрессии" (раздел 13.1), установив на шаге 2.5 флажок Output options (Параметры вывода) в положение Variance Inflationary Factor (Коэффициент инфляции). В этом случае надстройка PHStat2 вычислит коэффициент инфляции для каждой комбинации объясняющих переменных и вставит его в ячейку В9 на каждом рабочем листе.
Применение Excel
Чтобы вычислить коэффициенты инфляции V/F, для каждой комбинации объясняющих переменных необходимо создать отдельный рабочий лист, затем применить процедуру, описанную в разделе "Вычисление коэффициентов множественной регрессии", следуя инструкциям из раздела ЕН.13.1. В заключение, на каждом рабочем листе, содержащем регрессионные статистки, в ячейку А9 необходимо вставить метку vif, а в ячейку В9 - формулу -1/ (1—В5).
УПРАЖНЕНИЯ К РАЗДЕЛУ
Изучение основ
14.12. Чему равна величина VIF, если коэффициент смешанной корреляции между двумя объясняющими переменными равен 0,20?
14.13. Чему равна величина VIF, если коэффициент смешанной корреляции между двумя объясняющими переменными равен 0,50?
Применение понятий
Задачи 14.14-14.17 следует решать с помощью программы Microsoft Excel.
14.14. Вычислите коэффициент VIF д,ля объясняющих переменных в задаче 13.5. Коллинеарны ли они? ftWARECOST.XLS.
14.15. Вычислите коэффициент VIF для объясняющих переменных в задаче 13.6. Коллинеарны ли они? ftAUTO.XLS.
14.16. Вычислите коэффициент VIF для объясняющих переменных в задаче 13.7. Коллинеарны ли они? ftADRADTV.XLS.
14.17. Вычислите коэффициент VIF для объясняющих переменных в задаче 13.8. Коллинеарны ли они? ftsTANDBY.XLS.
14.4. ПОСТРОЕНИЕ МОДЕЛИ
В этой и предыдущей главах описаны модели множественной линейной регрессии, модели квадратичной регрессии, модели с фиктивными переменными, а также модели, учитывающие взаимодействие между объясняющими переменными. Теперь мы рассмотрим процесс построения модели, содержащей несколько объясняющих переменных.
Для начала вспомним о задаче, в которой для предсказания объема простоя на телевизионной станции были учтены четыре объясняющие переменные (продолжительность работы в офисе, количество часов, проведенных на выезде, время, затраченное на озвучивание, и общее количество рабочих часов в неделе). Попробуем предсказать количество часов простоя, используя данные, приведенные в табл. 14.2
Таблица 14.2. Предсказание продолжительности простоя по количеству часов, проведенных в офисе, количеству часов, проведенных на выезде, количеству часов, затраченных на озвучивание, и общему количеству рабочих часов в неделе, ^standby . XLS
Неделя Простой Присутствие Отсутствие Озвучивание Всего
1 245 338 414 323 2 001
2 177 333 598 340 2 030
3 271 358 656 340 2 226
4 211 372 631 352 2 154
5 196 339 528 380 2 078
6 135 289 409 339 2 080
7 195 334 382 331 2 073
8 118 293 399 311 1 758
9 116 325 343 328 1 624
10 147 311 338 353 1 889
11 154 304 353 518 1 988
12 146 312 289 440 2 049
13 115 283 388 276 1 796
14 161 307 402 207 1 720
15 274 322 151 287 2 056
16 245 335 228 290 1 890
17 201 350 271 355 2 187
18 183 339 440 300 2 032
19 237 327 475 284 1 856
20 175 328 347 337 2 068
21 152 319 449 279 1 813
22 188 325 336 244 1 808
23 188 322 267 253 1 834
24 197 317 235 272 1 973
25 261 315 164 223 1 839
26 232 331 270 272 1 935
Прежде чем приступать к прогнозированию, необходимо учесть, что модель должна быть экономной. Это значит, что наша цель — разработать регрессионную модель, включающую в себя как можно меньше объясняющих переменных, позволяющих аде-
кватно интерпретировать интересующий нас отклик. Регрессионная модель с минимальным количеством переменных намного проще других и меньше страдает от коллинеарности переменных (см. раздел 14.3).
Кроме того, необходимо понимать, что модель с большим количеством объясняющих переменных порождает большие сложности при регрессионном анализе. Во-первых, оценка всех возможных регрессионных моделей становится крайне сложной вычислительной задачей. Во-вторых, даже если конкурентные модели удалось оценить, может оказаться, что единственной оптимальной модели не существует, а есть несколько одинаково хороших.
Начнем анализ простоев на телевизионной станции с оценки коллинеарности объясняющих переменных, вычислив коэффициент инфляции (14.8) для каждой из них. Результаты анализа показаны на рис. 14.10.
Анализ простоев
Регрессионные статистики
Присутствие и все остальные X Отсутствие и все остальные X Озвучивание и все остальные X Всего и все остальные X
Множественный R R-квадрат Нормированный R-квадрат Стандартная ошибка Наблюдения 0,64368 0,41433 0,33446 16,47151 26 0,43490 0,18914 0,07856 124,93921 26 0,56099 0,31471 0,22126 57,55254 26 0,70698 0,49982 0,43161 114,41183 26
| VIF 1,70743 1,23325 1,45924 1,99928
Панель А
J. ~2 L А Анализ простоев В... '1.1'2 с 1 1 г '—jy ]ё Г F G
3 Регрессионная статистика
4 Множественный R 0,78935
j R-квадрат 0,62308
6' Нормированный R-квадрат 0,55128
~7 Стандартная ошибка 31,83501
8 Наблюдения 26
9 10 Дисперсионный анализ
я" df SS MS F Значимость F
12 Регрессия 4 35181,79373 8795,44843 8,67857 0,00027
is* Остаток 21 21282,82166 1013,46770
лГ Итого 25 56464,61538
16
16 Коэффициенты \ Стандартная ошибка t-статистика Р-значение Нижние 95% Верхние 95%
17 jY-пересечение -330,83184 110,89536 -2,98328 0,00709 -561,451405 -100,212285
18 1Присутствие 1,24563 0,41206 3,02293 0,00647 0,388704 2,102554
191 Отсутствие Д,11842 0,05432 -2,17983 0,04080 -0,231392 Д,005444
20]Озвучивание Д ,29706 0,11793 -2,51891 0,01995 -0,542310 -0,051807
21 | Всего 0,13053 0,05932 2,20041 0,03911 0,007166 0,253904
Панель Б
, | . . .. ..... . А ,^'7 7^ /^' 1; .6
1 ^Вычисление статистики Дурбина-Уотсона
'Tjsum of Squared Difference of Residuals 47241.61261
^4 ISum of Squared Residuals 21282.82166
3j________________________
. S | Durbin-Watson Statistic
2.21971
Панель В
Рис. 14.10. Регрессионная модель для предсказания количества часов простоя по четырем объясняющим переменным с помощью программы Microsoft Excel
Обратите внимание на то, что коэффициенты VIF относительно малы и колеблются от 1,23 для часов, проведенных на выезде, до 2,0 для общего количества рабочих часов. Таким образом, используя критерий, предложенный Сни (Snee) [5], который предполагал, что коэффициенты VIF не должны быть больше пяти, мы можем утверждать, что объясняющие переменные не коллинеарны.
Пошаговый подход к построению регрессионной модели
Продолжим анализ задачи о простоях и попробуем определить такой набор объясняющих переменных, который позволил бы построить адекватную и точную модель без необходимости учитывать все переменные. Одним из основных способов построения таких моделей является пошаговая регрессия (stepwise regression), с помощью которой можно определить наилучшую регрессионную модель без перебора всех регрессионных моделей. После определения наилучшей модели для проверки проводится анализ остатков.
Напомним, что для оценки вклада переменных в модель множественной регрессии применяется F-критерий (см. раздел 13.5). В процессе шаговой регрессии F-критерий применяется к модели с любым количеством переменных. Важным свойством пошаговой процедуры является то, что объясняющие переменные, включенные в модель на предыдущих этапах, могут впоследствии исключаться из рассмотрения. Это значит, что на каждом этапе объясняющие переменные как включаются, так и исключаются из модели. Пошаговая регрессия останавливается, когда ни добавление, ни удаление объясняющих переменных не повышают точность модели.
На рис. 14.11 показаны результаты пошаговой регрессии, полученной с помощью программы Microsoft Excel при решении задачи о простоях на телевизионной станции.
2. 'з
......!------—
Пошаговый анализ простоев Таблица результатов
D ..
_G__
6 '7 ‘в 'д’
10 ii 12 13
14 1S .16
17
18
19 2Q 21 22
2Э 24
26
27
28 29
Штат
df SS MS F Значимость F
I Регрессия 1 20667.39798 20667.39798 13.8563159 0.00106
| Остаток 24 35797.21741 1491.550725
| Итого 25 56464.61538
| : Коэффициенты Стандартная ошибка t-статистика Р-значение Нижние 95% Верхние 95%
! Y-пересечение -272.38165 124.24020 -2.19238 0.03829 528.80077 -15.96253
Присутствие 1.42405 0.38256 3.72241 0.00106 0.63448 2.21362
Выезд
df SS MS F Значимость F
Регрессия 2 27662.54287 13831.27143 11.04501 0.00043
Остаток 23 28802.07251 1252.26402
Итого 25 56464.61538
Коэффициенты Стандартная ошибка t-статистика Р-значение Нижние 95% Верхние 95%
Пересечение 330.67483 116.48022 -2.83889 0.00930 -571.63220 -89.71747
Штат 1.76486 0.37904 4.65619 0.00011 0.98077 2.54896
Выезд -0.13897 0.05880 -2.36347 0.02693 -0'26060 -0.01733
Пошаговый анализ
завершен.
Рис. 14.11. Результаты пошаговой регрессии для задачи о простоях на телевизионной станции, полученные с помощью программы Microsoft Excel
При включении объясняющих переменных в модель и удалении их из нее уровень значимости был равен 0,05. Сначала проверяется переменная, обозначающая продолжительность работы в офисе (присутствие). Она сильно коррелирует с откликом. Поскольку /j-значение равно 0,001 и меньше 0,05, эта переменная включается в регрессионную модель.
На следующем этапе в модель включается вторая переменная. Она должна иметь наибольшее влияние на точность модели при условии, что первая объясняющая переменная (продолжительность работы в офисе) уже учтена. В данной задаче такой переменной оказалось количество часов, проведенных на выезде. Поскольку р-значение, соответствующее этой переменной, равно 0,027 и не больше 0,05, количество часов, проведенных на выезде (отсутствие), включается в модель.
Теперь необходимо определить, насколько велик вклад продолжительности работы в офисе и не следует ли исключить его из модели. Поскольку р-значение для этой переменной равно 0,0001, ее следует оставить в модели.
На следующем этапе необходимо решить, стоит ли включать в модель остальные переменные. Поскольку ни одна из оставшихся переменных не удовлетворяет F-критерию с 5% -ным уровнем значимости, в результате получаем регрессионную модель с двумя объясняющими переменными: продолжительностью работы в офисе (присутствие) и количеством часов, проведенных на выезде (отсутствие).
Процедура Excel: выполнение пошаговой регрессии
Для выполнения пошаговой регрессии следует применить процедуру PHStat1^ Regressions Stepwise Regression... (РН51а1рРегрессия^Пошаговая регрессия...).
Например, чтобы провести пошаговую регрессию для данных, приведенных в табл. 14.2, необходимо открыть рабочую книгу chapter 14 .xls на листе Простои и выполнить такие инструкции.
1. Выбрать команду PHStatsRegressionSStepwise Regression...
2. В диалоговом окне Stepwise Regression сделать следующее (см. иллюстрацию).
2.1. Ввести в диалоговом окне Y Variable Cell Range (Входной интервал Y) диапазон ячеек А1 ;А27.
2.2. Ввести в диалоговом окне X Variable Cell Range (Входной интервал X) диапазон ячеек В1:Е27.
2.3. Установить флажок First cells In both ranges contain a label (Первые ячейки обоих диапазонов содержат метки).
2.4. Ввести в диалоговом окне Confidence level for regression coefficients (Доверительный интервал для коэффициентов регрессии) число 0.95.
2.5. Установить переключатель Stepwise Criteria (Критерии пошаговой регрессии) в положение р values (р-значения).
2.6. Установить переключатель Stepwise Options (Параметры пошаговой регрессии) в положение General Stepwise (Полная пошаговая регрессия) и оставить в качестве р-значений число 0.05, как при включении в модель, так и при исключении их из нее.
Stepwise Regression jX|
Data
Y Variable Cell Range: [a17a27
X Variables Call Range: |вПЕ27 T] i
P First cells in both ranges contain label i
Confidence level for regression coefficients: [95% :
Stepwise Criteria p values <*' t values :
Stepwise Options
<* General Stepwise p value to enter: p value to remove
Г* Forward Selection
C Backward Elimination
• Output Options
> Title: IПошаговый анализ простоев i
Help j I LLgjLZjl Cancel |
2.7. Ввести в диалоговом окне Title (Заголовок) название листа.
2.8. Щелкнуть на кнопке ОК.
Эта процедура создает два рабочих листа, один из которых содержит модель множественной рег-- рессии, учитывающей все объясняющие переменные, а другой - результаты пошаговой регрессии.
Эти листы не являются динамически обновляемыми. Следовательно, если данные изменятся, все описанные выше действия необходимо выполнить заново.
Примечание, необходимо, чтобы объясняющие переменные хранились в соседних столбцах.
£a Chapter 14.xls
Результаты пошаговой регрессии содержатся на листе Рис14.11 в рабочей книге Chapter 14. xls.
Процедура пошаговой регрессии была предложена около тридцати лет назад, когда стоимость компьютерного времени была очень высока. В этих условиях она позволяла сократить объем перебора объясняющих переменных и широко использовалась. В настоящее время появились новые очень эффективные регрессионные модели. Так был разработан более общий подход к построению альтернативных регрессионных моделей, получивший название метода выбора наилучшего подмножества (best subsets analysis). В последнее время появилась новая методика исследования — иннтеллектуальный анализ данных (data mining) — способ анализа информации в огромных базах данных для поиска статистически значимых зависимостей среди огромного количества объясняющих переменных. В этих условиях метод выбора наилучшего подмножества становится непрактичным.
Метод выбора наилучшего подмножества
С помощью метода выбора наилучшего подмножества либо оценивают всевозможные регрессионные модели для заданного набора данных, либо определяют наилучшие подмножества моделей для заданного количества независимых переменных. На рис. 14.12 показаны результаты применения метода выбора наилучшего подмножества для решения задачи о простоях на телевизионной станции с помощью программы Microsoft Excel.
Обратите внимание на то, что максимальным значением скорректированного коэффициента г? является число 0,551. Оно достигается для модели, в которой учитываются четыре объясняющие переменные и эффект взаимодействия всех пяти оцениваемых параметров.
В качестве второго критерия часто используется статистика, предложенная Мэлло-усом (Mallows) [4]. Статистика С, определенная формулой (14.9), оценивает разность между эмпирической и истинной регрессионной моделями.
СТАТИСТИКА Ср
(\-R2A(n-T) . z ч.
С = 2(4 + 1)), (14.9)
где k — количество независимых переменных, включенных в регрессионную модель, Т — общее количество параметров (включая эффекты взаимодействия), включенных в полную модель регрессии, R[ — коэффициент множественной смешанной корреляции в регрессионной модели, содержащей k независимых переменных, R} — коэффициент множественной смешанной корреляции в полной регрессионной модели, содержащей все Г оцениваемых параметра.
А В С D "e " F.
1 .Анализ простоев методой наилучшего подмножества
2
3 J Intermediate Calculations
4 ,Я2Т 0.62308
5 1 -R2T 0.37692
6 п 26
X ,т 5
8 п-Т 21
9
10 Model Ср ы R Square Adj. R Square Std. Error
11 Х1 13.32152 2 0.36602 0.33961 38.6206
12X1X2 8.41933 3 0.48991 0.44555 35.38734
13'Х1Х2ХЗ 7.84181 4 0.53617 0 47292 34.50286
14jX1X2X3X4 5.00000 5 0.62308 0.55128 31.83501
15 -Х1Х2Х4 9.34492 4 0.50919 0.44227 35.49212
16 1X1X3 10.64856 3 0.44990 0.40206 36.74905
17X1X3X4 7.75166 4 0.53779 0.47476 34.44263
18 Х1Х4 14.79818 3 0.37542 0.32111 39.15789
19 Х2 33.20781 2 0.00909 -0.03220 48.28359
33JX2X3 32.30673 3 0.06116 -0.02048 48.00868
21 JX2X3X4 12.13813 4 0.45906 0.38529 37.26076
22 Х2Х4 23.24809 3 0.22375 0.15625 43.65405
”23X3 30.38835 2 0.05970 0.02052 47.03452
24]ХЗХ4 11.82309 3 0.42882 0.37915 37.44658
"25~Х4 24.18460 2 0.17105 0.13651 44.16192
Рис. 14.12. Результаты применения метода выбора наилучшего подмножества для решения задачи о простоях на телевизионной станции с помощью программы Microsoft Excel (обратите внимание на чрезвычайно маленькое значение коэффициента г2 и учтите, что скорректированный коэффициент г2 может быть отрицательным)
Вычислим статистику Ср для модели, содержащей продолжительность работы в офисе и количество часов, проведенных на выезде, используя формулу (14.9).
п=26, /г = 2, Т = 4 + 1 = 5, Я; =0,490 , Я*= 0,623.
Таким образом, (1-0.49)(26-5) _ 2+ 2
р 1-0,623 V V 77
Если отклонения регрессионной модели, содержащей k независимых переменных, от истинной модели являются случайными, среднее значение статистики Ср равно k+ 1, т.е. количеству параметров. Таким образом, при оценке многих альтернативных регрессионных моделей основная цель — найти модели, для которых величина Ср близка k + 1 или меньше этого числа.
Как показано на рис. 14.12, этому критерию соответствует лишь одна модель, содержащая все четыре независимые переменные. Следовательно, необходимо выбрать именно эту модель. Довольно часто статистика Ср выделяет не одну, как в данном случае, а несколько моделей, которые подлежат более глубокому анализу на основе критериев экономии, простоты и соответствия исходным предположениям (по результатам анализа остатков). Обратите также внимание на то, что значение статистики Ср для модели, выбранной по результатам пошагового анализа, равно 8,4. Эта величина намного превышает предполагаемый уровень k + 1 =3.
Поскольку данные собирались последовательно, необходимо вычислить статистику Дурбина-Уотсона и попытаться выявить автокорреляцию между остатками (см. раздел 12.6). Из рис. 14.10 следует, что статистика Дурбина-Уотсона D равна 2,22. Поскольку D > 2,0, положительная автокорреляция между остатками не наблюдается.
Процедура Excel: метод выбора наилучшего подмножества
Для анализа с помощью метода выбора наилучшего подмножества следует применить процедуру PHStat^Regression^Best Subsets... (PHStat^Perpeccnn^MeTOfl выбора наилучшего подмножества...).
Например, чтобы провести такой анализ для данных, содержащихся в табл. 14.2, необходимо открыть рабочую книгу chapter 14 . xls на листе Простои и выполнить такие инструкции.
1. Выбрать команду PHStat^Regression^Best Subsets....
2. В диалоговом окне Stepwise Regression сделать следующее (см. иллюстрацию).
2.1. Ввести в диалоговом окне Y Variable Cell Range (Входной интервал Y) диапазон ячеек А1:А27.
2.2. Ввести в диалоговом окне X Variable Cell Range (Входной интервал X) диапазон ячеек В1 :Е27.
2.3. Установить флажок First cells in both ranges contain a label (Первые ячейки обоих диапазонов содержат метки).
Best Subsets |Х]
Data .............. ...........
Y Variable Cell Range: [д17д27~ " _]
X Variables Cell Range: [bI7e27 T]
P First cells in each range contains label
Confidence level for regression coefficients: [95 %
Output Options - — —
Title: ^Анализ простоев методом выбора наилучшегс
2.4. Ввести в диалоговом окне Confidence level for regression coefficients (Доверительный уровень для коэффициентов регрессии) число 0.95.
2.5. Ввести в диалоговом окне Title (Заголовок) название листа.
2.6. Щелкнуть на кнопке ОК.
Эта процедура создает несколько рабочих листов, один из которых содержит результаты анализа по методу выбора наилучшего подмножества. Эти листы не являются динамически обновляемыми. Следовательно, если данные изменятся, все описанные выше действия необходимо выполнить заново.
Примечание: необходимо, чтобы объясняющие переменные хранились в соседних столбцах.
Содержимое компакт-диска
Результаты анализа по методу выбора наилучшего подмножества содержатся на листе Рис14.12 в рабочей книге chapter 14 . xls.
Определив объясняющие переменные, которые следует включить в модель, необходимо проверить ее точность с помощью анализа остатков. Результаты этой проверки приведены на рис. 14.13. Обратите внимание на то, что график остатков, зависящих от продолжительности работы в офисе, количества часов, проведенных на выезде, количества часов, затраченных на озвучивание, и общего количества рабочих часов в неделе, не демонстрирует никаких явных зависимостей. Кроме того, гистограмма остатков (не приведенная здесь) свидетельствует об умеренном нарушении условия о нормальном распределении ошибок.
Зависимость остатков от продолжительности отсутствия
.60 ------------1------------1------------1------------1-----------1------------f-------------1
0 100 200 300 400 500 600 700
Отсутствие
Зависимость остатков от продолжительности озвучивания
100 200 300 400
500 600
Озвучивание
Панель В
Зависимость остатков от продолжительности рабочей недели
Всего
Панель Г
Рис. 14.13. Графики остатков, построенные с помощью программы Microsoft Excel при решении задачи о простоях
Как следует из рис. 14.13, уравнение регрессии имеет следующий вид:
Y = -300,83 +1,2456Х„ -0,1184Х,, - 0,2971Х3, + 0,1305Х4, .
Проиллюстрируем оценку конкурирующих моделей, у которых величина статистики Ср меньше или равна k + 1, следующим примером.
ПРИМЕР 14.4. ВЫБОР СРЕДИ КОНКУРИРУЮЩИХ МОДЕЛЕЙ
Применяя метод выбора наилучшего подмножества, найдите в табл. 14.3 наилучший набор объясняющих переменных.
Таблица 14.3. Частичные результаты метода выбора наилучшего подмножества
Количество переменных R2 (%) Скорректированный R2 (%) Ср,% Переменные
1 12,1 11,9 113,9
1 9,3 9,0 130,4 X,
1 8,3 8,0 136,2 ^3
2 21,4 21,0 62,1 Х3 X,
2 19,1 18,6 75,6 X, х3
2 18,1 17,7 81,0 Хх х4
3 28,5 28,0 22,6 Х^Х,
3 26,8 26,3 32,4 Х^Х,
3 24,0 23,4 49,0 х2х3х4
4 30,8 30,1 11,3 Х,Х2Х3Х3
4 30,4 29,7 14,0 х.х.х.х.
4 29,6 28,9 18,3 Х,Х2ХхХ,
5 31,7 30,8 8,2 х.х.х.х.х.
5 31,5 30,6 9,6 Х.Х2Х3ХлХй
5 31,3 30,4 10,7 х^х.х.х.х.
6 32,3 31,3 6,8 ХхХ2Х,ХлХ,Х.
6 31,9 30,9 9,0 х.х^х.х.х.
6 31,7 30,6 10,4 х,х2х3х,хнх7
7 32,4 31,2 8,0 х.х.х.х^^х.
РЕШЕНИЕ. Среди этих наборов объясняющих переменных необходимо найти подмножества, для которых статистика Ср меньше или равна (/г+1). Этим критериям удовлетворяют две модели. Одна из них содержит шесть независимых переменных (Хр Х2, Х3, Х4, Х5, Хй). Ее статистика Ср равна 6,8 и не превосходит k = 6 + 1 = 7. Вторая модель является полной и содержит семь независимых переменных (Х15 Х2, Х3, Х4, Х5, Хв, Х7). Ее статистика Ср равна 8,0. Для окончательного выбора оптимальной модели необходимо определить набор переменных, являющийся общим для обеих моделей, и определить, является ли вклад дополнительных переменных статистически значимым. В данном случае полная модель отличается от частичной лишь одной переменной Х7. Следовательно, необходимо проверить, является ли значимым вклад этой переменной в регрессионную модель, учитывающую переменные (Хр Х2, Х3, Хр Х5, Xfi). Если включение новой переменной существенно повышает точность модели с шестью объясняющими переменными, следует предпочесть полную модель, если нет — частичную.
ВРЕЗКА 14.1. ЭТАПЫ ПОСТРОЕНИЯ РЕГРЕССИОННОЙ МОДЕЛИ
• Определить набор независимых переменных для включения в регрессионную модель.
• Построить полную регрессионную модель, учитывающую все независимые переменные, и вычислить коэффициент VIF для каждой из них.
• Определить, все ли независимые переменные имеют коэффициент VIF больше пяти.
• Возможны три варианта.
• Для всех независимых переменных коэффициент VIF больше пяти. Перейти к п. 5.
• Для одной независимой переменной коэффициент VIFбольше пяти. Исключить ее из модели и.перейти к п. 5.
• Для нескольких независимых переменных коэффициент VIF больше пяти. Исключить из модели независимую переменную, имеющую наибольший коэффициент VIF, и перейти к п. 2.
• Применить метод выбора наилучшего подмножества к оставшимся переменным и определить наилучшую модель (по величине Ср).
• Перечислить все модели, у которых Ср < к 4-1.
• Выбрать среди моделей, обнаруженных вп. 6, наилучшую (см. пример 14.4).
• Выполнить полный анализ выбранной модели, включая анализ остатков.
• В зависимости от результатов анализа остатков добавить квадратичные члены, преобразовать данные и выполнить повторный анализ.
• Применить полученную модель, чтобы предсказать значения зависимой переменной.
Эти этапы изображены на следующей схеме.
Выберите независимые переменные
Постройте полную регрессионную модель и вычислите коэффициенты -<*
VIF для всех независимых переменных
Если ли переменные, у которых коэффициент VIFp**^ больше & ' пяти?»
Несколько переменных имеют коэффи* JiS. циент VIF г больше пяти??
Исключите из модели переменную, имеющую наибольший коэффициент VIF
Нет
Нет
Примените метод выбора наилучшего подмножества и постройте модели, содержащие к слагаемых при заданном количестве независимых переменных
Исключите из модели переменную X
Перечислите все модели, удовлетворяющие условию Ср > (к + 1)
Выберите среди них наилучшую
«еевивд. - j
Выполните полный анализ выбранной модели, включая анализ остатков
В зависимости от результатов анализа остатков добавьте квадратичные члены, преобразуйте данные и выполните повторный анализ
Примените полученную модель для предсказания значений зависимой переменной
Рис. 14.14. Схема построения модели
УПРАЖНЕНИЯ К РАЗДЕЛУ 14.4
Изучение основ
14.18. Рассмотрим полную регрессионную модель с шестью независимыми переменными. Для ее построения используется выборка, содержащая 40 наблюдений. При анализе модели, содержащей две независимые переменные, получены следующие результаты:
п = 40, k = 2, Т = 6 + 1 = 7, R; = 0,274, R? = 0,653.
1. Вычислите величину Ср для модели, содержащей две независимые переменные. 2. Удовлетворяет ли эта модель критериям оптимальности? Обоснуйте свой ответ.
• 14.19. Рассмотрим полную регрессионную модель с четырьмя независимыми переменными. Для ее построения используется выборка, содержащая 30 наблюдений. Для модели, содержащей переменные А и Б, величина Ср равна 4,6.
Для модели, содержащей переменные А и В, величина Ср равна 2,4.
Для модели, содержащей переменные А, Б и С, величина Ср равна 2,7.
1. Какие модели удовлетворяют критериям оптимальности? Обоснуйте свой ответ.
2. Как сравнить модель, содержащую переменные А, Б и С, с моделью, включающей в себя независимые переменные А и Б?
Применение понятий
Задачи 14.20-14.26 рекомендуется решать с помощью программы Microsoft Excel.
14.20. Для предсказания продажной цены дома по его оценочной стоимости, периода, в течение которого он был выставлен на продажу, и состоянию (новый — 1, старый — 0) была разработана регрессионная модель. В файле ^HOUSEl. XLS приведены данные о 30 недавно проданных одноквартирных домах в небольшом городке на западе США (оценочная стоимость устанавливается один раз в год).
Постройте оптимальную регрессионную модель, позволяющую предсказать продажную цену дома. Выполните анализ остатков. Подробно объясните полученные результаты.
14.21. Файл ftcOLLEGES2002 .XLS содержит данные о 80 колледжах и университетах. В нем указаны стоимость обучения в течение года (тыс. долл.), среднее количество баллов, набранных студентами при сдаче теста на проверку умственных способностей (Scholastic Aptitude Test — SAT), вид заведения — государственное (0) или частное (1), а также сведения о количестве баллов, полученных при сдаче экзамена TOEFL (больше 550 или нет). Постройте оптимальную регрессионную модель, позволяющую предсказать стоимость годового обучения. Выполните анализ остатков. Подробно объясните полученные результаты.
14.22. Файл eiAUT02002.XLS содержит данные о 121 модели автомобилей, выпущенных в 2002 году. В частности, там хранятся данные о расходе топлива на милю пути, весе, длине каждой модели, а также типе: спортивный или нет. Постройте оптимальную регрессионную модель, позволяющую предсказать расход топлива на милю пути. Выполните анализ остатков. Подробно объясните полученные результаты.
14.23. В задаче 12.77 изучалось влияние демографической информации на объем продаж в магазинах спортивных товаров. Постройте оптимальную модель множественной регрессии, позволяющую предсказать ежемесячный объем продаж. Выполните анализ остатков. Подробно объясните полученные результаты. Сравните наилучшую модель множественной регрессии с наилучшей моделью простой линейной регрессией. ^SPORTING. XLS.
14.24. В задаче 12.78 с помощью модели простой линейной регрессии изучалась взаимосвязь между успеваемостью учеников в штате Огайо и тремя независимыми переменными. Постройте оптимальную модель множественной регрессии, позволяющую предсказать успеваемость учеников. Выполните анализ остатков. Сравните оптимальную модель множественной регрессии и наилучшую модель простой линейной регрессии. Подробно объясните полученные результаты, ftSCHOOLS. XLS.
14.25. Начальник отдела кадров крупной компании, выпускающей сложные промышленные инструменты, пытается применить регрессионные модели для правильного выбора менеджеров по продажам, возглавляющих торговые представительства в 45 регионах. Многие из них имеют научные степени в области электротехники, поэтому с учетом технического профиля компании некоторые руководители считают, что на должность менеджера по продажам следует принимать только специалистов с учеными степенями. Для этого во время интервью кандидатам предлагают пройти два теста. Поскольку проведение этих экзаменов требует дополнительных затрат, появилось предложение отменить один из них или оба. Для начала отдел кадров собрал информацию о каждом из 45 менеджеров по продажам, возглавляющих торговые представительства в данный момент. В эту информацию входит стаж работы, образование, а также оценки, полученные на обоих экзаменах. В качестве зависимой переменной выбран “индекс продаж”, представляющий собой отношение фактического объема продаж в регионе к плановому объему продаж, который каждый год устанавливается руководством компании на основании предыдущих результатов и емкости рынка в каждом регионе. Вся необходимая информация содержится в файле ft MANAGERS . XLS. В качестве независимых переменных выбраны следующие величины.
Продажи — отношение фактического объема продаж к плановому. Считается, что плановый объем продаж устанавливается на основе “реалистичных предположений”.
Первый тест — оценки, полученные менеджерами при сдаче первого теста (Wonder Personnel Test). Чем выше оценка, тем выше административные способности менеджера.
Второй тест — оценки, полученные менеджерами при сдаче второго теста (Strong-Campbell Interest Inventory Test). Чем выше оценка, тем выше заинтересованность менеджера в увеличении объема продаж.
1. Разработайте наиболее подходящую модель для прогнозирования объема продаж.
2. Следует ли компании проводить специальные экзамены? Аргументируйте свой ответ.
3. Можно ли на основании этих данных утверждать, что инженеры-электротехники лучше остальных менеджеров по продажам? Следует ли нанимать только инженеров-электротехников? Аргументируйте свой ответ.
4. Насколько важен стаж работы менеджера? Обоснуйте свой ответ.
5. Детально обоснуйте выбор регрессионной модели, на основе которой начальник отдела кадров должен принимать решение о найме менеджеров по продажам.
14.26. В файле ftpRINTERS.XLS приведены цена, скорость печати текста, стоимость печати текста, скорость печати цветной фотографии и стоимость печати цветной фотографии для 15 принтеров. Постройте наиболее точную модель множественной регрессии, позволяющую предсказать стоимость принтера.
14.5. ЛОВУШКИ И ЭТИЧЕСКИЕ ПРОБЛЕМЫ, СВЯЗАННЫЕ СО МНОЖЕСТВЕННОЙ РЕГРЕССИЕЙ
Ловушки множественной регрессии
Построение моделей является синтезом искусства и науки. Разные люди придерживаются разных точек зрения на оптимальность регрессионных моделей. В любом случае следует придерживаться схемы, изложенной во врезке 14.2. Однако применение этой схемы сопряжено с некоторыми ловушками. Трудности и этические проблемы, связанные с простой линейной регрессией, описаны в разделе 12.9. Перечислим теперь аналогичные проблемы, присущие моделям множественной регрессии.
ВРЕЗКА 14.2. ОСНОВНЫЕ ТРУДНОСТИ, СВЯЗАННЫЕ СО МНОЖЕСТВЕННОЙ РЕГРЕССИЕЙ
• Необходимо понимать, что при интерпретации коэффициента регрессии, соответствующего конкретной независимой переменной, остальные переменные считаются константами.
• Следует проводить анализ остатков для каждой независимой переменной.
• Нужно оценивать эффект взаимодействия и проверять, чтобы наклоны отклика по каждой из объясняющей переменной были одинаковыми.
• Необходимо вычислять коэффициенты VIF для каждой независимой переменной, включаемой в модель.
• Следует проверять несколько альтернативных моделей, используя метод выбора наилучшего подмножества.
Этические вопросы
В Этические вопросы возникают, когда модель множественной регрессии используется для предсказания величин, находящихся под управлением пользователя. Ключевым моментом в этом случае являются намерения исследователя. Кроме
ситуаций, перечисленных в разделе 12.9, возможны варианты, когда статистик преднамеренно не исключает из модели множественной регрессии коллинеарные
переменные и неправомерно применяет метод наименьших квадратов даже тогда, когда не выполняются необходимые условия.
РЕЗЮМЕ
В этой главе показано, как директор телевизионной станции может применять множественный линейный анализ для сокращения продолжительности простоев. Рассмотрены различные модели множественной регрессии, включая квадратичные модели, модели с фиктивными переменными, модели с эффектами взаимодействия. Изучены способы преобразования переменных, исследованы коллинеарные переменные и описан процесс построения регрессионной модели.
т
Г
‘Настройка множественной' | ~ регрессионной модели
1——-Ч—
Построение модели
Квадратичные Фиктивные члены i переменные
Преобразованные Эффекты
I переменные < j взаимодействия
'^Определение
'и интерпретация ' коэффициентов | регрессии
Пошаговая . регрессия
Метод выбора , наилучшего ^подмножества
I------
:.Скорректиро-ванный
j коэффициент
5
L q
двж ?, :»цjjiii Жнализ остатков.
Адекватна i ли модель?
Коллинеарност»^*^^
^Проверка значимости
Г;-, полной модели tМ): ₽1 = ₽2 =--- Q
I Проверка
К значимости Д-переменных
Значима г Нет ли модель?
Значим ли .. Нет коэффициент.
Применение модели для предсказания г и оценки
Оценка ^Оценка величины коэффициента > Р и предсказание 8, ,4 1 отклика/
Структурная схема главы 14
ОСНОВНЫЕ ПОНЯТИЯ
Извлечение квадратного корня, 949
Интеллектуальный анализ данных, 962
Коэффициент инфляции, 956
Логарифмическое преобразование, 951
Метод выбора наилучшего подмножества, 962 Пошаговая регрессия, 960
УПРАЖНЕНИЯ К ГЛАВЕ
Проверка знаний
14.27. Как выявить взаимодействие между независимыми переменными?
14.28. Чем пошаговая регрессия отличается от метода выбора наилучшего подмножества?
14.29. Как выбрать наилучшую модель, используя статистику Ср?
Применение понятий
Задачи 14.30—14.43 рекомендуется решать с помощью программы, Microsoft Excel.
14.30. Крейзи Дейв (Crazy Dave), популярный бейсбольный обозреватель, изучает статистические показатели разных команд на протяжении сезона 2002 года (см. задачу 13.57). В частности, он хотел бы определить, какие переменные важны для предсказания количества побед, одержанных командой. Для этого он решил использовать среднее количество очков (earned team average — ERA), набранных командой за сезон, количество удачных защит, пробежек, пропущенных бросков, пропущенных пробежек и ошибок в 2002 году. Эти данные записаны в файле fi>BB2002.XLS.
1. Постройте наиболее подходящую модель множественной регрессии, позволяющую предсказывать количество побед, одержанных командой. Тщательно выполните анализ остатков. Подробно объясните полученные результаты.
2. Постройте наиболее подходящую модель множественной регрессии, позволяющую предсказывать среднее количество очков (earned team average — ERA), набранных командой за сезон, по информации о количестве пропущенных ударов, пропущенных пробежек, ошибок и удачных защит в 2002 году. Тщательно выполните анализ остатков. Подробно объясните полученные результаты.
14.31. Последние несколько лет внимание публики приковано в неравенству доходов и размеров компенсаций, выплачиваемых игрокам в 30 бейсбольных командах высшей лиги. Общепризнанно, что наибольшее количество побед может одержать лишь та команда, в которой игроки получают крупную компенсацию и имеют большую прибыль. В файле BB2001.XLS собрана информация о денежных поступлениях команд за сезон, доходы местных теле- и радиостанций, другие местные доходы, размеры компенсаций, выплачиваемых игрокам, а также игровая статистика.
1. Постройте наиболее подходящую модель множественной регрессии для предсказаний количества побед, считая независимыми переменными перечисленные выше четыре показателя.
2. Сравните построенную модель с моделью, созданной при решении задачи 14.30, в которой для предсказания количества побед используется лишь игровая статистика. Какие объясняющие переменные позволяют точнее предсказать количество побед — доходы и компенсации игроков или игровая статистика? Аргументируйте свой ответ.
14.32. Профессиональный баскетбол стал поистине всемирным видом спорта. В Национальную баскетбольную лигу (NBA — National Basketball Association) приезжает все больше игроков из других стран. Например, в 2002 году на драфт был поставлен первый китайский игрок — Яо Мин (Yao Ming). Существует множество факторов, влияющих на количество побед, одержанных командами NBA. В файле ^NBA2002 . XLS собрана игровая статистика о командах NBA, в частности, количество очков, набранных за игру (командой, соперником и разница между этими показателями), процент попаданий (команды, соперника и разница между этими показателями), перехваты за игру (команды, соперника и разница между этими показателями), процент подборов под щитом соперника и процент подборов под своим щитом.
1. Следует ли включать в модель множественной регрессии количество очков, набранных за игру командой, количество очков, набранных за игру соперником, процент попаданий команды, процент попаданий соперника, разницу между количеством перехватов, сделанных игроками команды и соперниками, процент подборов под щитом соперника и процент подборов под своим щитом? Постройте оптимальную модель множественной регрессии, позволяющую предсказать количество побед на основе перечисленных объясняющих переменных.
2. Следует ли включать в модель множественной регрессии разницу между количеством очков, набранных за игру командой, и количеством очков, набранных за игру соперником, разницу между процентом попаданий команды и процентом попаданий соперника, разницу между количеством перехватов, сделанных игроками команды и соперниками, разницу между процентами подборов под щитом соперника у команды и соперника, а также разницу между процентами подборов под своим щитом у команды и соперника? Постройте оптимальную модель множественной регрессии, позволяющую предсказать количество побед на основе перечисленных объясняющих переменных.
3. Сравните результаты решения задач 1 и 2. Какая из указанн!х моделей точнее? Аргументируйте свой ответ.
14.33. Графство Нассау расположено приблизительно в 25 милях на запад от Нью-Йорка. До последней переоценки недвижимости, произведенной в 2002 году, налог на недвижимость начислялся по оценкам 1938 года либо по оценками того года, в котором было построено здание (если оно было построено позднее 1938 года). В файле ft>GLENCOVE. XLS собраны данные о стоимости (в 2002 г.), площадях земельных владений (в акрах), площадях зданий (в кв. футах), возрасте зданий, количестве комнат, количестве спален и количестве машин, запаркованных в гараже, для 30 одноквартирных домов, расположенных в поселке Глен-Коув (Glen Cove).
1. Постройте наиболее точную модель множественной регрессии, позволяющую предсказать стоимость дома.
2. Сравните полученные результаты с решением задач 14.34.1 и 14.35.1.
14.34. Аналогичные данные были собраны в поселке Рослин (Roslyn) ^ROSLYN. XLS.
1. Постройте наиболее точную модель множественной регрессии, позволяющую предсказать стоимость дома.
2. Сравните полученные результаты с последующим решением задач 14.33.1 и 14.35.1.
14.35. Аналогичные данные были собраны в поселке Фрипорт (Freeport) &FREEPORT. XLS.
1. Постройте наиболее точную модель множественной регрессии, позволяющую предсказать стоимость дома.
2. Сравните полученные результаты с решением задач 14.33.1 и последующим решением задачи 14.34.1.
14.36. Представьте себя на месте брокера, желающего сравнить стоимость владений в поселках Глен-Коув и Рослин (расположенных примерно в 8 милях друг от друга). Проанализируйте данные о домах, расположенных в этих поселках, записанные в файле ^GCROSLYN.XLS. Включите в модель фиктивную переменную, идентифицирующую поселок (Глен-Коув или Рослин).
1. Постройте наиболее точную модель множественной регрессии, позволяющую предсказать стоимость дома.
2. Какие выводы можно сделать, сравнив стоимость домов в поселках Глен-Коув и Рослин?
14.37. Представьте себя на месте брокера, желающего сравнить стоимость владений в поселках Глен-Коув, Фрипорт и Рослин. Проанализируйте данные о домах, расположенных в этих поселках, записанные в файле ^GCFREEROSLYN. XLS.
1. Постройте наиболее точную модель множественной регрессии, позволяющую предсказать стоимость дома.
2. Какие выводы можно сделать, сравнив стоимость домов в поселках Глен-Коув, Фрипорт и Рослин?
14.38. Файл ^COLLEGES2 002 .XLS содержит данные о 80 колледжах и университетах. Помимо всего прочего, в нем указаны стоимость обучения в течение года (тыс. долл.), первый (QJ и третий квартили (QJ баллов, набранных студентами при сдаче теста на проверку умственных способностей (Scholastic Aptitude Test — SAT), стоимость проживания в общежитии, вид собственности, количество баллов, набранных при сдаче экзамена TOEFL, и средний объем академической задолженности.
Разработайте оптимальную модель множественной регрессии для предсказания среднего объема академической задолженности. Выполните подробный анализ остатков. Объясните результаты.
14.39. Файл ^AUT02002 . XLS содержит данные о 121 модели автомобилей, выпущенных в 2002 году. Кроме всего прочего, в нем содержатся данные о расходе топлива на милю пути, мощности двигателя, ширине, длине, размере колесной базы, емкости багажника, радиусе поворота и разновидности модели (спортивная или нет).
Постройте оптимальную регрессионную модель, позволяющую предсказать расход топлива на милю пути. Выполните подробный анализ остатков. Объясните результаты.
14.40. На протяжении последних 30 лет резко возросло общественное беспокойство о загрязнении воздуха. Как правило, для удаления микрочастиц из пыли, тумана, дыма, выбросов газа и копоти используются газоочистители Вентури. На производительность газоочистителя влияют скорость потока воздуха, скорость потока воды (литров в минуту), скорость циркуляционного потока воды (литров в минуту) и проходное сечение дросселя (мм) в воздухозаборнике. Результаты измерений приведены в файле ^SCRUBBER. XLS.
Постройте оптимальную модель множественной регрессии, позволяющую предсказать количество удаленных частиц. Выполните анализ остатков. Объясните результаты.
Источник: Marshall, D.A., R. J. Sumner, and С. A. Shook, "Removal of SiO2 Particles with an Ejector Venturi Scrubber”, Environmental Progress 14 (1995): 28-32.
14.41. Для отбора проб газа с участка загрязненной почвы используется колпак из плексигласа. Диаметр промывной полости в этом колпаке — 2 фута. Для проверки предположения о выделении радона на подозрительном участке земли используется регрессионная модель, позволяющая предсказать концентрацию радона (пКи/л) по уровню излучения грунта (сГр/день), температуре поверхности почвы (°F), давлению пара (мбар), скорости ветра (миль в час), относительной влажности (%), точке росы (°F) и температуре окружающего воздуха (°F). Соответствующие данные содержатся в файле ft^RADON. XLS.
Постройте оптимальную модель множественной регрессии, позволяющую предсказать концентрацию радона. Выполните подробный анализ остатков. Объясните результаты.
14.42. В городке Оксфорд, штат Огайо, в 45 милях на северо-запад от Цинциннати, расположен университет Майами (Miami University). Кроме 16 000 студентов, в городе проживает около 20 000 постоянных жителей. В файле ©HOMES.XLS содержатся данные обо всех одноквартирных домах, проданных в этом городке на протяжении последнего года. В частности, там записаны значения следующих переменных.
Цена — продажная цена дома (тыс. долл.).
Район — рейтинг района от 1 (худший) до 5 (лучший).
Состояние — рейтинг состояния дома от 1 (худший) до 5 (лучший).
Спальни — количество спален в доме.
Ванны — количество ванн в доме.
Другие комнаты — количество других комнат в доме.
Выполните регрессионный анализ, используя в качестве отклика продажную цену дома, а в качестве объясняющих переменных — остальные пять переменных.
1. Сформулируйте уравнение множественной регрессии.
2. Объясните смысл наклонов отклика в этой модели.
3. Являются ли объясняющие переменные статистически значимыми при уровне значимости, равном 0,05? Какую модель регрессии следует применить для решения задачи?
4. Вычислите p-значения в задаче 3 и объясните их смысл.
5. Предскажите среднюю стоимость дома, состоящего из 3 спален, 2,5 ванных комнат, 4 других комнат, в районе, рейтинг которого равен 4, причем состояние дома также оценивается на 4.
6. Объясните смысл коэффициента множественной смешанной корреляции г};12345 .
7. Вычислите скорректированный коэффициент А
8. Выполните анализ остатков и определите адекватность модели.
9. Удалите из модели любую объясняющую переменную, не имеющую статистически значимого вклада, используя метод выбора наилучшего подмножества. Повторите решение задач 1-8. Какую модель следует предпочесть? Объясните свой выбор.
14.43. Посещаемость бейсбольных матчей команд высшей лиги зависит от многих факторов. К ним относятся время игры, погода, соперник, хорошо ли команда провела предыдущие матчи, а также проводились ли перед матчем рекламные мероприятия. В частности, в 2002 году перед матчами часто раздавались плакаты и бейсболки с фирменной символикой команд (Т. С. Boyd, and Т. С. Krehbiel, “Promotion Timing in Major League Baseball and the Stacking Effects of Factors that Increase Game Attractiveness”, Sport Marketing Quality, March 12, 2003). В файле ^BASEBALL. XLS записаны значения следующих переменных.
Команда — название команды (Kansan City Royals, Philadelphia Phillies, Chicago Cubs и Cincinnati Reds).
Посещаемость — посещаемость матчей.
Температура — температура воздуха в день матча (°F).
Победы хозяев, % — процент матчей, выигранных командой.
Победы соперника, % — процент матчей, выигранных соперником.
Уикэнд — фиктивная переменная (1 — игра проводилась в пятницу, субботу или воскресенье, 0 — игра проходила в другой день).
Реклама — фиктивная переменная (1 — рекламное мероприятие проводилось, 0 — не проводилось).
1. Постройте модель множественной регрессии для команды Kansas City Royals, рассматривая в качестве зависимой переменной посещаемость матчей, а в качестве независимых — пять остальных переменных.
2. Сформулируйте уравнение множественной регрессии.
3. Объясните смысл коэффициентов в этом уравнении.
4. Являются ли объясняющие переменные статистически значимыми при уровне значимости, равном 0,05?
5. Вычислите скорректированный коэффициент Р.
6. Выполните анализ остатков и определите адекватность модели.
7. Удалите из модели любую объясняющую переменную, не имеющую статистически значимого вклада, используя метод выбора наилучшего подмножества. Повторите решение задач 2-6, используя наиболее экономную модель. Какую модель следует предпочесть? Объясните свой выбор.
8. Повторите решение задач 1-7 для команды Philadelphia Phillies.
9. Повторите решение задач 1-8 для команды Chicago Cubs.
10. Повторите решение задач 1-8 для команды Cincinnati Reds.
11. Матчи какого клуба на протяжении 2002 года сопровождались наиболее эффективной рекламой (с точки зрения посещаемости)?
14.44. Заголовок передовицы в газете The New York Times 4 марта 1990 года гласил: “Wine Equation Puts Some Noses Out of Joint” (“Математика повергает дегустаторов вина в смятение”). В статье говорилось, что Орли Ашенфельтер (Orley Ashenfelter), профессор экономики из Принстонского университета, разработал модель множественной регрессии, позволяющую предсказывать качество знаменитого французского бордо по количеству зимних осадков, средней температуре воздуха на протяжении сезона и количеству осадков в период сбора урожая. Уравнение множественной регрессии выглядит следующим образом:
Q = -12,145 + 0,00117WR + 0,6164ТМР- 0,00386HR,
где Q — логарифмический индекс качества, WR — количество зимних осадков (с октября по март), измеренное в миллиметрах, ТМР — средняя температура воздуха на протяжении сезона (с апреля по сентябрь), измеренная в градусах Цельсия, HR — количество осадков в период сбора урожая (август-сентябрь), измеренное в миллиметрах.
Представьте, что вы на вечеринке, потягиваете стакан вина, и вдруг ваша подружка сообщает о том, что прочитала в газете. Она просит вас объяснить ей смысл коэффициентов регрессии и высказать свое мнение об анализе, описанном в газете. Что вы скажете ей в ответ?
Отчеты
14.45. В задаче 14.23 мы разработали модель множественной регрессии для предсказания ежемесячных объемов продаж в магазинах спортивных товаров. Напишите отчет о своих исследованиях. Дополните свой отчет диаграммами и другой статистической информацией. Для создания и вставки таблиц и диаграмм используйте программу Microsoft Excel и пакет Microsoft Office. Подготовьте презентацию с помощью программы Power Point. ^SPORTING. XLS.
Применение Интернет
14.46. Зайдите на сайт www .prenhall. com/levine. Выберите ссылку Chapter 14 и щелкните на ссылке Internet exercises.
1 ГРУППОВОЙ ПРОЕКТ
ТР.14.1. Файл данных ^MUTUAL FUNDS . XLS содержит информацию о 13 переменных, характеризующих 259 взаимных фондов.
Фонд — название взаимного фонда.
Вид — вид акций, принадлежащих взаимному фонду: малые, средние и крупные компании.
Цель — цель фонда (быстрый или медленный рост капитала).
Активы — в млн. долл.
Комиссия — да или нет.
Издержки — издержки, понесенные взаимным фондом (в процентах от среднего объема чистых активов).
Доходность 2 001 — доходность за двенадцать месяцев 2001 г.
Трехлетняя 2001 гг. доходность — среднегодовая доходность за период с 1999 по
Пятилетняя 2001 гг. доходность — среднегодовая доходность за период с 1997 по
Оборачиваемость — уровень торговой активности фонда: очень низкий, низкий, средний, высокий, очень высокий.
Риск — уровень риска: очень низкий, низкий, средний, высокий, очень высокий. Лучший квартал — квартал с наивысшей доходность за период с 1997 по 2001 гг.
Худший квартал — квартал с наименьшей доходность за период с 1997 по 2001 гг.
Постройте модели множественной регрессии, позволяющие предсказать для фондов со средним и высоким уровнями риска годовой доход в 2001 году, среднегодовой доход за последние три года и среднегодовой доход за последние пять лет на основе информации об издержках, целях и уровне риска. Другие фонды из рассмотрения следует исключить. Выполните анализ остатков. Подробно объясните полученные результаты. Дополните свой отчет диаграммами и другой статистической информацией. Для создания и вставки таблиц и диаграмм используйте программу Microsoft Excel и пакет Microsoft Office. Подготовьте презентацию с помощью программы Power Point.
КОРПОРАЦИЯ MOUNTAIN STATES РО1
Корпорация Mountain States Potato Company выращивает картофель в восточном Айдахо. В процессе производства образуется побочный продукт, осадок на фильтре, который можно использовать для откорма скота. Недавно один из фермеров, занимающихся скотоводством, пожаловался на то, что скот не прибавляет в весе, и решил, что это происходит из-за корма, продаваемого компанией Mountain States Potato Company.
Все, что было известно об осадке, хранилось в регистрационных записях. Из них следовало, что процент твердого вещества в жидкости раньше колебался около 12%. В настоящее время эта величина колеблется около 11% . Что именно повлияло на количество осадка, осталось загадкой. Однако, поскольку заводу требовалось остановить потери осадка, необходимо было предпринимать срочные меры, чтобы вернуть процент твердого вещества к прежнему уровню.
Исследователи, взявшиеся за эту работу, попытались определить, какие факторы могут влиять на количество осадка. В итоге, они выделили шесть переменных.
Переменная Комментарий
ОСАДОК Процент осадка в фильтре.
PH Кислотность. Влияет на активность бактерий в фильтрующейся жидкости. При увеличении бактериальной активности вырабатываются органические кислоты, которые измеряются с помощью показателя pH.
НИЖНЕЕ ДАВЛЕНИЕ Давление вакуума под линией тока в гравитационном смесителе.
ВЕРХНЕЕ ДАВЛЕНИЕ Давление вакуума над линией тока в гравитационном смесителе.
ТОЛЩИНА Толщина осадка в барабане.
ПРЕДЕЛ Предельная скорость вращения барабана. Может отличаться от показателя СКОРОСТЬ. Измеряется секундомером.
СКОРОСТЬ Скорость вращения барабана. Измеряется секундомером.
Данные, измеренные на протяжении 20 дней, записаны в файле POTATO. XLS. Разработайте регрессионную модель для предсказания процентного количества осадка. Напишите отчет, содержащий ваши выводы, и сформулируйте рекомендации, как вернуть процент осадка к 12% .
ПРИМЕНЕНИЕ WEB
Примените свои знания о моделях множественной регрессии для прогнозирования объема продаж батончиков OmniPovuer.
Разрабатывая кампанию пробного маркетинга в сети бакалейных магазинов, отдел маркетинга компании OmniFoods обратился к консультантам корпорации Соп-nect2Coupons. Консультанты пришли к выводу, что предварительный анализ, выполненный специальной группой по организации пробного маркетинга, был неверен, поскольку использовал данные некорректного вида. Кроме того, консультанты заявили, что виртуальный маркетинг с помощью Интернет повысит уровень продаж батончиков OmniPower еще больше, чем предсказывает специальная группа. В ответ группа заявила, что их заявления были обоснованными, и сообщила руководству компании OmniFood, что между виртуальной рекламой в Интернет и объемом продаж батончиков нет непосредственной связи.
Проанализируйте данные и заявления, размещенные на Web-сайте www. prenhall. сот/ Springville/Omni_OmniPowerMB. html), и ответьте на следующие вопросы.
1. Кто говорит правду? Кто лжет? Кто говорит правду, но заблуждается? Аргументируйте свой ответ результатами статистического анализа.
2. Какой способ продажи следовало бы применить, если бы их количество было неограниченным? Обоснуйте свой ответ.
3. Какой способ продажи следовало бы применить, если бы можно было использовать только один способ? Обоснуйте свой ответ.
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
1. Hocking, R. R., “Developments in Linear Regression Methodology: 1959-1982”, Technometrics 25(1983): 219-250.
2. Marquardt, D. W. “You Should Standardize the Predictor Variables in Your Regression Models” (Discussion of “A Critique of Some Ridge Regression Methods”, by G.Smith and F.Campbell), Journal of the American Statistical Association 75 (1980): 87-91.
3. Microsoft Excel 2002 (Redmond, WA: Microsoft Corporation, 2001).
4. Neter, J., M. H. Kutner, C. J. Nachsheim, and W. Wasserman, Applied Linear Statistical Models, 4th ed. (Homewood, IL: Irwin, 1996).
5. Snee, R. D., “Some Aspects of Nonorthogonal Data Analysis, Part I. Developing Predition Equations”, Journal of Quality Technology 5 (1973): 67-79.
Глава 15
Анализ временньлс рядов
ПРИМЕНЕНИЕ СТАТИСТИКИ: прогнозирование доходов трех компаний
15.1. ПРОГНОЗИРОВАНИЕ В БИЗНЕСЕ
15.2. КОМПОНЕНТЫ КЛАССИЧЕСКОЙ МУЛЬТИПЛИКАТИВНОЙ МОДЕЛИ ВРЕМЕННЫХ РЯДОВ
15.3. СГЛАЖИВАНИЕ ГОДОВЫХ ВРЕМЕНИ6/Х РЯДОВ
Скользящие средние
Экспоненциальное сглаживание Процедуры Excel: сглаживание временных рядов
15.4. ВЫЧИСЛЕНИЕ ТРЕНДОВ С ПОМОЩЬЮ МЕТОДА НАИМЕНЬШИХ КВАДРАТОВ И ПРОГНОЗИРОВАНИЕ
Модель линейного тренда
Модель квадратичного тренда
Модель экспоненциального тренда Процедуры Excel: предварительная обработка данных
Процедуры Excel: метод наименьших квадратов
Выбор модели на основе разностей первого и второго порядка, а также относительных разностей
15.5. ВЫЧИСЛЕНИЕ ТРЕНДА С ПОМОЩЬЮ АВТОРЕГРЕССИИ И ПРОГНОЗИРОВАНИЕ
Процедуры Excel: добавление запаздывающих независимых переменных
Процедуры Excel: построение авторегрессионных моделей
15.6. ВЫБОР АДЕКВАТНОЙ МОДЕЛИ ПРОГНОЗИРОВАНИЯ
Анализ остатков
Измерение абсолютной и среднеквадратичной остаточных погрешностей
Принцип экономии
Сравнение четырех методов прогнозирования Процедуры Excel: вычисление среднего абсолютного отклонения (МАД)
15.7. ПРОГНОЗИРОВАНИЕ ВРЕМЕННО РЯДОВ НА ОСНОВЕ СЕЗОННЫХ ДАННЫХ
Прогнозирование месячных и временных рядов с помощью метода наименьших квадратов Процедуры Excel: создание фиктивных переменных для предсказания значений месячных и квартальных временных рядов
15.8. ИНДЕКСЫ
Индекс цен
Составные индексы цен
Некоторые популярные индексы цен Процедуры Excel: вычисление индексов
15.9. ЛОВУШКИ, СВЯЗАННЫЕ С АНАЛИЗОМ ВРЕМЕННЫХ РЯДОВ
СПРАВОЧНИК ПО EXCEL. ГЛАВА 15
ЧЕМУ ДОЛЖЕН НАУЧИТЬСЯ СТУДЕНТ
• Понимать, как и когда можно применять метод скользящих средних и экспоненциальное сглаживание временных рядов.
• Применять модели временных рядов, использующие линейные, квадратичные и экспоненциальные тренды.
• Понимать концепцию запаздывающих переменных и уметь применять авторегрессионные модели.
• Выбирать для прогнозирования наилучшие модели временных рядов.
• Создавать модели, позволяющие прогнозировать сезонные данные.
• Понимать что такое индексы цен, и видеть разницу между взвешенными и невзвешенными индексами.
ПРИМЕНЕНИЕ СТАТИСТИКИ
Прогнозирование доходов трех компаний
для каждой компании? Как оценить
тов прогнозирования?
Представьте себе, что вы работаете аналитиком в крупной финансовой компании. Чтобы оценить инвестиционные перспективы своих клиентов, вам необходимо предсказать доходы трех компаний. Для этого вы собрали данные о трех интересующих вас компаниях — Eastman Kodak, Cabot Corporation и Wal-Mart. Поскольку компании различаются по виду деловой активности, каждый временной ряд обладает своими уникальными особенностями. Следовательно, для прогнозирования необходимо применять разные модели. Как выбрать наилучшую модель прогнозирования иционные перспективы на основе результа-
ВВЕДЕНИЕ
В главах 12-14 описаны регрессионные модели, позволяющие прогнозировать отклик по значениям объясняющих переменных. В этой главе мы покажем, как с помощью этих моделей и других статистических методов анализировать данные, собранные на протяжении последовательных временных интервалов. В соответствии с особенностями каждой компании, упомянутой в сценарии, мы рассмотрим три альтернативных подхода к анализу временных рядов.
Обсуждение начинается с анализа ежегодных данных. Демонстрируются два метода сглаживания таких данных: скользящее среднее и экспоненциальное сглаживание (см. раздел 15.3). Затем демонстрируется процедура вычисления тренда с помощью метода наименьших квадратов (см. раздел 15.4) и более сложные методы прогнозирования (см. раздел 15.5). В заключение, эти модели распространяются на временные ряды, построенные на основе ежемесячных или ежеквартальных данных (см. раздел 15.7).
15.1. ПРОГНОЗИРОВАНИЕ В БИЗНЕСЕ
Поскольку экономические условия с течением времени изменяются, менеджеры должны прогнозировать влияние, которое эти изменения окажут на их компанию. Одним из методов, позволяющих обеспечить точное планирование, является прогнозирование (forecasting). Несмотря на большое количество разработанных методов, все они преследуют одну и ту же цель — предсказать события, которые произойдут в будущем, чтобы учесть их при разработке планов и стратегии развития компании.
Современное общество постоянно испытывает необходимость в прогнозировании. Например, чтобы выработать правильную политику, члены правительства должны прогнозировать уровни безработицы, инфляции, промышленного производства, подоходного налога отдельных лиц и корпораций. Чтобы определить потребности в оборудовании и персонале, директора авиакомпаний должны правильно предсказать объем авиаперевозок. Для того чтобы создать достаточное количество мест в общежитии, ад-
15.2. Компоненты классической мультипликативной модели временных рядов 985 министраторы колледжей или университетов хотят знать, сколько студентов поступят в их учебное заведение в следующем году.
Существуют два общепринятых подхода к прогнозированию: качественный и количественный. Методы качественного прогнозирования (qualitative forecasting methods) особенно важны, если исследователю недоступны количественные данные. Как правило, эти методы носят весьма субъективный характер.
Если статистику доступны данные об истории объекта исследования, следует применять методы количественного прогнозирования (quantitative forecasting methods). Эти методы позволяют предсказать состояние объекта в будущем на основе данных о его прошлом. Методы количественного прогнозирования разделяются на две категории: анализ временных рядов и методы анализа причинно-следственных зависимостей.
Временной ряд (time series) — это набор числовых данных, полученных в течение последовательных периодов времени.
Метод анализа временных рядов (time-series forecasting methods) позволяет предсказать значение числовой переменной на основе ее прошлых и настоящих значений.
Например, ежедневные котировки акций на Нью-Йоркской фондовой бирже образуют временной ряд. Другим примером временного ряда являются ежемесячные значения индекса потребительских цен, ежеквартальные величины валового внутреннего продукта и ежегодные доходы от продаж какой-нибудь компании.
Методы анализа причинно-следственных зависимостей (causal forecasting methods) позволяют определить, какие факторы влияют на значения прогнозируемой переменной. К ним относятся методы множественного регрессионного анализа с запаздывающими переменными, эконометрическое моделирование, анализ лидирующих индикаторов, методы анализа диффузионных индексов и других экономических показателей. Рассмотрение этих методов выходит за пределы нашей книги [6]. По этой причине основное внимание мы уделим методам прогнозирования на основе анализа временных рядов.
15.2. КОМПОНЕНТЫ КЛАССИЧЕСКОЙ МУЛЬТИПЛИКАТИВНОЙ
МОДЕЛИ ВРЕМЕННЫХ РЯДОВ
Основное предположение, лежащее в основе анализа временных рядов, состоит в следующем: факторы, влияющие на исследуемый объект в настоящем и прошлом, будут влиять на него и в будущем. Таким образом, основные цели анализа временных рядов заключаются в идентификации и выделении факторов, имеющих значение для прогнозирования.
Чтобы достичь этой цели, были разработаны многие математические модели, предназначенные для исследования колебаний компонентов, входящих в модель временного ряда. Вероятно, наиболее распространенной является классическая мультипликативная модель (classical multiplicative model) для ежегодных, ежеквартальных и ежемесячных данных. Для демонстрации классической мультипликативной модели временных рядов рассмотрим данные о фактических валовых доходах компании Wm.Wrigley Jr. Company за период с 1982 по 2001 годы (рис. 15.1).
Как видим, на протяжении 20 лет фактический валовой доход компании имел возрастающую тенденцию. Эта долговременная тенденция называется трендом (trend).
Тренд— не единственный компонент временного ряда. Кроме него, данные имеют циклический и нерегулярный компоненты. Циклический компонент (cyclical component) описывает колебание данных вверх и вниз, часто коррелируя с циклами деловой активности. Его длина изменяется в интервале от 2 до 10 лет. Интенсивность, или амплитуда, циклического компонента также не постоянна. В некоторые годы данные могут быть вы-
ше значения, предсказанного трендом (т.е. находиться в окрестности пика цикла), а в другие годы — ниже (т.е. быть на дне цикла). Любые наблюдаемые данные, не лежащие на кривой тренда и не подчиняющиеся циклической зависимости, называются иррегулярными или случайными компонентами (irregular, or random, component). Если данные записываются ежедневно или ежеквартально, возникает дополнительный компонент, называемый сезонным (seasonal component).
Рис. 15.1. График фактического валового дохода компании Wm.Wrigley Jr. Company (млн. долл, в текущих ценах) за период с 1982 по 2001 годы
Все компоненты временных рядов, характерных для экономических приложений, приведены в табл. 15.1.
Классическая мультипликативная модель временного ряда (classical multiplicative time-series model) утверждает, что любое наблюдаемое значение является произведением перечисленных компонентов. Если данные являются ежегодными, наблюдение У, соответствующее i-му году, выражается уравнением (15.1).
КЛАССИЧЕСКАЯ МУЛЬТИПЛИКАТИВНАЯ МОДЕЛЬ ВРЕМЕННОГО РЯДА ДЛЯ ЕЖЕГОДНЫХ ДАННЫХ
У(15.1) где Tt — значение тренда, С, — значение циклического компонента в i-м году, It — значение случайного компонента в i-м году.
Компонент Вид Определение Причины Продолжительность
Тренд Систематический Описывает долговременное возрастание или убывание данных Изменения технологии, населения, благосостояния, рыночных цен Несколько лет
Сезонный Систематический Описывает четко выраженные периодические колебания, проявляющиеся ежегодно Погодные условия, социальное поведение, религиозные обычаи В течение года (возможно также, месяц или квартал)
Циклический Систематический Повторяющиеся колебания, имеющие четыре фазы: пик (процветание), спад (рецессия), дно (депрессия) и подъем (восстановление или рост) Взаимодействие многочисленных факторов, влияющих на экономическую активность Как правило, с переменной интенсивностью на протяжении 2-10 лет
Нерегулярный Несистематический Случайные колебания временного ряда, возникающие после учета систематических эффектов Случайные колебания данных или непредвиденные события, например, забастовки, ураганы и наводнения Кратковременные и однократные
Если данные измеряются ежемесячно или ежеквартально, наблюдение У(, соответствующее i-му периоду, выражается уравнением (15.2).
КЛАССИЧЕСКАЯ МУЛЬТИПЛИКАТИВНАЯ МОДЕЛЬ ВРЕМЕННОГО РЯДА ДЛЯ ДАННЫХ С УЧЕТОМ СЕЗОННОГО КОМПОНЕНТА
У^^хЗ.хС.х/, (15.2)
где Т — значение тренда, S, — значение сезонного компонента в i-м периоде, С, — значение циклического компонента в i-м периоде, 7 — значение случайного компонента в i-м периоде.
На первом этапе анализа временных рядов строится график данных и выявляется их зависимость от времени. Сначала необходимо выяснить, существует ли долговременное возрастание или убывание данных (т.е. тренд), или временной ряд колеблется вокруг горизонтальной линии. Если тренд отсутствует, то для сглаживания данных можно применить метод скользящих средних или экспоненциального сглаживания (см. раздел 15.3), позволяющий создать искусственный долговременный тренд. Если же реальный тренд существует, открывается возможность применять разнообразные методы прогнозирования (см. раздел 15.4 и 15.5) на основе ежегодных данных. Методы краткосрочного прогнозирования описаны в разделе 15.7.
15.3. СГЛАЖИВАНИЕ ГОДОВЫХ ВРЕМЕННА/* РЯДОВ
В сценарии мы упомянули о компании Cabot Corporation. Имея штаб-квартиру в Бостоне, штат Массачусеттс, она специализируется на производстве и продаже химикатов, строительных материалов, продуктов тонкой химии, полупроводников и сжиженного природного газа. Компания имеет 39 заводов в 23 странах. Рыночная стоимость компании составляет около 1,87 млрд. долл. Ее акции котируются на Нью-Йоркской фондовой бирже под аббревиатурой СВТ (Mergent’s Handbook of Common Stocks, 2002).
Таблица 15.2. Доходы компании Cabot Corporation в 1982-2001 годах (млрд, долл.)
Год Доход Год Доход Год Доход
1982 1 587,7 1989 1 936,9 1996 1 865,2
1983 1 558,0 1990 1 684,7 1997 1 636,7
1984 1 752,0 1991 1 488,0 1998 1 652,8
1985 1 407,5 1992 1 562,2 1999 1 699,0
1986 1 309,9 1993 1 618,5 2000 1 698,0
1987 1 424,0 1994 1 686,6 2001 1 523,0
1988 1 676,6 1995 1 840,9
Источник: Moody's Handbook of Common Stocks, 1992 и Mergent’s Handbook of Common Stocks, 2002.
Доходы компании за указанный период приведены на рис. 15.2.
Рис. 15.2. Доходы компании Cabot Corporation (в миллиардах долларов) за период с 1982 по 2001 годы
Как видим, долговременная тенденция повышения доходов затемнена большим количеством колебаний. Таким образом, визуальный анализ графика не позволяет утверждать, что данные имеют тренд.
В таких ситуациях можно применить методы скользящего среднего или экспоненциального сглаживания.
Скользящие средние
Метод скользящих средних весьма субъективен и зависит от длины периода!/, выбранного для вычисления средних значений. Для того чтобы исключить циклические колебания, длина периода должна быть целым числом, кратным средней длине цикла.
Скользящие средние (moving averages) для выбранного периода, имеющего длину!/, образуют последовательность средних значений, вычисленных для последовательностей длины L. Скользящие средние обозначаются символами MA(L).
Предположим, что мы хотим вычислить пятилетние скользящие средние значения по данным, измеренным в течение п = 11 лет. Поскольку L = 5, пятилетние скользящие средние образуют последовательность средних значений, вычисленных по пяти последовательным значениям временного ряда. Первое из пятилетних скользящих средних значений вычисляется путем суммирования данных о первых пяти годах с последующим делением на пять:
МА(5) =
}; + у2 + у3 + у4 + у5
5
Второе пятилетнее скользящее среднее вычисляется путем суммирования данных о годах со 2-го по 6-й с последующим делением на пять:
М4(5) =
У, + У, + У4 + У5 + Y6
Этот процесс продолжается, пока не будет вычислено скользящее среднее для последних пяти лет.
МА(5) =
5
Работая с годовыми данными, следует полагать число L (длину периода, выбранного для вычисления скользящих средних) нечетным. В этом случае невозможно вычислить скользящие средние для первых (L-1)/2 и последних (L-l)/2 лет. Следовательно, при работе с пятилетними скользящими средними невозможно выполнить вычисления для первых двух и последних двух лет.
Год, для которого вычисляется скользящее среднее, должен находиться в середине периода, имеющего длину L. Если n=ll,aL = 5, первое скользящее среднее должно соответствовать третьему году, второе — четвертому, а последнее — девятому. Рассмотрим следующий пример.
ПРИМЕР 15.1. ВЫЧИСЛЕНИЕ ПЯТИЛЕТНИХ СКОЛЬЗЯЩИХ СРЕДНИХ
Предположим, что приведенные ниже данные представляют собой общие доходы (млрд. долл, в ценах 1995 года) агентства по прокату машин за 11-летний период с 1992 по 2002 годы.
4,0 5,0 7,0 6,0 8,0 9,0 5,0 2,0 3,5 5,5 6,5
Вычислите пятилетние скользящие средние для этого временного ряда.
РЕШЕНИЕ. Вычислим среднее значение для первых пяти лет.
К + У, + К + У4 + У, 4,0 + 5,0 + 7,0 + 6,0 + 8,0 30,0 МА(5) - —!-------2---=--------------------=----= 6,0.
5 5 5
Поставим это число в соответствие средней точке — третьему году.
Затем вычислим среднее значение по годам со 2-го по 6-й.
^4(5) - + r4 + + Y6 _ 5,0 + 7,0 + 6,0 + 8,0 + 9,0 _ 35,0 _ у Q
5 " 5 5 " ’ ’
Поставим это число в соответствие новой средней точке — четвертому году.
Продолжим вычисления по указанным правилам.
лхх/гч К,+У+У. ^Уь + у1 7,0 + 6,0 + 8,0 + 9,0 + 5,0 35,0 „ о
МА(5 ) = -2 1—= ~ = —— = 7,0.
5 5 5
YA+Y.+Yf- ь У7 + к _6,0 + 8,0 + 9,0 + 5,0 + 2,0 зо,о , „
МА(5) = — L- 7 8 = —— = 6,0.
5 5 5
+- У8 + У9 8,0 + 9,0 + 5,0 + 2,0 + 3,5 27,5 с е
МА(5) = * 7- =—— = 5,5.
МЛ(Ъ _ + Y& + Y9 +_ 9,0 + 5,0 + 2,0 + 3,5 + 5,5 _ 25,0 _
Ш1Ъ _ Г7+Г8 + Г, + ^ + ^, _ 5,0 + 2,0 + 3,5 + 5,5 + 6,5 22,5 л c
Каждое из этих средних значений центрируется по соответствующим точкам — пятому, шестому, седьмому, восьмому и девятому интервалам. Обратите внимание на то, что для первых двух и последних двух лет вычислить скользящее среднее невозможно.
На практике, чтобы избежать утомительных вычислений, для получения скользящих средних применяется программное обеспечение, например, программа Microsoft Excel. На рис. 15.3 показаны графики 3- и 7-летних скользящих средних, вычисленные для доходов компании Cabot Corporation за период с 1982 по 2001 годы с помощью программы Microsoft Excel.
zi-A-o: т....... с. ..г \ р _
1 'Год Доход 3-летние МД 7-летние МА
2 |1982 1587,7 #Н/Д
3J1983 1558,0 1632,7
4'<1984 1752,5 1572,7
~Г|1985 1407,5 1490,0
ЭД 1986 1309,9 1380,5
’К; 1987 1424,0 1470,2
Т 1988 1676,6 1679,2
9'1989 1936,9 1766,1
"ТО 1990 1684,7 1703,2
“2,1991 1488,0 1578,3
12 i 1992 1562,2 1556,2
IT 1993 1618,5 1622,4
_t4 51994 1686,6 1715,3
15:1995 1840,9 1797,6
IS; 1996 1865,2 1780,9
17 1997 1636,7 1718,2
1Г 1998 1652,8 1662,8
19 1999 1699,0 1683,3
20^2000 1698,0 1640,0
2001 1523,0 #Н/Д
#Н/Д
#Н/Д
#н/д
1530,9
1580,8
1598,9
1561,1
1583,2
1627,3
1664,8
1688,3
1678,0
1671,2
1694,7
1714,2
1725,6
1702,2
#Н/Д
#Н/Д
#н/д
Ц-Л-Н.J\ J ‘! к TZk
Скользящие средние для доходов
1980 1985 1990 - 1995 2000 2005
ГОД
Рис. 15.3. Графики 3- и 7-летних скользящих средних, вычисленные для доходов компании Cabot Corporation с помощью программы Microsoft Excel
Обратите внимание на то, что при вычислении трехлетних скользящих средних проигнорированы наблюдаемые значения, соответствующие первому и последнему годам. Аналогично при вычислении семилетних скользящих средних нет результатов для первых и последних трех лет.
Кроме того, как показано на рис. 15.3, семи летние скользящие средние намного больше сглаживают временной ряд, чем трехлетние. Это происходит потому, что семилетним скользящим средним соответствует более долгий период. К сожалению, чем больше длина периода, тем меньшее количество скользящих средних можно вычислить и представить на графике. Следовательно, больше семи лет для вычисления скользящих средних выбирать нежелательно, поскольку из начала и конца графика выпадет слишком много точек, что исказит форму временного ряда.
Экспоненциальное сглаживание
Для выявления долговременных тенденций, характеризующих изменения данных, кроме скользящих средних, применяется метод экспоненциального сглаживания (exponential smoothing). Этот метод позволяет также делать краткосрочные прогнозы (в рамках одного периода), когда наличие долговременных тенденций остается под вопросом. Благодаря этому метод экспоненциального сглаживания обладает значительным преимуществом над методом скользящих средних.
Метод экспоненциального сглаживания получил свое название от последовательности экспоненциально взвешенных скользящих средних. Каждое значение в этой последовательности зависит от всех предыдущих наблюдаемых значений. Еще одно преимущество метода экспоненциального сглаживания над методом скользящего среднего заключается в том, что при использовании последнего некоторые значения отбрасываются. При экспоненциальном сглаживании веса, присвоенные наблюдаемым значениям, убывают со временем, поэтому после выполнения вычислений наиболее часто встречающиеся значения получат наибольший вес, а редкие величины — наименьший. Несмотря на громадное количество вычислений, программа Microsoft Excel позволяет реализовать метод экспоненциального сглаживания.
Уравнение, позволяющее сгладить временной ряд в пределах произвольного периода времени i, содержит три члена: текущее наблюдаемое значение У, принадлежащее временному ряду, предыдущее экспоненциально сглаженное значение Et х и присвоенный вес W.
ВЫЧИСЛЕНИЕ ЭКСПОНЕНЦИАЛЬНО СГЛАЖЕННОГО ЗНАЧЕНИЯ В AM ПЕРИОДЕ ВРЕМЕНИ
E^Yl}
Е'^WY' + tl-WyE'.^ i = 2, 3, 4, ..., (15.3)
где Е — значение экспоненциально сглаженного ряда, вычисленное для Аго периода, Е, х — значение экспоненциально сглаженного ряда, вычисленное для (i-l)-ro периода, У, — наблюдаемое значение временного ряда в Ам периоде, W — субъективный вес, или сглаживающий коэффициент (0 < W < 1).
Выбор сглаживающего коэффициента, или веса, присвоенного членам ряда, является принципиально важным, поскольку он непосредственно влияет на результат. К сожалению, этот выбор до некоторой степени субъективен. Если исследователь хочет просто исключить из временного ряда нежелательные циклические или случайные колебания, следует выбирать небольшие величины W (близкие к нулю). С другой стороны, если временной ряд используется для прогнозирования, необходимо выбрать большой вес W (близкий к единице). В первом случае четко проявляются долговременные тенденции временного ряда. Во втором случае повышается точность краткосрочного прогнозирования.
На рис. 15.4 показаны графики экспоненциально сглаженного временного ряда (W = 0,50 и W= 0,25) для данных о доходах компании Cabot Corporation за период с 1982 по 2001 годы, построенные с помощью программы Microsoft Excel.
2 1982 1587.7
3“ 1983 1558,0
4 1984 1752,5
5 1985 1407,5
6 1986 1309,9
7 1987 1424,0
8 1988 1676,6
9 1989 1936,9
10 , 1990 1684,7
111 1991 1488,0
12'; 1992 1562,2
"13 1993 1618,5
14 1994 1686,6
15* 1995 1840,9
16: 1996 1865,2
17 1997 1636,7
18' 1998 1652,8
19' 1999 1699,0
20 ’ 2000 1698,0
IT] 2001 1523,0
1587,7 1572,9 1662,7 1535,1
1422,5 1423,2 1549,9 1743,4
1714,1 1601,0 1581,6 1600,1
1643,3 1742,1 1803,7 1720,2
1686,5
1692,7 1695,4 1609,2
1587,7
1580,3
1623,3
1569,4
1504,5
1484,4
1532,4
1633,6
1646,3
1606,8
1595,6
1601,3
1622,7
1677,2
1724,2
1702,3
1689,9
1692,2
1693,7
1651,0
Е j F , i, G ; ,Н i I j J L. К I Л
Экспоненциально сглаженные доходы компании Cabot Corporation
2500 - - - - -
500
0 -------------,------------,-----------,-----------,------------,
1980 1985 1990 Год 1995 2000 2005
Рис. 15.4. Графики экспоненциально сглаженного временного ряда (W — 0,50 и W = 0,25) для данных о доходах компании Cabot Corporation, построенные с помощью программы Microsoft Excel
Допустим, что коэффициент сглаживания равен 0,25. Первое наблюдаемое значение, равное У1982 = 1 587,7, одновременно является первым сглаженным значением Е1982 = 1 587,7. Используя значение временного ряда для 1983 года (У1983 = 1 558,0), получаем следующее сглаженное значение:
Е1983 = ТУУ1983 + (1-Ж)£1982 = 0,25x1 558,0 + 0,75x1 587,7= 1 580,3.
Сглаженное значение временного ряда для 1984 года:
Я1984 = ГИУ1984 + (1-W) £1983 = 0,25x1 752,5 + 0,75x1 580,3 = 1 623,3.
Сглаженное значение временного ряда для 1985 года:
Я1985 = И%985 + (1-ИЭ Я1984 = 0,25x1 407,5 + 0,75x1 623,3 = 1 569,4.
Этот процесс продолжается до тех пор, пока не будут сглажены все 19 значений вариационного ряда, показанных на рис. 15.4.
Экспоненциально сглаженное значение, полученное для i-ro временного интервала, можно использовать в качестве оценки предсказанного значения в (Н-1)-м интервале.
ПРОГНОЗИРОВАНИЕ ЗНАЧЕНИЙ ДЛЯ (Я-1)-ГО ИНТЕРВАЛА
(15.4)
Для предсказания доходов компании Cabot Corporation в 2002 году на основе экспоненциально сглаженного временного ряда, соответствующего весу ТУ = 0,25, можно использовать сглаженное значение, вычисленное для 2001 года. Из рис. 15.4 видно, что эта величина равна 1 651,0 млн. долл. (Насколько точен этот прогноз? Для проверки достаточно обратиться к справочнику Mergent's Handbook of Common Stocks или найти ответ в World Wide Web.)
Когда станут доступными данные о доходах компании в 2002 году, можно применить уравнение (15.3) и предсказать уровень доходов в 2003 году, используя сглаженное значение доходов в 2002 году.
^2002 = W%002 + (1-ИЭДю01
Иначе говоря, формулы для прогнозирования выглядят следующим образом.
Текущее сглаженное значение =
=W х (текущее наблюдаемое значение) + (1-W) х (предыдущее сглаженное значение)
Новый прогноз = W х (текущее наблюдаемое значение) + (1-VT) х (текущий прогноз)
txcel: сглаживание временных рядов •' ' •
Чтобы сгладить временной ряд, сначала необходимо усреднить исходные данные, а затем построить график сглаженного временного ряда, используя Мастер диаграмм. Эти задачи выполняются вручную, поскольку в надстройке PHStat2 нет процедур для решения задач, связанных с временными рядами.
Например, чтобы сгладить временной ряд доходов компании Cabot Corporation, приведенный в табл. 15.2, необходимо сделать следующее.
Вычисление скользящих средних. Для вычисления скользящих средних применяется простая формула =СРЗНАЧ (диапазон ячеек, содержащих данные по усредняемым годам}. В табл. 15.3 показан шаблон рабочего листа Cabot_MA для вычисления 3- и 7-летних скользящих средних доходов компании Cabot Corporation. Трех- и семилетние скользящие средние значения находятся в столбцах с и D соответственно. В строках, соответствующих годам, для которых скользящие средние не вычисляются (например, в строке 1), записывается специальное значение #н/д. Для реализации этого шаблона следует открыть рабочую книгу Chapter 15.xls на листе Cabot и выполнить следующие действия .
1. Ввести в ячейку С1 заголовок 3-летние ССЗ, а в ячейку D1 — заголовок 7-летние ССЗ.
2. Записать в ячейки С2, D2, D3 и D4 значение #н/д.
3. Ввести в ячейку сз формулу =срзнач (В2 :В4) и скопировать ее в ячейки, расположенные ниже вплоть до строки 2 0.
4. Ввести в ячейку D5 формулу -срзнач (В2 : В8) и скопировать ее в ячейки, расположенные ниже вплоть до строки 20. Записать в ячейки D19, D20, С21 и D21 значение #н/д.
Таблица 15.3. Шаблон рабочего листа Cabot_MA для вычисления 3- и 7-летних
скользящих средних
А В С D
1 Год Доход 3-летние МА 7-летние МА
2 1982 1587,7 #н/д #н/д
3 1983 1558,0 =СРЗНАЧ(В2:В4) #н/д
4 1984 1752,5 =СРЗНАЧ(ВЗ:В5) #н/д
5 1985 1407,5 =СРЗНАЧ(В4:В6) =СРЗНАЧ(В2:В8)
6 1986 1309,0 =СРЗНАЧ(В5:В7) =СРЗНАЧ(ВЗ:В9)
...
17 1997 1636,7 =СРЗНАЧ(В16:В18) =СРЗНАЧ(В14:В20)
18 1998 1652,8 =СРЗНАЧ(В17:В19) =СРЗНАЧ(В15:В21)
19 1999 1699,0 =СРЗНАЧ(В18:В20) #н/д
20 2000 1698,0 =СРЗНАЧ(В19:В21) #н/д
21 2001 1523,0 #н/д #н/д
Построение графика скользящих средних. Инструкции, позволяющие построить график скользящих средних временного ряда, рассмотренного выше, приведены в разделе ЕН.15.1.
Вычисление экспоненциально сглаженных величин. Для вычисления экспоненциально сглаженных значений при конкретном значении коэффициента W используется процедура Сервис^Анализ данных... ^Экспоненциальное сглаживание. Эта процедура генерирует экспоненциально сглаженные значения, используя фактор затухания 1- И/ Например, чтобы сгладить данные о доходах компании Cabot Corporation, приведенные в табл. 15.2 , используя коэффициенты сглаживания И/= 0,50 и W= 0,25, необходимо открыть рабочую книгу chapter 13.xls на листе Cabot2 и выполнить следующие действия.
1. Ввести в ячейку С1 заголовок ЭС(W = 0,50).
2. Выбрать команду Сервис^
Анализ данных.... Выбрать пункт Экспоненциальное сглаживание в списке Анализ данных и щелкнуть на кнопке ОК.
3. В диалоговом окне Экспоненциальное сглаживание (см. иллюстрацию) выполнить следующие действия.
3.1. Ввести в окне редактирования Входной интервал диапазон В2 :В21.
3.2. Ввести в окне редактирования Фактор затухания число 0,5.
3.3. Ввести в окне редактирования Выходной интервал диапазон С2 :С21.
3.4. Щелкнуть на кнопке ОК.
Процедура Анализ данных вставляет в ячейку С2 специальное значение #Н/Д. Каждая из формул экспоненциального сглаживания относится к году, указанному на следующей строке. Для того чтобы настроить этот столбец так, чтобы формулы сглаживания и соответствующие данные находилась в одной и той же строке, необходимо сделать следующее.
4. Выделить ячейку С2, а затем выбрать команду Правка ^Удалить....
5. В диалоговом окне Удаление ячеек (см. иллюстрацию) установить переключатель Удалить в положение Ячейки, со сдвигом вверх и щелкнуть на кнопке ОК.
б. Скопировать формулу из ячейки С20 в ячейку С21.
Для того чтобы создать новый столбец сглаживающего коэффициента И/= 0,25, как показано на рис. 15.4, необходимо повторить описанную выше процедуру, оставаясь на модифицированном рабочем листе.
1. Ввести в ячейку С1 заголовок эс (W = 0,25).
2. Выбрать команду Сервис^Анализ данных.... Выбрать пункт Экспоненциальное сглаживание в списке Анализ данных и щелкнуть на кнопке ОК.
3. В диалоговом окне Экспоненциальное сглаживание (см. иллюстрацию) выполнить следующие действия.
3.1. Ввести в окне редактирования Входной интервал диапазон В2 :В21.
3.2. Ввести в окне редактирования Фактор затухания число 0,7 5 (1-0,25 = 0,75).
3.3. Ввести в окне редактирования Выходной интервал диапазон D2 : D21.
3.4. Щелкнуть на кнопке ОК.
Как и в предыдущем случае, для настройки формул необходимо сделать следующее.
4. Выделить ячейку D2, затем выбрать команду ПравкамУдалить....
5. В диалоговом окне Удаление ячеек (см. иллюстрацию) установить переключатель Удалить в положение Ячейки, со сдвигом вверх и щелкнуть на кнопке ОК.
6. Скопировать формулу из ячейки D20 в ячейку D21.
Построение графика экспоненциально сглаженных величин. В качестве источника для построения графика используется рабочий лист, содержащий экспоненциально сглаженные величины. Инструкции, позволяющие создать график экспоненциально сглаженных величин, изложены в разделе ЕН.15.2.
Chapter 15.xls
Графики сглаженных величин для доходов компании Cabot Corporation, изображенные на рис. 15.3 и 15.4, содержатся на листе Рис15.3 и Рис15.4 в книге Chapter 15 . xls.
Изучение основ
15.1. Предположим, что для прогнозирования доходов компании используется метод экспоненциального сглаживания временного ряда. Какой прогнозируемый доход получит компания в следующем году, если сглаженное значение дохода в этом году равно 32,4 млн. долл, в ценах 1995 года?
15.2. Предположим, что для сглаживания временного ряда используются 9-летние скользящие средние.
1. Какой год должен находиться в середине интервала, используемого для вычисления первого скользящего среднего?
2. Сколько лет будет проигнорировано при вычислении всех 9-летних скользящих средних?
15.3. Предположим, что для прогнозирования доходов компании используется метод экспоненциального сглаживания временного ряда. Кроме того, коэффициент сглаживания равен W = 0,20, а£2М2 = 0,20 х 12,1 + 0,80 х 9,4.
1. Чему равно сглаженное значение временного ряда для 2002 года?
2. Чему равно сглаженное значение временного ряда для 2003 года, если наблюдаемое значение в этом году равно 11,5 млн. долл, в ценах 1995 года?
Применение понятий
15.4. Приведенные ниже данные представляют собой количество сотрудников (тыс. чел.) в нефтедобывающей компании за период с 1983 по 2002 годы. ^OILSUPP. XLS.
Год Количество сотрудников (тыс. чел.) Год Количество сотрудников (тыс. чел.)
1983 1,45 1993 1,73
1984 1,55 1994 1,77
1985 1,61 1995 1,90
1986 1,60 1996 1,82
1987 1,74 1997 1,65
1988 1,92 1998 1,73
1989 1,95 1999 1,88
1990 2,04 2000 2,00
1991 2,06 2001 2,08
1992 1,80 2002 1,88
1. Постройте график временного ряда.
2. Вычислите 3-летние скользящие средние и постройте их график.
3. Примените метод экспоненциального сглаживания с коэффициентом W = 0,50 и постройте график.
4. Чему равно сглаженное значение прогноза в 2003 году?
5. Примените метод экспоненциального сглаживания с коэффициентом W = 0,25 и постройте график.
6. Чему равно сглаженное значение прогноза в 2003 году в задаче 5?
7. Сравните решения задач 4 и 6.
15.5. Данные, приведенные в файле ^FOODTIME. XLS, представляют собой объемы продаж (млн. долл.) в пищевой компании за период с 1977 по 2002 годы в ценах 1995 года.
1. Постройте график временного ряда.
2. Вычислите 7-летние скользящие средние и постройте их график.
3. Примените метод экспоненциального сглаживания с коэффициентом W = 0,25 и постройте график.
4. Чему равно сглаженное значение прогноза в 2003 году?
5. Примените метод экспоненциального сглаживания с коэффициентом W = 0,50 и постройте график.
6. Чему равно сглаженное значение прогноза в 2003 году в задаче 5?
7. Сравните решения задач 4 и 6.
15.6. Данные, приведенные в файле ^LOWERFIFTHINCOME . XLS, представляют собой доходы 20% беднейших семей в США за период с 1980 по 2002 годы (www .census.gov).
1. Постройте график временного ряда.
2. Вычислите 3-летние скользящие средние и постройте их график.
3. Примените метод экспоненциального сглаживания с коэффициентом W = 0,50 и постройте график.
4. Чему равно сглаженное значение прогноза в 2002 году?
5. Примените метод экспоненциального сглаживания с коэффициентом W— 0,25 и постройте график.
6. Чему равно сглаженное значение прогноза в 2002 году в задаче 5?
7. Сравните решения задач 4 и 6.
8. Зайдите на Web-сайт www. census . com и найдите фактическое значение дохода в 2000 году в таблице Министерства торговли США (U. S. Department of Commerce). Сравните эту величину с предсказанными значениями из задач 4 и 6. Объясните различия между ними.
9. Что можно сказать о тренде дохода 20% беднейших семей в США за период с 1980 по 2002 гг.?
15.7. Приведенные ниже данные представляют собой ставки казначейских векселей в США за период с 1991 по 2002 годы (www . f ederalreserve . gov).
Wtreasury.xls.
Год Ставка
1991 5,42
1992 3,45
1993 3,02
1994 4,29
1995 5,51
1996 5,02
1997 5,07
1998 4,81
1999 4,66
2000 5,66
Источник: www.federalreserve.gov
1. Постройте график временного ряда.
2. Вычислите 3-летние скользящие средние и постройте их график.
3. Примените метод экспоненциального сглаживания с коэффициентом W = 0,50 и постройте график.
4. Чему равно сглаженное значение прогноза в 2001 году?
5. Примените метод экспоненциального сглаживания с коэффициентом W = 0,25 и постройте график.
6. Чему равно сглаженное значение прогноза в 2001 году в задаче 5
7. Сравните решения задач 4 и 6.
15.8. Приведенные ниже данные представляют собой ставки трехмесячных депозитных сертификатов в США за период с 1991 по 2002 годы. ^CDRATE . XLS.
Годы Ставки
1991 5,83
1992 3,68
1993 3,17
1994 4,63
1995 5,92
1996 5,39
1997 5,62
1998 5,47
1999 5,33
2000 6,46
2001 3,71
2002 1,73
1. Постройте график временного ряда.
2. Вычислите 3-летние скользящие средние и постройте их график.
3. Примените метод экспоненциального сглаживания с коэффициентом W = 0,50 и постройте график.
4. Чему равно сглаженное значение прогноза в 2003 году?
5. Примените метод экспоненциального сглаживания с коэффициентом W = 0,25 и постройте график.
6. Чему равно сглаженное значение прогноза в 2003 году в задаче 5?
7. Сравните решения задач 4 и 6.
15.4. ВЫЧИСЛЕНИЕ ТРЕНДОВ С ПОМОЩЬЮ МЕТОДА НАИМЕНЬШИХ КВАДРАТОВ И ПРОГНОЗИРОВАНИЕ
Среди компонентов временного ряда чаще других исследуется тренд. Именно тренд позволяет делать краткосрочные и долгосрочные прогнозы. Как показано на рис. 15.1, для выявления долговременной тенденции изменения временного ряда обычно строят график, на котором наблюдаемые данные (значения зависимой переменной) откладываются на вертикальной оси, а временные интервалы (значения независимой переменной)— на горизонтальной. В этом разделе мы опишем процедуру выявления линейного, квадратичного и экспоненциального тренда с помощью метода наименьших квадратов.
Модель линейного тренда
Модель линейного тренда (linear trend model)
У, = p0 + piX+e, является простейшей моделью, применяемой для прогнозирования.
УРАВНЕНИЕ ЛИНЕЙНОГО ТРЕНДА
Y^b.+b.X,. (15.5)
Напомним, что метод линейного регрессионного анализа используется для вычисления выборочного наклона и сдвига Ьо. Вычислив уравнение Yt = + Ь]Х1 , в него можно подставлять значения X, чтобы определять отклик У.
Если при аппроксимации временного ряда с помощью метода наименьших квадратов первое наблюдение расположить в начале координат, поставив его в соответствие значению X = 0, интерпретация коэффициентов упрощается. Все последующие наблюдения получают целочисленные номера: 1, 2, 3, ..., так что n-е (последнее) наблюдение будет иметь номер п-1. Например, если временной ряд записывается на протяжении 20 лет, первый год обозначается цифрой 0, второй— цифрой 1, третий— цифрой 2 и так далее, а последний (20-й) год — числом 19.
В сценарии “Применение статистики” была упомянута компания Wm. Wrigley Jr. Company co штаб-квартирой в г. Чикаго, штат Нью-Йорк. Эта компания является крупнейшим производителем жевательной резинки в США, управляет 12 фабриками и продает свою продукцию в более чем 100 странах. Акции компании котируются на Нью-Йоркской фондовой бирже под аббревиатурой WWY. Рыночная стоимость компании составляет 13 млрд. долл. (Mergent’s Handbook of Common Stocks, 2002). Фактические доходы компании Wm. Wrigley Jr. Company в 1982-2001 годах приведены в табл. 15.4 и на
рис. 15.5. Затем с помощью индекса потребительских цен (Consumer Price Index — CPI), вычисляемого Бюро статистики Министерства труда США (Bureau of Labor Statistics), фактические доходы были преобразованы в реальные. Для этого следует умножить величину фактического дохода на коэффициент CPI/100. График реального дохода в ценах 1982-1984 гг. и график фактических доходов изображены на рис. 15.5.
Таблица 15.4. Фактические доходы компании Wm. Wrigley Jr. Company в 1982-2001 годах ^WRIGLEY. XLS
Год Доходы Год Доходы
1982 581,5 1992 1 301,3
1983 581,7 1993 1 440,4
1984 590,5 1994 1661,3
1985 620,3 1995 1 769,7
1986 699,0 1996 1 850,6
1987 781,1 1997 1 954,2
1988 891,4 1998 2 023,4
1989 992,9 1999 2 079,2
1990 1 110,6 2000 2 145,7
1991 1 148,9 2001 2 429,6
Источник: Moody's Handbook of Common Stocks, 1992 и Mergent's Handbook of Common Stocks, 2002. Публикуется с разрешения Службы финансовой информации (Financial Information Services) подразделения компании Financial Communications Company, Inc.
1 а ; Год в _ Код С. __ . ‘ Фактический доход D ' CPI-U Е Реальный : доход
2 1982 0 581,5 96,5 602,59
3" 1983 1 581,7 99,6 584,04
4 1984 2 590,5 103,9 568,33
5 1985 3 620,3 107,6 576,49
' 6 1986 4 699,0 109,6 637,77
7" 1987 5 781,1 113,6 687,59
8 ' 1988 6 891,4 118,3 753,51
9 1989 7 992,9 124,0 800,73
ю’ 1990 8 1110,6 130,7 849,73
ii 1991 9 1148,9 136,2 843,54
12 1992 10 1301,3 140,3 927,51
13 1993 11 1440,4 144,5 996,82
14 1994 12 1661,3 148,2 1120,99
Ts" 1995 13 1769,7 152.4 1161,22
16- 1996 14 1850,6 156,9 1179,48
17 1997 15 1954,2 160,5 1217,57
18 1998 16 2023,4 163,0 1241,35
19 1999 17 2079,2 166,6 1248,02
20 2000 18 2145,7 172,2 1246,05
21 ’ 2001 19 2429,6 177,1 1371,88
F
3000
2500
2000
5
500
1500 -
1000 -
Фактический и реальный доходы коипании Wm. Wrigley Jr.
Фактический доход
-♦—Реальный доход
0 — 1980
1985
1990 1995
Год
2000
2005
G
H
К
L
M
Рис. 15.5. Фактические и реальные доходы компании Wm. Wrigley Jr. Company в 1982-2001 годах (график построен с помощью программы Microsoft Excel)
Обозначим последовательные значения переменной X с помощью целых чисел от 0 до 19, а затем обработаем модифицированные данные с помощью программы Microsoft Excel. Как показано на рис. 15.6, уравнение линейной регрессии имеет следующий вид.
Yt = 498,656 + 45,485Хг,
где началом координат является 1982 год, а шаг переменной X равен одному году.
. А . . | В j. . . С 1 Модель линейного тренда для реального годового дохода . . 0 Е : F G
3 Регрессионная статистика
4 Множественный R 0,98391
5 R-квадрат 0,96807
6 Нориированный R-квадрат 0,96630
7 .Стандартная ошибка 50,20535
6 Наблюдения 20
10 Дисперсионный анализ
11 df SS MS F Значимость F
12 Регрессия 1 1375784,16173 1375784,16173 545,82110 6,48317Е-15
13 Остаток 18 45370,38740 2520,57708
14 Итого 19 1421154,54913
16
J6 Коэффициенты Стандартная ошибка t-статистика Р-значение Нижние 95% Верхние 95%
17 Y-пересечение 18 Код 498,65625 45.48459 21,63578 1,94688 23,04775 23,36281 8.21605Е-15 6.48317Е-15 453,20111 41,39435 544,11138 49,57484
Рис. 15.6. Модель линейной регрессии для предсказания реального дохода компании Wm. Wrigley Jr. Company по курсу 1982-1984 гг. (построена с помощью программы Microsoft Excel)
Регрессионные коэффициенты интерпретируются следующим образом.
• Сдвиг Ьо = 498,656 представляет собой предсказанное среднее значение реальных доходов (в ценах 1982-1984 гг.) компании Wm. Wrigley Jr. Company в 1982 году.
• Наклон = 45,485 представляет собой предсказанное уменьшение реальных доходов компании в среднем на 45,485 млрд. долл, в год.
Чтобы выполнить проекцию тренда реальных доходов компании Wm. Wrigley Jr. Company на 2002 год, следует подставить величину Х21 = 20 (номер 2002 года) в уравнение. В итоге получаем такой прогноз.
Yt = 498,656 + 45,485 х 20 = 1408,356 млрд. долл, в ценах 1982-1984 гг.
Линия тренда и временной ряд реальных доходов показаны на рис. 15.7.
Анализ рис. 15.7 показывает, что на протяжении ряда лет доходы компании линейно возрастали. Скорректированный коэффициент т* равен 0,966. Следовательно, все изменения реальных доходов хорошо описываются линейным трендом. Возникает вопрос: а нельзя ли выбрать еще более точную модель? Для ответа на него рассмотрим еще две модели — квадратичную и экспоненциальную.
Рис. 15.7. Линия тренда реальных доходов компании Eastman Kodak, вычисленная с помощью метода наименьших квадратов и программы Microsoft Excel
Модель квадратичного тренда
Модель квадратичного тренда (quadratic trend model), или полиномиальная модель второй степени
1>Р0+РЛ + М2+е;
является простейшей нелинейной моделью, применяемой для прогнозирования.
УРАВНЕНИЕ КВАДРАТИЧНОГО ТРЕНДА ^=Z>O+^X,.+Z>2X2,
(15.6)
где Ьо — оценка сдвига отклика Y, Ь, — оценка линейного эффекта, Ъ2 — оценка квадратичного эффекта.
Снова применим программу Microsoft Excel. Как показано на рис. 15.8, уравнение линейной регрессии имеет следующий вид.
У = 513,052 + 40,686Х,. + 0,253Х2,
где началом координат является 1982 год, а шаг переменной X равен одному году.
Чтобы применить квадратичную модель для прогнозирования, необходимо подставить величину Х21 = 20 (номер 2002 года) в уравнение регрессии. В итоге получаем такой прогноз.
Y, = 513,052 + 40,686x20 + 0,253х202 =1427,972 млрд. долл.
График квадратичного тренда и временной ряд реальных доходов показаны на рис. 15.9.
Рис. 15.8. Модель квадратичной регрессии для предсказания реального дохода компании Wm. Wrigley Jr. Company в ценах 1982-1984 гг. (построена с помощью программы Microsoft Excel)
Рис. 15.9. График квадратичного тренда реальных доходов компании Wm. Wrigley Jr. Company, вычисленный с помощью метода наименьших квадратов и программы Microsoft Excel
Этот график аппроксимирует временной ряд почти так же, как и линейный тренд. Скорректированный коэффициент г2 равен 0,965, а ^-статистика, учитывающая вклад квадратичного эффекта, равна 0,66 (соответствующеер-значение равно 0,521).
Модель экспоненциального тренда
Если временной ряд является возрастающим, а относительное изменение данных — постоянным, можно применять модель экспоненциального тренда (exponential trend model).
МОДЕЛЬ ЭКСПОНЕНЦИАЛЬНОГО ТРЕНДА
у, =PoPi4 , (15.7)
где ро — сдвиг, (р - 1)х100% — ежегодный уровень роста (%).
Модель экспоненциального тренда совершенно не похожа на модель линейной регрессии. Для того чтобы свести ее к линейной, следует применить логарифмическое преобразование по основанию 10 . Тогда уравнение экспоненциального тренда будет выглядеть следующим образом.
ПРЕОБРАЗОВАННАЯ МОДЕЛЬ ЭКСПОНЕНЦИАЛЬНОГО ТРЕНДА
log^ = log(pup-ve) = = log ₽,, + log р,' + log г, = (15.8)
= log Р„ + A, log Pj + log 8,.
Поскольку уравнение (15.8) является линейным, к нему можно применить метод наименьших квадратов. Применение логарифмического преобразования к зависимой и независимой переменным приводит к следующему уравнению.
УРАВНЕНИЕ ЭКСПОНЕНЦИАЛЬНОГО ТРЕНДА
logf = 6()(15.9, а)
где Ьо — оценка величины log Ро, т.е. 10л" = р() , Ь1 — оценка величины log рр т.е. 10л‘ = р,. Таким образом,
WoPf1, (15.9,6)
где I р] -11 х100% — ежегодный уровень роста (%).
Модель экспоненциальной регрессии для предсказания реального дохода компании Wm. Wrigley Jr. в ценах 1982-1984 гг., построенная с помощью программы Microsoft Excel, приведена на рис. 15.10.
Используя уравнение (15.9, а) и результаты, приведенные на рис. 15.10, получаем выражение
log = 2,7405 + 0,02205Х ,
где начало координат соответствует 1982 году, а шаг изменения переменной X равен одному году.
См. приложение А.
7 А В Модель экспоненциального тренда для реальных доходов С D Е F G
-з г г 8 Регрессионная статистика Множественный R 0,98085 R-квадрат 0,96206 Нормированный R-квадрат 0,95995 Стандартная ошибка 0,02662 Наблюдения : 20
9 10 Дисперсионный анализ
11 df SS MS F Значимость F
12 13 Регрессия Остаток 1 18 0,32342 0,01276 0,32342 456,40935 0,00071 3,07535Е-14
14 Итого 19 0,33617
15
16 Коэффициенты Стандартная ошибка t-статистика Р-значение Нижние 95% Верхние 9^%
17 18’ Y-пересечение Код 2,740515 0,022053 0,011472 0,001032 238,893442 5.71321E33 21,363739 ЗД7535Е-14 2,71641 0,01988 2,76462 0,02422
Рис. 15.10. Модель экспоненциальной регрессии для предсказания реального дохода компании Wm. Wrigley Jr. в ценах 1982-1984 гг. (построена с помощью программы Microsoft Excel)
Величины Ро и Pj вычисляются путем потенцирования регрессионных коэффициентов Ъо и Ьг (т.е. путем применения операции, обратной к логарифмированию. — Прим.ред).
Ро=Ю2 74О5 = 550,174 , р( = io002205 = 1,052 .
Таким образом, применяя формулу (15.9, б), получаем уравнение экспоненциального тренда
Y =550,174x1,052х' ,
где, как и прежде, начало координат соответствует 1982 году, а шаг изменения переменной X равен одному году.
Параметр сдвига р0 = 550,174 млрд. долл, представляет собой прогнозную величину реального дохода компании в базовом 1982 году. Величина (р1-1)х100% = 5,2% является оценкой темпа ежегодного роста реальных доходов компании Wm. Wrigley Jr. Company.
Чтобы применить экспоненциальную модель для прогнозирования, необходимо подставить величину Х21 = 20 (номер 2002 года) в уравнение (15.9, а) или (15.9,6). В итоге получаем такой прогноз.
log Y, = 2,7405 + 0,02205 х 20 = 3,1815 ,
Y. = 103,1815 = 1 518,798 млрд. долл.
График экспоненциального тренда и временной ряд реальных доходов показаны на рис. 15.11.
Рис. 15.11. График экспоненциального тренда реальных доходов компании Wm. Wrigley Jr. Company, вычисленный с помощью метода наименьших квадратов и программы Microsoft Excel
Экспоненциальная модель аппроксимирует временной ряд почти так же, как линейная и квадратичная модель. Скорректированный коэффициент г2 равен 0,960, в то время как для линейной модели этот коэффициент равен 0,966.
Процедуры Excel: предварительная обработка данных
Для применения метода наименьших квадратов исходные данные необходимо предварительно обработать. Эту процедуру приходится делать вручную, поскольку в надстройке PHStat2 эта возможность не предусмотрена.
Добавление закодированной переменной X. Для того чтобы добавить закодированную переменную X, вставьте в рабочий лист столбец, содержащий целые числа, начиная с нуля. Такие числа лучше всего вставлять с помощью команды Правка^Заполнить^Прогрессия.... Например, чтобы построить тренд фактических доходов компании Wm. Wrigley Jr. Company, представленных в табл. 15.4, необходимо открыть рабочую книгу Wrigley .xls на листе Данные и выполнить следующие действия.
1. Выделить ячейку В1 и выбрать команду Вставка ^Столбцы.
2. В новом (пустом) столбце в записать в ячейку В1 строку коды.
3. Ввести в ячейку В2 число 0 и снова выделить ее.
4. Выбрать команду Правка^Заполнить^ Прогрессия....
5. В диалоговом окне Прогрессия (см. иллюстрацию) сделать следующее.
5.1. Установить переключатель Расположение в положение По столбцам, а переключатель Тип -в положение Арифметическая.
5.2. Ввести в окне редактирования Шаг число 1.
5.3. Ввести в окне редактирования Предельное значение число 19.
5.4. Щелкнуть на кнопке ОК.
Для решения аналогичных задач следует задать другое предельное значение прогрессии.
Добавление переменной для вычисления квадратичного тренда. Чтобы добавить переменную для квадратичного тренда, вставьте в рабочий лист столбец, содержащий формулы, возводящие значение закодированной переменной Хв квадрат. Например, чтобы добавить переменную для квадратичного тренда фактических доходов компании Wm. Wrigley Jr. Company, представленных в табл. 15.4, необходимо открыть рабочую книгу Chapter 15. xls на листе Wrigley и выполнить следующие действия.
1. Выделить ячейку С1 и выбрать команду Вставка ^Столбцы.
2. В новом (пустом) столбце С записать в ячейку С1 строку Квадраты.
3. Ввести в ячейку С2 формулу =В2Л2 и скопировать ее во все нижележащие ячейки вплоть до строки 21.
Добавление переменной для вычисления экспоненциального тренда. Чтобы добавить переменную для экспоненциального тренда, вставьте в рабочий лист столбец, содержащий формулы, вычисляющие логарифм значений закодированной переменной X. Например, чтобы добавить переменную для экспоненциального тренда фактических доходов компании Wm. Wrigley Jr. Company, представленных в табл. 15.4, необходимо открыть рабочую книгу Wrigley.xls на листе Реальный_доход и выполнить следующие действия.
1. Выделить ячейку D1 и выбрать команду Вставка^Столбцы.
2. В новом (пустом) столбце Dзаписать в ячейку С1 строку LoglO.
3. Ввести в ячейку D2 формулу -LOGIC (С2) и скопировать ее во все нижележащие ячейки вплоть до строки 21.
4. Если рабочий лист ранее уже настраивался для вычисления квадратичного тренда, введите в ячейку Е1 строку Logic, а в ячейку Е2 - формулу -LOGIC (D2) и скопируйте эту формулу во все ячейки вплоть до строки 21.
Процедуры Excel: метод наименьших квадрате
Чтобы применить метод наименьших квадратов и построить диаграмму разброса, следует выполнить одну из процедур PHStatsRegressionSSimple Linear Regression... (PHStatsPerpeccnns Простая линейная регрессия...) или Сервис^Анализ данных... =>Регрессия, описанных в главах 12 и 13. Надстройка PHStat2 выполняет эти действия автоматически.
Применение Excel в сочетании с надстройкой PHStat2
Вычисление линейного тренда. Для построения линейного тренда следует выполнить процедуру PHStat2SRegressionSSimple Linear Regression.... Например, чтобы построить линейный тренд реальных доходов компании Wm. Wrigley Jr. Company, представленных в табл. 15.4, необходимо открыть рабочую книгу Chapter 15 . xls на листе Wrigley_MHK и выполнить следующие инструкции.
1. Выбрать команду PHStats Regressions Simple Linear Regression....
2. В диалоговом окне Simple Linear Regression сделать следующее.
2.1. Ввести в диалоговом окне Y Variable Cell Range (Входной интервалу) диапазон ячеек Е1 :Е21.
2.2. Ввести в диалоговом окне X Variable Cell Range (Входной интервал X) диапазон ячеек В1 :В21.
2.3. Установить флажок First cells in both ranges contain a label (Первые ячейки в обоих диапазонах содержат метки).
2.4. Ввести в окне редактирования Confidence level for regression coefficients (Доверительный уровень для коэффициентов регрессии) число 95.
2.5. Установить все четыре флажка в разделе Regression Tool Output Option (Параметры регрессионного анализа).
2.6. Ввести в диалоговом окне Title (Заголовок) название диаграммы.
2.7. Щелкнуть на кнопке ОК.
Чтобы построить график тренда и отобразить точки временного ряда, следует выполнить команду Диаграмма^Добавить линию тренда..., а затем, находясь в диалоговом окне Линия тренда, щелкнуть на корешке вкладки Тип и выбрать пункт Линейная в группе Построение линии тренда (аппроксимация и сглаживание). После этого необходимо щелкнуть на корешке вкладки Параметры, выбрать в группе Название аппроксимирующей (сглаженной) кривой пункт Автоматическое и щелкнуть на кнопке ОК.
Вычисление квадратичного тренда. Для вычисления квадратичного тренда следует выполнить процедуру PHStats Regressions Multiple Regression... и вызвать Мастер диаграмм. Например, чтобы построить квадратичный тренд реальных доходов компании Wm. Wrigley Jr. Company, необходимо открыть рабочую книгу Chapter 15.xls на листе Wrigley_MHK и выполнить такие инструкции.
1. Выбрать команду PHStatsRegressionSMultiple Regression....
2. В диалоговом окне Multiple Regression сделать следующее.
2.1. Ввести в диалоговом окне У Variable Cell Range (Входной интервал У) диапазон ячеек Е1:Е21.
2.2. Ввести в диалоговом окне X Variable Cell Range (Входной интервал X) диапазон ячеек Bl: С21 (диапазон ячеек, содержащих переменные Коды и Квадраты).
2.3. Установить флажок First cells in both ranges contain a label (Первые ячейки в обоих диапазонах содержат метки).
2.4. Ввести в окне редактирования Confidence level for regression coefficients (Доверительный уровень для коэффициентов регрессии) число 95.
2.5. Установить все четыре флажка в разделе Regression Tool Output Option (Параметры регрессионного анализа).
2.6. Ввести в диалоговом окне Title (Заголовок) название диаграммы.
2.7. Щелкнуть на кнопке ОК.
Чтобы построить диаграмму разброса и график тренда, следует воспользоваться процедурой, описанной в разделе ЕН.15.3, слегка изменив ее инструкции.
• На втором этапе диалога (п. 2.1) ввести в окно редактирования Диапазон данных диапазоны Al: А21, El: Е21. Не забудьте поставить запятую между диапазонами (пробел не нужен!).
• Находясь на рабочем листе, содержащем диаграмму разброса, выбрать команду Диаграмма^ Добавить линию тренда....
• Находясь в диалоговом окне Линия тренда, щелкнуть на корешке вкладки Тип и выбрать вариант Полиномиальная в группе Построение линии тренда (аппроксимация и сглаживание).
• Щелкнуть на корешке вкладки Параметры и установите переключатель Название аппроксимирующей (сглаженной) кривой в положение Автоматическое.
• Щелкнуть на кнопке ОК.
Вычисление экспоненциального тренда. Для вычисления экспоненциального тренда следует выполнить процедуру PHStat^Regression^Simple Linear Regression.... Например, чтобы построить экспоненциальный тренд реальных доходов компании Wm. Wrigley Jr. Company, необходимо открыть рабочую книгу Chapter 15. xls на листе Wrigley_MHK и следовать инструкциям.
1. Выбрать команду PHStat^Regression^Simple Linear Regression....
2. В диалоговом окне Simple Linear Regression сделать следующее.
2.1. Ввести в диалоговом окне Y Variable Cell Range (Входной интервалу) диапазон ячеек Fl : F21.
2.2. Ввести в диалоговом окне X Variable Cell Range (Входной интервал X) диапазон ячеек В1:В21.
2.3. Установить флажок First cells in both ranges contain a label (Первые ячейки в обоих диапазонах содержат метки).
2.4. Ввести в окне редактирования Confidence level for regression coefficients (Доверительный уровень для коэффициентов регрессии) число 95.
2.5. Установить все четыре флажка в разделе Regression Tool Output Option (Параметры регрессионного анализа).
2.6. Ввести в диалоговом окне Title (Заголовок) название диаграммы.
2.7. Щелкнуть на кнопке ОК.
Чтобы построить диаграмму разброса и линию регрессии, следует воспользоваться процедурами, описанными в разделе ЕН.15.4 и ЕН.15.5.
Применение Excel
Вычисление линейного тренда. Чтобы вычислить линейный тренд и построить диаграмму разброса, следует выполнить процедуру Сервис^Анализ данных... ^Регрессия. Например, чтобы построить линейный тренд реальных доходов компании Wm. Wrigley Jr. Company, необходимо открыть рабочую книгу Chapter 15. xls на листе Wrigley_MHK и следовать инструкциям.
1. Выполнить команду СервисЧ>Анализ данных....
2. В раскрывающемся списке Анализ данных выбрать пункт Регрессия и щелкнуть на кнопке ОК.
2.1. Ввести в диалоговом окне Входной интервал У диапазон ячеек Е1 :Е21.
2.2. Ввести в диалоговом окне Входной интервал X диапазон ячеек Bl: В21.
2.3. Установить флажок Метки.
2.4. Ввести в окне редактирования Уровень надежности число 95.
2.5. Установить переключатель Параметры вывода в положение Новый рабочий лист и ввести название диаграммы.
2.6. Установить флажки Остатки и График остатков.
2.7. Щелкнуть на кнопке ОК.
Чтобы построить диаграмму разброса и график тренда, следует воспользоваться процедурой, описанной в разделе ЕН.15.3, слегка изменив ее инструкции.
• На втором этапе диалога (п. 2.1) ввести в окне редактирования Диапазон данных диапазоны Al :А21, El:Е21. Не забудьте поставить запятую между диапазонами (пробел не нужен!).
• Открыть рабочий лист, содержащий диаграмму разброса, и выполнить команду Диаграмма^ Добавить линию тренда....
• Находясь в диалоговом окне Линия тренда, щелкнуть на корешке вкладки Тип и выбрать вариант Линейная в группе Построение линии тренда (аппроксимация и сглаживание).
• Щелкнуть на вкладке Параметры и установить переключатель Название аппроксимирующей (сглаженной) кривой в положение Автоматическое.
• Щелкнуть на кнопке ОК.
Вычисление квадратичного тренда. Чтобы вычислить квадратичный тренд и построить диаграмму разброса, следует выполнить процедуру Сервис=>Анализ данных...ч>Регрессия. Например, чтобы построить квадратичный тренд реальных доходов компании Wm. Wrigley Jr. Company, необходимо открыть рабочую книгу Chapter 15.xls на листе WrigleyJMHK и выполнить такие инструкции.
1. Выбрать команду Сервис^Анализ данных....
2. В раскрывающемся списке Анализ данных выбрать пункт Регрессия и щелкнуть на кнопке ОК.
2.1. Ввести в диалоговом окне Входной интервал Y диапазон ячеек Е1 :Е21.
2.2. Ввести в диалоговом окне Входной интервал X диапазон ячеек в 1: С21.
2.3. Установить флажок Метки.
2.4. Ввести в окне редактирования Уровень надежности число 95.
2.5. Установить переключатель Параметры вывода в положение Новый рабочий лист и ввести название диаграммы.
2.6. Установить флажки Остатки и Г рафик остатков.
2.7. Щелкнуть на кнопке ОК.
Чтобы построить диаграмму разброса и график тренда, следует воспользоваться процедурой, описанной в разделе ЕН.15.3, слегка изменив ее инструкции.
• На втором этапе диалога (п. 2.1) ввести в окне редактирования Диапазон данных диапазоны А1:А21,Е1 :Е21. Не забудьте поставить запятую между диапазонами (пробел не нужен!).
• Открыть рабочий лист, содержащий диаграмму разброса, и выполнить команду Диаграмма^ Добавить линию тренда....
• Находясь в диалоговом окне Линия тренда, щелкнуть на корешке вкладки Тип и выбрать вариант Полиномиальная в группе Построение линии тренда (аппроксимация и сглаживание).
• Щелкнуть на вкладке Параметры и установить переключатель Название аппроксимирующей (сглаженной) кривой в положение Автоматическое.
• Щелкнуть на кнопке ОК.
Вычисление экспоненциального тренда. Чтобы вычислить экспоненциальный тренд и построить диаграмму разброса, следует выполнить процедуру Сервис^Анализ данных... ^Регрессия. Например, чтобы построить экспоненциальный тренд реальных доходов компании Wm. Wrigley Jr. Company, необходимо открыть рабочую книгу chapter 15. xls на листе Wrigley__MHK и следовать инструкциям.
1. Выполнить команду Сервис^Анализ данных....
2. В раскрывающемся списке Анализ данных выбрать пункт Регрессия и щелкнуть на кнопке ОК.
2.1. Ввести в диалоговом окне Входной интервал Y диапазон ячеек Fl: F21.
2.2. Ввести в диалоговом окне Входной интервал X диапазон ячеек Bl: В21.
2.3. Установить флажок Метки.
2.4. Ввести в окне редактирования Уровень надежности число 95.
2.5. Установить переключатель Параметры вывода в положение Новый рабочий лист и ввести название диаграммы.
2.6. Установить флажки Остатки и Г рафик остатков.
2.7. Щелкнуть на кнопке ОК.
Чтобы построить диаграмму разброса и график тренда, следует выполнить процедуры, описанные в разделах ЕН.15.3 и ЕН.15.4.
Выбор модели на основе разностей первого и второго порядка, а также относительных разностей
Для аппроксимации данных о реальном доходе компании Wm. Wrigley Jr. Company мы применили три модели: линейную, квадратичную и экспоненциальную. Какая из этих моделей лучше? Кроме визуального впечатления и сравнения скорректированных коэффициентов г2, в качестве инструмента для оценки качества модели применяются разности первого, второго и третьего порядка. Свойства моделей перечислены во врезке 15.1.
ВРЕЗКА 15.1. ВЫБОР МОДЕЛИ НА ОСНОВЕ АНАЛИЗА РАЗНОСТЕЙ ПЕРВОГО И ВТОРОГО ПОРЯДКА, А ТАКЖЕ ОТНОСИТЕЛЬНЫХ РАЗНОСТЕЙ
Если исходные данные хорошо аппроксимируются линейной моделью, разность первого порядка должна быть постоянной. Иначе говоря, разности между двумя последовательными значениями одинаковы:
Если исходные данные хорошо аппроксимируются квадратичной моделью, разность второго порядка должна быть постоянной. Иначе говоря, разности между двумя последовательными разностями первого порядка одинаковы:
(У, - У,) - (У, - У,) = (У, - У3) - (У, - У,) = ... = (У. - У..,) - (У„ - У._г).
Если исходные данные хорошо аппроксимируются экспоненциальной моделью, относительная разность должна быть постоянной. Иначе говоря, относительные разности, вычисленные по двум последовательным наблюдениям, одинаковы:
у _ у у _у У - У
---ь X100% = 2- Х100% =... = " X100% .
у у У
Не следует ожидать, что модель будет идеально аппроксимировать конкретный набор данных. Несмотря на это, при выборе подходящей модели необходимо анализировать разности первого и второго порядка, а также относительные разности. Рассмотрим эти вопросы на примерах линейной, квадратичной и экспоненциальной моделей.
ПРИМЕР 15.2. ЛИНЕЙНАЯ МОДЕЛЬ, ИДЕАЛЬНО АППРОКСИМИРУЮЩАЯ ВРЕМЕННОЙ РЯД
Предположим, что приведенные ниже данные представляют собой количество пассажиров (млн. чел.), которые пользуются услугами некоей авиакомпании.
1991 1992 1993 Год 1996 1997 1998 1999 2000
1994 1995
Пассажиропоток 30,0 33,0 36,0 39,0 42,0 45,0 48,0 51,0 54,0 57,0
Оценим качество этой модели, пользуясь разностями первого порядка.
РЕШЕНИЕ. Разности первого порядка указаны в следующей таблице.
Год
1991 1992 1993 1994 1995 1996 1997 1998 1999 2000
Пассажиропоток 30,0 33,0 36,0 39,0 42,0 45,0 48,0 51,0 54,0 57,0
Разности первого порядка 3,0 3,0 3,0 з,о 3,0 3,0 3,0 3,0 3,0
Обратите внимание на то, что все разности первого порядка одинаковы.
ПРИМЕР 15.3. КВАДРАТИЧНАЯ МОДЕЛЬ, ИДЕАЛЬНО АППРОКСИМИРУЮЩАЯ ВРЕМЕННОЙ РЯД
Предположим, что приведенные ниже данные представляют собой количество пассажиров (млн. чел.), которые пользуются услугами некоей авиакомпании.
1991 1992 Год 1996 1997 1998 1999 2000
1993 1994 1995
Пассажиропоток 30,0 31,0 33,5 37,5 43,0 50,0 58,5 68,5 80,0 93,0
Оценим качество этой модели, пользуясь разностями второго порядка.
РЕШЕНИЕ. Разности второго порядка указаны в следующей таблице.
Год
1991 1992 1993 1994 1995 1996 1997 1998 1999 2000
Пассажиропоток 30,0 31,0 33,5 37,5 43,0 50,0 58,5 68,5 80,0 93,0
Разности первого порядка 1,0 2,5 4,0 5,5 7,0 8,5 10,0 11,5 13,0
Разности второго порядка 1,5 1,5 1,5 1,5 1,5 1,5 1,5 1,5 1,5
Обратите внимание на то, что все разности второго порядка одинаковы.
ПРИМЕР 15.4. ЭКСПОНЕНЦИАЛЬНАЯ МОДЕЛЬ, ИДЕАЛЬНО АППРОКСИМИРУЮЩАЯ ВРЕМЕННОЙ РЯД
Предположим, что приведенные ниже данные представляют собой количество пассажиров (млн. чел.), которые пользуются услугами некоей авиакомпании.
Год
1991 1992 1993 1994 1995 1996 1997 1998 1999 2000
Пассажиропоток 30,0 31,5 33,1 34,8 36,5 38,3 40,2 42,2 44,3 46,5
Оценим качество этой модели, пользуясь относительными разностями.
РЕШЕНИЕ. Относительные разности указаны в следующей таблице.
Год
1991 1992 1993 1994 1995 1996 1997 1998 1999 2000
Пассажиропоток 30,0 31,5 33,1 34,8 36,5 38,3 40,2 42,2 44,3 46,5
Разности первого порядка 1,5 1,6 1,7 1,7 1,8 1,9 2,0 2,1 2,2
Относительные разности 5,0 5,0 5,0 5,0 5,0 5,0 5,0 5,0 5,0
Обратите внимание на то, что все относительные разности одинаковы.
На рис. 15.12 приведены разности первого и второго порядка, а также относительные разности, вычисленные на основе данных о реальных доходах компании Wm. Wrigley Jr. Company за период с 1982 по 2001 гг. в ценах 1982-1984 гг.
.А .. В , , ... 1 0 . .1 Е ... ;
Год 1 2 1982 3 1983 Реальный доход 602.59 584.04 Разность первого порядка -18.55 Разность второго порядка Относительная разность
4 1984 568.33 -15.71 2.84 -3.08%
тг1985 576.49 8 16 23.87 -2 69%
6 1986 637 77 61,28 53,12; 1.44%
1987 687.59 49.82 -11.46 10.63%
' Е 1988 753 51 65 92 16.10 7 81%
~Е 1989 800.73 47.22 -18.70 9 59%
Т511990 849 73 49.00 1.78 6.27%
1111991 843 54 -6.19 -55.19 6 12%
J2: 1992 927.51 83.97 90.16 -0.73%
1311993 996,82 69.31 -14.66 9.95%
ТЕ1994 ТЕ 1995 1120 99 124.17 54.86 7.47%:
1161.22 ' 40.23 -83.94 12.46%
J§h996 1179.48 18 26 -21 97 3,59%
1?11997 1217 57 38 09 19.83 1.57%
ТЕ 1998 1241.35 23 78 -14.31 3.23%
1S]1999 1248.02. 6 67 -17 11 1.95%
26 j 2000 1246 05 -1.97 -8,64 0.54%
21 i2001 1371.88 125.83 127,80 -0.16%
Рис. 15.12. Разности первого и второго порядка, а также относительные разности, вычисленные на основе данных о реальных доходах компании Wm. Wrigley Jr. Company за период с 1982 по 2001 гг. в ценах 1982-1984 гг.
Анализ рис. 15.12 показывает, что разности первого и второго порядка, а также относительные разности практически постоянны. Итак, несмотря на то, что скорректированный коэффициент г* у всех трех моделей, рассмотренных в разделе 15.4, одинаков и приближенно равен 0,96, возможно, существуют более точные модели.
УПРАЖНЕНИЯ К РАЗДЕЛУ 15.4
Изучение основ
15.9. Предположим, что для прогнозирования доходов компании используется метод наименьших квадратов и временной ряд, содержащий 25 годовых наблюдений.
1. Какой код следует присвоить величине X, соответствующей первому году?
2. Какой код следует присвоить величине X, соответствующей пятому году?
3. Какие коды следует присвоить величинам X, соответствующим остальным годам?
4. Какой код следует присвоить величине X, если необходимо экстраполировать прогноз на 5 лет вперед?
15.10. Предположим, что для прогнозирования доходов компании используется метод наименьших квадратов и временной ряд, содержащий 20 годовых наблюдений за период с 1983 по 2002 годы (в ценах 1995 года). Линейный тренд задается следующим уравнением.
Yl=4,0 + l,5Xi
1. Объясните смысл параметра Ьо в модели линейного тренда.
2. Объясните смысл параметра Ьх в модели линейного тренда.
3. Чему равна прогнозная величина реального дохода, вычисленная для пятого года?
4. Чему равны прогнозные величины реального дохода, вычисленные для остальных лет?
5. Чему равна прогнозная величина реального дохода, вычисленная для третьего года, следующего за последним наблюдением?
15.11. Предположим, что для прогнозирования объемов продаж компании используется метод наименьших квадратов и временной ряд, содержащий 40 годовых наблюдений за период с 1963 по 2002 годы (в ценах 1995 года). Линейный тренд задается следующим уравнением.
Y, = 1,2 + 0,5А
1. Объясните смысл параметра Ьо в модели линейного тренда.
2. Объясните смысл параметра Ъх в модели линейного тренда.
3. Чему равен прогнозный объем продаж, вычисленный для десятого года?
4. Чему равен прогнозный объем продаж, вычисленный для последнего года наблюдения?
5. Чему равен прогнозный объем продаж, вычисленный для второго года, следующего за последним наблюдением?
Применение понятий
15.12. Приведенные ниже данные представляют собой индекс потребительских цен за период с 1965 по 2002 годы в ценах 1982-1984 гг. Эта величина измеряет среднее изменение стоимости фиксированной “корзины” товаров и услуг, предоставляемых городским жителям. ^CPI-U.XLS.
Индекс потребительских цен для городских жителей
Год Индекс Год Индекс Год Индекс
1965 31,5 1978 65,2 1991 136,2
1966 32,4 1979 72,6 1992 140,3
1967 33,4 1980 82,4 1993 144,5
1968 34,8 1981 90,9 1994 148,2
1969 36,7 1982 96,5 1995 152,4
1970 38,8 1983 99,6 1996 156,9
1971 40,5 1984 103,9 1997 160,5
1972 41,8 1985 107,6 1998 163,0
1973 44,4 1986 109,6 1999 166,6
1974 49,3 1987 113,6 2000 172,2
1975 53,8 1988 118,3 2001 177,1
1976 56,9 1989 124,0 2002 179,9
1977 60,6 1990 130,7
Источник: Bureau of Labor Stastics, U. S. Department of Labor.
1. Постройте график временного ряда.
2. Опишите изменение временного ряда на протяжении 38 лет.
15.13. Объем валового внутреннего продукта является главным показателем экономической активности. Он состоит из личных потребительских расходов, чистого объема экспорта товаров и услуг и государственных расходов. Данные, записанные в файле ^GDP.XLS, представляют собой объемы реального валового внутреннего продукта (млрд. долл, в ценах 1996 г.) в США за 27-летний период с 1975 по 2001 годы.
Источник: U.S. Census Bureau, www. census . gov.
1. Постройте график временного ряда.
2. Сформулируйте уравнение линейного тренда и постройте его график.
3. Чему равны прогнозные значения ВВП в 2002 и 2003 годах?
4. Опишите тренд реального ВВП.
15.14. Данные, записанные в файле ^FEDRECPT. XLS, представляют собой объемы федеральных денежных поступлений с 1978 по 2001 годы (в текущих ценах). К этим поступлениям относятся индивидуальные и корпоративные подоходные налоги, отчисления на социальное страхование, акцизный сбор, налоги на недвижимость, таможенные пошлины и депозиты федерального резервного банка.
Источник: U. S. Census Bureau, www. census . gov.
1. Постройте график временного ряда.
2. Сформулируйте уравнение линейного тренда и постройте его график.
3. Чему равны прогнозные объемы федеральных поступлений в 2002 и 2003 годах?
4. Опишите тренд федеральных поступлений за указанный период.
15.15. Данные, записанные в файле ^STRATEGIC.XLS, представляют собой объемы нефти, хранящейся в стратегическом резерве США на протяжении 20 лет с 1981 по 2000 гг.
Источник: www. f eelstat. gov.
1. Постройте график временного ряда.
2. Сформулируйте уравнение линейного тренда и постройте его график.
3. Сформулируйте уравнение квадратичного тренда и постройте его график.
4. Сформулируйте уравнение экспоненциального тренда и постройте его график.
5. Какая модель лучше других аппроксимирует данный временной ряд?
6. Используя наилучшую модель тренда, предскажите объем нефти, хранящейся в стратегическом резерве, в 2001 году. Проверьте точность своего прогноза, сравнив его с реальными данными, полученными в Интернет или библиотеке.
15.16. Данные, приведенные в файле ^COCACOLA. XLS, представляют собой величины реальной чистой годовой прибыли компании Coca-Cola (млрд. долл, в текущих ценах) за период с 1975 по 2002 годы.
Источник: Moody’s Handbook of Common Stocks, 1980, 1989, 1993, 1999 и Mergent’s Handbook of Common Stocks, Spring 2003.
1. Постройте график временного ряда.
2. Сформулируйте уравнение квадратичного тренда и постройте его график.
3. Чему равны прогнозные величины прибыли в 2003 и 2004 годах?
4. Заполните таблицу реальной прибыли, умножив фактическую прибыль на коэффициент 100/CPI, используя индекс потребительских цен, вычисленный в задаче 15.12. Полученный реальный доход выражается в ценах 1982-1984 гг.
5. Постройте график модифицированного временного ряда.
6. Сформулируйте уравнение линейного тренда реальной прибыли и постройте его график.
7. Сформулируйте уравнение квадратичного тренда реальной прибыли и постройте его график.
8. Сформулируйте уравнение экспоненциального тренда реальной прибыли и постройте его график.
9. Чему равны прогнозные величины реальной прибыли в 2003 и 2004 годах?
10. Сравните решения задач 3 и 9. Объясните разницу между ними.
11. Опишите изменения реальной и фактической прибыли за указанный период.
15.17. Приведенные ниже данные представляют собой значения индекса Доу-Джонса (Dow Jones Industrial Average) за период с 1979 по 2002 годы. ^DJIA. XLS.
Индекс Доу-Джонса, 1979-2002 гг.
Год DJIA Год DJIA
1979 838,7 1991 3 168,8
1980 964,0 1992 3 301,1
1981 875,0 1993 3 754,1
1982 1 046,5 1994 3 834,4
1983 1 258,6 1995 5 117,1
1984 1 211,6 1996 6 448,3
1985 1 546,7 1997 7 908,3
1986 1 896,0 1998 9 181,4
1987 1 938,8 1999 11 497,1
1988 2 168,6 2000 10 788,0
1989 2 753,2 2001 10 021,5
1990 2 633,7 2002 8 341,6
1. Постройте график временного ряда.
2. Сформулируйте уравнение линейного тренда и постройте его график.
3. Сформулируйте уравнение квадратичного тренда и постройте его график.
4. Сформулируйте уравнение экспоненциального тренда и постройте его график.
5. Какая модель наиболее точна?
6. Используя наилучшую модель тренда, предскажите значение индекса Доу-Джонса в 2003 году. Проверьте точность своего прогноза, сравнив его с реальными данными, полученными в Интернет или библиотеке.
15.18. Компания Procter&Gamble (P&G) является крупнейшим производителем и продавцом товаров широкого потребления. Объем рыночной капитализации компании равен 117,2 млрд, долл., а годовая прибыль — 41 млрд. долл. (Yahoo.com, April 29, 2003). Данные, приведенные в файле ^P&G.XLS, представляют собой стоимость акций компании за период с 1 января 1970 г. по 1 января 2003 г.
Источник: Yahoo, сот,April 15,2003.
1. Постройте график временного ряда.
2. Сформулируйте уравнение линейного тренда и постройте его график.
3. Сформулируйте уравнение квадратичного тренда и постройте его график.
4. Сформулируйте уравнение экспоненциального тренда и постройте его график.
5. Какая модель является наиболее точной?
6. Используя наилучшую модель тренда, предскажите стоимость акции компании по состоянию на 1 января 2004 года. Проверьте точность своего прогноза, сравнив его с реальными данными, полученными в Интернет или библиотеке. Какой прогноз вы даете на 2004 год?
15.19. Несмотря на то что моделей, идеально аппроксимирующих временной ряд, не существует, для выбора наилучшей можно воспользоваться анализом разностей первого и второго порядков, а также анализом относительных разностей. Соответствующие данные приведены в следующей таблице. ^TSMODELl. XLS.
Год
1993 1994 1995 1996 1997
Ряд 1 10,0 15,1 24,0 36,7 53,8
Ряд 2 30,0 33,1 36,4 39,9 43,9
Ряд 3 60,0 67,9 76,1 84,0 92,2
1998 1999 2000 2001 2002
Ряд 1 74,8 100,0 129,2 162,4 199,0
Ряд 2 48,2 53,2 58,2 64,5 70,7
Ряд 3 100,0 108,0 115,8 124,1 132,0
1. Постройте график временного ряда.
2. Сформулируйте уравнение тренда.
3. Предскажите значение тренда для 2003 года.
15.20. Модель тренда часто выбирается на основе анализа графика временного ряда. ^TSMODEL2 .XLS.
Год
1993 1994 1995 1996 1997
Ряд 1 100,0 115,2 130,1 144,9 160,0
Ряд 2 100,0 115,2 131,7 150,8 174,1
1998 1999 2000 2001 2002
Ряд 1 175,0 189,8 204,9 219,8 235,0
Ряд 2 200,0 230,8 266,1 305,5 351,8
1. Постройте график зависимости переменной Y от переменной X, а также график зависимости log У от переменной X. Определите, какая модель точнее: линейная или экспоненциальная. Подсказка: если зависимость log У от переменной X является линейной, более точной оказывается экспоненциальная модель.
2. Сформулируйте уравнение тренда.
3. Предскажите значение тренда для 2003 года.
15.21. Данные, приведенные в файле OgR0SSREV.XLS, представляют собой величины валового дохода коммунальных предприятий (млн. долл, в ценах 1995 г.) за период с 1989 по 2002 годы.
1. Сравните между собой разности первого и второго порядка, а также относительные разности и выберите наиболее точную модель.
2. Сформулируйте уравнение тренда.
3. На сколько выросли доходы за 14 лет?
4. Предскажите доходы в 2003, 2004 и 2005 годах.
15.22. В недавно опубликованной статье (B.Horovitz, “What’s Next? Fast-food Giants Hunt for New Products to Tempt Consumer”, USA Today, July 3, 2002, 1A-2A) обсуждалась необходимость постоянно разрабатывать новые продукты для того, чтобы увеличивать объемы продаж в сети ресторанов быстрого питания. ^FASTFOODSALES . XLS.
Годы Объемы продаж
1992 70,6
1993 74,9
1994 78,5
1995 82,5
1996 85,9
1997 88,8
1998 92,5
1999 97,5
2000 101,4
2001 105,5
1. Постройте график временного ряда.
2. Заполните таблицу реальной прибыли, умножив фактическую прибыль на коэффициент 100/CPI, используя индекс потребительских цен, вычисленный в задаче 15.12.
3. Постройте модифицированый график временного ряда.
4. Сформулируйте уравнение линейного тренда и постройте его график.
5. Сформулируйте уравнение квадратичного тренда и постройте его график.
6. Сформулируйте уравнение экспоненциального тренда и постройте его график.
7. Используя наилучшую модель тренда, предскажите уточненный объем в 2002 и 2003 годах.
15.5. ВЫЧИСЛЕНИЕ ТРЕНДА С ПОМОЩЬЮ АВТОРЕГРЕССИИ И ПРОГНОЗИРОВАНИЕ
Другой подход к прогнозированию основан на авторегрессионной модели (autoregressive modeling).2 Часто значения временного ряда в какой-то момент времени сильно коррелируют как с предшествующими, так и с последующими значениями. Автокорреляция первого порядка (first-order autocorrelation) оценивает степень зависимости между последовательными значениями временного ряда. Автокорреляция второго порядка (second-order autocorrelation) оценивает силу связи между значениями, разделенными двумя временными интервалами. Автокорреляция р-го порядка (pth-order autocorrelation) представляет собой величину корреляции между значениями, разделенными р временными интервалами. Авторегрессионная модель позволяет лучше оценить предысторию и получить более точный прогноз.
Метод экспоненциального сглаживания, описанный в разделе 15.3, и авторегрессионная модель, рассматриваемая в разделе 15.5, являются частными случаями моделей авторегрессионного интегрированного скользящего среднего (autoregressive integrated moving average model — ARIMA), разработанных Боксом (Box) и Дженкинсом (Jenkins ) [2].
АВТОРЕГРЕССИОННАЯ МОДЕЛЬ ПЕРВОГО ПОРЯДКА
У = Д + ДУ, j + 8,. (15.10)
АВТОРЕГРЕССИОННАЯ МОДЕЛЬ ВТОРОГО ПОРЯДКА
У, = Д + ДУ,, + ДУ, 2 + 8,. (15.11)
АВТОРЕГРЕССИОННАЯ МОДЕЛЬ р-ГО ПОРЯДКА
У, = Д + ДУ, t + ДУ, 2 + ... +AY,_р + 8,. (15.12)
Здесь У, — наблюдаемое значение временного ряда в i-й момент, У, х — наблюдаемое значение временного ряда в (i—1 )-й момент, У, 2 — наблюдаемое значение временного ряда в (г-2)-й момент, У,_р — наблюдаемое значение временного ряда в (г-р)-й момент, Д — фиксированный параметр, оцениваемый с помощью метода наименьших квадратов, Д, Д, ...,А, — параметры авторегрессии, вычисляемые с помощью метода наименьших квадратов, 8, — случайный компонент с нулевым математическим ожиданием и постоянной дисперсией.
Авторегрессионная модель первого порядка (15.10) внешне напоминает модель простой линейной регрессии (12.1), а авторегрессионные модели второго (15.11) и р-го порядков (15.12) похожи на модель множественной регрессии (13.2). В регрессионных моделях параметры регрессии обозначаются символами р0, ..., а их оценки —
символами 50, Ъх, ..., bk. В авторегрессионных моделях аналогичные параметры обозначаются символами Д,Д, ...,Д, а их оценки — символами а0, ах, ...,ар.
В авторегрессионной модели первого порядка (15.10) рассматриваются лишь соседние значения временного ряда. В авторегрессионной модели второго порядка (15.11) оценивается зависимость и корреляция как между соседними, так и между последовательными значениями временного ряда, разделенными двумя временными интервалами. В авторегрессионной модели р-го порядка (15.12) оценивается зависимость и корреляция между соседними значениями, последовательными значениями временного ряда, разделенными двумя временными интервалами, и так далее вплоть до последовательных значений временного ряда, разделенных р временными интервалами.
Выбор подходящей авторегрессионной модели представляет собой нелегкую задачу. В процессе ее решения необходимо оценить простоту модели и возможные потери вследствие игнорирования автокорреляции между данными. С другой стороны, модели высоких порядков сопряжены с оценками многочисленных параметров, которые могут оказаться бесполезными, особенно если длина п временного ряда не очень велика. Это происходит потому, что при вычислении параметра Ар каждое значение временного ряда У, сравнивается с его ближайшими соседями, расположенными не далее чем через р временных интервалов (т.е. величина У, сравнивается со значениями У, „ У, г, ..., У, р).
Для того чтобы продемонстрировать потерю данных, рассмотрим примеры 15.5 и 15.6.
ПРИМЕР 15.5. СХЕМА СРАВНЕНИЙ В АВТОРЕГРЕССИОННОЙ МОДЕЛИ ПЕРВОГО ПОРЯДКА
Рассмотрим следующий годовой временной ряд (н = 7).
Год
1 2 3 4 5 6 7
Ряд 31 34 37 35 36 43 40
Продемонстрируйте схему сравнений значений временного ряда при построении авторегрессионной модели первого порядка.
РЕШЕНИЕ. Схема сравнений приведена в следующей таблице.
Год Авторегрессионная модель первого порядка
i Сравнение У. с Ум
1 31«е
2 34 <- + 31
3 37< + 34
4 35 «е + 37
5 36 «е + 35
6 43 <- + 36
7 40 <- + 43
Поскольку значению не предшествует ничего, оно не учитывается в регрессионном анализе. Следовательно, авторегрессионная модель первого порядка использует только шесть пар наблюдений.
ПРИМЕР 15.6. СХЕМА СРАВНЕНИЙ В АВТОРЕГРЕССИОННОЙ МОДЕЛИ ПЕРВОГО ПОРЯДКА
Рассмотрим следующий годовой временной ряд (п = 7).
Год
1 2 3 4 5 6 7
Ряд 31 34 37 35 36 43 40
Продемонстрируйте схему сравнений значений временного ряда при построении авторегрессионной модели второго порядка.
РЕШЕНИЕ. Схема сравнений приведена в следующей таблице.
Год Авторегрессионная модель первого порядка
i Сравнение У; с Ум . и Х_2
1 31< + ...и31<+
2 34 <- + 31и34<+
3 37< + 34 и 37 <+ 31
4 35 <- + 37 и 35 <-+ 34
5 36 < + 35и36<+ 37
6 43 <-+ 36 и 43 <-+ 35
7 40 < + 43 и 40 <+ 36
Поскольку значению Y1 не предшествует ничего, в регрессионном анализе не учитываются два наблюдения. Следовательно, авторегрессионная модель второго порядка использует только пять пар наблюдений.
Выбрав модель и применив метод наименьших квадратов для вычисления оценок регрессионных параметров, необходимо оценить ее адекватность. Для этого можно использовать либо авторегрессионную модель конкретного порядка, которую уже применяли для похожих данных, либо сразу построить модель с несколькими параметрами, а затем последовательно исключать из нее параметры, не имеющие статистически значимого вклада. В последнем случае применяется /-критерий значимости параметра Ар, имеющего наивысший порядок в данной авторегрессионной модели. Нулевая и альтернативная гипотезы формулируются следующим образом:
Но:Д = О,
ИСПОЛЬЗОВАНИЕ f-КРИТЕРИЯ ЗНАЧИМОСТИ ПАРАМЕТРА АВТОРЕГРЕССИИ А, ИМЕЮЩЕГО НАИВЫСШИЙ ПОРЯДОК
а -А
t = -^-(15.13)
где Ар — гипотетическое значение параметра, имеющего наивысший порядок в регрессионной модели, ар — оценка параметра авторегрессии Ар, имеющего наивысший порядок, S„ — стандартная ошибка оценки а.
ир р
Тестовая f-статистика имеет /-распределение с п-2р-1 степенями свободы.3
При заданном уровне значимости а нулевая гипотеза отклоняется, если тестовая /-статистика больше верхнего или меньше нижнего критического уровня /-распределения. Иначе говоря, решающее правило формулируется следующим образом.
Если / > tn_2p_r или / < ~tn_2p_^ нулевая гипотеза Но отклоняется, в противном случае нулевая гипотеза не отклоняется.
Решающее правило, а также области отклонения и принятия гипотезы изображены на рис. 15.13.
Рис. 15.13. Области отклонения гипотезы для двустороннего критерия значимости параметра авторегрессии Ар, имеющего наивысший порядок
Тестовая t-статистика теряет р степеней свободы при оценке наклона и одну при оценке сдвига генеральной совокупности откликов. Еще р степеней свободы утрачиваются при сравнении значений временного ряда.
Если нулевая гипотеза (Ар = 0) не отклоняется, значит, выбранная модель содержит слишком много параметров. Критерий позволяет отбросить старший член модели и оценить авторегрессионную модель порядка р-1. Эту процедуру следует продолжать до тех пор, пока нулевая гипотеза Но не будет отклонена.
Уравнение, полученное путем регрессионного анализа авторегрессионной модели называется эмпирическим (fitted).
ЭМПИРИЧЕСКОЕ УРАВНЕНИЕ АВТОРЕГРЕССИИ р-ГО ПОРЯДКА
Y. = ч +...+«Лр ’ (15.14)
где Yt — предсказанное значение временного ряда в i-й момент, У, t — наблюдаемое значение временного ряда в (1-1 )-й момент, У 2 — наблюдаемое значение временного ряда в (г-2)-й момент, У р — наблюдаемое значение временного ряда в (1-р)-й момент, а0, at, ..., ар — оценки параметров авторегрессии Д, Д, ..., Ар.
Для предсказания значений временного ряда на j лет вперед на основании данных о предыдущих п временных интервалах используется уравнение (15.15).
ПРОГНОЗНОЕ УРАВНЕНИЕ АВТОРЕГРЕССИИ р-ГО ПОРЯДКА
где а0, at, ..., ар — оценки параметров авторегрессии Д,Д, ...»Д, j — номер года в будущем, Y„+J_p — предсказанное значение для j-p > 0, Yn+J_p — наблюдаемое значение Yn+l~f) дляу-р<0.
Таким образом, для того, чтобы предсказать значения временного ряда с помощью авторегрессионной модели третьего порядка, необходимо использовать лишь последние три наблюдаемых значения Уп, Уп, и У„ 2, а также оценки параметров Д, Д, Д и А3, полученные при множественном регрессионном анализе.
Для значения временного ряда на один год вперед уравнение (15.15) принимает вид:
К+1 = + a]Yn + O2^u-J + аЗ^;-2 *
Для значения временного ряда на два года вперед уравнение (15.15) принимает вид:
Для значения временного ряда на три года вперед уравнение (15.15) принимает вид:
^3= *0*^2 +*2^+^’
Авторегрессионная модель является весьма полезным инструментом для аппроксимации и предсказания значений временного ряда. Этапы авторегрессионного моделирования годовых временных рядов перечислены во врезке 15.2.
ВРЕЗКА 15.2. ЭТАПЫ АВТОРЕГРЕССИОННОГО МОДЕЛИРОВАНИЯ ГОДОВЫХ ВРЕМЕННЬ/Х РЯДОВ
• Выберите порядок р оцениваемой авторегрессионной модели с учетом того, что Z-критерий значимости имеет п-2р-1 степеней свободы.
• Сформируйте последовательность переменных р “с запаздыванием” так, чтобы первая переменная запаздывала на один временной интервал, вторая — на два и так далее. Последнее значение должно запаздывать на р временных интервалов (см. рис. 15.14).
• Примените программу Microsoft Excel для вычисления регрессионной модели, содержащей всер значений временного ряда с запаздыванием.
• Оцените значимость параметра имеющего наивысший порядок.
1. Если нулевая гипотеза отклоняется, в авторегрессионную модель можно включать все р параметров и применять ее для аппроксимации временного ряда (см. формулу (15.14)) и предсказания (см. формулу (15.15)).
2. Если нулевая гипотеза не отклоняется, отбросьте р-ю переменную и повторите п. 3 и 4 для новой модели, включающей р-1 параметр. Проверка значимости новой модели основана на t-критерии, количество степеней свободы определяется новым количеством параметров.
• Повторяйте п. 3 и 4, пока старший член авторегрессионной модели не станет статистически значимым.
Чтобы продемонстрировать авторегрессионное моделирование, вернемся к анализу временного ряда реальных доходов компании Wm. Wrigley Jr. Company за период с 1982 по 2001 гг. На рис. 15.14 показаны данные, необходимые для построения авторегрессионных моделей первого, второго и третьего порядка. Для построения модели третьего порядка необходимы все столбцы этой таблицы. При построении авторегрессионной модели второго порядка последний столбец игнорируется. При построении авторегрессионной модели первого порядка игнорируются два последних столбца. Таким образом, при построении авторегрессионных моделей первого, второго и третьего порядка из 20 переменных исключаются одна, две и три соответственно.
Выбор наиболее точной авторегрессионной модели начинается с модели третьего порядка, представленной на рис. 15.15.
Как следует из рис. 15.15, уравнение авторегрессии третьего порядка имеет следующий вид.
Y, = 54,6159 +1,0678 х - 0,0730 х Yt_2 - 0,0061 х .
Здесь начало координат соответствует 1985 году, а шаг по оси Y равен одному году.
Проверим значимость параметра А3, имеющего наивысший порядок. Его оценка а3 равна -0,0061, а стандартная ошибка равна 0,3262.
Для проверки гипотез Н0:Д = 0
и Н/Д + 0
вычислим Z-статистику:
я. - А t = -^—- = ^_0,0061_0 = 0,3262
При уровне значимости, равном 0,05, критические величины двухстороннего Z-критерия с 13 степенями свободы равны ±2,1604. Поскольку -2,1604 < t = -0,019 < +2,1604 ир = 0,9853 > а = 0,05, нулевую гипотезу Но отклонять нельзя. Таким образом, параметр
третьего порядка не имеет статистической значимости в авторегрессионной модели и должен быть удален.
Повторим анализ для авторегрессионной модели второго порядка, представленной на рис. 15.16.
Уравнение авторегрессии второго порядка имеет следующий вид.
Yt = 31,5007 +1,2107 х - 0,2053 х Уг2
Здесь начало координат соответствует 1984 году, а шаг по оси У равен одному году.
Оценка параметра, имеющего наивысший порядок, равна а2= -0,2053, а ее стандартная ошибка равна 0,2761.
Для проверки гипотез
Н0:Д = 0
и
НрД^О
вычислим i-статистику:
а? - -0,2053-0 .
t = _2—21. = —---------= -о,744 .
S* 0,2761
При уровне значимости, равном 0,05, критические величины двухстороннего i-критерия с 15 степенями свободы равны ±2,1315. Поскольку -2,1315 < t ==-0,744 < -2,1315 ир = 0,469 > а = 0,05, нулевую гипотезу Но отклонять нельзя. Таким образом, параметр второго порядка не является статистически значимым, и его следует удалить из модели.
Повторно применяя программу Microsoft Excel, построим авторегрессионную модель первого порядка, показанную на рис. 15.17.
А в С D Е
1 Год Реальный доход Lag1 Lag2 Lag3
2 ' 1982 602,59 #н/д #н/д #н/д
’3J 1983 584,04 602,59 #н/д #н/д
~4j 1984 568,33 584,04 602,59 #н/д
5 I 1985 576,49 568,33 584,04 602,59
J6 - 1986 637,77 576,49 568,33 584,04
Г\ 1987 687,59 637,77 576,49 568,33
1988 753,51 687,59 637,77 576,49
1989 800,73 753,51 687,59 637,77
«Г 1990 849,73 800,73 753,51 687,59
1991 843,54 849,73 800,73 753,51
12 1992 927,51 843,54 849,73 800,73
13 1993 996,82 927,51 843,54 849,73
14 1994 1120,99 996,82 927,51 843,54
15 1995 1161,22 1120,99 996,82 927,51
16 1996 1179,48 1161,22 1120,99 996,82
17 1997 1217,57 1179,48 1161,22 1120,99
fs" 1998 1241,35 1217,57 1179,48 1161,22
19 1999 1248,02 1241,35 1217,57 1179,48
20 2000 1246,05 1248,02 1241,35 1217,57
21 2001 1371,88 1246,05 1248,02 1241,35
Рис. 15.14. Построение авторегрессионных моделей первого, второго и третьего порядка для реальных доходов компании Wm. Wrigley Jr. Company (1982-2001 гг.)
Уравнение авторегрессии первого порядка имеет вид
Y.= 18,2612 +1,0245 х^
Оценка параметра, имеющего наивысший порядок, равна ах= 1,0245, а ее стандартная ошибка равна 0,0388.
i__ А. 1 Авторегессионная модель тре '2 Л. в тьего порядка С J P . I .. Е F G
3 Регрессионная ста т и стика
i f ,ч- jAOItO( ГЧ. |Ю ^Множественный R R-квадрат Нормированный R-квадрат Стандартная ошибка Наблюдения 0,98781 0,97576 0,97017 43,15039 17
9 10" Дисперсионный анализ
11 df SS MS F Значимость F
12 ’13" 'м' Регрессия Остаток Итого 3 13 16 974389,07541 24205,42962 998594,50503 324796,35847 1861,95612 174,43824 9,49611Е-11
15
16 Коэффициенты Стандартная ошибка * t-статистика Р-значение Нижние 95% Верхние 95%
17 18“ 19 20= Y-пересечение Переменная 1 Переменная 2 Переменная 3 54,61585 1,06783 -0,07299 -0,00613 43,85176 0,33091 0,54203 0,32624 1,24547 3,22697 -0,13465 -0,01878 0,23494 0,00662 0,89495 0,98530 40,12010 0,35294 -1,24397 -0,71093 149,35181 1,78271 1,09799 0,69867
Рис. 15.15. Параметры авторегрессионной модели третьего порядка, вычисленные с помощью программы Microsoft Excel
А ? 1 S . . J Р 1 D Е - F G
1 Авторегрессионная модель второго порядка 2 ’
3 Регрессионная статистика
4_ Множественный R 5 R-квадрат Нормированный R-квадрат Стандартная ошибка 8 Наблюдения 0,98833 0,97680 0,97370 42,50595 18
L 10 Дисперсионный анализ 11 12 Регрессия 13 Остаток 14 Итого 15 df 2 15 17 SS 1140836,3353 27101,3409 1167937,6762 MS 570418,16766 1806,75606 F 315,71399 Значимость F 5.51802Е 13
16 Коэффициенты Стандартная ошибка t-статистика Р-значение Нижние 95% Верхние 95%
J7 ^-пересечение 18 Переменная 1 19 .Переменная 2 31,50072 1,21066 -0,20533 38,75159 0,27326 0,27609 0,81289 4,43047 -0,74373 0,42900 0,00049 0,46853 -51,09638 0,62823 -0,79380 114,09783 1,79310 0,38313
Рис. 15.16. Параметры авторегрессионной модели второго порядка, вычисленные с помощью программы Microsoft Excel
А _! 8 _1 С .. ,_.L D : .... E_.'J ... .....F J .......G
яВ Авторегрессионная модель первого порядка
те Регрессионная статистика
Множественный R R-квадрат Нормированный R-квадрат Стандартная ошибка Наблюдения 0,98802 0,97618 0,97478 42,80936 19
Дисперсионный анализ
df SS F Значимость F
Регрессия Остаток Итого 1 17 18 1276636,4509 31154,8994 1307791,3502 1276636,451 1832,641 696,61017 ЗД8609Е-15
Коэффициенты Стандартная ошибка ; t-статистика Р-значение Нижние 95% ; Верхние 95%
| Y-пересечение ^Переменная 1 18,26124 1,02449 36,57084 0,03882 0,49934 26,39337 0,62394 3,08609Е-15 -58,89661 95,41908 0,94260 1,10639
Рис 15.17. Параметры авторегрессионной модели первого порядка для реальных доходов компании Wr. Wrigley Jr. Company, вычисленные с помощью программы Microsoft Excel
Для проверки гипотез
Но:Д = О и
вычислим ^-статистику:
При уровне значимости, равном 0,05, критические величины двухстороннего ^-критерия с 17 степенями свободы равны ±2,1098. Поскольку -2,1098 < t =26,39 < -2,1098 ир = 0,000000000000003086 < а = 0,05 (р = 3,08603Е-15), нулевую гипотезу Но следует отклонить. Таким образом, параметр первого порядка является статистически значимым, и его нельзя удалять из модели. Итак, модель авторегрессии первого порядка лучше других аппроксимирует исходные данные. Используя оценки а0 = 18,2614, аг = 1,0245 и значение временного ряда за последний год— У20= 1 371,88, с помощью формулы (15.15) можно предсказать величины реальных доходов компании Wm. Wrigley Jr. Company в 2002 и 2003 годах.
Yn+J = 18,2612 + 1,0245x1;^ .
2001: на один год вперед У21 = 18,2612 + 1,0245x1 371,88 = 1 423,75 млрд. долл.
2001: на два года вперед У22 =18,2612 + 1,0245x1423,75 = 1476,89 млрд. долл.
Предсказанные значения переменной У, полученные с помощью авторегрессионной модели первого порядка, изображены на рис. 15.18.
Рис. 15.18. Предсказанные доходы компании Wm. Wrigley Jr. Company, вычисленные с помощью авторегрессионной модели первого порядка и программы Microsoft Excel
Процедуры Excel: добавление запаздывающих независимых переменных
Для того чтобы добавить запаздывающие независимые переменные %и выполнить анализ авторегрессионной модели, следует использовать формулы, копирующие значения переменных /за предыдущий временной период. В надстройке PHStat2 эта процедура не предусмотрена.
Например, чтобы построить авторегрессионные модели первого, второго и третьего порядков для временного ряда реальных доходов компании Wm. Wrigley Jr. Company за период с 1982 по 2001 годы, необходимо открыть рабочую книгу Wrigley.xls на листе Реальный_доход и создать столбцы с, D и Е, как показано в таблице.
Обратите внимание на то, что ячейки С2, D2, D3, Е2, ЕЗ и Е4 содержат специальное значение #н/д, которое при попытке записи какого-либо числа в данные ячейки порождает сообщение об ошибке. Введите формулы в ячейки сз, D4 и Е5 и скопируйте их в нижележащие ячейки вплоть до строки 21.
1 Lag1 Lag2 Lag3
2 #н/д #н/д #н/д
Mill = B2 #н/д #н/д
lie® = ВЗ =В2 #н/д
5 =В4 = ВЗ = В2
lllllli =В5 =В4 = ВЗ
...
20 =В19 =В18 = В17
21 =В20 =В19 =В18
Процедуры Excel: построение авторегрессионных моделей
Для создания авторегрессионных моделей используются модифицированные процедуры регрессионного анализа, описанные в главах 12 и 13. Надстройка PHStat2 выполняет необходимые действия автоматически.
Например, чтобы построить авторегрессионную модель первого порядка для временного ряда реальных доходов компании Wm. Wrigley Jr. Company за период с 1982 по 2001 годы, необходимо открыть рабочую книгу Chapter 15. xls на листе Wrigley_Lag и выполнить одну из следующих процедур.
Применение Excel в сочетании с надстройкой PHStatZ
Для построения авторегрессионной модели первого порядка следует применить процедуры PHStat^ Regression^Simple Linear Regression... (PHStat Регрессия ^Простая линейная регрессия...) и выполнить следующие инструкции.
1 Выбрать команду PHStat^Regression^Simple Linear Regression....
2 . В диалоговом окне Simple Linear Regression выполнить такие действия (см. иллюстрацию).
2.1. Ввести в диалоговом окне Y Variable Cell Range (Входной интервалу) диапазон ячеек В1 :В21.
2.2. Ввести в диалоговом окне X Variable Cell Range (Входной интервал X) диапазон ячеек СЗ:С21.
2.3. Сбросить флажок First cells in both ranges contain a label (Первые ячейки обоих интервалов содержат метки).
2.4. Ввести в диалоговом окне Confidence level for regression coefficients (Доверительный уровень для коэффициентов регрессии) число 95.
2.5. Установить флажки Regression Statistics Table (Таблица регрессионных статистик) и ANOVA and Coefficients Table (Сводная таблица дисперсионного анализа и коэффициентов).
2.6. Ввести в диалоговом окне Title (Заголовок) название диаграммы.
2.7. Щелкнуть на кнопке ОК.
Чтобы построить авторегрессионную модель второго или третьего порядка для тех же данных, необходимо выполнить следующие действия.
1. Выбрать команду PHStat^Regression^Multiple Regression....
2. В диалоговом окне Multiple Regression выполнить такие действия (см. иллюстрацию).
2.1. Ввести в диалоговом окне Y Variable Cell Range (Входной интервалу) диапазон ячеек В4:В21 (для модели второго порядка) илив5:В21 (для модели третьего порядка).
2.2. Ввести в диалоговом окне X Variable Cell Range (Входной интервал X) диапазон ячеек с4 : D21 (для модели второго порядка) или С5:Е21 (для модели третьего порядка).
2.3. Сбросить флажок First cells in both ranges contain a label (Первые ячейки обоих интервалов содержат метки).
2.4. Ввести в диалоговом окне Confidence level for regression coefficients (Доверительный уровень для коэффициентов регрессии) число 95.
2.5. Установить флажки Regression Statistics Table (Таблица регрессионных статистик) и ANOVA and Coefficients Table (Сводная таблица дисперсионного анализа и коэффициентов).
2.6. Ввести в диалоговом окне Title (Заголовок) название диаграммы.
2.7. Щелкнуть на кнопке ОК.
Инструкции, позволяющие построить график временного ряда для авторегрессионной модели, изложены в разделе ЕН.15.6.
Применение Excel
1. Выбрать команду Сервио=>Анализ Данных....
2. В диалоговом окне Анализ данных выполнить такие действия (см. иллюстрацию).
2.1. Ввести - в диалоговом окне Входной интервалу диапазон ячеек ВЗ:В21 (для модели первого порядка) или В4:В21 (для модели второго порядка) или В5:В21 (для модели третьего порядка).
2.2. Ввести в диалоговом окне Входной интервал X диапазон ячеек СЗ:С21 (для модели первого порядка) или C4:D21 (для модели второго порядка) или С5:Е21 (для модели третьего порядка).
2.3. Сбросить флажок Метки.
2.4. Ввести в диалоговом окне Уровень надежности число 95.
2.5. Установить переключатель Параметры вывода в положение Новый рабочий лист.
2.6. Установить флажок Остатки.
2.7. Щелкнуть на кнопке ОК.
Инструкции, позволяющие построить график временного ряда для авторегрессионной модели, изложены в разделе ЕН.15.6.
УПРАЖНЕНИЯ К РАЗДЕЛУ 15.5
Изучение основ
15.23. Рассмотрим годовой временной ряд, содержащий 40 наблюдений. Требуется построить авторегрессионную модель пятого порядка.
1. Сколько сравнений будет потеряно при построении такой модели?
2. Сколько параметров необходимо оценить?
3. Какие из 40 значений временного ряда понадобятся для прогнозирования?
4. Формализуйте модель.
5. Напишите уравнение, позволяющее предсказывать значение временного ряда на у лет вперед.
15.24. Рассмотрим годовой временной ряд, содержащий 17 наблюдений, и авторегрессионную модель третьего порядка, аппроксимирующую эти данные.
а0 = 4,50, а1 = 1,80, а2 = 0,80, а, = 0,24, S, = 0,50, = 0,30, S = 0,10.
Оцените адекватность этой модели при уровне значимости, равном 0,05.
15.25. Примените авторегрессионную модель из задачи 15.24 для предсказания будущих значений временного ряда, если У15 — 23, У16 = 28, У17 = 34.
15.26. Предположим, что стандартные ошибки оценок параметров авторегрессионной модели третьего порядка, построенной в задаче 15.24, имеют следующие значения: Sa = 0,45, Sa = 0,35, £,=0,15.
1. Является ли авторегрессионная модель адекватной?
2. Можно ли применить ее для прогнозирования и как это сделать?
Применение понятий
15.27. Данные, записанные в файле ^STRATEGIC .XLS, представляют собой объемы нефти, хранящейся в стратегическом резерве США на протяжении 21 год с 1981 по 2000 гг. (задача 15.15).
1. Постройте авторегрессионную модель третьего порядка и проверьте значимость старшего члена, если уровень значимости равен 0,05.
2. Постройте авторегрессионную модель второго порядка и проверьте значимость старшего члена, если уровень значимости равен 0,05.
3. Постройте авторегрессионную модель первого порядка и проверьте значимость старшего члена, если уровень значимости равен 0,05.
4. Вычислите прогнозируемый объем запасов нефти в 2001, 2002 и 2003 годах.
15.28. Проанализируйте данные о величине реального дохода компании Coca-Cola (задача 15.16) за периоде 1975 по 2002 гг. f^COCACOLA.XLS.
1. Постройте авторегрессионную модель третьего порядка и проверьте значимость старшего члена, если уровень значимости равен 0,05.
2. Постройте авторегрессионную модель второго порядка и проверьте значимость старшего члена, если уровень значимости равен 0,05.
3. Постройте авторегрессионную модель первого порядка и проверьте значимость старшего члена, если уровень значимости равен 0,05.
4. Вычислите прогнозируемую величину реального дохода компании в 2003 и 2004 годах.
15.29. Проанализируйте данные об индексе Доу-Джонса (задача 15.17) за период с 1979 по 2002 гг. ©DJIA. XLS.
1. Постройте авторегрессионную модель третьего порядка и проверьте значимость старшего члена, если уровень значимости равен 0,05.
2. Постройте авторегрессионную модель второго порядка и проверьте значимость старшего члена, если уровень значимости равен 0,05.
3. Постройте авторегрессионную модель первого порядка и проверьте значимость старшего члена, если уровень значимости равен 0,05.
4. Вычислите прогнозируемые значения индекса в 2003, 2004 и 2005 годах.
15.30. Проанализируйте данные о стоимости акций компании P&G (задача 15.18) за период с 1970 по 2003 гг. ©P&G. XLS.
1. Постройте авторегрессионную модель третьего порядка и проверьте значимость старшего члена, если уровень значимости равен 0,05.
2. Постройте авторегрессионную модель второго порядка и проверьте значимость старшего члена, если уровень значимости равен 0,05.
3. Постройте авторегрессионную модель первого порядка и проверьте значимость старшего члена, если уровень значимости равен 0,05.
4. Вычислите прогнозируемую стоимость акции в 2004 году.
15.31. В задаче 15.22 обсуждались данные об объемах продаж в сети ресторанов быстрого питания с 1992 по 2001 гг. ©FASTFOODSALES . XLS.
1. Постройте авторегрессионную модель третьего порядка и проверьте значимость старшего члена, если уровень значимости равен 0,05.
2. Постройте авторегрессионную модель второго порядка и проверьте значимость старшего члена, если уровень значимости равен 0,05.
3. Постройте авторегрессионную модель первого порядка и проверьте значимость старшего члена, если уровень значимости равен 0,05.
4. Вычислите прогнозируемый доход компании в 2002, 2003 и 2004 годах.
15.6. ВЫБОР АДЕКВАТНОЙ МОДЕЛИ ПРОГНОЗИРОВАНИЯ
В разделах 15.4 и 15.5 описаны шесть методов прогнозирования значений временного ряда: модели линейного, квадратичного и экспоненциального трендов (раздел 15.4) и авторегрессионные модели первого, второго и третьего порядков (раздел 15.5). Существует ли оптимальная модель? Какую из шести описанных моделей следует применять для прогнозирования значения временного ряда? Во врезке 15.3 перечислены четыре принципа, которыми необходимо руководствоваться при выборе адекватной модели прогнозирования. Эти принципы основаны на оценках точности моделей. При этом предполагается, что значения временного ряда можно предсказать, изучая его предыдущие значения.
ВРЕЗКА 15.3. ПРИНЦИПЫ ВЫБОРА МОДЕЛЕЙ ДЛЯ ПРОГНОЗИРОВАНИЯ
• Выполните анализ остатков.
• Оцените величину остаточной ошибки с помощью квадратов разностей.
• Оцените величину остаточной ошибки с помощью абсолютных разностей.
• Руководствуйтесь принципом экономии.
Анализ остатков
Напомним, что остатком (residual) называется разность между предсказанным и наблюдаемым значением (см. разделы 12.5 и 13.2). Построив модель для временного ряда, следует вычислить остатки для каждого из п интервалов. Как показано на рис. 15.19, панель А, если модель является адекватной, остатки представляют собой случайный компонент временного ряда и, следовательно, распределены нерегулярно. С другой стороны, как показано на остальных панелях рис. 15.16, если модель не адекватна, остатки могут иметь систематическую зависимость, не учитывающую либо тренд (рис. 15.19, панель Б), либо циклический (рис. 15.19, панель В), либо сезонный компонент (рис. 15.19, панель Г).
о
01 23456789
Время (годы) Панель Б Не учитывается тренд
1 23456789 10
Время (годы)
Панель А
Случайно распределенные ошибки прогнозирования
01 23456789 10
Время (годы) Панель В Не учитывается циклический компонент
01 2345678
Время (годы) Панель Г Не учитывается сезонный компонент
Рис. 15.19. Анализ остатков
Измерение абсолютной и среднеквадратичной остаточных погрешностей
Если анализ остатков не позволяет определить единственную адекватную модель, можно воспользоваться другими методами, основанными на оценке величины остаточной погрешности [1,4]. К сожалению, статистики не пришли к консенсусу относительно наилучшей оценки остаточных погрешностей моделей, применяемых для прогнозирования.
Исходя из принципа наименьших квадратов, можно сначала провести регрессионный анализ (см. раздел 12.3) и вычислить стандартную ошибку оценки SXY При анализе конкретной модели эта величина представляет собой сумму квадратов разностей между фактическим и предсказанным значениями временного ряда. Если модель идеально аппроксимирует значения временного ряда в предыдущие моменты времени, стандартная ошибка оценки равна нулю. С другой стороны, если модель плохо аппроксимирует значения временного ряда в предыдущие моменты времени, стандартная ошибка оценки велика. Таким образом, анализируя адекватность нескольких моделей, можно выбрать модель, имеющую минимальную стандартную ошибку оценки SXY.
Основным недостатком такого подхода является преувеличение ошибок при прогнозировании отдельных значений. Иначе говоря, любая большая разность между величи-
нами Y. и Y при вычислении суммы квадратов ошибок SSE возводится в квадрат, т.е. увеличивается. По этой причине многие статистики предпочитают применять для оценки адекватности модели прогнозирования среднее абсолютное отклонение (mean absolute deviation — MAD).
СРЕДНЕЕ АБСОЛЮТНОЕ ОТКЛОНЕНИЕ
£М1
A£4D = -*-. (15.16)
п
При анализе конкретных моделей величина MAD представляет собой среднее значение модулей разностей между фактическим и предсказанными значениями временного ряда. Если модель идеально аппроксимирует значения временного ряда в предыдущие моменты времени, среднее абсолютное отклонение равно нулю. С другой стороны, если модель плохо аппроксимирует такие значения временного ряда, среднее абсолютное отклонение велико. Таким образом, анализируя адекватность нескольких моделей, можно выбрать модель, имеющую минимальное среднее абсолютное отклонение.
Принцип экономии
Если анализ стандартных ошибок оценок и средних абсолютных отклонений не позволяет определить оптимальную модель, можно воспользоваться четвертым методом, основанным на принципе экономии (parsimony). Этот принцип утверждает, что из нескольких равноправных моделей следует выбирать простейшую.
Среди шести рассмотренных в главе моделей прогнозирования наиболее простыми являются линейная и квадратичная регрессионные модели, а также авторегрессионная модель первого порядка. Остальные модели намного сложнее.
Сравнение четырех методов прогнозирования
Для иллюстрации процесса выбора оптимальной модели вернемся к временному ряду, состоящему из величин реального дохода компании Wm. Wrigley Jr. Company. Сравним четыре модели: линейную, квадратичную, экспоненциальную и авторегрессионную модель первого порядка. (Авторегрессионные модели второго и третьего порядка лишь незначительно улучшают точность прогнозирования значений данного временного ряда, поэтому их можно не рассматривать.)
На рис. 15.20 показаны графики остатков, построенные при анализе четырех методов прогнозирования с помощью программы Microsoft Excel. Делая выводы на основе этих графиков, следует быть осторожным, поскольку временной ряд содержит только 20 точек.
График остатков для линейной модели фафик остатков для квадратичной модели
Закодированный год Закодированный год
Панель А Панель Б
График остатков для экспоненциальной модели
Закодированный год
Панель В
График остатков для авторегрессионной модели первого порядка
Переменная X
Панель Г
Рис. 15.20. Графики остатков, построенные при анализе четырех методов прогнозирования с помощью программы Microsoft Excel
Как показывает анализ рис. 15.20, ни одна модель, кроме авторегрессионой модели первого порядка, не учитывает циклический компонент. Именно эта модель лучше других аппроксимирует наблюдения и характеризуется наименее систематической структурой.
Итак, анализ остатков всех четырех методов показал, что наилучшей является авторегрессионная модель первого порядка, а линейная, квадратичная и экспоненциальная модели имеют меньшую точность. Чтобы убедиться в этом, сравним величины остаточных погрешностей этих методов. На рис. 15.21 указаны фактические значения У,, предсказанные значения Yt , а также остатки е1 для каждой из четырех моделей. Кроме того, показаны значения SXY и MAD.
Для всех четырех моделей сравнение величин SXY и MAD приводит примерно к одинаковым результатам. Это сравнение ясно показывает, что экспоненциальная модель является худшей, а линейная и квадратичная модель превосходит ее по точности. Как и ожидалось, наименьшие величины SXY и MAD имеет авторегрессионная модель первого порядка.
Выбрав конкретную модель прогнозирования, необходимо внимательно следить за дальнейшими изменениями временного ряда. Помимо всего прочего, такая модель создается, чтобы правильно предсказывать значения временного ряда в будущем. К сожалению, такие модели прогнозирования плохо учитывают изменения в структуре временного ряда. Совершенно необходимо сравнивать не только остаточную погрешность, но и точность прогнозирования будущих значений временного ряда, полученную с помощью других моделей. Измерив новую величину Yt в наблюдаемом интервале времени, ее необходимо тотчас же сравнить с предсказанным значением. Если разница слишком велика, модель прогнозирования следует пересмотреть. Такие методы адаптивного управления описаны в работе [1].
А В C D , u E F G H J J К Тксп о ней ци аль н ая модель Прогноз Остатки 550,193 52,398 578,853 5,183 609,006 40,671 640,729 -64,242 674,106 -36,332 709,220 -21,632 746,164 7,344 785,032 15,694 825,925 23,807 868,948 -25,409 914,212 13,3 961,834 34,982 1011,937 109,048 1064,650 96,571 1120,108 59,369 1178,455 39,115 1239,842 1,508 1304,426 -56,407 1372,375 -126,324 1443,863 -71,983 L М N
.к 2 Реальный Год доход Линейная модель Прогноз Остатки 498,656 103,934 544,141 39,895 589,625 -21,29 635,110 -58,623 680,595 42,821 726,079 -38,491 771,564 -18,056 817,048 -16,323 862,533 -12,801 908,018 -64,479 953,502 -25,99 998,987 -2,17 1044,471 76,514 1089,956 71,264 1135,441 44,037 1180,925 36,645 1226,410 14,94 1271,894 -23,875 1317,379 -71,328 1362,864 9,017 Квадратичная модель Прогноз Остатки 513,052 89,539 553,99 30,046 595,434 -27,099 637,383 -60,896 679,837 42,063 722,796 -35,208 766,26 -12,752 810,229 -9,504 854,704 4,972 899,683 -56,144 945,168 -17,655 991,158 5,659 1037,652 83,333 1084,652 76,568 1132,157 47,32 1180,168 37,403 1228,683 12,667 1277,703 -29,684 1327,229 -81,177 1377,259 -5,379 /хвторегре* модель п Прогноз #н/д 635,610 616,602 600,516 608,868 671,655 722,690 790,224 838,599 888,805 882,460 968,491 1039,492 1166,702 1207,923 1226,627 1265,652 1290,014 1296,847 1294,831 ссионная ервого Остатки #н/д -51,574 48,267 -24,029 28,906 15,933 30,818 10,501 11,134 45,266 45,052 28,326 81,493 -5,481 -28,445 -9,056 -24,303 41,995 -50,796 77,049
3 ' 4' 5' б’ 7 В 9 10 11‘ 12 13 14 15 16 10 19 2ф 21 22 1982 602,59 1983 584,04 1984 568,33 1985 576,49 1986 637,77 1987 687,59 1988 753,51 I 1989 800,73 I 1990 849,73 I 1991 843,54 i 1992 927,51 ! 1993 996,82 \ 1994 1120,99 । 1995 1161,22 [ 1996 1179,48 ! 1997 1217,57 I 1998 1241,35 I 1999 1248,02 j 2000 1246,05 | 2001 1371,88
23 24 25 j SSE 45370,387 I SYX: 50,205 I MAD: 39,625 SSE 44250,604 SYX: 51,019 MAD: 38,253 SSE 63850,127 SYX: 59,559 MAD: 45,066 SSE 31154,828 SYX: 42,809 MAD: 34,654
Рис, 15.21. Сравнение четырех методов прогнозирования с помощью показателей SYX и MAD
Процедуры Excel: вычисление среднего абсолютного отклонения (МАР)
Для вычисления величины MAD сначала необходимо вычислить абсолютные величины остатков с помощью функции abs, а затем, вызвав функцию срзнач, найти среднее значение абсолютных разностей между фактическими и предсказанными значениями переменной Y, полученными с помощью линейной, квадратичной или авторегрессионной модели. Эти формулы реализуются вручную, поскольку в надстройке PHStat2 такая процедура не предусмотрена.
Вычисление среднего абсолютного отклонения для линейной, квадратичной или авторегрессионной модели. Сначала создайте регрессионную модель, руководствуясь инструкциями, приведенными ранее. Затем выделите на рабочем листе, содержащем регрессионные статистики, диапазон столбцов висс предсказанными значениями и остатками и скопируйте его на рабочий лист, содержащий исходные данные. После этого добавьте столбец, содержащий формулы =abs (ячейка), предназначенные для вычисления абсолютных величин остатков, и добавьте одну формулу =СРЗНАЧ (диапазон ячеек, содержащий абсолютные величины остатков) для вычисления среднего абсолютного отклонения.
Например, чтобы вычислить величину MAD для авторегрессионной модели первого порядка, построенной по данным о реальных доходах компании Wm. Wrigley Jr. Company за период с 1982 по 2001 гг., необходимо выполнить следующие инструкции.
1. Выделить диапазон ячеек В24 : С42 на рабочем листе, содержащем регрессионные статистики.
2. Выбрать команду Правкам Копировать.
3. Открыть рабочий лист Wrigley_Lag в книге Chapter 15.xls.
| 4. Щелкнуть правой кнопкой мыши на ячейке F2 и выбрать команду Вставить во всплывающем I контекстном меню. (Предсказанные и наблюдаемые значения, а также остатки располагаются на j рабочем листе, начиная со строки 2, поскольку данные запаздывают на один период времени.) i 5. Ввести в ячейку Н2 метку abs (Остатки).
6. Ввести в ячейку НЗ формулу =ABS(G3) и скопировать ее в нижележащие ячейки вплоть до строки 2 0.
7. Ввести в ячейку G21 метку mad, а в ячейку Н21 - формулу =срзнач (НЗ :Н20).
Этот рабочий лист можно настроить для создания других моделей. В любом случае последнее значение остатка должно находиться в строке 21, а формула для вычисления величины MAD- в строке 22.
Вычисление среднего абсолютного отклонения в экспоненциальной модели. Сначала создайте регрессионную модель, руководствуясь инструкциями, приведенными ранее в этой главе, а затем примените к предсказанным значениям У логарифмическое преобразование, следуя указаниям из раздела ЕН.15.4. Добавьте столбец, содержащий формулы =ABS (ячейка, содержащая величину Y, -ячейка, содержащая предсказанную величину Y), предназначенные для вычисления абсолютных величин остатков, И одну формулу =СРЗНАЧ (диапазон ячеек, содержащий абсолютные величины остатков) для вычисления среднего абсолютного отклонения.
Например, чтобы вычислить величины /1/М£>для экспоненциальной модели, построенной поданным о реальных доходах компании Wm. Wrigley Jr. Company за период с 1982 по 2001 гг., необходимо открыть рабочий лист Wrigley_MHK2 и в книге Chapter 15.xls выполнить следующие инструкции.
1. Ввести в ячейку Н1 метку ABS (Остатки).
2. Ввести в ячейку Н2 формулу -ABS (E2-G2) и скопировать ее в нижележащие ячейки вплоть до строки 21.
3. Ввести в ячейку G22 метку MAD, а в ячейку Н22 - формулу -СРЗНАЧ (Н2 : Н21).
Изучение основ
15.32. Приведенные ниже остатки вычислены после применения метода наименьших квадратов к годовому временному ряду, содержащему 12 наблюдений (объемы продаж, выраженные в млрд. долл, в ценах 1995 г.)
2,0 -0,5 1,5 1,0 0,0 1,0 -3,0 1,5 -4,5 2,0 0,0 -1,0
1. Вычислите величину S1A и объясните ее смысл.
2. Вычислите величину MAD и объясните ее смысл.
15.33. Предположим, что первый остаток в задаче 15.32 равен 12,0, а не 2,0, и последний ---------11,0, а не -1,0.
1. Вычислите величину SYX и объясните ее смысл.
2. Вычислите величину MAD и объясните ее смысл.
Применение понятий
15.34. В задаче 15.13 построена линейная модель временного ряда для объемов реального валового внутреннего продукта (млрд. долл, в ценах 1996 г.) в США за 27-летний период с 1975 по 2001 годы. ^GDP. XLS.
1. Выполните анализ остатков.
2. Вычислите стандартную ошибку оценки SYX.
3. Вычислите величину MAD для каждой модели.
4. Какую модель следует предпочесть для прогнозирования, учитывая результаты решения задач 1-3 и принцип экономии?
15.35. В задачах 15.15 и 15.27 построены линейная и авторегрессионные модели временного ряда для объемов нефти, хранящейся в стратегическом резерве США на протяжении 20 лет с 1981 по 2000 гг. ^STRATEGIC . XLS.
1. Выполните анализ остатков для каждой модели.
2. Вычислите стандартную ошибку оценки SYX для каждой модели.
3. Вычислите величину MAD для каждой модели.
4. Какую модель следует предпочесть для прогнозирования, учитывая результаты решения задач 1-3 и принцип экономии?
15.36. В задачах 15.16 и 15.28 построены линейная и авторегрессионные модели временного ряда для реального дохода компании Coca-Cola, ft COCACOLA. XLS.
1. Выполните анализ остатков для каждой модели.
2. Вычислите стандартную ошибку оценки SYX для каждой модели.
3. Вычислите величину MAD для каждой модели.
4. Какую модель следует предпочесть для прогнозирования, учитывая результаты решения задач 1-3 и принцип экономии?
15.37. В задачах 15.17 и 15.29 построены линейная и авторегрессионные модели временного ряда для индекса Доу-Джонса, ft DJIA. XLS.
1. Выполните анализ остатков для каждой модели.
2. Вычислите стандартную ошибку оценки SYX для каждой модели.
3. Вычислите величину MAD для каждой модели.
4. Какую модель следует предпочесть для прогнозирования, учитывая результаты решения задач 1-3 и принцип экономии?
15.38. В задачах 15.18 и 15.30 построены линейная и авторегрессионные модели временного ряда для стоимости акций компании P&G. ftp&G. XLS.
1. Выполните анализ остатков для каждой модели.
2. Вычислите стандартную ошибку оценки SYX для каждой модели.
3. Вычислите величину MAD для каждой модели.
4. Какую модель следует предпочесть для прогнозирования, учитывая результаты решения задач 1-3 и принцип экономии?
15.39. В задачах 15.22 и 15.31 построены линейная и авторегрессионные модели временного ряда для объемов продаж в сети ресторанов быстрого питания.
ftFASTFOODSALES.XLS.
1. Выполните анализ остатков для каждой модели.
2. Вычислите стандартную ошибку оценки SYX для каждой модели.
3. Вычислите величину MAD для каждой модели.
4. Какую модель следует предпочесть для прогнозирования, учитывая результаты решения задач 1-3 и принцип экономии?
15.7. ПРОГНОЗИРОВАНИЕ ВРЕМЕННЫХ РЯДОВ НА ОСНОВЕ СЕЗОННЫХ ДАННЫХ
До сих пор мы изучали временные ряды, состоящие из годовых данных. Однако многие временные ряды состоят из величин, измеряемых ежеквартально, ежемесячно, еженедельно, ежедневно и даже ежечасно. В частности, как показано в табл. 15.1, если данные измеряются ежемесячно или ежеквартально, следует учитывать сезонный компонент. В этом разделе мы рассмотрим методы, позволяющие прогнозировать значения таких временных рядов.
В сценарии, описанном в начале главы, упоминалась компания Wal-Mart Stores, Inc. В 2002 году эта компания управляла 1 736 универсальными магазинами, торгующими уцененными товарами, 888 супермаркетами и 475 клубами в США. Под ее контролем находятся также более тысячи магазинов в Канаде, Мексике, Европе, Южной Америке и Азии. Рыночная капитализация компании равна 229 млрд. долл. (Yahoo.com, September 1, 2002). Ее акции котируются на Нью-Йоркской фондовой бирже под аббревиатурой WMT. Финансовый год компании заканчивается 31 января, поэтому в четвертый квартал 2002 года включаются ноябрь и декабрь 2001 года, а также январь 2002 года. Временной ряд квартальных доходов компании приведен на рис. 15.22.
Таблица 15.5. Квартальные доходы компании Wal-Mart Stores, Inc. (млн. долл.) за период с 1994 по 2002 гг. Й WALMART. xls
Квартал 1994 1995 1996 1997 1998 1999 2000 2001 2002
1 13 920 17 690 20 440 22 772 25 409 29 819 34 717 42 985 48 565
2 16 237 19 942 22 723 25 587 28 366 33 521 38 170 46 112 53 269
3 16 827 20 418 22 913 25 644 28 777 33 509 40 432 45 676 51 754
4 20 361 24 448 27 550 30 856 35 386 40 785 51394 56 556 64 211
Источник: Standard & Poofs Stock Reports, November 1995, November 1999. (New York: McGraw-Hill ) и investor. walmartstores . com, September4, 2002.
Рис. 15.22. График квартальных доходов компании Wal-Mart Stores, Inc. (млн. долл.) за период с 1994 по 2002 гг.
Для таких квартальных рядов, как этот, классическая мультипликативная модель, кроме тренда, циклического и случайного компонента, содержит сезонный компонент.
Y, = Т, х S, х С, х I.
Прогнозирование месячных и временных рядов с помощью метода наименьших квадратов
Регрессионная модель, включающая сезонный компонент, основана на комбинированном подходе. Для вычисления тренда применяется метод наименьших квадратов, описанный в разделе 15.4, а для учета сезонного компонента — категорийная переменная (см. раздел 13.6).
Для аппроксимации квартальных временных рядов с учетом сезонных компонентов используется уравнение (15.17).
ЭКСПОНЕНЦИАЛЬНАЯ МОДЕЛЬ ДЛЯ КВАРТАЛЬНЫХ ДАННЫХ
Y, =р„р*р?р?=р?е,, (15.17)
где X, — закодированное квартальное значение, i = 0,1, ..., = 1 для первого квар-
тала и 0 для остальных, Q2 = 1 для второго квартала и 0 для остальных, Q3 = 1 для третьего квартала и 0 для остальных, р0 — сдвиг переменной Y, (р1-1)х100% — темп ежеквартального роста доходов (%), р2 — множитель первого квартала по отношению к четвертому кварталу, р3 — множитель второго квартала по отношению к четвертому кварталу, р4 — множитель третьего квартала по отношению к четвертому кварталу, в — величина случайного компонента в i-м временном интервале.
Модель (15.17) значительно отличается от модели линейной регрессии. Для того чтобы привести ее к линейному виду, необходимо выполнить логарифмирование по основанию 10.
ПРЕОБРАЗОВАННАЯ ЭКСПОНЕНЦИАЛЬНАЯ МОДЕЛЬ ДЛЯ АППРОКСИМАЦИИ КВАРТАЛЬНЫХ ДАННЫХ
log Y, = log(pop;v,0^0f Е,) = log р() + log р*' + log pf1 + log p? + log Pf’ + log E, = = log po + X, log p, + log p2 + Q2 log p3 + Q3 log p4 + log £,.
Модель (15.18) является линейной, поэтому к ней можно применить метод наименьших квадратов, считая log У, откликом, а величины X,, Q, и Q3 — независимыми переменными.
МОДЕЛЬ ЭКСПОНЕНЦИАЛЬНОГО РОСТА ДЛЯ КВАРТАЛЬНЫХ ДАННЫХ
log Y, = bl} + bxXi + b2Qx + b3Q2 + b4Q3, (15.19)
где b0 — оценка log Po (т.е. 1(Л = Po), \ — оценка log p4 (т.е. 1(T - [3,), b, — оценка log p2 (т.е. 106 - p, ), b3 — оценка log P3 (т.е. 106, = p3), b4 — оценка log p4 (т.е. IO*4 = p4).
Сл4. приложение A.
Для учета сезонного компонента при аппроксимации месячных данных можно использовать следующую модель.
ЭКСПОНЕНЦИАЛЬНАЯ МОДЕЛЬ ДЛЯ МЕСЯЧНЫХ ДАННЫХ
Y = , (15.20)
где Xt — закодированное месячное значение, i = 0, 1, ..., М1 = 1 для января и 0 для остальных месяцев, М2 = 1 для февраля и 0 для остальных месяцев, М3 = 1 для марта и 0 для остальных месяцев, ..., = 1 для ноября и 0 для остальных месяцев, 0О —
сдвиг переменной У, (01-1)хЮО% — темп ежемесячного роста доходов (%), 0,— множитель января по отношению к декабрю, 02 — множитель февраля по отношению к декабрю, 03 — множитель марта по отношению к декабрю, ..., 012 — множитель ноября по отношению к декабрю, £( — величина случайного компонента в i-м временном интервале.
Модель (15.20) отличается от модели линейной регрессии. Для того чтобы привести ее к линейному виду, необходимо выполнить логарифмирование по основанию 10.
ПРЕОБРАЗОВАННАЯ ЭКСПОНЕНЦИАЛЬНАЯ МОДЕЛЬ ДЛЯ АППРОКСИМАЦИИ МЕСЯЧНЫХ ДАННЫХ
logy; = iog(p„₽l'₽"'₽"!₽r₽"'₽;!'-₽;'-₽ )=
= log 0O + X, log 0, + Mx log 0, + M2 log 0. + M. Iog04 +
+ M4 log 05 + M5 log 06 + Mb log 07 + M7 log 0S +
+ 4 log 09 + M, log 01O + A/I0 log 0„ + log 0I2 + log
Модель (15.21) является линейной. Следовательно, к ней можно применить метод наименьших квадратов, считая log У откликом, а величины X, Мх, М2, ..., Мп — независимыми переменными.
МОДЕЛЬ ЭКСПОНЕНЦИАЛЬНОГО РОСТА ДЛЯ МЕСЯЧНЫХ ДАННЫХ
log Yt = bll+b]Xi + b,A4. +b2M, + b4Mx+b-M4 +b(M.+b1Mb +
(Ib.ZZ)
+ b^M2 + ЬЭМ^ + b^M^ + bnMw +
где b0 — оценка log 0n (т.е. 1 О*’ =0()), bx — оценка log 03 (т.е. 10л‘ = 0,), b2 — оценка log 02 (т.е. 1О/’;=02),63 — оценка log 03 (т.е. 10л' = 03),..., bX2— оценка log 012 (т.е. IO*12 =012).
Обратите внимание на то, что в модели, аппроксимирующей квартальный временной ряд, для учета четырех кварталов нам понадобились три фиктивные переменные Q2 и Q3, а в модели для месячного временного ряда 12 месяцев представляются с помощью 11 фиктивных переменных Мх, М2, ..., Мхх. Поскольку в этих моделях в качестве отклика используется переменная log У, а не У, для вычисления настоящих регрессионных коэффициентов необходимо выполнить обратное преобразование (т.е. потенцирование. — Прим.ред.).
На первый взгляд, эти регрессионные модели выглядят громоздкими. Однако при прогнозировании временного ряда для конкретного периода значения всех остальных фиктивных переменных полагаются равными нулю, и уравнения значительно упрощаются. Например, уравнение (15.19) принимает следующий вид.
Для первого квартала: log Yt = bj} + bxXt + b3Qx .
Для второго квартала: log Yt = bQ + b}Xi + b3Q2.
Для третьего квартала: log Yt = b0 + b}Xt + b4Q3.
Для четвертого квартала: log Yt = bn + b}X,.
При определении фиктивных переменных четвертый квартал является базовым и кодируется нулем.
Аналогично модель (15.22) для месячных временных рядов принимает следующий вид.
Для января: log Y=b^ + h.Xi + b,M} .
Для декабря: log Yt = /?() + b,Xi.
При определении фиктивных переменных базовым периодом считается декабрь, который кодируется нулем.
Чтобы проиллюстрировать процесс построения модели, аппроксимирующей квартальный временной ряд, вернемся к доходам компании Wal-Mart, приведенным в табл. 15.5. В этой таблице содержатся данные о квартальных доходах компании за период с 1994 по 2002 год. Параметры экспоненциальной модели, полученные с помощью программы Microsoft Excel, показаны на рис. 15.23.
Как показывает рис. 15.23, экспоненциальная модель довольно хорошо аппроксимирует исходные данные. Коэффициент смешанной корреляции г2 равен 99,4%, скорректированный коэффициент смешанной корреляции — 99,3%, тестовая F-статистика — 1 333,51, ар-значение равно 0,0000. Как видим, при уровне значимости, равном 0,05, каждый регрессионный коэффициент в классической мультипликативной модели временного ряда является статистически значимым. Применяя к ним операцию потенцирования, получаем следующие параметры.
Коэффициенты регрессии
Ьо: сдвиг отклика Y bY\ наклон
Ъ2: первый квартал д3: второй квартал Ь/ третий квартал
b, =logp, 4,265204 0,015614 -0,092927 -0,061211 -0,071851
р, = 10А
18 416,3687
1,0366
0,8074
0,8685
0,8475
А " 1 в 1 С : D |. Е .. f : . .. G
"Г "Г Регрессионный анализ квартальных доходов компании Wal-Mart Stores, Inc.
г Регрессионная статистика
4 Jr 'б_ 8* Множественный R R-квадрат Нормированный R-квадрат Стандартная ошибка : Наблюдения 0,997106742 0,994221055 0,993476287 0,013881364 36
9
1Q Дисперсионный анализ
11 ' df SS MS F Значимость F
12 .Регрессия 13 Остаток 4 31 1,02783 0,00597 0,256957203 0,000192692 1333,510803 3,33305Е-34
"14 Итого 35 1,03380
15
16 Коэффициенты Стандартная ошибка t-статистика Р-значение Нижние 95% Верхние 95%
17 '^-пересечение 1В Код Q 19 Q1 20. Q2 21 ОЗ 4,26520 0,01561 -0,09293 -0,06121 -0,07185 0,00629 0,00022 0,00658 0,00656 0,00655 678,4253636 69,70250597 -14,12664151 -9,3322773 -10,97367312 3.10356Е-66 1,2208Е-35 4,73136Е-15 1.62566Е-10 3.32943Е-12 4,25238 0,01516 -0,10634 -0,07459 -0,08520 4,27803 0,01607 -0,07951 -0,04783 -0,05850
Рис. 15.23. Параметры экспоненциальной модели для прогноза квартальных доходов компании Wal-Mart, полученные с помощью программы Microsoft Excel
Коэффициенты р0, р], р,, 03 и р4 интерпретируются следующим образом.
• Параметр р0 =18 416,3687, сдвиг зависимой переменной У, является значением некорректированного тренда квартальных доходов в первом квартале 1994 года, т.е. в первом временном периоде.
• Величина (р,-1) х 100% = 3,66% оценивает темп роста квартальных доходов.
• Величина р2 = 0,8074 представляет собой сезонный множитель для первого квартала по отношению к четвертому кварталу. Это число означает, что доходы, полученные в первом квартале, на 19,26% меньше, чем доходы, полученные в четвертом квартале.
• Величина р, = 0,8685 представляет собой сезонный множитель для второго квартала по отношению к четвертому. Это число означает, что доходы, полученные во втором квартале, на 13,15% меньше, чем доходы, полученные в четвертом квартале.
• Величина р4 = 0,8475 представляет собой сезонный множитель для третьего квартала по отношению к четвертому. Это число означает, что доходы, полученные во втором квартале, на 15,25% меньше, чем доходы, полученные в четвертом квартале.
Используя регрессионные коэффициенты b0, bx, b2, bs и Ь., а также уравнение (15.19), можно предсказать доход, полученный компанией в конкретном квартале. Например, предскажем доход компании для четвертого квартала 2002 года (X, = 35).
logf = b0 + btX, = 4,262504 + 0,015614x35 = 4,811694.
= 104,81169‘ = 64 817,757.
Таким образом, согласно прогнозу в четвертом квартале 2002 года компания должна была получить доход, равный 64 817,757 млн. долл. Для того чтобы распространить прогноз на период времени, находящийся за пределами временного ряда, например, на первый квартал 2003 года (X, = 36, = 1), необходимо выполнить следующие вычисления.
log5: = bQ + b.X, + b2Qt = 4,265204 + 0,015614x36 - 0,092927x1 = 4,734381.
У>10173138, = 54 247,659.
Следовательно, прогнозируемый доход компании в первом квартале 2003 года равен 54 247,659 млрд. долл.
Процедуры Excel: создание фиктивных переменных для предсказания знамений месячных и квартальных
Для создания фиктивных переменных, входящих в регрессионные модели для прогнозирования значений месячных и квартальных временнь/х рядов, используется последовательность формул, содержащих функцию если.
Например, чтобы создать фиктивные квартальные переменные для прогнозирования доходов компании Wal-Mart Stores, Inc. на основе данных из табл. 15.5, необходимо открыть рабочую книгу Walmart .xls на листе Данные. В таблице, приведенной ниже, показаны дополнительные столбцы F-н, в которых должны быть записаны значения фиктивных переменных Qv Q2 и Q3. Формулы для вычисления величины Q, проверяют значения, записанные в столбце в. Если они равны 1, переменная <3 также равна 1, в противном случае она равна 0. Аналогично выполняется проверка при вычислении значений переменных Q и Q3 - если в столбце в записаны числа 2 и 3, переменные Q и Q3 равны 2 и 3 соответственно, в противном случае они равны 0.
Формулы, приведенные в табл. 15.5, можно адаптировать для прогнозирования месячных временных рядов. Например, в качестве кодов месяцев в столбце в можно использовать их названия. В этом случае при вычислении значения переменной Ml формулы в строке 2 примут следующий вид: =ЕСЛИ (В2 = "январь", 1, 0). Соответственно при вычислении переменной МП формулы выглядят несколько иначе: =если (В2 = "ноябрь", 1, 0). (Поскольку названия месяцев являются текстовыми величинами, их следует брать в двойные кавычки.)
F G н
1 Q1 Q2 Q3
2 =ЕСЛИ(В2= 1, 1, 0) =ЕСЛИ(В2 = 2, 1, 0) =ЕСЛИ(В2 = 3, 1, 0)
3 =ЕСЛИ(ВЗ = 1, 1, 0) =ЕСЛИ(ВЗ = 2, 1, 0) =ЕСЛИ(ВЗ = 3, 1, 0)
35 =ЕСЛИ(В35 = 1,1,0) =ЕСЛИ(В35 = 2, 1, 0) =ЕСЛИ(В35 = 3, 1, 0)
36 =ЕСЛИ(В36= 1, 1, 0) =ЕСЛИ(В36 = 2, 1, 0) =ЕСЛИ(В36 = 3, 1, 0)
37 =ЕСЛИ(В37 = 1, 1, 0) =ЕСЛИ(В37 = 2, 1, 0) =ЕСЛИ(В37 = 3, 1,0)
?УП1»А>1ЙН1ЕНИЯ к РАЗДЕЛУ 15.7
Изучение основ
15.40. Предположим, что при прогнозировании значений месячного временного ряда, содержащего данные за пятилетний период с января 1998 года по декабрь 2002 года, используется следующая экспоненциальная модель.
log Yt = 2,0 + 0,01Х + 0,10 х January .
Выполните потенцирование коэффициентов.
1. Объясните смысл параметра |30.
2. Что представляет собой месячный темп роста?
3. Определите множитель для января.
15.41. Сколько фиктивных переменных необходимо ввести в модель для учета сезонной категорийной переменной WEEK при прогнозировании значений недельного временного ряда с помощью метода наименьших квадратов?
15.42. Предположим, что при прогнозировании значений квартального временного ряда, содержащего данные за пятилетний период с первого квартала 1998 года до четвертого квартала 2002 года, используется следующая экспоненциальная модель.
log Yt= 3,0 + 0,01%, - 0,25<2, + 0,20£>2 + 0,15Q3.
Точкой отсчета считается первый квартал 1998 года. Шаг переменной X равен одному кварталу.
1. Выполните потенцирование коэффициентов. Объясните смысл параметра 0().
2. Выполните потенцирование коэффициентов. Что представляет собой квартальный темп роста?
3. Выполните потенцирование коэффициентов. Определите множитель для второго квартала.
15.43. Рассмотрим экспоненциальную модель из задачи 15.42.
1. Чему равно предсказанное значение временного ряда в четвертом квартале 2000 года?
2. Чему равно предсказанное значение временного ряда в первом квартале 2001 года?
3. Выполните прогноз для четвертого квартала 2003 года.
4. Выполните прогноз для первого квартала 2004 года.
Применение понятий
15.44. Ниже приведены значения индекса курсов акций, вычисленные компанией Standard&Poor в конце каждого квартала за период с 1994 по первый квартал 2003 гг. &S&PSTKIN.XLS.
Индекс курсов акций, вычисленный компанией Standard&Poor
Квартал 1994 1995 1996 1997 1998
1 (март) 445,77 500,71 645,50 757,12 1 101,75
2 (июнь) 444,27 544,75 670,63 885,14 1 133,84
3 (сентябрь) 462,69 584,41 687,31 947,28 1 017,01
4 (декабрь) 459,27 615,93 740,74 970,43 1 229,23
Квартал 1999 2000 2001 2002 2003
1 (март) 1 286,37 1 498,58 1 160,33 1 147,38 848,18
2 (июнь) 1 372,71 1 454,60 1 224,38 989,81
3 (сентябрь) 1282,71 1 436,51 1 040,94 815,28
4 (декабрь) 1469,25 1 320,28 1 148,08 879,28
1. Постройте график временного ряда.
2. Сформулируйте уравнение экспоненциального тренда с учетом квартальных компонентов и постройте классическую мультипликативную модель временного ряда.
3. Предскажите значение временного ряда в третьем квартале 2003 года.
4. Предскажите значение временного ряда в четвертом квартале 2003 года.
5. Предскажите значение временного ряда в каждом квартале 2004 года.
6. Что представляет собой квартальный темп роста?
7. Какой смысл имеет второй квартальный множитель?
15.45. В файле ^REALGDP . XLS приведены значения объема внутреннего национального продукта, измеренные поквартально за период с 1993 по 2002 гг. (млрд. долл, в ценах 1996 года).
Источник: “GDP and Other Major NIPA Series, 1929-2002:1”, Table 2A, Bureau of Economic Analysis, U. S. Department of Commerce, August, 2002.
1. Постройте график временного ряда.
2. Сформулируйте уравнение экспоненциального тренда с учетом квартальных компонентов и постройте классическую мультипликативную модель временного ряда.
3. Предскажите значение временного ряда в третьем квартале 2002 года.
4. Предскажите значение временного ряда в трех последних кварталах 2002 года.
5. Что представляет собой квартальный темп роста?
6. Какой смысл имеет первый квартальный множитель?
15.46. Бюро статистики труда собирает данные о многих аспектах рынка рабочей силы. В файле ^DERATE . XLS приведены ежемесячные уровни безработицы в США за период с 1996 по 2003 гг. (с учетом сезонного фактора).
Источник: www .bls. gov.
1. Постройте график временного ряда.
2. Сформулируйте уравнение экспоненциального тренда с учетом квартальных компонентов и постройте классическую мультипликативную модель временного ряда.
3. Предскажите значение временного ряда в ноябре 2002 года.
4. Предскажите значение временного ряда в декабре 2002 года.
5. Предскажите значение временного ряда в каждом месяце 2003 года.
6. Что представляет собой месячный темп роста безработицы?
7. Какой смысл имеет июльский множитель?
8. Зайдите в Интернет и найдите реальные данные о безработице в 2003 году. Объясните разницу между прогнозируемыми и реальными значениями.
15.47. В следующей таблице приведены ежемесячные данные о количестве средств, зачисленных на популярные кредитные карточки в крупном банке, пожелавшем остаться неизвестным. ^CREDIT . XLS.
Объем средств, зачисленных на кредитные карточки (млн. долл.)
Месяц 2001 2002 2003
Январь 31,9 39,4 45,0
Февраль 27,0 36,2 39,6
Март 31,3 40,5
Апрель 31,0 44,6
Май 39,4 46,8
Июнь 40,7 44,7
Июль 42,3 52,2
Август 49,5 54,0
Сентябрь 45,0 48,8
Октябрь 50,0 55,8
Ноябрь 50,9 58,7
Декабрь 58,5 63,4
1. Постройте график временного ряда.
2. Опишите зависимость, которой подчиняется временной ряд.
3. Можно ли утверждать, что объем средств, зачисленных на банковские кредитные карточки, увеличивается или уменьшается? Обоснуйте свой ответ.
4. Обратите внимание на то, что в декабре 2002 года на банковских кредитных карточках было зачислено более 63 млн. долл., а в феврале 2003 года — менее 40 млн. долл. Насколько февральские показатели были близки к прогнозируемым?
5. Сформулируйте уравнение экспоненциального тренда с учетом месячных компонентов и постройте классическую мультипликативную модель временного ряда.
6. Что представляет собой месячный темп роста вкладов?
7. Какой смысл имеет январский множитель?
8. Предскажите объем средств, зачисленных на кредитные карточки в марте 2003 года.
9. Предскажите объем средств, зачисленных на кредитные карточки в апреле 2003 года.
10. Как применить анализ временных рядов такого типа в банковской практике?
15.48. Вфайле<>ТОУ5 -REV.XLS приведены ежеквартальные доходы (млн. долл.) компании Toys Я Us за период с 1992 г. по первый квартал 2002 г.
Источник: Standard & Poor;s Stock Reports, November 1995, November 1998, April 2003. New York: McGraw Hill, Inc.
1. Подвержены ли доходы компании Toys Я Us сезонным колебаниям? Объясните свой ответ.
2. Постройте график временного ряда. Подтверждает ли он ваш ответ на первый вопрос?
3. Сформулируйте уравнение экспоненциального тренда с учетом квартальных компонентов и постройте классическую мультипликативную модель временного ряда.
4. Что представляет собой квартальный темп роста?
5. Какой смысл имеют квартальные множители?
6. Предскажите значение временного ряда в каждом квартале 2003 года.
15.49. В файле Wf0RD-REV.XLS приведены ежеквартальные доходы компании Ford Motor Company (млн. долл.) с первого квартала 1992 года по четвертый квартал 2002 года.
Источник: Standard & Poor;s Stock Reports, November 1995, November 2000, April 2003. New York: McGraw-Hill, Inc.
1. Подвержены ли доходы компании Toys Я Us сезонным колебаниям? Объясните свой ответ.
2. Постройте график временного ряда. Подтверждает ли он ваш ответ на первый вопрос?
3. Сформулируйте уравнение экспоненциального тренда с учетом квартальных компонентов и постройте классическую мультипликативную модель временного ряда.
4. Что представляет собой квартальный темп роста?
5. Какой смысл имеют квартальные множители?
6. Предскажите значение временного ряда в каждом квартале 2003 года.
15.8. ИНДЕКСЫ
Индексы используются в качестве индикаторов, реагирующих на изменения экономической ситуации или деловой активности. Существуют многочисленные разновидности индексов, в частности, индексы цен (price indexes), количественные индексы (quantity indexes), ценностные индексы (value indexes) и социологические индексы (sociological indexes). В данном разделе мы рассмотрим лишь индекс цен.
Индекс (index) — величина некоторого экономического показателя (или группы показателей) в конкретный момент времени, выраженный в процентах от его значения в базовый момент времени.
Индекс цен
Простой индекс цен (simple price index) отражает процентное изменение цены товара (или группы товаров) в течение заданного периода времени по сравнению с ценой этого товара (или группы товаров) в конкретный момент времени в прошлом. При вычислении индекса цен прежде всего следует выбрать базовый промежуток времени (base period) — интервал времени в прошлом, с которым будут производиться сравнения. При выборе базового промежутка времени для конкретного индекса периоды экономической стабильности являются более предпочтительными по сравнению с периодами экономического подъема или спада. Кроме того, базовый промежуток не должен быть слишком удаленным во времени, чтобы на результаты сравнения не слишком сильно влияли изменения технологии и привычек потребителей. Индекс цен вычисляется по формуле (15.23).
ИНДЕКС ЦЕН
/,=-£-хЮ0, (15.23)
^баз
где / — индекс цен в i-м году, Р. — цена в i-м году, Рбаз — цена в базовом году.
Индекс цен (price index) — процентное изменение цены товара (или группы товаров) в заданный период времени по отношению к цене товара в базовый момент времени.
В качестве примера рассмотрим индекс цен на неэтилированный бензин в США в промежутке времени с 1980 по 2002 г. Соответствующие данные, включая индекс цен на бензин по сравнению с 1980 годом, представлены в табл. 13.15.
Таблица 15.6. Цена галлона неэтилированного бензина и простой индекс цен в США с 1980 по 2002 г. (базовые годы — 1980 и 1995) ^GASOLINE. XLS
Год Цена бензина Индекс цен - 1980 Индекс цен -1995
1980 1,25 100,0 108,7
1981 1,38 110,4 120,0
1982 1,30 104,0 113,0
1983 1,24 99,2 107,8
1984 1,21 96,8 105,2
1985 1,20 96,0 104,3
1986 0,93 74,4 80,9
1987 0,95 76,0 82,6
1988 0,95 76,0 82,6
1989 1,02 81,6 88,7
1990 1,16 92,8 100,9
1991 1,14 91,2 99,1
1992 1,14 91,2 99,1
1993 1,11 88,8 96,5
1994 1,11 88,8 96,5
1995 1,15 92,0 100,0
1996 1,23 98,4 107,0
1997 1,23 98,4 107,0
1998 1,06 84,8 92,2
1999 1,17 93,6 101,7
2000 1,51 120,8 131,3
2001 1,46 116,8 127,0
2002 1,31 104,8 113,9
Источник: Bureau of Labor Statistics, U.S. Department of Labor (www .bls . gov).
Для иллюстрации вычисления индекса цен для 1980 года применим к табл. 15.6 формулу (15.23).
Р 1 31
I = _2«2Lxioo = ——х 100 = 104,8.
го»? р . 25
'1980 1,х.^
Итак, в 2002 г. цена неэтилированного бензина в США была на 4,8% больше, чем в 1980 г. Анализ табл. 15.6 показывает, что индекс цен в 1982-2002 гг. в 1981 и 1982 гг. был больше индекса цен в 1980 г., а затем вплоть до 2000 года не превышал базового уровня. Поскольку в качестве базового периода в табл. 15.6 выбран 1980 г., вероятно, имеет смысл выбрать более близкий год, например, 1995 г. Формула для пересчета индекса по отношению к новому базовому промежутку времени приведена ниже.
ПЕРЕНОС БАЗЫ ДЛЯ ИНДЕКСА ЦЕН
(15-24)
* новая база
где 1кмый — новый индекс цен, 1етары6 — старый индекс цен, 1нояаяЛаза — значение индекса цен в новом базовом году при расчете для старого базового года.
Предположим, что в качестве новой базы выбран 1995 год. Используя формулу (15.24), получаем новый индекс цен для 2002 года.
= -^=- х 100 = X100 = 113,9.
/ 92,0
новая оспа ’
Итак, в 2002 г. неэтилированный бензин в США стоил на 13,9% больше, чем в 1995 г.
Невзвешенные составные индексы цен
Несмотря на то что индекс цен на любой отдельный товар представляет несомненный интерес, более важным является индекс цен на группу товаров, позволяющий оценить стоимость и уровень жизни большого количества потребителей.
Невзвешенный составной индекс цен (unweighted aggregate price index), определенный формулой (15.25), приписывает каждому отдельному виду товаров одинаковый вес.
Составной индекс цен отражает процентное изменение цены группы товаров (часто называемой потребительской корзиной) в заданный период времени по отношению к цене этой группы товаров в базовый момент времени.
НЕВЗВЕШЕННЫЙ СОСТАВНОЙ ИНДЕКС ЦЕН
1? = -^--хЮО, (15.25)
/=1 где t — период времени (0, 1, 2, ...), i — номер товара (1,2, ..., п), п — количество товаров в рассматриваемой группе, ^/’(/) — сумма цен на каждый из п товаров в пери-п
од времени £, ^7^(0) — сумма цен на каждый из п товаров в нулевой период времени, /=1
/'?) — величина невзвешенного составного индекса в период времени t.
В табл. 15.7 представлены средние цены на три вида фруктов за период с 1980 по 1999 гг. Для вычисления невзвешенного составного индекса цен в разные годы применим формулу (15.25), считая базовым 1980 год.
1980:
г (0) _ _2=1_
lU ~ 3
V
х100 = 0-692 + 0'342 + 0-365х100 = 1^х100 = 100,0, 0,692 + 0,342 + 0,365 1,399
ио
1985:
7(1) =
1и
х100 =
0,684 + 0,367 + 0,533 1,584
-2---------------1---х 100 = -----х 100 = 113,2,
0,692 + 0,342 + 0,365 1,399
1990:
х100 =
►(<))
0,719 + 0,463 + 0,570 1,752 „
—--------------------х 100 = -----х 100 = 125,2.
0,692 + 0,342 + 0,365 1,399
►(0)
1995: I™ =
хЮ0 =
>(0)
0,835 + 0,490 + 0,625 1,950 .
---------------------х 100 =------х 100 = 139,4,
0,692 + 0,342 + 0,365 1,399
>(<>)
.(4)
1999:/н>=^х100Л^+0^^
+ р<"» 0,692 + 0,342 + 0,365 1,399
Итак, в 1999 г. суммарная цена фунта яблок, фунта бананов и фунта апельсинов на 59,4% превышала суммарную цену на эти фрукты в 1980 г.
Таблица 15.7. Цены (в долл.) на три вида фруктов ^fruit . XLS
Год
1980 1985 1990 1995 1999
Фрукт pW p(i) ^<2) рО) р(4)
Яблоки 0,692 0,684 0,719 0,835 0,896
Бананы 0,342 0,367 0,463 0,490 0,491
Апельсины 0,365 0,533 0,570 0,625 0,843
Источник: Bureau of Labor Statistics, U. S. Department of Labor fwww.bls. gov),
Невзвешенный составной индекс цен выражает изменения цен на всю группу товаров с течением времени. Несмотря на то что этот индекс легко вычислять, у него есть два явных недостатка. Во-первых, при вычислении этого индекса все виды товаров считаются одинаково важными, поэтому дорогие товары приобретают излишнее влияние на индекс. Во-вторых, не все товары потребляются одинаково интенсивно, поэтому изменения цен на мало потребляемые товары слишком сильно влияют на невзвешенный индекс.
Взвешенные составные индексы цен
Из-за недостатков невзвешенных индексов цен более предпочтительными являются взвешенные индексы цен, учитывающие различия цен и уровней потребления товаров, образующих потребительскую корзину. Существуют два типа взвешенных составных
индексов цен. Индекс цен Лапейрэ (Laspeyres), определенный формулой (15.26), использует уровни потребления в базовом году.
Взвешенный составной индекс цен позволяет учесть уровни потребления товаров, образующих потребительскую корзину, присваивая каждому весу определенный вес.
ИНДЕКС ЦЕН ЛАПЕЙРЭ
= -^-----хЮО , (15.26)
где t — период времени (0, 1, 2, ...), i — номер товара (1, 2, ..., п), п — количество товаров в рассматриваемой группе, Q,0) — количество единиц товара i в нулевой период времени, ’ — значение индекса Лапейрэ в период времени t.
Таблица 15.8. Цены (в долл.) и количество (потребление в фунтах на душу населения) трех видов фруктов ^FRUIT. XLS
Год
1980 1985 1990 1995 1999
Фрукт р(<>) Q((,) а(,) р(2) 1 q:21 рО) р(4) Q!4>
Яблоки 0,692 19,2 0,684 17,3 0,719 19,6 0,835 18,9 0,896 18,8
Бананы 0,342 20,2 0,367 23,5 0,463 24,4 0,490 27,4 0,491 31,4
Апельсины 0,365 14,3 0,533 11,6 0,570 12,4 0,625 12,0 0,843 8,6
Источник: Bureau of Labor Statistics, U.S. Department of Labor (www.bls.gov) и Statistical Abstract of the United States, U. S. Census Bureau (www .census . gov).
Используя в качестве базового 1980 год, вычислим индекс Лапейрэ для 1999 года (t - 4) по формуле (15.26).
0,896x19,2 + 0,491x20,2 + 0,843x14,3 1ЛЛ 39,1763 „
—--------z-----г-------\-----------1_ х 100 = —-----х 100 = 154,2.
0,692 х 19,2 + 0,342 х 20,2 + 0,3 65 х 14,3 25,4143
Итак, индекс Лапейрэ равен 154,2. Это свидетельствует от том, что в 1999 году эти три вида фруктов были на 54,2% дороже, чем в 1980 году. Обратите внимание на то, что этот индекс меньше невзвешенного индекса, равного 159,4, поскольку цены на апельсины — фрукты, потребляемые меньше остальных, — выросли больше, чем цена яблок и бананов. Иначе говоря, поскольку цены на фрукты, потребляемые наиболее интенсивно, выросли меньше, чем цены на апельсины, индекс Лапейрэ меньше невзвешенного составного индекса.
Индекс цен Пааше (Paasche price index) использует уровни потребления товара в текущем, а не базовом периоде времени. Следовательно, индекс Пааше более точно отра-
жает полную стоимость потребления товаров в заданный момент времени. Однако этот индекс имеет два существенных недостатка. Во-первых, как правило, текущие уровни потребления трудно определить. По этой причине многие популярные индексы используют индекс Лапейрэ, а не индекс Пааше. Во-вторых, если цена некоторого конкретного товара, входящего в потребительскую корзину, резко возрастает, покупатели снижают уровень его потребления по необходимости, а не вследствие изменения вкусов. Индекс Пааше вычисляется по формуле (15.27).
ИНДЕКС ЦЕН ПААШЕ
=-^—---— xlOO , (15.27)
где t — период времени (0, 1, 2, ...), i — номер товара (1, 2, ..., п), п — количество товаров в рассматриваемой группе, Q('} — количество единиц товара i в период времени t, 1р} — значение индекса Пааше в период времени t.
Используя в качестве базового 1980 год, вычислим индекс Пааше для 1999 года (t = 4) по формуле (15.27).
ур(4)р(4)
.........х100 = O,896x|8,8 + O,491x31,4 + O,843x8,6x1qo = 39:5I2Ox|oo = Е^(0)2(4).0,692x18,8 + 0,342x31,4 + 0,365x8,6 26,8874
z=i
Итак, индекс Пааше равен 146,95. Это свидетельствует от том, что в 1999 году эти три вида фруктов были на 46,95% дороже, чем в 1980 году.
Некоторые популярные индексы цен
В бизнесе и экономике используется несколько индексов цен. Наиболее популярным является индекс потребительских цен (Consumer Index Price — CPU). Официально этот индекс называется CPU-U, чтобы подчеркнуть, что он вычисляется для городов (“urban”), хотя, как правило, его называют просто CPU. Этот индекс ежемесячно публикуется Бюро статистики труда (U. S. Bureau of Labor Statistics) в качестве основного инструмента для измерения стоимости жизни в США. Индекс потребительских цен является составным и взвешенным по методу Лапейрэ. При его вычислении используются цены 400 наиболее широко потребляемых продуктов, видов одежды, транспортных, медицинских и коммунальных услуг. В данный момент при вычислении этого индекса в качестве базового используется период 1982-1984 гг. В 2001 г. индекс CPI был равен 177,1. (Индексы цен в 1965-2001 гг. приведены в файле ftcPI-U. XLS.)
Важной функцией индекса CPI является его использование в качестве дефлятора (коэффициента пересчета в неизменные цены — Прим. ред.). Индекс CPI используется для пересчета фактических цен в реальные путем умножения каждой цены на коэффициент 100/CPI. Например, на рис. 15.5 представлены реальные доходы компании Wm. Wrigley Jr. Company, вычисленные на основе фактических величин. Это преобразование позволяет выявить действительное увеличение доходов компании, которое можно объяснить увеличением стоимости жизни.
Другим важным индексом цен, публикуемым Бюро статистики труда, является индекс цен производителей (Producer Price Index — PPI). Индекс PPI является взвешен-
ным составным индексом, использующим метод Лапейрэ для оценки изменения цен товаров, продаваемых их производителями. Индекс PPI является лидирующим индикатором для индекса CPI. Иначе говоря, увеличение индекса PPI приводит к увеличению индекса CPI, и наоборот, уменьшение индекса PPI приводит к уменьшению индекса CPI. Финансовые индексы, такие как индекс Доу-Джонса для акций промышленных предприятий (Dow Jones Industrial Average — DJIA), S&P 500 и NASDAQ, используются для оценки изменения стоимости акций в США. Многие индексы позволяют оценить прибыльность международных фондовых рынков. К таким индексам относятся индекс Nikkei в Японии, Dax 30 в Германии и SSE Composite в Китае.
Орш^^^Ы^хс^ййчйспениеиндексов "'У:;'; - У У"/У'У
Для вычисления индексов используются формулы, применяющие функцию сумм и другие арифметические операторы. Процедуры приходится реализовывать самостоятельно, поскольку в надстройке PHStat2 они не предусмотрены.
УПРАЖНЕНИЯ ОАЗДЕЛУ 15.8
Изучение основ
15.50. Простой индекс цен на товар в 2002 году равен 175, причем базовым является 1995 год. Объясните смысл этого показателя.
15.51. Ниже приведены цены на товар в течение 2000-2002 гг.
2000 5 долл.
2001 8 долл.
2002 7 долл.
1. Вычислите простой индекс цен в 2000-2002 гг., используя в качестве базового 2000 год.
2. Вычислите простой индекс цен в 2000-2002 гг., используя в качестве базового 2001 год.
15.52. Ниже приведены цены и уровень потребления товара в 1995 и 2002 гг.
Год
Товар 1995 2002
Цена, долл. Уровень Цена, долл. Уровень
потребления потребления
А 2 20 3 21
В 18 3 36 2
С 3 18 4 23
1. Вычислите невзвешенный составной индекс цен в 2002 г., используя в качестве базового 1995 год.
2. Вычислите составной индекс цен Лапейрэ в 2002 г., используя в качестве базового 1995 год.
3. Вычислите составной индекс цен Пааше в 2002 г., используя в качестве базового 1995 год.
Применение понятий
15.53. В файле ftcPI-U. XLS приведены ежегодные значения индекса потребительских цен в США, вычисленные за 37-летний период (1965-2002 гг.). В качестве базового периода выбран промежуток времени с 1982 по 1984 г. Этот индекс измеряет среднее изменение цен на фиксированный набор товаров и услуг, предоставляемых всем городским жителям — наемным работникам (т.е. конторским служащим, руководящим работникам, техническому персоналу, лицам свободной профессии и сезонным рабочим), безработным и пенсионерам.
Источник: Bureau of Labor Statistics, U. S. Department of Labor.
1. Вычислите индекс потребительских цен в США, используя в качестве базового 1965 год.
2. Перенесите базу на 1990 год и пересчитайте индекс потребительских цен в США.
3. Сравните результаты решения задач 1 и 2. Какой индекс цен дает более ясное представление об изменении потребительских цен в США? Обоснуйте свой ответ.
15.54. Приведенные ниже данные представляют собой ежегодные средние значения индекса Доу-Джонса для акций промышленных компаний (DJIA) на момент закрытия торгов, вычисленные за 24-летний период (1979-2002 гг.).
CIdjia.xls.
Индекс Доу-Джонса (1979-2002)
Год DJIA Год DJIA Год DJIA
1979 838,7 1987 1 938,8 1995 5 117,1
1980 964,0 1988 2 168,6 1996 6 448,3
1981 875,0 1989 2 753,2 1997 7 908,3
1982 1 046,5 1990 2 633,7 1998 9 181,4
1983 1 258,6 1991 3 168,8 1999 11 497,1
1984 1 211,6 1992 3 301,1 2000 10 788,0
1985 1 546,7 1993 3 754,1 2001 10 021,5
1986 1 896,0 1994 3 834,4 2002 8 341,63
1. Вычислите индекс Доу-Джонса для акций промышленных компаний, используя в качестве базового 1979 год.
2. Перенесите базу на 1990 год и пересчитайте индекс Доу-Джонса для акций промышленных компаний.
3. Сравните результаты решения задач 1 и 2. Какой из указанных индексов дает более ясное представление об изменении индекса Доу-Джонса для акций промышленных компаний? Обоснуйте свой ответ.
15.55. Приведенные ниже данные представляют собой ежегодные значения индекса потребительских цен и цен производителя в Японии, вычисленные за период с 1990 по 2001 годы. W JAPANCPIPPI. XLS.
Год Индекс потребительских цен Индекс цен производителя
1990 93,71 107,9
1991 96,38 105,9
1992 97,20 104,5
1993 98,58 101,4
1994 99,20 100,6
1995 98,90 99,8
1996 99,10 99,8
1997 101,60 100,9
1998 101,80 97,2
1999 101,10 96,6
2000 100,30 97,6
2001 99,80 96,1
Источник: w» . bo j .or.jp, September 19, 2002.
1. Вычислите индекс потребительских цен в Японии, используя в качестве базового 1990 год.
2. Перенесите базу на 2001 год и пересчитайте индекс потребительских цен в Японии.
3. Сравните результаты решения задач 1 и 2. Какая из указанных величин дает более ясное представление об изменении индекса потребительских цен в Японии? Обоснуйте свой ответ.
4. Вычислите индекс цен производителя в Японии, используя в качестве базового 1990 год.
5. Перенесите базу на 2001 год и пересчитайте индекс цен производителя в Японии.
6. Сравните результаты решения задач 1 и 2. Какая из указанных величин дает более ясное представление об изменении индекса цен производителя в Японии? Обоснуйте свой ответ.
7. Сравните результаты решения задач 1-5 с результатами решения последующей задачи 15.56.
15.56. Приведенные ниже данные представляют собой ежегодные значения индекса потребительских цен и цен производителя в Великобритании, вычисленные за период с 1990 по 2001 годы. ^UKCPI. XLS.
Год Индекс потребительских цен
1990 129,9
1991 135,7
1992 139,2
1993 141,9
1994 146,0
1995 150,7
1996 154,4
1997 160,0
1998 164,4
1999 167,3
2000 172,2
2001 173,4
Источник: www. statistics . gov. uk, September 19, 2002.
1. Вычислите индекс потребительских цен в Великобритании, используя в качестве базового 1990 год.
2. Перенесите базу на 2001 год и пересчитайте индекс потребительских цен в Великобритании.
3. Сравните результаты решения задач 1 и 2. Какая из указанных величин дает более ясное представление об изменении индекса потребительских цен в Великобритании? Обоснуйте свой ответ.
4. Сравните индексы потребительских цен в Великобритании и Японии.
15.57. Приведенные в файле ©COFFEEPRICE. XLS данные представляют собой средние цены фунта кофе в США за период с 1980 по 2003 годы.
Источник: Bureau of Labor Statistics, U. S. Department of Labor.
1. Вычислите простой индекс цен в 1980-2003 гг., используя в качестве базового 1980 год.
2. Объясните смысл простого индекса цен в 2003 г., используя в качестве базового 1980 год.
3. Вычислите простой индекс цен в 1980-2003 гг. по формуле (15.23), используя в качестве базового 1990 год.
4. Объясните смысл простого индекса цен в 2002 г., используя в качестве базового 1990 год.
5. Можно ли использовать в качестве базового 1995 год? Аргументируйте свой ответ.
6. Опишите тренд стоимости кофе в 1980-2003 гг.
15.58. Приведенные ниже данные представляют собой средние цены фунта свежих помидоров в США за период с 1980 по 2003 годы. ©TOMATOES . XLS.
Год Цена Год Цена Год Цена
1980 0,703 1988 0,871 1996 1,103
1981 0,792 1989 0,797 1997 1,213
1982 0,763 1990 1,735 1998 1,452
1983 0,726 1991 0,912 1999 1,904
1984 0,854 1992 0,936 2000 1,443
1985 0,697 1993 1,141 2001 1,414
1986 1,103 1994 1,604 2002 1,451
1987 0,943 1995 1,323 2003 1,711
Источник: Bureau of Labor Statistics, U. S. Department of Labor (www .bls. gov).
1. Вычислите простой индекс цен в 1980-2003 гг., используя в качестве базового 1980 год.
2. Объясните смысл простого индекса цен в 2003 г., используя в качестве базового 1980 год.
3. Вычислите простой индекс цен в 1980-2003 гг. по формуле (15.23), используя в качестве базового 1990 год.
4. Объясните смысл простого индекса цен в 2002 г., используя в качестве базового 1990 год.
5. Опишите тренд стоимости помидоров в 1980-2003 гг.
15.59. Приведенные в файле ^ENERGY2 . XLS данные представляют собой средние цены на энергоносители трех видов в США за период с 1992 по 2003 годы. К ним относятся электричество (долл, за 500 кВт.ч), природный газ (долл, за 40 термов) и горючее (долл, за галлон).
Источник: Bureau of Labor Statistics, U. S. Department of Labor (www.bls.gov/
1. Вычислите простой индекс цен на электричество в 1992-2003 гг., используя в качестве базового 1992 год.
2. Вычислите простой индекс цен на природный газ в 1992-2003 гг., используя в качестве базового 1992 год.
3. Вычислите простой индекс цен на горючее в 1992-2003 гг., используя в качестве базового 1992 год.
4. Вычислите простые индексы цен, указанные в задачах 1-3, используя в качестве базового 1996 год.
5. Вычислите невзвешенные составные индексы цен для группы, состоящей из энергоносителей трех видов, для периода 1992-2003 гг.
6. Вычислите индекс цен Лапейрэ в 2003 году для группы, состоящей из энергоносителей трех видов, если семья в 1992 году потребляла 5 000 кВт-ч электричества (10 единиц), 960 термов натурального газа (24 единицы) и 400 галлонов горючего (400 единиц).
7. Вычислите индекс цен Пааше в 2003 году для группы, состоящей из энергоносителей трех видов, если семья в 2003 году потребляла 6 500 кВт-ч электричества, 1 040 термов натурального газа и 235 галлонов горючего.
15.9. ЛОВУШКИ, СВЯЗАННЫЕ С АНАЛИЗОМ ВРЕМЕННЫХ РЯДОВ
Значение методологии, использующей информацию о прошлом и настоящем для того, чтобы прогнозировать будущее, более двухсот лет назад красноречиво описал государственный деятель Патрик Генри (Patrick Henry):
У меня есть лишь одна лампа, освещающая путь, — мой опыт. Только знание прошлого позволяет судить о будущем. — Речь в Конвенте штата Вирджиния, Ричмонд, Вирджиния, 23 марта 1775 года.
Анализ временных рядов основан на предположении, что факторы, влиявшие на деловую активность в прошлом и влияющие в настоящем, будут действовать и в будущем. Если это правда, анализ временных рядов представляет собой эффективное средство прогнозирования и управления.
Однако критики классических методов, основанных на анализе временных рядов, утверждают, что эти методы слишком наивны и примитивны. Иначе говоря, математическая модель, учитывающая факторы, действовавшие в прошлом, не должна механически экстраполировать тренды в будущее без учета экспертных оценок, опыта деловой активности, изменения технологии, а также привычек и потребностей людей (см. задачу 15.73). Пытаясь исправить это положение, в последние годы специалисты по эконометрии разрабатывали сложные компьютерные модели экономической активности, учитывающие перечисленные выше факторы. Однако эти модели выходят за рамки нашей книги [1, 2, 3].
Тем не менее, как показано в главе, методы анализа временных рядов представляют собой превосходный инструмент прогнозирования (как краткосрочного, так и долгосрочного), если они применяются правильно, в сочетании с другими методами прогнозирования, а также с учетом экспертных оценок и опыта.
РЕЗЮМЕ
В этой главе с помощью анализа временных рядов разработаны модели для прогнозирования доходов трех компаний: Wm. Wrigley Jr. Company, Cabot Corporation и Wal-Mart. Описаны компоненты временного ряда, а также несколько подходов к прогнозированию годовых временных рядов — метод скользящих средних, метод экспоненциального сглаживания, линейная, квадратичная и экспоненциальная модели, а также авторегрессионная модель. Рассмотрена регрессионная модель, содержащая фиктивные переменные, соответствующие сезонному компоненту. Показано применение метода наименьших квадратов для прогнозирования месячных и квартальных временных рядов.
Прогнозирование
Индексы
". с помощью
| временных рядоё
2^
Составной? j
Нет
Взвешенный?^
Нет
Невзвешенный : , индекс цен
Да
Простой индекс цен-|||
Тренд?
Нет
Экспоненциальное Скользящие
Есглаживание . , средние
Индекс Лапейрэ:
Индекс Пааше
Ежегодные ; Нет
Регрессионные модели ' для прогнозирования
Модели ,прогнозирования
Квадратичный . Экспоненциальный Авторегресионные тренд j тренд । модели
Линейный тренд
Выбор модели ;
Структурная схема главы 15
ОСНОВНЫЕ ПОНЯТИЯ
Автокорреляция р-го порядка, 1019 второго порядка, 1019 первого порядка, 1019
Авторегрессионная модель, 1019
Анализ временных рядов, 985
Анализ причинно-следственных зависимостей, 985
Временной ряд, 985
Индекс, 1049; 1050; 1051
Индекс цен
Лапейрэ, 1053
Пааше, 1053 составной взвешенный, 1053 невзвешенный, 1051; 1053; 1054
Классическая мультипликативная модель, 985
Компонент временного ряда сезонный, 986
случайный, 986
циклический, 985
Методы качественного прогнозирования, 985 Методы количественного прогнозирования, 985 Модель тренда
квадратичная, 1002
линейная, 999
экспоненциальная, 1004
Относительная разность, 1011
Принцип экономии, 1034
Разность
второго порядка, 1011
первого порядка, 1011
Скользящее среднее, 989
Среднее абсолютное отклонение, 1034
Стандартная ошибка, 1033
Экспоненциальное сглаживание, 992
УПРАЖНЕНИЯ К ГЛАВЕ 15
Проверка знаний
15.60. В чем проявляется важность методологии прогнозирования?
15.61. Что такое временной ряд?
15.62. Какие компоненты входят в классическую мультипликативную модель временного ряда и чем они отличаются друг от друга?
15.63. В чем заключается различие между методом скользящих средних и методом экспоненциального сглаживания?
15.64. В каких ситуациях следует выбирать метод экспоненциального сглаживания?
15.65. Чем регрессионная модель, описанная в этой главе, отличается от регрессионной модели, изложенной в главе 12?
15.66. Чем авторегрессионное моделирование отличается от других методов?
15.67. Какие существуют альтернативные методы прогнозирования?
15.68. Чем стандартная ошибка 8ХТ отличается от среднего абсолютного отклонения МАТУ?
15.69. Чем прогнозирование годовых временных рядов отличается от прогнозирования месячных и квартальных данных?
15.70. Что такое индекс?
15.71. Чем простой индекс цен отличается от составного?
15.72. В чем заключаются различия между индексами Лапейрэ и Пааше?
Применение понятий
15.73. В следующей таблице приведена частота заболеваний полиомиелитом (на 100 000 человек) за период с 1915 по 1955 годы. ftpOLIO. XLS.
Частота заболеваний полиомиелитом (на 100 000 человек)
Год 1915 1920 1925 1930 1935 1940 1945 1950 1955
Частота 3,1 2,2 5,3 7,5 8,5 7,4 10,3 22,1 17,6
Источник: данные взяты из книги В. Wattenberg, ed., The Statistical History of the United States, From Colonial Times to the Present, ser. B303 (New York: Basic Books, 1976).
1. Постройте график временного ряда.
2. Вычислите линейный тренд и постройте его график.
3. Какую частоту заболевания следовало ожидать в 1960, 1965 и 1970 гг. в соответствии с трендом?
4. Сравните фактическую частоту заболевания в 1960, 1965 и 1970 гг. с предсказанной в соответствии с трендом.
5. Почему механическая экстраполяция тренда, построенного с помощью метода наименьших квадратов, является неприемлемой?
15.74. В файле ftGAPAC. XLS приведены фактические доходы компании Georgia-Pacific Corporation за период с 1975 по 2002 годы (млрд. долл, в текущих ценах).
Источник: Moody's Handbook of Common Stocks, 1980, 1989, 1999. Mergent’s Handbook of Common Stocks, 2003. Публикуется с разрешения Службы финансовой информации (Financial Information Services), подразделения компании Financial Communications Company, Inc. и компании Standard and Poofs Corp. (New York: McGraw-Hill, Inc., December 2002).
1. Заполните новую таблицу, содержащую скорректированные (т.е. реальные) величины, умножив ежегодный доход на коэффициент 100/CPI. Годовые величины индекса потребительских цен CPI можно найти в таблице, помещенной в задаче 15.12. Реальные величины дохода выражаются в ценах 1982-1984 гг.
2. Постройте график скорректированного временного ряда.
3. Вычислите линейный тренд.
4. Найдите квадратичный тренд.
5. Вычислите экспоненциальный тренд.
6. Постройте авторегрессионную модель третьего порядка и проверьте значимость ее старшего члена, если уровень значимости равен 0,05.
7. Если необходимо, постройте авторегрессионную модель второго порядка и проверьте значимость ее старшего члена, если уровень значимости равен 0,05.
8. Если необходимо, постройте авторегрессионную модель первого порядка и проверьте значимость ее старшего члена, если уровень значимости равен 0,05.
9. Выполните анализ остатков для каждой из моделей в задачах 3-5 и для оптимальной авторегрессионной модели в задачах 6-8.
10. Вычислите стандартную ошибку 8УЛ. для каждой из моделей, упомянутых в задаче 9.
11. Вычислите среднее абсолютное отклонение MAD для каждой из моделей, упомянутых в задаче 9.
12. Используя решения задач 9-11 и принцип экономии, определите наилучшую модель для прогнозирования.
13. Предскажите доход компании в 2003 и 2004 годах, используя модель, выбранную в задаче 12.
15.75. В файле ft^PMORRIS .XLS приведены фактические доходы компании Philip Morris Companies, Inc. за период с 1975 по 2001 годы (млрд. долл, в текущих ценах). Источник: Moody's Handbook of Common Stocks, 1980, 1989, 1999, Mergent’s Handbook of Common Stocks, 2002.. Публикуется с разрешения Службы финансовой информации (Financial Information Services), подразделения компании Financial Communications Company, Inc. и компании Standard and Poors Corp. (New York: McGraw-Hill, Inc., December 2002).
1. Заполните новую таблицу, содержащую скорректированные (т.е. реальные) данные, умножив ежегодный доход на коэффициент 100/CPI. Годовые величины индекса потребительских цен CPI можно найти в таблице, помещенной в задаче 15.12. Реальные значения дохода выражаются в ценах 1982-1984 гг.
2. Постройте график скорректированного временного ряда.
3. Вычислите линейный тренд.
4. Определите квадратичный тренд.
5. Вычислите экспоненциальный тренд.
6. Постройте авторегрессионную модель третьего порядка и проверьте значимость ее старшего члена, если уровень значимости равен 0,05.
7. Если необходимо, постройте авторегрессионную модель второго порядка и проверьте значимость ее старшего члена, если уровень значимости равен 0,05.
8. Если необходимо, постройте авторегрессионную модель первого порядка и проверьте значимость ее старшего члена, если уровень значимости равен 0,05.
9. Выполните анализ остатков для каждой из моделей в задачах 3-5 и оптимальной авторегрессионной модели в задачах 6-8.
10. Вычислите стандартную ошибку SXY для каждой из моделей, упомянутых в задаче 9.
11. Вычислите среднее абсолютное отклонение MAD для каждой из моделей, упомянутых в задаче 9.
12. Используя решения задач 9-11 и принцип экономии, определите наилучшую модель для прогнозирования.
13. Предскажите доход компании в 2002 и 2003 годах, используя модель, выбранную в задаче 12.
15.76. В следующей таблице приведены фактические доходы компании MDonald's Corporation за период с 1975 по 2002 годы (млрд. долл, в текущих ценах). ^MCDONALD. XLS.
Фактические доходы компании McDonald's Corporation (1975-2002 гг.)
Год Доход (млрд, долл.) Год Доход (млрд, долл.)
1975 1,0 1989 6,1
1976 1,2 1990 6,8
1977 1,4 1991 6,7
1978 1,7 1992 7,1
1979 1,9 1993 7,4
1980 2,2 1994 8,3
1981 2,5 1995 9,8
1982 2,8 1996 10,7
1983 3,1 1997 11,4
1984 3,4 1998 12,4
1985 3,8 1999 13,3
1986 4,2 2000 14,2
1987 4,9 2001 14,9
1988 5,6 2002 15,4
Источник: Moody's Handbook of Common Stocks, 1980, 1989, 1999 и Mergens’s Handbook of Common Stock, Spring 1993. Публикуется с разрешения Службы финансовой информации (Financial Information Services), подразделения компании Financial Communications Company, Inc. и компании Standard and Poors Corp. (New York: McGraw-Hill, Inc., December 2002).
1. Заполните новую таблицу, содержащую скорректированные (т.е. реальные) данные, умножив ежегодный доход на коэффициент 100/CPI. Годовые величины индекса потребительских цен CPI можно найти в таблице, помещенной в задаче 15.12. Реальные величины доходы выражаются в ценах 1982-1984 гг.
2. Постройте график скорректированного временного ряда.
3. Вычислите линейный тренд.
4. Определите квадратичный тренд.
5. Вычислите экспоненциальный тренд.
6. Постройте авторегрессионную модель третьего порядка и проверьте значимость ее старшего члена, если уровень значимости равен 0,05.
7. Если необходимо, постройте авторегрессионную модель второго порядка и проверьте значимость ее старшего члена, если уровень значимости равен 0,05.
8. Если необходимо, постройте авторегрессионную модель первого порядка и проверьте значимость ее старшего члена, если уровень значимости равен 0,05.
9. Выполните анализ остатков для каждой из моделей в задачах 3-5 и для оптимальной авторегрессионной модели в задачах 6-8.
10. Вычислите стандартную ошибку SYX для каждой из моделей, упомянутых в задаче 9.
11. Вычислите среднее абсолютное отклонение MAD для каждой из моделей, упомянутых в задаче 9.
12. Используя решения задач 9-11 и принцип экономии, определите наилучшую модель для прогнозирования.
13. Предскажите доход компании в 2003 и 2004 годах, используя модель, выбранную в задаче 12.
15.77. В файле CfsEARS.XLS приведены фактические доходы компании Sears, Roebuck & Company за период с 1975 по 2002 годы (млрд. долл, в текущих ценах). Источник: Moody's Handbook of Common Stocks, 1980, 1989, 1999 и Megrent’s Handbook of Common Stocks, Spring 2003.. Публикуется с разрешения Службы финансовой информации (Financial Information Services), подразделения компании Financial Communications Company, Inc. и компании Standard and Poors Corp. (New York: McGraw-Hill, Inc., December 2002).
1. Заполните новую таблицу, содержащую скорректированные (т.е. реальные) данные, умножив ежегодный доход на коэффициент 100,0/СР1. Годовые величины индекса потребительских цен CPI можно найти в таблице, помещенной в задаче 15.12. Реальные величины доходы выражаются в ценах 1982-1984 гг.
2. Постройте график скорректированного временного ряда.
3. Вычислите линейный тренд.
4. Определите квадратичный тренд.
5. Вычислите экспоненциальный тренд.
6. Постройте авторегрессионную модель третьего порядка и проверьте значимость ее старшего члена, если уровень значимости равен 0,05.
7. Если необходимо, постройте авторегрессионную модель второго порядка и проверьте значимость ее старшего члена, если уровень значимости равен 0,05.
8. Если необходимо, постройте авторегрессионную модель первого порядка и проверьте значимость ее старшего члена, если уровень значимости равен 0,05.
9. Выполните анализ остатков для каждой из моделей в задачах 3-5 и для оптимальной авторегрессионной модели.
10. Вычислите стандартную ошибку SYX для каждой из моделей, упомянутых в задаче 9.
11. Вычислите среднее абсолютное отклонение для каждой из моделей, упомянутых в задаче 9.
13. Используя решения задач 9-11 и принцип экономии, определите наилучшую модель для прогнозирования.
14. Предскажите доход компании в 2003 и 2004 годах, используя модель, выбранную в задаче 12.
15.78. Общество учителей-пенсионеров г. Нью-Йорка предлагает своим членам несколько типов инвестиций. К типу А относятся инвестиции в акции, а к типу Б — инвестиции в корпоративные облигации и другие ценные бумаги с низким уровнем риска. В файле ©TRSNYC. XLS приведена стоимость ценных бумаг за период с 1984 по 2003 гг.
Год A Б
1984 13,111 10,342
1985 13,176 11,073
1986 16,526 11,925
1987 18,652 12,694
1988 15,564 13,352
1989 20,827 13,919
1990 24,738 14,557
1991 22,678 15,213
1992 28,549 15,883
1993 29,829 16,510
1994 31,199 16,970
1995 30,830 17,351
1996 39,644 17,682
1997 45,389 18,004
1998 54,882 18,341
1999 64,790 18,678
2000 74,220 18,962
2001 67,534 19,320
2002 57,709 19,673
2003 44,843 19,735
Источник: www. trs . nyc. ny. ua.
Для каждого временного ряда выполните следующие задания.
1. Постройте график временного ряда.
2. Создайте модель линейного тренда.
3. Создайте модель квадратичного тренда.
4. Создайте модель экспоненциального тренда.
5. Создайте авторегрессионную модель третьего порядка и проверьте значимость старшего авторегрессионного параметра при уровне значимости, равном 0,05.
6. Если необходимо, создайте авторегрессионную модель второго порядка и проверьте значимость старшего авторегрессионного параметра при уровне значимости, равном 0,05.
7. Если необходимо, создайте авторегрессионную модель первого порядка и проверьте значимость старшего авторегрессионного параметра при уровне значимости, равном 0,05.
8. Выполните анализ остатков для каждой модели в задачах 3-4 и оптимальной авторегрессионной модели.
9. Вычислите стандартную ошибку SYX для каждой модели.
10. Вычислите среднее абсолютное отклонение MAD для каждой из моделей, упомянутых в задаче 8.
11. Используя решения задач 8-10 и принцип экономии, определите наилучшую модель для прогнозирования.
12. Предскажите стоимость ценных бумаг в 2004 и 2005 годах, используя модель, выбранную в задаче 11.
13. Какую инвестиционную стратегию вы порекомендовали бы членам общества учителей-пенсионеров г.Нью-Йорка?
15.79. В файле ^BASKET.XLS приведены средние цены потребительской корзины за период с 1992 по 2002 гг. В частности, указаны цены (в долл.) однофунтовой буханки белого хлеба, фунта говядины, дюжины яиц и фунта кочанного салата.
Год Хлеб Говядина Яйца Салат
1992 0,726 1,926 0,933 0,573
1993 0,748 1,970 0,898 0,625
1994 0,768 1,892 0,917 0,506
1995 0,767 1,847 0,882 0,821
1996 0,860 1,799 1,155 0,769
1997 0,862 1,850 1,148 0,651
1998 0,855 1,818 1,120 1,072
1999 0,872 1,834 1,053 0,649
2000 0,907 1,903 0,975 0,748
2001 0,982 2,037 1,011 0,736
2002 1,001 2,151 0,973 1,003
Источник: Bureau of Labor Statistics, U. S. Department of Labor (www. bls . gov/
1. Вычислите простые индексы цен на хлеб в период с 1992 по 2002 г., считая базовым 1992 год.
2. Вычислите простые индексы цен на говядину в период с 1992 по 2002 г., считая базовым 1992 год.
3. Вычислите простые индексы цен на яйца в период с 1992 по 2002 г., считая базовым 1992 год.
4. Вычислите простые индексы цен на салат в период с 1992 по 2002 г., считая базовым 1992 год.
5. Вычислите простые индексы цен в задачах 1-4, считая базовым 1996 год.
6. Вычислите невзвешенные агрегированные индексы цен на товары, входящие в потребительскую корзину в период с 1992 по 2002 г., считая базовым 1992 год.
7. Вычислите индекс цен Лапейрэ (Laspeyres) в 2002 г. на товары, входящие в потребительскую корзину семьи, которая в 1992 г. съела 50 буханок хлеба, 22 фунта говядины, 24 дюжины яиц и 18 фунтов салата.
8. Вычислите индекс цен Пааше (Paasche) в 2002 г. на товары, входящие в потребительскую корзину семьи, которая в 1992 г. съела 55 буханок хлеба, 17 фунтов говядины, 20 дюжин яиц и 28 фунтов салата.
Отчеты
15.80. Трудовое соглашение, заключенное между игроками высшей бейсбольной лиги и ее владельцами, время от времени оспаривается. Это приводит к периодическим забастовкам. В файле ft^BBSALARY. XLS указаны средние зарплаты (тыс. долл.) игроков за период с 1979 по 2002 г., а также медиана зарплаты за период с 1983 по 2002 г.
1. Представьте себе, что владельцы лиги предложили вам подготовить отчет и показать, что зарплата игроков возрастает с космической скоростью. Постройте модель, подтверждающую этот вывод.
2. Представьте себе, что игроки бейсбольной лиги предложили вам подготовить отчет и показать, что с учетом индекса потребительских цен зарплата игроков возросла незначительно. Постройте модель, подтверждающую этот вывод.
3. Представьте себе, что владельцы спортивной телевизионной сети предложили вам объективно исследовать рост зарплаты игроков. Постройте соответствующую модель.
Замечание’, дополните ваш отчет графиками и диаграммами, иллюстрирующими статистическую информацию, извлеченную из данных. Для создания и вставки таблиц и диаграмм используйте программу Microsoft Excel и пакет Microsoft Office. Подготовьте презентацию с помощью программы Power Point.
15.81. Представьте себе, что вы работаете в фирме, торгующей валютой. Вам поручили изучить долговременные тренды, характеризующие поведение курсов канадского доллара, японской йены и английского фунта. В файле ^CURRENCY. XLS содержатся данные о курсе валют за 37-летний период с 1967 по 2003 гг. Все курсы выражаются в долларах США, лишь английский фунт выражен через центы.
Допустим, что вы решили разработать регрессионную модель для каждой из трех валют, используя данные из файла, и на их основе сделать прогноз на 2003 и 2004 гг. Напишите отчет и подготовьте презентацию для группы инвесторов. Опишите возможные ограничения, налагаемые на модели прогнозирования.
Применение Интернет
15.82. Зайдите на сайт www.prenhall.com/levine. Выберите ссылку Chapter 15 и щелкните на ссылке Internet exercises.
:ЖМЬ$КОЙЙ
ГАЗЕТА S7W/M
~ V ’г к '/ < :
Возрастающая стоимость доставки является важным фактором, влияющим на стратегию подписной кампании. Основная ответственность за мониторинг и прогнозирование стоимости доставки возложена на отдел маркетинга. В обязанности отдела входит анализ всех возможных трендов. Решая поставленную задачу, отдел маркетинга собрал данные о количестве подписчиков за последние два года. ^SH15 . XLS.
УПРАЖНЕНИЯ
Выполните следующие задания.
1. Проанализируйте данные и постройте статистическую модель для прогноза количества подписчиков в будущем. Учтите все предположения и ограничения, наложенные на выбранную модель. Предскажите количество подписчиков в следующие четыре месяца.
2. Не хотите ли распространить свой прогноз на один год вперед? Обоснуйте свой ответ.
3. Сравните тренды количества подписчиков и количества новых подписчиков, появившихся у газеты за последние два года. ^SH12.XLS Объясните разницу между ними.
ПРИМЕНЕНИЕ WEB
Примените свои знания о временных рядах для прогнозирования количества подписчиков газеты Springville Herald.
На протяжении многих лет газета Springville Herald конкурировала с журналом Oxford Glen Journal (OGJ). Недавно отдел распространения журнала OGJ заявил, что количество их подписчиков и объем продаж растут намного быстрее, чем количество подписчиков и объем продаж газеты Springville Herald, а местные рекламодатели предпочитают размещать свои объявления не в Springville Herald, а в OGJ. Отдел распространения газеты Springville Herald подал жалобу в Торговую палату г. Спрингвиль, попросив расследовать заявления их конкурентов.
Проанализируйте данные и заявления, собранные Торговой палатой г. Спрингвиль (www.prenhall.com/Springville/SCC_CirculationDispute.html), и ответьте на следующие вопросы.
1. Какое из изданий имеет право заявлять, что количество его подписчиков и объемы продаж растут быстрее, чем у конкурента? Аргументируйте свой ответ результатами статистического анализа.
2. Назовите самый сильный аргумент, свидетельствующий о росте количества подписчиков и объема продаж газеты Springville Herald. Назовите самый сильный аргумент, свидетельствующий о росте количества подписчиков и объема продаж газеты OGJ. Аргументируйте свой ответ.
3. Какие дополнительные данные было бы целесообразно исследовать при проверке заявления отделов распространения конкурирующих газет?
СПРАВОЧНИК ПО EXCEL ГЛАВА 15
ЕН.15.1. Создание графиков скользящих средних
Для построения графика скользящих средних используется Мастер диаграмм. Например, чтобы построить график 3- и 7-летних скользящих средних, вычисленных по доходам компании Cabot Corporation, приведенным в табл. 15.2, необходимо открыть рабочий лист Cabot_MA в книге Chapter 15.xls, выбрать команду Вставка^Диаграмма... и следовать инструкциям.
1. На первом этапе диалога осуществить такие действия.
1.1. Щелкнуть на корешке вкладки Стандартные, а затем выбрать пункт Точечная в раскрывающемся списке Тип. Выбрать первую (верхнюю) диаграмму во втором ряду, сопровождающуюся описанием: “Точечная диаграмма, на которой значения соединены отрезками”.
1.2. Щелкнуть на кнопке Далее>.
2. На втором этапе диалога выполнить следующее.
2.1. Щелкнуть на корешке вкладки Диапазон данных, а затем ввести в окне редактирования Диапазон ссылки на ячейки Al: D21.
2.2. Установить переключатель Ряды в положение В столбцах.
2.3. Щелкнуть на кнопке Далее>.
3. На третьем этапе диалога выполнить следующее.
3.1. Щелкнуть на корешке вкладке Заголовки. Ввести в окне редактирования Название диаграммы заголовок рисунка, в окне редактирования Ось X — строку Доходы (млрд. долл.), а в окне редактирования Ось У — строку Годы.
3.2. По очереди щелкнуть на корешках вкладок Оси, Линии сетки, Легенда и Подписи данных. Установить флажки и переключатели, как показано в разделе ЕР.6.
3.3. Щелкнуть на кнопке Далее>.
4. На четвертом шаге диалога выполнить следующее.
4.1. Установить переключатель Поместить диаграмму на листе в положение Отдельном.
4.2. Щелкнуть на кнопке ГОТОВО.
ЕН.15.2. Создание графиков экспоненциального сглаживания
Для построения графиков экспоненциального сглаживания используется Мастер диаграмм. Чтобы построить график экспоненциально сглаженных величин, вычисленных по доходам компании Cabot Corporation, приведенным в табл. 15.2, сначала необходимо открыть рабочий лист Cabot_ES в книге Chapter 15.xls. Затем следует выбрать команду Вставка^ Диаграмма... и следовать инструкциям.
1. На первом этапе диалога выполнить такие действия.
1.1. Щелкнуть на корешке закладки Стандартные, а затем выбрать пункт Точечная в раскрывающемся списке Тип. Выбрать первую (верхнюю) диаграмму во втором ряду, сопровождающуюся описанием: “Точечная диаграмма, на которой значения соединены отрезками”.
1.2. Щелкнуть на кнопке Далее>.
2. На втором этапе диалога выполнить следующее.
2.1. Щелкнуть на корешке закладки Диапазон данных, а затем ввести в окне редактирования Диапазон ссылки на ячейки Al: D21.
2.2. Установить переключатель Ряды в положение В столбцах.
2.3. Щелкнуть на кнопке Далее>.
3. На третьем этапе диалога выполнить следующее.
3.1. Щелкнуть на корешке закладки Заголовки. Ввести в окне редактирования Название диаграммы строку заголовок рисунка, в окне редактирования Ось X— строку Доходы (млн. долл.), а в окне редактирования Ось Y — строку Годы.
3.2. По очереди щелкнуть на корешках вкладок Оси, Линии сетки, Легенда и Подписи данных. Установить флажки и переключатели, как показано в разделе ЕР.6.
3.3. Щелкнуть на кнопке Далее>.
4. На четвертом этапе диалога выполнить следующее.
4.1. Установить переключатель Поместить диаграмму на листе в положение Отдельном.
4.2. Щелкнуть на кнопке Готово.
ЕН.15.3. Создание диаграмм разброса для трендов, построенных методом наименьших квадратов
Для построения диаграмм разброса используется Мастер диаграмм. Чтобы построить линейный тренд, вычисленный для доходов компании Wm. Wrigley Jr. Company, приведенных в табл. 15.4, сначала необходимо открыть рабочий лист Wrigley_MHK в книге Chapter 15.xls. Затем следует выбрать команду Вставка^Диаграмма и следовать инструкциям.
1. На первом этапе диалога выполнить такие действия.
1.1. Щелкнуть на корешке закладки Стандартные, а затем выбрать пункт Точечная в раскрывающемся списке Тип. Выбрать первую (верхнюю) диаграмму во втором ряду, сопровождающуюся описанием: “Точечная диаграмма, на которой значения соединены отрезками”.
1.2. Щелкнуть на кнопке Далее>.
2. На втором этапе диалога выполнить следующее.
2.1. Щелкнуть на корешке закладки Диапазон данных, а затем ввести в окне редактирования Диапазон ссылки на соответствующие ячейки.
2.2. Установить переключатель Ряды в положение В столбцах.
2.3. Щелкнуть на кнопке Далее>.
3. На третьем этапе диалога выполнить следующее.
3.1. Щелкнуть на корешке закладки Заголовки. Ввести в окне редактирования Название диаграммы строку заголовок рисунка, в окне редактирования Ось X— строку Доходы (млн. долл.), а в окне редактирования Ось Y — строку Годы.
3.2. По очереди щелкнуть на корешках вкладок Оси, Линии сетки, Легенда и Подписи данных. Установить флажки и переключатели, как показано в разделе ЕР.6.
3.3. Щелкнуть на кнопке Далее>.
4. На четвертом этапе диалога выполнить следующее.
4.1. Установить переключатель Поместить диаграмму на листе в положение Отдельном.
4.2. Щелкнуть на кнопке Готово.
ЕН.15.4. Логарифмическое преобразование
При создании экспоненциальной модели программа Microsoft Excel использует логарифмы предсказанных значений, а не фактические значения отклика, записанные на рабочем листе, содержащем регрессионную статистику. Для вычисления значений отклика по их логарифмам используется функция СТЕПЕНЬ (10; log Y), где значения логарифмов записаны в таблице остатков.
В табл. ЕН. 15.1 показаны дополнения, которые необходимо внести в рабочий лист Wrigley_MHK для создания диаграммы разброса для экспоненциального тренда, построенного для данных о доходах компании Wm. Wrigley Jr. Company, приведенных в табл. 15.4. Предполагается, что таблица остатков записана в ячейках В25 :В4 9 на рабочем листе SLR. Если регрессионные статистики находятся на другом рабочем листе, замените имя SLR.
Таблица ЕН.15.1. Дополнительный столбец G на рабочем листе Wrigley_MHK (показаны только первые и последние три строки)
' - - <5 ; :
1 Предсказанные значения Y
2 =СТЕПЕНЬ(10; SLR!B25)
3 =СТЕПЕНЬ(10; SLRIB26)
'' -
19 =СТЕПЕНЬ(10; SLR!B42)
20 =СТЕПЕНЬ(10; SLR1B43)
21 =СТЕПЕНЬ(10; SLRIB44)
ЕН.15.5. Создание диаграмм разброса с экспоненциальным трендом
Для построения диаграмм разброса с экспоненциальным трендом сначала необходимо создать экспоненциальную модель, выполнить логарифмическое преобразование отклика, руководствуясь инструкциями из раздела ЕН.15.4 и вызвать Мастер диаграмм. Например, чтобы построить диаграмму разброса с экспоненциальным трендом для доходов компании Wm. Wrigley Jr. Company, приведенным в табл. 15.4, сначала необходимо открыть рабочий лист Wrigley_MHK2 в книге Chapter 15 . xls и выполнить инструкции из раздела ЕН.15.3, введя на втором этапе диалога диапазоны ячеек В1 :В21,Е1 :Е21, Gl: G21 (обратите внимание на форму записи: без пробелов и с двумя запятыми).
Для того чтобы построить диаграмму разброса, щелкните правой кнопкой мыши на любой точке предсказанного значения отклика и выберите команду Формат рядов
данных... во всплывающем контекстном меню. (Если курсор мыши установлен правильно, на экране появится подсказка "Ряд "Предсказанный доход".) В диалоговом окне Формат рядов данных щелкните на корешке вкладки Вид, установите переключатель Линия в положение Обычная, а переключатель Маркер — в положение Отсутствует. Затем щелкните на кнопке ОК.
ЕН.15.6. Создание графиков для авторегрессионных моделей
Для построения графика авторегрессионной модели откройте рабочий лист с исходными данными и скопируйте в пустой столбец предсказанные значения У, содержащиеся в регрессионной таблице.
Например, чтобы построить график авторегрессионной модели первого порядка для доходов компании Wm. Wrigley Jr. Company, приведенных в табл. 15.4, сначала необходимо построить авторегрессионную модель, а затем открыть рабочий лист, содержащий регрессионные статистики, и следовать инструкциям.
1. Выделить диапазон ячеек В23:В4 3, содержащий предсказанные значения отклика У, а затем выбрать команду Правка^Копировать.
2. Открыть рабочий лист Wrigley_Lag, содержащий исходные данные.
3. Щелкнуть правой кнопкой мыши на ячейке F2 и выбрать команду Вставить из всплывающего контекстного меню.
4. Оставаясь на рабочем листе, выбрать команду Вставка^Диаграмма..., вызывая Мастер диаграмм.
5. На первом этапе диалога выполнить такие действия.
5.1. Щелкнуть на корешке закладки Стандартные, а затем выбрать пункт Точечная в раскрывающемся списке Тип. Выбрать первую (верхнюю) диаграмму во втором ряду, сопровождающуюся описанием: “Точечная диаграмма, на которой значения соединены отрезками”.
5.2. Щелкнуть на кнопке Далее>.
6. На втором этапе диалога выполнить следующее.
6.1. Щелкнуть на корешке закладки Диапазон данных, а затем ввести в окне редактирования Диапазон ссылки на ячейки АЗ:А21,ВЗ:В21,F3:F21. (Обратите внимание на форму записи: без пробелов и с двумя запятыми.)
6.2. Установить переключатель Ряды в положение В столбцах.
6.3. Щелкнуть на корешке вкладки Ряд. Выбрать пункт Ряд1 в раскрывающемся списке Ряд и ввести строку Доход в окне редактирования Имя. Выбрать пункт Ряд2 в раскрывающемся списке Ряд и ввести строку Предсказанный доход в окне редактирования Имя.
6.4. Щелкнуть на кнопке Далее>.
7. На третьем этапе диалога выполнить следующее.
7.1. Щелкнуть на корешке закладки Заголовки. Ввести в окне редактирования Название диаграммы строку Заголовок рисунка, в окне редактирования Ось X — строку Доходы (млн. долл.), а в окне редактирования Ось Y — строку Годы.
7.2. Затем по очереди щелкнуть на корешках вкладок Оси, Линии сетки и Подписи данных. Установить флажки и переключатели, как показано в разделе ЕР.6.
7.3. Щелкнуть на корешке вкладки Легенда и установить флажок Добавить легенду.
7.4. Щелкнуть на кнопке Далее>.
8. На четвертом этапе диалога выполнить следующее.
8.1. Установить переключатель Поместить диаграмму на листе в положение Отдельном.
8.2. Щелкнуть на кнопке Готово.
Для авторегрессионных моделей более высокого порядка предсказанные значения отклика У всегда следует копировать так, чтобы они заканчивались в строке 21 (следовательно, для модели второго порядка значения должны быть записаны, начиная со строки 4, а для модели третьего порядка— начиная со строки 5). Соответственно, необходимо уточнить диапазон данных, указываемый на втором этапе диалога с Мастером диаграмм.
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
1. Bowerman, В. L., and R. Т. O’Connell, Forecasting and Time Series, 3rd ed. (North Scituate, MA: Duxbury Press, 1993).
2. Box, G. E. P., G. M. Jenkins, and G. C. Reinsei, Time Series Analysis, Forecasting and Control, 3rded. (Englewood Cliffs, NJ: Prentice-Hall, 1994).
3. Frees, E. W., Data Analysis Using Regression Models: The Business Perspective (Upper Saddle River, NJ: Prentice Hall, 1996).
4. Hanke, J. E., D.W.Wichern and A. G. Reitsch, Business Forecasting, 7th ed. (Upper Saddle River, NJ: Prentice Hall, 2001).
5. Ittig, P., “A Seasonal Index for Business,” Decision Sciences, 1997, 28, 335-355.
6. Mahmoud, E. “Accuracy in Forecasting: A Survey,” Journal of Forecasting 3 (1984): 139-159.
7. Microsoft Excel 2002 (Redmond, WA: Microsoft Corporation, 2001).
Глава 16
Принятие решений
ПРИМЕНЕНИЕ СТАТИСТИКИ: выбор акций
16.1. ТАБЛИЦА ВЫИГРЫШЕН И ДЕРЕВО РЕШЕНИЙ
Процедуры Excel: вычисление упущенной выгоды
16.2. КРИТЕРИИ ПРИНЯТИЯ РЕШЕНИЙ
Ожидаемая прибыль
Ожидаемый размер упущенной выгоды
Отношение “доходность/риск”
Процедуры Excel: критерии принятия решения
16.3. ПРИНЯТИЕ РЕШЕНИЙ НА ОСНОВЕ ВЫБОРОЧНОЙ ИНФОРМАЦИИ
16.4. ПОЛЕЗНОСТЬ
СПРАВОЧНИК ПО EXCEL. ГЛАВА 16
ЧЕМУ ДОЛЖЕН НАУЧИТЬСЯ СТУДЕНТ
• Применять таблицы выигрышей и деревья решений для оценки альтернативных вариантов.
• Применять несколько критериев для выбора альтернативных вариантов.
• Применять теорему Байеса для уточнения вероятностей на основе выборочной информации.
• Понимать смысл концепции полезности.
ПРИМЕНЕНИЕ СТАТИСТИКИ
Выбор акций
Представьте себе, что вы работаете менеджером взаимного фонда и отвечаете за выбор и приобретение акций. Инвесторы вашего фонда ожидают больших прибылей от своих вложений. В то же время, они хотели бы минимизировать риск. Перед вами поставлена задача — I купить акции одной из двух компаний, j Экономист фонда оценил вероятную го-| довую доходность акций обеих компа-| ний для каждой из четырех возможных I ситуаций: спад, стабильность, умерен-! ный рост и экономический бум. Он так-I же оценил вероятность этих условий. | Как использовать эту информацию, что-
бы получить максимальную прибыль при минимальном риске?
ВВЕДЕНИЕ
В главе 4 мы изучили различные правила вычисления вероятностей, а также применили теорему Байеса для уточнения вероятностей с учетом новой информации. Кроме того, в главе 5 было введено понятие дискретного распределения. Теперь мы используем эти правила и теоремы для выбора конкретного плана действий. Процесс принятия решений характеризуется четырьмя основными свойствами.
1. Альтернативные планы действий. Прежде чем сделать окончательный выбор, лицо, принимающее решение, должно оценить несколько вариантов. Например, менеджер взаимного фонда в описанном выше сценарии должен решить, покупать акцию А или Б.
2. События или экономическое положение. Лицо, принимающее решение, должно перечислить возможные события и вычислить их вероятность. Например, для того, чтобы правильно выбрать компанию при покупке акций, экономист взаимного фонда перечислил четыре возможных сценария развития экономики в течение следующего года и указал их вероятность.
3. Таблица выигрышей. Для того чтобы оценить план действий, лицо, принимающее решение, должно сопоставить каждому событию возможный выигрыш или проигрыш. В деловых приложениях выигрыш и проигрыш обычно выражаются в терминах прибыли или убытка, хотя существуют и другие формы, например, моральное удовлетворение или польза. При покупке акций выигрыш выражается в виде доходности инвестиций.
4. Критерий принятия решения. Лицо, принимающее решение, должно установить критерий выбора наилучшего плана действий. В главе рассмотрено несколько таких критериев.
16.1. ТАБЛИЦА ВЫИГРЫШЕЙ И ДЕРЕВО РЕШЕНИЙ
Для того чтобы оценить альтернативные планы действий, следует составить таблицу выигрышей или построить дерево решений. В таблице выигрышей (payoff table) отражены все события, которые могут произойти в ходе реализации этих планов. Каждой комбинации плана и события следует сопоставить выигрыш или проигрыш. Рассмотрим эту процедуру на конкретном примере, связанном с рынком телевизоров.
ПРИМЕР 16.1. ТАБЛИЦА ВЫИГРЫШЕЙ ДЛЯ ПРИНЯТИЯ РЕШЕНИЯ, КАСАЮЩЕГОСЯ РЫНКА ТЕЛЕВИЗОРОВ
Менеджер по маркетингу, работающий в компании, производящей электронные бытовые приборы, должен решить, следует ли запускать в продажу новую модель телевизора. Ему известно, что это решение сопряжено с риском. Например, модель может оказаться неудачной и не пользоваться спросом. И, наоборот, модель может быть вполне успешной, а менеджер решит забраковать ее. Предположим, что на разработку новой модели телевизора уже потрачено 3 млн. долл. Если модель окажется удачной, то, руководствуясь прошлым опытом, менеджер прогнозирует получить прибыль в размере 45 млн. долл. (48 -3 млн. долл.). Если же модель плоха, потери составят 36 млн. долл. (33 млн. долл., затраченных на маркетинг, и 3 млн. долл., потраченных на разработку модели). Заполните таблицу выигрышей для двух альтернативных планов действий.
РЕШЕНИЕ. Выигрыши представлены в виде табл. 16.1. и
Таблица 16.1. Таблица выигрышей для оценки рыночной стратегии менеджера.
торгующего телевизорами
Альтернативные планы действий, млн. долл.
Событие Е, Продавать, А, Не продавать, А2
Удачная модель, Е{ +45 -3
Неудачная модель, Е2 -36 -3
Дерево решений (decision tree) представляет собой альтернативный способ описания событий для каждого из возможных планов действий. События и планы действий на дереве решений изображаются в виде ветвей и узлов, как показано на рис. 16.1.
ПРИМЕР 16.2. ДЕРЕВО РЕШЕНИЙ ДЛЯ ОЦЕНКИ РЫНОЧНОЙ СТРАТЕГИИ МЕНЕДЖЕРА, ТОРГУЮЩЕГО ТЕЛЕВИЗОРАМИ
Постройте дерево решений на основе таблицы выигрышей для оценки рыночной стратегии менеджера, торгующего телевизорами.
РЕШЕНИЕ. Соответствующее дерево решений изображено на рис. 16.1.
Дерево решений для оценки рыночной стратегии менеджера, торгующего телевизорами, содержит только два альтернативных плана действий и два возможных события. В принципе, дерево решений может состоять из произвольного количества планов и событий.
Вернемся к сценарию, описанному в начале главы. Представьте себе, что вы — менеджер взаимного фонда. Вам необходимо решить, акции какой из двух компаний принесут наибольший доход в течение следующего года. Экономист фонда предсказал доходность акций каждой компании при четырех сценариях развития экономической ситуации: спаде, стабильности, умеренном росте и экономическом буме. Прогнозируемая годовая доходность акций обеих компаний на 1 000 долл, инвестиций при упомянутых выше условиях показана в табл. 16.2.
Таблица 16.2. Прогнозируемая годовая доходность акций обеих компаний на 10ОО долл, инвестиций при реализации четырех сценариев развития экономической ситуации
Доходность акций, долл.
Экономическая ситуация А Б
Спад 30 -50
Стабильная экономика 70 30
Умеренный рост 100 250
Экономический бум 150 400
30 долл.
эконо^^. 70 долл.
Спад
иная
-50 долл, j
250долл. I
Рис. 16.2. Дерево решений для оценки выбора акций
Умеренный рост ,оо пппи |
^а£&ескийбум !
150 долл. I
Стабильная экономика 1 uU (Цилл.
Умеренный рост
400долл. I
Упущенная выгода (opportunity loss) — разница между наибольшим возможным доходом при определенном событии и фактическим доходом, полученным в результате осуществления выбранного плана действий.
ПРИМЕР 16.3. ВЫЧИСЛЕНИЕ РАЗМЕРА УПУЩЕННОЙ ВЫГОДЫ ПРИ ОЦЕНКЕ РЫНОЧНОЙ СТРАТЕГИИ МЕНЕДЖЕРА, ТОРГУЮЩЕГО ТЕЛЕВИЗОРАМИ
Постройте таблицу потерь, используя таблицу выигрышей, созданную при решении примера 16.1.
РЕШЕНИЕ. Максимальная прибыль, которую может получить компания, равна +45 млн. долл. Она соответствует “удачной модели”. Упущенная выгода возникает, если менеджер отказывается выпускать на рынок удачную модель телевизора. В этом случае размер упущенной выгоды равен разности между возможной прибылью и понесенными затратами, т.е. 45 - (-3) = 48 млн. долл. Если модель неудачна, лучше не выпускать ее на рынок. (В таком случае компания понесет убытки в размере -3 млн. долл.) Упущенная выгода, возникающая, если менеджер предлагает на рынке неудачную модель телевизора, равна -3 -(-36) = 33 млн. долл. Обратите внимание на то, что размер упущенной выгоды всегда представляет собой неотрицательную величину, поскольку он равен разности между прибылью, полученной при наилучшем решении, и прибылью, полученной (или не полученной) при любом другом решении. Потери, понесенные при реализации каждого из планов, приведены в табл. 16.3.
Таблица 16.3. Прогнозируемые размеры упущенной выгоды при различных действиях менеджера, торгующего телевизорами
Альтернативные планы, млн. долл.
Событие, Е( Оптимальное решение Прибыль при оптимальном решении, млн. долл. Предлагать Не предлагать
Удачная модель Предлагать 45 45 -45 = 0 45 -(- 3) = 48
Неудачная модель Не предлагать -3 -3 -(-36) = 33 -3-(-3) = 0
На рис. 16.3 приведена таблица упущенной выгоды, вычисленная с помощью программы Microsoft Excel.
А В С D E
1 Упущенная выгода при реализации планов иенеджера, торгующего телевизорами 2 3 Payoff Table:
4 Предлагать Не предлагать
6 Удачная модель 45
Б Неудачная модель 36 3
7 8 9 Opportunity Loss Table:
10 Optimum Optimum Alternatives
11 Action Profit Предлагать He предлагать
12 Удачная модель Предлагать 45 0 48
13 Неудачная модель Не предлагать 3 33 о]
Рис. 16.3. Таблица потерь при реализации планов менеджера, торгующего телевизорами
Процедуры Excel: вычисление упущенной выгоды
Для вычисления упущенной выгоды необходимо реализовать рабочий лист, использующий функции ИНДЕКС и поискпоз. Надстройка PHStat2 выполняет эту процедуру автоматически.
Например, для построения таблицы упущенной выгоды на основе таблицы выигрышей из примера 16.1 необходимо открыть пустой рабочий лист и выполнить одну из следующих процедур.
Применение Excel в сочетании с надстройкой PHStatl
Для вычисления упущенной выгоды используется процедура PHStat^>Decision-Making^>Opportunity Loss... (PHStatsПринятие решений^Упущенная выгода...). Чтобы выполнить ее, необходимо сделать следующее.
1. Выбрать команду PHStat^Decision-Making^Opportunity Loss....
2. Находясь в диалоговом окне Opportunity Loss (см. иллюстрацию), выполнить такие действия.
2.1. Ввести в окне редактирования Number of Events (Количество событий) число 2.
2.2. Ввести в окне редактирования Number of Alternative Actions (Количество альтернативных действий) число 2.
2.3. Ввести в окне редактирования Title заголовок таблицы.
2.4. Щелкнуть на кнопке ОК.
3. Описанная выше процедура создаст новый рабочий лист. Необходимо перейти на него и следовать приведенным ниже инструкциям (см. иллюстрацию).
3.1. Заменить метки событий Е1 и Е2, введя
В ячейке А5 строку Удачная модель, а В ячейке А 6 — строку Неудачная модель. Изменить ширину столбца А так, чтобы обе метки были видны полностью.
А В: С ! D
1 Упущенная выгода при реализации планов 2
3 Probabilities & Opportunity Losses:
4 Р А1 А2
5 Е1 0 0 0
6 Е2 0 0 0
3.2. Заменить метки альтернативных событий А1 и А2, введя в ячейку В4 строку Предлагать, а в ячейку с 4 - Не предлагать. Изменить ширину столбцов сие так, чтобы обе метки были видны полностью.
3.3. Ввести данные о возможных прибылях в диапазон ячеек В5: сб: в ячейку В5 - число 45, в ячейку вб - число -36, а в ячейки С5 и С6 - число -3.
3.4. Изменить ширину столбца в так, чтобы числа были видны полностью.
Применение Excel
Инструкции, позволяющие самостоятельно создать рабочий лист, выполняющий анализ упущенной выгоды, приведены в разделе ЕН.16.1.
^4 Содержимое компакт-диска
9 Данные, на основе которых выполнен анализ возможных потерь в примере 16.1, содержатся на листе Рис16.3 в рабочей книге Chapter 16.xls.
Руководствуясь описанными выше приемами, можно создать таблицу, содержащую размер упущенной выгоды при покупке акций, упомянутых в сценарии. Доходность акций зависит от экономической ситуации. Во время экономического спада акции компании А приносят доход в размере 30 долл., а акции компании Б — убыток в размере 50 долл. В стабильной экономической ситуации акции компании А снова оказываются выгоднее, поскольку они принесут 70 долл, на 1 000 долларов инвестиций, в то время как акции компании Б — только 30 долл. Однако в условиях умеренного роста или экономического бума акции компании Б намного выгоднее, чем акции компании А. В случае умеренного роста экономики доходность акций компании Б равна 250 долл., а акций компании А— 100 долл. При экономическом буме разница между показателями доходности этих компаний становится еще более заметной— 400 долл, у компании Б и 150 долл, у компании А. Размеры упущенной выгоды для разных вариантов развития событий приведены в табл. 16.4.
Таблица 16.4. Прогнозируемые потери при реализации планов менеджера.
торгующего телевизорами
Альтернативные планы, млн. долл.
Событие, Ej Оптимальное решение Прибыль при оптимальном решении,млн. долл. Компания А Компания Б
Спад А 30 30 - 30 = 0 30 - (-50) = 80
Стабильная экономика А 70 70 - 70 = 0 70 - 30 = 40
Умеренный рост Б 250 250- 100 = 150 250-250 = 0
Экономический бум Б 400 400- 150 = 250 400 - 400 = 0
УПРАЖНЕНИЯ К РАЗДЕЛУ 16.1
Изучение основ
16.1. Предположим, что поставленная задача описывается следующей таблицей выигрышей.
Действия, млн. долл.
Событие Компания А Компания Б
1 50 100
2 200 125
1. Создайте таблицу упущенной выгоды.
2. Постройте дерево решений.
16.2. Предположим, что поставленная задача описывается следующей таблицей выигрышей.
Действия, млн. долл.
Событие Компания А Компания Б
1 50 10
2 300 100
3 500 200
1. Создайте таблицу упущенной выгоды.
2. Постройте дерево решений.
Применение понятий
16.3. Производитель джинсов решает, какую фабрику строить в указанном месте — большую или маленькую. Доход, который приносит одна пара джинсов, равен Юдолл. Размер амортизационных отчислений на маленькой фабрике равен 200 тыс. долл, в год, а мощность производства— 50 тыс. пар джинсов в год. Размер амортизационных отчислений на большой фабрике равен 400 тыс. долл, в год, а мощность производства — 100 тыс. пар джинсов в год. Производитель рассматривает четыре варианта производственных мощностей — 10, 20, 50 и 100 тыс. пар джинсов в год.
1. Определите возможные уровни производственных мощностей маленькой фабрики, а также выигрыш, соответствующий каждому уровню.
2. Определите возможные уровни производственных мощностей большой фабрики, а также выигрыш, соответствующий каждому уровню.
3. Используя решения задач 1 и 2, создайте таблицу выигрышей, указав события и альтернативные планы действий.
4. Постройте дерево решений.
5. Создайте таблицу упущенной выгоды.
16.4. Автор нового романа решает, какому из двух издательств отдать права на издание своей рукописи. Компания А предлагает автору гонорар в размере 10 тыс. долл, и 2 доллара с каждой проданной книги. Компания Б предлагает гонорар в размере 2 тыс. долл, и 4 доллара с каждой проданной книги. Автор рассматривает пять вариантов тиража: 1 000, 2 000, 5 000, 10 000 и 50 000 экземпляров.
1. Определите выигрыш, соответствующий предложениям компаний А и Б.
2. Создайте таблицу выигрышей, указав события и альтернативные планы действий.
3. Постройте дерево решений.
4. Создайте таблицу упущенной выгоды.
16.5. Торговая сеть компании LeFleur Garden Center продает и покупает рождественские елки. Покупая елки за 10 долларов, она продает их за 20. Все елки, не проданные на Рождество, продаются за 2 доллара на дрова. Плантация компании может удовлетворить четыре уровня запросов: 100, 200, 500 и 1 000 елок.
1. Определите прибыль, полученную от продажи 100, 200, 500 и 1 000 елок.
2. Создайте таблицу выигрышей, указав события и альтернативные планы действий.
3. Постройте дерево решений.
4. Создайте таблицу упущенной выгоды.
16.2. КРИТЕРИИ ПРИНЯТИЯ РЕШЕНИЙ
Заполнив таблицы выигрыша и упущенной выгоды, необходимо выбрать оптимальный вариант действий. Для этого сначала требуется вычислить вероятность каждого события, используя статистические данные, экспертные оценки или знания о функции распределения. Выбор оптимального плана действий основывается на вероятностях событий и размерах упущенной выгоды при каждом варианте.
Ожидаемая прибыль
Уравнение (5.1) в разделе 5.1 показывает, как вычисляется математическое ожидание случайной величины, имеющей заданное распределение. Применим эту формулу для вычисления величины ожидаемой прибыли для каждого из альтернативных вариантов действий.
Ожидаемая прибыль (expected monetary value — EMV) для каждого варианта действий j представляет собой сумму доходов х(у, полученных при событии i, умноженных на вероятности Р,.
ОЖИДАЕМАЯ ПРИБЫЛЬ
= (16.1)
7=1
где EMV(j) — ожидаемая прибыль при варианте действий /, хч — выигрыш, полученный при варианте действий j и событии i, Р, — вероятность события i.
Применим эту формулу к задаче о выборе оптимальной рыночной стратегии, описанной в примере 16.4.
ПРИМЕР 16.4. ВЫЧИСЛЕНИЕ ОЖИДАЕМОЙ ПРИБЫЛИ ПРИ ОЦЕНКЕ РЫНОЧНОЙ СТРАТЕГИИ МЕНЕДЖЕРА, ТОРГУЮЩЕГО ТЕЛЕВИЗОРАМИ
Предположим, вероятность того, что модель телевизора окажется удачной, равна 0,60, а вероятность противоположного события равна 0,40. Вычислите ожидаемую прибыль для каждого из альтернативных вариантов действий и укажите оптимальный план.
РЕШЕНИЕ. Ожидаемая прибыль для каждого из альтернативных вариантов действий вычисляется по формуле (16.1). Результаты этих вычислений приведены в табл. 16.5.
Таблица 16.5. Ожидаемая прибыль для каждого из альтернативных вариантов
действий
Альтернативные планы, млн. долл.
Событие, Es Р, Продавать, А х„Р, Не продавать а2 х„Р,
Удачная модель, Е} 0,40 +45 45 х 0,4 = 18 -3 -3x0,4 = -1,2
Неудачная модель, Е2 0,60 -36 -36x0,6 = -21,6 -3 -3x0,6 = -1,8
EMV(AJ = -3,6 EMV(AZ) = -3
Ожидаемая прибыль для первого варианта действий (продавать новую модель) равна -3,6 млн. долл., а для второго варианта (не продавать новую модель) равна -3 млн. долл. Таким образом, если целью рыночной стратегии является получение максимальной ожидаемой прибыли, предлагать новую модель телевизора не следует (в этом случае потери будут наименьшими).
Вернемся к сценарию, описанному в начале главы, и таблице выигрышей, приведенной в примере 16.2. Допустим, что экономист компании оценивает вероятности различных вариантов развития экономической ситуации следующим образом.
Р(спад) = 0,10
Р(стабильная экономика) = 0,40
Р(умеренный рост) = 0,30
Р(экономический бум) = 0,20
В табл. 16.6 приведены величины ожидаемой прибыли для каждого варианта, вычисленные на основе информации, содержащейся в табл. 16.2.
Таблица 16.6. Ожидаемая прибыль для каждого из альтернативных вариантов действий при покупке акций
Альтернативные планы
Событие, Е; Р, Компания А х,Р, Компания Б xR
Спад 0,10 30 30x0,1=3 -50 -50x0,1=-5
Стабильная экономика 0,40 70 70x0,4=28 30 30x0,4=12
Умеренный рост 0,30 100 100x0,3=30 250 250x0,3=75
Экономический бум 0,20 150 150x0,2=30 400 400x0,2=80
EMV(A)= 91 EMV(B)=162
Таким образом, размер ожидаемой упущенной выгоды, соответствующий оптимальному решению, имеет особый смысл. Прибыль от покупки акций компании А составляет 91 долл., а для компании Б она равна 162 долл. Итак, следует предпочесть покупку акций компании Б, поскольку ожидаемая доходность ее акций равна 162/1 000, или 16,2%. Этот показатель почти в два раза превышает соответствующий показатель компании А, равный 91/1 000, или 9,1%.
Ожидаемый размер упущенной выгоды
В качестве альтернативы при оценке вариантов действий можно использовать таблицу упущенной выгоды, как показано в разделе 16.1. Ожидаемый размер упущенной выгоды (expected opportunity loss — EOL) вычисляется по формуле (16.2).
ОЖИДАЕМЫЙ РАЗМЕР УПУЩЕННОЙ ВЫГОДЫ
EOL(J) = f,L.,P, , (16.2)
где L — размер упущенной выгоды при варианте действий j и событии /, Р, — вероятность события i.
Критерий: следует выбрать вариант, минимизирующий величину EOL, т.е. максимизирующий величину EMV (см. формулу (16.1)).
Применим эту формулу для вычисления размеров упущенной выгоды при выборе рыночной стратегии продажи телевизоров.
ПРИМЕР 16.5. ВЫЧИСЛЕНИЕ ОЖИДАМОЙ УПУЩЕННОЙ ВЫГОДЫ ПРИ ОЦЕНКЕ РЫНОЧНОЙ СТРАТЕГИИ МЕНЕДЖЕРА, ТОРГУЮЩЕГО ТЕЛЕВИЗОРАМИ
Предположим, вероятность того, что модель телевизора окажется удачной, равна 0,40. Вычислите размер ожидаемой упущенной выгоды для каждого из альтернативных вариантов действий и выберите оптимальный план.
РЕШЕНИЕ. Как показано в табл. 16.7, наименьшая ожидаемая упущенная выгода соответствует отказу от предложения новой модели.
Таблица 16.7. Размер ожидаемой упущенной выгоды для каждого из альтернативных вариантов действий при продаже телевизоров
Альтернативные планы
Событие, Е, Pi Стратегия A, (продавать) l,p. Стратегия A2 (не продавать) l,p,
Удачная модель, Е2 0,40 0 0 X 0,4 = 0 48 48x0,4 = 19,2
Неудачная модель, Е2 0,60 33 33x0,6 = 19,8 0 Ox 0,6 = 0
EOL(A1)= 19,8 EOL(A2) = 19,2
Ожидаемая упущенная выгода, соответствующая оптимальному решению, имеет особый смысл в контексте принятия решений. Эта величина называется ожидаемой стоимостью полной информации (expected value of perfect information — EVPI).
ОЖИДАЕМАЯ СТОИМОСТЬ ПОЛНОЙ ИНФОРМАЦИИ
EVPI = ожидаемая прибыль в условиях полной определенности -- ожидаемая прибыль при оптимальном решении. (16.3)
Ожидаемая прибыль в условиях полной определенности (expected profit under certainty) представляет собой прибыль, которую можно было бы извлечь, если бы заранее было известно, какое именно событие произойдет.
ПРИМЕР 16.6. ВЫЧИСЛЕНИЕ ОЖИДАМОЙ ПРИБЫЛИ ПРИ ОЦЕНКЕ РЫНОЧНОЙ СТРАТЕГИИ МЕНЕДЖЕРА, ТОРГУЮЩЕГО ТЕЛЕВИЗОРАМИ
Вычислите ожидаемую прибыль при полной определенности.
РЕШЕНИЕ. Если бы менеджер был ясновидящим, то в 40% случаев (удачные модели) он получил бы прибыль, равную 45 млн. долл., а в 60% случаев (неудачные модели) — потерпел убытки в размере 3 млн. долл. Следовательно, ожидаемая прибыль при полной определенности равна 0,40 х 45 + 0,60 х (-3) = 18 - 1,8 = 16,2.
Эта величина представляет собой прибыль, которую получила бы компания, если бы менеджер точно знал, что модель телевизора будет удачной. Ожидаемая величина полной информации в этом случае равна EVPI = ожидаемая прибыль в условиях полной определенности - ожидаемая прибыль при оптимальном решении = 16,2-(-3) = 19,2 млн. долл. Эта величина является размером ожидаемой упущенной выгоды при отказе от выпуска новой модели телевизора. Величина EVPI является максимумом того, что менеджер должен заплатить за обладание полной информацией.
Вернемся к нашему сценарию и вычислим размер ожидаемой упущенной выгоды при покупке акций двух компаний.
Таблица 16.8. Размер ожидаемой упущенной выгоды для каждого из альтернативных вариантов действий при покупке акций
Альтернативные планы
Событие, Ej Р. Компания А Ч₽, Компания Б Чр.
Спад 0,10 0 0x0,1 = 0 80 80x0,1 =8
Стабильная экономика 0,40 0 0x0,4 = 0 40 40 х 0,4= 16
Умеренный рост 0,30 150 150x0,3 = 45 0 Ох 0,3 = 0
Экономический бум 0,20 250 250x0,2 = 50 0 0 х 0,2 = 0
ЕОЦА) = 95 ЕОЦБ) = EVPI = 24
Покупка акций компании Б уменьшает размер ожидаемой упущенной выгоды, что полностью соответствует решению, принятому на основе вычисления ожидаемой прибыли. Ожидаемая стоимость полной информации равна 24 долл, (на 1 000 долл, инвестиций). Это означает, что за обладание полной информацией менеджер должен быть готовым заплатить 24 долл.
Отношение "доходность/риск"
К сожалению, критерии выбора, основанные на вычислении ожидаемой прибыли или ожидаемой упущенной выгоды, не учитывают изменчивости выигрыша при разных событиях. Из табл. 16.2 следует, что доходность акций компании А изменяется от 30 долл, при спаде до 150 долл, при экономическом буме, в то время как доходность акций Б колеблется от 50 долл, убытков при спаде до 400 долл, при экономическом буме.
Для того чтобы учесть изменчивость экономической ситуации, можно вычислить дисперсию и стандартное отклонение доходности каждой акции, используя формулы (5.2) и (5.3) соответственно. Учитывая информацию, содержащуюся в табл. 16.7, и величину EMV(A) для акций компании А, равную = 91, получаем, что дисперсия доходности акций компании А равна
а’ = Х(X, - М): Р(Х,) = (30-91)’ х 0,1 + (70-91)’ х 0,4 +
+ (100-91)’ х 0,3 + (150-91)’ х 0,2 = 1 269.
Стандартное отклонение доходности акций компании А равно <зА = ^/1 269 = 35,62 . Для акций компании Б величина ЕМУ(Б) равна = 162. Дисперсия доходности акций компании Б равна
ст^ = р(^) = (-50-162)2 х 0,1 + (30-162)2 х 0,4 +
+ (250-162)2 х 0,3 + (400-162)2 х 0,2 = 25 116.
Стандартное отклонение доходности акций компании Б равно а, = ^25 116 = 158,48 .
Поскольку эти наборы данных имеют резко отличающиеся средние значения, следует оценить относительный риск, связанный с акциями каждой компании. Вычислив стандартное отклонение доходности акций, можно определить коэффициент вариации, введенный в разделе 3.2. Вычислим коэффициент вариации для генеральной совокупности показателя доходности акций компании А, подставляя в уравнение (3.11) величину S вместо параметра ст.
СУ. =—------х 100% = •^-^•х 100% = 39,1% .
А ЕМУ (А) 91
Коэффициент вариации показателя доходности акций компании Б вычисляется так.
СУ, = — х 100% = -1-58,48 х 100% = 97,8% .
ЕМУ (Б) 162
Таким образом, доходность акций компании Б колеблется намного больше, чем доходность акций компании А.
Поскольку коэффициент вариации характеризует относительную величину изменчивости по сравнению с арифметическим средним (или ожидаемой прибылью), для того чтобы выразить связь между доходом (или выигрышем) и риском (в виде стандартного отклонения), необходимы другие критерии. Одним из них является критерий, основанный на отношении доходности к риску (“доходность/риск”).
КРИТЕРИЙ "ДОХОДНОСТЬ/РИСК"
~ « / „ EMV(j)
Отношение доходность/риск =------— , (15.4)
а,
где EMV(j) — ожидаемая прибыль при выборе плана j, а о — стандартное отклонение прибыли при выборе плана /.
Отношение “доходность/риск” для акций компанииА составляет 91/32,62 = 2,55, для акций компании Б оно равно 162/158,48 = 1,02. Таким образом, учитывая относительный риск, выраженный через стандартное отклонение, следует признать, что акции компании А могут принести намного больше прибыли, чем акции компании Б. В то же время ожидаемая прибыль, которую могут принести акции компании А, меньше, чем ожидаемая прибыль компании Б. К тому же акции компании Б являются намного более рискованными. Итак, руководствуясь критерием “доходность/риск”, следует предпочесть акции компании А.
Результаты проведенных выше вычислений, полученные с помощью программы Microsoft Excel, показаны на рис. 16.4.
В
С
D
Е
G
A
1 Анализ потерь при выборе акций
3 _ Probabilities & Payoffs Table: 4 S’ 6 ' 7 “ 8
9 10 7 1Г 12 r 13 J4 1
15^
17 'Opportunity Loss Table: 18J 19, 20 21 , 22
______Спад Стабильная экономика ______Умеренный рост Экономический бум
P 0,1 0,4 0,3 0,2
Компания A
________30
________70
_________100
150
Компания Б
________50
________30
________250
400
_______Statistics for: Expected Monetary Value _______Variance _______Standard Deviation Coefficient of Variation Return to Risk Ratio
Компания A _______91 _______1269
35,6230 0,3915 2,5545
Компания Б
_________162 25116
158,4803 0,9783 1,0222
Calculations Area
For variance and std. deviation Компания А Компания Б 44944 17424 7744 56644
3721
441
81
3481
Optimum Action
Спад Компания А Стабильная экономика Компания А
Умеренный рост Компания Б
Optimum Profit
30
70
250
Alternatives Компания А Компания Б 80 40 0
0:
0
150
Рис. 16.4. Рабочий лист для вычисления ожидаемой прибыли
Процедуры Excel: критерии принятия решения
Для вычисления ожидаемой прибыли, ожидаемых потерь и оценки изменчивости на основе таблицы выигрышей и вероятностей событий необходимо создать рабочий лист, использующий функции индекс, поискпоз, суммпроизв и если. Надстройка PHStat2 выполняет эту процедуру автоматически.
Например, для того, чтобы вычислить эти величины на основе таблицы выигрышей из примера 16.1 и вероятностей перечисленных там событий, необходимо открыть пустой рабочий лист и выполнить одну из следующих процедур.
Применение Excel в сочетании с надстройкой PHStatZ
Для вычисления ожидаемой прибыли, ожидаемых потерь и оценки изменчивости на основе таблицы выигрышей и вероятностей событий используется процедура PHStat1^Decision-Making^Expected Monetary Value... (PHStat^ Принятие решений1^Ожидаемая прибыль...). Чтобы выполнить ее, необходимо сделать следующее.
1. Выбрать команду PHStat1^ Decision-Making^ Expected Monetary Value....
2. Находясь в диалоговом окне Expected Monetary Value (см. иллюстрацию), выполнить такие действия.
2.1. Ввести в окне редактирования Number of Events (Количество событий) число 4.
2.2. Ввести в окне редактирования Number of Alternative Actions (Количество альтернативных действий) число 2.
2.3. Ввести в окне редактирования Title заголовок таблицы.
2.4. Установить флажки Expected Opportunity Loss (Ожидаемый размер упущенной выгоды) и Measures of Variation (Оценки вариации).
2.5. Щелкнуть на кнопке ОК.
3. Описанная выше процедура создаст новый рабочий лист. Необходимо перейти на него и следовать приведенным ниже инструкциям (см. иллюстрацию).
3.1. Заменить метки El, Е2, ЕЗ и Е4, введя в ячейке А5 строку Спад, в ячейке А6 - строку Стабильная экономика, в ячейке А 7 — строку Умеренный рост, а в ячейке А8 — строку Экономический бум. Изменить ширину столбца А так, чтобы обе метки были видны
i' А Анализ потерь г В . |ри выбор С е акций : D !
Z 3 Probabilities & Payoffs Table:
4 р А1 А2
5 Е1
6 Е2
7 ЕЗ
“8 Е4
полностью.
3.2. Заменить метки альтернативных событий А1 и А2, введя в ячейку С4 строку Компания А, а в ячейку D4 — Компания Б. Изменить ширину столбцов так, чтобы все метки были видны полностью.
3.3. Ввести в диапазон ячеек В5:В8 данные о вероятностях: в ячейку В5 - число 0.1, в ячейку В6 - 0.4, в ячейку В7 - 0.3, а в ячейку В8 - 0.2.
3.4. Ввести данные из таблицы выигрышей. В ячейку С5 ввести число 30, в ячейку С6 - 70, в ячейку С7 - 100, в ячейку С8 - 150, в ячейку D5 - число -50, в ячейку D6 - 30, в ячейку D7 - 250, а в ячейку D8 - 400.
Применение Excel
Инструкции, позволяющие самостоятельно создать рабочий лист для вычисления ожидаемой прибыли, ожидаемых потерь и оценки изменчивости на основе таблицы выигрышей и вероятностей событий, приведены в разделе ЕН.16.2.
Содержимое компакт-диска
ж Данные, на основе которых произведены вычисления, содержатся на листе Рис16.4 в книге Chapter 16.xls.
Изучение основ
16.6. Предположим, что поставленная задача описывается следующей таблицей выигрышей.
Действия
Событие А Б
1 50 100
2 200 125
Вероятность событий 1 и 2 равна 0,5.
1. Вычислите ожидаемую прибыль (EMV) при действиях Ап Б.
2. Вычислите ожидаемый размер упущенной выгоды (EOL) при действиях А и Б.
3. Объясните смысл стоимости полной информации (EVPI) в этой задаче.
4. Какой вариант действий следует выбрать на основе показателей, вычисленных при решении задач 1 и 2? Почему?
5. Найдите коэффициент вариации для каждого варианта действий.
6. Вычислите отношение “доходность/риск” для каждого варианта действий.
7. Какой вариант следует предпочесть на основе критерий “доходность/риск”? Почему?
8. Сравните ответы на вопросы 4 и 7 и объясните различия между ними.
16.7. Предположим, что поставленная задача описывается следующей таблицей выигрышей.
Действия
Событие А Б
1 50 10
2 300 100
3 500 200
Вероятности событий 1, 2 и 3 равны 0,8, 0,1 и 0,1 соответственно
1. Вычислите ожидаемую прибыль (EMV) при действиях А и Б.
2. Вычислите ожидаемый размер упущенной выгоды (EOL) при действиях А и Б.
3. Объясните смысл стоимости полной информации (EVPI) в этой задаче.
4. Какой вариант действий следует выбрать на основе показателей, вычисленных при решении задач 1 и 2? Почему?
5. Найдите коэффициент вариации для каждого варианта действий.
6. Вычислите отношение “доходность/риск” для каждого варианта действий.
7. Какой вариант следует предпочесть на основе критерия “доходность/риск”? Почему?
8. Сравните ответы на вопросы 4 и 7 и объясните различия между ними.
9. Как вы считаете, были бы разными ответы на вопросы 4 и 7, если бы вероятности трех событий были равны 0,1, 0,1 и 0,8 соответственно?
16.8. Предположим, что объем потенциальных инвестиций равен 1 000 долл. Показатель EMV для акции некоей компании равен 100 долл., а стандартное отклонение составляет 25 долл.
1. Чему равен уровень доходности этих акций?
2. Чему равен коэффициент вариации доходности этих акций?
3. Чему равно отношение “доходность/риск”?
16.9. В таблице указана доходность акций некоей компании в разных экономических условиях.
Действия
Экономические условия Вероятность Доход, ДОЛЛ.
Спад 0,30 50
Стабильная экономика 0,30 100
Умеренный рост 0,30 120
Экономический бум 0,10 200
1. Вычислите ожидаемую прибыль.
2. Определите стандартное отклонение доходности.
3. Найдите коэффициент вариации.
4. Вычислите отношение “доходность/риск”.
16.10. В таблице приведены результаты анализа доходности акций двух компаний.
Компании
А, долл. Б, долл.
Ожидаемая прибыль 90 60
Стандартное отклонение 10 10
Акции какой компании следует предпочесть и почему?
16.11. В таблице приведены результаты анализа доходности акций двух компаний.
Компании
А, долл. Б, долл.
Ожидаемая прибыль 60 60
Стандартное отклонение 20 10
Акции какой компании следует предпочесть и почему?
Применение понятий
16.12. Поставщик, работающий на бейсбольном стадионе, должен решить, чем торговать на сегодняшнем матче — мороженым или лимонадом. Поставщик полагает, что его прибыль зависит от погоды. Таблица возможных выигрышей выглядит следующим образом.
Вариант действий
Событие Продавать мороженое, долл. Продавать лимонад, долл.
Холодно 50 30
Жарко 60 90
Поставщик предполагает, что вероятность жаркой погоды равна 0,60.
1. Вычислите ожидаемую прибыль (EMV) от продажи лимонада и мороженого.
2. Определите ожидаемый размер упущенной выгоды (EOL) от продажи лимонада и мороженого.
3. Объясните смысл стоимости полной информации (EVPI) в этой задаче.
4. Какой вариант действий следует выбрать на основе показателей, вычисленных при решении задач 1 и 2? Почему?
5. Найдите коэффициент вариации для каждого варианта действий.
6. Вычислите отношение “доходность/риск” для каждого варианта действий.
7. Какой вариант следует предпочесть на основе критерия “доходность/риск”? Почему?
8. Сравните ответы на вопросы 4 и 7 и объясните различия между ними.
16.13. Компания Islander Fishing Company приобретает моллюсков у рыбаков по 1,50 долл, за фунт, а затем продает их в различные рестораны Нью-Йорка по 2,50 долл, за фунт. Все моллюски, не проданные до конца недели, могут быть проданы местной компании по 0,50 долл, за фунт. В таблице приведены вероятности, соответствующие объемам заказов, поступивших от ресторанов.
Объем закупок (фунты) Вероятность
500 0,2
1 000 0,4
2 000 0,4
(Подсказка. Компания может закупить 500, 1 000 и 2 000 фунтов моллюсков.)
1. Вычислите размер ожидаемой прибыли или убытков для каждого объема закупок.
2. Определите оптимальный объем закупок моллюсков у рыбаков, руководствуясь критерием, основанным на вычислении ожидаемой прибыли. Обоснуйте свой ответ.
3. Вычислите стандартное отклонение доходности при закупке 500, 1 000 и 2 000 фунтов моллюсков.
4. Вычислите ожидаемые размеры упущенной выгоды (EOL) при закупке 500, 1 000 и 2 000 фунтов моллюсков.
5. Объясните смысл стоимости полной информации (EVPI) в этой задаче.
6. Найдите коэффициент вариации доходности при закупке 500, 1 000 и 2 000 фунтов моллюсков. Прокомментируйте полученные результаты.
7. Вычислите отношение “доходность/риск” при закупке 500, 1 000 и 2 000 фунтов моллюсков. Объясните свой ответ.
8. Выберите оптимальный размер закупок, руководствуясь ответами на вопросы 2 и 4. Обоснуйте свой выбор.
9. Сравните результаты решения задач 2, 4, 6 и 7. Объясните разницу между ними.
10. Предположим, что моллюски можно продать по Здолл. за фунт. Повторно решите задачи 1-8 и сравните результаты.
11. Как изменятся ответы на поставленные выше вопросы, если вероятности заказов, поступивших на 500, 1 000 и 2 000 фунтов моллюсков, равны 0,4, 0,4 и 0,2 соответственно?
16.14. Обладая определенным количеством денег, инвестор желает вложить их в акции. У него есть три варианта выбора. Выигрыши (и потери) от вложения капитала при разных экономических условиях приведены в следующей таблице.
Инвестиции
Событие А Б В
Экономический спад 500 -2 000 -7 000
Без изменений 1 000 2 000 -1 000
Экономический рост 2 000 5 000 20 000
Учитывая прошлый опыт, инвестор полагает, что вероятности каждой из экономических ситуаций распределены так:
Р(экономический спад) = 0,30,
Р(без изменений) = 0,50,
Р(экономический рост) = 0,20.
1. Сделайте оптимальный выбор, руководствуясь критерием, основанным на вычислении ожидаемой прибыли. Обоснуйте свой ответ.
2. Определите стандартное отклонение доходности для каждой инвестиции.
3. Вычислите ожидаемые размеры упущенной выгоды (EOL) для каждой инвестиции.
4. Объясните смысл стоимости полной информации (EVPI) в этой задаче.
5. Найдите коэффициент вариации доходности для каждой инвестиции.
6. Вычислите отношение “доходность/риск” для каждой инвестиции.
7. Выберите оптимальный вариант вложений капитала, руководствуясь ответами на вопросы 5 и 6. Обоснуйте свой выбор.
8. Сравните результаты решения задач 2 и 7. Объясните разницу между ними.
9. Предположим, что вероятности различных экономических условий распределены следующим образом:
а) 0,1, 0,6 и 0,3;
б) 0,1, 0,3 и 0,6;
в) 0,4, 0,4 и 0,2;
г) 0,6, 0,3 и 0,1.
Повторите решение задач 1-8 для каждого варианта распределения вероятностей и сравните полученные результаты с ответами к заданию 8. Объясните разницу между ними.
16.15. В задаче 16.3 была построена таблица выигрышей при строительстве маленькой и большой фабрик по производству джинсов. Предположим теперь, что вероятности заказов распределены следующим образом.
Объем заказов
10 000
Вероятность
0,1
20 000 0,4
50 000 0,2
100 000 0,3
1. Вычислите ожидаемую прибыль (EMV) от строительства маленькой и большой фабрик.
2. Вычислите ожидаемые размеры упущенной выгоды (EOL) при строительстве маленькой и большой фабрик.
3. Объясните смысл стоимости полной информации (EVPI) в этой задаче.
4. Используя ответы к задачам 1 и 2, определите, какую фабрику следует строить — маленькую или большую. Обоснуйте свое решение.
5. Найдите коэффициент вариации прибыли при строительстве маленькой и большой фабрик.
6. Вычислите отношение “доходность/риск” при строительстве маленькой и большой фабрик.
7. Выберите оптимальный вариант строительства, руководствуясь ответами на вопросы 5 и 6. Обоснуйте свой выбор.
8. Сравните результаты решения задач 4 и 7. Объясните разницу между ними.
9. Предположим, что вероятности различных заказов распределены следующим образом: 0,4, 0,2, 0,2 и 0,2. Повторите решение задач 1-8 при данном распределении вероятностей и сравните полученные результаты с предыдущими ответами. Объясните разницу между ними.
16.16. В задаче 16.4 была построена таблица выигрышей, позволяющая автору правильно выбрать издательство для публикации своей книги. Предположим, что вероятности заказов на книгу распределены следующим образом.
Объем заказов Вероятность
1000 0,45
2 000 0,20
5 000 0,15
10 000 0,10
50 000 0,10
1. Вычислите ожидаемую прибыль (EMV) от контракта с издательствами А и Б.
2. Определите ожидаемые размеры упущенной выгоды (EOL) от контракта с издательствами А и Б.
3. Объясните смысл стоимости полной информации (EVPI) в этой задаче.
4. Используя ответы к задачам 1 и 2, определите, с каким издательством следует заключить договор. Обоснуйте свое решение.
5. Вычислите коэффициент вариации прибыли от контрактов с издательствами АиБ.
6. Вычислите отношение “доходность/риск” для контрактов с издательствами АиБ.
7. Примите оптимальное решение, руководствуясь ответами на вопросы 5 и 6. Обоснуйте свой выбор.
8. Сравните результаты решения задач 4 и 7. Объясните разницу между ними.
9. Предположим, что вероятности различных заказов распределены следующим образом: 0,3, 0,2, 0,2, 0,1 и 0,2. Повторите решение задач 1-8 при данном распределении вероятностей и сравните полученные результаты с предыдущими ответами. Объясните разницу между ними.
16.17. В задаче 16.5 была построена таблица выигрышей от продажи 100, 200, 500 и 1 000 рождественских елок. Предположим, что вероятности заказов на разное количество елок распределены следующим образом.
Объем заказов Вероятность
100 0,20
200 0,50
500 0,20
1 000 0,10
1. Вычислите ожидаемую прибыль (EMV) от заказов на 100, 200, 500 и 1 000 елок.
2. Вычислите ожидаемые размеры упущенной выгоды (EOL) от заказов на 100, 200, 500 и 1 000 елок.
3. Объясните смысл стоимости полной информации (EVPI) в этой задаче.
4. Используя ответы к задачам 1 и 2, определите, сколько елок следует закупить — 100, 200, 500 или 1 000. Обоснуйте свое решение.
5. Найдите коэффициент вариации прибыли от закупки елок для каждого варианта заказа.
6. Вычислите отношение “доходность/риск” для каждого варианта заказа.
7. Руководствуясь ответами на вопросы 5 и 6, решите, сколько елок следует закупить — 100, 200, 500 или 1 000. Обоснуйте свой выбор.
8. Сравните результаты решения задач 4 и 7. Объясните разницу между ними.
9. Предположим, что вероятности различных заказов распределены следующим образом: 0,4, 0,2, 0,2 и 0,2. Повторите решение задач 1-8 при данном распределении вероятностей и сравните полученные результаты с предыдущими ответами. Объясните разницу между ними.
163. ПРИНЯТИЕ РЕШЕНИЙ НА ОСНОВЕ ВЫБОРОЧНОЙ
ИНФОРМАЦИИ
В разделах 16.1 и 16.2 рассмотрен процесс выбора оптимального решения на основе анализа нескольких альтернатив. Для этого были предложено несколько критериев, а также введено понятие ожидаемой стоимости полной информации. На основе прошлого опыта или субъективных оценок для каждого критерия были указаны вероятности каждого варианта событий. Напомним, что в разделе 4.3 изложена теорема Байеса, позволяющая уточнить априорную вероятность на основе вновь поступившей информации. Проиллюстрируем ее применение следующим примером.
ПРИМЕР 16.7. ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНОЙ РЫНОЧНОЙ СТРАТЕГИИ ТОРГОВЛИ ТЕЛЕВИЗОРАМИ НА ОСНОВЕ ВЫБОРОЧНОЙ ИНФОРМАЦИИ
Как показано в разделе 4.3, вероятность того, что модель телевизора будет пользоваться спросом, с учетом благоприятного прогноза равна 0,64. Таким образом, вероятность противоположного события равна 1-0,64 = 0,36. Вычислите ожидаемую прибыль для каждого варианта действий, используя уточненные вероятности, и решите, следует ли предлагать на рынке новую модель телевизора.
РЕШЕНИЕ. Поскольку в примере 16.4 для выбора оптимального решения были использованы исходные субъективные вероятности, размер ожидаемой прибыли следует вычислить снова на основе уточненных данных, как показано в табл. 16.9.
Таблица 16.9. Размер ожидаемой прибыли для каждого из альтернативных вариантов действий при продаже телевизоров
Альтернативные планы, млн. долл.
Событие, Е. Р. Продавать, х„Р, Не продавать, х„Р,
А, а2
Удачная модель, Ej 0,40 +45 45 х 0,64 = 28,8 -3 -3x0,64 = -1,92
Неудачная модель, Е2 0,60 -36 -36x0,36 = -12,96 -3 -3 х 0,36 = -1,08
EMV(Al) = - 15,84 EMV(A2) = -3
В данном случае оптимальным решением является предложение новой модели на рынке, поскольку средняя ожидаемая прибыль в этом случае составит 15,84 млн. долл. Противоположное решение принесет убытки в размере 3 млн. долл. Новое оптимальное решение отличается от предыдущего и базируется на выборочной информации, полученной при исследовании рынка. Как видим, благоприятный прогноз, сделанный в отчете о состоянии рынка, оказал существенное влияние на выбор оптимального решения.
Вернемся к сценарию, описанному в начале главы. Поскольку выбор акций для инвестирования сильно зависит от экономических условий, необходимо сделать предварительный прогноз на следующий год. Предположим, что прогноз ограничивается лишь двумя ситуациями — рост экономики (FJ и спад или застой (Г,). Прошлый опыт показывает, что в условиях спада предсказания экономического роста сбываются в 20% случаев, в условиях стабильной экономики — в 40%, в условиях умеренного роста — в 70%, и, наконец, в условиях экономического бума — в 90% случаев. Итак, если прогнозируется экономический рост, вероятности разных экономических ситуаций необходимо вычислить заново, используя теорему Байеса. Введем следующие обозначения:
Е, — спад,
Е2 — стабильная экономика,
Е3 — умеренный рост,
Ei — экономический бум,
Fx — экономический рост,
F2 — спад или застой.
Кроме того, сказанное выше можно сформулировать в виде формул:
Р(Е,) = 0,10, P(Fj Ех) = 0,20,
Р(Е2) = 0,40, P(Fj Е2) = 0,40,
Р(Е.) = 0,30, P(FX\E3) = 0,70,
Р(ЕХ) = 0,20, P(FjEJ = 0,90.
Применим теорему Байеса (4.10) и вычислим следующие вероятности.
Р(Е |К> =_____________________PU^PjE,)________________________
11 /’(/|£,)Р(Е,)+Р(/-|£2)Р(£2)+Р(/-|£э)Р(£,) + Р(£;|£4)Р(£4)
0,20x0,10
0,20x0,10 + 0,40x0,40 + 0,70x0,30 + 0,90x0,20
= 0,035.
р(£2|Л) =
_______________________P(f;|£,)P(£.)______________________
P(F, IЕ, )Р(Е,) + £(/• | Е2 )Р(Ег) + P(F, j Е, )Р(Е,) + P(Fl\Et)P(E,)
0,40x0,40
0,20x0,10 + 0,40x0,40 + 0,70x0,30 + 0,90x0,20
0,16
0,57
= 0,281
^зИ) =
_____________________Р(Л|^)^(^)______________________
P(FX\E})P(EX) + Р^\Е2)Р(Е2) + P(FX\E3)P(E3) + P(Fx\E4)P(E4)
0,70x0,30
0,20x0,10 + 0,40x0,40 + 0,70x0,30 + 0,90x0,20
0,21
0,57
= 0,368
Р^) =
________________________P(Fx\E4)P(E4)_______________________
P(Ej|EJ)P(E1) + P(Ej|E,)P(E2) + P(F1|E3)P(E3) + P(7^|E4)P(E4)
_________________0,90x0,20___________________= 0,18 _ 0 3 j 6 0,20x0,10 + 0,40x0,40 + 0,70x0,30 + 0,90x0,20_0,57 ’
Результаты вычисления этих вероятностей приведены в табл. 16.10 и на рис. 16.5.
Таблица 16.10. Результаты вычисления вероятностей по теореме Байеса при выборе акций
Событие, Eg Априорная вероятность, P(Ei) Условная вероятность, P(F,|E.) Совместная вероятность, Р<МЕ,)Р(Е,) Уточненная вероятность, Р(Е,|Р,)
Е, = Спад 0,10 0,20 0,02 0,02/0,57 = 0,035
Е9 = Стабильная 0,40 0,40 0,16 0,16/0,57 = 0,281
экономика
Е3 = Умеренный рост 0,30 0,70 0,21 0,21/0,57 = 0,368
Е, = Экономический бум 0,20 0,90 0,18 0,18/0,57 = 0,316
0,57
P(E1mF1) = P(F1|E1)P(E1) = (0,20) (0,10) = 0,02
P(E1hF2) = P(F2|E1)P(E1) = (0,80) (0,10) = 0,08
P(E2mF1) = P(F1|E2)P(E2) = (0,40) (0,40) = 0,16
P(E2mF2) = P(F2|E2)P(E2) = (0,60) (0,40) = 0,24
P(E3mF1) = P(F1|E3)P(E3) = (0,70) (0,30) = 0,21
P(E3mF2) = P(F2|E3)P(E3) = (0,30) (0,30) = 0,09
P(E4mF1) = P(F1|E4)P(E4) = (0,90) (0,20) = 0,18
P(E4mF2) = P(F2|E4)P(E4) = (0,10) (0,20) = 0,02
Рис. 16.5. Дерево решений при выборе акций на основе уточненных вероятностей
Поскольку для выбора оптимального решения на основе оценки ожидаемой прибы ли использовались прежние вероятности, приведенные в табл. 16.6, ожидаемую при быль необходимо вычислить заново, используя уточненные вероятности из табл. 16.10 Результаты новых вычислений приведены в табл. 16.11.
Таблица 16.11. Ожидаемая прибыль для каждого из альтернативных вариантов действий при покупке акций
Альтернативные планы
Событие, Е, Ps А, долл. х„Р, Б, дол. xijPi
Спад 0,035 30 30x0,035= 1,05 -50 -50x0,035 = -1,755
Стабильная экономика 0,281 70 70x0,281 = 19,67 30 30x0,281 = 8,43
Умеренный рост 0,368 100 100x0,368 = 36,80 250 250x0,368 = 92,00
Экономический бум 0,316 150 150x0,316=47,40 400 400x0,316 = 126,40
EMV(A) = 104,92 EMV(B) = 225,08
Итак, ожидаемая прибыль от покупки акций компанииА равна 104,92 долл., а от по купки акций компании Б — 225,08 долл. Используя этот критерий, следует признать, чтс покупка акций компании Б по-прежнему является наиболее выгодной. Однако это реше ние следует перепроверить, воспользовавшись критерием “доходность/риск” на основе уточненных вероятностей.
Используя уравнения (5.2) и (5.3) и учитывая, что EMV(A) = цл = 104,92 для акция компании А получаем следующий результат.
<г, = “И)2 Р(х<) = (30-104,92)2 х 0,035 + (70-104,92)2 х 0,281 +
+ (100-104,92)2 х 0,368 + (150-104,92)2 х 0,316 = 1 190,194.
Стандартное отклонение доходности акций компании А равно а 4 = ф. 190,194 = 34,50 .
Для акций компании Б величина EMV(A) равна = 225,08. Дисперсия доходности акций компании Б равна
с; = ~ М)2 Р( *,) = (-50-225,08)2 х 0,035 + (30-225,08)2 х 0,281 +
+ (250-225,08)2 х 0,368 + (400-225,08)2 х 0,316 = 23 239,39.
Стандартное отклонение доходности акций компании Б равно <зБ = у/23 239,39 = 152,445 .
Вычислив стандартное отклонение доходности акций, можно определить коэффициент вариации прибыли. С помощью формулы (3.11) получаем следующий результат.
__<7, EMV(A)
х100% =
СИЛ =
34 499
..~-х 100% = 32,88%.
104,92
Коэффициент вариации показателя доходности акций компании Б равен следующей величине.
EMV (Б)
х100%
152 445
-------х 100% = 67,73%.
225,08
Таким образом, как и в предыдущих вычислениях, доходность акций компании Б колеблется намного сильнее, чем доходность акций компании А.
Отношение “доходность/риск” для акций компанииА равно 104,92/34,50 = 3,041, а для акций компании Б — 225,08/152,445 = 1,476.
Итак, по отношению к величине риска, выраженной с помощью стандартного отклонения, доходность акций компании А намного выше, чем доходность акций компании Б. Руководствуясь критерием “доходность/риск”, при покупке следует предпочесть акции компании А.
УПРАЖНЕНИЯ К РАЗДЕЛУ163
Изучение основ
16.18. Предположим, что поставленная задача описывается следующей таблицей выигрышей.
Действия
Событие А Б
1 50 100
2 200 125
Допустим, Р{Е^ = 0,5, Р(Б2) = 0,5, P(P|P,) = 0,6, P(F\E2) — 0,4 и происходит событие F.
1. Вычислите заново вероятности P(PJ и Р(Б2), используя новую информацию.
2. Вычислите ожидаемую прибыль от покупки акций компаний А и Б.
3. Вычислите ожидаемый размер упущенной выгоды от покупки акций компаний А и Б.
4. Объясните смысл ожидаемой стоимости полной информации (EVPI) в этой задаче.
5. Используя ответы к задачам 2 и 3, определите, какие акции следует покупать — компании А или компании Б. Обоснуйте свое решение.
6. Вычислите коэффициент вариации доходности при покупке акций компаний А и Б.
7. Вычислите отношение “доходность/риск” при покупке акций компаний А и Б.
8. Выберите оптимальный вариант покупки, руководствуясь ответами на вопросы 6 и 7. Обоснуйте свой выбор.
9. Сравните результаты решения задач 5 и 8. Объясните разницу между ними.
16.19. Предположим, что поставленная задача описывается следующей таблицей выигрышей.
Действия
Событие А Б
1 50 10
2 300 100
3 500 200
Допустим, Р(Е,) = 0,8, Р(Е2) = 0,1, Р(ЕЯ) = 0,1, Р(Е,|Е,) = 0,2, P(F\E2) = 0,4, P(F\E3) = 0,4, и происходит событие F.
1. Вычислите заново вероятности Р(Ег), Р(Е2) и Р(Е3), используя новую информацию.
2. Вычислите ожидаемую прибыль от покупки акций компаний АиБ.
3. Вычислите ожидаемый размер упущенной выгоды от покупки акций компаний Аи Б.
4. Объясните смысл ожидаемой стоимости полной информации (EVPI) в этой задаче.
5. Используя ответы к задачам 2 и 3, определите, какие акции следует покупать — компании А или компании Б. Обоснуйте свое решение.
6. Вычислите коэффициент вариации доходности при покупке акций компаний Аи Б.
7. Вычислите отношение “доходность/риск” при покупке акций компаний А и Б.
8. Выберите оптимальный вариант покупки, руководствуясь ответами на вопросы 6 и 7. Обоснуйте свой выбор.
9. Сравните результаты решения задач 5 и 8. Объясните разницу между ними.
Применение понятий
16.20. В задаче 16.12 поставщик товаров на бейсбольном стадионе решает, чем торговать во время матча — мороженым или лимонадом. Предположим, что он решил воспользоваться прогнозом погоды, чтобы сделать окончательный выбор. По своему опыту он знает, что если в настоящее время стоит холодная погода, то прогноз холодной погоды сбывается в 80% случаев. Если же на улице установилась теплая погода, то прогноз теплой погоды сбывается в 70% случаев. Сегодняшний прогноз предсказывает холодную погоду.
1. Вычислите заново вероятности, на основе которых принимается решение.
2. Используйте эти вероятности для решения задачи 16.12.
3. Сравните полученные результаты с предыдущими.
16.21. В задаче 16.14 инвестор пытается сделать оптимальный выбор среди трех возможностей. Допустим, что перед принятием решения он обратился к своему биржевому брокеру. В прошлом, если экономика находилась в упадке, радужные прогнозы брокера сбывались в 20% случаев, а мрачные — в 80% . Если экономика пребывала в застое, благоприятные прогнозы брокера сбывались в 40% случаев. Если же экономика переживала подъем, оптимистические прогнозы брокера сбывались в 70% случаев. В данном случае брокер дал пессимистический прогноз.
1. Вычислите заново вероятности, на основе которых принимается решение.
2. Используйте эти вероятности для решения задачи 16.14.
3. Сравните полученные результаты с предыдущими.
16.22. В задаче 16.16 автор выбирал одно из двух издательств для публикации своего нового романа. Допустим, что перед принятием решения он обратился к опытному рецензенту и попросил его предсказать успех или неудачу романа. В прошлом среди романов, объем продаж которых был равен 1 000 экземпляров, лишь 1% получили благоприятный отзыв. Среди романов, объем продаж которых достигал 5 000 экземпляров, 25% имели благоприятный прогноз. Среди романов, проданных в количестве 10 000 экземпляров, 60% получили доброжелательную рецензию. И, наконец, среди романов, изданных 50 000 тиражом, 99% имели положительную оценку.
1. Вычислите заново вероятности, на основе которых принимается решение.
2. Используйте эти вероятности для решения задачи 16.16.
3. Сравните полученные результаты с предыдущими.
16.4. ПОЛЕЗНОСТЬ
До сих пор мы предполагали, что величина прибыли или убытков является постоянной. Однако в реальности это условие часто не выполняется. Большинство компаний предпринимают усилия, чтобы не допустить крупных потерь. В то же время они не возражают против очень больших прибылей. Такая дифференцированная оценка увеличивающихся прибылей или убытков называется полезностью (utility). Это понятие впервые ввел Даниэль Бернулли (Daniel Bernoulli) в 18-м веке [1]. Чтобы проиллюстрировать эту концепцию, предположим, что нам предстоит сделать выбор.
Выбор 1. Подбрасывается идеальная монета. Если выпадет герб, мы выигрываем 0,60 долл., если решка — проигрываем 0,40 долл.
Выбор 2. Не принимать участие в игре.
Какое решение следует принять? Ожидаемая прибыль игры составляет 0,60x0,50+ + (-0,40)х0,50 = +0,10. Ожидаемая прибыль в результате отказа от игры равна 0.
Большинство людей предпочтут принять участие в игре, поскольку ожидаемая прибыль является положительной величиной, а сама игра не требует большого количества денег. Предположим теперь, что ставки возросли: если выпадает герб, мы выигрываем 600 000 долл., если решка — проигрываем 400 000 долл. Ожидаемая прибыль игры теперь равна +100 000 долл. В таких условиях, несмотря на то что ожидаемая прибыль является положительной, большинство людей откажется играть, тяжело переживая возможную потерю 400 000 долл. Полезность каждого дополнительного доллара прибыли или убытков отличается от полезности предыдущих выигрышей. Крупные убыт-
ки большинство людей воспринимают негативно, в то же время полезность каждого дополнительного доллара прибыли постепенно снижается.
Построение кривой полезности каждого доллара является важной частью процесса принятия решений, однако эта тема выходит за пределы нашей книги [2, 3].
Существуют три основных типа кривых полезности: неприятие риска, ориентация на риск и нейтральное отношение к риску (рис. 16.6).
Количество денег Панель А: Кривая неприятия риска
Количество денег Панель Б: Кривая ориентации
на риск
Количество денег Панель В: Кривая нейтрального отношения к риску
Рис. 16.6. Три типа кривых полезности: неприятие риска (панель А), ориентация на риск (панель Б) и нейтральное отношение к риску (панель В)
Кривая неприятия риска демонстрирует резкое возрастание полезности первоначального объема денег, которое постепенно уменьшается по мере увеличения дохода. Эта кривая устраивает большинство бизнесменов, поскольку ценность каждого дополнительного доллара прибыли после достижения определенного уровня постепенно уменьшается.
Кривая ориентации на риск привлекает любителей риска. Она демонстрирует большую ценность крупной прибыли. Эта кривая описывает поведение бизнесменов, которые хотят разбогатеть моментально, многим рискуя.
Кривая, нейтральная по отношению к риску, описывает подход, основанный на оценке ожидаемой прибыли. В рамках этой модели каждый дополнительный доллар прибыли имеет одинаковую полезность.
Построив кривую полезности, лицо, принимающее решения, должно выразить денежные величины в терминах полезности и применить критерии, основанные на вычислении ожидаемой полезности, ожидаемой величины упущенной выгоды и отношения “доходность/риск”.
УПРАЖНЕНИЯ К РАЗДЕЛУ 16Д
Применение понятий
15.23. Как вы относитесь к риску: избегаете, любите или нейтрально?
15.24. Вернитесь к задачам 16.3-16.5 и 16.12-16.17. В каких из этих задач критерий, основанный на отношении “доходность/риск” (нейтральный), является неприемлемым? Почему?
РЕЗЮМЕ
Как показано на структурной схеме, в этой главе рассмотрен процесс принятия решений. Показано, как построить таблицу выигрышей и деревья решений, как применить различные критерии выбора оптимального решения, а также, как уточнить веро-
ятности с учетом вновь поступившей информации, используя теорему Байеса. В сценарии, описанном в главе, показано, как применить эти инструменты при покупке акций компаний А или Б. Оказалось, что акции компании Б приносят более крупную ожидаемую прибыль, минимизируют ожидаемые размеры упущенной выгоды, но характеризуются меньшим отношением “доходность/риск”.
Принятие решений Ц
Альтернативные варианты решений^
Таблица < Деревья
выигрышей г решений
L™_—i_______а
Полезность
I
Таблица . упущенной выгоды
решений
/Ожидаемая прибыль
/Ожидаемый размер Коэффициент упущенной выгоды s вариации
' Отношение
। “доходность/риск"
ОСНОВНЫЕ понятия
^Уточнение вероятностей на основе выборочной
информации
I /теорема Байеса), yj
Структурная схема главы 16
Альтернативные планы действий, 1076 Критерий
"доходность/риск", 1088
принятия решений, 1076
Ожидаемая прибыль, 1083
в условиях полной
определенности, 1086
Ожидаемая стоимость полной информации, 1085
Ожидаемый размер упущенной выгоды, 1085
Полезность, 1101
Событие или экономическое
положение, 1076
Таблица выигрышей, 1076
Упущенная выгода, 1079
УПРАЖНЕНИЯ К ГЛАВЕ 16 • '
Проверка знаний
16.25. В чем заключается разница между событиями и альтернативными планами действий?
16.26. Назовите преимущества и недостатки таблиц выигрыша и деревьев решений.
16.27. Как вычислить размер упущенной выгоды по таблице выигрышей?
16.28. Почему размер упущенной выгоды не может быть отрицательным?
16.29. В чем состоит разница между ожидаемой прибылью и ожидаемым размером упущенной выгоды?
16.30. Что такое ожидаемая стоимость полной информации?
16.31. Чем ожидаемая стоимость полной информации отличается от ожидаемой прибыли в условиях полной определенности?
16.32. Укажите преимущества и недостатки критерия, основанного на вычислении ожидаемой прибыли по сравнению с критерием “доходность/риск”.
16.33. Как уточнить вероятности на основе вновь поступившей информации, используя теорему Байеса?
16.34. В чем заключается разница между неприятием риска и ориентацией на риск?
16.35. Почему в некоторых условиях необходимо пользоваться критерием полезности, а не таблицей выигрышей?
Применение понятий
16.36. Сеть магазинов Shop-Quik Supermarkets приобретает большие партии белого хлеба для дальнейшей продажи в течение недели. Магазин покупает хлеб по 0,70 долл, за буханку, а продает — за 1,10 долл. Все буханки, не проданные до конца недели, могут быть проданы местным магазинам по 0,40 долл. Вероятности различных заказов приведены в следующей таблице.
Заказ (количество буханок) Вероятность
6 000 0,10
8 000 0,50
10 000 0,30
12 000 0,10
1. Создайте таблицу выигрышей, указав события и альтернативные варианты решений.
2. Постройте дерево решений.
3. Вычислите ожидаемую прибыль (EMV) при закупке 6 000, 8 000, 10 000 и 12 000 буханок.
4. Вычислите ожидаемый размер упущенной выгоды (EOL) при закупке 6 000, 8 000, 10 000 и 12 000 буханок.
5. Объясните смысл стоимости полной информации (EVPI) в этой задаче.
6. Используя решения задач 3 или 4, определите, сколько буханок следует закупить.
7. Найдите коэффициент вариации для каждого объема закупок.
8. Вычислите отношение “доходность/риск” для каждого объема закупок.
9. Выберите оптимальный размер закупок, руководствуясь ответами на вопросы 7 и 8. Обоснуйте свой выбор.
10. Сравните результаты решения задач 6 и 9. Объясните разницу между ними.
Заказ (количество буханок) Вероятность
6 000 0,30
8 000 0,40
10 000 0,20
12 000 0,10
Повторите решение задач 3-9 при новых вероятностях. Сравните полученные решения с предыдущими.
16.37. Владелец топливной компании должен решить, стоит ли предлагать своим клиентам солнечные батареи. Исходная цена такого оборудования равна 150 000 долл., причем каждый комплект приносит 2 000 долл, прибыли. Владелец компании оценил вероятности различных заказов.
Заказ (количество установок) Вероятность
50 0,40
100 0,30
200 0,30
1. Создайте таблицу выигрышей, указав события и альтернативные варианты решений.
2. Постройте дерево решений.
3. Постройте таблицу упущенной выгоды.
4. Вычислите ожидаемую прибыль (EMV) от установки солнечных батарей
5. Определите ожидаемый размер упущенной выгоды (EOL) от установки солнечных батарей.
6. Объясните смысл стоимости полной информации (EVPI) в этой задаче.
7. Вычислите отношение “доходность/риск” для каждого объема установок.
8. Определите оптимальное количество установок, руководствуясь ответами на вопросы 4 или 5 и 7. Обоснуйте свой выбор.
9. Как изменятся решения задач 1-8, если исходная стоимость оборудования равна 200 000 долл.?
16.38. Производитель картофельных чипсов должен решить, стоит ли менять на них упаковку. Менеджер по производству считает, что это решение может привести к трем последствиям: слабая, умеренная и сильная реакция рынка. Возможные выигрыши и проигрыши этого решения приведены в таблице.
Стратегия, млн. долл.
Событие Использовать новую упаковку Оставить старую упаковку
Слабая реакция -4 0
Умеренная реакция 1 0
Сильная реакция 5 0
Основываясь на прошлом опыте, менеджер определил вероятности всех событий: Р(слабая реакция) = 0,30, Р(умеренная реакция) = 0,60, Р(сильная реакция) = 0,10.
1. Постройте дерево решений.
2. Постройте таблицу упущенной выгоды.
3. Вычислите ожидаемую прибыль (EMV) от применения новой упаковки.
4. Определите ожидаемый размер упущенной выгоды (EOL) от применения новой упаковки.
5. Объясните смысл стоимости полной информации (EVPI) в этой задаче.
6. Вычислите отношение “доходность/риск” для новой упаковки.
7. Решите, стоит ли менять упаковку, руководствуясь ответами на вопросы 4 или 5 и 7. Обоснуйте свой выбор.
8. Как изменятся решения задач 3-7, если вероятности событий равны 0,6, 0,3 и 0,1 соответственно?
9. Как изменятся решения задач 3-7, если вероятности событий равны 0,1, 0,3 и 0,6 соответственно?
Прежде чем сделать окончательные выводы, менеджер решил оценить состояние рынка. В определенном городе в продажу поступили чипсы в новой упаковке. После этого менеджер оценил изменение объема продаж — увеличился, уменьшился или остался прежним. Ранее компания неоднократно применяла такой прием, однако это слабо влияло на состояние общенационального рынка. В то же время продажи в тестируемом городе уменьшились в 60% случаев, остались прежними в 30% случаев и увеличились в 10% случаев. В тех случаях, когда реакция национального рынка была умеренной, продажи в тестируемом городе уменьшились в 20% случаев, остались прежними в 40% случаев и увеличились в 40% случаев. Когда реакция национального рынка была сильной, продажи в тестируемом городе уменьшились в 5% случаев, остались прежними в 35% случаев и увеличились в 60% случаев.
10. Предположим, что объем продаж в тестируемом городе не изменился. Уточните априорные вероятности с учетом вновь поступившей информации.
11. Примените уточненные вероятности для решения задач 3-7.
12. Предположим, что объем продаж в тестируемом городе уменьшился. Уточните априорные вероятности с учетом вновь поступившей информации.
13. Примените уточненные вероятности для решения задач 3-7.
16.39. Предприниматель желает знать, насколько прибыльны садоводческие услуги в пригороде. Он полагает, что существуют четыре уровня спроса на эти услуги: очень низкий — 1% семей, низкий — 5% семей, умеренный — 10% семей и высокий — 25% семей.
Руководствуясь прошлым опытом, предприниматель так оценил вероятности спроса: Р(очень низкий спрос) = 0,20, Р(низкий спрос) = 0,50, Р(умеренный спрос) = 0,20, Р(высокий спрос) = 0,10.
Стратегия, долл.
Спрос Предложить новую услугу Не предлагать
Очень низкий (р = 0,01) -50 000 0
Низкий (р = 0,05) 60 000 0
Умеренный (р = 0,10) 130 000 0
Высокий (р = 0,25) 300 000 0
1. Постройте дерево решений.
2. Постройте таблицу упущенной выгоды.
3. Вычислите ожидаемую прибыль (EMV) от новой услуги.
4. Вычислите ожидаемый размер упущенной выгоды (EOL) от новой услуги.
5. Объясните смысл стоимости полной информации (EVPI) в этой задаче.
6. Вычислите отношение “доходность/риск” для новой услуги.
7. Решите, стоит ли предлагать новую услугу, руководствуясь ответами на вопросы 4 или 5 и 7. Обоснуйте свой выбор.
Прежде чем сделать окончательные выводы, предприниматель решил оценить состояние рынка. Для этого была сформирована выборка, состоящая из 20 семей. Три из них приняли предложение.
8. Уточните априорные вероятности с учетом вновь поступившей информации. (Подсказка-, для того, чтобы оценить вероятность результата, примените биномиальное распределение при каждом уровне заказов.)
9. Примените эти данные для решения задач 3-7.
16.40. Некая компания производит 10 000 дешевых фломастеров в день. Для того чтобы обеспечить максимальное качество своей продукции, производитель гарантирует бесплатный обмен неисправных фломастеров. Вычисления показывают, что стоимость замены несправного фломастера равна 20 центов. Руководствуясь прошлым опытом, менеджер компании так оценил вероятности различных уровней брака: очень низкий— 1%, низкий— 5%, умеренный— 10%, высокий — 20%.
Производитель может снизить уровень брака, отремонтировав станки в конце рабочего дня. Это позволяет снизить уровень брака на 1%, однако стоимость Ниже приведена таблица выигрышей, вычисленная на основании информации о дневном объеме производства (10 000 фломастеров) для каждой из двух альтернатив: вызывать механика или нет.
Действие
Уровень брака Вызвать механика, долл. Не вызывать механика, долл.
Очень низкий (1%) 20 100
Низкий (5%) 100 100
Умеренный (10%) 200 100
Высокий (20%) 400 100
Основываясь на прошлом опыте, менеджер предполагает, что каждый уровень брака одинаково вероятен.
1. Постройте дерево решений.
2. Постройте таблицу упущенной выгоды.
3. Вычислите ожидаемую прибыль (EMV) при вызове механика и отказе от его услуг.
4. Вычислите ожидаемый размер упущенной выгоды (EOL) при вызове механика и отказе от его услуг.
5. Объясните смысл стоимости полной информации (EVPT) в этой задаче.
6. Вычислите отношение “доходность/риск” при отказе от услуг механика.
7. Решите, стоит ли вызывать механика, руководствуясь ответами на вопросы 3 или 4 и 6. Обоснуйте свой выбор.
Предположим, что в конце рабочего дня из произведенной продукции формируется выборка, состоящая из 15 фломастеров, среди которых два являются неисправными.
8. Уточните априорные вероятности с учетом вновь поступившей информации. {Подсказка', для того, чтобы оценить вероятность результата, примените биномиальное распределение при каждом уровне брака.)
9. Примените эти данные для решения задач 3-7.
Применение Интернет
16.41. Зайдите на сайт www.prenhall.com/levine. Выберите ссылку Chapter 16 и щелкните на ссылке Internet exercises.
ПРИМЕНЕНИЕ WEB
Примените свои знания о теории принятия решений для проверки рекламных заявлений компании StockTout.
Компания StraightArrow Banking & Investments является конкурентом компании StockTout. В настоящее время она широко рекламирует свой фонд StraightDeal.
Посетите сайт компании StraightArrow (www.prenhall.com/Springville/SA_Home. htm) и проанализируйте правдивость их рекламных заявлений, используя статистические данные. Сравните эти заявления с заявлениями фондов StockTout Happy Bull и Worried Bear Funds (www . prenhall. com/Springville/ST_BullsandBears . htm), упомянутых в главе 5.
1. Можно ли утверждать, что фонд StraightArrow StraightDeal более эффективен, чем фонды компании StockTout? Подтвердите свои выводы результатами статистического анализа.
2. Прежде чем сформулировать окончательный вывод о эффективности фонда, сделайте прогноз экономической ситуации в следующем году. По общему мнению ведущих экономистов в следующем году ожидается экономический рост. В прошлом прогноз ведущих экономистов относительно экономического роста не оправдывался в 10% случаев, когда наступал спад, в 50% случаев, когда наблюдался застой, и полностью подтверждался только в 75% случаев. В 90% случаев прогноз благоприятной экономической ситуации “перевыполнялся” — наступал период бурного экономического роста.
Как влияет эта информация на ваши выводы, и влияет ли вообще? Аргументируйте свой ответ?
СПРАВОЧНИК ПО EXCEL. ГЛАВА 16
ЕН.16.1. Анализ упущенной выгоды
Вычислить упущенную выгоду позволит рабочий лист, использующий функции ИНДЕКС и П0ИСКП03. Формат этих функций выглядит следующим образом.
ИНДЕКС (диапазон индексов; 1; номер столбца)
Здесь диапазон индексов задает диапазон ячеек в строке, содержащий избранные величины, номер столбца указывает искомый столбец в указанном диапазоне индексов.
П0ИСКП03 (искомое значение; просматриваемый диапазон ячеек; 0)
Здесь параметр искомое значение задает искомое число, а параметр просматриваемый диапазон ячеек определяет область поиска.
В табл. ЕН.16.1 и ЕН. 16.2 представлен шаблон рабочего листа Упущенная_выгода, выполняющего анализ упущенной выгоды при выборе рыночной стратегии менеджера, торгующего телевизорами (табл. 16.1). В этом шаблоне для выбора оптимальной прибыли при каждом из событий используется функция МАКС. В свою очередь функция МАКС вызывает функцию ПОИСКПОЗ, которая в сочетании с функцией ИНДЕКС возвращает значение, содержащееся в указанном столбце внутри диапазона индексов В4 : С4.
В ходе реализации шаблона рабочего листа формулы в ячейках В12 и В13 необходимо вводить в одной строке, хотя в табл. ЕН.16.1 эти формулы записаны в двух строках.
Приведенный ниже шаблон можно настроить для решения аналогичных задач, вставив дополнительные строки и столбцы в таблицу выигрышей, а также исправив соответствующие формулы. Если в задаче предполагается другое количество событий, вставьте новые строки как в таблицу выигрышей, так и в таблицу упущенных возможностей, выбрав команду Вставка^Строки. Если в задаче предполагается другое количество возможных вариантов действий, выделите столбцы С и Е и выберите команду Вставка^Столбцы. В таблице упущенной выгоды столбец С следует оставить пустым, а формулы из ячеек столбца D — скопировать в новый столбец F.
Таблица ЕН.16.1. Шаблон рабочего листа Упущенная_выгода для задачи о телевизионном маркетинге (таблица выигрышей)
А В С
1 Оценка упущенной выгоды при выборе рыночной стратегии
2
3 Таблица выигрышей
4 Предлагать Не предлагать
5 Удачная модель 45 -3
6 Неудачная модель -36 -3
Таблица ЕН.16.2. Шаблон рабочего листа Упущенная_выгода для задачи о телевизионном маркетинге (строки 7 и 8 пусты)
А В С D Е
9 Таблица упущенной выгоды
10 Оптимум Оптимум Варианты
11 Действие Прибыль =В4 =04
12 =А5 = ИНДЕКС($В$4:$С$4;1; ПОИСКПОЗ(012;В5:05;0)) =МАКО(В5:С5) =$С12-В5 =$012-05
ИО =А6 =ИНДЕКС($В$4:$С$4;1; ПОИОКПОЗ(С13;Вб:Сб;0)) = МАКС(Вб:С6) =$013-Вб =$013-06
ЕН.16.2. Применение критериев принятия решений на основе таблицы выигрышей
Для вычисления ожидаемой прибыли, ожидаемого размера упущенной выгоды и коэффициента вариации прибыли на основе таблицы выигрышей и распределения вероятностей следует реализовать рабочий лист, использующий функции ИНДЕКС, ПОИСКПОЗ, СУММПРОИЗВ, ЕСЛИ, а также арифметические формулы. Функция СУММПРОИЗВ имеет следующий формат.
СУММПРОИЗВ (диапазон ячеек множителя; диапазон ячеек множимого)
В табл. ЕН.16.3-ЕН.16.7 показан шаблон рабочего листа Критерии, позволяющий вычислить ожидаемую прибыль, ожидаемый размер упущенной выгоды и коэффициент вариации в задаче о покупке акций, описанной в сценарии.
В формулах следует использовать как абсолютные, так и относительные ссылки на ячейки. Обратите внимание на то, что в формулах, записанных в ячейках D2 6 и Е2б используются двойные кавычки. Все формулы, которые изображены на двух строках, в реальном рабочем листе следует вводить в одной строке. В строках 10-15 столбца С, а также в ячейке С25 метки должны занимать одну строку.
Этот шаблон можно настроить для решения аналогичных задач, вставив дополнительные строки и столбцы в таблицу выигрышей, область вычислений, таблицу упущенной выгоды, а также исправив соответствующие формулы.
Таблица ЕН.16.3. Шаблон рабочего листа Критерии (вероятности и таблица выигрышей)
А В С D
1 Ожидаемая прибыль
II1II
3 Вероятности и таблица выигрышей
flgijlf Р А1 А2
5 Спад 0,1 30 -50
И Стабильная экономика 0,4 70 30
iiiii Умеренный рост 0,3 100 250
Hi Экономический бум 0,2 150 400
Таблица ЕН.16.4. Диапазон А10 :D15 шаблона рабочего листа Критерии (строка 9 пуста)
••••ч •: с , г : , , D
10 Статистика: =С4 =D4
11 Ожидаемая прибыль =СУММПРОИЗВ($В$5:$В$8;С5:С8) =СУММПРОИЗВ($В$5:$В$8;О5:Э8)
лл Дисперсия =СУММПРОИЗВ($В$5:$В$8;Е9:Е12) =СУММПРОИЗВ($В$5:$В$8;С9:С12)
13 Стандартное отклонение = К0РЕНЬ(С12) = K0PEHb(D12)
14 Коэффициент вариации =С13/С11 =D13/D11
15 Отношение "доходность/риск" =С11/С13 =D11/D13
Таблица ЕН.16.5. Столбцы F и G шаблона рабочего листа Критерии (первые пять строк должны оставаться пустыми)
6 Оценка упущенной выгоды
7 Дисперсия и вариация
8 =С4 =D4
9 = (С5-С$11)Л2 =(D5-D$11)A2
10 =(Сб-С$11)л2 = (D6-D$11)A2
ill = (С7-С$11)Л2 = (D7-D$11)A2
Bill = (С8-С$11)Л2 =(D8-D$11)A2
Таблица ЕН.16.6. Диапазон ячеек А17 : Е23 шаблона рабочего листа Критерии (строка 16 должна оставаться пустой)
A В с ' D E
lllill Оценка упущенной выгоды
III Оптимум Оптимум Варианты
iljlll Действие Прибыль =C4 = D4
jiliill =A5 =ИНДЕКС($С$4:$Э$4;1; ПОИСКПОЗ(С20;С5:О5;0)) =MAKC(C5:D5) =$C20-C5 =$C20-D5
21 =A6 =ИНДЕКС($С$4:$0$4;1; ПОИСКПОЗ(С21;Сб:06;0)) =MAKC(C6:D6) =$C21-C6 =$C21-D6
ЙЙ! =A7 = ИНДЕКС($С$4:$0$4;1; ПОИСКПОЗ(С22;С7:Э7;0)) =MAKC(C7:D7) =$C22-C7 =$C22-D7
23 =A8 =ИНДЕКС($С$4:$Э$4;1; ПОИСКПОЗ(С23;С8:О8;0)) =MAKC(C8:D8) =$C23-C8 =$C23-D8
Таблица ЕН.16.7. Строки 24:26 шаблона рабочего листа Критерии
A В С 0 .
24 =С4 = D4
25 Ожидаемый размер упущенной выгоды =СУММПРОИЗВ ($B$5:$B$8;D20:D23) =СУММПРОИЗВ ($B$5:$B$8;E20:E23)
liiiiii =ЕСЛИ(О25= MHH(($D$25:$E$25); “EVPI";'"') =ЕСДИ(Е25= MHH(($D$25:$E$25); "EVPI";"")
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
1. Bernstein, Р. L. Against the Gods: The Remarkable Story of Risk (New York: Wiley, 1996).
2. Render, B., R. M. Stair, and M.Hanna. Quantitative Analysis for Management, 8th ed. (Upper Saddle River, NJ: Prentice Hall, 2003).
3. Tversky, A. and D. Kahneman, “Rationale Choice and the Framing of Decisions,” Journal of Business, 59(1986): 251-278.
Глава 17
Статистические методы управления качеством и производительностью труда
ПРИМЕНЕНИЕ СТАТИСТИКИ: управление качеством обслуживания в отеле Beachcomber
17.1. ПОЛНЫЙ КОНТРОЛЬ КАЧЕСТВА
17.2. МЕТОД SIX SIGMA®
17.3. КОНТРОЛЬНЫЕ КАРТЫ
Процедуры Excel: построение контрольной р-карты
17.4. ПРОЦЕНТНЫЕ КОНТРОЛЬНЫЕ КАРТЫ
17.5. ЭКСПЕРИМЕНТ С КРАСНЫМИ ШАРАМИ: ВАРИАЦИЯ ПРОЦЕССА
17.6. КОНТРОЛЬНЫЕ КАРТЫ ДЛЯ РАЗМАХА И СРЕДНЕГО ЗНАЧЕНИЯ
Контрольная карта для размаха: В-карта
Контрольная X-карта
Процедуры Excel: построение карт для размаха и среднего значения
X7J7. ХАРАКТЕРИСТИКИ ПРОЦЕССА
Удовлетворение клиентов и допускае-
мые пределы
Показатели качества
Показатели мощности
Показатели CPL, CPU и Cpk
СПРАВОЧНИК ПО EXCEL
ЧЕМУ ДОЛЖЕН НАУЧИТЬСЯ СТУДЕНТ
• Владеть основными понятиями управления качеством и знать 14 принципов Деминга.
• Понимать основные аспекты метода Six Sigma®.
• Создавать различные контрольные карты.
• Знать, когда и как применяются конкретные контрольные карты.
• Измерять производительность процесса.
ПРИМЕНЕНИЕ СТАТИСТИКИ
Управление качеством обслуживания в отеле Beachcomber
Вернемся к сценарию, изложенному в главе 11. Поставьте себя на место управляющего отелем Beachcomber, прошедшего курс обучения методу Six Sigma®. Стремясь улучшить качество обслуживания постояльцев, вы желаете произвести на них приятное первое впечатление. Существуют два важных фактора, характеризующих качество обслуживания (Critical-To-Quality — CTQ) — готовность комнат к приему гостей и скорость доставки багажа. Значит, в номерах должны быть все необходимые аксессуары (мыло, полотенца и т.п.). Не менее важно, чтобы в номерах исправно работали
телевизор, радиоприемник и телефон. Кроме того, постояльцы, как правило, требуют, чтобы их багаж был доставлен в номер достаточно быстро. Для того чтобы удовлетворить потребности клиентов, администрация отеля должна собирать данные о степени готовности номеров и времени доставки багажа. Управляющий отелем должен постоянно анализировать эти данные и принимать необходимые решения. Например, вовремя ли доставляется багаж? Не изменяется ли время доставки багажа от случая к случаю? Если изменяется, то в какую сторону: увеличивается или уменьшается? Чем объясняются причины задержки — случайным стечением обстоятельств или серьезными недостатками в обслуживании? Если причины коренятся в плохой организации труда, необходимо принять экстренные меры, сократив время доставки багажа и улучшив качество обслуживания клиентов.
ВВЕДЕНИЕ
В этой главе мы сосредоточимся на управлении качеством и производительностью труда. Компании, производящие товары и оказывающие услуги, понимают, что качество и производительность труда становятся жизненно важными в глобальной экономике. Например, качество играет чрезвычайно важную роль в следующих отраслях производства и обслуживания.
• Проектирование, производство и надежность автомобилей.
• Услуги, предоставляемые отелями, банками, школами, магазинами и почтовыми компаниями.
• Производство все более мощных компьютеров.
• Средства передачи информации — пейджеры, факсы и сотовые телефоны.
• Средства диагностики и другое медицинское оборудование.
Начнем изучение методов управления качеством и производительностью труда с исторического обзора. В главе сформулированы 14 принципов Деминга, которые образуют основу для применения карт качества. Кроме того, здесь изложена весьма поучительная притча о красных шарах, которая иллюстрирует изменчивость, присущую наборам данных, и подчеркивает ответственность менеджера за постоянное улучшение работы.
17.1. ПОЛНЫЙ КОНТРОЛЬ КАЧЕСТВА
В середине 1980-х годов стало ясно, что в условиях глобальной экономики компании вступают в конкуренцию не только с национальными производителями, но и с иностранными компаниями во всем мире [5, 10]. Глобализация экономики стала результатом стечения многих обстоятельств, в частности, быстрого роста средств коммуникации и доступности мощных компьютерных систем. В этой экономической среде чрезвычайно важно, чтобы организация бизнеса гибко реагировала на изменение рыночных условий и внедрение новых эффективных методов менеджмента.
Развитие глобальной экономики возродило интерес к повышению качества продукции в США. Свидетельством этого стало соревнование за приз Малкольма Балдриджа (Malcolm Baldrige), который ежегодно присуждается компаниям, достигшим наивысших результатов в процессе улучшения качества своих товаров и услуг. К числу этих компаний относятся корпорации Motorola, Xerox, Federal Express, Cadillac Motor Company, Ritz-Carlton Hotels, AT&T Universal Card Services, Eastman Chemical Company и Los Alamos National Bank.
Принципы управления качеством были впервые сформулированы в 1950 году У. Демингом (W. Edwards Deming), Джозефом Джураном (Joseph Juran) и Каору Ишикава (Kaoru Ishikawa), принимавшими участие в процессе возрождения экономики Японии. В основе этого подхода лежат методы улучшения качества и системной оптимизации. Системный подход к управлению часто называют полным контролем качества (total quality management — TQM). Он характеризуется следующими свойствами (врезка 17.1).
ВРЕЗКА 17.1. ОСОБЕННОСТИ ПОЛНОГО КОНТРОЛЯ КАЧЕСТВА
• Основное внимание уделяется улучшению процесса производства.
• Основной причиной изменчивости характеристик процесса являются особенности системы, а не случайные обстоятельства.
• Коллективная работа является неотъемлемой частью контроля качества.
• Основной целью организационных усилий является удовлетворение потребностей клиентов.
• Все организационные преобразования направлены на повышение качества работы.
• Из организации необходимо изгнать страх.
• Повышение качества требует затрат на обучение персонала.
Наибольшее влияние на развитие теории полного контроля качества оказал известный статистик У. Деминг. Подводя итоги своей работы в Японии и США, он сформулировал 14 основных принципов, приведенных во врезке 17.2.
Первая рекомендация описывает процесс решения насущных и перспективных задач, стоящих перед организацией. Основное внимание уделяется постоянному улучшению качества продукции или услуг. Процесс улучшения качества продукции иллюстрируется циклом Шухарта-Деминга, изображенным на рис. 17.1. Непрерывный цикл Шухарта-Деминга состоит из этапов планирования, реализации, изучения и внедрения. Планирование представляет собой первую фазу изменений производственного процесса. В него вовлекаются работники из разных подразделений организации. Второй этап — реализация — описывает процесс внедрения запланированных изменений, желательно в небольшом масштабе. Третий этап — изучение — сводится к анализу результатов с помощью статистических инструментов. Четвертый этап — внедрение — означает принятие или отклонение предложенных изменений, а также дальнейшее изучение последствий преобразований при разных условиях. Отличительной чертой этого процесса является ориентация на клиента, представляющего собой наиболее важный элемент производства или обслуживания.
ВРЕЗКА 17.2. ПРИНЦИПЫ ДЕМИНГА
• Постоянно стремитесь к улучшению качества товаров и услуг.
• Овладевайте новым образом мышления. .
• Не полагайтесь на контрольные проверки.
• Не ориентируйтесь на цену товара. Вместо этого минимизируйте общие расходы, работая с одним поставщиком.
• Постоянно совершенствуйте планирование, производство и обслуживание.
• Обучение должно стать неотъемлемой частью работы.
• Поощряйте лидерство.
• Избавьтесь от страха.
• Устраните барьеры между подразделениями.
• Избегайте лозунгов, призывов и наставлений.
: • Не устанавливайте количественные нормативы.
.. • Устраните барьеры, лишающие людей гордости за свою работу. Отмените ежегодный рейтинг и систему оценки работника по заслугам.
• Внедряйте интенсивную программу обучения и самосовершенствования каждого сотрудника.
• Вовлекайте каждого сотрудника в процесс преобразований.
Рис. 17.1. Цикл Шухарта-Деминга
Второй пункт, рекомендующий осваивать новый образ мышления, отражает необходимость осознания новых экономических реалий в условиях глобальной конкуренции. Лучше предугадать кризис, чем реагировать на его негативные последствия. Рекомендация отвергает принцип “не сломалось — не ремонтируй”, а, напротив, понуждает постоянно работать над улучшением качества продукции и услуг, предупреждая дорогостоящий ремонт.
Третий пункт, призывающий не полагаться на контрольные проверки, основан на понимании того, что любые проверки, направленные на улучшение качества продукции, бессмысленны, поскольку проводятся слишком поздно — ведь продукция уже создана. Все нужно делать правильно с самого начала. Проверки качества порождают массу проблем — кроме высокой стоимости, они часто не позволяют отделить качественную продукцию от бракованной. Эти трудности иллюстрирует пример, описанный Шеркенбахом (Scherkenbach) [14] и представленный на рис. 17.2. Допустим, в предложении, приведенном на рис. 17.2, необходимо подсчитать количество вхождений буквы F. Выполните эту работу и укажите количество обнаруженных вхождений буквы F.
FINISHED FILES ARE THE RESULT OFYEARS OF SCIENTIFIC STUDY COMBINED WITH THE EXPERIENCE OF MANYYEARS
Рис. 17.2. Проверка предложения (источник: W. W. Scherkenbach, The Deming Route to Quality and Productivity: Road Maps and Roadblocks (Washington, D.C.: CEEP Press, 1986)
Как правило, люди обычно видят три или шесть вхождений буквы F. Правильный ответ— шесть букв. Количество обнаруженных вхождений зависит от метода, которым пользуются испытуемые. Скорее всего, читатели найдут три буквы F, если прочитают предложение вслух, и шесть — если тщательно пересчитают все буквы. Смысл этого примера заключается в том, что даже простейшая проверка может привести к неправильным результатам, что уж говорить о сложных процессах, протекающих в условиях неопределенности.
Четвертый пункт, рекомендующий отказаться от ориентации на цену товара, представляет собой полную противоположность подходу, в котором поощряются производители, предлагающие наиболее дешевый товар. Эта рекомендация означает, что в долговременной перспективе цена товара не может характеризовать его качество. Подход, в котором предпочтение отдается наиболее дешевой продукции, игнорирует преимущества, которые дает уменьшение колебаний цен в результате выбора одного поставщика, и не поощряет долговременные отношения между покупателем и поставщиком. Такие отношения стимулируют внедрение новшеств и делают покупателя и продавца партнерами, стремящимися к общему успеху.
Пятый пункт, подчеркивающий важность постоянного стремления к совершенствованию организации труда, ориентирует менеджеров на непрерывное улучшение процессов, описанных циклом Шухерта-Деминга. В основе этой рекомендации лежит твердое убеждение, что качество продукции закладывается уже на этапе планирования производства. Улучшение качества — бесконечный процесс, в котором уменьшение колебаний приводит к сокращению экономических потерь, являющихся следствием непостоянства характеристик продукции.
Шестой пункт, призывающий внедрять процесс обучения, касается всех сотрудников — начиная с рабочих и заканчивая инженерами и менеджерами. Руководство компании должно понимать разницу между случайными и неслучайными причинами отклонений (см. раздел 17.3). Это позволит адекватно реагировать на различные ситуации.
Пункты 8-12 рекомендуют руководителям избавиться от страха, устранить барьеры между подразделениями, избегать лозунгов, призывов и наставлений, не устанавливать количественные нормативы, устранить барьеры, лишающие людей гордости за свою работу (отменив ежегодный рейтинг и систему оценки работников по заслугам). Все эти рекомендации относятся к способам оценки производительности труда.
Тринадцатая рекомендация, призывающая заниматься образованием и самосовершенствованием, отражает общеизвестное мнение, что наиболее важным ресурсом любой компании являются ее сотрудники. Повышение квалификации персонала приводит к улучшению работы всей организации в целом.
Четырнадцатый пункт рекомендует вовлекать всех сотрудников в процесс улучшения производства. Он основан на убеждении, что процесс совершенствования бесконечен.
Весьма важным инструментом контроля качества являются карты контроля, позволяющие оценить изменчивость системы и принять правильное решение. Мы рассмотрим их в следующем разделе.
17.2. МЕТОД SIX SIGMA®
Метод Six Sigma® был изобретен компанией Motorola в середине 1980-х годов. Последние 10 лет он успешно используется компаниями General Electric и Allied Signal для сокращения затрат и повышения эффективности производства. Как и метод полного контроля качества, разработанный Демингом и другими исследователями, метод Six Sigma® использует статистику для выявления брака и уменьшения отклонений от нормы.
Метод Six Sigma® разбивает процесс на последовательные стадии. Он полностью исключает брак и приводит к практически идеальным результатам.
Метод называется Six Sigma®, потому что в результате его применения количество брака сокращается до 3,4 случаев на миллион единиц произведенной продукции *. Отличительной чертой метода Six Sigma® является стремление достичь итогового результата за период от трех до шести месяцев. Благодаря этому метод был горячо одобрен высшим руководством многих компаний [1, 7-9, 15].
Модель, используемая в методе Six Sigma® для улучшения производственных процессов, имеет пять компонентов: определение, измерение, анализ, улучшение и контроль (Define, Measure, Analyze, Improve and Control — DMAIC). Основные аспекты этой модели представлены во врезке 17.3.
ВРЕЗКА 17.3. МОДЕЛЬ DMAIC
• Определение. Необходимо четко сформулировать поставленную задачу, определить затраты, возможную прибыль и воздействие на клиента.
• Измерение. Необходимо дать определение важнейших качественных характеристик (Critical-To-Quality — CTQ). Кроме того, процедура измерения должна верифицироваться, чтобы все повторяющиеся измерения были непротиворечивы.
• Анализ. Необходимо обнаружить коренные причины брака, а также особенности производственного процесса, которые могут привести к браку. Данные, собранные для оценки производственных процессов, часто анализируются с помощью контрольных карт (разделы 17.3-17.6).
• Улучшение. С помощью спланированного эксперимента оценивается важность каждой изучаемой характеристики производственного процесса (см. главу 10). Целью этого этапа является определение наилучшего уровня каждой характеристики, который можно поддерживать долгое время.
• Контроль. Цель этого этапа — долговременный контроль производственного процесса и предотвращение потенциальных проблем, которые могут возникнуть при изменении его характеристик.
Метод Six Sigma® предполагает, что в долговременной перспективе производственный процесс может отклониться от нормы не более чем на 1,5 стандартного отклонения. Шесть стандартных отклонений минус 1,5 стандартного отклонения приводят в результате к 4,5 стандартного отклонения от нормы. Область фигуры, ограниченной гауссовой кривой на расстоянии 4,5 стандартного отклонения от математического ожидания, приблизительно равна 0,0000034 (это соответствует 3,4 случаям брака на миллион единиц произведенной продукции).
Метод Six Sigma® требует постоянного сбора и статистического анализа данных с помощью контрольных карт и спланированных экспериментов. Кроме того, необходимо обучить персонал. Как правило, на освоение этого метода уходит несколько месяцев.
17.3. КОНТРОЛЬНЫЕ КАРТЫ
При сборе данных на протяжении определенного интервала времени необходимо изобразить график интересующей нас переменной. Одним из наиболее распространенных способов построения такого графика являются контрольные карты, предложенные Шухартом.
Контрольная карта позволяет следить за колебаниями качества продукции и услуг стечением времени, а также выявлять причину этой изменчивости. Ее можно использовать как для ретроспективного анализа эффективности работы, так и для оценки текущего положения дел. Данные, на основе которых строятся контрольные карты, образуют фундамент для улучшения системы. Контрольные карты используются для разнообразных переменных — категорийных, например, для доли номеров отеля, не соответствующих установленным нормам, дискретных, например, для количества постояльцев отеля, зарегистрированных в течение недели, и непрерывных, например, для времени, затраченного на доставку багажа. Кроме того, для облегчения анализа данных контрольная карта предусматривает средства, позволяющие отделить случайные вариации от неслучайных.
Неслучайные вариации (special, or assignable causes of variation) представляют собой крупномасштабные или закономерные колебания данных, несвойственные процессу. Эти колебания часто объясняются изменениями самой системы, которые следует либо устранить, либо использовать.
Случайная вариация (chances of common causes of variation) представляет собой колебание, присущее процессу. Она является результатом действия многих незначительных и случайных причин.
Различие между случайными и неслучайными вариациями является принципиальным. Неслучайные вариации не являются частью процесса, поэтому их можно устранить или использовать, не изменяя саму систему. В то же время случайные вариации изначально присущи процессу и не могут быть ликвидированы без изменения системы. Систематические изменения, направленные на устранение случайных вариаций качества продукции, относятся к компетенции руководства компании.
Контрольные карты позволяют осуществлять мониторинг процесса и определять существование неслучайных вариаций. Это позволяет предотвратить ошибки двух видов. Ошибка первого типа возникает, когда исследователь считает, будто вариация является неслучайной, в то время как она имеет случайный характер. Это приводит к ненужной перестройке организации производства, что в результате вызывает еще большие отклонения. Ошибка второго типа возникает, когда исследователь считает случайную вариацию неслучайной и не вносит в производство необходимых корректив. Контрольные карты значительно снижают вероятность таких ошибок, хотя и не ис
ключают их полностью.
Наиболее типичная разновидность контрольных карт устанавливает контрольные границы, находящиеся на расстоянии трех стандартных отклонений от среднего значения интересующей нас величины2 (т.е. доли, размаха и т.п.).
КОНТРОЛЬНЫЕ ГРАНИЦЫ
Среднее значение ± 3 стандартных отклонения (17.1)
Верхняя контрольная граница = среднее значение + 3 стандартных отклонения.
Нижняя контрольная граница = среднее значение - 3 стандартных отклонения.
Карта контроля показывает, находятся ли наблюдаемые величины внутри контрольных границ. На рис. 17.3 показаны три примера карт контроля.
Исключительно случайные
Рис. 17.3. Примеры карт контроля
На панели А в распределении величин не наблюдается никакой зависимости и все точки лежат внутри контрольных границ. Следовательно, процесс является устойчивым и подвержен лишь случайным вариациям. Панель Б представляет собой полную противоположность панели А. На ней две точки выходят за контрольные границы, что может свидетельствовать о существовании неслучайных причин вариации. Несмотря на то что на панели В все точки графика находятся внутри контрольных границ, количество точек, расположенных над средним значением и под ним, приблизительно одинаково. К тому же график демонстрирует долговременный убывающий тренд. Эта ситуация требует энергичного вмешательства. Прежде чем приступать к изменениям системы, необходимо определить причины наблюдаемого явления.
Обнаружить тренд не всегда просто. В работах [7, 11] были сформулированы два простых правила, позволяющих распознать тренд: данные содержат тренд, если восемь последовательных точек лежат выше (ниже) средней линии или восемь последовательных точек расположены в убывающем (возрастающем) порядке.
Напомним, что для случайной величины, имеющей нормальное распределение, в интервале ц ± Зет находится 99,73% наблюдений (см. раздел 5.1).
Процесс, карта контроля которого свидетельствует о нарушениях границ контроля (точки лежат вне контрольных границ или образуют тренд), называется неконтролируемым.
Неконтролируемый процесс (out-of-control process) имеет как случайные, так и неслучайные вариации. Поскольку неслучайные причины вариации являются внешними по отношению к процессу, неконтролируемые процессы невозможно предсказать.
Когда процесс выходит из-под контроля, необходимо идентифицировать неслучайные причины. Если они отрицательно влияют на качество продукции или услуг, следует разработать мероприятия, направленные на их ликвидацию. Если же неслучайные причины повышают качество, их нужно использовать как составную часть процесса. В этой ситуации неслучайная причина становится источником случайных вариаций, а эффективность процесса повышается.
Процесс, контрольная карта которого не выявляет нарушений контрольных границ, называется контролируемым.
Контролируемый процесс (in-control process) имеет только случайные вариации. Поскольку случайные вариации изначально присущи процессу, его можно прогнозировать. Иногда контролируемые процессы называются процессами, поддающимися статистическому контролю (state of statistical control).
Если процесс является контролируемым, необходимо определить величину случайной вариации. Требуется, чтобы она была невелика. (В разделе 17.7 описаны статистические методы, позволяющие оценить величину случайной вариации.) Если величина случайной вариации достаточно мала, контрольную карту можно использовать для постоянного мониторинга процесса. В противном случае необходимо изменить сам процесс.
17.4. ПРОЦЕНТНЫЕ КОНТРОЛЬНЫЕ КАРТЫ
Для мониторинга процесса и выявления неслучайных и случайных вариаций применяются различные типы контрольных карт, в частности, карты контроля качественных признаков (attribute chart). Эти карты используются в ситуациях, когда единицы продукции разделены на бракованные и качественные. В данной главе рассматриваются р-карты, показывающие долю бракованных изделий в выборке.
Доли и биномиальное распределение рассмотрены в разделе 5.3. Напомним, что в разделе 6.3 выборочная доля определена как отношение Х/n, а стандартное отклонение пропорции вычисляется по формуле
Используя формулу (17.1), можно вычислить контрольные границы для бракован-
ных изделий3.
В этой главе термин “брак” используется вместо термина “успех”.
КОНТРОЛЬНЫЕ ГРАНИЦЫ ДЛЯ ДОЛИ
р±3.1^^~^ . (17.2)
N п
Верхняя и нижняя контрольные границы для р-карты вычисляются так:
НКГ= р-З^ , V п
ВКГ= р + 3.1^~Ё . V п
Для равных величин li = п, получаем: л ,=|
В общем случае эти величины вычисляются по формулам:
где X, — количество бракованных изделий в i-й подгруппе, nt — объем выборки или i-й подгруппы, р = Х1/п1 — доля бракованных изделий в i-й подгруппе, k — количество подгрупп, п —средний объем подгруппы, р —средняя доля бракованных изделий.
Отрицательное значение нижней контрольной границы означает, что ее вообще не существует. В качестве иллюстрации рассмотрим сценарий, изложенный в начале главы.
Чтобы применить р-карту для изучения готовности номеров в течение четырех недель, администрация отеля ежедневно формировала подгруппы, состоящие из 200 номеров. По методу Six Sigma® на этапе измерения для каждого номера, входящего в выборку, определялась степень его готовности к приезду гостей. На этапе анализа количество номеров и доля комнат, не готовых к приезду гостей, были занесены в табл. 17.1.
Таблица 17.1. Количество номеров и доля комнат, не готовых к приезду гостей f>HOTELl.XLS
День Количество исследованных комнат Количество неготовых комнат Доля День Количество исследованных комнат Количество неготовых комнат Доля
1 200 16 0,080 15 200 18 0,090
2 200 7 0,035 16 200 13 0,065
3 200 21 0,105 17 200 15 0,075
4 200 17 0,085 18 200 10 0,050
5 200 25 0,125 19 200 14 0,070
Окончание табл. 17.1
День Количество исследованных комнат Количество неготовых комнат Доля День Количество исследованных комнат Количество неготовых комнат Доля
6 200 19 0,095 20 200 25 0,125
7 200 16 0,080 21 200 19 0,095
8 200 15 0,075 22 200 12 0,060
9 200 11 0,055 23 200 6 0,030
10 200 12 0,060 24 200 12 0,060
11 200 22 0,110 25 200 18 0,090
12 200 20 0,100 26 200 15 0,075
13 200 17 0,085 27 200 20 0,100
14 200 26 0,130 28 200 22 0,110
Для этих данных имеем:
к
/г = 28, =2,315, и, = 77 = 200.
/—1
0,0827 ±3,
Поскольку все величины п. равны, получаем:
=1^ = 0,0827.
к^И‘ 28
Используя формулу (17.2), вычислим контрольные границы:
0,0827 х 0,9173
200
Следовательно,
ВКГ = 0,0827 + 0,0584 = 0,1411,
НКГ = 0,0827 - 0,0584 = 0,0243.
На рис. 17.4 показана карта контроля, соответствующая данным из табл. 17.1. Она построена с помощью программы Microsoft Excel. Анализ этой карты показывает, что процесс поддается статистическому контролю, все точки распределены вокруг значения р без какой бы то ни было закономерности и находятся внутри контрольных границ. Таким образом, на этапе контроля любое улучшение процесса подготовки комнат к приему гостей должно сопровождаться уменьшением случайных колебаний. Как указано выше, управление этим процессом находится в компетенции руководства компании. Помните: улучшения не наступят, пока весь процесс не будет успешно перестроен.
О 5 10 15 20 25 30
X
Рис. 17.4. Контрольная р-карта, построенная с помощью программы Microsoft Excel, для неготовых номеров отеля
Процедуры Excel: построение контрольной /жарты
Для вычисления данных, необходимых для создания р-карты, с помощью Мастера диаграмм следует создать два рабочих листа, использующих простые арифметические формулы. Надстройка PHStat2 выполняет эту процедуру автоматически.
Например, для построения контрольной р-карты, характеризующей степень готовности номеров отеля на основе данных, представленных в табл. 17.1, необходимо открыть рабочий лист Комнаты в книге Chapter 17. xls и выполнить одну из следующих процедур.
Применение Excel в сочетании с надстройкой PHStatZ
Для построения р-карты необходимо выполнить следующие действия.
1. Выбрать команду PH Stat ^Control Charts=i>p Chart... (PHStat^> Контрольные карты=>р-карта...).
2. Находясь в диалоговом окне р Chart (см. иллюстрацию), сделать следующее.
2.1. Ввести в окне редактирования Non Conformances Cell Range (Входной интервал брака) диапазон ячеек Cl:С2 9 и установить флажок First cell contains label (Первая ячейка содержит метку).
2.2. Установить переключатель Sample/Subgroups (Выборка/Подгруппы) в положение Size does not very (Постоянный объем).
р Chart
; Data -..-...—.....-...
Non-Conformances Cell Range p First cell contains label
I p Sample/Subgroups....-.....
; j Size does not vary
11 Sample/Subgroup Size:
11 Size varies
Output Options
Title: [р-картадля неготовых комнат
Help | [j,..OK j| Cancel
2.3. Ввести в окне редактирования Sample/Subgroup Size (Объем выборки/подгруппы) число 200.
2.4. Щелкнуть на кнопке ОК.
Если объем выборки или подгруппы является переменным, установите переключатель Sample/Subgroup в положение Size varies (Переменный объем) и введите соответствующий диапазон в окне редактирования Sample/Subgroup Cell Range (Диапазон выборки/подгруппы).
Применение Excel
Вычисление контрольных границ и координат точек на р-карте. Инструкции для вычисления контрольных границ и координат точек на р-карте приведены в разделе ЕН.17.1.
Создание р-карты. Инструкции для работы с Мастером диаграмм при построении вычисления р-карты приведены в разделе ЕН.17.2.
f £ Содержимое компакт-диска
ж Контрольная р-карта, представленная на рис. 17.4, содержится на листе Рис17.4 в рабочей
книге Chapter 17.xls.
В данном примере объемы подгрупп оставались постоянными, однако, как правило, со временем они изменяются. Если отклонение объемов подгрупп п. от среднего значения п не превышает 25% [7], для вычисления контрольных границ применяется формула (17.2). Если же отклонение объемов подгрупп превышает указанный предел, используются альтернативные формулы [7, 11, 13]. Проиллюстрируем сказанное примером, в которомр-карта применяется для контроля качества марлевых тампонов.
ПРИМЕР 17.1. ПРИМЕНЕНИЕ Я-КАРТЫ ДЛЯ КОНТРОЛЯ КАЧЕСТВА ПРИ НЕРАВНЫХ ОБЪЕМАХ ПОДГРУППП BsPONGE .XLS
В табл. 17.2 приведено количество ежедневно выпускаемых марлевых тампонов и количество бракованных изделий за 32 дня работы фабрики. Постройте карту контроля на основе этих данных.
Таблица 17.2. Количество бракованных изделий за 32 дня работы фабрики
День Количество марлевых тампонов Количество бракованных изделий Доля День Количество марлевых тампонов Количество марлевых изделий Доля
1 690 21 0,030 17 574 20 0,035
2 580 22 0,038 18 610 16 0,026
3 685 20 0,029 19 596 15 0,025
4 595 21 0,035 20 630 24 0,038
5 665 23 0,035 21 625 25 0,040
6 596 19 0,032 22 615 21 0,034
7 600 18 0,030 23 575 23 0,040
8 620 24 0,039 24 572 20 0,035
9 610 20 0,033 25 645 24 0,037
10 595 22 0,037 26 651 39 0,060
11 645 19 0,029 27 660 21 0,032
12 675 23 0,034 28 685 19 0,028
13 670 22 0,033 29 671 17 0,025
14 590 26 0,044 30 660 22 0,033
15 585 17 0,029 31 595 24 0,040
16 560 16 0,029 32 600 16 0,027
РЕШЕНИЕ. Для этих данных имеем:
/? = 32, =19 926,2^=679.
Следовательно, по формуле (17.2) получаем, что
п =
19 926
32
= 622,69
679
19 926
= 0,034
0,034±3,
Таким образом, контрольные границы равны:
0,034 х (1-0,034)
622,69
ВКГ = 0,034 + 0,022 = 0,056,
НКГ = 0,034 - 0,022 = 0,012.
Карта контроля качества марлевых тампонов, построенная с помощью программы Microsoft Excel, представлена на рис. 17.5. Анализ этой карты показывает, что 26-й день, в течение которого были произведен 651 тампон, в том числе 39 бракованных, выходит за контрольные границы. Следовательно, процесс стал неконтролируемым. Руководству компании необходимо установить причину такого неслучайного отклонения и принять меры, исключающие его повторение. После этого данные за 26-й день следует исключить из набора и построить карту заново.
Р-карта для бракованных тампонов
Рис. 17.5. Контрольная р-карта, построенная с помощью программы Microsoft Excel, для оценки качества марлевых тампонов
УПРАЖНЕНИЯ К РАЗДЕЛУ 17
Изучение основ
17.1. Предположим, что в течение 10 дней были собраны данные о бракованных изделиях.
День Объем выборки Брак День Объем выборки Брак
1 100 12 6 100 14
2 100 14 7 100 15
3 100 10 8 100 13
4 100 18 9 100 14
5 100 22 10 100 16
1. В какой день наблюдается наибольший процент брака? В какой день наблюдается наименьший процент брака?
2. Чему равны верхняя и нижняя контрольные границы?
3. Есть ли неслучайные причины вариации?
17.2. Предположим, что в течение 10 дней были собраны данные о бракованных изделиях.
День Объем выборки Брак День Объем выборки Брак
1 111 12 6 88 14
2 93 14 7 117 15
3 105 10 8 87 13
4 92 18 9 119 14
5 117 22 10 107 16
1. В какой день наблюдается наибольший процент брака? В какой день наблюдается наименьший процент брака?
2. Чему равны верхняя и нижняя контрольные границы?
3. Есть ли неслучайные причины вариации?
Применение понятий
17.3. Наблюдательная комиссия пассажиров железной дороги в течение месяца следила, насколько точно соблюдается график движения поездов в часы пик. Предположим, что опозданием считается задержка прибытия на 5 минут и больше. В течение месяца формировалась выборка, состоящая из 235 поездов. В таблице приведены данные, собранные в течение четырех недель (при 5-дневной рабочей неделе). ^Irrspc.xls.
День Опоздание День Опоздание
1 17 11 21
2 25 12 23
3 22 13 67
4 27 14 24
День Опоздание День Опоздание
5 32 15 35
6 23 16 18
7 16 17 23
8 24 18 24
9 20 19 26
10 36 20 35
1. Постройте контрольную р-карту для доли опозданий и определите, поддается ли процесс статистическому контролю.
2. Как изменится ответ на вопрос 1, если известно, что утром 13-го дня разразился 4-балльный шторм?
3. Как изменятся ответы на вопросы 1 и 2, если количество опозданий утром 13-го дня равно 47?
17.4. Частная курьерская служба гарантирует доставку пакетов не позднее 10:30 следующего дня. Предположим, что руководство компании решило оценить качество работы службы доставки в конкретном регионе и для этого собирало данные на протяжении четырех недель, состоящих из пяти рабочих дней. Общее количество пакетов, доставленных вовремя, и количество пакетов, доставленных с опозданием, приведено в файле OmaILPC . XLS.
1. Постройте контрольнуюр-карту для доли опозданий.
2. Контролируем ли процесс доставки пакетов?
17.5. Администратора больницы интересует время, затрачиваемое на обработку анализов, сданных пациентами. Выяснилось, что все результаты фиксируются на протяжении 5 дней после сдачи анализа. Любая запись, внесенная в базу данных по истечении пяти дней после сдачи анализа, считается опозданием. Количество пациентов, обслуженных за 30 дней, и количество записей, сделанных с опозданием, указаны в файле ^MEDREC . XLS.
1. Постройте контрольнуюр-карту для доли опозданий.
2. Контролируем ли процесс доставки пакетов? Почему?
3. Предположим, что процесс выходит из-под контроля и существует неслучайная причина вариации. Для ее устранения руководство компании приняло соответствующие меры. Исключите из набора данные, выходящие за контрольные границы, и повторите все вычисления.
17.6. Компания Sweet Suzy's Sugar less Cola фиксирует ежедневное количество бракованных банок, выпущенных разливочным и упаковочным автоматами. Бракованными считаются неполные, помятые и неправильно закатанные банки. Данные, собранные в течение одного месяца (при 5-дневной рабочей неделе), приведены в следующей таблице. ft^COLASPC . XLS.
День Количество неполных банок Количество поврежденных банок День Количество неполных банок Количество поврежденных банок
1 5 043 47 12 5 314 70
2 4 852 51 13 5 097 64
3 4 908 43 14 4 932 59
4 4 756 37 15 5 023 75
5 4 901 78 16 5 117 71
6 4 892 66 17 5 099 68
7 5 354 51 18 5 345 78
8 5 321 66 19 5 456 88
9 5 045 61 20 5 554 83
10 5 113 72 21 5 421 82
11 5 247 63 22 5 555 87
1. Постройте контрольную р-карту для доли бракованных банок, произведенных в течение месяца. Контролируем ли процесс?
2. Какие меры должно принять руководство компании, чтобы уменьшить долю бракованных банок?
17.7. Бухгалтер крупной больницы изучает причины ошибок при вводе данных в компьютерную систему. Для этого он каждый день формировал выборку, состоящую из 200 расчетных счетов, и проверял правильность их заполнения. Результаты, полученные за 39 дней, приведены файле. ^ERRORSPC . XLS.
1. Постройте контрольную р-карту для доли бракованных счетов, заполненных за 39 дней. Контролируем ли процесс?
2. Какие меры должно принять руководство компании, чтобы уменьшить долю ошибок?
17.8. Менеджер регионального офиса национальной телефонной компании несет ответственность за подключение, отключение и переключение телефонных номеров. Он сформировал группу, призванную улучшить качество обслуживания клиентов и выявить “узкие места” в работе компании. В течение 30 дней группа собирала информацию о числе заявок на ремонт и количестве несвоевременно устраненных повреждений. Данные приведены в следующей таблице. ФTELESPC. XLS.
1. Постройте контрольнуюр-карту для доли задержек. Контролируем ли процесс?
2. Какие меры должно принять руководство компании, чтобы уменьшить долю задержек?
17.5. ЭКСПЕРИМЕНТ С КРАСНЫМИ ШАРАМИ: ВАРИАЦИЯ ПРОЦЕССА
В начале главы были рассмотрены 14 принципов Деминга, метод Six Sigma®, а также описаны случайные и неслучайные причины вариации. Для иллюстрации карт контроля мы изучили р-карты. Теперь перейдем к исследованию двух типов вариации —
случайной и неслучайной. В качестве примера, демонстрирующего их сущность, рассмотрим знаменитый эксперимент с красными шарами (read beat experiment).
В ходе эксперимента шары извлекаются из урны, содержащей 4 000 шаров. Испытуемый не знает, что в урне 3 200 (80%) белых шаров и 800 (20%) красных. Существует несколько сценариев эксперимента. Один из них начинается с того, что экспериментатор, играющий роль бригадира, приглашает не менее четырех добровольцев на роль рабочих. Затем бригадир приглашает добровольцев на роли контролеров (два человека), главного контролера (один человек) и регистратора (один человек). Рабочий должен погрузить в урну решето, состоящее из пяти рядов, образованных десятью отверстиями. Таким образом, рабочий может извлечь из урны 50 шаров.
Пригласив добровольцев, бригадир разъясняет им их обязанности. Рабочий должен отбирать только белые шары, красные считаются бракованными. Стандарты качества для рабочих весьма строги — рабочий должен извлечь 50 белых шаров, ни больше ни меньше. Кроме того, руководство установило, что каждый рабочий не должен извлекать более 2 красных шаров (4% брака). После того как решето погружается в урну, из нее извлекаются 50 шаров. Затем решето передается двум контролерам. Каждый из них независимо от другого записывает количество красных шаров. После этого главный контролер сравнивает результаты проверки и объявляет аудитории окончательный результат. Регистратор записывает количество и долю красных шаров, извлеченных каждым рабочим.
Уяснив свои обязанности, рабочие приступают к “работе”. Предположим, что в первой попытке количество шаров, извлеченных каждым рабочим (назовем их Элисон, Дэвид, Питер и Шэрон), равно 9, 12, 13 и 7. Как руководство “компании” должно реагировать на эти результаты, учитывая, что допускаются не более двух красных шаров? Следует ли сделать выговор всем рабочим, или предупреждения должны получить только Дэвид и Питер?
Предположим, что эксперимент состоит из трех попыток. Их результаты приведены в табл. 17.3.
Таблица 17. 3. Результаты трех попыток, выполненных четырьмя рабочими
Попытка
Имя t 1 2 3 Все три попытки
Элисон 9(18%) 11 (22%) 6 (12%) 26(17,33%)
Дэвид 12(24%) 12(24%) 8(16%) 32(21,33%)
Питер 13(26%) 6(12%) 12 (24%) 31 (20,67%)
Шэрон 7(14%) 9(18%) 8(16%) 24(16,00%)
Все четверо рабочих 41 38 34 113
Среднее(X ) 10,25 9,5 8,5 9,42
Процент 20,5% 19% 17% 18,83%
Как следует из табл. 17.3, в каждой попытке результат некоторых рабочих был выше среднего, а других — ниже среднего. В первой попытке лучшей была Шэрон, а во второй — Питер (при том, что в первой попытке он имел наихудший результат). В третьей попытке лучшей оказалась Элисон.
Как объяснить все эти вариации? Ответ дает формула (17.2), выведенная дляр-карт. к
В данном случае k = 4 рабочих х 3 дня = 12, п = 50, = 113 . Таким образом,
113
50x12
= 0,1883.
Следовательно, контрольные границы равны
= 0Л883±ЗхР^в = 0,1883±0,1659.
N п \ 50
Итак,
ВКГ = 0,1883 + 0,1659 = 0,3542, НКГ = 0,1883 - 0,1659 = 0,0224.
На рис. 17.6 приведена контрольная р-карта, построенная на основе данных, содержащихся в табл. 17.3. Как видим, все точки лежат в пределах контрольных границ и не содержат каких-либо закономерностей. Разница в качестве работы сотрудников объясняется случайными причинами, присущими самой системе.
Рис. 17.6. Контрольная р-карта для эксперимента с красными шарами
ВРЕЗКА 17.4. ВЫВОДЫ ИЗ ЭКСПЕРИМЕНТА С КРАСНЫМИ ШАРАМИ
• Вариация представляет собой неотъемлемую часть производственного процесса.
• Сотрудники работают внутри слабо управляемой системы. Результаты их работы определяются самой системой и от рабочих не зависят.
• Изменить систему может только руководство.
• Всегда существуют рабочие, результаты которых превышают среднее значение, и рабочие, качество труда которых ниже среднего.
УПРАЖНЕНИЯ ОАЗДЕПУ 17.5
Изучение основ
17.9. Какой должна быть реакция менеджеров после первой, второй и третьей попыток?
17.10. Классная работа. Проведите эксперимент с красными шарами в своем классе.
1. Проведите эксперимент точно так же, как описано выше.
2. Перед началом эксперимента удалите из урны 400 красных шаров. Как изменятся результаты по сравнению с п. 1? О чем это говорит?
17.6. КОНТРОЛЬНЫЕ КАРТЫ ДЛЯ РАЗМАХА И СРЕДНЕГО ЗНАЧЕНИЯ
Если исследователя интересуют числовые характеристики, для мониторинга можно использовать карты контроля переменных. Поскольку числовые характеристики более информативны, чем доля или количество бракованных изделий, карты контроля переменных более чувствительны к случайным вариациям. Такие контрольные карты обычно применяются попарно. Одна карта используется для мониторинга вариации процесса, а вторая — для контроля за его средним значением. Первая карта должна анализироваться в первую очередь, поскольку именно она позволяет определить, не вышел ли процесс из-под контроля. Карта среднего значения для этой цели не подходит. Если необходимо исследовать как среднее значение, так и размах процесса, используются несколько карт контроля [7, 10, 13].
Контрольная карта для размаха: /?-карта
Прежде чем вычислять контрольные границы для среднего значения, необходимо построить карту контроля размаха, или R-карту (R-chart). Это позволит определить, контролируема ли вариация процесса и нет ли сдвига результатов по времени. Если процесс является контролируемым, эту карту можно использовать при построении карты контроля для среднего значения.
Из формулы (17.1) следует, что при построении контрольной карты необходимо получить оценку среднего размаха и стандартное отклонение размаха. Формула (17.4) показывает, что контрольные границы зависят от двух переменных — множителя d2 (d2 factor), описывающего отношение между стандартным отклонением и размахом при переменном объеме выборки, и множителя d3 (d3 factor), описывающего отношение между стандартным отклонением и стандартной ошибкой размаха при переменном объеме выборки. Величины этих множителей приведены в табл. Д.11. Контрольные границы для размаха k соседних последовательностей или периодов вычисляются по формулам (17.4) и (17.5).
КОНТРОЛЬНЫЕ ГРАНИЦЫ РАЗМАХА
R±3R^~. d. (17.3)
Следовательно, НКГ= R-3R^-, d2
ВКГ= R + 3R—, d.
где = • к ,=i
Эти вычисления можно упростить, введя множитель D3 (D3 factor), равный 1-3(d3/d2), и множитель D4 (D4 factor), равный l+3(d3/d2).
ВЕРХНЯЯ И НИЖНЯЯ КОНТРОЛЬНЫЕ ГРАНИЦЫ РАЗМАХА
НКГ=£3Д, (17.4, а)
ВКГ = D47? . (17.4,6)
Вернемся к сценарию, описанному в начале главы. Для того чтобы оценить качество обслуживания, менеджер отеля на протяжении четырех недель записывал время, затрачиваемое на доставку багажа (от регистрации до вручения). Для контроля были отобраны подгруппы, состоящие из пяти курьеров, работавших в вечернюю смену. Результаты измерений приведены в табл. 17.4.
Таблица 17.4. Средние значения и размах времени доставки для каждой из подгрупп
День Время доставки багажа, мин. Среднее Размах
1 6,7 11,7 9,7 7,5 7,8 8,68 5,0
2 7,6 11,4 9,0 8,4 9,2 9,12 3,8
3 9,5 8,9 9,9 8,7 10,7 9,54 2,0
4 9,8 13,2 6,9 9,3 9,4 9,72 6,3
5 11,0 9,9 11,3 11,6 8,5 10,46 3,1
6 8,3 8,4 9,7 9,8 7,1 8,66 2,7
7 9,4 9,3 8,2 7,1 6,1 8,02 3,3
8 11,2 9,8 10,5 9,0 9,7 10,04 2,2
9 10,0 10,7 9,0 8,2 11,0 9,78 2,8
10 8,6 5,8 8,7 9,5 11,4 8,80 5,6
11 10,7 8,6 9,1 10,9 8,6 9,58 2,3
Окончание табл. 17.4
День Время доставки багажа, мин. Среднее Размах
12 10,8 8,3 10,6 10,3 10,0 10,00 2,5
13 9,5 10,5 7,0 8,6 10,1 9,14 3,5
14 12,9 8,9 8,1 9,0 7,6 9,30 5,3
15 7,8 9,0 12,2 9,1 11,7 9,96 4,4
16 11,1 9,9 8,8 5,5 9,5 8,96 5,6
17 9,2 9,7 12,3 8,1 8,5 9,56 4,2
18 9,0 8,1 10,2 9,7 8,4 9,08 2,1
19 9,9 10,1 8,9 9,6 7,1 9,12 3,0
20 10,7 9,8 10,2 8,0 10,2 9,78 2,7
21 9,0 10,0 9,6 10,6 9,0 9,64 1,6
22 10,7 9,8 9,4 7,0 8,9 9,16 3,7
23 10,2 10,5 9,5 12,2 9,1 10,30 3,1
24 10,0 11,1 9,5 8,8 9,9 9,86 2,3
25 9,6 8,8 11,4 12,2 9,3 10,26 3,4
26 8,2 7,9 8,4 9,5 9,2 8,64 1,6
27 7,1 11,1 10,8 11,0 10,2 10,04 4,0
28 11,1 6,6 12,0 11,5 9,7 10,18 5,4
Для этих данных k = 28, а = 97,5. Таким образом,
Используя табл. Д.11, для п = 5 получаем, что d2 = 2,326 и d3 = 0,864. С помощью формул (17.3) вычисляем контрольные границы:
л = 19 926 = 622,69 и = 6 79 = 4
32 19 926
Следовательно,
ВКГ = 3,482 + 3,88 = 7,362,
НКГ = 3,482-3,88 <0.
Иначе говоря, нижней контрольной границы не существует.
В качестве альтернативы можно применить формулу (17.4), табл. Д.11 и множители D3 = 0, D4 = 2,114. Таким образом,
ВКГ = Di R = 2,114 х 3,482 = 7,36,
а нижней границы не существует. Обратите внимание на то, что нижняя контрольная граница для R не существует, поскольку размах не может быть отрицательным. На рис. 17.7 приведена контрольная Я-карта, построенная с помощью программы Microsoft Excel. Анализ рис. 17.7 показывает, что все точки находятся внутри контрольных границ.
Рис. 17.7. Контрольная R-карта, построенная с помощью программы Microsoft Excel, для оценки времени доставки багажа
Контрольная х-карта
Рассмотрим карту контроля среднего значения процесса, так называемую X -карту (X -chart). Карта контроля для величины X использует подгруппы одинакового объема п, полученные в течение k последовательных периодов времени. Из формулы (17.1) следует, что при вычислении контрольных границ для среднего значения необходимо оценить средние значения в каждой из подгрупп X и стандартное отклонение среднего стЛ. . Эти контрольные границы являются функциями множителя d2, описывающего отношение между стандартным отклонением и размахом при переменном объеме выборки. 4
В качестве оценки стандартного отклонения генеральной совокупности используется вели-
R Л Л R
чина — , а в качестве оценки стандартного отклонения среднего — величина -= .
d2 d2-Jn
КОНТРОЛЬНЫЕ ГРАНИЦЫ СРЕДНЕГО ЗНАЧЕНИЯ
J±3—, d2J7i
— | к _ _ J к _
где X - — , R=— ^R, , Xt — выборочное среднее для п наблюдений, полученных
£ /=1 к ;=i
в течение i-ro периода, R, — размах п наблюдений, полученных в течение i-ro периода, k — количество подгрупп.
Контрольные границы величины X можно также определить по следующим формулам:
НКГ = J-3—
d2J^
ВКГ=^ + 3—(17.5)
d2dn
Вычисления по формулам (17.5) можно упростить, введя множитель А2, равный з/(^).
ВЕРХНЯЯ И НИЖНЯЯ КОНТРОЛЬНЫЕ ГРАНИЦЫ СРЕДНЕГО ЗНАЧЕНИЯ, ВЫЧИСЛЕННЫЕ С ПОМОЩЬЮ МНОЖИТЕЛЯ А2
НКГ = X-A2R , (17.6, а)
ВКГ=^ + ЛЛ. (17.6,6)
Возвращаясь к сценарию, изложенному в начале главы, получаем, что k = 28,
А к _
а =97,5 и = 265,38 . Следовательно, ,=i (=i
С помощью табл. Д.11 для п = 5 определяем, что d2 = 2,326. Итак,
X ± 3—= 9,478 ± 3....3,4= 9,478 ± 2,008 .
d2Jn 2,326V5
Таким образом,
НКГ = 9,478 - 2,008 = 7,470,
ВКГ = 9,478 + 2,008 = 11,486.
В качестве альтернативы можно применить формулы (17.6, а и 6), табл. Д.11 и множитель А2 = 0,577. Следовательно,
НКГ = 9,478 - 0,577 X 3,482 = 9,478 - 2,009 = 7,469,
ВКГ = 9,478 + 0,577 х 3,482 = 9,478 + 2,009 = 11,487.
Результаты совпадают с точностью до ошибки округления. На рис; 17.8 приведена X -карта, построенная с помощью программы Microsoft Excel. Анализ рис. 17.8 показывает, что все точки находятся внутри контрольных границ, причем никакого тренда не существует, хотя в 28-й день наблюдалась сильное колебание средних значений. Поскольку R- и X -карты показывают, что процесс находится под контролем, колебание времени доставки багажа объясняется случайными причинами. Если руководство отеля решит сократить время доставки багажа, оно должно изменить сам процесс.
Рис. 17.8. Контрольная X -карта, построенная с помощью программы Microsoft Excel, для оценки времени доставки багажа
Процедуры Excel: построение карт для размаха и среднего значения
Для вычисления данных, необходимых для создания R- и X -карт, можно реализовать два рабочих листа, использующих простые арифметические формулы. Надстройка PHStat2 выполняет эту процедуру автоматически.
Например, для построения R- и X -карт, характеризующих скорость доставки багажа на основе данных, представленных в табл. 17., необходимо открыть рабочий лист Доставка_багажа в книге Chapter 17. xls и выполнить одну из следующих процедур.
Применение Excel в сочетании с надстройкой PHStat2
Для построения R- и X -карт необходимо выполнить такие действия.
1. Выбрать команду PHStat^Control Charts^ R & ХВаг Charts... (PHStatsКонтрольные карты^ R- и Х-карты...).
2. Находясь в диалоговом окне R & ХВаг Charts (см. иллюстрацию), сделать следующее.
2.1. Ввести в окне редактирования Sub-group/Sample Size (Объем подгруппы/выборки) число 5.
2.2. Ввести в окне редактирования Subgroup Ranges Cell Range (Входной интервал подгруппы) диапазон ячеек Н1 :Н29 и установить флажок First cell contains label (Первая ячейка содержит метку).
2.3. Установить переключатель Chart Options (Параметры карты) в положение R & ХВаг Charts (R- и Х-карты).
R and ХВаг Charts fx~|
- Data - - - - ----- -
Subgroup/Sample Size:
Subgroup Ranges Cell Range: |h 1:1-129 X]
P First cell contains label
- Chart Options
' c R Chart Only
<• R and XBar Charts
' Subgroup Means Cell Range: |g1:G29 :
i p First ceU contains label
- Output Options --------- -
i Title: [скоростГдоставки багажа i
Help | | Г.^picZjl Cancel |
2.4. Ввести в окне редактирования Subgroup Means Cell Range (Входной интервал средних по подгруппам) диапазон ячеек Gl: G2 9 и установить флажок First cell contains label (Первая ячейка содержит метку).
2.5. Ввести в окне редактирования Title (Заголовок) название диаграммы.
2.6. Щелкнуть на кнопке ОК.
Описанная выше процедура создает четыре рабочих листа: два из них содержат данные и результаты вычислений, а третий и четвертый — /?- и X -карты соответственно.
Применение Excel
Вычисление контрольных границ и координат точек на R-и X -картах. Инструкции для вычисления контрольных границ и координат точек на R- и X -картах приведены в разделе ЕН.17.3.
Создание на R- и X -карт. Инструкции для работы с Мастером диаграмм при построении вычисления R- и X -карт приведены в разделе ЕН.17.4.
Содержимое компакт-диска
Контрольные R- и X -карты, характеризующие скорость доставки багажа на основе данных, представленных в табл. 17.1, содержатся на листах Рис17.7 и Рис17.8 в рабочей книге Chapter 17.xls.
УПРАЖНЕНИЯ К РАЗДЕЛУ 17.6
Изучение основ
17.11. Предположим, что подгруппы содержат по 4 элемента. Чему равны следующие величины?
1. Множитель d2.
2. Множитель d3.
3. Множитель D2.
4. Множитель В3.
5. Множитель А2.
17.12. Предположим, что подгруппы содержат по 4 элемента. Данные собраны в течение 10 дней.
День Среднее Размах День Среднее Размах
1 13,6 3,5 6 12,9 4,8
2 14,3 4,1 7 17,3 4,5
3 15,3 5,0 8 13,9 2,9
4 12,6 2,8 9 12,6 3,8
5 11,8 3,7 10 15,2 4,6
1. Вычислите контрольные границы для размаха.
2. Наблюдаются ли неслучайные вариации процесса?
3. Вычислите контрольные границы для среднего значения.
4. Наблюдаются ли случайные вариации процесса?
Применение понятий
17.13. Менеджер местного филиала банка хотел бы оценить среднее время ожидания клиента в очереди к кассиру в час пик — с 12:00 до 13:00. Для этого была образована подгруппа, состоящая из четырех клиентов (по одному на каждый 15-минутный интервал), а затем определено, сколько минут прошло от момента прибытия до начала обслуживания. Результаты измерений за четыре недели приведены в таблице. ^BANKTIME. XLS.
День Время (мин.)
1 7,2 8,4 7,9 4,9
2 5,6 8,7 3,3 4,2
3 5,5 7,3 3,2 6,0
4 4,4 8,0 5,4 7,4
5 9,7 4,6 4,8 5,8
6 8,3 8,9 9,1 6,2
7 4,7 6,6 5,3 5,8
8 8,8 5,5 8,4 6,9
9 5,7 4,7 4,1 4,6
10 1,7 4,0 3,0 5,2
11 2,6 3,9 5,2 4,8
12 4,6 2,7 6,3 3,4
13 4,9 6,2 7,8 8,7
14 7,1 6,3 8,2 5,5
15 7,1 5,8 6,9 7,0
16 6,7 6,9 7,0 9,4
17 5,5 6,3 3,2 4,9
18 4,9 5,1 3,2 7,6
19 7,2 8,0 4,1 5,9
20 6,1 3,4 7,2 5,9
1. Вычислите контрольные границы для среднего значения и размаха.
2. Можно ли утверждать, что процесс является контролируемым?
17.14. Менеджер склада местной телефонной компании получает оборудование с центрального склада и отправляет его по месту назначения. Сокращение времени, затрачиваемого на перевозку оборудования, имеет весьма важное значение. В файле ftwAREHSE.XLS указано количество единиц оборудования, установленного каждой подгруппой, состоящей из пяти сотрудников, в течение 30 дней.
1. Вычислите контрольные границы для среднего значения и размаха.
2. Можно ли утверждать, что процесс является контролируемым?
17.15. В статье, опубликованной в журнале MidAmerica Journal of Business, проведен анализ операции разлива минеральной воды по бутылкам. Одной из характеристик этого производственного процесса является количество магния в воде, измеренной в частях на миллион. В таблице приведены данные о количестве магния, полученные в течение 30 часов для 30 подгрупп, состоящих из четырех бутылок каждая. ©AUTOREP . XLS.
Час 1 2 3 4
1 19,91 19,62 19,15 19,85
2 20,46 20,44 20,34 19,61
3 20,25 19,73 19,98 20,32
4 20,39 19,43 20,36 19,85
5 20,02 20,02 20,13 20,34
6 19,89 19,77 20,92 20,09
7 19,89 20,45 19,44 19,95
8 20,08 20,13 20,11 19,32
9 20,30 20,42 20,68 19,60
10 20,19 20,00 20,23 20,59
11 19,66 21,24 20,35 20,34
12 20,30 20,11 19,64 20,29
13 19,83 19,75 20,62 20,60
14 20,27 20,88 20,62 20,40
15 19,98 19,02 20,34 20,34
16 20,46 19,97 20,32 20,83
17 19,74 21,02 19,62 19,90
18 19,85 19,26 19,88 20,20
19 20,77 20,58 19,73 19,48
20 20,21 20,82 20,01 19,93
21 20,30 20,09 20,03 20,13
22 20,48 21,06 20,13 20,42
23 20,60 19,74 20,52 19,42
24 20,20 20,08 20,32 19,51
Час 1 2 3 4
25 19,66 19,67 20,26 20,41
26 20,72 20,58 20,71 19,99
27 19,77 19,40 20,49 19,83
28 19,99 19,65 19,41 19,58
29 19,44 20,15 20,14 20,76
30 20,03 19,96 19,86 19.91
Источник: Susan, К. Humphrey, and Timothy С. Krehbiel, “Managing Process Capability”, The Mid-American Journal of Business, 14, Fall 1999, 7-12.
1. Постройте контрольную карту для размаха.
2. Постройте контрольную карту для среднего количества магния.
3. Является ли процесс контролируемым?
17.16. В следующей таблице приведена прочность отрезов материи. Данные собраны в течение 25 часов в подгруппах, состоящих из трех отрезов. ^TENSILE. XLS.
Час 1 2 3
1 15,06 14,62 15,10
2 17,58 15,75 16,72
3 13,83 14,83 15,61
4 17,19 15,75 15,42
5 14,56 15,37 15,67
6 14,82 17,25 15,73
7 17,92 14,76 14,40
8 16,53 14,52 17,31
9 13,83 14,53 15,32
10 16,45 13,85 16,32
11 15,20 14,61 18,45
12 14,49 16,15 17,80
13 15,89 15,04 16,67
14 16,29 14,61 15,67
15 15,84 12,16 15,40
16 15,12 15,60 13,83
17 18,48 16,07 16,31
18 17,55 14,73 16,95
19 13,57 17,55 15,81
20 16,23 16,92 16,45
21 14,60 16,83 15,34
22 16,73 18,60 16,76
23 18,03 14,55 13,87
24 16,61 16,45 16,95
25 15,86 17,00 18,28
1. Постройте контрольную карту для размаха.
2. Постройте контрольную карту для средней прочности.
3. Является ли процесс контролируемым?
17.17. Заведующий радиологическим отделением крупной больницы составляет расписание работы рентгеновского оборудования. В среднем каждый день в отделение поступают 250 пациентов. Если пациенты обслуживаются не вовремя, возникает задержка. Время, которое затрачивается на доставку пациента, представляет собой интервал, прошедший между моментом, когда пациент покидает палату, и моментом, когда он поступает в отделение. Для исследования была создана выборка, состоящая из четырех пациентов, отбираемых ежедневно на протяжении 20 дней. Результаты измерений приведены в файле ^TRANSPORT .XLS.
1. Вычислите контрольные границы для среднего значения и размаха.
2. Можно ли утверждать, что процесс является контролируемым?
17.18. Упаковочная машина на чаеразвесочной фабрике заполняет приблизительно 170 коробок в минуту. Менеджер следит за весом упаковки. Для исследования была создана выборка, состоящая из четырех упаковок, отбираемых каждые 15 мин. На протяжении 25 последовательных интервалов. Результаты измерений приведены в таблице. ^ТЕАЗ . XLS.
День Вес (г)
1 2 3 4
1 5,32 5,77 5,50 5,61
2 5,63 5,44 5,54 5,40
3 5,56 5,40 5,67 5,57
4 5,32 5,45 5,50 5,42
5 5,45 5,53 5,46 5,47
6 5,29 5,42 5,50 5,44
7 5,57 5,40 5,52 5,54
8 5,44 5,61 5,49 5,58
9 5,53 5,25 5,67 5,53
10 5,41 5,55 5,51 5,53
11 5,55 5,58 5,58 5,56
12 5,58 5,36 5,45 5,53
13 5,63 5,75 5,46 5,54
14 5,48 5,44 5,45 5,60
15 5,49 5,57 5,43 5,36
16 5,54 5,62 5,66 5,59
17 5,46 5,46 5,38 5,49
18 5,72 5,36 5,59 5,25
19 5,58 5,50 5,36 5,40
20 5,43 5,51 5,37 5,32
21 5,59 5,58 5,60 5,46
22 5,42 5,41 5,40 5,69
23 5,64 5,59 5,42 5,56
24 5,62 5,38 5,75 5,47
25 5,51 5,54 5,73 5,77
1. Какие причины могут объяснить случайные вариации процесса?
2. Назовите неслучайные причины вариации.
3. Постройте контрольные карты для размаха и среднего значения.
4. Можно ли считать процесс контролируемым?
17.19. Производственная компания выпускает скобы для специализированной тары. Скобы образуют каркас и должны образовывать прямой угол с допустимым отклонением, равным одному градусу. Девяносто наблюдений распределены по 18 подгруппам, содержащим по пять чисел. Результаты записаны в файле ftANGLE. XLS.
17.7. ХАРАКТЕРИСТИКИ ПРОЦЕССА
Иногда возникает необходимость оценить величину случайных вариаций, возникающих в контролируемом процессе. В частности, требуется знать, достаточно ли мала величина случайных вариаций, чтобы удовлетворить большинство потребителей. Если случайная вариация слишком велика, многие клиенты могут быть недовольны качеством продукции, т.е. процесс необходимо изменить.
Для того чтобы ответить на эти вопросы, следует проанализировать характеристики процесса. Существует много методов анализа характеристик производственного процесса [2, 13]. Начнем с относительно простого способа, основанного на оценке процента качественных изделий. Позднее мы введем другие показатели качества.
Удовлетворение клиентов и допускаемые пределы
Качество определяется потребителем. Если клиент считает, что изделие или услуга соответствуют его ожиданиям, он остается удовлетворенным. Руководство компании должно прислушиваться к пожеланиям клиентов и устанавливать допустимые пределы колебания характеристик продукции.
Допускаемые пределы (specification limits) — это технические характеристики продукции, устанавливаемые руководством компании в соответствии с пожеланиями клиентов. Верхняя контрольная граница (ВКГ) — наибольшее допустимое значение характеристики продукции (upper specification limit — USL). Нижняя контрольная граница (НКГ) — наименьшее допустимое значение характеристики продукции (lower specification limit — LSL).
Например, производители мыла должны понимать, что клиенты ожидают от мыла определенного количества пены. Потребители будут разочарованы, если мыло будет мылиться либо слишком сильно, либо слишком слабо. Специалисты знают, что количество пены зависит от уровня свободных жирных кислот (free fatty acids — FFA). Следовательно, менеджер должен установить верхнюю и нижнюю контрольные границы концентрации свободных жирных кислот, содержащихся в мыле.
Сценарий, изложенный в начале главы, представляет собой пример процесса, для которого установлена лишь одна допустимая граница. Поскольку постояльцы желают, чтобы их багаж был доставлен как можно быстрее, менеджеры отеля должны установить лишь верхнюю контрольную границу (upper specification limit — USL). Как видим, в обоих случаях допустимая граница зависит от пожеланий клиентов. Если процесс полностью соответствует их требованиям, он называется удовлетворительным.
Мощность процесса (process capability) — это способность процесса удовлетворять потребности клиентов.
Для того чтобы оценить мощность процесса, можно оценить процент изделий или услуг, удовлетворяющих требованиям клиентов. В этом случае процесс должен быть контролируемым, поскольку предсказать мощность неконтролируемого процесса невозможно. Перед тем как приступить к анализу потенциала неконтролируемого процесса, необходимо установить и устранить причину неслучайной вариации. Любой неконтролируемый процесс считается неудовлетворительным и, следовательно, не может соответствовать ожиданиям клиентов. Для того чтобы оценить количество изделий, соответствующих установленным спецификациям, следует вычислить среднее значение и стандартное отклонение всех изделий или услуг. Оценка математического ожидания генеральной совокупности обозначается как X . Она представляет собой среднее значение всех выборочных средних в формуле (17.5). Стандартное отклонение генеральной совокупности равно величине R , деленной на число d2. Величины X и R вычисляются по контрольным X - и В-картам, а число d2 можно найти в табл. Д.11. В дальнейшем будем предполагать, что генеральная совокупность величин X является нормально распределенной. (Если данные не являются приближенно нормально распределенными, можно воспользоваться альтернативными подходами [2].) Допустим, что процесс является контролируемым, а величины X имеют нормальное распределение. Оценить вероятность того, что процесс выйдет за пределы допустимых границ, можно по формулам (17.7, а и б).
ОЦЕНКА МОЩНОСТИ ПРОЦЕССА
Если мощность имеет нижнюю и верхнюю контрольные границы, то
Р(мощность процесса не выходит за контрольные границы) =
= Р
НКГ-Х ВКГ-Х
R_ < < R_
d2 d2
(17.7, а)
Если мощность имеет только верхнюю допустимую границу, то
Р(мощность процесса не выходит за контрольные границы) =
= Р(Х<ВКГ} = Р Z <
R d2
(17.7,6)
Если мощность имеет только нижнюю контрольную границу, то
Р{мощность процесса не выходит за контрольные границы) = г \
= Р(НКГ<Х)= Р
НКГ-Х —=—<z
R d2
(17.7,6)
Здесь Z— случайная переменная, имеющая стандартизованное нормальное распределение.
В разделе 17.6 мы выяснили, что процесс доставки багажа является контролируемым. Предположим, что руководство отеля постановило, что 99% багажа должно доставляться за время, не превышающее 14 мин. Вычисления показывают, что
п = 5, X = 9,478 , R = 3,482, d2 = 2,326.
Таким образом,
Р(мощность процесса не выходит за контрольные границы) = Р(Х < 14) =
= Р
14-9,478
< 3,482
= P(Z<3,02).
2,326 J
Используя табл. Д.2, получаем, что P(Z < 3,02) = 0,99874.
Итак, вероятность того, что багаж будет доставлен вовремя, равна 99,874%. Следовательно, процесс доставки багажа удовлетворяет требованиям руководства отеля.
Показатели мощности
Для оценки процесса можно воспользоваться показателем мощности (capability index) — суммарным показателем, характеризующим соответствие процесса установленным спецификациям. Чем выше этот показатель, тем лучше. Чаще всего показатель качества обозначают символом Ср и вычисляют по формуле (17.8).
ПОКАЗАТЕЛЬ Ср
ВКГ - НКГ разброс спецификации
С =---рз-—г— =-------------------. (17.8)
61 R/сЦ 1 разброс процесса
Числитель в формуле (17.8) представляет собой расстояние между верхней и нижней контрольными границами, или размах спецификации (specification spread). Знаменатель равен шести стандартным отклонениям данных и называется размах процесса (process spread). (Напомним, что 99,73% всех нормально распределенных случайных величин лежит в интервале, концы которого отстоят на три стандартных отклонения от среднего значения.) Поскольку идеальный процесс должен полностью лежать в допустимом диапазоне, размах процесса должен быть как можно меньше. Следовательно, чем больше значение Ср, тем выше качество процесса.
Величина Ср оценивает потенциал процесса, а не фактическую мощность, поскольку он не зависит от текущего среднего значения. Допустим, что Ср= 1. Тогда, если процесс был бы центрированным, т.е. лежал посередине между границами НКГ и ВКГ, приблизительно 99,73% наблюдений лежали бы внутри допустимых границ. Если Ср> 1, значит, потенциал процесса настолько высок, что более 99,73% всех его значений может лежать внутри допустимых границ. Если Ср< 1, значит, потенциал процесса невысок, и даже если бы он был идеально центрирован, не более 99,73% всех его значений может лежать внутри допустимых границ. Многие компании требуют, чтобы величина Ср была больше или равна единице. По мере развития глобальной экономики, требующей повышения качества продукции, некоторые компании стали требовать, чтобы показатель Ср превышал 1,33, 1,5 и даже 2,0 (Six Sigma®).
Предположим, что компания, выпускающая безалкогольные напитки, разливает лимонад в 12-унциевые бутылки. Каждый час контролер извлекает одну бутылку, а затем вычисляет среднее значение и размах процесса. Нижняя допустимая граница равна 11,82 унции, а верхняя— 12,18 унций. Допустим, карта контроля показывает, что процесс находится под контролем, причем n = 4, X = 12,02 , R = 0,10 . Для того чтобы
вычислить показатель С , предположим, что данные имеют нормальное распределение. По табл. Д.11 для п = 4 находим, что d2 = 2,059. Используя формулу (17.8), получаем:
с ВКГ-НКГ 12,18-11,82 р~ ^R/d^ "6(0,10/2,059)“’
Поскольку показатель Ср превышает единицу, процесс разлива безалкогольных напитков имеет высокий потенциал, причем более 99,73% бутылок могут удовлетворять установленным спецификациям.
Итак, показатель Ср представляет собой суммарную меру потенциала процесса. Чем выше показатель Ср, тем лучше для потребителя. Иначе говоря, чем выше показатель Ср, тем меньше количество случайных вариаций и тем лучше процесс соответствует спецификациям. Для того чтобы достичь максимального потенциала, процесс должен колебаться вокруг среднего значения допустимого диапазона.
Показатели CPL, CPUv\ Cpk
Для измерения фактического потенциала процесса часто применяют показатели CPL, CPU и С ..
’ pk
ПОКАЗАТЕЛИ СР1ЛЛ CPU
CPL = , (17.9, a)
з(я/<д)
CPU = ~ (17.9, ff)
3(R/d2)
Поскольку при вычислении показателей CPL и CPU используется фактическое среднее значение, они характеризуют реальные свойства процесса, в отличие от показателя Ср, оценивающего лишь потенциал процесса. Если величина CPL (или CPU) равна единице, значит, среднее значение процесса отстоит от нижней (верхней) допустимой границы на три стандартных отклонения. Если процесс имеет только нижнюю допустимую границу, показатель CPL измеряет характеристики процесса и должен быть как можно больше. Если процесс имеет только верхнюю допустимую границу, показатель CPU измеряет характеристики процесса и тоже должен быть как можно больше.
Руководство отеля Beachcomber в нашем сценарии постановило, что 99% багажа должно доставляться за время, не превышающее 14 мин. Следовательно, характеристики качества процесса ограничены сверху числом 14, а нижней границы не существует. Поскольку ранее мы показали, что процесс доставки багажа является контролируемым, остается определить показатель CPU. Вычисления показывают, что X = 9,478 , R = 3,482, d2 = 2,326. Таким образом,
= 1МЛ78
3(Я/</2) 3(3,482/2,326)
Итак, показатель мощности процесса равен 1,01. Поскольку эта величина ненамного больше единицы, расстояние от верхней допустимой границы до среднего значения процесса слегка отличается от трех стандартных отклонений. Следовательно, необходимо изучить процесс доставки багажа и увеличить показатель CPU.
Вернемся к примеру, касавшемуся разлива безалкогольных напитков.
ПРИМЕР 17.2. ВЫЧИСЛЕНИЕ ПОКАЗАТЕЛЕЙ CPL И ОТ/ДЛЯ РАЗЛИВА БЕЗАЛКОГОЛЬНЫХ НАПИТКОВ
Процесс разлива напитков имеет следующие характеристики: п = 4, X = 12,02 , R = 0,10 , НКГ = 11,82, ВКГ = 12,18, d2 = 2,059. Вычислите показатели CPL и CPU.
РЕШЕНИЕ. Используя формулы (17.9, а и б), получаем:
X — НКГ 12,02 — 11,82
3(я/л) 3(0,10/2,059) ’ ’
сри = ВКГ-^ П^-П^ 3(Rld2) 3(0,10/2,059)
Оба показателя больше единицы. Следовательно, среднее значение процесса отличается от допустимых границ больше, чем на три стандартных отклонения. Поскольку показатель CPL меньше CPU, среднее значение процесса ближе к верхней допустимой границе, чем к нижней.
Наиболее распространенным показателем качества процесса является величина Cpk. Этот показатель измеряет фактическое качество процесса, имеющего нижнюю и верхнюю допустимые границы. Величина Срк представляет собой минимальное из двух показателей CPU и CPL.
ПОКАЗАТЕЛЬ Срк
Cpk = MIN[CPL,CPU]. (17.10)
Если величина Cpk равна единице, значит, среднее значение процесса отстоит на три стандартных отклонения от ближайшей допустимой границы. Если к тому же характеристика является нормально распределенной, значит, 99,73% текущих результатов лежат в допустимом диапазоне. Как и для всех остальных показателей качества, чем больше величина Cpk, тем лучше.
ПРИМЕР 17.3. ВЫЧИСЛЕНИЕ ПОКАЗАТЕЛЯ Срк ДЛЯ РАЗЛИВА БЕЗАЛКОГОЛЬНЫХ НАПИТКОВ
Вычислите показатель С^для процесса разлива напитков, описанного в примере 17.2.
РЕШЕНИЕ. В ходе решения примера 17.2 мы выяснили, что CPL = 1,37 и CPU = 1,10. Следовательно,
Срк = MIN\CPL,CPU] = M/7V[1,37,1,10] = 1,10 .
Итак, показатель Cpk больше единицы. Следовательно, фактические характеристики процесса удовлетворяют требованиям компании. Более 99,73% бутылок содержат от 11,82 до 12,18 унций напитка.
УПРАЖНЕНИЯ К РАЗДЕЛУ 17.7
Изучение основ
17.20. Предположим, что процесс является контролируемым, подгруппа содержит четыре элемента, X = 20 и R = 2. Чему равны следующие величины?
1. Математическое ожидание генеральной совокупности.
2. Стандартное отклонение генеральной совокупности.
17.21. Предположим, что процесс является контролируемым, подгруппа содержит три элемента, X = 100 и R = 3,386. Вычислите процент качественной продукции при следующих условиях.
1. НКГ = 98, ВКГ = 102.
2. НКГ = 93, ВКГ = 107,5.
3. НКГ = 93,8, ВКГ не существует.
4. ВКГ =110, НКГ не существует.
17.22. Предположим, что процесс является контролируемым, подгруппа содержит три элемента, X = 100 и R = 3,386. Вычислите показатели Сп, CPL, CPU и Cnh при следующих условиях.
1. НКГ = 98, ВКГ = 102.
2. НКГ = 93, ВКГ = 107,5.
Применение понятий
17.23. Вернемся к задаче 17.15. В журнале The MidAmerican Journal of Business недавно была опубликована статья, авторы которой утверждают: “Некоторые характеристики качественного процесса позволяют повысить степень удовлетворенности потребителей, увеличить производительность труда и сократить расходы”. Для подтверждения своей точки зрения авторы описывают анализ характеристик процесса разлива напитков в бутылки. Одной из интересующих его характеристик было количество магния в воде. Верхняя и нижняя допустимые границы содержания магния равны 18 и 22 частей на миллион соответственно. В файле ^SPWATER. XLS приведена концентрация магния (частей на миллион) в 30 подгруппах, содержащих по 4 бутылки, отобранных на протяжении 30 часов.
Источник: Humphrey, S. К., and Т. С. Krehbiel, “Managing Process Capability”, The MidAmerican Journal of Business, 14 (Fall 1999) 7-12.
1. Оцените процент качественной продукции.
2. Вычислите показатели С , CPL, CPU и С ..
17.24. Вернемся к задаче 17.16. В файле ©TENSILE.XLS приведены значения прочности ткани. Данные собирались в подгруппы по три отреза на протяжении 25 часов. Верхней контрольной границы не существует, а нижняя контрольная граница равна 13.
1. Оцените процент качественной продукции.
2. Вычислите показатели Ср, CPL, CPU и Cpk.
17.25. Вернемся к задаче 17.18, в которой описан процесс упаковки коробок на чаеразвесочной фабрике. Решая эту задачу, мы пришли к выводу, что производственный процесс является контролируемым. Номинальный вес коробки равен 5,5 г, нижняя допустимая граница равна 5,2 г, а верхняя допустимая граница — 5,8 г. Допустим, что менеджеры требуют, чтобы вес 99% упаковок находился в допустимом диапазоне. ^ТЕАЗ. XLS.
1. Оцените процент качественной продукции.
2. Предположим, что руководство компании ужесточило требования к качеству продукции и потребовало, чтобы 99,7% упаковок соответствовали стандарту. Удовлетворяет ли процесс новым требованиям? Обоснуйте свой ответ.
17.26. Вернемся к задаче 17.13, в которой описано обслуживание клиентов в отделении банка. Решая эту задачу, мы пришли к выводу, что процесс обслуживания клиентов является контролируемым. Допустим, что менеджеры банка требуют, чтобы пребывание клиента в очереди не превышало 5 мин., причем 99% клиентов обслуживалось вовремя. ^BANKTIME . XLS.
1. Оцените процент качественного обслуживания клиентов.
2. Предположим, что руководство компании ужесточило требования к качеству обслуживания и потребовало, чтобы 99,7% клиентов обслуживались вовремя. Удовлетворяет ли процесс новым требованиям? Обоснуйте свой ответ.
РЕЗЮМЕ
В главе рассмотрена теория контроля качества и принципы Деминга. Изучены различные типы карт контроля, позволяющие выделять случайные и неслучайные вариации. Кроме того, мы научились оценивать характеристики процесса, вычисляя процент качественной продукции и показатели мощности. В качестве иллюстрации рассмотрен сценарий, описывающий обслуживание постояльцев отеля Beachcomber. Показано, как выявлять проблемы и непрерывно улучшать качество обслуживания.
Является
••
Нет
5 . -' ;
Применяются Я-иХ-карты
L.
Мощность процесса \
ли переменная непрерывной?^
Применяется / р-карта
Структурная схема главы 17
ОСНОВНЫЕ ПОНЯТИЯ
Вариация качественных признаков, 1121
неслучайная, 1119 Показатель качества, 1145; 1146
случайная, 1119 Полный контроль качества, 1115
Допускаемый предел, 1143 Процесс
Контрольная граница контролируемый, 1121
верхняя, 1120; 1143 неконтролируемый, 1121
нижняя, 1120; 1143 поддающийся статистическому контролю.
Контрольная карта, 1119 1121
р-карта, 1121 Разброс
для переменных, 1132 процесса, 1145
для размаха, 1132 спецификации, 1145
для среднего значения X , 1135
УПРАЖНЕНИЯ К ГЛАВЕ 17
Проверка знаний
17.27. В чем заключается разница между случайными и неслучайными вариациями?
17.28. Что следует предпринять, чтобы устранить неслучайные вариации?
17.29. Что следует предпринять, чтобы устранить случайные вариации?
17.30. В каких ситуациях применяется р-карта?
17.31. В чем заключается разница между картой контроля качественных признаков и переменной картой контроля?
17.32. Почему X - и R-карты применяются вместе?
17.33. Какие принципы демонстрирует эксперимент с красными шарами?
17.34. В чем заключается разница между потенциалом и качеством процесса?
17.35. Некая компания требует, чтобы показатель Cnh превышал единицу. Какие изменения следует внести в процесс, если Ср = 1,5, a Cpk = 0,8?
17.36. Почему нельзя проводить анализ мощности неконтролируемого процесса?
Применение понятий
17.37. Исследователи университета Майами в штате Огайо (Miami University in Ohio) изучили применение р-карт для оценки рыночной доли компании и эффективности ее маркетинговой политики. Рыночной долей компании называется доля ее изделий в общем количестве продукции, представленной на рынке в данной категории. Если р-карта свидетельствует о том, что процесс является контролируемым, значит, рыночная доля компании является устойчивой. Например, компания RudyBird Diskette Company собрала данные о ежедневных продажах. Первые 30 дней компания собирала данные об общем количестве проданных дискет и количестве дискет, проданных компанией RudyBird Dickette Company. Последние 7 дней компания RudyBird Dickette Company проводила специальную рекламную акцию. Карта контроля позволила выяснить эффективность рекламной акции. ©RUDYBIRD. XLS.
Количество продукции, проданной до начала рекламной акции
День Всего RudyBird День Всего RudyBird
1 154 35 16 177 56
2 153 43 17 143 43
3 200 44 18 200 69
4 197 56 19 134 38
5 194 54 20 192 47
6 172 38 21 155 45
7 190 43 22 135 36
8 209 62 23 189 55
9 173 53 24 184 44
10 171 39 25 170 47
11 173 44 26 178 48
12 168 37 27 167 42
13 184 45 28 204 71
14 211 58 29 183 64
15 179 35 30 169 43
Количество продукции, проданной после начала рекламной акции
День Всего RudyBird
31 201 92
32 177 76
33 205 85
34 199 90
35 187 77
36 168 79
37 198 97
Источник: Crespy, С.Т., T.C.Krehbiel, and J. M. Stearns, “Integrating Analityc Methods into Marketing Research Education: Statisticsl Control Charts as an Example”, Marketing Educaiion Review, 5 (Spring 1995),p. 11 -23.
1. Постройте контрольную р-карту на основе данных о продажах продукции в течение первых 30 дней (до начала рекламной акции).
2. Является ли контролируемой рыночная доля компании RudyBird?
3. Постройте карту контроля на основе данных о продажах продукции в течение последних семи дней (после начала рекламной акции). Оцените эффективность рекламной кампании.
17.38. Производитель асфальтового кровельного покрытия “Boston” и “Vermont” построил карты контроля и провел анализ некоторых характеристик качества. В частности, руководство компании интересовала прочность материала, использованного для герметизации. Каждый рабочий день для проверки на прочность отбирались три покрытия. (Таким образом, каждая подгруппа соответствует отдельному рабочему дню и ее объем равен 3.) От верхней и нижней частей покрытия отрезались отдельные куски, затем они собирались вместе, имитируя покрытие крыши. Для герметизации покрытия использовалось нагревание. Нагретые куски покрытия испытывались на разрыв. Сила натяжения, при которой происходил разрыв, записывалась в журнал. Эта переменная называется силой герметизации. Нижний и верхний допустимые пределы равны 1,0 и 1,5 фунта соответственно. В файле ^SEALANT.XLS записаны результаты измерений, собранные на протяжении 25 дней для покрытия марки “Boston” и на протяжении 19 дней для покрытия марки “Vermont”.
1. Постройте карту контроля размаха прочности покрытия марки “Boston”.
2. Постройте карту контроля средней прочности покрытия марки “Boston”.
3. Является ли контролируемым процесс производства покрытия марки “Boston”?
4. Если процесс производства покрытия марки “Boston” является контролируемым, оцените процент покрытий, прочность которых находится внутри допустимых пределов.
5. Если процесс производства покрытия марки “Boston” является контролируемым, вычислите показатели Ср, CPL, CPU и Cpk.
6. Предположим, что руководство компании требует, чтобы прочность 99,7% покрытий марки “Boston” находилась внутри допустимых пределов. Проведите анализ мощности процесса, используя результаты решения задач 1-5.
7. Повторите решение задач 1-6 на основе данных, собранных на протяжении 19 рабочих дней для покрытия марки “Vermont”.
17.39. Профессиональный баскетболист решил оценить эффективность своих штрафных бросков. На протяжении 40 дней он выполнял по 100 бросков в день, записывая результаты. fi^FOULSPC. XLS.
День Попадания День Попадания День Попадания
1 73 15 73 29 76
2 75 16 76 30 80
3 69 17 69 31 78
4 72 18 68 32 83
5 77 19 72 33 84
6 71 20 70 34 81
7 68 21 64 35 86
8 70 22 67 36 85
9 67 23 72 37 86
10 74 24 70 38 87
11 75 25 74 39 85
12 72 26 76 40 85
13 70 27 75
14 74 28 78
1. Постройте контрольную р-карту для доли попаданий при выполнении штрафных бросков. Можно ли утверждать, что выполнение штрафных бросков поддается статистическому контролю? Если нет, то почему?
2. Допустим, что по истечении 20 дней баскетболист изменил манеру выполнения штрафных бросков. Можно ли сделать этот вывод на основе данных, представленных в таблице и на карте контроля?
3. Изменился бы способ построения р-карты, если бы вы заранее знали, что по истечении 20 дней баскетболист изменил манеру выполнения штрафных бросков?
>. Отдел движения средств между банками отслеживает время полного оборота средств. В процессе движения средств банк может играть роль отправителя, получателя или промежуточного звена. Отсчет времени начинается с момента поступления запроса на перевод денег. Получив запрос, банковский служащий планирует транзакцию, проверяет правильность информации и переводит средства. Затем он отчитывается о транзакции и закрывает ее. Очень важно, чтобы транзакция была закрыта в тот же день. Количество новых запросов, а также количество и доля вовремя закрытых транзакций записаны в файле ft^FUNDTRAN .XLS.
1. Постройте контрольную карту на основании этих данных.
2. Можно ли утверждать, что процесс является контролируемым? Объясните свой ответ.
3. Какие меры следует предпринять для улучшения процесса?
L. Брокер агентства недвижимости регистрирует количество нежелательных сделок, заключенных его сотрудниками. Сделка считается нежелательной, если документы оформлены неправильно. Такие сделки должны быть аннулированы и оформлены заново. Ошибки исправляются за счет брокера. Изучая проблему, менеджер желает знать, поддается ли статистическому контролю доля нежелательных сделок. Для этого на протяжении 30 дней он собирал данные, занося их в файл ^TRADE . XLS.
День Количество нежелательных сделок Общее количество сделок День Количество нежелательных сделок Общее количество сделок
1 2 74 16 3 54
2 12 85 17 12 74
3 13 114 18 11 103
4 33 136 19 11 100
5 5 97 20 14 88
6 20 115 21 4 58
7 17 108 22 10 69
8 10 76 23 19 135
9 8 69 24 1 67
10 18 98 25 11 77
День Количество нежелательных сделок Общее количество сделок День Количество нежелательных сделок Общее количество сделок
11 3 104 26 12 88
12 12 98 27 4 66
13 15 105 28 11 72
14 6 98 29 13 118
15 21 204 30 15 138
1. Постройте контрольную карту на основании этих данных.
2. Можно ли утверждать, что процесс является контролируемым? Объясните свой ответ.
3. Какие меры следует предпринять для улучшения процесса?
17.42. Представьте себе, что вы — менеджер крупной больницы. Вы только что вернулись с трехдневного семинара, посвященного повышению качества и производительности труда, и желаете внедрить новые идеи в практику вашей больницы. Для начала вы решили в течение ближайшего месяца построить карты контроля для следующих переменных: доли повторных анализов, проводимых в лаборатории (на 1 000 анализов, выполняемых ежедневно), времени между получением пробы и завершением анализа (на основе подгрупп, состоящих из 10 образцов). Данные собраны в файле ^HOSPADM.XLS.
Подготовьте презентацию для руководства вашей больницы. Изложите свои выводы в отчете. Укажите, какие еще переменные следует контролировать, чтобы повысить качество работы. Объясните, как принципы Деминга могут повысить качество обслуживания в вашей больнице.
17.43. Измеряйте свой пульс каждое утро и каждый вечер на протяжении четырех недель. Постройте X -иЯ-карты и определите, поддается ли ваш пульс статистическому контролю. Обоснуйте свой вывод.
17.44. Классная работа. Для имитации извлечения разноцветных шаров из урны можно использовать таблицу случайных чисел (табл. Д.1).
1. Выберите строку, номер которой соответствует текущему дню месяца, и прибавьте к нему год вашего рождения. Например, если вы родились 15 октября 1982 года, выберите строку под номером 15+82 = 97. Если результат превышает 100, вычтите из него число 100.
2. Выберите двузначные случайные числа.
3. Если случайное число лежит в диапазоне от 0 до 94, будем считать шар белым. Если случайное число больше или равно 95 и не превышает 99, будем считать шар красным.
Каждый студент должен выбрать 100 двузначных целых чисел и записать количество “красных шаров” в выборке. Карта контроля должна отображать количество или долю красных шаров. Что можно сказать о процессе извлечения красных шаров? Все ли студенты являются частью системы? Остался ли какой-нибудь студент за рамками системы? Если да, как объяснить, что он выбрал слишком большое количество шаров? Предположим, что лучшие 10% студентов (извлекших наименьшее количество красных шаров) получают премию. Как это повлияет на остальных? Объясните свой ответ.
Применение Интернет
17.45. Зайдите на сайт www.prenhall.com/levine. Выберите ссылку Chapter 15 и щелкните на ссылке Internet exercises.
РАЗБОР КОНКРЕТНОЙ СИТУАЦИИ --'/ ЛО КОМПАНИЯ HARNSWELLSEWING MACHINE COMPANY S3
Этап 1
Компания Harnswell Sewing Machine Company производит промышленные швейные машины и работает на рынке более 50 лет. Компания специализируется на автоматах, получивших название наметочных машин. Эти машины шьют однотипные образцы массовой продукции, такие как туфли, одежда и ремни безопасности. Компания продает как машины целиком, так и запасные части к ним. Компания имеет хорошую репутацию и благодаря этому может получать дополнительную прибыль.
Недавно Натали Йорк, управляющая компанией, приобрела несколько книг, посвященных контролю качества. Прочитав их, она стала интересоваться, возможно ли осуществить в ее компании программу действий, направленных на повышение качества. В данное время компания не имеет ни одной такой программы. При продаже или установке все запасные части подвергаются контролю. Однако Натали всегда интересовало, почему некоторых деталей (в частности, полудюймового кулачкового ролика) неизменно не хватает на целый год, несмотря на то, что они изготавливаются в количестве 7 000 штук при потребности в 5 000 штук.
Глубоко изучив вопрос и догадавшись о причинах этого явления, Натали решила обратиться к Джону Харнсвеллу, владельцу компании, с предложением внедрить программу мероприятий, направленных на повышение качества. В качестве испытательного полигона она предложила использовать цех, производящий запасные части. Придя на встречу в офис мистера Харнсвелла, Натали вспомнила, как в прошлом месяце он сказал ей: “Зачем вам учиться в школе бизнеса и получать степень магистра? Эта лишняя трата времени не принесет компании никакой пользы. Все эти профессора оторваны от мира и ничего не понимают в реальном бизнесе”.
Мистер Харнсвелл встретил Натали чрезвычайно вежливо и предложил ей сесть напротив него. “Ну, что еще взбрело вам в голову?” — спросил он инквизиторским тоном. Натали стала рассказывать о книгах, которые она прочитала, и об идеях, которые у нее возникли. Мистер Харнсвелл не дал ей закончить: “С тех пор, как я стал владельцем компании в 1955 году, дела всегда шли прекрасно. Я построил эту компанию на голом месте, а сейчас в ней работают более 100 человек. Зачем вы поднимаете волны? Помните — не сломано, не чини!”. Он выпроводил Натали из кабинета, предупредив напоследок, что уволит ее, если она еще раз явится к нему со своими странными идеями.
УПРАЖНЕНИЯ
Какие рекомендации Деминга нарушил мистер Харнсвелл?
Какие изменения могла бы осуществить Натали, если бы имела такую возможность?
НЕ ПРОДОЛЖАЙТЕ, ПОКА НЕ ОТВЕТИТЕ НА ЭТИ ВОПРОСЫ
Этап 2
Покинув офис мистера Харнсвелла, Натали медленно побрела на свое рабочее место, чувствуя себя униженной. “Он ничего не хотел слышать,” — думала она. В этот момент ее догнал Джим Мюрант, менеджер по продажам. “Неужели вы действительно надеялись, — сказал он, — что старик согласится выслушать вас? Я работаю в компании больше 25 лет. Единственный способ заставить его прислушаться к себе — продемонстрировать готовые результаты. Послушайте, что я предлагаю.”
Натали и Джим решили исследовать процесс производства кулачковых роликов, который требует большой точности. На последнем этапе выполняется шлифовка внутреннего диаметра кулачкового ролика. После шлифовки осуществляется настройка кулачка на конкретный образец изделия. В соответствии с техническими требованиями, предъявляемыми к полудюймовому кулачковому ролику, его внутренний диаметр должен быть равен 0,5075 ( в действительности применяется метрическая система, однако на фабрике принято называть кулачки полудюймовыми). Допускается отклонение минус 0,0003 дюйма. Таким образом, внутренний диаметр кулачка должен находиться в диапазоне от 0,5072 до 0,575 дюйма. Все кулачки, внутренний диаметр которых превышает указанный размер, считаются бракованными и относятся к более дешевой категории. Все кулачки, размеры которых меньше установленных, вообще невозможно использовать.
Шлифовка кулачков производится на единственном станке, настройка которого никогда не изменяется. Операцию выполняет Дэйв Мартин, старший механик, проработавший на фабрике более 30 лет. Поскольку продукция отгружается партиями, Натали и Джим решили отобрать из каждой партии пять образцов. В табл. HS.1 приведены данные о 30 партиях. ^HARNSWELL. XLS.
Таблица HS.1 Диаметры роликовых кулачков (в дюймах)
Партия 1 2 3 4 5
1 0,5076 0,5076 0,5075 0,5077 0,5075
2 0,5075 0,5077 0,5076 0,5076 0,5075
3 0,5075 0,5075 0,5075 0,5075 0,5076
4 0,5075 0,5076 0,5074 0,5076 0,5073
5 0,5075 0,5074 0,5076 0,5073 0,5076
6 0,5076 0,5075 0,5076 0,5075 0,5075
7 0,5076 0,5076 0,5076 0,5075 0,5075
8 0,5075 0,5076 0,5076 0,5075 0,5074
9 0,5074 0,5076 0,5075 0,5075 0,5076
10 0,5076 0,5077 0,5075 0,5075 0,5075
11 0,5075 0,5075 0,5075 0,5076 0,5075
12 0,5075 0,5076 0,5075 0,5077 0,5075
13 0,5076 0,5076 0,5073 0,5076 0,5074
14 0,5075 0,5076 0,5074 0,5076 0,5075
Окончание табл. HS. 7
Партия 1 2 3 4 5
15 0,5075 0,5075 0,5076 0,5074 0,5073
16 0,5075 0,5074 0,5076 0,5075 0,5075
17 0,5075 0,5074 0,5075 0,5074 0,5072
18 0,5075 0,5075 0,5076 0,5075 0,5076
19 0,5076 0,5076 0,5075 0,5075 0,5076
20 0,5075 0,5074 0,5077 0,5076 0,5074
21 0,5075 0,5074 0,5075 0,5075 0,5075
22 0,5076 0,5076 0,5075 0,5076 0,5074
23 0,5076 0,5076 0,5075 0,5075 0,5076
24 0,5075 0,5076 0,5075 0,5076 0,5075
25 0,5075 0,5075 0,5075 0,5075 0,5074
26 0,5077 0,5076 0,5076 0,5074 0,5075
27 0,5075 0,5075 0,5074 0,5076 0,5075
28 0,5077 0,5076 0,5075 0,5075 0,5076
29 0,5075 0,5075 0,5074 0,5075 0,5075
30 0,5076 0,5075 0,5075 0,5076 0,5075
УПРАЖНЕНИЯ
Ответьте на следующие вопросы.
1. Является ли процесс контролируемым?
2. Как улучшить производство кулачковых роликов?
НЕ ПРОДОЛЖАЙТЕ, ПОКА НЕ ОТВЕТИТЕ НА ЭТИ ВОПРОСЫ
Этап 3
Натали проанализировала X - и /?-карты, построенные на основе данных, приведенных в табл. HS.1. Изучение /?-карты показало, что процесс производства является контролируемым, однако X -карта выявила слишком низкое среднее значение в 17-й день. Это вызвало беспокойство у Натали, поскольку при низких значениях диаметра детали совершенно непригодны для эксплуатации. Натали пришла к Джиму Мюрранту и стала выяснять, что произошло с 17-й партией. Джим просмотрел записи и выяснил, когда была произведена данная партия. “Кажется, я понимаю в чем дело! — воскликнул он. — В то утро было очень холодно. Я отправился к мистеру Харнсвеллу с просьбой купить обогреватель. Он ответил, что настоящий холод был зимой 1952 года, а сейчас люди просто изнежены, и отказал мне.”
Натали чуть не упала в обморок от радости. Она поняла, что машинист не стал дожидаться, пока станок прогреется до нужной температуры, и приступил к шлифовке, когда было слишком холодно. К тому же Натали вспомнила, что в этот день бракованными оказались еще несколько дорогостоящих деталей. “Необходимо что-то предпринять. Ведь теперь мы знаем, в чем причина брака!” — воскликнула Натали. Она и Джим решили скинуться и купить обогреватель, не спрашивая разрешения у мистера Харнс-велла. Теперь они включают обогреватель за полчаса до начала работы.
УПРАЖНЕНИЯ
Какие меры должна предпринять Натали?
Объясните, может ли поступок Натали и Джима предотвратить возникновение новых проблем?
НЕ ПРОДОЛЖАЙТЕ, ПОКА НЕ ОТВЕТИТЕ НА ЭТИ ВОПРОСЫ
Этап 4
После того как данные о 17-й партии были исключены из карты контроля (поскольку причина неслучайной вариации была устранена), система стала устойчивой и подверженной лишь случайным колебаниям. Тогда Натали и Джим сели вместе с Дэйвом Мартином и еще несколькими механиками и стали обсуждать другие возможные причины брака. Натали по-прежнему беспокоилась о сборе данных. Она хотела понять, не являются ли технические требования завышенными (что приводит в пересортице) или заниженными (что приводит к браку). Натали размышляла о том, какие таблицы и диаграммы позволят ответить на эти вопросы.
УПРАЖНЕНИЯ
Выполните следующие задания.
1. Постройте распределение частот или диаграмму “ствол и листья” на основе диаметров кулачковых роликов. Объясните, почему вы предпочли табличное представление данных.
2. Постройте все необходимые диаграммы, характеризующие качество кулачковых роликов.
3. Напишите отчет и сформулируйте свои выводы. Укажите, соответствуют ли диаметры кулачковых роликов техническим требованиям.
НЕ ПРОДОЛЖАЙТЕ, ПОКА НЕ ОТВЕТИТЕ НА ЭТИ ВОПРОСЫ
Этап 5
Натали сразу заметила, что средний диаметр роликов в 17-й день равен 0,507527, что превышает верхний допустимый предел. Следовательно, ролики слишком велики и должны быть уценены. Фактически 55 из 150 роликов (36,6%) не соответствуют спецификации. Экстраполируя эти данные на весь год, Натали пришла к выводу, что 36,67% от 7 000 роликов, произведенных за год, т.е. 2 567 штук, продаже не подлежат. Таким образом, в продаже окажутся лишь 4 433 ролика. “Вот в чем кроется причина постоянного дефицита,” — подумала она. Натали также заметила, что ни один диаметр не вышел за нижний допустимый предел, равный 0,5072, т.е. ни один ролик не был выброшен на свалку.
Натали поняла, что это явление имеет свои причины. Вместе в Джимом Мюранте она решила показать результаты исследования Дэйву Мартину, главному механику. Тот сказал, что результаты его не удивляют. “Я знаю, что допустимое отклонение диаметра составляет всего 0,0003 дюйма. Если я буду стремиться попасть в середину диапазона от 0,5072 до 0,5075, много заготовок придется выбросить на свалку, поскольку их диаметр будет слишком маленьким. За это мистер Харнсвелл оторвет мне голову. Я понял, что если буду ориентироваться на размер 0,5075, то в худшем случае заготовки придется отправить на пересортицу, но, по крайней мере, брака не будет.”
УПРАЖНЕНИЯ
Правильно ли поступает машинист?
Какие меры должна предпринять Натали?
РАЗБОР КОНКРЕТНОЙ СИТУАЦИИ -ГАЗЕТА SPRINGVILLE HERALD
Этап 1
Для сокращения количества ошибок в рекламных объявлениях руководством газеты была создана рабочая группа, состоящая из сотрудников отдела рекламы. Особое внимание было обращено на нарушение сроков публикации рекламы. Сначала группа решила собирать данные о количестве ошибок, совершаемых ежедневно (за исключением воскресного выпуска, который существенно отличается от остальных номеров газеты). Данные об ошибках, совершенных в течение прошлого месяца, представлены в табл. SH. 17.1. SH 17 -1. XLS.
Таблица SH.17.1 Количество ошибок, обнаруженных заказчиками
День Количество объявлений, содержащих ошибки Количество ошибок День Количество объявлений, содержащих ошибки Количество ошибок
1 4 228 14 5 245
2 6 273 15 7 266
3 5 239 16 2 197
4 3 197 17 4 228
5 6 259 18 5 236
6 7 203 19 4 208
7 8 289 20 3 214
8 14 241 21 8 258
9 9 263 22 10 267
10 5 199 23 4 217
11 6 275 24 9 277
12 4 212 25 7 258
13 3 207
УПРАЖНЕНИЯ
Какие меры следует предпринять в первую очередь?
Выполните следующие задания.
1. Постройте карту контроля.
2. Является ли процесс контролируемым? Почему?
3. Какие меры рабочая группа должна предпринять во вторую очередь?
НЕ ПРОДОЛЖАЙТЕ, ПОКА НЕ ОТВЕТИТЕ НА ЭТИ ВОПРОСЫ
Этап 2
Рабочая группа исследовалар-карту, построенную по данным, приведенным в табл. SH. 17.1, и обнаружила 8 точек, выходящих за контрольные границы. Оказалось, что ошибки были сделаны работниками, временно привлеченными к созданию рекламных объявлений вместо заболевших сотрудников отдела рекламы. Группа проанализировала ситуацию и рекомендовала провести обучение сотрудников, привлекаемых для работы в отделе рекламы. Впоследствии такие подготовленные сотрудники смогут качественно заменять отсутствующих специалистов.
УПРАЖНЕНИЯ
Какие меры следует предпринять отделу рекламы?
Объясните, каким образом рекомендация рабочей группы позволит избежать будущих ошибок.
Какая еще информация нужна для анализа ошибок в рекламных объявлениях?
НЕ ПРОДОЛЖАЙТЕ, ПОКА НЕ ОТВЕТИТЕ НА ЭТИ ВОПРОСЫ
Этап 3
Производственный отдел подготовил программу действий, направленных на улучшение качества. После нескольких рабочих совещаний группа решила в качестве первого проекта исследовать насыщенность шрифта. Каждый день исследователи должны измерять насыщенность шрифта с помощью денситометра по стандартной шкале и записывать результаты в журнал наблюдений. Для анализа выбираются пять экземпляров газеты, в каждом из которых производятся необходимые измерения. Результаты за 20 дней представлены в табл. SH.17.2.
Таблица SH.17.2 Насыщенность шрифта газеты на протяжении 20 дней
Насыщенность
День 1 2 3 4 5
1 0,96 1,01 1,12 1,07 0,97
2 1,06 1,00 1,02 1,16 0,96
3 1,00 0,90 0,98 1,18 0,96
4 0,92 0,89 1,01 1,16 0,90
5 1,02 1,16 1,03 0,89 1,00
6 0,88 0,92 1,03 1,16 0,91
7 1,05 1,13 1,01 0,93 1,03
Окончание табл. SH. 17.2
Насыщенность
День 1 2 3 4 5
8 0,95 0,86 1,14 0,90 0,95
9 0,99 0,89 1,00 1,15 0,92
10 0,89 1,18 1,03 0,96 1,04
11 0,97 1,13 0,95 0,86 1,06
12 1,00 0,87 1,02 0,98 1,13
13 0,96 0,79 1,17 0,97 0,95
14 1,03 0,89 1,03 1,12 1,03
15 0,96 1,12 0,95 0,88 0,99
16 1,01 0,87 0,99 1,04 1,16
17 0,98 0,85 0,99 1,04 1,16
18 1,03 0,82 1,21 0,98 1,08
19 1,02 0,84 1,15 0,94 1,08
20 0,90 1,02 1,10 1,04 1,08
21 0,96 1,05 1,01 0,93 1,01
22 0,89 1,04 0,97 0,99 0,95
23 0,96 1,00 0,97 1,04 0,95
24 1,01 0,98 1,04 1,01 0,92
25 1,01 1,00 0,92 0,90 1,11
УПРАЖНЕНИЯ
Выполните следующие задания и ответьте на вопросы.
1. Постройте карту контроля.
2. Является ли процесс контролируемым? Почему?
3. Какие меры рабочая группа должна предпринять во вторую очередь?
СПРАВОЧНИК ПО EXCEL. ГЛАВА 17
ЕН.17.1. Вычисление контрольных границ и координат точек на р-карте
Для построения контрольных р-карт необходимо реализовать два рабочих листа, использующих простые арифметические формулы.
Шаблон этих рабочих листов показан в табл. ЕН.17.1 и ЕН.17.2. В них содержатся данные, характеризующие степень готовности отеля к приему постояльцев (см. табл. 17.1). В табл. ЕН.17.1 представлен шаблон рабочего листа рКарта, предназначенного для вычисления нижней контрольной границы, средней линии и верхней контрольной границы. Некоторые формулы ссылаются на ячейки рабочего листа ДляРКарты, показанного в табл. ЕН.17.2. Второй шаблон содержит первые три строки табл. 17.1 и использует формулы, записанные в столбцах Е и G для преобразования контрольных границ, вычисленных на рабочем листе рКарта. (Эти преобразования облегчают дальнейшее использование Мастера диаграмм при построениир-карты.)
Таблица ЕН.17.1. Шаблон рабочего листа рКарта
А В
1 р-карта, характеризующая готовность комнат
2
3 Промежуточные вычисления
4 Сумма объемов подгрупп =СУММ(ДляРКарты!В:В)
5 Количество подгрупп =СЧЁТ(ДляРКарты!В:В)
6 Средний объем выборки (подгруппы) =В4/В5
7 Средняя доля комнат, не подготовленных к приему гостей =СУММ(ДляРКарты!С:С)/В4
8 Три стандартных отклонения =3*КОРЕНЬ(В7*(1-В7)/В6)
9
10 Контрольные границы р-карты
11 Нижняя контрольная граница = В7-В8
12 Среднее значение = В7
13 Верхняя контрольная граница =В7+В8
Таблица ЕН.17.2. Шаблон рабочего листа ДляРКарты (показаны только первые три и последние две строки)
III В С D Е F G
1 День Объем Брак Р НКГ Среднее ВКГ
2 1 200 16 =С2/В2 =ЕСЛИ(рКарта!$В$11<0,"", рКарта!$В$11) =рКарта!$В$12 =рКарта!$В$13
3 2 200 7 =СЗ/ВЗ =ЕСЛИ(рКарта!$В$11<0,"", рКарта!$В$11) =рКарта!$В$12 =рКарта!$В$13
...
28 27 200 20 =С28/В2 8 =ЕСЛИ(рКарта!$В$11<0,"", рКарта!$В$11) =рКарта!$В$12 =рКарта!$В$13
29> 28 200 22 =С29/В29 =ЕСЛИ(рКарта!$В$11<0,"", рКарта!$В$11) =рКарта!$В$12 =рКарта!$В$13
Сначала следует создать первые три строки рабочего листа ДляРКарты. Затем необходимо создать рабочий лист рКарта и завершить реализацию листа ДляРКарты. Формулы, записанные в нескольких строках, в рабочем листе ДляРКарты должны занимать одну строку. Обратите внимание на использование двойных кавычек.
ЕН.17.2. Создание р-карт
Создав рабочий лист на основе шаблона ДляРКарты, следует вызвать Мастер диаграмм, открыть рабочий лист ДляРКарты и выбрать команду Вставка^Диаграмма.
1. На первом этапе диалога нужно выполнить следующие действия.
1.1. Щелкнуть на корешке вкладки Стандартные, а затем выбрать пункт Точечная в списке Тип.
1.2. Выбрать первый вариант на панели Вид, сопровождаемый надписью “Точечная диаграмма позволяет сравнить пары значений”.
1.3. Щелкнуть на кнопке Далее>.
2. На втором этапе диалога необходимо выполнить такие действия.
2.1. Щелкнуть на корешке вкладки Диапазон данных. Ввести в диалоговом окне Диапазон ячейки Al: А2 9, DI: G2 9 и установить переключатель Ряды в положение В столбцах. Пробел перед запятой не нужен.
2.2. Щелкнуть на кнопке Далее>.
3. На третьем этапе диалога следует выполнить такие действия.
3.1. Щелкнуть на корешке вкладки Заголовки. Ввести в диалоговом окне Название диаграммы строку р-карта, характеризующая степень готовности номеров, в диалоговом окне Ось X (категорий) — строку День, а в диалоговом окне Ось У (значений) — строку Доля.
3.2. По очереди щелкнуть на корешках вкладок Оси, Линии сетки, Легенда, Подписи данных и установить желаемые настройки.
3.3. Щелкнуть на кнопке Далее>.
4. На четвертом этапе диалога следует выполнить следующие действия.
4.1. Установить переключатель Поместить диаграмму на отдельном листе и ввести название нового рабочего листа.
4.2. Щелкнуть на кнопке Готово.
Мастер диаграмм создает рабочий лист с р-картой, характеризующей степень готовности номеров отеля. Эта карта содержит несколько ошибок форматирования: маркеры точек загромождают линию верхней контрольной границы, среднюю линию и линию нижней контрольной границы.
Исправление контрольной линии. Линии верхней и нижней контрольных границ должны быть пунктирными, средняя линия, а также линии верхней и нижней контрольной границы выделены неверным цветом. Для того чтобы исправить эти недостатки, следует открыть рабочий лист ДляРКарты и выполнить следующие действия.
1. Установить курсор на линию верхней контрольной границы и щелкнуть правой кнопкой. (Если курсор мыши установлен правильно, на экране появится подсказка, начинающаяся словами “Ряд. ..”.)
2. Выбрать во всплывающем меню команду Формат рядов данных.... Щелкнув на корешке вкладки Вид, осуществить следующие манипуляции.
2.1. Установить переключатель Маркер в положение Отсутствует.
2.2. Выбрать пунктирную линию в списке Тип линии из группы Линия.
2.3. Выбрать синий цвет в списке Цвет из группы Линия.
2.4. Щелкнуть на кнопке ОК.
3. Установить курсор на линию нижней контрольной границы и щелкнуть правой кнопкой. (Если курсор мыши установлен правильно, на экране появится подсказка, начинающаяся словами “Ряд. . . ”.) Выполнить п. 2.
Исправление контрольной линии. Для исправления средней линии необходимо сделать следующее.
1. Щелкнуть правой кнопкой на средней линии. (Если курсор мыши установлен правильно, на экране появится подсказка, начинающаяся словами “Ряд. . .”.) Выполнить п. 2.
2. Выбрать во всплывающем меню команду Формат рядов данных.... Щелкнув на корешке вкладки Вид, осуществить следующие манипуляции.
2.1. Установить переключатель Маркер в положение Отсутствует.
2.2. Выбрать красный цвет в списке Цвет из группы Линия.
2.3. Щелкнуть на кнопке ОК.
Исправление меток контрольной и средней линии. Для исправления меток контрольной и средней линии необходимо сделать следующее.
1. Щелкнуть на правом конце линии верхней контрольной границы. (Если курсор мыши установлен правильно, на экране появится подсказка, начинающаяся словами “Ряд. . .”.) Затем, не перемещая курсор мыши, щелкнуть повторно, когда появится подсказка “Ряд “ВКГ” Точка “2 8”. Курсор мыши примет вид перекрещивающихся двунаправленных стрелок.
2. Щелкнуть правой клавишей мыши и выбрать команду Формат рядов данных... во всплывающем меню.
3. Находясь в диалоговом окне Формат ряда данных, выбрать вкладку Подписи данных, установить переключатель Включить в подписи в положение Имена рядов и щелкнуть на кнопке ОК.
4. Щелкнуть на метке 28. (Если курсор мыши установлен правильно, на экране появится подсказка, начинающаяся словами “Ряд. . .”.) Когда появится подсказка “ВКГ” Точка “2 8” Подпись данных”, щелкнуть второй раз.
5. Ввести в качестве подписи линии название ВКГ. (Символы, введенные пользователем, появятся в строке формул.)
6. Повторить п. 1-6 для средней линии и линии нижней контрольной границы.
Создав первую /2-карту, можно скопировать ее, а затем изменить, выбрав во всплывающем меню пункты Исходные данные и Параметры диаграммы. Всплывающее меню появляется после двойного щелчка правой кнопкой мыши.
ЕН.17.3. Построение R- и X -карт
Для построения R- и X -карт необходимо создать два рабочих листа, использующих простые арифметические формулы. Шаблоны этих рабочих листов показаны в табл. ЕН.17.3-ЕН.17.5. В них содержатся данные, характеризующие скорость доставки багажа (см. табл. 17.). В табл. ЕН.17.3 представлен шаблон рабочего листа RXKapTbi, предназначенного для вычисления нижней контрольной границы, средней линии и верхней контрольной границы на R- и X -картах. Некоторые формулы ссылаются на ячейки рабочего листа ДляРКарты, показанного в табл. ЕН.17.4 и ЕН.17.5. Второй шаблон содержит первые три строки табл. 17. и использует формулы, записанные в столбцах Е-G для преобразования контрольных границ, вычисленных на рабочем листе РХКарты. (Эти преобразования облегчают дальнейшее использование Мастера диаграмм при построении р-карты.)
Таблица ЕН.17.3. Шаблон рабочего листа RXKapTbi
- А . . ... ... В
1 Анализ скорости доставки багажа
2
3 Данные
4 Объем выборки/подгруппы 5
5
1И1 Промежуточные вычисления для /?-карты
7 RBar =СРЗНАЧ(ДляРКарт!С;С)
8 Множитель D3 0
9 Множитель D4 2,114
10
11 Контрольные границы для /?-карты
12 Нижняя контрольная граница =В8*В7
13 Среднее значение =В7
14 Верхняя контрольная граница = В9*В7
15
Окончание табл. ЕН. 17.3
16 Промежуточные вычисления для ХЬаг-карты
17 Средние значения подгрупп =СРЗНАЧ(ДляРКарт!В:В)
18 Множитель А2 0,577
19 Множитель А2 * RBar = В18*В7
20
21 Контрольные границы для ХВаг-карты
22 Нижняя контрольная граница =В17-В19
23 Среднее значение =В17
24 Верхняя контрольная граница = В17+В19
Таблица ЕН.17.4. Шаблон рабочего листа ДляКарт — столбцы А: F (показаны только первые три и последние две строки)
А В ’ С D Е ' F - ''
ililj День ХВаг Размах НКГ-R Среднее-R ВКГ-R
2 1 5,32 3,85 =ЕСЛИ(РХКарты!$В$12<0;""; РХКарты!$В$12) = RXKapTbi!$B$13 =RXKapTbi!$B$14
3 2 6,59 4,27 = ЕСЛИ(РХКарты!$В$12<0;""; РХКарты!$В$12) =RXKapTbi!$B$13 = RXKapTbi!$B$14
йж| 27 6,94 4,57 =ЕСЛИ(РХКарты!$В$12<0;""; РХКарты!$В$12) =РХКарты!$В$13 = RXKapTbi!$B$14
29 28 5,71 4,29 =ЕСЛИ(РХКарты!$В$12<0;""; РХКарты!$В$12) =RXKapTbi!$B$13 =RXKapTbi!$B$14
Таблица ЕН.17.5. Шаблон рабочего листа ДляКарт — столбцы G: I (показаны только первые три и последние две строки)
- j'' ' , <Si ,, .. . ' .. H ' । :-
1 НКГ-Х Среднее значение-Х ВКГ-Х
2 = ЕСЛИ(РХКарты!$В$22<0;""; RXKapTbi!$B$22) =RXKapTbi!$B$23 = RXKapTbi!$B$24
3 = ЕСЛИ(РХКарты!$В$22<0;""; RXKapTbi!$B$22) =RXKapTbi!$B$23 = RXKapTbi!$B$24
28 =ЕСЛИ(РХКарты!$В$22<0;""; RXKapTbi!$B$22) =RXKapTbi!$B$23 = RXKapTbi!$B$24
29 ==ЕСЛИ(РХКарты!$В$22<0;""; RXKaPTbi!$B$22) = RXKapTbi!$B$23 = RXKapTbi!$B$24
Формулы, записанные в нескольких строках, на реальном рабочем листе должны занимать одну строку.
ЕН.17.4. Создание R- и X -карт
Инструкции по созданию контрольных R- и X -карт совпадают с инструкциями по созданию /2-карт.
Например, чтобы создать контрольные R- и X -карты для данных о скорости доставки багажа, представленных в табл. 17., откройте рабочий лист ДляКарт из книги Chapter 17.xls и выполните команду Вставка^Диаграмма....
1. На первом этапе диалога выполните следующие действия.
1.1. Щелкните на корешке вкладки Стандартные, а затем выберите пункт Точечная в списке Тип.
1.2. Выберите первый вариант на панели Вид, сопровождаемый надписью “Точечная диаграмма позволяет сравнить пары значений”.
1.3. Щелкните на кнопке Далее>.
2. На втором этапе диалога выполните такие действия.
2.1. Щелкните на корешке вкладки Диапазон данных. Введите в диалоговом окне Диапазон ячейки Al: А2 9, Cl: F2 9 (для R-карт) или Al :В2 9, Gl: 12 9 (для X -карт) и установите переключатель Ряды в положение В столбцах.
2.2. Щелкнуть на кнопке Далее>.
3. На третьем этапе диалога сделайте следующее.
3.1. Щелкните на корешке вкладки Заголовки. Введите в диалоговом окне Название диаграммы заглавие контрольной карты, в диалоговом окне Ось X (категорий) — строку День, а в диалоговом окне Ось Y (значений) — строку Минуты.
3.2. По очереди щелкните на корешках вкладок Оси, Линии сетки, Легенда, Подписи данных и установите желаемые настройки.
3.3. Щелкните на кнопке Далее>.
4. На четвертом этапе диалога выполните такие действия.
4.1. Установите переключатель Поместить диаграмму на отдельном листе и введите название нового рабочего листа.
4.2. Щелкните на кнопке Готово.
Мастер диаграмм создает рабочий лист, который может содержать несколько ошибок форматирования: маркеры точек загромождают линию верхней контрольной границы, среднюю линию и линию нижней контрольной границы, линии проведены не пунктиром и имеют неправильный цвет. Для того чтобы исправить эти ошибки, необходимо выполнить инструкции, приведенные в разделе ЕН. 17.2.
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
1. Arndt, R., “Quality Isn’t Just for Widgets,” Business Week, July 22, 2002, 72-73.
2. Bothe, D. R., Measuring Process Capability (New York: McGraw-Hill, 1997).
3. Deming, W. E., Out of the Crisis (Cambridge, MA: MIT Center for Advanced Engineering Study, 1986).
4. Deming, W. E., The New Economics for Business, Industry, and Goverments (Cambridge, MA: MIT Center for Advanced Engineering Study, 1993).
5. Friedman, Т. L., The Lexus and the Olive Tree: Understanding Globalization (New York: Farrar, Straus and Giroux, 1999).
6. Gabor, A. The Man Who Discovered Quality (New York: Time Books, 1990).
7. Gitlow, H., A. Oppenheim, R. Oppenheim, and D.Levine, Tools and Methods for the Improvement of Quality, 3nd ed. (Homewood, IL: Irwin, 2005).
8. Gitlow, H., and D. Levine, A Course in Six Sigma® Management (Upper Saddle River, NJ: Financial Times-Prentice Hall, 2005).
9. Hahn, G. H., N. Doganaksoy, and R. Hoerl, “The Evolution of Six Sigma,” Quality Engineering, 2000,12, 317-326.
10. Halberstam, D., The Reckoning (New York: Morrow, 1986).
11. Levine, D. M., P. P. Ramsey, and R. K. Smidt, Applied Statistics for Engineers and Scientists Using Microsoft Excel and Minitab (Upper Saddle River, NJ: Prentice Hall, 2001).
12. Microsoft Excel 2002 (Redmond, WA: Microsoft Corporation, 2001).
13. Mitra, A., Fundamental of Quality Control and Improvement, 2nd ed. (Upper Saddle River, NJ: Prentice Hall, 1998).
14. Scherkenbach, W. W., The Deming Route to Quality and Productivity: Road Maps and Roadblocks (Washington, DC: CEEP Press, 1987).
15. Snee, R.D., “Impact of Six Sigma on Quality,” Quality Engineering, 2000, 12, ix-xiv.
16. Walton, M. The Deming Management Method (New York: Pedigree Books, Putnam, 1986).
Ответы на избранные вопросы
В этом разделе содержатся ответы на избранные вопросы.
Глава 1
1.2. 338 505 855 551 438 855 077 186 579 488 767 833 170 897 340 033 648 847 204 334 639 193 639 411 095 924 707 054 329 776 100 871 007 255 980 646 886 823 920 461 893 829 380 900 796 959 453 410 181 277 660 908 887 237 818 721 426 714 050 785 223 801 670 353 362 449 406.
Примечание: все числа, превышающие 902, отбрасываются.
1.4. Для личного собеседования метод простого случайного выбора менее эффективен из-за транспортных расходов (если, конечно, кандидаты не оплачивают свой проезд сами).
1.6. Вероятность извлечь любой элемент генеральной совокупности одинакова, поэтому выбор является случайным. Однако выбор двух разных элементов не является независимым, например, если элемент А уже включен в выборку, то элемент В будет включен в выборку, а элементы CvlD — нет.
1.8. 1. 2323 6737 5131 8888 1718 0654 6832 4667 6510 4877 4579 4269 2615 1308 2455 7830 5550 5852 5514 7182 0989 3205 0514 2256 8514 4642 7567 8896 2977 8822 5438 2745 9891 4991
4523 6847 9276 8646 1628 3554 9475 0899 2337 0892 0048 8033 6945 9826 9403 6858 7029
7341 3553 1403 3340 4205 0823 4144 1048 2949 8515 7479 5432 9792 6575 5760 0408 8112
2507 3742 1110 0023 4012 8607 4697 9664 4894 3928 7072 5815 3687 1507 7530 5925 7143
1738 1688 5625 8533 5041 2391 3483 5763 3081 6090 5169 0546. Примечание: все числа, превышающие 5000, отбрасываются. 2. 089 189 289 389 489 589 689 789 889 989 1089 1189 1289 1389 1489 1589 1689 1789 1889 1989 2089 2189 2289 2389 2489 2589 2689 2789 2889 2989 3089 3189 3289 3389 3489 3589 3689 3789 3889 3989 4089 4189 4289 4389 4489 4589 4689 4789 4889 4989. 3. За исключением счета № 0989, счета из случайной и систематической выборки не совпадают. Крайне маловероятно, что при случайном выборе систематически будут извлекаться одни и те же элементы.
1.12. 1. Время загрузки МРЗ-файла из Интернет является числовым, или количественным, показателем. 2. Время загрузки представляет собой переменную, измеренную по шкале отношений, поскольку истинная нулевая точка измерений представляет собой нуль.
В задачах 1.14-1.16 денежные суммы можно считать дискретными.
1.14. 1. Числовая, непрерывная, шкала отношений. 2. Числовая, дискретная, шкала отношений. 3. Числовая, непрерывная, шкала отношений. 4. Категорийная, номинальная шкала. 5. Категорийная, номинальная шкала. 6. Числовая, дискретная, шкала отношений. 7. Категорийная, номинальная шкала. 8. Числовая, дискретная, шкала отношений. 9. Категорийная, номинальная шкала. 10. Категорийная, номинальная шкала.
1.16. 1. Числовая, непрерывная, шкала отношений. 2. Числовая, дискретная, шкала отношений. 3. Категорийная, номинальная шкала. 4. Числовая, непрерывная, шкала отношений. 5. Категорийная, номинальная шкала. 6. Числовая, дискретная, шкала отношений. 7. Категорийная, номинальная шкала.
1.18. 1. В первом опросе измерения производятся по шкале отношений, а во втором — по порядковой. 2. Доход можно считать дискретным, если суммы округляются. В противном случае суммы можно считать непрерывными величинами. 3. Формат ответов, полученных в ходе первого опроса, является более предпочтительным, поскольку ответы измеряются по более точной шкале. 4. Второй вид анкеты предъявляет меньше требований к респондентам, поэтому количество ответов будет больше.
1.20. 1. В генеральную совокупность входят все работающие женщины, делающие покупки в универмаге. Из нее следует извлечь систематическую или случайную выборку женщин, делавших покупки в течение конкретного периода времени, например, в течение месяца.
1.22. 1. В выборку попадают только сотрудники конкретного подразделения компании. 2. Руководство компании не предприняло попыток уговорить сотрудников, отказавшихся отвечать на вопросы, заполнить анкету. 3. Выборочные статистики, полученные по данной выборке, никогда не совпадут с истинными параметрами генеральной совокупности. 4. Вопросы анкеты сформулированы неоднозначно.
1.24. Кто финансировал исследование? Зачем оно проводится? Из какой генеральной совокупности извлечена выборка? Каков объем выборки? Какой метод выбора был использован? Что представляет собой опрос: личное интервью, телефонный опрос или анкетирование по почте? Проводилось ли обучение интервьюеров? Проводилось ли пробное анкетирование? Какие дополнительные вопросы задавались респондентам? Были ли эти вопросы ясными, точными, непредвзятыми и корректными? Сколько респондентов отказалось отвечать на вопросы?
1.26. Кто финансировал исследование? Зачем оно проводится? Из какой генеральной совокупности извлечена выборка? Каков объем выборки? Какой метод выбора был использован? Что представляет собой опрос: личное интервью, телефонный опрос или анкетирование по почте? Проводилось ли обучение интервьюеров? Проводилось ли пробное анкетирование? Что означает выражение “адаптация к работе”? На какие вопросы отвечали респонденты? Были ли эти вопросы ясными, точными, непредвзятыми и корректными? Сколько респондентов отказалось отвечать на вопросы?
1.28. Кто финансировал исследование? Зачем оно проводится? Из какой генеральной совокупности извлечена выборка? Каков объем выборки? Какой метод выбора был использован? Что представляет собой опрос: личное интервью, телефонный опрос или анкетирование по почте? Проводилось ли обучение интервьюеров? Проводилось ли пробное анкетирование? Что означает выражение “бесплатный источник”? Какие вопросы задавались респондентам? Были ли эти вопросы ясными, точными, непредвзятыми и корректными? Сколько респондентов отказалось отвечать на вопросы?
1.48. Несмотря на дешевизну, скорость и высокую активность респондентов, люди принимают участие в Интернет-опросах по собственной инициативе. Поскольку такие респонденты, как правило, не выражают общественную точку зрения, данные, собранные в ходе Ин-тернет-опроса не позволяют делать корректных статистических выводов о генеральной совокупности.
1.50. 1. Генеральная совокупность состоит из всех рабочих. 2. Основу опроса можно сформировать с помощью списка сотрудников, полученного в отделе кадров. 3. В данном опросе можно применить метод простого случайного выбора. 4. Ответ является категорийной переменной. 5. Данный показатель является статистикой, поскольку он оценивает долю респондентов, нашедших работу путем личного или сетевого общения.
1.52. 1. При низкой активности респондентов следует учесть систематическую ошибку, связанную с отказами от ответов. Низкая активность респондентов приводит к увеличению ошибки выборочного обследования. 2. Исследователи должны связаться с респондентами, отказавшимися отвечать на вопросы, по почте или с помощью телефона, и попытаться уговорить их заполнить анкету. 3. Исследователям следует заручиться поддержкой начальника полиции и президента Общества полицейских и попросить их повлиять на подчиненных, подчеркнув важность проводимого опроса. Начальники подразделений должны издать соответствующий приказ. С той же целью начальники подразделений в течение недели должны напоминать подчиненным о необходимости принять участие в опросе.
1.54. 1. Прежде чем делать выводы о результатах опроса, следует выяснить: 1) какова цель опроса; 2) какой метод выбора был использован; 3) какова активность респондентов; 4) что является основой опроса и 5) как были сформулированы вопросы. 2. Генеральная совокупность состоит из всех работающих женщин, в том числе, использующих гибкий график работы и не проживающих в данном географическом регионе. Основу опроса можно создать с помощью списка женщин, полученного в налоговой администрации региона. Эта генеральная совокупность состоит из двух естественных страт: женщин, использую-
щих гибкий график работы, и женщин, не имеющих такой возможности. Следовательно, для лучшего представления генеральной совокупности необходимо применить метод стратифицированного выбора.
1.56. 1. Прежде чем делать выводы о результатах опроса, следует выяснить: 1) какова цель опроса; 2) какой метод выбора был использован; 3) какова активность респондентов; 4) что является основой опроса и 5) как были сформулированы вопросы. 2. Примером категорийной переменной является ответ на вопрос: “Считаете ли вы, что причиной безработицы является экономическое положение страны?”. 3. Примером числовой переменной является величина начальной зарплаты. Уровень измерений: шкала отношений. 4. Данная величина является статистикой, поскольку она описывает свойство выборки. 5. Следует применить метод стратифицированного выбора. Работодателей следует разделить на две страты в соответствии с отраслями промышленности. Студентов следует разделить на страты в соответствии с полом и образованием.
1.58. 1. Генеральная совокупность, которую мы хотим описать, состоит из граждан, имеющих право голоса и действительно желающих принять участие в выборах. 2. Можно сформировать случайную выборку, состоящую из избирателей, уже посетивших избирательный участок. 3. К числу возможных проблем относятся ошибка охвата и систематическая ошибка, связанная с отказом отвечать на вопросы. Это не позволяет правильно предска-затыисход будущих выборов.
1.60. 1. Генеральная совокупность: владельцы кошек. 2. Основа опроса: домовладельцы, живущие в США. 4. а) категорийный; б) категорийный; в) числовой; г) категорийный.
Глава 2
2.4. 50 74 74 76 8189 92.
2.6. 1. 5, 6, 10, 11, 11, 12, 13, 14, 14, 14, 15, 15, 15, 15, 16, 16, 16, 16, 17, 17, 17, 19, 19, 20, 22, 23, 25, 28, 30, 34. 3. Диаграмма “ствол и листья” содержит больше информации, чем упорядоченный массив, поскольку она характеризует распределение данных в массиве. 4. Нет, не кажется. Есть два вида акций, у которых показатель Р/Е не превышает 10, и два — у которых он превосходит 30.
2.8. 1. 0 0 5 5 5 5 5 5 6 6 6 7 7 7 8 8 9 9 9 10 10 10 10 10 12 12. 3. Диаграмма “ствол и листья” более информативна, поскольку она позволяет оценить распределение данных в массиве. 4. Величина ежемесячной оплаты банковских услуг концентрируется в окрестности 7 долл., при этом у 22 банков стоимость обслуживания колеблется между 5 и 10 долл.
2.10. 1. Границы групп: 10 — 20, 20 — 30, 30 — 40, 40 — 50, 50 — 60, 60 — 70, 70 — 80, 80 — 90, 90 — 100. 2. 10. 3. Срединные точки групп: 15, 25, 35, 45, 55, 65, 75, 85, 95.
2.12. 9. Ежемесячная стоимость потребления электричества концентрируется между 140 и 160 долл. В этом интервале находится более четверти всех значений. 10. Процентная диаграмма, построенная в задаче 4, явно демонстрирует верхнюю и нижнюю границы семи интервалов, а также процентную долю счетов, лежащих в каждом интервале. Например, процентный полигон, построенный в задаче 5, точнее демонстрирует типичное значение, присущее каждому интервалу (срединную точку). Однако, поскольку точки на графике не сопровождаются метками, полигон лишь аппроксимирует процентное распределение электрических счетов, попадающих в каждый интервал. Оба графика дают визуальное представление о распределении счетов за электричество. Стрелка, изображенная на кривой распределения, построенной в задаче 8, концентрирует внимание на распределении интегральных процентов. Однако, поскольку количество счетов накапливается, этот график не позволяет четко выявить распределение отдельных счетов за потребление электричества.
2.14. 6. Большинство продаж бензина концентрируется в интервале от 11 до 11,9 галлонов.
2.16. 5. Да, работа пресса соответствует стандартам, поскольку только одна заготовка из 100 является дефектной.
2.18. 2. Да, между величинами X и У существует положительная зависимость.
2.20. 2. Нет, между ценой и стоимостью электроэнергии не существует положительной зависимость. 3. Нет, нельзя.
2.22. 2. Нет, между емкостью батареек и продолжительностью телефонных разговоров нет никакой зависимости. 3. Нет, данные не подтверждают предположение о том, что разговоры по мобильному телефону, имеющему большую емкость батареек, должны быть более продолжительными.
2.24. 2. Наблюдается убывающий тренд индекса S&P 500 в период с января 2002 г. по июль 2002 г. С 7 января 2002 г. по 8 июля 2002 г. этот индекс потерял около 20%. В период с 8 июля по 30 декабря 2002 г. индекс колебался около 900 пунктов. 4. С 7 января по 6 мая 2002 г. цены были практически стабильными. До 28 мая они слегка росли, а после этой даты снижались вплоть до 30 декабря 2002 г. 6. Стоимость акций компании Target Corporation возрастала с 7 января по 19 февраля 2002 г. После этой даты тренд стал убывающим. 8. Стоимость акций компании Sara Lee с 7 января по 1 июля 2002 г. была практически стабильной. Затем за две недели она снизилась на 16%, а впоследствии ее тренд стал возрастающим вплоть до 30 декабря 2002 г. 9. В целом, тренд индекса S&P, как и стоимость акций компании Target Corporation, в период с 7 января по 8 июля 2002 г. были слабо убывающими. Стоимость акций компаний Sears и Sara Lee была практически стабильной с 7 января по 1 июля 2002 г. Затем стоимость акций компании Sears стала падать, а акций компании Sara Lee — расти.
2.26. 2. Объем лимонада имеет убывающий тренд. 3. Вероятно, объем лимонада в следующей бутылке будет равен приблизительно 1,87 л. 4. Более точным является прогноз, данный в задаче 3.
2.30. 4. Диаграмма Парето является более информативной, чем круговая или линейчатая, поскольку содержит не только частоты, упорядоченные по убыванию, но и полигон накопленных частот. Диаграмма Парето ясно показывает, что более 90% всех электронных переводов были выполнены с банковских карточек Visa, Master Card и American Express.
2.32. 4. Если требуется сравнивать частоты, предпочтительнее линейчатая диаграмма. Если требуется исследовать долю определенной категории, следует выбрать круговую диаграмму.
2.34. 4. Диаграмма Парето является более информативной, чем круговая, поскольку содержит не только частоты, упорядоченные по убыванию, но и полигон накопленных частот. Диаграмма Парето ясно показывает, что 44% ошибок соискателей работы связано с отсутствием знаний о компании.
2.36. 2. Чтобы уменьшить общее количество жалоб, администрация больницы должны сосредоточить внимание на улучшении качества питания, которое является предметом более 30,5% жалоб. Следующими по важности факторами являются медленное реагирование на вызовы больных и хамство персонала (18,5 и 16,1% жалоб соответственно). В совокупности, эти три фактора являются предметами более 65% всех жалоб.
2.40. 3. В целом, объем розничных продаж в швейной промышленности в период с апреля 2001 по апрель 2002 г. демонстрировал умеренный рост. Исключение составляют компания Talbots, объем продаж которой слабо уменьшался, и компания Gap, объем продаж которой упал на почти 200 млн. долл.
2.42. 4. Общая таблица позволяет компенсировать эффект, возникающий вследствие неодинакового размера групп. Кроме того, она демонстрирует, что количество недостоверных анализов, проведенных днем и вечером, сильно отличается от количества правильных анализов. Например, днем были проведены 40% всех недостоверных и 68% всех правильных анализов. 5. Директор лаборатории мог бы уменьшить количество брака, сократив количество вечерних анализов, которые чаще других оказываются недостоверными.
2.48. 1. Полицейский из Вашингтона изображен не только более высоким, но и более крупным. Это искажает реальную разницу между размерами полицейских департаментов. Намного лучше было бы использовать простую линейчатую диаграмму.
2.62. 6. Да, время принятия решения характеризуется большой изменчивостью. Длительность рассмотрения жалобы изменяется от 1 до 165 дней. Хотя 72% жалоб рассматриваются на протяжении 50 дней, остальные 28% рассматриваются в среднем 115 дней. 7. Следует сообщить президенту компании, что более 50% жалоб рассматриваются в течение месяца, и указать, что изучение некоторых жалоб растягивается на три и даже четыре месяца.
2.64. 4. 97,50% партий соответствует стандарту.
2.66. 1. Посещаемость большинства игр колебалась от 9 000 до 17 000. Распределение имеет положительную асимметрию, причем только семь игр посетило более 29 000 человек. 2. Посещаемость большинства игр колебалась от 9 000 до 17 000. Распределение имеет положительную асимметрию, причем только семь игр посетило более 29 000 человек. 3. При сравнении нескольких наборов данных процентный полигон более предпочтителен, чем гистограмма. Если рассматривается только один набор данных, то одинаково приемлемыми являются как процентная гистограмма, так и процентный полигон. 4. Посещаемость игр, сопровождавшихся рекламными мероприятиями, колебалась от 9 000 до 25 000, в то же время посещаемость большинства игр, не сопровождавшихся рекламными мероприятиями, колебалась от 9 000 до 17 000. Рекламные мероприятия повышают посещаемость матчей.
2.68. 11. Результаты решения задач 9 и 10 свидетельствуют, что среди автомобилей, использующих обычный бензин, процент автомобилей с передним приводом, выше, чем процент автомобилей с задним приводом.
2.70. 7. Процентный полигон и процентный полигон отображают, в сущности, одну и ту же информацию. Преимущество процентного полигона заключается в том, что на одном рисунке можно изобразить несколько графиков одновременно. Если накопленный процент не превышает требуемой величины, следует применять процентный полигон. Кроме того, процентный полигон позволяет сравнивать несколько групп. 8. Между количеством побед и размерами выплат игрокам существует положительная зависимость.
2.72. 5. Единственной переменной, позволяющей правильно предсказать стоимость принтера, является стоимость печати текста. Между ценой принтера и стоимостью печати текста существует отрицательная зависимость. Чем выше стоимость печати текста, тем ниже цена принтера.
2.74. 7. Наиболее предпочтительной является диаграмма Парето, на которой представлены не только частоты, упорядоченные по убыванию, но и полигон накопленных частот. 8. Ближний Восток, обладающий 60% запасов нефти, является крупнейшим резервуаром. Среди стран крупнейшими запасами обладает Саудовская Аравия, за ней следуют Ирак, Объединенные Арабские Эмираты и Кувейт. На эти четыре страны приходится более половины разведанной нефти в мире.
2.76. 3. Внешне обе диаграммы очень похожи и различаются только шкалой оси X. Если требуется исследовать только абсолютное количество уникальных пользователей, позволяющее обосновать количество рекламных объявлений, предпочтительнее использовать линейчатую диаграмму абсолютных величин. Если же требуется оценить долю компании на рынке, необходимо построить линейчатую диаграмму процентов Интернет-аудитории.
2.78. 3. Сравнивая два набора данных, следует применять параллельную линейчатую диаграмму. 4. Наибольшая доля доходов на рынке принадлежит компании AT&T, за ней следуют компании MCI, Sprint, Verizon и VarTec. Кроме того, компании AT&T принадлежит наибольшая доля частных клиентов, за ней следуют компании MCI, Verizon, Sprint и VarTec.
2.80. 1. Более 80% рекламаций вызвала марка 23575R15. 2. Большинство рекламаций (70%) вызвано отслоением протектора. 3. У шин модели АТХ 70% рекламаций вызвано отслоением протектора. 4. Количество рекламаций довольно равномерно распределено среди трех видов происшествий, причем на неизвестные (другие) происшествия приходится почти 40% рекламаций, 35% рекламаций связано с отслоением протектора, а разрыв шины стал причиной около 25% рекламаций. 5. Диаграмма Парето демонстрирует, что модель АТХ марки 23575R15 вызвала более 80% рекламаций. Основной причиной аварий, связанных с этой маркой шин АТХ, является отслоение протектора. Для модели Wilderness невозможно выделить какой-то конкретный основной вид происшествий. Отслоение протектора у шин модели АТХ стало причиной 1365/2504 = 54,5% рекламаций.
Глава 3
3.2. 1. Среднее = 7, медиана = 7, мода = 7. 2. Размах = 9, межквартильный размах = 5, дисперсия = 10,8, коэффициент вариации = (3,286/7) х 100% = 46,94%, стандартное отклонение = 3,286. 3. Поскольку среднее значение и медиана совпадают, распределение является симметричным.
3.4. 1. Среднее = 2, медиана = 7, мода = 7. 2. Размах =17, межквартильный размах =14,5, дисперсия = 62, коэффициент вариации = (7,874/2) х 100% = 393,7% , стандартное отклонение = 7,874. 3. Поскольку среднее значение меньше медианы, распределение имеет отрицательную асимметрию.
3.6. 19,58%.
3.8. 1. Гамбургеры: среднее = 34,29, медиана = 35, (^ = 31, Q3 = 39. Куриное мясо: среднее =20,64, медиана = 18, Qi = 15, Q3 = 27. 2. Гамбургеры: S2 = 60,905, S = 7,804, размах = 24, межквартильный размах = 8, коэффициент вариации = 22,76% . Куриное мясо: S2 = 95,455, S = 9,770, размах = 32, межквартильный размах = 12, коэффициент вариации =47,34%. 3. Данные, характеризующие жирность куриного мяса, обладают положительной асимметрией. Данные, характеризующие жирность гамбургеров, обладают отрицательной асимметрией. 4. В целом, гамбургеры жирнее куриного мяса. Наименьшая жирность гамбургеров на 50% превышает среднюю жирность куриного мяса. Жирность примерно 25% гамбургеров превышает наибольшую жирность куриного мяса.
3.10. 1. Среднее = 16,83, медиана = 16, мода = 15, размах = 29, дисперсия = 41,18, стандартное отклонение = 6,42. 2. Среднее отношение Р/Е для 30 видов акций, котируемых на Нью-Йоркской фондовой бирже, равно 16,83. В большинстве случаев отношение Р/Е равно 15, в то время как отношение Р/Е, имеющее средний ранг, равно 16. Среднее значение квадратов разностей между всеми значениями отношения Р/Е в выборке и выборочным средним равно 41,18.
3.12. 1. Среднее = 44,69, медиана = 46,25. Моды не существует. 2. Размах = 60, S2 = 370,4241, 8= 19,2464. 3. Средний процент повторно используемого кода равен 44,69%. Процент повторно используемого кода, имеющий средний ранг, равен 46,25. Ни одно конкретное значение не повторяется более одного раза. Среднее значение квадратов разностей между всеми выборочными значениями и выборочным средним равно 370,4241. По эмпирическому правилу приблизительно две трети процентов повторно используемого кода колеблется между 19,25 и 44,69%.
3.14. 1. Среднее = 4,287, медиана = 4,5, Qx = 3,20, Q3 = 5,55. 2. Дисперсия = 2,683, стандартное отклонение = 1,638, размах = 6,08, межквартильный размах = 2,35, коэффициент вариации = 38,21% . 3. Поскольку среднее значение меньше медианы, распределение имеет отрицательную асимметрию. 4. Среднее значение и медиана превышают 5 мин. Это означает, что относительно малые величины встречаются реже, чем относительно большие. Однако в шести из 15 банков, образующих выборку (40%), время ожидания превышает 5 мин. Итак, несмотря на то, что, вероятнее всего, клиент будет обслужен менее, чем за 5 мин., менеджер банка слишком уверенно заявил, что клиент наверняка будет обслужен быстрее, чем за 5 мин. 5. В соответствии с эмпирическим правилом от 90 до 95% наблюдений лежат в интервале, границы которого отстоят от математического ожидания на два стандартных отклонения. Следовательно, округляя результат выражения 4,287 + 2x1,638= 7,563, получаем, что приблизительно в 5% случаев клиент получит компенсацию за несвоевременное обслуживание.
3.16. 1.-1,245%. 2.-1,667%. 3. Средняя геометрическая норма прибыли точнее оценивает изменение стоимости акций с течением времени.
3.18. 1. 3,67%. 2. 4,11% . 3. 1,61%. 4. Тридцатимесячный депозитный сертификат имеет наиболее высокую норму прибыли за три года, за ним следуют годовой сертификат и депозитный сертификат денежного рынка, имеющий наименьшую норму прибыли. 5. С 2000 по 2002 годы депозитные сертификаты и сертификаты денежного рынка имели наибольшую норму прибыли. Вложения в драгоценные металлы были менее выгодными. Наименьшую прибыль приносили акции компаний.
3.20. 1. Математическое ожидание = 6. 2. Дисперсия генеральной совокупности = 9,4, стандартное отклонение генеральной совокупности = 3,066.
3.22. 2. Математическое ожидание = 10,28. 3. о2 = 4,1820, о = 2,045. 4. 64% . 5. 94%. 6.100%. 7. Процентная доля меньше, чем ожидалось по эмпирическому правилу.
3.24. 1. Математическое ожидание = 8,24. Средняя 52-недельная доходность пяти крупнейших облигационных фондов равна 8,24%. 2. Дисперсия генеральной совокупности = 1,86, стандартное отклонение генеральной совокупности = 1,36. Средний квадрат разностей между значениями доходности и математическим ожиданием равна 1,86. В большинстве случаев 52-недельная доходность колеблется от 1,36 до 8,24%. 3. Поскольку стандартное отклонение генеральной совокупности не превышает 1/7 математического ожидания, изменчивость доходности пяти крупнейших облигационных фондов меньше, чем изменчивость большинства фондов, 52-недельная доходность которых колеблется от 1,36 до 8,24%.
3.26. 1. Среднее =-18,59. В среднем 52-недельная доходность 10 крупнейших акционерных фондов не превышает 18,59%. 2. Дисперсия = 24,98, стандартное отклонение = 5,00. Средний квадрат разностей между значениями 52-недельной доходности и математическим ожиданием равна 24,98. Если распределение является приближенно симметричным, около 68% значений 52-недельной доходности будут отличаться от -18,59% не более чем на 5% . 3. Пять базовых показателей: -24,3, -21,6, -19,9, -17,1 и -6,6. Поскольку распределение не симметрично, для объяснения изменчивости данных следует применить правило Бьенамэ-Чебышева. В соответствии с правилом Бьенамэ-Чебышева, как минимум 75% наблюдений лежит в окрестности математического ожидания на расстоянии, не превышающем двух стандартных отклонений, т.е. между -28,58 и -8,59, и как минимум 88,89% наблюдений отличаются от математического ожидания не более чем на три стандартных отклонения, т.е. лежат в интервале от -33,58 до -3,60. В данном наборе данных 90% наблюдений расположено в интервале от -28,58 до -8,59, а все наблюдения лежат в интервале от -33,58 до -3,60. 4. Поскольку 90% наблюдений расположено в окрестности математического ожидания на расстоянии, не превышающем двух стандартных отклонений, и все наблюдения отличаются от математического ожидания не более чем на три стандартных отклонения, данный набор данных не содержит выбросов. 5. Пять крупнейших облигационных фондов, приведенных в табл. 3.1, приносят наибольший доход. Десять крупнейших акционерных фондов характеризуются наибольшей изменчивостью доходности.
3.28. 1. Пять базовых показателей: 2 3 7 8,5 9. 2. Распределение имеет отрицательную асимметрию. 3. Расстояние от Qj до медианы больше, чем от медианы до Q3. Это подтверждает вывод об отрицательной асимметрии распределения.
3.30. 1. Пять базовых показателей: 0 3 7 9 12. 2. Распределение имеет отрицательную асимметрию. 3. Анализ блочной диаграммы показывает, что расстояние от Qj до медианы больше, чем от медианы до Q3. Это подтверждает вывод об отрицательной асимметрии распределения.
3.32. 1. Пять базовых показателей: 264 307,5 451 553,5 1 049. 2. Распределение имеет положительную асимметрию. 3. Поскольку набор данных невелик, одна крупная величина (1 049) смещает распределение вправо.
3.34. 1. Пять базовых показателей: 15 20 22 26 30. 2. Распределение сумм возвращенных чеков имеет слабую положительную асимметрию. 3. Пять базовых показателей: 0 5 7 10 12. 4. Распределение ежемесячной оплаты имеет отрицательную асимметрию. 5. Средняя величина суммы возвращенных чеков превышает среднюю ежемесячную оплату. В то время как распределение сумм возвращенных чеков является практически симметричным, распределение ежемесячной оплаты смещено влево, причем несколько банков установили весьма низкую величину ежемесячной оплаты услуг или не взимают ее совсем.
3.36. 1. Минимум = 308, Q, = 593, медиана = 895,5, Q3 == 1 425, максимум = 1 720. 2. Расйределе-ние имеет положительную асимметрию.
3.38. 1. Пять базовых показателей: 0,38 3,2 4,5 5,55 6.46. 2. Распределение имеет отрицательную асимметрию. 3. Пять базовых показателей: 3,82 5,64 6,68 8,73 10,49. 4. Распределение имеет слабую положительную асимметрию. 5. Средняя величина ожидания в отделе-
нии банка, расположенном в промышленном районе, меньше, чем в отделении, расположенном в жилом районе. Время ожидания в отделении банка, расположенном в жилом районе, немного дольше, поскольку в выборке, характеризующей скорость обслуживания клиентов в отделении банка, расположенном в промышленном районе, содержится несколько очень маленьких величин.
3.40. В соответствии со статьей между темпами роста биржи NASDAQ и объемом инвестиций в информационные технологии на протяжении 90-х годов существовала положительная корреляция. Индекс NASDAQ представляет собой взвешенное среднее стоимости акций высокотехнологичных компаний, и, следовательно, быстрый рост инвестиций в информационные технологии положительно влиял на его величину.
3.42. 1. г =-0,2810. 2. Между ценой и стоимостью электроэнергии существует очень слабая отрицательная корреляция.
3.44. 1. г= 0,3409. 2. Между продолжительностью разговоров и емкостью батарей существует очень слабая положительная корреляция. 3. Предположение о том, что владельцы более емких батареек разговаривают дольше, не подтверждается данными.
3.46. 1. Среднее = 25. 2. Стандартное отклонение = 11,01.
3.48. 1. Март: среднее = 4 720, апрель: среднее = 4 400.
2. Март: стандартное отклонение = 2 250,0794, апрель: стандартное отклонение = 2 657,2965.
3. Среднее арифметическое уменьшилось на 320 долл., а стандартное отклонение увеличилось на 407,2171 долл.
3.50. 1. Подразделение А: среднее = 40,4348. Подразделение Б: среднее = 36,8310. 2. Подразделение/!: стандартное отклонение = 11,0969. Подразделение Б: стандартное отклонение = 8,3341. 3. Средний возраст сотрудников и его изменчивость в подразделении А больше, чем в подразделении Б.
3.61. 1. Среднее значение = 43,89, медиана = 45. 2. Q, = 18,3, Q3 = 63. 3. Размах = 76, межквартильный размах = 45, дисперсия = 639,2564, стандартное отклонение = 25,28, коэффициент вариации = 57,61% . 5. Распределение имеет положительную асимметрию, так как некоторые страховки оформляются чрезвычайно долго. 6. В среднем процесс оформления страховки продолжается 43,89 дня, причем 50% страховок оформляются не более 45 дней. Кроме того, 50% страховок оформляются от 18 до 63 дней. Около 67% заявок на оформление страховок рассматриваются от 18,6 до 69,2 дня.
3.63. 1. С рекламной кампанией: среднее = 20 748,93, стандартное отклонение = 8 109,50. Без рекламной кампании: среднее = 13 935,70, стандартное отклонение = 4 437,92. 2. С рекламной кампанией: минимум = 10 470, = 14 905, медиана = 19 775, Q3 = 24 456, максимум =40 605. Без рекламной кампании: минимум = 9 555, = 11 779, медиа-
на = 12 952, Q3 = 14 367, максимум = 28 834. 4. Рекламная кампания повышает среднюю посещаемость на 6 813, причем изменчивость посещаемости матчей, сопровождаемых рекламными мероприятиями больше, чем посещаемость обычных матчей. Существует много факторов, влияющих на посещаемость матчей: погода, время проведения матча, уровень соперников и т.д.
3.65. 1. Среднее = 1 723,4, медиана = 1 735, размах = 348, стандартное отклонение = 89,55. 2. Средняя выборочная величина силы, необходимой для разрушения изолятора, равна 1 723,4 фунта. Упорядоченная средняя величина силы, необходимой для разрушения изолятора, равна 1 735 фунтов. Разность между наибольшей и наименьшей величиной силы, необходимой для разрушения изолятора, равна 348 фунтов. Приблизительно в 68% случаев сила разрушения, необходимая для разрушения изолятора, лежит в интервале от 89,55 до 1 723,4 фунтов. 3. Пять базовых показателей: 1 522 1 662 1 735 1 784 1 870. 4. Распределение имеет отрицательную асимметрию. 5. Во всех наблюдаемых случаях изоляторы разрушались, если к ним прикладывалась сила, превышающая 1 500 фунтов. Это полностью соответствует стандартам компании.
3.67. Типография А. 1. Среднее =9,382, медиана = 8,515. 2. Первый квартиль = 7,29, третий квартиль = 11,42. 3. Размах = 17,2, межквартильный размах = 4,13, дисперсия = 15,981, стандартное отклонение = 3,998, коэффициент вариации = 42,61% . 5. Распределение имеет положительную асимметрию. Типография Б. 1. Среднее = 11,354, медиана = 11,96. 2. Первый квартиль = 6,25, третий квартиль = 14,25. 3. Размах = 23,45, межквартиль-
ный размах = 8, дисперсия = 26,277, стандартное отклонение = 5,126, коэффициент вариации = 45,15%. 5. Распределение длительности производства в типографии Б имеет отрицательную асимметрию. 6. Длительность производства в типографиях А и Б отличаются друг от друга. Длительность производства в типографии Б имеет более широкий размах, большую дисперсию, большую медиану, больший третий квартиль и большее экстремальное значение, чем типография А.
3.69. Стоимость порции сухого корма для собак. 1. Среднее = 0,549, медиана = 0,54. 2. Первый квартиль = 0,49, третий квартиль = 0,65. 3. Размах = 0,69, межквартильный размах = 0,16, дисперсия = 0,0226, стандартное отклонение = 0,150, коэффициент вариации = 27,41%. Стоимость порции консервированного корма для собак. 1. Среднее = 1,990, медиана= 1,555. 2. Первый квартиль = 1,39, третий квартиль = 1,96. 3. Размах = 7,41, межквартильный размах =0,57, дисперсия = 2,108, стандартное отклонение = 1,452, коэффициент вариации = 72,98%. Стоимость порции сухого корма для кошек. 1. Среднее = 0,27, медиана = 0,26. 2. Первый квартиль = 0,2, третий квартиль = 0,29. 3. Размах = 0,46, межквартильный размах =0,09, дисперсия = 0,0106, стандартное отклонение = 0,103, коэффициент вариации =38,15%. Стоимость порции консервированного корма для кошек. 1. Среднее = 1,095, медиана = 0,84. 2. Первый квартиль = 0,68, третий квартиль = 1,39. 3. Размах = 2,09, межквартильный размах = 0,71, дисперсия = 0,354, стандартное отклонение = 0,595, коэффициент вариации = 54,32%. Содержание белка в порции сухого корма для собак. 1. Среднее = 65,393, медиана = 65,5. 2. Первый квартиль = 59, третий квартиль = 69. 3. Размах = 30, межквартильный размах = 10, дисперсия = 61,136, стандартное отклонение = 7,819, коэффициент вариации = 11,96%. Содержание белка в порции консервированного корма для собак. 1. Среднее = 92,042, медиана =92. 2. Первый квартиль = 81, третий квартиль = 103. 3. Размах = 86, межквартильный размах = 22, дисперсия = 400,563, стандартное отклонение = 20,014, коэффициент вариации = 21,74%. Содержание белка в порции сухого корма для кошек. 1. Среднее = 35,846, медиана = 36,5. 2. Первый квартиль = 35, третий квартиль = 38. 3. Размах =14, межквартильный размах = 3, дисперсия = 8,935, стандартное отклонение = 2,989, коэффициент вариации = 8,34%. Содержание белка в порции консервированного корма для кошек. 1. Среднее = 45,421, медиана = 45. 2. Первый квартиль = 38, третий квартиль = 51. 3. Размах = 29, межквартильный размах = 13, дисперсия = 75,924, стандартное отклонение = 8,713, коэффициент вариации = 19,18%. Содержание жира в порции сухого корма для собак. 1. Среднее = 34,607, медиана = 32,5. 2. Первый квартиль = 29, третий квартиль = 41. 3. Размах = 24, межквартильный размах = 12, дисперсия = 43,062, стандартное отклонение = 6,562, коэффициент вариации = 18,96%. Содержание жира в порции консервированного корма для собак. 1. Среднее = 53,125, медиана = 52. 2. Первый квартиль = 42, третий квартиль = 67. 3. Размах = 57, межквартильный размах = 25, дисперсия = 245,245, стандартное отклонение = 15,660, коэффициент вариации = 29,48%. Содержание жира в порции сухого корма для кошек. 1. Среднее = 14,731, медиана = 14. 2. Первый квартиль = 12, третий квартиль = 16. 3. Размах = 13, межквартильный размах = 4, дисперсия = 13,085, стандартное отклонение = 3,6, коэффициент вариации = 24,56%. Содержание жира в порции консервированного корма для собак. 1. Среднее = 23,947, медиана = 26. 2. Первый квартиль = 19, третий квартиль = 27. 3. Размах = 20, межквартильный размах = 8, дисперсия = 27,608, стандартное отклонение = 5,254, коэффициент вариации = 21,94%. 5. Стоимость всех видов корма, кроме сухого корма для собак, имеет положительную асимметрию. Особенно сильную асимметрию имеет стоимость консервированного корма для собак. Распределение стоимости консервированного корма для кошек также имеет заметную положительную асимметрию. Распределение содержания белка в консервированном корме для кошек и сухом корме для собак имеет слабую положительную асимметрию, в то же время распределение содержания белка в сухом корме для кошек имеет отрицательную асимметрию. Распределение жира в консервированном корме для кошек имеет слабую отрицательную симметрию, в то время как распределение жира в сухом корме для собак и кошек имеет положительную асимметрию. 6. В среднем, консервированный корм для собак стоит больше, чем сухой корм для собак. Кроме того, консервированный корм для кошек также стоит больше, чем сухой корм для собак. В среднем, в консервированном корме для собак больше белка, чем в сухом корме для собак, а в консервированном корме для кошек — больше, чем в сухом корме для кошек. В среднем, содержание жира в консервированном корме для собак больше, чем в сухом корме для собак, а содержание жира в
консервированном корме для кошек больше, чем в сухом корме для кошек. Размах стоимости одной порции консервированного корма для собак и кошек больше, чем размах стоимости сухого корма для собак и кошек. Размах содержания белка в одной порции консервированного корма для собак и кошек больше, чем размах содержания белка в одной порции сухого корма для собак и кошек. Аналогично размах содержания жира в одной порции консервированного корма для собак и кошек больше, чем размах содержания жира в одной порции сухого корма для собак и кошек.
3.71. Время проезда. 1. Среднее = 22,428, медиана = 22,50. 2. Первый квартиль = 20,10, третий квартиль = 24,30. 3. Размах = 15,80, межквартильный размах = 4,20, дисперсия = 12,536, стандартное отклонение = 3,541, коэффициент вариации = 15,79%. Дома с восемью комнатами. 1. Среднее = 15,835, медиана = 15,50. 2. Первый квартиль = 12,0, третий квартиль =19,50. 3. Размах = 20,70, межквартильный размах =7,50, дисперсия = 26,312, стандартное отклонение = 5,130, коэффициент вариации = 32,39%. Оплата дома составляет более 30% дохода. 1. Среднее = 25,128, медиана = 24,80. 2. Первый квартиль = 21,40, третий квартиль = 27,10. 3. Размах = 23,50, межквартильный размах = 5,70, дисперсия = 24,381, стандартное отклонение = 4,938, коэффициент вариации = 19,65%. Медиана семейного дохода. 1. Среднее = 40 794,255, медиана = 39 480,00. 2. Первый квартиль = 36 385,00, третий квартиль = 45 654,00.3. Размах = 25 657,00, межквартильный размах = 9 269,00, дисперсия = 41 471 014,794, стандартное отклонение = 6 439,799, коэффициент вариации = 15,79%. 5. Распределение всех переменных имеет небольшую положительную асимметрию.
3.73. г= 0,0210. 2. г = -0,2255. 3. Цена и стоимость электроэнергии не связаны друг с другом, а между ценой и стоимостью фильтра существует слабая обратная зависимость.
3.75. Все модели. Пробег в милях на галлон топлива. 1. Среднее = 20,703, медиана = 21. 2. Первый квартиль = 18, третий квартиль = 22. 3. Размах = 31, межквартильный размах =4, дисперсия = 21,894, стандартное отклонение = 4,679, коэффициент вариации = 22,60% . Длина. 1. Среднее = 187,190, медиана = 187. 2. Первый квартиль = 177,5, третий квартиль = 194,5. 3. Размах =72, межквартильный размах =17, диспер-
сия = 173,939, стандартное отклонение = 13,188, коэффициент вариации = 7,05% . Ширина. 1. Среднее = 71,339, медиана =71. 2. Первый квартиль = 69, третий квартиль =73. 3. Размах =15, межквартильный размах = 4, дисперсия = 10,426, стандартное отклонение = 3,229, коэффициент вариации = 4,53%. Грузоподъемность. 1. Среднее = 27,508, медиана = 18. 2. Первый квартиль = 14, третий квартиль = 37. 3. Размах = 79, межквартильный размах = 23, дисперсия = 362,633, стандартное отклонение = 19,043, коэффициент вариации = 69,23%. Радиус поворота. 1. Среднее = 39,926, медиана = 40. 2. Первый квартиль =38, третий квартиль = 41. 3. Размах =19, межквартильный размах = 3,
дисперсия = 7,669, стандартное отклонение = 2,769, коэффициент вариации = 6,94%. Вес. 1. Среднее = 3 616,074, медиана = 3 530. 2. Первый квартиль = 3 162,5, третий квартиль = 3 990. 3. Размах = 5 120, межквартильный размах = 827,5, дисперсия = 515 343,003, стандартное отклонение = 717,874, коэффициент вариации = 19,85%. 5. Распределения ширины, емкости багажника и веса имеют положительную асимметрию. Распределение пробега в милях на галлон топлива и радиуса поворота имеют слабую положительную асимметрию. Распределение длины является симметричным. 7. Автомобили, не являющиеся спортивными моделями. Пробег в милях на галлон топлива. 1. Среднее = 22,156, медиана = 21. 2. Первый квартиль =19, третий квартиль = 23. 3. Размах = 24, межквартильный размах = 4, дисперсия = 8,740, стандартное отклонение = 4,329, коэффициент вариации = 19,54%. Длина. 1. Среднее = 187,978, медиана =189. 2. Первый квартиль = 178, третий квартиль = 198. 3. Размах = 60, межквартильный размах = 20, диспер-
сия =161,438, стандартное отклонение = 12,706, коэффициент вариации = 6,76%. Ширина. 1. Среднее = 71,00, медиана =71. 2. Первый квартиль = 68, третий квартиль =73. 3. Размах = 14, межквартильный размах =5, дисперсия = 9,865, стандартное отклонение =3,141, коэффициент вариации = 4,42%, Грузоподъемность. 1. Среднее = 22,394, медиана =15. 2. Первый квартиль =13, третий квартиль = 19. 3. Размах = 70,5, межквартильный размах = 6, дисперсия = 323,784, стандартное отклонение = 17,994, коэффициент вариации = 80,35%. Радиус поворота. 1. Среднее = 39,700, медиана = 40. 2. Первый квартиль =38, третий квартиль = 41. 3. Размах = 12, межквартильный размах = 3, диспер-
сия = 6,325, стандартное отклонение = 2,515, коэффициент вариации = 6,33%. Вес. 1. Среднее = 3 391,722, медиана = 3 457,5. 2. Первый квартиль = 3 095, третий квартиль = 3 750. 3. Размах = 2 165, межквартильный размах = 655, дисперсия = 232 210,765, стандартное отклонение = 481,883, коэффициент вариации = 14,21%. 5. Распределения пробега и емкости багажника имеют положительную асимметрию. Распределение длины и веса имеют отрицательную асимметрию. Распределение ширины имеет небольшую отрицательную асимметрию, а распределение радиуса поворота является симметричным. Спортивные модели. Пробег в милях на галлон топлива. 1. Среднее = 16,484, медиана =16. 2. Первый квартиль =15, третий квартиль =18. 3. Размах =12, межквартильный размах = 3, дисперсия =7,258, стандартное отклонение = 2,694, коэффициент вариации = 16,34% . Длина. 1. Среднее = 184,903, медиана = 183. 2. Первый квартиль = 175, третий квартиль = 190. 3. Размах =64, межквартильный размах =15, дисперсия = 209,557, стандартное отклонение = 14,476, коэффициент вариации = 7,83% . Ширина. 1. Среднее = 72,323, медиана = 72. 2. Первый квартиль =70, третий квартиль =74. 3. Размах =13, межквартильный размах = 4, дисперсия = 11,093, стандартное отклонение = 3,331, коэффициент вариации =4,61%. Грузоподъемность. 1. Среднее = 42,355, медиана = 37,5. 2. Первый квартиль = 34,5, третий квартиль = 45,5. 3. Размах = 56, межквартильный размах = 11, дисперсия = 183,753, стандартное отклонение = 13,556, коэффициент вариации = 32,00%. Радиус поворота. 1. Среднее = 40,581, медиана = 40. 2. Первый квартиль = 39, третий квартиль =41. 3. Размах =15, межквартильный размах = 2, дисперсия = 11,318, стандартное отклонение = 3,364, коэффициент вариации = 8,29% . Вес. 1. Среднее = 4 267,419, медиана =4 135. 2. Первый квартиль = 3 590, третий квартиль = 4 715. 3. Размах = 4 215, межквартильный размах = 1 125, дисперсия = 783 086,452, стандартное отклонение = 884,922, коэффициент вариации = 20,74% . 5. Распределение всех переменных, за исключением пробега, имеет положительную асимметрию.
Глава 4
4.2. 1. Простым событием является извлечение красного шара. 2. Извлечение белого шара.
4.4. 1. 0,4. 2. 0,35. 3. 0,6. 4. 0,1. 5. 0,3. 6. 0,35. 7. 0,65. 8. 0,75. 9. 0,9.
4.6. 1. Взаимоисключающие, но не исчерпывающие. 2. Не взаимоисключающие, не исчерпывающие. 3. Взаимоисключающие, но не исчерпывающие. 4. Взаимоисключающие и исчерпывающие. 5. Взаимоисключающие и исчерпывающие.
4.8. 1. Плата является качественной. 2. Плата является качественной и на матрице нет частиц. 3. Плата является некачественной. 4. Плата может быть качественной, и в то же время на матрице могут обнаружиться частицы. 5. 0,8889. 6. 0,2578. 7. 0,1778. 8. 0,7111. 9.0,92. 10.0,2889. 11. Вероятность события “плата является качественной или на матрице нет частиц” зависит от вероятностей событий “плата является качественной и на матрице нет частиц”, “плата является качественной и на матрице есть частицы” и “матрица является некачественной и на матрице нет частиц”.
4.10. 2. Крупная компания. 3. Крупная компания, предлагающая фондовые опционы членам своих правлений в рамках безналичного компенсационного пакета. 4. Крупная компания, не предлагающая фондовые опционы членам своих правлений в рамках безналичного компенсационного пакета. 5. Компания может быть крупной и в то же время предлагать фондовые опционы членам своих правлений в рамках безналичного компенсационного пакета. 6. 0,5122. 7. 0,2249. 8. 0,1084. 9. 0,3713. 10. 0,6287. 11. 0,5962. 12. Вероятность события “компания является крупной или предлагает фондовые опционы” зависит от вероятностей событий “компания является крупной и предлагает фондовые опционы”, “компания является крупной, но не предлагает фондовые опционы” и “компания не является крупной и предлагает фондовые опционы”.
4.12. 2. Поскольку простое событие должно удовлетворять только одному критерию, в качестве примера можно привести одно из следующих событий: а) “респондент— мужчина”, б) “респондент — женщина”, в) “респондент любит покупать одежду” и г) “респондент не любит покупать одежду”. 3. Поскольку совместное событие удовлетворяет одновременно двум критериям, в качестве примера можно привести одно из следующих событий:
а) “респондент — мужчина и любит покупать одежду”, б) “респондент — мужчина и не любит покупать одежду”, в) “респондент — женщина и любит покупать одежду” и г) “респондент — женщина и не любит покупать одежду”. 4. Событие “респондент не любит покупать одежду” является дополнительным к событию “респондент любит покупать одежду”. 5. 0,48. 6. 0,72. 7. 0,448. 8. 0,208. 9. 0,792. 10. 0,552. 11. 1,00.
4.14. 1. 0,33. 2. 0,33. 3. 0,67. 4. События А и Б являются статистически независимыми.
4.16. 0,5.
4.18. События А и Б не являются статистически независимыми.
4.20. 1. 0,5475. 2. 0,8240. 3. Эти условные события являются взаимно обратными. 4. События “респондент добирается на работу на автомобиле” и “респондент является домовладельцем” не являются статистически независимыми.
4.22. 1. 0,5179. 2. 0,1871. 3. Эти условные события являются взаимно обратными. 4. События “уволенный рабочий — белый” и “уволенный рабочий заявил о несправедливости” не являются статистически независимыми.
4.24. 1. 0,0417. 2. 0,0375. 3. Эти два события не являются статистически независимыми.
4.26. 1. 0,0045. 2. 0,012. 3. 0,0059. 4. 0,0483.
4.28. 0,095.
4.30. 1.0,736.2.0,997.
4.32. 1.0,4615.2.0,325.
4.34. 1. Р(Огромный спрос | Благоприятный отзыв) = 0,2157. Р(Умеренный успех | Благоприятный отзыв) = 0,3050. ^(Самоокупаемость | Благоприятный отзыв) = 0,3486. Р(Убытки | Благоприятный отзыв) = 0,1307. 2. Р(Благоприятный отзыв) = 0,459.
4.38. 59049.
4.40. 1. 128. 2. 279 936. 3. В задаче 1 существуют два взаимоисключающих и исчерпывающих исхода, в задаче 2 — шесть.
4.42. 24.
4.44. 120.
4.46. 1320.
4.48. 35
4.50. 1 140.
4.51. Априорная вероятность успеха основана на априорном знании исследуемого процесса. Эмпирическая вероятность использует наблюдения. Субъективная вероятность оценивает шансы, приписываемые событию конкретным лицом.
4.59. 1. 0,7. 2. 0,54. 3. 0,315. 4. 0,265. 5. 0,45. 6. События “хорошие отношения с начальником” и “респондент — мужчина” не являются статистически независимыми. Ни одно из утверждений о факторах, влияющих на успех работы, не зависит от пола респондента.
4.61. 1. 0,227. 2. 0,688. 3. 0,42. 4. 0,4. 5. 0,118. 6. 0,84. 7. 0,8571. 8. 0,3797. 9. Эти события не являются статистически независимыми. 10. Эти события не являются статистически независимыми.
4.63. 1. 0,68. 2. 0,24. 3. 0,32. 4. 0,655. 5. 0,035. 6. 0,7443. 7. 0,233. 8. 0,2557. 9. Результаты решения задач 1-3 относятся ко всем потребителям, в то время как решения задач 6-7 относятся только к тем потребителям, которые изменили свои предпочтения.
4.65. 0,6024.
Глава 5
5.2. 1. Распределение В: р=2,00. Распределение Г: ц = 2,00. 2. Распределение В: <5=1,141. Распределение Г: о = 1,095. 3. Распределение В является равномерным и симметричным. Распределение В является одномодальным и симметричным. Математические ожидания обоих распределений совпадают, а дисперсии различаются.
5.4. 1.2,00.2.1,18321596.
5.6. 4. При каждом способе игры проигрыш равен -0,167 долл.
5.8. 1. 90 долл. 2. 30 долл. 3. 126,10. 4. 10,95. 5. -1 300. 6. 120 долл. 7. 115,84.
5.10. 1. Е(Р) = 56 долл., = 37,47, CV = 66,91% . 2. Е(Р) = 84 долл., СУ = 63,93% .
3.CV = 14,29%.
5.12. 1. 71 долл. 2. 97 долл. 3. 61,88. 4. 84,27. 5. 5 113. 6. Акции У приносит инвестору больший ожидаемый доход, чем акции X, однако доход акций У имеет большее стандартное отклонение. Инвестор, избегающий риска, должен выбрать акции X, а инвестор, предпочитающий рисковать, может ожидать более высокого дохода от акций У. 7. Е(Р) = 94,40 долл., ст,, = 81,92. 8. Е(Р) = 89,20 долл., ст,, = 77,28. 9. Е(Р) = 84,00 долл., ст,, = 72,73. 10. Е(Р) = 78,80 долл., стр = 68,2. 11. Е(Р) = 73,60 долл., ст,, = 63,98. 12. Если единственным критерием при выборе решения является ожидаемая прибыль, то, основываясь на результатах решения задач 7-11, следует рекомендовать портфель акций, 10% которого составляют акции X и 90% — акции У. При этом необходимо иметь в виду, что при увеличении ожидаемого дохода риск также увеличивается.
5.14. 1. 0,5997. 2. 0,0016. 3. 0,0439. 4. 0,4018. 5. 0,3874.
5.16. 0,0312.
5.18. 1. Термин “знали" означает, что телезрителей предупредили о предстоящей премьере. 2. Поскольку числа 68 и 24% получены в результате опроса, проведенного среди зрителей, их можно классифицировать как эмпирическую классическую вероятность. Сериал “Преступный умысел”. 3. 0,000014. 4. 0,9721. 5. 0,3426. 6. 0,000447. 7. 13,6. Шоу “Тайны Шварца”. 3. 0,4561. 4. 0,0103. 5. 0,0000022. 6. 0,00000. 7. 4,8.
5.20. 1. 0,0010. 2. 0,0156. 3. 0,2373. 4. 0,8965. 5. Два предположения: 1) ответы должны быть независимыми; 2) исходов должно быть два — правильный ответ или неправильный. 6. Среднее = 1,25, стандартное отклонение = 0,968. 7. 0,00000016, или 1,6423x107.
5.22. 1. 0,2381. 2. 0,2. 3. 0,1591. 4. 0,0083.
5.24. 1. 0,4691. 2. 0,5854. 3. 0,0279. 4. 0,1090. 5. Вероятность того, что проверке подвергнется вся генеральная совокупность, сильно зависит от истинного количества нарушений. Если количество нарушений очень мало (А = 5), вероятность также очень мала (0,0279). Если количество нарушений увеличивается, вероятность того, что вся генеральная совокупность подвергнется проверке, возрастает в 21 раз (0,5854).
5.26. 1. 1,31Е-06. 2. 0,080192. 3. 0,9198. 4. 2,28Е-06. 0,3128. 0,6872.
5.28. 1. 0,4396. 2. 0,8462. 3. 0,9231. 4. 1,33.
5.30. 1. 0,5940. 2. 0,9863. 3. 0,9098. 4. 0,9817. 5. 0,2650.
5.32. 1. Для того чтобы случайная переменная X, описывающая количество жалоб, поступающих в течение часа, имела распределение Пуассона, необходимо предположить, что 1) вероятность того, что в течение одного часа в систему поступит звонок, одинакова для всех интервалов времени, длина которых равна одному часу; 2) количество звонков, поступивших в систему в течение одного часа, не зависит от количества звонков, поступивших в систему в течение любого другого интервала времени, длина которого равна одному часу; 3) вероятность того, что в течение одного интервала времени в систему поступит несколько звонков, при уменьшении длины этого интервала стремится к нулю. 2^0,6703. 3. 0,2681. 4. 0,0536. 5. 0,0079. 6. 0,99994. В 99,99% всех интервалов времени, длина которых равна одному часу, в систему поступит не больше четырех звонков.
5.34. 1. 0,285057. 2. 0,160623. 3. 0,714943. 4. 0,294476. 5. 1) 0,440493. 2) 0,17546. 3) 0,559507. 4)0,350935.
5.36. 1. 0,00623. 2. 0,01499. 3. 0,99377. 4. 0,97877.
5.51. 1. 0,006047. 2. 0,040311. 3. 0,120932. 4. 0,16729. 5. 0,000105. 6. Если вероятность того, что случайно выбранный абонент захочет автоматически переключиться на оператора, равна 40%, то вероятность того, что это сделают 10 абонентов, практически равна нулю. Следовательно, число 40% , фигурирующее в статье, не относится к конкретной системе.
5.53. 1.0,121577. 2.0,28518. 3.0,593244. 4.1,9. 1,240564. 5.1)0,018228. 2)0,089782. 3)0,89199.4)3,3. 1,486943.
5.55. 1. 0,000272. 2. 0,228878. 3. 0,469581. 4. 0,530419. 5. 0,240703. 6. 4,4.
5.57. 1. Для того чтобы количество возвращенных дневников являлась случайной величиной, имеющей биномиальное распределение, должны выполняться следующие предположения: 1) вероятность возврата одинакова у любого дневника, и 2) возврат одного дневника никак не влияет на возврат другого. 2. 32,6. 3. 4,6875. 4. 0,3308. 5. 0,0626. 6. 0,0478. 7. 0,4778. 8. 1) 1. Для того чтобы количество возвращенных дневников являлась случайной величиной, имеющей биномиальное распределение, должны выполняться следующие предположения: 1) вероятность возврата одинакова у любого дневника, и 2) возврат одного дневника никак не влияет на возврат другого. 2.40. 3.4,8990. 4.0,0248. 5. 0,0012. 6. 0,4567. 7. 0,1647.
5.59. 1. 0,74. 2. 0,74. 3. 0,3898. 4. 0,0012. 5. В период экономического роста стоимость акций с годами увеличивается, а в периоды застоя или спада — уменьшается. Следовательно, вероятность того, что стоимость акций в течение года возрастет, не зависит от конкретного года.
5.61. 1. 7,39941x10 °. 2.3,84769Е-7. 3. 1,73886Е-6. 4.0,0001704084. 5.0,001199814.
6. 0,004159356. 7. 0,006598978. 8. 0,019230769. 9. 0,968638543.
5.63. 1.0,67032. 2.0,26813. 3.0,06155. 4.0,00006. 5.0,85214. 6.0,13634. 7.0,01151. 8. 0,00000.
Глава 6
6.2. 1. 0,0901. 2. 0,8790. 3. 0,3790. 4. 0,1210. 5. 0,7889. 6. 0,1875.
6.4. 1. 0,1401. 2. 0,4168. 3. 0,3918. 4. 0,8349. 5. 0,1151. 6. Поскольку нормальное распределение является симметричным относительно математического ожидания, половина площади фигуры будет лежать левее значения Z = 0,0. 7. -1,00.
6.6. 1. 0,9599. 2. 0,0228; 3. 0,0301. 4. 0,2857. 5. Р(Х < 40) = 0,0062, Р(Х > 55) = 0,1056, Р(Х < 40) + Р(Х > 55) = 0,1118. 6. 43,42. 7. 46,64 и 53,36. 8. 45,84.
6.8. 1. 0,4082. 2.0,0669. 3. 0,2508. 4. 749 грузовиков. 5. 39,92 тыс. миль. 6. Чем меньше стандартное отклонение, тем больше значение Z. 1)0,4452; 2)0,0603. 3)0,1815; 4) 819 грузовиков; 5) 41,6 тыс. миль.
6.10. 1. 0,9878. 2. 0,8185. 3. 0,1359. 4. 86,16% . 5. Первый вариант: поскольку 81 балл соответствует величине Z= 1,00, которая не превышает минимальное значение Z = 1,28, вероятность получить высшую оценку очень мала. Второй вариант: поскольку 68 баллов соответствуют величине Z = 2,00, которая превышает минимальное значение Z = 1,28, вероятность получить высшую оценку на втором экзамене выше, чем на первом. Итак, следует предпочесть второй вариант.
6.12. 1. 0,0526. 2. 0,5954. 3. 53,08. 4. 41,03 и 90,37. 5. Разумно предположить, что продолжительность посещения является нормально распределенной случайной величиной.
6.14. При 19 наблюдениях площадь фигуры, ограниченной нормальной кривой и 18-м по величине наблюдением, равна 0,9. Соответствующее Z-значение равно +1,28. Площадь фигуры, ограниченной нормальной кривой и наибольшим наблюдением, равна 0,95. Соответствующее Z-значение равно +1,645, +1,64 или 1,65, в зависимости от правила выбора.
6.16. Площадь фигуры, ограниченной нормальной кривой: 0,1429; 0,2857; 0,4286; 0,5714; 0,7153; 0,8571. Стандартизованный нормальный квантиль: -1,07; -0,57; -0,18; +0,18; +0,57; +1,07.
6-18. 1. Повреждения на станции: X = 2,214; 5 = 1,718. Пять базовых показателей: 0,52; 0,93; 1,54; 3,93; 6,32. Распределение имеет положительную асимметрию. 2. Повреждения на линии: X = 2,011; 5= 1,892. Пять базовых показателей: 0,08; 0,60; 1,505; 3,75; 7,55. Распределение имеет положительную асимметрию.
6.20. 1. Данные не подчиняются приближенному нормальному распределению. 2. Данные не подчиняются нормальному распределению.
6.22. 1. В целом, свойства рассматриваемых данных довольно близки к свойствам нормального распределения. 2. Данные подчиняются приближенному нормальному распределению.
6.24. 1.0,2.2.0,1.3.5.4.2,8868.
6.26. 1. 0,6667. 2. 0,1333. 3. 0,4667. 4. 17,5. 5. 4,3301.
6.28. 1. 0,3. 2. 0,6. 3. 0,1. 4. 0. 5. 1. 6. 0,5774.
6.30. 1. 0,9502. 2. 0,0498. 3. 0,0473. 4. 0,9527.
6.32. 1. 0,9179. 2. 0,5661. 3. 0,9502 и 0,6329. 4. 0,7769 и 0,3941.
6.34. 1. 0,5276. 2. 0,9765. 3. 0,7135 и 0,9981.
6.36. 1. 0,5034. 2. 0,3499. 3. 0,2953.
6.38. 1.0,0062. 2.0,0994. 3.0,1357. 4.0,3830. 5.99,22. 6.1)0,0228; 2)0,1359; 3)0,1894; 4)0,3108; 5) 99,05.
6.40. 1. Распределение выборочных средних представляет собой распределение средних значений всевозможных выборок, состоящих из 25 сумм. 2. Распределение выборочных средних представляет собой распределение средних значений всевозможных выборок, состоящих из 25 записей. 3. Распределение выборочных средних представляет собой распределение средних значений всевозможных выборок, состоящих из 25 объемов продаж.
6.42. 1. 0,3085. 2. 0,1747. 3. 1,2664 и 1,3336. 4. 1,30 и 0,01. 5. Приближенно нормальное распределение. 6.0,0228. 7.0,15735. 8.1,2916; 1,3084. 9. Увеличение объема выборки п приводит к уменьшению доли. 10. Стандартная ошибка выборочного распределения средних для выборок, состоящих из 16 элементов, равна 1/4 стандартного отклонения отдельных значений. Это значит, что выборочное распределение концентрируется вокруг математического ожидания генеральной совокупности в более узкой области. 11. Оба события имеют одинаковую вероятность (р = 0,1587), поскольку при увеличении объема выборки п выборочные средние располагаются все ближе к математическому ожиданию распределения и Z = 1 во всех случаях.
6.44. 1. 0,3830. 2. 0,3944. 3. 0,6826. 4. При увеличении объема выборки с и = 25 до п = 100 выборочные средние располагаются все ближе к математическому ожиданию генеральной совокупности. Стандартная ошибка выборочного распределения при п = 100 намного меньше стандартной ошибки выборочного распределения при п = 25, поэтому вероятность того, что выборочное среднее будет отличаться от математического ожидания не более чем на 0,2 мин., для выборок, имеющих объем 100 (вероятность равна 0,6826), намного выше, чем для выборок, имеющих размер 25 (вероятность равна 0,3830). 5. Более вероятно, что сеанс связи с сервером электронной почты превысит 11 мин.
6.46. 1. 0,0855. 2. 0,9938. 3. 0,7532 и 0,8468. 4. 0,8468. 5. 0,9969. 6. 0,0142. 7. 2,3830 и 2,6170. 8.2,6170. 9. Поскольку объем выборки равен 30, нет необходимости предполагать, что распределение генеральной совокупности загрузок является нормальным.
6.48. 1.0,0207. 2.0,1685. 3.0,9543. 4.28,7922 и 41,6078. 5.26,9757 и 43,4243. 6.25,4002 и 44,9998.
6.50. 1.0,30.2.0,0693.
6.52. 1.0,1635. 2.0,8461. 3.0,1151. 4. При увеличении объема выборки в четыре раза стандартная ошибка уменьшается в два раза. 1) 0,0250; 2) 0,9793; 3) 0,0082.
6.54. 1. 0,7242. 2. 0,9708. 3. 0,0146. 4. 1) 0,5588; 2) 0,8764; 3) 0,0618.
6.56. 1. 0,9285. 2. 0,9997. 3. 0,0000. 4. 1) 0,7975; 2) 0,9897; 3) 0,0025.
6.58. 1. 0,7887. 2. 0,1342 и 0,2658. 3. 0,1216 и 0,2784.
6.60. 1. 0,1826. 2. 0,7518. 3. 0,1241. 4. 0,3626. 5. 0,9816. 6. 0,0092.
6.62. Биномиальное распределение можно аппроксимировать нормальным, только если пр и п(1-р) больше или равны пяти.
6.64. 1.0,2051. 2.0,8281. 3.0,3770. 4.0,1719. 5.0,6230. 6.0,8281. 7.1)0,2045. 2)0,8286. 3)0,3759. 4)0,1714. 5)0,6241. 6)0,8284. 8. В задаче 7 биномиальное распределение хорошо аппроксимируется нормальным.
6.66. 1. 0,216. 2. 0,288. 3. 0,352. 4. 0,936. 5. 0,7864. 6. 0.0852. 7. 0,1932.
6.68. 1. 0,0821. 2. 0,5438. 3. 0,1841. 4. 0,6803.
6.70. 1. 0,0223. 2. 0,9927. 3. Сделанные предположения: 1) вероятность того, что видеокассета будет возвращена, является постоянной и не зависит от конкретного дня; 2) количество кассет, возвращенных в конкретный день, не зависит от количества видеокассет, возвращенных в любой другой день; 3) вероятность, что в один и тот же период времени бу-
дут возвращены несколько кассет, стремится к нулю при уменьшении длины временного интервала. 4. 1) 0,0257. Биномиальное распределение очень хорошо аппроксимируется нормальным. 2)0,9812. Биномиальное распределение очень хорошо аппроксимируется нормальным.
6.72. Если объем выборки, извлеченной без возвращений из генеральной совокупности, состоящей из 400 элементов, равен 100, он оказывает больше влияния на уменьшение стандартной ошибки.
6.74. 0,1479.
6.76. 1.0,2563.2.0,0824.
6.91. 1.0,2734. 2.0,2260. 3.0,0401. 4.0,00058. 5.0,7471. 6.0,4999. 7.0,00009.
8. Практически нуль. 9. Практически нуль. 10. 0,7518.
6.93. 1. 0,2734. 2. 0,2038. 3. 4,404 унции. 4. 4,188 и 5,212 унции. 5. 0,8944. 6. 4,6168 и 4,7832 унции. 7. 4,6408.
6.95. 1. 0,1587. 2. 0,0304. 3. 0,1056. 4. 0,0062. 5. -16,7330. 6. 0,2524. 7. -25,6797 и 5,6797.
6.97. 1. 0,3446. 2. 0,0495. 3. 0,0000. 4. -15,0335. 5. -13,2738. 6. Если из генеральной совокупности извлекаются выборки, состоящие из четырех элементов, то к ним нельзя применить ни один метод, изложенный в главе, не предположив заранее, что доходность взаимных фондов является нормально распределенной случайной величиной.
Глава 7
7.2. 114,68 <|д< 135,32.
7.4. Для того чтобы любой возможный интервал содержал математического ожидания, необходимо выбрать всю генеральную совокупность.
7.6. Примерно 5% всех интервалов не содержат математическое ожидание. Поскольку математическое ожидание неизвестно, мы не знаем наверняка, содержится ли оно в построенном интервале, т.е. между 10,99408 и 11,00192.
7.8. 1. 325,5005 < р < 374,4995. 2. Нет. 3. Нет. 4. Доверительный интервал является оценкой математического ожидания, полученной по выборке, состоящей из 64 лампочек, а не оценкой индивидуальной продолжительности работы. 5. 1). 330,4 < ц < 369,6. 2). Нет.
7.10. 1. 2,2622. 2. 3,2498. 3. 2,0395. 4. 1,9977. 5. 1,7531.
7.12. 38,9499 <ц< 61,0501.
7.14. Исходные данные: -0,1229 < ц< 11,8371, измененные данные: 2,0022 < ц< 5,9978. Наличие выброса в исходных данных увеличивает выборочное среднее и сильно влияет на стандартное отклонение.
7.16. 1. 1,52 < р < 1,82. 2. Владелец магазина может быть на 95% уверен, что математическое ожидание цен поздравительных открыток больше 1,52 долл, и меньше 1,82 долл.
7.18. 1. 33,89 < р< 53,89. 2. Генеральная совокупность должна быть нормально распределенной. 3. График нормального распределения и блочная диаграмма свидетельствуют, что генеральная совокупность не является нормально распределенной и имеет положительную асимметрию. 4. Поскольку объем выборки равен 27, а распределение генеральной совокупности является асимметричным, метод, примененный при решении задачи 1, ненадежен, и, следовательно, любое сравнение с решением задачи 2.64 становится некорректным.
7.20. 1. -0,000566 < р < 0,000106. 2. Генеральная совокупность должна быть нормально распределенной. Однако, поскольку размер выборки равен 100, по центральной предельной теореме t-распределение можно применять, даже если генеральная совокупность не является нормально распределенной. 3. График нормального распределения и блочная диаграмма свидетельствуют, что генеральная совокупность имеет положительную асимметрию. 4. Поскольку нуль принадлежит доверительному интервалу, можно быть на 95% уверенным в том, что заготовка соответствует стандартам.
7.22. 0,19 < р< 0,31.
7.24. 1. 0,2189 <р < 0,3211. 2. Менеджер телефонной компании может прийти к выводам, что доля домовладельцев, желающих установить дополнительную телефонную линию, если цена будет снижена, лежит между 0,22 и 0,32 с 99% -ным доверительным уровнем.
7.26. 1. 0,3810 <р < 0,4388. 2. 0,3856 <р < 0,4342. 3. 95%-ный доверительный интервал шире, поскольку критическое значение, используемое при построении доверительного интервала, увеличивается при увеличении доверительного уровня.
7.28. 1. 0,4163 <р < 0,5037. 2. 0,0737 <р < 0,1263.
7.30. 1. 0,4192 <р < 0,4808. 2. Можно быть уверенным на 95%, что доля работающих женщин в Северной Америке, полагающих, что компании должны резервировать место работы для женщин, находящихся в декретном отпуске, на срок более 6 месяцев, колеблется от 0,4192 до 0,4808.
7.32. 35.
7.34. 1041.
7.36. 1.246.2.984.
7.38. 97.
7.40. 1.167.2.97.
7.42. 62.
7.44. 1. 423. 2. 601. 3. 1 068. 4. В целом, если требуется более высокий доверительный уровень при прочих равных условиях, необходимо создавать более крупные выборки. Чем большая точность требуется, тем крупнее должна быть выборка.
7.46. 1. 547. 2. 944. 3. 2 185. 4. 3 774. 5. При прочих равных условиях для повышения доверительного уровня и уменьшения ошибки выборочного обследования требуется более крупный объем выборки.
7.48. 1. 0,5053 < р < 0,5347. 2. Можно быть уверенным на 95% , что доля семей, владевших акциями в 2001 году, колеблется от 0,5053 до 0,5347. 3. 9 589.
7.50. Ю 721,53 долл. < сумма элементов генеральной совокупности < 14 978,47 долл.
7.52. 1.р < 0,0545. 2.р < 0,0586. З.р < 0,0663.
7.54. 543 176,96 долл. < сумма элементов генеральной совокупности < 1 025 223,04 долл.
7.56. 5 125,99 долл. < общая сумма скидок < 54 546,57 долл. Замечание: t-значение, равное 2,6092 при 95%-ном доверительном уровне, и величина df = 149 вычислены с помощью программы Microsoft Excel.
7.58. 1. р < 0,0542. 2. Поскольку верхняя граница превышает допустимый уровень, аудитор должен потребовать для проверки более крупную выборку.
7.60. 67,63 <ц< 82,37.
7.62. 1. 322,6238 < ц < 377,3762. 2. 92. 3. 1) 322,9703 < ц < 377,0297; 2) 88.
7.64. 1. 0,2285 <р < 2,3715. 2. 186. 3. 1) 0,2265 <р < 0,3735; 2) 205.
7.66. 1. 1,9804 < р < 2,0000. 2. 92. 3. 1) 1,9807 <р < 1,9993; 2) 88.
7.74. 1. Генеральной совокупностью, из которой извлечена выборка респондентов, являются подписчики журнала Redbook^ посещавшие его Web-сайт. 2. Нет. 3. Нет
7.76. 1. 0,5116 < р< 0,6484. 2. 0,4307 < р< 0,5963. 3. 0,1626 < р< 0,2774. 4. 0,1356 < р< 0,2444.5. 2 401.
7.78. 1. 14,085 < ц < 16,515. 2. 0,530 < р < 0,820. 3.25. 4.784. 5. Следует использовать более крупную из двух выборок (п = 784).
7.80. 1. 8,049 < ц < 11,351. 2. 0,284 < р< 0,676. 3.35. 4.121. 5. Следует использовать более крупную из двух выборок (п = 121).
7.82. 1. 25,80 < ц < 31,24. 2. 0,3037 < р< 0,4963. 3.97. 4.423. 5. Следует использовать более крупную из двух выборок (п = 423).
7.84. 1. 36,66 < ц < 40,42. 2. 0,2027 < р< 0,3973. 3. 110. 4. 423. 5. Следует использовать более крупную из двух выборок (п = 423).
7.86. 1.р< 0,2013. 2. Поскольку верхняя граница превышает допустимый уровень, аудитор должен потребовать для проверки более крупную выборку.
7.88. 1. 27. 2. 737 655,50 долл. < сумма элементов генеральной совокупности < 838 275,58 долл.
7.90. 1. 8,41 < Li < 8,43. 2. Можно быть уверенным на 95%, что среднее расстояние между боковыми сторонами профиля, колеблется от 8,41 до 8,43 дюйма.
7.98. 1. 0,2425 < ц < 0,2856. 2. 0,1975 < р< 0,2385. 3. Распределение веса гранул, потерянных кровельными плитками, произведенными в Бостоне и Вермонте, имеет положительную асимметрию. 4. Средний вес гранул, потерянных кровельными плитками, произведенными в Бостоне, больше, чем средний вес гранул, потерянных кровельными плитками, произведенными в Вермонте.
Глава 8
8.2. Символом Л, обозначается альтернативная гипотеза.
8.4. Вероятность ошибки второго рода обозначается символом р.
8.6. Символ а обозначает вероятность ошибки первого рода.
8.8. Мощность критерия является дополнением по отношению к вероятности ошибки 2-го рода.
8.10. Поскольку отдельное выборочное значение может попасть в область принятия гипотезы, даже если она является ложной, существует возможность принять ложную нулевую гипотезу.
8.12. При прочих равных условиях, чем ближе гипотетическое математическое ожидание к фактическому, тем выше риск совершить ошибку 2-го рода.
8.14. Во французской судебной системе, в отличие от американской, нулевая гипотеза заключается в том, что обвиняемый виновен, а альтернативная гипотеза утверждает, что он невиновен. Таким образом, риски аир следует поменять местами.
8.16. Но: ц = 20 минут, ц * 20 минут.
8.18. Гипотеза Но отклоняется.
8.20. Если Z < -2,58 или Z > +2,58, гипотеза Но отклоняется.
8.22. 0,0456.
8.24. 0,1676.
8.26. 1. Но: ц = 70 фунтов, Hr: ц + 70 фунтов; 2. Поскольку 2и1к. = -1,80 лежит между критическими значениями ±1,96, гипотеза Но не отклоняется. З.р = 0,0718. 4. Поскольку Zmic = -3,60 < -1,96, гипотеза Но отклоняется. 5. Поскольку Zmk. = -2,00 < -1,96, гипотеза Но отклоняется.
8.28. 1. Но: р = 375 часов, Нх: р * 375 фунтов; 2. Поскольку Zcak = -2,00 меньше критического значения -1,96, гипотеза Но не отклоняется. 3. с = 0,0456. 4. 325,50 < ц < 374,50. 5. Результаты совпадают.
8.30. 1. Но: ц = 8 унций, Н,:ц^8 унций; 2. Гипотеза Но отклоняется, если <-1,96 или Z,.alc > 1,96. Поскольку Z.ak = 0,8 лежит между критическими значениями ±1,96, гипотеза Но не отклоняется. З.р = 0,4229. 4. Гипотеза Но отклоняется, если Zrak. < -1,96 или Zc,ilt > 1,96. Поскольку Z<jik = -2,40 < -1,96, гипотеза Но отклоняется. 5. Гипотеза Но отклоняется, если Zailc < -1,96 или Z.ak. > 1,96. Поскольку Z^ — -2,26 < -1,96, гипотеза Но отклоняется.
8.32. 2,33.
8.34. -2,33.
8.36. 0,0228.
8.38. 0,0838.
8.40. 0,9162.
8.42. 1. Но: р > 2,8 футов, Н\: р < 2,8 футов. 2. Поскольку Zt.jik. = -1,75 < Zml = -1,645, гипотеза Но отклоняется. 3. Поскольку р = 0,0401 < а = 0,05, гипотеза Но отклоняется. 4. Вероятность обнаружить выборку, среднее значение которой не превышает 2,73 футов, если нулевая гипотеза является истинной, равна 0,0401. 5. Тот же вывод.
8.44. 1. Но: ц > 8 унций, Нх: ц < 8 унций. 2. Решающее правило: если Z < -1,645, гипотеза Но отклоняется. Поскольку Z = -0,80 > Z(.rit = -1,645, гипотеза Но не отклоняется. 3. Поскольку р = 0,2119 > а = 0,05, гипотеза Но не отклоняется. 4. Вероятность обнаружить выборку, среднее значение которой не превышает 7,983 унций, если нулевая гипотеза является истинной, равна 0,2119. 5. Тот же вывод.
8.46. 2,00.
8.48. 1. = ±2,1315. 2. fcnt = +1,7531.
8.50. Нет, для проверки нулевой гипотезы, заключающейся в том, что математическое ожидание генеральной совокупности, распределение которой имеет отрицательную асимметрию, равно 60, нельзя применять t-критерий, потому что размер выборки (п = 21) меньше 30. Основное предположение t-критерия заключается в том, что если исследуемая генеральная совокупность не является нормально распределенной, то большой объем выборки компенсирует этот недостаток. Если объем выборки невелик (п < 30), t-критерий применять нельзя, поскольку выборочное распределение не удовлетворяет условиям центральной предельной теоремы.
8.52. 1. Но: ц < 300 долл., Нг: ц > 300 долл. Если t > 1,2902, то нулевая гипотеза Ноотклоняется. Поскольку t€aK = 3,5648 больше критического значения t= 1,2902, гипотеза Но отклоняется. 2. Но: ц < 300 долл., Н^. ц > 300 долл. Если t > 1,6604, то нулевая гипотеза Но отклоняется. Поскольку tralr = 2,0533 больше критического значения t= 1,6604, гипотеза Но отклоняется. 3. Но: ц < 300 долл., Нх: ц > 300 долл. Если t> 1,2902, то нулевая гипотеза Но отклоняется. Поскольку tcak = 1,1829 больше, критического значения t = 1,2902, гипотеза Но отклоняется.
8.54. 1. Но: р = 22,2, Нг: 22,2. Если 111 > 1,6766, то нулевая гипотеза Но отклоняется. Поскольку | 11 > 1,6766, нулевая гипотеза Ноотклоняется.
8.56. 1. Но: р < 20, Ht: р > 20. Если t > 1,6766, то нулевая гипотеза Но отклоняется. Поскольку t > 1,6766, гипотеза Ноотклоняется. 2. Распределение генеральной совокупности должно быть нормальным. 3. График нормального распределения свидетельствует о положительной асимметрии. 4. Даже если распределение генеральной совокупности не является нормальным, согласно центральной предельной теореме результаты решения задачи 1 остаются правильными, поскольку объем выборки равен 50.
8.58. 1. Но: р = 45, Н^: р # 45. Если 111 > 2,0555, то нулевая гипотеза Наотклоняется. Поскольку |t|< 2,0555, гипотеза Но не отклоняется. 2. Распределение генеральной совокупности должно быть нормальным. 3. Блочная диаграмма свидетельствует о положительной асимметрии. 4. Решение задачи 1 не противоречит решению задачи 3.61.
8.60. 1. Но: р = 5,5, Нг: р 5,5. Если 111 > 2,068, то нулевая гипотеза Ноотклоняется. Поскольку | 11 < 2,068, гипотеза Но не отклоняется. 2. 5,46 < р < 5,54. С вероятностью 99% математическое ожидание веса чайных пакетиков лежит где-то между 5,46 и 5,54 г. 3. Выводы совпадают.
8.62. 0,22.
8.64. Но: р - 0,20, Н^. р * 0,20. Если Z < -1,96 или Z > 1,96, то нулевая гипотеза Но отклоняется. Поскольку ZLalc = 1,00 лежит между критическими значениями Z = ±1,96, гипотеза Но не отклоняется.
8.66. 1. Но: р = 0,50, Нг: р * 0,50. Если Z < -1,96 или Z > 1,96, то нулевая гипотеза Но отклоняется. Поскольку Z.ak. = 3,4061 меньше критического значения Z = -1,96, гипотеза Но отклоняется. 2. 0,00066. 3. Нп: р < 0,50, Н/. р > 0,50. Если Z > 1,645, то нулевая гипотеза На отклоняется. Поскольку Zak = 3,968 больше критического значения Z = 1,645, гипотеза Но отклоняется. 4. 3,6260Е-5. 5. Но: р < 0,55, р > 0,55. Если Z > 1,645, то нулевая гипотеза Но отклоняется. Поскольку Z.ak = 1,13 меньше критического значения Z = 1,645, гипотеза Ноне отклоняется. 6. 0,1301.
8.68. 1. Но: р < 0,101, Нг: р > 0,101. Если Z > 1,645, то нулевая гипотеза Наотклоняется. Поскольку Z ,, ^ 0,8917 меньше критического значения Z= 1,645, гипотеза Но не отклоняется. 2. Но: р < 0,082, Нр р > 0,082. Если Z > 1,645, то нулевая гипотеза Ноотклоняется. Поскольку Zrak = 2,2164 больше критического значения Z = 1,645, гипотеза Ноотклоняется.
8.70. 1. Н0\р > 0,22, Нг'.р< 0,22. Если Z< -2,3263, то нулевая гипотеза На отклоняется. Поскольку Zak = -3,3296 меньше критического значения Z = -2,3263, гипотеза Наотклоняется. 3. 0,00043.
8.89. 1. Компания La Quinta Inns совершает ошибку 1-го рода, когда приобретает неподходящий участок. В этом случае компания упускает выгоду, которую могла бы получить, купив подходящий участок. 2. Компания La Quinta Inns совершает ошибку 2-го рода, когда
отказывается приобрести подходящий участок. В этом случае компания упускает выгоду, которую могла бы получить, купив его. 3. Руководство компании La Quinta Inns стремится избежать ошибки 1-го рода, принимая очень строгое правило принятия решения и приобретая лишь те участки, которые могут принести высокую прибыль. Участки, которые могли бы принести умеренную прибыль, классифицируются как неподходящие. 4. Если бы компания приняла более мягкое правило принятия решений и стала приобретать участки, которые компьютерная программа оценивает как умеренно или высоко прибыльные, то вероятность совершить ошибку 1-го рода возросла бы. В этом случае многие участки, которые программа оценивает как умеренно прибыльные, могут не принести прибыли вообще. С другой стороны, более мягкое правило принятия решения снижает вероятность ошибки 2-го рода, поскольку теперь компания может приобретать больше потенциально прибыльных участков.
8.91. 1. Но: ц = 10,0 галлонов, ц* 10,0 галлонов. Если t< -2,0010 или t > 2,0010, то нулевая гипотеза Но отклоняется. Поскольку t= 3,2483 больше верхнего критического значения t = 2,0010, гипотеза Ноотклоняется. 2. 0,0019. 3. Но: р > 0,20, Нг: р < 0,20. Если Z < -1,645, то нулевая гипотеза отклоняется. Поскольку Zrak. = -0,32 больше критического значения Z = -1,645, гипотеза Но не отклоняется. 4. Но: ц= 10,0 галлонов, Н{\ 10,0 галлонов. Если
t < -2,0010 или t > 2,0010, то нулевая гипотеза Но отклоняется. Поскольку trak. = 0,7496 лежит между критическими значениями t = ±2,0010, гипотеза Нп не отклоняется. 5. Но: р > 0,20, р < 0,20. Если Z < -1,645, то нулевая гипотеза Ноотклоняется. Поскольку Zak. = -1,61 больше критического значения Z = -1,645, гипотеза Нп не отклоняется.
8.93. 1. Нп: 5 мин., Нг: ц < 5 мин. Если t < -1,7613, то нулевая гипотеза Ноотклоняется. Поскольку trak = -1,6867 больше верхнего критического значения t = -1,7613, гипотеза Ноне отклоняется. 2. Для применения t-критерия необходимо предположить, что данные являются случайными и приближенно нормально распределенными. 3. За исключением одной экстремальной точки, данные являются приближенно нормально распределенными. 4. 0,0569.
8.95. 1. Но: ц - 30, Нг: р #= 30. Если | 11 > 2,0555, d.f. = 26. Поскольку | 11 > 2,0555, нулевая гипотеза Но отклоняется. 2. Для применения t-критерия необходимо предположить, что данные независимо друг от друга извлечены из нормально распределенной генеральной совокупности. 3. Блочная диаграмма свидетельствует о том, что распределение имеет положительную асимметрию. Поскольку размер выборки равен 27, t-распределение плохо аппроксимирует распределение выборочных средних. 4. Поскольку распределение имеет положительную асимметрию, применение t-критерия не корректно. Менеджер должен остерегаться некорректных выводов и потребовать более крупную выборку, которая соответствовала бы требованиям центральной предельной теоремы.
8.97. 1. Но: ц > 0,35, Нг: ц < 0,35. Нулевая гипотеза На отклоняется, если t < -1,690, d.f- = 35. Поскольку t = -1,4735 > 1,690, нулевая гипотеза Но не отклоняется. 2. 0,0748. 3. Но: ц> 0,35, Н{: ц < 0,35. Если t < -1,6973, d.f. = 30. Поскольку t = -3,10 < -1,6973, нулевая гипотеза 77О отклоняется. 4. 0,0021. 5. Для применения t-критерия необходимо предположить, что данные независимо друг от друга извлечены из нормально распределенной генеральной совокупности. Поскольку объемы выборок равны 36 и 31 соответственно, т.е. достаточно велики, распределение генеральной совокупности не слишком асимметрично, t-распределение хорошо аппроксимирует распределение выборочных средних. 6. Блочная диаграмма свидетельствует о том, что распределение имеет положительную асимметрию, причем для бостонских плиток асимметрия выражена сильнее. Желательно увеличить объемы выборок.
8.99. 1. Но: ц = 0,5, И,: р 0,5. Нулевая гипотеза На отклоняется, если 111 > 1,9741. Поскольку t = -21,60 < 1,9741, нулевая гипотеза Но отклоняется. 2. р-значение практически равно нулю. 3. Нп: р = 0,5, 77,: р^ 0,5. Нулевая гипотеза Но отклоняется, если |t|> 1,977, d.f. = 139. Поскольку t = -27,19 <-1,977, нулевая гипотеза Но отклоняется. 4. р-значение практически равно нулю. 5. Для применения t-критерия необходимо предположить, что данные независимо друг от друга извлечены из нормально распределенной генеральной совокупности. Поскольку объемы выборок равны 170 и 140 соответственно, т.е. достаточно велики, t-распределение хорошо аппроксимирует распределение выборочных средних, даже несмотря на то, что генеральная совокупность не является нормально распределенной.
Глава 9
9.2. Поскольку Zcalc = 1,73 лежит между критическими значениями Z =±2,58, нулевая гипотеза Нп не отклоняется.
9.4. 1.1 = 3,8959. 2. df=21. 3. Если t> 2,5177, гипотеза Но отклоняется. 4. Поскольку tcalc = 3,8959 > t = 2,5177, гипотеза Но отклоняется. 5. Выборки извлекаются из двух независимых генеральных совокупностей, имеющих нормальное распределение и одинаковую дисперсию. 6. 3,7296 < < 12, 2704.
9.6. 1. Поскольку Zral(. = 5,20 больше критического значения, равного 2,33, гипотеза На отклоняется. 2.р = 0,0000.
9.8. 1. Поскольку tralc = -9,8541 меньше нижнего критического значения -1,6456, гипотеза Но отклоняется. 2. р-значение практически равно нулю. 3. -483,2044 < Pj-p-j < -322,7956.
9.10. 1. Поскольку р-значение равно 0,000293 и не превышает 5%-ного уровня значимости, нулевая гипотеза отклоняется. 2.р-значение равно 0,000293. 3. Необходимо предположить, что обе генеральные совокупности являются нормально распределенными. 4. -4,2292 < р, -р2<-1,4268. 5. Поскольку 95%-ный доверительный интервал не содержит нуль, нулевая гипотеза о том, что время ожидания в отделении банка № 1 и № 2 одинаково, должна быть отклонена при 5%-ном уровне значимости. Этот вывод совпадает с решением задачи 1. 6. Поскольку р-значение не превышает 5%-ный уровень значимости, нулевая гипотеза отклоняется. 7. Оба t-критерия приводят к одинаковым результатам.
9.12. 1. Поскольку = 4,8275 превышает верхнее критическое значение, равное 1,9752, нулевая гипотеза Но отклоняется. (Предположение о равенстве дисперсий может нарушаться, поскольку выборочная дисперсия стоимости домов в поселке Фармингдейл в четыре раза превышает выборочную дисперсию стоимости домов в поселке Левиттаун, а выборки имеют довольно большие объемы. Несмотря на это, результаты применения критерия для проверки гипотезы о разностях двух математических ожиданий являются достоверными (р-значение практически равно нулю). 3. 11,2202 < ц, -р2 < 26,7598.
9.14. 1. Поскольку tcal(. = -2,1522 не превышает нижнее критическое значение, равное -2,0211, нулевая гипотеза Нд отклоняется. 2. Необходимо предположить, что обе независимые генеральные совокупности являются нормально распределенными. 3. Поскольку р-значение равно 0,041 < 0,05, нулевая гипотеза Но отклоняется. 4. В предположении, что дисперсии равны, выполняется неравенство -4,52 < -ц2 < -0,14.
9.16. d.f. = 19.
9.18. 1. Поскольку tcalc = -2,1748 не превышает нижнее критическое значение, равное -2,093, нулевая гипотеза Но отклоняется. 2. Необходимо предположить, что распределение разностей между средней стоимостью аренды гостиничного номера в мае 2000 года и июне 2002 года имеет приближенно нормальное распределение. 3. р-знаЧение равно 0,0425. 4. -24,4317 < цо< -0,4683. 5. Поскольку 95%-ный доверительный интервал для разности между средней стоимостью аренды гостиничного номера в мае 2000 года и июне 2002 года не содержит нуля, нулевую гипотезу можно отклонить. Тот же вывод следует сделать в задачах 1 и 4. 6. 1) поскольку t .al[. = 0,7223 лежит между критическими значениями ±2,093, нулевая гипотеза Но не отклоняется; 2) необходимо предположить, что распределение разностей между средней стоимостью проката автомобиля в мае 2000 года и июне 2002 года имеет приближенно нормальное распределение; 3)р-значение равно 0,1489; 4)-2,9234 < pD < 1,4234; 5) поскольку 95%-ный доверительный интервал для разности между стоимостью проката автомобиля в мае 2000 года и июне 2002 года не содержит нуля, нулевую гипотезу можно отклонить. Тот же вывод следует сделать в задачах 1 и 4; 6) между средней стоимостью аренды гостиничного номера в мае 2000 года и июне 2002 года есть существенная разница, а между средней стоимостью проката автомобиля в мае 2000 года и июне 2002 года — нет.
9.20. 1. Поскольку = 0,1169 лежит между критическими значениями ±2,0687, нулевая гипотеза Но не отклоняется. 2. Необходимо предположить, что распределение разностей между средними измерениями имеет приближенно нормальное распределение. 3. Распределение не является нормальным. 4.р-значение = 0,9079. 5. -0,0545 < цо< 0,0487.
9.22. 1. Пять базовых показателей, вычисленных с помощью программы Microsoft Excel, не демонстрируют никаких нарушений предположения о нормальности распределения. Среднее значение и медиана совпадают, коэффициент асимметрии почти равен нулю. Итак, даже без применения графических средств, таких как диаграмма “ствол и листья”, блочная диаграмма и график нормального распределения, учитывая крупный объем выборки (п = 35), можно применять парный двухвыборочный t-критерий. Результаты применения парного двухвыборочного t-критерия, полученные с помощью программы Microsoft Excel, свидетельствуют о значительном повышении средней производительности труда. Вычисленная t-статистика, равная -2,699, не превышает нижнего критического значения -1,6909, соответствующего 5%-ному уровню значимости, ар-значение равно 0,005376.
9.24. 1. Поскольку Z„-k = -0,58 лежит между критическими значениями Z = ±2,58, гипотеза Но не отклоняется. 2. -0,2727 < ps - ps < 0,1727.
9.26. 1. Поскольку Zciik = -13,53 меньше критического значения Z = -1,96, гипотеза Но отклоняется. 2. р-значение практически равно нулю. 3. -0,2841 < ps - ps < -0,2615.
9.28. 1. Поскольку Z я1с = -0,6266 больше верхнего критического значения Z == -1,645, гипотеза Но не отклоняется. 2. р-значение, вычисленное с помощью программы Microsoft Excel, равно 0,2655.
9.30. 1. Поскольку Zruk = -3,8819 меньше критического значения Z = -1,96, гипотеза Ноотклоняется. 2. р-значение равно 0,0001. 3. -0,1501 < ps - ps < -0,0499.
9.32. 1. Fv = 2,20. 2. Fv = 2,57. 3. FL, = 3,09. 4. Fu = 3,50. 5. По мере уменьшения величины а область отклонения гипотезы сужается, а область принятия гипотезы расширяется, при этом величина Fl; увеличивается.
9.34. F= 0,826.
9.36. FL = 2,27; FL = 0,441.
9.38. 1. Нет, поскольку распределение генеральной совокупности имеет сильную положительную асимметрию, а F-критерий для проверки гипотезы о разностях между дисперсиями очень чувствителен к отклонениям от нормального распределения.
9.40. 1. Поскольку Z(uik= 2,008 больше, чем Ри= 1,556, гипотеза Но отклоняется. 2. р-значение = 0,0022. 3. Предполагается, что обе генеральные совокупности имеют нормальное распределение. 4. Следует применять t-критерий, использующий раздельную дисперсию.
9.42. 1. Поскольку £сяк = 0,8248 лежит между FL = 0,3958 и Ри = 2,5264, гипотеза Ноне отклоняется. 2. р-значение = 0,6789. 3. Предполагается, что обе генеральные совокупности имеют нормальное распределение. Графики нормального распределения и блочные диаграммы показывают, что длительность ремонта в обоих подразделениях не является нормально распределенной случайной величиной. Следовательно, F-критерий для проверки гипотезы о разности между дисперсиями, который очень чувствителен к нарушениям предположения о нормальности генеральных совокупностей, применять нельзя. Блочная диаграмма и пять базовых показателей свидетельствуют о том, что длительность ремонта в обоих подразделениях имеет одну и ту же дисперсию, хотя в первом подразделении наблюдается больший размах. Следовательно, для сравнения средних значений необходимо применить t-критерий, использующий суммарную дисперсию. 4. Для сравнения средней длительности ремонта в обоих подразделениях следует применять t-критерий, использующий суммарную дисперсию.
9.44. Поскольку Znh. — 5,76 больше, чем Fv = 2,5437, гипотеза Но отклоняется. Дисперсия веса консервов, произведенных на линии А больше, чем дисперсия веса консервов, произведенных на линии Б.
9.52. 1. Но: ст* > ст* , а* < ст, . 2. Ошибка 1-го рода: отклонить истинную нулевую гипотезу о том, что дисперсия цен музыкальных компакт-дисков, установленных виртуальными розничными торговцами, применяющими Интернет, не меньше, чем дисперсия цен музыкальных компакт-дисков, установленных традиционными физическими продавцами. Ошибка 2-го рода: не отклонить ложную нулевую гипотезу о том, что дисперсия цен музыкальных компакт-дисков, установленных виртуальными розничными торговцами, применяющими Интернет, не мень-
ше, чем дисперсия цен музыкальных компакт-дисков, установленных традиционными физическими продавцами. 3. Можно применить F-критерий для проверки гипотезы о разности между двумя дисперсиями. 4. Следует предположить, что обе генеральные совокупности имеют нормальное распределение. 5.1)Н0: Pj>p2, ц,< ц2. Средняя цена компакт-дисков на электронном рынке меньше, чем средняя цена диска на физическом рынке. 2. Ошибка 1-го рода: отклонить истинную нулевую гипотезу о том, что средняя цена музыкальных компакт-дисков на электронном рынке меньше, чем средняя цена на физическом рынке. Ошибка 2-го рода: не отклонить ложную нулевую гипотезу о том, что средняя цена музыкальных компакт-дисков на электронном рынке меньше, чем средняя цена на физическом рынке. 3. Можно применить парный двухвыборочный J-критерий для проверки гипотезы о разности между двумя средними. 4. Следует предположить, что распределение разностей между средней ценой компакт-диска на электронном и физическом рынке имеет приближенное нормальное распределение.
9.54. 1. После просмотра рекламного ролика исследователи могут попросить подростков оценить степень опасности курения по шкале от 0 до 10. 2. Но: ц,. > ps, Но: цг < ps. 3. Ошибка 1-го рода: сделать вывод, что государственная реклама более эффективна, чем реклама, произведенная компанией Philip Morris, когда на самом деле это не так. Риск, связанный с ошибкой 1-го рода, заключается в том, что подростки могут потерять возможность лучше осознать опасность курения, просмотрев рекламные ролики компании Philip Morris, и государственные деньги будут израсходованы неэффективно. Ошибка 2-го рода: сделать вывод, что реклама, произведенная компанией Philip Morris, не менее эффективна, чем государственная реклама, когда на самом деле это не так. Риск, связанный с ошибкой 2-го рода, заключается в том, что подростки могут потерять возможность лучше осознать опасность курения, просмотрев государственные рекламные ролики. 4. Поскольку рекламные ролики были продемонстрированы обоим группам подростков, более предпочтительным является парный двухвыбочный t-критерий для проверки гипотезы о разности между математическими ожиданиями.
9.56. 1. 3,74< цу < 11,86 . 2. Поскольку t.iil(, = 1,9463 < 2,0150, гипотеза Но не отклоняется.
3. Поскольку 0,107 < Рн1г = 1,08 < 7,39, т.е. лежит между двумя критическими значениями, гипотеза Но не отклоняется. 4. Критерий предполагает, что оба распределения являются нормальными. 5. Поскольку -2,2622 < t(.alc = -0,3610 < 2,2622, т.е. лежит между двумя критическими значениями, гипотеза Но не отклоняется. 6. Следует предположить, что оба распределения являются нормальными и имеют одинаковую дисперсию. 7. 2)р = 0,0546; 3)0,9102; 5) 0,7264; 8)-5,0867 < цл - < 3,6867; 9) нет оснований ут-
верждать, между средней продолжительностью выполнения заданий в бухгалтерии и исследовательском отделе есть существенная разница. С 95%-ной вероятностью можно утверждать, что средняя продолжительность выполнения заданий в бухгалтерии колеблется от 3,74 до 11,86 с. Нельзя утверждать, что средняя продолжительность выполнения заданий в исследовательском отделе на 6 с больше, чем в бухгалтерии. Кроме того, нет оснований утверждать, что дисперсии генеральных совокупностей продожительности выполнения заданий в бухгалтерии и исследовательском отделе существенно отличаются друг от друга.
9.58. 1. 348,19 < ц < 396,81. 2. 480,24 < ц < 539,76. 3. Поскольку р-значение практически равно нулю, при 5%-ном уровне значимости нулевая гипотеза отклоняется. 4. Поскольку р-значение практически равно нулю, при 5%-ном уровне значимости нулевая гипотеза отклоняется. 5. Необходимо предположить, что, во-первых, обе выборки являются случайными, и, во-вторых, что дисперсии обеих генеральных совокупностей равны. Поскольку объем обеих выборок больше 30, предположения о нормальности распределения не требуется. 6. 66,1961 < цм - ц„ < 127,8039. 7. -211,551 < цм - ци, <-140,449. 8. Поскольку р-значение равно 0,0711 > 0,05, нулевая гипотеза не отклоняется. 9. Поскольку р-значение практически равно нулю, при 5%-ном уровне значимости нулевая гипотеза отклоняется. 10. Поскольку объем обеих выборок больше 30, предположение о нормальности распределения не требуется. Необходимо лишь предположить, что обе выборки являются случайными и независимыми. 11. Существуют достаточные основания утверждать, что среднемесячная продолжительность разговоров по мобильному и домашнему телефонам у мужчин и женщин существенно различается.
9.60. 1. Поскольку trelc = 7,8735 превышает верхнее критическое значение, равное 2,3598, нулевая гипотеза Но отклоняется. 2. р-значение, вычисленное с помощью программы Microsoft Excel, практически равно нулю. 3. Поскольку р-значение практически равно нулю, нулевая гипотеза Но отклоняется. Можно утверждать, что средняя зарплата у мужчин выше, чем средняя зарплата у женщин.
9.62. Блочная диаграмма и пять базовых показателей свидетельствуют о том, что данные имеют симметричное, но не нормальное распределение. Результаты применения F-критерия для проверки гипотезы о разности между дисперсиями показывают, что при 5%-ном уровне значимости нет достаточных оснований утверждать, что дисперсии совпадают. Поскольку обе выборки извлечены из двух независимых генеральных совокупностей, для проверки гипотезы о разности между средними продолжительностями работы лампочек, произведенных на разных заводах, наиболее предпочтительным является t-критерий, использующий суммарную дисперсию. При 5%-ном уровне значимости следует отклонить нулевую гипотезу о том, что между средними продолжительностями работы лампочек, произведенных на разных заводах, нет статистически значимой разницы. Следовательно, средние продолжительности работы лампочек, произведенных на разных заводах, существенно отличаются друг от друга.
9.64. Из задачи 3.70 следует, что распределения всех переменных являются асимметричными. Поскольку F-критерий для проверки гипотезы о разности между дисперсиями очень чувствителен к нарушению условия нормальности распределений, его применять нельзя. Кроме того, дисперсии всех параметров, характеризующих спортивные и обычные модели, значительно отличаются друг от друга. Следовательно, необходимо применить t-критерий для проверки гипотезы о разности между математическими ожиданиями, использующий суммарную дисперсию. Пробег: поскольку р-значение практически равно нулю, нулевая гипотеза Но отклоняется. Длина: поскольку р-значение равно 0,2985 и превышает 5% -ный уровень значимости, нулевая гипотеза Но не отклоняется. Ширина: поскольку р-значение равно 0,0587 и превышает 5%-ный уровень значимости, нулевая гипотеза Но не отклоняется. Вес: поскольку р-значение практически равно нулю, нулевая гипотеза Но отклоняется. Емкость багажника: поскольку р-значение практически равно нулю, нулевая гипотеза Но отклоняется. Радиус поворота: посколькур-значение равно 0,1892 и превышает 5%-ный уровень значимости, нулевая гипотеза Но не отклоняется.
9.66. Цены. Блочная диаграмма, график нормального распределения и пять базовых показателей свидетельствуют о том, что распределения цен на все сорта пива, произведенного в США и импортированного из-за рубежа, имеют положительную асимметрию. Предположение о нормальности распределения грубо нарушается. Следовательно, F-критерий для проверки гипотезы о разности между дисперсиями применять нельзя. Однако анализ выборочных дисперсий показывает, что они значительно отличаются друг от друга. Объем выборки, состоящей из сортов американского пива, равен 54, а объем выборки, состоящей из сортов импортированного пива, равен 15. Строго говоря, ни парный двухвыборочный t-критерий, использующий суммарную дисперсию, ни парный двухвыборочный t-критерий, использующий раздельную дисперсию, применять нельзя. Тем не менее мы все же применили t-критерий, использующий раздельную дисперсию. Поскольку р-значение равно 0,00063 и не превышает 5%-ный уровень значимости, можно утверждать, что средние цены на американское и импортированное пиво значительно отличаются друг от друга. Калории. Блочная диаграмма, график нормального распределения и пять базовых показателей свидетельствуют о том, что распределения калорийности всех сортов пива, произведенного в США и импортированного из-за рубежа, имеют отрицательную асимметрию. Оба распределения являются несимметричными. Предположение о нормальности распределений грубо нарушается. Следовательно, F-критерий для проверки гипотезы о разности между дисперсиями применять нельзя. Однако анализ выборочных дисперсий показывает, что они незначительно отличаются друг от друга. Для анализа данных можно применить парный двухвыборочный t-критерий, использующий суммарную дисперсию. Поскольку р-значение равно 0,587 и превышает 5%-ный уровень значимости, нулевую гипотезу отклонять нельзя. Следовательно, у нас нет оснований утверждать, что средние калорийности американского и импортированного пива значительно отличаются друг от друга. Содержание алкоголя. Блочная диаграмма, график нормального распределения и пять базовых показателей свидетельствуют о том, что рас-
пределения содержания алкоголя на все сорта пива, произведенного в США и импортированного из-за рубежа, имеют отрицательную асимметрию. Оба распределения являются несимметричными. Предположение о нормальности распределений грубо нарушается. Следовательно, F-критерий для проверки гипотезы о разности между дисперсиями применять нельзя. Однако анализ выборочных дисперсий показывает, что они незначительно отличаются друг от друга. Для анализа данных можно применить парный двухвыборочный t-критерий, использующий суммарную дисперсию Поскольку р-значение равно 0,429 и превышает 5%-ный уровень значимости, нулевую гипотезу отклонять нельзя. Следовательно, у нас нет оснований утверждать, что содержание алкоголя в американском и импортированном пиве значительно различается.
9.68. 1. Поскольку р-значение = 0,000361 < 0,05, нулевая гипотеза Но отклоняется. 2. Поскольку предположение о равенстве дисперсий делать нельзя, следует применить t-критерий, использующий раздельную дисперсию для проверки гипотезы о разности между двумя математическими ожиданиями. Поскольку р-значение практически равно нулю, нулевая гипотеза На отклоняется. 3. Можно утверждать, что при 5%-ном уровне значимости посещаемость матчей, сопровождающихся рекламными акциями, значительно отличается от посещаемости обычных матчей.
9.70. График нормального распределения показывает, что обе генеральные совокупности не являются нормально распределенными. Следовательно, F-критерий для проверки гипотезы о разности между дисперсиями применять нельзя. Выборочные дисперсии веса гранул, вычисленные для бостонских и вермонтских плиток, равны 0,0203 и 0,015. Следовательно, для проверки гипотезы о разности между математическими ожиданиями можно применить парный двухвыборочный t-критерий, использующий суммарную дисперсию. Поскольку р-значение = 0,0028 < 0,05, нулевая гипотеза Но отклоняется. Следовательно, между весом гранул, потерянных в ходе испытаний плитками, произведенными в Бостоне и Вермонте, существует значительная разница.
Глава 10
10.2. 1.150.2.15.3.5.4.3.
10.4. 1.2.2.18.3.20.
10.6. 1. Если F>2,95, гипотеза Н(1 отклоняется. 2. Если F>2,95, гипотеза Но отклоняется. 3. Поскольку F я1< = 4,00 > 2,95, гипотеза Нп отклоняется. 4. Распределение имеет четыре степени свободы в числителе и 28 — в знаменателе. 5. Приблизительно 3,90 при четырех степенях свободы в числителе и 28 — в знаменателе. 6. Критический размах = 6,166.
10.8. 1. Поскольку р-значение = 0,003835 < 0,05, нулевая гипотеза Но отклоняется. 2. Q = 3,95. При 5% -ном уровне значимости применение критерия множественных сравнений Тьюки-Крамера показывает, что между средней доходностью акций, выбранных экспертами и читателями, а также читателями и лицами, применявшими жеребьевку, существует значительная разница. 3. Средняя доходность акций, выбранных экспертами, равна 6,475%, а средняя доходность акций, выбранных читателями, равна -42,5%. Доходность акций, выбранных по жребию, равна 22,6%. Однако по разности между выборочными средними нельзя делать вывод о том, что между математическими ожиданиями доходности акций, выбранных экспертами и по жребию, существует статистически значимая разница. 4. Посколькур-значение = 0,905 > 0,05, нулевая гипотеза не отклоняется.
10.10. 1. Поскольку р-значение практически равно нулю, нулевая гипотеза Но отклоняется. 2. 3,79, критический размах = 4,446. Существует статистически значимая разница
между прочностью мешков марки Kroger и Tuffstuff, Glad и Tuffstuff, а также Hefty и Tuffstuff. 3. Поскольку р-значение = 0,2443 > 0,05, нулевая гипотеза Ноне отклоняется. 4. Мешки марки Tuffstuff имеют наименьшую среднюю прочность. Их покупать не следует.
10.12. 1. Поскольку р-значение практически равно нулю, нулевая гипотеза Но отклоняется. Между средними рейтингами рекламных объявлений пяти разновидностей существует статистически значимая разница. 2. Q = 4,17, критический размах — 4,668. Существует статистически значимая разница между средними рейтингами рекламных объявлений А и В, Ап Г, Б и Г, а также Г и Д. 3. Поскольку р-значение = 0,137 > 0,05, нулевая гипотеза
Ноне отклоняется. 4. Между средними рейтингами рекламных объявлений А и Б нет статистически значимой разницы, причем их рейтинг превышает остальные. Между средними рейтингами рекламных объявлений В и Г нет статистически значимой разницы, причем их рейтинг меньше остальных. Следовательно, наиболее предпочтительными являются рекламные объявления А и Б, а наименее предпочтительными — Ви Г.
10.14. 1. Решающее правило: d.f.: 3; 36. Нулевая гипотеза Но отклоняется, если FcaU > 2,866. Поскольку FrMr = 53,03 превышает верхнее критическое значение, нулевая гипотеза Но отклоняется 2. QU(I 10) = 3,79, критический размах = 5,1967. При 5%-ном уровне значимости можно утверждать, что между средними расстояниями, которые пролетают мячи для гольфа, произведенные по разным технологиям, кроме третьей и четвертой, существует статистически значимая разница. 3. Предполагается, что, во-первых, выборки являются случайными и независимыми, во-вторых, генеральные совокупности являются нормально распределенными, и, в-третьих, дисперсии генеральных совокупностей одинаковы. 4. Поскольку р-значение = 0,1182 > 0,05, нулевая гипотеза Но не отклоняется. 5. Для - производства мячей, пролетающих максимальное расстояние, следует предпочесть третью или четвертую технологии.
10.16. 1. 40. 2. 60. 3. 55. 4. 10. 5. 10. 6. 1,00. 7. 6,0. 8. 5,50.
10.18. 1. SSAB = 8. 2. Фактор А : d.f. = 1, MS = 18, F=9. Фактор В : d.f. = 4, MS =16, F=8. Эффект взаимодействия: d.f. = 4, MS = 2, F = 1. Ошибка: d.f. = 30, MS = 2. Сумма:: d.f. = 39 3- Лгзо) = 7,56. 4. 30) = 4,02. 5. F(430) = 4,02. 6. Поскольку F,ik. = 9,00 > F = 7,56, гипотеза Ho
отклоняется. 7. Поскольку Fmle = 8,00 > F = 4,02, гипотеза Ho отклоняется. 8. Поскольку F„ik = 1,00 < F = 4,02, гипотеза Ho не отклоняется.
10.20. 1. F(230) = 3,32. 2. Fa 30) = 2,69. 3. F(g>30) = 2,27. 4. Поскольку FCBk. = 16,00 > F = 3,32, гипотеза отклоняется. 5. Поскольку F lr =-11,00 > F = 2,69, гипотеза Ho отклоняется. 6. Поскольку F.b1c = 2,00 < F = 2,27, гипотеза Но не отклоняется.
10.22. 1. Решающее правило: нулевая гипотеза Но отклоняется, если F вк > 7,709. Поскольку Fmic = 1,2857 < 7,709, гипотеза Но не отклоняется. 2. Решающее правило: нулевая гипотеза Но отклоняется, если F.,llr> 7,709. Поскольку F = 24,14 > 7,709, гипотеза Но отклоняется. 3. Решающее правило: нулевая гипотеза Но отклоняется, если F„lc> 7,709. Поскольку FBk = 240,143 > 7,71, гипотеза Нп отклоняется. 5. При 5%-ном уровне значимости длительность приготовления, как и разновидность спагетти, увеличивает вес. Не существует статистически значимого эффекта взаимодействия между длительностью приготовления и разновидностью спагетти, с одной стороны, и весом, с другой стороны.
10.24. 1. Поскольку F = 1,0245 < 3,88529 и р-значение = 0,3883 > 0,05, гипотеза Но не отклоняется. 2. Поскольку F= 0,0873 < 3,88529 и р-значение = 0,917 > 0,05, гипотеза Но не отклоняется. 3. Поскольку F = 1,9847 < 4,7472 и р-значение = 0,1843 > 0,05, гипотеза Но не отклоняется. 5. Не существует статистически значимого эффекта взаимодействия между способами очистки и травления, а также между способами очистки и травления, с одной стороны, и объемом производства, с другой.
10.26. 1. 4. 2. 6. 3. 24. 4. 34.
10.28. 1. Между группами: d.f. = 4, 88 = 60, MS= 15, F = 4,8. Между блоками: d.f. = 6, SS=75, MS = 12,5, F = 4,0. Ошибка: d.f. = 24, 88 = 75, MS = 3,125. Сумма: d.f. = 34, 88 = 210. 2. Решающее правило: нулевая гипотеза Но отклоняется, если F>2,78. 4. Поскольку F(Mk = 4,80 > 2,78, нулевая гипотеза Но отклоняется. 5—6. Решающее правило: нулевая гипотеза На отклоняется, если F > 2,51. 7. Поскольку F^ = 4,0 > 2,51, нулевая гипотеза Но отклоняется.
10.30. 1. 2. 2. 6. 3. 12. 4. 20.
10.32. Между группами: d.f. = 3, SSA= 240, F= 5,185. Между блоками: d.f. = 7, MSBL= 77,1427. Ошибка: d.f. = 21, SSE = 324, MSE = 15,4286. Сумма: d.f. = 31, SST= 1104.
10.34. Решающее правило: нулевая гипотеза На отклоняется, если F>3,01. Поскольку Рлк.= 26,42 > 3,01, нулевая гипотеза Но отклоняется. QU(2^ = 3,9, критический размах = 1,303. Пары средних, отличающихся при 5-ном уровне значимости, помечены звездочкой. |ХЛ-ХЯ| = 1,56‘, |ХЯ-ХВ| = О,89 , |%л-%г| = 2,56*, |Х£ - %в| = 2,45*, |%я - А>| = 4,12* ,
|ХД -А"г| = 1,67* . Марка Б имеет наивысший рейтинг, причем ее средний выборочный рейтинг равен 25,56.
10.36. 1. Решающее правило: нулевая гипотеза Но отклоняется, если F > 3,44. Поскольку Fcnl(. = 2,6023 < 3,44, нулевая гипотеза Нп не отклоняется. 2. Необходимо предположить, что выборки случайно и независимо извлечены из нормально распределенных генеральных совокупностей, дисперсии генеральных совокупностей приближенно равны, и между условиями и блоками нет взаимодействия. 3. Менеджер может прийти к выводу, что агенты хорошо подготовлены, а их оценки недвижимости несущественно отличаются друг от друга.
10.38. 1. Решающее правило: нулевая гипотеза Но отклоняется, если F> 3,114. Поскольку Fcnlc = 228,26 > 3,114, нулевая гипотеза Но отклоняется. 2. QU(3 QU(3 fi0= 3,4, критический размах — 0,1651. |J,-Х,| = 0,5531 , |%,-Х3| = 1,5685 , |-Х3| = 1,0154 . При 5%-ном уровне значимости все сравнения являются статистически значимыми. 3. RE = 2,558. 5. Прочность бетона на сжатие возрастает в течение трех временных периодов.
10.39. Межгрупповая дисперсия MSA описывает вариацию средних между группами. Внутригрупповая дисперсия MSW измеряет вариацию внутри каждой группы.
10.49. 1. Нулевая гипотеза Но отклоняется, если F > 2,51. Поскольку Fcal(. = 3,18 > 2,51, гипотеза Но отклоняется. 2. Нулевая гипотеза Но отклоняется, если F>3,01. Поскольку Fralc = 26,55 > 3,01, гипотеза Но отклоняется. 3. Нулевая гипотеза Но отклоняется, если F>3,40. Поскольку Fciilr = 43,57 > 3,40, гипотеза Но отклоняется. 5. Значительные эффекты взаимодействия затрудняют исследование основных эффектов. 6. Ткачихи создают ткани разной прочности в зависимости от станков. Можно применить комбинацию из 12 пар ткачих и станков в качестве единого фактора и полностью проанализировать данные с помощью однофакторного дисперсионного анализа. 7. Нулевая гипотеза Но отклоняется, если F > 3,2849. Поскольку Fcalc = 11,366 > 3,2849, гипотеза Но отклоняется. Эти результаты не противоречат результатам решения задач 1-6, в которых прочность ткани зависит от вида станков, мастерства ткачих и эффекта взаимодействия между ними.
10.51. Этап 1.1. Поскольку р-значение = 0,0224 < 0,05, нулевая гипотеза Но отклоняется. 2. Нулевая гипотеза Но отклоняется, если F > 3,47. Поскольку Frak = 2,60 < 3,47, нулевая гипотеза Но отклоняется. 3. Процедуру Тьюки применять нельзя, поскольку нулевая гипотеза в задаче 2 не отклоняется. 4. Определенные выводы о разности между средним временем чтения на основе размера файла делать нельзя. Этап 2.5. Нулевая гипотеза Но отклоняется, если F > 3,55. Поскольку Fralc = 4,0835 > 3,55, нулевая гипотеза Но отклоняется. 6. Нулевая гипотеза Но отклоняется, если F>4,41. Поскольку = 131,8529 > 4,41, нулевая гипотеза Но отклоняется. 7. Нулевая гипотеза Но отклоняется, если F > 3,55. Поскольку Fcjik. = 19,5403 > 3,55, нулевая гипотеза Но отклоняется. Можно утверждать, что среднее время чтения зависит от размера файла. 8. Если бы эффект взаимодействия был значительным, при некоторых размерах файла и буфера чтение выполнялось бы быстрее. Нельзя определенно утверждать, что размер файла или буфера (основные эффекты) сильно влияют на среднюю скорость чтения. 9. Нельзя определенно утверждать, что размер файла или буфера влияют на среднюю скорость чтения, поскольку между этими факторами существует взаимодействие. 10. В полностью рандомизированном эксперименте между средней скоростью доступа при чтении и тремя размерами файла нет статистически значимой связи. В двухфакторном эксперименте между размером буфера и размером файла существует статистически значимое взаимодействие. Учитывая эффекты взаимодействия, можно утверждать, что размер файла и размер буфера в совокупности влияют на скорость доступа при чтении файла.
Глава 11
11-2. 1. 25; 25; 25; 25. 2. Гипотеза Но отклоняется, если вычисленное значение %2 > 3,841. Поскольку вычисленное значение %2 = 4,00 > 3,841, гипотеза Но отклоняется.
11.4. Гипотеза Но отклоняется, если вычисленное значение %2 > 3,841. Поскольку вычисленное значение %2 = 183,07 > 3,841, гипотеза Но отклоняется. 2. Величина р практически равна нулю. 3. Результаты решения задач 1-3 совпадают с решением задачи 9.26.
11.6. Гипотеза На отклоняется, если вычисленное значение %2 > 3,841. Поскольку вычисленное значение %2 = 15,0693 > 3,841, гипотеза Но отклоняется. 2. Величина р практически равна нулю. 3. Результаты решения задач 1-3 совпадают с решением задачи 9.30.
11.8. Гипотеза Но отклоняется, если вычисленное значение %2 > 3,841. Поскольку вычисленное значение %2 = 33,33333 > 3,841, гипотеза Но отклоняется. 2. Величина р практически равна нулю.
11.10. Ожидаемые частоты в первой строке равны 20, 30 и 40. Ожидаемые частоты во второй строке равны 30, 45 и 60. 2. %2 = 12,500 > 5,991. Критическое значение при двух степенях свободы и 5%-ном уровне значимости равно 5,991. Результат является статистически значимым. 3. Признаки А и Б, а также признаки А и В отличаются друг от друга.
11.12. Поскольку вычисленное значение %2 = 8,3827 > 7,8147, гипотеза Но отклоняется. 2. При 5%-ном уровне значимости попарных отличий не существует. 3. Даже если критерий %2 позволяет выявить статистически значимую разницу между пациентами, прошедшими разные курсы лечения, процедура Мараскуило не позволяет идентифицировать различия между конкретными парами лекарств, поэтому администратор должен выбрать наименее дорогое.
11.14. 1. Гипотеза Но отклоняется, если вычисленное значение %2 > 5,9915. Поскольку вычисленное значение %2 = 16,5254 > 5,9915, гипотеза Но отклоняется. 2. Величина р = 0,0003. 3. Существуют статистически значимые различия между возрастными группами 32-54 и старше 54, а также группами моложе 35 лет и старше 54 лет. 4. Магазины могут использовать эту информацию для уточнения своей маркетинговой стратегии, направленной на группы покупателей, совершающих покупки в субботу и другие дни. 5. 1. Гипотеза Но отклоняется, если вычисленное значение \ > 5,9915. Поскольку вычисленное значение %2 = 4,1314 < 5,9915, гипотеза Но не отклоняется. 2. Величина р = 0,1267. 3. Чем больше объем выборки, тем выше вероятность отклонить ложную нулевую гипотезу.
11.16. 1. Поскольку вычисленное значение %2 = 4,582 < 5,991, гипотеза Но не отклоняется. 2. Величина р = 0,101. 3. Поскольку вычисленное значение %2 = 3,5 < 5,991, гипотеза Но не отклоняется. 4. Величина р = 0,174. 5. Поскольку вычисленное значение %2 = 0,755 < 5,991, гипотеза Но не отклоняется. 6. Величина р = 0,686. 7. Поскольку для всех трех факторов нулевая гипотеза не отклоняется, нет необходимости применять процедуру Мараскуило. 8. 1. Поскольку вычисленное значение %2 = 9,163 > 5,991, гипотеза Но отклоняется. 2. Величина р = 0,01. 3. Поскольку вычисленное значение %2= 7,0 > 5,991, гипотеза Но отклоняется. 4. Величина р = 0,03. 5. Поскольку вычисленное значение %2 = 1,51 < 5,991, гипотеза Но не отклоняется. 6. Величина р = 0,470. 7. Процедура Мараскуило для первого фактора: между долями отелей, регистрирующих имена постояльцев, в Гонконге и Нью-Йорке обнаружена статистически значимая разница. Процедура Мараскуило для второго фактора: между долями отелей, правильно определяющих плату за пользование минибарами, в Гонконге и Нью-Йорке обнаружена статистически значимая разница. 9. Чем больше объем выборки, тем больше мощность критерия.
11.18. 1. 21,026. 2. 26,217. 3. 30,578. 4.23,209. 5. 23,209.
11.20. 1. Гипотеза Но отклоняется, если вычисленное значение %2 > 13,277. Поскольку вычисленное значение %2 = 9,931 < 13,277, гипотеза Но не отклоняется. 2. Гипотеза Но отклоняется, если вычисленное значение %2 > 9,488. Поскольку вычисленное значение //= 9,831 < 9,488, гипотеза Но отклоняется.
11.22. Гипотеза Но отклоняется, если вычисленное значение %2 > 21,026. Поскольку вычисленное значение %2 = 129,520 > 21,026, гипотеза Но отклоняется.
11.24. 1. 31; 59. 2. 29; 61. 3. 25; 65. 4. Чем меньше уровень значимости а, тем шире область принятия гипотезы.
11.26. 1. 31. 2. 29. 3. 27. 4. 25. 5. Чем меньше уровень значимости а, тем шире область принятия гипотезы.
11.28. 40; 79.
11.30. 1. Выборка 1: 1; 2; 4; 5; 10. Выборка 2: 3; 6,5; 6,5; 8; 9; 11. 2. 22. 3. 44. 4. 66.
11.32. Поскольку = 22 превышает нижний критический уровень, равный 20, гипотеза Но не отклоняется.
11.34. 1. Поскольку Z як. = 1,714 лежит между критическими значениями, гипотеза Но не отклоняется. 2. Необходимо, чтобы обе генеральные совокупности имели приблизительно одинаковую изменчивость. 3. Между количеством опозданий на обеих железных дорогах нет статистически значимой разницы.
11.36. 1. Нулевая гипотеза Но отклоняется, если Znik. < -1,645. Поскольку Zcji]c =-4,118 <-1,645, нулевая гипотеза Но отклоняется. 2. Необходимо, чтобы обе генеральные совокупности имели приблизительно одинаковую изменчивость. 3. Парные двухвыборочные /-критерии, использующие суммарную и раздельную дисперсии, позволяют отклонить нулевую гипотезу и заявить, что в задаче 10.14 средний размер трещины в деталях, классифицированных как целые, меньше, чем в деталях, признанных треснутыми. Ранговый критерий Уилкоксона также позволяет отклонить нулевую гипотезу.
11.38. 1. Нулевая гипотеза На отклоняется, если Zc l(. < -1,96 или Zcalc > 1,96. Поскольку Zh1c = 0,6627 лежит между критическими значениями, нулевая гипотеза Нп не отклоняется. 2. Необходимо, чтобы обе генеральные совокупности имели приблизительно одинаковую изменчивость. 3. Парные двухвыборочные /-критерии, использующие суммарную и раздельную дисперсии, позволяют отклонить нулевую гипотезу и заявить, что в задаче 10.11 средняя продолжительность ремонта в первом и втором подразделении незначительно отличаются друг от друга. Ранговый критерий Уилкоксона также позволяет не отклонять нулевую гипотезу.
11.40. 1. Нулевая гипотеза Наотклоняется, если Я > %£, = 15,086. 2. Поскольку Нлк = 13,77 < 15,086, нулевая гипотеза На не отклоняется.
11.42. 1. Нулевая гипотеза Но отклоняется, если Я > %^, = 7,815. 2. Поскольку = 11,91 > 7,815, нулевая гипотеза Но отклоняется.
11.44. 1. Поскольку р-значение = 0,78 > 0,05, нулевая гипотеза Но не отклоняется. 2. Решая задачу 1, мы определяли, существует ли статистически значимая разница между медианами долговечности разных сплавов, а в задаче 11.11 речь шла о математических ожиданиях.
11.47. 1. 5,229. 2. 3,427. 3. 2,167. 4. 40,113. 5. 34,170. 6. 13,277.
11.49. 10,417.
11.51. 1.6,262 и 27,488. 2. 7,261.
11.53. Для того чтобы применить критерий “хи-квадрат”, необходимо, чтобы данные извлекались из нормально распределенной генеральной совокупности. Если это предположение не выполняется или выборка имеет малый объем, точность критерия значительно падает.
11.55. 1. Нулевая гипотеза Ноотклоняется, если %2 < 12,401 или х2 > 39,364. Поскольку статистика xL/< = 33,849 лежит между критическими значениями, нулевая гипотеза Но не отклоняется. 2. Для того чтобы применить критерий “хи-квадрат”, необходимо, чтобы данные извлекались из нормально распределенной генеральной совокупности. З.р = 0,1748.
11.57. 1. Нулевая гипотеза Но отклоняется, если %2 < 13,848. Поскольку статистика Х^. = 12,245 лежит между критическими значениями, нулевая гипотеза Но не отклоняется. 2. Диаметры являются нормально распределенными. 3. р = 0,0230.
11.59. 1. Нулевая гипотеза Но отклоняется, если %2 >• 30,144. Поскольку статистика Х(2о/( = 21,492 лежит между критическими значениями, нулевая гипотеза Н(] не отклоняется. 2. Для того чтобы применить критерий “хи-квадрат”, необходимо, чтобы данные извлекались из нормально распределенной генеральной совокупности. З.р = 0,3103.
11.61. х*-р-1 = 68,1407. х(?и/ = 15,0863. Поскольку 68,1407 > 15,0863, гипотеза Но отклоняется.
11.64. xL^-i = 19,4698. х2«/ = 9,4877. Поскольку 19,4698 > 9,4877, гипотеза Но отклоняется.
11.72. 1. Нулевая гипотеза Но отклоняется, если %2 > 3,841. Поскольку =0,412 <3,841, нулевая гипотеза Но не отклоняется. 2. Нулевая гипотеза Но отклоняется, если %2 >3,841. Поскольку %2аЛ. — 2,624 < 3,841, нулевая гипотеза Но не отклоняется. 3. Нулевая гипотеза Нп отклоняется, если %2 > 5,991. Поскольку xL/<- = 4,956 < 5,991, нулевая гипотеза Но не отклоняется. 4. Величина р = 0,0839. 5. Поскольку пицца и пиццерия выбирались независимо друг от друга, процедуру Мараскуило применять нецелесообразно.
11.74. 1. Хорошие отношения с начальником. Нулевая гипотеза Но отклоняется, если
<-1,96 или Zak. > 1,96 либо %2 > 3,841. Поскольку Zcalc =-4,830 <-1,96, а Х2а/ё. = 23,33 > 3,841, нулевая гипотеза Но отклоняется. Современное оборудование. Нулевая гипотеза отклоняется, если Z.ak < -1,96 или Zak. > 1,96 либо х2 > 3,841. Поскольку ZHk. = -3,294 < -1,96, a xL/r = 10,8504 > 3,841, нулевая гипотеза Но отклоняется. Достаточные ресурсы. Нулевая гипотеза Нп отклоняется, если Zak. < -1,96 или Zcak. > 1,96 либо х2 > 3,841. Поскольку Z.ik = -6,278 < -1,96, a xL/c = 39,4133 > 3,841, нулевая гипотеза Но отклоняется. Удобное расположение офиса. Нулевая гипотеза Ноотклоняется, если Zalc < -1,96 или Z.alc > 1,96 либо х2 > 3,841. Поскольку Zcalc =-3,807 <-1,96, а Хёа/ё = 14,493 > 3,841, нулевая гипотеза Но отклоняется. Гибкий график работы. Нулевая гипотеза Но отклоняется, если Z 11г < -1,96 или Z!ik. > 1,96 либо х2 > 3,841. Поскольку Zciilc = -4,121 < -1,96, а хГ«/<- = 16,983 > 3,841, нулевая гипотеза Но отклоняется. Возможность работать дома. Нулевая гипотеза II(] отклоняется, если Zak < -1,96 или Z 11с >1,96 либо х2 > 3,841. Поскольку Zilc = -4,603 < -1,96, а х2о/< ==21,19>3,841, нулевая гипотеза Но отклоняется. 2. Можно утверждать, что доли женщин и мужчин по каждому фактору значительно отличаются.
11.76. 1. Нулевая гипотеза Но отклоняется, если х? > 3,841. Поскольку xL, = 12,026 > 3,841 нулевая гипотеза Но отклоняется. 2. Величина р = 0,000525. 3. Нулевая гипотеза Но отклоняется, если х2 > 3,841. Поскольку xfa/t = 7,297 > 3,841, нулевая гипотеза Но отклоняется. 4. Величина р = 0,00691.
11.78. 1. Нулевая гипотеза Ноотклоняется, если х2 > 12,592. Поскольку xL/c = 11,895 < 12,592, нулевая гипотеза Но не отклоняется. 2. Нулевая гипотеза Но отклоняется, если X2 > 12,592. Поскольку xL/< = 3,294 < 12,592, нулевая гипотеза Нй не отклоняется.
11.80. 1. Нулевая гипотеза Но отклоняется, если х2 > 7,815. Поскольку xLc = 11,635 > 7,815, нулевая гипотеза Но отклоняется. 2. Величинар = 0,00874. 3. Нулевая гипотеза Ноотклоняется, если х2 > 3,841. Поскольку xLc = 10,94 > 3,841, нулевая гипотеза Но отклоняется. 4. Величина р = 0,0000941. 5. Нулевая гипотеза Но отклоняется, если х?> 3,841. Поскольку
Х2а/ё. = 0,612 < 3,841, нулевая гипотеза II (] не отклоняется. 6. Величина р = 0,4341. 7. Поскольку х2о/< = 3,454 < 3,841, нулевая гипотеза Нп не отклоняется. 8. Величинар = 0,063.
Глава 12
12.2. 1. Если X — 0, оценка ожидаемой средней величины У равна 16. 2. При увеличении переменной X на единицу оценка ожидаемой средней величины У уменьшается на 0,5. 3. 13.
12.4. 2. Ьо = -2,3697, Ь, = 0,0501; 3. При увеличении объема груза на один кубический фут оценка ожидаемого среднего количества рабочего времени увеличивается на 0,5 часа.
12.6. 2—3. Y = 76,54+ 4,3331Д'. 4. При увеличении суммы кассового сбора на один млн. долл, оценка ожидаемого среднего количества проданных видеокассет увеличивается на 4,3331 тысячи. 5. 163 202 единиц. 6. Для прогноза могут также оказаться полезными такие факторы, как длительность проката, рейтинг кинофильма, объем затрат на рекламу и т.п.
12.8. 2. Y = 6,0483 + 2,0191Х. 3. При увеличении твердости на одну единицу по Рокуэллу, оценка ожидаемой средней прочности увеличивается на 2,0191 тыс. фунтов на кв. дюйм. 4. 142,382 тыс. фунтов на кв. дюйм.
12.10. SST = 40 и г2 = 0,90. Итак, вариация зависимой переменной на 90% объясняется вариацией независимой переменной.
12.12. г = 0,75. Итак, вариация зависимой переменной на 75% объясняется вариацией независимой переменной.
12.14. 1. ^ = 0,684. Итак, вариация зависимой переменной на 68,4% объясняется вариацией независимой переменной. 2. 0,308. 3. Результаты решения задач 1 и 2 показывают, что модель можно применять для предсказания объемов продаж.
12.16. г2 = 0,9731. Итак, вариация зависимой переменной на 97,31% объясняется вариацией независимой переменной. 2. 0,7258. 3. Результаты решения задач 1 и 2 показывают, что модель можно применять для предсказания количества заказов.
12.18. 1. г2 = 0,723. Итак, вариация зависимой переменной на 72,3% объясняется вариацией независимой переменной. 2. 194,6. 3. Результаты решения задач 1 и 2 показывают, что модель можно применять для предсказания количества заказов.
12.20. Анализ остатков не выявил никаких закономерностей. Условия применения регрессии выполняются.
12.22. 1—2. Анализ остатков подтверждает адекватность модели.
12.24. 1. Анализ остатков не выявил никаких закономерностей. Линейная модель вполне адекватна. 2. График остатков не выявил нарушений условия гомоскедастичности. График нормального распределения выявил левый хвост, более тяжелый, чем у нормального распределения, однако асимметрия не наблюдается.
12.26. 1—2. Анализ остатков подтверждает адекватность модели. График нормального распределения показывает, что условие нормальности нарушено.
12.18. 1. Существует положительная линейная зависимость. Критические значения статистики Дурбина-Уотсона равны dL = 1,08 и dv = 1,36. 2. D = 0,109. 3. Поскольку D = 0,109 < dL = 1,08, между остатками существует сильная положительная автокорреляция.
12.30. 1. Нет, поскольку данные собраны во многих магазинах в течение одного и того же периода. 2. Если в течение определенного периода времени изучается отдельный магазин, причем размер полок изменялся во времени, необходимо применить статистику Дурбина-Уотсона.
12.32. 2. Ьо = 0,458, bt = 0,0161. 3. При увеличении количества заказов на единицу ожидаемая средняя стоимость перевозок увеличивается на 0,0161 тыс. долл. 4.72,908. 5. г2 = 0,844. Итак, вариация зависимой переменной на 84,4% объясняется вариацией независимой переменной. 6. 5,218; 9. D = 2,08 > 1,45. Нет оснований утверждать, что между остатками есть положительная автокорреляция. 10. Анализ остатков подтверждает адекватность модели.
12.34. 2. Ьп = -2,535, Ьх = 0,060728. 3. При увеличении температуры на один градус по Фаренгейту оценка ожидаемого объема продаж увеличивается на 0,060728 тыс. долл. 4.2 505,40. 5. 0,1461. 6. г2 = 0,94. Итак, вариация зависимой переменной на 94% объясняется вариацией независимой переменной. 9. D = 1,64 > 1,42. Нет оснований утверждать, что между остатками есть положительная автокорреляция. 10. Анализ остатков демонстрирует существование кластеров, состоящих из положительных и отрицательных остатков, следовательно, более подходящей является нелинейная модель. 11. Ъо = -2,6281, = 0,061713. При
увеличении температуры на один градус по Фаренгейту оценка ожидаемого объема продаж увеличивается на 0,061713 тыс. долл. Y = 2,4941, или 2 494,10 долл. г2 = 0,929. Итак, вариация зависимой переменной на 92,9% объясняется вариацией независимой переменной. Syx = 0,1623, D= 1,24. Результаты применения критерия Дурбина-Уотсона являются неубедительными. Анализ остатков демонстрирует существование кластеров, состоящих из
положительных и отрицательных остатков, следовательно, более подходящей является нелинейная модель. Выводы аналогичны результатам решения задач 1-10.
12.36. 1. MSR = 60, MSE = 2,222; F = 27. 2. Fl>18 = 4,41. 3. Гипотеза Но отклоняется. 4. г2 = 0,6, г=-0,7746. 5. Гипотеза Но отклоняется, если | tealc | > 2,1009. Поскольку tealf = ~ 5,196 < 2,1009, гипотеза Нп отклоняется.
12.38. При увеличении индекса S&P 500 на 1% стоимость акций компании Poctor and Gamble увеличивается в среднем на 0,626%, компании Ford Motor— на 1,074%, компании IBM — на 1,132%, компании LSI Logic — на 1,705%. 2. Если абсолютная величина коэффициента 0 больше единицы, акция является более рискованной, чем фондовый рынок в целом. Этот факт можно использовать для оценки изменчивости курса акций в зависимости от поведения всего фондового рынка.
12.40. 1. Поскольку teale = 16,5223 > t34 = 2,0302, гипотеза На отклоняется. 2. 0,0439 < 0j< 0,0562.
12.42. 1. Поскольку tcalc = 8,65 > t28 = 2,0484, гипотеза Но отклоняется. 2. 3,3073 < 0] < 5,3589.
12.44. 1. Поскольку р = 7,26497Е-06 < 0,05, гипотеза HQ отклоняется. 2. 1,2463 < 0,< 2,7918.
12.46. 1. г = -0,4014. 2. t = -1,8071, р = 0,0885 > 0,05. Гипотеза Но не отклоняется. 3. Нет оснований утверждать, что между производительностью металлоискателей и количеством выявленных нарушений существует линейная зависимость.
12.48. 1. г = 0,4838. 2. t = 2,5926, р = 0,0166 < 0,05. Гипотеза Но отклоняется. 3. Чем выше стоимость аккумулятора, тем выше сила пускового тока. 4. Данные подтверждают предположение о том, что более мощные батареи стоят дороже.
12.50. 1. 15,95 < цУХ < 18,05. 2. 14,651 < У, < 19,349. 3. В этой задаче интервалы шире, поскольку переменная X изменяется в более широком диапазоне.
12.52. 1. 20,7990 < цух < 24,5419. 2. 12,2755 < Y, < 33,0654. 3. В задаче 2 оценивается индивидуальное значение отклика, а в задаче 1 — среднее.
12.54. 1. 100,96 < цух < 138,77. 2. 20,01 < Y, < 219,72. 3. В задаче 2 оценивается индивидуальное значение отклика, а в задаче 1 — среднее.
12.56. 1. 116,7082 < цух < 178,0564. 2. 111,5942 <Yt < 183,1704. 3. В задаче 2 оценивается индивидуальное значение отклика, а в задаче 1 — среднее.
12.66. j = 24,84, Ь4 = 0,14. 3. Y = 24,84+0,14Х. 4. При увеличении количества контейнеров на единицу время доставки увеличивается на 0,14 мин. 5. Y = 45,84. 6. Нет. Число 500 выходит за пределы диапазона, для которого построено уравнение регрессии. 7. Е = 0,972. Итак, вариация зависимой переменной на 97,2% объясняется вариацией независимой переменной. 8. Поскольку bt > 0, г = 0,986. 9. Syx= 1,987. 10. Закономерности нет. Модель является адекватной. 11. Поскольку t = 24,88 > t18 = 2,1009, гипотеза Но отклоняется. 12. 44,88 < щ,х < 46,80. 13.41,56 < У, < 50.14.0,1282 < 0, < 0,1518.
12.68. 1. Ьп = -44,172, bj = 1,78171. 2. При увеличении оценочной стоимости на один доллар продажная цена увеличивается на 1,78 долл. 3. Y = 80,458. 4. Syx = 3,475. 5. г2 = 0,926. Итак, вариация зависимой переменной на 92,6% объясняется вариацией независимой переменной. 6. г =+0,962. 7. Закономерности нет. Модель является адекватной. 8. Поскольку t = 18,66 > t28 = 2,0484, гипотеза Но отклоняется. 9. 78,707 < цух < 82,388. 10. 73,195 < Y, < 87,900. 14. 1,5862 < 01 < 1,9772.
12.70. 1. Ьп = 0,30, b4 = 0,00487. 2. При увеличении оценки GMAT на один балл оценка GPI увеличивается на 0,00487 балла. 3. Y = 3,2225. 4. SYX = 0,1559. 5. г2 = 0,7978. Итак, вариация зависимой переменной на 79,78% объясняется вариацией независимой переменной. 6. г =+0,893 7. Закономерности нет. Модель является адекватной. 8. Поскольку t = 8,428 > г18 = 2,1009, гипотеза Но отклоняется. 9. 3,144 < < 3,301. 10. 2,886 < У, < 3,559.
11. 0,00366 < 0J < 0,00608. 12. Ьо = 0,258, Ь{ = 0,00494. При увеличении оценки GMAT на один балл оценка GPI увеличивается на 0,00494 балла. Y = 3,221. SYX = 0,147. г2 = 0,820. Итак, вариация зависимой переменной на 82% объясняется вариацией независимой переменной. г =+0,906. Закономерности нет. Модель является адекватной. Поскольку t = 9,06 > = 2,1009, гипотеза Но отклоняется. 3,147 < цух < 3,295; 2,903 < У, < 3,539;
0,00380 < 0j < 0,00609.
12.72. 1. Между температурой воздуха и степенью повреждения уплотнительного кольца нет явной зависимости. 3. В задаче 2 в 16 случаях кольцо не было повреждено. Если бы мы изучали лишь такие наблюдения, это свидетельствовало бы о том, что между температурой воздуха и степенью повреждения уплотнительного кольца нет явной зависимости. С учетом всех наблюдений выясняется, что отсутствие повреждения уплотнительного кольца искажает зависимость. Таким образом, при изучении степени риска полетов следует сосредоточиться лишь на полетах, в которых уплотнительное кольцо оказывалось поврежденным. 4. Прогноз нельзя распространять на интервал температур ниже 31 °F, поскольку в этом интервале не было наблюдений. 5. Y = 18,036 - 0,240Х. 7. Для этих данных более предпочтительной является нелинейная модель. 8. Последовательность отрицательных и положительных вычетов, лежащих на прямой линии, имеющей положительный наклон, свидетельствует о том, что для прогноза следует применять сильно нелинейную модель.
12.74. 2. Y = -2 269,222 + 82,4717Х. 3. При увеличении диаметра бочонка на один сантиметр вес семечек увеличивается на 82,4717 г. 3. У= 2 319,080. 5. Между весом семечек и диаметром бочонка существует положительная зависимость. 6./ = 0,9373. Итак, вариация зависимой переменной на 93,73% объясняется вариацией независимой переменной. 7. SYX = 277,7495. 8. Между весом семечек и диаметром бочонка существует нелинейная зависимость. 9. Поскольку р-значение практически равно нулю, гипотеза Но отклоняется. 10. 72,7875 < Pj < 92,1559.11. 2 186,9589 <щ,А.< 2 451,2020.12.1 726,5508 < Y, < 2 911,6101.
12.76. 1. У = -13,6561 + 0,8932Х. 3. Параметр Ьо смысла не имеет. При увеличении рейтинга на единицу стоимость обеда на одну персону увеличивается на 0,8932 долл. 3. У= 31,01. 5. SYX — 7,0167. 6. г2 = 0,4246. Итак, вариация зависимой переменной на 42,46% объясняется вариацией независимой переменной. 7. г =0,6516. 8. Нарушается условие гомоскеда-стичности. 9. Поскольку р-значение практически равно нулю, гипотеза Но отклоняется. 10. 29,07 <цГА.< 32,94. 11. 16,95 < Y, < 45,06. 12. 0,6848 < р2 < 1,1017. 13. Линейная модель адекватна. Между стоимостью обеда и рейтингом ресторана существует сильная линейная зависимость.
12.78. 1. Между количеством учеников, прошедших тестирование, и посещаемостью существует явная положительная зависимость. 2.Ьо= -771,5868, Ь, = 8,8447. Y = -771,5868 + 8,8447Х. 3.^ = 8,8447. Это означает, что при увеличении посещаемости на 1% количество учеников, прошедших тестирование, увеличивается на 8,8447%. 4. SYX = 10,5787. 5./ = 0,6024. Итак, вариация зависимой переменной на 60,24% объясняется вариацией независимой переменной. 6. г=+0,7762. Между посещаемостью и количеством учеников, прошедших тестирование, существует сильная положительная линейная зависимость. 7. Остатки распределены по всему диапазону посещаемости. Условие гомоскедастичности не нарушается. Распределение остатков имеет отрицательную асимметрию. Однако, за исключением двух выборов, распределение остатков имеет не слишком явную асимметрию. 8. Гипотеза Но отклоняется, если 111> 2,0141. Поскольку t = 8,2578 > 2,0141, гипотеза На отклоняется. 9.6,6874 < Pj < 11,0020. 10.1. Между количеством учеников, прошедших тестирование, и зарплатой учителей существует слабая положительная зависимость. 2. Y = 23,065 + 0,001 IX. 3. Ь} = 0,0011. Это означает, что при увеличении зарплаты учителей на один долл, количество учеников, прошедших тестирование, увеличивается на 0,0011%. 4. SYX = 16,3755. 5./ = 0,0474. Итак, вариация зависимой переменной на 4,74% объясняется вариацией независимой переменной. 6. г =+0,2177. Между зарплатой учителей и количеством учеников, прошедших тестирование, существует слабая положительная линейная зависимость. 7. Остатки распределены по всему диапазону посещаемости. Условие гомоскедастичности не нарушается. Распределение остатков имеет слабую отрицательную асимметрию. Распределение остатков имеет не слишком явную асимметрию и близко к нормальному. 8. Гипотеза Но отклоняется, если |г|> 2,0141. Поскольку t = 1,496 < 2,0141, гипотеза Но не отклоняется. 9. -0,000375 < pj < 0,002542. 11.1. Между количеством учеников, прошедших тестирование, и величиной расходов на одного ученика существует слабая положительная зависимость. 2. Y = 35,7843 + 0,0109Х. 3. Ьх = 0,0109. Это означает, что при увеличении расходов на одного ученика на один долл, количество учеников, прошедших тестирование, увеличивается на 0,019%. 4. SYX = 15,9984. 5. / = 0,0907. Итак, ва-
риация зависимой переменной на 9,07% объясняется вариацией независимой переменной. 6. г = +0,3012. Между величиной расходов на одного ученика и количеством учеников, прошедших тестирование, существует слабая положительная линейная зависимость. Остатки распределены по всему диапазону посещаемости. Условие гомоскедастичности не нарушается. 7. Распределение остатков имеет слабую отрицательную асимметрию. За исключением максимального отрицательного вычета, гистограмма является симметричной. 8. Гипотеза Но отклоняется, если |f|> 2,0141. Поскольку t = 2,1192 > 2,0141, гипотеза Нп отклоняется. 9.0,00054 < Pj < 0,02129. 12. Для прогнозирования количества учеников, прошедших тестирование, наиболее предпочтительной является модель, учитывающая посещаемость. В этом случае вариация зависимой переменной на 60,24% объясняется вариацией независимой переменной.
12.80. 1.GM и Ford: г= 0,947235, GM и IAL: г = 0,33972, GM и Microsoft: г = 0,177661, Ford и IAL: г= 0,402114, Ford и Microsoft: г= 0,25265, IAL и Microsoft: г= 0,29521. 2. Между стоимостью акций компаний GM и Ford существует сильная положительная корреляция, равная 0,9472, между стоимостью акций компаний Ford и IAL существует умереная положительная корреляция, равная 0,4024, между стоимостью акций компаний GM и IAL существует слабая положительная корреляция, равная 0,3397, между стоимостью акций компаний Ford и Microsoft существует слабая положительная корреляция, равная 0,2527, между стоимостью акций компаний IAL и Microsoft существует слабая положительная корреляция, равная 0,2952, между стоимостью акций компаний GM и Microsoft существует слабая положительная корреляция, равная 0,1777. 3. Нецелесообразно включать в портфель акции, между которыми существует сильная положительная корреляция. Это увеличивает инвестиционный риск.
Глава 13
13.2. 1. При фиксированной переменной Х2 увеличение переменной на единицу уменьшает среднее значение отклика У на 2 единицы. При фиксированной переменной X, увеличение переменной Х2 на единицу уменьшает среднее значение отклика У на 7 единиц. 2. Сдвиг отклика У, равный 50, оценивает значение отклика, когда X] и Х2 равны нулю. 3. 40% вариации отклика У можно объяснить вариацией переменных Xj и Х2.
13.4. 1. 68% полной вариации эффективности рабочей группы с поправкой на количество объясняющих переменных и объем выборки можно объяснить опытом. 78% полной вариации эффективности рабочей группы с поправкой на количество объясняющих переменных и объем выборки можно объяснить ясностью целей. 97% полной вариации эффективности рабочей группы с поправкой на количество объясняющих переменных и объем выборки можно объяснить опытом и ясностью целей. 3. Модель 3 лучше других предсказывает эффективность рабочей группы, поскольку у нее наибольший коэффициент г21рр .
13.6. 1. Y = 58,15708 - О,11753Х1 - 0,00687Х2. 2. При фиксированном весе увеличение мощности на одну лошадиную силу уменьшает пробег на галлон топлива в среднем на 0,11753 мили. При фиксированной мощности увеличение веса на одну единицу уменьшает пробег на галлон топлива в среднем на 0,00687 мили. 3. Коэффициент Ьо не имеет практического смысла, поскольку невозможно оценить пробег автомобиля на один галлон топлива при нулевой мощности и нулевом весе. 4. Y = 37,365 мили. 5. 35,453 < цгх < 39,276. 6. 28,747 < У, < 45,981. 7. 12 = 0,7494. Итак, 74,94% вариации зависимой переменной
объясняется вариацией мощности и веса. 8. г2 = 0,7388.
13.8. 1. Y = -330,675 + 1,764865Х1 - 0,13897Х2. 2. При фиксированном количестве рабочего времени, проведенного на выезде, увеличение количества времени, проведенного в офисе, увеличивает продолжительность простоя в среднем на 1,764865 ч. При фиксированном количестве рабочего времени, проведенного в офисе, увеличение количества времени, проведенного на выезде, уменьшает продолжительность простоя в среднем на 0,13897 ч. 3. Коэффициент Ьо не имеет практического смысла, поскольку невозможно оценить продолжительность простоя, если сотрудники ни разу не появлялись в офисе и не были на выезде. 4. Y = 160,845. 5.141,7856 <цгх< 179,9074. 6.85,2014 < У, < 236,4915. 7. г}п = 0,4899. Итак, 48,99% вариа-
ции зависимой переменной объясняется вариацией времени, проведенного в офисе и на выезде- 8- = 0,4456.
13.10. Анализ остатков демонстрирует наличие квадратичной зависимости между расходом топлива на милю пути, мощностью и весом автомобиля.
13.12. 1. Анализ остатков подтверждает адекватность модели. 2. Никакой закономерности не существует. 3. D = 1,79. 4.7)= 1,79 > 1,55. Положительной автокорреляции остатков не существует.
13.14. 1. MSR=15, MSE = 12. 2. F = 1,25. 3. Поскольку F = 1,25 < F = 4,103, гипотеза Hn не отклоняется.
13.16. 1. MSR = 1 684, MSE = 22,7. F = 74,13. Поскольку F = 74,13 > FU(22i Z1) = 3,467, гипотеза Но отклоняется. 2. Вероятность того, что F-статистика, имеющая две степени свободы в числителе и 21 — в знаменателе, попадает в область отклонения гипотезы, когда она верна, меньше 0,001.
13.18. 1. MSR = 1 014 016, MSE = 25 251. F = 40,16. Поскольку F = 40,16 > FU(2 22.2.l} = 3,522, гипотеза Но отклоняется. 2. Вероятность того, что F-статистика, имеющая две степени свободы в числителе и 19 — в знаменателе, попадает в область отклонения гипотезы, когда она верна, меньше 0,001.
13.20. 1. Угол наклона переменной Х2, равный 2,5 величины t-статистики, больше угла наклона переменной Хр равного 1,25 величины t-статистики, 2. 0,85225 < 04 < 9,14755. 3. Для переменной Хх: t = 2,50 > t22 = 2,0739, следовательно, гипотеза Но отклоняется. Для переменной Х2: t = 1,25 < t22 = 2,0739, следовательно, гипотеза Нп не отклоняется. Вклад переменной Х2 в модель, уже содержащую переменную X,, является статистически незначимым. Таким образом, в модель следует включить лишь переменную ХР
13.22. 1. 0,65400 < Pj < 0,92832. 2. Для переменной ХР t = 12,57 > t12 = 2,1788, следовательно, гипотеза Но отклоняется. Для переменной Х2: t = 8,43 > t)2 = 2,1788, следовательно, гипотеза Нп отклоняется. Таким образом, в модель следует включить обе переменные.
13.24. 1. -0,18311 < Pj < -0,05195. 2. Для переменной ХР t = -3,605 < t47 = -2,0117, следовательно, гипотеза Но отклоняется. Для переменной Х2: t = -4,91 < t47 = -2,0117, следовательно, гипотеза Но отклоняется. Таким образом, в модель следует включить обе переменные.
13.26. 1. 0,9809 < Р4 < 2,5489. 2. Для переменной X,: t = 4,66 > t23 = 2,0687, следовательно, гипотеза Но отклоняется. Для переменной Х2: t = -2,36 < -t23 = -2,0687, следовательно, гипотеза Но отклоняется. Таким образом, в модель следует включить обе переменные.
13.28. 1. Для переменной ХР F = 1,25 > FV(J J0) = 4,965, следовательно, гипотеза Но не отклоняется. Для переменной Х2: F = 0,833 < FU(110) = 4,965, следовательно, не гипотеза Но отклоняется. Таким образом, в модель не следует включать обе переменные. 2. 2 = 0,1111. При
фиксированной переменной Х2 11,11% вариации отклика можно объяснить вариацией переменной ХР г*2 { = 0,0769. При фиксированной переменной Х4 7,69% вариации отклика можно объяснить вариацией переменной Х2.
13.30. 1. Для переменной ХР F = 12,96 > FU(i 47) = 4,047, следовательно, гипотеза Но отклоняется. Для переменной Х2: F = 24,04 > FU(i 10) = 4,047, следовательно, гипотеза Но отклоняется. 2. Гу] 2 = 0,2162. При фиксированной переменной Х2 21,62% вариации отклика можно
объяснить вариацией переменной ХР rf2, = 0,3384. При фиксированной переменной Х4 33,84% вариации отклика можно объяснить вариацией переменной Х2.
13.32. 1. Для переменной Х4: F = 21,68 > FVil 23) = 4,279, следовательно, гипотеза Но отклоняется. Для переменной Х2: F = 5,586 > F( (12j) = 4,279, следовательно, гипотеза Но отклоняется. Обе переменные следует включить в модель. 2. r}i2 = 0,4852. При фиксированной переменной Х2 48,52% вариации отклика можно объяснить вариацией переменной ХР гг2 1 = 0,1954. При фиксированной переменной Х4 19,54% вариации отклика можно объяснить вариацией переменной Х2.
13.34. 1. Сначала необходимо построить модель множественной регрессии, используя в качестве переменной Xt количество баллов, набранных студентом при сдаче теста SAT, а в качестве переменной Х2 — фиктивную переменную, равную 1, если студент получил хорошую оценку. Если коэффициент при фиктивной переменной значительно отличается от нуля, необходимо построить модель, учитывающую член ХгХ2, и убедиться, что коэффициент при переменной Х1 не является статистически значимым, если Х2 = 1 или Х2 = 0. 3. Если студент получил хорошую оценку по статистике, то его ожидаемая оценка по бухгалтерскому учету будет в среднем на 0,30 балла выше, чем у студента, набравшего те же баллы при сдаче теста SAT, но не получившего хорошей оценки по статистике.
13.36. 1. Y = 43,737 4- 9,219Xj 4- 12,697Х2, где Хх— количество комнат, Х2— местоположение (восток = 0). 2. При фиксированном местоположении каждая дополнительная комната увеличивает стоимость дома в среднем на 9,219 тыс. долл, больше. При фиксированном количестве комнат дом, расположенный на западе, стоит на 12,697 тыс. долл, больше. 3. 126 710; 109,5600 < < 143,8551. 121,4714 < цж=г < 131,9437. 4. Анализ остатков
подтверждает адекватность модели. 5. Поскольку F = 55,39 > F(217) = 3,5915, гипотеза отклоняется. 6. Для переменной X,: t = 8,95 > t17 = 2,1098, гипотеза Но отклоняется. Для переменной Х2: t = 3,59 > i17 = 2,1098, гипотеза Нп отклоняется. В регрессионную модель следует включить обе переменные. 7. 7,0466 < Pj < 11,3913. 5,2377 < Р2 < 20,1557. 8. Гу ]2 = 0,867. Итак, 86,7% вариации стоимости дома объясняется вариацией количества комнат и местоположения. 9. г* =* 0,851. 10. Гу]2 = 0,825. Итак, при фиксированном местоположении 82,5% вариации стоимости дома объясняется вариацией количества комнат. Гу2} = 0,431. Следовательно, при фиксированном количестве комнат 43,1% вариации стоимости дома объясняется вариацией местоположения. 11. Наклон стоимости дома по отношению к количеству комнат не зависит от его местоположения. 12. Y = 53,95 4- 8,032Х! - 5,90Х2 4- 2,089XjX2. Для фактора Х,Х2 р-значение равно 0,330. Гипотеза Но не отклоняется. 13. Следует применять модель с двумя переменными.
13.38. 1. Y = 8,0100 4- 0,0052Xj - 2,1052Х2, где Хг— глубина (в футах) Х2— вид бурения (мокрое = 0, сухое = 1). 2. При фиксированном виде бурения каждый дополнительный фут глубины увеличивает время бурения в среднем на 0,0052 мин. При фиксированной глубине сухое бурение уменьшает время бурения на 2,1052 мин. 3. Сухое бурение: Y = 6,4276 мин.; 4,92304 <Y,< 7,9322; 6,2096 < щх< 6,6457. 4. Анализ остатков подтверждает адекватность модели. 5. F = 111,109, Е297 = 3,09, р-значение практически равно нулю. Гипотеза Но отклоняется. 6. Для переменной Xt: t = 5,0289 > ig7 = 1,9847, гипотеза Но отклоняется. Для переменной Х2: £ = -14,0331 > £„7 = -1,9847, гипотеза Но отклоняется. В регрессионную модель следует включить обе переменные. 7. 0,0032 < < 0,0073. -2,4029 < р2 <-1,8075.
8. гу?,2 = 0,6961. Итак, 69,61% вариации дополнительной продолжительности бурения объясняется вариацией глубины скважины и вида бурения. 9. г* = 0,6899. 10. 2 = 0,2068.
Итак, при фиксированном виде бурения 20,68% вариации дополнительной продолжительности бурения объясняется вариацией глубины скважины. г?2 ,= 0,6700. Следовательно, при фиксированной глубине скважины 67% вариации дополнительной продолжительности бурения объясняется вариацией вида бурения. 11. Наклон дополнительной продолжительности бурения по отношению к глубине скважины не зависит от вида бурения. 12. Y = 7,9120 4- 0,0060Х1 - 1,9091Х2 - 0,00015XjX2. Для фактора XtX2 р-значение равно 0,4624 > 0,05. Гипотеза Но не отклоняется. 13. Следует применять модель с двумя переменными.
13.40. 1. У = 31,5594+ 0,0296Xt + 0,0041Х2+1,7159x10 5XSX2, где Хг ~~ объем продаж, Х2 — количество заказов. Для Х^^-значение равно 0,3249 > 0,05. Гипотеза Но не отклоняется. 2. Следует применить модель из задачи 13.5.
13.42. 1. Y = -1 293,3105 + 43,6600Х; + 56,9335Х2 - 0,8430X^2, где Х} — затраты на рекламу по радио, Х2 — затраты на рекламу в газетах. Для XtX2р-значение равно 0,0018 < 0,05.
Гипотеза Но отклоняется. 2. Следует применить модель, разработанную при решении данной задачи.
13.44. 1. Y = -63,9813 + l,1258Xj - 22,2887Х2 + 8,0880Х3, где X,— оценка на вступительном экзамене, Х2 — фиктивная переменная, кодирующая традиционный вид обучения, Х3 — фиктивная переменная, кодирующая новый вид обучения. 2. При фиксированном виде обучения каждый дополнительный балл, полученный на вступительном экзамене, увеличивает оценку, полученную на выпускном экзамене, в среднем на 1,1258 балла. При фиксированной оценке, полученной на вступительном экзамене, применение традиционного метода понижает оценку, полученную на выпускном экзамене, в среднем на 22,2887 балла по сравнению с оценками, полученными после обучения по методике, использующей Интернет. При фиксированной оценке, полученной на вступительном экзамене, применение метода, использующего компакт-диски, повышает оценку, полученную на выпускном экзамене, в среднем на 8,0880 балла по сравнению с оценками, полученными после обучения по методике, использующей Интернет. 3. Y =48,5969 мин. 4. Анализ остатков демонстрирует квадратичную зависимость. График нормального распределения не выявил серьезных отклонений от предположения о нормальности. 5. F = 31,77, р-значение практически равно нулю. Гипотеза Нп отклоняется. 6. Для переменной Хр t= 7,0868, р-значение практически равно нулю. Гипотеза Но отклоняется. Для переменной Х2: i =-5,1649, р-значение практически равно нулю. Гипотеза Но отклоняется. Для переменной Х3: t— 1,8765, р-значение = 0,07186. Гипотеза Но не отклоняется. В регрессионную модель следует включить оценку, полученную на вступительном экзамене, и фиктивную переменную, кодирующую традиционный метод обучения. 7. 0,7992 < pj < 1,4523. -31,1591 < р2 <-13,4182, -0,7719 < Р3 < 16,9480. 8. гД2 = 0,7857. Итак, 78,57% вариации оценки, полученной на выпускном экзамене, объясняется вариацией оценки, полученной на вступительном экзамене, и видом обучения. 9. гД =0,7610. 10. ryL23 = 0,6589. Итак, при фиксированном виде обучения 65,89% вариации оценки, полученной на выпускном экзамене, объясняется вариацией оценки, полученной на вступительном экзамене. 13 = 0,5064. Следовательно, при фиксированной оценке, полученной на вступительном экзамене, 50,64% вариации оценки, полученной на выпускном экзамене, объясняется разницей между традиционным обучением и обучением по методике, использующей Интернет. Гу312 = 0,1193. Следовательно, при фиксированной оценке, полученной на вступительном экзамене, 11,93% вариации оценки, полученной на выпускном экзамене, объясняется разницей между методиками обучения, использующими компакт-диски и Интернет соответственно. 11. Наклон оценки, полученной на вступительном экзамене, по отношению к оценке, полученной на выпускном экзамене, не зависит от методики обучения. 12. F = 0,8122, р-значение равно 0,46 > 0,05. Гипотеза Нп не отклоняется. 13. В регрессионной модели следует учитывать оценку, полученную на вступительном экзамене, и фиктивную переменную, кодирующую традиционное обучение.
13.46. Проверка значимости полной регрессионной модели включает в себя одновременную проверку значимости каждой независимой переменной. Оценка вклада каждой независимой переменной сводится к проверке вклада, который вносит каждая независимая переменная, после учета остальных независимых переменных.
13.52. 1. Y =-44,988+ 1,7506Х] +0,368Х2, где X, — оценочная стоимость (тыс. долл.), Х2— период времени (месяцев). 2. При фиксированном периоде времени каждая дополнительная тысяча долларов в оценочной стоимости повышает продажную цену дома в среднем на 1,7506 тыс. долл. При фиксированной оценочной стоимости каждый дополнительный месяц увеличивает продажную цену дома на 0,368 тыс. долл. 3. 81,969 тыс. долл. 4. Все четыре графика остатков подтверждают адекватность модели. 5. Поскольку F = 223,46 > Ги(227) = 3,35, нулевая гипотеза На отклоняется. 6. Значениер не превышает 0,001. 7. г}?12 = 0,943 . Итак, 94,3% вариации продажной цены можно объяснить вариацией оценочной стоимости и периода времени. 8. = 0,939. 9. Для переменной X,: t = 20,41 > t27 = 2,0518, гипотеза Но отклоня-
ется. Для переменной Х2: t = 2,873 > t27 = 2,0518, гипотеза Но отклоняется. Обе переменные следует включить в модель. 10. Для переменной X, р-значение не превышает 0,001. Для переменной Х2 р-значение равно 0,008. 11. 1,575 < Pj < 1,927; 12. /у2!2 = 0,9392 . При фиксированном периоде времени 93,92% вариации продажной цены можно объяснить вариацией оценочной стоимости. г221 =0,2342 . При фиксированном периоде времени 23,42% вариации продажной цены можно объяснить вариацией временного периода.
13.54. 1. Y = 63,7751 +10,7252 -0,2843Х2 , где %! — площадь (тыс. кв. футов), Х2— возраст (лет). 2. При постоянном возрасте каждая дополнительная тысяча квадратный футов увеличивает оценочную стоимость в среднем на 10,7252 тыс. долл. При фиксированной площади каждый дополнительный год возраста уменьшает оценочную стоимость в среднем на 0,2843 тыс. долл. 3. 79,702 долл. 4. График остатков, построенный на основе возраста дома, демонстрирует потенциальную закономерность. На каждом графике существует выброс. 5. Г = 28,58 >Г11(212) = 3,89, гипотеза Но отклоняется. 6.р< 0,001. 7. /г212 = 0,8265. Итак, 82,65% вариации оценочной стоимости дома объясняется вариацией его площади и возраста. 8. гД = 0.7976. 9. Для переменной Хх: t = 3,558 > t12 = 2,1788, гипотеза Н„ отклоняется. Для переменной Х2: t = -3,400 <-t12 = -2,1788, гипотеза отклоняется. Таким образом, в модель необходимо включить обе переменные. 10. Для переменной Хх значение р равно 0,004. Для переменной Х2 значение р равно 0,005. 11. 4,158 < 0t < 17,293. 12. гГ12 = 0,5134. Итак, при фиксированном возрасте дома 51,34% вариации оценочной стоимости дома объясняется вариацией его площади. гГ2, = 0,4907. Следовательно, при фиксированной площади дома 49,07% вариации оценочной стоимости дома объясняется вариацией его возраста. 13. Нет. Возраст дома вносит статистически значимый вклад в оценочную стоимость.
13.56. 1. Пробег автомобиля на галлон топлива = 40,8765 - 0,0121 х Длина -0,0050 х Вес.
2. &! =-0,0121. При фиксированном весе увеличение длины автомобиля на один дюйм приводит к увеличению пробега в среднем на 0,0121 мили. Ь2 = -0,0050. При фиксированной длине увеличение веса автомобиля приводит к уменьшению пробега в среднем на 0,0050 мили. 3. Предсказанный пробег = 23,6603 мили на галлон. 4. Анализ остатков длины показывает, что условие гомоскедастичности нарушено. Анализ остатков веса показывает, что между пробегом и весом существует квадратичная зависимость. 5. Да, при 5%-ном уровне значимости между пробегом и двумя объясняющими переменными существует статистически значимая зависимость, поскольку р-значение в Г-критерии практически равно нулю. 6. р-значение практически равно нулю. 7. 61,17% полной вариации пробега объясняется вариацией веса и длины. 8. гд2 = 0,6051. 9. В модель следует включить только вес. 10. Для длины и веса p-значения практически равны нулю. 11. 95%-ный доверительный интервал имеет следующий вид: [-0,0059, -0,0040]. 12. /у, 2 = 0,0018, ГП1 = 0,4706. При фиксированном весе 0,18% вариации пробега можно объяснить длиной автомобиля. При фиксированной длине автомобиля 47,06% вариации пробега можно объяснить весом автомобиля.
13.58. 1. Y = 170,80225 - 3,0654 х Xj- 19,9941 х Х2, где Хх— фиктивная переменная, кодирующая лигу (0 — Американская, 1 — Национальная), Х2 — показатель ERA. 2. При фиксированном показателе ERA среднее ожидаемое количество побед команды в Американской лиге на 3,0654 больше, чем в Национальной лиге. При фиксированной лиге увеличение показателя ERA на единицу уменьшает среднее ожидаемое количество побед на 19,9941. 3. Приблизительно 81 победа. 4. Анализ остатков показывает, что модель адекватна. 5. F = 20,257, р = 4,23207Е-06 < 0,05. Гипотеза Но отклоняется. 6. Для переменной Хх: t == -0,9755, р = 0,3380 > 0,05. Гипотеза Но не отклоняется. Для переменной Х2: t = -6,3616, р = 8,20671Е-07 < 0,05. Гипотеза Но отклоняется. В модель следует включить показатель ERA, но не фиктивную переменную, кодирующую лигу. 7. -9,5130 < 0Х < 3,3823, -26,4429 < 02 <-13,5453. 8. Гу12 = 0,6001. Итак, 60,01% вариации количества побед
можно объяснить вариацией лиги и показателя ERA. 9. гкорр — 0,5705. 10. г,712 =0,0340. Следовательно, при фиксированном показателе ERA 3,4% вариации количества побед объясняется вариацией лиги. /у2 j = 0,5998. Следовательно, при фиксированной лиге 59,98% вариации количества побед объясняется вариацией показателя ERA. 11. Наклон количества побед по отношению к показателю ERA не зависит от лиги. 12.р — 0,7290. Гипотеза Но не отклоняется. 13. Следует применять модель, учитывающую только показатель ERA.
Глава 14
14.2. 2. Y = -7,556 + 1,2717Х-0,0145Х2. 3.18,52. 4. Анализ остатков выявил закономерности распределения остатков в зависимости от скорости, квадрата скорости и отклика. 5. F = 141,46 > Г22, = 3,39. Гипотеза Нп отклоняется. Полная модель является статистически значимой, р < 0,001. 6. t = -16,63 < -t25 = -2,0595. Гипотеза Но отклоняется. р< 0,001. 7. г;12= 0,919 Итак, 91,9% вариации пробега можно объяснить квадратичной зависимостью между пробегом и скоростью. 10. r~jpp = 0,912.
14.4. 2. Y = 6,643 + 0,895Х - 0,0041Х2. 3. 49,17. 4. Анализ остатков не выявил закономерностей. Однако распределение остатков отличается от нормального. 5. F = 157,32 > Г29 = 4,26. Гипотеза Но отклоняется. Полная модель является статистически значимой, б.р < 0,001. Следовательно, вероятность F-статистики, превышающей 157,32, если pj = 0 и р2 = 0, меньше 0,001. 7. t = -4,27 < -t9 = -2,2622. Гипотеза Но отклоняется. Квадратичный эффект является значимым. 8.р = 0,002. Следовательно, вероятность t-статистики с абсолютным значением, превышающим 4,27, если р2 = 0, равна 0,013. 9. г212 = 0,972. Итак, 97,2% вариации урожая можно объяснить квадратичной зависимостью между урожаем и количеством внесенных удобрений. 10. г*орр = 0,966.
14.6. 1. 1 511,22. 2. При фиксированной переменной Х2 увеличение натурального логарифма переменной Х} на единицу приводит к увеличению натурального логарифма отклика Y в среднем на 0,9. При фиксированной переменной Xj увеличение натурального логарифма переменной Х2 на единицу приводит к увеличению натурального логарифма отклика Y в среднем на 1,41.
14.8. 1. Y = 9,04 + 0,852^/х^ . 2.15,36 миль на галлон. 3. Анализ остатков выявил явную квадратичную зависимость. Модель плохо приближает данные наблюдений. 4. t = 1,35 < t№ = 2,0555. Гипотеза Но не отклоняется. Модель не является статистически значимой. 5. г2 = 0,066. Только 6,6% вариации пробега можно объяснить вариацией квадратного корня скорости. 6. = 0,030. 7. Квадратичная регрессионная модель, построенная в задаче 14.2,
намного лучше. Квадратный корень скорости не позволяет хорошо аппроксимировать наблюдаемые данные.
14.10. 1. In У = 2,475 + 0,018546Хг 2.32,95 фунтов. 3. Анализ остатков демонстрирует четкую квадратичную зависимость. 4. t = 6,11 > t10 = 2,2281. Гипотеза Но отклоняется. Модель является статистически значимой. 5. г2 = 0,798. Следовательно, 78,7% вариации натурального логарифма урожая можно объяснить вариацией количества внесенных удобрений. 6. г* =* 0,768. 7.Квадратичная регрессионная модель, построенная в задаче 14.4, является намного более точной.
14.12. 1,25.
14.14. VIF1 = 2,778, VIF2 = 2,778. Нет причин подозревать коллинеарность.
14.16. VIFX = 1,009, VIF2 = 1,009. Нет причин подозревать коллинеарность.
14.18. 1. 35,04. 2. Величина Ср намного превышает k+ 1 = 3 (количество параметров, включая сдвиг), поэтому данную модель можно далее не рассматривать в качестве кандидата на лучшую модель.
14.20. 1. Пусть У — продажная цена, Х4 — оценочная стоимость, Х2 — период времени, Х3 — фиктивная переменная, кодирующая новый дом (0 — да, 1 — нет). Используя полную регрессионную модель, учитывающую все переменные, выясняем, что показатели VIF (1,3; 1,0 и 1,3 соответственно) не превышают 5. Нет причин подозревать коллинеарность. Используя метод наилучшего подмножества, определяем, что наилучшая модель должна учитывать оценочную стоимость (XJ и временной период (Х2). Анализ остатков не выявил никаких четких закономерностей. Итоговая модель: Y = -44,9882 + ^ТбОбХ^ 0,3680Х2. = 0,9434.
гкорР = 0,9388. Значимость модели: F = 233,4575, р < 0,001. При 5%-ном уровне значимости каждая независимая переменная является статистически значимой.
14.22. 1. Пусть У — пробег в милях на галлон топлива, Хг — вес, Х2 — ширина, Х3 — длина, Х4 — фиктивная переменная, кодирующая спортивные модели (1 — да, 0 — нет). Используя полную регрессионную модель, учитывающую все переменные, выясняем, что VIFX — 5,1, VIF2= 4,8, VIF2= 4,6, VIF = 2,6. Переменная Xt исключена из модели. В регрессионной модели, учитывающей оставшиеся переменные, все показатели VIF не превышают пяти. Используя метод наилучшего подмножества, определяем, что единственная модель, учитывающая Х2, Х3 и Х4, имеет показатель Ср < £+1. Анализ остатков выявил нарушение условия гомоскедастичности. Между пробегом и длиной, а также между пробегом и шириной автомобиля существуют квадратичные зависимости. Маленькие p-значения квадрата длины и квадрата ширины в регрессионной модели свидетельствуют о том, что длина и ширина являются при 5%-ном уровне значимости статистически значимыми. Итоговая модель: Y = 236,01 - 0,2072^^- 2,0024Х3 - 4,0526Х1 + 0,00000026 Х22 + 0,0051 Х32 , г2= 69,3%,
г* = 68% . Значимость модели: F = 51,92, значениер практически равно нулю. Анализ остатков показывает, что нарушение условия гомоскедастичности не устранено.
14.24. Пусть У— успеваемость, Х4 — посещаемость занятий, % , Х2 — зарплата, Х3 — затраты. Построим полную регрессионную модель, учитывающую все переменные. У всех переменных коэффициенты VIF меньше пяти. Следовательно, у нас нет оснований подозревать коллинеарность между ними. Модель, построенная с помощью метода наилучшего подмножества, имеет вид: У =-771,5869 + 8,8447Х,. График остатков показывает, что наиболее точной является нелинейная модель. График нормального распределения демонстрирует, что, несмотря на относительно “тяжелый” левый хвост, распределение ошибок является почти нормальным. Существуют основания утверждать, что квадратичная модель имеет 5%-ный уровень значимости. Наиболее точной является следующая квадратичная модель: У == 6 672,8367 + 150,56947Х1 + 0,8532(Х1)2.
14.26. 1. Пусть У — цена, Xt — скорость печати текста, Х2 — стоимость печати страницы текста, Х3 — время печати цветной фотографии, X, — стоимость печати цветной фотографии. Используя полную регрессионную модель, учитывающую все переменные, выясняем, что все показатели VIF меньше пяти. Итак, нет причин подозревать коллинеарность между какой-либо парой переменных. Используя метод наилучшего подмножества, определяем следующую модель: Y = 326,8080 - 23,8570Xj- 10,2344Хя . Анализ остатков не выявил никаких закономерностей.
14.30. 1. Анализ линейной регрессионной модели, учитывающей все шесть независимых переменных, показывает, что у показателя ERA. и количества попаданий показатели VIF больше пяти. Они равны 7,0 и 5,38 соответственно. Поскольку показатель ERA имеет наибольший показатель VIF, его следует исключить из модели. Анализ оставшейся линейной регрессионной модели показывает, что ни у одной из независимых переменных показатель VIF не превышает пяти. Используя метод наилучшего подмножества, определяем, единственную модель, у которой показатель Ср не превышает /г+1. Проверяя p-значения для i-статистик, соответствующих каждому наклону коэффициентов, определяем, что при 5% -ном уровне значимости ошибками можно пренебречь. Наилучшей является следующая модель: У = 123,9173 + 0,0828Х2-0,0699Х3-0,0432Х4+0,4457Х., где Х2— количество очков, Х3— количество пропущенных бросков, Х4— количество пробежек, Х5— количество удачных защит. При 5%-ном уровне значимости все коэффициенты существенно отличаются от нуля. Тестовая F-статистика для полной модели равна 103,40, имеет 4 степени свободы в числителе и 25 — в знаменателе, ар-значение меньше 0,001. Анализ остатков не выявил никаких закономерностей.
/у2345 = 0,9430, г* = 0,9339. Распределение вычетов имеет отрицательную асимметрию.
2. Анализ показывает, что у количества пробежек, количества попаданий, количества обходов и количества удачных защит показатели VIF превышают 5. Метод поиска наилучшего подмножества приводит к следующей модели: Y = -3,8666 + 0,0046Xj + 0,0029Х2, где Х1 — количество попаданий, аХ2 — количество обходов. Тестовая F-статистика для полной модели равна 77,19, имеет 2 степени свободы в числителе и 27 — в знаменателе, ар-значение меньше 0,001. Анализ остатков не выявил никаких закономерностей. Гу 35 = 0,8511, г^ирр = 0,8401. Распределение вычетов не имеет никаких закономерностей.
14.32. 1. Пусть У — количество побед, Хх — количество очков, набранных командой, Х2 — количество очков, набранных соперниками, Х3 — количество очков, набранных командой за игру, %, X, — количество очков, набранных соперниками за игру, %, Х7 — разница в количестве перехватов, Х6 — количество подборов в нападении, %, Х7 — количество подборов в защите, %. Используя полную регрессионную модель, учитывающую все переменные, выясняем, что 777^=9,81, VIF = 9,21, VIF.= 3,57, VIF.= 4,54, VIF= 2,92, VIF(=- 1,35, VIF7= 1,42. Поскольку переменная Xt имеет наибольший показатель VIF, она исключена из модели. Пусть теперь У — количество побед, Хх — количество очков, набранных соперниками, Х2— количество очков, набранных командой за игру, %, Х3 — количество очков, набранных соперниками за игру, % , Х4 — разница в перехватах, Х5 — количество подборов в нападении, %, Х6 — количество подборов в защите, %. Анализ множественной регрессионной модели, учитывающей оставшиеся переменные, показывает, что все показатели VIF не превышают пяти. Следовательно, нет оснований подозревать коллинеарность между какими-либо переменными. Используя метод наилучшего подмножества и шаговой регрессии, определяем, что наиболее предпочтительной является следующая модель: Y = 13,6936 + 4,0274Х,-3,4149Х3 - 3,4150Хг 2. Пусть У — количество побед, X. — разница в очках, Х2 — разница в количестве очков, набранных за игру, % , Х3 — разница в количестве перехватов, X. — количество подборов в нападении, %, X. — количество подборов в защите, %. Используя полную регрессионную модель, учитывающую все переменные, выясняем, что П7’1=9,42, VIF2= 6,18, V77’3= 2,84, VIF^ 1,33, VIF,= 1,18. Поскольку переменная Хх имеет наибольший показатель VIF, она исключена из модели. Пусть теперь У — количество побед, Хх — разница в количестве очков, набранных за игру, %, Х2 — разница в количестве перехватов, Х3 — количество подборов в нападении, %, X. — количество подборов в защите, %. Анализ множественной регрессионной модели, учитывающей оставшиеся переменные, показывает, что все показатели VIF не превышают пяти. Следовательно, нет оснований подозревать коллинеарность между какими-либо переменными. Используя метод наилучшего подмножества и шаговой регрессии, определяем, что наиболее предпочтительной является следующая модель: Y = 40,9507 + 3,7221Х1-3,4242Х3. 3. Коэффициент г* в обеих моделях равен 0,8347 и 0,8390 соответственно. Вторая модель является более точной, поскольку объясняет большую долю вариаций количества побед с учетом поправки на количество независимых переменных и объем выборки.
14.34. Пусть У — стоимость дома, X, — площадь участка, Х2 — внутренняя площадь, Х3 — возраст дома, X. — количество комнат, Х5 — количество ванных комнат, Хв — площадь гаража. 1. Рослин. Используя полную регрессионную модель, учитывающую все переменные, выясняем, что все показатели VIF не превышают пяти. Значит, нет причин подозревать коллинеарность. Используя методы наилучшего подмножества и шаговой регрессии, определяем, что наилучшая модель, позволяющая предсказывать стоимость дома в поселке Рослин, имеет следующий вид: Y = 93,131 + 660,0916Х1+ 0,1428Х2. 2. Коэффициенты г^орр в моделях, разработанных при решении задач 14.33.1, 14.34.1 и 14.35.1, равны 0,81, 0,8252 и 0,8383 соответственно. Модель, созданная при решении задачи 14.35.1, является наиболее точной с учетом поправки на количество переменных и объем выборки.
14.36. Пусть У — стоимость дома, Xt — площадь участка, Х2 — внутренняя площадь, Х3 — возраст дома, Х( — количество комнат, Х5 — количество ванных комнат, Х6 — площадь гаража, X- — фиктивная переменная, кодирующая местоположение дома (Глен-Коув — 0, другие поселки — 1). 1. Используя полную регрессионную модель, учитывающую все переменные, выясняем, что все показатели VIF не превышают Значит, нет причин подоз-
ревать коллинеарность. Используя методы наилучшего подмножества и шаговой регрессии, определяем, что наилучшая модель, позволяющая предсказывать стоимость дома, имеет следующий вид: Y = 102,8870 + 398,2023^+0,1278^+ 38,3694Х5- 140,7485Х7 2. При прочих равных условиях дом в поселке Глен Коув стоит на 140,75 тыс. дешевле, чем в поселке Рослин.
14.38. Анализ линейной регрессионной модели, учитывающей все независимые переменные, показывает, что первый квартиль оценки SAT имеет показатель VIF, равный 61,04, третий квартиль оценки SAT имеет показатель VIF, равный 55,23, а общая стоимость обучения имеет показатель VIF, равный 6,02. Поскольку первый квартиль оценки SAT имеет наибольший показатель VIF, его следует исключить из модели. Анализ оставшейся линейной регрессионной модели показывает, что годовая стоимость обучения имеет показатель VIF, равный 5,83. Его следует исключить из модели. Анализ оставшейся линейной регрессионной модели показывает, что у всех оставшихся переменных показатель VIF не превосходит пяти. Пусть Х1 — фиктивная переменная, кодирующая форму собственности университета (0 — государственный, 1 — частный), Х2 — третий квартиль оценки SAT, Х3 — стоимость проживания в общежитии и питания. Используя шаговую регрессию, определяем, что в модели следует оставить только переменную Хг Наилучшей является следующая модель: Y = 15 822,0333 + 1 763,6067Хг Анализ остатков не выявил никакой четкой закономерности и нарушений условия нормальности распределения.
14.40. Анализ линейной регрессионной модели, содержащей все возможные переменные, показывает, что коэффициент инфляции всех независимых переменных не превышает 5,0. С помощью метода наилучшего подмножества выделяем несколько наборов переменных, коэффициент Ср которых не превышает k+ 1. К числу наиболее значимых переменных относятся следующие показатели: Х\ — поток воздуха, Х2 — поток воды. Тестовая F-статистика полной модели имеет р-значение, практически равное нулю. Количество удаленных частиц сильно зависит от обеих переменных. Индивидуальные t-статистики для каждой из двух независимых переменных свидетельствуют о том, что при 5%-ном уровне значимости только поток воздуха имеет статистическое значение. Для потока воды р-значение, соответствующее тестовой t-статистике, равно 0,137. Следовательно, эту переменную следует удалить из модели. В результате получаем следующую модель: Y = 0,1860 + 0,7209Хр F= 0,9571, гД,/? = 0,9544. Анализ остатков не выявил никакой четкой закономерности и нарушений условия нормальности распределения. График нормального распределения показывает, что ошибки имеют нормальное распределение.
14.42. 1. Пусть Xj — район, Х2 — состояние, Х3 — спальни, Х4 — ванные, Х5 — другие комнаты. Y = -64 558,50 + 25 533,35^+ 10 124,57Х2+ 8 842,66Х3+ 17 202,56Х4+ 3 173,66Х5.
2. Сдвиг. Поскольку ни одна независимая переменная не может быть равной нулю, сдвиг следует интерпретировать как долю цены, которая варьируется в зависимости от других факторов, которые отличаются от указанных выше независимых переменных. Район. Если остальные независимые переменные фиксированны, при увеличении рейтинга района на единицу, средняя продажная стоимость дома увеличивается на 25 533,35 долл. Состояние. Если остальные независимые переменные фиксированны, при увеличении оценки состояния дома на единицу средняя продажная стоимость дома увеличивается на 10 124,57 долл. Спальни. Если остальные независимые переменные фиксированны, каждая дополнительная спальня увеличивает среднюю продажную стоимость дома на 8 842,66 долл. Ванные. Если остальные независимые переменные фиксированны, каждая дополнительная ванная увеличивает среднюю продажную стоимость дома на 17 202,56 долл. Другие комнаты. Если остальные независимые переменные фиксированы, каждая дополнительная комната увеличивает среднюю продажную стоимость дома на 3 173,66 долл. 3. Но: Р;=0, Н,: р;*0, / = 1, 2, 3, 4, 5. При 5%-ном уровне значимости статистически значимыми являются район, состояние дома, количество спален и ванных комнат. 4. Для каждой независимой переменной р-значение представляет собой вероятность того, что оценке коэффициента чистой регрессии & соответствует t-статистика, которая превышает t-статистику, вычисленную по исходным данным, если нулевая гипотеза является истинной.
5. Y = -64 558,50 + 25 533,35x4+ 10 124,57x4+ 8 842,66x3+17 202,56x2,5+ 3 173,6x4 =1 60 302,18; 153 755,46 <цУЛ.< 166 848,90; 121 786,37 < Y, < 198 817,98. 6.82,53% вариации продажной цены можно объяснить вариацией пяти независимых переменных. 7. /;< =0,8161. 8. Все пять независимых переменных, за исключением переменной Состояние, предполагают наличие более точной нелинейной, возможно, квадратичной, зависимости между продажной ценой и каждой независимой переменной. 9. На основе величины Ср и коэффициента^, можно утверждать, что наилучшей регрессионной моделью является модель, учитывающая все пять независимых переменных.
Глава 15
15.2. 1. Первое центрированное скользящее среднее можно вычислить для 1959 года. 2. При вычислении всех 9-летних скользящих средних будет проигнорировано 8 лет.
15.4. 4. 1,94 тыс. сотрудников. 6. 1,90 тыс. сотрудников. 7. Тот же результат.
15.6. 4. 17 861 долл. 6. 17 427,53 долл. 7. Экспоненциально сглаженный прогноз при коэффициенте сглаживания W, равном 0,25, выше, чем при коэффициенте W, равном 0,5.
15.8. 4. 3,27. 6. 4,28. 7. Экспоненциально сглаженный прогноз при коэффициенте сглаживания W, равном 0,25, выше, чем при коэффициенте W, равном 0,5.
15.10. 1. Сдвиг отклика Ъо= 4,0 отражает реальный полный доход (в млн. долл, по курсу 1995 г.) на протяжении базового года. 2. Наклон bt = 1,5 означает, что с каждым годом реальная полная доход увеличивается на 1,5 млн. долл. 3. 10 млн. долл. 4. 37,0 млн. долл.
15.12. 2. На протяжении 38 лет индекс потребительских цен в США возрастал. В конце 1970-х, середине 1980-х и конце 1990-х годов темпы роста увеличивались, однако в начале 1980-х и 1990-х они стабилизировались.
15.14. 2. Y = 281,1013 + 69,0691Х. 3. Прогноз федеральных поступлений на 2002 и 2003 годы таков: 1 928,7594 и 2 007,8285 млрд. долл, соответственно. 4. Между 1978 и 2001 годами тренд индекса потребительских цен был возрастающим и нелинейным. Для исследования следует выбрать либо квадратичную, либо экспоненциальную модель.
15.16. 3.2003:23,4927 млрд, долл., 2004: 24,6110 млрд. долл. 9. Линейный тренд в 2003 г.: 12,3704; линейный тренд в 2004 г.: 12,6431, квадратичный тренд в 2003 г.: 13,1194, квадратичный тренд в 2004 г.: 13,5470, экспоненциальный тренд в 2003 г.: 12,9549, экспоненциальный тренд в 2004 г.: 13,3815. 10. Прогноз фактической чистой прибыли выше, чем прогноз реальной чистой прибыли, поскольку реальная прибыль учитывает инфляцию. 11. На протяжении всего периода объем чистой прибыли в целом возрастал, испытывая небольшие спады в 1980-1982, 1995-1998 и 2001-2003 гг.
15.18. 5. Исследование первой, второй и процентной разностей не отдает предпочтения никакой трендовой модели. Более точным кажется экспоненциальный тренд, который лучше остальных аппроксимирует данные в начале временного периода. 6. Экспоненциальная модель дает прогноз У2001 = 105,07 долл.
15.20. 1. Временной ряд I: график зависимости переменной У от переменной X более линеен, чем график зависимости логарифма переменной У от переменной X, поэтому следует применить линейную модель. Временной ряд II: график зависимости логарифма переменной У от переменной X более линеен, чем график зависимости переменной У от переменной X, поэтому следует применить экспоненциальную модель. 2. Временной ряд1: Y = 100,082 + 14,9752 х X. Временной ряд II: Y = 99,704 х 1,1501х. 3. Временной ряд I: 279,834. Временной ряд!!: Y =403,709.
15.22. 7. Линейный тренд в 2002 г.: 60,9329; линейный тренд в 2003 г.: 61,9559, квадратичный тренд в 2002 г.: 60,6284, квадратичный тренд в 2003 г.: 61,4854, экспоненциальный тренд в 2002 г.: 61,1614, экспоненциальный тренд в 2003 г.: 62,3071.
15.24. Поскольку t = = ~~~ = 2,40 > £10;0 025 = 2,2281, нулевая гипотеза Но отклоняется. Сле-
дует применить авторегрессионную модель третьего порядка.
15.26. 1. Поскольку t = ~ =1,60 > t100025= 2,2281, нулевая гипотеза Но не отклоняется.
Следует применить авторегрессионную модель третьего порядка. 2. Следует построить авторегрессионную модель второго порядка и проверить ее адекватность.
15.28. 1. Поскольку р-значение = 0,53 > 0,05, нулевая гипотеза На о том, что А3 = 0, не отклоняется. Параметр авторегрессии третьего порядка не является статистически значимым. 2. Поскольку р-значение = 0,18 > 0,05, нулевая гипотеза Но о том, что А2 = 0, не отклоняется. Параметр авторегрессии второго порядка не является статистически значимым. 3. Поскольку р-значение практически равно нулю, нулевая гипотеза Но о том, что А4 = 0, отклоняется. Параметр авторегрессии первого порядка является статистически значимым. 4. 2003: 11,0188, 2004: 11,1387.
15.30. 1. Поскольку р-значение = 0,73 > 0,05, нулевая гипотеза Но о том, что А, = 0, не отклоняется. Параметр авторегрессии третьего порядка не является статистически значимым. 2. Поскольку р-значение = 0,44 > 0,05, нулевая гипотеза Но о том, что А2 = 0, не отклоняется. Параметр авторегрессии второго порядка не является статистически значимым. 3. Поскольку р-значение практически равно нулю, нулевая гипотеза Но о том, что At = 0, отклоняется. Параметр авторегрессии первого порядка является статистически значимым. 4.92,0576.
15.32. 1. 2,121 млрд. долл, в неизменных ценах 1995 г. 2. 1,5 млрд. долл, в неизменных ценах 1995 г.
15.34. 1. 238,7385; 3. 194,1732. 4. Остатки линейного тренда образуют последовательности положительных и отрицательных значений. Вероятно, следует применить модель авторегрессии.
15.36. 2. Линейный тренд: 0,8747, квадратичный тренд: 0,8333, экспоненциальный тренд: 0,8329. AR(1): 0,4913. 3. Линейный тренд: 0,7172, квадратичный тренд: 0,6007, экспоненциальный тренд: 0,6314. AR(1): 0,3585. 4. Остатки линейного тренда образуют последовательности положительных и отрицательных значений. Руководствуясь принципом экономии, вероятно, следует применить модель авторегрессии, которая, как правило, хорошо аппроксимирует исторические данные. Авторегрессионная модель имеет наименьшее значение MAD.
15.38. 1. Линейный тренд: 18,13, квадратичный тренд: 9,94, экспоненциальный тренд: 12,39. AJR(l): 8,31. 3. Линейный тренд: 15,11, квадратичный тренд: 6,93, экспоненциальный тренд: 5,34. AR(1): 4,28. 4. Остатки линейного тренда образуют последовательности положительных и отрицательных значений. Руководствуясь принципом экономии, вероятно, следует применить модель авторегрессии, которая, как правило, хорошо аппроксимирует исторические данные. Авторегрессионная модель имеет наименьшее значение MAD и SSE.
15.40. 1. Ьо = 100. Это число представляет собой приближенное значение для января 1998 г., которое затем уточняется с помощью соответствующего множителя. 2. Ьх = 1,0233. Месячный темп роста равен 2,33%. 3. Ь2 = 1,2589. Значение временного ряда в январе на 25,89% превышает значение, определенное с помощью месячного темпа роста.
15.42. 1. Ъо = 1,000. Это число представляет собой приближенное значение для января 1998 г., которое затем уточняется с помощью соответствующего множителя. 2. д, = 1,2589. Месячный темп роста равен 25,89%. 3. Ь3 = 1,5849. Значение временного ряда во втором квартале на 58,49% превышает значение, определенное с помощью квартального темпа роста.
15.44. 2. log10 Y =2,7471 + 0,01150 х X - 0,01229 х Q1 + 0,01252 х Q2 - 0,01549 х Q3. 3. 1 408,4488; 4. 1 531,2552; 5. 2003: 1 531,2552; 1 474,1520; 1 568,6511. 2004: 1 565,7969; 1 702,3229; 1 638,8403; 1743,8966. 6. bx = 1,0268. Прогнозируемый квартальный темп роста равен 2,68%. 7. Ъ = 1,0292. Значения временного ряда во втором квартале в среднем на 2,92% превышают значения временного ряда в четвертом квартале.
15.46. 2. log Y = 0,6770 + 0,000199 х X - 0,004042 хМ, + 0,004270 х М2 + 0,002576 х М--0,007265 х М4 - 0,009982 хМ5- 0,009627 х Мъ - 0,01006 х М, - 0,009588 х М8--0,008657 х М10- 0,004355 х Мп. 3. 4,8859%. 4. 4,9374%. 5. Прогнозы на 2003 г.: 4,9858%, 4,9907%, 4,9736%, 4,8944%, 4,8363%, 4,8484%, 4,8398%, 4,8473%, 4,8284%, 4,8622%, 4,9128%, 4,9646% . 5. Ьг = 1,0005. Прогнозируемый месячный темп роста 0,05%.
6. Ья = 0,9771. Значения временного ряда в июле в среднем на 2,29% меньше значений временного ряда в декабре.
15.48. 1. Розничная торговля подвержена сильным сезонным колебаниям. В частности, объем продаж компании Toys Я зависит от отпускного сезона. 2. Временной ряд значительно зависит от сезонных колебаний. 3. У, = 2944,3104x1,0177Л' х0,3947й х0,3901~! xO,4252Q' . 4. = 1,0177. Квартальный темп роста равен 1,77% . 5. Ь2 = 0,3947. Значения временного ряда в первом квартале в среднем на 60,53% меньше значений временного ряда в четвертом квартале: 63 = 0,3901. Значения временного ряда во втором квартале в среднем на 60,99% меньше значений временного ряда в четвертом квартале. = 0,4252. Значения временного ряда в третьем квартале в среднем на 57,48% меньше значений временного ряда в четвертом квартале. 5. Прогнозы на 2003 год: 2 511,74; 2 526,41; 6 707,42.
15.50. Стоимость товаров в 2002 г. была на 75% выше, чем в 1995 году.
15.52. 186,96; 2. 162,16; 3. 154,42.
15.54. 3. Индекс, использующий в качестве базового 1990 год, более точен. Индекс DJIA за 23 года вырос более чем на 100% .
15.56. 3. Оба индекса полезны. Индекс, использующий в качестве базового 1990 год, иллюстрирует рост индекса CPI в процентах к базовой величине. Индекс, использующий в качестве базового 2001 год, иллюстрирует рост индекса CPI в процентах к текущей величине. Поскольку индексы цен используются для оценки роста цен по сравнению с базовым периодом, более полезным является индекс, использующий в качестве базового 1990 год. 4. Индекс потребительских цен в Великобритании за период с 1990 по 2001 г. вырос на 33,49% , а в Японии — на 6,5% .
15.58. 2. Средняя цена за фунт свежих помидоров в 2003 г. на 143,39% больше, чем в 1983 г. 3. Средняя цена за фунт свежих помидоров в 2003 г. на 1,38% меньше, чем в 1983 г. 5. Стоимость свежих помидоров за период с 1980 по 2002 г. возрастала.
15.74. 3. Y = 4,7180 + 0,2460 хХ. 4. Y = 5,7790 + 0,001168 хХ + 0,009069 х X2.
5. Y = 5,1777 х 1,0303х 6. Поскольку р-значение = 0,90 > 0,05, гипотеза Но о том, что As = 0, не отклоняется. Третье слагаемое можно исключить из модели. 7. Поскольку р-значение = 0,32 > 0,05, гипотеза Но о том, что Аг = 0, не отклоняется. Второе слагаемое можно исключить из модели. 8. Поскольку р-значение практически равно нулю, гипотеза Но о том, что Д = 0, отклоняется. Наиболее подходящей является авторегрессионная модель первого порядка. 10. Линейный тренд: 1,1989, квадратичный тренд: 1,0874, экспоненциальный тренд: 1,1183. AR(1): 0,9508. 11. Линейный тренд: 0,8657, квадратичный тренд: 0,7597, экспоненциальный тренд: 0,7597. AR(1): 0,7037. 12. Анализ остатков, проведенный для трех прогнозных моделей, демонстрирует наличие строк, состоящих из последовательных положительных и отрицательных чисел. Наиболее подходящей является авторегрессионная модель, остатки которой распределены совершенно случайным образом. Кроме того, эта модель имеет наименьшую стандартную ошибку, а также наименьшие коэффициенты MAD и SSE. Основываясь на принципе экономии, для прогнозирования следует выбрать именно авторегрессионную модель. 13. Прогноз на 2003 г.: 13,0360 млрд, долл., прогноз на 2004 г.: 13,1166 млрд. долл.
15.76. 3. Y = 1,3786 + 0,2540 хХ. 4. Y = 1,9972 + 0,1112 х X + 0,005287 х X2.
5. Y = 2,0454 х 1,0575 х . 6. Поскольку р-значение = 0,87 > 0,05, гипотеза Но о том, что А3 = 0, не отклоняется. Третье слагаемое можно исключить из модели. 7. Поскольку р-значение = 0,10 > 0,05, гипотеза Но о том, что А2 = 0, не отклоняется. Второе слагаемое можно исключить из модели. 8. Поскольку р-значение практически равно нулю, гипотеза Н(, о том, что Aj = 0, отклоняется. Наиболее подходящей является авторегрессионная модель первого порядка. 10. Линейный тренд: 0,4041, квадратичный тренд: 0,2522, экспоненциальный тренд: 0,2799. AR(1): 0,2032. 11. Линейный тренд: 0,3266, квадратичный тренд: 0,1943, экспоненциальный тренд: 0,2078. AR(1): 0,2078. 12. Анализ остатков, проведенный для трех прогнозных моделей, демонстрирует наличие строк, состоящих из последовательных положительных и отрицательных чисел. Наиболее подходящей является авторегрессионная модель, остатки которой распределены совершенно случайным образом. Кроме того, эта модель имеет наименьшую стандартную ошибку, а также наименьшие коэффициенты MAD и SSE. Основываясь на принципе экономии, для прогно-
зирования следует выбрать именно авторегрессионную модель. 13. Прогноз на 2003 г.: 8,8902 млрд, долл., прогноз на 2004 г.: 9,2269 млрд. долл.
15.78. Переменная А. 2. У = 7,6841 + 2,9579 х X. 3. Y = 9,5309 + 2,3423 х X + 0,03240 х X2. 4. Y = 13,2289 х 1,0938х. 5. Поскольку р-значение = 0,38 > 0,05, гипотеза Но о том, что А3 = 0, не отклоняется. Третье слагаемое можно исключить из модели. 6. Поскольку р-значение = 0,014 < 0,05, гипотеза Но о том, что А, = 0, не отклоняется. Второе слагаемое можно исключить из модели. 7. Поскольку р-значение практически равно нулю, гипотеза Нп о том, что Aj = 0, отклоняется. Наиболее подходящей является авторегрессионная модель первого порядка. 10. Линейный тренд: 8,4464, квадратичный тренд: 8,6287, экспоненциальный тренд: 9,3458. AR(1): 5,5173. 11. Линейный тренд: 6,0278, квадратичный тренд: 5,5613, экспоненциальный тренд: 5,2940. AR(2): 0,0556. 12. Анализ остатков, проведенный для линейной прогнозной модели, демонстрирует наличие строк, состоящих из последовательных положительных и отрицательных чисел. Наиболее подходящей является квадратичная, экспоненциальная или авторегрессионная модель, остатки которых распределены совершенно случайным образом. Кроме того, модель AR(2) имеет наименьшую стандартную ошибку, а также наименьший коэффициент MAD. Основываясь на принципе экономии, для прогнозирования следует выбрать именно авторегрессионную модель. Прогноз на 2004 г.: 35,2726, прогноз на 2005 г.: 29,1261. Переменная Б. 2. Y = 11,3178 + 0,4938 х X. 3. Y = 10,3259 + 0,8244хХ-0,0174 хХ2. 4. Y = 11,5490 х 1,0330х. 5. Поскольку р-значе-ние = 0,18 > 0,05, гипотеза Но о том, что А3 = 0, не отклоняется. Третье слагаемое можно исключить из модели. 6. Поскольку р-значение = 0,28 < 0,05, гипотеза Но о том, что А2 = 0, не отклоняется. Второе слагаемое можно исключить из модели. 7. Поскольку р-значение практически равно нулю, гипотеза Но о том, что = 0, отклоняется. Наиболее подходящей является авторегрессионная модель первого порядка. 10. Линейный тренд: 0,5510, квадратичный тренд: 0,0939, экспоненциальный тренд: 0,8208. AR(1): 0,0856. 11. Линейный тренд: 0,4397, квадратичный тренд: 0,0722, экспоненциальный тренд: 0,6627. AR(1): 0,0650. 12. Анализ остатков, проведенный для линейной и экспоненциальной прогнозных моделей, демонстрирует наличие строк, состоящих из последовательных положительных и отрицательных чисел. Наиболее подходящей является квадратичная или авторегрессионная модель, остатки которых распределены совершенно случайным образом. Кроме того, модель AR(1) имеет наименьшую стандартную ошибку, а также наименьший коэффициент MAD. Основываясь на принципе экономии, для прогнозирования следует выбрать именно авторегрессионную модель. Прогноз на 2004 г.: 19,9734, прогноз на 2005 г.: 20,1963.
Глава 16
16.4. 1—4. Таблица выигрышей: событие 1— 12 000 долл.; 6 000 долл., событие 2 — 14 000 долл.; 10 000 долл., событие 3— 20 000 долл.; 22 000 долл., событие 4 — 30 000 долл.; 42 000 долл., событие 5 — 110 000 долл.; 202 000 долл.
16.6. 1. 125; 112,50. 2. 25; 37,50. 3. Полная информация позволяет правильно предсказать событие 1 или 2. Если известно, какое из событий произойдет, размер ожидаемой прибыли увеличивается. Это позволяет выбрать оптимальное решение на основе правильного прогноза. При наличии полной информации EMV = 150, EVPI = 25. 4. Вариант А. 5. 60%, 11,11%. 6. 1,667; 9,0. 7. Вариант Б. 8. Выбор наилучшего решения зависит от используемого критерия.
16.8. 1. 10%; 2. 25%; 3.4,0.
16.10. Следует выбрать портфель А.
16.12. 1. 56; 66. 2.18, 8. 3. Величина EVPI представляет собой максимальную сумму денег, которую клиент готов заплатить за полную информацию о том, какое событие обязательно произойдет 4. Следует выбрать продажу мороженого. 5. 8,748%; 44,536% . 6.11,431; 2,245.
16.14. 1.1050; 1400; 1400. 2. 522,02; 2 498,00; 9 656,09. 3. 4 100,3 750,3 750. 4. EVPI = 3 750. Инвестору не следует платить больше 3 750 долл, на полную информацию. 5.49,72%, 178,43%, 689,72% 6. 2,01; 0,56; 0,14. 7-8. Действия Б и В являются оптимальными с точки зрения доходности, при этом действие А минимизирует коэффициент вариации и максимизирует отношение “доходность/риск”.
16.16. 1. 25 200; 32 400. 2. 10 700; 3 500. 3. 3 500. 4. Следует подписать контракт с издательством Б, поскольку он принесет наибольшую прибыль (32 400 долларов) и минимизирует упущенные возможности (3 500 долларов). 5.114,25%, 177,73%. 6. 0,8752, 0,5627. 7. Контракт с издательством Б минимизирует авторский риск и, следовательно, увеличивает отношение “доходность/риск”. 8. Коэффициент EMV у издательства Б больше, чем у издательства А, но выбор издательства Б сопряжен с более высоким риском и, следовательно, уменьшает отношение “доходность/риск”.
16.18. 1. 0,6; 0,4. 2. 110; 110. 3. 30; 30. 4. 30. 5. Оба варианта имеют одинаковый коэффициент EMV. 6. 66,8%, 11,1%. 7. 1,497; 8,981. 8. Вариант Б максимизирует отношение “доходность/риск”. 9. Оба варианта имеют одинаковый коэффициент EMV, однако у варианта Б больше отношение “доходность/риск”.
16.20. 1.0,64; 0,36. 2. EMV: 53,6; 51,6. EOL: 10,8; 12,8. EMV с полной информацией: 64,4; EVPI = 10,8. Клиенту не следует платить за полную информацию больше 10,8 долл. Для того чтобы получить максимальную прибыль с минимальным риском, следует продавать безалкогольные напитки. СИ: 8,96%, 55,81%. Отношение доходность/риск: 11,1667, 1,7917. Уточненные вероятности изменяют решение поставщика, поскольку прогнозируется холодная погода. В этих условиях он принимает решение продавать лимонад, что позволяет максимизировать ожидаемую прибыль и минимизировать размер упущенной выгоды.
16.22. 1.0,5590; 0,2484; 0,1412; 0,0502, 0,0013. 3. Уточненные вероятности влияют на решение автора. В новых обстоятельствах контракт с издательством А максимизирует ожидаемую прибыль (14 658,60 долл.), минимизирует ожидаемую упущенную выгоду (1 004,40 долл.), минимизирует риск и приносит большую прибыль, чем контракт с издательством Б.
16.36. 3.2 100, 2 660, 2 520, 1 960. 4.980, 420, 560, 1 120. 5. EVPI = 420 долларов. 6. Купить 8 000 буханок. 7. 0, 15,79%, 35,57% , 57,14% . 8. Отношение “доходность/риск” не определено, 6,333, 2,811, 1,750. 9. Купить 8 000 буханок. Повторное решение. 3. 2 100, 2 380, 2 100, 1 540. 4.700, 490, 770, 1 330. 5.£ИР7 = 490. 6. Купить 8 000. 7.0%, 26,96%, 51,64%, 85,76%. 8. Отношение “доходность/риск” не определено, 3,71, 1,94, 1,17. 9. Купить 8 000 буханок.
16.38. 3.-100 000, 0. 4.1200 000, 1 100 000. 5. EVPI = 1 100 000. 6.-3,0356, не определено. 8. Использовать старую упаковку. EMV = 1 600 000, 0; EOL = 2 400 000, 800 000. Повторное решение. 3. -1 600 000, 0. 4. 2 400 000, 800 000. 5. EVPI = 800 000. 6. -0,5101, не определено. 8. Использовать старую упаковку. Повторное решение. 3. 2 900 000, 0. 4. 400 000, 3 300 000. 5. EVPI = 400 000. 6. 0,9953, не определено. 8. Использовать новую упаковку. 10. 0,2466, 0,6575, 0,0959. Повторное решение. 3. 150 600, 0. 4. 986 400, 1 137 000. 5. EVPI = 986 400. 6. 0,0570, не определено. 8. Использовать новую упаковку. 12.0,5902, 0,3934, 0,0164. Повторное решение. 3.-1885 400, 0. 4.2 360 700, 475 400. 5. EVPI = 475 400. 6. -0,7288, не определено. 8. Использовать старую упаковку.
16.40. 3.180, 100. 4.20, 100. 5. EVPI = 20; 6. 1,2665, не определено. 7. Вызвать механика. 8.0,0143; 0,2100; 0,4159; 0,3598. Повторное решение. 3. 248, 100. 4.1,15, 149,53. 5. EVPI = 1,15; 6. 2,0544, не определено. 7. Вызвать механика.
Глава 17
17.2. 1. Наибольший процент брака наблюдается в 4-й день, а наименьший — в 3-й день.
2. НКГ = 0,039719, ВКГ = 0,245995. 3. Доля брака находится внутри контрольных границ, поэтому вариация является обычной.
17.4. 1. НКГ не существует, ВКГ = 0,0988. 2. Хотя ни одна точка не выходит за контрольные
границы, в распределении точек наблюдается закономерность, поскольку первые восемь точек находятся ниже средней линии, а остальные точки — выше средней линии. Таким образом, перед изменением системы следует определить причину этой закономерности.
17.6. 1. НКГ = 0,00817, ВКГ = 0,01759. Доля бракованных банок в 4-й день выходит за ниж-
нюю контрольную границу. В распределении точек наблюдается определенная закономерность, поскольку первые восемь точек находятся ниже средней линии, а остальные точки — выше средней линии. Таким образом, перед изменением системы следует определить причину этой закономерности. 2. После удаления выбросов и стабилизации
процесса, для улучшения системы следует применить 14 принципов Деминга. Необходимо также разобраться в причинах брака в 4-й день.
17.8. 1. НКГ = 0,0752, ВКГ = 0,1431. Точки 9, 26 и 30 лежат выше верхней контрольной гра-
ницы. 2. После удаления выбросов и стабилизации процесса, для улучшения системы следует применить 14 принципов Деминга.
17.12. 1. НКГ = 0. ВКГ не существует. ВКГ = 9,05954. 2. Все точки лежат внутри контрольных
границ и распределены случайным образом. 3. НКГ = 11,05587, ВКГ = 16,84413. 4. Выборочное среднее на 7-й день лежит выше верхней контрольной границы. Это свидетельствует о слишком сильной вариации.
17.14. 1. Для размаха: ВКГ =574,09, НКГ не существует. Для среднего: НКГ =41,97,
ВКГ = 355,36. 2. Все точки лежат внутри контрольных границ и распределены случайным образом.
17.16. 3. Все точки лежат внутри контрольных границ и распределены случайным образом.
Следовательно, процесс является контролируемым.
17.18. 4. Процесс является контролируемым, хотя некоторые точки лежат вне контрольных
границ.
17.20. 1.20; 2. 0,9713.
17.22. 1,Ср = 0,3333, CPL = 0,3333, CPU =0,3333, Срк = 0,3333. 2. Ср= 1,2083, CPL= 1,1667, CPU = 1,25, Ср„= 1,1667.
17.24. 1. 0,9832; 2. CPL = 0,7073, С „ = 0,7073.
17.26. Поскольку процесс, описанный в задаче 17.13, не поддается статистическому контролю, решение задачи теряет смысл. Если бы мы все же решили задачу, то ответ был бы равен 0,286. 2. Процесс не позволяет достичь цели при уровне качества, равном 99%, даже если повысить требование до 99,7% , процесс не станет эффективным.
17.38. 1. ВКГ = 0,33063, НКГ не существует. 2. ВКГ = 1,3447, НКГ = 1,0820. 3. Одна точка ле-
жит ниже НКГ и одна — выше ВКГ. Таким образом, процесс вышел из-под контроля и требует вмешательства. 4. Поскольку процесс не поддается контролю, нет смысла оценивать долю плиток, удовлетворяющих стандарту. 5. Поскольку процесс не поддается контролю, вычисление выполнять нецелесообразно. 6. Поскольку процесс не поддается контролю, нет смысла проводить анализ. 7. 1. ВКГ = 0,31984, НКГ не существует. 2. ВКГ= 0,31984, НКГ не существует. 3. Поскольку на всех диаграммах все точки лежат между контрольными границами, процесс является контролируемым. 4.0,9988. 5.Ср = 1,136, CPL = 1,015, CPU = 1,257. 6. Поскольку все точки лежат между контрольными границами, процесс поддается контролю и достигает цели в 99,7% случаев. Кроме того, С, НКГ, ВКГ и Срк больше единицы, что свидетельствует об эффективности процесса.
17.40. 1. НКГ = 0,301, ВКГ= 0,480. 2. Процесс поддается статистическому контролю. Доля за-
крытых транзакций ниже контрольной границы на 2- и 16-й день, а на 22- и 23-й день эта доля превышает верхнюю контрольную границу. 3. Особые выбросы следует исследовать и исключить. Необходимо провести дополнительные исследования и улучшить процесс выполнения транзакций.
17.42. Время обработки анализов. Контрольная карта для размаха: НКГ = 0,802, ВКГ = 6,392. Контрольная карта для среднего: НКГ = 1,1575, ВКГ = 3,3732. Все значения размаха и среднего лежат внутри контрольных границ и распределены случайным образом. Доля повторных анализов: Д = 0,04737, НКГ= 0,02721, ВКГ= 0,06752. Доля повторных анализов на 6- и 29-й день превышает верхнюю контрольную границу. Таким образом, сначала необходимо исследовать причины выбросов, а затем внести изменения в систему. Устранив причину неустойчивости процесса, необходимо построить диаграммы течения процесса и глубже изучить его свойства. Для улучшения системы можно применить 14 рекомендаций Деминга.
Приложение А
Некоторые правила алгебры и арифметики
1.1. ПРАВИЛА ВЫПОЛНЕНИЯ АРИФМЕТИЧЕСКИХ ОПЕРАЦИЙ
Правило Пример
1. а + Ь = сиЬ + а = с. 2. а + (Ь + с) - (а + Ь) + с. 3. а- Ъ = с, но b - а * с. 2+1-3 и1+2 = 3. 5+ (7 + 4) = (5 + 7)+ 4. 9 -7 = 2, но 7 -9= 2.
4. а х b = b х а. 7 х 6-6 х 7.
5. а х (Ь + с) = (а х Ь) + (а х с}. 6. а 4- Ь * Ь 4- а. 2 х (3 + 5) = (2 х 3) + (2 х 5) = 16. 12 + 3^34-12.
„ a+b а b 7. = - + с с с 7 + 3 7 3 =-+-=5. 2 2 2
о а а а 8. ^- + - . b + c b с 3 3 3 —1— . 4 + 5 4 5
„ 1 1 Ь+а 9. - + - = . a b ab 1 1 5 + 3 _ 8 3 + 5~ 3x5 “15 *
а с ахс 10. — х— . b d bxd 2 6 2х6_12 3Х7~Зх7-21 ’
Л а , с _axd b d bxc 5.3_5х7_35 8 7~8хЗ~24 ’
1.2. ПРАВИЛА ВОЗВЕДЕНИЯ В СТЕПЕНЬ И ИЗВЛЕЧЕНИЯ КОРНЯ
Правило Пример
1. Ха х Хь = Ха+Ь. 42 х 43 = 45.
2. (ха)ь = ХаЬ . (22)3 = 26 .
3. ^- = ха-ь хь 4=з2- з3
4. — = Х°=1 . ха 4- = 3°=1 . з4
5. 4xy = 4x4y . л/25х4 =725 а/4 =10.
6. II Д = Д = 0,40. V100 V100
1.3. ПРАВИЛА ВЫЧИСЛЕНИЯ ЛОГАРИФМОВ
Десятичный логарифм
Обозначим десятичный логарифм символом LOG.
Правило Пример
1. LOG(104)=A. LOG(100)= LOG(102) = 2.
2. Если LOG(A) = В, то A = 10й. Если LOG(A) = 2, то A = 102 = 100.
3. LOG(A x B) = LOG(A) + LOG(B). LOG(IOO) -- LOG(10 x 10)= LOG(10) + LOG(IO) = 1 + 1= 2.
4. LOG(A*) = В x LOG(A). LOG( 1000) = LOG( 103) = 3 x LOG( 10) = 3 x 1 = 3.
5. LOG(A/B) = LOG(A) - LOG(B) . LOG(IOO) = LOG(IOOOZIO) = LOG(IOOO) - LOG(IO) = 3 - 1 =2.
Пример. Возьмите десятичный логарифм от обеих частей следующего уравнения.
Решение. Применим правила 3 и 4.
LOG(K) = LOG( p()p;v£) = LOG(PJ + LOG( pf ) + LOG(s) = = LOG(P0) + X x LOG(P,) + LOG(e).
Натуральный логарифм
Обозначим натуральный логарифм символом LN. Основанием натурального логарифма является константа Ейлера е = 2,178282.
Правило Пример
1. LN(ez,)=A. LN(7,389056) = LOG(e2) = 2.
2. Если LN(A) = В, to A = eB. Если LN(A) = 2, to A = e~ = 7,389056.
3. LN(A x B) = LN(A) + LN(B) . LN(100) = LN(10 x 10)= LN(10) + LN(10) = 2,302585 + 2,302585 =
=4,605170.
4. LN(Afi) = В x LN(A). LN(1000) = L(103) = 3 x LN(10) = 3 x 2,302585 = 6,907755.
5. LN(A/B) = LN(A) - LN(B) . LN(100) = LN( 1000/10) = LN(1000) - LN(10) = 6,907755 - 2,302585 =
=4,605170.
Пример. Возьмите натуральный логарифм от обеих частей следующего уравнения.
L = PoP1Ve.
Решение. Применим правила 3 и 4.
LN(Y) = LN( рХ’ ) = LN(Pfl) + LN( P;v) + LN(e) = LN(P0) + X x LN(pJ + LN(e).
Приложение Б
Правила суммирования
Поскольку суммирование часто встречается в статистических вычислениях, его обозначают отдельным символом S. Предположим, например, что мы имеем набор величин, состоящий из п значений некоторой переменной X. Выражение ^Х, означает i=i
сумму п значений переменной X. Иначе говоря, ^Х,=Х1+Х2+- + Хп‘ i=l
Проиллюстрируем суммирование следующим примером. Допустим, что мы имеем пять значений переменной Х:Х1 = 2,Х2 = 0, Х3 = -1,Х4 = 5иХ5 = 7. Таким образом,
^Х, = X1+X2+X3 + Jf4 + Ar5 =2 + 0 +(-1) + 5 +7 = 13 . /=1
В статистических вычислениях также часто встречается сумма квадратов значений некоей переменной.
±х2=х?+х22+...+х2.
i=l
В нашем примере сумма квадратов значений переменной X вычисляется так:
= Х2+Х2+Х2 + Х2 + Х2 = 22 + 02 + (-1)2 + 52 + 72 = 4 + 0 + 1 + 25 + 49 = 79 .
1=1
Обратите внимание на то, что сумма квадратов ^Х^ не равна квадрату суммы :
Z=1 \ Z=1 /
и ( п V
В нашем примере сумма квадратов равна 79. Она не равна квадрату суммы 132 = 169.
Не менее часто в статистических вычислениях встречается сумма произведений величин. Предположим, что мы имеем п значений двух переменных — X и Y. Тогда сумма произведений этих значений вычисляется так:
yXY=XY+X2Y2+... + XYn . II 11 2 2 П П
1=1
Вернемся к предыдущим примерам и предположим, что вторая переменная Y имеет значения Ух = 1, У2 = 3, У3 = -2, У4 = 4 и У5 = 3. В этом случае сумма произведений значений переменных X и У вычисляется так:
+ ОД + ОД + ОД = (=1
= 2x14-0x3 + (-1) х (-2) + 5x4 + 7x3 = 2 + 0 + 2 + 20 + 21 = 45.
п
Вычисляя сумму произведений ^XY , следует иметь в виду, что первое значение ;=1
переменной X умножается на первое значение переменной У, второе значение переменной X умножается на второе значение переменной У, и т.д. После этого эти попарные произведения суммируются. Кроме того, сумма попарных произведений значений переменных X и У не равна произведению сумм этих значений. Иначе говоря,
5 5
В нашем примере = 13 , а Yt = 1 + 3 + (-2) + 4 + 3 = 9 . Таким образом,
/=1 Z = 1
- 13x19 = 117 . В то же время, Yt - 45 .
V /=1 ) \ /=1 ) /=1
Прежде чем сформулировать четыре основных правила суммирования, представим значения переменных X и У в виде следующей таблицы.
Наблюдение Л Yi
1 2 1
2 0 3
3 -1 -2
4 ' 5 5 4 7 3
Правило 1. Сумма п сумм значений двух переменных равна сумме двух сумм п значений каждой переменной в отдельности.
/=1 z=-l z=l
В нашем примере это правило применяется следующим образом.
£(Х, + у,) = (2 + 1) + (0 + 3) + (-1 + (-2)) + (5 + 4) + (7 + 3) = z=i
= 3 + 3 + (-3) + 9 + 10 = 22 = Yx, =13 + 9 = 22. /=1 /=1
Правило 2. Сумма п разностей значений двух переменных равна разности сумм п значений каждой переменной в отдельности.
Правила суммирования 1221
В нашем примере это правило применяется так.
Х(^,->:) = (2-1) + (0-3) + (-1-(-2)) + (5-4) + (7-3) = 7=1
= 1 + (-3) + 1 + 14-4 = 4= ^Xt =13- 9 = 4. 7=1 7=1
Правило 3. Сумма п значений переменной X, умноженных на константу с, равна сумме п значений переменной X, умноженной на константу с.
п п
^сХ^е^Х, . 7=1 7=1
Предположим, что в нашем примере с = 2.
^сХ1 =j^2Xi=2x2 + 2xO + 2x (-1) + 2х 5 + 2х 7 = /=1 /=1
= 4 + 0 + (-2) + 10 + 14 = 26 = = 2 х 13 = 26.
7 = 1
Правило 4. Сумма п констант равна произведению числа п на суммируемую константу.
н
=ИС .
7=1
Предположим, что с = 2. Тогда
= 2 + 2 + 2 + 2 = 2 = 10 = 5 х 2 = 10.
7=1
Продемонстрируем эти правила на примере вычисления арифметического среднего. Как известно (см. раздел 3.2),
=0.
/=1
Докажем это свойство, выполнив следующие вычисления.
Из формулы (3.1) следует, что
77+ '
Применяя правило 2, получаем
Пх,-х^±х,-±х.
7=1 7=1 7 = 1
2. Поскольку для любого фиксированного набора данных величина X является константой, применяя правило 4, получаем
±Х = пХ.
7=1
Следовательно,
7=1 7=1
3. Учитывая формулу (3.1), получаем
Следовательно,
=> пХ = ^Х, .
/=1
Таким образом,
У(х.-х] -±х. ±х .
/=1 /=1 /=1
/=1
Задача
Даны шесть значений переменных X и У: = 2, Х2 = 1, Х3 = 5, Х4 = -3, Х5 = 1, Х6 = -2 и У, = 4, У2 = 0, У3 = -1, У4 = 2, У5 = 7, У6 = -3. Вычислите значения следующих выражений.
D ±х.-
2)
/=1
3) tx-
4) ix-
5)
/=|
6) £(*.+*:)•
/=1
7) £(X,-Y,).
/=1
s) £(х,-3i; + 2x2).
,=1
9) ^сХ, , где с = -1.
<=1
10) £(Х, - ЗУ + с), где с = 3.
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
1. Bashaw, W. L., Mathematics for Statistics (New York: Wiley, 1969).
2. Lanzer, P., Video Review of Arithmetic (Hicksville, NY: Video Aided Instruction, 1990).
3. Levine, D., The MBA Primer: Business Statistics (Cincinnati, OH: Southwestern Publishing, 2000).
4. Levine, D., Video Review of Statistics (Hicksville, NY: Video Aided Instruction, 1989).
5. Shane, H., Video Review of Elementary Algebra (Hicksville, NY: Video Aided Instruction, 1990).
Приложение В
Статистические обозначения и греческий алфавит
3.1. СТАТИСТИЧЕСКИЕ ОБОЗНАЧЕНИЯ
Сложить
Вычесть
Равно
Приближенно равно
Больше
Больше или равно
х Умножить
ч- Поделить
Ф Не равно
Меньше
Меньше или равно
3.2. ГРЕЧЕСКИЙ АЛФАВИТ
Г реческая буква Название Английский эквивалент Греческая буква Название Английский эквивалент
А а Альфа а N v Ню п
в р Бета b S Кси X
Г у Гамма g О о Омикрон о
А 5 Дельта d П к Пи р
Е £ Эпсилон ё Р Р Ро г
Z С Дзета Z S о Сигма S
н л Эта ё Т х Тау t
0 0 Тэта th Y о Ипсилон U
I i Йот i Ф ф Фи Ph
К к Каппа k х % Хи ch
A X Лямбда 1 Пси ps
М ц Мю m Q со Омега б
Приложение Г
Обзор компакт-диска
К изданию прилагается компакт-диск, на котором записано программное обеспечение, предназначенное для обучения читателей статистике. Содержание диска записано в файле readme, расположенном в корневом каталоге.
Excel Data Files
Каталог содержит рабочие книги Microsoft Excel, упомянутые в тексте. Подробный список этих файлов приводится ниже.
Instructional Files
В каталоге содержатся все файлы, упомянутые в “Справочнике по Excel”, обучающие файлы и все остальные файлы, упомянутые в книге и приложении 3.
Visual Explorations in Statistics
Каталог содержит файлы, необходимые для запуска программы Visual Explorations in Statistics. Для ее запуска достаточно открыть рабочую книгу Visual Explorations. xla либо непосредственно на компакт-диске, либо предварительно скопировав ее на жесткий диск вместе с файлом Veshelp. hip в один и тот же каталог.
PHStatZ
Каталог PHStat содержит инсталляционную программу и сопутствующие файлы, которые позволяют установить на компьютере статистическое программное обеспечение PHStat2, широко использованное в тексте книги (инструкции по установке программы PHStat2 изложены в приложении Ж).
CD-ROM Topics
Каталог содержит дополнительные главы, представленные в виде файлов в формате Adobe PDF. Для чтения этих файлов необходима программа Acrobat Reader, записанная на компакт-диске.
Очевидно, наиболее часто читатели будут обращаться к каталогам Excel. С ними можно работать как непосредственно на компакт-диске, так и записав их на жесткий диск. Если читатели предпочтут второй вариант, следует позаботиться, чтобы жесткий диск содержал не менее 10 Мб свободного места. При копировании файлы имеют статус “только для чтения”. Это не создаст больших проблем — файлы можно изменять и сохранять под другими именами с помощью команды Фа ЙлФ Сохранить как.... Впрочем, статус файлов можно изменить, выполнив следующие действия.
1. Открыть папку на жестком диске, содержащую рабочие файлы.
2. С помощью команды Правка ^Выделить все выбрать файлы для чтения-записи.
3. Выбрать команду Файл^Свойства. В открывшемся диалоговом окне Свойства сбросить флажок Только чтение и щелкнуть на кнопке ОК.
Файлы, содержащиеся в каталоге Excel
Ниже в алфавитном порядке приведены все файлы, содержащиеся в каталоге Excel. Все файлы из каталога Excel в тексте сопровождаются пиктограммой ft.
ACCESS Продолжительность чтения (в мс), размер файла, код программистской группы и размер буфера (глава 10).
ACCRES Время обработки в секундах и тип задания (исследовательский отдел — 1, бухгалтерия — 0) (глава 9).
ADVERTISE Объем продаж (тыс. долл.), затраты на рекламу на радио (тыс. долл.), затраты на рекламу в газетах (тыс. долл.) в 22 городах (глава 13).
AIRCLEANERS Название, цена, стоимость потребления электроэнергии и стоимость фильтра (главы 2, 3).
ALLOY Долговечность четырех сплавов (главы 10, 11).
AMPHRS ANGLE Емкость батарей (глава 9). Номер подгруппы и величина угла (глава 17).
ANSCOMBE Наборы данных А, Б, В и Г, состоящие из 11 пар значений переменных X и У (глава 12).
APARTMENT AUTO Размер ежемесячной ренты (глава 6). Пробег в милях на галлон топлива и вес 50 моделей автомобилей (глава 13).
AUT02002 Модель, тип (спортивный — да, другие — нет), тип привода, мощность, тип топлива, пробег на галлон топлива, длина, ширина, вес, грузоподъемность и радиус поворота (главы 2, 3, 10, 13 и 14).
BANK1 Время ожидания (в минутах), проведенное 15 клиентами банка во время ленча (главы 3, 8, 9 и 11).
BANK2 Время ожидания (в минутах), проведенное 15 клиентами банка в вечернее время (главы 3, 9 и 11).
BANKCOST1 Название банка, минимально допустимая сумма депозита, стоимость обслуживания возвращенного чека, стоимость обслуживания валютного банкомата, сетевой доступ (глава 2).
BANKCOST2 Название банка, минимальный баланс, не требующий оплаты, ежемесячная стоимость обслуживания, стоимость обслуживания валютного банкомата, сетевой доступ (глава 2).
BANKRETURN Год, доходность 30-дневного депозитного сертификата, доходность 30-месячного депозитного сертификата и доходность денежного рынка (глава 3).
BANKTIME Среднее время ожидания клиентов в четырех банках в течение дня на протяжении 20-дневного периода (глава 17).
BASEBALL Хозяева, посещаемость, высокая температура воздуха в день игры, процент побед хозяев, процент победы соперников, игра проводится в пятницу, субботу или воскресенье (0 — нет, 1 — да), рекламная акция (0 — нет, 1 — да) (глава 14).
BASKET Год, стоимость хлеба, говядины, яиц и салата (глава 15).
BATFAIL Продолжительность работы до момента отказа (низкая, нормальная, высокая и очень высокая) (глава 11).
BATTERIES Продолжительность работы до момента отказа (в часах) для 13 батареек (главы 3 и 8).
BATTERIES2 BB2001 Название, стоимость, сила тока (глава 2, 3 и 12). Команда, лига (Американская — 0, Национальная — 1), количество побед, среднее количество очков, количество пропущенных пробежек, пропущенных ударов, собственных пробежек, удачных защит и ошибок, средняя цена билетов, размер членского взноса в фан-клубе, стоимость абонемента, доходы местных теле- и радиостанций, кабельной сети, дру-
гие местные доходы, компенсация и премии игроков, общенациональные и местные затраты, доход от деятельности, связанной с бейсболом (главы 2, 12, 13 и 14).
ВВ2002 Команда, лига (Американская — 0, Национальная — 1), количество побед, среднее количество очков, количество пропущенных пробежек, пропущенных ударов, обходов, удачных защит и ошибок (глава 13).
BBSALARY Год, средняя зарплата, медиана зарплаты, минимальная зарплата (глава 15).
BEARING Автоколебание (слабое — 0, сильное — 1), нагревание (слабое — 0, сильное — 1), длительность работы подшипников (глава 10).
BEER Марка, стоимость в долларах, количество калорий, содержание алкоголя (светлое — 1, эль — 2, импортное легкое — 3, обычное — 4, ледяное — 4, легкое — 5, безалкогольное — 5), страна производства (США — 1, импорт — 1) (главы 3, 9 и 10).
BIGBONDFUNDS Год и пятилетняя доходность пяти крупнейших облигационных фондов (глава 3).
BIGBONDFUNDS2 BIGSTOCKFUNDS BONDRATE Год и годовая доходность пяти крупнейших облигационных фондов (глава 3). Год и годовая доходность пяти акционерных фондов (глава 3). Дата, изменение доходности 10-летних облигаций, изменение индекса Доу-Джонса (глава 12).
BREAKSTW Прочность ткани на разрыв (операторы — строки, машины — столбцы) (глава 10).
BUBBLEGUM Диаметр пузыря для четырех марок жевательных резинок и шести студентов (глава 10).
BULBS Продолжительность работы 40 электрических ламп, произведенных компанией А (код — 1), и 40 электрических ламп, произведенных компанией Б (код — 2) (главы 2 и 9).
CABOT Год и прибыль корпорации Cabot (глава 15).
CDRATE CELLPHONE Год и ссудный процент (глава 15). Название, тип (CDMA или TDMA), цена, продолжительность разговора, емкость батарей (главы 2, 3 и 9).
CEREALS CHANGE2003 CHEMICAL CIRCUITS Название, стоимость, количество калорий, клетчатки и сахара (глава 2). Взаимный фонд и изменение стоимости акций (глава 8). Вязкость химических веществ из разных партий (главы 2 и 7). Толщина полупроводниковых плат в зависимости от партии и расположения (глава 10).
COCACOLA Год, закодированный год и текущие поступления компании Coca-Cola (млрд, долл.) (глава 15).
COFFEE Рейтинг кофе в зависимости от экспертов и марки (глава 10).
COFFEEPRICE COLA Год и цена фунта кофе в США (глава 15). Объемы продаж со средних стеллажей и стеллажей, расположенных в глубине зала (глава 9).
COLASPC День, общее количество заполненных консервных банок, количество бракованных банок (в течение 22 дней) (глава 17).
COLLEGECOST Университет и изменение стоимости обучения в 2001-2002 и 2002-2003 гг. (глава 3).
COLLEGES2002 Школа, тип (0 — государственная, 1 — частная), первый квартиль оценки SAT, третий квартиль оценки SAT, стоимость проживания в общежитии и питания в столовой, общая стоимость обучения и средняя величина академической задолженности (главы 10, 13 и 14).
COMPTIME Время выполнения задания лидером текущего рынка и новым программным обеспечением (глава 9).
COMPUTERS COMPUTERS2 CONCRETEl
CONCRETE2 CONTEST2001 CPI-U
CRACK
CREDIT
CURRENCY
CUSTSALE
DELIVERY DENTAL
DIFFTEST
DISCOUNT DISPRAZ
DJIA
DOWCAPITA1
DRILL
DRINK
ELECUSE
ENERGY ENERGY2 ERRORSPC
ESPRESSO
FASTFOOD FASTFOODSALES FEDRECPT
FFCHAIN
FIFO
FLYASH
FOODTIME FORCE
Время загрузки комьютеров трех марок (глава 10).
Время загрузки, марка и браузер (глава 10).
Прочность бетона через 2 и 7 дней (глава 9).
Прочность бетона через 2, 7 и 28 дней (глава 10).
Доходы экспертов, читателей и метателей жребия (глава 10).
Год, закодированный год, значение индекса потребительских цен, значения индекса цен производителей (глава 15).
Тип и размер трещины (главы 9 и 11).
Месяц, закодированный месяц и объем расходов, осуществленных с помощью кредитных карточек (глава 15).
Год, закодированный год и средний ежегодный курс обмена на доллар США для канадского доллара, японской иены и английского фунта (глава 15).
Номер недели, номер клиента и объем продаж (в тыс. долл.) на протяжении 15 последовательных недель (глава 12).
Номер клиента, количество контейнеров и время доставки (глава 12). Ежегодные расходы семей 10 сотрудников на стоматологические услуги (глава 7).
Разница между объемами по счетам и объемами реальных продаж на основе выборки, содержащей 50 расписок (глава 7).
Объем скидок, вычисленных по 150 счетам (глава 7).
Цена, квадрат цены и объем продаж одноразовых бритв в 15 магазинах (глава 14).
Год, закодированный год и показатель Доу-Джонса в конце года (глава 15). Название компании, аббревиатура и рыночная капитализация компаний, стоимость акций которых учитывается индексом Доу-Джонса (глава 3). Время, необходимое для бурения дополнительных 5 футов, глубина и тип скважины (глава 13).
Объем безалкогольных напитков, разлитых в 50 двухлитровых бутылок, следующих одна за другой (главы 2 и 8).
Объем потребленной электроэнергии (в киловаттах) и средняя температура (по Фаренгейту) на протяжении 24 последовательных месяцев (глава 12).
Штат и объем потребления электроэнергии на душу населения (главы 2 и 3).
Год, стоимость электроэнергии, газа и нефти (глава 15).
Количество ошибок и общее количество счетов, обработанных за 39 дней (глава 17).
Наполнение (расстояние в дюймах между дном и верхом фильтра) и время (количество секунд, в течение которых нижняя, средняя и верхняя часть напитка остаются разделенными) (глава 12).
Разновидность блюда и процент калорий за счет жирности (главы 2 и 3).
Год и объем продаж в США (млрд, долл.) (глава 15).
Дата, год, закодированный год и федеральные поступления (млрд. долл, в текущих ценах) (глава 15).
Эксперты и рейтинги ресторанов (глава 10).
Цены (в долларах) и оценочная стоимость (в долларах) для выборки, состоящей из 120 инвентарных единиц (глава 7).
Процентное содержание зольной пыли, квадрат процентного содержания зольной пыли и прочность бетона (глава 14).
Год, закодированный год и годовые объемы продаж (глава 14).
Сила, необходимая для разрушения изолятора (главы 3, 7 и 8).
FORD-REV
FOULSPC
FREEPORT
FRUIT
FUNDTRAN
FURNITURE
GAPAC
GASOLINE GCFREEROSLYN
GCROSLYN
GDP
GEAR
GLENCOVE
GOLFBALL
GPIGMAT
GRANULE
GROSSREV
HARDNESS HARNSWELL
HOMES
HOSPADM
HOTEL1
HOTEL2
HOUSE1
HOUSE2
Квартал, закодированный квартал, доход и три фиктивные переменные для кварталов (глава 15).
Количество штрафных бросков, выполненных в течение 40 дней, и количество попаданий в кольцо (глава 17).
Адрес, оценочная стоимость, полезная площадь (акры), размер дома, возраст, количество комнат, количество ванных комнат и количество автомобилей, которые можно парковать в гараже (глава 14).
Цена фунта яблок, бананов и апельсинов (глава 15).
День, количество новых и закрытых транзакций в течение 30-дневного периода (глава 17).
Количество дней, прошедших с момента получения жалобы до момента ее удовлетворения (главы 2, 3, 7 и 8).
Год, закодированный год и доходы корпорации Georgia-Pacific (млрд, долл.) (глава 15).
Год, стоимость бензина и индекс цен по отношению к 1980 г (глава 15).
Адрес, оценочная стоимость, полезная площадь (акры), размер дома, возраст, количество комнат, количество ванных комнат и количество автомобилей, которые можно парковать в гараже в поселках Глен-Коув, Фрипорт и Рослин, штат Нью-Йорк (глава 14).
Адрес, оценочная стоимость, полезная площадь (акры), размер дома, возраст, количество комнат, количество ванных комнат и количество автомобилей, которые можно парковать в гараже в поселках Глен-Коув и Рослин, штат Нью-Йорк (глава 14).
Год, закодированный год и реальный валовой национальный продукт (в миллиардах неизменных долларов в ценах 1996 года) (глава 15).
Размер зубьев, установка деталей и деформация шин (глава 10).
Адрес, оценочная стоимость, полезная площадь (акры), размер дома, возраст, количество комнат, количество ванных комнат и количество автомобилей, которые можно парковать в гараже в поселке Глен-Коув (глава 14). Расстояния на схемах 1-4 (глава 10).
Количество баллов, набранных 20 студентами при сдаче тестов GMAT и GPI (глава 11).
Вес гранул, потерянных бостонскими и вермонтскими плитками главы 2, 7, 8 и 9).
Год, закодированный год и реальные годовые доходы (глава 15).
Прочность и твердость алюминиевых образцов (глава 12).
День и диаметр кулачковых роликов (в дюймах) для выборок, состоящих из пяти запасных частей, принадлежащих 30 разным партиям (глава 17). Цена, местоположение, наличие системы кондиционирования, количество спален, ванных и остальных комнат (глава 14).
День, количество анализов, средняя продолжительность обработки (в часах), размах продолжительности, доля повторных анализов в течение 30 дней (глава 17).
День, количество комнат, количество неподготовленных комнат в течение 28 дней, доля неподготовленных комнат (глава 17).
День, средняя скорость доставки и размах, вычисленные для подгруппы, состоящей из пяти багажей, в течение 28 дней (глава 17).
Продажная цена (тыс. долл.), оценочная стоимость (тыс. долл.), тип (новый — 0, старый — 1) и продолжительность продажи 30 домов (главы 12 и 13).
Оценочная стоимость (тыс. долл.), обогреваемая площадь (в тысячах квадратных футов) и возраст 15 домов (главы 12 и 13).
H0USE3 Оценочная стоимость (тыс. долл.), обогреваемая площадь (в тысячах квадратных футов) и наличие камина в 15 домах (главы 14).
HTNGOIL Месячное потребление мазута (в галлонах), температура (по Фаренгейту), высота чердака (в дюймах) и стиль (0 — не усадьба, 1 — усадьба) (глава 13).
ICECREAM Дневная температура (по Фаренгейту) и объем продажи мороженого (тыс. долл.) за 21 день (глава 12).
INDPSICH Время реакции, измеренной разными методами (глава 11).
INSURANCE INVOICE Время обработки страхового полиса (главы 3, 7 и 8). Количество обработанных заказов и продолжительность их обработки (в часах) на протяжении 30 дней (глава 12).
INVOICES Объем продаж, зарегистрированный в выборке, состоящей из 12 чеков (глава 7).
ITEMERR Количество ошибок (в долларах), содержащихся в выборке, состоящей из 200 элементов (глава 7).
JAPANCPIPPI Год, индекс потребительских цен и индекс цен производителей (глава 15).
LAUNDRY Количество грязи (в фунтах), удаленное с помощью стирального порошка (строки) и время стирки (столбцы) (глава 10).
LOCATE Объем продаж товаров, расположенных на передних, средних и задних стеллажах (в тыс. долл.) (главы 10 и 11).
LOWERFIFTHINCOME Год и доход 20% беднейших семей (глава 15).
MAIL Вес пакета и количество заказов (главы 2 и 12).
MAILSPC День, общее количество пакетов и количество пакетов, доставленных не вовремя в течение 20 дней (глава 17).
MANAGERS Продажи (отношение фактического и планового объемов годовых продаж), оценка, полученная при сдаче теста Wonderlic Personnel, оценка, полученная при сдаче теста Strong-Campbell Inventory, стаж работы до вступления в должность менеджера по продажам, наличие у менеджера научной степени в области электротехники (глава 14).
MCDONALD Год, закодированный код и общая годовая прибыль компании McDonald’s (млрд, долл.) (глава 15).
MEASUREMENT Выборка, производственные измерения и лабораторные измерения (глава 9).
MEDICARE Разность между фактической и предписанной компенсацией затрат на медицинское обслуживание (глава 7).
MEDREC День, количество обслуженных пациентов и количество записей, не обработанных в течение 30-дневного периода (глава 17).
METALRETURN Год, доходность платины, золота и серебра (главы 3).
MOISTURE Содержание смеси, используемой для производства кровельного покрытия в бостонском и вермонтском филиалах компании (глава 8 и 9).
MOVIE Стоимость проданных билетов (млн. долл.) и количество проданных видеокассет (тыс. штук) для 30 кинофильмов (глава 11).
MOVING Количество рабочих часов и объем груза (в кубических футах), перевезенного конкретной компанией, вычисленные по выборке, состоящей из 36 клиентов (глава 12).
MUTUAL FUNDS Название фонда, тип, цель, активы, сборы, доля затрат, доходность в 2001 г., трехлетняя, пятилетняя доходность, оборот, риск, лучший квартал и худший квартал (главы 2, 3, 6, 7, 9, 10, 13 и 14).
NBA Название команды, количество побед, количество очков, набранных за игру (для команды, соперника и разность очков), потери мяча за игру (для команды, соперника и разность между количеством подборов, сделанных командой и соперником), перехваты в нападении и защите (глава 14).
NEIGHBOR Продажная цена (тыс. долл.), количество комнат и местоположение (восток — 0, запад — 1) 20 домов (глава 14).
NET-CHG Ежедневное изменение стоимости акций (глава 6).
NYSE OILSUPP OMNI Компания и количество проданных акций (глава 6). Год, закодированный год и количество сотрудников (тыс. чел.) (глава 15). Количество проданных батончиков, цена, затраты на рекламу (глава 13).
O-RING Номер запуска, температура воздуха и степень повреждения уплотнительного кольца (глава 15).
P&G Год, закодированный год и уточненная цена акции (глава 15).
PAGEVIEW PAIN-RELIEF PALLET Компания, доход и количество посетителей Web-страницы (глава 12). Температура, марка лекарства и время растворения (глава 10). Вес кровельного покрытия, произведенного в Бостоне и Вермонте (главы 2, 7, 8 и 9).
PARACHUTE PARACHUTE2 PASTA PE Прочность парашютов, поставленных компаниями 1-4 (глава 10). Прочность волокон (строки) и поставщики (столбцы) (глава 10). Вес спагетти (строки) и длительность приготовления (столбцы) (глава 10). Символ и отношение рыночной цены к чистой прибыли в расчете на одну акцию (главы 2 и 3).
PEN Пол, вид рекламы и рейтинг товара (глава 10).
PERFORM Производительность труда до и после специализированного обучения (глава 9).
PETFOOD Расстояние между полками (в футах), недельный объем продаж (в сотнях долларов) и местоположение стеллажей (сзади — 0, впереди — 1) (главы 12 и 14).
PETFOOD2 Стоимость, количество белка и жира в сухом и консервированном корме для кошек и собак (главы 3 и 9).
PHONE Продолжительность устранения повреждений телефонной линии (в минутах) и номер телефонной станции (I и II) для 20 разновидностей зафиксированных повреждений (главы 3, 6 и 9).
PHOTO Концентрация проявителя (строки) и длительность проявления (столбцы) (глава 10).
PIZZA Продукт, вес, стоимость, количество калорий и количество жира в граммах для трех категорий продуктов для 40 образцов (главы 2 и 3).
PLUMBINV Разность между фактическим объемом зарегистрированных продаж и объемом продаж, занесенным в компьютерную систему для 100 чеков (глава 7).
PMORRIS Год, закодированный год и текущие доходы компании Philip Morris, Inc (млрд, долл.) (глава 15).
POLIO Год и количество зарегистрированных заболеваний полиомиелитом на 100 000 человек (глава 15).
POTATO Процентное содержание осадка в фильтре, кислотность, давление под линией тока, давление над линией тока, толщина осадка, предельная скорость вращения барабана и скорость вращения барабана. Файл содержит результаты 54 измерений (глава 14).
PRINTERS Название, цена, скорость печати текста, стоимость печати текста, скорость печати цветной фотографии, цена печати цветной фотографии (главы 2, 3 и 14).
PROTEIN Калорийность (в граммах), количество белка, процент калорий за счет жирности, процент калорий за счет насыщенного жира и количество холе-стерола (в миллиграммах) в 25 популярных белковых продуктах (глава 2).
PUMPKIN Диаметр бочонка и вес семечек (глава 12).
RADON Уровень излучения грунта, температура поверхности почвы, давление пара, скорость ветра, относительная влажность, точка росы и температура окружающего воздуха (глава 14).
RAISINS Вес упаковок с изюмом (глава 9).
REALGDP Данные о закодированных кварталах, квартальный объем внутреннего национального продукта (в миллиардах долларов по курсу 1996 года) и три фиктивные переменные (глава 15).
REAPPR3 Оценочная стоимость, данная тремя агентами (глава 10).
REDWOOD Вес, диаметр и толщина коры дерева (глава 13).
REFRIGERATOR Название, тип, цена и стоимость годового потребления электроэнергии (главы 2, 3 и 12).
RENT Месячная рента (в долларах) и площадь апартаментов (в квадратных футах) для выборки из 25 апартаментов (глава 12).
RESTRATE Местоположение, оценка качества пищи, оформления блюд, уровня обслуживания и стоимость обеда для одного человека (главы 3, 9, 12 и 14).
RETURNS Дата закрытия торгов, курс акций компании General Motors, Ford, International Aluminium, Health Care и Retirement Group. Inc (глава 12).
REUSE ROSLYN Процент повторно используемого программного обеспечения (глава 3). Адрес, оценочная стоимость, полезная площадь (акры), размер дома, возраст, количество комнат, количество ванных комнат и количество автомобилей, которые можно парковать в гараже в поселках Рослин, штат Нью-Йорк (глава 14).
ROYALS RRSPC Игра, посещаемость, проводилась ли рекламная акция (глава 2). Количество опозданий и общее количество прибытий в течение 20 дней (глава 17).
RUBBER Вес резиновой прокладки (глава 6).
RUDYBIRD День, общее количество проданных дискет, количество проданных дискет компании Rudybird (глава 17).
S&PSTKIN Закодированный квартал, индексы курсов акций, вычисленные компанией Standard&Poor в конце каждого квартала, и три фиктивные переменные (глава 15).
SALARIES Вид работы, зарплата мужчин и зарплата женщин (глава 9).
SCHOOLS Район, процент учеников, успешно прошедших тестирование, посещаемость, зарплата учителей и затраты на учеников (главы 12 и 14).
SCRUBBER Скорость потока воздуха, воды, циркуляционного потока воды и проходное сечение дросселя в воздухозаборнике (глава 14).
SEALANT Номер выборки, герметичность покрытия, произведенного в Бостоне и Вермонте (глава 17).
SEARS Год, закодированный год и совокупный годовой доход компании Sears, Roebuck & Company (млрд, долл.) (глава 15).
SECURITY Город, производительность металлоискателя, количество нарушений на миллион пассажиров (главы 2, 3 и 12).
SH2 SH7 День и количество звонков, поступивших в справочную систему (главы 2 и 3). Суммы, которые 46 потенциальных респондентов согласны платить (в неделю) за подписку в течение 90-дневного испытательного срока (глава 7).
SH8 SH9 Насыщенность шрифта (глава 8). Продолжительность раннего телефонного звонка (с), продолжительность позднего телефонного звонка (с) и разность между ними (с) (глава 9).
SH10-1 Звонок, план презентации (структурированный — 1, полуструктуриро-ванный — 2, неструктурированный — 3), продолжительность разговора (с) (глава 10).
SH10-2
SH12
SH13
SH15
SH17-1
SH17-2
SITE
SP500
SPEED
SPONGE
SPORTING
SPWATER STANDBY
STATES
STEEL
STOCKRETURN
STOCKS2002 STRATEGIC TAX
TAXES
TEA3
TREABAGS
TELESPC
TENSILE
TESTRANK
TEXTBOOK
TOMATOES
Пол звонящего человека (мужчина — 1, женщина — 2), тип приветствия (личное, но формальное — 1, личное, но неформальное — 2, безличное — 3) (глава 10).
Продолжительность телемаркетинга (часов в месяц) и количество новых подписчиков в месяц за 2 года (глава 12).
Продолжительность телемаркетинга (часов в неделю, количество новых подписчиков и вид презентации) (глава 13).
Месяц и количество домашних подписчиков за 2 последних года (глава 15). День, количество рекламных объявлений, содержащих ошибки, и количество ошибок, совершенных в течение 25 дней (глава 17).
День и насыщенность шрифта в каждом из пяти экземпляров в течение 20 дней (глава 17).
Номер магазина, площадь магазина (в квадратных футах) и объемы продаж (тыс. долл.) (глава 12).
Неделя и изменение за неделю индекса S&P 500, а также стоимости акций компаний Exxon, Mobil, International Aluminium, Sears, BancOne и General Motors (глава 12).
Пробег на галлон топлива и скорость (миль в час) автомобилей (глава 14). День, количество произведенных тампонов, количество бракованных тампонов за 32-дневный период и доля бракованной продукции (глава 17). Объемы продаж, возраст, годовой рост населения, процент жителей, имеющих среднее образование, а также процент жителей, имеющих высшее образование (главы 12 и 14).
Номер выборки и объем магния (глава 17).
Общее количество часов простоя за неделю, общее количество человекочасов в рабочей неделе (присутственные часы), общее количество часов, отработанных сотрудниками вне центральной станции (часы, проведенные на выезде) за 26 недель (глава 14).
Штат, время, затраченное на переезды, процент домов, имеющих более 8 комнат, медиана доходов, процент домов, стоимость которых превышает 30% семейного дохода (глава 2 и 3).
Разность между фактической и номинальной длиной (главы 2, 6 и 7). Неделя, индекс Доу-Джонса, S&P 500, Russell 2000 и Willshire 5000 (глава 3).
Неделя, индекс S&P 500, Sears, Target и Sara Lee в конце недели (глава 2).
Год и количество баррелей нефти в стратегических запасах США (глава 15). Еженедельные поступления налогов с продаж, выплаченные 50 компаниями (глава 3).
Муниципальные налоги (в долларах) и возраст (в годах) для 19 одноквартирных домов (глава 12).
Номер выборки и вес чайной упаковки (глава 17).
Вес чайной упаковки (главы 3, 7 и 8).
Количество заказов и количество исправлений, сделанных в течение 30 дней (глава 17).
Номер выборки и прочность (глава 17).
Рейтинги 10 работников, обученных с помощью традиционного метода (Т — 0), и 10 работников, обученных с помощью экспериментального метода (Т — 1) (глава 11).
Учебник, стоимость книги в магазине и стоимость книги в интернет-магазине Amazon.com (глава 9).
Год и цена фунта помидоров в США (глава 15).
TOMYLD2 Количество удобрений (в фунтах на 100 квадратных футов) и урожай (в фунтах) на 12 участках земли (глава 14).
TOYS-REV Квартал, закодированный квартал и три фиктивные переменные (глава 15).
TRADE Дни, количество нежелательных сделок и общее количество сделок за 30-дневный период (глава 17).
TRADES День, количество входящих звонков и количество сделок, заключенных за день, в течение 35-дневного периода (глава 12).
TRAIN2 Отклонение от расписания (в минутах) для 10 электричек компании Long Island Railroad (0) и 12 электричек компании New Jersey Trains (1) (глава 11).
TRAINING Продолжительность сборки и программа обучения (коллективная — 0, индивидуальная — 0) (главы 9 и 11).
TRANSPORT Дни и скорость доставки пациентов (в минутах) измеренные по выборкам, содержащим по четыре пациента. Данные охватывают 30-дневный период (глава 17).
TRASHBAGS TRAVEL TRAVEL2 Вес, при котором разрываются мешки (глава 10 и 11). Город, стоимость проживания в гостинице и проката автомобиля (глава 7). Город, стоимость аренды гостиничного номера и стоимость проката автомобиля (глава 7).
TREASURY TROUGH TRSNYC TSMODEL1 TSMODEL2 UERATE UKCPI Год и ссудный процент (глава 15). Ширина профиля (главы 3 и 7). Год, значение переменной А и значение переменной Б (глава 15). Годы, закодированные годы и три временных ряда (I, II и III) (глава 15). Годы, закодированные годы и два временных ряда (I и II) (глава 15). Год, месяц и уровень безработицы по месяцам в 1995-1999 гг. (главы 2 и 15). Год, индекс потребительских цен и индекс цен производителя в Великобритании (глава 15).
UNDERWRITING Оценка на вступительном экзамене, оценка на выпускном экзамене и метод обучения (глава 13).
UTILITY VB Расходы на содержание 50 трехкомнатных апартаментов (глава 6). Время разработки и запуска программы на языке Visual Basic, которое потребовалось 9 студентам (в минутах) (глава 9).
WALMART Квартал, закодированный квартал, квартальная прибыль, Quarter 1, Quarter 2 и Quarter 3 (глава 15).
WARECOST Стоимость распространения (тыс. долл.), объем продаж (тыс. долл.) и количество заказов за 24 месяца (главы 12 и 13).
WAREHSE Количество единиц, обработанных за день, день и количество сотрудников (глава 17).
WEEKLIES Журнал, количество рекламных страниц в текущем году и количество текущих страниц в прошлом году (глава 9).
WIP Продолжительность производства в каждой типографии (А — 1, В — 2) для выборки, состоящей из 20 книг (главы 3, 6 и 9).
WRIGLEY Год, закодированный год, фактический доход, индекс цен производителя и реальный доход (глава 15).
YARN Прочность пряжи, уровни давления (30, 40 и 50 фунтов на кв. метр), выборка и направление потока (попутный — 1, встречный — 2) (глава 10).
YIELD ZIPCODES Этап очистки, этап травления и объем производства (глава 10). Город, стоимость дома в 2001 г. и стоимость дома в 2002 г. (глава 9).
Приложение Д
Таблицы
Д.1 Таблица случайных чисел
Д.2 Кумулятивное стандартизованное нормальное распределение
Д.З Критические значения ^-статистики
Д.4 Критические значения х2-статистики
Д.5 Критические значения F-статистики
Д.6 Таблица биномиального распределения
Д.7 Таблица распределения Пуассона
Д.8 Нижние и верхние критические значения статистики Т, в ранговом критерии Уилкоксона
Д.9 Критические значения стьюдентизованного размаха Q
Д.10 Критические значения dL и dv статистики Дурбина-Уотсона D
Д.11 Множители контрольных карт
Д.12. Стандартизованное нормальное распределение
Таблица Д.1. Случайные числа
Столбцы
Строки 00000 12345 00001 67890 11111 12345 11112 67890 22222 12345 22223 67890 33333 12345 33334 67890
01 49280 88924 35779 00283 81163 07275 89863 02348
02 61870 41657 07468 08612 98083 97349 20775 45091
03 43898 65923 25078 86129 78496 97653 91550 08078
04 62993 93912 30454 . 84598 56095 20664 12872 64647
05 33850 58555 51438 85507 71865 79488 76783 31708
06 97340 03364 88472 04334 63919 36394 11095 92470
07 70543 29776 10087 10072 55980 64688 68239 20461
08 89382 93809 00796 95945 34101 81277 66090 88872
09 37818 72142 67140 50785 22380 16703 53362 44940
10 60430 22834 14130 96593 23298 56203 92671 15925
11 82975 66158 84731 19436 55790 69229 28661 13675
12 39087 71938 40355 54324 08401 26299 49420 59208
13 55700 24586 93247 32596 11865 63397 44251 43189
14 14756 23997 78643 75912 83832 32768 18928 57070
15 32166 53251 70654 92827 63491 04233 33825 69662
16 23236 73751 31888 81718 06546 83246 47651 04877
17 45794 26926 15130 82455 78305 55058 52551 47182
18 09893 20505 14225 68514 46427 56788 96297 78822
19 54382 74598 91499 14523 68479 27686 46162 83554
20 94750 89923 37089 20048 80336 94598 26940 36858
21 70297 34135 53140 33340 42050 82341 44104 82949
22 85157 47954 32979 26575 57600 40881 12250 73742
23 11100 02340 12860 74697 96644 89439 28707 25815
24 36871 50775 30592 57143 17381 68856 25853 35041
25 23913 48357 63308 16090 51690 54607 72407 55538
Столбцы
Строки 00000 12345 00001 67890 11111 12345 11112 67890 22222 12345 22223 67890 33333 12345 33334 67890
26 79348 36085 27973 65157 07456 22255 25626 57054
27 92074 54641 53673 54421 18130 60103 69593 49464
28 06873 21440 75593 41373 49502 17972 82578 16364
29 12478 37622 99659 31065 83613 69889 58869 29571
30 57175 55564 65411 42547 70457 03426 72937 83792
31 91616 11075 80103 07831 59309 13276 26710 73000
32 78025 73539 14621 39044 47450 03197 12787 47709
33 27587 67228 80145 10175 12822 86687 65530 49325
34 16690 20427 04251 64477 73709 73945 92396 68263
35 70183 58065 65489 31833 82093 16747 10386 59293
36 90730 35385 15679 99742 50866 78028 75573 67257
37 10934 93242 13431 24590 02770 48582 00906 58595
38 82462 30166 79613 47416 13389 80268 05085 96666
39 27463 10433 07606 16285 93699 60912 94532 95632
40 02979 52997 09079 92709 90110 47506 53693 49892
41 46888 69929 75233 52507 32097 37594 10067 67327
42 53638 83161 08289 12639 08141 12640 28437 09268
43 82433 61427 17239 89160 19666 08814 37841 12847
44 35766 31672 50082 22795 66948 65581 84393 15890
45 10853 42581 08792 13257 61973 24450 52351 16602
46 20341 27398 72906 63955 17276 10646 74692 48438
47 54458 90542 77563 51839 52901 53355 83281 19177
48 26337 66530 16687 35179 46560 00123 44546 79896
49 34314 23729 85264 05575 96855 23820 11091 79821
50 28603 10708 68933 34189 92166 15181 66628 58599
51 66194 28926 99547 16625 45515 67953 12108 57846
52 78240 43195 24837 32511 70880 22070 52622 61881
53 00833 88000 67299 68215 11274 55624 32991 17436
54 12111 86683 61270 58036 64192 90611 15145 01748
55 47189 99951 05755 03834 43782 90599 40282 51417
Столбцы
Строки 00000 12345 00001 67890 11111 12345 11112 67890 22222 12345 22223 67890 33333 12345 33334 67890
56 76396 72486 62423 27618 84184 78922 73561 52818
57 46409 17469 32483 09083 76175 19985 26309 91536
58 74626 22111 87286 46772 42243 68046 44250 42439
59 34450 81974 93723 49023 58432 67083 36876 93391
60 36327 72135 33005 28701 34710 49359 50693 89311
61 74185 77536 84825 09934 99103 09325 67389 45869
62 12296 41623 62873 37943 25584 09609 63360 47270
63 90822 60280 88925 99610 42772 60561 76873 04117
64 72121 79152 96591 90305 10189 79778 68016 13747
65 95268 41377 25684 08151 61816 58555 54305 86189
66 92603 09091 75884 93424 72586 88903 30061 14457
67 18813 90291 05275 01223 79607 95426 34900 09778
68 38840 26903 28624 67157 51986 42865 14508 49315
69 05959 33836 53758 16562 41081 38012 41230 20528
70 85141 21155 99212 32685 51403 31926 69813 58781
71 75047 59643 31074 38172 03718 32119 69506 67143
72 30752 95260 68032 62871 58781 34143 68790 69766
73 22986 82575 42187 62295 84295 30634 66562 31442
74 99439 86692 90348 66036 48399 73451 26698 39437
75 20389 93029 11881 71685 65452 89047 63669 02656
76 39249 05173 68256 36359 20250 68686 05947 09335
77 96777 33605 29481 20063 09398 01843 35139 61344
78 04860 32918 10798 50492 52655 33359 94713 28393
79 41613 42375 00403 03656 77580 87772 86877 57085
80 17930 00794 53836 53692 67135 98102 61912 11246
81 24649 31845 25736 75231 83808 98917 93829 99430
82 79899 34061 54308 59358 56462 58166 97302 86828
83 76801 49594 81002 30397 52728 15101 72070 33706
84 36239 63636 38140 65731 39788 06872 38971 53363
85 07392 64449 17886 63632 53995 17574 22247 62607
Окончание табл.Д.1
Столбцы
Строки 00000 12345 00001 67890 11111 12345 11112 67890 22222 12345 22223 67890 33333 12345 33334 67890
86 67133 04181 33874 98835 67453 59734 76381 63455
87 77759 31504 32832 70861 15152 29733 75371 39174
88 85992 72268 42920 20810 29361 51423 90306 73574
89 79553 75952 54116 65553 47139 60579 09165 85490
90 41101 17336 48951 53674 17880 45260 08575 49321
91 36191 17095 32123 91576 84221 78902 82010 30847
92 62329 63898 23268 74283 26091 68409 69704 82267
93 14751 13151 93115 01437 56945 89661 67680 79790
94 48462 59278 44185 29616 76537 19589 83139 28454
95 29435 88105 59651 44391 74588 55114 80834 85686
96 28340 29285 12965 14821 80425 16602 44653 70467
97 02167 58940 27149 80242 10587 79786 34959 75339
98 17864 00991 39557 54981 23588 81914 37609 13128
99 79675 80605 60059 35862 00254 36546 21545 78179
00 72335 82037 92003 34100 29879 46613 89720 13274
Источник: таблица является фрагментом книги “A Million Random Digits with 100,000 Normal
Deviates” (Glencoe, IL. The Free Press, 1955).
Таблица Д.2. Кумулятивное стандартизованное нормальное распределение
Элементы таблицы представляют собой площади, ограниченные кривой кумулятивного стандартизованного нормального распределения от —оо до Z
Z 0,00 0,01 0,02 0,03 0,04 0,05 0,06 0,07 0,08 0,09
-3,9 0,00005 0,00005 0,00004 0,0000’4 0,00004 0,00004 0,00004 0,00004 0,00003 0,00003
-3,8 0,00007 0,00007 0,00007 0,00006 0,00006 0,00006 0,00006 0,00005 0,00005 0,00005
-3,7 0,00011 0,00010 0,00010 0,00010 0,00009 0,00009 0,00008 0,00008 0,00008 0,00008
-3,6 0,00016 0,00015 0,00015 0,00014 0,00014 0,00013 0,00013 0,00012 0,00012 0,00011
-3,5 0,00023 0,00022 0,00022 0,00021 0,00020 0,00019 0,00019 0,00018 0,00017 0,00017
-3,4 0,00034 0,00032 0,00031 0,00030 0,00029 0,00028 0,00027 0,00026 0,00025 0,00024
-3,3 0,00048 0,00047 0,00045 0,00043 0,00042 0,00040 0,00039 0,00038 0,00036 0,00035
-3,2 0,00069 0,00066 0,00064 0,00062 0,00060 0,00058 0,00056 0,00054 0,00052 0,00050
-3,1 0,00097 0,00094 0,00090 0,00087 0,00084 0,00082 0,00079 0,00076 0,00074 0,00071
-3,0 0,00135 0,00131 0,00126 0,00122 0,00118 0,00114 0,00111 0,00107 0,00103 0,00100
-2,9 0,0019 0,0018 0,0018 0,0017 0,0016 0,0016 0,0015 0,0015 0,0014 0,0014
-2,8 0,0026 0,0025 0,0024 0,0023 0,0023 0,0022 0,0021 0,0021 0,0020 0,0019
-2,7 0,0035 0,0034 0,0033 0,0032 0,0031 0,0030 0,0029 0,0028 0,0027 0,0026
-2,6 0,0047 0,0045 0,0044 0,0043 0,0041 0,0040 0,0039 0,0038 0,0037 0,0036
-2,5 0,0062 0,0060 0,0059 0,0057 0,0055 0,0054 0,0052 0,0051 0,0049 0,0048
-2,4 0,0082 0,0080 0,0078 0,0075 0,0073 0,0071 0,0069 0,0068 0,0066 0,0064
-2,3 0,0107 0,0104 0,0102 0,0099 0,0096 0,0094 0,0091 0,0089 0,0087 0,0084
-2,2 0,0139 0,0136 0,0132 0,0129 0,0125 0,0122 0,0119 0,0116 0,0113 0,0110
-2,1 0,0179 0,0174 0,0170 0,0166 0,0162 0,0158 0,0154 0,0150 0,0146 0,0143
-2,0 0,0228 0,0222 0,0217 0,0212 0,0207 0,0202 0,0197 0,0192 0,0188 0,0183
-1,9 0,0287 0,0281 0,0274 0,0268 0,0262 0,0256 0,0250 0,0244 0,0239 0,0233
-1,8 0,0359 0,0351 0,0344 0,0336 0,0329 0,0322 0,0314 0,0307 0,0301 0,0294
-1,7 0,0446 0,0436 0,0427 0,0418 0,0409 0,0401 0,0392 0,0384 0,0375 0,0367
-1,6 0,0548 0,0537 0,0526 0,0516 0,0505 0,0495 0,0485 0,0475 0,0465 0,0455
-1,5 0,0668 0,0655 0,0643 0,0630 0,0618 0,0606 0,0594 0,0582 0,0571 0,0559
-1,4 0,0808 0,0793 0,0778 0,0764 0,0749 0,0735 0,0721 0,0708 0,0694 0,0681
-1,3 0,0968 0,0951 0,0934 0,0918 0,0901 0,0885 0,0869 0,0853 0,0838 0,0823
-1,2 0,1151 0,1131 0,1112 0,1093 0,1075 0,1056 0,1038 0,1020 0,1003 0,0985
-1,1 0,1357 0,1335 0,1314 0,1292 0,1271 0,1251 0,1230 0,1210 0,1190 0,1170
-1,0 0,1587 0,1562 0,1539 0,1515 0,1492 0,1469 0,1446 0,1423 0,1401 0,1379
-0,9 0,1841 0,1814 0,1788 0,1762 0,1736 0,1711 0,1685 0,1660 0,1635 0,1611
-0,8 0,2119 0,2090 0,2061 0,2033 0,2005 0,1977 0,1949 0,1922 0,1894 0,1867
-0,7 0,2420 0,2388 0,2358 0,2327 0,2296 0,2266 0,2236 0,2206 0,2177 0,2148
-0,6 0,2743 0,2709 0,2676 0,2643 0,2611 0,2578 0,2546 0,2514 0,2482 0,2451
-0,5 0,3085 0,3050 0,3015 0,2981 0,2946 0,2912 0,2877 0,2843 0,2810 0,2776
-0,4 0,3446 0,3409 0,3372 0,3336 0,3300 0,3264 0,3228 0,3192 0,3156 0,3121
-0,3 0,3821 0,3783 0,3745 0,3707 0,3669 0,3632 0,3594 0,3557 0,3520 0,3483
-0,2 0,4207 0,4168 0,4129 0,4090 0,4052 0,4013 0,3974 0,3936 0,3897 0,3859
-0,1 0,4602 0,4562 0,4522 0,4483 0,4443 0,4404 0,4364 0,4325 0,4286 0,4247
-0,0 0,5000 0,4960 0,4920 0,4880 0,4840 0,4801 0,4761 0,4721 0,4681 0,4641
Продолжение табл. Д.2
Элементы таблицы представляют собой площади, ограниченные кривой кумулятивного стандартизованного нормального распределения от —оо до Z
Z 0,00 0,01 0,02 0,03 0,04 0,05 0,06 0,07 0,08 0,09
0,0 0,5000 0,5040 0,5080 0,5120 Ю,5160 0,5199 0,5239 0,5279 0,5319 0,5359
0,1 0,5398 0,5438 0,5478 0,5517 0,5557 0,5596 0,5636 0,5675 0,5714 0,5753
0,2 0,5793 0,5832 0,5871 0,5910 0,5948 0,5987 0,6026 0,6064 0,6103 0,6141
0,3 0,6179 0,6217 0,6255 0,6293 0,6331 0,6368 0,6406 0,6443 0,6480 0,6517
0,4 0,6554 0,6591 0,6628 0,6664 0,6700 0,6736 0,6772 0,6808 0,6844 0,6879
0,5 0,6915 0,6950 0,6985 0,7019 0,7054 0,7088 0,7123 0,7157 0,7190 0,7224
0,6 0,7257 0,7291 0,7324 0,7357 0,7389 0,7422 0,7454 0,7486 0,7518 0,7549
0,7 0,7580 0,7612 0,7642 0,7673 0,7704 0,7734 0,7764 0,7794 0,7823 0,7852
0,8 0,7881 0,7910 0,7939 0,7967 0,7995 0,8023 0,8051 0,8078 0,8106 0,8133
0,9 0,8159 0,8186 0,8212 0,8238 0,8264 0,8289 0,8315 0,8340 0,8365 0,8389
1,0 0,8413 0,8438 0,8461 0,8485 0,8508 0,8531 0,8554 0,8577 0,8599 0,8621
1,1 0,8643 0,8665 0,8686 0,8708 0,8729 0,8749 0,8770 0,8790 0,8810 0,8830
1,2 0,8849 0,8869 0,8888 0,8907 0,8925 0,8944 0,8962 0,8980 0,8997 0,9015
1,3 0,9032 0,9049 0,9066 0,9082 0,9099 0,9115 0,9131 0,9147 0,9162 0,9177
1,4 0,9192 0,9207 0,9222 0,9236 0,9251 0,9265 0,9279 0,9292 0,9306 0,9319
1,5 0,9332 0,9345 0,9357 0,9370 0,9382 0,9394 0,9406 0,9418 0,9429 0,9441
1,6 0,9452 0,9463 0,9474 0,9484 0,9495 0,9505 0,9515 0,9525 0,9535 0,9545
1,7 0,9554 0,9564 0,9573 0,9582 0,9591 0,9599 0,9608 0,9616 0,9625 0,9633
1,8 0,9641 0,9649 0,9656 0,9664 0,9671 0,9678 0,9686 0,9693 0,9699 0,9706
1,9 0,9713 0,9719 0,9726 0,9732 0,9738 0,9744 0,9750 0,9756 0,9761 0,9767
2,0 0,9772 0,9778 0,9783 0,9788 0,9793 0,9798 0,9803 0,9808 0,9812 0,9817
2,1 0,9821 0,9826 0,9830 0,9834 0,9838 0,9842 0,9846 0,9850 0,9854 0,9857
2,2 0,9861 0,9864 0,9868 0,9871 0,9875 0,9878 0,9881 0,9884 0,9887 0,9890
2,3 0,9893 0,9896 0,9898 0,9901 0,9904 0,9906 0,9909 0,9911 0,9913 0,9916
2,4 0,9918 0,9920 0,9922 0,9925 0,9927 0,9929 0,9931 0,9932 0,9934 0,9936
2,5 0,9938 0,9940 0,9941 0,9943 0,9945 0,9946 0,9948 0,9949 0,9951 0,9952
2,6 0,9953 0,9955 0,9956 0,9957 0,9959 0,9960 0,9961 0,9962 0,9963 0,9964
2,7 0,9965 0,9966 0,9967 0,9968 0,9969 0,9970 0,9971 0,9972 0,9973 0,9974
2,8 0,9974 0,9975 0,9976 0,9977 0,9977 0,9978 0,9979 0,9979 0,9980 0,9981
2,9 0,9981 0,9982 0,9982 0,9983 0,9984 0,9984 0,9985 0,9985 0,9986 0,9986
3,0 0,99865 0,99869 0,99874 0,99878 0,99882 0,99886 0,99889 0,99893 0,99897 0,99900
3,1 0,99903 0,99906 0,99910 0,99913 0,99916 0,99918 0,99921 0,99924 0,99926 0,99929
3,2 0,99931 0,99934 0,99936 0,99938 0,99940 0,99942 0,99944 0,99946 0,99948 0,99950
3,3 0,99952 0,99953 0,99955 0,99957 0,99958 0,99960 0,99961 0,99962 0,99964 0,99965
3,4 0,99966 0,99968 0,99969 0,99970 0,99971 0,99972 0,99973 0,99974 0,99975 0,99976
3,5 0,99977 0,99978 0,99978 0,99979 0,99980 0,99981 0,99981 0,99982 0,99983 0,99983
3,6 0,99984 0,99985 0,99985 0,99986 0,99986 0,99987 0,99987 0,99988 0,99988 0,99989
3,7 0,99989 0,99990 0,99990 0,99990 0,99991 0,99991 0,99992 0,99992 0,99992 0,99992
3,8 0,99993 0,99993 0,99993 0,99994 0,99994 0,99994 0,99994 0,99995 0,99995 0,99995
3,9 0,99995 0,99995 0,99996 0,99996 0,99996 0,99996 0,99996 0,99996 0,99997 0,99997
Таблица Д.З. Критические значения f-статистики
Элементы таблицы представляют собой критические значения t-статистики с заданным количеством степеней свободы, соответствующие указанной площади фигуры, ограниченной правым хвостом распределения Стьюдента (а)
2 Площадь фигуры, ограниченной правым хвостом распределения Стьюдента
Степени свободы 0,25 0,10 0,05 0,025 0,01 0,005
1 1,0000 3,0777 6,3138 12,7062 31,8207 63,6574
2 0,8165 1,8856 2,9200 4,3027 6,9646 9,9248
3 0,7649 1,6377 2,3534 3,1824 4,5407 5,8409
4 0,7407 1,5332 2,1318 2,7764 3,7469 4,6041
5 0,7267 1,4759 2,0150 2,5706 3,3649 4,0322
6 0,7176 1,4398 1,9432 2,4469 3,1427 3,7074
7 0,7111 1,4149 1,8946 2,3646 2,9980 3,4995
8 0,7064 1,3968 1,8595 2,3060 2,8965 3,3554
9 0,7027 1,3830 1,8331 2,2622 2,8214 3,2498
10 0,6998 1,3722 1,8125 2,2281 2,7638 3,1693
11 0,6974 1,3634 1,7959 2,2010 2,7181 3,1058
12 0,6955 1,3562 1,7823 2,1788 2,6810 3,0545
13 0,6938 1,3502 1,7709 2,1604 2,6503 3,0123
14 0,6924 1,3450 1,7613 2,1448 2,6245 2,9768
15 0,6912 1,3406 1,7531 2,1315 2,6025 2,9467
16 0,6901 1,3368 1,7459 2,1199 2,5835 2,9208
17 > 0,6892 1,3334 1,7396 2,1098 2,5669 2,8982
18 0,6884 1,3304 1,7341 2,1009 2,5524 2,8784
19 0,6876 1,3277 1,7291 2,0930 2,5395 2,8609
20 0,6870 1,3253 1,7247 2,0860 2,5280 2,8453
Продолжение табл. Д.З
2 Площадь фигуры, ограниченной правым хвостом распределения Стьюдента
Степени свободы 0,25 0,10 0,05 0,025 0,01 0,005
21 0,6864 1,3232 1,7207 2,0796 2,5177 2,8314
' 22 0,6858 1,3212 1,7171 2,0739 2,5083 2,8188
23 0,6853 1,3195 1,7139 2,0687 2,4999 2,8073
24 0,6848 1,3178 1,7109 2,0639 2,4922 2,7969
25 0,6844 1,3163 1,7081 2,0595 2,4851 2,7874
26 0,6840 1,3150 1,7056 2,0555 2,4786 2,7787
27 0,6837 1,3137 1,7033 2,0518 2,4727 2,7707
28 0,6834 1,3125 1,7011 2,0484 2,4671 2,7633
29 0,6830 1,3114 1,6991 2,0452 2,4620 2,7564
30 0,6828 1,3104 1,6973 2,0423 2,4573 2,7500
31 0,6825 1,3095 1,6955 2,0395 2,4528 2,7440
32 0,6822 1,3086 1,6939 2,0369 2,4487 2,7385
33 0,6820 1,3077 1,6924 2,0345 2,4448 2,7333
34 0,6818 1,3070 1,6909 2,0322 2,4411 2,7284
35 0,6816 1,3062 1,6896 2,0301 2,4377 2,7238
36 0,6814 1,3055 1,6883 2,0281 2,4345 2,7195
37 0,6812 1,3049 1,6871 2,0262 2,4314 2,7154
38 0,6810 1,3042 1,6860 2,0244 2,4286 2,7116
39 0,6808 1,3036 1,6849 2,0227 2,4258 2,7079
40 0,6807 1,3031 1,6839 2,0211 2,4233 2,7045
41 0,6805 1,3025 1,6829 2,0195 2,4208 2,7012
42 0,6804 1,3020 1,6820 2,0181 2,4185 2,6981
43 0,6802 1,3016 1,6811 2,0167 2,4163 2,6951
44 0,6801 1,3011 1,6802 2,0154 2,4141 2,6923
45 0,6800 1,3006 1,6794 2,0141 2,4121 2,6896
46 0,6799 1,3022 1,6787 2,0129 2,4102 2,6870
47 0,6797 1,2998 1,6779 2,0117 2,4083 2,6846
48 0,6796 1,2994 1,6772 2,0106 2,4066 2,6822
49 0,6795 1,2991 1,6766 2,0096 2,4049 2,6800
50 0,6794 1,2987 1,6759 2,0086 2,4033 2,6778
2 Площадь фигуры, ограниченной правым хвостом распределения Стьюдента
Степени свободы 0,25 0,10 0,05 0,025 0,01 0,005
51 0,6793 1,2984 1,6753 2,0076 2,4017 2,6757
52 0,6792 1,2980 1,6747 2,0066 2,4002 2,6737
53 0,6791 1,2977 1,6741 2,0057 2,3988 2,6718
54 0,6791 1,2974 1,6736 2,0049 2,3974 2,6700
55 0,6790 1,2971 1,6730 2,0040 2,3961 2,6682
56 0,6789 1,2969 1,6725 2,0032 2,3948 2,6665
57 0,6788 1,2966 1,6720 2,0025 2,3936 2,6649
58 0,6787 1,2963 1,6716 2,0017 2,3924 2,6633
59 0,6787 1,2961 1,6711 2,0010 2,3912 2,6618
60 0,6786 1,2958 1,6706 2,0003 2,3901 2,6603
61 0,6785 1,2956 1,6702 1,9996 2,3890 2,6589
62 0,6785 1,2954 1,6698 1,9990 2,3880 2,6575
63 0,6784 1,2951 1,6694 1,9983 2,3870 2,6561
64 0,6783 1,2949 1,6690 1,9977 2,3860 2,6549
65 0,6783 1,2947 1,6686 1,9971 2,3851 2,6536
66 0,6782 1,2945 1,6683 1,9966 2,3842 2,6524
67 0,6782 1,2943 1,6679 1,9960 2,3833 2,6512
68 0,6781 1,2941 1,6676 1,9955 2,3824 2,6501
69 0,6781 1,2939 1,6672 1,9949 2,3816 2,6490
70 0,6780 1,2938 1,6669 1,9944 2,3808 2,6479
71 0,6780 1,2936 1,6666 1,9939 2,3800 2,6469
72 0,6779 1,2934 1,6663 1,9935 2,3793 2,6459
73 0,6779 1,2933 1,6660 1,9930 2,3785 2,6449
74 0,6778 1,2931 1,6657 1,9925 2,3778 2,6439
75 0,6778 1,2929 1,6654 1,9921 2,3771 2,6439
76 0,6777 1,2928 1,6652 1,9917 2,3764 2,6421
77 0,6777 1,2926 1,6649 1,9913 2,3758 2,6412
78 0,6776 1,2925 1,6646 1,9908 2,3751 2,6403
79 0,6776 1,2924 1,6644 1,9905 2,3745 2,6395
80 0,6776 1,2922 1,6641 1,9901 2,3739 2,6387
Окончание табл. Д.З
2 Площадь фигуры, ограниченной правым хвостом распределения Стьюдента
Степени свободы 0,25 0,10 0,05 0,025 0,01 0,005
81 0,6775 1,2921 1,6639 1,9897 2,3733 2,6379
82 0,6775 1,2920 1,6636 1,9893 2,3727 2,6371
83 0,6775 1,2918 1,6634 1,9890 2,3721 2,6364
84 0,6774 1,2917 1,6632 1,9886 2,3716 2,6356
85 0,6774 1,2916 1,6630 1,9883 2,3710 2,6349
86 0,6774 1,2915 1,6628 1,9879 2,3705 2,6342
87 0,6773 1,2914 1,6626 1,9876 2,3700 2,6335
88 0,6773 1,2912 1,6624 1,9873 2,3695 2,6329
89 0,6773 1,2911 1,6622 1,9870 2,3690 2,6322
90 0,6772 1,2910 1,6620 1,9867 2,3685 2,6316
91 0,6772 1,2909 1,6618 1,9864 2,3680 2,6309
92 0,6772 1,2908 1,6616 1,9861 2,3676 2,6303
93 0,6771 1,2907 1,6614 1,9858 2,3671 2,6297
94 0,6771 1,2906 1,6612 1,9855 2,3667 2,6291
95 0,6771 1,2905 1,6611 1,9853 2,3662 2,6286
96 0,6771 1,2904 1,6609 1,9850 2,3658 2,6280
97 0,6770 1,2903 1,6607 1,9847 2,3654 2,6275
98 0,6770 1,2902 1,6606 1,9845 2,3650 2,6269
99 0,6770 1,2902 1,6604 1,9842 2,3646 2,6264
100 0,6770 1,2901 1,6602 1,9840 2,3642 2,6259
110 0,6767 1,2893 1,6588 1,9818 2,3607 2,6213
120 0,6765 1,2886 1,6577 1,9799 2,3578 2,6174
9С 0,6745 1,2816 1,6449 1,9600 2,3263 2,5758
Элементы таблицы представляют собой критические значения ^-статистики с заданным количеством степеней свободы, соответствующие указанной площади фигуры, ограниченной правым хвостом у-распределения (а)
Площадь фигуры, ограниченной правым хвостом х2-распределения (а)
Степени свободы 0,995 0,99 0,975 0,95 0,90 0,75 0,25 0,10 0,05 0,025 0,01 0,005
1 0,001 0,004 0,016 0,102 1,323 2,706 3,841 ' 5,024 6,635 7,879
2 0,010 0,020 0,051 0,103 0,211 0,575 2,773 4,605 5,991 7,378 9,210 10,597
3 0,072 0,115 0,216 0,352 0,584 1,213 4,108 6,251 7,815 9,348 11,345 12,838
4 0,207 0,297 0,484 0,711 1,064 1,923 5,385 7,779 9,488 11,143 13,277 14,860
5 0,412 0,554 0,831 1,145 1,610 2,675 6,626 9,236 11,071 12,833 15,086 16,750
6 0,676 0,872 1,237 1,635 2,204 3,455 7,841 10,645 12,592 14,449 16,812 18,458
7 0,989 1,239 1,690 2,167 2,833 4,255 9,037 12,017 14,067 16,013 18,475 20,278
8 1,344 1,646 2,180 2,733 3,490 5,071 10,219 13,362 15,507 17,535 20,090 21,955
9 1,735 2,088 2,700 3,325 4,168 5,899 11,389 14,684 16,919 19,023 21,666 23,589
10 2,156 2,558 3,247 3,940 4,865 6,737 12,549 15,987 18,307 20,483 23,209 25,188
11 2,603 3,053 3,816 4,575 5,578 7,584 13,701 17,275 19,675 21,920 24,725 26,757
12 3,074 3,571 4,404 5,226 6,304 8,438 14,845 18,549 21,026 23,337 26,217 28,299
13 3,565 4,107 5,009 5,892 7,042 9,299 15,984 19,812 22,362 24,736 27,688 29,819
14 4,075 4,660 5,629 6,571 7,790 10,165 17,117 21,064 23,685 26,119 29,141 31,319
15 4,601 5,229 6,262 7,261 8,547 11,037 18,245 22,307 24,996 27,488 30,578 32,801
Площадь фигуры, ограниченной правым хвостом %2-распределения (а)
Степени свободы 0,995 0,99 0,975 0,95 0,90 0,75 0,25 0,10 0,05 0,025 0,01 0,005
16 5,142 5,812 6,908 7,962 9,312 11,912 19,369 23,542 26,296 28,845 32,000 34,267
17 5,697 6,408 7,564 8,672 10,085 12,792 20,489 24,769 27,587 30,191 33,409 35,718
18 6,265 7,015 8,231 9,390 10,865 13,675 21,605 25,989 28,869 31,526 34,805 37,156
19 6,844 7,633 8,907 10,117 11,651 14,562 22,718 27,204 30,144 32,852 36,191 38,582
20 7,434 8,260 9,591 10,851 12,443 15,452 23,828 28,412 31,410 34,170 37,566 39,997
21 8,034 8,897 10,283 11,591 13,240 16,344 24,935 29,615 32,671 35,479 38,932 41,401
22 8,643 9,542 10,982 12,338 14,042 17,240 26,039 30,813 33,924 36,781 40,289 42,796
23 9,260 10,196 11,689 13,091 14,848 18,137 27,141 32,007 35,172 38,076 41,638 44,181
24 9,886 10,856 12,401 13,848 15,659 19,037 28,241 33,196 36,415 39,364 42,980 45,559
25 10,520 11,524 13,120 14,611 16,473 19,939 29,339 34,382 37,652 40,646 44,314 46,928
26 11,160 12,198 13,844 15,379 17,292 20,843 30,435 35,563 38,885. 41,923 45,642 48,290
27 11,808 12,879 14,573 16,151 18,114 21,749 31,528 36,741 40,113 43,194 46,963 49,645
28 12,461 13,565 15,308 16,928 18,939 22,657 32,620 37,916 41,337 44,461 48,278 50,993
29 13,121 14,257 16,047 17,708 19,768 23,567 33,711 39,087 42,557 45,722 49,588 52,336
30 13,787 14,954 16,791 18,493 20,599 24,478 34,800 40,256 43,773 46,979 50,892 53,672
Если количество степеней свободы (df) больше 30, для вычисления площади фигуры, ограниченной правым хвостом ^распределения, можно применять формулу Z = - y/2df -1. Значение Z можно найти в таблице кумулятивного стандартизованного нормального распределения (табл. Д.2).
Элементы таблицы представляют собой критические значения F-статистики для каждой __________________I Л
комбинации степеней свободы в числителе и знаменателе, соответствующие указанной площади 0 /4/(a,df1,df2)
фигуры, ограниченной правым хвостом F-распределения
Знаменатель, Числитель, df,
1 2 3 4 5 6 7 8 9 10 12 15 20 24 30 40 60 120 ос
1 161,40 199,50 215,70 224,60 230,20 234,00 236,80 238,90 240,50 241,90 243,90 245,90 248,00 249,10 250,10 251,10 252,20 253,30 254,30
2 18,51 19,00 19,16 19,25 19,30 19,33 19,35 19,37 19,38 19,40 : 19,41 19,43 19,45 19,45 19,46 19,47 19,48 19,49 19,50
3 10,13 9,55 9,28 9,12 9,01 8,94 8,89 8,85 8,81 8,79 8,74 8,70 8,66 8,64 8,62 8,59 8,57 8,55 8,53
4 7,71 6,94 6,59 6,39 6,26 6,16 6,09 6,04 6,00 5,96 5,91 5,86 5,80 5,77 • 5,75 5,72 5,69 5,66 5,63
5 6,61 5,79 5,41 5,19 5,05 4,95 4,88 4,82 4,77 4,74 4,68 4,62 4,56 4,53 4,50 4,46 4,43 4,40 4,36
6 5,99 5,14 4,76 4,53 4,39 4,28 4,21 4,15 4,10 4,06 4,00 3,94 3,87 3,84 3,81 3,77 3,74 3,70 3,67
7 5,59 4,74 4,35 4,12 3,97 3,87 3,79 3,73 3,68 3,64 3,57 3,51 3,44 3,41 3,38 3,34 3,30 3,27 3,23
8 5,32 4,46 4,07 3,84 3,69 3,58 3,50 3,44 3,39 3,35 3,28 3,22 3,15 3,12 3,08 3,04 3,01 2,97 2,93
9 5,12 4,26 3,86 3,63 3,48 3,37 3,29 3,23 3,18 3,14 3,07 3,01 2,94 2,90 2,86 2,83 2,79 2,75 2,71
10 4,96 4,10 3,71 3,48 3,33 3,22 3,14 3,07 3,02 2,98 2,91 2,85 2,77 2,74 2,70 2,66 2,62 2,58 2,54
11 4,84 3,98 3,59 3,36 3,20 3,09 3,01 2,95 2,90 2,85 2,79 2,72 2,65 2,61 2,57 2,53 2,49 2,45 2,40
12 4,75 3,89 3,49 3,26 3,11 3,00 2,91 2,85 2,80 2,75 2,69 2,62 2,54 2,51 2,47 2,43 2,38 2,34 2,30
13 4,67 3,81 3,41 3,18 3,03 2,92 2,83 2,77 2,71 2,67 2,60 2,53 2,46 2,42 2,38 2,34 2,30 2,25 2,21
14 4,60 3,74 3,34 3,11 2,96 2,85 2,76 2,70 2,65 2,60 2,53 2,46 2,39 2,35 2,31 2,27 2,22 2,18 2,13
О ^(a.dfndfz)
Знаменатель, df2 Числитель, df, ос
1 2 3 4 5 6 7 8 9 10 12 15 20 24 30 40 60 120
15 4,54 3,68 3,29 3,06 2,90 2,79 2,71 2,64 2,59 2,54 2,48 2,40 2,33 2,29 2,25 2,20 2,16 2,11 2,07
16 4,49 3,63 3,24 3,01 2,85 2,74 2,66 2,59 2,54 2,49 2,42 2,35 2,28 2,24 2,19 2,15 2,11 2,06 2,01
17 4,45 3,59 3,20 2,96 2,81 2,70 2,61 2,55 2,49 2,45 2,38 2,31 2,23 2,19 2,15 2,10 2,06 2,01 1,96
18 4,41 3,55 3,16 2,93 2,77 2,66 2,58 2,51 2,46 2,41 2,34 2,27 2,19 2,15 2,11 2,06 2,02 1,97 1,92
19 4,38 3,52 3,13 2,90 2,74 2,63 2,54 2,48 2,42 2,38 2,31 2,23 2,16 2,11 2,07 2,03 1,98 1,93 1,88
20 4,35 3,49 3,10 2,87 2,71 2,60 2,51 2,45 2,39 2,35 2,28 2,20 2,12 2,08 , , 2,04 1,99 1,95 1,90 1,84
21 4,32 3,47 3,07 2,84 2,68 2,57 2,49 2,42 2,37 2,32 2,25 2,18 2,10 2,05 2,01 1,96 1,92 1,87 1,81
22 4,30 3,44 3,05 2,82 2,66 2,55 2,46 2,40 2,34 2,30 2,23 2,15 2,07 2,03 1,98 1,94 1,89 1,84 1,78
23 4,28 3,42 3,03 2,80 2,64 2,53 2,44 2,37 2,32 2,27 2,20 2,13 2,05 2,01 1,96 1,91 1,86 1,81 1,76
24 4,26 3,40 3,01 2,78 2,62 2,51 2,42 2,36 2,30 2,25 2,18 2,11 2,03 1,98 1,94 1,89 1,84 1,79 1,73
25 4,24 3,39 2,99 2,76 2,60 2,49 2,40 2,34 2,28 2,24 2,16 2,09 2,01 1,96 1,92 1,87 1,82 1,77 1,71
26 4,23 3,37 2,98 2,74 2,59 2,47 2,39 2,32 2,27 2,22 2,15 2,07 1,99 1,95 1,90 1,85 1,80 1,75 1,69
27 4,21 3,35 2,96 2,73 2,57 2,46 2,37 2,31 2,25 2,20 2„13 2,06 1,97 1,93 1,88 1,88 1,79 1,73 1,67
28 4,20 3,34 2,95 2,71 2,56 2,45 2,36 2,29 2,24 2,19 2,12 2,04 1,96 1,91 1,87 1,87 1,77 1,71 1,65
29 4,18 3,33 2,93 2,70 2,55 2,43 2,35 2,28 2,22 2,18 2,10 2,03 1,94 1,90 1,85 1,81 1,75 1,70 1,64
30 4,17 3,32 2,92 2,69 2,53 2,42 2,33 2,27 2,21 2,16 2,09 2,01 1,93 1,89 1,84 1,79 1,74 1,68 1,62
40 4,08 3,23 2,84 2,61 2,45 2,34 2,25 2,18 2,12 2,08 2,00 1,92 1,84 1,79 1,74 1,69 1,64 1,58 1,51
60 4,00 3,15 2,76 2,53 2,37 2,25 2,17 2,10 2,04 1,99 1,92 1,84 1,75 1,70 1,65 1,59 1,53 1,47 1,39
120 3,92 3,07 2,68 2,45 2,29 2,17 2,09 2,02 1,96 1,91 1,83 1,75 1,66 1,61 1,55 1,50 1,43 1,35 1,25
ТО 3,84 3,00 2,60 2,37 2,21 2,10 2,01 1,94 1,88 1,83 1,75 1,67 1,57 1,52 1,46 1,39 1,32 1,22 1,00
^(a.df^dfa)
Знаменатель, Числитель, df.
df2 1 2 3 4 5 б 7 8 9 10 12 15 20 24 30 40 60 120 ос
1 647,80 799,50 864,20 899,60 921,80 937,10 948,20 956,70 963,30 968,60 976,70 984,90 993,10 997,20 1001,00 1006,00 1010,00 1014,00 1018,00
2 38,51 39,00 39,17 38,25 39,30 39,33 39,36 39,39 39,39 39,40 39,41 39,43 39,45 39,46 39,46 39,47 39,48 39,49 39,50
3 17,44 16,04 15,44 15,10 14,88 14,73 14,62 14,54 14,47 14,42 14,34 14,25 14,17 14,12 14,08 14,04 13,99 13,95 13,90
4 12,22 10,65 9,98 9,60 9,36 9,20 9,07 8,98 8,90 8,84 8,75 8,66 8,56 8,51 .8,46 8,41 8,36 8,31 8,26
5 10,01 8,43 7,76 7,39 7,15 6,98 6,85 6,76 6,68 6,62 6,52 6,43 6,33 6,28 6,23 6,18 6,12 6,07 6,02
6 8,81 7,26 6,60 6,23 5,99 5,82 5,70 5,60 5,52 5,46 5,37 5,27 5,17 5,12 5,07 5,01 4,96 4,90 4,85
7 8,07 6,54 5,89 5,52 5,29 5,12 4,99 4,90 4,82 4,76 4,67 4,57 4,47 4,42 4,36 4,31 4,25 4,20 4,14
8 7,57 6,06 5,42 5,05 4,82 4,65 4,53 4,43 4,36 4,30 4,20 4,10 4,00 3,95 3,89 3,84 3,78 3,73 3,67
9 7,21 5,71 5,08 4,72 4,48 4,32 4,20 4,10 4,03 3,96 3,87 3,77 3,67 3,61 3,56 3,51 3,45 3,39 3,33
10 6,94 5,46 4,83 4,47 4,24 4,07 3,95 3,85 3,78 3,72 3,62 3,52 3,42 3,37 3,31 3,26 3,20 3,14 3,08
11 6,72 5,26 4,63 4,28 4,04 3,88 3,76 3,66 3,59 3,53 3,43 3,33 3,23 3,17 3,12 3,06 3,00 2,94 2,88
12 6,55 5,10 4,47 4,12 3,89 3,73 3,61 3,51 3,44 3,37 3,28 3,18 3,07 3,02 2,96 2,91 2,85 2,79 2,72
13 6,41 4,97 4,35 4,00 3,77 3,60 3,48 3,39 3,31 3,25 3,15 3,05 2,95 2,89 2,84 2,78 2,72 2,66 2,60
14 6,30 4,86 4,24 3,89 3,66 3,50 3,38 3,29 3,21 3,15 3,05 2,95 2,84 2,79 2,73 2,67 2,61 2,55 2,49
Fu(a,dfi,df2)
Знаменатель, df2 Числитель, df,
1 2 3 4 5 6 7 8 9 10 12 15 20 24 30 40 60 120 ос
15 6,20 4,77 4,15 3,80 3,58 3,41 3,29 3,20 3,12 3,06 2,96 2,86 2,76 2,70 2,64 2,59 2,52 2,46 2,40
16 6,12 4,69 4,08 3,73 3,50 3,34 3,22 3,12 3,05 2,99 2,89 2,79 2,68 2,63 2,57 2,51 2,45 2,38 2,32
17 6,04 4,62 4,01 3,66 3,44 3,28 3,16 3,06 2,98 2,92 2,82 2,72 2,62 2,56 2,50 2,44 2,38 2,32 2,25
18 5,98 4,56 3,95 3,61 3,38 3,22 3,10 3,01 2,93 2,87 2,77 2,67 2,56 2,50 2,44 2,38 2,32 2,26 2,19
19 5,92 4,51 3,90 3,56 3,33 3,17 3,05 2,96 2,88 2,82 2,72 2,62 2,51 2,45 2,39 2,33 2,27 2,20 2,13
20 5,87 4,46 3,86 3,51 3,29 3,13 3,01 2,91 2,84 2,77 2,68 2,57 2,46 2,41 2,35 2,29 2,22 2,16 2,09
21 5,83 4,42 3,82 3,48 3,25 3,09 2,97 2,87 2,80 2,73 2,64 2,53 2,42 2,37 2,31 2,25 2,18 2,11 2,04
22 5,79 4,38 3,78 3,44 3,22 3,05 2,93 2,84 2,76 2,70 2,60 2,50 2,39 2,33 2,27 2,21 2,14 2,08 2,00
23 5,75 4,35 3,75 3,41 3,18 3,02 2,90 2,81 2,73 2,67 2,57 2,47 2,36 2,30 2,24 2,18 2,11 2,04 1,97
24 5,72 4,32 3,72 3,38 3,15 2,99 2,87 2,78 2,70 2,64 2,54 2,44 2,33 2,27 2,21 2,15 2,08 2,01 1,94
25 5,69 4,29 3,69 3,35 3,13 2,97 2,85 2,75 2,68 2,61 2,51 2,41 2,30 2,24 2,18 2,12 2,05 1,98 1,91
26 5,66 4,27 3,67 3,33 3,10 2,94 2,82 2,73 2,65 2,59 2,49 2,39 2,28 2,22 2,16 2,09 2,03 1,95 1,88
27 5,63 4,24 3,65 3,31 3,08 2,92 2,80 2,71 2,63 2,57 2,47 2,36 2,25 2,19 2,13 2,07 2,00 1,93 1,85
28 5,61 4,22 3,63 3,29 3,06 2,90 2,78 2,69 2,61 2,55 2,45 2,34 2,23 2,17 2,11 2,05 1,98 1,91 1,83
29 5,59 4,20 3,61 3,27 3,04 2,88 2,76 2,67 2,59 2,53 2,43 2,32 2,21 2,15 2,09 2,03 1,96 1,89 1,81
30 5,57 4,18 3,59 3,25 3,03 2,87 2,75 2,65 2,57 2,51 2,41 2,31 2,20 2,14 2,07 2,01 1,94 1,87 1,79
40 5,42 4,05 3,46 3,13 2,90 2,74 2,62 2,53 2,45 2,39 2,29 2,18 2,07 2,01 1,94 1,88 1,80 1,72 1,64
60 5,29 3,93 3,34 3,01 2,79 2,63 2,51 2,41 2,33 2,27 2,17 2,06 1,94 1,88 1,82 1,74 1,67 1,58 1,48
120 5,15 3,80 3,23 2,89 2,67 2,52 2,39 2,30 2,22 2,16 2,05 1,94 1,82 1,76 1,69 1,61 1,53 1,43 1,31
□с 5,02 3,69 3,12 2,79 2,57 2,41 2,29 2,19 2,11 2,05 1,94 1,83 1,71 1,64 1,57 1,48 1,39 1,27 1,00
Знаменатель, df2 1 2 3 Числитель, df, 60 120 ос
4 5 6 7 8 9 10 12 15 20 24 30 40
1 4052,00 4999,50 5403,00 5625,00 5764,00 5859,00 5928,00 5982,00 6022,00 6056,00 6106,00 6157,00 6209,00 6235,00 6261,00 6287,00 6313,00 6339,00 6366,00
2 98,50 99,00 99,17 99,25 99,30 99,33 99,36 99,37 99,39 99,40 99,42 99,43 99,45 99,46 99,47 99,47 99,48 99,49 99,50
3 34,12 30,82 29,46 28,71 28,24 27,91 27,67 27,49 27,35 27,23 27,05 26,87 26,69 26,60 26,50 26,41 26,32 26,22 26,13
4 21,20 18,00 16,69 15,98 15,52 15,21 14,98 14,80 14,66 14,55 14,37 14,20 14,02 13,93 13,84 13,75 13,65 13,56 13,46
5 16,26 13,27 12,06 11,39 10,97 10,67 10,46 10,29 10,16 10,05 9,89 9,72 9,55 9,47 9,38 9,29 9,20 9,11 9,02
6 13,75 10,92 9,78 9,15 8,75 8,47 8,26 8,10 7,98 7,87 7,72 7,56 7,40 7,31 7,23 7,14 7,06 6,97 6,88
7 12,25 9,55 8,45 7,85 7,46 7,19 6,99 6,84 6,72 6,62 6,47 6,31 6,16 6,07 5,99 5,91 5,82 5,74 5,65
8 11,26 8,65 7,59 7,01 6,63 6,37 6,18 6,03 5,91 5,81 5,67 5,52 5,36 5,28 5,20 5,12 5,03 4,95 4,86
9 10,56 8,02 6,99 6,42 6,06 5,80 5,61 5,47 5,35 5,26 5,11 4,96 4,81 4,73 4,65 4,57 4,48 4,40 4,31
10 10,04 7,56 6,55 5,99 5,64 5,39 5,20 5,06 4,94 4,85 4,71 4,56 4,41 4,33 4,25 4,17 4,08 4,00 3,91
11 9,65 7,21 6,22 5,67 5,32 5,07 4,89 4,74 4,63 4,54 4,40 4,25 4,10 4,02 3,94 3,86 3,78 3,69 3,60
12 9,33 6,93 5,95 5,41 5,06 4,82 4,64 4,50 4,39 4,30 4,16 4,01 3,86 3,78 3,70 3,62 3,54 3,45 3,36
13 9,07 6,70 5,74 4,21 4,86 4,62 4,44 4,30 4,19 4,10 3,96 3,82 3,66 3,59 3,51 3,43 3,34 3,25 3,17
14 8,86 6,51 5,56 5,04 4,69 4,46 4,28 4,14 4,03 3,94 3,80 3,66 3,51 3,43 3,35 3,27 3,1*8 3,09 3,00
15 8,68 6,36 5,42 4,89 4,56 4,32 4,14 4,00 3,89 3,80 3,67 3,52 3,37 3,29 3,21 3,13 3,05 2,96 2,87
16 8,53 6,23 5,29 4,77 4,44 4,20 4,03 3,89 3,78 3,69 3,55 3,41 3,26 3,18 3,10 3,02 2,93 2,84 2,75
17 8,40 6,11 5,18 4,67 4,34 4,10 3,93 3,79 3,68 3,59 3,46 3,31 3,16 3,08 3,00 2,92 2,83 2,75 2,65
18 8,29 6,01 5,09 4,58 4,25 4,01 3,84 3,71 3,60 3,51 3,37 3,23 3,08 2,00 2,92 2,84 2,75 2,66 2,57
19 8,18 5,93 5,01 4,50 4,17 3,94 3,77 3,63 3,52 3,43 3,30 3,15 3,00 2,92 2,84 2,76 2,67 2,58 2,49
а = 0,01
0
^U(a,dfi,df2)
Знаменатель, df2 1 Числитель, df, 120 ос
2 3 4 5 6 7 8 9 10 12 15 20 24 30 40 60
20 8,10 5,85 4,94 4,43 4,10 3,87 3,70 3,56 3,46 3,37 3,23 3,09 2,94 2,86 2,78 2,69 2,61 2,52 2,42
21 8,02 5,78 4,87 4,37 4,04 3,81 3,64 3,51 3,40 3,31 3,17 3,03 2,88 2,80 2,72 2,64 2,55 2,46 2,36
22 7,95 5,72 4,82 4,31 3,99 3,76 3,59 3,45 3,35 3,26 3,12 2,98 2,83 2,75 2,67 2,58 2,50 2,40 2,31
23 7,88 5,66 4,76 4,26 3,94 3,71 3,54 3,41 3,30 3,21 3,07 2,93 2,78 2,70 2,62 2,54 2,45 2,35 2,26
24 7,82 5,61 4,72 4,22 3,90 3,67 3,50 3,36 3,26 3,17 3,03 2,89 2,74 2,66 2,58 2,49 2,40 2,31 2,21
25 7,77 5,57 4,68 4,18 3,85 3,63 3,46 3,32 3,22 3,13 2,99 2,85 2,70 2,62 2,54 2,45 2,36 2,27 2,17
26 7,72 5,53 4,64 4,14 3,82 3,59 3,42 3,29 3,18 3,09 2,96 2,81 2,66 2,58 2,50 2,42 2,33 2,23 2,13
27 7,68 5,49 4,60 4,11 3,78 3,56 3,39 3,26 3,15 3,06 2,93 2,78 2,63 2,55 2,47 2,38 2,29 2,20 2,10
28 7,64 5,45 4,57 4,07 3,75 3,53 3,36 3,23 3,12 3,03 2,90 2,75 2,60 2,52 2,44 2,35 2,26 2,17 2,06
29 7,60 5,42 4,54 4,04 3,73 3,50 3,33 3,20 3,09 3,00 2,87 2,73 2,57 2,49 2,41 2,33 2,23 2,14 2,03
30 7,56 5,39 4,51 4,02 3,70 3,47 3,30 3,17 3,07 2,98 2,84 2,70 2,55 2,47 2,39 2,30 2,21 2,11 2,01
40 7,31 5,18 4,31 3,83 3,51 3,29 3,12 2,99 2,89 2,80 2,66 2,52 2,37 2,29 2,20 2,11 2,02 1,92 1,80
60 7,08 4,98 4,13 3,65 3,34 3,12 2,95 2,82 2,72 2,63 2,50 2,35 2,20 2,12 2,03 1,94 1,84 1,73 1,60
120 6,85 4,79 3,95 3,48 3,17 2,96 2,79 2,66 2,56 2,47 2,34 2,19 2,03 1,95 1,86 1,76 1,66 1,53 1,38
X 6,63 4,61 3,78 3,32 3,02 2,80 2,64 2,51 2,41 2,32 2,18 2,04 1,88 1,79 1,70 1,59 1,47 1,32 1,00
^l/(a,dft,df2)
Знаменатель, Числитель, df,
1 2 3 4 5 6 7 8 9 10 12 15 20 24 30 40 60 120 ос
1 16211,0 20000,0 21615,0 22500,0 23056,0 23437,0 23715,0 23925,0 24091,0 24224,0 24426,0 24630,0 24836,0 24490,0 25044,0 25148,0 25253,0 25359,0 25465,0
2 198,50 199,00 199,20 199,20 199,30 199,30 199,40 199,40 199,40 199,40 199,40 199,40 199,40 199,50 199,50 199,50 199,50 199,50 199,50
3 55,55 49,80 47,47 46,19 45,39 44,84 44,43 44,13 43,88 43,69 43,39 43,08 42,78 42,62 42,47 42,31 42,15 41,99 41,83
4 31,33 26,28 24,26 23,15 22,46 21,97 21,62 21,35 21,14 20,97 20,70 20,44 20,17 20,03 19,89 19,75 19,61 19,47 19,32
5 22,78 18,31 16,53 15,56 14,94 14,51 14,20 13,96 13,77 13,62 13,38 13,15 12,90 12,78 12,66 12,53 12,40 12,27 12,14
6 18,63 14,54 12,92 12,03 11,46 11,07 10,79 10,57 10,39 10,25 10,03 9,81 9,59 9,47 9,36 9,24 9,12 9,00 8,88
7 16,24 12,40 10,88 10,05 9,52 9,16 8,89 8,68 8,51 8,38 8,18 7,97 7,75 7,65 7,53 7,42 7,31 7,19 7,08
8 14,69 11,04 9,60 8,81 8,30 7,95 7,69 7,50 7,34 7,21 7,01 6,81 6,61 6,50 6,40 6,29 6,18 6,06 5,95
9 13,61 10,11 8,72 7,96 7,47 7,13 6,88 6,69 6,54 6,42 6,23 6,03 5,83 5,73 5,62 5,52 5,41 5,30 5,19
10 12,83 9,43 8,08 7,34 6,87 6,54 6,30 6,12 5,97 5,85 5,66 5,47 5,27 5,17 5,07 4,97 4,86 4,75 4,64
11 12,23 8,91 7,60 6,88 6,42 6,10 5,86 5,68 5,54 5,42 5,24 5,05 4,86 4,76 4,65 4,55 4,44 4,34 4,23
12 11,75 8,51 7,23 6,52 6,07 5,76 5,52 5,35 5,20 5,09 4,91 4,72 4,53 4,43 4,33 4,23 4,12 4,01 3,90
13 11,37 8,19 6,93 6,23 5,79 5,48 5,25 5,08 4,94 4,82 4,64 4,46 4,27 4,17 4,07 3,97 3,87 3,76 3,65
14 11,06 7,92 6,68 6,00 5,56 5,26 5,03 4,86 4,72 4,60 4,43 4,25 4,06 3,96 3,86 3,76 3,66 3,55 3,44
15 10,80 7,70 6,48 5,80 5,37 5,07 4,85 4,67 4,54 4,42 4,25 4,07 3,88 3,79 3,69 3,58 3,48 3,37 3,26
16 10,58 7,51 6,30 5,64 5,21 4,91 4,69 4,52 4,38 4,27 4,10 3,92 3,73 3,64 3,54 3,44 3,33 3,22 3,11
17 10,38 7,35 6,16 5,50 5,07 4,78 4,56 4,39 4,25 4,14 3,97 3,79 3,61 3,51 3,41 3,31 3,21 3,10 2,98
18 10,22 7,21 6,03 5,37 4,96 4,66 4,44 4,28 4,14 4,03 3,86 3,68 3,50 3,40 3,30 3,20 3,10 2,89 2,87
19 10,07 7,09 5,92 5,27 4,85 4,56 4,34 4,18 4,04 3,93 3,76 3,59 3,40 3,31 3,21 3,11 3,00 2,89 2,78
а = 0,005
0
^(a.dfndfz)
Знаменатель, df2 Числитель, df,
1 2 3 4 5 6 7 8 9 10 12 15 20 24 30 40 60 120 oc
20 9,94 6,99 5,82 5,17 4,76 4,47 4,26 4,09 3,96 3,85 3,68 3,50 3,32 3,22 3,12 3,02 2,92 2,81 2,69
21 9,83 6,89 5,73 5,09 4,68 4,39 4,18 4,01 3,88 3,77 3,60 3,43 3,24 3,15 3,05 2,95 2,84 2,73 2,61
22 9,73 6,81 5,65 5,02 4,61 4,32 4,11 3,94 3,81 3,70 3,54 3,36 3,18 3,08 2,98 2,88 2,77 2,66 2,55
23 9,63 6,73 5,58 4,95 4,54 4,26 4,05 3,88 3,75 3,64 3,47 3,30 3,12 3,02 2,92 2,82 2,71 2,60 2,48
24 9,55 6,66 5,52 4,89 4,49 4,20 3,99 3,83 3,69 3,59 3,42 3,25 3,06 2,97 2,87 2,77 2,66 2,55 2,43
25 9,48 6,60 5,46 4,84 4,43 4,15 3,94 3,78 3,64 3,54 3,37 3,20 3,01 2,92 2,82 2,72 2,61 2,50 2,38
26 9,41 6,54 5,41 4,79 4,38 4,10 3,89 3,73 3,60 3,49 3,33 3,15 2,97 2,87 ‘ 2,77 2,67 2,56 2,45 2,33
27 9,34 6,49 5,36 4,74 4,34 4,06 3,85 3,69 3,56 3,45 3,28 3,11 2,93 2,83 2,73 2,63 2,52 2,41 2,29
28 9,28 6,44 5,32 4,70 4,30 4,02 3,81 3,65 3,52 3,41 3,25 3,07 2,89 2,79 2,69 2,59 2,48 2,37 2,25
29 9,23 6,40 5,28 4,66 4,26 3,98 3,77 3,61 3,48 3,38 3,21 3,04 2,86 2,76 2,66 2,56 2,45 2,33 2,21
30 9,18 6,35 5,24 4,62 4,23 3,95 3,74 3,58 3,45 3,34 3,18 3,01 2,82 2,73 2,63 2,52 2,42 2,30 2,18
40 8,83 6,07 4,98 4,37 3,99 3,71 3,51 3,35 3,22 3,12 2,95 2,78 2,60 2,50 2,40 2,30 2,18 2,06 1,93
60 8,49 5,79 4,73 4,14 3,76 3,49 3,29 3,13 3,01 2,90 2,74 2,57 2,39 2,29 2,19 2,08 1,96 1,83 1,69
120 8,18 5,54 4,50 3,92 3,55 3,28 3,09 2,93 2,81 2,71 2,54 2,37 2,19 2,09 1,98 1,87 1,75 1,61 1,43
X) 7,88 5,30 4,28 3,72 3,35 3,09 2,90 2,74 2,62 2,52 2,36 2,19 2,00 1,90 1,79 1,67 1,53 1,36 1,00
Источник: цитируется по книге Е. S. Pearson and Н. О. Hartley, eds., Biometrica Tables for Statisticians, 3rd ed., 1966 с разрешения издательства Biometrica Trustees.
Таблица Д.6. Таблица биномиального распределения
При заданных параметрах пир ячейка таблицы содержит вероятность конкретного значения случайной переменной X. Если р <0,50, то параметр р следует искать в верхней строке таблицы, а параметры X и п — на левом поле. Если р >0,50, то параметр р следует искать в нижней строке таблицы, а параметры X и п — на правом поле.
Р
n X 0,01 0,02 0,03 0,04 0,05 0,06 0,07 0,08 0,09 0,Ю 0,11 0,12 0,13 0,14 0,15 0,16 0,17 0,18 X п
2 0 0,9801 0,9604 0,9409 0,9216 0,9025 0,8836 0,8649 0,8464 0,8281 0,8100 0,7921 0,7744 0,7569 0,7396 0,7225 0,7056 0,6889 0,6724 2
1 0,0198 0,0392 0,0582 0,0768 0,0950 0,1128 0,1302 0,1472 0,1638 0,1800 0,1958 0,2112 0,2262 0,2408 0,2550 0,2688 0,2822 0,2952 1
2 0,0001 0,0004 0,0009 0,0016 0,0025 0,0036 0,0049 0,0064 0,0081 0,0100 0,0121 0,0144 0,0169 0,0196 0,0225 0,0256 0,0289 0,0324 0 2
3 0 0,9703 0,9412 0,9127 0,8847 0,8574 0,8306 0,8044 0,7787 0,7536 0,7290 0,7050 0,6815 0,6585 0,6361 0,6141 0,5927 0,5718 0,5514 3
1 0,0294 0,0576 0,0847 0,1106 0,1354 0,1590 0,1816 0,2031 0,2236 0,2430 0,2614 0,2788 0,2952 0,3106 0,3251 0,3387 0,3513 0,3631 2
2 0,0003 0,0012 0,0026 0,0046 0,0071 0,0102 0,0137 0,0177 0,0221 0,0270 0,0323 0,0380 0,0441 0,0506 0,0574 0,0645 0,0720 0,0797 1
3 0,0000 0,0000 0,0000 0,0001 0,0001 0,0002 0,0003 0,0005 0,0007 0,0010 0,0013 0,0017 0,0022 0,0027 0,0084 0,0041 0,0049 0,0058 0 3
4 0 0,9606 0,9224 0,8853 0,8493 0,8145 0,7807 0,7481 0,7164 0,6857 0,6561 0,6274 0,5997 0,5729 0,5470 0,5220 0,4979 0,4746 0,4521 4
1 0,0388 0,0753 0,1095 0,1416 0,1715 0,1993 0,2252 0,2492 0,2713 0,2916 0,3102 0,3271 0,3424 0,3562 0,3685 0,3793 0,3888 0,3970 3
2 0,0006 0,0023 0,0051 0,0088 0,0135 0,0191 0,0254 0,0325 0,0402 0,0486 0,0575 0,0669 0,0767 0,0870 0,0975 0,1084 0,1195 0,1307 2
3 0,0000 0,0000 0,0001 0,0002 0,0005 0,0008 0,0013 0,0019 0,0027 0,0036 0,0047 0,0061 0,0076 0,0094 0,0115 0,0138 0,0163 0,0191 1
4 — — 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0001 0,0001 0,0001 0,0002 0,0003 0,0004 0,0005 0,0007 0,0008 0,0010 0 4
5 0 0,9510 0,9039 0,8587 0,8154 0,7738 0,7339 0,6957 0,6591 0,6240 0,5905 0,5584 0,5277 0,4984 0,4704 0,4437 0,4182 0,3939 0,3707 5
1 0,0480 0,0922 0,1328 0,1699 0,2036 0,2342 0,2618 0,2866 0,3086 0,3280 0,3451 0,3598 0,3724 0,3829 0,3915 0,3983 0,4034 0,4069 4
2 0,0010 0,0038 0,0082 0,0142 0,0214 0,0299 0,0394 0,0498 0,0610 0,0729 0,0853 0,0981 0,1113 0,1247 0,1382 0,1517 0,1652 0,1786 3
3 0,0000 0,0001 0,0003 0,0006 0,0011 0,0019 0,0030 0,0043 0,0060 0,0081 0,0105 0,0134 0,0166 0,0203 0,0244 0,0289 0,0338 0,0392 2
4 — 0,0000 0,0000 0,0000 0,0000 0,0001 0,0001 0,0002 0,0003 0,0004 0,0007 0,0009 0,0012 0,0017 0,0022 0,0028 0,0035 0,0043 1
5 — — — — — 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0001 0,0001 0,0001 0,0001 0,0002 0 5
При заданных параметрах пир ячейка таблицы содержит вероятность конкретного значения случайной переменной X. Если р <0,50, то параметр р следует искать в верхней строке таблицы, а параметры X и п — на левом поле. Если р >0,50, то параметр р следует искать в нижней строке таблицы, а параметры X и п — на правом поле.
п X
6 о
1
2
3
4
5
6
7 О
1
2
3
4
5
6
7
8 О 1
2
3
4
5
6
7
8
_______________________________________________________________Р______________________________________________________________
0,01 0,02 0,03 0,04 0,05 0,06 0,07 0,08 0,09 0,10 0,11 0,12 0,13 0,14 0,15 0,16 0,17 0,18
0,9415 0,8858 0,8330 0,7828 0,7351 0,6899 0,6470 0,6064 0,5679 0,5314 0,4970 0,4644 0,4336 0,4046 0,3771 0,3513 0,3269 0,3040
0,0571 0,1085 0,1546 0,1957 0,2321 0,2642 0,2922 0,3164 0,3370 0,3543 0,3685 0,3800 0,3888 0,3952 0,3993 0,4015 0,4018 0,4004
0,0014 0,0055 0,0120 0,0204 0,0305 0,0422 0,0550 0,0688 0,0833 0,0984 0,1139 0,1295 0,1452 0,1608 0,1762 0,1912 0,2057 0,2197
0,0000 0,0002 0,0005 0,0011 0,0021 0,0036 0,0055 0,0080 0,0110 0,0146 0,0188 0,0236 0,0289 0,0349 0,0415 0,0486 0,0562 0,0643
— 0,0000 0,0000 0,0000 0,0001 0,0002 0,0003 0,0005 0,0008 0,0012 0,0017 0,0024 0,0032 0,0043 0,0055 0,0069 0,0086 0,0106
— — — — 0,0000 0,0000 0,0000 0,0000 0,0000 0,0001 0,0001 0,0001 0,0002 0,0003 0,0004 0,0005 0,0007 0,0009
— — — — — — — — — 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000
0,9321 0,8681 0,8080 0,7514 0,6983 0,6485 0,6017 0,5578 0,5168 0,4783 0,4423 0,4087 0,3773 0,3479 0,3206 0,2951 0,2714 0,2493
0,0659 0,1240 0,1749 0,2192 0,2573 0,2897 0,3170 0,3396 0,3578 0,3720 0,3827 0,3901 0,3946 0,3965 0,3960 0,3935 0,3891 0,3830
0,0020 0,0076 0,0162 0,0274 0,0406 0,0555 0,0716 0,0886 0,1061 0,1240 0,1419 0,1596 0,1769 0,1936 0,2097 0,2248 0,2391 0,2523
0,0000 0,0003 0,0008 0,0019 0,0036 0,0059 0,0090 0,0128 0,0175 0,0230 0,0292 0,0363 0,0441 0,0525 0,0617 0,0714 0,0816 0,0923
— 0,0000 0,0000 0,0001 0,0002 0,0004 0,0007 0,0011 0,0017 0,0026 0,0036 0,0049 0,0066 0,0086 0,0109 0,0136 0,0167 0,0203
— — — 0,0000 0,0000 0,0000 0,0000 0,0001 0,0001 0,0002 0,0003 0,0004 0,0006 0,0008 0,0012 0,0016 0,0021 0,0027
— — — — — — — 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0001 0,0001 0,0001 0,0002
— — — — — — — — — — — — — — 0,0000 0,0000 0,0000 0,0000
0,9227 0,8508 0,7837 0,7214 0,6634 0,6096 0,5596 0,5132 0,4703 0,4305 0,3937 0,3596 0,3282 0,2992 0,2725 0,2479 0,2252 0,2044
0,0746 0,1389 0,1939 0,2405 0,2793 0,3113 0,3370 0,3570 0,3721 0,3826 0,3892 0,3923 0,3923 0,3897 0,3847 0,3777 0,3691 0,3590
0,0026 0,0099 0,0210 0,0351 0,0515 0,0695 0,0888 0,1087 0,1288 0,1488 0,1684 0,1872 0,2052 0,2220 0,2376 0,2518 0,2646 0,2758
0,0001 0,0004 0,0013 0,0029 0,0054 0,0089 0,0134 0,0189 0,0255 0,0331 0,0416 0,0511 0,0613 0,0723 0,0839 0,0959 0,1084 0,1211
0,0000 0,0000 0,0001 0,0002 0,0004 0,0007 0,0013 0,0021 0,0031 0,0046 0,0064 0,0087 0,0115 0,0147 0,0185 0,0228 0,0277 0,0332
— — 0,0000 0,0000 0,0000 0,0000 0,0001 0,0001 0,0002 0,0004 0,0006 0,0009 0,0014 0,0019 0,0026 0,0035 0,0045 0,0058
— — — — — — 0,0000 0,0000 0,0000 0,0000 0,0000 0,0001 0,0001 0,0002 0,0002 0,0003 0,0005 0,0006
— — — — — — — — — — — 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000
X п
6
5
4
3
2
1
О 6
7
6
5
4
3
2
1
О 7
8
7
6
5
4
3
2
1
О 8
При заданных параметрах пир ячейка таблицы содержит вероятность конкретного значения случайной переменной X. Если р <0,50, то параметр р следует искать в верхней строке таблицы, а параметры Хи п — на левом поле. Если р >0,50, то параметр р следует искать в нижней строке таблицы, а параметры X и п — на правом поле.
п X Р X п
0,01 0,02 0,03 0,04 0,05 0,06 0,07 0,08 0,09 0,10 0,11 0,12 0,13 0,14 0,15 0,16 0,17 0,18
9 0 0,9135 0,8337 0,7602 0,6925 0,6302 0,5730 0,5204 0,4722 0,4279 0,3874 0,3504 0,3165 0,2855 0,2573 0,2316 0,2082 0,1869 0,1676 9
1 0,0830 0,1531 0,2116 0,2597 0,2985 0,3292 0,3525 0,3695 0,3809 0,3874 0,3897 0,3884 0,3840 0,3770 0,3679 0,3569 0,3446 0,3312 8
2 0,0034 0,0125 0,0262 0,0433 0,0629 0,0840 0,1061 0,1285 0,1507 0,1722 0,1927 0,2119 0,2295 0,2455 0,2597 0,2720 0,2823 0,2908 7
3 0,0001 0,0006 0,0019 0,0042 0,0077 0,0125 0,0186 0,0261 0,0348 0,0446 0,0556 0,0674 0,0800 0,0933 0,1069 0,1209 0,1349 0,1489 6
4 0,0000 0,0000 0,0001 0,0003 0,0006 0,0012 0,0021 0,0034 0,0052 0,0074 0,0103 0,0138 0,0179 0,0228 0,0283 0,0345 0,0415 0,0490 5
5 — — 0,0000 0,0000 0,0000 0,0001 0,0002 0,0003 0,0005 0,0008 0,0013 0,0019 0,0027 0,0037 0,0050 0,0066 0,0085 0,0108 4
6 _ — — — — 0,0000 0,0000 0,0000 0,0000 0,0001 0,0001 0,0002 0,0003 0,0004 0,0006 0,0008 0,0012 0,0016 3
7 — — _ _ _ — _ — — 0,0000 0,0000 0,0000 0,0000 0,0000 6,0000 0,0001 0,0001 0,0001 2
8 — — _____ — — — — — — — — 0,0000 0,0000 0,0000 1
9 — — — — — — — — — — — — — — — — — — 0 9
10 0 0,9044 0,8171 0,7374 0,6648 0,5987 0,5386 0,4840 0,4344 0,3894 0,3487 0,3118 0,2785 0,2484 0,2213 0,1969 0,1749 0,1552 0,1374 10
1 0,0914 0,1667 0,2281 0,2770 0,3151 0,3438 0,3643 0,3777 0,3851 0,3874 0,3854 0,3798 0,3712 0,3603 0,3474 0,3331 0,3178 0,3017 9
2 0,0042 0,0153 0,0317 0,0519 0,0746 0,0988 0,1234 0,1478 0,1714 0,1937 0,2143 0,2330 0,2496 0,2639 0,2759 0,2856 0,2929 0,2980 8
3 0,0001 0,0008 0,0026 0,0058 0,0105 0,0168 0,0248 0,0343 0,0452 0,0574 0,0706 0,0847 0,0995 0,1146 0,1298 0,1450 0,1600 0,1745 7
4 0,0000 0,0000 0,0001 0,0004 0,0010 0,0019 0,0033 0,0052 0,0078 0,0112 0,0153 0,0202 0,0260 0,0326 0,0401 0,0483 0,0573 0,0670 6
5 — _ 0,0000 0,0000 0,0001 0,0001 0,0003 0,0005 0,0009 0,0015 0,0023 0,0033 0,0047 0,0064 0,0085 0,0111 0,0141 0,0177 5
6 — — 0,0000 0,0000 0,0000 0,0000 0,0001 0,0001 0,0002 0,0004 0,0006 0,0009 0,0012 0,0018 0,0024 0,0032 4
7 _ — _____ — 0,0000 0,0000 0,0000 0,0000 0,0000 0,0001 0,0001 0,0002 0,0003 0,0004 3
8 — — _____ — — — — — — 0,0000 0,0000 0,0000 0,0000 0,0000 2
9 — — — — — — — — — — — — — — — — — — 1
10 _ — _ _ _ ________ — — _ 0 10
п X 0,99 0,98 0,97 0,96 0,95 0,94 0,93 0,92 0,91 0,90 0,89 0,88 0,87 0,86 0,85 0,84 0,83 0,82 X и
При заданных параметрах пир ячейка таблицы содержит вероятность конкретного значения случайной переменной X. Если р <0,50, то параметр р следует искать в верхней строке таблицы, а параметры Хип — на левом поле. Если р >0,50, то параметр р следует искать в нижней строке таблицы, а параметры Хип — на правом поле.
Р
п X 0,19 0,20 0,21 0,22 0,23 0,24 0,25 0,26 0,27 0,28 0,29 0,30 0,31 0,32 0,33 0,34 0,35 0,36 X п
2 0 0,6561 0,6400 0,6241 0,6084 0,5929 0,5776 0,5625 0,5476 0,5329 0,5184 0,5041 0,4900 0,4761 0,4624 0,4489 0,4356 0,4225 0,4096 2
1 0,3078 0,3200 0,3318 0,3432 0,3542 0,3648 0,3750 0,3848 0,3942 0,4032 0,4118 0,4200 0,4278 0,4352 0,4422 0,4488 0,4550 0,4608 1
2 0,0361 0,0400 0,0441 0,0484 0,0529 0,0576 0,0625 0,0676 0,0729 0,0784 0,0841 0,0900 0,0961 0,1024 0,1089 0,1156 0,1225 0,1296 0 2
3 0 0,5314 0,5120 0,4930 0,4746 0,4565 0,4390 0,4219 0,4052 0,3890 0,3732 0,3579 0,3430 0,3285 0,3144 0,3008 0,2875 0,2746 0,2621 3
1 0,3740 0,3840 0,3932 0,4015 0,4091 0,4159 0,4219 0,4271 0,4316 0,4355 0,4386 0,4410 0,4428 0,4439 0,4444 0,4443 0,4436 0,4424 2
2 0,0877 0,0960 0,1045 0,1133 0,1222 0,1313 0,1406 0,1501 0,1597 0,1693 0,1791 0,1890 0,1989 0,2089 0,2189 0,2289 0,2389 0,2488 1
3 0,0069 0,0080 0,0093 0,0106 0,0122 0,0138 0,0156 0,0176 0,0197 0,0220 0,0224 0,0270 0,0298 0,0328 6,0359 0,0393 0,0429 0,0467 0 3
4 0 0,4305 0,4096 0,3895 0,3702 0,3515 0,3336 0,3164 0,2999 0,2840 0,2687 0,2541 0,2401 0,2267 0,2138 0,2015 0,1897 0,1785 0,1678 4
1 0,4039 0,4096 0,4142 0,4176 0,4200 0,4214 0,4219 0,4214 0,4201 0,4180 0,4152 0,4116 0,4074 0,4025 0,3970 0,3910 0,3845 0,3775 3
2 0,1421 0,1536 0,1651 0,1767 0,1882 0,1996 0,2109 0,2221 0,2331 0,2439 0,2544 0,2646 0,2745 0,2841 0,2933 0,3021 0,3105 0,3185 2
3 0,0222 0,0256 0,0293 0,0332 0,0375 0,0420 0,0469 0,0520 0,0575 0,0632 0,0693 0,0756 0,0822 0,0891 0,0963 0,1038 0,1115 0,1194 1
4 0,0013 0,0016 0,0019 0,0023 0,0028 0,0033 0,0039 0,0046 0,0053 0,0061 0,0071 0,0081 0,0092 0,0105 0,0119 0,0134 0,0150 0,0168 0 4
5 0 0,3487 0,3277 0,3777 0,2887 0,2707 0,2536 0,2373 0,2219 0,2073 0,1935 0,1804 0,1681 0,1564 0,1454 0,1350 0,1252 0,1160 0,1074 5
1 0,4089 0,4096 0,4090 0,4072 0,4043 0,4003 0,3955 0,3898 0,3834 0,3762 0,3685 0,3601 0,5313 0,3421 0,3325 0,3226 0,3124 0,3020 4
2 0,1919 0,2048 0,2174 0,2297 0,2415 0,2529 0,2637 0,2739 0,2836 0,2926 0,3010 0,3087 0,3157 0,3220 0,3275 0,3323 0,3364 0,3397 3
3 0,0450 0,0512 0,0578 0,0648 0,0721 0,0798 0,0879 0,0962 0,1049 0,1138 0,1229 0,1323 0,1418 0,1515 0,1613 0,1712 0,1811 0,1911 2
4 0,0053 0,0064 0,0077 0,0091 0,0108 0,0126 0,0146 0,0169 0,0194 0,0221 0,0251 0,0283 0,0319 0,0357 0,0397 0,0441 0,0488 0,0537 1
5 0,0002 0,0003 0,0004 0,0005 0,0006 0,0008 0,0010 0,0012 0,0014 0,0017 0,0021 0,0024 0,0029 0,0034 0,0039 0,0045 0,0053 0,0060 0 5
При заданных параметрах пир ячейка таблицы содержит вероятность конкретного значения случайной переменной X. Если р <0,50, то параметр р следует искать в верхней строке таблицы, а параметры X и п — на левом поле. Если р >0,50, то параметр р следует искать в нижней строке таблицы, а параметры X и п — на правом поле.
Р
п X 0,19 0,20 0,21 0,22 0,23 0,24 0,25 0,26 0,27 0,28 0,29 0,30 0,31 0,32 0,33 0,34 0,35 0,36 X п
6 0 0,2824 0,2621 0,2431 0,2252 0,2084 0,1927 0,1780 0,1642 0,1513 0,1393 0,1281 0,1176 0,1079 0,0989 0,0905 0,0827 0,0754 0,0687 6
1 0,3975 0,3932 0,3877 0,3811 0,3735 0,3651 0,3560 0,3462 0,3358 0,3251 0,3139 0,3025 0,2909 0,2792 0,2673 0,2555 0,2437 0,2319 5
2 0,2331 0,2458 0,2577 0,2687 0,2789 0,2882 0,2966 0,3041 0,3105 0,3160 0,3206 0,3241 0,326 7 0,3284 0,3292 0,3290 0,3280 0,3261 4
3 0,0729 0,0819 0,0913 0,1011 0,1111 0,1214 0,1318 0,1424 0,1531 0,1639 0,1746 0,1852 0,1957 0,2061 0,2162 0,2260 0,2355 0,2446 3
4 0,0128 0,0154 0,0182 0,0214 0,0249 0,0287 0,0330 0,0375 0,0425 0,0478 0,0535 0,0595 0,0660 0,0727 0,0799 0,0873 0,0951 0,1032 2
5 0,0012 0,0015 0,0019 0,0024 0,0030 0,0036 0,0044'0,0053 0,0063 0,0074 0,0087 0,0102 0,0119 0,013 7 0,0157 0,0180 0,0205 0,0232 1
6 0,0000 0,0001 0,0001 0,0001 0,0001 0,0002 0,0002 0,0003 0,0004 0,0005 0,0006 0,0007 0,0009 0,0011 0,0013 0,0015 0,0018 0,0022 0 6
7 0 0,2288 0,2097 0,1920 0,1757 0,1605 0,1465 0,1335 0,1215 0,1105 0,1003 0,0910 0,0824 0,0745 0,0672 0,0606 0,0546 0,0490 0,0440 7
1 0,3756 0,3670 0,3573 0,3468 0,3356 0,3237 0,3115 0,2989 0,2860 0,2731 0,2600 0,2471 0,2342 0,2215 0,2090 0,1967 0,1848 0,1732 6
2 0,2643 0,2753 0,2850 0,2935 0,3007 0,3067 0,3115 0,3150 0,3174 0,3186 0,3186 0,3177 0,3156 0,3127 0,3088 0,3040 0,2985 0,2922 5
3 0,1033 0,1147 0,1263 0,1379 0,1497 0,1614 0,1730 0,1845 0,1956 0,2065 0,2169 0,2269 0,2363 0,2452 0,2535 0,2610 0,2679 0,2740 4
4 0,0242 0,0287 0,0336 0,0389 0,0447 0,0510 0,0577 0,0648 0,0724 0,0803 0,0886 0,0972 0,1062 0,1154 0,1248 0,1345 0,1442 0,1541 3
5 0,0034 0,0043 0,0054 0,0066 0,0080 0,0097 0,0115 0,0137 0,0161 0,0187 0,0217 0,0250 0,0286 0,0326 0,0369 0,0416 0,0466 0,0520 2
6 0,0003 0,0004 0,0005 0,0006 0,0008 0,0010 0,0013 0,0016 0,0020 0,0024 0,0030 0,0036 0,0043 0,0051 0,0061 0,0071 0,0084 0,0098 1
7 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0001 0,0001 0,0001 0,0001 0,0002 0,0002 0,0003 0,0003 0,0004 0,0005 0,0006 0,0008 0 7
8 0 0,1853 0,1678 0,1517 0,1370 0,1236 0,1113 0,1001 0,0899 0,0806 0,0722 0,0646 0,0576 0,0514 0,0557 0,0406 0,0360 0,0319 0,0281 8
1 0,3477 0,3355 0,3226 0,3092 0,2953 0,2812 0,2670 0,252 7 0,2386 0,2247 0,2110 0,1977 0,1847 0,1721 0,1600 0,1484 0,1373 0,1267 7
2 0,2855 0,2936 0,3002 0,3052 0,3087 0,3108 0,3115 0,3108 0,3089 0,3058 0,3017 0,2965 0,2904 0,2835 0,2758 0,2675 0,2587 0,2494 6
3 0,1339 0,1468 0,1596 0,1722 0,1844 0,1963 0,2076 0,2184 0,2285 0,2379 0,2464 0,2541 0,2609 0,2668 0,2717 0,1756 0,2786 0,2805 5
4 0,0393 0,0459 0,0530 0,0607 0,0689 0,0775 0,0865 0,0959 0,1056 0,1156 0,1258 0,1361 0,1465 0,1569 0,1673 0,1775 0,1875 0,1973 4
5 0,0074 0,0092 0,0113 0,0137 0,0165 0,0196 0,0231 0,0270 0,0313 0,0360 0,0411 0,0467 0,0527 0,0591 0,0659 0,0732 0,0808 0,0888 3
6 0,0009 0,0011 0,0015 0,0019 0,0025 0,0031 0,0038 0,0047 0,0058 0,0070 0,0084 0,0100 0,0118 0,0239 0,0162 0,0188 0,0217 0,0250 2
7 0,0001 0,0001 0,0001 0,0002 0,0002 0,0003 0,0004 0,0005 0,0006 0,0008 0,0010 0,0012 0,0015 0,0019 0,0023 0,0028 0,0033 0,0040 1
8 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0001 0,0001 0,0001 0,0001 0,0001 0,0002 0,0002 0,0003 0 8
При заданных параметрах пир ячейка таблицы содержит вероятность конкретного значения случайной переменной X. Если р <0,50, то параметр р следует искать в верхней строке таблицы, а параметры X и п — на левом поле. Если р >0,50, то параметр р следует искать в нижней строке таблицы, а параметры X и п — на правом поле.
Р
п X 0,19 0,20 0,21 0,22 0,23 0,24 0,25 0,26 0,27 0,28 0,29 0,30 0,31 0,32 0,33 0,34 0,35 0,36 X п
9 0 0,1501 0,1342 0,1199 0,1069 0,0952 0,0846 0,0751 0,0665 0,0589 0,0520 0,0458 0,0404 0,0355 0,0311 0,0272 0,0238 0,0207 0,0180 9
1 0,3169 0,3020 0,2867 0,2713 0,2558 0,2404 0,2253 0,2104 0,1960 0,1820 0,1685 0,1556 0,1433 0,1317 0,1206 0,1102 0,1004 0,0912 8
2 0,2973 0,3020 0,3049 0,3061 0,3056 0,3037 0,3003 0,2957 0,2899 0,2831 0,2754 0,2668 0,2576 0,2478 0,2376 0,2270 0,2162 0,2052 7
3 0,1627 0,1762 0,1891 0,2014 0,2130 0,2238 0,2336 0,2424 0,2502 0,2569 0,2624 0,2668 0,2701 0,2721 0,2731 0,2729 0,2716 0,2693 6
4 0,0573 0,0661 0,0754 0,0852 0,0954 0,1060 0,1168 0,1278 0,1388 0,1499 0,1608 0,1715 0,1820 0,1921 0,2017 0,2109 0,2194 0,2272 5
5 0,0134 0,0165 0,0200 0,0240 0,0285 0,0335 0,0390 0,0449 0,0513 0,0583 0,0657 0,0735 0,0818 0,0904 0,0994 0,1086 0,1181 0,1278 4
6 0,0021 0,0028 0,0036 0,0045 0,0057 0,0070 0,0087 0,0105 0,0127 0,0151 0,0179 0,0210 0,0245 0,0284 0,0326 0,0373 0,0424 0,0479 3
7 0,0002 0,0003 0,0004 0,0005 0,0007 0,0010 0,0012 0,0016 0,0020 0,0025 0,0031 0,0039 0,0047 0,0057 0,0069 0,0082 0,0098 0,0116 2
8 0,0000 0,0000 0,0000 0,0000 0,0001 0,0001 0,0001 0,0001 0,0002 0,0002 0,0003 0,0004 0,0005 0,0007 0,000^ 0,0011 0,0013 0,0016 1
9 — — — — 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0001 0,0001 0,0001 0 9
10 0 0,1216 0,1074 0,0947 0,0834 0,0733 0,0643 0,0563 0,0492 0,0430 0,0374 0,0326 0,0282 0,0245 0,0211 0,0182 0,0157 0,0135 0,0115 10
1 0,2852 0,2684 0,2517 0,2351 0,2188 0,2030 0,1877 0,1730 0,1590 0,1456 0,1330 0,1211 0,1099 0,0995 0,0898 0,0808 0,0725 0,0649 9
2 0,3010 0,3020 0,3011 0,2984 0,2942 0,2885 0,2816 0,2735 0,2646 0,2548 0,2444 0,2335 0,2222 0,2107 0,1990 0,1873 0,1757 0,1642 8
3 0,1883 0,2013 0,2134 0,2244 0,2343 0,2429 0,2503 0,2563 0,2609 0,2642 0,2662 0,2668 0,2662 0,2644 0,2614 0,2573 0,2522 0,2462 7
4 0,0773 0,0881 0,0993 0,1108 0,1225 0,1343 0,1360 0,1576 0,1689 0,1798 0,1903 0,2001 0,2093 0,2177 0,2253 0,2320 0,2377 0,2424 6
5 0,0218 0,0264 0,0317 0,0375 0,0439 0,0509 0,0584 0,0664 0,0750 0,0839 0,0933 0,1029 0,1128 0,1229 0,1332 0,1434 0,1536 0,1636 5
6 0,0043 0,0055 0,0070 0,0088 0,0109 0,0134 0,0162 0,0195 0,0231 0,0272 0,0317 0,0368 0,0422 0,0482 0,0547 0,0616 0,0689 0,0767 4
7 0,0006 0,0008 0,0011 0,0014 0,0019 0,0024 0,0031 0,0039 0,0049 0,0060 0,0074 0,0090 0,0108 0,0130 0,0154 0,0181 0,0212 0,0247 3
8 0,0001 0,0001 0,0001 0,0002 0,0002 0,0003 0,0004 0,0005 0,0007 0,0009 0,0011 0,0014 0,0018 0,0023 0,0028 0,0035 0,0043 0,0052 2
9 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0001 0,0001 0,0001 0,0001 0,0002 0,0002 0,0003 0,0004 0,0005 0,0006 1
10 — — — — — — — 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0 10
п X 0,81 0,80 0,79 0,78 0,77 0,76 0,75 0,74 0,73 0,72 0,71 0,70 0,69 0,68 0,67 0,66 0,65 0,64 X л
При заданных параметрах пир ячейка таблицы содержит вероятность конкретного значения случайной переменной X. Если р <0,50, то параметр р следует искать в верхней строке таблицы, а параметры Хип — на левом поле. Если р >0,50, то параметр р следует искать в нижней строке таблицы, а параметры Хип — на правом поле.
п X Р п
0,37 0,38 0,39 0,40 0,41 0,42 0,43 0,44 0,45 0,46 0,47 0,48 0,49 0,50
2 0 0,3969 0,3844 0,3721 0,3600 0,3481 0,3364 0,3249 0,3136 0,3025 0,2916 0,2809 0,2704 0,2601 0,2500 2
1 0,4662 0,4712 0,4758 0,4800 0,4838 0,4872 0,4902 0,4928 0,4950 0,4968 0,4982 0,4992 0,4998 0,5000 1
2 0,1369 0,1444 0,1521 0,1600 0,1681 0,1764 0,1849 0,1936 0,2025 0,2116 0,2209 0,2304 0,2401 0,2500 0 2
3 0 0,2500 0,2382 0,2270 0,2160 0,2054 0,1951 0,1852 0,1756 0,1664 0,1575 0,1489 0,1406 0,1327 0,1250 3
1 0,4406 0,4382 0,4354 0,4320 0,4282 0,4239 0,4191 0,4140 0,4084 0,4024 0,3961 0,3894 0,3823 0,3750 2
2 0,2587 0,2686 0,2783 0,2880 0,2975 0,3069 0,3162 0,3252 0,3341 0,3428 0,3512 0,3594 0,3674 0,3750 1
3 0,0507 0,0549 0,0593 0,0640 0,0689 0,0741 0,0795 0,0852 0,0911 0,0973 0,1038 0,1106 0,1176 0,1250 0 3
4 0 0,1575 0,1478 0,1385 0,1296 0,1212 0,1132 0,1056 0,0983 0,0915 0,0850 0,0789 0,0731 0,0677 0,0625 4
1 0,3701 0,3623 0,3541 0,3456 0,3368 0,3278 0,3185 0,3091 0,2995 0,2897 0,2799 0,2700 0,2600 0,2500 3
2 0,3260 0,3330 0,3396 0,3456 0,3511 0,3560 0,3604 0,3643 0,3675 0,3702 0,3723 0,3738 0,3747 0,3750 2
3 0,1276 0,1361 0,1447 0,1536 0,1627 0,1719 0,1813 0,1908 0,2005 0,2102 0,2201 0,2300 0,2400 0,2500 1
4 0,0187 0,0209 0,0231 0,0256 0,0283 0,0311 0,0342 0,0375 0,0410 0,0448 0,0488 0,0531 0,0576 0,0625 0 4
5 0 0,0992 0,0916 0,0845 0,0778 0,0715 0,0656 0,0602 0,0551 0,0503 0,0459 0,0418 0,0380 0,0345 0,0312 5
1 0,2914 0,2808 0,2700 0,2592 0,2484 0,2376 0,2270 0,2164 0,2059 0,1956 0,1854 0,1755 0,1657 0,1562 4
2 0,3423 0,3441 0,3452 0,3456 0,3452 0,3442 0,3424 0,3400 0,3369 0,3332 0,3289 0,3240 0,2185 0,3125 3
3 0,2010 0,2109 0,2207 0,2304 0,2399 0,2492 0,2583 0,2671 0,2757 0,2838 0,2916 0,2990 0,3060 0,3125 2
4 0,0590 0,0646 0,0706 0,0768 0,0834 0,0902 0,0974 0,1049 0,1127 0,1209 0,1293 0,1380 0,1470 0,1562 1
5 0,0069 0,0079 0,0090 0,0102 0,0116 0,0131 0,0147 0,0165 0,0185 0,0206 0,0229 0,0255 0,0282 0,0312 0 5
При заданных параметрах пир ячейка таблицы содержит вероятность конкретного значения случайной переменной X. Если р <0,50, то параметр р следует искать в верхней строке таблицы, а параметры X и п — на левом поле. Если р >0,50, то параметр р следует искать в нижней строке таблицы, а параметры X и п — на правом поле.
п X Р п
0,37 0,38 0,39 ОДО 0,41 0,42 0,43 0,44 0,45 0,46 0,47 0,48 0,49 0,50
6 0 0,0625 0,0568 0,0515 0,0467 0,0422 0,0381 0,0343 0,0308 0,0277 0,0248 0,0222 0,0198 0,0176 0,0156 6
1 0,2203 0,2089 0,1976 0,1866 0,1759 0,1654 0,1552 0,1454 0,1359 0,1267 0,1179 0,1095 0,1014 0,0937 5
2 0,3235 0,3201 0,3159 0,3110 0,3055 0,2994 0,2928 0,2856 0,2780 0,2699 0,2615 0,2527 0,2436 0,2344 4
3 0,2533 0,2616 0,2693 0,2765 0,2831 0,2891 0,2945 0,2992 0,3032 0,3065 0,3091 0,3110 0,3121 0,3125 3
4 0,1116 0,1202 0,1291 0,1372 0,1475 0,1570 0,1666 0,1763 0,1861 0,1958 0,2056 0,2153 0,2249 0,2344 2
5 0,0262 0,0295 0,0330 0,0369 0,410 0,0455 0,0503 0,0554 0,0609 0,0667 0,0729 0,0795 0,0864 0,0937 1
6 0,0026 0,0030 0,0035 0,0041 0,0048 0,0055 0,0063 0,0073 0,0083 0,0095 0,0108 0,0122 0,0138 0,0156 0 6
7 0 0,0394 0,0352 0,0314 0,0280 0,0249 0,0221 0,0195 0,0173 0,0152 0,0134 0,0117 0,0103 0,0090 0,0078 7
1 0,1619 0,1511 0,1447 0,1306 0,1211 0,1119 0,1032 0,0950 0,0872 0,0798 0,0729 0,0664 0,0604 0,0547 6
2 0,2853 0,2778 0,2698 0,2613 0,2524 0,2431 0,2336 0,2239 0,2140 0,2040 0,1940 0,1840 0,1740 0,1641 5
3 0,2793 0,2838 0,2875 0,2903 0,2923 0,2934 0,2937 0,2932 0,2918 0,2897 0,2867 0,2830 0,2786 0,2734 4
4 0,1640 0,1739 0,1838 0,1935 0,2031 0,2125 0,2216 0,2304 0,2388 0,2468 0,2543 0,2612 0,2676 0,2734 3
5 0,0578 0,0640 0,0705 0,0774 0,0847 0,0923 0,1003 0,1086 0,1172 0,1261 0,1353 0,1447 0,1543 0,1641 2
6 0,0113 0,0131 0,0150 0,0172 0,0196 0,0223 0,0252 0,0284 0,0320 0,0358 0,0400 0,0445 0,0494 0,0547 1
7 0,0009 0,0011 0,0014 0,0016 0,0019 0,0023 0,0027 0,0032 0,0037 0,0044 0,0051 0,0059 0,0068 0,0078 0 7
8 0 0,0248 0,0218 0,0192 0,0168 0,0147 0,0128 0,0111 0,0097 0,0084 0,0072 0,0062 0,0053 0,0046 0,0039 8
1 0,1166 0,1071 0,0981 0,0896 0,0816 0,0741 0,0672 0,0608 0,0548 0,0493 0,0442 0,0395 0,0352 0,0312 7
2 0,2397 0,2297 0,2194 0,2090 0,1985 0,1880 0,1776 0,1672 0,1569 0,1469 0,1371 0,1275 0,1183 0,1094 6
3 0,2815 0,2815 0,2806 0,2787 0,2759 0,2723 0,2679 0,2627 0,2568 0,2503 0,2431 0,2355 0,2273 0,2187 5
4 0,2067 0,2157 0,2242 0,2322 0,2397 0,2465 0,2526 0,2580 0,2627 0,2665 0,2695 0,2717 0,2730 0,2734 4
5 0,0971 0,1058 0,1147 0,1239 0,1332 0,1428 0,1525 0,1622 0,1719 0,1816 0,1912 0,2006 0,2098 0,2187 3
6 0,0285 0,0324 0,0367 0,0413 0,0463 0,0517 0,0575 0,0637 0,0703 0,0774 0,0848 0,0926 0,1008 0,1094 2
7 0,0048 0,0057 0,0067 0,0079 0,0092 9,0107 0,0124 0,0143 0,0164 0,0188 0,0215 0,0244 0,0277 0,0312 1
8 0,0004 0,0004 0,0005 0,0007 0,0008 0,0010 0,0012 0,0014 0,0017 0,0020 0,0024 0,0028 0,0033 0,0039 0 8
При заданных параметрах пир ячейка таблицы содержит вероятность конкретного значения случайной переменной X. Если р <0,50, то параметр р следует искать в верхней строке таблицы, а параметры Хип — на левом поле. Если р >0,50, то параметр р следует искать в нижней строке таблицы, а параметры Хип — на правом поле.
п X Р п
0.37 0.38 0.39 0.40 0,41 0.42 0,43 0,44 0,45 0,46 0,47 0,48 0,49 0.50
9 0 0,0156 0,0135 0,0117 0,0101 0,0087 0,0074 0,0064 0,0054 0,0046 0,0039 0,0033 0,0028 0,0023 0,0020 9
1 0,0826 0,0747 0,0673 0,0605 0,0542 0,0484 0,0431 0,0383 0,0339 0,0299 0,0263 0,0231 0,0202 0,0176 8
2 0,1941 0,1831 0,1721 0,1612 0,1506 0,1402 0,1301 0,1204 0,1110 0,1020 0,0934 0,0853 0,0776 0,0703 7
3 0,2660 0,2618 0,2567 0,2508 0,2442 0,2369 0,2291 0,2207 0,2119 0,2027 0,1933 0,1837 0,1739 0,1641 6
4 0,2344 0,2407 0,2462 0,2508 0,2545 0,2573 0,2592 0,2601 0,2600 0,2590 0,2571 0,2543 0,2506 0,2461 5
5 0,1376 0,1475 0,1574 0,1672 0,1769 0,1863 0,1955 0,2044 0,2128 0,2207 0,2280 0,2347 0,2408 0,2461 4
6 0,0539 0,0603 0,0671 0,0743 0,0819 0,0900 0,0983 0,1070 0,1160 0,1253 0,1348 0,1445 0,1542 0,1641 3
7 0,0136 0,0158 0,0184 0,0212 0,0244 0,0279 0,0318 0,0360 0,0407 0,0458 0,0512 0,0571 0,0635 0,0703 2
8 0,0020 0,0024 0,0029 0,0035 0,0042 0,0051 0,0060 0,0071 0,0083 0,0097 0,0114 0,0132 0,0153 0,0176 1
9 0,0001 0,0002 0,0002 0,0003 0,0003 0,0004 0,0005 0,0006 0,0008 0,0009 0,0011 0,0014 0,0016 0,0020 0 9
10 0 0,0098 0,0084 0,0071 0,0060 0,0051 0,0043 0,0036 0,0030 0,0025 0,0021 0,0017 0,0014 0,0012 0,0010 10
1 0,2578 0,0514 0,0456 0,0403 0,0355 0,0312 0,0273 0,0238 0,0207 0,0180 0,0155 0,0133 0,0114 0,0098 9
2 0,2529 0,1419 0,1312 0,1209 0,1111 0,1017 0,0927 0,0843 0,0763 0,0688 0,0619 0,0554 0,0494 0,0439 8
3 0,2394 0,2319 0,2237 0,2150 0,2058 0,1963 0,1865 0,1765 0,1665 0,1564 0,1464 0,1364 0,1267 0,1172 7
4 0,2461 0,2487 0,2503 0,2508 0,2503 0,2488 0,2462 0,2427 0,2384 0,2331 0,2271 0,2204 0,2103 0,2051 6
5 0,1734 0,1829 0,1920 0,2007 0,2087 0,2162 0,2229 0,2289 0,2340 0,2383 0,2417 0,2441 0,2456 0,2461 5
6 0,0849 0,0934 0,1023 0,1115 0,1209 0,1304 0,1401 0,1499 0,1596 0,1692 0,1786 0,1878 0,1966 0,2051 4
7 0,0285 0,0327 0,0374 0,0425 0,0480 0,0540 0,0604 0,0673 0,0746 0,0824 0,0905 0,0991 0,1080 0,1172 3
8 0,0063 0,0075 0,0090 0,0106 0,0125 0,0147 0,0171 0,0198 0,0229 0,0263 0,0301 0,0343 0,0389 0,0439 2
9 0,0008 0,0010 0,0013 0,0016 0,0019 0,0024 0,0029 0,0035 0,0042 0,0050 0,0059 0,0070 0,0083 0,0098 1
10 0,0000 0,0001 0,0001 0,0001 0,0001 0,0002 0,0002 0,0003 0,003 0,0004 0,005 0,0006 0,0008 0,0010 0 10
п X 0,63 0,62 0,61 0,60 0,59 0,58 0,57 0,56 0,55 0,54 0,53 0,52 0,51 0,50 X п
При заданных параметрах пир ячейка таблицы содержит вероятность конкретного значения случайной переменной X. Если р <0,50, то параметр р следует искать в верхней строке таблицы, а параметры X и п — на левом поле. Если р >0,50, то параметр р следует искать в нижней строке таблицы, а параметры X и п — на правом поле.
Р
п X 0,01 0,02 0,03 0,04 0,05 0,06 0,07 0,08 0,09 0,10 0,11 0,12 0,13 0,14 0.15 0,16 0,17 0,18 X п
20 0 0,8179 0,6676 0,5438 0,4420 0,3585 0,2901 0,2342 0,1887 0,1516 0,1216 0,0972 0,0776 0,0617 0,0490 0,0388 0,0306 0,0241 0,0189 20
1 0,1652 0,2725 0,3364 0,3683 0,3774 0,3703 0,3526 0,3282 0,3000 0,2702 0,2403 0,2115 0,1844 0,1595 0,1368 0,1165 0,0986 0,0829 19
2 0,0159 0,0528 0,0988 0,1458 0,1887 0,2246 0,2521 0,2711 0,2818 0,2852 0,2822 0,2740 0,2618 0,2466 0,2293 0,2109 0,1919 0,1730 18
3 0,0010 0,0065 0,0183 0,0364 0,0596 0,0860 0,1139 0,1414 0,1672 0,1901 0,2093 0,2242 0,2347 0,2409 0,2428 0,2410 0,2358 0,2278 17
4 0,0000 0,0006 0,0024 0,0065 0,0133 0,0233 0,0364 0,0523 0,0703 0,0898 0,1099 0,1299 0,1491 0,1666 0,1821 0,1951 0,2053 0,2125 16
5 — 0,0000 0,0002 0,0009 0,0022 0,0048 0,0088 0,0145 0,0222 0,0319 0,0435 0,0567 0,0713 0,0868 0,1028 0,1189 0,1345 0,1493 15
6 — — 0,0000 0,0001 0,0003 0,0008 0,0017 0,0032 0,0055 0,0089 0,0134 0,0193 0,0266 0,0353 0,0454 0,0566 0,0689 0,0819 14
7 — — — 0,0000 0,0000 0,0001 0,0002 0,0005 0,0011 0,0020 0,0033 0,0053 0,0080 0,0115 0,0160 0,0216 0,0282 0,0360 13
8 — — — — — 0,0000 0,0000 0,0001 0,0002 0,0004 0,0007 0,0012 0,0019 0,0030 0,0046 0,0067 0,0094 0,0128 12
9 — — — — — — — 0,0000 0,0000 0,0001 0,0001 0,0002 0,0004 0,0007 0,0011 «0,0017 0,0026 0,0038 11
10 — — — — — — — — — 0,0000 0,0000 0,0000 0,0001 0,0001 0,0002 0,0004 0,0006 0,0009 10
11 — — — — — — — — — — — — 0,0000 0,0000 0,0000 0,0001 0,0001 0,0002 9
12 — — — — — — — — — — — — — — — 0,0000 0,0000 0,0000 8
13 — — — — — — — — — — — — — — — _ _ _ 7
14 — — — — _ — — — — _ — _ _ — _ 6
15 — — — — — — — — — — — — — — — — — — 5
16 — — — — — — — — — _______ _ — _ 4
17 _______________ _ — _ 3
18 _______________ _ _ _ 2
19 _______________ _ _ _ 1
20 _______________ _ _ _ 0 20
п X 0,99 0,98 0,97 0,96 0,95 0,94 0,93 0,92 0,91 0,90 0,89 0,88 0,87 0,86 0,85 0,84 0,83 0,82 X п
При заданных параметрах пир ячейка таблицы содержит вероятность конкретного значения случайной переменной X. Если р <0,50, то параметр р следует искать в верхней строке таблицы, а параметры X и п — на левом поле. Если р >0,50, то параметр р следует искать в нижней строке таблицы, а параметры X и п — на правом поле.
Р
п X 0,19 0,20 0,21 0,22 0,23 0,24 0,25 0,26 0,27 0,28 0,29 0,30 0,31 0,32 0,33 0,34 0,35 0,36 X п
20 0 0,0148 0,0115 0,0090 0,0069 0,0054 0,0041 0,0032 0,0024 0,0018 0,0014 0,0011 0,0008 0,0006 0,0004 0,0003 0,0002 0,0002 0,0001 20
1 0,0693 0,0576 0,0477 0,0392 0,0321 0,0261 0,0211 0,0170 0,0137 0,0109 0,0087 0,0068 0,0054 0,0042 0,0033 0,0025 0,0020 0,0015 19
2 0,1545 0,1369 0,1204 0,1050 0,0910 0,0783 0,0699 0,0569 0,0480 0,0403 0,0336 0,0278 0,0229 0,0188 0,0153 0,0124 0,0100 0,0080 18
3 0,2175 0,2054 0,1920 0,1777 0,1631 0,1484 0,1339 0,1199 0,1065 0,0940 0,0823 0,0716 0,0619 0,0531 0,0453 0,0383 0,0323 0,0270 17
4 0,2168 0,2182 0,2169 0,2131 0,2070 0,1991 0,1897 0,1790 0,1675 0,1553 0,1429 0,1304 0,1181 0,1062 0,0947 0,0839 0,0738 0,0645 16
5 0,1627 0,1746 0,1845 0,1923 0,1979 0,2012 0,2023 0,2013 0,1982 0,1933 0,1868 0,1789 0,1698 0,1599 0,1493 0,1384 0,1272 0,1161 15
6 0,0954 0,1091 0,1226 0,1356 0,1478 0,1589 0,1686 0,1768 0,1833 0,1879 0,1907 0,1916 0,1907 0,1881 0,1839 0,1782 0,1712 0,1632 14
7 0,0448 0,0545 0,0652 0,0765 0,0883 0,1003 0,1124 0,1242 0,1356 0,1462 0,1558 0,1643 0,1714 0,1770 0,1811 0,1836 0,1844 0,1836 13
8 0,0171 0,0222 0,0282 0,0351 0,0429 0,0515 0,0609 0,0709 0,0815 0,0924 0,1034 0,1144 0,1251 0,1354 0,1450 0,1531 0,1614 0,1678 12
9 0,0053 0,0074 0,0100 0,0132 0,0171 0,0217 0,0271 0,0332 0,0402 0,0479 0,0563 0,0654 0,0750 0,0849 0,0952 0,1056 0,1158 0,1259 11
10 0,0014 0,0020 0,0029 0,0041 0,0056 0,0075 0,0099 0,0128 0,0163 0,0205 0,0253 0,0308 0,0370 0,0440 0,0516 0,0598 0,0686 0,0779 10
11 0,0003 0,0005 0,0007 0,0010 0,0015 0,0022 0,0030 0,0041 0,0055 0,0072 0,0094 0,0120 0,0151 0,0188 0,0231 0,0280 0,0336 0,0398 9
12 0,0001 0,0001 0,0001 0,0002 0,0003 0,0005 0,0008 0,0011 0,0015 0,0021 0,0029 0,0039 0,0051 0,0066 0,0085 0,0108 0,0136 0,0168 8
13 0,0000 0,0000 0,0000 0,0000 0,0001 0,0001 0,0002 0,0002 0,0003 0,0005 0,0007 0,0010 0,0014 0,0019 0,0026 0,0034 0,0045 0,0058 7
14 — — — — 0,0000 0,0000 0,0000 0,0000 0,0001 0,0001 0,0001 0,0002 0,0003 0,0005 0,0006 0,0009 0,0012 0,0016 6
15 — — — — — — — — 0,0000 0,0000 0,0000 0,0000 0,0001 0,0001 0,0001 0,0002 0,0003 0,0004 5
16 — — — — — — — — — — — — 0,0000 0,0000 0,0000 0,0000 0,0000 0,0001 4
17 — — — — — — — — — — — — — — — — — 0,0000 3
18 — — — — — — — — — — — — — — — — — — 2
19 — — — — — — — — — — — — — — — — — — 1
20 — — — — — — — — — — — — — — — — — — 0 20
п X 0,81 0,80 0,79 0,78 0,77 0,76 0,75 0,74 0,73 0,72 0,71 0,70 0,69 0,68 0,67 0,66 0,65 0,64 X п
При заданных параметрах п и р ячейка таблицы содержит вероятность конкретного значения случайной переменной X. Если р <0,50, то параметр р следует искать в верхней строке таблицы, а параметры Хип — на левом поле. Если р >0,50, то параметр р следует искать в нижней строке таблицы, а параметры Хип — на правом поле.
п X Р X п
0,37 0,38 0,39 0,40 0,41 0,42 0,43 0,44 0,45 0,46 0,47 0,48 0,49 0,50
20 0 0,0001 0,0001 0,0001 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 — — — 20
1 0,0011 0,0009 0,0007 0,0005 0,0004 0,0003 0,0002 0,0001 0,0001 0,0001 0,0001 0,0000 0,0000 0,0000 19
2 0,0064 0,0050 0,0040 0,0031 0,0024 0,0018 0,0014 0,0011 0,0008 0,0006 0,0005 0,0003 0,0002 0,0002 18
3 0,0224 0,0185 0,0152 0,0123 0,0100 0,0080 0,0064 0,0051 0,0040 0,0031 0,0024 0,0019 0,0014 0,0011 17
4 0,0559 0,0482 0,0412 0,0350 0,0295 0,0247 0,0206 0,0170 0,0139 0,0113 0,0092 0,0074 0,0059 0,0046 16
5 0,1051 0,0945 0,0843 0,0746 0,0656 0,0573 0,0496 0,0427 0,0365 0,0309 0,0260 0,0217 0,0180 0,0148 15
6 0,1051 0,1447 0,1347 0,1244 0,1140 0,1037 0,0936 0,0839 0,0746 0,0658 0,0577 0,0501 0,0432 0,0370 14
7 0,1812 0,1774 0,1722 0,1659 0,1585 0,1502 0,1413 0,1318 0,1221 0,1122 0,1023 0,0?25 0,0830 0,0739 13
8 0,1730 0,1767 0,1790 0,1797 0,1790 0,1768 0,1732 0,1683 0,1623 0,1553 0,1474 0,1388 0,1296 0,1201 12
9 0,1354 0,1444 0,1526 0,1597 0,1658 0,1707 0,1742 0,1763 0,1771 0,1763 0,1742 0,1708 0,1661 0,1602 11
10 0,0875 0,0974 0,1073 0,1171 0,1268 0,1359 0,1446 0,1524 0,1593 0,1652 0,1700 0,1734 0,1755 0,1762 10
11 0,0467 0,0542 0,0624 0,0710 0,0801 0,0895 0,0991 0,1089 0,1185 0,1280 0,1370 0,1455 0,1533 0,1602 9
12 0,0206 0,0249 0,0299 0,0355 0,0417 0,0486 0,0561 0,0642 0,0727 0,0818 0,0911 0,1007 0,1105 0,1201 8
13 0,0074 0,0094 0,0118 0,0146 0,0178 0,0217 0,0260 0,0310 0,0366 0,0429 0,0497 0,0572 0,0653 0,0739 7
14 0,0022 0,0029 0,0038 0,0049 0,0062 0,0078 0,0098 0,0122 0,0150 0,0183 0,0221 0,0264 0,0314 0,1370 6
15 0,0005 0,0007 0,0010 0,0013 0,0017 0,0023 0,0030 0,0038 0,0049 0,0062 0,0078 0,0098 0,0121 0,0148 5
16 0,0001 0,0001 0,0002 0,0003 0,0004 0,0005 0,0007 0,0009 0,0013 0,0017 0,0022 0,0028 0,0036 0,0046 4
17 0,0000 0,0000 0,0000 0,0000 0,0001 0,0001 0,0001 0,0002 0,0002 0,0003 0,0005 0,0006 0,0008 0,0011 3
18 — — — — 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0001 0,0001 0,0001 0,0002 2
19 — — — — — — — — — — 0,0000 0,0000 0,0000 0,0000 1
20 — — — — — — — — — — — — 0 20
п X 0,63 0,62 0,61 0,60 0,59 0,58 0,57 0,56 0,55 0,54 0,53 0,52 0,51 0,50 X п
Таблица Д.7. Таблица распределения Пуассона
Ячейки таблицы содержат вероятность конкретного значения X при заданной величине X
X
X 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0
0 0,9048 0,8187 0,7408 0,6703 0,6065 0,5488 0,4966 0,4493 0,4066 0,3679
1 0,0905 0,1637 0,2222 0,2681 0,3033 0,3293 0,3476 0,3595 0,3659 0,3679
2 0,0045 0,0164 0,0333 0,0536 0,0758 0,0988 0,1217 0,1438 0,1647 0,1839
3 0,0002 0,0011 0,0033 0,0072 0,0126 0,0198 0,0284 0,0383 0,0494 0,0613
4 0,0000 0,0001 0,0003 0,0007 .0,0016 0,0030 0,0050 0,0077 0,0111 0,0153
5 0,0000 0,0000 0,0000 0,0001 0,0002 0,0004 0,0007 0,0012 0,0020 0,0031
6 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0001 0,0002 0,0003 0,0005
7 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0001
X
X 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0
0 0,3329 0,3012 0,2725 0,2466 0,2231 0,2019 0,1827 0,1653 0,1496 0,1353
1 0,3662 0,3614 0,3543 0,3452 0,3347 0,3230 0,3106 0,2975 0,2842 0,2707
2 0,2014 0,2169 0,2303 0,2417 0,2510 0,2584 0,2640 0,2678 0,2700 0,2707
3 0,0738 0,0867 0,0998 0,1128 0,1255 0,1378 0,1496 0,1607 0,1710 0,1804
4 0,0203 0,0260 0,0324 0,0395 0,0471 0,0551 0,0636 0,0723 0,0812 0,0902
5 0,0045 0,0062 0,0084 0,0111 0,0141 0,0176 0,0216 0,0260 0,0309 0,0361
6 0,0008 0,0012 0,0018 0,0026 0,0035 0,0047 0,0061 0,0078 0,0098 0,0120
7 0,0001 0,0002 0,0003 0,0005 0,0008 0,0011 0,0015 0,0020 0,0027 0,0034
8 0,0000 0,0000 0,0001 0,0001 0,0001 0,0002 0,0003 0,0005 0,0006 0,0009
9 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0001 0,0001 0,0001 0,0002
X
X 2,1 2,2 2,3 2,4 2,5 2,6 2,7 2,8 2,9 3,0
0 0,1225 0,1108 0,1003 0,0907 0,0821 0,0743 0,0672 0,0608 0,0550 0,0498
1 0,2572 0,2438 0,2306 0,2177 0,2052 0,1931 0,1815 0,1703 0,1596 0,1494
2 0,2700 0,2681 0,2652 0,2613 0,2565 0,2510 0,2450 0,2384 0,2314 0,2240
3 0,1890 0,1966 0,2033 0,2090 0,2138 0,2176 0,2205 0,2225 0,2237 0,2240
4 0,0992 0,1082 0,1169 0,1254 0,1336 0,1414 0,1488 0,1557 0,1622 0,1680
5 0,0417 0,0476 0,0538 0,0602 0,0668 0,0735 0,0804 0,0872 0,0940 0,1008
6 0,0146 0,0174 0,0206 0,0241 0,0278 0,0319 0,0362 0,0407 0,0455 0,0504
7 0,0044 0,0055 0,0068 0,0083 0,0099 0,0118 0,0139 0,0163 0,0188 0,0216
8 0,0011 0,0015 0,0019 0,0025 0,0031 0,0038 0,0047 0,0057 0,0068 0,0081
9 0,0003 0,0004 0,0005 0,0007 0,0009 0,0011 0,0014 0,0018 0,0022 0,0027
10 0,0001 0,0001 0,0001 0,0002 0,0002 0,0003 0,0004 0,0005 0,0006 0,0008
11 0,0000 0,0000 0,0000 0,0000 0,0000 0,0001 0,0001 0,0001 0,0002 0,0002
12 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0001
X
X 3,1 3,2 3,3 3,4 3,5 з.б 3,7 3,8 3,9 4,0
0 0,0450 0,0408 0,0369 0,0334 0,0302 0,0273 0,0247 0,0224 0,0202 0,0183
1 0,1397 0,1340 0,1217 0,1135 0,1057 0,0984 0,0915 0,0850 0,0789 0,0733
2 0,2165 0,2087 0,2008 0,1929 0,1850 0,1771 0,1692 0,1615 0,1539 0,1465
3 0,2237 0,2226 0,2209 0,2186 0,2158 0,2125 0,2087 0,2046 0,2001 0,1954
4 0,1734 0,1781 0,1823 0,1858 0,1888 0,1912 0,1931 0,1944 0,1951 0,1954
5 0,1075 0,1140 0,1203 0,1264 0,1322 0,1377 0,1429 0,1477 0,1522 0,1563
6 0,0555 0,0608 0,0662 0,0716 0,0771 0,0826 0,0881 0,0936 0,0989 0,1042
7 0,0246 0,0278 0,0312 0,0348 0,0385 0,0425 0,0466 0,0508 0,0551 0,0595
8 0,0095 0,0111 0,0129 0,0148 0,0169 0,0191 0,0215 0,0241 0,0269 0,0298
9 0,0033 0,0040 0,0047 0,0056 0,0066 0,0076 0,0089 0,0102 0,0116 0,0132
10 0,0010 0,0013 0,0016 0,0019 0,0023 0,0028 0,0033 0,0039 0,0045 0,0053
11 0,0003 0,0004 0,0005 0,0006 0,0007 0,0009 0,0011 0,0013 0,0016 0,0019
12 0,0001 0,0001 0,0001 0,0002 0,0002 0,0003 0,0003 0,0004 0,0005 0,0006
13 0,0000 0,0000 0,0000 0,0000 0,0001 0,0001 0,0001 0,0001 0,0002 0,0002
14 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0001
X
X 4,1 4,2 4,3 4,4 4,5 4,6 4,7 4,8 4,9 5,0
0 0,0166 0,0150 0,0136 0,0123 0,0111 0,0101 0,0091 0,0082 0,0074 0,0067
1 0,0679 0,0630 0,0583 0,0540 0,0500 0,0462 0,0427 0,0395 0,0365 0,0337
2 0,1393 0,1323 0,1254 0,1188 0,1125 0,1063 0,1005 0,0948 0,0894 0,0842
3 0,1904 0,1852 0,1798 0,1743 0,1687 0,1631 0,1574 0,1517 0,1460 0,1404
4 0,1951 0,1944 0,1933 0,1917 0,1898 0,1875 0,1849 0,1820 0,1789 0,1755
5 0,1600 0,1633 0,1662 0,1687 0,1708 0,1725 0,1738 0,1747 0,1753 0,1755
6 0,1093 0,1143 0,1191 0,1237 0,1281 0,1323 0,1362 0,1398 0,1432 0,1462
7 0,0640 0,0686 0,0732 0,0778 0,0824 0,0869 0,0914 0,0959 0,1002 0,1044
8 0,0328 0,0360 0,0393 0,0428 0,0463 0,0500 0,0537 0,0575 0,0614 0,0653
9 0,0150 0,0168 0,0188 0,0209 0,0232 0,0255 0,0280 0,0307 0,0334 0,0363
10 0,0061 0,0071 0,0081 0,0092 0,0104 0,0118 0,0132 0,0147 0,0164 0,0181
11 0,0023 0,0027 0,0032 0,0037 0,0043 0,0049 0,0056 0,0064 0,0073 0,0082
12 0,0008 0,0009 0,0011 0,0014 0,0016 0,0019 0,0022 0,0026 0,0030 0,0034
13 0,0002 0,0003 0,0004 0,0005 0,0006 0,0007 0,0008 0,0009 0,0011 0,0013
14 0,0001 0,0001 0,0001 0,0001 0,0002 0,0002 0,0003 0,0003 0,0004 0,0005
15 0,0000 0,0000 0,0000 0,0000 0,0001 0,0001 0,0001 0,0001 0,0001 0,0002
X
X 5,1 5,2 5,3 5,4 5,5 5,6 5,7 5,8 5,9 6,0
0 0,0061 0,0055 0,0050 0,0045 0,0041 0,0037 0,0033 0,0030 0,0027 0,0025
1 0,0311 0,0287 0,0265 0,0244 0,0225 0,0207 0,0191 0,0176 0,0162 0,0149
2 0,0793 0,0746 0,0701 0,0659 0,0618 0,0580 0,0544 0,0509 0,0477 0,0446
3 0,1348 0,1293 0,1239 0,1185 0,1133 0,1082 0,1033 0,0985 0,0938 0,0892
4 0,1719 0,1681 0,1641 0,1600 0,1558 0,1515 0,1472 0,1428 0,1383 0,1339
5 0,1753 0,1748 0,1740 0,1728 0,1714 0,1697 0,1678 0,1656 0,1632 0,1606
6 0,1490 0,1515 0,1537 0,1555 0,1571 0,1584 0,1594 0,1601 0,1605 0,1606
7 0,1086 0,1125 0,1163 0,1200 0,1234 0,1267 0,1298 0,1326 0,1353 0,1377
8 0,0692 0,0731 0,0771 0,0810 0,0849 0,0887 0,0925 0,0962 0,0998 0,1033
9 0,0392 0,0423 0,0454 0,0486 0,0519 0,0552 0,0586 0,0620 0,0654 0,0688
10 0,0200 0,0220 0,0241 0,0262 0,0285 0,0309 0,0334 0,0359 0,0386 0,0413
11 0,0093 0,0104 0,0116 0,0129 0,0143 0,0157 0,0173 0,0190 0,0207 0,0225
12 0,0039 0,0045 0,0051 0,0058 0,0065 0,0073 0,0082 0,0092 0,0102 0,0113
13 0,0015 0,0018 0,0021 0,0024 0,0028 0,0032 0,0036 0,0041 0,0046 0,0052
14 0,0006 0,0007 0,0008 0,0009 0,0011 0,0013 0,0015 0,0017 0,0019 0,0022
15 0,0002 0,0002 0,0003 0,0003 0,0004 0,0005 0,0006 0,0007 0,0008 0,0009
16 0,0001 0,0001 0,0001 0,0001 0,0001 0,0002 0,0002 0,0002 0,0003 0,0003
17 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0001 0,0001 0,0001 0,0001
X
X 6,1 6,2 6,3 6,4 6,5 6,6 6,7 6,8 6,9 7,0
0 0,0022 0,0020 0,0018 0,0017 0,0015 0,0014 0,0012 0,0011 0,0010 0,0009
1 0,0137 0,0126 0,0116 0,0106 0,0098 0,0090 0,0082 0,0076 0,0070 0,0064
2 0,0417 0,0390 0,0364 0,0340 0,0318 0,0296 0,0276 0,0258 0,0240 0,0223
3 0,0848 0,0806 0,0765 0,0726 0,0688 0,0652 0,0617 0,0584 0,0552 0,0521
4 0,1294 0,1249 0,1205 0,1162 0,1118 0,1076 0,1034 0,0992 0,0952 0,0912
5 0,1579 0,1549 0,1519 0,1487 0,1454 0,1420 0,1385 0,1349 0,1314 0,1277
6 0,1605 0,1601 0,1595 0,1586 0,1575 0,1562 0,1546 0,1529 0,1511 0,1490
7 0,1399 0,1418 0,1435 0,1450 0,1462 0,1472 0,1480 0,1486 0,1489 0,1490
8 0,1066 0,1099 0,1130 0,1160 0,1188 0,1215 0,1240 0,1263 0,1284 0,1304
9 0,0723 0,0757 0,0791 0,0825 0,0858 0,0891 0,0923 0,0954 0,0985 0,1014
X
X 6,1 6,2 6,3 6,4 6,5 6,6 6,7 6,8 6,9 7,0
10 0,0441 0,0469 0,0498 0,0528 0,0558 0,0588 0,0618 0,0649 0,0679 0,0710
11 0,0245 0,0265 0,0285 0,0307 0,0330 0,0353 0,0377 0,0401 0,0426 0,0452
12 0,0124 0,0137 0,0150 0,0164 0,0179 0,0194 0,0210 0,0227 0,0245 0,0264
13 0,0058 0,0065 0,0073 0,0081 0,0089 0,0098 0,0108 0,0119 0,0130 0,0142
14 0,0025 0,0029 0,0033 0,0037 0,0041 0,0046 0,0052 0,0058 0,0064 0,0071
15 0,0010 0,0012 0,0014 0,0016 0,0018 0,0020 0,0023 0,0026 0,0029 0,0033
16 0,0004 0,0005 0,0005 0,0006 0,0007 0,0008 0,0010 0,0011 0,0013 0,0014
17 0,0001 0,0002 0,0002 0,0002 0,0003 0,0003 0,0004 0,0004 0,0005 0,0006
18 0,0000 0,0001 0,0001 0,0001 0,0001 0,0001 0,0001 0,0002 0,0002 0,0002
19 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0001 0,0001 0,0001
X
X 7,1 7,2 7,3 7,4 7,5 7,6 7,7 7,8 7,9 8,0
0 0,0008 0,0007 0,0007 0,0006 0,0006 0,0005 0,0005 0,0004 0,0004 0,0003
1 0,0059 0,0054 0,0049 0,0045 0,0041 0,0038 0,0035 0,0032 0,0029 0,0027
2 0,0208 0,0194 0,0180 0,0167 0,0156 0,0145 0,0134 0,0125 0,0116 0,0107
3 0,0492 0,0464 0,0438 0,0413 0,0389 0,0366 0,0345 0,0324 0,0305 0,0286
4 0,0874 0,0836 0,0799 0,0764 0,0729 0,0696 0,0663 0,0632 0,0602 0,0573
5 0,1241 0,1204 0,1167 0,1130 0,1094 0,1057 0,1021 0,0986 0,0951 0,0916
6 0,1468 0,1445 0,1420 0,1394 0,1367 0,1339 0,1311 0,1282 0,1252 0,1221
7 0,1489 0,1486 0,1481 0,1474 0,1465 0,1454 0,1442 0,1428 0,1413 0,1396
8 0,1321 0,1337 0,1351 0,1363 0,1373 0,1382 0,1388 0,1392 0,1395 0,1396
9 0,1042 0,1070 0,1096 0,1121 0,1144 0,1167 0,1187 0,1207 0,1224 0,1241
10 0,0740 0,0770 0,0800 0,0829 0,0858 0,0887 0,0914 0,0941 0,0967 0,0993
11 0,0478 0,0504 0,0531 0,0558 0,0585 0,0613 0,0640 0,0667 0,0695 0,0722
12 0,0283 0,0303 0,0323 0,0344 0,0366 0,0388 0,0411 0,0434 0,0457 0,0481
13 0,0154 0,0168 0,0181 0,0196 0,0211 0,0227 0,0243 0,0260 0,0278 0,0296
14 0,0078 0,0086 0,0095 0,0104 0,0113 0,0123 0,0134 0,0145 0,0157 0,0169
15 0,0037 0,0041 0,0046 0,0051 0,0057 0,0062 0,0069 0,0075 0,0083 0,0090
16 0,0016 0,0019 0,0021 0,0024 0,0026 0,0030 0,0033 0,0037 0,0041 0,0045
17 0,0007 0,0008 0,0009 0,0010 0,0012 0,0013 0,0015 0,0017 0,0019 0,0021
18 0,0003 0,0003 0,0004 0,0004 0,0005 0,0006 0,0006 0,0007 0,0008 0,0009
19 0,0001 0,0001 0,0001 0,0002 0,0002 0,0002 0,0003 0,0003 0,0003 0,0004
20 0,0000 0,0000 0,0001 0,0001 0,0001 0,0001 0,0001 0,0001 0,0001 0,0002
21 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0001 0,0001
X 8,1 8,2 8,3 8,4 8,5 8,6 8,7 8,8 8,9 9,0
0 0,0003 0,0003 0,0002 0,0002 0,0002 0,0002 0,0002 0,0002 0,0001 0,0001
1 0,0025 0,0023 0,0021 0,0019 0,0017 0,0016 0,0014 0,0013 0,0012 0,0011
2 0,0100 0,0092 0,0086 0,0079 0,0074 0,0068 0,0063 0,0058 0,0054 0,0050
3 0,0269 0,0252 0,0237 0,0222 0,0208 0,0195 0,0183 0,0171 0,0160 0,0150
4 0,0544 0,0517 0,0491 0,0466 0,0443 0,0420 0,0398 0,0377 0,0357 0,0337
5 0,0882 0,0849 0,0816 0,0784 0,0752 0,0722 0,0692 0,0663 0,0635 0,0607
6 0,1191 0,1160 0,1128 0,1097 0,1066 0,1034 0,1003 0,0972 0,0941 0,0911
7 0,1378 0,1358 0,1338 0,1317 0,1294 0,1271 0,1247 0,1222 0,1197 0,1171
8 0,1395 0,1392 0,1388 0,1382 0,1375 0,1366 0,1356 0,1344 0,1332 0,1318
9 0,1256 0,1269 0,1280 0,1290 0,1299 0,1306 0,1311 0,1315 0,1317 0,1318
10 0,1017 0,1040 0,1063 0,1084 0,1104 0,1123 0,1140 0,1157 0,1172 0,1186
11 0,0749 0,0776 0,0802 0,0828 0,0853 0,0878 0,0902 0,0925 0,0948 0,0970
12 0,0505 0,0530 0,0555 0,0579 0,0604 0,0629 0,0654 0,0679 0,0703 0,0728
13 0,0315 0,0334 0,0354 0,0374 0,0395 0,0416 0,0438 0,0459 0,0481 0,0504
14 0,0182 0,0196 0,0210 0,0225 0,0240 0,0256 0,0272 0,0289 0,0306 0,0324
15 0,0098 0,0107 0,0116 0,0126 0,0136 0,0147 0,0158 0,0169 0,0182 0,0194
16 0,0050 0,0055 0,0060 0,0066 0,0072 0,0079 0,0086 0,0093 0,0101 0,0109
17 0,0024 0,0026 0,0029 0,0033 0,0036 0,0040 0,0044 0,0048 0,0053 0,0058
18 0,0011 0,0012 0,0014 0,0015 0,0017 0,0019 0,0021 0,0024 0,0026 0,0029
19 0,0005 0,0005 0,0006 0,0007 0,0008 0,0009 0,0010 0,0011 0,0012 0,0014
20 0,0002 0,0002 0,0002 0,0003 0,0003 0,0004 0,0004 0,0005 0,0005 0,0006
21 0,0001 0,0001 0,0001 0,0001 0,0001 0,0002 0,0002 0,0002 0,0002 0,0003
22 0,0000 0,0000 0,0000 0,0000 0,0001 0,0001 0,0001 0,0001 0,0001 0,0001
X 9,1 9,2 9,3 9,4 9,5 9,6 9,7 9,8 9,9 10,0
0 0,0001 0,0001 0,0001 0,0001 0,0001 0,0001 0,0001 0,0001 0,0001 0,0000
1 0,0010 0,0009 0,0009 0,0008 0,0007 0,0007 0,0006 0,0005 0,0005 0,0005
2 0,0046 0,0043 0,0040 0,0037 0,0034 0,0031 0,0029 0,0027 0,0025 0,0023
3 0,0140 0,0131 0,0123 0,0115 0,0107 0,0100 0,0093 0,0087 0,0081 0,0076
4 0,0319 0,0302 0,0285 0,0269 0,0254 0,0240 0,0226 0,0213 0,0201 0,0189
5 0,0581 0,0555 0,0530 0,0506 0,0483 0,0460 0,0439 0,0418 0,0398 0,0378
6 0,0881 0,0851 0,0822 0,0793 0,0764 0,0736 0,0709 0,0682 0,0656 0,0631
7 0,1145 0,1118 0,1091 0,1064 0,1037 0,1010 0,0982 0,0955 0,0928 0,0901
8 0,1302 0,1286 0,1269 0,1251 0,1232 0,1212 0,1191 0,1170 0,1148 0,1126
9 0,1317 0,1315 0,1311 0,1306 0,1300 0,1293 0,1284 0,1274 0,1263 0,1251
Окончание табл. Д. 7
Ячейки таблицы содержат вероятность конкретного значения X при заданной величине X
X
X 9,1 9,2 9,3 9.4 9,5 9.6 9.7 9.8 9.9 10.0
10 0,1198 0,1210 0,1219 0,1228 0,1235 0,1241 0,1245 0,1249 0,1250 0,1251
и 0,0991 0,1012 0,1031 0,1049 0,1067 0,1083 0,1098 0,1112 0,1125 0,1137
12 0,0752 0,0776 0,0799 0,0822 0,0844 0,0866 0,0888 0,0908 0,0928 0,0948
13 0,0526 0,0549 0,0572 0,0594 0,0617 0,0640 0,0662 0,0685 0,0707 0,0729
14 0,0342 0,0361 0,0380 0,0399 0,0419 0,0439 0,0459 0,0479 0,0500 0,0521
15 0,0208 0,0221 0,0235 0,0250 0,0265 0,0281 0,0297 0,0313 0,0330 0,0347
16 0,0118 0,0127 0,0137 0,0147 0,0157 0,0168 0,0180 0,0192 0,0204 0,0217
17 0,0063 0,0069 0,0075 0,0081 0,0088 0,0095 0,0103 0,0111 0,0119 0,0128
18 0,0032 0,0035 0,0039 0,0042 0,0046 0,0051 0,0055 0,0060 0,0065 0,0071
19 0,0015 0,0017 0,0019 0,0021 0,0023 0,0026 0,0028 0,0031 0,0034 0,0037
20 0,0007 0,0008 0,0009 0,0010 0,0011 0,0012 0,0014 0,0015 0,0017 0,0019
21 0,0003 0,0003 0,0004 0,0004 0,0005 0,0006 0,0006 0,0007 0,0008 0,0009
22 0,0001 0,0001 0,0002 0,0002 0,0002 0,0002 0,0003 0,0003 0,0004 0,0004
23 0,0000 0,0001 0,0001 0,0001 0,0001 0,0001 0,0001 0,0001 0,0002 0,0002
24 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0001 0,0001 0,0001
X X =20 X Х=20 X Х=20 X Х=20
0 0,0000 10 0,0058 20 0,0888 30 0,0083
1 0,0000 и 0,0106 21 0,0846 31 0,0054
2 0,0000 12 0,0176 22 0,0769 32 0,0034
3 0,0000 13 0,0271 23 0,0669 33 0,0020
4 0,0000 14 0,0387 24 0,0557 34 0,0012
5 0,0001 15 0,0516 25 0,0446 35 0,0007
6 0,0002 16 0,0646 26 0,0343 36 0,0004
7 0,0005 17 0,0760 27 0,0254 37 0,0002
8 0,0013 18 0,0844 28 0,0181 38 0,0001
9 0,0029 19 0,0888 29 0,0125 39 0,0001
Таблица Д.8. Нижние и верхние критические значения статистики Т, в ранговом критерии Уилкоксона
П2 a n,
Односторонний Двусторонний 4 5 6 7 8 9 10
0,05 0,10 11; 25
4 0,025 0,05 10; 26
0,01 0,02 9
0,005 0,01 , 4,
0,05 0,10 12; 28 19; 36
5 0,025 0,05 11; 29 17; 38
0,01 0,02 10; 30 16; 39
0,005 0,01 15; 40
0,05 0,10 13; 31 20; 40 28; 50
6 0,025 0,05 12; 32 18; 42 26; 52
0,01 0,02 11; 33 17; 43 24; 54
0,005 0,01 10; 34 16; 44 23; 55
0,05 0,10 14; 34 21; 44 29; 55 39; 66
7 0,025 0,05 13; 35 20; 45 27; 57 36; 69
0,01 0,02 11; 37 18; 47 25; 59 34; 71
0,005 0,01 10; 38 16; 49 24; 60 32; 73
0,05 0,10 15; 37 23; 47 31; 59 41; 71 51; 85
8 0,025 0,05 14; 38 21; 49 29; 61 38; 74 49; 87
0,01 0,02 12; 40 19; 51 27; 63 35; 77 45; 91
0,005 0,01 11; 41 15; 53 25; 65 34; 78 43; 93
0,05 0,10 16; 40 24; 51 33; 63 43; 76 54; 90 66;105
9 0,025 0,05 14; 42 22; 53 31; 65 40; 79 51; 93 62; 109
0,01 0,02 13; 43 20; 55 28; 68 37; 82 49; 97 59;112
0,005 0,01 11; 45 18; 57 26; 70 35; 84 45; 99 56;115
0,05 0,10 17; 43 26; 54 35; 67 45; 81 56; 96 69;111 82; 128
10 0,025 0,05 15; 45 23; 57 32; 70 42; 84 53; 99 65; 115 78; 132
0,01 0,02 13; 47 21; 59 29; 73 39; 87 49;103 61;119 74; 136
0,005 0,01 12; 48 19; 61 27; 75 37; 89 47; 105 58;122 71; 139
Источник: таблица 1 из книги F. Wilcoxon, R. A. Wilcoxon, Some Rapid Approximate Statistical Procedures (Pearl River, NY.’Lederle Laboratories, 1964). Публикуется с разрешения компании Amercan Cyanamid Company.
Таблица Д.9. Критические значения стыодентизованного размаха Q
Верхние 5% значений (а=0,05)
Числитель, df,
Знаменатель, df. 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
1 18,00 27,00 32,80 37,10 40,40 43,10 45,40 47,40 49,10 50,60 52,00 53,20 54,30 55,40 56,30 57,20 58,00 58,80 59,60
2 6,09 8,30 9,80 10,9 0 11,7 0 12,4 0 13,0 0 13,5 0 14,00 14,40 14,70 15,10 15,40 15,70 15,90 16,10 16,40 16,60 16,80
3 4,50 5,91 6,82 7,50 8,04 8,48 8,85 9,18 9,46 9,72 9,95 10,15 10,35 10,52 10,69 10,84 10,98 11,11 11,24
4 3,93 5,04 5,76 6,29 6,71 7,05 7,35 7,60 7,83 8,03 8,21 8,37 8,52 8,66 8,79 8,91 9,03 9,13 9,23
5 3,64 4,60 5,22 5,67 6,03 6,33 6,58 6,80 6,99 7,17 7,32 7,47 7,60 7,72 7,83 7,93 8,03 8,12 8,21
6 3,46 4,34 4,90 5,31 5,63 5,89 6,12 6,32 6,49 6,65 6,79 6,92 7,03 7,14 f,24 7,34 7,43 7,51 7,59
7 3,34 4,16 4,68 5,06 5,36 5,61 5,82 6,00 6,16 6,30 6,43 6,55 6,66 6,76 6,85 6,94 7,02 7,09 7,17
8 3,26 4,04 4,53 4,89 5,17 5,40 5,60 5,77 5,92 6,05 6,18 6,29 6,39 6,48 6,57 6,65 6,73 6,80 6,87
9 3,20 3,95 4,42 4,76 5,02 5,24 5,43 5,60 5,74 5,87 5,98 6,09 6,19 6,28 6,36 6,44 6,51 6,58 6,64
10 3,15 3,88 4,33 4,65 4,91 5,12 5,30 5,46 5,60 5,72 5,83 5,93 6,03 6,11 6,20 6,27 6,34 6,40 6,47
11 3,11 3,82 4,26 4,57 4,82 5,03 5,20 5,35 5,49 5,61 5,71 5,81 5,90 5,99 6,06 6,14 6,20 6,26 6,33
12 3,08 3,77 6,20 6,51 6,75 6,95 5,12 5,27 5,40 5,51 5,62 5,71 5,80 5,88 5,95 6,03 6,09 6,15 6,21
13 3,06 3,73 4,15 4,45 4,69 4,88 5,05 5,19 5,32 5,43 5,53 5,63 5,71 5,79 5,86 5,93 6,00 6,05 6,11
14 3,03 3,70 4,11 4,41 4,64 4,83 4,99 5,13 5,25 5,36 5,46 5,55 5,64 5,72 5,79 5,85 5,92 5,97 6,03
Верхние 5% значений (а=0,05)
Числитель, df,
Знаменатель. df7 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
15 3,01 3,67 4,08 4,37 4,60 4,78 4,94 5,08 5,20 5,31 5,40 5,49 5,58 5,65 5,72 5,79 5,85 5,90 5,96
16 3,00 3,65 4,05 4,33 4,56 4,74 4,90 5,03 5,15 5,26 5,35 5,44 5,52 5,59 5,66 5,72 5,79 5,84 5,90
17 2,98 3,63 4,02 4,30 4,52 4,71 4,86 4,99 5,11 5,21 5,31 5,39 5,47 5,55 5,61 5,68 5,74 5,79 5,84
18 2,97 3,61 4,00 4,28 4,49 4,67 4,82 4,96 5,07 5,17 5,27 5,35 5,43 5,50 5,57 5,63 5,69 5,74 5,79
19 2,96 3,59 3,98 4,25 4,47 4,65 4,79 4,92 5,04 5,14 5,23 5,32 5,39 5,46 5,53 5,59 5,65 5,70 5,75
20 2,95 3,58 3,96 4,23 4,45 4,62 4,77 4,90 5,01 5,11 5,20 5,28 5,36 5,43 5,49 5,55 5,61 5,66 5,71
24 2,92 3,53 3,90 4,17 4,37 4,54 4,68 4,81 4,92 5,01 5,10 5,18 5,25 5,32 5,38 5,44 5,50 5,54 5,59
30 2,89 3,49 3,84 4,10 4,30 4,46 4,60 4,72 4,83 4,92 5,00 5,08 5,15 5,21 5,27 5,33 5,38 5,43 5,48
40 2,86 3,44 3,79 4,04 4,23 4,39 4,52 4,63 4,74 4,82 4,91 4,98 5,05 5,11 5,16 5,22 5,27 5,31 5,36
60 2,83 3,40 3,74 3,98 4,16 4,31 4,44 4,55 4,65 4,73 4,81 4,88 4,94 5,00 5,06 5,11 5,16 5,20 5,24
120 2,80 3,36 3,69 3,92 4,10 4,24 4,36 4,48 4,56 4,64 4,72 4,78 4,84 4,90 4,95 5,00 5,05 5,09 5,13
ОС 2,77 3,31 3,63 3,86 4,03 4,17 4,29 4,39 4,47 4,55 4,62 4,68 4,74 4,80 4,85 4,89 4,93 4,97 5,01
Верхние 5% значений (а=0,05)
Числитель, df,
Знаменатель, df7 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
1 90,00 135,0 0 164,00 186,00 202,00 216,00 227,00 237,00 246,00 253,00 260,00 266,00 272,00 277,00 282,00 286,00 290,00 294,00 298,00
2 14,00 19,00 22,30 24,70 26,60 28,20 29,50 30,70 31,70 32,60 33,40 34,10 34,80 35,40 36,00 36,50 37,00 37,50 37,90
3 8,26 10,60 12,20 13,30 14,20 15,00 15,60 16,20 16,70 17,10 17,50 17,90 18,20 18,50 18,80 19,10 19,30 19,50 19,80
4 6,51 8,12 9,17 9,96 10,60 11,10 11,50 11,90 12,30 12,60 12,80 13,10 13,30 13,50 13,70 13,90 14,10 14,20 14,40
5 5,70 6,97 7,80 8,42 8,91 9,32 9,67 9,97 10,24 10,48 10,70 10,89 11,08 11,24 11,40 11,55 11,68 11,81 11,93
6 5,24 6,33 7,03 7,56 7,97 8,32 8,61 8,87 9,10 9,30 9,49 9,65 9,81 9,95 10,08 10,21 10,32 10,43 10,54
7 4,95 5,92 6,54 7,01 7,37 7,68 7,94 8,17 8,37 8,55 8,71 8,86 9,00 9,12 9,24 9,35 9,46 9,55 9,65
8 4,74 5,63 6,20 6,63 6,96 7,24 7,47 7,68 7,87 8,03 8,18 8,31 8,44 8,55 8,66 8,76 8,85 8,94 9,03
9 4,60 5,43 5,96 6,35 6,66 6,91 7,13 7,32 7,49 7,65 7,78 7,91 8,03 8,13 8,23 8,32 8,41 8,49 8,57
10 4,48 5,27 5,77 6,14 6,43 6,67 6,87 7,05 7,21 7,36 7,48 7,60 7,71 7,81 7,91 7,99 8,07 8,15 8,22
И 4,39 5,14 5,62 5,97 6,26 6,48 6,67 6,84 6,99 7,13 7,25 7,36 7,46 7,56 7,65 7,73 7,81 7,88 7,95
12 4,32 5,04 5,50 5,84 6,10 6,32 6,51 6,67 6,81 6,94 7,06 7,17 7,26 7,36 7,44 7,52 7,59 7,66 7,73
13 4,26 4,96 5,40 5,73 5,98 6,19 6,37 6,53 6,67 6,79 6,90 7,01 7,10 7,19 7,27 7,34 7,42 7,48 7,55
14 4,21 4,89 5,32 5,63 5,88 6,08 6,26 6,41 6,54 6,66 6,77 6,87 6,96 7,05 7,12 7,20 7,27 7,33 7,39
15 4,17 4,83 5,25 5,56 5,80 5,99 6,16 6,31 6,44 6,55 6,66 6,76 6,84 6,93 7,00 7,07 7,14 7,20 7,26
16 4,13 4,78 5,19 5,49 5,72 5,92 6,08 6,22 6,35 6,46 6,56 6,66 6,74 6,82 6,90 6,97 7,03 7,09 7,15
17 4,10 4,74 5,14 5,43 5,66 5,85 6,01 6,15 6,27 6,38 6,48 6,57 6,66 6,73 6,80 6,87 6,94 7,00 7,05
18 4,07 4,70 5,09 5,39 5,60 5,79 5,94 6,08 6,20 6,31 6,41 6,50 6,58 6,65 6,72 6,79 6,85 6,91 6,96
19 4,05 4,67 5,05 5,33 5,55 5,73 5,89 6,02 6,14 6,25 6,34 6,43 6,51 6,58 6,65 6,72 6,78 6,84 6,89
Верхние 5% значений (а=0,05)
Числитель, df,
Знаменатель, df2 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
20 4,02 4,64 5,02 5,29 5,51 5,69 5,84 5,97 6,09 6,19 6,29 6,37 6,45 6,52 6,59 6,65 6,71 6,76 6,82
24 3,96 4,54 4,91 5,17 5,37 5,54 5,69 5,81 5,92 6,02 6,11 6,19 6,26 6,33 6,39 6,45 6,51 6,56 6,61
30 3,89 4,45 4,89 5,05 5,24 5,40 5,54 5,65 5,76 5,85 5,93 6,01 6,08 6,14 6,20 6,26 6,31 6,36 6,41
40 3,82 4,37 4,70 4,93 5,11 5,27 5,39 5,50 5,60 5,69 5,77 5,84 5,90 5,96 6,02 6,07 6,12 6,17 6,21
60 3,76 4,28 4,60 4,82 4,99 5,13 5,25 5,36 5,45 5,53 5,60 5,67 5,73 5,79 5,84 5,89 5,93 5,98 6,02
120 3,70 4,20 4,50 4,71 4,87 5,01 5,12 5,21 5,30 5,38 5,44 5,51 5,56 5,61 5,66 5,71 5,75 5,79 5,83
oc 3,64 4,12 4,40 4,60 4,76 4,88 4,99 5,08 5,16 5,23 5,29 5,35 5,40 5,45 5,49 5,54 5,57 5,61 5,65
Величина размах/S ~ а.ц-уД равна размеру выборки, по которой вычисляется размах, а значение v представляет собой количество степеней свободы случайной величины S.
Источник: цитируется по книге Е. S. Pearson, Н. О. Hartley, eds., Biometrika Tables for Statisticians, Vol.l, 3rd ed., 1966, Table 29 с разрешения издательства Biometrika Trustees, London.
Таблица Д.10. Односторонние критические значения dL и d0 статистики Дурбина-Уотсона D.
а =0,05 a =0,01
п к dL =1 du к dt =2 du к dL =3 du к dL =4 du к dt =5 du к dL =1 du к dL =2 du к dL = 3 du к dL = 4 du к =5
d, d0
15 1,08 1,36 0,95 1,54 0,82 1,75 0,69 1,97 0,56 2,21 0,81 1,07 0,70 1,25 0,59 1,46 0,49 1,70 0,39 1,96
16 1,10 1,37 0,98 1,54 0,86 1,73 0,74 1,93 0,62 2,15 0,84 1,09 0,74 1,25 0,63 1,44 0,53 1,66 0,44 1,90
17 1,13 1,38 1,02 1,54 0,90 1,71 0,78 1,90 0,67 2,10 0,87 1,10 0,77 1,25 0,67 1,43 0,57 1,63 0,48 1,85
18 1,16 1,39 1,05 1,53 0,93 1,69 0,82 1,87 0,71 2,06 0,90 1,12 0,80 1,26 0,71 1,42 0,61 1,60 0,52 1,80
19 1,18 1,40 1,08 1,53 0,97 1,68 0,86 1,85 0,75 2,02 0,93 1,13 0,83 1,26 0,74 1,41 0,65 1,58 0,56 1,77
20 1,20 1,41 1,10 1,54 1,00 1,68 0,90 1,83 0,79 1,99 0,95 1,15 0,86 1,27 0,77 1,41 0,68 1,57 0,60 1,74
21 1,22 1,42 1,13 1,54 1,03 1,67 0,93 1,81 0,83 1,96 0,97 1,16 0,89 1,27 0,80 1,41 0,72 1,55 0,63 1,71
22 1,24 1,43 1,15 1,54 1,05 1,66 0,96 1,80 0,86 1,94 1,00 1,17 0,91 1,28 0,83 1,40 0,75 1,54 0,66 1,69
23 1,26 1,44 1,17 1,54 1,08 1,66 0,99 1,79 0,90 1,92 1,02 1,19 0,94 1,29 0,86 1,40 0,77 1,53 0,70 1,67
24 1,27 1,45 1,19 1,55 1,10 1,66 1,01 1,78 0,93 1,90 1,04 1,20 0,96 1,30 0,88 1,41 0,80 1,53 0,72 1,66
25 1,29 1,45 1,21 1,55 1,12 1,66 1,04 1,77 0,95 1,89 1,05 1,21 0,98 1,30 0,90 1,41 0,83 1,52 0,75 1,65
26 1,30 1,46 1,22 1,55 1,14 1,65 1,06 1,76 0,98 1,88 1,07 1,22 1,00 1,31 0,93 1,41 0,85 1,52 0,78 1,64
27 1,32 1,47 1,24 1,56 1,16 1,65 1,08 1,76 1,01 1,86 1,09 1,23 1,02 1,32 0,95 1,41 0,88 1,51 0,81 1,63
28 1,33 1,48 1,26 1,56 1,18 1,65 1,10 1,75 1,03 1,85 1,10 1,24 1,04 1,32 0,97 1,41 0,90 1,51 0,83 1,62
29 1,34 1,48 1,27 1,56 1,20 1,65 1,12 1,74 1,05 1,84 1,12 1,25 1,05 1,33 0,99 1,42 0,92 1,51 0,85 1,61
30 1,35 1,49 1,28 1,57 1,21 1,65 1Д4 1,74 1,07 1,83 1,13 1,26 1,07 1,34 1,01 1,42 0,94 1,51 0,88 1,61
a =0,05 а =0,01
n k = 1 k = 2 k = 3 k = 4 k = 5 k = 1 k = 2 k = 3 k = 4 k = 5
dL do dL d0 dL do dL do dt do dL do dt do dL do dL do dt du
31 1,36 1,50 1,30 1,57 1,23 1,65 1,16 1,74 1,09 1,83 1,15 1,27 1,08 1,34 1,02 1,42 0,96 1,51 0,90 1,60
32 1,37 1,50 1,31 1,57 1,24 1,65 1,18 1,73 1,11 1,82 1,16 1,28 1,10 1,35 1,04 1,43 0,98 1,51 0,92 1,60
33 1,38 1,51 1,32 1,58 1,26 1,65 1,19 1,73 1,13 1,81 1Д7 1,29 1Д1 1,36 1,05 1,43 1,00 1,51 0,94 1,59
34 1,39 1,51 1,33 1,58 1,27 1,65 1,21 1,73 1,15 1,81 1,18 1,30 1,13 1,36 1,07 1,43 1,01 1,51 0,95 1,59
35 1,40 1,52 1,34 1,58 1,28 1,65 1,22 1,73 1,16 1,80 1,19 1,31 1,14 1,37 1,08 1,44 1,03 1,51 0,97 1,59
36 1,41 1,52 1,35 1,59 1,29 1,65 1,24 1,73 1,18 1,80 1,21 1,32 1,15 1,38 1,10 1,44 1,04 1,51 0,99 1,59
37 1,42 1,53 1,36 1,59 1,31 1,66 1,25 1,72 1,19 1,80 1,22 1,32 1,16 1,38 1,11 1,45 1,06 1,51 1,00 1,59
38 1,43 1,54 1,37 1,59 1,32 1,66 1,26 1,72 1,21 1,79 1,23 1,33 1,18 1,39 1,12 1,45 1,07 1,52 1,02 1,58
39 1,43 1,54 1,38 1,60 1,33 1,66 1,27 1,72 1,22 1,79 1,24 1,34 1,19 1,39 1,14 1,45 1,09 1,52 1,03 1,58
40 1,44 1,54 1,39 1,60 1,34 1,66 1,29 1,72 1,23 1,79 1,25 1,34 1,20 1,40 1,15 1,46 1,10 1,52 1,05 1,58
45 1,48 1,57 1,43 1,62 1,38 1,67 1,34 1,72 1,29 1,78 1,29 1,38 1,24 1,42 1,20 1,48 1,16 1,53 1,11 1,58
50 1,50 1,59 1,46 1,63 1,42 1,67 1,38 1,72 1,34 1,77 1,32 1,40 1,28 1,45 1,24 1,49 1,20 1,54 1,16 1,59
55 1,53 1,60 1,49 1,64 1,45 1,68 1,41 1,72 1,38 1,77 1,36 1,43 1,32 1,47 1,28 1,51 1,25 1,55 1,21 1,59
60 1,55 1,62 1,51 1,65 1,48 1,69 1,44 1,73 1,41 1,77 1,38 1,45 1,35 1,48 1,32 1,52 1,28 1,56 1,25 1,60
65 1,57 1,63 1,54 1,66 1,50 1,70 1,47 1,73 1,44 1,77 1,41 1,47 1,38 1,50 1,35 1,53 1,31 1,57 1,28 1,61
70 1,58 1,64 1,55 1,67 1,52 1,70 1,49 1,74 1,46 1,77 1,43 1,49 1,40 1,52 1,37 1,55 1,34 1,58 1,31 1,61
75 1,60 1,65 1,57 1,68 1,54 1,71 1,51 1,74 1,49 1,77 1,45 1,50 1,42 1,53 1,39 1,56 1,37 1,59 1,34 1,62
80 1,61 1,66 1,59 1,69 1,56 1,72 1,53 1,74 1,51 1,77 1,47 1,52 1,44 1,54 1,42 1,57 1,39 1,60 1,36 1,62
85 1,62 1,67 1,60 1,70 1,57 1,72 1,55 1,75 1,52 1,77 1,48 1,53 1,46 1,55 1,43 1,58 1,41 1,60 1,39 1,63
90 1,63 1,68 1,61 1,70 1,59 1,73 1,57 1,75 1,54 1,78 1,50 1,54 1,47 1,56 1,45 1,59 1,43 1,61 1,41 1,64
95 1,64 1,69 1,62 1,71 1,60 1,73 1,58 1,75 1,56 1,78 1,51 1,55 1,49 1,57 1,47 1,60 1,45 1,62 1,42 1,64
100 1,65 1,69 1,63 1,72 1,61 1,74 1,59 1,76 1,57 1,78 1,52 1,56 1,50 1,58 1,48 1,60 1,46 1,63 1,44 1,65
п — количество наблюдений, k — количество независимых переменных.
Источник: цитируется по журналу Biometrika, 41 (1951): 173,175 с разрешения издательства Biometrika Trustees.
Таблица Д.11. Множители контрольных карт
Количество наблюдений в выборке d2 D3 d4 a2
2 1,128 0,853 0,000 3,267 1,880
3 1,693 0,888 0,000 2,575 1,023
4 2,059 0,880 0,000 2,282 0,729
5 2,326 0,864 0,000 2,114 0,577
6 2,534 0,848 0,000 2,004 0,483
7 2,704 0,833 - 0,076 1,924 0,419
8 2,847 0,820 0,136 1,864 0,373
9 2,970 0,808 0,184 1,816 0,337
10 3,078 0,797 0,223 1,777 0,308
11 3,173 0,787 0,256 1,744 0,285
12 3,258 0,778 0,283 1,717 0,266
13 3,336 0,770 0,307 1,693 0,249
14 3,407 0,763 0,328 1,672 0,235
15 3,472 0,756 0,347 1,653 0,223
16 3,532 0,750 0,363 1,637 0,212
17 3,588 0,744 0,378 1,622 0,203
18 3,640 0,739 0,391 1,609 0,194
19 3,689 0,733 0,404 1,596 0,187
20 3,735 0,729 0,415 1,585 0,180
21 3,778 0,724 0,425 1,575 0,173
22 3,819 0,720 0,435 1,565 0,167
23 3,858 0,716 0,443 1,557 0,162
24 3,895 0,712 0,452 1,548 0,157
25 3,931 0,708 0,459 1,541 0,153
Источник: цитируется по отчету ASTM-15D с любезного согласия Американского общества испытаний и материалов (American Society for Testing and Materials).
Таблица Д.12. Стандартизованное нормальное распределение
Элементы таблицы представляют собой площади, ограниченные кривой стандартизованного нормального распределения от математического ожидания до Z
Z 0,00 0,01 0,02 0,03 0,04 0,05 0,06 0,07 0,08 0,09
0,0 0,0000 0,0040 0,0080 0,0120 0,0160 0,0199 0,0239 0,0279 0,0319 0,0359
од 0,0398 0,0438 0,0478 0,0517 0,0557 0,0596 0,0636 0,0675 0,0714 0,0753
0,2 0,0793 0,0832 0,0871 0,0910 0,0948 0.0987 0,1026 0,1064 0,1103 0,1141
0,3 0,1179 0,1217 0,1255 0,1293 0,1331 0,1368 0,1406 0,1443 0,1480 0,1517
0,4 0,1554 0,1591 0,1628 0,1664 0,1700 0,1736 0,1772 0,1808 0,1844 0,1879
0,5 0,1915 0,1950 0,1985 0,2019 0,2054 0,2088 0,2123 0,2157 0,2190 0,2224
0,6 0,2257 0,2291 0,2324 0,2357 0,2389 0,2422 0,2454 0,2486 0,2518 0,2549
0,7 0,2580 0,2612 0,2642 0,2673 0,2704 0,2734 0,2764 0,2794 0,2823 0,2852
0,8 0,2881 0,2910 0,2939 0,2967 0,2995 0,3023 0,3051 0,3078 0,3106 0,3133
0,9 0,3159 0,3186 0,3212 0,3238 0,3264 0,3289 0,3315 0,3340 0,3365 0,3389
1,0 0,3413 0,3438 0,3461 0,3485 0,3508 0,3531 0,3554 0,3577 0,3599 0,3621
1,1 0,3643 0,3665 0,3686 0,3708 0,3729 0,3749 0,3770 0,3790 0,3810 0,3830
1,2 0,3849 0,3869 0,3888 0,3907 0,3925 0,3944 0,3962 0,3980 0,3997 0,4015
1,3 0,4032 0,4049 0,4066 0,4082 0,4099 0,4115 0,4131 0,4147 0,4162 0,4177
1,4 0,4192 0,4207 0,4222 0,4236 0,4251 0,4265 0,4279 0,4292 0,4306 0,4319
1,5 0,4332 0,4345 0,4357 0,4370 0,4382 0,4394 0,4406 0,4418 0,4429 0,4441
1,6 0,4452 0,4463 0,4474 0,4484 0,4495 0,4505 0,4515 0,4525 0,4535 0,4545
1,7 0,4554 0,4564 0,4573 0,4582 0,4591 0,4599 0,4608 0,4616 0,4625 0,4633
1,8 0,4641 0,4649 0,4656 0,4664 0,4671 0,4678 0,4686 0,4693 0,4699 0,4706
1,9 0,4713 0,4719 0,4726 0,4732 0,4738 0,4744 0,4750 0,4756 0,4761 0,4767
Окончание табл. Д. 12
Элементы таблицы представляют собой площади, ограниченные кривой стандартизованного нормального распределения от математического ожидания до Z
2,0 0,4772 0,4778 0,4783 0,4788 0,4793 0,4798 0,4803 0,4808 0,4812 0,4817
2,1 0,4821 0,4826 0,4830 0,4834 0,4838 0,4842 0,4846 0,4850 0,4854 0,4857
2,2 0,4861 0,4864 0,4868 0,4871 0,4875 0,4878 0,4881 0,4884 0,4887 0,4890
2,3 0,4893 0,4896 0,4898 0,4901 0,4904 0,4906 0,4909 0,4911 0,4913 0,4916
2,4 0,4918 0,4920 0,4922 0,4925 0,4927 0,4929 0,4931 0,4932 0,4934 0,4936
2,5 0,4938 0,4940 0,4941 0,4943 0,4045 0,4946 0,4948 0,4949 0,4951 0,4952
2,6 0,4953 0,4955 0,4956 0,4957 0,4959 0,4960 0,4961 0,4962 0,4963 0,4964
2,7 0,4965 0,4966 0,4967 0,4968 0,4969 0,4970 0,4971 0,4972 0,4973 0,4974
2,8 0,4974 0,4975 0,4976 0,4977 0,4977 0,4978 0,4979 0,4979 0,4980 0,4981
2,9 0,4981 0,4982 0,4982 0,4983 0,4984 0,4984 0,4985 0,4985 0,4986 0,4986
3,0 0,49865 0,49869 0,49874 0,49878 0,49882 0,49886 0,49889 0,49893 0,49897 0,49900
3,1 0,49903 0,49906 0,49910 0,49913 0,49916 0,49918 0,49921 0,49924 0,49926 0,49929
3,2 0,49931 0,49934 0,49936 0,49938 0,49940 0,49942 0,49944 0,49946 0,49948 0,49950
3,3 0,49952 0,49953 0,49955 0,49957 0,49958 0,49960 0,49961 0,49962 0,49964 0,49965
3,4 0,49966 0,49968 0,49969 0,49970 0,49971 0,49972 0,49973 0,49974 0,49975 0,49976
3,5 0,49977 0,49978 0,49978 0,49979 0,49980 0,49981 0,49981 0,49982 0,49983 0,49983
3,6 0,49984 0,49985 0,49985 0,49986 0,49986 0,49987 0,49987 0,49988 0,49988 0,49989
3,7 0,49989 0,49990 0,49990 0,49990 0,49991 0,49991 0,49992 0,49992 0,49992 0,49992
3,8 0,49993 0,49993 0,49993 0,49994 0,49994 0,49994 0,49994 0,49995 0,49995 0,49995
3,9 0,49995 0,49995 0,49996 0,49996 0,49996 0,49996 0,49996 0,49996 0,49997 0,49997
Приложение Е
Установка и настройка программы Microsoft Excel
Е.1. ВВЕДЕНИЕ
В разделе изложены инструкции, позволяющие установить и настроить программу Microsoft Excel так, как описано в основном тексте. Если вы используете программу Microsoft Excel совместно с другими пользователями, учтите, что ваши настройки повлияют на их приложения.
Е.2. НЕОБХОДИМЫЕ УСЛОВИЯ ИНСТАЛЛЯЦИИ
Прежде чем приступать к работе, проверьте номер версии программы Microsoft Excel. Запустите программу и выберите команду Справка^О программе. Первая строка в диалоговом окне содержит номер версии, номер выпуска и другую информацию. Запишите эти номера для того, чтобы ссылаться на них в будущем. Если вы работаете с версией Microsoft 97, следует применять выпуски SR с номером 2 или выше. (Свежие выпуски и пакеты для программы Microsoft Excel можно загрузить с Web-сайта компании Microsoft.)
В тексте книги широко применяются надстройки программы Microsoft Excel, которые поставляются вместе с основной программой. Для проверки корректности установки надстроек необходимо выбрать команду Сервис^Надстройки... и убедиться, что в списке Надстройки установлены флажки Пакет анализа и Analysis ToolPack— VBA. Если эти флажки сброшены, их следует установить и щелкнуть на кнопке ОК. (Диалоговое окно Надстройки приведено на иллюстрации.)
Надстройки
Доступные надстройки:
ОК
Пакет анализа Пересчет в евро Поиск решения Помощник по Интернету
Отмена
Обзор...
I Автоматизация... 1
Analysis ToolPak - VBA
Функции VBA для работы пакета анализа
Если в списке вообще нет пунктов Пакет анализа и Analysis ToolPack — VBA, их необходимо установить. Для этого требуется повторить процесс инсталляции программы Excel. (Подробности изложены в справочной системе программы Excel.)
Е.З. ОБЩИЕ ПАРАМЕТРЫ
Все приложения, описанные в основном тексте, реализуются при условии, что программа Microsoft Excel настроена определенным образом. Для того чтобы убедиться, что параметры установлены правильно, необходимо выполнить следующее.
Для проверки настроек, касающихся вычислений, правки и дисплея, выберите Сервис^Параметры.... В открывшемся диалоговом окне Параметры выполните такие действия.
1. Щелкните на корешке вкладки Вычисления и убедитесь, что на ней установлен флажок Автоматически.
2. Щелкните на корешке вкладки Правка и убедитесь, что на ней установлены все флажки, за исключением флажков Фиксированный десятичный разряд при вводе и Автоматический ввод процентов. (В программе Excel 97 флажок Автоматический ввод процентов не предусмотрен.)
3. Щелкните на корешке вкладки Общие и убедитесь, что на ней сброшен флажок Стиль ссылок R1C1 и установлен флажок Защита от макровирусов (только в версии Excel 97). Кроме того, в окне редактирования Листов в новой книге следует ввести число 3, выбрать пункт Arial Суг (или другой подходящий шрифт) в списке Стандартный шрифт, выбрать пункт 10 в списке Размер и при желании изменить значения в окнах редактирования Рабочий каталог и Имя пользователя.
4. Щелкните на кнопке ОК.
Е.4. НАСТРОЙКА ИНТЕРФЕЙСА
Приведенные ниже инструкции позволяют настроить интерфейс программы Microsoft Excel.
Настройка окна приложения. Для настройки окна приложения выберите команду Сервис^ Параметры... и выполните следующие инструкции.
1. Щелкните на корешке вкладки Вид. Если в группе Отображать флажок Строку формул не установлен, установите его.
2. Щелкните на корешке вкладки Вид. Если в группе Отображать флажок Строку состояния не установлен, установите его.
3. Щелкните на корешке вкладки Вид. Если в группе Отображать флажок Область задач при запуске не установлен, установите его.
4. Выполните команду Вид^ Панели инструментов. Если флажок Стандартная панель не установлен, установите его.
5. Выполните команду Вид ^Панели инструментов. Если флажок Форматирование не установлен, установите его.
Если панели не выровнены надлежащим образом, переместите их на верхнюю кромку экрана, пока границы панелей не превратятся в тонкую полоску маленьких точек, и отпустите кнопку мыши. Панель закрепится на месте. (Если вы работаете с версией программы Microsoft Excel 2000, придется дополнительно настроить меню и панели. Для этого выберите Сервис^Настройка... и сбросьте флажок Стандартная панель и панель форматирования в одной строке во вкладке Параметры. После этого щелкните на кнопке ОК.)
Установка и настройка программы Microsoft Excel 128 7
Настройка рабочей области. Для настройки внешнего вида рабочего листа, выберите команду Сервис^ Параметры... и, находясь в диалоговом окне Параметры, щелкните на корешке вкладки Вид (см. иллюстрацию) и установите все флажки в группе Параметры окна, кроме флажков Авторазбиение на страницы и Формулы. Затем щелкните на кнопке ОК.
Параметры [ ? |fx|
> „ .Международные Сохранение h Проверка ошибок $ Орфография ji Безопасность
Вид ! Вычисления Правка Общие Переход Списки Диаграмма Цвет j Отображать .............
; 0 область задач при запуске 0 строку формул 0 строку состояния 0 окна на панели задач : Примечания
О не отображать С*) только индикатор
1 Объекты
(*) отображать О только очертания
: Параметры окна
0 авторазбиение на страницы 0 заголовки строк и столбцов ! 0 формулы 0 символы структуры
j 0 сетка 0 нулевые значения
Цвет линий сетки:; Авто v.
О примечание и индикатор -
О не отображать
0 горизонтальная полоса прокрутки i
0 вертикальная полоса прокрутки i
0 ярлычки листов \
Если выяснится, что формулы, введенные вами в ячейку рабочего листа, появляются с задержкой, вернитесь в диалоговое окно Параметры на вкладку Вид и установите на время флажок Формулы.
Е.5. УСТАНОВКИ ПЕЧАТИ
Программа Microsoft Excel позволяет настроить свойства печати с помощью команды Файл^Параметры страницы.... Ниже приведены некоторые полезные советы, касающиеся четырех закладок, расположенных в диалоговом окне Параметры страницы.
Вкладка Страница. Если страница содержит слишком много столбцов, выберите ориентацию Альбомная или измените ширину страницы.
Вкладка Колонтитулы. Пользователь может задать содержание верхнего и нижнего колонтитула или сформатировать их, щелкнув на кнопках Создать верхний колонтитул и Создать нижний колонтитул.
Вкладка Лист. Чтобы изменить внешний вид страницы, подлежащей выводу на печать, установите флажки Сетка и Заголовки строк и столбцов.
Вкладка Поля. Чтобы установить поле страницы, подлежащей печати, можно изменить значения в окнах редактирования Левое, Правое, Верхнее и Нижнее.
Чтобы сохранить установки, необходимо щелкнуть на кнопке ОК.
Приложение Ж
Дополнительные сведения о программе PHStat
Ж.1. ВВЕДЕНИЕ
Надстройка PHStat2 позволяет свободно работать с программой Microsoft Excel, сосредоточиваясь лишь на статистических вопросах и не вникая в технические подробности, связанные с применением Excel. Используя ее в сочетании со стандартной надстройкой Пакет анализа, можно решить практически любую статистическую задачу.
Надстройка PHStat2 выполняет все низкоуровневые операции автоматически. В отличие от других надстроек, она выводит результаты не в виде текстовых меток, скрывающих детали применения программы Microsoft Excel, а в виде полноценных рабочих листов и диаграмм. Это свойство делает надстройку PHStat2 особенно полезной для дальнейшего освоения программы Microsoft Excel.
Надстройка PHStat2, последняя версия программы PHStat, является приложением для операционной системы Windows. Для того чтобы запустить программу PHStat2, необходимо выбрать пункт меню PHStat и ввести соответствующие числа и диапазоны.
Программа PHStat2 создает новые рабочие листы и диаграммы с результатами анализа. Многие из этих листов содержат формулы и являются интерактивными, т.е. позволяют изменять исходные данные и получать новые результаты без повторного запуска процедуры.
Надстройка PHStat2 совместима со всеми версиями Microsoft Excel, начиная с версии 97.
Ж.2. УСТАНОВКА ПРОГРАММЫ PHSTAT2
К работе с надстройкой PHStat2 и к ее инсталляции предъявляются разные технические требования.
Требования к применению программы PHStat2
• Windows 98/98SE/ME/NT 4.0/2000/ХР Home/XP Pro Computer System.
• Microsoft Excel 97/2000/2002(Office XP)/2003 и более поздние версии. Пользователи программы Excel 97 должны применять версию SR-2 и более поздние обновления. Надстройка PHStat? не совместима с версией Microsoft Windows 95 и версией программы Microsoft Windows для компьютеров Macintosh.
• Рекомендуется установить разрешение экрана равным 800 на 600 или 1024 на 748 пикселей. Надстройка PHStat2 работает при любом разрешении экрана, однако применение крупных шрифтов и грубое разрешение экрана могут привести к обрезанию сообщений, а также искажению окон и рабочих листов.
• Необходимо инсталлировать надстройки Microsoft Excel Data Analysis ToolPak и Analysis ToolPak-VBA (см. приложение E).
• Необходимо установить средний уровень безопасности (см. раздел Ж.4).
• Рекомендуется установить антивирусную программу.
Требования к инсталляции надстройки PHStat!
• Привод CD-ROM или DVD-ROM.
• Приблизительно 10 Мб свободного пространства на жестком диске при запуске инсталляционной программы и 3 Мб после установки программы. В некоторых старых версиях системы Windows для замены системных файлов может потребоваться еще 3 Мб свободного места.
• Номер пользователя системы Windows с привилегиями администратора (для пользователей операционных систем Windows NT/2000/XP или сетевых пользователей). Обратите внимание на то, что обычные сетевые пользователи не имеют указанных привилегий. Если вы хотите инсталлировать надстройку PHStat2 в сети, обратитесь к системному администратору.
• Доступ в Интернет (для загрузки обновлений).
Ж.З. ЗАПУСК ИНСТАЛЛЯЦИИ ПРОГРАММЫ PHSTAT2
Прежде чем устанавливать программу PHStat2, следует ознакомиться с приложением Е и настроить программу Microsoft Excel. Убедитесь, что технические требования, указанные в предыдущем разделе, выполнены. (Необходимая информация содержится также в файле PHStat2 readme . rtf.) Затем необходимо запустить инсталляционную программу Setup.exe, расположенную в каталоге PHStat2 на компакт-диске, используя пиктограмму Мой компьютер или Window Explorer.
Инсталляционная программа открывает диалоговое окно, приветствующее вас и приглашающее продолжить процесс инсталляции. Проходя этапы диалога, следует внимательно читать все сообщения и щелкать на кнопках Далее>. В процессе установки программы пользователь имеет возможность указать рабочий каталог для файлов программы PHStat2 (по умолчанию в качестве рабочего каталога используется папка \Program Files\PHStat2).
После успешного завершения процесса инсталляции будут созданы пиктограмма и пункт меню для программы PHStat2. Теперь программа PHStat2 готова к применению. Некоторые устаревшие системы могут потребовать перезагрузки.
Ж.4. ПРИМЕНЕНИЕ ПРОГРАММЫ PHSTAT2
Инсталлировав надстройку PHStat2, убедитесь, что установлен средний уровень безопасности макросов. Для этого следует выбрать команду Сервис^Макрос^Безопасность..., щелкнуть на корешке вкладки Уровень безопасности, установить переключатель в положение Средняя и щелкнуть на кнопке ОК.
Для запуска программы PHStat2 достаточно дважды щелкнуть на пиктограмме PHStat2 или выбрать соответствующую команду в меню Пуск. При запуске программы PHStat2 большинство версий программы Microsoft Excel выводит на экран сообщение о том, что макросы могут содержать вирусы. Чтобы продолжить работу, следует щелкнуть на кнопке Не отключать макросы. Запуск программы PHStat2 создает новый пункт PHStat2 в строке меню программы Microsoft Excel. Теперь пользователь может работать с программой PHStat2.
Для проверки надстройки PHStat2 выберите команду About PHStat2 в меню PHStat2. Убедитесь, что в диалоговом окне указаны номер версии и информация об авторских правах. Для того чтобы закрыть окно, щелкните на кнопке ОК. Для генерации рабочих листов, содержащих распределения случайных данных, выберите команды Probability & Prob. Distributions и Simple & Joint Probabilities.
Если эти команды выполняются правильно, процесс инсталляции можно считать успешным. Если возникнут проблемы, читайте раздел “Дополнительная информация”.
Ж.5. ПОДГОТОВКА ДАННЫХ ДЛЯ АНАЛИЗА С ПОМОЩЬЮ ПРОГРАММЫ PHSTAT2
Многие процедуры программы PHStat2 требуют тХредварительной подготовки рабочих листов. При этом данные должны содержаться в столбцах. Если пользователь хочет выделить только часть столбца, этот фрагмент необходимо скопировать в отдельный столбец. Это позволит избежать некоторых довольно распространенных ошибок.
Программа Microsoft Excel требует, чтобы рабочий лист, подлежащий анализу, был указан до вызова процедуры PHStat2. Если пользователь забудет сделать это, программа может выдать сообщение об ошибке. Правда, некоторые процедуры игнорируют это обстоятельство. Кроме того, если процедура требует данных, записанных в двух столбцах, например, при выполнении регрессионного анализа, следует убедиться, что оба столбца расположены на одном и том же рабочем листе.
Ж.6. ЧЕГО НЕ МОЖЕТ ПРОГРАММА PHSTAT2
Программа PHStat2 не является коммерческим статистическим пакетом и не предназначена для замены программ SAS или SPSS®. Поскольку программа PHStat2 в первую очередь применяется для обучения, она использует приемы вычисления, позволяющие проследить за их выполнением и проконтролировать результаты. В других ситуациях программа PHStat2 использует методы, предусмотренные в программе Microsoft Excel, которые слишком трудно реализовать вручную. Таким образом, результаты, полученные с помощью программ PHStat2 и Microsoft Excel, могут быть не такими точными, как результаты, вычисленные коммерческими пакетами, использующими методы высокой точности. В большинстве случаев эта разница не очень заметна. Студенты должны применять программу PHStat2 только к данным, приведенным в тексте, или использовать ее под руководством преподавателя. В этом случае программа PHStat2 гарантирует результаты, позволяющие делать правильные статистические выводы.
Ж.7. ДОПОЛНИТЕЛЬНАЯ ИНФОРМАЦИЯ
Технические требования и другая необходимая информация содержится в файле PHStat2 readme.rtf на компакт-диске, а также на Web-странице www.prenhall. com/phstat. Любой владелец этой книги и компакт-диска может свободно загружать новые версии программы PHStat2. Более подробные инструкции содержатся на Web-странице.
(К сожалению, надстройка PHStat2 не учитывает особенностей локализованной версии программы Microsoft Excel. В частности, она не распознает числа, представленные в русском стандарте, т.е. с десятичной запятой, а не точкой. Для того чтобы надстройка работала корректно, существуют две возможности: 1) изменить стандарт представления чисел в папке Панель управления Ф Языки и стандарты на Английский (США), указав в качестве страны расположения США (в этом случае все числа следует вводить с десятичной точкой); 2) не изменяя стандарта представления чисел, вводить дробные числа
в научном формате, например, число 0.95 необходимо представить как 95е-02. Кроме того, необходимо выполнить команду Сервис^Параметры, щелкнуть на вкладке Международные и установить флажок Использовать системные разделители. К сожалению, процедуры Multiple-Sample Tests^Levene’s Test... и Multiple-Sample Tests^ Tukey-Kramer Procedure... в локализованной версии программы Microsoft Excel не работают. Вместо них рекомендуется применять шаблоны рабочих листов, приведенные в соответствующих разделах книги. — Прим.ред.)
Приложение 3
Подготовка отчетов и презентаций с помощью пакета Microsoft Office
3.1. РАБОТА С ПАКЕТОМ MICROSOFT OFFICE: ОБМЕН ДАННЫМИ МЕЖДУ ПРОГРАММАМИ MICROSOFT EXCEL
И MICROSOFT WORD
Во многих ситуациях электронные таблицы и диаграммы, построенные с помощью программы Microsoft Excel, необходимо вставлять в отчеты. Если для редактирования такого отчета используется текстовый процессор Microsoft Word, выберите пункт меню Правка^Копировать, а затем — либо пункт Правка^Вставить, либо пункт Специальная вставка. Для простого копирования, а также для установления связей между программами Microsoft Word и Microsoft Excel используются разные варианты вставки. Такие команды позволяют автоматически обновлять объекты, вставленные в документ Microsoft Word, при изменении оригинала, хранящегося на рабочем листе Microsoft Excel.
Копирование и вставка таблиц. Выделите диапазон ячеек, подлежащих копированию, и выполните команду Правка^Копировать. Откройте документ Microsoft Word, укажите место вставки, а затем выполните команду Правка^Вставить. В результате документ Microsoft Word будет содержать форматированный текст и числа, хранящиеся в указанном диапазоне ячеек. В процессе копирования все формулы, содержащиеся в заданном диапазоне ячеек, заменяются их значениями.
Например, в результате копирования содержимого ячеек A3-.D9 из рабочего листа Образец (рис. 3.1, панельА), принадлежащего книге Techniques.xls, в документе текстового процессора Word создается таблица, изображенная на рис. 3.1, панель Б. В ходе этой операции формулы из ячейки В9 и формулы в столбцах С и D заменяются их текущими значениями. ^TECHNIQUES .XLS.
A | В |~C
D
1 Образец таблицы
_3 А .5 2 L 8
Всего ll’ SC Gl MC TK
Цель
~ 42
37
28
20
12j
Процент "3066% 27jQt% 18,98% 14,60% . 8,76%
Интегральный %!
эо.66%;
57.66%
76j64%
91,24%
jsM
Всего Цель Процент Интегральный %
IL SC GI МС ТК 42 37 26 20 12 30,66% 27,01% 18,98% 14,60% 8,76% 30,66% 57,66% 76,64% 91,24% 100,00%
Общий итог 137
Панель А Панель Б
Рис. 3.1. Копируемый диапазон ячеек (панель А) и документ Word после вставки (панель Б)
Копирование и установка связи с электронными таблицами. Выделите диапазон ячеек, подлежащих копированию, и выполните команду Правка^Копировать. Откройте документ Microsoft Word, укажите место вставки, а затем выполните команду Правка^Специальная вставка.... В открывшемся диалоговом окне Специальная вставка (рис. 3.2) следует установить переключатель в положение Связать, выбрать в списке Как пункт Лист Microsoft Excel Объект и щелкнуть на кнопке ОК.
Специальная вставка
Источник: Лист Microsoft Office Excel
SLR!C1:C2
Как:
0 Вставить: iMmeiiA
О Связать' j Текст в формате RTF ' >
- ’ i Неформатированный текст ; о
i Рисунок (метафайл Windows)
Точечный рисунок । Метафайл Windows (EMF)
Формат HTML
И®!
Отмена
□ в виде значка
Результат
।—к Вставка в документ содержимого буфера обмена с ] возможностью редактировать его как "Лист I Microsoft Office Excel".
Рис. 3.2. Диалоговое окно Специальная вставка в программе Microsoft Excel 2002 при копировании таблиц
Выбор других пунктов в списке Как может повлиять на внешний вид таблицы. (Более подробную информацию читатели найдут в разделе Результат, расположенном в нижней части диалогового окна Специальная вставка и в справочной системе программы Microsoft Excel.) Если вы работаете со старыми версиями текстового процессора, или ваш компьютер не оснащен достаточно большим объемом памяти, не следует выбирать пункт Лист Microsoft Excel Объект в списке Как, поскольку он позволяет непосредственно редактировать электронную таблицу, не запуская программу Microsoft Excel, а это может сильно замедлить работу.
Копирование диаграмм. Выделите диапазон ячеек, подлежащих копированию, и выполните команду Правкам Копировать. Для большей эффективности рекомендуется все операции вставки выполнять с помощью команды Правка^Специальная вставка.... В диалоговом окне Специальная вставка (рис. 3.3) установите один из переключателей Вставить или Связать. Затем выберите в списке Как пункт Диаграмма Microsoft Excel Объект и щелкните на кнопке ОК. Как и при копировании диапазона ячеек, остальные варианты, предлагаемые в списке Как, могут изменять внешний вид диаграммы при ее отображении, форматировании и выводе на печать.
Рис. 3.3. Диалоговое окно Специальная вставка в программе Microsoft Excel 2000 при копировании диаграмм
3.2. ПРИМЕНЕНИЕ ПАКЕТА MICROSOFT OFFICE: ИСПОЛЬЗОВАНИЕ ТАБЛИЦ И ДИАГРАММ, СОЗДАННЫХ ПРОГРАММОЙ MICROSOFT EXCEL, ДЛЯ ПРЕЗЕНТАЦИЙ MICROSOFT POWERPOINT
Как вы уже знаете, многие отчеты содержат таблицы и диаграммы, созданные программой Microsoft Excel. Для этого между нею и текстовым процессором Microsoft Word обеспечивается обмен информацией. Аналогично таблицы и диаграммы можно вставлять в слайды презентаций, создаваемые программой Microsoft PowerPoint. Для этого предназначены команды Правкам Копирование и Правка ^Вставить.
Например, чтобы сгенерировать электронный слайд, содержащий точечную диаграмму (см. рис. 3.2), сначала необходимо открыть файл Chapter 3.xls на листе Рис. 3.2. Затем нужно запустить программу Microsoft PowerPoint 2002. Первое окно приложения зависит от версии программы. На рис. 3.4 показано типичное окно Microsoft PowerPoint 2002, содержащее панель задач и пустой заголовок.
В старых версиях приложения Microsoft PowerPoint необходимо установить переключатель Создать новую презентацию, используя пустую презентацию и щелкнуть на кнопке ОК. Если вы не видите область задач, выберите команду Файл ^Создать, а затем установите переключатель Создать новую презентацию, используя пустую презентацию. Если вы работаете с версией Microsoft Excel 2000, находясь в диалоговом окне PowerPoint, установите переключатель Создать новую презентацию, используя пустую презентацию и щелкните на кнопке ОК. (Если вы работаете с версией Microsoft Excel 97, щелкните на пиктограмме Blank Presentation .pot и на кнопке ОК.)
S Microsoft PowerPoint - [Презентация!]
файл орайкв "вставка Форде- Сдрвис Показ слайдов Окно Справке
Ж 48%
тор _| Создатьслацд ^
Й Office Online
Заголовок слайда
Подзаголовок слайда
* Подключиться к веб-узлу Microsoft Office Online
* Последние сведения об использовании Power Point
ч Автоматически обновлять этот список из Веба
f Искать:
Пример: "Печать нескольких копий"
^Заметки к слайду
Открыть.,.
Слайд 1 из 1 Оформление по умолчанию русский (Россия)
Рис. 3.4. Первое диалоговое окно программы Microsoft PowerPoint 2002
j е i а
Применить разметку слайда: Макеты текста
0 Показывать при вставке слайдов
Открыв новую презентацию, выберите команду Вставка^ Создать слайд. В программе PowerPoint 2002 панель Разметка слайда находится на панели задач (см. иллюстрацию). В предыдущих версиях программы содержание этой панели аналогично. Щелкните правой кнопкой мыши на первом пункте списка в разделе Макеты текста и выберите команду Добавить новый слайд.
Программа PowerPoint вставляет новый слайд и позволяет его редактировать в области, показанной на рис. 3.5, панель А. Выделите рамку вокруг текста “Двойной щелчок вводит диаграмму” (рис. 3.5, панель Б). Переключитесь в программу Microsoft Excel с помощью комбинации клавиш <Alt+Tab>. Находясь в программе Microsoft Excel, щелкните на точечной диаграмме и выберите команду Правка^Копировать. Вернитесь в программу Microsoft PowerPoint (снова используя комбинацию клавиш <Alt+Tab>) и выберите команду Правка^Вставка, чтобы создать слайд, показанный на рис. 3.6. Чтобы минимизировать затраты системных ресурсов, выберите пиктограмму Вставить, которая появляется под вставленной диаграммой, и выберите команду Рисунок диаграммы (меньший размер файла) во всплывающем меню.
Размер вставленных диаграмм и таблиц можно изменять, перемещая прямоугольные маркеры, окружающие вставленный объект. (Размер заголовка и поясняющего текста также можно изменять.) Чтобы дополнить презентацию новым слайдом, необходимо выбрать Вставка ^Создать слайд, а сохранить презентацию можно с помощью команды Файл ^Сохранить как....
Диаграмма Microsoft Excel (вся книга)
Рисунок диаграммы (меньший размер файла)
Панель А
Рис. 3.5. Область редактирования перед (панель А) и после (панель Б) выбора рабочей области
Панель Б
Рис. 3.6. Слайд после вставки диаграммы (панель А) и изменения ее размера (панель Б)
3.3. ИСПОЛЬЗОВАНИЕ ПАКЕТА MICROSOFT OFFICE: СОХРАНЕНИЕ РАБОЧИХ ЛИСТОВ В ВИДЕ WEB-СТРАНИЦЫ ДЛЯ БРАУЗЕРА INTERNET EXPLORER
Для сохранения рабочих листов, созданных с помощью программы Microsoft Excel, в виде Web-страниц, предназначенных для браузера Internet Explorer, необходимо выбрать команду Файл ^Сохранить как... выбрать в списке Тип файла параметр Веб-страница. (В программе Microsoft Excel 97 этой команды нет.) Начиная с версии Internet Explorer 4.01, электронные таблицы могут сохранять интерактивные возможности, т.е. допускают редактирование. Для этого необходимо, чтобы пользователь, просматривающий таблицу, предвари
тельно установил соответствующие компоненты пакета Microsoft Office (или программы Microsoft Excel). Web-компоненты доступны только лицензированным пользователям пакета Microsoft Office/Excel, но не всем пользователям браузера Internet Explorer. По этой причине мы не будем рассматривать эту возможность слишком подробно.
Для иллюстрации команды Сохранить как... откройте книгу chapter 12 . xls. В виде Web-страниц можно сохранять как отдельные листы, так и диаграммы этой книги. Например, откроем рабочий лист Рис12.4, не содержащий никаких формул и средств диалога. Для того чтобы сохранить его в виде Web-страницы, выберите команду ФайлФ Сохранить как..., В открывшемся диалоговом окне Сохранение документа следует выбрать в списке Тип файла пункт Веб-страница, ввести в окне редактирования Имя файла строку Рис12.4 . htm и щелкнуть на кнопке Сохранить (рис. 3.7).
Рис. 3.7. Диалоговое окно Сохранение документа
Программа Microsoft Excel создает форматированную Web-страницу, которую можно просмотреть с помощью браузера Internet Explorer 4.01 и более поздних версий.
Сохранение листов диаграмм в виде Web-страниц. Для того чтобы сохранить лист диаграммы, необходимо выполнить все инструкции, указанные выше. Программа Microsoft Excel создает Web-страницу, представляющую собой копию диаграммы. Несмотря на то что эту страницу можно вставить обратно в электронную таблицу, возможности редактировать диаграмму при этом утрачиваются.
Чтобы не потерять возможность редактирования диаграммы, необходимо сохранить ее интерактивные свойства. Например, для того, чтобы сохранить рабочий лист Рис12.5, следует выбрать Файл^Сохранить как... и в диалоговом окне Сохранение документа установить флажок Добавить интерактивность. Затем в открывшемся диалоговом окне Сохранение документа в списке Тип файла нужно выбрать пункт Вебстраница, ввести в окне редактирования Имя файла строку Рис12.5 . htm и щелкнуть на кнопке Сохранить (рис. 3.9).
Программа Microsoft Excel создает форматированную Web-страницу, содержащую диаграмму, которую можно редактировать как обычно (рис. 3.10). Ее можно просмотреть с помощью браузера Internet Explorere 4.01 и более поздних версий. Обратите внимание на то, что при создании Web-страницы метки исходной диаграммы искажаются.
Ц Chapter 1 2 - Microsoft Internet Explorer
l-je®
Файл Правка Вид Избранное Сервис Справка
вгесм Остановить Обновить Домой
Адрес ‘ G:\browse\Instructional Files\Figure 12.4.html
Поиск Избранное Медиа Журнал
vj Ссылки **
Анализ данных о магазинах
Регрессионная статистика
Множественный!? 095088
R-киадаат 050418
Нормированный R-квадрат 0 89619
Стандартная ошибка 056638
Наблюдения 14
Дисперсионный анализ df SS MS F
Регрессия 1 105.74761 105.74761 113233
Остаток 12 1120668 053389
Итого 13 11655429
Жзэффицшнты ОнанЭартноя ошибка f-статистика Р-Значапн
^пересечение 0564474 052619 183293 0Л91
Площадь 1.669862 0.15693 10454112 0000
«<>» Обзор Данные Рмс12.3 Рмс12.4 Рнс12.5 Рис12.И Рис1212 Рис12.14 Продажи Рис12 15 Рис12.16 Рис1217 Рис в '.......Мой компьютер
Рис. 3.8. Web-страница, созданная из рабочего листа Рис12.4
Рис. 3.9. Диалоговое окно при сохранении рабочего листа Рис12.4 в виде Web-страницы
3i D:\DIMA\Books\LEVINE\CD-ROM-RUS\browse\lnstructional_Files\Figure 12.5.htm - Microsoft Internet Explorer |
Файл Правка Вид Избранное Сервис Справка
© © • Э й й
Остановить Обновить Домой
Адрес: ; G:\browse\Instructional Files\Figure 12.5.htm
Поиск Избранное Медиа
Рис. 3.10. Интерактивная Web-страница, созданная из рабочего листа Рис12.5
Сохранение рабочих листов с добавлением интерактивности. Рабочие листы также можно сохранять, не теряя возможности интерактивного редактирования. Однако лучше всего это получается, если рабочий лист не содержит формул, ссылающихся на ячейки других рабочих листов. Если попытаться сохранить рабочий лист с такими формулами, на экране появится диалоговое окно, изображенное на рис. 11.29. Если щелкнуть на кнопке ОК, формулы, содержащие “внешние ссылки”, будут заменены их текущими значениями.
Отмена
Например, при сохранении рабочего листа Рис12.22 с добавлением интерактивных свойств будет создана Web-страница, изображенная на рисунке. Формулы, ссылающиеся лишь на ячейки этого же листа, сохраняют свои динамические свойства. Однако многие формулы будут заменены текущими значениями. При изменении исходных данных значения этих формул станут неверными. Следовательно, сохраняя рабочие листы, содержащие внешние ссылки, следует проявлять осторожность.
3.4. ПРИМЕНЕНИЕ ПАКЕТА MICROSOFT OFFICE: ИЗВЛЕЧЕНИЕ ФОРМАТИРОВАННЫХ ТАБЛИЧНЫХ ДАННЫХ ИЗ WORLD WIDE WEB С ПОМОЩЬЮ БРАУЗЕРА
С течением времени данные меняются, особенно во временных рядах, которые изменчивы по своей природе. Экономические и демографические данные можно извлекать не только из письменных источников, но и из World Wide Web.
Поиск Web-сайтов. Сначала необходимо определить Web-страницу, содержащую нужные данные. Для этого можно воспользоваться поисковой машиной. Эти машины представляют собой Web-сайты, генерирующие список гиперссылок на другие Web-страницы, соответствующие заданному критерию. .Например, на рис. 3.11 показана часть результатов поиска по запросу “U.S. Census Bureau data”. Вполне естественно, что первой ссылкой является Web-сайт самого Бюро переписи населения США. В некоторых случаях результаты поиска могут быть неверными, но хорошо сформулированные запросы, как правило, приводят к цели. Например, чтобы найти обновленные версии данных, использованных при решении задач, можно попробовать напечатать название набора данных и/или название исходного файла.
Shortcuts Advanced
Results 1 - 20 of about 11,900 for '‘U.S. Census Bureau data" Search took 0.15 seconds.
1. U.S. Bureau of the Census
government agency who produces the United States' demographic data
Category U S. Census Bureau
www census.gov/ - 22 k - Cached - More pages from this site
2. TIGER Mapping Service high-quality, detailed maps of anywhere in the United States, with multiple layers and elective marker placement.
Category. U S Census Bureau > Geographic Data Access Tools tiger census gov/ - 8k - Cached
3. US Census Bureau. State & County QuickFacts US Census Bureau- State & County QuickFacts The US Census Bureau Web site, State and County QuickFacts, provides "quick, easy access to facts about people, business, and geography." Users can . .
Category U S Census Bureau
Рис. 3.11. Частичные результаты поиска по запросу "U.S. Census Bureau data"
Соединившись с выбранным Web-сайтом, необходимо найти нужную Web-страницу, содержащую искомые данные. Презентация WEBSITE NAVIGATION. РРТ, расположенная в каталоге Instructional Files, демонстрирует процесс навигации, который позволяет найти данные о доходах семей в США в начале 2001 года, предоставленные Бюро переписи населения США. Полученные данные могут быть записаны в разных форматах. Легче всего использовать данные, записанные в формате электронных таблиц Microsoft Excel (xls), электронных таблиц Lotus 1-2-3 (wk4) или в виде записей, разделенных запятой (scv), а затем непосредственно открыть их с помощью программы Microsoft Excel.
Иногда интересующие нас данные записываются в формате, определенном браузером Intemer Explorer, и не содержатся в загружаемом файле. Если данные хранятся в виде обычной или html-таблицы, как, например, данные о штате Вашингтон на рис. 3.12, панель А, их можно скопировать и вставить в электронную таблицу. Для этого необходимо выделить данные, затем выбрать команду Правка ^Копировать, переключиться в программу Microsoft Excel, открыть соответствующий рабочий лист и выполнить команду Правкам Вставка. После этого может понадобиться несложное форматирование (см. рис. 3.12, панель Б). Если решетка данных представляет собой отдельный объект, размещенный на Web-странице, его можно сохранить с помощью программы Internet Explorer, а затем открыть с помощью программы Microsoft Excel, как обычный файл.
А В С
Number of school districts and K-12
1 __________enrollment, by type________
alZBSZZT 3 County Office 4 Elementary 5 Unified_______
6 High__________
7 ;CYA* 8 State Special T- Total
Number
______58 566 327
______93
_______9
_______3
1,056
Панель Б
Enrollment
67.920 1,240,932 4,263,546
568,965
5,094
_________918
6,147,375
Панель А
Рис. 3.12. Таблица в окне браузера Internet Explorer (панель А) и в окне программы Microsoft Excel (панель Б)
3.5. ПРИМЕНЕНИЕ ПАКЕТА MICROSOFT OFFICE: ИЗВЛЕЧЕНИЕ ДАННЫХ ИЗ WORLD WIDE WEB С ПОМОЩЬЮ БРАУЗЕРА
К сожалению, как правило, данные, публикуемые правительственными органами, записываются в виде текста для отображения с помощью браузера Internet Explorer. Извлечение данных в этих случаях обычно сопровождается утомительным процессом форматирования. Продемонстрируем это на примере данных статистического исследования, которые содержатся на Web-странице http://ferret.bls.census.gov/ macro/032002/hhinc/new06_000 . html. Сохраним эту страницу под именем HINC-06 . htm. (Этот файл записан на компакт-диске в каталоге Instrumental Files.)
Первичная настройка сохраняемой Web-страницы
1. Прокрутите рабочий лист и определите графические элементы, расположенные в начале и конце. (Таким элементом является логотип Бюро переписи населения США.) Выберите каждый графический элемент и удалите его. Графические элементы “плавают” поверх рабочего листа, как диаграммы, и не привязаны к конкретной ячейке.
2. Удалите строки от 51 до 57, не содержащие фактических данных, с помощью команды Правка^Удалить.... На этом этапе рабочая область будет выглядеть как настоящий рабочий лист, хотя простая проверка показывает, что “таблица” содержит лишь длинные метки в колонке А.
3. Выберите команду Файл ^Сохранить как.... В диалоговом окне Сохранить как (см. иллюстрацию) следует выполнить следующую операцию.
3.1. Выберите в раскрывающемся списке Тип файла пункт Текст Юникод (*.txt).
3.2. Введите имя файла в окне редактирования Имя файла (или согласитесь с предложенным).
3.3. Щелкните на кнопке ОК.
4. Щелкните на кнопке Ок в окне сообщения программы Microsoft Excel.
5. Если на экране появится сообщение о возможной несовместимости файла с форматом Юникод (*.txt), щелкните на кнопке Да.
6. Завершая настройку, выберите команду Файл^Закрыть, чтобы закрыть исходную таблицу, извлеченную из Web-страницы. Щелкните на кнопке Нет в диалоговом окне, предлагающем вам сохранить изменения.
Применение Мастера текстов
1. Выполните команду Файл<=>Открыть, чтобы открыть файл, сохраненный в п. 3. Чтобы увидеть нужный файл, выберите в списке Тип файлов пункт Текстовые файлы (см. иллюстрацию.)
2. На первом этапе диалога с Мастером текстов (импорт) установите переключатель Укажите формат данных в положение Фиксированной ширины, значение счетчика Начать импорт со строки сделайте равным единице и щелкните на кнопке Далее>. (Если установки отличаются от указанных, вернитесь к предыдущему этапу.)
3. На втором этапе диалога с Мастером текстов (импорт) (см. иллюстрацию) выполните следующие действия.
3.1. Дважды щелкните на первой линии со стрелками, чтобы удалить разделитель столбцов. Остальные столбцы должны остаться неизменными.
3.2. Щелкните на кнопке Далее>.
Мастер текстов (импорт) - шаг 1 из 3
@®
Данные восприняты как список значении фиксированной ширины.
Если это eepHOj нажмите кнопку "Далее в противном случае укажите формат данных.
Формат исходных данных
Укажите формат данных:
О с вазделителями * значения полей отделяются знаками-разделителями
©^к^рованной щ^иньН - поля имеют заданную ширину
Начать импорт со строки: j 1
Формат файла:
Windows (ANSI)
Предварительный просмотр файла D:\DIMA\Books\LEVINE\CD-ROM-4edition\browse\Instructional_Files\l-
1 All Races White
Z. Mean :.'йг:
3 . Number Income Number 1
4
5 Income of Household
•1 .... - .i" . • ЖР
[ отмена ] /Н'зЗ' л [ Далее > j [ Готово ]
4. На третьем этапе диалога с Мастером текстов (импорт) следует установить переключатель Формат данных столбца в положение Общий и щелкнуть на кнопке Готово.
Элементы, стоящие в столбцах А им нового рабочего листа, заключены в двойные кавычки. Чтобы избавиться от них, выделите столбец А, выберите команду Правка ^Удалить..., выделите столбец L (бывший столбец м) и выберите команду Правка ^Удалить... вторично. Выровняйте ширину столбца, отредактируйте метки и сохраните лист в виде рабочей книги (xls).
Предметный указатель
С
Среднее, 179 арифметическое, 180
F
F-критерий
в однофакторном анализе, 646
для фактора А, 667
для фактора В, 667
для эффекта взаимодействия факторов
А и В, 667
F-критерий для наклона, 828
F-распределение, 611
Р
р-значение, 529
Т
t-критерий
для коэффициента корреляции, 831
для наклона, 827 t-критерий для математического ожидания при неизвестном су, 540 t-распределение, 582; 597
Z
Z-критерий, 604
Z-критерий для математического ожидания при известном о, 526
Z-критерий для проверки гипотезы о доле признака, 551
А
Автокорреляция, 816 р-го порядка, 1019 второго порядка, 1019
первого порядка, 1019
Авторегрессионная модель, 1019
Альтернативные планы действий, 1076
Анализ временных рядов, 985
Анализ причинно-следственных зави-
симостей, 985
Асимметрия
отрицательная, 196
положительная, 196
Аудит, 480
Б
Базовые показатели, 213
В
Вариация
взаимодействия, 666
внутригрупповая, 643; 645
межгрупповая, 643; 645
необъяснимая, 806
неслучайная, 1119
объяснимая, 806
полная, 644; 665; 806
случайная, 1119
фактора А, 665
фактора В, 665
Вероятность, 253
безусловная, 255
доверительная, 523
ошибки 1-го рода, 523
ошибки 2-го рода, 523
совместного события, 256
условная, 266
Временной ряд, 985
Выбор
без возвращения, 46
с возвращением, 46
Выборка
вероятностная, 45
детерминированная, 44
кластерная, 49
систематическая, 48
стратифицированная, 49
Выборки
зависимые, 596
независимые, 581
парные, 595
Выборочное пространство, 254
Г
Гипотеза
альтернативная, 521
нулевая, 520
Гипотеза о разности двух дисперсий
F-критерий, 611
Гипотеза о разности математических ожиданий
зависимые группы
t-критерий, 597
Z-критерий, 596
независимые группы
t-критерий
использующий объединенную диспер-
сию, 581
использующий раздельную диспер-
сию, 588
Z-критерий,581
Гистограмма, 111
Гомоскедастичность, 811
График нормального распределения, 369
Графический хлам, 143
Графическое представление данных, 142
д
Дерево решений, 267
Диаграмма
блочная, 214
круговая, 125
линейчатая, 125
параллельная, 136
Парето, 126
точечная, 182
Диаграмма разброса, 793
Диаграмма:, 100
Дисперсионный анализ, 643
двухфакторный, 664
однофакторный, 643
Дисперсия, 187
MSA, 666
MSAB, 666
MSB, 666
MSE, 666
выборочная, 190
генеральной совокупности, 206
дискретной случайной величины, 296
суммы двух случайных величин, 301
Доверительный интервал
для доли признака, 466
односторонний, 487
для математического ожидания
при известном стандартном отклоне-
нии, 451
при неизвестном стандартном отклонении, 458
для математического ожидания откли-
ка, 836
для общей суммы, 481
для полной разности, 484
для предсказанного значения отклика,
837
односторонний, 487
разность математических ожиданий,
588
средняя разность, 601
Доверительный уровень, 451
Дополнение, 254
Допускаемый предел, 1143
3
Закон больших чисел, 388
И
Извлечение квадратного корня, 949
Индекс, 1049; 1050; 1051
Индекс цен
Лапейрэ, 1053
Пааше, 1053
составной
взвешенный, 1053
невзвешенный, 1051; 1053; 1054
Интеллектуальный анализ данных, 962
Интервал группирования, 105
Информативность рисунка, 142
Источник данных
вторичный, 42
К л
Квантиль стандартизованного нормального распределения, 370
Квартиль, 185
первый, 185
третий, 186
Класс, 105
Классическая мультипликативная мо-
дель, 985
Ковариация, 300
Компонент временного ряда
сезонный, 986
случайный, 986
циклический, 985
Контрольная граница
верхняя,1120; 1143
нижняя, 1120; 1143
Контрольная карта, 1119
р-карта, 1121
для переменных, 1132
для размаха, 1132
для среднего значения X ,1135
качественных признаков, 1121
Коэффициент
вариации,194
корреляции, 222
регрессии, 796
смешанной корреляции, 808
Коэффициент инфляции, 956
Коэффициент множественной смешанной корреляции, 879
Коэффициент частной корреляции, 903
Коэффициент чистой регрессии, 876
Кривая распределения, 113
Критерий
двусторонний, 527
для проверки гипотезы о доле признака в генеральной совокупности, 551 Крускала-Уоллиса, 748 направленный, 535 односторонний, 535
Уилкоксона, 748
устойчивый, 547
Критерий "доходность/риск", 1088
Критерий Левенэ, 656
Критерий принятия решений, 1076
Критерий хи-квадрат
для проверки независимости, 730
для сравнения двух долей, 710
Критический размах, 653
Критическое значение, 452; 523
Логарифмическое преобразование, 951
м
Математическое ожидание, 206;
387; 430
дискретной случайной величины, 295
суммы двух случайных величин, 301
Медиана, 183
Метод выбора наилучшего подмножества, 962
Методы качественного прогнозирования, 985
Методы количественного прогнозиро-
вания, 985
Множественное сравнение, 675
Мода, 184
Модель тренда
квадратичная, 1002
линейная, 999
экспоненциальная, 1004
Мощность критерия, 524
н
Наклон, 793
Непараметрическая процедура, 587
Нормирующее преобразование, 587
О
Обратное преобразование, 370
Общее среднее, 644
Объем выборки
для оценки доли признака, 474
для оценки среднего, 471
Ожидаемая прибыль, 1083
Ожидаемая прибыль в условия полной
определенности, 1086
Ожидаемая стоимость полной инфор-
мации, 1085
Ожидаемый размер упущенной выго-
ды, 1085
Остаток, 812
Отбрасывание данных, 558
Отклик,792
Относительная разность, 1011
Оценка
интервальная, 449
несмещенная, 386
точечная, 448
общей суммы, 481
Очистка данных, 558
Ошибка
1-го рода, 523
2-го рода, 523
выбора систематическая, 58
выборки, 59
измерения, 59
связанная с отказами от ответов, 58
связанная с охватом исследования, 58
случайная, 666
эксперимента, 643
Ошибка выборочного обследова-
ния, 471
п
Переменная
зависимая, 792
независимая, 792
объясняющая, 792
План
полностью рандомизированный, 642
факторный, 642
Плотность
нормального распределения, 349 стандартизованного нормального распределения, 350
Повторные измерения, 595
Подтасовка данных, 558
Подход
априорный, 253
субъективный, 253
эмпирический, 253
Показатель качества, 1145; 1146
Полезность, 1101
Полигон
накопленных частот, 113
процентный, 112
Полный контроль качества, 1115
Портфельные инвестиции, 302
ожидаемая доходность, 302
риск,302
Пошаговая регрессия, 960
Правило
сложения вероятностей, 258
сложения вероятностей взаимоисклю-
чающих событий, 258
сложения вероятностей исчерпывающих событий, 259
умножения вероятностей, 270
умножения вероятностей независимых
событий, 271
Принцип экономии, 1034
Проверка гипотез, 520
Процедура
ANOVA
двухфакторная, 664
однофакторная, 643
апостериорного сравнения, 653
множественного сравнения, 653
Тьюки-Крамера, 653
Процесс
контролируемый, 1121
неконтролируемый, 1121
поддающийся статистическому кон-
тролю, 1121
Пуассоновский процесс, 320
Р
Разброс
процесса, 1145
спецификации, 1145
Размах, 188
межквартильный, 189
средний,189
Разность
второго порядка, 1011
первого порядка, 1011
Ранговый критерий Уилкоксона
для больших выборок, 740
для малых выборок, 739
Рандомизация, 557
Распределение
асимметричное, 196
биномиальное, 307
выборочное, 386
выборочной доли, 403
гипергеометрическое, 316
дискретное, 294
накопленных процентов, 108; 113
нормальное, 347
относительных частот, 107
процентное, 107
Пуассона, 320
равномерное, 379
симметричное, 196
стандартизованное нормальное,
350;456
Стьюдента, 456
частот, 105
экспоненциальное, 382
Регрессия
множественная, 792
простая линейная, 792
Реплика, 664
С
Сводная таблица ANOVA, 647
Сдвиг, 793
Скользящее среднее, 989
Скорректированный коэффициент г2,880
Случайная величина, 52
дискретная, 52
категорийная, 52
непрерывная, 52
числовая, 52
Событие
достоверное, 253
невозможное, 253
совместное, 254
элементарное, 254
Событие или экономическое положение, 1076
События
взаимоисключающие, 257
исчерпывающие, 257
Совокупность
основная, 43
Сочетания, 308
Среднее
выборочное, 180
геометрическое, 186
Среднее абсолютное отклонение, 1034
Среднеквадратическая ошибка, 809
Средняя разность, 484
Стандартная ошибка, 1033
доли признака, 402
среднего, 389
Стандартное отклонение
выборочное, 190
генеральной совокупности, 207; 387
дискретной случайной величины, 296
суммы двух случайных величин, 301
Стандартное отклонение разностей, 484
Статистика Дурбина-Уотсона, 820
Статистическая назависимость, 269
Статистический пакет, 35
Страта, 49
Сумма квадратов
внутригрупповая, 645
межгрупповая, 645
ошибок, 666; 806
полная, 645; 665; 806
регрессии, 806
соответствующая фактору А, 665
соответствующая фактору В, 665
средняя,646
учитывающая взаимодействие между
факторами А и В, 665
т
Таблица
перекрестной классификации, 254; 709 перекрестной классификации с двумя входами, 134
сводная, 124
сопряженности признаков, 134;
254;709
факторная, 134; 254; 709
Таблица выигрышей, 1076
Таблица случайных чисел, 46
Тенденция, 223
Теорема Байеса, 276
У
Упорядоченный массив, 99
Упущенная выгода, 1079
Уровень
доверительный, 523
значимости, 523
наблюдаемый, 529
риска, 524
Ф
Фактор, 642
Фактор лжи, 143
Фокус-группа, 43
Формула преобразования, 350
ц
Центральная предельная теорема, 394
ч
Частный F-критерий, 898
э
Эксперимент
полностью рандомизированный, 642
факторный, 665
Экспоненциальное сглаживание, 992
Эффект
взаимодействия, 670; 910
главный, 670
условий эксперимента, 643
Научно-популярное издание
Дэвид М. Левин, Дэвид Стефан, Тимоти С. Кребиль, Марк Л. Беренсон Статистика для менеджеров с использованием Microsoft Excel 4-е издание
Литературный редактор Верстка Художественный редактор Корректоры
О.Ю. Белозовская
О.В. Мишутина
С.А. Чернокозинский
З.В. Александрова, Л.А. Гордиенко, О.В. Мишутина, Л.В. Чернокозинская
Издательский дом “Вильямс”.
101509, Москва, ул. Лесная, д. 43, стр. 1.
Подписано в печать 27.12.2004. Формат 70X100/16. Гарнитура Times. Печать офсетная.
Усл. печ. л. 107,07. Уч.-изд. л. 83,00.
Тираж 3000 экз. Заказ № 58.
Отпечатано с диапозитивов в ФГУП “Печатный двор” Министерства РФ по делам печати, телерадиовещания и средств массовых коммуникаций. 197110, Санкт-Петербург, Чкаловский пр., 15.
2005
Статистика для менеджеров с использованием
Microsoft* Excel
ЧЕТВЕРТОЕ ИЗДАНИЕ
Учебник Статистика для менеджеров с использованием
Microsoft" Excel произвел переворот в обучении бизнес-статистике. Это первый учебник, использующий программу Microsoft* Excel в качестве инструмента для статистического анализа.
Книга быстро стала бестселлером. В ней рассмотрены методы анализа данных, дана интерпретация результатов, полученных с помощью программы Microsoft* Excel, а также указаны основные статистические концепции, позволяющие принимать обоснованные решения.
Новинка! Углубленное описание программы Excel
Для интерпретации результатов статистического анализа в каждой главе широко используется программа Excel. Книга содержит четкие и ясные инструкции, позволяющие проводить статистические расчеты как с помощью стандартных средств программы Microsoft* Excel, так и с помощью надстройки PHStat2. В каждую главу включены разделы справочника по Excel, содержащие подробное описание программы.
Новинка! Более полное описание проверки гипотез
В главах 8 и 9 теперь описаны все критерии, использующие нормальное распределение и Г-раопределение. F-критерий помещен в конец главы 9, что позволяет преподавателям создавать более гибкие учебные планы. Описания критерия "хи-квадрат" и непараметрических критериев объединены в одной главе.
PEARSON
Prentice Hall
Посетите Издательский дом "Вильямс"
Internet по адресу: http y/wvcw.wIBamipcitahl ng.com
Посетит» Prentke Hill
Internet no адресу: httpj'/www.pwhaU.com
StudentAid.ed.gov