Author: Райзер Ю.П.
Tags: электричество магнетизм электромагнетизм физика
ISBN: 5-02-014615-3
Year: 1992
Text
ТО. П. РАЙЗЕР
ФИЗИКА
КАЗОВОГО
РАЗРЯДА
ИЗДАНИЕ ВТОРОЕ,
ПЕРЕРАБОТАННОЕ И ДОПОЛНЕННОЕ
МОСКВА «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИ И1КО М АТГМ АТИЧЕСКОЙ ЛИТГ РАТУРЫ
1992
ББК 22 33
Р18
УДК 537(075.8)
Рекомендовано Государственным komuiетом СССР
по народному образованию
для использования в учебном процессе
студентами физических специальностей
высших учебных заведений
Г < цензент
дом эр физико-математических наук А В Елецкий
Раизер Ю П Физика газовою разряда: Учеб руководство: Для ву-
зов — 2 е изд, перераб и доп — М На^ка. Гл. ред. физ.-мат. лит, 1992 —
536 с —ISBN 5-02 014615 3.
На современном уровне рассмотрен широкий круг проблем физики га-
зово] о разряда: элементарные процессы, взаимодействие постоянного и пе-
ременных электрических полей с электронами плазмы, разряды всевозмож-
ных типов и другие Цель руководства — разъяснить сущность явлений, об-
легчить изучение специальной литературы, дать необходимые сведения для
исследовательской работы, для чет о приводится много фактических и спра-
вочных данных, формулы доведены до расчетного вида Новое издание
(1 е изд— 1987 т) существенно переработано и дополнено результатами
последнего времени за счет сокращения вспомогательного материала.
Для студентов и аспирантов физических и технических специальностей
вузов, а также для научно технических работников в области газовой элект-
роники и физики плазмы
Табл 28 Ил 269. Библиогр : 217 назв
Учебное издание
РАЙЗЕР Юрии Пегрозич
ФИЗИКА ГАЗОВОГО РАЗРЯДА
Иведующт й редакцией Л И Гладнева
Редакторы Н А Михалина, Д А Миртова, Л П Русанова
М 1ацший редактор В А Кузнецова Художественный редактор Г. М Коровина
3схн1ческ[й 1 едактор Л В Лихгчева Корректор Т К Кармаъулова
НЬ X 112^8
( i<iно в набор 09 09 91 Подписано к печати 2е* 10 92 Формат 60x90/16 Бумага
uni X 2 Гарнитура обыкновенная Печать высокая Усл печ т 33,5 Усл кр-
он > Уч изд I 6,->з Тираж 1026 экз Заказ № 1006 С—^92
II орле и < ко и рои родственное и книготорговое объединен ie «Наука»
Г hi иная р г пан я а т 1 гчо математической литературы
117071 Miiihiii В-71 книнский проспект, 15
Ч(1вер1)я 1 пно! р ) |н I гздательства «Наука»
( 0077 । 11ово( ибн।(। ул Станиславского, 2э
1604050000 092 'С) «Наука» Физматлит 198”;
I* (У53|()2) -92 89-91 с изменениями, 1992
ISBN 5-02-0Vi615-3
ОГЛАВЛЕНИЕ
Предисловие ко второму изданию 8
Предисловие к первому изданию 9
Глава! Введение 11
§ 1 Что изучает физика 1азового разряда 11
§ 2 Типичные разряды в постоянном электрическом поле 12
§ 3 Классификация разрядных процессов 14
§ 4 Коротко 0(5 истории исследования разрядов 15
Ч \ С Т Ь I ЭЛЕМЕНТАРНЫЕ ПРОЦЕСС Ы И ЭЛЕМЕНТЫ РАЗРЯД-
НЫХ ПРОЦЕССОВ
Глава 2 Столкновения электронов и ионов с атомами, молекулами
и друг с другом , 18
§ 1 Основные понятия физит и атомных стол! новепии и i и нети
ческой теории i азов 4 18
§ 2 ^пруюе рассеяние элет тропов центральными атомами и мо
лекулами * 22
§ 3 Столкновения ионов с центральными чкппрчи 26
§ 4 Упругие столкновения мс i iy заряженными частицами 29
§ 5 Неупрунге столкновения злектропов с атомами и молекула
ми 32
Глава 3 Дрейф, энергия и диффузия заряженных частиц в постоям
ном поле 40
§ 1 Дрейф элет тронов в слабоиопизоваппом газе 41
§ 2 Проводимость иопизоваппого газа 44
§ 3 Энергия электронов 45
§ 4 Диффузия )лектропов 51
§ 5 Попы 54
§ 6 Амбиполярная щффузия 58
§ 7 Протекание электрическою тока в плазме в присутствии про
дольных градиентов плотности зарядов 61
§ 8 Гидродинамическое описание электронов 64
§ 9 Движение зарядов в газе в присутствии магнитного поля 65
Глава 4 Образование и гибель заряженных частиц в газе 68
§ 1 Ионизация электронным ударом в постоянном поле 68
§ 2 Другие механизмы ионизации 75
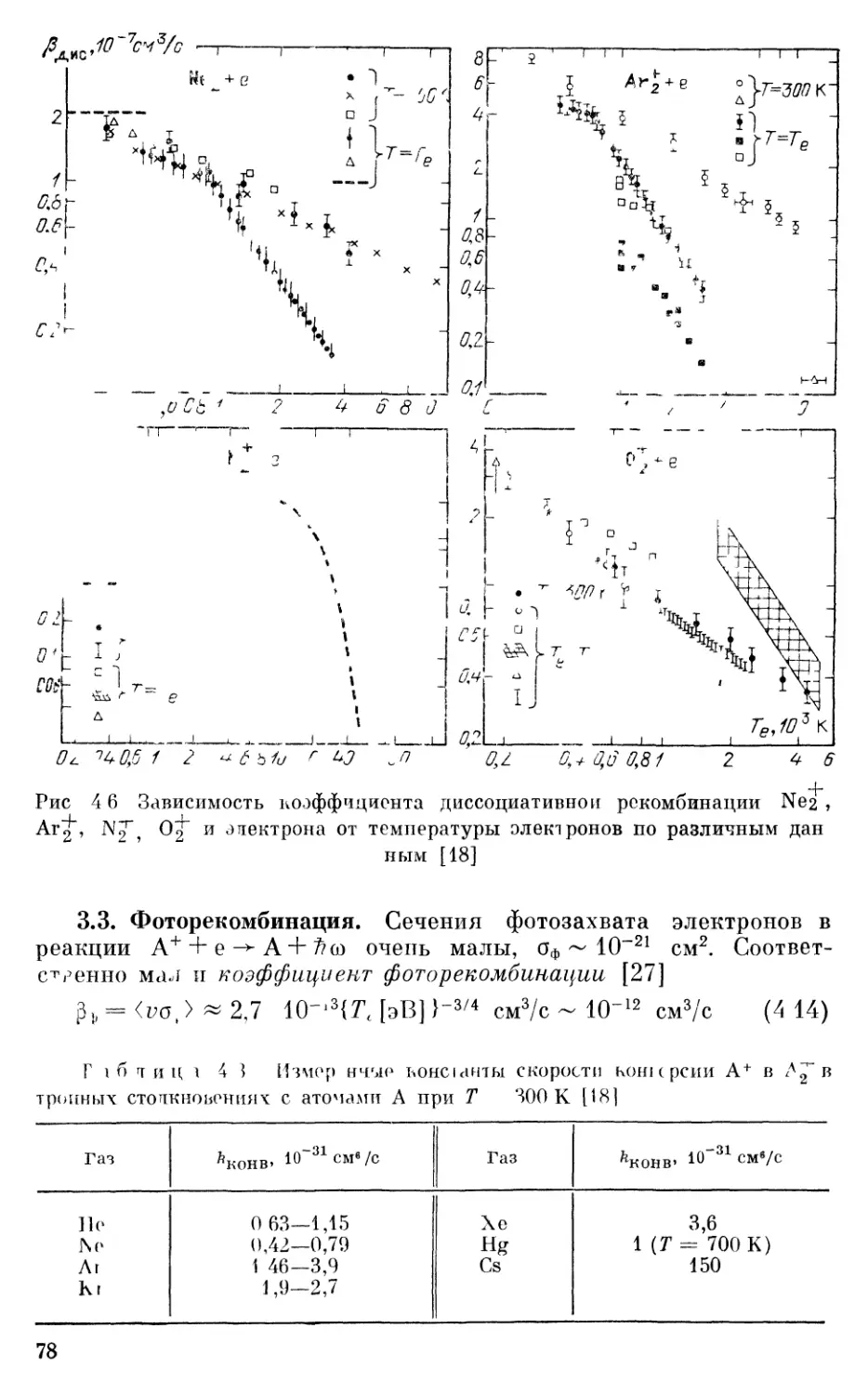
§ 3 Объемная рекомбинация . . ... 77
3
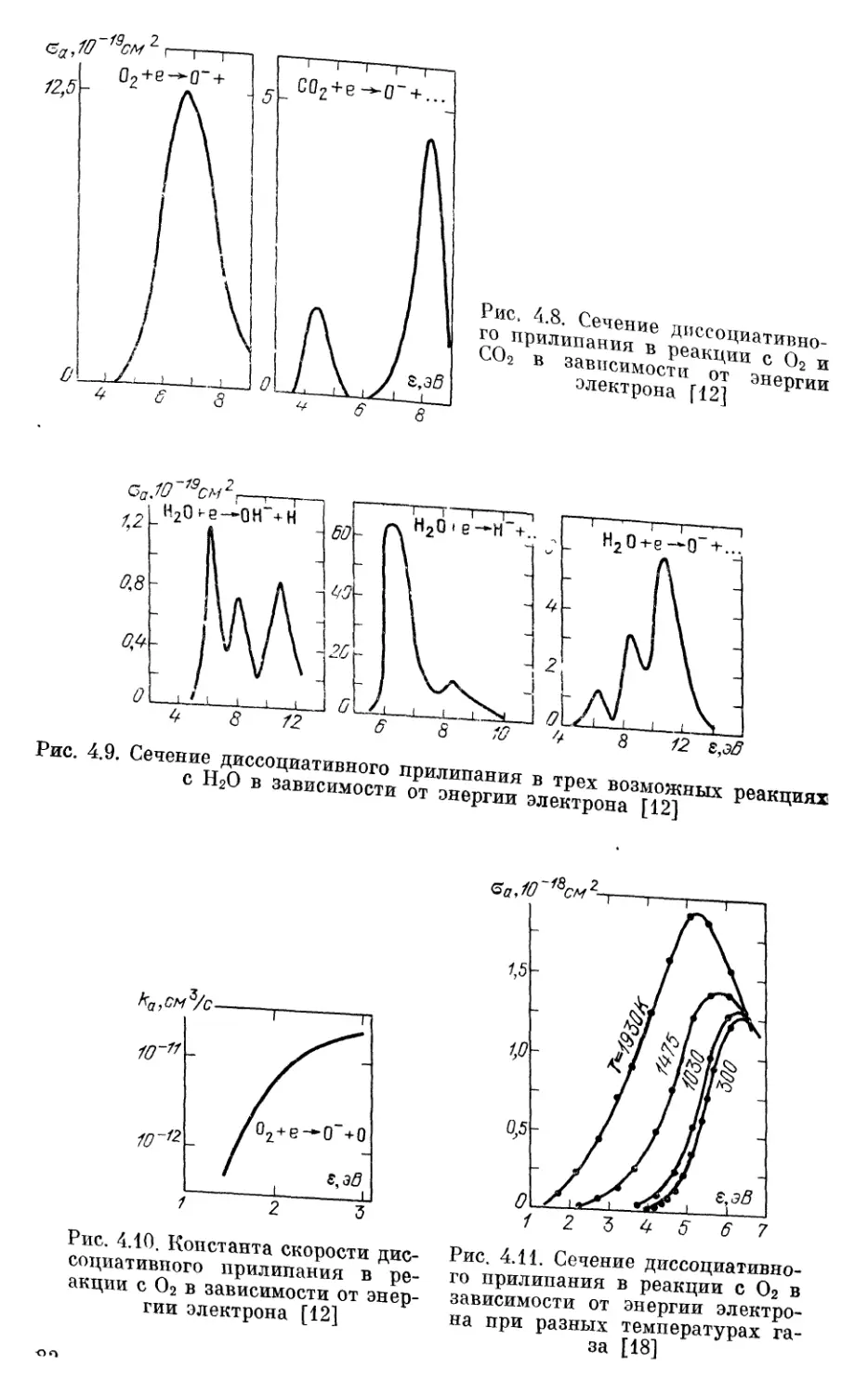
\ Обр । ion инк II разрушение отрицательных ионов НО
5 Диффу шопныс потери зарядов 85
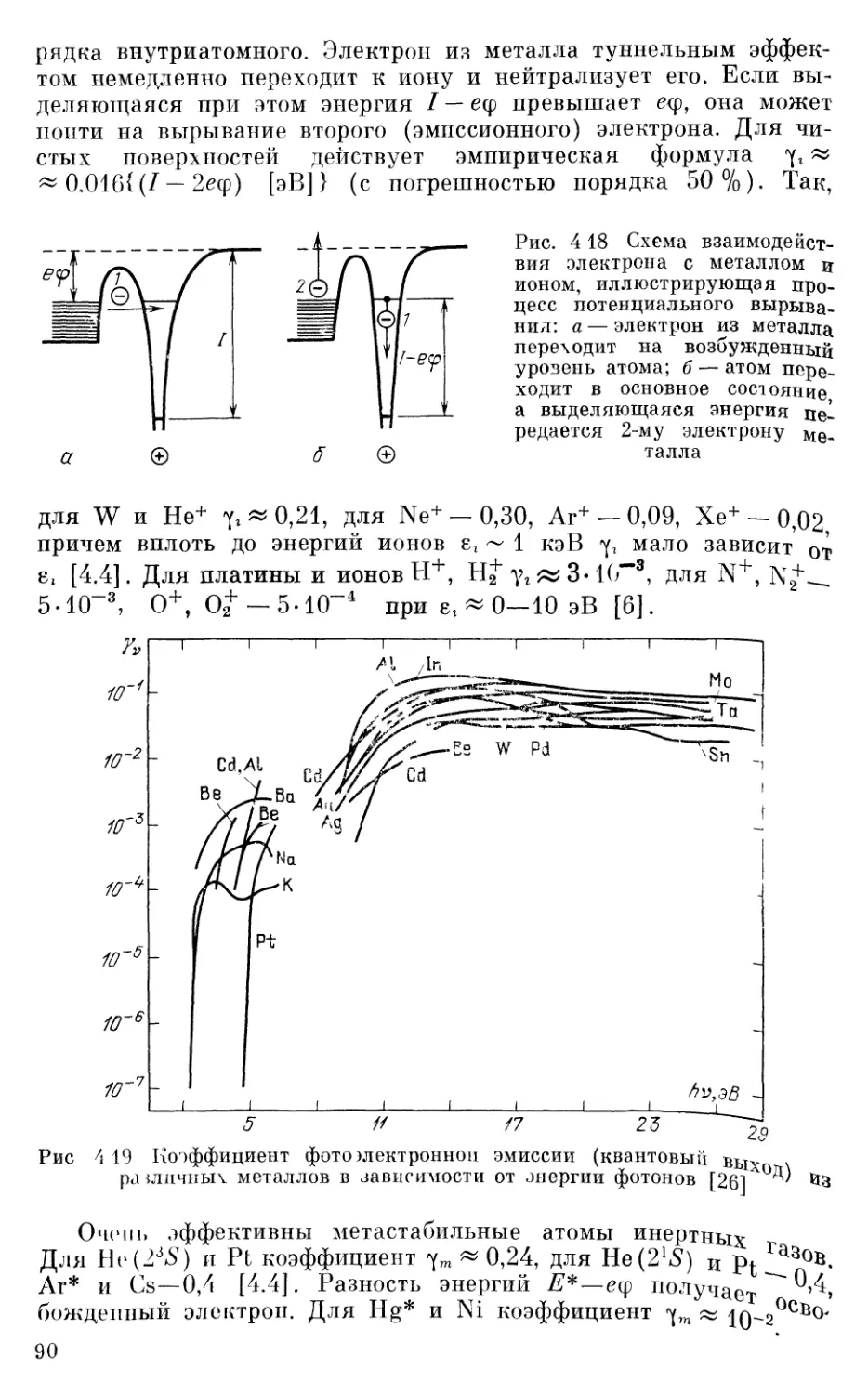
§ 6 Эмиссия электронов из твердых тел 86
§ 7 Размножение зарядов в газе через вторичную миссию ’И
Глава 5 Взаимодействие электронов ионизованного газа с перемен
ными электрическими полями и электрома! питыми излучениями 95
§ 1 Колебания электронов в осциллирующем ноле 95
§ 2 Энергия электронов . 97
§ 3 Основные уравнения электродинамики сплошных сред 101
§ 4 Высокочастотные проводимость и диэлектрическая проницае-
мость плазмы 104
§ 5 Распространение электромагнитных волн в плазме • 109
§ 6 Полное отражение электромагнитной волны от плазмы 111
§ 7 Плазменные колебания и волны ИЗ
§ 8 Обмен квантами меж ту полем излучения и свободными
электронами в газе 117
§ 9 Полуклассичеспий способ нахождения квантовых коэффици
ентов 121
§ 10 Фактические границы применимости классического подхо
да к эффектам взаимодействия 123
I лава 6 Излучение п поглощение света плазмой
§ 1 Типы радиационных переходов 123
§ 2 1ормозное излучение при столкновениях электронов с
ионами 124
§ 3 Рекомбинационное излучение . . . 125
§ 4 Полное испускание в непрерывном спектре 128
§ 5 Поглощение в непрерывном спектре 130
§ 6 Излучение спектральных линий 135
§ 7 Селективное поглощение 140
§ 8 Молекулярные спектры 142
§ 9 Перенос излучения выход его из плазменного объема ра
диациопные потери 145
§ 10 Принцип действия лазера 152
ЧАСТЬ II ФУНДАМЕНТАЛЬНЫЕ МЕТОДЫ ТЕОРЕТИЧЕСКОГО
И ЭКСПЕРИМЕНТАЛЬНОГО ИССЛЕДОВАНИЯ РАЗРЯДНОЙ
ПЛАЗМЫ 155
Глава 7 Кинетическое уравнение для электронов в слабоионизо-
ванном газе, находящемся в поле 155
§ 1 Описание электронных процессов при помощи функции
распред* пения по скоростям 155
§ 2 Формулировка кинетического уравнения 156
] Приб in 1 t пие для угловой зависимости функции распреде
лепил 161
§ '\ X о 1 вне ии< щя энергетического спектра электронов 164
§ > Ьрикрии справедливости уравнения для спектра 169
§ Ь ( р ник кис некоторых выводов вытекающих из кипетическо-
к) \р inn inn с результатами элементарной теории 172
4
§ 7 Стационарный спектр электронов в поле при действии од-
них упругих потерь..........................................174
§ 8. Численные расчеты для азота и воздуха •...........................................177
§ 9. Пространственно неоднородные поля произвольной силы . 182
§ 10. Квантовое уравнение для электронного спектра и переход
к классике................................................• 184
Глава 8. Электрические зонды . . . •...................................187
§ 1. Введение. Схема эксперимента.......................................................187
§ 2. Вольт-амперная характеристика одиночного зонда . • . 189
§ 3. Теоретические основы диагностики разреженной плазмы по
электронному току............................................191
§ 4. Техника измерения функции распределения ..... 195
§ 5. Ионный ток на зонд в разреженной плазме .... 197
§ 6. Ток в вакуумном диоде и слой пространственного заряда око-
ло заряженного тела..........................................199
§ 7. Двойной зонд .....................................................................203
§ 8. Зонд в плазме повышенного давления.................................................206
ЧАСТЬ III. РАЗРЯДЫ РАЗНЫХ ТИПОВ.............................................................212
Глава 9. Пробой газов в полях различных частотных диапазонов 212
§ 1. Сущность явления...................................................................212
§ 2. Пробой и зажигание самостоятельного разряда в постоянном
однородном поле при не слишком больших произведениях
давления на длину промежутка . ...... 214
§ 3. Эксперименты по пробою в СВЧ полях.................................................223
§ 4. Интерпретация результантов экспериментов по СВЧ пробою
па основе элементарной теории*.......................• . 226
§ 5. Вычисление частот ионизации и порогов пробоя па основе ки-
нетического уравнения.....................................• 231
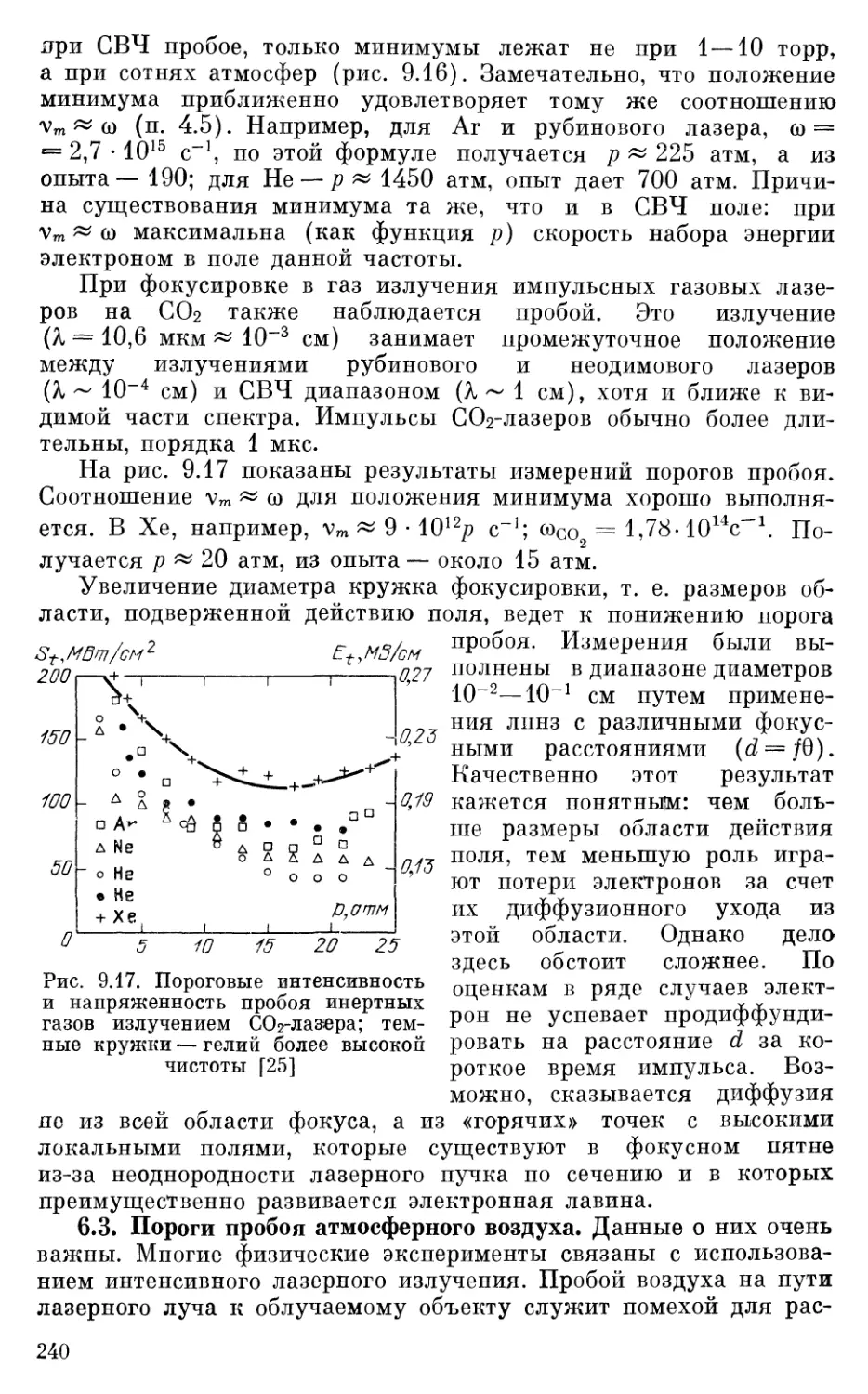
§ 6. Оптический пробой....................•.............................................237
§ 7. Способы возбуждения высокочастотного поля в разрядном
объеме..................................................... 245
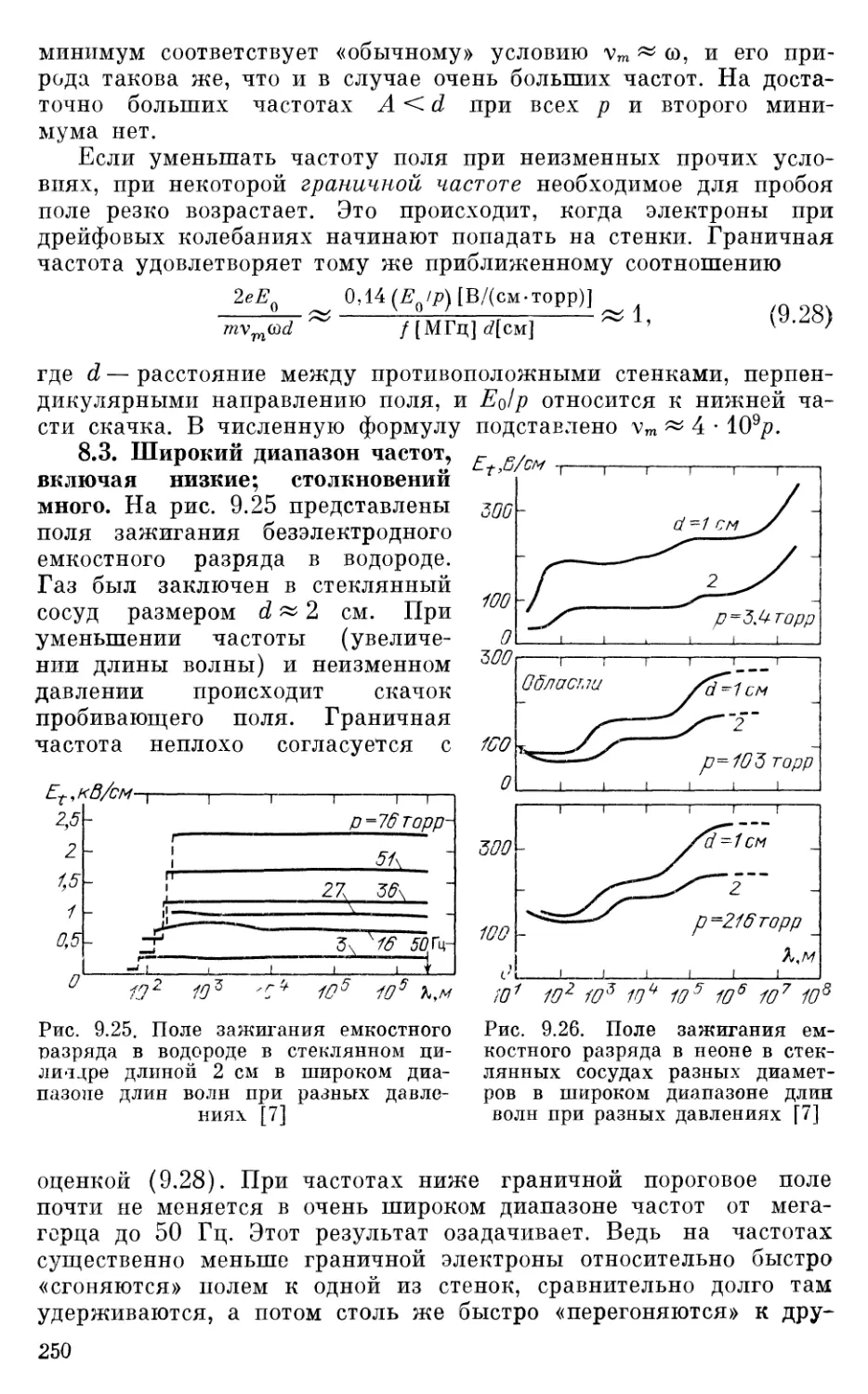
§ 8. Пробой в полях высокочастотного и низкочастотного диапа-
зонов ......................•................................247
Глава 10. Стабильный тлеющий разряд.........................................................252
§ 1. Общая структура и внешний вид . •................................................252
§ 2. Вольт-амперная характеристика разряда между электродами 258
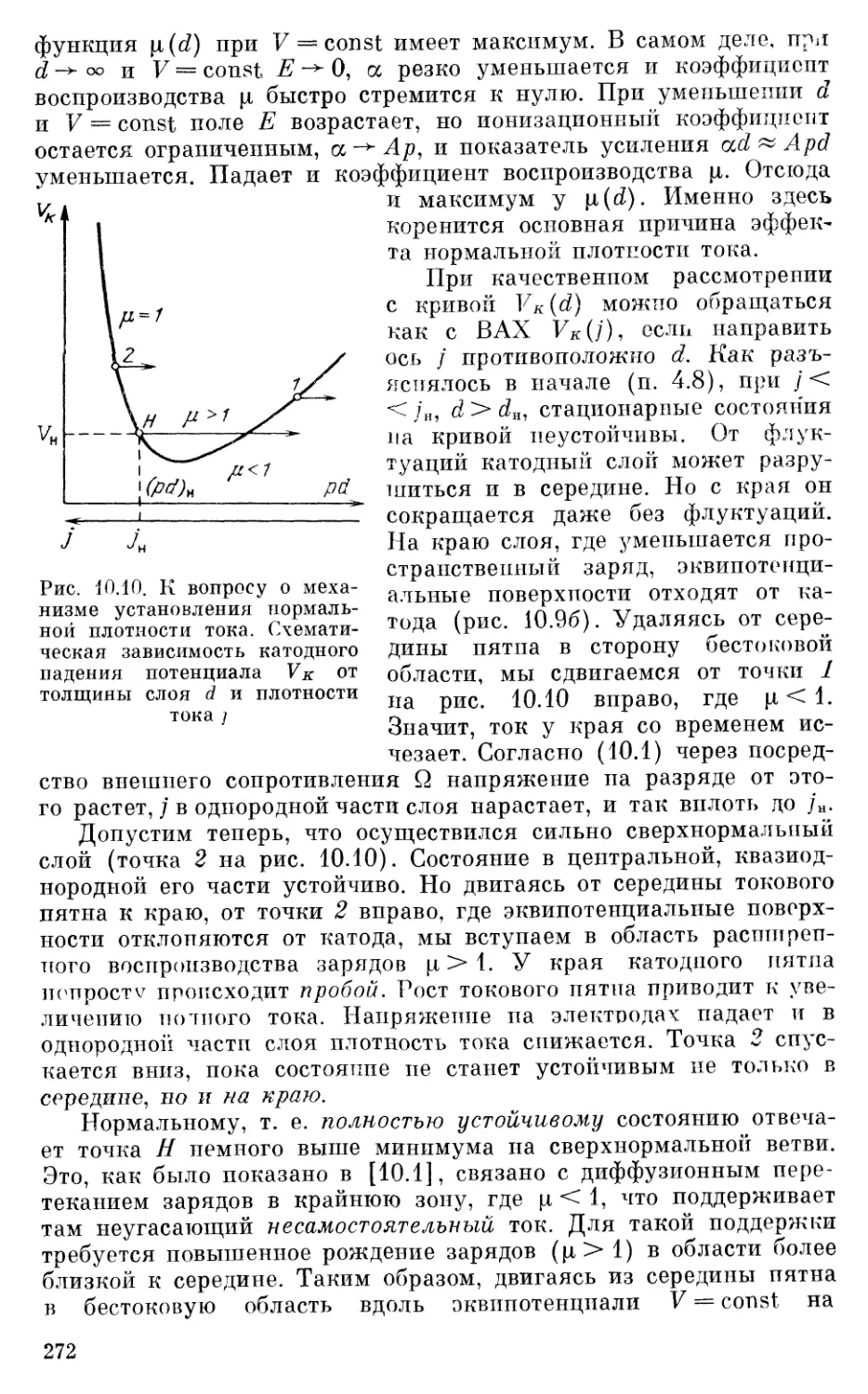
§ 3. Темный разряд и роль пространственных зарядов в образо-
вании катодного слоя................................260
§ 4. Катодный слой . •...................................................264
§ 5. Переходная область между катодным слоем и однородным
положительным столбом............................... 277
§ 6. Положительный столб . . •.....................................280
§ 7. Влияние нагрева газа на поле и ВАХ положительного
столба........................................«... 286
§ 8. Плазма электроотрицательных газов ....... 292
§ 9. Разряд в быстром потоке газа.297
§ 10. Анодный слой . 299
5
J'л пв a 11. Неустойчивости тлеющего разряда и их последствия . 300
§ 1. От чего возникают и к чему приводят неустойчивости . 3<М>
§ 2. Квазистационарпыс параметры.....................................................• 304
§ 3. Возмущения поля и электронной температуры в условиях ее
квазистационарносги.................................................................• 307
§ 4. Ионизационно-перегревная неустойчивость.......................................................................309
§ 5. Прилипательная неустойчивость . . ...... 313
§ 6. Некоторые другие часто действующие дестабилизирующие
факторы................................................315
§ 7. Страты...................................................................................................317
§ 8. Контракция положительного столба . ...... 327
Глава 12. Дуговые разряды...................... ... 332
§ 1. Определение и отличительные признаки дуги .... 332
§ 2. Виды дуг . . . •..........................................................................................333
§ 3. Зажигание дуги.......................................................• . 335
§ 4. Угольная дуга в свободном воздухе . ... • . . . 337
§ 5. Прикатодные процессы в дуге с горячим катодом . . . 338
§ 6. Катодные пятна и вакуумная дуга..............................................................................345
§ 7. Анодная область ....... .... 353
§ 8. Дуга низкого давления с искусственным накалом катода . 355
§ 9. Положительный столб дуги высокого давления (эксперимен-
тальные факты)..............................................358
§ 10. Температура плазмы и ВАХ столба дуги высокого давления 362
§ 11. Отрыв электронной и газовой температур в равновесной
плазме.............................................................................................................373
Глава 13. Поддержание и генерация равновесной плазмы в разря-
дах различных частотных диапазонов ........................376
§ 1. Введение. Баланс энергии плазмы...............................................................................376
§ 2. Столб дуги в постоянном поле...............• . . . 378
§ 3. Высокочастотный индукционный разряд ...... 379
§ 4. Сверхвысокочастотные разряды . . •............................387
§ 5. Непрерывный оптический разряд...........................................................................393
§ 6. Генераторы плотной низкотемпературной плазмы — плазмо-
троны ..................................................... 403
§ 7. Некоторые общие черты равновесных разрядов в потоке газа 408
Глава 14. Искровой и коронный разряды...............................................................................412
§ 1. Общие представления . . . •.............................................................................412
§ 2. Одиночная электронная лавина................................................................................417
§ 3. Понятие о стримере . . •...............................................................................423
§ 4. Пробой и стример в электроотрицательных, газах (воздухе)
в не очень длинных промежутках с однородным полем . 427
§ 5. Искровой канал............................• . . . 431
§ 6. Коронный разряд..................•...........................................................................433
§ 7. Модели распространения стримера..............................................................................440
§ 8. Пробой длинных воздушных промежутков с сильно неод-
нородным полем (эксперимент) •..............................449
§ 9. Лидерный механизм пробоя длинных промежутков . . 453
§ 10. Обратная волна (возвратный удар).............................................................................460
§ 11. Молния . . . . •.......................................................................................461
§ 12. Oi рпцательпый ступенчатый лидер.............................................................................466
6
Глава 15 Высокочастотный емкостный разряд 468
§ 1 Дрейфовые качания электронного газа 468
§ 2 Идеализированная модель протекания быстропеременного то
ка через длиннып плоский промежуток при повышенных
давлениях 471
§ 3 ВАХ однородного положительного столба . 475
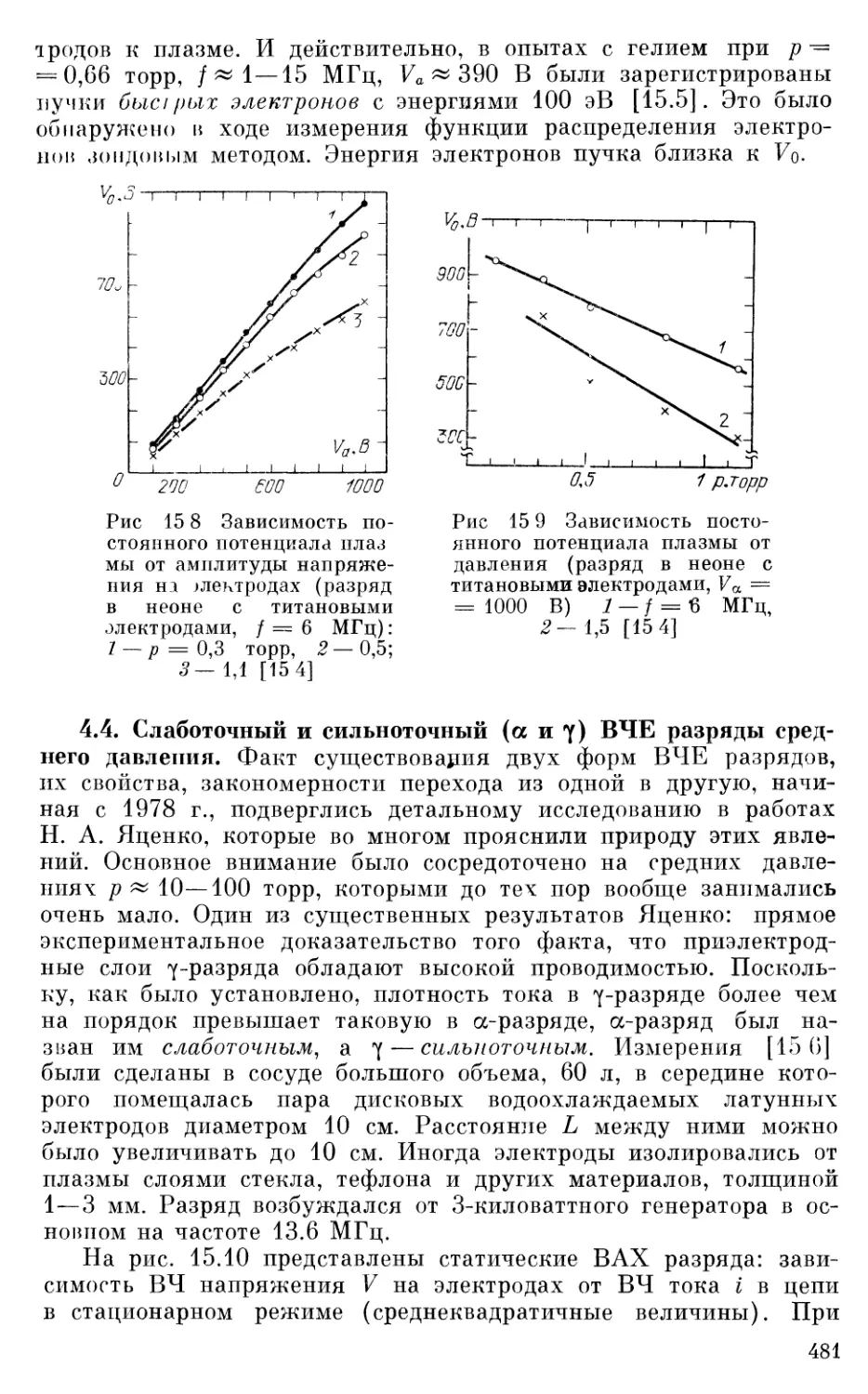
§ 4 Эксперимент — о двух формах существования ВЧЕ разрядов
и постоянном положительном потенциале пространства 478
§ 5 Электрические процессы в непроводящем приэлектродном
слое и механизм замыкания тока 486
§ 6 Постоянный положительный потенциал плазмы слаботочно
го разряда 490
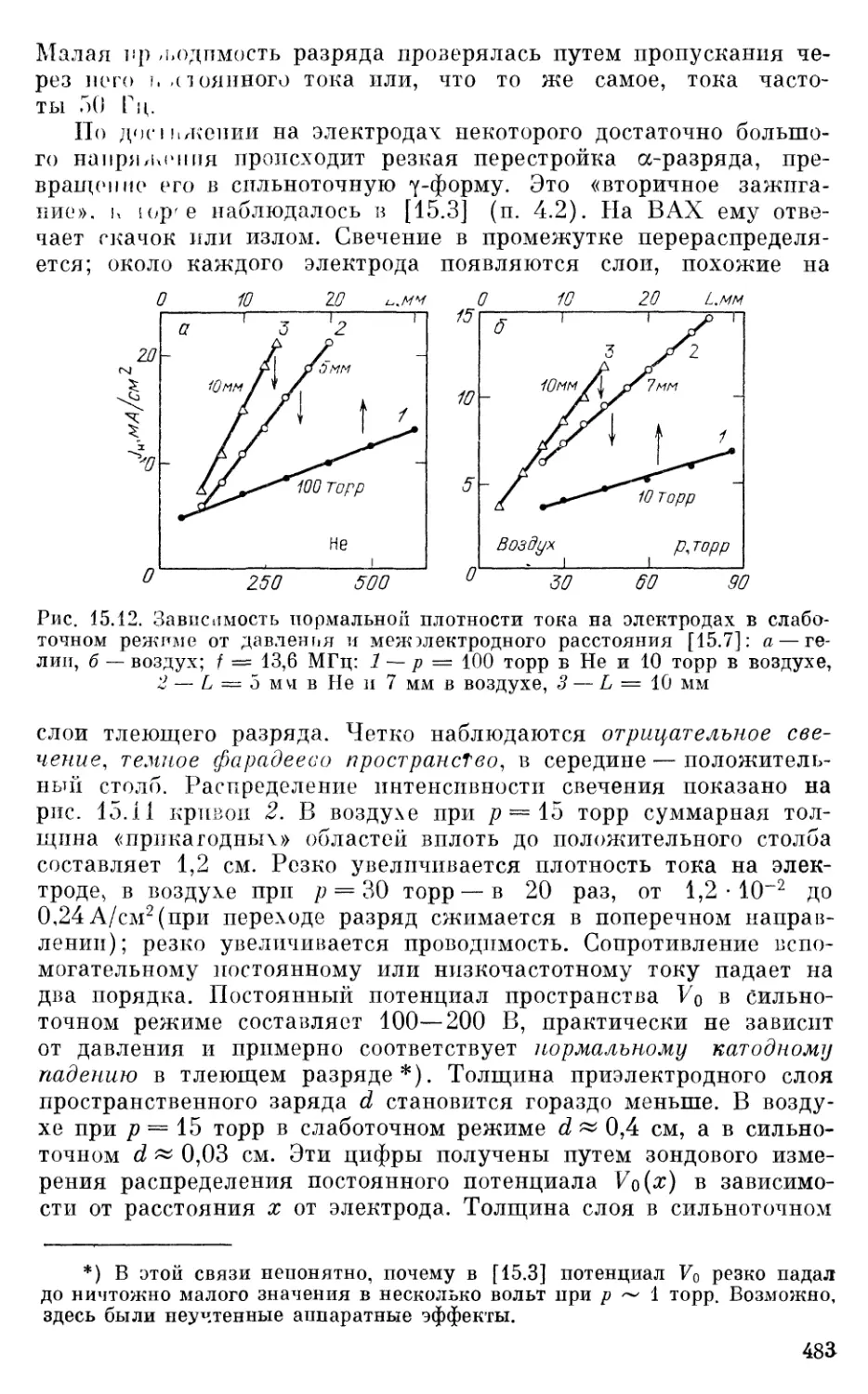
§ 7 Сильноточный режим 492
§ 8 Структура разряда среднего давления по результатам чис
лепною моделирования 499
§ 9 Нормальная плотность тока в слаботочном режиме и преде
лы его существования 503
Глава 16 Разряды в мощных СО2 лазерах непрерывною дейстгия 505
§ 1 Принцип работы электроразрядного лазера на СО2 505
§ 2 Два типа лазеров различающихся способом теплоотвода 507
§ 3 Способы борьбы с неустойчивостями 511
§ 4 Пути ор анизации разряда в больших объемах с протоком
газа . 514
Дополнение Принцип работы магнитогидродинамического гене-
ратора 521
Приложение 523
Список литературы 528
Примечания при копрекгуре 535
ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
За годы, истекшие со времени подготовки первого издания,
появились новые результаты, автор ознакомился с рядом преж-
них, отвечающих строю книги, но выпавших тогда из его поля
зрения, у него возникло более ясное понимание некоторых об-
суждаемых вопросов*). Для отражения всего этого требовался
дополнительный объем. Между тем, издательство настаивало на
сокращении книги, в конечном счете — па 13 %.
Чтобы выйти из положения, пришлось изъять материал, ме-
нее обязательный для проникновения в суть самих разрядных
явлений. Опущены главы о незондовых методах диагностики
плазмы, о термодинамических и переносных свойствах равно-
весной плазмы, сокращено разъяснение закономерностей раз-
личного рода столкновений между частицами, эмиссии электро-
нов из твердых тел. Однако фактический и справочный матери-
ал по элементарным процессам, нужный для эрудиции и работы
в области газовых разрядов, сохранен и даже пополнен.
Главы, посвященные поведению заряженных частиц в поле,
зондам, излучению плазмы, непосредственно разрядным явлени-
ям и процессам, не только не сокращены, но в соответствии
со сказанным в той или иной степени расширены. В наибольшей
мере последнее относится к искровому, тлеющему, высокочастот-
ному емкостному разрядам, в чем сказались нынешние привя-
занности автора при невозможности объять необъятное. Много
нового по сравнению с первым изданием содержится в § 8, 9
гл. 7, § 4—7 гл. 10, гл. И, § 5, 7 гл. 13, § 7-9 гл. 14, § 4,
7—9 гл. 15 (по нумерации второго издания).
В качестве руководства для занимающихся разрядами второе
издание, будем надеяться, окажется более полезным, чем первое.
Но студенту, начинающему с азов, рекомендуем не пренебрегать
п первым (в некоторых местах мы к нему отсылаем).
Автор признателен А. В. Елецкому, прочитавшему рукопись
второго издания, за многие полезные замечания и Э. М. Вазе-
лину за ценные обсуждения обновленной главы об искровом
разряде.
*) (’м примечания при корректуре в конце книги.
8
ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
Наука о газовых разрядах необходима многим физикам. Опа
нужна инженерам, специализирующимся по электротехнике, ра-
диотехнике, энергетике, электронике, светотехнике, лазерам,
нлазмохимии, сварке Изучают газовый разряд по нескольким
книгам из числа приведенных в списке литературы под началь-
ными номерами К тем же книгам обращаются за разъяснения-
ми и справками в процессе работы И хотя книги эти приобрели
заслуженную популярность, неизбежно сказывается давность их
написания Дело не в том, что устарел и потерял ценность со-
держащийся в них материал — это произошло лишь в неболь-
шой степени Сама паука сильно продвинулась в «ширину и
глубину», и в ней песко гько сместились акцепты.
Журнальная литература по разрядам выросла необозримо,
монографическая, напротив, скудна, но и та и другая чаще всего
трудны для восприятия, в особенности когда дело касается тео-
рии, тем более что газоразрядные эффекты на редкость сложны,
многогранны и запутаны Нужны новые руководства, система-
тически охватывающие широкий круг вопросов, который ныне
подключен к физике газового разряда, ясные, доступные мало-
подготовленному читателю, студенту, и вместе с тем несущие
столько и, главное, той информации, которая будет полезна и
работающим специалистам.
Такими качествами мы стара тись в рамках отпущенного объ-
ема наделить предлагаемую книгу, которая по замыслу должна
служить учебником и руководством Большое внимание в пей
уделяется четкости изложения фактов, разъяснению физической
сущности явлений и закономерностей Из необъятного материала
отобрано по возможности то, что способствует углубленному
пониманию физики и с чем чаще приходится сталкиваться со-
временному исследователю Мы стремились включить в книгу
как можно больше полезных для работы сведений: эксперимен-
тальных фактов и результатов расчетов, характерных значений
различных величин, данных справочного характера, выбирая из
всей их массы то, что удобнее иметь собранными в одном томе
под рукой Все нужные для оценок формулы доведены до ясного
расчетного вида.
9
Пз за ограниченности объема о некоторых видах разряда
пришлось говорить менее подробно, чем они тою заслуживаю!,
<i некоторых, менее распространенных форм не ь.юаться вообще.
Мы сочли целесообразным полностью отказаться от рассмотре-
ния практических схем, техники, методики (но не идейной сто-
роны) экспериментов и измерений, чтобы сосредоточиться па
физике самих исследуемых процессов. По той же причине мы
не затрагиваем чисто технических приложений газового разряда.
Ссылки на оригинальные статьи даются только при изло-
жении чьих-то конкретных результатов не очень давнего вре-
мени или указаний на таковые. В остальных случаях чаще всего
указываются книга или обзор, где ссылки имеются, или же
откуда был взят какой-то график или другой справочный мате-
риал. При таком охвате тематики давать сколько-нибудь полную
библиографию было бы немыслимым. Достаточно сказать, что
в книге Н. А. Капцова 1950 г. содержится 2524 ссылки. Сейчас
при такой же полноте цитирования их было бы на порядок
больше.
Автор глубоко благодарен А. В. Елецкому и Л. Д. Цендину,
которые прочли рукопись и сделали много полезных замечаний,
а также Н. М. Сериковой за большую помощь при ее подготовке.
Октябрь 1986 г.
Глава 1. ВВЕДЕНИЕ
§ 1. Что изучает физика газового разряда
Термин «газовый разряд» происходит от обозначения процесса
разрядки конденсатора через цепь, включающую в себя газовый
промежуток между электродами. При достаточно высоком на-
пряжении в газе происходит пробой и возникает ионизованное
состояние. Со временем разрядом стали называть всякий про-
цесс протекания электрического тока через ионизованный газ,
а также любой процесс возникновения ионизации под действием
приложенного электрического поля. Поскольку в достаточной сте-
пени ионизованный газ светится, стали говорить: зажигается раз-
ряд, горит, гаснет.
Протекание электрического тока обычно ассоциируется с
представлением о цепи, составленной из проводников. Но в бы-
стропеременных электрических полях, а тем более в поле элек-
тромагнитных излучений для направленного движения зарядов,
т. е. электрического тока, вовсе не требуется присутствия зам-
кнутой цепи и электродов. Вместе с тем многие эффекты, ко-
торые наблюдаются в газе при действии переменных полей и
электромагнитных волн: пробой, поддержание состояния иони-
зации, диссипация энергии поля, в принципе не отличаются от
того, что происходит в постоянном поле. Все подобные процессы
теперь называют разрядными и включают в физику газового
разряда. Вообще факт протекания незамкнутых электрических
токов в полях электромагнитных волн не имеет никакого зна-
чения. О диссипации энергии поля в этих случаях говорят не
как о выделении джоулева гепла электрическим током, а как
о поглощении излучения.
Итак, современная физика газового разряда изучает процес-
сы, связанные с протеканием электрического тока в газах, с воз-
никновением и поддержанием под действием поля самой спо-
собности газа проводить электричество и поглощать электромаг-
нитные излучения.
Физика газового разряда охватывает великое множество слож-
ных, запутанных, многогранных явлений, насыщена невообрази-
мым количеством экспериментальных фактов и теоретических
построений. Приступая к их изучению, целесообразно выделить
основные типы разрядных процессов и классифицировать их.
11
§ 2. Типичные разряды
в постоянном электрическом поле
( пс( ьоиышми важнейшими видами разрядов можно позна-
комнндя П1)н помощи сравнительно простого эксперимента. Два
Mei <» । л и чес кн \ электрода А и К, подключаемых к источнику по-
сюянпок) напряжения, вводят в стеклянную трубку (рис. 1.1).
Трубку можно откачивать и наполнять разными газами при раз-
ных давлениях При проведении опыта измеряют напряжение
на электродах и ток в цепи. Это классическое устройство уже
150 лет служит для изучения разрядных процессов и не утра-
тило своего значения и поныне.
Если подать па электроды небольшое напряжение, скажем
десятки вольт, никаких видимых эффектов не произойдет, но
сверхчувствительный прибор зарегистрирует протекание чрезвы-
чанно слабого тока, может быть 10 15 А. Под действием косми-
ческого излучения и естественной радиоактивности в газе обра-
зуются заряды. Поле вытягивает их к электродам противополож-
ного знака, что дает ток. Можно получить ток до 10-6 А, если
специально облучать газ радиоактивным или рентгеновским ис-
точником. Но все равно соответствующая ионизация слишком
мала, чтобы газ светился. Разряд и электрический ток, которые
возникают только благодаря действию постороннего ионизую-
щего агента или в результате эмиссии электронов или ионов
с электродов под действием посторонних причин (например,
вследствие накаливания катода), называют несамостоятельными.
При увеличении напряжения несамостоятельный ток сначала
возрастает, так как все большую часть зарядов удается вытя-
нуть па электроды до того, как они прорекомбинируют. Но ког-
да поле успевает вытягивать все образующиеся заряды, ток
перестает расти и достигает насыщения, ибо он лимитируется
скоростью образования ионов
Далее, если увеличивать напряжение, при некотором его зна-
чении ток резко возрастает и появляется свечение Это проис-
ходит пробой — один из важнейших разрядных процессов При
давлении р ~ 1 торр 1 мм рт. ст. и межэлектродном расстоя-
нии L ~ 1 см напряжения пробоя составляют несколько сотен
вольт. Пробой начинается с некоторого числа случайных или
______________________ искусственно впрыснутых электро-
@ нов, когда хотят стимулировать
_______________________Z/ процесс Но разряд немедленно
Рис 1 1 Газоразрядная трубка приобретает самостоятельность и
пе нуждается больше в посторон-
ней поддержке. В поле электрон ускоряется и набирает энергию.
Достигнув потенциала ионизации атомов, он вырывает другой
электрон, затрачивая на это приобретенную энергию. В резуль-
тате такого акта ионизации появляются два медленных элект-
рона Они повторяют тот же цикл, и т. д. Так развивается элек-
тронная лавина и происходит размножение электронов За 10~7—
12
10~3 с газ ионизуется заметным образом, и электрический ток
вырастает на несколько порядков.
Дальнейший ход процесса зависит от ряда условий. При не-
больших давлениях (например, 1 —10 торр) и большом элек-
трическом сопротивлении внешней цепи, которое не позволяет
течь большому току, в результате пробоя зажигается тлеющий
разряд — один из наиболее распространенных и важных типов
разряда. Для него характерны небольшая сила тока (i ~ 10-ь—
10“1 А в трубках радиусом R ~ 1 см) и довольно высокое на-
пряжение (сотни и тысячи вольт). В достаточно длинной трубке
(скажем, L ~ 30 см) при р ~ 1 торр образуется однородный по
длине, красиво светящийся столб. Так делают красочные рек-
ламные трубки для улиц.
Практически повсюду, за исключением приэлектродпых об-
ластей, ионизованный газ в столбе электропейтрален, т. е. пред-
ставляет собою плазму. Это — так называемый положительный
столб тлеющего разряда. Плазма в нем ионизована очень слабо,
до степени ионизации 10~8—10~6, н в двух отношениях не рав-
новесна. Электроны, непосредственно приобретающие энергию от
поля, обладают средней энергией j ~ 1 эВ и температурой Те ~
~ 104 К. Между тем температура газа, в том числе и ионов.
Т не на много/превышает температуру окружающей среды 300 К.
Такое неравновесное состояние с сильным отрывом электронной
и газовой температур поддерживается из-за малой скорости вы-
деления джоулева тепла при относительно больших теплоемкости
газа и скорости его естест^ппого охлаждения. Неравновесна
и степень ионизации. Она па много порядков ниже термодина-
мически равновесной величины, соответству ющей температуре
электронов. Это происходит из-за большой скорости гибели за-
рядов в холодном газе.
.Если давление газа высоко, порядка атмосферного, а сопро-
тивление внешней цепи мало, з а к что цепь может пропустить
сильный ток, вскоре после пробоя обычно зажигается дуговой
разряд. Для дуги характерны сильный ток (г > 1 А), низкое
напряжение (десятки вольт) и ярко светящийся столб. В дуге
г.ыделяется большая мощность, стеклянная трубка довольно ско-
ро разрушается от перегрева. Поэтому, зажигая дуговой разряд
в замкнутом сосуде, нужно позаботиться об интенсивном отводе
тепла от его стенок. Дуту часто зажигают прямо в открытом
воздухе. Тогда тепло рассеивается в пространстве. В дуге атмо-
сферного давления обычно образуется термодинамически рав-
новесная, так называемая низкотемпературная плазма с Те ~
Xi Т ~ 104 К и соответствующей таким температурам равновесной
степенью ионизации 10“3—IO"1. Дуговой разряд существенно от-
личается от тлеющего механизмом э гектронной эмиссии с катода
(без катодной эмиссии не мог бы течь постоянный ток). В тле-
ющем разряде электроны вырываются с поверхности холодного
металла под действием вытягиваемых на катод положительных
ионов. В дуговом разряде из-за сильного тока катод разогревает-
13
ся либо по всей поверхности, либо локально, и происходит тер-
моэлектронная эмиссия.
При давлениях р ~ 1 атм, расстояниях между электродами
L > 10 см и достаточно высоких напряжениях происходит иск-
ровой разряд. Пробой при этом осуществляется путем быстрого
прорастания плазменного капала от одного электрода к другому.
Потом происходит как бы короткое замыкание электродов силь-
ноионизованным искровым каналом. Грандиозной формой искро-
вого разряда является молния, для которой «электродами» слу-
жат заряженное электричеством облако и земля. В сильно не-
однородных полях, недостаточных для пробоя всего промежутка,
может возникнуть коронный разряд. Светящаяся корона появ-
ляется около острий, где концентрируется поле, проводов, нахо-
дящихся под напряжением, около линий электропередач.
§ 3. Классификация разрядных процессов
Разряды в постоянном поле можно разделить на несамостоя-
тельные и самостоятельные. Последние гораздо более распро-
странены, разнообразнее и богаче физическими эффектами. Ими
мы и будем заниматься. Среди стационарных или квазистацпо-
нарпых самостоятельных разрядов постоянного тока выделяются
тлеющие и дуговые. Принципиально они различаются катодными
процессами, как отмечалось в § 2. К тлеющему разряду отно-
сительно близок темный таунсендовский разряд. Ток в нем сов-
сем слабый (катод, естественно, холодный). Особняком стоит
коронный разряд, тоже самостоятельный и слаботочный. Корона
у катода имеет общие черты с тлеющим и темным разрядами.
Среди быстротечных разрядов резко выделяется искровой.
Многие черты объемных плазменных (т. е. пеэлектродпых)
процессов, характерных для пробоя в постоянном электрическом
поле, для тлеющего и дугового разрядов, свойственны разрядам
в быстропеременных полях, где присутствие электродов вообще
не является обязательным. Поэтому целесообразно провести так-
же классификацию, минуя признаки, связанные с электродными
эффектами. В основу классификации положим два признака:
состояние ионизованного газа и частотный диапазон приложен-
ного поля.
По первому признаку будем различать: 1) пробой газа,
2) поддержание полем неравновесной плазмы, 3) поддержание
равновесной плазмы. По признаку частоты — 1) постоянные, низ-
кочастотные и не слишком кратковременные импульсные элек-
трические поля, 2) высокочастотные поля, в зарубежной литера-
туре их называют радиочастотные (частоты / ~ 105—108 Гц),
3) сверхвысокочастотные, или микроволновые (/~ 109—1011 Гц;
длины воли Л ~ 102—10"1 см), 4) оптические (от далекого ин-
фракрасного до ультрафиолетового). Поля каждого из диапазонов
могут взаимодействовать с каждым из типов разрядной плазмы.
Всего получается 12 вариантов. Все они реализуются на опыте,
14
многие нашли широкое применение в физическом эксперименте
и технике. Типичные условия, в которых проявляется каждый
из вариантов, сведены в табл. 1.1. Большинство из указанных
вариантов будет рассматриваться в соответствующих главах, хотя
ограниченность объема вынуждала нас проходить мимо большого
количества фактов из практики газового разряда и теории. По
той же причине мы не касаемся разрядов и поведения плазмы
в магнитном поле. Магнитное поле — не частый атрибут в тра-
диционных видах разряда (за исключением магпптогидродипа-
Таблица 11. К к гассификации разрядов
Частотный диапазон приложенного поля Состояние ионизованного iaia
пробой н< равновес ная и 1азма рарпови ная плазма
Постоянное и ни )- кочастотное a ickiрпческое позе Зажигание тлею- щего ра {ряда в трубке 11оложи 1°ЛЫ ыи сю 16 «леющею ра{ряда 11о !О,Ки юпъпыи (ТОЮ ДУ1 И BIJ- ( ОКО! о Р1В 1О11ПЯ
Высокие частоты Залипание ВЧ разряда в сta \ цах с pa ц ежен HUM 1 а ИА! ВЧ емкое iiibie ра i ря р>1 1 ра ще ,пенных 1 а ; а ! !пд\ кционная л ia именная ю резка
СВЧ диапазон Пробои В ВО !НОВО- дах и ре юна ю рах ( ВЧ ра {ряды в ра {реяченных 1 а {ах СВЧ плазмотрон
Оптический диапа- зон Пробои Iазов ^а юрным и?луче Н1 см Лше| шающая ста- дия он гическси о Т! । обоя Непрерывный опд тическии разря-
мнческих генераторов). Плазма в магнитном поле, высокотемпе-
ратурная плазма с Г ~10б К, предназначенная для термоядер-
ного синтеза,— все это стало объектом специальной пауки —
физики плазмы. Впрочем, четко разделить сферы влияния фи-
зики плазмы и физики газового разряда не всегда возможно.
Все же если обратиться к оглавлениям книг по физике плазмы,
разделение просматривается, и в ту область мы вторгаться не
будем.
§ 4. Коротко об истории исследования разрядов
Если не считать молнии, люди впервые столкнулись с разря-
дами, когда заметили, что заряженные трением изолированные
проводники постепенно теряют заряд. Это наблюдали еще в
1600 г. В 1785 г. Кулон опытами доказал, что заряд уходит
через воздух, а не вследствие несовершенства изоляции. Теперь
мы знаем, что здесь происходит несамостоятельный разряд. В те-
чение XVIII в. проводили отдельные опыты с искрами, которые
получали, заряжая тела при помощи электростатических машин,
а также обращаясь к атмосферному электричеству.
15
В начале XIX в. появились достаточно мощные электриче-
ские батареи и был открыт дуговой разряд. В. В. Петров, ра-
ботавший в Санкт-Петербургской медико-хирургической акаде-
мии, сообщил об этом в 1803 г. Дуга получалась при соприкос-
новении и последующем разведении угольных электродов, под-
соединенных к батарее. Через несколько лет дугу в воздухе по-
лучил и исследовал Дэви в Англии. Разряд был назван
дуговым, так как ярко светящийся горячий столб изгибался,
всплывая своей серединой под действием архимедовой силы.
В 1831 —1835 гг. Фарадей открыл и исследовал тлеющий раз-
ряд. Фарадей работал с трубками, откачанными до р ~ 1 торр,
и источниками напряжения до 1000 В.
История физики газового разряда конца XIX — начала XX вв.
не отделима от истории атомной физики. Опыты Крукса с ка-
тодными лучами, установление Дж. Дж. Томсоном отношения
elm привели к пониманию того факта, что ток в газе перено-
сится главным образом электронами. Изучение явлений в раз-
рядных трубках дало много сведений об элементарных процессах
с участием электронов, иопов, атомов, в том числе и возбуж-
денных, светового излучения.
Начиная с 1900 г., ученик Дж. Дж. Томсона Таунсенд, ос-
нователь школы физики газового разряда, установил законо-
мерности ионизации и однородного (его называют таунсендов-
ским) пробоя газа в электрическом поле. Накапливались многие
экспериментальные данные по сечениям различных электрон-
атомных столкновений, скоростям дрейфа электронов и ионов,
их рекомбинации и т. д. Все это составило основу современного
справочного материала, без которого немыслима работа иссле-
дователя в области разрядов. Понятие плазмы было введено в
1928 г. Лэнгмюром и Тонксом. Лэнгмюр оставил большой след
в физике газового разряда: зондовый метод исследования плазмы
и многое другое.
Что касается различных частотных диапазонов, то хроноло-
гически освоение генераторов поля и изучение соответствующих
разрядов шло в порядке следования диапазонов. Высокочастот-
ный разряд наблюдал Тесла в 1891 г. Разряд легко получить,
если внутрь соленоида поместить откачанный сосуд и пропу-
стить через катушку ток высокой частоты. Под действием элек-
трического поля, индуцированного переменным магнитным, в ос-
таточном газе возникает пробой и зажигается разряд. Однако
механизм зажигания разряда стал в достаточной мере понятным
значительно позже, фактически в результате работ Дж. Дж. Том-
сона 1926—1927 гг. Индукционные разряды мощностью в де-
сятки киловатт были получены к 1940 г. Г. И. Бабатом в Ле-
нинграде.
Развитие радарной техники вызвало большой интерес к яв-
лениям в СВЧ диапазоне. С конца сороковых годов С. Браун
в США начал систематическое исследование микроволнового про-
боя. Разряды в оптическом диапазоне были получены только
16
после изобретения лазеров. Когда луч рубинового лазера, даю-
щего так называемый гигантский импульс (мощностью более
10 МВт) сфокусировали линзой, в воздухе вспыхнула искра.
Это было в 1963 г.
Непрерывный оптический разряд, в котором происходит ста-
ционарное поддержание плотной равновесной плазмы, питаемой
энергией излучения, был впервые создан в 1970 г. при помощи
лазера непрерывного действия на углекислом газе (СОг-лазера).
Оптические разряды, названные так вследствие большой общно-
сти их эффектов с обычными разрядными явлениями, с самого
начала привлекли к себе пристальное внимание. Как и разряды
в СВЧ диапазоне, они изучены не в меньшей степени, чем раз-
ряды в постоянном электрическом поле, которыми скрупулезно
занимаются чуть ли не сто лет.
Физика тлеющего разряда, одного из самых старых и, ка-
залось бы, изученных, в последние 20 лет испытала небывалый
подъем, вскрывший массу новых сторон этого явления. Подъем
связан с использованием тлеющего разряда в электроразрядпых
лазерах, в особенности мощных на СО2, предназначенных для
лазерной технологии. Подобным же образом стимулом для рас-
ширения и углубления исследований дуговой плазмы с р ~ 1 атм,
Т ~ 104 К и аналогичных разрядов во всех частотных диапазонах
явилось применение генераторов плотной низкотемпературной
плазмы — плазмотронов в металлургии, плазмохимии, для плаз-
менной сварки и резки и др. Это также произошло в последние
десятилетия. Требования современной энергетики и техники вы-
соких напряжений (в частности, задачи молниезащцты) сти-
мулировали углубленное изучение искрового разряда, кстати,
одного из самых сложных и трудно постигаемых явлений в
области газовых разрядов. Отмеченные и многие другие прак-
тические приложения физики газового разряда поставили ее в
ряд наук, которые являются фундаментом современной техники.
На приложениях газового разряда, за исключением СОг-лазеров
и плазмотронов, мы останавливаться не будем. Очерк техниче-
ских приложений газового разряда имеется в [11].
2 Ю. П Райзер
Часть!. ЭЛЕМЕНТАРНЫЕ ПРОЦЕССЫ И ЭЛЕМЕНТЫ
РАЗРЯДНЫХ ПРОЦЕССОВ
Глава 2 СТОЛКНОВЕНИЯ ЭЛЕКТРОНОВ И ИОНОВ
С АТОМАМИ, МОЛЕКУЛАМИ И ДРУГ С ДРУГОМ
§ 1. Основные понятия физики атомных столкновений
и кинетической теории газов
Столкновения атомных частиц могут иметь упругий и не-
упругий характер. При упругом соударении меняются направле-
ния движения партнеров, происходит обмен импульсом и кине-
тической энергией, но внутренние энергии и состояния частиц
остаются неизменными. При неупругом ударе внутренняя энер-
гия и состояние одной из частиц (реже — обеих) изменяются.
Формально к неупругим можно отнести и такие столкновения,
которые сопровождаются не только превращением энергии, по и
превращениями самих частиц, например ионизацией атома.
1.1. Эффективное сечение. Для характеристики вероятности
столкновений частиц в газе служат такие величины, как длина
свободного пробега, среднее время между соударениями, частота
столкновений. Все они зависят как от свойств частицы, так й
от плотности газа.
Мерой вероятности индивидуального акта определенного рода
(скажем, упругого соударения, ионизации и т. д.) является со-
ответствующее эффективное сечение. Это понятие вводится сле-
дующим образом. Представим себе, что на одну частицу-мишень
налетает однородный в пространстве поток ударяющих частиц
со скоростью относительно мишени v' [см/с] и плотностью
[см~3]. Вообразим, далее, что выбитая со своего места или
претерпевшая какое-либо изменение частица-мишень немедленно
заменяется новой. Число ударов определенного рода, которое
испытывает такая «неуязвимая» мишень в 1 с, Уг [с-1] тем боль-
ше, чем больше проходит за это время частиц через 1 см2. Число
соударений пропорционально именно плотности потока частиц
Nxv' в месте расположения мишени, а не полному потоку. В са-
мом деле, если увеличить полный поток вдвое, но пропустить
вторую партию значительно дальше от мишени, чем первую,
число ударов практически не изменится. Коэффициент пропор-
циональности о между V2 и N\v',
V2 = (5N\V', [см2], (2.1)
18
имеющий размерность площади, называется эффективным сече-
нием данного процесса или, для краткости, просто сечением-
Сечение зависит от индивидуальных особенностей партнеров, за-
конов их взаимодействия и скорости относительного движения v'*
Физическии смысл эффективного сечения выступает особен-
но явственно на примере соударения твердых шаров радиусами
Г1 и Г2 (рис. 2.1). Чтобы налетающий
шар 1 задел шар-мишень 2, линия движе-
ния его центра должна пройти от центра
мишени па расстоянии, не превышающем
т\ + ^*2. Значит, в секунду произойдет V2 =
= л(г! + r^N^u' ударов и сечение столкно-
вения есть о = л (ri + г<2)7. Если налетаю-
щий шар очень маленький (и < 7*2), он дол-
жен попасть в площадь диаметрального се-
чения мишени о — л/2 Таким образом, эф-
фективное сечение процесса численно сов-
падает с площадью диаметрального сечения,
которой должна была бы обладать частица-
мишень, чтобы попадание в этот кружок точечной ударяющей
частицы привело к ожидаемому результату.
Модель твердых шаров удобна для описания газокинег <ческих
столкновений Jr. е. упругих соударении молекул в газе, так как
неплохо имитирует этот процесс В газе из частиц одного сорта
= г2 и о = лй2, где d — эффективный диаметр молекулы. Тео-
ретическое вычисление эффективных сечений па основе законов
взаимодействия сталкивающихся частиц составляет задачу ме-
ханики, классической или квантовой, в зависимости от конкрет-
ного процесса, рода частиц, их скорости. Разумеется, без теории
нельзя обоптись, когда нужно понять, как происходит сам акт
столкновения. Но когда, как в физике разряда, требуются конк-
ретные числовые данные по сечениям, как правило, прибегают
не к теоретическим вычислениям, которые чаще всего сложны
и несовершенны, а к результатам измерений. Часто для оире~
Таблица 21 Га акинетические параметры *)
Рис 2 1 Схема, пояс-
няющая понятие эф-
фективного сечения
Газ d, 10-8см о, 10~15 см2 1, 1 О-3 см г, 104 см/с v, 106 с~1 т, 10—7 с
Не 2.15 1,45 13,2 12,0 9 09 1,10 1,94 1,25 0,54 °,99 1,13
Ne 3,54 3,93 9 41 5,35 5,68
Аг 3,58 4,02 4,76 3,80 7,98
н2 2,70 2,29 8,41 16,0 21,1
N2 3,70 4,31 4,47 4,53 10,1
О2 3,56 3,98 4 81 4,25 8,83
*) Представлены е _ . , -----------
кости, газокинетические сечения о, средние длины свободного пробега I, средние'т
скорости v, частоты газокинетических столкновений v, времена между столкни л°вЬ1е
при Т == О °C и р = 1 торр Вениями т
эффективные диаметры молекул d, найденные из данных
ГА ГРирИИЯ ГГ РПАТТТТМА TTTTITWKT ЛТЭлАлттГГА ПЛ ППлКлпо 1 - По Ндд
'евиями
2*
19
деления сечений служат косвенные пути. Например, газокинети-
ческие сечения находят из измерений вязкости газов (табл. 2.1).
Эти цифры полезны для дальнейшего в том числе и тем,
чю служат ориентиром для суждений о вероятностях различных
процессов. Когда говорят, что «сечение такого-то процесса мало»,
то мысленно сравнивают его с газокинетическим. «Большое се-
чение»— (значит, порядка или больше газокинетического.
1.2. Частота столкновений. Число соударений определенного
рода, которые данная частица (назовем ее 1) в среднем совер-
шает в 1 с, двигаясь в газе из частиц-мишеней 2, называют
частотой столкновений. Чтобы найти это число, представим себе,
подобно предыдущему, что пучок частиц 1 со средней плот-
ностью и скоростью и' налетает на газ из неподвижных ча-
стиц-мишеней со средней плотностью Л^2- В соответствии с (2.1)
в 1 см3 в 1 с происходит A^2V2 = NiN2vfe(v') актов соударений.
Каждая из налетающих частиц 1 совершает в 1 с
vi = N2v'g(v') (2.2)
ударов. Выражения (2.1) и (2.2) симметричны, поскольку ча-
стоты столкновений, испытываемых соударяющимися частицами,
пропорциональны плотностям партнеров, а в остальном зависят
от взаимной величины — скорости относительного движения.
В общем случае формула (2.2) еще не решает поставленной
задачи. Говоря о частоте столкновений, которые испытывает дан-
ная частица, подразумевают, что это — частица с определенной
энергией или скоростью движения в системе координат, где по-
коятся не отдельные молекулы, а газ в целом. Поэтому выра-
жение (2.2) нужно усреднить по скоростям частиц-мишеней,
которые на самом деле совершают тепловое движение. Проще
всего дело обстоит, когда речь идет о частоте столкновений элек-
трона. Из-за малости массы электрона m даже при сравнимых
энергиях его скорость гораздо больше скоростей тяжелых частиц,
поэтому v' практически совпадает со скоростью электрона, и Ча-
стота его столкновений есть
v === Nve(y),
(2.3)
где для общности опущены все индексы.
В случае газокинетических столкновений молекул друг с дру-
гом произведение и'в (и') усредняется по скоростям относитель-
ного движения. Распределение частиц массы М по абсолютным
скоростям описывается максвелловской функцией. Число частиц
в 1 см3, обладающих скоростями в интервале от и до и + dv,
равно
, ч f М 3/2 I Mv2\ 2 , м
где Т — термодинамическая температура, к — постоянная Больц-
20
мана. Средняя тепловая скорость молекулы равна
v = (SkT/nM]1/2. (2.5)
Распределение по относительным скоростям v' определяется той
же функцией (2.4), если заменить М на приведенную массу Мг =
= МХМ2/ (Мj + М2). При столкновении одинаковых частиц ==
= М2 = Л/, Mr = М/2 и средняя скорость относительного движе-
ния v' = l/2v. Для молекул — твердых шаров эффективное се-
чение равно в(и') = const = nd2. При усреднении, которое обо-
значим угловыми скобками, получим <и'о(у') > = v'a. Средняя
частота газокинетических столкновений в газе из молекул одно-
го сорта равна
v = Nv'nd2 = ] 2 Nvnd2 = Т2 Nvo. (2.6)
Среднее время между столкновениями есть r = v-1. Когда газ
состоит из частиц разных сортов или представляет интерес ча-
стота нескольких видов столкновений (например, частота возбуж-
дений нескольких молекулярных уровней), следует суммировать
парциальные частоты: v 2^гЬ’ог.
1.3. Длина свободного пробега. Если частица движется в га-
зе со скоростью/?; и совершает в среднем v столкновений в 1 с,
то на пути 1 см она испытывает v/v столкновений. Между столк-
новениями она проходит расстояние
I = v/v = = 1/2Vcf, (2.7)
которое называют длиной свободного 'пробега (по отношению к
какому-либо процессу). Соотношение (2.7) между длиной сво-
бодного пробега и сечением строго справедливо лишь для бы-
стрых частиц, в частности электронов, когда нет вопроса об
усреднении по скоростям частиц-мишеней.
В газокинетпческой теории длина пробега определяется при-
менительно к молекуле, движущейся со средней тепловой ско-
ростью v. Для молекул — твердых шаров согласно (2.6)
I = v/v - 1/V2 No = lp/2Nnd2. (2.8)
В смеси газов суммируются обратные длины: Z = (2Л\О{) Х-
В силу случайного характера столкновений, вероятность частице
пройти путь х без столкновения равна ехр(—#//), а вероятность
осуществления свободного пробега от х до х + dx — exp (—x/l)dx/l.
1.4. Числа столкновений при нормальных условиях. В лите-
ратуре по разрядам сечения столкновений часто заменяют одно-
значно связанными с ними числами Р столкновений, которые ча-
стица испытывает на пути 1 см, если плотность газа соответству-
ет давлению р = 1 мм рт. ст. = 1 торр и температуре Т = О °C,
No = 3,54 • 1016 см-3:
Р = 3,54 1016о см"1-торр-1, о = 2,83 • 10"17Р см2. (2.9)
21
Величину Р называют вероятностью столкновений. Плотность,
которая выражается большими числами, очень удобно характе-
ризовать давлением в" торрах. В этом и состоит целесообразность
введения Р; длина пробега в сантиметрах тогда просто равна
I = ]JPp [торр] см. (2.10)
Но необходимо помнить о том, что однозначное соответствие
N и р и буквальное выполнение формулы (2.10) требуют одно-
значности температуры. Фигурирующее в формуле давление, ко-
торое отнесено к 7 = 0 °C, называют приведенным. Иногда про-
исходит небольшая путаница, ибо нередко указывают реальное
давление, которое скорее соответствует комнатной температуре
20 °C. а не 0 °C. Тогда давлению 1 торр отвечает немного мень-
шая плотность У20 = 3,30 • 1016 см-3. Вообще,
р (приведенное) = р (истинное) (273/7[К]). (2.11)
§ 2. Упругое рассеяние электронов
нейтральными атомами и молекулами
2.1. Сечения упругих столкновений. Эти сечения, как правило,
гораздо больше сечении неупругих столкновений. Сечения
упругих столкновений ис зависят от скорости v (или энергии е =
= mv2/2) электрона и определяются действием на электрон
Рис. 2.2. Вероятности и сечения уп-
ругих столкновений электронов с
атомами инертных газов в зависимо-
сти от энергии электронов [24]
Рис. 2.3. Вероятности и сечепия
упругих столкновений в Щ и Не
в зависимости от энергии элект-
ронов [24]
сложного силового поля атома, молекулы. Рассмотрение этого
эффекта и вычисление сечений составляет предмет квантово-ме-
ханической теории столкновений, так как при типичных энергиях
е ~ 1 эВ дебройлевская длина волны электрона сравнима с раз-
мерами атома.
22
В практической работе, как правило, пользуются сече
для электронов, которые найдены опытным путем (рис. 2 2-^ЯМ11
С помощью этих данных легко сосчитать частоты упругих ’
повений: столд-
(рис. 2.5). В области энергий в
сечения всегда уменьшаются с
— = 5,93 • 107Уе [эВ] Рср [торр] с'1 (2д2)
десятки электронвольт упруго
ростом 8 — более энергичный
Рис. 2.4. Вероятности упругих столкновений в зависимости
электронов: а — в Ог, N2 и СО; б в СО2 и 1N2O; в — в парах
таллов; г — в парах Hg, Zn и Cd [6]
Рс,ом 1-торр 1 1—I--------1---1--1---г
от «скорости»
щелочных ме-
электрон труднее «сбить с пути»; укорачивается и длительность
действия молекулярного поля. У некоторых атомов и молекул
наблюдаются глубокие минимумы сечений в области энергий е «
23
~ 0,1— 1 эВ; это называют эффектом Рамзауэра, который обна-
ружил минимумы в 1923 г., измеряя сечения на опыте. В су-
ществовании минимумов проявляются волновые свойства элек-
трона.
Рис. 2 5 Частоты упругих столкновении в зависимости от анергии электро-
нов (р = 1 торр): а — в Н2 и Не, б — в инертных газах; штриховые ли-
нии— удобная аппроксимация при расчетах [24]
2.2. Транспортное сечение и потери импульса. При упругом
столкновении с атомом электрон может отклониться от направ-
ления своей начальной скорости v на разные углы 0. Вероят-
ность рассеяния на угол 0, или дифференциальное сечение do =
= (do/dQ)dQ, где dQ = 2л sin0d0 — элемент телесного угла, обыч-
но сложным образом зависит от угла рассеяния (рис. 2.G). Что-
бы выяснить, как сказывается угловое распределение на резуль-
Рис. 2.6. Дифференциальное сечение уп-
ругого рассеяния электронов в СО2 в
зависимости от угла рассеяния [6]
тирующем эффекте многих
столкновений, решим глав-
ный вопрос, за который не-
сут ответственность упругие
столкновения: как быстро
электрон растрачивает свою
направленную скорость, свой
импульс. Имея в виду, что
электрон гораздо легче и го-
раздо быстрее движется, чем
молекула, будем считать по-
следние неподвижными.
В результате рассеяния
скорость электрона становит-
ся равной v', а импульс ме-
няется на Ap = m(v' —v).
Скорость изменения импуль-
са, обязанная упругим
векторной сумме Ар по всем
столкновениям, (dp/dt)c равняется
столкновениям, которые электрон совершает в единицу времени.
Проводить такое суммирование точно было бы не реальным, по-
этому подойдем к вопросу статистически. Усредним Ар по всем
24
столкновениям, т. е по всевозможным углам рассеяния в одном
акте, и умножим результат на число актов в единицу времени
(на частоту столкновений vc):
(dp/dt) с = m< Av>vc = m<v' — v>vc.
Чтобы произвести усреднение, разложим вектор v' на состав-
ляющие, параллельную и перпендикулярную направлению на-
чальной скорости v, которая фиксирована и усреднению не под-
лежит* vz : v i Vj . Отклонения вправо и влево на один и тот
же угол 0 равновероятны, т. е — 0. Как будет показано
в п 2 3, вследствие большого различия масс электрона и моле-
кулы, электрон теряет при упругом соударении ничтожную до-
лю своей энергии. Поэтому значение его скорости при рассеянии
остается почти неизменным, и (v v cos 0. Средний косинус угла
рассеяния cos 0 находится путем усреднения cos 0 по телесному
углу с учетом углового распределения рассеяния.
Введя величины
(1—cosO) dQ ^ас(1 — cos0), \т \<-(1 cos^^7
(2.13)
представим искомый результат в виде
(dp/d/)c = — mv(i — cos 0)\с = —mvvm = —pvm (—14)
Величину o/r называют транспортным сечением, a
эффективной частотой столкновений, О сечении сцг и
ющей длине пробега lm = 1/Notr иногда* говорят, как о с_
онных или для передачи импульса Все влияние угловог
пределепия рассеяния
учитывается одним параметром
ie
Рис 2 7 Вероятности упругих столкновений электронов (штрих(°сплоп1яь1в
вые) и вероятности, соответствующие транспортным сечениям
кривые), в Не, Ne и Аг в зависимости от энергии электрон
Если рассеяние изотропно (или симметрично) относительно пло-
скости 0 = 90°, cos 0 = 0, Otr = ос, ут = ус. Если электрон рас-
сеивается преимущественно вперед, cos0~l, ут < ус и требуется
много столкновений, чтобы электрон растратил свой начальный
импульс. Если электрон рассеивается строго назад, cos 0 = — 1,
скорость потери импульса вдвое больше, чем при изотропном
рассеянии. У большинства газов при энергиях электронов е ~
~ 1 —10 эВ, характерных для разрядов, транспортные сечения
па 1 —10 % меньше истинных, в области более высоких энер-
гий— раза в полтора (рис. 2.7).
2.3. Упругие потери энергии. Эти потери хотя и малы, но во
многих случаях играют важную роль, определяя скорость пере-
дачи энергии от электронов газу тяжелых частиц. Когда при
рассеянии электрон теряет импульс Др, молекула такой же им-
пульс приобретает. Если молекула вначале покоилась, вместе
с импульсом она получит энергию Ле = (Др)2/2Л/, которую элек-
трон теряет. Поступая так же, как и при вычислении (dp/dt)CJ
запишем скорость уменьшения энергии электрона за счет упру-
гих потерь в виде
(М = - 2Й «А₽)2> v' = - S? <<Av)2X’ Av = v' — v.
Проведем усреднение с учетом того, что электрон теряет в
одном акте только очень малую долю своей энергии:
<(Av)2> = v'2 — 2r'rcos0 fy2 = 2y2(l—cos0),
/ d& \ 2ms. -------------2m (2-15)
Ыс ~ H1 - COS0)fcVc = - M eV«-
В каждом соударении электрон теряет в среднем долю
(2т/М) (1 — cos 0) от своей энергии е, а в каждом «эффектив-
ном» соударении долю 2т/М. Величина эта очень мала, порядка
10-4. Чтобы отдать значительную часть своей энергии атомам,
электрон должен совершить порядка М]т ~ 104 упругих столкно-
вений. В этом кроется причина того, что температура элект-
ронов, которые фактически только и получают энергию от поля,
сильно превышает температуру газа, а выравниваются темпера-
туры довольно медленно.
§ 3. Столкновения ионов с нейтральными частицами
3.1. Поляризационное сечение. Сечения упругого рассеяния
медленных ионов с энергиями порядка тепловой (как это чаще
всего бывает в условиях разряда) определяются поляризацион-
ными силами. Взаимодействие частиц можно рассматривать на
основе классической механики, так как длины волн де Бройля
в чанном случае много меньше характерного радиуса взаимо-
действия.
26
Находясь на расстоянии г от молекулы, однозарядный ион
своим электрическим полем е/r2 индуцирует в молекуле диполь-
ный момент d = ae/r2, где а— поляризуемость молекулы
(табл. 2.2). Положительный ион подтягивает молекулярные элек-
троны ближе к себе, отрицательный отодвигает их от себя.
Ион притягивается к молекуле полем диполя 2 с?/г3, обладаю-
щим потенциалом ф = —ае/2г4. Обозначим через р0 расстояние,
Таблица 22 Поляризуемость а атомов и мо текут в основном состоя-
нии и длпотьяьтй момент dv молекул *)
Атом a/а3 0 Моле- кула a/ao /<«0 Атом а/а1 Моле- кула a/uo d0/eaQ
Н 4,5 н2 5,52 0 О 512 СО2 17,5 0
Не (В5) 1,39 N2 11,8 0 Хе 2,76 П,0 9,8 1,84
Не(215)**) 800 о, 10 6 0 Ai И,1 NHt 15,4 1,46
НеГ235)**) 316 со 13,1 0.1 Кг 16,8
N 7,6 NO 11,5 0,16 Хе 27,2
*) Взято из киши Г26]
**) Для сравнения приведены огромные поляризуемости возбужденных атомов
гелия Такого же порядка и по шризуемости атомов щелочных металлов в основном
состоянии
на котором кинетическая энергия относительного движения иона
и молекулы е' Л/'г/2/2 равняется потенциальной <з!ф1, ро =
= (ае2/2е')1/4. Ецли ион подлетает к молекуле с прицельным рас-
стоянием^) р < ро, он подвергается сильному воздействию и рас-
сеивается на значительный угол, ес ш р > ро — ион подвергается
слабому воздействию и рассеивается на малый угол. По порядку
величины транспортное сечение рассеяния равно Otr « лр0. С уче-
том уточняющего оценку множителя 2V2 [26]
atr = 2л Vае2/е' =- 2 V2ла„ К(а/д®) (7н/г'). (2ОО
В последнем преобразовании мы гыразили е2 через боровский
радиус uq = ti2!me2 = 0,529 • 10~8 см и потенциал ионизации ато-
ма водорода /н = e2/2aQ = 13,6 эВ, чтобы выделить характерный
масштаб сечений атомных столкновений — площадь первой боров-
ской орбиты — 0,880-10~16 см2.
При поляризационном взаимодействии сечение щг ~ 1/р', а ча-
стота столкновений vm = Nv'o(v') = const. Когда при увеличе-
нии скорости (энергии) иона характерный радиус поляризацион-
ных сил ро становится меньше размеров молекулы, а соответ-
ствующее сечение меньше газокипетического, рассеяние проис-
ходит при «соприкосновении» частиц. Поляризационное сечение
♦) Так называется минимальное расстояние, на котором частица про-
шла бы мимо мишени, если бы между ними не было взаимодействия
27
сменяется газокинетическим, которое от о' зависит слабо; теперь
vm ~ v'. В Не, Ar, N2, О2 это происходит при e'>gK«
~ 0,5—0,6 эВ, в Ne— ек~0,15 эВ, в Н2— 0,9 эВ. Таким обра-
зом, далыюдеиствующее притяжение уступает близкодействую-
щем у отталкиванию при температурах примерно выше 4000 К.
Несимметричные молекулы обладают постоянным дипольным
моментом do (табл. 2.2). На ион со стороны молекулы действуют
я см"1 торр г-----------1----------1— (2.10 *6СМ2
0
| i I V£,3B^
0 5 10 15 20
Рис 2 8 Вероятности и сечения
столкновении ионов в инертных га-
зах в зависимости от энергии элект-
ронов 1 — упругое рассеяние, 2 —
in резарядка, 3— их сумма [15]
поля постоянного и индуци-
рованного моментов То из
них, которое окажется более
сильным, и определяет се-
чение рассеяния. Оценку
можно сделать так же, как
и выше (см. 1-е изд., с. 46).
В случае постоянного мо-
мента G/r ~ 1/z/2, т. е. при
достаточно малых энергиях,
преобладает действие посто-
янного момента В СО, NO
это происходит при энерги-
ях меньше тепловых, т. е.
сечение всегда поляризаци-
онное но в парах воды —
при е' < 2, 3 эВ.
3.2. Резонансная переза-
рядка. Двигаясь в собствен--
пом газе (Не+ в Не, N^ в
N2), ионы интенсивно теря-
ют импульс в результате ре-
зонансной перезарядки. Ус-
коренный полем ион на
лету отбирает электрон у
нейтральной молекулы и
нейтрализуется Это проис
ходит так быстро, что новый
ион (бывшая молекула) не
успевает «сдвинуться с ме-
ста». Сечение перезарядки
Опер обычно даже больше
сечения упругих столкнове-
ний (рис 2 8). Оно медлен-
но уменьшается с ростом
скорости (см. 1-е изд., с. 49).
В системе центра масс мо-
лекула и ион движутся с
одинаковыми скоростями навстречу друг другу, а после
перезарядки заряд с той же скоростью движется в противопо-
ложном направлении. Это эквивалентно рассеянию на 180°, по-
этому при перезарядке afr = 2апер. Резонансная перезарядка
28
сильно влияет на скорость потери импульса ионов и существенно
уменьшает их подвижность в собственном газе.
Перезарядка возможна и в случае разнородных частиц, но та-
кого типа акты чаще всего являются одноразовыми. Действи-
тельно, если потенциал ионизации атома А больше потенциала
ионизации атома В, то перезарядка А+ + В А + В+ энергети-
чески позволена, а В+ + А В + А+ — нет. Перезарядка ионов
в собственном газе тем и замечательна, что, подобно упругим
столкновениям, не сопровождается превращениями энергии и по
своему результату вполне эквивалентна упругому удару.
3.3. Потери импульса и обмен энергией при упругих столк-
новениях. В случае ионов решение этих вопросов не столь про-
стое, как для электронов, из-за сравнимости масс иона Мг и мо-
лекулы М. Отсылая за выводами формул к 1-му изд., приведем
лишь результаты, нужные для изучения дрейфа ионов в поле
(§ 5 гл. 3). Скорость потери импульса рг = Л/гу2 иона (dpt/dt)c
определяется величиной W<vV(jlr(i/)>, где усреднение прово-
дится по тепловым скоростям молекул при фиксированной ско-
рости иона V». Для поляризационных сил, когда щг ~ 1/к' и ча-
стота столкновений ут = Nv'otr не зависит от скорости, <v'> = vt и
(dpjdt) с =—М'угут. (2.17)
Формула (2.17) отличается от (2.14) лишь тем, что в пей стоит
приведенная масса. В случае Мг < Л/, когда М' = Мг, она пре-
вращается в (2.14).
Энергии ионов в разрядных условиях из-за интенсивного об-
мена чаще всего мало отличаются от энергий молекул. Обмен
имеет двусторонний характер, т. е. при столкновениях и ион
может отдавать часть энергии молекуле, и молекула — иону,
все зависит от соотношения скоростей партнеров. При условии
vm = const скорость изменения средней энергии 8г иона за счет
упругих столкновений с молекулами равняется
2МгМ
+ М)2
(Ci — ем)
Vm,
(2.18)
где 8М = (3/2) кТ — средняя тепловая энергия молекул.
Мг <с М и 8г > 8М (2.18) превращается в (2.15)*).
В случае
§ 4. Упругие столкновения между заряженными частицами
Из всех сил взаимодействия между атомными частицами мед-
леннее всего спадают с расстоянием (как 1/г2) кулоновские си-
лы. Они обладают наибольшим дальнодействием. Это практиче-
*) В п. 2.3 предполагалось, что энергия электрона велика по сравнению
с температурой газа, как это всегда бывает в слабоионизованном газе, на-
ходящемся в поле. При выключении поля или в сильноионизованной плазме
энергии электронов становятся сравнимыми с энергиями атомов, ионов
В этом более общем случае и в формулу (2.15) вместо е следует ввести
е— (3/2) кТ или (3/2) (Те — Т). Об этом, как и об истоках формулы (2.18)г
см. 1-е изд., § 5 гл. 2.
29»
ски единственный вид взаимодействия, при котором столкнове
пня с большими прицельными расстояниями, приводящие к рас-
сеянию па малые углы, вносят главный вклад в потерю им-
пульса частицы, причем интеграл транспортного сечения (2.13)
формально оказывается бесконечным. Реальные транспортные
се’кшия, которые, как мы увидим, конечны, во многих практи-
чески важных случаях оказываются гораздо больше газокине-
1ических. Это значит, что еще при далеко не полной ионизации
газа среди столкновений электрона с тяжелыми частицами на
первый план выступают столкновения с имеющимися в неболь-
шом количестве ионами.
4.1. Дифференциальное сечение. Оценим это сечение приме-
нительно к рассеянию электрона ионом при пролете электрона
па большом прицельном расстоянии р, когда угол рассеяния 0
мал. В течение времени взаимодействия t — р/г на электрон дей-
ствует сила /г ~ е2/р2, которая сообщает ему поперечную направ-
лению v скорость г±. Угол отклонения 0 связан с р соотноше-
нием
________С
v mv
de
е2 dp
ти~ p“
(2.19)
Электрон рассеивается в интервал углов от 0 до 0 + с/0, когда
попадает в кольцевую площадку с радиусами р и р + dp. Диффе-
ренциальное сечение рассеяния равно
do = ~~ dP. - 2лос/р~ ~ (2.20)
\т»2/ О3 \ти2/ О4 ' 7
Точное вычисление для любых комбинаций заряженных частиц
приводит к известной формуле Резерфорда-.
! е2 \2 t/Q ( е2 V t/Q /Q
do " I-----2 —i------tv —I------------, (2.21)
2M,vr2! sin4 (%/2) \ 4e / sin4 (x/2)
где x — угол рассеяния в системе центра масс. Для электрон-
ионных столкновений на малые углы (М' = т. и' = и, % = 0 1)
оценка (2.20) меньше (2.21) в четыре раза.
4.2. Кулоновские радиус и логарифм. Как мы сейчас увидим,
основной вклад в транспортное сечение дают малые углы. По-
этому в общую формулу (2.13) для о<г можно подставить уг-
ловую зависимость дифференциального сечения рассеяния (2.20),
справедливую для малых углов, распространив интеграл до не-
которого значения 0тах~1, до которого еще можно экстраполи-
ровать оценочное соотношение (2.20). Рассеянию на большие
5Г.1Ы 0^1 соответствует пролет электрона на расстояниях р,
меньших так называемого кулоновского радиуса го. Ему отвечает
примерное равенство кинетической mv2/2 и потенциальной ег/го
энергий электрона. Точное определение кулоновского радиуса
г0 сдЛ/ЭХ2 для общего случая соответствует рассеянию парт-
неров па угол 90° в системе центра масс. Заметив, что 1 — cos 0 ~
30
~ 02/2, и введя для расходящего со стороны малых углов ин-
теграла условный предел 0min, pmax, найдем
6mах ~1 Ртах
___ „ ( Г ^0 2 1 ^тах /о
—А —г- лг0 —- = лг01п——. (2.22)
\mv / J « Р 'о
бтт г0
Масштабом сечения служит площадь кружка с кулоновским ра-
диусом, что и естественно (ср. с. п. 3.1), но численно Gtr может
оказаться сколь угодно большим из-за логарифмического мно-
жителя.
Фактическим верхним пределом в интеграле (2.22) служит
то расстояние, до которого простирается кулоновское поле дан-
ного заряда в плазме. Заряд своим полем поляризует окружаю-
щую плазму, от чего поле поляризации уничтожает поле дан-
ного заряда на расстояниях г d. Потенциал заряда с учетом
экранировки соседями спадает уже не по кулоновскому закону
е/r, а как г-1 exp (—r/d). Величина
/ кт /Л1К]\1/2 /г [эВ]\ 1/2
d = \/ —6,90 ( -^-2 _ 743 (2.23)
V \ пе ) \ Пе )
называется дебаевским радиусом*). Подставив pmax = d и заме-
нив M'v'2 на 2кТ7 получим
In Л = 1пД -? г 7,47 ь 1,51g 7е|К| - 0,5 \gne.
го 2 Ул « «У
(2.24)
*
Для разрядных условий In Л ~ 4—11. Таково примерное соотно-
шение вкладов далеких и близких столкновений в транспортное
сечение.
4.3. Кулоновское сечение. Для частиц со средней тепловой
энергией это сечение равно
акул аг w1 = v яа°2 $ Г1п Л"2’87’10-14111 л (r I•’BJ)-2™2.
(2.25)
Применительно к электрон-ионным и электрон-электропным
столкновениям под Т следует понимать температуру электронов
Те. Например, при Те = 1 эВ = 11 600 К и пе = 1014 см-3, In А ~ 3
*) Дебаевский радиус выводится из решения уравнения Пуассона для
самосогласованного поля ср(/) вокруг данного заряда, которое создается
этим зарядом и его окружением При этом считается, что соседние заряды
распределяются в самосогласованном поле по больцмановскому закону ти-
па пе = Псо ехр (еу/кТе). Величина (2.23) соответствует неравновесной плаз-
ме, в которой Те >Т, п плотность малоподвижных ионов с низкой темпе-
ратурой считается неизменной («+ — const ~ псо). Если посчитать, что и
п+ = Поо ехр (—еу/кТ), что, быть может, имеет смысл для равновесной
плазмы с Т — Те, то для d получается величина, в [/2 раз меньшая (2.23).
31
и оьул 2,3 • 10~13 см2. Это па два порядка Польше обычных га-
зокинетических сечений и максимальных сечений упругих столк-
новений электронов с aioMdMii и пер i пых газов.
4.4. Обмен энергией между электронами и ионами. Если
Те > Т, то скорость передачи энергии от электронов ионам в плаз-
ме определяется формулой (2.15) с к = = п+геокул. При про-
извольном соотношении температур в соответствии с замечанием
на с. 29 (см. сноску)
dTe т~те 1___2m ?
dt тобм ’ тоСм М Vei'
250/1 (Те fK])3/2 3,15-108Л (Те [эВ])3/2
In А In А
(2.26)
где А — атомная масса иона. Например, при А =40 (аргон), Те =
= 104 К, п+ = Ю15 см~3 тоГм = 1,7 мкс. Уравнение (2.26) было
получено в 1936 г. Л. Д. Ландау.
§ 5. Неупругие столкновения электронов
с атомами и молекулами
5.1. Ионизация. Чтобы вырвать электрон из атома (молекулы),
необходимо затратить энергию, равную энергии его связи в атоме.
Эту величину называют потенциалом ионизации I (табл. 2.3).
На рис. 2.9—2.11 представлены измеренные на опыте сечения
ионизации (на практике обычно пользуются именно экспери-
ментальными сечениями). Особый интерес для разрядных про-
цессов представляют сечения, соответствующие небольшим пре-
вышениям энергии электрона г над пороговым значением е = /
Таблица 23 П)гнцш поншцши наклон сечении ионизации
вблизи порога
Атом, моле- кула I, эВ с\, 10~17см2/ В Облас ть применимости е, эВ Ат ом, моле- ку ia I, в сг, 10-17см2/эВ Область применимости е, эВ
н 13,6 Hg 2,7 10,5—28
Не 24 6 0,13 24.6-35 н2 15,4 0,59 16—25
Ne 21,6 0,16 21,6—40 n2 15,6 0,85 16—30
Аг 15,8 2,0 15—25 о2 12,2 0,68 13—40
Кг 14,0 со2 13.8
Хе 12,1 со 0,67 14-25
N 14,5 0,59 15—ЗП Na 5,1
С 13,6 0,6 14-25 К 4,3
Hg 10,4 7,9 10,5-13 Cs 3,9
(рис. 2.11). В большинстве случаев очень энергичных электро-
нов в газе бывает мало, и потому их роль в ионизации чаще
всего невелика. Впрочем, встречаются ситуации (например, в ка-
тодном слое тлеющего разряда), когда электроны достигают
энергий, значительно превышающих потенциал ионизации.
32
Вблизи порога сечения неплохо аппроксимируются прямой
ог = Сг(е-/), 8^/, (2.27)
чем пользуются при расчетах скорости ионизации (п. 1.2 гл. 4).
При максвелловском спектре масштабом сечения ог служит зна-
чение ог при 8~/+&Т\, а поскольку чаще всего ~ 1 эВ, то
численно 0г»С, если Сг выражено в см2/эВ (табл. 2.3).
В некоторых условиях существенную роль играет ионизация
возбужденных атомов, составляющая заключительный акт сту-
пенчатой ионизации (сначала электроны возбуждают атомы, по-
том ионизуют). Энергетических выгод это не дает, суммарная
энергия возбуждения и последа -
ющей ионизации все равно рав
на Z. Но оба акта могут совер-
шать более медленные электроны,
и сечения ионизации возбужден-
ных атомов при небольшом пре-
вышении е над порогом значи-
тельно больше, чем невозбужден-
ных (рис. 2.12, 2.13).
5.2. Возбуждение электронных
состояний. Процессы эти важны
как первичный /этап ступенчатой
ионизации, как/ источник потертГ
энергии электронов, как одна
из причин свечения плазмы. Сре-
ди возбужденных атомов и мо-*
лекул выделяются метастабилъ-
пые частицы. Самопроизвольный
переход из метастабильных со-
стояний в нижнее энергетическое
состояние, сопровождающийся
излучением кванта, запрещен,
т. е. имеет чрезвычайно мал'по
Рис. 2 9. Вероятности и сечения
ионизации атомов Не, Ne, Аг и
молекул Н, N2 электронным уда-
ром в широком диапазоне энер-
гий электронов [14]
вероятность. Метастабильная частица может жить долго,
пока не дезактивируется ударом электрона или атома, не перей-
дет в более высокое состояние, не ионизуется или не погибнет
на стенках.
Времена жизни метастабильных состояний по отношению к
высвечиванию превышают 10“4 с и достигают в некоторых слу-
чаях секунд (табл. 2.4), тогда как обычные возбужденные ато-
мы и молекулы высвечиваются через 10~8—10~7 с (если не будут
до этого дезактивированы ударом). Особенно велика роль мета-
стабильных частиц для процесса ступенчатой ионизации, так
как они живут долго и «ожидают» ионизующего удара.
Самый нижний из не метастабильных уровней называют
резонансным (табл. 2.4). Возможен такой процесс: атом излу-
чает квант света, возвращаясь в основное состояние. Этот квант
3 Ю. П Райзер
33
Рис 2.10. Вероятности ионизации различных молекул электронами в зави-
симости от энергии последних [15]
Рис 2 11. Поведение сечения
ионизации электронным ударом
вблизи порога; представлены от-
ношения сечении ионизации и уп-
ругих столкновений (последние
даны на рис 2 2 и 2 3) в зависи-
мости от энергии электронов [15]
с большой вероятностью поглощается соседним атомом, посколь-
ку происходит резонансное поглощение, и переводит его на тот
же самый резонансный уровень. Второй атом излучает квант,
и т. д. Так происходят блуждание (диффузия) резонансного из-
лучения и периодическое появление и исчезновение резонансно
возбужденных атомов. Процессу препятствует дезактивация (ту-
шение) резонансно возбужденных атомов ударами второго рода.
34
Рис 2 12 Сечения ионизации воз-
бужденных
электронами в
их энергии* —
эксперимент,
атомов Не (23S)
в зависимости от
сплошная кривая —
, штриховая — тео-
рия [12]
Рис 2 13 Сечения ионизации воз-
бужденных метастабильных ато-
мов Ne (ls5) электронами в зави-
симости от энергии последних
(теория) [12]
г' > 4 )и^пгл i нижгик метастабитьных и резонансных уровней
Атом молек^ ла (с< стояние) Энергии возбун дения, эВ Вр( мя я изни, с Ингерпо шция суммарного сечения возбуждения вблизи порогов о*, [см2], е, [эВ]
— —— 11(2^) Н(2Р) Jk(23Si) j:X2‘So) i1' i - Ar(4sPz) Кг Хе Нз 11а N2(43s£) N2(a1Su) o2CAs) o2(b*s+) 1 /к о* 1 о 1 - ' ' 2 1> * >. 21 1(> 62 * 1b 7 * 16,85 11,55 * 11,61 11,72 * 9,91 * 10,02 10,5 * 8,32 * 8,45 9,4 * 4,6 * 4,87 5,4 * 6,7 8,7 * 11,5 6,2 * 8,4* 0,°8 * 1,64* О '2 1 <> 10 2 10 >1,3 >1,3 1,3—2 6 0,э 2,7 103 12 25 10 LK (t — 101 ^4,6 10'18 (е — 20) •|1,5 10 18 (е — 16) ^7 10 18 (е — 11,5) °тах =1,7 10*16 при е = 6,5 }7,6 10-и (е- 8 7,
---' « -.л.пме уровни помечены звездочкой.
*> метаетабильнме^УР—----------------------
35
Эффективное сечение возбуждения о*(е) электронного со-
стояния называют иногда функцией возбуждения В зависимо-
сти от энергии электрона сечение возбуждения ведет себя в ка-
чесх венном отношении так же, как и сечение ионизации, только
максимум распо тагается ближе к порогу возбуждения Е*
(рис 2 14—2 16) Для некоторых атомов суммарные сечения воз-
буждения многих уровней недалеко от порогов можно грубо
интерполировать прямыми типа (2 27) — это бывает полезным
для оценок потерь энергии на возбуждение*) Надо сказать, что
измерение сечений возбуждения составляет гораздо более труд-
ную задачу, чем исследование ионизации, поэтому данные о him
значительно скуднее
5.3. Удары второго рода. Сталкиваясь с возбужденными ато-
мами, э нейтроны могут дезавуировать их приобретая п\ -шер
гию возбуждения Это называют неупр>гпми ударами вте рого
рода (в западной литературе — сверхупругими) Сечение этою
процесса 02 можно оценить, воспользовавшись принципом де-
тального равновесия и сечением возбуждения в форме о*(г) =
— С* (в—А*), как в табл 2 4 Это дает 02(e) ~ С* (в 3 E*)ga/g*.)
где ga и g* — статистические веса невоюх жденного и возоуж-
депного атомов При типичных для разряда энергиях 8 ~ 1 эВ <
~ 10 эВ 02^ C*E*g<Jg* и слабо зависит от энергии С i шс
но данным табл 2 4 02 ~ 10-16 см9
5.4. Возбуждение молекулярных колебаний. Этот процесс
играет исключительно важную роль в разрядах, происходящих
в молекулярных газах, будучи главным механизмом передачи
энергии от электронов молекулам Процесс возбуждения электро-
нами колебании в молекулах N2 и СО2 лежит в основе работы
электроразрядных газовых СО2 лазеров Аналогичным образом
работают и СО лазеры При энергиях э хектропа 8 ~ 1—5 эВ
сечения возбуждения колебаний довольно большие, в максимуме
они даже превосходят сечения электронного возбуждения и всего
на порядок меньше сечении упругих столкновении (рис 2 17 —
2 20) У молекул N2, Н2, СО, к ксторым относятся графики,
энергии колебательных квантов равны 0,29, 0,53, 0,27 эВ соот-
ветственно В молекулах возбуждаются не только первые, но и
высшие колебательные состояния, правда, в случае Н2 верой-
ности возбуждения высших состояний убывают с ростом кван-
тового числа v
Казалось бы, обмен энергией между легким электроном и ко-
лебательными степенями свободы тяжелых ядер должен быть
затруднен так же, как и обмен кинетической энергией, а гармо-
пическии осциллятор вообще воспринимает энергию по одному
кванту Парадокс разрешается следующим образом Процесс воз-
буждения молекулярных колебаний электронным ударом идет
*) В непосредственной близости к порогу по квантовой механике с1’ ~
~ 4е — I * по па играющие основною роль значения 8 — Е* 1 )В а < г
закон уже, по видимому, не распространяется
36
через промежуточное состояние. На первом этапе электрон объ-
единяется с молекулой, образуя молекулярный hoh:N7, Н2,
СО-. Будучи неустойчивыми, перечисленные отрицательные
ионы через короткое время распадаются, освобождая электрон
с энергией меньшей, чем начальная. Молекула при этом оста-
ется в возбужденном колебательном состоянии, причем это со-
стояние может соответствовать различным уровням. В пользу
электронами различных уровней атомов
(а) п Ne £б)
2.15. Сечения возбуждения электро-
[и различных уровней молекулы N2
этого предположения говорит и тот факт, что в азоте, например,
резкий рост сечения возбуждения начинается не от энергетиче-
ского порога 8 = йсокоп = 0,29 эВ, *а от -гораздо более высокой
энергии 8 ~ 1,8 эВ. По-видимому, порог определяется не столько
передаваемой в конечном
счете энергией колеба- б/
тельного кванта, сколько
энергией активации, необ-
ходимой для образова-
ния
Электроны возбуждают
и вращательные состоя-
ния молекул, но этот про-
цесс играет обычно зна- о,4-
чительно меньшую роль,
чем возбуждение колеба-
ний.
5.5. Диссоциация моле-
кул. Диссоциация не l
оказывает существенного рис
влияния на энергетиче- на
ский баланс электронов в
разряде, уступая в этом отношении возбуждению колебательных
уровней молекул. Но в определенных условиях диссоциация мо-
37
Рис. 2.16. Вероятности возбуждения и ионизации вблизи порогов: штрихо-
вые кривые — Аг и Н2, сплошные — Ne и Не [6]
лекул имеет большое непосредственное значение, будучи началь-
ным и наиболее ответственным этапом в цепочке последующих
химических превращений. Плазмохимия, т. е. получение химиче-
ских соединений в плазменных условиях при помощи разря-
дов,— новое важное направление в химической технологии. Для
многих реакций «узким местом», определяющим скорость всего
процесса, является образование из молекул атомов и свободных
радикалов, которые
Рис. 2.17. Суммарное се-
чение возбуждения пер-
вых восьми колебатель-
ных уровней N2 ударами
электронов [2.1]
потом уже достаточно быстро реагируют с
другими компонентами. Прохождению
этого этапа и способствует диссоциация
молекул ударами электронов в разряде.
Как и возбуждение колебаний, диссо-
циация идет двухступенчатым путем, но
не через захват электрона, а через воз-
буждение электронных или электронно-
колебательных состояний молекулы с
последующим распадом возбужденной мо-
лекулы на атомы. И порог у сечения оп-
ределяется не потенциалом диссоциации,
а потенциалом возбуждения низшего не-
стабильного электронного состояния
(рис. 2.21).
5.6. Замечание о возбуждении и ио-
низации ионами. Неупругие столкновения
ионов с атомами и молекулами сколь-
нибудь значительной роли в разрядах
не играют. Даже обладая энергией, до-
статочной для возбуждения или ионизации, ион проле-
тает мимо атома слишком медленно. Своим полем он медлен-
но (адиабатически) деформирует электронную оболочку, кото
38
Рис 2.18 Сравнение сечений различ-
ных процессов при столкновениях
электронов с молекулами N2 [2.1]:
Qtr — упругое транспортное, о46 и
0б4 — вращательные сечения возбуж-
дения с уровня ] = 4 на уровень
7 = 6 и дезактивации (Г = 77 К,
теория), gv — суммарное сечение
возбуждения восьми колебательных
уровней, Ge — суммарное сечение
возбуждения электронных уровней
с энергиями от 5 до 14 эВ, ог — се-
чение ионизации
5,10 ^см^—\—।—।—।
[2 1]
Рис. 2.20. Суммарное сечение воз-
буждения первых восьми колеба-
тельных уровней СО [19]
Рис. 2 21. Полные сечения диссоциации молекул электронным ударом че-
рез возбуждение различных электронных состояний [2.2]
рая, после удаления иона, возвращается в прежнее состояние,
вероятность неупругих ударов значительна только тогда, когда
скорость иона сравнима со скоростью движения электронов в
атоме, v ~ 108 см/с, для чего ион должен обладать энергией более
10 кэВ. В исключительных случаях при пересечении термов ква-
зимолекулы возможна ионизация и медленными тяжелыми ча-
стицами [18].
39
Глава 3. ДРЕЙФ, ЭНЕРГИЯ И ДИФФУЗИЯ ЗАРЯЖЕННЫХ ЧАСТИЦ
В ПОСТОЯННОМ ПОЛЕ
§ 1. Дрейф электронов в слабоионизованиом газе
В период между столкновениями электрон ускоряется вдоль
линии электрического поля Е. При столкновении он резко и слу-
чайным образом меняет направление своего движения, потом
ускоряется вновь и т. д. В слабоионизованиом газе встречи заря-
женных частиц друг с другом редки, сталкивается электрон в
основном с нейтральными молекулами (атомами), причем столк-
новения эти чаще всего оказываются упругими. Систематическое
движение вдоль направления действия внешней силы на фоне
беспорядочного движения называется дрейфом. В гл. 3, 5 пове-
дение электронов в поле рассматривается на основе элементарной
теории. Суть ее состоит в том, что внимание концентрируется на
одном «среднем» электроне. Рассматривается некое усредненное
поведение одного электрона, а когда требуется вычислить какие-
то величины, относящиеся к электронному газу в целом, все
электроны считаются одинаковыми. Строгий подход основан на
использовании кинетического уравнения для функции рас-
пределения электронов по скоростям и энергиям, чему будет по-
священа гл. 7.
1.1. Уравнение усредненного движения. Акт рассеяния длится
мгновение по сравнению со средним временем тс между столкно-
вениями*). Поэтому уравнение для истинной скорости данного
электрона ve можно записать в виде
пгче= — еЕ ^^тпЛуг8 (t — ti), AVi = \е—Че, (3.1)
i
где Avt — изменение вектора скорости при i-м столкновении, ко-
торое происходит в момент Л; 6 — дельта-функция, ve — скорость
после столкновения. Усредним уравнение, поскольку следить за
судьбой индивидуальной частицы просто немыслимо. Истинная
скорость ve превращается при этом в среднюю скорость у. Сумма
усредняется по моментам времени столкновений Л и углам рас-
сеяния 0 между векторами ve и ve. Она приобретает смысл сред-
него изменения импульса в единицу времени t?z<Av>vc, которое
вычислялось в п. 2.2 гл. 2. Это есть сила трения (сопротивление),
которая действует на электрон со стороны среды. Подставив ее
по формуле (2.14), получим уравнение для средней скорости
mv = —еЕ —mvvm, = vc(l — cos 0), (3.2)
где vm, напомним,— эффективная частота столкновений.
*) Размер атома а ~ 10~8 см, скорость электрона при е ~ 1 эВ и ~
108 см/с, время взаимодействия а/и ~ 10~16 с.
40
1.2. Скорость дрейфа. Проинтегрируем уравнение (3.2):
— (eE/mvm) [1 — ехр(—vmt) ] + v(0)exp (—vmt). (3.3)
После нескольких столкновений начальная направленная ско-
рость электрона v(0) исчезает (она хаотизируется). Средняя ско-
рость приобретает значение
уд = —eE/mvm, (3.4)
которое и представляет собою скорость дрейфа. Электрическая
сила при дрейфе компенсирует силу трения. Все предыдущие
рассуждения справедливы для электронов с определенным значе-
нием хаотической скорости v. Вообще говоря, сечение и частота
столкновений сложным образом зависят от энергии электрона
е = mv2/2 (см. рис. 2.1—2.5, 2.7), и формула (3.4) нуждается в
усреднении по спектру.
Последовательный подход к вычислению скорости дрейфа
основан на рассмотрении кинетического уравнения для функции
распределения электронов по скоростям. Такой путь указывает,
как нужно правильно усреднять формулу типа (3.4). При этом
оказывается, что допущение о независимости эффективной часто-
ты столкновений от скорости, во многих случаях вполне приемле-
мое, в точности сводит стрргое выражение для рд к формуле (3.4),
которую тогда вообще^йе нужно усреднять. Это обстоятельство
служит весьма веским оправданием T<yi широчайшей распростра-
ненности, которую получила предельно простая формула (3.4)
Таблица 31. Оценочные значения подвижное! и электронов, э^фекзив
ной частоты столкновений, проводимости, <плины. пробега *)
Газ Ю/', (М2-торр В-( 109(с-тор1 )-1 ор/ис, JQ-13T0PP - г м' £ ь р ’ СМ ГОрр 10 2<м-торр-
Ом
Не ]\е Аг Н2 N2 воздух со2 со *) Подвг гд(Е/р) законе к энергиям эл го разряда 0 86 1,5 0,33 0.37 0/12 0,45 1,1 0,31 гжности найде м Гд=цеЕ, vm ектронов в 1 — 2,0 1,2 5.3 4,8 4,2 3,9 1,8 5,7 ны путем ani и о вычислены -10 эВ, характ 1,4 2,4 0.53 0,58 0,67 0,72 1,8 0,5 эроксимацпи ; по ре. Длины Hj ерным для пол' 0 6—10 0/1-2 1 — 13 4-30 2—50 4-50 3—30 5—50 эксперимента,п робега 1 = (Nu ожительного сп о 12 3 2 3 3 3 >ных кривых относятся голба тлеюще-
при теоретических построениях и оценках. Для численных оце-
нок проще всего, пользуясь экспериментальными данными о
Ofr(e), относить vm к средней энергии электрона. Последняя за-
висит от поля, но па этот счет имеется справочный материал,
и можно делать оценки (§ 3).
41
Рис. 3 1. Скорость дрейфа электронов в Не, Ne, Аг, Н2, N2 и О2 как функция
отношения Е/р [6]
Рис. 3.2. Скорость дрейфа электронов в воздухе и молекулярных газах как
функция отношения Е/р [6]
42
1.3. Подвижность. Подвижностью называется коэффициент
пропорциональности между величинами скорости дрейфа заря-
женной частицы и поля. Подвижность электронов равна
е 1,76-1015 см2 о
~ v [с-1] "в^’ Рд ^Е-
т т 1 >
Поскольку средняя энергия электронов зависит от поля, зависи-
мость от Е не является строго линейной, и подвижность, опре-
деленная формулой (3.5), зависит от поля. Но при теоретиче-
ском рассмотрении различных разрядных процессов, как прави-
ло, пользуются удобной для этой цели линейной связью (3.5)
с Це = const. Для численных оценок подбирают разумное эффек-
тивное значение це (табл. 3.1). Обычно это не нарушает каче-
ственных выводов теории, хотя в некоторых случаях нелиней-
Рис 3 3 Скорость дрейфа электронов в Аг, Кг, Хе как функция отношения
Е/р [15]
1.4. Подобие, результаты измерений, дрейф в смесях газов
Частота столкновений vn пропорциональна плотности газа N или
его давлению р. Если частота постоянна, ~ р~х и ~ Е/р
Энергетический спектр и средняя энергия электронов также за-
висят от Е и N или р не порознь, а от комбинации Е/р (§ 3 и
гл. 7). Поэтому в любом случае скорость дрейфа является функ-
цией отношения Е/р. Законы подобия, как мы увидим проявля-
ются во многих закономерностях газового разряда. Они имеют
большое значение. Благодаря подобию сокращается объем изме-
рений и результаты представляются не в виде функции двух
переменных, скажем Е и р, а в виде функции Е/р, подобно v =
= рд(£7р). я
Окорость дрейфа всегда растет с увеличением отношения Е/р
(рис. 3.1—3.3), но не всегда этот рост близок к прямой пропор
4^
циональности, что связано с зависимостью vm и ид от электрон-
ного спектра. Так, например, в аргоне наблюдается аномально
быстрый дрейф при значениях Е/р ~ 10“3—10"1 В/(см торр),
для которых характерные энергии электронов приходятся на об-
ласть рамзауэровского минимума сечения столкновений (п. 2.1
гл. 2). Оценивая скорости дрейфа в смесях газов, следует усред-
нять с учетом процентного содержания компонент не сами ско-
рости или подвижности, а их обратные величины («сопротивле-
ния»), так как в смеси суммируются частоты столкновений. При
этом неизбежна небольшая ошибка, связанная с тем, что элек-
тронный спектр в смеси отличается от спектров в составляющих
ее газах.
§ 2. Проводимость ионизованного газа
2.1. Слабоионизованная плазма. Подвижности массивных ионов
в сотни раз меньше подвижностей легких электронов. Поэтому
вклад ионов в электрический ток пренебрежимо мал, за исклю-
чением тех нечастых случаев, когда плотности ионов
в соответствующее число раз превышают плотность электронов пе,
В плазме, где пе ~ п+, плотность тока j и проводимость о равны
/ = — епекД = епе\хеЕ = оЕ, (3.6)
?2Г1 Л [см~3]
о =ерепе=—^: _ 2,82.10-4-^——^Ом^-см-\ (3.7)
mVm v/ri
Проводимость слабоионизованного газа определяется в основном
степенью его ионизации ne!N.
2.2. Сильноионизованная плазма. Рассеяние электрона иона-
ми так же мешает его дрейфу вдоль поля, как и рассеяние моле-
кулами. При не слишком слабой ионизации и п+ = пе
vm = Nvatr + nevoKyJl, (3.8)
где о«ул — сечение электрон-ионных столкновений, которое опре-
деляется кулоновскими силами (§ 4 гл. 2). Из-за большой ве-
личины кулоновского сечения электрон-ионпые столкновения су-
щественны уже при степенях ионизации больше 10~3.
При еще больших степенях ионизации они играют главенст-
вующую роль. Поскольку в этом случае vm ~ пе, проводимость от
плотности электронов не зависит (точнее, зависит очень слабо
через кулоновский логарифм). По формуле (2.25) найдем про-
водимость:
е2
СУ —-------
тг?акул
- 1,9-10* Ом- .см-Ч (3.9)
4ne2mv In А 1п А
В численной формуле подставлена средняя тепловая скорость
электронов по (2.5) и уточнен примерно вдвое [3.1] коэффициент.
44
2.3. Почему электрон-электронные столкновения не вносят
вклада в электрическое сопротивление. Дело в том, что сопротив-
ление (или трение) при дрейфе электрона связано с потерей при
рассеянии импульса, направленного вдоль поля. Но суммарный
импульс любой пары взаимодействующих электронов (mvi + тчъ)
при рассеянии сохраняется, хотя скорости каждого из них меня-
ются и по величине, и по направлению. Отсюда следует, что при
столкновении не изменяется суммарный электрический «ток»
пары — evi — ev2. Значит, если бы электрон не испытывал ника-
ких иных столкновений, кроме как с другими электронами, дви-
жение электронного коллектива в поле было бы в среднем уско-
ренным, что и означает отсутствие электрического сопротивле-
ния. Заметим, что косвенным образом электрон-электронные
столкновения могут повлиять па проводимость — через воздейст-
вие на энергетический спектр электронного газа (его «максвел-
лпзацию»).
§ 3. Энергия электронов
3.1. Джоулево тепло. Над электроном, движущимся со ско-
ростью ve, в единицу времени поле совершает работу — eEve.
Представим скорость электрона в виде суммы хаотической v и
дрейфовой уд составляющих: уе = у + уд. По самому определению
в среднем по многим электронам <^> = 0 и <ve> — уд. Работа по-
ля в среднем равна — <сЕуд> — eEv^ При протекании тока в
1 см3 газа в 1 с выделяется энергия eEvAne= ]Е. Это и есть джоу-
лево тепло тока. Работа поля затрачивается на преодоление си-
лы трения. Джоулево тепло равняется диссипации энергии поля,
вызванной существованием трения (сопротивления).
3.2. Среднее приобретение энергии электроном в одном эффек-
тивном столкновении. Это приобретение энергии есть
е2Е2 „
Асе = “7“ ~—у == тгд (3.10)
vm д х 3
и по порядку величины совпадает с «кинетической энергией дрей-
фового движения» шГд/2. Полная кинетическая энергия электро-
на в среднем складывается из хаотической е и дрейфовой /2
составляющих:
/ \ / 2 \ mv2 _ mv2
\-2-z = VT/ + V =е + чб <vv«> = °-
Результат (3.10) качественно можно трактовать следующим
образом. Сразу после очередного столкновения («эффективного»)
скорость электрона полностью хаотизирована — вектор ее в сред-
нем равен нулю. К следующему столкновению электрон набирает
в поле направленную дрейфовую скорость и соответствующую ки-
нетическую энергию. При столкновении эти новые порции также
45
переходят в хаотическую часть — в электронное «тепло»—и все
начинается сначала.
3.3. Истинные изменения энергии электрона при столкнове-
ниях. Формула (3.10) отражает лишь конечный, результирующий
эффект различных, и притом резко противоположных ситуаций,
которые возникают в конкретных столкновениях. На самом деле
в период между двумя столкновениями электрон может и уско-
ряться полем и тормозиться, и набирать энергию и терять ее. Все
зависит от того, пришлось ли ему начать движение после столк-
новения в сторону действия силы пли против нее, с большой ско-
ростью или с малой. Поясним это на простейшем примере.
Зафиксируем внимание на двух электронах, которые сразу
после столкновения обладают одинаковыми по величине скоро-
стями v и летят параллельно полю, но в противоположных на-
правлениях. Начальные кинетические энергии у них одинаковы,
тк2/2 Тот электрон, который движется в направлении действия
силы (против поля), к следующему сто 1кновенпю набирает ско-
рость v + eElmx'm = v + ил и приобретает дополнительную энергию
ОТ(р+г)2 mr*
Af+ = ------------г /ПУ,'Д "Г1
Тот, который начал свое движение по полю, сначала, а может
и все время, тормозится и к следующему столкновению дости-
гает скорости — v + Кд. Он приобретает дополнительную энергию
mv2 ,
— = — ття -г —
которая оказывается отрицательной, если v > уд/2. В этом случае
электрон энергию теряет. Именно такая ситуация типична, ибо,
как мы увидим в п. 3.6, хаотические скорости v гораздо больше
дрейфовой.
В среднем по двум рассмотренным вариантам электрон полу-
чает дополнительную энергию
(Ле+ + Ле)
2
-= mvl,
которая не зависит от и всегда положительна и совпадаете (3.10).
Ясно, что электроны с любыми начальными векторами v можно
разбить на аналогичные пары с противоположно направленными
скоростями и получить, по крайней мере по порядку величины,
тот же результат.
Поскольку, как отмечалось со ссылкой на п. 3.6, средняя хао-
тическая скорость v > Кд, результирующий эффект приобретения
энергии из расчета на одно столкновение представляет собою
малую разность относительно больших истинных приобретений
и потерь, которые имеют порядок | Ае+ | « тии^ mv^. Сами
же ис hi иные изменения энергии I Де±1 в свою очередь малы по
сравнению со средней энергией электрона 8 ~ mv2/2. Указанные
46
величины относятся как
Дев J Ае±| уя (ЗЛ1)
| Ае^ | е v ’ е \ v /
3.4. Уравнение баланса энергии электрона. Получая энергию
от поля, электрон передает ее атомам и молекулам. При слабой
ионизации плотность тока и выделение джоулева тепла малы.
Газ при этом нагревается мало. Но средняя энергия (или темпе-
ратура) электронов в разряде не может стать слишком низкой.
Электроны тогда не смогут ионизировать атомы и поддерживать
в газе проводящее состояние. В таких случаях Те^> Т, и обмен
энергией при упругих столкновениях имеет односторонний харак-
тер — только от электронов газу. Воспользовавшись формулой
(2.15) для средней потери энергии электрона при упругом столк-
новении с молекулой и обозначив 6 = 2ш1М, запишем уравнение
баланса энергии «среднего» электрона, испытывающего только
упругие столкновения:
d& (л £ ч ( е2Е2, \
_=(Дея-бе)тт= _Se)vm. (3.12)
В разрядной плазме средние энергии электронов обычно дале-
ки от довольно высоких потенциалов возбуждения атомов £* и
ионизации, I ~ 10 эВ, и соответствующие неупругие потери энер-
гии малы. Ионизируют газ «сверхэцергичные» электроны, которых
очень мало. Поэтому в одноатомных газах основным механизмом
передачи энергии от электронов газу являются именно упругие
потери.
В молекулярных газах электроны* растрачивают приобретае-
мую энергию в основном путем возбуждения колебаний (и вра-
щений) молекул (п. 5.4 гл. 2). Передача энергии молекуле в акте
возбуждения колебаний несравненно больше средней упругой
передачи Дб>пр = (2ml М) 8 ~ 10~4 эВ. Она составляет один-два
колебательных кванта, т. е. несколько десятых электронвольта.
И хотя далеко не каждое столкновение оказывается неупругим,
все равно доля энергии 6, передаваемой молекуле из расчета на
одно любое (т. е. фактически на одно упругое) столкновение,
значительно больше 6упр = 2ш!М. Уравнение (3.12) можно со-
хранить и для молекулярных газов, причем 6 ~ 10“3—10“2, но
вычислить 6 теоретически с такой же легкостью, как для упру-
гих потерь, не удается. Обычно ее оценивают косвенным образом
из экспериментальных данных (п. 3.5) или путем расчетов на
основе кинетического уравнения.
3.5. Средняя энергия. Установившееся значение энергии
«среднего» электрона, которое соответствует компенсации при-
обретения энергии потерями, в данном приближении можно рас-
сматривать как среднюю энергию 8 электронов в поле (строгое
вычисление этой величины требует решения кинетического урав-
нения; см. гл. 7). Посчитаем не зависящими от энергии коэф-
47
фициент 6 и сечение рассеяния о/г, т. е. длину пробега электронов
l = При этом vm==v'll~l/e. Положим также для опре-
деленности то2 ~ (16/Зл) 8, как было бы в случае максвеллов-
ского спектра. Приравняв нулю правую часть (3.12), найдем
- 0,8^= 0,8-^А
4 V 6 ]/б
(3.13)
Средняя энергия пропорциональна E/N и в 1/У6 раз больше
энергии еЕ1, которую электрон приобретает иа длине пробега,
двигаясь в направлении действия электрической силы. Допуще-
нию о постоянстве длины пробега соответствует корневая зави-
симость скорости дрейфа от поля. Действительно, подставляя
в vm = Nvotr значение средней скорости v = (16s/3nm)1/2 и опре-
деляя о с помощью (3.13), по формуле (3.5) найдем
и ~ о 961/4/3 14)
д у 16 у \motrN j ’ ymotrNj ’ v '
С другой стороны, допущению о постоянстве частоты столкно-
вений, когда = const и ^д — EIN, отвечает квадратичная зави-
симость энергии от поля (если 6 = const). Из (3.12) в этом слу-
чае вытекает
- е2Е~ = е2 /_Е_\2 -
(3.15)
Таким образом, при выборе модели мы оказываемся перед ди-
леммой: либо считать
Ут, Це = const, 17д ~ E/N, 8 ~ б-1 (E/N)2,
либо считать
сщ, Z = const, рд~61/4(ЕА¥)1/2, 7~8-y2(E/N).
Реальные зависимости кд и 8 от отношения EIN, найденные
из опыта (и. 4.2) или полученные путем решения кинетического
уравнения, обычно сложны и в лучшем случае на отдельных
участках Е, N в тех или иных газах хорошо аппроксимируются
той пли иной моделью. Поэтому при теоретическом исследовании
различных эффектов, выяснении соотношений качественного ха-
рактера, направленном на более глубокое понимание физики про-
цессов, выбирают тот вариант, который удобнее для анализа.
Если эффекты определяются дрейфом, электрическим током,
целесообразно считать постоянными подвижность, проводимость.
Если внимание сосредоточено на энергетических аспектах пове-
дения электронов в поле, как в этом параграфе, лучше пользо-
ваться приближением I = const и очень наглядной формулой
(3.13), как мы и поступим ниже.
48
Формула (3.13) дает разумные числовые значения. Например,
в гелии (6 = 2,7 -10-4), где транспортное сечение мало меняется
в характерном диапазоне энергий и равно примерно Gir &
~ 5,5 • 10“16 см2 (I ~ 0,055//? [торр] см), при E/N = 3,3 • 10“17 В • см2
(Е/р = 1 В/ (см • торр)) получим 8 = 2,5 эВ. Из опыта следует
8 ~ 2 эВ. В случае молекулярных газов запросто вычислить 8
не удается, так как имеются значительные трудности в определе-
нии коэффициента потерь 6. Однако от этого формула (3.13)
не лишается ценности. Напротив, она открывает возможность
оценивать 6, поскольку существует независимый способ опреде-
ления 8 (п. 4.2). Так, например, в азоте при Е/р = 3 В/(см - торр)
8 ~ 1,5 эВ; сечение в характерном диапазоне энергий имеет по-
рядок Otr ~ 10~15 см2 (Z ~ 0,03/р [торр] см) и (3.13) дает 6~
~ 2,1 • 10-3, что согласуется с результатом, полученным другим
путем. Коэффициент упругих потерь в азоте 2т/М == 3,9 • 10-5
гораздо меньше.
•3.6. Соотношение между хаотической и дрейфовой скоростя-
ми. Это соотношение непосредственно вытекает из формул (3.5)
и (3.13):
= /б, (3.16)
v mv * о
Электрон набирает в поле хаотическую скорость, которая в
1/V6 (т. е. в десятки и сотни раз) больше дрейфовой. Соотноше-
ние (3.16), проясняющее физический смысл порядка малости
vjv, тесно увязано с показателями порядка малости энергетиче-
ских характеристик электронов. При столкновении^лектрон при-
обретает либо теряет энергию порядка k\s±I ~ V5s ~ е£7, кото-
рая соответствует проходимой им в том или ином направлении
разности потенциалов на длине свободного пробега. Энергия Де+
чуть больше |Де_1 на величину Д8Е~ Уб1Де±1, которую электрон
в среднем и набирает в одном столкновении.
Несколько слов о пределах применимости полученных соотно-
шений. Со стороны очень слабых полей она ограничена допуще-
нием об одностороннем характере обмена энергией между элек-
тронами и газом, 8 > кТ. Ведь в отсутствие поля электроны тер-
мализуются и приобретают температуру газа Т, если только до
этого не гибнут. В слабоионизованной разрядной плазме условие
8 > кТ обычно выполняется с большим запасом. В сильных по-
лях вступают в игру значительные неупругие потери на воз-
буждение электронных состояний, что происходит при энергиях
электронов 8^ 10 эВ. Даже из чисто формального перехода в
(3.13), (3.16) к пределу максимально возможных потерь 6«1
видно, что направленная и хаотическая составляющие скорости
становятся сравнимыми, стало быть, возникает сильная асиммет-
рия и в движении, и в обмене энергией между электронами и
полем. Электрон набирает на пробеге значительную энергию.
4 Ю. П Райзер 49
возбуждает или ионизует атом, теряя ее, и устремляется вперед
дальше. Это уже не совсем та картина, которая просматривалась
до сих пор. Подобные явления могут происходить в катодном
слое тлеющего разряда, однако здесь на этом мы останавливаться
не будем.
3.7. Релаксация энергии; критерии постоянства и однородно-
сти поля. Величину = 6vm называют частотой потерь энергии.
За время порядка
Ти = Vu1 = тот/б, (3.17)
т. е. примерно за 1/6 эффективных столкновений, электрон рас-
трачивает свою энергию, если «мгновенно» выключить поле.
За такое же примерно время очень медленный электрон набирает
в поле положенную энергию, так как в одном столкновении он
приобретает долю 6 от нее. Как видно из уравнения (3.12),
ти вообще характеризует скорость установления стационарной
энергии в данном поле. Это есть время релаксации энергии. Если
поле меняется за время ти мало, средняя энергия, а по существу,
и энергетический спектр электронов «следят» за изменениями
поля, т. е. являются квазистационарными; если быстро — следить
не успевают. Таким образом, критерий «постоянства» поля можно
сформулировать в виде условия
(dE/dt) ти < 1.
Поскольку электроны в среднем систематически сдвигаются
в направлении действия силы, процесс установления энергии про-
текает не только во времени, но и в пространстве. За время ре-
лаксации ти электроны сдвигаются вследствие дрейфа на рас-
стояние
Ли = кдти ~ О,8Убг7тт/6 = 0,8//Уб. (3 18)
Эту величину можно назвать длиной установления или дли-
ной релаксации энергии. В отличие от времени она не в 1/6,
а только в 1/У6 раз больше длины пробега электрона. Согласно
(3.13), (3.18)
8 = с£'Ли, (3.19)
т. е. свою среднюю энергию электрон приобретает, пройдя раз-
ность потенциалов на длине Ли.
Постоянное поле можно рассматривать как однородное, если
оно мало меняется на расстоянии порядка Ли, т. е. при условии
(dE!dx)Ku < 1.
В противоположном случае сильно неоднородных полей спектр
п шергия электронов уже не являются функциями только ло-
каиьпого отношения EIN. Энергия может определяться, напри-
мер, разностью потенциалов, проходимой электроном от точки
рождения.
50
В уравнении баланса энергии (3.12) слагаемое потерь в скоб-
ках растет с ростом 8, а слагаемое приобретений, в общем,
уменьшается; в предположении I = const — как 1/8. Значит,
энергия электронов всегда стремится к стационарному значению 8.
Если 8 < 8, то ds/dt>0; если 8 > 8, то dz/dt<0. Это свидетель-
ствует об устойчивости стационарного состояния, так как при
случайном отклонении 8 от 8 энергия будет неизменно возвра-
щаться к 8 (со скоростью релаксации).
§ 4. Диффузия электронов
4.1. Уравнение непрерывности. Когда плотность частиц, нахо-
дящихся в среде другого газа, неоднородна в пространстве, воз-
никает диффузионный поток, который стремится ее выровнять.
Полный поток складывается из дрейфовых и диффузионных со-
ставляющих. Плотности потоков положительно и отрицательно
заряженных частиц равны*)
r± = +z2pE-Z)Vn. (3.20)
Индексы ± у п, ц, D опущены. Коэффициенты диффузии равны
D = <z?2/3vm> « ZF/3, D - 1/р. (3.21)
Плотности частиц удовлетворяют уравнениям непрерывности
dnjdt +V = q, (3.22)
которые обобщают обычное уравнение диффузии; q — число актов
рождения или гибели частиц в 1 см3 в 1 с (источники).
4.2. Соотношение между коэффициентами диффузии, подвиж-
ностью и средней энергией. В предположении о постоянстве ча-
стоты столкновений согласно (3.5), (3.21) имеем
DJiie = mv*/3e = (2/3) е/е, (3.23)
где 8 — истинно средняя энергия электронов, независимо от их
энергетического спектра.
Если спектр максвелловский, равенство (3.23) справедливо
при любой зависимости vm(v). Нужно только подставить в него
строгое выражение для щ, вытекающее из кинетического урав-
нения (п. 6.1 гл. 7). Это и естественно, ибо в этом случае 8 =
= (3/2)кТе, и (3.23) сводится к соотношению Эйнштейна
Dl\i^kTle, (3.24)
которое имеет общий термодинамический характер. Действитель-
но, в состоянии термодинамического равновесия потоки отсутст-
вуют, а плотности зарядов в поле Е = —Vqp (ср — потенциал)
*) Если газ течет со скоростью и, к Г добавляются еще конвективные
потоки пи.
4* 51
W\
Е/р, В/(см-торр)
10~4 10~* 10" 2 10~1 10° 101
'.пв/Ре,в
Ne
10°
10~\
10 2
10
10~2° ftTl9 13-18 /0-17 10-16
10~^ 10~3 1СГ2 10° io1
T-| I I I I I ’ r-T-r— -I ГТ-] I r~~ g~
Ar e £
10°
10~1
x.
xe
Г,К
3Z7Z7
288
87
77
77
io~zV
I--X
ZZ7-27
—J—Jud_I- I 1 < t . t_L_UJ I 1. _X. -J. L. UX-1-L.
IO-20 10~ia 19~1& 10~17 10~16
10~2 10"1 ___10° , 101
10 ~15
10 0 r
10
\ к
JZ7J
cc2
□
g
1
> Г ® ® □ © □ @ ®
. л 5*^
-15
Л- '6
Рис 3.4 Отношение коэффициента диффузии к подвижности электронов,
характеризующее температуру электронов, как функция Е/р и E/N в Ne,
Аг и СО2 [20]
52
удовлетворяют закону Больцмана п± ~ ехр (Я^еу/кТ), отсюда и
получается (3.24).
При немаксвелловском спектре электронов и vm(n) const, как
обычно и бывает в слабоионизованиом газе, находящемся в по-
ле, величина (3/2)Д?/це также характеризует среднюю энергию
электронов, но не совпадает с нею точно. Отношение Del\ke, со-
ответшвующее электронной «температуре», называют характери-
стической энергией. Она, (как и спектр, зависит от Е/р.
Отношение Dj\ie измеряют на опыте, регистрируя диффузи-
онное расплывание электронов, дрейфующих в поле Е. На рас-
стоянии х *= vAt от места старта электронов пучок расширяется
в поперечном направлении до радиуса г — ^Det = У/)еж/пд =
= У (De/pe) (^/^) • На рис. 3.4, 3.5 показаны экспериментальные
Рис 3 5 Отношение температуры электронов к температуре газа как функ-
ция отношения Е/р: а — в N2, и воздухе, б — в Н2 и D2 [6]
зависимости De/^e от Е/р. Для No и Н2 в типичных для тлею
щего разряда диапазонах Е/р их удается с разумным щиближТ
нпем аппроксимировать законом пропорциональности Гпо
мощи (3.19) так можно получить представление о длинах пеЛГ
сации Аи энергии электронов. Имеем релак-
Ne: е »9.7 (£7р) эВ, £7р ~ 0,1 — 1,2 В/(см-торр)- д ~ 9-7
и ~ Лтовдсм,
Н2: 8 л; 0,17 (Е/р) эВ, Е/р ~ 0,5 — 13 В/(см-торр); Ди 0.17
“ ~ГГторр]СМ-
В молекулярном газе - водороде - релаксация ппоиехпю™
раздо быстрее, чем в атомарном - неоне, что является следстви'
ем интенсивного возоуждения молекулярных колебаний (п
4.3. Нахождение коэффициентов диффузии. Измерение скопУ
стеи дрейфа и характеристических энергий электпонот. ™ коро’
ляет вполне доступную задачу. Измерить прямым путем* кмф"
53
фициенты диффузии в присутствии поля, напротив, чрезвычайно
трудно. Фактически в прямом эксперименте измерялись только
коэффициенты диффузии термализованных электронов, пришед-
ших в тепловое равновесие с газом в отсутствие поля. При ком-
натной температуре 79етеп == К (105/р [торр]) см2/с, причем в Не
К - 2, Ne — 20, Аг — 6,3, Н2 — 1,3, N2 - 2,9, О2 — 12.
Величины De можно оценивать на основе данных по уд и
Delpe. Например, в Ne при Е/р = 1 В/ (см • торр) рд = 1,46 • 106см/с,
Те~5,5 эВ, откуда De ~ v^TJE ~ 8 • 106/р см2/с. В воздухе при
Е/р = 20, Уд = 8,5 • 106, Ге » 1,5 De * 6,3 • 105/р см2/с.
4.4. Продольная и поперечная диффузии. Отношения De/\be,
измеренные по диффузионному размытию пакета электронов
вдоль направления их дрейфа, систематически отличаю!ся от
величин, полученных путем регистрации поперечного расплыва-
ния. Физическая причина различия коэффициентов продольной
Dl и поперечной DT диффузии коренится в зависимости частоты
столкновений vm от энергии электронов е [3.2]. Согласно (3.20)
средняя скорость электрона складывается из дрейфовой и диф-
фузионной составляющих:
V = Ve/ne = Уд ~ Бе^Пе/Пе Уд + Удиф,
причем в нулевом приближении De—«обычный» коэффициент,
который характеризует диффузию в поперечном дрейфу направ-
лении. Когда имеется градиент пе вдоль поля, поле совершает над
электроном дополнительную по сравнению с дрейфовой состав-
ляющей работу —вЕудиф = eZZ (EvKe)/ке. Средняя энергия электро-
на 8 получает приращение Де, пропорциональное проекции гра-
диента на направление вектора Е, ^^пе. Если, как это чаще всего
бывает, возрастает с ростом 8, подвижность уменьшается на
величину Дце, пропорциональную VHne. Но это по своему эффекту
равносильно тому, как если бы скорость дрейфа осталась преж-
ней, а скорость продольной диффузии РдЖф!! = —DeV}]пе/пе получи-
ла приращение, пропорциональное Дцв ~ V(lne. Это в свою очередь
означает уменьшение коэффициента продольной диффузии. В пер-
вом приближении по малой величине градиента получим [3.2]
(Vm \ ~ d In Р™
‘"Ыг И (3'2Г”
Логарифмическая производная v,n характеризует крутизну функ-
ции. Так, если \m — 8ft, ут = /с. На опыте наблюдается уменьшение
Бъ по сравнению с DT до двух раз.
§ 5. Ионы
5.1. Подвижность в несильных полях. Имея в виду выраже-
ние (2.17) для скорости потери импульса иона при столкнове-
ниях с молекулами, запишем уравнение для средней скорости
54
положительного иона, аналогичное (3.2) :
Мгчг = еЕ - М\ут, М' МгМ/ (М, + М). (3.26)’
Для легких ионов в тяжелом газе Мг^М, и уравнение (3.26)
превращается в (3.2), только с другим знаком у заряда. Для
установившегося движения, приравнивая силы трения и поля,
получим скорость дрейфа и подвижность ионов, аналогичные
(3.4), (3.5):
р,д = еЕ1М'ут, ц, = e!M'vm. (3.27)
В отсутствие резонансной перезарядки с чисто поляризацион-
ным сечением (2.16) находим
= 2,7-104 Ух^м/Мг = -36 /1+М/М; см2
V^(a/ao) А р [торр] 1/(а/я^) Л р [атм] В’с
где А—молярная масса газа. Формула (3.28) с немного отлича-
ющимся коэффициентом была получена в 1905 г. Ланжевеном.
Она хорошо согласуется с опытом, правильно описывает влияние
О 20 60 100 100 180
Рис. 3.6. Зависимость подвижности ионов от их массы при дрейфе в N2 [6]
массы ионов на их подвижность в одном п том же газе (рис. 3.6).
Из общей закономерности щ(Л7г) согласно (3.28) систематически
выпадает только случай дрейфа ионов в собственном тазе: щ су-
щественно меньше, но также не зависит от поля. Это связано
с сильным влиянием перезарядки. Такое расхождение и привело
в свое время к теории дрейфа с перезарядкой, которая все по-
ставила на свои места (Л. Л. Сепа, 1946 г.).
Ионы часто склонны объединяться с молекулами и атомами
в комплексы типа N^", 0^", Ne^1", Не2+ (последние, в отличие от
Ne2, Нв2, достаточно устойчивы). Это влияет на подвижность,
так как отключает перезарядку (рис. 3.7, 3.8).
Рассмотрим в качестве примера дрейф Ne^ в Ne. У Ne
а/яо —2,76. Согласно (3.28) щ = 4,5 • 103/р [торр] см2/(В-с).
Опытное значение щ = 5 • 103/р. В характерном для тлеющего
разряда поле Е1р=Л В/(см-торр) ргд = 50 м/с. При Т = 300 К
тепловая скорость ргт = 400 м/с.
55
5.2. Средняя энергия. Составим уравнение для средней энер-
гии и опа 8?, аналогичное (3.12). Работа поля над положительным
ионом в 1 с есть еЕуг, или в среднем по vt — еЕигл. Скорость по-
терь энергии при упругих столкновениях с молекулами выража-
ется формулой (2.18). Подставляя ргд согласно (3.27), получим
уравнение 'баланса энергии «среднего» иона:
<4 е2 Е2 2М' /- -Ч
dt M'v2 Мг+М^г (З.^Э;
л * vm г
где ем = (3/2)кТ. В случае легких ионов в тяжелом газе Мг<^М
и при условии ?г'>кТ (3.29) не отличается от (3.12) с 6 =
= бупр = 2т/М.
Рис. 3.7. Подвижности Ne+ и NeJ
как функция отношения Е/р мри
дрейфе в Ne, Т = 300 К, подвиж-
ность атомарных ионов меньше из-за
действия резонансной перезарядки
[15]
(см2- атм)КВ с)г
О Ь 8 /2 16
8
Рис 3 8 Подвижности Не+ и Hej“
в Не, как функция О1ношения Е/р
[6]
Установившаяся энергия ионов равняется
3 +
2 2(М?/М) Мут
(3.30)
В пе очень сильных полях она лишь немного превышает тепло-
вую ЗкТ/2. Электроны, очень плохо обменивающиеся энергией
с газом, термализуются только в чрезвычайно слабых полях при
£7р ~ 10-3—10“2 В/(см-торр). Но ионы из-за сравнимости масс
Мг и М обладают температурой газа и в немалых полях при
Е/р ~ 1 —10 В/(см • торр).
В сильном поле, когда ион на длине^ свободного пробега I на-
бирает энергию eEl, гораздо большую 8М, его энергия 8г отрыва-
ется от тепловой Сечение столкновений при этом будет уже
порядка газокинетического и I ~ const. Например, при о =
3-10“В * * * * * * 15 см2 Z = 10~2/р [торр] см. При комнатной температуре
еЕ1 превышает 10ем ~ 0,4 эВ, если Е/р^^ В/(см торр). Такие
56
условия характерны для катодного слоя тлеющего разряда. Рас-
пространим приближенно формулу (3.30) и на случай, когда но
vm = const, а I = const. При этом vm = v/l ~ v. Заменив прибли-
женно v на /2гг/Мг, найдем
(1 + М JM\312
= J eEi,
2 (Мг/М)1/2
(3.31)
В пределе Мг<^М (3.31) превращается в (3.13) и 8г ~
~ (1/2) (М/Мг) шеЕ1 > еЕ1. Легкий ион в тяжелом газе, как и
э гектрон, накапливает хаотическую энергию, получая ее при
столкновениях от поля. Ион с массой Мг~ М энергии не накап-
ливает, он «сбрасывает» ее при каждом столкновении, и потому
8г ~ еЕ1.
Выражению (3.30) для средней энергии иона можно придать
характерный вид, при котором выступают различные ее состав-
ляющие (Ванье, 1953 г.). Исключим поле Е из (3.30), выразив
его через скорость дрейфа (3.27) в несильных полях. Получим
7 -А/Г । Mv^ ;
2 /г 2 ‘ 2 ’
Средняя энергия иона складывается^из трех частей: общей с мо-
лекулами и безотносительном к значению поля энергии тепло-
вето движения, энергии направленного дрейфового движения
(третье слагаемое) и дополнительной энергии беспорядочного дви-
жения, связанной с действием поля (второе слагаемое). В какой
пропорции распределяется работа ноля между энергиями направ-
ленного и хаотического движения зависит от соотношения масс
Mt и М. При одинаковых массах она распределяется поровну.
Легкие ионы в тяжелом газе, как уже говорилось, накапливают
хаотическую энергию, которая оказывается много больше энергии
дрейфа. Напротив, энергия, сообщаемая тяжелым ионам, в лег-
ком газе хаотизируется слабо — ударами легких молекул трудно
«сбить с пути» массивную разгоняемую полем частицу.
5.3. Дрейф в сильных полях. Полагая vm = v/l с I = const,
выражая скорость v через 8г, как при выводе формулы (3 31),
и подставляя в (3 27), находим скорость дрейфа:
Она пропорциональна не Е/р, как в несильных полях, а VЕ/р. При
Мг ~ М примерно совпадает со скоростью иона и У28г/3/.?
отвечающей его средней энергии, так как движение иона имеет
резко направленный характер. Однако легкие ионы в тяжелом
газе даже в сильном поле дрейфуют медленнее, чем движутся
хаотически: vtJv ~ [MJ(Мг + М) ]1/2 ~ VМг/М (ср, с форму-
лой (3.16)).
57
Переход от закона подвижности vlA~E/p к закону и1Л~УЕ/р
происходит постепенно (рис. 3.9). Он начинается при таких по-
лях, при которых энергии ионов достигают порядка 1 эВ и поля-
ризационные силы сменяются близкодействием, а сечение стано-
вится газокинетическим; при движении ионов в собственном газе
и преобладании перезарядки — когда энергия иона заметно пре-
вышает тепловую.
Рис. 3.9. Скорость дрейфа собственных атомов ионов в Не, Ne и Аг как
функция отношения Е/р, Т — 300 К; штриховые кривые слева соответст-
вуют нормальному дрейфу (игд ~ Е/р), справа — аномальному (г1Д ~ ^Е/р)
[15]
5.4. Диффузия. В несильных полях, когда ионы_ находятся
в тепловом равновесии с газом и их средняя энергия 8г ~ (3/2) /сУ7,
справедливо соотношение Эйнштейна (3.24). Прямые исследова-
ния диффузии ионов далеко не так многочисленны, как измере-
ния подвижности, поэтому коэффициенты диффузии Бг обычно
находят именно таким путем. При умеренных отношениях Е/р
Di меняются с Е/р столь же мало, как и цг. Для ионов азота в
азоте, например, цг ~ 1,5 • 103/р [торр] см2/(В-с), Dt~ ^Q/p см2/с.
(Подробнее о диффузии ионов см. 1-е изд., п. 6.4, 6.5 гл. 4).
§ 6. Амбиполярная диффузия
При очень низкой плотности заряженных частиц пе, п+ заря-
ды разных знаков диффундируют независимо друг от друга — это
называется свободной диффузией. Более подвижные электроны
58
диффундируют быстрее и при наличии градиента плотности заря-
дов в плазме могут оставить далеко позади своих менее подвиж-
ных партнеров. Однако, когда плотности пе, п+ не малы, в ре-
зультате разделения зарядов образуется значительный простран-
ственный заряд и возникающее поле поляризации препятствует
дальнейшему нарушению электроней-
тральности (рис. 3.10). Разделение заря-
дов и поле поляризации автоматически
так подстраиваются друг к другу, чтобы
поле сдерживало убегающие электроны,
подтягивало к ним тяжелые ионы и за-
ставляло их диффундировать только «вме-
сте». Такая диффузия называется амби-
полярной. Это понятие было ввведено
Шоттки в 1924 г.
6.1. Коэффициент амбиполярной диф-
фузии. Обратимся к общим выражениям
(.3.20) для плотностей потоков заряжен-
ных частиц. Будем интересоваться случая-
ми либо отсутствия внешнего поля, либо
диффузии в поперечном ему направлении.
Тогда поле Е, фигурирующее в этих фор-
мулах, связано исключительно с поляри-
зацией плазмы. Оно удовлетворяет урав-
нению электростатики
div Е = 4ле (тг+ — пе}. (3.33)
Рис. 3.10. Поляризация
плазмы при наличии
градиентов плотностей
электронов и ионов: а —
начальные распределе-
ния пе — п+; б — рас-
пределения пе, п+ и
плотности объемного за-
ряда р = е(п+ — пе)
спустя некоторое время.
Стрелки указывают на-
правление поля поляри-
Пусть разделение зарядов * мало:
1дг+ — пе\ < пе ~ п п. Чтобы оно не на-
растало заметным образом, плотности потоков (или просто пото-
ки) электронов и ионов также должны быть почти одинаковыми:
Г(Х~ Г+х~ Гх, где ось х направлена перпендикулярно внешнему
полю, если таковое присутствует. Исключим поле поляризации
из выражений
Гх « - ^ЕХП -De~, Гх « ^+ЕХП - D+
(3.34)
для чего разделим первое на второе — на ц+ и потом сложим.
В результате найдем, что поток заряженных частиц того и друго-
го знака записывается в обычной для диффузии форме
г ______ п дп л
1 X - дх , М
^+^ + ^4-
(3.35)
с неким эффективным коэффициентом Da — коэффициентом ам-
биполярной диффузии. Поскольку ре > p+, De > D+, величина
Da « D+ +De([i+/\ie) больше D+, но меньше De, в соответствии
со сказанным выше о «подтягивании» ионов и «сдерживании»
электронов. В равновесной плазме, где температуры электронов Те
и ионов Т одинаковы, с помощью соотношений Эйнштейна (3.24)
59
найдем, что Da = 27) 4. В неравновесной плазме, где «температу-
ра» электронов существенно выше ионной, которая совпадает с
температурой газа, получим
Da К De - D+ Е- = И+ = 4- И+₽е (эВ]. (3.36)
6.2. При каких условиях диффузия амбииолярна? Этот вопрос
очень важен, ибо коэффициенты свободной и амбиполярной диф-
фузии в неравновесной плазме различаются в десятки раз. Чтобы
несмотря на сильные неравенства De > D+, це ц+, поток Гех по
формуле (3.3 I) не превышал потока Г+х, диффузионный и дрей-
фовый члены в Гех, которые имеют противоположные знаки,
должны компенсировать друг друга с точностью до относительно
малой величины Г+х. Значит, то поле поляризации, которое авто-
матически устанавливается при амбиполярной диффузии, равно
р ~ 1 Ч Ч7\
/г дх е п дх eR ' 0 • /
где R — длина, характеризующая масштаб градиента плотности
зарядов. На этом расстоянии плотность меняется значительным
образом. Например, если плазма находится в трубке, R — ее ра-
диус, так как плотность на оси значительно больше, чем на стен-
ках трубки, где заряды нейтрализуются.
Поле поляризации образуется в результате разделения заря-
дов, которое в свою очередь вызвано беспорядочным (тепловым)
движением более быстрой компоненты — электронов и возникает
за счет их тепловой энергии. И действительно, разность потен-
циалов поля поляризации на всей длине R, где оно существует,
такова, что электрическая энергия заряда, приобретаемая на пей,
порядка тепловой энергии электрона: ебф ~ eExR ~ кТе. Поле по-
ляризации создается объемным зарядом ебп = е(п+ — пе), порядок
величины которого согласно (3.33) определяется из соотношения
EJR ~ 4лебя -= 4 л era (§п!п).
С помощью (3.37) найдем
1 _ I d V 7 _ ( \1/2
п 4ле2п R2 Е J ’ \
(3.38)
Величина d, как мы уже знаем (п. 4.2 гл. 2), представляет
собою дебаевский радиус плазмы. Он как раз и характеризует те
расстояния, на которых возможны сильные разделения зарядов и
поляризация плазмы. Если 7? » d, т. е. заметный перепад плот-
ности зарядов случается на расстояниях, больших дебаевского
радиуса, бп/тз < 1, нарушение электронейтральности мало и диф-
фузия имеет амбиполярный характер. При условии R < d элек-
троны и попы диффундирую^ независимо. Например, при Те =
-= 1 эВ, и, = 108 см"3, R = 1 см d = 0,052 см и бтз/п = 2,5 • 10"3,
т. е. днфф> шя явно амбиполя'на. Для тех же Те и R только при
пл 1Н0СГП пе < Ю6 см"3 заряды диффундируют свободно.
60
6.3. Определение понятия «плазмы». Условие (й/7?)2< 1, где
R — характерный размер области сильного перепада плотности
зарядов, является именно той количественной мерой, которая от-
личает «плазму», как электронейтральную ионизованную среду,
от иных случаев присутствия зарядов в газе.
§ 7. Протекание электрического тока в плазме
в присутствии продольных градиентов плотности зарядов
7.1. Уравнение непрерывности для электричества. Если к плаз-
ме приложено внешнее электрическое поле и идет ток, плотности
потоков электронов и ионов в отличие от п. 6.1 не одинаковы.
Плотность тока ] = е(Г+ — Ге). Из уравнений непрерывности
(3.22) для частиц данного сорта и того факта, что положитель-
ные и отрицательные заряды рождаются и исчезают только па-
рами (в отсутствие отрицательных ионов qe = q+), вытекает урав-
нение непрерывности для электричества:
dpldt + div j = 0, р •= е(п+ — пе). (3.39)
В электронейтральной среде, а в стационарных условиях вообще
всегда, ток не имеет источников *
div j = 0. (3.40)
В одномерном плоском случае вдоль направления тока z d]/dz = 0,
/(z) = const, т. е. плотность тока неизменна. Обычно она onje ге-
ляегся не локальными характеристиками, а условиями во всей
системе в целом, включая внешнюю по отношению к разряду
цепь. *
7.2. Диффузионный ток и искажение поля градиентами. В ус-
ловиях квазинейтральности, когда пс ~ п+ ~ п, согласно (3.20)
j/e = Г+ — Ге = (De — Z>+) V п Я (р,е + (Х+) Еп, (3.41)
Е = ---г---D'~D+ (3/j2)
е (Не + Н+) п Ь р+ п ' 7
Электрическое поле складывается из «внешнего», благодаря ко-
торому течет ток, и поля поляризации, вызванного присутствием
градиентов*). Эти составляющие, конечно, неразличимы — изме-
ряя поле в данном месте, скажем, при помощи зонда (гл. 8), мы
будем фиксировать полное поле (3.42).
Сильное падение плотности зарядов в направлении, противо-
положном внешнему полю, может привести к полному уничтоже-
нию последнего и даже к изменению направления поля по отно-
шению к току**). Электрический ток, с которым согласно (3.40)
*) Вообще говоря, существуют еще потоки, связанные с градиентами
температуры — термодиффузионные, но они обычно играют меньшую роль,
чем просто диффузионные.
**) Такие эффекты иногда наблюдаются в тлеющем разряде, низко-
вольтной дуге и др.
С1
при этом ничего не происходит, переносится в этом месте бла-
годаря диффузии электронов: при Е = 0 по (3.41) с учетом
De^> D+ плотность тока j ~ eDe^n. Диффузия при этом происхо-
дит свободно (амбиполярная — электричества не переносит). Дей-
ствительно, если нет поля, электроны не тянут за собою ионы.
Однако такое положение не может сохраняться на слишком
большом отрезке, что видно из (3.42). Заметим, что коэффициент
диффузии De зависит от электронного спектра, который в поле
устанавливается на длине релаксации энергии электронов Аи =
= 11Уб'>1 (п. 3.7). Строго говоря, это ужесточает обычное усло-
вие применимости диффузионных понятий — малость перепада п
на длине Z, во всяком случае требует проявления осторожности
при рассмотрении диффузии в резко неоднородном поле.
7.3. Уравнение для плотности плазмы. Подставляя (3.42)
в выражения (3.20) для Ге, Г+ и имея в виду определение (3.35),
находим
(3.43)
Потоки электронов и ионов складываются из одинаковых амбипо-
лярных диффузионных (они могут иметь составляющую и вдоль
тока) и потоков, обусловленных протеканием тока. Последние,
в отличие от амбиполярных, различаются сильно, в це/ц+ > 1 раз.
Подставляя любое из выражений (3.43) в соответствующее урав-
нение непрерывности (3.22) и имея в виду (3.40), получаем об-
щее уравнение баланса числа заряженных частиц в плазме
dnfdt — DaAn = q, п ~ пе ~ п+. (3.44)
Оно имеет вид обычного уравнения диффузии (с амбиполярным
коэффициентом) в присутствии объемных источников частиц и не
содержит никаких признаков того, что в среде может течь элек-
трический ток. Последний сказывается не на балансе, а на пото-
ках зарядов (3.43). Баланс не зависит от тока, потому что, образ-
но говоря, сколько электричества втекает в какое-то место, ровно
столько согласно (3.40) и вытекает.
7.4. Критерий электронейтральности. Он различен для двух
ситуаций. Если тока нет или он есть, но мал по сравнению с диф-
фузионным током электронов (поле поляризации больше «внеш-
него» в (3.42)), мы возвращаемся к ситуации, рассмотренной
в п. 6.2, и критерию (3.38) (d/JR)2 < 1. Если дрейфовый ток силь-
нее диффузионного, согласно (3.42) j ~ ецеЕп и в соответствии
с (3.40), (3.33) имеем
—EVrc = п div Е = 4летг (п+ — пе) « 4лепбп;
Ьп Е S * кте еЕ <Г____________________
п ~ faienL ~ 4пе^п hTeL ~ LAU \L ) Au’
(3.45)
где Аи—длина установления электронной температуры (средней
энергии электронов) (3.18), (3.19), а Л —длина вдоль поля, на
которой сильно (Меняются плотность электронов и проводимость.
Дебаевский радиус следует сравнивать со средним геометриче-
ским между L и Ли. Будет ли критерий (3.45) жестче или мягче
(3.38), зависит от конкретных условий, как и то, что сильнее
нарушает электронейтральность — градиенты вдоль тока или
поперек.
7.5. Амбиполярный поток зарядов вдоль неоднородного поля.
В отличие от диффузионного, амбиполярный поток имеет дрейфо-
вую природу и обусловлен присутствием пространственного за-
ряда [3.3]. Подставим в уравнения непрерывности (3.22) для
пе, п+ выражения (3.20) для потоков Ге, Г+. Умножив уравнение
для пе на Ц+/р1е и положив для простоты це, ц+ постоянными,
сложим результат с уравнением для п+. Интересуясь действием
пространственного заряда, который даже в квазинейтральной
(в смысле 8п/п<^1) плазме может быть сам по себе значитель-
ным, сохраним при суммировании дрейфовых потоков «малую»
разность 8п. Подставляя 6п = (4яе)-1 div Е и пренебрегая члена-
ми,, пропорциональными ц+/це<10"2, получаем уравнение
-^-4- divl_ ])^п _±.EdivEI = q, n^ne^n+, (3.46)
уточненное по сравнению c (3.44). Наряду с потоком амбипо-
лярной диффузии появляется поток «амбиполярного дрейфа».
В одномерном случае последний равен (ц^/8ле) дЕ2[дх.
С плотностью зарядов он непосредственно не связан. Однако в
силу постоянства тока вдоль его направления, j ~ епер.еЕ ~ const,
градиент поля неизбежно сопровождается градиентом плотности
плазмы. Поэтому амбиполярный др&йфдвый поток эквивалентен
некоему диффузионному
24 £1 = _ DЕ^~,DЕ = (3.47)
8ле дх члеп дх дх г
с эффективным коэффициентом диффузии который складыва-
ется с Da [3.4]. Сравнительная роль двух потоков характеризу-
ется отношением
Ш = E2l^nnkTe = {Е [В/см] }2/1,8 • 10"We [эВ], (3.48)
которое порядка (втрое больше) отношения энергии электриче-
ского поля и тепловой энергии электронов. Например, при п =
== 6 • 109 см-3, Те == 1 эВ амбиполярный дрейф преобладает над
амбиполярной диффузией, если Е > 102 В/см или, с учетом харак-
терных для плазмы значений Е/р ~ 1 —10 В/(см-торр), при р>
> 102—10 торр. Благодаря обоим эффектам, плазма перекачива-
ется из мест с более высокой плотностью и более слабым полем
в места с пониженной плотностью и более сильным полем. О при-
менении уравнения (3.46) см. п. 6.6 гл. 10.
63
§ 8. Гидродинамическое описание электронов
Частично ионизованный газ представляет собою трехкомпо-
нентную смесь, состоящую из электронов, ионов и нейтральных
частиц. Ее поведение в поле можно описывать на основе обычных
уравнений газовой динамики. Мы остановимся на упрощенном
и более употребительном для условий разряда варианте уравне-
ний, считая газ в целом покоящимся, слабопонизованным и ква-
зинеитральным. Тогда в сущности достаточно записать уравнения
для одного лишь электронного газа. Его состояние характеризу-
ется плотностью электронов пе, вектором макроскопической ско-
рости Ne и температурой Те (или давлением ре = ПекТе}.
8.1. Уравнения непрерывности и движения. Первое уже запи-
сывалось раньше—(3.22); в нем Ге == neNe. Второе имеет вид
dVg dNe дуе
тПе ~dt=~ n^E~ VPe~nemvcvm, — = — + (vey) Ve. (3.49)
Фактически, результат, вытекающий из (3.49), также использо-
вался выше. Из-за существования больших кулоновских сил,
обеспечивающих квазинейтральность плазмы (из-за возникнове-
ния поляризационного поля), электронный газ не может замет-
ным образом ускоряться относительно ионного, иначе происходи-
ло бы нарастающее со временем разделение зарядов. Значит,
ускорение dNeldt близко к ускорению ионного газа dw'dt, которое
подчиняется аналогичному уравнению движения
MnldNjdt = пгеЕ — ^рг~ пгМ'чгутг1 пг ~ пс.
Поскольку в правых частях уравнений движения стоят одинако-
вые по величине электрические силы, инерционный член в элек-
тронном уравнении (3.49) из^за крайне малой массы электрона
можно опустить. Но тогда (3.49) сводится к выражению (3.20)
для плотности потока Ге = neNe с учетом (3.21), (3.24), отличаясь
от (3.20) только присутствием дополнительного термодиффузион-
ного потока, пропорционального — ^Те. Последний чаще всего
меньше диффузионного из-за малости температурных градиен-
тов, поэтому мы его там и не учитывали.
8.2. Уравнение энергии. Оно имеет вид [27]
А (A nekTe} - d iv F = - пее (Eve) - ~ nekTevu - ql, (3.50)
F -= f- nekTeve - ЪуТе. К - -I- kneDe *). (3.51)
z z
Плотность потока электронной энергии F складывается из гидро-
*) Выражение для neNe, которое получается из (3.49) без инерцион-
ного члена, а также (3.51) для F и вытекают из кинетического уравне-
14’ч для электронов, если посчитать функцию распределения максвеллов-
ской и vm = const При I = const (Vm ~ коэффициент термодиффузии
по в чается вдвое меньшим [3.5], а коэффициент 5/2 в (3.51) заменяет-
ся на 2.
динамического потока энтальпии и потока теплопроводности;
— электронная теплопроводность. Слагаемые с кинетической
энергией электронов mvj2<^kTe опущены: согласно (3.16)
ve ~ v < V. Потери энергии электронов при столкновениях с мо-
лекулами записаны в (3.50) в соответствии с (3.12), (3.17). По-
следний член в (3.50) описывает затраты энергии на рождение
новых электронов; q — результирующая скорость рождения, ко-
торая фигурирует в уравнении непрерывности (3.22), I — потен-
циал ионизации.
Из комбинации (3.50), (3.51), (3.49), (3.22) вытекает урав-
нение для скорости нагревания движущейся «частицы» электрон-
ного газа:
4 k = — е (Eve) — ЪТ'Хи — div y?,ve +
+ A div XeVTe - ^Z + A ± (3.52)
где dTe/dt — субстанциональная производная типа (3.49). Оно
обобщает уравнение (3.12) учетом эффектов, связанных с про-
странственной неоднородностью: работой сил давления, теплопро-
водностью. Последний член, описывающий затраты энергии па
ионизацию и сообщение рожденному электрону тепловой энергии,
обычно мал по сравнению с фигурирующим и в (3.12) слагаемым,
пропорциональным vw.
8.3. Плазма с током. Скорость ve или поток пе\е в уравнениях
(3.50) — (3.52), (3.22) целесообразно представить в виде (3.43),
где из Ге выделен ток j, удовлетворяющий уравнению (3.40). Без
^чета амбиполярного термодиффузионного потока и с учетом
Р+ < Це
neNe = —j/e — D<yne, div j = 0. (3.53)
Входящее в (3.50), (3.52) поле в плазме согласно (3.42), (3.24)
с той же точностью есть
Е = ]!е\1еПе - (kTele) (Vne/ne). (3.54)
Рассмотренная здесь система уравнений будет использована в
§ 7 гл. И.
§ 9. Движение зарядов в газе
в присутствии магнитного поля.
Нельзя сказать, чтобы внешнее магнитное поле было частым
атрибутом в исследованиях и приложениях «обычного» газового
разряда. Это при создании «термоядерной» плазмы не обходятся
без него. Однако в такой важной области приложений физики
разрядов, как магнитогидродинамические генераторы, а также в
некоторых газоразрядных приборах и опытах магнитное поле
присутствует. Поэтому рассмотрим, как оно влияет на дрейф
*.0. П Райзер
электрический ток, диффузию зарядов, тем более что в сильных
магнитных полях характеристики этих процессов изменяются су-
щественным образом.
9.1. Дрейф в электрическом поле. Пусть на ионизованный
газ наложено посюянноэ однородное магнитное поле Н Введем
в уравнение движения электрона (3 2) лоренцеву силу, с которой
оно действует на движущимся заряд:
т\ = — еЕ — (е/с) [vH] — mvvrl.
(3 55)
Если поля Е п Н параллельны, то никакого влияния на дрейф
магнитное поле не оказывает, так как vI’EHH Поскольку уравнение
линейно и вектор Н всегда можно представить в виде суммы па
Рис 3 11 Дрейф
электронов в скре
щенных полях
раллельной и перпендикулярной Е составля-
ющих, достаточно рассмотреть случай скре-
щенных полей, когда Н-L Е. Направим ось х
вдоль Е, а ось z вдоль Н (рис 3 11) и от-
несем (3 55) к установившемуся состоянию
\ — 0. Тогда v представляет собою скорость
дрейфа уд. Спроецируем уравнение на коор-
динатпые оси.
—еЕх -Р e{v^ylc)IIz — mvAX\m = 0,
—в(кдХ/с)#г — тк,ух= 0, — 0
Составляющие скорости дрейфа равны
Fx г _ е
где pfc — обычная подвижность в отсутствие магнитного поля, а
= 1,76-10’Н |Э] с-1 (3.56)
— так называемая гиромагнитная, или циклотронная, частота.
С такой частотой электрон вращается в пустоте вокруг магнит-
ного вектора, если у него есть перпендикулярная этому вектору
составляющая скорости. Это легко усмотреть из уравнения (3.55),
положив в нем vm = 0.
Итак, в скрещенных полях ск рость дрейфа имеет иное на-
правление, чем электрическое поле, т е подвижность является
тензором Подвижность электронов в направлении электрическо-
го поля меньше обычной. Возникает дрейф в направлении, пер-
пендикулярном обоим полям В направлении магнитного поля
дрейфового движения нет. Поперечная обоим полям скорость v^v
появляется под действием лоренцевой силы. Скорость щх вдоль Е
уменьшается из-за того, что лоренцева сила все время стремился
отклонить дрейфующий вдоль Е электрон в сторону. Тем самым
помимо столкновении создается дополнительная помеха уско е-
нию наряда электрическим полем.
66
Количественное влияние магнитного поля характеризуется
отношением В слабом магнитном поле подвиж-
ность вдоль Е уменьшается немного и появляется лишь легкий
дрейф в сторону. В сильном магнитном поле подвижность вдоль
В падает как Я-2, а скорость поперечного к Е и Н движения не
.зависит от частоты столкновений и падает как Я-1. В последнем
с гучае роль столкновений, которые мешают ускорению заряда
па этот раз лоренцевои силой, полностью берет на себя магнит-
11 те поле, закручивающее частицу.
Значение магнитной напряженности Яе, которая служит гра-
ницей между «слабыми» и «сильными» полями, определяется из
равенства сон —vm, откуда Яе = с/це. При типичной частоте столк-
новений электронов vm ~ 2 • 109 р [торр] с"1 Не ~ 100 р [торр] Э. Вс^
сказанное остается в силе и для ионов, следует только заменить
/1 на М' и поменять знаки у пдх, v^y. Граничное поле дня ионов
Нг~с!рг в щ/щ, т. е. примерно на два порядка больше //<.
. 9.2. Проводимость и ток Холла. Плотность электрического тока
j = — рпе\л не совпадает с направлением Е. Проводимость, как и
подвижность, является тензором. Проводимости вдоль а к'ктрпче-
ского поля (Оц) и в поперечном Е*и Н направлении (Oj) даются
1 ыражениями
О' °Wvm ~ е2пе / • гт\
О' I. - -----, er I — О -----—О , ( .5/)
1 + 1 Н mVm
iде о — проводимость в отсутствие магнитного поля. Электриче-
ский ток, возникающий в скрещенных полях в направлении, пер-
пендикулярном Е и Н, /±&О1£, называется током Холла. Эю г
. ффект, носящий имя своего первооткрывателя, был обнаружен
?.оллом в 1880 г. в металлах. Джоулева тепла холловский юк
не выделяет, а поскольку продольный ток в присутствии попе-
речного магнитного поля становится меньше, уменьшается общее'
шерговыделение. Величину = Н/Не называют парамо/-
; ом Холла.
9.3. Диффузия. В диффузионном потоке заряженные частицы
обладают отличным от пуля вектором средней скорости, и в этом
отношении действие градиента плотности эквивалентно действию
электрического поля. Значит, магнитное поле влияет на диффу-
зию так же, как и на дрейф. Если градиент направлен вдоль Н,
никакого воздействия нет, если перпендикулярно — закручива-
йте частиц лоренцевой силой создает помеху для диффузии вдоль
градиента, появляется дополнительный поток в направлении дей-
ствия лоренцевой силы, перпендикулярном градиенту и Н (ана-
лог холловского тока). Коэффициент диффузии становится
тензором.
Эквивалентное электрическое поле Е', которое создает такую
же среднюю скорость движения заряда v, что и градиент плотно-
сти, определяется из равенства
, V , кТ, V
v = ± RE^- - + -^±44 (3.58)
5*
67
где D, ц, T относятся к случаю отсутствия магнитного поля,
а знаки соответствуют положительным и отрицательным зарядам.
По порядку величины |£"| ~kT!eR отвечает разности потенциа-
лов кТ1е на длине R перепада плотности, что вполне естественно,
если учесть тепловую природу диффузии (ср. с п. 6.2).
Остается повторить выкладки п. 9.1 применительно к «дрей-
фу» в эквивалентном поле Е'. Если направить ось z вдоль векто-
ра Н, а ось х вдоль вектора градиента плотности, то для состав-
ляющих потока частиц получим
р ____________£±__ dn Г _ __________ •^+(0H/V7n dn
Ж± l + V± + 1 + <0H/vmdX '
r2t = 0. (3.59)
Вдоль магнитного поля частицы диффундируют при наличии
продольного вектору Н градиента так же, как и без поля. В попе-
речном Н направлении градиента они диффундируют с коэффи-
циентом D±4- ~ D± (1 ~т (ОнДт)-1. В очень сильном поле, когда
и для электронов и для ионов ~ Но цик-
лотронная частота обратно пропорциональна массе частицы. По-
этому поперек очень сильного магнитного поля ионы диффунди-
руют быстрее электронов, вдоль поля — медленнее, как обычно.
На самом деле в присутствии сильного магнитного поля все
происходит гораздо сложнее, чем это рассказывалось здесь; тут
появляется масса тонких эффектов и запутанных взаимосвязей,
но углубляться в это не будем.
Глава 4. ОБРАЗОВАНИЕ И ГИБЕЛЬ ЗАРЯЖЕННЫХ ЧАСТИЦ
В ГАЗЕ
§ 1. Ионизация электронным ударом в постоянном поле
1.1. 'Скорость и частота ионизации. Ионизация невозбужден-
ных атомов и молекул ударами электронов — важнейший меха-
низм рождения зарядов в объеме газового разряда. Обозначим
ft(8)ей число электронов в 1 см3 с энергиями от 8 до 8 +ей;
ft(e)—это функция распределения электронов по энергиям, нор-
мированная на плотность электронов; пусть сЦе)—эффективное
сечение ионизации атомов, находящихся в основном состоянии,
электронами с энергией 8 = mv<2!2 (см. п. 5.1 гл. 2 и рис. 2.9—
2.11). Скорость ионизации, т. е. число актов ионизации, произво-
димых электронами в 1 см3 в 1 с, равна
оо
( dn \ (*
—- ’ = | 1Уиог (8) п (8) de = ktNne = чгпе. (4.1)
\ dt г J
О
Коэффициент кг при плотностях частиц, участвующих в ре-
акции, называется константой скорости реакции (это относится
к любым реакциям); хг = ktN— частота ионизации, т. е. число
68
ионизаций, которое электрон в среднем производит в 1 с. Ин-
тегрирование по энергиям в (4.1) фактически начинается не
от 8=0, а от потенциала ионизации /, так как ог = 0 при 8 С /.
Ионизующую способность электронов в данных условиях обыч-
но характеризуют частотой ионизации. Она пропорциональна
плотности газа и определяется энергетическим спектром элек-
тронов:
ОО . ОО < -1
уг = N (Ji (е) п (е) de Н п (8) de I = N == Nkp, (4.2)
о -о /
угловыми скобками обозначено усреднение по спектру. В слабо-
иопизованной плазме, находящейся в поле, электронный спектр
зависит от многих процессов упругих и неупругих столкновений.
Частоту ионизации для этих условий находят путем решения
кинетического уравнения для лг(е) (гл. 7) по формуле (4.2)
с известным экспериментальным сечением ионизации или же оп-
ределяют из опыта. Если ионизация электронами происходит при
неизменных условиях, так что v, = const, и гибель электронов
можно не учитывать, электроны размножаются во времени по
экспоненциальному закону: пе = тге(О)ехр(vt0- Развивается элек-
тронная лавина.
1.2. Частота ионизации при максвелловском спектре. Мак-
свелловский спектр устанавливается, когда степень ионизации
не слишком мала и существенны столкновения электронов друг
с другом. При максвелловском спектре
. оо
- 7=^77 '•'!> J «3)
зависимость v, от поля и процессов столкновений с молекулами
неявно заключена в электронной температуре, от которой и за-
висит частота ионизации. Обычно температура газоразрядной
плазмы существенно меньше потенциала ионизации /, так как
заметная ионизация наступает при kTei в 5—10 раз меньших /.
Ионизуют атомы высокоэпергичные электроны с 8 > кТе, при-
надлежащие хвосту максвелловского распределения. Поскольку
при этом п(е) спадает резко, в интеграл (4.2) можно подставить
линейный закон (2.27) для сечения щ(с), который неплохо пе-
редает поведение сечения при небольших превышениях е над
порогом. Это дает
уг = NvCt (Z + 2кТе)ехр (~11кТе), (4.4)
v = (8кТе/лпг)У2, (4.5)
где v — средняя тепловая скорость, а константы Сг представле-
ны в табл. 2.3.
Например, в Аг Сг = 2 • 10“17 см2/эВ. При Те = 1 эВ v —
= 6,7 • 107 см/с, кг = <i?at> = 3 • 10"16 см3/с. Если р = 50 торр и
69
7 = 300 К, N= 1,7 • 1018 см"3. Получаем vt = 510 с"1. Равновес-
ная степень ионизации при таких Те и N равна (ne)p/2V = 0,021.
1.3. Ионизационный коэффициент Таунсенда. В постоянном
поле электронная лавина, вызванная первичным электроном, раз-
вивается не только во времени, но и в пространстве вдоль на-
правления дрейфа рождающихся электронов, потому что все они
движутся с одной скоростью вдоль поля. Поэтому целесообраз-
нее характеризовать скорость ионизации не частотой vt, а иони-
зационным коэффициентом а — числом ионизаций, совершаемых
электроном на пути в 1 см вдоль поля. Очевидно,
а — Vi/рд, ^г = ард. (4.6)
Следует подчеркнуть, что первичной и всеобъемлющей харак-
теристикой скорости ионизации является не а, а частота уг.
Именно она, как и скорость дрейфа, вычисляется при помощи
функции распределения. Ионизационный коэффициент а — вели-
чина производная. Она находится по формуле (4.6). В быстро-
переменных полях а вообще особого смысла не имеет. Но, с дру-
гой стороны, в опытах с постоянным полем непосредственно
измеряют не уг, а именно а.
1.4. Измерения а и законы подобия. Поместим плоские элек-
троды на расстоянии d, приложим к ним напряжение V и будем
облучать катод ультрафиолетовым излучением, вырывающим УГэ
электронов в 1 с. Число электронов в лавине растет в направ-
Рис. 4 1 Экспериментальный график, де-
монстрирующий постоянство ионизацион-
ного коэффициента а и экспоненциальный
характер нарастания тока в разрядном
промежутке; ионизационные коэффициен-
ты определяются наклонами прямых [6]
Рис. 4.2. Ионизационный коэф^
фициент Таунсенда а в N2
как функции отношения Е/р
по разным измерениям
70
Рис. 4 3 Ионизационный коэффициент ъс в Не, воздухе, Лг, N2 как функция
отношения Е/р [26]
Рис. 4.4. Ионизационный коэффициент а в широком диапазоне значений
Е/р: а — 6Н2, N2 и в воздухе; б — в инертных газах [6]
71
лении к аноду по закону
dAf/dx = аЛ*, JV (ж) = Л"о ехр (аж). (4.7)
На анод поступает электронный ток i — eJV$ exp (ad). В стацио-
нарном состоянии рождающиеся в разрядном промежутке поло-
жительные ионы поступают на катод в том же количестве, что
и электроны на анод. Ток во всей замкнутой цепи одинаков
и равен I. Малоподвижные ионы скапливаются в промежутке
между электродами в гораздо большем количестве, чем быстро
вытягиваемые полем электроны. Поэтому в промежутке сосредо-
тачивается положительный пространственный заряд. Однако при
небольших токах вызванное им искажение поля мало, и поле
Е = Vid однородно и известно. Меняя d и V, измеряя i и строя
график In i в зависимости от d при неизменном Е, можно по
наклону получающейся прямой In i = const + ad определить
a(E).
Спектр, средняя энергия электронов, скорость дрейфа явля-
ются функциями отношения Е/р (п. 1.4, 3.5 гл. 3). Значит, для
¥г и а справедлив закон подобия типа а = pf(E/p). Поэтому на
опыте можно менять не d, а р, сохраняя неизменным отношение
Е/р-. In t = const + (a/p) (pd). Опыт показывает, что до известно-
го предела по pd точки хорошо ложатся на прямые линии
(рис. 4.1). Так были измерены а для многих газов (рис. 4.2—
4.5), хотя и имеются расхождения в результатах разных
авторов.
Рис 4 5. Ионизационный коэффициент как функция отношения Е/р в Н2
[26] и СО2 [6]
1.5. Интерполяционная формула для а. При теоретических
и численных исследованиях разрядов широко пользуются удоб-
ной эмпирической формулой, предложенной Таунсендом,
а = Ар ехр (-Вр!Е). (4.8)
Постоянные А и В определяют путем аппроксимации экспери-
ментальных кривых (табл. 4.1). Закономерности (4.8) в ряде
72
случаев можно приписать некоторый физический смысл. Допу-
стим, что электрон испытывает только ионизующие столкнове-
ния. Это имеет некий смысл при больших Е/р и энергиях элек-
тронов. На пути свободного пробега х электрон набирает энер-
гию еЕх, немного превышающую потенциал ионизации I. Ве-
роятность того, что он пройдет путь x^I/еЕ без столкновения
и потом совершит ионизирующее столкновение на пути dx, рав-
на adx = 1г' ехр(— I/eEl)dx, где I = IJp — средняя длина пробе-
га. Получаем формулу (4.8) с А = Z71’ В = 1/е1{. При о =
= 5 • 10"16 см2 1\ = 0,06 см •торр. Если 7=15 эВ, имеем А =17,
В = 250. Это похоже на табличные значения.
При максвелловском спектре доля электронов, способных
ионизовать атом, пропорциональна ехр(— 1/кТе). Если Те~Е/р
(п. 3.5 гл. 3), снова получаем зависимость и а от Е типа
(4.8), но с другим смыслом постоянной В. Как будет показано
в п. 4.7 гл. 9, приближенное решение кинетического уравнения
с учетом большой роли неупругих потерь энергии электронов
на возбуждение также приводит к закономерности типа (4.8),
но снова с другим смыслом В. В ^случае инертных газов иногда
применяют формулу [4.1]
а = ^ехр[-Д(р/£)1/2], (4.9)
которая лучше описывает экспериментальные данные, чем (4.8),
хотя для теории она менее удобна (табл. 4.1). Отметим полез-
ную эмпирическую формулу для воздуха при не очень больших
Е/р (см. также табл. 14.1)
а/р = 1,17 10~4 (Е/р — 32,2)2 см"1 торр"1,
Е/р = /И-176 В/(см торр). (4 10)
Т а б i и ц а 4 1 Эмпирические констан ни в формулах дня ион и {анион-
ною юэффлциенга и обмети применимости
Газ А, 1 (см* торр)-1 i 1 а а о g Е/р, В/(см-торр) С, (см* торр)-1 D, [В/(см торр)]1/2 Е/р< ВДсм торр)
Нр 3 34 20—150 4.4 14 100
Np 4 100 100—400 <8,2 17 250
Аг 12 180 100—600 29,2 26,6 700
Кг 17 240 100-1000 35,7 28,2 900
Хе 26 350 200—800 65,3 36,1 1200
Hg 20 370 200—600
н2 5 130 150—600
n2 12 342 Ю0-600
AV 8,8 275 27—200
воздух 15 365 100-800
со2 20 466 500—1000
Н2О 13 290 150—1000
73
1.6. Оптимальные условия для ионизации. Проходя в одно-
родном поле разность потенциалов 1 В, электрон рождает а/Е
электронов (пар ионов) Для рождения одной пары он должен,
следовательно, приобрести от поля энергию W = еЕ/а Функция
W(Е/р) имеет минимум В приближении (4 8) ТГт1П = ёеВ/А
при {Е/р)п^В где ё = 272 Даже при этих, наиболее благо-
приятных для размножения условиях на рождение одной пары
ионов затрачивается энергия ТУт1П {константа Столетова), ко-
торая в несколько раз превышает потенциал ионизацшт При-
чина в том, что электрону приходится тратить много энергии
на возбуждение атомов В воздухе, например, W 1 = 66 эВ на лару
иопов при {Е/р)т == 365 В! (см торр)*)
1.7. Очень сильные поля. Формула Таунсенда (4 8) неприме-
нима к очень сильным полям Она приводит к монотонному на
растаипю а от Е/р и при Е/р-^-ж дает aJp-^A Между тем,
в очень сильных полях электрон приобретает большую энергию,
которая переваливает за максимум кривой сечения ионизации
ог(е) (п 5 1 гл 2), и тогда ионизационная способность с ростом
поля падает Максимумы а на опыте наблюдаются при Е/р ~
~ 1000 В/(см торр) Конечно, столь большие значения Е/р для
разрядов пе типичны, но в некоторых условиях (например в ка-
тодном слое аномального тлеющего разряда и др ) встречаются
В очень сильных полях не лишено смысла приближение «мо-
ноэнергетических» электронов Предполагается, что в каждой
точке пространства вдоль оси х направления поля Е{х) присут-
ствуют электроны одной вполне определенной энергии и летят
они со скоростью и = У2&/т вперед в направлении оси х При-
ближение это оправдывается отчасти тем что при больших энер-
гиях 8 100 эВ сечения неупругих столкновении больше сече-
нии упругих ос, и рассеиваются электроны при упругих столкно-
вениях в основном вперед, так что транспортные сечения о/г еще
меньше ос При неупругих столкновениях электрон теряет энер-
гию возбуждения или ионизации и также продолжает лететь
вперед
В указанном приближении ионизационный коэффициент в
данной точке х просто совпадает с обратной величиной длины
пробега электрона для ионизации 1г при соответствующей этой
точке энергии 8 (х):
а = ЛГрщ (&)/v — Ngi = /Г1, k = k [e (я)] (4 11)
Саму энергию &(х) можно определить из приближенного урав-
нения
dz/dx = е\Е (r)\ —Це), L = NoJ [-N^o*kE*h, (4 12)
*) Не следует путать эту цифру с другой часто встречающейся вели
чинои — 33 эВ на пару ионов Последнюю тратит быстрый электрон с энергией
е > 4 кэВ, который замедляется в воздухе Потери на возбуждение у быст-
рых электронов меньше
74
где Л(е) — функция неупругих потерь, связанных с ионизацией
и возбуждением всевозможных уровней атомов*).
Ход функции потерь £(е) легко себе представить, мысленно
просуммировав все пеупругие сечения на рис. 2.14, 2.15 (по-
скольку всевозможные потенциалы Ek, I разнятся не очень
сильно). Как и все сечения функция £(е) имеет макси-
мум при энергиях 8™ порядка нескольких десятков электрон-
вольт. Это значит, что, двигаясь в поле Е > Е, р = е-1Лтех, элек-
трон будет неуклонно ускоряться, несмотря на неупругие потери
энергии. Этот эффект называется убеганием электронов. В азоте,
например, критическая для убегания величина (Е'/р)кр ~
~ 365 В/(см торр), в гелии — 63 В/(см-торр) [4.2]. В протя-
женном сверхкритическом поле убегающие электроны могут в
газе (не в вакууме!) приобретать весьма большую энергию —
порядка 103 эВ.
1.8. Ступенчатая ионизация. В слабоионизованном газе атомы
ионизуются преимущественно из основного состояния. При зна-
чительной степени ионизации образуется много возбужденных
атомов и молекул и может преобладать ступенчатая ионизация.
Атомы сначала возбуждаются электронным ударом, а потом ио-
низуются последующими. Большую роль при этом играют дол-
гоживущие метастабильные возбужденные частицы (табл. 2.4).
Сечения ионизации их довольно велики (рис. 2.12, 2.13). Вклад
ступенчатой ионизации зависит от концентрации присутствующих
в газе метастабилей. Последняя определяется не только ско-
ростью их рождения, но п скоростью гибели за счет дезактива-
ции ударами электронов, молекул и атомов, диффузионного ухо-
да па стенки. Один из случаев, * когда ступенчатая ионизация
играет важную роль, будет рассмотрен в § 6, 7 гл. 11. Надо
сказать, что ступенчатая ионизация чаще всего преобладает над
ионизацией из основного состояния в силыюпоппзоваппой плаз-
ме. Но в этом случае степень ионизации обычно бывает близкой
к термодинамически равновесной величине, и вопрос о кинетике
ионизации не столь актуален.
§ 2. Другие механизмы ионизации
2.1. Фотоионизация. Конкурировать с ионизацией электрон-
ным ударом в условиях разрядов фотоионизация не в состоя-
нии. Но иногда опа служит источником затравочных электронов,
от которых начинаются электронные лавины, в частности при
♦) В сущности, уравнение (4.12) эквивалентно уравнению (3.12) при
условии, что г?д = и, так как ds/dt = v^dzldx. Уравнение (3.12) тоже запи-
сывается для единственной (средней) энергии электронов, которые счита-
ются как бы моноэнергетическими. Но в слабых полях, где средняя энер-
гия 8 меньше потенциала ионизации I, приближение моноэнергетичности
не позволяет находить скорость ионизации. Ионизуют в слабых полях не
«средние» электроны, как в сильных, а те немногие, что обладают энергией,
значительно большей средней. Тут без знания спектра zz(e) никак не обой-
тись.
75
распространении стримеров (гл. 14). Сечения фотоионизации у
порога довольно велики (табл. 4.2), но обычно в газе бывает
мало квантов с энергиями Лео >7, способных произвести фото-
эффект.
Таблица 4.2. Сечение фотоионизации атомов и молекул из основного
состояния у порога
Газ эВ о X, А av, 10 18 см2 Газ /7(0 = 1, ЭВ о X, А (Tv, 10 18 смг
Н 13,6 912 6,3 Ся 3,89 3185 0,22
Не 24,6 504 7,4 N 14,6 852 9
Ne 21.6 575 4.0 О 13,6 910 2,6
Аг 15,8 787 35 О, 12,2 1020 -1
Na 5,14 2412 0,12 n; 15,58 798 26
К 4,34 2860 0,0! 2 Н2 15,4 805 7
2.2. Ионизация возбужденными атомами. Даже большая ки-
нетическая энергия медленных тяжелых частиц не эффективна
в отношении ионизации. Для ионизации нужны скорости атомов
и ионов, сравнимые со скоростью электрона в атоме 108 см/с,
чему соответствуют пе реализующиеся в разрядах энергии 10—
100 кэВ. Напротив, энергия возбуждения £* атома легко затра-
чивается на отрыв электрона от другого атома, если, конечно,
она превышает его потенциал ионизации I. Особенно эффектив-
ны в этом отношении резонансно-возбужденные атомы. Так, се-
чения ионизации Ar, Кг, Хе, N2, О2 атомами Не(217>) с Е* =
= 21,2 эВ(о~2-10“14 см2) гораздо больше газокинетических
[18]. Меньше сечения ионизации метастабильными атомами так-
же с Е* > I {эффект Пеннинга), но зато метастабильные атомы
присутствуют в газе в гораздо большем количестве, чем быстро
высвечивающиеся резонансные. Сечения ионизации Ar, Хе, N2,
СО2 метастабильными атомами Не(235) с Е* = 19,8 эВ достигают
значений 10“15 см2, а сечение ионизации Hg исключительно боль-
шое, 1,4 • 10“14 см2 [18].
2.3. Ассоциативная ионизация. Процесс типа А + А* -> А^ +
+ е, обнаруженный Хорнбеком и Молнаром в 1951 г., иногда
играет заметную роль в инертных газах. Отрыву электрона от
возбужденного атома способствует выделение небольшой энергии
связи порядка 1 эВ при объединении иона и атома в моле-
кулярный ион. В гелии реакция идет с участием атомов, воз-
бужденных до состояний с главным квантовым числом п = 3,
у которых энергии связи электрона равны 1,52—1,62 эВ. Энергия
связи Не^ — 2,23 эВ немного больше, и это обеспечивает отрыв
электрона. Сечения реакции при 7 = 400 К составляют 2 • 10“16—
2 • 10”15 см2. В парах ртути ассоциативная ионизация идет с уча-
стием двух возбужденных атомов:
Hg (б’Р,) + Hg (68Р0) -> Hg2+ + е,
76
причем первый находится на резонансном уровне с энергией’
возбуждения = 4,9 эВ, а второй — на метастабильном с —
= 4,7 эВ. Суммарной энергии 9,6 эВ не хватает для ионизации
атома (7Hg = 10,4 эВ), но вместе с энергией связи Hg^- 0,15 эВ
ее достаточно для ионизации молекулы (/Hg2 ~ 9,7 эВ). Ассоциа-
тивная ионизация иногда играет роль при распространении волн
ионизации и искровых разрядов в местах, где электронов еще
очень мало. Возбужденные атомы образуются там в результате
поглощения фотонов, излучаемых в уже ионизованных обла-
стях.
§ 3. Объемная рекомбинация
3.1. Распад плазмы. В отсутствие поля плотность зарядов
в плазме, лишенной электроотрицательных компонент, умень-
шается с течением времени по закону
(dn\ п® л
—₽^еп+, пе =-------——> д-. (4.13)
\ dt )г 1 h t->oo
Например, при коэффициенте электрон-ионной рекомбинации р =
— 10-7 см3/с и начальной плотности плазмы nQe~ 1010 см“3харак-
терное время распада трек = Ю-3 с. Коэффициент рекомбинации
можно определить из опыта, измерив ne(t) и построив график
в зависимости от t. Наклон прямой дает р.
3.2. Диссоциативная рекомбинация. Опа идет по схеме +
+ е—> А + А*. Это — наиболее быстрый механизм объемной ре-
комбинации в слабоиопизоваппой 'плазме, например в тлеющем
разряде. В этом случае газ — холодный и в плазме, как правило,
присутствуют молекулярные ионы. Выделяющаяся энергия свя-
зи переходит в основном в энергию возбуждения атома. Коэф-
фициент диссоциативной рекомбинации рдис ~ 10~7 см3/с, он
уменьшается при температурах от комнатной до нескольких ки-
локельвппов пропорционально а при более высоких — бы-
стрее, пропорционально TY312 (рис. 4.6). Даже в слабоионизо-
ванных инертных газах и парах металлов рекомбинация идет
именно таким путем. Молекулярные ионы образуются из рож-
дающихся при ионизации атомарных в ходе реакции конверсии
А+ + А + А -> А^ + А. Скорость реакции конверсии
(dN +ldt\ = ^конвАга+ А^аотнюдь пе мала (табл. 4.3). Так,
\ ^2 / /КОНВ
при р = 10 торр время жизни атомарного иона по отношению к
конверсии тКОНв~ (^конвАга) 4 с, при 100 торр — 10~6 с. Если
пе = 1010 см-3 и ^ис = Ю“7 см3/с, Тконв < Тдие = Ю“3 с. Конверсия
«мгновенно» пополняет запас молекулярных ионов, не задержи-
вая диссоциативной рекомбинации. В гелии рдис в 10—100 раз
меньше, чем в других газах. Конверсия приводит и к образо-
ванию сложных ионных комплексов Oj, Nj и др.
77
4-
Рис 4 6 Зависимость коэффициента диссоциативной рекомбинации Ne2 ,
Аг7(“, 0+ и электрона от температуры электронов по различным дан
ным [18]
3.3. Фоторекомбинация. Сечения фотозахвата электронов в
реакции А+ + е -> А + 7? со очень малы, оф ~ 10“21 см2. Соответ-
ственно мал и коэффициент фот о рекомбинации [27]
pv = <ro(>~2,7 10'13{7\ [эВ] }-3/4 см3/с~10"12 см3/с (4 14)
Г 16 лиц т 4 1 Измер нчыр коне i анты скорости конкрсии А+ в в
тропных столкновениях с атомами А при Т 300 К [18]
Газ ^КОНВ’ Ю см6/с Газ ^КОНВ’ 1® см6/с
Не 0 63-1,15 Хе 3,6
Хе 0,42—0,79 Hg 1 (Т = 700 К)
Аг 1 46—3,9 Cs 150
Кг 1,9—2,7
78
Чаще электроны захватываются на основной уровень атома с
испусканием кванта йсо ~ I в области вакуумного ультрафиолета
Л < 1000 А. Но возможны захваты и на высокие уровни с излу-
чением видимого света, длина волны которого Л ~ 4000—7000 А.
В газоразрядной плазме фоторекомбинация, если и важна, то
не как канал гибели электронов, а как механизм излучения света.
3.4. Ударно-радиационная рекомбинация в тройных столкно-
вениях. Этот процесс, идущий по схеме А+ + е + е А + е, яв-
ляется основным в плотной низкотемпературной равновесной
плазме, где Т ~Те~ 104 К и концентрация молекулярных ионов
слишком мала, чтобы шла диссоциативная рекомбинация.
В тройных столкновениях электроны захватываются ионами па
очень высокие уровни атома с энергией связи порядка кТ. За-
тем возбужденный атом постепенно дезактивируется ударами
электронов, «спускаясь вниз» по уровням, и, наконец, из нижнего
возбужденного состояния переходит в основное путем радиацион-
ного перехода. Этим завершается процесс рекомбинации, коэф-
фициент которой равен [27]
£гр - 8,75 • 10~27{Те [эВ] }~9/2лгс = 5,2 • 10"23{Те [103 К] }"9/2ие см3/с.
(4.15)
Согласно (4.14), (4.15) он превышает коэффициент фотореком-
бинации, если
пе > 3,1 • Ю13{Те [эВ] Р’75 = 3,2 • 109{Те [103 К] I3-73 см“3. (4.16)
Константа скорости рекомбинации в тройных столкновениях
с участием атома в качестве третьей частицы (^/7V) в 10z—
106 раз меньше f}Tp/ne согласно (4.15). Процесс этот пе типичен
для разрядных условий и может проявиться лишь при очень
слабой ионизации и высоких давлениях.
3.5. Ион-ионная рекомбинация. Она служит главным механиз-
мом нейтрализации зарядов в газах, где происходит интенсивное
прилипание электронов с образованием отрицательных ионов.
Таблица 4 1 Ко_>ф5>щионты парной ион-иониои рекомбинация при
Т — 300 К
Ионы |Зг-, 10 7 см3/г Ионы , 10 7 см3/с
Ъ О 203 + + + 4 + о оООД to I ю | ’ 1 3,9 2,7 2,6 4,2 1,6 о+п ОГ о+ + о- NO+ 4- О- NO+ + NO7 SF+4 SF? 2 1 4,9 5,1—1,8 0,39
79
к3 ~ 1.00 • 10 см /с при
#251—J_।_।—।—।—।—।—1—
0,1 0,4 1,6 6,4 рргпм
Рис. 4.7. Коэффициент ион-
ной рекомбинации в возду-
хе в зависимости от давления:
кривая — расчет, точки — экс-
перимент 118]
Для нее (dnjdt)r = — $гп+п_. Если п(<^п-, то п + п_ ж
При низких давлениях рекомбинация протекает
в парных столкновениях типа А" + В+-> А + В* (табл. 4.4). Про-
исходит нечто вроде перезарядки. Выделяющаяся энергия идет
на возбуждение бывшего иона В. Потом возбуждение снимается
при столкновениях. При средних давлениях рекомбинация идет
в тройных столкновениях типа Л“ + В+ + С -> А + В + С (теория
Томсона, 1924 г.). Коэффициент рекомбинации (У = /гтрАс ~ р.
Константа скорости рекомбинации ионов ОТ, 0^ в кислороде
р ~ 100 торр. Для ионов NOT NOT
в кислороде /€3 « 3,4 • 10‘26 см6/с,
в азоте — 1,0 • 10~25 см6/с, все значе-
ния даны при Т = 300 К.
При высоких давлениях частые
столкновения ионов с молекулами
мешают приблизиться им друг к
другу, что необходимо для взаимной
нейтрализации. Ионы дрейфуют по
направлению друг к другу в поле
взаимного притяжения Е = е/г2.
Скорость сближения партнеров в
этом приближении равна
drldt = — (ц+ + р-)е2/г2, (4.17)
где р+, р_ — их подвижности. Вре-
мя сближения с расстояния ri, рав-
ного среднему расстоянию между
ионами в газе, можно рассматривать как время жизни, скажем,
положительного иона по отношению к рекомбинации с отрица-
тельным: Трек =(рги-)_1. Интегрируя (4.17) и замечая, что по
определению 4nrjT?_/3 = 1, находим формулу Ланжевена (1903 г.)
рг = 4ле(ц+ + ц_) ~ р У
(4.18)
Таким образом, справедливый при средних давлениях вакон
р, ~ р при высоких сменяется па Максимальное значе-
ние Bmax ~ 10”6 см3/с достигается при р~1 атм (рис. 4.7).
§ 4. Образование и разрушение отрицательных ионов
4.1. Механизмы и сечения прилипания. Некоторые атомы и
молекулы: О, Н, О2, Н2О, Hg, Cs, галогены Cl, CI2 и др., гало-
генсодержащие соединения CCI4, SFe и др. обладают сродством
электрону с энергиями связи 0,5—3 эВ. Прилипание (attach-
ment) электрона к атомам или молекулам является важным,
а иногда даже главным механизмом гибели электронов в элек-
троотрицательных газах или газах с электроотрицательными до-
бавками. Прилипание затрудняет пробой, прохождение тока, под-
держание ионизованного состояния. Иногда этим намеренно поль-
80
зуются для повышения изолирующих свойств газа, для скорей-
шего устранения электронов в счетчиках ядерных частиц.
В газе из простых молекул прилипание идет либо в трой-
ных столкновениях, либо диссоциативным путем.
В холодном воздухе в отсутствие поля электроны прилипают
к молекулам кислорода в тройных столкновениях'.
е + О2 + М->ОГ 4- М, М - О2, N2, Но0,
(dne/dt)a = -*мМ\)2^м, '
/Со2 = 2,5-1О~30 сме/с, An2 = 0,16-10—3° см6/с, Л^о = 14- 10~зо.см6/с.
Приведенные константы скоростей км относятся к Те — Т = 300 К.
Плотность электронов уменьшается по закону
(dne/dt)a = — vane, пе = п® е\р (— Vat). (4.20)
В сухом воздухе при р = 1 атм частота прилипаний va = ko2No2 +
4-4'n27Vo2^n2 — 0,9-108 с"1, время жизни электрона по отноше-
нию к прилипанию та v,?1 =- 1,1 • 10~8 с.
Для диссоциативного прилипания к молекулам О2, СО2, Н2О,
которые сильно связаны, электрон должен обладать довольно
значительной энергией. Реакции идут по схемам
е + О2 + 3,6 эВ О + О", е + СО2 + 3,85 -> СО + О",
е + Н2О + 4,25 -> ОН + Н", е + Н2О + 3,6 -> Н2 + О", (4.21)
е + Н2О + 3,2-»Н + ОП-
с сечениями, показанными на рис. 4.8—4.11. В разрядах из-за
присутствия поля имеются достаточно энергичные электроны,
и эти процессы обычно идут быстрее, чем прилипание в тройных
столкновениях. При повышении температуры газа, начиная с
температуры Т ж 1000 К, порог реакций (4.21) понижается,
а сечение прилипания при данной энергии электрона становится
больше (рис. 4.11). Это объясняется включением в реакцию
колебательно-возбужденных молекул, энергия которых также
расходуется на превращение. Наличие нижней температурной
границы эффекта связано с необходимостью появления в газе
достаточного количества колебательно-возбужденных молекул.
В отличие от перечисленных молекул, потенциалы диссоциа-
ции молекул галогенов очень малы (1,5—2,5 эВ). Энергии срод-
ства электрона хватает на то, чтобы происходило диссоциативное
прилипание типа е + С12 -> С1 + С1". В иоде, например, при Те =
= 300 К сечение прилипания оа ~ 3,2 • 10“15 см2 и константа ско-
рости прилипания ка & т<5а ~ 3,4 • 10“8 см3/с. Прилипание в трой-
ных столкновениях, для которого va ~ р2, может превзойти дис-
социативное с va ~ р лишь при р 100 атм.
К сложным молекулам электрон может прилипать в парных
столкновениях без разрушения молекулы. Выделяющаяся энергия
6 Ю. П Райзер 81
Риса 6.8. Сечение диссоциативно-
го прилипания в реакции с О2 и
Си2 в зависимости от энергии
электрона [12]
Рис. 4.9. Сечение диссоциативного прилипания в трех возможных реакциях
с Н2О в зависимости от энергии электрона [12]
Рис. 4.10. Константа скорости дис-
социативного прилипания в ре-
акции с О2 в зависимости от энер-
гии электрона [12]
Рис. 4.11. Сечение диссоциативно-
го прилипания в реакции с О2 в
зависимости от энергии электро-
на при разных температурах га-
за [18]
связи при этом тотчас распределяется по ее колебательным
степеням свободы, и закон сохранения импульса не нарушается,
как было бы в случае превращения энергии связи в кинетиче-
скую Поэтому каждый захват электрона в парном столкновении
ведет к образованию стабильного отрицательного иона У наибо-
лее активных молекул CCI4, SFe при энергии электрона 8 ==
= 0,05 эВ Оа ~ 1,2 10“14 см2, причем оа ~ 1/8 Этому соответству-
ет константа скорости прилипания ka = \(jN ~ 1,6 10~7 см /с
В принципе энергия, выделяющаяся при прилипании, может
уноситься и фотоном, как при фоторекомбинации Однако сече-
ния этого процесса очень малы, 10~21 —10~23 см2, и в лаборатор-
ной плазме он роли не играет То же относится и к прилипанию
в тройных столкновениях с участием электрона в качестве треть-
ей частицы (см 1-е изд , § 8 гл 5)
4.2. Коэффициент прилипания. Подобно ионизации прилипа-
ние электронов в постоянном поле происходит на фоне их дрей-
фа Коэффициент пришпания a = vjv^ аналогичный а, дает чис
ло прилипаний па 1 см пути вчоль поля Для диссоциативного
прилипания справедлив тот же закон подобия a pf(Elp)
В случае тройных столкновении, которые преобладают в очень
с габых полях, а^р2!\{Е!р) (рис 412—415) Размножение
электронов в лавине определяется эффективным коэффициентом
сс)ф = сс — а Если а <я, чю бывает при Eip меньше определен-
ного для данного газа значения, размножение вообще невозмож-
но (п 2 5 гл 9)
4.3. Отлипание (detachment) Опыт показывает что для под-
держания стационарной слабоиопизованпой плазмы в электроот-
рицательных газах требуются значительно меньшие значения
Е!р, чем для поддержания кратковременных импульсных разря-
дов Это говорит о том, что в длительно существующих разря-
дах накапливаются активные частицы, скорее всего возбужден-
ные молекулы, которые при столкновениях с отрицательными
ионами освобождают электроны Частота и константа скорости
kd отлипания (разрушения) определяются равенствами
(dneldt)d = — (dn_/dt)d = vdn_ = kdNn^,
Из расчета на одну активную молекулу kd ~ 1О"10 см3/с
(табл 4 5) В воздухе и лазерных смесях СО2, Ns, Не, по види-
мому, эффективно действуют метастабильные молекулы
n2(/ps+), в воздухе — также молекулы О2(512'^) (табл 2 4)
Копстант kd для них, по-видимому, нет, но надо полагать, что
они имеют тот же порядок По косвенным данным (п 8 4 гл 10)
в разрядах из расчета на одну любую молекулу kd ~ 10“14 см3/с
Если /cdaKT — 10“10, концентрации активных частиц состав-
ляют 10“4
Ионы О“, образующиеся в лазерных смесях и воздухе, в ходе
реакций
0“ + СО2 + М->СО7 + М, к = 1,1-10”27 см6/с для М = СО2,
О~ + О2 -г М~>ОГ + М, к - 1,05-Ю”30 см6/с для М = О2, (4.22)
6* 83
а/p,CM I'TOpp 1 —|-"гТт-ггт[-----1---1 » I i i ТГ
Рис. 4.12. Коэффициент прилипания
электронов как функция отношения
Е/р в чистом кислороде при Т = 300 К
и разных давлениях [13]
Рис. 4.13. Вероятность h гибеЛ^
электрона вследствие прилипав#?
при столкновении с молекул0**
Н2О в парах воды при разнь*^
давлениях [6]
Рис. 4.14. Коэффициент прилипания
электронов как функция отношения
Е/р во влажном воздухе при разных
содержаниях паров воды: 1 — сухой
воздух, 2 — 150/2,5 (общее давление
150 торр, давление паров воды
2,5 торр), 5—150/5, 4—150/9, 5 —
150/15, 6 и 7 — воздух с незначитель-
ными следами паров [13]
Рис. 4.15. Коэффициент прилипаний
электронов как функция отношение
Е/р в СО2; данные на кривой 2 по
лучены в диапазоне давлений 25-
100 торр [14]
84
Таблица 4 5. Константы скоростей разрушения отрицательных ионов
при Т = 300 К
Реакция Выделение энергии, эВ Константа скорости 10~1осм3/с
О- и- О -+О2 - е 3.6 2
О- t Л NO 4 е 5,1 2
О- 1 NO -> NO2 -t е 1,4 1,6
О- f СО -+СО, ч- е 4 4
О~ 1 СО? -> СО3 4 е <0 10"3
о- 4 О2(*Лг)^О3 е *) 0,5 3
<>2~1 02->-02 | О2 е - 0,43 2,2 10~8, 600 К)
N2 -> О2 У, е — 0,43 1,8- 10-6(Г 600 К)
1 N ->NO2 । е 4,1 5
<vi О2(’Лг)-^О2 +- O2-i е 0,6 2
и- 1 Н Н2 1 Р 3,8 13
н- ] О, Н2О е 1,25 12
он- 1 О->НО2 е 0.9 2
ой- I Н Н,0 с 3,2 10
fc) O^Ag) — см табл 2 4
превращаются в более устойчивые комплексы — кластеры О3 ,
СО7- Как установлено, и это существенно для лазерных разря-
дов, молекулы СО, хорошо разрушающие ионы О', очень плохо
разрушают иопы СО^.
Заметим, что электронными ударами отрицательные иопы не
разрушаются, вернее, сечение такого процесса значительно толь-
ко при энергиях е — 100 эВ. Так происходит потому, что свобод-
ный электрон отталкивается отрицательным попом. Фотоотрыв
(аналог фотоионизации) в лабораторной плазме особой роли
не играет
§ 5. Диффузионные потери зарядов
При пробое и в разрядах низкого давления большую роль
обычно играют потери электронов, связанные с их диффузией
к стенкам. Оттуда они уже не возвращаются: в металл уходят,
к диэлектрикам прилипают, потом рекомбинируют там с ионами.
Среднее время жизни электрона по отношению к диффузионно-
му уходу равно тдиф = A2/D, где Л — длина порядка минималь-
ных размеров объема, D — коэффициент свободной, или амбипо-
лярной. диффузии. Для простейших геометрий величину Л мож-
но уточнить, решая стационарное уравнение диффузии типа
(3.44) с учетом источников ионизации:
D\ne + угпе = 0.
Положим, что поле однородно, т. е. vt(r) = const, а на стенках
85
пе = 0. Получается задача на собственные значения. Решается
она методом разделения переменных. Например, в цилиндре ра-
диуса R и длины L пе — J3(2,4r/T?)cos(.nz/L); Jo—функция Бес-
селя, z отсчитывается от середины осп. Стационарное решение
существует только при условии уг = v ДИф = DjA2, где
(1/Л)2 = (2,4/7?)2 + (л/£)2 — цилиндр,
(1/Л)2 = (л/7?)2, Л = 7?/л —шар, (4.23)
(1/Л)2 == (я/А])2 + (п/£2)2 + (п/Аз)2 — параллелепипед
(£123 — длины сторон). По смыслу ^диф^ Тдаф— средняя частота
диффузионных уходов; Л — характерная диффузионная длина.
Например, в положительном столбе тлеющего разряда в азоте
при р = 10 торр коэффициент амбиполярной диффузии 7£ =
= 200 см2/с.
Если разряд происходит в длинной трубке радиуса 7? = 1 см,
Л = 7?/2,4 = 0,42 см. Частота диффузионных уходов г’ДИф =
= 1,1 • 103 с-1. Заряды диффундируют к стенкам в среднем за
время Тдиф = 0,9 • 10“3 с. По формуле = D/А2 с Л по (4.23)
можно оценивать скорость диффузионных потерь (dnjdt) диф =
= ~и в более сложных и нестационарных случаях. Так,
если источник равномерно распределен по оси длинного цилинд-
ра, время диффузии частиц к стенкам всего в (2,4/2)2 = 1,44 ра-
за больше предыдущего.
§ 6. Эмиссия электронов из твердых тел
6.1. Работа выхода. Возможность протекания постоянного то-
ка в самостоятельном разряде обеспечивается эмиссией электро-
нов с поверхности катода. Для извлечения электрона из металла
необходимо затратить энергию, минимальное значение которой
называется работой выхода (табл. 4.6). Она зависит от состояния
поверхности, ее чистоты, шероховатости, у монокристаллов ме-
няется от грани к грани в пределах 1 В. Энергию связи элек-
трона в металле еср можно трактовать как работу е21ка против
притягивающей силы изображения e2lkr\ которую нужно затра-
тить при удалении электрона с расстояния а порядка межатом-
ного расстояния на бесконечность. Если имеется внешнее вытя-
гивающее поле £, на электрон действует суммарная сила F —
= e2[kr2 — eE. Начиная с расстояния гьр = (е/кЕ)1/2, где F = 0,
и дальше внешнее вытягивающее воздействие превышает силу
притяжения к поверхности. Значит, чтобы выбраться из тела,
электрону нужно преодолеть лишь расстояние гкр и энергию при-
тяжения
rk rk
Р Р / 2 \ 2
f F dr = ( - еЕ | dr = ег — е^Е1'2,
J J \4r2 / 4а
а а х 1
86
Работа выхода уменьшается по сравнению со случаем отсутствия
поля на
е А ср = ез/2^1/2 = 3>8.10-4{£ [,В/сМ] )1/2 эВ. (4.24)
Это явление называют эффектом Шоттки (1914 г.).
6.2. Термоэлектронная эмиссия. Эта эмиссия происходит при
нагревании металла, когда некоторые электроны приобретают
тепловую энергию, достаточную для вылета из потенциальной
ямы, каковой является для них металл. В отсутствие внешнего
поля вылетающие электроны скапливаются у поверхности и тю-
лем своего объемного щряда мешают вылету других. Объемный
заряд легко устраняется небольшим вытягивающим полем. Слу-
чаю беспрепятственного вылета соответствует ток насыщения
7Т = Л0ОТ,2е\р(-е<р//сП, А 120А/(см-К)2.
В этой формуле Ричардсона — Дэшмапа числовой множитель D
учитывает отражение электрона назад в металл от стенки по-
тенциальной ямы. Реально коэффициент Ax=AqD лежит в пре-
делах 15—300 (табл. 4.6, рис. 4.16). Электроны вылетают из
Таблица 46 Работа выхода для по 1якр гсталличсских веществ и по-
стоянная термоэлектронной эмиссии *)
Элемент еф, эВ Ап А/(см К)2 Элемент вф, эВ А,, А/(см К)2
С 4.7 30-170 Мо 4,3 60—150
А1 4,25 -В а 2,49 60
Fe 4,31 60-700 W 4,54 40—100
Ni 4,5 30-50 Р1 5,32 10—170
Си 4,4 60-100
*) Значения ф рекомендованы в справочнике [4 > ] на основании анализа измерений,
выполненных многими авторами.
Рис. 4.16. Зависимость плотности тока термоэлектронной эмиссии от темпе-
ратуры для нескольких материалов [4.4]
металла со средней энергией 2кТ. Эффект Шоттки может сильно
влиять на термоэмиссионный ток (табл. 4.7). Термоэлектронная
эмиссия действует в дуговых разрядах.
87
Таблица 4.7. Снижение работы выхода и токи термоэлектронной
автоэлектронной i \ и термоавтоэлектронной /ТА эмиссий *)
Е, 107 В/см Дф, в 7Т, А/см2 уд, А/см2 >ТА» А/см2
0 0 1,3-102 0 0
0,8 1,07 8,2-103 2-10-20 1,2-104
1,7 1,56 5,2-101 2,2-Ю'4 1,0-105
2,3 1,81 1,4-1()5 1,3-10° 2,1 -105
2,8 2,01 3,0-105 1,3-102 0.8-106
3,3 2,18 6,0-105 4,7-103 2,1-106
*) В расчетах принято:
Т = 3000 К, ф = 4 В, Ai -= 80 А/(см2-К2), eF = 7 эВ.
6.3. Автоэлектронная эмиссия. Вытягивающее электроны поле
превращает потенциальную яму в потенциальный барьер конеч-
ной ширины (рис. 4.17п), и это дает электрону возможность
выйти из холодного металла путем туннельного эффекта. Это
4
Термо
х
—=► Термо
с эфф. Шоттки
—^Термоивто
А б то
с эфф.
Шоттки
/7
5
2
1
б
Рис. 4.17. Потенциальная энергия электрона при наложении на металл
внешнего поля: а — без учета силы изображения: б — с учетом силы изо-
бражения; схема иллюстрирует явления авто- и термоавтоэлектронной
эмиссий
явление называется автоэлектронной эмиссией. Ток эмиссии да-
ется формулой Фаулера — Нордгейма (1928 г.); в численном виде:
A А/с.ч2.
Здесь Ер [2?] — граничная энергия Ферми, <р [22] — не возмущен-
ная полем работа выхода, £ (Дф/ф) — поправочный коэффициент,
учитывающий ее снижение; Е [В/см]. Ниже дан поправочный
множитель к формуле Фаулера — Нордгейма, учитывающий сни-
жение работы выхода [4]:
Дф/Ф 0 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1
I 1 0,95 0,9 0,85 0,78 0,70 0,60 0,50 0,34 0
Реально заметный ток получается при полях Е « 106 В/см, в де-
88
сятки раз меньших, чем это следует из (4.25) и табл. 4.7. При-
чина — в резком усилении приложенного поля около микроско-
пических выступов, всегда присутствующих на поверхности ме-
талла (п. 6.1 гл. 14). Автоэлектронная эмиссия обуславливает
пробой вакуумных промежутков.
6.4. Термоавтоэлектронная эмиссия. Когда у нагретой поверх-
ности металла имеется сильное вытягивающее поле, оба факто-
ра — высокая температура и поле — оказывают влияние на вы-
лет электронов, причем дело не ограничивается механизмами,
рассмотренными выше. На рис. 4.176 все возможные энергети-
ческие состояния электрона в металле разбиты на четыре груп-
пы. При Т = 0 электроны занимают состояния 1 с е eF. При
Т > 0 заполняются все четыре группы, хотя число электронов
быстро падает по мере превышения 8 над 8F. Электроны груп-
пы 7 испытывают автоэлектронную эмиссию, как и при Т = 0.
Электроны группы 4 вылетали бы путем термоэлектронной эмис-
сии даже в отсутствие поля. Электроны группы 3 за счет тепло-
вой энергии перепрыгивают через барьер, понизившийся в ре-
зультате действия поля. Что же касается электронов группы <2,
существующих только при нагревании, то они имеют повышен-
ную, по сравнению с электронами группы 7, вероятность про-
никнуть туннельным эффектом через барьер, который для них
уже и ниже.
Вылет этих электронов и дает ток термоавтоэлектронной эмис-
сии [3]. Простыми формулами он не выражается. Величины
/та, представленные в табл. 4.7, извлечены из результатов чис-
ленных расчетов [4, 5, 8], сделанных на ЭВМ для катодного
пятна дуги. При Т = 3000 К и /Г*>0,8 • 107 В/см преобладает
термоавтоэлектрониая эмиссия, причем тем сильнее, чем больше
ноле. При Е < 0,5 • 107 В/см вылетают в основном электроны
группы 5, что описывается формулой Ричардсона — Дэшмапа
с учеюм эффекта Шоттки.
6.5. Вторичная эмиссия. Она происходит под действием по-
ложительных ионов, возбужденных атомов, электронов, а также
фотонов. Вторичная эмиссия с холодного катода обеспечивает
пробои разрядных промежутков и протекание небольших посто-
янных токов, которые не в состоянии сильно разогреть катод,
а также привести к возникновению настолько высокого поля
у катода, чтобы вызвать термоавтоэлектронную эмиссию.
Важнейшим из вторичных механизмов является ионно-элек
тронная эмиссия. Она характеризуется коэффициентом уг — чис-
лом эмиттированных электронов из расчета на один падающий
положительный ион. Небольшая кинетическая энергия, которую
ионы приобретают в разрядах, не эффективна в отношении вы-
рывания электронов. Основным является потенциалъное вырыва-
ние (Пеннинг, 1928 г.). Приближаясь к поверхности на расстоя-
ние атомных размеров, ион своим полем трансформирует побли-
зости потенциальную яму и потенциальный барьер (рис. 4.18).
Барьер получается низким и узким, ибо поле — огромное, по-
89
рядка внутриатомного. Электрон из металла туннельным эффек-
том немедленно переходит к иону и нейтрализует его. Если вы-
деляющаяся при этом энергия Z — еср превышает е<р, она может
поити на вырывание второго (эмиссионного) электрона. Для чи-
стых поверхностей действует эмпирическая формула ~
~ 0,016{(/— 2вф) [эВ]} (с погрешностью порядка 50%). Так,
Рис. 418 Схема взаимодейст-
вия электрона с металлом и
ионом, иллюстрирующая про-
цесс потенциального вырыва-
ния: а — электрон из металла
переходит на возбужденный
уровень атома; б — атом пере-
ходит в основное сосюяние
а выделяющаяся энергия пе-
редается 2-му электрону Ме_
талла
для W и Не+ уг « 0,21, для Ne+ —0,30, Аг+— 0,09, Хе+ —- 0,02
причем вплоть до энергий ионов 8г ~ 1 кэВ мало зависит от
gj [4.4]. Для платины и ионов Н+, уг«3-1(~8, для N+,
5-1(Г3, О+, О2+-5-Ю~4 при е, да 0-10 эВ [6].
Рис 4 19 Коэффициент фотоэлектронной эмиссии (квантовый вых
различных металлов в зависимости от энергии фотонов [261 аз
Очень эффективны метастабильные атомы инертных
Для Не(235) и Pt коэффициент ут 0,24, для Не(215) и Газов.
Аг* и Cs—0,4 [4.4]. Разность энергий Е*—еср получает
бождеппый электрон. Для Hg* и Ni коэффициент Ю^2°Св<>
90
Фотоэффект с поверхности при Йсо > еср характеризуется
квантовым выходом — числом электронов на один фотон
(рис. 4.19). Для света в видимой и ближней ультрафиолетовой
областях спектра коэффициент фотоэлектронной эмиссии ~
~ 10"3, для дальнего ультрафиолета yv ~ 10-2—10”1. В первых
двух областях очень чувствителен к состоянию и чистоте по-
верхности и сильно снижается отражением. При пробое фото-
эмиссия часто играет определяющую роль. При пробое вакуума
высокочастотными полями существенна вторичная электронная
эмиссия — колеблющийся электрон поочередно ударяет то в одну,
ю в другую стенку. Для разных металлов коэффициенты вто-
ричной эмиссии уе ~ 0,4—1,6 при 8е до нескольких килоэлектрон-
вольт [4.4]. Электроны выбиваются и с поверхности диэлектри-
ков. Для стекла, кварца ~ 1—3, максимальные значения ле-
жат при 8е ~ 300—400 эВ. При 8е < 40 — 60 эВ уе<1 [7]. Па-
дающие электроны к диэлектрику прилипают, так что при уе < 1
поверхность заряжается отрицательно, при уе > 1 — положи-
тельно.
§ 7. Размножение зарядов в газе через вторичную эмиссию
7.1. Влияние вторичной эмиссии на усиление тока первичных
электронов. Вернемся к опыту по измерению ионизационного
коэффициента а (п. 1.4). Если с катода выходит фототок Iq =
— то в отсутствие вторичной эмиссии на анод поступает
ток i = iq ехр (ad). Вышедший с катода электрон рождает в про-
межутке ехр(ad)— 1 положительны^ ионов, и все они приходят
иа катод. В стационарном состоянии и на катоде ток равен Iq +
т io [ехр (ad) — 1 ] = /. Зависимость In i от d при р, Е = const яв-
ляется линейной. При повышении Е или d размножение быстро
возрастает и на значении тока начинает сказываться вторичная
эмиссия электронов с катода. Пусть это будет иоппо-электропная
эмиссия. Каждый из ехр(ad)—1 ионов, рожденных от одного
электрона, вылетевшего с катода, попадая на катод, вырывает
электронов, и этот ток вторичны^ электронов добавляется к то-
ьу Iq первичных от внешнего источника. Суммарный электронный
ток Zi с катода определяется из уравнения и = Iq + ^г1\ [ехр (ad) —
- 1]. На анод и во внешнюю цепь поступает ток (индекс у
опустим)
i = = iQead! [1 — y(ead — 1) ]. (4.26)
Формула подобного типа была впервые выведена Таунсендом
(1902 г.) для объяснения процесса зажигания самостоятельного
разряда. Благодаря вторичной эмиссии, In i после участка линей-
ного нарастания с увеличением d резко устремляется вверх
(рис. 4.20). Это происходит, когда знаменатель (4.26), не отли-
чающийся от единицы при небольших коэффициентах усиления
ad, по мере роста ad приближается к нулю. Обращение знаме-
нателя в нуль знаменует осуществление пробоя и зажигание
91
самостоятельного разряда: формально «г = 0/0 = const» при iQ =
= 0 (§ 2 гл 9) Достичь этого на опыте можно, повышая на-
пряжение на электродах Чтобы следовать вдоль определенной
кривой Е const на рис 4 20, нужно наращивать V и d одно-
временно и пропорционально Анализируя такой график с по-
мощью формулы (4 26) и известного значения а, найденного по
наклону линейного участка кривой, можно определить число у*).
t,A
Ю~10
10
10~9
10~12
2
Ъ
О
Рис 4 20 Влияние вторичной элект-
ронной эмиссии на усиление тока в
разрядном промежутке длиной d (воз
дух, р = 200 торр) [14 1]
7.2. Фотоэмиссия и эф-
фективный коэффициент 7»
В условиях разряда холод-
ный катод может эмиттиро-
вать электроны под действи-
ем всех возможных агентов,
и установить, какой из них
является главным в каждом
конкретном случае, далеко
не всегда оказывается воз-
можным Поэтому обычно
пользуются некоторым эф-
фективным коэффициентом
вторичной эмиссии рас-
считанным на один ион Он
характеризует весь сложный
процесс в целом, в отличие от тех характеристик элементарных
актов 7,, 7V и других, которые находят, бомбардируя мишени
пучками частиц и фотонов определенной энергии
Пусть на пути в 1 см вдоль поля электрон создает столько
возбужденных атомов, что в результате высвечивания появляется
av фотонов, способных вызвать эмиссию Полное число таких
фотонов, рожденных в конечном счете от одного вышедшего с
катода электрона, равно
d
Jeaxav^ = ^(ead-1).
О
Если кванты слабо поглощаются в газе, что случается при не-
больших давлениях, и § — средняя вероятность попадания их на
катод, то число вторичных электронов, эмиттироваипых с катода
из расчета па один первичный, составляет ^(7vav/a) [exp (ad) — 1].
Добавляя эту величину к [exp(ad)— 1], обязанную положи-
*) CiM Га^псепд д>мал, чго вторичным процессом который обеспе-
чивав! возможность перевода несамсслоятельного разряда с экспоненциаль-
ным усилением фототока z0 в са\юстоятельныи, является ионизация ато-
мов газа у дарами положительных ионов В теории наряду с а фигурировал
второ! иона зационны г козффициенг £ — для ионов Впоследствии многочис-
ленными опытами было доказано, чго ионизация газа ионами в разряде не-
возможна (по причине указанном в начале п 2 2) Or «а, £» перешли к
«а, 7» теории
92
тельным ионам, получим ту же формулу (4.26) с эффективным
кгафф.циентом 1_ъ + 1,?сМа. (427)
Аналогичным путем можно добавить к у вклад метастабильных
атомов.
7.3. Результаты измерений у. Положительные ионы или фо-
тоны? Результаты определения эффективного коэффициента у.
методом, изложенным в п. 7.1, собраны в [6, 21] и иллюстриру-
ются рис. 4.21 и табл. 4.8. Интерпретировать их нелегко. Метод
^аЖЖипиента ионно-электронной эмиссии от отно-
Рис. 4.21. Зависимость к,э.фЯДного эксперимента (п. 4.1): а —медный
шения Е!р, определена Lf2irlHHe металлы в Аг; в —различные ме-
катод в инертных газах, 6 - разлит
не позволяет отделить различные механизмы. Коэффициент
нерегулярным образом зависит от Е/р, весьма чувствителен к
состоянию поверхности катода. В ряде случаев -у совпадает по
порядку величины со значениями у., полученными в опытах по
бомбардировке мишеней ионными пучками. Указание на меха-
93
низм эмиссии удается получить, исследуя на опыте нестацио-
нарный процесс появления вторичных, третичных и т. д. элек-
тронов (вернее лавин) после выхода первичных, поскольку
времена прихода на катод ионов и фотонов существенно раз-
личны (п. 1.2 гл. 14).
Из совокупности данных можно сделать следующие ориенти-
ровочные заключения. При pd ~ 1 —10 см торр, для которых
характерны большие значения Е1р ^ 100—200 В/(см-торр), по-
видимому, преобладает ионно-электронная эмиссия с у ~ 10-1 —
10-3. Так бывает при пробое разреженных газов и в катодном
Таблица 48 талые коэффициенты вторичной эмиссии при
м репных и высоких сс н ых п )иядка атиос&ерпого *)
Газ Катод Состояние поверх- ности Условия в газе V Механизм
Е/р В/(см-торр) pd, см т орр
воздух N1 )ЧЧ]Ц 39—45 8 10-°—1,5 10"4
n2 Г 7 ЭЧМЩ 39—49 1,3 10-4—3,7 10"1
n2 Со ОЧ’НЦ Щ 1 5 10-6 ионы
N, ( U окнсл 59 >10-3 ионы
о2 У1 35,4 4 5 10-2
о2 Сп оч пц ~10-'
о2 Си ОЧ ТС’ 50 10 ( ти \
Н2 N1 ОЧ ПЦ 20,3 -25,1 d 2 Ми 2 1 п х О ЮНЫ
Н2 Си ОЧИ1Ц 50 ~М 6 1 О ЮНЫ
Н2 Си окнсл 50 5 10'5 фо ЮНЫ
органика:
спирт, метан, — 0 9
метилаль
*) Ссылки в [7]
слое тлеющего разряда. В инертных газах в случае чистого
(отожженного) катода 7 ~ и при высоких давлениях. не-
очищенной поверхности значения уг резко умет ыпаются и на
первый план часто выступает фотоэмиссия При давлениях по-
рядка атмосферного и отношениях Ещ — 30—40 В (см торр),
характерных для пробоя плотных газов, в большинстве газов,
за исключением инертных, действует фотоэмиссия Возможно,
вторичные электроны появляются благодаря фотопроцессам в са-
мом газе (п. 1.3 гл. 14). Данные по у несовершенны и часто
противоречивы. Однако неуверенность, которую обычно прихо-
дится испытывать, когда нужно выбрать у для расчета или ана-
лиза эксперимента, смягчается тем обстоятельством, что обыч-
но входит в формулы только под знаком логарифма (п. 2,4 гл. 9,
п 42 I г 10) Чаще всего полагают у ~ 10"1 —10"2.
94
Глава 5. ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОНОВ
ИОНИЗОВАННОГО ГАЗА
С ПЕРЕМЕННЫМИ ЭЛЕКТРИЧЕСКИМИ ПОЛЯМИ
И ЭЛЕКТРОМАГНИТНЫМИ ИЗЛУЧЕНИЯМИ
§ 1. Колебания электронов в осциллирующем поле
И уравнения электродинамики, и уравнение движения элек-
трона линейны относительно полей Е, Н и скорости электрона v.
Поэтому для них справедлив принцип суперпозиции. Поскольку
любое периодическое поле можно представить в виде совокуп-
ности гармонических компонент, достаточно рассмотреть сину-
соидальное, тем более, что на практике чаще всего имеют дело
именно с монохроматическими полями и волнами. Для нереля-
тивпстских движений магнитная сила волны e(v/c)H гораздо
меньше электрической еЕ. Кроме того, в разрядных процессах
амплитуда колебаний электронов обычно мала по сравнению с
длиной волны Л. Поэтому будем считать, что на электрон воз-
действует однородное в пространстве электрическое поле Е —
= Ео sin со£ с Ео = const.
1.1. Свободные колебания. Допустим, что электрон не испы-
тывает столкновений. Это имеет смысл, если частота колебаний
столь высока или столкновения столь редки, что за время между
столкновениями электрон успевает совершить много осцилляций,
со > vm. Проинтегрируем уравнение бесстолкновителыюго движе-
ния
mN = —еЕ0 sin со£, г = v,
которое имеет решение * *
еЕп еЕ
v = ^coscoZ+vo’ r = —^sinco^H-vot (5.1)
mco
Электрон осциллирует с частотой поля на фоне поступатель-
ного движения с произвольной скоростью Vo. Амплитуды смеще-
ния и колебательной скорости равны
а-еЕ^та2, и = еЕ^т^. (5.2)
Смещение находится в фазе с полем, а скорость сдвинута по
фазе на л/2. Предельный случай «бесстолкновительных» колеба-
ний приближенно реализуется на оптических частотах, а также
в СВЧ диапазоне при низких давлениях р < 10 торр.
1.2. Влияние столкновений. Столкновения нарушают строго
гармонический режим колебаний электрона, «сбивая» их фазу.
Резкое изменение направления движения при рассеянии мешает
электрону приобрести полный размах смещений (5.2), который
может вызвать приложенная сила, так как после каждого столк-
новения электрон начинает раскачиваться как бы заново: с но-
вой фазой, под новым углом по отношению к мгновенному на-
правлению скорости. Чтобы учесть это обстоятельство, включим
95
в уравнение движения «среднего» электрона эффективную ско-
рость потери импульса, связанную с действием столкновении.
Как и в случае постоянного поля (п. 1.1 гл. 3), запишем урав-
нение для средней скорости
mN = — еЕ0 sin r = v. (5.3)
Решение этих уравнений имеет вид
₽Е , vtn
v =--------- 0 cos (wi + ср), ср = arctg —,
т К “2 + vm
еЕ
г =--------- °-... _ sin (cof + ф).
ты у со2 +
(5.4)
Амплитуды смещения и скорости электрона в У 1 + Vm/со2 раз
меньше, чем для свободных, колебаний. Они тем меньше, чем
больше эффективная частота столкновений (последняя опре-
деляется скоростью хаотического движения, которая в разрядах
гораздо больше колебательной; см. § 2). Смещение сдвинуто по
фазе относительно поля. Фазовый сдвиг возрастает от 0 до л/2
при возрастании относительной роли столкновений vw/co от О
до оо.
Колебательные смещение и скорость (5.4) всегда можно пред-
ставить в виде двух составляющих, одна из которых пропорцио-
нальна самому полю E = Eosinco£, а другая—скорости его из-
менения Е = соЕо cos со£:
еЕ vm еЕ
г = - sin (fit + ~ —7-~——- cos ait
™(“+Vm) <om((o2 + v2m)
weE v еЕ
v = —/ '•? cos ----7—,—Ч-T sin tot
m((02 + v^)
(5.5;
Соотношение составляющих определяется относительной
ролью столкновений и однозначно связано с фазовым сдвигом ср.
Эта форма записи решения придаст большую наглядность ре-
зультатам последующих параграфов.
Из выражений (5.4), (5.5) видно, что роль столкновений
характеризуется соотношением между эффективной частотой
и круговой частотой поля со = 2л/, которая почти на порядок
больше собственно частоты /*). В пределе V™ со2 соотношения
(5.4), (5.5) приближаются к формулам (5.1) для свободные
колебаний. Для иллюстрации чисел приведем пример, относя-
щийся к этому случаю: СВЧ излучение частоты / = 3 ГГц-
*) При выяснении степени пространственной «однородности» поля
электромагнитной волны амплитуду смещения следует сопоставлять не с
длиной волны к = cjf, ас Х/(2л): а/7С = еЕ0/(тгш2:к) = и/с.
96
X = 10 см, (о = 1,9 1010 с-1 Пусть р = 1 торр, тогда vm ~
«3 109 с-1 < со; Eq = 500 В/см, что примерно соответствует
порогам СВЧ пробоя при таких давлениях По формулам (5 2)
а = 2,5 10"3 см, и = 4,7 107 см/с Видно, что а<Сл = 1,6 см,т. е.
поле в электромагнитной волне «однородно»
1.3. Дрейфовые колебания. В пределе очень частых столкно-
вений или относительно небольших частот поля, v2m со2, коле-
бательная скорость становится равной
— = —^Е(0 = уд(0- (5 6)
vm
Скорость колебательного движения в каждый момент времени
совпадает со скоростью дрейфа, соответствующей вектору поля
в этот момент Такие колебания электрона в режиме подвижно-
сти для краткости будем называть дрейфовыми Электрон ведет
себя так же, как в постоянном поле, он «следит» за его относи-
тельно медленной эволюцией Колебательное смещение электрона
r~AcosG)f, А = eEo/mvm(o = щЕо/со (5 7)
имеет амплитуду А, которая в > 1 раз меньше амплитуды
свободных колебаний в том же поле
Колебания электронов имеют дрейфовый характер в высоко-
частотном диапазоне полей (и, разумеется, при более низких
частотах) Так, например, при f ~ 10 МГц частота столкновений
~ 3 109р с-1 превышает со ~ 108 с-1, начиная с весьма низ-
ких давлений р ~ 0,03 торр Для поддержания слабоионпзовап-
нои плазмы невысокого давления ВЧ полем обычно требуются
значения Е0/р такого же порядка, как и Е/р в постоянном поле
Значит, при / ~ 10 МГц и Е&р~ 10 В/(см торр) А ~ 0,1 см не-
зависимо от давления.
§ 2. Энергия электронов
2.1. Бесстолкновителыюе движение. В отсутствие столкнове-
нии поле в среднем по времени работы над электроном не со-
вершает согласно (5 1)
<— eEv) — (eEo/mo) (sin o)Z cos g)£> — eEovo <sin otf) = 0
Электрическая сила лишь однажды, в стадии включения,
раскачивает электрон, после чего энергия электрона Tnv?l2 пуль-
сирует, в среднем оставаясь неизменной Средняя по времени
энергия <mz;?/2> складывается из энергии поступательного дви-
жения mv/j2, которая соответствует средней скорости v0 = <v(£)>,
и колебательной. Последняя для свободных колебаний равна
Есв кол = е-Е^/^ты2 = (5 £)
В примере, приведенном в конце п 12, / = 3 ГГц, Eq^-
= 500 В/с, энергия колебаний еСв кол = 0,31 эВ Она существенно
7 ю П Райзер 97
меньше тех средних энергий хаотического движения 8 ~ 1—10 эВу
которые нужны для поддержания разрядов. Итак, когда не г
столкновений, нет диссипации энергии поля, нет выделения энер-
гии в веществе.
2.2. Приобретение энергии от поля. Систематическая пере-
дача энергии электронам, сопровождаемая диссипацией энергии
поля, осуществляется благодаря актам рассеяния электронов.
Согласно (5.5) средняя за период колебаний ежесекундная ра
бота поля над электроном
е2Е2
<— eEv> = , ° - vm = Ae£vw (5.9)
2m (co- +
определяется той составляющей колебательной скорости, кото-
рая осциллирует в фазе с изменением поля и пропорциональ-
на vm. Слагаемое, сдвинутое по фазе на л/2, вклада в работу в
среднем за период не дает. Постоянное (хаотическое) движе-
ние — также. В одном эффективном столкновении электрон при-
обретает в среднем энергию Де^, которая вдвое больше средней
кинетической энергии колебательного движения:
р2 Е2 / 2 \
Де£ = Т~7 /'п = 2 \Т/ = 2е*ол- <5Л0)
Этот результат можно интерпретировать следующим образом.
В промежутке между столкновениями электрон под деиствием
электрической силы приобретает некую кинетическую энергию,
в среднем порядка 8К0Л. Если за период между столкновениями
электрон успевает совершить много колебании, то это величина
порядка энергии свободных колебаний (5.8). В акте упругого
рассеяния атомом электрон резко меняет направление своего
движения без изменения абсолютного значения скорости и энер-
гии. После этого поле начинает раскачивать электрон в новом
по отношению к скорости направлении, т. е. как бы заново сооб-
щает ему энергию порядка 8К0Л. Таким образом, в каждом акте
рассеяния порция энергии, в среднем приобретенной от поля с
момента предыдущего столкновения, переходит в энергию посту-
пательного, хаотического движения. Макроскопически — работа
поля затрачивается на преодоление силы трения, вызванной
столкновениями электрона. Все происходит так же, как и в по-
стоянном поле (п. 3.2 гл. 3), только роль энергии дрейфа вы-
полняет энергия колебаний.
2.3. Баланс энергии электрона. Этот, баланс складывается иэ
приобретения энергии от поля и передачи ее тяжелым частицам
в результате упругих и неупругих потерь. Если при каждом,
столкновении электрон теряет долю б от своей энергии 8. то
= (Де£ — бе) vm
(5.11)
98
где вместо амплитуды Eq введено среднеквадратичное поле Е,
которое определяется равенством Е2 = {Е2 (f)> = Е^/2. При со2
Vm уравнение (5.11) превращается в (3.12). Роль постоян-
ного поля в пределе со О выполняет среднеквадратичное
поле Е.
2.4. Средняя установившаяся энергия. В стационарных усло-
виях, когда электроны отдают всю ту энергию, которую получа-
ют от поля, у них устанавливается средняя энергия
е = Д?е/6 = 2екол'6 = e2E2/mb (со2 + v„). (5.12)
Поля низких частот со2<С^т не отличаются от постоянного
(§ 3 гл. 3); имеется подобие г=](Е1р). На больших частотах,
средняя энергия электронов не зависит от vm, р и вы-
полняется закон подобия по частоте поля: 8=/i(£’/co). Если
б = const, е~(Я/о))?. В эквивалентных ситуациях Е ~ со. Имен-
но по этой причине для пробоя газа на оптических частотах
со ~ 1015 с-1 требуются огромные поля в световой волне Е ~
~ 107 В/см, которые реализуются только при фокусировке ги-
гантских лазерных импульсов (§ 6 гл. 9). Ведь, чтобы развива-
лась электронная лавина, энергии электронов и 8 должны бызь
порядка I ~ 10 эВ.
2.5. Истинные изменения энергии эдектрона при столкнове-
ниях. В этом отношении ситуация в переменном поле также
аналогична тому, что происходит в постоянном (п. 3.3 гл. 3).
В отдельных столкновениях электрон может как приобретать
энергию от поля, так и отдавать ее полю, причем порциями,
которые значительно превышают средний по многим столкнове-
ниям прирост Дев. Приобретет электрон энергию или потеряет,
зависит от соотношения между направлениями движения и поля
и от фазы колебаний поля в момент столкновения. Этот факт
имеет принципиальное значение. В нем заключен классический
аналог таких, казалось бы, чисто квантовых явлений, как истин-
ное поглощение и вынужденное испускание фотонов (т. е. испу-
скание, стимулированное присутствием внешнего поля той же
частоты; см. § 9).
Поясним сказанное, вычислив прямым путем изменение энер-
гии электрона в результате столкновения. Пусть электрон испы-
тал последнее (эффективное) столкновение в момент t\ и сразу
после рассеяния обладал скоростью Vi и энергией 8Г = тщ]2.
Поскольку в результате «эффективных» столкновений, происхо-
дящих с частотой Vm, скорость каждый раз приобретает совер-
шенно произвольное направление, 81 есть энергия хаотического
движения в момент столкновения t\. В период вплоть
до момента t% следующего столкновения электрон движется под
действием силы — eEosinco^ со скоростью
v(Q = u(cos at — cos cd^i) + Vi, u = eEj/znco.
7* 99
Его энергия е = mv2[2 в каждый момент этого периода равна
8 (£) = (m/2) [к2 + 2v1u (cos mt — cos сой) +
+ и2 (cos2 mt — 2 cos mt cos сой + cos2 сой) ].
В момент t2 скорость снова приобретает произвольное направле-
ние, но вместе с энергией практически не меняется по величине.
Новое движение электрон начнет с энергией б(й), которую, как
и 81, следует рассматривать как энергию хаотического движе-
ния. Значит, изменение хаотической энергии от столкновения
к столкновению есть
Дб(й, t2) = б(й)~ 8i = mviu(cos mt2 — cos сой) +
+ (mu2/2) (cos2 сой — 2 cos mt2 cos cot1 + cos2 co11).
Допустим для простоты, что столкновения редки: vm <С со.
Тогда за время между столкновениями t2—t\ совершается много
колебаний и, в силу случайного характера столкновений, между
фазами поля в моменты столкновений сой, сой корреляция исче-
зает. Эти фазы могут быть любыми. В этом случае изменение
Де заключено в интервале между максимальным приобретением
энергии Де+ ~ 2mV[U и максимальной потерей Дб_ ~ — 2mviu,
причем наибольшим значениям отвечают параллельность ско-
ростей vi и и и определенные фазы сой, сой, такие, чтобы коси-
нусы превращались в ±1. Значения Ае± выписаны с точностью
до малых величин порядка ти2 (как уже было сказано, u^v).
При усреднении Де по многим столкновениям, т. е. по моментам
й, й, первое слагаемое более высокого порядка, mvu, исчезает и
остается только второе, положительное. Таким образом, в сред-
нем электрон приобретает энергию, причем в количестве
Д^н — <Дс (й? й)>й’й ~ — 2бсв кол,
которое найдено выше путем вычисления средней работы поля*).
Поскольку u/v<l, истинные изменения энергии электрона при
столкновении, положительные и отрицательные, имеют первый
порядок малости по отношению к самой энергии, I Де±1/е ~ и! о,
а результирующее положительное Дб^/б ~ (гг/к)2— второй. Оно
представляет собою малую разность двух относительно больших
величин; символически—Дб^^(Дб^ — IДб_|).
2.6. Почему электрон-электронные столкновения не приводят
к диссипации энергии поля. В слабоионизованном газе электро-
ны испытывают столкновения с атомами и молекулами. В силь-
ноионизованном — с ионами и друг с другом, причем примерно
*) В общем случае vm ~ со только одна из фаз является произвольной,
ибо между моментами последовательных столкновений существует корре-
ляция Вероятность интервала й—равна ехр [—vm(t2—ti)]vmdt2. С уче-
том корреляции при усреднении в Дер появляется дополнительный множи-
тель (о2/( со2 + см. (5 10). Предоставляем читателю самому проделать
это полезное для понимания эффекта вычисление.
100
d \fmv2 V
с одинаковыми частотами. Однако при рассмотрении эффектов
взаимодействия с полем следует учитывать одни лишь электрон-
ионные столкновения.
Для выяснения причины этого рассмотрим электронный газ
(можно даже более общий случай — газ из частиц с одинаковым
отношением е/т) и допустим, что электроны сталкиваются толь-
ко друг с другом. Просуммируем по всем электронам уравнение
движения /nV = — еЕ0 sin art + рст, где рст — скорость изменения
импульса электрона вследствие столкновений. Поскольку сум-
марный импульс взаимодействующих частиц сохраняется, полный
импульс газа 2 осциллирует как cos(o£, будучи сдвинутым
по фазе относительно поля на л/2. Принимая во внимание, что
суммарная энергия частиц при упругих столкновениях также
сохраняется, найдем скорость изменения энергии газа:
^-Ео sin 7ftv)~sin (at cos cousin 2coi.
Суммарная энергия частиц меняется периодически с удвоен-
ной частотой, как при бесстолкновительном движении, и в сред-
нем по времени остается неизменной. Диссипации энергии поля
нет. Напоминаем, что в случае постоянного поля электрон-элек-
тронные столкновения в сопротивление и выделение джоулева
тепла вклада также не вносят (п. 2.3 гл. 3). Как и в том случае,
электрон-электронные столкновения могут повлиять на дисси-
пацию косвенным образом, оказывая влияние на энергетический
спектр электронов и vm.
§ 3. Основные уравнения электродинамики сплошных сред
В § 1, 2 было рассмотрено, что происходит с электронами
ионизованного газа в присутствии переменного электрического
поля. Обратимся к другой стороне вопроса о взаимодействии
электронов с полем: как влияет ионизованное состояние на по-
ведение переменных полей и распространение электромагнит-
ных волн.
3.1. Уравнения Максвелла. Электромагнитное поле и состоя-
ние среды описываются векторами напряженностей Е, Н, элек-
трическим смещением D и магнитной индукцией В. По опреде-
лению D = Е 4- 4лР и В = Н + 4лМ, где Р и М — электрический
и магнитный дипольные моменты единицы объема. Векторы Е,
Н, D, В удовлетворяют системе уравнений Максвелла
rotH = (4л/с) j + с"1 5D/M, (5.13)
rotE = —с-1 dT&ldt, (5.14)
div В = 0, (5.15)
divD==4n:p, (5.16)
где р — плотность свободного объемного электрического заряда.
101
Система эта не вполне определена, ибо электрический ток j,
поляризованностъ Р и намагниченность М, которые вызываются
полем, зависят от свойств вещества. И опыт, и теория говорят
о том, что в постоянных и не слишком быстро меняющихся
полях действуют законы прямой пропорциональности: Р = /Е,
М = хН, j = оЕ. Вместо диэлектрической (/) и магнитной (х)
восприимчивостей вводят диэлектрическую (е = 1 + 4лх) и маг-
нитную (р,= 1 + 4лх) проницаемости. Вместе с уравнениями
связей
j = оЕ, D = eE, В = рН, (5.17)
где материальные константы с, ц и проводимость и считаются
известными, система (5.13) — (5.17) является замкнутой. В га-
зах и плазме с огромной точностью ц = 1 и В = Н.
3.2. Токи смещения, поляризации, проводимости зарядов.
Правую часть уравнения (5.13) можно трактовать как некую
плотность тока
j 1 4л dt ' dt * 4л dt 1 ( • )
помноженную на 4л/с. Величина (l/4n)5D/5^, добавленная Макс-
веллом к току проводимости в порядке постулата, была названа
нм током смещения. Без тока смещения уравнения (5.13), (5.16)
не согласуются с незыблемым законом сохранения заряда (3.39).
В переменном поле меняется во времени поляризация веще-
ства, которая заключается в смещении отрицательных зарядов
относительно положительных под действием электрической силы.
Но любое перемещение зарядов в пространстве есть ток, так чго
слагаемое dP/dt в токе смещения и в самом деле представляет
собою плотность тока — тока поляризации. Вместе с током про-
водимости j, они образуют полный ток зарядов Слагаемое
(1/4л)дЕ/д£, никак не связанное с движением зарядов, «током»
в буквальном смысле не является*).
Полный ток зарядов был разделен на две части: ток прово-
димости и ток поляризации, исключительно для удобства при-
менения уравнений к идеальным диэлектрикам, где о, j = 0. Та-
кое разделение вовсе не является обязательным. Для любой
электронейтральной среды можно определить вектор полной по-
ляризованности Pz, причем он связан с полным током зарядов jf,
так что достаточно оперировать одной из этих величин. В самом
деле, по определению
Р/ = У егтг, 2 ег = 0; h = 2 = d^t/dt, (5.19)
где гг — радиус-вектор заряда ег, vt = гг — его скорость и сумми-
рование распространяется на абсолютно все заряды (свободные,
связанные, электроны, ядра), содержащиеся в единице объема.
3.3. Разложение на гармоники. В достаточно быстро меняю-
щихся полях уравнения (5.17) теряют силу. Вследствие инер-
*) О его смысле еще пойдет речь в § 5 гл. 15.
102
циалъности те реальные процессы в среде, в результате которых
возникают поляризация и ток, не успевают «следить» за изме-
нениями поля. Поляризация и ток в момент t\ определяются
теперь не только и даже не столько значением E(fi), сколько
эволюцией E(f) в предыдущий период t<t\. Например, если в
течение длительного времени поле Е было направлено в одну
сторону, а потом его направление внезапно изменилось на про-
тивоположное, ток в течение некоторого времени, пока заряды
не затормозятся, еще будет течь по-прежнему — против «ново-
го» поля.
Задача установления уравнений связи с учетом эффектов
запаздывания сильно облегчается, поскольку движение зарядов
в веществе описывается линейными относительно Е, г, v уравне-
ниями. Поскольку уравнения Максвелла также линейны, все
зависящие от времени величины можно разложить на гармони-
ки в ряд или интеграл Фурье, и в силу принципа суперпозиции
оперировать только гармоническими компонентами, как это уже
было сделано в § 1, 2. Эволюция гармонических величин пол-
ностью определяется тремя параметрами: амплитудой, частотой
п фазой, и потому весь эффект запаздывания укладывается в
соотношения между этими параметрами для материальных вели-
чин и Поля. Если для определенной гармоники поле Е^ =
= Е^о sin (of, то полный ток jzco = З/шо sin ((of + фо), причем З/ш
и фо, являются функциями Ew0 п (о. Эти функции и задают не-
обходимую связь.
3.4. Уравнение связи для гармонических компонент. Ему
можно придать удобный и наглядный вид, если сохранить при-
вычные из практики обращения с постоянными полями понятия
проводимости и диэлектрической проницаемости. Полный ток
представляется в виде линейной комбинации sin cof и cos (of, что
отвечает линейной комбинации Е и dE/5f. Возращаясь к перво-
начальным понятиям о токе проводимости оЕ п токе поляриза-
ции dP/df, который в случае медленно меняющихся полей равен
[(е — 1)/4л] 5E/df, и снабжая новые коэффициенты о, 8 индек-
сом (о, поскольку они зависят теперь от частоты, запишем урав-
нение связи в виде
3/0 = о^Ею + [(ею — 1 )/4л] дЪа/dt, Ew = EWo sin (of. (5.20)
Величины do, 8W называются высокочастотными проводимо-
стью и диэлектрической проницаемостью среды. Именно эти ха-
рактеристики среды оказывают влияние на поведение в ней пе-
ременных полей.
3.5. Уравнение закона сохранения энергии. Умножим (5.13)
скалярно на Е, а (5.14)—на Н и вычтем потом друг из друга.
Поскольку Н rot Е — Е rot Н — div [ЕН], при условии линейных
связей D и Е, В и Н получим соотношение
£ ЕР + НВ + div [ЕН] = — jE. (5.21)
dt 8л 1 4лL J J v 7
J 03
Оно выражает закон сохранения энергии электромагнитного по-
ля. Величина (ED)/8n представляет собой плотность электриче-
ской энергии, (НВ)/8л — магнитной,
S = ^[EH] (5.22)
— плотность потока электромагнитной энергии (вектор Умова —
Пойнтинга), jE — выделение энергии в 1 см3 среды в 1 с, равное
убыли электромагнитной энергии. В гармонических полях в
среднем по времени диссипация энергии поля обязана только
току проводимости. Ток поляризации к диссипации не приводит,
так как он сдвинут по фазе относительно поля на л/2,
a <sin co^cos соО = 0 (ср. с результатами п. 2.1, 2.2).
§ 4. Высокочастотные проводимость
и диэлектрическая проницаемость плазмы
Результаты § 1 позволяют вычислить эти величины немед-
ленно. Сделаем прежде две оговорки. Будем считать ионы не*
подвижными, не учитывая их вклада в ток проводимости и по-
ляризацию. Далее, выделим и опустим слагаемое 8М — 1 в 8© — 1,
которое дают электроны, связанные в молекулах и ионах. По по-
рядку величины оно такое же, как и в неонизованных газах (раз-
ве что поляризуемость присутствующих в плазме возбужденных
молекул больше, чем невозбужденных). В воздухе при нормаль-
ных условиях 8М — 1 = 5,28 • 10“4, в Нг — 2,65 • 10"4, в Не —
0,67 • 10~4, при низких давлениях — еще меньше, так как 8М — I
пропорционально плотности. Эти цифры относятся к видимой
области спектра и более низким частотам. При сколько-нибудь
заметной ионизации вклад молекулярной части в объемную по-
ляризуемость плазмы очень мал.
4.1. Вычисление и еш. Подставим общее выражение (4.5)
для средней скорости электрона v в формулу (5.19) для тока
зарядов jt. Заменяя суммирование по всем электронам усредне-
нием с умножением на пе и сопоставляя полученное выражение
с (5.20), находим
Оо = e2nevm/m(a2 4- v™), (5.23)
8(о = 1 — кяе2пе/т (со2 + Vm). (5.24)
Эти формулы имеют фундаментальное значение для физики
взаимодействия электромагнитных полей с плазмой. Соотношение
амплитуд токов проводимости и поляризации
/пров о//поляр 0 4зТО©/(О I 8 © 11 Vт/ы (5.2о)
определяется отношением частот столкновений и поля.
4.2. Предел «больших» частот («бесстолкновительная» плаз-
ма). Он наступает, когда со2 v^, т. е. реально при не очень
больших частотах. Даже при атмосферном давлении это — СВЧ
104
или очень далекий инфракрасный диапазоны. Между тем, моле
кулярная поляризуемость большинства диэлектриков и неионпзо
ванных газов сохраняет свое значение, характерное для постояв
ного, поля, вплоть до оптических частот. В пределе большие
частот
е2пе 4ле2пе
О'о — 2 Vm, 8(0 =1 2~ ’ (5.26
mco mat
т. е. проводимость пропорциональна частоте столкновений, а ди
электрическая проницаемость от нее не зависит. Ток проводи
мости согласно (5.25) мал по сравнению с током поляризации
Этому пределу отвечает модель «бесстолкновительной» плазмь
(п. 1.1, 2.1).
4.3. Статический предел. При условии о)2 '«< Ут получим
е2п. 4ле2пг
асо = ч 8(0 = 1 —«
mvm
(5.27
Проводимость не отличается от обычной проводимости ионизо
ванного газа для постоянного тока. Диэлектрическая проннцае
мость также приобретает предельное, не зависящее от частоть
поля значение. Ток поляризации мал по сравнению с токол
проводимости и в пределе исчезает совсем.
4.4. Почему у диэлектриков обычно е > 1, а у плазмы е < 1
Все дело в том, что у диэлектриков электроны связаны в атома?
и молекулах, а в плазме (и металлах, где также 8< 1) часть ю
свободна. Абсолютно свободный, не, испытывающий столкновени!
электрон колеблется в фазе с полем (формула (5.1)). Он сме
щается от центра «равновесия» в направлении вектора Е, протш
направления действия электрической силы. Обладая отрицатель
ным зарядом, он придает среде отрицательную поляризуемост]
И 8 < 1.
Электроны в молекулах можно уподобить частицам, на кото
рые при смещении действует упругая возвращающая сила. Есл1
соо — частота собственных колебаний упруго связанного электро
на, то
*’ , 2
Г + 0)пГ =-----SIH O)L Г =------; --7- Sin COL
0 m
В статическом поле и при частотах, меньших собственной часто
ты (а последние обычно лежат в оптическом диапазоне), смеще
ние направлено против Е, так что поляризуемость положитель
на*), у жидких и твердых диэлектриков 8 обычно составляем
несколько единиц.
♦) При со > (о0 происходит обратное; с этим связано явление аномал!
ном дисперсии света.
10
§ 5. Распространение электромагнитных волн в плазме
В случае идеальных диэлектриков, где нет тока проводимости
и свободных зарядов, система уравнений Максвелла приводит к
волновым уравнениям для Е и Н. Они описывают распростра-
нение электромагнитных волн. В случае монохроматического по-
ля аналогичные уравнения получаются для электронейтральной
проводящей среды, каковой является плазма. Проще всего это
сделать, если перейти к комплексному представлению гармони-
ческих величин. Это вообще целесообразнее при наличии фазо-
вых сдвигов, так как избавляет от необходимости все время опе^
рировать комбинациями синусов и косинусов.
5.1. Комплексная диэлектрическая проницаемость. В случае
монохроматического поля Е, Н~ехр(—left) первое уравнение
Максвелла (5.13) вместе с уравнением связи (5.20) приобретает
вид
rotH = (4л/с)оЕ —f(coe/c)E; 8 == 8« (5.28)
(индексы со у со, 8W больше писать не будем). В (5.28) удобно
избавиться от тока проводимости, введя формально комплексную
диэлектрическую проницаемость
8х = 8 + i (4ло/со). (5.29)
Получающееся при этом уравнение
rot Н = — i ((08z/c)E (5.30)
внешне не отличается от соответствующего уравнения для ди-
электрика, где о = 0, 8х = 8.
5.2. Плоская электромагнитная волна. Подставим в (5.14)
дВ/д£ = —fwH. Взяв от получившегося уравнения rot, пользуясь
соотношением rot rot Е =—АЕ + grad div Е, замечая, что согласно
(5.16) при р = 0 divE = 0, п подставляя rotH согласно (5.30),
получим уравнение
AE + (8'co7c?)E = 0. (5.31)
Фактически это есть результат подстановки Е ~ ехр(—W) в вол-
новое уравнение для Е. Исключив из (5.13), (5.14) не Н, а Е,
с помощью (5.15) получим такое же уравнение (5.31) для Н.
Уравнение (5.31) допускает решение типа бегущей плоской вол-
ны Е, Н ~ ехр(—i^t + fkr), где к—волновой вектор. Коэффици-
ентами при экспонентах служат некоторые постоянные комплекс-
ные числа, характеризующие амплитуды полей и фазовый сдвиг
между ними. Подставляя эти выражения в исходные уравнения
(5.13) пли (5.30) и (5.14), найдем '
[кН] = - (ош'/с) Е, [кЕ] = (о/с)Н. (5.32)
Из этих равенств следует, что при е'^О все три вектора Е,
Н, к взаимно перпендикулярны, так как волна является попе-
речной. Если е' = 0 (что соответствует 8=0 в слабопроводящей
106
среде, где о~0), уравнения допускают существование продоль-
ных чисто электрических волн с Н = О, Е II к. Это — плазменные
волны (см. § 7).
5.3. Показатели преломления и затухания волны. Из равенств
(5.32) вытекает зависимость волнового вектора от частоты (дис-
персионное соотношение), а также соотношение между комплекс-
ными амплитудами полей:
* = (о)/с)У7, Н=1Т'Е. (5.33)
Волновой вектор — величина комплексная, поскольку е' комп-
лексна. Чтобы найти к = + гкъ, введем безразмерные числа п
и и по формуле ск]а = п + fx = Те'. Возведя это равенство в
квадрат, подставив е' согласно (5.29) и приравняв действитель-
ные и мнимые части, найдем
п2 — х2 == 8, 2тгх = 472о/со,
п = ь + х = ]/~е + (5.34)
Физический смысл величин п и х ясен из выражения для
бегущей волны:
Е,Н ~ ехр (—Utit + гкх) = ехр [—ко (t — пх/с) — хсогг/с].
Число п определяет фазовую скорость с/п и длину волны Л = Ло/п
в среде (Ло = 2лс/о—длина волны в вакууме). Оно соответ-
ствует показателю преломления. Число х характеризует затуха-
ние волны: амплитуда ее падает в е раз на пути Кх = \о/2лх
или в е* раз на расстоянии Ло. Числа п и х определяют соот-
ношение между амплитудами полей и фазовый сдвиг между
ними:
Н = (п + 1к)Е = Уп2 + х2 ег1*Е, г|) = arctg(x/n).
5.4. Закон ослабления потока энергии. Практический интерес
представляет лишь среднее за период колебаний значение плот-
ности потока энергии. Чтобы вычислить среднее от произведения
гармонических величин заданных в комплексной форме, нужно
взять половину действительной части произведения одного из
сомножителей на комплексно сопряженное другого*). В одно-
родной среде плотность потока энергии волны затухает по экспо-
ненциальному закону:
S = £ • 4 Re (ЕН^ = IE ЕЕ* = IЕ (°) I2 <5-35>
ег Л О JI О JI I
*) В самом деле, если А = Ао cos (cot + Фа), В = Бо cos (coi + срв). то
<АЯ> = (l/2)A0B0cos (фв— Фа).
В комплексном представлении А = Ло ехр (—Kirf + гфл), В — Во ехр (—zcof-}-
+ ирв) Отсюда
(1/2)Ве(ЛЯ*) = (1/2)Л^0Ве[ехр(-г(фв-фА))] =
— (l/2)A0BoCOS (фв —Фа) = <ЛВ>.
107
где знак усреднения у S опущен, Е(0) — амплитуда в точке
Щй = 2хсо/с = 4ло/пс (5.36)
— коэффициент поглощения. Поток энергии уменьшается в е раз
на длине Цш1.
Как следует из (5.35), а также из уравнения (5.21), если
произвести его усреднение по времени за период, для изменения
плотности потока энергии вдоль пути распространения волны
справедлив закон Бугера
dS/dx^-^S. (5.37)
В 1 см3 в 1 с диссипируется электромагнитная энергия
<}ЕУ «= сКЕ2> = щЛ, и эта энергия выделяется в среде. Пропор-
циональность между коэффициентом поглощения и проводи-
мостью вполне согласуется с пропорциональностью между про-
водимостью и скоростью выделения джоулева тепла.
В пределе непроводящей среды о = 0, диэлектрическая про-
ницаемость 8,==8 — действительная величина, лг = Уе, х=0,
go = 0. Среда абсолютно прозрачна. Волна в ней не затухает,
так как ток поляризации джоулева тепла в среднем за период
не выделяет.
5.5. Коэффициент поглощения волны в плазме. Если мнимая
часть 8х гораздо меньше действительной, 4ло/со8 < 1, причем 8
величина положительная, по формулам (5.34) получается Уе
и х ~ 2лс/(е/г< 1. Среда обладает обычным для диэлектрика по-
казателем преломления, но слабым поглощением, слабым в том
смысле, что волна лишь немного затухает на пути порядка 7..
Коэффициент поглощения определяется формулой (5.36), в кото-
рую можно подставить тг = Уе. Этот случай обычно реализуется
при распространении света, а отчасти и СВЧ (микроволнового)
излучения в лабораторной плазме*).
Коэффициент поглощения электромагнитной волны в ионизо-
ванном газе согласно (5.36), (5.23) равен
4ne\vm
mc(“2+vm)
0,106ив „ m CM-1.
“ + vm
(5.38)
=
Здесь положено п~ У8 « 1, как это чаще всего бывает в тех
условиях (слабая ионизация, слабое поглощение), когда форму-
*) Как ясно из предыдущего, для существования поглощения не обя-
зательно присутствие свободных электронов. Достаточно, чтобы по любой
причине диэлектрическая проницаемость содержала небольшую мнимую
часть. Так и получается в реальных диэлектрических материалах из-за су-
ществования некоторого «трения», которое испытывают молекулярные элек-
троны при колебаниях. Нагревание изоляционных материалов в перемен-
ных полях характеризуется отношением мнимой и действительной частей
8х, которое называется тангенсом угла потерь\Х£§ = 8мним/8действ« У сте-
кол, керамик в ВЧ диапазоне tg 6 ~ 10~3 — 1С~2.
108
ла (5.38) достоверно справедлива. Коэффициент поглощения
пропорционален плотности электронов. В пределе больших частот
со2 Ут для коэффициента поглощения характерна обратная
квадратичная частотная зависимость: ~ св-2 ~ Л2. Короткие
волны лучше проходят через плазму, чем длинные.
5.6. Квазистационарное поле и скин-слой. Допустим, что мни-
мая часть ez гораздо больше действительной, точнее, ее абсолют-
ного значения, так как в подобных случаях обычно е < 0. Так
получается в хороших проводниках в полях не слишком боль-
ших частот. При этом ток проводимости сильно преобладает над
током смещения:
| /лров |/| /смещ | — ^мним/1 Едейств | = 4hq/(D | 8 | 1.
В этом предельном случае согласно (5.34) га ~ х ~ У 2jw/(d и
поле сильно затухает на расстоянии порядка длины волны. Го-
ворить при этом о бегущей волне, о распространении волны нет
смысла. Существование электромагнитных волн обеспечивается
током смещения. Если его нет, как в данном предельном случае,
максвелловское уравнение (5.13) не отличается от уравнения
для магнитного поля постоянного тока. Это есть предел кваза-
стационарного поля.
Эффективная глубина проникновения квазистационарного по-
ля в проводник получается из формул для электромагнитной
волны как расстояние, на котором амплитуда «волны» с чисто
мнимой е' уменьшается в е раз:
сох —|/2лосо {о Юм”1.см"1] / [МГц]}1/- V ’
Эта величина называется толщиной скин-слоя. В хороших про-
водниках переменный ток течет только в поверхностном
(«скин»-) слое. Например, у меди о = 6 • 105 Ом-1 • см-1 и при
/ = 10 МГц 6 = 2 • 10“3 см. Однако рассматриваемый предельный
случай осуществляется не только в металлах, но и в достаточно
сильно ионизованной плазме в ВЧ диапазоне полей (§ 3 гл. 13).
§ 6. Полное отражение электромагнитной волны от плазмы
6.1. Непоглощающая среда с отрицательной диэлектрической
проницаемостью. Пусть в среде е < 0, а проводимость о, если и
не равна нулю, то столь мала, что выполняется условие
4зта/со 1 еI < 1. По формулам (5.34) в такой среде zz ~ 0, х ~ Ук;.
Как и в случае чисто мнимой s', электромагнитная волна в та-1
кую среду не проникает, хотя и по другой причине. Фазовая
скорость и длина волны стремятся к бесконечности при а -> 0,
поле осциллирует только во времени и экспоненциально умень-
шается по амплитуде при углублении в среду. Однако энергия
поля не диссипируется, в отличие от случая хорошего провод-
ника, когда амплитуда поля от границы уменьшается из-за силь-
109
ного поглощения энергии. Глубина проникновения в среду с
8 < 0, о ~ 0 не зависит от о и равна Х0/]Л|е|. Рассмотренная
ситуация соответствует полному отражению электромагнитной:
волны. Она нередко реализуется в «бесстолкновительной» плаз-
ме, когда Пусть, например, частота волны / = 3 ГГЦ,
Хо = 10 см, /> = 0,1 торр (7V = 3.3-1015 см"3). При слабой иони-
зации, когда электроны сталкиваются только с атомами, vm
~ 3 - 108 с-1 и тД/со2 ~ 10~4. Дело, стало быть, только за тем,
чтобы плотность электронов была больше некоторой величины.
6.2. Критическая плотность электронов. Представим диэлек-
трическую проницаемость (5.24) для бесстолкновительной плаз-
мы в виде
е-1— со2/со2, со2 = (4ле2тге/т)1/2 = 5,65- 104тгУ2с-1. (5.40)
Она отрицательна, если частота волны со < сор или плотность
электронов больше критической величины
пе кр = т^^пе2 = 1,24 • 104{/ [МГц] )2 =
= 1,11 • 1013{Мсм]}-2 см’3. (5.41)
Для рассмотренного примера neKp = 1,1 • Ю11 см-3. В область с
большей плотностью электронов волна Хо = 10 см проникнуть
не может, она испытывает от нее полное отражение. Если пе на-
растает в плазме в направлении оси х и в ту же сторону по
плазме распространяется электромагнитная волна, то она, грубо
говоря, дойдет до места, где ne = neWp, а оттуда отразится п пой-
дет назад. При этом в случае плоской симметрии имеет силу за-
кон отражения геометрической оптики, согласно которому угол
падения равен углу отражения (рис. 5.1).
х
Рис 5.1 Схема отражения электромагнитной вол-
ны от плазмы Нарастание плотности электронов
снизу вверх передается сгущением горизонталь-
ных линии: луч поворачивает назад приблизи-
тельно в гом месте, где плотность электронов
равна критической для частоты волны
Этот эффект имеет огромное практическое значение, он ши-
роко используется в физическом эксперименте и технике. Он
положен в основу одного из весьма действенных методов диаг-
ностики плазмы, лабораторной и ионосферной. Посылая в плаз-
му сигналы разной частоты, регистрируют, какие частоты через
нее проходят (со>соР), а какие нет (со<(оР). По частоте «от-
сечки» со = соР находят пе с помощью (5.40). Лабораторную
плазму невысокого давления («бесстолкновительную») с п€ ~
— 1011 —1015 см“3 можно диагносцировать СВЧ излучением с
Хо~ 10—0,1 см. Эффект лежит и в основе техники дальней ра-
диосвязи в средневолновом радиодиапазоне. В ионосфере пе ~
110
~ 104—105 см-3 и волны с частотами /<1 МГц и длинами
больше нескольких сотен метров от нее отражаются. Отражаясь
и от Земли, они зигзагообразным путем могут огибать Землю,
проникая в области, лежащие далеко за пределами прямой ви-
димости.
§ 7. Плазменные колебания и волны
Г
Ах
х
7.1. Плазменная частота. Как отмечалось в п. 5.2, уравнения
электродинамики допускают существование продольных воли
электрического поля при условии г =0. Колебания реализуются
в бесстолкновительной плазме на частоте определяемой фор-
мулой (5.40) (бесстолкновительной в смысле vm«cop). Частота
Юр, которая зависит только от плотности электронов, называется
плазменной или лэнгмюровской. Опа пред-
ставляет собой частоту собственных колеба?
ний электронов в плазме (Тонкс и Лэнг-
мтор, 1929). Действительно, вообразим пло-
ский слой однородной электронептральной
плазмы с плотностями электронов и поло-
жительных ионов пе = п+. Допустим, что в
начальный момент под действием какой-то
внешней импульсной силы все электроны
оказались сдвинутыми вправо относительно
ионов (рис. 5.2). Вследствие разделения
зарядов немедленно возникает кулоновская
сила их притяжения, которая стремится
вернуть заряды «на место». Цо будучи
разогнанными этой силой, электроны «проскакивают» положе-
ние равновесия п смещаются относительно ионов влево, и т. д.
Возникают собственные колебания электронного газа как целого
относительно ионов, которые с большой степенью точности
можно считать неподвижными.
Частоту колебаний легко вычислить с помощью схемы
рис. 5.2. Если Дх—смещение электронов из положения равно-
весия, то плотность поверхностного заряда на границах слоя
равна епекх, а напряженность электростатического поля полярп--
зацип Е = 4пепе\х. Возвращающая сила пропорциональна сме-
щению, следовательно, уравнение движения электрона
тАт = — еЕ = — 4ле2пеАт, Дх + ю^Дх = 0,
Рис. 5.2. Схема, пояс-
няющая возникнове-
ние плазменных ко-
лебаний и вывод
формулы для плаз-
менной частоты
описывает гармонические колебания с частотой юР по (5.40).
Плазменная частота, дебаевский радиус и тепловая скорость
электронов связаны соотношением
/ 4ле2пе кТе \1у2
с*) y) d — I I
\ m <ктсе2пе>)
- 0,62Ъ.
(5.42)
Скорость направленного движения электронов, совершающих ко-
111'
лебапия, хаотизируется с частотой столкновений vm, которая ха-
рактеризует, следовательно, скорость затухания свободных коле*
баний. Говорить о колебаниях имеет смысл, если vm < сор, или
пе > 2 • 109 (р торр)2 см”3. Плазменные колебания были обнару-
жены на опыте Пеннингом (1926 г.) и с тех пор много изу-
чались.
7.2. Волны. Колебания электронов могут приводить к волнам
поля и объемного заряда. Рассмотренные в п. 6.3 колебания
электронного газа как целого соответствуют бесконечной длине
волны. Рассмотрим волны малой амплитуды на основе гидроди-
намического приближения (§ 8 гл. 3). В нёвозмущенном состоя-
нии Е = 0, ие = 0, пе == п± = const. Считая малыми возмущения
Е, ve, 8п = пе — п+, 5Те по отношению к невозмущенной темпера-
туре Те, линеаризуем уравнения (3.49), (3.50), (3.22) с r = ?2evt,
(3.33). Опустим в них также все члены, связанные со столкно-
вениями электронов. Положим Е, ve, Ьп, 8Те ~ ехр(£со£ — iKx).
Подставив это в линеаризованные уравнения, в результате ре-
шения найдем дисперсионное соотношение, которое связывает ча-
стоту колебаний со с абсолютным значением волнового вектора К.
Здесь, однако, следует принять во внимание одну тонкость.
В отсутствие всяких столкновений при сжатии (разрежении)
электронного газа в продольной волне, движущейся в направле-
нии х, работа сил давления затрачивается на адиабатическое
изменение только яг-составляющей тепловой энергии электронно-
го газа (работа поля — величина второго порядка малости). По-
перечные у-, ^-составляющие скорости хаотического движения
изменений не претерпевают. Поэтому возмущение тепловой энер-
гии составляет не (3/2)/сб7\, как обычно, а только (1/2)
(К вариации давления ре = пекТе это не относится.) Учитывая
указанное обстоятельство при дифференцировании, найдем
со2 = со* + ЗК2 (кТе1т). (5.43)
Без его учета получили бы то же самое только без тройки, кото-
рая автоматически получается из решения на основе кинетиче-
ского уравнения. В пределе длинных волн Х — 2л//£->оо ИЛц
«холодных» электронов (7\->0) со шР, а фазовая скорость
волны Уф = (о/К оо.
7.3. Затухание Ландау. Плазменные волны могут затухать и
в отсутствие всяких столкновений (Ландау, 1946). Эффект свя-
зан с существованием распределения электронов по скоростям
и, следовательно, выходит за рамки гидродинамического прибли-
жения. Дело в том, что электроны, имеющие продольные ско-
рости vx < Уф, увлекаются волной, а имеющие скорость vx > уф —
удерживаются ею. Когда уф > у, что согласно (5.43), (5.42)
справедливо, если X > d, большинство электронов увлекается п
ускоряется, а волна теряет энергию.
112
§ 8. Обмен квантами между полем излучения
и свободными электронами в газе
8.1. Классический и квантовый подходы к проблеме взаимо-
действия. Все предыдущее рассмотрение взаимодействия элек-
тронов с электромагнитным излучением было сделано на основе
чисто классической электродинамики. Использование классиче-
ских представлений о механической работе, совершаемой силой
поля над движущимся зарядом, является вполне оправданным,
пока порции энергии, которыми обмениваются поле п электроны
в элементарных актах, намного превышают энергию кванта излу-
чения Лю. Скажем, кванты СВЧ излучения с Л =10 см, равные
Лю = 1,24 • 10~5 эВ, столь малы по сравнению с передачей энер-
гии электрону, рассчитанной на одно столкновение, Аее по фор-
муле (5.10), что сомнения в каком-либо несовершенстве класси-
ки в данном случае не могут и возникнуть. Более того, при ре-
альных значениях полей неравенство > Лео выполняется да-
же в далеком инфракрасном диапазоне частот, которому принад-
лежит излучение используемого в газоразрядном эксперименте
и на практике СОг-лазера (А, = 10,6 мкм, Лю =0,117 эВ).
Однако в районе видимой части оптического диапазона для
излучения неодимового (А =1,06 мкм, Лю = 1,17 эВ) и рубино-
вого (Л = 6943 А = 0,694 мкм, Лео = 1,78 эВ) лазеров соотноше-
ния между Ае£ и Лю становятся иными. Так, в сфокусированном:
гигантском импульсе рубинового лазера, который вызывает про-
бой в газах, электрическое поле световой волны имеет порядок
107 В/см. При амплитуде Ео = 107 В/см величина АеЕ = 0,024 эВ,
вычисленная по (5.10), в 74 раза меньше Лю (при вычислении
учтено, что ю2 v2m ). Но, согласно общим положениям квантовой
физики, минимальная энергия, которая может быть передана от
излучения веществу (и обратно), составляет Лю. Значит, воз-
можность использования выводов классической теории примени-
тельно к оптическому диапазону полей становится по меньшей
мере проблематичной. Во всяком случае, любая попытка обосно-
вать такую возможность, которая, как мы увидим в § 10, в не-
которых случаях все же имеется, требует рассмотрения эффектов
с квантовых позиций.
Основным механизмом нарастания энергии свободного элек-
трона в поле светового излучения является поглощение квантов
при столкновениях электрона с атомами (в сильноионизованной
плазме—с ионами). Как и в классической теории, столкновения
играют в этом отношении решающую роль. Изолированный элек-
трон не может поглощать кванты энергии — это несовместимо с
законом сохранения импульса. В самом деле, приобретая энер-
гию Лю, электрон получает и импульс порядка где v — его
скорость. Между тем импульс фотона ticalc чрезвычайно мал.
Следовательно, в акте его поглощения непременно должна уча-
ствовать еще одна частица, которая воспринимала бы импульс
отдачи.
8 Ю. П. Райзер
ИЗ
Наряду с актами поглощения происходят и акты вынужден-
ного {стимулированного) испускания квантов, также при столк-
новениях электрона с атомом, ионом. Согласно общим положе-
ниям квантовой теории, вынужденное излучение имеет точно
такие же характеристики, что и вынуждающее, т. е. испускается
квант тех же частоты, направления, поляризации, что и в поле
присутствующего в среде излучения внешнего источника. Разу-
меется, электрон, оставаясь свободным, не может испускать
квант энергии Йсо, превышающий его кинетическую энергию
8==mz;?/2, поэтому вынужденное испускание при столкновениях
с атомами возможно только при условии, что кванты внешнего
ПОЛЯ ЙО) < £.
И те и другие акты — поглощения квантов, вынужденного
испускания — имеют случайный характер. Вероятности их про-
порциональны интенсивности света — плотности потока энергии
в световой волне. Результирующий эффект, который проявляется
в нарастании энергии электрона и ослаблении светового потока,
определяется разностью между средними скоростями поглощения
и вынужденного испускания квантов, приобретения и отдачи
энергии электроном при столкновениях. В качественном отно-
шении ситуация, как видим, имеет большое сходство с тем, что
происходит в условиях справедливости классики, когда Аее ~
~ Де+- 1Ле_| (п. 2.5).
8.2. Интенсивность излучения, коэффициенты поглощения,
вынужденного и самопроизвольного испускания. Введем эти ос-
новные понятия, с помощью которых количественно описывают-
ся эффекты взаимодействия излучения с веществом. Пусть
Ц (Й) do dQ— энергия излучения в спектральном интервале от
со до со + dco и малом телесном угле dQ около направления рас-
пространения Й, проходящего в 1 с через площадку 1 см2,
перпендикулярную направлению распространения. Величина
7® эрг/(с • см2 • Гц • ср) называется интенсивностью излучения.
Для плоской монохроматической волны интенсивность формаль-
но бесконечна, так как интервалы dco, dQ нулевые. Физический''
смысл имеет конечное произведение do dQ эрг/(с-см2), кото-
рое совпадает с плотностью потока энергии излучения S. В кван-
товых терминах величина F = 5/7? со с-1 • см~2 — плотность потока
фотднов.
Вероятности поглощения и вынужденного испускания кванта
Пропорциональны потоку фотонов (или интенсивности излуче-
ния) и вероятности столкновений электрона с атомом, ионом.
Последние, естественно, зависят от скорости электрона. Пусть
q(v)dv — число электронов в 1 см3 со скоростями от v до v + dv,
со
У ф (г) dv = пе*
о
Энергию излучения из интервала dco dQ, которая поглощается
114 ”
в 1 см3 в 1 с электронами указанных скоростей, можно записать
в виде
Ц cZco dQ/Vq? (у) dva^ (v) эрг/(с • см3), (5.44)
где коэффициент пропорциональности а^и) представляет собой
коэффициент истинного поглощения света, рассчитанный на один
электрон и один атом. Совершенно аналогично вынужденное
испускание квантов определяется выражением
do cZQJVcp (v')dv'ba (v') эрг/(с • см3), (5.45)
где &co(z/) — коэффициент вынужденного испускания квантов Лю,
также из расчета на один электрон и один атом. Для процессов,
обратных друг другу, скорости и' и v свйзаны законом сохране-
ния энергии:
mr'2/2 = mr2/2 Ц-Йо, v'dv' = vdv: (5.46)
Электрон, обладающий энергией 8 > 7гсо, может испускать
кванты Йо и самопроизвольно (спонтанно), вне всякой связи с
присутствием внешнего излучения. Это тоже происходит при
столкновениях с тяжелыми частицами (§ 9). Такое излучение
называется тормозным потому, что электрон «тормозится» при
столкновении с частицей, теряя скорость и часть кинетической
энергии, которая расходуется на излучение. Обозначил!
dQa [эрг/с] количество энергии частоты со, которое излучается
одним электроном скорости v' в 1 с в спектральный интервал de>
во всех направлениях. В квантовых терминах dQJlud с-1 — ве-
роятность самопроизвольного испускания квантов с энергиями
от Йо до Tzco + dTzco. Вероятность удобно характеризовать сечени-
ем испускания do^ (v') = (do^/dei) do при помощи обычного опре-
деления:
dQ«> = ТшНи' daa(vf) эрг/с. (3.47)
Испускание в различных направлениях в среднем равнове-
роятно, так что в интервал dQ попадает доля dQ/4n от dQ^. Та-
ким образом, в 1 см3 в 1 с электронами со скоростями от v' до
v' + dv' в интервал do dQ. самопроизвольно излучается энергия
dQuty (и') dv' = ti^Nv' do^(v')^(v') dv' эрг/(с-см3). (5.48)
8.3. Принцип детального равновесия и соотношения между
коэффициентами. В условиях термодинамического равновесия
испускание света, самопроизвольное плюс вынужденное, компен-
сируется поглощением, а интенсивность излучения описывается
функцией Планка:
у- й, (О 1 /г/
wpaBH 4Л”2 e^/kT_f
Приравнивая сумму (5.48) и (5.45) выражению (5.44), подстав-
ляя максвелловское распределение <р (v) со v2e~mv^2kT, ПЛанков-
8* 115
ское (5.49) и принимая во внимание (5.46), получим соотноше-
ние между тремя коэффициентами b®, dojdti):
,2^0^') _ W2 va4> (») — v'ba (И
V da ~ e^!hT_i
Оно должно выполняться при любой температуре. Но поскольку
коэффициенты, характеризующие элементарные акты, от темпе-
ратуры не зависят, последняя должна выпасть из равенства. От-
сюда следует еще одно соотношение
и ( р W2
(у') = -?-ае)(у)={ а<0 (V), (5.50)
которое называется именем Эйнштейна*).
Коэффициент вынужденного излучения связан с сечением
самопроизвольного излучения равенством
<551)
Полное испускание складывается из спонтанного (5.48) и вы-
нужденного (5.45) с учетом (5.51):
n^Nv —-— ср (у ) dv асо -г- 1 ---^-1^ эрг/(с • см3). (5.52)
Спонтанная составляющая здесь соответствует единице в скоб-
ках, вынужденная — второму слагаемому, которое имеет физи-
ческий смысл числа фотонов определенной частоты со, на-
правления Q и поляризации в одной фазовой ячейке. Скорости
вынужденного и самопроизвольного эффектов относятся как
: 1. Если интенсивность излучения равновесна, это отношение
равно (e^kT—I)”1. Малые кванты (Лео < кТ) излучаются в
основном вынужденным путем, : 1 « кТ/Лео > 1, большие кван-
ты (Лео > кТ)— самопроизвольно, 1 ж е~*ы/кТ 1.
8.4. Результирующее поглощение световой волны. При вы-
нужденном испускании, которое, как и поглощение, пропорцио-
нально интенсивности, излучаются в точности такие же фотоны,
как и те, что присутствуют в световом луче. Различить их не-
возможно. Если, скажем, несколько квантов вынужденно излу-
чилось и столько же одновременно поглотилось, то нельзя при-
думать эксперимент, который бы показал, происходило это или
нет. Реально проявляется только разница между истинным по-
глощением и вынужденным испусканием.
Результирующий квантовый коэффициент поглощения света
свободными электронами, которым определяется ослабление по-
*) Еще задолго до создания квантовой механики, которая дает обосно-
вание существованию вынужденного излучения, Эйнштейн постулировал
такую возможность и с помощью принципа детального равновесия вывел
формулу Планка, получив связь коэффициентов (5.50).
116
тока излучения
Нсокв :
где
, описываемое законом (5.37), равен
”оо оо
= N J ф (y)dv (v) — J cp(zZ) dv'b^ (у') ,
-О
(5.53)
rmin
— наименьшая скорость, обладая которой электрон может излу-
чить квант Йсо. Если спектр электронов равновесный, т. е. макс-
велловский с температурой 7\, то
Нсокв — Рчоист(1 # *), Р'СОИСТ — Nne (5.54)
где Цоист — коэффициент истинного поглощения на единице дли-
ны, усредненный по Максвеллу. Вынужденное испускание при
этом уменьшает поглощение универсальным (не зависящим от
механизма взаимодействия) множителем 1 — е~Для боль-
ших квантов (Tzco > кТе) эффект вынужденного испускания
экспоненциально мал. Вынужденное испускание малых квантов
(Тио < кТе) почти полностью компенсирует истинное поглощение,
так что результирующее поглощение составляет лишь долю
Тм^кТе^ 1 от истинного.
8.5. Приобретение энергии электроном. В поле монохроматиче-
ской электромагнитной волны частоты со электрон, обладающий
энергией е — mv2/2 > Tzco, в 1 с приобретает энергию
(dz/dt)E = SN (и) - М^) ], (5.55)
которая пропорциональна плотности потока энергии 5 в волне
и определяется разностью между скоростями истинного поглоще-
ния п вынужденного испускания квантов.
Такова простейшая схема описания обмена энергией между
излучением и свободными электронами в газе, когда их взаимо-
действие имеет квантовый характер. Дело теперь за явными вы-
ражениями для коэффициентов поглощения и испускания.
§ 9. Полуклассический способ нахождения
квантовых коэффициентов
Нахождение коэффициентов П(О, &(0, doa/dcd требует рассмотре-
ния конкретного механизма взаимодействия, причем достаточно
вычислить только один из них. Строго говоря, это должно быть
сделано квантово-механическими методами. Подобные расчеты
сложны и мало наглядны. Возможен, однако, хотя и не слишком
ciporim, но зато простой и наглядный полуклассический подход
к этой задаче, который дает вполне удовлетворительные результа-
ты. Смысл его состоит в том, чтобы вычислить скорость тормоз-
ного излучения dQa по классической электродинамике, а потом
с определенной оговоркой перейти к сечению самопроизвольного
испускания кванта по связующей формуле (5.47). Коэффициенты
117
bw, аы после этого немедленно находятся по формулам (5.50),
(5.51).
Мы здесь могли бы поступить даже еще проще, поскольку пу-
тем рассмотрения механизма взаимодействия выше уже был най-
ден классический коэффициент поглощения — формула (5.38).
Тормозное излучение dQ^ можно вычислить и при помощи прин-
ципа детального равновесия, но только, в отличие от п. 8.3, сфор-
мулированного на чисто классической основе. Однако ввиду
принципиальной важности вопроса мы найдем dQ^ независимым
путем, а принцип детального равновесия используем для дру-
гой цели.
9.1. Тормозное излучение. Согласно выводам классической
электродинамики, излучение системы зарядов определяется вто-
рой производной ее дипольного момента d. При рассеянии элек-
трона «неподвижной» тяжелой частицей, атомом, ионом d =
== — er = — ew, где w(£) — ускорение электрона*). Bic ускорен-
но движущийся электрон излучает энергию 2e2w2/3c3. За все вре-
мя взаимодействия с рассеивающим центром электрон излучает
энергию
оо
= J [w(Z)]2 dt,
—оо
Если нас интересует спектральный состав излучения, нужно
подставить сюда разложение функции w(t) в интеграл Фурье и
произвести интегрирование по времени. В результате получим %
в виде интеграла по частотам. Подынтегральное выражение и
даст количество энергии, излученное в частотный интервал от
со до со + dco:
оо
dSa = 4r-^|w<o |2 dm, wo = Д f w(i) dt,
a c ZJL J ' '
— oo
где Wo — фурье-компонента вектора ускорения.
Будем интересоваться излучением частот со > vm. Тогда эффек-
ты последовательных относительно редких столкновений можно
считать независимыми. Имея в виду, что сам акт рассеяния про-
исходит очень быстро по сравнению с периодом осцилляций поля,
представим w(f) в виде дельта-функции времени: w(t) = Av6 (t) r
где Av — изменение вектора скорости при рассеянии (ср. с урав-
нением (3.1))**). Тогда ?гм = Ар/2л и
? 2
^ = з4т(^в- (5.56)
О J I Q
*) Электрон-электронные столкновения к излучению не приводят:
d = —eri — ег2 — —(e/m) (znVi + znv2) = 0
в силу сохранения импульса т\\ -f- mv2 = const (ср. с п. 2.6).
**) Время взаимодействия порядка 10~16 с, тогда как даже для видимо-
го света 2л/(о ~ 10-15 с.
118
Чтобы найти энергию, которую электрон излучает за 1 с в спек-
тральный интервал cZco во всех направлениях, нужно просуммиро-
вать d&w по всем столкновениям, происходящим в течение 1 с,
т. е. усреднить (5.56) по всевозможным углам рассеяния 0 и ум-
ножить на частоту столкновений v<>
На самом деле классическая теория излучения таит в себе
глубокое и неразрешимое в ее рамках противоречие, которое в
данном случае проявляется в том, что полное излучение во всем
спектре, т. е. интеграл от d%><* по о от 0 до °°, оказывается бес-
конечным. Этот результат, который в истории физики получил
название ультрафиолетовой катастрофы, в свое время явился
одним из серьезных побуждений к пересмотру классической фи-
зики. Противоречие устраняется квантовой теорией, которая ут-
верждает, что свободный электрон, имеющий скорость v, не мо-
жет излучать кванты, большие его энергии, т. е. частоты со >
Ютах 1TIV /2^2.
Если учесть это обстоятельство и не применять формулу (5.56)
к частотам ю > ютах, ею можно с успехом пользоваться, о чем
Свидетельствует сопоставление с результатом квантово-механиче-
ского расчета. Интеграл от d<S\ по частотам следует ограничить
верхним пределом ютах, и тогда получается правильное значение
полного излучения во всем спектре. Излучаемая энергия оказы-
вается малой не только по сравнению с энергией электрона, но
даже по сравнению с небольшой упругой потерей энергии при
рассеянии. Поэтому при усреднении (Av)2 абсолютное значение
скорости v можно считать неизменным, что дает <(Av)2> =
=• 2г>2(1 — cos 0). Помня, что vc(l — cos 0) = (п. 2.2 гл. 2), по-
лучим*) *
dQ^ = -------dco эрг/с, dQa = 0 При со > (5.57)
Q О - ' - ZfL '
9.2. Закон Кирхгофа. Такое название носит принцип деталь-
ного равновесия для излучения в классической физике. В услови-
ях термодинамического равновесия тормозное излучение компен-
сируется поглощением. В классике существует единый механизм
поглощения электромагнитной волны свободными электронами,
описываемый коэффициентом р^кл по формуле (5.38). Волна по-
глощается не отдельными электронами, как кванты, а электрон-
ным газом в целом, так что выражение для цокл, в которое входит
величина vm(v), следует усреднить по спектру электронов. Зна-
чит, с поглощением следует сопоставлять тормозное излучение,
также усредненное по скоростям электронов. В условиях равно-
весия распределение — максвелловское и
<ДОО> пе = /аравн d(S) cZQ <цакл> эрг/(с • см3), (5.58)
*) В случае со~ vm результаты последовательных столкновений не яв-
ляются независимыми и в формуле появляется знакомый нам множитель
<02/(®2 + Vm).
119
где /®равн — интенсивность равновесного излучения, но не план-
ковская (5.49), а та, которая следует из классической физики
и дается формулой Рэлея — Джинса: /®равн = ^kTlin^c2 (к ней
сводится (5.49) при Если подставим в (5.58) выраже-
ния (5.57) и (5.38) с co2»v™, убедимся в том, что при постоян-
ной часто’те столкновений vw(z;) = const равенство (5.58) действи-
тельно выполняется (</?w2> = ЗкТ). Ограничение vm(v) = const не
случайно: выражения (5.38) для |1®кл, (5.23), (5.24) для о®. е®
являются приближенными. Они совпадают со строгими соотно-
шениями, вытекающими из решения кинетического уравнения,,
только при условии Vm = const (п. 6.1 гл. 7).
9.3. Квантовые коэффициенты. Пользуясь выражением (5 57)
для dQa, по формуле (5.47) найдем сечение самопроизвольного»
тормозного излучения квантов электронами скорости и:
doo = 4--^— Qmda), (5.59)
c a co
Оно пропорционально транспортному сечению рассеяния электро-
на. Это и естественно, ведь квант излучается только при столкно-
вении электрона с тяжелой частицей. По формулам (5.51), (5 50)
найдем коэффициенты Ьа, аа. Выпишем только один из них —
коэффициент истинного поглощения (на один электрон и один
атом) при со2 v^:
2 8 + Й,СО 8 + fcCO Gm (8 + kco)
3 Ь °т (8) ’ (5.60)
Яюкл = РюклДУХ = 4ле2ш7П (v)/mca)2.
Мы намеренно так сгруппировали множители, чтобы выделить
классический коэффициент. На рис. 5.3 представлены результаты
0(0 (0 — 0(ОКЛ
Рис. 5.3. Коэффициенты ис-
тинного поглощения а® и
вынужденного испускания
6® квантов ha — 1,78 эВ,
рассчитанные на один
электрон и один атом Аг и
Не [25]
вычисления а® и &® для атомов аргона и гелия и частоты руби-
нового лазера в диапазоне энергий электронов, отвечающем усло-
виям оптического пробоя этих газов.
120
§ 10. Фактические границы применимости
классического подхода к эффектам взаимодействия
10.1. Предельный переход от квантовой теории к классической.
Привлекательные своей простотой и наглядностью формулы клас-
сической теории открывают больше возможностей для аналити-
ческого исследования закономерностей явлений, чем более слож-
ные формулы и зачастую нерешаемые уравнения квантовой тео-
рии. Поэтому важно знать истинные пределы применимости
классики с тем, чтобы, с одной стороны, не выйти за эти грани-
цы, а с другой — не обмануться, когда на первый взгляд пред-
ставляется, будто обращение к квантовому описанию является
неизбежным. Как мы сейчас увидим, в вопросе об обмене энергией
между излучением и свободными электронами в слабоионизован-
ном газе легко совершить перестраховку, отвергнув возможность
использования классических выражений.
В соответствии с квантовой трактовкой эффектов взаимодей-
ствия, поглощение световой волны свободными электронами в
ионизованном газе описывается результирующим коэффициентом
поглощения (5.53), а приобретение энергии электроном в поле
волны — формулой (5.55), где квантовые коэффициенты аы и Ьа
определяются приближенными формулами (5.60), (5.50). Перей-
дем к классическому пределу 7/(0 -> 0, для чего проведем во всех
формулах разложение по малому параметру йсо/g < 1. Получим,
что с точностью до малых порядка Й(о/е предельные коэффици-
енты истинного поглощения и вынужденного испускания одина-
ковы и равны
^о(е) ~ ~ (2е/ЗЙ(о)яЫКл 00 со-3.
Такая зависимость характерна для квантовых тормозных процес-
сов*). Разность коэффициентов в пределе составляет относитель-
но малую величину:
(е) da,. 1
-от- + = а<окл ~ W-2,
в точности равную классическому коэффициенту. Поскольку S ==
— скорость приобретения энергии (5.55) принимает клас-
сическое значение Ae^vw (см. (5.10), (5.11)); нужно только иметь
2 9 ,
в виду, что мы с самого начала повсюду оторасывали vm в от +
+ V^.
Предельное значение квантового коэффициента результирую-
щего поглощения получается равным
1 • ^ле2 С / \ з d \ л
- — -----2 vm(v) v*—\-jr\dv.
(о-»о 3mcco J av \ v )
о
*) Процесс поглощения излучения, обратный тормозному испусканию,
часто для краткости называют тормозным поглощением, хотя буквально та-
кое словосочетание неприемлемо: при поглощении электрон не тормозится,
а ускоряется.
121
В случае постоянной частоты столкновений vm = const интегри-
рование по частям с ср (°°) = 0 дает классическое значение р^кл»
которое как раз и справедливо при условии
ут = const*).
10.2. Критерий применимости формул классической теории.
Как показали чисто формальные вычисления предыдущего раз-
дела, квантовые формулы для рюкв и (de/dt)Е превратились в клас-
сические при условии 7zcd е. Значит, для справедливости клас-
сических формул вовсе не требуется, чтобы значение кванта было
мало по сравнению с энергией Дее, которая в среднем переда-
ется электрону при столкновении (энергией колебаний электро-
на). Не обязательно, чтобы квант был меньше и тех порций
энергий |Де+1, которыми электрон на самом деле обменивается
с полем в индивидуальных столкновениях с атомами. Достаточ-
но, чтобы значение кванта было мало лишь по сравнению с самой
энергией электрона е, а это условие значительно мягче, ибо
Е > I Де±1 > Деб ^екоч.
Однако сделанное заключение аргументируется доводами
лишь математического, но не физического характера, и заранее
вряд ли можно было бы на нем настаивать. Так уж получается,
что и при квантовом процессе результирующая скорость нараста-
ния энергии электрона совпадает с классической. Физическая
сущность процесса, безусловно, остается квантовой: в каждом
индивидуальном акте энергия электрона изменяется в ту или
другую сторону на 7/со **).
10.3. Статистическая трактовка классического выражения в
сугубо квантовом случае. Когда ДеЕ<Л(о, равенству (dzldt)E —
= Де£¥?п можно придать статистическую интерпретацию, как
это часто бывает при квантовом толковании результатов класси-
ческой физики. Поясним это на примере, который приводился
в п. 8.1. В поле излучения рубинового лазера при Eq = 107 В/см2,
чему соответствует плотность потока энергии 5 = 5- 1010 Вт/см2,
электрон при столкновении приобретает в среднем энергию Дег =
= 0,024 эВ, которая в 74 раза меньше энергии кванта //со =
= 1,78 эВ. Если энергия электрона е ~ 10 эВ, как это получается
при оптическом пробое газов, формальное условие применимости
классических формул е > Тгсо с какой-то степенью приближения
можно считать выполненным. «Противоречие» Деб<^(о разре-
шается так: в действительности электрон испытывает 73 столкно-
вения, не отбирая от поля никакой энергии, а на 74-й раз полу-
чает сразу полную порцию йсо = 74Дее.
*) Выписанное предельное интегральное выражение является более
общим Именно оно получается из рассмотрения кинетического уравнения.
**) Предельного перехода от истинного поглощения и вынужденного
испускания к соответствующим классическим величинам Де+, Де_ нет. Из-
ложенная квантовая теория оперирует только одноквантовыми процесса-
ми, тогда как классические порции энергии |Ае±| включают в себя много
квантов.
122
Оптический пробой газов (во всяком случае, излучениями
неодимового и рубинового лазеров) принадлежит к числу тех
квантовых процессов, где допустимо пользоваться классикой, ибо
характерные энергии электронов заметно больше 7zco. В гл. 6 мы
познакомимся с другим случаем. При рассмотрении теплового
излучения, поглощения света и лучистого теплообмена в низко-
температурной плазме классика абсолютно неприменима, так как
основную роль играют кванты энергии 7г со порядка нескольких
кТе ~ 1 эВ. Роль вынужденного излучения при этом экспоненци-
ально мала, и фактический, квантовый, коэффициент поглощения
Цфкв ~ (о-3 имеет существенно иную частотную зависимость, чем
классический Цо)КЛ ~ ю-2.
Глав а 6. ИЗЛУЧЕНИЕ И ПОГЛОЩЕНИЕ СВЕТА ПЛАЗМОЙ
§ 1. Типы радиационных переходов
энергетических
уровнен и перехо-
дов электрона в
поле положитель-
ного иона
Свойство разрядной плазмы светиться, быть источником излу-
чений различных диапазонов с давних пор широко используется
в физическом эксперименте, в спектроскопии, в осветительных
приборах и др. Потери энергии плотной низкотемпературной плаз-
мы на излучение нередко влияют на ее энергетический баланс,
температуру, а следовательно, и на протекание
разрядного процесса. Все это ставит вопрос
об оптических свойствах плазмы в ряд важ-
нейших для физики газового разряда.
Световые кванты появляются и исчезают
при радиационных переходах электррнов из од-
них энергетических состояний в другие, и клас-
сифицировать механизмы излучения и погло-
щения удобнее всего, перебирая возможные
варианты переходов. Плотная равновесная
плазма является более мощным излучателем,
чем слабоионизованная, и в отличие от послед-
ней взаимодействие электронов с ионами игра-
ет в ней очень большую роль, в том числе и в
отношении излучения. Что касается электрон-
электронных столкновений, то, как объясня-
лось в сноске на с. 118, ни излучения, ни по-
глощения света при этом не происходит.
Рассмотрим систему, состоящую из элек-
трона и «атомного остатка» или положитель-
ного иона. На рис. 6.1 изображена схе-
ма энергетических состояний (уровней) электрона. Энергия от-
считывается от границы непрерывного спектра, разделяющей
свободные п связанные состояния. Уровни связанных состояний
к границе сгущаются. Нижний соответствует основному состоя-
нию атома. Стрелками показаны возможные типы переходов:
свободно-свободные, связанно-свободные, связанно-связанные. Пе-
123
реходы сверху вниз сопровождаются излучением кванта энергии
Й(о, равной разности между энергиями верхнего и нижнего со-
стояний; переходы снизу вверх — поглощением.
Свободно-свободные переходы представляют собой тормозное
излучение при кулоновских столкновениях электронов с ионами
и обратные процессы тормозного поглощения. О природе тормоз-
ных процессов говорилось в § 9 гл. 5, правда, в применении к
столкновениям электронов с нейтральными атомами, но существа
дела это не меняет. Связанно-свободные переходы — это процессы
фотоионизации и фотозахвата. О них шла речь в п. 2.1, 3.3 гл. 4
как о механизмах рождения и гибели электронов. Свободно-сво-
бодные и связанно-свободные переходы дают непрерывные спект-
ры, или континуум, поскольку либо начальное, либо конечное,
либо оба этих состояния электрона лежат в непрерывном энерге-
тическом спектре. Связанно-связанные переходы электрона между
дискретными уровнями в атоме приводят к излучению и погло-
щению спектральных линий. Разновидностью линейчатых спект-
ров являются полосатые спектры молекул, которые также обяза-
ны своим происхождением связанно-связанным переходам. На-
сыщенность молекулярных спектров линиями, которые внутри
полосы располагаются очень тесно, обусловлена сложностью си-
стемы энергетических уровней молекулы. Каждому электронному
состоянию соответствует множество колебательных и вращатель-
ных, и возможно много вариантов переходов между ними.
Свободно-свободные и связанно-свободные переходы происхо-
дят и при взаимодействии электронов с нейтральными атомами.
Тормозное поглощение такого рода является главным механиз-
мом диссипации энергии электромагнитных волн и внешних из-
лучений в слабоионизованиом газе (§9, 10 гл. 5). Тормозное
излучение в оптическом диапазоне в слабоионизованиом газе яв-
ляется крайне слабым из-за малости числа электронов.
О связанно-свободных переходах в поле нейтральных частиц
также упоминалось в § 4 гл. 4 как о возможных механизмах
образования и разрушения отрицательных ионов {фотоприлипа-
ние, фотоотрыв). В качестве механизмов излучения и поглощения
света роль этих процессов в газоразрядной плазме не очень зна-
чительна (в отличие от звездных фотосфер). Необходимые для
дальнейшего общие понятия теории излучения: интенсивности
излучения, вынужденного и спонтанного испускания, коэффици-
ента поглощения света, закона Кирхгофа, выражающего принцип
детального равновесия для излучения, и другие были введены
в § 8, 9 гл. 5.
§ 2. Тормозное излучение при столкновениях
электронов с ионами
В п. 9.1 гл. 5 рассматривалось тормозное излучение электрона
при столкновениях с атомами. На основе чисто классической
электродинамики в приближении мгновенности акта рассеяния
была вычислена спектральная излучательная способность элек-
124
трона dQa [эрг/с] (см. (5.57)). Потом при помощи определяюще-
го соотношения (5.47) был сделан переход от dQ(i) к сечению dow
испускания квантов энергии й(о в интервал da) (см. (5.59)).
Выражения (5.57), (5.59) для dQ&, do^ можно с успехом при-
менить и к случаю рассеяния электрона ионами. Следует лишь
заменить частоту vm и сечение бт столкновений с атомами на
величины, описывающие кулоновские столкновения с ионами:
^кул = тг+1Юкуч (и), окул (v) = л [2гкул (и) ]2,
где гкул(v) = Ze2lmv2— характерный радиус кулоновского взаимо-
действия электрона с ионом, заряд которого равен Ze*). Такой
простой подход приводит к величинам dQ^, <io0, всего в л/УЗ =
== 1,8 раз меньше тех, которые дает вычисление на основании
фактического закона ускорения электрона в поле иона. С учетом
уточняющего множителя л/УЗ для дифференциального сечения
тормозного излучения получим
В 1 см3 в 1 с в спектральный интервал Jco тормозным меха-
низмом излучается энергия
dJ соторм =
о° о
р Z п.п /
= j 1i(im+neq(v)vdvd(5M(y) = С——exp da), (6.2)
гППП
С = = i'08*10"8 эрг-смЗ-К172,’
где ф(к)йк — нормированная на единицу функция максвеллов-
ского распределения электронов, z?min = (2^о/т)1/2 — наименьшая
скорость, имея которую электрон может испускать квант энер-
гии 7zcd. Спектр тормозного излучения определяется множителем
ехр(—h,u)lkT). В основном излучаются кванты энергии порядка
кТ. Больших квантов с энергией Тгсо > кТ излучается мало: их
способны испускать только очень энергичные электроны, принад-
лежащие хвосту максвелловского распределения.
§ 3. Рекомбинационное излучение
3.1. Сечение фотозахвата. При радиационном захвате электро-
на скорости v в связанное состояние с отрицательной энергией
Еп излучается квант энергии
= Ш + mv2/2. (6.3)
Найдем сечение этого процесса оСп, применив следующий, не
слишком строгий, но оправдывающий себя прием. Справедли-
*) В этой главе при рассмотрении радиационных процессов мы будем
учитывать множитель Z, имея в виду, что все результаты применимы и к
многозарядным ионам.
125
вость выражения (6.1), если рассматривать его как дифференци-
альное сечение тормозного излучения, ограничивается макси-
мальным квантом 7z(0max = nw2!2, испуская который электрон еще
остается свободным. Распространим формулу (6.1) и на испу-
скание квантов большей энергии. Электрон в таких случаях оста-
ется с отрицательной энергией, т. е. оказывается в связанном
состоянии. Если превышение 1ш над Л(отах невелико, электрон за-
хватывается на верхние возбужденные уровни атома.
Но при фиксированной начальной энергии электрона е = mv2i2
испускаются кванты с дискретными значениями энергий (6.3),
тогда как d<K — это сечение испускания квантов в сплошной
спектральный интервал dco. Чтобы выйти из положения, восполь-
зуемся тем обстоятельством, что верхние уровни атома распола-
гаются очень близко друг к другу, и будем интересоваться сум-
марным сечением испускания квантов в малый, но конечный
интервал До около (о. Электрон попадает при этом на один из
Ап уровней, принадлежащих энергетическому интервалу ДЕ ~
= 7?До около Еп==8 —7z(o. Если ДЕ<|ЕП|, захваты на все эти
Ап уровней почти равновероятны. Следовательно,
dor d(T_. А р
Д(О = ОспАп, в СП = (6.4)
dco сп 1 сп do ЪЛп х 7
Будем рассматривать водородоподобные системы. Электрон в
такой системе движется в поле точечного заряда Ze, и для нее
Еп = ~I^Z2ln2, где п — главное квантовое число. Полагая AEfAn ~
~ \dEnldn\ — 2IHZ2/n3, замечая, что /Н = иге4/2Е2, и пользуясь
формулой (6.1), получим сечение захвата:
16 л е10/4 1 _2,110-22(/Hz)2 ,
зУК’ЛЛи’ e/icon3 СМ ‘ ( '
Суммирование по п с учетом (6.3) и усреднение по v и приводят
к оценочной формуле (4.14) для коэффициента фоторекомбипации.
Использованный для вывода осп прием может показаться не-
сколько авантюристическим. Но он имеет некие обоснования, свя-
занные, в частности, с квазиклассичностыо движения электрона
по орбитам с большими квантовыми числами п, и согласуется
с так называемым принципом спектроскопической устойчивости.
Замечательно, что крайне громоздкая формула, которая получа-
ется в результате прямого квантово-механического вычисления
сечения фотозахвата электрона кулоновским центром, в пределе
п > 1 в точности превращается в (6.5). Еще более поразителен
тот факт, что классическая в своей основе формула (6.5), кото-
рая выведена для больших квантовых чисел п, хорошо согласу-
ется с квантово-механическим результатом даже в случае захвата
на основной уровень п = 1. И этот факт не единичен: сплошь и
рядом простые и наглядные формулы излагаемой здесь полу-
классической теории излучения оказываются пригодными и в
126
«сугубо квантовых» условиях. В этом состоит одно из больших
достоинств этой теории.
3.2. Излучательная способность. В результате фотозахвата
электронов со скоростями от и до v + dv на n-i'i уровень атомов
в 1 см3 в 1 с излучается энергия
J(ап = Й(ом+?геогеп <р (у) v dv —
= CZ^e-^hTeXn(2-^'}d0), (6.6)
г1/2 \ п J кТп2 ' 7
где константа С дается формулой (6.2). Первое выражение в (6.6)
раскрыто путем подстановки максвелловской функции ср(р), нСп
по формуле (6.5) и замены v на (о по формуле (6.3); mvciv^
= 7Ыо).
Кванты определенной энергии 7г (о могут излучаться при за-
хвате электрона на самые различные уровни, только его энергия
должна иметь избранные значения, рег-
ламентируемые равенством (6.3). По-
этому, интересуясь излучательной спо-
собностью газа в данном спектральном
интервале, выражение (6.6) следует
просуммировать по всем тем уровням,
захват па которые может привести к из-
лучению кванта данной энергии. В из-
лучении квантов Тгсо > 12?! I могут участ-
вовать все уровни от п == 1 до °°. Излу-
чить же квант Тгсо < |2?il электрон может ^>ис- ^2. ^пектР рекомби-
г панионного излучения как
только при захвате на достаточно вы^о- сумма (штриховые кри-
кие уровни с п > лг*. Самый нижний вые)
пз них, п*-й, определяется условием
\Еп* | < Йсо < | Еп*-! |. Таким образом, в результате всех возмож-
ных фотозахватов в 1 см3 в 1 с в интервал йсо излучается энергия
оо
J сорек d(S) — d(j) 2 J wt‘ (6.7)
3.3. Усреднение спектральной функции. Спектр рекомбинаци-
онного излучения, который дается функцией (6.7), показан на
рис. 6.2. При повышении частоты, начиная от какого-то значения
(оп— \En\lti, число слагаемых в сумме сначала сохраняется и из-
лучательная способность падает благодаря множителю
ехр (—7г(о/йТ), который присутствует в каждом слагаемом ]^п. Как
только (о достигает значения (оп-ь в излучение включаются за-
хваты на п — 1-й уровень, к сумме добавляется еще одно слагае-
мое и /сорек испытывает скачок, тем больший, чем ниже уровень,
т. е. чем больше (о. Лишь после последнего скачка при со = соi
испускание уменьшается монотонно до самого конца.
В области относительно малых квантов энергии, т. е. п* > 1г
зубцы и впадины спектрального «частокола» чередуются столь
часто, что нет смысла «разрешать» такую сложную спектральную
127
функцию. Ее естественно усреднить, сгладить, что автоматически
получается, если заменить суммирование по п интегрированием:
-
2хп[^хп\ | хп I х Л 1ъ(И /р о\
е ~ \ е dxn~e —1, х = ^-у. (6.8)
п* о
Здесь, в соответствии с определением п*, положено, что хп* ж
\Еп*\/кТ х. Энергетический разрыв между вторым и первым
уровнями велик, и при (о > IE2I приближение (6.8) теряет
смысл. В протяженной области х% < х < Xi сумма остается посто-
янной. При х > х\ основной вклад в сумму вносит слагаемое с
п = 1, которое необходимо учитывать индивидуально. При х > х%
имеем
2
Z2-l,
е*2-! +2x,eX1,
х2 <Zx<Z х19
х > хг.
(6.9)
Вообще, чем больше слагаемых в сумме (6.8) учитывать ин-
дивидуально, тем лучше будет описание истинной спектральной
функции.
§ 4. Полное испускание в непрерывном спектре
4.1. Спектральная излучательная способность. Она складыва-
ется из тормозной (6.2) и рекомбинационной (6.7) составляющих
и с учетом (6.8), (6.9) определяется следующей приближенной
формулой:
Jadu = c-—fe)dw3pr/(c.CM3), С = 1,08-IO-38, (6.10)
{Т [К]}1/2 \кт] 4 ' ’ ’ \ /
ТСг) =
1, х = кимкТ < Xg — | Eg | кТ,
e-(X-V) х <х<х
(^ । о *x'i) Til t*
le } + 2xre , x>xY = I;kT.
Поскольку на практике формулы подобного типа применяют для
сложных (неводородоподобных) атомов, где понятия главного
квантового числа недостаточно для характеристики уровня, энер-
гия связи нижнего возбужденного состояния обозначена \Eg\ вме-
сто \Е%\, а вместо |2?il введен потенциал ионизации I.
В области не очень больших квантов 7г (о < \Eg\ вклады сво-
бодно-связанных и свободно-свободных переходов в излучатель-
ную способность относятся как
*^орек* Аоторм [ехр (7г(о//ьТ) 1] . 1.
(6.11)
Следовательно, кванты ка)<0,7кТ излучаются в основном тор-
мозным механизмом, a 7z(o>0,7fc71— рекомбинационным. При
128
Т = 104 К кванты 1г(й ~ ~ 0,6 эВ (Z = 2 мкм) принадлежат
инфракрасной области спектра. Они существенно меньше значе-
ния |2?я1, которое для водорода, например, составляет 1^1
= 3,37 эВ (Л = 3700 А; это — область ближнего ультрафиолета).
Значит, согласно (6.11) излучение практически всего спектра, за
исключением инфракрасной области, обусловлено рекомбинацион-
ным механизмом. Такое положе-
ние типично для низкотемператур-
ной плазмы. Тормозные процессы
играют там небольшую роль и вы-
ступают на первый план лишь
при излучении в довольно дале-
ком инфракрасном и СВЧ диапа-
зонах.
4.2. Уточнения. Изложенная
простая теория служит идейной
основой для последующих уточне-
ний и усовершенствований, кото-
рые имеют главной целью при-
ложение ее к неводородоподобным
атомам. Результаты квантово-ме-
ханических расчетов сечений с
привлечением спектроскопических
данных об уровнях энергии ато-
мов в конечном счете представля-
ются в виде поправочного множи-
теля £(<о) к выражению (6.10).
В пределе малых частот, которые
излучаются при захвате электро-
нов па самые верхние уровни,
5 1, поскольку верхние уровни
всегда водородоподобны. Им соот-
ветствуют орбиты большого ра-
диуса, где поле атомного остат-
ка — кулоновское. Поправочные
множители меняются от атома к
атому нерегулярным образом и
при росте частоты в диапазоне
видимого света имеют значения
от 1/5 до 3 (рис. 6.3). При деталь-
ных расчетах несколько нижних
а гьно. Кроме того, вводят поправочный множитель eL
единицы, учитывающий снижение границы непрерывного спектра
из-за кулоновского взаимодействия заряженных частиц в плазме
и слияния уширенных верхних уровней Это снижение определя-
ется формулой Инглиса — Теллера (1939 г.) (см. п. 6 5):
Л/< = 1,0- 10~5/гД15 эВ, Az = 0,12ле4/15/Г [К];
подробнее об усовершенствованиях теории см. в [6.1].
9 Ю П Райзер
Рис 6 3 Частотная зависимость
поправочного множителя, на ко-
торый следует умножать коэффи-
циенты поглощения и излучения
для атома водорода, если приме-
нять множитель к реальным ато-
мам [6 1]
уровней учитывают индивиду-
?д* порядка
129
4.3. Интегральное излучение. Если интересоваться потерями,
энергии плазмы на тепловое излучение, выражение (6.10) сле-
дует проинтегрировать по всему спектру. Здесь, однако, необхо-
димо сделать существенную оговорку. Кванты, превышающие по-
тенциал ионизации атома, которые излучаются очень интенсивно
при захвате электрона на основной уровень, столь же интенсивно
поглощаются невозбужденными атомами (§ 5). При тех темпе-
ратурах, при которых вообще существуют неионизованные атомы,
подавляющее большинство их пребывает в основном состоянии.
Поэтому кванты 7гсо>/ не могут далеко уйти от места своего
рождения, разве если газ очень сильно разрежен. Значит, рас-
считывая потери энергии плазмы, чаще всего не следует вклю-
чать в них энергию, уносимую «нежизнеспособными» квантами
энергии Эта энергия тут же по соседству возвращается
в газ. По этой причине мы проинтегрируем (6.10) не до °°, а толь-
ко до (о = 111г. Получим, что 1 см3 плазмы в 1 с излучает в не-
прерывном спектре энергию
J = C^^Z2n+neJ W(x)dx^
о
^1,42-10“37 {T[K]y/2Z2n+ne(l -\-xg) кВт/см3, (6.12)
где Xg=\Eg\/kT. Единица в скобках соответствует вкладу в J
участка спектра от 0 до частоты ы8= \Её\/1г, которую называют
граничной. Слагаемое хб в скобках, обычно порядка нескольких
единиц, описывает вклад частот от до (щ. В то же время
единица соответствует вкладу тормозного излучения во всем
спектре от 0 до °°, а хё — вкладу рекомбинационного, от 0 до (щ.
Это видно, если проинтегрировать (6.2).
Приведем пример оценки радиационных потерь. Рассмотрим
аргон при р = 1 атм, Т = 12 000 К. При термодинамическом рав-
новесии по формуле Саха (см. Приложение) пе = п± =
= 6,7 • 1016 см-3 (Z = l). Энергия связи нижнего возбужденного
состояния 1^1 =4,3 эВ, так что ^ = 4,1. По формуле (6.12)
J = 0,36 кВт/см3. Чтобы ощутить масштаб этой величины, допу-
стим, что плазма остывает за счет высвечивания. Тогда pcPdTldt =
= где ср — удельная теплоемкость при постоянном давле-
нии, р — плотность. При начальной температуре рсР =
= 1,9 • 10“7 кДж/(см3 • К). Масштаб времени для заметного пони-
жения температуры составляет t = рсрТ11 = 6,3 • 10-3 с. На самом
деле радиационные потери могут быть в 2—3 раза больше из-за
излучения в линиях.
§ 5. Поглощение в непрерывном спектре
Принцип детального равновесия устанавливает связь между
характеристиками излучения и поглощения света. Поэтому все,
что касается поглощения при свободно-свободных и связанно-
130
свооодных переходах, можно получить, располагая результата-
ми § 2—4.
5.1. Тормозное поглощение. Соотношения (5.50), (5.51) для
тормозных коэффициентов, рассчитанных на элементарный акт,
справедливы и в случае столкновений электронов с ионами. С по-
мощью выражения (6.1) для da^ найдем коэффициент истинного
поглощения квантов Тгы, рассчитанный на один электрон скоро-
сти v и один ион:
16 л3 /У
3 УЗ cHa^v
(6.13)
Эта формула была выведена Крамерсом в 1923 г. и исторически
послужила основой для развертывания всей полуклассической
теории излучения плазмы в непрерывном спектре. Умножая
««(р) на п+пе и усредняя по скоростям v с максвелловским рас-
пределением, получим коэффициент тормозного поглощения света
в плазме:
= G
^соторм
71/2v3
CM \
= - 3'69-108 cmV(C3.^1/2). (6.14)
о \ o / m6' ^ck1'
В численной формуле мы перешли к частоте v = (о/2л в с”1, ко-
торой чаще пользуются в литературе при сообщении справочных
данных. ,
Для небольших по сравнению с кТ квантов, в частности, при-
менительно к инфракрасной области спектра, в формулу (6.14)
вводят уточняющий множитель — фактор Гаунта-.
g = У = 1,27(3, 38 + 1g Т [Я] - 11gпе).
В условиях плотной низкотемпературно!! плазмы g ~ 1,5—2,5.
5.2. Сечение фотоионизации. Обозначим сечение для ато-
мов, пребывающих в п-м состоянии; Nn — их плотность. В 1 см3
в 1 с происходит 4л (ЛоМы) d(£>6vnNn актов фотоионизации из п-го
состояния, совершаемых квантами Тгы в интервале dco. При этом
рождаются электроны со скоростями v в интервале dp, где и
определяется равенством (6.3), и mvdv == lido). На n-й уровень
атомов в 1 см3 в 1 с захватывается
n+ne<p(p)pdpaCn(l + 4л2с2/ш/Й(т>3)
таких электронов. Второе слагаемое в скобках описывает вынуж-
денные акты фотозахвата. Приравнивая скорости прямых и об-
ратных процессов, подставляя максвелловскую функцию <р(р),
нланковскую интенсивность 1^ и заменяя комбинацию nen+lNn
<)♦
131
по формуле Саха — Больцмана, в которой 1п = \Еп\*), получим
общую связь сечений фотоионизации и фотозахвата:
Gvn = (g+/gn) (тис1Ъ(й)2всп. (6.16)
У водородоподобного атома gn = 2/з2, g+ = 1, осп дается фор-
мулой (6.5). Отсюда сечение фотоионизации
Hvn —
8л e10mZ4
7,9-10~18-^J—Гем2,
Z2 \ /
(6.17)
3“/3 с&6Л5
где (оп =\Еп\/й — граничная частота, ниже которой вырывание
электрона с тз-го уровня атома невозможно. Сечение фотоэффекта
падает с увеличением частоты от порога (оп как со-3. Сечение вы-
рывания электрона из невозбужденного атома водорода (Z = 1г
73=1) имеет у порога порядок 10~17 см2. Как и сечение фото-
захвата (6.5), сечение фотоионизации (6.17) полностью совпа-
дает с результатом квантово-механического расчета при п > К
Неплохая точность получается даже для п = 1. Эксперименталь-
ные данные по фотоионизации невовбужденных атомов и моле-
кул приводились в табл. 4.2.
5.3. Полный коэффициент поглощения. Он складывается из
коэффициентов тормозного (6.14) и фотоионизационного х^ф по-
глощения:
оо
^(0 ~ ^соторм %соф? ^(£>ф " 2 Nn<hm- (6.18)
Последний представляет собою сумму парциальных коэффициен-
тов, которые относятся к атомам, пребывающим в различных
квантовых состояниях. Самый нижний уровень Еп*, который
еще участвует в поглощении данного кванта определяется
так же, как и для фотозахвата (п. 3.2). Спектр поглощения, как
и спектр излучения, имеет характер «частокола»—по мере уве-
личения частоты в поглощение включаются все менее и менее
возбужденные атомы.
Подставим в (6.18) сечения (6.17) и выразим с помощью фор-
мулы Саха — Больцмана плотности Nn через произведение пеп+г
*) Формулой Саха — Больцмана называют комбинацию формул Саха
и Больцмана, из которой исключена плотность нейтральных атомов Фор-
мула связывает равновесные числа пе, п+ и заселенность Nn п-го уровня
атома. В газе с одним сортом ионов
= £+ ЛГЗ/2ехр Л = 2/^^?/2
Nn gn е к кТе) \ )
где gn, g+ — статистические веса атома в n-ом состоянии и иона. Формула
содержит именно электронную температуру. Благодаря этому она примени-
ма и при Те Т, так как заселенность верхних уровней атомов находится
в равновесии со свободными электронами, даже если плотность последних
не равновесна.
132
чтобы привести xo$ к виду, подобному х^орм. В выражении для
Хоф при этом выделяется множитель С5, который фигурирует в
(6.14), а сумма приобретает вид (6.8). Применительно к квантам
Tzco < IE2I сгладим «частокол» путем замены суммирования инте-
грированием, как в (6.8). Для кван-
тов 7zcd > IE2I воспользуемся прибли-
жением (6.9). В результате этих
операций получим
Xq) —
Z2>n+ne
т1^3
= 4,05-10” 23
??п+пе е^т
------!--------—L
{Т [К]}7/2 х3
(6.19)
где функция Y (х) дается формула-
ми (6.10). В последнем выражении
(6.19) частотная зависимость хй це-
ликом представлена в безразмерной
форме, х = 7и&1кТ, что удобно для
вычислений. Вклады фотоионизаци-
ехЧ (х)
онного и тормозного механизмов в
поглощение при й(о<|ЕД характе-
ризуются тем же соотношением
(6.11): (еж- 1): 1.
При не слишком высоких темпе-
ратурах, когда степень ионизации
мала, произведение п+пе в (6.19)
удобно выразить с помощью форму-
лы Саха через плотность атомов N,
которая в этом случае непосредствен-
но определяется давлением р = NkT..
квантов (Ti(£)<\Eg\) получим
Рис 6.4. Коэффициент фото-
ионизационного поглощения
квантов в ксеноне из расчета
на один атом. Сплошные кри-
вые получены путем замены
суммирования по уровням ин-
тегрированием, штриховые —
путем непосредственного сум-
мирования с учетом фактиче-
ской схемы уровней [6 1]
Для не очень большпк
Хо) =
16л Z2eQkTN8+ /
--7- —7—5----ехр
зуз Лео3 ga \
I —
~~кТ J
= ^м-1, (6.20)
{Г[К])2^а х3
где х\ == ЦкТ, g+, ga — статистические веса иона и атома. Эта фор-
мула называется формулой Унзолъда — Крамерса (1938 г.). Сте-
пень приближения сглаженной спектральной функции типа
(6.19), (6.20) к фактическому «частоколу», рассчитанному с уче-
том конкретных особенностей системы уровней атомов, иллю-
стрируется рис. 6.4 на примере ксенона*).
*) В спектроскопии частоту света часто измеряют в см-1, заменяя ее
обратной длиной волны л-1 — v/c; 1 см-1 соответствуют v — 3 • 1010 с-1,
Йю = 1,24 • 10~4 эВ, кы/к = 1,44 К; 1 эВ соответствует X-1 = 8067 см-1.
133
Формулами (6.19), (6.20) обычно пользуются для сценок ко-
эффициента поглощения света нагретым газом*). Рассмотрим
для примера, как поглощается красный свет X = 6500 А в рав-
новесной водородной плазме атмосферного давления. Пусть Т =
= 104 К. При этом rie^N. N • 1017 см-3, х = 2,2 и по фор-
муле (6.20) с Z = 1, g+ = 1, ga = 2 = 5,5 • 10-5 см-1. Длина
пробега кванта до поглощения х^1 180 м — как видим, плазма
сильно прозрачна (в непрерывном спектре). При Т = 2 • 104 К
ионизация сильная и целесообразнее пользоваться формулой
(6.19), так как плотность оставшихся атомов N все равно при-
шлось бы вычислять. Имеем: пе = п+ = 2,0 • 1017 см-3, х = 1,1 и
%ы= 3,2 • 10-3 см-1. В этом случае заметна поправка на вынужден-
ное испускание и реальное поглощение описывается коэффициен-
том (п. 8.4 гл. 5)
>4 = х<а[1 — ехр(—Йм/йТ1)] = И<Д1 — ехр( — z)l
Длина пробега излучения (хо)—1«4,8м.
Поглощение света резко возрастает при нагревании газа. Это
связано с наличием множителя ехр [— (/ — 7z(o) /кТ} в формуле
(6.20), который имеет ясное происхождение. Поглощение обяза-
но в основном фотоэффекту. Квант Тгы может вырвать электрон
только из атомов с энергией возбуждения не менее / —Тгы. Число
их по закону Больцмана пропорционально указанной экспоненте.
5.4. Квантовая форма закона Кирхгофа. Коэффициент погло-
щения (6.19) можно получить чисто формальным путем из из-
лучательной способности (6.10) при помощи соотношения, кото-
рое в квантовой физике является эквивалентом закона Кирхгофа
(п. 9.2 гл. 5). Проделанный выше вывод (6.19) имел единствен-
ной целью сделать возможно более ясным содержание этой важ-
ной формулы. Обозначим Д количество энергии, которое излуча-
ется спонтанно в 1 см3 в 1 с в единичный интервал частот о и в
единицу телесного угла: = Л/4л. Как отмечалось в п. 8.3 гл. 5,
полное испускание складывается из спонтанного и вынужденного
и всегда для любого механизма составляет
Д (1 + 4л3с2/(ОМ(о3) эрг/(с • см3 • Гц • ср). (6.21)
В условиях термодинамического равновесия испускание (6.21)
компенсируется поглощением Хо/ю, а интенсивность излучения
имеет планковскую величину (5.49), откуда
з
V-'-'". (6.22)
4л с
В этом равенстве предполагается наличие термодинамического
равновесия в самом веществе, точнее, в тех степенях свободы,
с которыми взаимодействует излучение,— электроны, возбужден-
*) Формула (6.19) обладает большей общностью, чем (6 20). Ее, в от-
личие от (6 20), можно применять и при неравновесной ионизации, пони-
мая под Т электронную температуру.
134
ные состояния атомов. Ведь в (6.22) фигурирует температура,
с учетом последней оговорки — электронная температура; о том,
что оказывается возможным в особом случае неравновесной сре-
ды, см. в § 10
Из закона Кирхгофа, в частности, вытекает, что любые по-
правочные множители, которые появляются при уточнениях тео-
рии (п. 4.2) в равной мере относятся к и
§ 6. Излучение спектральных линий
Глядя на светящуюся плазму, мы во многих случаях воспри-
нимаем не непрерывный спектр, а наиболее интенсивные линии.
Именно линии придают разрядам цветовое многообразие и под-
час завораживающую красоту. Например, положительный столб
тлеющего разряда в аргоне имеет темно-красный цвет, в неоне —
кирпично-красный, в парах натрия — желтый, калия — зелени и,
ртути — зеленоватый. Источником линейчатых спектров для экс-
периментальных исследований, как правило, служит разряд в тех
или иных газах. На измерениях параметров линий основаны ши-
роко распространенные и эффективные методы диагностики плаз-
мы. Работами сравнительно недавнего времени (шестидесятых
годов) было показано, что излучение в линиях вносит сущест-
венный энергетический вклад в радиационные потери плазмы.
6.1. Вероятности радиационных переходов. При самопроиз-
вольном переходе атома из верхнего, n-го энергетического состоя-
ния в нижнее, /с-е, излучается квант, == Еп — Ек (см. рис. 6.1).
Скорость испускания атома в данной линии S [эрг/с] {сила, ин-
тенсивность линии) определяете^ вероятностью радиационного
перехода Апк [с-1]. По квантовой механике
5 = fa>nbAnh = | -г I h (6-23)
где dnft — матричный элемент дипольного момента атома d. Мат-
ричные элементы удается вычислить лишь для простейших си-
стем типа атома водорода. Для сложных атомов вероятности Ank
находят из опыта. В табл. 6.1 представлены данные для некото-
рых сильных линий, лежащих в видимой области спектра. Обрат-
ная величина т = Ank представляет собой время жизни атома
в 7?-ом возбужденном состоянии по отношению к радиационному
переходу п-+ к.
Вероятности переходов имеют масштаб 108 с-1, времена жиз-
ни— 10-8 с. Такие величины можно получить из (6.23), полагая,
что квадрат матричного элемента дипольного момента атома имеет
порядок среднего квадрата этой величины, т. е. порядок (е^о)2,
а частота (о ~ I^Jh.
6.2. Классическая модель излучающего атома. Если не под-
ставлять цифры, а раскрыть буквенные выражения для боров-
ского радиуса ао и постоянной Ридберга I^lh, увидим, что из мас-
135
штаба величины S выпадает постоянная Планка. Значит, эта
величина должна иметь определенный «классический» смысл.
И действительно, классика придает ей исключительно наглядное
физическое толкование и, вообще, позволяет уяснить многие су-
щественные закономерности явления.
Таблица 6.1. Параметры некоторых сильных атомных линий в види-
мом спектре
Атом, линия о к, А Переход W, эВ Sn Sh / Ank’ c
На 6563 2s — Зр 2 0,425 2,2-107
2р — 3s 12,09 6 0,014 4,2-106
2р — 3d 6 0,695 6,4-107
Насред 6563 2 — 3 18 8 0,641 4,4-107
Нр 4861 2s — 4р 12,75 2 0,102 9,5-106
2р — 4^ 6 0,003 1,8.10s
2р — kd 6 0,122 2,0-107
Врсред 4861 2—4 32 8 0,119 8,4-106
Не 5876 2/?Р° — 3dW 23,1 15 9 0,62 7,1 -107
Аг 6965 4s — 4р 13,3 3 6,8-106
Аг 4259 4s — 5р 14,74 1 4,1 • 106
Na 5890 3s — 2р 2 0,98 6,2-106
5896
Hg 5461 ftsftp — 6 pls 9 0,08 2,9-107
5791 6s6p — 6s6d 3 0,7 9,0-107
Моделью излучающего атома в классической физике служит
упруго связанный электрон, который совершает колебания около
положения равновесия (осциллятор). Эта схема не так уж далека
от квантовых представлений об электронном строении атома.
Вращение электрона по орбите можно разложить на колебания
вдоль декартовых осей около того же центра (ядра) с той же ча-
стотой. В нулевом приближении упруго связанный электрон со-
вершает гармонические колебания с собственной частотой соо
и обладает энергией W = mcog <г2>, где г — радиус-вектор, отсчи-
тываемый от точки равновесия. Его квадрат усредняется по
времени за период. Осциллирующий электрон движется с уско-
рением и, следовательно, излучает электромагнитную волну, при-
чем той самой частоты, с которой он колеблется. Как говорилось
в п. 9.1 гл. 5, в 1 с излучается энергия
2 /" \ 2
(6.24)
Классическая формула (6.24) очень похожа на квантово-механи-
ческую (6.23): удвоенному значению квадрата матричного эле-
136
мента дипольного момента соответствует средний за период квад-
рат момента.
В результате излучения энергия осциллятора убывает с те-
чением времени по закону
d W/dt = -S = -у W; W = WQe~^,
у = 2e2al/3mc3 = 2.47 • lO-2^ c-1, vri = ©0 2л. (6.25)
Здесь Wo — начальная энергия колебаний. Величина у, которая
характеризует время потери энергии т = 7-1, называется посто-
янной затухания. По своему смыслу она соответствует вероятно-
сти радиационной потери возбуждения Апк и для типичных атом-
ных частот v ~ 1015 с-1 имеет правильный порядок 7 ~ 108 с-1,
о
Например, для фиолетового света Л = 4000 A, v = 7,5 • 1014 с-1,
7 = 1,4 • 108 с-1. Условие слабого затухания у < то, которое лежит
в основе вывода (6.25), выполняется с большим запасом.
6.3. Естественные ширина и форма линии. Поскольку воз-
бужденное состояние атома не является строго стационарным,
а имеет конечное время жизни т, энергетический уровень Еп, со-
гласно квантово-механическому принципу неопределенности, раз-
мыт на величину ДЕ ~ Л/т. Следовательно, частоты излучения
в линии имеют разброс порядка Лео ~ ДЕ/Л ~ т--1 Эта
ширина линии, существующая независимо от внешних влияний,
называется естественной. Она очень мала: До ~ 108 с"1 < со ~
- 1015 с"1.
В классической модели линия также имеет ширину, причем
теория позволяет легко определить распределение излучения в
линии по частотам. Колебания электрона, гармонические лишь
в нулевом приближении, на самом деле слабо затухают: г ==
= гоехр(—y£/2)sin (ОоЕ где го — амплитуда в момент £ = 0, соот-
ветствующая начальной энергии TVo. Но затухающим колебаниям
отвечает не единственная частота ыо, а некий спектр. Цуг сину-
соидальных колебаний имеет теперь конечную длительность по-
рядка т = у-1. Это значит, что колебания разных частот в резуль-
тате сложения должны уничтожить друг друга при t > т. Для
этого за время т они должны набрать фазовый сдвиг примерно л,
откуда Дсот ~ л или Дю ~ у.
Спектральный состав излучения можно определить изложен-
ным в п. 9.1 гл. 5 стандартным методом — путем разложения в
интеграл Фурье вектора ускорения г. Как дает вычисление, за
время полного затухания от £ = 0 до £ = в определенный ча-
стотный интервал й(о излучается следующая доля начальной
энергии осциллятора Wo\
= (и) -----г. (6.26)
wo V ’ 2Я(<в_%)2 + (?/2)2 V >
Функция EL (со), нормированная в (6.26) на единицу по частоте
со, характеризует форму естественной линии, ее называют лорен-
137
mar
Рис. 6.5. Форма ес-
тественной спект-
ральной линии
пропорциональна
цевой. Она показана на рис. 6.5. Частотная ширина пика по по-
лувысоте равняется А<о = у. В шкале длин волн ширина не зави-
сит от частоты и составляет АХ = cAv/Vq = 4ле2/3те2 —1,2- 10~4А
Квантовая механика также дает для естественной линии лорен-
цеву форму (6.26); ширина у определяется суммарной шириной
уровней п и к.
6.4. Уширение линий. В реальных условиях линии, как пра-
вило, гораздо шире естественных. Тому есть несколько причин:
столкновения, тепловое движение, эффект
Штарка. При столкновении с какой-нибудь ча-
стицей колебания «осциллятора» сбиваются
случайным образом. Колебания после столкно-
вения никак не скоррелированы с предыдущи-
ми, т. е. фактически цуг синусоидальных коле-
баний имеет конечную длительность порядка
среднего времени между столкновениями ато-
ма в газе тс. Эффект столкновений в некотором
смысле равносилен действию затухания, также
ограничивающего длительность колебаний. По-
этому не удивительно, что линия, уширенная
столкновениями, имеет лоренцеву форму (6.26),
а ширина ее уэф складывается из естественной
у и столкновительной Асос ~ т^1. Последняя
плотности (давлению) и в не чрезмерно разре-
женном газе превышает естественную.
При высоких температурах газа преобладает доплеровский
механизм. Если излучатель движется со скоростью v навстречу
приемнику, его частота увеличивается на Ao = (z;/c) (о, если от
него — уменьшается. Случайный характер теплового движения
атомов приводит к сплошному размытию линии. Благодаря мак-
свелловскому распределению по скоростям, линия приобретает
гауссову форму с относительной шириной по полувысоте
Асор/о - AXD/X = 7,16 • 10-7УГ [К] /А,
где А — атомная масса. Этой формулой пользуются для оценки
температуры газа путем измерения ширины линий (предвари-
тельно убедившись в том, что уширение имеет именно доплеров-
скую природу).
Штарковское уширение связано со снятием вырождения и рас-
щеплением уровней атомов под влиянием статистических полей
соседних заряженных частиц. Эффект наиболее силен для атома
водорода и некоторых уровней гелия, когда расщепление пропор-
ционально первой степени поля Е. В подавляющем большинстве
остальных случаев эффект квадратичен по Е и слабее, так как
фактически речь идет о степени отношения Е к внутриатомному
полю Е{} = e^/al = 5,14-109 В/см, иЕД<1.
Разность энергий между наиболее удаленными компонентами
расщепленного п терма водорода составляет А8 = ЗеЕа$п(п — 1).
138
Физически она определяется разностью потенциалов, которая со-
здается полем Е в крайних точках zz-й атомной орбиты Аф«
~ Еа^п2. В плазме поле создается ближайшими зарядами и по
порядку величины равно Е ~ е г2 ~ е^е/3, где г ~ п^1/3 — сред-
нее расстояние между заряженными частицами. В силу стати-
стического характера полей, возможны разнообразные расщеп-
ления, поэтому излучающий уровень и сама линия оказываются
размытыми. Частотное штарковское уширение имеет порядок
Avs ~ Ae/Л. Для линии Яр с п = 4 уширение в шкале длин волн
имеет порядок
A%s = Avs^ ~ ~ 0,5 - 1(Г10^/3 А.
На самом деле такая оценка верна для описания действия
поля ионов, которые движутся медленно, в силу чего их поля
являются квазистатическими. Воздействие же свободных электро-
нов имеет ударный характер. Ударное уширение пропорционально
плотности электронов и логарифмическому множителю, который
уменьшается с ростом пе. Результирующее уширение довольно
хорошо аппроксимируется тем же законом ^/3, но его значение
раза в четыре больше, чем по приведенной оценке. Коэффициент
при п2е^ слабо зависит от Т и пе. В диапазоне Т ~ 5000—40 000 К
при изменении пе от 1014 до 1017 см-3 штарковская ширина ли-
нии Я3 по уровню половинной интенсивности меняется в интер-
вале
AZS «(1,8 - 2,3).1(Г1Ч2/3А.
Этой формулой наряду с теорией штарковского контура линии
широко пользуются для измерения плотности электронов в плаз-
ме. В исследуемый газ подмешивают немного водорода, снимают
контур линии Я3 и измеряют ее ширину. Метод применим, если
штарковский механизм уширения преобладает над доплеровским.
Первый не зависит от температуры, второй — от электронной
плотности. Для линии Яр, например, при Т = 104 К и пс -
= 1014 см-3 AXs = 0,42 А, АХр = 0,35 А; при пе == 1017 см-3 AXS =
= 48 А. Таким образом, для такой типичной температуры, как
1 эВ, измерение пе возможно, если пе > 1015 см-3.
6.5. Сдвиг границы серии. Исследуя спектры излучения можно
заметить, что число линий в серии, соответствующей переходам
электрона из состояний с различными п в определенное нижнее
состояние, ограничено. Это связано со снижением границы не-
прерывного спектра из-за кулоновского взаимодействия заряжен-
ных частиц и слияния уширенных уровней. Это снижение дается
формулой Инглиса — Теллера (п. 4.2). Они определяли снижение
из условия равенства штарковского расширения водородного
уровня Ае « ЗеЕаоп2 (п. 6.4) и расстояния между уровнями
2/нМ3 = е21а^~п?. Уточненное по сравнению с п. 6.4 значение сред-
139
него поля в плазме с однократно ионизованными атомами есть
Е ~ 3,7е(пе + тг+)2/3. Отсюда получается связь главного кванто-
вого числа самого высокого еще дискретного уровня nmax с плот-
ностью электронов в плазме
Пе [2 (З-ЗД)372^^]-1 « 0,91 • 1023Итах/3
и снижением границы непрерывного спектра = /н^тах (см.
л. 4.2).
6.6. Излучательная способность. В 1 см3 в 1 с в линии п -> к
излучается энергия Jnk = 1i^nkAnhNn. Обозначая через F(<о) нор-
мированную на единицу функцию формы любым образом уши-
ренной линии, мы можем записать спектральную излучательную
способность газа, обязанную данной линии, в виде
/ойо = (4л)'"1ЛсопкЛпкЛ^пГ((о)б/(о эрг/(с • см3 -ср). (6.27)
По существу, в этой записи отражен тот фундаментальный факт,
что уширение линии не меняет ее площади, т. е. площади кривой
рис. 6.5,— уменьшается высота пика. Физически это объясняется
тем, что полное излучение в линии, т. е. интеграл от (6.27) по со,
определяется вероятностью самопроизвольного внутриатомного
перехода, которая практически не зависит от внешних влияний.
Последние (например, неупругие удары) могут сказаться лишь
на числе Nn атомов, подготовленных к данному переходу. По-
дробнее о сохранении площади линии будет рассказано в сле-
дующем параграфе.
§ 7. Селективное поглощение
7.1. Эффективное сечение поглощения в линии, уширенной
столкновениями. Под действием поля электромагнитной волны
Е = Е0 sin упруго связанный электрон совершает вынужден-
ные колебания с частотой поля. При этом он непрерывно теряет
энергию на излучение. Кроме того, при каждом столкновении
происходит «сбой» колебаний, и электрон каждый раз как бы
раскачивается полем заново. Обе причины вызывают необходи-
мость в восполнении энергии электрона, которая черпается у по-
ля. Следовательно, электромагнитная волна поглощается. Точнее,
к поглощению, т. е. диссипации энергии в тепло, приводят только
столкновения. Затухание, в сущности, приводит к рассеянию све-
та, так как энергия волны переизлучается практически на той
же частоте.
Рассмотрим этот процесс так же, как в п. 1.2, 2.2 гл. 5, исходя
из уравнения движения электрона с учетом усредненных потерь
его импульса (действия «сил трения»), вызванных затуханием и
рассеянием при столкновениях:
тпг 4- тсодГ = — еЕ0 sin (о/ — тпг уЭф, уЭф= у + tJT1. (6.28)
140
Решение этого уравнения есть
г = —° sin(<ot + <p) arctg_^M. .
т ^-<0*
В среднем за период поле ежесекундно совершает над электро-
ном работу <—еЕг> = туэф<г2>. Такую энергию волна теряет в
1 с. Поделив ее на среднюю плотность потока энергии сЁЦ&к,
получим, по определению, сечение о© поглощения волны осцил-
лятором. Для частот со, близких к резонансной, |со — cool < соо,
найдем
пе2_______Уэф______
тс (“-%)2 + (W2)2‘
(6.29)
Линия поглощения имеет лоренцеву форму, в отсутствие столк-
новений (У'эф^у) совпадающую с (6.26), что и не удивительно,
ибо это следует из закона Кирхгофа*). В центре (со = соо) ес-
тественной линии сечение поглощения имеет колоссальное по
атомным масштабам значение о© max = ЗА2/2л ~ 10-9 см2 для ви-
димого света. Если линия сильно уширена столкновениями, се-
чение падает с ростом давления: (J© ~ тс ~ р~х,
7.2. Площадь «классической» линии. Из расчета на один
осциллятор площадь линии равняется универсальной величине,
которую, следуя традиции, приведем в виде интеграла по v:
Jo(BtZv = (2nr1Jo(B<?ffl = ^ = 2,64-10_2 см2/с. (6.30)
Поясним качественно, почему площадь линии не зависит от ча-
стоты столкновений. При со ~ со о раскачка колебаний электрона
полем имеет почти резонансный характер, а в этом случае амп-
литуда колебаний га растет пропорционально t от начала рас-
качки, т. е. от момента последнего столкновения. Значит, к мо-
менту следующего столкновения электрон набирает колебатель-
ную энергию W сю сю Тс, и она (в среднем!) переходит в хао-
тическую. В 1 с от поля отбирается энергия W/xc, так что с(., со
co]>F/тс<^ тс. Между тем Дсо сю т7\ откуда о©Асо 00 const. Уравне-
ние (6.28), в котором потеря импульса при столкновении «раз-
мазана» по времени, не описывает этого процесса в деталях,
а фиксирует лишь его средний результат. На рассматриваемую
ситуацию распространяются все те соображения о возможности
приобретения и отдачи энергии полю при индивидуальном столк-
новении и о классическом аналоге эффектов истинного погло-
♦) Осциллятор излучает усй!Г© [эрг/с], поглощает 4л/©с/соо0. В равенство
этих величин нужно подставить рэлей-джинсовскую интенсивность и Wo =
= ЗкТ (осциллятор трехмерный!). При действии столкновений осциллятор
излучает уэф^©, причем у в также следует заменить на уЭф. Заметим,
что, более строго, = у + 2т”1.
141
щения и вынужденного испускания, которые высказывались в
п. 2.5 гл. 5.
7.3. Сила осциллятора. Количество энергии, которое вне за-
висимости от характера уширения поглощается в данной линии
в 1 см3 в 1 с,
J 4л/т с?сох0 » J <&>,
определяется площадью линии поглощения (Nk — плотность ато-
мов-поглотителей). Именно эта величина служит мерой погло-
щательной способности вещества в линии *).
При помощи соотношения (6.22), выражения (6.27) и больц-
мановской связи между плотностями Nn, Nh ее можно выразить
через вероятность излучательного перехода:
= \oadv = l^~Ank. (6.31)
sk со J ш
Площадь линии очень удобно представлять в безразмерном ви-
де, взяв в качестве единицы измерения универсальный мас-
штаб— площадь линии одного классического осциллятора (6.30).
Выраженная в этих единицах площадь реальной линии, т. е.
число воображаемых классических осцилляторов, которое обеспе-
чило бы точно такое поглощение, как и реальная линия, назы-
вается силой осциллятора f (для поглощения). Для одноэлек-
тронных переходов в атоме силы осциллятора меньше единицы
и приближаются к единице для наиболее сильных линий. Они
представлены в табл. 6.1.
§ 8. Молекулярные спектры
Внутренняя энергия молекулы складывается из электронной
(как у атома), колебательной и вращательной. Каждый энерге-
тический уровень характеризуется набором электронных кванто-
вых чисел (обозначим наборы символически А, В, ...), колеба-
тельным числом v и вращательным j. При переходе Bv'j' ->
-+Av"j" излучается определенная спектральная линия
(рис. 6.6). Линии, отвечающие одинаковым Bv', Av", но разным
, образуют полосу. Разности вращательных энергий столь
малы, что линии внутри полосы располагаются чрезвычайно
*) В свое время при построении феноменологической теории излучения
и поглощения света Эйнштейн ввел равноценную величину
Bkn = (^“пйГ1 j dv-
Величины Ank, Bkn, а также Впк (для вынужденного излучения; см § 10}
называются коэффициентами Эйнштейна.
142
близко друг к другу, на расстояниях ДХ ~ 1 А в шкале длин
волн (рис. 6.7). При слабом разрешении регистрирующей аппа-
ратуры вращательная структура полосы вообще не различается
м спектр в ней кажется сплошным.
Рис. 6.6. Схема уровней и
радиационных переходов в
молекуле. Вертикальными
линиями показаны различ-
ные полосы
Совокупность полос, отвечающих определенному электронному
переходу В-+-А, но различным у', р", называется системой по-
лос. Наиболее важные системы имеют общепринятые названия,
например полосы Шумана — Рунге кислорода (переход >
Х327)’ вторая положительная система азота (С3Пи 53Щ).
Спектр испускания в последней Доказан на рис. 6.8. Полосы,
принадлежащие одной системе, также группируются, образуя
последовательности полос, каждой из которых отвечает опреде-
ленная разность kv = v' — v". Когда колебательные числа v',
и" пробегают ряд значений, но разность их фиксирована, раз-
ности энергий уровней отличаются меньше, поэтому полосы
одной последовательности располагаются ближе друг к другу,
чем полосы разных. Если бы частоты колебаний молекулы в
электронных состояниях А и В были строго одинаковыми и ко-
лебательные уровни были эквидистантными, как у идеаль-
ного гармонического осциллятора, все полосы последовательно-
сти вообще накладывались бы друг на друга (рис. 6.6). На са-
мом деле колебательные частоты различаются и проявляется
ангармоничность колебаний, поэтому полосы последовательности
раздвигаются.
Огромное множество всевозможных комбинаций из квантовых
-чисел верхнего и нижнего состояний ограничивается правилами
отбора, согласно которым вращательное число может изменять-
ся при переходе только на — //z ==0, ±1. Столь же строгого
правила отбора на колебательные числа нет, но среди возмож-
ных комбинаций vr, и" наиболее вероятными являются пере-
воды, которым отвечает вертикальное перемещение из одного
143
состояния в другое на схеме потенциальных кривых моле-
кулы. Это положение называется принципом Франка — Кон
дона [27].
Наиболее резко проявляющееся отличие молекулярных линий
от атомарных заключается в огромной разнице их высот, т е.
5ВД А
Рис 6 7 Спектр испускания в полосе 0—2 второй положительной систе-
мы N2 Каждая из линии вращательной структуры состоит из трех, в соот-
ветствии с мультиплетным расщеплением уровней
Рис 6 8 Спектр испускания системы ^2(2+) (см с\ему уровней ]\2 ва
рис 7.11)
абсолютных значений сечений поглощения или излучательных
способностей в центре линии. Дело в том, что одной атомной
линии, которая возникает при определенном электронном пере-
ходе, т. е. фиксированных 5, 4, соответствует множество моле-
кулярных, различающихся параметрами колебательных и вра-
щательных состояний у', /' — у", . Но вероятность радиацион-
ного перехода и сила осциллятора определяются преимуществен-
но свойствами именно электронных структур, а не колебатель-
ным или вращательным движением ядер. Поэтому, грубо говоря,
одна и та же «площадь линии», в случае атома сконцентриро-
ванная в единственном пике, у молекулы распределяется между
огромным числом линий, которое реально насчитывает десятки
144
тысяч. Ширины атомарных и молекулярных линий в общем име-
ют одинаковый порядок величины, силы осцилляторов — тоже»
Значит, высоты молекулярных линий на 4—5 порядков меньше
атомарных. Если в центрах атомарных линий лабораторная плаз-
ма часто бывает непрозрачной, в молекулярных полосах она
обычно прозрачна. По этой причине молекулярное излучение,
заполняя большие спектральные интервалы, вносит существен-
ный, иногда даже определяющий вклад в потери энергии на
излучение плазмы азота, воздуха и др.; подробнее об оптических
свойствах молекулярных газов см., например, [27]. Некоторые
фактические данные будут приведены в § 9.
§ 9. Перенос излучения, выход его из плазменного объема,
радиационные потери
9.1. Уравнение переноса излучения. При диагностике плазмы
спектральными методами, исследовании энергетического баланса
разряда неизменно возникает вопрос, сколько излучения выходит
с поверхности излучающего объема. В общем случае для на-
хождения интенсивности излучения служит уравнение, которое
мы сейчас сформулируем. Интенсивность излучения Д>(г, У),
распространяющегося в направлении J2, ослабевает вдоль пути s
вследствие поглощения и нарастает в результате испускания
средой, спонтанного и вынужденного*). Стационарное распреде-
ление Д> в пространстве устанавливается примерно за время
пролета света через среду, т. е. мгновенно по отношению к лю-
бым нестационарным процессам в самой среде. Поэтому явной
зависимости /() от t можно не учитывать. Из сказанного следует,
что
Исключив с помощью закона Кирхгофа (6.22), получим урав-
нение переноса излучения**):
dl^jds — (7op 1ю),
(6.32)
где = %to(l — е~п^кт}. Первое слагаемое в его правой части
описывает спонтанное испускание, второе — поглощение за вы-
четом вынужденного испускания. От местной температуры за-
висят и Xto, от местных оптических свойств —Эти вели-
чины, разумеется, могут меняться и во времени.
*) Рассеяние в плазме чрезвычайно мало по сравнению с поглощением.
**) В равновесной среде; о неравновесной см. в § 10.
Ю Ю. П Райзер 145
9.2. Интенсивность на выходе из тела. Будем регистрировать
с позиции А интенсивность излучения /оээ, выходящего из опре-
деленной точки О поверхности излучающего объема (рис. 6.9).
Направим ось х вдоль луча О А, отсчитывая координату от точ-
ки О в глубь тела, и введем оптическую координату
«А
Рис. 6.9. К вопросу о
выходе излучения из
нагретого тела
g = j* (z) = n^dx. (6-33)
6
Проинтегрируем получающееся из (6.32) уравнение dljdl, — 7м
= -Iap. Учитывая, что с задней поверхно-
сти x — d свет в тело не поступает и^там
ZM = 0, и относя решение к точке О, найдем
Тсо Р f
Но = f Лор [Та)] е-6 = J dx, (6.34)
о 0
где Tw — оптическая толщина тела в дан-
ных луче и спектральном участке.
9.3. Прозрачное тело. Если тело оптиче-
ски тонкое (то<1), в луче просто сумми_
руется испускание с каждого отрезка пу
ти dxt
Но « f Hpdl = J I^idx = J h dx. (6.35)
b b 0
Все излучение, рожденное в объеме, беспрепятственно
наружу. Если температура и оптические свойства везде
наковы,
IО о J(0 d = I (op^td d = /(op^CO Aop*
Интенсивность составляет малую долю то < 1 от равновеснощ
планковской величины Zwp. Когда тело прозрачно во всем
ре, потери его энергии на излучение имеют чисто объемн
рактер и полностью определяются интегральной по спектру
лучательной способностью 4л f j^du).
9.4. Абсолютно черное тело. Пусть тело обладает °^bn^0
оптической толщиной т© > 1 (непрозрачно) и температур
повсюду одинакова. На оптические коэффициенты к©? 7® т
ограничения не накладываем. Согласно (6.34) /©о — HOg
с поверхности во всех направлениях выходит излучение^
и той же, планковской интенсивности. Тело излучает тела
лютно черное*). С 1 см2 поверхности абсолютно черно
*) Если пет не учтенного нами отражения от поверхности. В п
в оптическом диапазоне отражение и в самом деле ничтожно.
146
в 1 с выходит энергия
Sp = J da j Лор cos cZQ = j яТ^р йй) = аТ4[эрг/(см2*с)], (6.36)
(2л)
где — угол между направлением 12 определенного луча и нор-
малью к поверхности; интегрирование ведется по полусфере; о —
постоянная Стефана — Больцмана. Полная потеря энергии телом
на излучение в 1 с равна oT4S, где 2 — площадь его поверхно-
сти. Этот привлекательный своей простотой вариант, который не
требует знания оптических свойств вещества, в разрядах прак-
тически не реализуется — плазма обычно празрачпа для излуче-
ния в непрерывном спектре*).
9.5. Самопоглощение. В общем случае полупрозрачного тела
на интенсивности выходящего излучения сказывается действие
эффекта самопоглощения {реабсорбции}. Излучение, рожденное
в точке х (рис. 6.9), частично поглощается по пути. Поверхно-
сти достигает лишь его доля ехр(—%), тем меньшая, чем с боль-
шей глубины оно идет, что и зафиксировано в формуле (6.34).
Последняя упрощается, если температура тела постоянна, и уп-
рощается еще больше, если постоянен также коэффициент по-
глощения:
/<00 - /ор(/) (1 - /<ор (1 - е~^\ (6.37)
Интенсивность у поверхности монотонно нарастает при увели-
чении оптической толщины тела, стремясь к планковской. Вы-
расти больше ей не позволяет самопоглощение.
Как правило, разрядная плазма бывает прозрачной в непре-
рывном спектре, но довольно часто — непрозрачной в линиях,
точнее, в центральных областях достаточно сильных линий.
Здесь происходит реабсорбция, которая приводит к искажению
формы наблюдаемой линии по сравнению с излученной. Пик ока-
зывается срезанным до планковской величины, тогда как крылья
сохраняют свою первозданную форму. Избежать такой деформа-
ции линии можно лишь путем уменьшения оптической толщи-
ны плазмы, либо за счет сокращения размеров, либо понижая
плотность газа. Эффекту реабсорбции линий приходится уделять
много внимания при использовании методов спектральной диаг-
ностики, при расчетах потерь на излучение теплообмена.
9.6. Степень черноты. Спектральный поток излучения с
поверхности полупрозрачного тела, который определяется ана-
логично (6.36) интегрированием интенсивности на полусфере,
зависит от геометрии тела. Это видно из рис. 6.10а, где изобра-
жен плоский слой. Для косых лучей слой менее прозрачен, чем
для нормальных к поверхности. Самым простым является случай
полусферического тела, если интересоваться выходом излучения
из центра основания (j)hc. 6.106). В этом случае, если Т, =
*) Исключение составляют лишь некоторые дуги сверхвысокого дав-
ления.
10* 147
= const, оптическая толщина для всех лучей одинакова и
J 700cos^dQ = 5rap(l -e~K“d), (6.38)
(2Л)
Рис. 6.10. К вопросу о сте-
пени черноты: а — плоский
•слой; б — полусферическое
тело
у которой коэффициент
где = лДор — спектральный поток с поверхности черного тела.
Удобной мерой интегрального потока излучения с поверхно-
сти полупрозрачного тела является степень черноты & — отно-
шение фактического потока во всем
спектре к стефан-больцмановскому. Ею
часто оперируют при представлении
результатов расчетов, измерений. Ка-
чественная зависимость степени черно-
ты от оптических свойств, давления,
размеров хорошо просматривается, ес-
ли вычислить ее для центра полусфе-
рического объема серого тела. Серой
называется идеализированная среда,
поглощения х' не зависит от частоты.
Из (6.38) для этого случая получим
8 = ^5 J rfo> = 1 - e~*'d.
(6.39)
9.7. Суммарные спектры и интегральное излучение. Суммар-
ными называют полные спектральные излучательные и погло-
щательные способности, обусловленные всеми действующими в
плазме механизмами, интегральными — величины, относящиеся
ко всему спектру в целом. В конце пятидесятых, шестидесятых
годах были подробно изучены радиационные свойства воздуш-
ной плазмы. Стимулировали эти исследования потребности ра-
кетной техники: когда космический аппарат с большой ско-
ростью движется в плотных слоях атмосферы, воздух перед ним
сильно нагревается и излучает. Попадая на поверхность аппара-
та, излучение поглощается, и это предъявляет дополнительные
требования к его теплозащите. Полученные в ходе этих иссле-
дований результаты вполне применимы и к разрядной плазме.
Приведем некоторые данные для воздуха и азота, полученные
в работах Л. М. Бибермана и его сотрудников [6.2].
На рис. 6.11 показаны коэффициенты поглощения воздуха
при Т = 6000 К и нескольких давлениях. Этот рисунок интере-
сен, в частности, тем, что на нем указаны спектральные участки,
в которых определяющий вклад в поглощение вносят те или
иные молекулярные системы полос. За исключением области
больших квантов, которые поглощаются в результате фотоиони-
зации невозбужденных частиц, во всем остальном спектре при
столь низкой температуре поглощение (а значит, и излучение)
имеет молекулярную природу. На рис. 6.12 даны коэффициенты
поглощения воздуха при р == 1 атм и Т = 8000, 14 000 К. Второй
из них демонстрирует вклад атомарных линий. Степень согласия
148
J'o), CM
1.0
10'
10
10
10'
Ю2
n2h
2-N2/, N?'
3 -NO/?,/, <?,£
4-N2 5-X
v,10\m 1
p„ ,,r™.^5— «*ж%г= :=”»«=
X= 6000 К. ОтмеЧ некоторые молекулярные полосы [6.2]
a
10 2
10
10'1 '
о _
10
10"1 -
10'3
10°
- 10 ~2
Ю'3
Uu*^
10 4
^r-™ 50 110_
'6i. Частая зависимость коэффициента^ тогло^ения^воздуха^ p^-—
a - T ~ 8000 *<;СпектральнЫХ лииий [6.2]
149
w,
рис. (
1 атм; a
расчетов с экспериментом иллюстрируется рис. 6.13. На рис. 6.11
показана степень черноты плоского слоя воздушной плазмы тол-
щиной d = l см. Она мала — плазма прозрачна. Рис. 6.15 дает
представление о вкладе различных механизмов в излучение слоя
толщиной d == 1 см азотной плазмы атмосферного давления. Са-
мое показательное здесь — роль атомарных линий, которые дают
большой вклад в интегральное излучение.
Рис. 6.13. Спектральная интенсивность излучения слоя воздуха 'го3111'1злУ*
d == 1 см, Т = 8000 К, р == 35 атм [6.1]. Численно она совпадает
нательной способностью /х (Вт/(см3 • ср • мкм)]. Кривые с цифрамя*^по-
четные вклады различных процессов: 1 — полосы О2; 2, 3, 8 — 10, ™
лосы NO; 4, 5 ~ полосы N2; 6, 7 — полосы N^; 11 — прилипание элеК в
к О; 12— то же для N; 13— тормозное и рекомбинационное излу4 jSs-
поле NO+; 14— то же для N+, О+; 15— тормозное излучение в ^jjjTp^"
2 — суммарная расчетная интенсивность, S' — то же для р == 38 атМороО
ховая кривая — 0,1 интенсивности излучения черного тела с Т °
точки — эксперименты при р == 38 атм
г
Для оценки интегральной излучательной способности _
ных газов с учетом вклада всей совокупности линий мо
жить формула, предложенная в [6.3] на основе опреД
теоретических соображений. Она отличается, от (6.1^)
множителя 1 + xg = 1 + \Её\/кТ на ехр(| Её\/кТ\ гДе
граничная энергия Eg выбирается так, чтобы обеспечи^
сие с экспериментом. Для этого граничным следует с ррУ#
нижний возбужденный уровень Eg1 а тесно расположен^
пу вторых возбужденных р-уровней атомов. У аргона
150
— 2,85 эВ, тогда как |2?J =4,3 эВ*). При Г =12000 К, р =
= 1 атм получается 7=1,1 кВт/см3, тогда как оценка в п. 4.3
по формуле (6.12), относящейся к непрерывному спектру, дала
0,36 кВт/см3. На рис. 6.16 показано интегральное излучение
аргона. Надо сказать, что данные
экспериментов весьма разноречивы.
9.8. Лучистый теплообмен. Не-
редко случается, в том числе и в га-
зоразрядных условиях, что излуче-
ние, рожденное в местах, где тем-
пература высока, поглощается в со-
седних, более холодных слоях, и это
приводит к их нагреванию. Так осу-
ществляется лучистый теплообмен —
перенос энергии в среде излучени-
ем. Бывает, что действие этого ме-
ханизма даже превышает эффект
теплопроводности вещества. Энер-
гетическое воздействие излучения
Рис. 6.14. Степень черноты
плоского слоя воздуха толщи-
нок d — 1 см при разных дав-
лениях [6.2]
на среду определяется в конечном
счете разностью между тем, сколько энергии поглощается,
и тем, сколько излучается:
оо
q = j j c/й (Za — Zwp) эрг/(с-см3). (6.40)
0 (4Л)
Эта интегральная по углам и по спектру величина представляет
собой плотность источников энергир в веществе. Как следует
Рис. 6.15. Вклад энергии раз-
личных процессов в изучение
плоского слоя азота при р =
= 1 атм (сплошные кривые)
и р = 0,1 атм (штриховые)
[28]: 7 — молекулярные поло-
сы и тормозное излучение в
поле нейтральных частиц; 2,
3 — рекомбинационное и тор-
мозное излучения в поле
ионов; 4 — линии атомов с % >
> 2000 А; 5 — линии атомов с
% < 2000 А; 6 — линии ионов.
Вклад, обозначенный цифрой,
характеризуется участком
между ближайшими кривыми
из уравнения переноса (6.32), q = — divS, где S — вектор плот-
ности интегрального по спектру потока энергии излучения.
) У Не |^| =3,6 эВ, у Ne—3,1 эВ, у Хе — 2,5 эВ.
151
Но если лучистый теплообмен оказывает существенное энер-
гетическое воздействие на среду, т., е. на распределение темпе-
ратуры, то уравнение переноса, в которое эта температура вхо-
дит, теряет свою самостоятельность. Оно образует с уравнениями,
описывающими поведение вещества, единую систему. Решение
задач подобного рода, как правило, представляет очень большие
вычислительные трудности. Физическое существо процесса, а бла-
годаря этому и математическое его описание, упрощаются в слу-
чаях, когда неравномерно нагретая плазма сильно непрозрачна
Рис, 6.16. Интегральная
по спектру излучатель-
ная способность аргона^
р = 1 атм [28]: 1, 6 —
только континуум, рас-
чет; 2, 5 — с учетом ли-
ний, расчет; 3— экспе-
римент без вакуумного
ультрафиолета, 0,2 <
< % < 6 мкм; 7 — то же,
0,2 < Л < 22 мкм; 4, 8,
9 — измерения; 10 — С
учетом вакуумного ульт-
рафиолета, оценка по
данным эксперимента
и интенсивность излучения повсюду близка кд0Т0Ка из-
личине, отвечающей местной температуре. ло « градиенту
S при это» оказывается
температуры, и перепое излучения пряобр -иые условия
стой теплопроводности. В газовом разряде Д (271.
встречаются редко; подробнее о лучистом те°Д°° ностики плаз-
Очерк спектроскопических <и. ДР^ жТ рассматриваются откло-
мы имеется в 1-м изд., гл. 12. Там ж р излучения из
нения плазмы от равновесия, вызванные вь Д
ее объема.
рассказывалось в этой
принцип лазерной ге-
что использование га-
§ 10. Принцип действия лазера
ЮЛ. Инверсия и усиление. Того, что
главе, вполне достаточно, чтобы уяснить
НеР(Щии. Сделать это тем более уместно, теды является
зового разряда для создания активной ла/’ и„ ,гЛ jg).
одним из важнейших его современных атоме или моле-
Рассмотрим радиационный псРех°Д/г^’ вынужденного
куле. Выразим выписанную в п. 5.4 скоробь
испускания через сечение Оью этого процесса.
ор). (6^)
152
Если среда равновесна, излучательная способность /© связана
с коэффициентом и сечением поглощения оаСо (х© — NhoaGi) за-
коном Кирхгофа (6.22), причем плотности Nn, Nk удовлетворяют
закону Больцмана. Отсюда вытекает связь сечений и <0™:
Оьш =(Л^Л/Лгп)равнехр(-Й(о/Л;77)оа£й = (gjga)oa£0*). (6.42)
Уравнение переноса излучения (п. 9.1), взаимодействующего
о атомами в п- и /с-состояниях, в отсутствие равновесия в среде
имеет вид
dl' Jds = /ю + Nсо -У/{Пасо-Ло = /со ~Ь 2 N1 ) ^йЦаи-Ло, (6.43)
где N2i=Nnlgn^ Ni=NjJgk — плотности атомов, которые занима-
ют определенные квантовые состояния, принадлежащие энерге-
тическим уровням п, к. В равновесном газе плотность N2 =
= TVj ехр (—fitolkT) < 2Vi, излучение поглощается с коэффициен-
том Х(о, исправленным на вынужденное испускание, и (6.43) сов-
падает с (6.32). Если же в верхнем состоянии атомов больше,
чем в нижнем N2 > Nx, что называется инверсной заселенностью,
то излучение, проходя через среду, не поглощается, а усилива-
ется. Интенсивность излучения в подобных случаях очень ве-
лика, и вынужденное испускание намного превышает спонтанное
(п. 10.3). В однородной среде с N2~Ni = const интенсивность
нарастает вдоль луча по закону
Zo=Z^as, . (6.44)
где a = (N2 — Ni)gkGa(ii — коэффициент усиления.
10.2. Условие генерации. Создание инверсной заселенности на
какой-нибудь паре уровней, что обеспечивает усиление излуче-
ния вместо обычного поглощения,— первое необходимое условие
лазерной генерации. Второе заклю-
чается в том, чтобы степень инверс-
пости и коэффициент усиления пре-
вышали определенный минимум.
Нужно, чтобы усиление преобладало
над потерями интенсивности, кото-
рые всегда существуют вследствие
рассеяния излучения, неполного от-
ражения от поверхностей и т. д.
Тогда интенсивность начального,
случайного луча света (скажем, теп-
лового происхождения) будет нара-
стать. Окончательная интенсивность
Рис. 6.17. Принципиальная
схема лазера: 1 — активная
среда, 2 — полностью отража-
ющее («глухое») зеркало, 3 —
полупрозрачное зеркало, 4 —
луч
будет тем выше исходной,
чем больший путь пройдет луч света в усиливающей среде. По-
этому активную среду помещают в резонатор, часто просто об-
разованный двумя параллельными зеркалами (рис. 6.17). Луч,
*) Таково же соотношение площадей линий вынужденного испускания
и поглощения и соответствующих коэффициентов Эйнштейна: Впь =
= (gh!gn)Bkn (СМ. сноску в п. 7.3).
153
испытывая отражения, много раз проходит через среду. Одно
зеркало делают полностью отражающим, другое — полупрозрач-
ным, чтобы выпускать усиленное излучение наружу. Такова
принципиальная схема лазера.
10.3. Температура лазерного излучения. Излучению данной
частоты можно приписать температуру Т&, определив ее такг
чтобы функция Планка (5.49) с Тм давала фактическую интен-
сивность Температура лазерного излучения имеет фантасти-
чески огромную величину. Пусть Р — лазерная мощность, d —
диаметр параллельного лазерного луча, 0 — угол его расходимо-
сти, который для излучения высокого качества близок к дифрак-
ционному 0 ~ K/d, Асо—частотная ширина лазерной линии. Име-
ем (с учетом кТа » Лев)
Исо2А:7\ / %\2
Zo/ZQAd лй2/(й02Асв » л^2 I j 1 Асв = кТ^Аы.
У хорошего рубинового лазера ширина линии Асв ~ 1010 с”1
(АЛ- 10"1 —10-2 А). При Р = 10 МВт = 1014 эрг/с ~ 1020 К!
В поле лазерного излучения спонтанное испускание меркнет по
сравнению с вынужденным:
Jмспопт/jовын ехр (Й(В/кТсо) 1 к(£)]кТ~ 10
Часть II. ФУНДАМЕНТАЛЬНЫЕ МЕТОДЫ
ТЕОРЕТИЧЕСКОГО И ЭКСПЕРИМЕНТАЛЬНОГО
ИССЛЕДОВАНИЯ РАЗРЯДНОЙ ПЛАЗМЫ
Глава 7. КИНЕТИЧЕСКОЕ УРАВНЕНИЕ ДЛЯ ЭЛЕКТРОНОВ
В СЛАБОИОНИЗОВАНИОМ ГАЗЕ, НАХОДЯЩЕМСЯ В ПОЛЕ
§ 1. Описание электронных процессов
при помощи функции распределения по скоростям
Поведение электронов в ионизованном газе в присутствии по-
стоянного и переменного электрических полей рассматривалось
в гл. 3 и 5 в рамках элементарной теории. Все внимание в ней
концентрируется на одном отдельном электроне, а при переходе
к макроскопическим величинам считается, что все электроны
ведут себя одинаково. Такой подход позволяет приближенно вы-
числить много важных характеристик ионизованного газа: элек-
трическую проводимость и диэлектрическую проницаемость, ко-
эффициент поглощения электромагнитных волн, скорость нагре-
вания электронов в поле. На основе этих результатов можно изу-
чать многие конкретные процессы: разряды разных типов, рас-
пространение радио- и световых волн в плазме и др. В дальней-
шем мы не раз будем обращаться к простым и наглядным пред-
ставлениям элементарной теории.
Однако указанный подход является весьма несовершенным.
В особенности это проявляется, когда возникает необходимость
в анализе более тонких и сложных эффектов: ионизации и воз-
буждения атомов электронным ударом, возбуждения колебаний
молекул в молекулярных лазерах и т. д. Здесь просто нельзя
обойтись без знания функции распределения электронов. Такое
знание позволяет значительно полнее и детальнее описывать
всевозможные эффекты взаимодействия электронов не только с
атомами и молекулами, но и с самим полем.
Функция распределения электронов по скоростям /(£, г, v)
определяется следующим образом. Величина fdrdv есть число
электронов, находящихся в момент t в элементе объема dr =
«dxdydz около точки г и обладающих компонентами скорости
от их до vx+dvx и т. д., причем dv dvxdvydvz. Интеграл от /
по всем скоростям равен плотности электронов ne(t, г). Посколь-
ку в пространстве имеется выделенное направление электриче-
ского вектора Е, скорость целесообразнее выражать не в декар-
товых, а в сферических координатах. Вектор v характеризуется
155
значением г, углом наклона 'ft к полярной оси Е и азимуталь-
ным углом <р (рис. 7.1). При этом dv = v2dvdQ, где dQ =
= sm#d#d(p — элемент телесного угла около направления v.
От функции /(v) легко перейти к функциям распределения
по абсолютным значениям скорости ф(р) и по энергиям п(е):
п (с) de == ф (i?) dv = v2dv J f (v) dQ. (7.1)
Они также нормированы на плотность электронов пе. Связь меж-
ду ними вытекает из равенства 8 = тцр2/2:
£ / п(г)== (p(v)/mv, ф(р) = и(е)У2тпе. (7.2)
/\ Зная функцию распределения, можно, в прин-
/ | ципе, вычислить любую величину, относящу-
/ j юся к электронному газу. Частота ионизации
• атомов и молекул выражается формулой (4.2).
/ । Аналогичными формулами, но со своими се-
х। чениями выражаются частоты любых неупру-
! гих столкновений, любых реакций. Плотность
\ I полного электрического тока, переносимого,
электронами, есть
Рис.
Рис. 7.1. Вектор
скорости в сфери-
ческих координа-
тах
j< = — е Jv/(v)dv.
Отсюда последуют выражения для проводимо-
сти и диэлектрической проницаемости. Они из-
-— —- ~ т'^ип г т тяя-г z-> ~
(7.3>
бавлены от неопределенности в выборе частоты столкновении
электронов, которая присуща формулам (5.23), (5.24) элемен-
тарной теории.
§ 2. Формулировка кинетического уравнения
Кинетическое уравнение для электронов представляет собой
частный случай общего кинетического уравнения Больцмана для
функции распределения частиц в газе. По своему смыслу оно
выражает баланс числа частиц в точке фазового пространства.
2.1. Уравнение баланса числа частиц. Выделим около фикси-
рованной точки фазового пространства г, v элементарный объем
«кубической» формы. Поскольку нарисовать шестимерный куб
невозможно, изобразим обычный трехмерный (фис. 7.2), но,
призвав на помощь воображение, будем себе представлять ше-
стимерный с координатами одной из «вершин» х, у, z, vx, vv, vz.
В момент t в кубическом объеме с/Г = dxdydzdvxdvydvz находится
/<2Г частиц, так что функция распределения / имеет смысл
плотности в фазовом пространстве.
Даже в отсутствие столкновений число частиц в кубе меня-
ется
няет
вает
156
с течением времени. Обладая скоростью v = г част
свое положение г, а подвергаясь действию силы F истыты'
ускорение w = v и меняет свою скорость v. Частица дви-
убыль частиц
Рис. 7.2. К выводу
уравнения балан-
са числа частиц
жется в фазовом пространстве, и, поскольку плотность f меняется
от точки к точке, через одну «грань» куба в него, вообще гово-
ря, втекает частиц больше или меньше, чем вытекает через
противоположную. Так происходит накопление или
в объеме. Столкновения приводят к тому же.
Одни частицы покидают объем вследствие рез-
кого изменения вектора скорости или гибели,
другие попадают в него после столкновения
или в результате рождения.
Через определенную грань куба (всего их
12), например нижнюю заштрихованную на
рис. 7.2, в 1 с в объем dT втекает
(/v2) zdxdydvxdvydvz
частиц. Индекс z у ^-составляющей плотности
потока fvz означает, что значение потока бе-
рется в точке z оси, «перпендикулярной» гра-
ни. Произведение пяти дифференциалов — это площадь грани
(грань пятимерна). Через противоположную грань (верхнюю за-
штрихованную) в 1 с вытекает
(fvz) z+dzdxdydvxdvydvz
частиц. Разница между втеканием и вытеканием
[ (fvz) * - (fvz)z+iz] dxdydvxdvydvz = - [d(fvz)/dz] dr
дает свой вклад в скорость накопления частиц в кубе (d]!dt}dV.
Аналогичным образом поступаем и с остальными пятью парами
граней.
Что касается столкновений, то их вклад в скорость измене-
ния числа частиц в объеме dV пропорционален самому объему;
обозначим это символически как (г///й^)стйГ. Собирая все члены
и сокращая па общий для всех множитель ^Г, получаем урав-
нение баланса числа частиц:
Оно вполне аналогично обычному уравнению непрерывности при
наличии источников, роль которых играет член столкновений.
В прямоугольных скобках стоит шестимерная дивергенция «плот-
ности потока». Введем в (7.4) производную dfldt вдоль траекто-
рии определенной группы частиц в фазовом пространстве. Это
можно сделать, рассматривая / как сложную функцию времени:
df______Of <9/ . I
'dt' ~~ ~dt ‘ dx dt "I" * ’ ’ dvx dt
=<+^+--- + ^<+
Операция d/dt соответствует субстанциональной производной в
157
гидродинамике. Получим
dt Г 1 дх Г * * ’ Г dvx Г ’ ’ ’ J \dt /ст'
(7-5)
Пары величин vx и х и т. д.— это независимые координаты
в фазовом пространстве, и vx не является функцией х. Если в
обычном пространстве имеется силовое поле F(r), ускорение
w = F/zn — функция координат х, г/, z, но не скорости. Даже
в присутствии магнитного поля лорепцева сила F сю [vH], и со-
ставляющая wx зависит от vy, vz, но не зависит от vx и т. д.
Стало быть, дивергенция «скорости» dvjdx + ... + dwjdvx + ... = 0.
Уравнение баланса (7.5) превращается в равенство
djldt==(dfldt)^
(7.6)
В отсутствие столкновений «плотность»
в определенной группе
частиц не меняется с течением времени вдоль траектории пере-
Рис 7 3 Пояснение теоре-
мы Лиувилля Прямоуголь-
ная в момент t0 область в
следующие моменты t2
превращается в параллело-
граммы той же площади
даннои совокупностью
мещения этих частиц в фазовом про-
странстве, djldt = 0. «Среда» в фазо-
вом пространстве является при этом
несжимаемой.
2.2. Теорема Лиувилля. Проследим
за совокупностью частиц, которые в
момент t занимали небольшой фазовый
объем А Г. В отсутствие столкновений,
число частиц в группе остается не-
изменным: d(JAr)/dt = 0. Но согласно
предыдущему, dfldt = 0. Следователь-
но, йАГ/й/ = О. В отсутствие столкно-
вений фазовый объем, занимаемый
частиц, перемещается в фазовом про-
странстве, деформируется, но по величине не изменяется. Это
положение носит название георемы Лиувилля. Оно наглядно по-
ясняется рис. 7.3, который относится к одномерному случаю
«г, рх, когда фазовое пространство укладывается на плоскости
рисунка.
2.3. Уравнение баланса применительно к электронам в поле.
Не будем рассматривать случаи, когда приложено сильное маг-
нитное поле (§ 9 гл. 3), хотя это и пе составляет труда. В полях
электромагнитных волн лоренцева сила обычно ничтожна по
сравнению с электрической. С F = — еЕ перепишем общее урав-
нение баланса для функции распределения электронов (7.6)
в виде
g- + vV/- — Vv/ = , (7.7)
dt 1 1 т VJ dt ст
где символом Vv обозначен градиент в пространстве скоростей.
Раскроем его теперь в сферических координатах:
V — д _L 1 JL I 1 д
v===Gv'dv ‘ v <9й ‘ е<р v sin О дер’
где ег о Ф — единичные векторы направлений (рис. 7.1). Будем
158
рассматривать только поля, однородные в пространстве. В случае
электромагнитных волн это приближение оправдывается тем, что
амплитуды колебаний электронов обычно малы по сравнению с
дпинами волн (§ 1 гл. 5) В однородном поле зависимость f
от пространственных координат может быть связана лишь с при-
сутствием стенок, диффузионных потоков, вызванных градиента-
ми Чтобы не отвлекалось внимание от нашей основной задачи —
выяснения влияния поля и столкновений на функцию распреде-
ления,— положим, что все в пространстве однородно Влияние
диффузионных потоков можно будет потом учесть простыми ме-
тодами Таким образом,
= Ш . (7 8)
dt т |_ dv v d (cos О) | \dt /Ст*
От угла ср функция f(t, и, '&) не зависит, ибо направление Е —
ось симметрии.
2.4. Разделение столкновений на упругие и неупругие. Зай-
мемся правой частью равенства (7 8). Будем считать газ иони-
зованным слабо и пренебрежем столкновениями электронов с
другими электронами и ионами, учитывая только столкновения
с нейтральными атомами. Это очень важное допущение, оно
чрезвычайно облегчает задачу решения кинетического уравнения,
так как делает его линейным Обычное уравнение Больцмана для
газа нелинейно, так как в его правую часть входят члены, опи-
сывающие столкновения частиц исследуемого сорта друг с дру-
гом В эти члены, естественно, входят произведения функций
распределения сталкивающихся частиц В нашем случае элек-
троны сталкиваются с посторонними частицами — тяжелыми
«покоящимися» атомами, у которых, как мы считаем, «пет» рас-
пределения. Вклады столкновений каждого рода в изменение
функции распределения просто суммируются Разделим все
столкновения на упругие и неупругие-.
/d/j М/Л 4./^.) =I(1\ \ QU). (7 9
Ui/ст \d Лупр M dt/неупр V> f V V
К группе неупругих столкновений, помимо процессов возбужде-
ния атомов и молекул, отнесем рождение новых электронов при
ионизации, возможные процессы исчезновения. Неупругие столк-
новения играют большую роль в формировании энергетического
спектра электронов, но случаются они гораздо реже, чем упру-
гие, и потому практически не влияют на взаимодействие элек-
тронов с полем и на изменения скорости и энергии электронов
под действием поля Неупругие процессы не влияют, следова-
тельно, на установление асимметричной части функции распре-
деления, которая связана с направленным действием поля и ча-
стыми упругими столкновениями Поэтому пока мы не будем
раскрывать выражение Q = (df/dt)^^ и сделаем это лишь
после того, как перейдем от функции распределения по векто-
рам скоростей к распределению по энергиям электронов.
159
2.5. Интеграл столкновений. Так называется слагаемое 1(f),
описывающее действие упругих столкновении Будем считать ато-
мы покоящимися и, кроме того, пока пренебрежем величинами
порядка mjM, полагая М = В этом приближении абсолютное
значение скорости электрона v и его энергия 8 при рассеянии
в точности сохраняются В дальнейшем, когда мы выведем окон-
чательное уравнение для спектра электронов, мы учтем упругие
потери При помощи простого физического рассуждения мы до-
бавим к уравнению дополнительный член упругих потерь, при-
чем этот результат будет точным Между тем если учитывать
изменение и при рассеянии с самого начала, то это не слишком
«существенное уточнение заметно усложняет вывод интеграла
столкновений
Интеграл столкновений Z[/(v)] учитывает изменение числа
электронов с данным вектором скорости v вследствие ухода элек-
тронов в другие точки фазового пространства
с другим вектором v' в результате рассеяния
на атомах, а также вследствие прихода из
всех других точек v' в v Поскольку модуль
скорости, согласно нашему допущению, при
рассеянии не меняется, скорость v достаточно
характеризовать единичным вектором направ-
ления Q Имея в виду, что все функции со-
держат еще в качестве аргумента одно и то
же абсолютное значение скорости р, вместо
/(v) = /(p, й) будем писать просто /(Q) Из
данного телесного угла dQ около рассматри-
ваемого направления скорости Й в 1 с вслед-
ствие рассеяния уходит /(O)dQvc(z?) электро-
нов, где г с — частота столкновений Уходят
возможные другие направления Пусть
ОНИ во все
(v Я, &')dQ—вероятность того, что при столкновении элек-
н летевший в направлении Я, приобретает направление Я'
^интервале dQ' Поскольку какое нибудь направление электрон
Ори рассеянии непременно приобретает, то
J </(Я, Я')с?Я' = 1
Число уходящих электронов можно подробно расписать в виде
/ (Я) dQvc = vc / (Я) dQq (Я, Я') dQ'
й'
Йз ДРУГИХ направлении Я' в данное Я в тот же интервал в 1 с
приходит
vc f f(Q')dQ'q(Q'. Q)dQ
Й'
ектроиов Разность между приходом и уходом и дает нам
160
Прежде чем выписывать разность, заметим, что вероятность
рассеяния из одного направления в другое зависит не от самих
направлений, а только от угла между ними—угла рассеяния 9
(рис. 7.4). Поэтому $(£2, £2,) = g(£2Z, S2)= q(0), и вероятность
можно с равным успехом интегрировать как по конечным £2',
так и по начальным £2 направлениям. Тогда, сокращая на диф-
ференциал dQ, по которому не ведется интегрирования, оконча-
тельно получаем
/ (/) = Vc (0 .( Г/ (Й') - / (Й)1 q (0) dQ'. (7.10)
Я'
Интегрирование здесь ведется по всем направлениям £2' при
фиксированном £2. Уравнение (7.8) с правой частью (7.9), в ко-
торой интеграл столкновений I дается формулой (7.10), а член
неупругих столкновений Q будет раскрыт ниже, представляет
собою искомое кинетическое уравнение.
§ 3. Приближение для угловой зависимости
функции распределения
Кинетическое уравнение, будучи интегро-дифференциальным
по углу й, в математическом отношении очень сложно. Причи-
ной, по которой функция распределения зависит от направления
скорости, т. е. от й, является поле. В его отсутствие распреде-
ление было бы изотропным. Ускоряя отрицательные заряды в
направлении, обратном направлению Е, поле создает избыток
электронов, движущихся в этом направлении, и недостаток —
в противоположном.
3.1. Симметричная и асимметричная части функции распре-
деления. Допустим, что поле не очень сильное и вызванная им
анизотропия функции распределения невелика. Учтем ее прибли-
женно в виде поправки к основной, симметричной части функ-
ции. Если совершать эту операцию математически строго, сле-
(ует представить угловую зависимость /(£, и, й) в виде разло-
жения в ряд по функциям, наилучшим образом описывающим
все усложняющуюся по мере уточнения асимметрию /(й). При-
менять для разложения нужно только систему ортогональных
и нормированных функций. Для угловой зависимости таковой
является система полиномов Лежандра: Pq = 1, Pi =cosй и т. д.
II порядке приближения ограничимся первыми двумя членами
разложения
f(t, v, й) = /о(£, ^) + /1(^ ^)соэй, (7.11)
I де /о и /1 — новые искомые функции, для которых необходимо
сог । а вить уравнения.
Новые функции имеют определенный физический смысл. Пер-
ной из них, симметричной частью, определяется энергетический
(Нскгр электронов. Согласно (7.1)
n(&)dz = q(v)dv = inv2fQ(v)dv. (7.12)
161
И l< >. I Г. Райзер
Асимметричная часть Дсозй1 определяет электрический ток.
Вследствие осевой симметрии /(v) ток направлен вдоль поля.
Согласно (7.3), (7.11)
it = — е J J vcos2r&f1-23W2dv sinOzW’ = — е § v3f±dv. (7.13)
Приближение (7.11) допустимо только в случае достаточно
слабой анизотропии функции распределения, т. е. при не слиш-
ком сильных полях. Количественный критерий понятия «не
слишком сильное» станет ясным после того, как мы найдем
поправку /1 к основной части / и потребуем, чтобы /1 < /о
(п. 5.1). Лоренц сформулировал кинетическое уравнение дтя
электронов в постоянном поле и на основе приближения (7.11),
которое называют лоренцевым, уточнил формулу (3.7) для про-
водимости.
3.2. Уравнения для функций /0, /х. Проще всего эти функции
вывести, воспользовавшись методом «моментов». Исходное урав-
нение для f умножается на полипом Лежандра и интегрируется
по углам с учетом свойств полиномов. В данном случае доста-
точно сделать это дважды: один раз просто проинтегрировать
уравнение (7.8) по телесному углу cZQ, так как нулевой полином
Ро = 1, а второй раз — умножить (7.8) на Pi=cosf> и снова
проинтегрировать. В результате первого интегрирования (точнее,
усреднения, т. е. операции j cZQ/4n с учетом того, что cos й = 0^
cos2 й = 1/3, sin2 й = 2/3) найдем
Ч
dt
еЕ I i
m \ 3 dv "Г"
2/Д
Й = Ш).
Интеграл ) IdQ в правой части автоматически обращается
в нуль. Он представляет собою изменение в результате упругих
столкновений числа электронов, движущихся во всех направле-
ниях. Но упругие соударения не меняют полного числа элек-
тронов. Член неупругих столкновений линеен по /, и вообще ре-
зультат неупругих соударений от направлений скорости не за-
висит, а зависит только от энергетического спектра. Поэтому
понятно, что он превратился просто в функцию от симметричной
части /о- Преобразовав выражение в скобках, перепишем полу-
ченное уравнение в виде
Оп _ еЕ 1 д(р2Л)
(9Z тп Зу2 dv
+ <?(U
(7.14)
При втором усреднении кинетического уравнения с весом
cosй получим
где мы пока просто переписали выражение (7.10), не используя.
162
(7.11), а вкладом неупругих столкновений в правую часть пре-
небрегли по сравнению с вкладом упругих.
Займемся правой частью (7.15). Внутренний интеграл по
берется по всем направлениям й' при фиксированном й. Но
с/й'
при
интегрировании по углам й' вовсе не обя-
зательно выбирать в качестве полярной; оси
вектор Е, как это было сделано при состав-
лении исходного кинетического уравнения.
В данном случае гораздо удобнее напра-
вить полярную ось по Й (рис. 7.5) и опи-
сывать направление О' углами 0 и ф', от-
считывая азимут ф' от фиксированной пло-
скости, которая проходит через векторы й рис 75 Направле-
и Е. В этих координатах элемент телесного НИя напряженности
угла поля и скоростей до
и после рассеяния
dQ' dq/ sin OdO,
что очень удобно, поскольку сомножитель q под знаком инте-
грала есть функция как раз 0. Подставив теперь (7.11), запи-
шем внутренний интеграл
J = J |/ (Q') — / (Й)] q (0) dQ' = fi\ (cos О' — cos О) q (0) dq' sin 0d0,
где угол О фиксирован. Подставим сюда cos О', выраженный
по известной формуле сферической тригонометрии,
cos О' = cos О cos 0 + sin 0 sin 0 cos ф'.
Учитывая, что при интегрировании по ф' слагаемое с созф' ис-
чезнет, находим
J = cos О i (cos 0 — 1) q (0) с/ф' sin OdO = cos О (cos 0 — 1).
Здесь cos 0 — по определению средний косинус угла рассеяния,
так как cos 0 усредняется в соответствии с вероятностью рассея-
ния д(0), нормированной по углам на единицу. Вводя эффектив-
ную частоту столкновений = vc (1 — cos 0) (заметим, что мы
только что проделали строгий вывод этой величины), подстав-
ляя внутренний интеграл J в (7.15) и проделывая еще интег-
рирование по dQ, получаем второе из искомых уравнений:
dfi , , __ еЕ
~t + Vm/X - —
(7.16)
dv ’
Итак, вместо интегро-дифференциального по углам уравне-
ния (7.8) мы получили два дифференциальных уравнения для
функций /о и /1, аппроксимирующих истинную функцию рас-
пределения равенством (7.11). Эти уравнения справедливы для
любой зависимости E(t)—и для постоянного поля, и для пере-
менного.
11*
163
§ 4. Уравнение для энергетического спектра электронов
4.1. Приближенное интегрирование уравнения для Д. Для
того чтобы продвинуться дальше, необходимо конкретизировать
зависимость поля от времени. Рассмотрим гармоническое поле
£ = £*0 sin Точное решение системы (7.14), (7.16) найти, ко-
нечно. невозможно, поэтому поступим следующим образом. По-
правка /1 к симметричной части функции распределения связана
с действием поля, которое периодически меняет свое направле-
ние. С той же частотой осциллирует и поправка: сначала боль-
ше электронов идет в одном направлении вдоль поля, через пол-
периода — в противоположном.
Следовательно, согласно (7.14) зависимость основной, симмет-
ричной функции /о от времени складывается из двух частей.
С одной стороны, это сравнительно медленная зависимость, свя-
занная с установлением энергетического спектра электронов
вследствие различных неупругих процессов, рождения и исчез-
новения электронов, а также, конечно, и набора энергии от поля.
Поскольку fi тоже гармоническая функция и она пропорцио-
нальна £о, первый член в правой части (7.14) имеет среднюю
за период составляющую, пропорциональную Е%, и осциллиру-
ющую составляющую. Средняя составляющая и обеспечивает
набор энергии. С другой стороны, /о содержит осциллирующую
часть, которая вызвана осциллирующей составляющей первого
члена в правой части (7.14). Она, как «мелкая рябь», наклады-
вается на медленное изменение /о(О- Ясно, что когда мы ин-
тересуемся энергетическим спектром электронов при достаточно
больших частотах (критерий — в п. 5.2), нас не должны волно-
вать колебания спектра в течение периода, т. е. указанная
«мелкая рябь». Физический интерес представляет сглаженная
функция </0>, усредненная за период колебаний поля.
При интегрировании уравнения (7.16) подставим усреднен-
ную за период функцию (dfjdv'). Высокочастотная составляющая
дала бы в /1 член высшего порядка по Е. Пренебрегая медлен-
ной зависимостью от времени величины (df^dv} по сравнению
с sin (of, проинтегрируем (7.16) как линейное уравнение, в кото-
ром <d/0/dz;> не зависит от времени. Получим
/1 =-----(® cos - Vm sin “0- (7.17)
+ vm) Х p z
Это выражение можно представить в виде
= a = arct< (7Л8)
т у со + \'~т т
Видно, что fi Е осциллирует с частотой со, но сдвинуто по
фазе относительно поля.
164
II предсиьиом c.iiy'iae <ii,ieof,ii > чтчог or 3> v,„ сдвиг по фазе
а л л/2 и
ej:„ z
Vid) \ dv /
Л
cos (oZ- — и 4 / cos coZ.
\ dv /
Но порядку величины df^dv ~ fo/v, где v — какая-то характер-
ная средняя скорость хаотического движения. Согласно (5.2)
еЕъ1тп($ = и представляет собой амплитуду колебательной скоро-
сти электрона в осциллирующем поле, так что по порядку ве-
личины
/1 ~(M/p)/o-
(7.19)
В противоположном предельном случае низких частот со2 <С v^,
сдвиг по фазе а мал и
/1
mvm \ д» /
sin coZ —>
со—*0
еЕ dfn
mvm dv’
Легко видеть, что то же самое получается непосредственно из
уравнения (7.16), если с самого начала считать поле постоян-
ным. Асимптотическое постоянное значение Д, которое устанав-
ливается примерно через время одного столкновения, есть
= еЕ df0 рд
1 frivm dv v '°’
(7.19')
где согласно (3.4) = eE!mvm — абсолютное значение скорости
дрейфа электронов. Формулы (7.19) дают критерий малости
/1//о (И. 5.1).
4.2. Уравнение для функции /0.* Теперь, после того как мы
выразили поправку /] через основную функцию /о, остается сде-
лать последний шаг — подставить ее в уравнение (7.14), и тогда
мы получим уравнение для симметричной части функции рас-
пределения, которая однозначно связана с энергетическим спект-
ром. В случае гармонического поля подставим (7.17) в (7.14}
и усредним полученное уравнение по времени за период осцил-
ляций для того, чтобы избавиться от «ряби» и выделить «мед-
ленную» временную зависимость спектра, которая только и пред-
ставляет интерес. Замечая, что
<cos coZ sin cdZ> = 0, <sin2 cdZ> = 1/2,
и опуская знак усреднения < > у /о, находим уравнение для
функции /o(Z, к).
дЦ_ _ J_ d_ е2 Е2 %
dt ~ dv зт2 (о2 + dv
(7.20)
где мы подставили вместо амплитуды Eq среднеквадратичное по-
ле E = EqI^2. В случае постоянного поля при подстановке
(7.19') в (7.14) получается то же самое уравнение (7.20), но с
165
co = О Иными словами, возможен точный предельный переход
от случая гармонического поля к случаю постоянного, если при
со О заменить среднеквадратичное поле постоянным, что, кста-
ти сказать, и интуитивно представляется естественным
4.3. Уравнение для функции я(е). Если в уравнении (7 20)
перейти к новой независимой переменной 8 = тг;2/2, с?8 = mvdv
и заменить функцию /oG, f) на функцию распределения по
энергиям n(t, б) с помощью соотношения (7 12), найдем урав-
нение для энергетического спектра
dt дг I дъ I 1 v
_ 2e2Ei vm _ е2^о
~ Зт + v2m Зт ш2 +
(7 21)
Случай постоянного поля также получается, если положить со =
= 0 и посчитать среднеквадратичное поле постоянным
4.4. Диффузионный характер уравнения. Раскроем производ-
ную от пе” 1/2 в уравнении (7 21) и перепишем его, введя обо-
значения для определенных комбинации величин
dn/dt = —dJ1дг + (Z J — —3)дп!дг + п°Ы,
^5= Ле, <Н = А[2 (722)
Уравнение (7 22) по своей структуре совершенно аналогично
уравнению одномерной диффузии частиц В самом деле, 8—это
координата, п — плотность частиц, J — поток, Q — источник, 2D —
коэффициент диффузии, который, правда, зависит от «точки»
(такое тоже можно себе представить скажем, плотность основ-
ного газа через который диффундируют частицы, меняется по
координате) °U — скорость «кинетического» потока, т е систе-
матического движения в одну сторону, например «сноса», кото-
рый может быть вызван течением среды
Физический смысл диффузионного характера набора энергии
в поле т е диффузионного движения электрона по «энергетиче-
ской оси», весьма нагляден Вп 33 гл Зин 25 гл 5 гово-
ритесь о том что в индивидуальных столкновениях электрон мо-
жет как приобретать энергию от поля, так и терять ее причем
порциями, по порядку величины равными тгк, где v — скорость
хаотического движения, а и — скорость направленного движения,
вызванного полем В высокочастотном случае и — амплитуда ко-
лебательной скорости электрона, в постоянном поле и = —
скорость дрейфа Поскольку приобретения и потери в среднем
происходят почти равновероятно изменение энергии электрона
имеет стохастический характер блужданий по оси 8 Коэффи-
циент обычной диффузии, который появляется при рассмотре-
нпи одномерных блужданий частицы, равен примерно D & Axz/x,
где Ах — скачок по оси х, а т — среднее время между скачками.
166
Применительно к нашему случаю
Ф & (mvu)2vm.
Подставляя сюда и = еЕо/та) в высокочастотном случае со2 >*
или и = v^ = eEim\'m (cnopocib дрейфа) в низкочастотном случае
Vm и учитывая, что 8 = mv2]2, получим для этих предель-
ных случаев коэффициент диффузии, определенный формулами
(7.22), (7.21) (с точностью до несущественного числового мно-
жителя) .
Физический смысл имеет и скорость «сноса» °U. Положитель-
ный кинетический поток, направленный в сторону увеличения 8,
связан с преобладанием набора энергии при столкновении по
сравнению с ее отдачей. В п. 3.3 гл. Зин. 2.5 гл. 5 мы видели,
что в среднем по многим столкновениям прирост энергии боль-
ше, чем отдача на величину Д8£ ~ ти\ которая в v/u раз мень-
ше самих средних скачков в ту или другую сторону тип. Ско-
рость систематического движения вверх по энергетической оси
<U ~ A8£Vm и в самом деле порядка
*U ~ ти2хт ~ (mvuyxjmv2 ~ We,
как было получено формальным путем при выводе формулы
(7.22).
4.5. Учет упругих потерь. После сделанных замечаний относи-
тельно диффузии по энергетической оси легко ввести в уравне-
ние для энергетического спектра член, описывающий упругие по-
тери. Ведь упругие потери также вызывают поток по энергетиче-
ской оси, причем всегда направленный в сторону уменьшения 8.
Средняя энергия, которую электрон теряет при упругом столкно-
вении, как было вычислено в п. 2.3 гл. 2, равна
А8упр = (2пъ/М) (1 — cos 9)8.
На столько электрон смещается «вниз» по оси 8 при каждом
столкновении. Время между столкновениями тс — v^1. Следова-
тельно, соответствующая скорость движения «вниз» равна
%пР = — Д8упр/тс = — \(2m/M)vmz,
а отвечающий ей кинетический поток есть Его и добавим
к потоку ] в формуле (7.22). Возвращаясь теперь от (7.22) обрат-
но к исходным уравнениям (7.20), (7.21), запишем их уже с уче-
том члена упругих потерь:
% = 12 dt р2 dv в2 F2 vmv2 dfQ . m 3 \ n (4 \ (n oq\ 3mi w2 + v^, dv + MVmP ^»J + (7-23^
dn д / л 3/2 д п 2т \ \
— = — Аг — —7- + — zvmn + Q (п),
dt д& I д&81/2 1 М I v v z’
. vm
Зт ы2 + <
(7-24)
167
Любопытно, что наше простое рассуждение привело к точному
учету упругих потерь. Если бы мы с самого начала составляли
интеграл столкновений с учетом конечности массы атома, мы по-
лучили бы в результате те же самые уравнения (7.23), (7.24).
4.6. Слагаемое неупругих столкновений. Раскроем содержание
величины Q, в которую мы включили все процессы, не связанные
с действиями поля и упругих столкновений. Уход электронов в 1 с
в 1 см3 из энергетического интервала r/s, вызванный актами воз-
буждения и ионизации атомов, равен n(s}dsx* (е) и га(8)с?8Уг(е),
где v*(e), уг(с) — частоты возбуждения соответствующего уровня
и ионизации при данной энергии электрона 8. В акте возбуждения
электрон теряет энергию Е*, равную потенциалу возбуждения,
плюс еще небольшую энергию, которая идет на сообщение атому
такой скорости, чтобы суммарный импульс электрона и атома не
изменялся. Эта дополнительная потеря энергии, как и при упру-
гом рассеянии, очень мала; по сравнению с Е* ею можно пре-
небречь. Если неупругое столкновение испытал электрон, обла-
давший энергией 87 = 8 + Е* в интервале dsf = ds, то после поте-
ри он попадает в рассматриваемый интервал ds около точки 8.
Таким образом, слагаемое в Q(n), связанное с возбуждением
определенного уровня, можно приближенно представить в виде
Q*(n) = — n(8)v*(e)+ n(8 + A'*)v*(8 + /?*), (7.25)
причем v*(e)=0, если 8 < E*. Такого же характера выражения
описывают и возбуждение колебательных уровней в молекулах.
Полная величина Q представляет собой сумму такого типа сла-
гаемых по всем уровням атомов и молекул, которые играют роль.
Сложнее выглядит слагаемое <Z(ft), описывающее ионизующие
столкновения. Пусть электрон обладает энергией с'>7. На от-
рыв электрона от атома он затрачивает энергию I, остаток s' — I
распределяется между ним и вновь рожденным (передача энер-
гии иону ничтожна мала). Пусть Ф(е', 8)^8 — вероятность того,
что вырванный из атома электрон получит энергию от 8 до 8 +
+ de, т. е.
ь'—I
J Ф (8', 8) С?8 = 1.
О
В тот же интервал попадает и ионизующий электрон, если
новый получает энергию от 8х — I — 8 — ds до 8 х — I — 8. Вероят-
ность 1акого события есть Ф(8Х, s' — I — s)ds. Составив Qtds из
членов прихода и ухода электронов в интервале от s до s + ds и
поделив на ds, найдем
со
(?г — П (b) Уг (8) + | П (8') Уг(е') [Ф (в', б) Ф (b', S' — I — 8)] ds'.
e+J
(7.26)
Выражение (7.26) приобретает форму (7.25), если допустить, что
168
ионизационный переход, как и возбуждение, принадлежит диск-
ретному спектру. Действительно, если новые электроны рождают-
ся с одинаковой энергией 8о и е' > / + 8о, то Ф (е', 8) = б (8 — 8о),
где б — дельта-функция. В этом случае с Л = I + 80
оо
Qi = — п (е) Vj (е) + п (е 4- Ц) уг (е + + 6 (е — е0) п (е') Vj (s') de'.
h
(7.26')
Третий дополнительный член описывает источник новых элект-
ронов.
Потери, связанные с рекомбинацией или прилипанием элект-
ронов, учитываются в Q элементарно, например слагаемым —
72(8)va(8), где va(s)—частота прилипаний к атомам или мо-
лекулам.
4.7. Пространственная диффузия электронов. Ее можно учесть
строго, если оставить в левой части исходного уравнения (7.8)
член v grad /, который присутствует в (7.7). Мы этого не сдела-
ли, чтобы не загромождать выкладок и сосредоточить внимание
на эффектах взаимодействия с полем. В окончательном уравне-
нии для спектра диффузионные потери электронов можно учесть
приближенным образом, включив в Q слагаемое типа
Qd = — п(8)^Де),
где Vd = D/A2—«частота диффузии», т. е. величина, обратная
характерному времени диффузионного ухода электронов из рас-
сматриваемого объема; D — и2/3^т — коэффициент диффузии
(в обычном пространстве!), Л— характерная диффузионная дли-
на (§ 5 гл. 5).
§ 5. Критерии справедливости уравнения для спектра
5.1. По величине поля. Лоренцево приближение (7.11), кото-
рое было положено в основу вывода уравнения, справедливо при
слабой асимметрии функции распределения /(v), когда /iZ/o^l.
Согласно (7.19), (7.19z) так бывает, когда направленная вдоль
поля скорость электрона (амплитуда колебательной скорости и в
случае быстроосциллирующего поля или дрейфовая кд в случае
постоянного) гораздо меньше хаотической скорости v. Члены с
высшими гармониками в разложении / по полиномам Лежандра
пропорциональны соответствующим степеням отношений u/v или
Кд/к. Эти отношения и служат теми малыми параметрами, по
которым производится разложение функции распределения / в
ряд. В большинстве практически интересных случаев указанные
условия выполняются. В самом деле, в однородном постоянном
поле, когда электрон при столкновении теряет лишь малую долю
своей энергии б, vjv ~ ]/б < 1 (см. (3.16)). Совершенно аналогич-
169
ное соотношение и/г;~Уб вытекает и из формул (5.2), (5.12)
для быстроосциллирующего поля.
Условия нарушаются, и функция распределения становится
существенно асимметричной (электроны движутся преимущест-
венно вдоль поля), когда электрон при столкновении теряет зна-
чительную часть своей энергии (формально 6 ~ 1). Так происхо-
дит, когда на длине пробега Z или в колебаниях электрон при-
обретает от поля энергию, большую энергии возбуждения элект-
ронных уровней или ионизации атома, скажем eEl I. Такие
ситуации встречаются в чрезвычайно сильных полях: в катодном
слое тлеющего разряда, при фокусировании сверхмощных опти-
ческих импульсов. Уравнения (7.23), (7.24) имеют границы при-
менимости и со стороны малых Е. В очень слабом поле «темпера-
тура» электронов может оказаться сравнимой с температурой
газа Г, которая считалась равной нулю. Кинетическое уравнение
с Т ¥= 0 рассматривалось Б. И. Давыдовым (1936 г.).
5.2. По частоте поля. В ходе вычислений в п. 4.1 мы игнори-
ровали модуляцию спектра с частотой поля со, усреднив симмет-
ричную часть функции распределения /о по времени за период
осцилляций. Это допустимо, если поле осциллирует быстро по
сравнению с временем установления энергетического спектра
электронов. Тогда на набор энергии в поле и на спектр оказывает
влияние только среднеквадратичное поле. Иными словами, усло-
вием применимости данного приближения является неравенство
со > vu = VmS, где ти = Vu1 — время релаксации спектра, равное ха-
рактерному времени для передачи энергии от электронов молеку-
лам (п. 3.7 гл. 3). Указанное неравенство лучше выполняется
в атомарных газах, чем в молекулярных. В СВЧ и, тем более,
в оптическом диапазоне частот оно выполняется практически
всегда. В ВЧ диапазоне для атомарных газов — почти всегда;
в случае же молекулярных газов — далеко не всегда. Например,
в азоте ~ 4,2 109 р с-1, б = 2,7 • 10-3, vu ~ 1,1 • 107 р с-1;
на частоте / = 13,6 МГц, ю = 0,85 • 108 с"1 приближение справед-
ливо лишь при р <С 10 торр.
В противоположном предельном случае со < vm6 энергетиче-
ский спектр и средняя энергия электронов пульсируют вместе с
колебаниями поля, «следя» за его сравнительно «медленными»
изменениями. В разрядной практике применяется диапазон / ~
~ 10 кГц, например в лазерах на «переменном токе» (п. 4.6
гл. 16). В этом случае поле является квазистационарным. Пре-
дельный переход от переменного поля к постоянному в п. 4 1
путем наложения более мягкого условия <о < vm вместо со <
< vm8 был сделан чисто формально.
5.3. По пространственной однородности. Когда группа электро-
нов дрейфует в постоянном поле, энергетический спектр в ней
устанавливается на длине релаксации энергии Ли~1/18
(п. 3.7 гл. 3). Поэтому постоянное поле должно быть однород-
ным на такой длине, иначе спектр будет зависеть не только от
170
значения поля, но и от распределения потенциала в простран-
стве (такая нелокалъностъ спектра проявляется в катодном слое
тлеющего разряда). Квазистационарное в смысле ю < vu поле в
отношении длины волны X заведомо однородно, так как Л = Х/2л^>
Ли(с Au. Влиянием вариаций поля на длине волны на
энергетический спектр электронов в электромагнитных волнах
больших частот часто можно пренебречь, но «бдительности» те-
рять не следует.
5.4. По степени ионизации. Одно из важнейших допущений,
сделанных при рассмотрении кинетического уравнения, это —
пренебрежение столкновениями электронов друг с другом, бла-
годаря чему уравнение является линейным. Межэлектронные
взаимодействия, как и в обычном газе, способствуют установлению
максвелловского распределения (максвеллизации электронов).
Именно так обстоит дело в достаточно сильно ионизованной, плот-
ной низкотемпературной плазме. При столкновениях друг с дру-
гом электроны обмениваются порциями энергии, которые порядка
самих энергий. Большие порции, также сравнимые с самими
энергиями, теряют электроны при неупругих столкновениях с ато-
мами и молекулами. Значит, в тех случаях, когда возможны
неупругие удары, межэлектронными столкновениями можно пре-
небречь, если их частота vee = (п. 4.3 гл. 2) гораздо мень-
ше частоты ^неупр. При энергиях электронов е ~ 5—10 эВ и боль-
ше, достаточных для электронного возбуждения молекул и ато-
мов (и ионизации), условие vee < хПелпр выполняется вплоть до
весьма значительных степеней ионизации ne/N ~ 10-4—10“3. Та
же оценка справедлива и при мецыпих энергиях (е ~ 1—5 эВ)
в случае молекулярных газов, где электроны возбуждают колеба-
ния молекул. К этому факту можно подойти и с другой стороны:
неупругие столкновения сильно нарушают максвелловское рас-
пределение электронов, уменьшая относительное число энергич-
ных электронов.
Иначе обстоит дело в атомарных газах при энергиях ниже
потенциала возбуждения Е* атомов (в инертных газах Е* ~
~ 10эВ). Здесь, в особенности в тяжелых газах, действуют толь-
ко очень слабые упругие потери энергии, и обмен энергией при
межэлектронных столкновениях активно включается в процесс
формирования спектра при гораздо меньших степенях ионизации.
В области энергий 8 < Е* условие применимости линейного кине-
тического уравнения выглядит примерно так: vee <С
ne/N < 10“6М, где А — атомная масса. При не очень слаб )й
ионизации в стационарных условиях спектр в зоне 8 < Е* может
приближаться к максвелловскому, и только при 8 > Е* он спа-
дает гораздо быстрее последнего. Но рассмотрение этих эффектов
требует усовершенствования кинетического уравнения путем угге-
та межэлектронных столкновений.
171
§ 6. Сравнение некоторых выводов,
вытекающих из кинетического уравнения,
с результатами элементарной теории
6.1. Проводимость и диэлектрическая проницаемость. Подста-
вим в (7.13) /1 по формуле (7.17). Та часть тока, которая нахо-
дится в фазе с полем, т. е. пропорциональна sin art и £', представ-
ляет собой ток проводимости. Слагаемое, пропорциональное cos со£,
т. е. dE/dt,— это ток поляризации. Сопоставим результат с фено-
менологической формулой (5.20) и приравняем по отдельности сла-
гаемые, пропорциональные sin и cos со£, подобно тому как это
было сделано в § 4 гл. 5. Полученные таким путем строгие выра-
жения для высокочастотных проводимости ow и диэлектрической
проницаемости имеют вид
— 4jtg2 f
“ 3m .) (у2 _|_ v2
0 w
dv /
(7.27)
dv.
C(D ---
16л2е2 f v3
3m w2 v2
0
В общем случае они зависят от энергетического спектра элект-
ронов. Однако если частота столкновений vm(v) не зависит от
скорости, содержащие vm множители можно вынести за знак
интеграла. Интегрируя оставшееся выражение по частям и при-
нимая во внимание, что электронов с бесконечной энергией нет,
т. е. /о 0 при v -* а также условие нормировки функ-
ции fo(v).
(7.28)
j* 4л^2 dvj^ (у) =
о
получаем формулы (5.23), (5.24) элементарной теории. Послед-
ние справедливы при любом спектре, если vm(y) = const. Прово-
димость в постоянном поле автоматически получается из (7.27),
если положить со = 0:
(7.29)
__ 4л е2 Г
3m J
v3 f
—TV--------т2 }dv.
vm(r) \ dv)
(7.30)
На практике, конечно, как правило, пользуются элементарны-
ми формулами (5.23), (5.24), (5.27), подбирая из тех или иных
соображений наиболее правдоподобное для реального спектра
значение характерной частоты столкновений. Но когда известен
спектр, формулы (7.27), (7.28), (7.30) позволяют осуществить
правильный выбор этой величины. Ими пользуются в точных
теориях и для установления поправочных коэффициентов к эле-
ментарным формулам.
172
6.2. Скорость изменения средней энергии спектра. По опреде-
лению средняя энергия электронов равна
ОО / ОО \ --1 оо
8 = гп (г) с/г j j* п (г) de I = j* гп (г) с/г. (7.31)
о ' о / о
Составим уравнение для скорости ее изменения, отвлекаясь от
влияния неупругих потерь и упитывая только действия поля и
упругих потерь. Для этого умножим на 8 уравнение (7.24), а еще
лучше (7.22) с добавочным слагаемым ft^Z/ynp в выражении для
потока 7, и проинтегрируем по всему спектру. Член неупругих
столкновений Q опустим. Проинтегрировав два раза по частям с
учетом условий п О, J 0 при 8 00 и поделив на пе, получим
de у ТтГ/ \ / vm \ ----\ п ээ\
rt = d? + - мм' v7>32)
где черта означает усреднение по спектру. При vm(8) = const это
выражение в точности совпадает с формулой (5.11) элементарной
теории для скорости изменения энергии «среднего» электрона
(поскольку речь идет об одних лишь упругих потерях, в (5.11)
& = 2т/М). Снова условие постоянства частоты столкновений
обеспечивает строгую правильность элементарной теории.
6.3. Законы подобия. Соотношения подобия для скорости дрей-
фа (п. 1.3 гл. 3), средней энергии электронов (п. 3.5 гл. 3, п. 2.4
гл. 5), ионизационного коэффициента (п. 1.4 гл. 4) и других ве-
личин находят в кинетическом уравнении свое подтверждение и
строгое обоснование. Рассмотрим сдучай постоянного поля со = 0.
Частоты любых неупругих столкновений, как и упругих, пропор-
циональны плотности газа N. Допустим, что пространственных
градиентов нет. Рекомбинация при малой степени ионизации роли
не играет. Тогда Q ~ N, Поделив уравнения (7.23) и (7.24) на N,
видим, что функции распределения /о(^) и я(е) содержат пара-
метры Е и N только в виде комбинации E/N. В нестационарном
случае
n(t, 8, Е, N)=n(Nt, 8, E/N).
При увеличении плотности газа времена пропорционально сокра-
щаются, чго и естественно, ибо все процессы связаны со столкно-
вениями.
В поле больших частот со2
n(t, 8, Е, N, со) = n(Nt, 8, Е/ы),
т. е. стационарный спектр от плотности вообще не зависит и опре-
деляется отношением Е/ы. В приближении постоянства частоты
столкновений vm(v) = const и при условии со > vm6 (п. 5.2) кине-
тическое уравнение и спектр для переменного поля со средне-
квадратичной величиной Е или амплитудой Eq = V2£’ тождествен-
173
ны уравнению и спектру в постоянном эффективном поле
£Эф = Е [4./(®2 + Vm)]1/2 < Е. (7.33)
Это позволяет иногда при исследовании разрядов в быстропере-
менных полях пользоваться имеющимися в большом количестве
расчетными и экспериментальными данными, полученными для
постоянных; для этого нужно сделать соответствующий пересчет
по формуле (7.33).
§ 7. Стационарный спектр электронов в поле
при действии одних упругих потерь
Результаты п. 6.1, 6.2 в общем свидетельствовали о высокой
эффективности элементарной теории. Теперь рассмотрим пример,
который демонстрирует ее несовершенство, ограниченность воз-
можностей по сравнению с теми, которые предоставляет кинети-
ческое уравнение.
Представим себе ионизованный газ, находящийся в перемен-
ном или постоянном поле, и отвлечемся от действия неупругих
столкновений. Рассмотрим стационарный спектр электронов, кото-
рый в конце концов устанавливается в результате точной компен-
сации набора энергии под действием поля и упругих потерь.
Нельзя сказать, чтобы такая ситуация была чересчур абстрактной.
Нечто подобное реализуется, если одноатомный (чтобы не было
возбуждения молекулярных колебаний) слабоионизованный газ,
занимающий большой объем, находится в слабом поле. Из-за
больших размеров диффузионные потери электронов невелики,
тем более, что при сколько-нибудь заметной ионизации диффузия
электронов имеет амбиполярный характер (§ 6 гл. 3) и происхо-
дит гораздо медленнее свободной. Для компенсации небольших
потерь электронов, что необходимо для поддержания стационар-
ного состояния, достаточно медленной ионизации, которую и обес-
печивает сравнительно слабое поле. Энергии электронов, следо-
вательно, в основном небольшие, и очень мало электронов обла-
дает энергиями, достаточными для возбуждения и ионизации
атомов. Значит, влияние неупругих столкновений на спектр не
очень существенно.
7.1. Что дает элементарная теория. Посмотрим сначала, что
дает применительно к данной ситуации элементарная теория,
в которой рассматривается поведение одного, «среднего» электро-
на и состояния всех электронов считаются одинаковыми. Энер-
гия электрона 8 меняется во времени по закону (5.11) с
б = 2тп/М-
— — (A8# А8уПр) vm
е2Е2 2m
--------- — — р
m(w2 + vm) М
\'т-
Приобретение энергии от поля в одном столкновении АеЕ от s
не зависит, упругая потеря А8упр 00 е. Следовательно, энергия
174
электрона достигает
7Х 8к Дбупр,
величины 8тах, определяемой равенством
М е2Е2
Ещах — о / 2 ।
(7.34)
и потом остается постоянной. Действительно, если по случайной
причине энергия электрона станет меньше 8тах, он сразу начнет
набирать энергию, dz/dt > 0; превысив етах, электрон будет те-
рять энергию (dz/dt < 0). Стационарному (и притом устойчивому)
состоянию соответствуют d&/dt = Q и делъта-об разная функция
распределения: все электроны имеют одинаковую энергию 8 =
= Етах. В силу исходного предположения значение 8тах должно
быть меньше потенциалов возбуждения, а тем более — потенциа-
ла ионизации атомов, иначе все будут определять не «упругие»,
а «неупругие» потери. Но тогда возникает вопрос, как же все-
таки происходит ионизация, если в газе нет ни одного электрона,
обладающего достаточной энергией? Ведь какая-то, пусть медлен-
ная, ионизация должна протекать, иначе вследствие всегда су-
ществующих потерь все электроны постепенно исчезнут, т. е. не
будет стационарного состояния. Элементарная теория здесь ста-
новится в тупик.
7.2. Решение кинетического уравнения (7.23). В стационар-
ном случае djo/dt = 0 и без учета неупругих процессов ((? = 0)
выражение в скобках (7.23) («поток»)—константа. Но при
[; -> °° /о и поток отсутствуют, значит, эта константа равна нулю.
Потока нет в каждой точке энергетической оси; при каждой
энергии 8 набор энергии от поля в точности компенсируется упру-
гими потерями. Второе интегрирование (7.23) дает
/о - Сехр
y(w2 + v2m)dv
Me Е *J
0
(7.35)
где постоянная интегрирования С определяется условием норми-
ровки (7.29). Функция распределения (7.35) приобретает особен-
но простую форму в случае vm (v) = const, когда она получается
максвелловской:
/о -= С ехр
3m2(<o2 + v^) ml?
Ме2Е2
(7.36)
с температурой Те и средней энергией 8, равными
7 __ 3 ьт _ м _
г — KI е — 2 2 \ 8та\.
J О) + )
(7.37)
Средняя энергия совпадает с единственной энергией электрона
Етах, которую дает элементарная теория. Точное совпадение про-
изошло более или менее случайно, при других предположениях
Относительно функции vm(v) совпадение 8 с 8тах получается лишь
Но порядку величины.
175
Как видим, «истинный» спектр размыт около 8тах; в нем при-
сутствуют электроны с большими энергиями («хвост» максвеллов-
ского распределения), которые обеспечивают ионизацию и под-
держание стационарного состояния; есть и электроны с 8 < smax.
Причина появления в стационарном спектре электронов с отлич-
ными от 8щах энергиями связана с тем, что в кинетическом урав-
нении строго учтено силовое воздействие поля на электроны, ко-
торое, как мы видели в п. 2.5 гл. 5, допускает возможность боль-
ших приобретений анергии, превышающих среднее А8е, а также
отдачу больших порций энергии при столкновениях. Энергичные
электроны с 8 > 8шах «живут» за счет таких «индивидуальных»
приобретений As > Ase, медленные, с 8 < smax,— благодаря боль-
шим «индивидуальным» потерям.
7.3. Распределение Дрюйвестейна. В физике газового разряда
чаще рассматривается другой частный случай распределения
(7.35), в котором не зависящей от энергии считается не частота
столкновений, а длина свободного пробега электрона I = vhm,
т. е. транспортное сечение. В этом предположении
и интегрирование в (7.35) дает
/о = С ехр
Зт3
(р4 f-2zAo2Z2)
(7.38)
s
Рис. 7.6. Функции распределе-
ния электронов по энергиям
Максвелла пм(&) и Дрюйвес-
теина гсд(е)
Это так называемое распределение Маргенау (1946 г.), на кото-
ром мы останавливаться не будем.
В случае постоянного поля распределение Маргенау превра-
щается в распределение Дрюйвестейна (1930 г.):
/0 = Сехр(— ъй = еЕ1, (7.39)
\ ео '
которое в свое время было получено прямым путем. Параметр 80
представляет собою энергию, которую электрон приобретает от
поля на длине пробега. Средняя энер-
гия 8, как следует из (7.39), при-
обретается примерно на ^М/тп про-
бегах (ср. с (3.13)). Легко видеть,
что по порядку величины она также
совпадает с той единственной энерги-
ей етах, которую может приобрести
электрон по элементарной теории.
Только теперь сама величина 8тах
отличается от (7.34), ибо Ass =
= e2E2lmx1/е.в отличие от высоко-
частотного случая, когда Ase = const.
Для распределения Дрюйвестейна ха-
рактерно гораздо более быстрое спадение числа электронов в
«хвосте», чем в максвелловском распределении (82 в экспоненте
вместо 8); см. рис. 7.6.
176
7.4. Указание о приближенном аналитическом решении для
атомарных газов в случае преобладания неупругих потерь. Ре-
шение будет получено в § 5 гл. 9 при рассмотрении пробоя. Оно
примечательно использованным приближением «бесконечного
стока». В определенном смысле этот случай противоположен рас-
смотренному в п. 7.2, 7.3.
§ 8. Численные расчеты для азота и воздуха
Для получения аналитических решений кинетического урав-
нения (7.23) всегда приходится идти на существенные упрощения
и допущения, как в § 7 (см. также § 5 гл. 9). В случае молеку-
лярных газов, где, помимо электронного, необходимо учитывать
колебательное и вращательное возбуждение, на аналитическое
решение и вовсе не остается надежд. Однако возможности совре-
менной вычислительной техники делают доступным численное
интегрирование, хотя такие расчеты требуют известных квалифи-
кации и затрат труда. Из вопросов физического характера на
первый план здесь выступает анализ подлежащих учету процес-
сов и выбор наиболее достоверных данных по сечениям. Имеются
довольно значительные расхождения между результатами разных
авторов, что связано со сложностью соответствующих эксперимен-
тов. Именно недостаточность сведений о сечениях служит глав-
ным источником погрешностей при решении кинетического
уравнения.
Действенным стимулом для производства расчетов явились
потребности современной техники молекулярных лазеров. В этой
связи проведены вычисления для многих смесей типа СОг + N2 +
+ Не (см. § 8 гл. 10). Наряду с лазерными смесями исследова-
лись и такие широко употребляемые в разрядной практике моле-
кулярные газы, как азот и воздух. Результаты расчетов для азота
[7.1] и для воздуха [7.2] приведем здесь и в целях иллюстрации
применения кинетического уравнения, и как представляющие
практический интерес для изучения разрядов.
Численно интегрировалось уравнение (7.23) для стационарных
условий и постоянного поля (из соображений удобства чуть пре-
образованное) .
8.1. Колебательно невозбужденные газы. Результаты для азо-
та представлены на рис. 7.7—7.10. Набор заложенных в расчеты
сечений близок к показанным на рис. 2.15, 2.17, 2.18. На рис. 7.7,
построенном в полулогарифмической шкале, даны энергетические
спектры электронов. Отложена функция хр = е-1/2тг (е)/тге. Смысл
ее делается наглядным, если учесть, что в случае максвелловско-
го распределения функция хр(е) = 2л“1/2(&7\)“3/2 ехр(—ь/кТе) с
точностью до постоянного множителя есть больцмановская экспо-
нента. На рассматриваемом полулогарифмическом графике она
дала бы прямую линию, тем больше наклоненную к горизонтали,
чем меньше Те.
12 ю. П Райзер
177
На рис. 7.8 представлены рассчитанные по формулам (7.30),
(7.31) скорость дрейфа, электронная «температура» как 2/3 от
«редней энергии е и характеристическая энергия, равная отно-
шению коэффициента поперечной диффузии к подвижности
, (п. 4.2 гл. 3). Коэффициент диффу-
^(е).эв —।------1------1 зии определен как <z;2/vm>, подвиж-
ность — как ид/Е. Отличие Те от De/\ie
связано с немаксвелловским характе-
ром спектра.
На рис. 7.9 показана константа
скорости ионизации кг, вычисленная
при помощи формулы (4.2), и коэф-
фициент Таунсенда. На рис. 7.10 —
доли энергии, которые передаются от
электронов в разные степени свобо-
ды. Видно, что в широком диапазоне
Е/N подавляющая часть работы поля
превращается в энергию молекуляр-
ных колебаний. Это — факт принци-
пиального значения. На этом свой-
стве слабоионизованной плазмы в
поле основана работа электроразряд-
пых молекулярных лазеров.
Для различного рода вычислений
Рис 7.7. Функция распределе-
ния электронов в азоте ip(e) =
= Е~1/2п(&) /пе
и оценок полезны построенные в
[7.3] по результатам расчетов интер-
поляционные формулы для констант
скоростей к ряда реакций*). Приво-
и метастабильного
дим к для ионизации из основного (kt) и метастабильного
(kiA) состояний, а также для возбуждения указанного ме
тастабильного (&1)и53Д (&в) состояний (рис. 7.11). Из послеп-
него молекула через излучение кванта быстро переходит в мета-
стабильное Л-состояние (эти данные дают возможность оценивать
роль ступенчатой ионизации; см. § 6 гл. 10).
1g кг - - 8,3 - 34,8 (ME), lgkiA = -6,1- 27,5 (N/E),
lg к*А = _ 8,35 - 14,9 (ДО), 1g к*в = - 8,2 - 15,6 (N/Е). (7Л0>
Е/N, 10“16 В • см2; к, см3/с.
На рис. 7.12—7.14 показаны некоторые результаты расче
для сухого воздуха без учета паров воды, содержание котот/03
может меняться от опыта к опыту. Функции распределения ^Ь1Х
чественно похожи на азотные. Ка~
8.2. Колебательно-возбужденный азот. При значительном
делении джоулева тепла в азоте образуется много колебательно^
*) В статье [7 3] дан подробный обзор расчетов электронных СПе
в разных газах. Р°в
178
возбужденных молекул. Высокой их концентрации способствует
замедленный характер колебательной релаксации, благодаря чему
нередко возникает ситуация, когда колебательная температура
Tv в азоте на порядок превышает поступательную. Вообще говоря,
распределение молекул по высшим колебательным состояниям
Рис. 7 8. Зависимость скорости дрейфа ид электронов (а), характеристиче-
ской энергии De/[ie и электронной температуры Те (б) от отношения E/N
в азоте; точки — эксперимент
7 2 4 О 10 20 4Z7 102
E/N,10~16в-см2
Рис. 7.9. Зависимость кон-
станты скорости ионизации
кг = <огг> и коэффициента
Таунсенда a/N = кг/ид от
отношения Е/N в азоте
Рис. 7.10. Зависимость доли энергии
в азоте, которая передается элект-
ронами во вращения (7), колеба-
ния (2), затрачивается на электрон-
ное возбуждение (5), ионизацию (4),
от отношения E/N
v > 1 не больцмановское, но под Tv можно подразумевать вели-
чину, определяющую отношение чисел молекул на уровнях с v = 1
и и — 0, z = ехр(— litoJkTv), где сок — частота колебаний молеку-
лы. Так, в азоте Йсок = 0,29 эВ и z = 0,5 при Tv = 4906 К.
12*
179
Присутствие колебательно-возбужденных молекул уменьшает
потери энергии электронов на возбуждение колебаний, что обога-
щает спектр энергичных электронов. Кроме того, пороги электрон-
ного возбуждения и ионизации у колебательно-возбужденных мо-
лекул ниже, чем у невозбужденных. Все это приводит к ускоре-
Рис. 7.11. Схема уровней молекулы азота
(7 31
ия. Согласно l'-UJ
нию ионизации и электронного воз бу ж дон г 7 41)
фект описывается интерполяционной фор^ У ft&JkTv) ? '
lg[fc(7’„)/fc(0)] = 43,5z(W)2, z==exp( ” аведлив°й
ЛА-16 В • СМ ) и
единой для всех к (Е/N измеряется iv (7.40),
До Т 5000 К. отях и форМУ*а; efleKTpe
Надо сказать, что ошибка в Расчет^, так как а
(7.41) резко возрастает при уменьшении
180
при этом остается все меньше энергичных электронов, способных
производить электронное возбуждение и ионизацию (рис. 7.7).
При Е/N ~ (3 20) • 10-16 В • см2 относительная погрешность
расчетов и формул для к оценивается в 100 %, при еще меньших
Рис 7 12. Зависимость скорости
дрейфа и характеристической
энергии от отношения E/N
в воздухе: 1 — расчет, 2 и 3 —
эксперимент
Рис 7.13. Ионизационный
коэффициент Таунсенда
a/N в воздухе как функция
отношения E/N
E/N — она значительно больше. Между тем, именно малые зна-
чения E/N ~ (1 6) 10~16 В • см2 реализуется в положительном
столбе тлеющего разряда и представляют наибольший интерес.
Это сильно усложняет задачу выяснения роли механизмов, влияю-
щих на ионизацию: ступенчатых процессов, нагрева газа, колеба-
тельного возбуждения, ассоциативной ионизации (§ 6, 7 гл. ЮТ
Рис. 7.14. Зависимость доли энергии в
воздухе, которая передается электрона-
ми в колебания О2 (7), вращения О2 и
N2 (2), упругие потери (3), колебания
N2 (4), затрачивается на электронное
возбуждение N2 (5) и О2 (6), иониза-
цию О2 и N2 (7)
Из-за крайне резкой зависимости скоростей реакций от Е/N теопр
тически легче установить, какая в данной ситуации должна быт'
скорость ионизации, чем указать точное значение Е/N, котоп
ее обеспечивает. Это — типичная трудность в теории слабоион °
зованной плазмы.
181
§ 9. Пространственно неоднородные поля
произвольной силы
В слабоионизованном газе сильные неоднородные поля воз-
никают в катодном слое тлеющего разряда (гл. 10), в приэлект-
родных слоях высокочастотного емкостного разряда (гл. 15),
в высоковольтных импульсных разрядах. Рассматривавшееся до
сих пор лоренцево приближение при этом теряет силу, так как
функция распределения электронов оказывается сильно анизо-
тропной. Кроме того, спектр приобретает нелокальный характер
(§ 5). Это вынуждает вернуться к исходному общему кинетиче-
скому уравнению. Главная трудность его решения связана
с угловой зависимостью функции распределения и интегро-
дифференциальным характером уравнения по углу. На пре-
одоление именно этой трудности и направлено лоренцево при-
ближение.
Наиболее подходящим способом решения кинетического урав-
нения общего вида в настоящее время признан метод Монте-Кар-
ло. Это — вычислительная процедура, которая с помощью ЭВМ
воспроизводит запечатленный в кинетическом уравнении стоха-
стический процесс блуждания частицы в фазовом пространстве
при задаваемых распределении поля, вероятностях столкновений
и сопровождающих их изменениях направления скорости и энер-
гии частицы. Расчеты методом Монте-Карло (с их результатами
мы познакомимся в § 5 гл. 10) очень сложны, требуют больших
затрат машинного времени и мало кому доступны. В качестве
альтернативы методу Монте-Карло может быть предложен упро-
щенный подход к задаче, так же как и лоренцев, основанный на
приближенном описании углового распределения электронов.
Задача при этом сводится к вполне доступным уравнениям, не
более сложным, чем уравнения лоренцева приближения. Будучи
пригодным для рассмотрения поведения электронов в любых по-
лях, сильных и слабых, неоднородных и однородных, с сохране-
нием всех качественных особенностей и следствий строгого урав-
нения, упрощенный способ дает более оперативный, чем метод
Монте-Карло, инструмент для исследования указанных выше раз-
рядных явлений.
Упрощенное уравнение формулируется в приближении «впе-
ред-назад». Считается, что все электроны движутся вдоль на-
правления поля (вдоль оси х). При упругих столкновениях они
рассеиваются либо вперед, либо с вероятностью g назад. При не-
упругих столкновениях: возбуждающих, ионизующих — электроны
теряют энергию, но не отклоняются от направления своего перво-
начального движения. Тогда функция распределения по скоро-
стям состоит из двух составляющих. Вперед в положительном
направлении оси х(Е ^== Ех < 0) со скоростями от v до v + dv ле-
тит ф1(р, х, t)dv электронов в 1 см3. Назад, с той же скоростью
v по величине,— я, t)dv. Плотности электронов пе, потока
182
Ге и электронного тока je определяются формулами
оо оо
пе{х, t) = | (<Р1 + ф2)^, Ге = — ~ = J(<Pi — <p2)z^. (7.42)
о о
Уравнения для функций ф1, <р2 легко составить, повторяя вывод
кинетического уравнения для настоящей функции распределения
(§2). Можно поступить и чисто формально, подставив в строгое
уравнение (7.8) функцию распределения /(р, й) в виде суммы
6-функций по й при 0 = 0, л. Нужно только в (7.8) сохранить
опущенное там слагаемое с пространственным градиентом
vxdfldx = - v cos 'ftdfjdx. Раскрывая интеграл столкновений (7.10),
находим
дф еЕдц> 1 ( х у щ \
+ t’ ^7 - - — - 7 vnl (ф2 ~ Ф1) -г <2 (Ф1),
л л л (7-43)
Й*Р2 а<р eEd(f2 1 , . , п/ .
~дГ - V~dl + ^^7 = 2 Vm
причем роль эффективной частоты столкновений играет величи-
на vm = 2Nvgc(v) Вероятность £ следует выбирать, исходя из
реального среднего косинуса угла рассеяния: £ = (1 — cos 0)/2.
Например, при изотропном законе рассеяния £ = 1/2 и vm — vc.
Член упругих потерь энергии введем в уравнение для энергети-
ческого спектра, как и в п. 4.5. Слагаемые неупругих столкнове-
ний Q определяются так же, как и в уравнении лоренцева при-
ближения в п. 4.6.
Перейдем к распределениям электронов, летящих вперед и
назад, по энергиям:
П1>2(е)йе = <pi.2(^)dp, Г1,2(с)= nl>2 (е) v = (pi>2(t;)/m,
где Г1,2 — односторонние спектральные потоки. С учетом упру-
гих потерь энергии уравнения для спектральных функций при-
обретают вид:
дп. дГ л / о™ о \ л
-ЛГ + ir1 + # I - е£Г1 - т- г! | = 4- (Г, - I\) + Q (ГО,
dt 1 дх 1 дг I 1 М lm 1 I 2lm ' 2 1/ । v \ 1/,
я ,г (7.44)
d d £_ г) / РтГ) р \ 4
55Т--^ + ;гИГ2- Г2 = £- (Г1-Г2) + <?(Г2),
dt дх 1 del 2 ML 2 2ZW v 1 27 1 v ' 27
\ lib / lit
где Zm =(27Voc^)-1 — zVvm — длина пробега для передачи импуль-
са, определяемая транспортным сечением <зт = 2^ас. Система
(7.44) для двух спектральных функций п\, п2 и подлежит реше-
нию, подобно системе (7.14), (7.16) для двух функций /о, /ь
В пределе слабых полей, когда ускорение электронов полем
вперед мало, а рассеяние назад действует в полную силу, спект-
ральные потоки вперед и назад мало отличаются друг от друга.
При этом сумма Г1 + Г2 = пр (где п = п\ + п2 — спектральная
плотность) соответствует симметричной части лоренцевой функ-
183
ции распределения, а разность Г = Г1 — Г2 (или спектральный
поток)—малой асимметричной части. Поскольку энергии элект-
ронов в слабом поле в основном малы, частоты упругих столкно-
вений гораздо больше частот неупругих, а также обратного вре-
мени установления спектра. Вычитая уравнения (7.44) и опуская
малые величины, получим приближенно
г = + (7.45)
в полной аналогии с лоренцевой связью типа (7.19'). Первое сла-
гаемое определяет диффузионный поток, который в (7.19') был
опущен, второе — дрейфовый.
Интегрируя (7.45) по спектру для случая vm(v) = const и имея
в виду, что nv2 -> 0 при v 0, находим выражение для плотно-
сти потока
Ге = — ^Ix^dnjdx — (eE/mVm) ^е, (7.46)
которое совпадает с (3.20). Выражение для скорости дрейфа по-
лучается точным, а коэффициент диффузии — втрое больше на-
стоящего, так как хаотическое движение не трехмерно, а одно-
мерно*). Подробности см. [7.4]; результаты расчета приводятся
в § 5 гл. 10.
В очень сильных и достаточно протяженных полях электроны
разгоняются до больших энергий, неупругие столкновения проис-
ходят чаще упругих, рассеиваются электроны преимущественно
вперед. Из двух уравнений (7.44) в этом случае можно оставить
только первое, без члена упругих столкновений. Из него вытекает
уравнение (4.12), записанное в приближении «моноэнергетиче-
ских» электронов, если под е подразумевать среднюю энергию.
10.1. Формулировка уравнения. Как и в случае «классиче-
и переход к классике
10.1. Формулировка уравнения. Как и в случае «классиче-
ского» взаимодействия электронов с полем электромагнитной вол-
ны, строгое описание эффектов взаимодействия с полем фотонов
требует решения соответствующего кинетического уравнения для
функции распределения электронов по энергиям п (8, t). На опы-
те квантовые эффекты проявляются в основном при взаимодей-
ствии электронов с лазерным излучением. В этом случае спон-
танное излучение пренебрежимо мало (п. 9.3 гл. 5). Взаимодей-
ствие состоит в обмене квантами энергии 7г со в актах истинного
поглощения света и вынужденного испускания. Опуская индекс
со у коэффициентов Ь<^ рассчитанных на один электрон и один
*) По строгому определению Но v2 =v2 ==...= и2/3.
У нас же v* — v2.
184
атом (§ 8 гл. 5), запишем кинетическое уравнение
dnldt = FN[—a(&)n(&) + b(& + + Йсо) —
— &(e)n(&) + a(e — ^co)n(e — ^co)]+ Qi, (7.47)
где ^[c-1 cm-2] — плотность потока фотонов, TV [см-3] — плотность
атомов. В 21 включено то, что не имеет отношения к взаимодей-
ствию электронов с полем излучения: упругие потери, действие
неупругих ударов, рождение, гибель электронов. Смысл слагае-
мых в скобках ясен: уход электрона из состояния с данной энер-
гией 8 в состояние с 8 + Тгсо вследствие поглощения кванта энер-
гии, приход «сверху» в результате вынужденного испускания
кванта, уход «вниз», приход «снизу».
В результате случайных актов поглощения и вынужденного
испускания квантов электрон «блуждает» вдоль энергетической
оси 8, совершая случайные скачки то вверх, то вниз на величину
As = Йсо. Интервалы между скачками та, ть характеризуются
частотами
va = Та 1 = FNa, vb = тГ1 = FNb, (7.48)
которые весьма близки друг к другу. Например, для света руби-
нового лазера Йсо = 1,78 эВ, аргона с плотностью N =
= 5,3 1019 см-3, (р = 1,5 атм), потока квантов F =
= 3,4 1029 с-1 • см-2, при котором происходит пробой в таких
условиях (среднеквадратичное поле в световой волне Е =
= 6 • 106 В/см), и энергии электронов 8 = 10 эВ по данным
рис. 5.3 va ~ Уь ~ 5,4 • 1011 с-1, Та ~ ть ~ 1,8 • 10-12 с. Хотя вероят-
ности скачков вверх и вниз по оси энергии более или менее оди-
наковы, в средне^ электрон все же движется вверх, т. е. набира-
ет энергию от поля. Этот процесс вполне аналогичен одномерной
диффузии частицы в газе от непроницаемой стенки, когда с тече-
нием времени частица в среднем удаляется от нее. Роль «стенки»
здесь играет нуль энергии электрона.
10.2. Диффузионное приближение. Конечно-разностное урав-
нение (7.47) можно существенно упростить, превратив его в диф-
ференциальное, если функция распределения п(е) мало меняется
на длине одного скачка //со по оси 8, т. е. при условии, что Йсо
значительно меньше типичных значений 8, например средней
энергии спектра. Вместе с тем операция над уравнением, связан-
ная с использованием условия малости кванта энергии, должна
приближать нас к классике. Сейчас мы убедимся в том, что это
действительно так и есть на самом деле. Прежде, однако, заме-
тим, что неравенство Йсо < 8 реализуется в наиболее интересном
случае. Квантового рассмотрения требует в первую очередь ис-
следование пробоя газов под действием лазерного излучения
(§ 6 гл. 9). Для того чтобы произошел пробой, т. е. развилась
электронная лавина, необходимо, чтобы энергия электронов до-
стигла величины, превышающей потенциал ионизации атомов.
У аргона, например, I = 15,8 эВ, у гелия — 24,6 эВ. Эти значе-
185
ния на порядок превышают энергии квантов рубинового
(Тгсо = 1,78 эВ) и тем более неодимового (1,17 эВ) лазеров, так
что с разумным приближением условие Тгсо < е можно считать
выполненным.
Пользуясь этим неравенством, разложим в уравнении (7.47)
все функции от аргументов 8 ± Тш в ряд около точки 8, сохранив
члены второго порядка малости по Тгсо/8. Опуская члены более
высокого порядка малости, чем (Тгсо/е)2, получим дифференциаль-
ное уравнение второго порядка для функции распределения
n(t, е), которое, так же как и в классическом случае, имеет вид
уравнения диффузии по оси энергии, но с иными коэффициен-
тами:
d^ = -^ + Q j = ^2)'^ + n6U’ (7.49>
S)- (1/2) FN [а (8) + &(P)J,
= FN(fa)[a(e)~ b(t)]-d0'/de. (
Мы отметили 3' и °U' штрихом, чтобы не путать их с «клас-
сическими» коэффициентами (7.22). Квантовые коэффициент диф-
фузии 3' и скорость кинетического потока °U' имеют очень яс-
ную физическую интерпретацию. Действительно, величина
FN (а + Ь) =Таъ— это вероятность электрону либо поглотить, ли-
бо испустить квант энергии и совершить скачок по координате.
Следовательно, таь — среднее время его жизни по отношению к
такому шагу. Квант Тгсо — это значение скачка, и 3' =
= (Йсо)2/2та6— это просто точное значение коэффициента одно-
мерной диффузии D = Д.г2/2т. Далее, Йсо/та—это средняя ско-
рость одностороннего движения вверх по оси 8, Тгсо/ть— вниз.
Разность этих скоростей
7гсо/та — 7гсо/ть = FNTia) (а — Ь)
характеризует систематическое движение вверх, в сторону увели-
чения энергии. Кроме того, если коэффициент диффузии зависит*
от точки, то в обычном диффузионном потоке частиц
] = —d(Dn)Jdx = —Ddn/dx — ndDIdx
появляется составляющая типа кинетического потока со ско-
ростью, равной — dD/dx. Для суммарной скорости W получаем
в точности выражение (7.50).
10.3. Предельный переход. Остается сделать еще один шаг —
перейти к пределу 7г со 0 в значениях квантовых коэффициен-
тов 3' и °ЦУ и мы завершим переход к классике. Прежде всего,
независимо от конкретного вида коэффициентов поглощения и
вынужденного испускания, в пределе & с помощью общего
соотношения (5.50) между а и Ъ находим
3' =FN^)2a^}, =FN^)2a^)J2E=3'/2s.
Связь величин °и' и 3' получается точно такой же (7.22), как
186
в классике. Если подставить сюда коэффициент истийного по-
глощения а(е) по формуле (5.60) и перейти к пределу Tzco/e 0,
заметив, что = сЕ2[^л, получим классические выражения
(7.22) для Ф и °U.
Таким образом, в добавление к § 10 гл. 5 мы еще раз пока-
зали, теперь уже с помощью кинетического уравнения, что клас-
сической теорией взаимодействия электромагнитной волны с
электронами в ионизованном газе формально можно пользовать-
ся при условии /гео < е, а не при условии Тгсо < екол, как это ка-
залось сначала (п. 8.1 гл. 5). Это весьма существенный резуль-
тат, он служит обоснованием возможности применения (с извест-
ными оговорками) классической теории к такому, казалось бы,
типично «квантовому» процессу, как пробой газа излучениями
оптического диапазона. Если же условие Tzco е нельзя считать
выполненным, как, например, в случае квантов ультрафиолетово-
го диапазона, необходимо пользоваться квантовым уравнени-
ем (7.47).
Глава 8. ЭЛЕКТРИЧЕСКИЕ ЗОНДЫ
§ 1. Введение. Схема эксперимента
Все методы диагностики плазмы призваны определять на опы-
те ее параметры. Главные задачи состоят в измерении плотности
электронов пе, их температуры 7\, если таковой они обладают,
в общем случае—функции распределения /о(к). Для исследова-
ний разряда большой интерес представляют распределения по-
тенциала и электрического поля в пространстве. При благоприят-
ных условиях эти задачи решает зондовый метод, развитый в
1923 г. Ленгмюром. Зондовый метод (практически единственный
среди всех диагностических приемов) позволяет непосредственно
находить локальные характеристики плазмы, т. е. пространствен-
ное распределение параметров, и в этом состоит его особая
ценность.
При зондовом исследовании в определенное место плазмы
вводится электрод, на который подаются различные потенциалы.
Это металлический проводник, почти до конца покрытый изоля-
цией. Оголенной поверхности зонда, которая соприкасается с
плазмой, придают разные формы: плоскую, цилиндрическую,
шарообразную. Потенциал зонда, задаваемый источником напря-
жения, фиксируется относительно опорного электрода: анода, ка-
тода или заземленной металлической стенки разрядной камеры,
если таковая имеется.
На рис. 8.1 изображена схема измерений. В данной схеме
зондовый ток замыкается через анод 4, поэтому полярность
источника напряжения для зонда выбрана так, чтобы потенциал
зонда был ниже потенциала анода,— промежуточным между по-
187
тенциалами анода и катода К, как в плазме. Потенциал зонда
варьируется при помощи потенциометра. Эксперимент заключает-
ся в измерении токов, протекающих через зонд, и приложенных
к нему напряжений — в снятии зондовой вольт-амперной харак-
теристики (ВАХ).
На рис. 8.2 показано несколько вариантов конструкций зон-
дов. Изготавливают зонды преимущественно из тугоплавких ме-
Рис. 8.1. Схема зондовых измерений
таллов: вольфрама, молибде-
на, тантала; цилиндрические
зонды — из проволоки диа-
метром 0,5—0,05 мм. В ка-
честве изолятора используют
специальные сорта стекла,
которым можно покрыть про-
волоку, керамику, кварц,
алунд (99 % АЬОз) и др.
Правильная конструкция
зонда (рис. 8.2в) в отличие
от неправильной (рис. 8.2г)
уменьшает влияние краевые
эффектов. Ведь при обработке результатов измерений приходится
задаваться значением площади токособирающей поверхности. Раз-
меры сферических и плоских зондов имеют порядок 1 мм.
Простота технических средств и эксперимента являются до-
Недостаток его — в сложности
теории, с помощью которой ив
данных измерений извлекаются
характеристики плазмы. Пра-
вильнее сказать так: лишь в
ограниченном диапазоне усло-
вий теория не чрезмерно слож-
Рис 8.2. Конструкции зондов: а — на. За пределами этого диапазо-
ну — правильная, г — неправильная; на сложность ее такова, что
1 — зонд, 2 — изолятор становится значительной вероят-
ность некорректных измерений
или ошибочной интерпретации их результатов. При измерении ка-
кой-нибудь величины всегда следует стремиться к тому, чтобы в
основе метода лежала простая, не вызывающая сомнений теория с
минимумом допущений и нечетких ограничений. В этом отношении
зондовый метод работает с достаточной надежностью лишь в слу-
чае разреженного газа, когда длина свободного пробега заряжен-
ных частиц больше характерных размеров зонда и возмущенной
области плазмы вокруг него*). Но в принципе с помощью зондов
*) Именно к этому случаю относятся теория Ленгмюра. Зонды вводили
в разрядную плазму и раньше, еще в начале века. Электростатическими
способами измеряли разность нохенциалов между зондом и катодом или
анодом. По потом стало ясно, что потенциалы зонда и плазмы не совпада-
ют, хотя разность потенциалов между соседними точками так определять
можно Лишь теория Ленгмюра сделала зонды эффективным методом ко-
личественной диагностики.
188
можно исследовать плазму в весьма широком диапазоне условий:
р ~ 10-5—102 торр, пе ~ 106—1014 см-3.
Если в плазме присутствует магнитное поле, теория сильно
усложняется и интерпретировать измерения бывает трудно. То же
относится и к случаю, когда имеются отрицательные ионы. В от-
сутствие опорного электрода, как, например, в безэлектродном
высокочастотном разряде или в распадающейся плазме с отклю-
ченным полем, одиночный зонд ничего не дает. В этих случаях
пользуются двойными зондами (§ 7).
§ 2. Вольт-амперная характеристика одиночного зонда
На рис. 8.3 представлена несколько идеализированная зондо-
вая характеристика — зависимость электрического тока ц проте-
кающего через плоский зонд, от его потенциала V. Откуда отсчи-
тывать потенциал — значения не имеет, лишь бы точка отсчета
была четко фиксированной. Именно для этой цели и служит
опорный электрод. Дадим качественную
сти Z(F). Допустим, что в отсутствие
зонда плазма электронейтральна, пе =
= п+ = tiq. Потенциал плазмы (про-
странства) в том месте, куда помещен
зопд, обозначим Es и будем отсчиты-
вать его от опорного электрода. Пусть
Vs мало меняется на протяжении той
области, которая возмущена присут-
ствием зонда, т. е. потенциал ближай-
шей невозмущенной плазмы вокруг зон-
да равен Vs. Измеряемый на опыте по-
интерпретацию зависимо-
Рис. 8.3. Типичная зондо-
вая характеристика
тенциал зонда относительно опорного
электрода есть V = VP + Vs, где Vp — потенциал зонда относи-
тельно невозмущенной плазмы в его окрестности (рис. 8.1).
Зонд только собирает заряды из плазмы. Он их не испускает.
Будем оперировать абсолютными значениями электронного и
ионного токов на зонд /е, i+. Условимся о таком знаке зондового
тока: i = ie — f+, ему соответствует ориентация кривой рис. 8.3,
Если потенциал зонда совпадает с потенциалом пространства и
токособирающая поверхность параллельна направлению внешнего
поля между анодом и катодом, заряды попадают на зонд исклю-
чительно благодаря своему тепловому движению. Но электроны
движутся гораздо быстрее ионов, тем более что их температура
в слабоионизованной плазме гораздо больше ионной (газовой) Т.
Поэтому при V = Vs зондовый ток практически совпадает с
электронным: i ~ ie. Подчеркнем сам факт: в отсутствие разности
потенциалов между проводником и окружающей плазмой провод-
ник собирает электрический ток (электронов).
Когда на зонд подан положительный относительно плазмы по-
тенциал V > Fs, ионы отталкиваются от зонда, ионный ток исче-
189
зает, а электроны притягиваются. Около зонда образуется слой
отрицательного объемного заряда, который экранирует потенциал
Vp. Падение потенциала от V до Vs и поле зонда сосредотачи-
ваются в области слоя пространственного заряда, асимптотически
исчезая при переходе в невозмущенную плазму. Эффект совер-
шенно аналогичен поляризации плазмы вокруг заряда и экрани-
ровке поля заряда в плазме на расстояниях, больших дебаевско-
го радиуса.
Введем условную внешнюю поверхность слоя — границу, даль-
ше которой плазму можно приближенно считать нейтральной,
а поле — отсутствующим. Электроны попадают извне на границу
слоя, а потом и на зонд, в основном благодаря тепловому дви-
жению, чем и определяется их поток, который слабо зависит от
потенциала зонда. Зондовый ток совпадает с более или менее
постоянным электронным током насыщения £енас- Этому соответ-
ствует верхняя пологая часть ВАХ АВ. В идеальном случае «без-
граничной» плоскости /енас = const и эта часть ВАХ была бы го-
ризонтальной. В случае небольшого зонда ток нарастает с ростом
положительного потенциала, но медленнее, чем в крутой час-
ти ВАХ.
Если создать на зонде отрицательный относительно плазмы
потенциал, электронный ток резко падает по мере возрастания
I Vp\, так как все меньше электронов обладает скоростями, доста-
точными для преодоления тормозящего поля. Так возникает кру-
тая часть характеристики С. Место верхнего «излома» ВАХ (точ-
ка В, соответствующая VP ~ 0) фиксирует потенциал простран-
ства Vs. Его так и можно найти на опыте. Передвигая зонд, по
разности потенциалов Vs в соседних точках определяют электри-
ческое поле.
При некотором отрицательном потенциале Vp = Vf (точка D
на рис. 8.3) ток исчезает. В этом состоянии поток на зонд не-
большого количества энергичных электронов, способных преодо-
леть тормозящий потенциал, компенсирует поток ионов. Такой по-
тенциал Vf (он называется плавающим) приобретает помещенное
в плазму изолированное тело. Возвращаясь к сноске в § 1,
можно сказать, что в опытах с зондом без питания измеряли
не потенциал плазмы, а более отрицательный плавающий по-
тенциал.
При еще больших отрицательных потенциалах зонд отталки-
вает практически все электроны. Ионы он притягивает. Зонд окру-
жает ионный слой положительного объемного заряда, который
экранирует большой отрицательный потенциал VP. Ток на зонд
является чисто ионным, причем определяется он потоком ионов,
попадающих на границу слоя из окружающей плазмы. Поток
этот мало зависит от потенциала зонда, который заэкрани-
рован, т. е. зондовый ток меняется медленно и совпадает с
ионным током насыщения. Этому соответствует нижняя пологая
часть ВАХ.
190
§ 3. Теоретические основы диагностики
разреженной плазмы по электронному току
3.1. Электронная температура. Рассмотрим крутую часть зон-
довой характеристики С, где ток — электронный, а потенциал для
электронов — тормозящий. Пусть электроны пересекают слой по-
ложительного объемного заряда без столкновений. При напряже-
ниях на зонде, соответствующих крутой части характеристики,
толщина слоя имеет порядок дебаевского радиуса. При ~ 1 эВ,
пе ~ 109 см-3 по формуле (2.23) d ~ 10-2 см. Если, как обычно,
длина пробега электронов 1е такова, что 1ер ~ 0,03—0,01 см - торр,
то le~> d при р < 10-1 — 1 торр. Вычислим электронный ток на
зонд, для простоты полагая, что слой — тонкий по сравнению с
радиусом кривизны или размерами токособирающей поверхности.
В этом случае задачу можно считать плоской. В п. 3.4 будет по-
казано, что полученный результат справедлив для любой выпук-
лой поверхности, например для маленького сферического зонда.
Полагаем, что поверхность металла полностью поглощает (не
отражает) заряды.
Электрон, попадающий с тепловой скоростью из невозмущен-
ноц плазмы на внешнюю границу слоя, подвергается тормозяще-
му действию нормального к поверхности поля, Е = —dy/dx.
В соответствии с уравнением движения
1П dt dx 2 е dx
он может достичь поверхности зонда,только если обладает в на-
чале составляющей скорости vx такой, что е | Vp | =
т. е. vx vt = (2е| VP\/m)1/2. Если на внешней границе слоя
функция распределения электронов есть f(vx, vy, vz), то плот-
ность тока на зонд равна
оо оо оо
je = e j dvy j dvz§ f(vx, Vy, vz)vxdvx cm-2-c-1 (8.1)
oo —oo Vf
Интегрируя (8.1) с максвелловским распределением (см. прило-
жение) и умножая результат на площадь поверхности S, находим
зондовый ток:
i = S(enove/4:)exp(eVp/kTe), vc = (8кТе/лт)1/2. (8.2)
Эта формула, описывающая крутую часть ВАХ, была получена
Лэнгмюром и широко применяется на практике. Сняв зондовую
характеристику и построив график In i в зависимости от У, по
углу наклона получающейся прямой можно определить электрон-
ную температуру Те. Вместе с тем линейность зависимости In i от
V свидетельствует о максвелловском характере распределения
электронов.
3.2. Ток насыщения; потенциал и плотность зарядов в плаз-
ме. Место верхнего излома ВАХ, как отмечалось выше, определи-
191
ет потенциал пространства Vs. При V > Vs, когда поле становится
ускоряющим, формула (8.2) теряет силу, так как по vx в (8.1)
теперь нужно интегрировать от нуля независимо от Vp. Зондовый
ток при этом совпадает с электронным током насыщения, кото-
рый отвечает отсутствию поля, т. е. Vp = 0 в (8.2):
i = ie нас = Sen0Ve/^. (8.3)
Эта величина соответствует плотности потока частиц в газе, пере-
секающих площадку с одной стороны, nv/^к. Один из множителей
1/2 в 1/4 появляется из^за того, что только половина всех частиц
летит в нужную сторону, другой — в результате усреднения по
полусфере косинуса угла й между направлением скорости v и
нормалью к площадке. Зная тепловую скорость электронов ve из
измерения Те по крутой части ВАХ и значение тока в точке В
излома ВАХ, по формуле (8.3) можно найти плотность зарядов
в плазме по.
3.3. Критерий «разреженности» плазмы. Чтобы по можно бы-
ло трактовать как плотность электронов в невозмущенной плазме,
необходимо, чтобы присутствие зонда не нарушало в точках
последнего столкновения, после которого электроны приходят к
зонду. Они отстоят от зонда на расстоянии порядка длины про-
бега. Но плотность частиц в какой-то точке формируется в ре-
зультате прихода их из сферы с радиусом порядка I. Своей по-
верхностью S зонд «затемняет» долю 5/4л/2 этой сферы, тем са-
мым обедняя источник формирования плотности. Нужно, чтобы
эта доля была малой; 5/4л/2 < 1, т. е. чтобы длина пробега / бы-
ла больше характерного линейного размера зонда V5. Другим
условием разреженности плазмы является малость размеров слоя
объемного заряда по сравнению с I.
3.4. Нахождение функции распределения электронов. В слу-
чае произвольного, но почти изотропного распределения электро-
нов в невозмущенной плазме, f(yx, vy, vz)^ fo(v), в выражении
(8.1) для потока электронов на поверхность зонда целесообразнее
оперировать значением скорости v и углом ее наклона к внутрен-
ней нормали к поверхности й. Замечая, что vx= v cos й, предста-
вим (8.1) в виде
Л/2 оо
je=~e f cosй-2л sin й с/й | р3/0 (у) dv. (8.4)
О г^/cosft
Меняя порядок интегрирования с сохранением области, охваты-
ваемой двойным интегралом, проинтегрируем (8.4) по р = cos й:
1 ОО ОО 1
je = 2л£ J р d\i z;3/0 (р) dv -=- 2лс z?3/0 (у) dv р dp =
о Vf v't/v
оо
= (8.5)
192
Максвеловокая функция /0=(т/2л Т,)™ ехр(-трдам пре-
вращает (8.5) в (8.2). Как и (8.2), формула (8.5) справедли-
а только при Vp 0. Если Vp > 0, интегрировать по v в (8.4)
едует от нуля независимо от Vр. Это дает ток насыщения (8.3)
с немаксвелловской средней скоростью ve,
родифференцировав (8.5) по Vp два раза, получим
fZ'~' о2ле3 / 2elVI
< (8-C)
Для нахождения функции распределения электронов следует
снять зондовую характеристику, дважды продифференцировать ее
в каждой точке крутого участка и приписать точке потенциал Vp,
отсчитанный от точки В верхнего излома. Вторая производная
даст число /о(р) при v = (2е|Vp\/m)1/2. ___________________
Этот метод, впервые примененный
Дрюйвестейном (1930 г.), с некоторы-
ми усовершенствованиями и ныне ис-
пользуется на практике (§4).
3.5. Применимость теории крутой
части ВАХ к зондам малых размеров.
Покажем, что основная для диагности-
ки формула (8.5), выведенная выше
путем рассмотрения «плоской» геомет-
рии, справедлива и в случае зондов, ма-
лых по сравнению с размерами обла-
сти объемного заряда. Необходимо толь-
ко, чтобы зондовая поверхность бвгла
выпуклой. Возможность применения не-
больших зондов крайне благоприятна,
ибо они меньше нарушают естествен-
ные условия в исследуемой плазме. Необходимость втопж
плазму — один из существенных недостатков зондовой ме 6НИЯ В
Не все из тех электронов, которые влетают в слой 5 ТОДИКИ-
заряда, окружающий зонд конечных размеров, попадают УИИого
Часть пролетает мимо (рис. 8.4). Задача не плоская НЭ 3°НД’
вывод формулы (8.5) нужно пересмотреть. Сделаем эт ПОЭТомУ
[8.2]. Обозначим: гР — координаты точки зондовой пон°’ СЛедуя
vp и /(гР, vp)—скорость и функция распределения элр7₽ХН°СТИ’
поверхности. Плотность тока на зонд в точке гр есть КТР°НОВ У
Л/2 сю
А = е J Vp cos <гр> vp) 2л sin й dftvl dv
0 0 р Р-
Рис 8 4. Траектории частиц
около отталкивающего сфе-
рического или цилиндриче-
ского зонда
(8.7)
Вследствие выпуклости электроны прихопят и
всей полусферы 0 < л/2 *). д на Поверхность со
*) На вогнутых участках некоторые углы «затенены» п
пуклостями, и их нужно выделять из интеграла. сос^дними вы-
13 ю. П Райзер
193
В точку гр со скоростью vp, направленной к поверхности, элек-
трон приходит без столкновения из какой-то точки г невозмущен-
ной плазмы, где он обладал скоростью v. Вследствие потенциаль-
ного характера тормозящей силы изменение кинетической энергии
электрона на этом пути не зависит от пространственного распреде-
ления потенциала и формы траектории:
mzy/2 = тк2/2 — е | Vp |. (8.8}
Но согласно (7.6) в отсутствие столкновений функция распределе-
ния не меняется вдоль траектории частицы в фазовом простран-
стве. В невозмущенной плазме она изотропна и равна /о(к). Сле-
довательно, /(гр? vp)=/(r, v) = /o(^). Заменяя в (8.7) / на /о (у),
Ур по формуле (8.8), vpdvp на vdv и интегрируя по й, получаем
последнее выражение (8.5). Плотность тока на всех участках
выпуклого зонда одинакова, т. е. i = Sje, где S — площадь поверх-
ности зонда.
3.6. Почему не насыщается ток на маленький зонд. В идеаль-
ном плоском случае, реально — если толщина слоя объемного за-
ряда мала по сравнению с радиусом кривизны и размерами токо-
собирающей поверхности, достаточно подать на зонд небольшой
положительный потенциал Vp, чтобы электронный ток достиг не
зависящего от потенциала значения (8.3), соответствующего на-
зонда малы по сравнению с размерами
(радиусом) области объемного заряда
электронный ток продолжает расти при
увеличении положительного потенци-
ала, хотя и медленнее, чем в крутой
части ВАХ, отвечающей уменьшению
тормозящего потенциала. Причина тако-
го поведения ВАХ состоит в том, что
не все электроны, влетающие в слои
объемного заряда, аде они подвергаются
действию притягивающего поля, попа-
дают на зонд. Часть из них пролетает
мимо и вылетает из слоя, не задев зон-
да. Но, конечно, чем выше ускоряющий
потенциал Ер, тем сильнее электроны
притягиваются к зонду, тем большая их
часть, вступив в слой, собирается зон-
дом — растет и ток.
около притягивающего сфе-
рического или цилиндриче-
ского зонда
Это положение иллюстрируется рис. 8.5, на котором схемати-
чески показаны траектории частиц в притягивающем поле сфе-
рического или длинного цилиндрического зонда. В последнем
случае изображены проекции траекторий на плоскость, перпен-
дикулярную оси. Если частица приближается к слою с прицель-
ным расстоянием р, превышающим радиус слоя R (эффективную
границу, вне которой поле как бы отсутствует), прямолинейный
путь ее не искривляется. Если частица влетает в слой (р</?)г
194
юна может либо пролететь мимо, либо удариться о зонд. Это за-
висит от ее начальной скорости i?o, прицельного расстояния р,
значения и характера распределения потенциала по радиусу V(r).
Чем энергичнее электрон, тем меньше должно быть его прицель-
ное расстояние или тем выше должен быть потенциал, чтобы
электрическая сила сумела притянуть его к зонду. Очень медлен-
ные электроны с любым р < R собираются зондом.
Все это регламентируется законами сохранения энергии и мо-
мента импульса
_о = ---еу mvr sjn q = (8.9)
где г — расстояние от текущей точки траектории до центра, v —
текущая скорость, 0 — угол между ее направлением (касательной
к траектории) и радиус-вектором г, проведенным в точку траек-
тории из центра. Наименьшее расстояние гтщ, на которое частица
приближается к центру, удовлетворяет равенствам (8.9)
с sin 0=1, так как касательная к траектории перпендикулярна
к rmin. Если rmin меньше радиуса зонда а, частица непременно уда-
рится о его поверхность, если больше — пролетит мимо.
Надо сказать, что описанные эффекты, свойственные зарядам
обоих знаков, представляют больший интерес в случае ионов.
Электронная часть зондовой характеристики (с УР>0), соответ-
ствующая притяжению электронов зондом, мало используется
на практике. Чтобы уменьшить воздействие зонда на плазму,
желательно применять маленькие зонды, а электронный ток в об-
ласти V > У5 весьма силен и расплавляет их. Поэтому для из-
мерения плотности зарядов в плазме больше используется ионная
часть ВАХ (§ 5).
§ 4. Техника измерения функции распределения
4.1. Наложение небольшого переменного напряжения. Прямое
дифференцирование экспериментальной кривой £(У), тем более
двукратное, сопряжено с большой погрешностью. Поэтому для
определения d^i/dV2 пользуются обходными путями. Так, целе-
сообразно к постоянному напряжению на зонд Vc добавить не-
большую переменную составляющую: V = Vc + yasin соЛ Если
К « Ус,
i (t) ж i (Ус) + fУа sin otf + 4" {““И sin2
\av)vc \dV /vc
при каждом значении Ус. В среднем по времени
дг- = <i> _ 1(VC) = А VI
Vй /Vc
Основную составляющую тока £(УС) для большей точности ис-
ключают экспериментально при помощи компенсационной схемы.
13* 195
То
тУДе Va прямо пя°ртВпеМеНИ дойавка к Т0КУ при известной ампли-
ИзмерениА дает „ВТ0РУЮ производную.
"Рй высокой М9Лг?И постоянной Добавки к току возможно только
^овеопгр^ стабильности
рятенствовать,
параметров разряда. Метод можно
.> низкой частотой
если промодулировать
dV2
70-
А
1g г*
304
О
"30-
-70-
lg/
-3
КВ
100 ~
d2i
cfV2
Рис. 8.6. ВАХ
ском масштабе
ная тока. Разряд в парах ртути;
проволочный зонд диаметром 0,03 мм
и длиной 6 мм— на оси трубки [8.1]
в полулогарифмиче-
и вторая производ-
/7
ЮО
О
₽ЙС. 8.7
ные j
во
20
во
10 о
20
ПРимеры ф в /О ° 10 г,зО
по энергиям в неоне, получен-
’ /Р 1 ГтоТп И,’ а~~.р = 1 Т°РР> Z =Ю°мА;б~р = 1 торр,
максВрЛтгп РР’ г = 25 мА; 1 — измеренное распределение,
а^Плцт К°е ° Т°й Жв средней энергией [8.1]
т°тно^ COs С’М). ^Ого напряжения высокой частоты со: Va ==
ОсЦиллипущтттЛ1?а ВТоРая производная связана с низкочас-
РУЮц*еи составляющей тока
Из^ерИть 2 \dT/2
196 °РУю проте г>К1
• пь1сокочастотные колебания тока усред-
Va0 COSG)^,
няются аппаратурой автоматически, ибо она их не разрешает.
В опытах, о которых сейчас пойдет речь, применялась несущая
частота со/2л = 8,4 • 104 Гц, низкая — coi/2n = 500 Гц.
4.2. Пример результатов. В целях иллюстрации применения
зондовой методики приведем результаты измерения функции
распределения электронов в положительном столбе тлеющего раз-
ряда [8.1]. Разряд создавался в стеклянной трубке диаметром
2,5 см, длиной 50 см. В центральную часть трубки параллельно
оси вводились впаянные цилиндрические зонды диаметрами
0,03, 0,06 мм и длиной 6 мм. На рис. 8.6 показаны типичная
ВАХ (в полулогарифмическом масштабе) и вторая производная
тока. В месте излома ВАХ d2ildV2 меняет знак (рис. 8.3), и это
даже облегчает установление точки излома и потенциала про-
странства.
На рис. 8.7 даны пересчитанные из /о(^) функции распреде-
ления по энергиям п(е) в неоне при р — 1 и 1,6 торр. Они
представлены в относительных единицах, величина 100 приписана
максимуму. Там же показаны соответствующие максвелловские
распределения. Температура для них определялась по имеющимся
на графиках In i от V прямолинейным участкам в области неболь-
ших энергий электронов 8 = el Vp|. Видно, как содержание энер-
гичных электронов в спектре обедняется по сравнению с макс-
велловским, что является следствием потерь энергии электронов
на возбуждение.
§ 5. Ионный ток на зонд в разреженной плазме
Пусть на зонд подан отрицательный потенциал, настолько
превышающий электронную «температуру» (скажем, на порядок),
что все электроны отталкиваются от зонда и вклада в ток не
дают. Зонд окружен слоем положительного объемного заряда.
Допустим, что слой тонкий, так что площадь его внешней гра-
ницы мало отличается от площади зонда S. Если длина про-
бега ионов много больше размеров зонда (и, тем более, слоя),
окружающая плазма возмущена мало и, казалось бы, ионный
ток можно оценить по формуле (8.3), заменив в ней ve на теп-
ловую скорость ионов г?+= (8&77л7И)1/2. Однако плотность заря-
дов гсо в слабоионизованной плазме, определенная таким способом
по измереннему ионному току в нижней пологой части ВАХ,
оказывалась систематически завышенной по сравнению со зна-
чением, вычисленным на основе формулы (8.3) по электронному
току насыщения (в точке верхнего излома В).
Выяснению этого вопроса было посвящено много теоретических
исследований, в том числе и самого Ленгмюра с сотрудниками.
Четкий ответ был дан в работах Бома, Бархопа и Мэсси (1949 г.).
Различные варианты детальной теории, которая включает иссле-
дование траекторий ионов в слое объемного заряда (п. 3.6) и рас-
пределения потенциала в нем, очень сложны [8.2—8.4]. Мы рас-
смотрим процесс в самой упрощенной форме, имея в виду лишь
197
выяснить физическое существо явления и дать оценочную фор-
мулу для ионного тока.
5.1. Ток насыщения. В слабоионизованной плазме температура
газа и ионов Т в десятки раз меньше температуры электро-
нов 7\ ~ 1 эВ. Электронейтральность плазмы вдали от зонда на-
чинает нарушаться там, где электроны испытывают заметное тор-
Рис 8 8 Распределения по-
тенциала и плотностен
электронов и положитель-
ных ионов около отрица-
тельного зонда
кТ < \eV\ < кТе. Плазма
можение в поле отталкивания, т. е.
там, где отрицательный потенциал от-
носительно невозмущенной плазмы ра-
вен примерно \Vg\ кТе!е. Это и есть
внешняя «граница» слоя объемного за-
ряда (рис. 8.8). Плотность электронов
на границе по закону Больцмана есть
ng = по ехр (—е\ Vg\/kT) ~ /г0/ё,
где ё — экспонента. Снаружи от этой
границы малоэнергичные ионы «под-
страиваются» к более энергичным элек-
тронам так, чтобы сохранялась квази-
нейтральность, т. е. плотность ионов
на границе близка к ng.
Но поскольку кТ < кТе ~ el Fg|, ио-
ны подвергаются относительно сильно-
му воздействию поля и вне «слоя», а
именно в том наружном «пределов», где
потенциал V заключен в пределах
там квазинейтральна, однако ионы под
действием поля приобретают скорость, значительно большую
тепловой. Они вступают из «пределоя» в «слой» нормально к гра-
ничной поверхности со скоростью
v+~ (2e\Vgl/M)y2 (2kTeIMy/2~ (TJTy/2v,.
Таким образом, ионный ток насыщения в идеализированном
«плоском» случае равен примерно
£+нас ~ Sengv+ ~ (]/2/e)SenoVkTe/M. (8.10)
Более детальные расчеты дают тот же результат и даже очень
близкое значение числового коэффициента, который в (8.10)
равен У2/ё = 0,52. В случае маленького сферического или тонкого
цилиндрического зонда ионный ток растет с ростом отрицатель-
ного потенциала по причинам, изложенным в п. 3.6.
5.2. Измерение плотности зарядов в плазме. Плотность удобно
определять по измеренному ионному току в нижней пологой
части ВАХ и Те при помощи формулы (8.10) или по тем уточ-
ненным, но более сложным формулам, которые дает теория зондов
малых размеров*). Этот способ, в особенности, когда ионный ток
*) Здесь, правда, возникают трудности при оценке соответствия экспе-
риментальных условий границам применимости той или ином приближен-
ной формулы, которые сами определены не вполне четко.
198
не сильно зависит от потенциала, ВАХ полога и применима про-
стая формула (8.10), в основном и используется на практике
для определения по. Электронный ток насыщения, как видно из
сопоставления формул (8.3) и (8.10), примерно в l/M/m ~ 102 раз
больше ионного. Как уже отмечалось, он сильнее возмущает плаз-
му и расплавляет маленькие зонды. Формулой (8.10) пользуются
для быстрого нахождения пространственного распределения плот-
ности зарядов в плазме. Электронная температура чаще всего
выравнена в пространстве, так что определять ее в каждой
точке не обязательно.
5.3. Плавающий потенциал. В случае максвелловского распре-
деления электронов электронный ток при отрицательном потен-
циале зонда дается формулой (8.2), ионный определяется форму-
лой (8.10). Приравнивая эти выражения, найдем отрицательный
потенциал зонда относительно плазмы, который соответствует
отсутствию тока на зонд:
еI Vf |/кТе « In [ (ё/V4n) ~ In (0,77Ш/m). (8.11)
Для водорода плавающий потенциал У/[В] «—3,3 Те [эВ], для
аргона — 6,3 Те. Самый простой способ измерить на опыте про-
странственное распределение потенциала плазмы Vs — определить
в каждом месте напряжение на зонде V, при котором исчезает
зондовый ток. Добавление к измеренной величине IVJ по фор-
муле (8.11) и дает потенциал пространства. Если температура
электронов (в более общем случае — средняя энергия) вырав-
нена в пространстве, т. е. Vf « const постоянное смещение потен-
циала не влияет на распределение электрического поля, которое
определяется разностями V в соседних точках.
§ 6. Ток в вакуумном диоде и слой пространственного заряда
около заряженного тела
Оценка возможности применения простейших формул теории
зондов, относящихся к плоскому случаю, базируется на сопостав-
лении толщины слоя объемного заряда с размерами зонда. Мы
оценим толщину слоя в наиболее простых и вместе с тем пред-
ставляющих главный интерес для зондовой диагностики крайних
ситуациях, когда на зонд идет поток частиц того же знака, каков
и знак объемного заряда. Это случаи положительного или до-
статочно большого отрицательного потенциалов, т. е. случаи
«токов насыщения». В области крутой части ВАХ, где объемный
заряд у отталкивающего электроны зонда положительный, а ток —
электронный, последний не зависит от геометрии слоя (и. 3.5).
Подходящей моделью для рассмотрения слоя около зонда, а так-
же других аналогичных ситуаций, например катодного слоя ду-
говых разрядов (гл. 12), может послужить классическая задача
о токе в вакуумном диоде,
6.1. Ток в вакуумном промежутке, ограниченный действием
пространственного заряда. Пусть к плоским электродам, отстоя-
199
щим на растоянии Л, приложено напряжение V. Один электрод
под действием посторонних причин эмитирует заряды, и благо-
даря этому в цепи течет постоянный ток. Эта модель является
прообразом реального устройства — вакуумного диода с накален-
ным катодом, испускающим термоэлектроны. Если накал слабый
и ток эмиссии мал, электронов в пространстве также мало. Они не
создают сколько-нибудь заметного поля, и потенциал ср распре-
деляется в промежутке так же, как и в отсутствие зарядов:
Ф = —Ех, где Е = — V/h — поле, ср и х отсчитываются от катода
(кривая 1 на рис. 8.9). —
поле вытягивает на анод
эмиссии
При не слишком низком напряжении
все электроны. Ток совпадает с током
от
V не зависит.
(плотности /э) и
Л
Рис. 8.9. Распределение потенциала в плос-
ком вакуумном промежутке, когда катод
эмитирует электроны: 1 — очень малый
ток эмиссии, поле не искажено простран-
ственным зарядом, 2 — возникновение по-
тенциального барьера для электронов, ког-
да они вылетают из катода с конечной
скоростью, 3 — электроны вылетают с ну-
левой скоростью
При сильном токе эмиссии промежуток заполняется большим
количеством зарядов, которые создают свое поле. Распределение
потенциала ф(я) определяется пространственным зарядом. Рас-
пределение плотности электронов пе, в свою очередь, зависит
от ср(гс). Эта самосогласованная картина описывается уравнениями
Пуассона, непрерывности тока и энергии электронов mv2l2 =
= mv^/2 Ц- £<р, которое определяет их скорость v(x). Со ско-
ростью ко электрон вылетает из катода. Если положить для про-
стоты, что у всех электронов она одинакова, то плотность тока
(абсолютное значение) / = enev = const. Таким образом,
<Гф , 4л/
dx2 и
кл]'
%(1 + 2ecp/mz?2)1/2’
(8.12)
причем ср(О) = 0, что было уже использовано при записи равен-
ства для к (я), а ф(й) = V.
Посмотрим, как ведет себя функция ф(я). Вблизи катода,
где электроны еще не успели ускориться полем, возникает их
скопление. Этот отрицательный заряд отталкивает электроны
металла вглубь от поверхности, в результате чего образуется
двойной слой: «плюс» на металле, «минус» вблизи. У катода по-
является обратное поле Е > 0, которое тормозит вылетающие
электроны, потенциал ф падает ниже потенциала самого катода
ф = 0. Но на аноде ф > 0, следовательно, ф(^) проходит через
минимум фт < 0 (кривая 2 на рис. 8.9). Перед электронами пред-
стает потенциальный барьер — есрт, который они должны преодо-
леть за счет своей начальной энергии тпд%/2.
200
Какой может быть высота этого барьера? Допустим, что
] £ф™ | > я^;о/2. Тогда ни один электрон не сможет его перейти
и тока не будет. Такое возможно только при очень низком на-
пряжении 7, и этот случай нас не интересует. Пусть |ефт|<?ш‘о/2.
Тогда, в предположении о моноэнергетичности вылетающих элект-
ронов, все они проскочат через барьер и пойдет просто ток насы-
щения /э. Интересующий нас промежуточный вариант, когда про-
странственный заряд ограничивает ток, но не запирает его: 0 <
< j < А, осуществляется, если высота барьера (в предположении
об одинаковости энергий электронов) в точности совпадает с их
начальной энергией. При этом электроны проходят через пик
барьера с формально нулевой скоростью, плотность их в этом
месте бесконечна, но j = «О • <»» — конечное число. Решение
(8.12), удовлетворяющее указанному условию dyldx = 0 при
ф = фт = — тпи^/2е, отбирает тот ток, который в состоянии про-
пустить промежуток при напряжении 7, когда пространственный
заряд не позволяет достичь анода всем эмитированным элект-
ронам *).
Введем в (8.12) безразмерный потенциал ф = 2^/z?Wo:
_ 4 1
dx~ 9^2 ”|/1 + 'Ф7
mvo
18 ле/
(8.13)
Физический смысл масштаба длины аг0 сейчас станет ясным. За-
мечая, что
d\_ id (d^ldx}2
dx2'^ 2 dip ’
проинтегрируем (8.13). Для определения произвольной постоян-
ной воспользуемся сформулированным условием d^ldx = 0 при
‘ф = —1. Получим
(+) при ^ф2х(тШ).
Проинтегрируем эти два уравнения. В уравнении со знаком
«минус» постоянную находим из условия 4 = 0 при х = 0. Ре-
зультат показывает, что минимум = — 1 достигается на рас-
стоянии гг(т1П) = х$ от катода. Постоянную в решении уравнения
со знаком «плюс» найдем, потребовав, чтобы решение прошло
через ту же точку х$, 4 = Так получим распределение по-
тенциала, которое изображается кривой 2 на рис. 8.9:
2б?ф Г , / X Л \"|4/3 л / , X /о я /X
—±—— 1 —1, (±) при х^х0. (8.14)
mvi L Vo /J
*) Реально эмитированные электроны обладают разными скоростями,
барьер же устанавливается вполне определенный—|ефт|. Те электроны,
у которых начальная энергия больше, преодолевают его, остальные заво-
рачиваются назад. Соответствующее решение получается только числен-
ным интегрированием, но в пределе |фт| результат получится тот же
[3, 4].
201
Отнеся (8.14) со знаком «плюс» к координате анода х = h,
где ср = V, получим соотношение, которое определяет ток j(V,
Л, Vo). Практически всегда eV тщ/2 ~ кТ, где Т — темпера-
тура катода, т. е. десятые доли вольта. Значит, h > хо и единицами
в (8.14) можно пренебречь везде, за исключением самой близкой
к катоду области. Отсюда ср °° ^4/3, Е #1/3, v ^2/3, пе °° х~2/\
а ток равен
1 1 /2? У3/2 о Q/ .п_6 {У [В]}3/2 Л s 9 ZQ/IK.
z—Q-J/--------о- -2,34-10 у--- зт А/см2. (8.15)
J 9л Г щ д2 {Мем]2}
Это соотношение, которое определяет ток в плоском вакуум-
ном диоде, ограниченный действием пространственного заряда,
называют законом Чайлда — Ленгмюра (1913 г.) или законом
трех вторых — ток пропорционален У3/2. В этом приближении
исчезающе малый минимум ср сливается с катодом. Закон (8.15)
можно получить элементарным путем, интегрируя (8 12) с до-
полнительным условием Е = 0 при х = 0, которое равносильно
предположению о том, что электроны вылетают из катода с «ну-
левой» скоростью. Независимость j от уэ следует понимать так,
будто эмиссионная способность катода неисчерпаема. Справед-
ливость (8.15) со стороны высоких напряжений и токов ограни-
чена условием ] < /э, а со стороны низких — eV > кТ и требо-
ванием, чтобы пространственный заряд оказывал сильное воз-
действие на ток.
Приведем для иллюстрации численный пример. При Т -=-
= 1000 К ~ 0,1 эВ оксидный катод дает эмиссию уэ ~ 1 А/см9.
Если к промежутку h = 1 см приложить V = 100 В, он пропустит
ток всего лишь j ~ 2,3 10-3 А/см2; только 2 электрона из 1000
прорвутся через ими самими же воздвигнутый барьер.
Для сферического и цилиндрического диодов остается в силе
закономерность (8 15) i <*> У3/2, но вместо № фигурирует произ-
ведение на функции отношения радиусов электродов R\!R^
они табулированы [3, 4]. Формула (8.15) применима и к случаю
эмитера ионов, надо только тп заменить на М, а V на I У|.
6.2. Оценка толщины плоского слоя. Для этой цели можно
использовать предыдущий результат (в случае сферического и
цилиндрического зондов — соотношения для соответствующих
диодов). Зонд играет роль электрода, собирающего заряды.
Роль эмитирующего электрода выполняет граница квазинейтраль-
ной плазмы, из которой частицы поступают в слой пространствен-
ного заряда. Правда, меняется задаваемая величина. В диоде
фиксировано расстояние между электродами, а значение тока
«подстраивается» к приложенному напряжению. В слой около
зонда поступает определенный ток «насыщения», который задает-
ся тепловым газокинетическим потоком электронов в случае по-
ложительного потенциала на зонде или также не зависящим
от Vp потоком ионов из предслоя в слой — в случае большого
отрицательного потенциала. Граница же слоя, т. е. его толщи-
на h, «подстраивается» к потенциалу зонда.
202
Для Vp > 0 и максвелловского распределения электронов по
формулам (8.3), (8.15) найдем
h (8/9)1/2>(eVp/kTe)3/4d, d = (кТе/4ле2п0)1/2.
Масштабом толщины слоя отрицательного объемного заряда яв-
ляется дебаевский радиус d, но толщина растет с ростом потен-
циала. Для большого отрицательного потенциала, когда весь ток
создается ионами, толщина слоя положительного заряда по фор-
мулам (8.10), (8.15) равна (с М вместо т)
h^^el9Y/2(e\Vp\/kTe^^d.
В данном случае гораздо выше потенциал IVp\. Он примерно
на порядок больше электронной температуры, чтобы электронный
ток был меньше ионного. Поэтому толщина ионного слоя на
порядок больше дебаевского радиуса.
Похожие в качественном отношении результаты получаются
для сферы и цилиндра, но когда эти случаи сильно отличаются
от плоского, т. е. когда h больше радиуса зонда, теория очень
сложна [8.3, 8.4].
§ 7. Двойной зонд
Двойной зонд, предназначенный для исследования плазмы
в отсутствие опорного электрода, был впервые применен незави-
симо в работах [8.5, 8.6]. Два ленгмюровских зонда 1, 2 вво-
дятся в плазму и подсоединяются Через потенциометр к источ-
нику постоянного напряжения так, чтобы можно было менять
не только напряжение между зондами V, но и полярность
(рис. 8.10).
7.1. Характеристика. На рис. 8.11 показана измеренная ха-
рактеристика двойного зонда, полученная в безэлектродном ВЧ
разряде. Разберем ее физический смысл в предположении об
одинаковости самих зондов и параметров плазмы в местах, где
они находятся. Симметричность приведенной характеристики
свидетельствует о том, что эти условия выполнялись в данном
эксперименте с хорошей точностью. Если потенциалы плазмы К
в местах расположения зондов одинаковы, то в отсутствие напря-
жения, V = 0, ток через зондовую цепь не течет: i = 0. В данном
случае это условие также выполнялось: видимо, зонды были рас-
положены достаточно близко, и градиент потенциала в плазме
был мал. Оба зонда при этом находились под одним и тем же
плавающим потенциалом Vf < 0 (рис. 8.12 а).
Обозначим потенциал левого зонда относительно плазмы PTPi,
правого — VP2. Условимся о направлении отсчета напряжения:
V = VPi — VP2. Электрический ток i будем считать положитель-
ным, когда он течет из плазмы в левый зонд; iei i+ — по-преж-
пему абсолютные значения электронного и ионного токов на
203
зонд*). Сколько положительного заряда втекает из плазмы в
один из зондов, столько вытекает из другого в плазму; поэтому
j ^+1 iel = (^+2 ^е2) 7 ^4-1 “Ь ^+2 = lei + 1е2- (8.16)
Потенциал ни одного из зондов не может быть положительным.
В самом деле, при Vp > 0 на зонд течет электронный ток насыще-
ния. Согласно (8.16) на другом зонде он должен замыкаться
Рис. 8 11. Характеристика симмет-
ричного двойного зонда. Снята по
схеме рис. 11.10 в безэлектродном
ВЧ разряде [8.4]
Рис 8.10. Схема под-
ключения двойного
зонда с применением
кругового потенцио-
метра
ионным током, который существенно меньше. Таким образом, не
только зондовая система в целом «плавает», т. е. заряжена
отрицательно относительно плазмы, но и каждый из зондов не-
пременно «отрицателен». Пусть на левый зонд от источника
подан «минус», на правый—«плюс» (V < 0). Ток в плазме течет
ог «плюса» к «минусу». Значит, на левом зонде преобладает
ионный ток, на правом—электронный. Если напряжение I V\
большое (по сравнению с кТ!е}, левый зонд сильно отрицателен,
правый — менее отрицателен, чем плавающий (рис. 8.12 6). На
лезый идет чисто ионный ток насыщения. Зависимость ^(У)
при этом слабая. Этому соответствует левая пологая часть ВАХ.
При небольших отрицательных V иоин яй ток на левый зонд
частично компенсируется электронным. Но последний сильно
зависит от потенциала зонда по больцмановскому закону (8.2).
На этом участке ВАХ ведет себя круто; ток резко уменьшается
до нуля при У -> 0. Правая часть ВАХ в точности повторяет
левую и соответствует перемене полярности — подаче «плюса»
на левый зонд, а «минуса» на правый (рис. 8.12 в).
*) Знаки i и V согласованы в соответствии с ориентацией кривой
рис. 8.11.
204
Поскольку потенциалы на обоих зондах отрицательны относи-
тельно плазмы, для описания электронных токов м, ie2 применима
формула Ленгмюра (8.2). В соответствии с (8.16)
I = i+i (VPi) — ieHac exp(eVpi/A77e) = —i+2(Vp2)+ ^нас ехр(еУр2/^Л),
(8.17)
где ионные токи относительно слабо зависят от ускоряющего ионы
отрицательного потенциала зонда.
7.2. Измерение параметров плазмы. Продифференцируем пер-
вое равенство (8.17) по V в точке симметрии ВАХ, где i = 0.
При этом iei(Vf)= i+i(V/); обозначим
эту величину (г+)о. Имеем
( di_ \ Г / ^+1 \____£_/ • \ ] I dVvl
\dV /0 кТе^+)о\\ dV )Q'
(8.18)
Если зондовый ток исчезает при нуле-
вой разности потенциалов У, то при
перемене полярности напряжения зон-
ды просто меняются ролями. Поэтому
потенциалы зондов, помимо равенства
V = VPi — Vp2, связаны еще функцио-
нальным равенством УР1(У) = Vp2(~V).
Дифференцируя эти равенства по V,
находим
1 = (dVpl/dV)v- (dVp2/dV)v„
(dVpl/dV)v = -(dVp2/dV)-v.
Отсюда следует, что в точке симмет-
Рис. 8.12. Потенциалы
двойного зонда: а — плава-
ющее состояние, тока через
зонды нет; б — зонд 1 силь-
но отрицателен, на него
рии (dVpJdV^ = 1/2. Из (8.18) полу-
е/кТе = (^+i)o [(di^-j/d^ рг)0 2 (бй/с/Р)0].
(8.19)
идет ионныи ток насыще-
ния; в — перемена поляр-
ности, зонд 2 сильно отри-
цателен
Эту формулу используют для измере-
ния электронной температуры. Произ-
водную (dildV)o находят по наклону из-
меренной ВАХ в точке, где i = 0.
Ионный ток и его производную, которая, кстати сказать, гораз-
до меньше производной от полного тока, можно определить пу-
тем линейной экстраполяции пологой части ВАХ к точке сим-
метрии (рис. 8.11). При этом предполагается, что в области боль-
ших отрицательных напряжений V ~ УР1, т. е. измеренную в этой
области функцию г+1(У) можно рассматривать как /+1(Ур1), что
и позволяет экстраполировать эту зависимость.
Применяется еще один способ нахождения Те, который похож
на используемый в однозондовом методе. Поделим второе ра-
205
венство (8.16) на м, воспользуемся формулой Ленгмюра (8.2)
для электронных токов и прологарифмируем результат:
1пр.±1+.!±а._1К^. (8.20)
\ 1~ г+1 ) е
Определяя ионные токи путем экстраполяции и построив полулога-
рифмический график (8.20) как функцию 7, по наклону «пря-
мой» в области точки симметрии можно найти Те-
Плотность зарядов в плазме находят, как в однозондовой ме-
тодике, при помощи формулы (8.10) для ионного тока насы-
щения, по измеренному на пологой части ВАХ току i ~ i+Hac и
известной Те.
7.3. Измерение электрического поля. Когда в плазме имеется
градиент потенциала, потенциалы пространства в местах распо-
ложения зондов 7«i, Vs2 различны. Чтобы оба зонда «плавали»
и на них не шел ток, на зонды нужно подать разность потен-
циалов
&V=Vpl-Vp2 = Vsl-Vs2.
Добиваясь прекращения зондового тока путем вариации напря-
жения и зная расстояние между зондами Аж, можно найти
электрическое поле EX = AV/Ax. Потенциал же плазмы двух-
зондовым методом в принципе нельзя определить. Способы на-
хождения Те и по при А7 =/= 0 остаются в силе. Просто на оси 7
смещается на А 7 точка симметрии ВАХ, где i = 0. К ней и сле-
дует «привязываться» в (8.19), (8.20).
Поскольку ток в двойном зонде гораздо меньше электронного
тока в одиночном зонде, двойной зонд меньше везмущает плазму.
Поэтому им пользуются и при исследовании нестационарных
явлений, когда возмущения особенно нежелательны, так как
могут исказить всю картину эволюции состояния плазмы.
§ 8. Зонд в плазме повышенного давления
Говоря о повышенных давлениях, мы имеем в виду ситуацию,
в которой длины пробега электронов 1е и ионов Z+ очень малы по
сравнению с размерами зонда. Зонд будем считать сферическим
радиуса а. Например, при р = 30 торр 1е ~ 10~3 см, Z+ ~ 10“4 см.
тогда как а ~ 10“1 — 1 см. При типичных разрядных условиях
Тс ~ 104 К, по ~ 109—1010 см“3 дебаевский радиус d =
= (/£Ге/4ле2А1о)1/2 ~ 10“2 см, так что I < d <£. а. В плотном газе
потоки заряженных частиц к зонду формируются в результате
диффузии и дрейфа. Теория в этом случае, пожалуй, еще слож-
нее, чем в разреженной плазме, и не вполне разработана. Кроме
того, для получения количественных результатов приходится
привлекать данные по длинам пробега или подвижностям, что
вносит дополнительные погрешности в извлекаемые величины.
Не вдаваясь в детали теории, остановимся на некоторых общих
моментах, способствующих пониманию физических процессов.
206
8.1. Приближенное равновесие в электронном газе. Потоки
заряженных частиц можно представить в виде сумм диффузион-
ного и дрейфового (см. (3.20)). Электрическое поле Е создается
приложенным к зонду напряжением и поляризацией плазмы
вследствие отрыва более быстрых электронов от ионов. Пусть
на зонд подан отрицательный потенциал, который тормозит
электроны. Если потенциал совпадает с плавающим, потоки
электронов и ионов из плазмы к зонду в точности одинаковы.
Если потенциал отрицательнее плавающего, электронный поток
меньше ионного. Если выше плавающего, но не на много —
поток электронов больше ионного, но сравним с последним по
величине. В тех случаях, когда потенциал зонда не является
положительным или слабоотрицательным, ионный слой положи-
тельного объемного заряда около зонда переходит в слой также
возмущенной, но квазинейтральной плазмы, постепенно пере-
ходящей в невозмущенную с плотностью зарядов п0.
Возмущение от зонда в квазинейтральном слое проявляется
в виде присутствия градиента плотностей ~ п+ ~ п. Плотности
уменьшаются по направлению к зонду, что обеспечивает диффу-
зионный поток зарядов из отдаленной области к поглощающему
их телу зонда. Сама же квазинейтральность является следствием
малости дебаевского радиуса по сравнению с характерной длиной
перепада плотности, которая порядка размеров тела.
Как уже отмечалось, в случае достаточно большого отрицатель-
ного потенциала зонда электронный ток сравним с ионным или
меньше его. Но коэффициент диффузии De и подвижность цР
у электронов гораздо больше, чем у ионов D+l ц+. Следовательно,
противоположно направленные большие диффузионный и дрей-
фовый электронные потоки компенсируют друг друга с точностью
до относительно малой величины результирующего электронного
потока Ге, который сравним с ионным потоком Г+ или меньше
его. Имея в виду соотношение Эйнштейна (3.24) между Dc и
и полагая в (3.20) приближенно Ге ~ 0, находим
— « — Е --V7, пе « ехр кТ^ , (8.21)
где V(г) <0 — потенциал, отсчитываемый от невозмущенной
плазмы. Таким образом, распределение плотности электронов
в отдаленной окрестности отрицательного зонда приближенно под-
чиняется больцмановскому закону.
8.2. Пространственное распределение плотности зарядов и по-
тенциала в квазинейтральной области вокруг отрицательного
зонда. Электрическое поле в квазинейтральной, квазиравновесной
для электронов области связано с градиентом пе первой форму-
лой (8.21). Пользуясь тем, что п+ ~ пе ~ п, введем эту величи-
ну Е в равенство (3.20) для потока ионов. Полный ионный ток
через сферическую поверхность есть
[кт 1 Л
Z)+ + p+_±|-g-. (8.22)
207
Выражение в квадратных скобках представляет собой не что
иное, как коэффициент амбиполярной диффузии (3.35), в кото-
ром > ц+. Если зонд находится под плавающим потенциалом
и потоки электронов и ионов к зонду одинаковы, поток зарядов
к поглощающему телу фактически и является результатом амби-
полярной диффузии (§ 6 гл. 3). При ином потенциале потоки
зарядов разнятся на величину, сравнимую с амбиполярным по-
током. Но так или иначе, ионный поток в квазинейтральной зоне
совпадает по величине с потоком амбиполярной диффузии. В не-
равновесной плазме, где Те > Z, дрейфовая составляющая ионного
потока, пропорциональная второму слагаемому в (8.22), в
TJT > 1 раз больше диффузионной, и можно говорить о «чистом»
дрейфе ионов в суммарном поле Е зонда и поляризации. Малое
слагаемое с D+ в (8.22) опустим.
В стационарных условиях и в пренебрежении относительно
медленными процессами рождения и гибели зарядов в возмущен-
ной зондом области плазмы (г) = const. Интегрируя (8.22),
найдем распределение зарядов в квазинейтральной зоне, асимп-
тотически переходящей при г в невозмущенную плазму:
££ j р = _________+_______
г /’ 4лгп0ц+ (кте/е) *
(8.23)
Физический смысл величины R сейчас станет ясным. Согласно
(8.21), (8.23) и пе ~ п, распределения потенциала и поля в ква-
зинейтральной области имеют вид
кТ' л кТ п2 4
V=--------In 7... б, ; Е =---------2. Л. 1 •
е 1 — R/r' eR 1 — R/r
(8.24)
Они нарастают от нуля при приближении из бесконечности к
зонду, имеют масштабами кТе1е и kTe!eR и формально устрем-
ляются к — оо при г -> Д, когда формально п -> 0.
Радиус Д, при приближении к которому выражения (8.23),
(8.24) утрачивают силу, соответствует границе слоя пространст-
венного заряда, которым зонд отделен от квазинейтральной об-
ласти. В самом деле, квазинейтральность нарушается там, где
тормозящий электроны потенциал I Е(г) I достигает нескольких
электронных температур кТе1е. Но на таком радиусе 1 — Rlr <С 1,
т. е. г « Д. Таким образом, Д можно рассматривать как эффек-
тивный радиус слоя, и второе соотношение (8.23) связывает
ионный ток на зонд с этой величиной.
8.3. Ионный ток насыщения и оценка плотности зарядов
в плазме. Чем выше отрицательный потенциал зонда |ЕР1, тем
больше толщина слоя положительного объемного заряда h —
= Д —а и больше Д. Согласно (8.23) ионный ток растет с рос-
том Д. Однако, если слой тонкий, Д приближенно совпадает с
радиусом зонда а и ионный ток от потенциала не зависит. Соот-
ветствующая величина представляет собой ионный ток насы-
щения. Случается такое либо если зонды больших размеров,
208
т. е. толщина слоя h, которая, в общем, характеризуется дабаев-
ским радиусом d, мала по сравнению с а, либо если мал дебаев-
ский радиус, т. е. достаточно велика плотность зарядов в плазме.
Выражая в (8.23) туодвижность ионов через длину пробега:
[i+ = el^/Mv+l где г?+ =4 (8кТ/пМ)У2, и вводя площадь зонда
S = 4ля2, представим ионный ток насыщения в виде
_ / 4. \i/2 / кТо \1/2 / то \ 1/2
а
(8.25)
^+нас •— &
ую в (8.25) электронную температуру,
чена в гораздо более узком диапазоне
1 эВ), чем плотность зарядов, которая может
ери изменении разрядных условий.
Он отличается от (8.10) для разреженной плазмы двумя послед-
ними множителями. Первый из них (Т^/Г)172 не превышает 10,
второй, согласно исходному предположению,— величина очень
малая, гораздо меньше АО-1. Следовательно, ионный ток насы-
щения в плотном ионизованном газе меньше, чем в разреженном,
причем тем меньше, чем выше давление.
Зондовая характеристика при повышенных давлениях в ка-
чественном отношении ^похожа на ВАХ в разреженной плазме,
и нижняя пологая ее чДсть соответствует ионному току. Форму-
лой (8.25) можно воспользоваться для оценки плотности заря-
дов по по измеренному I ионному току. Даже если не удается
хорошо измерить входящ
известно, что она заклкг
значений (Tt
изменяться на порядки п
8.4. Об оценке электронной температуры по электронному
току на зонд. Когда отрицательный потенциал зонда выше пла-
вающего, электронный ток, быстро нарастающий с уменьшением
тормозящего потенциала |УР|, больше ионного. Как и в раз-
реженной плазме, при этом i = ie — i+ ~ Ze. Этому соответствует
крутая часть ВАХ, которая присутствует и при повышенных
давлениях. Электроны непосредственно попадают на зонд после
последнего столкновения, т. е. со сферы радиуса и ~a+Ze, от-
стоящей от поверхности зонда на малом расстоянии порядка
длины пробега 1е <С а. Обозначим zzei, Vi плотность электронов
и потенциал на радиусё г\. Поскольку электроны идут от сфе-
ры ri на зонд без столкновений, их ток на зонд можно пред-
ставить формулой, которая аналогична (8.2):
ie ~ 5(^1Ге/4)ехр [e(Vp — Vx}lkTe\. (8.26)
Электронная температура и ге(Те) возмущаются гораздо меньше,
чем плотность.
Если проэкстраполйровать формулу (8.21) для равновесной
плотности электронов tae.(V) вплоть до сферы радиуса гь где
V = Vi, тем самым определив пе\, получим из (8.26) в точности
выражение (8.2) для тока на зонд, exp(eVp/kTe). Это дает на-
дежду на возможность использования крутой части ВАХ для
оценки электронной температуры (по наклону полулогарифми-
ческого графика Ini от Ур). Более детальное рассмотрение [8.7]
с учетом отличия от руля электронного потока в (3.20) показы-
14 ю. п. Райзер \ ' 209
вает, что электронный ток уменьшается/ по сравнению с (8.2)
в у ~ 1 + a(hlle) (kTJeVp) раз, где а -ф числовой коэффициент
около 0,5. Уменьшение может быть и значительным, порядка 10,
но от Vp оно зависит гораздо слабее, чей больцмановская экспо-
нента в (8.2). Это и позволяет оценивать Те по крутизне электрон-
ной части зондовой характеристики. /
8.5. Слой положительного пространственного заряда. Чтобы
оценить толщину или радиус слоя, отделяющего зонд от квази-
нейтральной плазмы, необходимо интегрировать уравнение Пуас-
сона. Пренебрегая малой плотностью электронов в ионном слое,
запишем
АЕ = 4ле«+, £=.--^<0. (8.27)
г2 dr j dr v 7
Плотность ионов, как и в § 6, выразим^ через ионный поток, на
этот раз дрейфовый: п+ = T+Zp+I^l *). Введя сохраняющуюся
величину ионного тока по (8.23), найдем
1 д- кТ. r
п+ = —-----------= _„ 4. (8.28)
4лг"е|1+(— £) 1 еЕ г“
В качестве граничных условий к уравнениям (8.27), (8.28)
можно считать, что на границе между слоем и квазинейтральной
областью при г = R поле и потенциал равны нулю. Такое при-
ближение отражает факт малости этих величин по сравнению с
l^pl и |УР| на поверхности зонда при г = а.
Даже при сделанных упрощениях компактная формула для
толщины слоя h = R — а получается, только если слой тонкий,
т. е. является «плоским»; при этом г2 ~ const « а2 и
h/a = [ (3/2V2) (б/М) (е\Vi0\/kTe) ]2/3. (8.29)
В бесстолкновительном слое по формуле (8.15) |V|3/4. При-
ближение «плоского» слоя справедливо, । пока h < а. Например,
при d ~ 10~2 см, а ~ 10-1 см, aid = 10 нарастающая с потенциалом
толщина слоя становится сравнимой с радиусом зонда, hja « 1,
при elVpl ~ 10 кТе. С учетом сферичности формулы получаются
весьма громоздкими, хотя принципиальных трудностей интегри-
рование не представляет. В случае толстого слоя радиус его R
связан с потенциалом зонда Vp грубо приближенным соотно-
шением [
eVp/kTe — (2/3)1/2 (a/rf) (Ж) (Ж - 1). (8.30)
Например, с a/d =12,3 R/a = 1,5 при е| VL\/kTe = 7,5; 2 — при 20
В пределе больших I Ур| R/a VIVPI и согласно (8.23) зондовый
ТОК £ ~ £+ оэ У| VP|.
*) При очень больших отрицательных потенциалах Vp поле в слое мо-
жет оказаться столь большим, что дрейф ионов будет иметь аномальный
характер: и+д со У|Е| (§ 5 гл. 3). /
210 /
8.6. Плавающий потенциал и измерение распределения по-
тенциала. Приравнивая выражения для ионного тока (8.25)
и электронного (8.2) с учетом уменьшающего множителя у,
о котором говорилось в п. 8.4, получим соотношение, аналогич-
ное (8.11):
(8.31)
KI е I jl //б у 1 е j J
которое определяет плавающий потенциал. Он имеет порядок 10
(Ще).
Измерение абсолютного значения потенциала в плотной плаз-
ме — задача непростая, но пространственное распределение по-
тенциала снять легко. Для этого можно, например, без всякого
источника питания подсоединить зонд к опорному электроду
через очень большое сопротивление Q. Почти изолированный
зонд находится при этом под плавающим потенциалом. Измеряя
малый зондовый ток i, найдем разность потенциалов между зондом
и опорным электродом iQ = Vs + Vf. Если плавающий потенциал
везде одинаков, передвигая зонд, найдем с точностью до констан-
ты Vf распределение потенциала плазмы относительно опорного
электрода Vg. По разности потенциалов в соседних точках по-
лучим распределение поля.
Часть III. РАЗРЯДЫ РАЗНЫХ ТИПОВ
Глава 9. ПРОБОЙ ГАЗОВ В ПОЛЯХ РАЗЛИЧНЫХ ЧАСТОТНЫХ
ДИАПАЗОНОВ
§ 1. Сущность явления
В самом общем смысле электрическим пробоем называется
процесс превращения непроводящего вещества в проводник в ре-
зультате приложения к нему достаточно сильного поля. Ионизо-
ванное состояние, в которое приходит газ при пробое, может
возникать за разные промежутки времени — от 10~9 с до несколь-
ких секунд, но чаще всего это происходит за 10“4 — 10-8 с. Иони-
зация достигает заметной величины, столь заметной, что пробой,
как правило, сопровождается видимой невооруженным глазом
световой вспышкой. Определенные ее варианты по-житейски на-
зывают «искрой». Если внешнее поле прикладывается на достаточ-
но длительное время, в результате пробоя может зажечься разряд,
который будет гореть, пока действует поле. Так происходит в лю-
бых электрических полях: постоянном, импульсном, периоди-
ческом, в поле электромагнитной волны, световой. Предел, до
которого нарастает ионизация, диктуется конкретными условиями.
Ее степень может быть порядка 10“8, как при зажигании тлею-
щего разряда, ток которого ограничен большим сопротивлением
внешней цепи. Это может быть и полная однократная ионизация
всех атомов, как случается при пробое под действием интен-
сивного лазерного импульса.
Первичным и главным элементом подчас комплексного и слож-
ного процесса пробоя является электронная лавина, которая раз-
вивается в газе под действием поля. Лавина начинается с неболь-
шого количества затравочных электронов, которые появляются
случайно, скажем под действием космических лучей. Ее может
начать даже один электрон. Для облегчения пробоя при экспери-
ментальных исследованиях, чтобы надежно спровоцировать воз-
никновение лавины, пользуются искусственными источниками
первичных электронов (например, облучают катод или газ ультра-
фиолетовым излучением, вызывающим фотоэффект). Под дейст-
вием электрического поля электрон набирает энергию. Достигая
энергии, несколько превышающей потенциал ионизации, он
ионизует молекулу, теряя при этом свою энергию. В результате
появляются два медленных электрона. Они снова ускоряются
212
тюлем и также производят ионизацию — получается четыре
электрона, и т. д. Происходит ли это в ходе систематического
дрейфового сноса лавины, если поле постоянное, или электроны
в основном «топчутся на месте», совершая колебания в быстро-
переменном поле, принципиального значения не имеет, хотя на
деталях и внешней стороне процесса это существенным образом
отражается.
Явление пробоя имеет резко выраженный пороговый характер.
Это значит, что пробой происходит только при полях, превышаю-
щих определенное для каждых конкретных условий значение.
Так, повышая напряжение на разрядном промежутке или интен-
сивность электромагнитного излучения, мы до поры до времени
не замечаем каких-либо изменений в состоянии среды. Й вдруг,
при определенных значениях напряжения или интенсивности,
бурно развивается ионизация, приборы регистрируют ток, наблю-
дается вспышка. Существование порога связано с резкой зависи-
мостью скорости ионизации атомов электронным ударом от зна-
чения поля и тем, что наряду с ионизацией, обеспечивающей
размножение электронов, имеются механизмы, которые ставят
препятствия на пути развития лавины.
Лавину тормозят потери энергии электронов и потери самих
электронов. Первые замедляют приобретение в поле энергии, до-
статочной для ионизации. Вторые приводят к обрыву цепей в цеп-
ной реакции размножения. Электроны теряют энергию на возбуж-
дение электронных состояний атомов и молекул, молекулярных
колебаний и вращений, а также при упругих столкновениях.
Электронные цепочки обрываются в результате диффузионного
ухода электронов из области действия поля (в частности, на
стенки), прилипания в электроотрицательных газах. При пробое
газа между электродами, к которым приложено напряжение,
электроны устраняются в результате вытягивания их полем па
анод. Рекомбинация не принадлежит к числу тех механизмов
гибели электронов, которые оказывают существенное влияние на
порог пробоя. Судьба лавины, будет она развиваться или нет,
решается на ранней ее стадии, когда электронов и ионов так
мало, что их встреча маловероятна. Скорость рекомбинации про-
порциональна квадрату плотности зарядов. При малых плотно-
стях рекомбинация намного уступает механизмам гибели, линей-
ным по плотности электронов: выносу полем на анод, диффузии
на стенки, /прилипанию. Однако возрастающая после рождения
очень многих поколений электронов рекомбинация может по-
ставить предел дальнейшей ионизации и тем самым зафиксировать
уровень, которого достигает степень ионизации при пробое.
Потери энергии электронов скорее следует рассматривать как
фактор, уменьшающий частоту ионизации. Формально они не
закрывают возможности размножения, лишь замедляют его, хотя
практически в недостаточно сильных полях сводят на нет ско-
рость ионизации. Исчезновение электронов обрывает цепи, и это
ставит предел самой возможности осуществления цепной реакции
213
размножения. Идет соревнование между рождением и гибелью
электронов. Скорость рождения электронов, которая определяется
частотой ионизации, чрезвычайно резко зависит от напряжен-
ности поля. Скорость гибели зависит от поля значительно сла-
бее. Значит, преобладание положительного или отрицательного
факторов для развития лавины очень чувствительно к значению
поля. Даже если поле чуть ниже порогового, скорость ионизации
заметно меньше скорости гибели и размножения не происходит.
Если же поле больше порогового, процесс ионизации катастрофи-
чески разгоняется. Чем выше степень «надпороговости», тем
легче и быстрее развивается пробой.
Порог пробоя определяется соотношением между скоростями
рождения и гибели электронов лишь при достаточно длительном
воздействии поля, когда заведомо хватает времени на рождение
многих поколений электронов. В случае очень кратковременных
импульсов поле должно быть настолько сильным, чтобы обеспе-
чить рождение достаточного, «макроскопического» числа электро-
нов за время импульса даже при полном отсутствии их потерь.
Так, например, получается при пробое газа сфокусированными
«гигантскими» лазерными импульсами, которые длятся всего
(2—4) • 10~8 с. Видимая вспышка появляется, если в области фо-
куса нарождается около 1013 электронов.
В этой главе будут рассмотрены эффекты пробоя газов во всех
частотных диапазонах, от постоянного поля до оптического. Од-
нако важнейшие явления пробоя разрядных промежутков под
действием поданного на электроды напряжения будут затронуты
только частично, а именно в той части, которая связана с про-
боем всего объема промежутка и зажиганием самостоятельного
разряда в газах не высокого давления. Пробой относительно
длинных промежутков, заполненных газами высокого (атмос-
ферного) давления,— так называемый стримерный, или искровой^
когда от электрода к электроду прорастает тонкий ионизованный
канал,— будет рассмотрен в гл. 14.
§ 2. Пробой и зажигание самостоятельного разряда
в постоянном однородном поле
при не слишком больших произведениях давления
на длину промежутка
2.1. Несамостоятельный ток в разрядном промежутке. Рас-
смотрим, что происходит в плоском газовом промежутке, вклю-
ченном в цепь с источником питания, если постепенно повышать
напряжение V на электродах. Приложенное электрическое поле
будем считать однородным: E=Vld, где d — расстояние между
электродами. Время от времени у катода появляются случайные
электроны. Поле движет их к аноду. Электрон может и не достичь
анода: попасть на боковые стенки разрядного сосуда, прилипнуть
к электроотрицательной молекуле. Ионы могут рекомбинировать.
Гибнет по пути тем меньшая доля зарядов, чем быстрее они
214
Рис 91 ВАХ не-
самостоятельного
разряда между
плоскими элект-
родами
проходят промежуток, т е чем сильнее поле Поэтому электри-
ческий ток i в цепи, который определяется числом зарядов,
достигающих электродов в 1 с, растет с повышением V Начиная
с какого то напряжения, практически все заряды, электроны и
ионы, рождающиеся в объеме, попадают на электроды Ток до-
стигает насыщения и перестает зависеть от V Он определяется
скоростью появления зарядов под действием посторонних источ-
ников, космического излучения или искусственного ионизатора.
Разряд этот является несамостоятельным Его
статическая волът амперная характеристика
изображена на рис 9 1 Статическая — значит
отвечающая установившемуся, стационарному
состоянию Предполагается, что напряжение
мы повышаем настолько медленно, что при
каждом его значении успевает установиться ста
ционарное состояние
При еще больших напряжениях начинается
ионизация молекул электронным ударом, что
приводит к усилению тока, происходящего от
внешних источников Пусть, для определенно-
сти, катод освещается ультрафиолетовым
излучением лампы, что создает фототок zq,
и прилипания нет, о влиянии последнего
см в п 2 5 Электроннный ток на аноде и ток i
по сравнению с током электронов, вылетающих с катода, в ead
раз, где а— ионизационный коэффициент Таунсенда (§ 1 гл 4)
z = zo exp(acZ) Полный ток на катоде в стационарном состоянии
также равен i Он складывается и5 тока электронов iq и тока ио-
нов, рождающихся в ходе ионизации и вытягиваемых полем на
катод, z0(exp(ad) — 1) (п 7 1 гл 4) Вертикально растущая ВАХ
становится более пологой При дальнейшем повышении напря-
жения вступают в игру вторичные процессы — рождение элект-
ронов под действием тех частиц, которые появляются в резуль-
тате первичного процесса ионизации газа электронами Особенно
активно влияют вторичные процессы на усиление, если приводят
к эмиссии электронов с катода Эмитированный электрон прохо-
дит весь путь от катода до анода и потому производит больше
ионизаций, чем рожденный «на полпути» С учетом вторичной
эмиссии стационарный разрядный ток определяется формулой
(4 26),
i = iQead/ [1 —у (ead — 1)],
где у — эффективный коэффициент вторичной эмиссии с катода,
которая происходит под действием положительных ионов, фото-
нов и метастабильных атомов, рождающихся в газе в результате
ионизации и возбуждения атомов электронами Ток по-прежнему
остается несамостоятельным, пока знаменатель положителен. Он
нарастает с V еще круче, чем в области простого усиления,
благодаря уменьшению знаменателя, равного единице при не-
больших коэффициентах усиления ad.
215
2.2. Условие зажигания самостоятельного разряда. Если по-
дать на электроды такое напряжение V > Vt, при котором коэф-
фициент воспроизводства ц = 7 [ехр (ad) — 1] >1 и знаменатель
в предыдущей формуле отрицателен, формула не имеет физи-
ческого смысла. Это значит, что при таком напряжении ток не
может быть стационарным. С другой стороны, при V < V t, когда
ц < 1, течет стационарный несамостоятельный ток. Условие пе-
рехода ц = 1, или
y(ead— 1) = 1, ad = ln(l/y + 1), (9.1)
эквивалентно условию протекания стационарного самостоятельно-
го тока в однородном поле Et = Vt/d, где соответствующее напря-
жение Vt определяется из равенства (9.1).
В самом деле, формально при V = Vt I = 0/ 0 =/= 0, когда
г’о = 0, т. е. ток течет даже в отсутствие постороннего источника
электронов. Процессы в разрядном промежутке при этом сами без
посторонней помощи обеспечивают воспроизводство электронов,
устраняемых полем. От одного электрона, вылетевшего с катода,
рождается ead — 1 ионов, и, приблизившись к катоду, каждый
вырывает у электронов (если эмиссия ионно-электронная). На
смену одному первичному появляется один вторичный (ц =
= 7 (ead — 1) = 1) и т. д. Переход несамостоятельного разряда в
самостоятельный можно в то же время рассматривать и как
насту пленив пробоя. Условие (9.1) через известные функцию
а(Е} и у определяет пробивное напряжение Vt в зависимости от
длины промежутка d. Для зажигания самостоятельного разряда
электрон должен совершить на длине промежутка ad/ln2 ~
~1п7-1/1п2 актов размножения, 3—10 актов, если у ~ 10—1 —
- IO"3 (п. 7.3 гл. 4).
2.3. Протекание процесса пробоя во времени. Подать на элект-
роды напряжение, в точности равное У^ которое обеспечивает лишь
простое воспроизводство электронов, ц = 1, для осуществления
пробоя, строго говоря, недостаточно. Ничтожный «затравочный»
ток с катода не вырастает до макроскопической величины, како-
вую только и можно рассматривать как ток самостоятельного
разряда. Чтобы это произошло, требуется хотя бы небольшое
«перенапряжение» ДУ=У — У/> 0, которое обеспечило бы рас-
ширенное воспроизводство электронов, ц > 1. Тогда, если в на-
чальный момент с катода вышел, скажем, один электрон, в сле-
дующем цикле выйдет ц > 1 вторичных электронов, потом щ
и т. д. Ток и ионизация в газе будут нарастать, пока это не
будет остановлено действиями рекомбинации или внешнего оми-
ческого сопротивления Q. На последнем по мере роста тока па-
дает все возрастающая часть напряжения источника питания iQ,
и напряжение на электродах У уменьшается. Когда У упадет до
величины Уь рост I прекратится, самостоятельный ток станет
стационарным. Так зажигается так называемый темный таунсен-
довский разряд (п. 2.2, 3.1 гл. 10). Это происходит, когда внешнее
сопротивление столь велико, что разрядный ток ограничивается
216
/ ц — 1 М _ 1 1
\ р Т / Ll — 1 J
очень малой величиной, при которой внешнее поле не искажается
накапливающимся в промежутке положительным пространствен-
ным зарядом. В противном случае возникает пространственная
неоднородность поля и зажигается тлеющий разряд (§ 3, 4 гл. 10).
Описанный процесс пробоя также называют таунсендовским (в
отличие от стримерного).
Найдем закон нарастания тока в стадии пробоя, пока пере-
напряжение еще можно считать неизменным. Допустим, что эмис-
сия происходит под действием положительных ионов. Ионы
рождаются в основном вблизи анода, где число электронов вслед-
ствие размножения максимально. Обозначим т время вытягивания
на катод ионов от самого анода. Эмиссия электронов с катода
в момент t обязана тем ионам, которые рождались от электронов,
эмитированных в период от t — т до t. Для электронного тока ii
с катода можно составить приближенное уравнение:
И (0 ~ io + |lUi (t — т) ~ io + ц [ii (t) — rd/i/бй],
где io — затравочный ток от внешнего ионизатора. Интегрируя
с начальным условием i\ (0) = io в момент включения поля, на-
ходим разрядный ток (Шаде, 1937 г.)
i (t) (t) exp (ad) — i0 exp (ad) —exp
[И 1
(9.2)
Ток нарастает co временем по экспоненциальному закону,
причем тем быстрее, чем выше степень перенапряжения и ц — 1.
Масштабом времени нарастания тотСа служит величина т/(ц— 1).
Если эмиссия происходит под действием фотонов, т имеет по-
рядок времени дрейфа не ионов, а электронов, т. е. пробой раз-
вивается на два порядка быстрее. Ионизационный коэффициент а
резко зависит от поля, а усиление exp(ad) и коэффициент вос-
производства ц вдобавок экспоненциальным образом зависят от а.
Поэтому достаточно небольшого перенапряжения в несколько
процентов, чтобы ц заметно превысила единицу и пробой разви-
вался достаточно быстро. По этой причине критическая вели-
чина Vt, определенная из условия ц = 1 (см. (9.1)), с доста-
точной степенью определенности характеризует порог пробоя.
Реальное время развития пробоя после включения напряжения
состоит из двух частей: только что рассмотренного, масштабом
которого служит т/(ц—1), и времени ожидания затравочного
электрона (если не применяется достаточно интенсивный ис-
кусственный источник). Последнее имеет статистический раз-
брос. Обычно времена запаздывания таунсендовского пробоя
имеют порядок 10-5 — 10-3 с.
Процесс развития таунсендовского пробоя имеет характер раз-
множения размножающихся электронов — размножения лавин.
Каждый цикл от момента выхода индивидуального электрона
с катода и до ухода всех exp(ccd) происходящих от него элект-
217
ронов в анод можно рассматривать как единичную лавину. Если
пробой начался с одного случайного электрона, то после первой
лавины во втором цикле пройдет в среднем ц > 1 лавин, в третьем
ц2, еще больше, и т. д. Поскольку каждая лавина несколько
расплывается в поперечном направлении вследствие диффузии
электронов, новая лавина начинается в общем с другого места
катода (в случае фотоэмиссии — может, и далекого). Кроме того,
реально начало процессу не всегда кладет один-единственный
электрон, их может вылетать несколько, с разных мест. Поэтому
таунсендовский пробой чаще всего диффузно охватывает весь
объем промежутка. Этим он внешне отличается от искрового,
когда между электродами прорастает тонкий проводящий ка-
нал — миниатюрная молния, а соседние участки, также находя-
щиеся в поле, остаются неионизованными.
2.4. Потенциал зажигания. Так называют пробивающее на-
пряжение Vt. Эта величина и соответствующее поле пробоя Et
зависят от рода газа, материала катода, давления и длины раз-
рядного промежутка. Чтобы найти явные зависимости, восполь-
зуемся формулой (4.8) для а. Подставляя ее в (9.1), получим
у __ В (^) ______В_____ г» _ in____________/Q
* C + ln(pd)’ р С 4-ln(prf) ’ 1п(1-|-1/у)* '
Потенциал зажигания Vt и Et/p определяются только произ-
ведением pd. В этом проявляется закон подобия. Вычисление
Vt по формуле (9.3) с экспериментальными значениями констант
А и В (табл. 4.1) дает удовлетворительное согласие с опытом.
Экспериментальные зависимости Vt(pd)—так называемые кри-
вые Пашена — показаны на рис. 9.2—9.4. Существует минималь-
ное напряжение пробоя разрядного промежутка. Согласно (9.3)
параметры точки минимума таковы (ё = 2,72):
(pd)mm = (—+ 11 ) = В, Утш == --г-1п ( 1 г —1
/пнп д Y 1 /’ \ р /тт ’ шш А \ У I
(9.4)
Значение Е/р в минимуме соответствует точке Столетова
(п. 1.6 гл. 4), где ионизационная способность электрона ц =
= а/Е = А/Вё максимальна. Промежуток пробивается при этом
легче всего, потому что оптимальны условия для размножения.
В отличие от 7min и (pd)m^ величина (E7p)min не зависит от
материала катода (от у), что подтверждается опытом (рис. 9.3).
Сопоставим оценку по формулам (9.4) с экспериментом. Для
воздуха А = 15, В = 365. С у =10-2 по формулам (9.4) полу-
чается С = 1,18 и
(pd)min = 0,83 торр-см, (£7/>)min = 365 В/(см-торр), Ут1П = 300В,
Опытные значения в случае железного катода:
(pd)mln = 0,57 торр • см, Vmm = 330 В, (Е/р)min = 580 В/(см • торр).
218
Рис. 9.2. Потенциал зажигания в различных газах в широком диапазоне
значении pd (кривые Пашена)
Рис 9.3. Влияние материала катода на напряжение пробоя аргона. Штрих-
пунктирная прямая соединяет точки минимума. Ее наклон 45° соответству-
ет независимости (Е/р)т1п от материала катода [6]
Рис. 9.4. Кривые Пашена в укрупненном масштабе [6]
219
У инертных газов (pd)min больше, a Vmin меньше. Так, в аргона
с железным катодом
(pd)min = l,5 торр-см, Vmin = 265B, (£7p)min = 176 В/(см-торр).
В области относительно больших pd, на правой ветви кривой
Пашена пороговая величина Et/p довольно медленно, по лога-
рифмическому закону уменьшается с ростом pd. Соответственно
напряжение пробоя возрастает почти пропорционально pd (не-
много медленнее). Такое поведение пороговых величин объяс-
няется тем, что в случае повышенных давлений, длинных проме-
жутков электрон имеет возможность совершить много ионизующих
столкновений даже при не очень высоких Е/р. Но в этом случае а
резко зависит от Е/р и условие необходимого усиления (9.1)
довольно жестко фиксирует значения Е/р.
Напротив, при малых pd, на левой ветви возможностей для
столкновений мало. Для достижения должного усиления требует-
ся очень большая величина а/p, т. е. очень сильное поле. Напря-
жение пробоя быстро растет с уменьшением pd. Отсюда и мини-
мум напряжения. В силу ограниченности эффективного сечения
ионизации, ионизационный коэффициент также ограничен (вели-
чиной Ар). Поэтому в случае достаточно малых pd ни при каких
полях не может быть обеспечено нужное усиление. В рамках
данного приближения Vt °о, когда pd сверху уменьшается до»
предельного значения:
(рй)Пред = 1п(1/у + 1) = (рй)тш/ё. (9.5)
Реальное нарастание Et/p и Vt на левых ветвях кривых Пашена
происходит медленнее и, разумеется, не до бесконечности. «Левее»
левых ветвей вступают в действие совершенно иные механизмы
(п. 2.6).
2.5. Пробивающие поля в воздухе и других электроотрицатель-
ных газах атмосферного давления в случае не слишком длинных
промежутков; предельные pd для таунсендовского механизма
пробоя. Для последнего характерны пониженные давления и не
слишком большие pd < 1000 торр • см. В случае недлинных про-
межутков (и однородных полей) механизм размножения лавин
действует и при атмосферном давлении. В комнатном воздухе
в плоских промежутках он реализуется примерно до d < 5 см
{pd < 4000 торр-см). Напряжение пробоя при столь больших
pd меняется более или менее пропорционально pd, т. е. про-
бивающее поле не сильно зависит от pd, и для газов атмосферного
давления характерны определенные значения пробивающих по-
лей или {E/p)t. На рис. 9.5 представлены результаты измерений
для комнатного воздуха в области d, где еще действует
таунсендовский механизм. Для промежутков сантиметровых
размеров характерны цифры {E/p)t ~ 32 кВ/(см • атм) =
= 42 В/(см-торр). В случае длинных промежутков в десят-
ки сантиметров пробивающее поле в воздухе при комнатной
220
температуре снижается до предельного значения Et « 26 кВ/смг
но при d > 6 см действует уже стримерный механизм (гл. 14).
Предельные значения пороговых полей Et « 32—26 кВ/см для
достаточно больших pd не случайны. Имеется их явная связь
с возможностями размножения электронов в газе, где происхо-
дит прилипание электронов. Коэффициент прилипания а, опре-
деленный аналогично ионизационному а (п. 4.2 гл. 4), обычно
Рис 9 5. Пробивающие поля в плоском
воздушном промежутке в зависимости
от его длины d при р = 1 атм по дан-
ным разных авторов [21]
Рис 9 6. Частоты ионизации и
прилипания в воздухе, рассчи-
танные на основе решения ки-
нетического уравнения, в за-
висимости от поля
также заметным образом возрастает q ростом Е/р, но гораздо сла-
бее, чем а. Кривые а/p и а/p как функции Е/р пересекаются при
некотором значении (Е/р)\. Результаты расчета коэффициентов
для воздуха на основе кинетического уравнения, расчета, подоб-
ного тому, о котором говорилось в § 8 гл. 7, показаны на
рис. 9.6*). Точка пересечения лежит при значении (Е/р)\~
«41 В/(см-торр). Эта цифра близка к предельным значениям
для порога пробоя воздуха, хотя и несколько завышена, возмож-
но вследствие несовершенства данных по сечениям многочислен-
ных процессов, которые закладываются в расчет. Измерения эф-
фективного коэффициента ионизации аэф = а — а, который фигу-
рирует в уравнении лавины (4.7), если учесть в нем прилипание:
dNe/dx = (а — a)Ne, Ne °° exp [(а — а)х],
указывают, что аэф 0 при (E/p)i«35 В/(см-торр), что как
раз соответствует (Е/р)иред « 26 кВ/(см-атм). При Е/р<(Е/р)\
размножение электронов, очевидно, невозможно, и это наклады-
вает отпечаток на пределы пробоя.
Измерения показывают, что пороги пробоя сильно электроот-
рицательных галогенсодержащих газов при атмосферном давле-
*) Сравните с аналогичными графиками в § 8 гл 10 для лазерных сме-
сей, содержащих электроотрицательный компонент СО2
221
нии очень высоки. Это видно из табл. 9.1, где представлены так-
же данные для газов, в которых прилипание отсутствует. При
низких давлениях (малых pd) величины (Elp)t значительно
Таблица 91 Ориентировочные пороги пробоя ia-
зов при высоких давлениях
Газ Постоянное поле, недлин- ные промежутки, p~i атм СВЧ, р-100— 300 торр
Et/p, кВ/(см атм) Et/p, В/(см торр) Et/P, В/(см торр)
Не 10 13 3
Ne 1,4 1.9 3-5
V 2 7 3,6 5—10
Но 20 26 10-15
No 35 46 -25
о; 30 40 35
Воздух 32 42 -30
С12 76 100
CC12F2 (фреон) 76 100
CSF4 150 200
СС14 180 230
SFb (элегаз) 89 117
больше (Е/р)\ (рис. 9 5), ос заметно выше п, поэтому электроот-
рицательные свойства газов проявляются не столь резко, как при
больших pd. Свойство высокой электрической прочности электро-
отрицательных газов находит важные практические применения.
Рис 9 7 Поле (7) и напря-
жение (2) пробоя вакуум-
ного промежутка между
шаром диаметром 2,5 см и
диском диаметром 5 см из
стали в зависимости от дли-
ны промежутка [3]
2.6. Пробой вакуумных промежутков. При pd < 10-3 торр • см
электрон пролетает промежуток практически без столкновений и
никакого размножения в объеме нет. Это не значит, однако, что
вакуумный промежуток может служить идеальным изолятором.
Если приложить большое напряжение к малому зазору, возни-
кают сильные поля, которые могут вызвать автоэлектронную
222
эмиссию с катода (п. 6.3 гл. 4). Поля дополнительно усиливают-
ся вблизи микроскопических выступов. Более длинные проме-
жутки пробиваются при полях, недостаточных даже для выры-
вания электронов из металла. Случайный электрон разгоняется
в поле, выбивает ион из анода или излучает при торможении
рентгеновский квант. Те, в свою очередь, вырывают электрон из
Рис. 9 8. Напряжения пробоя
коротких промежутков между
стальными электродами в за-
висимости от давления запол-
няющего их водорода. Неза-
висимость от р свидетельству-
ет о вакуумном характере про-
боя Загиб вниз верхней кри-
вой соответствует переходу к
левой кривой Пашена [12.3]
катода и т. д. Так происходит размножение без участия остаточ-
ного газа. Возможен также процесс, при котором под ударами ра-
зогнанных полем частиц испаряются электроды и промежуток
наполняется парами металла, от чего и происходит газовое уси-
ление. Результаты эксперимента показаны на рис. 9.7, 9.8.
§ 3. Эксперименты по пробою в СВЧ полях
*
Нарушая порядок рассмотрения диапазонов, пропустим слу-
чай высокочастотных полей, который более сложен и многообра-
зен. Вообще говоря, классифицировать эффекты пробоя в пере-
менных полях следует не просто по частотным диапазонам, а пу-
тем сопоставления характерных длин. Но признак частоты при
этом является наиболее определяющим. Для СВЧ диапазона ха-
рактерна малость амплитуды колебаний электрона по сравнению
с размерами разрядного объема. По этой причине электроны и
ионы в своем движении под действием поля не касаются стенок,
поле не толкает энергичные частицы к поверхностям, эмиссион-
ные процессы роли не играют. Электронная лавина локализова-
на, т. е. в каждом месте развивается независимо, обособленно.
Например, для типичной СВЧ длины волны Л = 10 см, / = 3 ГГц,
со ==• 1,9 • 1010 с-1 в характерном для пробоя при р ~ 1 торр поле
Eq = 500 В/см амплитуда колебаний электронов (свободных)
а = еЕъ1ты = 2,5 • 10-3 см (п. 1.2, гл. 5). Она гораздо меньше
размеров сосудов, которые порядка длины волны. Такой объем-
ный процесс сравнительно прост, и для него достигнута хорошая
степень понимания и теоретического описания, тем более, что
имеется богатый и четко оформленный экспериментальный мате-
риал для анализа.
223
3.1. Постановка опытов. При экспериментальном определении
пороговых полей, вызывающих пробой газа, СВЧ мощность, ге-
нерируемую магнетроном непрерывного (или импульсного) дей-
ствия, через волновод или коаксиальную линию подводят к резо-
натору. На пути ставится делитель мощности, который позволяет
отводить часть ее в сторону, причем долю эту можно менять. Та-
ким способом варьируют поле в резонаторе. Пороговое поле дан-
ной частоты зависит от размеров разрядного объема. Вызвано это
влиянием потерь электронов вследствие их диффузионного ухода
на стенки, где электроны гибнут. Они оседают на стенках, а по-
том рекомбинируют с диффундирующими туда ионами. Если
стенки металлические, электронный заряд мйжет отводиться в
металл. Скорость диффузионных потерь определяется диффузи-
онной длиной Л. Она вычисляется по формулам (4.23).
Вообще говоря, размеры резонатора для электромагнитного
поля всегда связаны с длиной его волны и сравнимы с ней. По-
Рис. 9.9. Распре-
деление электри-
ческого поля в ре-
этому не всякая геометрия позволяет менять
размеры камеры при неизменной частоте, без
чего нельзя проверить на опыте зависимость
порогового поля от размеров при прочих рав-
ных условиях. Эту трудность удается избе-
жать, применяя цилиндрический резонатор,
возбуждаемый на такой моде, что резонансная
частота зависит от радиуса цилиндра, но не
зависит от высоты. Электрическое поле при
этом направлено вдоль образующей цилиндра
(рис. 9.9). Напряженность Е максимальна на
зонаторе экспери- оси и спадает по радиусу г к поверхности про-
ментального уст- порционально функции Бесселя Jo (2,4г//?),
роиствэ Деизме- обращаясь в нуль при r = R Диффузионную
СВЧ пробоя Длину Л можно менять, меняя высоту цилинд-
ра при неизменных радиусе и частоте поля.
Резонатор наполняют различными газами при разных давле-
ниях. Установка снабжается измерительной техникой, позволяю-
щей измерять частоту, поле в резонаторе и мощность, проходя-
щую через резонатор «насквозь». По последней величине и реги-
стрируют факт пробоя. Увеличивая поле в резонаторе путем уве-
личения подаваемой в него мощности, фиксируют параметры, при
которых проходящая мощность резко падает. Это свидетельству-
ет о наступлении пробоя. Газ в объеме становится проводящим,
и в нем диссипируется электромагнитная энергия. Пробой насту-
пает раньше всего в центральной части резонатора, вблизи оси,
где поле Е имеет максимальное значение. Именно ее и прини-
мают в качестве пороговой. Систематические исследования СВЧ
пробоя, экспериментальные и теоретические, были проведены,
начиная с конца 40-х годов, С. Брауном и его сотрудника-
ми [6, 24].
3.2. Результаты измерений. На рис. 9.10 приведены типичные
результаты экспериментов — пороговые для пробоя поля (сред-
224
иеквадратичные). Зависимость порогового поля от давления все-
гда имеет минимум. На левой ветви, где порог падает с ростом
давления, он тем ниже, чем больше размеры разрядного объема
и чем меньше частота поля. То же относится и к значению ми-
нимума. На меньших частотах минимум располагается при более
низких давлениях. На правой ветви, где порог растет с повыше-
нием давления, зависимость порогового поля от размеров и час-
тоты становится все менее заметной и в пределе больших давле-
ний почти совсем исчезает: все кривые асимптотически
сливаются.
Рис 910 Зависимость
пороговых полей СВЧ
пробоя от давления* а —
воздуха (/ — 9,4 ГГц);
б — нескольких газов
(/ = 0,99 ГГц, Л =
~ 0,63 см), в — Нед-га-
за (Л == 0,6 см) [24]
Обращает на себя внимание легкость, с которой при повы-
шенных давлениях пробиваются смеси из гелия или неона с не-
большой добавкой аргона (рис. 9.10, б). Здесь сказывается эф-
фект Пеннинга, благодаря которому неупругие потери энергии
электронов на возбуждение атомов основного газа (Не, Ne) поч-
ти не тормозят развития лавины. При столкновениях с атомами
15 Ю П Райзер
22
Ас возбужденные атомы Не*, Ne* затрачивают свою энергию на
отрыв электрона от Аг. Скорость такого двухступенчатого про-
цесса ионизации пропорциональна не только плотности основного
газа, но еще и плотности добавки, поэтому эффект проявляется
тем сильнее, чем выше давление, о чем и свидетельствует
рис. 9.10, б.
3.3. Heg-газ. Аналогичным образом протекает ионизация в так
называемом Heg-газе — смеси Не с добавкой паров ртути
(рис. 9.10, в). Сечение ионизации Hg метастабильными атомами
Не (235) с энергией возбуждения £* ~ 19,8 эВ аномально вели-
ко (и. 2.2, гл. 4), так что каждый акт возбуждения Не, можно
сказать, немедленно ведет к появлению электрона — размноже-
нию. Частота ионизации газовой смеси электронами уг при этом
фактически совпадает с частотой возбуждения атомов основного
газа — гелия. Неупругих потерь как бы вовсе нет. Это обстоя-
тельство является крайне благоприятным для опытной проверки
ряда существенных положений теории. Самым трудным момен-
том для теории является учет неупругих потерь, для чего тре-
буется привлечение кинетического уравнения, да и решение его
при этом усложняется. В случае Heg-газа эта трудность отпа-
дает. Поскольку неупругие потери вносят скорее количественные,
чем качественные изменения в ход развития электронной лави-
ны, анализировать закономерности пробоя удобнее всего на этом
примере, что и будет сделано в § 4.
§ 4. Интерпретация результатов экспериментов
по СВЧ пробою на основе элементарной теории
4.1. Уравнение кинетики ионизации. Плотность электронов;
как функция координат и времени подчиняется уравнению диф-
фузии с объемными источниками:
dneldt = DAne + (Vi — va) ne. (9.6)
Частоты ионизации vt и прилипания va зависят от энергетиче-
ского спектра электронов, который устанавливается в поле, и в
предположении о квазистационарном характере спектра опреде-
ляются значением поля — среднеквадратичного Е или амплитудой
Eq. Коэффициент диффузии электронов (свободной, ибо послед-
них мало) также усредняется по спектру, но он от поля зависит
слабее. Этой зависимостью можно пренебречь по сравнению с
v,(£), va(E).
Положим для простоты, что поле однородно в пространстве,
так что частоты vt, va не зависят от точки. Усредняя (9.6) по
объему, в соответствии с результатами § 5 гл. 4 получаем урав-
нение для средней плотности или, что то же самое, для полного
числа электронов Ne в разрядном объеме:
dNe/dt - va - vd)Ne, vd = D/A2, (9.7)
226
где vd— частота диффузионных потерь электронов. Это уравне-
ние описывает кинетику ионизации газа.
4.2. Стационарный критерий пробоя. Допустим, что внешнее
поле включается быстрее по сравнению с характерным временем
размножения и остается постоянным в течение времени развития
лавины. Под такое ограничение подпадают не только стационар-
ные, но и не слишком кратковременные импульсные поля (с до-
статочно крутым фронтом нарастания). В этом предположении
vt(£), va(t) = const после момента t — 0 включения поля и урав-
нение (9.7) имеет экспоненциальное решение, характерное для
лавинообразного процесса:
Ne == Neo exp [ (vt — Va — Vd) t] = Ne0 exp (t/&). (9.8)
Здесь 0 — постоянная времени лавины, Neo — число затравочных
электронов, которые начинают лавину*). В опытах с короткими
импульсами, когда вероятность попадания электрона в область
действия поля в нужный момент невелика, пробой затрудняется
и для инициирования лавины приходится искусственно впрыски-
вать небольшое количество электронов. Для этого пользуются
слабым радиоактивным источником.
Согласно (9.8) лавина развивается при условии vz — va — vd>
> 0, которое выполняется, если поле превышает пороговую вели-
чину Et, определяемую стационарным критерием пробоя-.
v^Et) = vd-va(Et), (9.9)
Рассмотрим для примера пробой гелия при р = 1 торр СВЧ по-
лем сЛ = 3 см. Длина диффузий Л=1 см, D ~ 2 • 106 см2/с,
время диффузии к стенкам vj1 5 • 10“7с, частота диффузии
vd ~ 2 • 106 с-1, прилипания нет. Лавина развивается при условии
~ 2 - 106 с-1. Но как будет показано чуть ниже, даже в
наиболее благоприятном для размножения случае отсутствия вся-
кие потерь энергии у электронов частота ионизации \\^Е2.
В присутствии потерь, в особенности неупругих, зависимость v\
от Е гораздо более резкая. Значит, при увеличении поля на 10 %
по сравнению с Et 0-1—— vd 0,2vd ~ 4 • 105 с”1. Через каж-
дый период 0/1п 2 С 1,7 мкс число электронов удваивается. Это
весьма быстрый темп. Во многих случаях его достаточно, чтобы
надежно осуществился пробой. Поэтому стационарный критерий
(9.9), подобно стационарному критерию (9.1), с хорошей точ-
ностью определяет порог пробоя газа не слишком короткими им-
пульсами.
Оценим пороговые поля для Heg-газа.
*) Скорость образования электронов в атмосфере под действием косми
ческого излучения на уровне моря порядка 10 с-1 • см~3. В неэлектроотри-
цательных газах обычно в 1 см3 присутствуют 10—102 электронов В воз-
ду ve они тотчас прилипают к кислороду и заряды присутствуют в виде
ионов; их концентрации порядка 103 см~3.
15*
227
4.3. Низкие давления. В этом случае коэффициент диффузии
D^l/p велик и диффузионные потери электронов значительны.
Для их компенсации требуется большая скорость ионизации, т. е.
сильное поле. Но в сильном поле роль упругих потерь энергии
электрона несущественна. Действительно, энергии электронов е
не превышают величины порядка энергии возбуждения атома ге-
лия AIJe == 19,8 эВ, так как при 8>> /:Не электрон с большой ве-
роятностью совершает неупругое столкновение и теряет энергию.
Упругая передача энергии атому при столкновении ограничена
величиной (Л8уПр)тах — (2т/М) ЕЦе Приобретение энергии Д8д
при столкновении согласно (5.10) пропорционально Е2. В доста-
точно сильных полях, необходимых для компенсации больших
диффузионных потерь, Д8Е » Аеупр.
В отсутствие потерь электрон набирает энергию от поля со
скоростью dz/dt — Энергии АНе он достигает за время
Те = ''in1- Поскольку за этим без промедления следу-
ют акты возбуждения и пеннинговской ионизации, частота иони-
зации определяется просто временем тЕ:
Vj = ТЁ1 = (Аев/Е'не) Vm =- е2Е2ут/шш2Е^е. (9.10)
Здесь учтено, что при низких давлениях v^<Cco2- В соответствии
с (9.9) среднеквадратичное пробивающее поле
Dm(£> \ 1/2 / тЕ^е \ со со
При вычислении использованы выражения для коэффициента
диффузии D — lv/З = Z2vm/3 и длины пробега l = (NGm)~i электро-
на. Пороговое поле пропорционально частоте и обратно пропор-
ционально плотности (давлению) газа и размерам разрядного
объема в полном согласии с опытом. Более того, если подста-
вить в формулу сечение столкновений вт = 4 • 10-16 см2, соответ-
ствующее середине электронного спектра, 8 Е^/2 « 10 эВ, по-
лучается неплохое количественное совпадение с данными
рис. 9.10. Формула (9.11) правильно описывает асимптотические
прямые на логарифмическом графике, к которым приближаются
левые ветви зависимости Et(p) при разных со и А.
4.4. Высокие давления. В этом случае диффузионные потери
электронов незначительны и даже не слишком большая скорость
ионизации обеспечивает пробой. На первый план выступают по-
тери энергии, в случае Heg-газа — чисто упругие. Они и ограни-
чивают частоту ионизации. Если рассуждать с позиции элемен-
тарной теории, электрон не может приобрести в данном поле
энергию, которая превышает предел (5.12), диктуемый сущест-
вованием упругих потерь. В случае высоких давлений, когда
Vm » О)2,
emax = (М/2т) e2E2/mvm оэ (Е/р)2. (9.12)
228
Если эта энергия меньше ^не- электрон не сможет возбуждать
атомы гелия и лавина не разовьется. Следовательно, возможность
пробоя определяется условием £тах(^)^^не и пороговое поле
вычисленное из этого равенства, есть
Et = (тчт/е)(2Ене/мУ/2 со р. (9.13)
Пороговое поле пропорционально р и не зависит ни от размеров
объема Л (в рамках данного приближения; см. п. 4.7), ни от час-
тоты, снова в качественном соответствии с опытом. Количествен-
ное согласие для Heg-газа также получается удовлетворитель-
ным. Порог не зависит от частоты, так как при со2<с хД перемен-
ное поле по своему действию на электроны не отличается от
постоянного.
4.5. Положение минимума. В грубом приближении положение
минимума пороговой кривой Et(p) можно установить на основа-
нии того условия, которое в какой-то мере разграничивает пре-
дельные случаи низких и высоких давлений, когда << со2 и
v^^xo2 соответственно. Это условие заключается в равенстве по
порядку величины частот столкновений и поля: vm ~ со. При этом
скорость приобретения энергии электроном от поля (d&/dt)E как
функция давления проходит через максимум. Условия для про-
боя, следовательно, наиболее благоприятны, и пороговое поле са-
мое низкое. Частота, при которой порог минимален, пропорцио-
нальна давлению газа. Этот результат качественно подтверждает-
ся опытом. В СВЧ диапазоне газы легче всего пробиваются при
р ~ 1—10 торр. *
4.6. Неупругие потери; молекулярные, электроотрицательные
газы. В качественном отношении неупругие потери, которые иг-
рают важную роль в большинстве газов, влияют на пороговые
поля примерно таким же образом, как и упругие. Об этом свиде-
тельствует даже полнейшее внешнее сходство графиков Et(p)
для Heg- и других газов (рис. 9.10). При низких давлениях по-
роги определяются главным образом диффузией. Пороговые поля
велики, и электрон при наборе энергии быстро проскакивает
«опасную» энергетическую зону между потенциалами возбужде-
ния и ионизации, возбуждая атомы с не чрезмерно большой веро-
ятностью. Пороговое поле при этом определяется формулой типа
(9.10), в которой ^не следует заменить потенциалом ионизации.
При высоких давлениях диффузия происходит медленно и по-
рог в основном определяется потерями энергии. Скорость неупру-
гих столкновений, как и упругих, пропорциональна давлению.
Из условия компенсации энергетических потерь приобретением
энергии от поля вытекает, что при со2<С средняя энергия элек-
тронов есть функция Е/р (см. (5.12)). Чтобы шла ионизация,
средняя энергия не должна быть слишком малой по сравнению
с потенциалом ионизации, что в какой-то мере фиксирует вели-
чину Е/р. Значит, пороговое поле Et ~ р; оно не зависит от о,
229
если co2 <Cv™, и в рамках приближения не зависит от Л, как в
случае чисто упругих потерь.
Для СВЧ пробоя молекулярных газов требуются более высо-
кие поля, чем для атомарных, так как электрону приходится за-
трачивать много энергии на возбуждение колебательных и более
низко лежащих в молекулах электронных уровней, и это тормо-
зит набор энергии в поле. В электроотрицательных газах пороги
также высокие, поскольку существуют дополнительные потери
электронов на прилипание.
4.7. Близость пороговых величин в постоянном и пере-
менных полях при высоких давлениях и зависимость их от раз-
меров. Если при больших давлениях переменное поле действует
на электроны как постоянное и если пороговые значения Et/p в
СВЧ диапазоне мало зависят от р и Л, есть все основания ожи-
дать, что и числа Etlp близки к таковым для случая постоянного
поля и больших pd, когда они тоже слабо зависят от pd. Опыт в
общем подтверждает это заключение. Правые ветви кривых СВЧ
пробоя соответствуют правым ветвям кривых Пашена вдали от
минимумов. Числа Et/p различаются раза в полтора-два
(табл. 9.1),
Следует подчеркнуть, и это важно для понимания существа
дела, что независимость Et/p от диффузионной длины Л в (9.13)
возникла исключительно из-за несовершенства элементарной тео-
рии. Отсутствие Л в формуле эквивалентно отсутствию потерь
электронов: Л = о°, vd = 0. Но поскольку в спектре всегда имеет-
ся какое-то число энергичных электронов, ионизация, пусть ма-
лая, идет в сколь угодно слабом поле. Поэтому при полном от-
сутствии потерь самих электронов у пробоя не было бы порога.
Число электронов, обладающих энергиями 8 ~ достаточными
для ионизации, экспоненциально мало: при максвелловском рас-
пределении оно пропорционально ехр(—е/ео), при дрюйвестей-
новском — ехр(—82/8q). Масштабы 8о ориентировочно совпадают
со средними энергиями спектра или 8тах элементарной теории и
возрастают с ростом поля. Потому и реальная частота ионизации
имеет характерную экспоненциальную зависимость от Е типа
exp [—const//(Elp) ].
Примем для примера таунсендовский закон «>
сч°/;е.\р( — const р!Е). То, что это не далеко от истины, показано
в п. 5.7 этой главы. Из условия пробоя vt = vd найдем
Etlp = const/(const' + In/>Л), const > 0. (9.14)
Эта логарифмическая зависимость, слабая при больших /?Л, со-
вершенно аналогична зависимости от pd в (9.3) и обеспечивает
формальное обращение порога в нуль, когда длины Л, d °°.
По существу, длины Л и d играют качественно одинаковые роли,
характеризуя скорости устранения электронов из разрядного объ-
ема. Поле выносит электрон на анод за время от 0 до div* (рд —
скорость дрейфа) в зависимости от того, с какого места он начал
230
движение. Обратная величина vjd служит масштабом «частоты
выноса»—частоты потерь. Таунсендовский критерий (9.1),
ad = k, где к — число порядка нескольких единиц, a a = vt/uA,
можно трактовать, подобно (9.9), как условие равенства частот
ионизации и потерь: kv^/d = Средняя частота выноса
в к раз больше минимальной vjd, поскольку большинство элек-
тронов в лавине рождается ближе к аноду.
§ 5. Вычисление частот ионизации и порогов пробоя
на основе кинетического уравнения
5.1. Вывод уравнения кинетики из кинетического уравнения.
Исходя из соотношений (7.24)—(7.26), представим кинетическое
уравнение для функции распределения электронов по энергиям
п(е, t) в следующей, удобной для анализа форме:
- <2* + <2г — va (е) п — vd (е) п,
J = - Аг + ±Ап + пЖупр, (9.15)
2 e2E2vm _ 2т
А -'З <о2 + ’ ^УПР ~ “ ~М~ т'
Поток J по энергетической оси связан с приобретением энергии
от поля и упругими потерями. Слагаемое Q* описывает возбуж-
дение атомов, Qx — ионизацию, va(e)n — прилипание, vd(8)ft—
диффузионные потери.
Вследствие неизбежных актов возбуждения и ионизации при
энергиях, превышающих соответствующие потенциалы, электро-
ны не достигают очень больших энергий. Функция распределе-
ния весьма быстро убывает при 8 чем обеспечивается ко-
ею
нечность плотности электронов пе = n(F,t)ds. Стремится к ну-
о
лю и поток: /(°°) = 0. Далее, источники частиц в уравнении
(9.15) распределены по оси 8. Сосредоточенных источников элек-
тронов с нулевой энергией нет. Отрицательных кинетических
энергий не бывает. Значит, поток в точке 8=0 отсутствует:
7(0) = 0. Если проводить аналогию с одномерной диффузией ча-
стиц в обычном пространстве х = 8, то этому соответствует нали-
чие непроницаемой и неэмитирующей частицы стенки при х = 0.
Имея в виду сказанное, проинтегрируем уравнение (9.15) по
всему спектру от 0 до °°. Интеграл от <2* автоматически обраща-
ется в нуль — акты возбуждения не меняют числа электронов.
При интегрировании по 8 первого слагаемого в (7.26) для Qi
получим —хгАге, где Vt — средняя по спектру частота ионизации.
Второе слагаемое даст 2хгпе, в чем легко убедиться, если поме-
нять порядок интегрирования в двойном интеграле. В акте иони-
зации один электрон как бы исчезает, а два новых появляются.
231
В результате получим уравнение кинетики для электронной
плотности:
dne!dt =(уг-~ Va — Vd)rte, (9.16)
эквивалентное (9.7); va, vd—также средние по спектру частоты.
5.2. Разделение переменных. Строго говоря, в качестве на-
чального условия к (9.15) следует задать функцию распределе-
ния начальных электронов тг(8, 0). Физически ясно, однако, что
после рождения одного-двух поколений электронов начальный
спектр «забывается» и устанавливается новый спектр, отвечаю-
щий воздействиям поля и столкновений. Действительно, время
установления (релаксации) спектра характеризуется средним
временем, в течение которого медленный электрон проходит по
оси 8 весь путь от 8 ~ 0 до самых больших реализующихся энер-
гий. Но это, в сущности, и есть время, необходимое для иониза-
ции и размножения. Интересуясь сколько-нибудь развитой ста-
дией лавины, нет смысла вникать в детали релаксационного про-
цесса, а следует прямо искать установившийся спектр, т. е. ис-
кать решение нестационарного уравнения в виде гс(8, t) =
= тг(е)Ф(О-
Подстановка в уравнение (9.15) дает
n(s, t) = n(s)exp(£/0), (9.17)
где константа 0 имеет смысл постоянной времени лавины,
а спектральная функция п(ъ) нормирована на начальную плот-
ность пео. Решение вида (9.17) было бы точным всегда, если бы
спектр начальных электронов совпадал с тем. которому суждено
установиться. Согласно (9.16), (9.17) константа 0 связана со
средними по спектру частотами очевидным равенством
0-1 = vt — va — vd. (9.18)
5.3. Уравнение для спектральной функции. Подставим (9.17)
в (9.15) и заменим 0 согласно (9.18). Диффузионньш уход элек-
тронов на стенки учтен в (9.15) приближенным образом, с тем
чтобы не усложнять и без того сложного уравнения зависимо-
стью функции распределения от пространственных координат.
Поэтому вряд ли стоит сохранять не сильную и не имеющую
принципиального значения зависимость коэффициента простран-
ственной диффузии и Vd(c) от энергии. Заменим Vd(e) в (9.15)
на среднюю величину vd. Тогда в результате подстановки (9.17),
(9.18) в (9.15) член диффузионных потерь вообще выпадет из
уравнения для спектральной функции тг(е), и для нее получится
уравнение
(vt — va)n = —dJ/d& + 2* + Qi~ va(e)n. (9.19)
Спектр и частота ионизации в этом приближении не зависят от
геометрии, размеров объема и не отличаются от тех, которые по-
лучались бы в бесконечном пространстве с однородным полем.
Так всегда и поступают при решении кинетического уравнения.
232
Решение (9.19) дает спектр п(&) и частоту ионизации уг в
зависимости от поля и характеристик газа. Равенство (9.18) оп-
ределяет скорость размножения (или исчезновения) электронов
в зависимости от поля и диффузионных потерь. Условие 0-1=О
отвечает стационарному состоянию и стационарному критерию
пробоя (9.9). Подчиняя решение этому условию, можно найти
пороговое поле Et. Однако полученная таким путем зависимость
\\(Е) имеет более общее значение. Ее можно использовать и при
изучении других процессов, например положительного столба
тлеющего разряда*).
5.4. Законы подобия. Как отмечалось в п. 6.3 гл. 7 и видно
непосредственно из соотношений (9.15), (9.19), установившийся
спектр в пределе низких частот со2 v™ (и в постоянном поле)
описывается функцией п(е, Е1р), а в пределе высоких со2 >> v™—>
функцией az(е, £7со). Соответственно частота ионизации в пер-
вом случае есть функция типа уг = pf\(E/p), а во втором —
vt = pf2{E/(d). В предположении о постоянстве частоты столкно-
вений хп(е)= const частота ионизации в переменном поле vt<B
выражается через частоту ионизации в постоянном поле Vio пу-
тем введения эффективного поля Еэф по формуле (7.33):
vlfi)(co, р, £’) = vl0(p, Еэф) = pf^E^/p). (9.20)
В газе без прилипания, исходя из стационарного критерия про-
боя (9.9) и зависимости Vd°° 1/рЛ2, найдем, что в пределе низких
давлений (высоких частот) пороговое поле Et = coFi (рЛ), а в
пределе высоких давлений (малых частот) Et = pF2(pA). Асимп-
тотический вид функций Fi, F2 дается формулами (9.11), (9.14)
или (9.3). Законы подобия для частоты прилипания такие же,
что и для частоты ионизации. Поэтому в электроотрицательном
газе при высоких давлениях, когда прилипание преобладает над
диффузией, порог пробоя Et/p = const.
5.5. Постановка упрощенной задачи о влиянии неупругих по-
терь на частоту ионизации. Уравнение (9.19) в сколько-нибудь
полной постановке можно решать только численными методами.
Громоздкие и трудоемкие расчеты такого рода стали доступными
лишь благодаря применению электронно-вычислительных машин.
Разумеется, численные решения дают ценную для практики ни
формацию, однако зачастую даже очень грубое, но аналитиче-
ское решение больше способствует пониманию природы законо-
мерностей и уяснению механизмов влияния различных факторов.
С этой целью мы построим упрощенное решение, которое нагляд-
но демонстрирует воздействие неупругих потерь на скорость
ионизации,— то, что недоступно элементарной теории.
Будем рассматривать тяжелые инертные газы (аргон, ксе-
нон), в которых нет прилипания, нет низко лежащих уровней
энергии и несущественна роль упругих потерь; последними пре-
*) Следует только помнить, что при развитой ионизации диффузия име-
ет амбиполярный характер и vj существенно меньше.
233
небрегаем. Частоту упругих столкновений vm считаем постоян-
ной. Допустим, что частота возбуждения атома v* также не за-
висит от энергии, если последняя превышает величину Е1Ч не-
много большую потенциала возбуждения. Допустим, что элек-
трон, достигший энергии 7ц немного превышающей потенциал
ионизации, «мгновенно» совершает неупругое столкновение, с ве-
роятностью ионизуя атом и с вероятностью 1 — — возбуждая
его. Величины Е± , /1? v*, Р можно подобрать разумным образом,
рассматривая кривые сечений о*(е), ог(е). Для инертных газов
Ег, 7, на 1 — 2 эВ превышают соответствующие потенциалы £*,
I (₽~0,2).
Допущение о мгновенности неупругого столкновения при
8 >71, которое отнюдь не является чересчур грубым, ибо соот-
ветствующие частоты велики, позволяет исключить из рассмотре-
ния область 8 >71, заменив действие распределенных в ней отри-
цательных источников <2* + Qi адекватным граничным условием.
Тогда для электронов, движущихся по оси энергии, в точке
8=71 имеется «сток бесконечной мощности», отчего в этой точке
?г(71) = 0. «Соберем» в точку 8 = 0 реальные положительные ис-
точники Q* + Qz, расположенные в области малых энергий. Те-
перь поток 7(0) будет отличным от нуля. Он связан с потоком
7(71) или частотой ионизации, которая по смыслу равна
/11 \ “1
Vj = РJ (7J Н п (8) ds I . (9.21)
\о J
В самом деле, «сток» при e=7i в 1 св 1 см3 достигают 7(71)
электронов. Они незамедлительно совершают неупругие столкно-
вения, ионизующие п возбуждающие, в результате чего с «нуле-
вой» энергией появляется 2[37(Zi) + (l — p)7(7i) электронов. Кро-
ме того, с «нулевой» энергией оказываются электроны, совершив-
шие акт возбуждения в зоне £1<8<71. Таким образом,
Л
J (0) = (1 + Р) J + V* J п (е) <?. с-1, см-3- (9.22)
Е1
Это — второе граничное условие. Из самого уравнения (9.19) вы-
падают члены упругих столкновений, прилипания, ионизации и
распределенные источники в области 0<8<£1. Оно прини-
мает вид
хгп -- — dJ/ds при 0 < 8 < £*,
хгп =—dJ/ds— v*n при £*<8<Z1, (9.23)
J = Asdn/ds An/2, A = 2e2E2vm/3m (co2 + v^).
Легко проверить, интегрируя (9.23) по 8 от 0 до Zi, что незави-
234
симым является только одно из соотношений (9.21), (9.22). Дру-
гое следует из результата интегрирования.
5.6. Результаты решения. Отсылая за подробностями к [25],
отметим, что уравнения (9.23) интегрируются в функциях типа
exp (±const Ve). Подчинение общего решения условиям на грани-
цах п (Л) = 0 и (9.23), а также непрерывности п и J на стыке
областей г Е± приводит к довольно громоздкому трансцен-
дентному уравнению для частоты ионизации vl(£'). Однако в
двух крайних случаях его удается разрешить аналитически,
и получающиеся выражения имеют весьма наглядный физиче-
ский смысл, хорошо поясняя сущность процесса.
Назовем величину
vE = Че
АЛ
2 Л
(9.24)
1
Е
"!(“2 +vm)/l
частотой наборов энергии. Медленному электрону потребовалось
бы время чЕ = v#1, чтобы в отсутствие всяких потерь энергии
приобрести под действием поля энергию Ц, необходимую для со-
вершения акта ионизации. Неравенство v* < отвечает малой
вероятности неупругих потерь во время набора энергии иониза-
ции. В этом предельном случае получается \г ~ 00 Е2. Элект-г
рон почти беспрепятственно проскакивает «опасный» участок
£'1<<8<;Z1, где может быть нарушено его продвижение по оси
е к энергии Zi, и затем с вероятностью р совершает ионизацию.
Для размножения требуется время тг = ₽ ^е- Резуль-
тат — очевидный. *
В противоположном случае больших неупругих потерь
(v* > VE)
on J (Л) п Г 1 / 6V* \1/2] /Q or\
v, «a2P|ivK, (i =« 2« exp I-----------— —— , (9.2o)
J / E i J [_ \ VE / J
где a = (A/Z\ )1/2— число, равное примерно 1,2 для всех инерт-
ных газов. Фактор ц < 1 — отношение потоков в конце и начале
«опасной» зоны—представляет собой вероятность электрону про-
скочить эту зону, не потеряв энергии на возбуждение атома.
Электрон в среднем ц-1 раз совершает почти полный цикл на
бора энергии, каждый раз безрезультатно теряя ее на возбужде-
ние, прежде чем ему удастся прорваться сквозь заслон неупругих
потерь и с обеспеченной вероятностью (3 совершить акт иониза-
ции. С точностью до несущественного множителя а2 порядка еди-
ницы для размножения требуется время тч = ~ т^/Рр. Значе-
ние результата (9.25), разумеется, состоит не в констатации это-
го, также очевидного, факта, а в том, что он дает возможность
вычислить вероятность ц. Примечательно, что выражение для ц
можно преобразовать к виду, характерному для стохастического
235
процесса, каковым согласно (9.15) является движение электрона
по энергетической оси [25].
В общем случае трансцендентное уравнение для \\ приходит-
ся решать численно. Но в силу существования законов подобия
Рис. 9.11. Универсальная
функция для вычисления
частоты ионизации в зави-
симости от отношения Ve/v*,
пропорционального квадра-
ту поля [25]
это достаточно сделать один раз, по-
скольку числа аир для большинства
газов близки. На рис. 9.11 представле-
на универсальная зависимость безраз-
мерной частоты ионизации Vx/v* от
безразмерной частоты наборов энергии
Ve/v* — в сущности от квадрата эффек-
тивного поля (7.33). Принято а =1,2,
= 0,2 (представлен также вариант
Р = 1, полезный для некоторых случа-
ев оптического пробоя; см. § 6).
5.7. Сравнение вычисленных частот
ионизации и порогов пробоя с экспери-
ментом. Имея в виду связь ионизацион-
ционного коэффициента Таунсенда а
для постоянного поля с частотой иони-
зации и скоростью дрейфа а = vt/vA =
= vxmvmleE, сопоставим теоретическую
формулу (9.25) с имеющимися экспе-
риментальными данными по а. Пола-
гая со — 0 и выделяя давление по фор-
*
мулам vm = Vmip, v = ViP, с помощью
(9.25) составляем ионизационный коэффициент:
а/р = Ai (Е/Р) ехР (— Вгр!Е\
л 2ea3fi _ 2а3р 0,68 R
(9.26)
В± = -—- ( «1-10 8(/1Ут1Ъ)1/2 В/(см-торр).
а \ е /
Формулы (9.25), (9.26), описывающие случай сильных неупру-
гих потерь, отвечают небольшим значениям Ejp ~ 5—20. И хотя
экспоненциальный множитель в (9.26) по виду совпадает с ин-
терполяционной формулой Таунсенда (4.8), константа В\ суще-
ственно отличается от данных табл. 4.1, которые относятся к
большим значениям Ejp> 100. И смысл Bi, связанный в первую
очередь с сечением возбуждения, не имеет ничего общего с той
полукачественной интерпретацией, которая придается таунсен-
довской константе В (п. 1.5 гл. 4).
Если аппроксимировать функцией (9.26) экспериментальную
кривую а для аргона в области Е!р~Ь—20 В/(см • торр)
(рис. 4.6, 4.9), получим В\ = 31, Л1 = 0,01. Для аргона 1\ =
= I + 1 = 16,8 эВ, vm = 7 • 109/? с-1, v* ~ 2,6 • 108р с-1, что дает
Bi = 53, Л1 = 0,04. Такое согласие весьма упрощенной теории g
236
опытом следует признать удовлетворительным, в особенности ес-
ли учесть, что в расчете не было использовано ни одного «подго-
ночного» параметра. Еще лучшее согласие получается для ксено-
на. Выбирая на основе данных по сечениям 71 = 13,1 эВ, vm =
= 1,5 • 1010р с-1, v* = 4-108/? с-1, получим Вх = 85, Л1=0,05.
Аппроксимация экспериментальной кривой а дает В\ = 85,
Л1 = 0,1.
Ряс. 9.12. Зависимость
пороговых полей СВЧ
пробоя от давления: а —
аргона (1 — f — 2,8 ГГц,
Л = 0,15 см, 2 — f =
= 0,99 ГГц, Л =-
= 0,63 см); б — ксенона
(/ = 2,8 ГГц, Л =
= 0,10 см; сплошные
кривые — расчет, штри-
ховые и крестики — экс-
перимент) [25]
На рис. 9.12 сопоставлены расчетные и измеренные пороги
СВЧ пробоя аргона и ксенона. Вычисления сделаны на основе
изложенной теории частоты ионизации и стационарного критерия
Vi = vd. В области высоких давлений, в конце правых ветвей,
Vm <о2, Е/р — 10, действует асимптотическая формула (9.25).
Расчет хорошо согласуется с экспериментом. Верно описывается
и область минимума, где приходится пользоваться рис. 9.11.
Сильнее расхождение при низких давлениях, где неупругие по-
тери малы и действует другая асимптотическая формула
Vi = [Зуе. Но при р < 10-1 торр длина пробега электрона сравни-
вается с диффузионной (размерами резонатора), нарушается тео-
рия диффузионных потерь, становятся существенными столкно-
вения электрона со стенками, когда он движется поперек элек-
трического поля, так что здесь и нельзя ожидать хорошего
согласия.
§ 6. Оптический пробой
Открытие эффекта оптического пробоя (Мэйкер, Терхун, Сэ-
видж, 1963 г.) стало возможным только после создания лазеров
с модулированной добротностью, которые дают световые импуль-
сы огромной мощности, названные гигантскими. Когда луч тако-
го (рубинового) лазера пропустили через фокусирующую линзу,
237
в воздухе в области фокуса вспыхнула искра, как при электри-
ческом пробое разрядного промежутка (рис. 9.13). Открытие это-
го явления было для физиков полнейшей неожиданностью, и в
то время сообщение о
Рис. 913. Фотография ла-
зерной искры в воздухе
нем вызвало сенсацию. Теперь этому
не приходится удивляться. Для пробоя
газов на оптических частотах требуют-
ся колоссальные поля в световой вол-
не 106—107 В/см, о чем до изобрете-
ния лазеров нельзя было даже и по-
мышлять. Более того, для создания со-
ответствующих интенсивностей света
105 МВт/см2 понадобилось хорошо сфо-
кусировать луч не обычного лазера,
а работающего в режиме гигантского
импульса. Новый эффект вызвал ис-
ключительный интерес среди физиков.
За короткий срок он был исследован
экспериментально и теоретически на-
столько [25], что сейчас мы знаем о
нем не меньше, чем о его ближайшем
аналоге — СВЧ пробое.
6.1. Постановка опытов. Постановка первых опытов по изме-
рению порогов пробоя (Мейерэнд, Хот, 1964 г.) типична для
многих последующих экспериментов, поэтому расскажем о ней
подробнее (рис. 9.14). Рубиновый стержень длиной 15 см и диа-
метром 1,3 см «накачивался» четырьмя импульсными ксеноновы-
ми лампами, через каждую из которых разряжалась конденса-
торная батарея. Добротность квантового генератора модулирова-
лась при помощи поляризатора и ячейки Керра. В результате
получался гигантский импульс со следующими параметрами:
Рис 9 14. Схема опыта по измерению порогов оптического пробоя: 1 — ру-
биновый стержень, 2 — ксеноновые лампы, 3 — поляризатор, 4 — ячейка
Керра, 5 — зеркало, £ —фокусирующая линза, 7— собирающие электроны,
8 — окно
энергия 1 Дж, длительность 30 нс = 3 • 10-8с, максимальная (пи-
ковая) мощность 30 МВт = 3 • 1014 эрг/с. Эти параметры типич-
ны и для современных стандартных установок умеренной мощно-
сти*). Энергия импульса определялась калориметрически. Фор-
ма его, грубо говоря, треугольная, колоколообразная с более
крутым передним фронтом, чем задним.
*) В настоящее время созданы твердотельные лазеры, дающие тысячи
мегаватт в течение нескольких наносекунд.
238
Чтобы повысить плотность потока излучения, луч фокусиру-
ют. Диаметр кружка фокусировки d определяется углом расхо-
димости исходного светового луча 0 и фокусным расстоянием
линзы f; d = /0. Обычно 0 ~ 10“3—10~2 рад, 3—10 см. В опи-
сываемых опытах б/ ~ 2 • 10~2 см. Диаметр измерялся по размеру
отверстия, которое луч прожигал в тончайшей золотой фольге
толщиной 0,05 мкм. При пиковой мощности 30 МВт плотностг
потока энергии в фокусе составляла S ~ 105 МВт/см2 =
= 1018 эрг/(с-см2), среднеквадратичное поле в световой волне
Е = (4nS/c)1/2 = 19(5 [Вт/см2])1/2 В/см ~ 6 - 106 В/см,
плотность потока фотонов рубинового лазера (Йео = 1,78 эВ)
F = 3,4 10185 [Вт/см2] « 3,4 • 1029 с"1 • см"2.
Луч света фокусировался внутрь камеры, наполняемой иссле-
дуемыми газами при разных давлениях. Факт пробоя устанавли-
вался по появлению видимой вспышки (она длилась 50 мкс)
Для объективной регистрации фокус заключался между napoi
электродов, к которой прикладывалось напряжение 100 В. Прт
пробое из области фокуса вытягивалось 1013 электронных заря
дов*). Мощность облучения менялась при помощи ослабителя
чтобы можно было «поймать» порог пробоя, который выражег
очень резко.
Рис. 9.15. Пороги пробоя Аг и Не
излучением рубинового лазера
[25]
Рис. 9.16. Пороги пробоя Ar, N2, Не рз
биновым лазером в широком диапазон
давлений (длительность импульса 50 н<
диаметр фокуса 0,1 мм)
6.2. Результаты экспериментов. На рис. 9.15 показаны порог]
пробоя аргона и гелия излучением рубинового лазера, измерен
ные в описанном опыте. Пороговое поле монотонно уменьшаете]
при повышении давления. Но так происходит только в ограни
ченном диапазоне давлений. Когда прошлись по более широкому
диапазону от нескольких атмосфер до двух тысяч (Гилл и Ду
гал, 1965 г.), обнаружилось, что порог имеет минимум, как i
*) При пробое также уменьшается мощность проходящего через фоку
излучения — образующаяся плазма его поглощает.
23
яри СВЧ пробое, только минимумы лежат не при 1—10 торр,
а при сотнях атмосфер (рис. 9.16). Замечательно, что положение
минимума приближенно удовлетворяет тому же соотношению
vm ~ со (и. 4.5). Например, для Аг и рубинового лазера, со =
= 2,7 -1015 с-1, по этой формуле получается р ~ 225 атм, а из
опыта— 190; для Не — р~ 1450 атм, опыт дает 700 атм. Причи-
на существования минимума та же, что и в СВЧ поле: при
Vm ~ со максимальна (как функция р) скорость набора энергии
электроном в поле данной частоты.
При фокусировке в газ излучения импульсных газовых лазе-
ров на СО2 также наблюдается пробой. Это излучение
(Л = 10,6 мкм ~ 10“3 см) занимает промежуточное положение
между излучениями рубинового и неодимового лазеров
(X ~ 10-4 см) и СВЧ диапазоном (А — 1 см), хотя и ближе к ви-
димой части спектра. Импульсы СО2-лазеров обычно более дли-
тельны, порядка 1 мкс.
На рис. 9.17 показаны результаты измерений порогов пробоя.
Соотношение Vm ~ со для положения минимума хорошо выполня-
ется. В Хе, например, vm ~ 9 • 1012р с-1; соСо2 = 1,78- 1014с \ По-
лучается р ~ 20 атм, из опыта — около 15 атм.
Увеличение диаметра кружка фокусировки, т. е. размеров об-
ласти, подверженной действию поля, ведет к понижению порога
ВМ3/см
200
130
100
50
О
Рис. 9.17. Пороговые интенсивность
и напряженность пробоя инертных
газов излучением СОг-лазера; тем-
ные кружки — гелий более высокой
чистоты [25]
пробоя. Измерения были вы-
полнены в диапазоне диаметров
10~2—10-1 см путем примене-
ния линз с различными фокус-
ными расстояниями (d == /0).
Качественно этот результат
кажется понятным: чем боль-
ше размеры области действия
поля, тем меньшую роль игра-
ют потери электронов за счет
их диффузионного ухода из
этой области. Однако дело
здесь обстоит сложнее. По
оценкам в ряде случаев элект-
рон не успевает продиффунди-
ровать на расстояние d за ко-
роткое время импульса. Воз-
можно, сказывается диффузия
нс из всей области фокуса, а из «горячих» точек с высокими
локальными полями, которые существуют в фокусном пятне
из-за неоднородности лазерного пучка по сечению и в которых
преимущественно развивается электронная лавина.
6.3. Пороги пробоя атмосферного воздуха. Данные о них очень
важны. Многие физические эксперименты связаны с использова-
нием интенсивного лазерного излучения. Пробой воздуха на пути
лазерного луча к облучаемому объекту служит помехой для рас-
240
пространения света, так как плазма поглощает его. По этой при-
чине во многих экспериментах с мощным излучением, скажем
при воздействии на мишени с целью достижения термоядерных
температур, приходится подавать излучение к мишени через ва-
куум. Для гигантского импульса рубинового лазера при обычном
радиусе кружка фокусировки 10-2 см пороговая интенсивность
составляет St ~ 1011 Вт/см2, а поле Et ~ 6 • 106 В/см.
Пороговая интенсивность пробоя неочищенного воздуха сфо-
кусированным излучением СО2-лазера примерно 2 • 109 Вт/см2,
очищенного от пыли—не менее 1010 Вт/см2. Мельчайшие пылин-
ки, присутствующие в атмосфере, в высшей степени облегчают
пробой излучением ССЬ-лазера, тогда как в случае неодимового,
и особенно рубинового лазера влияние пыли незначительно. При-
чина такого различия состоит в том, что коротковолновое излу-
чение твердотельных лазеров «само себе» создает затравочные
электроны, необходимые для начала лавины. Длинноволновое из-
лучение СОг-лазера в чистом газе этого сделать не может.
6.4. Многоквантовый фотоэффект. Можно представить себе
два совершенно различных механизма ионизации газа под дей-
ствием интенсивного светового излучения. Один из них — разви-
тие электронной лавины, по своей природе не отличается от того,
что происходит при пробое во всех других полях. Имеются лишь
различия в деталях механизма приобретения энергии электрона-
ми от поля, связанные с квантовым характером светового поля.
Второй механизм ионизации характерен именно для световых
частот, он имеет чисто квантовую природу. Электроны могут от-
рываться от атомов в результате многоквантового фотоэффекта,
т. е. при одновременном поглощений* сразу нескольких фотонов.
Одноквантовый фотоэффект невозможен в случае частот видимо-
го диапазона, так как потенциалы ионизации атомов в несколько
раз превышают энергии квантов. Так, например, для рубинового
лазера Йсо = 1,78 эВ, а потенциал ионизации аргона ZAr = 15,8 эВ,
т. е. для отрыва электрона требуется девять квантов. Обычно
многофотонные процессы маловероятны, но скорость их очень
резко повышается при увеличении плотности фотонов (интенсив-
ности света), и при тех исключительно высоких интенсив-
ностях, при которых наблюдается оптический пробой, ве-
роятность многофотонных процессов может достигать значитель-
ной величины^
И расчеты (см. ниже), и опыт показывают, что в случае на-
носекундных (и более длительных) лазерных импульсов при дав-
лениях выше десятых долей атмосферы всегда происходит лавин-
ная ионизация. Скорость ее оказывается достаточной для пробоя
газа при таких полях, которые еще недостаточны для интенсив-
ной многофотонной ионизации. Последняя, однако, играет важ-
ную роль, обеспечивая появление первых, затравочных электро-
нов, необходимых для начала лавины. Попадание случайного
электрона в маленькую область фокуса в момент кратковремен-
ного импульса — событие практически невероятное.
16 Ю П Райзеп
241
Выше неоднократно говорилось о том, что возбуждение ато-
иов ударами электронов оказывает тормозящее действие на раз-
витие лавины, так как электрон теряет свою энергию и вынуж-
ден снова и снова ее набирать, прежде чем ему удастся проско-
чить зону возбуждения и достичь потенциала ионизации. Так
происходит во всех полях, кроме светового. В световом поле, ког-
да энергия кванта велика, может оказаться достаточным неболь-
шого числа квантов, чтобы путем многоквантового фотоэффекта
вырвать электрон из возбужденного атома. В этом случае воз-
буждение даже ускоряет развитие лавины, так как электрону
достаточно достичь потенциала возбуждения, а не ионизации.
Например, в аргоне /Лг = 15,8 эВ, а потенциал первого воз-
бужденного состояния EAy = 11,5 эВ. Для отрыва электрона от
возбужденного атома нужна энергия 4,3 эВ, т. е. требуется одно-
временное поглощение трех квантов рубинового лазера или че-
тырех квантов неодимового (Tzco = 1,17 эВ). Четырехквантовый
процесс маловероятен, но на чистоте рубинового лазера в опре-
деленных условиях трехквантовый процесс может идти. Имеются
экспериментальные и теоретические свидетельства в пользу су-
ществования подобного механизма.
6.5. Нестационарный критерий пробоя. В случае чрезвычайно
коротких импульсов, как в рассматриваемых условиях, поле, ко-
торое диктуется стационарным критерием (9.9), может оказаться
недостаточным для заметной ионизации газа. Ведь если за время
импульса родится два-три поколения электронов, это еще нельзя
будет квалифицировать как пробой. Ионизация должна достичь
заметной величины. В повседневном понимании пробой даже свя-
зывается с появлением видимой вспышки. Так, в опытах, опи-
санных выше, было установлено, что вспышка и пробой соответ-
ствуют появлению 1013 электронов. Если считать, что лавина на-
чинается от одного электрона, то при пробое за время импульса
рождается lg2 Ю13 ~ 43 поколения электронов. Поле должно
быть настолько сильным, чтобы постоянная времени лавины 0
была в In 1013 ~ 30 раз короче длительности импульса t\ ~
3 • 10-8 с, т. е. 0 « 1 нс.
Пороговое поле должно определяться из условия, что за вре-
мя действия поля t\ лавина, начавшаяся с No электронов, успе-
вает дорасти до N\:
t\/& (Et) = (vt - va - vd) t. = In (NJN0). (9.27)
Пороговое поле мало чувствительно к не слишком определенной
величине N\/Nq, поскольку она стоит под логарифмом. При рас-
четах можно положить £1/0 ~ 30. Нестационарный критерий
(9.27) обобщает стационарный (9.9) и сводится к нему при
£1 -> оо. В случае же чрезвычайно коротких импульсов порог ока-
зывается очень высоким и роль потерь электронов становится не-
существенной: va, Vd < vt. Нестационарный критерий еще сильнее
обостряет пороговый характер пробоя. При уменьшении частоты
242
Рис. 9.18. Расчет порогов
пробоя Аг рубиновым
лазером в предположе-
нии, что возбужденные
атомы мгновенно иони-
зуются излучением; точ-
ки — эксперимент с од-
номодовым лазером [25]
ионизации Vt вдвое, для чего требуется небольшое уменьшение-
поля, вместо 43 родится только 21 поколение, т. е. электронов
появится на 6—7 порядков меньше.
6.6. Расчеты пороговых полей. В сущности, рассмотрение,
проведенное в предыдущих и этой главах, дает все элементы, не-
обходимые для теоретического анализа оптического пробоя.
В § 8 гл. 5 было рассмотрено, как электрон набирает энергию в
поле фотонов, то поглощая, то вынужденно испуская кванты.
В § 10 гл. 7 тот же процесс был рассмот-
рен на основе квантового кинетиче-
ского уравнения. Была обоснована воз-
можность применения классического урав-
нения — при условии Йсо е, которое не
вызывает сомнений в случае СО2-лазера,
достаточно хорошо выполняется для нео-
димового и с некоторыми оговорками
можно считать выполненным в случае
рубинового (8 ~ Zi/2 ~ 8—13 эВ в Аг,
Не). Это позволяет применить для расче-
та теорию, изложенную в § 5, использо-
вав нестационарный критерий (9.27).
В случае рубинового лазера представля-
ется правдоподобным предположение о
быстрой трехфотонной ионизации воз-
бужденных атомов. Процесс пробоя при
этом уподобляется пробою Heg-газа: не-
упругие потери отсутствуют; [} = 1. В слу-
чаях неодимового и, конечно, СОг-лазеров
неупругие потери действуют, как и для
СВЧ. Для СОг-пробоя справедлив стацио-
нарный критерий (9.9). На рис. 9.18, 9.1
сопоставлены с экспериментом. Согласи
удовлетворительным. Это свидетельствует о большом сходстве
процессов пробоя в оптическом и СВЧ диапазонах.
6.7. Мост между СВЧ и светом. Особенно убедительным в от-
ношении последнего утверждения является тот эксперименталь-
ным путем установленный факт, что классический закон подобия
ею St со со2 для пороговых величин выполняется в широком
диапазоне оптических частот, вплоть до смыкания с СВЧ. Для
самого СВЧ диапазона закон St <*> со2 справедлив только при низ-
ких давлениях р < 10 торр, отвечающих левым ветвям пороговых
кривых. Обобщая, следует считать St со (со2 4- v™). Что же касает-
ся оптического, то здесь даже десятки атмосфер — давление низ-
кое, и, к примеру, весь график 9.15 изображает левую ветвь.
На рис. 9.20 около линии, соответствующей St со (со2 -f- vj»),
которая в логарифмическом масштабе вырождается в прямую
при << со2, проставлены экспериментальные точки для воздуха.
В дополнение к многочисленным данным по пробою атмосферно-
16* 243
результаты расчетов
получается вполне
то воздуха излучениями рубинового, неодимового и СОг-лазеров
представлены данные для лазеров на D2O (X = 385 мкм =
— 0,38 мм—самый «неосвоенный» диапазон) и HF, DF
(л == 2,7 мкм, 3,8 мкм). Как видим, точки хорошо группируются
Рис. 9.19 Расчет порогов пробоя- « — Аг, неодимовый лазер, точки — экспе-
римент, А= 16,4 мкм; б — Аг и Хе, СС^-лазер, точки — эксперимент дли-
тельность импульса 1 мкс, диаметр фокуса 80 мкм [25]
около теоретической прямой, хотя строгого выполнения закона
ожидать нельзя, ибо условия разных экспериментов не идентич-
ны. Заметим, что точки D2O лежат на пределе выполнения уело-
вия О)2 > У2т: со = 4,9-1012 с"1, vm « 3,8 • 1012 с"1.
Закон St со о)2 явно нарушается в середине видимой и ультра-
фиолетовой области спектра: на вторых гармониках неодима
Рис. 9.20. Пороговая интен-
сивность пробоя атмосфер-
ного воздуха в зависимости
от длины волны разных ла-
зеров. Штриховая кривая —
классическая зависимость
(/гео = 2,34 эВ) и особенно рубина
(Tzco = 3,56 эВ), где вступают в игру
квантовые эффекты [25].
6.8. Длинная искра. При не слиш-
ком большой надпороговой мощности
для получения пробоя лазерное излу-
чение приходится фокусировать корот-
кофокусной линзой. Если же лазер
очень мощный, интенсивности хватает
на то, чтобы пробить воздух на боль-
шой длине вдоль каустики длиннофо-
кусной линзы. Так получают весьма
впечатляющую картину протяженного
оптического пробоя — длинную искру.
Искра рекордной длины — более
60 метров! — была создана в 1976 г.
при помощи неодимового импульса с
энергией 160 Дж, средней мощностью
5 ГВт и линзы с / = 40 м.
Луч выпускали прямо в институт-
ский двор (рис. 9.21). Длинные искры
не получаются сплошными, ионизован-
ные участки чередуются с непробитыми. Вероятно, это связано со
статистическим характером появления затравочных электронов,
а также пространственно-временной и угловой неоднородностями
луча. Длинную искру получают и при помощи СОг-лазера, она
244
возникает при интенсивностях (1—2) • 108 Вт/см2; в очищенном
воздухе порог повышается до 3 • 109 Вт/см2. С помощью длинной
лазерной искры удается эффективно инициировать пробой в про-
тяженных промежутках между электронами. Поле пробоя возду-
ха постоянным напряжением снижается при этом до 250 В/см.
Рис. 9 21. Фотография длинной искры, полученной с помощью неодимового
лазера Длина искры 8 м, фокусное расстояние линзы 10 м [9.2]
Вообще при совместном действии лазерного излучения и, СВЧ
или постоянного поля пробой существенно облегчается. Так мож-
но создать направленный и даже изломанный канал пробоя меж-
ду электродами *). *
§ 7. Способы возбуждения высокочастотного поля
в разрядном объеме
Способы возбуждения можно разбить на две основные группы
по признаку того, замыкаются ли силовые линии электрического
поля в разрядной плазме или нет, иначе — является ли поле
вихревым или потенциальным. К первой группе относятся индук-
ционные методы, основанные па использовании явления электро-
магнитной индукции.
Типичный и наиболее распространенный путь воплощения
этого принципа заключается в следующем (рис. 9.22, а). Через
катушку-соленоид пропускают ток высокой частоты (на практике
катушка вполне может состоять из одного или нескольких вит-
ков). Магнитное поле этого тока, также переменное, внутри ка-
тушки направлено вдоль ее оси. Под действием переменного
магнитного потока внутри катушки индуцируется вихревое элек-
трическое поле. Силовые линии его представляют собою замкну-
*) Некоторые подробности обо всем сказанном и ссылки имеются в об-
зоре [9.1].
245
тые окружности, концентрические с витками катушки. Это элек-
трическое поле может зажигать и поддерживать разряд, причем
токи также замкнуты и протекают вдоль круговых линий элек-
трического поля. Практически в катушку вставляют диэлектриче-
скую трубку, наполненную исследуемым газом, и при соответст-
вующих условиях в газе возникает пробой и может стационарно
гореть однажды зажженный разряд. Разряд можно сделать им-
пульсным, если подать в катушку достаточно сильный импульс
Рис. 9 22. Схемы возбуждения
ВЧ разрядов: а — индукционный
(при помощи соленоида); б — на-
пряжение подается на электроды,
соприкасающиеся с плазмой; в —
электроды изолированы от плаз-
мы (безэлектродный, емкостной
способ)
тока. Описанный разряд называют индукционным или Я-типа.
Буква Я символизирует определяющую роль магнитного поля.
Индукционные разряды, естественно, являются безэлектродными.
В методах второй группы высокочастотное (и вообще любое
переменное) напряжение подают на электроды. В простейшей и,
кстати, наиболее употребительной геометрии это два параллель-
ных плоских электрода. Электроды могут быть оголенными и не-
посредственно соприкасаться с разрядной плазмой, а могут быть
изолированными от плазмы диэлектриками (рис. 9.22, б, в). Си-
стема двух электродов ведет себя по отношению к переменному
напряжению как конденсатор, «емкость», поэтому разряды дан-
ной категории, в отличие от индукционных, называют емкостны-
ми или Я-типа. Буква Е символизирует определяющую роль
электрического поля.
Емкостный разряд зажигают и в трубке, создавая продольное
поле при помощи пары кольцевых электродов, наложенных по-
верх стекла у концов трубки. Это позволяет наблюдать разряд
через торцы.
Индукционное электрическое поле возрастает с увеличением
частоты, в отсутствие плазмы — пропорционально ей. На низких
частотах таким путем трудно создать большие поля, нужно про-
пускать слишком сильный ток через индуктор. Поэтому индук-
ционный способ, как правило, употребляют лишь в «истинно»
ВЧ диапазоне 102 МГц. На низких частотах труднее
создать и безэлектродный емкостный разряд, так как изолирую-
щие диэлектрики в этом случае представляют большое емкостное
сопротивление и на них «садится» большая доля подаваемого
напряжения. На частотах /<10 кГц чаще пользуются оголен-
ными электродами. Имеется, правда, возможность использовать
для изоляции электродов тонкие слои из вещества с большой
диэлектрической постоянной (например, титанат бария), но тех-
нически это не всегда осуществимо. Впрочем, трудности возника-
246
ют лишь тогда, когда нужно приложить к разрядному промежут-
ку много киловольт, т. е. при больших длинах и высоких давле-
ниях. Когда дело касается сотен вольт, киловольта, проблем осо-
бенных нет. Разрядная практика в ВЧ дипазоне сложилась та-
ким образом, что индукционный способ чаще применяют для
поддержания плазмы при высоких давлениях порядка атмосфер-
ного (§ 3 гл. 13), а емкостной — при средних и низких давле-
ниях (гл. 15).
Как и при исследовании разрядов в постоянном поле, конфи-
гурация электродов может быть самой различной: два шара, шар
и плоскость, проволока и концентрический цилиндр и т. д.
Во всех этих случаях поле получается неоднородным, и это вно-
сит дополнительные трудное!и в интерпретацию результатов.
Для обработки результатов эксперимента, оценок и теории наи-
более удобны плоские параллельные электроды с относительно
малым зазором, т. е. плоская геометрия.
§ 8. Пробой в полях высокочастотного
и низкочастотного диапазонов
Картина процесса подчас весьма резким образом меняется в
зависимости от многих условий: частоты, давления, способа вве-
дения поля в разрядный объем, геометрии и размеров последне-
го, ориентации электрического вектора.
В какой-то мере классифицировать явления можно путем
сопоставления характерных длин. Их три: размеры объема cZ,
длина свободного пробега электронов, Z, амплитуда их свободных
колебаний а или дрейфовых А (п. 1.3 тл. 5). Выбор между а и
А определяется тем, что больше, частота поля со или частота
столкновений электронов vm*). Если давления так малы, что
2 > d, электрон не испытывает столкновений с атомами газа. Для
типичных размеров d ~ 1 см и большинства газов верхней грани-
цей области столь низких давлений (Z ~ d) служит р~ 10-2торр.
Рассмотрим очень кратко несколько вариантов условий, которые
приводят к более или менее ярко выраженным картинам явления.
8.1. Амплитуда колебаний электронов мала; столкновений
много. Это — случай а, А < cZ, Z < d. Он реализуется на достаточ-
но больших частотах, при не слишком низких давлениях и мало
отличается от рассмотренного выше процесса СВЧ пробоя. На
рис. 9.23 представлены измеренные амплитудные значения по-
тенциалов зажигания Vt разряда в неоне на частоте /==158 МГц
при давлениях до 50 торр и расстояниях между плоскими элек-
тродами d = 0,5—2 см. Зависимость Vt от р при фиксированном
*) Длину волны колебании поля можно использовать для характеристи-
ки частоты, но она мало что определяет. Для ВЧ и более низких частот
1 > 1 м, А > d 1 см, т е. колебания не вносят дополнительной неодно-
родности в пространственное распределение поля.
247
расстоянии, т. е. фактически Et = Vt/d от р, очень похожа на
изображенную на рис 9 10 для СВЧ
Тому есть все основания Амплитуда дрейфовых колебаний в
конце правых ветвей
А = еЕп1т\ты ~ 2,6 10~3 * * * * В см <С d
(со = 109 с’1, Е[р~3 В/(см торр); vm ~ 2 109р с-1 для таких
Е1р). В области минимумов (Е/р « 50—100, ут ~ 4 109/>) ампли-
туда на порядок больше (2,5 10-2 см), но все равно мала по
сравнению с с/ ~ 1 см Положение минимумов неплохо удовлетво-
ряет обсуждавшемуся выше соотношению vm & со, из которого
получается (p)min~2,5 торр Пороговые значения Et/p при по-
вышенных давлениях ~ 50 торр в конце правых ветвей
(Еtip = 2,2 В/(см торр) при d = 2 см, Etlp = k,b при б/ = 0,5см)
также близки к таковым в СВЧ диапазоне и постоянном поле
(табл. 9 1). По-видимому, мы имеем дело с типичной картиной
объемного пробоя, в котором электроны гибнут в результате
диффузии.
Рис 9 23 Потенциалы за-
жигания Vt емкостного ВЧ
разряда в неоне в зависи-
мости от давления Штри-
ховые кривые — напряже-
ние горения Vm установив-
шегося разряда [7]
На рис. 9 23 нанесены измеренные в тех же опытах напряже-
ния горения уже зажженного разряда В процессе стационарного
горения ионизация, которая определяется той же частотой Vi(E)r
тоже компенсирует диффузионный уход электронов, но теперь
плотности зарядов значительны и диффузия, будучи амбиполяр-
ной, происходит гораздо медленнее Поэтому после зажигания
напряжение на разряде падает *)
*) О том, что для поддержания горящего разряда достаточно более сла-
бого поля, чем для пробоя газа, см также в п 6 3 гл 10 Каждый может
убедиться в этом путем простого, но очень показательного эксперимента.
Если Вы когда-нибудь принимали физиотерапевтическую процедуру УВЧ
(это поле частотой 40 МГц), то знаете, как проверяют, работает ли аппарат
В область между электродами вдвигают маленькую лампочку — запаянный
сосуд с неоном при низком давлении, и если все в порядке, она зажигается
красным светом Приблизьте медленно контрольную лампочку к электроду
или проводу, пока она не вспыхнет Потом медленно отодвиньте ее по тому
же пути Разряд будет сокращаться в размерах и угасать Он полностью ис-
чезнет гораздо дальше от места зажигания, там, где поле слабее
248
8.2. Амплитуда колебаний сравнима с размерами; столкнове-
ний много. Такая ситуация возникает на меньших частотах. Дав-
но было замечено, что на кривых F«(p), подобных изображенным
на рис. 9.23, иногда появляется дополнительный минимум. Изме-
рения, показанные на рис. 9.24, были сделаны в длинной
(30 см) цилиндрической трубке с внешними электродами (ем-
костной разряд). Когда электроды располагались за торцами (по-
ле направлено вдоль оси), картина не отличалась от рис. 9.23.
Рис. 9.24. Потенциалы зажигания Vt емкостного ВЧ разряда в зависимости
от давления для различных длин волн колебаний [7]
Второй минимум (справа), который фигурирует на кривых Vt(p)
при не слишком высоких частотах, появлялся, только если поле
прикладывалось поперек трубки. В этом случае амплитуда коле-
баний электронов сравнима с расстоянием до стенок в направле-
нии движения электронов — с диаметром трубки d = 2 см.
Если двигаться по шкале давлений справа налево, то сначала
мы находимся на обычной правой ветви типа изображенной на
рис. 9.23, отвечающей диффузионным потерям. При понижении
давления амплитуда дрейфовых колебаний электронов вырастает
до величины с//2 и электроны при каждом колебании попадают
на стенку. Потери их от этого увеличиваются, ибо диффузия вы-
носит электроны на стенки медленнее. Для зажигания требуется
более сильное поле; пробивающий потенциал возрастает. Поло-
жение скачка и минимума определяется очевидным соотношени-
ем А = еЕъ1тпУт& ~ d/2, откуда Е0/ра) ~ const. Эта закономерность
по данным рис. 9.24 действительно выполняется, и численное
совпадение получается удовлетворительным. Например, на часто-
те f = 3 МГц (А =100 м) со = 1,9 • 107 с"1, Е/р 100, vm ~
~ 4 • 109р, А ~ 1 см. Левее скачка мы движемся влево по «пра-
вой» ветви, отвечающей повышенным потерям. Левый, основной
249
минимум соответствует «обычному» условию ут ~ со, и его при-
рода такова же, что и в случае очень больших частот. На доста-
точно больших частотах А < d при всех р и второго мини-
мума нет.
Если уменьшать частоту поля при неизменных прочих усло-
виях, при некоторой граничной частоте необходимое для пробоя
поле резко возрастает. Это происходит, когда электроны при
дрейфовых колебаниях начинают попадать на стенки. Граничная
частота удовлетворяет тому же приближенному соотношению
2eEQ ~ 0,14 (EQ/p) [В/(см-торр)]
mvm(Dd ~ /[МГц]б?[см]
(9.28)
где d — расстояние между противоположными стенками, перпен-
дикулярными направлению поля, и Ео/р относится к нижней ча-
сти скачка. В численную формулу подставлено vm ~ 4 • 109р.
8.3. Широкий диапазон частот,
включая низкие; столкновений
много. На рис. 9.25 представлены
поля зажигания безэлектродного
емкостного разряда в водороде.
Газ был заключен в стеклянный
сосуд размером d ~ 2 см. При
уменьшении частоты (увеличе-
нии длины волны) и неизменном
давлении происходит скачок
пробивающего поля. Граничная
частота неплохо согласуется с
Et, кв/см
2 -
1,5-
р=16 торр-
______5К_ '
27, ’
0,5-
5йГц-
__i__....i_„7t —
70 5 105 К,м
Рис. 9.26. Поле зажигания ем-
костного разряда в неоне в стек-
лянных сосудах разных диамет-
ров в широком диапазоне длин
волн при разных давлениях [7]
Рис. 9.25. Поле зажигания емкостного
разряда в водороде в стеклянном ци-
линдре длиной 2 см в широком диа-
пазоне длин волн при разных давле-
ниях [7]
о ^2 ^5
оценкой (9.28). При частотах ниже граничной пороговое поле
почти не меняется в очень широком диапазоне частот от мега-
герца до 50 Гц. Этот результат озадачивает. Ведь на частотах
существенно меньше граничной электроны относительно быстро
«сгоняются» полем к одной из стенок, сравнительно долго там
удерживаются, а потом столь же быстро «перегоняются» к дру-
250
гой, и т. д. Подавляющее время в объеме нет электронов. Если
бы ионизация в эти периоды прекращалась, пробить газ было бы
труднее. Похоже на то, что в объеме остается какой-то другой
ионизующий агент.
В неоне в широком диапазоне частот порог несколько повы-
шается (рис. 9.26). После размытого «скачка» на граничной ча-
стоте (первый подъем слева) он возрастает в 1,5—2 раза при из-
менении частоты на 3—5 порядков. Для объяснения указанных
и ряда других сложных и запутанных обстоятельств, присущих
низкочастотным разрядам, привлекаются эффекты, связанные с
фотонами, возбужденными атомами, фотоэмиссией со стенок
и т. д. [7], однако до полной ясности здесь далеко.
На низких частотах порядка 1 кГц и менее, в особенности в
случае оголенных электродов, пробой в каждом полупериоде про-
исходит заново и примерно так же, как в постоянном поле. По-
казательно в этом отношении, что по данным рис. 9.25 при повы-
шенном давлении р = 76 торр среднеквадратичная пороговая ве-
личина в водороде Et/p ~ 22 В/(см - торр) близка к соответствую-
щему значению в постоянном поле (табл. 9.1). И вообще, потен-
циалы зажигания при повышенных давлениях зависят от pd, по-
добно правым ветвям пашеновских кривых, и близки к ним по
величине.
8.4. Пробой «вакуума». В случае сильно разреженного газа,
когда электрон испытывает очень мало столкновений (Z>d),
размножение происходит в ре-
зультате вторичной электрон-
ной эмиссии со стенок. Ди-
электрические материалы (стек-
ла) дают достаточно сильную
эмиссию, так что пробиваются
и изолированные от электро-
дов объемы. В результате про-
боя в остаточном газе зажига-
ется разряд, появляется свече-
ние и регистрируется измене-
ние тока через генератор пере-
менного напряжения. Но про-
бой случается только на часто-
тах выше граничной /гр
(рис. 9.27).
Это можно объяснить. Что-
бы происходило размножение,
энергия е ударяющего электро-
на должна быть достаточной
для вырывания более одного
электрона на один ударяющий,
тело и там остается (отражение
множению не ведет и в расчет е
ной эмиссии требуется е ек -
Рис. 9.27. Поле зажигания ВЧ раз-
ряда в вакууме в стеклянных труб-
ках длиной d параллельно оси (во-
дород, р = 10~3 торр) [7]
который при этом внедряется в
падающих электронов к раз-
ie принимается). Для эффектив-
100 эВ (п. 6.5 гл. 4). Кроме
251
того, электроны должны пересекать промежуток согласованно
с полем. К моменту прихода ускоренного электрона от одной
стенки к другой поле должно изменить направление с тем, что-
бы эмитированный электрон в свою очередь начал ускоряться
в сторону первой.
Пусть электрон вылетает от стенки х = 0 со скоростью х = О
в момент ^о = я;/(о, когда поле Ех = EG sin coi меняет направление,
начиная ускорять эмитированный электрон. Согласно (5.1) он
достигает противоположной стенки х = d со скоростью ик ==
= (2скМ)1/2 в момент следующего изменения направления поля
t\ = 2л/со, если 2еЕъ1т(й — vK, cud =* п(еЕо//па)) (второе равенство
соответствует (9.28) только для свободного движения). При ск =
= 100 эВ, ph = 5,8 • 108 см/с, отсюда получается частота отсечки
/гр ~ 140/е/ [см] МГц и пороговое поле Ео ~ 120/d [см] В/см
в разумном согласии с рис. 9.27 и эмпирической связью /гр ~
« 80/rf МГц.
При f < /гр электрон достигает противоположной стенки в мо-
мент, когда ускоряющая сила все еще направлена по его движе-
нию. Эмитированный электрон оказывается безнадежно «запер-
тым». Возможности для размножения ограничены очень жестко.
Если же / > /гр, электрон начинает тормозиться до прихода к
стенке. Это дело поправимое: нужно сообщить ему до этого боль-
ше энергии, что достигается увеличением поля. Поэтому при
/ > /гр пробой возможен, но порог возрастает с увеличением
/— Лр (см. Рис- 9.27). Подробнее о пробое в ВЧ и низкочастот-
ных полях см. [7].
Глава 10. СТАБИЛЬНЫЙ ТЛЕЮЩИЙ РАЗРЯД
§ 1. Общая структура и внешний вид
1.1. Отличительные черты. Тлеющий разряд—это самопод-
держивающийся разряд с холодным катодом, испускающим элек-
троны в результате вторичной эмиссии, главным образом под
действием положительных ионов. Его отличительным признаком
является существование вблизи катода слоя определенной тол-
щины с большим положительным объемным зарядом, сильным
полем у поверхности и значительным падением потенциала:
100—400 В (и более). Оно называется катодным падением. Тол-
щина слоя катодного падения обратно пропорциональна плотно-
сти (давлению) газа. .Если межэлектродное расстояние достаточ-
но велико, между катодным слоем и анодом образуется электро-
нейтральная плазменная область, где поле относительно неболь-
шое. Серединную, однородную часть ее называют положительным
столбом. От анода он отделяется анодным слоем. Положительный
столб тлеющего разряда постоянного тока — наиболее ярко выра-
женный и распространенный пример слабоионизованной неравно-
252
веской плазмы, которая поддерживается электрическим полем.
В отличие от катодного слоя, без которого тлеющий разряд су-
ществовать не может, положительный столб не является его не-
отъемлемой частью. Если в результате образования катодного
слоя промежуток между электродами оказывается исчерпанным,
столба нет Но если не хватает расстояния на формирование
должного катодного слоя, тлеющий разряд не загорается
1.2. Разрядные устройства. Тлеющий разряд — один из наибо-
лее изученных и широко применяемых на практике типов газово-
го разряда В течение многих десятилетий для его получения и
исследования служил классический прибор — разрядная трубка
(рис 11). Для тлеющего разряда в трубках радиуса R ~ 1 см,
длины L ~ 10—100 см при типичных давлениях
— 10“2—102 торр характерны напряжения на электродах V ~
- 102—103 В и токи i - 10-4—10"1 А
Тлеющим разрядом всегда много занимались Он привлекал
богатством электронных процессов и возможностями использова-
ния в газосветных приборах и др Но с конца 60-х годов эта ус-
тоявшаяся было область физики разряда переживает период бур-
ного возрождения. Новый этап связан с применениями, которые
нашел тлеющий разряд в мощных электроразрядных СО2 лазерах.
Рис 10 1 Типичная геометрия тлеющего разряда в электроразядных СО2-
лазерах а — поперечный разряд (ток идет перпендикулярно газовому пото-
ку направлениям), верхняя плата усеяна катодными элементами К, ниж-
няя служит анодом А, б — продольный разряд катодные элементы К рас-
положены вверх по потоку, анодом А служи! трубка
В ряде современных лазерных устройств геометрия разрядной
камеры отличается от традиционной трубки Разрядный объем
имеет форму плоского канала, через который прокачивается газ
(последнее не является принципиальным моментом для самого
разрядного процесса). Электроды могут располагаться как на
больших поверхностях канала, так и у узких его концов
(рис 10 1). Конфигурация электродов далека от параллельных
дисков, обычных для разрядных трубок Электрод может состо-
ять из многих раздельных элементов различной формы, рассеян-
ных по той или иной плоскости, может быть сделан в виде длин-
ной трубки Масштабы тока и напряжения иные, когда разряд-
ный канал большой амперы и киловольты, давление — повышен-
ное Но главные отличительные признаки тлеющего разряда —
катодный слой со свойственной ему структурой, область электро-
нейтральной слабоионизованной неравновесной плазмы, запол-
253
Темное астоново
пространство
уемное катодное
' пространство
Темное фа рад неб о
пространство
Темное анодное
пространство
( I / . { Полон отельный Х к ।
V \ х сто с в р
Катодное Отрицательное Анодное
свечение свечение свечение
няющая пространство между приэлектродными слоями,— и в та-
ких условиях сохраняются. Для однородной электронейтральной
области сохранен привычный термин— «положительный столб».
Именно он служит активной средой лазера (гл. 16). Поскольку
главные свойства тлеющего разряда мало чувствительны к кон-
кретным условиям, при
их изучении мы будем
ориентироваться пре-
имущественно на клас-
сический разряд в
трубке.
1.3. Картина свече-
ния. Тлеющему разряду
свойственно определен-
ное чередование темны\
и светящихся слоев,
каждый из которых по-
лучил свое собственное
название. Наблюдать
эту картину хорошо
при низких давлениях,
когда слои растяну! ы
по длине трубки,— ведь
все процессы в разряде
связаны со столкнове-
ниями. Расстояния от
характерных точек до
катода определяются
числом укладывающих-
ся на них длин пробе-
га электронов I ~ р~1.
Поэтому координате
границы какого-то слоя
Х[ отвечает определен-
ное значение pxi. Слои-
стая картина растягива-
ется па сантиметры при
давлениях р ~ 1СН торр.
Она схематически изо-
бражена в верхней ча-
гти рис. 10.2. К катоду
прилегает очень узкое
Рис. 10 2. Картина тлеющего разряда в труб-
ке и распределения интенсивности свечения
3, потенциала ср, продольного поля Е, плот-
носгеи электронного и ионного токов /е, j-t
и зарядов пе, п+, объемного заряда р =
= е(п+ — пе)
темное астоново прост-
ранство. Затем следует тонкий слой катодного свечения. После
него идет темное катодное пространство. Следующая за ним об-
ласть отрицательного свечения резко отделена от темного катод-
ного пространства. В направлении анода отрицательное свечение
затухает и переходит в темное фарадеево пространство. За ним
начинается светящийся положительный столб. Положительный
254
столб иногда имеет правильную слоистую структуру — это так
называемые страты, но страты образуются (или видны) далека
пе всегда, и когда их нет, положительный столб светится одно-
родно вплоть до анодной области. Там он иногда сменяется не-
большим темным анодным пространством, а у поверхности анода
видна узкая пленка анодного свечения.
При низких давлениях (р ~ 10~2торр) и не слишком больших
расстояниях между электродами для положительного столба ме-
ста нет и видна в основном область отрицательного {тлеющего}
свечения. От нее разряд и получил свое название тлеющего
(glow discharge, die Glimmenlladung). Спокойное, иногда слегка
подрагивающее свечение тлеющего разряда завораживает своей
красотой. Положительный столб обычно менее яркий, чем отри-
цательное свечение, и имеет другой цвет. В гелии катодное све-
чение — красное, отрицательное свечение — зеленое, положитель-
ный столб — красно-фиолетовый. В неоне соответственно — жел-
тое, оранжевое, красный; в азоте — розовое, голубое, красный.
Каждый газ имеет свои окраски, что связано с особенностями
спектров, и это используется в цветных рекламных трубках.
В длинных трубках при не чрезмерно низких давлениях виден
в основном положительный столб. В очень широких трубках или
сферических сосудах положительный столб часто не виден. Лишь
умозрительно можно себе представить, как протягивается токо-
вый путь от отрицательного свечения до анода.
1.4. Изменение условий. При повышении давления все слои
сжимаются и стягиваются к катоду. При р ~ 100 торр кажется,
будто горит сам катод, хотя это — отрицательное (тлеющее) све-
чение газа. Различается более протяженное темное фарадеево
пространство, вся остальная часть трубки или канала занята
положительным столбом. При повышенных давлениях столб сжи-
мается к оси, при небольших — диффузно заполняет сечение
трубки. Если сближать электроды при постоянном давлении, со-
кращается положительный столб. Промежуточные области между
столбом и катодом (их называют отрицательными} до поры до
времени остаются неизменными. Они перемещаются вместе с
катодом, если сдвигать именно этот электрод.
Более того, если в широком сосуде с закрепленным анодом
поворачивать катодный диск, все отрицательные слои поворачи-
ваются вместе с ним, как будто они приклеены к его поверхно-
сти, а положительный столб искривляется, чтобы достичь анода.
Так же получается и в сосудах сложной конфигурации. Отрица-
тельные слои «приклеены» к поверхности катода, а положите ть-
ный столб находит себе путь, чтобы соединить конец фарадеева
пространства с анодом. По мере сближения электродов, после
столба «съедается» сначала фарадеево пространство, потом отри-
цательное свечение. Когда не остается места хотя бы для катод-
ного края последнего, разряд гаснет. Для поддержания его нуж-
но повышать напряжение. Такой разряд называется затруд-
ненным.
255
1.5. Распределения параметров по длине. С расположением
слоев и распределением яркости свечения по длине трубки на
рис. 10.2 сопоставлены распределения основных параметров раз-
ряда. Картина эта — качественная, но в достаточной мере досто-
верная. Она подтверждается зондовыми измерениями и теорети-
ческими соображениями. Один из главнейших моментов в ней —
большой пространственный заряд и сильное поле у катода, кото-
рое почти линейно спадает до очень малого значения около ка-
тодной границы отрицательного свечения. Эта область называется
катодным слоем, но уже не по такому внешнему признаку, как
свечение, а по «объективным» показателям — распределению
электрического поля.
Далее следует зона очень слабого поля, оно иногда бывает
даже слегка отрицательным, т. е. направленным к аноду. В фара-
деевом пространстве продольное поле возрастает и потом остается
постоянным на протяжении положительного столба. Последний
может быть сколь угодно длинным, лишь бы хватало напряже-
ния источника питания, чтобы обеспечить должную разность по-
тенциалов в столбе. Постоянство осевого градиента потенциала в
столбе, проверенное зондовыми измерениями, свидетельствует об
электронейтральности плазмы. Около анода имеется область не-
большого анодного падения потенциала.
1.6. Качественная интерпретация картины свечения. Из като-
да электроны вылетают с энергией порядка 1 эВ. Они пе в со-
стоянии возбуждать атомы. Так появляется темное астопово про-
странство. Ускоряясь в поле, электроны приобретают энергию,
достаточную для возбуждения,— возникает катодное свечение
Появляются даже два-три слоя катодного свечения. Они соответ
ствуют возбуждению различных уровней атомов, ближе к като-
ду — более низких, дальше — более высоких. Цвета таких слоев
различны. Потом энергия ускоряемых электронов «переваливает»
максимумы функций возбуждения, где сечения падают (рис. 2.14,
2.15). Электроны перестают возбуждать атомы — образуется тем-
ное катодное пространство. Здесь электроны преимущественно
ионизуют атомы и происходит основное их размножение. Рож-
дающиеся ионы движутся в поле гораздо медленнее и накаплива-
ется большой положительный объемный заряд. Ток переносится
в основном ионами.
К концу катодного слоя нарождается большой поток электро-
нов, причем в силу лавинообразного характера размножения
большинство электронов рождается именно в конце слоя, где
поле уже не столь сильно и ослабевает. Энергии этих электронов
не слишком велики и находятся в области максимумов функций
возбуждения. Появляется отрицательное свечение. Еста вблизи
катода энергия электронов нарастает по мере удаления от катода
и сначала появляются легко возбуждающиеся спектральные ли-
нии (первое, второе катодные свечения), то за катодным слоем
энергии электронов, напротив, уменьшаются при удалении о г
катода. В отрицательном свечении сначала появляются те линии,
256
которые излучаются с более высоких уровней атомов, а потом —
с более низких, в порядке, обратном катодному свечению {пра-
вило 3велигера). По мере того как электроны растрачивают свою
энергию, акты возбуждения происходят все реже и реже, ибо
повой энергии в слабом поле электроны не приобретают. Отри-
цательное свечение переходит в темное фарадеево пространство.
В области отрицательного свечения имеются электроны не
только умеренных энергий, хотя их большинство. Сюда попада-
ют и энергичные электроны, которые родились в глубине катод-
ного слоя и у катода и прошли зону катодного падения, пе со-
вершив многих неупругих столкновений. Они ионизуют атомы,
и благодаря этому за катодным слоем получается повышенная
плотность электронов, больше, чем в положительном столбе.
В фарадеевом пространстве продольное поле постепенно на-
растает до значения, свойственного положительному столбу.
В столбе устанавливается характерное для неравновесной слабо-
понизованной плазмы хаотическое распределение электронов по
скоростям, в которое вносит небольшую асимметрию дрейф к
аноду. Средняя энергия электронного спектра в положительном
столбе составляет 1—2 эВ. Но в спектре имеется и некоторое чис-
ло энергичных электронов. Они возбуждают атомы и обусловли-
вают свечение столба. Анод ионы отталкивает, а электроны из
столба вытягивает. Образуется область отрицательного объемного
заряда и повышенного поля, ускоряющего электроны. Это при-
водит к анодному свечению.
1.7. Направляющее действие зарядов, оседающих на стенках.
Опыт показывает, что разряд может гореть в трубке весьма за-
мысловатой конфигурации. Электроны (и ионы), переносящие
электрический ток, обязаны двигаться по газовому тракту, но
вдоль силовых линий электрического поля. Между тем силовые
Рис. 10.3, Тлеющий разряд в трубках сложной конфигурации: а — линии
напряженности приложенного поля; б — линии напряженности результи-
рующего поля (приложенного плюс поля, осевшего на стенках отрицатель-
ного заряда), в — эквипотенциальные поверхности в прямой трубке (с уче-
том поля осевшего на стенках отрицательного заряда)
линии приложенного внешнего поля протягиваются от анода к
катоду своим собственным путем. Они сплошь и рядом пересе-
кают стенки разрядной трубки (рис. 10.3а). Как же идет ток?
Дело в том, что заряды, преимущественно электроны, в нача-
ле процесса увлеченные силовой линией внешнего поля к ди-
электрической стенке, оседают там и накапливаются до тех пор,
пока не начинают отталкивать от стенки последующие заряды
17 Ю. П Райзер 257
того же знака. Электростатическое поле осевших зарядов, скла-
дываясь векторным образом с внешним, направляет часть сило-
вых линий результирующего поля вдоль доступного для зарядов
пути вдоль трубки (рис. 10.3, б, в). Благодаря этому эффекту
продольное поле в прямой трубке или в плоском канале стано-
вится более однородным по сечению. Поперечная (радиальная)
составляющая поля в разряде все же присутствует. В частности,
в длинном положительном столбе она однородна по длине и на-
правлена от оси к отрицательно заряженной стенке. Эквипотен-
циальные поверхности в трубке выпуклы и обращены выпук-
лостью к катоду. Иногда можно заметить, что так выглядят гра-
ница между положительным столбом и темным фарадеевым про-
странством и страты. Границы отрицательных слоев у плоского
катода обычно плоские, что, по-видимому, свидетельствует оз от-
сутствии здесь поперечной составляющей поля.
§ 2. Вольт-амперная характеристика разряда
между электродами
Продолжим рассмотрение ВАХ разряда постоянного тока, на-
чатое в § 2 гл. 9, и будем продвигаться в сторону увеличения
тока. По достижении на электродах пробивающего напряжения
V = Vt в газе зажигается самостоятельный разряд. В рамках той
идеализированной схемы, которой мы пользовались в п. 2.2 гл. 9,
при V = Vt ток устремляется к бесконечности. В реальной цепи,
помимо разрядного промежутка, всегда имеется омическое сопро-
тивление Q (специально включенное, сопротивление проводов,
источника питания), и это ставит абсолютный предел достижимо-
му току при заданной электродвижущей силе источника (S. По-
скольку масштаб разрядного тока во многом определяет сам тип
разряда, ибо с величиной тока связана степень ионизации газа,
от сопротивления Q зависит, какой разряд загорится после
пробоя.
2.1. Нагрузочная прямая. Электрическое уравнение замкнутой
цепи, включающей разрядный промежуток, имеет вид
ё = V + iQ. (10.1)
На графике V, i это уравнение изображается прямой линией
(рис. 10.4), которая называется нагрузочной прямой. Она падает
тем круче, чем больше внешнее сопротивление, и отсекает на оси
абсцисс значение предельного тока ^/Q. Реализуются те значе-
ния i и У, которым отвечает пересечение нагрузочной прямой *и
ВАХ У(0.
2.2. Темный таунсендовский разряд. Допустим, что сопротив-
ление Q столь велико, что цепь в состоянии пропустить лишь
исключительно слабый ток. Плотности пе, п+ при этом ничтожны
и пространственный заряд столь мал, что не искажает внешнего
поля. Так, если расстояние между плоскими электронами (в этой
главе мы будем обозначать его А) мало но сэаз^еппю с их но-
253
перечными размерами, поле Е(х) ~ const = VIL, как и в отсут-
ствие ионизации. Для поддержания такого самостоятельного раз-
ряда к электродам должно быть приложено напряжение, равное
потенциалу зажигания Vt. Именно оно обеспечивает стационарное
воспроизводство электронов, вылетающих с катода и вытягивае-
мых на анод (п. 2.2 гл. 9). Пока поле не зависит от плот-
ностей зарядов (от тока), ВАХ разряда есть У(0 = const = Ft
Рис. 10 4 ВАХ разряда между
электродами в широком диапазо
не токов и нагрузочная прямая
А — область несамостоятельного
разряда, ВС — темный таунсен-
довский разряд, DE — нормаль
ный тлеющий разряд, EF — ано
мальный тлеющий разряд, FG —
переход в дугу, GH — дуга
Этой ситуации отвечает участок ВС на рис. 10 4*) Такой само-
стоятельный разряд действительно наблюдается на опыте, в обыч-
ных трубках — при токах i ~ 10~10—10-5 А. Он называется тем
ным таунсендовским. Из-за чрезвычайной малости ионизации газ
совсем не светится. Ток регистрируют высокочувствительными
приборами.
2.3. Тлеющий разряд. Будем увеличивать ток Практически
это можно осуществить, уменьшая нагрузочное сопротивление Q
или увеличивая ЭДС источника <S. Начиная с какого-то тока, на-
пряжение на электродах падает. Пбтом падение прекращается
и в довольно большом диапазоне токов (иногда в несколько по
рядков) почти не меняется. Этот участок DE на ВАХ соответст-
вует так называемому нормальному тлеющему разряду. Нижней
части; переходного участка CD отвечает поднормальный тлеющий
Г азряд.
Нормальный разряд обладает замечательным свойством. При
изменении разрядного тока плотность его на катоде остается не-
изменной. Меняется площадь на катоде, в которую втекает ток
Меняя Q или в ту или другую сторону, можно видеть, как
светящееся токовое пятно на поверхности катода расширяется
или сокращается.
Когда на катоде не остается свободного места, для увеличе-
ния тока приходится повышать напряжение, чтобы вырывать с
единицы площади катода больше электронов. Ведь теперь должна
расти плотность катодного тока. Такой разряд называется ано-
мальным. Ему соответствует нарастающий участок EF ВАХ Ип-
*) Обращаем внимание на то, что мы сейчас рассматриваем ВАХ ус-
тановившегося, стационарного процесса Никакого перенапряжения (п 2 3
гл 9) по сравнению с потенциалом зажигания быть не должно Перенапря-
жение требуется для развития пробоя, т е осуществления нестационар-
ного процесса нарастания тока В коде пробоя, koi да V > V/, ток как раз и
। арастает до такой величины, чтобы ликвидировалось перенапряжение
17* 259
тересно наблюдать переход к аномальному режиму. Видно, как
тлеющее свечение охватывает сначала всю поверхность катода,
обращенную к аноду, потом отыскивает любое не защищенное
Рис 10.5. Измеренные ВАХ раз-
ряда в неоне между медными
дисками диаметром 9,3 см с рас-
стоянием между ними 1,6 см:
плато слева — темный разряд,
плато внизу (область миниму-
ма) — нормальный тлеющий раз-
ряд, подъем справа — аномаль-
ный тлеющий разряд [8]
диэлектриком место на боковой,,
внутренней сторонах, на ножке и
лишь когда все исчерпано, стано-
вится более протяженным и на-
сыщенным, что свойственно ано-
мальному разряду. При i ~ 1 А
тлеющий разряд срывается в дугу.
Участок FG описывает пеяехсд,
участок GH— дуговой разряд.
Мы проследили за лодом ВАХ,
как бы «крутя ручку», меняю-
щую Q или <S. В эксперимент^ в
момент включения ЭДС в цепи
стоит определенное сопротивление,
и если <S превышает потенциал
зажигания, то немедленно после
пробоя ус1апавливается тот ре-
жим, который соответствует точ-
ке пересечения ВАХ и нагрузоч-
ной прямой. На рис. 10.4 ВАХ
изображена схематически. На
рис. 10.5 показаны реальные ВАХ,
полученные в эксперименте. Ох-
вачены темный, нормальный и,
частично, аномальный режимы.
Чем выше давление, тем шире
диапазон токов, в котором осуществляется нормальный режим
(почему — станет ясно ниже; см. п. 4.4). В Н2, N2, Аг наблю-
далась примерно та же картина, что и в Ne.
§ 3. Темный разряд и роль пространственных зарядов
в образовании катодного слоя
Главное отличие тлеющего разряда, в котором ток имеет уме-
ренную силу, от темного, где ток исключительно мал, состоит в
резко неравномерном распределении приложенной к электродам
разности потенциалов по длине промежутка. Чтобы понять, nd-
чему и каким механизмом осуществляется перераспределение по-
ля между электродами, рассмотрим для начала темный разряд,
где внешнее поле не искажено.
3.1. Распределение зарядов в слаботочном темном разряде.
Будем считать промежуток небольшим по сравнению с попереч-
ными размерами электродов. Ось х направим от катода к апочу.
Исходим из уравнений непрерывности (3.22), (3.20) для плот-
ностей зарядов. Диффузионные потоки малы по сравнению с
дрейфовыми, диффузия в боковом направления лакже несуще
260
ственна, рекомбинация — тем более. Объемные источники зарядов
связаны лишь с ионизацией газа: q = угпе = аиедПе, потоки — чи-
сто дрейфовые. Будем оперировать плотностями тока je = —eneve^
j+ = еп+и+д. В стационарном случае
djjdx = aje, dj+/dx = —ajei je + j+ = j = const. (10.2)
Третье равенство, говорящее о постоянстве плотности полного
тока, является следствием первых двух. Граничное условие на
катоде (х = 0) описывает вторичную эмиссию, на аноде (х = L) —
отсутствие ионной эмиссии
/еК = у/+к = ['Т/(1 + 7)]Л 7+л = 0, jeA=j. (10.3)
Если начать интегрировать уравнение (10.2) для /е от катода
с учетом первого условия (10.3), при ] = const получим
ie = т4- , 7+ = 7 (1 - И. (Ю.4)
Удовлетворить условию (10.3) на аноде можно только при вы-
полнении уже знакомого нам по п. 2.2 гл. 9 критерия зажигания
(самоподдержания):
eaL — 1 = 1/у, aL = In (1 + 1/y) . (10.5)
Перепишем (10.4), используя (10.5):
je/j = jjj = 1 _ e-a(L-x)^ ea(L-x) _ 1
На большей части промежутка, начиная от катода, ионный
ток значительно превышает электронный (рис. 10.6). Например,
Рис. 10.6. Распределения плот-
ностей электронного и ионно-
го токов (а) и зарядов (б),
когда поле в промежутке не
искажено действием прост-
ранственного заряда
при у = 10~2, aL = 4,6 плотность ]е достигает /+ только при
х = 0,85L. Еще сильнее различие в плотностях зарядов. С ре/р+ =
= 100, найдем, что п+!пе = (щ/ц+) (/+//е) = 1 только при х =
=- 0,9981/. В подавляющей части промежутка п+ > пе (рис. 10.6).
В темном разряде практически все пространство заряжено поло-
жительно, но объемный заряд мал в силу малости у и п+. Вели-
чины эти произвольны, они определяются током, который может
пропустить цепь, и площадью электродов (§ 2).
3.2. Искажение внешнего поля. Его вносит пространственный
заряд. Оценим эффект, взяв в качестве нулевого приближения
распределения плотностей зарядов, полученные в предположении
Е(х) = const. Распределение поля в пространстве определяется
уравнением
dEjdx = 4ле(тг+ — пе), Е^ЕХ. (10.6)
9Д4
Полагая приближенно п+ > ne, |/+| » |/el, п+& jlev+A^ i!e\i+E и
обозначая Ек поле у катода, найдем
Е = Ек /1 - xjd, d = и+£1/8л/. (10.7)
В области анода поле уменьшается, в области катода — возра-
стает, причем тем сильнее, чем больше плотность тока (рис. 10.7).
Плоскость х = d, где экстраполированная величина E(d) обра-
щается в нуль, при слабых токах располагается далеко за преде-
лами разрядного промежутка. При росте j она приближается к
аноду и при значении ]ь = совпадает с анодом (d =
= £). При дальнейшем возрастании /, когда d<L, поле по
(10.7) формально обращается в нуль уже внутри промежутка,
Рис. 10 7. Эволюция поля под
действием пространственного
заряда: 1 — неискаженное по-
ле, / -> 0; 2 — слабый ток, / <
< ]l, 3 — ]=]L; 4—переход
к тлеющему разряду, / > /ь
тем ближе к катоду, чем больше ток (рис. 10.7). Но в этом
случае распределение (10.7) на участке d<x<L лишено смыс-
ла, так как теряют силу исходные допущения. На самом деле
распределения пе, п+ и Е приобретают вид, изображенный па
рис. 10.2.
3.3. Предельный ток существования темного разряда. При
столь слабых токах, что искажение поля мало, поле у катода Ек,
как, впрочем, и везде, близко к невозмущенному Et, которое
пробивает данный промежуток. По мере возрастания тока значе-
ние Ек все сильнее отклоняется от Et, но пока d> L, оно со-
храняет тот же порядок (см. сноску в п. 3.5). Поэтому в выра-
жении для jL, которое соответствует предельному условию d = L,
можно для оценки подставить Et вместо Ек- Плотность тока, при
которой происходит существенная перестройка поля и структуры
разряда и которая знаменует начало перехода от темного разря-
да к тлеющему, определяется оценочной формулой
Ъ ~ (Ц+Р)(ЗД2
8л (PL) 8л, (pL)3' k
Ей придана форма, отвечающая законам подобия. Например,
в азоте по формуле (4 8) для а с А = 12 см"1 • торр'1, В =
= 342 В/(см торр), взятыми из табл. 4.1, и у = 10'2 при pL=-
= 100 см торр по формулам (9.3) Etlp^=^2 В/(см-торр), Vt=*
= 6200 В. Со значением = 1,5 • 103 см2 • торр/ (В • с) найдем
7i7p2 = 2,5 10'9 А/(см2 торр2). Скажем, при р = 10 торр, А =
= 10 см ]ь = 2,5 • 10"7 А/см2. Если площадь электродов 100 см2,
предельный ток темного разряда i = 2,5 • 10~5 А.
9Д9
L
J Е dx
о
3.4. Условие самоподдержания разряда в плоском промежутке
в случае неоднородного поля. Оно непосредственно вытекает из
уравнений (10.2), (10.3):
L
( a (z)] dx = In (1 k 1/y). (10.9)
0
Равенство (10.9) обобщает (10.5) и выражает тот же факт.
В электронной лавине, распространяющейся от катода к аноду,
должно рождаться определенное число поколений. Это число оп-
ределяется только коэффициентом вторичной эмиссии и не за-
висит от того, однородно поле или нет. Интеграл в (10.9) в точ-
ности совпадает со значением &(Е\)£, отвечающим пробою дан-
ного промежутка в однородном поле. Поскольку а(Е) — функция
возрастающая, а при искажении поля пространственным зарядом
\Е(х) I — падающая, у катода \ЕК\ >Et, а у анода IEaI <Et.
3.5. Что происходит с напряжением в результате действия
пространственного заряда. Качественная тенденция видна из рас-
смотрения интеграла (10.9), интеграла напряжения V =
и зависимости а от Е по формуле (4.8). В несильных полях при
росте Е функция сс~ехр(—BplE) идет вверх с нарастающей
крутизной d2aldE2 > 0, в очень сильных — с убывающей: а ->
const. Точка перегиба а (2?) лежит при Е = Вр!2. Если неиска-
женное пробивающее поле Et<-Bp!2, перераспределение потен-
циала облегчает условия для размножения: усиленное поле до-
бавляет в интеграл (10.9) больше, чем ослабленное отнимает.
И обратно, интеграл (10.9) сохраняет свое значение, если раз-
ница \ЕК\—Et меньше, чем Et—I^aI. Но если в одном месте
усилить поле меньше, чем ослабить его в другом, разность по-
тенциалов уменьшается. В случае Et > Bpl2 все получается на-
оборот: в результате перераспределения размножение затрудня-
ется и напряжение возрастает.
В правильности этих качественных рассуждений легко убе-
диться на примере слабой неоднородности, вычисляя по форму-
лам (10.9), (10.7), (4.8) с помощью разложения по малому па-
раметру j7jl = Lfd^ 1 (в общем случае интеграл не берется)*).
Малое изменение напряжения на промежутке по сравнению с
потенциалохМ зажигания Vt = EtL в однородном поле равно
V - Vt = - (1/48) (Bp!2Et - 1) (/7Л)2. (10.10)
Условие Et < В/?/2, при котором напряжение на горящем раз-
ряде падает по сравнению с потенциалом зажигания, согласно
(9.3) выполняется для промежутков с pL > е(pd)min4 где (pd)mln
соответствует минимальному напряжению пробоя. Для проме-
*) Поле у катода находится из равенства интеграла (10.9) и a(Et)L;
|£к| = Et [1 + £/4d + О (Ltd)]. Члены второго порядка необходимо сохра-
нить. Вопрос впервые рассматривался в [1, 5].
263
жутков с pL < e(pd)V > Vt. Поскольку на опыте чаще всего
имеют дело со случаем длинных в указанном смысле промежут-
ков, напряжение при переходе от темного разряда к тлеющему
уменьшается (рис. 10.4, 10.5).
§ 4. Катодный слой
4.1. Что дает катодный слой. При пробое плоского промежут-
ка и слаботочном темном разряде в восполнении потерь зарядов,
связанных с их вытягиванием на электроды, принимает участие
вся длина промежутка, вплоть до анода. Но в случае больших
в смысле p/7>(pd)mm промежутков такое положение, которое
явтяется следствием однородности поля, явно не оптимально. Для
удовлетворения условия самоподдержания (10.9) требуется не-
оправданно большое напряжение. Можно обойтись и меньшим,
если сконцентрировать падение потенциала, ведь в сильном поле
размножение идет эффективнее.
Идеальным явилось бы такое распределение потенциала по
длине, при котором разность потенциалов, равная минимальному
напряжению пробоя Уппп, сосредоточилась бы на соответствующей
длине (pcZ)min У катода. Тем самым было бы обеспечено воспро-
изводство при минимальных затратах напряжения. Для поддер-
жания дальнейшего протекания электронного тока, зарождающе-
гося в таком катодном слое, через остальную часть промежутка
потребовалось бы приложить к ней напряжение, которое необхо-
димо, чтобы скомпенсировать благодаря небольшой ионизации
неминуемые потери электронов вследствие ухода на стенки, ре-
комбинации, прилипания. Поразительно, сколь целесообразно
устроена природа. В нормальном тлеющем разряде осуществля-
ется приближение к идеалу. Одним из главных механизмов оп-
тимизации распределения потенциала по длине промежутка слу-
жит действие пространственного заряда, который автоматически
образуется у катода и создает там повышенные поле и падение
потенциала, как было описано в § 3.
4.2. «Вольт-амперная» характеристика. Теория катодного па-
дения потенциала была развита Энгелем и Штеенбеком (1934 г.)
и имеет большое значение для физики тлеющего разряда. После-
дующие уточнения и углубленное проникновение в ход процесса
ничуть не опровергают главной сути схваченных в ней моментов.
Мы изложим теорию в простейшей и наиболее прозрачной для
понимания природы явлений форме. Рассмотрим сформировав-
шийся стационарный слой катодного падения. Допустим, что дав-
ления и токи пе слишком низки, так что токовое пятно на ка-
тоде большое, а слой тонкий. Тогда его можно считать плоским
и одномерным. На анодном краю слоя при х = d поле E(d) су-
щественно меньше, чем у катода E(Q)^EK. Пусть E(d)~0. До-
пустим, что со стороны анода в слой если и втекает, то лишь
малый ионный ток (в электронейтральной части промежутка
7\//в == к+д/кед = р^/ре ~ 10~2). Тогда слой представляет собой ав-
264
топомную систему, в которой выполняется условие самоподдер-
жания тока (10.9). Нужно только заменить в (10.9) расстояние
между электродами L толщиной слоя d. Зарождающийся в этой
системе электронный ток идет уже до самого анода. С точностью
до малой величины порядка ц+/це он совпадает с полным раз-
рядным током*). Катодное падение составляет
d
VK=\Edr, Л'==|£т|, (10.11)
о
Энгель и Штеенбек разрешали • систему уравнений (10.9),
(10.11), (10.6), принимая закон (4.8) для а(£) и задаваясь, со
ссылкой на зондовые измерения, линейным распределением поля
= EK{i — x/d), dEldx ~ 4летг+ ~ const. (10.12)
Интеграл (10.9) с (10.12) в элементарных функциях не выража-
ется. Те же, в принципе, результаты, отличающиеся только чис-
ловыми коэффициентами порядка единицы, но зато в наглядной
аналитической форме, можно получить, полагая при вычислении
интеграла (10.9) Е{х) = const ~ Ек, Е = 0 при х> d. Тогда (10.9)
превращается в (10.5) с d вместо L. Но поскольку поле в слое
принято однородным, использование (4.8) и следующего из (10.11)
тривиального соотношения VK = EKd дает просто формулы (9.3)
для пробоя промежутка в однородном поле:
VK -= ГЕЕ с = In . . (10.13)
С -J- In (pd) Р C-E^(pdy In (1 4- 1/у) v z
Они связывают катодное падение* VK с «толщиной» катодного
слоя pd.
Установим теперь связь этих величии с плотностью тока па
катоде /. Согласно п. 3.1 в области, где осуществляется необходи-
мое для самоподдержания размножение, п+ > ие, j+»je. По
(10.6) плотность ионов в слое приближенно равпг!
п+ ~ (4ле) ~xdE/dx ~ EKlkn>ed,
причем здесь уже принято во внимание, что поле в слое па са-
мом деле пе постоянно, а уменьшается от Ек до пуля. Отсюда
j = (1 + ?)еи^р+£к да (1 + ?) d да (1 у) р+Ук/4л d3.
(10.14)
Эта формула вместе с (10.13) определяет параметрическую зави-
симость катодного падения V к и поля на катоде Ек от плотности
тока /. Параметром служит толщина слоя d. По (10.13) функция
VK{pd) имеет минимум. В данном приближении она описывает
кривую Пашепа (п. 2.3 гл. 9), и Vmin совпадает с минимальным
напряжением пробоя разрядного промежутка.
*) В силу уравнения непрерывности (3.39) в стационарном процессе
div j = 0, i = const; в одномерном случае и / (х) = const.
265
Согласно (10.13), (10.14) VK проходит через минимум и как
функция у с тем же значением Vmin. Эти формулы удобно пред-
ставить в безразмерном виде, введя в качестве размерных масш-
табов величины, отвечающие минимальному падению. Мы пометим
их индексом «н» вместо «min» (именно они реализуются в нор-
мальном разряде), а безразмерные величины — знаком «тильда»:
у = 7=^.
Fh Ен'Р (Pd)H 7Н
Масштабы VH, Ejp, (pd)a определяются формулами (9.4),
а масштаб плотности тока с учетом законов подобия:
4 = + Y) (Р+Р) F2H (1 т т) (ц+р) У* а и 0 14')
р2 4л (pd)^ 9 10й 4л (pd)^ см2 торр2 4
Параметрические связи величин через параметр d имеют вид
У =-----Е =-----------7 —--------------1 (10.15)
1 + In d 1 + In d d (1 -г In dY
Зависимости F, Ё и d от у, выражаемые этими формулами, пока-
заны на рис. 10.8. Кривая V(j) дает «вольт-амперную» харак-
Рис. 10.8 Катодное па-
дение потенциала, поле
на катоде и толщина ка-
тодного слоя в зависимо-
сти от плотности тока
в безразмерных перемен-
ных
теристику катодного слоя. Кавычки по-
ставлены потому, что аргументом служит
не ток, а его плотность.
4.3. Нормальные катодное падение и
плотность тока. Формально по (10.15) и
рис. 10.8 при уменьшении j от ун Ук и d
возрастают, а Ек падает. Когда толщина
слоя d вырастает до размеров промежут-
ка L, решение (10.15) смыкается с ре-
шением § 3; у по (10.14) примерно срав-
нивается с ]L по (10 8). Казалось бы,
прослежена эволюция между темным
разрядом и тлеющим.
Опыт с определенностью показывает,
что ничего подобного пе происходит. Па-
дающая ветвь кривой F(y), левее точки
] = 1, 7 =7н, не реализуется. При токах i,
меньших SKjn, где SK — площадь катода,
устанавливается режим, отвечающий точ-
ке минимума «ВАХ» катодного слоя. Так
получается и при варьировании тока,
и когда <5 и Q таковы, что после зажига-
ния состояние попадает в область DE на рис. 10.4. На катоде ав-
томатически загорается пятно такой площади S. чтобы плотность
тока в нем составляла Jh — i/S, а катодное падение—Ун. ВАХ
реального разряда не имеет ничего общего с левой ветвью
рис. 10.8 (как было бы, если бы ток i шел через весь катод,
i = SK]). Напряжение на разряде при не полностью занятом ка-
266
тоде пе зависит от тока и превышает VH на величину падения в
положительном столбе. Если последнее незначительно (низкое
давление, короткая трубка), напряжение на электродах почти не
отличается от FH. Такой тлеющий разряд называется нормаль-
ным, так же называются соответствующие значения катодного
падения и плотности тока.
Теоретические значения 7Н, /н, (pdK несколько зависят от
тех предположений о профиле Е(х), которые были заложены в
расчет. В простейшем приближении, сделанном в и. 4.2, Ин и
(pd)H в точности совпадают с параметрами минимума кривой
Пашена 7min, (pd)mm, а /н дается формулой (10.14). В расчете
Энгеля и Штеенбека с аппроксимацией (10.12) получается VH =
= 1,1 Vmm, (pd)n = l,4(pd)mln, а /и в 1,8 раза больше значения,
полученного по (10.14')*). Любая разумная теория, так же каки
опыт, дают для нормальных катодного падения и толщины слоя
Таблица 10 1. Нормальное катодное падение VH [В]
Катод Воздух Аг He н2 Hg Ne n2 o2 CO co2
А1 229 110 140 170 245 120 180 311
Ag 280 130 162 216 318 150 233 — — —
Au 285 130 165 247 — 158 233 — — —
Bi 272 136 137 240 — — 210 — — —
С — — — 240 475 — — — 526 —
Си 370 130 177 214 447 220 208 — 484 460
Fe 269 165 150 250 298 150 215 290 — —
Hg — — 142 — 340 — 226 — — —
К 180 64 59 94 — 68 170 — 484 460
Mg 224 119 125 153 — 94 188 310 — —.
Na 200 — 80 185 — 75 178 — — —
Ni 226 131 158 211 275 110 197 — — —
Pb 207 124 177 223 — 172 210 — — —
Pt 277 131 165 276 340 152 216 364 490 475
w — — — — 305 125 — — — —
Zn 277 119 143 184 — — 216 354 480 410
Стекло *) 310 i — — 260 — — — — — —
*) Тонкий мягкий стеклянный диск,
нагретый до 300 °C. То же в табл. 10 2, 10 3.
значения более или менее близкие к Fmin, (prf)mm пробоя плоско-
го разрядного промежутка в том же газе при том же материале
катода. Вычисления с указанными числовыми коэффициентами,
выведенными Энгелем и Штеенбеком па основе аппроксимации
(10.12), при подстановке чисел А, В из табл. 4.1 и у ~ 10-1 —
10-2 (от 7 зависимость логарифмическая) дают неплохое согла-
*) С линейным законом распределения поля (10.12) (pd)n
= 3,8 A-1 In (1 4~ V1)- Заметим, что в первоисточнике [1] в указанной фор-
муле по непонятной причине стоит коэффициент 0,82 вместо 3,8. Ошибка
переночевала и ц популярную книгу [6].
267
Таблица 102. Нормальная толщина катодного слоя (pd)H [торр см]
при комнатной температуре
Катод Воздух Аг н2 Не Hg n2 Ne о2
А1 0,25 0,29 0,72 1,32 0,33 0,31 0,Р4 0,24
С — — 0,9 — 0 69 —. — —
Си 0,23 — 0,8 — 0,6 — — —
Fe 0,52 0,33 0,9 4 .30 0,31 0,42 0,72 0,31
Mg — — 0,61 1.45 — 0,35 — 0,25
Hg — — 0,9 — — — — —
Ni — — 0,9 — — — — —
Pb — — 0.84 — — — — —
Pt — — 1,0 — — — — —
Zn — — 0,8 — — — — —
Сток 70 0 3 — 0,8 — — — — —
Таблица 10 3 Нормальная плотность тока 2 [мкА/(см2 торр2)]
при комнатной температуре
Катод Воздух Аг н_, Не Hg n2 О2 Ne
AL 330 90 4
Аи 570 — НО — — — — —
Си 240 — 64 — 15 — — —
Fe, Ni — 160 72 2 2 8 400 — 6
Mg — 20 — 3 — — — 5
Pt — 150 90 5 — 380 550 18
Стекло 40 — 80 — — — — —
сие с опытными параметрами нормального разряда, которые при-
ведены в табл. 10.1 —10.3.
4.4. Аномальный разряд. Когда заполняется весь катод, даль-
нейшее увеличение тока неминуемо сопровождается ростом его
плотности на катоде по сравнению с нормальной. Такому ано-
мальному разряду отвечает правая ветвь кривой F (у) рис. 10.8,
которая теперь и на самом деле описывает ВАХ слоя и разряда
без положительного столба, ибо i = const у = SKj. Теоретическая
кривая согласуется с экспериментом (область EF на рис. 10.4).
Асимптотически (при J -> оо) толщина катодного слоя по (10.15)
уменьшается до конечного значения d = е~~х = 0,37, V и Ё растут
как у~1/2. Реально при катодных падениях порядка 10 кВ и плот-
ностях тока порядка 10—102 А/см2 катод сильно разогревается
и происходит переход в дугу. Экспериментальные ВАХ аномаль-
ного разряда можно видеть на рис. 10.5.
4.5. В каком диапазоне токов существует нормальный разряд.
Темный разряд занимает весь катод, так же как и нормальный
па верхнем пределе своего существования. Поэтому от области
268
перехода между темным и нормальным до точки перехода от нор-
мального к аномальному ток увеличивается примерно в jJjL раз.
По формулам (10.8), (10.14) у\Ж ~ £(1 + In £)2, где Г = рЫ
/(pd)n. Стало быть, диапазон токов в нормальном режиме (в об-
ласти DE рис. 10.4) тем больше, чем выше давление и длиннее
трубка (рис. 10.5). Например, применительно к одному из пока-
занных на рис. 10.5 экспериментальных вариантов, при р =
= 15 торр, L = 1,6 см, (м)н~0,7 см • торр £ = 34 и отношение
jiJjb — 700 в согласии с опытом.
4.6. Поднормальный разряд. Эта переходная область между
тлеющим и темным разрядами, (но более близкая к нормально-
му), соответствует столь слабым токам, что размеры «квазинор-
малыюго» катодного пятна оказываются сравнимыми с толщиной
катодного своя. Уход зарядов в боковом направлении ухудшает
условия для размножения, и необходимое для самоподдержаппя
разряда напряжение на слое оказывается повышенным по срав-
нению с нормальным.
4.7. Затрудненный разряд. Он возникает при малых межэлект-
родных расстояниях L и очень низких давлениях, когда зпаче
ние pL оказывается меньше толщины нормального слоя (pd)H.
Такие условия, грубо говоря, отвечают левой ветви кривой Па-
шена, где V > Ущщ. Для «нормального» размножения пе хватает
места, и приходится повышать напряжение по сравнению с нор-
мальным. Если этого не сделать, разряд гаснет.
4.8. Нормальный разряд и принцип минимума мощности. По-
чему на незаполненном катоде ток занимает такую площадь, что-
бы плотность его была неизменной? Как это ни удивительно, но
до самого последнего времени (даж$ к моменту 1-го издания этой
книги) не было вполне вразумительного ответа па этот безуслов-
но принципиальный вопрос, который возник более полувека тому
назад. В сущности, он сводится к физическому обоснованию по-
стулата теории Энгеля и Штеепбека о реализации в нормальном
разряде минимально возможного катодного падения. Именно та-
кое предположение хорошо объясняет экспериментальные факты.
Почему не наблюдаются состояния с плотностью тока на катоде
меньше нормальной, разъяснили еще создатели теории [1]. Со-
стояния эти неустойчивы, поскольку относятся к падающей ветви
кривой К (у) рис. 10.8 (разрядам с падающей ВАХ вообще своп
ствепно появление неустойчивых состояний, п. 7.5). Действитель-
но, если на каком-то участке поверхности катодного с^оя возни-
кает флуктуация бу > 0, для поддержания тока / + бу понадобит-
ся меньше напряжения, чем есть на самом деле, начнет
развиваться ионизация и у будет расти. При б/< 0 фактическое
напряжение окажется меньше необходимого, вынос зарядов из
слоя превысит рождение и плотность тока упадет еще сильнее.
Но в этом смысле состояния с у > ун на растущей ветви ВАХ
вполне устойчивы. Между тем, на незаполненном катоде никогда
не возникает «аномальных» катодных пятен с плотностью тока
больше нормальной. Надо полагать, нестабильной оказывается
269
соседняя бестоковая область Но как все происходит и что ста-
билизирует границу нормального катодного пятна?
Двадцать лет спустя Энгель [5], не возвращаясь к аргументам
об устойчивости, говорил о непонятности явления и апеллировал
к «принципу минимума мощности» Последний оставил заметный
след в физике разряда, к нему иногда обращаются и поныне,
и па нем следует остановиться подробнее
В объеме катодного слоя выделяется мощность
d
PK=S\]Edx = S1VK(j) = iVK{])
О
Если варьировать площадь 5, сохраняя полный ток i, мощность
оказывается минимальной как раз при нормальной плотности то
ка, когда Ук(/) = тш Существуют и другие явления в газовом
разряде, когда реализуются именно такие состояния, которые тре
буют наименьших напряжении и (или) мощности, например
страты (§ 7 гл 11) На основании таких фактов, демонстрирую
щих замечательную целесообразность в устройстве природы, Ште-
енбек (1932 г) выдвинул указанный принцип Однако впос тед-
ствии, возможно, в силу большого авторитета Штеепбека прин-
ципом стали иногда пользоваться не то еько в целях лучшей
иллюстрации наблюдаемых фактов, но и в качестве недостающего
условия при построении теоретических моделей Это, как ока за
лось, чревато возможностью ошибки (завуалированной кажущим-
ся согласием с экспериментом), ибо принцип не вытекает из
фундаментальных законов физики Но в нем и нет необходимо-
сти, когда удается проникнуть в механизм явления и построить
теорию обычным способом Именно так обстояло дело со страта-
ми, каналами дуги (§ 10 гл 12) индукционного (§ 3 гл 13) и
СВЧ разрядов Так же следует подходить и к вопросу о нормаль-
ной плотности тока
4.9. Механизм установления нормальной плотности тока. Он
прояснился в результате работ последнего времени [10 1 —
10 4а]*) Обсу/кдаемыи эффект i/S = const проявляется и при
численном моделировании тлеющего разряда на основе уравнений
(3 22), (3 20) (3 33) для пе, п+, Е = —V<p с граничными ус ю
виями типа (10 3) и а по (4 8) [10 2, 104] При достаточно
больших токе и поверхности катодного слоя, как на рис 10 9,
середина слоя уже имеет квазиодномерный характер, и его пара-
метры там неплохо описываются формулами одномерной теории
[1]**)
Обратимся к карте эквипотенциальных поверхностей
(рис 10 9) и схематической зависимости напряжения VK па
катодном слое от его толщины d (рис 10 10) Последняя следует
*) Проблема обсуждалась в [10 5], но в то время ясносзи еще ве бы-
ло Не были разрешены возникшие противоречия, см [10 4]
**) С учетом поправки, указанной в сноске к п 4 3
270
из равенства типа (10.9), которое запишем в виде
р, = у ехр
d(r)
J a[E(l)]dl
о
= 1,
(10.16)
- 1
где ц — коэффициент воспроизводства зарядов (п. 2.2 гл. 9). Ин-
тегрирование здесь ведется вдоль линии тока, втыкающейся в
какую-то точку г катодной поверхности. Если отвлечься от диф-
фузии зарядов, линии тока совпадают с силовыми линиями поля.
Рис 10 9 Рассчитанная двумерная структура стационарного осесимметрич-
ного столба тлеющего разряда между плоскими электродами [10 4] Азот,
р — 15 торр, расстояние между электродами 0,75 см, ЭДС— 2500 В, внешнее
сопротивление 300 кОм Катод внизу, анод вверху. На электродах получи-
лось V — 250 В, ток i — 7,Ь мА. Представлены линии равных плотностей
электронов Ti ионов пг (а), жвипотенциали через каждые V/10 = 25 В
(б), радиальные распределения плотностей тока jK на катоде, jA — на ано-
де (в), радиальные распределения пг на катоде, пе на аноде (г); распреде-
ления пе, пг, ф вдоль оси разряда (д)
При Е(1) = const зависимость VK(d) совпадает с «пашеновскоп,>
(10.13). Линейный закон (10.12), кстати, неплохо подтверждае-
мый и одномерными [10.6] и двумерными [10.2, 10,4] расчетами,
дает кривую [1], которая не сильно отличается от (10.13).
Стационарному протеканию тока отвечает кривая рис. 10.10
(ц = 1). Выше ее ц>1, ниже — ц<1. Это является следствием
ограниченности коэффициента ионизации сс(£') при Е -+ оо, отчего
271
функция ц(й) при V =const имеет максимум. В самом деле, при
d -> оо и у = const Е 0, а резко уменьшается и коэффициент
воспроизводства ц быстро стремится к нулю. При уменьшении d
и V = const поле Е возрастает, но ионизационный коэффициент
остается ограниченным, сх->Ар, и показатель усиления ad~Apd
уменьшается. Падает и коэффициент воспроизводства ц. Отсюда
Рис. 10.10. К вопросу о меха-
низме установления нормаль-
ной плотности тока. Схемати-
ческая зависимость катодного
падения потенциала VK от
толщины слоя d и плотности
тока /
и максимум у p(d). Именно здесь
коренится основная причина эффек-
та нормальной плотности тока.
При качественном рассмотрении
с кривой VK(d) можно обращаться
как с ВАХ VK(j), если направить
ось j противоположно d. Как разъ-
яснялось в начале (п. 4.8), при /<
< /н, d > da, стационарные состояния
на кривой неустойчивы. От флук-
туаций катодный слой может разру-
шиться и в середине. Но с края он
сокращается даже без флуктуаций.
На краю слоя, где уменьшается про-
странствепный заряд, эквипотенци-
альные поверхности отходят от ка-
тода (рис. 10.96). Удаляясь от сере-
дины пятна в сторону бестоновой
области, мы сдвигаемся от точки 1
на рис. 10.10 вправо, где ц<1.
Значит, ток у края со временем ис-
чезает. Согласно (10.1) через посред-
ство внешнего сопротивления Q напряжение па разряде от это-
го растет, / в однородной части слоя нарастает, и так вплоть до /н.
Допустим теперь, что осуществился сильно сверхнормальный
слой (точка 2 на рис. 10.10) . Состояние в центральной, квазиод-
нородной его части устойчиво. Но двигаясь от середины токового
пятна к краю, от точки 2 вправо, где эквипотенциальные поверх-
ности отклоняются от катода, мы вступаем в область расширен-
ного воспроизводства зарядов ц>1. У края катодного пятна
непростv происходит пробой. Рост токового пятна приводит к уве-
личению полного тока. Напряжение па электродах падает и в
однородной части слоя плотность тока снижается. Точка 2 спус-
кается вниз, пока состояние пе станет устойчивым не только в
середине, но и на краю.
Нормальному, т. е. полностью устойчивому состоянию отвеча-
ет точка И немного выше минимума на сверхнормальной ветви.
Это, как было показано в [10.1], связано с диффузионным пере-
теканием зарядов в крайнюю зону, где ц < 1, что поддерживает
там неугасающий несамостоятельный ток. Для такой поддержки
требуется повышенное рождение зарядов (р> 1) в области более
близкой к середине. Таким образом, двигаясь из середины пятна
в бестоковую область вдоль эквипотенцпали V = const на
272
рис. 10.10, мы, начиная от точки Н па левой ветви, где ц — 1,
сначала проходим область ц> 1, потом пересекаем кривую VK(d)
на правой ветви, где снова ц= 1, и, наконец, переходим в область
и < 1, где ток постепенно исчезает. В отсутствие диффузии точ-
ка 2 спустилась бы вниз до конца, ничего бы этого не было,
нормальное состояние совпало бы с минимумом VK, а край ка-
тодного пятна должен был бы стать резким. Но такая ситуация
несовместима с электростатикой. Эквипотенциальные поверхности
не могут идти параллельно вплоть до обрыва зоны пространствен-
ного заряда и начать отклоняться только за ее пределами.
Стационарное сосуществование токовой и бестоковой зон па
катоде имеет много общего с явлением контракции (§ 8 гл. 11),
когда в поле рядом сосуществуют области, где идет ток и где
тока нет, несмотря на присутствие поля. Применение такого под-
хода к задаче о токовом пятне па катоде в [10.1] позволило мно-
гое прояснить в природе эффекта нормальной плотности тока.
4.10. Нелокальный характер электронного спектра и иониза-
ционного коэффициента в катодном слое. Выше, при установле-
нии условий самоподдержания разряда и интегральных харак-
теристик слоя V к, d, j ионизационный коэффициент а счпт1 гея
функцией локального поля Е (х). Сама таунсепдовская зависи-
мость сх(Е') бралась, как это обычно и делается, из экспериментов
по ионизации в однородном поле. Такого приближения достаточ-
но, чтобы дать правильные интегральные характеристики, но оно
совершенно искажает картину ионизации, производимой электро-
нами в конце катодного слоя и примыкающей к нему области,
что мешает пониманию процессов в последней (§ 5). Дело в том,
что поле в катодном слое меняется в 102—103 раз на толщине
слоя, которая составляет не более 10 длин пробега для пеупругих
столкновений. Грубо говоря, толщина слоя составляет 1п(И-
+ 1/у)~3 «длины ионизации» сх-1. При столь резкой простран-
ственной неоднородности поля не успевает устанавливаться рав-
новесный энергетический спектр, соответствующий локальному
полю Е(х), как было бы при слабой неоднородности. Отличен от
таупсендовского а [7? (.г)] и фактический ионизационный коэф-
фициент, по определению равный а(^)==д/Ге, где q—число ак-
тов ионизации электронами в 1 см3 в 1 с, а Ге — плотность их
потока.
Поскольку электроны движутся в сторону падения поля, их
спектр жестче равновесного, а ионизационный коэффициент боль-
ше, ибо всего за длину пробега до прихода в данное место
электроны набирали энергию в более сильном поле и «не забы-
вают» об этом. В предельном случае очень малого числа неупру-
гих столкновений энергия электронов определяется даже не по-
лем, а пройденной разностью потенциалов. Благодаря нелокаль-
ным эффектам, на выходе из катодного слоя, где поле слабое,
присутствуют электроны со значительными энергиями, в том чис-
ле есть и такие, которые, родившись у катода, пронизали весь
слой, не совершив ни одного неупругого столкновения. Послед-
18 ю. П Райзер
273
ние обладают энергией eVh, т. е. в сотни электронвольт. Их дав-
но обнаружили на опыте и называют пучком. Правда, таких
электронов мало.
Современные усилия в теории катодного слоя направлены на
учет нелокальных эффектов*). Строгий подход возможен только
на основе решения кинетического уравнения для электронов в
Рис. 10.11. Энергетические спектры электронов на разных расстояниях х
от катода в катодном слое нормального тлеющего разряда, полученные пу-
тем расчета стохастического процесса движения электронов методом Мон-
те-Карло [10 8]. Разряд в гелии при р — 1 торр. В расчете принято: Рн =
— 150 В, поле в катодном слое 0 < х < 1,3 см, Е — 230(1 — д?/1,3) + 1 В/см,
при 1,3 < х < 1,5 см до анода Е = 1 В/см. При удалении от катода пик
«пучка» быстро падает и в масштабе рисунка исчезает. На выходе из ка-
тодного слоя он составляет 10-3 от функции распределения при е = 0
неоднородном поле. Одно из приближений состоит в замене ло-
кального поля Е(х) в таунсендовском коэффициенте а средним
полем на участке предыдущего пути Лгг, где электрон набирает
энергию \x_^xeEdx, равную потенциалу ионизации [10.7]. Наибо-
лее полную и достоверную информацию дает сильно продвинутое
в последнее время моделирование стохастического процесса в ка-
тодном слое методом Монте-Карло [10.8, 10.9], что, в сущности,
*) Это уже не имеет отношения к вопросу о нормальной плотности тока.
274
Рис. 10.12. Распределение средней энергии электронов е по координате к а-
тодного слоя: 1 — упругое рассеяние считалось изотропным, 2 — упругое
рассеяние считалось неизотропным, с преобладанием рассеяния вперед
[10.8]. На выходе из слоя е «__10 эВ. Без учета нелокальных эффектов на
выходе из слоя было бы е = 2,5 эВ, так как на границе Е/р ==
= 1 В/(см • торр) (п. 3.5 гл. 3)
а/ррм торр
/,5
42
О,Ъ
42
1.5
Рис. 10.13. Распределе-
ние ионизационного ко-
эффициента Таунсенда
а(я), вычисленного на
основе спектра, изобра-
женного на рис. 10.9.
Без учета нелокальных
эффектов на выходе
из слоя при рх =
= 1,3 торр • см было бы п
а « 0 [10.8]
18*
275
представляет собою способ численного решения кинетического
уравнения. Решение сопряжено с большими и трудоемкими рас-
четами, возможными благодаря применению мощных ЭВМ.
Результаты расчетов, хотя и сделанных с рядом упрощений,
открывают перед нами препарированную анатомическую картину
процесса (рис. 10.11—10.13). На выходе из слоя обнаруживаются
электроны с энергиями от малых и до 10—20 эВ, имеется и не-
большой пучок. Реальный ионизационный коэффициент на гра-
нице слоя в показанном варианте всего вдвое меньше максималь-
ного значения в середине, тогда как равновесный, а [Е(х) ], мак-
Рис 10.14. Рассчитанное на основе при-
ближенного кинетического уравнения
распределение скорости рождения за-
рядов в промежутке L — 5,5 см Поле
падает с х по линейному закону от Е =
= 130 В/см при х = 0 до Е = 1 В/см
при х = 2,2 см Вследствие нелокаль-
ны* эффектов половина всех зарядов
рождается в области слабого поля Е =
= 1 В/см за пределами катодного слоя
х > 2,2 см
симален у катода и равен 1,7 см-1, а у границы, где поле слабое,
на много порядков меньше, практически нулевой. Однако де-
тального согласия выходного спектра с опытом нет. В том же
нормальном разряде в гелии на выходе из катодного слоя были
зарегистрированы три группы электронов: со средней энергией
2 эВ (их подавляющее большинство), со средней энергией 22,5 эВ
(их на два порядка меньше) и слабый пучок с 8 = 150 эВ = еГн
[10.10].
В недавних работах [10.9] методом Монте-Карло рассмотрена
самосогласованная задача, в которой распределение поля Е(х)
в катодном слое задается не искусственным образом, как в [10.8],
а находится в результате численного интегрирования совместной
системы уравнений для функции распределения электронов,
плотности ионов ;г+(гг) и электростатики (3.33) для Е(гг). Рас-
четы также сделаны для гелия при р = 1 торр, причем охвачены
режимы аномального разряда. Межэлектродное расстояние взято
большим, Ь = Ъ см, что позволяет ионизации идти и далеко за
пределами катодного слоя в области слабого поля (тем дальше,
чем больше катодное падение VK и жестче электронный спектр).
Как и в самосогласованном расчете [10.6] с таунсендовским
коэффициентом, поле в катодном слое получилось падающим по
закону, близкому к линейному (10.12), лишь в конце слоя оно
затухает плавным образом.
В § 9 гл. 7 рассказывалось об упрощенном кинетическом урав-
нении для электронов в сильных резко неоднородных полях. Оно
было проверено на варианте, представленном графиками
рис. 10.11 —10.13 и дало удовлетворительное с ними согласие
[7.4]. Таким образом был рассмотрен катодный слой в рамках
276
«полусамосогласованной» задачи. Поле в слое задается линейным
по (10.12), но с заранее неизвестными Ек и с/, а вне слоя —
небольшим, только чтобы вытягивать заряды на электроды. Па-
раметры Ек, d, VK = EKdl2 находятся на основании равенства
потока ионов на катод n+\k+EK и числа их рождений во всем
промежутке \Qqdx. Па принятом для гелия при р = 1 торр рас-
стоянии £ = 5,5 см в значительной мере исчерпывается ионизую
щая способность большинства высокоэнергичных электронов, хо-
тя даже в нормальном разряде почти половина зарядов рождае!-
ся уже за пределами катодного слоя (рис. 10.14). Рассчитанные
ВАХ катодного слоя в гелии при р = 1 торр, нормальные пара-
метры Рн ~ 140 В, /н ~ 1,5 • 10-6 А см2 п аномальная ветвь не-
плохо согласуются с экспериментом (dH = 2,2 см получилось в
1,7 раза завышенным). (См. примечите при корректуре.)
§ 5. Переходная область между катодным слоем
и однородным положительным столбом
Имеются в виду области отрицательного свечения и темного
фарадеева пространства. Эти названия отражают внешние при-
знаки. Нас же будут интересовать процессы, ответственные за
продольную структуру разряда: распределение поля, плотность
зарядов вдоль оси х, перепое тока. В этом отношении обе области
представляют собою единое целое (рис. 10.2).
5.1. Определяющая роль энергичных электронов, поступающих
из катодного слоя. Растрачивая энергию на возбуждение и иони-
зацию газа, энергичные электроны вызывают интенсивное свече-
ние и создают резко повышенную ионизацию в области, где нет
достаточного для того электрического поля (рис. 10.14). Повы-
шенная ионизация со своей стороны является причиной резкого
ослабления поля, ибо в одномерном стационарном разряде плот-
ность тока вдоль направления его протекания остается неизмен-
ной (это справедливо для разряда в трубке). Значит, в рамках
часто оправдывающегося допущения о постоянной подвижности
пеЕ = const. Отсюда поле Е в точке Летах слабее, чем в поло-
жительном столбе, где пе меньше, как и показано на рис. 10.2,
схематически отражающем результаты экспериментов.
Роль нелокальных эффектов, которые приводят к появлению
мощного источника электронов, не обусловленного действием ме-
стного поля, выступает особенно явственно, если поинтересовать-
ся, что было бы, если бы мощность источников повсюду моно-
тонно уменьшалась при уменьшении поля, как в случае иониза-
ции с равновесным таунсендовским коэффициентом. Распределе-
ния пе, п+, Е вдоль оси х в промежутке описываются при этом
уравнениями (10.2), (10.6), (10.3). Только в (10.2) следует
включить члены потерь зарядов, чтобы обеспечить возможность
появления в длинном промежутке однородного положительного
столба, в котором ионизация компенсирует потери (§ 6). И ка-
277
чественный анализ, и численное интегрирование системы показы-
вают, что поле монотонно уменьшается от катода до значения,
соответствующего положительному столбу, а пе тоже монотонно
возрастает. Получается непосредственный переход от катодного
слоя к положительному столбу без области провала поля [10.5].
Можно сказать, что без потока энергичных электронов за пределы
слоя с сильным полем, т. е. в отсутствие нелокальных эффектов,
не было бы фарадеева пространства.
5.2. Данные зондовых измерений. Эти данные немногочислен-
ны. На рис. 10.15 показаны распределения плотности электронов
в отрицательном свечении и фарадеевом пространстве в гелии
на оси трубки радиуса R = 1,35 см при р = 1,5 торр [10.11, 8].
Координата х отсчитывается от катодной границы отрицательного
свечения в сторону анода. По тем же измерениям температура
Рис. 10.15. Измеренные распре-
деления плотности медленных
электронов в отрицательном
свечении и фарадеевом прост-
ранстве на оси трубки радиу-
са 1,35 см. Координата х от-
считывается от начала отрица-
тельного свечения к аноду
[10.11, 8]
Рис. 10.16. Зондовые измерения
распределений температуры
электронов (7) и продольного по-
ля (2) в фарадеевом пространст-
ве на оси трубки радиусом 1,5 см;
разряд в Не, р = 1 торр, I =
= 15 мА [10.12]
электронов почти постоянна по длине, мало зависит от тока и
составляет Те ~ 0,12 эВ, повышаясь вдвое вблизи катодной гра-
ницы х ~ 0. Потенциал ср почти не меняется на участке 2 < х <
< 10 см, и там, судя по наклону ф(а:), Е]р, по-видимому, не пре-
вышает 0,01 В/(см-торр). Такое Е]р слишком мало, чтобы обес-
печить дрейфовый перенос тока, и в этой области, возможно, дей-
ствует диффузионный механизм (п. 5.3). Численная интерпре-
тация этих результатов довольно затруднительна из-за неточ-
ности Е.
Медленные электроны являются максвелловскими, так как
частота электрон-электронных столкновений при столь низких
температурах значительно превышает частоту потерь энергии
(3.17) при столкновениях с атомами. Это те электроны, которые
родились в самом конце катодного слоя, где уже почти пет поля.
278
от которого они могли бы почерпнуть энергию, а также родив-
шиеся от энергичных электронов на выходе из слоя и растеряв-
шие свою энергию Их называют конечными Зондовые измерения
функции распределения указывают на существование второй
группы электронов с ~ 3—4 эВ Плотность их в 100—200 раз
меньше Эти электроны называют вторичными. Они рождены не-
сколько глубже в катодном слое и еще немного ускоряются в
поле Возможно к ним принад тежат и не слишком энергичные
эчектроны, испытавшие неупругое столкновение и оставшиеся с
такой энергией Третья группа, очень немногочисленная, это —
пучок (о трех группах говорилось также в п 4 10)
Недавно исс хедовалось фарадеево пространство в гечии в
близких условиях (р = 1 торр, R = 1,5 см, L = 50 см), но при
более сильном токе i=15 мА [10 12] Нельзя сказать, что эти
результаты (рис 10.16) вполне согл суются с описанными выше
Измененные Те и Е/р существенно выше, а участок по х короче
Большая неопределенность возникает при привязке начал отсчета
.г = 0 На рис 10 16 за х = § принята кажущаяся граница межд.у
отрицательным свечением и фарадеевым пространством, но, судя
по всему, правый конец участка — это уже переход от фарадеева
пространства к положительному сто i6y Количественная интер
претация результатов, сделанная в 4 [10 12], показывает, что ток
здесь преимущественно дрейфовый Гоки электронных диффузии
и термодиффузии раза в 3—4 меньше и компенсируют друг дру-
га, будучи направленными в разные стороны
5.3. Роль электронной диффузии. Наличие резкого максимума
электронной плотности с последующим большим спадом ее в сто-
рону анода (рис 10 15) может привести к тому, что ток в области
спада будет переноситься электронной диффузией, как это было
описано в п 7 2 гл 3 *) Поле при этом уничтожается Вследствие
падения электронной плотности диффузионный поток постепенно
уменьшается, поле восстанавливается (формула (3 42)), диффу-
зия постепенно уступает место дрейфу и фарадеево пространство
переходит в положительный столб (если анод еще далеко,
рис 10 2) Подобная ситуация возникает также в пространстве
низковольтной дуги Опа приближенно рассчитана в [10 13,
10 14, 8] Падение пе от максимума в сторону анода отчасти вы
звано потерями электронов, не восполняемыми отсутствующей
ионизацией При низких давлениях электроны гибнут вследствие
амбиполярной диффузии зарядов к стенкам с последующей ней-
трализацией на стенках При высоких давлениях, когда диффу
зия затруднена, на первый план выступает объемная рекомбина-
ция, в электроотрицательных газах — прилипание Длина пере-
ходной области (отрицательного свечения плюс фарадеева про-
*) В некоторых работах [8] говорится об участии пучка в переносе то-
ка Но в пучок превращается лишь малая доля электронов эмитированных
с катода кроме того са i электронный ток с катода составляет малую долю
7/(1 + у) от полного Ускорение элекхронон пучка до больших скоростей их
тока не увеличивает,— соответственно уменьшается их плотность
279
странства) практически совпадает с расстоянием от катода до
начала положительного столба. Она растет с понижением давле-
ния и увеличением тока. Произведение ее на давление имеет по-
рядок 10 см • торр.
5.4. Основные факторы, определяющие продольную структуру
разряда в длинном промежутке. Итак, три обстоятельства важны
для формирования перехода от катодного слоя к однородному
положительному столбу через отрицательное свечение и фара-
деево пространство. 1. Наличие мощного источника ионизации в
конце катодного слоя, не связанного со значением местного поля.
2. Локальные потери зарядов, не связанные с их переносом к
электродам. 3. Диффузия электронов вдоль направления тока.
Неучет любого из пих не даст возможности построить адекватную
теорию переходной области, которая, надо сказать, продвинута
весьма слабо. Старые работы рассматриваются в [8]. Проблема
обсуждается в [10.5]. (См. примечание при корректуре.)
5.5. Разряд с полым катодом. Если сделать два катода в виде
параллельных пластин, анод вынести в сторону, и сближать ка-
тоды, то, начиная с некоторого расстояния, ток возрастает в сот-
ни, тысячи раз. Это происходит, когда перекрываются две сначала
отдельных области отрицательного свечения. Свечение становится
гораздо интенсивнее. Напряжение меняется мало. Аналогичный
эффект можно получить, если сделать катод в виде полого ци-
линдра, а анод отодвинуть вдоль оси. Давления должны быть
такими, чтобы толщина катодного слоя была сравнимой с диа-
метром цилиндра. В полом катоде вследствие кумуляции у оси
сходящихся электронных потоков происходят интенсивные иони-
зация и возбуждение газа. Играет роль и фотоэмиссия с катода
под действием рожденного в этой области ультрафиолетового
излучения. Подробнее см. [10.15].
§ 6. Положительный столб
6.1. Его предназначение; причинные связи. Положительный
столб замыкает электрическую цепь в пространстве между катод-
ным слоем и анодом, и единственно в этом заключается его
функция. Состояние плазмы в достаточно длинном столбе совер-
шенно пе зависит от того, что делается в приэлектродных обла-
стях. Оно определяется местными процессами и значением про-
пускаемого тока. Неизбежные потери носителей тока в столбе —
электронов — в стационарном режиме должны восполняться иони-
зацией*). Поскольку скорость ионизации через зависимость от
электронного спектра зависит от поля, причем весьма резко, это
фиксирует значение поля Е, которое необходимо для поддержа-
*) Строго говоря, это утверждение относится только к длинному одно-
родному столбу. В противном случае присутствуют градиенты вдоль тока,
потери могут восполняться и за счет поступления зарядов из катодных ча-
стей путем амбиполярных диффузии и дрейфа или, наоборот, излишек рож-
денных зарядов может выноситься амбиполярными механизмами (п. 6.6).
280
ния стационарной плазмы. Тем и определяются продольный гра-
диент потенциала и падение напряжения в однородном столбе
данной длины. Если спектр максвелловский, описанную связь
можно расчленить на два причинных звена: 1. Требование ком-
пенсации потерь ионизацией показывает, какой температурой Те
должны обладать электроны. 2. Поле обязано снабдить электроны
должной энергией. Связь Е и Те вытекает из условия баланса
электронной энергии (§ 3 гл. 3). Газовая температура Т опре-
деляется балансом энергии газа в целом. В положительном стол-
бе тлеющего разряда Те > Т.
Процессы рождения и гибели электронов в столбе разыгры-
ваются на фоне их непрекращающейся смены в результате дрей-
фового движения от катода к аноду. Нельзя сказать, чтобы в
столбе тлеющего разряда рождалась значительная часть носи-
телей тока. Скорее наоборот, большинство электронов, достигаю-
щих анода, поступает в столб извне, из катодных областей. Ве-
роятность им погибнуть по пути невелика, за исключением слу-
чаев каких-то чрезмерно больших расстояний между электродами.
6.2. Баланс числа зарядов в газах б£з прилипания. Рассмот-
рим длинный положительный столб в трубке (или плоском ка-
нале), столь длинный, что его можно считать однородным вдоль
направления тока х. В стационарных условиях согласно (5.14)
rot Е = 0, откуда следует, что однородное по х продольное поле
не зависит от поперечных координат (поперечным полем поля-
ризации вообще пренебрегаем). Плотность зарядов в квазипей-
тральной плазме столба описывается уравнением (3.44), где q
включает ионизацию и объемную рекомбинацию. Отметив зна-
ком -1- поперечную часть лапласиана, получим уравнение
Dat^n + v,(£) п — $п2 = 0. (10.17)
Допустим, что гибель зарядов на стенках важнее, чем в объ-
еме. О таких случаях говорят: разряд контролируется диффузией
и <и рекомбинацией на стенках. Без слагаемого $п2 и с гранич-
ным условием п = 0 при г = 13 уравнение (10.17) дает бесселевый
радиальный профиль га ~ 7о(2,4г/7?) и условие
(Е) = DJA2 ^vda, А = 7?/2,4, (10/8)
равенства частоты ионизации и эффективной частоты диффузи-
онных уходов (Шоттки, 1924 г.)*). Случай fin < Vda реализуется
при небольших давлениях и поперечных размерах (vda ~ 1, рА9),
при не слишком больших токах, когда п невелико, и легче в
одноатомных газах, где объемная рекомбинация происходит мед-
леннее, чем в молекулярных.
Приведем пример. В азоте ц+р ~ 1,5 • 103 см2 • торр/(В с),
Те ~ 1 эВ, Dap = (ц+р) Те ~ 1,5 • 103 см2 торр/с. При р = 10 торр,
13 = 1 см, Da ~ 150 см2/с имеем ~ 900 с-1. С коэффициентом
*) В плоской геометрии профиль косинусоидальный, а Л дается форму-
лой (4.23).
281
рекомбинации (диссоциативной; п 3 2 гл 4) [3 = 1,6 10-7 см3/с
условие fin < vda выполняется вплоть до п « 6 109 см-3, чему
соответствует плотность тока j = е (рер) пе(Е/р) ~ 2 мА/см2 (цер~
~ 4,2 105 см2 Toppz(B с); для оценки положено Е/р^Ъ ВХ
Х(см торр)-1 Полный ток мА Если ток меньше
этого значения, разряд контролируется диффузией, если боль-
ше — объемной рекомбинацией
Вероятность электрону, совершая дрейф вдоль столба длины
L, погибнуть на стенках равна vda£, где t = L/v^ — время дрейфа.
С помощью формул (3 36), (3 21), (3 16) ее можно выразить че
рез характеристики газа и размеры
j /£ ~ p+ _ Q,4ZL_ p+
Л\ He 3 л2 Не ^Л2]/б Р/ k * 7
В нашем примере вероятность составляет 7 10-4 на 1 см длины.
Даже через метровый столб проходит 93 % электронов (если
мала объемная рекомбинация, при оценке принято 1р = 0,03 см X
Хторр, 6 = 1,2 10"3).
Когда У > vdG, рекомбинация зарядов в объеме преобладает
над их диффузией к стенкам Если опустить диффузионное сла-
гаемое в (10 17), получим, что уг(Е) = т е плотность постоян-
на по сечению. На самом деле около поглощающих стенок по-
являются сильный градиент п, и там пренебречь диффузией
нельзя. Плотность мало меняется в основной части сечения, но
вблизи стенок резко падает На основании (10 17) можно запи-
сать интерполяционное уравнение баланса, которое включает оба
предельных случая и обеспечивает непрерывный переход между
ними:
x2(^)-vda-^z = 0 (10 20)
6.3. Поле в столбе и ВАХ. В столбе, контролируемом диффу-
зией, поле Е определяется из равенства (10 18) и формально не
зависит от плотности электронов, а следовательно, и от тока Так
получается потому, что скорости и рождения, и гибели электро-
нов пропорциональны п ВАХ столба в данном приблпже ши изо-
бражается горизонтальной прямой, как и ВАХ всего разряда,
если он является нормальным: V(i) = VH + EL = const Для поля
в столбе (рис 10 17, 10 18) справедлив закон подобия Е/р =
= f(pA), который вытекает из зависимостей vt=pfi(E/p), Vda
— lzp\2. Уменьшение Е/р при возрастании тока на порядок, вид-
ное из рис 10 17, связано с повышением температуры газа оз
джоулева нагрева, в результате чего происходит тепловое рас-
ширение разрядной плазмы (§ 7) Ведь на самом дече в законы
подобия входит плотность газа или приведенное давление Р20
(п 1 гл 2), которое является ее мерой Между тем на гра-
фиках фигурирует фактическое начальное давление в трубке р
Например, если из за нагрева от сильного тока температура газа
в разряде повысилась от комнатной при слабом токе до 650 К,
отношение Е/р^ станет вдвое больше, чем Е/р, и кривая Е/р^
282
сместится вверх. Этим, отчасти, объясняются и кажущиеся слиш-
ком низкими значения Е/р для молекулярных газов (см. также
п. 7.7).
Особенное внимание на рис. 10.18 привлекает факт сущест-
вования разряда в воздухе при низких Е/р, вплоть до 13 В X
Х(см •торр)-'1. Как мы знаем из п. 2.5 гл. 9, ионизация в воздухе
Рис. 10.17. Измеренные значения
Е/р для положительного столба
в трубках в инертных газах в за-
висимости от параметра pR [5]
Рис. 10 18. Измеренные значения
Е/р для положительного столба
в трубках в молекулярных газах
в зависимости от параметра
pR [5]. Штрихпунктирные кри-
вые — расчет [1]
преобладает над прилипанием, что необходимо для горения раз-
ряда, лишь при Е/р >35 В/(см-торр). Здесь, помимо нагрева,
а скорее всего в первую очередь, проявляется другой эффект.
В стационарных условиях, к которым относятся измерения, на-
капливается много молекул, активных в отношении отлипания
(§ 8). Прилипание при этом в значительной мере компенсиру-
ется отлипанием, и потери электронов меньше, чем при пробое
или в кратковременных разрядах. Соответственно для поддержа-
ния стационарного разряда требуются меньшие значения Е’р.
Подчеркнем, что поле, необходимое для поддержания плазмы
в столбе, всегда меньше нужного для пробоя газа в тех же ус-
ловиях. При пробое электроны диффундируют к стенкам свобод-
но. В сформировавшемся разряде диффузия амбиполярна и про-
исходит существенно медленнее. С этим положением мы уже по-
знакомились в п. 8.1 гл. 9 на примере высокочастотного разряда.
При значительных разрядных токах возрастает степень иони-
зации газа и вступает в действие объемная рекомбинация. ВАХ
столба при этом описывается общим соотношением
(10.21)
которое вытекает из (10.20). В разряде, контролируемом объем-
283
ной рекомбинацией (хг > vda) Е медленно растет с j. Такой ре-
жим скорее осуществим в молекулярных газах, где сильна ре-
комбинация; в инертных — раньше происходит контракция, стя-
гивание положительного столба в токовый шнур (§ 8 гл. 11).
Растущую из-за рекомбинации ВАХ удается наблюдать в крат-
ковременных разрядах или на ранней стадии длительных. Как
только газ прогревается, ВАХ стационарного разряда становится
падающей из-за теплового расширения (§ 7).
6.4. Электронная температура и ее связь с полем. Рассмотрим
разряд, контролируемый диффузией, и допустим, что спектр
электронов — максвелловский. Подставив в (10.18) выражения
(4.4) для уг при максвелловском спектре и (3.36) для 7?а, поле-
чим уравнение для Те
(ЕГД1/2 т С- / 87 W2 N
(-1 <10-22>
Рис. 10.19. Универсальная кривая для
вычисления Те в положительном стол-
бе в зависимости от cpR [5]. Констан-
ты для нескольких газов приведены в
тексте
Оно определяет универсальную для всех газов зависимость TJI
от cpR (рис. 10.19), где с — своя для каждого газа постоянная,
которая вычисляется на
основе данных о ц+, Сг-
и I (Энгель и Штеен-
бек, 1934 г.). Констан-
ты с равны: Не — 4 X
X IO’3, Ne - 6 • 10"3,
Аг - 4 • 10-2, Н2 - 1X
ХЮ-2, N2- 4 • 10“2.
Например, в азоте при
R = 1 см, р === 10 торр
находим Те = 0,9 эВ =
— 10 400 К. С увеличе-
нием радиуса трубки и
давления электронная
температура падает, так
как уменьшаются диф-
фузионные потери, и
поэтому достаточно
меньшей скорости иони-
зации. Понятно, почему в широких сосудах положительный столб
не светится: слишком низка электронная температура.
Вопрос о связи между энергией (или температурой электро-
нов) и полем рассматривался в п. 3.5 гл. 3. В предположении
о независимости длины пробега электрона от энергии Te^E/N.
Показанные на рис. 10.18 расчетные кривые полечены в [1]
именно таким путем по формулам (10.22), (3.13) с использова-
нием экспериментальных значений б. Впрочем, в свете поздней-
ших исследований отличному согласию расчета с экспериментом,
по крайней мере в случае азота, не следует придавать особого
значения, оно может быть и иллюзорным. Механизм ионизации
в азоте гораздо сложнее (п. 7.7). Теория, по-видимому, больше
284
подходит для атомарных газов. Спектр электронов близок к макс-
велловскому, если частота электрон-электронных столкновении
vee заметным образом превышает частоту потерь энергии vu =
= 6vm (п. 3.7 гл. 3), что легче осуществляется в атомарных га-
зах. Но для понимания качественных закономерностей явления
изложенная простая старая теория в высшей степени полезна.
6.5. Почему степень ионизации в слабоионизованной газораз-
рядной плазме сильно неравновесна. В диффузном положитель-
ном столбе тлеющего разряда (диффузным называют столб пе
контрагированный, заполняющий все сечение трубки) плотности
электронов имеют порядки пе ~ 108—1011, максимум 1012 см-3.
При р ~ 1 —10 торр, N ~ 3 • 1016—3 • 1017 см-3 степени ионизации
газа составляют 10-8—10-7. Между тем, фактическим электрон-
ным температурам Те ~ 1—3 эВ отвечают термодинамически рав-
новесные степени ионизации 10~2— 1. Причина такого несоответ-
ствия состоит в том, что резко нарушено первейшее требование,
которое обусловливает достижение термодинамического равнове-
сия: в главных реакциях прямые и обратные процессы должны
быть уравновешены.
В тлеющем разряде атомы ионизуются преимущественно
электронными ударами, часто — из основного состояния. Гибнут
же заряды в холодном разреженном газе на стенках или путем
диссоциативной рекомбинации. Как было оценено в п. 6.2, при
пе < Ю10 см-3 частота диффузионных потерь vda ~ Ю3 с-1. Поте
и электронная температура, подстраиваясь к потерям, обеспечи-
вают такую же скорость ионизации. Но рекомбинация в тройных
столкновениях с захватом электрона в основное состояние атома,
которая обратна процессу ионизации*, дает в этом случае частоту
гибели 10-10 с"1. Это на 13 порядков меньше! Быстро происхо-
дящей гибели (диффузионной, диссоциативной) пе противопо-
ставлены соответствующие обратные процессы ионизации. Так
ассоциативная ионизация не идет, если газ холодный и не воз-
бужден. Потому плотность электронов и не вырастает.
Другое дело — плотная, сильноионизованная равновесная
плазма. Там диффузия и диссоциативная рекомбинация не су-
щественны, потому что газ плотный, горячий, мало молекулярных
ионов. Плотность зарядов велика, и преобладает ударно-радиа-
ционная рекомбинация с захватом электронов на верхние уровни
(п. 3.4 гл. 4). Ионизуются атомы в результате обратного ей про-
цесса — ступенчатой ионизации из возбужденных состояний. Так
достигается термодинамически равновесная ионизация.
6.6. Неоднородный плазменный столб. При сложной геомет-
рии разрядного объема, сложной конфигурации электродов,
в присутствии быстрого поперечного газового потока, когда он
сносит и искривляет токовый капал, а такие условия встречаются
в современных мощных лазерах (п. 4.2 гл. 16), плазменный
столб между электродами может оказаться весьма неоднородным,
хотя и в достаточной степени электронейтральным. В таких слу-
чаях для нахождения пространственных распределений плотно-
285
сти плазмы и поля Е ==—V<p нецелесообразно пользоваться об-
щей системой уравнений (3.22), (3.20), (3.33), ибо уравнение
Пуассона (3.33) будет содержать малую разность п+ — пе отно-
сительно больших величин. Вместо двух близких плотностей
п+ следует оперировать одной, п ~ пе ~ п+, отчего система трех
уравнений сведется к двум, (3.46), где q зависит от Е, и (3.40)*).
Последнее в предположении це = const сводится к div(nE) = 0.
Если разряд горит в газовом потоке скорости и, к потоку плазмы
под знаком div в (3.46) следует добавить конвективную состав-
ляющую пм.
Исключение п+ — пе из системы отвечает фактической при-
чинной связи явлений. При малой плотности пространственного
заряда поле в неоднородной проводящей среде определяется не
местными зарядами, а распределением токов и граничными ус-
ловиями. Пространственный заряд, наоборот, сам «подстраивает-
ся» к неоднородностям поля, и по найденному полю его можно
определить при помощи уравнения электростатики (3.33).
Неоднородный плазменный столб образуется и между пло-
скими электродами при пе слишком больших pL < 10 торр • см,
когда не хватает места для формирования однородного столба,
рассмотренного выше. При этом может наблюдаться резкий дис-
баланс между рождением и потерями электронов в плазме. Так,
в случае, показанном на рис. 10.9, ионизация в столбе, в общем
незначительная, все равно оказывается гораздо более силь оч,
чем рекомбинационные и диффузионные потери. То же с^мое
показал одномерный расчет [10.6], где потери и диффузия вооб-
ще не приняты во внимание, а по результатам расчета — малы.
Плазменная зона в коротких (в смысле pL} промежутках не
является прообразом «положительного столба», если под послед-
ним понимать область, где поддерживается локальное равновесие
между рождением и гибелью зарядов.
Учет нелокальных эффектов (п. 4.10) в одномерной модели
короткого промежутка, аналогичной [10.6], в качественном от-
ношении продольной структуры разряда не изменил [10.1С].
В свете сказанного в п. 5.4 это и не удивительно.
§ 7. Влияние нагрева газа на поле
и ВАХ положительного столба
В стационарных условиях вся та энергия, которую электроны
получают от поля, в результе их столкновений с атомами и
молекулами переходит в газ. В 1 см3 в 1 с выделяется энергия,
равная jE = вЕ2 (п. 3.1 гл. 3). Это есть джоулево тепло. Часть
его расходуется на возбуждение молекулярных колебаний, но
если последние релаксируют быстро, а так иногда и происходит
*) Распределение токов квазистационарно даже в нестационарных плаз-
менных процессах из-за большой скорости релаксации объемного заряда
(п. 2.2 гл. 11). Поэтому мы вправе отказаться от уравнения (3.39) в поль-
зу (3.40).
286
Т
R О R
Рис. 10.20. Распределение
газовой температуры в
трубке при небольших на-
греваниях
(важное исключение составляет азот!), можно говорить о единой
газовой температуре Т даже в молекулярном газе.
7.1. Теплопроводностями вывод джоулева тепла. В трубке без
протока газа тепло отводится к стенкам, которые, при небольшом
энерговыделении имеют комнатную температуру То. Температу-
ра газа равномерно спадает от оси к
стенкам (рис. 10.20). Плотность тепло-
вого потока в стенки равна JR =
= —к(дТ/дг)r=R, где X — теплопровод-
ность. Если оперировать средней по се-
чению температурой Т, то потеря энер-
гии газом в 1 с из расчета на 1 см3
(2|я7?/л/л7?2) с точностью до числового
коэффициента равна Х(Т—То)//?2. Ее
можно представить в виде NcPi(T —
— To)vr эрг/(с • см3), где ср\ — теплоем-
кость при постоянном давлении, рас-
считанная на одну молекулу, a vT — величина, обратная времени
вывода тепла из объема. Частота теплоотвода Ут %/ где
X = 'klNcp\ — температуропроводность, a At ~ /?/Т8 ~ /?/2,8. Она
аналогична частоте диффузии vd = D/А2 (теплопроводность и диф-
фузия описываются одинаковыми уравнениями). Небольшое раз-
личие Ат и А ==/?/2,4 связано с процедурой усреднения.
7.2. Конвективный теплоотвод. Возможен еще один механизм
вывода тепла из разряда, который используется в современных
мощных лазерных установках,—прокачка газа через разряд
(п. 1.2). Этот механизм называют конвективным охлаждением.
Собственно, никакого охлаждения Данной массы газа не проис-
ходит. Напротив, макроскопическая частица газа, пролетая через
разряд, нагревается, и температура в ней неуклонно растет во
времени или вдоль пути пролета. Речь идет о выводе тепла из
разрядного объема. Если по-прежнему оперировать средней по
длине L\ потока температурой 7, то скорость теплоотвода из
разрядного объема можно записать в том же виде Ncp\ (Т — То) vf.
Теперь То — температура газа, вступающего в разряд, a vF ~
~ 2н/Л1, где и — скорость потока. Двойка учитывает, что в сред-
нем тепло выводится «с полпути». В продольном разряде
(рис. 10.16) Li совпадает с расстоянием L между электродами.
7.3. Баланс энергии газа. Для большей ясности запишем сна-
чала нестационарное уравнение баланса. Учтем только, что пе-
редача энергии от электронов молекулам происходит гораздо
скорее, чем из газа наружу. Поэтому баланс электронной энер-
гии будем считать стационарным, даже если температура газа
меняется во времени. Упрощенное уравнение для газовой тем-
пературы есть
Ncpidlldt = jE - АсР1 (7 - То)vT>F. (10.23)
В стационарных условиях средняя температура определяется из
287
равенства
NcPl (Г — То) vf,t = jE = iv*). (10.24)
7.4. Падающая ВАХ. Опыт показывает, что в разряде, конт-
ролируемом диффузией, ВАХ изображается не горизонтальной
линией, а слегка падающей кривой: при увеличении тока напря-
жение несколько уменьшается. Это является следствием нагре-
вания газа. У оси плотность тока больше, чем у стенок, так как
там больше плотность электронов (поле же одинаково по сече-
нию). Энерговыделение и температура газа на оси также выше,
чем у стенок. Но давление выравнено в пространстве (даже в
разряде с потоком газа скорости обычно намного меньше скорос-
ти звука). Следовательно, в областях с большей температурой
плотность газа меньше. Поскольку частота ионизации фактиче-
ски зависит не от Е/р, а от Е/N, для поддержания ионизации в
основной части токового сечения требуется меньшее поле; умень-
шается и напряжение. Установить оценочный закон падения
можно на основании равенств (10.24), р = NkT == const и при-
ближенного условия EjN^ET ~ const, вытекающего из (10.18).
Найдем
77/о = (Е0/Е)3/2(Е0/Е-1). (10.25)
Здесь Ео — поле, нужное для поддержания очень слабого тока
(7 0), когда нагревание газа ничтожно и его температура не
отличается от комнатной То;
/о ~ Norpi^ ovt/Eq, w0 =— JqEq, (10.26)
Это характерные масштабы плотности тока и сюрости вы тле-
ния джоулева тепла. При таком энерговыделении газ нагрева-
ется до температуры Т, вдвое выше температуры стенок.
7.5. Устойчивое и неустойчивое состояния. Когда ВАХ имеет
падающий характер, нагрузочная прямая зачастую пересекает
ее не в одной, а в двух точках (рис. 10.21). Одно из состояний,
а именно 7, является неустойчивым и потому не реализуется.
В самом деле, если по какой-либо причине ток случайно повы-
шается, для его поддержания достаточно будет напряжения,
*) Если разряд горит в потоке или в малой части большого объема, а вре-
мя колебательной релаксации . vp1, ка £ это бывает, например,
в азоте, колебательная энергия вообще не участвует в балансе. Она выно-
сится пз разряда потоком или диффузией возбужденных молекул (следует
только иметь в виду, что вероятность тушения колебательно-возбужденных
молекул азота при ударах о степки (и металл, и диэлектрик) мала— 10~3—
10-4). В этом случае }Е в (10.23), (10.24) нужно умножить на долю джоу-
лева тепла, которая переходит в поступательные и вращательные степени
свободы. В общем случае приходится исходить из системы отдельных урав-
нений для поступательно-вращательной и колебательной энергий. Заметим,
что при больших энерговыделениях обмен между ними может существенно
ускоряться из-за ангармонизма верхних колебательных уровней, интенсив-
но заселяемых в результате быстрого обмена квантами при столкновениях
молекул (п. 7.7).
288
меньшего фактического, которое при данных ЭДС и внешнем
сопротивлении непременно соответствует нагрузочной прямой.
Возникает дисбаланс между ионизацией и гибелью электронов,
ионизация начнет расти, сопротивление разряда падать, ток рас-
ти, пока состояние не достигнет нижней точки пересечения. При
отрицательной флуктуации тока 61 электроны начнут гибнуть,
пока разряд не погаснет. Состояние 2
6пе > 0 напряжение станет меньше не-
обходимого и повышенная гибель вер-
нет степень ионизации в исходное со-
стояние.
7.6. Температура газа и масштабы
электрических параметров в диффузном
тлеющем разряде. Одним из наиболее
характерных свойств такого разряда яв-
ляется резкое различие электронной и
газовой температур. Почему электрон-
ная температура обязана быть высокой,
мы уже обсуждали: электроны должны
ионизировать атомы. Тем же определя-
ются и порядки величин Е/р в столбе:
Е/р ~ 0,2—20 В/ (см торр). Темпеоату-
ра Т определяется балансом энерговы-
устойчиво. При 61 > О,
Рис 10.21. ВАХ с учетом
нагревания газа и нагру-
зочная прямая. Верхняя
точка пересечения 1 отве-
чает неустойчивому состоя-
нию
деления и теплообмена (10.24). Относительное превышение ее
над температурой стенок (комнатной) равно
(Г — Tq)/Tq — w/wq — jE/jsE^.
(10.27)
Масштабами энерговыделенля дт плотности тока /0 служат
величины (10.26). Им соответствует повышение температуры
вдвое. Посмотрим, что это за числа. При Т ~ 300—600 К тепло-
проводность большинства газов л~(2—5) - 10—4 Вт(см-К).У од-
ноатомных газов сР1 = (5/2)/г, у двухатомных — (7/2)к. С про-
межуточными значениями X = 3 • 10-4, ср[ = Зк температуропро-
водность % =-= 220/р см2/с. Для трубок (или каналов) с R = 1 см
теплоотвод в стенки характеризуется частотой vr ~ 1,3 • 103/р с-1.
Отсюда масштабы энерговыделения и плотности тока при типич-
ном значении Е/р = 3 В/(см-т(рр) равны = 0,5 Вт/см3, /о =
= 170//? мА/см2. По формулам (3.6), (3.7) для проводимости с
vm = 3 • 109 р с-1 масштабом плотности электронов является ве-
личина ~ 6- 1011//? СМ 3.
Опыт показывает, что разряд в большом объеме редко сохра-
няет диффузную форму, если газ в нем нагревается заметным
образом, скажем вдвое. Происходит контракция, стягивание стол-
ба в шнур, где степень ионизации, плотность тока и газовая тем-
пература резко повышаются,— это преддверие к переходу тлею-
щего разряда в дугу при еще больших токах. Приведенные
масштабы характеризуют верхние границы реализации слабо-
ионизованной холодной плазмы диффузного тлеющего разряда.
Чем выше давление, тем ниже по току и плотности электронов
19 ю. П. Рай зер
289
эта верхняя граница, тем сильнее нагревается газ при данном
токе. Значит, для осуществления неравновесной слабоионизован-
нои плазмы благоприятны низкие давления, для осуществления
равновесной — высокие, порядка атмосферного, о чем и свиде-
тельствует разрядная практика.
При конвективном теплоотводе зависимость масштабов от дав-
ления иная: vF, /о и от давления не зависят, a Wq00 р. На-
пример, при L\ = 10 см, и = 50 м/с Vf ~ Ю3 c~l, Wo ~ 0,4р Вт/см3.
Со значением Е/р ~ 10, более реальным для подобного рода слу-
чаев, у ~ 40 мА/см2, п® « 1,5-1011 см~3.
7.7. Состояние газа и механизмы ионизации в положитель-
ном столбе разряда в азоте. По ряду причин, среди которых не
последнее место занимают приложения в газовых лазерах и
плазмохимии, к азоту приковано внимание исследователей кине-
тики электронных, колебательных и ионномолекулярных процес-
сов в слабоионизованной неравновесной разрядной плазме. Экс-
перименты и усилия по их теоретической интерпретации указы-
вают на многообразие и сложность ионизационных механизмов
в плазме положительного столба, которые далеко не всегда укла-
дываются в простейшую схему ионизации невозбужденных ато-
мов и молекул электронным ударом, как обычно считают при
общем описании разрядного процесса. Недостаточность этого ме-
ханизма немедленно проявляется при попытке объяснить на-
блюдаемые значения Е/N в столбе.
Табл. 10.4, в которой отражены результаты измерений и рас-
четов [10.17] для положительного столба в длинных трубках
(А ~ 30—60 см) радиуса R =- 1,6 см, дает весьма полное пред
ставление о состоянии плазмы азота особой чистоты — 99,998 %.
Продольное поле Е измерялось двумя зондами, температура га-
за Т — термопарой, плотность электронов пе — СВЧ методом,
плотность метастабилей А 2(А3 2J-) = N А — спектроскопическим.
Плотность газа А рассчитана по Т и измеренному давлению*).
Все эти величины относятся к оси трубки. Относительные засе-
ленности a = NJN состояний с колебательными квантовыми чис-
лами v получены расчетным путем; — средняя колебательная
энергия молекулы. Колебательная температура (п. 8.2 гл. 7)
Тъ — 5000 К — весьма высока. Это связано с тем, что чуть ли не
все джоулево тепло идет на накачку колебаний, а колебательная
релаксация идет замедленно. ВАХ столба, E(i) при данном р,
имеет падающий характер в соответствии со значительностью
нагрева газа. Главным результатом эксперимента, который и
подлежит анализу, является эффективная константа скорости
ионизация /сгэф. Она определена из соотношения дп ТеРь = #ион =
= k^Nne, эквивалентного (10.20), путем расчета скорости по-
терь электронов дпот [см-3 с-1] за счет амбиполярной диффузии
*) В столбце с EIpzq, р2о— это давление при данной плотности 2V, при-
веденное к комнатной температуре 20 °C (п. 1 5 гл 2)
290
к стенкам и диссоциативном рекомбинации (в данных устовиях
первая важнее) Эффективная частота ионизации v Эф = kt^N со-
ставляет при низшем давлении примерно 104с-1, при среднем
4 103 и при верхнем 2 103
Скорости ионизации электронным ударом, вычисленные по
формулам (7 40), (7 41) при верхних наблюдаемых значениях
Таблица 1)4 Сэе; >я i г* ташы и пар ш тры почо кигс явного сю 16а
в азоте в трубке
и й а ео Ху 10-3 7
а о о •
& о а. 7 мА J мА/ Г В/с т к ! N 10 E/N 10 16 . ° 2 ьзга С 10 2 civ 1 10 °5 РР го i j? эф CM3/t
0 65 75 9 5 10 450 1 4 7 1 23 2 0 4 1 410 !8( И 1 0 1 0 ’0
30 3 8 12 390 1 6 7 5 2э 0 67 3 9 '30 190 5 0 60 0 60 6
10 1 3 15 370 1 7 8 8 29 0 22 3 2 /00 180 2 1 0 20 0 32 6
2 0 7 5 9 5 17 520 3 7 4 6 15 2 6 2 1 480 200 6 5 0 73 0 65 1
30 3 8 >3 450 4 3 5 3 17 1 0 2 0 )40 2 )() 4 2 0 48 0 44 1
10 1 3 29 350 5 5 > 7 17 0 33 2 ~ 610 201 2 2 0 26 0 30 0 4
3 9 75 9 5 23 650 5 8 4 0 13 9 9 1 2 >20 ! 90 4 < 0 62 0 60 0 5
30 3 8 31 4э0 8 5 3 (> 12 1 1 1 0 300 180 2 6 0 35 ) 38 0 2
10 1 3 41 420 ) 0 4 > ’5 0 ° 1 2 э80 186 4 о 0 18 G 23 0 2
E!N~(J—8) 10-16 В см2, примерно соответствуют эксперимен
тальным Но при малых значениях Л77У ~ 3,6—4,5 10-16 В см2,
которые реализуются при повышенных давлениях, они на много
порядков меньше экспериментальных Не спасает положения и
учет ступенчатой ионизации метастаби 1ьных молекул, которая
при таких EIN сравнима с прямой ионизациеи \ ведь при дав
лениях в десятки тор реализуются еще меньшие значения EIN,
вплоть до (1,5—2) 1016 В см2 [10 18, 10 19]
В столь слабых полях ионизация идет в ассоциативных реак-
циях типа 1\2 е с участием молекул в высоко
возбужденных колебательных (и > 32) и электронных состоя-
ниях При этом электронно возбужденные молекулы зачастую
образуются не электронным ударом, а при столкновениях коле-
бательно возбужденных молекул с >15 Присутствие в шазме
большого числа молекул с очень высокими и связана с быстро
той обмена колебательными квантами при столкновениях моле-
кул Электронными ударами в разряде возбуждаются низкие ко-
лебательные уровни, что не требует больших значении Е/N При
малых v V — Т релаксация (превращение колебательной энергии
в поступательную) происходит очень медленно Благодаря быст-
рому У — У обмену, идет заселение верхних уровней Там же
в силу ангармоничности колебаний колебательные кванты малы
и именно оттуда происходит гораздо более быстрая, чем внизу,
19* 291
V — Т релаксация. Так осуществляется непрерывный поток мо-
лекул вверх по оси р, который приводит к установлению так на-
зываемого триноровского распределения по колебательной энер-
гии, при котором заселенности верхних уровней больше, чем при
больцмановском.
Все эти и другие процессы детально рассматриваются в ра-
ботах [10.17 — 10.22] в целях наилучшего объяснения механиз-
ма ионизации при низких значениях Е/N, причем в ряде случаев
удается добиться согласия с опытом. Однозначной точки зрения
по поводу конкретного главенствующего механизма, пожалуй,
нет, тем более что роль тех или иных реакций зависит от кон-
кретных условий (Г, N, пе, Те и т. д.) и допущений об их ско-
ростях. Кое-что зависит от ионного состава. Известно, что коэф-
фициент диссоциативной р'екомбинации ионов N^“, которые в
основном присутствуют при низких температурах и высоких
плотностях, на порядок выше, чем для ионов N^:
p(Nt)^i,8.io“\re/3oo)~0’4, KN^-Ke-io-^r./aoo^’W.c"1.
§ 8. Плазма электроотрицательных газов
8.1. Разряд, контролируемый прилипанием. Бывают случаи,
когда основным механизмом гибели электронов является их при-
липание, причем отлипания нет, и прилипание действует в ни-
чем не затемненном виде. Так происходит в кратковременных
разрядах, на ранней стадии (t < 10-5—10-3 с) длительных, пока
не успевает накопиться достаточное количество активных в от-
ношении отлипания молекул. Давление должно быть не слиш-
ком низким, р 10 торр, чтобы не было диффузионных потерь.
Ток и плотность электронов должны быть не чрезмерно больши-
ми, пе < 1012—1013 см 3, чтобы рекомбинация уступала прилипа-
нию. Газ при этом нагреться не успевает.
Прилипание чаще всего идет диссоциативным механизмом,
с затратой энергии (§4 гл. 4). Для реакции СО2 + е
СО + О", основной в лазерных смесях СО2 + N2 + Не, требует-
ся 3,85 эВ*). По этой причине частота va и коэффициент прили-
пания а = Va/Vjj, довольно сильно возрастают с ростом Е/р, хотя
и не стель резко, как частота и коэффициент ионизации, уг, а,
ибо потенциал ионизации в несколько раз больше. В лазерной
смеси ионизуются молекулы СО2, обладающие самым низким
потенциалом Zco2 — 13,8 эВ. Стационарному состоянию отве-
чает равенство скоростей рождения и гибели электронов:
\г(Е/р) = уа(Е/р), а (Е/р) = а(Е/р).
На рис. 10.22, 10.23 показаны результаты расчетов коэффи-
циентов а и а для нескольких смесей на основе решения кине-
*) Ионы О- потом объединяются с молекулами СО2 в устойчивые ком-
плексы со~.
292
Рис. 10.22. Коэффициенты ионизации и прилипания для нескольких лазер-
ных смесей, рассчитанные на основе решения кинетического уравнения
[10.23, 10.24]
тического уравнения. Точка пересечения кривых ионизации и
прилипания определяет ^значение Е/N, необходимое для поддер-
жания разряда, контролируемого прилипанием. Аналогичные ре-
зультаты для другого важного электроотрицательного газа —
воздуха — приводились в п. 2.5 гл. 9. Отношение Е/р для стацио-
нарного разряда, а также отвечающие ему частоты ионизации
и прилипания сведены в табл. 10.5. Данные эти интересны,
Рис 10 23. Констанзы скоростей иони-
зации и прилипания и Те (шкала вни-
зу), рассчитанные на основе решения
кинетического уравнения для смеси
СО2 * N2: Не == 1 : 7 : 12. Кривые кг, ка
пересекаются при E/N = 2,8 • 10“16 В\
X см2, Те = 1,6 эВ, что соответствует
разряду, конзролируемому прилипани-
ем При сильном отлипании, т е. в раз-
ряде, контролируемом рекомбинацией,
кг = (ne/N)^e. При этом Е/N = 1,65 X
ХЮ’16 В • см2, Л = 09 эВ, nel~N =
= 10“7 [10 25]
I________________________________________________________, (
0,5 1,0 1,5 2,0 2,5
293
Таблица 10 5. Поля и частоты ионизации в разряде, кон-
тролируемом при пп«анипм *)
CO2: N2: He Рас чет Эьсперимент
Е/р, В/(см-торр) _ ь'р. 104с торр-1
Е/р, В/(см-торр)
1 : 7 : 30 ** 7.9 0 052 9,1
1:1:8 8.6 0 35 9.5
4:7:12 9,2 8,2
1:2: 3 16,5 1,1 17
1:2:1 23,5
: : 7 : 0 25 28
1:0:9 6
Азот ***) 22,3
Азот 1 °6 H2O 97
В03Д5 x 41 30
*) Расчеты [10 24], за иск печением смеси 1 7 12 [10 25] и воз-
духа (п 2 5 гч 9), эксперимент [10 2J ]
**) Отношение чисе i молекул
***) Технический азот (не очень чистый, примесь О_> и др. 0,2 %).
в частности, тем, что указывают верхние пределы, поскольку
отлипание снижает потери и облегчает поддержание плазмы.
В табл. 10.5 приведены и опытные данные [10.23], которые
неплохо согласуются с расчетом. Измерения были сделаны в им-
пульсных разрядах между плоскими медными электродами пло-
щадью 29 см2, разделенными расстояниями 1,2—4,2 см при дав-
лениях 100—1200 торр. При таких больших давлениях напря-
жения на разряде велики, достигают 10 кВ. Катодное падение —
200 В, так Что почти все падение потенциала приходится на
положительный столб. Менее чем за 0.1 мкс от момента зажи-
гания устанавливалось квазгЛзтационарное напряжение на элек-
тродах, и оно держалось порядка 10 мкс. Напряжение и Е!р
в данной смеси не зависели от значения тока при его изменении
на несколько порядков: j/p ~ 10”1 —102 мА/(см2 • торр) (строго
горизонтальная ВАХ). При добавлении долей процента паров
воды отмечалось повышение напряжения, вызванное возрастани-
ем прилипания.
8.2. Зарядовая кинетика при действии отлипания. При тех не
слишком низких давлениях р > 10 торр, которые обычно исполь-
зуются в лазерных разрядах, диффузионные потери зарядов иг-
рают подчиненную роль. Объемные процессы с участием отрица-
тельных ионов, которые в целом определяют плотность электро-
нов и проводимость смеси, описываются системой уравнений
кинетики для плотностей зарядов пе, п_, п+:
dnjdt = kflrie — kaNne + kdNn_ — $enen+,
dn_.ldt — kaNnc — kdNn_ — $-n_n+, (10.28)
dn+ldt = kvNne — (fiene + $_n-)n+.
294
Здесь ktN = Vi, kaN = ya, kd — константа скорости отлипания, рас-
считанная на одну любую молекулу (предполагается, что кон-
центрация активных молекул стабилизировалась), и р_—
коэффициенты электронно-ионной и ион-ионной рекомбинации.
Независимых дифференциальных уравнений только два; третье
эквивалентно ус товию электронейтральности пе + п_ = п+. На ос-
нове этих уравнений можно рассматривать и нестационарные
процессы, скажем распад плазмы.
8.3. Эффективный коэффициент рекомбинации. Если процес-
сы отлипания идут быстро и в значительной мере компенсируют
прилипание, систему (10.28) можно приближенно свести к одному
уравнению кинетики для плотности электронов [10.26]. Допус-
тим, что отрицательные ионы разрушаются в актах отлипания
гораздо скорее, чем рекомбинируют, kdN $_п+. Тогда устанав-
ливается приближенное динамическое равновесие между прили-
панием и отлипанием: капе ~ kdn_. Отношение чисел электронов
и отрицательных ионов сохраняется постоянным, n_lne~kalkd^
= ц, хотя сами числа пе, п_ могут медленно изменяться. В таких
условиях п+ ~ пе (1 + ц) и третье уравнение (10.28) дает
dne dt = kzNne (1 ц) — (ре p_rj) Пе. (10.29)
Первый член справа можно трактовать так, как будто в акте
ионизации рождается не один электрон, а меньше. Те электроны,
которые быстро исчезают вследствие прилипания, как бы вовсе
«не рождаются». Скорость рекомбинации электронов как бы воз-
растет из-за того, что, объединившись с молекулой, электрон
пропадает в ходе ион-ионной рекомбинации. Если рассматривать
распад плазмы, когда нет первого члена, описывающего рожде-
ние, то величина
рэф=ре+Р-П, v} = kjkd, (10.30)
играет роль эффективного коэффициента рекомбинации. Ести же
рассматривать стационарное состояние, то уравнение баланса
числа электронов можно представить так:
krNne (1 ц) - р_ц) п2е Р.фИе. (10.31)
Оно выглядит так, как будто ионизация идет обычным порядком
с истинной частотой уг = kzN, отрицательных ионов вообще нет,
но электроны рекомбинируют с еще более высоким эффективным
коэффициентом
Рзф = (1 -г ц) (Ре Р-Ц)< Ц (10.32)
8.4. ВАХ; зарядовый состав плазмы и скорость отлипания.
Можно лишь строить предположения о том, какие частицы ак-
тивно разрушают отрицательные ионы (п. 4.3 гл. 4). Данные о
константе скорости отлипания в настоящее время получают кос-
венным путем, сопоставляя экспериментальную ВАХ стационар-
ного разряда в электроотрицательном газе с расчетами, сделан-
295
ными в разных предположениях о kd. Пример такого анализа
[10.27], который дает и зарядовый состав плазмы, демонстри-
руется рис. 10.24. Треугольниками и кружками показаны экспе-
риментальные ВАХ разряда в смеси СО2: N2: Не = 1 : 7 : 12 при
давлениях 40 и 20 торр соответственно [10.28]. Разряд (продоль-
ный) горел в плоском
Рис. 10 24 Эксперименталь-
ные [10 28] и расчетные
[10 27] ВАХ разряда в сме-
си СО2 • N2 • Не = 1 7 • 12
Цифры вдоль кривых, вы-
бранных в качестве «совпа-
дающих» с эксперимен-
том,— значения Е/N в
10"16 В • см2 (выбрано kd —
= 9 • 10"15 см3/с)
канале сечением 5X15 см2 и длиной
вдоль поля 46 см (рис. 10.16). В том
же направлении прокачивался газ со
скоростью 100 м/с, с целью вывода теп-
ла из разрядного объема. Газовый по-
ток не оказывает сильного воздействия
па сам разряд и лишь предотвращает
перегрев газа. Согласно эксперимен-
тальным ВАХ отношение Е/р в дан-
ных условиях довольно слабо зависит
от тока и давления и равно в сред-
нем Е/р ~ 7 В/ (см • торр) (Е/N ~ 2,1 X
X 10-16 В см2).
На том же рис. 10.24 представлены
результаты расчета ВАХ на основе ста-
ционарных равенств (10.28). Констан-
ты скоростей кг, ка взяты с рис. 10.23,
положено = 10“7 см3/с, учтены
такие детали, как прпэлектродпые па-
дения потенциала, нагрев газа, и вы-
бран ряд значений kd от 0 до Видно,
чю оба крайних предположения — отли-
пания нет (kd = 0) и отлипание пол-
ностью компенсирует прилипание (kd =
= 00)— противоречат эксперименту.
Наилучшее согласие с опытом получа-
ется при значении kd = 9 • 10-15 см3/с.
Если предположить, что сечение отлипания — газокинетическое,
число активных молекул составляет порядка 10~4 от их полного
числа, что представляется разумным. Экспериментальному значе-
нию Е/р~1 соответствуют константы скоростей кг = 1,5 X
X 10“14 см3/с, ка = 6 • 10~14 см3/с. При р = 20 торр N = 6,7 • 1017 см“3
и частоты vt = Ю4 с-1, va = 4 • 104 с-1. В плазме присутствует
много отрицательных ионов: ц = п_/пе = ka/kd ~ 5,3. Эффективный
коэффициент рекомбинации электронов [Гф 40(Je ^4-10 6 см3/с
очень велик, в 40 раз больше фактического (из-за прилипания).
Отлипание на 80 % компенсирует прилипание.
Демонстрацией сильного действия отлипания служит ВАХ
стационарного разряда в трубке, наполненной воздухом
(рис. 10.18). Об этом говорилось в п. 6.3.
296
§ 9. Разряд в быстром потоке газа
Газ прокачивают через разряд с целью вывода джоулева теп-
ла, предотвращения перегрева самого газа и стенок разрядной
камеры. Опыты свидетельствуют о разной степени влияния ско-
рости потока на горение стационарного разряда, однако все схо-
дя! ся на одном: с увеличением скорости напряжение горения в
большей или меньшей мере, но только повышается. Это говорит
об увеличении потерь зарядов, которое должно быть скомпенси-
ровано повышенной ионизацией. Мыслимы несколько механиз-
мов воздействия потока.
9.1. Турбулентный вынос зарядов к стенкам. В достаточно
быстром потоке газ турбулизуется. Зачастую, в особенности в
мощных лазерных установках, намеренно организуют ме гко-
масштабную турбулентность, так как это способствует повыше-
нию устойчивости разряда и увеличению верхнего предела энер-
ювклада. Действие турбулентного перемешивания объемов ила j
мы сродни амбиполярной диффузии. Оно выносит сильнее
ионизованные объемы из центральных областей к стенкам и,
наоборот, слабее ионизованные — с периферии к оси. Этот меха-
низм может оказать воздействие в случае разряда без потока,
контролируемого диффузией, т. е. при пониженных давлениях,
в тонких трубках или узких каналах. Описать эффект можно
путем добавления к коэффициенту амбиполярной диффузии Da
коэффициента турбулентной.
Для последнего в газовой динамике существует несколько
эмпирических формул (влияние слабой ионизации на турбулент-
ность вряд ли существенно). В частности, если и [см/с] — сред-
няя скорость потока, а [см] — радикс трубки или половина высо-
ты птоского канала, то
Отзрб ~ 0,009 аи см2/с. (10.33)
В опыте, о котором шла речь в п. 8.4, например, а = 2,5 см, и =»
= 104 см/с, £>тхрб = 225 см2/с. Это значение в несколько раз боль-
ше Da^lb см2/с при р = 40 торр, но все равно частота суммар-
ных «диффузионных» потерь vdr = (Da + DTvp6) (л/2а)2 ~ 120 с"1
меньше частоты объемных (104 с-1), так что в данных конкрет-
ных условиях роль турбулентной диффузии невелика.
9.2. Конвективный вынос зарядов. Потеря зарядов из токово-
го канала, связанная с увлечением их газовым потоком, может
сказаться, если длина разряда вдоль потока L\ мала. Такое слу-
чается в поперечных разрядах, когда длина по крайней мере
одного из электродов гораздо меньше расстояния между электро-
дами. «Частота конвективного выноса» равна vF ~ 2u/L\. По-ви-
димому, этот механизм действовал в опытах [10.29] с воздухом,
результаты которого показаны на рис. 10.25. Катодом служила
узкая (вдоль потока) полоса 0,4X40 мм2, анод — сплошная
297
Рис. 10.25. Зависимость на-
пряжения горения попереч-
ного разряда в воздухе oi
скорости потока [10 29]
пластина, расстояние между электродами 3 см. Если в области
положительного столба Li ~ 1 см, то при и ~ 100 м/с vF ~
— 104 с"1, что сравнимо с частотой объемных потерь. Значения
Е/р, оцененные по данным рис. 10.25, возрастают от 15 до 25 в
диапазоне и ~ 50—180 м/с. В случае протяженных вдоль потока
поперечных разрядов, когда геометрия разряда близка к показан-
ной на рис. 10.1а, напряжение горения мало зависит от скорости
потока. Действительно, в каком-нибудь
серединном поперечном сечении кана-
ла заряды слева приходят в слой, спра-
ва уходят из него, а в целом их проте-
кание баланса пе нарушает.
9.3 Влияние на накопление актив-
ных в отношении отлипания молекул.
Оно сходно с действием времени, о чем
говорилось в п. 8.1. Если макроскопи-
ческая газовая частица, протекающая
через разряд, проводит в нем мало вре-
мени, в ней не успевает накопиться то
число активных молекул, которое соот-
ветствует установившимся условиям.
Тогда чем быстрее протекает газ через
разряд, тем в меньшей степени прили-
пание электронов компенсируется отлипанием, что эквивалентно
росту потерь (на прилипание). Если характерные времена уста-
новления стационарной концентрации активных молекул состав-
ляют 10-5 —10“3 с, то скорость должна влиять на разряд в элект-
роотрицательных газах, если время пролета газовой частицы через
разряд LJu как раз такого порядка. Не исключено, что этот
эффект действовал наряду с конвективным выносом в опыте
[10.29]; рис. 10.25.
В длинных продольных самостоятельных разрядах не отме-
чалось заметного влияния скорости потока на напряжение го-
рения разряда (рис. 10.26). В этих опытах [10.30] разряд горел
/2
I । ।----1-----г
р = 25 торр
и-120 м/с 220
8\______L_
О 0,10
о,ъо
i,A
0.50
Рис 10.26. ВАХ продольного разря-
да в потоке для смеси СО2: N2 • Не —
= 1 : 2,5 • 15 [10 30]
в плоском канале (рис. 10.16) высотой 5,5 см, шириной 76 см
и с расстоянием между электродами L = L\ = 65 см. Время про-
лета даже при и = 220 м/с весьма велико: rF = L\/u = 3 • 10~3 с.
Видимо, концентрация активных молекул в используемой смеси
СО2: N2 : Не = 1 : 2,5 : 15 стабилизировалась. Частота диффузион-
ных и турбулентных потерь в данных условиях невелика: Da-\-
+ -DTvpG«650 см2/с, Vdr ~ 220 с-1. В более коротких разрядах
наблюдается рост напряжения при увеличении скорости (в само-
298
стоятельном разряде). В несамостоятельном (п. 4.5 гл. 16) — за-
висимость V от и всегда сильная. Надо сказать, что вопрос о
влиянии скорости на характеристики продольного разряда изу-
чен еще недостаточно. Разрядам в поперечном потоке посвящен
обзор [10.31].
§ 10. Анодный слой
10.1. Рождение ионов. Поскольку анод пе эмитирует и от-
талкивает положительные ионы, у самой поверхности металла их
нет. Между анодом и электронейтральноп плазмой положитель-
ного столба имеется слой отрицательного объемного заряда, в ко-
тором поле уменьшается в направлении от анода к столбу.
Плотность электронного тока ]е изменяется в слое на незначи-
тельную величину (ц+/це)/, а плотность ионного /+ вырастает
от нуля до /+с = (ц+/ре) / в плазме. Ионный ток /+с, втекаю-
щий в положительный столб, образуется в результате рождения
зарядов в анодном слое, причем для этого электрону достаточно
произвести ничтожное число ионизаций ц+/це. В самом деле,
dj^ldx = aje ж а;, /+с ~ 7 adx, j adx = ц+/це.
Это число на три порядка меньше числа поколений электронов,
которые рождаются в катодном слое. Поэтому анодное падение
потенциала VA много меньше катодного.
10.2. Падение потенциала и плотность тока. Согласно старым
измерениям [5, 10.32] в трубках при р < 1 —10 торр, ~ Ю—
20 В, причем значение анодного Падения в каждом газе сопоста-
вимо с его потенциалом ионизации. Плотность тока на аноде
имеет порядок 10-4—10~3 А/см2; в азоте вблизи анода измерены
поля Е/р ~ 600—200 В/(см торр), чему отвечает толщина слоя
dA~ 0,05/р см порядка длины пробега электрона I. В работах
последнего времени показано, что при средних давлениях анод-
ное падение увеличивается с ростом давления, в электроотрица-
тельных газах больше (рис. 10.27). Согласно [10.33] в азоте в
диапазоне р ~ 5—30 торр плотность тока на аноде ]!р2 ~ 4,3 X
ХЮ-4 Azz(cm • торр)2; в воздухе при р~8—60 торр /7р?~2,7Х
X 10~4 А/(см • торр)2, независимо от значения тока. (Исследовался
разряд между плоскими стальными электродами диаметром 1,6 см.)
Измеренные значения j/p2 очень близки к нормальным значе-
ниям на катоде (табл. 10.3). По всей видимости в условиях,
когда диаметр токового сголба в промежутке не меньше меж-
электродного расстояния, нормальный катодный слой навязывает
значение j всему столбу, включая анод. По расчетам [10.4] в
таких случаях на аноде повторяется даже радиальное распреде-
ление j(r), задаваемое катодом (рис. 10.6). Рассчитанное в азоте
анодное падение (рис. 10.6) хорошо согласуется с измеренным
(рис. 10.27). При малых токах анодное пятно получается ма-
леньким. Его радиус гА по результатам численного эксперимен-
299
Рис. 10.27. Анодное падение разря-
да в азоте и воздухе в зависимости
от давления [10.33]
та [10.4] определяется размытием вследствие поперечной (ради-
альной) диффузии электронов и связан с толщиной анодного
слоя (pdA & 0,25 торр • см) характерным для диффузии соотно-
шением гА ~ (DedA!v^)~
^^(Л/СА)1/2*).
10.3. Пронизывают ли поло-
жительный столб ионы, рож-
денные в анодном слое? Очень
часто — нет. Вероятность иону
погибнуть в раз больше,
чем электрону,— во столько раз
дольше ион дрейфует через
столб. В примере, приведенном
в п. 6.2 (формула (10.19)), ве-
роятность составляет 0,2 на 1 см
длины столба, т. е. столб длиною 5 см ионы не пропускает. Мы
отвлекаемся здесь от возможных процессов резонансной переза-
рядки, в результате которой один ион незамедлительно заме-
няется точно таким же другим,— это уже пе «гибель» в обычном
понимании.
В продольных разрядах, горящих в потоке газа, поток чаще
всего направляют от катода к аноду, дабы сразу же выносить
из разряда возмущения, которые рождаются в анодной области.
Используемые в нынешней практике скорости и ~ 100—200 м/с
сравнимы со скоростями дрейфа ионов г+д. Например, в самосто-
ятельном разряде в смеси СО2: N2: Не = 1: 7 :12 Е!р~
ж 7 В/(см • торр), для основных положительных ионов GOtр+д ~
^220 м/с. Быстрый поток тормозит ионы, а при и > г+д вооб-
ще должен «сдувать» их. Положительные ионы при этом, во-
преки естественному <оду вещей, увлекаются потоком против по-
ля, в сторону анода. Это, однако, не может помешать протеканию
электрического тока в разряде, ибо он переносится электрона-
ми [10.5].
Глава И. НЕУСТОЙЧИВОСТИ ТЛЕЮЩЕГО РАЗРЯДА
И ИХ ПОСЛЕДСТВИЯ
§ 1. От чего возникают и к чему приводят неустойчивости
Однородное состояние положительного столба тлеющего раз-
ряда часто оказывается неустойчивым, в особенности, когда раз-
ряд происходит в больших объемах, при повышенных давлениях,
когда сильны ток и выделение джоулева тепла. Случайные воз-
мущения катастрофически нарастают, и плазма переходит в иное.
пространственно неоднородное состояние. Вызываемые неустой-
*) Результаты [10.4] не подтверждают теоретическую модель, предло-
женную в [10.33].
300
чивостями неоднородные формации: страты — разбиение положи-
тельного столба вдоль тока на чередующиеся светлые и темные
слои, контракция — стягивание плазмы в ярко светящийся то-
ковый шнур, известны давно. Но в последнее время эти эффек-
ты стали объектом особого внимания из-за тех затруднений, ко-
торые они вызывают при создании мощных газовых лазеров. На
лазерную генерацию неустойчивости оказывают губительное дей-
ствие. Преодоление тенденции к шнурованию разряда вылилось
в центральную и самую трудную проблему при создании мощ-
ных электроразрядных лазеров (гл. 16). Эффективная борьба за
устойчивость требует глубокого проникновения в природу раз-
рядных процессов и механизмов неустойчивостей. Современные
усилия в этом направлении существенным образом расширили
знания, касающиеся такого классического объекта, как тлеющий
разряд*).
1.1. Феноменологический признак устойчивости или неустой-
чивости. Неоднородность плазмы нередко видна па глаз. Неоди-
наковость свечения вызывается в первую очередь неодинаковой
плотностью электронов. Стало быть, причины, приводящие к не-
однородности, связаны с процессами, которые управляют плот-
ностью электронов, их рождением, гибелью, переносом в прост-
ранстве. Запишем символическое уравнение кинетики элект-
ронов
dneldt = Z+ —Z-. (11.1)
Стационарному состоянию отвечает равенство скоростей их
рождения и гибели: Z Z,. Скорости зависят от пе и других
параметров: электронной температуры пли поля, плотностей от-
рицательных ионов, возбужденных атомов и т. д., причем эта
Рис 11 1 Качественная кар-
тина расположения кривых
скоростей рождения и гибели
электронов в окрестностях ус-
тойчивого («) и неустойчиво-
го (б) состоянии
зависимость может выражаться через дифференциальные урав-
нения, как (10.28). Поэтому в общем случае говорить о функ-
циональной связи Z+, Z- с пе можно лишь качественно. Точке
пересечения символических функций Z±(ne) (рис. 11.1) соответ-
ствует стационарная плотность электронов , которая в ко-
нечном счете определяется внешними условиями: ЭДС источни-
ка, геометрией, более непосредственно — значением тока, пропус-
камого через разряд.
Об устойчивости стационарного состояния можно судить по
взаимному расположению кривых в его окрестности. Если при
*) Мы вынуждены лишь кратко остановиться на самых общих, ключе-
вых моментах этой обширной темы. Ей посвящены обзоры [11.1—11.5], где
имеется подробная библиография.
301
ne Z> nf* кривая гибели Z_ проходит выше, а при пе <Z п^ —
ниже кривой рождения Z+ (рис. 11.1а), состояние устойчиво,
ибо при случайном отклонении от равновесия, система к нему
возвращается. В противном случае, показанном на рис. 11.16,
состояние не устойчиво: при случайном возрастании пе рожде-
ние становится больше гибели и число электронов увеличивается
еще сильнее. Важно лишь взаимное расположение кривых Z+,
Z_, но не их абсолютный ход.
1.2. Стабилизирующие и дестабилизирующие факторы. Ука-
занные соображения позволяют качественно квалифицировать
влияние различных факторов на устойчивость. Пусть электроны
рождаются путем ионизации атомов электронным ударом из ос-
новного состояния, причем электронная температура не чувстви-
тельна к пе\ при этом Z+ = уг (Ге) пе — пе. Объемная рекомбина-
ция Z_ = $п] способствует устойчивости разряда, так как она
придает гибели более сильную, квадратичную зависимость от тге.
Стабилизирует разряд внешнее сопротивление', если пе и ток
возрастают, напряжение, поле, электронная температура и, как
следствие, частота ионизации уг уменьшаются. Благодаря такой
цепочке связей функции Z+ (пе) растет с пе медленнее, чем про-
порционально пе. По этой причине однородный разряд, контроли-
руемый амбиполярной диффузией, когда Z_ = ydne — тге, до поры
до времени оказывается устойчивым. То же относится и к разря-
ду, контролируемому объемной рекомбинацией. Диффузия и теп-
лопроводность помогают рассасыванию неоднородностей плотно-
стей частиц и температуры и потому принадлежат к числу ста-
билизирующих факторов.
Дестабилизирующую роль играет нагрев газа. Поскольку
давление в газе выравнивается быстро, локальное повышение
газовой температуры сопровождается уменьшением плотности
(тепловым расширением). На значении поля это непосредствен-
но не сказывается, но отношение Е/N и зависящая от него элект-
ронная температура возрастают. Это ведет к усилению иониза-
ции, локальному повышению проводимости, плотности тока и
выделения джоулева тепла. В результате газ нагревается еще
сильнее. Это — так называемая ионизационно-перегревная неус-
тойчивость, наиболее распространенная и опасная.
Дестабилизируют разряд ступенчатая ионизация и накопле-
ние метастабильных атомов и молекул. При повышении пе рож-
дается больше возбужденных частиц, и к ионизации из основного
состояния присоединяется ионизация возбужденных частиц, ко-
торая протекает гораздо легче, ибо энергия связи электрона у
них меньше. Скорость рождения электронов Z+ растет с пе, сле-
довательно, быстрее, чем уг{Те}пе. В дальнейшем будут указаны
и другие механизмы дестабилизации разряда. В сущности, вопрос
об устойчивости состояния решается тем, кто выйдет победите-
лем в соревновании дестабилизирующих и стабилизирующих
факторов.
302
Рпс. 11.2 Схемы продольных (а)
и поперечных (б) возмущений
электронной плотности
области с из-
1.3. Продольные и поперечные неоднородности и их резуль-
таты. Развитие неустойчивости, т. е. катастрофическое нараста-
ние первоначально малого возмущения,— процесс нестационар-
ный. К чему-то он должен привести. Здесь мыслимы и действи-
тельно реализуются две возможности: система приходит к
новому, более устойчивому стационарному состоянию или ста-
ционарность вообще не наступает, но поскольку нестационарный
процесс не может развиваться в одном направлении вечно, уста-
навливается периодически изменяющееся состояние*).
Цепочки причинных связей между различными процессами
при развитии возмущений и тот или иной их конечный резуль-
тат зависят от ориентации неоднородностей относительно выде-
ленного направления в разрядном
пространстве — вектора электриче-
ского поля и тока. Если парамет-
ры разряда, скажем плотность
электронов, меняются вдоль поля
(рис. 11.2и), осуществляется вто-
рой случай, т. е. образуются стро
ты — чередующиеся в простра
стве и времени области повыше-
ния и уменьшения пе и других
параметров разряда. Иногда воз-
никают домены — периодически
зарождающиеся и бегущие вдоль
мененными параметрами, например домены сильного поля.
В результате нарастания поперечных полю возмущений
(рис. 11.26) происходит контракция и образуются шнуры с
резко повышенной плотностью тока. Вдоль шнуров в основном
и течет разрядный ток, который при этом возрастает. В трубках
в силу симметрии образуется один шнур на осп, в плоских
каналах шнуров бывает несколько (часто они «бегают»).
1.4. Принципы анализа на устойчивость. Проследить за по-
ведением разряда от начала развития малого возмущения и
вплоть до конечного результата эволюции — дело, как правило,
чрезвычайно сложное. Нередко бывает затруднительной даже
формулировка адекватной физической системы уравнении, не
говоря уже о математических трудностях ее решения. Чаще все-
го ограничиваются куда более скромной задачей: указать области
значений параметров стационарного состояния, отвечающих ус-
тойчивым и неустойчивым состояниям, и в линейном приближе-
нии вычислить начальную скорость нарастания малых возмуще-
ний — инкремент развития неустойчивости. Иногда удается
независимо исследовать конечное, неоднородное состояние, стаци-
онарное или периодическое. Однако решение первой задачи дает
немалую информацию, ибо по начальной скорости в общем мож-
*) В принципе возможна еще нерегулярная, стохастическая периодич-
ность.
303
но судить и о масштабе времени всего перехода к конечному
состоянию через нелинейную стадию.
Пусть однородному стационарному состоянию разрядной си-
стемы соответствуют параметры л4°\ ^е0) и т. д. Для анализа
на устойчивость уравнения, которые описывают поведение пе,
Те ... во времени и пространстве, линеаризуют, представляя
параметры в виде пе = nf* 4~ ... и считая возмущения .
малыми. Решение линейной системы ищут в виде плоской волны
= (6тге)а ехр [j (со£ — Кг) ], где волновой вектор К считают
ориентированным вдоль или поперек поля (косые волны можно
векторно разложить). Физически это следует воспринимать так.
Допустим, нас интересует реакция разряда на определенным об-
разом ориентированное возмущение с пространственным разме-
ром Л (рис. 11.2). В силу линейности уравнений возмущение
всегда можно разложить в интеграл Фурье по плоским волнам и
исследовать каждую из компонент независимо. Ясно, что волно-
вые векторы К при этом направлены вдоль той координаты, по
которой изменяются пе, Те, ..., а в наибольшей мере в интеграле
представлены длины волн порядка Л или К ~ Л-1.
Подстановка волновых решений в линеаризованные уравне
ния дает систему пг однородных алгебраических уравнений отно-
сительно m амплитуд (бпе)а, (STe)a, ... Из условия равенства
нулю детерминанта системы следует дисперсионное уравнение,
связывающее со с К. Если среди пг его комплексных корней най-
дется хотя бы один, у которого Q = Re zco > 0, возмущения будут
нарастать как exp(Q£)- Если таких корней несколько, инкремен-
том послужит наибольшая из Q. Характерное время развития
неустойчивости т = Й^х. Обычно быстрее всего нарастают
длинноволновые возмущешуц которые медленнее рассасываются
диффузией и теплопроводностью. Верхний предел длинам волн
ставят наименьшие размеры разрядного объема (диаметр труб-
ки, высота канала).
§ 2. Квазистационарные параметры
2.1. «Быстрые» и «медленные» процессы. Состояние плазмы,
в особенности в электроотрицательном молекулярном газе, харак-
теризуется большим набором параметров: пе, п_, п+, Те, Т, коле-
бательной температурой 7\, которая может отличаться от посту-
пательной температуры газа Т вследствие замедленности колеба-
тельной релаксации, N, Е, плотностью возбужденных молекул
N*. Все они подчиняются нестационарным уравнениям, которые
в общем случае взаимосвязаны (примером может служить сокра-
щенная система (10.28)). Анализ соответствующего детерминан-
та пг-то порядка с пг ~ 10 был бы немыслимым. Положение об-
легчается тем, что одни процессы в плазме протекают -очень
быстро, другие — медленно. При рассмотрении неустойчивости,
связанной с каким-то определенным процессом и развивающейся
304
за время т, более быстрые процессы приближенно можно счи-
тать релаксирующими «мгновенно». Их параметры подстраива-
ются к мгновенным значениям медленно эволюционирующих,
т. е. в каждый момент являются как бы стационарными (квази-
стационарными). Напротив, очень медленные процессы, мало
развивающиеся во время роста данных возмущений, можно счи-
тать вообще не развивающимися, т. е. «замороженными».
2.2. Временные масштабы различных процессов. Представле-
ние о них дает табл. 11.1. Поясним происхождение некоторых
Таблица I* 4 1. Временные масштабы различных разрядных процессов
в условиях, типичных для разрядов в лазерах непрерывного действия на СО2:
газ — СО2 — N2 К Не, р ~ 10—100 торр, N — 101* см~3, Т « 300—500 К,
Е/р - 10В/(см юрр), Те 1 эВ, Тъ ~ 2000—5000 К, пе ~ 1010см"3, Л — 1 см*)
Процессы Характерное время т, с
I. Релаксация п'Чемнзго заряда 11. Передача энергии при столкно- вениях 1) релаксация температуры элект- Та ('гиг1 io-10—io-9
ронов - (б'™)’1 10 9—10"8
2) нагрев газа ТТ -= 10-3—Ю-2
3) накачка колебаний молекул Ту = NMcvTv'oE2 Ю-3—10-2
4) колебательная релакгац тя III. Кинетика столкновений Тут 10-4—10-2
I) ионизация ц - (у)-’ 10-5 _Ю-4
2) прилипание ц* (W1 10 щ-5
3) отлипание \i - (^’1 10-6—ю-5
4) электронное возбуждение т ♦ — (k *Х')~Г 10-6—10-4
5) электрон-ионная рекомбинация трек (Рел+/) 10-4-10-3
6) ион-ионпая рекомбинация IV. Процессы переноса трек ~ (Р-/г+) 1 10-4—10-3
1) выравнивание давления (звук) A ‘s 10-5—10-4
2) теплопроводность газа тх - X2 Z 10-2
3) амбиполярная диффузия ~da ~ 10-2
4) электронная теплопроводность А = А5 * * 10-5
*) Взято из [И 1]. Некоторые цифры заменены более реальными.
масштабов. Рассасывание объемного заряда р = е (п+ — пе — п_)
в среде с постоянной проводимостью о определяется уравнениями
непрерывности, электростатики и законом Ома:
4- div j = о div Е = ~~ + 4лпр = 0,
dt 1 J dt dt 1 r 2}
p (0 = p (0) exp (— f/Ta), та = (4na)~1.
Время исчезновения объемного заряда та называют плазменным
или максвелловским. Время накачки молекулярных колебаний
20 Ю. П Райзер 305
аналогично времени нагрева газа, нужно только подставить ко-
лебательную теплоемкость съ и плотность молекул 7VM. Колеба-
тельная релаксация характеризуется временем обмена энергией
тут между колебательными и поступательными степенями сво-
боды. Давление выравнивается в пространстве со скоростью зву-
ка cs. Электронная теплопроводность в слабоионизованном газе
приближенно равна Хе = (5/2) kneDe\ соответствующая темпера-
туропроводность = De.
2.3. Квазистационарность тока. Основные неустойчивости раз-
рядной плазмы связаны с кинетикой рождения и гибели электро-
нов, изменением температуры газа, возбуждением электронных и
колебательных уровнен атомов и молекул. Как видно из
табл. 11.1, все это происходит гораздо медленннее, чем рассасыва-
ние объемного заряда. Это позвотяет считать процесс рассасы-
вания «быстрым». Допустим, что в ходе развития неустойчиво-
сти с характерным временем т > га в пространстве как-то пере-
распределяются пе и о. Обобщив (11.2) на случай непостоянства
о, запишем
ор/dt + 4лор + EVq = 0. (11.3)
Объемный заряд р, который отсутствует в однородном стаци-
онарном состоянии, сам является «возмущением». Он, как и все
другие возмущения, изменяется со скоростью нарушения одно-
родности плазмы. Следовательно, первый чтен в (11.3) имеет
порядок р/т, и он гораздо меньше второго, р/та. Последние два
очень больших по абсолютному значению слагаемых, которые в
сумме образуют div j, компенсируют друг друга с точностью до
относительно малой величины р/т. Значит, в (11.3) можно пре-
небречь производной dpl^t и в каждый момент времени считать
div j = 0, как и в истинно стационарных устовиях.
В одномерных случаях плотность тока всегда однородна в
пространстве и может зависеть только от времени. В направле-
нии, перпендикулярном Е, электрическая цепь разомкнута и по-
перечного тока, следовательно, вообще быть не может, даже если
проводимость в этом направлении претерпевает какие-то изме-
нения (как при шнуровании). Поперечный ток отсутствует
вследствие компенсации дрейфовой и диффузионной составляю-
щих (§ 6 гл. 3). Последняя в (11.2), (11.3) не включена.
В случае продольных неоднородностей (страты) j вдоль поля
остается неизменной. Если мы «навязываем» продольным возму-
щениям вид плоских волн, = 0. При КИЕ, К #= 0 dj = 0, т. е.
ток не меняется не только в пространстве, но и во времени.
2.4. Квазистационарность электронной температуры. Установ-
ление средней энергии электронов в результате столкновений
является одним из самых быстрых процессов, особенно в моле-
кулярном газе. Как видно из табл. 11.1, он уступает по скорости
только релаксации объемного заряда. Поэтому при развитии боль-
шинства неустойчивости электронная температура остается ква-
зистанционарной. Она «следит» за более медленными изменениями
306
других величин. В упрощенном уравнении баланса энергии элект-
рона (3.12) (с учетом (3.17)) dzldt — Те[х. При т > тм — боль-
шие, порядка Те!хи, слагаемые в правой части компенсируют
друг друга с высокой точностью. Таким образом, Те связана с
Е/N соотношением, вытекающим из (3.12) при условии стацио-
нарности энергии электрона. Получается та же формула (3.15),
только теперь мы не будем делать допущения о независимости
vm и 61 от Те:
E/N = (3mkTeVmVu/2e2)1/2, vm и (Те) =xm U/N. (11.4)
Во избежание путаницы долю энергии, теряемую электроном при
столкновении, в этой главе обозначаем 6ь
2.5. Нарушения квазистационарности Те. Они возможны,
когда поле заметно меняется на длине установления электронной
температуры Аи (3.18). Чтобы выяснить, когда это случается, со-
поставим порядки величин различных слагаемых в общем урав-
нении энергии электронов (3.52) с (3.19), где в отличие от (3.12)
принята во внимание пространственная неоднородность. Сравним
конвективный член в dljdt, содержащий (с ним совпадает
по порядку величины и член электронного давления), скорость
теплопроводностного тепчообмена в электронном газе и скорость
передачи энергии молекулам. Поскольку кТе ~ еЕАи, эти слагае-
мые относятся как 1 : Ам/А: А/Аи. Очень мелкие неоднородности
с А « Аи быстро выравнивает теплопроводность. В случае А > Аи
преобладает локальная передача энергии молекулам и Те квази-
стационарна. Так бывает в молекулярных лазерных разрядах
(при р = 30 торр длина пробега электронов Z ~ 10“3 см, 61 ~
~ 10~2, Аи~10~2 см, а А~1 см). Если же А ~ Аи и все три
слагаемых имеют один порядок, локальной квазистационарной
связи между Те и Е не существует. Температура электронов из-
меняется вдоль направления изменения А1, «отставая» от изме-
нений Е из-за относительной медленности релаксации. Так про-
исходит в стратах в инертных газах, когда I ~ 10~2 см, §i~ 10-1—
10~5, Аи ~ 1 см, а А порядка диаметра трубки, тоже 1 см.
§ 3. Возмущения поля и электронной температуры
в условиях ее квазистационарности
3.1. Потенциальность поля. В стационарном процессе могут
возникать переменные магнитные поля, связанные с изменениями
электрического поля и возможными изменениями тока проводи-
мости. С помощью уравнений Максвелла (5.13), (5.14) и данных
табл. 11.1 легко оценить, что индуцируемое вихревое электриче-
ское поле составляет ничтожную долю от возмущений §Е. Воз-
мущенное электрическое поле с колоссальной точностью является
потенциальным и удовлетворяет стационарному уравнению
rotE = 0. Как следует из этого уравнения, в одномерных случаях
претерпевать изменения в пространстве может только составля-
20*
307
ющая Е вдоль направления изменения всех параметров. Это и
не удивительно. Возмущения поля вызываются объемными заря-
дами, и поле поляризации ориентировано вдоль направления
смещения зарядов. Для плоских волн получаем [КбЕ] = 0, отку-
да при К =/= О 6ЕНК.
3.2. Поперечные неоднородности. Если К -Ь Е, то 6Е -L Е. Воз-
мущение абсолютного значения поля
б|Е| = VE2 + (6E)2-E~ (6£)W
имеет второй порядок малости, можно сказать отсутствует. Вдоль
направления дрейфа электронов все параметры неизменны и ус-
тановлению Те ничто не мешает. Температура электронов квазп-
стационарна. При практически неизменной величине поля, она
может измениться только в результате изменения плотности га-
за N Так и происходит при нагревании газа. Вследствие тепло-
вого расширения, электронная температура и скорость иониза-
ции возрастают.
Согласно (11.4) возмущение Те связано с возмущением плот-
ности газа соотношением
е__ £ 6Л _ 2 ___ d In V
~е = — * Л"' 1-Г I ; ’ v = d in •
(И-5)
Числовой коэффициент § всегда положителен и имеет порядок
единицы. Если Z(Te) = const и 6i (Те) = const, то vmu ~ VТе, g = 1.
3.3. Связь продольных возмущений Те, Еппе В случае
продольных неоднородностей поле возмущается, причем ЙЕНЕ, но
ток остается неизменным (п. 2.3). Значит, 8Е/Е = — бо/о *). Про-
дольные неустойчивости развиваются обычно за счет механизмов
нетепловой природы, которые действуют гораздо быстрее, чем
успевают произойти какие-либо изменения температуры и плот-
ности газа. Поэтому N в данном случае является параметром
замороженным. Согласно (11.4)
8Те/Те = &Е/Е, (11.6)
температура Те выше там, где сильнее поле Варьируя о =
= е2пе1тпчт с N = const, получаем
бо/о = 8пе1пе — vm8Te!Te = —8Е/Е,
и исключая 8EIE с помощью (11.6), свяжем возмущения темпе-
ратуры и плотности электронов [11.1]:
^ = — l+vu — Vm (11.7)
ТВ Vu П(
Множитель 2/х tz. = 2/(1 + 6Х) безусловно положителен и
имеет порядок единицы. Таким образом, в случае продольных
неоднородностей поле и электронная температура понижаются в
*) Мы пренебрегаем диффузионным током электронов /Диф, ибо в тех
случаях, когда Л » Аи и Те квазпстационарна, он мал по сравнению с дрей-
фовым Действительно, согласно (3 41), (3 24), (3 19) ;Диф/оЕ — Лм/Л 1
308
местах с повышенной плотностью электронов, и наоборот. Физи-
ческий механизм, который к этому приводит, поясняется рис. 11.3.
Рис. 11.3. Схема, поясняющая причину
уменьшения Е и Тс в области повышения
пе. Сдвиг пе (штриховая кривая) относи-
тельно п+ (сплошная кривая) обязан
дрейфу электронов В области впадины п
ноле поляризации ЬЕ складывается с внеш-
ним полем Е, в области горба поля вычи-
таются
Предполагается, что размер неоднородности Л гораздо больше
дебаевского радиуса dD (при Те 1 эВ, пе ~ 1010 см-3 dD ~
~ 10~2 см), так что плотности тге, п± возмущаются «вместе».
§ 4. Ионизационно-перегревная неустойчивость
Ионизационно-иерегревную неустойчивость иногда кратко на-
зывают тепловой. Это — наиболее распространенный, можно ска-
зать, универсальный механизм, который мешает однородному
горению разряда при повышенных давлениях и достаточно силь-
ных токах и в атомарных, и в молекулярных газах, и в трубках,
и в {плоских каналах. Он неизменно приводит к контракции
разряда, образованию токовых шнуров, в которых степень иони-
зации и температура газа резко повышены по сравнению с обыч-
ным тлеющим разрядом. Развивается неустойчивость из попереч-
ных неоднородностей. Поле Е остается однородным вдоль на-
правления тока и изменяется по величине только в связи с
уменьшением напряжения на электродах вследствие возрастания
тока и падения напряжения на внешнем сопротивлении. Впервые
тепловая неустойчивость исследовалась еще до возникновения
проблемы мощных лазеров применительно к разряду в трубке,
контролируемому диффузией зарядов к стенкам [11.6].
Механизм неустойчивости, разъясненный в п. 1.2, отражается
следующей замкнутой цепочкой причинных связей, которую мож-
но начать с любого звена:
Ьпе\ - 6 (/£) f - Ш ёМ + 6 (£/7V) t - 8Тл ё^Л. (11.8)
Стрелки вверх (вниз) символизируют возрастание (уменьшение)
величины. Скорость нарастания возмущений лимитируется наи-
более медленным звеном — нагреванием газа. Плотность элект-
ронов, электронную температуру, как и связь газовой темпера-
туры с плотностью через постоянство давления p~NkT = const,
можно считать квазистационарными, соответствующими мгновен-
ному значению EIN.
4.1. Порог и инкремент. Установим критические (пороговые)
условия для возникновения нестабильности и оценим инкремент
309
ее нарастания. Определяющим параметром является газовая
температура Г, которая подчиняется уравнению баланса энергии
газа. Уравнение баланса (10.23) записано для усредненных по
пространству величин, но это делу не мешает. Мелкие простран-
ственные неоднородности не представляют большой опасности,
так как быстро рассасываются теплопроводностью. Наиболее
опасны возмущения с длиной волны Л порядка размеров объема.
Но уход тепла из всего объема в уравнении (10.23) учитывается
(этот фактор — стабилизирующий).
Составить уравнение для возмущений 8Т проще всего, про-
варьировав уравнение (10.23) на фоне стационарного состояния
(10.24). В случае теплопроводностного выноса тепла vT ~ х ~
~ N~\ в случае конвективного — NvF ~ Nu — const в силу закона
сохранения массы (постоянства расхода в потоке). В обоих слу-
чаях произведение NvT F не возмущается. В слагаемом JE = gE2
будем варьировать только наиболее резко меняющийся сомножи-
тель — пе. Частоту столкновений приближенно считаем постоян-
ной, так как при варьировании произведения vm = Nvm(Te) ва-
риации сомножителей согласно (11.5) имеют разные знаки и час-
тично компенсируют друг друга. Полагая после варьирования
6Т ~ exp Qt, получим
о о 61nzz. о ОА2 у-1оЕ2 Qx
Q -= V! тег - VT'F- = = —V’ (119)
0 — 1
где vt ~ — ооратное значение характерного времени на-
гревания газа вдвое при невозмущенном значении Т; 7 — показа-
тель адиабаты. Чтобы связать пе и Т, опишем гибель электронов
при помощи эффективного коэффициента рекомбинации (10.32).
Поскольку рождение и гибель электронов — процессы быстрые по
сравнению с нагреванием, плотность электронов квазистацио-
нарна:
= v,[Te(£,A9]p^ N = P!kT. (11.10)
Проварьируем эти равенства в предположении рэф(7’(,) =
= const, что впочне допустимо. С учетом (11.5) находим
6 In пе ~ 6 In Те — d In
дТпТ = — v’ 6 In Л = ^V1? d In Те-
(11.11)
Плотность электронов гораздо более чувствительна к нагреванию,
чем Те, так как в отличие от g, vt — число большое. Физический
смысл его очень нагляден в случае максвелловского распределе-
ния электронов, когда
Ч - exp(-Z/*Te), vx = I!kTe ~ 5-10. (11.12)
Подставляя (11.11) в (11.9) и полагая для краткости £ == 1, по-
лучаем очень простую и наглядную формулу
Q = — vr,F, J in v^d In (T/7V). (11.13)
310
Выписанное определение хг справедливо в предположении Те ~
~E/N. Это удобно при аппроксимации vz(E/N) таунсендовской
функцией.
Согласно (11.13) неустойчивость возникает (Q>0), только
когда ток и тепловыделение превышают некоторый порог:
]Е > Nc^Tvt,^ «(0,1-0,2)NcpiTvTF. (11.14)
Порог этот согласно (10.24) соответствует нагреванию газа на
10—20%. Вследствие резкой зависимости частоты ионизации от
Те ~ Е/N ~ Г, именно такое повышение температуры приводит к
сильному возрастанию скорости ионизации, в е раз, что и ведет
к «разгону» системы. Теплоотвод стабилизирует процесс, его уве-
личение повышает порог неустойчивости. При теплопроводност-
пом механизме охлаждения, как в трубках, уг = т71~ р"1 и по-
рог (]Е)кр от давления не зависит. Поскольку Е/р & const, по-
роговый ток 7кр ~ р~1. Опыт подтверждает этот результат: при
высоких давлениях труднее получить однородный разряд, столб
стягивается к оси трубки при меньших токах. При конвективном
теплоотводе (/£')кр ~ р, а пороговый ток укр(р) « const. Порог тем
выше, чем быстрее прокачивается газ. При заметном превыше-
нии энерговыделения над порогом инкремент Q«VtVi~103—
— 104с“-1 (табл 11.1), т. е. тепловая неустойчивость развива-
ется за Ю-4 — 10-3 с. То же получается и в результате анализа
нелинейной стадии развития шнура [11.3].
4.2. Молекулярный газ с замедленной колебательной релакса-
цией. Таковым является азот. В этом*случае тепловое расшире-
ние наступает с запаздыванием. Джоулево тепло сначала куму-
лируется в колебательных степенях свободы молекул, а потом в
ходе нарастания возмущений (если превзойден соответствующий
порог) с ускорением переходит в поступательную энергию газа,
ибо колебательная релаксация с ростом температуры ускоряется.
Нарастает п скорость ионизации. Получается нечто вроде тепло-
вого взрыва, когда по мере повышения температуры все быстрее
идет химическая реакция, а это в свою очередь ускоряет рост
температуры.
4.3. Стабилизирующее действие ионизации внешним источни-
ком. Применение несамостоятельного разряда, в котором иониза-
ция в газе создается посторонним источником (в особенности
пучком быстрых электронов), позволило существенно повысить
ток и энерговклад в разряд без наступления тепловой неустой-
чивости (гл. 16). Стабилизирующее действие обусловлено резким
ослаблением обратной зависимости скорости «самостоятельной»
ионизации от плотности газа*). Пусть под действием внешнего
источника в 1 см3 объема в 1 с образуется S пар ионов. Теперь
*) Линейная теория устойчивости несамостоятельного разряда была
впервые сформулирована в [11.7].
311
уравнение баланса числа электронов (11.10) выглядит так:
5 +уг[Г<;(£’ЛУ)|«е--р'ф^, N — p/kT. (11.15)
Проварьируем эти равенства, положив для краткости Те ~ Е/N и
5 = 1. Пусть, как это бывает при ионизации электронным пучком
S ~ N. Имеем
6 In пе — S/Угпе —
~ 1 + 2S/vjie < Vi'
Плотность электронов теперь менее чувствительна к нагреву,
а в пределе S > угпе, когда пе )/ 5/|3Эф, даже уменьшается при
нагреве как Ni/2 ~ Т~У2. В выражении для инкремента
_ П v7 — *S7v 'Vr'v, Svt
в " '’тЪзтЙ - - Trffe - ^77 -v" *11ЛС>
величина первого, дестабилизирующего слагаемого уменьшается
по сравнению с (11.13). Кроме того, помимо теплоотвода vT f
появляется еще одно стабилизирующее слагаемое (второе в по-
следнем выражении). При S > угяе, т. е. в резко несамостоятель-
ном разряде, пороговые значения тока и энерговклада, т. е. Лу,
при том же теплоотводе vT F больше, чем в самостоятельном.
Фактически неустойчивость возникает, когда скорость внешней
ионизации сравнивается со скоростью обычной, т. е. несамостоя-
тельный разряд близок к самостоятельному. При S <
(11.16) превращается в (11.13).
4.4. Повышенная устойчивость разрядов в переменных нолях.
При прочих равных условиях высокочастотный емкостной раз-
ряд (гл. 15) стабильнее по отношению к тепловой неустойчи-
вости, чем разряд постоянного тока,— это экспериментальный
факт. Вследствие резкой зависимости уг от Е, ионизация в пере-
менном поле происходит в моменты максимумов поля. В те
стадиях, когда поле слабее, плазма преимущественно распада-
ется. В установившемся разряде баланс между рождением и ги-
белью зарядов соблюдается лишь в среднем за период. Плот-
ность электронов при этом слегка пульсирует около среднего
стационарного значения пе. Тепловая неустойчивость может раз-
виваться лишь во время ионизации. Но поле в эти моменты силь-
нее, чем то постоянное поле, которое дало бы постоянную плот-
ность пе, равную средней пе в переменном поле. Действительно,
усиленное ионизующее поле должно восполнить нехватку иони-
зации в моменты, когда ионизации нет. Между тем, крутизна
функции Уг(Е) и величина уг в более сильных полях меньше
(см. формулу (11.12)). Согласно (11.14) пороговое энерго-
выделение (так называемый предельный энерговклад) при
этом выше.
Энергетический порог возникновения неустойчивости оказы-
вается еще более высоким в несамостоятельном разряде постоян-
312
ного тока, в котором газ ионизуется кратковременными повто-
ряющимися высоковольтными импульсами, а энергия вкладыва-
ется постоянным током. Причина стабилизации та же, но эффект
выражен сильнее, так как для поддержания той же средней
плотности электронов амплитуды импульсов, разделенных отно-
сительно длительными паузами, должны быть еще более высо-
кими. Использование этого принципа организации разряда по-
зволило на порядок повысить энерговклад в разряд без наруше-
ния его однородности и создать на этой основе мощный лазер
(п. 4.5 гл. 16). Изложенные соображения о повышении стабиль-
ности подтверждаются расчетом [10.27].
§ 5. Прилипательная неустойчивость
5.1. Устойчивость разряда, контролируемого прилипанием.
Само по себе прилипание к неустойчивости не приводит. Частота
прилипайия va растет с Е/N не так круто, как частота иониза-
ции, и va < Vi. При продольных неоднородностях Е/N и Те обрат-
ным образом зависят от пе (п. 3.3), поэтому в случае чистого
прилипания осуществляется устойчивая ситуация (рис. 11.1а).
В самом деле, пренебрегая пространственной неоднородностью
и варьируя уравнение кинетики электронов dne]dt = — Va)
около точки стационарного состояния хг = va и полагая §пс ~
~ exp Qf, находим
(dv, dvn \ 6ТР 6 In 7\ , — — х
Й = \dFe — TtJ ПеёТе = “ VaVa)' v»-=va- (И.17)
Например, в смеси СО2: N2: Не = 1: 7 : 12 кривые хг и va пере-
секаются при Те = 1,6 эВ (рис. 10.19). Потенциал ионизации
/со2 ~ 13,3 эВ. Частота диссоциативного прилипания электрона
к молекуле СО2 va ~ exp ( — U/kTe), где U = 3,85 эВ (п. 4.1 гл. 1).
В точке пересечения хг = 8,3, va = 2,4. В соответствии с (11.7),
(11.17) Q < 0. Возмущения затухают весьма быстро: |Q| ~ 10va.
Пусть возникло поперечное возмущение. Нагрев и тепловое
расширение происходят значительно медленнее, чем развивается
ионизационно-прилипательная кинетика, так что плотность газа N
можно считать замороженной. При этом 61п Те/& In nt = 0
(п 3.2) и в (11.17) Q = 0. Это неопределенное равновесие ста-
билизируется внешним сопротивлением (п. 1.2). Стабильность
разряда, контролируемого прилипанием, подтверждается экспе-
риментом [10.23], о котором говорилось в п. 8.1 гл. 10.
5.2. Механизм неустойчивости. Прилипательная неустойчи-
вость может проявиться в том случае, когда прилипание в зна-
чительной степени компенсируется отлипанием. Электронная
температура стационарного состояния при этом заметно ниже
той, при которой хг = va, поскольку ионизация должна компен-
сировать лишь малую разность между прилипанием и отлипани-
ем. Продольные возмущения могут нарастать из-за того, что
313
скорость отлипания не зависит от Те. Пусть где-то повысилась
плотность электронов. Электронная температура в этом месте
стала меньше. Конечно, скорость ионизации уменьшается, но это
может слабее повлиять на баланс числа электронов, чем умень-
шение прилипания. Последнее оставляет нескомпенсированным
не изменившееся отлипание, и электроны продолжают поступать
в плазму за счет разрушения отрицательных ионов. Число элек-
тронов растет, а Е и Те уменьшаются еще сильнее. Это отобра-
жается цепочкой причинных связей
бяЛ 6ГЛ хЛ (Z+ - z_) f 6яЛ. (И 18)
5.3. Инкремент. Рассматриваемый нестационарный процесс
описывается системой двух из уравнений кинетики (10.28) для
пе и п-. Третье эквивалентно условию электронейтральности
п+ = пе + п_. Их общий анализ [11.1, 11.2] приводит к весьма
сложным выражениям. Ограничимся существенно более простым
предельным случаем, когда положительные ионы рекомбинируют
гораздо медленнее, чем происходят процессы прилипания и от-
липания и чем развивается неустойчивость [11.8]. В этом случае
параметр п+ можно считать замороженным, бя_ = —б?ге, и из
двух уравнений кинетики (10.28) остается одно, для пе. Варьи-
руя его в предположении пространственной однородности, как
и в п. 5.1, находим инкремент
б In г z - ~ х б In г
С учетом f9.7) п приближенного равенства скоростей прилипа-
ния и отлипания vane ~ представим Q еще и так:
dk1!dTi
lk^df(
(11.20)
Первое слагаемое в (11.19) по виду совпадает с (11.17), только
теперь v2 С va и оно может быть положительным. Согласно
(11.20) это возможно, только когда dkJdTе< dkJdTе. Для смеси
СО2: N? : Не = 1: 7 : 12 это неравенство выполняется при Те <
<1,05 эВ [10.25, 11.2] (рис. 10.19). Если Те заметно ниже этол
величины, первое слагаемое в (11.19), (11.20) представляет со-
бою достаточно большую положительную величину и может пре-
высить второе, пропорциональное п+1п_. Нужно только, чтобы
отношение п+1п_, которым определяется стабилизирующий эф-
фект, не было чересчур большим.
Расчеты [10.25, 11.2] очертили область неустойчивости для
указанной смеси: пе < 1010 см-3, 10-1 < п-1пе < 10, Те<1 эВ.
При пе > 1010 слишком сильна рекомбинация, которая всегда
играет стабилизирующую роль (п. 1.2). При п-!пе < 10”1,
njn- > 10 слишком мал резервуар связанных отрицательных
зарядов, высвобождение которых при отлипании могло бы при-
вести к неустойчивости. При п-!пе> 10 и данной плотности
314
электронов слишком много положительных ионов, сильна реком-
бинация, для ее компенсации требуются большая скорость иони-
зации и Те > 1 эВ. От этого исчезает дестабилизирующий эф-
фект. Масштабом времени развития неустойчивости, если ohi
возникает, служит согласно (11.20) время прилипания та = v"1»
5.4. Домены. Прилипательная неустойчивость приводит обыч-
но к образованию доменов. Если в неустойчивом состоянии с от-
носительно большим числом отрицательных ионов возникает
флуктуация Ьпе > 0 или < 0, они начинают неудержимо рас-
падаться. Появляется много электронов, проводимость резко воз-
растает, а поле в этом месте падает. Получается домен слабого
поля. Если в неустойчивом состоянии с относительно малым
числом п- возникает флуктуация бпе < 0 или §Те > 0, столь же
неудержимо растет прилипание, проводимость падает, поле воз-
растает. Образуется домен сильного поля. Домены движутся к
аноду с фазовой скоростью, которая может быть на несколько
порядков меньше, чем скорость дрейфа электронов. Для ее вы-
числения следует учитывать эффекты пространственной неодно-
родности. С тем, как они проявляются, мы познакомимся в § 7
при рассмотрении движения страт. Обычно домены периодиче-
ски зарождаются, бегут, потом исчезают. Па глаз они не видны,
по приборы регистрируют осцилляции тока. В чистых Ar, Не, N2,
где нет прилипания, домены не наблюдаются.
§ 6. Некоторые другие часто действующие
дестабилизирующие факторы
*
6.1. Ступенчатая ионизация. Действие ее продемонстрируем
на примере разряда, контролируемого диффузией. Снова опуская
для простоты и краткости слагаемые, учитывающие простран-
ственную неоднородность плазмы, запишем уравнения кинетики
для плотностей электронов и возбужденных атомов
дпо *
— — kzNne + кг]\т*пе—vdne (11.21)
dN*jdt = k*Nne — kzN*ne — v*aN*. (11.22)
Здесь kl = vJN, k* = v*/N — константы скоростей ионизации и
возбуждения атомов из основного состояния, кг, к2— ионизации
и дезактивации возбужденных метастабильных атомов электро-
нами, vd — частота потерь возбужденных атомов, не вызванных
ударами электронов (за счет диффузии на стенки, дезактивации
ударами атомов). В (11.22) учтено, что Аг<сА*2, поскольку для
ионизации электрон должен обладать достаточной энергией, а для
дезактивации — нет. Если неустойчивость развивается медленнее,
чем гибнут возбужденные атомы, а так оно в общем и получа-
ется. плотность А* «следит» за нарастанием пе, будучи квази-
315
стационарной:
k*Nn
N'“ TV* [ne (t)] «-----Ч- (11.23)
к2Пе + Vd
Проварьируем уравнения (11.21), (11.23) около точки ста-
ционарного состояния, пренебрегая слабой по сравнению с кг, к*
зависимостью кг и кг от Те. Полагая ~ ехр (Й£), находим
5 In Г.,- - * ч
Й = -^Ц------hxi—Ь’Л v*k*N*). (11.24)
v*ne 1 6 In Пе 4 г г ' ' 7
Первое положительное слагаемое Q(+), связанное с иониза-
цией накапливающихся возбужденных атомов и квадратичное
по N*, обуславливает дестабилизирующий эффект ступенчатой
ионизации. Как функция пе оно имеет максимум при значениях
Ыопт = v*d/k2, (ДГ*)0ПТ = v*/2A’2 = Nt/2, (11.25)
оптимальных для развития неустойчивости. Здесь JVp — равно-
весная больцмановская плотность возбужденных атомов, соот-
ветствующая Те. Она удовлетворяет принципу детального равно-
весия k*Nne =- k2N^ne. Величина
= к*гх*/'1к2 =- А-* (7V*)onT/2 -- *Х/4 (11.26)
дает верхнюю оценку инкремента неустойчивости. С такой ско-
ростью развивалась бы неустойчивость в наиболее благоприят-
ных условиях, в отсутствие стабилизирующих факторов. Но и
при действии последних вдали от границ области устойчивости Q
имеет порядок йтах-
Чтобы получить представление о порядках величин, рассмот-
рим пример. Пусть р = 3 торр, N = 1017 см-3. В трубке радиуса
R = 1 см частота амбиполярной диффузии зарядов к стенкам,
которая контролирует разряд в инертном газе, vd ~ 5 • 103 с-1.
Примерно такова же, следовательно, и частота ионизации
Частота возбуждения v* ~ 105 с-1 больше vt, так как Е* ~ 311^
к* ~ 10“9 см3/с кг « 5 • 10“14 см3/с, ибо энергия связи возбуж-
денных атомов 1 — Е*~1!бт, к% ~ 10~8 см3/с, TVp 1013 см“3, v*
^3-103с~1. Отсюда (?ге)опт ~ 3 • 1011 см-3, (Аг*)опт ~ 5 • 1012 см-3,
£2max ~ 3-103 с”1. Инкремент имеет порядок vd ~ уг.
Что касается второго, ионизационного слагаемого в (11.24),
то, как и в (11.17), (11.19), в случае продольных возмущений
оно отрицательно и оказывает стабилизирующее действие. Это
влияние необходимо преодолеть, что ограничивает область воз-
можного проявления неустойчивости. Подробнее о стабилизирую-
щем действии ионизации пойдет речь в п. 7.2. В случае попереч-
ных возмущений, когда Те связана с пе только через теплозое
расширение, данный стабилизирующий эффект ионизации
исключается.
316
6.2. Максвеллизация электронов. В слабоионизированном газе
распределение электронов по энергиям устанавливается в ре-
зультате приобретения энергии от поля и ее потерь при упругих
и неупругих столкновениях с нейтральными частицами. Ни одно
из таких столкновений не придает электрону энергии, каждое
ведет лишь к потере. Особенно велики потери при больших
энергиях, когда электрон возбуждает электронные уровни и иони-
зует атомы и молекулы. Поэтому при энергиях порядка потен-
циала ионизации функция распределения спадает очень резко,
и соответствующая частота ионизации, рассчитанная на один
средний электрон, относительно невелика. При больших плотно-
стях электроны начинают взаимодействовать друг с другом, об
мениваясь при этом большими порциями энергии. Появляется
новый механизм приобретения энергии отдельным электроном.
Распределение по энергиям стремится к максвелловскому, и чис-
ло энергичных электронов резко возрастает. Повышается и ско-
рость ионизации, что в свою очередь еще сильнее приближает
функцию к максвелловской и способствует нарастанию числа
быстрых частиц, способных производить ионизацию. При доста
точно больших пе (токах) такая неустойчивость может привести
и к контракции и к образованию страт, как и ступенчата/!
ионизация.
6.3. Удары второго рода. Еще один процесс связан с насыще-
нием заселения возбужденных состояний молекул и атомов, ко-
лебательных и электронных. При больших плотностях электро-
нов и частых актах возбуждения число возбужденных атомов
может вырасти настолько, что станут существенными столкнове-
ния с ними электронов. При столкновении с возбужденной ча-
стицей электрон может отбирать у нее энергию возбуждения
(удары второго рода). Может возникнуть ситуация, когда резер-
вуар возбужденных частиц столь велик, что электроны начнут
черпать из него свою энергию, вместо того, чтобы только отда-
вать ее. Электронная температура начнет повышаться, и это
приведет к ускорению ионизации и еще большим заселению и
отбору энергии от возбужденных частиц. Снова возникает не-
устойчивость. Подробнее см. [11.5, 11.4].
§ 7. Страты
7.1. Наблюдения. Положительный столб разряда в трубках
стратифицирован (рис. 11.4) гораздо чаще, чем это видно нево-
оруженным глазом. Как правило, страты движутся. В инертных
газах при р ~ 10“1 —10 торр—со скоростями порядка 100 м/с,
в направлении от анода к катоду. Поскольку интенсивность све-
чения осциллирует во времени с частотами порядка 1 кГц, глаз
этого не разрешает, и столб выглядит однородным. Страты бы-
вают и неподвижными. Тогда видно, как вдоль трубки череду-
ются светлые и темные слои. Так, собственно, страты и были
обнаружены. Страты стоят на месте, когда в разряде имеется
317
какой-то локальный постоянно действующий источник сильного
возмущения, например зонд под большим отрицательным потен-
циалом пли резкое изменение сечения трубки. Иногда роль та-
кого возмущения играет прикатодпая область. Стоячие страты
выстраиваются в сторону анода от места возмущения, постепен-
но затухая. В некоторых случаях затухают только несколько
первых, начиная от катода, а потом затухание прекращается.
‘ ** - . «вЖИйЙШЖвв4»' > •
♦ * ПУЩ OTf'7TjГПУ •> .
.j® *.<<ПУ* *»_. »-
«iHgi „
Рис 11 4. Внешний вид разряда со стратами [3]
Длина одной страты, т. е. расстояние между соответствующими
точками соседних страт, составляет обычно несколько радиусов
трубки R. Это относится как к стоячим, так и к бегущим стратам.
Страты существуют в ограниченном диапазоне условий по
значению тока, роду газа, давлению, радиусу трубки. От тех же
параметров зависят и амплитуда колебаний свечения, длина вол-
ны страт, скорость их распространения. Вблизи границы суще-
318
ствования амплитуда колебании свечения, которая в какой-то
мере отражает и амплитуду колебания плотности электронов^
невелика. Колебания при этом близки к синусоидальным. Неред-
ки страты большой амплитуды, в которых плотность электронов
изменяется во времени и вдоль длины трубки на порядок, и рас-
пределения параметров далеки от синусоидальных. Соотношение
между стратами малой и большой амплитуд примерно такое же.
как между звуковыми (акустическими) и сильными нелинейны-
ми волнами в газовой динамике. Вне области существования
страт положительный столб устойчив и однороден, хотя путем
внешнего возмущающего воздействия можно возбудить страты
и в небольшой окрестности за пределами области естественного
существования. Обширный экспериментальный материал по стра-
там содержится в обзорах [11.9—11.11].
7.2. Условия возникновения. Страты представляют собой
ионизационные колебания и волны. Это значит, что периодиче-
ские изменения электронной плотности вызваны не перераспре-
делениями фиксированного количества электронов, как в плаз-
менных волнах, а чередованием областей, в которые электроны
преимущественно рождаются и преимущественно гибнут. Меха-
низмы неустойчивостей, вызывающие возникновение страт, свя-
заны с ионизационными процессами. Стратификацию могут вы-
звать ступенчатая ионизация, максвеллизация функции распре-
деления электронов (§ 6) — все, что приводит к раскачке про-
дольных неоднородностей. Ступенчатая ионизация действует
только при не слишком больших токах, когда метастабильные
атомы, рождаемые электронными ударами, гибнут в результате
диффузии к стенкам. При более высоких токах (в инертных
газах при 100 мА) пе вырастает настолько, что метастабили
разрушаются электронными ударами. В этом случае согласие
(11.23) их плотность перестает расти с ростом пе, что является
залогом развития неустойчивости через нелинейную зависимость
скорости ионизации газа от пе. Ступенчатая ионизация при этом
уступает место максвеллизации или каким-то другим меха-
низмам.
Движущиеся страты — процесс волнового характера, и реша-
ющую роль здесь играют пространственные неоднородности в
плазме, причем неоднородности продольного типа. Важным мас-
штабом длины, присущим плазме, является Аи = оЛти ~ 1/1/—
длина установления электронной температуры (энергетического
спектра) в поле. Именно она, помимо другого (геометрического)
масштаба — радиуса трубки R — во многом определяет возник-
новение пространственных неоднородностей и их масштаб. Свя-
зано это в конечном счете с тем, что в случае продольных воз-
мущений резкий рост скорости ионизации с Те является факто-
ром стабилизирующим (см. формулу (11.24) и замечание в кон-
це п. 6.1). В самом деле, из-за постоянства / в месте, где повы-
шается пе, падает поле (п. 3.3). Если вместе с Е падает и Те,
319
скорость ионизации уменьшается, и положительная флуктуация
пе затухает.
Но электронная температура в данном поле приходит к со-
ответствующему этому полю значению на длине релаксации Аи.
В случае длинных волн или малых волновых чисел К, КАи 1,
этот стабилизирующий фактор действует в полную силу. Соглас-
но (11.7) 6 In 7\/6 In ~ —2 и его величина 2v2vt существенно
больше £2тах- Дестабилизация за счет ступенчатой ионизации
со стабилизирующим действием прямой ионизации справиться
не может. На коротких волнах, КАи > 1, роль стабилизации
ионизацией ослабевает, так как Те не успевает упасть до вели-
чины, соответствующей уменьшенному полю. На очень коротких
волнах. КАи» 1, Те вообще безучастна к колебаниям Е, и ни-
какой стабилизации прямой ионизацией нет. Этот механизм огра-
ничивает сверху длины волн страт длиной релаксации электрон-
ной энергии. Величины КАи в стратах всегда больше нескольких
единиц. Но длины волн ограничены и снизу. Чрезмерно корот-
кие по сравнению с радиусом трубки R волны также нежизне-
способны, так как возмущения пе активно рассасываются про-
дольной амбиполярной диффузией. Поэтому страты могут суще-
ствовать только в некотором ограниченном интервале длин волн.
Наиболее благоприятны для них в инертных газах значения
ЯЛм«5-10, KR ~ 1.
В молекулярных газах, где доля энергии 61, передаваемая
электроном молекуле при столкновении, имеет повышенное зна-
чение, длина Аи очень мала. Неоднородности пс, не подвержен-
ные стабилизации понизацйонным фактором, слишком мелкие,
они хорошо рассасываются диффузией, и потому возникновение
страт затруднено. Другое дело — атомарные инертные газы, где
61 = 2ш!М—очень малая величина, и длина Аи, в особенности
при небольших давлениях 10-2—10 торр, значительна. Именно
этот случай, когда Аи превышает 7?, благоприятен для возник-
новения крупномасштабных пространственных неоднородностей.
И действительно, стратификация типична как раз для инертных
газов, хотя узкие страты наблюдаются и в водороде. Надо ска-
зать, что стратами начали заниматься еще в начале века, но
понимание истинной природы этого распространенного явления
было достигнуто не столь давно, пожалуй, в 60-х годах.
7.3. Теория ионизационных волн малой амплитуды. Она осно-
вана на линеаризации уравнений, описывающих поведение элек-
тронного газа в плазме. В гидродинамическом приближении —
это уравнения (3.44) для пе, (3.52) для Те с (3.49) для d/dt,
(3.53) для ve, (3.54) для Е. В уравнениях непременно должен
присутствовать дестабилизирующий фактор. Если это — ступен-
чатая ионизация, в качестве источника зарядов q в (3.44) можно
взять правую часть уравнения (11.21) с 7V* по (11.23). Диспер-
сионное соотношение для со(7£) находится так, как говорилось
в п. 1.4. причем волны с самого начала следует считать направ-
320
ленными вдоль Е. Требование положительности инкремента очер-
чивает границы области существования страт. Такой расчет по-
следовательно доведен до конечного результата в [11.12, 11.10].
Расчет [11.13] с дестабилизацией механизмом максвеллизации
при повышенных токах дал не только качественное, но и хоро-
шее количественное согласие с результатами измерений зависи-
мости длины волны страт от частоты и границ их существова-
ния в аргоне.
Система уравнений (3.44), (3.52), (3.53), (3.54) имеет вто-
рой порядок, от чего для со получается квадратное уравнение.
Однако, если подставить волновое решение для 8Те в (3.52),
видно, что временное и конвективное слагаемые относятся как
3(ЦЬКие « 3^ф/5?;д. Здесь = а/К — по определению фазовая
скорость волны. И опыт, и последующее решение показывают,
что скорость движения страт гораздо меньше скорости дрейфа
электронов, поэтому есть все основания опустить член с dTe)dt.
Тогда дисперсионное соотношение приобретает первый порядок.
Оно следует из (3.44) и для механизма ступенчатой ионизации
отличается от (11.24) только слагаемым, обусловленным амби-
полярной диффузией плазмы. Последняя стремится выравнять
неоднородности и оказывает стабилизирующее действие, давая
в отрицательный вклад:
/со = Q(+)+ (6 In Те/б In пе) (7^ + v*/c*7V*) - DaK2. (11.27)
Дестабилизирующий член Q(+) уже рассматривался в п. 6.1.
Сделаем несколько упрощений, чтобы недостающая в (11.27)
связь 6Те и Ьпе была не слишком громоздкой. Пусть vm, це, vu =
= 6ivm от Те не зависят (в атомарном газе 6i = 2mlМ = const).
Поскольку Da^De, пренебрежем в (3.53) амбиполярным пото-
ком. Тогда neve = — Це = const и вариации не подлежит (п. 2.3).
Пренебрежем затратами энергии на ионизацию по сравнению с
ее передачей атомам. Это справедливо при хг vM, т. е. при не
слишком низких давлениях, ибо ~ vd ~ р~\ а уи ~ р. Варьируя
(3.54), (3.52) без dTJdt около точки стационарного однородного
состояния, с учетом кТе~ еЕКи по (3.19), находим связи между
комплексными амплитудами возмущений:
бШ = (-1 + 1ККЦЪпе1пе, (11.28)
=+ / (11.30)
61пре (5/2) к2\2и + 1 + i (5/2) К\и
Эти связи очень показательны и подтверждают качественные
утверждения п. 7.2. В пределе KXU < 1 они практически квази-
стационарны и локальны. Связи превращаются в те, что даются
формулами (11.6), (11.7) (vm = 0, vu=l, g = 2). Стабилизация
ионизацией в (11.27) с б In ТЦЬ In пе ~ — 2 очень сильна. Длин-
21 Ю. п. Райзер
321
ные волны затухают. В общем случае волны 5ne, $Е, 6Те сдви-
нуты друг относительно друга по фазе. В этом, как мы сейчас
увидим, залог их движения. Отделим действительную и мнимую
части в (11.30), для упрощения—применительно к предельно-
му случаю КАи > 1, который только и может осуществиться,
е=-----+ (Н.31)
6 In пе 5AAu
Действительное отрицательное слагаемое, которому пропор-
ционален стабилизирующий фактор, становится очень малым,
что и открывает возможность существования незатухающих волн.
Мнимая часть определяет частоту волн, которая пропорциональ-
на их длине: со ~ К~\ Стабилизация ионизацией, пропорциональ-
ная К~\ тем слабее, чем короче волна. Но чрезмерно короткие
волны хорошо стабилизируются диффузией, действие которой
согласно (11.27) пропорционально К2. Следовательно, суммар-
ный стабилизирующий фактор, обозначим его в зависимости
от К имеет минимум при некотором значении Хопт. Если
волны могут существовать, а уравнение Q(+) =
= Q(“)(7Q ограничивает с двух сторон область возможных длин
волн вокруг 7£опт*).
По формулам, которые получаются из (11.27), (11.31), опти-
мальное для раскачки колебаний волновое число удовлетворяет
соотношению
Я0ПТЛ ^(Л/Ли) 1/2(2?г/5)1/2,
где Л = 7?/2,4—длина диффузии для трубки радиуса R. В ато-
марных газах при р ~ 1 —10 торр и R = 1 см Аи ~ Z/V51 «
~ 1—10 см, Л ~ 0,3 см; уг ~ 10. Оптимальная длина волны страт
составляет несколько диаметров трубки, что подтверждается
опытом. При этом #ОптЛи ~ 5—10, что оправдывает приближение
КАи » 1.
7.4. Почему страты движутся. Поясним, в чем состоит физи-
ческая причина того, что волны бегут, и, как правило, от анода
к катоду. В реальных, сравнительно коротких волнах, градиенты
плотности значительны. Относительное разделение зарядов, ко-
торое существует несмотря на высокую степень электронейтраль-
ности плазмы, определяется не дрейфом, а диффузией (рис. 11.5).
Возникающее поле поляризации 8Е складывается с постоянным
невозмущенным полем Е на том склоне, где пе уменьшается в
сторону падения потенциала, и вычитается из Е на другом скло-
*) В известном обзоре [11.9] в рамках аналогичной постановки задачи,
но без учета ступенчатой ионизации или какого-либо иного дестабилизирую-
щего механизма, сделан вывод о положительности инкремента Q в некото-
ром небольшом интервале коротких волн с КАи 1. Он повторен в обзоре
[11.14] со ссылкой на [11.9]. Это не так, и получилось из-за неучета элект-
ронной теплопроводности, которая на самом деле приводит к затуханию ко-
ротковолновых возмущений.
322
не. По этой причине волна ЬЕ сдвинута на четверть своей длины
в сторону катода относительно волны 8пе (рис. 11.5, формула
(11.28)). Энерговыделение ]'Е в электронном газе распределено
так же, как и Е, поскольку / = const.
Рис 115. Схема, поясняющая причину
движения страт от анода к катоду. Рас-
пределения пе (штриховая кривая) и
п+ (сплошная кривая) соответствуют
преобладанию диффузии электронов
над дрейфом в случае коротких волн.
Максимумы поля Ё и энерговыделения
]Е сдвинуты вправо, к катоду, относи-
тельно горба п
Из различных составляющих в балансе энергии электронов
(п. 2.5) доминирующую роль в коротких волнах с 7ГЛи > 1
играет теплопроводность. От усиленного источника 5 IjE} = j$E
электронное тепло растекается в обе стороны, и распределение
Те почти повторяет распределение источника тепла и Е. Волна
находится почти в фазе с волно!! 6Е (это видно и из фор-
мул (11.28)—(11.31)). Почти в фазе с нею находится и скорость
ионизации тг(7\)пе, ибо к Те она гораздо чувствительнее, чем
к пе. Значит, наиболее интенсивная ионизация происходит в точ-
ке мгновенного «равновесия» пс на оси х, где Апе ~ 0, a /s мак-
симально. Через четверть периода в этой точке пространства §пе
вырастет до амплитудного значения, т. е. в нее, передвигаясь в
направлении Е, придет горб распределения пе.
7.5. Оценка скорости и частоты страт. Ее целесообразно сде-
лать не формальным путем, продолжая выкладки п. 7.3, а не-
посредственно, исходя из высказанных только что соображений.
Это позволяет лучше уяснить сущность явления. Очень короткие
волны §пе и дЕ сдвинуты на четверть периода. В комплексном
направлении связь этих параметров чисто мнимая. Согласно
(11.28)
8Е/Е ~ iKAubnelne. (11.32)
Из баланса между дополнительным тепловыделением и тепло-
проводностным растеканием тепла — старшими членами при ва-
риации (3.52) — имеем: jSE « К2ХебГе. Подставляя j = епереЕ,
=(5/2) kneDe и kTe = EAU1 находим
_ 2
Те ~ 5£2А2 Е
2
(11.33)
Благодаря выравниванию температуры теплопроводностью, отно-
сительное изменение Те гораздо слабее изменения поля. Оно
слабее и изменения плотности плазмы, хотя и в меньшей
степени.
21* 323
Дополнительная скорость ионизации, обязанная усиленному
нагреву, равняется
dvz - ^Те
б (угпе) ж пе -^-ЬТ е пе\1уг
За четверть периода, т. е. за время t ~ где иф = ь)/К—
фазовая скорость волны, пе вырастает на величину 6пе порядка
амплитудной: 8(угпе)1 ~ $пе. Отсюда
рф ~ vtViX_1|6 In Те/6 In пе\.
Подставляя сюда (11.33), получаем скорость и частоту страт:
(11.34)
Ф 5 5 KAU v 7
Частота колебаний пе и других величин в стратах пропорцио-
нальна длине их волны, скорость — ее квадрату. Масштабом
частоты служит частота ионизации, поскольку для страт харак-
терны КХи ~ 10, а тг ~ ~ 10. При невысоких давлениях в
инертных газах электроны гибнут за счет амбиполярной диф-
фузии к стенкам, так что хг ~ Vd = DJ№ ~ DJR. Значит, со — по-
рядка частоты диффузии. В более строгих решениях [11.10г
11.13] качественное ядро выражений для (o(7Q и та'ково же,
как и в (11.34). Из опыта и на основании расчета [11.13] в
аргоне в трубке R = 1,5 рм при р == 0,5 торр и токе I = 3,6 А при
увеличении частоты со/2л от 1,4 до 2 кГц длина волны страт
2п!К вырастает от 6 до 9 см, а скорость — от 80 до 180 м'с.
Оценки дают верный порядок величин. Интересно, что группо-
вая скорость страт z?rp = d^fdK < 0, т. е. направлена противопо-
ложно фазовой и (в рамках данного приближения) равна ей по
модулю. Поэтому какая-нибудь метка (например, более яркая
область от импульсного локального возмущения) в отличие от
самих страт бежит к аноду. Волны малой амплитуды, подчиняю-
щиеся линейной теории, чаще существуют при условиях, кото-
рые соответствуют углублению в область неустойчивости не
слишком далеко от ее границ. Там стабилизирующие факторы
еще сильны, и они сдерживают рост амплитуды. Вдали от гра-
ниц могут возникать и сильные, нелинейные волны большой
амплитуды.
7.6. Страты большой амплитуды. Как следует из предыду-
щего, страты — это движущиеся по газу ионизационные волны,
сменяющие друг друга области ускоренной и замедленной иони-
зации, обязанной своим существованием волнам усиленного и
ослабленного поля. В стратах большой амплитуды в общем про-
исходит то же, что и в слабых волнах, но все процессы гипер-
болизированы до крайности. Области сильного поля обострены
до резких скачков потенциала, в следующих за ними (ближе к
аноду) областях поле не только полностью уничтожается, но да-
же становится отрицательным.
324
В областях сильного поля ионизация ускоряется настолько,
что плотность электронов резко вырастает на порядок. Эту ярко
светящуюся сравнительно узкую зону называют головой страты.
За нею ионизация прекращается, поскольку поле исчезает,
и электроны, вследствие диффузии к стенкам, гибнут. Плотность
их постепенно падает на тот же порядок вплоть до головы сле-
дующей страты. Эта темная зона гораздо длиннее светлой, так
как гибнут электроны медленнее, чем рождаются. По мере па-
дения пе поле восстанавливается (/(#) = const), и все повторя-
ется. Описанная картина качественно похожа на то, что проис-
ходит однократно и без движения в катодных частях разряда
(§ 5 гл. 10). Катодный слой с отрицательным свечением соот-
ветствуют голове страты, темное фарадеево пространство — про-
тяженной области вплоть до следующей головы, только вместо
нее появляется положительный столб с умеренными полем и
свечением (если он не стратифицирован).
7.7. Эксперимент и его интерпретация. На рис. 11.6 показаны
результаты зондовых измерений мгновенных распределений пещ Те
Рис. 11.6. Страты большой амплитуды в аргоне в трубке радиуса R =
= 0,85 см: а — распределение потенциала вдоль оси в направлении от ано-
да к катоду; б — распределения пе и Те в пределах одного периода; в — рас-
пределение потенциала в том же масштабе, совмещенное с графиком б по
координате. Поле Е получено путем дифференцирования потенциала ф
[11.15]
и потенциала ср вдоль оси х разрядной трубки с сильными стра-
тами. Там же нанесено распределение Е, полученное путем диф-
ференцирования кривой ср (я). Измерения сделаны на оси длин-
ной трубки. Страты движутся от анода к катоду со скоростью
= 60 м/с. С такой скоростью изображенные распределения
перемещаются слева направо как целое. Длина одной страты
325
d — 5,5 см. Распределение интенсивности свечения приблизитель-
но повторяет распределение пе. Оценка пространственного заря-
да на основе двукратного дифференцирования кривой ср (я) пока-
зывает, что даже в местах с большими градиентами степень элек-
тронейтральности высока: \пе — п+\ < 10“4тге. В среднем по длине
страты и всего столба <Е1рУ =0,22 В/(см - торр).
Максимум Е и скорости ионизации локализуется в месте
наиболее крутого спада пе, на правом склоне горба. Именно
поэтому пик (ne)max? как и вся страта, перемещаются направо,
к катоду. На правом склоне пе очень силен диффузионный ток
электронов eDe\dneldx\ ~ 530 мА/см2 (Z9e ~ 2,5 • 106 см/с), кото-
рый направлен против фактического тока i. С учетом бесселевого
радиального профиля пе(г) плотность тока на оси трубки j = 2,3 X
X z/n7?2=77 мА/см2. Диффузионный ток перекрывается дрейфовым
е\х(псЕ = 530 + 77 = 610 мА/см2 ровно на столько, чтобы обеспе-
чить должную плотность тока/. Отсюда с це = 1,7 • 105 см2/(с • В)
получается (Е/р)тах~ 8 В/(см-торр), что в 36 раз больше сред-
него {Е1р\ Когда механизмом гибели электронов является диф-
фузия к стенкам, их плотность за головой страты, где рождение
замедлено, должна падать по закону v^dne!d\х\ = — VdTte. Отсюда
d (^ф/Vd) In (/Ze mln) • (11.35)
В условиях эксперимента р+ ~ 250 см2/(с • В), Те~ 1,3 эВ,
Da = р+Те = 320 см2/с, Vd = 2,42Д7-Й2 = 2,6 • 103 с"1. Измеренные
значения гф, d и перепада плотности nemax/nemin ~ 10 превосход-
но согласуются с оценкой (11.35). Так количественно «расшиф-
ровывается» полученная на опыте картина. Следует подчеркнуть,
что в сильных стратах с резкими перепадами поля, как, впрочем,
и в слабых с КАи > 1, функция распределения электронов имеет
нелокальный характер, т. е. определяется не просто местным
мгновенным значением поля Е, а зависит от поведения потен-
циала в пространственно-временной «окрестности» (как в катод-
ном слое, п. 4.10 гл. 10). Этот эффект уже сам по себе может
приводить к стратификации и влиять на структуру сильных
страт [11.16, 11.17].
7.8. Чем «выгодно» стратифицированное состояние. Если по-
ложительный столб, имея полную возможность пребывать в од-
нородном состоянии — возможность, обеспеченную выполнением
всех законов сохранения, «предпочитает» состояние слоистое,
значит, в последнем есть какая-то целесообразность. Состоит
она в том, что при равном значении тока напряжение V и вы-
деление мощности IV в стратифицированном столбе меньше, чем
в однородном. В стратах большой амплитуды рождение и гибель
электронов разнесены в пространстве и во времени. Баланс меж-
ду ними выполняется лишь в среднем по всей страте, либо в
среднем за период колебаний в данном сечении трубки. Из-за
резкой крутизны функции vl(£') для рождения определенного
числа электронов, которое компенсирует их гибель, требуется
326
Edx = AV
меньший интеграл j Е dt за период t\, если поле сильное, но
действует в течение короткого времени. Падение напряжения AV
на длине страты
Ч
Гф Е dt =
о о
меньше, чем на такой же длине однородного столба с постоян-
ным полем.
«Целесообразность» стратификации сродни «целесообразно-
сти» сосредоточения всей функции самоподдержания разряда в
катодном слое (п. 4.1 гл. 10). Можно пояснить дело и так.
Электрону легче приобрести энергию, необходимую для иониза-
ции, если он пройдет нужную разность потенциалов в сильном
поле на коротком пути. Он испытает меньше столкновений, ко-
торые мешают его ускорению. С этой точки зрения выгоднее
распределить разность потенциалов в виде резких скачков, чем
размазать ее по той же длине с постоянным градиентом. Явление
страт удовлетворяет принципу .минимума мощности (п. 4.8
гл. 10). Но ему дано независимое принципиальное объяснение
на основе анализа самих процессов. Причина образования страт
коренится в неустойчивости однородного состояния при опреде-
ленных условиях.
§ 8. Контракция положительного столба
Систематическое исследование йерехода диффузного тлеющего
разряда в контрагированное состояние сделано только в трубках.
При работе с плоскими каналами обычно ограничиваются фикса-
цией критического тока, при котором происходит срыв однород-
ного горения. Условия для исследования в каналах крайне не-
благоприятны: геометрия шнуров не всегда воспроизводится от
опыта к опыту, заранее не известно, где шнур возникнет, шнуры
«бегают». В трубках же все жестко определено идеальной сим-
метрией. Но надо полагать, что основные свойства шнуров в
общем одинаковы в разрядах любой геометрии.
8.1. Результаты эксперимента. Приведем результаты работы
[11.18], где получена весьма полная информация о явлении.
Изучался разряд в неоне при р = 75—200 торр в трубке радиуса
R = 2,8 см. Напряженность поля измерялась зондами, распреде-
ление плотности электронов по радиусу — по тормозному излу-
чению при рассеянии на нейтральных атомах, интенсивность
которого пропорциональна neN. При этом учитывался радиаль-
ный профиль плотности газа У (г), связанный с распределением
газовой температуры Т (г) постоянством давления р = NkT. Это
существенно, потому что газ нагревался сильно. Для нахождения
Т (г) решалось уравнение теплопроводности с истинным распре-
делением источников тепла ](Е)Е. Трубка термостатировалась,
327
ее стенки поддерживались при температуре То = 300 К. Электрон-
ная температура на оси определялась по измеренному полю и
N(0) из равенства (3.13), вытекающего из баланса энергии
электронов. Транспортное сечение неона довольно слабо зависит
от энергии и равно примерно от ~ 2,3 • 10“16 см2; газ атомарный,
61 = 2т] М.
На рис. 11.7 показана ВАХ положительного столба. Левая
часть до скачка соответствует диффузному разряду, заполняю-
щему всю трубку с той степенью однородности, которая присуща
Рис. 11.7. ВАХ разряда в
трубке в области перехода
из диффузного в контраги-
рованное состояние [11.18]
(неон, радиус трубки R =
— 2,8 см). Сплошная кри-
вая в районе скачка снята
при уменьшении тока,
штриховая — при повыше-
нии
Рис. 11.8. Измеренные профили пе
в условиях рис. 11.7: 1 — ilR —
= 4,8 мА/см2; 2 - 15,4; 3 — 26,8;
4 — 37,5; 5—42,9; 5 — 57,2; 7 — 71,5.
Переход из диффузного в контраги-
рованное состояние произошел в об-
ласти между кривыми 4 и 5
разряду, контролируемому диффузией, когда пе(г) ~ 7о(2,4г/Я)
(п. 6.2). ВАХ — падающая, что типично для разряда, контро-
лируемого диффузией, при сравнительно больших токах, когда
газ сильно нагревается (п. 7.4 гл. 10). При критическом значе-
нии тока поле и напряжение скачком уменьшаются, чему соот-
ветствует скачкообразный переход однородного столба в контра-
гированную форму. У оси появляется ярко светящийся шнур,
а остальная часть трубки темнеет. Переход происходит при сред-
ней по сечению плотности тока примерно 5,3 мА/см2. Плотность
критического тока на оси в соответствии с бесселевым профилем
/(г) в 2,3 раза больше, 12 мА/см2. Критическая плотность элек-
тронов на оси пе (0)~1011 см“3. Наблюдается явление гистере-
зисного характера. Во время увеличения тока переход в контра-
328
гированное состояние происходит при несколько большем токе,
чем переход к диффузному при уменьшении тока. Это говорит
о двузначности состояний в области скачка и их возможной ме-
тастабильности *).
На рис. 11.8 показаны относительные радиальные распреде-
ления пе, а в табл. 11.2 даны параметры на оси, все при р =
— ИЗ торр. Видно, насколько резко сжимается при контракции
токовый канал, который характеризуется проводимостью или пе,
Таблица 11.2. Параметры разряда в трубке R — 2,8 см при р =
— ИЗ торр
г мА Те(0), эВ Т(0), К пДО), 1011 см~3 i мА ТД0), эВ Т(0), К пе(0), 1011 см-3
13,5 3,0 440 0,12 120 3,0 1200 54
43 75 3,3 3,6 650 840 0,39 0,93 160 2,6 1300 72
96 3,7 930 1,2 200 2,5 1400 93
п< ереход про исходит пр и токе 105—1 15 мА.
и как резко подскакивает степень ионизации, чуть ли не на два
порядка. Эффективный радиус шнура по уровню пе = пе(0) /2
в 20 раз меньше радиуса трубки. Газовая температура на оси
немного возрастает при переходе, причем в контрагированном
разряде она спадает от оси круче, чем в диффузном. Половина
перепада температур между осью „и стенками в диффузном раз-
ряде приходится на радиус (0,7—0,8)7?, в контрагированном —
на 0,57?. Это и естественно: источники тепла в последнем случае
сосредоточены у оси. Электронная температура при контракции
несколько уменьшается из-за уменьшения поля. Весьма близкая
к описанной картина наблюдалась и в аргоне.
Несколько иначе происходит при добавке в инертный газ мо-
лекулярного (рис. 11.9). До скачка ВАХ сначала падает, как
обычно, вследствие нагревания, но потом становится растущей.
Видимо, это связано с переходом от диффузионных потерь к ре-
комбинационным по мере роста пе. Разряду, контролируемому
объемной рекомбинацией, свойственна растущая ВАХ (п. 6.2
гл. 10). Диффузному состоянию отвечают очень низкие Е/р~
~ 0,12 В/(см-торр). По-видимому, здесь сказывается действие
ионизации (ступенчатой) метастабильных молекул азота, облег-
чающее рождение электронов. В контрагированном состояние
после скачка на оси образуется токовый шнур радиуса 0,5 мм
Добавка азота чем-то стабилизирует разряд, в чистом ксеноне
переход происходил при гораздо более слабом токе, 1 мА вместе
19 мА, как с азотом.
*) Вспомним фазовый переход между жидкостью и паром (перетретьи
пар, переохлажденная жидкость).
32
Рис. 11.9. ВАХ разряда в трубке радиусом
R = 5 см в Хе + 0,12 % N2, р = 120 торр
[11.19]
обеспе-
от оси
8.2. Что необходимо для возникновения контракции. Для то-
го чтобы подавляющая часть электронов оказалась сосредоточен-
ной в тонком канале около оси трубки (или в том месте плоско-
го канала, где образовался шнур), необходимо выполнение по
крайней мере двух условий.
1. Электроны должны рождаться преимущественно там, где
высока их плотность. Должна существовать какая-то нелинейно
возрастающая зависи-
мость скорости рожде-
ния от пе, более быст-
рая, чем обычная —
угпе с уг(Е) = const. Ча-
стота ионизации Vi
должна резко падать от
оси к периферии. Если
нет зависимости Vi от
радиуса г, кат; в диф-
фузном разряде, источ-
ники электронов рас-
пределяются по объему
пропорционально пе, и
сами электроны запол-
няют сечение более или
менее равномерно^ Под-
черкнем, что
чить спад Vi
может зависимость только от пе. Продольное поле при контрак-
ции остается однородным по сечению, поскольку rotE = 0.
2. Гибель электронов должна иметь объемный характер, при-
чем быть достаточно быстрой, чтобы, будучи рожденным в шну-
ре, электрон не мог далеко продиффундировать из него в сторо-
ну. В противном случае даже при сосредоточенных на оси источ-
никах рождения электроны заполнили бы объем благодаря диф-
фузии (амбиполярной). Электроны обязаны гибнуть неподалеку
от места рождения. По этой причине контракция возникает толь-
ко при достаточно сильных токах и больших пе, когда объемная
рекомбинация преобладает над рекомбинацией на стенках. Ра-
диус шнура определяется большей из двух длин: радиусом обла-
сти, где сосредоточиваются источники рождения электронов,
и расстоянием ________ _________ ________________
Нк « УДхТрек ~ УDa[$ne, ИЛИ 7?к УDaTa,
на которое электрон может продиффундировать за время жизни
по отношению к рекомбинации или прилипанию. Контракция
возможна только при условии, что jRk < R. Это дает оценку
пв>10и см-3, которая согласуется с опытом. Тот факт, что кон-
тракция происходит в чистых инертных газах, свидетельствует
в пользу образования молекулярных ионов типа NeJ, Аг^э
иначе рекомбинация была бы слишком медленной.
330
8.3. Механизмы нелинейного рождения. Они те самые, кото-
рые приводят к неустойчивости диффузного разряда: ионизаци-
онно-перегревный, ступенчатая ионизация, максвеллизация. Все
обеспечивают возрастание с пе частоты ионизации, т. е. скорости
ионизации, рассчитанной на один электрон.
Для ступенчатой ионизации и максвеллизации это разъясня-
лось в § 6. Для теплового механизма зависимость уг от пе имеет
характер х\ ~ ехр (—I/kTe) ~ ехр [—const/ (То + const пе) ], где То —
температура газа в случае очень слабого тока (комнатная). Так
получается благодаря очевидным закономерностям: Те ~ Е/N ~ Т
при р ~ NT = const и Т — То ~ оЕ2 ~ пе. Все три механизма на-
чинают проявляться при плотностях пе больше величины поряд-
ка 1011 см-3, и выбрать среди них главный довольно трудно.
Не исключено, что действуют они одновременно, хотя опыт по-
зволяет в тех или иных случаях отдать какому-то предпочтение.
Так, в описанных в п. 8 1 экспериментах в неоне (и аргоне) все
удалось объяснить без привлечения теплового механизма, хотя
перегрев газа был огромным — в три раза.
Наблюдаемый гистерезис при переходе из диффузной формы
разряда в контрагированную и обратно (рис. 11.7) связан с дву-
значностью состояний в зоне перехода. Данный ток i можно осу-
ществить двумя способами: можно распределить его по всему
сечению трубки с низкой плотностью, можно сосредоточить в ма-
лой части сечения у оси. В обоих случаях теплоотвод сбаланси-
рован с тепловыделением от тока. Переход из одного состояния
в другое «запаздывает», поскольку он начинается лишь при до-
вольно сильном вторжении в область двузначности и нестабиль-
ности одного из состояний. Лишь в этом случае инкремент нара-
стания неустойчивости достаточно велик и переход провоцируется
любой малой флуктуацией (см. сноску в п. 8.1).
8.4. Контракция в разряде с потоком. В плоских каналах с
быстрым протоком лазерных смесей четко наблюдается зависи-
мость предельного энерговклада, при котором происходит шну-
рование, от скорости потока и. Чем больше и, тем меньше вре-
мени проводит газовая частица в разряде, тем меньше времени
имеется как для нагревания газа, так и для развития неустой-
чивости, тем стабильнее оказывается разряд, тем сильнее можно
поднять ток до срыва его однородности. В продольном разряде
в плоском канале, описанном в п. 9.3 гл. 10, отмечается четкая
корреляция между срывом и температурой газа на выходе из
него. Контракция наблюдалась всякий раз, когда температура
повышалась примерно на 100 К. Все это говорит в пользу тепло-
вой природы контракции в этих условиях.
Наглядное представление о том, как выглядит шнурование в
таких условиях, дает цветная фотография, приведенная в книге
[10]. О способах борьбы с контракцией, которые были найдены
в ходе разработки мощных лазеров, будет рассказано в § 3. 4
гл. 16.
331
8.5. Шнур и дуга. Хотя в американской литературе явление
контракции тлеющего разряда часто называют «arcing»—дуго-
образование, плазма в шнуре отличается от типичной равновес*
ной плазмы дугового разряда с Те~ Т « 6000—10 000 К. По сво-
им характеристикам шнур занимает промежуточное положение
между сильно неравновесной плазмой диффузного тлеющего раз-
ряда и равновесной дуговой. В шнуре остается сильный отрыв
температур: Те ~ 1—3 эВ, а Т « 2000—3000 К, но он слабее, чем
в тлеющем разряде. Степень ионизации пе ~ 1013—1014 см“3,
и ток больше, чем в последнем, но меньше, чем в дуге. Поле
меньше, чем в тлеющем, но выше чем в дуговом разрядах. Об-
щим с дугой является сосуществование токовой области и бесто-
кового окружения при одинаковости продольного поля в обеих
областях. В этом смысле тонкий столб дуги тоже «контрагп-
рован».
Глава 12. ДУГОВЫЕ РАЗРЯДЫ
§ 1. Определение и отличительные признаки дуги
Дуговыми называют разряды, как правило, самоподдержива-
ющиеся, в которых катодное падение потенциала имеет относи-
тельно низкое значение порядка потенциалов ионизации или
возбуждения атомов, т. е. порядка 10 эВ. Этим дуговой разряд
отличается от тлеющего, у которого катодное падение составляет
сотни вольт. Малое значение катодного падения является резуль-
татом действия иных, чем в тлеющем разряде, механизмов ка-
тодной эмиссии. Эти механизмы в состоянии обеспечить большой
электронный ток с катода, близкий к полному току разряда.
Тем самым отпадает необходимость в значительном усилении
электронного тока, что является функцией большого катодного
падения в тлеющем разряде. Катоды дуг испускают электроны
в результате термоэлектронной, автоэлектронной и термоавтоэлек-
тронной эмиссии. Возможно, существуют еще какие-то более
сложные, комбинированные процессы рождения электронов
у катода.
Дуговым разрядам свойственны большие токи (£ ~ 1—105 А),
намного превышающие типичные токи в тлеющих разрядах
(Z~10“4—10-1 А). Велики по сравнению с тлеющим разрядом
плотности тока на катоде. В одних формах дуг они составляют
/к~ 102—104 А/см2, в других — /к~ 104—107 А/см2. Для сравне-
ния укажем, что даже при высоком для тлеющего разряда дав-
лении р = 1 атм нормальная плотность тока на медном катоде в
воздухе 155 А/см2 соответствует самой нижней границе дугового
диапазона. Напряжения горения дуг чаще всего низкие. В ко-
ротких дугах они не превышают 20—30 В, в некоторых фор-
мах — всего несколько вольт. Вольт-амперные характеристики
дуг во многих случаях падающие, но не всегда.
332
Катоды дуг либо целиком, либо местами и кратковременно
получают от тока много энергии и обладают высокой температу-
рой. Они разрушаются с уносом материала (эрозией) и испаря-
ются. Если спектр излучения прикатодной области тлеющего
разряда совпадает со спектром газа, в котором происходит раз-
ряд, то в спектре дуг присутствуют линии паров материала элек-
тродов. Вакуумные дуги вообще горят в парах испаренного ме-
талла. Что касается состояния плазмы положительного столба —
области между приэлектродными слоями,— то наряду с равно-
весными дугами сплошь и рядом бывают неравновесные. Это
зависит от давления газа. Можно сказать, что равновесность плаз-
мы в разряде постоянного тока характерна только для дуги, а не-
равновесность свойственна и тлеющему разряду, и дуговому, когда
последний происходит при низком давлении.
§ 2. Виды дуг
Под определение дуги как разряда с низким катодным паде-
нием подпадают чуть ли не все разряды постоянного тока, кро-
ме тлеющего. Поэтому разновидностей разрядов, которые при-
числяют к типу дуговых, довольно много. Их можно классифи-
цировать по характеру процессов на катоде, состоянию плазмы
положительного столба, по роду среды (газ или пары материала
катода), в которой протекает ток.
2.1. Дуга с горячим термоэмиссионным катодом. Катод в та-
кой дуге бывает нагретым целиком до температуры около 3000 К
и даже выше, так что сильный ток дуги получается просто за
счет интенсивной термоэлектронной эмиссии. Токовое пятно за-
нимает на катоде сравнительно большую площадь. Плотность
его там ]к ~ 102—104 А/см2. Дуга привязана к одному и тому же
месту катодной поверхности, и токовая площадка стационарна.
Столь высокую температуру в течение длительного времени спо-
собны выдержать только тугоплавкие, с трудом испаряющиеся
вещества: углерод (графит, уголь, сажа), который вообще не
плавится при обычных давлениях (температура его кипения
7\ип^4000 К), особенно широко применяемый на практике
вольфрам (температура плавления Тпл ~ 3700 К, Т^ип 5900 К),
молибден, цирконий, тантал и др. Дуги с горячими вольфрамо-
выми катодами применяют в электродуговых устройствах, часто
высокого давления, когда требуется большой ресурс работы (ма-
лая эрозия) электродов: в плазмотронах, сварочных аппаратах,
для некоторых видов дуговой плавки металлов и др.
2.2. Дуги с внешним накалом катода. Это частный случай
горячего термоэмиссионного катода, но катод нагревается не то-
ком разряда, а от постороннего источника. Разряд, естественно,
является несамостоятельным. Для снижения температуры накала
используют активированные катоды, как в электронных лампах.
От вакуумного диода дугу с внешним накалом отличает присут-
ствие проводящей газовой среды. При увеличений тока, когда
333
ток разогревает катод сильнее, чем подвод внешней энергии,
разряд может перейти в самостоятельный. Дуги такого типа
используют в ряде приборов низкого давления, в термоэмиссион-
ных преобразователях тепловой энергии в электрическую.
2.3. Дуги с «холодным» катодом и катодными пятнами. Ток в
таких дугах протекает через одно или много маленьких, быстро
и беспорядочно перемещающихся, возникающих и исчезающих
пятен на катоде. Плотность тока в пятнах очень велика, ]к ~
~ 104—107 А/см2. На короткое время локализации пятна металл
в данном месте сильно разогревается, разрушается, испаряется,
но по соседству с пятнами и в целом катод остается сравни-
тельно холодным. Пятна всегда образуются на катодах из легко-
плавких металлов: меди, железа, серебра, жидкой ртути и др ,
которые не могли бы выдержать температуры, нужной для рабо-
ты в режиме горячего термоэмиссионного катода (у Си Та31 ~
~ 2570 К). Но при слабых токах и низких давлениях пятна
появляются и на тугоплавких материалах: W, Мо и др Основ-
ным механизмом эмиссии катодных пятен, по-видимому, явля-
ется термоавтоэлектронная.
2.4. Вакуумная дуга. Это дуга с катодными пятнами, кото-
рая зажигается между электродами, находящимися в вакууме,
но горит в плотных металлических парах электрода, которыми
немедленно заполняется разрядный промежуток вследствие силь-
ной эрозии и испарения электродов. Вакуумные дуги возникают
в вакуумных выключателях (прерывателях) сильноточных элек-
трических цепей. Это одна из важных областей приложения
дуговых разрядов.
2.5. Дуга высокого давления. Имеются в виду давления выше
р ~ 0,1—0,5 атм, для которых характерно образование равновес-
ной плазмы в положительном столбе. Среди такого типа дуг
особенно распространены дуги атмосферного давления, в том
числе и в свободном воздухе. Столб дуги атмосферного давле-
ния — наиболее типичный и распространенный образец плотной
низкотемпературной равновесной плазмы, поддерживаемой элек-
трическим полем. Обычные температуры—Т ~ 6000—12 000 К,
но в специальных условиях достигаются и более высокие, вплоть
до 50 000 К (п. 2 8).
2.6. Дуга сверхвысокого давления, 10 атм. Этот вариант,
принадлежащий к группе высоких давлений, следует отметить
особо. Столь плотная плазма излучает так сильно, что в столбе
дуги в излучение перерабатывается до 80—90 % выделяющегося
джоулева тепла. При атмосферном давлении, например, выход
излучения существенно меньше. Указанное свойство нашло важ-
ное применение: на этой основе созданы лампы высокого (сверх-
высокого) давления Дуга горит в ксеноне или парах ртути, ко
торые обладают наиболее подходящими для этой цели излуча-
тельными характерно!иками и высоким светоэлектрическим КПД.
2.7. Дуги низкого давления. Это давления р ~ 10“3—1 торр,
при которых в положительном столбе получается сильно нерав-
334
новесная плазма, в принципе не отличающаяся от плазмы тлею-
щего разряда как в отношении отрыва температур так
и степени ионизации, которая много меньше равновесной. Одна-
ко последняя выше, чем в тлеющем разряде, так как токи в ду-
гах гораздо сильнее.
2.8. Особые виды. Сюда относятся сильно нестандартные ва-
рианты, например дуга Гердиена (1922 г.). Такая дуга горит в
закрученном водяном вихре, отжимающем токовый канал от уз-
кой диафрагмы, через отверстие которой проходит канал. Вслед-
ствие испарения воды дуга горит практически в водяных парах.
В усовершенствованной дуге Гердиена при токе 1,5 кА в диа-
фрагме диаметром 2,5 мм была получена на оси канала самая
высокая из наблюдавшихся в дуговом разряда температур —
50 000 К.
§ 3. Зажигание дуги
3.1. Способы инициирования. Дугу проще всего зажечь, при-
водя в контакт, а потом разъединяя электроды, подключенные к
соответствующему источнику питания, который в состоянии дать
достаточно сильный ток. В момент короткого замыкания элек-
троды в месте контакта сильно раскаляются, частично испаря-
ются, дают эмиссию, и в момент разведения в парах, которые
обычно ионизуются легче, зажигается дуга. Потом пары замеща-
ются газом, если таковой присутствует.
Для зажигания сильноточных дуг применяют вспомогатель-
ный анод, который вставляется между основными электродами
так, чтобы он касался катода, а после подачи напряжения его
быстро удаляют. Когда облако образующихся в момент короткого
замыкания ионизованных паров достигает основного анода, зажи-
гается дуга.
Можно прямо подавать на находящиеся на своих местах
электроды высокое напряжение, достаточное для пробоя газа в
промежутке. При этом источник питания и внешняя цепь долж-
ны допускать горение дугового разряда в соответствии с общей
ВАХ, изображенной на рис. 10.4, и нагрузочной прямой. Напря-
жения обычной сети 220 В бывает достаточным для зажигания
таким способом дуг низкого давления и ртутных ламп. Высокое
давление в последних возникает постепенно по мере испарения
ртути, а вначале зажигается тлеющий разряд, который по мере
разогрева катода переходит в дуговой.
3.2. Переход из тлеющего разряда в дуговой. Он описывается
участком FG ВАХ, изображенной на рис. 10.4. Переход при
постепенном увеличении тока вызывается разогревом катода, бла-
годаря все возрастающей плотности тока в аномальном тлеющем
разряде. В какой-то стадии начинается термоэлектронная эмис-
сия. В случае тугоплавких (термоэмиссионных) катодов переход
происходит более или менее плавно. Если катод сделан из легко-
плавкого металла, который ведет себя в дуге как «холодный»,
335
происходит резкий срыв тлеющего разряда в дугу с мгновенным
возникновением катодных пятен. Это случается при меньших
токах 0,1 1 А), чем в случае токов с термоэмиссионных
катодов (I — 10 А).
На рис. 12.1 показана ВАХ разряда в ксеноновой лампе
(/? = 5 атм) в стадии перехода. Тлеющий разряд при столь вы-
Рис. 12.1. ВАХ в ксеноно-
вой лампе в области пере-
хода от тлеющего разряда
в дуговой [22]
соком давлении стабилизировался при
помощи дополнительного большого
внешнего сопротивления. При токах
i — 10~2—10-1 А горит аномальный
тлеющий разряд. При г —0,1—0.2 А
он теряет стабильность и срывается в
дугу. Напряжение на электродах при
этом резко падает, а ток возрастает.
Один и тот же разрядный ток I — 0,2 А
в переходной неустойчивой области
требует напряжения 250 В, если меха-
низмом его поддержания является вто-
ричная эмиссия с размножением элек-
тронов в катодном падении, и лишь
70 В, если действуют дуговые меха-
низмы эмиссии. Последнее «выгоднее»,
поэтому и происходит самопроизволь-
ный срыв в дугу — наглядный пример действия неустойчивости
(на этот раз катодного процесса).
3.3. Кратковременное прерывание тока. Дуги с горячим и хо-
лодным катодами ведут себя совершенно по-разному при преры-
вании тока. В первом случае разряд восстанавливается без сбли-
жения электродов после сравнительно долгого перерыва, в слу-
чае угольных электродов — до 1 с. Во втором случае даже очень
кратковременный перерыв производит необратимый эффект. Дуга
с медными электродами не восстанавливается уже через 10~3 с,
а с ртутным катодом — при перерыве 10“8 с.
3.4. Дуга переменного тока. При не слишком сильных токах
и не очень коротких межэлектродных промежутках дуга в тече-
ние периода дважды гаснет и снова зажигается. Гаснет она,
когда ток становится меньше некоторого критического значения.
Зажигается — когда напряжение превышает определенный порог,
отчего возникают пики напряжения. В случае угольной дуги в
воздухе длиною 2,6 мм со средней силой тока 2 А на частоте
50 Гц дуга гаснет при i < 0,7 А, а зажигается вновь при
7^110 В. Наблюдается гистерезис: в стадии после зажигания
при росте тока напряжение горения в момент с данным током
больше, чем в стадии уменьшения тока перед погасанием. Это
связано с тем, что после зажигания плазма еще не полностью
разогрелась и условия для протекания тока менее благоприятны,
чем позднее при полном разогреве. В коротких сильноточных
дугах разогрев столба от раскаленных электродов столь велик,
что благодаря тепловой инерционности плазмы исчезают пики
336
зажигания и гистерезисные явления. Осциллограммы тока и на-
пряжения приближаются к синусоидам, как если бы сопротивле-
ние дуги оставалось неизменным в течение периода.
§ 4. Угольная дуга в свободном воздухе
Угольная дуга — классический образец дугового разряда.
Именно она была создана первой (§ 4 введения) и известна под
названием вольтовой дуги. Угольную дугу с умеренным током
зажигают, разводя соприкасающиеся вначале угольные электро-
ды, сильноточную — при помощи вспомогательного анода (п. 3.1).
Дугой разряд был назван потому, что при горизонтальном рас-
положении электродов нагретый токовый канал изгибается,
Рис. 12 2. Угольная дуга в воздухе при i — 200 А: а — теплеровская фото-
графия; б — измеренное поле температур [22]
всплывая серединной частью под действием архимедовой силы.
Угольная дуга в атмосфере принадлежит к типу дуг высокого
давления с горячим катодом. На рис. 12.2а представлена фото-
графия дуги при вертикальном ее расположении, когда картина
осесимметрична.
На рис. 12.3 показаны ВАХ угольной дуги. Катодное падение
составляет примерно 10 В, анодное—11 В, что в сумме равня-
ется 21 В, остальная часть напряжения приходится на положи-
тельный столб. При расстоянии между электродами L > 0,5 —
1 см напряжение горения повышается линейно с ростом L, что
свидетельствует о постоянстве продольного градиента потенциала
в столбе. Например, при i = 7 А поле в длинном однородном
столбе Е ~ 22 В/см. При увеличении тока поле падает. При не-
которой силе тока происходит скачкообразное уменьшение на-
22 Ю П Райзер 337
пряжения горения, ВАХ из падающей превращается в почти
горизонтальную и появляется характерное шипение. Звук вызы-
вается интенсивным испарением анода в образующихся быстро
перемещающихся анодных пятнах, где велика плотность тока.
Плазма столба в воздухе атмосфернего давления равновесна.
На рпс. 12.26 показано измеренное поле температур в сфотогра-
фированной дуге; L = 4,6 см, i = 200 А. В приосевой области
Т« 10 000 К, в максимуме вблизи катода12 000 К. Радиус
Рис. 12.3. ВАХ угольной дуги в воздухе [22]
высоконагретого, а следовательно, ионизованного и в основном
проводящего электрический ток канала составляет примерно
0,5 см; от катода к аноду канал несколько расширяется. Темпе-
ратура катода 7\~3500 К, анода — ТА ж 4200 К (до «шипе-
ния»). На заостренном катоде дуга привязана к острию. При
небольших токах z‘~ 1—10 А плотность тока на катоде jK~
~ 470 А/см2, на аноде /А~ 65 А/см2. С увеличением тока jK
растет вплоть до « 5 • 103 А/см2 при i ~ 400 А, но при даль-
нейшем росте тока не повышается — расширяется токовая пло-
щадь на катоде.
§ 5. Прикатодные процессы в дуге с горячим катодом
5.1. Назначение катодного слоя. Оно, в принципе, такое же,
что п в тлеющем разряде. В отсутствие постороннего накала
катода катодный слой призван создать условия для самоподдер-
жания тока, в данном случае — сильного. Осуществляется это
предназначение иным путем. В катодном слое тлеющего разряда
рождается столько пар зарядов, сколько необходимо, чтобы их
воспроизводство было обеспечено вторичной эмиссией под дей-
ствием ионного потока. При термоэлектронной эмиссии ионы.
338
рожденные в катодном слое, обязаны сообщать катоду энергию,,
необходимую для поддержания должной температуры. Такой
способ извлечения электронов из катода ионами (не путем инди-
видуального вырывания, а посредством нагрева металла) более
эффективен. Вторичная эмиссия дает только у ~ 10~3—10-1 элек-
тронов на ион, и потому доля ионного тока на катоде в тлею-
щем разряде составляет без малого единицу, 1/(1 + 7), электрон-
ного— у/(1 + 7) ~ 10-3—10-1. В дуге с горячим катодом термо-
электронная эмиссия, как показывает анализ, дает долю S «1
~ 0.7—0,9 полного тока, а ионы приносят на катод 1 — 5 ~ 0,1—
0,3 тока. От одного иона с катода эмитируется 5/(1 —5) ~2—9
электронов. Но столь эффективное действие ионов возможно
только при большом токе, сильно нагревающем катод.
С большой разницей в соотношении электронного и ионного
токов на катоде тлеющего разряда и дуги связано различие в
значении катодного падения Vк. В электронейтральной плазме
вслед за катодным слоем практически весь ток переносится элек-
тронами. Чтобы поднять долю электронного тока от у/(1 + 7)~
~ 10“3—10"1 до единицы, в катодном слое тлеющего разряда
должно родиться несколько поколений электронов, а для этого
требуются сотни вольт напряжения, ибо на рождение пары ионов
в слабоионизованиом газе расходуется в среднем 30—50 эВ.
В катодном слое дуги доля электронного тока должна вырасти
всего на 1 — 5 « 10—30%. Тут не нужно даже одного дополни-
тельного поколения. Поэтому катодное падение в дуге порядка
или даже меньше потенциала ионизации. Но вместе с тем обой-
тись вообще без катодного слоя тоже* нельзя. Доля ионного тока
в электронейтральной плазме положительного столба ничтожно
мала, ц+/ (це + ц 4.) ~ 10-2. Столь слабый ионный ток, даже вместе
с чисто тепловым потоком энергии, не смог бы нагреть катод.
И действительно, доля ионного тока вырастает в слое практи-
чески от нуля и до 10—30 %.
Катодный слой дуги выполняет свою функцию главным обра-
зом тем, что ионы здесь рождаются в большом количестве и при-
обретают в поле кинетическую энергию, которую несут к катоду,
в дополнение к другим источникам: потенциальной энергии ней-
трализации ионов, тепловому потоку из плазмы. Но этим роль
слоя не исчерпывается. Он выполняет и другие задачи, причем
все оказывается взаимосвязанным. Температура газа у поверх-
ности катода совпадает с температурой металла и по крайней
мере вдвое ниже, чем в положительном столбе (рис. 12.4).
За счет одной лишь термической ионизации заряды рождаться
здесь никак не могут. Между тем скорость рождения в слое
должна быть даже большей, чем в столбе, ибо нужно создать
сильный ионный ток. Это происходит в катодном слое за счет
нетермического механизма сообщения энергии эмитированным
электронам. Кроме того, сильное электрическое поле, которое
образуется у поверхности катода, благодаря эффекту Шоттки
(и. 6.1 гл. 4) уменьшает работу выхода и тем облегчает термо-
22* 339
электронную эмиссию. Само поле, как и катодное падение, воз-
никает, в свою очередь, благодаря повышенной скорости рожде-
ния ионов в слое и накоплению положительного пространствен-
ного заряда из-за различия в скоростях устранения электронов
и ионов.
5.2. Структура катодного слоя. Ее основная особенность опре-
деляется большой плотностью тока на катоде. Вблизи катода об-
Рис. 12.4. Схематические
распределения темпера-
туры, потенциала и по-
ля в дуге от катода до
анода
разуется очень большой положительный
пространственный заряд. Он обусловлива-
ет резкое падение поля и потенциала в
исключительно тонком слое, который да-
же меньше длины свободного пробега
ионов и электронов. На этот бесстолкно-
вительный слой приходится значительная
часть катодного падения потенциала. Бес-
столуновительный слой у поверхности
отделен от положительного столба более
протяженным промежуточным слоем, где
плазма квазинейтральна, поле гораздо сла-
бее, чем у катода, и где происходит уси-
ленная ионизация атомов электронами. По-
следние ускорены в бесстолкновительном
слое если не до потенциала ионизации, то
до значительной его части (рис. 12.5).
Остальное приобретается в столкновени-
ях с другими электронами. Здесь сосре-
доточен основной источник рождения
ионов, которые несут ток к катоду.
В бесстолкновительном слое, где нет источников зарядов,
электронная и ионная составляющие полного тока остаются не-
изменными и такими же, как на катоде. В соседней части катод-
ного слоя доля электронного тока вырастает от 5 до це/(це + р + ) ~
~ 1, а доля ионного падает от 1 — 5 до ц+/(ре + ц+)< 1. Плот-
ности зарядов пе ~ п+ здесь возрастают в направлении к поло-
жительному столбу вследствие их интенсивного рождения. По-
скольку электроны здесь уже испытывают рассеивающие столк-
новения, часть их возвращается обратно к катоду. Они образуют
небольшой обратный ток. Затормаживаясь полем в бесстолкнови-
тельном слое, электроны все же частично достигают катода. Это
похоже на поток электронов из плазмы на отрицательно заря-
женный зонд. Значение обратного тока описывается тэй же фор-
мулой Ленгмюра (8.2).
5.3. Поле у катода. Рассмотрим бесстолкновительный слой
у катода. Ось х направим от катода. Плотности электронного и
ионного токов в слое постоянны и равны
je = Sj = eneve, 7+= (1-5)7 =^en+v+. (12.1)
Допустим, что все катодное падение потенциала VK сосредоточи-
вается в бесстолкновительном слое. Поле Епл_ на границе с плаз-
340
мой гораздо меньше поля Ек на границе с катодом. Энергии и
скорости зарядов определяются проходимой ими разностью по-
тенциалов:
ve = (2eV/zn)1/2, = [2е(7к - V)/M]1/2.
Подставим (12.1), (12.2) в уравнение Пуассона:
d2V faij Г(1 — S)~\/M $ 1/т
- —i = 4ле(«+ - пе} = i----------------------v—
dx у
Замечая, что d2V/dx2 = (!/2)dE2/dV, интегрируя (12.3)
yvK-v
с граничным условием Е ~ Еил_ ~ 0 при
V = VK и относя результат к катодной
границе, где V = 0, находим поле у като-
да (Маккоун, 1929 г.):
М- = ~ [(1 - 5) VMS Vm] VV^.
(12.2)
один раз
Рис. 12.5. Схематические
распределения плотно-
стей зарядов, токов и
поля в катодном слое
дуги: 1 — бесстолкнови-
тельная часть слоя, 2 —
квазин ейтральная
(12.4)
Положительный объемный заряд, со-
здаваемый ионами, способствует усиле-
нию поля у катода. Отрицательный заряд
электронов частично компенсирует этот
эффект. Однако при реальных для любых
дуг значениях S ~ 0,7—0,9 степень ком-
пенсации мала. Описывающий действие
электронов второй член в формуле (12.4)
составляет не более нескольких процен-
тов от первого, и его можно без ущерба
опустить. В численном виде
Ек = 5,7- 10M1/4 (1 — 5)1/2 Fk/47V2,
h = 4УК/ЗЕК, (12.5)
где А — атомная масса иона, Ек [В/см],
Ук [В], / [А/см2]. Величина h представ-
ляет собою толщину рассматриваемого
слоя. Ее легко найти, если проинтегрировать (12.3) без электрон-
ного слагаемого дважды. Ситуация в бесстолкновительной части
катодного слоя аналогична процессу в вакуумном диоде (п. 6.1
гл. 8). и формула (12.5) соответствует закону «трех вторых»
(8.15). Роль эмиттера зарядов в данном «диоде» выполняет не ка-
тод, а примыкающая к слою плазма, которая посылает в слой
положительные ионы, как в случае отрицательного зонда (и. 6.2
гл. 8)*).
*) Закономерность (12.5) свойственна столь сильному току, что слой
пространственного заряда очень тонкий и ионы движутся в нем без столк-
новений. В случае сравнительно слабого тока и протяженного слоя, когда
ионы совершают дрейф, dE^lx = 4л/+/ц+Е'. Отсюда Ек = (8л/+/г/ц+)1/2,
341
Равенства (12.4) или (12.5), которые, кстати сказать, спра-
ведливы и для катодного пятна, вместе с другими соотношения-
ми, описывающими процессы у катода, образуют единую систему
уравнений. Однако для оценок неизвестные величины можно
взять из эксперимента. Например, при типичных для дуг с го-
рячим катодом параметрах j = 3 • 103 А/см2, S = 0,8, VK = 10 В,
А = 28 (азот) получаем Ек = 5,7 • 105 В/см, h = 2,3 • 10-5 см.
По формуле Шоттки (4.24) от такого поля работа .выхода умень-
шается на еАф = 0,27 эВ. При Т — 3000 К скорость термоэлек-
тронной эмиссии возрастает в ехр (еАсрДТ) ~ 3 раза.
5.4. Баланс энергии на катоде и доля ионного тока. Темпе-
ратура катода, от которой в основном зависит плотность тока
термоэмиссии, а также соотношение ионной и электронной со-
ставляющих тока определяются из системы уравнений, описы-
вающих баланс энергии на катоде, рождение зарядов в катодном
слое; см. (12.4) и др. Расчету такого рода весьма несовершенны
из-за многообразия и сложности процессов и неполноты знаний
о важных величинах. Они дают результаты, которым можно
придавать скорее качественное значение [12.1]. Получить ори-
ентировочное представление об одной из наиболее интересных
величин — S — можно, составляя баланс энергии упрощенным
образом.
Каждый ион приносит к катоду свою кинетическую энергию,
которую он приобрел в катодном падении Vк. Какую-то часть
ее Pi он отдает катоду при ударе; [Ji называется коэффициентом
аккомодации. При нейтрализации иона выделяется энергия, рав-
ная потенциалу ионизации I образующегося атома за вычетом
работы выхода ф, которая затрачивается на извлечение нейтра-
лизующего электрона из металла. Какая-то доля ее ^2 также
отдается катоду. Доли 1 — Pi, 1 — ^2 остаются у отлетающего ато-
ма. О коэффициентах аккомодации кинетической (Pi) и потен-
циальной (Р2) энергии мало что известно, но на основании не-
которых аналогий и косвенных соображений можно предпола-
гать, что они порядка единицы. С каждым эмитированным элек-
троном катод теряет энергию eq (плюс небольшую энергию 2кТк,
с которой электрон вылетает). Если допустить, что энергия, вно-
симая в катод ионами, как раз и затрачивается на эмиссию элек-
тронов, и положить Pi = Р2 = 1, найдем
i Vt, + I — Ф
7> = /+(Гк + /-Ч)), S = = v ^-1 ' (12-6)
Например, при 7=14 В, VK = 10 В, ф = 4 В S = je/j = 0,83,
7+/j = 0,17. Это — разумные величины, которые не противоречат
другим данным. Однако в действительности в балансе энергии
VK = 2EKh/3. Вместо (12 5) получается Ек = (12л7 + Ук/ц+)1/3, а ток, огра-
ниченный действием пространственного заряда, в «газонаполненном» диоде
вместо (8 15) равен /+ = (9р,+/32л) У2/Д3, как в катодном слое тлеющего раз-
ряда (10 14).
342
катода имеются и другие составляющие. В катод поступает из
плазмы теплопроводностный поток QT, вызванный перепадом
температур между плазмой (Г 6000—12 000 К) и катодом
(Тк » 3000 К). Поступает и поток излучения <2ИЗл- От эмити-
рующей поверхности катода тепло отводится в глубь металла
теплопроводностным потоком <2П, так как противоположная
часть тела катода холоднее из-за охлаждения. Какую-то энер-
гию 2изл к катод излучает.
Величины Q имеют размерность мощности [Вт]. Отнесем их
к току дуги i [А] и введем обозначение q = Q/i[B]. По смыслу
это потоки, которые приходятся на один электронный заряд,
протекающий с электрическим током (численно — энергии в
электрон-вольтах). Баланс энергии на катоде из расчета на еди-
ничный протекающий заряд имеет вид ({Ji = £2 = 1)
= (1 - S) (Ук +1 - ф) + qT - дизл - 5ф - qH3JI к. (12.7)
Учет всех этих факторов не меняет порядка величины S по
сравнению с оценкой (12.6). Подробные расчеты баланса вмес-
те с другими уравнениями, в которых связаны входящие в
(12.7) величины, показывают, что при увеличении тока дуги
температура и плотность тока на катоде возрастают, а катод-
ное падение потенциала, поле у катода и
уменьшаются [12.1].
Рис. 12.6. Зависимость катодного падения Потен-
циала от силы тока дуги (вольфрамовый катод
в атмосфере гелия, р — 1 атм). Получено зон-
довым (7), калориметрическим (2) методами и
путем сближения электродов (5). Кривая 4 —
вольтов эквивалент теплового потока дп в катод
[12-1]
доля ионного тока
Заметим, что при вычислении доли ионного тока часто при-
бегают к оценке баланса энергии не на самом катоде (12.6),
а в катодном слое [12.1]. Предполагают, что вся энергия, при-
обретаемая электронами в катодном падении, затрачивается на
ионизацию, т. е. на рождение ионов, потом падающих на катод.
Это дает
/еГк = /+/, 5 = 7/(/+Ук), 7+/7 = Ук/(7+Ук). (12.8)
С теми же числами, которые были взяты при оценке по (12.6),
получается S = 0,58, j+/j = 0,42. Надо полагать, что оценка ион-
ного тока по (12.8) завышена, поскольку из-за возбуждающих
столкновений на образование пары ионов в среднем тратится
энергия, превышающая потенциал ионизации.
5.5. Результаты измерений. На рис. 12.6 представлены изме-
ренные разными методами падения потенциала у вольфрамового
343
Рис. 12 7. Распределение
температуры по радиусу
рабочей торцевой поверх-
ности стержневого вольф-
рамового катода в атмосфе-
ре арюна [ 12 1]
катода в атмосфере гелия при р = 1 атм в зависимости от тока
дуги I. Калориметрический способ заключается в измерении кало-
риметрическим методом потока тепла (мощности), отводимого
теплопроводностью от поверхности в глубь катода Qn [Вт]. Катод-
ное падение VK восстанавливается на основе этого измерения и
известного тока i путем привлечения теоретических соображений
о балансе энергии на катоде. На рис. 12.6 представлена также
измеренная величина дп == которую называют вольтовым
эквивалентом теплового потока в катод. Она связана с VK соот-
ношением баланса энергии (12.7). В методе сближения электро-
дов измеряется уменьшение напряжения на электродах при
сокращении расстояния между ними.
Считается, что перед самым моментом
короткого замыкания, после которого
напряжение резко падает до долей
вольта (что соответствует сопротивле-
нию контакта), положительный столб
полностью исчезает и напряжение рав-
няется просто сумме катодного и анод-
ного падений. Последнее определяется
отдельно и вычитается. Все методы
указывают на уменьшение VK с уве-
личением тока, но числовые резуль-
таты не совпадают. Наиболее досто-
верным является, по-видимому, резуль-
тат зондовых измерений.
На рис. 12.7 показаны радиальные
распределения температуры на торце-
вой токовой поверхности стержневого
вольфрамового катода диаметром
0,6 см и длиной 2,5 см. В центре тем-
пература превышает 4000 К. Видно,
как расширяется высокотемператур-
при возрастании тока. Температу-
ру поверхности измеряют в основном по яркости ее свечения.
Плотность тока на вольфрамовом катоде составляет 103—
104 А/см2. Ее находят по известному полному току и измеренно-
му распределению температуры, которое показывает площадь,
занимаемую током на катоде. Расчет контролируется при помощи
формулы для тока термоэлектронной эмиссии. Долю ионного то-
ка измерить прямыми путями невозможно. Ее извлекают из ана-
лиза баланса энергии и других измеренных величин. Так полу-
чаются цифры 1 — S ~ 0,1—0,3.
Одной из важнейших для практики мощных электродуговьтх
устройств является проблема эрозии электродов, в особенности
катода. Даже тугоплавкие материалы подвержены разрушению
и испарению. Резко повышает эрозию присутствие в газе кисло-
рода, паров воды, даже в малых концентрациях порядка 0,1 %,
что вызывает окисление. Тем более это относится к такой
344
ная токовая площадь
распространенной среде, как воздух. Стойкость катода характе-
ризуется удельной эрозией — потерей массы из расчета на проте-
кание заряда 1 Кл. Удельная эрозия зависит от многих условий.
Для стержневых вольфрамовых катодов в инертных газах при
токах в сотни ампер и не низких давлениях она имеет порядок
10"7 г/Кл. Это значит, например, что при токе 300 А катод те-
ряет 0,1 г в час.
5.6. Полый катод. При низких давлениях р < 1 торр даже на
тугоплавком вольфраме образуются катодные пятна (§ 6), мате-
риал в которых разрушается гораздо сильнее, чем при работе
в режиме горячего катода. Поэтому в практических устройствах
стержневые катоды из тугоплавких материалов применяют
только при высоких давлениях. При низких давлениях приме-
няются конструкции, разработанные по принципу полого катода.
В простейшем варианте полый катод представляет собой отре-
зок трубки, к внутренней поверхности которой «привязывается»
дуга, как в тлеющем разряде (п. 5.4 гл. 10). С применением
продувания газа сквозь полые катоды, чтобы создать внутри
газовую атмосферу, удалось добиться очень высокой стойкости
тугоплавких электродов в электродуговых устройствах [12.1].
Она характеризуется рекордно малой удельной эрозией 10“9 —
10~10 г/Кл.
§ 6. Катодные пятна и вакуумная дуга
Концентрированные токовые центры возникают на катоде в
условиях, когда нужно перенести значительный ток, а катод по
тем или иным причинам не может -быть нагретым целиком до
высокой температуры. Причины эти могут заключаться в легко-
плавкости металла, как чаще всего и бывает, в сравнительно
малом токе, который способен вызвать эмиссию на катоде, толь-
ко будучи собранным на маленькой площади, в низком давлении
окружающей среды. В последнем случае необходимо впрыснуть
в промежуток некоторое число атомов (паров катода), иначе
неоткуда будет взяться ионному потоку, несущему на катод
энергию, без чего катод не может выполнять свою эмиссионную
функцию. Но для эффективного испарения металла энергия
также должна быть сконцентрированной. И действительно,
ориентировочно при 1<1 —10 А, р<1 торр катодные пятна
образуются даже на тугоплавких веществах, которые при по-
вышенных токах, более высоких давлениях ведут себя как тер-
моэмиссионные, рассмотренные в § 5. Последнее называют диф-
фузной привязкой дуги к катоду, в отличие от привязки к пят-
ну. На легкоплавких металлах пятна образуются при любых
давлениях и токах.
6.1. Основные экспериментальные факты. Эволюция пятен.
На ранней стадии разряда на катоде возникают маленькие,
быстро, беспорядочно и независимо друг от друга перемещаю-
щиеся пятна. Размеры их г ~ 10-4—10-2 см, скорости v ~ 103—
345
Рис. 12.8. Фотография вакуумной ду-
ги между медными электродами ди-
аметром 2,5 см; ток 6 кА [12.3]. Вид-
ны яркие катодные пятна
104 см/с. Эрозию поверхности они вызывают незначительную и,
по-видимому, нетермической природы. Высказывалось предпо-
ложение, что эрозия связана с микровзрывами мельчайших
выступов на поверхности под действием сконцентрированного
тока в самом выступе. Через время порядка 10“4 с характер
пятен меняется. Маленькие
пятна объединяются в более
крупные и менее подвижные ас-
социации, скорости которых
10—102 см/с. Эрозия в таких
укрупненных ячеистых пятнах
существенно больше и имеет
уже термический характер, бу-
дучи вызванной нагревом и ис-
парением макроскопических
участков поверхности за счет
энергии, приносимой ионным
током из плазмы паров.
Пороговый ток, размножение.
Через отдельное пятно не мо-
жет течь слишком малый ток.
Существует минимальный, пороговый ток на одно пятно, а следо-
вательно, дуги в целом: гт1П « 0,1 — 1 А. При уменьшении тока до
Zmin весь он концентрируется в одном-единственном пятне, а при
i < Jmm Дуга гаснет. Отмечена эмпирическая закономерность,
согласно которой для многих неферромагнитных материалов
fmin^2,5 10"4ТкипПА,
где X [Вт/ (см • К) ] — теплопроводность. Физический смысл зако-
номерности не очень ясен, как и многое другое, касающееся
катодных пятен. Значение среднего тока, пропускаемого одним
пятном, лежит в диапазоне от 1 А (на жидкой ртути) до 300 А
(на вольфраме). При увеличении тока разряда число пятен воз-
растает (рис. 12.8). Пятна образуются, как правило, не на новых
местах, а размножаются путем «деления». Время жизни пятна
по отношению к делению зависит от скорости нарастания тока.
При dl!dt~ 105—107 А/с оно имеет порядок 10“5 с. Пятна иногда
распадаются и исчезают.
Плотность тока. Если через пятно протекает ток Z ~ 10 А,
а радиус пятна г ~ 10~3 см, плотность тока составляет / « i/nr2 &
~ 3 • 106 А/см2. Приводимая различными авторами плотность
тока в пятнах лежит в диапазоне / ~ 104—107 А/см2, а на ме-
ди— даже до 108 А/см2. Данные по / крайне неопределенны, не-
совершенны и противоречивы. Для определения / обычно доби-
ваются существования одного пятна, чтобы был известным ток
i через него, однако трудность состоит в определении размеров.
Для этого применяют высокоскоростную фотографию, и тогда
приходится отождествлять размер токового пятна с размером
светящейся области, что является весьма проблематичным. Оце-
346
нивают размеры по эрозионным следам на поверхности катода,
которые исследуются после выключения дуги (метод автогра-
фов); здесь также нет никакой уверенности в правильности
отождествления.
Испарение. Катодные пятна, в которые с ионным током по-
ступает концентрированный поток энергии, являются источником
интенсивных струй пара. На 10 эмитированных электронов ис-
паряется примерно 1 атом. Скорости струй имеют порядок
105—106 см/с. Удельная эрозия в больших ассоциациях пятен
на меди составляет 10-4 г/Кл. В единичных пятнах на ранней
стадии разряда эрозия, как говорилось, существенно меньше:
для меди 5 • 10~7 г/Кл.
Температура, плотность частиц. Крайне противоречивы дан-
ные по температуре поверхности металла в пятне. Температуры
находят путем измерений яркости свечения либо же на основа-
нии оценок плотности и давления паров у поверхности. Для
пятна на ртути приводят цифры от 700 до 2000 К, на меди —
2400—3300 К. Плотность паров, оцененная по давлению насы-
щения, должна быть порядка 1017—1019 см-3*). Определение
концентрации нейтральных частиц по ослаблению электронного
пучка в вакуумной дуге на железном катоде дало 1016—1017 см-3.
Измерения плотности заряженных частиц над пятнами на по-
верхности (по штарковскому уширению и отношению интенсив-
ностей спектральных линий атомов и ионов меди) дало пе«
« 5 • 1017 см-3, что характерно для плотной низкотемпературной
плазмы. Значит, плотность паров и степень ионизации весьма
высоки. Аналогичные измерения дают электронную температуру
Те « 1-2 эВ.
Катодное падение. Катодное падение измеряют двумя спосо-
бами: при помощи зонда и методом сближения электродов
(п. 5.5), в частности по напряжению горения короткой вакуум-
ной дуги. Предполагается, что в вакуумной дуге анодное паде-
ние мало. Замечено, что катодное падение особенно мало для
металлов, у которых имеются низкие метастабильные уровни.
Это говорит в пользу ступенчатой ионизации атомов металличе-
ского пара. В табл. 12.1 собраны некоторые параметры катод-
ных пятен для нескольких металлов. Указаны либо усредненные
величины, либо приведен диапазон, если результаты разных ав-
торов расходятся очень сильно или значение существенно зави-
сит от условий измерения. Среди множества данных, получен-
ных на протяжении десятилетий, в таблицу отобраны по воз-
можности результаты измерений после 1960 г.
ВАХ. На рис. 12.9 представлены ВАХ металлических ваку-
умных дуг. В отличие от многих дуг они — возрастающие. Поче-
му — объяснений нет. Подробно с результатами экспериментов
(и попытками их объяснить) можно ознакомиться в [12.2, 12.3,
3], где имеется и библиография.
*) По расчетам Т и N для меди ближе к верхним цифрам.
347
Пятно в магнитном поле. Одно из любопытнейших явлений,
на которое обратил внимание еще Штарк (1903 г), наблюдав-
ший катодные пятна на поверхности жидкого ртутного катода,—
это обратное движение пятна дуги в магнитном поле, направ-
ленном касательно к поверхности. Пятно движется в направле-
нии, противоположном магнитной силе [iH], действующей на ток.
Удовлетворительного объяснения эффекта, даже качественного,—
нет (несмотря на множество попыток).
Таблица 12.1. Некоторые характеристики катодов с катодными пят-
нами
Металл Си Ag Zn Hg Fe W
Потенциал иониза- ции, В 7,68 7,54 9,36 10,39 7,83 7,98
Потенциал возбуж- дения метаста- бильных уров- ней, В * 4 4,7—4,9
Катодное паде- ние, В 15-21 12-16 10-11 8-9,5; 19 *) 17—18 16—22
Температура кипе- ния, К 3150 2436 1046 630 3045 5900
Теплопроводность, Вт/(см-К) 4,1 4.17 1,13 0,104 0,84 1,67
Пороговый ток пят- на, А 1,6 1,2 0,3 0,07 1,5 1,6
Средний ток на пятно, А 75-200 60-100 9 0,5-2 60-100 100-300
Плотность тока, А/см2 104-108 ЗЛО4 104—106 107 104—10е
Удельная эрозия при токе 100— 200 А, г/Кл Ю-4 1,3-10~4 1,3-10’5
Скорость струи, 10 км/с 1,5 0,9 0,3-0,5 0,1-4 0,9 1,3-3
Наблюдаются два режима с ® 8—9,5 и 19 В.
6.2. Состояние теории катодных пятен. Немного найдется
явлений в газовом разряде, которые породили бы такое количе-
ство гипотез, моделей и теоретических построений. Ни одно из
них не объясняет всей совокупности экспериментальных фак-
тов. Теории рисуют, подчас правильно, лишь какие-то стороны
картины, но не отвечают на многие вопросы — почему? Почему
пятна делятся, почему смещаются «не туда» в магнитном поле,
откуда берутся колоссальные плотности тока 108 А/см2, если
348
только можно верить этим цифрам, и т. д. Один из исследовате-
лей дугового разряда еще в 1968 г. насчитал 17 различных и
даже взаимоисключающих объяснений явлений в катодных пят-
нах [12.3], а с тех пор появилось еще множество работ. Такое
положение, безусловно, связано
с крайней сложностью и запу-
танностью картины, в которой
тесно переплетаются твердо-
тельные, поверхностные, меж-
фазные, плазменные, электри-
ческие, тепловые процессы*).
Картина явлений в области
пятна во многом похожа на то,
что происходит у горячего ка-
тода. В пятно поступает ион-
ный ток. Ионы приносят кинети-
ческую энергию, которую при-
обрели в катодном падении.
Вместе с потенциальной энер-
гией, выделяющейся при ней-
трализации, она идет на разо-
грев металла. Это в совокупнос-
ти с действием сильного поля
(п. 6.3) вызывает эмиссию и,
с другой стороны, испарение
металла. Пары создают в слу-
чае вакуумного промежутка ту
Рис 12 9 ВЛХ слаботочных вакуум-
ных дуг при различных материалах
катода [12 3]. Диаметр электродов
равен 1 27 см, расстояние между ни-
ми L = 0,5 см
среду, которая ионизуется эмитированными электронами, ускорен-
ными в катодном падении. Это, в свою очередь, является источ-
ником ионного тока. Процесс испарения из локализированного
нагретого центра зависит от теплопроводностного оттока энертии
в соседние слои металла и других составляющих энергетического
баланса, и т. д. Многие элементы этой картины рассчитываются в
разумном согласии с опытом, хотя до недавнего времени в теориях
присутствовали те или иные параметры, определяемые из опыта.
В последнее время доведена до логического завершения
гидродинамическая модель катодного пятна, в которой картина
процессов воссоздается в замкнутом виде без привлечения эм-
пирических параметров [12.2, 12.4]. Гидродинамическая теория
описывает и катодные пятна на пленочных катодах, которые мно-
го изучались на опыте [12.5]. Пленочные катоды часто исполь-
зуют на практике. Кроме того, не редки случаи, когда катодное
*) Впрочем, впечатление какой го уникальной сложности явления ка-
тодного пятна усугубляется еще и тем4 что к нему, ввиду большой практи-
ческой важности, приковано внимание исследователей Мимо многих слож-
ных и непонятных явлений в газовом разряде просто проходят из-за их не-
достаточной значимости Быть может — до поры до времени, пока не возник
практический стимул, как это случилось, например, с неустойчивостями
тлеющего разряда (гл И).
349
пятно, присутствующее на казалось бы массивном катоде, на
самом деле горит на покрывающей его пленке окислов или
загрязнений. На пленке пятно появляется с большей легкостью:
легче происходит локальный разогрев из-за затрудненности от-
вода теплоты в массив под пленкой. По мере выгорания участ-
ка пленки пятно предпочитает переброситься на другой участок,
чем остаться на поверхности массива. Это является одной из
причин перемещения пятен, наряду с переброской с одного
микровыступа на другой после тепловою разрушения первого.
6.3. Механизм эмиссии. Этот вопрос, безусловно, является
кардинальным. Среди известных механизмов эмиссии только
термоавтоэлектронная в состоянии дать плотности тока ] ~
~ 106 А/см2 без нереалистических допущений о существовании
сверхвысоких температур и полей у поверхности*). Из
табл. 4 8 видно, что при Т = 3000 К и работе выхода ф = 4 В
плотности тока эмиссии имеют нужный порядок 106 А/см2 даже
без предположений об усилении* поля вблизи микровыступов на
поверхности. Существование последних в развитом пятне, по-
видимому, вообще является проблематичным, так как микровыс-
тупы оплавляются, разбрызгиваются и испаряются в первою
очередь.
Плотность тока на пятне 7, доля ионной составляющей 1 — S,
поле у поверхности Е, температура металла Т связаны системой
уравнений, описывающих эмиссию je = S]=F(T, Е), поле по
(12.5) Е = СУ]’+==СУ](1 —S), баланс энергии. В 1959 г. Ли
[4.5, 8] выполнил серию расчетов на ЭВМ на основе первых
двух уравнений, задаваясь Т, работой выхода ср и константой С,
ориентировочно соответствующей меди {А = 63, VK=10 В). Ре-
зультаты этих расчетов, которые дали возможные наборы пара-
метров пятна, показывают, что на основе представлении о термо-
автоэлектронной эмиссии и уравнения (12.5) для поля можно
без особых натяжек получить не находящиеся в резком противо-
речии с экспериментом результаты. Несколько таких наборов
представлено в табл. 12.2**). Надо сказать, что при понижен-
ных значениях / и Е требуются, по-видимому, нереально боль-
шие доли ионного тока. С другой стороны, при самых высоких
значениях / и £, когда доля 7+/у правдоподобна, катодное паде-
ние, чтобы дать сильное поле, должно сосредоточиться в слое
толщиной h ~ VKlE ~ 10/3,3 107 ~ 3 10“7 см, т. е порядка десят-
ка атомных диаметров’ Чтобы получить 108 А/см2, потребовалось
бы Е « 1,5 • 108 В/см, Л ~ 6 10~8 см, что уже трудно себе пред-
ставить (это порядка толщины границы тела); о некоторых
*) Еще в 1923 г , до возникновения квантовой механики, Ленгмюр вы-
сказал мысль о вырывании электронов из катодного пязна дуги полем прост-
ранственного заряда Когда стало известно о квантовомеханическом эффек-
те автоэлектронной эмиссии (1928 г , см п 6 3 гл 4), Маккоун в развитие
гипотезы Ленгмюра вывел формулу (12 4) для поля у катода
**) На основе этих данных, более подробно приведенных в [8], была по-
строена табл 18.
•350
других моделях и теориях см. в [8, 12.3], но в настоящее вре-
мя больше склоняются к выше изложенной, которая, по-види-
мому, может объяснить ток ] ~ 106 А/см2.
Рассмотренная модель относится к материалам типа медиг
обладающим умеренной летучестью (отношение работы выхода
Таблица 122 Согласованные по плотностям токов
]+ и полю Е у катода наборы параметров катодного пятна дуги при
.заданных Т и ф
т, к ср, В Е, Ю7 в/см j, 106 А/см2
3000 4 3,3 4 0,30
3000 4 2,8 2 0,45
3000 4 0,8 0,1 0,83
3500 4 2,6 4 0,23
3500 4 2,3 2 0,30
3500 4 0,8 0,1 0,45
3000 3,5 2,5 4 0,20
3000 3,5 2,1 2 0,25
3000 3,5 0,6 0,1 0,45
ф к энергии испарения атома ф5 ф/фв = 1,4). В случае нелету-
чих веществ (вольфрам, ф/фз = 0,6) или сильно летучих (ртуть,
ф/ф5 = 8) описанным механизмом эмиссии объяснить параметры
катодного пятна в вакуумной дуге не удается. При температуре
6000 К, необходимой для испаренгГя W, без чего неоткуда
взяться ионам, плотность тока термоэлектронной эмиссии значи-
тельно превышает реальную. В этом случае у катода вообще не
возникает сильного вытягивающего электрического поля [12.6]
Образующийся отрицательный пространственный заряд ликви-
дирует сильное поле и ограничивает ток с пятна, как в вакуум-
ном диоде, где действует закон трех вторых (§ 6 гл. 8). Напро-
тив, Hg, где даже •критическая температура составляет 1753 К,
механизмы термоавтоэлектронной и, тем более, термоэлектронной
эмиссии мало что дают. Для действия одной лишь автоэлектрон-
ной эмиссии требуются нереально сильные поля. И. И. Беилис
выдвинул гипотезу об отсутствии в ртутной дуге катодного слоя
в обычном понимании и о возникновении неподалеку от жидкой
поверхности двойного электрического слоя на толщине, меньшей
длины свободного пробега частиц. Привнесение в плазму
энергии ионами, ускоренными в двойном слое, создает согласно
этой модели условия для термической ионизации и образования
плазменного катода.
6.4. Взрывная эмиссия. Об этом не так давно обнаруженном
явлении (Г. А. Месяц, 1966 г.) уместно рассказать здесь, ибо
оно имеет общие черты с тем, что происходит в катодном пятне
вакуумной дуги [12.7.] Опыты показали, что при импульсном
351
пробое вакуумного промежутка с сильно заостренным катодом
резкое нарастание тока после некоторой задержки от момента
приложения напряжения неизменно сопровождается взрывом
кончика острия и выбросом из него плазменного сгустка — ка-
тодного факела. Аналогичные процессы происходят и в случае
массивных катодов, только взрываются микроскопические высту-
пы на поверхности. Это все исследуется при помощи высокоско-
ростной осциллографии, фотоэлектронной и электронно-оптиче-
ской техники с временным разрешением 1О“10—10-9 с. У воль-
фрамового острия с радиусом закругления кончика 0,2 мкм и
полем около него 1,2 • 108 В/см задержка тока и время «индук-
ции» взрыва составляют 1 нс. Задержка тем длительнее, чем
меньше поле и особенно ток.
В результате многократного приложения импульсов напря-
жения длительностью порядка 10 нс с временем нарастания
переднего фронта 1 нс вершина острия разрушается, сглажива-
ется, но на ней образуются новые микровыступы, около которых
поле еще усиливается на порядок. Поэтому та же задержка в
1 нс пробоя и тока происходит уже при макроскопическом поле
около острия Ю7 В/см. В случае массивного катода поле у мик-
роостриев усиливается в сотни раз и тот же эффект поручается
при макроскопическом поле 106 В/см. Плазменный сгусток раз-
летается во все стороны со скоростью примерно 2 • 106 см/с, по-
ступает в него (2—3) • 10~3 г/с. Плотности тока с острия, окру-
женного плазмой, достигают 108—109 А/см2, сам ток составля-
ет 102—103 А с площадки 10~6 см2.
Взрыв металла происходит в результате выделения в кончи-
ке острия или микровыступе большого количества джоулева
тепла от тока автоэлектронной, а по мере нагревания — термо-
автоэлектронной эмиссии. Тот факт, что эти токи очень велики,
установлен экспериментально. Так, при длительности импульса
напряжения 5 нс с острия радиуса 0,1 мкм и с углом раствора
конуса 10° удавалось получить без разрушения острия, т. е.
только за счет автоэмиссии, до 4 • 109 А/см2. Когда электроны
вылетают с поверхности, на их место изнутри металла приходят
новые, т. е. в самом металле у эмитирующей поверхности проте-
кает ток примерно той же огромной плотности. Он и нагревает
металл до взрывообразного испарения микровыступа, а задержка
связана с накоплением должной энергии.
Интересно, каков же все-таки механизм эмиссии в той ста-
дии после взрыва, когда обычно происходит резкое усиление
тока. Было установлено, что в импульсе тока переносится в
10—103 раз больше электронов, чем имеется атомов в плазмен-
ном сгустке. Значит, дело не в ионизации испаренного материа-
ла. По-видимому, здесь, как и в случае катодного слоя дуги,
происходит поляризация плазмы факела, образование положи-
тельного пространственного заряда у поверхности металла, еще
большее усиление поля и еще более быстрая термоавтоэлектрон-
ная эмиссия, как в катодном пятне вакуумной дуги. Эффект
352
взрывной эмиссии применяется в технике генерирования мощ-
ных электрических импульсов наносекундноп длизельности,
мощных электронных пучков. Уже сейчас созданы установки,
ь которых достигаются мощности порядка 1013 Вт.
§ 7. Анодная область
Процессы на аноде также сложны и многообразны. Как и на
катоде, здесь существуют две формы привязки дуги к по-
верхности.
Диффузная привязка. Ток при этом занимает на аноде срав-
нительно большую площадь, плотное!ь его у ~ 102 А/см2. Так
бывает, когда анод обладает большой поверхностью Эрозия ма-
териала при диффузной привязке незначительна, так как плот-
ность потока энергии к поверхности невелика.
Анодные пятна. Пятно образуется, когда анод неболыпоп,
и по мере повышения тока последний вынужден захватывать
края, «неудобные» боковые места и т. д. При какой-то силе тока
происходит срыв, разряд на поверхности ано i,a ьонтрагируется.
Плотность тока в пятне имеет порядок у ~ 104—105 А/см2. Число
пятен обычно растет с ростом тока дуги и давления. Инотда
возникает много пятен, которые симметрично выстраиваются,
образуя правильные узоры. Пятна иногда двигаются, также по
правильным траекториям типа концентрических кругов и др.
Анодные пятна ярко светятся, из них вырываются струн раска-
ленного пара.
7.1. Падение потенциала. Слой пространственного заряда.
Анодное падение складывается из два х частей. Одна связана с
возникновением слоя отрицательного объемного заряда у самой
поверхности анода из-за того, что анод отталкивает положитель-
ные ионы в сторону катода. Эта часть ано тного падения призва-
на восполнить отсутствие ионною тока у анода за счет повы-
шенной ионизации атомов газа или паров и с( ответствующего
небольшого увеличения электронного тока Опа пмеет порядок
потенциалов ионизации или возбуждения атомов паров или га-
за. При диффузной привязке анодное падение может этим
и О1раничиться. Иногда при диффузной привязке падение сов-
сем мало или даже отрицательно, 1—3 В. Так случается, ког та
анод обладает большой поверхностью, к нему прилегает плот-
ная сильноионизованная плазма и нет необходимости в допол
нительных затратах энергии для подведения электронною тока
к аноду.
Геометрическое падение. Когда анод обладает маленькой по-
верхностью, которая меньше сечения положительного столба,
пли когда дуга сильно контрагирована на аноде, токовый канал
должен сжаться от столба к аноду. Практически весь ток пере-
носится электронами. Сжатие капала при сохранении полною
тока i~ nepPESx (где 5К — площадь сечения канала) возможно,
если возрастают плозность электронов, скорость дрейфа, т. е.
23 ю П Райзер 353
поле, или обе эти величины. И на дополнительное рождение
электронов, чтобы скомпенсировать возрастающую с пе реком-
бинацию, и на ускорение дрейфа требуется повышенное поле,
т. е. дополнительное напряжение. Так появляется в анодной
области вторая составляющая падения потенциала. Она имеет
скорее геометрическую природу и не связана с образованием
пространственного заряда у электрода, так что, строго говоря,
ее не следовало бы присоединять
к анодному падению, но в лите-
ратуре обе составляющие иногда
объединяют (на опыте их не
всегда удается разделить; в тлею-
щем разряде — также).
Влияние привязки на ВАХ.
На рис. 12.10 показаны ВАХ ва-
куумной дуги с большим и ма-
леньким анодами. В случае боль-
шого анода получается диффуз-
ная привязка, при малых токах
анодное падение совсем мало.
Почти все напряжение дуги па-
дает в катодном слое. Анодное па-
дение постепенно возрастает по
мере увеличения тока. В случае
маленького анода анодная часть
Рис 12 10 ВАХ вакуумной дуги
с большим (7) и маленьким (2)
анодами [12 31 На большом ано-
де привязка диффузная, на ма-
леньком при повышении тока
происходит переход от диффуз-
ной привязки к анодному пятну.
Вычитание катодного падения на-
пряжения (3) из полного напря-
жения практически дает анодное
падение [12 3]
напряжения резко возрастает при
росте тока, потом происходит
срыв и возникает анодное пятно.
Это сопровождается резким умепь_
шением напряжения за счет
уменьшения анодного падения.
Привязка к пятну «выгоднее»,
чем диффузная.
7.2. Анод угольной дуги.
В угольной дуге в воздухе до из-
вестного предела по току (ВАХ
на рис. 12.3) привязка к аноду диффузная, у ~ 40 А/см2, полное
падение в анодной области составляет 36 В, из них 16 В—«гео-
метрического» и 20 В — в области отрицательного пространствен-
ного заряда. При i~ 15—20 А образуется анодное пятно, где у ~
~ 5 • 104 А/см2. Дуга становится шипящей (§ 3). Анодное падение
при этом уменьшается примерно на 10 В. Пятно движется со ско-
ростью 300 м/с. При дальнейшем увеличении тока из пятна исхо-
дит факел раскаленных паров; температура в пятне 4200 К. Если
угольный анод содержит присадки из солей или окислов церия
или других редкоземельных элементов, при токах порядка 100 А
образуется глубокий ярко светящийся кратер, пз которого выхо-
дит язык пламени. Яркость поверхности кратера соответствует
яркости Солнца^ он излучает до 6 кВт/см2. В случае не очень
354
длинных дуг 70 % мощности дуги излучается анодом. Это ис-
пользуют в светотехнике, в прожекторах. Анодное падение по-
тенциала около металлических анодов в воздухе составляет
1,5—2 потенциала ионизации атомов пара.
7.3. Баланс энергии. В области анода, куда поступает ток,
выделяется энергия. Она складывается из кинетической энергии
электронов, которую электроны приобретают в анодном падении,
и потенциальной энергии связи, которая выделяется при нейтра-
лизации электронами положительного заряда ионов металла.
Эта составляющая равна работе выхода. Всего — порядка 10 эВ
на один электрон тока. Значит, в пятне при j ~ 104 А/см2
плотность потока энергии составляет 104 • 10 = 105 Вт/см2. Тем-
пература в анодных пятнах вакуумных металлических дуг
Т 2700-3300 К.
§ 8. Дуга низкого давления
с искусственным накалом катода
Такого рода разряд применяется в газотронах, которые слу-
жат для выпрямления переменного тока, тиратронах и др.
Обычно используются оксидные катоды. Газотроны наполняют
аргоном или смесью Хе, Кг при давлениях порядка 1 торр
(раньше выпускались газотроны с ртутными парами). Напря-
жение горения составляет 10—20 В, ток i ~ 1 А. Значительную
часть напряжения составляет катодное падение; анодное паде-
ние 2—3 В. На положительном столбе, который в данном случае
не является «столбом», ибо разрядный сосуд широкий, падение
потенциала небольшое.
8.1. В чем смысл газового наполнения. Сопоставим дугу с
искусственно накаливаемым катодом, горящую между плоскими
электродами, с аналогичным устройством, но полностью лишен-
ным газа. Это — вакуумный диод, рассмотренный в п. 6.1 гл. 8,
для которого справедлив закон «трех вторых» (8.15). Допустим,
что катод дает ток эмиссии /э = 0,1 А/см2. Из-за ограничиваю-
щего ток действия пространственного заряда, чтобы получить
ток j такого же порядка при расстоянии между электродами
L = 1 см, потребовалось бы приложить к ним напряжение
V = 1200 В.
При газовом наполнении газ пробивается и превращается в
плазму. В инертных газах и при больших поперечных размерах
сосуда потери зарядов из плазмы невелики, и для их восполне-
ния, т. е. для поддержания электронейтрального положительного
столба, требуется Е/р~0,3 В/(см-торр). При р = 1 торр,
L = 3 см напряжение на плазме падает всего на 1 В. За выче-
том еще небольшого анодного падения потенциал анода «пере-
носится» хорошо проводящей плазмой прямо к катоду. Большая
часть напряжения падает в катодном слое, точнее, в бесстолк-
новительной его части у поверхности металла, толщиной поряд-
ка или меньше длины пробега заряженных частиц. По той же
23* 355
формуле (11.15) для вакуумного диода, если применить ее к
«вакуумированному» бесстолкновительному слою толщины h =
= 0,05 см, получится, что для переноса тока / = 0,1 А/см2 по-
требуется не 1200, а всего лишь 18 В.
Эффект газового наполнения состоит в том, что ионы, в боль-
шом количестве образующиеся в результате ионизации газа
электронами, компенсируют отрицательный пространственный
заряд электронов в подавляющей части пространства. Тем са-
мым облегчается прохождение к аноду эмитированных с катода
электронов.
8.2. Катодный слой как вакуумный промежуток с биполяр-
ным током, ограниченным пространственным зарядом. Назна-
чение катодного падения в несамостоятельной дуге существенно
отличается от такового в обычной дуге. Здесь нет нужды в ра-
зогреве катода ионным током и обеспечении катодной эмиссии.
Эта функция возложена на источник накала. Роль катодного
слоя — только ускорить термоэлектроны, чтобы они поддержи-
вали нужную степень ионизации в плазме. А поскольку потери
в плазме невелики, достаточно относительно небольшом частоты
ионизаций. Поэтому катодное падение имеет величину порядка
потенциала ионизации илп потенциала возбуждения, если иони-
зация происходит ступенчатым путем, а иногда даже ниже
(п. 8.3; такая дуга называется низковольтной). Толщина
же бесстолкновительного слоя катодного падения устанавли-
вается в соответствии с задаваемым всей цепью током. Этот ток
должен быть пропущен слоем, содержащим пространственный
заряд.
Процесс в бесстолкновительном слое несамостоятельной дуги
отличается от такового и в обычном диоде, и в бесстолкнови-
тельном слое самостоятетьной дуги. В обычном диоде накален
катод, но ионного тока нет. Пространственный заряд отрица-
тельный. поле па катоде практически равно нулю, а на аноде —
значительное (п. 6.1 гл. 8). В слое самостоятельной дуги ион-
ный ток из плазмы, где поля практически нет, слабее электрон-
ного с катода, но не настолько, чтобы пространственный заряд
стал отрицательным. Заряд положителен, и потому поле на
катоде очень сильное. Такая ситуация отвечает назначению
слоя: ведь нужно обеспечить сильную эмиссию и вытянуть все
электроны. Это отражается уравнением Маккоуна (12.5).
В несамостоятельной дуге, как и в самостоятельной, поля со
стороны хорошо проводящей плазмы нет. Плазма посылает в
направлении катода ионный ток. Однако этот ток не должен
быть слишком сильным, ибо катод не нуждается в дополнитель-
ном воздействии со стороны разряда (пока разрядный ток j
меньше тока эмиссии создаваемого накалом). Напротив, ток
эмиссии нужно ограничить пространственным зарядом. Поэтому
заряд вблизи катода отрицательный, а поле близко к нулю, как
и в диоде с накалом катода. Итак, поля нет ни на том, ни па
другом конце слоя. Значит, в середине напряженность поля
356
Рис. 12.11. Распределе-
ния поля и пространст-
венного заряда в катод-
ном слое дуги с искусст-
венным накалом катода
должна иметь максимум, а пространственный заряд — менять
знак. Эта картина изображена на рис. 12.11.
Она описывается теми же уравнениями (12.1) — (12.3), кото-
рые в результате одного интегрирования с условием Е = 0 на
плазменной границе слоя приводят к соотношению (12.4) для
поля на катоде. В рассматриваемом случае
оно слабое. Полагая в (12.4) Ек = 0, на-
ходим, каково должно быть для этого со-
отношение ионного и электронного токов:
j+/je = (1 _ S) /S = 1М7Й « 3 • IO-3- 10-2.
(12. 9)
Существенное увеличение ионного то-
ка по сравнению с этим значением при-
вело бы к появлению положительного
пространственного заряда и поля на ка-
тоде. Так и получается, когда разрядный
ток превышает ток эмиссии и начинается
переход к самостоятельной дуге. Опыт
показывает, что в несамостоятельной ду-
ге ионный ток в два-три раза больше,
чем это диктуется соотношением (12.9),
сит вклад в полный ток всего лишь порядка процента*). Од-
нако на токе, ограниченном действием пространственного за-
ряда, присутствие ионов отражается гораздо значительнее.
Медленно движущиеся ионы заметным образом нейтрализуют
отрицательный пространственный за*ряд электронов и тем самым
облегчают пролет электронов от катода до границы слоя с
плазмой.
Проделаем соответствующее вычисление. Проинтегрируем
(12.3) один раз, как эго было сделано в п. 5.3, применим гра-
ничное условие на катоде Е(0) = 0 и используем (12.9). По-
лучим
= {16л/ / V^-V L /у - (12.10)
Интегрирование (12.10) сводится к квадратуре. Относя ре-
зультат к анодной границе слоя х = /г, где V = VK, и разрешая
полученное соотношение относительно тока, находим
но все равно он вно
. 7 1 1/2е VK2 7 9 ___________dz__________
С 9л г т ь2 16 1 — — 1)1/2 ’
(12.11)
*) Результат (12.9) показателен еще в одном отношении. Он дает пред-
ставление о нижнем пределе числа ионизации, которые должен совершить
электрон, влетая из слоя катодного падения в плазму. Если бы не было
потока ионов на стенки и дру:их потерь, каждый электрон должен был бы
совершить всего лишь ^т!М ~ 10-2 актов рождения ионов.
357
Пропускаемый ток, который в отличие от униполярного в диоде
(переносимого зарядами одного знака) является биполярным,
оказался в 1,86 раз больше, чем вычисленный по закону Чайл-
да-Ленгмюра (8.15). В этом проявилбсь нейтрализующее
действие ионов.
8.3. Эксперимент. В опытах с дугой в аргоне при р = 0,05 торр
измерялись напряжение и толщина слоя катодного падения. Ок-
Рис. 12.12. ВАХ дуги с искусст-
венным накалом катода в сфе-
рическом сосуде радиуса 5 см
в аргоне при давлении в не-
сколько торр. Расстояние меж-
ду электродами L — 1 см;
верхняя кривая — более сла-
бый ток накала и меньшая
температура катода [5]
сидный катод имел активную поверх-
ность 2,9 см2. В интервале токов i
от 1 до 4 А напряжение оставалось
неизменным (1~13 В), а толщина
слоя катодного падения h уменьша-
лась от 0,031 до 0,012 см. Вычисле-
ние по формуле (12.11) (/ = 0,35 —
1,4 А/см2) дает для указанного интер-
вала h = 0,025—0,012 см в хорошем
согласии с опытом [8]. На рис. 12.12
показаны ВАХ дуги в аргоне при
более высоком давлении, несколько
торр [5]. Ток идет между оксидиро-
ванным нитевым катодом и плоским
никелевым анодом, помещенным в
сферический сосуд радиуса 5 см.
Расстояние между электродами 1 см.
В диапазоне i ~ 0,5—2,5 А ВАХ так-
же горизонтальна, но напряжение
ниже 7—8 В, даже меньше потенциала возбудения аргона (низ-
ковольтная дуга). Для несамостоятельной дуги характерно умень-
шение напряжения при возрастании давления в каком-то диапа-
зоне. Неизменность V свидетельствует об уменьшении толщины
слоя h при росте тока.
Как показывают все эксперименты, напряжение горения (при
не слишком малых токах) остается неизменным, только пока
ток разряда не превышает тока эмиссии, обеспечиваемого нака-
лом. При i > i9 ВАХ идет вверх. Рост связан с необходимостью
вызвать дополнительную эмиссию с катода. Стало быть, горизон-
тальный участок ВАХ, который обычно и используется в при-
борах, простирается тем дальше по току, чем сильнее накал
катода.
§ 9. Положительный столб дуги высокого давления
(экспериментальные факты)
9.1. Стабилизация. В столбе дуги выделяется значительная
мощность, например, в воздухе при р = 1 атм и токе i = 10 А
поле Е = 20 В/см. Значит, в 1 см длины выделяется П/=Е7 =
== 200 Вт/см. Чтобы процесс был стационарным, эта энергия
должна отводиться от разряда. Непосредственно из токового ка-
пала джоулево тепло выносится теплопроводностью (при сверх-
358
высоких давлениях — излучением). Дальнейшая судьба теплово-
го потока зависит от организации разряда. Если, как это часто
бывает при исследованиях, дуга заключена в трубку, наполнен-
ную газом, тепло поступает в стенки, которые необходимо ох-
лаждать, дабы предотвратить от разрушения. Во многих экспе-
риментах и приложениях столб дуги обдувают потоком холодно-
го газа (бывает и жидкости), который уносит энергию. Особен-
но эффективно действует закрученный поток; он надежно от-
жимает столб нагретого газа от стенок. Когда дуга горит в сво-
бодной атмосфере, тепло рассасывается в пространстве благода-
ря возникающим конвективным течениям. В короткой дуге
энергия поступает в основном в электроды, которые в случае
необходимости охлаждают. О перечисленных вариантах осу-
ществления стационарного состояния говорят: дуга стабилизи-
рована стенками, потоком, электродами.
9.2. Степень равновесности плазмы. Она зависит от рода газа,
давления, силы тока. При р < 0,1 атм и небольших токах А
плазма всегда неравновесна. Плазма воздуха и других молеку-
лярных газов, паров металлов при давлениях р 1 атм практи-
чески при любых токах бывает равновесной. Это обусловлено
интенсивным обменом энергией между электронами и молекула-
ми через возбуждение колебаний и вращений, а в парах метал-
ла — большими сечениями упругого рассеяния электронов. В па-
рах Hg равновесие наступает уже при р 0,1 атм. В инертных
газах отрыв температур сильнее из-за относительной малости
сечений рассеяния электронов атомами. Только при больших
токах, когда степень ионизации велика и сильно взаимодействие
электронов с ионами, отрыв исчезает. Так, в Аг при р — 1 атм
электронная и газовая температуры совпадают (Те ~ Т » 8000 К)
только при i > 10А, когда пе > 3 • 1015 см-3. При меньших токах
Рис. 1213. Отрыв температур в
положительном столбе дуги в Аг
или Аг с добавкой Н2 при р =
= 1 атм в зависимости от силы
тока или плотности электронов на
оси: Те — температура электро-
нов, Тт — температура газа, Tw со-
ответствует температуре заселен-
ности верхних уровней, Td — ниж-
них уровней, Тг связана с ие(0)
по формуле Саха [8]
Т примерно вдвое меньше Те (рис. 12.13). Еще хуже устанавли-
вается равновесие в Не, где заметный отрыв температур при
р = 1 атм наблюдается, начиная с малых токов и вплоть до i -
— 100 А (Л- 9000—10 000 К, Т-4000—5000 К). Только при
i — 200 А, когда пе & 5 • 1016 см"3, отрыв исчезает, Те~ Т ~
~ 10 000 к.
359
9.3. Радиальные распределения температуры и плотности
электронов. Они максимальны на оси столба и спадают к стен-
кам. Но из-за чрезвычайно резкой зависимости равновесной сте-
пени ионизации от температуры, тге ехр (—7/2&Г), плотность
Рис 1214 Распределение темпе-
ратуры по радиусу в столбе ду-
ги в Аг + 5 % Н2 при р = 1 атм,
i ~ 50 А в условиях, близких к
равновесным, когда все темпера-
туры совпадают [8]
Рис 12 15 Распределения
плотности электронов по
радиусу в столбе* дуги в
Аг + 5 % Н2
электронов спадает от оси неизмеримо быстрее, чем сама темпе-
ратура, которая более или менее равномерно уменьшается от
~ 10 000 К на оси к Tw — 1000 К у стенок, если последние
хорошо охлаждаются. Так же, как пе, ведет себя и яркость све-
чения. Таким образом, токопроводящий и ярко светящийся столб
дуги представляет собой относитель-
но тонкин капал у оси. Это иллю-
стрируется рис. 12.14, 12 15, па кото-
рых показаны измеренные радиаль-
ные профили Т и пе в столбе дуги
в смеси Аг + 5 % Н2 при р =~1 атм.
Обращаем внимание па то, что рез-
кость спада пе(г) завуалирована при-
нятым на рис 12.15 логарифмиче-
ским масштабом для пе.
9.4. ВАХ. Поле в столбе находят,
изменяя расстояние между электро-
дами L при неизменном токе. При
L>0,5—1 см напряжение линейно
зависит от £, так что Е = dVfdL ~
const. Это свидетельствует о про-
дольной однородности длинного стол-
ба. На рис. 12.16 показаны ВАХ
столба в воздухе при разных давлениях. Увеличение давления
при фиксированном токе приводит к увеличению поля. Это вы-
звано возрастанием потерь на излучение и, быть может, некото-
рым увеличением теплопередачи от плазмы к стенкам, что тре-
бует повышения погонной мощности W = Ei. На рис. 12.17 со-
поставлены ВАХ в различных газах. Одни кривые относятся
Рис 12 16 ВАХ положительно-
го столба дуги в воздухе при
разных давлениях [8]
360
к разряду в трубке радиуса 2 см, другие — к разряду в большом
объеме, т. е. как бы в свободной атмосфере, не ограниченной
стенками. При одном и том же токе для поддержания плазмы
в трубке требуется более сильное поле, так как теплоотдача
выше и нужно вкладывать больше мощности. В водороде поле
сильнее, чем в других газах, также из-за более высокой тепло-
проводности и более интенсивного теплоотвода от столба. В до-
полнение к рис. 12.14, 12.15 на рис. 12.18 представлена ВАХ
для той же смеси.
Рис. 12 18 ВАХ поло-
жительного столба
дуги в Аг + 5 % Нг
[3]
Рис 12 17. ВАХ положительного столба дуги в
различных газах в трубках радиусом R = 2 см
и в свободной атмосфере (R = оо) [5]
9.5. Излучение столба. Излучательная способность и ин-
тегральный выход излучения из столба зависят от газа, давле-
ния и силы тока. В каком-то приближении они пропорциональ-
ны п2е. В азоте, воздухе при р = 1 атм потери на излучение
составляют от одного до нескольких процентов вкладываемой
мощности. В аргоне при 1 атм они становятся заметными (более
15%) при мощностях W > 150 Btzcm. Среди различных газов
своими высокими излучательными свойствами выделяются пары
ртути. Экспериментальное исследование баланса мощности ртутной
дуги в кварцевой трубке с внутренним диаметром 4,1 см и длиной
50 см при р = 0,88 атм, i = 6 А, Е = 5,8 В/см показало, что из
мощности W = 35 Вт/см 10 Вт/см отводится теплопроводностью
в стенки, 18 Вт/см выходит в виде излучения, а остальные
7 Вт/см, по-видимому, выносятся из плазмы в резонансных ли-
ниях Hg 1850 и 2537 А и поглощаются в кварце [8]. И вообще,
при высоких давлениях теплопроводность выносит из ртутных
паров 10 Вт/см независимо от диаметра трубки и давления.
Очень велико излучение столба дуги при сверхвысоких дав-
лениях р 10 атм (и, конечно, при достаточно больших мощ-
ностях), в особенности в Hg, Хе, Кг. Эю используется в ртут-
ных и ксеноновых лампах. Приводим эмпирические формулы
361
для мощности излучения столба дуги для нескольких газов, вы-
веденные из результатов измерений [8] :
Hg, р > 1 атм 1УИзл [Вт/см] = 0,72{W [Вт/см] - 10},
Хе, р = 12 атм ТУизл-0,88 (W - 24), W> 35,
Кг, р - 12 атм Жизл = 0,72 (W - 42), W > 70,
Аг, р=1 атм 1УИ31 = О,52 (17-95), W > 150
§ 10. Температура плазмы и ВАХ столба дуги
высокого давления
Плотная равновесная низкотемпературная плазма привлека-
ет внимание физиков и инженеров в не меньшей, а быть может
даже в большей степени, чем слабоионизованная неравновесная.
Ее исследуют в лабораториях, используют в экспериментах и тех-
Рис 1219 Температурная зависимость
удельной электрической проводимости рав
новесной плазмы Аг, р == 1 атм точки —
эксперименты, кривые — расчеты разных
авторов [28]
нике Сейчас ее получают
в полях любых частотных
диапазонов (гл 13), од-
нако дуговой способ по-
прежнему остается самым
простым, доступным и рас-
пространенным Первей-
шей характеристикой рав-
новесной плазмы является
ее температура, и задача
состоит в том, чтобы по-
нять, чем она определя-
ется, как связана с элект-
рическими параметрами
разряда током, мощ-
ностью, как эти связи от-
ражаются в ВАХ столба
10.1. Термическая ио-
низация. Описание состо-
яния равновесной плаз-
мы, баланса ее энергии,
которым определяется но-
ле, необходимое для стационарного поддержания, в некоторых
отношениях проще, чем в случае неравновесной плазмы тлеющего
разряда. Мы избавлены от необходимости вникать в сложные
механизмы и кинетику рождения и гибели зарядов. Электропро-
водность плазмы однозначным образом определяется ее темпе-
ратурой и давлением; последнее обычно известно просто из ус-
ловий эксперимента (рис. 12.19—12 21)*).
*) При не слишком высокой степени ионизации, когда проводимость
определяется столкновениями электронов с нейтральными атомами, о ~ пе.
Поскольку плотность электронов равновесна, основная температурная за-
висимость о определяется формулой Саха о ~ пе ~ ехр (—II2kT) При
сильной ионизации а не зависит от пе и пропорциональна Z3/2(§ 2 гл 3).
362
Сам характер процесса ионизации отличен от того, что про-
исходит в слабоионизованной неравновесной плазме. Там моле-
кулы ионизуются электронами, которые приобрели необходимую
для того энергию непосредственно от поля. В сильноионизован-
ной плотной плазме действие поля как бы «обезличивается».
Поле поставляет энергию всему электронному газу в целом.
Электроны термализуются в результате столкновений друг с
другом, приобретая максвелловское распределение. Ионизуют
газ те из них, которые получили достаточно энергии не от поля,
а в ходе обмена с другими частицами. Термическая ионизация
происходит совершенно независимо от того, каким путем энер-
гия поступает в плазму.
Рис. 12.20. Температурная зависимость удельной электрической проводимо-
сти равновесных воздуха, N2, О2, Н2, р -= 1 атм* точки— эксперименты, кри-
вые — расчеты [28]
10.2. Уравнения столба равновесной плазмы. Рассмотрим
длинный цилиндрический столб дуги в продольном поле Е. Пусть
дуга стационарно горит в неподвижном газе, заключенном в
охлаждаемую трубку радиуса R. Подобные условия часто встре-
чаются в разрядной практике, но даже если дуга горит в сво-
363
бодной атмосфере или оодувается потоком, такая модель дает
представление о состоянии в токопроводящем канале, ибо темпе-
ратура на оси разряда не очень чувствительна к внешним ус-
ловиям. Будем интересоваться не слишком высокими давления-
ми, для определенности — атмосферным, и не слишком сильными
токами, когда температура плазмы не превышает И ООО—12 000 К.
Потери на излучение при этом в большинстве случаев заметно
уступают теплопроводностному выносу энергии из столба, поэто-
му и учитывать их не станем.
Рис. 12.21. Температурная зависимость удельной электрической проводимо-
сти равновесной плазмы N2 (расчет) [12,5]
Поскольку rot Е = 0, электрическое поле в однородном по
длине столбе постоянно по сечению. Радиальное распределение
проводимости о, плотности тока ] = оЕ, источников джоулева
тепла w —jE = оЕ2 [Вт/см3] определяется только распределени-
ем температуры через зависимость о (Г). Баланс энергии плазмы
описывается уравнением теплопроводности с энерговыделением
за счет джоулева тепла:
---г^^ + сг(П^ = о, <12-12)
где X — теплопроводность (рис. 12.22—12.24)*).
*) Немонотонности в зависимости % от температуры связаны с дейст-
вием так называемой реактивной теплопроводности в тех диапазонах
температур, где существенны диссоциация и ионизация молекул (рис. 12 23).
Так, равновесная ионизация в более нагретых местах выше, чем в холод-
ных Возникает амбиполярный диффузионный поток зарядов. В более хо-
лодных местах они рекомбинируют, отчего там выделяется тепло. Соответ-
364
Граничные условия к (12.12): при г = R Т = TW, где Ти —
температура стенки; при г=0 dTjdr=^Q вследствие симметрии.
Температура токопроводящей плазмы гораздо выше температу-
ры стенок, так что, по существу, можно положить Ти — 0. Раз-
рядный ток равен
R
i = E^o-2nrdr. (12.13)
О
Сила тока регулируется на опыте и потому является зада-
ваемым параметром. Поле находится в результате решения по-
Рис. 12.22 Температурная зависимое!ь теплопроводности воздуха, N2, Н2
и Аг, р — 1 атм точки—эксперимент, кривые —- расчеты [28]
ставленной задачи, которая при известных характеристиках ве-
щества о (Г), вполне определена. Так получится ВАХ
столба Е(1). Введение потенциала теплового потока
0 - f X dT
о
(рис. 12.25) позволяет ограничиться одной материальной функ-
цией о(0) вместо двух. Уравнение (12.12) называют уравне-
нием Эленбааса — Геллера (1934 г.).
ствующий тепловой поток можно оценить как поток потенциальной энергии:
/ион ==: IDff Пе —IDa(dne'dT) pVТ = —XjiohVT.
Дифференцируя в формуле Саха только основной, экспоненциальный мно-
житель, найдем (дпе!дТ)р = (7//cZ2) дгеАа/(2^а + где Na — плотность ней-
тральных атомов. Так находится XR ИОй и аналогично — ДИс- Функция
KR(T) имеет максимум: не->0, при Т оо Аа-^0.
365
Рис 12.23. Температурная зависимость составных частей полной теплопро-
водности X кислорода, р = 1 атм: точки — эксперименты, кривые — расчеты;
Хо соответствует обычному переносу, X/? дис и XR ион — реактивные состав-
ляющие, связанные с переносом энергии диссоциации и ионизации [28]
Рис. 12.24. Температурная зависимость теплопроводности N2 (расчет) [12.5]
10.3. Каналовая модель и принцип минимума мощности. Не-
линейный характер реальных функций о(0) не позволяет ре-
шить уравнение (12.12) в общем виде аналитически. С начала
30-х годов, когда была сформулирована задача о столбе дут и,
стали разрабатываться различные формальные методы ее реше-
ния, основанные на линеаризации функции о(0), разбиении
366
области интегрирования на отдельные численные зоны [28].
Для того чтобы лучше понять природу закономерностей, обра-
тимся к хорошо отвечающей существу дела Качаловой модели
дуги, предложенной Штеенбеком в 1932 г.
При не очень высоких температурах проводимость исчезаю-
ще мала. При Т ~ 4000—6000 К она становится заметной и
быстро нарастает с увеличением Т.
Благодаря действию теплового пото-
ка, температура спадает от оси к
стенкам более или менее равномерно.
Ток же фактически протекает толь-
ко в приосевой части трубки, где
температура достаточно высока. Это
иллюстрируется рпс. 12.26, при
взгляде на который каналовая мо-
дель напрашивается сама собой Вве-
дем эффективный радиус токопрово-
дящего канала го и приближенно по-
ложим, что вне канала (при г>/})
о = 0 и тока нет. Внутри канала (при
0 < г < го) проводимость высока и
близка к величине —п(Гк), соог-
Л, Вт/(см К)
3, кВт !с, 1
Рис 12 25. Температурная за-
висимость теплопроводности %
и потенциала теплового пото-
ка 0 в воздухе, р = 1 атм
[25]
ветствующей температуре па оси
7\==r(0). Каналовая модель сводится к приближенной замене
истинного распределения а (г) ступенчатым, показанным па
рис. 12.26 штриховой линией.
В этом приближении выражение (12.13) для силы тока при-
обретает вид
i = о^Елго,
(12.14)
а уравнение (12.12) в бестоковой зоне (го<г<Л) лет ко ин-
тегрируется. Полагая приближенно на границе канала
Т(г0) ~ Т(0) = 7\ и у стенки Tw = 0, находим
2л Г0 ЛГ0аК J
о
(12.15)
где W =Ei — выделение мощности в 1 см столба.
Два уравнения (12.14), (12.15) содержат три неизвестные
величины: Тк, r0, Е; ток i является задаваемым параметром, как
и радиус трубки R. Для получения недостающего соотношения
Штеенбек предложил использовать принцип минимума мощно-
сти. При заданных i и R в трубке должно установиться такое
распределение температуры, а в рамках каналовой модели —
такие температура плазмы Гк и радиус канала го, чтобы мощ-
ность W и поле E — W/i оказались минимальными. Расчеты
ВАХ дуги на основе принципа минимума дали хорошее согласие
с опытом (рис. 12.27), и, в частности, это послужило причиной,
367
по которой принцип приобрел известную популярность (см. так-
же п. 4.8 гл. 10).
Однако вопрос о его правомерности, не переставая волновать
пытливых исследователей, послужил предметом многих изыска-
ний и дискуссий вплоть до наших дней. Попеки обоснований
привели к связи с термодинамикой необратимых процессов. При-
менительно к уравнениям столба дуги было показано, что прин-
цип справедлив. Однако возможность его использования должна в
ские распределения тем-
пературы Т и проводи-
мости о по радиусу
столба дуги. Штриховая
линия — замена о (г)
ступенькой в каналовой
модели
каждом случае подтверждаться специаль-
ным анализом. Так, неосмотрительное при-
менение принципа минимума к индукци-
9
Рис. 12.27. ВАХ положитель-
ного столба дуги в азоте в
трубке радиуса R = 1,5 см.
Сплошная кривая — экспери-
мент, штриховая — расчет с
привлечением принципа мини-
мума [22]
очному и СВЧ разрядам в рамках моделей, совершенно аналогич-
ных каналовой, в отличие от дуги привело к ошибочным резуль-
татам, причем их ошибочность оказалась завуалированной ка-
жущимся согласием со здравым смыслом и опытом в каких-то
диапазонах параметров [25].
10.4. Баланс энергии в токопроводящем канале. Не останав-
ливаясь больше на вопросе о принципе минимума (подробнее
см. в [25]), рассмотрим, чем же определяется температура
плазмы. Для этого нет нужды в привлечении дополнительных
принципов. Ведь вся информация о столбе заложена в уравне-
ниях (12.12), (12.13). Начав их приближенное решение путем
профилирования функции о (г) ступенькой, нужно последова-
тельно довести его до конца. Интегрирование уравнения (12.12)
в бестоковой зоне дало соотношение (12.15). Рассмотрим теперь
область, где течет ток. Выделяющаяся в канале мощность W
выносится через его границу тепловым потоком Jo: W = 2лго/о.
Поток из канала определяется реально существующим, вопреки
сделанному при выводе (12.14), (12.15) допущению, небольшим
перепадом температур ДТ = Тк — То. По порядку величины /о ~
где Если уточнить эту оценку, проинтегри-
368
ровав (12.12) в области О<г<го с прежним допущением об
однородности источников оЕ2, получим
4 л АО = W « 4лХкАТ, А© = 0К - 0О. (12.16)
10.5. Количественное определение понятия канала и замыка-
ние системы уравнений каналовой модели. Новое соотношение
(12.16) принесло новую неизвестную: АТ или Tq. Но до сих пор
не было четко определено, что же такое канал. Умозрительное
введение его характеристик — радиуса го и температуры Гк — еще
не дает базы для вычисления этих величин. Следует количествен-
но установить, как мы разграничиваем условные понятия прово-
дящая — непроводящая среды. Поскольку до решения задачи мы
не знаем распределения тока по радиусу столба, условную гра-
ницу естественно провести в том месте распределения плотности
тока о (г), где она уменьшается в определенное число раз
по сравнению с максимальным значением па оси канала. Если
принять во внимание большую крутизну функции этому
будет соответствовать не слишком большой перепад темпера-
тур АТ,
Пусть, например, ток дуги слабый, температура и степень
ионизации плазмы невелики и электрон-атомные столкновения
сказываются на сопротивлении сильнее, чем электрон-ионпые.
Тогда о со пе и
о (7) = С ехр (~I/2kT), С(Т)~ const. (12.17)
Полагая для конкретности, что оо = о(7о) меньше ок в е раз.
и имея в виду, что 1)2кТ > 1, находим
А7 = Тк - Tq (2kTJI) ТК. (12.18)
При более сильных токах, когда степень ионизации больше про-
цента, основную роль играют электрон-ионные столкновения и
зависимость в(Т) становится иной. Однако в каком-то интерва-
ле температур ее можно описать той же формулой (12.17), по-
добрав эффективное значение «потенциала ионизации»
путем аппроксимации графика в(Т). Так, в воздухе, азоте и ар-
гоне, р = 1 атм, в характерном для дуг диапазоне температур с
достаточной для оценок точностью можно описать о одной и
той же интерполяционной формулой:
о « 0,83 • 102 ехр (-36 000/7 [К]) Ом"1 • см"1,
8000-14000 К, /эф « 6,2 эВ. (12.19)
Требование, чтобы в относительно небольшом интервале тем-
ператур АТ < Т величина о изменялась существенно, например
вдвое, можно представить в общей дифференциальной форме, не
конкретизируя вида функции б (7):
Ar«l, (12.20)
О \dT )T=T* 7К \дЛъТ]Тъ
24 ю. П. Райзер
369
С учетом (12.17) соотношение (12 20) превращается в (12.18).
Исключая Л Г из равенств (12.16), (12.20), получаем равен-
ство
4лЛксук = W (do/dT)T^T^ (12.21)
которое замыкает систему уравнений каналовой модели душ и
определяет максимальную температуру Гк. Замечательно, что
формальное применение принципа минимума мощности
(dkr/dro)i=const = 0 к функциональным связям (12.14), (12.15)
приводит точно к (12.21). Поскольку справедливость принципа
для дуги хотя и очень сложным путем, но была доказана, это
может служить подтверждением правильности простых и нагляд-
ных рассуждений, изложенных в п 10 4, 10 5*).
Все же в этих рассуждениях содержится элемент произвола,
связанный с выбором конкретных чисел ок/по = е в (12 18) или
единицы в правой части (12 20). Этой неопределенности лишено
приближенное интегральное соотношение
j GXdT = 1У(Ук/4л. (12.22)
о
которое является более общим, нежели дифференциальное (12 21),
и по самому своему выводу (§ 2 гл. 13) соответствует наилучшеи
замене тока, распределенного по сечению трубки, током, сосредо-
точенным в канале.
10.6. Температура плазмы. Любое из приближенных соотно-
шений — (12.18) вместе с (12.16), или (12.21), или (12.22) (в по-
рядке улучшения точности) — определяют максимальную темпе-
ратуру плазмы в столбе дуги Тк в зависимости от вкладываемой
в единицу длины мощности W. При фиксированной мощности
не зависит от радиуса трубки и согласно (12 22) мало чув-
ствительна к теплопроводностным свойствам газа в непроводя-
щей ток периферийной области. В более грубом приближении,
которое описывается формулами (12.21), (12.16), (12.18), тем-
пература Гк вообще к ним не чувствительна.
Температура Тк устанавливается такой, чтобы тесно связан-
ный с ней соотношением (12 20) и функцией проводимости с(Г)
*) Предостерегаем от встречающейся в некоторых теоретических рабо-
тах ошибки, когда при аппроксимации о(Т) ступенчатой функцией о = 0,
const при Т То жестко фиксируют положение ступеньки То При рассмот-
рении рис 12 19, 12 20 действительно возникает искушение положить, на
пример, То — 9000—10 000 К. На самом деле температура «возникновения
проводимости» То скользит вместе с максимальной температурой плазмы Тк,
если изменяются сила гока, мощность Мы имеем право закрыть глаза на
какую то долю тока, протекающую впе основного токопроводящего канала,
но недопустимо оставить за пределами канала определенное количество то-
ка Так может возникнуть абсурдная ситуация, если, скажем, То = 9000 К,
а Тк = 9010 К— весь ток потечет вне канала, или другая- TQ = 9000 К,
а Гк - 15 000 р, когда подавляющая часть канала будет переносить ничтож-
ную долю тока и, следовательно, не будет каналом
370 \
\
перепад температур в зоне энерговыделения обеспечил сбалан-
сированный теплоотвод из канала в бестоковую зону. Подчерк-
нем — только за пределы токопроводящего канала. Дальнейшая
судьба энергии на максимальной температуре отражается мало
(если зафиксирована мощность). Отсюда можно заключить, что
температура мало чувствительна к способу охлаждения дуги,
к условиям организации разряда — в свободной атмосфере, с об-
дуванием холодным потоком. Непосредственное влияние на
Тк оказывает только вклад мощности в плазму, который уже
в свою очередь зависит (и притом сильно) от интенсивности
охлаждения. Чем больше можно отвести тепла от горячего газа,
тем больше мощности в него можно вложить, сохраняя стацио-
нарное состояние.
Из-за резкой зависимости проводимости от температуры для
достижения более высоких температур приходится непропорцио-
нально увеличивать мощность. Это видно из общих формул
(12.21), (12.22), но становится еще более наглядным, если наити
явную зависимость 7^(И7) путем задания функции а(Т) в фор-
ме (12.17) (при низких температурах с настоящим, при более
высоких — с эффективным потенциалом ионизации):
= Л//8лОЖ- (12.23)
Температура растет в среднем даже медленнее, чем 1У1/2, так
как в общем теплопроводность повышается с ростом Т. Сдела-
ем оценку для угольной дуги в атмосферном воздухе при токе
/ = 200 А, когда измерения показали Тк~ 10 000—12 000 К
(рис. 12.2). Согласно ВАХ на рис. 12.17 поле в этих условиях,
по-видимому, составляет Е ~ 2,5 В/ем, откуда W = 500 Вт/см.
Со значением = 1,5 • 10-2 Вт/ (см • К) и /аф = 6,2 эВ (см. (12.19))
по формуле (12.23) найдем Тк = 9800 К, в разумном согласии
с измерениями.
При относительно слабом токе (г =10 А) в воздухе
(р = 1 атм), согласно ВАХ на рис. 12.16, Е = 20 В/см, W =
= 200 Вт/см. Формула (12.23) дает оценку ~ 7000 К (Хк«
« 2 • 10“2 Вт/(см • К), 7эф « 10 эВ выше, так как степень иони-
зации мала (2 • 10-4)).
10.7. Закономерности столба. Полученные выше формулы
решают задачу. Задаваясь W, по формуле (12.23) или более об-
щим (12.21), (12.22) находим Гк, потом из первого соотношения
(12.15) получаем го, а по второй формуле (12.15)—/. Поле рав-
но E = W/i. Справедлив закон подобия: при фиксированной
мощности W радиус канала го Пропорционален радиусу трубки
/?, да и все распределение Т (г) меняется подобным образом при
вариации R. На рис. 12.27 показаны результаты расчета ВАХ
столба по каналовой модели с использованием принципа мини-
мума мощности, т. е. формулы (12.21). Расчет сопоставлен с
экспериментом и с ним согласуется.
Непосредственно регулируемым и измеряемым на опыте па-
раметром является не мопуюсть, а ток, поэтому, чтобы уяснить
24* / 371
(12.25)
с i тоже
(12 26)
(12.27)
Радиус
(12.28)
закономерности столба, следует представить все его характе-
ристики в зависимости именно от тока Получить наглядное
представление о зависимостях можно, взяв функцию в ви-
де (12 17). Положим также для упрощения формул k = con&t,
0=Х71, что не вносит существенных качественных искажении *).
Из формул (12.23), (12.15), (12.17) найдем
ок = (/С/8л2Л/сГк)1/2 (i/R), (12.24)
т ______________1/2к___________
К (1/2) In (зЛт12//) — in (i/R)
Повышение силы тока сопровождается почти пропорциональ-
ным возрастанием проводимости, что и позволяет плазме про-
пустить ток. Однако в силу резкой зависимости о от температу-
ры последняя растет гораздо медленнее. Мощность, увязанная
с температурой балансом энергии в канале, повышается
медленно Поле Е = W/i соответственно падает:
ЗлХкТ^ ~______const_____
I [const — In (г/7?)]2 ’
Е _ 8лХА-Г2 __________const______
/ i г [const — ln(z/7?)]2
Формула (12 27) дает ВАХ столба; ВАХ —падающая
канала
r0 -= R (<тк/С)1/2 = R {1/8п2Ш1су-^ (i/Rj1'2
изменяется, грубо говоря, таким образом (/о оо г), что увеличе-
ние тока сопровождается увеличением занимаемой им площа-
ди, а не плотности тока j coi/tqCo которая возрастает столь
же медленно, как и температура. Все величины ТК, ок, W, Е яв-
ляются функциями отношения ijR. В более узкой трубке одна
и та же мощность вкладывается при пропорционально меньшей
силе тока.
Начиная с температур примерно 11000 -12 000 К и выше в
балансе энергии плазмы появляется новая статья — потери на
излучение. Для их компенсации в стационарном состоянии тре-
буется дополнительная мощность, более сильнее поле, и ВАХ
становится растущей.
10.8. Достижение возможна более высоких температур. Если
ставить такую цель, необходимо организовать интенсивный тепло-
отвод, чтобы можно было вложить в плазму большую мощность.
Достичь эффекта одним лишь наращиванием тока трудно: потре-
бовался бы слишком сильный ток. Улучшить теплоотвод можно
уменьшением радиуса трубки (увеличением градиента темпера-
*) Впрочем, при низких 1емпература!к (6000—8000 К) в молекулярных
газах могут возникать аномалии, связанные с немонотонным ходом h(T)
(рис 12 22—12 24) \
372 \
\
туры), обдуванием дуги быстрым потоком газа, а еще лучше —
воды, как в дуге Гердиена (п. 2.8). Очень высоких температур
в несколько десятков тысяч градусов легче достичь в кратковре-
менных импульсных разрядах, когда можно создать очень силь-
ный импульс тока и когда энергия, не успевая отводиться, накап-
ливается в плазме (нестационарный процесс).
Для получения в исследовательских целях высокотемператур-
ного стационарного дугового столба разряд пропускают через на-
бор охлаждаемых и изолированных медных щайб с отверстиями
диаметром несколько миллиметров. Медные шайбы перемежа-
ются диэлектрическими с такими же отверстиями. Получается
длинная «трубка» малого диаметра и с хорошим охлаждением.
В азоте (р = 1 атм) так получают температуру на оси до
15 000 К.
§ 11. Отрыв электронной и газовой температур
в равновесной плазме
В слабоионизованной неравновесной плазме, где Те > Т, обмен
энергией при столкновениях электронов с атомами идет в одно-
стороннем порядке: только от электронов — тяжелым частицам.
В равновесной плазме обмен двусторонний. При идеальном ра-
венстве Те = Т электроны в одних столкновениях получают от
тяжелых частиц ровно столько энергии, сколько отдают им в дру-
гих. В присутствии поля равенство Те = Т нарушается. От поля
энергию получают фактически одни лишь электроны. Они пере-
дают ее тяжелым частицам, а потом энергия отводится от газа
наружу — в стенки и далее. Подобная эстафета осуществляется
благодаря возникающим положительным разностям температур
между электронами и газом Те — Т, между газом и стенками
T — Tw. В § 10 мы пренебрегали различием Те и Т и оперирова-
ли общей температурой Т. Посмотрим, как можно проверить спра-
ведливость этого допущения.
11.1. Уравнение баланса энергии электронов, взаимодействую-
щих с полем и нагретым газом. Обобщение уравнения (3.12) на
случай Т Ф 0 вытекает из уравнения типа (2.18) (см. сноску
к п. 3.3 гл. 2):
е2Е2 3
2 к dt ~
vw.
(12.29)
Здесь под б по-прежнему следует понимать долю энергии, кото-
рую электрон в среднем передает при столкновении тяжелой ча-
стице, если та не обладает энергией. При » Т уравнение пре-
вращается в (3.12). В отсутствие поля оно обеспечивает установ-
ление устойчивого равновесия Те = Т.
11.2. Критерий равновесия. Применяя уравнение (12.29)
к стационарным условиям, а электронная температура устанавли-
вается быстро (табл. 11.1) и практически всегда квазистационар-
373
на, получаем связь между отрывом температур и напряженностью
поля:
те~т __ 2е2Е2 9 ,л2д (Е [В/см] Z,2
те ЗШету*т~ [ Те [эВ] j •
(12.30)
В последнем преобразовании мы перешли от частоты столкнове-
ний к длине пробега электрона I = и положили mv2j2 =
= ЗкТе12. Кроме того, принято б = 2ml М, где М — масса атома,
А — его относительная атомная масса. Присутствие небольшого
числа оставшихся молекул, если# до нагревания газ был молеку-
лярным, несколько усилит обмен (б будет больше) и уменьшит
отрыв температур. Формула (12.30) может служить для оценки
степени неравновесности плазмы по отношению к температурам.
Поле, необходимое для поддержания почти равновесной плаз-
мы, определяется балансом энергии ионизованного газа в целом
(§ 10). Зная Е и Т ~ Те для данного тока либо из расчета, либо
из эксперимента, по формуле (12.30) найдем фактически сущест-
вующий отрыв температур, который обеспечивает стационарную
передачу джоулева тепла от электронов газу. Если относитель-
ный отрыв превысит допустимые пределы, скажем 50%, при
расчетах придется отказаться от предположения о равновесности
плазмы и рассматривать систему уравнений энергии электронов
(12.30) и газа (12.12), но с настоящей проводимостью, которая
теперь уже будет зависеть не от Т, а от Те. Быть может, окажет-
ся нарушенным и ионизационное равновесие. Тогда придется
анализировать кинетику электронной плотности, как в гл. 10.
Именно так обстоит дело с процессами в контрагированных токо-
вых шнурах, образующихся в тлеющих разрядах (§ 8 гл. 11).
В дугах высокого давления плазма бывает довольно сильно
ионизованной. Существенную, а часто и основную роль играет
кулоновское рассеяние электронов ионами. В общем случае с уче-
том (3.8) имеем
= АЪт + 1,3 • [эВ]}"2 см"1, (12.31)
где первое слагаемое относится к нейтральным атомам. Кулонов-
ский логарифм положен равным In Л = 4,5, что соответствует
Те«104 К, пе ~ 1016—1017 см“3. Столкновения с ионами преоб-
ладают, если степень ионизации превышает значение
zze//V > 0,77 • 1013от{7\ [эВ] }2 ~ 10’2. (12.32)
Например, на оси столба Ar+5% Н2, р = 1 атм, при токе f =
= 50 А имеем Т ~ Те~ 104 К, пе ~ 2 • 1016 см“3 (рис. 12.14, 12.15),
N ~ 7,2 • 1017 см-3 nelN « 0,028. Согласно рис. 12.18 Е~6 В/см.
Столкновения —- кулоновские, Z ~ 3 • 10-4 см, отрыв (Те — Т)1Те —
= 3,5 % — в этом смысле плазма вполне равновесна.
11.3. Почему при одинаковых условиях для поддержания рав-
новесной плазмы требуется меньшее поле, чем для поддержания
неравновесной. Так, в положительном столбе азотной дуги атмо-
сферного давления, горящей в охлаждаемой трубке радиуса
374
Н = 1,5 см, при токе i = 10 А поле £'==10 В/см (рис. 12.27).
При этом Т ~ 8000 К, плотность газа N ~ 1018 см-3, пе ~
« 2 • 1015 см-3, ne/N & 2 • 10-3, т. е. преобладают столкновения
электрона с нейтральными частицами. В столбе тлеющего разряда
в азоте при тех же плотности и радиусе значение Е/N ~
— 2 • 10-16 В • см2 (п. 7.7 гл. 10); поле Е ~ 200 В/см на порядок
сильнее.
О том же говорит и формула (12.30), если для уравнивания
условий применить ее к случаю, когда столкновения с ионами
не существенны. Относительный отрыв температур пропорциона-
лен (EjNY2. В приведенном примере в случае дуги он на два
порядка меньше, чем в тлеющем разряде, ибо электронная тем-
пература не подвержена сильным вариациям. Она не может быть
ниже величины порядка 0,1 потенциала ионизации 7, иначе в
газе не будет электронов.
Физическая причина продемонстрированного различия отры-
вов коренится в различии механизмов приобретения электроном
энергии /, нужной для ионизации атомов. В неравновесной слабо-
ионизованной плазме электрон получает энергию непосредственно
от поля, e2E2/mXm ~ (Е/N)2 в каждом столкновении, в равновес-
ной — заимствует ее у других частиц, в том числе и тяжелых.
Каждый электрон коллектива приобретает от поля при столкно-
вении существенно меньшую порцию, так как (Е/N)2 на два по-
рядка меньше. Электроны снабжают энергией атомы, а потом
они все «в складчину» концентрируют при столкновениях энер-
гию в отдельных электронах, и те производят ионизацию или
сильное возбуждение. Короче, в неравновесной плазме поле долж-
но довести электрон до энергии Дав равновесной — только до
кТ<^1.
11.4. Когда плазма бывает равновесной. Итак, каждый элек-
трон в равновесной плазме получает от поля энергии гораздо
меньше, чем в неравновесной, но газ нагревается до температуры
гораздо более высокой, что, естественно, требует большого энер-
говыделения w~jE. Тепла выделяется много потому, что много
электронов, ток сильный (а не поле). Это хорошо видно из урав-
нения баланса энергии газа (12.12), если выразить в нем
<зЕ2 = пее2Е2/при помощи (12.30) через скорость передачи
энергии от электронов тяжелым частицам:
а£2 = А 5/с (Те - Т) vmne = (12.33)
Малый отрыв, отвечающий Т ~ 7\, достигается при больших
пе (при сильном токе). Тому же способствует и увеличение часто-
ты столкновений что ускоряет обмен энергией. Это одна из
причин, по которой плазма чаще получается равновесной при
высоких давлениях. Вторая, а по важности, бывает, и первая при-
чина — замедление диффузионных потерь электронов, что способ-
ствует повышению степени ионизации до равновесного уровня,
отвечающего Те.
375
Глава 13 ПОДДЕРЖАНИЕ И ГЕНЕРАЦИЯ
РАВНОВЕСНОЙ ПЛАЗМЫ В РАЗРЯДАХ
РАЗЛИЧНЫХ ЧАСТОТНЫХ ДИАПАЗОНОВ
§ 1. Введение. Баланс энергии плазмы
Равновесная плазма образуется в стационарных (и не слиш-
ком кратковременных) разрядах высокого давления. Для ее по-
лучения сейчас применяют поля всех четырех частотных диапа-
зонов: постоянное, высокочастотное, сверхвысокочастотное, опти-
ческое. Говоря «поддержание плазмы», мы подразумеваем про-
цесс, в котором энергия поля непрерывно выделяется в опреде-
ленной массе газа и благодаря этому в ней сохраняется плазмен-
ное состояние. Генерацией плазмы называем процесс непрерыв-
ного ее производства, превращения в плазму все новых и новых
масс холодного газа. Каждый процесс поддержания плазмы по-
лем можно использовать для ее генерации. Для этого следует
продувать холодный газ через область, где горит разряд,— оттуда
вытекает непрерывная плазменная струя. Подобного рода гене-
раторы плотной низкотемпературной плазмы — плазмотроны —
нашли широкое применение в физических исследованиях и
технике.
В этой главе мы познакомимся с процессами поддержания и
генерации равновесной плазмы в различных полях, подчеркнем
то общее, что всем им свойственно, рассмотрим, как решается
главная физическая задача определения температуры плазмы в
зависимости от характеристик приложенного внешнего поля.
1.1. Уравнение баланса энергии. В общем случае температура
газа подчиняется уравнениям газовой динамики, в которых долж-
ны быть учтены и негидродинамическпе механизмы переноса
энергии: теплопроводность, излучение. Однако во многих прак-
тически важных процессах плазма если и движется, то с неболь-
шой, дозвуковой скоростью, давление выравнено в пространстве
и постоянно во времени. В этих случаях газодинамическое урав-
нение энергии превращается в уравнение для температуры, в ко-
тором фигурирует удельная теплоемкость при постоянном дав-
лении Ср'.
pcpdT/dt = -div J + о<Е2> - Ф, J = -XVT. (13.1)
Здесь р = NM — массовая плотность газа, которая связана с тем-
пературой условием постоянства давления р = (N + ne)kT, X —
теплопроводность. Производная d/dt относится к определенной
массе газа. Если она движется со скоростью и,
dT/dt = dT/dt + (uV) Т, (13.2)
где d/dt относится к фиксированной точке пространства. Мы бу-
дем рассматривать помимо постоянного только синусоидальные
поля. В этом случае в выражении <jE> = о<Е2> для энерговыде-
ления в 1 см3 в 1 с под о подразумевается высокочастотная про-
376
водимость (§ 4 гл. 5), а скобки < > означают усреднение вели-
чины за период колебаний, который предполагается достаточно
коротким. Величина Ф в (13.1) описывает потери на излучение.
Как правило, учитывать их не будем, имея в виду, что при атмос-
ферном девлении и Т < 11 000—12 000 К пх роль не слишком
велика.
1.2. Закон сохранения полного потока энергии в стационарных
статических разрядах. Только в случае постоянного и однород-
ного поля, как в столбе дуги (§ 10 гл. 12), уравнение баланса
энергии можно исследовать и решать, рассматривая величину Е
как постоянный параметр. В общем случае распределение поля
подлежит определению, как и распределение температуры. Поле
удовлетворяет уравнениям Максвелла (§ 3 гл. 5), а они содер-
жат электродинамические характеристики среды о и 8, которые
зависят от температуры. Таким образом, температура и поле опи-
сываются системой взаимосвязанных уравнений.
Чаще всего температура плазмы в зоне, где непосредственно
выделяется энергия поля, мало зависит от того, движется газ
или нет. Поэтому для ее нахождения и установления зависимости
от приложенного поля достаточно бывает исследовать статические
режимы, когда разряд горит в неподвижном газе. Откладывая до
§ 7 рассмотрение разрядов в потоке и обоснование сделанного
утверждения, будем пока рассматривать стационарные статиче-
ские разряды без учета потерь на излучение. В этом случае (13.1)
принимает вид (ср. с (12.12))
—div J + о<Е2> =0, J = -XVZ. (13.3)
Обратимся к уравнению баланса энергии электромагнитного
поля (5.21), которое является следствием уравнений Максвелла.
В стационарных условиях
div <S> = —о<Е2>, S = (с/4л) [ЕН], (13.4)
где S — вектор плотности потока электромагнитной энергии.
Уравнение (13.4) говорит о том, что поток исчезает вследствие
диссипации энергии поля в среде. Комбинируя (13.3) и (13.4),
получаем равенство
div(J+ <S>)=0, (13.5)
которое свидетельствует об отсутствии источников у суммарного
потока тепловой и электромагнитной энергии. Сколько электро-
магнитной энергии втекает в какой-то объем и диссипируется там,
столько вытекает оттуда в виде тепла.
1.3. Интеграл потоков. В одномерных условиях уравнение
(13.5) интегрируется, и это дает первый интеграл системы урав-
нений поля и энергии плазмы — интеграл потоков:
rn(J + <*£>) = const. (13.6)
Здесь п = 0 для плоской геометрии, п = 1 — для цилиндрической,
п = 2 — для сферической. Постоянная интегрирования определя-
ется из граничных условий.
377
§ 2. Столб дуги в постоянном поле
Чтобы продемонстрировать большую общность закономерно-
стей, которые определяют температуру плазмы в любых равно-
весных разрядах, вернемся к рассмотренному в § 10 гл. 12 вопро-
су о температуре в столбе дуги. Подойдем к нему с новых пози-
ций, применив интеграл потоков (13.6). По условиям симметрии
на оси столба нет радиальных потоков, ни теплового, ни элект-
ромагнитного:
Л + Sr = О, -Ш!дг = -S. = (13.7)
где поток Sr выражен по (13.4) через электрическое поле Ez, ко-
торое направлено вдЪль оси, и магнитное II которое в случае
прямолинейного тока имеет азимутальное направление. Электро-
магнитная энергия втекает в токовый канал через боковую по-
верхность снаружи, диссипируется в плазме и выносится тепло-
проводностным потоком обратно. «Полевая» трактовка превраще-
ний энергии, согласно электродинамической концепции, эквива-
лентна представлениям о выделении джоулева тепла тока.
Выразим в (13 7) Ez через при помощи уравнения Максвел-
ла (5.13):
2 IT
rH*' s> = -~r4rH*- (13-8>
/ III 1ОЛ (J ' '
Умножим уравнение (13.7) на о, чтобы все явно зависящие от
температуры величины оказались в одной части равенства. Интег-
рируя по г от оси и до стенок трубки г = 7?, находим связь тем-
пературы плазмы на оси Тк с радиальным распределением поля:
С н d
v(T)k(T)dT ' М^(гЯф)</г, (13.9)
J 16л
Tw 0
где Tw ~ 0 — температура внутренней стенки трубки, в которую
заключен столб.
Точное интегральное соотношение (13.9) превратим в при-
ближенное, воспользовавшись представлениями каналовой модели
для вычисления правой части. Это даст возможность выразить
известную функцию искомой температуры 7\, стоящую в левой
части, через ток дуги ц которому пропорционально магнитное по-
ле. Согласно (13.8) вне канала Яф = Я1(го/г) (где Н\ = 21/стъ —
поле на границе проводника г = г0), внутри — Н^ = Н\ (т7г0).
Подставляя эти выражения в (13.9) и интегрируя, получаем со-
отношение (12.22):
J даю»
Tw-o о
о котором говорилось в и. 10.5 гл. 12. Оно замыкает уравнения
378
каналовой модели дуги без каких-либо допущений о виде функ-
ции и численном соотношении между проводимостями в точ-
ках г = 0 и г = го и оптимальным образом приближает упрощен-
ную каналовую модель к истине. Как мы увидим, соотношения
типа (13.10) определяют температуру плазмы и в других
разрядах.
§ 3. Высокочастотный индукционный разряд
3.1. Вводные замечания. Хотя дуговой способ получения плот-
ной низкотемпературной плазмы остается наиболее употреби-
тельным, в лабораторную практику и технику все шире проникают
высокочастотные (ВЧ) индукционные разряды. О принципе их
организации было рассказано в § 7 гл. 9. На основе индукцион-
ных разрядов созданы безэлектродные плазмотроны, которые об-
ладают рядом важных преимуществ по сравнению с дуговыми.
В отличие от последних, где плазма неизбежно загрязняется про-
дуктами разрушения электродов, в безэлектродных плазма полу-
чается чистой. Это открывает большие возможности для плазмо-
химического производства сверхчистых соединений, гранул туго-
плавких веществ также высокой чистоты, для тонкой металлур-
гии. Время работы безэлектродных плазмотронов практически не
ограничено, тогда как в дуговых большой мощности электроды
быстро разрушаются и выходят из строя. Но, конечно, реализа-
ция мощного ВЧ разряда — дело гораздо более сложное, чем
осуществление разряда постоянного тока. И источники питания
(мощные ламповые генераторы мегагерцевого диапазона) слож-
нее, дороже и капризнее.
Вопрос о значении и пространственном распределении тем-
пературы плазмы в индукционном разряде представляет двоякий
интерес. Как и в случае дуги постоянного тока, это важно для
понимания физических закономерностей поддержания плазмы по-
лем и для практических приложений. Но, кроме того, в ВЧ случае
возникает и иная проблема, не свойственная разрядам постоянно-
го тока, а именно необходимость согласования разряда как на-
грузки с ВЧ генератором, без чего последний не может эффектив-
но работать. Такие электрические параметры плазменной нагруз-
ки, как омическое сопротивление, самоиндукция, взаимоиндук-
ция, характеризующая магнитную связь с индуктором,— а они
влияют на работу всей электрической системы в целом, непо-
средственным образом связаны со значениями и распределения-
ми температуры и токов в разряде.
Принципиальная схема индукционного разряда показана на
рис. 9.22а. Индукторы делают разными, от одного-двух до многих
витков. Ток, который течет через индуктор после включения
источника питания, обычно бывает недостаточным для пробоя
газа атмосферного давления. Он достаточен лишь для поддержа-
ния уже горящего разряда, для чего всегда требуются более низ-
кие поля, и поэтому зажигать разряд приходится другим спосо-
379
бом. Вводят, например, на короткое время внутрь разрядной
трубки вспомогательный электрод. Он разогревается индуциро-
ванными ВЧ тонами Фуко, возможно, испаряется. При этом про-
биваются нагретые и потому разреженные пары металла или газа.
После зажигания разряда в основном газе электрод удаляется.
3.2. Уравнения разряда в длинном соленоиде. Рассмотрение
идеализированного одномерного процесса, подобно рассмотрению
длинного столба дуги, дает довольно полное представление об
энергетических и электродинамических закономерностях индук-
ционного разряда. Пусть в длинную катушку-соленоид вставлена
диэлектрическая трубка радиуса R (рис. 13.1). Плазма существу-
ет за счет выделения* джоулева тепла круговых токов, которые
индуцируются переменным магнитным полем тока высокой часто-
ты, текущего по катушке. Стационарное состояние поддерживает-
ся благодаря теплопроводностному выносу энергии к охлаждае-
мым стенкам трубки.
Рис 13 1 Индукционный разряд в трубке
радиусом 7?, вставленной в длинный со-
леноид; го — радиус плазмы, справа—рас-
пределение температуры по радиусу
Радиальное распределение температуры в газе внутри трубки,
схематически изображенное на том же рис. 13.1, описывается
уравнением (13.3):
-±J-rJr_! а<Л*) = 0, (13.11)
Оно совпадает по виду с уравнением (12.12) для столба дуги.
Только 1еперь электрическое поле является азимутальным, а маг-
нитное направлено по оси. В мегагерцевом диапазоне частот п
при атмосферном давлении высокочастотная проводимость (5.23)
не отличается от проводимости плазмы в постоянном поле, токи
поляризации и смещения малы по сравнению с токами проводи-
мости, комплексная диэлектрическая постоянная — чисто мнимая
(п. 5.1 гл. 5). Без тока смещения уравнения Максвелла (5.13),
(5.14) для цилиндрической геометрии и при Е, Н со е~гоК име-
ют вид
z 4л у-i 1 d y-i tj /л о j 9\
----;— -= — т~Г11^== —nz. (13.12)
dr c r dr c z ' 7
Граничные условия к системе (13.11), (13.12) таковы. На
оси (при г = 0) в силу симметрии Д = 0, = 0. При г = R
Т = Tw ~ 0. Магнитное поле в непроводящей холодной среде око-
ло стенки трубки такое же, как и внутри пустого соленоида:
Я2 (/?) Но = (4л/с) (IGn), (13.13)
где Iq — сила тока в катушке, п — число витков на единице ее
380
поле описывается теми
Рис. 13 2. Схематические рас-
пределения по радиусу тем-
пературы (а), проводимости
(б) и джоулева тепла (в) в
индукционном разряде; штри-
ховая линия — замена о (г)
ступенькой в модели металли-
ческого цилиндра, J — тепло-
вой поток, So— поток элект-
ромагнитной энергии, 6 — тол-
щина скин-слоя
длины*). Комплексные амплитуды /о, Яо здесь можно считать
действительными величинами. Сдвиг по фазе осциллирующих во
времени полей Hz, отсчитывается при этом от фазы поля Но
вблизи катушки.
3.3. Индукционный нагрев материалов. Этот метод широко ис-
пользуется в технике для закалки деталей, сушки, плавки и др.
Например, металлический стержень вставляют в индуктор, скажем
в ту же катушку-соленоид. Металл нагревается индуцированны-
ми токами. Из-за скин-эффекта (п. 5.6 гл. 5) поле не проникает
глубоко внутрь проводника, и джоулево тепло выделяется только
в поверхностном слое. Однако, благодаря хорошей теплопровод-
ности, металл вскоре прогревается целиком. В случае цилиндри-
ческой геометрии, когда длинный стержень радиуса го и проводи-
мости о вставлен в длинный соленоид,
же уравнениями (13.12). В непрово-
дящем зазоре между катушкой и
стержнем Hz(r)= const, так что гра-
ничное условие (13.13) переносится
прямо к поверхности проводника, где
Hz(ro)= Hq. Уравнения решаются в
функциях Бесселя от комплексного
аргумента, которые для этого случая
табулированы.
3.4. Модель металлического ци-
линдра. Она заключается в том, что
плазменный проводник уподобляется
металлическому с той лишь разни-
цей, что теперь радиус «стержня» го*
и его проводимость оь, которая счи-
тается в первом приближении посто-
янной и соответствующей максималь-
ной температуре плазмы на оси Тк,
заранее не известны. Данная модель
является буквальным аналогом ка-
наловой модели дуги и зиждется па
том же основании — крутой зависи-
мости о от Т, благодаря чему газ рез-
ко теряет проводящие свойства там,
где температура плазмы начинает заметно снижаться в направ-
лении к стенкам трубки. Если проводимость плазмы достаточно
высока, происходит скинпрование, и тепло индукционных то-
ков, как и в случае металла выделяется в каком-то кольцевом
слое. В середине кольца существует температурное плато вслед-
ствие теплопроводностного прогрева среды (рис. 13.2).
Модель металлического цилиндра позволяет отчасти расчле-
нить решение электродинамической и тепловой задач. При ре-
*) Это соотношение легко получить, применяя уравнение (5.13) к длин-
ному тонкому замкнутому контуру, лежащему в диаметральной плоскости
цилиндра (рис. 13.1) и охватывающему много витков катушки.
>84
шении первой ок и г0 рассматриваются как параметры. Не выпи-
сывая общего решения для случая цилиндрического проводника,
ограничимся рассмотрением случая сильного скин-эффекта, ког-
да поле проникает в проводник на малую глубину и геометрия
слоя является практически плоской. Условие справедливости та-
кого приближения б < го, где б = с/У2лосо — толщина скин-слоя
(5 39), обычно выполняется в индукционных разрядах на часто-
тах порядка промышленной /= 13,6 МГц. Отсчитывая координа-
ту х от поверхности в глубь слоя (против радиуса г) и направляя
ось z/ касательно к поверхности, перепишем уравнения (13.12):
dH 4-ТТ dE
= — оЕу, Hz. (13.14)
dx% с у dx с \ /
Теперь Н = Hq при х = 0 и Еу, Hz 0 при х °°. Уравнения
(13.14) описывают плоскую монохроматическую электромагнит-
ную волну в среде с чисто мнимой комплексной диэлектрической
проницаемостью. Выпишем их решение в комплексной форме,
как в § 5 гл. 5, а потом для наглядности перейдем к действи-
тельной:
Hz = Яоехр[—— х/8) — гг/б] -+ Ное~х/6 cos (со^ — х/д),
Еу = 1/2 exp [—j(со£ — х/5 + л/4) — х/б] -+
Яо(со/4лб) 1/2е~х/б cos(co£ — х/Ь + л/4). (13.15)
Амплитуды полей Яа, Еа экспоненциально убывают в глубь
плазмы, причем Еа На со сдвигом по фазе на л/4. Например,
дня воздуха при р = 1 атм и Т = 10 000 К о = 25 Ом"1 • см-1;
при f = 13,6 МГц б= 0,27 см, 4ло/со = 3,3 106 и Еа = 5,5 • 10“4 На.
Поток электромагнитной энергии направлен в глубь проводника
нормально к его поверхности и равен
<S> “ 50е-2х/б, 50 = (с/16л) (со 2лэ)’/2Яо. (13.16)
От индуктора в проводник поступает энергия
9 [(л’в)/смВ2 {/[МГц]}1/2
50 = 9,94- IO"2 1 ° Вт/см2. (13.17)
(о [Ом 1 см
В единице длины цилиндрического проводника выделяется мощ-
ность W = 2лго^о. Источники джоулева тепла сосредоточены в по-
верхностном слое эффективной толщины 6/2.
3.5. Радиус плазменного проводника. Его легко связать с
температурой плазмы Тк и мощностью W, рассматривая перенос
тепла через непроводящий зазор между проводником и трубкой.
Интегрируя (13.11) с о = 0, находим
0к-0w=(W2n)ln(fl/ro)« Аг50. (13.18)
Пока не раскрыто выражение для W, (13.18) не отличается от
аналогичного равенства (12.15) для дуги. При последнем пере-
ходе в (13.18) учтено, что в статическом индукционном разряде
382
цилиндрическое кольцо, в котором выделяется тепло, ооычно
приближено к трубке и зазор между плазмой и трубкой получает-
ся небольшим: Ar = R — го < R. В этом отношении скинирован-
ный индукционный разряд ведет себя иначе, чем дуга постоянного
тока, где ток течет в тонком приосевом канале.
3.6. Температура плазмы. Модель металлического цилиндра
не позволяет найти главного — проводимости плазменного провод-
ника или температуры плазмы. После обсуждения каналовой мо-
дели дуги в § 10 гл. 12 причины этого ясны. Температура опре-
деляется балансом энергии в самой зоне энерговыделения, а для
того чтобы рассмотреть, как тепло выводится из нее, необходи-
мо принять во внимание реально существующий перепад темпе-
ратур в модельном цилиндре и количественно разграничить поня-
тия проводящей и непроводящей среды.
Согласно (13.11) в середине плазменной области, куда ВЧ
поле не проникает и где источников тепла нет, T(r) = const =
(рис. 13.2). Весь перепад температур между осью и поверхностью
эквивалентного проводящего цилиндра АТ = Тк — То приходится
на поверхностный слой толщины 6/2, где выделяется энергия.
Тепловой поток, выходящий наружу из проводника, равен при-
мерно Jo ~ 2ХКА776 (ХК = Х(ТК)) и совпадает с потоком электро-
магнитной энергии So от индуктора. Отсюда получаем уравнение
баланса энергии самой проводящей плазмы, аналогичное (15.16)
для дуги,
2ЪДТ/д ~ So, 4лХкАГ « 1У(6/го). (13.19)
Поскольку функция о(Т) та же самая, что и для постоянного
поля дуги, сохраняется в силе условие (12.18) или (12.20), опре-
деляющее падение температуры АГ, при котором проводящая сре-
да, можно считать, превращается в «непроводящую». Объединение
одного из этих соотношений с (13.19) и дает равенство, из кото-
рого найдем температуру плазмы индукционного разряда. Так,
пользуясь (12.17) с эффективным потенциалом ионизации /
(п. 10.5 гл. 12) и формулами (13.16) для So, (13.13) для Но и
(5.39) для 6, выразим устанавливающуюся в разряде проводи-
мость плазмы через регулируемый на опыте параметр — ток
(ампер-витки) индуктора:
К (2кТ2к/1) ок = (Ion'2y. (13.20}
Поскольку о(Г)— функция резкая, и меняются в небольших
пределах и приближенно оксю(/о^)2. Температура же повышается
с ростом тока в индукторе медленно:
ут I/24 __ const /4 0 94 \
1п(4ЛкА:Г2б’/7)-1П(/оп) “ const - In (Z^) ’ Z
в полной аналогии с зависимостью (12.25) для дуги постоянного
тока. Как и там, достичь высокой температуры трудно: требуют-
383
ся большие ампер-витки, но кроме того, и высокие мощности:
W = 2лг050« 2л7?50 со Н20а~1/2 со 10п со о,'/2. (13.22)
От частоты поля температура плазмы не зависит (если скин-слой
тонкий).
3.7. Точное соотношение для температуры. Замечательно, что
в случае индукционного разряда сверх (13.6) существует и вто-
рой интеграл системы уравнений энергии плазмы и Максвелла
Это обусловлено тем, что уравнения без тока смещения (13.12)
позволяют представить поток электромагнитной энергии в диф-
ференциальной форме:
<5Г> = -
32л2ог
с2 dHl
64л2сг ’
(13.23)
где На — действительная амплитуда магнитного поля. Подставим
(13.23) в интеграл потоков (13.6), где const = 0, как и в случае
дуги (13.7), умножим все равенство на о и проинтегрируем по г
от 0 до R. С учетом (13.13) и того, что в условиях сильного ска-
нирования На~ 0 при г = О, получим
? с2Н2п ПХ2
v(T)^T)dT==—l= [If). (13.24)
Т^о 64я ' 2 '
Это соотношение, определяющее температуру плазмы в зави-
симости от тока в индукторе, было впервые получено в [13.1].
В отличие от (13.10) оно является точным. В случае дуги пра-
вую часть (13.9) нельзя проинтегрировать, так как согласно
(13.8) поток Sr не представляется в чисто дифференциальной
форме, но общность выражений (13.24) и (13.10)—налицо. При
задании а(Т) в виде (12.17) и Лф > кТк (13.24) практически сво-
дится к полученному выше упрощенным путем равенству
(13.20)*).
3.8. Примеры вычислений и экспериментальные измерения.
Сделаем оценки по полученным формулам. Пусть разряд горит
в воздухе (р = 1 атм) на частоте / = 13,6 МГц и температура
плазмы 7К = 10 000 К, КК = 1,4 • 10~2 Вт/ (см • К). Как уже отме-
чалось в п. 3.4, при этом ок = 25 Ом-1 • см-1, б = 0,27 см. Джоуле-
во топливо выделяется в кольце эффективной толщины 6/2 =
= 0,14 см. По (13.19), (12.18) для поддержания такой плазмы
в плазменный цилиндр должен поступать с поверхности поток
энергии 5о = 250 Вт/см2. Согласно (13.16), (13.13) такой поток
получается, если Но = 75 Э, hn = 60(А • в)/см. Наибольшая
*) Интегралы, содержащие больцмановскую функцию, приближенно
вычисляют способом Фрапк-Каменецкого, разлагая 71-1 в показателе экспо-
ненты около верхнего предела:
+ 7’2,
и вынося за знак интеграла все медленно меняющиеся множители с Т =• Ти.
384
.1 мплитуда электрического поля на внешней границе плазмы по
(13.15) Л'а~12 В/см. Наибольшая и ютность кольцевого тока в
и 1азме ]а ~ вкЕа 300 А/см2. Полны и кольцевой ток в плазме на
единицу длины столба /аб ~ 80 А/см. Он сравним с чоком в ин-
дукторе, также на единицу его длины, (»0 (А-в)/см Значит,
обратное, взаимоиндуктивное влияние пла i
мепною тока на процесс в цепи ВЧ генера-
юра весьма сильное.
Потенциал теплового потока плазмы 0К ~
« 0,14 кВт/см. Пусть разряд горит в трубке
радиуса R = 3 см. По (13.18) зазор между
п зазмой и трубкой относительно мал: Дг-=
= 0,56 см. Вклад мощности в единицу длины
п .азменпого столба по (13.22) В ~
3,8 кВт/см. Чтобы нагреть плазму до тем-
пературы не 10 000, а 12 000 К, надо по этим
расчетам увеличить мощность и ампер-витки
вдвое. Но при столь высокой температур с
появятся пе учтенные здесь потери на из пу-
чение и мощности потребуечся еще больше.
Температура в индукционных разрядах
обычно не превышает 10 000—11 000 К.
На рис. 13.3 показаны измеренные па
опыте радиальные распределения темпера-
тур и плотностей электронов. В ксеноне тем-
пература ниже, чем в аргоне, так как мень-
ше потенциал ионизации. Небольшой провал
Рис. 13 3. Изменен-
тсмпературы в центральной части разряде
примерно 50'0 К, связан с потерями энергии
на излучение. Джоулево тепло выдетяется
। олько в периферийном кольцевом слое, а по
тери на излучение, которые из-за прозрачно-
(ти плазмы имеют объемный характер, дей-
ствуют и в центральной части. Поэтому тем-
пература там понижается.
3.9. Пороговые условия существования
равновесной плазмы. Если уменьшать ток в
ные распределения
температур и элект-
ронных плотностей в
индукционном разря-
де в трубке радиусом
R — 3,5 см на часто-
те / = 11,5 МГц при
р — 1 атм: 1 — Аг,
вклад мощности в
плазму 4,7 кВт; 2,
3 — Аг, 7,2 кВт; 4,
5 — Хе, 6 кВт [13.2]
индукторе, начиная от таких значений,
при которых толщина скин-слоя б r0 ~ R, температура и прово-
димость плазмы, согласно (13.21), (13.22), будут уменьшаться,
а б — возрастать. Когда б достигнет величины порядка г0, 7?,
эффект скинирования исчезнет и указанные формулы потеряют
силу. В противоположном случае б R магнитное поле внутри
соленоида, как и в отсутствие плазмы, однородно и равно Но;
электрическое — по (13.12): Е(г)= 1ыНог/2с. В единице длины
плазменного цилиндра радиуса го выделяется мощность
R
TTZ I' /Z?2\ О 7 Яак‘°2яог^ Л3О <02)"4 (In)2
W = о <Е3> 2nrdr » —---------2-2- = ---2---°? 0 ’
J 16с2 с4
25 ю п г й
(13.25)
385
Теперь температура падает от Гк до Tq, соответствующей эффек-
тивной границе плазмы, на всем радиусе го, так что в отличие от
(13.19) и подобно (12.16)
W « 4лг0?1кАГ/г0 « 4лАкДГ « ЙлАД’Т^/Л (13.26)
Температура плазмы не может снизиться слишком сильно,
иначе исчезнет проводимость и перестанет выделяться энергия.
Следовательно, значение мощности по (13.26) теперь более или
менее стабильно, даже если падает проводимость. Радиус плазмы
в соответствии с равенствами (13.18), (13.24) уменьшается при
снижении температуры. Следовательно, по формуле (13.25) ток
в индукторе (или Iqu) обратным образом зависит от проводимости
температуры) плазмы и частоты
На протяжении большого интер-
измененпя проводимости, охваты-
Рис. 13 4. Качественная
зависимость ампер-вит-
ков от приводимости
плазмы
Рис. 13 5. Качественная
зависимость вклада
мощности в плазму от
проводимости
вающего оба случая (б <С R и б > R), зависимости Iqu и W от ок
и со будут выглядеть так, как это показано на рис. 13.4, 13.5 (при
б < R W сю 10п сю щ1/2).
Зависимость Iqu от ок (или Тк) проходит через минимум, кото-
рый соответствует месту смыкания кривых для двух рассмотрен-
ных отдельно предельных случаев, т. е. условию 6 ~ R. Сущест-
вует минимальное, пороговое значение тока в индукторе, при ко-
тором еще возможно поддержание равновесной плазмы в индук-
ционном разряде. Его можно оценить, экстраполируя формулу
(13.20) вплоть до такой пороговой температуры TK = Tt, при ко-
торой 6=7?:
/4
~ ~ ~ ] • (13.27)
\ л /ош /
Например, для воздуха, р = 1 атм, R = 3 см, /=13,6 МГц
(/от?)/ « 10 (А • в)/см. Пороговые температуры Tt ~ 7000—8000 К.
3.10. Устойчивые и неустойчивые состояния. Рис. 13.4 демон-
стрирует еще одно свойство, характерное для равновесных раз-
рядов различных типов. При данном токе в индукторе 7о>(7о)*
и прочих равных условиях существуют два стационарных состоя-
ния равновесного разряда. Одно из них соответствует выок й
386
проводимости и значительному скин-эффекту, другое — малой
проводимости и отсутствию скинирования. На опыте, однако,
реализуются только первые состояния. Состояния на левой ветви
при Т <Tt неустойчивы. Пусть, например, по какой-то случайной
причине температура несколько повысилась. Для поддержания
нового состояния будет достаточно меньшего тока в индукторе
чем фактический. Начнется разогрев плазмы, пока не будет до-
сглгнуто состояние, соответствующее правой ветви кривой
рис. 13.4, где Т > Tt. Как легко проверить путем аналогичные
рассуждений, оно является устойчивым.
§ 4. Сверхвысокочастотные разряды
4.1. Разряд в волноводе. Длительно существующие СВЧ раз-
ряды высокого давления были получены в начале 50-х годов, ког-
да были созданы необходимые для этого генераторы непрерывно-
го действия киловаттной мощности. Возможны различные спосо-
бы подвода энергии СВЧ поля к плазме. Одна из наиболее
употребительных схем показана на рис. 13.6. Волновод прямо-
угольного сечения пронизывает диэлектрическая трубка, прозрач-
ная для СВЧ излучения. Плазма поддерживается в области пере-
сечения за счет диссипации энергии электромагнитной волны.
Выделяющаяся теплота либо отводится теплопроводностью т
охлаждаемые стенки трубки, либо, как
продуваемым через трубку газом. По-
следний вариант представляет собою
СВЧ плазмотрон (§ 6).
Обычно применяют Н^\-моду бегу-
щей по волноводу электромагнитной
волны. Вектор электрического поля в
Рис. 13.7. Схема разряда 1
волноводе, поддерживаемо
го HOi волногй а — сечени<
волновода диаметрально)
плоскостью трубки, плазм;
затенена; б — раснределе
ние Е вдоль широкой стен
ки волновода
Рис. 13.6. Схема СВЧ раз-
ряда в волноводе: 1 — вол-
новод. 2 — диэлектрическая
грубка, 3 — разрядная
плазма
ней параллелен узкой стенке волновода. Напряженность поля г
этом направлении постоянна, а вдоль широкой стенки меняется
по закону косинуса (рис. 13.7). Разряд организуется посередине
сечения волновода, где электрическое поле максимально. Плаз-
менный столб вытягивается вдоль электрического вектора Е
25*
38'
Размеры волновода связаны с применяемой частотой. Для / —
= 2,5 ГГц (длина волны в вакууме Ло = 12 см) широкая стенка
имеет ширину 7,2 см, узкая — 3,4 см. Диэлектрическую трубку
делают диаметром примерно 2 см. Диаметр плазменного столба
получается при этом порядка 1 см.
Под действием осциллирующего электрического поля падаю-
щей волны в плазменном столбике возникает переменный ток. Ток
проводимости не замкнут, вернее, он замыкается током смещения.
Быстропеременный ток сам является источником электромагнит-
ного излучения. Так возникает рассеяние (и отражение) падаю-
щей волны от плазменного проводника, находящегося в волново-
де. Рассеянная волна интерферирует с падающей; плазму под-
держивает результирующее поле. Часть падающей волны прохо-
дит насквозь через плазму. Таким образом, мощность Ро, которая
поставляется генератором в падающую волну, делится между
отраженной и проходящей волнами и частично диссипируется в
плазме. В тонком хорошо проводящем стержне может диссипиро-
ваться половина мощности, четверть мощности при этом прохо-
дит, четверть отражается.
Эффективность разрядного устройства сильно повышается,
если поставить за разрядом о? ражателъ для проходящей волны с
тем, чтобы завернуть ее назад и заставить снова пройти через
плазму. В результате в волноводе в области разряда устанавлива-
ется стоячая волна. Расстояние между отражателем и разрядом
подбирают так, чтобы плазменный столб попадал в пучность
электрического поля. Так удается ввести в плазму 80—90 %
энергии, вырабатываемой генератором [13.3].
В такой системе при вкладе в плазму 1—2 кВт в воздухе
атмосферного давления получается температура Т ~ 4000 К,
а азоте — 5000 К. В аргоне наблюдается отрыв: Те ~ 6500—
7000 К, Т ~ 4500 К,— в атомарном газе (да еще при не очень
высоких температуре и электронной плотности) обмен энергией
между электронами и тяжелыми частицами происходит медленно
(ср. с § 9, 11 гл. 12). На большей частоте (Хо = 3 см) и соответ-
ственно в волноводе меньшего сечения температура несколько
выше, в азоте — 6000 К. Вообще, в СВЧ разрядах температура
всегда получается более низкой, чем в ВЧ. Это связано с резким
увеличением отражающей способности плазмы при возрастании
электронной плотности (п. 4.4).
4.2. Разряд в резонаторе. Это направление развивали П. Л. Ка-
пица с сотрудниками, также начиная с 50-х годов [13.4]. В ходе
работ был создан генератор непрерывной мощности 175 кВт на
частоте 1,6 ГГц (Хо = 19 см). В цилиндрическом резонаторе
(рис. 13.8) возбуждаются стоячие волны типа Е'оь Электрическое
поле на оси цилиндра направлено вдоль оси и изменяется по за-
кону косинуса с максимумом в середине цилиндра. При удалении
от оси по радиусу электрическое поле уменьшается. Разряд под-
жигается на оси в области наибольшего поля. Плазма вытягива-
ется вдоль электрического вектора и при больших мощностях
388
имеет вид шнура. Длина шнура составляет половину длины вол-
ны колебаний, около 10 см, диаметр — 1 см. При больших мощ-
ностях разряд извивается и «всплывает» под действием архиме-
довой силы. В целях его стабилизации газ в резонаторе закручи-
вают, это предотвращает всплывание и придает шнуру
устойчивость. В стабилизированный разряд в водороде, дейтерии,
гелии при давлениях от одной до нескольких атмосфер удается
вводить мощность до 20 кВт. Температура плазмы в основном не
превышает 8000 К.
Рис. 13.8. Схема разряда
в резонаторе. Приведены
линии напряженности
электрического поля в
колебаниях типа ^Оь
Плазма затенена [13.4]
4.3. Поддержание плазмы плоской электромагнитной волной.
Процесс в волноводе отягощен многими деталями, которые свя-
заны со сложностью геометрии и рассеянием волны на плазмен-
ном образовании. Большинство этих деталей влияет скорее на
количественную сторону дела, чем на качественную. Для выясне-
ния основных особенностей равновесных СВЧ разрядов рассмот-
рим простую одомерную модель. Допустим, что плоская электро-
магнитная волна проходит через прозрачную для нее плоскую
Рис. 13 9. Сз ема разряда, поддерживаемого электромагнитной волной: а —
распределение температуры, прозрачная диэлектрическая стенка заштри-
хована; б — соответствующее распределение плотности электронов; штри-
ховая линия — замена пе(х) ступенькой
диэлектрическую стенку и набегает на плазму. Выделяющееся в
плазме тепло выносится теплопроводностью к стенке, которая
охлаждается, и тем самым поддерживается стационарное состоя-
ние (рис. 13.9).
На первый взгляд кажется, будто такая модель слишком дале-
ка от реальности, но это не совсем так. Мы как бы вырезаем
участок трубки вместе с прилегающей поверхностью разряда, ко-
торый обращен прямо к падающей волне (рис. 13.6), и фиксиру-
ем на нем внимание. Если волна проникает в плазму не глубоко,
а при достаточно большой мощности волны температура полу-
чается повышенной, и это на самом деле так, искривление по-
верхности не столь существенно. Во всяком случае, при данной
идеализации сохраняются все важные качественные моменты,
а получающиеся числовые значения основных параметров дают
правильное представление о реальных величинах.
382
В плоской геометрии в глубине плазмы при х со темпера-
тура стремится к постоянному значению Тк, волна затухает, т. е.
в (13.6) const = 0, и
j + <s> = О, J = -MUdx. (13.28)
В СВЧ диапазоне существенны эффекты волнового характера:
отражение, интерференция; поле описывается волновым урав-
нением типа (5.31), но с комплексной диэлектрической прони-
цаемостью. Уравнения для комплексных амплитуд Еу, Hz моно-
хроматического поля имеют вид
+ (е + t 4 Еу = 0, (13.29)
tjxq о и е даются формулами (5.23), (5.24). В СВЧ разрядах
температура и степень ионизации не бывают большими и роль
электрон-ионных столкновений согласно (12.32) мало существен-
на. Тогда
о сю(1 — е)со сю ехр(—//2/сТ), (13.30)
где в случае однокомпонентного газа I — настоящий (не эффек-
тивный) потенциал ионизации. Граничные условия к системам
(13.3), (13.29) или же (13.28), (13.29) с определением S по
(13.4) гласят, что глубоко в плазме (при х -> °°) Е = 0, а у стен-
ки (при х = — яо) Т = Tw ж 0, и в падающей волне задан поток
энергии 5о. Он регулируется мощностью СВЧ генератора. Реше-
ние должно определить температуру плазмы ТК^Т(°°) и ту
часть потока электромагнитной энергии Si, которая затрачивает-
ся на ее поддержание, или, что одно и то же, коэффициент отра-
жения волны от плазмы р =(So — S\)/Sq.
4.4. Приближенное решение. Введем, как в каналовой модели
дуги и модели металлического цилиндра для индукционного раз-
ряда, эффективную границу плазмы, поместив ее в точке х = 0,
где температура Т = То, и положим о = 0, е = 1 при Т То, х
0 и о = ок е = ек при То Т С Тк, х 0, что соответствует за-
мене распределения пе(х} ступенькой (рис. 13.9). Коэффициент
отражения волны, нормально падающей из «вакуума» на резкую
границу однородной среды, равен
Р = [(„ _ 1)2 + х2]/ 1)2 + х2] (13.31)
Показатели п и х выражаются через о и е формулами (5.34) *).
Та часть электромагнитного потока, которая проникает в плаз-
му, затухает в ней по закону (5.37):
d<S>Jdx = -^<5), (13.32)
где коэффициент поглощения определяется формулой (5.36)
♦) Формула (13.31) выводится из граничных условий для векторов Е
и Н на границе раздела двух сред.
390
или (5.38). Энергия волны диссипируется в слое толщиной по-
рядка Zw = Ро1 у поверхности. В нем температура падает от Тк
до Tq. Баланс энергии в слое описывается приближенным равен-
ством = Jq ~ КДТ/Ц в полной аналогии с дуговым и ВЧ раз-
рядами. Температура Тк находится из уравнения
50 [1 - р Цк)] = Лк (2*^/7) рй (7К), (13.33)
аналогичного (13.20) для ВЧ разряда. Уравнение переноса тепла
от плазмы к стенке через «неионизованный» зазор (0К — 0ш =
= 51/х0) определит ширину зазора хо.
Таблица 13.1. Зтекграцанамические характеристики воздушной плазмы
р — 1 атм, f — 10 ГГц
т, 103 к пе, см—3 vm> 101° с'1 а, 101° с~1 е со|е| п X см Ро
3,5 6,6-1011 7,5 0,13 0,78 0,33 0,89 0,14 1,7 0,0089
4,0 4,4-1012 7,1 0,88 —0,53 3,3 0,81 1,1 0,22 0.28.
4,5 1,6-1013 6,6 3,3 —5,1 1,3 1,3 2,6 0,091 0,57
5,0 4,8-1013 6,4 9,9 -18 1,1 2,1 4,7 0,05 0,71
5,5 9,3-Ю13 6,0 19 -39 1,0 2,8 7,3 0,032 0,83
6,0 2,Ь1014 5,8 41 —88 со 4,3 И 0,022 0,88
В табл. 13.1, 13.2 приведены для иллюстрации результаты
расчета электродинамических характеристик воздушной плазмы
атмосферного давления и потоков СВЧ излучения, необходимых
для поддержания различных температур. Вычисления сделаны
для одной из применяемых на * опыте частот f = 10 ГГц
Таблищ 13 2. К расчету СВЧ разряда в воздухе
р — 1 атм, / = Ю ГГц
т, 103 к Х,10—2 Вт/(см-К) 0, 10“~2 кВт/см sr кВт/см3 Р »о- кВт/см2 Sj, ? кВт/см2 * s0, кВт/см2
4,2 0,92 1,1 0,2 0,2 0,25
4,5 0,95 1,4 0,045 0,4 0,075 0,23 0,38.
5,0 1,1 1,9 0.14 0,65 0,40 0,35 1,0
5,5 1.3 2,5 0,30 0,76 1,25 0,56 2,3
6,0 1,55 3,3 0,60 0,81 3,1 1,06 5,6
*) С учетом теплопроводностных потерь из столба плазмы радиуса
R = 0,3 см
(Хо = 3 см). Коэффициент отражения (13.31) обозначен р0. Вы-
числения сделаны с уточненным значением р, найденным при-
ближенно с учетом размытости границы плазмы (отражение при
этом немного уменьшается) [25].
При уменьшении температуры резко возрастает длина погло-
щения электромагнитной волны Zw сю п^1 exp (I/2kT). Когда она
391
сравнивается с радиусом R разрядного столба, плоская модель
теряет смысл. На поддержание «прозрачной» для волны плазмы
Z<o > R требуются все возрастающие мощности, причем соответ-
ствующие состояния неустойчивы. Все это аналогично ситуации
с ВЧ разрядом (п. 3.9, 3.10). Минимальная пороговая температу-
ра Tt для СВЧ разряда находится из условия /й(7\)~7?. Для
воздуха при R = 0,3 см Tt ~ 4200 К. Ей соответствуют пороговые
потоки в плазму ~ 0,2 кВт/см2 и в падающей волне Sot ~
~ 0,25 кВт/см2. Эти цифры согласуются с опытом. Возрастающее
с ростом температуры отражение электромагнитной волны от
плазмы ограничивает возможности достижения в СВЧ разряде вы-
соких температур. В воздухе температура не превышает
5000—6000 К.
4.5. Предел геометрической оптики. В общем случае, когда
действительная и мнимая части комплексной диэлектрической
проницаемости имеют один порядок, т. е. 4ло/colei ~ 1, поток
<S> нельзя представить в чисто дифференциальной форме (13.23)
или (13.32). В СВЧ разрядах чаще всего он и осуществляется
(табл. 13.1). Однако в пределе 4ло/сое < 1 ие«1, который воз-
можен на повышенных частотах, уравнение (13.32), строго спра-
ведливое в*однородной среде, имеет смысл и в случае неоднород-
ной, так как электромагнитная волна при этом слабо затухает
на расстоянии порядка длины волны Хо/п (х ~ 2n(j/cort < 1, п~
« Уе » 1; см. п. 5.5 гл. 5). Этот случай соответствует приближе-
нию геометрической оптики. При n « 1, х < 1, как следует из
(13.31), отражение мало: р < 1. В этом случае существует точ-
ный второй интеграл уравнений Максвелла и энергии, который,
подобно (13.24), позволяет выразить температуру плазмы через
параметры внешнего поля. Подставляя <5> по (13.32) в (13.28),
умножая все на о = cpu/4n и интегрируя, находим соотношение
J o(T)X(T)dT =^S0, (13.34)
которое стоит в одном ряду с (13.10) для постоянного и (13.24)
для ВЧ полей.
4.6. Предел квазистационарного поля (ВЧ разряд). Рассмот-
ренный в § 3 ВЧ разряд, когда в уравнении Максвелла можно
пренебречь током смещения, соответствует противоположному
предельному случаю 4ло/colei > 1. В этом случае, согласно
п. 5.6 гл. 5, тг ~ х ~ У2ло/со »1 и по (13.31) р ~ 1. Падающая
волна практически полностью отражается от плазмы, а прони-
кающее в нее поле затухает на толщине скин-слоя 8 = с (2лосо) “1/2.
Отсюда вовсе не следует, что в случае ВЧ разряда в плазму
вводится лишь малая доля энергии, вырабатываемой генерато-
ром. Прежде всего нет смысла говорить об индукционных разря-
дах в волновых терминах, ибо длина волны поля гораздо больше
размеров системы. Но если все-таки стать на «волновые» позиции,
392
то эффект можно трактовать так, как будто «отраженная» мощ-
ность возвращается обратно в генератор, и последний призван
восполнять только малую разность между «падающим» и «отра-
женным» потоками электромагнитной энергии. Иначе обстоит
дело в случае разрядов в волноводах. Здесь по техническим при-
чинам отраженную от плазмы волну приходится отводить от ге-
нератора, поэтому отражение снижает коэффициент использова-
ния вырабатываемой им энергии.
§ 5. Непрерывный оптический разряд
5.1. Особенности оптического способа поддержания плазмы.
Плотную равновесную плазму можно стационарно поддерживать
оптическим излучением так же, как и другими постоянными и
переменными полями. Точно так же, продувая через область раз-
ряда холодный газ, можно сделать генератор плазмы — оптиче-
ский плазмотрон. Возможность осуществления этих процессов бы-
ла теоретически обоснована в [13.5], и вслед за этим в 1970 г.
непрерывный оптический разряд был получен на опыте [13.6].
Для поддержания плазмы требуются довольно большие мощ-
ности излучения. Если стремиться к длительному эффекту, как
это получается во всех других полях, то пока можно рассчитывать
только на излучение ССЬ-лазера, ибо это единственный практи-
чески доступный мощный лазер непрерывного действия. Благода-
ря счастливому стечению обстоятельств, тот факт, что лазер на
СО2 дает длинноволновое инфракрасное излучение, для данной
цели является чрезвычайно благоприятным. (Коэффициент погло-
щения света в плазме быстро падает с ростом частоты. Видимое
излучение, например, поглощается в плазме атмосферного дав-
ления довольно слабо (п. 5.3). Для снабжения плазмы необходи-
мой энергией за счет поглощения видимого света потребовались
бы мощности в 102— 103 раз большие, чем мощность СС^-лазера.
Оптический способ снабжения плазмы энергией обладает ха-
рактерной особенностью, которая отличает его от всех прочих.
Для подвода энергии к плазме не нужны конструктивные эле-
менты: электроды, индуктор, волновод, резонатор. Оптическое
излучение можно транспортировать световым лучом прямо через
свободное пространство или атмосферу любого газа, и эта воз-
можность представляется привлекательной и перспективной для
приложений. В принципе, оптический разряд можно зажечь в
любом месте, вдали от каких-либо твердых предметов, можно за-
ставить разряд бежать по лучу, а можно локализовать его путем
фокусировки излучения и тем самым стабилизировать. Можно
двигать плазму в пространстве, передвигая луч, скажем фокус,
к которому «привязан» разряд. Можно, как говорилось, создать
оптический плазмотрон, продувая холодный газ через стабилизи-
рованный фокусировкой луча разряд, и получать непрерывную
плазменную струю очень высокой температуры. Температура
плазмы в оптическом разряде даже в стандартных условиях су-
393
щественно выше, чем в других (15 000—20 000 К). Наконец, бла-
годаря высокой температуре оптический разряд можно исполь-
зовать в качестве стабильного источника света очень большой
яркости, который, в принципе, можно расположить в свободном
пространстве.
Возможности получения непрерывного оптического разряда
при помощи световых источников нелазерного типа крайне огра-
ничены. Из-за малости коэффициента поглощения излучений
оптического диапазона для заметного выделения энергии в области
ограниченных размеров требуются весьма высокие степени иони-
зации газа, приближающиеся к полной однократной. Для этого
температура плазмы должна быть высокой (15 000—20 000 К).
Но источник, питающий плазму, должен обладать по крайней ме-
ре столь же высокой температурой. Ведь согласно второму закону
термодинамики свободная перекачка энергии от менее нагретого
тела к более нагретому невозможна. Так, например, фокусируя
солнечные лучи зеркалом или линзой сколь угодно большого диа-
метра и концентрируя сколь угодно большую мощность, все рав-
но нельзя поддерживать в веществе температуру выше солнеч-
ной — 6000 К. Но при столь низкой температуре свет в плазме
погдрщается настолько слабо, что, даже будучи однажды зажжен-
ной, плазма немедленно распалась бы из-за невосполняемых
потерь энергии.
5.2. Схема экспериментов. Луч СС^-лазера фокусирует лин-
зой, как изображено на рис. 13.10 (или зеркалом). Линза изго-
тавливается из NaCl или КС1, так как обычное стекло непрозрач-
но для инфракрасного излучения с X = 10,6 мкм. Чтобы зажечь
х Рис. 13 10. Схема опыта по получению непрерыв-
,_1_____ ного оптического разряда. Плазма (заштрихова-
I на) сдвинута от фокуса навстречу лазерному из-
---- лучению
разряд, необходимо создать начальный плазменный очаг (задача
поджига существует в любых равновесных разрядах). Это можно
сделать путем пробоя газа в области фокуса при помощи вспомо-
гательной системы либо вводя на короткое время в фокус воль-
фрамовую проволочку. Немного металла с поверхности испаряет-
ся, пары ионизуются и начинают поглощать лазерный луч. По-
том проволочка удаляется, а разряд продолжает гореть уже в
атмосфере газа. Плазма несколько сдвигается от фокуса навстре-
чу лазерному излучению до того сечения сходящегося светового
канала, где интенсивности луча еще достаточно для ее поддер-
жания. Размеры ее меняются от 1 мм на пределе существова-
ния до величины порядка 1 см и более при повышенных мощно-
стях лазера.
Чтобы можно было пользоваться разными газами и варьиро-
вать давление, луч через соляное окно вводится в камеру. Если
394
хватает лазерной мощности, непрерывный оптический разряд
можно зажигать прямо в свободном воздухе. Первые опыты [13.6]
были еде таны с помощью лазера маленькой по нынешним време-
нам мощности. 150 Вт. В ту пору (1970 г.) более мощные лазеры
были большой редкостью. Разряд был зажжен в ксеноне при
давлении в несколько атмосфер, для чего, согласно теоретическим
воззрениям, требуется небольшая лазерная мощность. Сейчас,
когда в руках исследователей имеются и более мощные лазеры,
разряд получают в разных условиях, в том числе и прямо в ком-
нате. Правда, для последнего требуется лазер большой даже по
нынешним временам мощности, не менее 5 кВт, а главное,—
нужен луч высокого качества (малой расходимости), который под-
дается хорошей фокусировке.
5.3. Поглощение излучения СО2-лазера в плазме. Малые, по
сравнению с кТ кванты СОгглазера Йсо = 0,117 эВ (Йсо/А =
= 1360 К) поглощаются в сильноионизованной плазме оптическо-
го разряда «тормозным» механизмом при столкновениях элект-
ронов с ионами. Соответствующий коэффициент истинного погло-
щения xw дается формулами (6.14), (6.15). Фактический коэффи-
циент поглощения исправленный на вынужденное испуска-
ние, получается из путем умножения на htoJkT. В численном
виде с учетом второй ионизации
Р<о(С02) =
2,82-10 2Х(п++4п++) [ 2,17 103Т [К] ]
{Г[К[}3/2 lg| „1/з (СМ
(13.35)
где плотности зарядов вычисляются на основе уравнений Са-
ха [27].
Рис 13.11 Температурная за-
висимость коэффициента по-
глощения излучения СО2 лазе-
ра в воздухе; максимальные
значения коэффициента Цштах
равны 0,85, 38, 1600 см-1
(сверху вниз)
На рис. 13.11 представлены коэффициенты поглощения для
воздуха. Существенным для дальнейшего является наличие макси-
мума у щДТ) при р = const. Максимум появляется, когда почти
заканчивается однократная ионизация атомов. При дальнейшем
повышении температуры в некотором интервале степень иониза-
ции почти не меняется. Вторая ионизация начинается при замет-
но более высоких температурах, а плотность газа и, следователь-
но, пе ~ при постоянном давлении уменьшаются как 1/7\
Таким образом, до начала второй ионизации цы падает как pw со
сю л2Т~3/2 сю Т~1/2. В ходе второй ионизации возникает новый
395
сильный подъем цо(Т), но столь высокие температуры в разряде
не достигаются.
Максимальный коэффициент ца тах растет с давлением несколь-
ко медленнее, чем р2. В воздухе при р = 1 атм ц^так ~ 0,85 см"1,
а наименьшая длина поглощения лазерного излучения к> тт
« 1,2 см. Для излучения неодимового лазера с X = 1,06 мкм
Ротах ~ 6 • 10"3 см, а /«тт ~ 170 см. Эти цифры ясно показывают,
почему для поддержания плазмы невыгодны коротковолновые
излучения: плазма для них слишком прозрачна.
Наличие максимума в коэффициенте поглощения свойствен-
но только излучениям достаточно высоких частот to >> vKya. В про-
тивоположном случае проводимость о и пропорциональный ей
коэффициент поглощения монотонно растет с повышением
температуры. При заметной ионизации, когда преобладают куло-
н вские столкновения электрона с ионами, и по завершении пер-
в й ионизации
сю о сю ГСгАкул 00 ne/n+VGKyJl <*> Т3/2
независимо от плотности и давления.
5.4. Температура плазмы и пороговая мощность. Геометрия
подачи энергии к плазме и самого разряда, как видно из
рис. 13.10, весьма сложна. Выбор подходящей одномерной модели
для оценочного аналитического расчета, как и в случае разряда
в волноводе, связан с известными натяжками. Все же основные
черты процесса неплохо отражаются сферической моделью, в осо-
бенности при фокусировке луча короткофокусной оптикой и мощ-
ностях излучения, близких к пороговым, когда плазма не в со-
стоянии отодвинуться от фокуса.
Рассмотрим плазменный шар радиуса го, высокая температура
в котором поддерживается за счет поглощения сферически сим-
метрично сходящихся лучей общей мощности Pq. Как и во всех
предыдущих случаях, будем считать, что вне шара, где Т < То,
поглощения нет (цы = 0), а внутри коэффициент поглощения pw
постоянен и соответствует наибольшей температуре в центре Тк.
Возможность аппроксимации функции цм(Г) ступенькой обуслов-
лена резким характером ее нарастания до области максимума.
При пороговых условиях плазма имеет маленькие размеры и по-
тому прозрачна для лазерного излучения. В плазме поглощается
мощность порядка Р\ ~ РоЦ^го. Из области энерговыделения она
выводится теплопроводностным потоком /о.
Вообще говоря, в оптическом разряде температура высока и
потери на излучение могут быть большими, но это относится в
основном к давлениям 5 —10 атм и выше и мощностям, заметно
превышающим пороговую. На пределе существования размеры
плазмы столь малы, что теплопроводностные потери, пропорцио-
нальные 4лго, больше потерь на излучение, которые вследствие
прозрачности плазмы пропорциональны излучающему объему
396
4лг'о/3. Таким образом,
Рг = 4лгоЛ 4лгоЛ0/го = 4лгоА0, (13.36)
где А0 = 0К — 0о — перепад потенциала теплового потока в
плазме.
Вне поглощающей сферы го имеем
~^r2d@/dr = РХ, 0 = Р1/4лг, 0о = Р1/4лго. (13.37)
Здесь принято во внимание, что на «бесконечности» газ холодный.
Из (13.36) и последнего равенства (13.37) следует, что А0 = 0о
или 0К = 2©о. Подставляя в равенство Р\ = 2лго0к поглощенную
мощность Р\ = находим связь лазерной мощности с тем-
пературой в центре плазмы:
Ро = 2л0(Л)/цД77к). (13.38)
Поскольку функция цо(Т) обладает максимумом, а 0(Г) мо-
нотонна, мощность Ро проходит через минимум (рис. 13.12). Ми-
нимум Роппп=Р/ лежит при температуре Тt, близкой к точке
|lu max- Это наименьшая (пороговая) мощность светового луча, ко-
торый, будучи сфокусированным, может стационарно поддержи-
вать плазму. Состояния на левой ветви кривой РО(ТК), где Т < Тк,
Рис. 13 12. Зависимость мощности сферически
симметрично сходящегося луча от максимальной
температуры плазмы при стационарном ее под-
держания (воздух, р = 1 атм, излучение СО2-
лазера) *
неустойчивы и потому не реализуются. В самом деле, при слу-
чайном повышении температуры фактическая мощность окажется
больше той, которая необходима для поддержания нового состоя-
ния. Плазма начнет разогреваться, пока состояние не перейдет
на правую ветвь. Как легко проверить путем аналогичных рас-
суждений, там состояния устойчивы. Ситуация типична для
равновесных разрядов.
Оценка радиуса плазмы г0 требует более детального рассмо-
трения [25]. Из уравнений (13.36) — (13.38) его найти нельзя.
Дело в том, что радиус плазмы связан с размером светового ка-
нала, в сферической модели — с радиусом кружка фокусировки р0.
В предыдущих рассуждениях он отсутствовал, ибо предполагалось,
что лучи сходятся точно в центр. Наименьший радиус плазмы, от-
вечающий пороговым условиям, равен rorain = rt ~ (4роМЗ)1/2.
При ро ~ 10-2 см, см о -1 мм, как в опытах.
5.5. Необходимые лазерные мощности. Оценочная формула
(13.38) позволяет предсказать мощность лазера, которая необхо-
дима для осуществления непрерывного оптического разряда в
тех или иных условиях. Она соо!ветствует примерно TK = Tt и
397
Цштах = Так, в воздухе атмосферного давления для излу-
чения СО2-лазера ц Мтах ~ 0,85 см-1, температура плазмы Tt~
~ 18 000 К, 0Z = 0(7\)^O,3 кВт/см; пороговая мощность Pt~
« 2,2 кВт. Эти цифры подтверждаются опытом. До известного
предела, пока не вступят в действие потери на тепловое излуче-
ние, пороговая мощность довольно быстро уменьшается с ростом
давления, поскольку растет цотах. Порог ниже в газах с низким
потенциалом ионизации и плохой теплопроводностью (меньше Tt
и 0f). Именно поэтому для первых опытов с маломощным лазе-
ром был выбран ксенон при р ~ 3—4 атм; при этом в Хе, Аг
достаточно 100—200 Вт. Чтобы поддерживать разряд в атмосфер-
ном воздухе на частоте неодимового лазера, потребовалось бы
300 кВт.
5.6. Почему в оптическом разряде получается необычно высо-
кая температура. В воздухе атмосферного давления в дуговом и
ВЧ разрядах Т « 10 000 К, в СВЧ — 5000 К, а в оптическом —
18 000 К. В аргоне Т ~ 20 000 А, что вдвое выше, чем в дуговом
и ВЧ разрядах. Причина связана с прозрачностью плазмы для
оптического излучения, что обусловлено зависимостью о)'2.
На более низких частотах энергия поля хорошо диссипируется
и при не слишком сильной ионизации, т. е. при не слишком высо-
кой температуре. Наоборот, в сильнопонизованную плазму поле
не проникает, и это мешает диссипации и разогреву. На оптиче-
ских же частотах для лучшей диссипации требуется полное рас-
ходование резерва электронов. По мере разогрева газ, оставаясь
прозрачным, поглощает свет все сильнее и сильнее, что в свою
очередь способствует разогреву, и так вплоть до полной однократ-
ной ионизации. Лишь при очень больших давлениях, когда велики
резко возрастающие с температурой потери на излучение, она не
может подняться высоко: Т « 13 000—15 000 К.
Необычно высокая температура в открытом газе, не затемнен-
ном стенками,— уникальное свойство непрерывного оптического
разряда, которое позволяет использовать его в качестве источника
света очень высокой яркости. Плазма оптического разряда све-
тится ослепительным белым светом, на нее невозможно смотреть
без темных очков. Особенно большой температуры (до 25 000—
30 000 К) следует ожидать в гелии, где исключительно высок
потенциал ионизации [13.7]. Это был бы мощный источник
ультрафиолетового излучения. Правда, в гелии высок и порог.
5.7. Измерения температур и порогов. На рис. 13.13 показана
фотография непрерывного оптического разряда, на рис. 13.14 —
поле температур в воздухе. Температура измерялась по излуче-
нию континуума в узком интервале длин волн около X = 5125 А
и по излучению в линиях атомов и ионов азота. Центр плазмы
сдвинут от фокуса навстречу лучу на 1,1 см. В Аг при давлении
2 атм температура в центре плазмы оказалась равной 18 000 К,
в Хе при 2 атм— 14000 К (ниже потенциал ионизации), в П2
при 6 атм— 21 000 К, в N2 при 2 атм — 22 000 К. Температура
398
всегда монотонно спадает от центра плазмы к периферии. Разме-
ры плазмы обычно порядка 3—15 мм, причем плазма вытянута
вдоль оптической оси, несколько повторяя форму светового
канала.
На рис. 13.15 показаны зависимости пороговых мощностей от
давления в Хе и Аг, а на рис. 13.16 — в молекулярных газах;
для сравнения приведены пороги д тя Лг. Пороговые мощности
Рис 13 13 Фотография непрерывного оптического разряда [13 9J: а — об-
щин вид через окно камеры диамегро i 8 см б — увеличенное изображение
плазмы, о що деление— 1 мм, лазерный луч идет справа налево
(нижние кривые) быстро спадают при р ~ 1 атм, но при р ~
~ 5 атм падение прекращается. Это связано со сменой механизма
потерь энергии. Потери на тепловое излучение Ф [Вт/см3] при
данной температуре возрастают с давлением примерно так же,
как и коэффициент поглощения лазерного света jlu, поскольку
обе величины пропорциоиа гьны ?v7+~ В условиях, близких
к пор^гэвь м, энерговыделение за счет поглощения лазерной энер-
гии компенсирует лучистые потери. Теперь ~ Ф, где S ==
== P/nR2 — интенсивность лазерного излучения, R — радиус све-
тового кана га в области расположения п шзмы. Но если и Ф
зависят от р примерно одинаковым образом, пороговая мощность
SnR2 от р зависит слабо, о чем и св щетельствуют нижние кривые
на рис 13 15, 13 16 В молекулярных газах пороги выше, чем в
тяжелых инертных, из-за сильном теплопроводности, в которую
большой вклад дает реактивная составляющая, связанная с пере-
носом энергии диссоциации молекул (рис. 12 22, 12.23).
П ища лазерный луч фокусируется линзой с не очень малым
фокусным расстоянием / ~ 8—10 см и больше, в некоторых газах
наблюдаются и верхние границы существования разряда по Р и
р (верхние кривые на рис. 13.15, 13 16). При мощностях, превы-
шающих верхний предел, и при давлениях выше точки, где схо-
399
дятся верхняя и нижняя кривые, стационарный разряд получить
пе удается. Это объясняется ослаблением интенсивности лазерно-
го луча вследствие поглощения при проникновении его в плазму.
Рис. 13.14. Измеренное пространственное распределение температуры в не-
прерывном оптическом разряде [13.8]. Воздух, р — 1 атм, мощность СОг-
лазера 6 кВт, фокусное расстояние линзы равно 15 см, луч идет справа на-
лево. Эффективная граница сходящегося светового канала показана штри-
ховой линией. Внизу — изотермы; х — оптическая ось, г — радиальное рас-
стояние от оси; вверху — распределение Т (х) на оси луча
Рис. 13.16. То же, что и на рис. 13.15,
для молекулярных газов. Для срав-
нения приведены кривые для Аг
[13.10]
Рис. 13.15. Пороговые мощности, не-
обходимые для поддержания непре-
рывного оптического разряда в ато-
марных газах (нижние кривые). По-
казаны и верхние границы сущест-
вования разряда (верхние кривые).
Область существования по Ро, р ле-
жит между верхней и нижней кри-
выми [13.9]
В глубине плазмы интенсивности при этом не хватает на ком-
пенсацию потерь на излучение [6.3]. В случае фокусировки луча
короткофокусными зеркалами с f = 1,5—2,5 см верхних пределов
по Р и р не наблюдалось (рис. 13.17) [13.11]. Ослабление лазер-
400
ной интенсивности из-за ее поглощения перекрывается увеличе-
нием за счет резкого схождения лучей. Поэтому источник вос-
полнения потерь на тепловое излучение, в отличие от предыду-
щего, не иссякает. Надо сказать, что в экспериментах [13.11]
лазерный луч направлен вертикально вверх, и это способствует
стабилизации разряда. Восходящий конвективный поток нагре-
того газа, связанный с действием архимедовой силы, сдвигает
Рис 13 17 Пороговые мощности для поддержания непрерывного оптическо-
го разряда при высоких давлениях [13 И]
плазму к фокусу, в зону повышенной* интенсивности. В экспери-
ментах [13.9, 13.10] луч горизонтален, конвективный поток стре-
мится вообще вывести плазму из светового канала, и это, напро-
тив, затрудняет горение разряда. Не исключено, что этот фактор
также ограничивает область существования разряда.
5.8. Двумерные расчеты и одномерная модель. Поле темпе-
ратур в оптическом разряде описывается уравнением баланса
энергии плазмы (13.1), где о<Е2> целесообразно заменить на
Геометрия разряда двумерна — температура Т(х, г) зависит от
координаты х вдоль оптической оси и радиуса г в поперечном
направлении (рис. 13.10, 13.14). Для упрощения распределение
интенсивности лазерного излучения S по сечению светового кана-
ла можно считать постоянным и оперировать мощностью jP(^) =
= SttR2 и коэффициентом поглощения pQ [Т (х, 0)] на оси. Тогда
член энерговыделения есть цшР/л7?2, причем Р удовлетворяет
уравнению дР/дх = — цюР, которое равносильно (13.4), (13.32)
для канала переменного сечения. Форма светового канала в на-
гретой области существенным образом отличается от конической
из-за рефракции лазерного излучения в создаваемой им плазме.
Поэтому в систему включается уравнение, описывающее радиус
канала R(x). Важную роль играет теплообмен излучением
(§ 9 гл. 6), вследствие чего слагаемое Ф представляет собою не
26 ю П Райзер
401
просто скорость объемного высвечивания, а разность между излу-
чением и поглощением тепловой радиации, Ф = — q по формуле
(6.40). Для нахождения Ф служит спектральное уравнение пере-
носа излучения (6.32). Оно также включается в систему урав-
нений.
Решение описанной задачи [13.12] для условий, соответствую-
щих рис. 13.14, хорошо согласуется с измеренным полем темпера-
тур. Оно позволило понять один загадочный момент. Дело в том,
что через плазму обычно проходит насквозь значительная часть
лазерной мощности, в данном случае 2,8 кВт из 6 кВт. Ее вполне
хватило бы для поддержания разряда в точке фокуса, для чего
требуется всего лишь 2 кВт (это порог для атмосферного возду-
ха). Однако на опыте никогда не наблюдается двух плазменных
областей, а в месте геометрического фокуса температура заметно
ниже, чем в центре плазмы (рис. 13.14). Как оказалось, из-за
рефракции конически сходящиеся лучи начинают расходиться
как раз в том месте, где Т ~ Гтах. Все становится на свои места —
наиболее горячая плазма располагается в наиболее узком месте
светового канала, где лазерное излучение сконцентрировано
сильнее всего. Просто само место «перетяжки» сходящегося-
расходящегося светового канала сдвигается от точки геометриче-
ского фокуса ближе к линзе, в отличие от рис. 13.10, где пока-
заны контуры невозмущенного канала. При этом наименьший
радиус искаженного светового канала на порядок превышает
радиус фокусировки лучей в отсутствие плазмы го ~ 10“2 см.
Показателен баланс энергии в разряде в атмосферном возду-
хе. Из 6 кВт лазерной мощности в плазме поглощается 3,2 кВт.
Происходит это в центральной зоне, где Т > 10 000 К. Практиче-
ски вся поглощенная энергия излучается, но ультрафиолетовая
часть излучения, в которой сосредоточено 1,9 кВт, поглощается
поблизости, в области, где 6000 < Т < 10 000 К. На «бесконеч-
ность» 2 кВт уносится теплопроводностью, 1,2 кВт — излучением.
Таким образом, теплообмен излучением в сильно нагретом газе
очень велик.
Двумерные расчеты сложны и трудоемки. Поэтому весьма по-
лезной оказалась упрощенная одномерная модель непрерывного
оптического разряда [13.13], которая позволяет более оперативно
решать многие вопросы и производить серийные расчеты, обеспе-
чивая вполне разумное согласие с экспериментом. В одномерной
модели рассматривается распределение температуры вдоль опти-
ческой оси х. Для этого радиальная часть дивергенции теплового
потока в уравнении (13.1) приближенно заменяется членом ра-
диальных теплопроводностных потерь Л0//?2, где 6(х) — потен-
циал теплового потока (п. 10.2 гл. 12), 7? (я)—текущий радиус
светового канала, А ~ 1,5—2 — числовой коэффициент, который
находится с учетом радиального профиля температуры. Основную
часть дивергенции целесообразно записать не в цилиндрических,
а в полярных координатах, что больше подходит для конусной
формы фокусированного светового луча.
402
Имея в виду применение одномерной модели и к разряду в
газовом потоке (п. 6.4), выпишем уравнение баланса энергии га-
за с учетом соответствующего слагаемого:
ат id,, ат л© ,
-^ = - М<оЛ Р =
(13.39)
Здесь р и и — плотность и скорость газа в точке х, причем р и
Т связаны уравнением р(р, Т) = const; сР — удельная теплоем-
кость при постоянном давлении. Для статического разряда и = 0.
Потери на излучение Ф в этой модели вычисляются на основе
двумерного уравнения переноса теплового излучения, которым
дополняются соотношения (13.39). Пример решения системы и
сопоставление с опытом даны в п. 6.4.
О непрерывном оптическом разряде см. также [25, 10, 9.1].
Ссылки на некоторые более поздние работы можно найти в стать-
ях [13.12, 13.13, 13.19].
§ 6. Генераторы плотной низкотемпературной плазмы —
плазмотроны
Как отмечалось в § 1, каждый статический разряд можно ис-
пользовать для создания плазмотрона, если продувать через него
холодный газ. Сейчас на практике применяют плазмотроны трех
типов: дуговые, ВЧ и СВЧ. Что касдется оптического, то здесь
дело находится в фазе экспериментов.
6.1. Дуговые плазмотроны. Они давно уже стали объектом
инженерного дела. Мощности их бывают самыми различными: от
сотен ватт до тысяч киловатт [28, 13.14]. Конструирование мощ-
ных машин связано с решением множества инженерных проблем:
стабилизации, охлаждения, повышения стойкости электродов,
материаловедческих и др. Принципиальная схема плазмотрона по-
казана на рис. 13.18а. Широко применяется схема рис. 13.18 6,
в которой анодом служит сам обрабатываемый материал. Такие
конструкции применяют для резки, сварки, плазменно-дуговой
плавки металлов.
6.2. ВЧ-плазмотрон. Принципиальная схема высокочастотного
плазмотрона мало отличается от схемы организации статического
разряда. Разряд горит в диэлектрической трубке, вставленной в
индуктор. В трубку подается холодный газ, из среза вытекает
плазменная струя, часто — в атмосферу. В своем современном
виде индукционная плазменная горелка, как ее иногда называют,
была сконструирована в 1960 г. Ридом (рис. 13.19). Главнейшим
конструктивным моментом в ней является применение танген-
циальной подачи газа. Дело в том, что в статическом ВЧ разряде
плазма очень близко подступает к стенкам трубки, и трубка на-
26*
403
ходится в условиях тяжелых тепловых нагрузок. Простая осевая
прокачка газа мало меняет это положение. При тангенциальной
подаче газ вводится в трубку на 20—30 см выше индуктора по
касательной к цилиндрической поверхности. Газ течет, совершая
винтовое движение. В результате действия центробежной силы
давление в приосевой области становится пониженным, и здесь
ооразуется завихрение — про-
дольное движение получается
слабым Холодный газ, проте-
кая вдоль трубки в основном в
Рис. 13 18 Принципиальные схемы ду-
говых плазмотронов: а — плазменная
струя 3 вытекает через отверстие в
аноде Л, К — катод, 1 — подача холод-
ного газа, 2 — разряд; б — анодом слу-
жит обрабатываемая деталь (разрезае-
мый лист металла)
Рис 1319 Принципиальная схе-
ма индукционного плазмотрона:
1 — поток холодного газа, 2 —
разряд, 3 — плазменная струя,
4 — индуктор, 5 — диэлектриче-
ская трубка
периферийном кольце, отжимает разряд от стенок, предохраняя
их от разрушительного действия высокой температуры. Расходы
обычно задаются такими, что средние продольные скорости холод-
ного газа имеют порядок 1 м/с. Плазменная струя вытекает в ат-
мосферу со скоростью несколько десятков метров в секунду. Сей-
час действуют индукционные плазмотроны с мощностями в десят-
ки и сотни киловатт. На рис. 13.20 показана фотография разряда
и плазменной струи.
6.3. СВЧ-плазмотроны. Устройство одного из них также не
отличается от схемы разряда в волн )воде (рис. 13.21 а). Через
диэлектрическую трубку, пересекающую волновод, продувают газ,
также закрученным потоком. Разряд отжимается от стенок,
и тепло выносится из трубки потоком с плазменной струей.
СВЧ-пДазмотроны обладают тем достоинством, что в них удается
получить высокий КПД, до 90 %. Это достигается, в частности,
путем заворачивания назад прошедшей через плазму волны
(п. 4.1). Температура плазмы 4000—6000 К, ниже, чем в ВЧ-
плазмотроне, где Т ~ 9000—10 000 К, но для многих целей этого
бывает достаточно. Плазма столь же чиста, как и в ВЧ-плазмо-
троне, в отличие от дуговой, где она загрязнена продуктами раз-
рушения электродов. В плазму вкладывают мощность в несколько
киловатт.
Схема, показанная на рис. 13.21 б, допускает получение боль-
ших мощностей [13.3]. Разряд горит на оси волновода круглого
сечения радиусом 5 см и длиной несколько десятков сантиметров.
404
По волноводу распространяется волна типа E’oi с длиной в вакуу-
ме X = 12,5 см. Внутренняя поверхность трубчатого волновода и
внешняя поверхность плазменного столба (радиус его около
1 см), образуют для электромагнитной волны коаксиальную ли-
нию. По волноводной трубе закрученным потоком продувается
Рис. 13.20. Фотография разряда и плазменной струи. Диаметр трубки ра-
вен 6 см, поток движется слева направо (воздух, р =- 1 атм, расход 2Х
ХЮ3 см3/с). Вклад мощности в плазму составляет 27 кВт, измеренная тем-
пература на оси у среза трубки 9800 К [13.15]
газ, и это стабилизирует разряд около оси. Труба заканчивается
соплом, через которое вытекает плазменная струя. Генерируемая
СВЧ-мощш сть почти полностью п гглощается плазмой. Поток
Рис. 13.21. Схемы СВЧ-плазмотронов: а — разряд 2 в диэлектрической труб-
ке 5, пересекающей волновод, 1 — поток холодного газа. 3 — плазменная
струя, 4—волновод; б —плашогрон коаксиального типа. Стрелками пока-
заны поток газа и электромагнитная волна, разрядный столб и плазменная
струя затенены
электромагнитной энергии втекает в разрядный столб с поверх-
ности по радиусу к оси так же, как в индукционном разряде или
разряде в резонаторе, а СВЧ-волна по мере распространения
вдоль трубы соответственно ослабевает. Температура плазмы
405
Т ~ 5000 К. Об СВЧ-плазмотронах и их расчетах см.
[13.16, 13.17].
6.4. Оптический плазмотрон. Его принципиальная схема, как
это было предложено в [13.5], показана на рис. 13.22. Газ про-
дувают через разряд в направлении распространения сфокусиро-
ванного лазерного излучения. Поток смещает плазму в сторону
Рис. 13.22. Схема оптического плаз-
мотрона: 1 — контур светового кана-
ла, 2 — линза, 3 — плазма, F — фо-
кус. Стрелками показаны направле-
ния лазерного излучения So и ско-
рости газового потока и
повышения интенсивности излучения, и это способствует стаби-
лизации разряда. Эффект аналогичен действию естественной кон-
векции при подаче излучения снизу вверх (п. 5.7), но выражен
Рис. 13.23. Расчет процесса в оптическом плазмотроне на основе уравнения
(13.39) [13.13] и сопоставление с экспериментом [13.18]. Представлены рас-
пределения температуры вдоль оптической оси. Луч и газовый поток на-
правлены слева направо; точка фокуса х — 0; аргон, р — 1 атм, лазерная
мощность Ро == 1,25 кВт, фокусное расстояние линзы / = 40 см; расходи-
мость излучения 2 мрад; коэффициент теплопроводностных потерь А — 2.
Отрезками показаны длины и положения светящейся области на фотогра-
фиях, v — скорость холодного газа
сильнее, так как скорости продувания обычно больше, чем кон-
векционные.
В опытах [13.18] с аргоном при р = 1 атм и мощности лазера
Ро = 1,25 кВт плазма разряда была сфотографирована при не-
406
скольких скоростях v набегающего холодного потока. Светящаяся
область имеет вытянутую вдоль луча и потока веретенообразную
форму. С увеличением скорости поток «вгоняет» плазму в фокус,
а горячая светящаяся струя простирается все дальше за фокус.
При v > 310 см/с плазма сдувается и разряд не существует. При
повышении скорости максимальная температура плазмы растет.
В случае фокусировки излучения длиннофокусной линзой с / =
= 40 см и р меньше некоторого нижнего предела ркр ~ 5 см/с
разряд не горит. В случае короткофокусной линзы f = 10 см раз-
ряд существует при сколь угодно малых скоростях, в том числе
и в неподвижном газе.
Рис 13 24 Двумерный газодина-
мический расчет течения в опти-
ческом плазмотроне [1319] Воз-
дух, р — 1 атм, мощность лазера
Ро — 6 кВт, фокусное расстояние
линзы / = 15 см, скорость одно-
родного холодного потока и =
= 1 м/с, Z — осевая координата,
отсчитываемая от точки геомет-
рического фокуса, г — радиаль-
ная Представлены линии тока
(кривые со стрелками), изотер-
мы, искаженный рефракцией кон-
тур светового канала (штриховые
кривые) Внизу для сравнения
даны изотермы в отсутствие по-
тока
Все эти закономерности проявились в расчете, сделанном на
основе изложенной в конце п. 5.8 относительно простой одномер-
ной модели (рис. 13.23). Сходящиися-расходящиися световой ка-
нал аппроксимировался двумя соприкасающимися усеченными
конусами. Поток считался прямым, что по закону сохранения
массы исключает из (13 39) скорость' ри = pov = const, где ро,
v — плотность и скорость газа в холодном набегающем потоке.
Расчет указал и на область существования разряда по мощности
Pq и скорости v в согласии с опытом. Все это говорит о правиль-
ности одномерной модели, отраженной в уравнениях (13.39).
Гораздо более совершенный уровень теоретического описания
процесса в оптическом плазмотроне дает численное моделирова-
ние на основе системы двумерных газодинамических уравнений
Навье — Стокса, непрерывности и баланса энергии (13.1), (13.2)
с учетом лучистого теплообмена и рефракции лазерного излуче-
ния в плазме (рис. 13.24). Конечно, в двумерной модели сильно
возрастают трудности расчета и затраты машинного времени.
В расчете проявилась интересная особенность газодинамического
процесса. Течение оказывается нестабильным. За центральной
частью плазмы все время возникают вихри, которые сносятся по-
током и зарождаются вновь. Расчет стационарной задачи дает
некое усредненное по времени поле течения. Поток обтекает об-
407
ласть эперговыделения, но некоторое количество таза протекает
через нее Двумерные расчеты усредненного стационарного тече-
ния делаются сейчас и для других плазмотронов (см., напри-
мер, [13.17]).
§ 7. Некоторые общие черты равновесных разрядов
в потоке газа
7.1. Обтекание или протекание? Две крайние и противополо/к-
ные идеализированные схемы могут служить отправным пунктом
для анализа сложной картины газодинамического течения в
плазмотронах. Можно себе представить, что разряд горит не
только в определенной пространственн )й области, задаваемой
источником электромагнитного поля, но и в определенной в сред-
нем неподвижной массе газа, которую снаружи обтекает поток.
Рис 13 25 Схема обтекания хо-
лодным газом статического раз-
ряда, горящего в определенной
массе газа
Такая ситуация похожа на процесс конвективного охлаждения
твердого тела, в котором выделяется тепло. Если разряд («на-
гретое тело») имеет цилиндрическую форму, картина обтекания
выглядит примерно так, как это показано на рис. 13.25. Тепло
передается теплопроводностью от нагретого объема в соприкасаю-
щиеся с ним слои обтекающего газа. Ясно, что температура в
смыкающейся, приосевой части струи за нагретым телом должна
быть близкой к температуре тела.
Из рассмотрения всех статических разрядов следует, что тем-
пература плазмы определяется в основном балансом энергии в
самой зоне энерговыделения. Она мало зависит от судьбы энергии
после того, как энергия выносится за пределы разряда в непогло-
щающую, бестоковую зону. Поэтому можно ожидать, что темпе-
ратура в разряде не будет очень чувствительной к тому, уходит
тепло в стенки, охлаждаемые снаружи, или уносится непосред-
ственно обтекающим разряд потоком. Иначе говоря, вопрос о
температуре плазмы разряда в режиме обтекания приближенно
решается расчетом соответствующего статического режима.
При протекании газа через разряд каждая масса газа, выхо-
дящая из плазмотрона, будучи нагретой до высокой температуры,
побывала в самом разряде и в ней непосредственно выделялась
энергия. Качественная картина предполагаемого течения показа-
на на рис. 13.26 применительно к индукционному плазмотрону.
Из скин-слоя, где происходит энерговыделение, тепло выносится
теплопроводностным потоком в радиальном направлении. Вслед-
ствие одновременного сноса тепла потоком в продольном направ-
лении, поверхность разряда, т. е. фактически какая-то изотерма,
408
отвечающая температуре «ионизации» («возникновения проводи-
мости») То ~ 8000 К, наклоняется относительно осевого потока.
Линии тока холодного газа, вступая в область повышенной тем-
пературы, искривляются, склоняясь в сторону оси. Они прелом-
ляются в слое, где происходит повышение температуры. Это вы-
зывается расширением газа при нагревании. Касательная к изо-
термической поверхности составляющая скорости при этом не
Рис 13 26. Качественная схема тече-
ния в индукционном плазмотроне в
предположении, что газ протекает
через разряд Переходная область о г
холодного газа к плазме и слой, где
про зсходит энерговыделепие, за-
штрихованы Показаны линии тока
газа, слева перед разрядом — завих-
рение
меняется. Нормальная же составляющая в силу сохранения плот-
ности потока массы, рокп = ркщ, резко увеличивается. Здесь ро —
плотность холодного газа, ип — скорость его втекания в разряд,
рк и — плотность и нормальная составляющая скорости горяче-
го газа на выходе из скин-слоя. Температура плазмы при проте-
кший также близка к температуре в статическом разряде. Как
все происходит на самом деле, будет рассказано в п. 7.3.
7.2. Нормальная скорость распространения разряда. Централь-
ным моментом в ка^ тине взаимодействия газового потока и раз-
ряда, типа изображенной на рис. 13.26, является процесс в каком-
то участке захптрихованного слоя, где происходит диссипация
. нергии поля и превращение холодного газа в нагретую плазму.
Рис. 13 27 Распределения температуры
п потока электромагнитной энергии в
плоек эм режиме разряда в поэоке га-
^а. Стрелками показаны направления
теплового потока /, скорости втекания
аза vn и потока электромагнитной
энергии 5С
Идеализированной моделью для рассмотрения этого процесса слу-
жит плоский стационарный режим в системе координат, связан-
ной с данным участком поверхности фронта разряда. Пусть в раз-
ряд пи нормали к поверхности втекают поток холодного газа рокп
и поток электромагнитной энергии плотности (рис. 13.27).
Диссипируемая энергия выносится теплопроводностью навстречу
газовому потоку, и это способствует нагреванию холодного газа
д> температуры ионизации То, при которой он приобретает спо-
собность интенсивно поглощать энергию поля. В результате
409
диссипации энергии поля газ нагревается от температуры То до
Тк. Максимальная температура плазмы Тк мало отличается от
той, которая получается в соответствующем статическом разряде.
Это связано с тем, что она определяется в основном балансом
энергии в самой зоне энерговыделения, где перепад температур
ДТ = Тк — То невелик и газ ускоряется мало.
В стационарном процессе газ втекает в разряд с вполне опре-
деленной нормальной составляющей скорости vn, которая связана
с Тк и 5о законом сохранения энергии. Если вся выделяющаяся
энергия поля в конечном счете уносится потоком, то 5о == pvvnwK,
где м« = ш(Тк)—удельная энтальпия нагретого газа (процесс
происходит при постоянном давлении). При теплопроводностном
механизме подготовки новых порций холодного газа к восприятию
энергии поля температура Тк определяется поступающим в разряд
потоком электромагнитной энергии 5о практически тем же соот-
ношением, что и в соответствующем статическом разряде. Для
индукционного разряда, например, это формула (13.19), где ДГ
дается формулой (12.18). Таким образом, равенство ип =
= So/pow(TK) определяет скорость ип в зависимости от 5о. Вместе
с (13.19), (12.18) ей можно придать характерную для теплопро-
водности форму:
2ХКДГ х 4ДТ сТк рк
О __ К /VK к рк К 1 к
П “ ~ 6Ро^К ~
где Xk==WPkCPk — температуропроводность горячего газа, сРк —
его теплоемкость, 6 — напоминаем, толщина зоны энерговыделе-
ния. Размерностным масштабом скорости ип служит характерная
скорость выноса тепла хн/6, хотя vn и много меньше этой вели-
чины. Как показывает множитель рк/ро 1, скорость vn лимити-
рует низкая температуропроводность плотного холодного газа /о
(ип можно представить и в виде ип ~ хо/6 с другой комбинацией
безразмерных множителей; Хо~Х»<Рк/ро).
Величина vn представляет собой скорость захвата разрядом
новых слоев холодного газа, или скорость распространения раз-
ряда по массе (п. 7.4). Ее называют нормальной скоростью рас-
пространения разряда. Для теплопроводпостного механизма рас-
пространения ип ~10—102 см/с. Подробнее см. [25,10], а также
1-е изд. с. 480.
7.3. Течение в плазмотроне. В отличие от идеализированных
предельных схем (п. 7.1) газ частично обтекает область разряда,
а частично проникает в зону энерговыделения, протекая через нее.
Это видно и из рис. 13.24, отражающего результат численного
моделирования процесса в оптическом плазмотроне (см. также
[13.20]). Попытаемся оценить количественно роли того и другого
элементов в картине течения.
Рассмотрим обращенную к набегающему потоку часть поверх-
ности фронта разряда. Она эффективно разграничивает холодную
и горячую области. В первой из них плотность и температура
410
газа равны ро, Too ~ 300 К, во второй — рк, Тк, причем в силу
приближенного постоянства давления ро/рк = ЦоТи/цкТоо ~ Ю2,
где ро, Рк — молярные массы холодного и горячего (диссоцииро-
ванного, если это воздух) газов.
Любые перепады давления Др в области сильно дозвукового
течения не зависят от самого давления р и определяются скорост-
ным напором набегающего потока: Др ~ ро^2, где v — скорость
невозмущенного газа. В критической точке горячего тела давле-
ние несколько выше давления на бесконечности. Благодаря это-
му скорость холодного потока на оси уменьшается до значения
vn. Поток заворачивается в стороны, обтекая тело. За фронтом
энерговыделения давление падает, и потому газ, проникающий в
разряд, ускоряется от vn до скорости связанной с vn законом
сохранения массы: porn = ркик. Скорость vn, с которой газ втекает
во фронт разряда, представляет собою нормальную скорость рас-
пространения, о которой говорилось в п. 7.2.
Соотношения между скоростями v, vn и ик легко получить,
если учесть, что для скоростного напора горячего газа нет иного
масштаба, кроме Др или скоростного напора холодного газа:
рк^к ~ Р Л Из этих двух соотношений следует, что v/vn ~ ujv ~
~Уро/рк~Ю, тогда как uK/i;n ~ ро/рк ~ 102. В отличие от одно-
мерного плоского режима (п. 7.2) на ограниченную в попереч-
ном направлении область стационарного разряда холодный газ
набегает не с нормальной скоростью vn, а быстрее в Урс/рк ~
— 10 раз. Из полного потока массы poizSo, набегающего на миде-
тюво сечение So горячей области, часть (порядка poi^nSo) прони-
кает через поверхность фронта. Таким образом, протекает чегез
разряд доля vjv ~ Урк/ро ~ 10 % набегающего потока, остальные
90 % обтекают нагретую область, как твердое тело Подробнее
см. [13.20].
7.4. Распространение разрядов. Процессы горения разряда в
потопе принадлежат к весьма обширному классу явлений рас-
пространения разрядов. Под распространением следует понимать,
в сущности, то же, что и под генерацией плазмы: движение гра-
ницы разряда по массе, захват все новых и новых масс холоди d
газа плазменным фронтом с переводом их в плазменное состоя-
ние. Движется ли фронт разряда в пространстве, где холодный
газ покоится, или стоит на месте, а газ в него втекает, принци-
пиального значения не имеет — это вопрос о выборе системы
координат для наблюдения эффекта.
Разрядам вообще свойственна тенденция к распространению.
Всегда существуют механизмы передачи энергии от разрядной
плазмы соседним неионизованным слоям газа, что способствует
их ионизации и приведению в состояние, когда в них может вы-
деляться энергия поля. Если эти слои и впрямь находятся в до-
статочно сильном поле, в них начинается диссипация, они за-
хватываются разрядом, который воздействует на следующий
слой, и т. д. Распространение разрядов в полях допробойной ин-
411
тенсивности непременно связано с действием какого-то механизма
переноса ионизующего агента.
К числу механизмов распространения принадлежит теплопро-
водность, ибо нагрев газа приводит к термической ионизации.
Теплопроводность является главной причиной распространения
равновесных разрядов высокого давления во всех рассмотренных
в этой главе случаях. Распространение может вызвать ионизация
атомов холодного газа тепловым излучением разрядной плазмы,
диффузия электронов, диффузия резонансного излучения и дру-
гие более сложные, комбинированные механизмы.
Эффекты распространения разрядов проявляются в самых
различных условиях и в любых диапазонах полей. Волны иони-
зации, движимые электронной теплопроводностью и электронной
диффузией, наблюдаются в постоянном поле. В волноводах, слу-
чается, бегут плазменные фронты, поддерживаемые СВЧ излу-
чением и движимые теплопроводностью при высоких давлениях
или диффузией резонансного излучения — при низких. Волны
оптического разряда, движимые теплопроводностью и тепловым
излучением, возникают и исследуются в опытах с лазерным из-
лучением. Подробности и ссылки см., в частности, в [25,9.1, 13.20].
Глава 14. ИСКРОВОЙ И КОРОННЫЙ РАЗРЯДЫ
§ 1. Общие представления
1.1. Внешняя картина. Искровой разряд возникает при давле-*
ниях порядка атмосферного и выше в пе слишком коротких про-
межутках порядка 1 см и более, т. е. при pd^ 103 торр • см, когда
к электродам прикладывается напряжение выше пробивного. Для
пробоя промежутков со столь большими pd требуются значитель-
ные напряжения, исчисляемые десятками и сотнями киловольт.
Разряд протекает быстро, нестационарным образом и в общем
представляет собою именно то явление, о котором в обиходе го-
ворят: «проскакивает искра». Грандиозной формой искрового раз-
ряда является молния, длина которой может составлять несколь-
ко километров. Молния пробивает промежуток между заряжен-
ным облаком и землей или между двумя облаками. По внешнему
виду искровой разряд в лабораторных условиях — та же молния
только в миниатюре. По достижении пробивного напряжения
промежуток между электродами «молниеносно» прорезывает топ-
кий, иногда зигзагообразный, иногда разветвленный светящийся
канал, и тут же гаснет. Искра сопровождается характерным
треском, как молния — раскатами грома. Звук вызывается удар-
ной волной. Источником ее служит резкое повышение давления
от интенсивного выделения джоулева тепла в искровом канале при
прохождении сильного разрядного тока.
Многим, вероятно, приходилось видеть на фотографиях и в
кино, как проскакивает искра между огромными металлическими
412
шарами, укрепленными на изоляторах (кинематографисты любят
это эффектное зрелище). Такие разрядника используют в технике
высоких напряжений, в частности, для измерения напряжения.
Разряд происходит при определенном минимальном напряжении,
которое зависит от диаметра шаров, расстояния между ними и
слегка — от атмосферных условий: давления, температуры, точ-
нее — плотности и влажности воздуха. Система эта отградуирова-
на, и показатели для измерений стандартизованы. Если между
электродами стоит препятствие в виде не очень толстой диэлект-
рической пластины из стекла или картона, искра может проло-
жить себе путь прямо через тело, пробив в нем отверстие. Искро-
вые разряды возникают и в однородном поле плоских промежут-
ков, привязываясь к случайным местам электродов, и в сильно
неоднородных полях: между острием и плоскостью, между тонкой
проволокой и концентрическим цилиндром, и т. д. В последних
случаях искровому разряду, если переходить ко все более высо-
ким напряжениям, предшествует коронный.
Корона — слаботочный слабосветящийся разряд — появляется
в окрестности острия, проволоки, где поле резко усилено. Только
в этой зоне происходит ионизация и газ светится. Электрический
ток замыкается потоком зарядов того или иного знака (в зави-
симости от полярности острия), которые рождаются в самопод-
держивающейся зоне вблизи острия и вытягиваются уже относи-
тельно слабым полем к другому электроду. Во внешней области
свечения нет. Коропа обычно возникает при давлениях порядка
атмосферного, в воздухе около проводов высоковольтных линий,
около громоотводов и мачт кораблей («огни святого Эльма»). Для
зажигания короны требуется определенное (достаточно высокое
напряжение, которое зависит от конкретных условий. При еще
более высоком напряжении пробивается остальная часть проме-
жутка и между электродами проскакивает искра.
Через сформировавшийся искровой канал протекает сильный
ток порядка 104—105 А. Вследствие падения напряжения на внеш-
нем сопротивлении или в результате быстрой разрядки конденса-
тора, если последний служит источником питания разряда, на-
пряжение на электродах резко уменьшается и разряд гаснет.
Если в результате погашения разряда напряжение на электродах
восстанавливается, пробой повторяется. Если же источник пита-
ния обладает достаточной мощностью и может обеспечить проте-
кание сильного тока в течение длительного времени, то от тока
искры образуется катодное пятно и зажигается дуговой разряд
(гл. 12). Вообще состояние плазмы в сформировавшемся канале
даже быстротечного искрового разряда похоже на состояние в
столбе дуги, так что иногда конечную стадию искрового разряда
можно рассматривать как импульсную дугу.
Искровой разряд — явление комплексное и очень сложное. Его
первой стадией с тужит процесс стримерного либо лидерного про-
боя, который протекает гораздо более сложным путем, чем при
низких давлениях, когда зажигается темный или тлеющий разряд.
4В
Потом, после формирования токопроводящего канала, что, кстати,
происходит поэтапно и тоже весьма «замысловатым» образом,
осуществляется разряд в буквальном смысле слова. Конденсатор
разряжается в результате переноса заряда сильным током по
замкнувшейся в области разрядника цепи.
Существуют искровые разряды, скользящие вдоль диэлектрика
(стекла, эбонита). Они образуются, когда один электрод, напри-
мер стержневой, опирается торцом на диэлектрическую пластину,
а другим электродом служит металлическая обкладка на другой
ее стороне. Разветвленные разрядные каналы в газе, прижимаясь
к диэлектрику, разбегаются от стержня и обтекают пластину
вплоть до обкладки на другой стороне. На пластине остается вет-
вистый след, вызванный деформациями материала под действием
температуры и давления в искровых каналах. След можно визуа-
лизировать; эти картины называются фигурами Лихтенберга.
Характер узора зависит от полярности стержня, а размеры — от
значения напряжения, что используется для измерении и при
исследовании грозовых разрядов.
1.2. Неприемлемость гауисепдовской схемы пробоя в случае
высоких давлений, длинных промежутков, значительных перена-
пряжений. Механизм пробоя, основанный па размножении лавин
через вторичную катодную эмиссию, действует преимущественно
при низких давлениях, ориентировочно при pd < 200 торр см.
Соответствующая теория, принципы которой были сформу шРова-
ны Таунсендом в начале века, объясняет многое Она дает убеди <
тельное толкование пашеновской зависимости пробивного напря-
жения Vt от pd с ее характерным минимумом (§ 2 гл. 9) и даже
неплохо согласуется с экспериментом количественно. Привнекая
дополнительные соображения о накоплении положительного про-
странственного заряда в промежутке и об искажении внешнего
поля при нарастании тока, можно, по крайней мере качественно,
проследить за процессом зажигания тлеющего разряда от начала
пробоя и до формирования катодного слоя. Для этого следует
рассматривать переход от темного таунсендовскою к тлеющему
разряду, анализируя не последовательность стационарных ик оя-
нии, отвечающих все возрастающему конечному току, как п § 3
гл. 10, а прослеживая динамику перехода и нарастание тока во
времени.
Однако по мере совершенствования техники эксперимента, ап-
паратуры и методов исследования быстропротекающих процессов
вскрывались все новые и новые факты, которые никак не уклады-
вались в рамки таунсендовской схемы. Проникновению в природу
пробоя в высшей степени способствовали изучение отдельных ла-
вин и серий размножающихся лавин в камере Вильсона (работы
Ретера и его школы [23]), регистрация видимых картин при
помощи фотоумножителей и электронно-оптических преобразова-
телей, ссциллографирование нарастающего во времени тока про-
боя, покадрогое фотографирование процесса при помощи высоко-
скоростной съемки. Было установлено, что при больших pd и
414
значительных перенапряжениях пробой в плоском промежутке
развивается намного быстрее, чем того требует размножение ла-
вин через катодную эмиссию Ионно электронная эмиссия вообще
сбрасывается со счетов поскольку за время пробоя ионы попросту
не успевают «сдвинуться с места» Но даже механизм фотоэмис-
сии оказывается недостаточно быстрым, ибо токопроводящий ка-
нал в указанных условиях образуется за время пролета электрона
от катода до анода или даже скорее На повторение лавин через
катодную эмиссию времени не хватает Высокоскоростная съемка
позволила наблюдать такой ионизованный светящийся канал, ко-
торый перекрывает промежуток вслед за прохождением первой же
мощной лавины
Против участия катодных процессов в механизме пробоя сви-
детельствует также независимость пробивающего искрового на-
пряжения от материала катода, установленная путем самых точ-
ных измерений Существуют условия, когда безучастность катода
в искровом пробое представляется и так очевидной Например,
пробои между острием анодом и удаленной плоскостью катодом
При пороговом напряжении поле у катода, да и вообще на зна-
чительной прилегающей к нему части промежутка, слишком ма то,
чтобы там могло происходить размножение электронов Оно идет
только далеко от катода в окрестности положительного острия,
где поле резко усилено Примером также может служить молния
Имеются и другие неувязки эксперимента с таунсепдовской тео-
рией Существуют, в частности, такие комбинации, например пары
метилаля или эфира с медным катодом, когда коэффициент вто
ричиой эмиссии с катода имеет иск почите тьно малое значение
(7э1)<10~8) и механизмом размножения лавин пробой объяснить
никак нельзя Уже к концу 30-х годов не оставалось сомнений в
том, что таунсендовская теория абсолютно неприменима при
больших pd и перенапряжениях, т е в тех самых условиях, когда
наблюдается искровои разряд
1.3. Стримерная теория. Основы повои теории, призванной
объяснить явление искрового пробоя, были заложены в работах
Леба, Мика, Ретера [2, 21, 23] примерно в 1940 г Опа базируется
на представлении о прорастании между электродами топкого
ионизованного канала — стримера (от английского «stream» —
поток), который прокладывает себе путь по положительно заря-
женному следу первой мощной лавины В след втягиваются элект-
роны множества вторичных лавин Лавины зарождаются вблизи
следа от электронов, рожденных под действием фотонов, которые
испускаются атомами, возбужденными при прохождении первой
и вторичных лавин В ходе последующих исследований было по-
лучено множество результатов, экспериментальных и теоретиче-
ских, вскрыты детали, существенно изменившие некоторые из
первоначальных представлений и оценок Многое можно почерп-
нуть в монографиях Э Д Лозанского и О Б Фирсова [26] и
новейшей — ЭМ Базеляна и И М Ражанского [33], пожалуй,
единственных в отечественной литературе на эту тему за послед-
415
ние 30 лет (в этих книгах подытожены и собственные работы
авторов в области искрового пробоя)*). Но идейные основы тео-
рии, отражающие фундаментальные показания опыта, остались
в общем непоколебленными. Нр обошлось и без крайностей, когда
вследствие успехов появившейся стримерной теории безоснова-
тельно умалялось значение таунсендовского механизма**). При
не очень больших pd (при pd < 200 торр • см — заведомо) и малых
перенапряженных действует именно он. Что касается конкретных
граничных значений pd, где происходит смена механизмов пробоя,
то литературные данные на этот счет весьма противоречивы п
мало обоснованы. Согласно [23] в атмосферном воздухе это про-
исходит при d ~ 5—6 см, т. е. стримерный механизм работает
только при pd > 4000 торр • см. В околограничном диапазоне pd ~
200—5000 торр • см скорее всего существуют и некоторые про-
межуточные формы, когда нет ни катодного размножения, ни
стримера и вторичным процессом служат объемные реакции:
возбуждение атомов резонансным излучением с последующей ас-
социативной ионизацией [26].
1.4. Лидер. В метровых воздушных промежутках с резко не-
однородным полем, в разряде молнии пробой осуществляется пу-
тем прорастания от одного электрода к другому лидера — тоже
канала, но проводящего гораздо сильнее стримерною. Лидерный
процесс является более сложным и масштабным, чем стримерный:
стримеры (в большом количестве) он включает в себя в качестве
составного элемента. От головки прорастающего лидерного капала
тонкие стримеры веером расходятся вперед. Лидерным процессом
мы займемся после § 7, а до того будем рассматривать только
стримерные. Последними дело чаще и ограничивается в недлин-
ных промежутках с более или менее однородным полем, в атмос-
ферном воздухе при d меньше десятка сантиметров.
1.5. Что считать пробоем. При низких давлениях (§ 2 гл. 9)
особой остроты в этом вопросе нет. Пробой, как правило, сопро-
вождается зажиганием самостоятельного разряда, и нет нужды
делать различие между этими событиями. В случае высоких дав-
лений — особенно в сильно неоднородных полях, когда одним или
обоими электродами служат острия, провода и т. д., не всякий
самостоятельный ток приводит к катастрофическим последствиям.
Например, зажигание коронного разряда, который является само-
стоятельным,— это еще не пробой. Ток идет весьма слабый, и на-
пряжение практически не меняется, хотя потери энергии па коро-
ну являются весьма нежелательным эффектом в случае высоко-
вольтных линий передач. Пробоем, который представляет реаль-
ную опасность в технике высоких напряжений, следует считать
*) Изучение работ Э. М. Базеляна и беседы с ним имели большое зна-
чение для авюра в его усилиях разобраться в ряде вопросов физики искро-
вого пробоя.
**) Детальный анализ дан в обзоре [14.1].
41С
эффект короткого замыкания, образование высокопроводящего
искрового канала, пропускающего столь сильный ток, что напря-
жение па разрядном промежутке резко падает*).
§ 2. Одиночная электронная лавина
Индивидуальная лавина является первичным и неотъемлемым
элементом любого механизма пробоя. Рассмотрим лавину в одно-
родном внешнем поле Ео между плоскими электродами. Пусть
она начинается от одного электрона, вылетевшего с катода в мо-
мент t = 0. Ось х направим от этого места катода в сторону анода.
Радиальное расстояние от оси х обозначаем г.
2.1. Числа и диффузионные пространственные распределения
зарядов. С учетом возможного образования отрицательных ионов
полные числа электронов и ионов нарастают по мере продвиже-
ния лавины как
dNeldx={a — a)Ne, dN+/dx==aNe, dN^jdx = aNe, (14.1)
A^ = exp[(a-«)z], ЛГ+ = -^_(ЛГе-1), Ar_=_A_(7ve-l),
(14.2)
где а и a — коэффициенты ионизации и прилипания. Все нарож-
дающиеся электроны летят к аноду одной группой со скоростью
дрейфа рд = це£о- Однако вследствие диффузии электронное об-
лако расплывается около центральной точки хо = vjt, г = 0. Плот-
ность электронов в облаке пе{х, г, t) подчиняется общему урав-
нению диффузии (3.22), (3.20), в котором должны быть приняты
во внимание дрейфовое движение и рождение. Решение уравнения
имеет вид [26]
п€ = (^iDet) 3/2 ехр
(х — р П2 + г2
1---------+ (a-a)^
(14.3)
Плотность пе падает с расстоянием от движущегося центра по
гауссову закону. Радиус сферы, на которой плотность ровно в е
раз меньше, чем плотность в центре пе(х$, 0, t), растет с течением
времени (или по мере продвижения лавины) по характерному для
диффузии закону
rnW- (14.4)
где по формуле (3.23) е — средняя энергия электронов.
*) Кстати сказать, при зажигании стационарного темного таунсендов-
ского разряда напряжение также несколько падает: снимается перенапря-
жение При зажигании тлеющего разряда напряжение снижается от про-
бивного до напряжения стационарного горения; в случае небольшого поло-
жительного столба — практически до минимального напряжения пробоя в
данном газе, к которому близко катодное падение (гл. 10).
27 ю. П Райзер 417
За время пролета лавины до анода ионы практически не успе-
вают сдвинуться с места. Поэтому в каждом месте они накапли-
ваются. Плотность положительных ионов составляет
t
п+ (х, r,t) = j* avnne (х, г, f) dt'.
о
Чтобы получить п_, нужно а заменить на а. Функция пе в инте-
грале задается формулой (14.3). В отсутствие прилипания в пре-
деле t 00 и не слишком далеко от оси приближенное вычисление
интеграла дает [26]
а [ г2 ]
п+ (х, г) =------— ехр lax----------L (14.5)
’ | I'-dWi2!
где rD(x) определяется формулой (14.4). Этот результат имеет
наглядный физический смысл. Плотность ионов в следе лавины
растет с расстоянием х от катода в соответствии с законом раз-
множения еах. В радиальном же направлении опа в каждом сече-
нии х спадает от оси по тому же диффузионному гауссову закону,
что и плотность рождающих ионы электронов в тот момент, когда
центр электронного облака проходил через данное сечение.
2.2. Видимые очертания лавины. Наряду с ионизацией элект-
роны возбуждают молекулы, которые, как и ионы, остаются
практически неподвижными. Пространственное распределение воз-
бужденных частиц, которые, высвечиваясь, могут дать изображе-
ние лавины, подобно распределению ионов (14.5). Глядя на эту
формулу, можно подумать, что видимые очертания лавины при-
мерно совпадают с характерным радиусом распределения rD(^),
т. е., что боковой контур лавины имеет параболическую форму
r = rD(x)<*> Ух, гладко переходя в закругление в области электрон-
ной головки лавины. Однако это не так. Каким бы способом мы
ни фиксировали на опыте изображение лавины (п. 2.4), граница
его будет соответствовать более или менее определенной абсолют-
ной, а не относительной плотности активных частиц (высвечиваю-
щихся молекул, ионов). Величина эта в общем определяется
чувствительностью регистрирующей аппаратуры. Поскольку
чувствительность подбирается достаточно высокой, минимальная
плотность, которая еще регистрируется, гораздо меньше плот-
ности частиц па оси далеко от катода, где ах » 1. Поэтому низкой
плотности частиц на видимом контуре лавины гк(гг) отвечает не-
большое значение показателя экспоненты (14.5), гораздо меныпее
ах. Следовательно, контур соответствует приближенному обра-
щению показателя в нуль и является не параболическим rD ~ Vх.
а клиновидным:
/ах = У8za!eEQx.
В области головки клин переходит в закругление (рис. 14.1).
2.3. Элементарный ток в цепи, содержащий разрядный про-
межуток. Вычислим ток i цепи, когда между электродами, к ко-
418
торым приложено напряжение V, движется один-единственный
электрон. Это позволит нам найти ток, создаваемый лавиной
(п. 2.4). Внешняя цепь подвергается электрическому воздействию
электрона, даже когда он находится вдали от обоих электродов.
Рис. 141. Электронная лавина: а — схематические очорхания и распределе-
ния зарядов в электронной лавине в два последовательных момента време-
ни и t2; стрелками указаны направления внешнего поля Ео и скорости уд
движения головки лавины; б — фотография лавины в камере Вильсона [23]
(газ СО2, р — 150 торр; горизонтальные полоски — электроды, расстояние
между ними L = 3,6 см, длительность импульса напряжения 250 нс)
Металл электродов поляризуется полем электрона, и на поверх-
ностях появляются индуцированные заряды противоположного
знака (рис. 14.2). Эффект этот тем сильнее, чем ближе к поверх-
ности находится заряд. Поэтому, по мере продвижения электрона
от катода к аноду, индуцированный положительный заряд на по-
верхности анода возрастает, а на ка-
тоде уменьшается. Это неминуемо
сопровождается перетеканием заряда
по проводам.
Для нахождения индуцированных
зарядов следует воспользоваться из-
вестной в электростатике теоремой
Рамо — Шокли (1938 г.) Заряд qK,
индуцированный изолированным за-
рядом q на поверхности проводника
К равен qK = — q (фмк/фк), где фмк —
Рис. 14 2. Схема протекания
тока в цепи при прохождении
заряда через газовый проме-
жуток
потенциал в точке М нахождения заряда д, который возникает,
если к проводнику К приложен потенциал фк, а другие провод-
ники системы (в данном случае А) обладают нулевым потенциа-
лом: фА = 0. Аналогично индуцированный заряд на электроде А
есть qA = — q (фМл/фл), причем фк = 0. В случае, изображенном
на рис. 14.2, фмк/фк == (d — x)jd\ ^ма/^а = x/d. Поскольку q = — e,
27*
419
qK = e(d — x)/d\ qA = exfd. Отсюда элементарный ток
i = qA = ~qK = exld = ev/d. (14.6)
Тот же результат можно получить путем феноменологического
рассуждения. Проходя путь dx = vdt, электрон приобретает от
внешнего поля Е = Vid энергию eEvdt. Эту работу совершает
источник питания, и она составляет tVdt, откуда i = evld. Вывод
прост, но в отличие от предыдущего не раскрывает механизма
эффекта.
В случае электродов произвольной формы, когда поле не од-
нородно,
i(t) = qA — —q^MAl^A = —q^^MA^I^A = q^lV, (14.6')
где v(£) — скорость заряда q в момент t, Е — поле в точке г, ко-
торую он проходит (заметим, что фактор Е/F зависит только от
геометрии, но не от напряженности поля).
2.4. Экспериментальное исследование лавин. Много ценной ин-
формации получено в ходе исследования одиночных лавин, лавин-
ных серий, размножения лавин, перехода лавины в стример в ка-
мере Вильсона [23]. В этом приборе используется тот факт, что
ионы обычно служат центрами конденсации пересыщенного пара.
Для регистрации лавин систему электродов помещают внутри
камеры, а в исследуемый газ добавляют немного паров воды,
спирта и пр. Синхронно с подачей напряжения и запуском лави-
ны производится адиабатическое расширение газовой смеси па
15—20 %, в результате чего пары становятся пересыщенными.
Облако из капелек жидкости воспроизводит по форме ионный
след лавины. Его фотографируют в свете постороннего источника.
Изображение получается благодаря рассеянию света на капель-
ках, плотность которых совпадает (или пропорциональна) плот-
ности ионов (рис. 14.1 б).
Остов лавины на фотографии имеет хорошо выраженную
клиновидную форму, которая переходит в закругленную головку.
Длину лавины (время ее движения) регулируют, задавая опре-
деленную длительность прямоугольного импульса напряжения на
электроды. По измеренному углу раствора клина (п. 2.2) и из-
вестному ионизационному коэффициенту а можно оценить сред-
нюю энергию электронов е. По измеренным длине и длительности
существования лавины можно найти скорость дрейфа электронов
Vn = xlt. «Фотографии» лавины получают и регистрируя ее собст-
венное свечение, обязанное возбуждению молекул и атомов. По-
скольку свечение очень слабое, для регистрации применяют
фотоумножители и электронно-оптические преобразователи.
В комплекс исследований входит измерение сверхчувствитель-
ными приборами и осциллографирование тока во внешней цепи.
В соответствии с результатом п. 2.3 лавина создает ток
i (t) = Ne(t) evjd = (evjd) exp [ (a — a) v J].
420
Регистрируя его, можно определить а — а, а в газе без прилипа-
ния — ос. Когда все электроны уходят в анод, идет гораздо более
слабый и длительный ток, вызванный движением ионов. Если ла-
вины размножаются, получаются последовательные импульсы
электронного тока с нарастающим средним значением. По времени
между импульсами иногда удается судить о том, участвуют ионы
в катодной эмиссии или нет.
2.5. Искажение поля пространственным зарядом. В лавине с
большим усилением еах возникают значительные пространствен-
ные заряды. Они создают собственное поле Е', которое векторно
складывается с внешним Ео, искажая его поблизости от лавины.
Когда эффект по мере размножения зарядов становится сильным,
это сказывается на всем дальнейшем ходе ионизации. Пространст-
венные заряды образуют нечто вроде диполя: все электроны со-
средоточены в головке лавины, основная масса положительных
ионов остается несколько позади. Расстояние, на которое элект-
роны отрываются от основной массы ионов, определяется длиной
ионизации ос-1, которую электрон в среднем проходит, прежде чем
образует пару ионов. Пока искажение внешнего поля Ео мало,
ос = a (Eq). При больших же усилениях а и пространственное рас-
пределение зарядов сами зависят от результирующего поля Е.
Распределения поля и зарядов описываются связанной системой
уравнений, решение которой представляет сложную задачу.
Рис. 14.3. Схематические изображения полей в присутствии электронной
лавины: а — линии напряженности внешнего поля Ео и поля пространст-
венного заряда лавины Е' по отдельности; б — линии напряженности ре-
зультирующего поля Е = Ео 4- Е'. Кружками условно показаны центры
пространственных зарядов
Качественная картина расположения пространственных заря-
дов и хода линий напряженности поля изображена на рис. 14.3.
Перед головкой и за областью сосредоточения основной массы
ионов поля Е' и Eq складываются и результирующее поле сильнее
внешнего. В зоне между центрами пространственных зарядов того
и другого знака Е' и Ео направлены в разные стороны и резуль-
тирующее поле слабее внешнего. У поля появляется радиальная
составляющая. Положим, что заряды каждого знака помещаются
в сфере радиуса R. Поле на ее поверхности равно Е' == eNeIR2.
421
Пока усиление и число элетронив в лавине IV е = еах не очень ве-
лики, за R можно принять диффузионный радиус (14.4). Предва-
рительное представление о масштабах величин можно получить,
если таким путем оценить рост поля Е' до значения внешнего
поля Eq. Например, при поле Eq = 31,4 кВ/см, пробивающем воз-
душный промежуток, х = 1 см, при р = 1 атм и е = 3,6 эВ по фор-
муле (14.4) rD = 1,8 • 10~2 см. Равенство Е' =Eq выполняется при
Ne = еах = 0,8 • 108, ах ~ 18. На самом деле при столь большом
числе Ne радиус R в несколько раз больше диффузионного, так
что Е' < Ео (п. 2.6).
Рис. 14.4. Схема электрического поля в промежутке после того, как лави-
на достигла анода и все электроны ушли в металл: а — линии напряженно-
сти поля пространственного заряда следа лавины Е' и его электрического
изображения в аноде; б — линии напряженности результирующего поля
Е = Ео 4- Е'
Когда лавина достигает анода, электроны уходят в металл и в
промежутке остается чисто положительный пространственный за-
ряд ионного следа. Его поле показано на рис. 14.4. Оно образует-
ся самим ионным зарядом и его «изображением» в аноде. Изобра-
жение в относительно удаленном от основной массы ионов катоде
играет значительно меньшую роль. У самого анода поле меньше
внешнего, поодаль — больше. Поле максимально на осевом рас-
стоянии от анода порядка длины ионизации ос-1. Приближенное
решение соответствующей электростатической задачи дано в [26].
2.6. Расталкивание электронов. При большом числе зарядов
Nc диффузионное расплывание облака электронов уступает их
электростатическому расталкиванию. Скорость последнего нарас-
тает с увеличением Ne, т. е. t и х, тогда как скорость диффузии
drD/dt ~ £~1/2 ~ х~х падает. Скорость расширения заряженной сфе-
ры за счет расталкивания определяется дрейфом электронов в
поле собственного пространственного заряда:
dRjdt = реЕ' = ере7?“2 ехр (осх), х = peEQt.
Интегрируя, находим закон расширения сферы R(t) или R(x),
422
а потом поле Е' и плотность электронов пе = ЗЛ^МлТ?3:
п /Зе \1/з [ах\ ЗЕ' /л / ^7\
R~= exp Hr- =------F", ne = . (14.7)
1 a£ у Г \ 3 / a kQ 4ne ' '
Поле E' растет так же, как и R, а средняя плотность электро-
нов при расталкивании с одновременным размножением остается
неизменной. Диффузионное расплывание по оценке сменяется
расталкиванием при Ne = еах ~ 106. ах ~ 14. Поле Е' при этом со-
ставляет 2—3 % от внешнего. На фотографиях лавин хорошо вид-
но, как, начиная с какой-то длины х, т. е. усиления, головка ла-
вины резко увеличивается, надо полагать из-за расталкивания.
Результаты измерений согласуются с оценками приведенного
типа [23].
Когда электронное облако вырастает до размеров порядка дли-
ны ионизации R ~ сс-1, отрыв электронов от ионов перестает быть
столь резко выраженным, как при R < ос1. Сдвиг между зарядами
обоих знаков теперь относительно невелик, и притягивающее дей-
ствие положительного заряда сдерживает дальнейшее расталкива-
ние электронов. Рост головки лавины замедляется, если не пре-
кращается вовсе. Таким образом, наибольший поперечный размер
головки лавины имеет порядок 7?тах ~ а~{ ~ 0,1 см, ибо в проби-
вающих при атмосферном давлении полях Eq обычно a(EQ)~
~ 10 см-1. Согласно (14.7) в момент прекращения роста головки
E'IEq~\I3. Если Ео ~ 30 кВ/см и ос ~ 10 см-1, при этом ~
-7-108, ах = In Ne 20, пе 2 • 1011 см~3.
При пробивающих полях d In а/d In Е ~ 4. Изменение поля на
1 % ведет к изменению ос на 4 %. Следовательно, на внешней гра-
нице электронного облака, обращенной к аноду, в усиленном поле
Е ~ Eq + Е' скорость ионизации в несколько раз больше а(Ео),
а на внутренней стороне, обращенной к ионному следу,— значи-
тельно меньше. Там не просто Е ~ Eq — Е', а скорее Е ~ Eq — 2Е',
так как из Eq вычитается еще и поле Е' ионного положительного
заряда (рис. 14.3). Резкое ослабление поля внутри головной части
лавины предрасполагает к возникновению там квазинейтралъиой
плазмы, т. е. стримера (направленного к аноду).
§ 3. Понятие о стримере
Стример представляет собой умеренно, можно даже сказать
слабоионизованный тонкий канал, который образуется из первич-
ной лавины в достаточно сильном поле и прорастает в ту или
другую или в обе стороны к электродам; у порога пробоя плоского
промежутка — от самого анода к катоду. Обладая некоторой про-
водимостью, стример по достижении электродов может так транс-
формировать поле, что откроется возможность резкого усиления
ионизации и тока, и это в конечном счете приведет к искровому
разряду в промежутке. Возникновение стримера и замыкание им
промежутка — не необходимое, но иногда достаточное условие для
осуществления пробоя.
423
Для перерождения лавины в стример в ней должно достигаться
достаточно высокое усиление. Поле пространственного заряда
должно вырасти до величины порядка приложенного, иначе не бу-
дет причин для нарушения нормального хода развития лавины.
В не слишком длинных плоских промежутках, при не очень боль-
ших перенапряжениях (по сравнению с пробивным), это случа-
ется, когда лавина исчерпывает весь резерв усиления, т. е. дости-
гает анода. Стример зарождается тогда у самого анода, в области
наибольшего пространственного заряда, и прорастает к катоду.
Такой стример называют катодонаправленным или положитель-
ным. В более длинных плоских промежутках, при больших пере-
напряжениях, число зарядов в первичной лавине становится до-
статочно большим раньше. Лавина перерождается в стример, не
достигнув анода. В этом случае стример прорастает к обоим элект-
родам. Если стример образуется, когда лавина еще недалеко ушла
от катода, он прорастает в основном в сторону анода. Такой стри-
мер называют анодонаправленным или отрицательным *).
3.1. Механизм образования катодонаправленного стримера. Он
поясняется рис. 14.5. Определяющая роль, согласно гипотезе, при-
надлежит энергичным фотонам, которые излучаются возбужден-
ными в лавине атомами и производят фотоионизацию поблизости
А .................... —-----------—---А
a б
Рис 14 5 Схема катодонаправленного стримера: а — стример в два последо-
вательных момента времени t\ и t2, показаны вторичные лавины, стремящие-
ся к положительной головке стримера, волнистые стрелки — фотоны, от ко-
торых появляются затравочные электроны для лавин; б — линии напря-
женности электрического поля около головки ci римера
от первичной лавины. (Рождение электронов у катода или далеко
от ионного следа интереса в данном случае не представляет, так
как ведет к образованию лавины, аналогичной первой.) Вырван-
ные фотонами электроны кладут начало вторичным лавинам, ко-
торые втягиваются в след, ибо результирующее поле направлено
именно таким образом (рис. 14.4). Электроны вторичных лавин,
смешиваясь с ионами первичной, образуют кзазинейтралъную
плазму. Они также возбуждают атомы, что приводит к излучению
новых фотонов. Ионы вторичных лавин приумножают на катод-
*) В [26], видимо, по недоразумению он назван положительным.
424
ном конце возникшего плазменного канала положительный заряд.
Последний создает поле, которое притягивает к себе электроны
последующих вторичных лавин, и т. д. Так растет стример. Про-
цесс нейтрализации ионного следа первичной лавины начинается
от того места, где положительный заряд и поле сильнее всего —
от анода, если только там достигнуто условие перерождения
Е' ~ Eq. Именно такая ситуация показана на рис. 14.5.
Плазменный стример в данном случае с самого начала сопри-
касается с анодом. Будучи проводником, он в электростатическом
отношении отчасти уподобляется металлической игле, выступаю-
щей с поверхности анода (идеально проводящая игла находилась
бы точно под потенциалом анода). У конца стримера поле резко
усилено, его линии напряженности веером расходятся от конца,
и это благоприятствует притягиванию вторичных лавин со всех
сторон и росту стримера. Механизмом некоторого выравнивания
потенциала в «игле» является поляризация проводника внешним
полем. Электроны сдвигаются к аноду, обнажая положительные
ионы на катодном конце. Поле образующегося диполя, обратное
внешнему, частично уничтожает последнее и сокращает разность
потенциалов на длине проводника. Собственно, это тот же эффект,
который приводит к картинам на рис. 14.3, 14.4.
Если источник фотонов и затравочных электронов для вторич-
ных лавин достаточно силен, а это, по-видимому, так, скорость
роста стримера лимитируется пе темпом зарождения лавин, а ско-
ростью нейтрализации положительного пространственного заряда
у катодного конца стримера. Но электроны втягиваются в эту
область со скоростью дрейфа, соответствующей имеющемуся там
полю. Поле заметно превышает внешнее, причем тем сильнее, чем
длиннее «игла»; это диктуется эл*ектростатикой. Опыт и в самом
деле показывает, что скорость распространения {прорастания)
стримера тем больше, чем он длиннее и чем сильнее внешнее
поле. Измеренные скорости имеют порядок 108 см/с, тогда как
скорости дрейфа во внешнем поле — 107 см/с. Диаметр стример-
ного канала сравним с размерами головки лавины в стадии ее
наибольшего расширения: 10~2—1СН см (п. 2.6). Плотность за-
рядов во всяком случае не меньше, чем наибольшая плотность в
лавине — порядка 1013 см~3.
Поскольку фотоны вылетают и поглощаются случайным обра-
зом, возможны ситуации, когда в какой-то момент появляется
новое преимущественное направление, по которому идет много
вторичных лавин. Так, видимо, появляются зигзагообразные изло-
мы стримера (и искрового канала), которые наблюдаются на
опыте.
3.2. Критерий возникновения. Как следует из всего предыду-
щего, стример образуется из лавины, если поле ее пространствен-
ного заряда достигает величины порядка внешнего. Соответствую-
щее приближенное равенство
Е' = eR~2 ехр [а(Е0)х] ~ Eq (14.8)
425
можно рассматривать как критерий возникновения стримера. Он
накладывает условие на параметры Eq и минимальную для дан-
ного Eq длину промежутка d = х. Численные результаты, выте-
кающие из (14.7), зависят от задания радиуса головки лавины R.
В старых работах Леба и Мика брался диффузионный радиус
Гв(^о) по формуле типа (14.4). Так получается известное условие
пробоя Мика
а(£0)^ ~ 18-20, Ne = е™ - 108
(14.9)
(ср. с численным примером в п. 2.5).
В теории Леба и Мика наступление пробоя отождествлялось
с фактом возникновения стримера. На самом деле это не всегда
так. Теперь известно, что при d < 5 см атмосферный воздух про-
бивается не стримерным, а таунсендовским механизмом размно-
жения лавин. Условие ad ~ 20 на коэффициент усиления лавины
к моменту образования стримера мало чувствительно выбору
величины 7?, ибо ad ”
Рис. 14.6. Схема анодонаправленного стри-
мера: а — фотоны и вторичные лавины пе-
ред головкой стримера в два последова-
тельных момента времени t\ и f2; б — ли-
нии напряженности электрического поля
около головки стримера
важный для стримерного процесса,
стоит в показателе экспоненты. Так, при
выборе R ~ a~l ~ НУ"1 см
(п. 2.6) получается Ne ~
— 109, но ad ~ 21 все рав-
но близко к (14.9). Надо
сказать, что обработка
экспериментов по пробою
о разных газов при р ~ 1 атм
и d ~ 1 —10 см приводит к
приближенной эмпириче-
ской связи a{EQ)d ~ 20,
равносильной критерию
Мика. Не следует, однако,
преувеличивать значение
этого обстоятельства, ибо
из любых критериев типа
(14.8) вытекает слабая
логарифмическая зависи-
мость ad от других входя-
щих в формулу величин.
Нельзя сказать, чтобы
конкретный механизм фо-
тоионизации газа,
был очень ясным. Ведь
нужно возбуждать атомы до энергий, превышающих потен-
циал ионизации, чтобы излученный фотон мог вырвать электрон
из невозбужденного атома, а такие акты происходят нечасто.
Предполагается, что в воздухе кислород ионизируется фотонами,
испущенными возбужденным азотом (/n2 = 15,6 эВ > Zq2 =
= 12,2 эВ), но прямых экспериментальных подтверждений этого,
пожалуй, нет. Не исключено, что затравочные электроны рожда-
ются сложным путем в ходе диффузии резонансного излучения и
426
столь
ассоциативной ионизации возбужденного атома при объединении
с певозбу ж денным.
3.3. Анодонаправленный стример. Если приложенное поле Eq
таково, что условия (14.8), (14.9) удовлетворяются на расстоя-
нии х от катода, меньшем длины промежутка d, лавина перерож-
дается в стример на «полпути». Механизм его прорастания в сто-
рону катода остается тем же самым (п. 3.1). При распростране-
нии к аноду характер процесса несколько отличен от предыдущего,
так как электроны здесь дрейфуют в ту же сторону, в которую
движется фронт плазменного стримера, а не навстречу ему, как
при прорастании к катоду. Под действием фотоионизующего
излучения вторичные лавины зарождаются перед отрицательно
заряженной головкой стримера, обращенной к аноду (рис. 14.6).
Передние электроны головки, быстро движущиеся в сильном сум-
марном поле Eq + E', входят в ионные следы вторичных лавин
и вместе с ними образуют плазму. В данном случае, по-видимому,
возможен механизм распространения и без участия фотонов. Плаз-
менный фронт распространяется благодаря ионизации передними
электронами, разогнанными сильным полем, а позади фронта в
плазме, где поле слабое, электроны не отрываются от ионов, т. е.
заряды образуют квазинейтральную плазму. Это похоже на рас-
пространение волны ионизации [25, 26]. О некоторых моделях,
призванных описать распространение стримеров, см. в § 7.
§ 4. Пробой и стример
в электроотрицательных газах (воздухе)
в не очень длинных промежутках с однородным полем
Прилипание электронов замедляет ход ионизации в лавине и
приводит к повышению пробивающих полей и граничных значе-
ний pd, при которых происходит смена таунсендовского и стри-
мерного механизмов. Весьма показательным в этом отношении
является анализ полученных на основании эксперимента величин
для атмосферного воздуха. По понятным причинам воздух пред-
ставляет исключительный интерес и много исследовался.
4.1. Пробивающие поля. На рис. 14.7 приведены результаты
измерений напряжений пробоя плоских промежутков различной
длины в воздухе при комнатной температуре. В отличие от
рис. 9.5, где диапазон ограничен значениями d = 3 см, здесь он
расширен до d = 30 см. Явственно выражено асимптотическое
стремление пробивающего поля к постоянному значению, около
26 кВ/см, Е/р^З^к В/(см-торр). Этот факт, несомненно, связан
с тем обстоятельством, что при чуть меньших отношениях Е/р
коэффициент прилипания а уже превышает ионизационный ос и
размножение электронов невозможно (п. 2.5 гл. 9). Точное зна-
чение (Е/т?)1, при котором пересекаются кривые ос/р и а/p как
функции Е/р, установить весьма трудно и опытным путем, и рас-
четным. Называют Цифру (экспериментальную) (E/p)i —
= 31 В/(см • торр) == 23,6 кВ/(см • атм). Ее можно рассматривать
427
как теоретический нижний предел для порога пробоя воздуха в
идеальном плоском промежутке. Однако реально это заключение
остается в силе лишь в ограниченном диапазоне давлений. При
р = 1 атм напряжение пробоя в однородном поле и в самом деле
стремится к Vt ~ E\d при росте d (рис. 14.7). Но при р ~ 10 атм,
Рис 14.7. Пороговое поле пробоя воздуха в плоском промежутке в зависи-
мости от его длины d при р — 760 торр + Ю торр Н2О, t — 20 °C по дан-
ным разных авторов [23]
начиная с некоторого значения р, которое зависит от d, пробиваю-
щее напряжение при данном d растет с р существенно медленнее,
чем по закону пропорциональности Vt ~ р. Значит, Etfp умень-
шается все больше и больше по сравнению с (£7p)i (рис. 14.8).
Природа эффекта не ясна. Имеются указания на то, что он связан
с существованием усиленных полей около выступов на катоде, где
и начинается размножение. Если это так, процесс происходит, как
в промежутке с сильно неоднородным почем (§ 8, 9).
4.2. Элегаз. Так называется электроотрицательный газ SFe.
Обладая высокой электрической прочностью и другими приемле-
мыми свойствами, элегаз применяется в качестве изолятора и име-
ет большое практическое значение. Теоретический нижний предел
порога пробоя, отвечающий равенству ос = а, у него очень высок:
(Е1р) 1 = 117,5 В/(см • торр) = 89 кВ/(см-атм); см. рис. 14.9. Эф-
фект уменьшения (E!p)t по сравнению с (Efp) i также наблюда-
ется при р 3 атм.
4.3. Размножение лавин или стример? В табл. 14.1 приведены
современные экспериментальные данные об эффективном коэф-
фициенте размножения аЭф = а — а лавины в сухом воздухе
(р = 1 атм) при полях, пробивающих промежутки различной дли-
ны d. Представлены числа электронов (усиления) в лавине, на-
428
чатой у катода одним электроном и дошедшей до анода. Таблица
ограничена значением d = 3 см, так как при меньших Е данные
об ссэф слишком ненадежны из-за близости к точке пересечения:
а — а < а, а. Мы уже знаем, что стример образуется, когда поле
Рис. 14.8. Амплитуда про-
бивного напряжения часто-
ты 50 Гц в воздухе в одно-
родном поле в зависимости
от pd при больших давле-
ниях [14.2]
Рис. 14.9. Коэффициенты ионизации
и прилипания в элегазе SF6 как
функция отношения Е/N: точки —
эксперимент, сплошные кривые —
расчет на основе кинетического урав-
нения [14.3]
пространственного заряда вырастает до величины внешнего, а это
случается, когда в лавине рождается критическое число Ne ~
~ 108—109 электронов (осэфй ~ 20). Как видно из табл. 14.1, в воз-
духе такого заведомо не происходит, если d < 3 см, но при d ~
Таблица 14 1 Размножение электронов в лавине при пробивающих
промежуток d полях [14.4]
Воздух, р - 1 атм
d, см pd, 102Х хторр. см кВ Ер кВ/см Etlv, В/(см-торр) а—а, см-1 (а—а)/р,10 2 см- i-Topp-1 (а—a)d
0,1 0,76 4,54 45,4 59,7 81 10,7 8J 3,3-103
0,3 2,3 36,7 48,4 31 4,1 9,3 1,1-ю4
0,5 3,8 17 34 44,8 20,5 2,7 10,2 2,8-10*
1 7,6 31,4 31,4 41,4 12,4 1,63 12,4 2,4-105
2 15 58.5 29.3 38,6 8,0 1,05 16 8,9-106
3 23 85,5 28,6 37,6 6,5 0,85 19,5 2,9-Ю8
-3 см ситуация приближается к «критической», хотя она не-
сколько сдвигается по d. Прямые данные, полученные на основа-
нии осциллографирования тока пробоя, говорят о том, что при
d < 5 см воздух пробивается механизмом размножения лавин и
лишь при d > 6 см — стримерным.
429
Изучение табл. 14.1 проясняет, почему в старых работах и
книгах Леба, Мика [2, 21], казалось бы, убедительно показыва-
ется, что пробой воздушного промежутка d = 1 см осуществляется
стримерным механизмом. В тех расчетах вообще не принималось
во внимание прилипание, а в качестве коэффициента размноже-
ния сс брались цифры из ранних экспериментов, где на этом так-
же не заострялось внимание. В частности, считалось, что а ~
~ 18 см-1 при Et = 31,4 кВ/см (d=l см). Между тем с учетом
прилипания при таком поле аЭф ~ 12,4, а это сразу уменьшает
на три порядка. Трудно в то же время допустить, что в диапазоне
d ~ 0,3—3 см действует механизм вторичной эмиссии с катода.
Для этого потребовалась бы исключительно резкая зависимость
коэффициента вторичной эмиссии у от -Et. Ведь по таунсендовско-
му условию пробоя (9.1) у « ехр(—a9$d), а эта величина, согласна
табл. 14.1, уменьшается в соответствующем диапазоне Et ~
~ 36,7—28,6 кВ/см на четыре порядка. Возможно, действует ме-
ханизм [26], о котором говорилось в конце п. 1.3.
4.4. Влияние перенапряжения на механизм пробоя. Под про-
бивающим полем обычно подразумевается минимальное значение,
при котором еще реально наблюдается пробой. Пороговые вели-
чины немного зависят от начального тока (числа затравочных
электронов) и от времени, которое отводится на ожидание пробоя.
Леб и Мик считают пробивающим такое напряжение, при котором
пробой реализуется с временем ожидания 30 с от момента подачи
напряжения, если начальная плотность тока с катода составляет
10~13 А/см2 ~ 1 электрон/(мкс • см2). Такую величину называют
статическим напряжением пробоя, поскольку процесс при этом
сначала развивается медленно. В силу резкой зависимости ос или
осЭф от Et достаточно перенапряжения, скажем, в 10 %, чтобы
стример возник и в таком промежутке, когда при статическом
напряжении пробой — таунсендовский.
Показательны в этом отношении эксперименты [14.5] по про-
бою азота в однородном поле. При р = 400 торр, d = 3 см и ста-
тическом пробивном поле Е1р = 3?)^ В/(см-торр), когда ad = 9
(в азоте прилипания нет), ток пробоя медленно нарастает с ха-
рактерным временем 1—2 мкс. На осциллограмме тока видны
пики от последовательных размножающихся лавин; на катоде
происходит фотоэмиссия. При тех же р и d, но при перенапряже-
нии более 17 % явно образуется стример. Так, при перенапря-
жении 19 %, когда Е/р = 45,2, уже через 0,2 мкс после пика пер-,
вой лавины регистрируется крутой рост тока. Между механизма-
ми размножения лавин и стримерным происходит соревнование,
и результат его различными способами можно склонить в ту или
другую сторону. В тех же опытах с азотом добавление в него
2,5 % метана снижает до 7—8 % перенапряжение, необходимое
для того, чтобы доминировал стримерный механизм. На а добав-
ка метана влияет мало, но коэффициент вторичной эмиссии у
она уменьшает в 102 раз, что и подавляет процесс размно-
жения лавин.
430
4.5. Влияние присутствия отрицательных ионов на образование
стримера. Осциллографирование тока в условиях стримерного про-
боя воздуха (d = Q см) обнаруживает следующий характерный
эффект [23] После короткого пика от первой лавины, в течение
сравнительного долгого времени, до 10 мкс, течет слабый «запаз-
дывающий» ток (как установлено, он переносится электронами)
Осциллограмма завершается скачкообразным ростом тока — про-
боем Задержка в образовании стримера и пробоя связана с при-
липанием После прохождения первой лавины положительный
заряд ионного следа в значительной мере компенсирован отрица-
тельными ионами Пространственного заряда не хватает для воз-
никновения стримера Однако отрицательные ионы, в основном
сосредоточенные на малом расстоянии cz^1 ~ 10-1 см от анода,
вытягиваются на анод со скоростью дрейфа порядка 105 см/с
Положительный ионный заряд обнажается, и поле постепенно
вырастает до значения, необходимого для образования стримера.
Запаздывающий электронный ток приписывают отлипанию элект-
ронов от отрицательных ионов в условиях возрастающего поля
пространственного заряда (о конкретном механизме отлипания
можно только строить догадки; см. п. 6.4).
§ 5. Искровой канал
Появлению сильноионизованной плазмы развитого искрового
разряда предшествует малоизученная стадия, на которой степень
ионизации в зоне первоначального стримерного канала быстро
вырастает Об этом свидетельствует крутой рост тока после замы-
кания промежутка стримером в условиях, когда происходит
стримерный пробой И это при том, что сам первозданный стри-
мерный канал большого тока пропустить пе в состоянии По
табл 3 1 проводимость слабоионизованпой плазмы о ~ 10~16пе/
Jp [атм] Ом”1 см-1 При р = 1 атм, пе ~ 1013 см-3 о ~ 10“3 Ом"1 X
Хсм-1 Если диаметр канала 2r ~ 10-1 см, а поле в нем Е ~
~ 10 кВ/см, то ток i = оЕ'лг2 ~ 10-2 А ничтожен
5.1. Обратная волна сильного поля и ионизации. Этот процесс,
который, по-видимому, кладет начало формированию искрового
канала, ярче выражен и лучше понятен в случае лидерного про-
боя, когда промежуток перекрывается гораздо сильнее проводя-
щим каналом (§ 10) Все же качественно дело можно предста-
вить себе так Потенциал вершины или головки стримера, про
ристающего от анода к катоду, меньше отличается от потенциала
анода, чем потенциал невозмущенного поля в той же точке.
Идеально проводящий стример, соприкасающийся с анодом, весь
находился бы под потенциалом анода По мере приближения
головки к катоду доля от приложенного к электродам напряже-
ния, которая приходится на непроводящий зазор между головкой
стримера и катодом, и поле в зазоре возрастают К моменту каса-
ния катода головкой поле становится столь сильным, что элект-
роны, вырванные из катода или из атомов фотонами, размножа-
431
ются с огромной скоростью. От катода вдоль канала первоначаль-
ного стримера распространяется в обратном направлении к аноду
фронт, за которым остается гораздо сильнее ионизованная плазма.
Идет как бы обратный стример, но уже с существенно более вы-
сокой ионизацией, чем первоначальный Хорошо проводящая
плазма обратного «стримера» находится под потенциалом, близ-
ким к потенциалу катода, и на фронте, следовательно, получаются
резкий перепад потенциала и очень сильное поле. Разгоняющиеся
в нем электроны и производят интенсивную ионизацию. Фронт
волны, как полагают, распространяется к аноду со скоростью по-
рядка 109 см/с. Это не есть скорость движения электронов, это —
фазовая скорость распространения скачка потенциала (волны
поля). Когда такой тонкий сильноионизованный канал достигает
анода и замыкает весь промежуток, создаются благоприятные
условия для протекания тока очень большой плотности, и это
кладет начало формированию «истинно» искрового канала. Теория
обратной волны разработана слабо.
5.2. Расширение искрового канала. Протекание тока большой
плотности сопровождается концентрированным выделением джоу-
лева тепла. Это ведет к сильному разогреву плазмы, ее термали-
зации, возможно, к дальнейшему росту ионизации уже термиче-
ским путем. Быстрое повышение температуры газа, не скомпенси-
рованное столь же быстрым теплоотводом, приводит к резкому
повышению давления в токовом канале Возникает цилиндриче-
ская ударная волна, как при взрыве нитевого заряда взрывчатого
вещества. На первых порах амплитуда ударной волны столь вели-
ка, что температуры за фронтом хватает для термической иониза-
ции газа. Граница токового канала при этом почти неотделима
от фронта ударной волны. Но вскоре, по мере расхождения от
оси, ударная волна ослабевает, перестает ионизовать газ и отрыва-
ется от медленно расширяющейся границы сильноионизованной
области — искрового канала. Канал расширяется теперь вследст-
вие радиального разлета газа, увлеченного ударной волной, и дей-
ствия теплопроводности.
Температура в канале достигает 20 000 К, плотность электро-
нов, согласно измерениям и оценкам, пе ~ 1017 см-3. Электропро-
водность при этом определяется кулоновскими столкновениями и
не зависит от пе. По формуле (3.9) о ~ 102 Ом”1 см-1. Ток на-
растает в основном из-за расширения канала и увеличения сече-
ния проводника, а не вследствие изменения своей плотности.
Радиус канала вырастает до значения г ~ 1 см, максимум тока
ъ ~ 104—105 А, ] ~ 104 А/см2, напряжение на электродах сущест-
венно меньше исходного, поле в канале Е ~ 102 В/см. На катоде,
по-видимому, возникает катодное пятно. Если источником питания
служит конденсатор, как это обычно бывает в лабораторных экспе-
риментах, после достижения максимума ток падает, причем
происходит несколько повторных затухающих осцилляций с
полупериодом порядка 10 мкс.
Описанная картина исследовалась во многих экспериментах.
432
Непосредственное опытное подтверждение факта возникновения
ударной волны в искровом разряде было впервые получено в
1947 г. [14.6]. На фоторазвертках искры ясно видны убегающий
фронт ударной волны и более медленно расширяющийся искровой
канал. На ранней стадии 10~7—10-6 с от начала пробоя канал
расширяется со скоростью порядка 1 км/с, потом — медленнее.
Теория газодинамического расширения искрового канала с учетом
ударной волны и энерговыделения от меняющегося во времени
тока разряда была впервые развита С. И. Драбкиной (1951 г.)
[14.7], более детально — С. И. Брагинским (1958 г.) [14.8]. Мно-
го экспериментального материала собрано в [21].
§ 6. Коронный разряд
Непременным условием возникновения коронного разряда яв-
ляется резкая неоднородность поля. Около одного или обоих
электродов поле должно быть значительно сильнее, чем в осталь-
ной части промежутка. Так обычно бывает, когда характерный
размер электрода г гораздо меньше межэлектродного расстояния
d. Например, параллельные провода радиуса г в воздухе кор о пи-
руют, если только dlr > 5,85. В противном случае при повышении
напряжения между проводами раньше проскакивает искра.
6.1. Распределения поля в простейших случаях. Имеющиеся
для простых геометрий точные решения уравнения электроста-
тики незаменимы при построении теорий короны и интерпретации
экспериментов. В пространстве между коаксиальными цилиндра-
ми радиусов г (внутреннего) и R, на радиальном расстоянии х
от оси поле равно
Е = Vlx In (Д/г), Дтах = У/r In (Д/г), (14.10)
где У — напряжение между цилиндрами. Между концентриче-
скими сферами радиусов г и Д
Е = VrR/x2(R-r), Emax^V/r при Д » г. (14.11)
Между шариком и удаленной плоскостью (R/r -> «>) Е~ Vrb2.
Между острием параболоидной формы с радиусом закругления г
и перпендикулярной плоскостью на расстоянии d поле на расстоя-
нии х от конца острия вдоль продолжения его оси равно
Е = (r + 2*)ln(2d/r+l) ’ ^max ~ rln(2d/r)' (14.12)
Если напряжение У приложено между параллельными про-
водами радиуса г, отстоящими на расстоянии d, или между про-
водом и параллельной плоскостью, отстоящей на расстояние h, то
поля у проводов (максимальные) соответственно равны
Дтах = (У/2г) In (d/r), Дтах = (V'/г) In (2Л/г). ( 14.13)
Поля одинаковы, если во втором случае У' = У/2, h = d!2, что и
естественно.
28 Ю П Райзер 433
6.2. Критерии зажигания. Когда приложенное напряжение V
меньше напряжения зажигания короны VK, в цепи можно заре-
гистрировать несамостоятельный ток порядка 10~14 А. Это вытя-
гиваются ионы, появляющиеся под действием космического излу-
чения и естественной радиоактивности. В воздухе на уровне моря
образуется примерно 10 пар ионов в 1 см3 в 1 с, стационарно при-
сутствует около 103 ионов в 1 см3. Зажигание короны в лабора-
торных условиях проявляется не только в виде свечения у коро-
нирующего электрода, которое можно и не увидеть, но и в виде
скачкообразного возрастания тока до значения порядка 10~6 А.
Коронный разряд принадлежит к числу самостоятельных, и усло-
вие его возникновения отражает физический механизм воспроиз-
водства электронов в той области усиленного поля, где происхо-
дит ионизация. Механизм размножения электронов существенно
зависит от полярности коронирующего электрода.
Если он является катодом (такую корону называют отрица-
тельной), происходит размножение лавин. Вторичным процессом
служит эмиссия с катода, а возможно, и фотоионизация в объеме
газа. Зажигание отрицательной короны, в принципе, не отличает-
ся от таунсендовского пробоя и зажигания темного таунсендовско-
го разряда (§ 3 гл. 10). Критерием зажигания служит равенство
типа (9.1), обобщенное на случай неоднородного поля. С учетом
эффектов прилипания
xi
f [а (гг) — а (ж)] dx = In (1 у”1), (14.14)
о
где у — эффективный коэффициент вторичной эмиссии. Область
интегрирования в (14.14) простирается от поверхности катода до
той точки х\, где а = а и прекращается размножение электронов.
В газе без прилипания область интегрирования формально рас-
пространяется до самого анода, но, вследствие чрезвычайно рез-
кого уменьшения а(Е') при удалении от проволоки, от острия —
до близлежащей эффективной точки х\, где поле заметно снижа-
ется и a [^(rci)] ~ 0. В области размножения электроны также
возбуждают молекулы. Вне ее в электроотрицательном газе элект-
ронов практически нет, они, пройдя малое расстояние, превра-
щаются в отрицательные ионы; в электроположительном газе
поле все равно слишком слабое, электроны медленные, поэтому
вне короны газ не светится.
Если острие, проволока являются анодом (положительная ко-
рона), удаленный большой катод, около которого поле слабое, не
принимает участия в размножении. Воспроизведение электронов
обеспечивают вторичные фотопроцессы в газе в зоне острия. В от-
личие от ровного свечения отрицательной короны в положитель-
ной наблюдаются светящиеся нити, разбегающиеся от острия (см.
рис. 14.12). Полагают, что это — стримеры. В качестве критерия
зажигания положительной короны можно принять условие воз-
никновения стримера (14.9), также обобщенное на случай
434
неоднородного поля:
J (a-a) da: ж 18-20. (14.15)
о
Несмотря на возможное различие в 2—3 раза в коэффициен-
тах усиления, т. е. в значениях интегралов (14.14), (14.15), на
критической напряженности поля у электрода это отражается не
сильно. Причина состоит в резкой зависимости а или а — а от Е,
вследствие чего даже небольшое изменение Е(х) сильно меняет
интеграл. И действительно, опыт показывает, что в ряде газов,
в частности в воздухе, напряжения зажигания положительной и
отрицательной корон различаются мало (для отрицательной Ук
меньше: видимо, Inf-1 < 20, 7 > 10"8).
6.3. Пороги в воздухе. Как ясно из вида критериев (14.14),
(14.15), они накладывают условие главным образом на значение
максимального поля около коронирующего электрода, которое
должно превышать некоторый нижний предел Ек. Пороговое на-
пряжение для зажигания короны VK связано с требуемым значе-
нием Ек электростатическим законом распределения поля в про-
межутке (14.10) — (14.13). Для критического поля зажигания
короны в воздухе между коаксиальными цилиндрами Пик (1929 г.)
установил эмпирическую закономерность
Ек ~ 316 (1 + 0,308/} б7) кВ/см. (14.16)
Здесь 6 — отношение плотности воздуха к нормальной, соответст-
вующей /2 = 760 торр, £ = 25°С; г[$м]—радиус внутреннею
электрода. Формула описывает эксперименты с гладко отполиро-
ванным внутренним электродом в диапазонах г ~ 10~2 — 1 см, р ~
~ 10-1 — 10 атм, в том числе и в переменных полях с частотами
до 1 кГц (Ек при этом — амплитуда поля). Наличие шероховато-
стей на электроде может снизить пороговую величину Ек па
10—20 %, так как поле дополнительно усиливается около мель-
чайших выступов. В общем виде (с другими числами) формула
применима к различным газам. Ее можно применять и к проме-
жутку между проводом и плоскостью. Напряжение зажигания Гк
связано с напряженностью Ек = Етах формулами (14.10),
(14.13).
Формула Пика несет в себе отпечаток физических критериев
типа (14.14), (14.15). Об этом говорит вычисление Ек [14.9] на
основе критериев (14.14), (14.15) с функцией Е(х) (14.10) и
аппроксимацией аэф для воздуха при Е!р < 150 В/(см-торр) =
= 110 кВ/(см • атм), принятой в электротехнике:
ос = 0,146{ (£ [кВ/см]/316)2 — 1} см"1. (14.17)
Рассмотрим в качестве примера воздушный промежуток между
проволокой г = 0,1 см и коаксиальным цилиндром R = 10 см, р =
= 1 атм, 6 = 1. По формуле Пика £к=61 кВ/см. По формулам
(14.10) Ик = 28 кВ, около внешнего электрода поле £(/?) =
28* 435
= 0,61 кВ/см. По разрядным масштабам, оно ничтожное: Е!р =
= 0,8 В/(см-торр). Размножение кончается на радиусе х\ =
= rEJE\ = 0,25 см (£5 ~ 24 кВ/см), т. е. толщина слоя около
провода, где происходит размножение, в стадии лавин, до форми-
рования стримеров, х\ — г « 0,15 см.
6.4. Запаздывание зажигания. Время запаздывания между по-
дачей напряжения и началом резкого роста тока складывается из
статистического времени ожидания затравочного электрона вблизи
острия и времени размножения лавин или образования стримеров.
Опыты указывают на большой и трудно интерпретируемый раз-
брос в случае отрицательной короны, что связывается с сильным
и неконтролируемым влиянием состояния поверхности катода.
В случае положительной короны время формирования стримеров
10~9 с явно мало по сравнению с измеренными временами за-
паздывания 10~8—10~6 с, которые следует отнести на счет вре-
мени ожидания затравочных электронов. Они образуются явно не
на катоде, так как время запаздывания, как правило, меньше вре-
мени дрейфа электрона от катода к положительному острию. Слу-
чайные электроны в воздухе быстро превращаются в отрицатель-
ные ионы. Полагают, что в сильном поле электроны отрываются
от ОТ при столкновениях с молекулами с максимальной эф-
фективностью при Е/р = 90 В/(см • торр)= 68,5 кВ/(см • атм).
Во влажном воздухе ионы гидратируются — образуют кластеры
с молекулами воды. Разрушаются в поле они при этом хуже.
6.5. Перенос тока за пределами области размножения и ВАХ.
Носители тока рождаются только в непосредственной близости от
коронирующего электрода, где имеется сильное поле. Через
остальное пространство («внешнюю» зону) ток переносится за-
рядами, которые вытягиваются имеющимся там слабым полем.
В положительной короне это положительные ионы, в отрицатель-
ной — отрицательные, или электроны, если газ лишен электроот-
рицательных примесей. Ток во внешней зоне коронного раз-
ряда является несамостоятельным, газ там не ионизован (не
«пробит»).
Ток короны зависит от приложенного напряжения, вернее, от
превышения его над потенциалом зажигания VK- Ограничивается
ток пространственным зарядом носителей тока во внешней зоне.
Область самостоятельного разряда у коронирующего электрода в
состоянии выработать и большой ток, большее число носителей,
но часть из них при движении к другому электрону заворачива-
ется назад пространственным зарядом того же знака. Ситуация
очень похожа на ограничение тока пространственным зарядом в
«вакуумном диоде» (§ 6 гл. 8), только здесь заряды движутся не
свободно, а дрейфуют. Изложенные соображения позволяют при-
ближенно установить ВАХ стационарного коронного разряда
(Таунсенд, 1914 г.).
Рассмотрим промежуток между коаксиальными цилиндрами.
Ток на единицу длины цилиндра через поверхность произвольного
радиуса х вне узкой зоны размножения равен i = 2пхеп\хЕ =
436
= const, где n — плотность носителей, pt — их подвижность. До-
пустим, что ток, плотность зарядов и искажение внешнего поля
пространственным зарядом не очень велики. Тогда для распреде-
ления Е(х) в первом приближении сохраняется закономерность
(14.10), отвечающая отсутствию тока, но фактическому напря-
жению V. В этом приближении
п = i/2ne[iEx = i In (Я/r) /2лецV = const.
Подставляя это в уравнение Пуассона х ld(xE)/dx = 4лт и ин-
тегрируя, найдем распределение поля в следующем прибли-
жении.
Постоянную интегрирования выберем так, чтобы в пределе
i -> 0 произведение хЕ выражалось формулой (14.10) через по-
тенциал зажигания VK:
г „211Л,Г>,
pV 2г х J
Интегрируя Е по х с учетом того, что в основной части проме-
жутка х2> г2, и разрешая полученное равенство относительно ц
найдем ВАХ короны:
. . ^(У-Ук)
R1 In (7?/г)
(14.18)
Закономерность (14.18) подтверждается опытом. Для ее про-
верки строят зависимость обратного сопротивления i/V от V (опа
называется редуцированной характеристикой) и убеждаются в ее
линейном характере. Экстраполяция полученной прямой к i/V = 0
позволяет определить потенциал зажигания Тк проще и точнее,
чем путем поиска порога возникновения короны. Поскольку под-
вижности положительных и отрицательных иопов более или менее
одинаковы, токи положительной и отрицательной корой в электро-
отрицательном газе при данном V также близки. В газе без при-
липания ток отрицательной короны, переносимый электронами,
существенно больше. Добавка электроотрицательной примеси сра-
зу его снижает.
Сделаем оценки для примера, рассмотренного в конце п. 6.3:
воздух, /2=1 атм, г = 0,1 см, R = 10 см, VK = 28 кВ. Положим
ц = 2 см2/ (В • с). Вокруг этой цифры с небольшими отклонениями
группируются подвижности 07, О^,О^ в О2; N^, N* в N2 при
1 атм. Пусть V = 40 кВ. При этом i = 4,6 мкА/см (1 А =
= 9 • 1011 В • см/с). Плотность ионов п = 2,6 • 108 см~3. Как пока-
зывает опыт, зависимость i(V) типа (14.18) справедлива и для
других геометрий. Так, в атмосферном воздухе для короны у
игольчатого катода с радиусом острия г = 3 10“3—4,5 • 10-2 мм
при перпендикулярном плоском аноде на расстоянии d ~ 4—16 мм
от конца иглы имеем
i ~ (52/d2)V(V — VK) мкА, (14.19)
причем VK & 2,3 кВ независимо от d [мм] [14.9].
437
6.6. Потери на корону в высоковольтных линиях. Этот вопрос
важен для энергетики. Потери на корону могут оказаться срав-
нимыми с потерями на выделение джоулева тепла в проводах.
Когда коронируют оба электрода, как в случае параллельных про-
водов противоположной полярности, ток во внешней зоне между
ними переносится движущимися навстречу ионами разных знаков.
Ток и потери энергии в такой биполярной короне гораздо сильнее,
чем в униполярной (с одним коронирующим электродом). Полной
Рис. 14.10. Потери мощности на
1 км длины на корону с провода
диаметром 2,5 см как функция
напряжения: 1 — хорошая сол-
нечная погода, 2 — слабый дождь
[14.2]
рекомбинации ионов обычно не
происходит, а взаимная нейтрали-
зация пространственного заряда
снижает степень ограничения то-
ка, ограниченного пространствен-
ным зарядом. Кроме того, отрица- #
тельные ионы, пройдя к положи-
тельному проводу, распадаются
в его сильном поле. Это там слу-
жит дополнительным источником
электронов и несколько облег-
чает зажигание разряда. Для слу-
чая двух параллельных проводов
по Пику
Е« = 29,86(1 + 0,301/УбГ) кВ/см.
r< 1 см, (14.20)
что несколько меньше, чем для
одного согласно (14.16). В элект-
ротехнике сейчас пользуются несколько иной, также эмпириче-
ской формулой. Для гладких проводов
Ек = 24,56 [1 + 0,65 (6г)-0 38] кВ/см.
(14.21)
Половина напряжения зажигания коронного разряда между про-
водами процентов на 10 меньше, чем между тем же проводом и
плоскостью посередине, хотя в отсутствие разряда в электроста-
тическом отношении обе ситуации эквивалентны.
В соответствии с ВАХ типа (14.18) в коронном разряде выде-
ляется мощность
P = iV^ const V2(V- VK).
На рис. 14.10 показаны потери мощности на 1 км длины для про-
водов линии высокого напряжения диаметром 2,5 см. В дождли-
вую погоду, зимой напряжение зажигания значительно умень-
шается, так как капельки дождя, кристаллики льда, осевшие на
проводах, создают дополнительные источники усиления поля. Ток
и потери при том же V резко возрастают.
6.7. Прерывистая корона. При некоторых условиях коронный
разряд, несмотря на постоянство напряжения, горит в виде перио-
дических импульсов тока с частотами повторения до 104 Гц, если
коронирует анод, и до 106 Гц, если катод. Прерывистые явления
438
были обнаружены в лаборатории Леба Тричелем, Кипом (1938 г.).
Леб и его школа внесли большой вклад в изучение искрового и
коронного разрядов. Периодические эффекты представляют и
практический интерес. Частоты их лежат в радиодиапазоне, и ко-
рона в линиях передач может оказаться источником радиопомех.
Для лабораторного изучения особенно удобна корона с острия на
плоскость в воздухе комнатной температуры.
Положительное острие. Приведем результаты типичного экспе-
римента. В случае острия радиуса г = 0,17 мм на расстоянии d =
= 3,1 см от плоского катода корона появляется при напряжении
К кВ и вплоть до напряжения Vi ~ 9,3 кВ имеет импульсный
характер [14.9]. У краев интервала FK—Vi частота повторения
мала, а в середине достигает максимальной величины 6,5 кГц.
Средний ток нарастает до 1 мкА при V\. Подобные импульсы
называют вспышечной короной. В интервале от V\ до Г2 ~ 16 кВ
импульсов нет. Идет стационарный ток. Он нарастает от 1 до
10 мкА при У2. Начиная от Г2 и вплоть до напряжения искрового
пробоя всего промежутка Vt ~ 29 кВ разряд снова протекает в
форме импульсов. Частота их монотонно возрастает от малого
значения до 4,5 кГц. Нарастающий с V средний ток достигает в
предпробойной стадии 100 мкА.
Вспышечная корона при небольших превышениях V над
связана с так называемыми предначалъными стримерами. Возни-
кающие в результате ионизации электроны втекают в острие-анод,
л вне узкой зоны, где разыгрываются процессы ионизации и по-
являются стримеры, накапливается пространственный заряд по-
ложительных ионов. Окружающий острие положительный слой
создает поле, которое с внутренней 'стороны слоя направлено
против внешнего, т. е. ослабляет поле острия, экранирует его.
Это нарушает критерий самоподдержания (14.15). Новые стри-
меры уже пе образуются, ток падает. По мере вытягивания ионов
к катоду сильное поле у острия восстанавливается (острие «обна-
жается»). Появляются стримеры, новый всплеск ионизации, ток,
и все начинается снова. Нечто подобное происходит и па втором
импульсном участке Г2—только с предпробойными стриме-
рами. В интервале V\ — Г2 условие самоподдержания выполняется
стабильно и течет постоянный ток. Ток между пиками вспышеч-
ной короны падает не до нуля, он обладает и постоянной состав-
ляющей.
Отрицательное острие. В некотором интервале напряжений и
средних токов, начиная от точки зажигания Гк, ток имеет им-
пульсный характер. Частота импульсов больше, чем в положи-
тельной короне, 105 Гц при 20 мкА, а сами импульсы короче
(10~7 с) и выше: пиковый ток достигает 10 мА. Импульсы имеют
очень регулярный характер. Их называют импульсами Тричеля.
При повышении напряжения импульсы исчезают и стационарная
корона существует вплоть до искрового пробоя промежутка.
Причина нестационарных явлений, в принципе, та же, что и в
случае положительной короны, хотя и есть особенности. При
439
росте лавин от острия-катода около острия располагается положи-
тельный пространственный заряд, а немного поодаль — отрица-
тельный. Если это электроны, они быстро вытягиваются к аноду,
а плотность отрицательного заряда очень низка. Экранирующего
действия на поле острия он не оказывает. Присутствие положи-
тельных ионов в непосредственной близости от острия только
усиливает там поле. Поэтому в электроположительных газах
(Ns, Аг) импульсы Тричеля не обнаруживаются. Другое дело
воздух. Там электроны, чуть удалившись от острия, попадают в
более слабое поле и прилипают к молекулам. Пространственный
заряд отрицательных ионов ослабляет поле острия, размножение
лавин и ток затухают. По мере вытягивания отрицательных ио-
нов к аноду, а положительных — на острие, внешнее поле восста-
навливается и создаются условия для нового импульса.
Коронный разряд приносит не только вред, как в линиях
передач. Он находит полезное применение в электрофильтрах,
электросепараторах, лежит в основе работы счетчиков Гейгера —
Мюллера (1929 г.), предназначенных для регистрации ядерных
частиц. По физике короны имеется хороший обзор [14.9], но.
к сожалению, он не переведен.
§ 7. Модели распространения стримера
Изолирована ли головка катодонаправленного стримера от ано-
да! Точнее сказать, насколько изолирована, и в какой мере потен-
циал анода переносится стримерным каналом к его положитель-
ной вершине? Это один из главных вопросов к теории, ибо от
этого зависит, сможет ли стримерный канал после перекрытия
промежутка трансформироваться в искровой (§ 5), т. е. осущест-
вим ли стримерный пробой. До недавнего времени рассматрива-
лись две модели стримерного процесса, основанные на крайних
предположениях: об абсолютной изоляции положительной стри-
мерной головки от анода*) и об идеальной проводимости стри-
мерного канала.
7.1. Модель самоподдерживающегося стримера (Даусон и Вин,
1965 г.) [14.10]. Головка катодонаправленного стримера пред-
ставляется сферой радиуса го, в которой содержится А+ положи-
тельных ионов. При движении она оставляет за собою квазиней-
тральный ионизованный канал, но считается, что проводимость
его исчезающе мала и головка лишена связи с анодом. Ставится
задача: найти, при каких условиях головка будет вести совер-
шенно автономное существование, т. е. продвигаться вообще без
внешнего поля, за счет втягивания лавин одним лишь своим соб-
ственным полем.
*) Здесь следует внести небольшое уточнение: имеется в виду, что изо*
ляция «наступает» после ухода самых первых электронов в анод в момент
образования стримера.
440
Пусть фотоэлектрон, начинающий лавину, родился на расстоя-
нии от центра положительной сферы по ходу ее движения
(рис. 14.11). От этого места под действием поля Е = eNJx2 на-
встречу сфере развивается электронная лавина. К точке х^ в ней
образуется
Ne = ехр j a dx
электронов. Пусть радиус лавины
rD растет по диффузионному
закону:
1/2
аг п
« We, rD (Z2) =
/ 7
4 „ : dx
Рис. 14.11. К модели самоподдер-
живающегося стримера
Когда «сферическая» электронная головка лавины вливается в
ионную головку стримера, па этом месте образуется квазиней-
тральная плазма, а ионный след
лавины превращается в новую
продвинутую дальше головку стри-
мера. Чтобы такой процесс про-
текал непрерывно и стационарно,
нужно, чтобы в момент касания
головкой лавины головки стриме-
ра, т. е. при условии Х2 = r0 + rD,
совпадали числа зарядов в обеих
головках, Ne = N^. s No, и их ра-
диусы, rD = г0. Место зарождения
лавины х\ задавалось искусствен-
но, в соответствии с длиной про-
бега фотонов, но с соблюдением
требования, чтобы поле Е(х\)
в воздухе было достаточным для ионизации: Е(х\)^ 30 кВ/см.
Самоподдерживающийся процесс в воздухе оказывается воз-
можным при следующих значениях параметров: «длина пробега
фотонов» х\ ~ 2 • 10~2 см, число ионов в головке стримера N+
= No ~ 108, ее радиус Го 2,7 • 10~3 см. Скорость распространения
стримера v = x^t, где t — время движения лавины от х\ до
v ~ 107 см/с. Цифры не выходят за рамки разумного, хотя и не
кажутся близкими к реальности. Слишком мал радиус стримера
г0, и слишком велика, соответственно, плотность зарядов в нем
пе ~ п+ ЗЛГо/4лТо ~ 2,6• 1015 см~3. Неучтенное расталкивание
электронов в лавине увеличит радиус, поле Е e7Vo/r0 упадет,
ионизация резко замедлится, т. е. все может «разбалансиро-
ваться».
7.2. Возможно ли строго стационарное распространение стри-
мера в отсутствие внешнего поля? Нет, для ионизации новых
объемов газа, захватываемых стримерным каналом, требуется
441
энергия, а черпать ее, кроме как извне, неоткуда. Рассмотрен-
ный процесс на самом деле является не стационарным, а лишь
квазистационарным, в том смысле, что все параметры мало ме-
няются на одном шаге продвижения головки па расстояние ее
размеров. По оценке [14.10] начального запаса энергии головки
(электростатической, e2N%/2r0 2,7-1011 эВ) с учетом затрат
на ионизацию и возбуждение хватает на продвижение стримера
примерно на 3 см. Примечательно, что последнее значение со-
гласуется с опытами [14.10], в которых исследовалось, сколько
проходит стример после отключения внешнего напряжения (па
электроды подавались импульсы конечной длительности с резки-
ми фронтами).
7.3. Положительный изолированный от анода стример в не-
однородном поле (стримерная корона). Модель Даусона и Вина
была существенным образом усовершенствована Галлимберти
(1972 г.) [14.11] путем последовательного учета баланса энергии
процесса при участии внешнего поля. Было также введено в
расчет приближенное описание фотоионизации, чтобы исключить
произвол в задании расстояния зарождения лавины. Как и в
[14.10], предполагалось, что образуется только одна «эквивалент-
ная» лавина. От анода положительная сфера также считалась
изолированной. В процессе распространения стримера в неодно-
родном поле параметры его (TVo, т*о) меняются. Уравнение балан-
са энергии выражает тот факт, что работа внешнего поля над
электронами компенсирует затраты энергии электронов на иони-
зацию, возбуждение, прилипание, передачу молекулам, а также
изменение потенциальной электростатической энергии положи-
тельного заряда стримерной головки, собственной и во внешнем
поле.
Довольно сложные уравнения были решены численно для
конкретных условий воздушной короны от положительного
стержня на плоскость. Рис. 14.12 демонстрирует превосходное
согласие с опытом. Длина стримера примерно И см, причем это
расстояние он проходит за 10~7 с. Первые 5 см в области особен-
но сильного поля 15—5 кВ/см стример движется со скоростью
примерно 2 • 108 см/с. Стример останавливается в месте, где поле
упало до 2 кВ/см. Число положительных зарядов в головке в.
максимуме достигает No ~ 1,6 • 109 (eNo ~ 2,5 • 10~10 Кл).
Была развита численная процедура Монте-Карло в прибли-
жении двух эквивалентных лавин, случайным образом зарождаю-
щихся в разных точках углового сектора около головки стримера
[14.12]. Так, посредством численного моделирования была полу-
чена ветвистая, зигзагообразная картина стримеров в тех же
условиях, еще более похожая на фотографию.
7.4. Внешнее поле, необходимое для распространения стриме-
ра. Как ясно из предыдущего, прорастающий стример нужно
питать энергией, и эту функцию выполняет приложенное полет
которое совершает работу над электронами. Макроскопически это
можно трактовать как энергию, выделяемую током стримера^
442
Исходя из такого представления, оценим необходимое поле.
В приближении концентрированной заряженной головки, движу-
щейся со скоростью v вдоль внешнего поля Е, стримерный ток
определяется формулами (14.6'), (14.6). При No ~ 109, v ~
~ 108 см/с в длинном разрядном промежутке с d ~ 1 м ток i ~
~ eNovfd — 10~4 А, в коротком промежутке с d — 10 см i ~ 10-3 А.
Рис. 14.12. Стример от положительного стсфжня диаметром 2 см на плос-
кость на расстоянии 150 см [14.11] при постоянном напряжении 125 кВ:
а — фотография; б — расчет, проведены эквипотенциальные поверхности,
цифры около кривых — доли от приложенного напряжения, отсчитанного
от плоскости
Расходуемая источником питания за время dt энергия IVdt =
*=eNovEdt (согласно (14.6') это равенство — точное) тратится на
ионизацию, возбуждение молекул во вновь образованном участке
стримерного канала длиной vdt. Если на образование электрона
в среднем тратится энергия w, то eN^vE = mtr^vw, причем плот-
ность образованных зарядов п ж ЗЛго/4л;Го- Отсюда для энергети-
ческого поддержания стримера требуется внешнее поле Es ~ w/ero,
удовлетворяющее требованию eEsrQ ~ w. Смысл его довольно про-
зрачен. Пройдя в поле источника путь г0, равный размеру уже
существующей стримерной головки, каждый электрон должен
приобрести энергию, нужную для рождения нового, причем поло-
жительный ион новой пары будет включен в новую головку, та-
кую же, если процесс квазистационарен.
443
Радиус заряженной головки и стримерного канала го опре-
деляется условием самоподдержания головки в создаваемом ею
сильном поле и от внешнего поля зависит мало. С w ~ 50 эВ
для воздуха и го ~ 10~2 см получаем оценку ~ 5 кВ/см. Де-
тальный расчет [14.11] применительно к случаю однородного
поля дал Es = 7 кВ/см.
Эти цифры находятся в разумном согласии с опытом. В со-
ответствии с [14.13] в сухом воздухе атмосферного давления
~ 4 кВ/см. По измерениям [14.14] для стабильного прора-
стания стримера в воздухе требуется среднее внешнее поле Es ~
~ 4,7 кВ/см, почти независимо от длины промежутка и степени
неоднородности поля. В техническом азоте (до 2 % О2) Es &
~ 1,5 кВ/см, в Аг — 0,4 кВ/см, все при 1 атм. На величину Е&
существенно влияет прилипание, ибо оно приводит к исчезно-
вению электронов. Дело в том, что отрицательный ион из-за
малой подвижности практически не смещается относительно по-
ложительного, так что пару тяжелых заряженных частиц, можно
сказать, не стоит даже считать «зарядами». Опа не участвует в
создании новой головки. При этом для размножения электро-
нов до должного числа Nq требуются более значительные энер-
гетические затраты*). Например, добавление 10 % О2 в Аг по-
вышает Es от 0,4 до 2,3 кВ/см. Напротив, при нагревании воз
духа до 1000 К, в результате чего электроны освобождаются из
отрицательных ионов, Es падает от 4,7 до 0,7 кВ/см [14.14].
Необходимое поле растет при увеличении влажности тоже из-за
прилипания. При содержании паров воды 2 • 10~5 г/см3 оно в
1,5 раза больше, чем в сухом воздухе.
7.5. Модель идеально проводящего стримерного канала. Пред-
положение об идеальной проводимости высказывалось еще Ле-
бом в ранние времена стримерной теории. На такой основе по-
строена одномерная теория распространения в поле ионизацион-
ной волны, моделирующей стример [14.15]. Двумерная модель
развита в [26] применительно к процессу прорастания стримера
из середины плоского промежутка к обоим электродам. Поверх-
ность идеально проводящего тела стримера эквипотенциальна.
На ней распределяются индуцированные внешним полем поверх-
ностные заряды (положительные на стороне, обращенной к ка-
тоду, отрицательные — к аноду). Предполагалось, что тело стри-
мера имеет форму вытянутого вдоль поля эллипсоида вращения,
а скорость движения поверхности в каждой точке направлена
по нормали наружу и совпадает со скоростью дрейфа электро-
нов в соответствующем поле (§ 3). Вычисленные скорости анод-
ного и катодного концов стримера совпали с результатами из-
мерений в неоне при р = 1 атм и внешних полях Е = 10—
15 кВ/см. Скорости возрастают с увеличением Е и длины стри-
мера Z; при I = 0,5 см v ~ 108 см/с.
*) Быть может, сказывается и уменьшение проводимости в канале-
стримера (см. п. 7.7), но это, конечно, не вписывается в теорию самоподдер-
живающейся стримерной головки.
444
Отметим полезную формулу для оценки усиленного поля Ет
около закругленного с радиусом г конца идеально проводящего
стержня длины Z, если стержень ориентирован вдоль однород-
ного внешнего поля Eq\
Ет/Еъ = 3 + 0,56i(Z/r)0 92, 10 < 1/г < 2000.
Формула построена путем аппроксимации расчетных полей [33].
Причина усиления поля у концов стержня, в силу идеальной
проводимости находящегося под постоянным потенциалом, ил-
люстрируется рис. 14.13. Чем тоньше стержень, тем меньше он
возмущает внешнее поле, тем ближе
к его концам восстанавливается ис-
ходный потенциал и тем круче по-
тенциал спадает у концов.
В начале п. 7.4 был оценен ток
стримера с «изолированной» от ано-
да головкой. Оценим теперь ток
идеально проводящего стримера, ко-
торый тянется от самого анода. Весь
проводник находится под потенци-
алом анода ср = V (на катоде ср = 0); Рис. 14 13. Схематическое рас-
продольного поля в канале нет.
Потенциал вдоль проводника вырав-
нивает сосредоточенный на нем по-
ложительный заряд. Заряд на еди-
нице длины q = CV, где С — погон-
пределение потенциала вдоль
линии идеально проводящего
тонкого стержня, помещенного
во внешнее поле Штриховая
кривая — потенциал в отсутст-
вие стержня
ная (линейная) емкость проводника,
которая меняется по длине. Ее можнб оценить по формуле С =
= [21п(Я/г0) ] !, справедливой для бесконечной нити радиуса го
в заземленном коаксиальном цилиндре радиуса R. Если длина
стримера I больше расстояния X до ближайшего заземленного
тела (катода), то можно положить R~X. Если г0 < I < X, то,
интересуясь погонным зарядом q на конце стримера, R следует
заменить на 21 (для середины—на Z).
При го-10"2 см и R = 60 см С = 0,057 = 6,4 • 10"14 Ф/см*).
Например, если V = 50 кВ, q = 3,2 • 10“9 Кл/см. Ток идеально
проводящего стримера длины х = I обязан непрерывающемуся
уходу электронов в анод и образованию нового участка поло-
жительного заряда у конца проводника: i = qv. При v = 108 см/с
i = 0,32 А. Эта величина существенно больше, чем в случае
изолированной стримерной головки.
7.6. Компенсационная зона. Надо сказать, что в представле-
нии о заряженной сфере, за которой простирается электроией-
тральный, но не проводящий канал (в духе модели Даусона и
Вина, п. 7.1), содержится противоречивый элемент.
*) Измерения [14.16] лучше всего согласуются с расчетом при С =
= 5 • 10~14 Ф/см.
445
На это обратили внимание Гриффитс и Фелпс*). Пусть весь
положительный заряд eNo сконцентрирован в сфере радиуса Го.
Созданный им потенциал, в максимуме равный cps = eNo/ro (при
Nq = 109, го=10~2 см <ps = 14 кВ), падает при удалении от сфе-
ры, в том числе и при удалении вдоль канала в сторону анода.
Очень сильное дополнительное поле Ег ~ eN^r^ ~ 103 кВ/см бу-
дет вытягивать к головке электроны из близлежащей окрестно-
сти канала, оставляя там ионный заряд.
Положительный заряд, следовательно, распределится по не-
Рис 14.14 К вопросу о ком-
пенсационной зоне. Распре-
деление потенциала вдоль
стримерного канала с ко-
нечной проводимостью
Пунктир — потенциал, ко-
торый получился бы в слу-
чае сферической заряжен-
ной головки у вершины
строго электропеитрально-
го канала с нулевой прово-
димостью
L у конца «непроводящего» капала так,
что потенциал на нем ср («г) окажется
выровненным на уровне примерно
Фо(£ — L) (рис. 14.14). За концом этого
участка, названного компенсационной
зоной, при х > I потенциал резко пада-
ет до уровня внешнего фо(0- Если
«скачок» потенциала на конце стриме-
ра ф1 ~ ф0(/ — Z) — фо(Z) ~ Eo(l)L ~
~ ф6 ~ 10 кВ, а внешнее поле здесь
Eq ~ 10 кВ/см, то L — 1 см. При С ~
~ 10“13 Ф/см q ~ 10"9 Кл/см и полный
заряд удлиненной вершины стримера
Q ~ qLI2 ~ 10“9 Кл больше, чем в слу-
чае сферической головки; 1,6 • 10“11 Кл
в модели п. 7.1 и 2,5 • 10“19 Кл в мак-
симуме по расчетам в и. 7.3.
7.7. Какая модель ближе к истине?
В сущности с этого вопроса был
начат § 7. Ответ на него могут дать
либо эксперимент, либо теория, где
принята во внимание конечная про-
водимость стримерного канала. Даже
в самых упрощенных физических
постановках стримерный процесс описывается столь слож-
ными уравнениями, что справиться с ними можно только чис-
ленными методами. В последнее время такие работы начали
появляться. Получен и некоторый экспериментальный материал.
В опытах [14.14] осциллографировался перенос заряда па ка-
тод при распространении одиночного стримера от анода, и это
позволяет определить ток стримера. В техническом азоте при
р = 1 атм в промежутке длиною d = 1 м между положитель-
ным стержнем и плоскостью во время пролета стримера в те-
чение t ~ 10~5 с зарегистрирован ток i ~ 10~3 А. При этом в тело
стримера внедряется заряд Q = idlv = it — 10"8 Кл. Он значи-
тельно больше заряда, получающегося в теории сферической го-
ловки. Если допустить, что I совпадает с током проводимости,
*) Их соображения изложены в обстоятельном обзоре [14 17] по искро-
вому пробою длинных промежутков.
446
текущим по каналу стримера, то из закона Ома i = уЕ с внеш-
ним полем Е ~ 1—10 кВ/см получается погонная проводимость
у = ягдО ~ 1СГ7 — 10~6 см/Ом
Радиус канала неизвестен Если го = 10 2 см, то при у —
= 106 см/Ом о = 3 • 10-3 (Ом см)-1, чему соответствует плот-
ность плазмы в канале тзе ~ 4 1013 см-3 Если го = 3 10 3 см,
пе = 4 1014 см-3 — это, по-видимому, верхняя оценка, тем более
что сам ток проводимости в канале наверняка меньше тока в це-
пи (в случае изолированной головки первого вообще нет, и пере-
нос электричества происходит так, как эго описано в п 2 3)
Измеренные значения i и Q слишком велики для модели изо-
лированной сферы, но слишком малы для модели идеально про-
водящего канала В условиях опыта V — 102 кВ у конца идеаль-
но проводящего стримера, прошедшего половину промежутка,
q ~ CV — 10-8 Кл/см и при v ~ 107—106 см/с i = qv~0,l— 1 А
Реальная ситуация занимает промежуточное положение между
двумя моделями и, надо полагать, соответствует значительной
изоляции стримерной вершины от анода и существованию там
компенсационной зоны
О том же свидетельствуют и численные расчеты, которые не
указывают на немонотонность потенциала ср (я) (что было бы
в модели сферы; рис 14 14) либо па уничтожение поля в канале,
как при идеальной его проводимости В [14 18] рассматривалась
двумерная задача о распространении плазменного капала в азо-
те при 1 атм в плоском промежутке d = 0,5 см с V = 30 кВ и
Ео = 60 кВ/см Вопросы самоподдержапия путем инициирования
вторичных лавин в результате фотоионизации не рассматрива-
лись Вместо этого задавался начальный фон электронов п =
= 108 см-3 В начальный момент задавался очаг плазмы у анода
с тзе ~ 1014 см-3 От него со скоростью и ~ 2 108 см/с к катоду
прорастал плазменной капал с пе ~ 1014 см-3 Па конце его поле
достигает 150 кВ/см, по внутри капала поле слабее внешнего
всего на 20—30 % В процессе прорастания капала сохранялся
его начальный, искусственно задаваемый радиус (порядка
10-2 см), т е данный расчет пе позволяет получить радикс
стримера г0 из самих уравнений*) Не удается пока измерить
его и на опыте — видимым на фотографиях радиус пет основа-
ний отождествлять с радиусом ионизованного, проводящего ка-
нала, который может быть и гораздо меньше (см п 7 8)
Искусственное задание Го есть слабое место и расчета [14 19]
для воздуха, правда, более полного в других отношениях, ибо
рассматривался процесс и в канале и вокруг головки стримера
с учетом фотоионизации Расчет был квазиодномерным, радиус
задавался равным го= 10~2 см Такие параметры стримера, как
скорость, плотность плазмы у вершины, поле вблизи нее со сто-
роны канала, ток определяются в модели потенциалом голов-
ки фг Сам же потенциал фг зависит от внешних условий, про-
*) В [14 18а] аналогичный расчет сделан для стримера в SF6
447
водимости в канале, которая определяется электронной кинети-
кой. Так, например, при срг = 9 кВ v = 1,4 • 108 см/с, Е = 4 кВ/см,
пе = 1015 см~3, 1 = 0,12 А.
В воздухе из-за прилипания погонная проводимость стример-
ного канала вдали от вершины не превышает 10-10 см/Ом. Об
этом свидетельствует исчезающе малый ток, менее 10~6 А, через
IO"7 с после касания стримером катода и «замыкания» проме-
жутка [14.14]. Прилипание не сильно сказывается только в ко-
ротких стримерах, либо на ранней стадии распространения длин-
ного. В воздухе при р = 1 атм частота прилипания уа ~ Ю7 с-1,
так что при v — 108 см/с пе должна заметно снижаться в канале
на расстоянии х ~ v/va ~ 10 см от вершины. По расчету [14.19]
при длине стримера /-8 см в канале лгс ~ 2 - 1014 см-3, а п_ ~
~ 1,5 • 1013 см-3.
Итак, в длинном (метровом) стримере в воздухе вершина
его всегда сильно изолирована от анода из-за прилипания
электронов и резкого падения проводимости в канале. Потому
п длинном воздушном промежутке и не бывает стримерного про-
боя — пробой неизбежно сопровождается возникновением лидера.
Относительно высокая проводимость стримерного канала была
зарегистрирована в очищенном от электроотрицательных при-
месей аргоне [14.14], у > 10~5 см/Ом, I ~ 10~2 А. Наблюдалось
и превращение стримерного канала в искровой, после достиже-
ния катода. Вообще стримерный (не лидерный) пробой надежно
наблюдался только в инертных газах. Только для них и имеет,
может быть, какой-то смысл модель идеально проводящего
«стримера.
7.8. Распад плазмы и радиус стримерного канала. Как мы
только что видели, проводимость канала в воздухе быстро умень-
шается с течением времени или по мере удаления от головки
стримера. Но даже в азоте, где прилипания пет, в условиях,
когда внешнее поле не сильно превышает предельное для рас-
пространения стримера Es ~ 1,5 кВ/см при р = 1 атм, плазма
в канале тоже распадается. Поле за головкой пе превышает
внешнего, а Е1р = 2 В/(смторр) в холодном азоте слишком ма-
ло для ионизации (п. 7.7 гл. 10). При коэффициенте диссоциа-
тивной рекомбинации р ~ 10~7 см3/с за время t ~ 10"5 с пролета
стримера через метровый промежуток пе от сколь угодно боль-
шего начального значения падает до пе ~ ([}£)-1 ~ 1012 см"\
Уменьшение проводимости канала, выраженное тем сильнее, чем
он длиннее и чем однороднее внешнее поле, препятствует стри-
мерному пробою длинных однородных промежутков.
Несмотря на некоторое сходство, стримерный канал со слабо-
ионизованной неравновесной плазмой нельзя уподобить поло-
жительному столбу тлеющего разряда. В столбе разряда иони-
зационные и энергетические процессы сбалансированы. Там осу-
ществляется самоподдерживающееся стационарное (или квазп-
стационарное) состояние. Канал же стримера является скорее
«пассивным» плазменным следом, который оставляет за собой
448
при продвижении самоподдерживающаяся стримерная вершина.
Радиус следа — канала г определяется, надо полагать, амбипо-
лярным диффузионным расширением плазмы от ее начального
размера — радиуса стримерной головки го ~ 3 • 10-3—10-2 см
(п. 7.1). Кажущаяся неизменной тонкость длинного канала со-
здает ложное впечатление о каком-то присущем ему самому
радиусе. На самом деле след просто пе успевает сильно расши-
риться: за время t ~ 10~5 с при 7)а ~ 2 см2/с г — Tq ~ }Dat ~
~ 4 • 10~3 см ~ Го.
Сохранение радиуса начального возмущения у прорастающе-
го плазменного канала в расчете [14.18], упомянутом в п. 7.7,
обусловлено возникающей структурой поля около капала; диф-
фузионное расплывание там ничтожно. Внешнее поле задано
столь высоким, Е ~ 402^, что ионизация в канале сильно преоб-
ладает над рекомбинацией. Итак, проблема стримера остается.
§ 8. Пробой длинных воздушных промежутков
с сильно неоднородным полем (эксперимент)
8.1. Влияние неоднородности поля на пробивные напряже-
ния. Неоднородность уменьшает пробивное напряжение при том
же расстоянии между электродами. Это иллюстрируется
рис. 14.15. Измерения сделаны на промышленной частоте 50 Гц.
Иестационарность поля практически не сказывается, так как
полупериод 10~2 с слишком велик по сравнению с временными
масштабами пробоя*). Полярность электродов чередуется, так
чю пробой происходит при той, которая его облегчает (см.
ниже). Касательная к кривой Vt(r) при г = R с наклоном
32 кВ/см соответствует примерно пробою плоских промежутков
с тем же размером d = 7? — г в однородном поле. По мере умень-
шения г, т. е. увеличения степени неоднородности, пороговая
кривая Vt(r) все больше отклоняется вниз от касательной. Сред-
нее пробивное поле Ecp = Vj(R— г) неуклонно уменьшается по
сравнению с 32 кВ/см. Причина такого действия неоднородности
связана с тем, что в любой критерий пробоя входит коэффици-
ент усиления исходных лавин J adx, очень чувствительный к
распределению Е(х) вследствие резко нарастающей зависимости
а(Е). Перераспределение поля по сравнению с однородным уве-
личивает усиление при сохранении J Е dx, либо уменьшает раз-
ность потенциалов при сохранении усиления. С этим обстоятель-
ством мы уже сталкивались неоднократно (гл. 10).
*) При измерениях электрической прочности промежутка по отношению
к постоянному или переменному (не импульсному) полю напряжение на
электродах (или амплитуду 50-герцового напряжения) поднимают постепен-
но, вплоть до минут, чтобы исключить влияние скорости «включения» на-
пряжения (п. 8 4)
29 ю П Райзер
449
Рис. 1415 показателен еще в одном отношении. Интервал
напряжений VK<V <Vt, в котором существует корона, сокра-
щается при увеличении г и уменьшении степени п^одгогодности
поля. При не очень сильной неодпоро щостч /Л’^0,1 корона
вообще пе появляется. Наращивание напряжения на электродах
ведет прямо к пробою. Напротив, при очень малом радиксе коро-
нпрующето электрода, когда неоднородность сильна, озрыв меж-
ду потенциалами зажигания короны и пробоя Vt велик.
Рис 14 15. Напряжения зажигания ко-
роны Ук и пробоя Vt воздушного про-
межутка между концентрическими ци-
линдрами в зависимости от радиуса
внутреннего электрода при радиусе
внешнего 5 см. Представлены амплиту-
ды переменного напряжения частоты
5') Гц, заштрихована область повышен
ног о разброса пробивных напряжении
[14 4]
Рис 14 16 Амплитуда пробивного
напряжения в зависимости от
длины а воздушною промежутка
м^жду стержнем и стержнем (7),
стержнем и плоскостью (2) [14.2]
Влияние степени неоднородности поля на электрическую
прочность промежутка проявляете;] и в том, что пробить про-
межуток между стержнем и плоскостью легче, чем между двумя
стержнями при одинаковом межэлектродном расстоянии d. На
рис. 14.16 показаны соответствующие пороговые напряжения
также частоты 50 Гц для больших d, до 10—12 м. Стержнем
служил металлический прямоугольный брусок квадратного се-
чения со стороной 1,27 см*). При одинаковых d электрическая
емкость системы стержень — плоскость больше, чем системы
стержень — стержень, так как больше объем, занятый полом.
Поэтому при одинаковом напряжении электрический заряд на
зтержне в первом случае больше, а поле у стержня, а также
степень его неоднородности выше.
Промежуток стержень — стержень с d и V по распределению
поля эквивалентен промежутку стержень — плоскость с d/2, К/2
*) Полдюйма — измерения стандартизованы.
450
(ср. с (14.13)). Это сказывается на соотношении пробивные пара-
метров в переменном поле, обеспечивающем полную симметрию
условий. Так, в случае стержень — стержень d = 6 м, У, =
= 2400 кВ, а стержень — плоскость d = 3 м, Vt = 1200 В. При
меньших размерах правило эквивалентности выполняется немно-
го хуже: в случае стержень — стержень d = 4 м, Vt 1850 кВ,
а стержень — плоскость d = 2 м, Vt =
= 850 кВ. Но все равно отклонение неве-
лико, т. е. пробивное напряжение в об-
щем определяется именно структурой по-
ля около электрода, где оно усилено.
8.2. Влияние полярности. Порог про-
боя в постоянном поле существенно зави-
сит от полярности «активного» электрода
(рис. 14.17). Пробивное напряжение для
отрицательного стержня примерно вдвое
больше, чем для положительного. Здесь
сказывается различие условий для раз-
Рис. 14.17. Амплитуда
пробивною напряжения
в зависимости от длины
d воздушного промежут-
ка между положитель-
ным стержнем (анод) и
плоскостью (7), отрица-
тельным стержнем и
плоскостью (2) [14.4]
вития лавин и стримеров около актив-
ного электрода. У стержня-анода лавипы
направлены извне к нему и попадают
по мере приближения в область все
более и более сильного поля. Это облег-
чает размножение электронов и стиму-
лирует переход лавины в стример. В слу-
чае стрежпя-катода лавины по мере раз-
множения удаляются от электрода и по-
падают в область все более слабого поля. Это тормозит
процесс размножения и затрудняет лавинно-стримерный пере-
ход. Кроме того, в случае положительного стержня электроны
уходят в металл, оставляя нескомпенсированный положительный
пространственный заряд, который усиливает поле электрода.
В случае отрицательного — поле соответствующего отрицатель-
ного пространственного заряда в какой-то мере компенсируется
полем полностью оставшихся в газе положительных ионов.
Приведенные выше данные почерпнуты из того материала,
который получают в лабораториях для нужд техники высоких
напряжений. Его используют при конструировании линий пере-
дач и других высоковольтных сооружений.
8.3. О чем говорит малость средних пробивных полей. Хотя
напряжения Vt, необходимые для пробоя длинных воздушных
промежутков, огромны — сотни и тысячи киловольт, средние
электрические поля,— если сравнивать с короткими промежутка-
ми (рис. 14.7),— на удивление низки. При d ~ 1 м E^=Vt'd^
~ 10 кВ/см для отрицательного острия и 4,5 кВ/см — для поло-
жительного (рис. 14.17); при d ~ 10 м на промышленной частоте
средняя амплитуда Ecv = 2 кВ/см (рис. 14.16). Таковы поля в
подавляющей части промежутка, а минимальные (у плоскости)
и того меньше. Но ведь мы знаем, что для ионизации воздуха
451
электронными ударами требуется по меньшей мере Е~
~ 24 кВ/см. Вывод отсюда однозначен. Ионизованный канал,
а в случае длинных воздушных промежутков это — лидер, воз-
никнув около активного электрода, где сконцентрировано поле,
пробивает себе путь к другому электроду безо всякого ионизую-
щего действия внешнего поля.
Роль приложенного напряжения в данном случае состоит не
в том, чтобы непосредственно обеспечить интенсивное размно-
жение электронов в любой части промежутка. Последнее необхо-
димо для пробоя идеального плоского промежутка с равномер-
ным полем при исчезающем перенапряжении*). Тогда суще-
ственна ионизация на каждом участке пути лавины; все участки
должны давать вклад в усиление, которое должно оказаться
достаточным то ли для воспроизводства лавин вторичной эмис-
сией, то ли для лавинно-стримерного перехода. Если же раз-
ность потенциалов распределяется в пространстве неравномерно,
она должна создать достаточное для интенсивного размножения
поле лишь в окрестности одного электрода. Возникнув там, плаз-
менный канал прорастает, вызывая необходимую ионизацию
газа, благодаря своему собственному полю, точнее, полю
своей заряженной вершины. Внешнее поле после этого долж-
но в основном снабжать прорастающий канал должной
энергией.
8.4. Влияние скорости нарастания напряжения. Сказанное
выше не означает, что пробивное напряжение определяется по-
лем, нужным лишь для возникновения лидера. По мере удли-
нения канала, поддерживать его рост становится все труднее
и труднее, и чтобы обеспечить продвижение лидера на большое
расстояние и достижение им противоположного электрода, на-
пряжение желательно все время повышать. Можно, конечно,
провести процесс и достичь пробоя при неизменном напряжении
Е/пост, но это потребует большего его значения, чем конечное,
в момент перекрытия каналом промежутка, если наращивать V
постепенно. Конечное напряжение, знаменующее пробой, зависит
от скорости нарастания V. Для каждой длины d существует
оптимальная средняя скорость подъема напряжения dV/dt, при
которой конечное, т. е. пробивное, напряжение оказывается ми-
нимальным Fimin. И слишком медленный, и слишком быстрый
подъем напряжения пробой затрудняют. Оптимальные времена
подъема положительного потенциала на стержне над зазем-
ленной плоскостью выражаются эмпирической формулой
Гопт ~ 50 d [м] мкс, надежно проверенной вплоть до d ~ 30 м
[33].
Поскольку наиболее благоприятным для пробоя является ре-
жим, когда лидерный канал прорастает при непрерывно повы-
шающемся с течением времени напряжении, экспериментальную
*) Кстати сказать, при больших d создать однородное поле и практи-
чески нереально.
452
величину Топт естественно трактовать как масштаб времени пере-
крытия каналом промежутка. Отсюда получаем скорость движе-
ния лидерпои вершины ил ~ d/x0WT ~ 2 • 106 см/с. К близким
цифрам приводят и прямые измерения (§ 9). Величины
в диапазоне до d« 10 м оказываются процентов на 30 % мень-
ше VfnoiT. Это принимается во внимание при расчетах электри-
ческой прочности воздушной изоляции, ибо ориентироваться
следует на наиболее опасные, т. е. наиболее благоприятные для
пробоя, условия. К пробою приводят и более кратковременные,
чем т0ПТ, импульсные воздействия, скажем, так называемый
«стандартный грозовой импульс» с длительностью 50 мкс и вре-
менем переднего фронта 1,2 мкс. Но при этом требуются более
высокие напряжения. Например, при d = 4 м — вдвое большее,
чем Vfmin ~ 1,1 МВ, чему отвечает т0ПТ ~ 200 мкс. Грубо говоря,
лидер в этом случае должен пересечь промежуток в четыре раза
быстрее.
При увеличении d рост пробивного напряжения замедляется
(кривая 2 на рис. 14.16). Поэтому для облегчения пробоя более
длинных промежутков скорость подъема напряжения надо умень-
шать. Если ДЛЯ иллюстрации ПОЛОЖИТЬ Ffmin ~ то
(dV/dt)onr — Е/тш/Топ-г ~ i/^d. Например, при с? ~ 20 м имеем
Г/тт ~ 2 MB, Tout ~ 1 МС, (dVjdt)0Trt « 2 КВ/МКС.
8.5. Сверхдлинные промежутки. Работа на открытой местно-
сти с генераторами импульсного напряжения (ГИН), дающими
импульсы в 5—6 МВ с длительностью до 10 мс, позволила про-
бивать и перекрывать «длинной искрой» расстояния в много
десятков метров. С импульсом длительностью 7,5 мс с передним
фронтом 2 мкс, по форме далеком ют оптимального, пробой про-
межутка длиной d = 65 м наблюдался при Vt = 4,5 МВ и Ес^ =
= 0,7 кВ/см [33]. По расчету [33] для оптимального режима
при tZ = 20—100 м F/min растет с d почти линейно, от 2 до
4 МВ. Темп прироста, около 200 В/см, характеризует и сред-
нее поле. Оно в несколько раз меньше измеренного, не опти-
мального.
§ 9. Лидерный механизм пробоя длинных промежутков
9Л. Недостаточность одного лишь стримерного процесса.
В § 5 рассматривалась простейшая схема стримерного пробоя,
как это представлялось на заре теории искры. Одиночный стри-
мер растет от анода; достигая катода, он вызывает распростра-
нение обратной волны сильной ионизации; это приводит к обра-
зованию искрового канала. Как постепенно было установлено,
нечто подобное реализуется лишь в случае промежутков не
слишком большой длины, полей с не слишком большой степенью
неоднородности, газов, в которых отсутствует прилипание
(п. 7.7). Проводимость канала стримера не столь велика, чтобы
в достаточной степени переносить потенциал анода к катоду,
30 Ю. П. Райзер 453
без чего у катода не могут образоваться сильное поле и обрат-
ная волна интенсивной ионизации. Кроме того, по мере продви-
жения от острия головка стримера вступает в область все более
слабых полей, и это ставит предел дальнейшему распростране-
нию. В электроотрицательном газе все это в высшей степени
усугубляется (§ 7).
В длинном сильно неоднородном воздушном промежутке, где
все складывается неблагоприятно для роста стримеров, послед-
ние, образовавшись у острия, останавливаются, не достигнув
другого электрода, как на фотографии стримерной короны
(рис. 14.12). Длина стримеров зависит от приложенного напря-
жения и ряда других условий, она может составлять 10—100 см
и более. Зная, что при росте напряжения стримеры удлиняются,
можно было бы подумать, что для пробоя воздуха нужно под-
нять поле повсюду выше Es = ^,l кВ/см (п. 7.4), чтобы стриме-
ры смогли пересечь весь промежуток. Однако, как мы видели
в § 8, длинные промежутки пробиваются раньше, при суще-
ственно меньших средних полях. Природа нашла иной выход —
и на него указывает высокоскоростное фотографирование длин-
ных лабораторных искр и молнии (исторически началось со
второго).
9.2. Лидер и его элементы. От активного электрода из обла-
сти сильного поля, по пути, прокладываемому предшествующими
стримерами, прорастает канал, проводимость которого гораздо
больше, чем у стримера. Он в гораздо большей степени, чем
стример, переносит потенциал электрода к своей вершине. Его
называют лидером. Этот канал как бы удлиняет острие электро-
да, продвигает его вместе с высоким относительно другого элект-
рода потенциалом к последнему электроду. Являясь, как и кон-
чик металлического острия, источником особенно сильного поля,
головка лидера источает множество разбегающихся от нее стри-
меров, которые подготавливают начальную, отнюдь не малую
плотность зарядов. Электроны интенсивно ионизуют газ в силь-
ном поле лидерной головки, создавая «новую» головку и тем
самым обеспечивая продвижение хорошо проводящего канала.
Когда он замыкает промежуток, от второго электрода (плоско-
сти) распространяется обратная волна, и это кладет начало пре-
вращению лидерного канала в искровой.
Нам сейчас приходится чуть ли не повторять те самые сло-
ва, которые раньше (в § 3, 5) говорились о стримерном механиз-
ме пробоя. И в самом деле, разница между стримером и лидером
не столько качественная, сколько количественная: в плотности
электронов, в величине пропускаемого тока, в температуре газа.
Стример захватывает лавины, лидер — стримеры, прямо как на
известном рисунке Питера Брейгеля «Большие рыбы пожирают
маленьких». В рассмотренную ранее цепочку процессов, подго-
тавливающих искровой разряд: лавины — стримеры — обратная
волна, включается еще одно звено: лавины — стримеры — ли-
дер — обратная волна.
454
которых электроны
Рис. 14.18. Схема ли-
дера, прорастающего
от положительного
острия. Структурные
элементы: 1 — канал
лидера, 2 — головка,
3 — стримеры стри-
мерной зоны, 4 —
стримеры чехла, 5 —
лавина, втягиваю-
щаяся в головку
стримера (показана
только одна лавина
у одного из многочис-
ленных стримеров)
Структура лидерной системы показана на рис. 14.18. Пред-
ставление о ней было во многом сформировано в работах [14.20].
Ярко светящаяся головка на фотографиях имеет диаметр при-
мерно 1 см. Диаметр канала вблизи головки 10-2 см, дальше
канал постепенно расширяется. Стримерная корона перед голов-
кой простирается на расстоянии порядка 1 м. Судя по фотогра-
фиям, сделанным с экспозицией 10-7 с, головка состоит из ко-
ротких, только что родившихся стримеров, в
еще не успели совершить прилипание [33].
В той стадии, когда лидерная головка про-
ходила через данное место длинного лидер-
ного канала, от нее веером исходили много-
численные стримеры. Они оставляли в про-
странстве заряд и плазму. Поэтому лидер-
ный канал оказывается окруженным «чех-
лом» из плазмы и пространственного заряда.
Благодаря наличию чехла результирующая
емкость единицы длины лидера раз в пять
возрастает по сравнению с линейной ем-
костью одиночного стримера или самого ка-
нала [14.23а].
9.3. О механизме образования лидера.
Первейшим условием образования лидера в
воздухе (стримерно-лидерного перехода) яв-
ляется повышение температуры газа, как
минимум, на столько, чтобы пресечь паде-
ние проводимости вследствие прилипания
электронов.
Когда с положительно заряженного
острия стартуют стримеры стримерной ко-
роны, они обычно ветвятся от одного ство-
ла. Выдвигалось предположение [14.21],
что электронный ток от всех стримеров,
сходящийся в этом канале, своим джоуле-
вым теплом разогревает газ до температу-
ры, достаточной для термической иониза-
ции. От этого газ сильно ионизуется, электроны уходят в
анод, в канале остается большой положительный заряд,
который создает вокруг сильное поле. Дальше все повторяется,
только новая стримерная корона отходит теперь уже не от ано-
да, а от вершины образовавшегося ионизованного канала. Так
начинается прорастание лидера. Однако, по оценкам, которые
сделаны в защиту гипотезы [14.4], ток стримеров нагревает воз-
дух в канале всего лишь до 3000 К. Этого явно недостаточно
для начала термической ионизации воздуха, для чего требуется
примерно 8000 К. И спектроскопические данные говорят о том,
что температура в стволе стримерной короны не столь высока.
В [14.22] предложен механизм низкотемпературного стример-
но-лидерного перехода. В этой модели также привлекается
30*
455
джоулев разогрев воздуха в стволе стримерной короны*), но
механизмом повышения проводимости служит интенсивный
отрыв электронов от большого числа ранее образованных отри-
цательных ионов. Для разрушения ионов 07 в сухом воздухе
достаточно температуры Т ~ 1500 К; при этом отлипание про-
исходит за 10“7 с. Во влажном воздухе образуются гидратиро-
ванные ионы 07 [Н2О]П, (п =1, 2, 3), причем энергия связи
электрона In в кластере растет с увеличением п, а связь моле-
кулы Н2О ^пн2о уменьшается. Так, /7 2,65 эВ, тогда как
для 07 /7 — 0,44 эВ; 2?3н2о = 0,23 эВ. Разрушение кластеров
сначала идет путем последовательного отщепления Н2О ударами
молекул. Для отлипания при Т ~ 1500—2000 К требуется
10“6—10-5 с, при более низких температурах гораздо больше.
Все это перекликается с тем, что говорилось в п. 7.4 по поводу
обнаруженного на опыте резкого увеличения проводимости стри-
мерного канала при искусственном нагревании воздуха.
Температура газа при прохождении тока повышается с уско-
рением. При низких температурах джоулево тепло запасается в
молекулярных колебаниях, по мере роста Т энергия все скорее
и скорее передается поступательным и вращательным степеням
свободы. Так, при влажности воздуха 0,8 • 10-5 г/см3, близкой к
нормальной, и Т == 300 К время колебательной релаксации тУТ ~
« 60- 10“5 с, при 1000 К —8-10~5 с, при 2300 К-10"5 с (ср.
с п. 4.2 гл. 11).
Повышение проводимости при росте температуры должно при-
водить к стягиванию тока, рассеянного в большой головке по
большой площади, в тонкий канал, который выходит из головки,
т. е. должно происходить нечто вроде контракции (§ 8 гл. 11).
9.4. Данные о параметрах лидера, извлеченные из экспери-
ментов. Информацию о лидере получают, расшифровывая резуль-
таты высокоскоростной фотографии с привлечением электронно-
оптической аппаратуры, одновременных электрических измерений
тока во внешней цепи, напряжения, измерений поля в канале
с помощью вспомогательных электродов-зондов или другими ме-
тодами, спектроскопических измерений и т. д. [14.12, 14.23, 33].
Представление о параметрах лидера дают следующие цифры
[14.17]. В воздушном промежутке d = 10 м между коническим
анодом и плоскостью-катодом при напряжении, нарастающем в
течение 200 мкс до 1,6 МВ, лидер распространяется со средней
скоростью рл ~ 2 106 см/с. В течение первые 100 мкс лидерный
канал расширяется с радиальной скоростью 104 см/с, потом рас-
ширение сильно замедляется до 2 • 102 см/с, радиус канала в
*) Слабый ток одиночного стримера вообще не в состоянии нагреть воз-
дух более, чем на 100 К. Ведь температура, до которой нагревав!ся тонкий
канал, где выделяется энергия, определяется в основном мощностью на
единице длины W — iE, что следует из уравнений теплоотвода; ср. с фор-
мулами (12.15), (12.23).
456
конце составляет г = 0,2 см. В течение 500 мкс пролета лидера
через промежуток течет ток А и выделяется мощность по-
рядка 1 МВт. Среднее поле в канале уменьшается по мере рас-
пространения лидера и, когда он проходит половину промежут-
ка, по оценке устанавливается на уровне Еч ~ 1 кВ/см. Исходя
из этих цифр проводимость в канале о ~ 10-2 Ом-1-см-1. По
расчету через 100 мкс заканчивается колебательная релаксация
и в канале устанавливается газовая температура Т ~ 5000 К;
при этом ~ 2 • 104 К. Плотность электронов, оцененная по о
и плотности газа при такой температуре и р = 1 атм, составляет
пе ~ 1013 см-3. Эта величина сопоставима с тем, что дают расче-
ты и анализ измерений и для канала стримера недалеко от го-
ловки, где электроны еще не исчезли из-за прилипания. Состоя-
ние же с сильным отрывом температур похоже на то, что де-
лается в контрагированном шнуре тлеющего разряда.
Из приведенных данных можно оценить погонный заряд ли-
дерного канала у вершины: q = i/v^ ~ 5 • 10-7 Кл/см. Падение
напряжения в канале длиной I = d/2 составляет ZX^/2 ~ 500 кВ,
значит, при V ~ 1,6 МВ потенциал головки в этот момент фл ~
~ 1 МВ, что дает для погонной емкости С = д/фл ~ 5 • 10-13 Ф/см.
Эта оценка не слишком противоречит результату С = 2,5 X
ХЮ-13 Ф/см, полученному в других измерениях [14.23а].
Приведенные цифры типичны для той стадии процесса, когда
стримеры еще не коснулись катодной плоскости, как на
рис. 14.18. Когда лидер приближается к катоду на расстояние,
меньшее длины стримеров, и стримеры втыкаются в катод (это
называют сквозной фазой), ситуация меняется. Лидер ускоря-
ется, ток подскакивает до 100—200 А, поле в канале падает до
Е:[ ~ 100 В/см. Иногда при приближении головки лидера к
электроду оттуда под действием сильно возросшего между ними
поля стартует встречный лидер. Встреча лидеров в принципе не
отличается от встречи лидера с электродом. Переход к сквозной
фазе, которая в не очень длинных промежутках может начаться
довольно рано, надежно обеспечивает пробой, почти независимо
от поведения внешнего напряжения, тогда как снижение его в
несквозной фазе пробой может предотвратить.
Состояние в развитом длинном лидерном канале на расстоя-
нии 10—20 м от вершины, видимо, похоже на состояние в дуге.
Поле там описывается эмпирической формулой £'л = (32 + 51/
/£[А]) В/см [33], имеющей нечто общее с ВАХ дуги в воздухе.
9.5. Из чего и как складывается ток лидера. Лидер объеди-
няет в одном канале токи множества стримеров, стартующих от
его вершины. Лишь общими усилиями стримеры могут нагреть
газ до должной температуры, почему, собственно, для пробоя
и требуется лидерный механизм. Короткие недавно родившиеся
стримеры, еще не потерявшие проводимость, дают свой вкчад
через ток проводимости, длинные, потерявшие электрический
контакт с лидером из-за прилипания — через ток смещения, как
описано в п. 2.3. Последних гораздо больше, так как они доль-
457
ше живут В песквознои фазе их головки со скоростью стримера
vc > кл пробегают путь I — 1 м до места, где поле лидерной вер-
шины падает ниже необходимой для продвижения величины
Es ~ 4,7 кВ/см (п 7 4) Там стримеры затормаживаются и на-
капливаются *)
Если длинный стример несет заряд Qc, а в воздухе по неза-
висимым измерениям Qc ~ 5 • 10-10 Кл, то, чтобы обеспечить весь
ток лидера гд ~ 1 А за счет одного лишь тока смещения, стриме-
ры короны должны рождаться с частотой vpo}Kfl ~ ijQc ~ 2 X
ХЮ9 с-1 [33] При времени до торможения тТ0рм ~ Uvc среД ~
~ 10-5 с на длине I ~ 1 м в короне присутствует Nc — \р0жДтТ0рм ~
~ 2 104 длинных стримеров Канал стримера теряет проводи-
мость, скажем, в 20 раз за время тпров ~ ЗгТ1 ~ 3 10“7 с, т е
число коротких, еще проводящих стримеров Nc пров — х’рождтПров ~
- 103 Если ток проводящих стримеров дает преобладающий
вклад в ц, то частоту л’рожд следует переопределить, но незави-
симые эксперименты подтверждают приведенную выше оценоч-
ную цифру
Иначе происходит в сквозной фазе, чем и объяснено в
[14 23а] наблюдаемое резкое повышение тока Теперь длинные
стримеры, грубо говоря, без торможения втыкаются в катод,
внося в него свой заряд Qc Если раньше лидерный ток составлял
Ч = Qc^c/tToim, то теперь он равен iл = (^ЛсАпрол, где Nc —
число таких макроскопических носителей заряда, а тпрол ~ ~
время пролета ими длины V между вершиной лидера и катодом
Полный заряд в объеме, занятом стримерными головками, есть
QCNC = С Гу', тде С' — погонная емкость объема, ф'— потен-
циал в нем Отсюда £л = С'ф'нс, тогда как в несквознои фазе
= Сфлкл Но потенциал ф' примерно таков же, что и потенциал
лидерной вершины фл раньше Погонные емкости зависят от
масштабных длин только логарифмически, и С' ~ С, поэтому
глЛл«Ус ул~ Ю2
9.6. Почему для облегчения пробоя нужно поднимать напря-
жение по мере продвижения лидера. Как и для стримера, ско-
рость и ток лидера определяются потенциалом фл его вер-
шины Известна эмпирическая зависимость кл = 1,2 106
(фч[МВ])1/2 см/с, причем при фл < 200—300 кВ лидер вообще
не образуется; ъл = Сфднл, где С — величина меньше подвержен-
ная вариациям (п 9 4; 7 5) Если V — мгновенное напряжение
на электродах, а Еч — среднее поле в лидерном канале длины Z,
то V = q)^ + EX При недостаточном потенциале фл ток очень
слабый, поле Ел сильно, и для обеспечения продвижения лидера
и тока требуется излишне высокое напряжение V При чрезмер-
но большом фл, несмотря на малость падения Ел1, также требу-
ется неоправданно большое напряжение Для каждой длины I
*) Быть может, какое то время они еще движутся со скоростью рл, с ко-
торой лидер продвшает вперед место, где Е = Е8
458
существует оптимальный потенциал <рл, при котором V мини-
мально. Это довольно стабильная величина в районе 1 МВ; для
Z ~ 20—100 м фЛопт слабо растет от 0,9 до 1,4 МВ [33]; при
этом рл ~ 1,5 • 106 см/с. Чтобы поддерживать оптимальный режим
с такими умеренными скоростью ул и током ~1 А (в несквоз-
ной фазе), нужно неуклонно поднимать напряжение по мере
удлинения лидера.
Слишком резкий подъем напряжения сопровождается сильным
током в начальной стадии и интенсивным нагнетанием положи-
тельного заряда в «чехол». Позднее, когда лидер продвинется
далеко, в этом месте появляется обратное радиальное поле, на-
правленное, вопреки обычному, к оси, и электронный ток, кото-
рому положено течь от вершины в анод, вместо того поворачи-
вает вбок и идет па нейтрализацию избыточного заряда чехла.
Канал в старых участках лидера оказывается перекрытым для
осевого тока, поле Ел там возрастает, от чего фл понижается.
«Исправить» положение можно поднятием общего уровня напря-
жения, но порог пробоя от этого становится выше. Сказанное
подтверждается расчетами [33].
9.7. В чем главное отличие лидера от стримера и почему в
лидерном процессе появляется промежуточное стримерное звено.
Вопросы эти принципиальны и, завершая обсуждение стримерно-
го и лидерного механизмов, в качестве резюме дадим на них по
возможности четкий ответ. Лидер и стример — образования од-
ного типа. Оба — плазменные каналы, самоподдерживающимся
образом прорастающие во внешнем поле, пе достаточном для
ионизации. Параметры вершинных частей каналов: плотности
электронов, радиусы — сопоставимы,* различаясь лишь на один-
два порядка. Принципиальное отличие состоит в тенденциях
плазмы. Плазма стримера склонна к потере проводимости, осо-
бенно в воздухе, из-за прилипания, плазма лидера — пет. Вер-
шина длинного стримера теряет электрический контакт с источ-
ником высокого потенциала, вершина лидера — пет. Отсюда не-
достаточность стримера для пробоя длинного промежутка.
Различие тенденций связано с температурой газа в вершине
капала, которая зависит от силы тока и мощности, выделяемой
на единице длины (ср. с формулой 12.23). Повышенная темпе-
ратура в лидерной головке подавляет эффект прилипания в воз-
духе. Это открывает путь к дальнейшему росту температуры и
ионизации (как при контракции тлеющего разряда).
Непосредственное образование из лавин канала с достаточ-
ным для нагрева газа током не осуществляется, так как еще до
этого происходит лавинно-стримерный переход. Стоит числу
электронов дорасти до некоторого не чрезмерно большого числа,
а радиусу лавины до весьма малого значения го, как лавина
тотчас превращается в стример с таким радиусом, слабым током
и малой погонной мощностью. Для лавинно-лидерного перехода
лавине нужно было бы порасти еще, но лавинно-стримерный
переход рост пресекает, Поэтому достаточно сильноточный ли-
45)
дерный канал может образоваться только путем объединения
стримеров.
Отметим в заключение оригинальную теорию распространения
лидера [14.24], в которой ионизация свежих порций газа, за-
хватываемого передним фронтом (головкой), связывается с на-
гревом его ударной волной. Источником последней служит вы-
деление джоулева тепла в лидерной головке. Этот механизм по-
добен световой детонации (см. о ней [25]). Однако при всей
привлекательности механизма его количественная аргументация
не представляется очень убедительной. Об отрицательном лиде-
ре см. § 12.
§ 10. Обратная волна (возвратный удар)
Это — заключительная стадия пробоя, после чего начинается
«искровой разряд» в буквальном смысле слова. Когда головка
лидера касается электрода, заряд ее немедленно нейтрализуется,
а вершина канала приобретает потенциал электрода. Если это
катод, электроны из него вырываются фотонами или сильным
полем, и образуется катодное пятно, если анод — электроны ли-
дера уходят в металл. По лидерному каналу распространяется
в направлении к острию обратная волна снятия потенциала и ис-
чезновения погонного заряда лидерного канала и его окружения
(чехла); заряд может нейтрализоваться и не полностью. Физи-
ческий механизм эффекта обратной волны лучше всего пояснить,
уподобляя процесс разряду заряженной длинной линии при за-
мыкании ее на землю. Именно такая трактовка явления приме-
нялась для модельных численных расчетов [14.23].
Пусть вдоль длинного провода распределен электрический
заряд q на 1 см. Емкость, индуктивность и омическое сопротив-
ление на 1 см обозначим С, Z, R. Потенциал U (по отношению
к «земле») и ток i как функции времени t и координаты х вдоль
провода описываются уравнениями
= + = (14.22)
дх с2 dt дх dt 1 ' 7
имеющими довольно прозрачный физический смысл (см. любой
курс теории электричества). В случае идеального проводника
(7? = 0) уравнения (14.22) сводятся к волновому:
дЧЦдР — v2d2U!dx2 = 0, (14.23)
где скорость волн и = с/УLC.
Если в начальный момент t = 0 равномерно заряженную ли-
нию go = CUq = const, в которой io = 0, замкнуть на землю, где
U = 0, то по линии со скоростью v побежит от земли волна сня-
тия потенциала и разряда линии (рис. 14.19). Сила тока за вол-
ной 1 = —С7о/р = —до*А где р = с"11/£/С—так называемое вол-
460
новое сопротивление. В такой идеализированной схеме потенциал
на фропте волны меняется
«бесконечно». Для провода радиуса
большом расстоянии Н зазем-
ленным цилиндром, L = C~X =
= 21н(Я/г) в абсолютных едини-
цах и v совпадает со скоростью
света с.
Реально, при наличии у про-
водника активного сопротивления,
заряда в чехле вокруг лидерного
канала, фронт волны имеет ко-
нечную ширину, поле там конеч-
но, а скорость, как показывают
опыт и оценочные расчеты
[14.23], v ~ 0,1 с. Именно это
от Uо до нуля скачком, а поле там
г в пустоте, окруженном па
сильное поле в «скачке» потен-
циала сообщает электронам боль-
шую энергию, а на макроскопи-
ческом языке — во фронте волны,
где одновременно велики и ток,
и поле, выделяется большое ко-
личество джоулева тепла W =
= Ei [Вт/см]. Эта проносящаяся
лю идеальной положительно за-
ряженной линии, моделирующая
обратную волну после прихода
на катод положительного лидера;
t — 0 — момент замыкания линии
на землю, Ц, t2— моменты движе-
ния волны Показаны эпюры то-
ка и потенциала
по каналу волна мощного энерговыделения и приводит к фор-
мированию искрового канала, как описано в § 5. Некоторые циф-
ры будут приведены применительно к разряду молнии (п. 11.5).
§ 11. Молния
11.1. Грозовое облако. Первопричиной электрических разрядов
в атмосфере является образование и пространственное разде-
ление положительных и отрицательных зарядов, благодаря чему
возникает электрическое поле. Если поле достигает значения,
достаточного для искрового пробоя воздуха, происходит разряд.
Примерно в 90 % случаев отрицательный заряд располагается
в нижней части облака, а основной положительный — в верхней.
Для грозового облака, изображенного па рис. 14.20, разности
потенциалов V между центрами положительного и отрицательно-
го зарядов Q, а также между отрицательной нижпей частью
облака и землей имеют порядок V ~ Q/L — 108 В (Q =40 Кл =
= 3,6-1011 В • см, L~2—5 км), средние электрические поля —
порядка ЕСТ) — VIL ~ 300 В/см. Такого порядка поля измеряют
и у земли под грозовыми облаками, и внутри облаков (с само-
летов).
Современные представления о происхождении атмосферного
электричества были заложены в 40-х годах Я. И. Френкелем
[14.26] (см. также [14.27]). Заряды в атмосфере появляются в
результате ионизации молекул или вырывания электронов из
461
макроскопических частиц под действием космического излуче-
ния. Возможна также электризация водяных капель при раз-
брызгивании во время падения. Отрывающиеся брызги уносят
преимущественно отрицательный заряд. Образовавшиеся при
ионизации воздуха отрицательные ионы склонны прилипать к
водяным каплям. Известно, что
полярные молекулы воды в по-
верхностном слое капли ориен-
тируются положительными кон-
цами вовнутрь, а отрицатель-
ными — наружу, отчего у по-
верхности образуется двойной
электрический слой. Внутри са-
мого слоя присутствует поле,
направленное в сторону возду-
ха; вне слоя поля нет. Следо-
вательно, в слое происходит
скачок потенциала Лер, причем
внутри капли ср выше, чем в
Рис. 14.20. Схема грозового облака
[14.25]; вероятное распределение
зарядов. Кружками обозначены
центры тяжести зарядов. Согласно
измерениям электрических полей
вблизи облаков вверху Q = +40 Кл,
внизу q — +10 Кл, Qo = —40 Кл
где г — радиус капли. При г =
окружающей среде; согласно
измерениям Аф = 0,26 В. Капля
захватывает отрицательные
ионы, пока не исчезнет раз-
ность потенциалов между жид-
костью и воздухом. Число по-
глощенных зарядов N опреде-
ляется равенством eN/r = Аф,
-3 см N ~ 2 • 103. Разделение за-
рядов в масштабе облака является следствием оседания отрица-
тельно заряженных капель под действием силы тяжести; многие
положительные заряды остаются в молекулярном виде и вниз не
стремятся.
Вообще говоря, искровые разряды внутри облака происходят
чаще, чем с нижней части облака па землю. Но по понятным
причинам экспериментальному изучению подверглись именно по-
следние, поэтому о них и пойдет речь.
11.2. Методы исследования. В 1900 г. Бойс сконструировал
камеру для скоростного фотографирования молнии. Под диском
с двумя объективами, расположенными на диаметральной прямой
по обе стороны от центра, лежит пленка. Диск вращается, и на
пленке получаются две фоторазвертки процесса. В 1929 г. Бойс
сделал камеру, в которой неподвижные объективы с помощью
призм отбрасывают изображение на движущуюся пленку. Плен-
ка укреплена на внутренней стороне вращающегося барабана*).
Первые фоторазвертки молнии, их теперь называют бойсограм-
*) В типичном современном скоростном фоторегис1раторе (СФР) непо-
движны и объектив и пленка, а луч бежит по пленке, отражаясь от вра-
щающегося зеркала.
462
мами, Бойсу удалось получить только в 1928 г. В основе совре-
менных представлений о ходе развития разряда молнии лежат
исследования Шопланда (1935—1940 гг.) с применением усо-
вершенствованных камер Бойса.
Наряду с фотографированием измеряют электрический ток
разряда. Лучше всего, когда это удается сделать при помощи
«молниеприемника», т. е. осциллографировать ток в том месте,
куда ударяет молния. Особенно ценны одновременно получен-
ные, синхронизированные фоторазвертки и осциллограммы то-
ка. Регистрируют с помощью антенн и других устройств элект-
рические и магнитные возмущения, вызванные разрядом, по
извлечение из них сведений о токе молнии — задача не простая.
Раньше широко применяли клидонографы — приборы, в которых
получаются фигуры Лихтенберга (п. 1.1). В СССР молнией мно-
го занимались И. С. Стекольников (с 30-х годов) и его школа.
Ее успехи во многом связаны с удачным сочетанием исследова-
ний молнии и лабораторных длинных искр [14 28, 14.23]. О ме-
тодах и аппаратуре см. также [14.25].
Рис 14 21 Схема разряда молнии. % — первый (ступенчатый) лидер идет
к земле со скоростью vb б—волна возвратного удара идет вверх со ско-
ростью v2, в — произошел внутриоблачныи пробой от канала возвратного
удара на левую часть облака, заряд правой части стек по искровому кана-
лу, г — второй лидер (стреловидный) идет со скоростью v3 по частично рас-
павшейся плазме искрового канала, и т. д
11.3. Ход событий. Световая вспышка молнии длится в сред-
нем 200 мс. Она состоит из нескольких импульсов по 10 мс с
интервалами примерно по 40 мс. Каждый импульс начинается с
прорастания от облака к земле лидерного канала (рис. 14.21).
Светится канал слабо, за исключением головной части. Лидер
переносит отрицательный заряд (из отрицательного облака),
и при этом течет ток порядка 100 А. По мере приближения к
земле канал ветвится, пути ветвей имеют зигзагообразный ха-
рактер. Когда основной лидер достигает земли или сталкивается
со встречным лидером, обратно, к облаку, по его пути с огром-
ной скоростью порядка 0,1—0,3 скорости света распространяется
ярко светящийся канал — обратная волна. Это явление называ-
ется возвратным ударом или главной стадией молнии. Ток мол-
нии при этом достигает максимальной величины порядка 100 кА.
Именно с этим, пиковым током связаны наиболее опасные воз-
463
действия молнии (перенапряжения в линиях передач и др )
Потом через образовавшийся искровой канал в течение 40 мс
небольшим током 200 А стекает на землю отрицательный заряд
облака Отток электричества из большого объема облака, с раз-
мерами порядка 1 км, возможен только благодаря освобожде-
нию электронов из отрицательно заряженных макроскопических
частиц и ионов, что происходит под действием сильного ноля
От тепловыделения в канале повышается давление, что сло-
жит источником ударной волны Акустическая волна, в которую
вырождается на больших расстояниях ударная, воспринимается
как гром При разряде молнии выделяется энергия QV/2 ~
~ 109—1010 Дж, которая соответствует энергии взрыва порядка
тонны взрывчатого вещества По спектроскопическим измерени-
ям, температура в искровом канале примерно 25 000 К, п ioi-
ность электронов (1—5) 1017 см-3 [14 25], что соответствует
полной однократной ионизации атомов
За один импульс в землю стекает только часть заряда облака,
расположенная ближе к месту, до которого доходит вершина
канала возвратного удара Подвод к ней зарядов из удаленные
районов требует времени, и потому разряд на землю на какой то
срок затихает Заряды из далеких частей облака приходят к
вершине канала в результате местных внутриобличных пробоев,
и, когда путь к дальним областям оказывается проложенным,
начинается следующий импульс молнии К этому моменту про-
водимость в искровом канале первого удара падает и по оста-
точному каналу распространяется от облака к земле новый ли-
дер Он увеличивает ионизацию в старом канале Второй и по
следующие лидеры не ветвятся Когда второй лидер доходит до
земли, происходит второй возвратный удар, и так повторяется
несколько раз, пока весь отрицательный заряд облака из все
более удаленных районов не стечет на землю Расположенный
совсем далеко (высоко) положительный заряд, по видимому,
остается, так как для столь большого расстояния от земли на-
пряжение между ним и землей слишком мало для пробоя
11.4. Несхожесть первого и последующих лидеров. Как сле-
дует из бойсограмм (рис 14 22), движение к земле первого от
рицательного лидера имеет прерывистый характер На фотогра-
фии быстро вспыхивает яркая полоска (ступень), соответствую-
щая натурной длине 50 м, потом на 50 мкс свечение пропадает,
и так повторяется систематически Такое впечатление, будто ли-
дер движется быстрыми рывками с паузами Он был назван
ступенчатым Средняя скорость продвижения переднего фронта
лидера к земле, определенная по наклону огибающей ярких по
лосок на фоторазвертках, составляет (1—2) 107 см/с Радиус
лидера, судя по фотографиям, имеет порядок 1 м, но, без сомне-
ния, радиус светящегося тела гораздо больше радиуса истинно
высокопроводящей зоны Лидеры второго и последующих ударов
движутся непрерывным образом, без всяких ступеней, и с го-
раздо большей скоростью (108—109 см/с) Они были названы
464
70мкс 60 мкс 1мс
20мс и ООмс ,2мсл ЪОмс
-----------------------------Hf-
Рис. 14.22. Схема бойсограммы, полученной путем фотографирования вспыш-
ки молнии камерой с движущейся пленкой: а — развертка; б — та же
вспышка, сфотографированная без развертки. Время идет слева направо,
для удобства шкала времени нелинейна [14.25]
стреловидными из-за некоторого внешнего сходства изображения
па бойсограмме со стрелой.
Рис. 14.22 дает представление о временных интервалах меж-
ду последовательными этапами процесса разряда, а табл. 14.2 —
Таблица 14.2. Основные параметры молнии с отрицательного облака
на землю *
Этапы процесса разряда Значение параметров
наименьшие | характерные наибольшие
Вспышка
Длительность, с 0,01 0,2 2
Число импульсов ' 1 3-4 26
Интервал между ними, мс 3 40 100
Полный переносимый заряд, Кл Ступенчатый лидер 3 25 90
Длина ступени, м 3 50 200
Пауза между ними, мкс 30 50 125
Средняя скорость, см/с 1.107 1,5-107 2,6-108
Переносимый заряд, Кл Стреловидный лидер 3 5 20
Скорость, см/с 1.108 2-Ю8 2,1-10°
Переносимый заряд, Кл Возвратный у dip 0,2 1 G
Длина канала, км 2 5 14
Скорость, см /с Пиковый ток, кX 2-io9 5-Ю9 1,4-1010
10—20 110
Длительность пика по пол овинному уровню, мкс 10 40 250
Перенос заряда, кроме непрерывно- го тока, Кл 0,2 2,5 20
*) Систематизировано в [14.25] по данным многих измерений.
об их характерных параметрах. Ток лидера i ~ Q^vld, где (?л —
переносимый заряд, v — скорость его распространения, d — длина
лидера, порядка высоты облака. При (?л = 5 Кл, d = 3 км, и =
465
= 1,5 107 см/с i ~ 250 А Погонный заряд лидера q = QJd~
~ 10“5 Кл/см, i ~ qv Поле в лидерном канале, по видимому,
имеет порядок 100 В/см
11.5. Возвратный удар. Этот процесс был рассмотрен в § 10
За волной, которая распространяется вверх от земли, течет силь-
ный ток, уносящий в землю заряд из лидерного канала и его
окружения; потенциал приближается к потенциалу земли Перед
волной сохраняется потенциал лидера, близкий к потенциалу об-
лака, а тока практически нет, ибо лидерный ток кончается вме-
сте с прекращением движения лидера Судя по фоторазверткам,
обратная волна молнии проносится вверх со скоростью v ~ 0,1 —
0,3с 3 104—105 км/с, т е за 102 мкс Переходная область
фронта волны, где происходит перепад потенциала и имеется
сильное поле, которая по этой причине ярко светится, имеет на
развертке протяженность I ~ 25—110 м Значит, поле там Е —
~ V/1 ~ 10 кВ/см Для сильноионизованной плазмы это очень
большая величина в канале дуги в воздухе Е — 10 В/см При
токе возвратного удара i = 20 кА энерговыделение в области
фронта составляет W = Ei = 2 108 Вт/см (в дуге W — 103 Вт/см).
Ясно, что при таком огромном тепловыделении плазменный ка-
нал быстро расширяется и превращается в развитый искровои
Энергия при этом идет в основном на нагревание и термическую
ионизацию окружающих слоев воздуха, а не на существенное
повышение температуры и ионизации в самой зоне выделения
тепла, где ионизация и без того полная, однократная.
§ 2. Отрицательный ступенчатый лидер
Если вглядеться в бойсограмму, можно увидеть, что яркие
полоски (ступени) тянутся по направлению к земле не следом
друг за другом, а «внахлест»: каждая начинается с «возвратом»,
с середины предыдущей Это не вяжется с простой интерпрета-
цией прерывистой картины* быстро движущееся светящееся об-
разование прописывает на фотопленке полоску, а потом на вре-
мя останавливается В книгах [2, 3, 21, 26, 14 25] вопрос о смыс-
ле, вкладываемом в термин «ступенчатый», молчаливо обходится
По поводу ступенчатого механизма движения лидера, начиная
с Шонланда (1938 г), выдвигали различные гипотезы, но все
рассуждения и оценки настолько туманны и расплывчаты, что,
видимо, не случайно в весьма обстоятельной книге Юмана
(1969 г) [14 25] их пересказ представляется лишенным физи-
ческого смысла *).
Дело еще и в том, что экспериментальное изучение такою
удаленного, случайного и неудобного объекта, каковым является
молния, не поставляет достаточной информации для проникно-
*) Сам Юман, говоря о теории молнии, подчеркивает бессодержатель-
ность употребления терминов «лидер пилот», «стример», которым подменя-
ется физическое объяснение явлении.
466
вения в детали сложнейших явлений искрового разряда. И дей-
ствительно, лабораторные исследования многометровых искр с
отрицательного острия, когда у лидера также появляются сту-
пени (при d = 6 м 3—
5 штук [14.23]), если не
позволяют пока пол-
ностью понять физиче-
ские причины, то по
крайней мере, в силу
лучшего разрешения,
дают возможность де-
тальнее восстановить
ход явления.
На основании элект-
ронно-оптических раз-
верток с одновремен-
ным осциллографирова-
нием лидерного тока
(и то и другое с очень
высоким разрешением)
вырисовывается следую-
щая картина (рис. 14.23)
[14.23]. Если в случае
положительного острия
или его «продолже-
ния» — положительного
лидера, которое притя-
гивает к себе лавины,
стримеры охотнее всего
образуются непосредст-
венно около вершин, то
в случае отрицательно-
го, от которого лавины
отталкиваются, лавин-
но-стримерный переход
может произойти толь-
ко на удалении от вер-
Рис. 14.23 Схема развития отрицательного
ступенчатого лидера, как это можно себе
шин острия или лидера.
На некотором расстоя-
нии от головки отрица-
тельного лидера возни-
кает яркое светящееся
плазменное образование
объемом около 1 см3.
От него отходят стри-
представить в результате расшифровки фото-
развертки процесса (приведена также осцил-
лограмма лидерного тока): 1 — головка кана-
ла лидера, 2 — канал лидера, 3 — катодона-
правленные стримеры, идущие от плазменно-
го сгустка (гипотетического направленного в
обе стороны «лидера»), 4— плазменный сгус-
ток, 5 — анодонаправленные стримеры, 6 —
ступень лидера [14.23]
меры, катодонаправлен-
ные — к головке лидера, анодонаправленные — к плоскому
электроду. Быть может, благодаря поляризации плазменного
сгустка внешним полем и усилению поля между положительным
467
зарядом диполя и головкой лидера, от плазмы навстречу основ-
ному отрицательному лидеру распространяется вторичный по-
ложительный. Когда лидеры сталкиваются, весь путь от острия
до противоположного конца вторичного лидера приобретает вы-
сокую проводимость, и это сопровождается броском тока, который
разогревает канал и дает вспышку (рис. 14.23). Головка основ-
ного лидера перескакивает на бывший плазменный сгусток, по-
лучается очередная ступень.
Конечно, модель не вполне убедительна, тем более что не
ясно происхождение гипотетического плазменного сгустка. Но,
вне всякого сомнения, понимание может быть достигнуто только
подобным путем целенаправленно поставленного лабораторного
эксперимента.
Понимание физики длинных искр, одного из самых сложных
явлений в газовом разряде, представляет не только познаватель-
ный интерес. Оно помогает решению практических задач техни-
ки высоких напряжений, молниезащиты. Не случайно над этой
проблемой работает международная европейская ассоциация
ученых «Группа Ренардье». Обширный отчет о ее недавних
работах см. [14.29].
Глава 15. ВЫСОКОЧАСТОТНЫЙ ЕМКОСТНЫЙ РАЗРЯД
§ 1. Дрейфовые качания электронного газа
1.1. Вводные замечания. В высокочастотных разрядах емко-
стного типа (ВЧЕ) ВЧ напряжение подается па электроды, чаще
всего — плоскопараллельные (рис. 9.20). Электроды могут со-
прикасаться с разрядом, могут быть изолированными от пего
твердыми диэлектриками. В этом смысле будем условно назы-
вать ВЧЕ разряды электродными или безэлектродными. Будем
ориентироваться в основном на наиболее употребительную «про-
мышленную» частоту /«13,6 МГц*) и средние давления 10—
100 торр, к которым сейчас проявляется большой интерес, от-
части в связи с перспективами применения ВЧЕ разрядов в
мощных лазерах (гл. 16). Плазма таких разрядов, как правило,
слабо ионизована, неравновесна и подобна плазме тлеющего раз-
ряда. Чтобы с пониманием воспринимать изложение результатов
наблюдений и измерений (§ 4), желательно иметь некоторые
самые общие представления о процессе ВЧЕ разряда. Их дают
излагаемая в п. 1.2 качественная схема и упрощенная теория
электротехнического толка (§2).
При давлениях р ~ 10 торр частота столкновений электронов
vm примерно в 103 раз превышает со = 2л/= 0,85 • 108 с”1, поэто-
*) Соответствующая длина волны X = 22 м принадлежит коротковол-
новому диапазону. Мощные ВЧ установки создают помехи для радиовеща-
ния и связи. Поэтому по международному соглашению для них выделили
несколько небольших интервалов частот, в том числе и около указанной.
468
му в осциллирующем поле типа Е = Еа sin cot электроны совер-
шают дрейфовые колебания (п. 1.3 гл. 3) с амплитудами скоро-
сти и смещений
гт 1 1 да №еР
Рда = Р^а, А = — - — - —
(15.1)
При Еа/р — 10 В/(смторр), что характерно для неравновесной
слаб’оионизованной плазмы молекулярных газов, и отмеченной о
амплитуда дрейфовых колебаний Л 0,1 см. Она мала по срав-
нению с типичными для экспериментов длинами разрядных про-
межутков вдоль поля L ~ 1—10 см. Дрейфовые скорости и амп-
литуды колебаний ионов в це/ц+~ 102 раз меньше, так что ко-
лебательное движение иопов во многих случаях вообще можно
не принимать во внимание. Даже при весьма низкой плотности
электронов пе = 108 см~3 и характерной для столкновительной
плазмы электронной температуре Те = 1 эВ дебаевский радиус
dD = 0,05 см < L. Поэтому в большей части разрядного проме-
жутка плазма электронейтралъна. Одпако около границ плоского
промежутка электронный газ, совершая
качания относительно «неподвижных» ^=0
ионов, периодически обнажает положи-
тельные заряды, подобно тому как при-
брежная волна, скатываясь, оголяет я.
песок. Это является первопричиной по- 2
явления приз лектродных слоев про-
странственного заряда. Приэлектродны- п
ми будем для краткости называть и
слои около диэлектриков, когда элект-
роды изолированы от плазмы. Ъп
1.2. Распределения пространствен- 2
ного заряда, поля и потенциала в плос-
ком промежутке. Допустим, что элект-
роды оголены. Те электроны, которые
в момент прохождения положения рав-
новесия при колебаниях отстояли от
электродов на расстояниях, меньших
амплитуды колебаний, после первых
же качаний «навсегда» уходят в ме-
талл [15.1]. В состоянии равновесия с
обеих сторон остаются слои нескомпен-
Рис. 15.1. Схема качаний
электронного газа. Распре-
деления 7?е(я) показаны че-
рез каждые четверть перио-
да. Предполагается, что
ионный газ неподвижен и
однороден. Время отсчиты-
вается от момента, когда
электроны проходят через
положение равновесия в
движении направо
сированного ионного заряда. Газ в целом оказывается заряженным
положительно*). При последующих качаниях электронный газ,
если отвлечься от медленного диффузионного процесса, только
«касается» электродов. На рис. 15.1 схематически изображена
картина качаний электронного газа в предположении, что ионы
*) Заметим, что в обычном тлеющем разряде постоянного тока газ в це-
лом также заряжен положительно в силу существования катодного слоя
(отрицательный заряд анодного слоя гораздо меньше). '
469
совершенно неподвижны и однородно распределены по длине
промежутка, а диффузионное движение электронов отсутствует.
На самом деле диффузия размывает границы между плазмой и
ионными с чоями. На рис. 15.2 построены соответствующие
рис. 15.1 распределения поля и потенциала в те же моменты
времени, через каждые четверть периода. Поле Е в однородной
электропейтральной части промежутка постоянно по его длине.
Потенциал для определенности отсчитывается от левого электро-
да. Можно себе представить, что он заземлен, а переменное на-
пряжение подается па правый. Значение и направление элект-
рического тока, можно считать, характеризуются напряжен-
ностью поля Е в плазме, так как чаще всего в самой плазме ток
проводимости преобладает над током смещения.
Рис. 15.2. Распределения
поля и потенциала по
длине промежутка, со-
ответствующие рис. 15.1
Как известно из разнообразных экспериментов, электроны, по-
падающие на поверхность диэлектрика (стекла и др.), прилипа-
ют к поверхности. Диэлектрик при этом заряжается отрицатель-
но до тех пор, пока возникающее поле пе начинает отталкивать
последующие электроны (п. 1.7 гл. 10). Так происходит и в ВЧЕ
разрядах с изолированными электродами, причем поверхность
изолятора способна воспринять все электроны, которые содержа-
лись бы в приэлектродном слое. Иными словами, рис. 15.1, 15.2
в равной мере относятся и к ВЧЕ разрядам с изолированными
электродами. Хотя прямым путем это и не наблюдалось, косвен-
470
пые экспериментальные подтверждения тому имеются (п 6 4)
Да и заметного различия между электродными и безэлектрод-
ными ВЧЕ разрядами опыт не обнаруживает*)
§ 2. Идеализированная модель протекания
быстропеременного тока через длинный
плоский промежуток при повышенных давлениях
2.1. Уравнения электрического процесса в безэлектродном слу-
чае. Рассмотрим плоский разря щыи про Юиуток достаточно
бо 1ьшоч h и i т I вдо ib тока и б\ дем считать ппоттесс одно мер
ным т е не зависящим от поперечз ых координат Ниже станет
ясно, для чего нужны оговорки д типпыи промежуток повышен
ные давления Пусть электроды изолированы от и а^иы щ
электрическими пластинами толщины I с диэлектрической про
ницаемостыо 8 (рис 15 За) В плазме положим 8 = 1 Из урав
нении непрерывности для плотности объемною заряда р, эки
ростатики и закона Ома для тока проводимости /1 в пл а м(,
ар ^7 п дЕ . г /1 )\
лт — О, — — 4лр, ]1 = оЕ, (1 ) 2)
dt дх 1 дх ‘ J1 ’ х '
следует, что сумма токов проводимости и смещения (п 3 2 i i
К = 31 Исм = 7(0 (1 • >)
в данный момент времени от координаты х пе зависит
Будем считать плазму электропеитральпои в> нем щ < ш
жутке, за исключением топких слоев у границ, i ( (осрс ци вш
ваются заряды, вызванные ее поляризацией Зэр i и б>дсм рас
сматривать как поверхностные Это эквивалентно < ii\iii(iiii') сю
однородности плазмы в объеме В самом де ie но (1 ) 2) (1 ) >)
если р = 0, то Е, ji, о от х не зависят И обр и о (ощипн
однородность промежутка, мы придем к выводу о) > к upon ir
ральпости плазмы в объеме Обозначим q\ и с/ и юн ости ши ( р\
постных зарядов в плазме и на электродах Пос к ц ш «собира
ются» из внешней цепи под действием при южын он )ДС
В плазму их не пускают изоляторы (см также п 2 2) Паправ
ления полям в диэлектриках Ел и знаки заря щм 7, q\ припп
*) Если к подобной системе с изолированными электродами приложите
постоянное пробивающее напряжение в газе происходит пробо i После это
го электроны из промежутка прилипают к диэлектрику покрывающему по
ложительныи электрод Возникшее поле эшго заряда будучи направленным
в области промегкутка противо олокчо приложенному частично уншттожа
ет последнее Поле в промежутке снижается до значения недостаточною
для поддержания ионизации а моакчт быть, и полностью исчезает и веко
ре все прекращается Пак показывает опыт, такая «дт э зектрическая ячейка»
может после этого сколь угодно долго «держать» приложенное сверхпро
бивнос напряжение без повторения пробоя или протекания сколько нибудь
заметного тока
471
шем один раз, в соответствии с мгновенной картиной, изобра-
женной на рис. 15.3а. В дальнейшем уравнения сами будут
управлять знаками алгебраических значений полей, зарядов и
токов.
Применяя общие уравнения электростатики (5.16), (5.17) к
границам Электрод — диэлектрик и диэлектрик — плазма и учи-
тывая, что поле в металле пренебрежимо мало из-за огромной
проводимости, находим
— 4лд, Е—sE^ — —4nqi. (15.4)
Применяя к тем же границам уравнение непрерывности, по-
лучас и
с/1 dqjdt = /1, q = i/S,
(15.5)
цепи, S — площадь электродов. Из ком-
где i — ток во внешней
бинации равенств (15.4),
(15.5) следует, что ток во
внешней цепи i(t) совпа-
дает с полными токами в
диэлектриках и промежут-
ке ]S (по (15.3)), что вы-
ражает закон сохранения
суммарного тока проводи-
мости и смещения вдоль
всей электрической цепи.
Рис 15 3 Схема безэлектродного ВЧЕ раз-
ряда а — конструкция разрядной камеры
(знаки поверхностных зарядов, направле-
ния полем и тока соответствуют фазе, в
которой заряд на верхнем электроде поло-
жительный и уменьшается); б — эквива-
лентная электрическая схема разрядного
устройства
В рамках допущения
о поверхностном характе-
ре зарядов у границ плаз-
мы, т. е. о «нулевой» тол-
щине слоев пространст-
венного заряда, не суще-
ствует падений потенциа-
ла в слоях. Откладывая
обсуждение вопроса о реальных слоях и падениях, заме-
тим. что пренебрежение любыми приэлектродными явлениями и
соответствующими падениями потенциала в какой-то мэре может
быть оправданным, если эти падения малы по сравнению с на-
пряжением 71= EL =(Elp)pL на однородной плазме, а занимае-
мая последней длина составляет значительную часть всего про-
межутка. Реально при средних давлениях приэлектродные паде-
ния потенциала в среднем за период не превышают 200 В, а тол-
щины неоднородных приэлектродных областей порядка 1 см
(§4). Следовательно, для достаточно больших pL (вспомним
оговорку) рассмотрение не лишено смысла. Оно вполне соответ-
ствует теории тлеющего разряда в случае больших pL, когда
внимание можно сосредоточить на положительном столбе, анало-
гом которого и является однородная плазма. Так и будем назы-
вать ее «положительным столбом».
472
В сделанных предположениях мгновенное напряжение па
электродах
V = 2EJ + EL. (15.6)
Исключая поля из (15.6), (15.4) и равенства ji=aE, получаем
систему уравнений
Ятг/ 1
V т7 1 Т’ 71 = 4л(Т0— 91)’ 91 = /|- '/ = /, (15.7)
которая описывает протекание тока. Ее следует дополнить урав-
нением внешней цепи—аналогом равенства (10.1), связываю-
щим V и j*). Системе (15.7) можно придать «электротехниче-
скую» форму. Введем вместо плотностей токи i = ]S, ii=jyS и
заряды Q = qS, Qi = q\S, омическое сопротивление разряда R =
= L!eS, емкости диэлектриков Сд = е£/4л/ и плазменного прост-
ранства С = S/faiL. Получим
^ = £^£1, = Q = i. (15.8)
Отвечающая им эквивалентная электрическая схема изображена
на рис. 15.36. Ток проводимости течет через активное сопротив-
ление, ток смещения — через плазменную емкость, причем
2.2. Уравнения в случае оголенных электродов. Если нет изо-
лирующих пластин, из эквивалентной схемы рис. 15.36 следует
изъять емкости Сд (рис. 15.4). Тогда
V = ikR, tlR=?-^l, Ci = h, Q — i. (15.9)
Вопрос о механизме замыкания тока на границе между плазмен-
ным и металлическим проводниками в данном приближении не
рассматривается. Токи зарядов
по разные стороны границы
не одинаковы. i=£ i\, и поверх-
ностный заряд на границе су-
ществует, Q — =/= 0, вследст-
вие различия проводимостей
плазмы о и металла («о = °°»).
Уравнениями (15.8), (15.9)
описываются не только ВЧ, но
вообще нестационарные разря-
ды, скажем, импульсные, лишь
бы при их характерной дли-
Рис. 15.4 Схема устройства (а) и эк-
вивалентная электрическая схема
(б) электродного ВЧЕ разряда, ана-
логичные рис. 15.3
тельности не нарушались сде-
ланные приближения. Например, смещения электронов должны
быть малыми по сравнению с L.
2.3. Решение для случая изолированных электродов. Плазма
в разрядном промежутке поддерживается полем, и, поскольку
*) Оно зависит от схемы подключения ВЧ генератора: заниматься этим
не синем
<31 ю П Райзер
473
поле осциллирует, периоды преимущественного рождения элек-
тронов чередуются с периодами преимущественной их гибели.
Допустим, что к электродам приложено синусоидальное напря-
жение V = sin d)t. Пусть за полупериод колебании плазма рас-
падается лишь в малой степени. На рассматриваемой частоте
/ ~ 107 с-1 это условие выполняется: характерные частоты гибе-
ли электронов в плазме тлеющего разряда не превышают 105 с-1.
Тогда глубина модуляции пе, о и R (с частотой 2/) незначитель-
на и R (t) ~ const. Уравнения (15.8) можно интегрировать, рас-
сматривая сопротивление плазмы как постоянный параметр (по-
ка нам неизвестный; § 3). Приведем результаты этого несложно-
го вычисления. Напряжение на плазме Fi, поле в плазме Е, ток
проводимости й, пропорциональные друг другу, определяются
формулой
= EL -= hR = —°- —г -Л sin (<ol цф), (15.10)
l+zc /Сд у 1Л_ ш-т2
т = R (CJ2 + С), ср = arctg сот.
Ток во внешней цепи (ток разряда)
у СОТ|01 + СО\2
?а = “/ГП ъ--7^х—.Г-------, Sin (со! + ср 4-Аф), 05.11)
Л 0 “ /сд» V 1 + огт2
т0 = RC = 1/4ло, Лер = arctg сота.
Амплитуда напряжения па плазме Fu тем меньше амплиту-
ды приложенного Fa, чем меньше емкость изоляторов (меньше
сот). Тем большую часть напряжения берут на себя изоляторы.
Напряжение Fi сдвинуто по фазе относительно V, так как через
диэлектрики цроходит исключительно ток смещения. По той же
причине, а также вследствие существования тока смещения в
плазме разрядный ток i сдвинут по фазе относительно F. Время
т характеризует инерционность всего конденсаторного устройст-
ва, изображенного на рис. 15.3. Если его зарядить, а потом со-
единить электроды накоротко, чтобы дать возможность разря-
диться, то при условии, что плазма не успеет распасться
(7? const), заряд будет релаксировать по закону Q = Q (0)е_//т.
Время та характеризует скорость рассасывания объемных за-
рядов в самой плазме (п. 2.2 гл. 11). Величиной сот(1 = со/4ло,
уже знакомой нам по п. 5.6 гл. 5, определяется отношение ам-
плитуд токов смещения и проводимости в плазме:
Ама —
Поскольку эти
и\ амплитуды,
474
- сотп. (15.12)
11а
1 + (0-т2
(О
токи сдвинуты по фазе на л/2, складываются не
, > 2 2
а квадраты амплитуд: ta 1х см.
2.4. Вариант с оголенными электродами. Аналогично преды-
дущему из (15.9) найдем
Vx = EL = ixR = V = Va sin at, (15.13)
z - J^7/?) 1 + gj2Tq sin (at k Аф). (15.14)
Сдвиг по фазе Аср между разрядным током i и полем в плазме Е
или током проводимости в ней i\ такой же, как и в случае изо-
лированных электродов, и дается формулой (15.11). Остаются
в силе и формулы (15.12). Однако теперь нет отличия между на-
пряжениями на плазме Fi и на электродах F. Ведь мы прене-
брегли возможной «изоляцией» электродов приэлектроднымл
слоями, которым приписали «нулевую» толщину.
§ 3. ВАХ однородного положительного столба
Решение § 2 показывает, какие поле и ток возникают в одно-
родной протяженной плазме с определенной проводимостью, если
к электродам приложено ВЧ напряжение. Другая сторона вопро-
са — это какая проводимость возникает в разрядном промежутке
в данном поле, или же какое поле требуется для поддержания
определенной плотности электронов. Это уже зависит от элект-
ронных процессов в плазме, и соответствующая связь пе и Е или
j и Е представит собой ВАХ положительного столба разряда.
При известных прочих условиях ее можно превратить в ВАХ
всего разрядного устройства. Условия поддержания неравновес-
ной однородной плазмы ВЧ разряд'а, в принципе, не отличаются
от таковых для положительного столба тлеющего разряда
(§ 6 гл. 10): ионизация должна компенсировать потери
электронов.
3.1. Частота ионизации ВЧ полем. Она определяется энерге-
тическим спектром электронов. Спектр зависит от частоты поля.
Он устанавливается со скоростью, которая характеризуется час-
тотой потерь энергии электрона vu = vm6 (п. 3.7 гл. 3). Если
со > vm6, спектр не успевает реагировать на осцилляции поля.
Как разъяснялось в п. 5.4 гл. 9, частота ионизации в ВЧ поле
vlB4 не отличается при этом от частоты ионизации чг(Е) в по-
стоянном поле Е, равном эффективному значению переменного
поля £эф. Последнее выражается через Еа, a, vm формулой
(7.33). В том диапазоне частот, где vw > со > vm6, Едф совпадает
со среднеквадратичным полем
EJ/2.
В противоположном пределе со < vm6 спектр «следит» за ос-
цилляциями поля, все время подстраиваясь к мгновенному зна-
чению E(t), а «мгновенная» частота ионизации совпадает с ча-
стотой ионизации в постоянном поле той же величины. В этом
Л*
475
случае нужно просто усреднить уг [Е (t) ] по времени:
2Л/С0 л/2
viB4 = 2^- f V{ (Еа | sin coi |) dt = J (Ea sin cp) dtp. (15.15)
о 0
Поскольку чг(Е)—функция очень крутая, ионизация фактиче-
ски происходит короткими всплесками в моменты амплитудных
значений поля. В остальное время преобладают потери электро-
нов. В молекулярных газах: N2, воздухе, лазерных смесях
СО2 + N2 + Не, при давлениях р > 30 торр ситуация близка ко
второму предельному случаю. Потери электронов при этом ха-
рактеризуются эффективным коэффициентом рекомбинации рэф
(§ 8 гл. 10). Если ионизационный коэффициент ос(Е) задан в
таунсендовской форме (4.8), разложением 1/sin ср около ср = л/2
получим полезную для расчетов формулу
vtB4 = (2Еа/яВр)У2уг(Еа), ^г(Е) ~ ехр(— BpfE), (15.15')
прямо выражающую vlB4 через частоту ионизации в постоянном
поле амплитудного значения. Коэффициент при хг(£'а) характе-
ризует долю времени, в течение которого фактически происходит
ионизация. Формула (15.15') тем точнее, чем меньше эта доля.
3.2. Пример расчета ВАХ. Рассмотрим положительный столб
разряда на частоте /= 13,6 МГц в лазерной смеси СО2 : N2: Не =
= 1:6:12 при р = 30 торр, что соответствует условиям в мощ-
ных быстропроточных СОг-лазерах [16.11, 16.13] (п. 4.4, 4.5
Рис. 15.5. Расчетная зависимость амплиту-
ды поля в плазме положительного столба
ВЧЕ разряда от плотности электронов (эк-
вивалент ВАХ столба). Смесь СО2: N2:
: Не = 1 : 6 : 12, р = 30 торр, [}эф = 4 X
X Ю~6 см3/с; сплошная кривая — элект-
ронный спектр «следит» за осцилляциями
поля (предел «низких» частот): штрихо-
вая — спектр не успевает пульсировать и
соответствует постоянному полю, равному
среднеквадратичному. На частоте 13.6 МГц
истинная зависимость близка к сплошной
кривой [15.2]
гл. 16). В такой плазме рэф ~ 4 • 10~6 см3/с. Для поддержания
электронной плотности пе требуется частота ионизации хгВч =
= рэф/ге, скажем, для пе = Ю10 см~3, 'vtB4 = 4-104 с-1. Эта величи-
на, которой характеризуется и скорость распада плазмы, столь
мала по сравнению с /, что пульсации пе около среднего значе-
ния ничтожны. Для данной смеси 6 ~ 0,8 • 10~2 и скорость уста-
новления электронного спектра ~ 6,4 • 108 с-1 почти на поря-
док больше со = 0,85 • 108 с-1. Поэтому спектр, можно считать,
осциллирует вместе с полем, и хгВЧ определяется формулой
(15.15). На рис. 15.5 сплошной кривой показана рассчитанная
таким образом «ВАХ», точнее, зависимость Eajp от плотности
476
электронов. Для сравнения штриховой кривой показана та же
зависимость, найденная в предположении, что электронный
спектр пе испытывает осцилляций и соответствует постоянно-
му полю
Е==Еа/У2,
как было бы в случае > со > При заведомом выполнении
неравенства vm ® истинная кривая лежит между проведенны-
ми, но, в соответствии с оценкой со < vm6,— ближе к сплошной.
Как видим, диапазон между предельными вариантами невелик.
Это и естественно, ибо в одном пределе «ионизует» поле
ЕМ 2 = 0,7£о,
в другом — чуть меньше Еа. При расчете отвод тепла от разряда
предполагался достаточно сильным и влияние нагрева газа на
ВАХ (§ 7 гл. 10) не учитывалось.
3.3. Пример расчета электрических параметров безэлектродно-
го разряда. Для иллюстрации «электротехнической» модели § 2
проделаем расчет разряда в том же газе при тех же р и /, что
и в п. 3.2, применительно к следующим геометрическим парамет-
рам установки [16.13] (п. 4.5 гл. 16): L==5,5 см, /=1 см, 8 = 5.
Остановимся на случае пе = 3 • 1010 см-3. При vm = 0,8-1011 с-1
проводимость о=1,0 10-4 Ом-1 • см-1. По рис. 15.5 для поддер-
жания плазмы с такой проводимостью требуется Eafp^
= 10 В/(см-торр). Плазменный параметр сота = 0,08. При этом
/1а//сма=13. Таким образом, в плазме течет в основном ток про-
водимости и амплитуда его плотнорти ja ~ о£а ~ 30 мА/см2. Энер-
говклад в плазму оЕа/2 = 4,9 Вт/см3.
Напряжение на столбе Via=l,6 кВ. Отношение емкостей
CJ2C = 14 и параметр сот = 1,2. Амплитуда напряжения на
плазме Via составляет 0,71 амплитуды приложенного Уа, так что
последняя равна Va = 2,3 кВ. Сдвиги по фазе между £, V] и V
<р = 50°, между током по внешней цепи и напряжением (i и V) —
ср + Аср = 55°.
В основе проделанного расчета лежит допущение о том, что
главным в разряде и в отношении падения напряжения и по
протяженности вдоль поля является «положительный столб» —
однородная плазма, свободная от влияния приэлектродных эф-
фектов. Так бывает при достаточно больших pL. На опыте часто
исследуются не слишком протяженные разряды и при не слиш-
ком больших давлениях, когда и приэлектродные падения потен-
циала существенны, и положительный столб занимает далеко не
всю длину промежутка. В этих случаях теория усложняется:
в частности, в равенство (15.6) следует включать падения на-
пряжения на приэлектродных слоях.
477
§ 4. Эксперимент — о двух формах существования
ВЧЕ разрядов и постоянном положительном потенциале
пространства
Экспериментально установлено, что ВЧЕ разряды горят в од-
ной из двух сильно различающихся форм. Внешне они отлича-
ются характером распределения интенсивности свечения по дли-
не промежутка, по существу — процессами в приэлектродных
с чоях и механизмами замыкания тока на электроды. Впервые на
этот факт обратил внимание С. М. Левитский (1957 г.) Его ра-
боты [15.1, 15.3] немало способствовали формированию совре-
менных представлений о природе явлений в ВЧЕ разрядах сред-
него давления.
4.1. Скачки на кривых потенциала зажигания. В опытах
[15.3] исследовались разряды в водороде и аргоне в стеклянном
Рис 15 6 Потенциал зажига-
ния электродного ВЧЕ разря-
да в зависимости от давления
(водород, f = 3 МГц, L —
= 2,64 см); левая ветвь до
скачка — ^-разряд, штриховая
кривая — потенциал вторично-
го зажигания (перехода а- в
7-форму) [15 3]
сосуде с введенными вовнутрь па-
раллельными оголенными дисковы-
ми электродами диаметром 4,2 см.
Расстояние L между ними варьиро-
валось до 10 см, частоты использо-
ванного 100-ваттного ВЧ генератора
/ ~ 1—70 МГц, давления р ~ 10~2—
10 торр. Измерялись потенциалы за-
жигания разряда Vt при разных /, р,
L причем особое внимание уделялось
области вблизи скачков на кривых
зажигания Ft(p) при данных со, L.
Скачки, обнаруженные еще в
экспериментах 30-х годов (п. 8.2
гл. 9), появляются при таких комби-
нациях параметров, когда размах ко-
лебании электрона в момент пробоя
2А =(иер) Vta/apL сравнивается с
расстоянием между электродами.
Если со, L фиксированы, то при бо-
лее высоких давлениях 2А < L и
электроны, раскачивающиеся из се-
редины; объема, не достигают элект-
родов. Потери их благодаря этому
меньше, только диффузионные, и Vt
падает по сравнению с более низки-
ми р, при которых 2А > Л, и электроны в ходе дрейфа попадают
на электроды. Эффект четко проявляется в Н2, но смазан в Аг,
по-видимому, из-за более сильной диффузии. На рис. 15.6 пока-
зана характеристика зажигания (нижняя сплошная кривая), на
которой хорошо выражен скачок.
4.2. а- и у-разряды. Наблюдения показали, что разряды, за-
жигаемые при давлениях слева и справа от скачка, не одинако-
вы. Справа — возникает диффузное свечение в середине проме-
478
жутка, а около электродов газ не светится. Напряжение на элек-
тродах при зажигании меняется мало, что указываем’ па слабую
проводимость ионизованного газа и малый разрядный ток. В раз-
ряде слева от скачка сильное свечение локализуется у эле^ ро-
дов и состоит из чередующихся слоев, по цвету и порядку следо-
вания очень похожих на слои в катодной области тлеющего раз-
ряда постоянного тока. Напряжение на электродах после зажи-
гания заметно падает, что говорит о значительной проводимости
разряда.
Эти особенности были истолкованы Левитским так. В разряде
со слабой проводимостью ток в приэлектродной области имеет
преимущественно емкостный характер и является током смеще-
ния, как и до зажигания. Зажигание разряда, следовательно, не
отражается на поведении электрода, который по-прежнему заря-
дов не испускает и не воспринимает. В хорошо проводящем раз-
ряде слева от скачка на отрицательный в данный момент элек-
трод идет ионный ток, там происходит вторичная эмиссия, и на
какое-то время до смены полярности около «катода» возникает
катодный слой, как в тлеющем разряде. На электроды, которые
попеременно служат катодами, ток из середины промежутка за-
мыкается теперь токами проводимости. Разряд с непроводящими
слоями Левитский назвал «а», с проводящими — «7», что симво-
лизирует роль вторичной эмиссии (у-процессов). При повышении
напряжения на горящем a-разряде последний внезапно перехо-
дит в у-форму. Происходит как бы вторичное зажигание. Харак-
теристика вторичного зажигания является продолжением харак-
теристики у-разряда слева от скачка; она показана на рис. 15.6
штриховой кризе й.
4.3. Постоянный потенциал пространства в ВЧЕ разряде низ-
кого давления. Еще в опытах 30-х годов было замечено, что в
ВЧЕ разрядах низкого давления происходит распыление электро-
дов, в результате которого слой металла оседает на стенках стек-
лянной трубки. Единственное объяснение этому могло заклю-
чаться в существовании некоторого постоянного поля, направлен-
ного из середины разряда к обоим электродам и разгоняющего
положительные ионы до больших энергий. Ионы с силой ударя-
ются об электроды и вызывают эффект, известный в тлеющих
разрядах постоянного тока как катодное распыление. Переменное
поле даже большой амплитуды в этом отношении бездейственно,
так как энергии колебательного движения ионов оказываются
слишком малыми. Присутствие постоянного, положительного по
отношению к электродам потенциала в середине разрядного про-
межутка было зафиксировано в ряде работ зондовыми методами.
На рис. 15.7 показан результат зондового измерения [15.1] в
той же установке, о которой шла речь в и. 4.1. При f = 68 МГц,
L = 10 см и р = 3,8 • 10~2 торр постоянный потенциал Vo падает
с ростом давления. В то же время он почти линейно возрастает
с ростом напряжения на электродах и раза в два меньше его
амплитуды Va. Измерение энергетического спектра ионов показа-
479
ло, что их средняя энергия сопоставима с Vo, а максимальная —
с Va
По мысли Левитского, причину появления постоянного поло-
жительного потенциала в ВЧЕ разряде следует усматривать в
образовании излишка ионов в промежутке из-за ухода части
электронов в электроды (§1) На основе предложенной им схе-
мы качаний электронного газа (рис 15 1) Левитский оценил
стоянного потенциала от
давления (водород, / =
= 68 МГц, L — 10 см)
[18 1]
постоянный потенциал Vo (п 6.2).
В этих соображениях в общем верно
схвачены некоторые ключевые момен-
ты Каждый из принятых во внима-
ние факторов: уход части электронов
из промежутка и качания электронно-
го газа — уже сам по себе может слу-
жить причиной появления постоянно-
го положительного потенциала плаз-
мы Первый — очевиден Если тело в
целом заряжено положительно, оно
обладает положительным потенциалом.
Но даже если газ в целом электро-
нейтрален, как было бы, если бы
электроны не прилипали к изоляторам
в безэлектродном разряде, он в сред-
нем по времени все равно обладает по-
ложительным потенциалом по отноше-
нию к границам; см п 6 4 Действи-
тельно, слой положительного заряда существенно толще слоя та-
кого же отрицательного, ибо электроны «прижимаются» полем к
изолятору, и падение напряжения в отрицательном слое меньше
Ясно, что изложенная модель соответствует только а-разряду
В у разряде, если около временного катода образуется катодный
слои, такой же как в обычном тлеющем разряде, то и положи-
тельный потенциал относительно «катода» на границе слоя с
плазмой должен быть порядка нормального катодного падения
Гн Поскольку «анодного» падения при этом нет или оно мало,
то в среднем за период Vo будет порядка Ен, что и наблюдается
при более высоких давлениях (п 4 4)
На рис 15 8, 15 9 приведены результаты [18 4] Измерения
сделаны зондовым методом в стеклянных трубках диаметром
5—8 см с дисковыми электродами Потенциал Vo падает с ростом
давления при прочих равных условиях Форма разряда в работе
не оговаривается, но примечательно, что наблюдается некоторая
зависимость Vo от материала электродов и рода газа Для тех
сочетаний металл — газ, для которых нормальное катодное паде-
ние выше, Ео больше, хотя и далеко по значению от Ен Наблю-
дается некоторая, в основном растущая зависимость Vo от часто-
ты (в диапазоне 1 —12 МГц).
Если постоянный положительный потенциал ускоряет ионы в
сторону электродов, то электроны разгоняются в сторону от элек-
480
1 родов к плазме. И действительно, в опытах с гелием при р —
= 0,66 торр, /«1—15 МГц, Va ~ 390 В были зарегистрированы
пучки быс!рых электронов с энергиями 100 эВ [15.5]. Это было
обнаружено в ходе измерения функции распределения электро-
нов зондовым методом. Энергия электронов пучка близка к Vo.
Рис 15 8 Зависимость по-
стоянного потенциала плаз
мы от амплитуды напряже-
ния на злеьтродах (разряд
в неоне с титановыми
электродами, / — 6 МГц):
1 — р = 0,3 торр, 2 — 0,5;
3 — 1,1 [154]
Рис 15 9 Зависимость посто-
янного потенциала плазмы от
давления (разряд в неоне с
титановыми электродами, Va ~
= 1000 В) 1 — / = 6 МГц,
2 — 1,5 [15 4]
4.4. Слаботочный и сильноточный (а и у) ВЧЕ разряды сред-
него давления. Факт существования двух форм ВЧЕ разрядов,
их свойства, закономерности перехода из одной в другую, начи-
ная с 1978 г., подверглись детальному исследованию в работах
Н. А. Яценко, которые во многом прояснили природу этих явле-
ний. Основное внимание было сосредоточено на средних давле-
ниях р~ 10—100 торр, которыми до тех пор вообще занимались
очень мало. Один из существенных результатов Яценко: прямое
экспериментальное доказательство того факта, что приэлектрод-
ные слои у-разряда обладают высокой проводимостью. Посколь-
ку, как было установлено, плотность тока в у-разряде более чем
на порядок превышает таковую в а-разряде, cz-разряд был на-
зван им слаботочным, а у — сильноточным. Измерения [15 6]
были сделаны в сосуде большого объема, 60 л, в середине кото-
рого помещалась пара дисковых водоохлаждаемых латунных
электродов диаметром 10 см. Расстояние L между ними можно
было увеличивать до 10 см. Иногда электроды изолировались от
плазмы слоями стекла, тефлона и других материалов, толщиной
1 — 3 мм. Разряд возбуждался от 3-киловаттного генератора в ос-
новном на частоте 13.6 МГц.
На рис. 15.10 представлены статические ВАХ разряда: зави-
симость ВЧ напряжения V на электродах от ВЧ тока i в цепи
в стационарном режиме (среднеквадратичные величины). При
481
самых малых напряжениях и токах V в ходе наращивания тока
почти не меняется Разряд в этих условиях не заполняет площа-
ди электродов Диаметр его в межэлектродном промежутке бли-
зок к диаметру пятна на электродах Светится средняя часть про-
межутка Около электродов,
в слоях пространственного
заряда интенсивность свече-
ния хменыпа ^тся(рис 15 11,
кривая 1) Это ТИПИЧНЫ!!
Рис 15 10 В\Х ЕЧЕ разряда на ча
стоте 13,6 МГц (средь еквадраэичные
величины) 1 — гели i, р = 30 торр,
L = 0,9 см, 2 — воздух, 30 торр,
0,9 см, 3 — воздух, 30 торр, 3 см,
4 — СО2, 30 торр, 0,9 см, 5 — СО2,
15 торр, 3 см 6 — воздух, 7 5 торр
1 см, электроды изолированы стек
лом, 7— воздух, 7,5 торр, 1 см,
электроды изолированы тефлоном
[15 6]
Рте 15 11 Распределение ин-
тенсивности свечения по дли-
не промежутка в установке
[15 6] (воздух, р = 10 торр,
L = 2 см, электроды латун-
ные) 1 — слаботочт ын режим,
2 — сильноточны г Средне-
квадратичные напцчж^ния на
электродах в обоих случаях
близки к 300 В
слаботочный а разряд с непроводящими приэлектродными
слоями При покрытии электродов диэлектриками все остается
неизменным *) При наращивании тока в этой стадии раз-
ряд расширяется в поперечном направлении, заполняя пло-
щадь электрода Плотность тока на электроде при этом остается
неизменной, т е в слаботочном разряде при неполном заполне-
нии электрода существует эффект типа рорма^ъ ил1 п'оти с>и
тока Последняя зависит от газа, давления и, 1,то любопытно, от
межэлектродного расстояния L (рис 15 12; § 9)
Когда электрод полностью заполняется током и диаметр раз-
ряда вырастает до диаметра электродов, для дальнейшего увели-
чения тока требуется большее напряжение, как в аномальном
тлеющем разряде, хотя здесь слои по-прежнему темные и непро-
водящие Толщины их в «нормальном» режиме d ~ 0,2—0,6 см.
G точностью до небольшого ионного тока насыщения (как на от-
рицательный зонд) ток замыкается на электрод током смещения.
*) Электроды вообще можно вынести наружу, за пределы разрядной
трубки,— такие опыты ставились издавна и многократно.
482
Малая isp жодпмость разряда проверялась путем пропускания че-
рез него в дзояиного тока или, что то же самое, тока часто-
ты 50 Гц.
По досшжении на электродах некоторого достаточно большо-
го напряжения происходит резкая перестройка cz-разряда, пре-
вращение его в сильноточную у-форму. Это «вторичное зажига-
ние», ь юр<е наблюдалось в [15.3] (и. 4.2). На ВАХ ему отве-
чает скачок или излом. Свечение в промежутке перераспределя-
ется; около каждого электрода появляются слои, похожие на
Рис. 15.12. Зависимость нормальной плотности тока на электродах в слабо-
точном режиме от давленья и меж электродного расстояния [15.7]: а — ге-
лии, б — воздух; f = 13,6 МГц: 1 — р = 100 торр в Не и 10 торр в воздухе,
2 — L — 5 м и в Не и 7 мм в воздухе, 3 — L = 10 мм
слои тлеющего разряда. Четко наблюдаются отрицательное све-
чение, темное фарадеево пространство, в середине — положитель-
ный столб. Распределение интенсивности свечения показано на
рис. 15.11 кривой 2. В воздухе при р = 15 торр суммарная тол-
щина «прикагодных» областей вплоть до положительного столба
составляет 1,2 см. Резко увеличивается плотность тока на элек-
троде, в воздухе при р = 30 торр — в 20 раз, от 1,2 • 10~2 до
0,24 А/см2(при переходе разряд сжимается в поперечном направ-
лении); резко увеличивается проводимость. Сопротивление вспо-
могательному постоянному или низкочастотному току падает на
два порядка. Постоянный потенциал пространства Vo в сильно-
точном режиме составляет 100—200 В, практически не зависит
от давления и примерно соответствует нормальному катодному
падению в тлеющем разряде*). Толщина приэлектродного слоя
пространственного заряда d становится гораздо меньше. В возду-
хе при р = 15 торр в слаботочном режиме d ~ 0,4 см, а в сильно-
точном d ~ 0,03 см. Эти цифры получены путем зондового изме-
рения распределения постоянного потенциала Vq(x) в зависимо-
сти от расстояния х от электрода. Толщина слоя в сильноточном
*) В этой связи непонятно, почему в [15.3] потенциал Vo резко падал
до ничтожно малого значения в несколько вольт при р ~ 1 торр. Возможно,
здесь были неучтенные аппаратные эффекты.
483
режиме сравнима с толщиной катодного слоя обычного тлеющего
разряда.
Для сильноточного режима также характерно существование
нормальной плотности тока, теперь уже подобно такому же эф-
фекту в обычном тлеющем разряде, однако значение плотности
тока в ВЧ разряде может быть существенно больше из-за добав-
ления тока смещения в «катодном» слое, где очень сильно поле
(п. 7.4). При наращивании тока электроды заполняются тлею-
щим свечением, диаметры токовых пятен на электродах и диа-
метр плазменного столба (довольно близкие) возрастают. Этому
отвечает последний участок постоянного напряжения на ВАХ
рис. 15.10, который соответствует нормальному режиму горения
тлеющего разряда. Впрочем, не всегда диаметр плазменного
столба беспредельно растет с увеличением тока. При некотором
значении тока может наступить контрайция, разряд стягивается
в тонкий токовый шнур, подобно тлеющему разряду постоянного
тока (п. 7.6) [15.8].
Недавние измерения [15.9] позволяют судить о частотной за-
висимости параметров срыва cz-разряда и перехода его в 7-форму.
Исследовался разряд в азоте между оголенными алюминиевыми
электродами в диапазонах /=15—55 МГц, р~ 10—50 торр, L &
~ 0,6—1,2 см. ВАХ ведут себя примерно так же, как и показан-
ные на рис. 15.10. С увеличением частоты при данном давлении
напряжение перехода Упер уменьшается, а ток /пер растет. Так
для L = 0,6 см, р = 35 торр среднеквадратичные значения равны:
при
/=15,4 МГц У пер = 440 В, ^пер = 45 мА;
/ = 20,4 МГц У у пер = 405 В, ^пер = 60 мА;
/ = 29,25 МГц У пер = 305 В, ^пер = 100 мА
С ростом давления на данной частоте Упер растет, а £пер па-
дает. Для L = 0,6 см, / = 29,25 МГц при
р = 25 торр УПеР — 270 В,
/2 = 55 юрр УпеР = 320 В,
/пер = 134 мА;
^пеР ~=г' 95 мА.
В момент перехода cz-разряд занимал па электроде площадь
1,5 см2, которая близка к его полной площади. При р = 55 торр
этому соответствует 7пер ~ 60 мА/см2. После перехода в 7-режиме
плотность тока подскакивала до 1 А/см2. Надо сказать, что
в этих опытах эффект нормальной плотности тока ь а-режиме,
по-видимому, не наблюдался. При наименьшем возможном токе
сс-разряд сразу охватывал почти всю площадь электрода.
4.5. Область существования слаботочного разряда. Экспери-
менты [15.6] показывают, что слаботочный разряд может гореть
только при значениях pL, меньших некоторого критического
(/>Л)кр (рис. 15.13). Последнее зависит от материала электродов
и рода газа. При pL^{pL)^ слаботочный разряд становится не-
484
устойчивым и либо переходит в сильноточную форму, либо гас-
нет. При pL > (pL)KV его зажечь вообще не удается, и реализует-
ся только сильноточный режим. При pL <(pL)Kp возможно суще-
ствование и того и другого режимов. Для молекулярных газов
критические значения невелики, для воздуха (щБ)кр ~ 40 торр • см.
В молекулярных смесях СО2 + N2 + Не
при средних давлениях и размерах
вдоль тока порядка нескольких санти-
метров реализуется, как правило, силь-
ноточная форма. Превращение слабо-
точного разряда в сильноточный обу-
словлено пробоем слоя пространствен-
ного заряда [15.6].
4.6. Безэлектродный электродный и
электродный безэлектродный разряды.
Это звучит как игра слов, однако отве-
чает существу дела. Разряд с оголен-
ными электродами в cz-режиме ничем
не отличается от разряда с изолиро-
ванными и является безэлектродным в
том смысле, что электроды никак себя
не проявляют. Как и на диэлектрике,
Рис. 15.13. Границы обла-
стей существования слабо-
точного разряда [15.6]: 1 —
азот, 2 — воздух, 3 — СО2,
4 — гелий; латунные элект-
роды, / — 13;6 МГц. Выше
и правее кривой возможен
только сильноточный ре-
жим
ток через слои пространственного за-
ряда замыкается на металл лишь током смещения. Но и «без-
электродный» разряд с изолированными электродами, оказывает-
ся, может гореть в 7-режиме со всеми признаками вторичной
эмиссии и размножения электронов в катодном слое: отрицатель-
ным свечением, темным фарадеёвым пространством,— подобно
обычному тлеющему и сильноточному ВЧ разряду с оголенными
электродами. Он не отличается от последнего ни по внешнему
виду, ни по плотности тока. О том же свидетельствует и
рис. 15.10, на котором представлены ВАХ и для случаев изоли-
рованных электродов. Амплитуда напряжения на электродах при
этом, естественно, больше обычного, так как часть напряжения
падает на диэлектриках.
Когда ионный ток из катодного слоя идет на металл, из него
вырываются электроны, нейтрализующие заряд ионов, и эмисси-
онные. Расход электронов из поверхностного слоя катода возме-
щается притоком их изнутри за счет поступления в анод. По-
скольку катодный слой заряжен положительно, в разряде посто-
янного тока на катоде содержится постоянный избыточный элек-
тронный заряд. В оголенных электродах ВЧЕ разряда также
имеется избыточный отрицательный заряд (п. 1.2), только он
меняется в ходе чередования катодной и анодной фаз. При за-
жигании «безэлектродного» разряда электроны из газа прилипа-
ют к поверхности диэлектриков, но изнутри тела притока заря-
дов» нет. В катодной фазе сильноточного режима прилипшие
электроны нейтрализуют падающие ионы, частично ими осво-
бождаются, в анодной — их запас пополняется.
485
Если во внешнюю цепь разряда с оголенными электродами
включить емкость, эквивалентную изолирующим плазму диэлек-
трикам, то в случае совпадения эмиссионных и нейтрализующих
ионы свойств поверхностей металла и диэлектрика разряды с
оголенными и изолированными от плазмы электродами должны
стать эквивалентными. Все это наглядно показывают результаты
численного моделирования структуры ВЧЕ разряда (§ 8).
§ 5. Электрические процессы в непроводящем
приэлектродном слое и механизм замыкания тока
В приближенном решении § 2 слои прост рана венного заряда
у границ разрядного промежутка фигурировали как поверхности
разрывов, на которых сосредоточены поверхностные заряды и где
ноле испытывает скачок. Посмотрим теперь на непроводящий
слой в слаботочном разряде как на образование конечной толщи-
ны, в котором имеется объемный заряд, а поле непрерывно, и
разберемся детально, как происходит замыкание тока между плаз-
мой и электродом. Как уже ясно из всего предыдущего, оно осу-
ществляется током смещения, и потому полезно лишний раз ос-
тановиться на вопросе о физическом содержании этого понятия.
5.1. Что такое ток смещения. В 60-х годах прошлого века,
формулируя систему уравнений для описания электромагнитных
явлений (§ 3 гл. 5) Максвелл столкнулся с той трудностью, что
уравнения магнитного поля постоянного тока и уравнение не-
прерывности для зарядов несовместимы, если поля — перемен-
ные. Чтобы устранить противоречие, Максвелл, не имея на то ни-
каких экспериментальных оснований, постулировал, что магнит-
ное поле порождается не только движением зарядов, но и изме-
нением электрического поля, подобно тому как электрическое
поле порождается изменением магнитного. Величину (l/4ft)dD/d£,
которую он добавил к току проводимости, Максвелл назвал то-
ком смещения. У явления электромагнитной индукции появился
«магнитоэлектрический» аналог, а уравнения (5.13), (5.14) обре-
ли замечательную симметрию. Так чисто умозрительным путем
был открыт один из фундаментальнейших законов природы,
следствием которого является существование электромагнитных
волн.
Но величина, именуемая током смещения, фигурирует в тео-
рии электричества и вне всякой связи с магнитными явлениями.
Из чисто электрических уравнений
dpldt + div j = 0, divD = 4np (15.16)
вытекает, что
Ы Ы“) = °-
Вектор, стоящий под знаком дивергенции в (15.17), обладает
всеми теми свойствами, которые присущи плотности постоянного
486
тока, подчиняющейся уравнению div j = 0. У вектора нет источ-
ников, линия тока его — замкнутая, даже если электрическая
цепь содержит непроводящие участки (линия тока может еще
уходить в бесконечность, как бы замыкаясь «через бесконеч-
ность»), произведение модуля вектора на площадь сечения токо-
вой трубки в любой момент времени одинаково вдоль всей цепи.
Векюр, следовательно, можно интерпретировать как плотность
«полного» тока — проводимости плюс смещения. Но это интер-
претация в значительной мере условная, ибо из двух составляю-
щих тока смещения (п. 3.3 гл. 5) величина (1/4л)d^jdt, в отли-
чие от тока поляризации cjP/ot, током в буквальном смысле сло-
ва не является.
Если отвлечься от подлинно физического назначения величи-
ны (1/4л)йЕ/сЯ быть источником вихрей магнитного поля, ника-
кой инои физической реальности она не отображает, никакого
иного физического смысла не имеет. Но, рассматривая протека-
ние переменного тока в квазипо! нщиалъном электрическом пол%
п< рождаемом преимущественно зарядами*), мы вообще «не зна-
ем» о существовании магнитного ноля. Имея дело с газообразны-
ми пр )водниками, т. е. разрядами, часто можно пренебречь нич-
тожным гоком поляризации, так как 8 ~ 1. Стало быть, оперируя
«чистым» током смещения (1/4л) dE/df, мы пользуемся поня-
тием, лишении м физического содержания?
Выходит, что' так. Механизм протекания переменного тока в
квазипотенциальном поле исчерпывающим образом расшифровы-
вается в терминах движения зарядов и электростатики при помо-
щи уравнений типа (15.16) без привлечения символического то-
ка смещения. Исключительно полезная его роль связана с тем,
что трактовка интеграла уравнений (15.16) или (15.17) как за-
кона сохранения полного тока чрезвычайно упрощает расчеты,
позволяет представить все в краткой, удобной и изящной форме.
Но если мы хотим познать, что происходит на самом деле, то за
словами типа «через емкость протекает ток смещения» необходи-
мо просматривать реальные физические процессы. Нужно пред-
ставлять себе, как электродвижущая сила источника питания
сдвигает электроны внешней цепи к одной из сторон этой емко-
сти, где они останавливаются, не пропускаемые дальше средой с
плохой проводимостью; как на другой стороне емкости за счет
ушедших электронов оголяется слой положительного заряда; как
*) Переменное электоическое поле не бывает строго потенциальным,
оно непременно содержит элемент вихревого Но если характерные размеры
L системы малы по сравнению с длино i волны X, поле является потенци-
альным приближенно В самом деле, ю уравнению (15 14) ^Ихр ~ (aHLIc.
По уравнению (5 13) Н ~ faijUc, откуда £Вкр~ 4жоА2у/с2 С друюй стороны
из уравнений (15.16) ^нотенц ~ 4лр£ л сор ~ y/L, откуда Т'Естенц ~4лу/со.
Следовательно,
Ецлхр/Е
потепц (aL/су = (2лЕ/Х)2 = (Ш)2
Например, в ВЧЕ разряде при L ~ 10 см, % = 22 м ^вихг/^потенц ~ 10-3.
487
между зарядами противоположного знака возникает электриче-
ское поле; как оно меняется во времени по мере того, как про-
исходит накопление (или рассасывание) зарядов; как в «прово-
дах» в это время течет сильный ток, а поля почти нет, а в среде
с плохой проводимостью ток не течет, но зато меняется сильное
поле,— и цепь рассуждений и цепь электрическая замкнулись.
Конечно, пример — тривиальный. Но видение подобного рода
картины должно стоять за каждым случаем, в котором мы хотим
досконально разобраться.
5.2. Поле в слоях. Разберем количественно ситуацию, изобра-
женную на рис. 15.1, 15.2. Решением (15.13), (15.14) § 2 можно
воспользоваться в качестве первого приближения. Следует только
иметь в виду, что на рисунках фаза сдвинута по сравнению с
(15.13), (15.14). Поле Е в плазме и разрядный ток i равны
Е = —Eacos(i)t, i ——Zacos((of+Дф) (15.18)
при тех же амплитудных величинах и Дф (по (15.11)). В прене-
брежении диффузионным размытием границы между ионным
слоем и плазмой*) поле в слое подчиняется уравнению дЕс^дх =
= ^пеп+. Положим для простоты, как и на рис. 15.1, п+(х) =
= const. В левом слое, на котором мы и зафиксируем внимание,
Есл(я, t) = E(t)—4nen+[d(t)—х], (15.19)
где d(t)—координата границы с плазмой, или толщина слоя.
У поверхности электрода
£о(О^^сл(О, t) = E(t)~^en+d(t). (15.20)
Граница с плазмой образована «крайними» электронами, ко-
торые колеблются под действием поля Е со скоростью дрейфа:
d = — [ieE. С учетом того, что d(0) = A,
d(t) = A(l + sin со£), A — [ieEa/(i). (15.21)
Подставляя (15.18), (15.21) в (15.20) и имея в виду, что п+
совпадает с пе в плазме, проводимость которой о = епе\ле, нахо-
дим поле у электрода:
£о = — /1 + со2т§ sin (coi Дф) — (15.22)
В случае хорошо проводящей плазмы, (ота<1, поле у электрода
почти все время велико по сравнению с полем у плазменной гра-
ницы слоя. И постоянная его составляющая, и амплитуда пере-
менной равны Е$а = Еа/ыХс, причем сдвиг последней по фазе от-
носительно Е составляет л/2.
5.3. Заряды и токи. Поле Eq создается поверхностным заря-
дом q на электроде, Eq = inq. Его переменная составляющая обя-
зана протекающему по внешней цепи разрядному току i = Sqr
*) Оценка диффузионных эффектов имеется в [15.2, 10].
488
постоянная — заряду тех электронов, которые попали из газа в
твердое тело. И действительно, постоянная составляющая плот-
ности заряда па электроде равняется заряду слоя в момент про-
хождения электронов через среднее положение или, что то же,
среднему по времени:
до == —^аМлсоТо == —еп+А, Ео пост = —4пеп+А.
Вычисленный на основании (15.22) разрядный ток
i = — SoEa V1 Н- (Ле cos (<at + Аф), S<jEa = Va/R, (15.23)
совпадает с решением (15.18), (15.14), найденным в первом при-
ближении. При (ота <£. 1 плазменный ток проводимости i\ = SoE
близок к разрядному I. Как видно из (15.22), положительный
заряд на электроде (Е > 0) появляется на тем меньшую долю
периода, чем меньше сота.
5.4. Реальность и символы. Итак, картина, описываемая при-
ближением разрывов (§ 2), не нарушилась и в результате заме-
ны разрыва изолирующим слоем пространственного заряда меж-
ду плазмой и электродом. Вместе с тем стал количественно яс-
ным механизм замыкания тока между плазмой и электродом, ка-
чественно понятный и из рис. 15.1. В той стадии, например, ког-
да отрицательный заряд на левом электроде накапливается (ток
течет налево), заряд все сильнее отталкивает электроны плазмы.
Граница плазмы, образуемая крайними электронами, отодвигает-
ся от электрода, а в оставшемся промежутке остается локально
нескомпенсированный ионный заряд. Суммарный положительный
заряд слоя также накапливается, пр не вследствие его концен-
трирования, а путем присоединения к слою новых положительно
заряженных участков. Положительный заряд в слой поставляет-
ся током проводимости из плазмы (уходом электронов): с/\ =
= en+d = —епе\1еЕ = i\IS. Внутри слоя никакого тока, естествен-
но, нет, но символическая величина — ток смещения — совпадает
с током разряда. Согласно (15.19)—(15.23)
cos + А<р) = 4~-
Вследствие конечной проводимости плазмы; меняющийся от-
рицательный заряд электрода q не успевает полностью нейтра-
лизоваться положительным зарядом слоя. Нескомпенсированный
заряд в области контакта плазменного и металлического провод-
ников q — q\= Е14п является источником поля Е внутри плаз-
мы, а различие в скоростях натекания зарядов q и gi, g —gi =
= Ё14п, порождающее переменность поля в плазме, символиче-
ски трактуется как ток смещения в самой плазме:
i i\ SEI4л iCM, t\ 4~ iCM = i.
5.5. Изолированные электроды. Рис. 15.1, 15.2 и все получен-
ные только что соотношения остаются в силе и в этом случае.
32 Ю. П Райзер 489
Только теперь постоянный заряд до оседает на поверхности ди-
электрика, обращенной к газу. Поле в газе у границ с изолято-
ром Ео = 4л (q + qo). Его постоянная (средняя по времени) со-
ставляющая 4лдо определяется осевшим разрядом, а перемен-
ная 4л# связана с переменным зарядом q на электроде.
Согласно (15.22) |#01 бЕа/(й ~ ]а/(я. В слаботочном режиме на
частоте / ~ 10 МГц ja ~ 10 мА/см2, откуда l#ol ~ 10"10 Кл/см2.
К 1 см2 поверхности диэлектрика прилипает порядка 10э элект-
ронов. Это мало по сравнению с поверхностной плотностью ато-
мов 10 6 см-2, т. е. поверхность усеяна осевшими э шктронами
не густо.
§ 6. Постоянный положительный потенциал плазмы
слаботочного разряда
6.1. Определение. Если к электродам приложено синусоидаль-
ное напряжение, разность потенциалов между ними в среднем по
времени равна нулю. Обращалась бы в нуль и средняя разность
потенциалов между любым местом плазмы и электродом, если
бы поле повсюду также было гармоническим. Поле и в самом
деле меняется по синусоидальному закону в электронейтральной
плазме, в изоляторе, но в приэлектродном слое поле не гармони-
ческое, и потому у плазмы появляется постоянный относительно
электрода потенциал Vo. Он равен среднему за период значению
разности потенциалов между какой-то точкой плазмы и электро-
дом. Средние значения от разностей потенциалов по участкам
с гармоническим полем (по плазме, по изолятору) исчезают.
Значит, постоянный потенциал плазмы относительно электрода
Vo, который измеряют на опыте, совпадает со средним значением
падения напряжения VK на приэлектродном слое. В случае сим-
метричного (плоского) промежутка оба электрода в среднем рав-
ноправны. Вычислим постоянный потенциал Vo = WK(t)} для
нескольких случаев.
6.2. Электроны совершают дрейфовые колебания, газ заря-
жен. Последнее означает, что из околограппчных слоев электроны
ушли в металл или прилипли к диэлектрику. Потенциал плаз-
менной границы слоя относительно электрода равен
d
VK =- — £сл дх ---------------------(1 + sin о/)2,
о
Здесь использованы формулы (15.18) — (15.22). Последний при-
ближенный переход соответствует случаю хорошо проводящей
плазмы: сот0< 1. В этом случае потенциал в течение почти всего
времени положителен. Постоянный потенциал, вычисленный пу-
тем усреднения VK при произвольном сота, равен
о £
VQ = 4-----— А = ЗлеиЛ2
0 4 сот„
Зл<? (щр)2 пе
(15.24)
490
Формула типа (15.24) была впервые получена Левитским,
только в [15.1], видимо, по ошибке величина Vo оказалась в два
раза больше. Порядок Vo по (15.24) в общем правильный. На-
пример, при пе = ЮВ * 10 см-3, А = 0,1 см Уо=14О В. Более де-
тальное сопоставление с опытом затруднено отсутствием доста-
точной экспериментальной информации для тех условий, к кото-
рым она относится. Но для понимания физики процессов и для
дальнейших усовершенствований теории вычисление (15.24),
безусловно, полезно.
6.3. Влияние неоднородности распределения ионов. Прибли-
жение п+(х) = const в слое является весьма грубым. Правда, оно
позволяет довести до конца все вычисления в простой и нагляд-
ной аналитической форме. На самом деле это не мало, ибо нет
лучшего способа проникнуть в сущность процесса. Но. конечно,
особой точности от полученных формул ожидать не приходится.
В действительности, как показывает численное моделирование
(§ 8), в слоях слаботочного режима т?+ монотонно падает от
плазмы до границ с электродами или изоляторами, уменьшаясь
в несколько раз. Слои при этом толще, чем в приближении
п+ = const, поле у границ слабее, но падения напряжения на
слоях и постоянный потенциал плазмы — почти вдвое больше.
6.4. Дрейфовые колебания, газ электронейтрален. Вернемся
к приближению п+ (х) = const и предположим, что электроны к
изоляторам не прилипают. В моменты равновесия со£ = 0, л слои
отсутствуют, а в моменты сй = л/2, Зл/2 электроны прижимаются
полем к поверхности, в отсутствие диффузии — вплотную. Для
левого слоя в катодный полупериод, * когда слой заряжен поло-
жительно, по-прежнему справедливы формулы (15.18) для поля
в плазме, (15.19), (15.20). Но поскольку теперь d(0) = 0, вместо
(15.21) d = A sin со£. Поле у поверхности изолятора определяется
формулой (15.22) без второго слагаемого, так как теперь у поля
Ео и заряда на электроде q нет постоянных составляющих.
В анодный полупериод толщина слоя отрицательного заряда ма-
ла, хотя поле Ео по величине — такое же. Поэтому при усредне-
нии разности потенциалов в слое по времени интегралом по анод-
ному полупериоду можно пренебречь. В результате
Т7 ^4'^ ,\ Бтах Л л2 /лг
Уо ? d —— впеА . (1о.2э)
В электронейтральном промежутке потенциал Уо в шесть раз
меньше, чем в заряженном. Опыт не указывает на существова-
ние больших различий в Уо для разрядов с изолированными и
оголенными электродами. Это можно рассматривать как косвен-
ное доказательство прилипания электронов к изоляторам в без-
электродном разряде.
6.5. Низкие давления. В этом случае и амплитуда колебаний
электрона, не обязательно дрейфовых, может оказаться сравни-
мой с межэлектродным расстоянием, и о протяженном положи-
тельном столбе говорить не приходится. В ходе электронных ка-
32*
491
чаний слой положительного пространственного заряда может
занимать чуть ли не весь промежуток. Но тогда возможна совсем
простая оценка Vo. Когда электроны смещаются направо, между
левым электродом и электронами образуется плохо проводящая
область, занятая ионами, и на ней падает почти все приложен-
ное напряжение V(t). Ему и равен приближенно мгновенный
потенциал прижатой к правому электроду плазмы относительно
Рис. 15.14 Зависимость постоянного положительного потенциала плазмы от
амплитуды напряжения на электродах при низких давлениях [15.10]:
сплошная кривая — 70 = Va/n, точки — эксперименты в Не и Н2 при низ-
ких давлениях
левого. В следующий полупериод разность потенциалов между
плазмой, прижатой к левому электроду, и этим электродом ста-
новится малой. Отсюда
л
го 2^ J Va sin Mt d(Mt) =
0
(15.26)
Постоянный положительный потенциал плазмы примерно втрое
меньше амплитуды приложенного напряжения. Этот результат
вытекает в качестве предельного случая из более детальной тео-
рии бесстолкновительного ВЧ разряда, построенной в [15.10] *).
На рис. 15.14 он сопоставлен с экспериментом.
§ 7. Сильноточный режим
7.1. Общее со слаботочным. Приэлектродные слои положи-
тельного пространственного заряда образуются в ВЧЕ разрядах
обеих форм. Причиной тому — качания электронного газа с раз-
махом, гораздо большим, чем у ионного, и обусловленный этим
уход части электронов в электроды. В любом случае при доста-
точно высокой проводимости плазмы поле в слоях подавляю-
щую часть времени движет ионы в сторону электродов. Попада-
ющий на электрод ион может вызвать вторичную эмиссию, и тог-
*) В [15.10] и ряде других работ развивается концепция постоянного
положительного потенциала как результата выпрямления ВЧ напряжения
на нелинейной проводимости слоев. Но эта радиотехническая аналогия не
должна заслонять реальной причины эффекта — качаний электронного га-
за относительно ионного.
492
да от эмитированного электрона в сильном поле слоя рождается
много электрон-ионных пар. Некоторые из электронов, проходя
без столкновений значительную разность потенциалов, достигают
больших энергий. Таким образом, в обоих режимах электрод, не-
смотря на смену знака приложенного напряжения каждые пол-
периода, большую часть времени ведет себя скорее, как катод*).
В любой из форм поле в слоях имеет переменную составляю-
щую и в них присутствуют токи смещения. Что касается уда-
ленной от электродов области, куда не доходят отзвуки приэлект-
родных явлений,— положительного столба, то, если для такового
есть место, процессы переноса и рождения зарядов в нем имеют
одинаково локальный характер. Локализация обусловлена ма-
лостью амплитуды смещения электронов А < L. Возможные ко-
лпчественные отличия в столбах разных режимов связаны с раз-
ницей в плотностях электронов и тока.
7.2. Сущность отличия. Все наиболее ярко выраженные осо-
бенности двух форм горения ВЧЕ разрядов определяются тем,
является ли процесс размножения электронов в результате вто-
ричной эмиссии с электрода самоподдерживающимся, удовлетво-
ряется ли в слое условие воспроизводства заряженных частиц
типа таунсендовского (9.1) — короче, «пробит» ли газ в слое.
В сильноточном режиме — пробит, в слаботочном — нет. В пер-
вом случае самостоятельный ток проводимости в слое развивает-
ся до сравнительно большого значения, примерно такого же, как
в нормальном тлеющем разряде. Во втором — ионный ток на
электрод мал, будучи связанным в основном с тепловым движе-
нием (диффузией) ионов. Восполняются эти небольшие потери
ионов скорее всего за счет ионизаций атомов электронами в ту
часть периода, когда электроны со стороны плазмы подступают
к электроду, частично — в результате потока ионов из положи-
тельного столба.
Повторяем еще раз, ибо это — момент существенный. В силь-
ноточном режиме, образно говоря, каждый электрон, эмитирован-
ный с электрода (или диэлектрика), и каждый ион, пропадающий
там, воспроизводятся за счет лавинного размножения непосред-
ственно в приэлектродном слое. В слаботочном режиме в балан-
се рождения и гибели зарядов участвует весь разряд, а размно-
жение в слое через вторичную эмиссию не сбалансировано. По-
чему в сильно! очном режиме протекает «сильный» ток, а в
слаботочном — «слабый», будет пояснено дополнительно в конце
п. 7.4.
Весь экспериментальный материал свидетельствует о том,
что в сильноточном разряде у обоих электродов формируются
*) Разумеется, только при условии А — iieEal^ < L. Если А L, раз-
ряд в течение каждого полупериода похож на разряд постоянного тока, и
электрод одинаково служит то катодом, то анодом. Закие низкочастотные
разряды (их называют разрядами переменного тока) применяют сейчас в
лазерной технике (п. 4.6 гл. 16).
493
с юи, очень погожие па катодный слой нормального тлеющего
разряда. К нормальным значениям с£н, VH близки измеренные
на опыте толщина слоя d и постоянный потенциал Vo, равный
среднему напряжению на слое. Подобно dH и VH, d^p~l, а Ио
не зависит от р. Обе величины не зависят от частоты. Хорошо
объясняется нормальная плотность тока (п. 7.4). Появляются
характерные области отрицательного свечения и темного фараде-
ева пространства. В слаботочном же разряде никакого самостоя-
тельного тока проводимости в слое быть не может, ибо толщина
слоя на порядок больше da и столь велика, что напряжения не
хватает для выполнения таунсендовского условия при фактиче-
ском pd. Толщина слоя d пропорциональна скорости дрейфа
электронов в плазме, от чего с£н не зависит. Кроме того, d 00 со-1
и почти не зависит от давления. Все это говорит о том, что опре-
деляющим d масштабом служит амплитуда смещения А =
= реЕа!чу, как это рассматривалось выше в модели, где нет на-
добности в ионном токе. (См. примечания при корректуре.)
7.3. Вторичное зажигание. Переход из слаботочного режима в
сильноточный происходит в результате таунсендовского пробоя
прпэлектродных слоев, при котором катодами служат электроды,
а приемниками электронов или «анодами» — плазма столба. Пе-
реход осуществляется, когда напряжение на слое (вероятно, про-
межуточное между максимальным VKmax и средним Vo) достига-
ет значения, примерно равного пашеновскому напряжению про-
боя Vt(pd). Величина pd в слаботочном разряде среднего
давления в молекулярных газах гораздо больше значения, отве-
чающего минимуму кривой Пашена, которое близко к pdn. По-
91 ому напряжение пробоя заметно выше VH*). После пробоя в
первоначально толстом ионном слое формируется «нормальный»
катодный слой, как при зажигании тлеющего разряда, т. е. зона
положительного пространственного заряда и падение напряже-
ния на ней сокращаются до оптимальных для самоподдержания
тока величин dn, VH, а остальная часть бывшего слоя превраща-
ется в электронейтральную плазму. См. конец п. 8.2.
Из ориентировочного условия вторичного зажигания Vo «
~ Vz (pd) вытекает ограничение на максимально возможную
плотность тока в слаботочном режиме [15.11]:
/ - со V0/ind < со Vt (pd) /ind. (15.27)
которое, в общем, подтверждается экспериментом. Чем выше час-
тота, тем больше предельные плотности тока и плазмы, при ко-
торых еще возможно существование a-разряда. Расчет пробоя
слоев с учетом движения и размножения электронов в меняю-
*) При pL < 10”1 торр • см в любых газах разрядный промежуток отно-
сится к той части левой ветви пашеновской кривой, где напряжение пробоя
довольно велико. Может быть, поэтому в экспериментах с очень низкими
давлениями р ~ 10~2 торр не замечали признаков сильноточного режима
(тока проводимости).
494
щемся во времени и пространстве поле [15.12] приводит к сле-
дующей оценочной формуле для критической плотности плазмы,
отвечающей сс — у-переходу в азоте при р = 15 торр: я1(р«4,5Х
X 108 (/[МГц])3/2 см"3, / ~ 1—30 МГц. На данной частоте и п >
или при данной плотности плазмы и / < /кр возможен только силь-
ноточный режим. В частности, в низкочастотном разряде перемен-
ного тока с / = 10 кГц cz-режим практически неосуществим.
7.4. Плотность тока. В тлеющем разряде нормальная плот-
ность тока на катоде 1н = С\р2, где С\—константа, своя для
каждой пары газ — металл (§ 4 гл. 10). Как показали измере-
ния [15.13], в сильноточном ВЧЕ разряде также имеется эффект
нормальной плотности тока, когда при изменении разрядного то-
ка пропорционально ему меняется площадь, занимаемая разря-
дом на электродах (в том числе и изолированных). Однако плот-
ность тока, как оказалось, может значительно превышать /н. Это
объясняется тем, что к току проводимости на электрода^ добав-
ляется неизбежный ток смещения. Ток проводимости должен
иметь значение, близкое к /н, поскольку толщина d и напряже-
ние V в слое пространственного заряда близки к нормальным
dH, Ен. Ток смещения в слое /см ~ соЕ/4лс/. Если учесть, что d~
~ d4 = С2р~\ где С2 — также константа для данной пары веществ,
а V ~ Ун от давления не зависит, то /см ~ (&V 1^пС2)р 00 р. Вслед-
ствие разной зависимости токов проводимости /н и смещения /См
от р, их относительный вклад в полный ток / меняется с р. По-
скольку /н и /см сдвинуты по фазе на л/2, среднеквадратичное
значение / есть
7 “= Е/н- 7см- Cj/r V1 2/?)2. (15.28)
На рис. 15.15, взятом из [15.13], расчет по этой формуле со-
поставлен с экспериментом. Для пары воздух — латунь, исполь-
зованной в измерениях (они сделаны на установке, о которой
Рис. 15 15 Зависимость нормальной
плотности тока ча электродах в
сильноточном режиме от давления
[15.131 (воздух, латунные электро-
ды, / =13 МГц). Точки около кри-
вой 2 — измеренные значения; кри-
вая 1 — /н для нормального тлеюще-
го разряда постоянного тока в воз-
духе с латунным катодом; кривая
2 — расчет по формуле (15.28) с уче-
том тока смещения
говорилось в п. 4.4), Ci = 2 • 10-4 А/(см2 • торр2), С2 ==
= 0,23 см торр; частота / = 13 МГц. В качестве напряжения
на слое взято значение V = 320 В, которое представляет собой
среднеквадратичное ВЧ напряжение на электродах, измеренное,
когда последние сближены настолько, что положительного столба
практически нет (есть слои и часть фарадеевых пространств;
495
L ~ 1—2 см). При этом большая доля приложенного напряжениям
падает на слоях. Экспериментальные среднеквадратичные значе-
ния ] хорошо ложатся на расчетную кривую 2. Вся кривая соот-
ветствует только сильноточному режиму. Видно, что при отно-
сительно низких давлениях р ~ 5 торр /см на порядок больше /н,
тогда как при р ~ 50 торр эти величины почти сравниваются.
Таким образом, большой ток сильноточного режима при неболь-
ших давлениях также замыкается на электрод током смещения.
Но сама возможность протекания сильного тока, связанная с от-
носительно высокой степенью ионизации газа, обеспечивается
размножением электронов в пробитых слоях, где созданы опти-
мальные для того условия, соответствующие нормальному катод-
ному слою.
Подчеркнем еще раз, что отличие сильноточного режима от
слаботочного вовсе не в соотношении токов проводимости и сме-
щения на электродах. Как мы видели, при низких давлениях и
в сильноточном разряде jCM намного превосходит /н. Главным ре-
зультатом пробоя приэлектродных слоев является не возникнове-
ние сильного ионного тока, а резкое сокращение толщины слоев
до значения, оптимального для размножения электронов и само-
поддержания тока, как это свойственно нормальному тлеющему
разряду. При сохранении порядка напряжения это приводит к
резкому увеличению поля у электрода, что позволяет течь току
смещения большой плотности. Толстый слой слаботочного раз-
ряда со слабым полем не в состоянии пропустить сильный ток
(смещения), а тонкий слой сильноточного разряда с сильным
полем — пропускает. В этом причина «сильноточности».
7.5. Простейшая модель функционирования «катодных» сло-
ев. Положим, что плотность ионов п± в слое постоянна, хотя и
отличается от плотности в положительном слое. Пусть граница
плазмы совершает колебания, лишь на мгновение касаясь элект-
рода. Проводимость плазмы высока, и амплитуда поля в ней
гораздо меньше, чем амплитуда поля у электрода. Допустим,
наконец, что ионный ток в электрод существует, но гораздо мень-
ше тока смещения. Тогда поле у левого электрода Eq, толщина
слоя d и падение напряжения в нем VK = E®dl2 описывается
такими же формулами, как в п. 5.2. Выражая все величины че-
рез амплитуду плотности разрядного тока / = 1?о/4л = — ja cos cof,
запишем
4 л/ 7
Eq —----------(1 Д- sin со/), d — —(1 -|- sin со£),
2я/2 вШП+ (15.29)
VK = (1 + sin at)2.
eos п.
Если в противоположность рассмотренному в § 2 случаю па-
дение напряжения на плазме мало, разность потенциалов на
электродах V = (8л ja/в(о2п+) sin cot
496
Поток ионов па электрод n+[i+Eo восполняется их рождением
в слое. При лавинном размножении через вторичную эмиссию
заряды рождаются г. основном вдали от катода, и если характер-
ная амплитуда смещений ионов А+ = р+^оа/о < da, иону требует-
ся много периодов, чтобы дойти от места рождения до электро-
да*). При этом стирается корреляция между фазами рождения
иона и прихода его к электроду. Игнорируя эффект запаздыва-
ния прихода ионов, запишем эквивалентное (10.9) условие само-
поддержания тока зарядов в слое [15.14]:
/ I (р(^ \ 1\
<^+ц+£'0(^)> = yn+\i+E()(t) jexp J a [EC}1 (x, t)] dx — 1 ? \
I \ о J '/
(15.30)
Усреднение здесь производится за период. В ионизационный
коэффициент а подставляется Есл = £о(1 — xfd); у— коэффици-
ент вторичной эмиссии. Основной вклад в интеграл размножения
дает короткий промежуток времени около момента, соответствую-
щего со£ = л/2, когда IEqI и d максимальны.
Уравнение (15.30) связывает V Ка И da или VКа и ja, посколь-
ку Еоа = 8л/а/со. «ВАХ» слоя VKa(ja) имеет минимум. По анало-
гии с теорией Энгеля и Штеенбека (§ 4 г.и. 10) естественно счи-
тать, что реализуется именно это, «нормальное» состояние. Как
и следовало ожидать, расчет по уравнениям (15.30), (15.29)
дает нормальные значения VKa, da, довольно близкие тому, что
получается из уравнения (10.9) при тех же А и В в формуле
(4.8) для сс и у. В рассчитанном дз [15.14] примере (воздух,
А =8,6, В = 254, у = 0,1, ц+р = 1,4 • 103) при /=13,6 МГц, р =
= 30 торр, нормальная амплитуда катодного падения (СК(7)н~
~ 280 В, средняя толщина слоя d^ ~ 0,02 см, нормальная плот-
ность тока /ан ~ 50 мА/см2. Плотность ионов определяется как
п+ = Eodfaieda. Амплитуда ионного тока /ш = еп+ рЛЕ^а, вычислен-
ная в следующем приближении, составляет 15 % от /ан.
Для нормальных параметров справедливы законы подобия:
(Ука)* от давления не зависит, (da)H~p-1, (ВОа)н^р, ток, сов-
падающий приближенно с током смещения /ан ~ Р, ионный ток
/ш ~ р2. Значит, при достаточно низких давлениях ионный ток
действительно составляет малую долю от полного. Но экстрапо-
лируя /см ~ р и /гн ~ р2 к высоким давлениям, следует ожидать
превышения /г над /см. Согласно представлениям [15.14], усло-
вию /\ /см отвечает переход от слаботочного режима к сильно-
точному, а вся построенная теория, относящаяся к случаю
/г < /1М, описывает слаботочный разряд.
Это пе так и противоречит опыту. Теория верна, но относит-
ся не к слаботочному, а к сильноточному режиму. Об этом гово-
рит использование таунсендовского условия самоподдержания
*) Максимальные (амплитудные) значения обозначаем ЕОа, da, VKa.
497
юка проводимости в слое (15.30) и выбор нормальных парамет-
ров по минимуму ВАХ катодного слоя. Экспериментальная кри-
вая рис. 15.15, на которой при низких давлениях 7г</См, цели-
ком принадлежит к сильноточному разряду. Последний легко
отличим на опыте от слаботочного по толщине слоев, характеру
свечения, плотности тока. Переход всегда сопровождается скач-
ками d и / на порядок. Рассчитанная выше малая толщина слоя
dH ~ 0,02 см свойственна именно сильноточному разряду. Для
тех же условий (воздух, р = 30 торр в слаботочном разряде d~
ъ 0,3 см, /а ~ 7 мА/см2) [15.6, 15.13].
Причина малости ионного тока по сравнению с током сме-
щения при небольших давлениях связана с тем, что иону требу-
ется много времени (периодов), чтобы пересечь слой толщины
dan от места преимущественного рождения до электрода. Между
сравнительно быстрым уходом в электрод ионов из прилежащей
области А+ ~ [i+EoJa) и приходом других им на смену как бы
образуется пауза, отчего около электрода получается недостаток
ионов. Ионный ток становится слабым, что и компенсируется
током смещения. И действительно, соотношение токов на элект-
род характеризуется соотношением указанных длин:
Ла ~ ^4-^+^Оа _
Ама w
При достаточно высоких давлениях, когда t00/?"1 сокращается
до амплитуды колебаний ионов Л+, которая от р не зависит, уход
ионов немедленно восполняется приходом рожденных в тот же
период, и ток проводимости выступает на первый план. Никаких
скачков и переходов при этом на опыте не наблюдается.
7.6. Контракция разряда и условия ее отсутствия. Как пока-
зали опыты [15.8], «беспредельно» наращивать ток и попереч-
ный размер (диаметр) токового столба «нормального» сильноточ-
ного разряда между большими плоскими электродами удается
лишь при условии, что межэлектродное расстояние L меньше
некоторого критического значения, L<LKp(p). Значение LKp тем
меньше (т. е. условия сохранения однородности разряда тем
жестче), чем выше давление. Так в воздухе для f = 13,6 МГц
£кр ~ 6; 2,5; 1 см при р = 15, 30, 90 торр соответственно. Если
L > Лкр, однородность сохраняется лишь до некоторого предель-
ного тока Zmax, которому соответствует диаметр Z)max, после чего
разряд контрагирует, сжимаясь в ярко светящийся шнур. Кон-
тракция происходит тем легче, чем выше давление и чем боль-
ше превышение L над Др. При р = 30 торр, например,
и L = 4 см Дпах = 3 см, Zmav ~ 3,5 А; при L = 8 см J9max ~ 2 см,
Aiax 2 А.
То, что контракция облегчается при росте давления, известно
и из практики тлеющих разрядов постоянного тока (гл. 10, 11);
причины здесь те же. Неожиданностью явилась ее связь с меж-
г ^т:тр >дным расстоянием. В работе [15.8] эффект объясняется
498
на основе анализа устойчивое! и разряда по отношению к попе-
речным возмущениям. Не вдаваясь в изложение теории, пояс-
ним качественно его природу. Причиной контракции является
ионизацией но перегревпая неустойчивость (§ 8 гл. 11). Стаби-
лизации однородного сосюяния способствует теплопроводностный
вынос тепла из разряда, скорость которого («частота») =
= х/Л2, где % — температуропроводность, а Л — характерная теп-
лопроводностная длина, которая близка к диффузионной. Для
цилиндрического столба по формуле (4.23) 1/Л2 = (л/Л)2 +
+ (4,8/7))2. Скорость рассасывания наиболее опасных длинновол-
новых возмущений при данной L тем меньше, чем больше
7), и потому, начиная с некоторого Z)max, вынос тепла уже не мо-
жет справиться с ростом температуры газа — наступает контрак-
ция. Однако при достаточно малом размере L частота vF велика
даже при «бесконечном» диаметре. Неустойчивость подавляется
одним лишь уходом тепла в электроды. Ведь скорость нараста-
ния температуры, пропорциональная плотности тепловыделения
<jE>, ограничена величиной, соответствующей нормальной плот-
ности тока. Так появляется условие отсутствия контракции
А 7>Кр.
Обсуждаемый эффект важен для практики. Если ставить пе-
ред собою задачу заполнить однородной плотной ВЧЕ плазмой
i озможно больший объем при возможно большем давлении, к че-
му обычно стремятся в лазерной технике, то шансы добиться это-
го без специальных ухищрений велики лишь в случае достаточно
узкой разрядной щели между большими плоскими электродами.
§ 8. Структура разряда среднего -давления
но результатам численного моделирования
8.1. Уравнения. В одномерном приближении, без учета диф-
фузии, в отсутствие прилипания распределения плотностей за-
рядов и поля в промежутке между плоскими электродами и их
эволюция во времени описываются системой уравнений
дпе дТе
-г- 4- — а | TJ — $пеп+, ГР = — neveE;
dt дх 1^1 । с -Г7 Г с,
дп, <ЭГ,
“Г ' лгл Г+=”+Г + Е;
дЕ . , .
Граничные условия на электродах или изолирующих поверхно-
стях говорят о том, что когда поле направлено к поверхности, на
ней происходит вторичная эмиссия, Ге = —уГ+, когда от поверх-
ности — нет ионного тока, Г+ = 0. К электродам приложено ВЧ
напряжение V; если они изолированы, напряжение делится меж-
ду газовым промежутком и диэлектриками. Для того чтобы на-
чался разрядный процесс, в начальный момент следует задать
499
начальную плотность электронов. На основе подобных уравнений
в [15.15] рассчитывался несамостоятельный ВЧ разряд с внеш-
ней ионизацией (в слаботочном режиме), в [15.16] — разряд пе-
ременного тока (п. 4.6. гл. 16). Мы здесь будем интересоваться
самостоятельным ВЧ разрядом в а- и у-режимах и переходом
между ними [15.12].
Интегрирование системы (15.31) показывает, что через неко-
торое время в большей части длинного промежутка (Л > d) об-
разуется однородный положительный столб, в котором в среднем
за период поддерживается ионизационно-рекомбинационное рав-
новесие. Интересуясь структурой приэлектродных слоев, доста-
точно задать вдали от твердой поверхности плотность плазмы
п = пе = п+ и поле в ней Е = Еа cos соЛ Амплитуда поля Еа связа-
на с п условием <хщеЕУ = $п (п. 3.2 и рис. 15.5). Это эквивалент-
но заданию не напряжения на электродах, а разрядного тока,
амплитуда которого ja выражается через п и Еа(п). Если ток
смещения в плазме мал, ja ~ епреЕа. Представленные ниже резуль-
таты расчетов [15.12] получены с набором входные данных
а = 12р ехр(—342р/£’) см-1 при Ejp > 100 В/(см-торр),
сс = 2,4/; ехр ( — 155р/£’) см"1 при £'//?< 100 В/(см-торр),
ре = 4,4 • 105/р, ц+ = 103/р см2/ (В • с),
£ = 2 • IO"7 см3/с, у = 0,01,
которым часто пользуются при моделировании разряда в азоте;
/=13,6 МГц, р = 15 торр. Расчет велся до установления строго
периодического решения, что требовало времени порядка 102—103*
периодов.
8.2. Результаты. В зависимости от задаваемых п или ja авто-
матически устанавливаются распределения, характерные для сла-
боточного или сильноточного режимов. Смена структуры проис-
ходит при /гкр ~ 8,72 - 109 см-3, /акр ~ 9,2 мА/см2*). На опыте в
воздухе при 30 торр переход был зафиксирован при /ahp ~
~ 17 мА/см2 [15.6], но при р = 15 торр, как в расчете, согласно
[15.11] / в 1,5 раза меньше, т. е. согласие с измерениями вполне
хорошее.
На рис. 15.16 показаны результаты для типичного слаботоч-
ного режима с ja = 4 мА/см2. В плазме при этом п = 3,7 • 109см-3,
Еа/р = 1А В/(см-торр). На электрод идет очень слабый ионный
ток, 10-3—10-4 от полного тока. Существует короткая «анодная»
*) Соответствующая величина (Еа1р)х? — 15 В/(см • торр) менее пока-
зательна, так как реальная ВАХ положительного столба может существен-
но озличаться от принятой из-за нагрева газа или действии колебательной
релаксации, влияния сложных механизмов ионизации (п. 7.7 гл 10). Все
это, однако, не влияет на структуру и параметры приэлектродных слоев.
Еще менее показательно обычно измеряемое на опыте напряжение пере-
хода (на электродах) (п. 4.4). Оно зависит от длины разрядного промежут-
ка L, от толщины диэлектриков, если электроды изолированы; как и Еа1р —
от харакзера охлаждения газа.
500
Рис 15 16 Левый приэлектродный слой слаботочного режима Представле-
ны токи проводимости (а) и смещения (б) в плазме, смещения на левом
электроде (а), ионный (г) и электронный (д) токи на левый электрод. По-
ложительными считаются ток и поле, направленные налево к электроду
Начало отсчета времени произвольно Верзикальными стрелками с цифра-
ми указаны моменты времени, для которых приводятся распределения пе
и Е Соответствующие кривые п(, Е помечены теми же цифрами Стрелки
у п показывают направление движения плазменного фронта Стрелки вверх
у / указывают, что поле растет во времени, вниз — уменьшается Пред-
ставлены также распределения средних за период (постоянных) поля Е
и потенциала V
501
стадия, когда плазма прижимается к электроду и на него идет
электронный ток. Количества выпадающего на поверхность поло-
жительного и отрицательного зарядов за период одинаковы. Плот-
ность ионов пульсирует во времени столь незначительно, что это
невозможно изобразить на рисунке такого масштаба. От поло-
жительного столба к электроду п+ падает вследствие системати-
ческого ухода ионов в электрод. Постоянный потенциал плазмы
Рис 15.17. Левый приэлектродный слои сильноточного режима. Представ-
лены токи проводимости в плазме (а), смещения па левом электроде (6),
электронный (в) и ионныи (г) токи на левый электрод. В остальном все,
как на рис. 15 16, только шкалы у ZT > О и Е' < О — разные
Ио ~ 45 В в 1,7 раза больше, чем полученный по форму ie
(15.24). Максимальная толщина слоя 0,3 см хорошо согласуется
с измеренной в воздухе — 0,35 см [15.11] — и вдвое больше той.
что получается в модели с п+ = const: 2А = ~ 0,16 см.
На рис. 15.17 показаны аналогичные результаты для типично-
го сильноточного режима с ]а = 0,12 А/см2 (п = 9 • 1010 см“3,
Еа/р= 18,6 В/(см - торр)). Подобные плотности тока измерены в
воздухе при 15 торр; получены следующие значения: 0,16 А/см2
в [io.ll], 0,11 A/cmz — в [15.13]. Ионный ток на электрод значи-
те тен, хотя и уступает току смещения. В «анодной» стадии весь
102
ток — электронный. Согласно [15.11] измеренный ток проводи-
мости в слое втрое меньше полного, что согласуется с расчетом.
Слой существенно тоньше, чем в слаботочном режиме, его мак-
симальное значение 0,05 см, а п+ имеет максимум внутри. В рас-
чете автоматически происходит процесс формирования «катодно-
го» слоя: после первых же качков плазменной границы от плазмы
к электроду распространяется волна ионизации, которая остав-
ляет за собою плазму и отодвигает слой пространственного заряда
к электроду. То же получается и при расчетах формирования
тлеющего разряда постоянного тока после пробоя (п. 4.9, гл. 10).
Структура разряда с изолированными электродами по расче-
там не отличается от случая оголенных. Расчеты с заданием си-
нусоидального напряжения на электродах при L = 2 см дают
практически то же самое, что и при задании синусоидального
тока. (См. примечания при корректуре.)
8.3. Нелокальные эффекты. В уравнениях (15.31) они пе уч-
тены (и. 4.10, гл. 10), и потому расчет дает лишь условное опи-
сание переходной зоны между слоем пространственного заряда
и положительным столбом (§ 5 гл. 10). Между тем, на опыте в
сильноточном режиме явно наблюдаются отрицательное свечение
и темное фарадеево пространство. Заметим, что в слаботочном
режиме переходная область светится ярче (рис. 15.11). Возмож-
но, слои слаботочного разряда также являются источником энер-
гичных электронов с энергиями порядка Со. Но и без учета не-
локальных эффектов максимум скорости ионизации и возб\ жде-
ния в слаботочном режиме (впрочем, как и в сильноточном)
приходится как раз на переходную зону [15.17]. (См. примеча-
ния при корректуре.) *
§ 9. Нормальная плотность тока в слаботочном режиме
и пределы его существования
9.1. Физическая причина. Этим эффектам (п. 4.4.) дается
следующее качественное истолкование [15.18]. В опытах ВАХ
положительного столба была падающей. Поскольку в плазме
сголба более или менее фиксировано значение Е/р, ВАХ столба
можно придать условную форму Уст = CpLj~m, где С и тп > 0 —
некие константы. У приэлектродного слоя, где течет ток смеще-
ния, ВАХ Ск = 4лй//й)_ растущая, так как толщина слоя d от
тока не зависит. С учетом сдвига фаз между VK и Уст напряже-
ние на электродах V = (Ест Ек)1^- ВАХ разряда Е(/)
имеет минимум при j = JH = (ь)Ср!Лпъ/1/(m+1). Естественно
предположить, что, когда электроды не заполнены током, реали-
з\ются, как и в разряде постоянного тока, минимальное напря-
жение УП||„ и нормальная плотность тока/н. Последняя тем выше,
чем больше pL, как на рис. 15.12. Но с ростом pL величины /н
н Vk вырастают до критических значений, при которых происхо-
503
дит пробой слоев и наступает сильноточный режим. Отсюда —
верхний по pL предел существования слаботочного.
9.2. О роли нагрева газа и расширении области существова-
ния слаботочного режима. Последнее было бы весьма желатель-
ным, ибо для использования в мощных лазерах (п. 4.7) благо-
приятнее именно этот режим. В непроводящих слоях нет потерь
мощности, и они не служат источниками возмущений для раз-
вития неустойчивости.
Чтобы слои оставались непроводящими, плотность разрядного
тока у не должна превышать /кр для перехода. Согласно сказан-
ному в п. 9.1, это возможно только при pL <(pL)Kp. Но причина
растущей зависимости /н от pL коренится в падающем характере
ВАХ положительного столба, что скорее всего связано с нагре-
вом газа (§ 7 гл. 10) Если частично подавить нагревание путем
быстрой прокачки газа через разряд, ограничение на pL станет
менее жестким. Слаботочный режим будет существовать и при
более высоких значениях рЛ, чем это было в опытах [15.6].
И действительно, расчет ВАХ разряда с учетом нагрева газа и
конвективного теплоотвода [15.19] подтверждает это предполо-
жение, но, конечно, решающее слово остатся за экспериментом.
По расчету, область существования слаботочного режима не-
сколько расширяется и при увеличении частоты.
Заметим, что расчет параметров а —у-перехода на ос но ю
модели пробоя слоев [15.12] и ВАХ положительного столба и
всего разряда с учетом нагрева газа, как в [15.19], дало удовле-
творительное согласие с результатами измерений [15.9], приве-
денными в конце п. 4.4. В зависимости от частоты и роли нагре-
ва в условиях конкретного эксперимента может и исчезать эф-
фект нормальной плотности тока в a-режиме, т. е. сх-разряд
может быть только аномальным. Все сказанное здесь говорит о
важности учета нагревания газа при более детальных расчетах
ВЧЕ разрядов. (См. примечания при корректуре.)
9.3. Замечание о разрядах низкого давления. Интерес к ним
сильно возрос в последнее время в связи с их применениями для
травления поверхностей и внедрения ионов при производстве по-
лупроводниковых материалов для микроэлектроники. В промыш-
ленных реакторах часто используются плоскопараллельные элек-
троды, разделенные расстояниями L ~ 10 см. Работа ведется в
диапазоне частот от 50 кГц до 50 МГц при давлениях 10~?—
1 торр; V 1000 В, у ~ 1 мА/см2. Для низких давлений харак-
терно очень малое падение напряжения на плазме положитель-
ного столба, значительно меньшее потенциалов ионизации газов.
Поэтому рождение электронов связывают с приэлектродными
слоями, на которых падает практически все напряжение [15.20].
Однако ясной картины процесса здесь еще, пожалуй, нет. ВЧЕ
разрядам и их применениям в плазмохимической технологии по-
священ специальный выпуск журнала [15.21]. (См. примечания
при корректуре.)
5 04
Глава 16 РАЗРЯДЫ В МОЩНЫХ СО2-ЛАЗЕРЛХ
НЕПРЕРЫВНОГО ДЕП( ГВИЯ
§ 1. При111и।и работы .икчстроразрядного лазера на СО2
Из всех сущее i ну ющп\ лазеров длительного действия наибо-
лее мощными, продвинутыми в практическом отношении и при-
способленными для резки материалов, сварки металлов, термиче-
ского упрочнения поверх пос гей деталей и ряда других техноло-
гических операций являю гея алоктроразрядные СОг-лазеры. За
25 лет, прошедших со времени создания первого образца (Пател,
1964 г.), их мощность в непрерывном режиме возросла от мил-
ливатта до многих килова! । Тех оологические лазеры с мощ-
ностью до нескольких киловатт и даже 10 кВт выпускаются
промышленностью [16.1]. Правда, ycianoBKii мощнее 10 кВт пока
немногочисленны. Пожалуй, ни одна из проблем прикладного
характера так не послужила в последние десятилетия прогрессу
науки о газовом разряде, как задача создания мощных СОг-ла-
зеров непрерывного действия.
1.1. Лазерный переход в молекуле СО2. Об общих принципах
лазерной генерации было рассказано в §10 гл. 6. Лазер на СО2
не является исключением, в нем з
только используется не элект- ЫО см
ценный, а колебательный пере-
ход между двумя колебатель-5
ними (точнее, колебательно-
вращательными) уровнями ос-
новного электронного состоя- 2.
ния молекулы СО2. Длина вол-
ны излучения X = 10,6 мкм
(Йо =0,117 эВ) принадлежит /
далекой инфракрасной области.
Линейная молекула СО2 может
совершать колебания трех ти-
о о
• с
Рис. 16 1. Схема низших колебатель-
ных уровней молекул СО2 и N2.
Сверху — направления движения
атомов молекулы СО2 в колебаниях
нов (их называют модами;
рис. 16.1). Частота vi соответст-
вует симметричным колебани-
ям, V2 — деформационным, уз —
асимметричным.
Лазерный
различных типов
квант излучается при переходе
пэ состояния 001 в 100; цифры означают колебательные кванто-
вые числа в модах vi, V2, Уз соответственно. Возможен еще пере-
ход 001020, % = 9,4 мтсм, но он обычно гораздо слабее.
Энергетический уровень молекулы определяется состоянием
не только колебательного, но и вращательного движения. Среди
вращательных состояний быстро устанавливается термодинами-
ческое равновесие. Поэтому по мере опустошения того враща-
тельного состояния, с которого происходит лазерный переход, ту-
да поступают молекулы; из других вращательных состояний, так
33 Ю П Райзер
505
что все вращательные уровни образуют как бы общий резервуар
энергии. При необходимости удается выделить одну колебатель-
но-вращательную линию. Энергия кванта составляет 41 % от
энергии верхнего уровня 001. Это есть принципиальный предел
для КПД СОг-лазера. Если бы все затраты энергии при создании
активной среды шли исключительно на возбуждение уровня 001
молекулы СО2 и каждый акт возбуждения сопровождался излу-
чением кванта, энергия лазерного излучения составила бы 41 %
от затрат. Реальный КПД обычно в несколько раз меньше.
1.2. Механизм создания инверсной заселенности. Верхний ла-
зерный уровень в электроразрядных СОг-лазерах заселяется пу-
тем возбуждения колебаний ударами электронов в плазме поло-
жительного столба тлеющего разряда. Мощность лазеров удалось
резко поднять благодаря смешению СО2 с азотом. Энергия пер-
вого колебательного уровня молекул N2, которые хорошо возбуж-
даются электронами в тлеющем разряде и медленно релаксируют,
очень близка к энергии верхнего лазерного уровня 001 СО2
(рис. 16.1). Это открывает возможность быстрой резонансной пе-
редачи колебательной энергии от N2 молекулам СО2 с прямым
заселением нужного уровня. Так, частота передачи колебатель-
ной энергии N2 в поступательную (скорость УТ-релаксации) да-
же при столкновении с исключительно активной в этом отноше-
нии молекулой воды Гут = 175рн2о fT0PP] тогда как
частота обмена квантами с молекулой CO2vo6m ^- 1,8- 104рСо г"* 1-
Находящаяся на верхнем лазерном уровне 001 молекула СО2
либо излучает квант, если нижний лазерный уровень заселен
меньше, либо испытывает УТ-релаксацию с частотой Vvt —
— 365рСо2 1Юри2 + 85рнеГ 1 (в смеси с гелием).
Достижение большой инверсной заселенности обусловливает-
ся не только интенсивным заселением верхнего уровня, но и дос-
таточно быстрым расселением нижнего уровня 100, куда все вре-
мя поступают молекулы, испустившие лазерный квант. С уровня
100 молекулы должны быстро переходить в другие состояния,
«освобождая» уровень для того, чтобы сохранялась значитель-
ная разница заселенностей TVooi — 2V1Oo (инверсностъ), которой
определяются коэффициент усиления и мощность излучения.
Нижнее состояние 100 СО2 расселяется за счет резонансного пе-
рехода энергии колебаний vi-моды в энергию V2-мoды (переход
100 + 020) с последующей УГ-дезактивацией колебаний (020 +
+ 010 + 000), а также за счет двухступенчатой УГ-дезактива-
ции (100 + 010 + 000).
1.3. Недопустимость сильного нагрева. Наряду с дезактивиру-
ющими столкновениями идут и обратные процессы, которые при-
водят к возбуждению нижнего лазерного уровня 100. В резуль-
*) При комнатной температуре; при столкновениях N* с N2, О2 vyr=
= 0,03pN ~г 0,28ро с"1; р[торр].
1 2 2
506
татр действия прямых и обратных процессов заселенность его
оказывается не очень далекой от равновесной, соответствующей
поступательной температуре газа Т. Значит, чтобы поддержива-
лась высокая степень инверсности, температура должна быть
достаточно низкой. Практически нежелателен нагрев газа более
чем на 150—200 °C. При Т > 450—500 К инверсия и лазерная
мощность резко снижается, а при Т > 600—650 К генерация
вообще становится невозможной. Обеспечение достаточно быст-
рого теплоотвода является необходимым условием работы лазера.
Ведь если КПД составляет 10—20%, то 90—80 % всей электри-
ческой мощности, вкладываемой в разряд, в конечном счете идет
на нагрев газа.
Снижение КПД по сравнению с идеальным (41%) происхо-
дит по ряду причин. Не вся энергия, приобретаемая электронами
от поля, затрачивается на возбуждение колебаний, хотя при оп-
тимальных составе газа и отношении Е/р (последнее порядка не-
скольких В/(см-торр)) в колебании N2 и 001 СО2 передается
примерно 80 % электрической мощности. Часть молекул 001 СО2
вместо испускания кванта испытывает релаксацию. Часть энер-
гии излучения теряется при отражении от зеркал и др. Выше
24 % КПД, по-видимому, никогда не был достигнут; реальные
цифры — 10—15 %.
1.4. Лазерная смесь. Опыт показывает, что для СОг-лазеров
очень полезно присутствие гелия. Легкий гелий, обладающий
высокой теплопроводностью, ускоряет вывод тепла из разряда,
улучшает свойства самого разряда. По-видимому, атомы гелия
ускоряют также дезактивацию нижнего лазерного уровня GO2.
Обычно лазерную смесь составляет из трех компонентов: СО2,
N2 и Не. Применяют самые различные составы, подбирая наи-
лучший для данной конструкции, например, в пропорциях СО2 :
• Na : Не = 1: 1: 8, 1:6:12 по числам молекул и др. Однако ге-
лий — газ дорогой, а расходуется его много, так как смесь в
лазерах приходится непрерывно обновлять. Поэтому в промыш-
ленных установках, где стоимость — фактор немаловажный, стре-
мятся сократить содержание гелия. Некоторые конструкции ра-
ботают вообще без гелия — здесь уже идет оптимизация по мно-
гим параметрам.
§ 2. Два типа лазеров, различающихся способом
теплоотвода
2.1. Лазеры с диффузионным охлаждением. Так называют
установки, в которых тепло из разряда выводится механизмом
теплопроводности. Во всех ранних конструкциях и теперь, когда
дело касается мощностей Р 1 кВт, всегда используется класси-
ческая схема тлеющего разряда в трубке (рис. 16.2). В длинной
стеклянной трубке с радиусом R ~ 1—3 см помещены внутри
ко (ьцевые электроды, чтобы не загораживать дорогу излучению.
507
Используется, например, смесь состава СО2 : N2: Не = 1 : 1 : 8
при р ~ 20 торр. С целью непрерывного обновления смеси газ
медленно прокачивают через трубку: в разряде происходит раз-
ложение молекул и образуются побочные продукты, оказываю-
щие неблагоприятное действие. Тепловой поток из разряда идет
к стенкам трубки, которые охлаждают проточной водой. Одно
Рис. 16.2. Схема СО2-лазера небольшой мощности с диффузионным охлаж-
дением: 1 — разрядная трубка, 2 — кольцевые электроды, 3 — медленная
прокачка лазерной смеси, 4 — разрядная плазма, 5 — внешняя трубка, 6 —
охлаждающая проточная вода, 7 — глухое зеркало, 8 — выходное полупроз-
рачное зеркало, 9 — выходящее излучение
из зеркал металлическое, вынесено за пределы трубки; излуче-
ние проходит к нему через соляное окно. Другим зеркалом, по-
лупрозрачным, через которое выводится излучение, служит окно
на противоположном конце. Его делают из NaCl, КС1, ZnSe,
AsGa [16.2].
Для сокращения длины лазера при повышенных мощностях,
когда длина труб достигает десятков метров, их складывают в
несколько колен, ставя отражатели излучения в местах поворотов
Рис. 16.3. Схемы многосекционных трубчатых лазеров, рассчитанных на
мощности 1 кВт и выше: а — последовательное соединение труб, 1 — раз-
рядные трубы, 2 — глухое зеркало, 3 — поворотные зеркала, 4 — полупроз-
рачное выходное зеркало, 5 — выходной луч; б — параллельное включение
труб в оптический резонатор, 1 — разрядные трубы, 2 — глухое зеркало,
3 — полупрозрачное выходное зеркало, 4 — выходные лучи, 5 — фокусирую-
щая линза
(рис. 16.3а). Питание подают независимо в отдельные не слиш-
ком длинные (метровые) секции, иначе потребовалось бы чересчур
высокое напряжение. Параметры разряда типичны для неконтра-
гированного диффузного положительного столба: пе ~ 1010 см-3,
Е/р & 2—4 В/(см • торр), j ~ 10 мА/см2, w ~ 0,5 Вт/см3. Лазеры
такого типа надежны в работе, неприхотливы, хорошо себя заре-
508
комендовали и выпускаются промышленностью в различных ва-
риантах на десятки, сотни ватт, вплоть до киловатта (иногда
больше.
Но по i учить от такой схемы большую мощностхэ можно, толь-
ко наращивая длину труб, что связано с недопустимостью нагре-
ва газа выше, скажем, АТ — 200 °C. Равенство скоростей энерго-
выделения и теплоотвода (10.24) дает
jE = Ncpi\Т!х. т « А2// = Аср1А2А, (16.1 >
где т в данном случае — теплопроводностное (диффузионное)
время вывода тепла из разряда, А — 7?/2,8 (п. 7.1 гл. 10). От-
сюда
piR2E = 1Е = (2,8) 2лХАТ, (16.2)
т. е. к данному АТ приводит определенный вклад мощности на
единицу длины трубы, который не зависит ни от давления (Х(р) —
— const), ни от радиуса трубы R. Таким образом, нельзя про-
извольно повышать ток, например, увеличивая R, или повышать
напряжение, увеличивая р,— наступит перегрев, и генерация пре-
кратится. В 1 м трубы нельзя вкладывать больше примерно
1 кВт электрической мощности и получить с него более 70—100 Вт
излучения.
Принцип диффузионного охлаждения получил и иное во-
площение [16.3]. Множество тонких трубок складывается в ком-
пактный пучок, и «включаются» они в резонатор не последова-
тельно, а параллельно (рис. 16.36). Система состоит из многих
независимых лазеров, каждый со своим электрическим питанием,
но общими резонатором и охлаждением. Пучок многих параллель-
ных лучей, каждый из которых несет мощность около 100 Вт
(а всего их в лазере 37 [16.3]), можно сфокусировать в одно
место линзой большого диаметра, тем самым сконцентрировав
суммарную мощность. На основе этой модели создан технологи-
ческий лазер.
2.2. Быстропроточные лазеры с конвективным охлаждением*
Применение быстрой прокачки газа через разряд резко сокращает
гремя т вывода тепла из разрядного объема и согласно (16.1)
позволяет поднять плотность энерговыделения, а следовательно,
и плотность энергосъема излучением. На этом пути были до-
стигнуты большие успехи в лазерной технике и созданы много-
киловаттные лазеры при умеренных размерах активной области.
Если длина зоны разряда вдоль газового потока L, а скорость
потока и, то т ~ Liu. Например, при L — 30 см, и = 100 м/с
т ~ 3 • 10-3 с, тогда как диффузионный вывод тепла при
р = 20 торр, R = 3 см дает т — 5 • 10“2 с (/ ~ 30 см2/с).
В газе плотности р, протекающем через разряд, в 1 с в 1 г
выделяется энергия /Ё7р. На выходе через время т температура
повышается на АТ в соответствии с первой формулой (16.1).
Существование температурного предела накладывает ограничение
на допустимый удельный энерговклад в разряд, т. е. на энергию,
509
которую разрешается вложить в 1 г газа, q — PeIQ [Дж/г]. Здесь
РЕ — мощность, вкладываемая в разряд, Q = puS [г/с] — массовый
расход протекающего газа; S — площадь поперечного сечения по-
тока. Неравенство Д77 < АТщах накладывает ограничение на па-
раметры системы:
ре _]ESL
Q puS
j Ex
P 1 — П
7max-
(16.3)
Здесь введен КПД т] = Р1РЕ, поскольку излучаемая мощность Р
в нагреве газа не участвует.
С ц ~ 15 % (/max ~ 700—800 Дж/г. Пусть, например, мы хо-
тели бы получить Р = 10 кВт излучения. Для этого нужно вкла-
дывать в разряд РЕ = Р1ц~Ю кВт, что требует расхода (? >
> Лг/^тах ~ ЮО г/с, реально — вдвое больше. На час работы
Рис. 16.4. Принципиальная
схема быстропроточного лазе-
ра на замкнутом цикле: 1 —
газовый контур, 2 — разряд-
ная камера с резонатором, 3 —
теплообменник, 4 — вентиля-
тор, 5 — напуск свежей смеси,
6 — откачка отработанной
смеси
Рис. 16.5. Схема разрядной каме-
ры быстропроточного лазера с
продольным разрядом, в котором
применен многопроходный резо-
натор [16.9]: 1 — разрядный ка-
нал, 2 — катодные штыри, напря-
жение на них подается через ин-
дивидуальные балластные сопро-
тивления (п. 3.2), 3— трубчатый
анод, 4 — направление газового
потока, 5 — зеркала; через по-
следнее, полупрозрачное зеркало
выходит лазерный луч 6
понадобилась бы почти тонна лазерной смеси! Потребность в столь
больших расходах газа в мощных лазерах, рассчитанных на дли-
тельную работу, вынуждает применять в них замкнутый цикл.
Лазерная смесь циркулирует по контуру, много раз проходя
через разрядную камеру (рис. 16.4). Для прокачки газа при-
меняют компрессоры, насосы, вентиляторы [16.1]. Газовый тракт
непременно включает теплообменник, где от газа отбирается
тепло, приобретенное в разряде. Смесь в контуре, как и в труб-
чатых лазерах, приходится медленно обновлять.
Разрядной камерой часто служит широкий плоский канал.
Поле и ток направлены либо перпендикулярно потоку (попереч-
ный разряд), либо вдоль него (продольный). Это схематически
показано на рис. 16.1. Луч в резонаторе пускают вдоль протя-
510
женной ширины канала'перпендикулярно газовому потоку и току.
Чтобы снять энергию с возможно большего объема активной
среды и удлинить резонатор, его часто делают многопроходным
(рис. 16.5). Два крайних зеркала образуют резонатор, проме-
жуточные (металлические) поворачивают луч обратно в разряд.
Для выпуска луча служит либо полупрозрачное зеркало, либо
кольцевое окно вокруг металлического. В последнее время по-
лучили широкое распространение и трубчатые лазеры с быстрой
продольной прокачкой. В трубе разряд получается более одно-
родным и качество излучения более высоким.
§ 3. Способы борьбы с неустойчивостями
3.1. Задача достижения принципиального предела по энер-
говкладу. Она остро стоит в быстропроточных лазерах. Ограни-
чение (16.3) ставит, можно сказать, принципиальный предел на-
ращиванию тока и электрической мощности при данных давле-
нии и массовом расходе газа, и здесь уже ничего не поделаешь —
температуру газа сильно повышать нельзя. При заданном вре-
мени пролета т = Liu предельному энерговкладу отвечают не
зависящие от давления максимально допустимые плотности элек-
тронов и тока. В самом деле,
q ~ jExlp сю пе(Е1рУх, / <*> пе(Е1р), (16.4)
а Е1р от р зависит слабо. Численно для типичных лазерных
смесей (скажем, 1:6: 12) и т ~ 3 • 10“3 с zzemax ~ 3 • 1010 см“\
Утах 20 мА/см2, Е1р~% В/(см-торр), ч;тах ~ 0,16 р Вт/см3.
Величины эти, казалось бы, не„чрезмерно высоки. При раз-
рядах в трубках (вообще в маленьких объемах) и при низких
давлениях они нередко получаются в лабораторных эксперимен-
тах. Но тогда встала задача достичь их в больших объемах:
в каналах с шириной порядка 100 см, длиной вдоль потока
20—40 см, высотой 5—10 см, при давлениях в десятки, сотню
торр, то оказалось, что это большая и сложная проблема. В про-
цессе повышения тока и мощности (/ и ш) еще задолго до
температурного предела (16.3) разряд становится неустойчивым
п теряет однородность (гл. 11). Чаще всего происходит контрак-
ция (шнурование; см. цветную вклейку в [10]). Шнурование
приводит к полному срыву лазерной генерации. Преодоление
неустойчивостей разряда представляет собой главную и наиболее
трудную проблему при создании лазеров большой мощности.
Развитию неустойчивостей очень способствует то, что газ заклю-
чен в замкнутый контур (где накапливаются провоцирующие их
продукты), и повышение давления, к чему всегда стремятся.
Ведь повышение плотности (давления) газа—наиболее це-
лесообразный путь к получению больших мощностей с сохране-
нием умеренных габаритов установки. Это видно из формулы
(16.3). Как можно увеличить расход Q = puS? Увеличение ско-
рости выше 200—250 м/с сопряжено с большими техническими
511
трудностями. С увеличением площади сечения S растут все га-
бариты. Вот и остается наиболее привлекательный путь — повы-
шать плотность, эффективнее используя объем. Но чем выше
давление, тем легче срывается однородный разряд. Остановимся
на некоторых способах стабилизации разряда, позволяющих
поднять предельные ток и мощность, выше которых разряд те-
ряет устойчивость.
3.2. Секционирование катода. Когда между какими-то местами
больших электродов возникает токопроводящий шнур и ток под-
скакивает, напряжение на электродах немедленно падает (фор-
мула (10 1)). Поле в других местах становится недостаточным
для поддержания стационарного разряда. Этот процесс удается
частично предотвратить и тем самым отчасти стабилизировать
разряд путем секционирования электродов, чаще — катода. На
каждый из элементов напряжение подается независимо через
индивидуальное балластное сопротивление. Последние сами по
себе оказывают на разряд стабилизирующее действие, гася
(флуктуации тока. В результате, когда от одного из катодов берет
начало шнур, по которому течет повышенный ток, это не при-
водит к столь катастрофическому падению напряжения на участ-
ках ряда, замыкающихся на других катодах.
Секционированными катодами пользуются во многих установ-
ках. Дело заключается еще и в том, что при повышенных дав-
лениях нормальная плотность тока на катоде /н оказывается в
10—100 раз больше допустимой плотности тока в положительном
столбе. Если в столбе она, как следует из оценки п. 3.1, порядка
10 мА/см2, то, скажем, при р = 40 торр /н ~ 2 -10“4 р2 А/см2 «
~ 300 мА/см2. Катоды выгодно использовать в режиме, гранича-
щем между нормальным и аномальным, при полном заполнении
площади. Это способствует стабилизации разряда вследствие рас-
тущего характера ВАХ аномального катодного слоя. Поэтому
площадь катодов все равно приходится делать гораздо меньшей
площади токового сечения в основной части разрядной камеры.
Чтобы равномернее распределить катодную поверхность по
токовому сечению камеры, катодные элементы рассредотачивают.
В поперечном разряде ими равномерно усеивают диэлектрическую
плату, встраивая в нее маленькие металлические элементы
«заподлицо», чтобы не возмущать потока (рис. 10.1а), в про-
дольном — на входе в разрядный канал выстраивают ряд катод-
ных штырей (рис. 10.16); форму их и число подбирают эмпири-
чески. Секционированные катоды обычно располагают именно на
входе в камеру, вверх по потоку. Наибольшую опасность пред-
ставляют возмущения, зарождающиеся на входе, а не на выходе,
так как последние скорее выносятся потоком за пределы разряда.
3.3. Управление потоком. Стабилизации разряда способствует
выравнивание поля скоростей, особенно в системах с продольным
разрядом Важно свести к минимуму возможные неоднородности,
которые могут положить начало развитию неустойчивости. По-
вышение скорости, т. е. сокращение времени пребывания газовой
512
частицы в разряде, вообще говоря, затрудняет развитие неустой-
чивости, хотя иногда слишком большое ускорение потока при-
водит к обратному эффекту [16.1, 16.2]. Благоприятное действие
оказывает создание интенсивной мелкомасштабной турбулентнос-
ти, которая, подобно диффузии и теплопроводности, оказывает
рассасывающее действие на зарождающиеся возмущения. Нуж-
ный масштаб турбулентности и конструкции турбулизаторов
(ряды штырей, сетки и т. д.) подбирают эмпирически.
Надо сказать, что когда добиваются стабилизации разряда и
улучшения его характеристик, многое решается на основе чисто
интуитивного экспериментального поиска, а не путем осуществле-
ния какой-то теоретической программы. Эксперимент здесь явно
опережает теорию, и реализация многих начинаний зависит от
опыта, физической интуиции и мастерства экспериментатора,
которые в лучших случаях граничат с искусством. Все это вообще
характерно для работы с разрядами, которые обладают мно-
жеством неуловимых особенностей.
3.4. Применение несамостоятельного разряда. И перечислен-
ные выше, и некоторые другие приемы, обычно используемые
комплексно, дают весьма положительные результаты. Примером
тому служит технологический пятикиловаттный лазер с самостоя-
тельным поперечным разрядом (п. 4.1). С помощью секциони-
рования электрода и сложной аэродинамической техники была
достигнута мощность 20 кВт в лазере с самостоятельным про-
дольным разрядом [16.4]. Но самым решительным шагом было
применение для накачки лазера несамостоятельного разряда с
пучком быстрых электронов в качестве постороннего ионизато-
ра*). Сделано это было первоначально (1970 г.) в импульсных
СОг-лазерах, и наиболее широкое распространение метод получил
в импульсной лазерной технике. Однако уже имеется немалый
опыт использования электронного пучка и в лазерах непрерыв-
ного действия [16.5, 16.6].
Смысл применения несамостоятельного разряда заключается
в том, чтобы разорвать цепочку развития неустойчивости (11.8)
в том последнем звене, которое единственное и поддается разрыву.
Если ионизация в газе поддерживается внешним источником, не
подверженным (или мало подверженным) влиянию плазменных
процессов, то изменение скорости ионизации «своими» электро-
нами, связанное с изменением Е/N, мало что изменит. Ведь иони-
зация электронами, ускоренными полем Е, играет подчиненную
роль. Тем самым парализуется наиболее опасная, ионизационно-
перегревная неустойчивость.
Когда ионизация создается внешним источником, пе и прово-
димость определяются его интенсивностью и не зависят от прило-
женного напряжения. Повышать ток и энерговыделение при
данных интенсивности источника и давления можно лишь путем
*) Для ионизации можно использовать также ультрафиолетовое из-
лучение
513.
увеличения напряжения на электродах, т. е. EIN. Как только EIN
приближается к значению, соответствующему самостоятельному
разряду, скорость ионизации электронами разряда становится
сравнимой с действием внешнего источника и восстанавливаются
все те причины, которые вызывают неустойчивость. Таким обра-
за м, метод имеет свои границы.
Несамостоятельный разряд выгоден еще и тем, что в нем
отделены функции поддержания ионизации и сообщения электро-
нам энергии, необходимой для эффективного возбуждения ко-
лебаний N2 и 001 СО2. В самостоятельном разряде обе функции
выполняются одним и тем же приложенным полем, в несамостоя-
тельном за полем остается только вторая функция. Можно под-
бирать значения E]N, оптимальные для лазерной накачки, а плот-
ность мощности IE со neN(Е/N)2 повышать не путем увеличения
напряжения; и EIN, а повышая давление р N. Однако ограни-
чения (16.3), (16.4) на разогрев и пе все равно остаются в силе.
§ 4. Пути организации разряда в больших объемах
с протоком газа
4.1. Поперечный самостоятельный разряд. Принципиальная
схема его показана на рис. 10.1а. Множество (бывает, что сотни)
специально сконструированных катодных элементов, подключен-
ных через индивидуальные балластные сопротивления, разме-
щают над единой анодной пластиной. Общее балластное сопротив-
ление должно составлять 20—30 % от сопротивления разряда.
К сожалению, на нем бесполезно теряется такая же доля электри-
ческой мощности. От каждого катода начинается расширяющаяся
струйка тока. На расстоянии 1 — 2 см они все перекрываются,
и общая плазма простирается до анода.
Однако, как показали исследования [10.31, 16.1, 16.2], плазма
сплошного положительного столба все равно не является однород-
ной, и это свойственно электроотрицательным газам в условиях
кратковременного пребывания газовой частицы в разряде. В плаз-
ме не успевают накапливаться активные молекулы, отрывающие
электроны от отрицательных ионов. Поэтому не устанавливается
баланс между прилипанием и отлипанием. На пути к аноду
электроны гибнут за счет прилипания, и эти потери не восста-
навливаются ни ионизацией, ни отлипанием. Проводимость по
направлению к аноду падает, а поле соответственно возрастает,
так как ток постоянен. В анодной области в усиленном поле
скорость ионизации, напротив, превышает скорость объемной ги-
бели зарядов, и избыток положительных ионов благодаря дрейфу
вносится в плазму. Таким образом, в отличие от классического
образца положительного столба, здесь пет локального баланса
между рождением и гибелью электронов, и плазма в столбе
является несамостоятельной. Так же получается и в коротких
продольных разрядах. В электроположительных газах этого эф-
фекта нет, локальный баланс существует. Имеется неоднород-
ен
ность и поперек тока: вниз по потоку температура газа растет,
плотность его уменьшается, и поле падает (до 1,5—2 раз).
ВАХ разряда почти горизонтальная или слабо возрастающая
(в отличие от падающей при разряде в трубке без потока).
Рассматриваемая схема разряда много и всесторонне иссле-
довалась, в том числе и в отношении нестабильности: возникно-
вения доменов и контракции [10.31]. Она положена в основу
первой серийной модели советских быстропроточных технологи-
ческих лазеров на замкнутом цикле, которые работают на ряде
предприятий [16.7]. Вот некоторые параметры этого лазера. Мощ-
ность Р ~ 5 кВт, длина разряда вдоль потока L = 20 см, ширина
а = 90 см, высота канала (она же и расстояние между электро-
дами) h = 4 см, р ~ 50 торр, и « 80 м/с, смесь СО2: N2: Не =
= 1: 20 : 20, w ~ 5,5 Вт/см3, q & 320 Дж/г; резонатор трехпроход-
ный. На той же принципиальной основе создан 10-киловаттный
лазер [16.8, 16.1] и разрабатываются новые усовершенствованные
модели.
4.2. Продольный самостоятельный разряд. Схема его показана
на рис. 10.16, а также на рис. 16.5, который приводился выше,
чтобы показать, как выглядит многопроходный резонатор, и на
котором изображена в общих чертах реальная установка [16.9].
Быстрая прокачка газа с замкнутым циклом применяется и в
трубчатых конструкциях типа изображенной на рис. 16.3а. В оп-
ределенном смысле такой разряд также следует причислить
к продольным. Так устроен советский серийный лазер «Карат»
мощностью 1,5 кВт [16.10, 16.1]. Своеобразно организован раз-
ряд в промышленных лазерах фирмы «Spectra Physics»; они
выпускаются на мощности 1,2; 2,5; кВт [16.1]. Катодом служит
трубка на входе в плоский канал (как анод на рис. 16.5), а анод
лежит на нижней плоскости канала, как на рис. 10.1а, причем
он выполнен в виде секционированных полос вдоль потока. Ток,
следовательно, искривляется, будучи у анода «поперечным», а у
катода «продольным».
4.3. Несамостоятельный разряд с ионизацией электронным
пучком. Для его организации пучок электронов, испускаемых рас-
каленной поверхностью металла и ускоряемых в вакууме высоким
напряжением Vi ~ 100 кВ, пропускают в разрядную камеру. По-
следняя отделяется от ускорителя тонкой мембраной (рис. 16.6).
Пройдя через сетчатый электрод, пучок вступает в газ. Напря-
жение Vi подбирается так, чтобы пробег электронов при давлении
лазерной смеси был сравним с расстоянием до другого электрода.
Тогда и энергия электронов eV\ используется почти полностью,
и объем ионизируется более однородно. Через электроды и иони-
зованный газ пропускается постоянный ток, энерговыделение от
которого дает лазерную накачку. Быстрые электроны ионизуют
газ не столько сами, сколько благодаря вторичным, более медлен-
ным электронам. В среднем с учетом возбуждения электронных
состояний на образование одной пары ионов затрачивается
Ei « 50 эВ.
515
МОЩНОСТИ Ге = lid — Ч К 1
Рис. 16.6. Принципиальная схе-
ма лазера с электронным пуч-
ком: 1 — эмитер электронов,
2 — мембрана, отделяющая ва-
куумную область ускорителя
5 от объема разрядной каме-
ры 6, 3 — сетчатый электрод
для несамостоятельного раз-
ряда, 4 — второй электрод, 7 —
направление газового потока,
8 — глухое зеркало, 9 — выход-
ное зеркало
HocMoipuM, какой требуется источник быстрых электронов
для поддержания плотности электронов пе в объеме Q активной
среди. Пусть в 1 см3 в 1 с рождается электронов и гибнут
они в результате прилипания и объемной рекомбинации с эффек-
тивным коэффициентом ^эф (§ 8 гл. 10). В стационарных уе-
ло шях = РэфГ?е. и, если пренебречь потерями, нужен источник
’ где i\ — ток пучка. Например, при
пе = 1011 см-3, Q = 103 см3 = 1 л и
рэф = 10“6 см3/с получается 51 =
= 1016 см~3 • с"1, Ре — 80 Вт; если
Vi = 100 кВ, то / = 0,8 мА.
Самое ценное преимущество
элеьтропонизационных лазеров со-
стоит в том, что благодаря устойчи-
вости разряда они могут работать при
давлениях порядка атмосферного (им-
пульсные — даже при более высоких).
Это резко сокращает размеры актив-
ной зоны. Затраты мощности на под-
держание ионизации ничтожны по
сравнению с той мощностью постоян-
ного тока РЕ. которую удается вло-
жить в объем для накачки колеба-
ний. Так, при р = 300 торр и выборе
напряжения на электродах, дающего
благоприятное для накачки Е!р =
(о ~ 10 '3 пе)р Ом"1 • см-1). Созда-
ны и успешно функционируют
10-киловаттные лазеры непрерывного действия на замкнутом
цикле [16.5, 16.6]. Но широкого распространения такие установ-
ки, в отличие от импульсных, пока не получили. Сдерживают
трудности технического характера: от непрерывной нагрузки раз-
рушаются мембраны, приходится изолировать работающий лазер
от людей из-за опасного рентгеновского излучения и др. Все
это побуждает непрестанно искать другие, более доступные пути
организации несамостоятельного или близкого к тому разряда.
4.4. Комбинированный разряд с постоянным и ВЧ полем.
Непрерывная мощность излучения 27 кВт, обязанная вкладу
электрической энергии 160 кВт, была достигнута в большом
лазере на замкнутом цикле с продольным разрядом постоянного
тока благодаря использованию вспомогательного ВЧ разряда
емкостного типа [16.11]. Исследования, предшествующие созда-
нию этого лазера [16.12], и их успешный результат стимулиро-
вали изучение физики ВЧЕ разряда (гл. 15). Приведем неко-
торые параметры этой установки, схема разрядной камеры ко-
торой показана на рис. 16.7: L = 53 см, а = 244 см, h = 6,3 см,
и = 140 м/с; смесь 1 : 6,4: 12,6, р = 30 торр. Частота ВЧ напря-
жения 13,6 МГц. Без ВЧ поля удалось вложить в разряд по-
516
5 В/(см • торр), PE = (j£'2Q « 75кВт
стоянного тока только 60 кВт (0,74 Вт/см3). При вкладе 60 кВт
ВЧ мощности мощность постоянного тока можно было поднять
до 100 кВт, т. е. в сумме 160 кВт или 2 Вт/см3. Разряд, пожа-
луй, нет смысла причислять к категории несамостоятельных:
мощности ВЧ и постоянного токов сравнимы, поэтому оба поля
(вернее, их векторная сумма) выполняют одновременно обе
функции: и ионизации газа и сообщения электронам энергии.
Судя по оценочной плотности ВЧ тока, 2—3 мА/см2, ВЧЕ разряд
следует отнести к слаботочной форме. Однако величина ph =
= 190 торр см кажется слишком большой для нее (п. 4.5
гл. 15). Возможно, здесь вследствие интенсивного конвективного
охлаждения проявился эффект расширения области существова-
ния a-режима, о котором говорилось в п. 9.2 гл. 15. Вопрос не
ясен, но интересен. К сожалению, на этот счет нет никакой
экспериментальной информации.
Никаких сведений о дальнейшем развитии указанного направ-
ления в лазерной технике (а также о 20-киловаттном лазере
[16.4]) в литературе больше не появлялось. Возможно, установка
оказалась слишком сложной.
4.5. Несамостоятельный разряд с ионизацией газа повторяю-
щимися емкостными импульсами. Такой, истинно несамостоя-
тельный заряд был осуществлен в большом лазере на замкнутом
цикле [16.13]. Схема разрядного устройства напоминает рис. 16.7.
Рис. 16 7. Схема быстропроточного ла-
зера с продольным разрядом постоян-
ного потока и вспомогательным попе-
речным ВЧЕ разрядом [16 11]: 1 — ди-
электрические пластины, образующие,
ра зряднып канал, 2 — ряды катодных
элементов (360 штук), 3 — анод (четы-
ре параллельные трубки), 4— электрод-
ные пластины для ВЧ напряжения, 5 —
направление газового потока. Зеркала
для многопроходного резонатора, разме-
щенные, как на рис 16 5, не показаны
Существенным элементом в нем является помещение электродов
конденсатора внутрь разрядной камеры; от плазмы они изоли-
рованы тонкими жаропрочными стеклами (рис. 16.8). Это во
много раз увеличивает емкость изоляторов, сокращает падение
напряжения на них, отчего возрастает ионизующее поле в плазме
(§ 2 гл. 15, рис. 15.3). Объем разрядной камеры 27 л: L = 63 см,
а = 76 см, h = 5,5 см; скорость потока и 230 м/с. На обкладки
конденсатора с частотой до 100 кГц подаются импульсы длитель-
ностью порядка 10~7 с и напряжением примерно 15 кВ. Они
поддерживают в объеме исключительно однородную плазму
с ~ 1010 см-3. Скважность импульсов достаточно высока для
того, чтобы их средняя мощность была небольшой, 1 кВт. Вместе
с тем в паузах 10“5 с плазма практически не распадается. Этот
безэлектродный разряд емкостного типа сам по себе является
517
вполне самостоятельным. Электрические процессы в нем имеют
общие черты с ВЧЕ разрядом [16.13, 15.2].
Большая мощность, идущая на лазерную накачку, вносится
постоянным продольным полем. ВАХ постоянного тока растет
почти линейно (рис. 16.9), так как пе и сопротивление плазмы
определяются посторонним ионизатором и от постоянного напря-
жения зависят мало. Так получается, пока постоянный ток далек
от самостоятельного. При приближении
к самостоятельности разряд шнуруется.
Применение постороннего ионизатора в
виде повторяющихся импульсов позво-
лило повысить мощность постоянного
Рис. 16.8. Схема быстропроточно-
го лазера [16.13]: 1 — толстые
прозрачные стекла, образующие
канал, 2 — металлические сетки,
на которые подаются высоко-
вольтные ионизующие импульсы,
3 — тонкие изолирующие жаро-
прочные стекла, 4 — катодные
элементы (50 штук), 5 — две
анодные трубки, 6 — отверстия
для установки зеркал многопро-
ходного резонатора. 7 — направ-
ление газового потока
Рис. 16 9. ВАХ несамостоя-
тельного постоянного тока в
установке, изображенной на
рис. 16.8 [16.13]. Частота
ионизующих импульсов
100 кГц. Смесь СО2: N2 • Не =
= 1:7:12, р = 30 торр. Кри-
вая Z — без потока, 2 — и »
= 60 м/с, 3—130 м/с, 4—
220 м/с. ВАХ самостоятельно-
го тока в той же установке
горизонтальна и от скорости
потока не зависит (рис. 10.26)
тока более чем на порядок, довести ее до РЕ ~ 70 кВт
(2,6 Вт/см3) при р = 50 торр в смеси 1:6:12 и получить
Р = 6 кВт излучения; в усовершенствованной модели этого ла-
зера — даже 10 кВт. На основе описанного принципа организации
разряда создан компактный технологический лазер комбиниро-
ванного действия [16.14]. Он может работать и в непрерывном
режиме, и в импульсно-периодическом, давая импульсы излу-
чения с частотой до 250 Гц. Последний режим полезен для свар-
ки, позволяет пробивать множество маленьких отверстий и т. д.
Примечательно, что разделенные относительно длинными пау-
зами высоковольтные импульсы поддерживают ту же ионизацию
в тех же условиях при гораздо меньшей средней мощности, чем
мощность ВЧ поля (пе ~ 1010 см-3 при 0,05 Вт/см3 и 1,4 Вт/см3
соответственно). Вследствие резкой зависимости частоты иони-
зации от поля достаточно увеличить поле в два-три раза —
и можно сократить время его действия и мощность в десятки раз,
518
получив то же самое число рожденных электронов. Поэтому им-
пульсы с удачно выбранными частотой и скважностью ионизуют
много эффективнее, чем почти «не прекращающееся» синусоидаль-
ное поле, в котором ионизация все равно происходит только
в короткие мгновения амплитудных значений. Разумеется, в лазе-
ре большая ВЧ мощность не пропадает, она расходуется на лазер-
ную накачку, как и энергия постоянного тока. Но вложить в раз-
ряд чуть ли не сотню киловатт ВЧ полем в техническом отно-
шении неизмеримо труднее, чем постоянным. В этом и состоит
целесообразность комбинации мощного несамостоятельного по-
стоянного тока с маломощными ионизующими импульсами по
сравнению с мощным самостоятельным ВЧЕ разрядом, который,
в принципе, можно было бы организовать в той же установке,
изображенной на рис. 16.8. По поводу механизма стабилизации
разряда импульсами и ВЧ см. п. 4.4 гл. 11 и [10.27].
4.6. Разряд переменного тока. Так называют электродный
или безэлектродный емкостный разряд на частоте / = 10 кГц.
Низкие частоты до 10 кГц обладают по сравнению с высокими
важным техническим преимуществом — они вырабатываются
генераторами, которые проще, дешевле и менее капризны, чем
ламповые ВЧ генераторы. По сравнению с постоянным током
низкие частоты обладают тем же ценным преимуществом, что и
ВЧ: для стабилизации разряда можно пользоваться реактивными
(емкостными) балластными сопротивлениями, в которых не вы-
деляется джоулево тепло и нет потерь мощности. Разряду пере-
менного тока свойственны стабилизирующие качества несамо-
стоятельного разряда, и вместе с тем он не требует применения
вспомогательного источника ионизации. Один источник питания
служит и для ионизации, и для* накачки лазерной среды энер-
гией, просто эти функции разнесены во времени. Электроны рож-
даются кратковременными вспышками в моменты амплитудных
значений ионизующего поля, а в остальное время энергия вкла-
дывается в рекомбинирующую плазму, уже не подверженную
воздействиям ионизационно-перегревной неустойчивости.
Целесообразность применения разряда переменного тока в
СОг-лазерах была отмечена в работе [16.15], с которой и на-
чалось подробное изучение этого процесса. Он занимает некое
промежуточное положение между разрядами постоянного тока
и ВЧЕ. Независимо от того, обнажены электроды пли изолиро-
ваны, около каждого из них в соответствующий полупериод каж-
дый раз должен происходить пробой и формироваться катодный
слой. Низкочастотный и потому слабый ток смещения не в со-
стоянии произвести замыкание тока на электроде. В этом отноше-
нии разряд похож на сильноточный ВЧЕ. Разряд переменного
тока можно использовать и в быстропроточных лазерах, и в труб-
чатых с диффузионным охлаждением; последний вариант более
продвинут. Создан многоканальный лазер переменного тока.
Схема его похожа на приведенную на рис. 16.36, но электроды
вынесены из трубок наружу, что сильно упрощает дело и по-
519
зволяет применить очень тонкие трубки, диаметром всего 5 мм
[16.16]. Лазер метровой длины и общего диаметра 7,5 см со-
держит 61 трубку и дает мощность 1,2 кВт. Балластом служат
емкости участков стекла под электродами. На основе этой модели
разработан технологический лазер. Подробнее об экспериментах,
теории, численных расчетах разрядного процесса, о многоканаль-
ном лазере переменного тока и о перспективах данного метода
см. [16.1, 16.2].
4.7. Самостоятельный высокочастотный емкостный разряд.
Он обладает рядом преимуществ по сравнению с разрядами по-
стоянного и переменного токов. ВЧЕ разряд устойчивее разряда
постоянного тока, и в нем достижим существенно больший эн *рго-
вклад. Балластным сопротивлениям, которые всегда оказывают
благотворное влияние на стабильность разряда, можно придать
емкостной (реактивный) характер, и это избавляет от бесполез-
ных потерь энергии, которые в обычных омических балластнпках
составляют примерно 30 % электрической мощности. В этом от-
ношении, конечно, ВЧ разряд не лучше низкочастотного, ибо
там тоже применяют емкостные сопротивления. Одно из су-
щественных преимуществ ВЧЕ разряда — это возможность изба-
виться от катодных слоев, свойственных разрядам и постоянного
и переменного токов. В катодных слоях бесполезно теряется часть
энергии, кроме того, в них обычно рождаются возмущения, о г
которых развивается неустойчивость. Но отсутствию «катодных»
слоев отвечает лишь слаботочная форма ВЧЕ разряда, в которой
ток из плазмы замыкается на электроды только токами смещения
(гл. 15). Поэтому для лазеров желателен именно слаботочный
режим. Это — недостаток, ибо ставит ограничения на плотность
тока, на длину промежутка и давление (§ 4.9 гл. 15).
Еще одно достоинство ВЧЕ разрядов, правда, свойственное
и емкостным низкочастотным разрядам,— это практическое удоб-
ство работы с длинными трубками. В трубках с быстрой осевой
прокачкой разряд обладает высокими устойчивостью и однород-
ностью. Последнее очень важно также и для качества излучения.
Приложение постоянного продольного поля, как в трубчатых ла-
зерах, требует напряжений в десятки киловольт. Если же по-
местить диэлектрическую трубку между двумя электродными по-
лосами или же вплотную покрыть ее сверху электродами, имею-
щими в сечении вид полуколец, то достаточно совсем небольших
ВЧ напряжений порядка 1 кВ и даже меньше. Очень легко мо-
дулировать интенсивность излучения путем модуляции подавае-
мого ВЧ напряжения, что немаловажно для практики.
ВЧЕ разряд широко и успешно применяется в лазерах не-
большой мощности*). Он особенно удобен для маленьких отпаян-
ных волноводных систем. Электроды располагают поверх тру-
бочки квадратного сечения примерно 2X2 мм2, вдоль нее
[16.18]. Созданы и ВЧЕ СОя-лазеры киловаттной (и более) мощ-
*) Одна из первых ВЧЕ СОг-установок (см. [16.17]).
520
ности [16.19, 16.20], с быстрым протоком газа. О нескольких
установках этого типа сообщается в [16.21]. Говорится даже о
том, что за последние 10 лет разработано новое поколение техно-
логических ССЬ-лазеров (имеются в виду ВЧЕ), которые более
компактны, легки, просты в конструкции и удобнее на прак-
тике, чем лазеры старого поколения на постоянном токе [16.22].
Во всяком случае несколько фирм уже выпускает технологиче-
ские ВЧЕ СОг-лазеры с мощностью 1 кВт и более. Весьма эффек-
тивен и компактный щелевой волноводный ССЬ-лазер средней
мощности 100—200 Вт с диффузионным охлаждением, в котором
ВЧ разряд возбуждается не в трубочке, а в протяженной щели
зигзагообразного сечения [16.23]. На ВЧ направление в лазерной
технике возлагаются большие надежды; обзор современного со-
стояния см. в [16.24].
Дополнение. ПРИНЦИП РАБОТЫ
МАГНИТОГИДРОДИНАМ ИЧЕСКОГО ГЕНЕРАТОРА
Он иллюстрируется рис. Д. 1. Ионизованный газ протекает
по каналу со скоростью и и пересекает линии напряженности при-
ложенного постоянного магнитного поля. В движущейся среде
индуцируется электрическое поле
Е' = с-1[иВ]. Вектор магнитной ин-
дукции В = цН не отличается от Н,
поскольку магнитная проницаемость
газа ц = 1*). Направление Е' харак-
теризуется координатным равенством
Еу = — uxBz/c, соответствующим*
рис. Д.1. Индуцированное поле Е'
движет электроны вверх. У верхней
стенки канала накапливается отри-
цательный пространственный заряд,
у нижней — положительный. Если
внешняя цепь между электродами, рИс. дл Принципиальная
помещенными на этих стенках, ра- схема МГД генератора
зомкпута, заряды накапливаются,
пока созданное ими электрическое поле Еж не уничтожает инду-
цированное (Ех = —£"). Потенциал нижнего электрода при этом
превышает потенциал верхнего на == E^L. Это напряжение
совпадает по величине с ЭДС генератора &=EyL — — (uxlc} (BZL)9
Если цепь замкнуть через нагрузочное сопротивление и обес-
печим» дос неточно высокую электронную эмиссию с нижнего
элек1рода, например путем его активирования и нагревания, в це-
*) Закон ин 1укции можно рассматривать как результат усреднения ло-
р<чщевои силы (<//с) fvH], которая действует на индивидуальным заряд д,
движущийся со скоростью v в локальном поле Н. При усреднении силы по
(uopociHM »11Н1иц появляется макроскопическая скорость среды и, по мик-
ро» коническому полю II — индукция В Действие усредненной силы экви-
в<» пен ню действию ноля Е'
34 и> и и |.
521
пи потечет ток. Реально электроны в газе непрерывным потоком
дрейфуют вверх, исходя из нижнего положительного электрода,
который в отличие от обычного разряда работает подобно катоду,
и внедряясь в верхний. Частичное устранение приэлектродного
пространственного заряда, уносимого током, приводит к уменьше-
нию напряжения на электродах V = EyL по сравнению с
В пренебрежении эффектом Холла (§ 9 гл. 3), в результате ко-
торого возникает ток по оси х 1 Е, В, плотность тока в газе
j = о(Е + Е') = о(Е + с-1 [иВ]), ]у = о(Еу — uxBJc) < О,
а ток в цепи i = jS, где S — в рассматриваемой прямоугольной
геометрии площадь электродов и сечения области действия маг-
нитного поля. Это равенство вместе со связью iR = V через сопро-
тивление нагрузки R позволяет найти ток i при задаваемых о,
и, В, R и геометрических параметрах.
При протекании тока на газ действует тормозящая пондеро-
моторная сила, в результате чего он и теряет энергию. Отноше-
ние мощности, выделяемой в нагрузке, к мощности, отбираемой
от газа:
iV __ V
(и/с) (JB) LS ~ Г
т. е. электрический кпд генератора тем выше, чем ближе си-
туация к режиму разомкнутой цепи. Но абсолютное значение
полезной мощности IV максимально, когда сопротивления на-
грузки и плазмы одинаковы и V = |<2Г|/2. Ток и полезная мощ-
ность уменьшаются в результате протекания холловского тока ух,
который возвращается по электродам. Этот нежелательный эф-
фект частично предотвращается секционированием электродов
вдоль оси х и замыканием каждой пары через индивидуальную
нагрузку.
мгд генератор предназначен для преобразования тепловой
энергии в электрическую без применения твердых движущихся
деталей, как в обычных паровых турбогенераторах. Он позволяет
поднять температуру, не превышающую в последних 850 К, до
2000—2500 К, и тем самым в принципе поднять КПД от обычных
30—40 % до 50—60 %. В одной из типичных схем поток горячего
газа образуется в результате сжигания горючего. Типичные зна-
чения: р ~ 0,1—1 атм, и ~ 1 км/с, 5 ~ 1 кГс, Е' « 10 В/см.
Чтобы генератор имел приемлемые размеры и отдавал во внеш-
нюю цепь 10 МВт с 1 м3 газа, требуется проводимость о ~
~ 0,1 Ом-1 • см”1, каковой продукты горения не обладают. В них
добавляют порядка 1 % легкоионизуемых щелочных элементов:
Cs, К. МГД генераторы пока не получили широкого применения
в энергетике из-за множества серьезных практических проблем;
подробнее см. в [31].
ПРИЛОЖЕНИЕ
Некоторые константы, формулы, соотношения между единицами,
часто встречающиеся и часто употребляемые в физике газового разряда
Фундаментальные константы
Скорость света
с = 2,998 • 1010 см/с.
Постоянная Планка
h — 6,625 • 10"27 эрг • с.
h = h/2n = 1,054 • 10"27 эрг • с.
Заряд электрона
е = 4,802 • 10-10 СГСЭ.
Масса электрона
т = 9,109 • 10"28 г.
Масса протона
Мр = 1,672 • 1б"24 г.
Атомная единица массы
Мо -= 1,660 • 10-24 г.
Постоянная Больцмана
к = 1,380 • 10~16 эрг/К.
Универсальная газовая постоянная
R = 8,314 • 107 эрг/(К • моль) = 1,986 кал/(К • моль).
Постоянная Авогадро
Na = 6,023-102s моль-1.
Атомные постоянные
Боровский радиус
h2 %2
% = 7Т”2 = — = 0,529 -10—8
0 4л те те
см.
Потенциал ионизации атома водорода
'H-2a0
2л2е4тп
е т
= —й- = 13,60 эВ.
212
34*
523
Постоянная Ридберга
Ry = ZH/A = 2nieimlhz = 3,290-1015 с”1.
Скорость электрона на первой боровской орбите
и0 = 2ле2/Л = e2/h = 2,187 • 108 см/с.
Классический радиус электрона
г0 = в2!тс2 -= 2,818 • 10~13 см.
Комптоновская длина волны
Хо = hlmc = 2,426 • 10“10 см, = Х/2л = h/mc — 3,862 • 10~и см.
Энергия покоя электрона
тс2 = 511 кэВ = 8,185 • 10~7 эрг
Постоянная тонкой структуры («число 137»)
ttc/e2 == 137,0.
Томсоновское сечение
Ф = 8лг2/3 = 6,65-10-25 см2.
Отношение масс протона и электрона
Mplm = 1836.
Электрическое поле на первой боровской орбите
е/а2 = 5,14-10® В/см.
Площадь спектральной линии с единичной силой осциллятора
пе2!тс = 0,0265 см2/с.
Атомная единица сечения
= 0,880-10“16 см2.
Формулы
Поток излучения с поверхности абсолютно черного тела
S = оТ4 = 5,67 • 10-5{7т[К] }4 = 1,03 • 1012{7т [эВ] }4 эрг/(с • см2).
Спектральная интенсивность равновесного излучения
Ivpdv = cUypdvIfai = 2/zv3c-2[exp (hvjkT) — 1]_ldv эрг/(с • см2 • ср)
(максимум при hv — 2,822 кТ).
Формула Саха
ПП, g_! I
= А -±- Т3/2 ехр ( - п [см~3],
па & а
А = 2 =4,85-1015 см~3-К“3/2 = 6,06-1021 см_3-эВ“3/2.
Функция максвелловского распределения, нормированная на единицу,
/ т \з/2 Г
Ж’ vz) dvx dvy dvz = ( Ж) ex₽
.m(vx + "y + vz)
2kT
dvx dvy dvz
524
Ф (р) dv 4л
©хр f v2 dv,
1 2кТ)
? I <* I р \
n (е) Je * . ii7at,xP гтт; ^е-
Скорость электрона
v„ 5,03 • WftTpBT см/с.
Скорость частицы с относительной атомное массой А
v «» 1,.Ш • 1(ЯУ< pH\!А см/с.
Средняя тепловая скорое и» электрона
- _ / 8ИЧ1/2 = 6 2| 1()» Т/У[Щ e,71 • 107 VTT^Bi см/с.
\ пт /
Средняя тепловая скорое i ь частицы
v = 1,45 • 1СМУ/ | К]Л4 — 1Л>(1 1()вуг[эВ]/А см/с.
Выражение эффективного сечения 0 через Р (среднее число столкнове-
ний на пути в 1 см при 1 мм рг ст. в О’С)
о = 2,83 • 10'17 Р см2, Р — 3,53 • 1 (),6о см'1 • торр'1.
Дебаевский радиус
dD —
кТе Y/2_c,nJrjK|!t/j
4ле2тге / ( пе ]
ТДэВ]11/2
, пе I
см.
Плазменная частота
сор = ^яе2пе/пг^1^2 = 5,65 loS/l/2 с"1.
Критическая плотность электронов
flLID А ) . 1Q __Л л
Пкр = = 1,24-104{/[МГц]}- (М ' 1,11-10 3 {1 [cmJ}—2cm~3.
Множитель в уравнении элоктроста i пни
<|I v Е = 4ле(п+ — пе)
4ле = 1,81 • IO'6 В • см, е = 1,44 • 10“7 В • см.
Электронная проводимость ионизованного газа
° ~ ( 2 ,—Г\ ~ 2,53- 108п -т-—с
+v^) ео>-
vm
= 2,82-10“4 пр—т---Ом“’1-см“1, vm, со [с-1].
Диэлектрическая проницаемость ионизованного газа
4ле2л ео2
8-1 + <o2 + v^‘
525
Коэффициент поглощения электромагнитной волны в ионизованном газе
тс ( а? -4- V2
4 ла vm
—— = О.Юблг -у-—- см'
с + v2m
d&
dt == (^eJS ~ ^8упр) vm =
Скорость нарастания энергии электрона в осциллирующем поле при
учете одних лишь упругих столкновений (Е = Еа1~]'2)
е2Е2 _ 2т
^е.
Приобретение энергии от поля в одном столкновении
vm’
е2Ё2 1,75-1015{£ [В/см]}2 6,34-10175 [Вт/см21
<o2 + v2m - w2 + v2ra 9В’
Подвижность электронов
е 1,76-1015
^ = ^='" vm см/(с-В), vm(c 1].
Толщина скин-слоя
____________________с_______________5,03___________
}/2ло(о {о [Ом“1-см~1] f [МГц]}1/2 М
Поток высокочастотной энергии в проводник, находящийся внутри со*
леноида (770, — амплитуды)
5 = = 9,94-ю-2 1)7—/[МГц1 - Д172 Вт/см2.
16л \2ла) 1° L см JJ [а [Ом—1-cm_х])
Магнитное поле внутри соленоида
Н = — in — 1,26гп [А-в^см] Э.
Характерная диффузионная длина А, определяющая «частоту» диффу-
зионных потерь Vd = D/A2,
1 /2,4\2 А2 = Ы + /Л \2 „ —цилиндр радиуса R и длины Ь9
1 ( л \2 /Л2 /Л\2 — j + 7“ 1 —параллелепипед со сторонами Lp ь2, \ L2 \ ь3/
= j2, А = — — шар радиуса 7?.
Коэффициент амбиполярной диффузии при Тв > Т
Da = ц+[см2/(с • В)]Те[эВ] см2/с.
Среднеквадратичное поле волны
Е = 19У5 [Вт/см2] В/см.
Частота ионизации электронами при максвелловском спектре и линей*
ном росте сечения ионизации о = С (г— I) от порога
V = Скт (-L + 2) v.N exp (— -L) « 2,2-107 fc • 10г7]х
’ \кТ ) е к кТ) I L эВ J J
X {Т [эВ]}1 /21 [эВ] р [торр] ехр ( — /-)I с-1,
526
Соотношения между единицами
Энергия в электрон-вольтах
Энергии <S = 1 эВ = 1,602 • 10“12 эрг соответствуют:
температура ff/k = 11610 К,
частота &/h = 2,418 • 1014 с-1,
длина волны hc/& = 1,240 • 10-4 см = 12 400 А,
волновое число <S/he = 8067 см'1.
1 эВ на молекулу соответствуют: 23,05 ккал/моль = 9,65 • 10н/р, эрг/г =»
= 96,5/р кДж/г (ц — относительная молекулярная масса).
Электрические единицы
Заряд 1 Кл = 3 • 109 абс. ед.= 6,25 • 1018 электронных зарядов =
*= 9 • 1011 В • см
Заряд электрона 1,60 • 10~19 Кл = 1,44 • 10“7 В • см (в формуле Е =
= е/г2).
Ток 1 А = 1 Кл/с = 3 • 109 абс. ед.= 6,25 • 1018 электронных зарядов в
секунду = 9 • 1011 В • см/с
Напряжение 1 В = 1/300 абс. ед
Напряженность электрического ноля Я[В/см] = 300#[абс. ед.].
Сопротивление 1 Ом = (1/9 • 1011)абс. ед.= 1/30 с; 1/с = 30 Ом.
Проводимость о [Ом"1 • см-1] = (1/9 • 1011) о [с-1]; о [с-1] = 9 • 10й а
[Ом-1 • см-1].
Емкость 1 Ф = 9 • 1011 абс. ед. (см.); 1 пФ = 0,9 см.
Индуктивность 1 Гн = 109 абс. ед. (см.); 1 мкГн = 1000 см.
Напряженность магнитного поля 13 = 1 абс. ед.
Энергия 1 Дж = 107 абс. ед. (эрг).
Мощность 1 Вт = 107 абс. ед. (эрг/с).
Барометрич еские единицы и соответствующие соотношения
Нормальная атмосфера 1 атм — 1,01-3 • 106 дин/см2 (эрг/см3).
При температуре 0 °C 1 атм = 760 мм рт. ст. = 760 торр — 1,013 X
X Ю5 Па = 0,1 МПа. 1 торр = 133,3 Па; 1 кПа = 7,5 торр.
Число молекул в 1 см3 при температуре 0°С и давлении 1 атм (число
Лошмидта) 2,687 • 1019 см-3.
Число молекул в 1 см3 при комнатной температуре 20 °C и давлении
1 торр 3,295 • 1016 см-3.
Е/р [В/(см • торр)] = 3,30 • 1016 Е/N [В • см2] = 0,33 Е/N [Тд].
Е/N [В • см2] = 3,03 • IO'17 Е/р [В/(см • торр)] = 10~17 Е/N [Гд].
Единица для E/N — таунсенд (Тд), 1 Тд = 10~17 В • см2.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
СПИСОК ЛИТЕРАТУРЫ
Руководства и книги общего характера,
охватывающие многие разделы физики газового разряда
Энгель А , Штеенбек М Физика и техника электрического разряда в га-
зах, т П/Пер с нем, Под ред Н А Капцова— М, Л ОНТИ, 1936
Леб Л Основные процессы электрических разрядов в газах/Пер с англ ;
Под ред Н А Капцова — М , Л Гостехиздат, 1950
Капцов Н А Электрические явления в газах и вакууме — М Гостех-
издат, 1950
Грановский В Л Электрический гок в газе — М Гостехиздат 1952
Энгель А Ионизованные газы/Пер с англ, Под ред М С Иоффе—М
Физматгиз, 1959
Браун С Элементарные процессы в плазме газового разряда/Пер с англ ,
Под ред Д А Франк-Каменецкого—М* Атомиздат, 1961
Френсис Г Ионизационные явления в газах/Пер с англ Под ред
А И Настюхи и Н Н Семашко — М Атомиздат, 1964
Грановский В Л Электрический ток в газе (установившийся ток; — М •
Наука, 1971
Смирнов Б М Физика слабоионизованного газа (в задачах с решения-
ми) — М Наука, 1985
Райзер Ю П Основы современной физики газоразрядных процессов —
М Наука 1980
Ховатсон А М Введение в теорию газового разряда/Пер с англ
И И Иванчика — М Агомиздаг, 1980
Cherrmgton В Е Gaseous Electionics and Gas Laser — Oxford, N. Y: Per-
gamon Press, 1982.
Книги и монографии, посвященные элементарным процессам
в газовом разряде, отдельным типам разрядов,
свойствам низкотемпературной плазм\ы
Атомные и молекулярные процессы/Под ред Д Бейтса/Пер с англ Под
ред Л М Бибермана и В А Фабриканта — М Мир, 1964
Хастед Дж Физика атом 1ых сголкновений/Пер с англ Под ред
Н В Ф(Доренко—М Мир 1965
Мак Даниель И Процессы столкновении в ионизованных газах/Пер с
англ Под ред Л А Арцимовита — М Мир 1967
Мак Даниель //, Мэзон Э По^виж! ость и диффузия ионов в газах/Пер
с англ , Под ред Б М Смирнова — М Мир, 1976
Хаксли Л, Кромптон Р Диффузия и дрейф электронов в газах/Пер с
англ , Под ред А А Иванова,— М Мир, 1977
Смирнов Б М Ионы и возбужденные атомы в плазме—М Атомиздат,
1974
Елецкий А В , Палкина Л А Смирнов Б М Явления переноса в ела-
боионизированной плазме—М Атомиздат, 1975
528
20 Dutton 1 Л Survey of Electron Swarm Data // J Phys Chem Ref Data —
1975 V \ 3 P 577-856
21 Mat Д, Крэ^с Д Электрический пробои в газах/Пер с англ; Под ред
В ( Комелгкова— М ИЛ, 1960
22 Финн елшоцрг В, Met кер Г Электрические дуги и термическая плазма/
Пер с ши Под ред В А Фабриканта — М ИЛ, 1961
23 Pet ер 1 )лсктронные лавины и пробой в газах/Пер с англ Под ред
В ( Комелькова — М Мир, 1968
24 Мак Доналд А Сверхвысокочасто 1иыи пробой в газах/Пер с англ , Под
ред М С Рабиновича — М Мир 1969
25 Райзер Ю П Лазерная искра и распространение разрядов — М Наука,
1974
26 Лозанский Э Д, Фирсов О Б Теория искры — М Атомиздат, 19/5
27 Зельдович Я Б, Райзер IO II Физика ударных волн и высокотемпера-
турных гидродинамические явл< пин — М Наука, 1966
28 Физика и техника низкотемпературном плазмы/Под ред С В Дресви-
на—М Атомиздат, 1972
29 Биберман Л М Воробьев В С, Чкубов И Т Кинетика неравновесной
низкотемпературно!! плазмы— М Наука 1982
30 Голант В Е Жил лне^ий А П Caiapoe С А Основы фиоики плазмы—
М Атомиздат 1977
31 Митчнер ¥, Ку^ер Ч Частично ионизованные газы/Пер с англ, Под
ред А А Иванова — М Мио, 1976
32 Велихов Е П Ковалев А С, Рахимов А Т Физические явления в га
зоразрядной плазме - М Наука 1987
33 Базелян Э М, Ражанский И Ч Искровой разряд в воздухе — Новоси
бцрек Наука, 1988
Специальная процитированная литература
(первая цифра в ссылке — номер главы)
2 1 Карнюшин В Н, Солоухин Р И Макроскопические и молекулярные
процессы в газовых лазерах — М Атомиздат, 1981
2 2 Словецкии Д И Сб Химия плазмы/Под ред Б М Смирнова — М
Атомиздат 1974 Вып 1
31 Спитцер Л Физика полностью ионизованного газа/Пер с англ, Под
ред М Л Левина — М Мир 1965
3 2 Parker J Н Lowke II /Phy Rev 19b9 V 181 P 290 302
3 3 Баркалов А Д, Самохин A A — Препринт ИАЭ, 1985, K° 4147/6
° 4 Сорока A V, Шапиро Г И Ц Письма ЖТФ 1979 Т 5 С 129
3 5 Брагинский С И Ц Вопросы теории плазмы/Под ред М А Леонто-
вича — М Атомиздат, 1963 Вып 1 С 183
41 Ward А I Ц J Appl Phys 1962 V 33 Р 2789
4 2 Бабич Л П, Станкевич Ю Л Ц ЖТФ 1972 Т 42 С 1669
4 3 Фоменко В С, Подчерняева И А Эмисионные и адсорбционные
свойства веществ и материалов Справочник — М Атомиздат 1975
4 4 Добрецов Л Н, Гэмоюнова М В Эмиссионная электроника — М На
ука, 1966
4 5 Lee Т Н // J Appl Phys 1959 V 30 Р 166
6 1 Биберман Л М, Норман Г Э Ц УФН 1967 Т 91 С 193
6 2 Оптические свойства горячего воздуха/Под ред Л М Бибермана —
М Наут а I )70
6 3 Козлов I И Кузнецов В А, Масюков В А Ц ЖЭ1Ф 1974 Т 66
С 954
7 1 Алексин Ц t // 7 Кончиков А М, Сон Э Е Ц Физ плазмы 1978
Т 4 ( ПЛ
7 2 Алексии ц в II Л и Ц Ц ГВТ 1981 Т 19 С 22
7 3 Александров И / ( и Э Е Сб Химия плазмы — М Атомиздат,
1980 Вып 7 ( Г>
7 4 Райзер Ю И lllm / ) р М II Ц Физ плазмы 1989 Т 15 С 318
529
8 1 Каган Ю М Сб Спектроскопия газоразрядной плазмы — Л : Наука,
1970
8 2 Каган Ю М, Перелъ ВИЦ УФН 1963 Т 81 С 409
8 3 Диагностика плазмы/Под ред Р Хаддлстоуна/Пер с англ; Под ред.
С Ю Лукьянова — М Мир, 1967
8 4 Методы исследования плазмы/Под ред В Лохте Хольтгревена/Пер с
англ, Под ред С Ю Лукьянова — М Мир, 1971
8 5 Биберман Л М, Панин Б Ц ЖГФ 1951 Т 21 С 12
8 6 Johnson L О , Mailer L Ц Рйуъ Bev 1950 V 80 Р 59
8 7 Козлов О В Электрическип ’оид в плазме — М • Атомиздат, 1969
9 1 Райзер Ю П Ц УФН 1980 Т 13? С 549
9 2 Парфенов В Н и др Ц Письма ЖГФ 1976 Т 2 С 731
10 1 Баранов В Ю,ВеЗеновА А , Низъев В Г Ц ТВТ 1972 Т 10 С 1156;
Ведение А А Физика электрораэрядных СО2 лазеров — М Энерго-
издат 1982
10 2 Гладуш Г Г Самохин 4 А Ц ПМТФ 1981 5. С 15
10 3 Мелехин В Н Наумов Н Ю // Письма ЖТФ 1986 Т 12 С 99
10 4 Райзер 10 П Суржиков С Т I/ Письма ЖТФ 1987 Т 13 С 452;
ТВТ 1988 Т 26 С 428
10 4а Мышенков ВИЦ ТВТ 1982 Т 20 С 642
10 5 Raizer Yu Р—Invited Papers of the 17th Internal Confer on Phenom,
m loms Gases — Budapest 1985 P 111, TBT 1986 T 24 C 984
10 6 Ward A L Ц Phys Rev 1958 V 112 P 1852
10 7 Бронин С Я, Ко гобое В M Ц Физ плазмы 1983 Т 9 С 1088
10 8 Всей] J Р, Marode Е Ц I Phy^ D Appl Phys 1982 V 15 Р 2169
10 9 Швейгерт В А, Шве^гррт И В Сб Мощные СО2 лазеры для плаз-
менных экспериментов и технологии—Новосибирск Наука 1986.
С 150 Физ пла°мы 1988 Т 14 С 347, ПМТФ 1988 № 4 С 16
10 10 Gill У, Webb С. Е \Ц J Phys D J Appl Phys 1977 V 10 Р 229
1011 Солнцев Г С, Орлов А И, Довженко В А Ц Радиотехи и электрон.
1970 Т 9 С 1980
10 12 Kagan Yu. М, Cohen С , Avivi Р Ц J Appl Phys 1988 V 63(1) Р 60
10 13 Недоспасов А В Ц ЖГФ 1956 Т 26 С 1202
1014 Ecker G, Emeleus К G Ц Ann Phys 1965 Bd 15 S 53
10 15 Москалев Б И Разряд с полым катодом— М Энергия, 1969
1016 Davies A J, Evans J G, Marode Е, Segur Р Ц ICDGA Edinburgh.
1980 V 2 Р 59
10 17 Полак Л С Сергеев И А , Словацкий Д И Ц ТВТ 1977 Т 15 С 15.
10 18 Голубовский Ю Б , Тележко В М Ц ТВТ 1984 Т 22 С 428
1019 Акишев Ю С и др Ц Физ плазмы 1985 ТИС 999
10 20 Brunet IE Hossa Serra J Ц J Appl Phys 1985 V 57 P 1574
10 21 Мнацаканян A X, Baud ic Г В Сб Химия плазмы—М Энергоатом-
издат, 1987 Вып 14 С 227
10 22 Бердышев А В, Кочетов И В, Папартович А П Ц Физ плазмы
1988 Т 14 С 741
10 23 Denes L J, Lowke J J Ц Appl Phys Lett 1973 V 23 P 130
10 24 Lowke 1 J, Phelps A V., Irwin В W. Ц J Appl Phys 1973 V 44
P 4664
10 25 Nighan W L, Wiegand W J Ц Phys Rev 1974 V A 10 P 922
10 26 Напартович А П, Наумов В Г Шашков В М Ц Физ плазмы 1975.
Т 1 С 821
10 27 Райзер Ю П Шапиро Г И Ц Фи* плазмы 1978 Т 4 С 810
10 28 Fckbreth А С, Blaszuk Р. R. Ц AIAA Paper 1972 V 72—723
10 29 Пашкин С В , Перртятъко II И Ц Квант электрон 1978 Т 5 С 1159
10 30 Генералов Н А и др Ц Физ плазмы 1980 Т 64 С 1152
10 31 Велихов Е П, Го губ'в В С Пашкин С В Ц УФН 1982 Т 137
С 117
10 32 Francis G The Glow Discharge at Low Pressure Encyclopedia of Phy-
sics/Ed S Flugge Handbuch der Physik — Berlin Springer, 1956
Bd XXII P 53-208
10 33 Акишев Ю С и др Ц TBT 1980 T 18 C 873
530
11.1. Haas R. А. Ц Phys. Rev. 1973. V. A8. P. 1017.
11.2. Nighan W. L. In Principles of Laser Plasmas/Ed. G. Bekefi.— N. Y.:
Wiley Interscience. 1976. Chapter 7.
11.3. Велихов E. П., Письменный В. Д., Рахимов А. Т. Ц УФН. 1977. Т. 122.
С. 419.
11.4 Елецкий А. В., Рахимов А. Т.: Сб. Химия плазмы/Под ред. Б. М. Смир-
нова.— М.: Атомиздат, 1977. Вып. 4. С. 123.
11.5. Напартович A. JL, Старостин А. Н.: Химия плазмы/Под ред.
Б. М. Смирнова.— М.: Атомиздат. 1978. Вып. 5. С. 153.
11.6. Ecker К., Kroll W., Zoller О. Ц Phys. Fluids. 1964. V. 7. P. 2001.
11.7. Басов H. Г. и др. // Письма ЖЭТФ. 1971. Т. 14. С. 421.
11.8. Мельников Г. Д.< Напаргович А. П. // Физ. плазмы. 1975. Т. 1. С. 891.
11.9. Пекарек Л. Ц УФН. 1968. Т. 94. С. 463.
11.10. Недоспасов А. В. Д УФН. 1968. Т. 94. С. 439.
11.11. Garscadden A. lo uzalion Waves: In Gaseous Electronics. V. 1. Electri-
cal Discharges/Eds M. N. Hirsh and H. J. Oskem.—N. Y.: Academic
Press, 1978.
11.12. Недоспасов А. В , Пономаренко Ю. Б. Ц ТВТ. 1965. Т. 3. С. 17.
11.13. Цендин Л. Д. // ЖТФ. 1970. Т. 40. С. 1600.
11.14. Allis W. Р. // Physica. 1976. V. С82. Р. 43.
11.15. Stewart А. В. // .1. Appl. Phys. 1956. V. 27. Р. 811.
11.16. Цендин Л. Д. // ЖТ<1>. 1982. Т. 52. С. 635, 643.
11.17. Недоспасов А. В , Ханг В. Д. Колебания и неустойчивости низкотем-
пературной платы.— М.: Паука, 1979.
11.18. Голубовский Ю. Б., Зинченко А. К., Каган Ю. М. Ц ЖТФ. 1977. Т. 47.
С. 1478.
11.19. Kenty С. // Phys. Rev. 1962. V. 126. Р. 1235.
12.1. Жуков М. Ф. и др. Приалектродные процессы в дуговых разрядах.—
Новосибирск: Наука, 1982.
12.2. Любимов Г. 4., Раховский В. И. Ц УФН. 1978. Т. 125. С. 665.
12.3. Вакуумные дуги/Под ред. Дж. Лафферти/Пер. с англ.; Под ред.
В. И. Раховского.— М.: Мир, 1982.
12.4. Бейлис И. И.— В кн.: МГД-преобразование энергии. Физико-техниче-
ские аспекты.— М.: Наука, 1983. ,С. 367; ДАН СССР. 1988. Т. 298.
С. 1108.
12.5. Кесаев И. Г.— Катодные процессы электрической дуги.— М.: Наука,
1968.
12.6. Бейлис И. И. // Письма в ЖТФ. 1988. Т. 14. С. 1124; ТВТ. 1988. Т. 25.
С. 1224.
12.7. Королев Ю. Д., Месяц Г. А. Автоэмиссионные и взрывные процессы
в газовом разряде.— Новосибирск: Паука, 1982.
12.8. Очерки физики и химии низкотемпературной плазмы/Под ред.
Л. С. Полака.— М.: Наука, 1971.
13.1. Ровинский Р. Е., Груздев В. А., Соболев А. П. // ПМТФ 1967. № 1.
С. 143.
13.2. Ровинский Р. Е. и др. Ц ТВТ. 1967. Т. 5. С. 557.
13.3. Блинов Л. М. и др.: Сб. Генераторы низкотемпературной плазмы.—
М.: Энергия, 1969.
13.4. Капица П. Л. // ЖЭТФ. 1969. Т. 57. С. 1801.
13.5. Райзер Ю. П. // Письма ЖЭГФ. 1970. Т. 11. С. 195.
13.6. Генералов Н. А. и др. Ц Письма ЖЭТФ. 1970. Т. И. С. 447.
13.7. Райзер Ю. П. // Письма ЖЭТФ. 1981. Т. 7. С. 938.
13.8. Keefer D. В., Henriksen В. В., Braerman W. F. Ц J. Appl. Phys. 1975.
V. 46. Р. 1080.
13.9. Генералов Н. А. и др. Ц ЖЭТФ. 1971. Т. 61. С. 1434.
13.10. Козлов Г. И., Кузнецов В. А, Масюков В. А. Ц ЖТФ. 1979. Т. 49.
С. 2304.
13.11. Ehlenbusch J. Invited Papers of the 16th Internal. Confer, on Phenom,
in loniz. Gases.— Dusseldorft, 1983. P. 119.
13.12. Райзер Ю. П., Силантьев 4. Ю. // Квант, электрон. 1986. Т. 13. С. «593.
13.13. Райзер Ю. П., Суржиков С. Т. Ц Квант, электрон. 1984. Т. 11. С. 2301;
ТВТ. 1985. Т. 23. С. 29.
531
13 14 Жуков М Ф, Смоляков В Я, Урюков Б А Электродуговые нагрева-
тели газа (плазмотроны) — М Наука, 1973
13 15 Кононов С В, Якушин М И // ПМТФ 1966 ДО 6 С 67
13 16 Лысов Г В Сб Зеория >лек1рической дуги в условиях вынужденно-
го теплообмена Ц Новосибирск Наука, 1977 С 270
13 17 Лелевкин В М, Оторбаев Д К Экспериментальные методы и теоре-
тические модели в физике неравновесной плазмы — Фрунзе Изд во
Илим, 1988
13 18 Герасименко М В и др // Письма ЖТФ 1979 Т 5 С 954
13 19 Райзер Ю П, Силантьев 4 Ю, Суржиков С Т Ц Письма ЖТФ 1986;
Т 12 С 134 ТВТ 1987 Т 25 С 454
13 20 Гуськов К Г, Райзер Ю П, Сурж ьков С Т Ц Квант электрон 1990.
Т 17 С 937
141 Маршак II С // УФН 1960 Т 71 С 631
14 2 Техника высоких напря кений/Под ред Д В Разевига — М Энергия.
1976
14 3 Бортник И М Кушко А Я, Лобанов А Н—Тез докл II Всесоюзн.
совещ по физике элпкгрического пробоя газов — Тарту, 1984 Ч II.
, С 270
14 4 Техника высоких напряжений/Под ред М В Костенко — М • Высшая
школа, 1973
14 5 Tholl Н Ц Zs Naturfoizsh 1964 Bd 19а S 346,704
(полный перевод статьи содержится в дополнении к книге [23])
14 6 Абрамсон И С и др Ц ЖЭТФ 1947 Т 17 С 862
14 7 Драбкина С И Ц ЖЭ1Ф 1951 Т 21 С 473
14 8 Брагинский С И // ЖЭТФ 1958 Г 34 С 1548
14 9 Goldman М., Goldman N Corona Discharges In Gaseous Elestromcs.
V 1 Electrical Discharges/Ed M N Hirsh and H J Oskam — N Y.:
A cad Am i c, Press 1978
14 10 Dawson G A Winn W P Ц Zs. Phys 1965 Bd 183, S 159 (полный
перевод статьи содержится в дополнении к книге [23])
14 И Gallimberti I. Ц J. Phys D. Appl Phys 1972 V 5 Р 2179
1412 Badaloni S, Gallimberti I Proc 11 th Internal Confer on Phenom in
lomz Gases — Prague, 1973 P 196
1413 Griffiths R F, Phelps С T — Quart J R Math Soc 1976 V 102 P 419.
14 14 Базелян Э M, Горюнов А Ю— Гез >окл II Всесоюзн совещ по фи^
зике электрического пробоя газов — Тарту, 1984 Ч 1 С 42, Электри-
чество 1986 ДО 11 С 27
1415 Khngbeil В D, Tilman A, Fernsler R F Ц Phys Fluids 1972 V 15.
Р 1969
14 16 Marode Е Ц J Appl. Phys 1975 V 46 Р 2005
14 17 Gallimberti 1 The mechanism of the long spark formation (Review) —
Journ de Physique Coll C7, Suppl ДО 7 1979 V 40 P 193
1418 Dhali S K, Williams P F Ц Phys Rev A 1985 V 31 P 1219
14 18a Dhali S К Pal 4 В // J 4ppl Phys 1988 V 63 P 1355
14 19 Гайворонскии А С Бажаны ий И M — Тез докл II Всесоюзн со-
вещ по физике электрического пробоя газов — Тарту, 1984 Ч II
С 244, ЖТФ 1986 Т 56 С 1110
14 20 Комельков В С Ц Изв АН СССР Отд техн наук 1947 ДО 8 С 955;
1950 № 6 С 851
14 21 Александров Г Н // ЖТФ 1965 Г 35 С 1225
14 22 Gallimberti I Ц Electra 1977 V 76 Р 5799
Всемирн электротехнич конгресс, Москва, 21—25 июня 1977, М, 1977
14 23 Базелян Э М Горин Б Н Левитов В И Физические и инженерные
основы молниезащиты — Л Гидрометеоиздат, 1978
14 23а Базелян Э М Ц Электричество 1987 ДО 5 С 20
14 24 Kekez М М , Savic Р Electrical Breakdown and Discharges in
Gases/Ed E Kunhardt and L H Luessen — h Y Plenum Press, 1983.
P 419
14 25 Юман M Молния/Пер с англ, Под ред H В Красногорской — М •
Мир, 1972
532
14 26 Френкель Я И Теория явлении атмосферного электричества—М
I (и 1е\и 1, 144 )
14 27 Чалмер( Дж Лiмоефериое >лсктричество/Пер с англ, Под ред
И М Нмяпнюва — Л Гидромегеоиздат, 1974
14 28 ( / (колышков 11 С Природа длинной искры—М Изд во АН СССР,
1960
14,29 Les Renardreres Group Ц IEEE Proc 1986 V 133, № 7 P 395—483
15 1 Левин кии С M /Ж1Ф 1957 T 27 C 1001
15 2 Райзер Ю П ЦФжз плазмы 1979 T 5 С 408
15 3 Левитскии С М Ц ЖТФ 1957 Т 27 С 970
15 4 Кузовников А А, Ковалевский В Л, Савинов В П Ц Вести Моск
ун та Сер Физ и астроном 1983 Т 24 № 4 С 28
15 5 Кузовников А А , Савинов ВВЦ Радиотехн и электрон 1973 Т 18
С 816
15 6 Яценко НАЦ ЖТФ 1981 Т 51 С 1195
15 7 Яценко НАЦ ЖТФ L982 Т 52 С 1220
15 8 Мышенков В И, Яценко НАЦ ЖГФ 1981 Т 51 С 2055
15 9 Viclaud, Р, Durrani S М А , Hall D R Ц J Phys D Appl Phys 1988
V 21 Р 57
1510 Год 1к В А, Кузовников А А Ц Физ плазмы 1975 Т 1 С 496
15 11 Яценко НАЦ ТВТ 1982 Т 20 С 1044
15 12 Райзер Ю П, Шнейдер М Н // Физ плазмы 1987 Т 13 С 471, 1988
Т 14 С 226
15 13 Яценко НАЦ ЖТФ 1980 Т 50 С 2480
15 14 Смирнов А С ЖТФ 1984 Т 54 С 61
15 15 Ковалев А С, Рахичов А Т, Феоктистов В А Ц Физ плазмы 1981.
Т 7 С 1411
15 16 Баркалов А Д и др Ц ТВТ 1978 Т 16 С 265
15 17 Ковалев А С и др Ц Физ плазмы 1986 Т 12 С 1264
15 18 Яценко Н А //ЖГФ 1988 Т 58 С 294
15 19 Райзер Ю П, Шнейдер М Н Ц 1 ВТ 1987 Т 25 С 1008
15 20 Gill М D Vacuum Techn 1984 V 34 Р 3j7
15 21 ТЕЕ Transactions on Plasm i Science, Special Issue on the Physics of
RF Discharges for Plasma Processing 1986 V PS 14 № 2
16 1 Абильсиитов Г А и др Мощные газоразрядные CO2 лазеры и их при-
менение в технологии — М . Наука, 1984
16 2 Веденов А А Физика электроразрядных СО2 лазеров — М • Энергоиз-
дат, 1982
16 3 Козлов Г И, Кузнецов В А, Масюков В А Ц Письма ЖТФ 1978.
Т 4 С 129
16 4 Hill А Е Ц Appl Phys Lett 1971 V 18 Р 194
16 5 Hoag Е et all Ц J. Quant. Electron 1973 V QE 9 P 652
16 6 Басов H Г и др Ц Квант электрон 1979 Т 6 С 772
16 7 Косырев Ф К, Косырева Н П Лунев Е И Ц Автомазич свар-
। а Т 9 С 72, Андриясин В М Ц Наука и жизнь 1977 № 11.
( 86
16 8 Абильсиитов Г А и др II Квант электрон 1979 Т 6 С 204
16 9 / (kbreth А С, Davis J W Ц Appl Phys Lett 1971 V 19 Р 101
1610 Алейников В С, Бибиков В В, Лысогоров О С Ц Электронная про-
мышленность 1981, вып 5—6 С 71
16 II Biown ( О Davis J W Ц Appl Phys Lett 1972 V 21 Р 480
16 I / ckbrdh A C, Blaszuk PR// AIAA Paper 1972 № 72 723
16 I J Геш pa ioe H А и др I/ Письма ЖГФ 1975 TIC 431, Физ плазмы
1977. 1 1 С 626, 634, 1980 Г 6 С 1152
16 I4 Генера юв НА и др Ц Квант электрон 1982 Т 9 С 1549
16 15 Гаври ши В Д и др Ц Квант электрон 1977 Т 4 С 2034
16 16 Анчюхои В В и др Ц Квант электрон 1981 Т 8 С 2234
16 17, Гойхман В \ Голъфарб В ¥ Ц Ж прикл спектроск 1974 Т 21.
С, 456
16 18 /h ZJ, Hill D В Ц Appl Phys Lett 1983 V 43 Р 723
533
16.19. Акиртава О. С., Джикия В. Д. и др. Ц Письма ЖТФ. 1981. Т. 43.
С. 1231; Акиртава О. С.. Голубев В. С. и др.: Сб. Тез. докл. Всесоюзн.
конф. «Применение лазеров в народном хозяйстве», Звенигород,
май 1985.— М.: Наука, 1985.
16.20 Schock W., Hugel Н., Hoffman Р. Ц Laser. + Electro-Opt. 1981. V. 13.
Р. 76.
16.21. Proc, of the 17th Internet. Congress Laser 85 Optoelektronik/Ed.
W. Waidelich.— Berlin: Springer Verlag, 1986.
16.22. Hoffmann P. Proc, of the 2nd Internet. Confer. Lasers Manuf., Birmin-
gham, March, 1985.— Amsterdam: Kempston, 1985.
16.23. Витрук Д. H., Яценко H. А. Ц Письма ЖТФ. 1989. T. 15. С. 1.
16.24. Яценко Н. А.— Газовые лазеры с высокочастотным возбуждением.
Препринт/ИПМ АН СССР.- М., 1989. № 381.
ПРИМЕЧАНИЯ ПРИ КОРРЕКТУРЕ (июнь 1992 г.)
К предисловию С момента (конец 1989 г) сдачи рукописи 2 ю издания
«Физика газового разряда» в Физматлит (английское издание киш и вышло
в издательстве «Шпрингер» в 1991 г) прошло довольно мною времени.
В связи с этим возникла потребность в некоторых изменениях и дополне-
ниях, что сделано частично в виде примечаний при корректуре бе j изме-
нений в тексте.
К § 5 и п. 4.10 гл. 10. Самосогласованный расчет структуры катодных
частей тлеющего разряда от катода через катодный слой (КС), области от-
рицательного свечения (ОС), фарадеево пространство (ФП) до однород-
ного положительного стотба (ПС) включительно с учетом отмеченных в
п. 5 4 факторов проделан в [П.1] для гелия при р == 1 торр в узкой и ши-
рокой трубках (R — 1,35 и 5 см). Это теперь позволяет количественно
объяснить все важнейшие особенности структуры. Нелокальные эффекты
описаны на основе кинетическою уравнения в приближении «вперед-на-
зад» (конец п. 4 10), медленные электроны — в диффузионно-дреифовом
(гидродинамическом) приближении. Приняты во внимание также элект-
ронная теплопроводность, термодиффузия, ступенчатая ионизация. Распре-
деления n+, Е, ф, Те в общих чертах похожи на рис. 10 2 (только п+
у катода много меньше nmax в ОС). Как и на рис. 10.14, значительная часть
зарядов рождается в области слабого поля. Пиковая плотность плазмы в
ОС почти на два порядка превышает п вг ПС и п+ у катода. Пик п обязан
ионизации энергичными электронами, рожденными в КС, и замедленности
рассасывания плазмы амбиполярной диффузией В ФП образуется доволь-
но протяженная область обратного поля: вследствие гибели электронов в
ФП слишком велик их диффузионный поток в сторону анода. Обратное
поле призвано уменьшить его путем обратного дрейфа до величины, со-
ответствующей плотности тока. Отсюда |ЕОбр| ~ KTeleR, а потенциальный
барьер Дф ~ кТе!е Обратное поле в ФП недавно было зарегистрировано
прямыми измерениями [П 2] Расчетная Те в ФП низка и имеет минимум
в согласии с измерениями Переход от ФП к ПС оказывается немонотон-
ным, что связано с отставанием роста Те и скорости ионизации при восста-
новлении поля
К п. 7.2 гл. 15. Соотношение ~ ^д/о) = ц^Е(;/ю остается в силе и для
у-разряда, только в этом случае правильнее записать гд « dco, ибо теперь
амплитуды скорости дрейфа и поля на границе слоя с плазмой определя-
ются нормальной толщиной слоя d ж dH.
К п. 8.2 гл. 15. В [П.З] численно прослежена эволюция формирования
а- и ^-режимов от одинаковых по виду условий: в полу бесконечном прост-
ранстве около электрода имеется однородная плазма плотности пив на-
чальный момент включается однородное синусоидальное поле с амплиту-
дой Еа, обеспечивающей ионизационно-рекомбинационное равновесие и не-
ишейный синусоидальный ток ]а — ещкеЕа Из графиков видно, как в
мвисимости от того, п или ia меньше или больше критических значений,
v )лектрода формируется характерный слой а- или ^-разряда, причем в по-
следнем ( iy чае все начинается с протяженного аслоя, который тотчас
пробивания и сокращается до «нормального» благодаря распространению
волны иопп ыции
555
К п. 9.2 гл. 15. ВАХ а разряда с учетом нагрева газа и колебательной
релаксации в случае азота, а также параметры а —у перехода на разных
частотах рассчитаны в [П 4, П 3] в согласии с измерениями [ 15 9] Это сде-
лано как на основе аналитической модели так и путем численного модели-
рования Замечательно, что в случае, когда ВАХ имеет минимум, числен-
ный счет, как и эксперимент, автоматически отвергает поднормальную не-
устойчивую ветвь и выбирает состояние на растущей аномальной При
задании напряжения меньше пэрмзлыюго начальная плазма в счете рас-
падается (разряд «не зажшается»)—в численном эксперименте все про-
исходит как на опыте
К п. 8.3 и 9.3 гл. 15. Нами проведено численное моделирование при-
электродной области у разряда с учетом нелокальных эффектов, почти пол-
ностью повторяющее расчет тлеющего разряда постоянного тока (см при-
мечание к § 5 гл 10) В < труктуре также проявились области ОС, ФП об-
ратного (в среднеvi а период; поля Последнее наблюдалось эксперимен-
тально при пониженных {явлениях [П 5] Поскольку ОС и ФП имеют впол
не определенную толщину, при пеболтшом расстоянии между электродами
или при низком давлении в разрядном промежутке нет места для ПС ВЧ
плазма в этих случаях — это плазма двух соприкасающихся ФП или даже
ОС Этим объясняется наблюдаемая исключительно низкая электронная
температура в плазме 7 разояда низкого {явления При ни ших давлениях
эффекта нормальной плотности тока в а разряде нет, ток заполняет элект-
роды полностью Причина в отсутствии протяженного ПС с падающей ВАХ,
отчего у ВАХ всею разряда нет минимума Зеперь наименьшему напряже
нию соответствует наименьшая плотность тока т е полное заполнение
электрода а — 7 переюд при низких давлениях происходит без скачка, так
как пробою а слоя отвечает левая ветвь кривой Папюна Формирование
нормально о 7 разряда сопровождающееся скачком потребовало бы не со
кращения слоя, как при средних давлениях а его расширения и значит
уменьшения плотности тока Но последнее исключено носколы у а разряд
перед пробоем уже заполняет весь электрод Статья выйдет в «Физике
плазмы», см также статью В А Годяка в [15 21] Недавно проведено пря
мое численное моделирование ВЧ разряда низкого давления кинетическое
уравнение для электронов решалось без всяких приближении [П 6]
СПИСОК ЛИТЕРАТУРЫ
II 1 Райзер Ю П, Шнейдер М Н ТВТ 1991 Т 29 С 1041
П2 Surendra М, Giaves D, Jellum G Phys Rev A 1990 V 41 P 1112
ПЗ Райзер Ю П, Шнейдер M H Физ плазмы 1991 T 17 С 1362
П4 Райзер Ю П, Шнейдер М Н Физ плазмы 1990 ТЫС 878
П5 Kaneda Т et all J Phys. D. Appl Phys 1990 V 23 P 1642
П6 Sommerer T et all. Phys. Rev Lett 1989 V 63 P 2361