Text
MAX PLANCK
EINFUHRUNG
IN DIE THEORETISCHE PHYSIK
IV
OPTIK
VERLAG VON S. HIRZEL
Leipzig. 1932
МАКС ПЛАНК
ВВЕДЕНИЕ
В ТЕОРЕТИЧЕСКУЮ ФИЗИКУ
ЧАСТЬ ЧЕТВЕРТАЯ
ОПТИКА
Перевод с немецкого
С. И. ЛЕЙТМАНА
Нарколтросом РОФОР
в качестве учебного пособия
вля еооуЭаротвенных университет»*
ОБЪЕДИНЕННОЕ НАУЧНО-ТЕХНИЧЕСКОЕ ИЗДАТЕЛЬСТВО
ГЛАВНАЯ РЕДАКЦИЯ ОБЩЕТЕХНИЧЕСКИХ ДИСЦИПЛИН
Мое кв а 1934 Ленинград
T 40-5-2
4-я тип. ОНТИ НКТП СССР «Красный Печатник». Ленинград, Международный др., 75а.
ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
Новое издание отличается от предыдущего лишь небольшими
изменениями и дополнениями.
Берлин — Грюневальд,
декабрь 1930 г. Автор
ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
При выборе содержания и характера изложения предлагаемой
книги я основывался на тех положениях, которые руководили
мною при составлении ранее появившихся в том же издательстве
трех частей настоящего труда, предназначенного для первого
серьезного введения в теоретическую физику. При том объеме,
который имеет в настоящее время теоретическая физика, и здесь
опять речь может итти лишь о скупом выборе из имеющегося
крайне богатого материала. При этом решающим было в первую
очередь ограничение рамками классической волновой теории
в ее применении к средам непрерывной плотности. Поэтому я
имел возможность уделить больше внимания систематическому
изложению и развитию высказываемых положений, а также их
связи с другими отделами теоретической физики. Этим обуслов-
обусловлены многочисленные ссылки на предшествующие тома насто-
настоящего труда, в которых цифр*а / указывает на общую механику,
2 — на механику деформируемых тел и 5 — на теорию электри-
электричества и магнетизма.
Но если в первых частях книги можно было рассматривать
материю как непрерывную среду с непрерывно меняющимися
свойствами, то при изложении дисперсии оказывается необхо-
необходимым отказаться от такого представления. Так как, однако,
при изложении теоретической оптики дисперсия не может быть
опущена, то в последней части книги я ввел атомистический
метод рассмотрения. При этом я пытался наметить также есте-
естественный переход и к квантовой механике. Мне кажется правиль-
правильным не только из педагогических соображений, но и по существу
дела подходить к квантовой механике, так же как и к теории
относительности, на основе классической теории при помощи
соответствующего обобщения.
В конце книги приведен, как и раньше, алфавитный указатель
всех определений и важнейших высказанных положений.
Берлян—Грюневальд,
июль 1927 г. Автор
ОГЛАВЛЕНИЕ
Стр.
Предисловие ко второму изданию 5
Предисловие к первому изданию —
Введение в теоретическую оптику 7
Часть первая
Оптика изотропных однородных сред
Глава I. Отражение и преломление 9
Глава II. Спектральное разложение, интерференция, поляризация .... 31
Глава Ш. Геометрическая оптика 50
Глава IV. Дифракция • 63
Часть вторая
Кристаллооптика
Глава I. Плоские волны 95
Глава II. Волновые поверхности 108
Глава III. Перпендикулярное падение 114
Глава IV. Наклонное падение 119
Часть третья
Дисперсия изотропных сред
Глава I. Основные уравнения 132
Глава П. Плоские волны • 137
Глава III. Геометрическая оптика неоднородных сред. Связь с квантовой
механикой 150
Указатель определений и важнейших положений 161
ВВЕДЕНИЕ В ТЕОРЕТИЧЕСКУЮ ОПТИКУ
§ 1. Физическая оптика образует специальный отдел электро-
электродинамики, охватывающий быстро меняющиеся поля. Особенное
ее значение состоит в том, что она обнимазт ту область физики,
где возможны наиболее тонкие измерения и вследствие этого
возможно наиболее глубокое проникновение в подробности фи-
физических процессов. Вместе с тем в оптике яснее, чем в других
областях физики, проявляется своеобразная тенденция научного
исследования—оставить первоначальную исходную точку—чув-
точку—чувственные ощущения — и построить наши физические понятия на
более объективных основаниях. В то время как важнейшие опти-
оптические понятия — понятия света и цвета — развились первона-
первоначально из впечатлений нашего глаза, в современной физике
понятия света и цвета не имеют ничего общего с непосредствен-
непосредственными ощущениями,, но относятся к электромагнитным волнам и
периодам колебаний; это развитие вполне оправдывается прине-
принесенными им богатыми плодами.
§ 2. В качестве исходной точки удобнее всего взять общую
систему уравнений Максвелла для электромагнитного поля
в покоящихся телах и притом в той специальной форме, кото-
которую они имеют для прозрачных немагнитных тел. Так как про-
прозрачность тела связана с отсутствием превращения электромаг-
электромагнитной энергии в теплоту, то все прозрачные тела являются
электрическими изоляторами, в которых вектор J электрического
тока (проводимости) везде и всегда равен нулю. Вместе с про-
проводниками исключаются из рассмотрения и все сильно намагни-
намагничиваемые вещества, а для остальных можно без заметной ошибки
отождествить магнитную индукцию В с напряжением магнитного
поля Н. Тогда уравнения поля согласно 3, C) принимают про-
простую форму:
D = crotH, H = —crotE A)
вместе с добавочными уравнениями 3, D9) и E1):
divD=O, divH = O. B)
Здесь Е обозначает напряжение электрического поля, Н —
напряжение магнитного поля, D—электрическую индукцию,
с — критическую скорость.
Эта система уравнений охватывает оптику всех прозрачных
веществ. Входящие в них переменные играют лишь роль вспо-
8 ВВЕДЕНИЕ В ТЕОРЕТИЧЕСКУЮ ОПТИКУ
могательных величин, так как они не могут быть непосредственно
измерены. Величиной, к определению которой сводятся все опти-
оптические измерения и вычисление которой является, в сущности
говоря, задачей каждой оптической теории, служит вектор по-
потока электромагнитной энергии 3, B6), равный:
S~[E, H], C)
который обусловливает интенсивность излучения по вели-
величине и направлению.
Для дальнейшего исследования этих уравнений надо принять
во внимание связь между вектором электрического напряже-
напряжения Е и вектором индукции D; эта связь и определяет характер
оптического поведения определенного вещества. В соответствии
с видом этой связи мы разобьем весь подлежащий рассмотре-
рассмотрению материал на три части и рассмотрим последовательно оптику
изотропных однородных сред, кристаллооптику и оптику неодно-
неоднородных сред вместе с явлениями дисперсии и абсорбции.
ЧАСТЬ ПЕРВАЯ
ОПТИКА ИЗОТРОПНЫХ ОДНОРОДНЫХ СРЕД
ГЛАВА I
ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ
§ 3. Для изотропного однородного вещества связь между
электрической индукцией и напряжением электрического поля
выражается уравнением 3, B8):
D=eE, D)
где в обозначает диэлектрическую постоянную.
Тогда уравнения поля A) переходят в
еЁ = с rot Н, Н = — с rot E. E)
Мы рассмотрим в качестве простейшего частного решения
этой системы диференциальных уравнений случай плоской волны,
которая распространяется вдоль одной из координатных осей,
например по положительному направлению оси х. Тогда все
слагающие поля независимы от у и z, и так как в оптике ста-
статические поля не принимаются во внимание, то из E) и B) по-
получается:
в то время как для других компонент имеют место диференци-
альные уравнения:
dt — " дх ' dt ~ " дх '
дНу dEz дНг дЕу
~~Ы С дх ' dt ~ С ~дх~ "
Таким образом из четырех компонент поля каждые две свя-
связаны попарно, именно Еу с //„ и Ez с Ну и для каждой пары
компонент имеет место то же самое диференциальное урав-
уравнение F):
Если мы обозначим
10 ОПТИКА ИЗОТРОПНЫХ ОДНОРОДНЫХ СРЕД
то из выведенного в 2, § 35 общего интеграла диференциального
уравнения F) получим наиболее общее выражение для плоской
волны, распространяющейся в однородной среде по положитель-
положительному направлению оси х в виде:
Н, = 0, j
(8)
где / и g—произвольные однозначные функции одного пере-
переменного.
Как видно, напряжения обоих полей перпендикулярны к на-
направлению распространения; волна называется поэтому „попе-
„поперечной". Она распадается на две в общем случае независимые
друг от друга составляющие, направленные вдоль координатных
осей; у каждой из них электрическое и магнитное напряжения
пропорциональны друг другу.
Знаки определяются согласно следующему правилу: напра-
направления напряжения электрического поля, напряжения магнитного
поля и направление распространения образуют правую систему
координат.
§ 4. Если мы теперь поставим вопрос о том, что можно из-
измерить в этой электромагнитной волне и какие ее свойства
могут быть объективно установлены, то окажется, что непосред-
непосредственно измеряемой величиной является вектор потока энергии C),
который в рассматриваемом случае сводится к л-компоненте:
Таким образом направление потока энергии в однородной
среде совпадает с направлением нормали к волне х, и коли-
количество энергии, протекшей за время dt через поверхность F,
лежащую в плоскости волны, равно:
Sa-F.dt=£.(f + g*).Fdt. (9)
Но так как заметные действия излучения происходят всегда
за конечный промежуток времени, то измерения дают не сам век-
вектор потока энергии, но его интеграл по времени или его среднее
значение, взятое за достаточно большой промежуток времени Т.
Если для сокращения обозначим средние значения через:
ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ 11
то лучистая энергия, проходящая в единицу времени через по-
поверхность F, равна:
Л
эта энергия может быть обнаружена каждым прибором, воспри-
воспринимающим лучистую энергию целиком и обладающим необхо-
необходимой чувствительностью (болометр, радиометр, термостолбик).
После того как измерен общий поток энергии волны, возни-
возникает задача о ее дальнейшем анализе; задача эта двойная: во-
первых, необходимо отделить обе слагаемые f2 и g2 друг от
друга, во-вторых, перейти от средних значений по времени
к самим функциям, т. е. исследовать вид волновых функций
fug. Для этих целей необходимы особые оптические установки,
теорию и способ действия которых мы разберем в дальнейшем.
Заранее о виде этих функций ничего нельзя сказать. В частности,
нет никаких оснований приписывать функциям fug какую-либо
периодичность. В действительности в оптике вообще не бывает
волны с резко определенным в математическом смысле периодом,
как это, например, имеет место в акустике. Поэтому мы пока
не будем рассматривать вопрос о форме волны; мы вернемся
к нему лишь тогда, когда это будет необходимо. Только одно
положение мы можем принять заранее, а именно, что средние
значения / и g равны нулю, т. е.:
/=0; g = 0. A2)
Если бы волновая функция имела среднее значение, отличное
от нуля, мы могли бы данную волну заменить другой волной,
подчиняющейся уравнениям A2), с наложенным на нее стати-
статическим полем, равным этому среднему значению. Это поле
может быть обнаружено вследствие его пондеромоторного вли-
влияния на заряженное пробное тело (электрон) и таким образом
отделено от собственно оптической волны.
§ б. Само собой понятно, что плоская волна с безграничным
сечением не может быть осуществлена в природе. Но все же
можно воспроизвести волны, которые по своим свойствам при-
приближаются к плоским волнам. Представим себе точечный источник
света, который начинает светиться в определенный момент вре-
времени, например при £=0. Так как предполагается, что окру-
окружающая среда однородна и изотропна, то свет будет распро-
распространяться равномерно во все стороны. Ту поверхность, до ко-
которой свет распространился за известный промежуток времени,
называют волновой поверхностью. Каждому моменту времени
соответствует, таким образом, определенная волновая поверхность
и все окружающее пространство заполнено системой волновых
поверхностей, следующих одна за другой и охватывающих одна
другую. В рассматриваемом случае волновые поверхности, оче-
очевидно, представляют собой сферы, концентрически охватывающие
источник света. Небольшой участок достаточно большой сфери-
12
ОПТИКА ИЗОТРОПНЫХ ОДНОРОДНЫХ СРЕД
Первая среда
£-0
Вторая среда
£-0
ческой поверхности может приниматься с достаточным приближе-
приближением за плоскую волну. Нормалью к последней служит соответ-
соответствующий радиус сферы и то же направление имеет и вектор луча S.
§ 6. Исследуем теперь явления, происходящие, когда плоская
волна (8) падает на плоскую границу двух изотропных сред.
Перпендикуляр к этой граничной плоскости возьмем за ось f
новой координатной системы; направим эту ось внутрь второй
среды, а точка О пусть будет общим началом координат систем
хуг и £»?£. Тогда мы можем, не уменьшая общности рассматри-
рассматриваемого случая» расположить как ось у, так и ось щ в так назы-
называемой плоскости падения, про-
проходящей через х и I, и взять эту
плоскость в качестве плоскости
рисунка (черт. 1). Все точки, для
которых КО (слева), находятся
в первой среде — в той, откуда
идет волна (8); все точки, для
которых £>0 (справа)—-во вто-
второй среде, все точки, для кото-
которых f = 0 (ось 1]), находятся в
плоскости, служащей границей
двух сред. Ось х совпадает с на-
направлением луча, приходящим
слева из первой среды; оиа
образует с перпендикуляром»
лежащим в плоскости падения, угол падения #. Ось у предста-
представляет собой след плоскости падающей волны, перпендикулярной
к плоскости чертежа; эта ось образует с плоскостью границы
также угол #, но на чертеже она не нанесена, чтобы не увеличи-
увеличивать числа начерченных направлений. Ось г совпадает с осью Г
и направлена от плоскости чертежа перпендикулярно к нему.
При решении поставленной задачи допустим, что каждая
система волн, удовлетворяющая диференциальным уравнениям
внутри обеих сред и граничным условиям, представляет собок»
явление, возможное в природе.
Чтобы удовлетворить диференциальным уравиениям во второй
среде, представим себе в ней плоскую волну, выражающуюся
уравнениями (8), но с направлением луча по хх (черт. 1), накло-
наклоненным к оси € под углом &х и с поверхностью волны у^, при-
причем гг опять совпадает с z и С. Тогда для шести компонент Е^,
Еу, Eit, H^, H9, HXf имеют место уравнения (8), но в правой
части этих уравнений должна стоять координата хх вместо х,
вместо волновых функций / и g должны стоять волновые функ-
функции fx и gv а вместо констант е и q—диэлектрическая посто-
постоянная £,, и скорость распространения во второй среде G):
A3)
Черт. 1.
ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ 13
Но этого недостаточно. Именно граничные условия требуют
согласно 3, § 6, чтобы для 1 = 0 значения тангенциальных компо-
компонент напряжения поля, т. е. величины £"ч, Ес, Н^ Hv в обеих
средах соответственно совпадали. Это дает четыре уравнения
между волновыми функциями, для удовлетворения которых в на-
щем распоряжении находятся только функции ft и g^, так как
функции fug заданы. Предполагаемое решение нужно поэтому
взять в более общем виде. Для этого допускаем, что в первой
среде существует еще одна волна, которая естественно опять
определяется уравнениями (8), но с измененным направлением
луча х', образующим с осью £ угол &' (черт. 1) и с плоскостью
волны y'z', .причем опять Z* == г. Тогда шесть компонент напря-
напряжения поля, Ех„ Еу„ Ег„ Нх„ Ну„ Hz,, заданы уравнениями (8),
если в них вставить волновые функции /'и g и вместо х коор-
координату х'\ константы е и q оставляем те же.
Теперь мы получили решение (как для точек внутри первой,
так и внутри второй среды) в достаточно общем виде и
можем приступить к составлению граничных условий. В первой
среде имеется электромагнитное поле, образованное наложением
обеих волн, принятых нами плоскими. Принимая во внимание,
что компоненты Ех, Нх, Ех,, Нх, равны нулю, получаем для инте-
интересующих нас остальных компонент в первой среде (£ <0):
Нп = Ну cos # + Ну, cos &' = — cos & ■ g—cos *' ■ g',
1
С другой стороны, принимая во внимание, что компоненты
Ех и Нх равны нулю, имеем для второй среды (£ > 0):
Ип = Ну cos #! = — cos &i • glr
Для граничной плоскости £ = 0 имеет место:
• р 4- р' = —
A4)
14 ОПТИКА ИЗОТРОПНЫХ ОДНОРОДНЫХ СРЕД
где для сокращения мы обозначили:
В этих четырех уравнениях содержится вся теория отражения
и преломления. Они, как это видно, распадаются на две группы,
из которых одна содержит только /-волны, другая только
#-волны. Таким образом эти группы волн ведут себя незави-
независимо друг от друга, и каждая из них повинуется своим соб-
собственным законам.
§ 7. Прежде всего, пользуясь последними четырьмя уравнени-
уравнениями, выразим неизвестные волновые функции /', ft, g', g1 через
заданные волновые функции fug. Получаем:
J
n(cos# — cos*')
cos^-n
s ncos^ —
Аргументами этих функций служат:
для / и g:
t— — ,
для Л и gt:
для /' и g':
При этом везде f = 0 и, Следовательно, при преобразовании
к координатам £, tj, f:
x' — г]sin&',
вследствие чего аргументы имеют следующие значения:
. г] sin & . т] sin &! rj sin &'
Я ' Яг ' Я ''
Так как уравнения A5) — A8) должны соблюдаться для лю-
любого времени t и для любых точек г\ граничной плоскости,
то необходимо, чтобы все три аргумента были равны между
собой. В этом можно убедиться и непосредственно, если взять
от одного из функциональных уравнений частную производную
ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ 1&
по t, потом частную производную по г] и полученные уравнения
разделить одно на другое. Следовательно, необходимо, чтобы
ГчГ я '
Отсюда получаем закон преломления:
Ж¥Г^У7- <20>
и закон отражения:
& = п~&. B1)
Если углом отражения назвать угол между отраженным лучом
и обратным направлением перпендикуляра к граничной плоскости,
то угол отражения равен углу падения.
§ 8. Закон преломления Снелиуса B0), утверждающий, что
отношение синуса угла падения & к синусу угла преломления &г
равно показателю преломления второй среды по отношению
к первой, или отношению скоростей распространения д и glt
подтверждается бесчисленными измерениями. Обыкновенно по-
показатель преломления какого-либо вещества относят к воздуху
(являющемуся „первой" средой). Так, показатель преломления
воды равен 1,3, стекла —1,5. Относительный показатель прелом-
преломления одного вещества по отношению к другому получим, раз-
разделив друг на друга их показатели преломления по отношению
к воздуху. Если вещества обменять местами, то показатель пре-
преломления принимает обратную величину. Показатель преломления
по отношению к вакууму, так называемый „абсолютный" пока-
показатель преломления, равен произведению показателя преломления
относительно воздуха и абсолютного показателя преломления
воздуха 1,0003. Очевидно, в большинстве случаев он мало отли-
отличается от обыкновенного показателя преломления.
Когда угол падения # меняется от 0 (нормальное падение)
до -^- (скользящее падение), то угол преломления 02 растет от 0
до arc sin — (предельный угол). При этом необходимо отметить
следующий важный момент. Предельный угол имеет действитель-
действительное значение лишь тогда, когда п>\, или, как говорят, когда
второе вещество оптически плотнее, чем первое. В этом случае
угол преломления #t всегда меньше угла падения &, т. е. луч
при преломлении приближается к перпендикуляру; предельный
угол — это наибольшее значение, которого достигает угол пре-
преломления. Если же я<1, что будет, если оба вещества обменять
местами, то меняются местами и углы падения и преломления;
в этом случае угол преломления больше угла падения и дости-
достигает значения -^, когда угол падения достигает величины пре-
предельного угла; и если угол падения увеличивать еще дальше,
то B0) дает мнимое значение для угла преломления и получен*
16 ОПТИКА ИЗОТРОПНЫХ ОДНОРОДНЫХ СРЕД
ное решение проблемы преломления теряет физический смысл
Но так как ничто не мешает дать углу падения любую величину
от О до -~-, то здесь возникает особый вопрос, обсуждение ко-
торого мы, однако, отложим до дальнейшего (§ 12), а пока огра-
ограничимся рассмотрением тех случаев, для которых закон прелом-
ления дает действительную величину угла преломления &1т
§ 9. Электромагнитная теория преломления света не только
указывает на независимость показателя преломления от вели-
величины угла падения, но также дает величину показателя прелом-
преломления; согласно B0) последний равен квадратному корню из
отношений диэлектрических постоянных; или для. абсолютного
показателя преломления
п = Уч- B2)
Однако, сравнивая это отношение с фактами, получаем в общем
резкое противоречие. Так, для воды имеем п = 1,3, et = 80. Но,
кроме этого, B2) не может быть всегда справедливо хотя бы
потому, что диэлектрическая постоянная по самому своему опре-
определению независима от формы волновых функций / и g, в то
время как показатель преломления п для всех веществ более
или менее сильно зависит от формы световой волны, т. е. от
цвета. Это явление (дисперсия) долгое время представляло серьез-
серьезное препятствие признанию максвелл о вской теории. Если же-
желательно учесть ее соответствующим образом в рамках изло-
изложенной здесь теории, то остается только принять, что для
быстрых оптических колебаний допущение D) в общем случае
не соответствует действительности. Это допущение пропорцио-
пропорциональности электрической индукции напряжению электрического
поля было сделано в начале настоящей главы для оптических
явлений в однородных изотропных средах. Чтобы получить удов-
удовлетворительную теорию дисперсии, мы должны будем заменить
это допущение более общим; это будет сделано в третьей части
этой книги. Обобщение это будет исходить из того, что пред-
представление об абсолютной непрерывности и однородности материи
не годно для объяснения оптических явлений во всех деталях, и
поэтому теория должна быть изменена так, чтобы были учтены
характерные особенности структуры среды.
С этой последней точки зрения соотношению B2) следует
приписать смысл предельного закона, выполняющегося тем лучше,
чем меньше заметна дисперсия. Это предположение, действи-
действительно, подтверждается более подробными исследованиями. Так,
в газах дисперсия меньше, чем в других веществах, и для них
формула B2) была хорошо подтверждена (впервые измерениями
Л. Больцмана). При этом особенно замечательно то, что у газов
зависимость от давления показателя преломления, с одной сто-
стороны, и диэлектрической постоянной — с другой, идет вполне
параллельно и в согласии с уравнением B2). Поэтому можно
с полвдш правом говорить об этом соотношении как о сущест-
ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ 17
венном подтверждении электромагнитной теории в пределах
определенной области ее применения.
§ 9а. Кроме направлений отраженного и преломленного
луча теория дает также и форму отраженной и преломленной
волны. Действительно, из теории следует, что волновые
функции последних пропорциональны соответствующим волно-
волновым функциям падающей волны. Если в формулах A5) — A8)
заменить показатель преломления п согласно B0) при помощи
углов # и #х, а угол •&' через п — #, то коэфициенты пропорцио-
пропорциональности принимают следующие значения:
для отраженной волны (f,g'):
8i
a~ si
для преломленной волны (Д,
sin 2^
!) cos (« — «0 ' CTl"~ sin (# + ^) •
Согласно этим так называемым френелевским формулам имеется
значительное различие между обеими волновыми функциями /
и g, которое соответствует тому физическому обстоятельству,
что согласно (8) у /-волны напряжение электрического поля
направлено в плоскости падения, а у ^-волны направлено пер-
перпендикулярно к плоскости падения. Первой соответствуют коэ-
коэфициенты ц, второй — а.
Для проверки теории мы должны обратиться к измерению
энергии лучей. Рассмотрим сначала отраженную волну.
Из уравнения A1) получается для отношения интенсивности
излучения отраженной волны к интенсивности излучения пада-
падающей волны или для так называемого „коэфициента отражения"
[при обозначениях A5) и A7)]:
7ч-F 7ч-?
Очевидно, значение коэфициента отражения q лежит между
значениями fi2 и а2, которые соответствуют предельным случаям,
-когда одна из волн / или g исчезающе мала. В общем случае
из измерений q можно найти отношение интенсивностей излу-
излучения для волн / и g:
f*--fz = ~^- B5)
Это отношение можно экспериментально проверить, измеряя
коэфициент отражения q для определенной падающей волны
(/, g) при различных углах падения #, вводя вычисленные со-
согласно B3) значения ц и а и исследуя, получается ли при всех
углах падения одно и то же отношение интенсивностей B5).
В действительности так всегда и оказывалось, если только по-
2 Введение ъ теоретическую физику, ч. IV
18 ОПТИКА ИЗОТРОПНЫХ ОДНОРОДНЫХ СРЕД
верхность применяемого тела была достаточно гладкой и если
были достаточно хорошо устранены химические загрязнения
поверхности, к которым относятся и загрязнения, возникающие
при действии полирующих веществ.
Когда свет приходит непосредственно от тела, нагретого до
каления, его называют „естественным"; в этом случае измерения
дают, как и следовало ожидать:
и поэтому
е--^. B6)
Зависимость коэфициента отражения q от угла падения #
дана уравнением B3). Для перпендикулярного падения, когда #
и #л бесконечно малы, получаем:
«-(&$№#• <27>
Отражение тем сильнее, чем больше показатель преломления
отличается от единицы, т. е. чем оптически разнороднее обе
среды. Для скользящего падения # = у и соответственно для
предельного угла #г = -" коэфициент отражения достигает своей
наибольшей величины, равной единице; в этих случаях вообще
никакое излучение не входит во вторую среду.
Но выводы теории и возможности ее применения идут еще
дальше. Именно оказывается, что если падающий свет был есте-
естественным, то отраженный свет не является естественным, но
согласно A5) и A7):
Только для перпендикулярного и скользящего падения (и
соответственно для предельного угла) это отношение равно еди-
единице и отраженный свет является естественным; это. вполне по-
понятно, так как в первом случае плоскость падения неопределен-
неопределенная и поэтому между волнами /' и ^Г\нет никакого физического
различия, а во втором случае отражается полностью весь свет.
Но в общем случае обе компоненты обладают различной интен-
интенсивностью, т. е. отраженное излучение ^поляризовано" и интен-
интенсивность /-волны, электрический вектор которой лежит в плос-
плоскости падения, меньше, чем интенсивность ^-волны. Притом
в случае, когда
0 + 0 ==* или tg# = «, B9)
т. е. когда отраженный луч перпендикулярен к преломленному
лучу, числитель B8) равен нулю, /-волна в отраженном свете
ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ 19
вообще отсутствует и остается лишь одна ^-волна. Излучение
называется тогда полностью поляризованным и притом поляри-
поляризованным прямолинейно (или линейно), потому что в этом слу-
случае электрическое и магнитное напряжения волны имеют вполне
определенные направления. Определяемый уравнением B9) угол
падения называется „углом поляризации", плоскость падения —
„плоскостью поляризации", а отражающее тело (зеркало) — „по-
„поляризатором". Если назвать „плоскостью колебаний" луча плос-
плоскость, проходящую через направление луча и направление на-
напряжения электрического поля, то в свете, отраженном при угле
поляризации B9), плоскость колебаний постоянна и перпендику-
перпендикулярна к плоскости падения (закон Брюстера). Это положение
может быть проверено непосредственно на опыте тем, что ли-
линейно поляризованный луч заставляют отражаться от второго
тела из того же вещества и опять при угле поляризации, но так,
чтобы при втором отражении падающий луч играл роль/-волны,
т. е. чтобы его плоскость колебаний совпадала с его новой
плоскостью падения. Это будет тогда, когда плоскость падения
при втором отражении перпендикулярна к плоскости падения
при первом отражении. В этом случае свет вообще не отра-
отражается (опыт Малюса с зеркалами). Второе отражающее тело
действует в этом случае, как „анализатор".
Отражение при угле поляризации дает возможность измерить
в заданном излучении отдельно волновые функции / и g.
Именно, приняв во внимание, что/' = 0, получим:
это — интенсивность отраженного света; ее можно измерить и
отсюда определить интенсивность ^"-волны; таким же образом
отражением в плоскости падения, повернутой на ~ (ось пово-
поворота — падающий луч), можно определить интенсивность /-волны.
При отражении под произвольным углом падения # отражен-
отраженный луч лишь чаетичнсцюляризован. Интенсивности обеих вол-
волновых компонент f2, и g'2 получаются путем умножения соответ-
соответствующих компонент /2 и g2 падающей волны на соответствую-
соответствующие коэфициенты отражения. Для света, колебания которого
происходят в плоскости падения (/-волна), коэфициент отра-
отражения равен:
для света, колебания которого перпендикулярны к плоскости
падения (^-волна):
2*
20 ОПТИКА ИЗОТРОПНЫХ ОДНОРОДНЫХ СРЕД
§ 10. Для излучения, прошедшего через граничную поверх-
поверхность двух сред, можно получить соотношения, аналогичные по-
полученным для отраженных лучей. Их можно свести к уже най-
найденным, если вспомнить, что на основании закона сохранений
энергии прошедщая энергия равна разности между энергией
падающего и отраженного света. Это имеет место потому, что
граничные условия уже обеспечивают отсутствие потерь лучи-
лучистой энергии (ср. 3, § 6). Если назвать коэфициентом пропуска-
пропускания ту часть падающей лучистой энергии, которая проходит
через границу во вторую среду, то для света, колебания кото-
которого происходят в плоскости падения (/-волна), он равен:
1 , 2 sin 2& • sin 2flt
1 е\\— l~v — ^tfW+^&^&W1
а для света, колебания которого перпендикулярны плоскости
падения (g- волна):
Само собой понятно, что коэфициент пропускания можно вы-
вычислить и непосредственно из отношения интенсивности волны,
проникшей во вторую среду flt или gt к интенсивности падаю-
падающей волны / или g. Только при этом соответствующие коэфи-
циенты пропускания нельзя считать, исходя из A6) и A8), рав-
равными jmx2 или of!2, но надо вернуться к выражению A1) для энер-
энергии, прошедшей в единицу времени через участок F, лежащий
в плоскости волны, так как при переходе во вторую среду ме-
меняется как скорость распространения д, так и величина поверх-
поверхности F, равная поперечному сечению цилиндра, образованного
лучами, причём легко сообразить из простых геометрических
рассуждений, что
F F
cosi = соИ^ • C!^)
В самом деле, это отношение равно величине площадки, на
которую опирается в плоскости границы как цилиндр падающих,
так и цилиндр преломленных лучей. Отсюда получается отно-
отношение прошедшей лучистой энергии к падающей согласно A1),
B0), C5) ,и A6) для /-волны:
™ COS&
и соответственно для g-t
sin &x q2 сю»,
qgtp sin# 1 cos* '
ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ 21
Эти выражения совпадают на основании B4) с C3) и C4).
Отношение обеих компонент интенсивности излучения в про-
прошедшем счете равно:
Так как это выражение не может равняться ни нулю ни бес-
бесконечности, то при падающем естественном свете прошедшее
излучение никогда не может быть полностью поляризовано, оно
всегда поляризовано только частично, и притом компонента с
колебаниями в плоскости падения является более сильной, в про-
противоположность тому, что имеется в отраженном свете.
Наконец, нужно указать еще на одно соотношение, которое
является выражением одного общего закона оптики. Как уравне-
уравнение B0) для закона преломления, так и значения коэфициентов
отражения и пропускания остаются неизменными, когда обе среды,
а вместе с ними и углы & и &и меняют местами, т. е. когда волну
заставляют падать в обратном направлении из второй среды на
границу первой среды. Другими словами, свет не только может
итти в обратном направлении, но при этом он разделяется в
прежнем соотношении на отраженное и прошедшее излучение.
Граница двух сред одинаково хорошо отражает в обе стороны
и одинаково хорошо пропускает в обе стороны; этот закон
является применением закона обратимости луча, высказанного
впервые Гельмгольцем, согласно которому ослабление, претерпе-
претерпеваемое определенным лучом на своем пути через различные среды
в результате отражения, преломления, рассеяния,, поглощения, не
зависит от направления, в котором пройден путь.
§ 11. После того как мы убедились, что обе взаимно перпен-
перпендикулярные компоненты fug заданной (8) плоской волны можно
измерить отдельно, и узнали, как это сделать, встает дальнейший
вопрос, определяется ли значением обеих интеисивностей /2 и g2
также интенсивность какой-либо компоненты света, колебание
которой направлено по какому-нибудь направлению, перпендику-
перпендикулярному к направлению распространения, подобно тому как за-
заданными двумя взаимно перпендикулярными компонентами какой-
либо силы задается ее компонента по любому направлению.
Мы увидим, что это не так, и выясним, какое здесь есть
отличие.
Чтобы ответить на поставленный вопрос, мы вновь рассмо-
рассмотрим общий случай (8) плоской волны, но в целях более удоб-
удобных обозначений возьмем в качестве направления распростране-
распространения ось z вместо оси л, так что плоскость ху будет плоскостью
волны, /-волна имеет колебания вдоль оси х, ^-волна — вдоль
оси у. Если теперь заменить оси х и у двумя другими осями л;'
и у' (взаимно перпендикулярными и лежащими в той же плос-
плоскости, перпендикулярной распространению), образующими угол <р
22 ОПТИКА ИЗОТРОПНЫХ ОДНОРОДНЫХ СРЕД
с прежними осями, то относящиеся к ним волновые функции /'
и g' согласно (8) преобразуются как компоненты напряжений
поля:
/' =/cos 93 4-jg-sin 9», C7)
g' = —/sin 9» -f g cos 9?, C8)
а соответствующие интенсивности преобразуются так:
/г =/2 cosa v + 2fgsm 9? cos q> + g* sin2 p,
g'z=:f2 sins 9? — 2fg sin 93 cos q> + g* cos2 9?.
Сложением получаем:
f* + £*=/* + £.
т. е. если сложим интенсивности двух взаимно перпендикуляр-
перпендикулярных компонент, то всегда получим интенсивность всей волны,
что ясно уже из того, что выбор начальной системы координат
ху вполне произволен. Но интенсивность какой-нибудь компо-
компоненты, например такой, направление колебаний которой образует
угол'9? с осью х, зависит не только от интенсивностей g* и/2,
но и от третьей величины fg. Если мы обозначим для сокращения
Г2=А, g~*=*B, fg^C, C9)
то интенсивность компоненты, колебания которой происходят
в азимуте <р, равна:
fb = Jv = A cos2 tp + B sin2 <p + 2C sin 95 cos 9?. D0)
Поэтому интенсивность излучения представляет собой не
вектор, но тензор второго ранга B, § 13, § 20) и притом плоский
тензор, имеющий только три компоненты и характеризующийся
тем, что величина D0) не зависит от выбора координат. Компо-
Компонента С может принимать любые значения между —У^АВ и
+ VAB, но не может превосходить эти пределы, так как J для
всех значений q> имеет положительную величину.
Для предельного значения С = ± YAB J согласно D0) пре-
превращается в полный квадрат:
J = (]/л cos q> ± У В sin tp J. D1)
В этом случае J = f2 обращается в нуль в азимуте <р, для кото-
которого tg <р = =р у -g и все излучение сводится к одной компо-
компоненте g'2, колеблющейся в перпендикулярном (? + тг ) азимуте.
Свет в этом случае поляризован линейно.
ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ 23
Из /'* = 0 следует /' = 0 и согласно C7):
, D2)
т. е. отношение волновых функций fug постоянно и не зависит
от их аргумента. В таком случае, когда одна волновая функция
вполне определяется второй, обе соответствующие компоненты
излучения называют вполне когерентными. Линейная поляризация
обусловливает поэтому полную когерентность обеих компонент,
на которые может быть разложен поляризованный луч. Из
соотношений A5)—A8) непосредственно вытекает, что линейно
поляризованный свет после преломления и отражения будет тоже
линейно поляризованным, так как тогда отношения fi'-gi и f :g'
также постоянны.
В общем случае свет лишь частично поляризован, так что
обе компоненты частично некогерентны. Противоположный край-
крайний случай представляет собой естественный свет, для него
интенсивность излучения Jv совершенно не зависит от азимута
колебаний. Для этого согласно D0) требуется, чтобы не только
имело место А = В, но также, чтобы С = 0.
Легко убедиться, что последнее условие действительно вы-
выполнено, если обе компоненты колебаний / и g совершенно не-
некогерентны, т. е. совершенно независимы друг от друга. Это
значит, что определенному значению / соответствует не одно
определенное* а бесконечное множество значений g, и что сред-
средняя величина всех этих значений g независима от взятого зна-
значения /. Поэтому математическим выражением полной некоге-
некогерентности / и g служит:
fg^f-g D3)
и согласно C9) и A2):
C=fg=0. D4)
Так как функции / и g однозначно зависят от их общего
аргумента, то для некогерентности fug необходимо, чтобы
определенному значению / или g соответствовало бесконечное
множество значений аргумента или чтобы любое определенное
значение волновой функции в течение времени очень часто по-
повторялось.
Если соотношение D4) является необходимым следствием пол-
полной некогерентности обеих функций / и g, то его совершенно
недостаточно, чтобы ручаться за некогерентность, так как мы
скоро (§ 20) увидим, что компоненты / и g могут быть совер-
совершенно когерентны, и все же уравнение D4) будет выполняться.
Само собой понятно, что / и g тогда не. пропорциональны одна
другой, как в D2), т. е. свет не является линейно поляризован-
поляризованным, но он все же вполне поляризован, так как одна компо-
компонента в каждый момент вполне определяется второй компонентой.
24 ОПТИКА ИЗОТРОПНЫХ ОДНОРОДНЫХ СРЕД
Вернемся теперь опять к рассмотрению общего случая. Легко
видеть, что интенсивность излучения Jv согласно D0) для опре-
определенных значений <р имеет максимум и минимум, которые оба
определяются из уравнения:
или согласно D0) из уравнения:
Эти два взаимно перпендикулярные направления называются
главными плоскостями колебаний луча, а соответствующие интен-
интенсивности,, т. е. максимум и минимум J, равные
D6)
называются главными интенсивностями луча.
Для плоскополяризованного света, как мы видели, С= ± УАВ.
Тогда согласно D6) максимальная интенсивность J = А + В,
а минимальная интенсивность У=0.
Для естественного света А = В и С = 0 и согласно D6)
J = А = В и главные плоскости колебаний согласно D5) дела-
делаются неопределенными.
Если координатные оси х и у направить по главным плоско-
плоскостям колебаний, то уравнение D5) удовлетворяется при q> = 0 и
9? = -g-» следовательно, тогда С=0 и компонента интенсивности
излучения в произвольном направлении согласно D0) равна:
Jv = A cos2 <p + В sin2 tp, D7)
причем А и В в согласии с D6) представляют собой главные
интенсивности. Так как в общем случае интенсивность излуче-
излучения Jv согласно D0) зависит от трех констант, то для характе-
характеристики поляризации излучения недостаточно измерений двух
компонент
У0=Л и J^ = B.
В действительности, например, когда А = В, свет может быть
или естественный или Линейно поляризованный в азимуте 45°
или же он может быть как-нибудь составлен из естественного
и линейно поляризованного света. Чтобы определить третью
компоненту тензора fg = С, требуется еще третье измерение,
например измерить компоненту, колебания которой направлены
под углом .^-:
J*. = ^+C D8)
Тогда А, В и С вполне определены.
ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ 25
§ 12. Чтобы закончить разбор вопросов, связанных с явлениями
отражения и преломления, нам остается рассмотреть еще один слу-
случай. Этот случай оставлен нами временно (в конце § 8) нерассмотрен-
нерассмотренным, так как найденное нами тогда решение к этому случаю не
могло быть применено. Это случай, когда sin & > п (причем п < 1).
В этом случае угол преломления #х согласно B0) получается мнимым.
Само собой понятно, что недостаточно сказать: так как угол
преломления мнимый, то никакого преломления нет и, следова-
следовательно, весь свет отражается. Действительно, мы не сможем
удовлетворить граничным условиям задачи, если волновые функ-
функции преломленной волны положим равными нулю, а волновые
функции отраженной волны равными волновым функциям па-
падающей волны. Вопроса о нахождении вида волновых функций,
удовлетворяющих всем условиям, требуемым теорией, таким
образом нельзя обойти. Кроме того, следует принять во внима-
внимание, что комплексное решение уравнения также является реше-
решением и что оно, не имея прямого реального смысла, может ука-
указать нам путь для нахождения действительного решения.
В самом деле, каждое уравнение с комплексными величинами
распадается на два уравнения с действительными величинами.
Примем во внимание, что как все уравнения между напряже-
напряжениями поля падающей, отраженной и преломленной волны, так
и условия внутри среды и на границе являются линейными и
однородными по отношению к напряжению поля и имеют дей-
действительные коэфициенты; из этого следует, что если все урав-
уравнения удовлетворяются комплексными значениями напряжения
поля, то и действительные части этих комплексных значений
удовлетворяют этим уравнениям и дают действительное физи-
физическое решение проблемы. Мы можем поэтому из любого ком-
комплексного решения получить сразу действительное решение, если
отбросим чисто мнимые части комплексных значений напряжений,
поля и оставим только действительные части.
Осуществляя эти соображения, мы должны помнить, что вслед-
вследствие комплексности угла преломления & как коэфициенты о
и /л, так и волновые функции преломленной и отраженной волны
будут комплексными величинами. В интересах полной общности
мы сделаем такое же допущение и относительно падающей
волны, т. е. под fug мы подразумеваем две произвольные ком-
комплексные функции одного и того же комплексного аргумента.
Обозначая действительную часть какой-нибудь комплексной ве-
величины поставленной впереди нее буквой R, получаем из (8) для
действительных компонент поли падающей волны выражения:
//. = 0,
±=
D9)
26
ОПТИКА ИЗОТРОПНЫХ ОДНОРОДНЫХ СРЕД
где в качестве аргумента для / и g опять служит t— —; ось х,
как и раньше, направлена по нормали к волне, ось у опять на-
находится в плоскости падения, ось z перпендикулярна к ней.
Что касается преломленной волны, то ее волновая нор-
нормаль хг является комплексной величиной (другими словами, угол ■&
комплексный). Поэтому мы сразу возьмем компоненты поля в дей-
действительной координатной системе £, щ, £, которая определена
перпендикуляром к границе | и плоскостью падения £щ (черт. 1).
Для эт(ого мы прежде всего выразим комплексные напряжения
«юля согласно уравнениям:
= ЕХ1' cos 0Х —
sin
Еп = EXi • sin #л -f- ESi • cos <
и т. д. и заменяем здесь компоненты Е , Еу , Е по образцу (8)
волновыми функциями /j и glt а эти опять согласно A6) и A8)
заменяем волновыми функциями падающей волны / и g. Тогда
для действительных компонент поля преломленной волны полу-
получаются выражения:
V Ч
R/н/ sin #ь И = Ralg sin
E = ~ - R/iJcos *„
V Ei
H = - Ra±gcos ^
E0)
Здесь аргументом / и g повсюду является t ——, где
хх = | cos #! -\-f] sin &v E1)
Наконец, для отраженной волны, нормаль которой х' дей-
действительна, мы получаем согласно (8), A5) и A7) действительные
компоненты поля:
Е* = 0, Н* = 0, j
V
x'
— для / и g.
•с аргументом t
% 13. Предшествующие уравнения в принципе разрешают
проблему полного внутреннего отражения, однако применить
теорию непосредственно к общему случаю волновых функций про-
произвольного вида не удается, потому что невозможно явно вы-
ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ 27
делить действительную часть комплексного выражения, пока
неизвестен вид этого последнего. Поэтому, если мы желаем пе-
перейти к действительным выражениям, мы вынуждены сначала
разобрать частные решения задачи, а потом соответствующим
обобщением частных ре,шений разрешить и общий случай. При
выборе частных .решений, могущих играть роль в задачах оптики,
мы должны помнить, что (согласно §11) для естественного света
нужно рассматривать волновые функции, очень часто принимаю-
принимающие все возможные для них значения. Мы выбираем поэтому
в качестве простейшего частного решения простую периодиче-
периодическую функцию, полагая
/ (f) = еш = cos cot + i sin cot, E3)
и рассматриваем обе волны / и g раздельно, принимая пока
gift = 0. E4)
Тогда согласно D9) имеем для падающей волны:
нх = и,
Е =
E5)
V е
£•.■=0, z (^)
Это частный случай синусоидальной волны с частотой со,
с числом колебаний v = ^ и длиной волны Я = — B, § 40).
Чтобы из E0) найти действительные компоненты поля для пре-
преломленной волны, мы вычисляем сперва комплексные значения
# и [хх. Для cos#i мы получаем из B0):
где через #' мы обозначили положительную действительную
величину:
#' = УШ1Г1 E6)
[не смешивать с углом отражения в (-21)].
Коэфициент /гг задан уравнением B4); мы выделим его дей-
действительную и мнимую части, написав его в виде:
2 sin & cos ё _2sina#cos2#=F i • 2 siq & cos & ■ &' ■ sin flt
^ ~ sin & cos & -\- sin &! cos &t ~ sin2 & cos2 & + &'* sin2 &± '
или если для сокращения мы положим
t (
shT¥^ T ^), E7)
то получим:
= 2 cos2 -5- =F i • 2 sin ■=■ cos -^ = 2 cos -^ e
28 ОПТИКА ИЗОТРОПНЫХ ОДНОРОДНЫХ СРЕД
Решение вопроса, взять ли верхний или нижний знак, полу-
получается из рассмотрения выражений E0). Последние содержат
величину /(/ ~\, где согласно E1):
Хх = ± г|#' + г} sin 0j,.
Если подставить выражение E3) для /, то в показателе е по-
получим действительный член ± ^j~, который, чтобы решение
было пригодно, должен обращаться в бесконечность при I = + оо,
т. е. в бесконечном удалении от плоскости границы. Поэтому
везде нужно взять нижний знак, и мы получим:
cos#! = — ffi' E8)
и соответственно:
ft1 = 2cos^etT. E9)
Таким образом для компонент поля преломленной волны по-
получаем согласно E0) следующие выражения:
ft—«
F0)
1 ■■ " ' j
,= о, I
Яе = 2 cos| • e-^cosf»^-^) +|]. F1)
Очевидно, и при полном внутреннем отражении во второй,
оптически менее плотной, среде имеют место заметные колеба-
колебания. Но эти колебания имеют ту особенность, что их фаза со-
совершенно не зависит от нормальной к границе координаты £.
В результате во второй среде волна распространяется парал-
параллельно плоскости границы вдоль оси щ и поэтому вообще не
проникает в глубину среды. Ее проникновение ограничивается
всегда граничным слоем, толщина которого имеет величину
порядка одной длины волны Я,. Чем больше угол падения, тем
менее глубоко волна проникает во вторую среду и тем медлен-
медленнее она распространяется вдоль граничной поверхности.
Для отраженной волны выражения получаются значительно
более простыми, так как для нее волновая нормаль
х' = — | cos & + п sin #, F2)
х'
входящая в аргумент t—r— волновой функции, является действи-
ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ 29
тельной величиной. Наоборот, на основании E8) и E7) для
коэфициента ц получается из B3) комплексное выражение:
/г = е*'. F3)
Отсюда на основании E2) получаем для компонент поля отра-
отраженной волны;
F4)
= 0, Нг. =
Ясно, что теперь, получив выражение для поля, можно убе-
убедиться непосредственной проверкой, что выражения E5), F0),
F1), F4) для падающей, преломленной и отраженной волны дей-
действительно удовлетворяют всем условиям внутри (|5g;0) и на
границе (I = 0) обеих сред.
Для отраженной волны характерно, что она имеет ту же
амплитуду, что и падающая волна, но в отличие от обыкновен-
обыкновенного отражения имеет фазу, смещенную на угол Ь.
Этот скачок фазы равен нулю согласно E7) для предельного
угла (sin ■& =j= п, &' = 0), где полное внутреннее отражение совпа-
совпадает с обыкновенным отражением, он растет вместе с увеличе-
увеличением угла падения # и достигает значения л для скользящего
падения
Изложенные результаты справедливы для /-волны, колеба-
колебания которой направлены в плоскости падения. Для ^-волны,
колебания которой направлены перпендикулярно к плоскости
падения, справедливы аналогичные законы; однако в этом слу-
случае имеются и характерные отличия от разобранного выше слу-
случая колебаний в плоскости падения. Так как ход вычисле-
вычислений остается тот же, то достаточно будет вкратце привести
результаты.
Если падающая волна представлена уравнениями:
= —coso>(* —у),
и если, далее, обозначить
F5)
= tg — @ < т < я), F6)
то получится из B4) и B3):
--e'^ , a = e\ F7)
30
ОПТИКА ИЗОТРОПНЫХ ОДНОРОДНЫХ СРЕД
Таким образом компоненты поля преломленной волны со-
согласно E0) равны:
£,= 0,
2 •
_ /> ei
<о6'|
#,= —
F8)
а компоненты поля отраженной волны согласно E2):
= 0, //„• = — cos \со(г!—-у) +*] . ^' = 0.
F9)
Таким образом ^-волна с колебаниями, направленными пер-
перпендикулярно к плоскости падения, претерпевает при полном
внутреннем отражении иной скачок фазы т, чем /-волна, коле-
колебания которой направлены в плоскости падения, причем в об-
общем случае согласно E2) и F6j ё > т. Только в случаях пре-
предельного угла (#1 = v) и скользящего падения (#= ^\ д и т
равны друг другу.
§ 14. Для полного решения вопроса о полном внутреннем
отражении полученные частные решения нужно еще распростра-
распространить на случай любых заданных волн f(t) и g(t). Это можно
сделать, если выражение E3) сперва умножить на произвольную
комплексную постоянную, вследствие чего колебание приобре-
приобретает произвольную амплитуду и произвольную фазовую постоян-
постоянную, и после этого произвести суммирование по целым кратным
значениям определенной частоты со. Вследствие этого действи-
действительная часть /(/) и соответственно g(t) принимает форму ряда
Фурье B, § 38):
со
(^f) G0)
n—l
а известно, что любая периодическая функция с периодом Т
может быть представлена таким рядом. Начальный член этого
ряда Св согласно* A2) взят равным нулю. То, что при этом
функции fug получаются периодическими, не является ограни-
ограничением, так как период Т можно взять столь большим, что для
СПЕКТРАЛЬНОЕ РАЗЛОЖЕНИЕ, ИНТЕРФЕРЕНЦИЯ, ПОЛЯРИЗАЦИЯ 31'
физических измерений будут иметь значения только моменты
времени t, лежащие внутри одного и того же периода, т. е.х
например, значения t между нулем и Т. Это имеет место, на-
например, если момент, когда источник света начинает действовать,
обозначить через t = 0, а момент окончания последнего измерений
обозначить через t=T.
ГЛАВА II
СПЕКТРАЛЬНОЕ РАЗЛОЖЕНИЕ, ИНТЕРФЕРЕНЦИЯ.
ПОЛЯРИЗАЦИЯ
§ 15. При выводе законов отражения и преломления, изло-
изложенных в предыдущей главе, не было сделано никаких предпо-
предположений относительно вида волновых функций / и g. Это отно-
относится также и к законам полного внутреннего отражения, так
как разложение волновой функции в ряд Фурье представляет
собой лишь особую форму математического изображения. В осо-
особенности не нужно думать, что волновые функции в пределах
большого основного периода Гдолжны обладать какими-нибудь
свойствами периодичности. В течение определенного времени
они даже могут быть равными нулю, а до этого и после этого
какими угодно. Отсюда следует также, что отдельным амплиту-
амплитудам Сп ряда Фурье G0) нельзя приписать объективного значе-
значения (для характеристики формы волновой функции), так же как
и основному периоду Т, от которого они зависят. Чтобы узнать
что-либо о форме волны, необходимы, следовательно, особые
измерения. Принципиально наиболее подходящим методом явля-
является метод, примененный Г. Герцем для исследования формы
открытых им электромагнитных волн: получение стоячих ко-
колебаний отражением от абсолютно проводящей и поэтому зер-
зеркальной поверхности C, § 92). При этом в периодическом ха-
характере волн можно убедиться по появлению узлов и пучностей,
лежащих на постоянных расстояниях, по которым можно изме-
измерить длину волны, а, таким образом, и частоту колебаний. Со-
Соответствующий опыт для оптических волн впервые удался
О. Винеру A890), который заставил фиолетовые лучи вольтовой
дуги падать перпендикулярно на серебряное зеркало. Чтобы об-
обнаружить образующиеся узлы и пучности электрического напря-
напряжения, на зеркало был наложен наклонно, под небольшим углом а,
очень тонкий, плоский светочувствительный слой из хлорно-
серебряного коллодия, который мало мешал световым колеба-
колебаниям (черт. 2). Оказалось, что в тех местах, где слой встречал
плоскость, в которой находятся узлы электрического напряже-
напряжения, например у самого зеркала, не было никакого фотографи-
фотографического действия, в местах же, лежащих в середине между ними,
где слоем пересекались плоскости пучностей (пунктир на черт. 2),
32 ОПТИКА ИЗОТРОПНЫХ ОДНОРОДНЫХ СРЕД
получался максимум почернения. Из расстояний между полосами
и угла наклона слоя относительно зеркала можно непосред-
непосредственно вычислить дли-
длину волны.
По причине малых
размеров длины све-
световой волны в оп-
Черт. 2. тике часто употреб-
употребляют в качестве еди-
единицы \0~*см=\р (микрон) и соответственно 1(Г7 см = 1 тпр
g О
(миллимикрон), или также единицу Ангстрема 10 см = 1А. Ви-
Видимый спектр простирается приблизительно от 0,4 ц (фиолетовые
лучи) до 0,8 ,« (красные).
§ 16. Описанным выше опытом был установлен периодиче-
периодический характер световой волны определенного цвета; но из этого
вовсе не следует, что ряд Фурье G0) для этого случая сводит-
сводится к одному единственному, например я-му, члену. Даже при
самых тонких спектральных линиях результаты измерения всегда
совместимы с наличием многих членов, которым соответствует
достаточно большая область порядковых чисел п, с частотами,
лишь незаметно отличающимися друг от друга. Именно, так как
G1)
и так как Т взято очень большим по сравнению с временем од-
одного светового колебания, то получаемые порядковые числа п
очень велики, и изменение п на одну или несколько единиц не
дает заметных изменений со.
Поэтому мы не должны считать свет определенного цвета
(так называемый однородный свет) волной с одним определен-
определенным периодом, как в акустике звуковую волну определенного
тона, а должны считать его сложным, состоящим из многих волн
с почти одинаковыми периодами. Понятие однородного света
имеет не абсолютный смысл, а только более или менее прибли-
приближенный. Условие однородности света с частотой соо — -^ мате-
математически выражается тем, что в ряде Фурье G0) отличны от
нуля лишь те амплитуды, для которых
G2)
Степень однородности определяется наибольшим значением,
которого достигает выражение G2) для таких я, для которых Сп
отлично от нуля. Особенно наглядное представление о характе-
характере волновой функции однородного света можно получить, если
в ряде Фурье G0) положить
« = «о +(« —«о)
СПЕКТРАЛЬНОЕ РАЗЛОЖЕНИЕ, ИНТЕРФЕРЕНЦИЯ, ПОЛЯРИЗАЦИЯ
33
и разложить косинус соответствующим образом. Тогда ряд G0)
можно изобразить одним членом:
G3)
где
однородном свете;
и считать его состоящим из колебаний одной частоты со0, с амп-
амплитудой Со и фазовой константой #0. Конечно, теперь Со и #0
не строго постоянны, но согласно G2) сравнительно медленно и,
вообще говоря, беспорядочно изменяются с временем t и притом
тем медленнее, чем однороднее свет. Здесь проявляется тесная
связь, существующая между колебаниями амплитуды и фазы,
с одной стороны, и степенью монохроматичности света — с другой.
Абсолютно постоянная амплитуда и строго определенная фаза
были бы возможны лишь при абсолютно
флюктуации(изменения)той
или другой связаны с не-
неполной однородностью.
§ 17. При помощи отра-
отражения света от прозрачной
плоскопараллельной пла-
пластинки или путем пропуска-
пропускания света сквозь нее можно
осуществить гораздо более
резкое и совершенное спек-
спектральное разложение, чем
при отражении от непро-
непрозрачного зеркала. Эта про-
проблема также может быть
разрешена при помощи вы-
вышеизложенных методов.
Если плоская волна па-
падает на прозрачную плоскую
пластинку толщиной D под
углом падения # (черт. 3),
то она частью отражается, Черт. з.
а частью проникает внутрь
пластинки. Волна, проникшая внутрь, будет распространяться
в пластинке взад и вперед между обеими ограничивающими ее
плоскостями и при каждой встрече с плоскостями будет частично
выходить в ту или другую сторону наружу из пластинки.
Полное решение задачи заключается в следующем. В первой
среде (воздух) находятся две волны: одна, направленная к пла-
пластинке под углом падения ■&, другая, идущая от пластинки под
В Введение в теоретическую физику, ч. IV.
ОтразкеннЬш
сбвтп'
Аз
\
А?
■\
б
0
6
-к
л
->■
Прошедший
сбетп
34 ОПТИКА ИЗОТРОПНЫХ ОДНОРОДНЫХ СРЕД
углом отражения #; во второй среде (стекло) также имеются две
волны, обе под углом &г к нормали к пластинке: одна, идущая
от передней грани к задней, другая, идущая в обратную сторо-
сторону; в третьей среде (воздух) распространяется одна волна в на-
направлении, параллельном первоначально падающей волне.
Эти пять волн связаны четырьмя граничными условиями, по
одному условию для электрического и магнитного векторов на
каждой границе. Поэтому при заданной падающей волне осталь-
остальные четыре волны определяются однозначно.
Достигнуть цели можно и более наглядным путем, хотя и не
таким прямым, как вышеизложенный, если рассмотреть, как
данное явление протекает во времени; этот метод имеет еще то
преимущество, что он может быть с успехом применен и тогда,
когда поперечное сечение падающей волны и поверхность пла-
пластинки не безграничны, как это всегда и имеет место в действи-
действительности. х .
Пусть падающая волна fit I представлена на черт. 3 од-
одним произвольно выбранным лучом, который встречает первую
грань пластинки в точке Аи так что х представляет собой вол-
волновую нормаль в точке Аг. Тогда отраженный луч (отраженная
волна) отразится обратно от точки А1 в воздух с коэфициентом
ослабления ц, известным из B3), в то время как преломленный
луч с коэфициентом ослабления [лг пойдет внутри пластинки до
точки Bv Здесь он опять расщепляется и частью выходит в воз-
воздух, частью возвращается обратно в пластинку к точке А2. Так
будет продолжаться и дальше, до тех пор пока энергия луча не
сделается настолько незначительной, что ею можно будет пре-
пренебречь. Таким образом четыре вышеупомянутые волны, волно-
волновые функции которых должны были быть вычислены из падаю-
падающей волны, могут быть представлены как четыре суммы беско-
бесконечно большого числа членов, каждый из которых известен и мо-
может быть вычислен.
Рассмотрим сначала прошедшую волну, выделив для этого
достаточно удаленную от пластинки плоскость волны В{ В2' Ва'.
Эта волна образована наложением волн, изображенных лучами
АХВХВ{, А1В1А2В2В.г',... Обозначим расстояние АгВх = ВгАг — Л2В2
и т. д. через 8, а расстояния Вф^, В2В2' через qu qs, ... Мы по-
получим в выделенной нами плоскости волны значения волновых
функций, соответствующих отдельным налагающимся лучам,
если в аргумент вставим указанный световой путь и, кроме того,
учтем коэфициенты ослабления при каждом отражении и пре-
преломлении ц, /*1г ц', цх [B3) и B4)]. Здесь ц' и ftt' обозначают
коэфициенты, относящиеся к переходу волны из стекла в воздух.
Они получаются из выражений для /л и /*, обменом мест углов & и &,.
Таким образом волновую функцию первого луча, который пре-
претерпел два преломления в Ах и Вх, для точки Вг' получаем в виде:
СПЕКТРАЛЬНОЕ РАЗЛОЖЕНИЕ, ИНТЕРФЕРЕНЦИЯ, ПОЛЯРИЗАЦИЯ 35
для второго луча, который претерпел два преломления в Аг
и В2 и два отражения — в Вг и Л2, для точки ба' получаем:
. х 3d р. \
—у—5-—т) ит-д-
Отсюда получаем для волновой функции всего прошедшего
света:
^f^^^) G4)
Коэфициенты цъ /л' и /*/ можно, пользуясь B3) и B4), свести
к одному коэфициенту ц при помощи уравнений:
/*' = —j«, jui = l+i«, ^' = 1— ц. G5)
Что же касается аргумента /, то в нем члены, содержащие
световые пути, можно, пользуясь A4), привести к общему зна-
знаменателю:
х+Bр+1Nп + е
и таким образом „привести к воздуху" световой путь.
Расстояния др+1 можно выразить через расстояние q1} если
воспользоваться понятными из черт. 3 соотношениями:
G7)
Наконец, для введенных величин д и е легко получить такие
выражения:
J
Обозначив еще для сокращения члены аргумента /, не завися-
зависящие от р, через а:
f_ « + *" + «, ga> (80)
и члены, содержащие р множителем, через ftp:
~^-р=Рр, (81)
получим волновую функцию G4) в виде:
3»
36 ОПТИКА ИЗОТРОПНЫХ ОДНОРОДНЫХ СРЕД
§ 18. Чтобы можно было провести суммирование, надо за-
задаться определенной формой /. Поэтому мы представим себе
функцию / разложенной в ряд Фурье и рассмотрим сперва один
член этого ряда с частотой со. Так как с показательными функ-
функциями часто удобнее производить вычисления, чем с тригоно-
тригонометрическими, то мы будем рассматривать действительное ко-
колебание как действительную часть „комплексного колебания",
т. е. положим:
eiat, (83)
причем для сокращения мы, как это часто делается, не будем
писать буквы R (действительная часть). Тогда выражение (82)
переходит в
а эта сумма равна:
A —
Действительная часть этого комплексного выражения и дает
искомую волну прошедшего света; так как переменные t a Qi
содержатся только в а, то получается простая периодическая
волна, волна с частотой со. Ее интенсивность согласно уравне-
уравнению A0) пропорциональна квадрату амплитуды. Проще всего
вычислить этот квадрат, если вспомнить, что он равен квадрату
абсолютного значения комплексной величины (84) или произве-
произведению (84) на комплексно сопряженную величину. Так как нас
интересует отношение интенсивности прошедшего света к интен-
интенсивности падающего света и так как абсолютное значение (83)
равно единице, то для интенсивности прошедшего света по от-
отношению к падающему мы получим:
1 _ „2 p-i°>P
1 — 2/х3 cos o/S + At4 *
При этом согласно (81), G8), G9) и B0):
следовательно."
atP^—cos^^S, (86)
где Ях—длина волны в веществе пластинки; и
СПЕКТРАЛЬНОЕ РАЗЛОЖЕНИЕ, ИНТЕРФЕРЕНЦИЯ, ПОЛЯРИЗАЦИЯ 37
Максимум интенсивности достигается при £ = 2пр, т. е. при
2^cos-&t=p, (88)
где р — целое число. Тогда У=1. Между ними лежат минимумы
интенсивности, имеющие величину:
у —
Разница между максимумом и минимумом тем больше, чем
ближе (j, к единице, т. е. чем большим взят угол падения &.
Но самой характерной для рассматриваемого явления и
наиболее важной для измерений чертой является острота
максимумов.
Она получается потому, что в большинстве случаев f в (86)
[а поэтому также р в (88)] очень большое число, когда D очень
велико по сравнению с Я. Поэтому интенсивность света быстро
меняется при изменении направления луча ■&.
Нужно теперь принять во внимание, что в оптике мы никогда
не имеем дела с лучом одного определенного направления
или одной системой параллельных волновых плоскостей, что вы-
вытекает уже из рассуждений § 5 и что дальше (§ 36) будет разъ-
разъяснено еще подробнее. На опыте всегда наблюдается конус лу-
лучей, хотя бы и узкий. Поэтому, если мы для лучей каждого на-
направления ■& найдем точку бесконечно удаленного экрана, к ко-
которой направлены все лучи этого направления, то всегда будет
освещено много таких точек ■&, лежащих близко одна от другой.
Так как У быстро меняется с изменением &, то на экране по-
появится ряд многочисленных максимумов и минимумов интенсив-
интенсивности, расстояния между которыми определяются следующими
друг за другом порядковыми числами р в (88). Если у, близко к
единице, то интенсивность У согласно (87) вообще мала, и лишь
тогда, когда условие (88) в точности выполнено, она делается
равной единице, то есть максимумы резко выделяются на
темном фоне.
Предыдущие рассуждения относятся к волне вполне опреде-
определенной частоты со, т. е. к вполне однородному свету.
В действительности, как мы видели, мы всегда имеем дело
с не строго монохроматическим светом; его можно представить
себе как наложение многих монохроматических — синусоидальных
волн, имеющих близкие частоты. Поэтому в наблюдаемой кар-
картине всегда налагаются многие системы максимумов и миниму-
минимумов рассмотренного выше рода, каждая с несколько другим рас-
расстоянием между максимумами и минимумами. В каждом луче
прошедшего света и соответственно в каждой точке # беско-
бесконечно удаленного экрана соединяется много лучей различного
цвета и, конечно, вообще говоря, различной интенсивности. При
этом может случиться, что в какой-нибудь определенной точке #
38 ОПТИКА ИЗОТРОПНЫХ ОДНОРОДНЫХ СРЕД
два различных цвета имеют свои максимальные интенсивности,
т. е. согласно (88):
или, отнесенные к воздуху:
pi = р'Х. (90)
Тогда р-и максимум для длины волны Я совпадает с р'-м
максимумом для длины волны Я''. Если Я и Я' мало отличаются друг
от друга, то и близлежащие максимумы обеих волн, порядок
которых лишь немногими единицами отличается от р и р', также
будут лежать близко один от другого. Поэтому на некотором
участке картины максимумов и минимумов этих двух систем бу-
будут примерно совпадать. Но если перейти к более высоким по-
порядкам, то даже малое различие в расстоянии между максиму-
максимумом и минимумом станет заметным, и максимумы обеих систем
разойдутся, причем максимумы большей длины волны, напри-
например Я', благодаря большим расстояниям между ними всегда будут
опережать максимумы меньшей длины волны Я соответствующего
порядка. Наконец, при достаточном увеличении порядка максиму-
максимума, максимум Я' порядка р' + г, так сказать, догонит максимум
для Я порядка р + г+ 1. Тогда опять получается совпадение обе-
обеих систем, но порядок максимумов Я увеличится на единицу
больше, чем порядок максимумов Я', т. е.
Из этого условия и из (90) получаем:
Таким образом, подсчитывая число максимумов между двумя
следующими друг за другом совпадениями максимумов двух сис-
систем, мы можем очень точно измерить разности длин волн.
Интенсивность света У, отраженного пластинкой, можно
найти тем же методом, как и для света, пропущенного ею. Од-
Однако нам нет надобности проводить подробно весь подсчет, так
как результат можно сразу получить из закона сохранения энер-
энергии, согласно которому сумма интенсивностей У отраженного
света и J пропущенного света равна интенсивности падающего
света (принимаемой равной единице); поэтому в силу (87):
Ьц* sin1 -|-
Отраженный свет является, как говорят, дополнительным к
пропущенному свету. Когда р, близко к единице, интенсивность
в минимумах равна нулю и минимумы резко выделяются на
окружающем фоне. В остальном здесь имеют место те же поло-
положения, что и для прошедшего света.
СПЕКТРАЛЬНОЕ РАЗЛОЖЕНИЕ, ИНТЕРФЕРЕНЦИЯ, ПОЛЯРИЗАЦИЯ
39
До сих пор мы рассматривали только/-волну — свет с коле-
колебаниями в плоскости падения. Ясно, что и для g-вопны— света
с колебаниями, перпендикулярными плоскости падения, справед-
справедливы те же заключения. Результат для g-волны отличается только
тем, что вместо коэфициента ц в него входит коэфициеит о (§ 9).
Положение максимумов и минимумов остается здесь то же, что
и у /-волны.
§ 19. Согласно уравнению (86) угол £, определяющий вели-
величину интенсивности света, зависит кроме длины волны 1± и на-
направления луча #! также и от толщины пластинки D. Это
ферометрах .переменной толщины об-
обстоятельство используется в интер-
(воздушная пластинка) для измерения
зависимости интенсивности света / от
толщины пластинки при перпенди-
перпендикулярном падении света (^ = 0). Тогда
согласно (88) толщина тех слоев, для
которых интенсивность проходящего
света имеет наибольшее значение,
равное единице, равна целому крат-
кратному половины длины в веществе слоя:
D = ^p. (93)
Это легко понять, если вспомнить,
что при толщине, кратной длине полу-
полуволны, фазы различных налагающихся
одна на другую волн, проходящих через слой после различного
числа отражений внутри слоя, отличаются на величину, кратную 2я,
и поэтому волны усиливают одна другую.
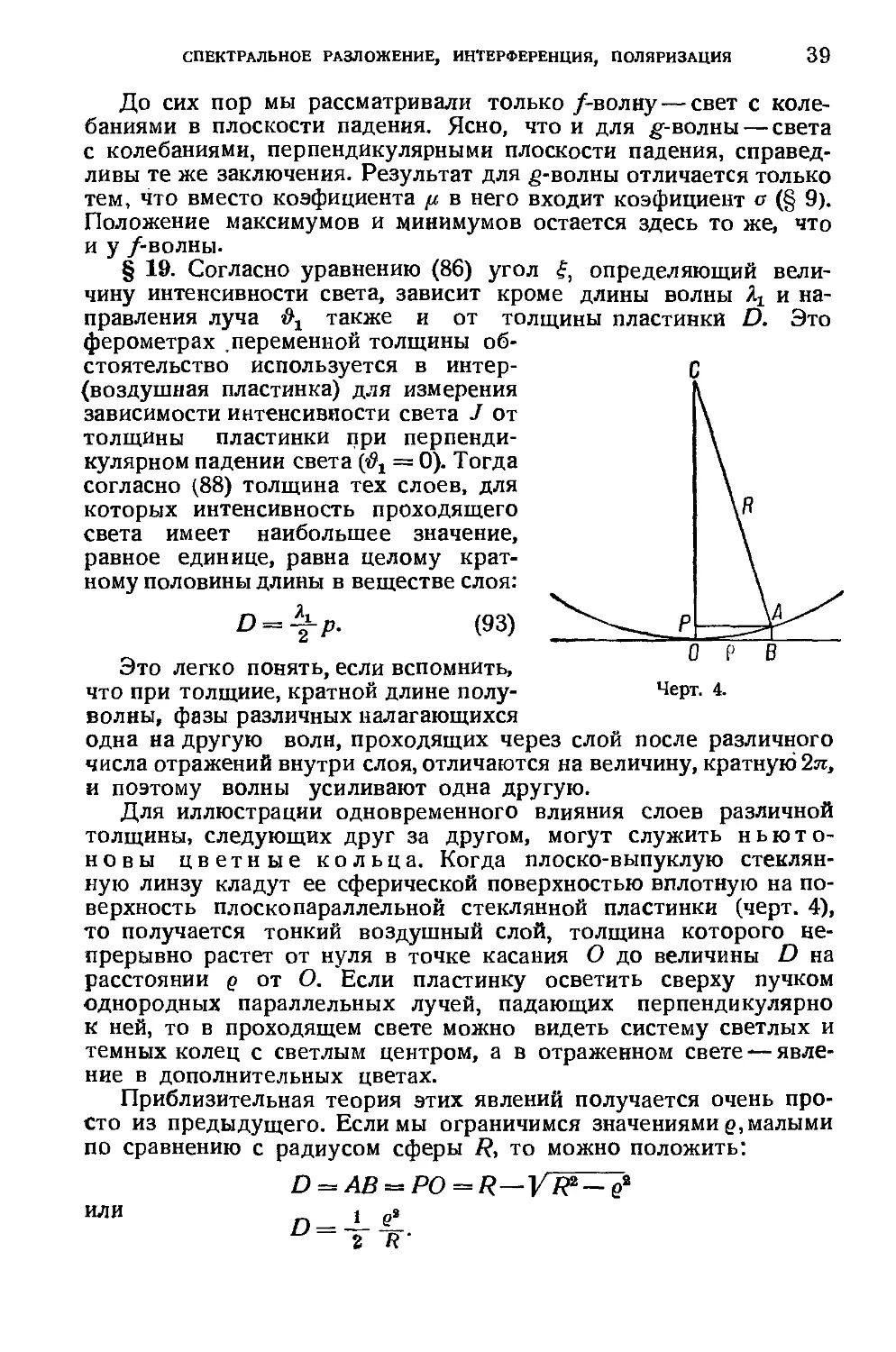
Для иллюстрации одновременного влияния слоев различной
толщины, следующих друг за другом, могут служить ньюто-
ньютоновы цветные кольца. Когда плоско-выпуклую стеклян-
стеклянную линзу кладут ее сферической поверхностью вплотную на по-
поверхность плоскопараллельной стеклянной пластинки (черт. 4),
то получается тонкий воздушный слой, толщина которого не-
непрерывно растет от нуля в точке касания О до величины D на
расстоянии q от О. Если пластинку осветить сверху пучком
однородных параллельных лучей, падающих перпендикулярно
к ней, то в проходящем свете можно видеть систему светлых и
темных колец с светлым центром, а в отраженном свете — явле-
явление в дополнительных цветах.
Приблизительная теория этих явлений получается очень про-
просто из предыдущего. Если мы ограничимся значениями q, малыми
по сравнению с радиусом сферы R, то можно положить:
или
ТГ
40 ОПТИКА ИЗОТРОПНЫХ ОДНОРОДНЫХ СРЕД
Следовательно, в силу (93) максимумы интенсивности в про-
проходящем свете и соответственно минимумы в отраженном свете
получатся на расстояниях от центра, равных:
(94)
где Я — длина волны в воздухе.
Итак, радиусы темных колец в отраженном свете относятся,
как квадратные корни из последовательных целых чисел.
Для двух цветов, лишь немного отличающихся друг от друга,
как, например, для двух компонент линии натрия, системы
колец несколько различны и по удалении от центра О посте-
постепенно разделяются и смазывают одна другую, пока при р, при-
приблизительно равном некоторому г, опять не наступает совпа-
совпадение максимумов и минимумов. Это можно обнаружить по вновь
появившейся резкости системы колец. Отсюда, пользуясь (91),
вычисляется относительная разность длин волн обеих натриевых
линий.
§ 20. Предшествующие рассуждения привели нас к необхо-
необходимости исследования действия многих накладывающихся друг
на друга и распространяющихся по одному направлению цугов
волн. Теперь мы подвергнем такую суперпозицию световых волн
более общему систематическому исследованию. Два луча с вол-
волновыми функциями /х 11 —J и fJt — \ распространяющих-
распространяющихся по общему направлению х и колебания которых происходят в
одном и том же направлении дают один луч с волновой функцией:
/=Л+Л. (95)
Отсюда следует, что интенсивность результирующего луча У»
выраженная в зависимости от интенсивностей У, и У2 обеих ком-
компонент (если отвлечься от не имеющего значения множителя),
равна:
У=Л + Л + 2Л7Г- (96)
Интенсивность результирующего луча, таким образом, вообще
говоря, отличается от суммы интенсивностей отдельных лучей.
Это явление называют „интерференцией" двух лучей / и 2.
В некоторых случаях интерференции не будет, именно, если вол-
волновые функции fx и /2 совершенно независимы друг от друга,
т. е. если лучи / и 2 некогерентны. В самом деле, в этом случае
[ср. D3)] имеем: _
Это имеет, например, место, когда лучи получаются от раз-
различных источников света. Поэтому два таких луча никогда не
интерферируют. Но некогерентность не является необходимым
условием для отсутствия интерференции. Интерференция может
СПЕКТРАЛЬНОЕ РАЗЛОЖЕНИЕ, ИНТЕРФЕРЕНЦИЯ, ПОЛЯРИЗАЦИЯ 41
отсутствовать и тогда, когда лучи „вполне корерентны", пони-
понимая под этим, что одна из двух волновых функций вполне опре-
определяется второй. Это имеет место, например, в случае одно-
однородного света, когда аргументы ft и /а отличаются на нечетное
кратное -^-; тогда/,/2 = 0, несмотря на полную когерентность (так
как sin cot ■ cos cot= 0). Более общим случаем является „частич-
„частичная когерентность", когда /, и /2, хотя и не независимы друг от
друга, но не вполне определяют друг друга.
§ 21. Тот же вопрос можно рассмотреть несколько иначе,
если обе волновые функции ft и /2 представить в виде рядов
Фурье, с одним и тем же основным периодом Т. Тогда и ре-
результирующая волновая функция /=/i +/2 сразу получится в
виде ряда Фурье, причем каждые две волны с одинаковыми ча-
частотами (соответствующие отдельным членам ряда) объединяются
в одну волну. Так, например, пусть имеем две волны с часто-
частотой со:
| (97)
При суммировании обоих этих выражений важную роль
играет разность фаз обеих волн:
»г — 0Я = А (98)
Вместо фазовой постоянной & в выражение волновой функ-
функции часто вводят постоянную d (некоторая длина) или постоян-
постоянную б (некоторое время) и пишут:
«cos H4-
ИЛИ
и тогда говорят о разности хода d1 — d2 обеих волн или о за-
запаздывании 8г—Eа второй волны по отношению к первой. Раз-
Разнице фаз 2я соответствует разность хода, равная одной длине
волны Я, или запаздывание на время одного колебания т. В резуль-
результате сложения обоих выражений (97) получается волна с часто-
частотой со:
a cos (со (t -) + #}, (99)
где
a cos # = at cos &г + а2 cos #a, \
a sin # = аг sin Фг + az sin #a
Амплитуда и фазовая постоянная результирующей волны
определяются соответствующими величинами для составляющих
42 ОПТИКА ИЗОТРОПНЫХ ОДНОРОДНЫХ СРЕД
совершенно так же, как определяются абсолютное значение и на-
направление вектора, являющегося суммой двух векторов.
Для квадрата амплитуды а мы получаем из A00) и (98):
й? = of + аг2 + 2аха2 cos Л. A01)
Это уравнение является выражением того, что две абсолютно
однородные волны одинаковой частоты с одинаковыми направ-
направлениями колебаний и распространения, вообще говоря, интерфе-
интерферируют одна с другой. Это обстоятельство не находится в про-
противоречии с тем положением (§ 20), что два луча, выходящие
из разных источников света, никогда не интерферируют друг
с другом, так как согласно § 16 в природе никогда не встречается
абсолютно однородный свет; наиболее однородный оптический луч
содержит очень много отдельных волн с близкими частотами коле-
колебаний, каждая из которых интерферирует с волной той же частоты
во втором луче. Если оба луча некогерентны, то разность фаз Л
беспорядочно меняется от одной пары волн к другой и никакого
заметного интерференционного эффекта не может получиться.
§ 22. Теперь мы разберем сложение двух волн с взаимно пер-
перпендикулярными колебаниями, распространяющихся по одному и
тому же направлению. Этот вопрос был рассмотрен в § 11, но
теперь в основу рассмотрения мы положим разложение в ряд
Фурье. Пусть, как и там, z будет направление распространения,
х и у— направления электрического напряжения первой и вто-
второй волны. Электрические напряжения обеих волн одной и той же
частоты со (соответствующих членам одного ;и того же порядка
в разложении / и g в ряд Фурье) можно представить, как в (97):
A02)
если только для х и у выбрать соответствующие единицы.
При этом мы можем, не теряя общности, принять, что: аг&&з=0.
Этот метод обозначения делает возможным наглядно представить
закон, по которому меняется со временем по величине и направ-
направлению результирующая электрического напряжения в определен-
определенной волновой плоскости z, так как она в каждый момент опре-
определяется положением подвижной точки х,у в плоскости z = const.
Что же касается пути этой точки, то он получается исключением
времени t из уравнений A02) проще всего, находя значение
cos colt 1 и sin со 11 —\, возвышая их в квадрат и при-
приравнивая их сумму единице. В качестве уравнения кривой пути
получаем:
3£2f A03)
* cos {ш(<--|-)+#,)= j/,
СПЕКТРАЛЬНОЕ РАЗЛОЖЕНИЕ, ИНТЕРФЕРЕНЦИЯ, ПОЛЯРИЗАЦИЯ 43
Это эллипс, который вырождается в прямую при А = гт, а
при А = \п-\- —\п оси эллипса совпадают с осями координат.
В общем случае угол у, образованный одной из осей с осью х,
определяется соотношением:
*2<Р-?5-^, (Ю4)
Это соотношение можно непосредственно получить из D5),
если там положить соответственно рассматриваемому случаю:
С =fg=-f cos А.
Скорость, с которой пробегается эллиптический путь, опре-
определяется из A02) диференцированием:
xdy—у их = ыаЬ sin A dt. A05)
Это значит, что точка х, у движется по закону площадей (/, § 50) и,
в зависимости от знака sinJ, в положительную, или отрицательную
сторону (так как ab > 0). Так как ось z нашей правой системы
координат указывает направление распространения света, то на-
направление вращения движущейся точки имеет определенный
физический смысл.
В оптике свет считается правовращающим, если движение
точки х, у представляется наблюдателю, смотрящему против
света, происходящим по часовой стрелке. Поэтому мы считаем
направление вращения правовращающего света отрицательным,
а левовращающего света положительным. Наглядное предста-
представление о том, как зависит движение точки х, у от координат
а, Ъ, А, можно получить, если а и Ъ оставить постоянными, а раз-
разность фаз вменять от 0 до 2л. При А = 0 согласно A04) или A02)
эллиптическое движение вырождается в прямолинейное колебание
в первой и третьей четверти наклонно к оси под углом:
9> = arctg|=s-j A05а)
с амплитудой Va? + b2.
С увеличением разности фаз А эллипс расширяется, и вра-
вращение происходит в положительном направлении. Свет, таким
образом, имеет левое вращение. Вместе с этим угол <р умень-
уменьшается, т. е. большая ось эллипса поворачивается к оси х. При
А = ~- эллипс достигает своей наибольшей ширины, его полу-
полуоси равны а и Ь, их направления совпадают с осями координат.
Когда А делается больше ^-1 большая ось переходит во вторую
и четвертую четверть, эллипс делается все более удлиненным,
44 ОПТИКА ИЗОТРОПНЫХ ОДНОРОДНЫХ СРЕД
пока при А = л опять не превратится в прямую, наклоненную
под углом A05а) к оси л:. Начиная отсюда, при дальнейшем
росте А форма эллиптического пути повторяется в обратном
направлении, что ясно уже из того, что уравнение пути A03)
остается неизменным, если А заменить через 2п — А. Эллипс
опять расширяется и его большая ось опять поворачивается к
оси х, которой она достигает при А = • Но теперь путь опи-
to
сывается в отрицательном направлении. Наконец, при А = 2л
опять получится движение, рассмотренное вначале. Поучительно
также разобрать случай, когда при определенной разности фаз А
меняются амплитуды а и b составляющих колебаний. Можно
видеть, между прочим, из A04), что тогда направление осей <р
зависит только от отношения амплитуд а и Ь и что то же самое
справедливо относительно отношения длин осей.
Условия, при которых движение делается круговым, легче
всего получаются из выражения для направления осей A04),
которое делается неопределенным в случае круга, т. е. прини-
принимает форму — ; это дает два условия для кругового колебания:
а = Ь, Д = [п+\)п, A06)
которые должны быть удовлетворены одновременно. В соответ-
соответствии с тем, будет ли п четным или нечетным, движение по
кругу будет происходить в положительном или отрицательном
направлении.
§ 23. Рассмотренное эллиптическое колебание представляет
собой также наиболее общий случай сложения скольких угодно
плоских световых волн одной и той же частоты со, распростра-
распространяющихся по направлению z. Каждое плоское колебание можно
разложить на два слагающих колебания по направлениям х и у
с разностью фаз 0; все же колебания по направлению х или у
согласно принципу суперпозиции (§ 21) образуют одно колеба-
колебание по тому же направлению.
Общий случай эллиптического колебания можно представить
себе замененным вместо двух плоских колебаний двумя колеба-
колебаниями по кругу, с противоположными направлениями вращения.
Это станет ясным, если вспомнить, что каждое плоское колеба-
колебание можно представить как сумму двух противоположно на-
направленных движений по кругу. Обе вращающиеся точки встре-
встречаются всегда в одних и тех же местах и эти места определяют
направление и половину амплитуды результирующего плоского
колебания. Таким образом для общего случая мы Получим
четыре вращения по кругу, из которых два, имеющие одинако-
одинаковое направление, можно, конечно, сложить в одно. Направление
вращения, получающееся от сложения двух вращений, опреде-
определяется, естественно, направлением вращения того кругового коле-
колебания, которое имело больший радиус.
СПЕКТРАЛЬНОЕ РАЗЛОЖЕНИЕ, ИНТЕРФЕРЕНЦИЯ, ПОЛЯРИЗАЦИЯ 45
§ 24. Рассмотрим вкратце еще зависимость электрических
напряжений х и у в A02) от волновой нормали z. При неизмен-
неизменном t эти уравнения дают так называемую „волновую линию",—
в рассматриваемом случае эллиптическую винтовую линию, и
согласно A05), если там заменить dt на — —, правый винт
B, § 32), если sin Л < 0, т. е. если направление вращения отрица-
отрицательно. Шаг винта равен длине волны Я.
Если принять во внимание сказанное в § 23 относительно
направления вращения правовращающего света, то получается,
что правовращающему свету соответствует правый винт, лево-
вращающему свету — левый винт. Движение точки х, у в плос-
плоскости z получится, если смещать винтовую линию вдоль оси z
со скоростью д и наблюдать ее мгновенную точку пересечения
с плоскостью z = const. Если взять обратное направление смеще-
смещения винтовой линии, то получается волна, распространяющаяся
в сторону отрицательных z и притом с вращением в противо-
противоположном направлении, так что опять правый винт соответствует
правовращающему свету, левый винт — левовращающему свету.
§ 25. Рассмотрим теперь вопрос о том, как можно получить
определенную разность фаз А между обеими составляющими
колебания х и у. Пусть мы имеем плоскополяризованную волну
с направлением колебания у в первой и третьей четверти, тогда
согласно A02) отношение амплитуд постоянно и равно:
4 = tg9>^l 007)
(ср. 105а) и разность фаз:
Эту волну заставляем отражаться под произвольным углом
падения так, чтобы колебания электрического напряжения х
происходили в плоскости падения. При обыкновенном отражении
(sin#<«) не получается никакого скачка фазы, разность фаз Л
остается равной нулю, и обе отраженные волны опять склады-
складываются в одну плоскополяризованную волну, но согласно A050а)
вследствие различия коэфициентов отражения /л и а с изменен-
измененным направлением колебания. Это было нами уже отмечено в § 11.
Дело обстоит совершенно иначе, если наша волна претерпе-
претерпевает полное внутреннее отражение (sin#>n). Здесь, наоборот,
остаются неизменными амплитуды а и b обеих волновых соста-
составляющих, но появляется разность фаз Л = 6 — т, значение кото-
которой получается из E7) и F6):
, А , 6 — т &' • cos & /1 по\
tgtg ж^. <108>
где &' определяется через E6).
Эта разность фаз А, как мы уже установили в конце § 13,
всегда положительна и исчезает в обоих предельных случаях:
46 ОПТИКА ИЗОТРОПНЫХ ОДНОРОДНЫХ СРЕД
для предельного угла 0' = 0 и для скользящего падения § = -£ .
to
Между ними она достигает максимума, который согласно A08)
получается при угле падения:
^A09)
величина этой наибольшей разности фаз равна:
А = л — 4 arc tg n,
@<arctg«<J).
Чем меньше показатель преломления п, тем большей разности
фаз можно достичь. После отражения обе составляющие коле-
колебания складываются в эллиптическое колебание; направление
осей tpr определяется из A04) и A07):
tg 2<p' =tg2<p. cos A. (Ill)
Для круговой поляризации света необходимо согласно A06),
чтобы разность фаз была равна ~. Наименьшее значение п,
которое необходимо для получения разности фаз ^, определяется
из (ПО):
n = tg|=V2-l. A12)
Его обратная величина К2+1 = 2,414; такой показатель пре-
преломления должно иметь вещество, чтобы при полном внутрен-
внутреннем отражении на его поверхности получить разность фаз -^
между /- и ^-волнами. Из известных веществ этому условию
удовлетворяет лишь алмаз.
Если при помощи однократного полного внутреннего отра-
отражения практически нельзя добиться разности фаз -^-, то этого
можно добиться сравнительно удобно при помощи двух после-
последовательных отражений, для чего особенно подходит паралле-
параллелепипед Френеля. Это — косоугольный параллелепипед из
прозрачного стекла (черт. 5), угол а которого выбран таким,
что луч света, падающий из стекла в воздух под углом падения
& = а, претерпевает полное внутреннее отражение с разностью
фаз А = -^ между обеими компонентами колебания. Согласно
A08) для данного сорта стекла это возможно при двух различ-
различных углах, из которых можно взять любой.
Если снизу (черт. 5) у точки А пустить перпендикулярно к
основанию параллелепипеда луч света, колебания которого, как
принято в начале этого параграфа, направлены под углом <р к
СПЕКТРАЛЬНОЕ РАЗЛОЖЕНИЕ, ИНТЕРФЕРЕНЦИЯ, ПОЛЯРИЗАЦИЯ
47
Черт. 5.
оси х, то уравнение A07) действительно для отношений ампли-
амплитуд как до, так и после вступления луча в параллелепипед-
Первое отражение происходит в точке О, на наклонной грани
под углом падения а с разностью фаз ~ и неизменными ампли-
амплитудами; затем в Р, на противоположной грани, происходит вто-
второе отражение с новой разностью фаз ~
и опять с неизменными амплитудами; нако-
наконец, в В луч по перпендикуляру выходит
в воздух с равномерно уменьшенными
амплитудами и неизменной разностью фаз,
равной -^ + ■£■ = —. Поэтому луч, выходя-
выходящий вверх в В, имеет эллиптические коле-
колебания, и его главные оси совпадают с
осями координат х (вправо) и у (напра-
(направлено за чертеж).
Так как было принято, что свет, падаю-
падающий в А, имел колебания в первой и
третьей четверти (о < q> г£ -у]»то свет, вы-
вышедший в точке В, имеет левое вращение.
Но если падающий свет колеблется во
второй и четвертой четверти (-j^y <гп,
то выходящий луч имеет правое вращение. При ?>=-?- или ~
получается tg ^ = ± 1, т. е. свет поляризован по кругу и имеет
левое или правое вращение.
§ 26. Все изложенные выше рассуждения относятся к све-
световому колебанию одной определенной частоты со, соответствую-
соответствующему одному члену разложения волновой функции в ряд Фурье.
Так как в природе даже наиболее однородная световая волна
содержит большое число отдельных синусообразных колебаний,,
то мы всегда должны суммировать по всем этим синусообраз-
ным колебаниям и таким образом получать соответствующие-
законы для результирующего колебания.
Вместо этого мы можем такое естественное „однородное"
световое колебание рассматривать, как в G3), как колебание
определенной частоты со0, у которого амплитуда и фазовая кон-
константа претерпевают со временем медленные беспорядочные
изменения; во многих случаях это дает более наглядную картину
явления. Из § 23 можно сделать вывод, что наиболее общая;
практически однородная световая волна может быть рассматри-
рассматриваема как одно эллиптическое колебание соответствующей
частоты с медленно и беспорядочно меняющимися длинами и
направлениями осей эллипса, или как два противоположно на-
направленных круговых колебания с медленно и беспорядочна
меняющимися радиусами.
48 ОПТИКА ИЗОТРОПНЫХ ОДНОРОДНЫХ СРЕД
Но так как вообще закономерности, выведенные в послед-
последних параграфах, начиная с § 22, совершенно независимы от
частного значения частоты колебания со, то они без дальнейшего
справедливы и при наложении многих синусообразных колебаний
с близкими частотами. В частности, это справедливо для отно-
отношения амплитуд A07) обеих компонент колебания синусообраз-
ной волны линейно поляризованного света, а также и для задан-
заданной A08) разности фаз А обеих компонент колебания, получаю-
получающейся при полном внутреннем отражении, и вместе с этим и
для направления A11) и для отношения длин обеих главных
осей результирующего эллиптического колебания (ср. конец § 22).
Все эти величины одинаковы для отдельных синусообразных
волн, поэтому они постоянны и не зависят от времени и для
результирующего колебания. Световые колебания с постоянным
направлением и отношением осей называют „эллиптически поля-
поляризованным светом". Под этим подразумевают не только то,
что световые колебания эллиптичны, — это само собой понятно,—
но также и то, что в эллипсе, описываемом при колебании,
хотя бы он менялся медленно и незакономерно, остаются неиз-
неизменными направление осей, отношение их длин и направление
вращения. Соответственно этому свет, поляризованный по кругу,
представляет собой круговые колебания с медленно и беспоря-
беспорядочно меняющимся радиусом. Чтобы получить из плоскополя-
ризованного света свет, поляризованный эллиптически или по
кругу, можно пользоваться описанным выше параллелепипедом
Френеля. Как мы видели, направление осей определяется плос-
плоскостью падения при полном внутреннем отражении, отношение
осей — азимутом поляризации падающего света. Отсюда легко
вывести заключение, что обе компоненты колебания такого света
вполне когерентны (§ 20).
§ 27. Мы в состоянии теперь на основании всех этих резуль-
результатов до известной степени проанализировать данную нам пло-
плоскую световую волну. Возьмем какую-нибудь реальную волну,
происхождения которой мы не знаем, и поставим себе задачу—
определить путем измерений ее форму, т. е. определить, как
можно полнее, свойства обеих волновых функций fug, из кото-
которых волна составлена.
Прежде всего мы производим спектральное разложение по
одному из вышеописанных интерферометрических методов.
После этого мы имеем дело только с однородным светом.
Для такой однородной световой волны мы определяем со-
согласно § 11 оба главных направления колебания и обе главные
интенсивности. При этом могут встретиться три случая. Первый
случай, когда одна главная интенсивность равна нулю. Тогда
свет линейно поляризован. Второй случай — противоположный,
когда обе главные интенсивности равны между собой. Тогда
свет или поляризован по кругу, или естественный, или предста-
представляет'собой смесь обоих — так называемый частично полярнва-
СПЕКТРАЛЬНОЕ РАЗЛОЖЕНИЕ, ИНТЕРФЕРЕНЦИЯ, ПОЛЯРИЗАЦИЯ 49
ванный по кругу свет. Чтобы узнать, с каким из этих случаев
мы имеем дело, пустим свет перпендикулярно на параллелепи-
параллелепипед Френеля (черт. 5). Если свет поляризован по кругу, то
амплитуды обеих компонент колебания fag равны между собой
аз равна ., или ^, смотря по тому, вправо
или влево вращается свет. После выхода света амплитуды
остаются равными, но разность фаз будет теперь л или 2тг, т. е.
выходящий свет линейно поляризован и колеблется во второй
и четвертой или первой и третьей четвертях под углом ф = -^г-
или — к оси х. Таким образом здесь начальная разность фаз
обеих компонент при помощи двойного отражения дополняется
до величины, кратной л, и параллелепипед Френеля действует
как „компенсатор".
Если же мы имеем дело с естественным светом, то никакой
компенсации не будет и выходящий свет, как и падающий, не
будет иметь никаких различий в различных направлениях коле-
колебания.
Наконец, если свет представляет собой смесь из естествен-
естественного и поляризованного по кругу, то естественная часть остается
неизменной, а часть, поляризованная по кругу, опять дает
плоскополяризованный свет, который колеблется в азимуте —
или j; его интенсивность определится из разности главных
интенсивностей выходящего света.
В третьем случае—общем, кргда обе главные интенсивности
данного света отличны от нуля и не равны друг другу, свет
пускают на параллелепипед Френеля так, чтобы направление
большей главной интенсивности совпадало с осью х (черт. 5).
Если свет эллиптически поляризован, то обе компоненты коле-
бания имеют разность фаз -~ или — и отношение амплитуд
равно —. Под влиянием компенсатора Получается плоскополя-
плоскополяризованный свет с направлением колебания у ■= =F arc tg —, ко-
которое образует с осью х угол < '-т. Если же свет представляет
собой смесь плоскополяризованного и естественного света, то
и в выходящем свете большее главное колебание направлено
по оси х.
Если, наконец, Свет частично эллиптически поляризован,
то в выходящем свете большее главное колебание образует
с осью х угол < ^ , который указывает отношение осей эллипса,
в то время как интенсивность поляризованной части опреде-
определяется из разности главных интеисивностей.
4 Введение в теоретическую (Двзику, ч. JV.
50 ОПТИКА ИЗОТРОПНЫХ ОДНОРОДНЫХ СРЕД
Таким образом во всех случаях можно определить свойства
данного луча в отношении его поляризации. Конечно, всегда
остаются элементы, не поддающиеся определению, которые
физически обусловлены сложностью элементарных процессов в
каждом источнике света и которые находят свое математическое
выражение в том, что в ряде Фурье имеется большое число
членов, не равных нулю.
ГЛАВА III
ГЕОМЕТРИЧЕСКАЯ ОПТИКА
§ 28. Изложенные выше законы отражения и преломления
довольно просты. Эта простота вызвана главным образом сде-
сделанным предположением, что как поверхности световой волны
(§ 5), так и поверхности, ограничивающие тела представляют
собой бесконечные плоскости. В действительности эти поверх-
поверхности не являются ни безграничными, ни плоскими, поэтому
строго говоря, указанные простые законы не применимы к слу-
случаям, встречающимся в природе. Однако, если указанные пред-
предпосылки выполняются хотя бы приблизительно, т.е. если сече-
сечения волновых и граничных поверхностей и радиусы кривизны
этих поверхностей очень велики по сравнению с длиной волны
рассматриваемого света, то эти законы являются очень хорошим
приближением к действительности. В оптике длина волны
вообще говоря, очень мала по сравнению с размерами рас-
рассматриваемых тел. Отсюда вытекает особая простота оптических
законов распространения, отражения и преломления, в противо-
противоположность тому, что имеет место в акустике, где законы волно-
волнового движения хотя и имеют силу, но указанные предположения
вообще говоря, не выполняются.
Геометрическая оптийа охватывает те закономерности, кото-
которые получаются, когда волновые поверхности света и поверх-
поверхности тел представляют себе разделенными на маленькие части
и к каждой применяют законы распространения, отражения и
преломления безграничных плоских волн на безграничных пло-
плоских поверхностях. Каждый такой маленький участок волновой
поверхности, рассматриваемый как часть плоскости, наглядно
изображают лучом, направленным по нормали к нему. Каждый
луч распространяется прямолинейно со скоростью, свойственной
данной среде; на поверхности раздела двух сред он отражается
и преломляется, сообразно с направлением нормали в этом
месте, как от плоскости. Поэтому геометрическая оптика назы-
называется также „лучевой оптикой" в отличие от боле.е общей, но
более сложной „волновой оптики".
§ 29, В качестве первого примера рассмотрим ход светового
луча через призму, т. е. через прозрачное тело, ограниченное i
ГЕОМЕТРИЧЕСКАЯ ОПТИКА
51
двумя плоскостями, наклоненными одна к другой под углом <р.
Согласно сказанному выше, мы должны исключить из рассмо-
рассмотрения явления, имеющие место непосредственно у ребра А
[которое мы представляем себе перпендикулярным к чертежу
(черт. 6)], потому что там радиус кривизны поверхности пре-
преломления бесконечно мал.
Луч, падающий в плоскости чертежа
в точку В под углом падения ■&, пре-
преломляется по направлению ВС и в точке
С вновь выходит в воздух под углом &'
к нормали в этом месте. Для обоих
преломлений имеем:
sin* = n sin^j, A13)
sintf'^/isiniV. A14)
При этом cvmm9 TDex углов треуголь-
треугольника ВАС:
Черт. 6.
01 + 01' = 9>- A15)
После построений вычисляется угол выхода •&' в зависимости
от угла входа $. Полное отклонение луча призмой 6, т. е. угол
между входящим и выходящим лучом, выражается так:
Принимая во внимание A15):
д = & + $'—<р. A16)
Исследуем зависимость полного отклонения 6 от угла входа #
пользуясь A13), A14) и (Пб), найдем производную:
dS I cos $* • cos $ч' .
— —— 1 — A1 / i
d& cos &t cos &' ' v '
Это выражение равно нулю при iS1' = !&1, а следовательно, и
■&' = •&, т. е. когда луч проходит призму симметрично, так что
расстояния АВ и АС равны между собой. Тогда отклонение
имеет максимум или минимум, равный д0. Результат зависит от
знака второй производной, которая получается вторичным дифе-
ренцированием A17) и при •&' = & равна:
jd*S\ _2sin(fl + fli)-sin(fl — flj
\dtrd/o sin ir cos »■ cos2 &i
Когда показатель преломления вещества'" призмы и>1, вто-
вторая производная при #' = # положительна и отклонение имеет
минимум.
Этот предельный случай можно довольно точно осуществить
экспериментально, если при неизменном направлении падающего
луча поворачивать призму вокруг оси, параллельной одному из ее
52 ОПТИКА ИЗОТРОПНЫХ ОДНОРОДНЫХ СРЕД
ребер, туда и назад и наблюдать направление выходящего луча.
Когда пробами найдено минимальное отклонение 80 из A16), A13)
и A15), вычисляется показатель преломления вещества призмы:
п = '—, A19)
sin2
§ 30. Прежде чем перейти к рассмотрению кривых волновых
поверхностей и кривых поверхностей тел, мы предпошлем даль-
дальнейшему несколько общих замечаний. Начальной поверхностью
волны в изотропном теле является сферическая поверхность.
От каждого точечного источника света распространяются сфе-
сферические световые волны, которые на достаточном расстоянии
от источника света могут быть представлены пучком расходя-
расходящихся лучей. После преломления или отражения на кривой
поверхности другого тела направления лучей в общем случае
не пересекаются в одной точке, т. е. пучок лучей уже является
не „гомоцентрическим", а „астигматическим". Если же, как это
бывает в особых случаях, пучок лучей оказывается опять гомо-
гомоцентрическим, то та точка, в которой лучи пересекаются, назы-
называется „оптическим изображением" источника света, действи-
действительным или мнимым, смотря по тому, сходятся ли лучи к точке
их пересечения или расходятся от нее. Так как свет всегда
может проделать и обратный путь (конец § 10), то источник
света и его изображение могут обменяться ролями. Поэтому они
называются „сопряженными" точками. Изображение бесконечно
удаленного источника света, или, что то же самое, точка пере-
пересечения лучей, образованных преломлением или отражением
пучка падающих параллельныхлучей, если она вообще существует,
называется „фокусом". Если фокус сделать местонахождением
источника света, то получится пучок параллельных лучей. На
этом основано получение на практике плоских световых волн.
§ 31. Теперь мы исследуем вопрос о преломлении света на
сферической поверхности, разделяющей две среды 1 и 2 (черт. 7).
Пусть будут пг и п2 показатели преломления этих двух сред,
С—центр сферы, r = PC — радиус ее. Найдем сперва изобра-
изображение светящейся точки Аъ лежащей на оси системы, т. е. на
прямой PC. Из всех лучей, выходящих из Аг, лишь осевой
луч АЛР проходит через сферическую поверхность без преломле-
преломления. Другой луч, выходящий из Л, под углом #! к оси, встречает
сферу в точке Q. Там он преломляется по закону
sin L-AiQC _я2
sin L AaQC ~ n,
и встречает ось в точке А2 под углом #2- Вычисление обоих сину-
сс^в при помощи треугольников AtQC и A2QC дает соотношение:
ГЕОМЕТРИЧЕСКАЯ ОПТИКА 53
Вообще с изменением &v а следовательно, и с изменением поло-
положения точки Q, изменится и положение точки Az, т. е. пучок
лучей, выходящий из А1г становится после преломления асти-
астигматическим. Но если #! взять достаточно малым, то можно в
A20) расстояния A±Q и A2Q с ошибкой второго порядка заме-
заменить расстояниями АгР и AJ^, обозначая расстояния Ах и А2
от Р через ег и е2, получим:
или
«1
A22)
Так как точка Q .здесь не фигурирует, то пучок лучей, выхо-
выходящий из точки А конусом с малым телесным углом, остается
гомоцентрическим и после преломления, и точка Аг имеет опти-
0, А,
Черт. 7.
ческое изображение: сопряженную ей точку As. Закон оптиче-
оптического изображения* выражается согласно A22) линейным уравне-
уравнением между обратными расстояниями сопряженных точек от
преломляющей сферической поверхности.
Когда Л, передвигается влево в бесконечность, А2 передви-
передвигается влево в фокус Fz, абсцисса которого
A23)
Пг
Когда Ах движется вправо, то Аа сперва уходит направо, уходя
в бесконечность, когда точка Аг приходит в фокус Ft с абсциссой
/, = "' ■ /-, A24)
но если Ах переходит через фокус Fx, преломленный пучок ста-
становится расходящимся, т. е. точка Аг лежит левее Аг и является
мнимым изображением А1г которое следует за* перемещающейся
вправо светящейся точкой Alt пока они не сольются в Р.
Точка Р сопряжена сама с собой, так же как и точка С, так
как лучи, выходящие из С, вообще не отклоняются.
Абсциссы /г и /2 фокусов связаны соотношениями
h~h = r, A25)
A. = ^i. A26)
54 ОПТИКА ИЗОТРОПНЫХ ОДНОРОДНЫХ СРЕД
Если их ввести вместо г и п, то закон изображения выра-
выражается так:
£+£ = 1. A27)
Все эти соотношения, как мы увидим, можно значительно
обобщить. Здесь отметим еще, что данные формулы справедливы
и для изображения, получаемого отражением на сферической
поверхности, если только положить
«! = —П2-
Когда лучи, выходящие из Аъ после преломления встречаются
в точке изображения А2, то угол расхождения пучка лучей в Ах
другой, чем у сопряженного пучка в А2. Из черт. 7 следует для
углов наклона к центральной оси обоих сопряженных лучей A±Q
и A2Q:
sin #! : sin •&2 = A2Q : AXQ
и с соответствующим приближением
sin #j : sin §2 = А2Р : AtP = е2 : ех. A28)
§ 32. Исследуем теперь изображение точки, не лежащей на
центральной оси. Пусть Ву (черт. 7) будет точкой, лежащей в
плоскости, проходящей через Аг и перпендикулярной к централь-
центральной оси. Вг так же, как и А1г имеет оптическое изображение
в сопряженной точке В2, находящейся на прямой ВЛС. Окруж-
Окружность, описанная точкой Вх при вращении вокруг центральной
оси А1А2, имеет своим оптическим изображением окружность,
образованную вращением В2. Поверхность круга с радиусом A±Bt
отображается куском определенной поверхности вращения, огра-
ограниченным окружностью В.2 с центром в А2. Если ограничиться
маленькими расстояниями от центральной оси, как мы это и
будем делать, то эту поверхность можно считать плоскостью, а
именно кругом, перпендикулярным к центральной оси с ради-
радиусом А2В2. Тогда светящаяся поверхность „подобно" отображается
на поверхности изображения и для отношения длины светя-
светящейся линии A tBt = 1г к длине линии изображения А^ ~ 12 имеем:
и согласно A21):
Это соотношение вместе с равенством A28) дает следующую
простую связь между линейными размерами и наклоном лучей
в двух сопряженных плоскостях:
пг1г sin #х = n2l2 sin#2. A29)
Если точка At находится в фокусе Fu то 1а = со и #2 = 0-
Две плоскости, проходящие перпендикулярно к оси через первый
и второй фокусы Ft и F2, называются фокальными плоскостями.
ГЕОМЕТРИЧЕСКАЯ ОПТИКА 55
§ 33. Все вышеизложенные законы могут быть легко обоб-
обобщены на случай многих преломляющих сферических поверхно-
поверхностей. Для этого необходимо только выбрать соответствующим об-
образом абсциссы двух сопряженных точек At и Аг. До сих пор мы
принимали абсциссы равными расстояниям ег ие2 от преломляющей
сферической поверхности, , причем считали положительные ег
влево, положительные ег вправо. Начало отсчета Р сопряжено
само с собою. Теперь для каждой из абсцисс мы выберем особое
начало отсчета, притом так, чтобы оба начала отсчета Ot и О8
были сопряженными точками. В остальном они могут быть вы-
выбраны произвольно. Кроме того, обе абсциссы хг и х2 мы будем
считать положительными, когда точки Ах и А2 лежат вправо от
своих начал отсчета. Если аг и аг обозначают расстояния новых
начальных точек Ог и Ог от сферической поверхности, то со-
согласно A27):
и новые абсциссы хг и х2 связаны со старыми ег и е2 следую-
следующим образом (черт. 7):
OLA, = ОгР—АХР =а1 — е1 = хъ
~ РА2 ~ POS = ег—аг = xz.
Подставив в A27) хъ хг вместо еъ е2 и приняв во внимание A30),
получим закон оптического изображения:
«1—Л | Л —g»_ ^ A31)
*2
Х1
т. е. опять-таки линейное соотношение между обратными
абсциссами обеих сопряженных точек.
§ 34. Теперь мы перейдем к исследованию системы, состоя-
состоящей из произвольного числа центрированных сферических
поверхностей. Система называется центрированной, когда центры
всех поверхностей лежат на одной прямой — центральной оси
системы. Если мы опять ограничимся лучами и светящимися
точками, близкими к центральной оси, т. е. малыми значениями &
и Z, то законы изображения можно вывести из вышеизложенных.
Возьмем сначала светящуюся точку, лежащую на оси, и узкий
пучок, идущий от нее в первой среде. Этой точке соответствует
определенная, лежащая на оси сопряженная точка, действитель-
действительная или мнимая, а пучку лучей соответствует определенный
сопряженный пучок лучей во второй среде. Этим последним
опять соответствуют определенные сопряженные величины в
третьей среде, и так постепенно приходим к определенной
сопряженной точке А' и определенному сопряженному пучку
лучей в последней среде,.
Так как обратные абсциссы двух последовательных сопря-
сопряженных точек по отношению к любой паре сопряженных точек
56 ОПТИКА ИЗОТРОПНЫХ ОДНОРОДНЫХ СРЕЛ
взятых в качестве начальных точек, связаны линейно между
собой, то это будет справедливо и для абсцисс х и х' сопря-
сопряженных точек А и А' в первом и последнем теле и закон отобра-
отображения имеет ту же форму, как в A31) г):
£+£-!■ 032)
Для х = О имеем л:' = 0. Тогда точки Л и А' совпадают с со-
сопряженными началами отсчета О и О'. Постоянные / и /' явля-
являются, очевидно, абсциссами фокусов точек в первой и послед-
последней средах. Когда фокусы лежат по разные стороны от начальных
точек, то / и f имеют противоположные знаки.
Длины / и /' двух сопряженных отрезков, проходящих че-
через А и А' перпендикулярно к центральной оси, очевидно, со-
согласно A29) связаны соотношением:
я/sin #=«'/'sin #', A33)
где и и и' — показатели преломления первой и последней сред,
# и #' — углы с центральной осью каких-либо сопряженных лу-
лучей, проходящих через А и А'.
Величины / и /' и углы # и §■' мы будем в дальнейшем счи-
считать положительными, когда они направлены в одну определен-
определенную (для всех тел) сторону. Это не внесет никакого изменения
в знаке в A33).
§ 34а. Постараемся теперь найти пару сопряженных точек,
лежащих на оптической оси, для которых Z = V. Ясно, что изоб-
изображение любой фигуры, лежащей в плоскости, проходящей через
одну из этих точек, перпендикулярно к центральной оси, полу-
получится в плоскости, проходящей через сопряженную точку, и бу-
будет совершенно конгруэнтно объекту (изображение будет без
1) В этом проще всего убедиться путем доказательства от п к п-\-\. Допу-
Допустим, что A32) имеет место для п — 1 преломлений и хп — абсцисса А„ относи-
относительно Оп — точки, сопряженной О„ и напишем A32) в виде:
Для п-го преломления имеем:
где а, Д а', /?' обозначают величины, аналогичные ах — fv /я—аг в A31). Исклю-
Исключая из этих уравнений х„ и оВозначая а" =-7-—д), /?" = -, _ ,, получим:
Отсюда и из того, что A32) справедливо для я = 1, следует, что A32) справед-
справедливо для любого числа п преломляющих поверхностей. Прим. ред.
ГЕОМЕТРИЧЕСКАЯ ОПТИКА 57
увеличения или уменьшения). Обозначим эти точки через Н и Н'
и найдем их абсциссы х их'. Из A33) получаем:
п sin & = п' sin &'.
Проведя через Н и Н' два каких-нибудь сопряженных луча
под малыми углами # и &' к центральной оси и обозначая через
/0 и /0' расстояния от оси точек их пересечения с плоскостями,
проходящими через начала координат О и О' перпендикулярно
оси (черт. 8), получим:
х х''
Отсюда, пользуясь A32), получаем:
A34)
Точки Н и Н' однозначно определяются этими уравнениями.
Они называются „главными точками", а проведенные через них
конгруэнтно отображающиеся
одна на другую плоскости назы- К
ваются „главными плоскостями" Ц \ ^ {'Г~^->^ Н'
системы. -^jV tf~F^^
Формулы значительно упро- \
щаются, если начала координат
О и О' поместить в главные точ- Черт- 8-
ки Н и Н'. В дальнейшем мы
будем предполагать, что начала координат выбраны именно
таким образом. Тогда в A34) х и х' равны нулю, а, с другой
стороны, /0=/0', следовательно:
/:/ = _«:«', A35)
т. е. фокальные точки лежат с противоположных сторон глав-
главных точек (обе внутри или обе вне их). Их расстояния (черт. 9)
от главных точек, так называемые фокусные расстояния, отно-
относятся, как s показатели преломления. Для закона изображения
A32) получаем:
--^' = ^-. A36)
х х /
Если первая среда одинакова с последней (например обе
воздух), то п- — п и оба фокусных расстояния равны друг другу,
и закон изображения принимает более простой вид:
-1 —V = -V. A36а)
х х' {
§ 35. Главным точкам Н и Н', характеризующимся тем, что
плоскости, проходящие через них, конгруэнтно отображают одна
58 ОПТИКА ИЗОТРОПНЫХ ОДНОРОДНЫХ СРЕД
другую, аналогичны в некотором отношении узловые точки. Это
две сопряженные точки К и Л", которые характеризуются тем,
что каждому лучу пучка, проходящего через К, сопряжен п а-
ралдельный луч пучка, проходящего через К', так что для
любых двух сопряженных лучей ■& = #'. Положение узловых то-
точек легко найти, если принять во внимание, что два параллель-
параллельных, взаимно сопряженных луча, проходящих через К и К> пере-
пересекают главные плоскости на одинаковом расстоянии /0 = 10' от
центральной оси, так что и абсциссы х и х' обеих узловых точек
равны между собою. Поэтому из A32) получается:
037)
т. е. обе узловые точки находятся на одинаковом расстоянии от
соответствующих главных точек, именно на расстоянии, равном
разности фокусных расстояний.
F НИ WH' F'
Черт. 9.
Примерное положение главных точек, фокусов и узловых
точек представлено на черт. 9, на котором абсциссы узловых
точек положительны, а фокусы лежат вне главных точек, так
что /+/' > 0, / < 0, /' > 0. Тогда
НК = Н'К = H'F' — HF.
Следовательно:
H'F' = НК + HF = FR,
т. е. пары точек FF', HfC и КН', которые все вместе называ-
называются „кардинальными точками", имеют общую для всех пар одну
и ту же среднюю точку, которая называется оптическим цент-
центром системы. Если имеется лишь одна преломляющая поверх-
поверхность (черт. 7), то эта поверхность отображается конгруэнтно
сама на себе, и, следовательно, в ней совпадают обе главные
плоскости. Вследствие этого совпадают и узловые точки, а именно
в другой самосопряженной точке — центре сферы С. Это видно
непосредственно, так как каждый проходящий через С луч со-
сопряжен с самим собой. При этом уравнения A35) и A37) для от-
отношения и разности фокусных расстояний непосредственно пе-
переходят в уравнения A26) и A25), найденные в § 31 и относя-
относящиеся к этому частному случаю.
ГЕОМЕТРИЧЕСКАЯ ОПТИКА 59
Если имеется система линз в воздухе, то фокусные расстоя-
расстояния равны между собой и узловые точки совпадают с главными
точками. Если имеется лишь одна тонкая линза, то главные
точки совпадают внутри самой линзы.
Вообще положение кардинальных точек дает простой гео-
геометрический метод нахождения точки Р', в последней среде со-
сопряженной с любой точкой Р, лежащей в первой среде (черт. 9).
Для этого только нужно для двух произвольных лучей, прохо-
проходящих через Р, начертить сопряженные лучи. Целесообразнее
всего взять луч РК, проходящий через узловую точку К- Лучом,
сопряженным с ним, является параллельный ему луч РК'. Кроме
того, можно воспользоваться лучом, проходящим через Р парал-
параллельно оси; сопряженный с ним в последней среде луч прохо-
проходит через фокус F' и встречает соответствующую главную плос-
плоскость на таком же расстоянии от центральной оси, на каком
начальный луч встречает главную плоскость в первой среде.
Таким образом точка Р' найдена. Можно рассмотреть также
луч PF. С ним сопряжен луч, параллельный оси и пересекающий
последнюю главную плоскость на таком же расстоянии от оси,
на каком первый луч пересекает первую главную плоскость.
§ 36. Полное изложение законов оптического изображения
должно касаться не только путей лучей, но также и интенсив-
интенсивности их. При рассмотрении этого вопроса необходимо иметь
в виду, что конечное количество энергии излучения никогда не
выходит из одной точки, а всегда из некоторой поверхности, и
распространяется вцутри некоторого конечного телесного угла,
а не в одном строго определенном направлении. Это обстоятель-
обстоятельство можно наглядно выразить, считая, что энергия пучка про-
пропорциональна числу лучей, входящих в пучок. Каждый пучок
лучей содержит бесконечное число с»4 лучей (бесконечное мно-
многообразие четырех измерений), так как поверхность, из которой
он исходит, определяет бесконечное число точек двух измере-
измерений (°°2), а каждая точка определяет конус с бесконечным чис-
числом направлений тоже двух измерений соа. При этом надо об-
обратить внимание на следующее обстоятельство. Лучи, выходя-
выходящие из одной светящейся точки по разным направлениям, коге-
когерентны между собой ввиду того, что точка эта является центром
волновой поверхности, на которой фаза всюду одна и та же.
Лучи же, идущие из двух различных точек поверхности объекта,
вообще говоря, некогерентны, во всяком случае, если объект
является источником света. Поэтому такие лучи не интерфери-
интерферируют друг с другом, их интенсивности просто складываются.
Однако бывают случаи (их иногда упускают из виду), когда две
различные точки поверхности излучают когерентный свет и, на-
наоборот, когда из одной точки поверхности в разных направле-
направлениях идут некогерентные лучи, например, когда поверхность
(отверстие, щель) освещена посторонним источником света; тогда
могут иметь место некоторые интерференционные явления, ко-
60 ОПТИКА ИЗОТРОПНЫХ ОДНОРОДНЫХ СРЕД
торые геометрическая оптика объяснить не в состоянии. По-
Поэтому будем предполагать, что поверхность самосветящаяся.
Когда источник света помещен в фокус, то получается пу-
пучок параллельных лучей, но согласно сказанному не в том смы-
смысле, что все лучи пучка параллельны, а в том смысле, что каж-
каждой точке светящейся поверхности соответствует особое направ-
направление лучей пучка, причем величина светящейся поверхности
определяет телесный угол конуса различных направлений лучей.
Наоборот, лучи, приходящие от практически бесконечно дале-
далекого источника света, например от солнца, не собираются все
в определенном фокусе, но в фокальной плоскости получается
малое изображение солнца, так как все параллельные между со-
собой лучи, исходящие из одной точки солнца, встречаются в од-
одной точке фокальной плоскости.
Рассмотрим интенсивность (поток энергии) У излучения, рас-
распространяющегося от малого элемента поверхности /, перпенди-
перпендикулярного к центральной оси в нормальном направлении, внутри
узкого конуса с телесным углом"" 12. Согласно сказанному она
равна:
J=K-f-£). A38)
Величина (конечная) К называется „удельной интенсивностью
излучения" или также „удельной яркостью"" пучка лучей.
Для сопряженного пучка лучей, падающего внутри сопря-
сопряженного конуса лучей Q' на сопряженную площадку /', имеет
место соответствующее соотношение:
A39)
Величины / и Q в первой и последней среде связаны согласно
законам оптического изображения уравнением A33). Так как
изображение подобно объекту, то форма поверхности не имеет
значения. Мы можем <взять ее в виде круга радиуса Z. Тогда
В качестве телесного угла Si возьмем телесный угол круго- ,
вого конуса с малым углом растворения ■&. Тогда
Q = 4тг sin2 — = ffin.
Точно так же Si' = #'2гг.
Пользуясь этими значениями Si и Si' и соотношением A33),
имеем:
nJSi = n'2f'Q', A40)
а принимая во внимание A38) и A39), получаем:
£ = ■!££. (Н1)
Если общая интенсивность излучения У (полный поток энергии)
ГЕОМЕТРИЧЕСКАЯ ОПТИКА 61
в обоих сопряженных пучках одинаковая (что, конечно, никогда
не может выполняться точно, хотя бы потому, что при каждом
преломлении излучение частью теряется), то
-£=■£ или7б7г = №г, A42)
т. е. яркости относятся обратно пропорционально квадратам
скорости распространения света. Для п — п' будет К=К'. «По-
«Поэтому путем оптического изображения яркость какого-либо пучка
никогда не может быть увеличена. В фокусе излучение хотя и
концентрируется на меньшей поверхности, зато оно рассеивается
по более расходящимся направлениям.
§ 37. Изложенные выше простые законы оптического изоб-
изображения системой центрированных сферических поверхностей
являются по большей части лишь первым приближением к ре-
реальным соотношениям, так как в практической оптике прихо-
приходится иметь дело с поверхностями конечного размера и с конеч-
конечными конусами лучей. К поправкам, вызываемым этими обстоя-
обстоятельствами, добавляются еще поправки, обусловленные зависи-
зависимостью показателя преломления от цвета лучей (§ 9). В связи
с необходимостью учитывать эти поправки возникает ряд слож-
сложных задач. Решение этих задач имеет громадное значение для
техники оптических инструментов. Однако все эти поправки
не вносят изменения в общие законы геометрической оптики
в том виде, как они обрисованы нами в § 28.
Общие законы геометрической оптики могут быть объединены
в одно простое и наглядное положение — принцип Ферма
(или принцип наименьшего времени распространения луча). Прин-
Принцип этот позволяет установить ход светового луча через произ-
произвольное число различных тел с любыми ограничивающими по-
поверхностями. Принцип Ферма состоит в следующем: время, по-
потребное свету, чтобы из определенной точки притти к какой-ни-
какой-нибудь другой точке, меньше на пути луча, чем на любом сосед-
соседнем пути. Заметим, что этот принцип является исторически од-
одним из первых примеров равноправности интегрального закона
с диференциальным (ср. 3, § 42).
Можно дать простое доказательство этого принципа, если
рассматривать поверхность волны, распространяющейся от све-
светящейся точки Р. Согласно § 5 каждому моменту времени t со-
соответствует определенная волновая поверхность. Независимо от
того, окружена ли точка Р одной средой или разными средами,
эта поверхность представляет собой границу, достигнутую к мо-
моменту t светом, вышедшим в момент t = О из точки Р. На вол-
волновой поверхности лежат концы всех лучей, вышедших из Р по
разным направлениям; каждый из этих лучей шел по своему
определенному пути. Пусть Q — некоторая точка волновой по-
поверхности, a PQ обозначает определенный (вообще говоря, не
прямой) луч; от точки Р до точки Q свет распространяется за
62 ОПТИКА ИЗОТРОПНЫХ ОДНОРОДНЫХ СРЕД
время t. Если бы свет из Р мог по какому-либо другому пути
достичь Q за время меньшее, чем t, то свет, выходящий из Р во
все стороны, за промежуток времени от 0 до t прошел бы
дальше Q, что противоречит самому определению волновой
поверхности. Поэтому t представляет собой минимум вре-
времени, необходимый свету, чтобы каким угодно путем дойти от Р
до Q.
Исходя из принципа Ферма, можно развить всю геометри-
геометрическую оптику, и притом даже для неоднородных и анизотроп-
анизотропных сред. Прямолинейное распростране-
распространение света в однородной изотропной
среде по принципу Ферма является
непосредственным следствием того, что
прямая линия есть кратчайшее расстоя-
расстояние между точками Р и Q. Рассмотрим
еще следующий пример перехода света
через плоскую границу двух однородных
изотропных сред. Пусть q и qx — ско-
скорости распространения, А и В— проек-
Черт, ю. ции точек Р и Q на плоскость границы,
С — точка прохождения луча через гра-
границу (черт. 10); наконец, 0 и &t — углы падения и преломления;
тогда время, потребное свету, чтобы притти из Р в Q, равно
(^ + S = Vi, A43)
причем
г2 = АР2 + АС2 и /jf = BQZ + ВС2. A44)
При смещении точки перехода С расстояния АР, BQ и АВ
остаются постоянными, в то время как АС=*а и ВС — b меня-
меняются так, что
da + 6b=*0, A45)
следовательно, согласно A43) и A44):
R
1 ^
1
1
A
8
^4
с
\
Д
V
в
1
i
1
\i
4
0
ГЯ ^ r,<7i
Полагая St = O а принимая во внимание A45),
получим:
q: qx = -^: — = sin &: sin &u
условие, совпадающее с B0).
*■) Заметим, что принцип Ферма сохраняет силу и для определения путей
лучей, испытывающих отражения. Нужно только иметь в виду, что в этом слу-
случае время прихода для пути луча всегда будет extremum, но может и не быть
минимальным (может быгь, например, наибольшим;. Прим. ред.
ДИФРАКЦИЯ 63.
Подобным же образом можно применить принцип Ферма
к определению путей распространения света в любых телах
с любыми поверхностями.
Если конечный пункт Q какого-нибудь луча, выходящего
из Р, совпадает с точкой, оптически сопряженной с Р, то путь
луча PQ неопределенный, и имеется бесчисленное множество
лучей от Рк Q. В соответствии с этим время, потребное свету для
прохождения от Р до Q, одинаково для всех этих путей, и опти-
оптическая поверхность волны, идущей от Р, имеет в Q особую точку.
ГЛАВА IV
ДИФРАКЦИЯ
§ 38. Законы геометрической оптики неприложимы в тех
случаях, когда волновые поверхности или поверхности тел нельзя
рассматривать как бесконечные по сравнению с длиной волны.
Понятие луча и его распространения теряет тогда смысл. В этих
случаях имеют место явления, называемые „дифракцией". Со-
Согласно сказанному в § 28 дифракция, вообще говоря, играет
тем большую роль, чем больше длина волны применяемого
света. Полная теория дифракции возможна только на основе
диференциальных уравнений для электромагнитных волн в рас-
рассматриваемой среде (мы будем теперь считать, что это вакуум
со скоростью распространения q = с) и граничных условий, вы-
выполняющихся на поверхности дифрагирующих тел.
Диференциальные уравнения поля внутри среды можно све-
свести к одному единственному диференциальному волновому
уравнению C, § 87):
у = с*А<р. A46>
Ему должна удовлетворять каждая компонента у любого век-
вектора поля.
Краевые условия могут быть различны; вид их зависит от
свойств дифрагирующих тел. Они имеют наиболее простой вид
для так называемых абсолютных проводников C, § 92); внутри
них электрическое поле равно нулю. Абсолютные проводники
действуют как идеальное зеркало. Противоположный крайний
случай представляют собой так называемые черные тела, они
поглощают весь падающий свет. Проблемы дифракции отно-
относятся к труднейшим в оптике. Строгое решение одной из этих
проблем было дано впервые А* Зоммерфельдом в 1895 г.
Волновую функцию (р всегда можно представить в виде ряда
Фурье и общее решение A46) свести к сумме частных решений,
каждое из которых соответствует определенной частоте со. Для
такого частного решения можно написать:
<p = Vei<at, A46а)
где yi обозначает определенную комплексную функцию простран-
64 ОПТИКА ИЗОТРОПНЫХ ОДНОРОДНЫХ СРЕД
ственных координат. Модуль или абсолютное значение у характе-
характеризует амплитуду, а аргумент — фазовую постоянную периодиче-
периодического колебания.
Из волнового уравнения A46) следует, что функция про-
пространственных координат щ> удовлетворяет диференциальному
уравнению:
ИЛИ
Av + tgV = O, A46b)
которое нужно интегрировать, приняв во внимание краевые
условия.
Строгие решения формулированной таким образом дифрак-
дифракционной проблемы очень сложны, нахождение их требует при-
применения достаточно сложного математического аппарата. По-
Поэтому очень важно, что приближенные решения, практически
вполне достаточные для коротких оптических волн, можно по-
получить, пользуясь принципом Гюйгенса. Идея принципа
Гюйгенса состоит в том, что каждая точка, до которой дошла
световая волна, сама делается источником новой световой волны,
распространяющейся от нее по концентрическим сферическим
поверхностям. Г. Кирхгоф в 1882 г. дал более точную формули-
формулировку принципа Гюйгенса; она представляет собой развитие
формулы Грина из теории потенциала, вывод которой мы сейчас
дадим.
§ 39. Пусть U и V представляют собой внутри некоторой
области пространства две однозначные непрерывные функции
пространственных координат х, у, z с непрерывными производ-
производными первого порядка. Тогда для этой области пространства
[согласно 2, § 18, (80) (где dx— элемент объема, da— элемент
поверхности и v—внутренняя нормаль к поверхности)] справед-
справедливо соотношение
Лди dV , dU dV , dUdV\, firdU . Слтлпл
s--a—h-r-1^—Г-3--3- \dx = — / V-—-da— 1 V Ли dx =
dx dx ' dy dy ' dz dz j J dv J
= - fu% da—.JuAVdx.
Следовательно:
f(ud^-Vd^)da = f(VAU-UAV)dx. A47)
Если взять U=—', где г, взятое с положительным знаком,—
расстояние точки х, у, z от произвольной точки А, лежащей вне
области интегрирования, то U удовлетворяет условиям одно-
однозначности и непрерывности; кроме того, U = — удовлетворяет
ДИФРАКЦИЯ 65
уравнению Лапласа [/, A29)] AU = O. Следовательно, из A47)
получается:
/ I—i V' —^—1do = — / uxt A48}
Если точка А лежит внутри рассматриваемой области про-
пространства, то, исключив при интегрировании очень маленькую
сферу с центром в точке А (где £/— — имеет разрыв непрерыв-
непрерывности), можно опять применить это уравнение. При этом правая
часть меняется лишь незначительно (ср. 7, § 33), к левой же ча-
части уравнения в качестве добавочного члена прибавляется ин-
интеграл по поверхности выделенной сферы (элемент ее da). При-
Принимая во внимание, что направленная внутрь области интегри-
интегрирования нормаль к этой сфере совпадает с г, получим этот
интеграл в виде:
J \r dr~*~ ' r» I af
Если радиус сферы взять достаточно малым, то этот интег-
интеграл ввиду конечности V и ^- сводится к интегралу:
где Vo обозначает значение V при /*=0, т. е. в точке А. При-
Прибавив этот член к левой части уравнения A48), получим фор-
формулу Грина:
Эта формула позволяет найти значение функции V в каж-
каждой точке А рассматриваемой области пространства, если даны
значения AV в каждой внутренней точке области и значения V
dV
и -г- на поверхности ее.
Если функция V удовлетворяет уравнению Лапласа AV = O,
то объемный интеграл пропадает и в правой части (М9) оста-
остаются лишь величины V и -^ на поверхности объема. В этом
случае формула Грина особенно полезна, однако ее значение
существенно ограничено тем, что значения V и -т- на поверх-
поверхности не могут быть выбраны независимо друг от друга. В са-
самом деле, известно, что решение уравнения Лапласа внутри не-
некоторой области вполне определено заданием как значений од-
одного только V на поверхности области C, § 19), так и заданием
значений одной только производной -т- на поверхности B, § 71).
5 Введееае в теоретическую фязвку, ч. IV
66 ОПТИКА ИЗОТРОПНЫХ ОДНОРОДНЫХ СРЕД
Но формула Грина при задании на поверхности либо только V,
либо только -5- может только в том случае служить непосред-
непосредственно для определения V во внутренних точках, если еще ка-
каким-нибудь образом можно определить для всех точек поверх-
поверхности недостающую величину.
§ 40. Формулу, выражающую принцип Гюйгенса, можно вы-
вывести непосредственно из формулы Грина. Для этого вставим
в последнюю вместо V некоторую волновую функцию, которую
нужно выбрать так, чтобы объемный интеграл в A49) можно
было свести к поверхностному. Этого нельзя сделать, если
вместо К просто" подставить решение <р волнового уравнения A46).
Как мы увидим, этот объемный интеграл удается свести к поверх-
поверхностному интегралу, если в качестве V в A49) взять какую-ни-
какую-нибудь функцию q> от х, у, z, t, удовлетворяющую волновому урав-
уравнению A40), но вместо t в качестве аргумента подставить t—■£-,
где г обозначает, как и прежде, расстояние точки х, у, z от
точки А, лежащей внутри области интеграции. Нужно, следова-
следовательно, иметь в виду, что теперь V зависит от координат х, у, z
двумя способами, во-первых, явно, так как у — функция коорди-
координат, во-вторых, неявно через г, так как аргумент:
t— 7 = т A50)
содержит расстояние г. Чтобы выразить это яснее, мы будем писать:
V=9r(x, у, z), A51)
причем мы пишем пространственные координаты в скобках .под
знаком функции, а временную координату ставим внизу в виде
индекса. Нам нечего опасаться смешения временного аргумента т
с элементом объема йт, так как последний скоро исчезнет из
формул. В этих обозначениях A49) приобретает такой вид:
у. A52)
Эта формула дает значение волновой функции q> в момент t
в какой-нибудь точке, лежащей внутри области интегрирования,
ограниченной поверхностью а с внутренней нормалью v. Чтобы
теперь свести объемный интеграл к поверхностному, вычислим
значение А<р^, которое, разумеется, не равно (А<р)г, вычисленному,
считая при диференцировании т постоянным.
Мы имеем:
дх \ ёх )х \ dt )х ' дх \дх)т с
И
^V«" (d1q>\ 2 / д*<р\ дг 1 /д*<р
~дх* ^ [дх?)т~~ с {dxdljr Fx + r* \dF)t\dxJ
ДИФРАКЦИЯ 67
Аналогичные выражения получаются для -^ и ~^~. Сло-
Сложением получаем:
2 1^9 or i &<Р дг , д*д> дг\ , 1 (д2<р\ 2 /д<р\
Если.из волнового уравнения A46) сюда вставить значение (Aq>\;
то выражение для А<рт можно представить как производную по
времени:
. _2_ д 1д<р Or , д^ дг_ , д<р дг l dip
У* I Ш \Ш дх~*~ ду ~dy~~t~~dz"dz~T~dt
ИДИ
. 2 д (д<Рг . <Рт
Таким образом объемный интеграл в A52) преобразуется в
. 2 д Гйг(д<рх <РГ
J
а если элемент объема dr выразить при помощи полярных коор-
координат с началом в точке А и через dm обозначить телесный угол
элементарного конуса с вершиной в А, то
dr = r2drdco,
и
/А д
/АЧ>% . 2
= ~ТШ/<*">■ Mo' A53)
После интегрирования по г, в выражение, стоящее в квад-
квадратных скобках, нужно еще подставить в качестве верхнего пре-
предела расстояние г элемента поверхности da от А, зависящее от
направления, а в качестве нижнего предела значения г — 0. Под-
Подстановка значения г = 0 дает нуль и остается только член, относя-
относящийся к поверхности. Элемент поверхности do связан с вели-
величиной телесного угла da> опирающегося на него элементарного
конуса следующим соотношением:
r2dco = — da- cos (r; v) — — da • ^ A54)
(знак минус, так как направления возрастающего г и возраста-
возрастающего v образуют между собой тупой угол).
Отсюда следует
68 ОПТИКА ИЗОТРОПНЫХ ОДНОРОДНЫХ СРЕД
Рассматриваемый элементарный конус da может пересекать
поверхность объема интегрирования больше одного раза, но
всегда нечетное число раз (если поверхность не везде выпуклая
наружу). В этом случае взятый по г интеграл в A53) распа-
распадается на отдельные части, и легко можно убедиться в том, что
соотношение A55) остается в силе, если только интегрирование
по da распространить на всю поверхность, охватывающую об-
область ^интегрирования. Примем, наконец, во внимание, что вхо-
дящая в A52) величина -г^ равна:
Ч (д<р\ 1 (д<р\ дГ
Теперь формула Грина A52) переходит в принцип Гюйгенса:
4я^@) = jQda, A57)
где согласно A55) и A56) для сокращения принято обозначение:
Я = \^ 7 *~vdi diЛ A58)
Вместо этого иногда пишут короче:
но в такой форме формула неверна, ибо при таком написании
не учтено, что в первом члене диференцирование q>f (x,у,z) по»
должно распространяться лишь на зависимость от аргумента т,
а не от координат *х, у, z.
Значение принципа Гюйгенса состоит в том, что согласно
ему волновая функция, удовлетворяющая внутри некоторой об-
области пространства волновому уравнению A46), вполне опреде-
определяется в какой-нибудь точке А внутри этой области в момент
времени t значениями <р, -~ и -~ на поверхности этой области;
да> дер ..
значения у, -~ и -~ на поверхности должны быть взяты в мо-
моменты времени т, различные для разных элементов поверхности;
эти моменты предшествуют моменту t на время, потребное свету,
чтобы дойти от соответствующих элементов до А.
Принцип Гюйгенса можно согласно только что сказанному
формулировать следующим образом: каждый элемент поверх-
поверхности da все время отсылает сферические волны, распространяю-
распространяющиеся во всех направлениях со скоростью света. Световое поле
этих волн определяется световым полем на элементе поверх-
поверхности da, испускающем их. Значение волновой функции в точке А
аддитивно складывается из значений в этой точке волновых
функций этих элементарных сферических волн, приходящих
ДИФРАКЦИЯ 69
к моменту * в точку А из всех элементов замкнутой поверхности а.
Нельзя, однако, упускать из виду, что эта картина справедлива
только для замкнутой поверхности а; поэтому не имеет физи-
физического смысла говорить о действии отдельных элементов по-
поверхности da, так как интеграл A57) может быть разложен на
свои диференциалы бесконечным числом способов. Значение
высказанного здесь ограничения становится особенно ясным
в том случае, если среди выходящих из А прямых имеются пря-
прямые, пересекающие поверхность больше чем в одной точке,
например в трех точках Р, Q, R (черт. 11).
В этом случае интегрирование не распространяется на область
PQ; между Р и Q волновое уравнение A46) может и не удовле-
удовлетворяться; более того, там могут нахо-
находиться любые тела, даже непрозрачные
для световых лучей. Тем не менее прин-
принцип Гюйгенса в форме A57) имеет место,
причем интегрирование нужно распростра-
распространить по всей поверхности а и нельзя
исключать элементы поверхности в Q и
R на том основании, что светот них не
может прямолинейно достичь точки А.
§ 41. Разделим область интегрирования
на две части 1 и 2 так, чтобы точка А на- Черт. и.
ходилась внутри части 7. При этом мы
получим две области пространства с элементами поверх-
поверхности dalt da2 и da0; при этом da0 обозначает элемент вве-
введенной поверхности раздела. Теперь принцип Гюйгенса можно
применить двумя способами, во-первых, можно применить его
к первоначальной поверхности с элементами day и da2, при
этом получится:
во-вторых, к поверхности области / с элементами dat и do0, при
этом имеем:
4*% @) = /ЧА + /Яо^о,
где vQl обозначает нормаль к поверхности раздела, направлен-
направленную внутрь объема /.
Вычитанием обоих уравнений получаем:
а так как гог и vn направлены в противоположные стороны, то
0 = fnvda2 + f®vado0. A60)
Но а2 и а0 образуют замкнутую поверхность объема 2. Та-
Таким образом получаем общее положение, что интеграл Гюйгенса,
70 ОПТИКА ИЗОТРОПНЫХ ОДНОРОДНЫХ СРКД
взятый для точки А, лежащей вне области интегрирования, равен
нулю. Это положение находится в полном соответствии с фор-
формулой Грина в форме A48).
§ 42. Теперь мы применим принцип Гюйгенса к области про-
пространства, ограниченной с одной стороны поверхностью, отде-
отделяющей все тела, принимаемые во- внимание при исследуемом
явлении: источники света, экраны и т. д., а с другой стороны —
очень большой сферической поверхностью радиуса R с центром,
лежащим в конечной части пространства. Уравнение A57) при-
применимо и в этом случае, если только во всей области интегри-
интегрирования удовлетворяется волновое уравнение A46). Интеграл
Гюйгенса распадается при этом на два интеграла: один по пер-
первой поверхности (точки которой находятся на конечном расстоя-
расстоянии) с элементом da и с нормалью v, направленной внутрь об-
области интегрирования и, следовательно, направленной к точке Л;
второй — по сферической поверхности радиуса R с элементом dS.
Без дальнейшего исследования второй интеграл нельзя считать
равным нулю при достаточно большом значении R, так как хотя
подинтегральное выражение Q и уменьшается безгранично при
увеличении R, но, с другой стороны, безгранично растет вели-
величина поверхности. Однако, если относительно формы волновой
функции <р сделать некоторое допущение, ни в какой степени не
ограничивающее действительное протекание явления, то этим
интегралом можно пренебречь. Для этого нужно только принять,
что для моментов времени t< — Т, где Т очень большой про-
промежуток времени, волновая функция у вместе с ее производными
всюду равна нулю, т. е. все источники света начали действовать
лишь в какой-то определенный момент времени. Тогда исчезает
значение^ вместе с ее производными для всех элементов по-
поверхности dS, если только
Следовательно, надо выбрать /?> G"+ t)c. Конечно, в вто уело,
вие входит переменная величина t, но это не создает труд-
трудности, ибо можно заранее выбрать R таким, что неравенство
будет выполнено даже для наибольших значений t, встречаю-
встречающихся при измерениях. Физически это означает, что R должно
быть выбрано таким, чтобы какое-либо исходящее от отдален-
отдаленной сферической поверхности воздействие к моменту t еще не
дошло до точки А.
После этих замечаний мы можем считать, что уравнение
A57) применимо и в том случае, когда точка А лежит по одну
сторону от поверхности о, а источники света, экраны и пр.
находятся по другую сторону этой поверхности.
Подводя итоги, мы можем сказать: принцип Гюйгенса в фор-
форме A57) применим всегда, когда поверхность а совершенно от-
отделяет точку А от действующих тел, так что нет никакого пути,
ДИФРАКЦИЯ 71
ведущего от какого-либо из этих тел к точке А, и не пересе-
пересекающего поверхности а.
§ 43. Интересующую нас проблему дифракции мы форму-
формулируем в общем случае следующим образом. На пути света от
данного источника поставлен непрозрачный экран с одним или
многими отверстиями определенной формы и положения. Тре-
Требуется найти интенсивность света в точке А позади экрана.
Прежде всего мы можем упростить задачу, приняв во вни-
внимание только одну точку С источника света, рассматривая источ-
источник как точечный; тогда (§ 36) интенсивности света, вызванные
другими точками источника, просто прибавляются к интенсив-
интенсивности, исходящей от С. Затем волновую функцию у света, иду-
идущего от источника, находящегося в точке С, можно предста-
представить в виде ряда Фурье и при расчете ограничиться одним
его членом. Это можно сделать потому, что при естественном
свете постоянной интенсивности отдельные члены ряда незави-
независимы друг от друга и не дают заметной интерференции.
Применяя принцип Гюйгенса к рассматриваемому случаю,
мы проводим поверхность Гюйгенса так, чтобы она отделяла
„точку дифракции" А от источника света и от экрана, и чтобы
она, кроме того, проходила вплотную к экрану и через отвер-
отверстия, со стороны, обращенной к точке А. Тогда, пользуясь A57J
и A58), мы можем интегрированием по поверхности Гюйгенса
вычислить значение <р в точке А.
Однако, чтобы продвинуться дальше в решении задачи, мы
вынуждены пожертвовать точностью этого решения. Положение
здесь такое же, как при применении формулы Грина (конец§39).
Для определения величины Q, стоящей в A58) под знаком инте-
интеграла, мы должны знать значение q> и ее производных по v и по t
во всех точках поверхности Гюйгенса, а это уже предполагает,
что проблема нахождения у частично разрешена. Эта трудность
особенно усугубляется еще тем, что значения <pt -^ и ~щ в опре-
определенной точке поверхности не независимы друг от друга и что»
вставляя в выражение Q какие-нибудь приближенные значения
этих величин, мы, вообще говоря, придем даже к внутреннему
противоречию. Действительно ли получается такое противоречие
и. какого оно характера, можно выяснить, переместив точку ди-
дифракции А на гюйгенсову поверхность и сравнив полученные из
A57) значения <р и его производных с первоначально вставлен-
вставленными в Q значениями их.
Несмотря на это, мы сможем пойти дальше по избранному
пути. Бесчисленные применения показали, что принцип Гюй-
Гюйгенса не только в его строгой формулировке, но даже при лишь
приблизительно верных значениях Q приводит к результатам,
вполне достаточным для потребностей практической оптики. Это
приближенное значение Q можно получить, если принять, что
в отверстиях экрана значения <р и его производных, входящих
72 ОПТИКА ИЗОТРОПНЫХ ОДНОРОДНЫХ СРЕД
в Q, таковы, каковыми они были бы в случае отсутствия экрана,
а что во всех других точках поверхности а они равны нулю.
Интеграл A57) нужно распространить тогда только на отверстия
экрана, а при вычислении Q при помощи A58) наличие экрана
можно вообще игнорировать.
% Естественно, A57) распадается на столько отдельных инте-
интегралов, сколько имеется отверстий, и каждый интеграл относится
только к одному отверстию. При этом легко убедиться в том,
что значение интеграла зависит только от края отверстия; в са-
самом деле, поверхности Гюйгенса moWho придать различную фор-
форму, лишь бы граница ее оставалась прежняя — край отверстия.
Поэтому можно с тем же успехом говорить о «дифрагирующем
отверстии*, как и о „дифрагирующем крае".
§ 44. Из сказанного выше вытекает, что теперь для решения-
задачи нужно только узнать волновую функцию и ее производ-
производные для всех точек отверстия, причем решать задачу так, как
будто экран отсутствует. Для этого достаточно простого инте-
интегрирования волнового уравнения A46). В качестве простейшей
формы частного решения этого уравнения, соответствующей
строго монохроматической волне, исходящей из светящейся точ-
точки С, мы согласно 2, B30) возьмем выражение:
9у , A61)
где rj — расстояние рассматриваемой точки от светящейся точки
С (в отличие от г, расстояния точки дифракции А от элемента
поверхности da). Величина А представляет собой некоторую ком-
комплексную постоянную, остальные обозначения те же, что и рань-
раньше [ср., например, (83)].
Вставляя выражение A61) для у в A56) и выполняя соот-
соответствующие диференцирования, мы увидим, что величина Q9
распадается на несколько членов, порядок величины которых
различен. Действительно, для оптических явлений длина волны
Д = — мала сравнительно с расстояниями г и гх точки дифрак-
дифракции А и светящейся точки С от дифрагирующего отверстия;
поэтому в Qv члены, содержащие со множителем, велики сравни-
сравнительно с остальными членами и эти последние можно отбросить
(ср. 2, § 88).
Наконец, вставив в качестве аргумента Qr везде вместо t
величину т = t г—, получим:
x dr
и в силу A57):
ДИФРАКЦИЯ 73
Для упрощения дальнейшей трактовки этого выражения мы
следующим образом специализируем проблему, сохранив все ха-
характерные черты дифракционных явлений. Именно, мы пред-
предположим, что, во-первых, дифракционный экран плоский и, во-
вторых, что свет падает перпендикулярно, параллельными луча-
лучами и параллельными волновыми плоскостями, т. е. что гг во всех
точках дифрагирующего отверстия имеет постоянное значение,
очень большое по сравнению с другими расстояниями. Тогда
-j^ = l, в то время как -^ =— cos#, где # обозначает „угол
дифракции" (знак минус, так как направление возрастающего v
образует тупой угол с направлением возрастающего г). Вставляя
эти значения, видим, что A62) обращается в
или
<pt(Q)=~e L ei(C—iS), A63)
где для сокращения положено:
г, 1 Г da „ & 2пг
С = -г- / — COS2— COS-jp,
-7 А A64)
Действительная часть A63) представляет периодическое (во
времени) синусообразное колебание; интенсивность его мы со-
согласно § 18 найдем, умножая комплексную величину A63) на вели-
величину, ей комплексно сопряженную. Так как нас интересует не
абсолютное значение интенсивности света, а отношение интен-
интенсивности дифрагированного света к интенсивности падающего,
то мы делим полученную таким образом величину на интенсив-
интенсивность падающего света, а именно на произведение комплексного
выражения A61) на сопряженную величину, т. е. на ^—~-.
Таким путем мы получаем следующее выражение для интен-
интенсивности дифрагированного света в точке А:
*. A65)
Проблема дифракции сведена таким образом к нахождению
обоих интегралов С и S, в которых da обозначает элемент по-
поверхности дифрагирующего отверстия, г — его расстояние от
точки наблюдения Л, & — угол дифракции.
§ 45. Наиболее важным в выражениях для С и S является
различие в характере зависимости содержащихся в них величин
от переменных интеграции. В то время как & и г меняются
74 ОПТИКА ИЗОТРОПНЫХ ОДНОРОДНЫХ СРЕД
сравнительно медленно, при переходе от одного элемента к
другому, тригонометрические функции, наоборот, вследствие
большой величины аргумента -^- изменяются быстро, колеблясь
между максимумом и минимумом. Единственным исключением
являются те элементы поверхности da, расстояние г которых от
точки А имеет минимум, потому что тогда г мало меняется с а-
Это справедливо для всех элементов поверхности da, которые
лежат в непосредственной близости от прямой линии, перпенди-
перпендикулярной к плоскости экрана, соединяющей светящуюся точку С
с точкой наблюдения А. Поэтому эта прямая АС, которую мы
назовем „центральной линией", и, в частности, точка пересече-
пересечения ее с поверхностью Гюйгенса играют существенную роль
при определении интенсивности света в А.
Но имеется случай, когда центральной линии вообще нет.
Это будет тогда, когда не только точка С, но и точка А лежит
в бесконечности. Тогда АС не обозначает никакой определенной
линии, но лишь определенное направление, и никакая точка
поверхности Гюйгенса не играет особенной роли. Интегралы С
и 5 при этом совершенно меняют свой характер. Этому случаю
соответствуют дифракционные явления, открытые Фраунгофером
и носящие его имя.
§ 46. Займемся прежде всего общим случаем, так называе-
называемым случаем дифракции Френеля. Разберем явление дифракции
от плоского экрана, ограниченного прямолинейным краем.
Ответ на этот вопрос представляет интерес и для общего случая
экрана, ограниченного краем любой формы, так как такой край
может быть представлен состоящим из прямолинейных отрезков,
если только кривизна его достаточно велика по сравнению с
длиною волны. Вместе с этим мы подходим к вопросу о границе
тени, образуемой телом любой формы.
Проведем плоскость черт. 12 через точку наблюдения А
перпендикулярно к краю экрана. Ось х направим по линии пе-
пересечения плоскости чертежа с экраном и положим начало ко-
координат О в точке края экрана. Край экрана, перпендикулярный
к плоскости чертежа, возьмем в качестве оси у, а ось z прове-
проведем в плоскости чертежа. Координаты точки наблюдения А на-
назовем х,у = 0, г, координаты какой-либо точки плоскости экра-
экрана |, 7], f =0. Если экран простирается в сторону положительных
значений х, интегрирование должно производиться по элементам
поверхности da == d£dr], лежащим в плоскости х, у и соответствую-
соответствующим положительным значениям I.
Отсюда пределы интеграции: для I — от 0 до оо, для rj —
от —оо до + оо. При вычислении интегралов A64) мы будем исхо-
исходить из характеризующих их свойств, указанных выше. Для этого
проведем центральную линию АС, пересекающую плоскость эк-
экрана в точке Р. Поверхностные интегралы A64), для которых пе-
переменными интеграции являются координаты | и t], мы разобьем
ДИФРАКЦИЯ
75
на две части следующим образом: пусть первый частичный инте-
интеграл охватывает точки, лежащие вблизи точки Р, расстояния ко-
которых от Р малы сравнительно
р
с АР — z; второй частич-
ный интеграл распростра-
няется тогда на все осталь-
остальные точки интегрируемой об-
области. Более четкое опреде-
определение границы первого ча-
частичного интеграла мы дадим
позже. Согласно сказанному
мы можем в этом интеграле
медленно меняющиеся вели-
величины г и i
лучаем:
i
i
i
1
_Л А >
г ~ г
Р,
Р2 О Р
Черт. 12.
заменить соответственно через z и 0 и тогда no-
cos
2пг
A66)
Здесь многоточия обозначают второй частичный интеграл.
Чтобы выполнить интегрирование по т], мы напишем:
#*=*(£- *)■ + (ч — yf + (С—zf;
или, так как у = 0 и f = 0:
где
A67)
A68)
остается постоянным при интегрировании. Интегрируем по г\ в
пределах от — ??' до + г\', полагая
Ч'<г. A69)
Так как согласно принятому rj <^L Q, то мы можем A67) раз-
разложить по степеням, откинув члены высших порядков:
Подставляя это в A66), имеем:
1ш 2 ~<р jnj2 . 2яв . пг?
COS -г- = COS -тг COS -,- Sit] -A Sin -; -.
/ A AQ A AQ
A70)
A71)
Таким образом мы сводим задачу к подсчету следующих
двух интегралов:
+ ч' t +ч'
У 3^ и j ^sin-A^- О72)
76 ОПТИКА ИЗОТРОПНЫХ ОДНОРОДНЫХ СРЕД
Положим для сокращения
j = «- A73>
Тогда мы приведем интегралы к виду:
+W +а'
У ^' f cos и2 da и y^f slnu*du. A74)
— и' — в'
Величину
мы можем без нарушения условия A69) принять очень большой
сравнительно с единицей, полагая
r,'^s>Vte. A76)
Делая это, мы дополняем приведенное выше определение
области интегрирования первого частичного интеграла в выра-
выражениях для С и S. Тогда оба интеграла в A74) принимают вид:
/ cosu2du и / smusdu. A77)
— со — ос
Оба эти „интеграла Френеля", как будет показано в следую-
следующем параграфе, имеют конечное значение, а именно каждый из
них равен 1/ -^-.
Вставив эту величину в A74), получим для обоих интегра-
интегралов A72) одно и тоже значение!/ -§-; согласно A68) можно на-
писать вместо него у -^-. Обращаясь теперь к A66) и приняв
во внимание A71), получим следующие выражения для С и S:
где для сокращения положено:
A78)
дифракция 77
Наконец, на основании A65) находим:
7= с»+ $■ + ... A79)
Таким образом задача сводится к вычислению обыкновенных
интегралов с и s, выраженных формулами A78). Аналогия их с
поверхностными интегралами С и S в A66) бросается в глаза.
Ясно, что ens, так же как С и S, представляют собой отвле-
отвлеченные числа.
В интегралах Френеля кажется удивительным то обстоятель-
обстоятельство, что они. простираясь в обе стороны в бесконечность, имеют
конечное значение, несмотря на то, что в данном случае под-
интегральные выражения их не исчезают в бесконечности, как
обычно бывает у подобных интегралов, но сохраняют конеч-
конечную величину, принимая поочередно положительные и отрица-
отрицательные значения. Но, несмотря на это, в результате получается
конечное значение для интеграла. Это объясняется тем, что при
возрастании и максимумы и минимумы +1 и — 1 сдвигаются
все ближе между собой, так что колебания значений интеграла
делаются все меньше. Такое своеобразное поведение является
математическим отображением некоторого, имеющего физический
смысл, обстоятельства. Последнее заключается в том, что влия-
влияние элементарных волн, соответствующих полоскам dr) поверх-
поверхности Гюйгенса, на величину волновой функции в точках А хотя
и сохраняет один и тот же порядок величины с удалением полосы
от центральной линии, но зато все быстрее меняет свой знак.
Это обстоятельство обусловливает недейственность тех элемен-
элементов поверхности do, координаты которых г) имеют величину по-
порядка if A76). Оно еще в большей степени будет иметь место
для тех элементов поверхности, которые еще дальше располо-
расположены от центральной линии, т. е. для которых координата »?>»?'.
Отсюда следует, что часть интеграла в выражениях A64) для С
и S, соответствующая интегрированию от »? = »?' до г/ — оо, не
влияет заметно на величину волновой функции в точке А. При
этом надо указать, что величины г и ■&, входящие в коэфициенты
при косинусе и синусе, также меняются по мере роста щ\ но их
изменения сравнительно так малы, что для интервала »?, который
охватывает много максимумов и минимумов косинуса и синуса,
ими можно пренебречь.
Отсюда вытекает, что мы можем откинуть многоточия во
всех наших формулах и в дальнейшем, во всех других случаях
дифракции Френеля, ограничиться при интегрировании только
теми элементами do поверхности Гюйгенса, которые лежат вблизи
центральной линии, соответственно условиям A69) и A76). Итак,
впредь мы будем пользоваться соотношением:
7 = ca + sa. A79а)
§ 47. В этом параграфе, имеющем вспомогательное значе-
значение, мы займемся исследованием интегралов Френеля. Прежде
78 ОПТИКА ИЗОТРОПНЫХ ОДНОРОДНЫХ СРЕД
всего мы должны вычислить определенные интегралы A77). Для
этого будем исходить из интеграла Лапласа:
:+оо
L= J e~aXtdx, A80)
— оо
где а> 0.
Мы можем также написать его в виде:
— оо
Умножением находим двойной интеграл
+ оо +оо
£г= j j" dxdye~
— оо — оо
Введя полярные координаты, имеем:
и
ею 2и
о
В результате интегрирования получаем:
L =У~. A81)
Интегралы Френеля могут быть найдены при помощи инте-
интеграла Лапласа, если в последнем заменить а на L
Ради краткости мы опускаем доказательство того, что урав-
уравнение A81) справедливо и для a — i. Из A80) получаем:
Ls= I (cos л:2—isinx^dx
и из A81):
Приравнивая друг к другу последние выражения, находим
для обоих интегралов значения, указанные в предыдущем пара-
параграфе:
A82)
/
-оо
/" sintf
— оо
+ оо
ДИФРАКЦИЯ 7&
В дальнейшем нам потребуется знать величину интегралов
Френеля для переменных пределов, поэтому мы продолжим ис-
исследование несколько дальше.
Заметим прежде всего, что путем разбиения рассмотренного
интеграла на две части легко получить величину интеграла для
случая, когда один из пределов его равен нулю. Действительно,
так как (-|-к)г=.(—к)г, имеем:
О со со л
J'cos иг du == I' cos и2 du= J sin и2 du =-|-|/Г-|.. A83>
— oo 6 0
Но интеграл с переменным пределом и нельзя свести к эле-
элементарным функциям, и для вычисления необходимо воспользо-
воспользоваться разложением в ряд. С помощью интегрирования по частям
можно разложить интеграл, взятый в пределах от 0 до к, в схо-
сходящийся всюду ряд. Действительно, находим:
и и
I cos и2 du = и cos иг +2 f и? sin и? du,
о о
и и
I sin u2du — u sin ы2—2 / и2 cos и2 du.
о о
Продолжая преобразование интегралов, находящихся в пра-
правой части равенства, при помощи интегрирования по частям, по-
получаем в конце концов:
и
fcos и2 du = cos и2 • 2 + sin ы2 • Г, A84)
sin к2 du = sin и2 • I— cos ы2 • Г, A85}
где для сокращения положено:
2 = »-Ша5+тШа9---- <186>
и
f
Эти ряды сходятся для всех положительных и отрицатель-
отрицательных значений и, так как отношение двух последовательных чле-
членов ряда с возрастанием порядкового номера безгранично убы-
убывает. Однако эти ряды при сколько-нибудь больших значениях к
неудобны для вычислений вследствие быстрого роста показа-
показателя степени их членов. Поэтому при больших значениях и луч-
лучше употреблять другие ряды, расположенные по нисходящим
степеням и которые хотя и расходятся, но, как мы увидим*
80 ОПТИКА ИЗОТРОПНЫХ ОДНОРОДНЫХ СРЕД
часто оказываются очень удобными для вычислений. Так как ряд
с отрицательными степенями и для возрастающего и стремится
к нулю, то целесообразно здесь исходить из интеграла, имею-
имеющего границей и=оо. Применим в этом случае интегрирование
по частям в следующей форме:
к> 0 и и
оо оо оо
f
f
и и и
При последовательном применении этого приема к интегра-
интегралам правой части получаем:
оо
Г cos и2 da = cos и2 • уп — sin к2 • ап + Rt, A88)
U
оо
/'sin tfidu = sin и2 • у„ + cos и8 • а„ + #s- A89)
и
Здесь ряды
,. __ 1 1 3 1 , п„-1 1 • 3...DП — 5) t /1Qm
1 1 1-3-5 1 , , пп-1 1 -3...DП — 3) __2
расходятся и поэтому взяты с ограниченным определенным чис-
числом членов п. Остаточные члены их:
оо
г, _/_i\n 1 •■3---Dп— 1) fcosiPdu
l) P cos «
~'J и*
U
оо
fin a» «ft,
«• —I V 2-В-.- 2
Оба они с возрастающим л растут безгранично. Однако эти
ряды часто можно применять с успехом для вычислении, так как
при ближайшем рассмотрении оказывается, что для определен-
определенных значений порядкового числа п остаточные члены становятся
очень малы и поэтому могут быть откинуты без заметной ошиб-
ошибки. Прежде всего легко убедиться в том, что как /?„, так и R,
меньше по величине того выражения Rn, которое получится, если
в интегралах A92) и A93) заменить косинуЪ и синус единицей,
т. е. меньше, чем
р _ Ь2---DП — X) fdu_ Ъ3---DП— 3)
* —J =
fdu_
J Ы4п
и
f
2-Й... 2 J Ы4п= 2-2-•• 2 Г и*"-1'
и
ДИФРАКЦИЯ 81
Но это есть как раз последний член в ряде yh, который при
известных условиях представляет собой очень малое число, в
особенности, если и велико.
Существенным при этом является, конечно, выбор порядко-
порядкового числа п. Когда п растет, начиная от единицы, то Я„ снача-
сначала убывает благодаря степени 4л — 1 знаменателя, но дальше
растет безгранично вследствие наличия факториала в числителе.
Минимум /?„' имеет место для тех значений порядкового числа /п,
для которых отношение -S^ ближе всего к единице, т. е. когда
L. J_ приблизительно = 1,
а следовательно:
п приблизительно = -=-. A95)
Чем больше и, тем больше членов нужно взять в рядах у„ и ап,
для того чтобы остаточные члены их имели наименьшее возможное
значение. Притом это их наименьшее значение быстро убывает
с возрастанием величины и. Если ими пренебречь, то из A88)
и A89) получаются приближенные значения интегралов Френеля.
Такие ряды, которые, будучи расходящимися, все же до опреде-
определенного числа членов приближаются к некоторому пределу, вновь
удаляясь от него дальше, называются полусходящимися. Упо-
Употребление их часто удобнее^чем употребление сходящихся рядов.
Но, конечно, они имеют тот недостаток, что, пользуясь ими,
нельзя получить сколь угодно большого приближения, как для
сходящихся рядов, а только приближение до определенного пре-
предела. Тем не менее уже при не слишком больших значениях N
полусходящиеся ряды уп и ап оказываются более удобными для
определения приблизительных значений интегралов Френеля, чем
сходящиеся ряды Г и 2. Например, при к = 2 в сходящихся
рядах A86) и A87) нужно взять очень много членов, чтобы сде-
сделать колебания суммы достаточно малыми; в то же время остаточ-
остаточный член R разложения в расходящийся ряд, в котором на осно-
основании A95) надо положить п = 2, имеет значение согласно A94):
Эта величина уже достаточно мала сравнительно с единицей,
и при известных условиях ею, несомненно, можно пренебречь.
§ 48. Возвратимся теперь к задаче определения интенсивности
света У в точке А, где наблюдается явление дифракции. Для
этого вычислим интегралы ens, данные формулой П78). Выра-
Выразим предварительно д через переменную интеграции I, пользуясь
формулой A68). Согласно заключениям § 46 мы должны при ра-
расчете ограничиться точками, находящимися вблизи центральной
в Введение в теоретическую фишку, *. IT.
82 ОПТИКА ИЗОТРОПНЫХ ОДНОРОДНЫХ СРЕД
линии. Поэтому мы можем f — х принять малым по сравнению
с г, и тогда находим для q приближенное значение:
Q = z + ^-^p-. A96)
Отсюда следует:
2я(> 2яг п (f — x)s . 2я2 . я (f — х)*
Вставим это в выражение A78) для с; последнее выражается
тогда через два интеграла:
cos
причем оба эти интеграла должны быть взяты в пределах от
£ = О до | = оо. Введя новую переменную интеграции:
1§ A97)
приходим к интегралам:
^
И ^
~ f cos и* du и ]/~
— оо
Верхний предел их имеет значение, которое принимает и при
= 0, согласно A97), а именно:
Таким образом выражение A78) для с переходит в следующее
где для сокращения положено:
и и
С= J'cosu*du, 5= J'sin и* du. A99)
— оо —оо
Точно так же из A78) находим:
s= -pr[sin-r-C+cos-r-5 .
Уп \ л А I
Отсюда получаем согласно A79а) искомое значение интенсив-
интенсивности:
52). B00)
ДИФРАКЦИЯ 83
Таким образом задача сводится к вычислению интегралов
Френеля С и S, для которых переменная и имеет значе-
значение A98).
Интенсивность света J зависит только от и и, следовательно,
совершенно не зависит от у, что понятно само собой. Мы можем
поэтому ограничиться рассмотрением одной лишь плоскости
чертежа (черт. 12) _у=0. Кроме того, для каждой кривой
~ = const
Vz
интенсивность света имеет постоянную величину. Эта кривая
представляет собой одну ветвь параболы с вершиной в точке О.
В этой точке парабола касается края экрана (оси х) и более
или менее сильно искривлена в ней. Дадим постоянной все зна-
значения от —°° до -f °°. Vz всегда положителен, в то время как
абсцисса х точки наблюдения А может быть положительной или
отрицательной.
Поэтому прежде всего получим г = 0, х < О, т. е. точки»
лежащие непосредственно позади экрана. Затем идет ряд
ветвей парабол, простирающихся в сторону экрана. Далее для
const = 0 получаем положительную ось z, потом ветви парабол,
простирающиеся в сторону, не закрытую экраном, и, наконец,
положительную ось х-ов: z = 0, х > 0. Чтобы получить картину
зависимости интенсивности света У от места А, достаточно пере-
перемещать точку наблюдения А по какой-нибудь, параллельной
оси х, прямой: z = const. Тогда и согласно A98) дает меру для
абсциссы х точки наблюдения, т. е. для расстояния ОР централь-
центральной линии АР от края экрана.
Итак, будем перемещать точку наблюдения А по некоторой
прямой (черт. 12), проходящей справа налево через всю плос-
плоскость чертежа, и будем определять интенсивность с помощью
выражений B00) и A99).
1. Для очень больших положительных значений и, когда
точка А находится далеко справа, например в Ах, можно поло-
положить верхние пределы интегралов A99) бесконечными. Тогда из
A82) и B00) получаем У= 1. Отсюда следует, что на большом
расстоянии от экрана интенсивность света такая же, какая была
бы при отсутствии экрана, как и следовало ожидать.
2. Когда и принимает не слишком малые положительные зна-
значения, то, как мы видели выше, мы можем получить приближен-
приближенное значение интегралов Френеля при помощи разложения
в полусходящиеся ряды. При этом можно итти вплоть до й = 1,5,
так как для этого значения и остаточные члены Rc и Rs, кото-
которыми мы пренебрегаем, при п=\ согласно A94) остаются мень-
меньшими, чем
6*
84 ОПТИКА ИЗОТРОПНЫХ ОДНОРОДНЫХ СРЕД
Чтобы иметь возможность применить формулы A88) и A89),
мы пишем вместо A99):
+О0
С— Г cos u?du— Г cos u*du,
— со u
-f- со 4~°°
S— f sin u* du — f sin u*du.
Тогда, принимая во внимание A82), получаем следующие
приближенные значения для С я S:
С^УТ ~~Г«СО8Й8+ СТ,,Sin U\
, ПГ <20!>
S=*y у — ynsin»a — «recos«a.
Согласно B00) это дает:
/== ~ \тс—2\^пу cos [и? —%\-\-2\^яо sin (и8— — )+у *+<* а-1 B02)
Спросим себя, имеет ли интенсивность света J в каких-нибудь
местах рассматриваемого участка максимум или минимум? Та-
Такие места определяются согласно B00) из уравнения:
Так как на основании A99):
й~ -соей" и
то уравнение B03) переходит в следующее:
й~ -соей" и §-sin«». B04)
Выражение, стоящее в правой части этого уравнения, для
всех рассматриваемых значений и очень мало, следовательно,
уравнение удовлетворяется такими значениями аргумента, кото-
которые близки к одному из чисел ~, у*, у, у,--- Это дает сле-
следующие приближенные значения для
их = ЛГЩ, щ~ЛГ%, tu^V^, u^V—..- B06)
Первое и наименьшее из этих чисел и, = 1,535; оно как раз
лежит в рассматриваемом участке.
дифракция 85
Следовательно, мы имеем в этом участке бесконечное число
максимумов и минимумов интенсивности. Вопрос о том, чтб
именно имеет место, максимум или минимум, решается при помощи
подстановки найденных значений и в B02). Так как уп
и ап — малые положительные числа, то значение / определяется
главным образом членом, содержащим <rnsinlu*—-^J. При этом
знак перед синусом решает вопрос, имеет ли J максимум или
минимум, больше ли оно единицы или меньше. Поэтому J имеет
максимум для мест, где и равно ии щ, %,..., и минимум для
мест, где и равно щ, uit яв,...
Приближенные значения для максимумов и минимумов полу-
получаются из B02) и A90):
Согласно B06) это дает для максимумов:
I . , ?_ j , , 2
для минимумов:
у __ j
По мере роста » места максимумов и минимумов сближаются
друг с другом, как и значения для них интенсивности /. В конце
концов они сливаются между собой.
3. Пусть точка наблюдения А лежит так близко к оси г или
к границе тени экрана, что абсцисса и имеет малые положитель-
положительные или отрицательные значения, примерно между —1,5 и +1,5.
В этом случае для вычисления интегралов Френеля выгодно
применить разложение в сходящиеся ряды. Поэтому пишем A99)
в форме:
0 и
С= /cos и" du+ f cos u'.du,
— со О
0 и
5= / sin к2du+ fsinu'du,
и согласно A83), A84), A85) и B00) находим:
(йа_ £\+]/~^.г.5т(и?— j)+Z*+r*\ B07)
86 ОПТИКА ИЗОТРОПНЫХ ОДНОРОДНЫХ СРЯЛ
Решение вопроса о том, имеются ли в этом участке макси-
максимумы и минимумы для У, находится прежним путем. Оно приво-
приводит к условию:
или, согласно A86):
|)^(Н )а B08)
В этом уравнении первое слагаемое в пределах рассматривае-
рассматриваемого участка (—1,5< и< + 1,5) всегда положительно. Второе
слагаемое меняет свой знак в зависимости от знака и, но его
абсолютная величина никогда не достигает абсолютного значе-
значения косинуса. Чтобы убедиться в ^>том, достаточно вычислить
ряд S для крайнего случая и — 1,5. При этом можно установить
степень приближения, соответствующую взятому числу членов.
Для этого надо вычислить границу для пренебрегаемого оста-
остаточного члена, аналогично тому, как было получено уравне-
уравнение A94).
Вопрос о корнях уравнения -g- = 0 приобретает еще более
наглядное выражение, если зависимость функции / от и пред-
представить геометрически. Последняя вполне определена простыми
уравнениями B00) и B04), вместе с граничными условиями при
и — О. При этом С и 5 можно взять в качестве прямоугольных
Координат некоторой точки; тогда / выразится квадратом рас-
расстояния этой точки от начала координат.
Согласно сказанному выражение B08) имеет во всей рассма-
рассматриваемой области и знак, одинаковый со знаком косинуса, т. е.
оно положительно; таким образом для данной области -gj > 0
и интенсивность света при перемещении точки наблюдения от
отрицательных абсцисс к положительным монотонно возрастает
до достижения первого максимума при н,= щ. В непосредствен-
непосредственной близости от точки Аф лежащей яа границе геометрической
тени согласно B07) и A86):
Следовательно, в самой точке
4. Пусть, наконец, течка наблюдения А смещается влево не
сравнительно большое расстояние от границы тени («<■—1,5),
например в точку As. Тогда мы можем опять обратиться к полу-
полусходящимся рядам.
дифракция 87
При этом пишем:
— к'(и'> 1,5),
-и'
С=» / cos к2 du= I cos и2 du,
— оо и*
—И' оо
S— Г sinusdu=f sinutdu.
К этим выражениям можно применить формулы A88) и A89),
откинув в них остаточные члены. Это дает:
•/-■|(У„2+^2). BЮ)
Условие для максимума или минимума сводится при этом
согласно B03) и B04) к уп — 0. Оно не выполняется нигде, по-
поэтому при возрастании и' интенсивность света все время убы-
убывает. Наконец, для очень больших значений tC находим:
'-та*.
откуда для и = —оо
У = 0.
Полученные нами результаты определяют интенсивность света
и во всех других точках плоскости хг. Это следует из того, что
через каждую точку А рассмотренной нами прямой A2A0At про-
проходит ветвь определенной параболы семейства —р= = const. Во
всех точках этой параболы интенсивность света та же, что
и в точке А, вплоть до особой точки О, где все кривые касаются
одна другой. Следовательно, корда прямая А±АХ приближается
к оси х, все время оставаясь ей параллельной, то максимумы
и минимумы / сближаются все теснее между собой, не изменяя
своей величины; когда же прямая совпадает с осью х, то все они
сосредоточиваются в одной точке О, причем отрицательная ось х
представляет собой ветвь параболы с интенсивностью, равной
нулю, а положительная—с интенсивностью, равной единице.
Это вполне соответствует тем предпосылкам, из которых мы
исходили в § 43 при применении принципа Гюйгенса.
§ 49. Перейдем теперь от общего случая дифракции Фре-
Френеля к частному случаю дифракции Фраунгофера. При этом
мы воспользуемся замечаниями, сделанными в конце § 45. Явле-
Явления дифракции Фраунгофера представляют гораздо больший
интерес для практической оптики, чем явления дифракции Фре-
Френеля, и математическое исследование их значительно доступнее.
Исходной точкой в данном случае служат опять уравнения
A64) и A65), которые справедливы дли плоского дифракцион-
дифракционного экрана с перпендикулярно падающим на него светом. Но
88 ОПТИКА ИЗОТРОПНЫХ ОДНОРОДНЫХ СРЕД
теперь мы вводим специальное допущение, что не только светя-
светящаяся точка С, но также точка наблюдения А лежат в беско-
бесконечности. При этом мы сохраняем прежние обозначения, т. е.
проводим плоскость х, у в плоскости экрана и обозначаем коор-
координаты дифракционной точки через х, у, z, а координаты
точки отверстия в экране через £, т), £ = 0. В качестве начала
координат берем какую-либо точку отверстия.
Расстояние точки наблюдения от всех точек дифрагирую-
дифрагирующего отверстия должно быть бесконечно велико по сравнению
с линейными размерами отверстия. Поэтому мы приписываем
последнему конечные размеры. Тогда все лучи, идущие от точек
отверстия к точке А, можно считать параллельными между со-
собой. Их направление и определяет положение точки А, так как
величина расстояния точки А от экрана теперь не играет роли.
Поэтому, вместо того чтобы говорить о точке, где наблюдается
дифракция, мы можем говорить о направлении дифракции.
Оно характеризуется двумя полярными углами & и <р, входящими
в уравнения:
^г = sin # • cos 9», — = sin & • sin <p, -r=cos#, B12)
'o "o 'o
где x, у, z и r0 — расстояние О А — безгранично велики. При
подстановке этих выражений в A64) мы можем считать при
интегрировании г в знаменателе и Ь постоянными. В то же время
для отношения -£- изменения числителя имеют существенное
значение. Поэтому пишем:
г» = (х-£)* + (у-ч)а + B- О8 » roa-2*f - 2yv,
Подставив эти значения в A64), находим для С и S следую-
следующие выражения:
причем
с = jp cos2 у / da cos (af +
i » Г } B13)
5 = ~- cos2%-jdosin (af + fa),
2nx 2n sin & cos g> 2ny 2л sin fl sin у « ,~- ..
Величину интенсивности света У, ^ наблюдаемой в дифрак-
дифракционном направлении (#, д>), получаем согласно выражению A65):
У=зС*~М?. B151
дифракция 89
Входящие в B15) интегралы легко подсчитать, так как а и /5
при интегрировании остаются постоянными.
Для дифракционного угла & = 0 (точка наблюдения А лежит
на оси z) а ==/5 = 0, следовательно, также и 5=0. Отсюда мы
получаем „осевую" интенсивность света (т. е. света, распро-
распространяющегося вдоль „оси") с помощью B15) и B13):
^ B16)
где а обозначает величину площади отверстия. Согласно этому
выражению интенсивность света пропорциональна а2, а не а.
Это является парадоксальным, так как количество энергии,
посылаемое источником света через отверстие, должно быть
пропорционально а. Однако, кажущийся парадокс объясняется
тем, что Уо не есть непосредственно излученная энергия, так как
конечное излучение энергии всегда имеет место внутри опреде-
определенного конуса дифракционных направлений, (#, <р\ как уже
было установлено в § 18.
Для изучения явления дифракции абсолютная величина ин-
интенсивности света не имеет значения, поэтому удобнее выразить
ее через интенсивность, наблюдаемую вдоль оси. Тогда полу-
получим вместо B15):
S% B17)
B18)
где С и S имеют новые значения согласно B16) и B13):
С = cos* | • \jdo cos (a£ + /%),
S = cos21 • ^fdtr sin (of +
§ 60. В качестве примера рассчитаем дифракцию через
прямоугольное отверстие. Пусть ширина его Ь и длина его I,
откуда площадь его а =* Ы. Поместим начало координат О
в центре отверстия. Тогда имеем при интегрировании:
2""""" *^* я ^- т "о* t о "^ / ^" "Г *Н" •
Из B18) находим:
2 2
а из B17):
\~2
90 ОПТИКА ИЗОТРОПНЫХ ОДНОРОДНЫХ СРЕД
Таким образом, принимая во внимание B14), мы видим, что
интенсивность света У представляет собою функцию направления
{■&, <р), под которым наблюдается дифракция. Для # = 0 получа-
получается У=У0, как и должно быть. Интенсивность света, наблюдае-
наблюдаемого вдоль оси, является наиболее значительной, так как функ-
функция ^— имеет наибольшее значение для л- = 0. При возра-
возрастающем х интенсивность колеблется между постепенно убываю-
убывающими значениями максимумов и равным нулю минимумом, доходя
до полного исчезновения. При этом У изменяется двояким обра-
образом, так как мы имеем здесь две системы одинаково отстоящих
друг от друга точек, для которых интенсивность света равна
нулю. Одна из них определяется значениями а:
2nx 2n 4л 6я
}J"q b ' b ' b '' '''
другая значениями /?:
о 2лу 2я 4я 6я
гХл III
B20)
Между каждыми двумя точками, для которых интенсивность
равна нулю, лежит максимум, убывающий с возрастанием поряд-
порядкового числа. Сверх того, У постепенно уменьшается вследствие
возрастания дифракционного угла &.
Этот характер изменения интенсивности света можно сделать
доступным наблюдению следующим образом. Пропускают дифра-
дифрагированные лучи сквозь собирающую линзу. Тогда всем откло-
отклоненным по одному направлению (#, <р) лучам соответствует одна
точка в фокусной плоскости линзы. При этом в качестве ди-
дифракционной картины получается согласно сказанному светлый
крест с двумя системами темных полос с обеих сторон, симмет-
симметричных относительно сторон прямоугольника. Чем короче какая-
нибудь из сторон прямоугольника и чем больше длина волны
падающего света, тем дальше друг от друга лежат полосы.
Если прямоугольник длинный и узкий (щель), то полосы одной
системы исчезают и остается только другая система полос,
параллельных длине щели.
Ясно, что эта дифракционная картина не представляет со-
собой изображения дифрагирующего отверстия в том смысле,
в котором употребляется это понятие в геометрической оптике.
В данном случае мы не получаем оптически сопряженных точек
и поэтому здесь нельзя ожидать какого нибудь геометрического
подобия между дифракционной картиной и дифрагирующим
отверстием.
§ 60а. Явление дифракции Фраунгофера имеет практическое
значение для случая большого числа конгруэнтных дифраги-
дифрагирующих отверстий. Пусть у нас имеется N тождественных от-
отверстий произвольной формы, произвольным образом располо-
расположенных на экране, но одинаково ориентированных. Тогда интен.
ДИФРАКЦИЯ 91
сивнссть дифрагированного света J можно на основании
простого соображения выразить через интенсивность Jt дифра-
дифрагированного света от одного отверстия. Для этого выразим
координаты f, rj точки я'-го отверстия через координаты произ-
произвольно выбранной точки этого отверстия Оп, взятой в качестве
начала отсчета. Получим:
S =£. + ?, Ч^Ч. + Ч', B21)
где £„ и rjn суть координаты точки Оп относительно общего,
любым образом выбранного, начала координат О. Точки О„ во
всех других отверстиях мы берем в местах, соответствующих
данной выбранной точке Оп. Тогда каждый из двух интегралов
в B18) распадается на N интегралов, распространяемых на одно
отверстие с одинаковыми для всех интегралов пределами для
£' и j/. Таким образом мы получаем:
С = cos» |42/ fdrdr>'COS ta(f- + Г) +^rln + v')}- B22)
Суммирование здесь относится к индексу п, интегрирование
производится по координатам £' и г/. Оба эти действия совер-
совершенно независимы друг от друга и поэтому могут быть пере-
переставлены между собой. Положим для сокращения, аналогично B18):
cos2 f- • 1 f fdfdri' cos (af' + M) = Cu I
> B23)
cos21 ■ к ffdrdr>sin {ai'+pr>r)=5i>!
причем мы будем впредь обозначать индексом 1 величины, от-
относящиеся к одному отверстию. Положим также:
a=N-at B24)
и
B25)
sin (aSn + fan)
n=l
Согласно B22) получим:
С = jy (СКСг —
Точно таким же образом найдем:
92 ОПТИКА ИЗОТРОПНЫХ ОДНОРОДНЫХ СРЕД
Тогда находим согласно B17):
и, наконец, на основании B16) и B24):
J = ■/« (Cia + V) (<V + 5/). B26)
В соответствии с B17) мы можем также написать:
J^MCJ + SJ). B27)
Это простое соотношение дает возможность получить зна-
значение интенсивности света, дифрагированного системой отвер-
отверстий, зная интенсивность света, дифрагированного одним отвер-
. стием. Таким образом мы видим, что применение многих отвер-
отверстий не вызывает ни изменения распределения света в дифрак-
дифракционной картине, ни увеличения размеров ее. При этом меняется
исключительно величина интенсивности света сравнительно
с дифракционной картиной от одного отверстия. Но коэфициент
усиления интенсивности света может иметь, как мы увидим,
весьма различные значения, смотря по тому, расположены ли
отверстия на экране в определенном порядке или нет. Действи-
Действительно, согласно B25):
N N—1 N
2 2
N JV-1 iV .
^ 2
л=1 л=1 п'=т
JV-1 JV
= N + 2 J] 2 cos <a(f"' ~ *J + Pi4* — 4jl B28)
П—\ 7/=n+l
Пусть отверстия расположены совершенно беспорядочно,
как, например, когда отверстия проделаны на карте случай-
случайным образом одной и той же иглой. Тогда все члены двойной
суммы имеют частью положительные, частью отрицательные
значения. Поэтому величина суммы будет иметь значение, очень
малое по сравнению с первым членом (равным N). В результате
этого получается, что интенсивность дифрагированного света
согласно B27) в N раз сильнее света, дифрагированного одним
отверстием, если не считать местных колебаний.
Совершенно другой результат получится в случае правильно
расположенных отверстий. Пусть, например, точки Оп так распо-
расположены, что для определенных значений а и /3 все встречаю-
встречающиеся в B28) углы оказываются кратными 2jt. Тогда двойная
ДИФРАКЦИЯ 93
сумма превращается в N(N— 1) и, таким образом, при большом N
она имеет порядок величины Л/2.
Это своеобразное явление объясняется следующим образом.
При неправильном расположении отверстий лучи, отклонен-
отклоненные N отверстиями в определенном направлении, незначительно
интерферируют между собой, так что их интенсивности просто
складываются друг с другом. Наоборот, при правильном распо-
расположении отверстий эти N лучей могут иметь одну и ту же фазу,
так что складываются не интенсивности их, но абсолютные значе-
значения амплитуд напряжения поля. Так как результирующая интенсив-
интенсивность измеряется квадратом результирующей амплитуды, то она
в N2 раз больше интенсивности света от одного отверстия. Такое
большое изменение интенсивности света и обусловливает прак-
практическое значение дифракционных явлений Фраунгофера.
§ 51. Проведем еще подсчет для случая дифракции от ре-
решетки. Пусть Ъ — ширина отверстия щели, с—так называемая
постоянная ре'шетки, т. е. расстояние между соответствующими
точками двух соседних щелей. Последнее равно сумме ширины
щели и расстояния между двумя соседними щелями. Мы можем
в B25) считать все г\ равными нулю, в то время как
Суммирование обоих тригонометрических рядов B25) значи-
значительно упрощается, если мы вспомним, что выражение CJ + Sjf,
которое нас интересует, представляет собою квадрат абсолют-
абсолютного значения комплексной величины:
Л=1
Умножая на сопряженное мнимое выражение, мы получим
искомую величину. Таким образом согласно B27) интенсивность
дифракционного света:
У-Л-7~- B29)
sin2.-—
£
Максимумы интенсивности имеют место для:
_ 2п in 2tm
0
<230>
Их расстояния друг от друга равны между собой, прямо
пропорциональны длине волны и обратно пропорциональны по-
постоянной решетки. Свет, распространяющийся вдоль оси (# = 0),
имеет общий максимум для волн любой длины. Разложение на
цвета появляется лишь при ближайшем максимуме, для л=1,
т. е. в спектре первого порядка.
94 ОПТИКА ИЗОТРОПНЫХ ОДНОРОДНЫХ СРЕД
Значение максимума интенсивности для всех порядков равно
./V2/,. При этом нужно заметить, что множитель Jt в B29), обо-
обозначающий интенсивность света дифракции от одной щели,
не постоянен, но в свою очередь зависит от дифракционного
угла и ширины щели b согласно уравнению B19). Поэтому
решетки с одной и той же константой оказываются часто весьма
различными. Если, например, промежуток между двумя сосед-
соседними щелями равен по величине ширине щели (с = 2Ь), то точки,
для которых Jt согласно B20) равно нулю, совпадают с макси-
максимумами для четных значений порядка п в B30). Поэтому в ди-
дифракционной картине такой решетки отсутствуют все спектры
четного порядка.
ЧАСТЬ ВТОРАЯ
КРИСТАЛЛООПТИКА
ГЛАВА 1
ПЛОСКИЕ ВОЛНЫ
§ 52. Оптика кристаллов основывается на тех же уравнениях
электромагнитного поля A), B) и C), которые лежат в основе
оптики изотропных сред. Единственное различие состоит в том,
что связь между электрической индукцией D и напряжением
электрического поля Е, представляющая собой для изотропных
сред простую пропорциональность D), для кристаллов выражается
в более общей форме. Именно каждая компонента электриче-
электрической индукции является определенной линейной однородной функ-
функцией компонент электрического напряжения:
B31)
где константы е зависят от природы кристалла. Чем более высо-
высокой симметрией обладает кристалл B, § 26), тем большее число
соотношений существует между этими компонентами. Для пре-
предельного случая изотропного вещества еп = 623 = е^, а все ос-
остальные s—нули; в этом случае B31) переходит в D).
Однако и при отсутствии всякой симметрии из девяти вели-
величин е только шесть являются независимыми. В этом можно убе-
убедиться, применяя принцип сохранения энергии к какому-либо
электромагнитному процессу, происходящему внутри кристалла.
Именно, если мы выделим внутри кристалла некоторый объем и
применим к нему принцип сохранения энергии, как в 3, § 9, то по-
получим для энергии, втекающей в этот объем за промежуток времени
dt через все элементы поверхности da, величину [ср. 3, B5)]:
dtj doSJ=* — dtfdt • div S.
Применяя к этому выражению C) и A), приведем его к виду:
£п f dx (EJD. + EyDy + Ер, + Hji. + HyHy + ЯД). B32)
96 КРИСТАЛЛООПТИКА
Согласно принципу сохранения энергии эта величина должна
равняться изменению электромагнитной энергии, находящейся
внутри выделенной*части кристалла. Как видим, полученное вы-
выражение, так же как и для изотропных сред, состоит из двух ча-
частей, соответствующих электрической и магнитной энергии. Из-
Изменение плотности электрической энергии за бесконечно малый
элемент времени равно:
i {EadDx + EydDy + E,dD,), B33)
а изменение плотности магнитной энергии:
■^ (//. dHtt + Hv dHy + Н. dHz). B34)
В то время как плотность магнитной энергии, как указывает
сравнение с 3, C), в точности равна плотности этой энергии в изо-
изотропной среде с проницаемостью fi — l, плотность электрической
энергии принимает для кристалла гораздо более сложное выра-
выражение, так как подстановка B31) в B33) и интегрирование дают
для нее квадратичную форму от компонент электрического на-
напряжения/коэфициентами которой являются константы е. Но для
того чтобы интегрирование вообще было возможно, необходимо
чтобы козфициент при EadE,, был равен коэфициенту при EydEce
т. е. должно иметь место соотношение е1Я = %; точно так же
ДОЛЖНО быТЬ «Э3 = е82. е31=е18.
Тогда плотность электрической энергии равна:
~ («„£■.■ + еи£,« + eJ5* + 2е1В£Д, + 2ЧзЕуЕг + г^ВД)- B35)
Это выражение можно еще упростить, если в качестве осей
координат выбрать три взаимно перпендикулярные направления,
представляющие собой главные оси эллипсоида, определяемого
тензором B35). Они представляют собой три „главных оси" кри-
кристалла. В этом случае выражение для плотности электрической
энергии принимает форму:
Связь между электрической индукцией и напряжением элек-
электрического поля выразится тогда проще:
DX=HEX, Dy-4Ey, D^eaE,. B37)
Три постоянные, входящие в состав B36) и B37), называются
,главными диэлектрическими постоянными"; они всегда положи-
положительны. В дальнейшем мы будем пользоваться в качестве коор-
координатных осей исключительно главными осями.
ПЛОСКИЕ ВОЛНЫ 97
§ 53. Разберем теперь, возможны ли линейно поляризованные
волны в кристалле, и если возможны, то каким законам они
подчиняются. Для ответа на эти вопросы найдем выражения для
компонент поля такой волны и подставим их в уравнения поля
A) и B).
Пусть п будет нормалью плоской волны, a, /J, у— ее направ-
направляющие косинусы, так что
п = ах + 0у + yz; B38)
D — величина электрической индукции, £, »?, С — ее направляю-
направляющие косинусы, и, таким образом:
DS = DC; B39)
Е — напряжение электрического поля, (■', rf, £'—его направляющие
косинусы; имеем:
£■. = £■£', Ея=>Еч', Е,^ЕЦ\ B40)
наконец, Н—величина напряжения магнитного поля; Я, ц, v —
его направляющие косинусы, так что
Н.ГНК Н, = Нр, //, = №. B41)
Плоская линейно поляризованная волна определяется тем
условием, что величины D, Е и Н зависят кроме времени только
от расстояния п, причем все перечисленные направляющие коси-
косинусы остаются неизменными.
В этом случае уравнения поля A) принимают вид:
дН
B42)
B43)
Эти уравнения дают возможность ответить на все постав-
поставленные вопросы. В них через с0 обозначена скорость света в
пустоте, так как символ с впоследствии (§ 55) будет использован
в другом смысле.
§ 64. Направления векторов, характеризующих плоскую ли-
линейно поляризованную волну, могут быть определены из урав-
уравнений B42) и B43). Из них следует, что электрическая индук-
7 Введение в теоретическую физику, ч. IV.
98
КРИСТАЛЛООПТИКА
ция направлена перпендикулярно к волновой нормали и к
напряжению магнитного поля:
D_Ln и DJ_H. B44)
Из B43) следует далее, что напряжение магнитного поля на-
направлено перпендикулярно к волновой нормали и к напряжению
электрического поля:
Н1п и HJ_E. B45).
Эти положения являются следствиями уравнений поля B) и
получаются путем подстановки в них значений компонент напря-
напряжения поля. Кроме того, согласно C) вектор луча S направлен
перпендикулярно к напряжению элек-
В
трического поля
нитного поля:
и к напряжению маг-
SJL.E и SJ_H.
B46)
Все эти соотношения можно объеди-
объединить в одном положении, что напряже-
напряжение магнитного поля перпендикулярно
ко всем остальным векторам, т. е. по-
последние лежат в одной плоскости, при-
Черт. 13. чем электрическая индукция D перпен-
перпендикулярна к волновой нормали п, а на-
напряжение электрического поля Е перпендикулярно к лучу S.
Это соотношение уясняется черт. 13, в котором плоскость
чертежа пернендикулярна к напряжению магнитного поля, на-
направленному от рисунка к читателю; она называется, как и в слу-
случае изотропных сред, „плоскостью колебаний" (§ 9). В плоскости
колебаний находятся, таким образом, волновая нормаль, луч и
нормальные к ним электрическая индукция и напряжение элек-
электрического поля.
Мы видим, что направление напряжения магнитного поля играет
особую роль. Это объясняется тем, что направление его совпа-
совпадает с направлением магнитной индукции, в то время как на-
направление напряжения электрического поля, вообще говоря, не
совпадает с направлением электрической индукции. Если угол
между электрическим напряжением и электрической индук-
индукцией обозначить через д, то д будет также углом между лу-
лучом и нормалью волны, и так как главные диэлектрические по-
постоянные в B37) положительны, то й < —.
Физическое значение этого различия между направлениями
луча и нормали можно уяснить при помощи следующего рассуж-
рассуждения. Представим себе, что плоская волна ограничена с боков.
Для этого вырежем из одной из ее волновых плоскостей конеч-
конечный участок DA (черт. 13) и из каждой точки его проведем све-
световой луч под углом д к нормали. Совокупность этих всех лу-
ПЛОСКИЕ ВОЛНЫ У9
чей, исходящих из точек участка DA, образует световой цилиндр,
наклонный к плоскости волны. На черт. 13 сечение плоскости
волны цилиндром в различных местах его от ОА до РВ наме-
намечено пунктирными параллельными линиями.
Величина 8 согласно ее определению задана условием:
cos 8 = £Г + щ' + СС > 0. B47)
Кроме того, если обозначим направляющие косинусы луча S
через а', р у', то
COS д = аа' + #3' + у/. B48)
Входящие в эти уравнения величины £, ц, С, а, Р, у вместе с на-
направляющими косинусами Я, p.,v напряжения магнитного поля пред-
представляют собой косинусы трех взаимно перпендикулярных на-
направлений. То же относится и к £', »/, С; а', /?', у' и Я, р, v.
§ 55. Теперь мы перейдём от направлений рассматриваемых
векторов к их величинам. Для этого освободимся от направляю-
направляющих косинусов возведением в квадрат и сложением уравнений
B42) и B43). Сумма квадратов величин, стоящих в скобках в B42),
дает единицу, так как Н _L п. Для соответствующей суммы в B43)
это не имеет места, так как Е не перпендикулярно п. Эта сумма
квадратов равна:
- (Г2 + V'2 + С'2) • («2 + £2 + У2) - (Г« + г)'Р + С»2 =
= 1 — sin2d=cos2d.
Следовательно, мы получаем соотношения:
^ " с* (ж)' и Й* - 'о2 (^J- cos* 8. B49)
Следует обратить внимание на знаки при извлечении корня.
Их мзжно определить, рассматривая какой нибудь частный слу-
случай, например случай, когда нормаль направлена по оси х, элек-
электрическая индукция D — по оси у, а магнитное напряжение—по
оси z. Тогда а = 1, р = 0, у = 0, £ = 0, »? = 1, С = 0, Я = 0, ц = 0,
у=. 1, 9j' = cos й и уравнения B42) и B43) переходят в
Z> = -cog, Н = -с0со*д§. B50)
Эти соотношения согласно B49) имеют место и в общем случае.
Исключим из них Н, продиференцировав первое уравнение
ио t, а второе по п. Получим:
Wdfr B51)
С другой стороны, из B57) следует:
D • £ = е3 - ЕС'.
7*
100 КРИСТАЛЛООПТИКА
Выразив величину D через Е при помощи одного из этих со-
соотношений и вставив ее в B51), получим для Е знакомое вол-
волновое уравнение F) в форме:
причем квадрат скорости распространения света gz имеет следую-
следующее значение:
Введя „главные скорости распространения":
ei £a ea
получим:
f?* — fa* cos 0, r] 'q* = ф* cos д, £'q* =• Cc8cosd. B54)
Диференциальное уравнение B52), как известно B, § 35), имеет
решение:
£•=/(*-у), B55)
где /— произвольная функция аргумента t ~; она определяет
B56)
B57)
B58)
Таким образом, если найдено значение q, удовлетворяющее
всем трем уравнениям B54), то это значит, что в кристалле воз-
возможна волна произвольной формы, направления распространения
и поляризации которой связаны друг с другом определенным
образом.
§ 66. Посмотрим теперь, можно ли найти такие выражения
для различных констант, которые бы удовлетворяли всем необ-
необходимым условиям и прежде всего уравнениям B54).
Легко видеть, что, взяв какое-либо направление электриче-
электрической индукции D, мы тем самым однозначно задаем все осталь-
остальные величины. Для нахождения величины q умножим каждое из
уравнений B54) на £, q, £ и сложим; приняв во внимание B47),
получим:
- - B59)
форму
Из
и при
волны.
уравнения B55)следует:
дЕ
дп ~ '
1
подстановке в B50) получаем
И— -^-
ч
• COS
• COS
дЕ
dt
:
й-
д-
Ё,
Е.
ПЛОСКИЕ ВОЛНЫ 101
Далее, из B54) получается направление напряжения поля Е
£': ?':£'- аЧ: Ъ*ц: сЧ. B60)
Но направления D и Е дают нам плоскость колебаний, а зна-
значит, и перпендикулярное к ней направление Н, а также и напра-
направления п и S. Таким образом волна определена полностью кроме
.ее формы, которая остается произвольной.
Теперь выведем выражения для направляющих косинусов вол-
волновой нормали а, /?, у. Так как волновая нормаль п лежит в од-
одной плоскости с напряжением поля Е и индукцией D, то ее на-
направление определяется условием:
а :0: у = (f'
где х обозначает определенное число. С другой стороны, волно-
волновая нормаль перпендикулярна к индукции, следовательно:
a£+pri + y£ = O. B61)
Отсюда, приняв во внимание B47), получаем:
х = — cos 8.
Следовательно:
а:/?:у «=(£' — fcos<5):(j/ — vcos8):(£' — Uos8).
Из этого следует согласно B54):
bz — tf2)>?:(с2 - tf2K- B62)
§ 57. Поставим теперь вопрос, насколько определена пло-
плоская волна, если задано направление волновой нормали. В дан-
данном случае дело сводится к тому, чтобы выразить все величины
при помощи а, р, у, а для этого, как мы видели, достаточно
определить направляющие косинусы вектора индукции $, rj, С.
Они получаются из B62):
*:**--^:-p^:-s^r. B63)
Остающаяся в этом уравнении неопределенной скорость рас-
распространения q находится согласно B61) из уравнения:
Я -^+^ = 0. B64)
Как показывает исследование подобного уравнения C, § 25),
корни его дают два действительных положительных значения
для q2. Вместе с этим и q получает два действительных поло-
положительных значения. Оба они лежат в двух интервалах, ограни-
ограниченных значениями постоянных а, Ь, с. Назвав их qx и q2, можно,
не уменьшая общности, положить, что
B65)
102 КРИСТАЛЛООПТИКА
Каждому из двух значений qt и дл соответствует согласно B63)
определенное направление индукции Du и D2, а этим согласно
§ 56 уже определены направления всех остальных векторов, ха-
характеризующих волну.
Направления индукции Dt и Da, соответствующие одной и
той же волновой нормали а, /S, у, находятся в простом соотно-
соотношении друг с другом, а именно: если в уравнение B61) подста-
подставить для £, г), £ значения £„ щ, £v а для a, р, у значения B62),
выражаемые через q2 и £z, V& t%, то получается:
Таким же образом получается:
(а2 - д& £tf 2 + (й2 - qt*) вд2 + (с2 - ft2) £& = 0.
Отсюда вычитанием получаем:
fA + 4.4« + tit»«0, B66)
a2 fifa + & пы + с2 £Л = 0. B67)
Из первого уравнения следует, что D!_LD^ из второго, что
_LEa и D2 J_Ei. Отсюда получается также, что Hi II D2 и Н2 || ГХ^
§ 58. Связь между всеми этими направлениями и соответ-
соответствующими величинами скоростей распространения qx и qu мо-
может быть наглядно представлена при помощи так называемого
„эллипсоида поляризации" Коши. Этот эллипсоид, уравнение
которого
а2*2 + b*y* + c*z* = 1, B68)
имеет полуоси
JL JL 1
а' ь • Т*
Если мы хотим для какого-нибудь определенного направле-
направления волновой нормали п найти обе соответствующие волны, про-
проводим диаметральную плоскость эллипсоида, перпендикулярную
к п. Тогда направления обеих осей эллипса, полученного в сече-
сечении, дают направления электрической индукции Dt и D2, а вели-
величины, обратные длинам его полуосей, дают соответствующие
скорости распространения дх и q2. Действительно, если вместо
координатной системы х, у, z ввести новую прямоугольную сис-
стему х', У, г' с тем же началом, причем ось z' направлена по
нормали п, а х? и у' по направлениям электрической индукции
Dt и D2, то уравнения преобразования имеют вид:
ПЛОСКИЕ ВОЛНЫ 103
Подставив эти выражения в B68) и положив г' = 0, получаем
на основании B67) уравнение полученного в сечеиии эллипса в
форме:
(аг!г* + b V + c2d V2 + (аЧ2а + &2%2 + сЧЯУ* =• 1,
откуда согласно B59) получаются дг и q2 как величины, обрат-
обратные полуосям.
Так как напряжение магнитного поля Н перпендикулярно к
п и к D, то каждая из осей полученного в сечении эллипса дает
также направление магнитного напряжения, соответствующее
электрической индукции, направление которой совпадает с дру-
другой осью. В то же время направление напряжения электрического
поля Е согласно B60) задается нормалью к эллипсоиду в конце
той оси, которая определяет электрическую индукцию. Наконец,
направление Луча S определяется, касательной к эллипсоиду, ко-
которая лежит в плоскости колебаний, определенной данными п,
D и Е.
Когда одна из главных осей кристалла, например ось х, яв-
является волновой нормалью, то две другие оси у и z дают на-
направление индукции с соответствующими скоростями распростра-
распространения b и с.
Все эти положения, конечно, сохраняют свою силу и в случае,
когда a = b = c. Тогда среда оптически изотропна, эллипсоид по-
поляризации превращается в сферу, эллипс сечения переходит в
круг, каждый диаметр которого является осью, а скорость рас-
распространения q—a.
§ 59. До сих пор мы задавались значениями а, /?, у и вычис-
вычисляли соответствующие величины qt и qz. Но может быть случай,
когда заранее заданы значения qx и да [разумеется, внутри гра-
границ B65)] и требуется найти соответствующие значения а, /3, у
для волновой нормали.
Для решения этой задачи уравнение B64) напишем в следую-
следующей форме:
а2 (й2 — $2) (с2 — q*) + P* (с2 — q*) (а2 — qz) + у» (аа—q*) (b* — ?2)=
B69)
Это равенство выражает, что qt и q% являются корнями урав-
уравнения B64). Смотря по тому, положим ли мы q равным a, b
или с, получим из B69):
2 (a" — q-f) • (a* — t
B70)
Таким образом аа, jS2 и у* определены, если заданы qt и qz.
Легко убедиться при помощи B65), что значения направляющих
104 КРИСТАЛЛООПТИКА
косинусов а, р, у получаются всегда действительные. Эти зна-
значения определяют в зависимости от их знака восемь различных
направлений, лежащих каждое в особом октанте координатной
системы, оси которой совпадают с главными осями, или, — если
объединить вместе каждые два противоположных направления,—■
четыре различных направления. Значениями а, /3, у определяются
согласно § 58 направления электрической индукции и т. п., со-
соответствующие данным qt или д2.
Особенно интересен частный случай, когда qx = qs. Тогда со-
согласно B65):
qi = qz = b, B71)
и направляющие косинусы соответствующей нормали:
"о л— С2 + £2 > го — "» Уо — а^ч?"
Эти. уравнения определяют четыре направления, лежащих в
плоскости х, г. Из них два, образующие острые углы с осью z,
которой соответствует наименьшая скорость распространения, на-
называются „оптическими осями" кристалла. Для них имеет место:
е|. B73)
Кристалл называется „оптически положительным", если обе
оптические оси образуют между собой острый угол. В этом
случае у0 > у j, откуда
*->^. B74)
В противном случае кристалл называется „оптически отрица-
отрицательным".
В эллипсоиде поляризации Коши оптические оси образуют
нормали двух, проходящих через ось у диаметральных плоско-
плоскостей, которые рассекают эллипсоид по кругу с радиусом -g. Так
как круг имеет бесконечное множество направлений осей, то
волна, нормаль которой совпадает с оптической осью, имеет беско-
бесконечное множество направлений электрической индукции, так же
как и в изотропной среде. Поэтому можно сказать, что в случае
совпадения оптической оси кристалла с волновой нормалью кри-
кристалл ведет себя в известной степени, как изотропное тело.
Однако между изотропным телом и кристаллом для этого
случая имеется и существенная разница. В изотропном теле на-
напряжение электрического поля совпадает с направлением индук-
индукции, а следовательно, и луч с направлением нормали; в кри-
кристалле же электрическое напряжение, т. е. нормаль к эллипсоиду
поляризации в какой-нибудь точке круга сечения, в общем слу-
случае не совпадает с электрической индукцией, т. е. с радиусом
ПЛОСКИЕ ВОЛНЫ 105
круга в этой точке. Более того, каждому из бесконечного мно-
множества направлений индукций соответствует свое особое напра-
направление напряжения поля и свое особое перпендикулярное к нему
направление луча. Таким образом, когда оптическая ось является
волновой нормалью, то ей соответствует бесконечное множество
лучей, расположенных по образующим некоторого конуса. Среди
образующих этого конуса находится также и сама оптическая
ось, потому что в точке круга сечения, лежащей на оси у, нор-
нормаль к эллипсоиду совпадает с радиусом круга, т. е. напряжение
электрического поля совпадает по направлению с электрической
индукцией, а следовательно, и луч с волновой нормалью.
Когда из трех главных скоростей распространения а, Ь, с две
равны между собой, кристалл называется „оптически одноосным"
ипритом согласно B74) „положительным", если а = Ь>с, и
„отрицательным", если а > b = с.
Для численного расчета обычно применяют не значения глав-
главных скоростей распространения, но значения „главных показа-
показателей преломления". По отношению к вакууму они равны:
-£ = /!„- ■£ = «* £=я. B75)
или согласно B53):
«г = \ Ч» «г = \Ч 1 «з = \ Ч • B76)
При этом согласно B65):
пх < п2 < п3.
При я, = »а кристалл положительный одноосный, при »2 = и3 он
отрицательный одноосный.
Оптические свойства кристалла тесно связаны с его упругой
структурой, так как каждый род кристаллографической сим-
симметрии влечет за собой соответствующую симметрию в оптиче-
оптическом отношении. Поэтому кристаллы асимметрической, моносим-
моносимметрической и ромбической систем B, § 26) оптически двуосны
(топаз — положителен, арагонит, слюда — отрицательны), а кри-
кристаллы гексагональной и тетрагональной систем оптически одно-
осны (кварц, лед, циркон — положительны, исландский шпат,
турмалин —отрицательны). Кристаллы правильной системы опти-
оптически изотропны (каменная соль, сильвин).
§ 60. Физическое значение скорости распространения q ста-
становится особенно наглядным при рассматривании черт. 13 (§ 58).
Положим, что плоскость волны ОА за единицу времени пере-
переместилась в РВ. Тогда величина q будет представлена соответ-
соответствующим приращением нормали и, т. е. отрезком OQ. Если
измерять скорость не по направлению нормали, а по направле-
направлению луча, то она определяется отрезком ОР, который мы обо-
обозначим q'.
106 КРИСТАЛЛООПТИКА
Между обеими скоростями имеет место соотношение:
i' f277)
Целесообразность принятого здесь обозначения ясна из того
обстоятельства, что каждое из полученных нами соотноше-
соотношений между направляющими косинусами и скоростями распро-
распространения сохраняет свое значение, если в них заменить все
штрихованные направляющие косинусы соответствующими не-
штрихованными и наоборот, и, кроме того, q заменить через —,
q' — через— и а, Ь, с— через — , -j , — . При этом направле-
направление магнитного напряжения А, /л, v остается неизменным, так же
как и угол 8. Справедливость изложенного делается ясной, если
вспомнить, что согласно § 54 для штрихованных направляющих
косинусов имеют место те же соотношения, как и для нештрихо-
ванных, и что уравнения B54), служащие для определения ско-
скорости распространения q, остаются согласно B77) справедливыми,
если в них произвести указанную замену.
В этом обстоятельстве выражается имеющий повсюду место
дуализм, представляющий собою общий принцип взаимности,
который часто может быть использован для получения новых
соотношений, характеризующих волну. На основании принципа
взаимности мы можем без вывода высказать ряд положений,
которые но своему значению не уступают ранее рассмотренным.
Важнейшие из них мы здесь приведем.
Каждому направлению луча а', /3', у соответствуют скорости
распространения дх' и q/, причем
a>ql'>b>qs'>c. B78)
Эти значения скоростей являются корнями уравнения:
Они равны по величине полуосям эллипса, который полу-
получается при пересечении эллипсоида
диаметральной плоскостью, перпендикулярной к направлению и,
Р', у'. Направления осей эллипса дают направления соответствую-
соответствующих электрических напряжений, в то время как направление
электрической индукции совпадает с нормалью к эллипсоиду в
конечной точке оси. Направление волновой поймали опреде-
определяется касательной в этой точке к эллипсоиду, лежащей в плос-
плоскости колебаний, которая в свою очередь определяется лучом
и напряжением электрического поля. Напряжение магнитного
ПЛОСКИЕ ВОЛНЫ 107
поля перпендикулярно к плоскости колебаний, следовательно,
совпадает с другой осью эллипса.
Обратно, каждым двум произвольно заданным, удовлетворяю-
удовлетворяющим условиям B78) значениям <// к q2' соответствуют восемь
рчправлений луча, из которых каждые два друг другу противо
положны. Они определяются следующими уравнениями:
с-') • (о2 — с-) ' !
Чх Яг'~ №2 — с") ■ (о2 — а-)
Если <7i' и ^й' одинаковы, то согласно B78):
?/ = а2' = Ъ. B82)
В этом случае уравнения B81) определяют особые направле-
направления луча, которые называются „вторичными оптическими осями"
кристалла:
«о =±7Г
А/= () = &, [ B83)
Эти оси являются нормалями двух проведенных через ось у
диаметральных плоскостей, которые пересекают эллипсоид B80)
по кругам радиуса Ь. Сравнение с направляющими косинусами
Go> f'oj Уо первичных оптических осей показывает, что угол с
осью z для вторичных осей меньше, чем для первичных, следо-
следовательно, вторичные оси расположены ближе к оси z.
Для одноосных кристаллов эти оси совпадают с первичными
осями, причем у положительных кристаллов (а = Ь) они совме-
совмещаются с осью г, а у отрицательных (Ь = с) они направлены по
положительной и отрицательной осям л. Вторичной оптической
оси в качестве луча соответствует целый конус волновых нор-
нормалей, к образующим которого принадлежит также и луч. Каж-
Каждой такой нормали соответствует определенная плоскость коле-
колебаний, проходящая через нее и через луч. В этой плоскости
лежат напряжение электрического поля и электрическая индукция.
Само собой разумеется, что все эти положения могут быть
получены непосредственно, без применения принципа взаимности,
если повторить ход мыслей § 56 и следующих за ним, с заменой
всюду нештрихованных величин штрихованными.
108 КРИСТАЛЛООПТИКА
ГЛАВА II
ВОЛНОВЫЕ ПОВЕРХНОСТИ
§ 61. Плоские волны в природе невозможны, хотя бы по
причине их безграничной протяженности в поперечном сечении.
Но плоские волны можно осуществить с определенной, как
угодно далеко идущей степенью приближения при помощи того
же приема, который мы раньше применяли для изотропных сред.
Именно мы представляем себе где-нибудь внутри достаточно
большого кристалла точечный источник света О, который начи-
начинает светить в момент времени t = 0, и называем волновой по-
поверхностью с центром в О ту поверхность, окружающую точку О,
до которой свет успел распространиться за время t. Выбрав
t достаточно большим, мы можем на волновой поверхности вы-
выделить участок произвольной величины, размеры которого малы
сравнительно с расстоянием его от О и который может счи-
считаться плоским. Тогда вся волновая поверхность окажется со-
составленной из таких плоских участков, для каждого из которых
справедливы законы распространения плоских волн.
Тот, кому трудно представить себе точечный источник света
внутри кристалла, может его представить себе находящимся на
поверхности кристалла, откуда свет распространяется внутрь
кристалла. Тогда получатся не полные замкнутые волновые по-
поверхности, но лишь части их, ограниченные поверхностью кри-
кристалла. Для дальнейших рассуждений это безразлично, так как
они будут относиться главным образом к одному плоскому
участку волны.
Такой плоский участок волны распространяется в кристалле
согласно выведенным нами в предыдущей главе законам. Его
скорость и поляризация определяются его положением относи-
относительно главных осей кристалла совершенно таким же образом,
как это имело место для ограниченного участка плоской волны,
который мы на черт. 13 (§ 54) обозначили через РВ. При этом
ОР, так же как и ОБ (так как РВ<^ОР), обозначает направле-
направление луча, OQ—направление волновой нормали, причем OP=q''t,
a OQ = q ■ t. To обстоятельство, что вблизи источника света
волновая поверхность не может быть представлена состоящей
из достаточно больших плоских участков, не создает никаких
затруднений, так как время t можно выбрать столь большим,
что расстояния OQ и ОР могут быть приняты пропорциональ-
пропорциональными времени t.
При помощи таких рассуждений можно полностью опреде-
определить волновую поверхность, соответсгвующую определенному,
достаточно продолжительному промежутку времени t, напри-
например t =1, и притом определить двумя различными способами.
При первом способе используется скорость распространения
по лучу: в произвольных направлениях а', /?', / откладывают
ВОЛНОВЫЕ ПОВЕРХНОСТИ 109
отрезки, равные скорости q'\ тогда все концы Р таких отрезков
образуют искомую волновую поверхность. Второй способ исполь-
использует скорость распространения по нормали: в произвольном на-
направлении а, /3, у откладывают отрезок, равный q, и проводят
через конец Q этого отрезка перпендикулярную к нему плоскость.
Все полученные таким образом плоскости являются касатель-
касательными плоскостями искомой волновой поверхности. Первый спо-
способ дает уравнение волновой поверхности в точечных коорди-
координатах, второй — в плоскостных координатах.
На основе этого построения можно без особых расчетов
установить некоторые свойства волновых поверхностей. Так как
каждому лучу соответствуют два значения скорости распростра-
распространения дгг и q2', то каждая прямая, проведенная из О, пересекает
волновую поверхность в двух точках Рг и Р2, т. е. волновая
поверхность состоит из двух замкнутых поверхностей, из кото-
которых наружная образована точками Pv а внутренняя точками Р2.
Касательные плоскости к волновым поверхностям в точках Р\
и Р2 образуют волновые плоскости, соответствующие лучу OPtPz,
а перпендикуляры к ним — волновые нормали. Но имеются
четыре особых направления, а именно: направления вторичных
оптических осей B83) и направления, им прямо противополож-
противоположные, которые пересекают волновую поверхность только один
раз на расстоянии b от точки О. Таким образом волновая по-
поверхность имеет в плоскости xz четыре особых точки, в кото-
которых встречаются обе замкнутые поверхности. Так как каждому
из особых лучей соответствует бесконечное множество напра-
направлений нормали, то волновая поверхность имеет в особой точке
бесконечное множество касательных плоскостей, т. е. целый
конус касательных, который придает волновой поверхности
вблизи этой точки воронкообразный вид. Внешняя поверхность
волны в этом месте оказывается вогнутой внутрь, внутренняя —
выгнута наружу.
К образующим конуса касательных принадлежит также и
сама вторичная оптическая ось.
С другой стороны, каждому произвольному направлению вол-
волновой нормали соответствуют две перпендикулярные к ней плос-
плоскости волны, проходящие на расстояниях qx и q2 от О. Отрезки,
соединяющие точки касания с точкой О, дают направление и
величину скорости распространения двух соответствующих лучей.
Но имеются четыре особых касательных плоскости, перпенди-
перпендикулярные к оптическим осям B73) и находящиеся на расстоянии b
от точки О, для которых расстояния q1 и qz совпадают по вели-
величине и равны Ь. Каждой такой особой касательной плоскости
соответствует бесчисленное множество лучей, следовательно, и
бесконечное множество точек касания с волновой поверхностью,
т. е. эта плоскость касается волновой поверхности по кривой
Поэтому указанная выше воронка обладает плоским краем, ее
можно полностью закрыть плоским листом. К образующим ко-
110 КРИСТАЛЛООПТИКА
нуса, определяемого кривой касания, принадлежит также сама
оптическая ось.
Все изложенные здесь положения, с необходимостью выте-
вытекающие из рассуждений последних параграфов, получают в даль-
дальнейшем подтверждение и большую наглядность в применении
к частным случаям.
§ 62. Мы составим теперь уравнение поверхности световой
волны в координатах х, у, z для t = I, применив к данному
случаю первый из двух упомянутых методов. Каждая точка вол-
волновой поверхности определяется координатами:
x = ra\ y = rp\ z = ry',
причем
Подставляя отсюда значения а', /3', у' в уравнение B79), по-
получаем уравнение, волновой поверхности:
я*
Эта поверхность, очевидно, имеет центр симметрии О и рас-
распадается на восемь симметричных октантов. Чтобы выяснить
порядок поверхности, умножаем B84) на общий знаменатель.
Получается выражение шестой степени, но легко заметить, что
он содержит множитель г\ и если его откинуть, то получается
из B84):
+ (л? +у* + 2а) (а2*2 + Ь V + Л2) = 0. B85)
Итак, получается поверхность четвертого порядка, что со-
согласуется с тем обстоятельством, что луч, выходящий из точки О,
пересекает ее в двух точках.
Форму поверхности световой волны можно представить себе
всего нагляднее при рассмотрении пересечения ее с тремя глав-
главными плоскостями. Начнем с плоскости х, у. При 2 = 0 уравне-
уравнение B85) переходит в следующее:
(а2й2—а2*2 — Ъ V) (с2 — х% — у*) = 0. B86)
Кривая пересечения волновой поверхности с плоскостью рас-
распадается на эллипс:
1
аг ~ 1
с полуосями b и а и находящуюся внутри него окружность:
с радиусом, равным с.
ВОЛНОВЫЕ ПОВЕРХНОСТИ
111
Эта кривая представлена на черт. 14. Эллипс своими точ-
точками Р, образует след внешней замкнутой поверхности волны,
круг своими точками Ра— след внутренней поверхности. Лучу S,
проходящему через точки Рг и Р2, соответствуют в качестве
плоскостей волны плоскости, касательные к поверхности волны
в точках Рг и Р2. Эти плоскости, конечно, перпендикулярны к
плоскости ху. При помощи их легко могут быть определены обе
соответствующие лучу взаимно перпен-
перпендикулярные плоскости колебаний, про-
проходящие через луч и волновую нор-
нормаль п. Плоскость колебаний в точке Рг
есть плоскость ху\ в точке Р2, для кото-
которой совпадают луч и нормаль,-—это
плоскость, перпендикулярная к первой.
Напряжение электрического поля Е и
электрическая индукция D лежат в
плоскости колебаний, причем первое
перпендикулярно S, вторая перпенди-
перпендикулярно п. В точке Р1 оба эти вектора
лежат в плоскости чертежа (черт. 14),
в Р2 они перпендикулярны к ней и сов-
совпадают между собой. Наоборот, напря-
напряжение магнитного поля Н в Рг пер-
перпендикулярно к плоскости чертежа, а
в Р2 совпадает с ней.
Аналогично можно разобрать кри- Черт. 14.
вые пересечения поверхности волны
с двумя другими главными плоскостями. Разберем сначала пере-
пересечение с плоскостью уг. При х = 0 уравнение B85) переходит в
2_3/2_ 2а)=: Q
B87)
Здесь мы имеем в качестве следа внешней поверхности волны
окружность:
у2 + г2 = а2
с радиусом о, а в качестве следа внутренней поверхности эллипс:
-£+1
с полуосями с и Ь. Соответствующее изображение дано на черт. 15;
оно отличается от черт. 14 только тем, что здесь для точки Р2
внутренней поверхности волны колебания происходят в плос-
плоскости чертежа, а для точки Рг внешней поверхности—в плос-
плоскости, перпендикулярной к ней.
§ 63. Наиболее интересным является сечение волновой по-
поверхности плоскостью xz, т. е. той, в которой лежат наиболь-
наибольшая и наименьшая скорости. Оба конических сечения, по кото-
112
КРИСТАЛЛООПТИКА
рым пересекается плоскость у
определяются уравнением:
В этом
получается
Черт. 15.
= 0 с поверхностью волны B85),
(b^ — zs~-xz) = 0. B88)
эллипс с полуосями с и а и
окружность с радиусом Ъ, пе-
пересекающиеся в четырех дей-
действительных точках, как пред-
представлено на черт. 16. Для
каждого луча, идущего из
точки О к такой точке пере-
пересечения, обе скорости q{ и
q2' совпадают между собой и
равны Ь. Два из этих лучей,
которые образуют с осью z
острый угол, представляют
собою вторичные оптические
оси кристалла. След внешней
поверхности волны предста-
представлен частью двумя дугами
эллипса, выступающими из
окружности, и частью двумя
дугами окружности, выступаю-
щими из эллипса. Для внутренней поверхности волны имеет
место обратное.
Первичные оптические оси, так же
как и вторичные, лежат в плоскости xz
и образуют нормали тех касательных
плоскостей, которые касаются поверх-
поверхности волны по целой кривой. Расстоя-
Расстояние этих плоскостей от точки О равно
Я\ — <7а = Ь. Угол между первичными
оптическими осями согласно B83) боль-
-х ше, чем между вторичными. Кривая ка-
касания представляет собой край описан-
описанной в конце § 61 воронки, встречающий
плоскость чертежа в точках А и В, а
вообще идущий перпендикулярно к пло-
плоскости чертежа. На черт. 16 он обозна-
обозначен пунктиром.
Черт. 16. Идущие от точки О до точек кри-
кривой касания прямые линии образуют
соответствующий оси ОА конус лучей, к образующим которого
относится и сама оптическая ось ОА.
Чтобы найти форму кривой касания, мы будем считать точку С
на чертеже подвижной и будем перемещаться из точки А по пе-
передней части кривой до точки В, а потом по остальной части
кривой обратно в точку А. При каком-либо положении точки С
ВОЛНОВЫЕ ПОВЕРХНОСТИ 113
ОС означает направление луча, плоскость О АС—соответствую-
АС—соответствующую ему плоскость колебаний, а лежащее в ней перпендику-
перпендикулярное к ОА направление АС есть направление электрической
индукции. Длина отрезка АС получается из прямоугольного тре-
треугольника ОАС:
Согласно B47) вследствие перпендикулярности направления
волновой нормали а„, /30, у0 к направлению электрической
индукции i, щ £ имеем:
причем
a^+M + Yif-0. B89
Из этого согласно B60) следует:
AC—h
приняв во внимание, что в данном случае # = Ъ и Р0 = 0,
имеем согласно B59) и B89):
АС = *=^у£. B90)
Этим соотношением искомая кривая касания вполне опреде-
определена, так как для каждого значения направляющего косинуса,
а значит, и для каждого направления прямой АС, вращающейся
около точки А, находим соответствующую величину расстоя-
расстояния АС. Когда С совпадает с А, АС = 0 и С = 0, т. е. касатель-
касательная к кривой в точке А перпендикулярна к оси z, а так как она
также перпендикулярна к оптической оси ОА, то она совпадает
по направлению с осью у, перпендикулярной к плоскости чер-
чертежа. Когда С перемещается в точку В, угол между АС и осью z
уменьшается, причем С увеличивается до своего наибольшего
значения, которое достигается при совпадении С с В. Так как
ABJ_OA, то в этом случае £=а0 и согласно B90):
Г B91)
При обратном движении точки С по другой дуге кривой те же
самые значения будут пройдены в обратном порядке, пока С
опять не совпадет с А. Соотношение B90 получится еще проще,
если ввести вместо С угол CAB. Это угол между направлением
АС (с направляющими косинусами £, г\, С) и направлением АВ (с на-
направляющими косинусами у0, 0, а0). Следовательно:
cos/_ CAB = — yj +a0C
и согласно B89):
сое z. едя-
8 Введение в теоретическую физику, ч. IV >
114 КРИ СТАЛЛООПТИКА
Последнее вместе с B90) и B91) дает:
AC = AB cos Z. CAB.
Из этого следует, что в треугольнике ABC угол С прямой и
кривая касания АСВ является окружностью. Поэтому конус лу-
лучей ОС не является круговым конусом, так как круговое сече-
сечение АСВ перпендикулярно к образующей конуса. Для величины
угла расхождения между лучами конуса получается простейшее
выражение, если обозначить через со угол между лучами ОА и ОВ:
. _ АВ _ о"-с2
и согласно B73):
tgco — р . B92)
Аналогичные положения можно получить при помощи прин-
принципа взаимности (§ 60) для вторичных оптических осей и соот-
соответственно для особых точек поверхности световой волны. В каж-
каждой особой точке особому лучу, идущему к ней из точки О,
соответствует бесконечное множество волновых плоскостей и
волновых нормалей, которые образуют конус с углом со', причем
аналогично B92):
или
tgco =JLi JA L. B9d)
ГЛАВА Ш
ПЕРПЕНДИКУЛЯРНОЕ ПАДЕНИЕ
§ 64. Отражение и преломление света у поверхности кристалла
происходит по гораздо более сложным законам, чем для изо-
изотропных сред, поэтому всего удобнее начать с рассмотрения наи-
наиболее простых случаев. Мы начнем с простейшего случая пер-
перпендикулярного падения монохроматической плоской световой
волны из воздуха на поверхность кристалла, которая может быть
как угодно ориентирована относительно его главных осей.
Согласно принятым нами условиям все точки поверхности
кристалла одновременно и в одной фазе возбуждаются падаю-
падающей волной. Поэтому внутри кристалла волновая плоскость
и волновая нормаль сохраняют свое прежнее направление. Осо-
Особенность заключается в том, что внутри кристалла распростра-
распространяются две волны с вполне определенными скоростями распро-
ПЕРПЕНДИКУЛЯРНОЕ ПАДЕНИЕ 115
странения дг и д2 и вполне определенными направлениями напря-
напряжений поля и индукции, которые можно вычислить из приведен-
приведенных ранее законов, соответственно данному направлению волно-
волновой нормали.
При выходе из кристалла каждая из обеих волн следует
своему собственному закону отражения и преломления. Можно
поэтому использовать различие обеих скоростей распространения
в кристалле, чтобы совершенно разделить обе волны, пользуясь,
например, тем, что одна из них при падении на противополож-
противоположную поверхность кристалла претерпевает полное внутреннее
отражение, в то время как вторая выходит
наружу согласно обычным законам преломле-
преломления. Это имеет место в призме Николя и яв-
является простейшим методом преобразования
естественного света в линейно поляризован-
поляризованный. Рассмотрим теперь шлифованную плоско-
плоскопараллельную кристаллическую пластинку.
В этом случае и при выходе из кристалла
обе волновые плоскости остаются параллель-
параллельными поверхностям пластинки. Так как элек-
электрические индукции обеих волн перпен- Че т 17
дикулярны друг к другу и к волновой '
нормали, то они лежат в плоскости пла-
пластинки. Сечения пластинки в направлении этих двух векторов
называются главными оптическими сечениями пластинки. Через
них проходят плоскости колебаний обеих волн, обозначенные
на плоскости черт. 17, которую надо себе представить парал-
параллельной плоскости пластинки, через / и //. Световые волны
надо представить себе падающими на пластинку сзади и выхо-
выходящими по направлению к читателю. Когда падающий свет
является естественным, тогда и прошедший свет будет есте-
естественным, если пренебречь потерями при отражении, как мы
и будем здесь делать. Но иначе получится, если будет падать
поляризованный свет, например свет, прошедший через призму
Николя, которая в этом случае играет роль поляризатора.
Плоскость колебаний падающего на кристалл поляризованного
света обозначена на черт. 17 ОР и образует угол у с главным
сечением /. При вступлении в кристалл волна расщепляется на
две волны с плоскостями колебаний / и //, скоростями распро-
распространения qx и q& с одинаковыми фазами и отношением ампли-
амплитуд, равным cos у: sin <p (§ 22). Пройдя сквозь кристаллическую
пластинку толщины D, эти две волны выйдут из кристалла
с разностью фаз:
(££Ы B94)
где со обозначает частоту, Яо — длину волны в воздухе, щ и »2—
показатели преломления. Поэтому, слагаясь в воздухе, эти две
волны дают в общем случае эллиптически поляризованную волну,
8*
116 КРИСТАЛЛООПТИКА
(§ 26), направление осей которой существенно зависит от йели-
чины А. Только тогда, когда Л является кратным п, получается
в результате опять плоскополяризованная волна. Если А равно
нечетному числу ^-, оси эллипса имеют направления главных
сечений / и //; если, кроме того, угол <р = j или -— , полу-
получается свет, поляризованный по кругу. Поэтому такая пластинка
соответствующей толщины (например пластинка слюды) предста-
представляет собой простое средство для превращения линейно поляризо-
поляризованного света в циркулярно поляризованный или, наоборот, она
применяется, как компенсатор для анализа эллиптически поляри-
поляризованного света путем превращения его в линейно поляризо-
поляризованный.
Пропустим прошедший сквозь кристаллическую пластинку
свет через вторую призму Николя, действующую в качестве ана-
анализатора, причем оси ее ориентированы так, что она пропускает
только волны с направлением колебаний (черт. 17), образующим
угол у> с главным сечением /. От волны / с амплитудой cos <p
пройдет через анализатор лишь компонента cos ц> -cosy), а от
волны // с амплитудой sin <p пройдет компонента sin <p • sin y>.
Обе эти волны имеют колебания ОА и обладают согласно A01)
следующей интенсивностью, считая интенсивность света, давае-
даваемого поляризатором за единицу:
J = cos2 <p cos2 y> + sin2 <p sin2 y> + 2 cos <p cos y> sin <p sin y> cos А
или
J = cos2 (<р — у>) — sin 2<p sin 2y sin2 у. B95)
Особого интереса заслуживает случай, когда направления
колебаний ОА и ОР взаимно перпендикулярны, т. е. поляриза-
поляризатор и анализатор скрещены. Тогда у — <р + ^ и из B95) полу-
получается:
/!=sin229>sin2-|-. B96)
В атом случае, если Л = 0, то и У = 0. Поэтому прохождение
света сквозь пластинку между двумя скрещенными николями
является доказательством того, что разница фаз А, а вместе
с этим и qx и q, отличны от нуля. Это дает один из самых чув-
чувствительных методов для исследования оптической анизотропии
веществ. Направления главных сечений могут быть в этом слу-
случае непосредственно определены, так как согласно B96) прохо-
проходящий свет имеет максимальную интенсивность при <р= ~ и <р =
= ■£, в то время как при ^ = 0и у = -^ свет, естественно, це-
целиком пропадает.
ПЕРПЕНДИКУЛЯРНОЕ ПАДЕНИЕ
117
Черт. 18.
§ 65. До сих пор при рассмотрении световых волн в кри-
кристалле мы обращали внимание лишь на волновые нормали, но
не на лучи. Это допустимо, пока сечение волны принимается
бесконечным. Но если сечение волны имеет конечные размеры,
то тогда необходимо принять во внимание то обстоятельство, что
энергия волны распространяется не в направлении волновой
нормали, а в направлении луча, как это уже
и было разъяснено в § 54 при помощи черт. 13.
В кристалле определенному направлению
нормали соответствуют в общем случае два
различных луча. Поэтому те две волны, на
которые расщепляется при входе в кристалл
падающий нормально на пластинку плоский
пучок лучей, рано или поздно, в зависи-
зависимости от величины поперечного селения
пучка, разделяются в пространстве и выхо-
выходят из противоположной стороны кристалла
в виде отдельных пучков лучей. Это пред-
представлено на черт. 18. Поэтому кристаллическая пластинка и при
перпендикулярном падении лучей является двоякопреломляющей,
хотя волновые нормали всех лучей как внутри, так и вне кри-
кристалла сохраняют одно и то же направление. Следовательно,
в этом случае преломление определяется не различием двух гра-
граничащих веществ, как в случае изо-
изотропных сред, но обусловливается при-
природой самого кристалла.
§ 66. Особенно интересен случай,
когда кристаллическая пластинка, на-
например из арагонита, отшлифована
перпендикулярно одной из оптиче-
оптических осей кристалла. Тогда плос-
плоскости падающей волны, параллельной
плоскости пластинки, соответствует
бесконечное множество лучей, и луч
после входа в кристалл распростра-
распространяется не по двум направлениям, а по многим, если он перво-
первоначально не был поляризован. В этом случае лучи образуют по-
поверхность конуса, соответствующего оптической оси в качестве
нормали. К образующим конуса принадлежит и сама оптическая ось.
На черт. 19 плоскость чертежа содержит в себе (как и плос-
плоскость черт. 16 в § 36) кроме оптической оси также направле-
направления наибольшей и наименьшей главной скорости распространен
ния, т. е. совпадает с плоскостью xz. Направления ОА и ОБ
обозначают, как и там, оптическую ось и наиболее уклоняю-
уклоняющийся от нее луч конуса. Так как сечение поверхности пластинки
(как особой плоскости касания волновой поверхности) с конусом
лучей дает окружность, то лучи, выходящие в воздух, образуют
поверхность кругового цилиндра, диаметр которого АВ согласна
В
Черт.
118 КРИСТАЛЛООПТИКА
черт. 19 равен D-tgco, где D — толщина пластинки, а со — угол
расхождения лучей конуса-, tgw можно заменить выражением B92).
Описанное явление, которое представляет собой одно из наи-
наиболее блестящих подтверждений теоретической кристаллооптики,
называется „конической рефракцией" и, в частности, „внутрен-
„внутренней" конической рефракцией, так как распадение света на конус
лучей происходит при входе в кристалл.
§ 67. Всякой закономерности, относящейся к направлению
лучей в кристалле, соответствует аналогичная закономерность,
относящаяся к направлению нормалей. Это имеет место и для
только что рассмотренного явления конической рефракции, при-
причем в данном случае это основывается на том,
что двум определенным особым лучам соответ-
соответствуют не две, а бесчисленное множество раз-
различных волновых нормалей. Чтобы осуществить
такой случай, надо получить луч, направление
которого совпадает со вторичной оптической
осью. Для этого может быть следующим обра-
образом употреблена та же пластинка арагонита,
которая употреблялась для опыта, описанного
в предыдущем параграфе.
Помещают точечный источник света О на
ерт. 20. поверхность кристалла, для чего покрывают
поверхность непрозрачным экраном, имеющим
небольшое отверстие, и этот экран освещают со всех сторон.
Тогда из точки О распространяются в кристалле лучи по
всем направлениям. Если противоположную сторону пластинки
также покрыть непрозрачным экраном с отверстием Р в каком-
либо месте, то из кристалла может выйти только один луч,
именно ОР. Этому лучу, как мы знаем, соответствуют в кри-
кристалле в общем две нормали, следовательно, две волновые пло-
плоскости, образующие с ним некоторые углы; каждая из них пере-
переходит в воздух согласно особому закону преломления, с кото-
которым мы ближе познакомимся в следующей главе. Следовательно,
мы получаем в Р два луча, выходящих по разным направлениям.
Но если направление ОР как раз совпадает со вторичной опти-
оптической осью кристалла, то лучу ОР соответствует в кристалле
бесконечное множество различно направленных нормалей и вол-
волновых плоскостей. Так как каждая из них при выходе наружу
преломляется особым образом, то свет распространяется из
точки Р в виде конуса по бесконечному числу различных на-
направлений (черт. 20). Это явление известно как „внешняя" ко-
коническая рефракция, потому что здесь расщепление луча проис-
происходит при выходе из кристалла.
Чтобы найти соответствующее направление Р, естественно,
нужно один из экранов сделать подвижным и двигать его до
тех пор, пока линия ОР, соединяющая оба отверстия, не совпа-
совпадает со вторичной оптической осью.
НАКЛОННОЕ ПАДЕНИЕ 119
Само собой понятно, что при конической рефракции как
внутренней, так и внешней каждый из лучей цилиндра или ко-
конуса, выходящий в воздух, обладает определенной плоскостью
колебаний и плоскостью поляризации, которые получаются сог-
согласно известным законам распространения и преломления.
ГЛАВА IV
НАКЛОННОЕ ПАДЕНИЕ
§ 68. Законы перехода плоской световой волны из изотроп-
изотропной среды в кристалл или из кристалла в изотропную среду
можно получить тем же методом, которым мы пользовались
в первой части книги. Для этого мы сначала составляем выра>
жение для плоских волн внутри обеих граничащих друг с дру-
другом сред и налагаем граничные условия, имеющие место для
плоскости раздела. Последние заключаются в непрерывности
тангенциальных слагающих напряжений электрического и маг-
магнитного полей. Таким путем, если произвольным образом задана
падающая волна, получаются определенные выражения для пре-
преломленной и отраженной волны.
Чтобы сохранить прежние обозначения, мы и теперь возьмем
в качестве осей координат главные оси кристалла. Поэтому мы
уже не можем, как для изотропных сред, взять нормаль к падаю-
падающей волне в качестве оси х. Мы назовем направляющие коси-
косинусы этой нормали а0, ро, у0, а скорость распространения в пер-
первой изотропной среде д0. Тогда падающая волна определенной
поляризации характеризуется, как в (8), ее волновой функцией
(выражающей напряжение магнитного поля):
B97)
причем / является произвольно заданной функцией одного аргу-
аргумента. Нормаль к плоскости раздела имеет направляющие коси-
косинусы и, v, w. Требуется найти волновые функции для преломлен-
преломленной волны:
(^ B98)
и отраженной волны:
f(t— *'х+Ь'У+Гл*.\. B99)
Так же как и для изотропных сред, задача здесь распадается
на две части: требуется, во-первых, найти направления, по кото-
которым распространяются преломленная и отраженная волны, и во-
вторых, определить волновые функции /г и /'. Обе задачи раз-
разрешаются путем составления граничных условий, выражающих
120 КРИСТАЛЛООПТИКА
равенство напряжений электрического и магнитного поля по обе
стороны от плоскости раздела:
их + vy + шг = 0. C00)
Отсюда находим два уравнения, так же как A5) и A6), линей-
линейные и однородные относительно /, Д и /'; из них следует, что /г
и / пропорциональны /.
§ 69. Рассмотрим сначала направления преломленной и отра-
отраженной волны. Так как пропорциональность между /г, /' и /
должна иметь место во все моменты времени t и во всех точках
граничной плоскости C00), то аргументы этих функций должны
быть равны между собой, как это имело место в § 7, т. е. на
границе должно быть:
_ Qc + fi/y +yo'z Q
Первое равенство дает:
Если бы это имело место для любых значений х, у, z, то
все величины в скобках должны были бы равняться нулю. Но
х, у, г связаны между собой уравнением C00). Поэтому можно z
при помощи C00) выразить через х и у, подставить в C02)
и приравнять нулю коэфициенты при х и у. Целесообразнее,
однако, применить, как в 1, § 97, симметрический метод исклю-
исключения Лагранжа, состоящий в том, что выражение C00), умно-
умноженное на некоторую постоянную Я, прибавляют к C02) и при-
приравнивают нулю коэфициенты при х, у, z в отдельности. Это
дает три уравнения:
{-*+*-<>.
C03)
Эти равенства допускают следующее простое геометрическое
толкование. Во-первых, три заданных направляющими косину-
косинусами направления лежат в одной плоскости, т. е. нормаль пре-
преломленной волны лежит в плоскости падения, проходящей через
нормаль к падающей волне, и перпендикуляр к плоскости гра-
границы. Во-вторых, умножением отдельных уравнений на соответ-
соответствующие направляющие косинусы линий пересечения плоско-
плоскости падения и плоскости границы и сложением полученных выра-
выражений получаем:
НАКЛОННОЕ ПАДЕНИЕ 121
где & и #0 обозначают углы обеих волновых нормалей с перпен-
перпендикуляром к граничной плоскости. Таким образом закон прелом-
преломления Снеллиуса сохраняется и при преломлении в кристалле,
поскольку он прилагается к нормали преломленной волны. Но
в данном случае он не имеет того практического значения, ка-
какое он имеет для случая изотропной среды, поскольку скорость
распространения q неизвестна и сама зависит от искомого угла
преломления #. Поэтому для нахождения направления прелом-
преломленной волны надо принять во внимание связь д с а, /3, у, выра-
выраженную в B64). Всего проще и очевиднее это можно сделать,
введя сокращения:
-Р —- г=*,
C05)
где, конечно, х, у, z имеют другое значение, чем прежде. Тогда
из C03) следует:
(*-Й:(»-1И—?)—=•=• • C06>
а из B64):
Первое уравнение выражает, что точка Р, представленная
координатами х, у, z, лежит на прямой, проходящей через
точку А с координатами ^ , ~° , ^ , перпендикулярно к пло-
плоскости границы. При этом отрезки ОД и ОР (черт. 21) имеют
направления нормалей падающей и преломленной волны и вели-
величины, обратные соответствующим скоростям распространения
q0 и q. Второе уравнение говорит о том, что точка Р лежит на
поверхности C07). Сравнение с B84) показывает, что эта поверх-
поверхность может быть рассматриваема как поверхность световой
волны некоторого воображаемого кристалла с главными скоро-
скоростями распространения —, -^ , —.Ее называют „поверхностью
индексов" действительного кристалла, имеющего главные ско-
скорости распространения а, Ь% с, так как главные показатели пре-
преломления пи ng, n3 согласно B75) обратно пропорциональны
величинам а, Ь, с.
Поверхность индексов находится в таком же отношении
к волновой поверхности, в каком находится эллипсоид с полу-
полуосями а, Ь, с (§ 60) к поляризационному эллипсоиду с полуосями
— , -г , — (§ 58). Поэтому все те следствия, которые вытекают
из общего принципа взаимности, могут быть применены к свой-
свойствам поверхности индексов. Так, например, первичные оптиче-
122
КРИСТАЛЛООПТИКА
ские оси поверхности индексов являются вторичными оптическими
осями волновой поверхности, и наоборот.
§ 70. Предыдущие положения дают простой метод геометри-
геометрического построения направления и скорости распространения
преломленной волны. Через центр О поверхности индексов кри-
кристалла проводят плоскость параллельно плоскости падения
и принимают ее за плоскость чертежа (черт. 21). Эта плоскость
содержит нормаль а,,, /30, у0 падающей волны и перпендикуляр
к плоскости границы и, v, w. Пересечение ее с обеими частями
поверхности индексов представлено на рисунке двумя кривыми,
охватывающими одна другую.
В направлении а0, /30, у0 отклады-
откладывают отрезок О А = — и прово-
проводят через А параллель к перпен-
перпендикуляру и, v, w. Каждая из
двух точек пересечения с поверх-
поверхностью индексов Pt и Р& дает
'uvvj два отрезка ОРг и OPZ, которые
определяют направление а, /S, у
и обратную величину скорости
распространения — для нормали
Черт. 21.
преломленной волны. Таким об-
образом в общем случае имеются две различные преломленные
волны, на которые расщепляется падающая волна при входе
в кристалл. Каждой из двух волновых нормалей соответствует
определенный луч, направление которого представлено нормалью
к поверхности индексов в точке Р", в общем случае он выходит
из плоскости падения. Точно так же каждой нормали соответ-
соответствует и определенная плоскость колебаний, проходящая через
нормаль и луч; этим самым определяются направления напряже-
напряжения электрического и магнитного полей и индукции.
Если q0 не слишком велико сравнительно с главным^ скоро-
скоростями распространения а, Ь, с, может случиться, что точка А
лежит вне внутренней или даже внешней замкнутой поверхности
индексов. Тогда возможно, что одна точка Р2> либо обе точки
Рг и Р2 делаются мнимыми и наступают условия для полного
внутреннего отражения.
Чтобы наглядным образом проверить описанный здесь метод
построения, применим его к преломлению света изотропной сре-
средой, которую можно рассматривать как частный случай кри-
кристалла.
Для изотропной среды оба сечения поверхности индексов
совпадают с окружностью радиуса —. Отрезки О А и ОР дли-
ны — и
— образуют с перпендикуляром к границе и, v, w
углы
НАКЛОННОЕ ПАДЕНИЕ 123
Из соотношения между этими углами и получается закон
преломления Снеллиуса:
sin #0: sin ■&=qit;q.
§ 70а. Для отраженной волны второе уравнение C01) дает:
К' — а0) х + (,V — PJy + (у0' - у0) г = 0.
Отсюда при помощи рассуждения, аналогичного предыдущему,
получается, что нормаль отраженной волны лежит в плоскости
падения, а угол ее с перпендикуляром к плоскости границы
определяется из условия:
sin #0' = sin #0.
Таким образом:^
т. е. угол отражения равен углу падения, так же как для изе-
тропных сред.
§ 71. Точно так. же как мы здесь исследовали преломление
и отражение волны, падающей из изотропной среды на кристалл,
можно исследовать и противоположный случай, когда волна,
распространяющаяся внутри кристалла, падает на поверхность
изотропной среды. Тогда тем же самым методом получаются
соответствующие- этому случаю законы преломления и отраже-
отражения, которые характерным образом отличаются от прежних. Так,
в общем случае получаются две различные волны, которые
Отражаются от поверхности границы обратно в кристалл; в одно-
однородную среду выходит лишь одна волна, направление которой
можно непосредственно определить при помощи закона пре-
преломления Снеллиуса.
§ 72. Полученные здесь для кристаллов законы преломления
и отражения допускают большое число применений. Мы коснемся
лишь немногих из них. Ради простоты мы ограничимся рассмотре-
рассмотрением одноосного и притом положительного кристалла. В этом
случае согласно § 59:
а = Ь > с C08)
и уравнение B64) переходит в
{(«2 + F) (с2-Я2) + У2 («2- tf2)} • (а2 — Я2) = 0.
Корнями его являются:
Яг — а> \
Волну с постоянной скоростью распространения а = Ях назы-
называют „обыкновенной", волну с переменной скоростью распро-
распространения Яъ—„необыкновенной". Обозначим через & угол волно-
волновой нормали с оптической осью, которой в данном случае является
124 КРИСТАЛЛООПТИКА
ось г. Тогда y = cos#. Отбросив для простоты индекс 2 у #а>
получим для скорости распространения необыкновенной волны:
q2 = a2 cos2 ft + с2 sin2 ft. C10)
Уравнение B85) поверхности световой волны при а = Ь пере-
переходит в
(а?*? + а*у* + cW ~ аЧ2)- (х2 +у* +z2 — as) = 0. C11)
Эта поверхность распадается на вытянутый эллипсоид вра-
z щения с полуосями с, с, а:
са+^-+^-—1 C12)
и на сферу радиуса а, касающуюся эллип-
эллипсоида в концах его оси:
Эллипсоид образует внутреннюю зам-
замкнутую поверхность волны, сфера — внеш-
внешнюю. Первичные и вторичные оптические
оси совпадают с осью z.
Черт. 22. На черт. 22 нарисованы обе волновые
плоскости, которые соответствуют опреде-
определенной волновой нормали OQ. Они касаются волновых поверх-
поверхностей в точке Р внутренней и Q внешней поверхностей волны.
ОР и OQ — соответствующие им лучи. Плоскость колебаний
необыкновенного луча ОР совпадает с плоскостью чертежа,
которая представляет собой главное сечение кристалла, прохо-
проходящее через его оптическую ось. Колебания обыкновенного луча
происходят в перпендикулярной к ней плоскости. Поэтому элек-
электрическая индукция лежит в Я в плоскости чертежа, а в Q—
перпендикулярно к ней (ср. черт. 14 и 15).
Угол обыкновенного луча OQ с осью z равен углу волновой
нормали ft. Угол &' необыкновенного луча ОР с осью г легко
вычисляется, если принять во внимание, что на черт. 22 угол #
обозначает направление нормали к эллипсоиду в конце полу-
полудиаметра ОР, проведенного под углом &. Следовательно:
^^ C13)
Отсюда находим:
Л1 С2 COS* ,„...
cosfl — .. —■ . C14)
j/Vcos'^l^sin1*
Для угла д между лучом и нормалью необыкновенной волвы
получается:
cos д — cos (ft—ft )== ■ _ ■- г, C15)
v "* ]Aa«cos'# + c4sin8# v
НАКЛОННОЕ ПАДЕНИЕ
а для скорости распространения по направлению луча:
125
Само собой понятно, что при вычислении этих величин можно
воспользоваться и теми соотношениями, которые вытекают из
общего принципа взаимности (§ 60). Так, из уравнения (ЗЮ)
можно прямо получить следующее соотношение:
1 COS2*' . Sina#'
А'
правильность которого легко может быть установлена.
§ 73. Теперь мы рассмотрим прохождение плоской монохро-
монохроматической волны через плоскопараллельную пластинку одно-
одноосного положительного кристал-
кристалла, отшлифованную перпендику-
перпендикулярно оптической оси.
Обозначим угол падения че-
рез #0. Плоскость падения, кото-
которая в то же время является глав-
главным сечением кристалла, примем
за плоскость чертежа (черт. 23),
причем ось z совпадает с опти-
оптической осью. Падающий луч
идет через пластинку снизу с ле-
вой стороны вверх в правую сто-
сторону. Будем считать волну, как
и пластинку, неограниченной с боков, тогда можно не останав-
останавливаться на направлении луча, а ограничиться рассмотрением
волновой нормали.
Луч естественного света, который снизу падает на пластинку
в точке А, расщепляется в ней согласно закону преломления
Снеллиуса на обыкновенную волну:
C18)
черт. 2з.
?»- = ft,
gt a
и на необыкновенную волну:
sin &ь q0
где qz и &2 взаимно связаны соотношением C10).
Каждая из этих двух волн проходит через кристалл и дает
при выходе через противоположную, проходящую через точку А,
поверхность луч, направленный вверх вправо. Этот луч парал-
параллелен падающему в точку А лучу, так как при преломлении
у второй поверхности кристалла получаются те же углы, что и
у первой поверхности его, но в обратной последовательности.
Таким образом обе волны опять соединяются в воздухе в одну
126 КРИСТАЛЛООПТИКА
волну, параллельную падающей. Но так как путь по волновой
нормали для обеих волн различен, то разность фаз при выходе из
пластинки у них другая, чем при входе. Подсчитаем это смещение
фаз А, которое получается при прохождении через пластинку.
Нормаль обыкновенной волны представлена на черт. 23 от-
отрезком АС, причем угол САА'=&г. В точке С происходит вто-
второе преломление, посредством которого восстанавливается пер-
первоначальное направление нормали, образующее угол #0 с осью z.
Нормаль необыкновенной волны в кристалле представлена
отрезком АВ, причем угол ВАА' = #?. В точке В волна вы-
выходит в воздух опять в направлении % к оси г. Плоскость волны
прошедшего света СС перпендикулярна к волновой нормали ВС.
Искомая разность фаз А получится, если мы выберем две опре-
определенные плоскости волны, из которых одну возьмем до вступ-
вступления луча в пластинку, например плоскость, проходящую через
точку А. Другую возьмем после прохождения луча через пла-
пластинку, пусть она проходит, например, через точку С. Сравним
те изменения, которые претерпевает аргумент волновой функции
colt ) для каждой из двух волн в« промежутке между этими
двумя волновыми плоскостями. В этом промежутке нормалью
обыкновенной волны служит прямая АС, нормаль необыкновен-
необыкновенной волны представлена ломаной ABC, участок которой АВ
пробегается волной со скоростью q2, участок ВС — со скоростью д0
и притом без изменения фазы при преломлении. Отсюда полу-
получается искомое смещение фазы:
Величина отрезков АВ, ВС, АС, как и скорости распростра-
распространения <7g, получается из угла падения #0. Для простоты мы при-
принимаем #0 малым и ограничиваемся членами второго порядка
относительно него. Тогда из C18) следует".
из C19):
На основании C10) получаем:
откуда
и
*-1
НАКЛОННОЕ ПАДЕНИЕ 127
Далее, обозначив через D толщину пластинки, найдем:
D ,
в то время как
ВС =
является величиной порядка D • #02 и поэтому может быть откинуто.
Найденные величины, будучи вставлены в C20), дают:
/1 г\ &D аа — & а »
или, если ввести главные показатели преломления пг и л2 и длину
волны в воздухе Яо:
^(^^)V. C21)
Плоскость колебаний необыкновенной волны, так же как и
электрическая индукция, лежит в главном сечении, т. е. в пло-
плоскости падения; плоскость колебаний обыкновенной волны —
в плоскости, перпендикулярной к главному сечению. Поэтому
необыкновенная волйа получается из той компоненты падающей
волны, колебания которой происходят в плоскости падения, а обык-
обыкновенная волна—из компоненты, перпендикулярной к первой.
Пусть падающий свет линейно поляризован, например, при
помощи призмы Николя, употребленной в качестве поляриза-
поляризатора, плоскость колебания которого образует угол <р с плоско-
плоскостью падения. Тогда разность фаз обеих волн при входе в пла-
пластинку равна нулю, а амплитуды их относятся, как cos q>: sin q>,
если пренебречь ослаблением света благодаря отражению. При
выходе из пластинки разность фаз, как подсчитано, равна Л, так
чточвыходящий луч в общем случае является эллиптически по-
поляризованным. Если после этого пропустить свет через вторую
призму Николя как через анализатор, плоскость колебаний ко-
которого образует угол у с плоскостью падения, то интенсивность
прошедшего света получается, как в B95), равной:
/= cos2 (<р — у) — sin 2<p • sin 2y> • sin2 ^, C22)
где Л дано посредством C21), а интенсивность падающего света
принята за единицу.
Когда николи скрещены, получается подобно B96):
/=sin22ip>- sin2-. C23)
Если свет проходит еще через собирательную линзу, распо-
расположенную параллельно кристаллической пластинке, то световые
лучи соединяются в такой точке фокальной плоскости, положе-
128 КРИСТАЛЛООПТИКА
ние которой определяется углом #0; последний пропорционален
расстоянию этой точки от осевой точки, т. е. от фокуса лучей,
перпендикулярных к пластинке, прошедших через нее без пре-
преломления.
На основании изложенного объясняется следующее световое
явление: возьмем пучок лучей, падающих почти перпендику-
перпендикулярно на плоскопараллельную кристаллическую пластинку, выре-
вырезанную из одноосного кристалла перпендикулярно к оптической
оси и находящуюся между двумя скрещенными николями.
В этом случае мы имеем в пучке лучей бесконечное множество
плоскостей падения, каждой из которых соответствует опреде-
определенное значение <р. Поэтому интенсивность прошедшего спета /
зависит, кроме #0, также о г азимутального угла tp плоскости паде-
падения. Благодаря этому в фокальной плоскости линзы получается
черный крест (при <р = 0, 9>==т) с налегающими на него кон-
концентрическими черными кольцами, радиусы которых определя-
определяются теми значениями А, которые являются кратными 2гг. При
других положениях призм Николя значение /получается из C22).
§ 74. До сих пор мы занимались изучением направления
и скорости распространения волн, отраженных и преломленных
кристаллом.
Возвращаясь к рассуждениям § 68, поставим теперь вопрос
о величине волновых функций. С этой целью мы должны,
как и для случая изотропных сред, принять во внимание осо-
особую форму условий на границе. Но задача здесь гораздо слож-
сложнее, потому что теперь невозможно преломление и отражение
компоненты, совершающей колебания в плоскости падения, рас-
рассматривать сонершенно отдельно от компоненты, колебания ко-
которой перпендикулярны к плоскости падения, тем более, что
в общем случае каждая из этих двух компонент претерпевает
двойное преломление при вступлении в кристалл.
Однако мы можем, как увидим далее, разбить задачу на две
.независимые части и этим значительно упростить вычисления.
При этом мы должны исходить не из определенной компоненты
падающей из изотропной среды волны, а обратить свое вни-
внимание прежде всего на одну из двух распространяющихся в к р и-
сталле волн. Направление распространения и поляризация,
равно как и скорость распространения обеих преломленных
волн, могут быть определены на основании положений последнего
параграф i. Поэтому мы можем постаэить себе следующий вопрос:
какими свойствами должна обладать падающая волна, чтобы
в кристалле получилась только одна из двух преломленных волн?
Будем считать известными направления нормали п, напряже-
напряжения электрического и магнитного полей и индукции, а также
скорость распространения одной из двух преломленных волн, и
определим соответствующую ей падающую и отраженную
волну. Это может быть сделано при помощи условий на границе,
НАКЛОННОЕ ПАДЕНИЕ 129
выражающих непрерывность тангенциальных компонент напря-
напряжений поля.
Обозначая напряжение магнитного поля преломленной
волны через
"=/i(*—у)' C24>
имеем для напряжения электрического поля волны согласно B57):
Выразим направление напряжения электрического поля, кото-
которое мы считаем известным, при помощи направляющих косину-
косинусов $, г], С углов, образуемых им со следующими тремя взаимно
перпендикулярными направлениями: перпендикуляром к гра-
границе (I), линией пересечения плоскости падения с плоскостью
границы (»?) и нормалью к плоскости падения (£) (ср. черт. 1 .
Тогда из двух касательных к граничной плоскости компонент
электрического напряжения та, которая находится в плоскости
падения, равна:
Л • V, C26)
а перпендикулярная к плоскости падения равна:
Напряжение магнитного поля перпендикулярно, во-первых,
напряжению электрического поля с направляющими косинусами
I, г], С, во-вторых, к лежащей в плоскости падения нормали
волны п, с направляющими косинусами: cos#, sin#, 0; его на-
направляющие косинусы поэтому равны:
С sin 9 — С cos & rj cos 9 — g sin 9 (V)K\
ccs<f' с<кй ' cos 6 ' ^ '
Правильные знаки получаются из рассмотрения частного слу-
случая, например, когда 6 = 0, & = 0, ?? = 1. Следовательно, со-
согласно C24) и C28) та касательная к границе компонента маг-
магнитного напряжения, которая лежит в плоскости падения, равна:
-Л
а перпендикулярная к плоскости падения:
Теперь найдем соответствующие величины для падающей
волны, которую также примем линейно поляризованной. Обозна-
Обозначив ее магнитное напряжение через/, имеем согласно (8) и G) для
9 Введение в теоретическую фвзику, ч. IV.
130 КРИСТАЛЛООПТИКА
электрического напряжения величину/-~. Если плоскость коле-
колебаний образует с плоскостью падения угол у, то касательная
к границе компонента электрического напряжения, находящаяся
в плоскости падения, равна:
^cos9> cos^o, C31)
а перпендикулярная к плоскости падения равна:
ff-situp. C32)
Соответствующие выражения для магнитного напряжения такие:
—/sin ^ cos ^0 C33)
и
f-cos<p. C34)
Наконец, для отраженной волны мы получаем аналогич-
аналогичные выражения, которые мы для отличия будем обозначать штри-
штрихом. Л ри этом следует заметить, что #о' = 0е и 0' = я— ■&. Для
электрического напряжения получаются компоненты:
C35)
-и
и
/'^sin/, C36)
а для магнитного напряжения компоненты:
/'sin/ cos % C37)
и
f'cosy'. C38)
На границе касательные компоненты всех напряжений поля
должны быть непрерывны, так что напряжения падающей и от-
отраженной волны равны напряжению поля преломленной в_>лны.
Отсюда получаются следующие четыре граничных условия: во-
первых, для компоненты электрического напряжения, лежащей
в плоскости падения, согласно C31), C35), C26):
\г). C39)
Во-вторых, для компоненты электрического напряжения, пер-
перпендикулярной к плоскости падения согласно C32), C36), C27):
fq0 sin 9 + fq0 sinV = ^/.f. C49)
В-третьих, для компоненты магнитного напряжения, лежащей
в плоскости падения, согласно C33), C37), C29):
/sin <p cos A, -b/'siny' cos0o = ~h~^- C41)
НАКЛОННОЕ ПАДЕНИЕ 131
Наконец, в-четвертых, для компоненты магнитного напряже-
напряжения, перпендикулярной к плоскости падения, согласно C34>,
C38), C30):
;/ C42)
Полагая, как в § 7:
Г = И/ и h = fHf, C43)
видим, что все четыре уравнения могут быть удовлетворены
при определенных значениях q>, <р', ц и ц1- Таким образом мы
приходим к выводу, что, действительно, имеется падающая волна
определенной формы и поляризации, которая кроме отраженной
волны другой определенной формы и поляризации дает в* кри-
кристалле только одну, рассмотренную здесь преломленную волну.
Искомые величины получаются, принимая во внимание C04),
при помощи следующих формул:
t£07_ Csin(ffl0 + ffl)
BY j?(sin0ocos0ocos#+ sin#) — S sin#o«>s#osin0'
£ sin (fflp — 9)
f sin &0 cos #„ sin & — rj (sin »B cos #0 cos & — sin
sin у sin (ffl0 — fl)
P Ш^' ' sin @o-!-0)'
siny • cos 6 • sin 20o
Для того частного случая, когда напряжение электрического
поля преломленной волны перпендикулярно к волновой нормали
и лежит в плоскости падения (£ = — sin^, r\ = cos^, С = 0, «5 = 0),
выражения для ц и ц^ приобретают вид B3) и B4), где #0 — угол
падения, ■&—угол преломления; углы у и у' при этом равны нулю.
§ 75. Теперь спро„сим себя: какой должна быть падающая
волна, чтобы при том же самом угле падения #0 получилась
лишь вторая из обеих преломленных волн? Мы получим ответ
тем же самым путем, если будем исходить из волновой функции
второй преломленной волны: g111— — I. Соответствующие рас-
расчеты опять дадут определенную падающую волну g^, плоскость
колебаний которой имеет азимут уг и определенную отраженную
волну g1 с азимутом колебаний <р2'- Обозначим, как в § 7:
g' = Og И g1 =
тогда последние четыре уравнения предыдущего параграфа, если
подставить в них вычисленные для второй преломленной волны
значения #, 8, |, ц, £, дадут соответствующие величины для <р2>
у2' а и ах.
Для того частного случая, когда напряжение электрического
поля преломленной волны перггендикулярно как к волновой нор-
9*
132 КРИСТАЛЛООПТИКА
мали, так и к плоскости падения A = 0, щ = 0, f = 1, 8 = 0), вы-
выражения для <5 и eL принимают вид B3) и B4), причем оба угла
<р2 и ф2' делаются равными ■-.
Отсюда получается и решение общей задачи: найти для про-
произвольно заданной падающей волны форму обеих преломленных
волн, а также форму и поляризацию отраженной волны. Для
этого разлагают падающую волну на две компоненты / и g, из
которых каждая, независимо одна от другой, дает согласно опре-
определенному закону одну преломленную и одну отраженную волну.
При этом колебания нужно разлагать не по азимутам 0 и -^
(т. е. в плоскости падения и перпендикулярно к ней), как для
изотропных сред, но по азимутам q>x и 9V Величина последних
находится из C44), если туда вставить вместо #, I, щ, f те зна-
значения, которые получаются для обеих преломленных волн, при
угле падения #0 согласно § 69. Тогда цх ■ /и ot • g являются вол-
волновыми функциями для обеих преломленных волн, в то время
как ц ■ f и о • g, нормаль которых одна и та же, соответственно
значениям их азимутов g?i' и q>2', складываются в одну отражен-
отраженную волну. Если падающий свет был линейно поляризованным,
то таким же будет и отраженный свет; если падал естественный
свет, то отраженный свет будет частично поляризован.
При помощи полученных таким образом результатов могут
быть произведены подсчеты, аналогичные тем, которые мы про-
проделали для изотропных сред. Так, например, можно подсчи-
подсчитать коэфициенты отражения и пропускания (q и 1—q), разо-
разобрать случай перпендикулярного падения (#0= 0) и скользящего
падения (#0 = ^)> найти угол полной поляризации (е = 0), угол
полного внутреннего отражения (# — мнимое). Однако углубле-
углубление 1в эти вопросы завело бы нас слишком далеко.
ЧАСТЬ ТРЕТЬЯ
ДИСПЕРСИЯ ИЗОТРОПНЫХ СРЕД
ГЛАВА I
ОСНОВНЫЕ УРАВНЕНИЯ
§ 76. Возвращаясь снова к рассмотрению изотропных сред,
мы займемся теперь явлением, которое наблюдается в той или
иной степени во всех случаях преломления света, а.именно, дис-
дисперсией. До сих пор мы принуждены были игнорировать это
явление, так как ему не было отведено никакого места в перво-
первоначальной теории Максвелла. Выше, в § 9, нам встретилось это
обстоятельство, и мы уже тогда указывали единственный выход
из связанных с ним затруднений для теории: мы должны отка-
отказаться от представления о пространстве, как о совершенно не-
непрерывно заполненном материей, и перейти к атомистическому
представлению о нем.
Таким образом мы решительно оставляем ту точку зрения,
которой мы держались в предыдущих рассуждениях, и вступаем
в область, для продвижения в которой нам необходимо с самого
начала обратиться к более или менее произвольным гипотезам.
Тут трудность заключается в самой природе вещей. Ее возможно
до известной степени уменьшить тем, что мы заранее считаем
атомы, или, вообще говоря, наименьшие элементарные частицы
материи, крайне малыми и чрезвычайно многочисленными. При
помощи этого допущения создается, с одной стороны, возмож-
возможность приписать материальному телу, построенному из атомов,
новые, прежней теорией не объясняемые свойства. С другой сто-
стороны, мы можем считать, что тело ведет себя практически, как
вполне однородное, если рассматриваемые явления происходят
внутри участков, не слишком малых по своим размерам. Хоро-
Хорошим примером тут служит распространение звуковой волны в
среде, состоящей из атомов. Для такой среды в случае не слиш-
слишком малой длины волны совершенно точно справедливы те за-
законы, которые действительны для абсолютно однородной среды
той же плотности и упругости. С этой точки зрения вся рас-
рассмотренная до сих пор теории является предельной теорией,
годной для относительно медленно протекающих явлений гру-
грубого характера. Наша теперешняя задача состоит в том, чтобы
134 ДИСПЕРСИЯ ИЗОТРОПНЫХ СРЕД
область, в которой теория справедлива, несколько расширить
в сторону явлений, протекающих более быстро и имеющих более
тонкую природу.
§ 77. Чтобы не терять связи с прежним изложением, мы со-
сохраним, как и в кристаллооптике, уравнения A), B) и C), но
вместо уравнения D), выражающего пропорциональность между
электрической индукцией D и электрическим напряжением Е,
введем более общее соотношение. Это соотношение делается
легко понятным при помощи того наглядного физического
толкования, которое можно дать согласно 3, § 26 различию
между индукцией и напряжением поля, а именно, полагая со-
согласно 3, A41):
5^ = М, C48)
ми можем рассматривать М как электрический момент единицы
объема, т. е. как сумму моментов всех бесконечно малых элек-
электрических диполей, которые согласно нашему представле-
представлению содержатся в единице объема, выбранной достаточно
малой.
Мы сделаем, далее, еще один шаг и припишем этим единич-
единичным диполям реальное физическое существование, т. е. мы при-
принимаем не бесконечно большое количество бесконечно малых со-
соприкасающихся друг с другом диполей, относительно размеров
которых не имеет смысла и спрашивать, но мы предполагаем их
число, их величину и их взаимные расстояния реальными и ко-
конечными.
Самым важным следствием из этой гипотезы является
то, что теперь имеется только одна непрерывная среда, в на-
настоящем смысле этого слова, — вакуум, в котором протекают все
проявления электромагнитного поля. Материальные среды играют
р этих процессах лишь промежуточную роль, которая состоит
в том, что их электрически заряженные составные части, ионы
и электроны, перемещаются в вакууме. Благодаря этому крити-
критическая скорость, — скорость распространения света в вакууме,
получает более глубокое значение, чем в прежней теории, где
она являлась одной из многих скоростей.
§ 78. Обратимся теперь к вопросу о том, каким образом за-
заменить уравнение D) соотношением, вытекающим из обрисован-
обрисованных нами новых представлений. Заметим прежде всего, что со-
согласно D) электрический момент всех диполей, содержащихся
в единице объема, пропорционален существующему в этот мо-
момент времени электрическому напряжению. Однако, приписывая
диполям реальное существование, мы должны дать им некото-
некоторую самостоятельность. Поэтому мы не можем требовать, чтобы
электрический момент диполя мгновенно повторял все колебания
действующего на него электрического поли. Мы придадим закону
связи между электрическим моментом и возбуждающим электри-
ОСНОВНЫЕ УРАВНЕНИЯ 135
ческим полем более общее значение, проводя различие между
колебаниями электрического момента диполя и колебаниями воз-
возбуждающего электрического поля. Первые, конечно, опреде-
определяются последними, но не при помощи простой пропорциональ-
пропорциональности, а при помощи определенного уравнения колебания, в ко-
котором играют роль и индивидуальные особенности диполей, в
особенности их инерция. Мы имеем ряд возможностей для вы-
выбора формы уравнения колебания. Например, можно диполи
считать жесткими и способными вращаться, сохраняя постоянный
электрический момент. Тогда в уравнение колебания входят мо-
моменты инерции диполей. Нейтральное в электрическом смысле
состояние характеризуется совершенно неупорядоченной ориен-
ориентацией диполей.
Для целей рассмотрения явлений оптической дисперсии, по
крайней мере в первом приближении, удобнее всего колебания
диполя выразить уравнением вынужденного колебания. Мы пред-
представляем себе диполь в виде точечного осциллятора, состоящего
из массы т, соединенной с электрическим зарядом е и колеблю-
колеблющейся около определенного положения равновесия, в котором
находится такой же величины заряд противоположного знака.
Уравнение его колебаний в векторной форме 2, B03) имеет вид:
/иг + тсо0Ч = еЕ'. C49)
Здесь а>0 обозначает собственную частоту осциллирующего
диполя, г — его расстояние от положения равновесия. Поэтому,
согласно 3, § 26, ег—его электрический момент и если в еди-
единице объема находится N таких диполей, то
N • е • г = М C50)
представляет собой электрический момент единицы объема.
Возбуждающее электрическое поле Е' надо отличать от сум-
суммарного напряжения поля Е, так как первое происходит от элек-
электрических зарядов, находящихся вне рассматриваемого диполя
(диполь не может возбуждать сам себя), второе же содержит,
кроме того, и то поле, которое происходит от самого рассматри-
рассматриваемого диполя. Различие между Е' и Е было бы исчезающе
малым, если бы достаточно малый объем v внутри себя не
возбуждал никакого поля. Но в действительности этого нет.
Наоборот, напряжение поля, которое имеется внутри произвольно
малой, равномерно поляризованной, сферы с моментом М на еди-
единицу объема, равно повсюду одной и той же величине [3, A89)]
— тг М, т. е. не зависит от величины сферы. Прибавив эту
величину к возбуждающему напряжению Е', получим полное
напряжение поля Е:
Е = Е'-^М. C51)
136 ДИСПЕРСИЯ ИЗОТРОПНЫХ СРЕД
Соединяя вместе три последних уравнения, получаем связь между
электрическим моментом М и электрическим напряжением Е, а
именно, уравнение колебания в форме
тМ + (ты0* — ^ Afe2) M = Ne?E. C52)
Вместе с C48) это дает искомое обобщение основного урав-
уравнения D).
Часто к левой части уравнения колебания прибавляют член
затухания, содержащий М с положительным коэфициентом, как
в 7, B0j или 3, C75). Благодаря этому учитывается затухание
колебаний, происходящее или вследствие излучения электро-
электромагнитной энергии, или по причине столкновений с соседними
осцилляторами. Однако мы здесь откажемся от этого добавления.
Для сокращения мы положим:
i^ = «, C53)
cV-l^cV2; C54)
тогда уравнение колебания примет более простой вид:
М ^Е. C55)
Уравнения (.1), B), C), C48J и C55) составляют основу изла-
излагаемой здесь теории дисперсии, в основных чертах данной
Г. А. Лорентцом. Первым следствием ее является то, что
«,?>—-, иначе в статическом поле D и Е имели бы различные
О
знаки; благодаря этому устанавливается верхняя граница для
плотности N распределения осцилляторов определенного рода.
§ 79. Чтобы установить переход к первоначальной теории
Максвелла, рассмотрим явления, протекающие столь медленно,
что в уравнении колебания C55) можно пренебречь членом М
по сравнению с членом, содержащим М. Это соответствует тому
случаю, когда частота вынужденных возбуждающей волной коле-
колебаний диполя мала по сравнению с его собственной частотой.
Тогда из C55) следует:
Д| . - Е
m ~~ 4жоо'2 '
а принимая во внимание C48), получим:
Это уравнение равносильно уравнению D), устанавливающему
строгую пропорциональность между электрической индукцией и
ПЛОСКИЕ ВОЛНЫ 137
электрическим напряжением. Коэфициент пропорциональности —
диэлектрическая постоянная, имеет значение:
— 1 + -£г- C56)
Область этих явлений и есть та область, на которую распро-
распространяются следствия, полученные в § 9. Для них диспереия
полностью исчезает, и согласно B2) получаем для показателя
преломления:
«2=1 + ^. C57)
Формулы C56) и C57), как можно видеть, выясняют физи-
физическую сущность диэлектрической постоянной, а поэтому также
и электрической индукции. Их можно экспериментально прове-
проверить путем изучения зависимости диэлектрической постоянной
и показателя преломления, от N—плотности распределения ди-
диполей. При этом надо обратить внимание на то, что согласно
C53) и C54) как а, так и щ'г зависят от N.
Подставляя соответствующие значения в C57), получаем:
Так как константы е, т и ш0 независимы от N, то это соот-
соотношение очень удобно для установления зависимости между
величинами п и N. Оно. получено независимо один от другого
Г. А. Лорентцом и датским физиком Л. Лоренцом и в достаточ-
достаточной степени подтверждается на опыте.
§ 80. В дальнейшем при изучении общего случая удобно
исключить из уравнений A) и C48) магнитное напряжение Н и
электрическую индукцию D. При помощи B) это дает:
Ё + 4я:М = сМЕ. C59)
Это уравнение вместе с C55) может служить для решения
задач дисперсии.
ГЛАВА II
ПЛОСКИЕ ВОЛНВД
§ 81. Теперь на основании полученных нами основных урав-
уравнений выведем важнейшие законы, относящиеся к электромаг-
электромагнитным процессам в диспергирующей среде. При этом обра-
обратимся к тому ходу мыслей, которому мы следовали в § 3 при
рассмотрении изотропной среды. Возьмем сперва плоскую волну,
т. е. предположим, что из пространственных координат х, у, г
лишь координата х играет роль. Кроме того, мы принимаем волну
138 ДИСПЕРСИЯ ИЗОТРОПНЫХ СРЕД
линейно поляризованной, а именно считаем колебания направлен-
направленными вдоль оси у. как раньше принимали для волны /. Тогда
Е, = О, Ez = 0, Нх = 0, Ну = 0, и уравнения C55) и C59) сводятся
к таким:
- 2^Es
Эти диференциальные уравнения, установленные нами для
диспергирующей среды, имеют существенное отличие от дифе-
ренциального уравнения F). Оно заключается в том, что невоз-
невозможно удовлетворить этим диференциальным уравнениям, не
задавшись определенными предположениями относительно формы
волновой функции /. Поэтому нам не остается ничего другого,
как найти сперва частное решение этих уравнений, а потом со-
составить общее решение при помощи суммирования достаточно
большого числа частных решений. Таким образом, например, мы
поступили в § 12 при рассмотрении вопроса о полном внутрен-
внутреннем" отражении. Как и тогда, мы полагаем:
Е9 = е°(%-^ C62)
и соответственно
М9=ае%а\ с I. C63)
Эти уравнения выражают собой простую периодиче-
периодическую волну со скоростью распространения:
7Г = Я- C64)
Поэтому мы постоянную п называем показателем преломле-
преломления, как и для сред, не тлеющих дисперсии^. Мы увидим далее,
что, в отличие от прежнего, п может быть и мнимой величиной.
Тогда волна будет затухающей чз пространстве, как это имело
место в случае полного внутреннего Отражения.
Принятые нами выражения для Еу и Му удовлетворяют уравне-
уравнениям C60) и C61) при условии, что между константами суще-
существует следующее соотношение:
пг _ 1 = 4ла = —~ ,. C65)
Константы а и со0' заданы свойствами среды, поэтому какой-
нибудь частоте со волны соответствует определенный показатель
преломления п и определенная величина отношения а электри-
электрического момента М к напряжению поля Е. Для магнитного на-
напряжения получается из A):
Я, = пЕи. C66)
ПЛОСКИЕ ВОЛНЫ
139
§ 821 Поставим теперь вопрос о зависимости показателя пре-
преломления п от частоты вблны со. Согласно C65) п является или
действительной величиной или чисто мнимой. В первом случае
мы берем п положительным, т. е. мы берем волну, распростра-
распространяющуюся в положительном-направлении оси л:. Для очень малых
значений со мы, очевидно, получаем соотношение C57). По мере
роста со растет или притом безгранично, когда со приближается
к значению со0' (ср. черт. 24). После перехода через это значение
п является чисто мнимой величиной и равно — in, где к действи-
действительно и положитель-
положительно, так как- иначе, при
х = оо, Еу было бы бес-
бесконечно большим.
Это имеет место
до тех пор, пока со
не достигнет значения
j/ci>0'2 + а. В этом ин-
интервале к убывает не-
непрерывно от оо до О,
как показано на церт.
24 пунктирной линией.
После этого показа-
показатель преломления п
опять делается дей-
действительным и растет
от нуля до асимптоти-
асимптотического значения, рав-
равного единице, кото-
которого он достигает при со = оо. В результате получаем, что
вся область спектра от со = 0 до со = оо разделяется на три раз-
различные части „полосой поглощения", простирающейся от со = соо'
до со = У^со0'-2 + а (черт. 24). Для волн, частота которых лежит
в участках слева и справа от этой полосы, отсутствует погло-
поглощение, и показатель преломления растет вместе с ростом ча-
частоты; дисперсия, как говорят, является „нормальной". При этом
имеется существенное различие между двумя этими участками
спектра, а именно, слева для меньших частот показатель пре-
преломления всегда больше, чем \^е [ср. C56 ], в то время как справа
для больших частот он всегда меньше единицы. Для волн же,
частота которых лежит в самой полосе абсорбции, вообще нет
распространения энергии: получаются стоячие и затухающие в
пространстве колебания, как это происходит в случае полного
внутреннего отражения.
Что касается отношения а амплитуд момента диполя М и
напряжения поля Е, то следует заметить, что согласно C65) оно
слева от полосы абсорбции положительно, справа отрицательно
и превращается в нуль при е<л.= оо. Последнее значит, что при
-Ц.
Черт. 24.
140 ДИСПЕРСИЯ ИЗОТРОПНЫХ СРЕД
бесконечно больших частотах диполи вовсе не приходят в ко-
колебание и среда ведет себя оптически, как вакуум.
§ 83. Выведенные здесь законы дисперсии и абсорбции по-
получают некоторое обобщение, если в соответствии с уже выска-
высказанными в § 78 мыслями к левой части уравнения колебания
C55) прибавить еще небольшой член затухания AM, где k > 0.
Тогда в уравнении C60) прибавляется член kMy. Подстановка
выражений C62) и C63) в уравнения C60) и C61) приводит вме-
вместо C65) к такому соотношению между константами
л2 — 1 = Ana = -72—%-т-пг- • C67)
Соотношение C66) остается при этом неизменным. Единствен-
Единственная разница по сравнению с прежним состоит в том, что теперь
п не является уже действительным или чисто мнимым, но всегда
комплексным. Если мы вместо п напишем п—Ы, то п согласно
C62) будет опять иметь значение действительного показателя
преломления, к— показателя поглощения. Черт. 24 надо для
этого случая изменить, так как теперь п уже не растет сначала
до бесконечности, падая потом до нуля и оставаясь нулем для
всей полосы поглощения. Теперь п повсюду меняется непрерывно.
При вступлении в полосу поглощения п достигает крутого ма-
максимума и после этого непрерывно переходит к нулю, соответ-
соответственно так называемой „аномальной дисперсии". Кривая для
показателя поглощения « в обеих областях нормальной диспер-
дисперсии проходит вблизи от оси абсцисс и принимает заметную ве-
величину лишь в полосе абсорбции.
§ 84. Следующее обобщение, имеющее практическое значе-
значение, получается для формулы C67), если предположить, что
диспергирующая среда содержит колеблющиеся под действием
волны диполи разного рода, число которых в единице_объема
обозначим Nx, Ns, N3,... Тогда вместо C48) получается соот-
соотношение:
причем суммировать надо по всем родам диполей. Для каждого
рода диполей имеет место уравнение колебания типа C49), со-
содержащее или не содержащее член затухания, с особыми значе-
значениями для констант а>1} аи а также и для kv Уравнения C51) и
C59) получают при этом более общий вид:
Е + 4тс ^ Щ = с2АЕ. C70)
Подстановка выражения C62) для электрического напряжения
и выражения C63) для дипольных моментов М1з А?2)... с ампли-
ПЛОСКИЕ ВОЛНЫ 141
тудами аь а2, а3 приводит вместо C67) к более общим, соотно-
соотношениям:
.... C72)
при помощи которых для каждой волновой частоты со могут
быть определены комплексный показатель преломления п — Ы
и амплитуды колеблющихся диполей всех родов. Изображая гра-
графически, подобно тому как это сделано на черт. 24, соотноше-
соотношение между я, к и со, мы увидим, что каждый род осцилляторов
образует в спектре особую полосу абсорбции, определяемую его
собственными константами. Внутри каждой такой полосы имеет
место аномальная дисперсия и заметное поглощение, в то время
как вне полосы абсорбции дисперсия повсюду нормальна. При
этом получается та особенность, что в каждой промежуточной
области между двумя полосами абсорбции действительный пока-
показатель преломления растет от очень малых до очень больших
значений, в то время как во внешней области слева (малые со)
он всегда больше, чем Уе, а во внешней области справа (боль-
(большие со) он всегда меньше единицы. В общем можно сказать, что
каждая полоса абсорбции, частота которой превышает частоту
волны со, повышает действительный показатель преломления,
в то время как каждая полоса абсорбции, частота которой
меньше со, понижает показатель преломления. Поэтому показа-
показатель преломления, больший единицы, всегда указывает на нали-
наличие более высоких собственных частот.
Во всех дальнейших рассуждениях мы будем предполагать,
что комплексный показатель преломления п — Ы, который харак-
характеризует полностью оптическое поведение тела, нам известен.
§ 85. Законы преломления и отражения плоской периодиче-
периодической волны у поверхности диспергирующей среды или на гра-
границе двух соприкасающихся диспергирующих сред получаются
непосредственно из формул, относящихся к диспергирующим
средам. Это следует из того обстоятельства, что уравнения C62)
и C66), при помощи которых мы выразили электрическое и маг-
магнитное напряжения волны, распространяющейся в диспергирую-
диспергирующей среде, содержатся как частньГе случаи в уравнениях (8),
а кроме того, граничные условия на плоскости раздела, тре-
требующие непрерывности тангенциальных слагающих напряжения
поля, остаются такими же для диспергирующих сред, как и для
не диспергирующих. Отсюда ясно, что все прежде полученные фор-
формулы для отраженной и преломленной волны сохраняют свою силу
и теперь. Единственное отличие здесь состоит в том, что вместо
показателя преломления п, а вследствие этого согласно B0) и вме-
вместо угла преломления &v придется вставить в общем случае ком-
142 ДИСПЕРСИЯ ИЗОТРОПНЫХ СРЕД
плексную величину. Благодаря этому константы ц, о, ц-^, аи
определяемые уравнениями B3) и B4) для отраженной и прелом-
преломленной волны, являются комплексными, совершенно так же, как
при полном внутреннем отражении. Физическое значение этого
обстоятельства, как мы там видели, состоит в том, что при отра-
отражении и преломлении имеет место скачок фазы. Так как этот
скачок фазы для волны с колебаниями в плоскости падения,
/-волны, другой, чем для волны с колебаниями, перпендикуляр-
перпендикулярными плоскости падения, д-волны, то падающий линейно поля-
поляризованный свет отражается уже не линейно, а эллиптически по-
поляризованным. Можно измерить разность фаз обеих компонент
волны при помощи компенсатора, например параллелепипеда
Френеля (§ 27), или листочка слюды (§ 64). Вместе с изменением
угла преломления это дает два соотношения, необходимые, чтобы
вычислить две константы п и а, которыми определяются все
оптические свойства среды.
Интенсивность отраженного и преломленного света согласно
общим соображениям, высказанным в § 18, определяется ква-
квадратами абсолютных значений коэфициентов ju и а. Поэтому
величины:
1Н2 = ец и \о\* = ех C73)
дают непосредственно коэфициенты отражения обеих компонент
волны. Коэфициент пропускания для преломленной волны можно
проще определить согласно § 10 из коэфициента отражения,
чём из величин /^ и а1ш Для частного случая перпендикулярного
падения (& = 0) из B3) получается
— —
Gn Q,
tWx)— (n— Ы)
1*1)+("—!*)
_ _(Яд —„
C74)
Отсюда видно, между прочим, что коэфициент отражения
лишь тогда равен нулю, когда одновременно пх = п и кг = к, т. е.
когда между обоими соприкасающимися телами вообще нет опти-
оптического различия. Поэтому „черное" тело, т. е. такое, которое
поглощает весь падающий на него свет, не может обладать пло-
плоской поверхностью. Однако коэфициент отражения может быть
как угодно близким к единице. Это будет в том случае, когда из
четырех величин пг, п, к, кх одна очень велика по сравнению с
другими. В этом случае говорят о „металлическом" отражении,
оно имеет место, например, у поверхности абсолютного провод-
проводника электричества C, § 92).
§ 86. При выводе законов дисперсии и абсорбции на осно-
основании сделанных нами гипотез относительно природы и распо-
расположения участвующих в колебаниях диполей мы воспользовались
определенным методом расчета. Этот метод можно заменить со-
ПЛОСКИЕ ВОЛНЫ 143
вершенно другим и с помощью его проверить правильность
полученных ранее результатов.
Применяя первый метод, мы получили сначала общие дифе-
ренциальные уравнения для электромагнитных процессов, проис-
происходящих внутри среды, и затем искали частные интегралы их.
При выводе этих диференциальных уравнений мы должны были
совершить переход от атомистического представления о струк-
структуре среды к представлению о непрерывном ее строении. Более
углубленное понимание изучаемых физических явлений требует
переход этот проделать позже, изучив раньше непосредствен-
непосредственно те электромагнитные волны, которые излучаются отдельными
колеблющимися диполями среды. При таком переходе мы имеем
дело лишь с одной средой, в которой распространяются волны:
с вакуумом. В нем помещено большое количество колеблющихся
диполей, каждый из которых является центром сферической вол-
волны, распррстраняющейся по известным законам, независимо от
остальных диполей, так как согласно 3, C96) электромагнитное
поле, возбуждаемое диполем, колеблющимся с моментом f(t),
однозначно определено для любого места и для любого момента
времени. Этим путем мы приходим к частному решению проб-
проблемы, удовлетворяющему уравнениям C62) и C63). При этом мы
принимаем, что в вакууме имеется, во-первых, периодическая
„первичная" волна, распространяющаяся вдоль оси х, с колеба-
колебаниями в направлении оси у, частотой со и скоростью распростра-
распространения с; во-вторых, большое число сферических ^вторичных"
волн, которые излучаются отдельными диполями, колеблющимися
с той же частотой, и налагаются друг на друга и на первичную
волну. В результате получается „эффективная" волна, у которой
напряжения поля Е и Н получаются путем векторного сложения
соответствующих напряжений поля первичной и вторичной волн.
Так как диполи находятся крайне близко друг от друга, можно
сложение заменить интегрированием.
Взаимодействие диполей друг с другом и с первичной волной
выражается, как и ранее, уравнением C49), которое устанавли-
устанавливает связь между моментом колеблющегося диполя и напряже-
напряжением возбуждающего его поля Е'. Зависимость между Е и Е'
определяется опять уравнением C51) или C69).
Из этих соотношений вытекает вполне определенный закон
распространения эффективной волны в рассматриваемой среде.
Если теория лишена внутренних противоречий, то этот зако»
должен быть идентичным с ранее полученным, хотя мы здесь не
пользовались ни диференциальными уравнениями дисперсии, ни
понятием электрической индукции, а только законами распро-
распространения волн в чистом вакууме. Так оно и есть на самом деле,
в чем можно убедиться прямым подсчетом. При этом следует
подчеркнуть, что векторное сложение посылаемых диполями вто-
вторичных сферических волн дает, как и следует быть, две волны:
во-первых, одну волну, распространяющуюся со скоростью с, ко-
144 ДИСПЕРСИЯ ИЗОТРОПНЫХ СРЕД
торая равна и противоположна первичной, также распространяю-
распространяющейся со скоростью с, и поэтому ее уничтожает; во-вторых, вол-
волну, распространяющуюся со скоростью -jj-, где п определяется
из C65) или C71). По всем другим направлениям, отличным от
•оси х, вторичные волны взаимно уничтожаются вследствие ин-
интерференции.
Мы видим, что новый способ распространения дает непосред-
непосредственное понимание сущности дисперсии; но его физическое зна-
значение гораздо глубже, он ведет к новому выводу законов пре-
преломления и отражения. Представим себе, ради простоты, плоскую
периодическую волну, падающую из вакуума под углом # на
поверхность диспергирующей среды. Эта волна, которую мы опять
обозначим первичной, проходит без всяких препятствий сквозь
среду, так как она распространяется, как и прежде, в вакууме,
г. е. со скоростью с. С этой новой точки зрения вообще нельзя
говорить о поверхности или границе. Влияние среды сказывается
исключительно в виде колебаний его диполей, и мы опять полу-
получаем эффективную волну, как суперпозицию первичной волны
с вторичными сферическими волнами, получаемыми от колеблю-
колеблющихся диполей среды. При этом наши предположения относительно
моментов диполей должны, конечно, удовлетворять уравнению ко-
колебания C49). При подсчете полученные в предыдущих парагра-
параграфах совершенно другим путем законы подтверждаются во всех
их деталях. Действительно, результатом суперпозиции вторичных
сферических волн является, во-первых, плоская волна, целиком
уничтожающая первичную волну вследствие интерференции; во-
вторых, плоская волна, распространяющаяся по направлению
луча, преломленного согласно закону Снеллиуса; в-третьих-, вол-
волна, отраженная в вакуум под углом &. Амплитуды волн получаются
также в согласии с предыдущими вычислениями.
Эгот метод получения законов отражения и преломления
сложнее, чем прежний, в отношении вычислений; но зато он
имеет большее физическое значение. Не требуя никаких условий
на границе, он прямо дает полное объяснение явлений отраже-
отражения и преломления, представляя их как действие излученных
во-вне и особым образом интерферирующих сферических волн.
§ 87. Все предыдущие рассуждения относятся исключительно
к таким частным решениям уравнений поля, которые соответ-
соответствуют простым гармоническим периодическим волнам. Обра-
Обратимся теперь к исследованию более общего случая непе-
непериодических плоских волн, распространяющихся вдоль
оси х внутри диспергирующей среды. Раньше всего надо отме-
отметить, что здесь понятие о скорости распространения совершенно
теряет тот общий смысл, который оно имело для недиспергирую-
щей среды. Действительно, для диспергирующей среды волновая
функция не всегда может быть представлена в виде определен-
определенной функции единственного аргумента, зависящего только от х
ПЛОСКИЕ ВОЛНЫ 145
и t, как это имеет место в уравнении (8). Другими словами,
волна не остается неизменной при распространении, но дефор-
деформируется с течением времени, и нельзя какой-нибудь, отмечен-
отмеченный в некоторый момент времени пункт волны вновь безоши-
безошибочно опознать в другой момент времени.
Из этого сразу вытекает, что можно произвольным образом
определить бесконечное множество различного рода скоростей
распространения, смотря по тому, на какой характеристический
признак обращать внимание при распространении волны. Так,
например, можно заметить в какой-нибудь точке х в момент
времени t напряжение поля Еу и искать соседнюю точку л; + dx,
в которой в момент времени t + dt будет иметь место то же на-
напряжение поля {Еу = const). Отсюда для скорости распростра-
распространения напряжения поля Е получим:
дЕу
ах dt
dt дЕу
дх
C75)
Для недиспергирующих сред эта величина постоянна. Но
для сред, имеющих дисперсию, она постоянна лишь в случае
простой гармонической периодической волны и поэтому не имеет
общего физического значения. Это же замечание будет иметь
место, если рассматривать скорость распространения максимума
или минимума напряжения поля. Она получается из C75), если
туда вставить -д у вместо Еу, и в общем случае отличается
от C75).
Из этих рассуждений следует, что. вообще невозможно для
диспергирующей среды определить скорость распространения
постоянную во времени и пространстве, если не ввести каких-
нибудь предположений относительно особой формы волны.
Легко видеть также, что для различных форм волны скорость
распространения может быть определена весьма различным
образом. Мы установим это для некоторых особенно важных
случаев.
Обращаясь теперь к вопросу об общем интеграле волнового
уравнения C60) и связанного с ним уравнения колебания C61),
мы можем сказать, что в основных чертах достаточный ответ
находится тем же путем, который привел нас к цели в случае
полного внутреннего отражения (§ 14). Мы можем любую функ-
функцию для сколь угодно большого интервала ее аргумента напи-
написать в виде ряда Фурье. Каждый член этого ряда представляет
собой простой гармонический процесс, который распространяется
согласно найденным выше законам. Так как диференциальные
уравнения C60) и C61) линейны и однородны, то отдельные
процессы налагаются друг на друга. Таким образом любая волна,
распространяющаяся в диспергирующей среде, может быть рас-
ВвоДеняв в теоретическую физику, ч. IV г 10
146 ДИСПЕРСИЯ ИЗОТРОПНЫХ СРЕД
сматриваема как состоящая из элементарных гармонических
периодических волн, из которых каждая распространяется,
не изменяясь, с постоянной во времени и в пространстве
скоростью —. Но так как п для различных волн различно, то
фазы отдельных волн смещаются друг относительно друга и
отсюда получается деформация суммарной волны.
§ 88. Рассмотрим теперь следующий частный случай. Пусть
имеется диспергирующая среда, простирающаяся от х = 0 до
х = оо. Вначале она ничем не возбуждается, но с некоторого
момента £=0 на нее падает в течение продолжительного вре-
времени, перпендикулярно к ее поверхности, простая периодическая
волна частоты со. С какой скоростью возмущение распростра-
распространится внутрь среды? Неверно будет предположение, кажущееся
правильным на первый взгляд, что волна просто войдет в среду
с
со скоростью —, как это имеет место для периодической, дол-
п
гое время распространявшейся волны. В рассматриваемом слу-
случае мы имеем дело с непериодической волной, которая дефор-
деформируется при распространении. Полное решение этого вопроса
при помощи разложения волны в интеграл Фурье дано А. Зом-
мерфельдом х). Но мы можем без особых вычислений найти
ответ на поставленный выше вопрос, если воспользуемся спо-
способом рассуждения, подробно изложенным в § 86.
Первичная волна в диспергирующей среде распространяется
со скоростью с, так же как и вторичные волны, вызванные
диполями, колеблющимися вместе с волной. Но результат взаимо-
взаимодействия их получается не такой, как для периодической волны,
длящейся продолжительное время. Диполи колеблются не перио-
периодически—в самом начале они находятся в покое и вследствие своей
инерции приходят в колебание лишь постепенно и притом тем
позже, чем больше их абсцисса х. Колебания эти принимают
постоянный характер, строго говоря, лишь через бесконечно
большое время и тогда только создают простое периодическое
гармоническое волновое движение, распространяющееся со
скоростью с. Пока это не достигнуто, первичная волна не
уничтожается вторичными, и она проявляется как возмущение,
распространяющееся в диспергирующей среде со скоростью с.
С другой стороны, вторичные волны, какую бы форму они ни
имели, также распространяются со скоростью с. Из этого сле-
следует, что искомая скорость, с которой распространяется в среде
начало волны, так называемая „фронтовая скорость", всегда
равна с.
В противоположность фронтовой скорости можно гово-
говорить о фазовой скорости —, которую имеет элементарная
х) A. So mm erf eld, Weber-Festschrift, В. G. Teubner, S. 338, 1912.
ПЛОСКИЕ ВОЛНЫ 147
периодическая, длящаяся продолжительное время волна; мы ее
будем обозначать:
и=~. C76)
Не нужно видеть внутреннего противоречия теории в том,
что фазоаая скорость и может быть больше, чем фронтовая
скорость с(и<1); Волна не является строго периодической и
фронт проникающей в среду волны не обладает постоянной
фазой. Поэтому не может быть речи о том, чтобы задние, рас-
распространяющиеся с фазовой скоростью части волны определили
фронт, распространяющийся с фронтовой скоростью. Из сказан-
сказанного выше следует, что скорость распространения светового
сигнала, посланного в среду, не может быть больше с. Она
достигает этого наивысшего значения только для случая наи-
наиболее чувствительного детектора, т. е. для приемника, реагирую-
реагирующего на малейшее возбуждение. В ином случае скорость сигнала
можно считать меньшей, смотря по чувствительности прием-
приемника. Величину фазовой скорости при этом вообще не прихо-
приходится принимать во внимание, так как нельзя передавать сигна-
сигналов при помощи простых периодических гармонических волн.
§ 89. Теперь мы рассмотрим еще более важный случай
непериодической волны, и именно случай- почти гармони-
гармонической волны. Во всех так наз. монохроматических лучах
(§ 16) в действительности имеет место именно этот случай.
Общее выражение для такой приблизительно гармонической волны,
распространяющейся в диспергирующей среде, согласно C62):
2 C77)
m = l
причем
-*L_L<C1. C78)
Здесь т — порядковое число, вместе с которым растет частота
колебаний; общее количество N различных частот колебаний
произвольно велико, Ст есть комплексная постоянная. Рассмотрим
сначала форму такой волны. Для этого Еу, как функцию х для
определенного момента времени t, представим в виде кривой
с абсциссой х. Эта кривая образована наложением определен-
определенного числа простых синусоид с приблизительно одинаковой
длиной волны. Результатом будет, как подробно выяснено в § 16,
почти гармоническая кривая, с той же длиной волны и с медленно
и в общем беспорядочно меняющимися амплитудой и фазой.
Разберемся в этом несколько ближе. Амплитуда и фаза резуль-
результирующей волны определяются различием фаз, с которыми нала-
налагаются друг на друга отдельные гармонические волны. Выделим
одну из них с частотой со и фазовой скоростью —. Фаза какой-
148 ДИСПЕРСИЯ ИЗОТРОПНЫХ СРЕД
нибудь другой парциальной волны с частотой со' и фазовой
скоростью -дг согласно C77) может быть представлена для
любой точки х и любого момента t фазой первой волны с при-
прибавкой разности фаз:
(со' — со) t — ■—■ {со'п'—сап) + ■&' — Л C79)
Здесь &' и ■& представляют собой угловые аргументы ком-
комплексных постоянных с' и с. Пока эта разность фаз не меняется
заметно для любых комбинаций из каждых двух парциальных
колебаний, парциальные волны интерферируют одинаковым обра-
образом, и результирующая волна имеет постоянную амплитуду и
фазу. Будем считать время t постоянным, тогда разность фаз
меняется лишь в зависимости от абсциссы х. При переходе от
точки х к соседней точке xt > x разность фаз C79) меняется
на величину.
-сап). C80)
Пусть обе точки лежат так близко друг от друга, что для всех
пар парциальных колебаний имеет место:
C81)
Тогда результирующая волна между обеими точками образует
простую синусоиду с длиной волны:
, 2пС 2пс
Л = -^Г— ИЛИ -7—, ,
что согласно C78) дает практически одно и то же.
Но если точка хх переместится по оси абсцисс так далеко,
что соотношение C81) уже будет не действительно, то интерферен-
интерференционное действие парциальных волн изменится, и результирующая
волна будет иметь другую амплитуду и другую фазовую константу.
Сообразно с этим можно сказать следующее: форма результи-
результирующей волны Еу в какой-нибудь момент времени t может быть
представлена состоящей из ряда лежащих одна за другой групп
простых синусоидальных гребней и впадин. Каждая группа в от-
отдельности простирается на такой отрезок по оси абсцисс, для
которого выполняется соотношение C81). Любая пара парци-
парциальных колебаний имеет в ней определенную разность фаз C79),
поэтому каждая такая группа обладает определенной ампли-
амплитудой и определенной фазовой постоянной. Но от группы к группе
эти величины меняются. Число длин волн, укладывающихся на
протяжении одной группы, согласно C82) равно:
х*~х = (х*~х>'"<а.) C83)
если х и х{ обозначают начальную и конечную ее точки. Это
ПЛОСКИЕ ВОЛНЫ 149
число может быть очень велико, так как на основании B79)
соотношение
вполне совместимо- с соотношением C81).
Рассмотрим теперь изменения, происходящие в определенной
точке пространства х с течением времени t При помощи рас-
рассуждения, аналогичного вышеприведенному, получаем, что
в интервале времени tx—t столь малом, что для каждой пары
парциальных колебаний:
результирующее напряжение поля Еу колеблется синусоидально
с частотой а. Но для более поздних моментов времени £, насту-
наступает изменение амплитуды и фазовой постоянной. Можно при-
придать этому явлению большую наглядность, если обратить вни-
внимание не на одну определенную точку пространства х, а на
определенную фазу результирующей волны, например на вер-
вершину волнового гребня. Этот гребень распространяется с фазовой
скоростью —; он сохраняет свою величину и свою скорость
распространения на определенном участке, который может охва-
охватывать много длин волн. Но со временем меняются как его
величина, так и скорость его распространения. Последняя всегда
остается близкой к фазовой скорости, величина же гребня может
как угодно расти и убывать. Другими словами, определенным
образом выбранный гребень волны не остается" с течением вре-
времени в одной и той же группе, но переходит в соседнюю
группу.
При помощи этого представления решается вопрос о том,
с какой скоростью распространяется какая-нибудь определенная
группа. Ответ получается на основании вышеуказанного свойства
группы, что для нее разность фаз C79) для каждой комбинации
двух парциальных колебаний сохраняет определенное неизменное
значение.
Возьмем разность фаз C79) для х и t и приравняем ее соот-
соответствующей величине для хх и tv Тогда найдем, что отношение
хх —х К—со) с
|—f- со'п-соп
независимо от х и t. Это и есть искомая групповая скорость,
постоянная для любого места и времени. Выражение для нее
можно на основании C78) написать так:
^ C87)
150 ДИСПЕРСИЯ ИЗОТРОПНЫХ СРЕД
Между групповой и фазовой скоростью согласно C76) имеется
соотношение:
Различие между и и v, естественно, основывается на том, уже
указанном обстоятельстве, что определенный отмеченной вол-
волновой гребень, распространяющийся с фазовой скоростью, с те-
течением времени переходит от группы к группе. Лишь для сред,
не имеющих дисперсии ^~ =0j, v~u и каждый гребень дол-
долгое время остается в пределах своей группы. При нормальной
дисперсии (^ > 0J, v<u, т. е. определенный волновой гребень
переходит с течением времени из своей группы в ближайшую,
впереди находящуюся группу и обгоняет, таким образом, одну
группу за другой. При аномальной дисперсии имеет место об-
обратное. При этом надо помнить, что группа не представляет со-
бёй образования, сохраняющегося все время. Отношение разно-
разностей C86) не равно в точности отношению диференциалов
в C87), но имеет несколько различное значение для каждой ком-
комбинации двух парциальных колебаний. Поэтому для большого
интервала времени^ — £ проделанный путь xt — л: для различных
пар колебаний будет в значительной степени неодинаков, т. е.
группа распадается. Следовательно, в течение больших проме-
промежутков времени происходит постепенный обмен и между груп-
группами, причем каждая группа со временем распадается и сливается
частично с впереди идущей группой, частично — с следующей
позади.
ГЛАВА III
ГЕОМЕТРИЧЕСКАЯ ОПТИКА НЕОДНОРОДНЫХ СРЕД.
СВЯЗЬ С КВАНТОВОЙ МЕХАНИКОЙ
§ 90. Оптически неоднородная среда характеризуется тем,
что для нее показатель преломления п определенным образом
зависит от пространственных4 координат х, у, z. Мы предпола-
предполагаем также, что среда обладает дисперсией, т. е. принимаем п
зависимым от длины волны. Но зато мы будем считать среду изо-
изотропной; тогда п в определенной точке среды и для определен-
определенной частоты одинаково для всех направлении. Законы рас-
распространения света в такой среде вообще крайне сложны. Но
можно достигнуть значительного упрощения, если ограничиться
областью геометрической или лучевой оптики, охватывающей
согласно § 28 те явления, для объяснения которых достаточны
законы, действительные для плоских волн.
ГЕОМЕТРИЧЕСКАЯ ОПТИКА НЕОДНОРОДНЫХ СРЕД 151
Мы начнем опять с простых гармонических периодических
колебаний. Всякая волновая функция имеет в этом случае фазу:
cot — (р {х, у, z) = 6, C89)
где со—частота, а <р есть функция точки, обобщающая выраже-
выражение C62). Она называется „эйконал".
Назовем волновой поверхностью такую поверхность, все
точки которой в определенный момент t имеют одну и ту же
фаёу 0. Тогда волновая поверхность определяется уравнением:
<р (х, у, z) = const. C90)
Семейство волновых поверхностей, которое получается, когда
постоянная пробегает всевозможные значения, остается неизмен-
неизменным для всякого момента времени и поэтому неподвижно нахо-
находится в среде. Если взять какую-нибудь определенную фазу 0,
то она согласно C89) в момент t имеет место на поверхности
y = cot—0. Поэтому она со временем равномерно перемещается
в направлении от меньших значений ц> к большим. Если же взять
определенную точку пространства х, у, г, то в ней фаза равно-
равномерно растет со временем:
*=»■ C91)
Для геометрической оптики характерно положение, что каж-
каждый достаточно малый элемент волновой поверхности можно
рассматривать как плоскую волну, распространяющуюся в на-
направлении нормали с соответствующей данному месту фазовой
скоростью «=—. Так как среда изотропна, то направление
нормали вместе с тем является направлением луча. Поэтому,
если какая-нибудь волновая поверхность известна, то мы полу-
получим поверхность, бесконечно близкую к ней, откладывая по на-
направлению нормали из каждой точки данной волновой поверх-
поверхности отрезок и • dt и соединяя концы всех этих отрезков. Та-
Таким образом, обозначая через ds расстояние по нормали между
обеими поверхностями, получим:
ds= и dt.
С другой стороны, фаза 0 при распространении волновой
поверхности осталась неизменной, так как а есть фазовая ско-
скорость. Тогда из C89) находим:
со dt — dtp = 0.
Это уравнение вместе с предыдущим дает нам производную
для ср по нормали:
д<р to run _ дв
ds - И= ~ ds-
152 ДИСПЕРСИЯ ИЗОТРОПНЫХ СРЕД
Полученное таким образом диференциальное уравнение назы-
называется уравнением эйконала. С его помощью можно из одной дан-
данной волновой поверхности получить остальные, так как п задано
как функция х, у, z. В нем, в сущности, заключена в скрытой
форме вся геометрическая оптика, так как если известна система
волновых поверхностей, то ее ортогональные кривые предста-
представляют собой лучи, распространяющиеся сквозь среду.
§ 91. Законы геометрической оптики могут быть получены
как из уравнения C92), так и при помощи принципа Ферма. При-
Приведем вывод последнего в той форме, как это сделано для бо-
более специального случая в § 37.
Согласно принципу Ферма время, потребное для того, чтобы
определенная фаза с присущей ей скоростью и перешла от
определенной точки среды Р к другой определенной точке Q
меньше по пути луча, идущего от Р к Q, чем по любому дру-
другому пути, соединяющему Р и Q; или
Q Q
8 /"А = о = Л /" nds. C93)
р р
Вставим в это уравнение вместо вариаций их выражения:
. дп . дп s . дп .
Затем, как в /, в § 108, при помощи интегрирования по ча-
частям, перейдем от bdx, 8dy, 8dz к дх, 8у, 8z и коэфициенты при
них приравняем по отдельности нулю. Тогда диференциальные
уравнения для пути луча, идущего от Р до Q, получатся
в форме:
При помощи этих уравнений может быть вычислен путь
луча, если заданы начальная точка и начальное направление
его. Они заключают в себе все законы геометрической оптики
и совершенно идентичны с уравнением C92) для волновых по-
поверхностей. В этом можно убедиться и непосредственно, если
мысленно представить себе построение по данной поверхности
другой, близкой к ней, как описано в § 90. Вычисляя происхо-
происходящее при этом изменение направления нормалей волновой
поверхности по сравнению с нормалями первоначальной, мы как
раз и получим соотношение C94).
§ 92. Чтобы с большей уверенностью итти дальше, мы не-
несколько точнее сформулируем условия, при которых допустимо
применение геометрической оптики. Диференциальные уравнения
дисперсии C59) и C55) имеют силу в общем случае. Первое из
ГЕОМЕТРИЧЕСКАЯ ОПТИКА НЕОДНОРОДНЫХ СРЕД 153
них содержит универсальную постоянную с, во-втором мы при-
принимаем константы со0' и а заданными для неоднородной среды
как функции пространственных координат х, у, z. Оба диферен-
циальных уравнения можно удовлетворить при помощи следую-
следующего обобщения подстановок C62) и C63), которые мы приме-
применяли для случая плоских волн в однородной среде
Е = % М = тр. C95)
В данном случае а является определенной функцией коорди-
координат, в то время как волновая функция у> есть некоторая функция
пространства и времени.
При помощи подстановки этих выражений в C55) и C59)
получаем:
ау> + юо'2ау = £ V C96)
и
гр + ^птр = съЛгр
или
^ C97)
где п связано с а опять п{эи помощи C65).
Введем теперь предположение, что процесс является перио-
периодическим по времени, т. е.
v, = e«(«'-rt> C08)
где функция места у в обобщение C89) может быть теперь
комплексной. Тогда
у = — со2у C98а)
и соотношение C96) приводит к тому же значению для п, как
соотношение C65), полученное для плоских волн в однородных
средах. Вследствие этогр вся проблема в общем случае сводится
к диференциальному уравнению C97), определяющему волновую
функцию ip.
Подстановка в него выражения C98) дает:
или, если обозначить опять через ds элемент длины нормали
к поверхности <р = const:
с"
Это соотношение переходит в основное уравнение геометри-
геометрической оптики C92) тогда и только тогда, когда можно прене-
пренебречь членом, содержащим Atp.
154 ДИСПЕРСИЯ ИЗОТРОПНЫХ СРЕД
Отсюда вытекают вследствие комплексности уравнения ,C99)
два условия. Во-первых, производные мнимой части tp должны
быть очень малы. Согласно C98) это значит, что амплитуда вол-
волновой функции должна медленно изменяться в пространстве.
Во-вторых, член, содержащий вторую производную действитель-
действительной части у, должен быть мал по сравнению с каждым из
остальных членов уравнения C99). Ввиду соотношения C82) это
значит: радиусы кривизны волновых поверхностей должны быть
велики по сравнению с длиной волны. Здесь мы имеем то же
требование, которое мы уже сформулировали в § 28. Иначе его
можно выразить так: радиусы кривизны лучей должны быть
велики по сравнению с длиной волны. Поскольку эти условия
выполнены, можно законы геометрической оптики применять'
в качестве первого приближения. Но как только они нарушены
в какой-либо точке, приходится иметь дело.с волновым уравне-
уравнением C97), выражающим явления с полной точностью.
§ 93. Оставим теперь простые гармонические лучи и обра-
обратимся к естественным монохроматическим, т. е. к почти гармо-
гармоническим лучам, о которых шла речь в § 89. Мы видели там,
что такой луч может быть представлен как ряд распространяю-
распространяющихся одна за другой групп простых синусоидальных греб-
гребней и впадин. Скорость распространения этих групп ■# характе-
характеризовалась условием, что разность ©' — 6 фаз каких-либо двух
парциальных колебаний частоты со' и со должна оставаться по-
постоянной.
Следовательно, согласно C89):
(со' — (а) • t — ($>'—<р) = const
или
Отсюда, приняв во внимание C92), получим:
ds ш'— а
V С
п'т'~пы
в полном согласии с C86), C87) и C88).
Так как групповая скорость v отлична от фазовой скорости и,
то точка, распространяющаяся с групповой скоростью, меняет
с течением времени свою фазу, для такой точки согласно C89):
ав _ дв , дв
F - Ж ~+"эГ v
и вследствие C91) и C92)
d&
_ = 0,
D00)
ГЕОМЕТРИЧЕСКАЯ ОПТИКА НЕОДНОРОДНЫХ СРЕД 155
Это дает вместе с C76) и C78):
d& ы ды
dt дп п
до о>
D01)
Производные здесь обозначены при помощи круглого д, так
как п зависит также от места.
Для недиспергирующей среды ^ = 0. Тогда фаза остается
постоянной, т. е. групповая скорость совпадает с фазовой. Это
имеет силу как для однородных, так и для неоднородных сред.
§ 94. Выведенные выше основные уравнения геометрической
оптики неоднородной диспергирующей изотропной среды обна-
обнаруживают с формальной стороны, для случая почти гармониче-
гармонического луча, замечательную аналогию с основными уравнениями
классической механики для свободной материальной точки,
движущейся в консервативном статическом силовом поле (/, § 49).
Аналогия эта состоит в том, что волновая группа (ограниченная
малым объемом) движется по направлению ее луча согласно
тем самым законам, которым следует материальная точка в ее
движении по своей траектории. Действительно, приравнивая
надлежащим образом оптические константы, можно достичь
полной идентичности оптических уравнений с механическими.
Мы покажем это в дальнейшем.
Для этой цели мы прежде всего рассмотрим оба уравнения
C91) и D01), которые выражают изменение по времени фазы 0
для покоящейся точки и для точки, перемещающейся вдоль
луча с групповой скоростью v. Этим уравнениям мы противопо-
противопоставим два соответствующих уравнения механики для интеграла
действия W, который мы будем считать функцией от х, у, z, t.
На основании [/, D20)] имеем:
™=-Е D02)
для покоящейся точки, и [/, D19)]
^ = f—2U D03)
для точки, перемещающейся согласно законам движения по
своей траектории [7, D19)]. При этом Е обозначает энергию,
а Я—2U—кинетический потенциал, или функцию Лагранжа, т. е.
разницу между кинетической энергией:
Е—и=\тР D04)
и потенциальной энергией U, которую мы рассматриваем как
заданную функцию координат х, у, z.
156 ДИСПЕРСИЯ ИЗОТРОПНЫХ СРЕД
К этим формулам для производных по времени от 0, с одной
стороны, и W, с другой стороны, присоединяются формулы для
их пространственных производных. Для 0 это есть уравнение
C92), для W—уравнения /, D17). Последние выражают собой,
что пространственный градиент равен импульсу движущейся
точечной массы. Из них следует, что скорость движения в каж-
каждый момент времени направлена по перпендикуляру к поверх-
поверхности W =const и что величина градиента -^- равна произве-
произведению массы на скорость:
~nw. D05)
Примем теперь скорость v перемещающейся точечной массы
идентичной по величине и направлению со скоростью распро-
распространения волновой группы, обозначенной ранее также через v.
Приняв во внимание, что луч направлен по перпендикуляру
к поверхности 0 —const, мы приходим к выводу, что можно по-
положить функции W у 6 пропорциональными одна другой. Из
этого вытекает путем сравнения C91) и D02), что и оптическая
константа со пропорциональна механической константе Е. Так как
обе эти величины имеют различные размерности, то коэфициент
пропорциональности не является отвлеченным числом. Мы полу-
получаем поэтому:
*=А.£, D06)
понимая под h определенную постоянную, размерность которой
равна произведению энергии на время. Уравнения C91) и D02)
делаются при этом идентичными, если мы положим еще:
W= — ~в. D07)
На основании этого устанавливается также соотношение
между уравнениями D05) и C92):
ds 2я ds 2пс с
Отсюда получается, если вычислить v из уравнения D04),
следующее выражение для показателя преломления:
п = -g- У 2т (Е— U). D09)
Зависимость показателя преломления от функции координат U
обусловливает неоднородность, а зависимость его от постоянной
энергии Е и вследствие этого от со, обусловливает дисперсию
среды, в которой распространяется рассматриваемая волновая
группа.
ГЕОМЕТРИЧЕСКАЯ ОПТИКА НЕОДНОРОДНЫХ СРЕД 157
Можно убедиться в том, что вследствие указанных соотно-
соотношений между механическими и оптическими величинами обе сис-
системы уравнений делаются вполне идентичными. В частности,
уравнение C87):
1 1 д(ем) _ 1 д(Еп)
v — с ~ды ~~ с дЕ V*l{J>
при помощи подстановки D09) приводит к идентичности груп-
групповой скорости с величиной v, данной уравнением D04). Точно
так же D01) непосредственно переходит в D03).
Мы можем, таким образом, сформулировать следующее, весьма
общее положение: согласно законам классической механики, ма-
материальная точка т движется в силовом поле с заданной потен-
потенциальной энергией U, так же как гармонический луч в не-
неоднородной диспергирующей изотропной среде с показателем
преломления:
Подобно тому как движение материальной точки опреде-
определяется начальным положением, начальным направлением движе-
движения и энергией Е, точно так же распространение соответствую-
соответствующего ей луча определяется начальной точкой, начальным напра-
влением его и частотой со = —^—.
Сказанным устанавливается далеко идущее сходство между
законами классической механики и законами геометрической оп-
оптики. Однако оно не полно. Мы имеем существенное различие
в следующем пункте. Классическая механика претендует на абсо-
абсолютную значимость, она представляет собой замкнутую в'себе
систему и не связана никакими предположениями о порядке
величин. Что касается геометрической оптики, то мы знаем, что
она не всегда имеет силу, но согласно § 92 лишь тогда, когда
длина волны C82), соответствующая частоте со луча, мала по
сравнению с радиусом кривизны пути луча. Лишь только это
условие нарушено, законы геометрической оптики теряют свою
силу, и приходится вновь вернуться к общему волновому уравне-
уравнению C97) или C99).
§ 95. Мы могли бы ограничиться этими результатами, если бы
классическая механика подтверждалась для всех происходящих
в природе динамических явлений. Но это не так.
Опытные факты заставляют принять, что очень быстрые дви-
движения мельчайших частиц материи происходят при условиях,
которые весьма отличаются от основных предположений класси-
классической механики. Можно привести в качестве примера тот факт,
что при движении электрона вокруг атомного ядра энергия Е
имеет предпочтительно некоторые особые, вполне определенные
значения, — факт, совершенно чуждый классической теории.
158 ДИСПЕРСИЯ ИЗОТРОПНЫХ СРЕД
Если, таким образом, оказывается необходимым изменить
классическую механику, то речь идет лишь об обобщении ранее
установленных ее законов, так как в пределе последние при
всех обстоятельствах сохраняют свое значение. Нужно при этом
заметить, что классическая механика не может получить такого
обобщения, исходя из себя самой, так как, как всякая замкнутая
система, она обладает внутренней законченностью и не содержит
в себе никаких новых возможностей для дальнейшего развития.
Толчок должен быть дан извне. Прекрасный пример предста-
представляет собой теория относительности, которая проникла в меха-
механику из оптики и прибавила к ней совершенно новую
страницу.
И в настоящем случае спасение пришло со стороны оптики.
Л. де-Бройль впервые привлек к объяснению квантовых явлений
давно уже известную аналогию между классической механикой
и геометрической оптикой, изложенную нами в предшествующем
параграфе. Шредингер эту мысль провел дальше. Он предполо-
предположил, что обобщение, которому должны подвергнуться законы
классической механики для согласования их с действительностью,
имеет тот же характер, как и расширение геометрической оптики,
применяемое при выходе за пределы области ее непосредствен-
непосредственного действия. Другими словами, законы новой механики нахо-
находятся просто при помощи дальнейшего проведения аналогии
между механикой и оптикой. Соответственно этому законы ста-
старой механики изменяются таким образом, что отмеченное в конце
предшествующего параграфа коренное различие между механи-
механикой и оптикой пропадает. Уравнения D06) и D11), характерные
для аналогии "механики с оптикой, остаются тогда в силе и вне
области применения геометрической оптики. Таким образом
классическая механика — механика лучевая — превращается в
волновую механику, включающую в себя первую как частный
случай. Ее характерной чертой является то, что движение
материальной точки уже не может быть представлено движе-
движением геометрической точки; но материальная точка некоторым
образом распадается на некоторое число волн определенного
рода совершенно так же, как световой луч, строго говоря, не
может быть представлен одной кривой, а является результатом
взаимодействия световых волн.
Первый большой успех этой идеи проявляется благодаря
введению волнового уравнения C97) в новую механику. При п,
определяемом D11), последнее принимает вид:
D12)
или, если вставить для у выражение C98):
a D13)
ГЕОМЕТРИЧЕСКАЯ ОПТИКА НЕОДНОРОДНЫХ СРЕД 159
Согласно D06) можно также написать:
^ 0. D14)
Особенность этого диференциального уравнения Шредингера
состоит в том, что коэфициент Е— (J при известных условиях
может сделаться отрицательным. Если постоянная Е взята столь
•большой, что для всех точек пространства (предполагая, что
волна не имеет границ в пространстве) (Е—U) > 0, то
уравнение имеет конечные и непрерывные решения. Если же
Е недостаточно велико, то для наибольших значений U этот
коэфициент отрицателен. В этом случае уравнение D14) имеет
всюду конечные и непрерывные решения у> только тогда, когда Е
принимает вполне определенные значения Еи Еъ Е3,.., так на-
называемые собственные значения. Этим значениям соответствуют
так называемые собственные функции ^,, ^а, %,... Кажущееся
сначала невероятным, это обстоятельство гораздо легче может
быть понято, если принять во внимание, что при отрицательных
значениях Е — U показатель преломления D09) получает мни-
мнимое значение и геометрическая оптика вообще теряет смысл.
Диференциальное уравнение D14) приобретает особенную
важность благодаря следующему обстоятельству: найденные из
него собственные значения Е во всех случаях совпадают в точ-
точности с теми собственными значениями, которые уже были ранее
получены Гейзенбергом, Борном и Иорданом при помощи соста-
составленных в матричной форме уравнений квантовой механики.
Последняя была построена независимо от каких бы то ни было
специальных гипотез физического характера, но основывалась на
экспериментальных фактах. Это совпадение результатов, получен-
полученных двумя совершенно различными путями, служит явным доказа-
доказательством их существенного значения. Не может быть никакого
сомнения в том, что при помощи диференциального уравнения
Шредингера, благодаря его близкой связи с классической меха-
механикой, удастся еще глубже проникнуть в сущность квантовых
явлений.
Конечно, в физической природе волновой функции у> остается
еще много неясного, и потребуется немало труда, чтобы
удовлетворительно ответить на все напрашивающиеся здесь
вопросы.
§ 96. В заключение покажем, каким образом можно при по-
помощи введенной в предшествующем параграфе гипотезы вычи-
вычислить порядок величины универсальной постоянной h в урав-
уравнении D06). Прежде всего понятно, что если взять h бесконечно
малым, то волновая оптика перейдет в геометрическую, а сле-
следовательно, и волновая механика в классическую. Это видно из
того, что при таком допущении со получает на основании D06)
при любом Е бесконечно большое значение. Согласно C82)
длина волны Я становится при этом бесконечно малой, а благо-
160 ДИСПЕРСИЯ ИЗОТРОПНЫХ СРЕД
даря этому всегда выполняется условие, что длина волны мала
сравнительно с радиусом кривизны траектории. Отсюда видно,
что значение h получится тем больше, чем больше радиус кри-
кривизны траектории, для которой заметны отступления от класси-
классической механики. Для нашего подсчета порядка величины h мы
примем, что для электрона, вращающегося вокруг заряженного
одним положительным зарядом ядра, отступления от классиче-
классической механики становятся заметны, когда радиус его пути до-
доходит до атомных размеров.
В нашем случае, если г обозначает радиус пути, v — скорость
движения по траектории, е—заряд, т — массу электрона, то по
законам классической механики при равномерном вращательном
движении центростремительная сила равна силе притяжения ядра.
Следо вательно,
v = -£= . D15)
С другой стороны, для длины волны Я, которая соответ-
соответствует рассматриваемому движению, получаем из C82), D11),
D06) и D04):
д ft h
и согласно D15):
Отсюда находим отношение длины волны Я к радиусу кри-
кривизны г.
! = —£=-. D17)
Чтобы это отношение имело заметную величину, числитель
и знаменатель дроби должны иметь одинаковый порядок вели-
величины, т. е.
D18)
= еу тг.
Подставляем сюда согласно принятому выше условию для г
величину 10~7 см и выражаем величины в элекромагнитной сис-
системе единиц:
j
е = 4,77 • 10~10(эрг - см)Г, т = 9,02 • 10-28 г.
Тогда получаем:
h ~ 4,5 • 10~27 эрг • сек. D19)
Более точное значение кванта действия:
А ~ 6,55 • 10~27 эрг • сек. D20)
УКАЗАТЕЛЬ
Анализатор 19.
Астигматический пучок лучей 52.
Брюстера закон 19.
Волна необыкновенная 123.
—■ обыкновенная 123.
— поперечная 10.
— почти гармоническая 147.
Волновав линия 45.
Волновая механика 158.
Волновая поверхность 11, 108 и ел.
Геометрическая оптика 50.
Главная скорость распространения 100.
Главные диэлектрические постоян-
постоянные 96.
Главные интенсивности 24.
Главные плоскости 57.
Главные точки 57.
Гомоцентрический пучок лучей 52.
Дисперсвя 16.
г- аномальная 140.
— нормальная 139.
Дифракции точка 71.
Дифракционная решетка 93.
— — ее постоянная 93.
Дифракция 63.
— Фраунгофера 87.
— Френеля 74.
Длины единицы в оптике 32.
Интегралы Френеля 76, 78.
Интенсивность излучения 8.
Интерференция 40.
Кардинальные точки 58.
Квант действия 160.
Когерентность 23.
Компенсатор 49.
Коэфицнент отражения 17, 142.
— пропускания 20, 142.
Металлическое отражение 142.
Опак, ч. IV.
Некогерентность 40.
Нормальное падение 16.
Ньютоновы пветные кольца 38.
Оптическое изображение 53.
Оптические оси кристалла 104.
— вторичные 107.
Оптический центр системы 58.
Параллелепипед Френеля 46.
Плоскопараллельная пластинка 33.
Плоскость колебаний 19, 98.
— поляризации 19.
Поверхность индексов 121.
Поглощения полоса 139.
Показатель поглощения 140.
— преломления 15.
— главный 105.
Полусходящиеся ряды 61.
Поляризатор 19.
Призма 50, 51.
— Николя 114, 115.
Принцип Гюйгенса 64.
— Ферма 61, 152.
Разность фаз 41.
Рефракция коническая 118.
— внешняя 118.
Свет естественный 18.
— левоврашающий 4S.
— линейно поляризованный 19.
— однородный 32-
— правовращающий 43.
— поляризованный по кругу 47.
— эллиптически поляризован-
поляризованный 48.
Системы центрированные 55.
Скорость главная распространения 100.
— групповая 149.
— светового сигнала 147.
— фазовая 146, 147.
— фронтовая 146.
Снеллиуса закон преломления 15.
Сопряженные точки 52.
Стоячие световые волны 31, 32.
Угол отражения 15.
— падения 12.
— преломления 15.
11
164
УКАЗАТЕЛЬ
— поляризации 19.
— предельный 15.
Узловая точка 58.
Уравнение Шредингера 159.
— эйконала 152.
Уравнения Масквелла 7.
Фокальная плоскость 54.
Фокус 52.
Фокусное расстояние 57.
Эллипсоид поляризации Коши 102.
Эйконал 151.
Яркость удельная 60.
Редакция Н. Д. Ершовой. Оформление С. Л. Дъшап.
Корректура Н. П. Загрядстеа. Выпускающий Л. Af. Вояквтн
Сдано в производство 16 сентября 1934 г* Подписано к печати S декабря 1934 г.
Количество бум. листов 6i/8. Авторских листов 12. Тираж 7 000. Формат бумаги 62 х 94*/ie
Количество веч. знаков в 1 бум. листе 96 000.
Заказ № 1121. ГТТИ Jft 145 Уполномоченный Главпита № В-100869.
4-я типография ОНТИ НКТП СССР .Красный Печатник". Ленинград, Международный, 75а.
ОБЪЕДИНЕННОЕ
НАУЧНО-ТЕХНИЧЕСКОЕ ИЗДАТЕЛЬСТВО
ННТП СССР
МАКС ПЛАНК
ВВЕДЕНИЕ
В ТЕОРЕТИЧЕСКУЮ ФИЗИКУ
ЧАСТЬ ПЕРВАЯ
ОБЩАЯ МЕХАНИКА
Пер. с немецкого под ред. проф. Н. П. Кастерина
Издание второе. 200 стр.
Москва—Ленинград. 1932 г. Ц. 2 р. 75 к.
ЧАСТЬ ВТОРАЯ
МЕХАНИКА ДЕФОРМИРУЕМЫХ ТЕЛ
Пер. с немецкого Л. Я. Штрума, под ред. проф. Н. П. Кастерина.
Издание второе. 184 стр.
Москва—Ленинград. 1932 г. Ц. 3 р.
ЧАСТЬ ТРЕТЬЯ
ЭЛЕКТРИЧЕСТВО и МАГНЕТИЗМ
Пер. с немецкого под ред. проф. Н. П. Кастерина
Издание второе, стереотипное
Москва—Ленинград. 1933 г. Ц. 3 р. 50 к.
часть п ятая
ОПТИКА
Пер. с немецкого П. Н. Успенского
ОБЪЕДИНЕННОЕ
НАУЧНО-ТЕХНИЧЕСКОЕ ИЗДАТЕЛЬСТВО
НКТП СССР
ГОТОВЯТСЯ К ПЕЧАТИ:
ИОСС
ТЕОРЕТИЧЕСКАЯ ФИЗИКА
Пер. с Немецкого под ред. Э. В. Шпольского
КЛЕМЕНС ШЕФЕР
ВВЕДЕНИЕ В ТЕОРЕТИЧЕСКУЮ ФИЗИКУ
г. I, ч. 2-я, пер. с немецкого под ред. В. К. Семенченко
Ю. Б. РУМЕР
ВВЕДЕНИЕ В ВОЛНОВУЮ МЕХАНИКУ
ч. 1-я
ГААЗ
ВВЕДЕНИЕ В ТЕОРЕТИЧЕСКУЮ ФИЗИКУ
Пер. с немецкого под ред. В. Б. Шулейкина
ПЕЧАТАЮТСЯ
КЛЕМЕНС ШЕФЕР
ВВЕДЕНИЕ Б ТЕОРЕТИЧЕСКУЮ ФИЗИКУ
т. I, ч. 1-я, пер. с немецкого под ред. К.