Author: Данко П.Е. Попов А.Г. Кожевниква Т.Я.
Tags: математика анализ высшая математика линейная алгебра аналитическая геометрия задачи по математике
ISBN: 5-06-003070-9
Year: 1999
Text
П.Е.ДАНКО А.Г.ПОПОВ
Т.Я.КОЖЕВНИКОВА
ВЫСШАЯ
МАТЕМАТИКА
в упражнениях
и задачах
В ДВУХ ЧАСТЯХ
часть!
Издание пятое, исправленное
Москва
«Высшая школа»
1999
УДК 516+517
ББК22. 11
Д17
Данко П.Е., Попов А.Г., Кожевником Т.Я.
Д 17 Высшая математика в упражнениях и задачах. В 2-х ч. Ч. I:
Учеб, пособие для втузов. —5-е изд., испр. —М.: Высш, шк.,
1999. — 304 с.: ил.
ISBN 5-06-003070-9
Содержание I части охватывает следующие разделы программы:
аналитическую геометрию, основы линейной алгебры, дифференциальное
исчисление функций одной и нескольких переменных, интегральное исчисление
функций одной переменной, элементы линейного программирования.
В каждом параграфе приводятся необходимые теоретические сведения.
Типовые задачи даются с подробными решениями. Имеется большое количество
задач для самостоятельной работы.
Учебное издание
Данко Павел Ефимович, Попов Александр Георгиевич,
Кожевникова Татьяна Яковлевна
ВЫСШАЯ МАТЕМАТИКА В УПРАЖНЕНИЯХ
И ЗАДАЧАХ
Часть I
Редактор А.М. Суходский
Художественный редактор ТА. Коненкова
Технический редактор Л.А. Овчинникова
ЛР № 010146 от 25.12.96. Изд. № ФМ-105 а. Сдано в набор и подл, в печать 16.11.98.
Формат 60x88'/и. Бум. газета. Гарнитура «Литературная». Печать офсетная.
Объем 18,62 усл. печ. л. 18,87 усл. кр.-отг. 20,8 уч.-изд. л.
Тираж!2000 экз. Заказ №215
Издательство «Высшая школа», 101430, Москва, ГСП-4,'Неглинная ул., 29/14.
Набрано на персональном компьютере издательства.
Отпечатано с диапозитивов в ОАО «Оригинал»,
101898, Москва, Центр, Хохловский пер., 7.
ISBN 5-06-003070-9 (ч. I) © Издательство «Высшая школа», 1999
ISBN 5-06-003072-5
ОГЛАВЛЕНИЕ
Предисловие . . . ..................................................... 5
Глава I. Аналитическая геометрия иа плоскости
§ 1. Прямоугольные и полярные координаты.......................... 6
§ 2. Прямая. ..................................................... 15
§ 3. Кривые второго порядка ..................................... 25
§ 4. Преобразование координат и упрощение уравнений кривых второ-
го порядка................. ...................................... 32
§ 5. Определители второго и третьего порядков и системы линейных
уравнений с двумя и тремя неизвестными . , , , ................... 39
Глава II. Элементы векторной алгебры
§ 1. Прямоугольные координаты в пространстве....................... 44
§ 2. Векторы и простейшие действия над ними........................ 45
§ 3. Скалярное и векторное произведения. Смешанное произведение . . 48
Глава III. Аналитическая геометрия в пространстве
§ 1. Плоскость и прямая ........................................... 53
§ 2. Поверхности второго порядка. , ............................... 63
Глава IV. Определители и матрицы
§ 1. Понятие об определителе л-го порядка........................ 70
§ 2. Линейные преобразования и матрицы........................... 74
§ 3. Приведение к каноническому виду общих уравнений кривых и по-
верхностей второго порядка........................................ 81
§ 4. Ранг матрицы. Эквивалентные матрицы......................... 86
§ 5. Исследование системы т линейных уравнений с п неизвестными . 88
§ 6. Решение системы линейных уравнений методом Гаусса......... 91
§ 7. Применение метода Жордана—Гаусса к решению систем линей-
ных уравнений................................................... 94
Глава V. Основы ливейиой алгебры
§ 1. Линейные пространства....................................... 103
§ 2. Преобразование координат при переходе к новому базису ... 109
§ 3. Подпространства............................................. 111
, § 4. Линейные преобразования..................................... 115
§ 5. Евклидово пространство..................................... 124
§ 6. Ортогональный оазис и ортогональные преобразования......... 128
§ 7. Квадратичные формы ......................•................. 131
Глава VI. Введение в анализ
§ 1. Абсолютная и относительная погрешности...................... 136
§ 2. Функция одной независимой переменной........................ 137
§ 3. Построение графиков функций................................. 140
§ 4. Пределы. •.................................................. 142
§ 5. Сравнение бесконечно малых................................ 147
§ 6. Непрерывность функции ... .................................. 149
Глава VII. Дифференциальное исчисление функций одной независимой пе*
ременной
§ 1. Производная и дифференциал............................. . 151
§ 2. Исследование функций ...................................... 167
§ 3. Кривизна плоской линии.................................... 183
§ 4. Порядок касания плоских кривых............................. 185
§ 5. Вектор-функция скалярного аргумента и ее производная . . . 185
§ 6. Сопровождающий трехгранник пространственной кривой. Кривиз-
на и кручение .......................................> . . . > 188
Глава VIII. Дифференциальное исчисление функций нескольких независи-
мых переменных
§ 1. Область определения функции. Линии и поверхности уровня . • 192
§ 2. Производные и дифференциалы функций нескольких переменных . 193
§ 3. Касательная плоскость и нормаль к поверхности ............. 203
§ 4. Экстремум функции двух независимых переменных ....... 204
Глава IX. Неопределенный интеграл
§ 1. Непосредственное интегрирование. Замена переменной и интегри-
рование по частям................................................ 208
§ 2. Интегрирование рациональных дробей........................ 218
§ 3. Интегрирование простейших иррациональных функций........... 229
§ 4. Интегрирование тригонометрических функций .................. 234
§ 5. Интегрирование разных функций ............................. 242
Глава X. Определенный интеграл
§ 1. Вычисление определенного интеграла......................... 243
§ 2. Несобственные интегралы.................................... 247
§ 3. Вычисление площади плоской фигуры.......................... 251
§ 4. Вычисление длины дуги плоской кривой........................ 254
§ 5. Вычисление объема тела..................................... 255
§ 6. Вычисление площади поверхности вращения.................... 257
§ 7. Статические моменты и моменты инерции плоских дуг и фигур . 258
§ 8. Нахождение координат центра тяжести., Теоремы Гульдена . . . 260
§ 9. Вычисление работы и давления ............................... 262
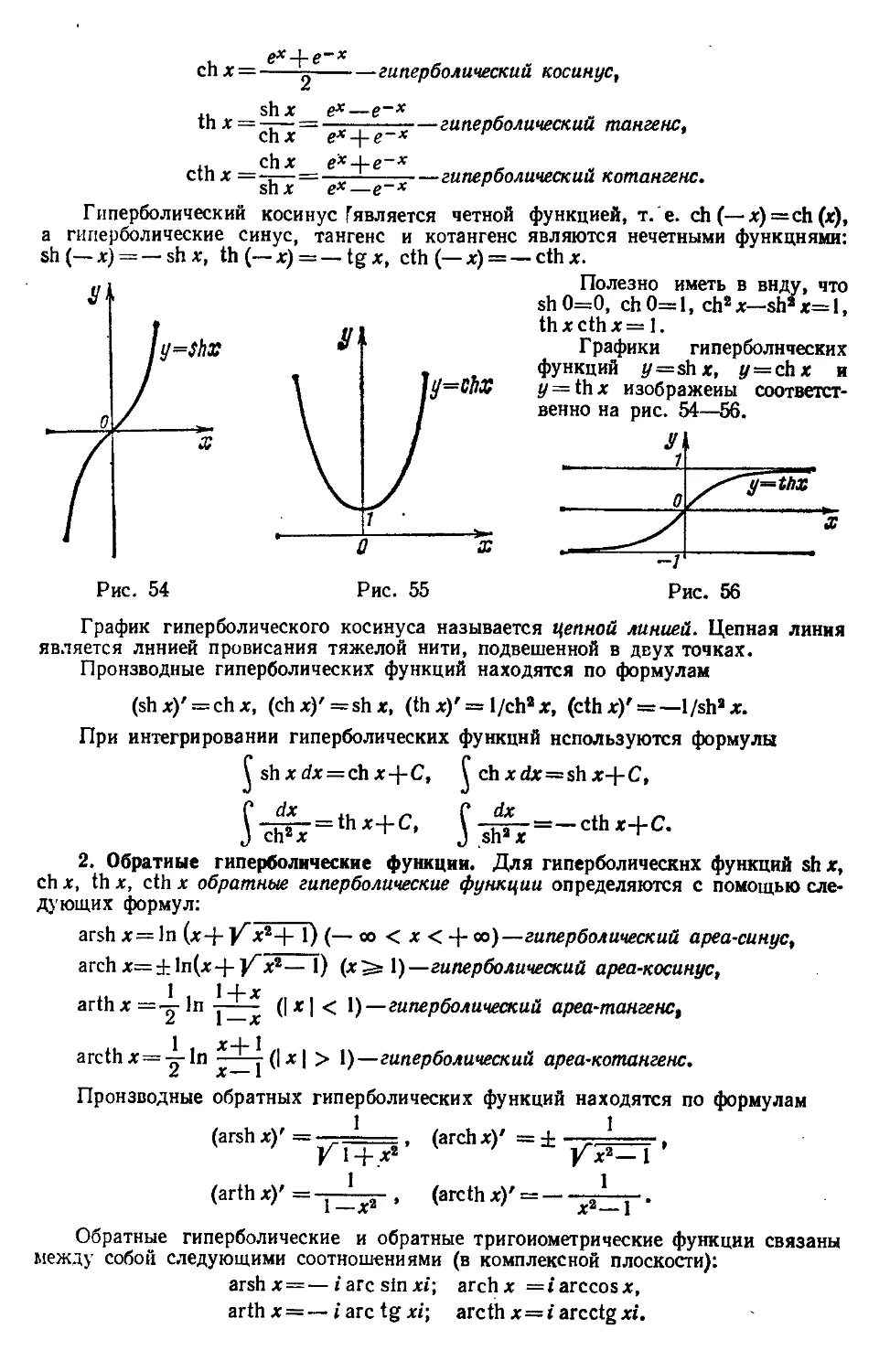
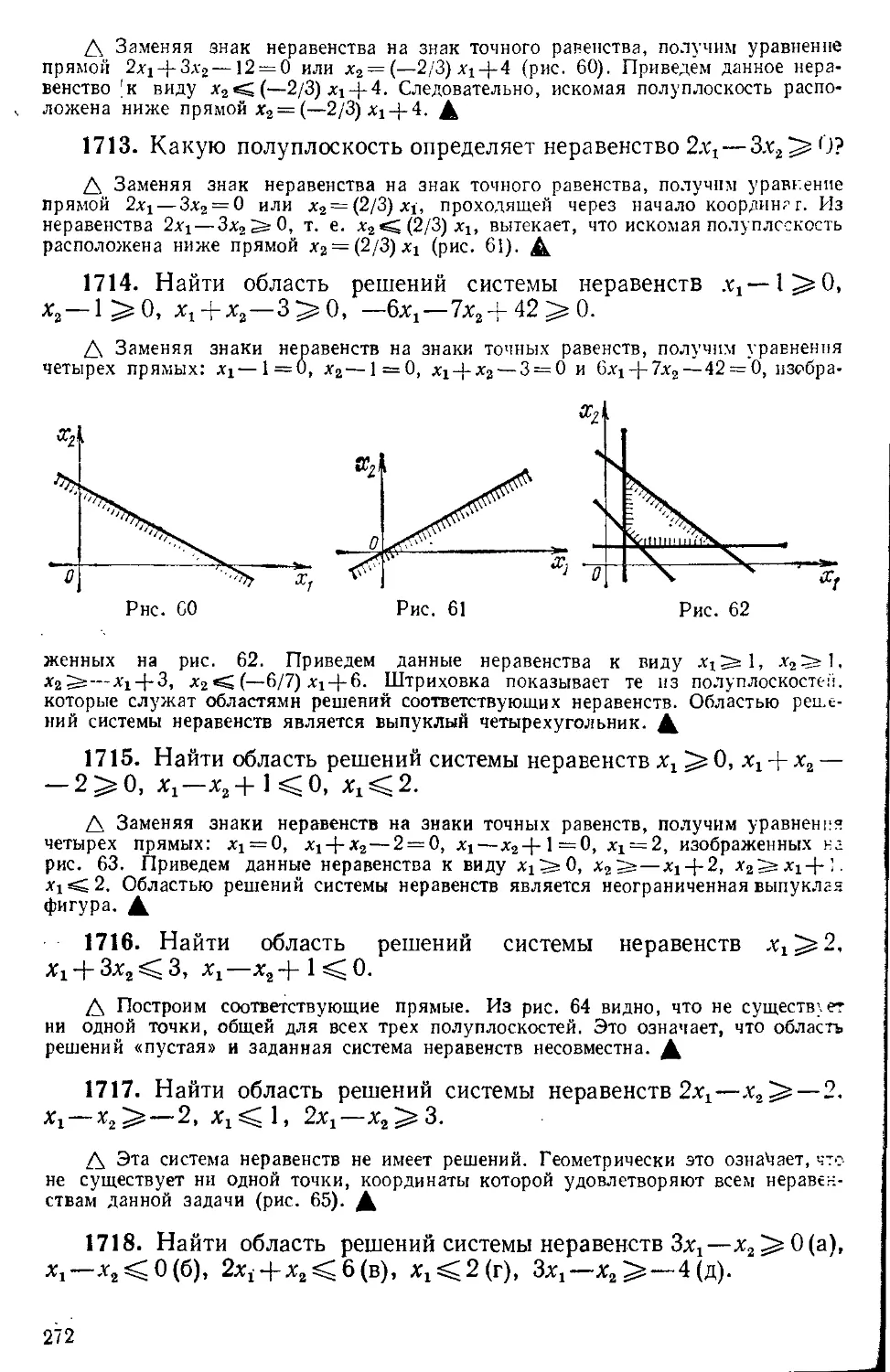
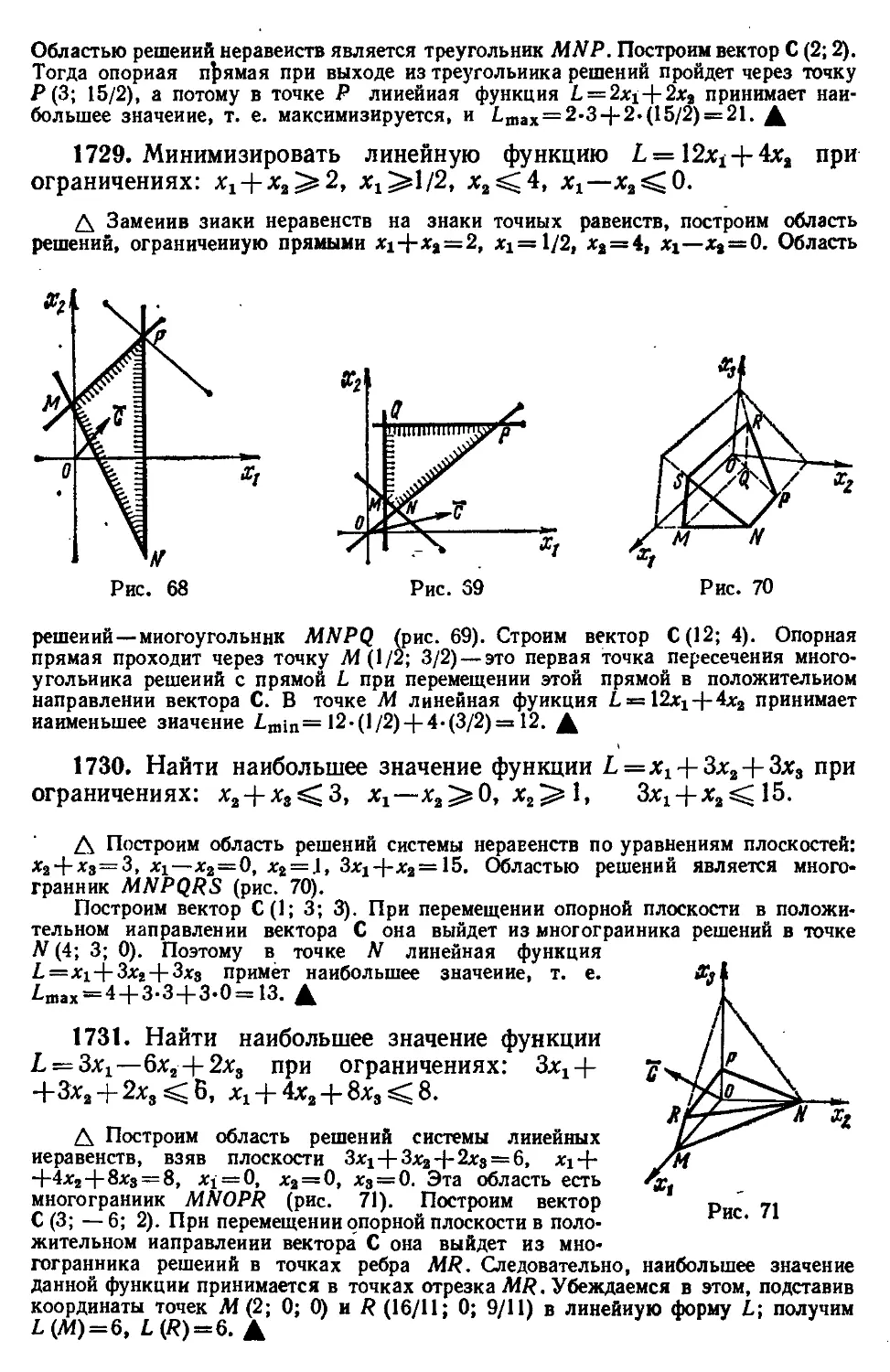
§ 10. Некоторые сведения о гиперболических функциях............. 266
Глава XI. Элементы линейного программирования
§ 1. Линейные неравенства и область решений системы линейных не-
равенств ..............•......................................... 271
§ 2. Основная задача линейного программирования.................. 274
§ 3. Симплекс-метод.............................................. 276
§ 4. Двойственные задачи......................,.................. 287
§ 5. Транспортная задача......................................... 288
Ответы.........................................................; . . 294
ПРЕДИСЛОВИЕ
При написании книги «Высшая математика в упражнениях и задачах» авторы
стремились раскрыть содержание основных понятий и теорем курса на специально
подобранных упражнениях и задачах.
В пособие включены типовые задачи и даются методы их решения. Каждому
параграфу предшествует краткое введение, состоящее из определений и основных
математических понятий данного раздела. При этом наиболее трудные вопросы
теории для лучшего усвоения сопровождаются раскрытием этих понятий (без до-
казательств).
Первое издание (в трех частях) вышло в 1967—1971 гт. Второе издание (в двух
частях) вышло в 1974 г., а третье и четвертое издания (также в двух частях) вышло
в 1974 г., а третье и четвертое издания (также в двух частях)—соответственно
в 1980 г. и 1986 г.
При написании пособия авторы использовали некоторые методические приемы
и задачи из книг: Фихтенгольц Г. М. Курс дифференциального и интегрального
исчисления, т. I — III; Курант Р. Курс дифференциального и интегрального исчисле-
ния, т. I, II; Гюнтер И. М. и Кузьмин Р. О. Сборник задач по высшей математике, т.
I — III; Демидович Б. П. и др. Сборник задач и упражнений по математическому
анализу; Фролов С. В. и Шостак Р. Я. Курс высшей математики.
В настоящее время перечисленные книги стали библиографической редкостью.
Поэтому в дополнение к данной книге рекомендуем студентам пользоваться со-
временной учебной литературой по высшей математике, список которой приведен
в конце II части.
В книге используются следующие обозначения: начало и конец решения задачи
отмечаются соответственно знаками Д и Д, а вместо слова "Указание” употребляется
знак ••
В пятом издании произведены некоторые улучшения методического характера,
а также исправлены замеченные опечатки.
Авторы считают своим приятным долгом выразить искреннюю признательность
студейтам и преподавателям высших учебных заведений, рецензентам всех изданий
книги, чьи поправки, критические замечания и предложения способствовали улучше-
нию данного пособия.
Авторы
ГЛАВА I
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
§ 1. ПРЯМОУГОЛЬНЫЕ И ПОЛЯРНЫЕ КООРДИНАТЫ
1. Координаты на прямой. Деление отрезка в данном отношении. Точку М
координатной оси Ох, имеющую абсциссу х, принято обозначать через М (х).
Расстояние d между точками Afi (xj и М2 (х2) оси при любом расположении
точек на осн определяется формулой
d = |x2—xj. (1)
Пусть на произвольной прямой задан отрезок АВ (А—начало отрезка, В —
его конец); тогда всякая третья точка С этой прямой делит отрезок АВ в неко-
тором отношении X, где Х=± | АС|:| СВ |. Если отрезки АС и СВ направлены
в одну сторону, то X приписывают знак « + »; если же отрезки АС и СВ направ-
лены в противоположные стороны, то X приписывают знаке — «.Иными словами,
X положительно, если точка С лежит между точками А н В и отрицательно,
если точка С лежит на прямой вне отрезка АВ. _
Если точки А и В лежат на оси Ох, то координата точки С (х), делящей
отрезок между точками A (xj) н В (х2) в отношении X, определяется по формуле
Xi 4- Хх2
1+Х •
(2)
В частности, при Х=1
получается формула для координаты середины отрезка:
~ Xi Хо
*=—2—-
(3)
1. Построить на прямой точки Л (3), В(—2), С(0), D (1^2),
£(-3,5).
2. Отрезок АВ четырьмя точками разделен на пять равных
частей. Определить координату ближайшей к А точ^и деления,
если Л(—3), В (7).
Л, Пусть С (х) — искомая точка; тогда Х= | АС |:| СВ | = 1/4. Следовательно,
по формуле (2) находим
—__х14-Хх2
1+Х
-3 + (1/4) 7 _
1 + 1/4
1, т. е. С(— 1). Д
3. Известны точки Л(1), В(5) — концы отрезка АВ; вне этого
отрезка расположена точка С, причем ее расстояние от точки Л
в три раза больше расстояния от точки В. Определить координату
точки С.
Л Нетрудно видеть, что Х = —|ЯС|:|5С|=—3 (рекомендуем сделать чер-
теж). Таким образом,
-==l z3 5 = 7> т. е С(7). А
Л о
4. Определить расстояние между точками: I) М (3) и /У(—5);
2) £(—11/2) и Q (-5/2).
5. Найти координаты середины отрезка, если известны его концы:
1) Л (—6) и В (7); 2) С (—5) и 7)(1/2).
6. Найти точку М, симметричную точке N (—3) относительно
точки Р(2).
7. Отрезок АВ двумя точками разделен на три равные части.
Определить координаты точек деления, если Л(—1), В (5).
8. Даны точки Л(—7), В(—3). Вне отрезка АВ расположены
точки С и D, причем |СЛ| = |BD| = 0,5|АВ\. Определить коорди-
наты точек С н D.
2. Прямоугольные координаты на плоскости. Простейшие задачи. Если на
плоскости задана прямоугольная декартова система координат хОу, то точку М
этой плоскости, имеющую координаты х и у, обозначают М (х; у).
Расстояние d между точками Afj (х^, у±) и Л12(х2; уг) определяется по фор-
муле
d = V ^-х^+^-у^. (1)
В частности, расстояние d точки М (х; у) от начала координат определяется
по формуле
4=/х2+у«. (2)
Координаты точки С(х; у), делящей отрезок между точками 4(xi', l/i) и
В (х2; у3) в заданном отношении % (см. п. 1), определяются по формулам
—___*1 + ^*2. —__Z/l + ^Z/2
14-Х ’ у~ 14-Х *
(3)
В частности, при Х=1 получаются формулы для координат середины отрезка:
—__*14-*2. —__1/14"1/2
z' у~~т~
(4)
Площадь треугольника с вершинами A (Xj; г/i), В (х2; у2), С(х3; у3) опреде-
ляется по формуле
S=-g-|Xi (у2—у3)4-х2 (у3—У1)4-х3 (yi—уг) |=а
=у К**—*т)(Уз—У1}~(х3—Xi) (уг—У1)|. (5)
Формулу для площади треугольника можно записать в виде
5=4* ДЬ (6)
где
Д =
1 1 1
Х1 х2 х3
У1 Уг Уз
*
(понятие об определителе третьего порядка дано в § 5 этой главы).
9. Построить на координатной плоскости точки А (4; 3), В(—2;5),
С (5; —2), D(—4; —3), £(—6; 0), £(0; 4).
10. Определить расстояние между точками А (3; 8) и В (—5; 14).
Л Воспользовавшись формулой (1), получим
d—V(—5 —3)24-(14 —8)2 = /644-36 = 10. А
7
11. Показать, что треугольник с вершинами А (—3;:—3), В (—1; 3),
С (11; —1) — прямоугольный.
Л Найдем длины сторон треугольника:
| АВ | = V(-1 +3)2 + (3 + 3)2 = V40,
| ВС | = (П4-1)24-(—1—З)2 = /’Тбб,
| АС| = У (114-3)2 + (—14-3)2= К20О-
Так как |ДВ|2 = 40, |5С|2=160, | АС |2 = 200, то | АВ |2 + | ВС |2 = | АС |2.
Таким образом, сумма квадратов длин двух сторон треугольника равна квадрату
длины третьей стороны. Отсюда заключаем, что треугольник АВС прямоуголь-
ный и сторона АС является его гипотенузой. А
12. Известны точки Л(—2; 5), В (4; 17) — концы отрезка АВ.
На этом отрезке находится точка С, расстояние которой от Л в два
раза больше расстояния от В. Определить координаты точки С.
Д Так как | АС | = 2 | СВ |, то Х = | АС |:| СВ | = 2. Здесь xi= —2, i/i = 5,
*2 = 4, у2=17; следовательно,
— —2 -|-2-4 — 5-|-2-17 „ । .
*— j_j_2 —2, у— ^2 —13, т. е. С(2, 13). Д
13. Точка С (2; 3) служит серединой отрезка АВ. Определить
координаты точки А, если В (7; 5).
Д Здесь х = 2, у = 3, х2 = 7, у2 = 5, откуда 2 = (Х!-|-7)/2, 3 = (уг4-5)/2. Сле-
довательно, %1 = —3, i/i = l, т. е. А (—3; 1). А
14. Даны вершины треугольника АВС:А(х1; yt), В (х2; у2),
С (х3; у3). Определить координаты точки пересечения медиан треу-
гольника.
Д Находим координаты точки D—середины отрезка АВ; имеем xD—(x14-х2)/2,
Ув = (У1-\-Уг)№- Точка М, в которой пересекаются медианы, делиг отрезок CD
в отношении 2:1, считая от точки С. Следовательно, координаты точки М опре-
деляются по формулам
~___*з4-2хо —_//з+2уо
14-2 ’ у~ 14-2 ’
т. е.
~___*з4-2 (Xi 4-х2)/2 —_?/з 4-2 (1/14-1/2)/2
х- 3 , у--------3 .
Окончательно получаем
~___,*1+*2-|- Хз —_У14-Уг+ Уз а
X з , у- 3 . А
15. Определить площадь треугольника с вершинами Л(—2; —4),
В (2; 8) и С(10; 2).
Д Используя формулу (5), получаем
s=y| (24-2) (2-1-4) —(104-2) (84-4) | = 1 (24 — 1441=60 (кв. ед.). £
16. Определить расстояние между точками: 1) А (2; 3) и В (—10;
—2); 2) С(И2;— И 7) и 0(2^2; 0).
в
17. Показать, что треугольник с вершинами А (4; 3), В(7; 6) и
С (2; 11) — прямоугольный.
18. Показать, что треугольник с вершинами Л (2; —1), В (4; 2)
и С (5; 1)—равнобедренный.
19. Даны вершины треугольника: Л(—1; —1), В(0; —6) и
С(—10; —2). Найти длину медианы, проведенной из вершины А.
20. Даны концы отрезка АВ:А(—3; 7) и В (5; 11). Этот отрезок
тремя точками разделен на четыре равные части. Определить ко-
ординаты точек деления.
21. Найти площадь треугольника с вершинами Л(1; 5), В (2; 7),
С(4; 11).
22. Даны три последовательные вершины параллелограмма:
Л(11; 4), В(—1; —1), С(5; 7). Определить координаты четвертой
вершины.
23. Даны две вершины треугольника Л (3; 8) и В (10; 2) и точка
пересечения медиан М (1; 1). Найти координаты третьей вершины
треугольника.
24. Даны вершины треугольника: Л (7; 2), В(1; 9) и С(—8; —11).
Найти расстояния точки пересечения медиан от вершин треуголь-
ника.
25. Точки L (0; 0), М (3; 0) и N (0; 4) являются серединами
сторон треугольника. Вычислить площадь треугольника.
3. Полярные координаты. В полярной системе координат положение точки М
на плоскости определяется ее расстоянием |ОЛ4 | = р от полюса О(р—полярный
радиус-вектор точки) н углом 0, образованным отрезком ОМ с полярной осью Ох
(0—полярный угол точки). Угол 0 считается положительным прн отсчете от по-
лярной оси против часовой стрелки.
Если точка М имеет полярные координаты р > 0 и О<0 < 2л, то ей же
отвечает и бесчисленное множество пар полярных координат (р; 04-2&л), где
k^Z.
Если начало декартовой прямоугольной системы координат совместить с по-
люсом, а ось Ох направить по полярной оси, то прямоугольные координаты х и у
точки М и ее полярные координаты р н 0 связаны следующими формулами:
x = pcos0, y = psin0; (1)
р = К^+7. tg0 = i//x. (2)
26. Построить точки, заданные полярными координатами:
А (4; л/4), В (2; 4л/3), С (3; —л/6), Z) (—3; л/3), Е (0; а),
F (— 1; — Зл/4).
27. Найти полярные координаты точки М (1; —КЗ), если полюс
совпадает с началом координат, а полярная ось—с положительным
направлением оси абсцисс.
Д На основании равенств (2) находим р = Р<1 2+(-К 3)2=2; tg0 = -K3-
Очевидно, что точка М лежит в IV четверти н, следовательно, 0=5л/3.
Итак, М (2; 5л/3). А
28. Найти прямоугольные координаты точки А (2К2; Зл/4),
если полюс совпадает с началом координат, а полярная ось направ-
лена по оси абсцисс.
9
Д_ Используя формулы (1), имеем х = 2^ 2 cos (Зл/4) =—2, у —
= 2)^ 2 sin (Зл/4) =2. Итак, Л(—2; 2). А
29. Найти полярныекоординаты точек: А (2^3; 2), В (0; —3),
С (—4; 4), D(/2, —^2), Е (—И2; —Иб), £(—7; 0).
30. Найти прямоугольные координаты точек: А (10; л/2), В (2; 5л/4),
С(0; л/10), D(l; —л/4), £(—1; л/4), £(—1; —л/4).
31. Определить расстояние между точками А4г (Pi; 0г) и Мл (р2; 02).
• Применить к треугольнику О/И1/И2 теорему косинусов.
32. Определить расстояние между точками М (3; л/4) и N (4; Зл/4).
33. Найти полярные координаты точки, симметричной точке
М (р; 0) относительно полярной оси.
34. Найти полярные координаты точки, симметричной точке
М (р; 0) относительно полюса.
35. Найти полярные координаты точек, симметричных точкам
(3; л/6), (5; 2л/3) н (2; —л/6): 1) относительно полюса; 2) относи-
тельно полярной оси.
36. Найти полярные координаты точки, симметричной точке
М (р; 0) относительно прямой, проходящей через полюс перпенди-
кулярно полярной оси.
4. Уравнение линии. Пусть некоторой линии на плоскости хОу, рассматри-
ваемой как множество точек, соответствует уравнение, связывающее координаты
любой точки М (х; у) («текущей точки»), лежащей на этой линии. Такое уравне-
ние называется уравнением данной линии.
Если в уравнение данной линии подставить координаты любой точки, лежа-
щей на этой линии, то уравнение обращается в тождество. Если же в уравнение
линии подставить координаты любой точки, не принадлежащей этой линии, то
уравнение не удовлетворяется.
37. Один конец отрезка перемещается по оси абсцисс, а другой—
по осн ординат. Найти уравнение линии, описываемой серединой
этого отрезка, если длина отрезка равна с.
Д Пусть М (х; у)—середина отрезка. Длина отрезка ОМ (длина медианы)
равна половние гипотенузы, т. е. | ОМ | =с/2. С другой стороны, | ОМ j = }^x2-f-i/4
(расстояние точки М от начала координат).
Таким образом, приходим к уравнению
У х2-\-у2 = с ft, илн x24-z/2=c2/4.
Это и есть уравнение искомой линии. Геометрически очевидно, что этой линией
является окружность радиуса eft с центром в начале координат. Д
38. Составить уравнение линии, расстояние каждой точки кото-
рой от точки £(0; 1/4) равно расстоянию этой же точки от прямой
1/ = —1/4.
Д Возьмем на искомой линии произвольную точку М (х; у). Расстояние
точки М от точки F определится по формуле расстояния между двумя точками:
|A4f|=]/(x-0)2 + ^-iy.
10
Расстояние точки М от прямой у=—1/4 найдется из простых геометриче-
ских соображений (рис. 1):
|Л4У| = |^|+|^|=уЧ-1.
Так как по условию равенство | MF | = | МN | выполняется для любой точки М,
лежащей на искомой линии, то уравнение этой линии можно записать в виде
или
т. е. у—х2.
Линия, определяемая уравнением у = х2, называется параболой. Д
39. Составить уравнение множества точек, произведение расстоя-
ний которых от точек F± (а; 0) и F2 (—а; 0) есть постоянная вели-
чина, равная а2.
Л Возьмем на искомой кривой произвольную точку М (х; у). Ее расстояния
от точек Fi (aj; 0) и F% (—а; 0) составляют r^ = У~(х—а)2-]-у2, г2 = У(х4-а)2~Н/2.
Из условия задачи следует, что г1г2 = а2. Та-
ким образом, искомая кривая имеет уравнение у
У (х-а)2+у2. У(х + а)2+у2 = а2.
Приведем это уравнение к рациональному виду:
(х2 -]- а2+у2—2ах) (х2 4- а2 + У2 +2ах) = a*t
т. е.
(х2 + а2+у2)2—4а2х2 = а*,
Рис. 1
или, наконец,
(х2+у2)2 = 2а2(х2—у2).
Найденная кривая называется лемнискатой. А
40. Составить уравнение лемнискаты в полярных координатах
и построить кривую.
Д В уравнении (х2-}-у2)2 = 2а2 (х2—у2) (см. предыдущую задачу) переходим
к полярным координатам по формулам x = pcos0, i/=psin0. Тогда получим
(p2cos20-]-p2sin20)2 = 2a2(p2cos20—p2sin20), или р2 = 2а2 cos 20.
Это—уравнение лемнискаты в полярных координатах.
Построим кривую. Разрешив уравнение относительно р, находим р=±а'/"2 cos 20.
Из того, что в правой части равенства стоит двойной знак «±», а также из того,
что уравнение не меняется при замене 0 на — 0, заключаем, что лемниската рас-
положена симметрично относительно осей Ох и Оу. Исследуем форму лемнискаты
для I четверти, т. е. для случая р^0, О<0 < л/2. Для этих значений р и 0
имеем р = аУ 2 - У cos 2в. Нетрудно видеть, что 0 может изменяться только
в промежутке от 0 до л/4. Таким образом, соответствующая часть кривой за-
ключена между полярной осью и лучом 0 = л/4. Если 0 = 0, то р = аУ 2. С воз-
растанием 0 от 0 до л/4 величина р убывает до значения р = 0.
Приняв во внимание соображения симметрии, мы можем построить лемни-
скату (рис. 2). А
11
41. Составить уравнение множества точек,, равноудаленных от
точек Л(1; 1) и В(3; 3).
Д Пусть точка М принадлежит искомому множеству; тогда | AM | = | Л4В |.
По формуле расстояния между двумя точками находим
| МА | = V(х-1)2+(//-1)2, | МВ | = V(х-3)2+(г/-3)Ч
и уравнение линии может быть записано в виде
Г (х-1)24-(!/-1)2 = v (х-3)2 + (//-3)2.
Возведя обе части последнего равенства в квадрат, получим
х2—2х-(-1 +?/2—2//+1 =х2—6х 4-9 4-f/2—61/4-9,
откуда после приведения подобных членов окончательно приходим к уравнению
х4-//—4 = 0. Итак, искомым множеством является прямая, которая, как известно,
служит серединным перпендикуляром к отрезку АВ. А
42. Точка М. равномерно перемещается по лучу, вращающемуся
равномерно около полюса. Составить уравнение линии, описанной
Рис. 3
точкой М, если в начальный момент вращающийся луч совпадает
с полярной осью, а точка М — с полюсом; при повороте же луча
на угол 0 = 1 (один радиан) точка М удалилась от полюса на рас-
стояние а.
Л Поскольку в начальный момент величины р и 0 равны нулю, а затем
обе возрастают пропорционально времени, нетрудно установить, что они связаны
прямой пропорциональной зависимостью: p/0 = const. Но р = а при 0=1; следо-
вательно, р/0 = а/1, т. е. р = а0. Кривая р = ав называется спиралью Архимеда. А
43. Окружность диаметра а катится без скольжения по внешней
стороне другой окружности такого же диаметра. Составить в по-
лярных координатах уравнение линии, описанной некоторой фикси-
рованной точкой катящейся окружности.
Л На рис. 3: Сг — первоначальное положение центра катящейся окружности;
А—первоначальное положение точки, описывающей искомую линию (точка А
диаметрально противоположна точке В, где в начальный момент соприкасаются
окружности); С2—центр неподвижной окружности; С3—центр катящейся окруж-
ности в новом положении; М — новое положение точки А, описывающей искомую
линию. (После перемещения окружности Ci в положение Са точка Р займет по-
12
ложенйе Q. Точка В займёт положение D, причем, поскольку качение происхо-
дит без скольжения, BQ=DQ, QCtB = QCsD.)
На чертеже показано положение полюса О и полярной оси Ох. Требуется
составить уравнение, которому удовлетворяют координаты любой точки М (р; 0)
искомой линии.
Легко установить, что MC3Q=OC2Q, в силу чего четырехугольник ОС2СаМ
является равнобедренной трапецией с меньшим основанием |С2С3|=а; С2С2 и
С3С3—перпендикуляры, опущенные из точек С2 и Сз на прямую ОМ. Итак,
р = | ОС21 +1 С2С31 + | ChM |=4 cos 0+ а+4 cos 0 =a(l-|-cos 0).
Таким образом, уравнение искомой линии в полярных координатах имеет вид
p = a(l+cos0); эта кривая называется кардиоидой.
Поскольку при замене 0 на — 0 уравнение кардиоиды не меняется, кардиоида
расположена симметрично относительно полярной оси. Если 0 изменяется от О
до л, то р убывает от 2а до 0. А
44. Найти уравнение множества точек, равноудаленных от точек
Л(2; 0) и В(0; 1).
45. Какая линия определяется уравнением х = у?
46. Какая линия определяется уравнением х =— у>
47. Составить уравнение множества точек, сумма квадратов рас-
стояний которых от точек А(2; 0) и В(0; 2) равна квадрату рас-
стояния между точками А и В.
48. Составить уравнение множества точек, сумма расстояний
которых от точек Л(1; 0) и В (0; 1) равна 2.
49. В полярной системе координат составить уравнение окруж-
ности с центром в полюсе.
50. В полярной системе координат составить уравнение полу-
прямой, проходящей через полюс и образующей с полярной осью
угол а.
51. В полярной системе координат составить уравнение окруж-
ности диаметра а, если полюс лежит на окружности, а полярная
ось проходит через центр окружности.
5. Параметрические уравнения линии. При отыскании уравнения множества
точек иногда оказывается более удобным выразить координаты х и у произволь-
ной точки этого множества через некоторую вспомогательную величину t (ее на-
зывают параметром), т. е. рассматривать систему уравнений х — <р (/), (t).
Такое представление искомой линии называется параметрическим, а уравнения
системы—параметрическими уравнениями данной линии.
Исключение параметра t из системы (если оно возможно) приводит к уравне-
нию, связывающему х и у, т. е. к обычному уравнению линии вида f (х, у)=0.
52. Составить параметрические уравнения окружности.
Л Рассмотрим окружность радиуса а с центром в начале координат (рис. 4).
Возьмем на ней произвольную точку М (х; у). Примем за параметр t угол, обра-
зованный с осью абсцисс радиусом ОМ. Из треугольника OMN следует, что
x = acost, y = asint. Таким образом, уравнения
x — acost, y=asint
являются параметрическими уравнениями окружности.
Исключив из этих уравнений параметр t, получим обычное уравнение окруж-
ности. В данном случае для исключения параметра достаточно каждое из урав-
нений возвести в квадрат и полученные уравнения сложить: x2-|-y2 = a2 cos2 't 4-
13
-J-a2sln2/, т. e. x2-j-y2 = a2. Последнее уравнение является уравнением окруж-
ности радиуса а с центром в начале координат. А
53. Составить параметрические уравнения кривой, описанной
фиксированной точкой окружности, катящейся без скольжения по
неподвижной прямой.
Д Пусть окружность радиуса а катится без скольжения вправо по горизон-
тальной прямой (рис. 5). Примем эту прямую за ось Ох, поместив начало коор-
динат в некоторой точке О оси. За фиксированную точку окружности (перемеще-
нием которой образуется искомая кривая) примем ту ее точку, которая совпадает
с точкой О при соответствующем положении окружности. За параметр t примем
угол поворота радиуса окружности, проходящего через фиксированную точку.
Рис. 5
Пусть в некоторый момент времени окружность касается оси в точке А.
Фиксированная точка окружности займет положение М (х; у), соответствующее
углу t поворота радиуса CM {t=ACM). Так как качение происходит без сколь-
жения, то | ОА [ — МА = а/. Используя это, выразим координаты точки М через t:
х = | ON ) = | О А ] — | N А | = МА— | NA \ = at—a sin / = а (/—sin f)t
у = \ NM | = | АР | = | АС | — | PC | = а—a cos t = а (1 — cos t).
Таким образом, параметрические уравнения искомой линии имеют вид
x = a(t—sin t), у=^а(\ — cost).
Эта линия называется циклоидой-, она изображена на рис. 5. А
54. Какая линия определяется параметрическими уравнениями
x = t2, ij = t2?
Исключая параметр t, приходим к уравнению у=х. В силу параметри-
ческих уравнений х'^0, у^О. Следовательно, данные параметрические уравне-
ния определяют луч—биссектрису I координатного угла. А
55. Какая линия определяется параметрическими уравнениями
x = cos/, z/ = cos2/?
Д Подставив х вместо cos t во второе уравнение, получаем уравнение пара-
болы у=х2. Из параметрических уравнений следует | х | < 1, 0 <;у < 1. Таким
образом, параметрические уравнения определяют дугу АОВ параболы у = х2, где
Л(-1; 1);В(1; 1). Д
56. Какая линия определяется уравнениями x = sin/, y=cosect?
Л Так как у= 1/sin t, то, исключив t, получаем уравнение у=\/х, выра-
жающее обратную пропорциональную зависимость величин хну. Учитывая, что
14
|х|<1, | у | 1, заключаем, что линия, заданная параметрическими уравнениями
x = sin/, i/ = cosec/, имеет вид, изображенный на рис. 6. Д
57. 'Какая линия определяется уравнениями x — 2t, y =
58. Кривая задана параметрическими уравнениями x = acost,
y=bsint. Найти ее уравнение в прямоугольной системе координат.
• Разделить первое уравнение, на а, второе—на Ь, а затем исключить t.
59. Кривая задана параметрическими уравнениями x = asec/,
y — bbgt. Найти ее уравнение в прямоугольной системе координат.
Рис. 6
60. Какая линия определяется уравнениями
x=cos21, z/ = sin2 Z?
61. Кривая, определяемая параметрическими
уравнениями x=acos3(, z/ = asin3/, называет-
ся астроидой. Исключив /, найти уравнение
астроиды в прямоугольной системе координат.
62. На круг, описанный из центра О радиу-
сом а, навернута по часовой стрелке нить; пусть
конец нити находится в точке А (а-, 0). Станем
развертывать нить (против часовой стрелки),
сматывая ее с круга и все время натягивая за
конец. Составить параметрические уравнения кри-
вой, описываемой концом нити, если за параметр
t взять угол между радиусом ОА и радиусом ОВ, проведенным
в точку касания окружности с натянутой нитью в произвольном
положении последней.
$ 2. ПРЯМАЯ
1. Общее уравнение прямой. Всякое уравнение первой степени относительно
х и у, т. е. уравнение вида t
Ах-\-Ву-\-С — 0 (1)
(где А, В и С—постоянные коэффициенты, причем А2 + В2^0) определяет на
плоскости некоторую прямую. Это уравнение называется общим уравнением прямой.
Частные случаи. 1. С = 0; Л # 0; В 0. Прямая, определяемая урав-
нением Лх+В//=0, проходит через начало координат.
2. Л=0; В # 0; С 5= 0. Прямая, определяемая уравнением Ву-)-С = 0 (или
У=Ь, где Ь —— С/В), параллельна оси Ох.
3. В = 0; А 0; С ?= 0. Прямая, определяемая уравнением Лх-|-С = 0 (или
х = о, где а = — С/А), параллельна оси Оу.
4. В = С = 0; А # 0. Прямая, определяемая уравнением Ах = 0 (или х = 0,
поскольку Л # 0), совпадает с осью Оу.
5. Л=С = 0; В Ф 0. Прямая, определяемая уравнением By=Q (или у — 0,
поскольку В 0), совпадает с осью Ох.
2. Уравнение прямой с угловым коэффициентом. Если в общем уравнении
прямой В # 0, то, разрешив его относительно у, получим уравнение вида
y = kx-]-b (2)
(здесь k=—A/В, b = —С/В). Его называют уравнением прямой с угловым коэф-
фициентом, поскольку fc = tga, где a—угол, образованный прямой с положи-
тельным направлением оси Ох. Свободный член уравнения b равен ординате точки
пересечения прямой с осью Оу.
15
3. Уравнение прямой в отрезках. Если в общем уравнении прямой С то,
разделив все его члены на — С, получим уравнение вида
(здесь а = —С/А, Ь = —С/В). Его называют уравнением прямой в отрезках', в нем
а является абсциссой точки пересечения прямой с осью Ox, а b—ординатой точки
пересечения прямой с осью Оу. Поэтому а и b называют отрезками прямой на
осях координат.
4. Нормальное уравнение прямой. Если обе части общего уравнения прямой
Ах-}-Ву-\-С = 0 умножить на число ц= 1/(± р<Л2 + В2) (которое называется нор-
мирующим множителем), причем знак перед радикалом выбрать так, чтобы вы-
полнялось условие цС < 0, то получится уравнение
х cos q> + У sin <р—р = 0. (4)
Это уравнение называется нормальным уравнением прямой. Здесь р—длина пер-
пендикуляра, опущенного из начала координат на прямую, а ф — угол, образо-
ванный этим перпендикуляром с положительным направлением оси Ох.
63. Составить уравнение прямой, отсекающей на оси ординат
отрезок Ь ——3 и образующей с положительным направлением оси
абсцисс угол а = л/6.
Д Находим угловой коэффициент: 6 = tg (л/6) = 1/)С 3. Воспользовавшись
уравнением (2) прямой с угловым коэффициентом, получаем у=(1/У 3) х—3;
освобождаясь от знаменателя и перенося все члены в левую часть, получаем
общее уравнение прямой х—V~3y—3 У 3=0. А
64. Составить уравнение прямой, отсекающей на осях коорди-
нат отрезки а = 2/5, Ь — —1/10.
Д Воспользовавшись уравнением (3) прямой в отрезках, имеем
_L+__£_=i.
2/5т(—1/10)
Это уравнение можно переписать в виде (5/2) х—10у=1, или 5х—20у—2 = 0
(общее уравнение прямой). А
65. Дано общее уравнение прямой 12%—5у—65 = 0. Написать:
1) уравнение с угловым коэффициентом; 2) уравнение в отрезках;
3) нормальное уравнение.
Л 1) Разрешив уравнение относительно у, получаем уравнение прямой с угло-
вым коэффициентом:
у = (12/5) х—13.
Здесь 6=12/5, &= —13.
2) Перенесем свободный член общего уравнения в правую часть и разделим
обе части на 65; имеем (12/65) х—(5/65) у=\. Переписав последнее уравнение
в виде
X у
-----1-------- 1,
65/12 (-65/5)
получим уравнение данной прямой в отрезках. Здесь а = 65/12, & = —65/5 = —13.
3) Находим нормирующий множитель |х= 1/'/"122-]-(—5)2=1/13. Умножив'
обе части общего уравнения на этот множитель, получаем нормальное уравнение
прямой
(12/13) х—(5/13) у— 5 = 0.
Здесь cosф= 12/13, sin ф = =5/13, р = 5. А
16
66. Построить прямые: 1) х—2г/ + 5 = 0; 2) 2x + 3z/ = 0; 3) 5х—
— 2 = 0; 4) 2z/ + 7 = 0.
Д 1) Полагая в уравнении х = 0, получаем у = 5/2. Следовательно, прямая
пересекается с осью ординат в точке В (0; 5/2). Полагая у = 0, получаем х =—5,
т. е. прямая пересекается с осью абсцисс в точке А (—5; 0). Остается провести
прямую через точки А и В (рис. 7).
2) Прямая 2x-J-3y = 0 проходит через начало координат, так как в ее урав-
нении отсутствует свободный член. Дадим х в уравнении прямой какое-нибудь
значение. Пусть, например, х = 3, тогда 6-|-3// = 0, т. е. у=—2; получим точку
.И (3; —2). Остается через начало координат и
точку М провести прямую.
3) Разрешив уравнение прямой относительно
х, получим х = 2/5. Эта прямая параллельна оси
срдинат н отсекает на осн абсцисс отрезок, рав-
ный 2/5.
4) Аналогично получаем уравнение у=—7/2;
эта прямая параллельна оси абсцисс. А
67. Уравнение прямой задано в виде
(x-j-2 К5)/4+ (у—2 И 5)/2 = 0. Написать:
1) общее уравнение этой прямой; 2) уравнение с угловым коэффи-
циентом; 3) уравнение в отрезках; 4) нормальное уравнение.
68. Какой угол образует с положительным направлением оси
абсцисс прямая 2x4-2//— 5 = 0?
69. Определить площадь треугольника, образованного прямой
4x-|-3z/—36 = 0 с осями координат.
70. Можно ли уравнение прямой 20x4-21// = 0 записать в отрез-
ках?
71. Построить прямые: 1) 4х—5г/4- 15 = 0; 2) 2х—г/ = 0; 3) 7х—
— 10 = 0; 4) 2//4-3 = 0.
72. Составить уравнение прямой, отсекающей на оси ординат
отрезок £>= 1 и образующей с положительным направлением оси
абсцисс угол а = 2л/3.
73. Прямая отсекает на осях координат равные положительные
отрезки. Составить уравнение прямой, если площадь треугольника,
образованного прямой с осями координат, равна 8 кв. ед.
74. Составить уравнение прямой, проходящей через начало коор-
динат и точку А (—2; —3).
75. Составить уравнение прямой, проходящей через точку А (2; 5)
т отсекающей на оси ординат отрезок b = 7.
76. Составить уравнения прямых, проходящих через точку
М(—3; —4) и параллельных осям координат.
77. Составить уравнение прямой, отсекающей на осях координат
равные отрезки, если длина отрезка прямой, заключенного между
осями координат, равна 5 J/2.
5. Угол между прямыми. Уравнение прямой, проходящей через две точки.
Острый угол между прямыми y^k^x-i-b^ и y — k2x-\-b2 определяется по формуле
tgaHnp^|- (1:)
Условие параллельности прямых имеет вид
Условие перпендикулярности прямых имеет вид #!=—1/fcj. .
17
Уравнение прямой, имеющей угловой коэффициент k и проходящей через точку
М (хх; У1), записывается в виде
у— yi = k(x—Хц). (2)
Уравнение прямой, проходящей через точки Мг (хх; yt) и Мг (хг; уг), записы-
вается в виде
У—Ух _ x—xj (3
Уа—Ух *г—Х1' ' ’
и угловой коэффициент этой прямой находится по формуле
Если Xi—х2, то уравнение прямой, проходящей через точки Л1х- и Мг, имеет
вид x=xt.
Если yi—Уг, то уравнение прямой, проходящей через точки Mi и М2, имеет
вид y—yi-
6. Пересечение прямых. Расстояние от точки до прямой. Пучок прямых.
Если Л1/Л2 BitBt, то координаты точки пересечения прямых Л1Х-|-В1у-|-С1=0
н Лгх+б2у+С2 = 0 находятся путем совместного решения уравнений этих прямых.
Расстояние от точки М (х^; у0) до прямой Лх 4-By 4-С=0 находится по формуле
I Лх0-|-Ву0-|-С | .j.
VА*+В* ’ ' ’
Биссектрисы углов между прямыми AjX-j-Biy-j-Ci =0 и Л2х4-ВаУ4-Са==0
имеют уравнения
'41*4~Д1У4~ Ci । Л2х4-бгУ4~ /2)
У Al+ В{ КЛ14-В?
Если пересекающиеся прямые заданы уравнениями Л1х4-В1у4-С1 = 0 и
Л2х4-В2у4-С2=0, то уравнение
Лхх4-В1у4-С14-Х(Л2х4-Вгу4-Са)=0, (3)
где X—числовой множитель, определяет прямую линию, проходящую через точку
пересечения заданных прямых. Давая в последнем уравнении X различные значе-
ния, будем получать различные прямые, принадлежащие пучку прямых, центр
которого есть точка пересечения заданных прямых.
78. Определить острый угол между прямыми у = —3x4-7 и
^ = 2x4-1.
Л Полагая kt=—3, kt — 2 в формуле (1) п. 5, получим
. I 2— (—3) I , л .
т. е.
79. Показать, что прямые 4х—6г/4-7 = 0 и 20х—30г/—11=0
параллельны.
Д Приведя уравнение каждой прямой к виду с угловым коэффициентом,
получаем
у = (2/3) х-^7/6 н у = (2/3) х—11/30.
Угловые коэффициенты этих прямых равны: Ах = А2 = 2/3, т. е. Прямые парал-
лельны. А
80. Показать, что прямые Зх—5г/4-7 = 0 и 10х4-6у—3 = 0 пер-
пендикулярны.
18
Л После приведения уравнений к виду с угловым коэффициентом получаем
у = (3/5) х + 7/5 и у=(—5/3) х+1/2.
Здесь ki =3/5, k2 =—5/3. Так как ^ =—1/й2, то прямые перпендикулярны. А
81. Составить уравнение прямой, проходящей через точки М (—1; 3)
N (2; 5).
Л Полагая *1 =—1, yi = 3, х2 = 2, у2 = 5 в уравнении (3) п. 5, получаем
у—3 х+ 1 у—3 х+ 1
5—3 2+Г’ или 2 3 '
Итак, искомое уравнение имеет вид 2х—Зу+11 =0.
Полезно проверить, что уравнение составлено верно. Для этого достаточно
оказать, что координаты точек М и N удовлетворяют уравнению прямой. Дей-
ствительно, равенства 2(—1)—3-3+11=0, 2-2—3-5+11=0 выполняются тож-
дественно. А
82. Составить уравнение прямой, проходящей через точки А (—2; 4)
В (—2; —1).
Д Так как х2 = х2 = —2, то прямая имеет уравнение х = —2 (параллельна
оси ординат). А
83. Показать, что прямые Зх—2г/+1=0 и 2х + 5г/—12 = 0 пе-
ресекаются, и найти координаты точки пересечения.
Д Так как 3/2 / (—2)/5, то прямые пересекаются. Решив систему уравнений
( Зх—2у+1 =0,
( 2х+5у—12 = 0,
аходим х=1, у = 2, т. е. прямые пересекаются в точке (1; 2). А
84. Определить расстояние от точки М (х0; у0) до прямой Ах +
+ Ву-\-С — 0, не пользуясь нормальным уравнением прямой.
Д Задача сводится к определению расстояния между точками М (хв; у0) и
X, где /V—основание перпендикуляра, опущенного из точки М на данную пря-
мую. Составим уравнение прямой MN. Так как угловэй коэффициент заданной
прямой равен — A/В, то угловой коэффициент прямой MN равен В/А (из условия
перпендикулярности) и уравнение последней имеет вид у—ув — (В/А)(х—хв). Это
уравнение может быть переписано в виде (х—х0)/А = (у—уд)/В.
Для определения координат точки N решим систему уравнений
Лх+Ву+С=0, (х—хв)/А = (у—ув)/В.
Введем вспомогательную неизвестную t:
(x—xB)/A = (y—yB)/B = t.
Тогда х = хд-$- At, y — yg-}-Bt. Подставив эти выражения в уравнение данной пря-
мой, получим А (х0 + Л/)+В (уо+ВО + С=0, откуда
/ = -(Лх0 + Вув + С)/(Л*+В*).
Подставив теперь значение t в уравнения х=х0 + Л/ и у=у0+В/, определим
жоордииаты точки /V:
г_х л Ахв-\-Вув-]-С __r Ахв-\-Вув-\-С
х Л Л2+В2 ’ у~у° ° А2+В*
19
Остается определить расстояние между точками Л4 и ./V:
______________d = V (х-хо)а4-(у-уо)8 =
-\/~( я Ах04"®Уо4"С \2 । ( о Ах04~ ^Уо 4~ С \ 2 .1 4хр4~By»4~СI л
- У А2 + в2 ) "Ц0 А2 + в* ) ~ ' Ж
85. Определить расстояние от точки Л4(1; 2) до прямой 20х—
— 21г/—58 = 0.
| 20-1 — 21-2—58 | 120—42— 58 | _ 1—801 _ 22 .
Л Г400 + 441 29 29 29 ‘ А
86. Дана прямая /:4х—Зу—7 = 0. Какие из точек А (5/2; 1),
В (3; 2), С (1; —1), D (0; —2), Е (4; 3), F (5; 2) лежат на этой прямой?
Д Если точка лежит иа прямой, то ее координаты должны удовлетворять
уравнению прямой. Имеем: А£1, так как 4(5/2)—3-1—7 = 0; B(£l, так как
4-3—3-2—7 # 0;С £ /, так как 4-1 — 3 (—1)— 7 = 0; D $ I, так как 4-0—3 (—2)—
— 7^0; Е£1, так как 4-4—3-3—7=0; F (£l, так как 4-5—3-2—7 4 0. Д
87. Составить уравнение прямой, проходящей через точку
М (—2; —5) и параллельной прямой Зх + 4у 4- 2 = 0.
Д Разрешив последнее уравнение относительно у, получим у =—(3/4) х—1/2.
Следовательно, в силу условия параллельности угловой коэффициент искомой
прямой равен —3/4. Воспользовавшись уравнением (2) п. 5, получаем
у-(-5)==(—3/4) [х-(-2)], т. е. 3x+4</ + 26 = 0. Д
88. Даны вершины треугольника: А (2; 2), В(—2; —8) и
С(—6 ;—2). Составить уравнения медиан треугольника.
Д Находим координаты середин сторон ВС, АС и АВ:
х' = (—2—6)/2 = —4, </' = (—8—2)/2 = —5; At (—4; —5);
х" = (2—6)/2 = —2, /' = (2—2)/2 = 0; Вг (—2; 0);
х"' = (2-2)/2 = 0; у'" = (2—8)/2 = —3; Q (0 ; —3).
Уравнения медиан находим с помощью уравнения прямой, проходящей через
две данные точки. Уравнение медианы ААг:
(у—2)/(—5 — 2) = (х—2)/(—4 — 2), или (у—2)/7=(х—2)/6, т. е. 7х—бу—2 = 0.
Находим уравнение медианы ВВг; поскольку точки В (—2; —8) и Bt (—2; 0)
имеют одинаковые абсциссы, медиана В Bi параллельна оси ординат. Ее уравне-
ние х -|-2 = 0.
Уравнение медианыCCii (у-\-2)/(—34*2)=(х+6)/(0+6), или х+6</+18 = 0. Д
89. Даны вершины треугольника: А (0; 1); В (6; 5) и С (12; —1).
Составить уравнение высоты треугольника, проведенной из вершины С.
По формуле (4) п. 5 найдем угловой коэффициент стороны АВ; имеем
fe = (5—1)/(6—0) = 4/6 = 2/3. В силу условия перпендикулярности угловой коэф-
фициент высоты, проведенной из вершины С, равен —3/2. Уравнение этой высоты
имеет вид
у+1=(—3/2) (х—12), или 3x4-2*/—34 = 0. А
90. Даны стороны треугольника: х4- Зу—7 = 0 (4В), 4х—у —
— 2 = 0 (ВС), 6х-|-8г/—35 = 0(40. Найти длину высоты, проведен-
ной из вершины В.
20
Л Определим координаты точки В. Решая систему уравнений х+Зу—7=0
и 4х— у—2 = 0, получим х=1, у=2, т. е. В (1; 2). Находим длину высоты BBi
как расстояние от точки В до прямой АС:
J6-1+8.2-35I
/б2 + 82
1,з. Д
91. Определить расстояние между параллельными прямыми Зх +
+ #—ЗИТО = О и 6x + 2z/ + 5ИТО = 0.
Д Задача сводится к определению расстояния от произвольной точки одной
прямой до другой прямой. Полагай, например, в_уравненни первой прямой х = 0,
получаем у = 3/10. Таким образом, М (0; 3/10)—точка, лежащая иа первой
прямой. Определим расстояние точки М до второй прямой:
^_16-о+2-з /То+5/Гб। н/То_55
“ /36 + 4 2 /10 ~ ‘ А
92. Составить уравнения биссектрис углов между прямыми
х+у—5 = 0 и 1х—у —19 = 0 (рис. 8).
Д Решим сначала эту задачу в общем виде. Биссектрисы углов, образован-
пых двумя прямыми, являются, как известно, множеством точек, равноудаленных
от этих прямых. Если уравнения заданных
прямых А1х^-В1у-[-С1=0 и Л2х + В2у +
+ С2 = 0 (Д1/Л2 Bj/B2, т. е. прямые _не
параллельны), то для всякой точки А4 (х; у),
лежащей на одной из
альзуя формулу для
ОТ точки до прямой):
I ДтУ + ^г I _ | Л2х + В2у + С2 |
КлЬЙв? "
биссектрис, имеем (ис-
определения расстояния
Поскольку М (х ; у) — произвольная точка бис-
сектрисы, ее можно обозначать просто через
М{х, у). Учитывая, что выражения, стоящие
в последнем равенстве под знаком абсолютной
из биссектрис уравне-
величины, могут иметь разные знаки, получаем для одной
ние
/л?7в? ~ /л17в! ’
а для другой — уравнение
Кя?+в? ~ Кл1+в1
Таким образом, уравнения обеих биссектрис можно записать в виде
Л1х + В1у+С1 Л2х + В2у+ С2 _о
/я^+в? Кл1+в1
Теперь решим поставленную конкретную задачу. Заменив Af, Bi, Ci, А2,
Сг их значениями из уравнений заданных прямых, получим
± ^=£~19=0, т. е. 5(х4-у—5) ± (7х—у —19) =0.
/1 + 1 /49+1 V ’
21
Уравнение одной из биссектрис записывается в виде
5(х-\-у—5)-|-(7х—у—19) =0, т. е. Зх-|-у—11=0,
а уравнение другой—в виде
5(*+у—5) — (7х—у—19) =0, т. е. х—3//4-3 = 0. А
93. Даны вершины треугольника: Д(1; 1), В (10; 13), С* (13; 6).
Составить уравнение биссектрисы угла А.
Д Воспользуемся другим (по сравнению с решением предыдущей задачи) спо-
собом составления уравнения биссектрисы.
Пусть D—точка пересечения биссектрисы со стороной ВС. Из свойства бис-
сектрисы внутреннего угла треугольника следует, что | BD |:| DC | = | АВ |:| АС |.
Но | АВ | = V(10— 1)2Ч-(13 —1)2= 15, | АС | = V(13-1)2+(6—1)2= 13. Следо-
вательно, % = | BD М £>С| = 15/13. Так как известно отношение, в котором точка
D делит отрезок ВС, то координаты точки D определятся по формулам
Ю4-(15/13) 13 _13 + (15/13)6
х~~ 1-4-15/13 ’ у 14-15/13 ’
или х = 325/28, </ = 259/28, т. е. D (325/28; 259/28). Задача сводится к составле-
нию уравнения прямой, проходящей через точки А и D:
259/28-1 = 325/28-1 ’ Т> е‘ 7х-9У+2 = °- А
94. Даны уравнения высот треугольника АВС: х+у—2 = 0,
9х—2>у—4 = 0 и координаты вершины Л (2; 2). Составить уравне-
ния сторон треугольника.
Д Легко убедиться в том, что вершина А не лежит ни на одной из задан-
ных высот: ее координаты не удовлетворяют уравнениям этих высот.
Пусть 9х—Зу—4 = 0—уравнение высоты BBj и х-\-у—2 = 0—уравнение
высоты CCt. Составим уравнение стороны АС, рассматривая ее как прямую, про-
ходящую через точку А и перпендикулярную высоте
ВВ{. Так как угловой коэффициент высоты ВВ{ равен
3, то угловой коэффициент стороны АС равен —1/3,
т. е. клс =—1/3. Воспользовавшись уравнением пря-
мой, проходящей через данную точку и имеющей
данный угловой коэффициент, получим уравнение
стороны АС:
у—2 = (—1/3) (х—2), или x-j-3z/—8 = 0.
Аналогично получаем kcci =—1, &4В = 1, и уравнение
стороны АВ имеет вид
у— 2=х—2, т. е. у = х.
Решив совместно уравнения прямых АВ и BBi,
а также прямых АС и CCj, найдем координаты вер-
шин треугольника: В (2/3; 2/3) и С(—1; 3). Остается
составить уравнение стороны ВС:
3=2fl-^S'’T'e'7' + 5!'-8='’'A
95. Составить уравнения прямых, проходящих
М(5; 1) и образующих с прямой 2х+У—4 = 0 угол
Д Пусть угловой коэффициент одной из искомых прямых
вой коэффициент заданной прямой равен —2. Так как угол между этими пря-
22
и
Рис. 9
У-2/3
через точку
л/4 (рис. 9).
равен k. Угло-
вши равен я/4, то
*4-2 1
1—2*1’
откуда
А±2=1 ИЛ±2=_
1—2* 1 1—2*
1.
Решая каждое из полученных уравнений, находим k ——1/3 и *=3. Итак,
уравнение одной из искомых прямых запишется в виде у—1=(—1/3) (х—5), т. е.
х4-3у—8 — 0, а уравнение другой прямой в виде у—1=3 (х—5), т. е. Зх—у —
— 14 = 0. Д
96. Найти прямую, принадлежащую пучку 2x4-3f/4-54-X,(x-|-
4-8#4-6) = 0 и проходящую через точку /И(1; 1).
Л Координаты точки М должны удовлетворять уравнению искомой прямой,
жатому для определения X получаем уравнение
2.14-3-14-54-Х(14-8-14-6) = 0, или 104-151=0,
т. е. Л=—2/3. Подставив значение X в уравнение пучка, получим уравнение
искомой прямой:
2x4-31/4-5—(2/3) (х4-8г/4-6) = 0, или 4х—7г/4-3 = 0. Д
97. Найти прямую, проходящую через точку пересечения пря-
мых Зх—4^4-7 =0 и 5x4-21/4-3 = 0 и параллельную оси ординат.
Л Прямая принадлежит пучку
Зх-4г/4-74-Х (5х4-2г/4-3) =0, т. е. (3-)-5Х) х-)-(—44-2А) г/4-(74-ЗХ) =0.
Так как искомая параллельна оси ординат, то коэффициент при у должен быть
равен нулю: —44-2Х=0, т. е. Х = 2. Остается подставить найденное значение Л
а уравнение пучка, откуда получаем искомое уравнение х-|-1=0. Д
98. Даны стороны треугольника: х4-2у4-5 = 0 (ДВ), 3x4-У+ 1 =
= 0(ВС) и x4-f/4-7 = 0 (АС). Составить уравнение высоты треуголь-
ника, опущенной на сторону АС.
Л Высота принадлежит пучку
x4-2i/4-54-A(Зх4-1/4-1) =0, т. е. (1-)-ЗХ) х-)-(24-Х) t/4-(54-A) = 0.
Угловой коэффициент прямой пучка равен—(14-ЗХ)/(2 4-X); так как угловой
коэффициент прямой АС равен—1, то угловой коэффициент искомой высоты ра-
вен 1 и для определениях получаем уравнение—(1 4-ЗХ)/(2-|-Х) = 1. Отсюда
14-ЗА4-2-|-Х = 0, т. е. Х = —3/4. Подставив найденное значение X. в уравнение
жучка, получим искомое уравнение высоты:
(1—|’)х+^2—г/-{-^5—-|-^=0, т. е. 5х—5у—17 = 0. Д
99. Даны вершины треугольника ДВС: Д (0; 2), В (7; 3) и С (1; 6).
Определить ВАС = а.
100. Даны стороны треугольника: х-\-у—6 = 0, Зх—5^4-14 = 0
5х—Зу—14 = 0. Составить уравнения его высот.
101. Составить уравнения биссектрис углов между прямыми
Зх-J- 4у—20 = 0 и 8x4-61/—5 = 0.
102. Даны вершины треугольника: Д (0; 0), В(—1; —3) иС(—5;
— 1). Составить уравнения прямых, проходящих через вершины
треугольника и параллельных его сторонам.
23
103. Составить уравнения прямых, проходящих через точку
М (2; 7) и образующих с прямой АВ, где Л(—1; 7) и В(8;—2),
углы 45°.
104. Определить расстояние от точки М (2; —1) до прямой, от-
секающей на осях координат отрезки а —8, Ь — б.
105. В треугольнике с вершинами А (3/2; 1), 23(1; 5/3), С(3; 3)
найти длину высоты, проведенной из вершины С.
106. При каком значении т прямые 1х—2у—5 = 0, х-\-1у—8 =
= 0 и тх + ту — 8 = 0 пересекаются в одной точке':*
107. Даны середины сторон треугольника: At(—1;—1), ВД1; 9)
и СД9; 1). Составить уравнения серединных перпендикуляров к
сторонам треугольника.
108. Найти острый угол, образованный с осью ординат прямой,
проходящей через точки А (2; У 3) и В (3; 2J/3).
109. Точки А (1; 2) и С (3; 6) являются противоположными вер-
шинами квадрата. Определить координаты двух других вершин
квадрата.
ПО. На оси абсцисс найти точку, расстояние которой от прямой
8х + 15«/ + 10 = 0 равно 1.
111. Даны вершины треугольника: Л(1; 1), В (4; 5) иС(13; —4).
Составить уравнения медианы, проведенной из вершины В, и вы-
соты, опущенной из вершины С. Вычислить площадь треугольника.
112. Найти прямые, принадлежащие пучку 2х+3«/ + 6 + Х(х—
— бу—6) = 0 и перпендикулярные основным прямым пучка.
113. Найти прямую, проходящую через точку пересечения пря-
мых х + 6«/ + 5 = 0, Зх—2«/+1 и через точку М (—4/5; 1).
114. Найти прямую, проходящую через точку пересечения пря-
мых х + 2«/ + 3 = 0, 2х + 3«/+4 = 0и параллельную прямой 5х +
+ 8«/ = 0.
115. Найти прямую, проходящую через точку пересечения пря-
мых Зх—у—1=0, хЗу + 1 = 0 и параллельную оси абсцисс.
116. Найти прямую, проходящую через точку пересечения пря-
мых 5х4-Зг/4-10 = 0, х 4-«/-^15 = 0 и через начало координат.
117. Найти прямую, проходящую через точку пересечения пря-
мых х + 2у + 1 = 0, 2х+ «/ + 2 = 0 и образующую угол 135° с осью
абсцисс.
118. Составить уравнения прямых, проходящих через точку
М (а; Ь) и образующих с прямой х + «/ + с = 0 угол 45°.
119. Даны стороны треугольника: х—у = 0 (АВ), х + У—2 = 0
(ВС), у = 0 (АС). Составить уравнения медианы, проходящей через
вершину В, и высоты, проходящей через вершину А.
120. Показать, что треугольник со сторонами х + «/КЗ + 1=0,
хКЗ + у + 1 = 0 и х—у—10 = 0 равнобедренный. Найти угол при
его вершине.
121. Даны последовательные вершины параллелограмма: Л (0; 0),
В (1; 3), С(7;1). Найти угол между его диагоналями и показать,
что этот параллелограмм является прямоугольником.
122. Даны стороны треугольника: х—«/ + 2 = 0 (АВ), х = 2(ВС),
24
х-£у — 2 = 0 (ДС). Составить уравнение прямой, проходящей через
вершину В и через точку на стороне АС, делящую ее (считая от
вершины Д) в отношении 1:3.
123. Показать, что треугольник с вершинами Д (1; 1), В (2; 1 +
Д-|ДЗ), С (3; 1) равносторонний, и вычислить его площадь.
124. Показать, что треугольник, стороны которого заданы ура-
внениями с целыми коэффициентами, не может быть равносторонним.
125. Дана вершина треугольника А (3; 9) и уравнения медиан:
у—6 = 0 и Зх —4z/ + 9 = 0. Найти координаты двух других вершин.
126. Составить уравнение гипотенузы прямоугольного треуголь-
ника, проходящей через точку М (2; 3), если катеты треугольника
расположены на осях координат, а площадь треугольника равна
12 кв. ед.
127. Составить уравнения трех сторон квадрата, если известно,
что четвертой стороной является отрезок прямой 4x-i-3y—12 = 0,
концы которого лежат на осях координат.
§ 3. КРИВЫЕ ВТОРОГО ПОРЯДКА
1. Окружность. Окружность — это множество всех точек плоскости, равноуда-
жнных от данной точки (центра). Если г — радиус окружности, а точка С (а; Ь)—
* центр, то уравнение окружности имеет вид
(Х_а)2 + (у_/,)2 = г2. (1)
В частности, если центр окружности совпадает с началом координат, то послед-
нее уравнение примет вид
X2+y2 = f2.
Если в левой части уравнения (1) раскрыть скобки, то получится уравнение
вида
х2 + у2 + 1х + ту-\-п =0, (2)
где / = —2а, т = —26, п = а24-62— г2.
В общем случае уравнение (2) определяет окружность, если /2-f-m2— 4п > 0.
Если /2 + т2 — 4n = Q, то уКазанное уравнение определяет точку (—Z/2; —т/2),
аеслн /2 + т2—4п < 0, то оно не имеет геометрического смысла. В этом случае
говорят, что уравнение определяет мнимую окружность.
Полезно помнить, что уравнение окружности содержит старшие члены х2 и
у2 с равными коэффициентами и в нем отсутствует член с произведением х на у.
Взаимное расположение точки Л1 (xt; гц) и окружности x2-J-y2 = r2 опреде-
ляется такими условиями: если х%-[-у2 = г2, то точка М лежит иа окружности;
если x? + yf > г2, то точка М лежит вне окружности, и если Xi-J-yf < г2, то
точка М лежит внутри окружности.
128. Найти координаты центра и радиус окружности 2x24-2z/2—•
— 8х + 5у — 4 = 0.
Д Разделив уравнение на 2 и сгруппировав члены уравнения, получим
X2—4х + ^2 + (5/2) у —2. Дополним выражения х2—4х и г/2 + (5/2) I/ до полных
квадратов, прибавив к первому двучлену 4 и ко второму (5/4)2 (одновременно к
правой части прибавляется сумма этих чисел):
(х2 _ 4х + 4) + ( у2 +4 У) = 2 + 4-4~т|
\ <4 1 V / Ю
25
или
('-2)’+(1'+4)’=-К-
Таким образом, координаты центра окружности а = 2, Ь~—5/4, а радиус окруж-
ности r= 11/4. А
129. Составить уравнение окружности, описанной около тре-
угольника, стороны которого заданы уравнениями 9х—2у—41=0,
7х + 4у + 7 = 0, х—Зу-|-1=0.
Найдем координаты вершин треугольника, решив совместно три системы
уравнений:
f 9х—2у—41=0, ( 9х—2у—41=0, ( 7х-)-4у4-7 = 0,
j 7х-|-4у4- 7 = 0; \ х—3//4- 1 = 0; ) х—Зу-|-1=0.
В результате получим А (3; —7), В (5; 2), С(—1; 0).
Пусть искомое уравнение окружности имеет вид (х—о)2-)-(у—Ь)г = гг. Для
нахождения а, b и г напишем три равенства, подставив в искомое уравнение
вместо текущих координат координаты точек А, В и С:
(3_fl)S + (_7_6)S = r2; (5—а)2-|-(2—6)2 = r2; (— 1 — a)* + b* = r*.
Исключая г2, приходим к системе уравнений
( (3—о)24-(—7—5)2 = (5—о)2 + (2—6)2, ( 4a+185 = —29,
\ (3—а)2 + (—7—6)2 = (— 1— a)2+62, ИЛИ I 8а—145 = 57.
Отсюда а = 3,1, 5=—2,3. Значение г2 находим из уравнения (—1—a)2+62 = r2,
т. е. г2 = 22,1. Итак, искомое уравнение записывается в виде (х—3,1 )2-f-(y-f-2,3)2=
=22,1. А
130. Составить уравнение окружности, проходящей через точки
А (5; 0) и В(1; 4), если ее центр лежит на прямой х-f-z/—3 = 0.
Д Найдем координаты точки М—середины хорды ЛВ; имеем хд! = (5+1)/2=3,
ИМ = (4+Q)/2 = 2, т. е. М (3; 2). Центр окружности лежит на серединном пер-
пендикуляре к отрезку АВ. Уравнение прямой АВ имеет вид
(У—0)/(4 —0) = (х— 5)/(1 — 5)7 т. е. х-\-у— 5 = 0.
Так как угловой коэффициент этой прямой есть —1, то угловой коэффициент
перпендикуляра к ней равен 1, а уравнение этого перпендикуляра у—2= IX
Х(х—3), т. е. х—у—1=0.
Очевидно, что центр окружности С есть точка пересечения прямой АВ с ука-
занным перпендикуляром, т. е. координаты центра определяются путем решения
системы уравнений х-^-у—5 = 0, х—у—1=0. Следовательно, х = 2, у = 1, т. е.
С (2; 1). Радиус окружности равен длине отрезка СА, т. е. г=уЛ^5—2)2+(1 — 0)2=
= Y10. Итак, искомое уравнение имеет вид (х—2)2 + (у—I)2 = 10. А
131. Составить уравнение хорды окружности х2 + у2 = 49, деля-
щейся в точке Л (1; 2) пополам.
Л Составим уравнение диаметра окружности, проходящего через точку А (1; 2).
Это уравнение имеет вид у = 2х. Искомая хорда перпендикулярна диаметру и
проходит через точку А, т. е. ее уравнение у—2 = (—1/2) (х— 1), или х + 2у —
— 5 = 0. А.
132. Найти уравнение окружности, симметричной с окруж-
ностью х2+у2 = 2х + 4у—4 относительно прямой х—у—3 = 0.
Л Приведем уравнение данной окружности к каноническому виду (х—1)2 +
+ (у—2)2=1; центр окружности находится в точке С(1; 2) и ее радиус равен 1.
26
Найдем координаты центра Ci (хц, t/i) симметричной окружности, для чего через
точку С (1; 2) проведем прямую, перпендикулярную прямой х—у—3 = 0; ее уравне-
ние y — 2 = k(x—1), где£ =—1/1=—1, откуда у—2 = — х+1, или х + р—3=0.
Решая совместно уравнения х—у—3 = 0 и х-\-у—3=0, получим х=3,у=0,
т. е. проекция точки С(1; 2) на данную прямую—точка Р (3; 0). Координаты же
симметричной точки получим по формулам координат середины отрезка: 3 =
= (I + Xj)/2, 0=(2+</j)/2; таким образом, ^=5, уг=—2. Значит, точка Ci (5; —2)—
митр симметричной окружности, а уравнение этой окружности имеет вид (х—52)-р
+(у4-2)2 = 1. Д.
133. Найти множество середин хорд окружности х2-]-у2= 4 (z/H-1),
проведенных через начало координат.
Д Уравнение множества хорд имеет вид y = kx. Выразим координаты точки
пересечения хорд с окружностью через k, для чего решим систему уравнений
» = Лх и х2+«/2—4у—4 = 0. Получим квадратное уравнение х2 (fe2+1)—4kx—4=0.
Здесь Xj+x2 = 4fe/(i 4-Л2). Но полусумма этих абсцисс дает абсциссу середины
хорды, т. е. x = 2k/(l-}-k2), а ордината середины хорды у = 2А2/(1 -ф-й2). По-
следние два равенства являются параметрическими уравнениями искомого
множества точек.
Исключив из этих равенств £ (для чего достаточно в соотношении х=2й/(1-|-£2)
положить k—y/x), получим х2+р2 — 2у = 0. Таким образом, искомым множеством
также является окружность. А
134. Определить координаты центров и радиусы окружностей:
1) х2 + у2 — 8х + 6// = 0; 2) л-2 + ;/2+10л-—4z/ + 29 = 0; 3) х° + у2 —
— 4х +14у + 54 = 0.
135. Найти угол между радиусами окружности х2 + г/24х—
— 6z/ = 0, проведенными в точки ее пересечения с осью Оу.
проходящей через точки
136. Составить уравнение окружности,
Л (1; 2), В (0; — 1) и С (—3; 0).
137. Составить уравнение окружности,
Л (7; 7) и В (—2; 4), если ее центр лежит
138. Составить уравнение общей хор-
ды окружностей x24-z/2=16 и (х—5)2Д-
+£/2 = 9.
139. Составить уравнения касательных
к окружности (х—3)2+ (у 4~2)2 = 25, про-
веденных в точках пересечения окруж-
ности с прямой х —z/ + 2 = 0.
140. Дана окружность х2^у2 = 4. Из
точки А {—2; 0) проведена хорда АВ,
которая продолжена на расстояние | ВМ | =
= |ЛВ|. Найти множество точек М.
проходящей через точки
на
прямой 2х—у—2=0.
2. Эллшс. Эллипсом называется множество всех точек плоскости, сумма расстоя-
ний которых до двух данных точек, называемых фокусами, есть величина постоян-
ная (ее обозначают через 2а), причем эта постоянная больше расстояния между
фокусами.
Если оси координат расположены по отношению к эллипсу так, как на рис. 10,
л фокусы эллипса находятся на оси Ох на равных расстояниях от начала коор-
динат в точках (с; 0) и F2 (—с; 0), то получится простейшее (каноническое)
уравнение эллипса:
а2 ‘Ь2
Здерр. а—большая,.b— малая полуось эллипса, причем а, b н с (с—половина
расстояния между фокусами) связаны соотношением а2'-Ь2-)-с2.
Форма эллипса (мера его сжатия) характеризуется его эксцентриситетом
е = с/а (так как с < а, то е < 1).
Расстояния некоторой точки эллипса М от его фокусов называются фокаль-
ными радиусами-векторами этой точки. Их обычно обозначают Г\ и г2 (в силу
определения эллипса для любой его точки ri + r2 = 2a).
В частном случае, когда а = Ь (с = 0, е = 0, фокусы сливаются в одной точ-
ке—центре), эллипс превращается в окружность (с уравнением х2-\-у2 = а2).
Взаимное расположение точки М (xj; гц) и эллипса х2/а2 + у2/Ь2 = 1 опреде-
ляется условиями: если xf/a2-f-z/?/Z>2 = 1, то точка М лежит на эллипсе; если
Xi/a2 у\/Ьг >1, то точка М лежит вие эллипса; если х*1а2-\-у\]Ь2 < 1, то
точка М лежит внутри эллипса.
Фокальные радиусы-векторы выражаются через абсциссу точки эллипса по
формулам гг — а—ех (правый фокальный радиус-вектор) и гг = а-\-ех (левый фо-
кальный радиус-вектор).
141. Составить каноническое уравнение эллипса, проходящего
через точки М (5/2; J/6/4) и N (—2; J/15/5).
Л Пусть x2/a2-)-y2/b2 — 1—искомое уравнение эллипса. Этому уравнению
должны удовлетворять координаты данных точек. Следовательно,
25+_1=1 ±+-£=1
4a2^8i2 ’ a=^562
Отсюда находим а2=10, 62=1. Итак, уравнение эллипса имеет вид х2/Ю4*
+ №=•• ▲
142. На эллипсе №/25 + у2/9 = 1 найти точку, разность фокаль-
ных радиусов-векторов которой равна 6,4.
143. Найти длину перпендикуляра, восставленного из фокуса
эллипса х2,/а2 + у2/Ь2=1 к большой оси до пересечения с эллипсом.
144. Составить уравнение прямой, проходящей через левый фокус
и нижнюю вершину эллипса x2/25-f-r/2/16 = 1.
145. Эллипс, отнесенный к осям, проходит через точку М (1; 1)
и имеет эксцентриситет е — 3/5. Составить уравнение эллипса.
146. Как расположены относительно эллипса х2/50 + г/2/32 = 1
точки /И (7; 1), N (—5; —4), Р (4; 5)?
147. Найти эксцентриситет эллипса, если фокальный отрезок
виден из верхней вершины под углом а.
148. На прямой х+5 = 0 найти точку, одинаково удаленную
от левого фокуса и верхней вершины эллипса х2/20 + у2/4 = 1.
149. Пользуясь определением эллипса, составить его уравнение,
если известно, что точки Fr (0; 0) и К2 (1; 1) являются фокусами
эллипса, а длина большой оси равна 2.
150. Составить уравнение множества точек, расстояния которых
от точки А (0; 1) в два раза меньше расстояния до прямой у—4=0.
151. Концы отрезка АВ постоянной длины а скользят по сто-
ронам прямого угла. Найти уравнение кривой, описываемой точ-'
кой М, делящей этот отрезок в отношении 1: 2.
3. Гипербола. Гиперболой называется множество всех точек плоскости, абсолют-
ная величина разности расстояний которых до двух данных точек, называемых фо-
кусами, есть величина постоянная (ее обозначают через 2а), причем эта постоян-
28.
ная меньше расстояния между фокусами. Если поместить фокусы гиперболы
з точках Ei (с; 0) и F2 (—с; 0), то получится каноническое уравнение гиперболы
где 62 = с2—а2. Гипербола состоит из двух ветвей и расположена симметрично
относительно осей координат. Точки Л1(а; 0) и А2 (—а; 0) называются верши-
нами гиперболы. Отрезок Л1Д2 такой, что | AjA2j = 2a, называется действитель-
ной осью гиперболы, а отрезок ВгВ2 такой, что | В1В2 | = 26, —мнимой осью (рис. 11).
Прямая называется асимптотой гиперболы, если расстояние точки М (х; у)
гиперболы от этой прямой стремится к нулю при х->~оо или х ->—оо. Гипер-
5?ла имеет две асимптоты, уравнения
I вторых у= ± (6/а) х.
Для построения асимптот гиперболы
строят осевой прямоугольник гиперболы
со сторонами х = а, х = — а, у = Ь,
у =— Ь. Прямые, проходящие через
противоположные вершины этого прямо-
угольника, являются асимптотами ги-
перболы. На рис. 11 указано взаимное
расположение гиперболы и ее асимптот.
Отношение e=c/a > 1 называется эксцен-
триситетом гиперболы.
Фокальные радиусы-векторы правой
ветви гиперболы: г\=ех—а (правый фо-
кальный радиус-вектор), г2-=ех4Га (ле-
гиперболы: г\ =— ех-\-а (правый
вый фокальный радиус-вектор).
Фокальные радиусы-векторы левой ветви
«жальный радиус-вектор), г2 = — ех—а (левый фокальный радиус-вектор).
Если а = Ь, то уравнение гиперболы принимает вид
х2—у2 = а2.
Такая гипербола называется равнобочной. Ее асимптоты образуют прямой угол.
Если за оси координат принять асимптоты равнобочной гиперболы, то ее урав-
нение примет вид ху=~т (т=±а2/2; при т >0 гипербола расположена в I
в III четвертях, при т< 0 — во II и IV четвертях). Так как уравнение ху = т
можно переписать в виде у = т/х, то равнобочная гипербола является графиком
обратной пропорциональной зависимости между величинами х и у.
Уравнение
х2 у2 f у2 х2 \
-Т — Т5-=— 1 ИЛИ — -2=1
а2 Ьг \ 62 а2 )
(2)
также является уравнением гиперболы, но действительной осью этой гиперболы
служит отрезок оси Оу длины 26.
Две гиперболы х2/а2—у2/62=1 и х2/а2—у2/Ь2 = — 1 имеют одни и те же
полуоси и одни и те же асимптоты, но действительная ось одной служит мни-
мой осью другой, и наоборот. Такие две гиперболы называют сопряженными.
152. На правой ветви гиперболы х2/16 — г/2/9 = 1 найти точку,
расстояние которой от правого фокуса в два раза меньше ее рас-
стояния от левого фокуса.
Д Для правой ветви гиперболы фокальные радиусы-векторы определяются
по формулам гх = ех—а и г2 = ех-|-а. Следовательно, имеем уравнение ех-|-а =
= 2 (ех—а), откуда х = 3а/е; здесь а = 4, е = с/а= уЛа2+ Ь2]а = 16-}- 9/4 =
= 5/4, т. е. х = 9,6.
Ординату находим из уравнения гиперболы:
у=± 4 =± । j/ (^Г-1б=± 4 rm.
•г ‘т Г Д v у v
29
Таким образом, условию задачи удовлетворяют две точки: Mi (9,6; О.бр^ 119)
и Мг (9,6; —0,6 /П9). А
153. Даны точки А (—1; 0) и В (2; 0). Точка М движется так,
что в треугольнике АМВ угол В остается вдвое больше угла А .
Найти уравнение кривой, которую опишет точка М.
Л Взяв точку М с координатами х и у, выразим tg В и tg А через коорди-
наты точек А, В и М:
Согласно условию, получаем уравнение tg S=tg 24, т. е. tg fi=2tg Л/(1—tg2A).
Подставив в это равенство найденные для tg В и tg Л выражения, приходим
к уравнению
у 2y/(x+D .
2—х 1— //7(1 4-х)2’
после сокращения иа у (у £ 0) н упрощения получаем х2—у2/3=1. Искомая
кривая — гипербола. А
154. Эксцентриситет гиперболы равен К2. Составить простейшее
уравнение гиперболы, проходящей через точку М (К3; J/2).
Д Согласно определению эксцентриситета, имеем с/а=У 2, или с2 = 2а2.
Но c2 = a24*t>2; следовательно, а2 4- Ь2 = 2а2, или а2=й2, т. е. гипербола равно-
бочная.
Другое равенство получим из условия нахождения точки М на гиперболе,
т. е. (У 3)2/а2—(У 2)2/й2=1, или 3/а2—2/62=1. Поскольку а2 — Ь2, получим
3/а2—2/а2 = 1, т. е. а2 = 1.
Таким образом, уравнение искомой гиперболы имеет вид х2—у2 = 1. А
155. Составить уравнение гиперболы, проходящей через точку
М (9; 8)^_ если асимптоты гиперболы имеют уравнения у—
= ±(2К2/3)х.
156. Найти уравнение гиперболы, вершины и фокусы которой
находятся в соответствующих фокусах и вершинах эллипса х2/8 +
+i/2/5=l.
157. Через точку М (0; —1) и правую вершину гиперболы
Зх2—4у2= 12 проведена прямая. Найти вторую точку пересечения
прямой с гиперболой.
158. Дана гипербола х2—у2 = 8. Найти софокусный эллипс, про-
ходящий через точку М (4; 6).
159. Дан эллипс 9х2 4-25г/2 = 1. Написать уравнение софокусной
равнобочной гиперболы.
160. Угол между асимптотами гиперболы равен 60°. Вычислить
эксцентриситет гиперболы.
161. На левой ветви гиперболы х2/64—у2/36 = 1 найти точку,
правый фокальный радиус-вектор которой равен 18.
162. Составить уравнение гиперболы, если ее эксцентриситет
равен 2 и фокусы совпадают с фокусами эллипса х2/25 4- у2/9 = 1.
163. Найти фокальные радиусы-векторы гиперболы №/16—z/2/9=
= 1 в точках пересечения ее с окружностью х2 + </2 —91.
164. Доказать, что длина перпендикуляра, опущенного из фо-
куса на одну из асимптот гиперболы, равна мнимой полуоси.
165. Доказать, что произведение расстояний от любой точки
гиперболы х2—л/® — 1 до ее асимптот есть величина постоянная.
166. Найти уравнение множества точек, равноотстоящих от
окружности x2-J-4x + </2 = 0 и от точки М (2; 0).
4. Парабола. Параболой называется множество всех точек плоскости, равноуда-
ленных от данной точки, называемой фокусом, и данной прямой, называемой
директрисой. Если директрисой параболы является прямая х— — р/2, а фоку-
сом — точка 0), то уравнение параболы имеет вид
Уг = 2рх. (1)
Эта парабола расположена симметрично относи-
тельно оси абсцисс (рис. 12, где р > 0).
Уравнение
хг = 2ру (2)
является уравнением параболы, симметричной отно-
сительно оси ординат. При р > 0 параболы (1) и
(2) обращены в положительную сторону соответству-
ющей оси, а при р < 0—в отрицательную сторо-
ну.
Длина фокального радиуса-вектора параболы у2 = 2рх определяется по фор-
муле г — х-^р/Ч (р > 0).
167. Составить уравнение параболы, симметричной относительно
оси Ох, с вершиной в начале координат, если длина некоторой
хорды этой параболы, перпендикулярной оси Ох, равна 16, а рас-
стояние этой хорды от вершины равно 6.
Л Так как известны длина хорды и расстояние ее от вершины, то, следо-
вательно, известны координаты конца этой хорды—точки М, лежащей иа пара-
боле. Уравнение параболы имеет вид у2 = 2рх; полагая в ием х=6, у = 8, иахо-
двм 82 = 2р-6, откуда 2р = 32/3. Итак, уравиеиие искомой параболы у2 = 32х/3. А
168. Составить уравнение параболы с вершиной в начале коор-
динат, 'симметричной относительно оси Оу и отсекающей на бис-
сектрисе I и III координатных углов хорду длиной 8 И 2.
Д Искомое уравнение параболы х* = 2ру, уравнение биссектрисы у = х. Таким
образом, получаем точки пересечения параболы с биссектрисой: 0(0; 0) и
М (2р; 2р). Длина хорды определяется как расстояние между двумя точками:
8 }^? = уЛ4р2-|-4р2, откуда 2р = 8. Следовательно, искомое уравнение имеет вид
х-’=8у. Д
169. Составить простейшее уравнение параболы, если известно,
иго ее фокус находится в точке пересечения прямой 4х—Зу—4 = 0
с осью Ох.
170. На параболе у2 = 8х найти точку, расстояние которой от
директрисы равно 4.
31
171. Составить уравнение параболы с вершиной в начале коор-
динат, симметричной относительно оси Ох и отсекающей от прямой
у = х хорду длиной 4 И 2.
172. Парабола у2 = 2х отсекает от прямой, проходящей через
начало координат, хорду, длина которой равна 3/4. Составить урав-
нение этой прямой.
173. Составить простейшее уравнение параболы, если длина
хорды, перпендикулярной оси симметрии и делящей пополам рас-
стояние между фокусом и вершиной, равна 1.
174. На параболе z/2 = 32x найти точку, расстояние которой от
прямой 4х + Зу + 10 = 0 равно 2.
175. Составить уравнение параболы с вершиной в начале коор-
динат, симметричной относительно оси Ох и проходящей через точку
М (4; 2); определить угол а между фокальным радиусом-вектором
этой точки и осью Ох.
§ 4. ПРЕОБРАЗОВАНИЕ КООРДИНАТ И УПРОЩЕНИЕ УРАВНЕНИЙ
КРИВЫХ ВТОРОГО ПОРЯДКА
1. Преобразование координат. При переходе от системы координат хОу к но-
вой системе х'Оху' (направление осей координат прежнее, за новое начало коор-
динат принята точка Oj (а; Ь); рис. 13) связь между старыми и новыми коор-<
динатами некоторой точки М плоскости определяется следующими формулами:
х = х'+а, y = y'-f-b; (1)
х' =х—а, у'—у— Ь. (2)
С помощью формул (1) старые координаты выражаются через новые, а с по-
мощью формул (2)— новые через старые.
При повороте осей координат на угол а (начало координат прежнее, причем
а отсчитывается против часовой стрелки; рис. 14) зависимость между старыми
координатами х, у и новыми х', у’ определяется следующими формулами:
х — х' cos а—у' sin а, у =х' sin ау' cos а; (3)
х' =xcos сх-j-z/ sin а, у'= —х sin а+у cos а. (4)
176. Сделан параллельный ’перенос осей координат, причем но-
вое начало расположено в точке О1 (3; —4). Известны старые коор-
динаты точки М (7; 8). Определить новые координаты этой же точки.
Л Здесь а=3, Ь=—4, х = 7, у = 8. По формулам (2) находим х' = 7—3=4,
/ = 8-(-4) = 12. А
32
177. На плоскости хОу дана точка М (4; 3). Система координат
повернута вокруг начала координат так, что новая ось прошла че-
рез точку М. Определить старые координаты точки Л, если известны
ее новые координаты х' = 5, у'—5.
/\ Так как | ОМ | = }^42 + 32 = 5, то sina = 3/5, cosa = 4/5; тогда формулы
(3) преобразования координат для дайной задачи примут вид х = (4/5)х'— (3/5) у’,
у = (3/5) х' + (4/5) у'. Полагая х'=у' = Ъ, находим х—1, у~7. А
178. Система координат повернута на угол а = л/6. Определить
новые координаты точки М (К3 ; 3).
А Используя формулы (4), получим
х' = }ЛЗ cos (л/6) +3 sin (л/6) =3/2+3/2 = 3,
у' = —УЗ sin (л/6)+3cos (л/6) = — У"3/2 + ЗУ"3/2 = У"3. А
179. Дана точка М (9/2; 11/2). За новые координатные оси при-
няты прямые 2х—1 = 0 (ось 0^'), 2у— 5 = 0 (ось 0^'). Найти
координаты точки М в новой системе координат.
180. Дана точка 44(4 1^5; 2J/5)- За новую ось абсцисс при-
нята прямая у — 2х, а за новую ось ординат—прямая у = —0,5 а:,
причем новые оси координат образуют с соответствующими старыми
осями острые углы. Найти координаты точки М в новой системе.
2. Парабола у = Ах2Вх С и гипербола у = (kx l)Kpx + q). У равне-
ние вида
у = Ах2 + Вх + С
преобразованием координат при параллельном переносе осей, т. е. по формулам
x = x'+a, y=--y'-{-b (а и b — координаты нового начала, х' и у' — новые коор-
динаты), преобразуется к каноническому виду уравнения параболы.
Парабола, определяемая уравнением у = Ах2 -\-Bx-\-C, имеет ось симметрии,
параллельную оси Оу (аналогично, уравнение х — Ау2-\-Ву-\-С определяет пара-
болу с осью симметрии, параллельной оси Ох).
Дробно-линейная функция
y = (kx+l)/(px+q)
определяет равнобочную гиперболу, если kq—pl + 0, р + 0; преобразованием
координат при параллельном переносе осей координат это уравнение преобразу-
ется к каноническому виду уравнения равнобочной гиперболы ху = т, т. е.
к уравнению равнобочной гиперболы, у которой оси координат ивляются асимп-
тотами. При т > 0 ветви гиперболы расположены в I и III четверти, а при
•л < 0 — во II и IV четверти.
181. Привести к каноническому виду уравнение параболы
у = 9х2—6х + 2.
А Заменим х на х’^-а и у на </' + &:
у' + b =9 (х' + а)2—6(х'+а)+2,
али
у' =9x'2 + 6x' (За — 1) + (9а2—6а + 2—&).
Найдем такие значения а и Ь, при которых коэффициент при х' и свободный
член обратятся в нуль: За—1=0, 9а2—6а + 2—6 = 0, т. е. а=1/3, 6 = 1. Сле-
довательно, каноническое уравнение параболы имеет вид х'2 = (1/9) у'. Вершина
параболы находится в точке Oj (1/3; 1) и р=1/18.
2-215
Другой способ решения таких задач заключается в том, что заданное урав-
нение вида у = Ах*-}-Вх-(-С (или х=Ау’+Ву+С) приводится к виду (х—а)г =
= 2р(у — Ь) [соответственно (у—Ь)г=2р (х—а)]. Тогда точка Oj (а; 6) служит
вершиной параболы, а знак параметра р определит, в какую сторону—положи-
тельную или отрицательную соответствующей оси (Оу или Ох)—направлена па-
рабола.
Так, уравнение у = 9х2—6х+2 преобразуется следующим образом:
/ IX2/ 1 X3 * s 1
у—1=9^х—-yj ; =д-(У—О-
Отсюда снова получаем, что вершина параболы находится в точке Oj(1/3; 1),
параметр р = 1/18, а ветвь параболы направлена в положительную сторону
оси Оу. А
182. Привести уравнение гиперболы у = (4х+5)/(2х—1) к виду
х'у' = k. Найти уравнения асимптот гиперболы относительно перво-
начальной системы координат.
Л G помощью параллельного переноса осей координат преобразуем данное
уравнение к виду
(у' + 6) (2х'+ 2а — 1) = 4х'+4а+5,
или
2х’у' + (26—4) х' + (2а—1) у' =4а-(-Ь—2ab-f-5.
.г
Найдем а и b из условий 2Ь—4=0 и 2а—1=0, т. е. а=0,5, 6 = 2. Тогда
уравнение гиперболы в новой системе координат примет вид х'у'=3,5. Асимпто-
тами гиперболы служат новые оси координат, а поэтому их уравнения х'=0,5,
у'=2.
Другой способ решения таких задач заключается в том, что уравнение вида
у = (£х+/)/(рх+у) преобразуется к виду (х—а) (у—6)=/п; центр гиперболы на-
ходится в точке О* (а; 6); ее асимптотами служат прямые х=а и у = Ь, знак т
по-прежнему определяет, в каких углах между асимптотами находятся ветви ги-
перболы.
Так, уравнение у = (4х+5)/(2х— 1) преобразуется следующим образом:
(2х—1)у—— (4х+5)=0; 2(х—0,5) (у—2) =7.
Значит, уравнение гиперболы приведено к виду (х—0,5) (у—2) =3,5; центр
гиперболы находится в точке Ог (0,5; 2), ветви гиперболы расположены в I н III
четвертях между ее асимптотами х—0,5 = 0, у—2=0. А
183. Привести к каноническому виду уравнения парабол:
1) г/ = 4х—2х*;2)у = —х* + 2х-[-2; 3) х= —4уг + у, 4)х = у* + 4у + 5.
184. Преобразовать уравнения гипербол к виду х'у' —mt
1) г/= 2х/(4х—1); 2) у = (2х + 3)/(3х—2); 3) у = (10*+2)/(5х + 4);
4) // = (4х + 3)/(2х+1).
3. Пятичлениое уравнение кривой второго порядка. Уравнение второй сте-
пени вида
Ax»+Cys+2Dx+2£y + F = 0
(не содержащее' члена ху с произведением координат) называется пятичленным
уравнением кривой второго порядка. Оно определяет на плоскости хОу эллипс,
34
гиперболу или параболу (с возможными случаями распада и вырождения этих
кривых) с осями симметрии, параллельными осям координат, в зависимости от
знака произведения коэффициентов А и С.
1. Пусть АС > 0; тогда определяемая этим уравнением кривая есть эллипс
(дейсвительиый, мнимый или выродившийся в точку); при А=С эллипс превра-
щается в окружность.
2. Пусть АС < 0; тогда соответствующая кривая является гиперболой, кото-
рая может вырождаться в две пересекающиеся прямые, если левая часть урав-
нения распадается ва произведение двух линейных множителей;
Ах2+Су2+2Dx+2Ey+F = (ajx + bry+Ci) (a2x-f-b2у+c2).
3. Пусть AC — G (т. e. либо A=0, C/0, либо C=0, \A 0); тогда уравне-
ние определяет параболу, которая может вырождаться в две параллельные пря-
мые (действительные различные, действительные слившиеся или мнимые), если
левая часть уравнения не содержит либо х, либо у (т. е. если уравнение имеет
вид Ax2+2Dx-]-F = 0 или Cy2Jr2Ey-\-F = 0).
Вид кривой и расположение ее на плоскости легко устанавливаются преоб-
разованием уравнения к виду А (х—х0)24-С(</—y<>)2 = f (в случае АС > 0 или
АС < 0); по виду полученного уравнения обнаруживаются и случаи распада или
вырождения эллипса и гиперболы.
В случае невырожденных кривых переносом начала координат в точку
Of (*«; Уч) полученное уравнение эллипса или гиперболы можно привести к кано-
ническому виду.
Случай АС = 0 подробно рассмотрен в предыдущем параграфе, поскольку
уравнение невырожденной параболы здесь может быть записано в виде
у=а1х2^-Ь1х-}-с или х = а1у2 + Ь1у-\-с{.
185. Какую линию определяет уравнение 4х24-9#2—8х—
— 36у + 4 = 0?
А Преобразуем данное уравнение следующим образом:
4 (х2—2х)+9 (у2—4у)~ —4;
4 (х2—2х+1 —1)+9 (у2—4# 4-4 —4) = — 4;
4 (х—1)24-9 (у—2)2 = -44-44-36; 4 (х— I)2-J-9 (у—2)2 = 36.
Произведем параллельный перепое осей координат, приняв за новое начало
координат точку О' (1; 2). Воспользуемся формулами преобразования координат:
х=х'4-1, у=у'-\-2. Относительно новых осей уравнение кривой примет вид
4х'24-9у'а = 36, или x,2/9-|-j/,2/4 = 1.
Таким образом, заданная кривая является эллипсом. А
186. Какую линию определяет уравнение х2—9#2 4-2х-)-36#—
— 44 = 0?
А Преобразуем данное уравнение так:
(^4-2x4-1 — 1)—9 (у2—4у+4—4) =44;
(х4-1)2—9(у—2)2 = 444-1—36, (х-1-1)2—9(у—2)2 = 9.
Произведем параллельный перенос осей координат, приняв за новое начало
точку О’ (—1; 2). Формулы преобразования координат имеют внд х = х' — 1,
#=1/4-2. После преобразования координат получим уравнение
х'2—9у'2 = 9, или х'2/9—у'2= 1.
Кривая является гиперболой. Асимптотами этой гиперболы относительно новых
осей служат прямые /=± (1/3) х'. А
Установить, какие кривые определяются нижеследующими урав-
нениями. Построить чертежи.
187. 36х2-|-36#2—36х—24#—23 = 0.
188. 16x»4-25#2—32x4-50#—359s=0.
1 i о
189. + =0.
190. х2 + 4г/2—4х—8г/4-8 = 0.
191. х24-4г/24-8у+5 = 0.
192. х2—у2—6x4-10 = 0.
193. 2х2—4x4-2г/—3 = 0.
194. х2—6x4-8 = 0.
195. х2 4-2х-{-5 = 0.
4. Приведение к каноническому виду общего уравнения кривой второго по-
рядка. Если кривая второго порядка задана уравнением
Ах2 + 2Вху -|- Су2+2Е>х-|- 2Еу -|- F = 0,
то, применив преобразование поворота осей координат с использованием формул
х = х’ cos а—у' sin а, у = х' sin а4-у' cos а, следует при надлежащем выборе а
освободиться в уравнении от члена с произведением координат.
Дальнейшие преобразования были рассмотрены в предыдущем разделе.
Случай распада кривой второго порядка на две прямые может быть легко
установлен по исходному уравнению следующим образом: [рассматривая уравне-
ние как квадратное относительно у (предполагая, что коэффициент при у2 отли-
чен от нуля), разрешают его относительно у; если при этом под корнем окажется
точный квадрат некоторого двучлена ах-\-Ь, то корень извлечется, и для у полу-
чатся два значения: У1 = й1Х-|-61: уг — кгх4-Ьг. Это и покажет, что кривая рас-
падается на две прямые.
Данное уравнение может быть разрешено и относительно х. Если в общем
уравнении кривой второго -порядка А=С — 0 (естественно, что В Ф 0), то ука-
занное уравнение определяет пару прямых тогда и только тогда, если B/D = 2E/F.
В этом случае левая часть уравнения разлагается на линейные множители.
196. Показать, что уравнение 9x2-f-24xy-|- 16г/2—25 = 0 опреде-
ляет совокупность двух прямых.
Л Перепишем уравнение в виде (Зх-|-4у)2—25 = 0. Разложив левую часть на
множители, получаем (Зх-|-4у + 5) (Зх+4у—5) = 0. Таким образом, заданное
уравнение определяет прямые Зх-|-4у-|-5 = 0 и Зх-|-4у—5 = 0. А
197. Показать, что уравнение Зх24-8хг/—Зг/2—14х—2г/4-8 = 0
определяет совокупность двух прямых.
Л Перепишем уравнение в виде Зу2—2 (4х— 1) у—(Зх2— 14х-|-8) =0. Разре-
шим уравнение относительно у.
4х-1 ± у-(4х-1)2+(9х2-42х+24) 4х-1 ± (5х-5)
У — 3 , НД н у — 2 •
Получаем уравнения прямых у=3х—2 и у = (—х-|-4)/3. Эти уравнения
можно записать в виде Зх—у—2 = 0, х-|-Зу—4=0. А
198. Какая линия определяется уравнением хг/4-2х—4у— 8 = 0?
Л Запишем уравнение в виде х(г/-|-2)—4(у-|-2)=0, или (х—4)(р-|-2)=0.
Таким образом, уравнение определяет две прямые х—4 = 0 и i/-f-2 = 0> одна нз
которых параллельна осн Ох, а другая параллельна оси Оу. А
199. Привести к каноническому виду уравнение
5х2 + 4ху 4- 8у2 + 8х +14у 4- 5 = 0.
36
А 1. Преобразуем это уравнение, воспользовавшись формулами (3) п. 1
поворота осей координат. Имеем
5 (х' cos а—y'"sin а)2-|-4 (х' cos а—у' sin а) (х' sin а-^-у' cos а)4-
+8 (х' sin а-|-у' cos а)2-)-8 (х' cos а—у' sin а) +14 (х' sin а-|-у' cos а)-)-5 = 0,
ли
(5 cos2 а-f-4 sin a cos а4-8 sin2 а) х'2-)- (5 sin2 а—4 sin a cos а-|-8 cos2 а) у'2-)-
4- [6 sin a cos а 4 (cos2 а—sin2 а)] х'у' 4- (8 cos а 4-14 sin а) х'
4-(14cosa—8sina)y'-|-5 = 0.
Найдем а из условия 4 (cos2 а—sin2 а) 4-6 sin a cos а=0, т. е. приравняем
улю коэффициент при х'у'. Получаем уравнение 2tg2a—3tga—2=0. Отсюда
tgai = 2, tga2 =—1/2.
Заметим, что эти значения tg а соответствуют двум взаимно
ым направлениям. Поэтому, взяв tga = 2
место tga = —1/2, мы только меняем ролями
оси х' и у' (рис. 15). _
Пусть tg a = 2, тогда sin a = ±2/ У 5 ,
cos a =4; l/]/"5 ; возьмем положительные зна-
чения sin а и cos a. Тогда уравнение принима-
ет внд
9х'2 4-4у'24- х' -J= у' 4-5 = 0,
У 5 У о
жди
перпендикуляр-
У'*
1
-±=У
2. Выражения в скобках дополним до полных квадратов:
о ( , , 2 V , и ( > 1 V 3S . 1 ,
91 х “|—т=. ) +4 I у------1 =-=——б
\ К 5 / \ 4 К 5 / б1 20
жди
а /
I +4(/
/ 2 № / 1 \а 9
9fx'+-== 1 +4( у'----!— 1=4-.
\ Кб/ V 4 Кб/ 4
Приняв за новое начало точку О' (—ъу 5; 1/(4 уг5)),_применим формулы пре-
сбразовання координат х'=х"—2/|<5, у' =у"-|- 1/(4 Кб"); получим 9х"2-|-4у"2 =
у"2
= 9/4, или -jyy-f~gy[g = 1 (уравнение эллипса). А
200. Привести к каноническому виду уравнение
6ху-\-8у2—12х—261/4- 11=0.
А 1. Преобразуем это уравнение, воспользовавшись формулами (3) п. 1
поворота осей координат:
6 (х' cos a—у' sin a) (х' sin а-\-у' cos a)-|-8 (x' sin a4-y' cos a)2—
—12 (x' cos a—y' sin a)—26 (x' sin a-|-y' cos a)-|-ll =0,
ли
(6 sin a cos a-|-8 sin2 a) x'2 4- (8 cos2 a—6 sin a cos a) y'2-f- -
4-[16 sin a cos a-рб (cos2 a—sin2 a)] x'y' —
— (12 cos a-|-26 sin a) x' — (26 cos a—12 sin ajy7 -)-l 1 =0.
37
Приравнивая нулю коэффициент при х'у', имеем
16 sin a cos а+6 (cos2 а—sin2a) = 0, или 3tg2a—8tga—3 = 0.
Отсюда tgai=3, tga2 =—1/3; примем tga = 3, тогда sin а— ± З/р^Ю,
cosa=± l/У ГО; возьмем положительные значения sin а и cos а. Тогда уравне-
ние принимает вид
Эх'2—у'2—9 }<l0 x' + KiOy' + n =0,
или
9(х'2—К10 х') — (у'2— рЛ10у')=—11.
2. Выражения в скобках дополним до полных квадратов:
или
Кюу Л., _ Ую\2 п
2 ) V 2 )
Приняв за новое начало точку_О' (У 10/2; У10/2), применим формулы преобра-
зования координат х'=х"+рЛ 10/2, у'=у"4-уг 10/2; получим 9х"2—у"2 = 9, или
х"2—у"2/9=1 (уравнение гиперболы). Д
201, Привести к каноническому виду уравнение
х2—2ху + «/2— 10х—6^4-25 = 0.
Л 1. Преобразуем уравнение с помощью формул поворота осей:
(х' cos a—у7 sin a)2—2 (х' cos a—у' sin a) (x' sin a+y' cos a) 4-
-f-(x' sin a-j-y' cos a)2—10 (x' cos a—y' sin a) —6 (x' sin a-j-y' cos a)-{-25 = 0,
или
(cos2 a—2 sin a cos a-|-sin2 a) x'2-|-(sin2 a -|- 2 sin a cos a-|-cos2 a) y'2+
-f- 2 (sin2 a—cos2 a) Х'у' — (10 cos a-|-6sina)x'-|-(10sina—6 cos a) у' 4- 25=0.
Приравнивая нулю коэффициент при произведении х'у', имеем (2 sin2 a—cos2a)=0,
откуда tg2a = l, т. е. tgai = l, tga2=—1. Возьмем tga=l, откуда а=л/4 и
sin а = 1/^2, cosa=l/prF. Тогда уравнение принимает вид
2у'2—8]<2 х'+21<2 у'+25 = 0, или 2(у,г + У2 у')—8 У2 х'4-25 = 0.
2. Выражение в скобках дополним дэ полного квадрата:
/ тЛТХ2 ,__________ / ViTX2 ,________/ 3 \
2\У' +^2 / =8 У2 х'—24, или^у'4-ly-J =4 У2
Приняв за новое начало точку О' (З/КЯ;—У 2 /2_), применим формулы преобра-
зования координат х*=х"—ЗУ2, у'у"-j-У 2/2; получим у"2=4рл2х*
(уравнение параболы). А
Показать, что нижеследующие уравнения определяют кривые,
распадающиеся на пару прямых, и найти уравнения этих прямых:
202. 25х24~ 10xz/4-z/2—1=0.
203. х2 4- 2ху+уъ 4- 2х -f- 2у -f-1 = 0.
204, 8х2—18ху 4- 9у* 4- 2х—1 = 0.
Привести к каноническому виду уравнения следующих кривых:
205. 14x2 + 24xy + 21ff2—4x+ 18^—139 = 0.
206. 16*+ 12у—36 = 0.
207. 9х2—24ху4-1 бу2—20*+ИОу—50 = 0.
f 5. ОПРЕДЕЛИТЕЛИ ВТОРОГО И ТРЕТЬЕГО ПОРЯДКОВ
СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ С ДВУМЯ
ТРЕМЯ НЕИЗВЕСТНЫМИ
1. Определители второго порядка и системы линейных уравнений. Определи-
тель второго порядка, соответствующий таблице элементов у1 определяется
\а2 о2у
равенством
£|=а1Ь2-аЛ-
Система двух линейных уравнений с двумя неизвестными
Г а1х-{-Ь1у=а,
I a,x+b2y=c2i
I at Ь< I , n
если ее определитель D = | . / 0, имеет единственное решение, которое нахо-
I аг °г I
днтся по формулам Крамера
Ci bi ai С1
Dx с2 Ь2 • 1! * а2 С2 /1\
Х D ' at bl ’ у D 41 bi • W
а2 b2 b2
Если определитель Z)—0, то система является либо несовместной, либо неоп-
ределенной. В последнем случае система сводится к одному уравнению (например,
первому), второе же уравнение является следствием первого.
Условие несовместности системы можно записать в виде Oila2 — bilb2^Cilc2,
а условие неопределенности—в виде Oi/n2 = 6i/6»=Ci/c2.
Линейное уравнение называется однородным, если свободный член этого урав-
нения равен нулю.
Рассмотрим систему двух линейных однородных уравнений с тремя неиз-
вестными
( OiX+biy-i-CiZ — Oi
( а2х-У-Ь1у+с2г = О.
1. Если ai/a2=bf/b2=ci/c2i то система сводится к одному уравнению (напри-
мер, первому), из которого одно из неизвестных выражается через два других,
значения которых остаются произвольными.
2. Если условие ai/a2 = bi/b2 = ci/c2 не выполнено, то решения системы нахо-
дятся по формулам
у = - |а< *1./, 2 = |fli*U (2)
IЬ2 с21 ’ | а2 с21 I вг Ь21 ’ ' ’
где t может принимать любые значения. Эти решения можно записать также
в виде
х _ у __ г
bi С11 | ах а I I 01 bi
b2 с21 | п2 с2 I" | а2 Ь2
39
»При этой форме записи решений следует помнить, что если один из знамена-
телей обращается в нуль, то следует приравнять нулю и соответствующий чис-
литель.
208. Решить систему уравнений
( (а-{-Ь)х—(а—b)y = 4ab,
I (а-6)х+(а+&)у = 2(аг-62).
Л Находим определитель D системы и определители Dx и Dy, входящие
в числители формул (1):
|=<«+Ч,+(»-Ч1“2 («’+»’>.
М2( “« " »+»’
— 2ab2 + 2&з = 2 (a3 *+a2b + ab2 + Ь3) = 2 (а2 + Ь2) (а + Ь),
Dy = 1 “ + bh \ab \=2а3-\-2a2b— 2ab2—2b3—
J \a — b 2 (a-— b2) |
—4a2b-l-4ab2 = 2(as—a2b + ab2—b3) = 2(a2 + b2) (a — b).
Отсюда x = Dx/D = a-{-b, y = Dv/D=a—b. A
209. Решить систему линейных однородных уравнений
f 3x-|-4y-|-5z = 0,
| х-\-2у—3z = 0.
Д Используя формулы (2), находим
* = |2 -з|;< = -22<. У — ~11-зр = 14'. * = |i
где t можно придавать любые значения. А
Решить системы уравнений:
210.
212.
214.
216.
( 5х— Зу — 1,
I х-|-11у = 6.
/ ах—by = a2-\-b2,
| bx-\-ay = a2-\-b2.
( х—2у+ г = 0,
( Зх—5у-\-2г = 0.
( a2x—2(a2 + b2)y + b2z = 0,
( 2х—|—2г/—Зг = 0.
( 2x+j/=1/5.
11 • 1 4х + 2у=1/3.
213 J Зх+2у=1/6,
‘ I 9хЦ-6у=1/2.
2|5 Г xcosa—у sin a = cos 2а,
\ х sin a -f- у cos а — sin 2а.
2. Определители третьего порядка и системы линейных уравнений. Определи-
ла! br Ci\
тель третьего порядка, соответствующий таблице элементов ( а2 Ь2 с2 ), опреде-
\а3 Ьз с3/
ляется равенством
0-2
аз
&1 Ci
b2 с2
Ьз с3
=ai
р2 М 6|a2 с2|+ |аг J2I
I &з сзI I аз С3 | | аз Ьз I
Минором данного элемента определителя третьего порядка называется опре-
делитель второго порядка, который получится, если в исходном определителе
вычеркнуть строку и столбец, содержащие данный элемент. Алгебраическим до-
43
полнением данного элемента называется его минор, умноженный на (—1)й, где
к—сумма номеров строки и столбца, содержащих данный элемент.
Таким образом, знак, который при этом приписывается минору соответст-
вующего элемента определителя, определяется следующей таблицей:
+ — +
- + -
+ - +
В приведенном выше равенстве, выражающем определитель третьего порядка,
в правой части стоит сумма произведений элементов 1-й строки определителя на
их алгебраические дополнения.
Теорема 1. Определитель третьего порядка равен сумме произведений
элементов любой его строки или столбца на их алгебраические дополнения.
Эта теорема позволяет вычислять значение определителя, раскрывая его по
элементам любой его строки или столбца.
Теорема 2. Сумма произведений элементов какой-либо строки (столбца)
определителя на алгебраические дополнения элементов другой строки (столбца)
разна нулю.
Свойства определителей.
1°. Определитель не изменится, если строки определителя заменить столб-
цами, а столбцы—соответствующими строками.
2°. Общий множитель элементов какой-нибудь строки (или столбца) может
быть вынесен за знак определителя.
3°. Если элементы одной строки (столбца) определителя соответственно
равны элементам другой строки (столбца), то определитель равен нулю.
4°. При перестановке двух строк (столбцов) определитель меняет знак на
противоположный.
5°. Определитель не изменится, если к элементам одной строки (столбца)
прибавить соответственные элементы другой строки (столбца), умноженные на
одно и то же 'число (теорема о линейной комбинации параллельных рядов опре-
делителя).
Решение системы трех линейных уравнений с тремя неизвестными
( a2x-\-b2y-\-c1z=d-i.,
а2х ~|— Ь.2у ~|— c2z — cig,
I a3x + b3y+c3Z=d3
находится по формулам Крамера
x=^Dx/D, y=Dy/D, z=DzlD,
где
at bi Ct
a2 b2 Cj
аз b3 c3
Dz =
at 6i
a2 61
a3 b3
dr
d}
^3
(1)
При этом предполагается, что D уЬ 0 (если 0=0, то исходная система либо
неопределенная, либо несовместная).
Если система однородная, т. е. имеет вид
=0,
а2х b2y -К c2z = О,
а3х4-^зУ+сзг = 0,
и ее определитель отличен от нуля, то она имеет единственное решение х = 0,
у = 0, г = 0.
Если же определитель однородной системы равен нулю, то система сводится
либо к двум независимым уравнениям (третье является их следствием), либо к
одному уравнению (остальные два являются его следствиями). Первый случай
имеет место тогда, когда среди миноров определителя однородной системы есть
хотя бы один отличный от нуля, второй—тогда, когда все миноры этого опреде-
лителя равны нулю.
41
В обоих случаях (см. п. 1) однородная система имеет бесчисленное множество
решений.
217. Вычислить определитель третьего порядка
5 3 2
—12 4.
7 3 6
Л Разложив определитель по элементам I-й строки, получим
5 3
—1 2
7 3
4 =5|з б|~3| 7 б| + 2| 7 з| =5.0-3(-34) + 2(-17)=68. А
218. Вычислить тот же определитель на основании теоремы
о линейной комбинации элементов строк (столбцов).
Д К элементам 1-й строки прибавим соответствующие элементы 2-й строки,
умноженные иа 5, а к элементам 3-й строки—соответствующие элементы 2-й стро-
ки, умноженные иа 7:
2 О
3
2
3
5
—1
7
4 = —1
6 О
13 22
2 4
17 34
Разложив определитель по элементам 1-го столбца, получаем
О 13 22
-12 4
О 17 34
-’11? м|+‘-|п SI+’Ts
219. Решить систему уравнений
х + 2у 4-2=8,
3x-f-2//-|-z= 10,
4х-|-3</—2г = 4.
Д По формулам (1) находим
14
220. Решить систему линейных однородных уравнений
"4х+ у+ 2 = 0,
X-|-3t/+ 2 = 0,
, х+ 1/+2г = 0.
42
4 1 1
Д Здесь £>= 1 3 1 . Для вычисления этого определителя к элементам
1 1 2
1-й строки прибавим элементы 3-й строки, умноженные на —4, а к элементам 2-й
строки—элементы 3-й строки, умноженные на —1:
0
О
1
—3
2
1
D =
—7
—1
2
—3
2
Jl=17-
= 1-
Так как D Ф 0, то
система
имеет
только нулевое
решение х = р = г = 0. А
221. Решить
систему
уравнений
(3x-|-2t/— г=0,
x4-2t/4-9z = 0,
x-f- y-]-2z = 0.
Л Имеем
3
1
1
D=
— 154-14-1-1=0.
2
2
1
—1
9
2
= 3
Следовательно, система имеет решения, отличные от нулевого. Решаем систему
первых двух уравнений (третье уравнение является их следствием);
(3x4-2t/— г = 0,
| х4-2р4-9г = 0.
Отсюда по формулам (2) п. 1 получаем
* = |з 9|,/==2(W’ y==-ll = 2 = |f 2|,/ = 4ЛА
I £ V I I 1 v | ll£|
1 2 —1
222. Вычислить определитель
ментам 3-й строки.
3 7 2
2 3—7
1 1 1
, разложив его по эле-
223. Вычислить определитель
2 3 4
4 9 16
линейной комбинации строк (столбцов).
2 3
224. Вычислить определитель
Решить системы уравнений:
2 а4-3
2 с4-3
, использовав теорему о
4
*4-4 ,
d-f-4
(5х— у— г = 0,
x4-2j/-f-3z=14,
4х4-3р4-2г= 16.
С—5x4- z = 0,
227. ] х~ бу 4- z = 0,
( х4- у—7г = 0.
(ax-f-by-^-cz =а—Ь,
bx-^-cy -f-az — b— с,
ex 4-ai/4- bz = c —а,
если а 4- b -|- с 0.
(x-j-Зу—6г— 12,
Зх 4-2р 4-5г = —10,
2х4-5р—Зг= 6.
( х4- у+ г = 0,
228. ] Зх 4-61/4-5г=О,
( х4-4(/4-Зг = 0.
7 ax4-5t/4-(^+^) г=0,
230. ] &x4-aj/4-(a4-Z>) г = 0,
I *+ г/4-2г=о.
ГЛАВА II
ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ
§ 1. ПРЯМОУГОЛЬНЫЕ КООРДИНАТЫ В ПРОСТРАНСТВЕ
Если в пространстве задана прямоугольная декартова система координат Охуг^
то точка М пространства, имеющая координаты х (абсцисса), у (ордината) и г (ап-
пликата), обозначается М (х; у, г).
Расстояние между двумя точками A (xf, у2\ zj и В (х2; у2; г2) определяется по
формуле
d=V (х2— xi)2 —({/а—У1)2 + (гз — г1)“- (О
В частности, расстояние точки М (х; у\ г) от начала координат О определя-
ется по формуле
(2)
Если отрезок, концами которого служат точки А (х,; у*; гг) и В(х2; у.2; г2),
разделен точкой С (х; у, г) в отношении X (см. гл. I, § 1), то координаты точки
С определяются по формулам
- xI + Xx2. ~__У1 + 1Уа . + zQi
Х~ 1+1 ’ У~ 1+1 ’ Z~ 1+1 '
’ В частности, координаты середины отрезка определяются по формулам
— Х1+хг . — У! + у2. г1~^~г2
* — 2 » У 2 9 £ 9* ‘ ’
231. Даны точки Aft (2; 4; —2) и М„(—2; 4; 2). На прямой
М2М2 найти точку М, делящую отрезок Mv-W2 в отношении Х = 3.
Л Воспользуемся формулами деления отрезка в данном отношении:
„ *1+1*г _2+3(—2) ( _ У1 + 1у2 4+3-4 _4
Л1~ 1+1 ~ 1 + 3 ~ *’ УЛ1~ 1 + 1 “ 1+3
, — ____—2 + 3-2
м 1+1 — 1+3
Следовательно, искомая точка М (—1; 4; 1). А
232. Дан треугольник: Л(1; 1; 1), В (5; 1; —2), С (7; 9; 1).
Найти координаты точки D пересечения биссектрисы угла А со
стороной СВ.
/\ Найдем длины сторон треугольника, образующих угол А:
| АС | = V(хс-хл)2 + (ус-ул)2 + (гс-гд)2 = /(7-1)2 + (9-Г)2+(1 -1)2 = 10;
МВ|=/(хл-хл)2 + (ув-ул)2+(гй-гл)2=К(5-1)2 + (1-1)2 + (-2-1)2 = 5.
44
Следовательно, | CD |:| DB | = 10:5 = 2, так как биссектриса делит сторону СВ
на части, пропорциональные прилежащим сторонам. Таким образом,
*с+74-2-5 17 _УсА-^Ув__94-2-1__11
D~ 1 + л “ 14-2 ~3 ’ yD 14-Л 14-2 3 ’
__гс4~^гв__1 4~ 2 (—2)__
D 14-Х 14-2
искомая точка D (17/3, 11/3, —1). Д
233. На оси Ох найти точку, равноудаленную от точек А (2;
— 4; 5) и В(—3; 2; 7).
Д Пусть М— искомая точка. Для нее должно выполняться равенство | AM |=
= | МВ|. Так как эта точка лежит на оси Ох, то ее координаты (х; 0; 0), а по-
тому имеем
| АМ | = V(х—2)24-(—4)24-5г, | МВ | = /(х4-3)24-2г4-7«.
Отсюда после возведения в квадрат получаем
(х—2)2-4-41 = (х-f-3)*-f-53, или 10х=—17, т. е. х = —1,7.
Таким образом, искомая точка М (—1,7; 0; 0). А
234. Даны точки Л (3; 3; 3) и В(—1; 5; 7). Найти координаты
точек С и D, делящих отрезок АВ на три равные части.
235. Дан треугольник: Л (1; 2; 3), В(7; 10; 3), С(—1; 3; 1).
Показать, что угол Л—тупой.
236. Найти координаты центра тяжести треугольника с верши-
нами Л (2; 3; 4), В(3; 1; 2) и С(4; —1; 3).
237. В каком отношении точка М, равноудаленная от точек
Л (3; 1; 4) и В (—4; 5; 3), разделит отрезок оси Оу от начала ко-
ординат до точки С (0; 6; 0)?
238. На оси Ог найти точку, равноудаленную от точек МД2;
4; 1) и А42(—3; 2; 5).
239. На плоскости хОу найти точку, равноудаленную от точек
Л (1; —1; 5), В(3; 4; 4) и С (4; 6; 1).
§ 2. ВЕКТОРЫ И ПРОСТЕЙШИЕ ДЕЙСТВИЯ НАД НИМИ
Свободный вектор а (т. е. такой вектор, который без изменения длины и на-
правления может быть перенесен в любую точку пространства), заданный в коор-
динатном пространстве Охуг, может быть представлен в виде
a = axi -f-aj + ^k.
Такое представление вектора а называется его разложением по осям координат,
или разложением по ортам.
Здесь ах, ау, аг — проекции вектора а на соответствующие оси координат
(их называют координатами вектора а), 1, }, к—орты этих осей (единичные век-
торы, направление каждого из которых совпадает с положительным направлением
соответствующей оси).
Векторы axi, ayj и a2k, в виде суммы которых представлен вектор а, назы-
ваются составляющими (компонентами) вектора а по осям координат.
Длина (модуль) вектора а обозначается а или | а | и определяется по формуле
а
45
Направление вектора а определяется углами v., и у, образованными им с
осями координат Ох, Оу' и Ог. Косинусы этих углов (так называемые направляю-
щие косинусы вектора) определяются по формулам;
cos a — —=— l... a-v ; cosp = —cosy=—.
a « 'a
Направляющие косинусы вектора связаны соотношением
соз2 а + соз2 3 -f- cos2 у = 1.
Если векторы а и b заданы их разложениями по ортам, то их сумма и раз-
ность определяются по формулам
а+b = (ах + & v) (+ (а„ + & ,у) ] + (а, + Ь2) к,
а—b = (ах—bx) i + (а'и — by) j + (аг — Ь2) к.
Напомним, что сумма векторов а и Ь, начала которых совмещены, изобра-
жается вектором с тем же началом, совпадающем с диагональю параллелограмма,
сторонами которого являются векторы а н Ь. Разность а—Ь этих векторов изо-
бражается вектором, совпадающим со второй диагональю того же параллелограм-
ма,. причем Начало этого вектора находится в конце вектора Ь, а конец—в
конце вектора а (рис. 16).
Сумма любого числа векторов может быть найдена по правилу многоуголь-
ника (рис. 17).
Произведение вектора а на скалярный множитель т определяется формулой
/па — тах1 + та у j ma2k.
Напомним, что векторы а и та параллельны (коллинеарны) и направлены “в
одну и ту же сторону, если т > 0, и в противоположные стороны, если т < 0.
В частности, если т=\/а, то вектор a/а имеет длину, равную единице, и на-
правление, совпадающее с направлением вектора а. Этот вектор называют единич-
ным вектором (ортом) вектора а и обозначают а0. Нахождение единичного векто-
ра того же направления, что и данный вектор а, называется нормированием век-
тора а.
Таким образом, ао = а/а, или а = аао.
Вектор ОМ, начало которого находится в начале координат, а конец—в точ-
ке М (х; у; г), называют радиусом-вектором точки М и обозначают г (М) или
просто г. Так как его координаты совпадают с координатами точки М, то его
разложение по ортам имеет вид
r = xi+l/j+zk.
Вектор АВ, имеющий начало в точке A (xt; ус, zj и конец в точке В (х2;
уг; г2), может быть записан в виде АВ=гг—гх, где г2 — радиус-вектор точки В,
46
а Г£—радиус-вектор точки А. Поэтому разложение вектора АВ по ортам имеет вид
~АВ = (хг —xi) i + (j/2 — t/i) j + (z2—Zi) k.
Его длина совпадает с расстоянием между точками А и В'.
| АВ | = d = У (х2—хО2 + (J/г—J/i)2 + (z2 — zO2.
В силу приведенных выше формул направление вектора АВ определяется направ-
ляющими косинусами:
X.,—Xi „ y2—yt Z2 — Zi
cosa = ~"j....; cos ; cos v = —1.
d ’ d ' d
240. В треугольнике ABC сторона AB точками M и N разделена
натри равные части: | AM | = I MN | = | NB |. Найти вектор СМ,
если СА = а, СВ = Ъ.
А Имеем АВ=Ь—а. Следовательно, AM = (Ъ—а)/3. Так как СМ — СА -|-АлГ,
то C.'W=a-f-(b—a)/3 = (2a + b)/3. А
241. В треугольнике АВС прямая AM является биссектрисой
угла ВАС, причем точка М лежит на стороне ВС. Найти AM,
если АВ = Ъ, АС = с.
Д Имеем ВС=с—Ь. Из свойства биссектрисы внутреннего угла треугольника
следует, что \ВМ |:| МС\ = Ь:с, т. е. | ВМ |:|ВС| = &:(Ь4-с). Отсюда получаем
ВМ=-г-^—(с—Ь). Так как АМ = АВ-\-ВМ, то
О ~р с.
-гг. <. > b . .. &c-f-cb .
АМ — Ь-\--—— (с—Ь) = —т—у—. Д
1 Ь-\-с ' ' b-A-с “
242. Радиусами-векторами вершин треугольника АВС являются
гп г2 и г3. Найти радиус-вектор точки пересечения медиан треу-
гольника.
Д Имеем ВС = г3—г2; ВО = (г3—r2)/2 (О—середина стороны ВС); АВ =
= г2—г2; ЛО = ВО-!-ЛВ = (г3—г2)/2-!-г2--г1 = (г2+г3—2г2)/2; ЛЛ4 = (2/3)АО
(Л4—точка пересечения медиан), поэтому /.M = (r2-f-r3—2г2)/3. Итак,
г = О/И=г1-|-ЛЛ1 = (r2-j-r3 —2Г1)/3-]-Г1, или r = (ri-f-r2-f-r3)/3. А
243. Найти длину вектора a = 20i-j-30j— 60k и его направляю-
щие косинусы.
Д а = У202H-302-f-602 = 70; cos а = 20/70 = 2/7,
cos ₽ =30/70 = 3/7, cos у = —60/70 = — 6/7. Д
244. Найти вектор а —АВ, если А (1; 3; 2) и В (5; 8; —1).
А Проекциями вектора АВ на оси координат являются разности соответст-
венных координат точек В и А: ах=5—1=4, ау = 8—3 = 5,аг = —1—2 = — 3.
Следовательно, АВ = 41-)-5} — 3k. Д
245. Нормировать вектор а = 3i 4j — 12k.
Л Найдем длину вектора а:
I а | = + = У32+42 + (-12)2 = 13.
47
Искомый единичный вектор имеет вид
a 3i + 4j— 12k 3 . , 4 . 12, .
а“= |ТГ=------13----=Тз' +ТзJ -Тзк“ А
246. Дан треугольник АВС. На стороне ВС расположена точка
М так, что | ВМ |: | МС | = К. Найти AM, если АВ = Ь, АС = с.
247. Дано АВ = а~г 2Ъ, ВС = — 4а—b, CD = — 5а — ЗЬ. Дока-
зать, что ABCD—трапеция.
248. Найти проекции вектора а на оси координат, если а =
= ЛВ4-СД Л (0; 0; 1), В(3; 2; 1), С (4; 6; 5) и £>(1; 6; 3).
249. Найти длину вектора a = mi4-(m-|- 1) 1) k.
250. Даны радиусы-векторы вершин треугольника АВС: гА =
= i + 2j4-3k, rB = 3i + 2j+к, гс = i 4- 4j-j- к. Показать, что треу-
гольник АВС равносторонний.
251. Вычислить модуль вектора а = i 4- 2j 4- k — (1 /5) (4i 4- 8j 4~ 3k)
и найти его направляющие косинусы.
252. Даны точки Л4г(1; 2; 3) и Л42 (3; —4; 6). Найти длину
и направление вектора /Иг/И2.
253. Дан вектор a = 4i—2j4-3k. Найти вектор Ь, если b = a,
bu = av и bx = 0.
254. Радиус-вектор точки М составляет с осью Оу угол 60 ,
а с осью Oz угол 45°, его длина г —8. Найти координаты точки Л1,
если ее абсцисса отрицательна.
255. Нормировать вектор a = i—2j—2k.
§ 3. СКАЛЯРНОЕ И ВЕКТОРНОЕ ПРОИЗВЕДЕНИЯ.
СМЕШАННОЕ ПРОИЗВЕДЕНИЕ
1. Скалярное произведение. Скалярным произведением двух векторов а п b
называется число, равное произведению длин этих векторов на косинус угла ф
между ними:
а-b — ab cos ф.
Свойства скалярного произведения.
1°. а-а = а1 2, или а2 = а2.
2°. а-Ь = 0, если а = 0, либо Ь = 0, либо a J_b (ортогональность ненулевых
векторов).
3®. a-b = b-a (переместительный закон).
4°. а-(Ь4-с) = а'Ь4-а<с (распределительный закон).
5°. (ma)-b = a-(mb) = m (а-b) (сочетательный закон по отношению кскалярному
множителю).
Скалярные произведения ортов осей координат:
i2 = j2 = k2 = 1, i - j = i • k = j • k = 0.
Пусть векторы а и b заданы своими координатами: a —xIi4-:/ij-Lz1k, b =
= x2i4-p2j4*z2k. Тогда скалярное произведение этих векторов находится по фор-
муле
а-Ь=х1х24-</1у24-г1г2.
2. Векторное произведение. Векторным произведением вектора а на вектор b
называется третий вектор с, определяемый следующим образом (рис. 18):
1) модуль вектора с равен площади параллелограмма, псстроенного на век-
торах а и b (с~ ab sin ф, где ф —угол между векторами а и Ь);
2) вектор с перпендикулярен векторам а и Ь;
3) векторы а, Ь, с после приведения к общему началу ориентированы по от-
48
ношению друг к другу соответственно как орты i, j, к (в правой системе коор-
динат образуют так называемую правую тройку векторов).
Векторное произведение а на b обозначается через axb.
Свойства векторного произведения.
1°. Ьха = — axb, т. е. векторное произведение ие обладает переместительным
свойством.
2°. aXb = 0, если а = 0, либо b =0, либо аIIb (коллинеарность ненулевых век-
торов).
3°. («a)Xb = aX(mb) — т (axb) (сочетательное свойство по отношению к ска-
лярному миожителю).
4°. ax(b-f-c)=aXb-f-aXc (распределительное свойство).
Векторные произведения координатных ортов I, j и к:
iXi=jXj=kxk = O,
iX} = —)Xi=k; )хк = — kXj = i; kXi=—iXk = j.
Векторное произведение векторов а = х^ i -f- t/ij + Zik и b = x2i -|- y2j + z2k удобнее
всего находить по формуле
axb =
i J к
Х1 У1 Zt
хг Уз Z2
3. Смешанное произведение. Смешанным произведением векторов а, b и с на-
зывается скалярное произведение вектора axb на вектор с, т. е. (aXb)-c.
Смешанное произведение трех векторов а, Ь, с по модулю равно объему па-
раллелепипеда, построенного на этих векторах.
Свойства смешанного произведения.
1°. Смешанное произведение трех векторов равно нулю, если:
а) хоть один из перемножаемых векторов равен нулю;
б) два из перемножаемых векторов коллинеарны;
в) три ненулевых вектора параллельны одной и той же плоскости (компла-
нарность) .
2°. Смешанное произведение не изменяется, если в нем поменять местами
знаки векторного (X) и скалярного (•) умножения, т. е. (axb)-c = a-(bxc).
В силу этого свойства смешанное произведение
векторов а, b и с условимся записывать в виде с=цхЪ
3°. Смешанное произведение не изменяется, ес-
ли переставлять перемножаемые векторы в круго-
вом порядке:
abc=bca=cab.
4°. При перестановке любых двух векторов
смешанное произведение изменяет только знак:
Рис. 18
Ьас = — abc; cba = — abc; acb = — abc.
Пусть векторы заданы их разложениями по ортам: a=Xil-f-yij + zik; b =
= -Ч*+^2)+г2к; c = x3i-f-</3j4~z3k. Тогда
abc =
xi yi Zi
хг Уч гч •
хз Уз гз
Из свойств смешанного произведения трех векторов вытекает следующее:
необходимым и достаточным условием компланарности трех векторов служит
условие abc = 0;
объем Vf параллелепипеда, построенного на векторах а b и с, и объем V2
образованной ими треугольной пирамиды находятся по формулам
Vi = l abc |, Ks=lri=-g-|abc|.
49
256. Найти скалярное произведение векторов а = 314-4] + 7k и
b = 2i —5j + 2k.
Д Находим а-Ь = 3-2+4(—5) + 7-2 = 0. Так как а-Ь = 0 и а О, Ь £ 0, то
а Д_Ь*. А
257. Даны векторы a = ml + 3j + 4k и b = 4i + mj—7k. При ка-
ком значении т эти векторы перпендикулярны?
Д Находим скалярное произведение этих векторов: a-b = 4«+3m—28; так
как aj_b, то а-Ь = 0. Отсюда 7т—28 = 0, т. е. т = 4. Д
258. Найти (5а + ЗЬ)-(2а—Ь), если а = 2, Ь = 3, а_|_Ь.
Д (5а+ЗЬ)-(2а—Ь) = 10а2—5a-b + 6a-b—3b2 = 10а2—ЗЬ2 = 40—27 = 13. Д
259. Определить угол между векторами а = i + 2j + 3k и b =
= 6i + 4j—2k.
& * b
ДТактака.Ь=аЬсозф, to cos<p=-^y Имеем a-b = 1-6+2-44-3 (—2)=8j
а—У 1+4+9 = К14, &= K36+16 + 4 =2^14.
r- 8 2 2 .
Следовательно, cos<p = —--====-=- и <p = arccos -=-. ▲
У14-2K14 7 7
260. Найти векторное произведение векторов а = 21 + 3] +5k и
b = i + 2j + k.
Д Имеем
i j k
aXb =235
1 2 1
т. e. aXb =— 7i + 3J4-k. Д
261. Вычислить площадь параллелограмма, построенного на век-
торах а = 61 + 3j—2k и b = 3i—2j + 6k.
Д Находим векторное произведение а иа Ь:
axb = 6
3—2 6
2 “б I - i I 3 “б I + k 13 -21 = 14i—42j—21k.
Так как модуль векторного произведения двух векторов равен площади
построенного на них параллелограмма, то S = | axb | = рг142-{-422 + 212 =
=49 (кв. ед.). Д
262. Вычислить площадь треугольника с вершинами Л(1; 1; 1),
В (2; 3; 4), С (4; 3; 2).
Д Находим векторы АВ и АС:
АВ = (2—1) i+(3-l) j+(4-l) к= 14-2J + Зк*
ДС=(4—1) i + (3-l) J + (2— l)k=3i+2j+k.
Площадь треугольника АВС равна половине площади параллелограмма,
построенного на векторах АВ и АС, поэтому находим векторное произведение
этих векторов:
i 1 k
3 2 1
50
Следовательно,
SADC^\ABxAC\=^V 16 + 64+16=^24 (кв. ед.) А
263. Вычислить площадь параллелограмма, построенного на век-
торах а + ЗЬ и За + b, если |а| = |Ь|=1, (а, Ь) = 30°.
Д Имеем
(а+ЗЬ)Х(За+Ь) = ЗаХа + ахЬ+9ЬХя + ЗЬхЬ +
= 3-0+axb—9ахЬ + 3-0 = — 8ахЬ
(поскольку aXa = bxb = 0, Ьха=—axb). Итак,
5 = 81 axb | = 8-1 • 1-sin 30° = 4 (кв. ед.). А.
264. Найти смешанное произведение векторов а — 2i — j—k,
h=i + 3j — k, c = i + j + 4k.
Д abc =
2 —1 —1
1 3 —1
1 1 4
= 2 |f “ll+l'IJ -4|-1-|1 1|= 26 + 5 + 2 = 33. A
265. Показать, что векторы a —2i + 5j + 7k, b = i + j — k, c =
=i + 2j + 2k компланарны.
Д Находим смешанное произведение векторов:
2 5 7
abc = 1 1 —1
1 2 2
= 2 | 2 “ г|- 5| I1 “ 2|+7| 1 2| =8-15 + 7 = 0.
.Так как abc = 0, то заданные векторы компланарны. А
266. Найти объем треугольной пирамиды с вершинами А (2; 2; 2),
Я (4; 3; 3), С (4; 5; 4) и D (5; 5; 6).
Л Найдем векторы АВ, АС и AD, совпадающие с ребрами пирамиды,
сходящимися в вершине А: ДВ = 21+) + к, AC = 2i + 3j + 2k, XD = 3i + 3j + 4k.
Находим смешанное произведение этих векторов:
2 1 1
ABACAD =232
3 3 4
— 213 I 1.| 21 . । I 2 31 _2.6 , .2 1.3 = 7
|з 4| 1 |3 4| +1 13 31 2 ° 1 1 15 ’
(Так как объем пирамиды равен 1/6 объема параллелепипеда, построенного на
екгорах АВ, АС и AD, то У = 7/6 (куб. ед.). А
267. Вычислить (а—b)(b—с)(с—а).
Д Так как (а—b) + (b—с)+(с—а) = 0, то эти векторы компланарны (рис. 19).
Следовательно, их смешанное произведение равно нулю: (а—Ь) (Ь—с) (с—а)=
= о. А
268. Найти скалярное произведение векторов За—2Ь и 5а—6Ь,
если а = 4, 5 = 6 и угол между векторами а и b равен л/3.
269. Определить угол между векторами а = 3i + 4j + 5k и b =
= 4i + 5j —3k.
270. При каком значении т векторы a = /ni + j и b==3i—3j+4k
перпенд и кул я р ны?
51
271. Найти скалярное произведение векторов 2а4-ЗЬ4-4с и
5a + 6b-i-7c, если а=1, Ь = 2, с = 3, а (а7^Ь) = (а, с) = (Ь, с)=л/3.
272. Найти работу силы F на перемещении s, если F — 2, s = 5,
<p=(F, s) = n/6.
273. Найти единичный вектор, перпендикулярный векторам
я = i + j + 2k и b = 2i -|- j-|- k.
274. Векторы a, b, с имеют равные длины и образуют попарно
равные углы. Найти вектор с, если а = i + j, b = j4-k.
275. Даны, векторы a = 2i-f-2j-|-k и b = 6i 4-3j + 2k. Найти npab
и прьа-
276. Даны радиусы-векторы трех последовательных вершин па-
раллелограмма Л BCD: гл=1-Н+к, rB=i+3j+5k, rc=7i+9j+1 Ik.
Определить радиус-вектор четвертой верши-
ны D.
-т/ Показать, что векторы а и b не
а / могут быть перпендикулярными, еслиа-1>0,
/_________ a-j>0, a-k>0, b i < 0, b j<0; bk<0.
278. Показать, что векторы а = i + j + /як,
b = i + j + (m+l)k и c = i—j + mk ни при
Рис> 19 каком значении т не могут быть компла-
нарными.
279. Могут ли отличные от нуля числа х1( хг, x3, yt, yv у3, zlt
г2, zs удовлетворять уравнениям
xi Hi ?1 + + Z1Z2 = 0 >
y2 z2 =0, х1хз~\-у1Уз-\-г1гз = 0,
x3 Уз 2з хгхз-\- у2Уз_Ьг2гз = 0?
280. Найти векторное произведение векторов а — 2i + 5j 4- k
и b=i-r2j—3k.
281. Вычислить площадь треугольника с вершинами А (2; 2; 2),
В (4; 0; 3) и С (0; 1; 0).
282. Найти смешанное произведение векторов a=i — j-bk, b =
==i + j + k. с = 2i + 3j + 4k.
283. Показать, что векторы a = 7i—3j + 2k, b = 3i—7j4-8k,
c = i—j + k компланарны.
284. Вычислить объем треугольной пирамиды с вершинами
А (0; 0; 1), В (2; 3; 5), С (6; 2; 3) и D (3; 7; 2). Найти длину
высоты пирамиды, опущенной на грань BCD.
285. Показать, что точки А (5; 7; —2), В (3; 1; —1), С (9; 4; —4)
и D (1; 5; 0) лежат в одной плоскости.
ГЛАВА III
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
f 1. плоскость И ПРЯМАЯ
1. Плоскость. 1) Уравнение плоскости в векторной форме имеет вид
г-п = р.
! Здесь r = xi4-i/j + zk — радиус-вектор текущей точки М (х; у, г) плоскости; п =
• = i cos a-j- j cos P+k cos у—единичный вектор, имеющий направление перпенди-
< гуляра, опущенного на плоскость из начала координат; а, (}, у—углы, образо-
(инные этим перпендикуляром с осями координат Ох, Оу, Ог; р—длина этого
ерпендикуляра.
При переходе к координатам это уравнение принимает вид
xcos a-|-i/cos P + zcos у—р = 0 (1)
/формальное уравнение плоскости)
2) Уравнение всякой плоскости может быть записано также в виде
Ax4-Bj/+Cz4-D = 0, (2)
«ли А2Ц-В2-|-С2 Ф 0 '(общее уравнение). Здесь А, В, С можно рассматривать
как координаты некоторого вектора N = Ai4-Bj + Ck, перпендикулярного плос-
g «doth (нормального вектора плоскости). Для приведения общего уравнения плос-
кости к нормальному виду надо все члены уравнения умножить на нормирую-
щий множитель
и=± 1/ЛГ=± 1/у" Л2 + В24-С2, (3)
жж знак перед радикалом противоположен знаку свободного члена D в общем
уравнении плоскости.
3) Частные случаи расположения плоскости, определяемой общим уравнением
AxA-By+Cz 4-0 = 0;
А = 0; параллельна оси Ох;
В~0; » » Оу;
С = 0; » » Ог;
0 = 0; проходит через начало координат;
А = В = О; перпендикулярна оси Ог (параллельна плоскости хОу);
А = С = О; » » Оу ( » » хОг);
В = С = О; » » Ох ( » » уОг);
А = 0 = 0 проходит через ось Ох;
B~D = 0 » » » Оу;
C~D = Q » » » Ог;
A = B = D — O; совпадает с плоскостью хОу (г — О);
А = С = О = 0; » » » хОг (у = 0);
В = С = О = 0; » » » уОг (х = 0).
Если в общем уравнении плоскости коэффициент О уО, то, разделив все
члены уравнения на —О, уравнение плоскости можно привести к виду
_£+4+± = 1 (4)
а Ь ' с 4 '
Ддесь а = —D/А, Ь = —D/В, с ——D/С). Это уравнение называется уравнением
плоскости в отрезках; в нем а, Ь и с—соответственно абсцисса, ордината и ап-
жликата точек пересечения плоскости с осями Ох, Оу и Ог.
53
4) Угол <р между плоскостями 41x-J-Biz/+C1z-(-Di = 0 и А2х-}-В2у—С2г-{-
4-О2 = 0 определяется по формуле
cos <р = ---- а^ + в^ + С1С2 ..................... (5)
К л214-в?4-с1И а1+в%+с%
Условие параллельности плоскостей:
И1/Л2 = В1/В2 = С1/С2. (6)
Условие перпендикулярности плоскостей:
Л1Л2 + В1В2 + С1С2 = 0. (7)
5) Расстояние от точки Мо (х0; у0; z0) до плоскости, определяемой урав-
нением Ax-T-By-\-Cz-\-D = O, находится по формуле
d = । ^л-о~1~5Уо4~^го4~ Д I zg\
У Д* + в*+С*
Оно равно взятому по абсолютной величине результату подстановки координат
точки в нормальное уравнение плоскости; знак результата этой подстановки ха-
рактеризует взаимное расположение точки и начала координат относительно дан-
ной плоскости: «плюс», если точка /Ио и начало координат расположены по раз-
ные стороны от плоскости, и «минус», если они расположены по одну сторону от
плоскости.
6) Уравнение плоскости, проходящей через точку Мй (х0; у0; г0) и перпенди-
кулярной вектору N = Л( J-BjJ-Ck, имеет вид
Л (х—x0)4-B(r/—г/0)4-С(г—го)=О. (9)
При произвольных значениях Л, В и С последнее уравнение определяет некото-
рую плоскость, принадлежащую связке плоскостей, проходящих через точку М3.
Его поэтому часто называют уравнением связки плоскостей.
7) Уравнение
А]Х В1У~}~ 014“^ (А2х~]~ В2у~]-С2г-]~ В>з) = 0 (1®)
при произвольном значении X определяет некоторую плоскость, проходящую
через прямую пересечения плоскостей
>4ix4-B1z/4-Ciz4-Di = 0 (0 и Л2х4-В2у4-С2г4-Р2 = 0, (П)
т. е. некоторую плоскость, принадлежащую пучку плоскостей, проходящих через
эту прямую (в силу чего такое уравнение часто называют уравнением пучка
плоскостей}. Если плоскости, определяемые уравнениями (I) и (II), параллельны,
то пучок плоскостей превращается в совокупность плоскостей, параллельных
этим плоскостям.
8) Уравнение плоскости, проходящей через три заданные точки Mi (<i), M2(r2).
М3(г3) (здесь r1 = x1i4-z/1J4-z1k; r2 = x2i4-r/2j4-z2k; r3 = x3i4-y3j4-z3k), проще
найти из условия компланарности векторов г—п, г2—г2, г3—п, где г = х!4-
4-t/j4-zk—радиус-вектор текущей точки искомой плоскости М;
(г—п) (г2— г 0 (г3—Г1)=0,
или в координатной форме:
X— Xi
х2 — Х1
*3 —*1
У—Hi
Уз—У1
У3—У1
z—zi
z3—zi
z3—Z1
= 0.
(10
286. Уравнение плоскости 2x4-3z/—6г 4-21= 0 привести к нор-
мальному виду.
Находим нормирующий миожитель (который берем со знаком «минус».,
поскольку 0 = 21 >0): р, =—l/V"224-324- 62 =— 1/7. Итак, нормальное уравне-1
ние заданной плоскости имеет вид —(2/7) х—(3/7) у-\- (6/7) г—3 = 0. А
54
287. Определить расстояние от точки Л40 (3; 5; —8) до плос-
кости 6х—3^4-2г—28 = 0.
Л Используя формулу (8) расстояния от точки до плоскости, находим
^_|6.3—3-54-2-(—8) —28|_41
~ у бг + 32 + 2а ~1
Так как результат подстановки координат точки Мо в нормальное уравнение
плоскости отрицателен, то Л40 и начало координат лежат по одну сторону от
заданной Плоскости. Ж
288. Составить уравнение плоскости, проходящей через точку
М (2; 3; 5) и перпендикулярной вектору N = 41 4-3j 4-2k.
Д Достаточно воспользоваться уравнением (9) плоскости, проходящей через
данную точку и перпендикулярной данному вектору:
4 (х—2)4-3(у—3)4-2(г—5) =0, т. е. 4x4-3y-}-2z—27 = 0. Ж
289. Найти уравнение плоскости, проходящей через точку М (2;
3; —1) параллельно плоскости 5х—Зг/4- 2г —10 = 0.
Д Запишем уравнение (9) связки плоскостей, проходящих через данную точку:
Л (х—2)-}-В(у—3) 4-С (z-}-1)= 0.
Нормальный вектор искомой плоскости совпадает с нормальным вектором п =
= (5; —3; 2) данной плоскости; следовательно, А = 5, В = —3, С —2 и уравне-
ние искомой плоскости примет вид
5(х—2)—3(у—3)4-2(z-{-1) = 0, или 5х—3y4-2z4-l=0. Ж
290. Из точки Р (2; 3; —5) на координатные оси опущены
ерпендикуляры. Составить уравнение плоскости, проходящей через
х основания.
Д Основаниями перпендикуляров, опущенных на координатные плоскости,
служат следующие точки: Aff(2; 3; 0), М2 (2; 0; —5), М3 (0; 3; —5). Используя
соотношение (11), запишем уравнение плоскости, проходящей через точки Mt,
Aft» Afgi *
х—2 у—3 z
0 —3 —5
—2 0 —5
= 0, или 15х-}-Юу—6г—60 = 0. Ж
291. Составить уравнение плоскости, проходящей через точку
А (5; 4; 3) и отсекающей равные отрезки на осях координат.
Д Используя уравнение (4) плоскости в отрезках, в котором а = Ь=с, имеем
х/а-\-у1а-\-г/а= 1. Координаты точки А удовлетворяют уравнению искомой плос-
кости, поэтому выполняется равенство 5/а 4/а 3/а = 1, откуда а =12. Итак,
получаем уравнение х-\-у-\-г—12 = 0. Ж
292. Составить уравнение плоскости, проходящей через линию
пересечения плоскостей х-|-^4-5г—1=0, 2x4-3^—z-f-2 = 0 и че-
рез точку М (3; 2; 1).
Л Воспользуемся уравнением (10) пучка плоскостей:
х4-у4-5г—14-Z (2х4-3у—г4-2) =0.
55
Значение X определяем из условия, что координаты точки М удовлетворяют этому
уравнению: 34-24-5— —1Ц-2) = 9 + 13Х = 0, откуда Х =—9/13. Та-
ким образом, искомое уравнение имеет вид
g
х-f-//-}-5г—1—у= (2х-~3у—z-|-2) = 0, или 5x4-14//—74г-|-31=0. Д
293. Составить уравнение плоскости, проходящей через линию
пересечения плоскостей х-|-3//4-5г— 4 = 0 и х—у—2г4-7 = 0 и
параллельной оси Оу.
Л Воспользуемся уравнением пучка плоскостей:
х4-Зу-|-5г—4-f-X(x—у—2г 4-7) =0;
(14-Х) *4* (3 — X) у-\- (5—2Х) г 4- (7Х—4) =0.
Так как искомая плоскость параллельна оси ординат, то коэффициент
при у должен быть равен нулю: 3—Х = 0, т. е. Х = 3. Подставив найденное зна-
чение X в уравнение пучка, получаем 4х—г-{-17 — 0. А
294. Найти уравнение плоскости, проходящей через точки
А (2; —1; 4) и В (3; 2; —1) перпендикулярно плоскости х-|-//4-2г—
—3 = 0.
Д В качестве нормального вектора N искомой плоскости можно взять век-
тор, перпендикулярный вектору ДВ = {1; 3; —5} и нормальному вектору п =
= {1; 1; 2} данной плоскости. Поэтому за N примем векторное произведение
АВ и п:
N=4Sxn= 1
1
= 111 — 7j— 2k.
Остается воспользоваться уравнением плоскости, проходящей через данную точку
(например, А) перпендикулярно заданному вектору N={11; —7; —2}:
11 (х—2)—7(г/4-1)—2(г—4) = 0, или Их— 1у—2г—21 =0. Д.
295. Составить уравнение плоскости, проходящей через точку
М (3; —1; —5) и перпендикулярной плоскостям Зх—2у 4- 2г 4- 7 =
= 0 и 5х—4//4-Зг4-1 =0.
Д Очевидно, что в качестве нормального вектора N искомой плоскости можно
взять векторное произведение нормальных векторов щ = {3; —2; 2} и п2={5; —4; 3}
данных плоскостей:
N = п1хп2 =
i J
3 —2
5 —4
1—2 21 .12 31 13 —2
4 з| + *|з 5| + к|5 —4
= 2i4-j— 2к.
Теперь, используя уравнение плоскости, проходящей через данную точку М (3
— 1; —5) перпендикулярно вектору N = {2; 1; —2}, получаем
2(х—3)4-(У4-1)—2(г4~5) = 0, или 2x4-*/—2г—15 = 0. А
296. Привести к нормальному- виду уравнения следующих пло-
скостей: 1) х-\-у—г—2 = 0; 2) 3x4-5//—4г 4-7 = 0.
297. Найти расстояние от точки Л40 (1; 3;—2) до плоскостж
56
2r—Зу — 4г 4-12 = 0. Как расположена точка Мо относительно пло-
скости?
298. Найти длину перпендикуляра, опущенного из точки Мо(2;
3; — 5) на плоскость 4х—2у + 5г—12 = 0.
299. Найти уравнение плоскости, проходящей: 1) через точку
.И ( — 2; 3; 4), если она отсекает на осях координат равные отрезки;
2) через точку N (2; — 1; 4), если она отсекает на оси Ог отрезок
вдвое больший, чем на осях Ох и Оу.
300. Найти уравнение плоскости, проходящей через точки Р (2;
0; — 1) и Q(l;—1; 3) и перпендикулярной плоскости Зх + 2у— г +
+ 5 = 0.
301. На плоскости 2х—5у + 2г + 5 = 0 найти такую точку М,
чтобы прямая ОМ составляла с осями координат равные углы.
302. Найти уравнение плоскости, зная, что точка Р (4; — 3; 12)
служит основанием перпендикуляра, опущенного из начала коорди-
жат на эту плоскость.
303. Найти уравнения плоскостей, проходящих через оси коор-
динат перпендикулярно плоскости Зх—4г/ + 5г—12 = 0.
304. Найти уравнение плоскости, точки которой одинаково уда-
лены от точек Р(1; — 4; 2) н Q (7; 1; — 5).
305. Найти уравнение плоскости, проходящей через точки Р (0;
2; 0) и Q(2; 0; 0) и образующей угол 60° с плоскостью х = 0.
306. Вычислить угол между плоскостями, проходящими через
точку Л4(1; — 1; — 1), одна из которых содержит ось Ох, а дру-
гая— ось Ог.
307. Найти уравнение плоскости, проходящей через начало коор-
динат и через точки Р (4; — 2; 1) и Q (2; 4; — 3).
308. Найти уравнение плоскости, проходящей через точку пере-
сечения плоскостей 2л' + 2у + г—7 = 0, 2х—у-\-Зг — 3=0, 4х + 5г/—
—2г —12 = 0 п через точки М (0; 3; 0) и N (1; 1; 1).
309. Составить уравнение плоскости, проходящей через линию
пересечения плоскостей х + 5г/+9г—13 = 0, Зх—у—5г+1=0 и
через точку М (0; 2; 1).
310. Составить уравнение плоскости, проходящей через линию
пересечения плоскостей х + 2у + 3г— 5 = 0 и Зх—2у— г + 1 = 0 и
отсекающей равные отрезки на осях Ох и Ог.
311. Составить уравнение плоскости, проходящей через линию
ересечения плоскостей (1 +К2)х + 2у + 2г — 4 = 0, х+г/ + г + 1= 0
в образующей с координатной плоскостью хОу угол 60°.
312. Составить уравнение плоскости, проходящей через линию
ересечения плоскостей 2х—у — 12г — 3 = 0 и Зх + «/—7г — 2 = 0 и
перпендикулярной плоскости х + 2у + 5г — 1=0.
313. Составить уравнение плоскости, проходящей через линию
ересечения плоскостей Л1х + В]// + С1г + О1 = 0 и А2х-\-В2у-]-С2г +
+ D, = 0 и через начало координат.
314. Составить уравнение плоскости, проходящей через точку
ЛИ (0; 2; 1) и параллельной векторам а = i + j + к и b = i + j — k.
315. Какой угол образует с плоскостью х + у + 2г — 4 = 0 вектор
а = j щ 2j + k?
57
2. Прямая. 1) Прямая может быть задана уравнениями двух плоскостей
Aix+В\У+C-iZ+Dj = О,
А2Х -|- C2z -|- О2 = О,
пересекающихся по этой прямой.
2) Исключив поочередно х и у из предыдущих уравнений, получим уравнения
x = az-\-c, y = bz-\-d. Здесь прямая определена двумя плоскостями, проецирую-
щими ее на плоскости хОг и yOz.
3) Уравнения прямой, проходящей через две точки Mi (хх; уг-, г2) п Л12 (х2;
у2; г2), имеют вид
X — Xj _ У — У1 _ Z—Zj
х2—Xi У2—У1 Z2—Z1 v
4) Так называемые канонические уравнения
x—x, y—yt z—zt 2)
I т п
определяют прямую, проходящую через точку Л4 (х2; у^’, гг) и параллельную
вектору s = /i + mj-|-nk. В частности, этн уравнения могут быть записаны в виде
х—х, _ t/—t/i z—zt
cos a cos р cos у ’л
где а, Р и у—углы( образованные прямой с осями координат. Направляющие
косинусы прямой находятся по формулам
I а т п
cos п. = — cosp= — cos у = .................(3)
}^/24-/n2 + n2 }^/2 + m2 + л2 /V2-|-m2-|-n2
5) От канонических уравнений прямой, вводя параметр t, нетрудно перейти
к параметрическим уравнениям-.
( х=И-|-хт,-
•! y = mt-\-yit (4)
\z = n< + zl.
6) Угол между двумя прямыми, заданными их каноническими уравнениями
(x—x1)/li = (y—y1)lmi = (z—zi)/n1 и (х—x2)//2 = (t/—t/2),'m2 = (z—z2)/n2, определя-
ется по формуле
cos ф = + -------, (5)
К /2Ч-т2+ niyif+ml+nl *
условие параллельности двух прямых:
Ii/l2 = mi/m2 = ni/n2', (6)
условие перпендикулярности двух прямых:
/j/2-|-mim2-|-«in2 = 0. (7)
7) Необходимое и достаточное условие нахождения двух прямых, заданных
их каноническими уравнениями, в одной плоскости (условие компланарности двух
прямых):
х2— Xi У2 — У1 z2—Zi
li тг П1 = 0
I2 m2 n2
(8)
Если величины lit т^, п± не пропорциональны величинам /2, тг, пг, то ука-
занное соотношение является необходимым и достаточным условием пересечения
двух прямых в пространстве.
58
8) Угол между прямой (х—х1)/1 = (у—y1)/m = (z—z1)/n и плоскостью
Jbc-^-By-^-Cz-[-D = Q определяется по формуле
sin ф=—---------------------- (9)
К>424-В2 + С2 •
условие параллельности прямой и плоскости:
Л/4-В/п+Ся=0; (10)
условие перпендикулярности прямой и плоскости:
А/1 = В/т = С/п. (11)
9) Для определения точки пересечения прямой (х—хо)/1 = (у—уо)/т =
(г—г0)/п с плоскостью Ax-j-By-]-Cz-{-D~0 нужно решить совместно их уравне-
эя, для чего следует воспользоваться параметрическими уравнениями прямой
x—lt-i-xo, y=mt+y<>, z—nt-\~2a:
а) если А1+ВтА-Сп^0, то прямая пересекает плоскость;
б) если Л^+В/п + Сп = 0 и Лхо+Вуо+Сго + О^О, то прямая параллельна
вескости;
в) если Л/+В/п + Сп = 0 и Лх0 + 5уо + Czo + D = 0, то прямая лежит в пло-
скости.
316. Уравнения прямых 2х—у + Зг—1=0 и 5х-|-4^—г—7 =
= 0 привести к каноническому виду.
Л I способ. Исключив сначала у, а затем г, имеем
13x4-112—11=0 и 17x4-Пу—22 = 0.
Если разрешить каждое нз уравнений относительно х, то получим
„_,П(У-2) „11(2-1) х____у-2 г-1
— 17 — 13 ’ — 11 17 ~ 13 ’
II способ. Найдем вектор 5 = /1-|-/п)4-пкЛпараллельный искомой прямой.
Так как он должен быть перпендикулярен нормальным векторам Nj = 2i — j-|-3k
N2=5i4-4j—к заданных плоскостей, то за s можно принять векторное произ-
ведение векторов Nt и N2:
1
2
5
1
— 1
4
k
3
— 1
s=NtxN2 =
= - 1114-17)4-13k.
Таким образом, 1=—11; m=17; n=13.
В качестве точки Мг (х2; yt: zi), через которую проходит искомая прямая,
ожно взять точку пересечения ее с любой из координатных плоскостей, напри-
мер с плоскостью уОг. Так как при этом xi = 0, то координаты yt и zt этой точки
•иределятся из системы уравнений заданных плоскостей, если в них положить
х=0;
f — j/4-3z—1=0,
\iy—z—7 = 0.
Решая эту систему, находим г/i = 2, 22=1. Итак, искомая прямая определяется
уравнениями х/(—11) = (у—2)/17=(г—1)/13. А
317. Построить прямую {^+g+^9==00’
Д Искомую прямую можно построить как линию пересечения плоскостей. Для
этого запишем уравнения этих плоскостей в отрезках, на осях: x/4,5-|-y/34-z/3 =
= 1, х/2-|-у/44-г/8= 1. Построив данные плоскости, получим искомую прямую
(рнс. 20). Д
318. Из начала координат опустить перпендикуляр на прямую
(х—2)/2 = (у—1)/3.= (г—3)/1.
точки
т. е.
ДИспользуя условие (11) перпендикулярности прямой и плоскости и полагая
A = l, В = т, С = п, D — 0, составим уравнение плоскости, проходящей через
начало координат и перпендикулярной заданной прямой. Это уравнение имеет
вид 2х+Зу+г = 0.
Найдем точку пересечения этой плоскости и данной прямой. Параметрические
уравиения прямой запишутся так: x = 2t-(-2, у—31-1-1, г=/+3. Для определе-
ния t имеем уравнение 2 (2< + 2)-|-3 (3<+1) +
+< + 3 = 0, откуда / = —5/7. Координаты —..................................
пересечения х=4/7, у= — 8/7, г = 16/7,
М (4/7; — 8/7; 16/7).
Остается составить уравиения прямой,
ходящей через начало координат и через
М\ используя соотношения (1), получим
х/(4/7)=у/(—8/7) = г/( 16/7), или х/1 =у/(-2) =
про-
точку
319. В уравнениях прямой х/2 =
—уК—3) — г/п определить параметр п так,
чтобы эта прямая пересеклась с прямой
(х + 1 )/3 = (у + 5)/2 = г/1, и найти точку
их пересечения.
А Для: нахождения параметра п используем условие (8) пересечения двух
прямых; полагая Xi =—1, уг =—5, Zi = 0, х2 = 0, у2 = 0, г2 = 0, 4 = 3, т\ = 2,
«1=1. 4*=2> m2 = — 3, п2 = п, получим
5 О
1
3
2
1 =0, или 2п+10+3—15п = 0, т. е. п=1.
п
, Чтобы найти координаты точки пересечения прямых х/2 = !//(— 3) = г/1 и
(5<+l)/3=(y+5)/2 = z/l, выразим из первых уравнений х и у через г: х = 2г,
у=—Зг. Подставляя эти значения в равенство (х+1)/3 = (y-j-5)/2, имеем
(2г-|-1)/3=:(—Зг+5)/2, откуда 2=1. Зная г, находим х = 2г = 2, у =—Зг =
=—3. Следовательно, М (2; —3; 1). Д
320. Составить уравнения прямой, проходящей через точку
М (3; 2; — 1) и пересекающей ось Ох под прямым углом.
Д Так как прямая перпендикулярна оси Ох и пересекает ее, то она проходит
через точку N (3; 0; 0). Составив уравнения прямой, проходящей через точки
М и N, получаем (х—3)/0=(у—2)/(—2)=(г+ 1)/1. Д
321. Дана плоскость х+у—2г—6 = 0 и вне ее’точка М (1; 1; 1).
Найти точку А/, симметричную точке М относительно данной пло-
скости.
А Запишем уравнения любой прямой, проходящей через точку Л4; (х—1)// =
= (у—1)//п = (г—1)/я. Координаты {/; т; я} направляющего вектора прямой,
перпендикулярной плоскости, можно заменить координатами нормального вектора
п = {1; 1;—2} данной плоскости. Тогда уравнения этой прямой запишутся
в виде (х—1)/1 = (у—1)/1 =(г—1)/(—2).
Найдем проекцию точки М иа данную плоскость, решив совместно уравнения
x+y-2z-6 = 0, (х-1)/1 = (у-1 )/1 = (г-1)/(- 2).
60
Перепишем уравнения прямой в виде х = < + 1, y = t-{-1, z = —2/4-1. Подставляя
эта выражения для х, у и z в уравнение плоскости, найдем 7=1, откуда х = 2,
у=2, z = — 1.
Координаты симметричной точки найдутся из формул х = (хм + х^)/2, у =
= (yM+yN)/2,'z = (zM+z^)/2, т. е. 2 = (1 +хЛ)/2, 2 = (1 +^/2, — 1 =(1 + zN)/2,
откуда х.у=3, yN=3, гц=—3. Следовательно, N (3; 3; —3). А
322. Дана прямая (х—l)/2 = z//3 = (г 4-1)/(—1) И вне ее точка
5f(l; 1; 1). Найти точку N, симметричную точке М относительно
ланной прямой.
Д Уравнение плоскости, проецирующей точку М на данную прямую, имеет
ад
Л(х-1) + В(у-1)+С(г-1) = 0.
Координаты нормального вектора {Д; В; С} плоскости, перпендикулярной прямой,
ямеиим координатами направляющего вектора {2; 3; — 1} данной прямой; тогда
вэлучим
2 (х—1)+3(у—1) — (z — 1) = 0, или 2х+3у—z—4 = 0.
Найдем проекцию точки М на прямую, для чего совместно решим систему урав-
нений
2x+3y-z-4=0, (х-1)/2=у/3 = (г+1)/(-1).
Параметрические уравнения данной прямой имеют вид х = 2/-|-1, y=3t, г =
=—t—I. Подставляя х, у и г в уравнение плоскости, найдем / = 1/14. Отсюда
*=8/7, у=3/14, г = —15/14.
Тогда координаты симметричной точки можно найти,'используя формулы для
оордингт середины отрезка, т. е. 8/7 = (1-^хд0/2, 3/14 = (14-у,у)/2,—15/14 =
= (1+гд,)/2, откуда ху=9/7, Ум ——4/7, гуу=—22/7.. Итак, N (9/7; —4/7;
s -22/7). А
323. Через прямую (х4-1)/2 = (г/—1)/(—1) = (г—2)/3 провести
лоскость, параллельную прямой х/(—1) = Q/4~2)/2 = (г—3)/(—3).
Д Запишем уравнения первой из заданных прямых с помощью уравнений
жух плоскостей, проецирующих ее соответственно на плоскости хОу и уОг:
i (х+1)/2 = (у-1)/(-1), или х+2у-1=Р;
। (У—!)/(—!) = (г—2)/3, или Зу+г—5 = 0.
1 Уравнение пучка плоскостей, проходящих через эту прямую, имеет вид
х-[-2у—1 -|-к(Зу+г—5)=0, илн x+(2+3A) y-\-kz—(1+5А)=0.
Используя условие параллельности прямой и плоскости, определим к так,
чтобы соответствующая плоскость пучка была параллельна второй из заданных
к «вямых. Имеем —1 • 1 4-2 (24-Зл)—ЗА = 0, илн ЗХ4-3 = 0, откуда А =—1. Таким
I Аразом, искомая плоскость определяется уравнением х—у—z+4 = 0. А
Г 324. Найти уравнения проекции прямой (х—1)/1 =(у+ 1)/2 = г/3
f ва плоскость х + у + 2г—5 = 0.
А Запишем уравнения заданной прямой в виде уравнений двух плоскостей,
проецирующих ее соответственно на плоскости хОу н хОг:
(х—1)/1 =(«/+ 1)/2, или 2х—у—3 = 0;
(х—1)/1=г/3, или Зх—г—3 = 0.
j Уравнение пучка плоскостей, проходящих через данную прямую, запишется
I • "виде
2х—у—3-(-Х(Зх—г—3) = 0, или (2-|~ЗА.)х—у—кг—3(1 4-Х) = 0.
61
Используя условие перпендикулярности плоскостей, выберем из этого пучка
плоскость, проецирующую данную прямую на заданную плоскость. Имеем l-(2-f-
-f-3X)+l(—1) + 2(—А) = 0, илн A-j-1 = 0, откуда А=—1.Итак, уравнение проеци-
рующей плоскости имеет вид
2х—у—3 + (— 1)-(Зх—г—3) = 0, или х-\-у—г = 0.
Искомую проекцию можно определить как линию пересечения двух плоскос-
тей— заданной и проецирующей:
/*+у+2г—5 = 0,
V+y—г = 0.
Приведя эти уравнения прямой к каноническому виду, окончательно получим
х/1 = (у—5/3)/(—l) = (z—5/3)/0. Д
325. Составить уравнения прямой, проходящей через точку
М (5; 3; 4) и параллельной вектору s = 2i + 5j—8k.
Л Воспользуемся каноническими уравнениями прямой. Полагай в равенствах
(2)/=2, т = 5, п =—8, Xi = 5, yi = 3,- Zi = 4, получаем (х—5)/2 = (у—3)/5 =
= (г-4)/(-8). ±
326. Составить уравнения прямой, проходящей через точку
Л1 (1; 1: 1) и перпендикулярной векторам s1 = 2i + 3j + k и s2 = 3i+
+ j + 2k.
Л Прямая параллельна вектору s1Xsa = 5f—j—7k, поэтому она определяет-
ся уравнениями (х—1)/5 = (у—1)/(— 1) = (г—0/(~Ъ- Д
327. Найти уравнения проекций прямой
/х+2у+3г—26 = 0,
\3x+z/-f-4z—14 = 0
на координатные плоскости.
328. Привести к каноническому виду уравнения прямой
(2х+3у— 16г— 7=0,
\3х+у—17г=0.
329. Вычислить углы, образованные с осями координат прямой
(х—2у—5=0,
V—Зг + 8 = 0.
330. Найти уравнения прямой, проходящей через точку М (1;
—2; 3) и образующей с осями Ох и Оу углы 45° и 60°.
331. Найти уравнения прямой, проходящей через точку N (5;
—1; —3) и параллельной прямой
(2х~\-Зу-\-г—6 = 0,
\4х—5у—z+2 = 0.
332. Найти точку пересечения прямых (х—1)/(— 1) = (у—2)/5=
=(г + 4)/2 и (х—2)/2 = (у—5)/(—2) = (г—1)/3.
333. Даны три последовательные вершины параллелограмма:
4(3; 0; — 1), В(1; 2; —4) и С(0; 7; —2). Найти уравнения сторож
AD и CD.
334. Найти параметрические уравнения прямой, проходящей че-
рез точки М (2; —5; 1) и N (—1; 1; 2).
335. Вычислить расстояние между параллельными прямыми
х/1 =(//—3)/2 = (г—2)/1 и (х—3)/1 =(^4-1)/2 = (г—2)/1.
336. Даны точки Л(— 1; 2; 3) и В (2; —3; 1). Составить урав-
нения прямой, проходящей через точку М(3; —1; 2) и параллель-
ной вектору АВ.
337. Найти угол между прямыми
/4х-у-г4-12 = 0, „ /Зх-2у+16=0<
\у—г—2 = 0 и /Зх—г=0.
338. В плоскости уОг найти прямую, проходящую через начало
v „ (2х—у = 2,
жоординат и перпендикулярную прямой |У+2г=—2.
339. Даны две вершины параллелограмма ABCD: С (—2; 3; —5)
a D(0; 4; —7) и точка пересечения диагоналей Л1(1; 2; —3,5).
Найти уравнения стороны АВ.
340. Треугольник АВС образован пересечением плоскости
x4-2z/4~4z — 8 = 0 с координатными осями. Найти уравнения сред-
ней линии треугольника, параллельной плоскости хОу.
341. Даны точки Л (1; 1; 1), В(2; 3; 3) и С(3; 3; 2). Составить
уравнения прямой, проходящей через точку Л и перпендикуляр-
ной векторам АВ и АС.
342. Составить уравнения прямой, проходящей через точку
И (0; 2; 1) и образующей равные углы с векторами a = i4-2j4-2k,
b = 3j, c = 3k.
343. Найти уравнение плоскости, проходящей через прямую
(x4-l)/3 = (z/—2)/(—l) = z/4 и перпендикулярной плоскости 3x4-//—
— z 4~ 2 = 0.
344. Найти уравнения проекции прямой х/2 = (//4-3)/1 =
=(г—2)/(—2) на плоскость 2x4-3//—г—5 = 0.
9 2. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
1. Сфера. В декартовой системе координат сфера, имеющая центр в точке
С (а; Ь; с) п радиус г, определяется уравнением
(х—а)24-(у—Ь)24-(г—с)2 = г2. (1)
Если центр сферы находится в начале координат, то ее уравнение имеет вид
х24-у24-г2 = г2. (2)
345. Найти координаты центра и радиус сферы, заданной урав-
нением
х2 4-//2 4-г2—х 4-2//4-1=0.
д Приведем уравнение сферы к каноническому виду (1), для чего дополним
* полных квадратов члены, содержащие х, у, и г, т. е. перепишем уравнение
в следующем виде:
(х2-х4-1) -14-(у2+2у +1)-14-г24-1 =0.
ш
(x-iy+(y4-1)24-22=j-
Следовательно, центр сферы—точка С (1/2;— 1; 0), а ее радиус г = 1/2. А
346. Составить уравнение сферы, проходящей через точки А (1;
2; —4), В(1; —3; 1) и С (2; 2; 3), если ее центр находится в плос-
кости хОу.
Д Так как точки А, В к С принадлежат сфере (х—«)2+(?/—6)2-|-(г—с)г = г2,
центр которой находится в плоскости хОу (откуда с = 0), то их координаты долж-
ны обращать искомое уравнение в тождество; поэтому получаем уравнения
(1— а)2Д-(2—&)2 + (— 4)2 = r2, (1—а)2Д-(— 3—&)2_|_ 12 = г2,
(2—а)2Д-(2—6)2Д-32 = г2.
Отсюда
(1 —а)2 +(2—6)2 Д-16= (1 —а)2-|-(—3 —ft)2 Д-1,
(1 —a)2 i (2 —fe)2+16 = (2 —а)2 + (2 —&)2 + 9,
или
(2 —6)2—(—3—ft)2 = —15, т.е. 106=10;
(1—а)2—(2—а)2 = —7, т.е. 2а = —4,
Итак, а = —2, 6=1. Следовательно, центр сферы—точка С(—2; 1; 0). Далее,
находим г2 = (1—а)2-|-(2—ft)2 Д- 16 = (1Д-2)2Д-(2—1)2Д-16 = 26. Таким образец,
искомое уравнение имеет вид (х-|-2)2Д-(г/—1)2Д-г2 = 26. А
347. Найти координаты центра и радиус окружности
((х-З)2 Д-(у + 2)2 Д- (г-1)2 = 100,
( 2х—2у—гД-9 = 0.
Л Из центра сферы С (3; —2; 1) опустим на плоскость 2х—2у—г Д-9 — 0
перпендикуляр, уравнения которого можно записать в виде
(х—3)/2 = (уД-2)/(—2) = (г—1)/(—1) (»)
(в качестве направляющего вектора этого перпендикуляра можно взять нормаль-
ный вектор заданной плоскости).
Теперь найдем координаты точки пересечения прямой (*) с плоскостью
2х—2у—гД-9 = 0. Эта точка и есть центр окружности, являющейся сечением
сферы данной плоскостью.
Записав уравнения прямой в параметрическом виде x=2f-|-3, y = —2t— 2,
г = —f-|-l и подставив х, у, г в уравнение плоскости, получим
2 (2f Д-З)—2 (—2f—2) —(—f Д-1) Д-9 = 0, т. е. t = — 2.
Следовательно, х = 2(—2)-)-3 = — 1, у = —2 (—2) — 2 = 2, г = —(—2)Д-1=3,
т.е. центр окружности находится в точке С(—1; 2; 3).
Найдем теперь расстояние d от центра сферы С (3; —2; 1) до плоскости
2х—2у—гД-9 = 0:
, 2-ЗД-2-2—1Д-9 „
224-22Д-1
Радиус окружности г определится из равенства г2 = /?2—d2, где R — радиус сфе-
ры; таким образом, г2 = 100—36 = 64, т.е. г = 8. А
348. Определить координаты центров и радиусы сфер, заданных
уравнениями: 1) (хД- 1 )2Д-(уД-2)2 Д-г2=25; 2) х2Д-у2Д-г2—4хД-6у Д-
Д- 2г — 2 = 0; 3) 2х2 Д-2у2Д-2г2 Д-4у—Зг Д-2 = 0; 4) х2 Д- уг Д- г2 = 2х;
5) х2 Д- у2 Д- г2 = 4г — 3.
349. Как расположена точка Л4(1;—1; 3) относительно сфер:
1) (х—1)2Д-(у + 2)2Д-г2= 19; 2) x2 + y2 + z2—x + y = 0; 3) х2Д-у2 +
д- г2—4хД-у—2г = 0?
64
350. Составить уравнение сферы, если точки И (4; —1; —3) и
N (0; 3; —1) являются концами одного из ее диаметров.
35L Составить уравнения окружности, образующейся в сечении
сферы (х—1)2 + (у— 1)24- (г — 3)2 = 25 координатной плоскостью z = 0.
352. Найти координаты центра и радиус окружности х2+у2 +
4-г2 =100, 2х + 2у—г =18.
2. Цилиндрические поверхности и конус второго порядка. Уравнение ви-
да F (х, у) = 0 в пространстве определяет цилиндрическую поверхность, у
которой образующие параллельны оси Ог. Аналогично, уравнение F (х, г)=0
определяет цилиндрическую поверхность с образующими, параллельными оси
Су, н F (у, г) = 0—цилиндрическую поверхность с образующими, параллель-
ными оси Ох.
Канонические уравнения цилиндров второго порядка:
№ w®
— +'^2' = 1 —эллиптический цилиндр,
л-2 г/2
— -=- = 1 —гиперболический цилиндр,
у2 = 2рх—параболический цилиндр.
Образующие всех трех цилиндров, определяемых этими уравнениями, парал-
лельны оси Ог, а направляющей служит соответствующая кривая второго поряд-
ка (эллипс, гипербола, парабола), лежащая в плоскости хОу.
Следует помнить, что кривую в пространстве можно задать либо параметри-
чески, либо в виде линии пересечения двух поверхностей. Например, уравнения
направляющей эллиптического цилиндра, т. е. уравнения эллипса в плоскости
хОу, имеют вид
a2"t- b-2 — *•
2 = 0.
Уравнение конуса второго порядка с вершиной в начале координат, осью кото-
рого служит ось Ог, записывается в виде
а2 1 Ь2 с2
Аналогично, уравнения
являются уравнениями конусов второго порядка с вершиной в начале коорди-
нат, осями которых служат соответственно оси Оу и Ох.
353. Какую поверхность определяют в пространстве уравнения:
1) x2 = 4z/; 2) z2 = xz?
1) Уравнение № = 4г/ определяет параболический цилиндр с образующими,
параллельными оси Ог. Направляющей цилиндрической поверхности является
парабола х2 = 4у, г~0.
2) Уравнение г2=хг может быть представлено в виде г (г—х) и распадается
иа два уравнения: 2 = 0 и г = .х, т. е. оно определяет две плоскости—плоскость хОу
и биссектральную плоскость г = х, проходящую через ось Оу.
354. По какой линии пересекается конус х2-гу2—2z2 = 0 с пло-
скостью у = 2?
3-213 65
Д Исключив из системы уравнений у, получим х2+4 —2z2=0,. или э?/2 —
— ж2/4=1. Следовательно, искомой линией пересечения является гипербола,'лежа-
щая в плоскости у—2; ее действительная ось параллельна оси Ог, а мнимай—
оси Ох. А
355. Составить уравнение конической поверхности, вершиной
которой служит точка М (0; 0; 1), а направляющей—эллипс х2/25 +
+ //‘79=1, 2 = 3.
Л Составим уравнение образующей AM, где А (х0; у0; z0)—точка, лежащая
иа эллипсе. Уравнения этой образующей имеют вид x/*0=y/y0 = (z—l)/(z0—1).
, Так как точка А лежит иа эллипсе, то ее координаты удовлетворяют уравнениям
эллипса, т. е. *2/25-|-у2/9= 1, z0 = 3.
Исключив теперь х№, у0 и га из системы
*/*o = (z—Wo— 0. У/Уо = (г-1)/(го—1). х2/25+у2/9 = 1, г0=3,
получим уравнение искомого конуса: х2/25+у2/9—(z—1)2/4=0. А
356. Установить, какие поверхности определяются следующими
уравнениями, и построить эти поверхности: 1) х2+//2 = 4; 2) х2/25 +
+ «/2/16=1; 3) х2—i/2=l; 4) у3 — 2х; 5) z3=y, 6) г + х2 = 0; 7) х2 +
+ у3 = 2у, 8) ха+у3 = 0-, 9) х2—г2 = 0; 10) у3 = ху.
357. Составить уравнения линий пересечения конуса х2—y2 + z2 =
= 0 с плоскостями: 1) г/= 3; 2) 2 = 1; 3) х = 0.
358. Составить уравнение конуса с вершиной в начале коорди-
нат, направляющие которого заданы уравнениями: 1) х=а, y3 + z3 —
= Ь3\ 2) у — Ь, х24-г2 = а2; 3) г = с, х2/а2 + «/2/Ь2 = 1.
3. Поверхности вращения. Поверхности второго порядка. Если лежащая
в плоскости уОг кривая F (у, г) = 0, х=0 вращается вокруг оси Ог, то уравнение
образуемой ею поверхности вращения имеет вид
г)=0.
Аналогичйо, уравнение F(x, у2-J-г2) =0 определяет поверхность, образо-
ванную вращением вокруг оси Ох кривой F (х, у)=0, z=0; уравнение F(Y"x3+г3,
у) = 0—поверхность, образованную вращением той же кривой вокруг оси Оу.
Приведем уравнения поверхностей вращения второго порядка, образуемых
вращением эллипса, гиперболы и параболы вокруг их осей симметрии.
Эллипсоид вращения
х2+у2 , z2_
Q2 -Гс~2—*>
осью вращения служит ось От; эллипсоид сжат при а > с и удлинен при а < с
(при а = с он превращается в сферу).
Однополостный гиперболоид вращения
х3+у3 г3
а3 с2 ’
осью вращения является ось Ог (служащая мнимой осью гиперболы, вращением
которой образована эта поверхность).
Двуполостный гиперболоид вращения
х3 + у3 г3 _
а3 с3
осью вращения является ось Ог (служащая действительной осью гиперболы, вра-
щением которой образована эта поверхность).
С6
Параболоид вращения
х2+уа = 2рг;
осью вращения служит ось Ог.
/Поверхности вращения второго порядка являются частным случаем
Иосией второго порядка общего вида, канонические уравнения которых
1 Эллипсоид (трехосный)
поверх-
таковы:
Г2 , г2 .
ЛГ-ГГГ— *•
Однополостный гиперболоид
а2 Ь2 с2 1
второго
второго
Двуполостный гиперболоид
а2“г Ьа с2 —
Эллиптический параболоид
y+^-=2z (р > 0, <7 > 0).
Кроме этих четырех поверхностей второго порядка, трех цилиндров
порядка (эллиптического, гиперболического и параболического) и конуса
порядка', существует еще одна поверхность второго порядка—гиперболический
параболоид, каноническое уравнение которого имеет вид
~p~q~^z (р > 0, q > 0).
Таким образом, всего существует девять различных поверхностей второго
порядка.
359. Найти уравнение поверхности, полученной при вращении
прямой x4-2z/ = 4, 2 = 0 вокруг оси Ох.
Л Поверхностью вращения является конус с вершиной в точке М (4; 0; 0).
Пусть произвольная точка А искомой поверхности имеет координаты X; У; Z;
ей соответствует на данной прямой точка В (х; у, 0). Точки А и В лежат в одной
плоскости, перпендикулярной осн вращения Ох. Тогда Х=х, У2-|-22 = у2.
Подставляя выражения для х и у в уравнение данной прямой, получим урав-
еиия искомой поверхности вращения: ХЦ-2 J^y2^-^2 =4, или 4(У24-22)—
— (X —4)2 = 0, т. е. 4T24-4Z2 — (X—4)2 = 0. А
360. Какую поверхность определяет уравнение х2 — уг>
Произведгм поворот координатных осей вокруг оси Ох на угол а = 45°
(от осп Оу к осн Ог против часовой стрелки). Формулы преобразования координат:
х = х', у —у' cos а—г'sin а, г = у' sina-f-г' cosa. Так как sina = cosa= 2/2,
то х=--х’, // = (/ 2/2) {у' — г’), г = (У 2/2) (р'4-z').
Подставив эти выражения в уравнение поверхности, получим х' =у' /2—г' /2,
вли х'2—у' /24~г'2;2 = 0 (конус с вершиной в начале координат, осью которого
является ось ординат). А
361. Найти уравнение поверхности, полученной при вращении
прямой 2у4-2— 2 = 0, х = 0 вокруг оси Oz.
362. Найти уравнения линий пересечения поверхности г = х2—у2
плоскостями 2 = 1, у= 1, х=1, г = — 1.
363. Какие поверхности определяются уравнениями: 1) z — xy,
2) г2 = ху?
ф Произвести поворот вокруг оси Ог на угол 45°.
364. Найти уравнение эллиптического параболоида, имеющего
вершину в начале координат, осью которого является ось Ог, если
на его поверхности заданы две точки М (—1; —2; 2) иУ(1; 1; 1).
365. Составить уравнение эллипсоида, осями симметрии которого
служат оси координат, если на его поверхности заданы три точки
Л (3; 0; 0), В (—2; 5/3; 0) и С (0; —1; 2/И 5).
366. Найти уравнения линии пересечения поверхностей г = 2 —
— х2—у2 и г — х2 + у2.
367. Исследовать, какие поверхности определяет уравнение г2 +
+ х2 = т (г2 + у2) при: 1) т = 0; 2) 0 < т < 1; 3) т > 1; 4) т <0;
5) т = 1.
4. Общее уравнение поверхности второго порядка. Общее уравнение второй
степени относительно х, у и г имеет внд
А х2 + By3+С г2 + 2Dyz+2Ехг + 2F ху+2Gx+2Ну+2Кг+L = 0.
Это уравнение может определять сферу, эллипсоид, однополостный или двупо-
лостиый гиперболоид, эллиптический или гиперболический параболоид, цилиндри-
ческую или коническую поверхность второго порядка. Ойо может также опреде-
лять. совокупность двух плоскостей, точку, прямую или даже ие иметь геометри-
ческого смысла (определять «мнимую» поверхность).
При Z>=0, £ = 0, F = 0 общее уравнение принимает вид
Ах3 + By2+Сг2+2Gx+2ffy+ 2№+L = 0.
В этом случае уравнение легко упрощается с помощью параллельного переноса
осей координат, что позволяет сразу установить его геометрический смысл.
368. Каков геометрический смысл уравнения
х2 + 4у2 4- 9г2 + \2уг + 6xz + 4ху—4х—8у— 12г + 3 = 0?
Л Данное уравнение можно записать в виде
(х+2у+3г)2-4 (х+2у+Зг)+3 = 0.
Разложим иа множители левую часть уравнения: (x-j-2y-f-3z—l)(*+2y+3z—3)==
= 0. Таким образом, уравнение определяет совокупность двух плоскостей x+2y~t~
+ 3г—1=0, х+2у+3г—3=0. X
369. Каков геометрический смысл уравнения
х2 + у2 + г2—уг —хг —ху — 0?
Л Умножая иа 2, перепишем уравнение в виде
2х2 + 2у2+2г2—2уг—2хг—2ху=0,
или
(х—у)2 + (у—г)2 + (х—г)2 = 0.
Этому уравнению удовлетворяют координаты только тех точек, для которых
выполняются равенства х=у, у —г, х — г. Таким образом, уравнеиие определяет
прямую x=y=z. А
370. Каков геометрический смысл уравнения
х2 + у2 + 4г2—2ху—8г 4-5 = 0?
Л Перепишем уравнеиие в виде (х—у)2+4(г—1)2=—I. Это уравнение
не имеет геометрического смысла, так как его левая часть не может быть отрица-
тельной ни при каких действительных значениях х, у и г. А
68
371. Привести к каноническому виду уравнение
4х2 + 9у3 + 36z2—8х — 18у—72z + 13 = 0.
Л Сгруппируем члены с одинаковыми координатами:
4(х2—2x)+9(z/2—2у)+36(г2—2г) = — 13.
Дополнив до полных квадратов выражения в скобках, получим
4 (х2—2х+ 1)+9 (у3—2 г/+1)4-36 (г2—2г-|- I) = — 13 + 4+9+36,
ли 4(х—1)2+9(у—1)2 + 36(г—1)2 = 36.
Произведем параллельный перенос осей координат, приняв за новое начало
координат точку О' (1; Г, 1). Формулы преобразования координат имеют вид
х=х' + 1, у = у'-т-1, г = г' + 1. Тогда уравнение поверхности запишется так:
4х'‘+9у'‘ + 36г'2 = 36, или х'’/9+у'*/4+г'* = 1.
Это уравнение определяет эллипсоид; его центр находится в новом начале
координат, а полуоси соответственно равны 3, 2 и 1. Д
372. Привести к каноническому виду уравнение
х3—у3—4% + 8//—2г =0.
Д Сгруппируем члены, содержащие х и у. (х2—4х)—(у3—8у) = 2г. Допол-
няем до полных квадратов выражения в скобках:
(х2—4х+4) — (у2—8//+16) = 2г+4—16, или (х—2)2—(у—4)2 = 2 (г—6).
Произведем параллельный перенос осей координат, приняв за новое начало
точку О' (2; 4; 6). Тогда х = х' + 2, у = у'+4, г = г'+6. В результате получаем
уравнение х'*—г/'2 = 2г', определяющее гиперболический параболоид. А
373. Какая поверхность определяется уравнением
4х2—у3 + 4г2—8х + 4у + 8г + 4 = 0?
Д Выполнив соответствующие преобразования, получим
4 (х2—2х) — (z/2—4у) + 4 (г2 + 2г) = — 4;
4(х2—2х+1) —(z/2—4у+4)+4(г2 + 2г+1)= —4+4—4+4;
4(х— I)2 — (у—2)2+4(г+1)2 = 0.
Произведем параллельный перенос осей координат, приняв за новое начало
точку О' (1; 2; —1). Формулы преобразования координат 2x = xj' +1, ху = у'+ 2,
г = £' — 1. Тогда данное уравнение примет вид 4х' —у’ +4г' =0, или
х'*—у'‘/4+г'2 = 0. Это уравнение конической поверхности. Д
Выяснить, какие поверхности определяются следующими уравне-
ниями:
374. X2—ху—хг + уг — 0. 375. х2 + г2— 4х—4г+ 4 = 0.
376. х3 + 2у3 + г3—2ху—2уг = 0. 377. x2 + i/2—г2—2г/ + 2г = 0.
378. х2 + 21/2 + 2г2—4г/ + 4г + 4 = 0.
379. 4х2+ у2—г2—24х —4г/ +2г + 35 = 0.
380. х3 + у2—г3—2х—2у + 2г + 2 = 0.
381. х3 + у3—6х + 6у—4г + 18 = 0.
382. 9х2 — г2—18х— 18у—6г = 0.
ГЛАВА IV
ОПРЕДЕЛИТЕЛИ И МАТРИЦЫ
§ 1. ПОНЯТИЕ ОБ ОПРЕДЕЛИТЕЛЕ n-ГО ПОРЯДКА
Определитель четвертого порядка, соответствующий таблице элементов
Оц olt а13 ац\
а31 я 32 а33 а34
а41 а42 а43 а44'
, определяется равенством
аН ait а1в а14
а2г а22 аг3 а24
а31 а32 а33 а34
а41 а43 а44
= а11
п22 Пгз ам
азг °зз ам
а42 а43 а44
а21 а33 аМ
ati а22
«24
—а12 а31 а33 а34 +а13 а31 а32 а34—а14 а31 а32
а41 а43 аЫ
а41 а«
а44
°4f а42
агз
а33
O43
“ti ott
С помощью определителей четвертого порядка можно аналогично ввести понятие
определителя пятого порядка и т. д.
Для определителей любых порядков остаются в силе определения минора и
алгебраического дополнения некоторого элемента и обе теоремы об алгебраических
дополнениях, сформулированные для определителей третьего порядка.
Таким образом, обозначая через М,* минор, а через —алгебраическое
дополнение элемента ац определителя n-го порядка (т. е. элемента, находящегося
в »-й строке и Л-м столбце этого определителя), имеем
А'4 = (- 1У<+ЛМ№-
Пусть D—определитель n-го порядка. Раскрывая его сначала по элементам
»-й строки, а затем по элементам k-ro столбца, в силу теоремы 1 (см. с. 41)
получим
— a<iA/-i-f-a(-2A/24-... 4-а<пЛ|-п;
4"а2»А2* -f-... -f- Опц^-пь-
С другой стороны, при j 7= i и k I в силу теоремы 2 (см. с. 41) имееем
в/1'4/14-4/2А/24-. •. +а/пА(П = 0.
+ • • • +°nft^nZ = 0.
Свойства определителей второго и третьего порядка, сформулированные на
с. 41, справедливы и для определителей любого порядка.
Решение системы линейных уравнений
а11х14~а1!Х2 4* • • • Ч* а1П*п = >
а21*1 + а22*2 + • • - + Я2П*П =
.ап1х1 + аи2*2 4- • • • 4- аППХП = 1>пг
определитель которой
D =
а11 а12
а21 аМ
^1П
а2п /О,
ani ап% ••• апп
находится по формулам
Xi~Di/D\ x^-D^/D' •••> Хп~Вп[В'
В этих формулах D—определитель системы, a Dk(k=l, 2, ..., п)—определи-
тель, полученный из определителя системы заменой /г-го столбца (т. е. столбца
коэффициентов при определяемом неизвестном) столбцом свободных членов:
Ли а12 ... al k^i bi al tt+i ... ai„
Dk= а21 а22 ••• а2, fc-t Ьг а2, ft + t ••• °2л
ani ат ••• ап, fe-t bn вц, k+i ... апп
383. Вычислить определитель
3 5 7 2 '
1 2 3 4
—2—332-
1 3 5 4 -
Д Произведем следующие действия: 1) из элементов 1-й строки вычтем
утроенные элементы 2-й строки; 2) к элементам 3-й строки прибавим удвоенные
Элементы 2-й строки; 3) из элементов 4-й строки вычтем элементы 2-й строки.
Тогда исходный определитель преобразуется к виду
D —
О —1 —2 —10
12 3 4
0 1 9 10
0 12 0
Разложим этот определитель по элементам 1-го столбца:
—2 —10
9 10
2 О
Прибавляя к элементам 1-й строки элементы 3-й строки и вычитая из эле-
ментов 2-й строки элементы 3-й строки, получим
О 0 —10
0 7 10
1 2 0
Разложим определитель по элементам 1-го столбца:
р=—1° ~1о|=—70-А
384. Вычислить определитель
12 0 0 0
3 2 3 0 0
0 4 3 4 0
0 0 5 4 5
0 0 0 6 5
Л Вынесем за знак определителя общие множители 2, 4 и 5-го столбцов:
Р = 2-2-5-
110 0 0
3 13 0 0
0 2 3 2 0
0 0 5 2 1
0 0 0 3 1
71
Вычтем из элементов 2-го столбца
элементы 1-го столбца н разложим полу*
ченнып определитель по элементам 1-й строки:
0 = 20
Г
3
О
О
О
0 0 0 0
—2 3 0 0
2 3 2 0
0 5 2 1
0 0 3 1
-2 3 0 0
2 3 2 0
0 5 2 1
0 0 3 1
Прибавим к элементам 2-й строки элементы 1-й строки, вынесем —2 (общий
множитель элементов 1-го столбца) за знак определителя, а затем разложим по-
лученный определитель по элементам Г-го столбца:
О = —40
1 3 О
0 6 2 0
6 2 0
5 2 1
О 3 1
0 5 2 1
0 0 3
Вычтем из элементов 2-й строки элементы 3-й строки, вынесем 2 (общий мно-
житель элементов 1-й строки) за знак определителя и разложим полученный опре-
делитель по элементам 3-го столбца:
О = — 80
3 1 О
5-10
О 3 1
= -80|s -1|=640- А
385. Найти у из системы уравнений
’ х-)-2^4-Зг= 14,
у+ 2г + 3/ = 20,
z 2t Зх = 14,
<4-2х4-3{/= 12.
/\ Запишем систему в виде
/ х4- 24/4- Зг4-0 / = 14,
0,*4- 4*4- 2*4- 31 = 20,
' Зх+0.{/4- г+ 2< = 14,
_ 2x4- Зу4-0-г4- 1 = 12.
Найдем
12 3 0
п- 0 1 2 3
3 0 1 2 •
2 3 0 1
Из элементов 2-го столбца вычтем удвоенные элементы 1-го столбца; из эле-
ментов 3-го столбца вычтем утроенные элементы 1-го столбца:
1 000
0 12 3
3—6—8 2
2—1—6 1
1 2 3
—6 —8 2
-1 -6 1
= (-2)(-1)
1 2 3
3 4-1
1 6 -1
Из элементов 2-го столбца вычтем удвоенные элементы 1-го столбца; из элемен-
тов 3-го столбца вычтем утроенные элементы 1-го столбца:
0 = 2
1 О
О
3 —2 —10
1 4 —4
= 2|-1 | = 2 (84-40) =96.
Находим
1 14 3 0 1 7 3 0
п — 0 20 2 3 — 9 0 10 2 3
У~~~ 3 14 1 2 — & 3 7 12-
2 12 0 1 2 6 0 1
72
Из элементов 3-й строки вычтем утроенные элементы 1-й строки; из элементов 4-й
строки вычтем удвоенные элементы 1-й строки:
7 3 0
^ = 2
10 2 3
— 14 —8 2
—8 —6 1
10 2 3
—14 —8 2
—8 —6 1
= 2-2-2
5 1 3
—7 —4 2
—4 —3 1
Из элементов 1-й строки вычтем утроенные элементы 3-й строки; из элементов
2-й строки вычтем удвоенные элементы 3-й строки:
0^ = 8
17
1
—4
10 О
2 О
—3 1
= 8|1р0|=192.
Отсюда у = Dy/D = 192/96 = 2. А
386. Вычислить определитель
1111
У__ abed
а2 Ь2 с2 d2
а3 Ь3 с3 d3
& Вычтем из 2-й строки 1-ю, умноженную на а; из 3-й строки 2-ю, умно-
женную на а; из 4-й строки 3-ю, умноженную на а:
1 1
О
0.
Ь—а
Ь2—ab
О b3—ab2
1 1
с—a d—а
с2—ас d2—ad
с3—ас2 d3—ad2
— (b—а) (с—a) (d—а)-
1 1 1
bed
b2 с2 d2
Вычтем из 2-й строки 1-ю, умноженную на Ь; из 3-й строки
вую иа Ь:
2-ю, умиожен-
V = (b—а) (с —a) (d—a)
1 1
О с—b
О с2— be
1
d—b
d2—db
V =
= (&—а) (с—а) (d—a) (c—b) (d—b) |
— (b—а) (с—a) (d—a) (c—b) (d—b) (d—c).
Нетрудно видеть, что рассматриваемый определитель равен нулю тогда и только
тогда, когда среди чисел a, b, с, d имеются равные. А
Вычислить определители:
1 —2 3 4 —1 —1 —1 —1
387. 2 1 3 -4 —4 —1 - 3 -2 388. —1 —2 —4 —8 —1—3 —9 —27 •
4 3 2 - -1 —1 —4 —16 —64
10 2 0 0 0
12 10 2 0 0 1 +a 1 1 1 1 - 1 1 1
389. 0 12 0 0 10 2 12 10 0 2 390. 1 1 —a 1 1 1 1-p 111 1 1
0 0 0 12 10 1 1 1 1 —0
Решить системы уравнений:
' у—3z-}-4/ = —5,
х—2z-|- 3t = — 4,
Зх+2у— 5t= 12,
k4x-|-3y—5z = 5.
392.
r x—3y-|-5z—7Z=12,
3x—5y+7z— t= 0,
5x—7y+ z—3t— 4,
„ 7x— y + 3z- ^ = 16.
73
393.
х-|- 2у = 5,
Зу+ 4z = 18,
5?+ би = 39,
7«+ 8ц = 68,
9t>+ 10х = 55.
394.
'2*4-3^—3z4-4f= 7,
2x4- У— z+2Z= 5,
6x4-2;/4- г = 4,
,2x4-3^—5f =—11.
§ 2. ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ И МАТРИЦЫ
С помощью равенств
х=апх'4-а12/(
£ = а21х'4-а22/
значения переменных х и у можно выразить линейно через значения переменных
х' и у'. Эти равенства принято называть линейным преобразованием переменных
х' и у'. Их можно рассматривать также как линейное преобразование координат
точки (или вектора) иа плоскости.
Таблица
л = / ап «12 \
\ ^21 ^22 /
называется матрицей рассматриваемого линейного преобразования, а определитель
Ол = |а“ аЧ
I «21 «22 I
— определителем линейного преобразования. В дальнейшем будем предполагать,
что Ьд 4 0.
Можно также рассматривать линейное преобразование трех переменных (т. е.
для пространства)*
х = ацх' 4- #13?',
у = fl2ix' 4- аггу’ + a23z',
z=a3iXr 4- азгУ' 4~«ззг,>
где
(«11 «12 «13\ аП а12 «13
£21 £22 «23 j и D д = а21 а22 £2з .
£31 £32 £зз' £з1 £32 азз
/ \ / Ли
f«и £12 \ „ I „
и £21
\ «21
Х«31
— соответственно матрица и определитель этого преобразования.
Матрица А называется невырожденной (неособой), если Эд / 0. Если же
Dz!=0, то матрица называется вырожденной (особой).
Матрицы
£12 а1з\
а22 «гз I
£32 £зз'
называются квадратными матрицами соответственно второго и третьего порядков.
Для большей общности ряд определений будет дан для матриц третьего по-
рядка; применение их к матрицам второго порядка не вызывает затруднений.
* Часто линейным преобразованием называют равенства более общего вида
х=апх' 4-auj/' 4-ai3z' ~-&i,
У = «21*' -г аг1у' 4- а23г' 4- Ь2,
z — £з1Х' 4- а3,у' 4- а33г' 4- Ь3.
Здесь рассматривается линейное преобразование, для которого Ьх = &2 = &3 = 0.
В курсах функционального анализа такое линейное преобразование называют
линейным оператором.
74
Если элементы квадратной матрицы удовлетворяют условию атп — апт, то
матрица называется симметрической.
Две матрицы
/аП а12 а1з’
Л=( fl21 fl22 ^23
\О31 а32 а33
/&ц &12
И В = ( ftgi &22
\&31 ^32
&1з\
&23 j
&зз/
считаются равными (А = В) тогда и только тогда, когда равны их соответствен-
ные элементы, т. е. когда атп=Ьтп (т, п=1, 2, 3).
Суммой двух матриц А и В называется матрица, определяемая равенством
^а11 а13 «1з\ /Ь11 ^12 ^1з\ /а11АгЬ11 £12 + ^12 а13*Ь&1з\
I а21 а22 а23 ) + ( &21 Ъгг &23 )=( ^2t+^21 а22 + ^22 ^гз + ^23 )•
'Оз! а32 а33' '^31 ^32 &33' \а31~Ь^31 а32 ~Ь ^32 ^33*Ь^ЗЗ'
П роизведением числа т на матрицу А называется матрица, определяемая
равенством
/аи а12 Л1з\ [matt malt
т I П21 ^22 ^23 ) = ( та%\ та%2
\Лз1 лз2 П33/ \та31 та32
та13\
тагз ).
та33/
Произведение двух матриц А
равенством
и В обозначается символом АВ и определяется
/ЯЦ Я12
АВ = 1 fl2t ^22
\Я31 а32
&t2 ^13'
&22 &23
&32 &33
2
J=l
3
2 в1Л2
j=l
3 3
2 2 a2j^j2
j=I j=l
3 3
2 аз^1 2 °зАг
(j=l j=l
т. e. элемент матрицы-произведения, стоящий в i-й строке и k-м столбце, ра-
вен сумме произведений соответственных элементов i-й строки матрицы А и k-eo
столбца матрицы В.
По отношению к произведению двух матриц переместительный закон, вообще
говоря^ не выполняется: АВ ?= ВА.
Определитель произведения двух матриц равен произведению определителей
этих матриц.
Нулевой матпиией называется матрица, все элементы которой равны нулю:
/О 0 0\
(ООО 1 = 0.
\о о о/
Сумма этой матрицы и любой матрицы А дает матрицу At Л + 0 = Л.
Единичной матрицей называется матрица
/1 ° °\
£= 0 10).
\0 0 17
При умножении этой матрицы слева или справа на матрицу Л получается
матрица Л: ЕА = АЕ = А. Единичной матрице отвечает тождественное линейное
преобразование: х — х', у —у', г —г'.
75
Матрица В называется обратной по отношению к матрице А, если произве-
дения АВ и ВА равны единичной матрице: АВ —ВА —В.
Для матрицы, обратной по отношению к матрице А, принято обозначение
Л-1, т. е. S —Л~х.
Всякая невырожденная квадратная матрица А имеет обратную матрицу. Об-
ратная матрица находится по формуле
/ Atl/DA A21/Da Лз1/Од\
Л-1 =4 Ah/Da A22/D д A32/Da \
'Ли/D^ A23/Da A33'D а/
где Атп—алгебраическое дополнение элемента матрицы атп в ее определителе,
т. е. произведение минора второго порядка, полученного вычеркиванием /л-й строки
и и-го столбца в определителе матрицы Л, иа (—1)'”+".
Матрицей-столбцом называется матрица
Mi\
Х=( х2 1.
\х3/
Произведение АХ определяется равенством
/Оц 012
Л X — ( а21 а22
'°31 а32
a13\ /Xl\ /аПХ1 -ЬЙ12Л'2"Г
й23 Х2 1=4 й21^-1 ”!~й22'^2 ~ГЙ23-^3
Йзз4 \Хз/ \аз1Х| -\-а32х2 4-аззЛ'з
Система уравнений
( ай*1 + й1г*г + а13*з = ^1.
ч a2ixi -f-o22x2 -|-а2ЯХз = Ь2,
' й31*1 + а32х2+а33х3=^3
может быть записана в виде АХ —В, где
fati а12 а13\ /х,\ fbi
Л=^ Й21 а22 а23 к Х = ( х2 1, В — ( Ь2
хоз! Оз2 а33/ \х3/ \4>з
Решение этой системы имеет вид Х — А~1В (если DA # 0).
Характеристическим уравнением матрицы
аи а12 а13
°2i а22 а23
Оз1 а32 а33
называется уравнение
Корни этого уравнения Xi, Х2, Х3 называются характеристическими числами
матрицы; они всегда действительны, если исходная матрица является симметричес-
кой.
Система уравнений
(Оц — X) £1 4-012^2+ й13?»== О»
a2ti»l -|- (а22 — ?2 й23ъ3 ~
аз111-|-азг^2-|- (а33 — X) ёз = 0,
в которой X имеет одно из значений Xf, Xj, Х3 и определитель которой в силу
этого равен нулю, определяет тройку чисел (gi; g2; g3), соответствующую дан-
ному характеристическому числу.
76
Эта совокупность трех чисел (Jt; £t; £3) с точностью до постоянного множи-
теля определяет ненулевой вектор r = |ii + 52J + 5sk, называемый собственным
вектором матрицы.
395. Дано линейное преобразование х=х' + у' + г', у = х' + у',
г = х’ и даны точки в системе координат х', у’, г’: (1; —1; 1),
(3; —2; —1), (—1; —2; —3). Определить координаты этих точек в
системе х, у, г.
Подставив координаты точек в равенства, определяющие данное линейное
преобразование, получаем: если х' = 1, у'=—1, г' = 1, то х = 1, у = 0, г=1,т. е.
(1; 0, 1); если х' = 3, у' =—2, г' = — 1, то х = 0, у — 1, г = 3, т. е. (0; 1; 3); если
х'=—1, у' ——2, г'=—3, то х = —6, у ——3, г =—1, т. е. (—6; —3; —1). А
396. Написать линейное преобразование предыдущей задачи для
перехода от координат х, у, г к координатам х', у , г'.
Л Имеем x' = z (из третьего равенства); у' =у—г (вычитаем из второго ра-
венства третье); г'=х—у (вычитаем из первого равенства второе). Д
397. Дано линейное преобразование х — х' + 2у', у = Зх' + 4/.
У каких точек оно не меняет координат?
Д Нужно иайти х и у, если х = х', у = у', т. е. х = х+2у, ^ = Зх+4^. Сле-
довательно, х=х' = 0, у = у' = 0. А
398. У каких точек линейное преобразование х = 3х'—2г/', у =
= 5х' —4у не меняет координат?
Д Имеем х = 3х—2у, у = 5х—4у. Следовательно, х — у = х' =у', т. е. линей-
ное преобразование не меняет координат у точек (/; t) с одинаковыми координа-
тами. А
399. Найти сумму матриц
А
/3+1
Д л+в= 2+2
<4-1
/3 5 7\ Г 1 2 4\
= 2—1 0 , В —( 2 3 —2 .
<4 3 2/ <—1 0 1/
5 + 2 7+4\ /4 7 ИХ
— 1+3 0—2 = 4 2 —2 . А
3+0 2+1J <3 3 3/
400. Найти матрицу 2А + 5В, если
л = (43?). в-(?4).
Д2Л_(И), »-('?_;§), «+»-(!* Л). А
401. Найти произведения матриц АВ и ВА, если
/1 3 1\ /2 1 0Х
Д = 1 2 0 4 , 5=1—12.
<12 3/ <3 2 1/
/Ь2+3-1 + 13 Ы+3(—1)+1-2 1-0+3-2+1-1Х /80
Д ЛВ = 2-2+0-1+4-3 2-1+0(—0 + 4-2 2-0+0.2+4-1 )= 16 10
\1.2 + 2-1+3-3 Ы+2(—0 + 3-2 1-0+2-2+3-1/ <13 5
/2-1 + 1-2 + 0-1
ВЛ = 1-1 —1-2+21
<3-1+2-2+11
2-3+10 + 0.2 2.1 + 1-4+0-3\ /4 6 6\
1.3—1.0+2-2 1-1 —1-4+2-3 >=( 1 7 3).
3-3+2.0+1-2 3-1+2-4+1-3/ <8 11 14/
Л
4 ),
7/
77
402. Найти А3, если A = (i 4).
Л л2_/3 2Л /3 2\_/9 + 2 6+ 8\_/11 14\
Л л “<1 4J <1 4;-<3 + 4 2+ 16/ ~ < 7 18/’
лз_л2 л_/П 14\ /3 2\ /33+14 22 + 56\_/47 78\ А
л -а а-^ 7 18д j 4;-^21 + 18 14 + 72J “<39 86/ А
403'. Найти’ значение матричного многочлена 2А2 + 34 + 5£’ при
/1 1 2\
= (1311, если Е—единичная матрица третьего порядка.
/1 1 2\ /1 1 2\ /10 6 5\ /20
А А2 = 13 113 1= 8 11 6 , 2Л2 = 16
\4 1 1/\4 1 1/ \ 9 8 10/ \18
/ 3 3 6\ / 1 0 0\ /5 0 0\
ЗЛ = 3 9 3 , 55=5 0 1 0 = 0 5 0,
\12 3 з/ \0 0 1/ \0 0 б/
/28 15 16\
2А2+ЗЛ+5£= 19 36 15 . к
\30 19 28 J
12 10\
22 12 ,
16 20/
404. Даны два линейных преобразования х = а1Гх' + ai2y', у =
= а^х' + а22у' и х'=&nX’ + &tay', У' ^Ь^х” + Ьг2уя. Подставляя х' и
у' из второго преобразования в первое, получим линейное преобра-
зование, выражающее х и у через х' и у". Показать, что матрица
полученного преобразования равна произведению матриц первого и
второго преобразований.
Д Имеем
х = аи (Лцх’+bijt/")+а12 (^21х’+йггУ*) = (aii^ii+ °i2^2i) ^’+ (an^ia+^ia^s) У*.
У = а21 (ЛцХ" —|- &12у") + 4722 (&21*’+ Ь22у") = (ацЬц +<>22^21) X* + (<>21^12 + а22^2») У*•
Матрица полученного линейного преобразования имеет вид
/ ЯцЬ11+й12&21 а11Л12 + Я12&22 \
\П21Ь11 + а22&21 °21^12+а22^22 /
т. е. она является произведением матриц 1 1 и , . А
\°2i «22/ \&2i Ъгг) m
/ □ 2, 2\
405. Дана матрица А=( 1 3 11. Найти обратную матрицу.
\5 3 4/
Д Вычисляем определитель матрицы Л:
3 2 2
рл= 1 з j =27+ 2—24 = 5.
5 3 4
Находим алгебраические дополнения элементов этого определителя:
^11 — |з4| = ^’ ^21 = —
Л12 = —| 5 I [ = 1, А22 =
=—2, Л31= =—4,
__2 _____ 3 2 __ ।
— *» Л32-----| | — —1>
Л13 = |‘ 8|=—12, Ли=-|^| = 1, Л33 = |^| = 7.
Следовательно,
/ 9/5 —2/5 —4/5\
Л-! = ( 1/5 2/5 —1/5 ). А
\—12/5 1/5 *7/5/
78
408. Решить систему уравнений
2x+3j/4-2z = 9.
х-\-2у—Зг=14,
Зх-|-4у+ г—16,
представив ее в виде матричного уравнения.
Д Перепишем систему в виде АХ = В, где
/2 3 2\ .'х\ / 9\
Л = I 2 —3 Х = ( у \ В=[ 14 .
\3 4 1/ \г/ \16/
Решение матричного уравнения имеет вид Х = А~1В. Найдем Л-1. Имеем
Da =
2-3 2
1 2 —3
3 4 1
= 28 —30— 4 = —6.
Вычислим алгебраические дополнения элементов этого определителя:
. 12 —31 1Л . 3 2 к . 13 21
Лц = |4 ] | = 14, Л21 =— 4| —5, Л31 —12 _3|---13,
Л12 = —|з =-Ю, Л22= з 2 =—4, Л32 = — | f _?| =8,
Таким образом,
, / 14 5 —13\
Л-‘= —4-1 —10 —4 8 1,
6 \ —2 1 1 /
откуда
. / 14 5—13\/ 9\ . / 126+70—2084 . /—12\ / 2\
Х = -4- —10—4 8 14 =—4- —90—55+128 =—4- —18 = 3 .
6 \ —2 1 1Д16/ b 18+14+16 ) 12/ \—2/
Следовательно, х = 2, </ = 3, z =—2. А
407. Дана матрица (43). Найти ее характеристические числа и
собственные векторы.
Д Составляем характеристическое уравнение
j57X3_\|=°- нли (5—Х)(3 —л)—8 = 0, т. е. Z2—8/+7 = 0;
характеристические числа = 1, Х2 = 7. Собственный вектор, соответствующий
первому характеристическому числу, находим из системы уравнений
( (5-X1)g; + 2j2 = 0,
I 4g;+ (3-1052=0;
так как 11 = 1, то и £2 связаны зависимостью 2g[ + g; = 0.
Полагая g;=a(a^0—произвольное число), получаем |^ = —2a и собствен-
ный вектор, соответствующий характеристическому числу lt= 1, есть Г! = а1—2aj.
Найдем второй собственный вектор. Имеем
j (5—12) si + 2c2 =0,
14g;+(3-12) g;=o.
79
Подставив значение Х2 = 7, приходим к соотношению cj—£2 = 0. т.е. Ь =
= Й = ₽# 0. Собственным вектором, соответствующим второму характеристиче-
скому числу, служит r2 = ₽i + ₽j. Д
408. Найти характеристические числа и собственные векторы
/ 3 —1 1\
матрицы ( — 1 5 —1 \
Д Составляем характеристическое уравнение
3—X
— 1 5—X
—1 3—X
-1 =0,
1
или
(3—X) [(5—X) (3—X)—1] + (— 3+Х+1) + (1— 5+Х) = 0.
После элементарных преобразований уравнение приводится к виду (3—X) (X2 —
— 8Х-1- 12) =0, откуда Х] = 2, Х2 = 3, Х3 = 6.
Находим собственный вектор, соответствующий характеристическому числу
Xi = 2. Из системы уравнений
Z — £г+£з = 0,
| -61'+з&-&=о,
X £1— 5г+£з = О
(одно из уравнений этой системы есть следствие двух других и может быть от-
брошено), получим g2=0, = —gi. Полагаем £i=a, тогда £2 = 0, gs = —а и
ri = ai—ak.
Находим собственный вектор, соответствующий значению Х2 = 6, Получаем
систему уравнений
( -?;+ fe'=o,
I -Й4-2Й-Й = 0,
I Ь'-Й=о
(одно из этих уравнений—следствие двух других). Отсюда Ь —£з = £з = Р и г2 =
= pi + pj + ₽k.
Находим собственный вектор, соответствующий значению Х8 = о. Составляем
систему уравнений
/ -3gl”-1г" + Ь'"=о,
•I —Si —ёг — |з =0,
v Ь —it —3|з =0
(снова одно из уравнений—следствие двух других). Решая эту систему, находим
it”= — 2у, £з” = Т и г3 —yi — 2yj + yk.
Итак, собственные векторы заданной матрицы имеют вид ri = a(i — к); г2 =
— р (j_|_j_|_k); r3 = y(i— 2j—к), где a, р, у—произвольные отличные от нуля
числа. А
409. Даны два линейных преобразования х — апх'-j-а12у'+ а13г',
у = a21x' + а22у’ + a23z’, z = a31x' + а32у' + a33z'; х' = b^x" + b12y" + b13z",
y' = b21x" + b22y' + b23z", z' = b31x" + b32y" + b33z". Подставляя x', у и
z' из второго преобразования в первое, получим линейное преобра-
зование, выражающее х, у, г через х", у", г". Показать, что мат-
рица полученного преобразования равна произведению матриц пер-
вого и второго преобразований.
80
410. Дано линейное преобразованиех = 6х'4- у'—2z' ,у — —18х' 4-
4-2у' + &z', z = 2х' + 2у . Координаты каких точек удваиваются в
результате этого преобразования?
411. Даны два линейных преобразования: х = х’ -^у' -т2г', у =
— х'+ 2у'+ 6г', z = 2x'-гЗу'-, x — 2x' + 2z', у — х'-^Зу'-[-4г', z —
= х' + Зу' + 2z'. Найти точки, для которых каждое из этих преоб-
разований дает один и тот же результат.
412. Найти точки, координаты которых не меняются при при-
менении линейного преобразования х — х cos а—у' sin а, у' = х' sin а-f-
4- у' cos а.
413. Найти множество точек, координаты которых меняются ме-
стами при применении линейного преобразования х —x'cosa—
— у'sin а, у — х sin а -f- у cos а.
/5 8 4А
414. Дана матрица Д=\ 3 2 5 Какую матрицу В нужно при-
\7 6 0'
бавить к матрице А, чтобы получить единичную матрицу?
/2 1 1\
415. Дана матрица А—- ^1 2 | Найти сумму матриц Д2 4- zl -\-Е.
/10 20 —30\
416. Дана матрица Д = ^ 0 10 20 j. Найти обратную матрицу.
417. Решить систему уразнений
( Зх + 4у= 11,
I 5у + 6г = 28,
( ж 4-2г = 7,
представив ее в виде матричного уравнения.
418. Найти характеристические числа и нормированные собст-
венные векторы матрицы (5 б)-
419. Найти характеристические числа и собственные векторы
/1 1 ЗУ
матрицы U 5 1 ).
f 3. ПРИВЕДЕНИЕ К КАНОНИЧЕСКОМУ ВИДУ ОБЩИХ УРАВНЕНИЙ
КРИВЫХ И ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА
Выражения вида
«ll'-'3-r2<’12*y-r<’22.V'2
И
Оцх24- о2,у2 -и o33z2 4- 2<»t,xi/4- 2в, Зхг 4- 2aMyz
называются квадратичными формами соответственно от двух и трех переменных.
Симметрические матрицы
Л(2у / Oil \
г — . где я21 = я1?,
\ а21 а-22 /
и
/аи. °12 а1л\
Дз*— I в»1 я22 fl23 .» где ^21 = 012. И й32=^23-
\я31 а и о33/
называются матрицами этих форм.
81
Квадратичные формы с помощью линейного преобразования переменных можно
преобразовать к виду, не содержащему произведений новых переменных (при-
вести, как говорят, к алгебраической сумме квадратов); иными словами, квадра-
тичная форма двух переменных может быть приведена к виду Xix'24-?.2z/'", а
квадратичная форма трех переменных — к виду 'к1х'г-\-'к^у'г-\-'к3г'~.
Для того чтобы коэффициенты при xj были характеристическими числами,
линейное преобразование должно быть произведено следующим образом: опреде-
ляют тройку (для квадратичной формы двух переменных—пару) нормированных
попарно ортогональных собственных векторов, соответствующих характеристичес-
ким числам Xj, Xj, Х3:
e^aJ + PiJ + Yik,
е2 = a2i 4- fJ2i 4- y2k,
ез = аз' + Зз)+Уз1<-
В силу нормированное™ и ортогональности векторов ех, е2, е3 должны выпол-
няться тождества:
a?+?‘+Vi = l (* = 1. 2, 3); ajay+PfPy+vrYy=0 (i, j = l, 2, 3, i # у).
Тогда матрица преобразования переменных имеет вид
/ CCj CCg GCg\
s=( Pl P2 Ps ;
\yi Yi Уз/
иными словами, надо положить
х = aix' -j- a2i/' 4- «зг'.
У — Pi-x+PsV' 4-Рзг',
z = yix'4-y#4-Ysz'
(для случая двух переменных все формулы соответственно упрощаются). Такое
преобразование переменных носит название линейного ортогонального преобразо-
вания: в этом случае определитель матрицы S равен ±1: £>$=±1.
Линейное ортогональное преобразование используется для приведения к ка-
ноническому виду общего уравнения кривой илн поверхности второго порядка,
причем если хотят сохранить взаимную ориентацию новых координатных осей, то
налагают на матрицу преобразования S дополнительное условие: D$—l.
Преобразование уравнения кривой или поверхности второго порядка к кано-
ническому виду производят следующим образом:
а) находят то линейное ортогональное преобразование координат, которое
приводит квадратичную форму старших членов уравнения кривой или поверхно-
сти к сумме квадратов, и выполняют в уравнении соответствующую замену.
В результате этого преобразования из уравнения исчезают члены с произведе-
ниями координат;
б) производя после этого параллельный перенос новых осей координат (в про-
странстве иногда приходится, кроме того, делать дополнительный поворот двух
осей в одной нз координатных плоскостей), приводят уравнение к требуемому
каноническому виду.
420. Привести к каноническому виду уравнение кривой
5х2 4- 4ху 4- 8у2 — 32х—56г/ 4- 80 = 0.
А В данном случае матрица старших членов имеет вид А = в)‘ достав-
ляем характеристическое уравнение матрицы:
|5уХ 82J=°. т- е. X2—13X4-36 = 0.
8)
Находим характеристические числа Xi = 4, А2 = 9. Полагая Xi=4, для опре-
деления соответствующего собственного вектора получаем систему уравнений
J li + ^s=0,
I 2Ь+4В„ = 0.
Отсюда £!==—2£2; полагая _|2 =—а, находим 51 = 2а и г2 = а(21—j). Нормируя
вектор Г1, имеем e1 = (2/pr5) i—(Г/Кб) J.
Полагая 7^—9, для определения второго собственного вектора получаем си-
стему уравнений
/ —41,14* 2т}2 = О,
1 2т)1-- Па = °-
Отсюда i]s = 2r]f и rs = P(i-|-2j). Нормируя, определяем е2=(1/Кб)4 4-
4-(2/Кб)). Легко проверить, что скалярное произведение е1-е2 = 0, т. е. век-
торы ej и е, ортогональны.
Используем собственные нормированные ортогональные некторы для построе-
ния матрицы преобразования координат
S = f DS-I.'
k-l/KS 2/К5 )
Отсюда
х = (2//Т) х' 4-(1 /Кб) у', у = (-1/Кб) х' 4-2/(К5")У'-
Найденные для к и у выражения подставим в уравнение кривой:
2 , , 1 , ./ 2 , , 1 ,\ / 1 , 2 X .
5 I ~ г— хЧ->=• У +4 I ~7-' х' 4-7=- У 1 I--7= * Н---7= У 1 +
\Кб Кб / \Кб Кб Д Кб Кб /
(1 2 \2 / 2 I \ / j
“3Ч7Г’’+7Т!'')-“(-7Г''+
+7Г’')+М“’’
откуда после раскрытия скобок н приведения подобных членов получим
4х'2 4- 9(/'2-Д=- *'-у' 4- 80=0.
Кб Кб
Заметим, что в преобразованном уравнении коэффициентами при х'2 и у1*
оказались (как и следовало ожидать) характеристические числа kj и А*. Перепи-
шем уравнение в виде
4(х'2-у^ х')+9 (у,2~ТТ у') 4-80=0.
Выражения в скобках дополним до полных квадратов:
4(х,2_'А’х'+т_т)+9(у,2~тту,+¥-¥)+80=0’
\ У 5 о о у у 5 о о у
кли
4^ —’ y_4+9f/—А.
\ Кб/5 \ Кб
8_ф+80=0,
или окончательно
/ 1 V / 8 Xs
4 ( х'---Аг) 4-9 (К--------7=-) =36.
\ Кб / \ Кб /
Произведем параллельный перенос осей координат, полагая х* = *' — 1/Кб,
у" —у'—8/Кб; получаем 4х"24-9у’г = 36, или х*2/94-К2/4= 1 (каноническое
уравнение эллипса). Д
«3
421. Привести к каноническому виду уравнение кривой
9х2 4- 24ХД/+ 16д/* — 230х+ ПОд/—225 = 0.
Л Характеристическое уравнение имеет вид
|9~Х 1=0. или Х2-25Х = 0, т. е. ^ = 0, Ь2 = 25.
I 12 1о—Л |
При Х = 0 получаем систему
f 9&14-12^ = 0,
I 12^4-16^=0.
Каждое из этих уравнений сводится к уравнению 5i/4 = 5s/(—3). Следовательно,
собственным вектором матрицы служит вектор r = a(4i—3j), а при а =
= 1/У4г + (—3)2=1/5 находим собственный нормированный вектор ef = (4/5) 1 —
~(3/5)j.
Прн X = 25 получаем систему
/ —16t]j4-12Пз==0,
( 12г)!— 9г]2 = 0.
Из этой системы аналогичным образом находим второй собственный нормирован-
ный вектор е2 = (3/5) i-J-(4/5) j (ei-e2 = 0).
Матрица преобразования координат имеет вид
s-(_3/s ijt)
формулы преобразования х=(4/5)х'4-(3/5)у', у — (—3/5)х'4*(4/5)у'.
Переписав уравнение кривой в виде
(3x4-4^)2—230x4-110^—225=0,
перейдем к новым координатам:
25^-230 f J-х'4-J y'Vllof-|x'4-| x'V225 = 0 .
D у у D D. /
После приведения подобных членов и сокращения на 25 приходим к уравне-
нию
у'2—10х'—2у'—9 = 0.
Последнее уравнение можно переписать в виде (у'—1)*= 10(x'-j-1). Произведя
параллельный перенос осей, примем за новое начало координат точку О'(—1, 1).
В итоге приходим к каноническому уравнению заданной кривой у"2=10х’ (пара-
бола). Д
422. Привести к каноническому виду уравнение поверхности
Зхг 4- 5у2 4- Зг2 — 2ху + 2хг — 2уг — 12х — 10 = 0.
А Здесь матрица старших членов уравнения поверхности имеет вид
/ 3 —! 1\
( -1 5-1 );
\ 1 -1 3/
характеристические числа матрицы определяются из уравнения
3—X
— 1
1
— 1 1
5—X —1
— 1 3—X
которое приводится к виду (3—X) (^2—81-j-12) = 0; отсюда находим 11 = 2, Х2=3,
Хд = 6.
84
При 1 = 2 получаем систему
/"U|—it24~«s = 0.
1 —U|-|"3u2—Ug = O,
Иг 4-И8 = О.
Указанному значению X соответствует собственный вектор (а; 0; —а). После
нормирования приходим к вектору e1 = (l/pr2) i — (l/|^2)k.
При 1 = 3 получаем систему
( — vs + v2 = 0,
1 — t>i4-2t'2—1'3 = 0,
( t'j—vs=0.
Отсюда находим второй собственный нормированный вектор es = (l/V3)i +
4-(1/У^З) F^3) к. Векторы ех и е2 ортогональны: ере2=0.
При 1 = 6 получаем систему
{—3a>j—a>s4- «’з = 0.
— а>!—wt— и>3 = 0,
а>!—wt—Зи>з==0.
Соответствующим собственым нормированным вектором (третьим) служит вектор
е, = (1/ргб’) I — (2/У^в} j4~(l/Vr6’)к, который ортогонален векторам ei и е^
e1-e8=0, е2-е8 = 0. Находим матрицу преобразования координат:
/ 1/V2 1/Кз i/Kf\
S=l о 1//3 — 2/|/*6 )
\- 1/V2 I/Уз 1/Уб)
Отсюда получаем формулы преобразования координат:
х = (1//2)х'4-(1/К^)у'4-0/Кб’)£. 4’ = (1/КЗ)у'-(2/Кб')2\
г = (-1/К2)х'4-(1//3)у'4-(1/Кб)2'.
Подставив выражения для х, у и г в уравнение поверхности, после упрощений
получим
2х'*4-3у'24-6г'2—б/Тх'—4КЗ у'—2/б г' —10=0.
Коэффициентами при х'2, у'2, г'2, как и должно быть, являются соответствеи-
о числа 11, 12, 18. Перепишем уравнение в виде
2 fx'2--£=х' Wsf у'2----£=у' Vefг'2-----Д=-2Л = 10,
\ /2 ) V /3 / \ Кб /
что после дополнения выражений в скобках до полных квадратов дает
/ 3 \2 / 2 \2 / IX®
2( х'——) 4-3 ( у' —) 4*6 ( 2'—-7=.) =24.
\ 2) V /3 / \ ^6)
Произведя параллельный перенос осей координат по формуламх'=х’4-3/}^2’»
=у"4-2// 3 , г' = г’4*1/)^6 и разделив уравнение на 24, приходим к канони-
ческому уравнению эллипсоида х’2/124*у"2/8 4-г'2/4= 1. А
Привести к каноническому виду уравнения кривых:
423. 5х34~ 6ху4-5«/2—16х—16у—16 = 0.
424. 7х24-16ху — 23у* — 14х— 16у — 218 = 0.
425. х*-]-2ху + уг—8x4-4 = 0.
Привести к каноническому виду уравнения поверхностей!
426. х2 4- 5^2 4- z2 4- 2x^4- 6xz 4- 2уг — 6 = 0.
85
ф Формулы преобразования координат: x = (l/J/"3) х'(1 / ) г'.
i,= _(l/Vry)x'H-(2/J<6).I/', г = (1/КЗ’)л-' + (1/Кб)/-(1,У'2)г'.
427. 2.V2 + У2 + 2z2 — 2ху — 2yz -f- х — 4у — 3z + 2 = 0.
ф Формулы преобразования координат: х =—(1/^6 ) х'— (1/}^2 ) у’-J-
+ (1/ГЗ) г', х'=х"; р=-(2/Гб)_х'-(1/КЗ)г', /=у"+1/К2’; * =
= -(l/Kb)x' + (l/K2)y' + (l/K3)z', 2' = г"+1//3.
§ 4. РАНГ МАТРИЦЫ. ЭКВИВАЛЕНТНЫЕ МАТРИЦЫ
Дана прямоугольная матрица
/ °11 Я12 • • • Я1Л
\ °21 °22 • • • а2П
I ........................
\^/я1 ^/»2 • • • атп
Выделим в этой матрице k произвольных строк и k произвольных столбцов
(£<т, Л<«)- Определитель k-ro порядка, составленный из элементов матрицы
А, расположенных на пересечении выделенных строк и столбцов, называется
минором k-ro порядка матрицы А. Матрица А имеет С^.С* миноров k-ro порядка.
Рассмотрим всевозможные мнноры матрицы А, отличные от нуля. Рангом
матрицы А называется наибольший порядок минора этой матрицы, отличного от
нуля. Если все элементы матрицы равны нулю, то ранг этой матрицы принимают
равным нулю.
Всякий отличный от нуля минор матрицы, порядок которого равен рангу этой
матрицы, называется базисным минором матрицы.
Ранг матрицы А будем обозначать через г (А). Если г(Л) = г(В), то матрицы
А и В называются эквивалентными. В этом случае пишут А ~ В.
Ранг матрицы не изменится от элементарных преобразований. Под элементар-
ными преобразованиями понимают:
1) замену строк столбцами, а столбцов—соответствующими строками;
2) перестановку строк матрицы;
3) вычеркивание строки, все элементы которой равны нулю;
4) умножение какой-либо строки на число, отличное от нуля;
5) прибавление к элементам одной строки соответствующих элементов другой
строки.
/1 2 3 4 \
428. Определить ранг матрицы ( 2 4 6 8 1.
\3 6 9 12/
Д Все миноры второго и третьего порядков данной матрицы равны нулю,
так как элементы строк этих миноров пропорциональны. Мнноры же первого по-
рядка (сами элементы матрицы) отличны от нуля. Следовательно, ранг матрицы
равен 1. А,
/1 0 0 0 5
429. Определить ранг матрицы I 0 0 0 0 о
\2 0 0 0 11
Д Вычеркнув из этой матрицы 2-ю строку, а затем 2, 3 и 4-й столбцы.
/1 5 \ ’ 115 1
получаем матрицу ( _ ), эквивалентную заданной. Так как „ =1^0, то
у 11j 1^111
ранг данной матрицы равен 2. А
/3 5 7\
430. Определить ранг матрицы Л=( 1 2 3 ).
\1 3 5/
вб
/\ Сложим соответствующие элементы 1-й и 3-й строк, а затем разделим
a i элементы 1-й строки:
/3 5 7\ /4 8 12\ /1 2 3\
А = ( 1 2 3 ) ~ I 1 2 3 ) ~ 1 2 3).
\1 3 5 У \1 3 5 У \1 3 5 J
Из элементов 1-й строки вычтем соответствующие элементы 2-й строки,
зосле чего вычеркнем 1-ю строку:
II 21
Ранг последней матрицы равен 2, так как, например, L 0. Следова-
тельно, и ранг данной матрицы равен 2. Д
/4
431. Определить ранг матрицы Л=(о
3 2 2\
2 11)
0 3 3/
Л Вычтем из элементов
вем 4-й столбец:
/4 3
Л= 0 2
\0 0
4-го столбца элементы 3-го
столбца, а затем вычерк-
2 2\ /432
1 1)~ 0 2 1
3 3/ \0 0 3
0\ /4 3 2\
О ) ~ 0 2 1 ).
Оу \0 0 3/
4
О
О
3
2
О
2
1
3
Так как
= 24^0, то ранг матрицы равен 3. Д
432. Определить ранг
и найти базисные миноры матрицы
/1 0 2 О 0\
А = о 1 0 2 0 )
\2 0 4 О 0 /
Л Имеем
/1 0 2 О 0\ /1 0 2 0\ /1 0 2 0\ /1 0 2 0\
0102 0)~ О 1 0 2 ~ О 1 0 2 ~ О 1 0 2)
\2 0 4 0 Оу \2 0 4 0/ \1 0 2 О/ \0 О О О/
Базисными минорами являются миноры второго порядка этой матрицы, отличные
ст нуля:
II 01 11 01 10 21 12 01 10 1) 10 21 11 01 10 21
|0 1 I’ 10 2| |1 Ор |0 2|’|2 0|>|2 0|’ |о 41> |4 0|
Таким образом, матрица А имеет 8 базисных миноров. Д
433. Сколько миноров второго порядка имеет матрица
/011 а12 013\
А = \ a-ц ам а-,3 .?
\О-1 о 32 O33J
Выписать все эти миноры.
Л Матрица имеет С3С3 — 3-3 = 9 миноров второго порядка:
I Оц а»з I IО21 о23 I I021 о231 | O12 <Т1з I
J O32 ОззГ I Q31 Озз Г I а31 О32 I ’ I Оз, О3з |’
oil 013 I I 011 012 I I 012 013 I I 011 013 I |оц 012
О31 O33 I ’ I O31 032 I I O22 O23 I I O21 O23 I ’ |o.2i O22
87
/. X 5Х —Х\
434. Определить ранг матрицы Л=1 2Х X ЮХ I.
\—X —2Х —ЗХ/
/1 2 3 6\
435. Определить ранг матрицы (2 3 1
/О 2 0 0\
436. Определить ранг матрицы ® 4J и найти ее базис-
ные мнноры.
/1 2 1 3 4\
437. Определить ранг матрицы А = 3 4 2 6 найти ее
базисные миноры.
§ 5. ИССЛЕДОВАНИЕ СИСТЕМЫ т ЛИНЕЙНЫХ УРАВНЕНИЙ С п НЕИЗ-
ВЕСТНЫМИ
Дана система т линейных уравнений с п неизвестными
' а11х1 + О12х2 + • • • +
, fl21*l + Я22Х2 + • • • + ОгпХп = Ь2, 0)
1-^1 2-^24~ • • • а mrixn = bmi
Решением этой системы называется совокупность п чисел (xt; хг; ...; хп), кото-
рые, будучи подставлены вместо неизвестных в уравнения, обращают эти уравне-
ния в тождества. Система уравнений называется совместной, если она имеет
хотя бы одно решение (xi; хг; ...; х„). Если же система не имеет ни одного
решения, то она называется несовместной.
Совместная система называестя определенной, еслиона имеет только одно решение,
и неопределенной, если она имеет больше одного решения.
Матрицы
(Оц 012 • • • “1л \ / Я11 а12 • • • «1л \
Я21 Огг ••• огп ] н Ai = | °21 °22 в2п I
ат1 ат2 ••• атп / \aml атг ••• атп bm J
называются соответственно матрицей и расширенной матрицей системы (1).
Для совместности системы (1) необходимо и достаточно, чтобы ранг матрицы
этой системы был равен рангу ее расширенной матрицы (теорема Кроне-
кера—Капелл и). Итак, система (1) совместна тогда и только тогда, когда
г (А) = г (Ai) = г. В этом случае число г называется рангом системы (1).
Если b-t — b2 = ... =Ьт = 0, то система линейных уравнений (1) называется
однородной. Однородная система уравнений всегда совместна.
Если ранг совместной системы равен числу неизвестных (т. е. г = п), то сис-
тема является определенной.
Если же ранг совместной системы меньше числа неизвестных, то система — неопре-
деленная. Остановимся на последнем случае. Итак, предположим, что система
(1) совместна, причем г < п. Рассмотрим какой-нибудь базисный минор матрицы А.
Выделим в этом миноре произвольную строку. Элементы этой строки являются
коэффициентами при г неизвестных в одном из уравнений системы (1). Эти г
неизвестных назовем базисными неизвестными рассматриваемой системы уравнений.
Остальные п—г неизвестных системы (1) назовем свободными неизвестными.
Выделим из системы (1) систему г уравнений, среди коэффициентов которых
содержатся элементы базисного минора. Базисные неизвестные в выделенной
системе оставим в левых частях уравнений, а члены, содержащие свободные
неизвестные, перенесем вправо. Из полученной системы уравнений выразим
88
базисные неизвестные через свободные неизвестные (например, по формулам
Крамера).
Таким образом, придавая свободным неизвестным произвольные значения,
можно найти соответствующие значения базисных неизвестных. Следовательно
(об этом уже сказано выше), система (1) имеет бесчисленное множество решений.
438. Исследовать систему уравнений
( Xi + 3x2 + 5x3-|-7x44-9x6 = 1,
1 Xj—2х24-Зх3—4х4 + 5х6 = 2,
\ 2х4-}~ 11х212хд 25х4-}~ 22х^ = 4.
Л Определим ранги матрицы и
расширенную матрицу
/1 3
Л1= 1 —2
\2 11
расширенной матрицы системы. Выпишем
5 7 9 1\
3 —4 5 2)
12 25 22 4/
Вертикальной чертой мы отделили элементы матрицы системы (матрицы А) от
свободных членов системы.
Прибавим к элементам 2-й строки соответствующие элементы 3-й строки, а
затем разделим все элементы 2-н строки на 3:
/13579
Ах~ 3 9 15 21 27
\2 11 12 25 22
1\ /1357914
6 ) ~ 1 3 5 7 9 2).
4/ \2 11 12 25 22 4/
Вычтем из элементов 2-й строки соответствующие элементы 1-й строки:
/1 3 5 7 9 1\ /1 3 5 7 9\ . з - _ q
АМ~ 0 0 0 0 0 1 ); А~ 0 о 0 0 0 )—(’ f ° 7 УХ
\2 11 12 25 22 4^ \2 11 12 25 22/ 11 12 20
Нетрудно видеть, что г (А) =2, r(Ai)=3, т.е. г (А) /г(Ах); следовательно, сис-
тема несовместна .А
439. Исследовать систему уравнений
Xj -|- 2х2 4* Зх3 = 14,
3xi4-2x2 + Хд = 10,
< Х1 -f- Х2 -f- Х3 = 6,
2xi + Зх2 — Хд — 5,
. Xi -}~ х2 == 3.
Л Расширенная матрица системы имеет вид
/1 2 3 14
/3 2 1 10
Л1= 1 1 1 6
\ 2 3 — 1 5
XI 1 0 3
Прибавим элементы 2-й строки к соответствующим элементам 1-й и 4-й строк
а затем разделим элементы 1-й строки на 4, а элементы 4-й строки на 5:
/4
/ 3
А1~ 1
\ 5
XI
4
2
1
5
1
4
1
1
0
0
24\ /1 1 1
10 \ /321
6 ~ 1 1 1
15 / \ 1 1 0
3/ XI 1 0
6\
1° \
6
3 /
3/
Вычтем из элементов 3-й строки соответствующие элементы 1-й строки, а из
ыементов 5-й строки вычтем, элементы 4-й строки; после этого вычеркнем 3-ю и
89
5-ю строки:
Al
(1 1
3 2
О О
1 1
О О
1
1
О
О
о
6\
10 X /1 1 1
О ~ 3 2 1
3 / \1 1 О
О/
/1 1 Г
А ~ 3 2 1
\1 1 О
Найдем определитель последней матрицы:
О 0 1
3 2 1
1 1 О
1 1 1
3 2 1
1 1 О
= 1 £ 0.
Следовательно, г(А)=3. Ранг расширенной матрицы также равен 3, так как
найденный определитель является минором матрицы Ах.
Итак, система совместна. Для ее решения возьмем, например, первое, третье
и пятое уравнения:
f *1+2*г + 3*з— 14,
•j *1 + *2 4* *3 = 6,
\ *1 + *2 = 3.
Отсюда легко находим, что *1 = 1, *2 = 2, *3 = 3. А
440. Исследовать систему уравнений
( *i 4* 5*2 4- 4*з 4- 2*4— 1*
I 2X1— *2 + 2*3 — *4=0,
у 5*14- 3*2 4- 8*з 4- *4 = 1.
Д Здесь /1 5 4 3 1\
Ai= 2 — 1 2 — 1 ° .
\5 3 8 1 1J
Вычтем из 3-й строки 1-ю: 4 5 4 3 1\
Ai ~ — 1 2 — 1 0 ].
— 2 4 — 2 0?
из полученной 3-й строки 2-ю;
Разделим элементы 3-й строки на 2 н вычтем
затем вычеркнем 3-ю строку:
Нетрудно видеть, что г (A) = r (А 0 =2. Следовательно, система совместна.
Возьмем первое и второе уравнения заданной системы:
( *i 4- 5*2 4- 4*з 4~ 2*4 = 1»
1 2*1— *24-2*з— *4=0.
За базисные неизвестные примем *1 н *□. Это можно сделать, так как опре-
1151
делитель | ___] из коэффициентов при этих неизвестных отличен от нуля.
Свободными неизвестными служат *3 и *4. Переписав систему в виде
*1 + 5*2 = 1 —4*з — 3*4,
2*1 —*2 — — 2*3 + *4,
00
сразим X] и х2 через х3 и х4:
II—4х3—Зх4 51
I —2хз+ *4 —11
ж,= м
11 1—4х3—Зх4|
I 2 —2х3-|-х4 I
6 8 1
и*з и*4 п»
6 , 7 , 2
- п'з+п^’н-
Полагая х3=и, х4=о, получим решение системы в виде
6,8 1 6.7,2
*1— — Ц *'”’”11 ° И’*2 —и> х4—V-
Придавая и и v различные числовые значения, будем подучать различные реше-
на данной системы уравнений. А
Исследовать системы уравнений:
441. <
к
442.
(
443. 1
Зх4 -|~ 2х3 — 4,
*1—4х2 = — 1,
7xi -|~ 10х2 = 12,
5x1-f-6x3 = 8,
3xi—16х2 = —5.
Xi -f- 5х3 -f- 4х3 = 1,
2xi Ч~ 10х2 -|~ 8х3 = 3,
3xi -|- 15х2 -|- 12х3 = 5.
Xi—Зх2 + 2хз = — 1>
Xi -f- 9х2 -f- 6х3 = 3,
Xi -f- Зх2 -f- 4х3 = 1.
( в. РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ МЕТОДОМ ГАУССА
Численное решение линейных алгебраических уравнений с помощью опреде-
лителей удобно производить для систем двух и трех уравнений. В случае же
систем большего числа уравнений гораздо выгоднее пользоваться методом Гаусса,
который заключается в последовательном исключении неизвестных. Поясним смысл
итого метода на системе четырех уравнений с четырьмя неизвестными:
anx+a]2p+ai3z+ai4w=ai5, (а)
а21*"Ь°22У_Ьа23г-Ьа24и =О25> (Ф
a3ix+a3ty -|- a33z+a34a = a33, (в)
. °41Х+°42У "Ь°43г+а44м =О45- (г)
Допустим, что an / 0 (если ац = 0, то изменим порядок уравнений, выбрав
первым такое уравнение, в котором коэффициент при х не равен нулю).
I шаг: делим уравнение (а) иа an, умножаем полученное уравнение на att
а вычитаем из (б); затем умножаем иа a3i и вычитаем из (в); наконец, умножаем
а a4i и вычитаем из (г). В результате I шага приходим к системе
*+зг 4~ bnU = blit (Д)
b33y-]- b33z -|- b3iu = b3i, (e)
bsiy+b33z -f- 634a = b33> (Ж)
ЬцУ + bt3z -f- 644a = 643, (3)
кричем bij получаются из a/у по следующим формулам:
6iy=aiy/an (/ = 2, 3, 4, 5);
6,y=a/y—a/Ay (i = 2, 3, 4; / = 2, 3, 4, 5).
II шаг: поступаем с уравнениями (е), (ж), (з) точно так же, как с уравне-
ниями (а), (б), (в), (г) и т. д. В итоге исходная система преобразуется к так на-
зываемому ступенчатому виду:
' Х + ^12{/"Т'^13г+
У+C23Z + c2iu — с23,
г + — dm
u=et!i.
Из преобразованной системы все неизвестные определяются последовательно без
труда.
444. Решить систему уравнений
( 36,47* + 5,281/ + 6,34г = 12,26, (а)
•! 7,33* + 28,741/+ 5,86г = 15,15, (б)
( 4,63х +6,311/+ 26,17г = 25,22. (в)
Д Разделив уравнение (а) на 36,47, получим
x + 0,1447t/+0,1738z = 0,3361. (*)
Умножим уравнение (*) на 7,33 и результат вычтем из (б); получим
27,6793t/+ 4,586г = 12,6864;
теперь умножим уравнение (*) на 4,63 и результат вычтем из (в); получим
5,64{/+25,3653г= 23,6639.
Таким образом, приходим к системе уравнений
( 27,67931/+4,586г= 12,6864, (г)
I 5,64t/+25,3653г= 23,6639. (д)
Разделив уравнеиие (г) на 27,68 имеем
у + 0,1657г —0,4583. (**)
Умножая уравнение (м) на 5,64 и вычитая из (д), получим 24,4308г=21,0791.
Следовательно, г = 0,8628. Тогда
у= 0,4583- 0,1657-0,8628 = 0,3153,
*•=0,3361—0,1447-0,3153 — 0,1738-0,8628 = 0,1405.
Таким образом, * = 0,1405, у = 0,3153, г = 0,8628.
Практически удобнее приводить к ступенчатому виду не саму систему урав-
нений, а матрицу из коэффициентов при неизвестных и свободных членов:
36,47 5,28 6,34 12,26\
7,33 28,74 5,86 15,15).
4,63 6,31 26,17 25,22 /
Введем 5-й, так называемый контрольный столбец, каждым элементом кото-
рого является сумма четырех элементов данной строки:
'36,47
7,33
Ч 4,63
5,28
28,74
6,31
6,34 12,26
5,86 15,15
26,17 25,22
60,35\
57,08 .
62,33 )
При линейных преобразованиях элементов матрицы такому же преобразованию
должны подвергнуться и элементы контрольного столбца. Нетрудно видеть, что
каждый элемент контрольного столбца преобразованной матрицы равен сумме
элементов соответствующей строки. Переход Ьт одной матрицы к другой будем
92
записывать с помощью знака эквивалентности:
36,47 5.28
7,33 28,74
. 4,63 6,31
6,34 12,26 60,35' \ /1 0,1447 0,1738 0,3361 1.6547
5,86 15,15 57,08 ~ 7,33 28,74 5,86 15,15 57,08
26,17 25,22 62,33 / \4,63 6,31 26,17 25,22 62,33
/1 0,1447 0,1738 ' 0,3361 1,6547\
0 27,6793 4,586 12,6864 44,9516 ~
V 5,64 25,3653 23,6639 54,6688/
/1 0,1447 0,1738 0,3361 1,6547\
0 1 0,1657 0,4583 1,6240 ~
\0 5,64 25,3653 23,6639 54,6688/
(\ 0,1447 0,1738 0,3361 1,6547 \ /1 0,1447 0,1738 0,3361 1,6547 \
'0 1 0,1657 0,4583 1,6240 - J 0 1 0,1657 0,4583 1,6240
/0 0 24.4308 21,0791 45,5094 / \0 0 1 0,8628 1,8629,
Используя полученную матрицу, выписываем преобразованную систему и нахо-
дим решение:
г = 0,8628,
у = 0.4583 — 0,1657-0,8628 = 0,3153,
х --= 0,3361 — 0,1738-0,8328 — 0,1447-0,3153 = 0,1405. ±
Если система имеет единственное решение, то ступенчатая система уравнений
приведется к треугольной, в которой последнее уравнение содержит одно не-
известное. В случае неопределенной системы, т. е. такой, в которой число неиз-
эестных больше числа линейно независимых уравнений, допускающей поэтому
бесчисленное множество решений, треугольной системы не получается, так как
юследнее уравнение содержит более одного неизвестного.
Если же система уравнений несовместна, то после приведения к ступенча-
тому виду она содержит хотя бы одно уравнение вида 0=1, т. е. уравнение,
в котором все неизвестные имеют нулевые коэффициенты, а правая часть отлична
от нуля. Такая система не имеет решений.
445. Решить систему уравнений
( Зх2i/г = 5,
{ х+у-г=0,
V 4*—{/+5г = 3.
А Преобразуем матрицу в эквивалентную:
1 5
— 1 0
5 3
11 \ /1
1 3
11/ \4
1
2
— 1
—1 0 1\
15 11)
5 3 11/
(для упрощения вычислений мы поменяли местами первое и второе уравнения).
Вычитаем из остальных двух строк 1-ю строку, умноженную на 3 п на 4:
— 1 0 1
4 5 8
9 3 7
Изменив знаки во 2-й строке и умножив ее на 5, прибавляем к 3-й:
/1 >
° I
\0 0
0
—5
— 22
1\ /1
-8 )~1 О
—33/ \0
1
1
о
— 1 0 1\
-4 _5 -8 )
1 2 3/
(мы разделили на —11 последнюю строку).
Система уравнений приняла треугольный вид:
х + у—г = 0,
У—4z= — 5,
г = 2.
93
Она имеет единственное решение. Из последнего уравнения имеем г=2; под-
ставляя это значение во второе уравнение, получаем у—3 и, наконец, из перво-
го уравнения находим х =— 1. А
Решить системы уравнений:
г 2xt+ Хг— х3 = 5,
446. J Х1-2х2+Зхз>»-3,
I 7X1+ ха— х3=10.
{3xi— ха+х3+2х3== 18$
2X1 —5х2+х4+ х5=—7,
Xi— х4 + 2х5=8,
2х2+х3+ х4— х6=10$
Х1 +х2—Зх3 + х4=1.
I 0,04х—0,08у+ 4г = 20,
450. ! 4х+0,24у—0,08г = 8,
I 0,09х+ Зу—0,15г = 9.
447.
449.
' xl+xz~ х3+ х4 = 4$
2xi —х2 + Зх3—2х4 = 1,
xt— х3 + 2х4 = 6,
. 3x1— ха + х3— х4 = 0.
4xi + 2ха + Зх3 —• —2,
2х1 + 8х2— х3 = 8,
9.<1+ х2 + 8ха = 0.
г 3,21х+0,71у+0,34г = 6,12$
451. < 0,43х+4,11у+0,22г = 5,71$
I 0,17х + 0,16у+4,73г = 7,06.
§ 7. ПРИМЕНЕНИЕ МЕТОДА ЖОРДАНА—ГАУССА К РЕШЕНИЮ
СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
При решении системы линейных уравнений методом Гаусса был рассмотрен
матричный метод с контрольным столбцом, в результате чего данная система
уравнений сводилась к треугольной ристеме (см. с. 92). Для последующего изло-
жения важно познакомиться с модифицированным методом Жордана—Гаусса,.
позволяющим находить непосредственно значения неизвестных.
Пусть дана система линейных уравнений
' оп Х1 + °1г х?+ ... +#inx„ =bi,
. Otl xl + fl22 хг+ . . • +a2«Xn = b2, 'll
, amlxl + am2X2+ ... -\-amnxn — bm.
В матрице А этой системы выберем отличный от нуля элемент апр. Этот элемент
называется разрешающим элементом, р-н столбец матрицы А—разрешающим
столбцом, а <?-я строка—разрешающей строкой.
Рассмотрим новую систему уравнений
' 011X1 +#12X2 + . . . +й1лХ„ = Ьц
fl21Xl -]~a-22x2 + • • • + fl2«Xn = fc2,
Omtxi + атгХг + ... + атпхп — Ьт
с матрицей А'; коэффициенты и свободные члены этой системы определяются по
формулам
, О/ „ Uq ] \
ail^ai'---
a- bP (’ если
В частности, a(y = 0, если ij=q. Если же i = q, то принимаем a'qj^aqj,
b'q — bq. Таким образом, q-e. уравнения в системах (1) и (2) одинаковы, а коэф-
фициенты при хр во всех уравнениях системы (2), кроме q-ro, равны нулю.
Следует иметь в виду, что системы (1) и (2) одновременно совместны или не-
совместны. В случае совместности эти системы равносильны (их решения совпадают).
Для определения элемента ац матрицы А' полезно иметь в виду так назы-
ваемое «правило прямоугольника».
Рассмотрим 4 элемента матрицы A: (элемент, подлежащий преобразова-
нию), вдр .(разрешающий элемент) и элементы а(р и a4j. Для нахождения эле-
мента a'ij следует из элемента а/у вычесть произведение элементов а,р и a4i, распо-
ложенных в противоположных вершинах прямоугольника, деленное на разрешаю-
щий элемент ai/p:
а
а
ij\............ia‘P
4j.............aqp
Аналогичным образом можно преобразовать систему (2), приняв за разрешаю-
щий элемент матрицы А' элемент £ 0, причем s Ф q, г р. После этого пре-
образования все коэффициенты при хг, кроме aSr, обратятся в нуль. Полученная
система может быть снова преобразована и т. д. Если г = п (ранг системы равен
числу неизвестных), то после ряда преобразований придем к системе уравнений
вида
^1*Т —^i>
^2^2 ~^2*
• • » • •
из которой находятся значения неизвестных. Описанный метод решения, основан-
ный на последовательном исключении неизвестных, называется методом Жордана —
Гаусса.
452. Дана матрица системы линейных уравнений
/5 4 6 —1 7\
. / 8 13 2 0)
0 15 3 —1
\7 —5 5 —4 3/
При решении этой системы методом Жордана — Гаусса за разрешаю-
щий элемент приняли а23 = 3. Найти элементы ам, а'13, а'и преобра-
заванной матрицы.
Д Так как a2i—элемент разрешающей строки, то ац=аи — 2. Элемент aJ3
принадлежит разрешающему столбцу; поэтому а13 = 0. Элемент ац определяем
по правилу прямоугольника:
5 4 6 — 1 7
8 1 | 3 |-2 О
О 1 И 3 -1
7 —6 5—-;—4 3
аи = ац
__a2iQj3_______.___2-5_______1_ »
агз ~ 3 ~ 3 •ж
453. Решить систему уравнений
(Xj + х2—Зл'3-3-2x4 = 6,
Xi — 2х2 — х4 =—6;
Л*2 Ц- Х3-[~Зх4=16,
2xi—Зх2-|-2х3 —6.
Д Запишем коэффициенты, свободные члены и суммы коэффициентов и сво-
бодных членов (S — контрольный столбец) в следующую таблицу:
95
Х1 Хг *3 Xi ь V
111 1 —3 2 6 7
1 —2 0 — 1 —6 —8
0 1 1 3 16 21
2 —3 2 0 6 7
Мы взяли за разрешающий элемент коэффициент при в первом уравнении.
Перепишем без изменения строку таблицы, содержащую этот элемент (разрешаю-
щую строку), а все элементы 1-го столбца, кроме разрешающего, заменим нулями.
Применив правило прямоугольника, заполняем остальные клетки таблицы (это
же правило применяем и к столбцу 2):
XI Хг х3 Ч b V
1 1 —3 2 6 7
0 —3 3 —3 -12 — 15
0 1 1 3 16 21
0 —5 8 —4 —6 —7
Отметим, что в контрольном столбце получаются суммы элементов соответст-
вующих строк. Разделив на —3 элементы 2-й строки, получаем таблицу:
Х1 Хг Хз Xi Ь 2
1 1 —3 2 6 7
0 111 — 1 1 4 5
0 1 1 3 16 21
0 —5 8 —4 —6 —7
96
Примем за разрешающий 2-й элемент 2-й строки. 1-й столбец перепишем без
измеиеиия, элементы 2-го столбца, кроме разрешающего, заменим нулями, 2-ю (раз-
решающую) строку перепишем без измеиеиия, элементы остальных клеток таблицы
преобразуем по правилу прямоугольника:
Xi *2 х3 xt b 2
1 0 —2 1 2 2
0 1 — 1 1 4 5
0 0 2 2 12 16
0 0 3 1 14 18
Разделим элементы 3-й строки на 2:
Xi х2 х3 Xi b 2
1 0 —2 1 2 2
0 1 — 1 1 4 5
0 0 111 1 6 8
0 0 3 1 14 18
Преобразуем таблицу, приняв за разрешающий 3-й элемент 3-го столбца:
Xi Хз x3 Xi b 2
1 0 0 3 14 18
0 1 0 2 10 13
0 0 1 1 6 8
0 0 0 —2 —4 —6
97
4-215
Разделим элементы 4-й строки на—2:
Хз *3 *4 ь ' 2
1 0 0 3 14 18
0 1 0 2 10 13
0 0 1 1 6 8
0 0 0 111 2 3
Преобразуем таблицу, приняв за разрешающий 4-й элемент 4 й строки:
*1 Ха *3 х* 2
1 0 0 0 8 9
0 1 0 0 6 7
0 0 1 0 4 5
0 О 0 1 2 3
В результате получим си ( 1 1 0 1 0 т. е. *1 = 8, х2=6, х3 = 4, Xj 454. Решить систему < Д Составим таблицу 1 5 1 "2 “ + + + + | Т 1 1 Т ® О О 7 о И S? Н О £ £ g to to to м ® eeeoaeeejj | | + | S + + + + g кэ 20е О О О Ф X Н >t Л Л 1 Л “ со со u to Н И К Н S lit! to to to се да Utt +++ + аь Й* *» ль м» Q Q о II 1 II II >< А £ * ~ -° ~ II II 0 II ЬЭ 4*. 05 00
И 1 —2 1 1 2
1 —3 1 1 0 0
4 —1 —1 —1 1 2
4 3 —4 —1 2 4
98
1-й элемент 1-го столбца — разрешающий:
1 1 —2 1 1 2
0 .—4 3 0 — 1 —2
0 —5 7 —5 —3 —6
0 —1 4 —5 —2 —4
Изменим знаки в 4-й строке:
1 1 —2 1 1 2
0 —4 3 0 —1 —2
0 —5 7 —5 —3 —6
0 1-1 —4 5 2 4
4-й элемент 2-го столбца — разрешающий:
1 . 0 2 —4 —1 —2
0 0 — 13 20 7 14
0 0 — 13 20 7 14
0 1 —4 5 2 4
Вычтем из 3-й строки 2-ю и вычеркнем 3-ю строку:
1 0 2 —4 —1 —2
0 0 —13 [Ml 7 14
0 1 —4 5 2 4
4-й элемент 2-й строки — разрешающий:
1 0 —0,6 0 0,4 0,8
0 0 —13 20 7 14
0 1 -0,75 0 0,25 0,5
Матрица имеет ранг, равный 3, следовательно, система содержит три базисных
неизвестных х4, х2 и х4 и одно свободное неизвестное х3. Получаем систему урав-
нений
г 1-Х1+(Ьх2—0,6xs + 0-x4 =0,4,
г 0-Xi-\-0-x2—13х, -|~20х4 =7,
I 0-Х1+Ьх2—0,75xs+0-x4 = 0,25.
Отсюда
х4 = 0,4 + 0,6х3, х2 = 0,254-0,75x3, х4 = 0,35 4-0,65xs.
Итак, решение системы имеет вид
х1 = 0,44-0,6«, х2 = 0,25-|-0,75и, х3 = и, х4=0,354-0,65«2
где и—произвольное число. А
455. Решить систему уравнений
' 6х— 5у4-7г4-81 = 3,
Зх4-11{/4-2г 4-4/=6,
3x4- 2у4-Зг4-4/ = 1,
Л Составим таблицу: х4- у4- г =0.
6 —5 7 8 3 19
3 11 2 4 6 26
3 2 3 4 1 13
III 1 1 0 0 3
4-й элемент 1-го столбца — разрешающий:
0 —11 ш 8 3 1
0 8 —1 4 6 17
0 —1 0 4 1 4
1 1 1 0 0 3
100
1-й элемент 3-го столбца — разрешающий:
0 —11 HI 8 3 1
0 —3 0 12 9 18
0 —1 0 4 1 4
1 12 0 —8 —3 2
Изменим знаки элементов 3-й строки на противоположные:
0 —11 1 8 3 1
0 —3 0 12 9 18
0 ш 0 —4 —1 —4
1 12 0 —8 —3 2
3-й элемент 2-го столбца—разрешающий:
0 0 1 —36 —8 —43
0 0 0 0 6 6
0 ш 0 —4 —1 —4
1 0 0 40 9 50
В результате приходим к системе
О-х+О.у+l-z—36/ = —8,
0-х4-0-у4-0-г4-0</=6,
0-х4-1-у4-0-г—4</=—1,
. 1-х+0-у4-0-г+40/=9.
Легко видеть, что второму уравнению не удовлетворяют никакие значения х,
у, г и /. Таким образом, полученная система уравнений и заданная система
«совместны. А
456. Применить метод Жордана—Гаусса к определению ранга
матрицы
7 —1 3 5\
1 3 5 7 ]
4 1 4 бу*
.3 —2 —1 —1/
101
Л Составим таблицу
7 —1 3 5 14
13 3 5 7 16
4 1 4 .6 15
3 —2 -1 —1 —1
В последнем (контрольном), столбце записаны суммы элементов соответствую*
щих строк, 2-й элемент 1 го столбца —разрешающий:
0 —22 —32 —44 -,98
1 3 5 7 16
0 —11 —16 —л22 —49
0 —11 —16 —22 —49
Разделим элементы 1-й строки на—2, вычтем элементы 1-й строки из соот-
ветствующих элементов 4-й и Эй строк и '.вычеркнем 3-ю и 4-ю строки. Тогда
получим
0 1 11 1 16 1 1 22 1 49
1 1 3 1 5 1 7 1 16
Любой определитель второго порядка полученной матрицы отличен от нуля.
Следовательно, г (А) =2
457.
Методом Жордана — Гаусса решить системы уравнений:
*1 + 2гг+ хз =8, / хг— *1+ Хз— Xi = —2,
х2-)-Зхз+ х4=15, ЛЧЯ J :2хэ—Xi=—5,
4х4 + х3+ Xf= 11, ‘ j .2х4— х2—Зхз + 2х4 = —1,
Х14- х2 -(-.йх^^.ЭЗ, A xi -J- 2х2 -J- Зх3—6х4 =—10.
{xj + 5х2 — 2хз—Зх4 = 1,
7xi + 2х2 — Зх3 —>4х4 — 2,
Xj-|- x2-j- Хз+ х4—.5,
2xi Ч- Зх2 2х3 —‘Зх4 =^4,
Х1— х2 — х3— х4 = —2.
460. Методом Жордана—Таусса определить ранг матрицы
/1 2 3 1\
I 2313]
I 3 1 2 5 J
\2 2 2 3/
ГЛАВА V
ОСНОВЫ ЛИНЕЙНОЙ АЛГЕБРЫ
| 1. ЛИНЕЙНЫЕ ПРОСТРАНСТВА
I. Основные-понятия. Рассмотрим такое множество R элементов х, у, ж, ...,
в котором для любых двух элементов н y£R определена сумма x+ygR и
для любого элемента x£R и любого действительного числа А определено произве-
дение Ax£R.
Если сложение элементов множества R и умножение элемента этого множества
иа действительное число удовлетворяет следующим условиям:
1°. х + у = у4-х;
2°. (х+у)4-я = х4-(у+1);
3°. существует такой элемент 0£R (нуль-элемент), что х4-0 = х для любого
x£R;
4°. для каждого элемента xg R существует элемент y£R такой что х+у = 0
(в дальнейшем будем писать у = —х, т. е. х+(— х)=0);
5». 1-х = х;
6’. А (рх) = (Ар) х;
7е. (А + ц)x = Ax-i-ux;
8°. А(х + у) = Ах-|-Лу,
то множество R называется линейным (или аакторомш) пространством, а элемен-
ты х, у, ж, ... этого пространства—векторами.
Например, множество всех геометрических векторов является линейным про-
странством, так как для элементов этого множества определены действия сложения
умножении на число, удовлетворяющие сформуллровваным условиям
Разностью двух векторов хну линейного пространства иаашиетс* такой
вектор v этого пространства, что y+v = x. Разность векторов хну обовиачают
через х—у, т. е. х—y=v. Легко доказывается, что х—у = х + (— у).
Справедливы также следующие теоремы:
1. В каждом линейном пространстве существует только одйн нумнзммвят.
2. Для каждого момента линейного пространства суиуеетвует только один
мротивоположный злемент.
3. Для каждого злемента x£R выполняетсяравенстео 0-х = 0.
4. Для любого действительного числа А и OfR выполняется-равенство А-0 = 0.
5. Из равенства Ах = 0 следует одно из двух равенств: А = 0 или х=О.
6. Элемент (— 1)-х является противоположным для злемента х
461. Имеется множество всевозможных систем действительных
чисел (£n ...; £„), Оъ; т),; . .; т)„), (U ••-;£.)..........Сум-
ма двух любых элементов определяется равенством (£>; gt; ...; ?„) +
+ 01.; И.; •••; Hn) = (5i + T|v 5» + п»: •••; 5» + n»). а произведение
любого элемента на любое число —равенством g,; ...; g„) =
= А?,; ...; Ag„). Доказать, что это множество является линей-
ным пространством.
А Обозначимx-($i;b; -••: ?«). у=(»и; Пя; • ••; nJ. *=(Ci; Са; •••;£»).
Проверим выполнение сформулированных выше условий 1°—8°.
1°.х+у=(Si+rh;.g»+п»; •••; £»+*!„). у+х=(пх4-6а; ч»+• ••;гя+5п),
т. е. х+у=у+х.
2°. х+у = (gi+пь 6»+п»; •••; Бп+Лп)- у+*—(41 + Ci; п»+k; •••; пп+Сп)>
(»+у)+«=($1+П1+Сь Ь+пя+Ся; •••; 5»+ii»+tn). x+(y+») = (£i + »h+ti;
бя+Пя+U; •••; 6n + n» + C»)- Такнм образом, (х + у) + ж = х + (у+ж).
103
3°. Нуль-элементом является 0=(0, 0 0). Действительно, х-}-0 = (£14-0;
I2 + O; •••; £п4~0)=х-
4°. Элемент (—£1; — £2; •••; — Sn) является противоположным элементу (gu
£2! •••; In), так как (gj; g2; U + (—Sil —£2! •••;—Вл) = (О; 0; б)=О. ‘
5». l.x = (l.gi; Н2; Ц„)х.
6°. l(,ux)=l(p.g1; р?2;...; p.gn) = (Xii|1; •••; = (М х.
7°. (1 + н)х = ((1+(х)|1; (l + p)g2; (Х+ц)U = (^i + ^i! ^2 + ^2; •••;>
*£»+hU = (*&;^2;. • •;^»)+ Ш & • • •; U+и &; . •:.
fe„) = >.x+jix.
8°. 1 (х+у)=1 (Bi+ш; ^+пг; •••;Bn+n») = (^i+A.m;^г+Мг;---: *&+ ,
+ — (^11; • •; ^л) + (^т]1> • • > ^Лл)—(£1> 1г; • • •; In) 4*^ (пх; лг; • • ••
»]л)=Хх+1у. д
462. Доказать, что множество всех комплексных чисел является
линейным пространством.
463. Является ли линейным пространством множество систем че-
тырех действительных чисел (gjj g2; 0; 0), (т^; т]2; 0; 0)» (Сп ?2> 0: 0).
где g2, Ли Лг> £х» Сг—всевозможные действительные числа? Сло-
жение элементов и умножение на действительное число определены |
так же, как и в задаче 461.
464. Образует ли линейное пространство множество элементов
(gi; u 1; 1), (Л1; л2; 1; 1). Сх; k; i; 1)?
465. Является ли линейным пространством множество всевозмож-
ных многочленов второй степени а0/24-а!/ 4-а2, Ро^ + Р^ + Р,, W’ +
+ У1^ + ?2’ • ’ ?
466. Образует ли линейнсе пространство множество всех много-,
членов не выше третьей степени?
467. Даны функции f3 (/), .... Является ли множество
этих функций линейным пространством, если эти функции образуют:
1) совокупность всех непрерывных функций на отрезке Га, &]; 2) со-
вокупность всех дифференцируемых функций на отрезке [а, &J; 3) со-
вокупность всех элементарных функций; 4) совокупность всех неэле-
ментарных функций?
468. Дано множество всевозможных пар положительных чисел: ’
х = (^; t2), У = (Лх; Лг)’ z = (CiJ С2)» ••• • Является ли это множество
линейным пространством, если сложение двух элементов определяет-
ся равенством х4-у = (^1т]1; |2т]2), а умножение на действительное
число — равенством Xx=(|j; g£)?
469. Может ли линейное пространство состоять: 1) из одного век-
тора; 2) из двух различных векторов?
470. Из линейного пространства исключен вектор х. Может ля
полученное после этого исключения множество векторов остаться ли- ,
нейным пространством? ]
471. Из линейного пространства исключено бесчисленное множе- j
ство векторов. Может ли полученное после этого исключения мно-;
жество векторов быть линейным пространством? f
472. В резерв проводников вагонов для выдачи им ежедневно по-
ступают со склада: 1) сахар; 2) чай; 3) печенье; 4) сухари; 5) дре-
весный уголь. Пусть gj, g2, gs, g4, —соответственно приращения за
день количества (в кг) этих поступлений. Если > 0, то соответст-
вующего продукта или угля поступило больше, чем выдано в этот
день, а если < 0, то их выдано больше, чем поступило со склада-
104
Является ли совокупность систем чисел |2; |3; |4; |5) линей-
ным пространством? Что означает вектор (—100; 5; 0;—200; 3)?
473. Образует ли линейное пространство совокупность троек целых
чисел (g4; g2; g3)?
474. В парк вагонного депо ежедневно прибывают вагоны разных
типов: багажные, почтовые, жесткоплацкартные, купированные и мяг-
кие, из которых ежедневно формируются и отправляются пассажир-
ские и скорые поезда. Пусть gx, g2, g3, g4, g5 — приращения за сутки
числа соответствующих вагонов. Является ли совокупность чисел
ISii ё2; Вз; 115 В») линейным пространством?
475. Образуют ли линейное пространство все геометрические век-
торы, имеющие общее начало в начале координат и расположенные
в I октанте?
476. Доказать, что множество всех решений системы линейных
„ (fl1x4-fe1u+ciZ = 0, л
однородных уравнении <fl y-f-c г=0 °оразУет линейное прост-
ранство.
• Доказать, что если (х4; z/i; Zj) н (х2; t/2; z2)— решения этой системы, то
г*!-1-х2; У1 + (/2; ?i-]-z2) и (Xxi; Xyf, Izi) при любом 1 также являются решениями
системы.
477. Доказать, что все функции уг(х), у2(х), у3(х), ..., удовлет-
воряющие дифференциальному уравнению Аоу{п > + А1у'п~" + Апу = 0
|Ле, Аг Ап—функции от х) образуют линейное пространство.
2. Линейно независимые векторы. Пусть х, у, г, ..., и—какие-нибудь векто-
ры линейного пространства R. Вектор, определяемый равенством
v = ах + Ру+yz -J-...-)- lu,
где а, Р, у...1—действительные числа, также принадлежат линейному прост-
ранству R. Этот вектор называется линейной комбинацией векторов х, у, z.и.
Пусть линейная комбинация векторов х, у, z, ..., и является нуль-вектором, т. е.
ax-]-Py-]-yz-|-...+1и = 0. (1)
Векторы х, у, z, ..., и называются линейно независимыми, если равенство (1)
выполняется лишь при а = В = у = ... =1 = 0. Если же равенство (1) может вы-
полняться н в том случае, когда не все числа a, Р, у.1 равны нулю, то говорят,
что векторы х, у, z, ..., и линейно зависимы.
Легко доказывается, что векторы х, у, z и линейно зависимы тогда и только
тогда, когда одни из этих векторов может быть представлен в виде линейной ком-
бинации остальных векторов.
478. Показать, что если среди векторов х, у, z, ..., и имеется
нуль-вектор, то рассматриваемые векторы линейно зависимы.
Д Пусть х=0. Так как равенство ax-f-Py-|-yz4-...+1и = 0 может выпол-
няться при a 0, р = у = ... = 1 = 0, то векторы линейно зависимы. А
479. Элементами линейного пространства являются системы упо-
рядоченных действительных чисел xz = (g1Z, g2Z, .... g„z)(i=l, 2,
3, ...). Какому условию должны удовлетворять числа (i = l,
2, ..., n; k = 1, 2, ..., n) для того чтобы векторы х,, х2, ..., х„ были
линейно независимы, если сумма векторов и произведение вектора на
число определяются равенствами xz4-x4 = (g1Z-[-glft; g2< + £2ft;
6./ + ^). 4 = (^lZ; Xg£Z; ...; Xg„z)?
105
Рассмотрим равенство a^-f-ccjXj-f-... 4-апх„ = в. Оно равносильно сис-
теме уравнений
а1£11 + аг£1г + • • + ап£1л = 0-
а1£и4* aa£i2 + • • • + аи£гл =
. alSnl+a2^n2+ • • • +алБлл=0-
В случае линейной независимости векторов х1( х2, ..
иметь единственное решение ccL = a2 = ... — an — 0, т. е.
х„ эта система должна
£п
£п
£ni
£12 •••
£12
• • • •
£л1
£in
£in
5*0.
В частности, векторы (£ч; £21) и (£i2; £2J) линейно независимы тогда и только
тогда, когда £n£22 — £u£ii # 0. А
480. Рассматривается линейное пространство многочленов не выше
второй степени. Доказать, что векторы Р2 = 1 + 21 + 3/\ Р2 = 2 + 3t +
-|- 4Р и Р, = 3 + 5/~|-7/2 лииейио зависимы.
Д В данном случае можно сразу заметить, что Р3 = 1 -₽i+ 1 -Р2; следовательно,
векторы ₽!, Р2 и Р3 линейно зависимы. А
481. В каком случае векторы x = (£j; |2) и у = (т]1; т|2), определен-
ные в условии задачи 468, линейно зависимы?
Д Из равенства х = 1у следует, что (£,; £i)=M»h; ’ll)- илн (5ь £г) = (»1ь П*)»
т. е. 5i=T]i, £i = t]i. Отсюда заключаем, что In £i-ln r]2 = ln Tji-ln £2. А
482. Доказать, что три компланарных вектора а, b и с линейно
зависимы.
• Привести векторы к общему началу и разложить один из векторов на со-
ставляющие, соответственно коллинеарные двум другим векторам.
483. Доказать, что три иекомпланарных вектора а, b и с линейно
независимы.
484. Доказать, что любые четыре вектора а, Ь, с и d линейно
зависимы.
Д Если три из четырех векторов компланарны, то задача решается просто.
Предположим, что эти векторы некомпланарны. Приведем все четыре вектора к
общему началу О. Построим параллелепипед, диагональю которого является вектор
de ребрами иа прямых, содержащих а, Ь и с. Нетрудно видеть, что d = aa-f-Pb-f-
+ ?с. А
485. Доказать, что если п векторов линейного пространства х, у,
z, ..., и линейно зависимы, то п+1 векторов «того пространства
х, у, z, ..., u, v также линейно зависимы.
3. Размерность и базис линейного пространства. Если в линейном простран-
стве R имеется л линейно независимых векторов, но любые n-|-1 векторов этого
пространства линейно зависимы, то пространство R называют л-мерным. Принято
также говорить, что размерность пространства R равна л, и писать d(R)=n. Про-
странство, в котором можно найти сколь угодно много линейно независимых век-
торов, называется бесконечномерным. Если R—бесконечномерное пространство, то
106
Совокупность п линейно независимых векторов «-мерного линейного простран-
ства называется базисом. Справедлива следующая теорема: каждый вектор ли-
лейного п-мерного пространства может быть единственным образам представлен
в виде линейной комбинации векторов базиса. Так, если ei, е2, ..., ел—базис
л-мерного линейного пространства R, то любой вектор х£/? может быть единст-
венным образом представлен в виде
X = ёте14- &>е2 + • • • + Елел.
Таким образом, вектор х в базисе ei, е2, ..., ел определяется единственным
образом с-помощью чисел Эти числа называются координатами
вектора х в данном базисе.
Если х = £ier+ g.eH- • -4-®лел, У=т)1ег+г1гег+ • • • +ПлСл, то
x-ry=(5i+T]i)-ei-b(g24-T]2).e24- 4-11л) е„, >.х=Ц1еН-1с2ег+ ... +xg„e„.
Для определения .размерности линейного пространства полезно использовать
следующую теорему: если любой вектор линейного пространства R может быть
представлен в виде линейной комбинации линейно независимых векторов е,, е2, ....
е„, mocti (R)—n .(а следовательно, векторы ei, е2..... образуют базис в про-
странстве R).
486. Дано линейное .пространство всевозможных пар упорядочен-
ных действительных чисел Xj = (su; g21), х2= (g12; £я), х3 = (|13; £„), ...,
причем сложение векторов и умножение вектора на действительное
число определены равенствами + ^гг+^гь)', =
= ХН2/). Доказать, что векторы е, = (1; 2) ,и е2 = (3; 4) образуют
базис данного линейного пространства. Найти координаты вектора
х = (7; 10) в этом базисе.
Д Векторы ei = (l; 2) и е> = (3: 4) линейно независимы (см. задачу 479). Рас-
смотрим какой-нибудь вектор у = (гг. т]2). Покажем, что для любых 1)! и i)2 можно
определить числа /. и р так, чтобы выполнялось равенство у = >.ег-(-ре2, или
(т)х; т),) = (л-!-Зр; 2л4-4р).
Нетрудно видеть, что существует единственная пара значений (Z; р), для ко-
торой выполняется это равенство. .Это следует из того, что система уравнений
/.4-3p=ni,
2л J-4р = т]2
является определенной.
Итак, векторы е2 и е, образуют базис. Определим координаты вектора х = (7; 10)
а этом базисе. Задача сводится к определению л и р из системы уравнений
1 + Зр = 7,
2Х4-4р= 10.
Отсюда находим Х = 1, р = 2, т. е. x = e!-i-2e2. А
487. .Показать, что линейное пространство, элементами которого
являются векторы х = (^; Е,; ...; %п) (см. задачу 479), имеет своим
базисом совокупность векторов et = (1; 0; 0; ...; 0), е2 = (0; 1; 0;...; 0),
е, = (0; 0; 1; ...; 0)....еП = (0; 0; 0; .... 1).
Л Нетрудно видеть, что
х = ?г (1; 0; 0; ...;0)-Н,(0; 1; 0; ...; 0)+.. (0; 0; 0; ...; 1),
т. е. x = |iei-f-£2е2-{-... 4-£лел. Таким образом, любой вектор может быть пред-
ставлен в виде линейной комбинации векторов ej, е2, ..., е„. Векторы ei, е2,...,
е„ линейно независимы, так как определитель, составленный из’ координат
этих векторов, равен 1, т. е. отличен от нуля. Итак, эти векторы образуют ба-
зис, а пространство R является «-мерным. А
107
488. Из каких элементов состоит линейное пространство с бази-
сом 1, t, t2, 1п~г, tn, если сложение элементов и умножение
элемента на действительное число понимать в обычном смысле?
489. Показать, что множество всех матриц второго порядка яв-
ляется линейным пространством четвертого измерения.
490. Показать, что матрицы е1== (q , е2 = о) , е3 = (чз о) •
е4= (о 4) образуют базис линейного пространства, рассмотренного
в задаче 489.
491. Показать, что элементы et = (1; и е2 = (10; 1) линейного
пространства, рассмотренного в задаче 468, являются базисными.
Найти координаты вектора х=(2; 3) в этом базисе.
Л Так как In 1-1п 1—In 10-1п 10 0, то векторы ei и е2 линейно независимы
(см. задачу 481). Пусть любой вектор у = (щ; Чг) представлен в виде линейной
комбинации векторов е2 и е2. Покажем, что существует такая пара чисел (Z; ц),
для которой выполняется равенство у = -|-j.ie2, или (тц; г)г) = (1^- 10**; 10^- 1Ц).
Следовательно, р. = 1gтцД = 1gт]г- В частности, х-~е£ 1g 3-f-е2 lg2. Таким образом,
(1g 3; lg 2) — координаты вектора х в базисе е2, е2. А
492. Показать, что за базис «-мерного пространства, рассмотрен-
ного в задаче 479, могут быть приняты векторы ех — (1; 1; 1;..., 1;
1), е2 = (0; 1; 1; ...; 1; 1), е3 = (0; 0; 1; ...; 1; 1)..en_x = (0; 0;
0; ...; 1; 1), е„=(0; 0; 0; ...; 0; 1).
• Рассмотреть векторы е; = е2—е2, е'=е2 — е3.е’п_г = сп-1—еп, е' = е„.
4. Изоморфизм линейных пространств. Рассмотрим два линейных пространст-
ва R и R'. Элементы пространства R будем обозначать через х, у, х, ..., а эле-
менты пространства R' — через х', у', z', ... .
Пространства R и R' называют изоморфными, если между их элементами х.
у, х', у' можно установить такое взаимно однозначное соответствие х<-»х'; у<->у',
при котором х + у «-> х'4-у', Хх«-»1х' (1—любое действительное число). Следует
отметить важную теорему, с помощью которой легко устанавливается изомор-
физм конечномерных линейных пространств: для того чтобы два конечномерных
пространства R и R' были изоморфными, необходимо и достаточно, чтобы их
размерности были одинаковыми.
493. Даны два линейных пространства R и R'. Элементами про-
странства R являются всевозможные дифференцируемые функции
аргумента i, обращающиеся в нуль при ( = 0. Элементами же про-
странства R' являются производные функций, принадлежащих про-
странству R. Доказать, что пространства R и R' изоморфны.
Л Пусть (/), f2 (/), f3 (I), ... —функции пространства R, а <р2 (/), <р2 (0.
Фз (t), ...—функции пространства R'. Из того, что эти функции снабжены индек-
сами, не следует делать заключение, что R и R' — сче!ные множества.
I
Пусть ф1(0 = /1(0’> тогда ft (/) = ф; (/) dt. Таким образом, между элемеит»-
о
ми линейных пространств R н R' (доказательство их линейности предоставляя»
выполнить самостоятельно) установлено взаимно однозначное соответствие.
108
С помощью равенств1
t
Ф/Ю+ФНО = 1Л-(0+М)Г. М04-М0 = $ [ф/(О+ф»(О]dt,
6
t
Ц>» (О = [Ui (ОГ. Ki (t) = $ Хф/ (о л
о
установлены взаимно однозначные соответствия: (ОЧ-^(О*“>ф| (О+ф*(О«
Ifi (/) 1ф,- (/). Итак, R и /?' —изоморфные пространства. А
494. Доказать, что множества всех геометрических векторов и
многочленов не выше второй степени—изоморфные линейные про-
странства.
495. Даны изоморфные линейные пространства R и R'. Между
элементами этих пространств установлены взаимно однозначные со-
ответствия х <-»х', у<-»у', ... . Доказать, что ax + Py-f-yzwax'-f-
-^Py' + yz' при любых действительных а, Р и у.
496. Пусть R и R' — изоморфные линейные пространства, причем
х<-»х'. Доказать, что (—х)ч->(—х').
497. Даны изоморфные пространства R н R’, причем 0 и О'—
нуль-элементы этих пространств. Доказать, что 0ч-»0' независимо
от того, как установлены взаимно однозначные соответствия между
другими элементами этих пространств.
498. Даны всевозможные пары действительных чисел: (£2; t]j),
т]2), (£3; т]3), ... . Построены два линейных пространства: про-
странство R с элементами Xj = (Si; t)i)> х2 = (£»‘. Л»)» х» = (В»; Лэ). •••»
в котором сложение векторов и умножение вектора на число опре-
делены равенствами Xi + x2 = + g2; rh-T-ib). A.x1 = (Xg1; Xrjj), и про-
странство R’, состоящее из векторов Xi = (e~S*; e~Th), x2 = (e-5«; е-ч»),
х^ = (е~$г; е-ть), .... в котором соответствующие действия опреде-
лены равенствами Х14-Х2 = (е_^_Ь; е-n.-n.), Xxi = (e_x6‘; Хт>*). Дока-
зать, что пространства R и R’ изоморфны.
499. Изоморфны ли линейные пространства R и /?'; если эле-
ментами R являются векторы х, у, г, ..., а элементами R'—векторы
2х, 2у, 2z,...? Показать, что пространства R н R' состоят из
одних и тех же элементов.
9 2. ПРЕОБРАЗОВАНИЕ КООРДИНАТ ПРИ ПЕРЕХОДЕ
К НОВОМУ БАЗИСУ
Пусть в n-мерном линейном пространстве /?" имеются два базиса: ej, е2, е3,...
(старый) и е', е', е', ... (новый). Даиы зависимости, выражающие каждый вектор
ового базиса через векторы старого базиса:
е2 = On*i 4"fl2i*2 -f-... 4- anieni
е2 = 012*14" а22е2 + • • • 4"ап2*п>
= 01пе1+а2п*14‘«• • 4'аппел-
109
Матрицу
Яц 012 • • • «1п
021 Я22 • • а2п
&П1 @п2 • • • ®пп
называют матрицей перехода от старого базиса к новому.
Возьмем какой-нибудь вектор х. Пусть (§i: |г; • • •! In)— Координаты этого
вектора в старом базисе, а (£'; — его координаты в новом базисе. При
этом старые координаты вектора х выражаются через новые координаты этого
вектора по формулам
11 =allll + a12l2 + • • • + alnl„>
|г = a21S4+ fl22l2 + • • • + ^2nl^*
In—anlli + fln2l2 + • ’ • ~\~annSn>
которые называются формулами преобразования координат.
Нетрудно видеть, что столбцы матрицы А являются координатами в форму-
лах перехода от старого базиса к новому, а строки этой матрицы—координатами
в формулах преобразования старых координат через новые.
500. Дан вектор х = е4 + е2 + е3 + е4. Разложить этот вектор по
новому базису ej, е2, е3, е4, если е{ = е2 + е3 4-е4, е2 = е1 + е3 + е1,
е3 = е4 + е2 + е4, е; = е4 + е2 + е3.
Д I способ. Выпишем матрицу перехода от старого базиса к новому:
/° 1 1 1\
А- 1 0 1 И
110 1/*
М 1 1 о'
Строки этой матрицы являются коэффициентами в формулах преобразовании
координат:
11 = + 1з -4’ I2 = ll+l3+l4’ ~3 — 11 + 12 + 14, |4=11+12 + 13-
Так как Si = l2 = ls = l4 = l. то> решив систему уравнений, находим li = l2 = lj=
= g;=l/3 и х = (1/3)(е; + е' + е;+е;).
II способ. Исключив ei, е2, е3, е4 нз системы уравнений
х = ei е2 -J- е3 + е4,
=0-в1 + 62 + 63 +е4>
e2 = ei+0-e2 + e3 + e4,
e3=ei + e2+0-e3 + e4,
e4 = ei + e2 + e3 + 0-e4
получаем
х 1 1 1 1
е4 0 1 1 1
е' 1 0 1 1
е' 1 1 ° !
е; 1 1 1 о
= 0.
Остается раскрыть этот определитель по элементам 1-го столбца и выразить х че-
Рез е', е', е' и е;.
ПО
уравнениями
i1
31
Рис.
чх)
I
X
HI способ. Так как ej + ei + e^+e, = 3ei + 3et+3es + 3e4, то ei4-*»4-*»4-
+ е4==(1/3)(е;Н-^Н-е;+е;). Отсюда х = (1/3) (е^+^+е^+ер. Д
501. Дан вектор х = 8е14-6е,4-4е,—1ве4. Разложить этот вектор
по новому базису, связанному со старым
ei «= —Зе4 4* еа 4-®» 4- е4, =2е(—4еа4-е»4-
+е4, е; = е4 + 3е,—5е, + е4, 'е; = е1 + е1+ ,
4-4е,—6е4. *
502. Дан вектор х== 2<е, + е,+ • • -+en).
Разложить вектор х по базису ei, ei......
ei, если ei = e14-es, ei = e,4-ea, ei = e.,4-
4-е.......е;-т = ев_,+еп, е; = ея + е,.
503. Система координат хОу повернута
вокруг начала координат на угол а (рис. 21).
Выразить координаты вектора а = х<4-
4-z/j в новой системе через его координаты в старой системе.
Л Разложим векторы I’ и J' по ортам i и j:
l' = icosa + Jsina,
j'=.i cos (y+a^+J sin ^y-f-a).
Запишем матрицу перехода от старого базиса i. J к новому базису 1', j':
Zcosa —sina\
\staa сова/
Отсюда получаем
x=t'co»a—у'sin а, у = x'eta a4-y'cos a,
т. е.
jt'=xcosa4-ysina, у' = — xstaa-j-ycosa. Д
504. Даны зависимости ei = aet, ei = 0ea, ei = ye., е4 = 6е5, e^ee^
Написать формулы, связывающие старые координаты (£lt £а;
£а) вектора к с новыми координатами (£4 54 £4 £4 5») этого же
вектора.
505. Возможны ли зависимости ei = е,—еа, ej = e,—e1,ei = e1—еа
между старым базисом е4, е„ е, и новым базисом ei, ei, ei?
$ 3. ПОДПРОСТРАНСТВА
1. Подпространство лвиейиого пространства. Линейное пространство /?' назы-
вается подпространством линейного пространства R, если элементами простран-
ства Я' являются только элементы пространства R.
Например, множество всех векторов, параллельных одной и той же плос-
кости, является подпространством всех геометрических векторов пространства.
Если к, у, х, ..., а—какие-нибудь векторы линейного пространства R, то
все векторы ах4-₽у4-.. .4-?л, где а, Р.Л—всевозможные действительные
числа, образуют подпространство пространства R. Множество всех линейных ком-
бинаций векторов ах4-Ру4—-4-Аи называется линейной оболочкой вектороа х,
у, .... и и обозначается через £(х, у, .... и).
Если Ri—подпространство линейного пространства R, то d(Ri)<d(R).
Пусть в линейном пространстве R имеются два подпространства Ri н Rt.
Пересечением подпространств Ri и Rt называется множество R» всех элементов,
одновременно принадлежащих Ri и Rt. Запись ₽а=₽1ПЯ« означает, что R»
является пересечением подпространств Ri и Rt. Суммой подпространств Ri и Rt
111
называется множество /?4 всех элементов вида х + у, где x£Ri, a y^R3- Запись
Я4 = R, означает, что множество Rt является суммой подпространств Т?4 иТ?2-
Доказывается, что пересечение R3 и сумма Т?4 являются подпространствами
пространства R. Следует иметь в виду, что d (Ri)-rd (R3) = d (R3)-Jrd(Ri).
506. Может ли подпространство линейного пространства R
состоять из одного элемента?
507. Дано линейное пространство R, элементами которого явля-
ются всевозможные системы действительных чисел: х = (^4; £2; £3;
11). У = (П1; П2; Пз! nJ. z = (?4; £2; £3; £J, .... Сложение двух эле-
ментов и умножение элемента на число определены равенствами
x + y = (IU + ni; £з + п2; ?з + Пз’. S4 + nJ, Хх = (^4; А£3; Ц4).
Доказать, что множество R3 элементов Xj=(0; |2; £3; В4), у4 =
= (0; т]2; Пз; nJ. z4 = (0; ?2; Ц; £J, ... и множество R2 элементов
x2 = (Si; 0; g3; g4), y2 = (nt; 0; т)3; nJ. z2 = (^; 0; £3; £4), ...являются
подпространствами линейного пространства R.
508. Для линейного пространства R, рассмотренного в задаче 507,
найти пересечение R3 и сумму /?4 подпространств Rt и R2.
509. Показать, что для подпространств задач 504 и 505 выпол-
няется равенство d (/?4) + d (R2) = d (R3) + d (Rt).
510. Дано линейное пространство, состоящее из всех геометри-
ческих векторов. Является ли подпространством этого пространства
множество векторов с началом в начале координат и расположен-
ных в I октанте?
511. Дано линейное пространство R, элементами которого являются
координаты точек Р — (х\ у, z) I октанта, не лежащих на коорди-
натных плоскостях. Сложение двух каких-нибудь элементов Р± =
= (х4; у2, z4) и Р2 = (х2, у2, г2) определено равенством Р1-}-Р2 =
= (xixz> УтУг’ zizz)> а умножение элемента Р = (х; у; г) на действи-
тельное число X—равенством ХР = (хх; «/•; гк). Доказать, что мно-
жество Rt точек этого пространства, расположенных на плоскости
2=1, является подпространством пространства R.
512. Дано линейное пространство R многочленов не выше пятой
степени. Доказать, что множество /?4 многочленов вида и
множество R2 многочленов Ь3Р 4- Ь2Р + Ь2 являются подпространствами
пространства R, если сложение элементов и умножение элемента на
число понимать в обычном смысле.
513. Найти подпространства R3 = R$ П R2 и Rt = Rt -f- R$ по условию
предыдущей задачи.
514. Рассматриваются два подпространства пространства R всех
геометрических векторов: Rt—множество векторов, параллельных
координатной плоскости хОу, и R2—множество векторов, парал-
лельных плоскости хОг. Найти R3 = П R2 и /?4 = Rt + R2.
515. Пусть и R2—подпространства линейного пространства R,
а R{ и R2—подпространства линейного пространства R'. Известно,
что подпространства Rr и R[, а также R2 и R2 изоморфны. Дока-
зать, что изоморфны подпространства /?3 = /?4п/?2 и R3 = Ri П Rt,
а также Rt = R± +R2 и R[ = +R2.
112
516. Дано множество функций/(х), непрерывных и положительных
на отрезке [—а, а\. Доказать, что это множество является линейным
пространством, если за сумму векторов принять произведение соот-
ветствующих функций, а за произведение вектора на действительное
число к-—результат возведения в степень X соответствующей функции.
Является ли подпространством множество всех четных функций этого
пространства? Множество всех нечетных функций этого пространства?
517. Рассматривается линейное пространство геометрических век-
торов. Образует ли подпространство этого пространства множество
всех векторов а = Xi + Yj 4-Zk, где X, Y и Z—рациональные числа?
2. Подпространства, образованные решениями однородной линейной системы
уравнений. Рассмотрим однородную линейную систему уравнений
' а11х1 +a12*2 -Y ~kaLnxri — О,
а21Х1 + О22х2 + • • • “F а2пхп = О,
(1)
<гяИ*1 4'<гт2*2 4' • • • -Yamnxn — 0.
Пусть Xf = М, х2 = ^2, • ••, х,п = Ьп — какое-нибудь решение системы. Запишем это
решение в виде вектора f = (Xi; Х2; ... Хп). Совокупность линейно независимых
решений fi, fa.f„ системы уравнений (1) называется фундаментальной систе-
мой решений, если любое решение системы уравнений (1) может быть представлено
з виде линейной комбинации векторов ft, f2.f„.
Теорема о существовании фу н да ментальной системы ре-
зец и й. Если ранг матрицы
ац ai2
а21 а22
,ат1 ат2
жныие п, то система (1) имеет ненулевые решения. Число векторов, определя-
ющих фундаментальную систему решений, находится по формуле k = n—г, где
г — ранг матрицы.
Таким образом, если рассматривается линейное пространство R’1, векторами
доторого являются всевозможные системы п действительных чисел, то совокупность
дсех решений системы (1) является подпространством пространства Rn. Размерность
этого подпространства равна k.
518. Найти базис и размерность подпространства решений
линейной однородной системы уравнений
Xi4“ 2х2 4~ Зх3 4x4 = 0,
(1/2) xj-|- х2(3/2) х3-|- 2x4 = 0,
(1/3) xi (2/3) х2 4- Хз4-(4/3) х4 = 0,
(1/4) *14-О/2) х2-[-(3/4) Хз4" х4 = 0,
Л Ранг матрицы
1 2 3 4 \
1/2 1 3/2 2)
1/3 2/3 1 4/3 /
1/4 1/2 3/4 1 /
завей 1, поскольку все миноры матрицы, кроме миноров первого порядка, равны
жулю. Число неизвестных равно 4; поэтому размерность подпространства решений
t'=n—г —4—1 =3, т. е. это подпространство является трехмерным. Так как г=1,
до из этой системы достаточно взять какое-нибудь одно уравнение.
113
Возьмем первое уравнение системы и запишем его в виде *•> = — 2х-—Зх3— 4х4.
Если х2 = 1, х3 = 0, х4=-0, то Х]= — 2; если хг = 0, х3=1, х4 = 0, то хд-- —3;
если х2 = 0, х3 = 0, х4=1, то х4“ —4. Итак, мы получили линейно независимые
векторы ft = (—2; 1; 0; 0), f2 = (— 3; 0; 1; 0), f3=(— 4; 0; 0; 1), которые обра-
зуют базис трехмерного подпространства решений дайной системы. Д
519. Показать, что вектор f = f4 — 2f,4- f3 удовлетворяет системе
уравнений задачи 518.
520. Найти базис и размерность подпространства решений системы
уравнений
(х*1— 2х2+ х3 = 0,
2x1— *«— х3 = 0,
— 2xi + 4х2—2х3 = 0.
Л Ранг матрицы
( 2 —1 —1 )
2 4 —2/
равен 2, так как определитель третьего порядка, образованный элементами мат-
рицы, равен нулю, а среди мииоров второго порядка имеются отличные от нуля.
Размерность подпространства решений k = n — г = 3 —2=1. Так как г —2, то доста-
точно взять два уравнения нз заданных трех. Отбросим третье уравнение, поскольку
его коэффициенты пропорциональны соответствующим коэффициентам первого
уравнения.
В системе
f xi—2х, = —х3,
} 2xi— х3= х3
полагаем х3=1, тогда решение системы
есть Xi=l, х,= 1.
I (Итак,[ подпространство
Xi — 2х2 = — 1,
2xi — х2 = 1
решений определяется одним базисным вектором
521. Найти размерность и базис подпрсстранства решений
системы уравнений
(Х1+х2— х34-х4=0,
xi—х24-х3—х4 = 0,
3xj 4-х2—х3+х4=0,
3xt — х» + х» —х4 = 0.
Д Определяем ранг матрицы
/1 1 -1 1\
1-1 1-11
3 1-1 1 •
\3 —1 1—1/
Вычитаем из 3-й строки 2-ю, а из 4-й строки 1-ю:
/1 1 -1 1\
. 1-1 1-11
Л 2 2 —2 2 •
\2 —2 2—2/
Так как элементы 3-й строки пропорциональны соответствующим элементам
1-й строки, а элементы 4-й строки пропорциональны элементам 2-й строки, то
114
З-Ю и 4-ю строки можно вычеркнуть:
ч: j -О-
Таким образом, ранг матрицы А равен 2 и k = n— г — 4 — 2 = 2.
Итак, размерность подпространства решений равна 2. Так как г=2, то из
четырех уравнений возьмем два:
J —*з+х4 = 0, или / х1-^-х2 = х, х
( Х1Т-Х2 + *3 — Х1 = 0, 1 х1 — х2= — *s+x4-
Полагая х3= 1, х4 = 0, получим систему < Xl+X2 — j’ Следовательно, х4 = О,
I #2 = •
Х2=1 и f4 = (0; 1; 1; 0).
Полагая теперь х3 = 0, х4 = 1, имеем/ 1’ Таким образом, х4 = 0,
х, = — 1 и f2 = (0; —1; 0; 1). За базисные векторы подпространства могут быть
приняты векторы f4 = (0; 1; 1; 0), f2 = (0; —1; 0; 1). Общее решение системы урав-
нений определяется вектором f = Cifi+c2f2, т. е. f=(0; с4—с2; с4; с2). Ак
522. Определить размерность подпространства решений, базис
и общее решение системы уравнений
J Xi -|- 2х2 + х3 х4+х5 = 0,
[х4 —2х2+х34-х4—х3 = 0.
$ 4. ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ
1. Основные понятия. Будем говорить, что в линейном пространстве R зада-
но преобразование А, если каждому вектору х£/? по некоторому правилу постав-
лен в соответствие вектор Ax£R. Преобразование А называется линейным, если
для любых векторов х и у и для любого действительного числа Л выполняются
равенства
А (х + у) = Ах+Ау, А(Хх) = ЛАх.
Линейное преобразование называется тождественным, если оно преобразует
любой вектор х в самого себя. Тождественное линейное преобразование обознача-
ется через Е. Таким образом, Ех = х.
523. Показать, что преобразование Ах = ах, где а—действитель-
ное число, является линейным.
Д Имеем А (х + у) = а (х + у) = ах + ау = АхЦ-Ау, А (?,х) = а (?.х) = Л (ах) —
= ЛАх. Итак, оба условия, определяющие линейное преобразование, выполнены.
Рассмотренное преобразование А называется преобразованием подобия. А
524. Преобразование А в линейном пространстве /? определено
равенством Ах = х + х0, где xa£R — фиксированный ненулевой век-
тор. Является ли преобразование А линейным?
А Из равенств Ax = x-J-x0, Ау = у-]-х0, А (х+у) = х+у+хо, А(х + у) =
= Ах-|-Ау заключаем, что x-j-y+xo=(x-l-xfl)-[-(y-[-Xo). Отсюда следует, что
х» = 0, но это противоречит условию. Следовательно, преобразование А не явля-
ется линейным. А
525. Дано линейное пространство геометрических векторов. Пре-
образование А состоит в замене каждого вектора его составляющей
по оси Ох. Является ли это преобразование линейным?
115
Д Пусть a = X)i + y1j + Z1k н b = X2i4-y2j-{-Z2k—произвольные векторы,
а X—произвольное действительное число. Так как
а+ b = (Xf4~ А2) 14-(У14_У2)]-|-(Zi4-Z2) к, Ха = ХХ414-ХУ4-|-XZik,
то
A(a-{-b) = (X1 + X2) i = X1i-|-X2i = Aa + Ab, А (Ха) = AAJ = ХАа.
Итак, А—линейное преобразование. А
526. Является ли линейным преобразованием замена каждого
геометрического вектора его зеркальным отображением относительно
координатной плоскости хОу?
527. Является ли линейным преобразованием умножение каждого
геометрического вектора на его длину?
528. В каком случае преобразование А является линейным, если
Ах = х0, где х0—произвольный вектор линейного пространства R,
а х0—фиксированный вектор?
529. Дано линейное пространство векторов х = + £2е2 4- £,е3 4*
+ &4е4, где g2, g3, g4—всевозможные действительные числа.
Пусть а—фиксированное действительное число. Является ли линей-
ным преобразование А, определяемое равенством Ах = 4-4-
+ £зе3 +
530. Дано линейное пространство векторов х = ^ej 4- 4* £,е3 4*
4-&4е4. Преобразование А состоит в том, что у каждого вектора
меняются местами вторая и третья координаты, т. е. Ах = 4-
4-g3e24-g2e34-B4e4. Является ли преобразование А линейным?
531. Пусть А—линейное преобразование. Доказать, что преоб-
разование В, определяемое равенством Вх = Ах—2х, является
линейным.
2. Матрица линейного преобразования. Пусть в п-мер ном линейном пространстве
R, базис которого е2, е2,...,е„, задано линейное преобразование А. Так как Ае1(
Ае2,...,Ае„—векторы пространства R, то каждый из них можно разложить
единственным способом по векторам базиса:
Ае4 = Оце1-|-а21е24-... -}-ап1е„,
Ае2 = а42е14-a22ei-{-... 4-Яп2ел»
Аеп = а1пе14-П2пв2 4- • •+ал«ея.
Матрица
(011 О1г ... fli„ \
Пи • • • о!п |
Oni оп% • •. опп /
называется матрицей линейного преобразования А в базисе ej, eg, ..., е„. Столбцы
этой матрицы составлены из коэффициентов в формулах преобразования базисных
векторов. Возьмем в пространстве R какой-нибудь вектор x = xiei-|-x2eg4-• ••
хпеп. Так как Ах£Я, то и вектор Ах можно разложить по векторам базиса:
Ах = х'е4 4- х'е2 4-... 4-х; е„.
Координаты ... ;х;) вектора Ах выражаются через координаты (х2; х2;.,,
...; хп) вектора х по формулам
Xj = Я11Х14-П12Х24- ... 4-И1Пхп,
*2 — в2Л 4~ оггхг 4-... 4-а2пхп,
*Я =а»1Х14'ап2Х2 4' • • • 4-П„пХп.
116
Эти и равенств можно назвать линейным преобразованием А в базисе еь е2,...
..., е„. Коэффициенты в формулах этого линейного преобразования являются
элементами строк матрицы А.
532. Найти матрицу тождественного преобразования Е в «-мер-
ном пространстве.
Д Тождественное преобразование не меняет базисных векторов: ej = elr
еа~е2> ез = ез...еп ==е«’ т- е-
е; = 1.е1 + 0.е2+...+0-еп,
с2 = 0 ei +1' е2 + • • • + 0 • ел,
е; =0.ei+0.e2 + ... + len.
Следовательно, матрицей линейного преобразования служит единичная матрица
/10 0
/010
£= 0 0 1
ООО
533. Найти матрицу преобразования подобия Ах = ах в «-мер-
ном пространстве.
534. В четырехмерном линейном пространстве рассматривается
линейное преобразование А. Записать это преобразование в коорди-
натной! форме, если Ae1 = e3-f-e4, Ae2 = ex + e4, Ae3 = e4-f-e2, Ае4 ==
= е2 -f- е3.
А Матрица преобразования А имеет вид
0 110
0 0 11
10 0 1
110 0
Следовательно, преобразование А в координатной форме записывается так: х' =
= Х2А-Х3, Х'2 = Х3-[-Х4, Х;=Х1+Х4, + А
535. Линейное преобразование совокупности всех векторов на
плоскости хОу заключается в повороте каждого вектора против ча-
совой стрелки на угол а (рис. 22). Найти
матрицу этого линейного преобразования
в координатной форме.
Д Так как Ai = icosa + jsin a, Aj= —isln a+
-j-jcosa, to
cos a —sin a
sin a cos a
A =
Таким образом, рассматриваемое линейное пре-
образование имеет вид
х' =х cos a—у sin а; у' = xsin a 4-1/cos a. A
536. Рассматривается линейное пространство векторов x = x1e1-f-
4-х2е24-х3е34-х4е4, где хг, х3, х4 — всевозможные действительные
117
числа. Доказать, что преобразований А, определяемое равенством
Ax = x2e14-x3e2 + x1e3-f-x'1e4, является линейным, и найти его мат-
рицу.
3. Действия над линейными преобразованиями. В приведенных ниже опреде-
лениях примем следующие обозначения: А и В — произвольные линейные преоб-
разования в линейном пространстве R, ?.— произвольное действительное число,
—любой элемент.
Суммой линейных преобразований А и В называется преобразование Clt
определяемое равенством С!Х = Ах-[-Вх. Обозначение: Ci = A + B.
П роизведением линейного преобразования А на число к называется преобразо-
вание С2, определяемое равенством С2х = ХАх. Обозначение: С2 = ХА.
Произведением линейного преобразования А на линейное преобразование В
называется преобразование С3, определяемое равенством С3х = АВх. Обозначение:
С3 = АВ.
Преобразования Сь С2 и С3 являются линейными. Матрицы линейных преоб-
разований Ci, С2 и С3 определяются из равенств Ci = A-|-B, С2 = кА, СЯ = АВ.
При сложении линейных преобразований выполняется переместительный закон;
произведение же АВ, вообще говоря, отличается от произведения ВА.
Перечислим некоторые свойства операций над линейными преобразованиями
в пространстве R:
А(ВС) = (АВ)С; АЕ = ЕА = А; (А-[-В) С = АС+ВС; С (А+ В) =СА + СВ.
Если для линейного преобразования А найдутся такие линейные преобразо-
вания В и С, что ВА = Е, АС = Е, то В=С. В этом случае обозначают
В = С = А-1, а линейное преобразование А-1 называют обратным линейным пре-
образованием по отношению к. линейному преобразованию А. Таким образом,
А~1А = АА-1 = Е.
Линейное преобразование А в конечномерном пространстве называют невырож-
денным, если определитель матрицы этого преобразования отличен от нуля. Сле-
дует иметь в виду, что каждое невырожденное линейное преобразование А имеет
обратное преобразование А-1 и притом только одно.
Если невырожденное линейное преобразование А в координатной форме опре-
деляется равенствами
Х' — 011х + ЯцУ + • • + UinU,
у' ~ П21х + аггУ + • • + а2пи,
и' = ап1х^-ап2уД---+аппи>
то обратное линейное преобразование А-1 имеет вид
А,, , A2i . А,,, ,
X = \A\X+~A\y+---+TA\U'
Ain А „о , , , А, ,п ,
у = х' 4-т—гт- (/+••• +гтт и ’,
* | А | | А ' |А| ’
....................... t
.,_ । А2л , , Апп ,
U-\A\ +|АТг/ ~"'+ГаТ ’
Здесь Ajj—алгебраическое дополнение элемента а,-у матрицы A, J А |—определи-
тель матрицы А.
Матрица линейного преобразования А-1 является обратной по отношению к
матрице А и определяется равенством
/Aii А2< ,.. Ani
л-i__ I I Ala А22 ... Ап2
|А|1 .................
\А1Л Ал2 ,.. Алл
118
537. Преобразование А заключается в повороте каждого вектора
плоскости хОу на угол а = л/4. Найти в координатной форме пре-
образование А + Е.
Л Имеем
Al = icos (л/4) +J sin (л/4) = (К2/2)2+ (К^/2) J;
Aj = i cos (Зя/4) + j sin (Зл/4) = —(К 2/2) i + (К 2/2) j.
Следовательно,
~К2/2\
2/2 V 2/2/
_ г. Л 0\
Так как £=1^1, то
A-k£ = ^2/2 + 1 “KJ/2 \
+ \V 2/2 К 2/2+1/
Таким образом, линейное преобразование А-\-Е можно записать с помощью
равенств г'= (К2/2+1)*—(К2/2) у, у' = (К2/2) х + (/’2/2 + 1) у. Д
538. Даны два линейных преобразования:
х' = *+2y + 3z, х' — х+ Зу + 4,5г,
у'^4х+5у + 6г, (А) и У'= &* + 7*+ 9г,
г'=7*+8у+9г г' = 10,5х+12у+ 13г.
(В)
Найти ЗА — 2В.
539. Даны линейные преобразования:
х'=х+у, х'=у+г,
У'=У+г, (А) и y’=x+z, (В)
г'=г-|-х г'=х+у.
Найти преобразования АВ и ВА.
Л Матрицы данных преобразований имеют вид
/1 1 0\
А = ( 0 1 1 ),
\1 0 1/
Найдем произведения этих матриц:
/1 1 2\
АВ = 2 1 1 ),
\1 2 1/
/О 1 1\
£ = (10 1).
\1 1 0/
/1 1 2\
В А = ( 2 1 1 ).
\1 2 1/
В данном случае АВ — ВА, поэтому линейные преобразования АВ и ВА сов-
падают. Координатная форма преобразования АВ записывается следующим образом:
х'=х+у+2г, у' = 2«+y+z, х'=х+2у+г. Д
540. Пусть над совокупностью векторов u = xi+yj на плоско-
сти хОу производятся два линейных преобразования: А—замена
вектора его составляющей по оси Ох; В—зеркальное отображение
вектора относительно биссектрисы I и III координатных углов.
Найти преобразования АВ и ВА.
119
Л, Согласно условию, Au = xi, Ви=х)---0. Таким образом, Ai — i, Aj=O,
Bi = j, Bj = i, t. e.
Итак, преобразование AB определяется равенствами x'=y, y'~-Q,a преобра-
зование BA — равенствами x' =0, y'—x. Рекомендуем получить эти равенства из
геометрических соображений. А
541. Преобразование А заключается в повороте каждого вектора
плоскости хОу на угол а. Найти матрицу преобразования .А2 (т. е. А А).
Л Так как Ai = i cos a-f- j sin a, Aj = —i sin a-}- j cos a, to
, /cos a —sin a
A = .
\sina cos a
Следовательно,
cos2 a — sin2 a — 2sinacosa\ / cos 2a —sin 2a
2 sin a cos a cos2 a — sin2 a/ sin 2a cos2a
Таким образом, преобразование А2 в координатной форме определяется ра-
венствами х' =х cos 2a—у sin 2a, у’ =--х sin 2a-)-i/ cos 2a. Эти результаты могут
быть получены и из чисто геометрических соображений. Д
542. Линейное преобразование А заключается в повороте на
угол л/4 каждого вектора плоскости хОу. Найти матрицу линейного
преобразования В = А2 + К2А-|-Е.
= -К~2/2\=К2/2/1 -1\ Д2 = (О-Ц.
Л \У~2/2 У~2/2 ) \1 1/’ U 0Г
e = b оН 1M01M2 2ЛЧ1 1М
543. Дано пространство геометрических векторов. Пусть линей-
ное преобразование А —поворот пространства вокруг оси Ог на
угол л/4, а линейное преобразование В — поворот пространства во-
круг оси Ох на тот же угол. Найти матрицу линейного преобра-
зования АВ.
Л Имеем Ai=i cos (л/4)+) sin (л/4)=(У 2/2) i-f- (У 2/2) j, Aj=— i sin (л/4) -f-
+ jcos(n/4) = — (У 2/2)i+(K 2/2) j, Ak = k; Bi = i, Bj = (K 2/2) j+(K 2/2)k,
Bk = —(y 2/2) j~r(y 2/2) к. Следовательно,
(у 2/2 — У1/2 o\ /1 ° 0 \
-4=4 У 2/2 У~2/2 0 j. B=4 0 У~2/2 — У1/2 )(
\ 0 ° \J \0 yi/2 yi/2 J
fУ 2/2 —1/2 1/2
-48, = у 2/2 1/2 —1/2
\0 У 2/2 У 2/2
544. Дано линейное преобразование А: х' = — 0,5 (у 4- г), у’ =
— —0,5 (х' + г), г' — — 0,5 (х4-у). Найти матрицу обратного линей-
ного преобразования.
120
545. Рассматривается совокупность всех геометрических векто-
ров. Линейное преобразование .А — зеркальное отображение этих
векторов относительно плоскости Р. Найти А-1.
546. В линейном пространстве с базисом еп е2 дано линейное
преобразование А. Найти матрицу обратного преобразования, если
Аех = е2, Ae2 = ev
547. Линейное преобразование А заключается в повороте каж-
дого вектора плоскости хОу на угол а. Найти матрицу В = А + А-1.
548. Дано линейное преобразование А: х' = х-{-у, у' =2(xJry).
Найти обратное линейное преобразование.
549. Линейное преобразование А заключается в повороте каж-
дого вектора плоскости хОу на угол л/4. Найти матрицу А~2.
550. При каком значении % линейное преобразование х' = — 2x4*
+ у + г, у' — х—2у-\-г, г' = х4- у + ^г не имеет обратного?
4. Характеристические числа и собственные векторы линейного преобразова-
ния. Пусть R—заданное n-мерное линейное пространство. Ненулевой вектор х^/?
называется собственным вектором линейного преобразования А, если найдется
такое число к, что выполняется равенство Ах = Хх. Само число к называется
характеристическим числом линейного преобразования А, соответствующим век-
тору х.
Если линейное преобразование А в базисе ej, .. е„ имеет матрицу
(«11 «12 • • • «1п
«21 «22 • • • «2П
«Ю1 «п2 • • • «пп
то характеристическими числами линейного преобразования А служат действи-
тельные корни Xi, Х2> .... Ап уравнения n-й степени, которое можно записать
в виде
«11 «12 • • • «1п
«21 «22—Л. ••• «2П =0.
«П1 «п2 ••• «пп—
Оно называется характеристическим уравнением, а его левая часть—характери-
стическим многочленом линейного преобразования А. Собственным вектором х*,
соответствующим характеристическому числу X*. является любой вектор gjei -f-
~ 1ге2+• • • + Snen. координаты которого удовлетворяют системе линейных одно-
родных уравнений
(«11 — £1 4" «12?2 + • • • +«1п?п =0>
«21?1 4" («22 — &2-f- • • • + «2П&Л ==
«л1£14-«п2&24~ • • • ~f-(«nn—£п—
Отметим следующие важные теоремы.
Характеристический многочлен линейного преобразования не зависит от вы-
бора базиса.
Если матрица А линейного преобразования А является симметрической, то
асе корни характеристического уравнения | А — ХЕ|=0—действительные числа.
551. Найти характеристические числа и собственные векторы
линейного преобразования А, определяемого уравнениями х' = 5x4-
4-4^, у' = 8х+9«/.
121
(5 4\
). Характеристическое
о У j
уравнение имеет вид
|5т\ 4J=°. "ли X*—14X4-13 = 0;
I о У — Л I
характеристические числа Xi = l, Х2=13.
Для определения координат собственных векторов получаем две системы ли-
нейных уравнений:
((5-X1)6i + 46a=O, ((5-X2)5i + 46a = O,
18Ь + (9 - М J2 = 0; ) 851 + (9 -Х2) 5а = 0.
Так как Xj — 1, то первую систему можно записать следующим образом:
J 451+4?а = 0,
I 851 + 85г т=0.
Таким образом, значения 51 и 5, должны удовлетворить уравнению 5t + 5а=0,
или £, = —61- Следовательно, решение этой системы имеет вид 51=Сь 5а — — ci<
где Ci—произвольная величина. Поэтому характеристическому числу Х=1 соот-
ветствует семейство собственных векторов u=Ciej—Cje,, т. е. u=ci(ei—е,).
Значение Х,= 13 приводит к системе уравнений
J-85i + 45a = O,
I 851 - 45а = 0,
т. е. 5а = 251- Полагая 5i=c2, получаем 5а = 2са- Следовательно, характеристи-
ческому числу Х = 13соответствуетсемействособственных векторов v = c, (ei + 2e2).
Итак, придавая в равенствах u = Ci(ei — е2), v = с, (ех4-2е,) величинам Ci и
с, всевозможные числовые значения, будем получать всевозможные собственные
векторы линейного преобразования А. Д
(ос 0\
0 р ) . Найти
характеристические числа и собственные векторы этого преобразо-
вания.
553. Найти характеристические числа и собственные векторы
линейного преобразования с матрицей А = 2$) •
554. Найти характеристические числа и собственные векторы
линейного преобразования с матрицей А = ~д) •
555. Определить характеристические числа и собственные век-
торы линейного преобразования с матрицей А = 2
1
Л Составим характеристическое уравнение:
2-Х -1 1
—1 2-Х —1 =0,
0 0 1—X
т. е.
(1— Х)[(2—Х)»-1]=0, (1— Х)’(3—Х)=0, Xi, ,= 1, Xs = 3.
ЕслиХ=1, то для определения координат собственного вектора получаем
систему уравнений
6i-5a + 5a = O,
—61 +5а—£э = 0.
ь=о.
122
Таким образом, характеристическому числу 1=1 соответствует семейство
собственных векторов u =Cj (ei4-е2).
Если 1 = 3, то для определения координат собственного вектора получаем
систему уравнений
(— £1 — ?2 + 5з = 0,
{ —S1— |2 + 5з = 0,
’ £з = 0.
Семейство собственных векторов, соответствующих этому характеристическому
числу, определяется равенством v = c2(ei— е2). А
556. Определить характеристические числа и собственные век-
/1 1 3\
торы линейного преобразования А с матрицей А = 15 1].
\3 1 1/
/Оц <712 а13\
557. Доказать, что если ( a2i °22 «23] — симметрическая матрица,
^°31 ° 32 а33'
а действительные числа а, р и у отличны от нуля, то все корни
характеристического уравнения матрицы
/ац ai2a/P О1з^/у\
А = ( a2ifVa а22 а2зР/Т )
\а31у/а а32у/В а33 J
являются действительными числами.
Л В базисе е1( е2, е3 рассмотрим линейное преобразование А с матрицей А.
Тогда
Aet = cnei + (a2i₽/a) е2 + (а31у/а) е3,
Ae2 = (oi2a/P) ei+a2?e2 + (a32y,'P) е3,
Ae3 = (ai3a/y) ei-f-(°гзР/т) е2-|-а33е3
жли
A (aej = аиав! 4-а21[5е2 + a3iye3,
А (Ре2)=а12ае1+а22Ре24-а32уе3,
A (Yes) — а135се1 + а2зРе2 4-аЗзТеЗ.
Полагая aei = ei, Ре2=е2, уе3 = е3, имеем
Aei = аце1 H-a2ie2' + a31e3,
Ае2 = aj2ei -р <т22е2 ^зг^з»
Ае3 — aj3ei -f- о23е2 -|-a33e3.
Таким образом, матрицей линейного преобразования А в базисе ej, е2, ез служит
симметрическая матрица
/°11 а12 «13\
А1 = ( о21 о22 п23 ].
ХО31 Я32 а33'
Следовательно, характеристическое уравнение линейного преобразования А
з базисе ец е2, е3 имеет только действительные корни. Так как при переходе
к базису ei, е2, е3 характеристические числа не меняются, то те же корни имеет
1 характеристическое уравнение матрицы А. А
558. Линейное преобразование А заключается в повороте про-
странства на угол л/3 вокруг оси Ог. Найти характеристические
числа и собственные векторы этого преобразования.
ф Показать, что матрица этого линейного преобразования имеет вид
/ J/2 — /3/2 0\
А =( К3/2 1/2 0 ) •
\ 0 0 1/
559. Зная характеристические числа линейного преобразования А,
найти характеристические числа обратного линейного преобразова-
ния А-1.
ф Показать, что из уравнения |Л-1—Х£| = 0 следует | А —(1/Х)£ |=0.
560. Найти характеристические числа и собственные векторы
/0 1 0 0\
- . . . / 0 0 1 о \
линейного преобразования А с матрицей А =1 0 0 0 j I-
о о о/
561. Найти характеристические числа и собственные векторы
/« Р
линейного преобразования с матрицей А = ( т « ₽ ).
\р у а/
§ 5. ЕВКЛИДОВО ПРОСТРАНСТВО
Линейное пространство R называется евклидовым, если имеется правило, кото-
рое позволяет для каждых двух векторов х и у из /? построить действительное
число, называемое скалярным произведением векторов х и у и обозначаемое (х, у),
причем _ _
1°.
2°.
3°.
это правило удовлетворяет следующим условиям:
(х. У) = (У> х);
(х, у+в) = (х, у>+(х, z);
(Хх, у) = X (х, у) для любого действительного числа X;
(х, х) > 0, если х 0.
условий 1°—4° следует, что:
Из
а) (У 4-х, х) = (у, x) + (z, х):
б) (х, Ху) = Х(х, у);
в) (0, х) —0 для любого вектора х.
Скалярное произведение любого вектора x£R иа себя называется скалярным
квадратом вектора х.
Длиной вектора х в евклидовом пространстве называется квадратный корень
из скалярного квадрата этого вектора, т. е. |х| = /(х, х).
Если X—любое действительное число, а х—любой вектор евклидова про-
странства, то | Хх | = | X |-| х |.
Вектор, длина которого равна единице, называется нормированным. Если
x£R—ненулевой вектор, то нетрудно видеть, что -j—г-• х (можно обозначить
у является нормированным вектором.
Для любых двух векторов х и у в евклидовом пространстве выполняется
неравенство (х, у)’<(х, х) (у, у), называемое неравенством Коши—Буняковского,
Равенство (х, у)’ — (х, х) (у, у) имеет место тогда и только тогда, когда век-
торы х и у линейно зависимы.
(х v)
Из неравенства Коши—Буняковского следует, что —1 <| у | 1 ’ ^Г0Л(Р’
fa
определяемый равенством cos<p= v .’-ЛЧ- н принадлежащий отрезку [0, я], на-
I в I | у I
зывается углом между векторами х и у. Еслихиу—ненулевые векторы, а <р=я/2,
то (х, у) = 0. В этом случае говорят, что векторы х и у ортогональны, н пишут
124
Для произвольных векторов хну евклидова пространства имеют место сле-
дующие важные соотношения:
1. |х4~у|<|х|4-|у| (неравенство треугольника).
2. Пусть <р—угол между векторами х и у; тогда | х—у |* = | х |2-Ь| У I’ —
— 21 х |-| у | cos <р (теорема косинусов). Если х_[_у, то получается равен-
ство |х—У |2 = | х 1*4-1 УI2. Заменяя в последнем равенстве у на —у, получаем
I x-j-y |* = | х |*4~| У |2 (теорема Пифагора).
562. Дано линейное пространство, рассмотренное в задаче 461.
Можно ли скалярное произведение двух произвольных векторов
X = (L; в2; - - -; Е„) и у = (Т) 1; Т)2 ...; Т)п) определить равенством (х, у)=
= + fa'Ha + • • • Ч-^пЛи (Для того чт°бы это пространство стало
евклидовым)?
Д Проверим выполнение условий Г—4°.
1°. Так как (у, х) =Л1?14-Л2?24-• • •+л«5«, то (х, у) = (у, х).
2°. Пусть z = (£i; ?2; •••; £п)- Тогда y + z = (T)1-|-£l; Лг + ^г! •••; Лп4*?п) и
(х, у4*2) = £1Л14~ 51Л1 + 4~ ёгЫ* • • • 4" 1>пЛп4~£п£п —
— (^1Л14- ^гЛг 4~ • • • + £пЛп)4~(^i?i + ^2?2+ • • • 4-£п£п) = (х, У)4-(х, z)-
3°. (Jix, у) =Х^1т)14-Л?2т)24-• • ^пЛп = ^(?1Т)1 + ^2Т)2+• • •+ ?пЛп)=^ (*» У)-
4°. (х, х) = 514-Й4-...4-5л Ф о, если хотя бы одно из чисел g1( g2 .... g„
отлично от нуля.
Значит, в заданном пространстве с помощью указанного равенства можно
определить скалярное произведение. Д
563. Дано евклидово пространство, рассмотренное в задаче 562.
Пусть |2, ..., — количество п видов изделий, выпускаемых
ежедневно заводом, а т],, т)2, ..., т)я—соответственно цены этих
изделий. Как можно истолковать скалярное произведение векторов
x = (li; ?2; •••;!„) и y=0h; ъ; •••; *!„)?
564. Дано линейное пространство, векторами которого являются
всевозможные системы, состоящие из п положительных чисел: х =
= (£i; В2; • ••; U- У=0к; и»; •••; nJ. z=(£2; ---, U, ... .
Сложение векторов и умножение вектора на число определены равен-
ствами х4-У = (?iT]i. В,П2. •••> 1„т1п)- Ьх = (51, ...,^). Можно ли
сделать это пространство евклидовым, определив скалярное произ-
ведение равенством (х, у) = In tx lnih4~ In |21пт)24-... 4- In In-q„?
Д Проверим выполнение условий Г—4°.
1°, (х, у) = In In т]! 4-In 5г In Лг 4- ••• + 1п£п 1пт)«. (у, х)=1пл11п£1 +
4-In т)г In g2 4-4-1п1Ъ.1п£п, т. е. (х, у) = (у, х).
• 2°. Так как у 4-* = (Л1С1; Лг£2; •••; Л«£и). то
(х, у 4~ z) = In In (Л1£1) 4- In ?2 In (л г Ег) 4- ••+•" In (Лп£л) ==
= In gi In Л14- In ?2 In Лг 4-+ In in In Ли4- In In 5x4-
4-In In £24-... 4-In g„ln £n = (x, y)4-(x, z).
3° Так как Xx = (g^; g2; ..., $), то
(Xx, у) = In In Л14" In ?2 In л2 4" • • • 4" In In Лп =
= Л (In In Л14~'п £2 In Ла4-• • •+ln ?n In Лп) =MX, У)-
4°. (x, x) = ln*g14-ln2g2+...4-lnagnSs=0.
Следовательно, рассматриваемое пространство является евклидовым. А
565. Рассматривается линейное пространство непрерывных в про-
межутке [а, 6] функций x = x(i)> У = У(О. z = z(/), .... Можно ли
125
сделать это пространство линейным, определив скалярное произве-
ь
дение двух любых векторов х и у равенством (х, у) = х (?) у (?) dt?
а
566. Является ли множество всех геометрических векторов
евклидовым пространством, если скалярное произведение двух
векторов, определить как произведение их длин?
567. Образует ли множество всех геометрических векторов евкли-
дово пространство, если определить скалярное произведение двух
произвольных векторов а и b как произведение длины вектора а и
утроенной проекции вектора b на направление вектора а?
568. Задано линейное пространство, рассмотренное в задаче 562,
при п — 4. Определить угол между векторами х = (4; 1; 2; 2) и
У = (1; 3; 3; -9).
А |х| = /(хГ^) = /16+1+4+4 = 5; |у | = /(/¥) = /1+9+9+81 =10;
(х, у)=4+3 + 6—18=—5; cosq) = .-^’ —0,1; <p = arccos(—0,1) =
= 174°15'. А У
569. Задано евклидово пространство, рассмотренное в задаче 562.
Определить угол между векторами х = (1; /3; V5; ...; И2п — 1)
и у — (1; 0; 0; ...; 0).
570. Рассматривается евклидово пространство непрерывных функ-
ций х (t), y(t), z(t), ... на отрезке [—1, 1]. Скалярное произведе-
I
ние определено равенством (х, у) = f х (?) у(?) dt. Найти угол между
— 1
векторами х = 3?2— 1, у = 3t—5?3.
1
Д Имеем (х, у) = (З/2—1) (3t—5t3)dt. Нетрудно видеть, что (х, у)=0, так
— 1
Как подынтегральная функция является нечетной. Следовательно, векторы х и у
ортогональны. А
571. Задано евклидово пространство, рассмотренное в задаче 562,
при /1 = 6. Проверить справедливость теоремы Пифагора для орто-
гональных векторов х = (1; 0; 2; 0; 2; 0) и у = (0; 6; 0; 3; 0; 2).
А Имеем
| х | = /1 +0+4 + 0+4 + 0 = 3, | у | = /0 + 36+0+9 + 0+4 = 7;
х+у = (1; 6; 2; 3; 2; 2); | х + у | = /1+36 +4 + 9 + 4 + 4 = /58.
Итак, |х|2 + |у |2 = |х + у |2. А
572. В евклидовом пространстве непрерывных функций, соответст-
вующих условию задачи 565, рассматриваются два вектора: х= ?2+1,
у = Х?2+ 1. Найти значение X, при котором векторы х и у ортого-
нальны на отрезке [0, 1], и проверить справедливость теоремы
Пифагора для этих векторов.
Л Составам скалярное произведение
1
(х, у)=р/=+1)(Х/*+1)Л = Х/5+а+1>/3+1.
о
Из условна (к, у)=0 определяем X; имеем X/5-f-(X-f-l)/3+1=0, откуда
1=—5/2.
Найдем теперь длины векторов х = /24-1, у = — (5/2)/2-{-1 н х+у=»
«_(3/2)Р + 2:
о
jyi-]/ j(?<•-»+!)«- / 4-4+1- /J.
l«+y|-J/ j (4- «--6Л+4 ) Л- ]/ |-2+«- / g.
О
Таким образом, | х|2 = 28/15, ]у |*=7/12, ( х+у |2 = 49/20, т. е. | х 1 у |2 =
--1х+у1’-А
573. Рассматривается множество всевозможных упорядоченных
систем геометрических векторов a* = (ai‘, а,; ..а„), Ь* =ХЬЖ; Ь,;...
Ь„)....Является ли это множество евклидовым пространст-
вом, если сложение элементов, умножение элемента на число н
скалярное произведение определить равенствами а*4-Ь* = (а1 + Ь1;
*1 + Ь,; . • • ;ап + Ь„),Za’= (Xaf, Хаа; •. Xa„), (a*, b‘) =alb1+a„ba+...
.-banb„ (правая часть последнего равенства представляет собой
сумму скалярных произведений геометрических векторов)?
574. Доказать справедливость неравенств:
К (St+п.)’+0.+V + • • -I+(5„ + ч«)’ <
< П! + S> + • -+SS + /tf+n?+---+nJ;
(S’+SI + • • • + Sn) (ч*+н? + • • • + Ля) (Si4t + Ss^> + • • • + Sa1)»)1,
где Bi, .... I),, i)„ ..., i)„—действительные числа.
• Воспользоваться неравенствами треугольникам Коши—Бупяковского для
евклидова пространства, рассмотренного в аадаче 562.
575. Рассматриваются всевозможные непрерывные на отрезке
[0, 1] функции х((), у (/), г (2), ... Доказать справедливость не-
равенств:
(x+yydt < у JxW+I/ \y»dt ,
0 0 0
о \о ✓ \0
, если х (0) =#= 0.
127
§ 6. ОРТОГОНАЛЬНЫЙ БАЗИС И ОРТОГОНАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ
1. Ортогональный базис. Базис ej, ..., е„ евклидова пространства назы-
вается ортогональным, если (е;, е^) = 0 при i 7= k.
Справедлива следующая теорема:во всяком евклидовом пространстве имеется
ортогональный базис. Если ортогональный базис состоит из нормированных век-
торов, то этот базис называется ортонормированным. Для ортонормированного
базиса в], в2, е„ выполняются равенства
, , ( 0 при i 7= k,
(е!’ еП1 при j =fc.
Если в л-мерном евклидовом пространстве известен какой-нибудь базис ft,
h, .. •, fB, то в этом пространстве всегда можно найти н ортонормированный базис
«1, е2, е„.
Любой вектор х евклидова пространства, заданный в ортонормироваином ба-
зисе, определяется равенством
х = £1е1 + &2е2 + • • • + Snen-
Длина вектора х находится по формуле
|*| = 1//' + £2+ • • • + ?«•
Два вектора х = ^ + g2e2 + ... -Н„еп и у = T)iei + T]sC2 + . +т]пеп линейис
независимы (коллинеарны, пропорциональны) тогда и только тогда, когда
?1/Т)1=б2/Т)2=..-=^П/Т)Я.
Условие ортогональности векторов хну имеет вид
В1"П1 + + • • • 4- £пЛп — 0.
Угол между двумя векторами х и у находится по формуле
rn<5 __________^iTli4- ^2Т12 4~ • • • 4~ £пЦп_
г £1 4~ &2 + • • • 4~ &П ’ У 111 + Т)2 + • • • + Ли
В следующих задачах ортонормированный базис «-мерного евклидова прост-
ранства обозначается через е2, е2, еп.
576. Найти длину вектора x = 4et—2е24-2е3 —е4.
577. Нормировать вектор х = et 4-2 К 2 е, 4- 3КЗ е3 4- 8е4 4- 5И5е5.
/—2/7 3/7 6/7\
578. Дана матрица А = 6/7 —2/7 з/7 j перехода от ортонор-
мированного базиса еп е2, е3 к базису ej, е2, е3. Доказать, что ба-
зис е,', е2, е3—ортонормированный.
579. Нормировать вектор х= в! sin3 а-]-е2 sin2 а cos а4-е3 sin а cosa-J-
+ е4 cos а.
58О. _ Определить угол между векторами х = е1И74-е2Иб4-
+ е3И34-е4 и у = е1К74-е2/5.
581. Найти нормированный вектор, ортогональный векторам х=
= 3et е2 е3 е4, у = е4—Зе24-е3-]-е4, z = e14_e2—Зе34~е4.
582. При каком значении X векторы x = Xej4~Xe2—е3—Хе4 н
у=е4—е,4-Хе3—е4 имеют одинаковые длины?
128
583. В четырехмерном пространстве дан базис fy, f2, f3, f4.
С помощью векторов этого базиса построить ортонормированный
базис того же пространства.
Д Сначала построим в заданном пространстве какой-нибудь ортогональный
базис ft, g2, g3, g4.
Положим gi—fi, g2 = ^2 + agi- Подберем действительное число а так, чтобы
выполнялось условие g2 J_gi- Умножив скалярно на gy обе части последнего ра-
венства, получим
(gi. g2) = (gi. h)+a (gy, gi).
Так как (gy, g2j = 0, то a=—(gy, f2)/(gi, gi).
Далее, в равенстве g3 = f3 + Pigi + P2g2 подберем Pi и р2 так, чтобы выпол-
нялись условия gs_l_gi, gaj_g2- Йз равенств
(gi, g3) = (gi, h)-f-Pi (gi> gi)H~P2 (gi. g3).
(g2> gs) = (g2> fs) + Pl (gl> 82) + P2 (g2> 82)
получим Pl = —(gi, f3)/(gi> gi). p2=—(g2, h)/(g2, 82).
Наконец, из равенства g4 = f4 + Tigi +7282 + Yaga находим уу = — (gi, f4)/(gf, gi),
T2=—(g2. h)/(g2. g2). Ya=—(ga. f4)/(gs. gs) •
Итак, при сделанном выборе а, р1( р2, Yi, Тг, Тз векторы gi, g2, g3, g4 по-
парно ортогональны. Значит, векторы ei=gi/| gi |, e2=g2/| g2 |, e3=g3/| g3 |, e4=g4/|g4|
образуют ортонормированный базис. A
584. Рассматривается евклидово пространство многочленов не
выше второй степени. Скалярное произведение двух произвольных
многочленов х = х (() и у = у (() определено равенством (х, у) =
1
= х (t) у (t) dt. Использовав базис f2 = t, f3 = l и применив
о
метод решения, рассмотренный в задаче 583, построить для этого
пространства ортонормированный базис.
Д Сначала построим ортогональный базис gi, g2, g3. Положим gi=fy, т. е.
gy = t2, g2=f2+agy = /+aia. Тогда
1 1 1
f g2t2dt =Л (3<«+<Д t2dt.
000
В силу ортогональности векторов gy и g2 левая часть последнего равенства обра-
щается в нуль. Таким образом, а=—5/4 и g2 — t—5Р/4.
Найдем теперь g3. В равенстве g3 = 1-f-Pi^2 + Рг —5/г/4) значения Pi и Р2
определяем из условий ортогональности
1 1
р р ! Ч \
\ g3/M/=0 и \ g3( i —t2] dt = O.
о о
Таким образом,
1 ! I !
0= Cpd/+Pi и 0=^ —f-/2)^+p2 j (/--|-/2)л.
о о о о '
Отсюда ₽i = -5/3, Р2= -4, g3= 1—5/2/3—4 ((-5i2/4), т. е. g3= 1-4/ + 10Р/3.
S-215 129
Находим длины векторов gx = Z2, g2 = t—5/2/4 и g3 = l—41+ЮР/З:
Таким образом, векторы ex=gx/| gx 1 = У 5t9, e2=g2/| g2 1 = У 3(4—5fa),
®»=gi/|g»| = 3—12< +10Z®, образуют ортонормированный базис. A
585. При каком значении X базис, образованный векторами
gi = Xe1 + e2 + e3+e4, g2 = ex + Xe2 + e3 + e4, g3 = e1 + e3+Xe3 + e4, g4 ==
=ei + e2+ е» + Хе4, является ортогональным? Нормировать этот базис.
Д Из условия (е/, е*) = 0 (при i # fe) получаем уравнение Х+Х+1+1= 0.
Следовательно, >.= —1 и gi= — ех + еа + е3+е4, g2 = ei—е2 + е3 + е4, g3 =
= ®i+e»—e3+e4, g4 = ex + e3+e3—e4, | g,1 = У 14-1 + 1 + 1=2.
Таким образом, векторы ех = 0,5 (—ех + е3 + е3 + е4), е3=0,5(ех—ej + ej+ej,
e’ = 0,5 (ei + es—es+e^, e' = 0,5 (ex + e3 + e3—e^ образуют ортонормированный
базис. A
586. При каких значениях а и Р базис, образованный векторами
ех = уех 4---д— е, + Ре,, е,= —— ех+₽е2+ у е3, е3 = Рех + ув3 +
+ —д— е3, является ортонормированным?
Л Из условий | е' | = 1, (е', е*) =0 (при 1 # fe) получим систему уравнений
а’ + (1— а)»+9₽’=9,
а (1—а) + 3 (1—а) Р+За0 = О.
Из последнего уравнения находим р=—а (а—1)/3. Подставив это значение
Р в первое уравнение, имеем
а’+(1— а)«+а’(1— а2)2=9; 1— 2(1—а)а+а2 (1— а)’=9; (1—а+а’)’ = 9.
Так как 1—а+а* > 0 при действительных значениях а, то 1—а+а’=3,т. е.
а2 —а—2=0. Следовательно, ах =— 1, а2=2, рх =—2/3, ps = 2/3.
Итак, получаем два ортонормированных базиса:
1,2 2 2 2 1
e<i> = ех+у е2-у е„ е<»=у ех - у е, - у е„
2 1 9 1 2 2 2 2 1
е12)=3' ех—д е»+уе», е«>=-у ех+уе2+уе3, е<32>=у ех+у е2-у е3. А
2. Ортогональные преобразования. Линейное преобразование А евклидова про-
странства называется ортогональным, если оно сохраняет скалярное произведе-
ние любых двух векторов х и у этого пространства, т. е. (Ах, Ау) = (х, у). Длина
вектора х при этом не изменяется, т. е. |Ах| = |х|. Таким образом,
(х, у) (Ах, Ау)
|х||.У| |Ах|-|Ау1*
Из последнего равенства следует, что ортогональное преобразование А не изме-
няет угла между любыми двумн векторами х и у.
130
Ортогональное преобразование переводит любой ортонормированный базис
а ортонормированный. Наоборот, если линейное преобразование переводит какой-
нибудь ортонормированный базис в ортонормированный, то оно ииляется орто-
гональным.
587. Является ли ортогональным преобразование, переводящее
каждый геометрический вектор в вектор, симметричный относительно
кекоторой фиксированной плоскости?
588. Является ли ортогональным преобразование, заключающееся
в повороте любого вектора, лежащего в плоскости хОу, на фикси-
рованный угол а?
589. При каких значениях X преобразование А, определяемое
равенством Ах = Хх, является ортогональным?
590. Является ли ортогональным преобразование А, определяе-
мое в каком-нибудь ортонормированном базисе е4, еа, е, матрицей
(аа aii <чз\
а22 «23 у, если «Ц«12 + «21«22 + «31«32 = «11«13 «21<*23 +
a3i «32 «33 /
+ «31«зз = 0. «й«й + а22а23 + «з2«зз = 0, eJi + <4i+a&= 1, «12 + 022 +
+ «32 = 1 > «13 + «23 + «33 — 1?
591. Является ли ортогональным преобразование Ах — — Siei +
+ 12еа + |3е3 + |4е4, где х = + £аеа + £3е3 + g4e4 — произвольный
вектор, а еа, е2, е3, е4—ортонормированный базис?
592. Пусть е4, еа, е3, е4, е5, ев—ортонормированный базис. Дока-
зать, что А—ортонормированное преобразование, если Ае^е*,
Aej=—еа, Ae3 = e3cosa + e4sina, Ае4==—e3sina+e4cosa, Ае5 =!
= e5cosP + eesinP, Аев = —е5 sinP-|-ee cosp.
I 7. КВАДРАТИЧНЫЕ ФОРМЫ
Квадратичной формой действительных переменных х4, х2, ..., хп называется
иогочлен второй степени относительно этих переменных, не содержащий сво-
бодного члена и членов первой степени.
Если f (xi, х2.х„)—квадратичная форма переменных хл, х2, ..., х„, а
X—какое-нибудь действительное число, то f (Xxi,Xx2, •• .,Ххя) = Ха/ (xi,x2.хп).
Если п = 2, то
/ (xi, х2) —auXi-j-2ai22XiX2-j-a22x2.
Если и = 3, то
f (х2, х2, х2) = «11Х1+«22Х2+«ззХз + 2л42х4х2 4~ 2Л1зХ4х3-|- 2а23х2х3.
В дальнейшем все необходимые формулировки и определения приведем для
квадратичной формы трех переменных.
Матрица
/ an ait «is\
А=( а$£ а22 а22 1,
'«31 «32 а3з/
у которой ащ—а/ц, называется матрицей квадратичной формы f (xj, х2, х3), а
соответствующий определитель—определителем этой квадратичной формы.
Так как А—симметрическая матрица, то корни Xi, Х2 и Х3 характеристиче-
ского уравнении
ац—X 012 «!з
a2i а22—Л» а2з
«з< «31 «зз—X
= 0
являются действительными числами.
Пусть
е' = Ьцп+&а1еа+&3iCs ,
е' = Ь12п+Ь23П + 6зге8,
ej = bian -|- &2je2 + b33t3
— нормированные собственные векторы, соответствующие характернстическаз
числам If, 12, 1з в ортонормнрованном базисе [ei, е2, е3. В свою очередь, век-
торы е', е', е' образуют ортонормированный базис. Матрица
/Ьц ba bis \
В = I b3i b33 btt j
\&si b33 b33 /
является матрицей перехода от базиса ei, е2, е3 к базису е’, е', е*.
Формулы преобразования координат при переходе к новому ортонормирован-
ием у базису имеют вид
xi = Ьах^+612х' +
ха=621Х' + &22х' + ,
хз = b3ix' Ь33х* Ь33х'.
Преобразовав с помощью этих формул квадратичную форму f (ха х2, х3), полу-
чаем квадратичную форму
f (Х1> ха> Хз)=^1Х^ +^з*2 +^з*2 >
не содержащую членов с-произведениями х^х*, х^х^, х*х'.
Принято говорить, что квадратичная форма f (xlf хг, х3) приведена к кано-
ническому виду с помощью ортогонального преобразования В. Рассуждения про-
водились в предположении, что характеристические числа If, 12, Хз различим.
При решении задач будет показано, как следует поступать, если среди характе-
ристических чисел имеются одинаковые.
593. Привести к каноническому виду квадратичную форму
f — 21 х* — + Зх2.
Л Здесь au = 27, ai3 ——5, а22=3. Составим характеристическое уравнение
127-1 —5 | 0> иди v_30X+56 = 0>
| —□ и — Л, [
т. е. характеристические числа 11 = 2, 1а = 28.
Определяем собственные векторы. Если 1=2, то получаем систему уравнений
( 25^-5Ь = 0,
I -5Ь+ 6з = 0.
Таким образом, £2=5gj> Полагая £i = c, имеем £а = 5с, т. е. собственный вектор
u = c(ei+5e2).
Если 1=28, то приходим к системе
I -61- 5g2 = o,
I -5gi-25ga = 0.
В этом случае получаем собственный вектор v=c(—5ei-f-e2).
Для того чтобы пронормировать векторы и и V, следует принять с =
= 1/рЛ1, + 5, = 1/^26- Итак, мы нашли нормированные собственные векторы
el = (ei+5e2)/K26, ei = (-5ei+ea)/K26.
Матрица перехода от ортонормированиого базиса е2, е2 к ортоиормировав-
ному базису е', е2 имеет вид
/ 1/К26 — 5/У"2д\
\5/j/"26 1/К26/
132
Отсюда получаем формулы преобразования координат: х1=(1/^Л2б) х[—(5/^26) х2,
*1 =(5//"2б)*1 + (1/К2б)x't- Таким образом,
1 5 Д2 ,п/ 1 , 5 Д/ 5 , , 1 Д.
Х^гё*1 |<26Ха/ \У~2&Х1 К26* /
+3 Л-Д=х.' +~Д= < У=2х/+28х;2.
\|<26 1 |<26 2J 1 2
Этот результат можно было получить'сразу, так как f = lix'2-f-lax'2. Д
594. Привести к каноническому виду квадратичную форму
/ = 2х2 -|~ 8XjX2 -|- 8ха.
А Здесь aii = 2, aia=4, ааа = 8. Решаем характеристическое уравнеиие:
12_________________1 д
. я . =0. Ла=О, Ха = 10.
О ”“А
Определяем собственные векторы. При 1=0 получаем систему
I 2Ы-4Ь = 0,
1 «i+8ga = 0,
которая имеет решение ?i=2c, £а = — с, т. е. и=с(2ех—еа).
При 1=10 имеем
/ -85i+4ga=0,
I 4gi-2ga=0,
откуда £i = с, ga = 2c, т. е. v=c(ej+2ea).
Приняв c=l/p^2a_4-l2= 1/^5> находим нормированные собственные век-
торы el = (2ei—еа)/К5 . ej = (ei + 2еа)/У 5.
Матрица перехода к новому базису (матрица ортогонального преобразования)
имеет вид
Bf ууъ 1//5Л
X-l/KS’ 2/y5j
Формулы преобразования координат запишутся так: xi = (2/^5) Xi -f-
Ч-(1//'5’)х1, х2=— (l/K5)xi+(2/K5)xa. Следовательно,
Эту задачу можно решить проще. Заметим, что f = 2 (xi-|-2xa)2; поэтому
можно принять xa = (xi+2xa)/yrl+4 = (xi + 2xa)/yr5, xj = (2xi—х2)/У5 (вто-
рое равенство написано с учетом ортогональности преобразования). Так как
Xi+2xa=yr5 Хз, то /=10х/.
595. Привести к каноническому виду квадратичную форму
f — Зх? + 2х|+х£ + 4Х]Х2 + 4хаха.
Д Здесь ац — 3, ааа = 2, а38 = 1. вхг = 2, fli2=0, ааа = 2. Составляем харак-
теристическое уравнеиие
3—1 2
2 2—1
О 2
О
2
1-1
= 0; (3—1) (2—1) (1—1)—4 (1—1)-|-4 (3—1) =0;
133
(3—1) (2-1) (1—1)—8 (2—1) = 0; 2—1) (I2—41+3—8) =0),
(2—1) (Is—41—5) =0; 1! = 2, 1, = —1, 1з = 5.
Определяем собственные векторы, соответствующие найденным характеристиче-
ским числам. Для определения координат собственных векторов получаем три
системы линейных уравнений:
1)1=2, 2) 1= — 1, 3)1=5,
( £i+2£2 = 0, ( 4^+252=0, ( -251+2^=0,
1 2Ei+2gs=0, ] 25i+3g2 + 2gs=0, ) 2gi-3g2+2&8 = 0,
\ 2£.-Ь=0; I 2&a+2&s=O, \ 2g2-4g2=0;
li = 2c, Ь=—с, 1з=—2с, ^i = c, g2 = —2с, 5з = 2с, |i=2c, £2=2с, Ь=с,
u=c(2ei—е2—2es), v=c(ei—2e2+2es), w=c (2ej+2e2+es),
ei=^’(2ei—e2—2es); e'=-g-(ei—2ег+2ез); ea =-g- (2ei + 2e2 + ea).
Матрица ортогонального преобразования имеет вид
/ 2/3 1/3 2/3\
В = (_1/3 —2/3 2/3).
\—2/3 2/3 1/3/
Формулы преобразования координат таковы: x1 = (2/3)x'+(l/3)x' + (2/3)xJt
*2= —(1/3) х[—(2/3) х' + (2/3) х',%= —(2/3) х; + (2/3) х' + (1/3) х'.Следовательно,
f=2xf—х^’ + бх'1. ±
596. Привести к каноническому виду квадратичную форму
/ = бх* + 3xJ + Зха + 4ХрХя + 4Х1Ха—8X2X3.
Л Здесь ац=6, a2i = 3, Язз = 3, ait — 2, ais=2j
ристическое уравнение
«23 = —4. Решив характе-
6—1
2
2
2 2
3—1 —4
—4 3—1
= 0,
находим характеристические числа 11 = 12 = 7, lj = —2.
При 1=7 приходим к системе
Г -£1+2£2+2Ь = 0,
1 251-4?2-4Ь = 0,
I 2£1-4£2-4£з = 0,
которая сводится к одному уравнению £i = 2g2+2£a. Решение этой системы можно
записать в виде il = 2a + 2b, ^2 = а, £а = 6. В результате получаем семейство соб-
ственных векторов u = 2(a+6) ei+ae2+6es, зависящее от двух параметров а и Ь.
При 1=—2 получаем систему
( 8£1+2£2 + 2£з = 0,
{ 2£1+5£2-4£з = 0,
I 2gi-4g2+5gs = 0.
Решив, например, два последних уравнения, имеем — —18) = 1з/(—18),
или gi = —£2/2= — £з/2; £i = c, g2 = —2с, £а =—2с. Таким образом, получим
однопараметрическое семейство собственных векторов v = c(ei—2е2—2еа).
Из семейства собственных векторов и =2 (а+й) ei+ae2+6ea выделим два
каких-нибудь ортогональных вектора. Полагая, например, а = 0, 6=1, получим
собственный вектор tii=2ei+e3. Подберем параметры а и Ь так, чтобы выполня-
лось равенство (u, Ui) = 0. Тогда получим уравнение 2-2(а+6)+6 = 0, т. е.
4а+56 = 0. Теперь можно принять а = 5, Ь = —4; отсюда находим другой собст-
венный вектор рассмотренного семейства: и2=-2е1+5е2—4е8.
Итак, мы получили три попарно ортогональных вектора: ui = 2ei+es,
u2 = 2ei + 5e2—4е3, v = ei—2е2—2е8. Собственные векторы щ и и2 соответствуют
характеристическому числу 1=7, а собственный вектор v—характеристическому
числу 1=—2 при с=1.
Пронормировав эти векторы, получим новый ортонормированный базис, при*
чем матрица перехода к новому базису имеет вид
/2/К5 2/(3 У 5") 1/3\
В=( О V5/3 —2/3 1-
\1/К5 -4/(3 К5) —2/3/
Применив формулы преобразования координат хр= (2/У 5) х1+(2/(зУ5Г)) xs-f-
+ (1/3)х;, x2 = (V5/3)"ха —(2/3) Хз, х8=(1/У5)х;-(4/(3 У5)) xi-(2/3) х£
к заданной квадратичной форме, получаем /=7х' -|-7х' — 2х' . А
597. Привести к каноническому виду уравнение линии 17х2 +
+ 12ху + 8у*—80 = 0.
Д Группа старших членов уравнения образует квадратичную форму
17x2-f-12xy-f-8y2 с матрицей Д = (^.Составим характеристическое уравнение
j17?1 в—1|=°’ “ЛИ Х2—25Х+,00=0-
т. е. характеристические числа li = 5, 12=20. Следовательно, квадратичная форма
17х2+12xy-f-8y2 преобразуется к каноническому виду 5х'*-|-20у'2, а данное урав-
нение—к виду
5х'2-|-20у'2—80=0, или х'*/16+у'2/4=1,
откуда ?2 = — 2gi. По-
u=c(ef—2е2).
— 2ga, т. е. собствен-
т. е. заданная линия является эллипсом.
Найдем базис, в котором уравнение эллипса принимает канонический вид,
для чего определим собственные векторы.
, _ / 125i4-6J2=0,
При 1=5 имеем систему уравнений <
I 6ё1+Зё8 = 0,
лагая |1= с, получим ?2 =—2с, т. е. собственный вектор
( —ЗЕ,+ 6Е. = 0,
При 1=20 имеем систему j _0 откуда
иый вектор v=c(2ef+ea). _
Приняв c—\lV 12-|-22 = 1/У5 , находим нормированные собственные векторы
е1'=(е1— 2е2)/У5 и е8' = (2е£+е2)/У5 .
Матрица ортогонального преобразования имеет вид
в( Х1уГ*
\-2/У5 1/Кб/
Формулы преобразования координат запишутся так: х=(1/У5)х' + (2/У5)у/,
у= — (2/Уб) х' + (1 /У5)у'. Следовательно,
17
17х2+ 12ху+8у2—80=^ (х'+2у')2+
и
. ^(х'+гуЭ (-2х' +/)+! (—2х'+у')2-80 = 5х'2+20у'2-80.
1 □ о
Этот же результат можно было получить сразу, как только были найдены
1Ц и A,: lix'2+W2-80 = 0. А
Привести к каноническому виду уравнения линий:
598. 6х*+2^5 ху+2у'—21=0. 599. 4ху + 3у2+ 16 = 0.
600. 5х2 + 4 lz6’xi/+7y2—44 = 0.
ГЛАВА VI
ВВЕДЕНИЕ В АНАЛИЗ
§ 1. АБСОЛЮТНАЯ И ОТНОСИТЕЛЬНАЯ ПОГРЕШНОСТИ
Пусть а — приближенное число, заменяющее собой в вычислениях точное
число А.
Абсолютной погрешностью приближенного числа а называется абсолютная
величина разности между ним и соответствующим точным числом: |А—а|.
Предельной абсолютной погрешностью называется возможно меньшее число А,
удовлетворяющее неравенству \А—а|<:А.
Точное число А находится в границах а—А<А<а±А, или А = а ± А.
Относительной погрешностью приближенного числа а называется отношение
абсолютной погрешности этого числа к соответствующему точному числу:
| А—а \/А.
Предельной относительной погрешностью называется возможно меньшее
число 6, удовлетворяющее неравенству |А—а|/А<6.
Так как практически А хл а, то за предельную относительную погрешность
принимают число 6 = А/а (выражаемое обычно в процентах).
Справедливо неравенство а(1—6) < А < а (I 4-6).
Говорят, что положительное приближенное число а, записанное в виде деся-
тичного разложения, имеет п верных знаков (цифр), если абсолютная погрешность
этого числа не превышает половины единицы n-го разряда.
При п > I за предельную относительную погрешность приближенного числа а
1 / 1 \«~1
с первой значащей цифрой k можно принять число 6=^( )
Если известно, что
то число а имеет п верных знаков.
Предельная абсолютная погрешность алгебраической суммы нескольких чисел
равна сумме предельных абсолютных погрешностей слагаемых.
Относительная погрешность суммы положительных слагаемых не превышает
наибольшей из относительных погрешностей этих слагаемых.
Предельная относительная погрешность произведения и частного приближен-
ных чисел равна сумме предельных относительных погрешностей этих чисел.
Предельная относительная погрешность степени приближенного числа равна
произведению предельной относительной погрешности этого числа на показатель
степени.
601. Угол, измеренный теодолитом, оказался равным 22°20'30"±
±30". Какова относительная погрешность измерения?
Л Абсолютная погрешность А = 30". Тогда относительная погрешность
Л 30"
6=y=2F20W100%=°’04%-А
602. Определить число верных знаков и дать соответствующую
запись приближенной величины ускорения силы тяжести g = 9,806 ...
при относительной погрешности 0,5%.
13G
Л Так как первая значащая цифра есть 9, то, воспользовавшись неравенств
вом (1), получим О’005 < 2Л0 \ ) > г. е. п = 2. Значит, g=9,8. А
603. Известно, что предельная относительная погрешность числа
И19 равна 0,1%. Сколько верных знаков содержится в этом числе?
А Здесь первая значащая цифра есть 4, предельная относительная погреш-
1 I 1 Х"-1
иость 6 = 0,001 = 10-3. На основании неравенства (1) имеем 0,001 \ ТО J ’
откуда п = 3. Следовательно, У19 =4,36 (по четырехзначным таблицам У19 =
= 4,3589). А
604. Сколько верных знаков содержит число А = 3,7563, если
относительная погрешность равна 1%?
1 Z 1 \в-1
Д Первая верная цифра есть 3, поэтому (XOKgTg* (foy » 0ТКУДа л=2.
Число А следует записать так: А = 3,8. А
605. Площадь квадрата равна 25,16 см* (с точностью до 0,01 см*).
С какой относительной погрешностью и со сколькими верными зна-
ками можно определить сторону квадрата?
А Искомая сторона х = У25,16. Относительная погрешность стороны квадрата
6 = (1/2)-(0,01/25,16), где 0,01 — абсолютная погрешность площади, т. е. 6 = 0,0002.
Первая значащая цифра числа, измеряющего сторону квадрата, есть 5. Решив нера*
венство (1) при k = 5, получим (5±1)-0,0002 < l/lO”-1, или l,2-10_*< l/lO»-1.
Отсюда п — 3. А
606. Со сколькими верными знаками можно определить радиус
круга, если известно, что его площадь равна 124,35 см* (с точностью
до 0,01 см*)?
607. Найти предельную относительную погрешность при вычисле-
нии полной поверхности усеченного конуса, если радиусы его основа-
ний Я = 23,64 ±0,01 (см), г = 17,31 ±0,01 (см), образующая / =
— 10,21 ± 0,01.(см); число л = 3,14.
608. Число g = 9,8066 является приближенным значением уско-
рения силы тяжести (для широты 45°) с пятью верными знаками.
Найти его относительную погрешность.
609. Вычислить площадь прямоугольника, стороны которого 92,73±
±0,01 (м) и 94,5 ±0,01 (м), Определить относительную погрешность
результата и число верных знаков.
| 2. ФУНКЦИЯ ОДНОЙ НЕЗАВИСИМОЙ ПЕРЕМЕННОЙ
Действительными (или вещественными) числами называются рациональные и
иррациональные числа. Множество всех действительных чисел обозначается бук-
вой R. Каждое действительное число может быть изображено точкой на числовой
прямой.
Пусть даиы два непустых множества X и У. Если каждому элементу х из
множества X по определенному правилу ставится в соответствие один и только
один элемент у из У, то говорят, что иа множестве X задана функция (или отоб-
ражение) со множеством значений Y. Это можно записать так: х£Х, X —>- У или
f: X —> У, где множество X называется областью определения функции, а мно-
137
жество Y, состоящее из всех чисел вида y — f (х), —множеством значений функции.
Если у является функцией от х, то пишут также y — f(x) или у=<р(х). Буквы f
или <р характеризуют то правило, по которому получается значение у, соответст-
вующее заданному аргументу х. Область определения функции f обозначается че-
рез D(f), а множество значений—через Е(/). Значение функции f(x) при х=а,
где a(?D(f), называется частным значением функции и обозначается f(a).
Область определения функции в простейших случаях представляет собой: ин-
тервал (открытый промежуток), ]а, й[, т. е. совокупность значений х, удовлетво-
ряющих условию а < х < Ь; сегмент (отрезок или замкнутый промежуток) (а, 6],
т. е. совокупность значений х, удовлетворяющих условию а Ь; полуинтервал
]а, 6] (т. е. в<х<6) или [а, й[ (т. е. а<х < Ь)\ бесконечный интервал
1в,+ ооj (т. е. а < х <4-оо) или ] — оо, 6[ (т. е. —оо < х < Ь) или ]—оо, +°°1
(т. е. —оо < х < + оо); совокупность нескольких интервалов или сегментов и т. п.
Основными элементарными функциями называются следующие функции:
П степенная функция у=х®, где a^R;
2) показательная функция у=ах, где а—любое положительное число, отличное
от единицы: а > 0, а 1;
3) логарифмическая функция y=logax, где а—любое положительное число,
отличное от единицы: а > 0, а =£ 1;
4) тригонометрические функции у = sin х, у = cos х, у = tg х, у = ctg х, у — sec х,
у=cosec х;
5) обратные тригонометрические функции у — arcsln х, у = arccos х, у=arctg х,
y=arcctgx.
Элементарными функциями называются функции, получающиеся из основных
элементарных функций с помощью четырех арифметических действий н суперпо-
зиций (т. е- формирования сложных функций), примененных конечное число раз.
Примером иеэлемеитариой функции может служить абсолютная величина (мо-
дуль) действительного числа х:
( х при х^О,
у=х =< п
’ 1 ( —-х при х < 0.
Геометрически |х| равен расстоянию на числовой прямой от точки с координатой
х до начала отсчета. В общем случае |х—а\ есть расстояние между точками с
координатами х и а.
Графиком функции y = f(x) называется множество точек плоскости хОу с коор-
динатами (х; f(x)), где x£D(f).
Функция f(x), область определения которой симметрична относительно нуля,
называется четной (нечетной), если для любого значения x£D(f) f (— x) = f (х)
[соответственно f (— х) = — f (х)]. Г рафик четной функции симметричен относительно
оси ординат, график нечетной функции— относительно начала координат.
Функция f(x) называется периодической, если существует такое число Г#б, что
для любых xeD(/), x-TeD(f), x+TeD(f) выполняются равенства/(х)«/(х-7)-
=f(x+7). Основным периодом функции называется наименьшее положительное чис-
ло т, обладающее указанным свойством.
,610. Найти f если Нх) = *2-
Д Найдем значения данной функции при х—а и x — bt f(a)—a>, f(b) = b*.
Тогда получим
f(b)-f(a)_b*-a* .
b—a b—a ‘
611. Найта область определения функции f(x) =
д Данная функция определена, если 2х—1 О, т. е. если х 1/2. Таким
образом, областью определения функции является объединение двух интервалов:
/>(/)—(—оо, l/2)U(l/2, +оо). ▲
612. Найти область определения функции /(х)=
136
Л Функция определена, если х—1 / 0 и 1 -}-х > 0, т. е. если х 1 и х >— 1.
Область определения функции есть объединение двух интервалов: D (f) =
=(-1, 1)U(1, +а>).: Д
613. Найти область определения функции
f (х) = ]/ 1—2х + 3 arcsin ^1.
Л Первое слагаемое принимает действительные значения при 1—2x^.0, а
второе—при—1<(3х—1)/2=с1. Таким образом, для нахождения области опре-
деления заданной функции необходимо решить систему неравенств: 1—2x^0,
(Зх— 1)/2< 1; (Зх— 1)/23г — 1. В результате получаем х< 1/2, х< 1, xSs—1/3.
Следовательно, область определения функции есть отрезок I—1/3, 1/2]. А
614. Найти множества значений функций:
О /(х) = х2—6x4-5; 2) f (х) = 2 4- 3 sin х.
Л (1) Выделяя нз квадратного трехчлена полный квадрат, получим f (х) =
= х2—6x4-9—4 = (х—З)2—4. Первое слагаемое при всех х является неотрица-
тельным числом, поэтому функция принимает значения, не меньшие—4. Итак, мно-
жество значений функции—бесконечный промежуток [—4, +<ю).
2) Так как синус принимает значения, не превосходящие по модулю единицы,
то получаем неравенство | sin х | < 1, или — К sin х < 1. Умножив все части этого
двойного неравенства на 3 и прибавляя к ним по 2, имеем—3<3sinx<3;
— 1 <2-|-3sinx«c5. Следовательно, Е (/) = [ — 1, 5]. А ’
615. Найти основные периоды функций:
1) f(x) — cos 8х; 2) f (х) = sin 6х 4- tg 4х.
Д 1) Так как основной период функции cosx есть 2л, то основной период
функции f (x) = cos8x равен 2л/8, т.е. л/4.
2) Здесь для первого слагаемого основной период равен 2л/6 = л/3, а для
второго он равен л/4. Очевидно, что основной период данной функции есть наи-
меньшее общее кратное чисел л/3 и л/4, т. е. л. А
616. Установить четность или нечетность функций:
l)7(x) = x2^x4-2sinx; 2) f(x) = 2*4-2~*; 3) f(x) = |x|—5е*’;
4) f(х) = Xs4-5х; 5) f(x) = lg^f.
Д В рассматриваемых примерах область определения каждой из функций
симметрична относительно нуля: в первых четырех примерах D (f) = (—со, + оо),
а в последнем примере D (/) = (—оо, — 3)(J(3, +<ю). _
1)3аменяяхна —х,получим/(—х) = (—х)2 р/(—x)-[-2sln(—х) =— х2у/х—
— 2sinx т. е. f (— х) = — f (х). Значит, данная функция является нечетной.
2) Имеем f (— х) = 2“*-|-2-<-х>=2-*4-2*, т.е, /(-х)=/(х). Итак, данная
функция—четная. . _ , л
3) Здесь f(—x) = |x|—5e<-*)2 = |xf—5e*2, т.е. f(—x)=f(x). Следовательно,
f (х)—четная функция.
4) Имеем f (— х) = (— х)2-|-5(— x)=xz—5х. Таким образом, /(—х)//(х) и
f (— х) Ф — f (х), т.е. заданная функция не является ни четной, ни. нечетной.
5) Находим
. . . -х+З . х—3 . /х+ЗХ-1 1 *4-3
/(—*)-,2_А._3-,бх_|_3 3/ gx—3’
т.е. f(— х) = — / (х), и, следовательно, данная функция—нечетная. А
139
617. Найти области определения функций:
1) f(x)= И4—№ + у; 2) f(x) = arccos^ — 1);
3) /(х) = ——; 4) f(x) = ^-; 5) / (х) = —2*‘±Ь--;
' zv ' xe* cos2x x—4
6) f (x) = 1g (3x—1) + 21g (x+ 1); 7) f (x) =
618. Найти множества значений функций:
1) f(x) = |x|+l: 2)f(x)==5/x; 3) /(x) =/Тб=^;
4) /(x) =— x*+8x—13; 5) f(x)=l— 3cosx; 6) f(x) = 4-*2.
619. Установить четность или нечетность функций:
1) / (х) = х4 sin 7х; 2) f(х) = 5|х|—З^х5; 3) f(х) = х4—Зх8 + х;
4) /(х) = |х| + 2; 5) /(х) = |х + 2|; 6) f(x) = lgcosx;
620. Найти основные периоды функций:
1) /(x)==sin5x; 2) f(x) = —2cos(x/3)+1;
3) f (x) = 1g cos 2x; 4) f (x) = tg 3x + cos 4x.
$ 3. ПОСТРОЕНИЕ ГРАФИКОВ ФУНКЦИЙ
При построении графиков функций применяются следующие приемы: построе-
ние «по точкам»; действия с графиками (сложение, вычитание, умножение графи-
ков); преобразования графиков (сдвиг, растяжение).
Исходя из графика функции y=f (х), можно построить графики функций:
1) y—f (х—а)—первоначальный график, сдвинутый вдоль оси Ох иа вели-
чину а;
2) y-f(x)-\-b—тот же график, сдвинутый вдоль оси Оу иа величину Ь;
3) y—Af(x)—исходный график,
растянутый в А раз вдоль оси Оу.
4) y — f (kx)— тот же график, рас-
тянутый в l/k раз вдоль оси Ох.
Таким образом, можно по .графи-
ку функции y = f (х) построить график
функции вида y=Af[k(x—a)]-f-6.
621. Построить график функции у = 2х-|-1+cosx.
Л График дайной функции можно построить сложением графиков двух функ-
ций: у=2х4-1 и y = cosx. График первой функции есть прямая, ее можно по-
строить по двум точкам, график второй функции—косинусоида (рис. 23). А
140
622, Построить график функции
{2—х при х^З,
0,1 х* при х>3.
А При х<3 графиком является луч, а при х^З—ветвь параболы. Иско-
мый график изображен на рнс. 24. А
623. Построить график функции z/ = 2sin(2x—1).
Д Преобразуем данную функцию к виду y = 2sln2(x—1/2). Здесь А = 2,
4 = 2, а =1/2. В качестве исходного возьмем график y=slnx. Затем строим гра-
фик функции y=sln2x сжатием вдоль оси абсцисс в два раза. После этого стро-
им график функции y=sin2(x—1/2) сдвигом на 1/2 вправо и, иакоиец, растяже-
нием в два раза вдоль оси ординат последнего графика получаем искомый график
функции y=2stn(2x— 1) (рис. 25). ±
Построить графики функций:
624. у = на отрезке [—4, 4].
625. у = хг(2—х)‘ на отрезке [—3, 3].
626. г/ = Кх+^4—х в области определения.
627. у = 0,5х + 2~* на отрезке [0, 5].
628. у = 2(х—I)8, исходя из функции г/ = х5.
629. 630.
631. f/ = sin(3x—2)4-1. 632. у = — 2cos(2x4-l).
633. y = arcsin(x—2).
634. y = x-f-l 4-sin(x— 1). 635. y = sinx4-cosx.
(—х*
e3e- Н а*
при х < 0,
при х^О.
637.
У =
’4—х при
5 при
х44-5 при
х< — 1,
— 1<х<0,
х>0.
141
§ 4. ПРЕДЕЛЫ
Число а называется пределом последовательности xt, хг,... , хп,... , если
для всякого сколь угодно малого положительного числа е найдется такое поло-
жительное число N, что |хл—а \ < е при п > N. В этом случае пишут limx„=a.
л->оо
Число А называется пределом функции f(x) при х—>-а, если для любого
сколь угодно малого е > 0 найдется такое о > О, что | / (х)—А | < е при 0 < | х —
— а| < 6. Это записывают так: Um/(x) = A.
х-*а
Аналогично Um/(x) = A, если |/(х)—А \ < е при |х| > N.
х->оо
Условно записывают Um f (х) = оо, если | f (х) | > М при 0 < | х—а | < 6, где
х->а
М—произвольное положительное число.
В этом случае функция / (х) называется бесконечно большой при х —> а.
Если Uma(x)=0, то функция а(х) называется бесконечно малой при х—t-a.
х-т
Если х < а и х —► а, то употребляют запись х —► а—0; если х > а и х —>- а
— запись х—>а4-0. Числа f (а—0)= lim f (х) и /(a-|-0) = Um f (х) называются
x-+a—Q х-нл-О
соответственно левым и правым пределом функции f (х) в точке а.
Для существования предела функции f (х) при х —> а необходимо и достаточ-
но, чтобы f(a—0)=/(a-|-0).
Практическое вычисление пределов основывается иа следующих теоремах.
Если существуют Um f (х) и lim g(x), то
1) Дт [/ W+g WJ = Um f W+Jimg (x)j
2) Um [/ (x)-g (x)] = Um / (x). Um g (x);
x->a x->a x-hj
Um / (x)
Используются также следующие пределы:
Um *= 1 (первый замечательный предел);
х-*о х
Um ( 1-|—— )*= Um (l + <x)I/a =e = 2,71828... (второй замечательный предел).
х_оо\ х / а—о
Логарифм числа х по основанию е называется натуральным логарифмом и
обозначается 1пх.
При решении примеров полезно иметь в виду следующие равенства:
1п(1+х) , „ ах—1 . .. (1+х)® —1 т
lim —-—!—-=1, Um------------=lna, lim -—1— ------=m.
x-*e x x-»o x хч-о x
638. Показать, что при n—► оо последовательность 3, 2у, 2 у,
2-^, ... , 2 + , ... имеет пределом число 2.
А Здесь я-й член последовательности есть хл = 24-1/я. Следовательно, хп—
— 2= 1/я. Зададим заранее положительное число в. Выберем я настолько боль-
шим, что будет выполнено неравенство 1/я < в. Для этого достаточно принять
я > 1/е. При таком выборе я получим |х„—2| < е. Значит, Umx„ = 2. Д
639. Показать, что при п—>-оо последовательность 7/3, 10/5,
13/7, ... (3n-f-4)/(2n-|-1), ... имеет пределом число 3/2.
А Здесь х„—3/2 = (Зя + 4)/(2я+1)—3/2 = 5/[2(2я+1)]. Определим, при ка-
ком значении я выполняется неравенство 5/(2 (2я-|-1)1 < в; так как 2 (2я+1) >
142
> 5/e, то n > 5/(4 e) —1/2. Итак, если n > 5/(4e) —1/2, to |x„—3/2f<e, т.е.
lim x=3/2.
rt“>O0
Полагай е = 0,1, заключаем, что неравенство |x„—3/21< 0,1 выполняется
при n > 12 (например, при п=13), Аналогично, неравенство |х„—3/21< 0,01
выполняется при п> 124,5 (например, при п = 125), а неравенство |хл—3/21 <
< 0,001—при п > 1249,5 (например, при п = 1250). А
Найти следующие пределы:
640.
Л Так как х—>-4, то числитель дроби стремится к числу 5*44-2 = 22, а зна-
। О по
менатель—к числу 2.44-3=11. Следовательно, 11m ———2. А
х-+4 2х-|-3 11
Д Числитель и знаменатель дроби неограниченно возрастают при х—>оо.
В таком случае говорят, что имеет место неопределенность вида оо/оо. Разделив
на х числитель и знаменатель дроби, получаем
Пт lim 1+5/*—J.,
л->оо2х-|-7 х-*<» 2-|“7/х 2
так как при х —► оо каждая из дробей 5/х и 7/х стремится к нулю. Д
642.
х->-3 х । °*
А Здесь числитель и знаменатель дроби при х—► З стремятся к нулю (не-
определенность вада 0/0). Имеем
х*—9 ^_(х—3) (х-|-3)_х4-3 .
х4—Зх х(х—3) х "
если х^З, то 11m 4-~ -= Hmii®. Но при х—>-3 дробь стремится к
х_>з х* —Зх х->-3 х х
числу 2. Итак, Нт -х ~^=2. А
3 x-*-3 х4 — Зх
643. lim
А Здесь имеет место неопределенность вида 0/0. Разложим иа множители
числитель и знаменатель дроби:
Um Пт
х»4-х4-х-1 1 * (*+ D-(*+ О
цт Пт 0 —0. А
Х-1 (X—1) (х—(—I)4 x-И х4-1 2
алл к- 1000___
644*ЛТо Xs—2бх»4-100х •
Д Это—также неопределенность вида 0/0. Имеем
Xs—1000 (х-10) (х44- Юх-ЦОО) г,т х*4- 10х+100
JLiox»—20х44-100х~х-Ю х.(х— IO)2 х-ио х(х—10)
x(X~ 10)2
143
Числитель дроби стремится к 300, а знаменатель стремится к нулю, т. е. яв-
ляется бесконечно малой величиной, следовательно, рассматриваемая дробь—бес-
, х3—1000 .
конечно большая величина и lim ——-— ---- — оо. ▲
«юх3-20х44-100х
645. lim О+4~2 .
х-0 *
Л Умножим числитель и знаменатель дроби на сумму 4-^-2:
Цт(^^-^^Й + 2^== ]im-..*+lr4 = lim. _J_ =1 . Л
х-о х(угх4-4+2) х->.0х(/х+4-]_2) х-0 /х4-4-|-2 4
м». и,, .
Х-0 *
Л Положим 1-|-х=у5; тогда у—► 1 при х—»-0. Значит,
Um
х-»о
Umlim ..... <8+у+1_________=1
X ,-ну5-1 y4+l/3+fZ2+fz+l 5
647.
x-»0 x
Л Используя первый замечательный предел, имеем
sin mx .. msinmx т sinmx
Um--------= Um-----------=m Um-----------=m
x->-o x x^-o mx x-+o mx
648.
x->0 x
Д Имеем
Um 1 -cos Um 2sln* (5*/2>=2 lim (sln (5x/2)V=2.(A?=? • A
«-*o x2 x-»-o хг x-*o \ x J \ 2 / 2
Здесь мы воспользовались результатом предыдущего примера, приняв
Л1 = 5/2. А
х»+2х44-Зх+4
4х®+3х4+2х+1
649. lim
Х-.00
Д Это—неопределенность вида оо/оо. Разделим числитель и знаменатель дро-
би на старшую степень х, т. е. на х’:
х»+2х4+Зх+4 ,.т 1+2/х+3/х4+4/х’_ 1 А
х^» 4x3-|-3*4+2x+ f 4+3/х+2/х4+1/х? 4 ж
650. lim
X-»-®
Зх4—2
ух«4->3x4-4 '
Л Разделим числитель и знаменатель на х4:
lim J**"2 Um _3-2^ _-3_з. А
Х-+® )<x84-3x4-4 х-*® уг14-3/х’4-4/х« 1
651. lim (/х44-8х4-3—/х44-4х4-3).
Х-*00
144
Л Здесь имеет место неопределенность вида оо — оо. Умножим и разделим
данное выражение на )Лх24-8х 4-З4-Уг*24-4х4-3:
Jim (/х24-8х4-3—/+ 4x4-3) =
= lim (^+8x+3-yrx1‘+4x+3)(^+8x+3+Vrx<‘+4x+3) __
*->» /х24-8х4-34-угх24-4х-|-3
= Jim х2 + 8х-Ь_3-х2-4х-3 _ Цш Jx
уд*+8х-|-34-угх24-4х4-3 *->-«> Ух24-8x4-34- Угх24-4х4-3
= lim — . —— -^А—2. ±
**» У14-8/х4-з/х24-У14-4/Х4-з/ха 2
“•да)'
Л Делением числителя дроби на знаменатель выделим целую часть:
х24-5х4-4_ . 8х—3
х2—3x4-7“1 +х2-3x4-7 ’
Таким образом, при х—► оо данная функция представляет собой степень,
основание которой стремится к единице, а показатель—к бесконечности (неопре-
деленность вида 1”). Преобразуя функцию так, чтобы использовать второй заме-
чательный предел, получим
lim
х-*а>
х2 4-5x4-4 V
Xs—3x4-7 )
= lim
= lim
х‘-Зх + 71 -МЗх-З)
. . 8х — 3 \ 8х—3 х2-Зх+7
1 х2—3x4-7/ J
— Нт
л-*<ю
хж-3*+7
8х—3 \ 8х-з
х2—3x4-7/
8-3/х
1 -З/х + 7/х2
__2
Так как -5—=—г-=—>0 при х—► оо, то
х2—3x4-7 г
х*-Зх+7
lim Г1+ в*~3 8*-3 =е.
х-+а> \ х®—Зх-{-7 /
Учитывая, что lim -——==8, находим lim (
х-« 1—3/Х4-7/Х2 Z-оо \Х2—3x4
правый пределы функции f(x)
X
1
653. Найти левый и
при X—нЗ.
Л Если х—► 3—0, то
lim f(x) = l/3. Если же
>-♦3 — 0
lim f(x) = 0. А
1/(х—3)—►—оо и 21/(*-3)—►О. Следовательно,
х—^34-0, то 1/(х—3)—>4-00, 21/(*-3)—♦4-00 и
654. Найти левый и правый пределы функции f (x) = eI/(*-a> прн
х—+а.
143
Л Если х—►а—0, то 1/(х—а)—►— со и lim f(x) = O. Если же х—►а-}-0,
. х-*а-0
то 1/(х—в) —» -j- со и lim f (х) = Ц-00 • А
х-*а+0
655. Показать, что при п—► <» последовательность 1/2, 5/3,
9/4, , (4п—3)/(n+ 1), ••• имеет предел, равный 4.
656. Показать, что при п—>оо последовательность 1, 1/3, 1/5,...
.... 1/(2п—1), ... является бесконечно малой.
Найти следующие пределы:
657. lim e58< Hm К1,+х+х«—Kl—.
659. lim ^5x+6. 660. lim *’~e*?± V*"6.
X-+3 9 x4—3x4-2
661. lim sMa+2ft)-2sin(a+ft)+Sinaj 662> Hin tgmx .
h->o A JC_>osinnx
663. lim ^-*-=tg*°. 664. lim *“*=“’*.
x-x. x——Xq л_л/4 Л-4*
«05. Um 000. lim^+ff+g-6.
Х-+-Я/2 я x->-a> *’ + >i*4 + 7x—1
• Положить л/2—x = a.
667 lim (2x’+4x+5) (x44-x-|-1) .. x2—7x+10
e®7- А® (Г+2Й?+Ъ’+7х4+х-1) 668- 1^^87+12-
669. lim 1Г1±Х+Х*~2. 670. lim to*sta*->.
X—1 *+l x_0 x
671. lim T7'-=^-—. 672. lim K1.+*+*8~H7x+2x—x4
хм.о/14-X-l X_2 X4—2x
673. limlz^Jl*. 674. lim
XM-ol— c°s3* л_0 x*
675. lim.-to"1*). 676. lim g±|.
X-.0 x x->±oo 2 —J
677. lim (Их4 + ах + &—Их’ + сх + d).
678. lim (sinjAr+ 1—sin Их).
X-*»
679. lim (J/x+T—l/l). 680. lim
681. lim . 682. lim .
6* 5* In (1-|-x)
683. lim 5^. 684. lim *~1-
X-*0 X x-M X—1
• Положить x = t*.
685. lim . 686. lim
*_±o|x| Sint
687. lim *. 688. lim 10V<*-»>.
x->0 In («4-1) x-»5-0
146
689. lim sin x. 690. lim —-.
X-*® X->1 --I
691. Найти lim/({/a—1) (где />0).
/-*00
• Положить x=l/t, где x—»-0.
692. lim .
694. lim (—Ц-—А-Л
x-3 \*-3 *s—9J
693. lim (1+-Y.
X-*-<X> \ x )
695. lim
x-0 **+*
• Привести дроби к общему знаменателю.
696. lim . 697. lim ln(1~-3x).
л-0 х
ф Учесть, что х* = ел1пл,
698. lim ЙЙЙТ- б»»-
;->«2х‘+Зх4+1 Л_о X
700. lim 701. lim (2—cosa)co8ec’“.
702. Найти lim (^Y+C. 703. lim f * Y/u-a).
t-KO \X + °J x—2 \ i J
§ 5. СРАВНЕНИЕ БЕСКОНЕЧНО МАЛЫХ
Пусть a(x) и Р (х)—бесконечно малые при х—»-а.
1. Если lim(a/p) = 0, то говорят, что а является бесконечно малой высшего
х~*а
порядка по сравнению с р. В этом случае пишут <х = о(р).
2. Если lim (<х/р) = т, где т—число, отличное от нуля, то говорят, что а и
х-»а
Р—бесконечно малые одного и того же порядка. В частности, если lim(a/p)=l,
х-*а
то бесконечно малые аир называются эквивалентными. Запись а ~ р означает,
что а и р—эквивалентные бесконечно малые.
Если а/р—► оо. то это означает, что lim (P/a)=0. Таким образом, р являет-
ся бесконечно малой высшего порядка по сравнению с а, т. е. Р = о(а).
3. Если а* и р—бесконечно малые одного и того же порядка, причем k > 0,
то говорят, что бесконечно малая р имеет порядок k по сравнению с а.
Отметим некоторые свойства бесконечно малых:
1° . Произведение двух бесконечно малых есть бесконечно малая высшего поряд-
ка по сравнению с сомножителями, т. е. если у = ар, то у=о(а) и у=о(Р).
2° . Бесконечно малые аир эквивалентны тогда и только тогда, когда их
разность а—Р = у является бесконечно малой высшего порядка по сравнению с а
и р, т. е. если у=о (а), у=о(Р), то а~ р.
3° . Если отношение двух бесконечно малых имеет предел, то этот предел
не изменится при замене каждой из бесконечно малых эквивалентной ей беско-
нечно малой, т. е. если lim (а/р)=лг, a~aj, P~Pi> то lim (ai/pi)=/n.
x-t-a x-*a
Полезно иметь в виду эквивалентность следующих бесконечно малых: если
х—► 0, то
sin х ~ х, tg х ~ х, arcsln х ~ х, arctg х ~ xt In (1 -J-x) ~ х.
147
704. Пусть t—бесконечно малая. Сравнить бесконечно малые
а = 5/4 + 2П и 0 = 3P + 2f8.
а 54-2<’ 5
Д Имеем lim -я- —lim хтхТо.,== lim -х1г-оГ=Т • Так как предел отноше-
/-»0 Р t -*0 О* -|— /-*0 iJ-j-Zl о
ния а и р есть число, отличное от нуля, то а иР—бесконечно малые одного
того же порядка. А
705. Сравнить бесконечно малые а = t sin41 и 0 = 2t sin t при t —*0.
. Л Ct ,, t Sin* t 1 ,« , . а /П , A
Д Здесь lim-s-=lim ят-т~7=-к-Ит sin < = 0, т. e. a=o(P). ±
f P /^oxtstnt X f-»o
706. Сравнить бесконечно малые a = Hn (1 +1), 0 = t sin t при
Л Находим
In (1 + 0
lim « nmil^Uiim !МШ=Пга—Ц-
M P Z-0 *sln< Z-0 sta* /-0 SlnZ
t
t. e. a ~ p. A
707. Найти lim
X-*0 X
Л Заменим числитель и знаменатель дроби эквивалентными бесконечным!
малыми: In (1+3х sin х) ~ Зх sin х, tgx*~*a. Тогда получим
„ 1п (1+3*sin*) ,. 3xsinx „sin* _ .
lim — 1 --^=Нт 5—=31im---------—3. ▲
x-»o tgx* x-o x4 x-e x “
708. Определить порядок бесконечно малой у— хе* по сравнению
с бесконечно малой х. __________
709. Определить порядок бесконечно малой ^ = Hl+xsinx—1
по сравнению с бесконечно малой х. _____
710. Определить порядок бесконечно малой ^ = Ksin2* по срав-
нению с х при х —► 0.
711. Сравнить бесконечно малые а = t* sin41 и 3 = Mg t, если t —<- 0.
712. Сравнить бесконечно малые a = (l+x)m—1 и 0 = тх, если
х —>0 и т—рациональное положительное число.
713. Сравнить бесконечно мИлыеа = а*—1 и 0 = *1па, если х—>0.
Найти следующие пределы:
714- lira 'tt£ *• 715- lira
x-^0 X-.0 1П (1 +
ф Заменить числитель
и знаменатель эквивалентными бесконечно малыми.
eU-’ 717 lim 1п(1+*-Зх*+2**)
х“ 1 1п (1 +3*—4**+ха) ‘
sin (ех~1—1)
In *
716. lim j—r.—.
Л_о in (1-4*)
718. lim rnz,C°SX2; • 719. lim
x-.on(l+*4)
ф Представить cos* в виде
1 — (1 —cos *).
148
720. lim—И(1+^-1 . 721. ||Ш <5»-1)«»-1).
*-° (1-|-х)|/(1-|-х)2 — 1 а-*0(3“ —1)(6“—1)
722. Кт-^8+3^-2 .
х-о |/164-5х— 2
ф Разделить иа 2 числитель и знаменатель.
« в. НЕПРЕРЫВНОСТЬ ФУНКЦИИ
Функция Цх) называется непрерывной в точке а, если: 1) эта функция оп-
ределена в некоторой окрестности точки а; 2) существует предел lim / (х); 3) этот
Л-+а, . -
предел равен значению функции в точке а, т. е. lim f (x) = f (а).
х-+а
Обозначая х—а=&х (приращение аргумента) и f (х)—/ (a) = Az/(приращение
функции), условие непрерывности можно записать так: lim &у=0, т.,ё. функция
Дх-»-0
1 (х) непрерывна в точке а тогда и только тогда, когда в этой точнее бесконечно
•алому приращению аргумента соответствует бесконечно малое приращение
функции.
Если функция непрерывна в каждой Точке некоторой области: (интервала,
сегмента и т. п.), то она называется непрерывной в этой области.
Точка а, принадлежащая области определения функции илиявляющаяся
граничной для этой области, называется точкой разрыва, если ; в этой точке
ирушается условие непрерывности функции.
Если существуют конечные пределы lim f(x) — f(a—0) и lim / (х)=/(а4~0),
*-»а-0 х-мц-О
ернчем ие все три числа f(a), f (а—0), /(а 4-0) равны между собой, то а назы-
вается точкой разрыва I рода. .
Точки разрыва I рода подразделяются, в свою очередь, на точки, устрани-
мого разрыва (когда f(a—0) = f (а4-0) f (а), т. е. когда левый и правый , пре-
жлы функции в точке а равны- между собой, но не равны значению-' функции в
этой точке) и на точки скачка (когда f (а—0)^/(а4*0), т. е. когда левый и
правый пределы функции в точке а различны); в последнем случае разность
Г (в4-0)—f (а—0) называется скачком функции в точке а. Точки разрыва, не яв-
ляющиеся точками разрыва I рода, называются точками разрыва II рода. В точ-
ках разрыва II рода не существует хотя бы один из односторонних пределов.
Сумма и произведение конечного числа непрерывных функций есть функция
•епрерывная. Частное от деления двух непрерывных функций есть функция не-
прерывная во всех точках, где делитель не равен нулю.
723. Показать, что при х = 4 функция имеет разрыв.
X X
Л Находим lim -----7=—оо, lim - , = 4-оо. Таким образом, функция при
Х-.4-0 X—4 х-»4+0Х—4
я—>4 не имеет ни левого, ни правого конечного предела. Следовательно, х=4
шляется точкой разрыва II рода (рис. 26). А
724. Показать, что при х = 4 функция z/ = arctgимеет разрыв.
А Еслих—>4—0,то1/(х —4)—►—ос и lim у=—л/2. Если же х—»-44-0,
х-1-4-0
то 1/(х—4)—►4~оо и lim у = п/2. Итак, при х—>4 функция имеет как левый,
л->4 + 0
так и правый конечный предел, причем эти пределы различны. Следовательно,
х=4 является точкой разрыва I рода—точкой скачка. Скачок функции в этой
точке равен л/2—(—л/2) = л (рис. 27). А
149
-i__25
725. Показать, что при х = 5 функция у — имеет разрыв.
А В точке х=5 функция не определена, так как, выполнив подстановку,
получаем неопределенность 0/0. В других точках дробь можно сократить на
х—5, так как х—5 0. Следовательно, y=x-f-5 при х # 5. Легко видеть, что
Um У= Um у =10.
*-»5-0 Х-.5 + 0
Таким образом, при х=5 функция имеет устранимый разрыв. Он будет
устранен, если условиться, что у = 10 при х=5.
Итак, можно считать, что функция у=(х*—25)/(х—5) непрерывна при всех
значениях х, если считать, что равенство (х*—25)/(х—5)=x-f-5 справедливо при
всех значениях х, не исключая и х=5. В этом случае график функции есть
прямая у=х-}-5. Д
726. Найти точки разрыва функции у= •
727. Найти точки разрыва функции
728. Каков характер разрыва функции у— в точке х=1?
729. Каков характер разрыва функции 0=^уВ точ^е х=0?
tgxarctgj-tg
730. Найти точки разрыва функции у=—х (х^5)—‘
—. г, , ж. х»—&»+11х—в
731. Найти точки разрыва функции —•
X -4-1
732. Найти точки разрыва функции у = -f-6x*-f-1 lx'+'б *
733. Найти точки разрыва функции
734. Исследовать иа непрерывность функцию у=^х_р*ж —на
отрезке: 1) [2, 5J; 2) [4, 10]; 3) [0, 7].
735. Исследовать на непрерывность функцию у==м
отрезке: 1) [6, 10]; 2) [—2, 2]; 3) [—6, 6].
ГЛАВА VII
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ
ОДНОЙ НЕЗАВИСИМОЙ ПЕРЕМЕННОЙ
| 1. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ
1. Дифференцирование ивиых функций. Пусть xt и ха—значения аргумента,
• = и у,=/(х2)—соответствующие значении функции y=f(x). Разность
Ах==ха—Xi называется приращением аргумента, а разность Ду =yt—Ut=f (хг)—
— —приращением функции на отрезке [xj, ха].
Производной от функции у —f (х) по аргументу х называется конечный пре-
дел отношеияя приращения функции к приращению аргумента, когда последнее
стремится к нулю:
lira
Дх-»о Дх
/ =
f (хЧ-Дх)—f (х)
или f (х) = Um ———г-2—
' ' Дх-»о Дх
^производная обозначается также
Геометрически производная представляет собой угловой коэффициент каса-
тельной к графику функции у=/(х) в точке х, т. е. y'=tga.
Производная есть скорость изменения функции в точке х.
Отыскание производной называется дифференцированием функции.
Формулы дифференцирования основных функций
1. (хтУ = тхт~1
II. (Г7)'=-±
III. м у=_j_ \ X / х* *
IV. (е*)'=е*.
V. (аху = ах in а.
VI. (1пх)'=1.
VII. (10g«x)' xlna
VIII. (sin х)'= COS X.
IX. (cosx)'=—sinx.
X. (tgx)'=sec’x.
XI. (ctgx)'= — cosec1 x.
XII. (arcsinx)'=—
у 1— x1
XIII. (arccos x)' =-........
V 1-х»
XIV. (arctgx)'=-y-jL-.
XV. (arcctgx)'=—-j-jbj-.
XVI. (shx), = ^-~2e~xy = chx.
XVII. (ch x)' = ^-.^2e~xy =shx.
XVIII. (th x)'= =-i-.
' ' \chxy ch’x
X!X.
Основные правила дифференцирования
Пусть С—постоянная, « = «(х), v = v(x)—функции, имеющие производные.
Тогда:
1) С'=0; 2) х' = 1; 3) (u ± v)'=«' ± и'; 4) (С«)' = С«';
/ и V «'о—«t/
Б) (uvy=u'v+uv'; 6) j -------;
151
7) если y = f(u), u = u(x), т. e. y — f [и (x)J, где функции f(u) и u(x) имею»
производные, то
Ух=у’и-и'х
(правило дифференцирования сложной функции).
736. Исходя из определения производной (не пользуясь форму-
лами дифференцирования), найти производную функции у = 2х3 4-
4~5х2—7х—4.
Д Дадим х приращение Дх, тогда у получит приращение Ду:
у4-Ду = 2 (х-|-Дх)34-5 (х4-Дх)а—7 (х-|-Дх)—4.
Найдем приращение функции:
Ду = [2 (х+Ах)3+5 (х+Дх)3—7 (х+Дх) —4]—(2х® + 5х3—7х—4) =
= 6ха Дх-|-6х Дха + 2Дх3-|- ]0х Дх-|-5Дха—7Дх.
Находим отношение приращения функции к приращению аргумента;
-^-=6ха+6х Дх-|-2 Дха+ 10x4-5 Дх—7.
Найдем предел этого отношения прн Дх—>-0:
lira -г~ — lira (6ха-|-6хДх-|-2Дха4-10х4-5Дх—7)=6xa-f-10x — 7.
Дх — о Ах Дх -» о
Следовательно, по определению производной у'= 6x2-f-10x—7. А
737. Исходя из определения производной, найти производную
функции у = К*.
Л Находим приращение функции: Ду=угх-(-Дх—У х. Отсюда
Ду =£J+^-£x н Ит Д^= Пт Гм^-/х,
Дх Дх Лх о Дх Ах -> о Дх
Таким образом,
У'= lim (/Г+Д^+/^) .
Д*-о Дх(/"х-|- Дх-|- У х)
.. х-|-Дх—х 1 1
а* - о Ьх(Ух4- Дх+У^х) Ах -► о Ух-j- Лх-(-У х 2У х
.. , 1 .
Итак, у' = —т=- . А
2/ х
738. Исходя из определения производной, найти производную
функции у =— ctgx—х.
Л Находим
Ду = —ctg (х-|-Дх) —(x-|-Ax)-|-ctgx4-x = ctgx—ctg (х-|-Лх)—Дх.
Используй формулу ctg«—ctg Р = , получим
. _ sin (х4-Ах—х) sin Дх
~ sinxsin(x4-Ax) ~sinxsin (x-f-Дх)- ’
откуда
sin Дх
Ду = Дх______________
Дх sinxsln(x4-Ax)
152
t следовательно,
sin Ax
—Ax
Ау Ах . 1 ,
lim -т—= lim — -----—пп-------1=-г-®----*•
Дх.,0 Ах д*-.о Sin х sin (x-f-Ax) sin2x
Итак, у'— —г-i---l=ctg2x. A
sin2 x 6 “
Исходя из определения производной, найти производные функций:
739. у = 740. у = у/х2. 741. у — 5sinx-j-3cosx.
742. у = 5(tgx—х). 743. 744. у = 2*\
Применяя формулы и правила дифференцирования, найти произ-
водные следующих функций:
745. у = 2х3—5х2 + 7х + 4.
Д / = (2Х3)' - (5х2)' + (7х)' + (4)' = 2 (х3)' - 5 (х2)' + 7х' + 4' =
=2-Зх2—5-2х+7-1 + 0=6х2 — 10x4-7. А
746. t/ = x2e*.
Л у' =х2 (<?*)'4-ех.(х2)' =х2е*-|-2хе* =хе* * * х (x-f-2). А
747. «/ = x3arctgx.
Л у'=х3(arctgx)'4-arctgх-Сх3)'=х3-т-j-4-Зх2arctgx =
=т^+3х2агс1£х- А
748. t/ = xj/x(31nx—2).
Л Перепишем заданную функцию в виде у = х3^ (3 In х—2). Тогда у' =
*= х3-'2 -у4-у X»/» (3 ln-x-2) = 3xV2 + xi/a 1п х—Зх‘/а = 1 У 7 ]п х. А
749. »=:-arcslnx-.
х
Д у'
х- (arcsinx)'—arcsin х-(х)'
х2
1 arcsin х ,л, л v
।__хг х—У 1 — х2-arcsin х
х2 х2 У 1 —х2
___ sinx—cosx
У ~~ sinx -|- COSX ’
, (sinx-f-cos х) (cos x4-sln х)— (sinx—cos х) (cosx—sinx)
(sin X -|- cos x)2
(sinx4-cosx)24-(sinx—cosx)2 _________________
(sinx-f-cosx)2 (sinx-f-cosx)2 ‘
2
751. «/ = (2№4-5)4.
Л Обозначим 2x3-|-5 = «, тогда у —и*. По правилу дифференцирования слож-
ной функции имеем
у' =(«4);.(2х34-5);=4«3 (6х2) =24х2 (2х34-5)3. А
153
752. y=tg’x.
A y'=6tg»x.(tgx)'=6tg’xsec’x. A
753. y = cos2x.
A y'=2cosx(cosx)' = —2cosxsinx=—sin2x. A
754. t/ = sin (2x4-3).
A y' = cos(2x+3)-(2x+3)'=2cos(2»+3). A
755. z/=tglnx.
A y'=sec’lnx.(lnx)' =-i--sec2lnx. A
756. y=sin’4«
Д y> = 3 sin21. (sinf)' =3 sin’ f cos | ( £)' = sin21 cos |. A
757. # = ln(x24~5).
758. y = lntg|.
A ' mr "Tiihr-”’w2)-w2)'-
I _ 1 1
2 tg (x/2) cos2 (x/2) 2 sin (x/2) cos (x/2) sin x ‘
759. y = ln(x4-/^+T).
1 . 1 / 2x \
Д ** ~x4-/x2+"T=х4-/'х24Л V + 2/х24Й J
_ 1 . yr**+~l+x__ 1
x4-yrx24-'l ’ Vx*+T ’
760. y = ln(j/2sinx4-1 4-j/2sinx—1) .
Д y* . 1 ^ :=-(K2sinx4-14-K2sinX-i)' =
y^2sinx4-14-y^2sinx—1
____________1__________/ 2 cos x , 2 cos x \
~ yr2sinx4-l 4- V2sinx—1 \ 2 V2sinx4-l 2 Kasinx—1 /
____________1__________cos x (>^2sin x 4-l-j-1^2sin x—1) _
V2sinx4-14-К2sinx—1 K4Sin2x—1
COS X
~~y 4sin2x —1 ‘
761. у=|V"^+k4-4• In(x4-УхЧ^).
154
. , х 2х .1 1Г-гт-Е I k 1 /, , 2*
2 ‘ 2V"x?+k + 2 + +2’х4-/х2+Д 2К*2+*
ха Кx*+k . k 1
2 '*’2‘х + К«ГЙ
762. t/= arcsin , |х|<1.
(14-х4)-4х—2х2-4х3_ 1 4х(1—х4) 4х
(14-х4)1 у 1—2х44-х«’ 14- х* ~ 14-**
763. t/ = arctg
О
Д У' 14- (In2 х)/93х
3
х(94-1п2х)
764. t/ = e**arctge*—In К14-е2*.
Л Записав данную функцию в виде
y=e*arctge*—1- In (14*«**)<
&
золучим
765. у
У' =еХ • • ** + ** «rctg т-±55 е«х. 2 =
= 1 -|Х^ + е* arotg еХ - 'j = е* arctg е*. ±
sin х . । 14-slnx
cos2 х cos х
Л Преобразуем данную функцию:
_sin*—|_jn .j_j_slnх) —ln cosx.
’ cos2 x 1 4 1 '
Тогда
„Г = COs2 x cos *--Sin *-2 cos x. (- S.yn_^4-_!— cos X_1- (- sin X).
* COS4 X 1 14- Sin X COS X
ли
_cos2x4~2sln2x cos x (1 —slnx) sin x __cos2x4-2sln2x . 1 —slnx
COSSX ' 1—Sin2X "T~COSX COS3X cosx
. Slnx cos2X4-2sin2x ____L_=_2_ = 2sec3x. ▲
"I" COSX COS3X "I" cosx COS3X “
766. у = -7; tg2prx4-lncos/x.
A y' = tg У xsec2 у^~х—т=г4-~7= (—stn
&r r 2fx cosfx 2K x
=—~ tg Y"x (sec2 V"x— 1) = ;/=r tg3 / x.
2У x 2y x
767. t/=5sh3^ + 3sh6^.
Л Находим
/-l5!l’,B'l'r5-B+'5si’‘wd,ft-B-sh’rechB(,+sh,ft)’
откуда, используя соотношение ch2x—sh2x=l, окончательно получаем у’—
= sh2±ch3i.A
768. у = хх\
/\ Здесь основание и показатель степени зависят от х. Логарифмируя, по-
лучим 1пу=х31пх. Продифференцируем обе части последнего равенства по х.
Так как у является функцией от х, то In у есть сложная функция х и (In у)' =•
= — ^'.Следовательно,
-^-=х2--i-4-2xlnx, -^-=х(1-|-21пх)(
т. е.
. i,'=xy<l+21nx)=xx*2(14-21nx)=x*2+1(14-21nx). А
769. t/= (sinx)1®*.
А Имеем lny = tgx-lnslnx, откуда
•— = tg х——cos x-ksec2 x In sin x = 1 -4-sec2 x In sin x;
у sinx 1
y' =y (14-sec2 x In sin x) == (sin x)tg * (1 J-sec2 x In sin x). A
770. у =
a (5x-|-4)3 j/1 — x
Л Здесь заданную функцию также следует предварительно прологарифми-
ровать:
lny=3 In (2х—1)-|—In (3x4-2)—21n(5x-f-4)—-у 1п(1 —х);
.EL—___3 gi 1 3 ____2 $ I i •
у 2х—1 '2 3x4-2 5x-f-4 т 3(1—х) ’
, (2х—1)31^37+2 Г 6 3_______10 . 11 .
У ~ (5х4-4)2 у\^х L 2х—1 +2(Зх4-2) 5х4-4+ 3 (1— х) J * А
Найти производные функций:
771. у=^. 712. у = ^ХУ~х.
773. «/= уXsFx-ixsVx4-х’Vx.
774. у = (х2 + 2х+2) е~х. ,775. у = Зх3 In х—х3..
776. У~^. 777. # = x2sinx-[-2xcosx—2sinx.
778. г/==1п (2х34-Зх2). 779. г/ = /1—Зх2.
780. у = хarccosy—J/4—х2.
156
781
782
784
786
787
788
790
792
794
796
798
800
802
804
806
808
810
812
813
814
815
817
819
821
822
823
y= у x arcsin у x-f- V 1—x.
z/ = ^siny—cos-^ . 783. z/ = coss(x/3).
. . 2x4-1 ___ . i/"l-f-sinx
z/ = lntg—y—. 785. y = \ny
у = tg 2x + у tg3 2x + у tg6 2x.
z/ = ysin3K*—у sin’Kx-f-ySin’Kx.
z/ = In (3x2+K9x*+1). 789. z/ = у Кa2—x*4-y arcsin у.
у = 1п^ЕЁ-Ц^. 791. z/ = —ctg* y—2 In sin 4-.
У К 4 tg x-H+2 Ktg x » ь 2 2
у = arctg jAx2—1. 793. у = arctg •
1 — V" 1 г8 2X3
z/ = arctg—— ----. 795. у = arcsin , если | x| < 1.
Q y8
у = arccos gqyr • 797. y — e~x —sine-*cose-*.
y=aictg/iEf. 799. y-ln^-^
У _ 1 _e« » cos" 3x. SOI. у - In
z/ = ln(secx4-tgx). 803. y — — In (cosec x-|-ctg x).
z/ = e^(/2^-l). 805. zz = ln^y.
y_/ slnx \* 807t у_arcsin
y \14-cosx/' у 14-sin8x
y=—cosec*(x/2). 809. z/ = sin(lnx)-cos(lnx)—ln(l/x).
j, = (x»+ 3) [In (X»-1-3) — 1]. 811. z/ = arcsin/1—0,2x*.
у = 0,5 [(x 4- а)У х*4-2ах4-₽ +
4- (P—a*) In (x 4- а 4- j/x*4-2ax-|-0)].
у = arcsin e* 4- arcsin К1 —e**.
у = mV^ x* + 2ax + fi + (n—ma) In (х-|-а4-|'/х*4-2ах4-0).
у — . 816. z/ = x*4-2xsinxcosx4-cos*x.
у 1 — mx*
У = Ctg X cosec X 4- In (ctg X 4- cosec x). 818. у = •
z/ = 3xsin8x-|-3cosx—cos’x. 820. jr = ln
у=ex—sin e* cos* e*—sin3 ex cos e*.
i,=arctg(x+l)+p^LT.
у = X (In8 X—3 In* x + 6 In X—6).
157
824. t/=lnsinKxtg j/x—Kx. 825. y = arctgx* x *.
«2». у - X (tg-’ - ctg- ’)+1 (tg.± -ctg-A ) + A In tg-J-
827. у-In tgf+cosx + lcos-x. 828. y—
829. t/ = 4-tg2sinx-|-lncossinx. 830. t/ = ln( 1 — •
831. у = In ^_^2x . 832. у = 2x tg 2x 4- In cos 2x—2x2.
833. у — arccos (2e2x—1). 834. z/ — ln lnx(ln Inlnx—1).
835. у = . 836. у = In }-.
57 x+e2* 27 xlnx+1
r3 ,2 sin Я
837. t/ = arctg'^-2. 838. i/= Intg ——j—•.
839. y = Y sin2 x + cos2 x —cos 2x.
840. z/= tg3 tgx + 3tg tgx. 841. y=arotgx—In
842. у = ^+_к. 843. у = Г2Т+Т[1п(2х + 1)-2].
844. у — sec х (1 4- In cos x). 845. у = e* У1 —e2jc—arcsin ex.
846. у^г™5’*-3'05*. 847. =
848. y — ~Y~—e ln*+1. 849. t/ = xsinxcosx4~y cos2x.
850., = ^.851., = lntg|_-^.
852. t/ —2(tgj/x— Ух). 853. «/ = ^ln^ + larctg-J.
854. у = In -O jf.. —* -. 855. у = e°-5 ‘к’ * cos x.
Ух*+1 + х2
856. у = arctg . 857. у = x2e** In x.
858. t/== arccos У 1—2х. 859. t/== log*. 2.
860. у = — tn У—хг + 2ах + ^ + (та + n) arcsin
_______________________________________ V a+₽
861. у =» logg sin2x. 862. t/ = loga(x + Kx2+9).
863. z/ = xarc’in*. 864,
887. у = [И +1) cos («Inx) + n sin (nInx)].
868. у — (x tg x + In cos x) • tg (x tg x + In cos x) 4-
4- In cos (x tg x4- In cos x).
869. у = (х cos х—sin х) [In (х cos х— sin х)—1 ].
870. #=3sin(xe*—6х)—sin3(хг*—г*).
871. у — arCcos (2хК1—х2). 872. у — |х| (х#=0).
873. y = \f(x)\. 874. г/ = |3х—5|.
.875. = 876. t/ = |x| + | х—2|.
877. у = хе* (sinx—cosx) -j-г*cosx.
878. t/ = ln[xsinx + cosx+]/r(xsinx+cosx)2 +1].
879. z/ = p-(xlnx—х—1). 880. у = logcosxsinx.
881. у = log,» (xB + j/x,B+ 1) 882. у = log-, e.
883. t/ = log,.x. 884. z/=log*»x*. 885. t/ = x1/ln*.
886. t/ = x*. 887. г/ = х"*-2*-х2.
888. t/ = xIn*. 889. y =-x2yrf
(x— I)3 J/5x—1
890. Показать, что (secx)' = secxtg x.
891. Показать, что (cosec x)' = — cosec xctgx.
892. Показать, что (u°y = vu°~l-u'+ u°-v' Inu.
893. Вывести формулы дифференцирования arcsec x и arccosecx.
894. Чему равно выражение и = у* + у'* + 4у*/у'*, если г/= 2 cosx?
895. Показать, что функция у — (х2 +1) (г*-(-С) обращает урав-
нение у' —= е* (х2 +1) в тождество.
2. Дифференцирование неявных функций. Пусть уравнение F (х, tfi = 0 опре-
деляет у как неявную функцию от х. В дальнейшем будем считать эту функцию
дифференцируемой.
Продифференцировав по х обе части уравнения F (х, у) — 0, получим уравне-
ние первой степени относительно у'. Из этого уравнения легко находится jr, т. е.
яроизводиая неявной функции для всех значений х и у, при которых множитель
при у' в уравнении не обращается в нуль.
896. Найти производную у’х из уравнения x2-|-t/2 = 4.
Л Так как у является функцией от х, то будем рассматривать у2 как слож-
ную функцию от х. Следовательно, (y2)' = 2w'. Продифференцировав по х обе
части данного уравнения, получим 2х-(-2уу'=0, т.е. у' ——х/у. А
897. Найти производную ух из уравнения х2-|-1пг/—х'еУ—Ъ.
Л Дифференцируя по х обе части уравнения, получаем
Зх2 + ——xWy'—2хеХ=0, т.е. у'у, д
у \—х2уеУ
Найти производную у’х от неявных функций:
898. х3+ «/3—Зхг/ = 0.
899. Ах2 + 2Вху + Су2 + 2Dx + 2Еу + F = 0.
900. х4—6х2г/2 + 9г/4—5х2+15г/2—100 = 0.
901. з&—г/* = 0. 902. xsint/ + t/sinx = O.
903. e* + es'—2*^—1 =0. _____
904. sin(y—х2)—ln(y—х2) + 2Ку—x2—3 = 0.
159
905. + еУх — У 7=0. 906. x’S + У2 In х—4 = 0.
907. х2 sin у 4-г/3 cos х—2х—3 г/4-1=0.
3. Дифференцирование функций, заданных параметрически. Если функция
аргумента х задана параметрическими уравнениями x=<f(t), у = ф(/), то
dy
! tit dy dt
Ух=-^Т, ИЛИ -г——;—.
х' dx dx
ИГ
908. Найти у' = ^, если х— t3-\-3i-}-1, у — ЗГ-г513-Г 1.
Л Найдем -^- = 3Z2 + 3, 15/44- 15/2. Следовательно,
dt dt dx 3/--[-3
= 5/2. А
909. Найти г/' = ^, если x = ncos/, z/ = asin<.
910. Найти у' = ~ , если x — e~l sin t, y = etcost.
J dx J
911. Найти p'=^, если p=f4-j/a + Ha> 0 = l/^e1/“.
flu \ О j
912. Найти у' = , если х=сЦ z/ = sM.
n dx ’ J
4. Приложения производной к задачам геометрии и механики. Если кривая
задана уравнением y=f(x), то /'(x0) = tga, где а— угол, образованный с поло-
жительным направлением оси Ох касательной к кривой в точке с абсциссой х„-
У равнение касательной к кривой y~f(x) в точке Л10(х0; у0) имеет вид
У—Уо ~Уо (х— х0).
где уо есть значение производной у' при х--=х0.
Нормалью к кривой называется прямая, перпендикулярная касательной и
проходящая через точку касания.
Уравнение нормали имеет вид
1 / ч
У—Уо —----г (х—х0).
Уо
Углом между двумя кривыми y = ft(x) и y — f-ztx) в точке их пересечения
Л40 (х0; Уо) называется угол между касательными к этим кривым в точке Мо. Этет
угол находится по формуле'
{g(p= /2(Хо)-Л' (Х0) _
1 +/1 (*о) /2 (Хо)
Если при прямолинейном движении точки задан закон движения s = s(t), тс
скорость движения в момент t0 есть производная пути по времени: v = s'(t0).
913. Какой угол образует с осью абсцисс касательная к кривой
«/=(2/3) х6— (1/9)х3, проведенная в точке с абсциссой х=1?
Л Находим производную у' — (10/3) х4—(1/3) х2; при х=1 имеем у'= 3, т. е.
tga = 3, откуда a = arctg 3 х 71°34'. А
914. Какой угол образует с осью абсцисс касательная к пара-
боле у = х2— Зх-)-5, проведенная в точке М (2; 3)? Написать урав-
нение этой касательной.
160
915. Составить уравнения касательной и нормали к кривой
х* +2xz/2 + 3z/4 = 6 в точке М(1; —1).
Л Из уравнения кривой найдем производную:
хА- и*
2x-j-2y2-j-4xyy'-j-12y3y'= 0, т.е.
1+(-1)2 1
^едовательно, ув=- .у_—
Уравнение касательной
«/+1=-^-(х—1), или х — 4у—5 = 0.
Уравнение нормали
«/+1=—4 (х—1), или 4х-]-у—3 = 0. Д
916. Найти угол между параболами у = 8—х2 и у — х2.
Л Решив совместно уравнения парабол, находим точки их пересечения
.4(2; 4) и В(—2; 4). Продифференцируем уравнения парабол: у' = —2х, у'=2х.
Найдем угловые коэффициенты касательных к параболам в точке А (т. е. значе-
44-4 8
яия производных прих = 2):А1 =— 4, k2= 4. Следовательно, tg <pi = -:—lte5=—те,
1 — lu 10
f!=arctg(—8/15). Так же определяется угол между кривыми в точке В: <р2 =
= arctg(8/15). А
917. Найти уравнение нормали к параболе у2—2рх в точке
.И (ха, у0).
918. Составить уравнение касательной к гиперболе х2/9—t/2/8=l,
проведенной в точке М (—9; —8).
919. Составить уравнения касательной й нормали к астроиде
х = И2 cos3t, у = 1^2 sin3t, проведенных в точке, для которой t=n/4.
920. Составить уравнения касательной и нормали к циклоиде
х=/—sin t, у=\—cost, проведенных в точке, для которой t=n/2.
921. Составить уравнения касательной и нормали к полукуби-
ческой параболе x=t2, у — 13, проведенных в точке, для которой
1 = 2.
922. Показать, что уравнение касательной к эллипсу х2/а2 +
+ y*/b2 = 1 в точке М (х0; у0) имеет вид xxja2 4- yyjb2 = 1.
923. Какой угол образует с осью абсцисс касательная к кривой
y = shx, проведенная в точке (0; 0)?
924. Составить уравнения касательной и нормали к цепной ли-
нии у — ch(х/2) в точке, где х = 21п2.
925. Составить уравнение касательной к равносторонней гипер-
боле x = chl, у = sh t в точке 1 = 10.
926. Найти угол между кривой z/ = x—х3 и прямой z/ = 5x.
927. Найти угол между кривыми у — х3 и z/ = l/x2.
928. Найти угол между линиями у — 1 + sinx, у=1.
929. Найти угол между кривыми х2 4- г/® = 5, у2 = 4х. _
930. Найти угол между кривыми у = И 2 sin х, z/ = j/2cosx.
931. Зависимость пути от времени при прямолинейном движе-
нии точки задана уравнением s= 15/54- (2/л) sin (л!/8) (1—в секундах,
6-215 1б1
s—в метрах). Определить скорость движения в конце второй се-
кунды.
Л Находим производную пути по времени:
ds ... 1 nt
_=<4 + _COS^.
При 1=2 имеем 2 я 16,18. Следовательно, о « 16,18 м/с. А
932. По параболе у = х(8—х) движется точка так, что ее абс-
цисса изменяется в зависимости от времени t по закону х — t И t
(t—в секундах, х—в метрах). Какова скорость изменения орди-
наты в точке М (1; 7)?
Д'Найдем закон изменения ординаты; заменив в уравиеиии параболы х иа
t V t, получим y=8t}^t—t3. Скорость изменения ординаты есть производная
от ординаты по времени: у\ = 12 3tl. Для точки М (1; 7) значение t равно 1.
Следовательно, y't—x = 9, т. е. скорость измерения ординаты равна 9 м/с. А
933. Зависимость пути от времени задана уравнением s =
= /ln(/-|-l) (t—в секундах, s—в метрах). Найти скорость движения
в конце второй секунды.
934. По кубической параболе у = х3 движется точка так, что ее
ордината изменяется в зависимости от времени t по закону у —at3.
Какова скорость изменения абсциссы в зависимости от времени?
5. Нахождение угла между радиусом-вектором и линией. Пусть плоская линия
задана в декартовых координатах уравиеиием y=f(x). Направление линии в дан-
ной точке М (х; у) определяется касательной в этой точке, т. е. углом а между
касательной и положительным направлением осн Ох (отсчитываемым против часо-
вой стрелки), причем tga = z/'. Угловой коэффициент радиуса-вектора точки М
составляет tg<p = y/x, а угол между радиусом-вектором и касательной к линии
в этой точке есть ш = а—<р. Следовательно,
tg ш— tg ср _ х __xy'—y_xdy—ydx
l+tgatg<p , , х+УУ' xdx+ydy’
-t-y • x
Если линия задана в полярных координатах уравиеиием г —г (у), то х =
= гсозф, y = rsin<p, xdy—ydx = r3dtp, xdx-)-ydy=rdr, откуда
. r3 dtp г
tgco=——ь=—.
r dr г
935. Найти угол между параболой у —4—х3 и ради усом-векто-
ром точки М (1; 3) этой линии.
Л Находим
tg ш=ХУ'—У_Х (—2х)—у —2х3—у
х+УУ' х+у(—2х) х—2ху *
В точке М (1; 3) получаем tg ш=~1 т. е. со=-?- . А
1—о 4
936. Найти угол между окружностью г = аи радиусом-вектором
любой ее точки.
Д Имеем г—0; значит, tgw = r//=a/0 = oo, т. е. <о = л/2. А
162
937. Найти угол между равносторонней гиперболой хг—у2 = 36
н радиусом-вектором точки М (10; 8).
Д Так как 2х—2г/г/'=0, у' = х/у, то
♦gta _Х~(Х/У)—У^х2—у2^ 36 ^18
*+У-(*/У) 2дгу 2ху ху ’
18
а в точке М (10; 8) имеем tgco = —^= 0,225, т. е. co = arctg 0,225. ±
Ю’О
938. Найти угол между кардиоидой г = а(1—cos<p)n радиусом-
вектором точки М (За/2; 2л/3).
. „ • . . г а(1—coscp) . <р „
Л Здесь r = a sin <p, tg<o =—= —---— = tg-!-. В данной точке М по-
г a sin <р 2
лучаем tgco = tg (л/3), со = л/3. А
939. Найти угол между параболой z/2 = 8x и радиусом-вектором
точки М. (2; 4).
940. Найти угол между спиралью Архимеда г = а<р и радиусом-
вектором любой ее точки.
941. Найти угол между окружностью r = cos<p и радиусом-век-
тором любой ее точки.
942. Найти угол между окружностью (х—7)2 + (z/—5)2 = 2 и
радиусом-вектором точки М (6; 6).
943. Найти угол между спиралью /• = аеЯ1Ч’ и радиусом-вектором
любой ее точки.
944. Найти угол между эллипсом х2/100Ц-г/2/Зб= 1 и радиусом-
вектором точки Л4 (6; 4,8).
6. Производные высших порядков. Производной второго порядка (второй про-
изводной) функции y = f(x) называется производная от ее производной. Вторая
, j. й2и ,
производная обозначается так: if, или , или f (х).
Если s — f(t)—закон прямолинейного движения точки, то вторая произвол-
dzs
пая пути по времени есть ускорение этого движения.
Аналогично производная третьего порядка функции у = f (х) есть производная
от производной второго порядка: у"' = (у")'.
Вообще, производной п-го порядка от функции y = f(x) называется производ-
ная от производной (л — 1)-го порядка: t^n) — (^п~1))'. Обозначается n-я произ-
dnu
водная так: у<я) или , или /<я) (х).
Производные высших порядков (вторая, третья и т. д.) вычисляются после-
довательным дифференцированием данной функции.
Если функция задана параметрически: x = <p(t), у=ф(/), то производные
Ух, у......вычисляются по формулам
„’—У* _{y’xxit
Ух — , » Ухх — > 9 Уххх — ,
Xt Xt Xt
Производную второго порядка можно вычислить также по формуле
» _yttxt—x"ttyt
УXX----------------------------/ '\3 •
(*i)
и т. д.
945. у=х*-\-2х*—Зх8—х’—0,5x4-7. Найти у', у", у'", ••
Л у'= 5х44-8х3—9х2—2х—0,5,
у*=20х84-24х2—18х—2,
у"'=60х24-48х—18,
0>v= 120х-Н8, yv=120, yVi=yVU = ..,=o. Д
946. у = 1пх. Найти у{п}.
а , 1
Л У ~—=х~1,
4Г=-1х-’,
у'" = 1-2х-8,
yW=— Ь2-Зх-‘,
y<">=l-2-3...(«-l)(-l)n~1^~B = (-0n~1-(W^1-- ▲
947. х = 2*. Найти у{п).
& {/=2*1112,
у* = 2* In2 2,
у'” = 2* In3 2,
у<«> = 2* In” 2.
948. y = sinx. Найти у{п}.
Л y'=cosx=sin »
у" = —sinx = sin ^x-f-2~^ ,
у'" =—cosx = sin ^х4-3~^ ,
......., •............. •
y<»)=Sin^X4-«-y^ . А
949. Найти у' = , у' = т|, если x = acos8/, у = a sin3/.
3 ах ’ а dxa я
. , _dy_ (a sin8i)t За sin21 cos t _. .
dx (acos8<)f —3a cos21 sin t ’
У»_(— tgOf _ —sec2/ _ 1 .
dx2 (a cos8 i)t —3a cos21 sin t 3a sin t cos41
Найти производные второго порядка:
950. у = —-^g. 951. y = -tx2(21nx-3).
952. у=ух2И1 —х24--|-И1 —x?4-xarcsinx.
953. у = — yxsin3x—^cos3x.
164
954. y = x1n (x+Kx2+a2)— Ух2 + а2.
ncc (x~a(t— sin/), f х=агссозКГ,
\y = a(l — cost). \y==]ft—72.
957. Показать, что функция z/ = sin Inx-f-coslnx удовлетворяет
уравнению x2y” -\-xy' -\-y = Q.
958. Показать, что функция i/ = x-|-sin2x удовлетворяет урав-
нению /4-4*/ = 4х.
959. При прямолинейном движении точки зависимость пути от
времени задана уравнением s = K/- Найти ускорение точки в конце
4-й секунды.
Найти производные третьего порядка:
9в0- »-вЙ0'
962. у = (2х+З)8 /2x4-3. 963. у = sh2 х.
• Учесть, что sh2x = 2shxchx.
Найти производные n-го порядка:
964. у = хп]/гх. 965. У = 2х+1 ' & = 5—3cos2x.
967. у = 2* + 2~*. 968. У=^^~. 969. у^е**.
( х— In t, ( x=at + b,
970. j/ = cosx. 971. < ... 972. { ,
\y=l/t. \y = ata + fit + y.
973. Показать, что функция y = ex-\-2e2x удовлетворяет уравне-
нию у”'—бу" + 11у'—бу — 0.
974. Показать, что функция */ = х* удовлетворяет уравнению
У4 А-У^+У''' + / + /+// = Xs + 3х2 + 6х + 6.
8. Дифференциалы первого и высших порядков. Дифференциалом (первого
приращения, линейная
порядка) функции y = f (х) называется главная
относительно приращения аргумента. Дифферен-
циалом аргумента называется приращение аргу-
мента: dx = Ax.
Дифференциал функции равен произведению
ее Производной иа дифференциал аргумента:
dy=y'dx.
Геометрически дифференциал представляет
собой приращение ординаты касательной к гра-
фику функции в точке М (х; у) (рис. 28).
Основные свойства дифферен-
циала
1°. dC = 0, где С = const.
часть
ее
2». d(Cu) = Cdu.
3°. d (и ± о) = du ± do.
4°. d(uo) = udv-(-odu.
vdu—и do
v • и I — | — о
\V J V2
6». df (u)=f'(u)du.
(» 0).
165
Если приращение Дх аргумента мало по абсолютной величине, то Ду я dy и
f (х+Дх) я / (х)-]-(х) Дх.
Таким образом, дифференциал функции может применяться для приближен-
ных вычислений.
Дифференциалом второго порядка функции y=f(x) называется дифференциал
от дифференциала первого порядка: d2y=d(dy).
Аналогично определяется дифференциал третьего порядка: <Py=d (d?y).
Вообще, dny=d(dn~1y).
Если y=f (х) и х—независимая переменная, то дифференциалы высших по-
рядков вычисляются по формулам
d2y=y" (dx)2, d3y = y'" (dx)8, dny—tf-n’> (dx)n.
975. Найти дифференциал функции t/ = arctgx.
A dy=(arctgx)'-dx = j-^r. A
976. Найти дифференциал функции s = et’.
Д ds=e*3-3<2d<. А
977. Найти дифференциалы первого, второго и третьего поряд-
ков функции у = (2х—З)3.
Л dy = 3(2x—3)2-2dx = 6(2x—3)2dx,
d2y= 12 (2x—3)-2dx2 = 24 (2x—3) dx2,
d3y=24-2dx2 = 48dx3. A
978. Найти дифференциалы первого и второго порядков функции
v = e2t.
Л dv — 2e2tdt, d2t>=4e2t-dt2. А
979. Сравнить приращение и дифференциал функции у = 2х8+5х2.
Л Находим
Ду=2 (х+Дх)8+5 (х-]-Дх)2—2х3—5x2=(6x2-f-10х) Дх+(6х-{-5) Дх2 + 2Дх*,
dy—(бх2-}-1 Ox) dx.
Разность между приращением Ду и дифференциалом dy есть бесконечно малая
высшего порядка по сравнению с Дх, равная (6х-|-5) Дх2-]-2Дх3. А
980. Вычислить приближенное значение arcsin 0,51.
Л Рассмотрим функцию y=arosinx. Полагая х=0,5, Дх = 0,01 и применяя
формулу arcsin (х-|- Дх) я arcsin х-{-(arcsin х)' Дх, получаем
arcsin0,51 я arcsin 0,54-—— * -0,01 =j-4-0,011 =0,513. А
У7! —(0,5)2 6
981. Вычислить приближенное значение площади круга, радиус
которого равен 3,02 м.
Л Воспользуемся формулой S — пД2. Полагая R=3, AR = 0,02, имеем
AS я dS = 2nR-AR = 2n-3 0,02 = 0,12n.
Следовательно, приближенное значение площади круга составляет 9л+0,12л
= 9,12л я 28,66 (м2). А
Найти дифференциалы функций:
982. у = arcsinу. 983. х=11п—|.
984. у = 2 In ch (х/2). 985. у = arctg е2х
986. Найти dy, d2y, d?y, если i/ = x(lnx—1).
987. Найти (Ру, если у = 1п (x-\-Vrxt+ 4).
988. Сравнить приращение и дифференциал функции у~1/х.
989. Вычислить &у и dy для функции у = х2—2х при х = 3 и
Дх = 0,01.
990. Найти приближенное значение объема шара радиуса 2,01 м.
991. Найти приближенное значение х из уравнения 13sinx —
— 15cosx=0.
Найти приближенное значение:
992. arctg 1,05. 993. tg 46°.
994. Intg47°15'. 995. УТбД ’
f 2. ИССЛЕДОВАНИЕ ФУНКЦИЙ
1. Теоремы Ролля, Лагранжа, Коши и формула Тейлора.
Теорема Ролля. Если функция f (х) непрерывна на отрезке [а, Ь],
дифференцируема в интервале ]а, Ь[ и f (а) = f (b), то в интервале ]а, най-
дется хотя бы одно значение х—1, при котором f (g) = 0.
Если, в частности, f(o) = 0, f (ft) = 0, то теорема Ролля означает, что между
двумя корнями функции содержится хотя бы одни корень ее производной.
Теорема Лагранжа (о к о и е ч и о м п р и р ащеи и и). Если функция
'(х) непрерывна на отрезке [в, Ь] и дифференцируема в интервале ]а, fe[, то
л этом интервале найдется хотя бы одно значение х = g, при котором выполня-
ется равенство
f(b)-f(a) = (b-a)f(l).
Эти теоремы имеют такой геометрический смысл: на дуге АВ непрерывной
кривой y—f(x), имеющей в каждой внутренней точке определенную касательную
(не параллельную оси Оу), найдется хотя бы одна внутренняя точка, в которой
касательная параллельна хорде АВ. (Для теоремы Ролля и хорда АВ, и каса-
тельная параллельны оси Ох.)
Теорема Коши. Если функции f (х) и <р (х) непрерывны на отрезке [a, ft]
дифференцируемы в интервале ]а, &[, причем <р' (х) # 0, то в этом интервале
вайдется хотя бы одно значение х= g, при котором
f(b)-f(a) f' (g)
tp(b)—<р(а) <р' (g)
, где а < g < b.
Формула Тейлора. Функция f (х), дифференцируемая n-f-1 раз в неко-
тором интервале, содержащем точку а, может быть представлена в виде суммы
многочлена п-й степени и остаточного члена Rn:
f (х) = f (а)+^ (х-а) (х-а)2+... (х-а)»+₽я(
R
лп+1>(ё)
а («+1)1
(х-а)»+\
где точка g лежит между точками а и х, т. е. g = a-f-0(x4-a), причемО<0<1;
rtt
При. а = 0. получается ф о р м у л а Ма к л о р е н а .
Р _ Лп + 1) (0Х) п + 1 о < 0 < 1
(п+1) I х ’ и<0< Ь
Приведем разложения* некоторых функций по формуле Маклорена:
1* 1*2 уЗ р0Х\
еХ=1+к+2!+зГ+-+^|+^ ^=(ЙП)!хП+1:
, х х3 , х5 . (_ 1)/»+1х2'»-1 , _
sinx-ц 31+5! ••• + (2/п—1)! +*2Я”
у2/я +1
.Я2я> = (-1)'я c°s 0x-(2m+ 1)!’
, X2 . X* Xе (—1)/» Х2я , _
COSX-1 2| +41 б!+"’+ (2т)! +/?2'" + 1:
и2/Л + 2
«2»+1 = (-1)в’+1сО8 0х.^-р^;
(1 + = j +« x+=L^=ll x3+m(m--A)!(m-2)x3+...
_l «(и—l)-..[m—(п—1)] x„
nl
_ т(т— 1).. .(т—п) ,
Rn = —----, ,т;------'-Xn + l (14-0x)'"-"-1
(п+1)1
(всюду О < 0 < 1).
996. Выполняется ли теорема Ролля
— 6х+100, если а= 1, 6 = 5? При каком
Д Так как функция f (х) непрерывна и дифференцируема при всех значениях х
и ее значения на концах отрезка [1, 5] равны: f (1) = / (5) = 95, то теорема Ролля
на этом отрезке выполняется. Значение £ определяем из уравнения f (х) = 2х—6 =
для функции f(x),= x2—
значении £?
997. Выполняется ли теорема Ролля для функции f (х) = у/8х—х’,
если а —О, Ь = 8? При каком значении £?
А Функция f(x)=y 8x—x2 непрерывна при всех значениях х и имеет про-
изводную f (х) = (8—2х)/(з yf(8х—х2)2) при х 5^ 0, х 8, т. е. дифференцируема
в интервале (0, 8). Кроме того,/(0)=/(8)=0. Таким образом,.теорема Ролля на
отрезке [0, 8] выполняется; действительно, f (х) = 0 при х = £ = 4. А
998. Дана функция /(х)=|/(х—8)2. Пусть а = 0, Ь= 16. Тогда
f (Q) — f (16) = 4. Однако производная f (х) = 2/(3 f/х—8) не обра-
щается в нуль ни в одной точке интервала (0, 16). Противоречит ли
это теореме Ролля?
А Нет, так как в точке х = 8 интервала (0, 16) производная ие существует,
и условия теоремы Ролля нарушены. А
999. Показать, что производная многочлена f(x) = x3—х2—х + 1
имеет действительный корень в интервале (— 1, 1)..
168
Д Найдем корни данного многочлена: х3—х2—x-J-1 =0 или (х— t)2(х-|-1^0,
т. е. х1 = х2 = 1, х3 =—1. Так как f (— 1) = /(1) = 0, то по теореме Ролля f (х)
имеет корень в интервале (—1, IV. Найдем корни производной: /'(х)=3х2—2х—
— 1=0, т. е. Xt = — 1/3, х2 = 1. Таким образом, между корнями функции —1 и I
содержится корень производной, равный —1/3. А
1000. На дуге АВ кривой у = 2х—х2 найти точку М, в которой
касательная параллельна хорде АВ, если Л(1; 1) и В(3; —3).
Д Функция у — 2х—х2 непрерывна и дифференцируема при всех значениях х.
По теореме Лагранжа между двумя значениями а = 1 и Ь = 3 существует значе-
ние x=g, удовлетворяющее равенству y(b)—y(a) = (b—а) у’ (g), где у'= 2—2х.
Подставив соответствующие значения, получим у(3)—«/(1) = (3— 1) у' (g);
(2.3-З2) — (2-1-12) = (3—1)-(2—2g); -4 = 4(1-1). Отсюда g = 2, f/(2)=0.
Таким образом, точка М имеет координаты (2; 0). А
1001. На дуге АВ кривой, заданной параметрическими уравне-
ниями x = t2, y = t2, найти точку М, в которой касательная парал-
лельна хорде АВ, если точкам А и В соответствуют значения t = 1
и t = 3.
А Угловой коэффициент хорды АВ равен , а угловой коэффициент
' (&) —*
касательной в точке М (при t = g) равен —775г , где х\ = 2t, y't = 3t2.
xt (»)
Для определения g по теореме Коши получаем уравнение
У(3)-у(1) 27-1 3g2
х(3)-х(!) х;а)’ИЛИ9-1 2g
или
13 — _3
4 — 2
т. е. g = 13/6. Найденное значение £ удовлетворяет неравенству 1 < £ < 3.
Подставив значение f = g в параметрические уравнения кривой, получаем
х= 169/36, «/ = 2197/216. Итак, искомая точка М (169/36; 2197/216). А
1002. Представить функцию f(x)=l/ х в виде многочлена пятой
степени относительно двучлена х—1.
Д Вычислим значения функции f(x)=x1^ и ее производных до пятого
порядка включительно при а=1: /(1) = 1, /'(х) = (1/3)х-2/3, f (1) = 1/3; Г(х) =
= —(2/9)х~5/3, Г(1) = —2/9; (х) = (10/27)х~8/з, Г (1) = 10/27; fw (х) =
= — (80/81) х-11/3, fIV(l) = —80/81; /v (х) = (880/243) х-14/3, fv (1) = 880/243.
Следовательно, по формуле Тейлора получим
з /— 1 2 10
V х=1+ з'(х— 0—972г(х— 02+ 27.3! (х~ О3—
— 8Ь4Г (Х~1)4 + 243-51 (х—5)5 +
где R5 = £l^.(x-l)» = --lg^r.g-i’/3 (ж—1)% 1<?<х. А
1003. Представить функцию f(x) = ax (а>0) в виде многочлена
третьей степени относительно х.
А Имеем
f(x) = ax,
f (х) = ах !п а,
f"(x)=ax In2 а,
f” (х)=ах In3 а,
fIV (х) = ах In4 а,
f(0) = l,
f (0) = In а,
Г(0) = 1п2а,
(0) = !п3 а,
fw (0х)=1п4а-а9*.
169
По формуле Маклорена получаем
„ . . х21п2а , х31п3а „
a* = 14*xlna-|---gj--1---------b₽8,
где ° д9*, 0 < 0 < 1. А
1004. Вычислить с точностью до 10-3 приближенное значение
/29.
А Представим заданный корень так: у 29—у/274*2 = 3 14-/57У^. Вос-
пользуемся биномиальным разложением
/,1ч». , , т । т(т— 1) _ , , т(т— 1)...[т—«4*11 „ , _
(14- х)» = 14- — х4-Ь-_—х2 4-... 4- -i----хп 4- яп.
Отсюда получаем приближенное равенство
. т . т(т— 1) . , , т (т — 1).. Ат—п4-1) _
(14-х)т « 1 + 17 *1——-х + • • • И—s-----------------— хп,
погрешность которого
Яп = —----(п+Т)!-----"~Х
может быть сделана как угодно малой при |х| < 1 и при достаточно большом п.
Полагая х=2/27 и т=1/3, получим
Уа -3<1 1 2 2,2 I 2’2’2‘5 25,5 ' 4-Р
29 ^l+g! 81-81+ 813 .81* + -" + /?яу) *
Оценивая величины последовательных ошибок вычисления 3|7?„|, находим
3 |Ri | < < 0.002. 31 Т?21< ^2-2;-2-’5 < 0.0003.
Следовательно, для вычисления с заданной точностью достаточно взять трж
члена, которые предшествуют остатку Т?2, т. е. /29 « 3 (14*0,024—0,0006) =
= 3,072. А
1005. Вычислить У~е с точностью до 0,0001.
где
А Воспользуемся формулой Маклорена для функции е*:
е*-!+ п-+^г + ---+тй+7?'”
евх
р — с
" («+1)1
х”+1, 0 < 0 < 1. Полагая х = 1/2, получаем
е = 1 +‘2йт+2Г21+^М1+ • • • +^1+ Rn‘
где
<
е0/2
7?я==2я + 1(п4-1)! ’ ° < 0 < Ь
е1/г ,/»
Так как 0 < 0 < 1, 2 < е < 3, то ’R„ < KL-i'f, пп • Но е1'2 < 2, поэтому
1 2 (П-|-1) I
2« (д 4- j )4 ‘ Требуется опРВДелить п так, чтобы выполнялось неравенство
0,OWL ’
170
n—4, » Rt < 16.12o ; < 1920’
« = 5- ’ ^<зЙ2б:^<0’0в01-
Для определения У е с точностью до 0,0001 получаем приближенное
равенство
Произведем суммирование, обратив все слагаемые в десятичные дроби с одним
лишним (запасным) знаком. В результате получим У е ~ 1,6487. А
1006. Дана функция f (х), непрерывная вместе со своими произ-
водными до (п—1)-го порядка включительно на отрезке [а, 6] и
имеющая производную n-го порядка в интервале (а, 6), причем для
этой функции выполняются равенства f (а) = f (xj = f (х2) = ... =
= f (xn_t) = / (b), где а < х± < х2 < ... < хп_± < Ь. Доказать, что в
интервале (а, о) найдется по крайней мере одна такая точка £,
для которой /<пГ(&) = 0.
1007. Рассмотреть частный случай предыдущей задачи, если
f(x) = (x—1) (х—2) (х—3) (х—4), а— 1, хг — 2, х2 = 3, 6 = 4. Опре-
делить £.
1008. Представить в виде многочлена третьей степени относи-
тельно х—х0 (хо^=О) функцию 1/х.
1009. В какой точке дуги АВ кривой у = х*—Зх касательная
параллельна хорде АВ, если А (0; 0), В (3; 18)?
Вычислить с точностью до 10~*i
1010. cos 41°. 1011. р/Т21.
1012. j/7. 1013. {/129. 1014. sin 36°.
2. Правило Лопиталя раскрытия неопределенностей. Пусть в некоторой
окрестности точки х0 (кроме, быть может, самой точки х0) функции f (х) и <р (х)
дифференцируемы и <р' (х) # 0. Если lim f (х) = lim q> (х) = 0 или lim f (х) =
X-t-X,
= lim ф(х) = оо, т. е. частное f (х)/ф (х) в точке х=х0 представляет собой неоп-
ределенность вида 0/0 или оо/оо, то
если предел в правой части этого равенства существует.
Если частное f (х)/ф' (х) в точке х = х0 также есть неопределенность вида 0/0
нли оо/оо и производные f' (х) и ф' (х) удовлетворяют соответствующим условиям,
то следует перейти к отношению вторых производных и т. д.
В случае неопределенности вида 0. оо или оо — оо следует алгебраически пре-
образовать данную функцию так, чтобы привести ее к неопределенности вида 0/0
или оо/оо и далее воспользоваться правилом Лопиталя.
В случае неопределенности вида 0° или оо° или 1” следует прологарифмиро-
вать данную функцию и найти предел ее логарифма.
171
Найти следующие пределы:
1015. lim 1 +—.
х-ы ^-e
А Числитель и знаменатель стремится к нулю при х —► 1, а потому имеем
неопределенность вида 0/0. Воспользуемся правилом Лопиталя, т. е. рассмотрим
предел отношении производных заданных функций:
lim **-1 + 1п*= Jim А
х->-1 е*—е х->-1 ех е
1016. lim х-?1пх
п X3
А Это—неопределенность вида 0/0. Имеем
lim х~^х = lim lim ’
Х-»-0 X3 х->-0 Зх’ х+о 6х 6
так как Um SJfli—i. Здесь правило Лопиталя применено дважды. Д
л-* О X
1017. lim —г, если п—целое положительное число.
6х
А Это—неопределенность вида оо/оо. Применим правило Лопиталя п раз:
lim lim lim lim n(n-l)(n-2).,.l^n д
Х-* 00 е*
Ю18. lim -£-=•.
А В данном случае также имеет место неопределенность вида оо/оо. Находим
ХрХ/г
Пт---------== lim
о» x-f-e* хс
= lim
ех
2+4 1
lim -
lim ------У2--..
2 х->« (1/2) еУ1
=-L цт ——
2 05 fXl2
1019. lim(x’lnx).
х-*0
Д Здесь мы имеем неопределенность вида 0-оо. Представим произведение
функций в виде частного, а затем, получив неопределенность вида со/оо, приме-
ним правило Лопиталя:
X lim
2 х-*о
lim (х’1пх) = Пт XLX= Ит —1/Х-
х-*о x-*ol/x2 Х-+0— 2/х3
1020. lim (-—-Д-Л.
х-о\* е* —1 /
Д Это неопределенность вида оо— оо. Для того чтобы найти предел функ-
ции, приведем дроби к общему знаменателю, а затем, получив неопределенность
вида 0/0, применим правило Лопиталя:
lim пт _еХ~' = lim =_L д
х->о х(е*—1) х->ое*—14-хе* х->ое*(2+х) 2’ж
172
1021. lim (sinx)*.
x-* 0
' Л Это—неопределенность вида 0°. Обозначим данную функцию через у, т. е.
। y=(sinx)x, и прологарифмируем ее:
, , In sin х
in п = х Insin х=———.
1/х
i Вычислим предел логарифма данной функции, применяя правило Лопиталя (здесь
имеем неопределенность вида со/оо):
lim In у = lim lim cosx/stox^
х->о x-*o 1/x x->0 —1/x2
x’cosx I „ x \ n
=— lim --------=— lim I x-cosx-—— 1=0.
x->o sinx x-*o\ sinx/
Следовательно, lim y=e°=l. A
x-*0
1022. lim (tgx)2C0SX.
X-* Я/2
Д Это—неопределенность вида co0. Положим (fgx)2C0sx = t/ и прологариф-
мируем:
i о 1 » 21ntgx
lnn = 2cos x-lntgx=——— .
я 6 '1/cosx
Применяя правило Лопиталя, получим
lim In у = 2 lim lim
Х-*Я/2 X—-я/2 secx Х-+Я/2 secxtgx
=2 lim ^£±=2 lim = lim cosx=0,
x->n/2tg2x x->n/2 2tgxsec2x х->я/2
т. e. lim y=e°—l. Ж
Х-*Я/2
1023. lim (l-|-x),nx.
x-*0
Д Это—неопределенность вида 1". Логарифмируя и применяя правило Лопи-
таля, получим
lim 1пу= lim (inxln (l-J-x)) = lim *П^~ЬХ) __
х->о х-*о х-*о 1/1пх
= lim _кР+х) lim Lln>*=_ lim
x-. о — l/(x ln2x) x-*0 x+1 x—Ol+l/X
=_ lim lim 1LJ=2 lim -V* =Q.
x-M —1/X2 X-*O 1/X x — 0 — 1/x2
Таким образом, lim y=e° — l. A
о
Найти пределы следующих функций:
Неопределенность вида 0/0.
1024. lim . 1025. lim т—.—-—.
х-> 1 х3—4х2+3 x-Ioln(l+x)
1026. lim я-г,:,с18л . х-><» е3/х — 1 1027. lim 2-^+e-x)cosx X->0 **
1028. Пш е3х-^~ 1. 1029. lim -s-^—^.+3x;_
х^0 sln25x x_. 0 arctg x—sin x—xF/fi
Неопределенность вида oo/oo.
1030. lim 1031. lim (n>0). X-*CD X
173
,032- Ит Г+2Ыпх- 1033- lim ГнХ/21 • 1034- lim
0 * + * |п Slnx х__ ! 1П(1—X) х_)_ J ctg лх
Неопределенность вида 0-оо.
1035. lim(xctgnx). 1036. lim (arcsin х-ctg х).
1037. lim (1 — cos х) • ctg х.
л-*0
Неопределенность вида оо— оо.
1038. Нт ('-А--*'). Ю39. Нт 1^— —
1040. lim (A-_ctg2x\
х-+ 0 \ х /
Неопределенности вида 0°, оо°, 1”.
1041. Нт (л—2x)cosx. 1042. Нт (cos2x)3/*’.
Х-+Л/2 Х-.0
1043. Нт (х + 2*)1/*. Ю44. lim
Х-* о» Х-* 0 \ Х /
3. Возрастание и убывание функции. Экстремум функции. Функция f (х) на-
зывается возрастающей в точке х0, если при любом достаточно малом й > 0 вы-
полняется условие ((х0—й) < f (х0) < /(х0-|-й) (рис. 29).
Функция /(х) называется убывающей в точке х0, если при любом достаточас
малом й > 0 выполняется условие /(х0—й) > f (х0) > /(х0+й) (рис. 30).
Функция f (х) называется возрастающей в интервале (а, Ь), если для любых
двух точек xt и х2 из указанного интервала, удовлетворяющих неравенству Xt < х*.
выполняется неравенство f(xi) < f (х2).
Функция f (х) называется убывающей в интервале (а, Ь) , если дли любых
точек xi и xt из указанного интервала, удовлетворяющих неравенству Xi < х»
выполняется неравенство /(xi) > f (х2).
Признаки возрастания и убывания функции.
1) Если f (х0) > 0, то функция f(x) возрастает в точке х0.
2) Если f (х0) < 0, то функция f (х) убывает в точке х0.
Значение f (х0) называется максимумом функции f (х), если при любом доста-
точно малом й>0 выполняются условии /(х0—й) < f (х0) и f (х04-й) < f (х^.
Точка Хо называется в этом случае точкой максимума функции f (х) (рис. 31 и
Значение f(x9) называется минимумом функции f(x), если при любом доста-
точно малом й>0 выполняются условия / (х0—й) >/(х„) н f (х04-Л) >f (х^.
Точка х0 называется в этом случае точкой минимума функции /(х) (рис. 32t
Максимум или минимум функции называется экстремумом функции. Точка
максимума или минимума функции называется точкой ее экстремума.
Необходимое условие э к ст р ем у м а. Если функция f (х) в точке я,
имеет экстремум, то производная f (х0) обращается в нуль или не существует.
174
Точка Xq, в которой f (хо) = О, называется стационарной точкой. Точки,
в которых f'(x)=O или (х) не существует, называются критическими точками.
Не всякая критическая точка является точкой экстремума.
> ।___I—
Xg-tl
Рнс. 31
xs-h х, xsh л
Рис. 32
Достаточные условия экстремума.
Правило 1. Если х0—критическая точка функции f (х) и при произвольном
достаточно малом h > 0 выполняются неравенства f' (х0—й) > 0, f (х„+й) < О,
то функция f (х) в точке х0 имеет максимум; если же г (х0—й) < 0, f (х0 -j-й) > О,
то функция f (х) в точке х0 имеет минимум.
Если знаки f (xj—й) и f (хь+й) одинаковы, то функция f (х) в точке х0
вкстремума не имеет.
Правило 2. Если f (х0) = 0, f (х0) / 0, то функция f (х) в точке х0 имеет
вкстремум, а именно максимум, если f" (Xq) < 0, и минимум, если f (х0) > 0.
Правило 3. Пусть f (х0) = 0, f"(xo) = O, ..., (х0) =0, /(п)(хо)#0.
В этом случае функция f (х) имеет в точке х0 экстремум, если п — четное число,
а именно, максимум при р"> (х0) < 0 и минимум при f<n> (Xq) > 0. Если же п —
нечетное число, то функция f (х) в точке х0 экстремума не имеет.
Для нахождения наибольшего (наименьшего) значения функции f (х) на отрезке
[а, Ь] нужно из значений функции на границах отрезка и в критических точках,
принадлежащих этому отрезку, выбрать наибольшее (наименьшее).
1045. Даны точки х = 3, х=1, х ——:1, х = 0,5. В каких из пе-
речисленных точек функция i/ = xs—Зх2 возрастает? Убывает?
Л Найдем производную у' =3х2—6х. Имеем:
если х=3, то /= 9>0 — функция возрастает;
» х = 1 » у' — — 3<0 — » убывает;
» х =—1 » у' =9 >0— » возрастает;
» х = 0,5 » у'=—2,25 < 0— » убывает. А
1046. Найти интервалы возрастания и убывания функции у =
= х(1 +/х).
Д Находим у' = 1 +(3/2) х1/2. Так как производная положительна в про-
межутке [0, + оо) , то функция возрастает во всей области определения. А
1047. Найти интервалы возрастания и убывания функции у =
= х—2sinx, если 0^х^2л.
Д Найдем производную: у' = \—2cosx. Очевидно, что у* > 0 в интервале
(я/3, 5я/3) и у' < 0 в интервалах (0, я/3) и (5я/3, 2я). Таким образом, в интер-
вале (я/3, 5я/3) данная функция возрастает, а в интервалах (0, я/3) и (5я/3, 2я) —
убывает. А
1048. Исследовать на экстремум функцию у — (х—5)е*.
Д Находим производную: у'=(х—4) е*. Приравниваем ее нулю и находим
стационарную точку; ех (х—4) = 0, х = 4; у' (4—й)=—йе*~А < 0, у' (4+й) =
«=йе4+А > 0. Согласно правилу 1 заключаем, что в точке х=4 функция имеет
минимум утщ = — е*. А
175
1049. Исследовать на экстремум функцию y — x}f 1—х2.
Л Функция определена при —1 < х < 1. Найдем производную: tf =
= (1—2x2)/J^I—х2‘, у' =0 при 1—2х2 = 0; отсюда xt =—I/J^2, х2=1/уг2
(стационарные точки); у' = оо при х=± 1, т. е. на границах области определе-
ния функции.
Найдем вторую производную: tf = x (2х2—3)/(1—х2)3''2. Вычислим значения
второй производной в стационарных точках. Прих=1/уг 2 имеем
if (1 /У 2)= b(1—-------< 0;
V 2(1 —1/2J3/2
следовательно, согласно правилу 2 заключаем, что в точке х=1/|Л 2 функции
имеет максимум </тах = (1/Р^ 2) У" 1/2 =1/2. При х =— 1/У 2 получим
J-(l—3)
V 2(1 —1/2)3'2
if (-1/К 2)=
т. е. в точке х =—\/У 2 функция имеет минимум ymin =—1/2.
В критических точках х = ± 1 экстремума нет, так как по определению точ-
ками экстремума могут быть лишь внутренние точки области определения функ-
ции. Д
1050. Исследовать на экстремум функцию у = (х—I)4.
Д Найдем производную: у' = 4(х—I)3; (х—1)3 = 0; х=1—стационарная
точка. Вторая производная у"=12(х—I)2 при х=1 равна нулю. Третья произ-
водная у'"=24(х—1) при х=1 также обращается в нуль. Четвертая производ-
ная ylv = 24>0. Следовательно, согласно правилу 3 заключаем, что в точке
х=1 функция имеет минимум ymin = 0. А
1051. Исследовать на экстремум функцию у=1— (х—2)4/6.
4 4
Л Находим у' =—=-(х—2)_,/5=-----Производная не обращаете®
° 5 ух—2
в нуль ни при каких значениях х и не существует лишь при х = 2 (критическая
точка).
Так как при достаточно малом h > 0 выполняются неравенства у' (2—й) >0
и у' (2-f-Л) < 0, то согласно правилу 1 заключаем, что при х = 2 функция имеет
максимум t/max—!• А
1052. Исследовать на экстремум функцию у = (х—2)2/3 (2х1;
AU , 10 Х~1 V
Л Находим у• -т- . Критические точки х=1 (производная равна
° у х—2
нулю) и х = 2 (производная не существует). При достаточно малом Л > 0 выпол-
няются неравенства у' (1— й) > 0, у' (I-f-й) < 0, ; у' (2—й) < 0, у' (2 + й) > 0.
Следовательно, в точке х=1 функция имеет максимум (/тах = 3, а в точке
х=2—минимум </min = 0. А
1053. Найти наибольшее и наименьшее значения функции f (х) =
= Зх—х3 на отрезке [—2, 3].
Л Находим производную: f (х)=3—Зх2; 3—Зх2 = 0, т. е. х=± 1— стацио-
нарные точки. Определяем значения функции в этих точках: f (1) = 2, /(—1)=—2.
Вычисляем значения данной функции на границах промежутка: /(—2) = 2,
/(3)=—18. Из полученных четырех значений выбираем наибольшее и наименьшее.
Итак, наибольшее значение функции на данном отрезке равно 2, а наименьшее
равно—18. А
176
1054. Найти такой цилиндр, который имел бы наибольший объем
при данной полной поверхности S.
Л Пусть радиус основания цилиндра равен х, а высота равна у. Тогда
S = 2лх2 + 2 лху, т. е. у=—~—2лх .
~ я 2лх 2л \ х J
Следовательно, объем цилиндра выразится так:
1 / с \ с
у = у (х) = лх2 •-f—-2лх ) = -п-х—лх3.
' ' 2л \ х J 2
Задача сводится к исследованию функции V (х) на максимум при х > 0.
„ „ dV S „ „
Найдем производную —w**2 и приравняем ее нулю, откуда х =
=]As7(taj.
Найдем вторую производную: 2 =—блх. Так как при x=J^S/(6n) вы-
d2y
полняется условие < 0, то объем имеет наибольшее значение, причем
у=—.2jI"?/(6ji) = 2 |Л$/(6л) =2х,
2л У5/(6л)
т. е. осевое сечение цилиндра должно быть квадратом. А
Найти интервалы возрастания и убывания функций:
1055. t/ = 2—Зх + х3. 1056. //=(х2 —1)3/2.
1057. у = хе~х. 1058. г/= (2—х)(х+1)2-
Найти экстремумы функций:
1059. у = хг(\ — хУ~х). 1060? у=х-\-УЗ—х. 1061. у = In (х2+ 1).
1062. w = ch2x. 1063. у = ^—. 1064. у = хе~х2'3.
v V In X V
1065. у=(х— I)’/’. 1066. у—(2х— l)j/(x—З)2.
1067. у — х*—Фх’ + бх2 — 4х. 1068. у — х—2sin2x.
1069. t/ = e1-6 ”'пх.
1070. Найти наименьшее и наибольшее значения функции
y = xi—2х2 + 3 на отрезке [—3, 2].
1071. На оси Оу найти точку, из которой отрезок АВ виден под
наибольшим углом, если А (2; 0), В (8; 0).
1072. Пункт В находится на расстоянии 60 км от железной до-
роги. Расстояние по железной дороге от пункта А до ближайшей
к пункту В точки С составляет 285 км. На каком расстоянии
от точки С надо построить станцию, чтобы затрачивать наименьшее
время на передвижение между пунктами А и В, если скорость дви-
жения по железной дороге равна 52 км/ч, а скорость движения
по шоссе равна 20 км/ч?
1073. Найти стороны прямоугольника наибольшей площади,
который можно вписать в эллипс х2/25 + «/2/9 = 1.
1074. Проволока длиною I согнута в прямоугольник. Каковы
размеры этого прямоугольника, если его площадь наибольшая?
177
1075. Найти наибольший объем конуса, образующая которого
равна I.
1076. Найти наибольший объем цилиндра, у которого полная
поверхность равна S.
1077. Турист идет из пункта А, находящегося на шоссейной
дороге, в пункт В, расположенный в 8 км от шоссе. Расстояние
от Л до В по прямой составляет 17 км. В каком месте туристу
следует свернуть с шоссе, чтобы в кратчайшее время прийти
в пункт В, если скорость его по шоссе 5 км/ч, а по бездорожью
3 км/ч?
1078. Канал, ширина которого 27 м, под прямым углом впадает
в другой канал шириною 64 м. Какова наибольшая длина бревен,
которые можно сплавлять по этой системе каналов?
1079. На какой высоте над центром круглого стола радиуса а
следует поместить электрическую лампочку, чтобы освещенность
края стола была наибольшей?
ф Яркость освещения выражается формулой I = (k sin <р)/г2, где <р — угол
наклона лучей, г—расстояние источника света от освещаемой площадки, k—сила
источника света.
4. Выпуклость, вогнутость. Точка перегиба. График функции y = f (х) назы-
вается выпуклым в интервале (в, Ь) , если он расположен ниже касательной, про-
веденной в любой точке этого интервала (рис. 33).
----
Рис. 33 Рнс. 34
График функции y — f(x) называется вогнутым в интервале (а, Ь~) , если он
расположен выше касательной, проведенной в любой точке этого интервала (рис. 34).
Достаточное условие выпуклости (вогнутости) графика
функции. Если f" (х) < 0 в интервале (а,Ь)., то график функции является
выпуклым в этом интервале-, если же f (х) > 0, то
/Хг в интервале (а. Ъ) график функции—вогнутый.
У Предположим, что функция f (х) дифференцируема
Jp на интервале (а, Ь) и хд в (а, i). Точка (xgi f (х0)) графика
I функции у—/(х) называется точкой перегиба этого гра-
/у фика, если существует такая окрестность точки хд оси
ч'—-—' абсцисс, в пределах которой график функции / (х) слева
рнс 35 и справа от точки хд имеет разные направления выпук-
лости (рис. 35).
Если хд — абсцисса точки перегиба графика функции у»/(х), то вторая произ-
водная равна нулю или не существует. Точки, в которых /* (х) — 0 или f (х) не
существует, называются критическими точками II рода.
Если х0—критическая точка П роДа й при произвольном достаточно малом
h > 0 выполняются неравенства /" (х0—А) < 0, /" (Xp-f-й) > 0 (или неравенства
f (х0—й) > 0, f” (х0+й) < 0), то точка кривой у=[(х) с абсциссой х0 является
точкой перегиба.
Если же Г (ха—h) и f” (х0 + Л) имеют одинаковые знаки, то точка кривой
y**f(x) с абсциссой х0 точкой перегиба не является.
1080. Найти промежутки выпуклости и вогнутости графика функ-
ции у = х’ + 5х—о.
178
Д Имеем г/' = 5х44-5, tf = 20х3. Если х < О, то ?/" < 0 и кривая выпукла;
если же х > 0, то у" > 0 н кривая вогнута. Итак, кривая выпукла в промежутке
(—оо,0). и вогнута в промежутке (О, +оо) • А
1081. Найти экстремумы функции «/=(х+1)2(х—2) и точки пе-
региба ее графика.
, Л Найдем первую производную: у' = 3(х2—1). Корни первой производной:
Х1 = —1, х2=1. Найдем вторую производную: tf — бх. Вычислим значения вто-
рой производной в стационарных точках: if (—1) = — 6< 0, т. е. ушах=0; у" (])=
=6 > 0, т. е. (/mln= — 4.
Найдем точку перегиба, для чего вторую производную приравняем нулю:
6х=0, т. е. х = 0. Слева от точки х = 0 имеем у" (0—Л) < 0—кривая выпукла,
а справа от точки х = 0 имеем г/" (O-f-Zi) > 0—кривая вогнута; следовательно,
точка с абсциссой х = 0 является точкой перегиба; ут.пер =— 2. А
1082. Найти точки перегиба кривой г/ = (х—5)6/34-2.
10
7^
Л Находим у'—~(х—5)2/3
и
. Вторая производная не обра-
щается в нуль ни при каких значениях х и не существует в точке х = 5. Значе-
ние х = 5 является абсциссой точки перегиба, так как tf (5—Л) < 0, if (5-|-Л) > 0.
Таким образом, (5; 2)—точка перегиба. А
1083. Найти интервалы выпуклости и вогнутости кривой у = хех.
1084. Найти точки перегиба кривой у = (х—4)6 4-4x4-4.
1085. Найти точки перегиба кривой у=(х—l)j/(x—1)в.
1086. Найти точки перегиба кривой у = х*—8х34-24х2.
5. Асимптоты. Прямая L называется асимптотой кривой y=f(x), если рас-
стояние точки М (х; у) кривой от прямой L стремится к нулю при неограничен-
ном удалении этой точки по кривой от начала координат (т. е. при стремлении
хотя бы одной из координат точки к бесконечности).
Прямая х = а является вертикальной асимптотой кривой y=f(x), если
lim /(х) = +оо или lim f(x) = — оо.
а х-t- а
Прямая у = Ь является горизонтальной асимптотой кривой y = f(x), если
существует предел lim /(х)=6или Пт f(x) = b.
Х-+ + со X — 00
Прямая у = kx является наклонной асимптотой кривой y = f(x), если
существуют пределы
А= lim , b— lim [/(•*)—kx]
X-*+oo X X->+Q0
ВЛИ
k = lim ^3, b= lim lf(x)—kx],
x->—x ®
1087. Найти асимптоты кривой у = У x3/(x—2).
Д Функция определена в интервалах (—оо, 0) и (2, +оо)'- Так как
lim У*®/(*—2) = 4- оо, то прямая х = 2 является вертикальной асимптотой
х->2 + о
кривой.
Горизонтальных асимптот кривая не имеет, так как lim Ух3/(х—2) и
______________ X ->• + 00
lim У х3Цх—2) не являются конечными величинами.
- 00
179
Определим, существуют ли наклонные асимптоты. Находим:
1) ^i= lim LW— Пт 2) _ цт -»/ х
Х-* + а> X х->+оо X х-*+а> г х — 2
*1= Пт (/(*)—Пт ( |/\*L_je'\=.
.. х (К *—к*—2) х(х—*4-2)
Пт ———т=£=--------- = Пт . , ,
х->+ <ю Ух—2 х-» + оо Ух — 2 (У *+ У х—2)
Таким образом, существует правая наклонная асимптота у = *4-1;
n- um Ш_ Bm VSEES.= Bn ПОЗ.
X —► — СО *- X -> — 00 % X — СО 1
(разделили числитель и знаменатель на положительную величину —х), т. е.
‘=—Е™У Т^2Я — '•
bt = lim (/(x)—fea x] = lim
lim
lim
у 2—х
lim
y2=i
x(-x—2-j-x)
у2— x (У—х+ У2— x)
Итак, существует левая наклонная асимптота у — — х—1 (рис. 36). А
— 1.
1088. Найти асимптоты кривой «/ = x4-2arctgx.
Д Нетрудно видеть, что вертикальных »
горизонтальных асимптот кривая не имеет. Ищем
наклонные асимптоты:
lHi= Um * + 2arctgx^
х -> + 00 Х
= Jim
bi= lim (*+2 arctgx—x) = 2 (л/2)=л;
X -► + 00
ys=x-{-n—правая наклонная асимптота;
2) fe2.^ lim * + 2агс1£* =
X -► — 00 X
= lim (1 + ^ESlEi.Vi,
X -* — оо \ X J
b2= lim (x+2arctgx—x) = 2(—л/2) = —к;
X -»• — 00
y~x—л—леваи наклонная асимптота. 4k
180
1089. Найти асимптоты кривой у = х2е~х.
Д Очевидно, вертикальных асимптот нет. Если х—►«>, то у—>-0. Следова-
тельно, ось Ох является горизонтальной асимптотой данной кривой. Определим,
существует ли наклонная асимптота:
k = lim
X -► 00 %
lim -;=0-
е*
Таким образом, имеетси только горизонтальная асимптота у = 0. ±
х2__2х4-3
1090. Найти асимптоты кривой у = —х_^2 '
т. е. х =—2—вертикальная асимптота.
/X Если х—>—2, то у—►
Найдем невертнкальные асимптоты:
. х2 —2x4-3
«= пт ------—г-яг—=1, Ь —
х(х-|-2)
х2 —2х-
*4-2
4.
Таким образом, наклонная асимптота имеет уравнение у=х—4. А
Найти асимптоты кривых:
1091. у = 2х—^~. 1092. у = {~~3х. 1093. # = j/x3 — 6ха.
1094. i/ = 0,5x+arctgx. 1095. у — — xarctgx.
6. Построение графиков функций по характерным точкам. При построении
графика функции y = f(x) полезно выяснить его характерные особенности. Для
этого надо:
1) найтн область определения функции;
2) исследовать функцию на четность и нечетность;
3) найти точки пересечения графика функции с осями координат;
4) исследовать функцию на непрерывность; найти точки разрыва (если они
существуют) и установить характер разрыва; найтн асимптоты кривой у = f (х);
5) найти интервалы возрастания и убывания функции и ее экстремумы;
6) найти интервалы выпуклости и вогнутости кривой и точки ее перегиба.
__х3 4*4
х2-’
1096. Построить график функции у
Д 1) Область определения функции—вся ось Ох, за исключением точки х=0,
т. е. О(у) = (-оо, 0)0(0, +оо) .
2) Функция не является четной или нечетной.
дрЗ I _
3) Найдем точки пересечения графика с осью Ох, имеем —=0; х = —j/ 4.
4) Точка разрыва х = 0, причем limy=oo; следовательно, х=0 (ocj> Оу) яв-
.х — о
ляется вертикальной асимптотой графика.
Найдем наклонные асимптоты:
. f(x) х34-4 .
fc = lim !-*-£= lim —5—=1;
х-е х х3
(уЗ I А
* -
\ 4
х ) иа lim —j ~0,
/ . Х“*°°
Наклонная асимптота имеет уравнение у = х.
5) Найдем экстремумы функции и интервалы возрастания и убывания. Имеем
у' = (—8/х3 = (х3—8)/х3; у'=0 при х = 2; у'=оо при х = 0 (точка разрыва функ-
ции). Точки х = 0 и х = 2 разбивают числовую ось на промежутки (—оо, 0),
181
(0,2) н (2, + ао), причем у' > 0 в промежутках (—оо, 0) и (2, +оо) (функция
возрастает) и у' < 0 в промежутке (0, 2) (функция убывает).
Далее, находим у = 24/х4; tf (2) > 0,’следовательно, х=2—точка минимума;
Z/min 3.
6) Найдем интервалы выпуклости и вогну-
тости кривой и точки ее перегиба. Так как
у” > 0,' то график функции всюду вогнут. Точек перегиба кривая не имеет.
Используя полученные данные, строим график функции (рис. 37). А
1097. Построить график функции y=f/l—х3.
1) Область определения—вся ось Ох, т. е. D(y)= (—со, +оо).
2) Функция не является четной или нечетной.
3) Точки пересечения с осями координат: если х=0, то у=1; если у=0, то
х — 1.
4) Точек разрыва и вертикальных асимптот нет. Имеем:
yzl—
k= lim —---
•1;
_______1
Ь= Пт (/Г=№+х)= Пт
=0.
Итак, наклонная асимптота у = — х.
5) Находим р'=—х21 (1 —х3)2; у' = 0 при x = Q\y' = оо при х= 1. В окрест-
ности критических точек производная ие меняет знака, экстремумов нет. Так как
у' < 0 при всех х ф 0, то функция убывает иа всей числовой оси.
6) Находим tf=—2xly (1— х3)6;У=0 при х=0; tf=ao при х=1; tf(—h) > О;
0*(Л) < 0, tf(l — Л) < 0; 0*(l-f-h) > 0. Следовательно, в промежутках (—оо, Щ
и (1, +оо) кривая вогнута, а в промежутке (0,1)—выпукла. Точки перегиба
имеют координаты (0; 1) и (1; 0).
Используя полученные данные, строим искомый график (рис. 38). Д
Построить графики функций:
1098. y = sin2x. 1099. у=3у/~х—к.
1100. у = \пх—1п(х—1). 1101. у = 1п^у.
1102. у = -^—. 1103. у = ^.
9 ха—4 а у *
1104. 16х(х—I)3. П05. у=(х—1)Кх.
182
1106. У = х + е~х. 1107. у = In (х+/F+I).
1108. у = е^~х*. 1109. у = . *30.г-
» » (х—2)2
§ 3. КРИВИЗНА плоской линии
Углом смежности дуги АВ плоской линии называется угол <р между каса-
тельными, проведенными в точках А и В этой линии (рис. 39). Отношение угла
смежности к длине,з дуги АВ называется
средней кривизной дуги АВ, т. е. fccp=<p/s.
Кривизной дайной линии в точке А на-
зывается предел средней кривизны дуги АВ
при В—* А, т. е. £ = lim(<p/s).
s->0
Кривизна окружности ^окр=1/о, где
а—радиус окружности; кривизна прямой
равна нулю.
Если линия задана уравнением y = f(x)t
то ее кривизна вычисляется по формуле
А=_1^1
(1+У'‘)3/а
Если линия задана параметрическими
уравнениями х=<р(/), у=ф(/), то
А I*»—У*1
-1.^)3/» •
• dx • dy •• (Рх - <Ру
где х- dt , у- dt , х-dta , у- dfi .
Если линия задана в полярных координатах уравнением р=/(в), то
ь_ |Р2+2Р,2~ РР*1
(р2+р'2)3/2 ’
, dp , d*p
где р'=^, р’=-^-
Радиусом кривизны называется величина, обратная кривизне: R= 1/| k |.
Окружностью кривизны данной линии в ее точке А называется предельное
положение окружности, проходящей через три точки А, В, С кривой, когда
В—>А и С—* А.
Радиус окружности кривизны равен радиусу кривизны. Центр окружности
кривизны называется центром кривизны и находится иа нормали к линии, про-
веденной в точке А в сторону вогнутости этой линии.
Координаты £ и т) центра кривизны линии y=f(x) вычисляются по формулам
^х-^1,
У У
Эволютой линии называется множество ее центров кривизны. Формулы для
координат центра кривизны можно рассматривать как параметрические уравнения
эволюты (где параметром является абсцисса х исходной линии).
1110. Найти кривизну линии у = —х8 в точке с абсциссой х=1/2.
Л Имеем у' = — Зх8, у*=—6х. При х= 1/2 эти прЬизводные принимают зна-
чения у1 =—3/4, у"=—3 и
I —3 I 3 _192 .
1(14-9/16)*/® |=125/64- 125- А .
1§3
1111. Найти кривизну в любой точке циклоиды х=а(/—sin/),
у = а(1—cos t).
Л х — а(1— cos/), i'=asin/, y = aslnt, y=acost,
ху—yx=a2 (cos /—cos2 /—sin2 /) = — a2 (1 —cos /),
х24-</2 = а2 О —2 cos /4-cos2 /4-sin2 /) = 2а2 (1 —cos /),
_ I —а2 (1—cos /) I______________1_______ .
I 23/2 a3(l — cos/)3/2 I 23/2a(l — cos/)1/2
1112. Найти координаты центра кривизны линии x> + yt = 2
в точке М (1; 1).
Л Продифференцируем уравнение данной линии дважды:
3x24-4j/V = 0 (*), 6x-]-12y2y,i-[-4y3y"=0 (**).
Так как х=1, у=1, то из уравнения (*) находим у' = —3/4, а из уравнения (*»)
получаем 64-27/44*4tf — 0, т.е. у" = —51/16. Тогда
. (И-/*)/ . (14-9/16) (-3/4) _43
6 у" —51/16 ~‘68’
„_„,1+у'2 и. 1+9/16 26
П = </+-у-=1+^5171б-=5Г.
т. е. С (43/68, 26/51). А
1113. Составить уравнение эволюты параболы 2i/2 = 2x4-1.
Л Продифференцируем дважды уравнение параболы:
4W' = 2, у'=>±; 4y'‘-j-4yy”=O, y" = -L-=_^L.
Определяем координаты центра кривизны:
(1+/*)•</'
6 JT
. 1 + </'*
2 1
!/2-y-
—1/(4у3)
+у-Н_3|Л
-1/(4^) У’
у~4у3—у = —4у3.
Получаем уравнение эволюты в параметрической форме: | = Зу2, t) =—4у*.
Исключив параметр у, найдем уравнение эволюты в явном виде: t)2 = 16g3/27. А
1114. Найти радиус кривизны эллипса х2/25 4- у2/9 = 1 в точке
М (0; 3).
1115. Найти радиус кривизны в любой точке кардиоиды р =
= a (1 4- cos 0) (а > 0).
1116. Найти кривизну линии x = etsin/, у — е(соз1 в точке / = 1.
M(W* координаты центра кривизны линии у = 1/х в точке
1118. Составить уравнение эволюты кривой x = /sin/4-cost
y=t sin/—sint
184
§ 4. ПОРЯДОК КАСАНИЯ ПЛОСКИХ КРИВЫХ
Если кривые y = f(x) и t/ = <p (х) имеют общую точку М (х0; у0), т. е. у0 =
= f (х0) = ф (•*<>), и касательные* к указанным кривым, -проведенные я.тояве» Л1 (х0;
ул), не совпадают, то говорят, что кривые y = f (х) и </ = Ф (•*) пересекаются в точке М.
Условие пересечения этих кривых в точке М (х0; у9) таково:
f (хо) = ф (*o). Г (Хо) * ф' (*<>)•
Если же эти кривые имеют общую точку М. (хл; ул) н касательные в этой
точке к обеим кривым совпадают, то говорят, что кривые касаются в точке М.
Условие касания кривых в точке М (х0; уа) таково:
/ (*о) = ф(*о)> 7'(*о) = ф'(*о)-
Если, наконец,
f (xa) = <f(Xo)< Г (Xo) = <f’(Хо), f" (xo)=<f" (Хо), Гп} (Хо) = <?п> (Хо),
НО /<” + !> (Хо) £ (х0), то принято говорить, что в точке М (хо; Уо> кривые
y — f(x) и у = <р (х) имеют касание n-го порядка.
Если «3^2, то кривые y = f(x) н y=<f(xj в точке М (х0; у9) имеют не только
общую касательную, но и одинаковую кривизну.
1119. Какой порядок касания имеют кривые у = е~х и ху=\!е
в точке х= 1?
Л Пусть f(x)=e~x, ф (х) = \/(ех). Найдем последовательные производные
этих функций: f'(х) — — е~х, f" (х)=е~х, ф' (х)=—1/(ех2), <р" (х) = 2/(ех3).
Теперь вычислим значения данных функций и их производных в точке х=1;
имеем f (1)=е-1, f (1) = — е-1, f (1)=е-1; ф (1)=е-1, <р' (1) = —е-1, ф’(1)=2е-1.
Таким образом, f(l) = ф (1), f (1) = <р' (1), но (1) £ <р" (1). Следовательно, ука-
занные кривые имеют касание первого порядка. А
1120. При каком выборе параметра а кривая у = е°х имеет в точке
х = 0 касание первого порядка с прямой y — 2x-j-l?
Д Пусть f(x)=eax и ф(х) = 2x-f-l. Для того чтобы указанные линии имели
в точке х = 0 касание первого порядка, необходимо выполнение равенств /(0)=<р(0)
и f (0) =ф' (0), т. е. еа*0 = 2.0-|-1 и ае° = 2. Отсюда а = 2. А *
Определить порядок касания заданных кривых:
1121. i/=14-cosx и у = 2—хг в точке х = 0.
1122. z/ = sin2x и оси Ох в точке х = 0.
1123. Цепной линии y=(ex-sre~x)/2 и параболы t/ = 14-0,5xa
в точке х = 0.
1124. Окружностей х2+у2 — 2у и х24-у2 = 4у в точке х = 0.
1125. Параболы у = х* и оси Ох в точке х = 0.
1126. i/ = ln(14-x) и параболы у = х—х2 в точке х = 0.
§ 5. ВЕКТОР-ФУНКЦИЯ СКАЛЯРНОГО АРГУМЕНТА
И ЕЕ ПРОИЗВОДНАЯ
Пространственную кривую можно задать параметрическими уравнениями
x = x(t), y—y(t), z = z(t) или векторным уравнением
r = x(0i + t/(0J4-2Wk-
Последнее уравнение определяет переменный вектор г как вектор-функцию
скалярного аргумента t, т. е. г=г(/)- Кривая, заданная уравнением г=г(/), на-
зывается годографом переменного вектора г.
185
Производной вектор-функции г=г(<) по скалярному аргументу t называется
новая вектор-функция, определяемая равенством
, ... dr Дг
г (0=я7= lim -д7«
dt д/->о Д/
Производная вектор-функции может быть вычислена по формула
dt~~ dt + dt dt
dr
Производная есть вектор, направленный по касательной к годографу век-
тора г в сторону возрастания параметра t.
„ . dr d2r
Если t есть время, то —вектор скорости конца вектора г, а ^ — вектор
ускорения.
Основные правила дифференцирования вектор-функции скалярного аргумента:
Ю d ir д_, dri_l_dro drs.
1 • ~dt <г1+г»-г’)—dt + If-It •
de
2°. , где c—постоянный вектор;
3°. (1г)=^тт+г-т 1 гДе X = X(0—скалярная функция от t;
ut СИ СИ
^-4<r‘xr’>“Slxr'+r"x§-
Уравнения касательной к пространственной кривой r=x (t) 14-1/ (О J+*(0 k
в точке Л1о(*о; Уо', zo) записываются в виде
(х—Хо)/Хо = (у—Уо)/Уо = (г—го)/го,
где жо = х(/о), Уо — У^о), «o = z(/o), io=x'(Oo. Уо=Уг (<о). zo = z'(M-
Нормальной плоскостью называется плоскость, проходящая через точку каса-
ния и перпендикулярная касательной. У равнение нормальной плоскости имеет вид
хо (*—хо) -Но (у—Уо) 4- z (г— го) = 0.
Дифференциал дуги пространственной кривой вычисляется по формуле
ds = Kia4-?4-zadt
1127. Какая линия является годографом вектор-функции г =
=а\ cos t + aj sin 14- c/k?
Л Эта линия имеет параметрические уравнения x—acost, y=asint, z=ct,
определяющие винтовую линию. Д
Найти годографы вектор-функций:
1128. r = icosf4-j-|-ksinL 1129. r = /(14-j + k).
ИЗО. r = 14-j-Hk. 1131. r = ichf4-jsht
1132. Найти производную скалярного произведения векторов
r1 = 3«4-2j4-5k и ra = 2i —3/j4-k.
Л Имеем
d(rpra)_ dra dri
—dt------ri‘Tt+ti'Tt~
= (3 Z i 4- 2j 4- 5k) • (-3j) 4- (21 - 3tj 4- k) -31=-6 4-6=0.
186
Полученный результат объясняется тем, что скалярное произведение грг^—5,
т.е- является постоянной величиной. А
1133. Показать, что векторы г = i cos t 4- j sin 14-k и •^•перпен-
дикулярны.
Л Имеем —=—i sin f-f-jcos t Находим скалярное произведение;
r--^-=—cos t sin i-f-sin t cos /-{-1.0=0.
„ , rdr .
Следовательно, г | -гт. А
at
1134. Найти производную вектор-функции r = ich* /-|-jsh/ch/4-
4- ksh’1.
1135. г = 1 sh t + j ch t + k ]/cha/ —3sh2/. Найтн
1136. п = 1/ + j/*4- k/3, r, = i/a4-j/34-k/- Найти d(r**r*\
1137. Составить уравнения касательной и нормальной плоскости
к кривой x = asin3/, y = bsintcost, z = ccos2t в точке t = n/4.
Л Находим x = asia2t, y=b cos 2/, г —— с sin 2/. При / = л/4 имеем: х0=а/2,
Уо — Ь/2, z0=c/2, Хо = а, уо = О, го = — с.
Уравнения касательной:
(х— а/2)/а = (у—b/2)/0 = (z—с/2)/(— с).
Уравнение нормальной плоскости:
/ а \ ( с \ - а2—с2 _ .
al х —у 1—с( z—2 7 °, или ах~сг------§—=°‘ *
1138. Составить уравнения касательной и нормальной плоскости
к винтовой линии г = 1 cos t + j sin t + К 3 tk в точке t = л/2.
1139. На кривой х=/4-1, y=t2 — 1, z — t2 найти точку, к кото-
рой касательная параллельна плоскости x4-2//4-z—1=0.
1140. Какой угол образует с плоскостью хОу касательная в вин-
товой линии x=cos/, y = sint, z — 2]/^2t в точке / = л/4?
1141. Составить уравнения касательной и нормальной плоскости
к кривой х= (1/К2) е* sin t, y=l, z — (ll]^2)etcost в точке t = Q.
1142. Составить уравнения касательной к кривой x = ef(cos* +
4-sin/), y = et(sint—cos/), z=e* в точке / = 0.
1143. Составить уравнения касательной к кривой г =/*14-/’j+
4-/*k в точке /=1.
1144. Показать, что кривые г = (и 4-1) 14- u*j 4- (2и—1) к и г =
=2v*i-|-(3v—'2) j4-oak пересекаются, и определить угол между кри-
выми в точке их пересечения.
1145. Составить уравнения винтовой линии, если радиус осно-
вания цилиндра R = 4, шаг Л = 6л, и найти дифференциал ее дуги.
Л Уравнения винтовой линии имеют внд x=4cos/, y=4sln/, z—3t, так
как z=h при / = 2л. Продифференцируем эти уравнения: i= — 4sin/, у=4cos/,
z«=3. Следовательно,, дифференциал дуги равен
<fe=J/>+y*+z*d/=/16 sin*/4-16 cos’ /4-9 Л=
=К 16(sin*/+cos*/)+9d/=5d/. А
1146. Найти дифференциал дуги кривой x = acos*/, ffsa
==p/a’+b’sintcos/, z = bsin*t.
1147. При каком шаге Л длина дуги одного витка винтовой линии
x = cosf, 0 = sinf, z — ct равна 4л?
ф Воспользоваться тем, что при развертывании цилиндра на плоскость одни
виток винтовой линии превращается в отрезок прямой.
1148. Уравнение движения имеет вид г = 3i cos t + 3jsin t + 4fk,
где t—время. Определить скорость и ускорение движения в произ-
вольный момент времени.
1149. Уравнение движения имеет вид г =/14-/2j+/Зк. Опреде-
лить скорость и ускорение движения в момент t— 1.
$ в. СОПРОВОЖДАЮЩИЙ ТРЕХГРАННИК ПРОСТРАНСТВЕННОЙ КРИВОЙ.
КРИВИЗНА И КРУЧЕНИЕ
Во всякой точке M(x; у, г) пространственной кривой г—г(/) можно постро-
ить три взаимно перпендикулярных единичных вектора (рис. 40); единичный век-
тор касательной (тангенциальный единичный
вектор)
dr dr/di .
ds \dr/dt I ’
единичный вектор главной нормали
_ dr/ds
V~ I dr/ds I ;
единичный вектор бинормали
0=tXv.
Соответствующие иеедииичиые векторы можно найти по формулам:
Т=^- (вектор касательной),
„ dr d*r , , ,
В=(вектор бинормали),
N = BxT (вектор главной нормали).
188
Плоскость, содержащая векторы гит, называется соприкасающейся плоско-
стью; содержащая векторы v и 0,— нормальной плоскостью; содержащая векторы
0 и т,— спрямляющей плоскостью.
Трехгранник с вершиной в точке М, образованный соприкасающейся, нор-
мальной и спрямляющей плоскостями, называется сопровождающим трехгранни-
ком пространственной кривой (рис. 41).
Кривизной линни в точке М называется число К= где Ф—Угол
поворота касательной (угол смежности) на дуге MN, As—длина этой дуги.
Если кривая задана уравнением r=r(s), то K=|-jg-|.
Если уравнение кривой имеет вид r=r(i), то
1*^1
„ |dfXdf*|
** I Л- 13 •
Q
Кручением кривой в точке М называется число <т= Пт -т—, где 0 —угол
Д$—0 As
поворота бинормали (угол смежности второго рода) на дуге MN.
Если r = r(s), то а=Т -^-1, где знак «минус» берется в случае одинакового
dB
направления векторов и V, знак «плюс»—в случае их противоположного
направления.
Если r=r(t), то
dr dar <Pr
dt dt* dt3
a
I dr d*r I* ’
I dt Х-Л*|
1150. Найти тангенциальный вектор т кривой г = 1*1 + Isj 4- t*k
в точке 1 = 1.
А Имеем
^ = 2/1 +3/*j+6/6k, |-^ |=y^4/«4-9#«4-36/ie.
При t = 1 находим
£=a+3H-«. |*|=r<+9+M-7. Д
1151. Найти тангенциальный единичный вектор кривой r = 5H-f-
+ 12j cos 1 + 12k sin 1 в произвольной точке.
1152. Найти тангенциальный единичный вектор кривой х=1 sin 1+
4-cosl, y=tcost—sin 1, z = 1*j/2 в точке 1 = л/2.
1153. Найти вектор т винтовой линии x = acos1, y = asint,
z = \^R*—a*t, R > a > 0 в произвольной точке.
Д r=ai cos /4-aj sin t-j-У R*—a3tk, sin i-f-a] cos f-f-y'’/?*—a*k,
189
R
1-^-^У a2sin2 /4-a2cos2/4-R2—a2=R,
_ dr/dt —ai sin/4-aJ cos/4-J^R2—a2 к
| drldt |
_ a sin/. a cos/ У R2— a2 .
“ R + R J+ R A
1154. Найти вектор 0 винтовой линии в произвольной точке.
ДИмеем ~дГ—— fli sin Z-J-aj cos/4- У R2—a2k, — ei cos/—ajsin/.
Найдем векторное произведение этих векторов:
dr , d2r
В=-згХ-т7«-= —a sin/ a cos/
dt Л dt2~
— a cos /
—a sin /
к
yR2—a2
О
= aVR2—a2sin /-i—а У R2—a2 cos /-J4-a2k;
I В | = |-^г X —1= У a2 (R2—a2) sin2 /4-а2 (R2—a2) cos2/4-a4=aR.
Следовательно,
„ В а УR2—a2 i sin/—a/R2—a2] cos /4-aak
P = — ---------------------------------------=
VR’-a* . , ,
=—R— sin/’1---------x-
1155. Найти вектор v винтовой
Л Так как v = 0 X т, то
aR
У R2—a2
линии в произвольной точке.
v=
i
У R2—a* sin /
УR2—a2 cos /
R
a sin /
R
1156. Найти
R
a cos /
~~R~
k
а
~R
R
кривизну К ВИНТОВОЙ линии.
Л В задачах
поэтому
1153 и 1154 было найдено, что
d’rl
|*X^I
„ | dt х dt2 I aR a
------—--“—-=—-
dr I? — R3 R2
1
1157. Найти кручение а винтовой линии.
Л Имеем
—aisln /4-ojcost-^УR2—a2 k,
-r^-e—ai cos/—aisln/, -^^ai sin /—al cos /.
dt2 dt3-
Найдем смешанное произведение этих векторов:
dr d2r (Pr
~dt dt2 dP
— a sin/ a cos/ У R2—a2
— a cos / —a sin / 0
a sin / — a cos / 0
= a* уR*_a2.
В задаче 1154 было найдено, что -тг X-тяг ==я/?. Следовательно,
| a/ dt‘ |
I dr „ d2r I * x а2 УR2—a2 У R2-a2 .
ГЛ X 574 =a R • Таким обРазом- <7=—~^Ri “ Ri—-A
1158. Составить уравнение соприкасающейся плоскости винтовой
линии в произвольной точке.
Л Эта плоскость проходит через точку (a cos/; a sin/; У R2—а2 /) и пер-
У R2—a2 sin / . У Ъ2—а2 cos t. a
~R R k’
пендикулярна вектору бинормали 0
Поэтому уравнение соприкасающейся плоскости таково:
|/^> sin / (X—acos /) —^--2 q2.cos * (Г—asin/)+-^- (Z—УR2—a2 /)=0,
А А А
или X У R2— a2 sin t—У У R2—a2 cos /-f-aZ—а УR2— а2 / = 0. А
1159. Составить уравнение спрямляющей плоскости винтовой
линии в произвольной точке.
Л Эта плоскость проходит через точку (acos/; a sin/; У R2—а2 /) перпен-
дикулярно вектору главной нормали v = —1 cos t—j sin /. Поэтому искомое урав-
нение имеет вид
— (X—a cos /) cos /—(У—a sin /) sin / = 0, т. е. X cos i-f-Y sin /—a — 0. A
1160. Составить уравнение нормальной плоскости винтовой
линии в произвольной точке.
. -ч - . a sin / , ,
Л Эта^ плоскость перпендикулярна вектору касательной т =-——i
, a cos /
+ ~R~
Поэтому искомое уравнение имеет вид
asln/.„ ...acos/.,. , л , V^R2—а2л „
----(X —acos/)-|—(У—asln/)+~—-------------\Z — V R2—a2 /) = 0,
l/" п2_,
J4--—р--------к и проходит через точку (acos/; a sin/; У R2—а2 /).
или Ха sin/—Ya cost—zy R2—a2 4-(/?2—a2)/ = 0. A
1161. Найти вектор т кривой x — Gt, y = 3t2, z = t3 в точке t — l.
1162. Найти вектор 0 той же кривой при t = 1.
1163. Найти вектор v той же кривой при / = 1.
1164. Найти кривизну К той же кривой при t = l.
1165. Найти кручение а той же кривой при t= 1.
1166. Составить уравнение соприкасающейся плоскости той же
кривой при t =1.
1167. Составить уравнение спрямляющей плоскости той же кри-
вой при t = 1.
1168. Составить уравнение нормальной плоскости той же кри-
вой при t = 1.
ГЛАВА VIII
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ
НЕСКОЛЬКИХ НЕЗАВИСИМЫХ ПЕРЕМЕННЫХ
§ 1. ОБЛАСТЬ ОПРЕДЕЛЕНИЯ ФУНКЦИИ.
ЛИНИИ И ПОВЕРХНОСТИ УРОВНЯ
Пусть даны два непустых множества D и U. Если каждой паре действитель-
ных чисел (х; у), принадлежащей множеству D, по определенному правилу ста-
вится в соответствие один и только один элемент и из U, то говорят, что на
множестве D задана функция! (или отображение) со множеством значений U. Прк
этом пишут D-1+U, или f: D—► U, или u = f(x, у). Множество D называется
областью определения функции, а множество U, состоящее из всех чисел вида
f(x, у), где (х; у) £ D,— множеством значений функции. Значение функции
u = f(x, у) в точке М (х0; уй) называется частным значением функции и обозна-
чается f(x0, уа) илн f (М).
Область определения функции u = f(x, у) в простейших случаях представляет
собой либо часть плоскости, ограниченную замкнутой кривой, причем точки этой
кривой (границы области) могут принадлежать или не принадлежать области
определения, либо всю плоскость, либо, наконец, совокупность нескольких частей
плоскости хОу. Геометрическим изображением функции и = /(х, у) в прямоуголь-
ной системе координат Охуи (графиком функции) является некоторая поверхность.
Аналогично определяется функция любого конечного числа независимых
переменных u = f(x, у, г,..., I).
Линией уровня функции u = f(x, у) называется линия f (х, у) = С на пло-
скости хОу, в точках которой функция сохраняет постоянное значение и = С-
Поверхностью уровня функции u = f(x,y,z) называется поверхность
/(х, у, г) —С, в точках которой функция сохраняет постоянное значение и = С.
1169. Найти область определения функции u — V^a2—х2—у2.
Л Функция и принимает действительные значения при условии а2 —х2—уа^0
т. е. ха4-«/а<аа. Областью определения данной функции является круг радиуса s
с центром в начале координат, включая граничную окружность. А
1170. Найти область определения функции и — arcsin (х/у2).
Л Эта функция определена, если у Ф 0 и —1 <х/«/2< 1, т. е. —£а<х<£*.
Областью определения функции является часть плоскости, заключенная между
двумя параболами у2—х и у2~ — х, за исключением точки 0(0; 0). А
1171. Найти область определения функции u = ln(2za—6ха —
-Зу2-Ь}.
Л Данная функция зависит от трех переменных и принимает действительные
значения при 2га—6ха—Зу2—6 > 0, т. е. ха/1+ «/а/2—za/3 < —1. Областью опре-
деления функции является часть пространства, заключенная внутри полостей
двуполостного гиперболоида. А
1172. Найти линии уровня функции и — х2-\-уг.
Л Уравнение семейства линий уровня имеет вид х2-)-у2 = С(С > 0). Прида-
вая С различные действительные значения, получим концентрические окружное™
с центром в начале координат. А
192
1173. Найти поверхности уровня функции u = x2 + z2—у2.
Л Уравнение семейства поверхностей уровня имеет вид xa-|-za—у2 = С. Если
С = 0, то получаем xa4-za—у2 = 0—конус; если С > 0, то xa + z2 —i/a = C—
семейство однополостных гиперболоидов, если С < 0, то ха4-га—у2 = С—семей-
ство двуполостных гиперболоидов. А
Найти области определения функций:
1174. M = /xa + r/2 — 1.
1176. w = arcsin (x-j-r/).
1178. и = In (—
1180. и = /а2—х2—i/2—za.
1182. u = 1/1п(1— х2 —у2 — z2).
Найти линии уровня функций:
1184. z = 2x + y. 1185.
1187. z = Vx/y- 1188.
z = xly.
z — e?u.
1175. M = l/J/’1— х2— у2.
1177. и = /cos (х2 + z/2).
1179. м = г/ + /х .
1181. и = arcsin (z IVх2 -f- у2)
1183. u = Vx-]-y-]-z.
1186. z = lnVy/x.
Найти поверхности уровня функций:
1189. и = х + у + Зг. 1190. и = х2у2г2. 1191. и = х2—у2 — г2.
§ 2. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ФУНКЦИЙ
НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
1. Частные производные первого порядка. Частной произзодной от функции
z — f(x, у) по независимой переменной х называется конечный предел
Дх -» 0 ZXX ОХ
вычисленный при постоянном у.
Частной производной по у называется конечный предел
lim /(х,У + А//)-/(х,У)=^ -
Ду-о Ау ду 'У'”"
вычисленный при постоянном х.
Для частных производных справедливы обычные правила и формулы диф-
ференцирования.
1192. и = х2—Зху—4у2—x-]-2i/+l. Найти’и —-.
А Рассматривая у как постоянную величину, получим |^=2х—Зу — 1
Рассматривая х как постоянную, найдем = —8y-J-2. А
1193. г = ех'+У*. Найти и
дх ду
Д Й-=еХ,+ у,(^+У’)х = 2«Х’+у’. ^=^+^^+УЧу~2у^+^. Д
7-215
193
1194. p = u4cosaq>. Найти и
A -^£-=4a3cos*<p, -|&-=a4-2cos<p(— sin<p)= — u4sln2<p. Д
1195. Показать, что функция z = 01n(*a—у2} удовлетворяет
1 dz , 1 dz z
уравнению
Д Находим
dz , 2xy £L- In f-л ..ay 2ya
dx x*—y* ’ dy х*—у^’
Подставим найденные выражения в левую часть уравиения:
1 2ху 1 Г. . . ~__ЗУ8 1 __ 2У 2У । In (ха-уа) г
X ха—уа у [ ' V ' ха—y’J ха—уа ха—уа + у уа"
Получаем тождество, т. е. функция г удовлетворяет данному уравнению. А
1196. Показать, что функция г=уу/х sin (у/х) удовлетворяет урав-
, dz . dz
нению x^ + xy-g^yz.
Л Находим
Ш+г’"'-'] •“ (f)+
Подставим найденные выражения в левую часть уравиения:
— х* -^.y^Mny-sin ха--^-у|'/хсоз(-=0 +
+xy~-y*'/*“1-sln f-^-^+xy.y-y^.lny-sln +
Л \ " / <* \ •* /
+*У,у,У*'/х cos
=yy»/*sinfyjeyz.
Получаем тождество; следовательно, функция г удовлетворяет данному
уравнению, Д
1197< u = x*H-2z/a—Зху—4x4-20+5. Найти
1198, r = pasin40. Найти %-, .
• dp оо
плп х* х тт . du du
1199. u = -j--. Найти -г-, -г-.
У* У dx dy
1200. z~e*y <*•+»•>. Найти .
dx dy
1201. в-ЗуГГ+Зр"/?. Найти
1202, и=е«Л+е-й. Найта
194
1203. z = arctg . Найти , g-.
1204. г — e(xa+^\ Найти 4^-, 4~.
ox oy
1205. u = (x— y)(x~z)(y—z). Найти-g, -g, g.
1206. и = езх,+^~хУ. Найти , ~.
1207. u = e*je>sin —. Найти
•г X oy
1208. Показать, что функция z = £- + 4+4’—T Удовлетворяет
*>У £ х у
,дг , . дг х3
уравнению х2 .
1209. Найти
дх дх
др дО
ду ду
др дв
если x = pcos0, 0 = psinO.
2. Полный дифференциал. Полным приращением функции z — f(x, у) в точке
М (х; у) называется разность Дг=/(х+Дх, у-}-Ау)—f(x, у), где Дх и Ду—про-
извольные приращения аргументов.
Функция г=/(х, у) называется дифференцируемой в точке (х; у), если в этой
точке полное приращение можно представить в виде
да — А Ax-J-B Ду-f- о (р), где р — У foe2-}-Ау2.
Полным дифференциалом функции z = f(x,y) называется главная часть пол-
ного приращения Дг, лйнейная относительно приращений аргументов Дх и Ду,
т. е. dz = A Ах-}-В Ау.
Дифференциалы независимых переменных совпадают с их приращениями, т. е.
dx = Ax и dy = Ay.
Полный дифференциал функции z = f(x, у) вычисляется по формуле
. дг . , дг .
dz=-s- dx-}- -j— dy.
дх'ду
Аналогично, полный дифференциал функции трех аргументов u — f(x, у, г)
вычисляется по формуле
. ди . , ди . , ди ,
du=-^-dx-}--^--dy-}--5—dz.
дх 1 ду 1 дг
При достаточно малом р = УДха4-Дуа для дифференцируемой функции
z — f(x, у) справедливы приближенные равенства
Дг я dz; f (x-J-Дх, у+Ду) я f (х, y)-}-dz.
1210. z = arctg-^g. Найти dz.
Л. Найдем частные производные:
дг _______1______—2у у дг _________________I________2х х
Эх~1 . /х+у\а> (х—у)а ха+уа ’ ду"*! । М+у\*' (х—у) а“ха +уа‘
'Дх—у] У/
Следовательно, dz=^-dy=X^ . . Д,
’ дх 1 ду ха+у*
1211. и — хУ*г. Найти du.
Л Имеем du=^dx-\-^-dy-[-~d2, где
^ = и2г-хУ,/-1, ^—•хУ12Лпх.2уг, ^-—хУ2гЛпх-у*.
дх 3 ду ог
Следовательно,
du = уггхУ*г ~1dx-j-2yz- хУ*г • In х dy+у*хУ2г -In xdz.
1212. Вычислить приближенно Ksin* 1,55 + 8е®’018, исходя из
значения функции z = prsin2x + 8e>' при х = л/2« 1,571, г/ = 0.
Л Искомое число есть наращенное значение функции г прн Дх = 0,021.
Ду = 0,015. Найдем значение г прн х = я/2, у~0; имеем г = p^sln2 (л/2) + 8е° = 3.
Находим приращение функции:
. , дг . . дг . s\n2x Ьх-\-8еУ &у 8-0,015 n по
Дг га dz=^- Дх4-ч- Ду=-... ——г—=0,02.
дх 1 ду 2/sln2x+8eX 6
Следовательно, J^sin21,55+8е0,018 а;3,02. Д
1213. Вычислить приближенно arctg (1,02/0,95), исходя из зна-
чения функции z = arctg (уlx) при х=1, у=\.
Д Значение функции г при х=1, у=1 есть z=arctg (1/1) = л/4«0,785.
Найдем приращение функции Дг прн Лх = —0,05, Ду=0,02:
. , дг . . дг . у Ьх х Ьу хку—уЬх 1 • 0,02+1-0,05 пп
Дг^г=.-Дх+^ДУ=-^+^=-^_=--------------------------2------=0,03э.
Следовательно, arctg (1,02/0,95) = г+Дг и 0,785 + 0,035 = 0,82. Д
1214. г = in (х2 + у2). Найти dz.
1215. г = In tg (у/х). Найти dz.
1216. г = sin (х2 + у2). Найти dz.
1217. г = хУ. Найти dz.
1218. и — 1п(х + Ух2 + у2). Найти du.
1219. z = ex (cosy + xs'my). Найти dz.
1220. г — ё^У (хcosy+уsinx). Найти dz.
1221. г = arctg 2/*~*~sl,n . Найти dz.
х х sin у
1222. и = ехУг. Найти du.
1223. Вычислить приближенно 1,02*’°’, исходя из значения функ-
ции г = хУ при х=1, у=4 и заменяя ее приращение дифферен-
циалом.
1224. Вычислить приближенно In (0,09s + 0,99s), исходя из зна-
чения функции г = In (х3 + у3) при х = 0, у = 1.
1225. Вычислить приближенно ^/1,022 + 0,052, исходя из значе-
ния функции г = у/х2 + у2 при х= 1, у = 0.
1226. Вычислить приближенно Ибе9’02+ 2,03*, исходя из значе-
ния функции z = \^5ex + у2 при х = 0, у = 2._____
1227. Вычислить приближенно И 1.041’99 + In 1,02, исходя из зна-
чения функции u= Кх>'+In г при х=1, у = 2, г=1.
196
3. Частные производные н дифференциалы высших порядков. Частными Про-
изводными второго порядка от функции г = Цх, у) называются частные производ-
ные от ее частных производных первого порядка.
Обозначения частных производных второго порядка:
д (дг\ д2г , д f дг\ д2г . . .
дх \дх)~д2х~ ду\дх)~ дхду~ ^у <х’
д (дг\ д2г . д Iдг\ д2г .
дх\ду Jdydx ~ h* <х’ ду \ду )~ду2~ (х’
Аналогично определяются н обозначаются частные производные третьего н
высшнх порядков, например:
д (д2г\ <Рг д fd2z\ dPz .
дх \ дх» / дх3 ~ I*** ду\д&) ~ дх2 ду ~ (х’ и Тф Д'
Так называемые «смешанные» производные, отличающиеся друг от друга лишь
последовательностью дифференцирования, равны между собой, если онн непре-
д2г д2г
рывны, например 5—4-= 5—5-.
г дхду дудх
Дифференциалом второго порядка от функции z = f(x, у) называется диффе-
ренциал от ее полного дифференциала, т. е. d2z — d(dz).
Аналогично определяются дифференциалы третьего н высших порядков:
d3z = d(d?z); вообще dnz = d(dn~1z).
Если х и у—независимые переменные и функция f(x, у) имеет непрерывные
частные производные, то дифференциалы высшнх порядков вычнсляютси по фор-
мулам
м ^2г j « । о 52г , , , д2г , ,
d2z= st dx24-2 5—5- dx dy-i-s-s dy2;
dx2 1 дхду я Г ду2
д®г=-О- dx*+3 -5^- dx2 dy+3 <^2+ттзг №
дх® 1 дх2ду 3 1 дхду2 3 1 ду3 ’
Вообще, имеет место символическаи формула
dnz=[ s-dxA-s-dy \ г,
\дх 'ду }
которая формально раскрывается по биномиальному закону.
1228. г = г/1пх. Найти Д4-, 44.
дх2 дхду ду2
А Найдем частные производные: ^=—;
дх х
торно, получим
dz
^=1пх. Дифференцируя пов-
= Ллпй = о- — д(у\ -1
дх2 дх\х } х2 ’ ду2 ду' ' ’ дхду dy\xj х'
1229. г = In tg (уlx). Найти
- дг ’ 1 , . , . ( у \ у 2
dx-'tg (у/х) ’ 860 ^Х^ \ ~~ х2 )~ х2 ’ sln(2t//x)’
д2г 1 2 у —2 cos (2у/х) • (2/х)
дхду~ x»*sln(2y/x) х2 * sln2(2y/x) ~~
2
3". «/о , ч ’ (2у cos (2ylx) —х sin (2г//х)). ▲
Xs sin* (2у/х) ' я ' \ si /> м
197
1232.
1233.
1234.
1235.
1236.
1237.
1238.
1239.
1240,
1241.
1242.
1230. z = sinxsiny. Найти 4?z.
Л |j==COSXSlny, g^ = slnxcosy,
д2г , , д2г д2г
^-=-sinxsiny, ^^=cosxcosy; -sin х sin у,
d.2z = —sin х sin у dx24-2 cos x cos ydxdy—sin x sin ydy2. A
1231. z = x2y. Найти tPz.
.dz „ д2г „ д3г n dz r~" d2z .
& dx~2xy’ dx2~~2y’ dx3-0, dy~X ’ dy2~°’
*£=0 -^=2 -L^-=o-
dy3 ' dx2 dy ' dx dy2 ’
<Pzr==0-dx^-[-3'2dx2 dy-{-3‘0-dX'dy2-j-0-dy3 = 6dx2 dy. Д
« = 4x® 4-3x2y 4-3xy2—у3. Найти
u = xy + sin(x + y). Найти
и = In tg (x + у). Найти ~-y.
z = arctg x+y-. Найти
» 1— xy dxdy
z = x2\n(x-\-y). Найти д^-.
' 1 13' дхду
. , Т Т . д2и
u = xsinxy-i-ycosxy. Наити
д3и
w = sin (х 4-cos у). Найти
г = 0,51п(х2 + у2). Найти d2z.
z = cos(ху). Найти d2z.
z = cos (ах + еУ). Найти
х* — 8x1/* и „ д3и
и=-----х-2-. Наити д , 3 .
х—2у дх2ду
г = х2у3. Проверить, что чЛч-л—дЛ 5-?.
» г г дуз дуз дхг
г — х2-\-у2—ху—2x4- У 4- 7. Найти d2z.
1243.
1244.
1245. Показать, что функция z = <p(x)g(y) удовлетворяет урав-
d2z дг дг
нению г т-5- = д- • д-.
дх ду дх ду
1246. Показать, что функция z = g(x)-\-yg' (х) удовлетворяет
dz дг . д2г
уравнению г = ?- + 1/т-т-
дх ду ^дхду 2 2
1247. Показать, что функция и—уех2~У удовлетворяет уравнению
1 ди 1 ди_____ и
х * дх + ~у ‘ ду~~у2’
1248. Показать, что функция u = -^=e~x*^ia,C) удовлетворяет
уравнению = а2
J r dt дх2
1249. Найти (?u. 1250. a=ln(x4-*/)- Найти d*u.
1251. u<=ylx. Найти <Pu. 1252. u — xyz. Найти d*u.
1253. u = xlny. Найти d4u. 1254. u=?t+>'. Найти d*u.
4. Дифференцирование сложных функций. Пусть x=f(x, у), где х=ф(/),
у—Ф(0 ,н функции \f (х, у), <р(О>ф(О дифференцируемы. Тогда производная
сложной функции х=/[ф (0, ф (/)] вычисляется по формуле
dz_dz dx.dx dy
dt Зх * dt+dy ’ dt’
Если г=/(х, у), где у=ф(х), то полная производная от г по х находится
по формуле
dz дг , дг dy
dx^Sx+Sy ’ dx-
Если же г—[(х,у)( где х=ф(£, Т|), у=(Е, л), то [частные производные
выражаются так:
дг дг дх . дг ду дг дг дх , дг ду
Э1вБ • al+sy • " ^“Эх* Эп+^ *
1255. z=e**+/, где x—ac.ost, y=as’mt. Найти
Л Имеем
2? “Й * й+й ’ йве*2+у2,2х (~а sta 0+**2+А2У (а со8 0-
= 2ае**+У* (у cos t—х sin 0.
Выразив х и у через t, получим
—=2aeat (asln tcost—a cos/sin 0=0. A
1256. z = ln(x’-y2), где y = e*. Найти g, g
Л Имеем
дг
Зх
2x
x2—у2
. Используя формулу полной производной, находим
—=—4-^г.^= %* Х12(х~
dx=dx-'Зу * dx х4—у* х*—у±яа х2—у* '
1257. z = yln£, где « = tg»x, D = ctg»x. Найти g.
1258. z = где у = 3x4-1. Найти
х24-у ° г dx
1259. z=x*y, где у=cosx. Найти и
1260. z = 1п*~^^2_~, где # = xcosa. Найти
х+у х*—у* ах
1261. z = x*+y*, где х = Е4-т], y=l—1|. Найти
1262. и = 1п(х*4-#*), где х=£т], у=|. Найти
1263. Показать, что функция и = 1п(1/г),' где г =
«К(х—а)24- (у—Ь)*, удовлетворяет уравнению ^+^ = 0-
199
5. Производная в данном направлении. Градиент функции. Производной ф>-нв-
ции z = f(x, у) в точке М (х; у) в направлении вектора 1 — ММ± называется
предел
37= “га ' , ,гп—г "= Ьт — , где р=у Дхг+Дуг-
dl |мм,|-*о |MMi | p-о р
Если функция f (х, у) дифференцируема, то производная в данном направ-
лении вычисляется по формуле
дг дг , дг ,
зт=з- cos а4-з- sin a,
dl дх 1 ду
три a—угол, образованный вектором 1 с осью Ох.
В случае функции трех переменных u = f(x, у, г) производная в данном на-
правлении определяется аналогично. Соответствующая формула имеет вид
ди ди , ди „ , ди
57= з- cos a-i-д- cos р-1—д- cos у,
dl дх 1 ду г I дг 1
где cos a, cosfJ, cosy—направляющие косинусы вектора 1.
Градиентом функции z — f(x, у) в точке М (х; у) называется вектор с на-
чалом в точке М, имеющий своими координатами частные производные функции z:
. дг . , дг ,
grad 2=з- 1+5- 1.
6 дх 1 ду-
Градиент функции и производная в направлении вектора I связаны формула*
Зг .
^ = npzgradz.
Градиент указывает направление иаибыстрейшего роста функции
„ дг л
точке. Производная в направлении градиента имеет наибольшее
равное
в даивз*
значение,
I = |gradz|
наиб
2
М (1; 1)
В случае функции u = f (х, у, г) градиент функции равен
. ди ,, ди, , ди,
gradu = -=- i-J-з- j+-5~k«
6 дх 'ду'дг
1264. Найти производную функции г = х2—уг в точке
в направлении вектора I, составляющем угол а = 60° с положитель-
ным направлением оси Ох.
Л Найдем значения частных производных в точке М: ^=2х,
= 2, ) = — 2. Так как cos a=cos 60°=1/2, sin a=sin60°=yr3/2, то
\dxjM \dyjM
-=2
dl *
1265. Найти производную функции и = хугг3 в точке М (3; 2; 1)
в направлении вектора MN, где 7V (5; 4;2).
Л Найдем вектор ММ н его направляющие косинусы: AfV = i = (5—3)i +
+ (4—2)j-f-(2—l)k=2i + 2J4-k; cos a = 2/K 22-f-22+ l2 = 2/3; cos₽ = 2/3;
200
1 —К3 и-0,7. А
cos у =1/3. Вычислим значения частных производных в точке Л4:
ди « ч п , ди „ » „ (ди\
~-=»2z3; ^- — 2хугг; -^-=3ху2г2-, = =4
дх * ’ ду * ’ дг я \dxjM
=36.
м
п ди___. 2 , , л 2 , „„ 1 _ «л 2 *
Следовательно, st=4--^-4-12—4-36—=-22-^-.
д1 3 3 3 3
1266. Найти производную функции z = ln (х2 + /) в точке М (3; 4)
в направлении градиента функции г.
Л Здесь вектор 1 совпадает с градиентом функции z = ln (х24-г/2) в точке
М (3; 4) и равен
, f 2х \ , . f 2у \ 6.8
grad z-^+уа + {ха+уа j-25 +25 j.
Следовательно,
дг , . . -1/7 6 V ./ 8 V 2 .
d/“,grad2l— Г (,25) +\25/ 5'^
1267. Найти величину и направление градиента функции ы —
= tgx—x4-3siny—sin3«/4-z-|-ctgz в точке М (л/4; л/3; л/2).
Л Найдем частные производные
ди „ , ди „ ди , ,
=sec2x—1, ^-=3cosu—3 sin2 у cos у, = = 1—cosec2 z
дх ду дг
и вычислим их значения в точке At (л/4; л/3; л/2):
(ди\ (ди\ _ 1_3 !ди\ =
\дх)м~2 Х~'’\ду)м. 2 4 '2 /’2 8’ \дг)и
Следовательно,
(grad «)Ж = 1 +4 j; | grad и |ж = V 12+(3/8)2 = /73/8;
О
18 3
,cosa=——=—cos8 —sina=——А
/73/8 /73 ' /73
1=0.
1268. Найти производную функции z = x2—х«/ + «/2 в точке
М (1; 1) в направлении вектора I = 6i + 8j. ______
1269. Найти производную функции ц = arcsin (z//x2 + y2) в точке
М (1; 1; 1) в направлении вектора MN, где Л/(3;2;3).
1270. Найти производную функции и = In (х2 + у2 + г2) в точке
/И(1; 2; 1) в направлении вектора г = 21 + 4] + 4k.
1271. Найти величину и направление градиента функции u=l/r,
где г = /х2 + / + г2, в точке М (х0; у0\ г„).
1272. Найти величину и направление градиента функции и = хуг
в точке М (2; 1; 1).
1273. Найти производную функции и = х/2 + у/3 + z/б в направ-
лении 1 = 6i + 3j—6k в произвольной точке.
6. Дифференцирование неявных функций. Производная г неявной функции
у = «/(х), заданной с помощью уравнения F (х, у)=0, где F (х, у)—дифференци-
руемая функция переменных хну, может быть вычислена по формуле
, dF/дх dF n
Ч = -dF/fy ПРИ УСЛ°ВИИ & •
201
Производные высших порядков неявной функции можно найти последова-
тельным дифференцированием указанной формулы, рассматривая при этом у как
функцию от х.
Аналогично, частные производные неявной функции двух переменных
г=<р(х, у), заданной с помощью уравиения F (х, у, г)=0, где г (х, у, г)—диф-
ференцируемая функция переменных х, у и z, могут быть вычислены по формулам
дг _ dF/dx дг_________dF/dy
dF/дг' ду~ dF/dz
при условии
дг
1274. cos (х4*1/) + у = 0. Найти у'.
Д Здесь F (х, у)=соз(х+у)+у. Найдем —sin (x-j-y), ~
=—sin (x-f- у) +1. Следовательно,
, —sin(x+y)= sln(x+y) .
У 1— sln(x+y) 1— sin(x+y)’ ж
1275. у—s\ny = x. Найти у' и у".
dF
Л Здесь F (х, у)=у—sin у—х. Имеем
откуда
I, = cosy=2 sin’-j
y,g=-2sin4/2)=?coseci
Найдем вторую производную:
у"=-£--2созес у Г — созес
у/ = --|-cosec*-|ctg-|.. ▲
1276. z3—3xyz = a3. Найти и
Л Здесь F (х, у, г) — г3—3хуг—а3. Находим Д—=—Зуг,-££-=—Зхг,
ох оу OZ
= Зг* — Зху. Тогда
дг —Зуг уг дг ___ — Зхг _ хг .
дх~ 3г*—3ху~ г*—ху ’ ду~ 3г*—3ху~ г*—ху ‘
1277. хуг = х+у + г. Найти dz.
. . дг . . дг . . дг дг
Л Как известно, dz=^ах-\-^ау, поэтому найдем сначала^ н :
дг уг—1 дг хг—1
дх~ху— 1 ’ ду ху—1 ’
Следовательно,
dz^--~[(yz—V)dx+(xz—\)dy]. £
лу — 1
1278. x*4-t/s4-ln(xs + «/s) =а*. Найти у'.
1279. (y/x) + s\n(y/x) = a. Найти у’.
1280. (ху—а)* + (ху—^)* = г*. Найти у', у*.
1281. х^ + 2у*—2ху^2ху+ 1 =0. Найти у’.
1282. lntg^/x)—ylx = a. Найти у'.
1283. (х*+у*—bx)* — a*(x* + y*). Найти у' в точке М (Ь; Ь).
1284. 3sin(Кх/у)—2cos1 =0. Найти у'.
202
1285. 0,51n(x24-y2)—arctg (уlx) =0. Найти у'.
1286. x2—x-2^+1 + 4«'—х4-2^ + 2 = 0. Найти у'.
1287. х + у—е^ — О. Найти у', у".
1288. х + у + г = ег. Найти zx, zy.
1289. х3 +г/8-|-г3—Зхг/г = 0. Найти zx, zy .
1290. х = г In (г/г/). Найти dz.
1291. х sin г/4-г/sin х + г sin х = а. Найти г».
1292. xy + xz + yz = 1. Найти dz.
1293. хег'4-//е*+ге* = а- Найти zx.
1294. г = х+ arctg—— . Найти
1 & г —х дх
§ 3. КАСАТЕЛЬНАЯ ПЛОСКОСТЬ И НОРМАЛЬ К ПОВЕРХНОСТИ
Касательной плоскостью к поверхности в точке М называется плоскость, прохо-
дящая через точку М поверхности, если угол между этой плоскостью и секущей,
проходящей через точку М и любую точку М\ поверхности стремится к нулю, когда
Mi стремится к М.
Касательная плоскость к поверхности в точке М содержит касательные ко всем
кривым, проведенным на поверхности через точку М.
Нормалью к поверхности в точке М называется прямая, проходящая через
М перпендикулярно касательной плоскости в этой точке.
Если поверхность задана уравнением F (х, у, г) = 0 и в точке М (х0; уа‘, г0)
{ dF \ ( dF \ ( dF \ А
частные производные , -я— конечны и не обращаются
н \ дх Jm \ ду Jm \ dz ]м
в нуль одновременно, то уравнение касательной плоскости к поверхности в точке
At (-х0; Уо, z0) записывается в виде
( dF \ , , , ( dF \ . . , / dF \ . v „
-я— I (х—*о) + ( -я— I [и—У о) 4* ) (г—го) = О>
\ dx )м' 0/ Г\ dy Jm \ dz Jм' ’
а уравнения нормали к поверхности в этой же точке—в виде
X—ха У—Уо _z—гв
( dF \ ~ (dF\ ~ fdF\ ’
\ dx )м \dy Jm \dzjM
Если же уравнение поверхности задано явным образом: z = f (х, у), тдечаст-
ные производные 1 и ( tyJM в точке Af (х0; у0\ гв) конечны (нмогутбыть
равны нулю одновременно), то уравнение касательной плоскости в точке М запи-
сывается в виде
fdz\ , . , fdz\ . .
г~г° = Ым (Х-Хо) + Ым
а уравнения нормали—в виде
х —х0 _ у—у0 __ г—Zo
f dz \ / dz\ —1 ’
\~дх )м \ду)м
Равенство нулю, например ( j , означает, что касательная плоскость парал-
лельна оси Ох, а нормаль лежит в плоскости х=х0.
1295. Дана поверхность г = х2—2хг/-|-г/2—х+2г/. Составить урав-
нение касательной плоскости и уравнения нормали к поверхности
в точке А4(1; 1; 1).
203
Л Найдем частные производные ^=2х—2у—1 и —2*+ 2^4-2 и “
., . .. / дг \ , / dz \ п
вначения в точке М (1; 1; 1): = | = — 1 — =2.
' ’ ’ ' \dxjM \dy/M
Уравнение касательной плоскости:
г—1 = — (х—1)4-2 (у— 1), или х —2у+г = 0.
Уравнения нормали:
(х—!)/(—!) = ((/—1)/2 = (г—1)/(—1). А
1296. К поверхности х2 + 2у2 + Зг2 = 11 провести касательные
плоскости, параллельные плоскости x-]-y + z=l.
Л Здесь F (х, у, z) =x2-^-2y2-f-3z2—11. Найдем частные производные:
dF . dF л dF с
~^-—2х, -^—=4у, -^-=6г. Из условия параллельности касательной плоскости
и данной плоскости следует, что (dF;dx)/l=(dF/dy),il—(dF/dz)/l, или (2х)/1 =
= (4</)/1 =(6г)/1. Присоединив к этим уравнениям уравнение поверхности х2—-
-\-2у2Зг2 = 11, найдем координаты точек касания: Mi(V 6; У 6/2; У 6/3) и
Л42(—У 6; —У 6/2; —У 6/3). Следовательно, уравнения касательных плоско-
стей имеют внд
1 (х ± У 6) + 1 • (у ± У 6/2) + 1 -(г ± У 6/3) =0,
т. е.
ж+у4-г+1 1/У 6 = 0 и —11/У 6 = 0. А
1297. Найти уравнения касательной плоскости и нормали к по-
верхности z = 1 -j- х2 4- У1 в точке Л4(1; 1; 3).
1298. Найти уравнения касательной плоскости и нормали к по-
верхности х24-*/2—г2 =— 1 в точке М (2; 2; 3).
1299. Найти уравнения касательной плоскости и нормали к по-
верхности г = 1п (х2-|-//2) в точке М (1; 0; 0).
1300. Найти уравнения касательной плоскости и нормали к по-
верхности z — sin х cos у в точке М (л/4; л/4; 1/2).
1301. Составить уравнения касательных плоскостей к поверх-
ности х24-2у24-3г2 = 21, параллельных плоскости х 4-+ 6г =*0.
1302. Доказать, что касательные плоскости к поверхности У х+
Ч-Уу + Уг = Уа(а>0) отсекают на осях координат отрезки, сум-
ма которых постоянна.
1303. В какой точке эллипсоида x2/4 + y2/4-{-z2 = 1 нормаль к нему
образует равные углы с осями координат?
1 олл п дг cos« dz cos 6 о
1304. Доказать, что 5-=-------, 3-=-------- , если cos a, cosp,
дх cos у ’ ду cos у г
cosy—направляющие косинусы нормали к поверхности z = f(x, у).
§ 4. ЭКСТРЕМУМ ФУНКЦИИ ДВУХ НЕЗАВИСИМЫХ ПЕРЕМЕННЫХ
1. Экстремум функции. Функция z — f(x,y) имеет максимум (минимум)
в точке Мв (х0; ув), если значение функции в этой точке больше (меньше), чем
ее значение в любой другой точке М (х; у) некоторой окрестности точки /И0,т. е.
f (хо, Уо) > f (х, у) [соответственно f (х0, у0) < f (х, г/)] ДЛЯ всех точек М (х; у), удо-
влетворяющих условию | МаМ | < 6, где 6—достаточно малое положительное число.
Максимум или минимум функции называется ее экстремумом. Точка Мв,
в которой функция имеет экстремум, называется точкой экстремума.
204
Если дифференцируемая функция z=f(x, у) достигает экстремума в точке
Л40 (х0; у0), то ее частные производные первого порядка в этой точке равны
нулю, т. е.
dfjxp, Уо) п Уо) 0
дх ’ ду
(необходимые условия экстремума).
Точки, в которых частные производные равны нулю, называются стационар-
ными точками. Не всякая стационарная точка является точкой экстремума.
Пусть Л40(х0; ув)—стационарная точка функции z = f(x, у). Обозначим
, _57 (хь, Уо) „ _ 5а/(х0, у,) _ d*f(xa, ув)
д& ’ дхду ' 5уа
и составим дискриминант А = АС—В*. Тогда:
если Д > 0, то функция имеет в точке Мй экстремум, а именно максимум
при А < 0 (или С < 0) и минимум при А > 0 (или С > 0);
если Д <0, то в точке Мо экстремума нет (достаточные условия
наличия или отсутствия экстремума);
если Д=0, то требуется дальнейшее исследование (сомнительный случай).
1305. Найти экстремум функции г = хг + ху + уг—Зх—6г/.
. .. 5г _ , „ дг
Д Находим частные производные первого порядка: -^=2х~1~у—3,
=x-j-2y—6. Воспользовавшись необходимыми условиями экстремума, находим
стационарные точки:
(2х-(- у—3 = 0,
1 х4-2у—6 = 0,
откуда х=0,у=3; М (0; 3).
Находим значения частных производных второго порядка в точке Л4:
5*г „ 51 2г дгг _.
дхг~~ ’ду*~~ ’дхду
и составляем дискриминант Д = ЛС—Ва = 2-2—1 =3 >0; А > 0. Следовательно,
в точке М (0; 3) заданная функции имеет минимум. Значение функции в этой
точке zmin = —9. 4
1306. Найти экстремум функции
г = (47—х—у) (у+-|).
Л Находим частные производные первого порядка:
дг_ 1 _2_ 47 дг 1__________1_ , £7
дх~ 12У 3 Х' 3 ’ ду^ 2У 12* '4 *
Воспользовавшись необходимыми условиями экстремума, находим стационар*
ные точки:
__1, _2_ , 47_0
12У 3 3 ’ (8х+ у =188,
1 t ЛП ИЛИ <
_±„_±х_|_£=0 I х+6у=141.
2 У 12 Т 4 ’
Отсюда х = 21, у = 20; стационарная точка М (21; 20).
„ , ., 2 дЧ
Найдем значения вторых производных в точке /И:
1 d2z 1
= —а-, Tor*a Д = ЛС—Ва = (—2/3) (— 1/2) —(—1/12)2= 1/3-
л ил иу 1 л
— 1/144 > 0.
Так как Л < 0, то в точке М (21; 20) функция имеет максимум: гтах== 282.
205
Найти экстремумы функций»
1307. z = xy2(l—х—у). 1308. z = x®4-z/s — 15xz/.
1309. z = 4—(x2 + z/2)2/®. 1310. z = (x2 + z/2)(e-<x’+^ —1).
1311. z = V\a—x) (а—у) (x+y—a).
2. Условный экстремум. Наибольшее н наименьшее значения функции
в замкнутой области. Условным экстремумом функции z = f(x,y) называется
экстремум этой функции, достигнутый при условии, что переменные хну связаны
уравнением <р(х, у)—0 (уравнение связи).
Отыскание условного экстремума можно свести к исследованию на обычный
экстремум так называемой функции Лагранжа u = f(x, y)-|-X<p(x, у), где X—не-
определенный постоянный множитель.
Необходимые условия экстремума функции Лагранжа имеют вид
дх дх 1 дх
ду ду ду
К <р(х, у)=0.
Из этой системы трех уравнений можно найти неизвестные х, у и X.
Для того чтобы найти наибольшее и наименьшее значения функции в замк-
нутой области, надо:
1) найти стационарные точки, расположенные в данной области, и вычислить
значения функции в этих точках;
2) найти наибольшее и наименьшее значения функции на линиях, образующих
границу области;
3) из всех найденных значений выбрать наибольшее и наименьшее.
1312. Найти экстремум функции z = xy при условии, что х и у
связаны уравнением 2%+3z/—5 = 0.
А Рассмотрим функцию Лагранжа и =ху+Х (2х-|-Зу—5). Имеем|^=у4-2Х,
|^=х-|-ЗХ. Из системы уравнений (необходимые условия экстремума)
( y-f-2X=0,
4 х+ЗХ=0,
V2x+3y—5 =0
находим Х =—5/12, х=5/4, у=5/6. Нетрудно видеть, что в точке (5/4; 5/6) функ-
ция z—xy достигает наибольшего значения zmax = 25/24. А
1313. Из всех прямоугольных треугольников с заданной пло-
щадью S найти такой, гипотенуза которого имеет наименьшее зна-
чение.
А Пусть х и у—катеты треугольника, а г—гипотенуза. Так как z2=x2-f-y2,
то задача сводится к нахождению наименьшего значения функции х2+у2 при
условии, чтохиу связаны уравнениемxy/2 = S, т. е. ху—2S = 0. Рассмотрим функ-
цию и = х2+у24-Х(ху—23) и найдем ее частные производные
g=2x+Ay, g==2y+Xx.
Так как х > 0, у > 0, то из системы уравнений
{2х-|-Ху = 0,
2у-|-Хх = 0,
xyft = S
получаем решение Х =—2, x=y = pr2S.
206
Таким образом, гипотенуза имеет наименьшее значение, если катеты треуголь-
ника равны между собой. Д
1314. Найти наименьшее и наибольшее значения функции z=*
= хг + угв круге (х—К2)2 + 0/—рЛ2)2^9.
Л Здесь рассматривается область D, ограниченная окружностью (х—yr'2)2-f-
4- (у—У 2)2=9, включая и точки окружности.
Найдем стационарные точки данной функции; имеем ^-=2х,
dz _
д^=2у, в силу
необходимых условий экстремума находим х=0, у=0.
Нетрудно видеть, что в точке (0; 0) функция г—хг-\-у2 имеет наименьшее
значение гнаим = 0, причем указанная точка является внутренней точкой области D.
Исследуем на условный экстремум функцию г=хг-\-у2, если х к у связаны
соотношением (х—У^)г-^-(у—У~2)г=9. Рассмотрим функцию и—х2-}-у2-±-
4-Х[(х— У~2)2+(у— У 2)2—9]. Находим частные производные 2х+
-|-2Х(х— У 2), ^=2^4-2Х(у—У~5). Для определения х, у и X получаем си-
стему уравнений
х + Х(х— У 2)=0,
у+Му- К2)=0,
(х_/-2)а+(у- }/"2)2=9.
Эта_система имеет два решения: х—у=ЬУ 2/2, Х = —5/3 и г = 25; х=у =
= — У 2/2, Х=—1/3 и г=1. Значит, наибольшее значение функция принимает
в точке (5 К 2/2; 5/"5/2). Итак, гяаим = 0. *иаиб=25. ±
1315. Найти экстремум функции z = x2-f-z/2, если х и у связаны
уравнением х/4 + z//3 = 1.
Найти наименьшее и наибольшее значения функций:
1316. z = x2—ху + у2—4х в замкнутой области, ограниченной
прямыми х = 0, y = Q, 2х4-3у—12 = 0.
1317. г= ху + х+у в квадрате, ограниченном прямыми х=1,
х = 2, у = 2, у==3.
1318. г = ху в круге x24-i/2^l.
1319. z= х2 + 3#2 4- х—у в треугольнике, ограниченном прямыми
х=1, у—1, х+у=1.
1320. z — 1—х2—уг в круге (х—1)2 + («/—1)2^1.
1321. z= sinx + sint/ 4- sin(x-j-t/) в области 0^х^л/2,
O^t/^ л/2.
1322. z= sinx+sint/+ cos (х-|-1/) в области 0<х<Зл/2,
0<С«/<13л/2.
1323. z = cos х cost/cos (х-}-//) в области 0<х<л, 0<у<л.
1324. Из всех треугольников, вписанных в круг, найти тот,
площадь которого наибольшая.
1325. Из всех треугольников, имеющих данный периметр, найти
наибольший по площади.
1326. Из всех прямоугольников с заданной площадью S найти
такой, периметр которого имеет наименьшее значение.
1327. Найти размеры прямоугольного параллелепипеда, имею-
щего при данной полной поверхности <$ максимальный объем.
ГЛАВА IX
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
§ 1. НЕПОСРЕДСТВЕННОЕ ИНТЕГРИРОВАНИЕ.
ЗАМЕНА ПЕРЕМЕННОЙ И ИНТЕГРИРОВАНИЕ ПО ЧАСТЯМ
1. Непосредственное интегрирование. Функция F (х) называется первообраз-
ной для функции f(x), если F' (x) = f(x) или dF (х) = f (х) dx.
Если функция f (х) имеет первообразную F (х), то она имеет бесконечное мно-
жество первообразных, причем все первообразные содержатся в выражении
F(x)4-C, где С—постоянная.
Неопределенным интегралом от функции f (х) (или от выражения f (х) dx)
называется совокупность всех ее первообразных. Обозначение: / (х) dx = F (х)+С.
Здесь J—знак интеграла, / (х)—подынтегральная функция, f(x)dx—подынтег-
ральное выражение, х—переменная интегрирования.
Отыскание неопределенного интеграла называется интегрированием функции.
Свойства неопределенного интеграла
(правила интегрирования)
1°. (p(x)dx)' = /(х).
2°. d(p(x)dx}=/(x)dx.
3°. dF (x) = F (х)4-С.
4°. J af (x)dx=a J f (x) dx, где a—постоянная.
5е. J [/i (x) ± ft (x)] dx = pi (x) dx ± p2 (x) dx.
6°.Если p(x)dx = F (x) + C и u = <p(x), to p(a) du = F (u)-j-C.
Таблица основ н-ы x интегралов
I. \dx = x+C. VIII. J slnxdx =—cosx-f-C.
II. ( * Xя* +1
| x” dx:=‘£+i+c npH m * ~L IX. $ cos x dx = sin x -|- C.
III. j£-l»W+C. X. $ sec2 x dx = tg x+C.
IV. C dx . , „ J -q^T-arctgx+C. XI. ( । cosec2xdx = —ctgx-f-C.
4 • —=arcsin x4- C. /1-х2 XII. J shxdx=chx-f-C.
VI. J e*dx=e*-}-C. XIII. J chxdx=shx-f-C.
VII. \a*dx=-?—+C. J Ina 1 XIV. C dx .. , „ Jd^=thx+C-
XV. Ccthx+C. J sh2x 1
208
1328. Найти интеграл J (2х®—5х24~7х—3) dx.
Д Используя свойства 4° н 5°, получаем
J (2х3—5х2Ц-7х—3)dx=2 J x3dx—5 J x2dx-f-7 §xdx—3 J dx.
К первым трем интегралам правой части применим формулу II, а к четвер-
тому интегралу—формулу I:
г* х$ х^
I (2Х3—5x2+7x-3)dx = 2.^--5-i-4-7~-3x+C =
1329. Найти интеграл J *+ ^*dx.
л J (V dx=J(х+2’77г+^5’) dx=
= J (х-}-2х1/*-}-х~2/3) dx = J xdx-}-2 J х1?3 dx-j- J x-2^3 dx —
„2 „’/• „1/3 „2 12 6 z— з z—
-^+2- Wt73-+c=t+t' /-+3 S'+C. *•
1330. Найти интеграл J 2* • З2* • 5s* dx.
e p ' p 2250*
Д \ 2*-32*-53* dx = \ (2.32.5s)* dx= I 2250* dx =, о^п+с- ▲
J J J In 2250
Свойство 6° позволяет значительно расширить таблицу основных интегралов
с помощью приема подведения функции под знак дифференциала.
1331. Найти интеграл J (1 + х2)1/2 xdx.
А Этот интеграл можно привести к формуле II, преобразовав его так:
j (l-f-x2)1/2xdx=y J (l+x3)1/2-2xdx=-^ J (14-x2)1/2d(14-x2).
Теперь переменной интегрирования служит выражение 14-х2 и относительно
этой переменной получается интеграл от степенной функции. Следовательно,
С (1 +х2)1/2 Xdx =±.(1±7^—Ч-С = 1 (1 + х2)3/2+С. ,Д
1332. Найти интеграл J (х2—Зх-|-1)10 (2х—3) dx.
Л Здесь, поступая так же, как и в предыдущем примере, имеем
J (х2—Зх+1)1» d (х2—Зх+1) = ^(х2—Зх4-1)п+С. Д
1333. Найти интеграл ^(111/)*^.
Д Выражение -^- можно записать как d(lnf), поэтому
C (ln7)«d(ln0=l(ln06+C. А
209
1334. Найти интеграл J e8C0,xsinxdx.
Л Заданный интеграл можно представить так:
j е8 « sin х dx=1 j.e’со* *-3 sin х dx,
но 3slnxdr®— d(3cosx), а потому
У е9 ео* ? sin х dx = — у У е®* d (3 cos ж),
т. е. переменной интегрирования является Зсозх. Следовательно, интеграл ба»
рется по формуле VI:
У е®со’* sin х dx--~е®“’«+С. А
1335. Найти интеграл J (2 sin х 4-3 cos х) dx.
Л Находим
J (2sinх4-3 cos ж) dx = 2 J sinxdx4-3 J cosxdx =— 2cosx4-3sinx4-C
(см. формулы VIII н IX). A
1336. Найти интеграл J (tgx4-ctgx)2dx.
Д Имеем
J (tgx4-ctgx)*dx= J (tg2x4-2ctgxtgx4-ctg’x)dx=
= J (tg*x4-14-14-ctg®*)d* = J (tg*x4-l)dx4- J (14-ctg2x)dx=
= J sec*xdx4- J cosec2 xdx=tgx—ctgx-f-C
(см. формулы X и XI). A
Найти интегралы:
1337. (x^xdx. 1338. f-r^. 1339. f^jQ^-dx.
J J у x J У 1 — x2
1340. j£=£dx. 1341. ye«-3*dx. 1342. jtg2xdx.
1343. J(shx—slnx)dx. 1344. —у^У^'
1345. J (2 tg x 4- 3 ctg x)2 dx. 1346. J x cos (x2) dx.
1347. 1348. ^ax' + b)V*-xdx.
1349. J Ksinx cos x dx. 1350. sin (a 4- bx) dx.
1351. J cos (sin x) • cos x dx.
2. Замена переменной в неопределенном интеграле. Замена переменной в неопр*
деленном интеграле производится с помощью подстановок двух видов:
1) х=<р (0, где <р (t)—монотонная, непрерывно дифференцируемая функция
новой переменной /. Формула замены переменной в этом случае имеет вид
р(л)Л/-5'ПФ(О)Ф‘(0Л1
210
2) и=ф(х), где и—новая переменная. Формула замены переменной при такой
подстановке:
J / [ф W1Ф' (х) dx = J / (н) du.
1352. Найти интеграл I s 3/—Х dx.
J у х2
Л Произведем подстановку t=y х, т. е. x=t3. Эта подстановка приведет
к тому, что под знаком синуса окажется переменная интегрирования, а не корень
нз нее. Найдем дифференциал dx=3t2dt. Отсюда получаем
f sin у/ х . f З/2 sin t (* „
J з/— —t2—^ = 3j sin^ = — 3cosf+C.
Ответ должен быть выражен через старую переменную х. Подставляя в ре-
з /~
зультат интегрирования t=y X, получим
г. 3/~
( sin у X . „ з/—
I —„ dx =— 3cosy х-}-С. А
J V х2
1353. Найти интеграл J (2x+l)20dx.
Д Этот интеграл можно найти н не производя замены переменной. Здесь
достаточно развернуть выражение (2х+1)20 по формуле бинома Ньютона и при-
менить почленное интегрирование. Однако этот прием связан с большим количе-
ством вычислений. С помощью замены переменной можно сразу свести данный
интеграл к табличному.
Полагая 2х-|-1=/, имеем 2dx—dt, т. е. dx—(l/2) dt. Отсюда получаем
j (2х+1)2»dx=± j t2° dt=^.^t21+ С=± (2х+ 1)21+С. А
Вообще, если интеграл f (х) dx является табличным, то интеграл J / (ах-]-6) dx
может быть легко найден с помощью подстановки ax-}-b — t.
Например, применим эту подстановку к интегралу J sin (ах-]-6) dx. Имеем
ax-j-b = t, adx=dt н dx — (l/a) dt. Следовательно,
У sin (ах-]-6) sin У sin t dt = — ~cos *4-C.
Возвратившись к старой переменной, получаем
У sin (ах6) dx= — cos (ах-]-Ь)-]-С.
Аналогично можно показать, что
У cos (ax-\-b) dx = ± sin (ах-]-6)-]-С, § eax+i dx =~eax+t-(-C и т. д..
При нахождении интеграла J f (ах-]-6) dx записи самой подстановки ax-j-b=t
можно фактически н не производить. Здесь достаточно принять во внимание, что
dx=±-d (ax->-b). Таким образом,
У f (ах -]- 6) dx= F (ах-]- Ь) -]-С,
где F—первообразная для /.
211
1354. Найти интеграл J х* К*8 + 5 dx.
& Положим V х*+5 = £; тогда х8+5 = /8. Дифференцируем обе части раве»-
ства: 3x8rfx = 2/<W. Отсюда х* dx = (2/3) t dt и, следовательно,
^x*V"J?+5dx= § =
= JР+С=4(/7+5)а+С=-|(х’+5) /?+5+С.
Данный интеграл можно найти нс помощью подстановки х®4-5 = Л Эта под-
становка сразу приводит интеграл к табличному вследствие того, что первый мно-
житель подынтегрального выражения хг отличается от производной подкоренного
выражения х®+& только постоянным множителем 1/3, т. е. ха = (1/3) (х3-)-5)'. А
Вообще, если подынтегральная функция является произведением двух мно-
жителей, одни из которых зависит от некоторой функции ф (х), а другой является
производной ф (х) (с точностью до постоянного множителя), то целесообразв»
сделать замену переменной по формуле ф (х) = t.
1355. Найти интеграл j <21п*+3) ^х.
Д Перепишем данный интеграл в виде § (21nx4-3)8-^-rfx. Так как производ-
ная выражения 21пх-]-3 равна 2/х, а второй множитель 1/х отличается от этой про-
изводной только постоянным коэффициентом 2, то нужно применить подстановку
21пх+3 = /. Тогда 2~=Л, ^=-g-df. Следовательно,
J (21nx+3)8y=J j ? Л=-§-^+С==-§-(21пх+3)‘+С- ▲
1356. Найти интеграл ^j-^dx.
Л Произведем подстановку f(x) = t. Тогда f (х) dx=di и
j dx=§ "=1п 1t l+C= In I / (X) 1+ С.
Например,
f xdx 1 f 2xdx 1 . 2 _
j *+l = -2 j ^+T=-2 ’"(x’+D+C.
Здесь знак модуля опущен, так как ха+1 >0. А
1357. Найти интеграл J '
& Положим f(x) = t. Тогда f'(x)dx = dt и
f ^==rfx= f-^L= fr^8dt=.-^-+C = 2 KH-C = 2 /Tw+C.
J V f(x) J у t J 1/2
Заметим, что. данный интеграл можно было найти с помощью подстановки
К/(х)=/. ▲
a dx
1358. Найти интеграл j *а_|_аа» если ^¥=0-
212
& Для того чтобы свести интеграл к табличному (см; формулу IV),' разде-
лим числитель н знаменатель подынтегрального выражения на а2:
0 dx Г (dx)/a2 1 Г d(x/a)
J x«+a»“J 1+(х/а)« a J 1 + (х/а)2 ’
Мы подвели постоянный множитель 1/а под знак дифференциала. Рассматри-
вая xja как новую переменную, получим
С dx 1 . х . _
\ тп—» = —arctg—
J х2-\-а2 а а
К этому же результату мы пришли бы н с помощью подстановки х=а(. А
1359. Найти интеграл f -/* - , если а > 0.
J К а2—х2
Разделив числитель и знаменатель на а, получаем
С dx_________Г (dx)/a Г d (х/д)
J Уа2^2 ~ J УТ^(х/а)2 J У 1 —(х/а)а ’
Принимая х/а за новую переменную, получим
dx
У а2—х2
arcsin —-]-С. А
Дополним теперь таблицу основных интегралов следующими формулами
‘^dx=ln|/(x)|+C.
XWLj
XVIII. C dx 1 x , „ J x2+a~ a arctg a +C
XIX J ‘ ln|£=£|+c. xa—a* 2a |x-|-a| 1
XX. J. dx . x . „ =arcsin kC. Va2~ x« «
XXI. ( dx =1п|х+Ух* + М+С. у А» Л
XXII. 1 7^7= 1пНе 4|+С = 1п 1 cosecx—ctgx Ц-С. j oil* X j X |
XXIII. J^=ln|tg(4+j)|=ln|secz+tgx|+c-
XXIV. J tgxdx=— In | cosx|-]-C.
XXV. 1 Г ctg x dx= In ] sin x | -j-С.
Формулы I—XXV нужно знать наизусть, так как большинство интегралов,
используемых на практике, сводится к интегралам, берущимся по этим формулам.
1360. Найти
интеграл
dx
х/2х^9 ’
213
Л Произведем подстановку У2x—9 = /; тогда 2x—9 = t2, x — (t2-}-9)/2 и
dx—tdt. Итак,
—=2
Применив формулу XVIII, получим
C dx 2 . t 2 . У 2x—9
\ —7===Tarct^+C=Tarc,S----------------
J x У2x—9 3 3 3
1361. Найти интеграл С -J—.
J У3—cos4x
А Произведем подстановку cos2x = i; тогда
Sin 2x dx = — dt. Теперь находим
Г sin 2x , C dt t
I — dx = — I '=—arcsin —7=
J У3 —cos4x J У3—t2 У t
(мы использовали формулу XX). A
1362. Найти интеграл (2 sin — + 3^2с
Л Применим подстановку 2sin (х/2)-|-3=/; тогда cos (x/2) dx=dt и
Cf2sin4+3Ycos4^=C/2r» = l/3+C=-|-f2sin4+3Y-|-c- ▲
J \ £ ] *• J \
1363. Найти интеграл С х dx
J К*10-2
Д Применим подстановку x2 — t\ тогда 5x*dx=dt, х4 dx = (l/5) dt и
С ' f -/-—=4- ln’l <+ У^2 l + C
JKx10-2 5JK<2—2 5 ' r
(см. формулу XXI). Итак,
[ =4 In | x5-|- Ух^21 + C. A
J Ух1а-2 о
1364. Найти интеграл j* x4_|*2x*-|-5 ’
Д Преобразуя знаменатель дроби, получим х4 + 2х2+5 = (х24-1)24-4. Про-
изведем подстановку х2-|-1=/; тогда х dx = (l/2) dt. Отсюда
С xdx 1 С dt 11. t „
J х4 + 2х2 + 5 — 2 J /2+4 — 2”IT31"0 g 2 + °
(см. формулу XVIII). Таким образом,
У xdx 1 . >
х4 + 2х2 + 5—Tarctg-
А Положим e2x — t, тогда е2х dx — (1/2) dt
Г е2х dx 1 С dt 1 1
1 е4*—5
3
— 2cosxsinxdx = d/, т. e.
- COS2X
-|- C = — arcsin
dx.
2
и
t2~5 2’2р<51П
+C
214
(мы применили формулу XIX). Итак,
С e**dx 1
J е«_5-4)/-5
е»х/5
е**+К5
+<?. А
1366. Найти интеграл
ea*dx
e**+S •
Л Произведя ту же подстановку, что и в предыдущем примере, получим
' e^dx 1 Г dt 1 . t . - 1 „ . еа* L/, .
. , - I jq i tt r— arctg "дг I С=з= —- arctg _ -4-C. A
e«*+5 2 J /«+5 2/5 f5T 2/5 /5
1367. Найти интеграл Г *dx.
r J /xsin2/ x
Л Полагая /x=f, x=ts, dx=2tdt, получим
f stn^ x+cos К x dxC (sin Z+cos 0-2/
J /xsin2/x J *sin2*
Г sin H-cos ( dt~C( I tg f 4+t^ l+ln I ‘e4l+C
J sin t cos t J \ cos tn sin t j | \ 2 1 4 } | ' | “ 2 | 1
(см. формулы XXII и XXIII). Возвращаясь к старой переменной, получим
J /х sin 2 /х
tg (-^+у) 1+in I tgXL Lc. А
\ 4 *t / 1 I & I
Найти интегралы:
1368. I 1 dx. 1369. х» (1 — 2х‘)3 dx.
J/2x— I - ' 7
1370. J sin (2—Зх) dx. 1371. $ xch (5xa + 3) dx.
1372. J (*+^* . 1373. p(xa+I)3'2dx.
1374. 1375. f rxJL_-. 1376. Г
1 xa—I I i/x1— 1 J cos* 2X-f-4
1377; f----1378. . .
J (x—7) /x J /16—e*
1379
ф Представить интеграл в виде суммы интегралов.
1380. С.. . 1381. Г У dx.
J /2—Зх’ J /3—ха
1382- • 1звз.1|13±1л. нм-У-^г.
3. Интегрирование по частям. Интегрированием по частям называется иа«
хождение интеграла по формуле
J Udo =uv— J о du,
215
где u = q> (х), о=ф (х) — непрерывно дифференцируемые функции от х. С помощь»
этой формулы нахождение интеграла и dv сводится к отысканию другЬго интеграла
J vdu; ее применение целесообразно в тех случаях, когда последний интеграл
либо проще исходного, либо ему подобен.
При этом за и берется такая функция, которая прн дифференцировании упро-
щается, а за dv—та часть подынтегрального выражения, интеграл от которой и>
вестей или может быть найден.
Так, например, для интегралов вида J Р (х) еах dx, J Р (х) sin ахсх.
J Р (х) cos ах dx, где Р (х)—многочлен, за и следует принять Р (х), аза dv —
соответственно выражении еах dx, sinaxdx, cosaxdx; для интегралов
J P(x)lnxdx, J P (x) arcsin x dx, J P (x) arccos x dx за и принимаются соответст-
венно функции In х, arcsin х, arccos х, а за dv—выражение Р (х) dx.
1385. Найти интеграл In xdx.
Л Положим u = lnx, dv = dx; тогда у=х, du=^. Используя формулу ин-
тегрирования по частям, получаем
х
dx , (•
Х-—=х In х— \ dx=
=xlnx—х-|-С=х(1пх— 1)+С. А
1386. Найти интеграл J arctg xdx.
Л Пусть и = arctg х, dv = dx, тогда du= 2 , v=x. По формуле интег-
рнрования по частям находим
У arctg xdx=x
j^r=xarctgx—у In (1 -f-x2)-f-G. Л
1387. Найти интеграл ^xsinxdx.
Л Положим и=х, do = sinxdx; тогда du — dx, х=—cosx. Отсюда
J xsin xdx = — xcos x-|- J cos xdx =—xcos x-|-sin x-|-C.
Если бы выражения и и dv мы выбрали иначе, например u = sinx, dv—xdx.
то получили бы du = cosxdx, о = (1/2)х2, откуда
У xsin xdx=-^ x2sinx—у у х2 cos xdx=-i-x2sinx—у х2cosxdx,
и пришли бы к интегралу более сложному, чем исходный, так как степень со-
множителя при тригонометрической функции повысилась на единицу. А
1388. Найти интеграл \x2exdx.
& Положим н=х2, dv = exdx; тогда d« = 2xdx, v=ex. Применяем формулу
интегрирования по частям:
f х2ех dx = x2ex—2 С хех dx.
216
Мы добились понижения степени х на единицу. Чтобы найти хе* dx, при-
меним еще раз интегрирование по частям. Полагаем и=х, dv=e* dx; тогда du =
= dx, v=e* и
J x2e* dx=x*e* —2 (^xe*— J e*dx^ =x2e*—2xe*-}-2e*-\-C = e* (x2—2x-]-2)-j-C. Д
1389. Найти интеграл /=Je*sinxdx.
Л Пусть u—e*, dv = sinxdx; тогда du = e*dx, v = —cosx. Следовательно,
I = —e* cos x-f- J e* cos xdx.
Создается впечатление, что интегрирование по частям не привело к цели, так
как интеграл не упростился. Попробуем, однако, еще раз проинтегрировать по
частям. Приняв и=е*, dv —cos xdx, откуда du—e*dx, v = sinx, получаем
/ = —e*cosx-|-(e*sinx—I), т. e. /=—e*cosx-|-e*sinx—I.
Применив дважды операцию интегрирования по частям, мы в правой части
снова получили исходный интеграл. Таким образом, приходим к уравнению с не-
известным интегралом /. Из этого уравнения находим
е*
21 ——е* cos x-f-е* sin х, т. е. /=-^-(sinx—cosx)-|-C.
В окончательном результате мы прибавили к найденной первообразной функ-
ции произвольную постоянную. А
1390. Найти интеграл J —x2dx, если а>0.
% dx
Л Положим и—у а2—х2, dv = dx, откуда du =-------- , и=х. Следо-
у а2—х2
вательно,
или
С Уа2—x2dx=x Уа2—х2 —С }^а2—x2dx-\-a2arcsin.
Отсюда получаем
2 у У a2—x2dx = x /"а2—х2-|-а2 arcsin^-,
т. е.
У а2—х2 dx=-^ х У а2—х2-]—arcsin —+С. А
Sdx
8 а
(X -f-a )п
Л Заданный интеграл можно преобразовать так:
, (* dx if а2+х2—х2
п~ J (х2+а2)« ~ a2 J (х2+а2)" =
_____1 Р dx___________1 Р x-xdx _____ 1 1 Р xdx
a2 J (х2+ а2)"-1 а2 J (х2-\-а2)п а2 ' n~l~ a2 J Х’ (х2-|-а2)и *
217
Положим ц=х, dt>=. , тогда du=dx,
(х’+а*)'*
j (x*+«*)-" d (*а+«а) =~ ^~Г}' 1
откуда
. 1 , , 1 Г_________х___________1 Р dx 1
'я“-£Г'п-Ц-а, [2(л—1) (х^-(-а’)п-1 2(л—1) J (х«+а«)п-Ч'
ИЛИ
, 1 , X 1 г
n = '^‘ '"-l+W(л-1) p+aSj»-i: 2а2(л-1)
t. e.
r x (1 2n—3 r
/п“2а*(л—1) (х*+а|)""1+‘^’2n—2 "-1,
Полагая n = 2, получаем выражение интеграла /2 через элементарные функ-
ции. Полагая теперь л=3, находим интеграл /3 (ведь интеграл /» уже найден).
Таким образом, можно найтн 1п при любом целом положительном л. Д
Найти интегралы:
1392. Jxlnxdx. 1393. J arcsin х dx.
1394. jx’arctgxdx. 1395. ^(xH-l)e*dx.
1396. Jx’sinxdx. 1397. §х*е**(1х. 1398. J j/xa4-kdx.
ф Положить x* — t.
1399. J (xa + 2x + 3)cosxdx. 1400. $e**cosxdx.
1401. Jsinlnxdx. 1402. J sinKx dx.
ф Положить y~x=t.
§ 2. ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ДРОБЕЙ
1. Интегрирование простейших дробей. Рациональной дробью называется дробь
вида P(x)/Q(x), где Р(х) и Q (х)—многочлены. Рациональная дробь называется
правильной, если степень многочлена Р (х) ниже степени многочлена Q (х); в про-
тивном случае дробь называется неправильной.
Простейшими (элементарными) дробями называются правильные дроби сле-
дующего вида:
I.
А
х—а ’
П. г--~^
(х— а)1Я
где т—целое число, большее единицы;
III.
Ax-j-S
x*+px+q ’
о3
где ------q < 0, т. е.
квадратный трехчлен x’+px-l-g не
имеет действительных корней;
IV. где л—целое число, большее единицы, и квадратный
(ха+рх+ q)n
трехчлен x*-}-px-}-q не имеет действительных корней.
Во всех четырех случаях предполагается, что А, В, р, q, а—действительные
числа. Перечисленные дроби будем соответственно называть простейшими дробяме
I, II, III и IV типов.
218
Рассмотрим интегралы от простейших дробей первых трех типов. Имеем
I- j^^=^ln|x-a|+C;
п (* Adx — А__________1 I г-
, ' J (х— а)т т — \(х—а)т~^' ’
HL С , А ...=г arctg 2х+Р=+С-
J х2-|-рх+<7 У 4q—р2 У4q—р2
Действительно, для этого частного случая простейшей дроби III типа полу-
чаем
х2+рх+<7=(*+у) +<7—тр. или x2-\-px+q = t2+a2,
, । р Уtq—р2 , р2 гл
где / = х+у, а = ——% (здесь q < 0), откуда
f dx С dt 1 . t . п 2 2*+р
Jx2+px_|_9 Jt2-{-a2 а а ' /4?— р2 /49—р2
1403. Найти интеграл j •хз+^_|.25- •
л Г ** Г dx -С rf<*+3) _ 1 arctg *+3 । с ▲
J х»+6х + 25 “J (х+3)2+16 J (х+3)2+16 4 е 4 ж
1404. Найти интеграл j 2х2-2х-\-3 ’
к f dx 1 f dx If dx
Л I 2x2-2x+3 T I ~ ~T~*2" I I 1 \2 . ( 3 I '
J Jx2-x+-
1 Г ^\X F/ 1 2 X 2
-7J (x_|y+(j^y =7'гт'агс,г w +c“
Покажем, как интегрируются в общем виде простейшие дроби III типа.
Требуется найти j* ------Я < Выделим в числителе дроби
производную знаменателя. Для этого числитель представим в виде
Ах+В = (2х+р)Л-^-ув.
Тогда
С Ах+В я,-Л С 2х+р dXA_(в- Л/? К dx
}x2+px+qaX 2 }x2+px+qaX+\D 2 }}x2^px+q'
В первом интеграле числитель является производной знаменателя; поэтому
С ~2~Г~(*2+/’•*+'?) +С.
J x2-j-px-f-q ' 1 1 1
так как x2-f-px-j-q > 0 для любого значения х. Второй интеграл, как уже было
отмечено, находится по формуле
С dx 2 . 2х+р , _
Jx2 + px + 7 y4q-p2 y4q—p2^
Итак,
^2+Х+'/х=41п(х2+рх+?)
2В—Ар
V^—p*
arctg
2х+р
y~4q—p3
С.
О Оу_____1
1405. Найти интеграл j x2_4^qi~8 ^х‘
Г Зх—1 f 4 (2х~4)-1 + 6
д J тате- J х2-4х+8...............Л=
= -2 3 x2-4x+8 *+5J 2 1п {x 4х+8) + 5 J (х-2)2+22
= у1п(х2—4x+8)+-|-arctg А
1406. Найти интеграл J2xa_^^+ 5 -
С xdx Г-4<4х+2) — у if 4х+2 . 1 f <fr _
Л J2x2+2x4-5~j 2x2+2x+5 4j2x2+2x-|-5 2 J 2x2+2x-|-5
= 1 ln(2x24-2x+5)-l-l- f--g- = -J-ln(2x2+2x+5)-
J x2+x+y
~tL *iV^r?-+"^’+2*+^-T,^1,c<e^+c-
J («++ +(+
=-|ln(2x2+2x+5)—|arctg ^±1-^0. A
1407. Найти интеграл f
J -f- 1
Л Предварительно в этом интеграле произведем замену переменной х2 = Г,
тогда 2xdx=dt, xdx = (1/2)dt. Следовательно,
(* (2x24-3)xdx 1 f(2/+3)dt 1 С (2*+l) + 2
J x«4-x2+l 2 J /«+*+1 2 J /«4-/4-1
-4УЛт+Л+ j^+1-т'"<'+'+'>+ J, 5у+/гз?~
V+-2 J +k~2“/
_4ln((.+,+1)+_^arctg/^.+c-
= ±ln (x<4-x24-l)+-A.arctg 3£±L+C A
Рассмотрим теперь частный случай интеграла от простейшей дроби IV типа.
j- (я—целое положительное число) имеет место
следующая рекуррентная формула:
/ _ 1 1 । 1 2«—3 j
п 2а2 (я — 1)' (/24-а*)п-1 + а2‘2я—2'/п-1,
тг , г dt
Для интеграла 1п=\ , д8;
220
Эта формула позволяет после (п — 1)-кратного применения свести данный
, К f dt
интеграл 1п к табличному интегралу \ •
1408. Найти интеграл /s=j (х3+1)5 ‘
Л Здесь я = 3. После первого применения рекуррентной формулы получаем
1 х 2-3—3 , 1 х , 3
,3~2 (3—1)' (x3+l)3-i
.. . С dx
К интегралу 4 = j (х34~1 j'3 снова
лагаем л = 2):
, »_____________х
* 2(2-1) (х3+1)2-1
х , 1 р dx х ,1
~ 2(х3 + 1) + 2J х34-1 ~ 2(х3+1) "г "2
2-3—3 , _ 1 х , „ ,
2-3—2 3-1 4 (х3 + 1)з+ 4 а‘
применяем рекуррентную формулу (здесь по-
2-2—3 _ 1 х 1
2-2—2 2"г 2 х3+1 +2
arctg х-|-С.
Итак,
Р dx _ х
J (х2 +1)3 ~ 4 (х2 +1)3
Окончательно имеем
2 (x3-f-1) + 2 arctg *]
х
х . Зх .3
|з“ ~ 4 (х3+ I)3 + 8 (х2+1) + 8
Покажем теперь в общем виде, как интегрируются простейшие дроби IV типа.
Р Ах I ff р2
Требуется найти \ . , , - ,—г—dx, ------q < 0.
J (х2+рх4-<7)п 4 7
Выделим в числителе производную от квадратного трехчлена, стоящего в зна-
менателе:
С Лх+В [ -g-(2х+р) + ^В _
J (х3+рх+q)n * J (х3+рх+<7)« Х
——Г 2х+д / „. Ар_ \ Р dx
~ 2 J (х3+дх+<7)« 2 /.J (х3+дх+<?)п '
Первый интеграл в правой части равенства легко находится с помощью под-
становки x*-\-px-\-q = t, а второй преобразуем так:
f* dx Г dx
p p^
Полагая теперь x-(-y = t, dx=dt и обозначая q—!^-=а3, получаем
e dx r* dt
J (x2 + px+<7)« “J (t2+a.2)« '
Таким образом, интегрирование элементарной дроби' IV типа может быть
выполнено с помощью рекуррентной формулы.
1409. Найти интеграл J
221
Л Имеем
е 3x-l-2 fy(2x+2) + (2-3)
I _____дх=. I ±_______________(fx =
J(x’ + 2x+10)2 J (x2 + 2x+10)2
-1 C 2x+2 Иг- C dx
~2 J (x2+2x + 10)a ax J [(x-|-l)24-9]2'
В первом интеграле произведем замену х24-2х-|-10 = z, (2x4-2)dx=dz, а во
втором интеграле положим х4-l=f, dx = dt. Отсюда
Г* Зх-(-2 , 3 Р dz f* dt _________3 Г , . Р dt
J (х24-2х4-10)2 йх~~2 J 'z2J (124-9)2 2 J 2~ аг~} (t'+S)»^
3 Г 1 t 1 2-2—3 Г dt
~ 2Z [ 2 (2—1)-9 ' (l24-9)s-1 9'2-2—2 ' J /24-9 J
3 11 1 1 , t , _
~ 2г 18’124-9 18’3 arctg 3+С’
Возвращаясь к старой переменной, получаем
С 3*+2_________ з 1 х-Н _1 t Х±1
J (х24-2х4-10)2 2 (х24-2х 4-10) 18 (х-Н)24-9 54 в 3
3 1 х4~ 1 1 > х 4-1 t а
2 (х24-2x4-10) “ 18‘ х24-2x4-10 54 g ~3 А
Найти интегралы:
lain С dx 14Ц С dx 1412 С А*
J (х— I)4 • J(2x-|-3)3" Jx2-6x4-18’
1413- f j, v ♦ 1414‘ Г» *Гл.7^-
J х«4-2х®4-3 J х2—4x4-7
1415. f оо- dx. 1416‘ f ; alt1 , . dx.
J x2+ 10x4-29 J 5x2 + 2x+l
1417. f -Гз?-О<з- - 1418-
J (x2-|-2)3 J (x24-2x-(-5)2
2. Интегрирование рациональных дробей с помощью разложения иа простей-
шие дроби. Перед интегрированием рациональной дроби Р (x)/Q (х) надо сделать
следующие алгебраические преобразования н вычисления:
1) если дана неправильная рациональная дробь, то выделить из нее целую
часть, т. е. представить в виде
Р (х) .. Pi (х)
e« = "«+-QW'
где М (х)—многочлен, a Pf(x)/Q(x)— правильная рациональная дробь;
2) разложить знаменатель дроби на линейные и квадратичные множители:
Q (х) = (х—а)” ... (х24-рх4-<7)« ...,
где ------q < 0, т. е. трехчлен х24-рх-|-<7 имеет комплексные сопряженные корни;
3) правильную рациональную дробь разложить на простейшие дроби:
Pi (х) _ А । Аг , Ат
Q (х) (х—а)т' (х—а)и-1 ' ' х—а"1”’**
I 5jX-|~Ci ।__________В2х -|- Cg_. Впх-}-Сп . е
(х24-рх4-<7)п "г" (х24-рх4-<7)п~1 ’Г’-” ' х24-рх-(-<7 ' ’
4) вычислить неопределенные коэффициенты Аг, ...5 Ат, ..., Bi, Ci,
Ct, ... , Bn, Cn, ..., для чего привести последнее равенство к общему зиаме-
нателю, приравнять коэффициенты при одинаковых степенях х в левой й правой
частях полученного тождества и решить систему линейных уравнений относи-
тельно искомых коэффициентов. Можно определить коэффициенты и другим спо-
собом, придавая в полученном тождестве переменной х произвольные числовые
значения. Часто бывает полезно комбинировать оба способа вычисления коэффи-
циентов.
В результате интегрирование рациональной дроби сведется к нахождению
интегралов от многочлена и от простейших рациональных дробей.
Случай 1. Знаменатель имеет только действительные различные корни,
т. е. разлагается на неповторяющиеся множители первой степени.
1419. Найти интеграл
Д (Так как каждый из двухчленов х— 1, х—2, х—4 входит в Знаменатель
в первой степени, то данная правильная рациональная дробь может быть пред-
ставлена в виде суммы простейших дробей I типа:
х34-2х-|-6 А ._________В.____С_
(х—1) (х—2) (х—4) х—1 ' х—2 ' х—4'
Освобождаясь от знаменателей, получим
х24-2х-(-6 = Л (х—2) (х—4) 4-В (х—1) (х—4) + С (х— 1) (х—2). (♦)
Следовательно,
х?4-2х+6 = Л (х2—6х + 8)+В(х2—5х+4) + С(х«—Зх+2),
Сгруппируем члены с одинаковыми степенями:
х2+2х+6 = (4+В + С)х2 + (— 6Л — 5В —ЗС)х+(84+4В+2С).
Сравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений
( Л+ В+ С=1,
J — 6Л—5В—ЗС = 2,
I 8Л+4В+2С=6,
з которой найдем Л = 3, В = —7, С=5.
Итак, разложение рациональной дроби на простейшие имеет вид
х2 4-2x4-6 _ 3________7 . 5
(х—1) (х—2) (х—4) х—1 х—2 ' х—4'
Неизвестные Л, В, С в разложении можно было определить и иначе. После
освобождения от знаменателя можно придать х столько частных значений, сколько
содержится в системе неизвестных, в данном случае—три частных значения.
Особенно удобно придавать х значения, являющиеся действительными корнями
знаменателя. Применим этот прием к решению данного примера. После освобожде-
ния от знаменателя мы получили равенство (♦). Действительными корнями зна-
менателя являются числа 1, 2 и 4. Положим в этом равенстве х=1, тогда
134-2.14-6 = Л (1—2) (1— 4)4-В(1 — 1) (1— 4)4-С(1 — 1) (1-2),
откуда 9 = ЗЛ, т. е. Л=3. Полагая х = 2, получаем 14 = —2В, т. е. В = —7;
полагая х = 4, имеем 30 = 6С, т. е. С = 5. В результате получились те же зна-
чения, что и при первом способе определения неизвестных.
Таким образом,
( х24-2x4-6 р dx р dx , р р dx
J (х—1) (х—2) (х—4)" Jx-1 Jx—2‘ J X— 4“
s=31n|x—11—71n|x—2|4~51n|x—4|4-C = lnl |+C. Д
223
Случай 2. Знаменатель имеет лишь действительные корни, причем некото-
рые из них кратные, т. е. знаменатель разлагается на множители первой степени
и некоторые из них повторяются.
1420. Найти интеграл j (ж_ dx.
Д Множителю (х—I)3 соответствует сумма трех простейших дробей г------7-3 +
(X 1)
Q Q
——^-|—-—— , а множителю х-|-3—простейшая дробь • Итак,
х2+1 _ А В С , D
(х— 1)3(х-|-3) (х-1)3 + (х— 1)г+х— 1+х4-3’
Освободимся от знаменателя:
х2-(-1=Л (х+3)4-В(х— 1)(х4-3)-|-С(х — 1 )2 (x-J-3)-}-£> (х— I)3.
Действительными корнями знаменателя являются числа 1 и —3. Полагая
х=1, получаем 2 = 4Л, т. е. Л = 1/2- При х = —3 имеем 10 = —64D, т. е.
D = — 5/32.
Сравним теперь коэффициенты при старшей степени х, т. е. при х3. В левой
части нет члена с х3, т. е. коэффициент при х3 равен 0. В правой части коэф-
фициент прн х3 равен C-\-D. Итак, С4-О = 0, откуда С = 5/32.
Остается определить коэффициент В. Для этого необходимо иметь еще одно
уравнение. Это уравнение можно получить путем сравнения коэффициентов при
одинаковых степенях х (например, прн х2) или придав х какое-нибудь числовое
значение. Удобнее взять такое значение, при котором вычислений будет возможно
меньше. Полагая, например, х = 0, получаем
о с q
l=3A-3B-\-3C—D, или 1=4-35+^+^, т. е. В = -~-.
£ 04 о
Окончательное разложение данной дроби на простейшие имеет вид
х2 +1 _ 1 3 5 5
(х —I)3 (x-j-З) “ 2 (х—I)3 + 8 (х—I)2 "г 32 (х—1) “ 32(х-|-3) ’
Таким образом, получим
х2+1 , 1 Р dx 1 3 Р dx
(х-1)3(х-3) - ~~2 J (х-1)3 +Т J ’(7=1
- 1 3 -4- 5 1
4(х— I)2 8(х—1) +32
, 5 Г dx 5 Р dx
2+32jx—1 32Jx+3
Случай 3. Средн корней знаменателя имеются простые комплексные корни,
Т. е. разложение знаменателя содержит квадратичные неповторяющнеся множители.
1421. Найти интеграл £ -
Л Разложим знаменатель на множители:
х3—х2 = х2 (х3—1)=х2 (х—1) (х24-х+1).
Тогда
1 ___________1___________ Л В________С . Рх + В
X3 —X2 X2 (х—1) (Х24-х4-1) X2 ' х +х—1 + х2 + х+1
Освобождаемся от знаменателя:
1=Л(х—1)(х2 + х+1)4-Вх(х—1)(х2+х+1) +
4-Сх2 (х24-х+1) + (Рх4-£) х2 (х—1).
224
Действительными корнями знаменателя являются числа 0 и 1.
Прн х = 0 имеем 1=—А, т. е. А = —1; при х = 1 имеем 1 =ЗС, т. е. С=1/3.
Перепишем предыдущее равенство в виде
1 = А (х*—1) + В (х*—х) + С (х*+х3+х2) + Dx*+£х* — Ох*—£х8.
Сравнивая коэффициенты при х*, х®, х8, получаем систему уравнений.
, в+с+о=о,
/ А + С+Е—D = Qt
I С—£ = 0,
из которой найдем В = 0, D = —1/3, £=1/3. Итак,
1 1,1 х—1
х5—х8 х8 + 3(х—1) 3(х8+х + 1) •
Следовательно,
С
J х5—х8
dx , 1 f rdx
хг+3‘ J х—1
1 f* x-1
3 J x84-x+l
1,1,, ,. 1 C2x4-1— 3 .
——“4“"V In I 1 I 1 « , I , dx—
x 1 3 1 1 6 J x84-x-f-l
=7+yin|(x-i)l—§-ln(x84-x4-i)+y [y-----
1,1. (x—I)8 , 1 ...t_ 2x+l
х + б Пха4-х4-1^1<"з g i<3
Случай 4. Среди корней знаменателя имеются кратные комплексные корни,
т. е. разложение знаменателя содержит повторяющиеся квадратичные множители.
1422. Найти интеграл J ^~^g- dx.
Л Так как x8-f-l есть двукратный множитель, то
х8—2х Ах+В ,Cx+D
(х84-1)8 (ха4-1)« + х84-1 *
Освобождаясь от знаменателей, получим
Xs—2x = 4x4-B4-(Cx-f-D) (х84-1).
Приравняем коэффициенты при одинаковых степенях х:
Xs
х8
X
X»
1=С,
0 = 0,
—2 = Л4-С;
0 = В4-О;
А=— 3,
В = 0.
Следовательно,
f Xs—2х j. С —3x'dx , (‘ xdx _ 3 (* d(x8-f-l) , 1 (,d(x84*l)_
J (x84-1)8 J (x84-1)8 x84-1~ 2 J (x84-1)8+2 J x84-l
= 2(Д1)+1-1П^+1) + С-
Заметим, что данный интеграл можно было иайти проще с помощью подста-
новки х2 4-1 =/. ^
1423. Найти интеграл С dx.
J х "Г2
Л Выделим целую пасть данной неправильной рациональной дроби}
х»4-Зх»4-5х4-7|х»-|-2
** 4-2х Зх-4-1
з*»+Зх+7 x+3+jrp2
~3х» +6
3x4-1'
Итак,
х*+Зх»+5х+7 _ Зх-Ц
х»+2 '
Отсюда находим
(*+^+7.<Ч(»-Н+№>-
J ха+2 J \ х*+2/
f а 1 *> С t РЗх+1 . 1 . . о . 3 Г 2xdx . С dx
= J xdr+3 j dx+ j -r±-dx=yx«+3x+yJ-jrpy+J
‘ д«+3*+4in(x«+^+ ‘ arctg*+C. ▲
* £ у 2 У 2
1424. Найти интеграл J пх+б' dy'
Л Так как подынтегральная функция является правильной дробью, то ее
следует сразу представить в виде суммы простейших дробей. Легко видеть, что
многочлен х*-(-6х84-11х-(-6 обращается в нуль при х=—1, поэтому он делится
без остатка на х-]-!. Выполним деление:
х»4-6х»4-11x4-61 х4-1
**+ х*_______хг 4-5x4- 6
5х*4-11х
5ха-- 5х
6х-|-6
~ 6x4-6
Следовательно,
X» 4-бх» 4- 11x4-6=(х4-1) (x«4-5x-f-6) = (х4-1) (x-f-2) (x-f-3);
x-f-4 x-f-4 А . В । С
х»4-6х»4-11x4-6 —(х4-1) (x-f-2) (x-f-3)_"х+~Г"'*4-2"‘x-f-3’
Освобождаясь от знаменателей, получим
*4-4 = A (x-f-2) (х4-3)-|-В (х-|-1) (х-f-3)4-С (x-f-1) (x-f-2).
Полагая х=—1, найдем 3 = 24, т. е. 4=3/2. Если х =—2, то получим
2 =— В, т. е. В =—2. При х=—3 получим 1=2С, т. е. С=1/2.
Итак,
С х+4 . _ 3 С dx _ f dx .1 f* dx
J x*4-6x»4-11x4-6 dx~'2 J x4-l~ J x4-2+2 J x4-3=a.
= | in |x-f-11-2 in | x-f-214-1 In |x-f-3 |4-C. A
A X® I 1
1425. Найти интеграл 16 dx.
226
Л Прежде всего нужно выделить целую часть:
х®4-1 |х*—8х®4-16
х3—8х®4-16х 8х3— 16x4-1
вх3 — 16x4-1 * + х* _ 8х»4-16
Следовательно,
х®4-1 ,8х3—16x4-1 8х3—16x4-1
х4—8х34-16-Х+х4—8х34- 16~*+ (х—2)3(x-f-2)« '
Разложим теперь правильную дробь на простейшие:
^х®—16x4-1 А , В , С . . D
(х—2)« (х4-2)3 - (х—2)® +х-2-’-(х4-2Я+х4-2*
Освободимся от знаменателей:
8х®—16x4-1 =4 (х4-2)а4-В (х-2) (х4-2)®4-С (х—2)®4-О (х— 2)3 (х4-2).
Полагая х=2, найдем 33 = 164, т. е. 4=33/16; При х=—2 получим
—31 = 16С, т. е. С = —31/16; Если х=0, то 1 =44—8В4-4С4-8О. Заменив 4
и С их значениями, получаем
1=^—8В—j4-8D, нли —1654-160=1.
Для того чтобы найтн В н D, составим еще одно уравнение. Сравнив коэф-
фициенты прн х®, получим 8 = 5-(-О. Решив систему уравнений
( В-j- D = 8,
(—1684-160=1,
находим 0=129/32, В =127/32.
Итак,
С х5+1 . С Г , 33/16 , 127/32 31/16 , 129/32 1
J х«—8х®4-16 J L (х—2)®")-Т^2' (Х4-2)®"1- х4-2 J
х® 33 . 127 , 31 , 129. .
2 16(х—2)+32 П'Х ' + 16(х4-2)”*" 32 ,п1*+21+С-А
1426. Найти интеграл j • ,.
Д Подынтегральная функция является правильной рациональной дробью
и можно было бы найти интеграл, представив эту дробь в виде суммы простейших
дробей. Однако нахождение интеграла можно значительно упростить, если произ-
вести замену переменной х—1=/; тогда x=t-j-l иdx—dt. В результате получаем
f x'dx Clt + VfdtCtt+it + l С dt ? dt С dt
J (x— 1)»~J « “J Й t3 +2J ti^_
_ 1 2 1 c_ 1 2
2t3 3t3 ~ 4t* + 2(x—1)® 3(x— I)3
1 , n- 6x®—4x4-1 , r .
4 (x—1)*+ 12(x—1)* *
1427. Найти интеграл J '^4^84.5 •
А Преобразуем знаменатель: x*4-6x®4-5 = (x®4-3)®—4. Теперь имеем
f* xdx _C xdx
J x«4-6x»4-5 “ J (x»4-3)® -4 ’
227
Произведем замену х* 4-3 = 1, тогда 2xdx=dt и
С xdx f* xdx 1 f* dt
J x«+6x« + 5 ~ J (x» + 3)« -4“ 2 J P-4
1 .-^+1 ,
8 lnxa + 5’,-C’
1 > i
= -S- • -J- In
2 4
Из последних двух примеров видим, что иногда перед интегрированием рацио-
нальной дроби следует произвести замену переменной. Д
Найти интегралы:
С 2x» + x+3
J (x+2)(x»+x+l) *
p dx
1431. Нгт*
J x3—8
1428. i \<dx. 1429.
J х(х— 3)
Г5х»-17х«+18х-5 .
ИЗО. j (х—j)» '(x—2) ' dx-
*432- ,433-taA)i-
1434- l435-1
I43e-
ф Представить знаменатель в
виде х4-|-4 = (х’4-2)2—4х’.
1438. С 1439. \^ы<1х.
J х2—6x4-5 J х* —16
1440. C3x»+x2j-5x+l^
3. Интегралы вида § R (ех) dx, где R — рациональная функция. С помощью
подстановки ex = t, откуда exdx = dt, dx=-^-=-~, интеграл указанного вида
преобразуется в интеграл от рациональной функции
1441. Найти интеграл
Д Положим ex = t-, тогда ех dx=dt, dx=—p, откуда
Г ЗР* 4-е* 4-1 f ЗР-Н4-1 dt
J е2*_2е*—3 J /(Р —2/ —3)
Так как t (Р—2/—3) = /(/ + !)(/— 3), то разложение иа простейшие дроби
имеет вид
ЗР + /+1 А , В , С
3) t + <4-1 "* t— 3 ’
Освобождаясь от знаменателей, получим
3P+<+l=4(f+l)(Z-3) + S;(f—3) + CZ (f-f-1)-
Если / = 0, то1=—ЗЛ, т. е. Л=—1/3, если же 1, то 2=4В, т. е.
В = 1/2, наконец, если t=3, то 31 = 12Cf т.ё. С = 31/12.
Итак,
ЗР4-/4-1 »,/3..|! 1/2 31712
“t(P— 2t—3) t З1
и значит,
^-^.Ine^+lln^ + n+^nl^-Sl+C»
=-|+4!п(0*+!)+й!п|еХ~3|+с- *
Найти интегралы:
1442.
J е*х —16
1ЛЛЧ С_______2еХ+3
(2e2x_ex — i) (e^ + l)dx’
§ 3. ИНТЕГРИРОВАНИЕ ПРОСТЕЙШИХ ИРРАЦИОНАЛЬНЫХ ФУНКЦИЙ
1. Интегралы вида J R (х, (ax+b)mt/nt, (ах+Ь)т,/"г,...) dx, где R — рацио-
нальная функция; mi, пь m2. nt, ...— целые числа. С помощью подстановки
ax-j-b = it, где s —наименьшее общее кратное чисел пг, пг, ... , указанный интег-
рал преобразуется в интеграл от рациональной функции.
1444. Найти интеграл / = С----ттп—------пт •
И J (2х + 1)2/3 —(2х+1)|/2
Л Здесь 14 = 3, пг = 2; поэтому s = 6. Применим подстановку 2х-(-1 =/*; тогда
х=(/®—1)/2, dx=3i5di н, следовательно,
Г 3/»Л Г t*dt Р/а-1 + 1
'~J 14TT7F-3J 1~Т-3 j /-1 dt~
=3 у _|__L_) d/=4/»+з/+з1п|е-11+c.
Возвратимся к старой переменной. Так как i = (2x+l)I/6, то
/=3.(2х+1)1/3 + 3(2х+1)*/6+31п|У2х+1-1|+С. А
л
2. Интегралы вида J -рг=========-. Такие интегралы путем выделения
полного квадрата нз квадратного трехчлена приводятся к табличным интегралам
XX или XXl.
Г dx
1445. Найти интеграл | —г===
J К*8+2*+5
Л Преобразуем квадратный трехчлен к виду ха + 2х+5 = (х+1)2+4. Тогда
У тзйтН 1,+' +к“+2,+5 |+с-А
f* dx
1446. Найти интеграл | .
F J / —Зх*+4х—1
w . J 2 \
г dx d x—т
д f : . -—f ~? i . 2V-
=—т=г arcsin *~2^3+C=-j=- arcsin (Зх—2) + C. A
КЗ 1/3 ]Гз
229
Г Лх-1 В
3. Интегралы вида I .; ~r dx. Для нахождения этого интеграла
J Уах’+&х+<?
выделим в числителе производную квадратного трехчлена, стоящего под знаком
корня, и разложим интеграл на сумму двух интегралов:
A Ah
Г Ах+В с^(2ах+Ь)+в~^.
I -7==- dx— I ------- , dx=a
j y^ax3-j-bx-{-c J y^axa-j-bx-j-c
, A f d(axa + &x+c) । f q_ Ab \ Г_dx____
2e J ^aX2-!-bx-j-c \ 2° / J y~ax2-j-bx-j-c
Первый из полученных интегралов есть табличный интеграл XVII, а второй
рассмотрен в п. 2 § 3.
Г5х______з
^=-dx.
Y 2xs 4-8x+l
Л Выделим в числителе производную подкоренного выражения:
р 5х—3 « •ф’(4*+8)—13
I —7====- dx= 1 ——--- ,. dx=
J К2хг+8*+1 J K2xs+8x+1
5 C 4x+8 „ C dx
=1-1 r—..... =-dx—13 I —- , —=a
4 J j<2x»+8x+1 J У 2x» + 8x+l
=4 /2x’+8x+l------yLr- f- dx =
2 К 2 J ,/ ... ,1
J/ xa+4x+-g
K2x*+8x+l—^=-ln |x+2+ |Лх«+4x4-1 |+C- ▲
1448. Найти интеграл f - -.. 3*~h4 dx.
J'Y-x2+Gx-8
r 3x+4 —J (-2x+6) + 13
A I dx= I .......... — dx =
J V— x2+6x—8 J У — x«+6x—8
_ _ 3_ Г —2x+6 Г dx_______
2 J У-х»+6х-8 + J Y1 —(x-3)a
= —3 Y — xa+ 6x— 8+13 arcsin (x—3) + C.
, „ f dx -
4. Интегралы вида I-------- . С помощью подстановки x —
J (x—a) Yax2+bx+c
— a = l/t этот интеграл приводится к рассмотренному в п. 2.
f dx
1449. Найти интеграл | —т==-.
J х/5ха—2х+1
Л Положим х= 1/1, тогда dx=—(i/t2)dt и
Г dx = Г (dt)/t2
J хКб*а—2х+1 J (1//) У5//8—2/1+1
— У гЛ,+5“~1'+
—in|4-i+ Y з~4+5| +с“- |п | +с- *
230
1450. Найти интеграл |. л „ ~ •
J (х-ОК-^+Зх+З
Л Полагаем х—1 = 1//, тогда x = l/f-f-l и dx=— (lfl*)dt. Следовательно,
1451. Найти интеграл /=1------...
J (х-f-!) Кх*+3х+3
Д Записав числитель подынтегральной функции в виде 3x4-2=3 (х 4-1) —1,
получим
/=f_____З(х-М)-1
J (х+1) Кх«+Зх+З
Представим данный интеграл как разность двух интегралов:
j=3 С dx__________С dx_______
J Кх*4-3х4-3 J (х4-1)Кх*4-Зх4-3 ’
К первому интегралу применим формулу XXI, а ко второму—подстановку
х4-1 = 1Д:
/=3 talx+4+r«‘+Si+S|+ [ . , < -
1 1 J Т /(!-') +3(т-')+3
=з1п|х4~|-4-К х»+3х4-з|4-1п | f-f-y+K i’-н-Ы |+с=
=з1п|х4-|-4-Гх»+Зх4-з 4-ш |-±r4-|4-JCi^±l +с. а
I Л I * “1“ I «* «* 1
5. Интегралы вида (* &х-. t Гдё Рл (х) — многочлен п-й степени.
J у ах*+Ьх+с
Интеграл такого вида находится с помощью тождества
f , ^|^) -[ dx=Q„_j (х) Гах»-рх+с+Х f ,
J У ах* 4- i>x4- с J уах*-4-Ьх-}-с
231
где QB_j (х)--многочлен (n—1)-й степени с неопределенными коэффициентами,
1—число.
Дифференцируя указанное тождество н приводя результат к общему знамена-
телю, получим равенство двух многочленов, из которого можно определить коэф-
фициенты многочлена Qn-i(x) н число X.
1452. Найти интеграл (*х3+2х
J К x»+2x±2
Л Здесь п = 3, поэтому соответствующее тождество имеет вид
С **+2**,+3*±j dx=(M’+M+M Ух»+2х+2+Х f dx ..............-rr .
J V\»+2x+2 ve-ri-ra/r т т т j уха_|_2х+2
Дифференцируя обе его части, получаем
= (2М+ Ь1) V х*+2х+2 +
у х®4-2х4-2
-НМ’+*1*+ М ; Х~171-----ИХ—------ 1 .- ,
TV о -Г 1 т Ух»+2х+2 Ух*+2х+2
Освобождаемся от знаменателя:
х® -]- 2х® Зх 4* 4 — (26qX-|“ 6i) (х®4- 2x4-2) -|~ (6qX®4- ^1Л4~ ^а) (*4“ 04“^»
илн
х® 4-2х® 4-3x4-4=36дх® 4“ (56q4“2^i) х®4- (46g 4-^6i 4“ ^s) *4~ (26j 4“ 62 4_^)*
Сравнивая коэффициенты при одинаковых степенях х, получим
36g— 1,
56о 4~ 261 ~ 2»
460-]-36i4-^a ^З»
2614-6g 4“^ = 4.
Решая систему, найдем 60 = 1/3, 6Х = 1 /6, 63 = 7/6, X —5/2. Следовательно,
С & 4“ 2х® 4-3x4-4 j /. 1 « . 1 . 7 \ _< 2 о I о I
I —^====-<й= -=- Х*4~г-х4--г У X®4-2x4-24-
J /х’+2х-Ь2 к 3 6 6 )
Найти интегралы:
1453. С-7==Az==-
J V 1— 2x— у 1— 2x
..ее f dX ..
6/—
— —- dx.
l+¥x
dx
5х+3
V — x»—2x+8
а Г 3*4~2
dx.
dx
dx
х—1
(x-f-2)/x2-|-2x
-------------- dx.
(x-H) yx» +1
х Y2хг — 2x— 1
f 4+2x+3-^
6. Интегралы от дифференциальных бииомон хт (a^-bx”}p dx, где т, п,
р — рациональные числа, Как доказал П. Л. Чебышев, интегралы от дифференци-
альных биномов выражаются через элементарнее функции Только в трех случаях:
232
1) р—целое число, тогда данный интеграл сводится , к интегралу от рацнр.
иальной функции с помощью подстановки x = ts, где з —наименьшее общее кратное
знаменателей дробей m,и п;
2) (т-|-1)/л—целое число, в этом случае данный интеграл рационализируется
с помощью подстановки а+6хп = /л;
3) (m-f-l)/n4-p—целое число, в этом случае к той же цели ведет подстанов-
ка ах-п4-Ь = 1л, где з—знаменатель дроби р.
1463. Найти интеграл
Л Здесь подынтегральную функцию можно записать в виде х“1/2(х1/44-1)-10»
т. е. р = —10—целое число. Значит, имеем первый случай интегрируемости диф-
ференциального бинома. Поэтому следует применять подстановку x = t*; тогда
dx=4t3dt н искомый интеграл принимает вид
tdt
К + 1)10 '
Последний интеграл находится так:
Г tdt _С*+1 — l.._f Л С л
J К +010 J K+i)w J к.+о* J к+о1о=я
Таким образом,
f_________________.______1_____I *________I Q А
J Vх(/х+1)10 2(У7+1)8+9(У х+1)о+ ' А
1464. Найти Интеграл С---
. . J (а2—х2)/а2—х2
Д Переписав подынтегральную функцию в виде х® (а®—х2)"®/*, имеем т=3,
л = 2, р =— 3/2. Так кдк (т + 1)/л = (34-1)/2 = 2—целое, число, < то < имеет место
второй случай интегрируемости. Используя подстановку а3—x3 = t*, получим
— 2хdx=21 dt, xdx = —tdt, x2 = a2—t3. Следовательно,
j x3 (a2—x8)-B/8<ix= — j (a2— t3)t~3-tdt = -^^-dt =
Г.. Г dt <S+al _ir 2a2—x2 .
=J dt~a3 j _«1+t+C=—r-4-C=p== + C. A
1465. Найти интеграл f 4.
Л Здесь m=-rr4, n = 2, p~— 1/2 и (m+iy/n+p=(—4-|-l)/2—1/2= —2
—целое число. Поэтому имеет место третий случай интегрируемости дифференциаль-
ного бинома. Полагаем х-2+1 = /2; тогда — 2х~аdx=2tdti x~3dx=—tdt.
Преобразуем данный интеграл таким образом:
/=(—=== (* Х-« (14-х2)-1/8 dx =
J х*у 1 4-х2 J
= Jx-*[x2(x-24-l)]-1/2dx=yx-2(x-24-l)-1/2x-8dx.
233
Следовательно,
/=—j (F—1) /-ЧЛ=—J(/2—1)Л =
в=ут+^’ Ии-**)3 . г (2xj-1)VT+F, г .
х Зх3 Г Зх3 *
Найти интегралы:
1466. (-7тД—п- 1467. f;> dx-
Jx(/*+i)’ Jrri+i
1468. f т-. 1469. f..— .
J /1+*»_________ J*K1+*3
1470. f У1}^5хУ~х+3(1х. 1471. f.........
J J x3 v 2—x3
f 4. ИНТЕГРИРОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЯ
1. Интегралы вида j/?(iinx, coex)<fx, где Я — рациональна» функция.
Интегралы указанного вида приводятся к интегралам от рациональных функц^
с помощью так называемой универсальной тригонометрической подстановхя
tg(x/2) = /. В результате этой подстановки имеем:
В1ПХ
2tg(x/2) 2t
14-tg1 (х/2)=ГТТ8 ’
x=2arctg t;
CO3 l-tg2(*/2) J~<2.
cos*-l+tg2(x/2)“l-|-/2’
dx=
2dt
l + t2'
1472. Найти интеграл fj—:—r4~----------rr
r J 4 sin x-l-3 cos x-l-5
Л Подынтегральная функция рационально зависит от sin х и cos х; примени
2t 1 — t* 2 dt
подстановку tg (x/2) = t, тогда sin x = '«, cosx=—-js, rfx= j--; и
2 di
i 4slnx-f-3cosx-|-5
2t ЖЧ
+ /»+3‘l-Hl+5
- 1 j-C.
4-i
di
P+2? t-
Возвращаясь к старой переменной, получим
1
tg(x/2)+2
4 sin x-l-3 cos x-f-5
1473. Найти интеграл j •
234
Л Полагая tg(x/2) = l, получим
Р Р 2dt
J ^+^)-(a^)eosx J
_»С _ dt________________? di д
-J (a2-f- fc2) (i -f- Р) —(о2—ft») (1 — Р) J a2P-f-b*
)+е-±
Универсальная подстановка tg(x/2)=l во многих случаях, приводит к слож-
ным вычислениям, так как при ее применении sin х и c'os х выражаются через t
в виде рациональных дробей, содержащих t*.
В некоторых частных случаях Нахождение интегралов вида J flfSlnx, coSx)dx
может быть упрощено.
1. Если ₽(slnx, cbsx)—нечетная функция относительно Slnx, т. е. если
R (— sin х, cos х) = — R (sin х, cos х), то интеграл рационализируется подстановкой
cosx—t.
2. Если /?(sinx, cosx)—нечетная функция относительно cosx, т. е. если
₽(sinx, —cosx) = —R (slnx, cosx), то интеграл рационализируется с помощью
подстановки sin х== t.- .;,
3. Если R (sin х, cosx)—четная функция относительно sinx и cosx, т. е.'
если R (— sin х, — cos x) — R (sin x, cos x), то к цели приводит подстановка tg х = t.
;. и » (* (sin x-f-sin3x) dx
1474. Наити интеграл \ ---------з^х — ’
Л Так как подынтегральная функция нечетна относительно синуса, то пола-
гаем cos х = Е Отсюда sin2x=l— Р, cos2x = 2cos2x—1 = 2Р—1, dt ——sinxdx.
Таким образом,
С (sin x-f-sin’x) dx _ f (2— Р)(— dt) _ Г (Р—2)dt
J cos 2х — J 2Р—1 J 2Р—1 =*
1 (* 2Р—4 If 3 f dt
~ 2J2P—1 Г 2 J at 2J2P—i —
=£_____3 rd(//2)^l 3 1/2-1
2 2/2J 2Р—1 2 2/2 1/ 2-f-l
Следовательно,
Г (sin x-f-sin2 x)d« 1
J cos 2x — "2
3
COS*~2/1
In
/ 2cosx—1
/"2 cos x-f-1
+C.
Отметим, что в рассматриваемом случае интеграл всегда может быть записан
в виде J R* (sin2 х, cos х) sin х dx. А
, тт f (cossx4-cos*x)dx
1475. Наити интеграл 1 -—; .
r J sin2 x-f-sin4 X
Л Здесь подынтегральная функция является нечетной относительно косинуса.
Поэтому применяем подстановку sinx=l; тогда cos2x=l—sin2x=l—/2,
cosxdx = dl. Следовательно,
f (cos3 x-f-cos5 х) dx f cos2 x (1 -f-cos2 x) cos x dx_f (1 — i2) (2—P) dt
J sin2x-f-sin4x ~~ J sin2 x-f-sin4x J P-f-P ‘
235
Окончательно получаем
Г (cos^+costx)^^ 2 _6 c
J sin1 x+sin* x sinx
Отметим, что в рассматриваемом случае интеграл всегда может быть записав
в виде J R* (sin х, cos1 х) cos х dx. Д
Sdx
sin1 x+2sin xcos х-сБ^Г-
Д Подынтегральная функция четна относительно синуса и косинуса. Пола-
tg х t 1
гаем tgx=t; тогда sinx= — =—,1 - ; cosx= .-.„z;—
Kl+‘g*x Ki+<* Ki + ‘g’«
= , 1 - ; x = arctg t; dx= Отсюда
14-/1 W
Л /» dt
I __________dx_________ I _____T+77
1 sin1 x-f- 2 sin x cos x—cos1 x 1 t* . 2t . 1
J J i + t’^KT+T1 ’ KT+71
= C____<“___
J /« + 2Г-1
Далее, имеем
1
1-f-t1
dt f d(f+D 1 , _
/’+2/—1 J (f-f-ijs—(/2)s 2^T 2
/+1 + Г 2
и, следовательно,
Г____________________dx_______________1_
’ sin1 x+2sinxcosx—cos’x 2 ^"2
tgx+l-K 2
tgx+1 + Г 2
+C.
Заметим, что нахождение интеграла можно упростить, если в исходном интег-
рале разделить числитель и знаменатель на cos’x:
Г Г Г
। __________dx____________I cos1 х_________I d (tg x) .
J sin1 x+2sinxcosx—cos’x-J tg’x-|-2tgx—1— J tg*x+2tgx— 1 ’ *
2 . Интегралы вида j sin” x cos"x dx. Выделим здесь два случая, имеющие
особенно важное значение.
Случай 1. По крайней мере одни из показателей т или л—нечетное.поло-
жительное число.
Если п—нечетное положительное число, то применяется подстановка sinx=r,
если же т—нечетное положительное число,— подстановка cosx=/.
1477. Найти интеграл J sin* х cos5 х dx.
Л Полагая sinx=/, cosxdx=dt, получим
J sin*xcos5xdx= J sin*x(l—sin1 x)1 cosxdx = <*(l—t^dt^
=J t*dt—2^ t*dt + ^ <’Л=у/5-у f-f-y <94-C=s
1 2 1
=-=-sifl5r—-=-sin’jr4--“Sta9jr+C. A
V l У
236
1478. Найти интеграл
Л Имеем
sin** Л?
?/----*
cos* у cos *
—Г sin**cos”*/* *d*= (*(1—cos**) cos”*/* *sin«4*.
cos * у cos * J J
Полагая cos*=f, — Sinxdx=dt, получим
Г —sin**d* __ Г (1 ,-vs di = _ (* dt + f dt=t
J COS X у COS X J J J
= 3f~1'z*4-g-/*/8+C= a >j-=+~Fcos*’ cos**4-C. A
5 у cos * 5
Случай 2. Оба показателя степени т н л—четные положительные числа.
Здесь следует преобразовать подынтегральную функцию с помощью формул
sin * cos*=~ sin 2*. (1)
sin’*==-y (1— cos2*), (2)
cos* *=y (• 4-cos 2*). (3)
1479. Найти интеграл J sin* x cos’ x dx.
Л Из формулы (1) следует, что
/1 \* 1
sin* * cos* * = (sin * cos *)* = i у sin 2* j =y sin* 2*.
Применив теперь формулу (2), получаем
. • . 11 —cos 4* 1 ...
sin** cos* *=— --g---=s-g-(l—cos4*).
Итак,
J sin**cos**</*=£• У (1—cos4*)d*=
=-|-Jd*—cos4*d*=-g-*—^sin4*4-C. Д
1480. Найти интеграл J cos’ * dx.
А Используя формулу (3), получим
. « vij f 714-cos2*У .
(cos* *)* dx = \ ( — 2 --1 J dx=
cos**rf*=
=-|- у (14- 3 cos 2* 4-3 cos* 2* 4- cos* 2*) dx =
cos2xdx+"|' J costZxdx-t-—^ cosa2xdx—
l±^d*4-
+4- С (1—sin*2^cos2xdx=4-x+^sin2x-f’
О J О ID
+Л Cdx+Л f cos4xdx+4" Ccos2xdx—
10 J 10 J О J
—4* sih*2*-4-<i(sin2«)=4’*+^s,n2*+
o J 2 о 10
3 3 11
+ 16х+6481п4х+Тб s’n2*~48Sins2«+C=
= 5 x+‘ sin2x+^sin4x-lsln*2x+C. ±
lb 4 04 4o
1481. Найти интеграл J sin’xcos* xdx.
Д \ sin8 x cos* x dx— l (sin x cos x)* cos* x dx= \ ( sin 2x j -2-=
«= 4* \ sin* 2x dx-l-4- sin’ 2* cos 2x dx =
о J ° J
1 C 1 —cos 4x . . 1 r , . „ 1 . . , „ .
= 7 J —~2— <**+ 7 J sln d (sln =
= -^y dx~jQ § cos4xdx+^y sin* 2xd(sin 2x) =
=V-(ksin4x+is,nS2x+c-A
3. Интегралы вида J tg"xdx n ctg"xdx, где m — целое положительное
число. При нахождении таких интегралов применяется формула tg*x = sec*x—1
(или ctg* х=cosec* х— 1), с помощью' которой последовательно понижается сте-
пень тангенса или котангенса.
1482. Найти интеграл J tg’xdx.
Л Jtg’xdx=ytgsx(sec*x—l)dx = y tg’xd(tgx) — § tgsxdx =
=”Т“~У tg’xfsec’x—1) dx=^^—+ У tgx(sec*x—l)dx =
_^_^+!^+1„|co„l+c. д
1483. Найти интеграл J ctg*xdx.
Л У ctg* xdx = § ctg* x (cosec* x— 1) dx=— J ctg* x d (ctg x)—ctg* x dx =
==— —y——У ctg* x (cosec* x—1) dx=*
ctg*x . ctg*x . Г . , ... ctg’x . ctg*x . , „ .
«-----1—I—I—Fj (cosec* x—l)dx =------1—I—|-------ctgx—x+C. ±
4. Интегралы вида tgMx sec"xdxи ^ctgM~x cosec" xdx, где л —четное поло-
жительное число. Такие интегралы находятся аналогично рассмотренным в п. 3
с помощью формулы sec*x=l-|-tg*x (или cosec*x=l-|-ctg*x).
1484. Найти интеграл J fg4jrsec6xdr.
Д J tg4xsec’xdx = tg4xsec4x-sec’xdx =
= J tg4x(l+tg*x)*d(tgx)=J t8**4(tg^+2j tg6xd(t8«)+$t88*4(tgx) =
= ltg»x+ytg’x+ltg9x+C. Д
1485. Найти интеграл J .
Л У cosec*xdx=y cosec’ x-cosec’ xdx—^ (l+ctg*x) cosec*xdx =
= C cosec* xdx— C ctg* x d (ctg x) =—ctg x—ctg* x-|-C. Д
5. Интегралы вида J sec*"+1 xdx и j cosec’"+1 xdx. Интегралы от нечетной
положительной степени секанса или косеканса проще всего находятся по рекур-
рентным формулам:
С sec*"+1 xdx = J- Sln^-+fl— C sec*"-’xdx, (1)
J 2л cos*" x 1 \ 2л } J ' '
cosec*"+lxdx =— -y-« -f-f 1—4-^ Г cosec*"-1 xdx. (2)
2л sin*" x ' \ 2л/ J ' '
i486. Найти интеграл J cosec5 xdx.
Д Применяя рекуррентную формулу (2) при 2л-|-1=5, т. е. прн п — 2,
получим
С . . 1 cosx . 3 (* , .
\ cosec5xdx = —т • —гт \ cosec’xdx;
J 4 sin’x 4 J
полагая теперь 2л-}-1 =3, т. е. л=1, по той же формуле имеем
J cosec’xdx = -4 . jcosecxdx.
Так как cosecxdx=J ^—^-=1п | tg у |-{-С, то
У cosec’xdx=-^4-lln|tgA| + c,
Г . . cos х 3cos х , 3 , I. x I , „ .
I cosec5 x dx—— -g—3-g-/ y -4—к- In tg-=- H-C. A
J 4sin4x 8sin*x 1 8 2 e
6. Интегралы вида j sinmxcosnxdx, J cosmxcosnxdx, sinmxsinnxdx.
Тригонометрические формулы
sin a cos 0 = 4 (sin (a-f-₽)-f-sin (a—₽)], (1)
cos a cos 0 = 4 Icos (®+₽)+cos (“—₽)]< (2)
sin asin 0 = 4 lcos (a—•₽)~cos (a + ₽)l (3)
дают возможность произведение тригонометрических функций представить в виде
суммы.
239
1487. Найти интеграл J sin2xcos5xdx.
Л Используя формулу (1), получим
У sin2*cos5xdx=-2-у [sin 7x+sin (—3x)]d«=
=-^- J sin 7хdx—-yj sin3*d* =—^cos7*+-g-cos3*4-C. A
1488. Найти интеграл J cos x cos у cos-^-dx.
Л Применим к произведению cos x cos у формулу (2):
p x x , If/ 3x , * \ x ,
I COS*COS-yCOS yd* = -y \ ( COS у -f-COS Y ) C0S “x~
3* x . , 1 f x x
cos -я- cos -r dx-J-— \ cos cos -r- dx.
2 4 2 J 2 4
Снова используя ту же формулу, находим
* х j If/ 7* . 5*\ j , 1 f [ Л Зх , пх \ .
COS * COS у COS yd* = у \ ( cosy + cosy ) d*+y \ I cos у +cos j dx =
1 , 7* . 1 . 5* . 1 , 3* , , x , „ .
e_SinT4._-sin-+ysinT+sinT+C. A
_1_ P
2 J
Найти интегралы:
1AfiQ C
J 3 + 5sin *+3cos x '
1491 C «***<<*
J sin8*-|-4sin* cos* ‘
• Положить ctg* = /.
« jao Г sin 2x dx
J cos3*— sin8*—1’
1496. J sin8 (x/4) cos8 (x/4) dx.
1498. Jtg4(x/2)dx.
1500. J sec*xdx.
1502. J sec* xdx.
1504. J sin 3x sinxdx.
1490.
J 1—sn
cos8 xdx
sin8*+sinx
1494. fsin* xdx. 1495. Ccos.8x,/'
J J sinx
1497. $ cos* xdx.
1499. J ctg83xdx.
1501. f £?^dx.
J sin4*
1503. ctg8xcosecxdx.
1505. J cos (x/2) cos (x/3) dx.
7. Тригонометрические подстановки. Интегралы вида J/? (*, a*— xa)dx,
J Я (*, У a2-j-x2) dx, j R(x, Ух2—a2)dx приводятся к интегралам от рацио-
нальной относительно sin i и cos t функции с помощью надлежащей тригоно-
метрической подстановки: для первого интеграла *=asin f («ли *=acosi). для
второго *=atg/ (или *=actg/) и для третьего *=asec/ (или x=acosec t).
1506. Найти интеграл I — f—-----— dx.
Л Положим x = nsin/, тогда dx = a cos t dt и заданный интеграл примет вид
1 =
У а2 — a2 sin2t
a sin t
a cos t dt =
cos21
sin t
dt=a
1 —sin21 C dt
---:—— dt=a \ -—j —
sin t J sin г
sin t dt =
=a In | cosec t — ctg t |-|-я cos /+С.
TT 0 dt . . f d/
Для нахождения интеграла I -—- мы воспользовались формулой > -7—7 =
J S1П I v SIП I
= In | cosec t — ctg t l+C, так как с ее помощью легче перейти к прежней пере-
менной х.
Таким образом, получаем
, , I 1 cos t I , , , п
1 = a In —7-----:—т + a cos t + С,
sin г sm /
где sin t — xja, cos t = У a2— x2/a. Следовательно,
I n_______________________1/" д2 _у 2 I ~ t
7 = a in 2A
1507. Найти интеграл 7= С—7^=.
Jx у a2+ x2
Л Применим подстановку x — atgt, откуда dx —a sec2 t dt. Тогда получим
j _ Г a sec21 dt _____ 1 C sec2 t dt__
~ J a tgt y^a2tg2 t~J »g t sec t ~
1 С sec t ,, 1 C dt 1 . , , , ,, , „
— — \ —7 dt = — \ , = — In cosec t — ctg t 14- C,
a J tg t a J sin t a 1 1 1
где \gt = xja и, следовательно, ctg/ = a/x, cosec t = У1 +ctg2 t = У a2 -j-x2/x.
Итак,
7=±in|lC^±Zzz£l+c. A
a I x I m
1508. Найти интеграл 7 — f- x d— .
J У x2— a2
А Применим подстановку x = asect, откуда dx = a sec t tg t dt. Тогда получим
, Г a2 sec2 t-a sec t tg t , f „ ,
I — I -----d/ = a2 1 sec3 t dt.
J }^a2 sec2/ —a2 J
Далее применим рекуррентную формулу (1) п. 5 при n= 1:
С з, ,, 1 sin / . 1 f sin / . 1 р dt
J sec tdt~ 2 cos2 /+ 2 Jsec/ d/~2cos2 /+ 2 J cos t~~
”2Яп+т|”1“',+'в'1+с'
где sec t=x/a, cos t=ajx, sin / = Ух2 — a2lx, tg/ = '/'x2—а2!а. Следовательно,
, a2 sin t . a2 . . . , , , 1 , -
7=-2OT+Tln|SeC/ + tg/| + C =
x r-j----2 I a2t Ix + Z’x2— a21 r
r*2-«2+yln|--------------l+C. A
9-215
241
Найти интегралы:
1509. С—-—.
J (1-х*)2/*
151°- j(a2+x2)3/2
§ 5. ИНТЕГРИРОВАНИЕ РАЗНЫХ ФУНКЦИЙ
Найти интегралы:
1512. j sin2xsin 3xdx. 1513. $ (2x2—2x4-l)e_x/2dx.
1514. 1515. P x2 2 ^+1 arctg xdx.
1516. (2x*—l)cos2xdx. 1517. J x In2 x dx.
i5ig, j —2ex—3 1519. arctg К x dx.
15zu. J|/2* —Idx. 1521. p dx
J У 14-х4
1522. $K6 + 4x—2xldx. 1524 C 1523. 1525. J e2* sin ex dx. sin 2x In cosxdx.
J cos* x Y 2-J-5 tg2x
1526. (x-f-2) cos(x2+4x+l)dx. 1527. P x cos x dx J sin’x *
1528. f—gL^dx. 1529. J In (x2 4- x) dx.
1530. f-г^Ц-. 1531. J cos In x dx.
J^+x*
,532' 1533. J e“x sinpxdx.
1534. J e“* cos px dx. 1535. f* dx
J a* cos2x-|-b2sin2x
1536. 1537. C dx U1 _L_ v2\2 •
ГЛАВА X
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
§ 1. ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Пусть функция f(x) определена на отрезке [a, &]. Разделим отрезок [а, Ь]
на п произвольных частей точками а = х0 < *! < х2 < ... < xn-i < *n — b, выбе-
рем на каждом элементарном отрезке [Xfc_f,xs] произвольную точку g* и найдем
длину каждого такого отрезка: Дх£ = Х£—*л-1- Интегральной суммой для функ-
п
цнн f (х) на отрезке [а, 1>] называется сумма вида о= 2 /(Вл) ДхЛ> причем эта
*=1
сумма имеет конечный предел I, если для каждого е > 0 найдется такое число
6 > 0, что при тахДх£<6 неравенство |а—/|<е выполняется при любом
выборе чисел 5л-
Определенным интегралом от функции / (х) на отрезке [а, 6] (или в пределах
от а до Ь) называется предел интегральной суммы прн условии, что длина наи-
большего из элементарных отрезков (max Дх^) стремится к нулю:
& п
J={f(x)dx= lim а= lim Т Д*Л-
* max Дх^-^-0 шах ]
Если функция f (х) непрерывна на [а, 6], то предел интегральной суммы сущест-
вует н не зависит от способа разбиения отрезка [а, Ь] на элементарные отрезкь
и от выбора точек (теорема существования определенного
I н те г р а л а).
Числа а н b соответственно называются нижним и верхним пределами ин-
тегрирования.
ь
Если f (х) >0 на [a, &], то определенный интеграл f (х) dx геометрически
а
представляет собой площадь криволинейной трапеции—фигуры, ограниченной
линиями y~f(x), х=а, х=Ь, у = 0 (рис. 42).
Основные свойства определенного интеграла
а b
ъ ь ь
4°. f [fl (х) ± ft (*)] dx= f fl (x) dx ± f ft (x) dx.
V V V
a a a
b b
5°. J C>f (x)dx=C*^f (x)dx, где С—постоянная*
а в
6°. Оценка определенного интеграла-, если т</(х)<Л1 на [a, ft], то
ь
т(Ь — а) < J f(x)dx < М (6—а).
а
Правила вычисления определенных интегралов
1. Формула Ньютона—Лейбница-.
Ь ь
\f(x)dx=F(x) =F(b)—F(a),
а а
где F (х)—первообразная для f (х), т. е. F'(x)—f(x).
2. Интегрирование по частям-,
ь ьь
J и dv = uv — du,
а а а
где и = и(х), v = v(x) — непрерывно дифференцируемые функции на отрезке [а, 6].
3. Замена переменной-.
Ь ₽
р W dx= р [<р (01 Ф' (0 dt,
а а
где х = ф(/)—функция, непрерывная вместе со своей производной ф' (/) на от-
резке а = ф(а), Ь — ф (0), f [ф (/)]—функция, непрерывная на [а, 0].
4. Если f (х) — нечетная функция, т. е. f (—х) = — f (х), то
а
J f(x)dx = 0.
— а
Если f (х)—четная функция, т. е. /(—x) = f (х), то
а а
J f (х) dx = 2 J / (х) dx.
— а 0
1
1538. Вычислить интеграл J x*dx как предел интегральной
о
суммы.
Л Здесь f (x) = x’t а = 0, ft = l; разделим отрезок [0, 1] на п равных частей,
тогда Дх^ = (6—а)/п=1/л; выберем ^ = х*. Имеем:
„ п 1 2 П~1 п <
%<з 0» Xi , х2—• ....*л—1~----, хп——- —1;
п п п п
Следовательно,
1
(* . . 12 + 2’+32+.., +«’
\ x*dx= lim —I----!—=-!----1—=
J «-►<» n3
о
л(п-Н) (2n-f-l) ( ’+Т J p+'nj 1
“л1™ -----fo?—-=Л"1 -----------6 -------- 3 •
Здесь использована формула суммы квадратов натуральных чисел.
244
я/4
dx
1539. Вычислить \ по формуле Ньютона—Лейбница.
л/6
я/4
Р dx . |л/4 л Л ,
я/6
3 •
18
1540. Оценить интеграл J
io ' "I"
А Так как | cos х | < 1, то при х> 10 получим неравенство
Следовательно,
18
Р cos хdx
VT+x*
< 8* 10-* < 10-1, t. e.
18
P cos x dx
cos x
Я/2
1541. Оценить интеграл J 3*05’х‘
о
Л Поскольку 0 < cos’ х < 1, имеем
я/2
1 1 ^.1 а_ С dx л
8 **5+3cos’x** 5 " 16** J 5+3cos’х*5 10'
о
1
1542. Вычислить J хе~х dx.
о
А Воспользуемся методом интегрирования по частям. Положим и = х, dv=e~xdx,
откуда du=dx, v = — е~х. Тогда
I 1
С хе~х dx=— хе-* Р+С е-х dx=—е~1—е~х I ——2е~’+1=——.
J |о J Ю е
1543. Вычислить Ji^dx.
1
Д Положим 1пх=/; тогда ^=dt; если х=1, то / = 0; если х=е, то / = 1
Следовательно,
е
1
f /’Л= */з|1=4(г-°з)=1
J V 10 V д
1
1544. Вычислить J Иг*—x*dx.
о
245
& Положим x = rsin/; тогда dx—r cos tdt; если x = 0, то / = 0; если x=r,
то 1=п/2. Поэтому
г л/2 л/2
р^г2—х2 dx = J У г2—г2 sin2/ г cos t dt=r2 j cos2 tdt =
оо о
Л/2
e=-^-r2 J (l+cos2/)d/ =-y r2 p4-i-sin2/1 ' =s
о
=5 [(y+4sinii)-(o+4sino)]=4-- a
Л/3
1545. Вычислить / = t —*”* dx.
J COS2 X
-л/3
л/3
C x sin x
Л Подынтегральная функция—четная, а потому 1 = 2 \ COs2 x ^x' Интегрн-
o
. sin xdx . . 1 ~
руем по частям, полагая u — x, dv=-3; тогда du = dx, v =-. Отсюда
cos2x ' cosx
находим
л/3 л/3
C xsinx __ X |л/з_ Г dx п /х_ л.^|я/3_
J cos2 х cos х |о J cos х 3 cos (л/3) n®’V2-‘"47lo
о о ' 1
2л , . л 2л , . бл
B=T_lnt^_+_j+lntg_=___infg_,
Следовательно, 1 = 2
1546. Вычислить /=
J / 1+х2
— 1
А Подынтегральная функция—нечетная, следовательно, 1 = 0. Д
1
1547. Вычислить Jxdx как предел интегральной суммы,
о
1
1548. Вычислить ^^dx как предел интегральной суммы,
о
1
1549. Оценить интеграл $х(1—x)2dx.
о
л/2
1550. Оценить интеграл J es,n'xdx.
о
л
1551. Оценить интеграл С ^^dx.
Л/2
Вычислить интегралы!
з I
1552. f х3 dx. 1553.
J J 1 T x
1 0
2 I
1554. J^dx. 1555. p*+e*dx.
i о
ея/2 л/6
1556. f cos Inxdx. 1557. f S-^dx.
tj COS X
1 0
2 In 2 2Л
1558. C dx-.-. 1559. C cos5xcosxdx.
J ex—1 J
In 2 о
л/3 Л/4
1560. C cos3xsin2xdx. 1561. j i^cosx^**
о 0
2 Я/2
1562. 1563. С e*cosxdx.
J x3+x J
1 0
3 I
1564. {X^ly~dx. 1565. Cx arctgxdx.
J x2+l J
-3 -I
• Использовать свойство иечет- ф Использовать свойство четной
ной функции. функции.
1566. Доказать, что
Л
f , 10 при т # п,
\ sin mx sin nxdx=< F '
J [ л при fn = fl
-л
(т и п—целые положительные числа).
§ 2. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
1. Основные понятия. Несобственными интегралами называются: 1) интег-
ралы с бесконечными пределами; 2) интегралы от неограниченных функций.
Несобственный интеграл от функции / (х) в пределах от а до —00 опреде-
ляется равенством
+ ® 6
f f(x)dx= lim {f(x)dx.
J b-++ 00 V
a a
Если этот предел существует и конечен, то несобственный интеграл назы-
вается сходящимся', если же предел не существует или равен бесконечности,—рас-
ходящимся.
Аналогично,
b ь +» ь
f f(x) dx= lim f f(x) dx и f f (x) dx= lim f f (x)dx.
J a~* — oo J J д - да J
-® a -a> b^. + a>a
247
Если функция f (х) имеет бесконечный разрыв в точке с отрезка [а, 6] и непре-
рывна при а < х< с н с < х < й, то по определению полагают
Ь с-а ь
f/(x)dx=lim С /(x)dx+ lim f f(x)dx.
J a->0 J B->0 J
a a p c+3
b
Несобственный интеграл f (x) dx (где f (с) = оо, a < с < b) называется cxo-
a
дящимся, если существуют оба предела в правой части равенства, и расходящим-
ся, если не существует хотя бы один из них.
+ 00
1567. Вычислить несобственный интеграл cosxdx (или устаио-
о
вить его расходимость).
Л Имеем
ь
lim \ cosxdx = lim sinx = lim (sin b—sinO) = lim sin ft,
b-*- +00 q b-* +00 10 b—*• + oo b-> + co
т. e. предел ие существует. Следовательно, несобственный интеграл расходится. А
-1
“2-
— оо
Л Найдем
-I
т. е. несобственный интеграл сходится. А
1569. Найти С , г-.
J 1+х2
Л Подынтегральная функция—четная.
dx
C dx _
J T+^- Тогда
0
ь •
Г dx . |ь , л
\ ТТ „2 = lim arctgx = lim arctg&=—.
J i “I x /)—>4-00 I® 1)—>4 00 *•
C dx
) 1 -4- y2 ~
g I ( "r Q _ T . iz—r T
+ ao
- C dx . м
Таким образом, \ > у = л, т. е. несобственный интеграл сходится. Д
1570. Найти
J х
о
Д Подынтегральная функция f(x) — \/x в точке х=±0 неограничена, а по-
тому имеем
dx .. С dx
—— lim \ —
х а_оJ х
= lim In x =lim(lnl — lna) = + oo,
o-<-0 1“ a-*0
a
0
т. e. несобственный интеграл расходится. A
248
1571. Найти j хе~х'dx.
о
Д Имеем
+ со Ъ
С xe~x‘dx = lim \xe~x2dx = lim Г — 4-«_дг21„= . l'm (~п----<ye~bi
J ь-»+®1 2 Jo 6-*+® \ *
t. e. несобственный интеграл сходится. Д
Вычислить несобственные интегралы:
+ 00 0
1572. 1574. С ^ xdx J l-j-х2 ах- 0 2 (* x’dx 1573 С dx .
J ,4+*2 ' -> 30 1 1575 С dx 157fi 1 f dx
J К4—х2 ‘ 0 J J/x(l -X) J *2 -1
1 + 00
1577. J х In2 х dx. 0 1578 C dx
J (x2+l)(x2 + 4)' — 00
2. Признаки сравнения. При исследовании сходимости несобственных интег-
ралов пользуются одним из признаков сравнения.
1. Если функции f (х) и <р(х) определены для всех х^а и интегрируемы на
отрезке [а, А],, где А^а, и если 0</(х)<ф(х) для всех х^а, то из сходи-
+ 00
мости интеграла J (р (x\dx вытекает сходимость интеграла J f (г) dxt причем
а а
+ « + 00
f (х) dx < J ф (х) dx.
а а
2. (а) Если при х—>•+» функция f (х)Э»0 является бесконечно малой по-
+ ®
рядка р > 0 по сравнению с 1/х, то интеграл f (x)dx сходится при р > 1 и
а
расходится при р < 1.
(б) Если функция f (х)^0 определена и непрерывна в промежутке а^х < b и
является бесконечно большой порядка р по сравнению с 1/(6—х) при х—»-6—О,
Ь
то интеграл J f (x)dx сходится при р < 1 и расходится при р^1.
а
1579. Исследовать сходимость интеграла \
J хр
а
Л По определению
+ оо А
С lim [x~Pdx= lira Г—Ц-гХ
J ХР А->+со J А-»+а> L —Р-Н
а а
=----Ц-r lira A~p+i---------Ц-гй-/’
А
249
Допустим, что р> 1; тогда lim А~р+1 = 0. Значит, при р> 1 интеграл
Л-* + оо
+ 00
сходится. Пусть р< 1; тогда lim A~p+1 = оо, т. е. интеграл \ —- прир<1
Л->+оо V хР
а
расходится. Д
+ 00
1580. Исследовать сходимость интеграла J sin (х2) dx (интеграл
о
Френеля).
+ 00 +00
— С 1 С sin Т
Л Пусть тогда 1 sin (хг) dr. Представим стоящий
о о ' т
справа интеграл в виде суммы:
+ оо л/2 + оо
f sint. С sinx . . f sin х .
\ —z=dx= \ -^=ах + \ —— dr.
iJ Гт oJ
Первое слагаемое есть собственный интеграл, так как lim ^= = 0- а ко
х—о у х
второму применим интегрирование по частям, полагая и=1/К т, da = sinxdx:
+ 00 + 00 + 00 + 00
С sin т dr cos т I______1_ С cos г dr 1 Г* cos т dr
J У X У Г ) % U У Г3 2 J т3/2
л/2 ' ' п/2 л/2 ' л/2
+ оо
г, COS X 1 С dr
Последний интеграл сходится, так как з/2 С 3;2 , а интеграл 1 сходит-
л/2
+ оо
ся. Поэтому \ dr сходится на основании признака (2а), а следовательно,
о V ’
данный интеграл также сходится. А
+ 00
1581. Исследовать сходимость интеграла \ й.
J 1т*
1
Л Подынтегральная функция f (x) = l/(l+*10) в промежутке интегрирования
+ оо
меньше, чем <р (х) = 1/х10, а интеграл J является сходящимся. Следователь-
1
ио, данный интеграл также сходится.
ь
С* dx
1582. Исследовать сходимость интеграла \ —-г= (а<Ь).
J (° х)г
а
Л По определению
Ь Ь-8
\ тг--—= lim \ 7T-----— -------—- lim (b~x) /’+ll =
J (6—x)P e-,0 J (6—x)P —p-ple->o |a
a a
s=—Ц-Нтв~/’+,4------Ц-т (b~-а)~Р^г.
P— 1 8-0 1 — p+1
250
Если р < 1, то lims“/’+J = 0; если же р > 1, то lim е~/’+1 = оо; если, нако-
е—►(} е-+0
нец, р = 1, то
Ь-8
С dx . |Ь—8
lim \ т---=— limln(6—х) =оо,
е-о J Ь—х 8->о |а
а
b
С dx
Следовательно, при р< 1 интеграл J сходится, а при 1—рас-
а
ходится. A j
f* COS2 X
1583. Исследовать сходимость интеграла \ , dx.
О V 1-х2
Д'Подынтегральная функция является бесконечно большой при х—>-1.
Представим ее в следующем виде:
{, ч cos2 х 1 __ cos2 х
W ~ 3/7V * л/',-----— 3/7V ' л —и2/3 ’
у 1+* V 1 —х V 1+* —х'
т. е. порядок этой бесконечно большой функции при х—> 1 по сравнению с 1/(1—х)
равен р=1/3 < 1. Поэтому данный интеграл сходится на основании призна-
ка (26). А
• / 3 7“\
1584. Исследовать сходимость интеграла J * dx.
о е ~
Л Подынтегральная функция /(х) в промежутке интегрирования положи-
тельна и f (х) —► оо при х —► 0. Пользуясь теоремой об эквивалентных беско-
нечно малых, преобразуем числитель и знаменатель подынтегральной дроби; имеем
InG-f-p^ х)~х1/3, a esinx—l ~sinx при х—► 0, откуда
lim 1п(1 + т/х) = нт
х^о esmjc— 1 *-о х х->о х2/3
т. е. f (х) является бесконечно большой порядка р=2/3 по сравнению с 1/х. Сле-
довательно, по признаку (26) заданный интеграл сходится. А
Исследовать сходимость следующих несобственных интегралов:
1585. f (ill+i! dх 1586. C 1587. f x"c,ex Hr.
S r J « J +
4- CO + CD
1588. J fl—cosy)dx. 1589. j ±^dx.
i i
1590. —. 1591. f dx—.
J У x J tgx—x
о ev *_i о
§ 3. ВЫЧИСЛЕНИЕ ПЛОЩАДИ ПЛОСКОЙ ФИГУРЫ
Площадь криволинейной трапеции, ограниченной кривой у— f (х) [/ (х)^ 0],
прямыми х=а и х=& и отрезком [а, &] оси Ох, вычисляется по формуле
ь
S --=^f(x) dx.
а
251
Площадь фигуры, ограниченной кривыми y — fi(x) и у = 1г(х) [Л (х)</2(х)]
и прямыми х = а и х=Ь, находится по формуле
ъ
S = ^lfi(x)~fi(x)]dx.
а
Если кривая задана параметрическими уравнениями x=x(f), y=y(f), то
площадь криволинейной трапеции, ограниченной этой кривой, прямыми х=а,
х=Ь и отрезком [а, 6] оси Ох, выражается формулой
t,
S=^y(f)x' (0 dt,
tt
где и t2 определяются из уравнений a=x(/i), b=x(t2) [y(i)^G при
Площадь криволинейного сектора, ограниченного кривой, заданной в поляр-
ных координатах уравнением р = р(0) и двумя полярными радиусами 0 = а,
0=₽ (а < ₽), находится по формуле
s=4^p2rf0-
а
1592. Найти площадь фигуры, ограниченной параболой у—4х—х*
и осью Ох.
Л Парабола пересекает ось Ох в точках 0(0; 0) и М (4; 0). Следовательно,
4
S = J (4х—х2) dx= [ 2xs —-i-xs (кв. ед.). А
о L J
1593. Найти площадь фигуры, ограиичеииой параболой у = (х—Г<*
и гиперболой х2—i/2/2=l.
Л Найдем точки пересечения параболы и гиперболы, для чего решим сов-
местно уравнения этих кривых:
х2—^2^ ~’ или ,*4—4х3+4х2—4х-)-3=0.
Левую часть последнего уравнения можно разложить на множителе
(х—1) (х—3) (х2+1)=0, откуда Xi=l, х2=3 и #1 = 0, уа = 4. Таким образом,
заданные кривые пересекаются в точках А (1; 0) и В (3; 4) (рис. 43). Следовательно,
з
3 = J [/2(х2—1)—(х—l)2]dx=
1
^[х/^1+1п|х+Г^Й |]3-1[(х-1)3]? =
[з /8+1п(3+К'8)]-4=т+^? 1п(3+/8) « 4,58 (кв. ед.). А
1594. Вычислить площадь плоской фигуры, ограниченной одной
аркой циклоиды х=2 (/—sin t), у—2(1 — cos/) (см. рис. 5) и осью Ох.
252
Л Здесь rfx = 2(l—cos f) dt, a i изменяется от ^ = 0 до /2 = 2л. Следова-
тельно,
2л 2л
5=^ 22(1—соз02Л = 4^ (1—2 cos 7-|-cos2 t) dt =
о о
1595. Найти площадь плоской фигуры, ограниченной лемниска-
той p2 = 2cos20 (см. рис. 2).
Л Четвертой части искомой площади соответствует изменение 0 от 0 до л/4,
а потому
л'4
I Г* |л/4
S=4-~2 \ 2 cos 29 d0 = 2 sin 20 =2 (кв. ед.). А
о
Вычислить площади фигур, ограниченных заданными линиями:
1596. у = — х2, х4-{/ —2 = 0.
1597. у=16/х2, у—\7 — х2 (I четверть).
1598. у2 = 4х3, у = 2х2.
1599. ху = 20, х2-гу2 = 41 (I четверть).
1600. z/ = sinx, у = cosx, х = 0.
1601. у = 0,25х2, у = 3х—0,5х2.
1602. лт/ = 4К2, х- — 6х~г(/2 = 0, у = 0, х = 4.
1603. х= 12cos t + 5 sin i, z/ = 5cos/ — 12sin/.
1604. x = acos3/, y = asin3/.
1605. p = 4/cos(0—л/6), 0 = л/6, 0 = л/3.
1606. p = acos0, p = 2acos0.
1607. p = sin2 (0/2) (справа от луча 0 = л/2).
1608. p = asin30 (площадь одной петли).
1609. P = 2cos0, р = 1 (вне круга р=1).
253
§ 4. ВЫЧИСЛЕНИЕ ДЛИНЫ ДУГИ ПЛОСКОЙ КРИВОЙ
Если кривая y=f (х) на отрезке [а, 6]—гладкая (т. е. производная у' —f (х)
непрерывна), то длина соответствующей дуги этой кривой находится по формуле
ь ________
L = J Vl + y’*dx.
а
При параметрическом задании кривой x=x(f), y—y(t) [x(f) и у (t)—непре-
рывно дифференцируемые функции] длина дуги кривой, соответствующая моно-
тонному изменению параметра t от до /2, вычисляется по формуле
_____
6
Если гладкая кривая задана в полярных координатах уравнением р = р (0),
а<0<Р, то длина дуги равна
L = J /p2 + p'2d0.
а
1610. Найти длину дуги кривой у2 — х3 от х — 0 до х=1 (г/^0).
Л Дифференцируя уравнение кривой, найдем / = (3/2) х1'2. Таким образом,
1611. Найти длину дуги кривой x = cos5/, y = sin5/ от /2 = 0 до
tt = л/2.
Л Найдем производные по параметру t: х =—5cos4/sin/, y=5sin4fcost
Следовательно,
Л/2 Л/2
L = J У (—5 cos4 t sin t)2 -|- (5 sin41 cos t)2 dt = 5 J sin t cos t У sin* i+cos° t dt =
о 0
Л/2 __________ Л/2
j sin 2/ |/ 1-l-y cos22/Л =—у j У1 + 3cos22/d(cos2/) =
0 0
5 Г1/"*Я ______— 1 — “1 л/2
=— -Ц^соз2// 1+3COS22/+4 ln(/3.COS2/+/1+3cos22t) =*
О У О I £> £> JO
__5Го In (2-/3)1 .
8[ y~3
1612. Найти длину дуги кривой р = sin3 (0/3) от 0Х = О до 02 = Л/2.
254
л Имеем р'= sin2 (0/3) cos (0/3). Следовательно,
L
Г j/^sin*f-f sin2cosd0= У sin2-|-d0 =
о 4 о
Л/2
z j \ о / z l а о j о о
О
Вычислить длины дуг кривых:
1613. y = lnsinx от х = л/3 до х = л/2.
1614. у = (2/5) х у/х—(2/3) у/х3 между точками пересечения
с осью Ох.
1615. у = х3/2 от х = 0 до х==1.
1616. у=1—Incosx от х = 0 до х = л/6.
1617. y = chx от х = 0 до х=1.
1618. x=ts/3—t, y = t3-\-2 от / = 0 до t = 3.
1619. x = e*cos/, у = е*sint от / = 0 до / = 1пл.
1620. x = 8sin/-|-6cos/, r/ = 6sin/—8cos/ от / = 0 до t = n/2.
1621. х = 9(/—sin/), г/ = 9(1—cos/) (длину дуги одной арки
циклоиды).
1622. р = 02 от 0 = 0 до 0 = л.
1623. p = asinO.
1624. р = a cos3 (0/3) от 0 = 0 до 0 = л/2.
1625. р= 1—cos0.
§ 5. ВЫЧИСЛЕНИЕ ОБЪЕМА ТЕЛА
1. Вычисление объема тела по известным площадям поперечных сечений.
Если площадь сечения тела плоскостью, перпендикулярной оси Ох, может быть
выражена как функция от х, т. е. в виде S = S(x) (а <;х <;/>), то объем части
тела, заключенной между перпендикулярными оси Ох плоскостями х=а и x=bt
находится по формуле
Ь
V= J S(x)dx.
а
2. Вычисление объема тела вращения. Если криволинейная трапеция, огра-
ниченная кривой y=f(x) и прямыми у = 0, х = а, х=Ь, вращается вокруг оси Ох,
то объем тела вращения вычисляется по формуле
ь
Vx= п J у2 dx.
а
Если фигура, ограниченная кривыми У1 = /у(х) и y2 = f2(x) [0< fy (х)< f2 (х)]
и прямыми х = а, х=Ь, вращается вокруг оси Ох, то объем тела вращения
ь
Vx=n (уг2~yi) dx.
а
255
1626. Найти объем тела, образованного вращением вокруг оси Ох
фигуры, ограниченной кривой д/2 = (х—I)3 и прямой х = 2 (рис. 44).
2 2
Л У = л J y2dx = rt § (х—l)3dx=-^-л (х—I)4 | =-^- л (куб. ед.). А
1 1
1627. Найти объем тела, в основании которого лежит равно-
бедренный треугольник с высотой h и основанием а. Поперечное
сечение тела есть сегмент параболы с хордой, равной высоте сег-
мента (рис. 45).
ДИмеем |ЛВ| = а, |ОС|=Л, | МК | = | DE |, | ОК | = х. Выразим площадь
поперечного сечения как функцию от х, для чего предварительно найдем уравне-
ние параболы. Длину хорды DE можно найти из подобия соответствующих тре-
угольников, а именно: | DE \/а— (h—x)/h, т.е. |О£| = а(й—х)/Л = |Л4К|.
Положим |D£| = m, тогда уравнение параболы в системе координат uKv
4
примет вид v=m — — и2. Отсюда находим площадь поперечного сечения данного
тела:
т/2
С ! 4 \ 9 2 a2 (h— х)2
S = 2 I (т—-и2] du =4 т2, или S (х)=-=-. -- А , .--2-.
J \ mJ 3 3 h2
о
Таким образом,
h h
V = ^S(x)dx = ^.-^(h-x-)2dx=~a2h. А
о о
Найти объемы тел, образованных вращением вокруг оси Ох фи-
гур, ограниченных линиями:
1628. 2641fi , х2 = 8и.
47 х2+16 ’ у
1629. г/2 = х, х2 = у.
1630. у = Ухё*, х= 1, у = 0.
1631. у = хг!2, у = х31$.
256
1632. Найти объем тела, ограниченного
плоскостями х=1, х — 3, если площадь его
поперечного сечения обратно пропорциональ-
на квадрату расстояния сечения от начала
координат, а при х = 2 площадь сечения рав-
на 27 (кв. ед.).
1633. Найти объем цилиндрического кли-
на по его размерам, указанным на рис. 46
(задача Архимеда).
1634. В цилиндрический стакан с водой
вложен параболоид вращения вершиной вниз.
Основание и высота параболоида совпадают
с основанием и высо-
той цилиндра. Найти объем оставшейся в стакане воды, если ра-
диус основания равен г, а высота равна h.
§ 6. ВЫЧИСЛЕНИЕ ПЛОЩАДИ ПОВЕРХНОСТИ ВРАЩЕНИЯ
Если дуга гладкой кривой y = f(x) (а<х^Ь) вращается вокруг оси Ох, то
площадь поверхности вращения вычисляется по формуле
b _______
Sx — 2л у У \-\-y'2 dx.
а
Если кривая задана параметрическими уравнениями х = х (/), у = у (/) (Zi <
то
^2 _____
Sx = 2л у У х2-\- у2 dt.
tt
1635. Найти площадь поверхности, образованной вращением вокруг
оси Ох дуги синусоиды у = sin 2х от х = 0 до х = л/2.
А Находим у' = 2 cos 2х; тогда
л/2
Sx=2n sin 2х У1 -]-4 cos2 2х dx.
о
Произведем замену переменной: 2cos2x = Z, — 4 sin 2xdx — dt, sin 2xdx — (—1/4) di.
Найдем пределы интегрирования no t: если х=0, то /=2; если х = л/2, то
i=i—2. Таким образом,
-2 2
S —2л j уТТ*5 (-!)<«=-£ J /7+72^ =
2 -2
=т[4 /ЙН2+11п(^+ГТ+72)]12 =
= У 5+4 1п£|±|)=4 [2 У 5 + 1П (К5 + 2)] (кв. ед.). А
Найти площади поверхностей, образованных вращением вокруг
оси Ох дуг кривых:
1636. t/ = 2ch(x/2) от х = 0 до х = 2.
1637. у — х3 от х = 0 до х— 1/2.
257
1638. х*1аг + уг1& =1.
1639. x—t—sin/, i/=l—cos/ (площадь, образованную враще-
нием одной арки).
§ 7. СТАТИЧЕСКИЕ МОМЕНТЫ И МОМЕНТЫ ИНЕРЦИИ
ПЛОСКИХ ДУГ И ФИГУР
Пусть на плоскости хОу задана система материальных точек Ai (xj; t/i),
А2(х2; у2)...А„(х„; уп) с массами mlt тг, т„. Статическим моментом Мх
этой системы относительно оси Ох называется сумма произведений масс этих точек
на нх ординаты:
k=n
мх = 2
*=1
Аналогично (как сумма произведений масс точек на нх абсциссы) определяется
статический момент системы относительно оси Оу.
k=n
Ми= 2 т*х*-
k= 1
Моментами инерции 1Х н 1у системы относительно осей Ох н Оу называются
суммы произведений масс точек на квадраты нх расстояний от соответствующей
осн. Таким образом,
k—n
k=i k=i
За статические моменты и моменты инерции плоских дуг н фигур принима-
ются соответствующие моменты условных масс, равномерно распределенных вдоль
этих дуг н фигур с плотностью (линейной или плоскостной), равной единице.
Статические моменты н моменты ннерцнн дуги плоской кривой у=/(х)
(а<х<&) вычисляются по формулам
6 b b Ь
Mx=^ydL; My=^xdL; fx=^ytdL; Iy=^xidL,
a a a a
где dL = y l+y'2dx—дифференциал дуги кривой.
Статические моменты н моменты инерции криволинейной трапеции, ограничен-
ной кривой y=f(x), осью Ох и двумя прямыми х—а и х = Ь, вычисляются по
формулам
b ь ь ь
Мх = ±- ^ydS=^^yidx, Му = ^ xdS= xydx,
а а а а
b b b
Ix=±-{y3dx, /„= С x3dS={ x*ydx.
О <J * J J
a a a
В этих формулах dS = ydx—дифференциал площади криволинейной трапеции.
1640. Найти статический момент и момент инерции полуокруж-
ности у = Угг—хг (—г^х^г) относительно оси Ох.
ь
Д Статический момент Мх будем вычислять по формуле Mx=^ydL, где
а
258
dL = V \~]-yrtdx, yr = — х/Уr2—x2. Тогда получим
г____________________________________________г
мх= § /г2—х2 у dx=r dx=2r*-
-г -г
Находим момент инерции относительно оси Ох:
ь г____________
Ix = ^y2dL=^ (r2-x2) j/ \+-p^dx~
а —г
г г
= г Уr2-—x2dx = 2r J У r2—x2dx.
-г О
Введем подстановку x = rsln/, dx = r cos/dt', если x = 0, то / = 0; еслих=г,
то t=^n./2. Следовательно,
Л/2
1х = 2г У г2—г2 sin2 / г cos / <//=
о
Л/2
р Г 1 1 л/2 №
= т3 \ (l-|-cos2/)d/ = r3 /-]-—sin2/ =—<j—• А
о
1641. Найти момент инерции площади эллипса x = aco3t,
y = bsint относительно оси Оу.
а
Л Момент инерции площади эллипса относительно оси Оу равен Iy = х2 dS,
—а
где dS = 2ydx. Из параметрических уравнений эллипса находим dS = 2b sin tX
Ха (— sin /) dt = —2аЬ sin21 dt, откуда
о о
/j, = 2 a2cos2/(—2ab sin2 t) dt = — 4a3b J sin2 t cos2 t di =
л/2 Л/2
Л/2
1 С „ л t\ jj Tta3b
=-^-a3b \ (1—cos4/)d/=—7—. A
2 J 4 е
о
1642. Найти статические моменты и моменты инерции дуги астро-
иды x — acos3t, y = asiri3t, лежащей в I четверти (рис. 47).
Л В силу симметрии астроиды относительно координатных осей Mx = Myt
1х = 1у. Поэтому достаточно вычислить моменты относительно оси Ох. Для I чет-
верти имеем 0</<л/2. Находим
dL = х'*-\-у'* dt = За sin t cos t dt^
b л/2 л/2
Mx = § ydL — J a-sin3/-Sesin t cos t dt—-^- sin61 | =-|-a2(
a о о
b n/ч Л/2
/л=\ t/2dL= C a2sin3/-Заsin/cos/d/ = 4-a3sin8/ =4-a3.
J J О | о
a 0 0
Итак, Mx = My = (3/5) a2; Ix = ly = (3/8) a3. Д
259
1643. Найти момент инерции параболического сегмента, у кото-
рого хорда равна а, а стрелка относительно хорды равна h (рис. 48).
Д Имеем | АВ\ = а, |ОС|=/г. Уравнение параболы записывается в виде
y = h— .\'х2, где неопределенный коэффициент N можно найти, пользуясь тем, что
точка В(а,2; 0) принадлежит параболе: 0 = Л — Nd2/4, или N = 4h/a2; следова-
тельно, y = h—4/ix2,a2. Теперь находим искомый момент инерции:
/х=у S (h~^ х2У dx=xiah3-
-а 2 0
1644. Найти статический момент и момент инерции дуги цепной
линии z/ = y (еЛ/а + е-Л' а), где 0<Ух<Уа, относительно оси Ох.
1645. Найти статический момент и момент инерции треугольника
с основанием а и высотой h относительно его основания.
1646. Найти момент инерции параболического сегмента, ограни-
ченного параболой г/ = 4 — х2 и прямой z/ = 3, относительно оси Ох.
1647. Найти момент инерции прямоугольника со сторонами а и b
относительно осей симметрии прямоугольника.
1648. Найти полярный момент инерции круга диаметра d, т. е.
момент инерции относительно оси, проходящей через центр круга
и перпендикулярной его плоскости.
§ 8. НАХОЖДЕНИЕ КООРДИНАТ ЦЕНТРА ТЯЖЕСТИ. ТЕОРЕМЫ ГУЛЬДЕНА
Координаты центра тяжести однородной дуги плоской кривой у = /(х)(а^
sCx<b) выражаются формулами
ь
ь
У =
а
а
где dL = l//'l ~i~y'S dx, a L — длина дуги.
Координаты центра тяжести криволинейной трапеции вычисляются по формулам
У =
а
а
х = \ х dS = \ xydx,
J J □ J
а а
где dS = ydx, a S — площадь фигуры.
Теоремы Гульдена
Теорема 1. Площадь поверхности, полученной при вращении дуги плоской
260
кривой вокруг оси, лежащей в плоскости этой кривой и не пересекающей ее, равна
длине дуги кривой, умноженной на длину окружности, описанной центром
тяжести дуги.
Теорема 2. Объем тела, полученного при вращении плоской фигуры вокруг
оси, не пересекающей ее и расположенной в плоскости фигуры, равен произведению
площади этой фигуры на длину окружности, описанной центром тяжести фигуры.
1649. Найти координаты центра тяжести дуги цепной линии
y = ach(x/a), —as^xs^a.
Д Так как кривая симметрична относительно оси Оу, то ее центр тяжести
лежит иа оси Оу, т. е. х = 0. Остается найти у. Имеем у' = sh(x/a); тогда dL =
= У1 + sh2 (х/а) dx = ch (х/а) dx-, длина дуги
а а а
L— § У 1 -j-y'1 dx — 2 § ch dx = 2a sh | =2ash 1.
-а о о
Следовательно,
a a a
У=п * , V a ch2 -dx = -^-r C ch2— = f ( 1 -|-ch — dx =
2a sh 1 J a sh 1 J a 2 sh 1 J V 1 a j
-а о o'
1 Г . a , 2x|o a ( . 1 \ a(2+sh2) , 1O .
s=n~Tznr I Н’тт’sh — I == n t_ г I I *4““л* sh 2 ) ... i_ . & 1,18л»
2sh 1 [ * 2 a Jo 2sh 1 \ 1 2 / 4shl ’
1650. Найти координаты центра тяжести фигуры, ограниченной
дугой эллипса x = acos/, у —bsmt, расположенной в I четверти,
и осями координат.
Д В I четверти при возрастании х от 0 до а величина t убывает от л/2
до 0; поэтому
а 0
- 1 С 1 с
х=-$ \ xydx=-§- \ acos f.ftsin t (— asin f)dt —
0 л/2
Л/2 л/2
a26 (* . , • .. aab 1 . a*b
=— J s>nt<cos<^=^-3-sin3/ =35-
о 0
Воспользовавшись формулой площади эллипса S — nab, получим "х =
= (4a26)/(3naft) = (4a)/(3n).
Аналогично находим
а 0
*2sin2/(— asint)dt =
ZO U Z<j %)
0 Л/2
0
2ab2 С/, ,л./ л 26 Г t 1 1,1° 46
&---Г- \ (1—cos2 /) d (cos Л =- cos/----cos3 / .
nab J ' ' ' л I 3 Jn/2 3л
л/2 J
Таким образом, x=4a/(3n), у=46/(3л). A
1651. Найти площади поверхностей и объемы колец (торов),
образованных вращением круга (х—а)2 + (у—b)2^Zr2 вокруг осей Ох
и Оу (a^r, Ь^г).
Д Если круг вращается вокруг оси Ох, то центр тяжести круга отстоит от
оси вращения на, расстоянии Ь; поэтому площадь поверхности, согласно первой
2^1
теореме Гульдена, равна Sx = 2w-2nb=4n2br, а объем, согласно второй теореме
Гульдена, равен Ух = лг2-2лЬ = 2я2Ьг2.
Если же вращение производится вокруг оси Оу, то расстояние центра тяжести
круга от оси Оу равно а. Тогда 8у = 2яг-2яа=4я2аг, Уу=яг2-2яа = 2я2аг2. Д.
1652. Пользуясь теоремой Гульдена, найти координаты центра
тяжести четверти круга х2 + у2^г2.
Д При вращении четверти круга вокруг осн Ох получим полушар, объем
которого равен Г = (1/2)-(4лг3/3) = 2лг3/3. Согласно второй теореме Гульдена,
V = (№/4)-(2m/). Отсюда y = 2V/(n2r2) = 2-2лг3/(Зл2г2) =4г/(3л). Центр тяжести
четверти круга лежит на оси симметрии, т. е. иа биссектрисе I координатного
угла, а потому х=у=4г/(3л). А
1653. Найти координаты центров тяжести полуокружности у —
= Kr2—х2 и полукруга, ограниченного этой полуокружностью и
осью Ох.
1654. Найти координаты центра тяжести фигуры, ограниченной
линиями х — 0, х — л/2, у = 0, y = cosx.
1655. Найти координаты центра тяжести параболического сег-
мента, ограниченного линиями у==4—х2, у — 0.
1656. Найти координаты центра тяжести дуги астроиды х —
= a cos3/, у —a sin31 (в I четверти).
1657. Найти координаты центра тяжести фигуры, ограниченной
линиями у = 2х—х2, у — 0.
1658. Найти координаты центра тяжести фигуры, ограниченной
линиями х = 0, х = л/2, у = 0, y = sinx.
1659. Пользуясь теоремой Гульдена,-^найти объем тела, образо-
ванного вращением полукруга радиуса г вокруг касательной, парал-
лельной диаметру.
1660. Пользуясь теоремой Гульдена, доказать, что центр тяжести
треугольника отстоит от его основания на одну треть высоты.
• Найти объем тела, полученного вращением треугольника вокруг основания.
1661. Пользуясь теоремой Гульдена, найти объем тела, получен-
ного при вращении прямоугольника со сторонами 6 и 8 вокруг оси,
проходящей через его вершину перпендикулярно диагонали.
§ 9. ВЫЧИСЛЕНИЕ РАБОТЫ И ДАВЛЕНИЯ
Работа переменной силы X = f(x), действующей в направлении оси Ох иа
отрезке [х0, xj, вычисляется по формуле
Xt
А = J / (х) dx.
Для вычисления силы давления жидкости используют закон Паскаля, согласно
которому давление'жидкости на площадку равно ее площади S, умноженной на
глубину погружения h, на плотность р и ускорение силы тяжести g, т. е.
P = pghS.
1662. Какую работу надо совершить, чтобы растянуть
262
пружину на 4 см, если известно, что от нагрузки в 1 Н она
растягивается на I см?
Д Согласно закону Гука, сила X Н, растягивающая пружину на х м, равна
X = kx. Коэффициент пропорциональности k найдем из условия: если х=0,01 м,
то X=l Н; следовательно, k— 1/0,01 = 100 и Х=100х. Тогда
0.04 ' 0,04
Л = J 100* dx = 50х2 =0,08 Дж. Д
о о
1663. С помощью подъемного крана извлекают железобетонную
надолбу со дна реки глубиной 5 м. Какая работа при этом совер-
шается, если надолба имеет форму правильного тетраэдра с ребром
1 м (рис. 49)? Плотность железобетона 2500 кг/м3, плотность воды
1000 кг/м3.
Д Высота тетраэдра h=y 6/3 м, объем тетраэдра V— У 2/12 м3. Вес
надолбы в воде с учетом действия архимедовой силы равен
Р = (1/12)-/2-2500.9,8— (1/12)-/2-1000.9,8= 1225 /2 (Н),
поэтому работа при извлечении надолбы до момента появления на поверхности
воды ее вершины составляет
Ло=1225/ 2(5—h) = 1225/ 2(5—/ 6/3) к 7227,5 (Дж).
Теперь найдем работу Af при извлечении надолбы из воды. Пусть вершина
тетраэдра вышла на высоту 5+«/; тогда объем малого тетраэдра, вышедшего из
воды, равен 3 / 3//8, а вес тетраэдра
Р (у) = 25°”29-- К 2- (1 / 2-1 у33 / з). 1000-9,8.
Отсюда A = A0 + Ai = 7227,5 Дж+2082,5 Дж = 9310 Дж = 9,31 кДж. Д
263
1664. Найти работу, совершенную при выкачивании воды из
корыта, имеющего форму полуцилиндра, длина которого а, радиус г
(рис. 50).
Л Объем элементарного слоя воды, находящегося на глубине х и имеющего
длину а, ширину т = 2У г2—х- и толщину dx, равен
dV = am dx = 2а У г2 — х2 dx.
Элементарная работа, совершаемая при поднятии этого слоя воды на высоту х,
равна dA — 2pgax У г2 — х2 dx, где р — плотность воды. Следовательно,
Г
A = 2pga\ xV72~^2dx = —pga f(г2 — х2)я ' 1 =ypgar3. ▲
0
1665. Водопроводная труба имеет диаметр 6 см; один конец ее
соединен с баком, в котором уровень воды на 1 м выше верхнего
края трубы, а другой закрыт заслонкой. Найти силу давления на
заслонку.
Л Заслонка представляет собой круг радиуса 0,03 м. Разобьем площадь
этого круга на элементы — полоски, параллельные поверхности воды. Площадь
одного такого элемента, находящегося на расстоянии у от центра, равна (с точ-
ностью до бесконечно малых высшего порядка) (/5 = 2^9—у2 dy. Найдем силу
давления, испытываемую этим элементом:
dP = 2pg(l,03 —у) V2^y2dy= 19600 (1,03—у) dy
(здесь р=1000 кг/м3). Следовательно,
з
Р=19600 (1,03—y)}/'T^y2dy =
-з
=» 19600 [ 1,03 КЭ^+4 arcsin j) +у <9-</2)3/2]’_3«
= 9 800-9,27л « 0,09л Н. £
1666. Найти силу давления воды на вертикальную стенку в форме
полукруга, диаметр которого 6 м и находится на поверхности воды
(рис. 51). Плотность воды р= 1000 кг/м3.
Д Дифференциал силы давления на элементарную площадку выразится так:
dP — 2pgx У 9—х2 dx — 19600х j/"9 — х2 dx.
Отсюда
з
Р=19600 ^хКЭ^Л=-^-Ц^(9-х2)3/2
О
3
= 176 400 Н-176,4 кН. Д
о
1667. Найти силу давления бензина, находящегося в цилиндри-
ческом баке высотой h — 3,5 м и радиусом основания г = 1,5 м, на
его стенки, если р = 900 кг/м3.
Л Элемент силы давления на поверхность стенки в выделенной полоске
выразится так: dP = pg-2.irx dx. Отсюда
Л
Р = 2лгр§ J xdx = npgrh2 = 9,8л-1,5-3,52-900 Н=161 700л Н = 161,7л кН. А
о
264
1668. Какую силу давления испытывает прямоугольная пластинка
длиной а и шириной b (а > Ь), если она наклонена к горизонтальной
поверхности жидкости под углом а и ее большая сторона находится
на глубине h (рис. 52)?
Л Площадь выделенной ва глубине х элементарной полоски равна dS =
= (a/sin a) dx. Следовательно, элемент силы давления dP = (axpg/sin a) dx (р —
плотность жидкости). Отсюда находим
ft+6 sin а
P=apg §
ft
xdx
sin а
h+b sin а
gpg 1 »
sin а ’ 2
ft
2S&-[^+2bh sin a+Z>* sin*a)—ft*] =
1669. Найти силу давления на пластин-
ку, имеющую форму равнобочной трапеции с основаниями а и b и
высотой h, погруженную в жидкость на глубину с (рис. 53).
- Д Площадь элементарной полоски выражается так: dS = (a+2/)dx, где / =
= (Ь—а) (х—с)/(2Л) (I определяется из подобия треугольников). Следовательно,
С
=[^-^сА+4"(а+26)] р^- а
1670. Найти работу, совершаемую при выкачивании воды из
конического сосуда, основание которого горизонтально и располо-
жено ниже вершины, если радиус основания равен г и высота
равна h.
1671. Из цилиндрической цистерны выкачивается жидкость.
Какую работу надо совершить при этом, если длина цистерны
равна а, а диаметр равен d?
1672. С помощью каната подъемным краном из воды поднимают
камень конической формы. Найти работу, совершаемую при полном
извлечении камня из воды, если вершина конуса находилась на
265
поверхности воды. Радиус основания конуса 1 м, высота 3 м, плот-
ность 2500 кг/м3.
• Здесь Р (у) = 14700+(9800/27) га/3, где Р выражается в ньютонах.
1673. Чугунный прямой конус высотой 0,4 м и радиусом осно-
вания 0,4 м находится на дне бассейна, наполненного до краев неф-
тяным маслом. Найти работу, которую надо совершить при извле-
чении этого конуса из бассейна, если плотность чугуна рх = 7220 кг/м3,
а плотность нефтяного масла ра = 890 кг/м3.
• Здесь Р (у) равна весу конуса без веса нефтяного масла, вытесненного
частью конуса, т. е. Р (у) = 4- n-0,43pig—(-=-л-0,43—т ЛУ3 ) Pag. где Р выра-
О \ о о У
жается в ньютонах.
1674. Цилиндрический баллон диаметром 0,24 м и длиной 0,8 м
наполнен газом под давлением 2 кПа. Какую работу надо совершить
при изотермическом сжатии газа до объема, в два раза меньшего?
1675. В жидкость с плотностью р погружена треугольная пла-
стинка вершиной вверх. Найти силу давления жидкости на пла-
стинку, если основание треугольника равно а, высота равна h. Вер-
шина треугольника расположена на поверхности.
1676. Найти силу давления бензина, находящегося в цилиндри-
ческом баке высотой й = 4 м и радиусом г —2 м (р = 900 кг/м3),
на стенки бака на каждом метре глубины.
1677. В жидкость с плотностью р погружена круглая пластинка
диаметром d, касающаяся поверхности жидкости. Найти силу дав-
ления жидкости на пластинку.
Составляя соответствующие интегральные суммы н производя
предельный переход, решить следующие задачи:
1678. Найти массу стержня длины 1 м, если линейная плотность
стержня меняется по закону 6 = 20х + 0,15х2, где х—расстояние от
одного нз концов стержня, в м; 6—в кг/м.
1679. Скорость точки меняется по закону v =100 + 8/ (где v
выражается в м/с). Какой путь пройдет эта точка за промежуток
времени ГО, 10]?
1680. Точка движется по оси Ох, начиная от точки М (1; 0),
так, что скорость ее равна абсциссе. Где она будет через 10 с от
начала движения?
1681. Скорость точки изменяется по закону о = 2(6—t) (где о
выражается в м/с). Каково наибольшее удаление точки от начала
движения?
§ 10. НЕКОТОРЫЕ СВЕДЕНИЯ О ГИПЕРБОЛИЧЕСКИХ ФУНКЦИЯХ
1. Гиперболические функции. Гиперболическими функциями называются функ-
ции, определяемые следующими равенствами:
ех_е-х
shx=-----5-----гиперболический синус,
266
chx =-------------гиперболический косинус.
sh х
thх = -г— — х I '-V—гиперболический тангенс,
сп х е "г е
.. chx е*4-е~х
cthх ~shx~~ex~ ё~*-------гиперболический котангенс.
Гиперболический косинус [является четной функцией, т. е. ch (—х) = ch (х),
а гиперболические синус, тангенс и котангенс являются нечетными функциями:
sh(—х) = —shx, th(—х) = —tgx, cth(—х) = — cthx.
Полезно иметь в виду, что
shO=O, ch 0=1, ch2x—sh2x=l,
th x cth x = 1.
Графики гиперболических
функций </=shx, y=chx и
y = thx изображены соответст-
венно на рис. 54—56.
Рис. 54 Рис. 55
График гиперболического косинуса называется цепной линией. Цепная линия
является линией провисания тяжелой нити, подвешенной в двух точках.
Производные гиперболических функций находятся по формулам
(sh x)z = ch х, (ch x)z = sh x, (th x)' = 1/ch2 x, (cth x)z = —1/sh2 x.
При интегрировании гиперболических функций используются формулы
J shхdx = chx-j-C, J chxdx=shx-j-C,
C-^- = thx+C, C-A-=—cthx+C.
J ch2x ' J sh2x 1
2. Обратные гиперболические функции. Для гиперболических функций shx,
ch х, th х, cth x обратные гиперболические функции определяются с помощью сле-
дующих формул:
arsh х — In (х-|- Yх2+ О (— оо < х < + оо)—гиперболический ареа-синус,
archx=±ln(x-|-^rx2—1) (х^= 1)—гиперболический ареа-косинус,
1 1 -I- х
arth х =-^- In —— (I х | < V)—гиперболический ареа-тангенс,
А 1 ~~Х
1 хЧ-1
arcthx=g- In - j(lx| > 1)—гиперболический ареа-котангенс.
Производные обратных гиперболических функций находятся по формулам
(arshx),=FrW (archx)'
(arth x)z = -|ЧХ2~ • <arcth *)' =-•
Обратные гиперболические и обратные тригонометрические функции связаны
между собой следующими соотношениями (в комплексной плоскости):
arshx = —fare sin xi; archx = iarccosx,
arthx = —jaretgxi; arcth x=i arcctgxt.
1682. Доказать справедливость равенства
sh (* + a) = sh x ch a + ch * sh a.
Л По определению гиперболического синуса имеем
e*+o_e-<x+o) ex-ea — e-x-e~a
sh (*H-a) =
2 ~ 2
Так как e* = ch*-}-sh*, e_* = ch*—sh*, e° = cha+sha, e-o = cha —she, to
sh (*4-a) (ch*+sh*) (chn-j-sha)—(ch*—sh*)(cho—she)
получаем
2
Выполнив алгебраические преобразования, получаем
sh (*+a) = sh*cha+ch*sha. Д
1683. Выразить ch(x + a) через гиперболические функции аргу-
ментов х и а.
Л Продифференцировав по * равенство
sh (*+e) = sh*cha-|-ch*sha,
ch (*-|-a) = ch*ch a-|-sh*sha. A
1684. Выразить sh2x и ch2x через shx и chx.
Л Имеем
sh 2* = sh (*+*) = sh*ch*+ch *sh*, ch2*=ch (*+*) = ch*ch*-|-sh*sh*,
T. e. sh 2x = 2 sh * ch *; ch 2* = ch2*-}-sh2*. A
1685. Выразить ch2 x и sh2x через ch2x.
Л Решив систему уравнений
Г ch2*+sh2* —ch 2*,
} ch2*—sh2*=l
относительно ch2* и sh2*, получаем
ch2*==(ch2*+l)/2, sh2*=(ch2*—1)/2. Д
1686. Выразить гиперболические функции chxi и shx»' мнимого
аргумента через sinx и cosx.
Л Находим
рх1_р-х1 pxi _p—xi е%1-Х-е“Х1
sh xi=--------— i---------- i sin *, ch xi — —---- cos *.
2 2t ’2
Итак, sh*t = isinx, chxi = cos*. A
1687. Выразить тригонометрические функции sinxi и cosx» мни-
мого аргумента через shx и chx.
Л Подставив в формулы sh*i = tsin* и ch*i — cos* (см. задачу 1686)
xi вместо *, получим sh*i2= i sin*i, ch*t2 = cos*i, т. e. sin*t = S =
= ishx, cosxi=ch(—*) = ch*. Итак, sin xi = i sh *, cosxt = chx. A
1688. Какая линия определяется параметрическими уравнениями
x=acht, y=askit при a>0?
Л Исключим из этих уравнений I, для чего из *2 вычтем у2:
*2—y2=a2(ch2/—sh2/), т. е. *2—у2=а2.
268
Кривая *•’—j/’жй4 является равносторонней гиперболой, асимптотами которой
служат прямые у— ± х, Данная кривая является правой ветвью этой гиперболы,
так как л-^och/ > 0 при любом i (рис. 57). £
1689. Точка М лежит на правой ветви равносторонней гиперболы
i/«=asht Из точки М опущен перпендикуляр MN на
ось абсцисс и эта же точка соединена отрезком ОМ с началом коор-
динат. Из вершины А гиперболы восставлен перпендикуляр АК до
пересечения в точке К с отрезком ОМ (рис. 58). Доказать, что
| NM |:a~shf, |OAT|:e-chf, | M|:a-th(.
Л | Л'Л! |;о wpia—sh t, | ON |:a=x:a = ch t,
|4A'|:e-»|M4|:|CW|«»(|JVAi|:e)/(|CW|;a)«»sh(/clU»th/. A,
1690. Точка M лежит на правой ветви равносторонней гиперболы
x*=-tich(, i/«=osh(. Вычислить площадь гиперболического сектора,
ограниченного ветвью гиперболы, осью абсцисс и отрезком ОМ
(рис. 59).
X
Л Имеем У^х. Так как x>«acht, p««esh<, то
а
dx«osh 1 dt, откуда
t t
S = A a1 sh Лей t —a3 sh’ / d/« у o’ sh 6ch t —y- f (ch 2t — 1) dt=*
b о
I 1 a* &Ч
•= 4 a’sh 2/-4-a’sh 2/+•=-/ - V.
4 4 2 2
Таким образом, t = 2S/a3. Итак, аргумент t гиперболических функций можно
рассматривать как частное от деления удвоенной площади гиперболического сек-
тора ОДА! на квадрат действительной полуоси. А
1691. Найти производные функций:
1) у = ln(chx + Kch’x+ 1); 2) ^ = 5sh3(x/15) + 3sh5 (х/15);
3) z/ = 2arctg (th (х/2)); 4) # = thx—j thsx-)--g-thsx;
5) у — arcctg (1/sh x); 6) z/ = lnth(x2/4).
269
1692. В какой точке цепной линии у — ch х касательная образует
с осью абсцисс угол а = л/4?
1693. Исследовать на экстремум функцию z/ = ch(x/2)— 1.
1694. Найти: 1) Jx2chxdx; 2)< J sh4xdx; 3) Jp^===dx;
4) Cshxsinxdx; 5) С /Ау-дл 6) ? sh3 (х/3) ch2 (х/3) dx.
• J •/ 1.11
1695. Вычислить определенные интегралы:
!п(1+У2) In 2 In 3
С ch х dx Г Г
1) J рч—X; 2) J th2xdr; 3) J xchxdr.
0 0 0
1696. Выразить sh (x—а) и ch (x—а) через гиперболические функ-
ции аргументов х и а.
1697. Выразить th(x+a) и th(x—а) через thx и th а. Найти th2x.
1698. Выразить через chx гиперболические функции половин-
ного аргумента sh(x/2), ch(x/2) и th(x/2).
1699. Привести к виду, удобному для логарифмирования, выра-
жения shx±shy, chx±ch^, thx±thi/.
1700. Выразить shx и chx через th(x/2).
1701. Представить произведения гиперболических функций
shxch^, shxsh#, chxchi/ в виде сумм.
1702. Вычислить площадь, ограниченную кривой z/ = shx и пря-
мыми х=1п5, у = 0.
1703. Найти длину дуги кривой y = ach (х/а), заключенной между
прямыми х = 0, х = а.
1704. На кривой x = acht, y = asht даны точки М и N, соот-
ветствующие значениям t — ti и t = Вычислить площадь
сектора 0MN.
1705. Какая линия определяется уравнениями x = a/cht, у —
= btht, если а>0, Ь>0?
1706. Какая линия определяется уравнениями x = ch21, y — sWf
1707. Дано sin а = th t. Выразить cos а и tga через t.
1708. Упростить выражение
(cos x ch у 4- i sin x sh y)2—(cos x sh у 4- i sin x cos y)2.
1709. Упростить выражение (x ch 14- у sh t)2—(x sh 14- у ch t)a.
1710. Доказать тождества:
(ch x 4- sh x)" = ch nx 4- sh nx; ch nx= <ch x+sh x)n + (ch * sh x)” .
shnx= (ch *+sh ~ (ch x—sh x)”
(gx_e~x)tt (ex-i-e~x)a
1711. Используя равенства sh"x = -——— ;сЬпх = 2—,
доказать, что
ch3 x = -j- ch 3x 4- 4- ch x, sh? x = 4 sh 5x —4 sh 3x 4- -4 sh x.
4 *4 lb 10 ‘0
ГЛАВА XI
ЭЛЕМЕНТЫ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
§ 1. ЛИНЕЙНЫЕ НЕРАВЕНСТВА И ОБЛАСТЬ РЕШЕНИЙ
СИСТЕМЫ ЛИНЕЙНЫХ НЕРАВЕНСТВ
Пусть задано линейное неравенство с двумя переменными и х2:
(1)
Если величины хх и хг рассматривать как координаты точки плоскости, то сово-
купность точек плоскости, координаты которых удовлетворяют неравенству (1),
называется областью решений данного неравенства. Областью решений неравен-
ства (1) является полуплоскость.
Для того чтобы установить, какая из двух полуплоскостей соответствует
неравенству (1), достаточно привести это неравенство к виду х2^kx^l или
к виду x2<Axi-|-/. В первом случае искомая полуплоскость лежит выше прямой
ajXi-|-a2x2+& = 0, во втором—ниже ее. Если же а2 = 0, то 'неравенство при-
водится к одному из видов Xi^sh или Xi^h, т. е. полуплоскость лежит справа
или слева от прямой xr = h.
В случае же, когда задана система неравенств
{Я11Л1 + аих2 + О,
а21х1 Ч~°22х2 +^2 0. (2)
amlxi -\~ат2х2 2s 0»
где т—конечное число, получим пересечевие конечного числа полуплоскостей,
образующее многоугольную область D. Область D называется областью решений
системы неравенств (2). Эта область не всегда бывает ограничена, она может быть
и неограниченной и даже пустой. Последний случай имеет место тогда, когда
система неравенств (2) противоречива. Могут быть также случаи лишних нера-
венств, входящих в совместную систему и определяющих прямые, не имеющие
с областью D общих точек. Такие неравенства можно исключить.
Область решений обладает важным свойством—она является выпуклой, т. е.
вместе с любыми своими двумя точками содержит и весь соединяющий их отрезок.
Прямая, которая имеет с областью по крайней мере одну общую точку, притом
так, что вся область лежит по одну сторону от этой прямой, называется опорной
по отношению к этой области.
Аналогично истолковывается геометрически и система неравенств с тремя
переменными:
' а11х1 + а12х2 + в13*3
а21Х1 -{-Я22х2 + а23*3 +^2^0>
. аЛ!1Л1 + аЛ!2х2 + атЗ*3'Ь^3^0-
Здесь каждое из неравенств выполняется для одного из полупространств, на кото-
рые разбивает все пространство соответствующая плоскость. Система неравенств (3)
представляет собой пересечение полупространств, т. е. многогранную область реше-
ний системы неравенств.
1712. Найти полуплоскость, определяемую неравенством 2хг +
+ 3х2 —12 < 0.
271
Д Заменяя знак неравенства на знак точного равенства, получим уравнение
прямой 2%1-|-Зл-2—12 = 0 или х2 = (—2/3)Xi-|-4 (рис. 60). Приведем данное нера-
венство 'к виду х2«С(—2/3)%i-|-4. Следовательно, искомая полуплоскость распо-
ложена ниже прямой х2 = (—2/3)х1-|-4. Д
1713. Какую полуплоскость определяет неравенство 2xt— Зх2^0?
Л Заменяя знак неравенства на знак точного равенства, получим уравнение
прямой 2xj — Зх2 = 0 или *2 = (2/3) *1, проходящей через начало координат. Из
неравенства 2лд— 3x2S=0, т. е. х2^ (2/3) л1( вытекает, что искомая полуплоскость
расположена ниже прямой x2 = (2/3)*i (рис. 61). Д
1714. Найти область решений системы неравенств .д—1^0,
х2 —1^0, х,+х2—3^0, —6х,—7х,-г42>0.
Д Заменяя знаки неравенств на знаки точных равенств, получим уравнения
четырех прямых: *1—1=0, х2—1=0, xi-j-x2— 3 = 0 и 6х!-|-7.Г2—42 = 0, изобра-
женных на рис. 62. Приведем данные неравенства к виду *1^1, хг^1,
—*т4-3, х2«С(—6/7)*i-|-6. Штриховка показывает те из полуплоскостей,
которые служат областями решений соответствующих неравенств. Областью реше-
ний системы неравенств является выпуклый четырехугольник. Д
1715. Найти область решений системы неравенств хг 0, хг + х2 —
— 2^0, хг —х2+1^0, «С2.
Л Заменяя знаки неравенств на знаки точных равенств, получим уравнения
четырех прямых: *i = 0, *i + x2—2 = 0, jq—*2-|- 1 =0, *i = 2, изображенных на
рис. 63. Приведем данные неравенства к виду луДэО, x2S=—.*1 + 2, ХгЭ=^1+!.
*i «С 2. Областью решений системы неравенств является неограниченная выпуклая
фигура. Д
1716. Найти область решений системы неравенств хг^2,
х^ 4~ Зх2 3, Х|—х2 -|- 1 0.
Д Построим соответствующие прямые. Из рис. 64 видно, что не существует
ни одной точки, общей для всех трех полуплоскостей. Это означает, что область
решений «пустая» и заданная система неравенств несовместна. Д
1717. Найти область решений системы неравенств 2хг—х2^—2.
Xi — х2> — 2, Xj С 1, 2xj—х2>3.
Д Эта система неравенств не имеет решений. Геометрически это означает, что
не существует ни одной точки, координаты которой удовлетворяют всем неравен-
ствам данной задачи (рис. 65). Д
1718. Найти область решений системы неравенств 3xj—х2^0(а),
Xi—х2^0(б), 2х,: + х2^6(в), Х!^2(г), 3xj — х24(д).
272
Л Пяти заданным неравенствам соответствует множество точек плоскости,
образующее треугольник ЛОВ (рис. 66). Неравенства (г) и (д) могут быть исклю-
чены, так как неравенство (д) определяет граничную прямую, не имеющую с тре-
угольником ЛОВ общих точек, а прямая, определяемая неравенством (г), имеет
одну общую точку с треугольником и является опорной. А
1719. Найти область решений системы неравенств хг 0, xt О,
х3>0, Xj + Xj— 1<0, Зх^Хз—Зх3>0.
Л Заменяя знаки неравенств иа знаки точных равенств, получим уравнения
плоскостей *! = 0, *2 = 0, x3 = 0, Xi + *2—1=0, 3xi-|-x:2—Зх3 = 0, которые изоб-
ражены на рис. 67. Областью решений системы неравенств служит выпуклый
четырехгранник ABOCD. А
1720. Как расположена полуплоскость, координаты точек кото-
рой удовлетворяют неравенству х3—х2 —10^0?
\ Найти область решений системы неравенств:
1721. Xi + Xa—5Z>0, хх—х2 — 5^0, xt^7.
1722. Xl—5ха + 5>0, Xi-|-3x2—3^0, х^б.
1723. Xj^3, x2Z>0, Xi + x2^0.
1724. Xi—х2 +1 Z>0, 2xi + x2—7^0, xt—2x2 + 4Z>0.
1725. x2^0(a), 4хх —x2>0(6), x2^6(b), 4xi + x2s^ 40(f),
Xi—х2 + 8>0(д).
1726. Xj^O, x2>l, x3Z>0, Xi-j-Xa + Xg—5^0.
1727. Xi^4, 2x2—x3^0, x2 + xs^3, x^O, xg>0.
10-215
273
§ 2. ОСНОВНАЯ ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Задача линейного программирования заключается в изучении способов отыс-
кания наибольшего или наименьшего значений линейной функции при наличии
линейных ограничений.
Функция, наибольшее или наименьшее значение которой отыскивается, назы-
вается целевой функцией, а совокупность значений переменных, при которых дости-
гается наибольшее или наименьшее значение, определяет так называемый опти-
мальный план. Всякая же другая совокупность значений, удовлетворяющая
ограничениям, определяет допустимый план (решение).
Пусть ограничения заданы совместной системой т линейных неравенств с п
переменными:
+ а12х2 + <>• + alnxn bii
a2lxl + а22Х2 + • • • + а2ПхП ^2,
amixi4"ат2х2 4" • • • ~}~атпхп Ьт.
Среди неотрицательных решений этой системы требуется найти такое решение
при котором линейная функция (целевая функция)
L = ад+с2х2 + ,., + спхп+сь
принимает наибольшее (наименьшее) значение илн, как говорят, максимизировать
(минимизировать) линейную форму L.
Покажем, как решается указанная задача геометрическим методом, для чего
ограничимся рассмотрением совместной системы линейных неравенств с двумя и
тремя переменными. Пусть, кроме того, задана линейная функция Z.=ciXi+c2x2-|-c0.
Найдем среди множества точек (*i; х2) из области решений совместной системы
неравенств такие, которые придают заданной линейной функции наименьшее (наи-
большее) значение. Для каждой точки плоскости функция L принимает фиксиро-
ванное значение L=Lj. Множество всех таких точек есть прямая ciXi4-c2x2-|-<?o=
перпендикулярная вектору C(ci; с2), выходящему из начала координат. Если эту
прямую передвигать параллельно самой себе в положительном направлении вектора С,
то линейная функция Z. = c1x1+c2x2+c0 будет возрастать, а в противоположном
направлении—убывать. Пусть при движении прямой L в положительном направ-
лении вектора С она впервые встретится с многоугольником решений в его вер-
шине, тогда в этом положении Lj прямая L становится опорной, и на этой
прямой функция L принимает наименьшее значение. При дальнейшем движении
в том же направлении (положительном) прямая L пройдет через другую вершину
многоугольника решений, выходя из области решений, и станет также опорной
прямой L2; на ней функция L принимает наибольшее значение среди всех значе-
ний, принимаемых на многоугольнике решений.
Таким образом, минимизация и максимизация линейной функции L = CiXj +
+ сгх2+со иа многоугольнике решений достигаются в точках пересечения этого
многоугольника с опорными прямыми, перпендикулярными вектору С (ст; с2).
Опорная прямая может иметь с многоугольником решений либо одну общую точку
(вершину многоугольника), либо бесконечное множество точек (это множество есть
сторона многоугольника).
Аналогично, линейная функция трех переменных L = сххх-|-с2х2 + с3х3 + с0
принимает постоянное значение из плоскости, перпендикулярной вектору С (q; с2; с3).
Наименьшее и наибольшее значения этой функции на многограннике решений
достигаются в точках пересечения этого многогранника с опорными плоскостями,
перпендикулярными вектору С (сх; с2; с3). Опорная плоскость может иметь с мно-
гогранником решений либо одну общую точку (вершину многогранника), либо
бесконечное множество точек (это множество есть ребро или грань многогранника).
1728. Максимизировать линейную форму L = 2xi + 2xi при огра-
ничениях; 3X1—2x^—6, 3xi + x2^3, Xi^3.
А Заменив знаки неравенств на знаки точных равенств, построим область
решений по уравнениям прямых 3xi—2х2-|-6 = 0, 3xi-j-x2—3=0, xi = 3 (рис. 68).
274
Областью решений неравенств является треугольник MNP. Построим вектор С (2; 2).
Тогда опорная прямая при выходе из треугольника решений пройдет через точку
Р(3; 15/2), а потому в точке Р линейная функция L — 2xi + 2xt принимает наи-
большее значение, т. е. максимизируется, и £шах = 2-3-|-2.(15/2) = 21. А
1729. Минимизировать линейную функцию L = 12xj + 4x2 при
ограничениях: х1 + ха'^2, Xj^l/2, х2^4, хг—х2^0.
Л Заменив знаки неравенств на знаки точных равенств, построим
решений, ограниченную прямыми Xi+x3=2, *1=1/2, х2 = 4, хх—х2 = 0.
область
Область
MNPQ (рис. 69). Строим
вектор
С (12; 4). Опорная
пересечения много-
решеиий—многоугольник
прямая проходит через точку М (1/2; 3/2) — это первая точка
угольника решений с прямой L при перемещении этой прямой в положительном
направлении вектора С. В точке М линейная функция £ = 12х1 + 4х2 принимает
наименьшее значение £ш;п = 12-(1/2)+ 4-(3/2)= 12. А
1730. Найти наибольшее значение функции £=х1 + Зх2 + Зх3 при
ограничениях: х2 + х3^3, хг—х2^0, х2^>1, З^Н-л^15.
Д Построим область решений системы неравенств по уравнениям плоскостей:
*2+ *3=3, xi—х2=0, x2 = .l, 3xi+x2=15. Областью решений является много-
гранник MNPQRS (рис. 70).
Построим вектор С (1; 3; 3). При перемещении опорной плоскости в положи-
тельном направлении вектора С она выйдет из многогранника решений в точке
N (4; 3; 0). Поэтому в точке N линейная функция
£=Х1+Зхг + Зх3 примет наибольшее значение, т. е.
£шах = 4 + 3-3+3-0= 13. 4
1731. Найти наибольшее значение функции
А = 3хх—6x2 + 2xs при ограничениях: Зхх +
+3х2 + 2х3 5, хх + 4х2 + 8х3 8.
Л Построим область решений системы линейных
неравенств, взяв плоскости Зхх + Зх2+2х3 = 6, хх +
+4х2+8х3 = 8, xi = 0, х2 = 0, х3 = 0. Эта область есть
многогранник MNOPR (рис. 71). Построим вектор
С (3; —6; 2). Прн перемещении опорной плоскости в поло-
жительном направлении вектора С она выйдет из мно-
гогранника решений в точках ребра MR. Следовательно, наибольшее значение
данной функции принимается в точках отрезка MR. Убеждаемся в этом, подставив
координаты точек М (2; 0; 0) и R (16/11; 0; 9/11) в линейную форму L; получим
Л(/И)=6, L(R) = 6. А
1732. Найти наибольшее значение функции L = Xj + 3x2 при огра»
ничениях: x1-f-4x2^4, Xj + x2^6, х2^2.
1733. Минимизировать функцию L = xr— х2 при ограничениях:
3<Xi + xa^7, 1<ха^4, хх^4.
1734. Найти наибольшее значение функции L — 3x1—4ха при
ограничениях: хх—2x2Z>6, х1 + 2х2'^0, х^б.
1735. Найти наибольшее значение функции £== — Xi + 2xa при
ограничениях: хх—8ха^10, Xi + x2>l, хх—5ха>—5, 3xi +
+ 10ха<30.
1736. Найти наибольшее значение функции L = 8xi—2х2 при
ограничениях: Зх1 + 4х2^18, Зхх—ха>3, х2<6, 2х1 + х2^18,
4хх—х2^24.
1737. Минимизировать линейную форму L = — 2хх—ха + Зх3 при
ограничениях: х1 + ха^2, 3xl + x2^6, х3^3.
1738. Найти наибольшее значение функции L = x1 + 2x2 + 3xs
при ограничениях: Xj + x2^3, хх + ха—х3^0, 3хх + 3х2—х3>0.
1739. Найти наибольшее значение функции L = 10xl4-x3 при
ограничениях: Зхх + 2х2 + х3 6, Зхх—Зх2 + х2^6, х3^3.
§ 3. СИМПЛЕКС-МЕТОД
1. Понятие о симплекс-методе. Решение основной задачи линейного програм-
мирования геометрическим методом является наглядным в случае двух и даже
трех переменных. Для случая же большего числа переменных геометрический
метод становится невозможным. Так называемый симплекс-метод принадлежит к
числу аналитических методов решения основной задачи линейного программиро-
вания. Система ограничений в вычислительных методах обычно задается системой
линейных уравнений
On*i+oi2*i+...+ofB*n = 6i,
а21Х1 + а22-*:г+ • • •-\-а1пХп = Ь2, m
. вЯ1Х1-|-аот2х2-|-... -\-атпхп = Ьт
и среди неотрицательных решений системы уравнений (1) надо иайти такие, кото-
рые максимизировали бы линейную функцию
L = Cj*!-|-сах2 + ... + с„хп+с0.
Выразим Xi, х2, ...,хг (г<т) через остальные переменные:
Xi = «1, г+ iXr+i + . • • + ащхп+bi,
x2=a2l r+iXr+i-f-... +взпхп-|-6а, ,п\
. xr=ar, r+iXr+i+ ... +ernxn-|-6r>
где 6i 0, 62 0, ..., 6, 0. Если ограничительные условия заданы неравен-
ствами, то их можно преобразовать в равенства путем введения новых неотрица-
тельных переменных, так называемых балансовых (выравнивающих). Например,
в неравенстве’ OiXi+ai2x2+ ... -f-anx„ < 6 достаточно добавить к левой части
некоторую величину хл+х^=0 и получится равенство
Oixi+oax2 +... -j-a„x„-[-xn+i=b.
Ограничительные условия могут задаваться и смешанным образом, т. е. нера-
венствами и уравнениями, тогда указанным путем их можно свести только к
, уравнениям. Переменные (неизвестные) хх, х2, ...,хг называются базисными, а
276
весь набор {xi, х2, ... -, хг}—базисом, остальные переменные называются свободными,
система ограничений (2) называется системой, приведенной к единичному базису.
Подставляя в линейную форму L вместо базисных переменных их выражения
через свободные из системы (2), получим
L =То + ?г + 1*г + 1+ • • • +?п*п-
Теперь, полагая все свободные переменные равными нулю, найдем значения
базисных переменных: xi = b[, х3 = Ь2,..., xr=b'r. Таким образом, решение (b'i,
b2....br, 0....0) системы является допустимым—оно называется базисным.
Для полученного базисного решения значение линейной формы LB = y0. Реше-
ние задачи с помощью симплекс-метода распадается иа ряд шагов, заключаю-
щихся в том, что от данного базиса Б мы переходим к другому базису Б' с таким
расчетом, чтобы значение Lb уменьшалось или, по крайней мере, не увеличи-
валось, т. е. LB, «cLb.
Идею метода проследим на конкретных примерах.
1740. Максимизировать линейную форму L = —x4 + xs при ограни-
чениях: Xi + xt—2х5 — 1, х2—2х4+*5 = 2, + Зх4 + х5 = 3.
Д Данная система уравнений-ограничений совместна, так как ранги матрицы
системы
/10 0 1 — 2\
(010—2 1)
\0 0 1 3 1/
и расширенной матрицы
/10 0 1—2 1\
1010—2 12)
\0 0 1 3 1 3/.
совпадают и равны 3. Следовательно, система уравнений совместна и три пере-
менные (базисные) можно линейно выразить через две свободные переменные.
Выразим, например xi, х2 и х3 через х4 и х5, т. е. приведем систему к единичному
базису:
( Х!= 1— х4-|~2х5,
< х2 = 2-|-2х4—х6, (*)
I х3 — 3—Зх4—х3.
Линейную форму L = — х4 + х5 выразим через свободные переменные х4 и х5
(в данном примере L уже выражена через х4 и х6). Теперь при х4 = 0, х5 = 0
найдем значения базисных переменных: хх = 1, х2 = 2, х3 — 3. Таким образом,
первое допустимое решение системы уравнений есть *1=1, хг = 2, х3 = 3, х4=0,
х5 = 0, или (1, 2, 3, 0, 0). При найденном допустимом решении линейная форма L
имеет значение 0, т. е. Lx = O.
Теперь попытаемся увеличить значение увеличение х4 уменьшит Lf, так
как перед х4 стоит отрицательный коэффициент, а увеличение хъ дает увеличение
и Li. Увеличим поэтому хь так, чтобы х4, х2, х3 не стали отрицательными, оставив,
х4 = 0. Из второго уравнения системы (*) следует, что х3 можно увеличить до 2.
Таким образом, получаем следующие значения переменных: хх = 5, х2=0, х3 = 1,
х4 = 0, х6 = 2 или (5, 0, 1, 0, 2).
Значение линейной формы L при этом допустимом решении равно L2 = 2, т. е.
при втором шаге оио увеличилось.
Далее, примем за свободные переменные х2 и х4, т. е. именно те переменные,
которые в новом решении имеют нулевые значения. С этой целью из второго
уравнения системы (*) выразим х3 через х2 и х4 и получим xs = 2—х2-|-2х4»'
277
Тогда
*i — 5—2*2 + 3*4;
*3 = 1 + *2 — 5*4,
*5 = 2—*2 + 2*4,-
Д = 2—*2+*4«
(»»)
Для увеличения значения L будем увеличивать *4. Из второго уравнения
системы (♦*) видно, что при условии неотрицательности *3 значение *4 можно
довести до *4=1/5. При этом условии новое допустимое решение есть *1 = 28/5,
*2=0, *з = 0, *4=1/5, *5=12/5 илн (28/5, 0, 0, 1/5, 12/5). Значение линейной
формы прн этом Д3=11/5.
Выразим теперь *!, *4, *5 через свободные переменные *2 и *3:
*i = 28/5—(3/5) *з—(7/5)*а,
*4=1/5—(1/5)*з+(1/5)*2,
*5= 12/5—(2/5)*3—(3/5)*2, <***>
L = 11/5—(1/5)*з—(4/5)*2.
Так как в последней линейной форме обе свободные переменные входят с от-
рицательными коэффициентами, то наибольшее значение L достигается при *2 = О,
*з=0. Это означает, что решение (28/5, 0, 0, 1/5, 12/5) является оптимальным
и £тах = Н/5. А
1741. Максимизировать линейную форму L = x2 + xs при ограни-
чениях: Xt—x2 + xs=l, х2—2х3 + %4 = 2.
Д Система уравнений-ограничений совместна, так как ранги матрицы систе-
мы уравнений и расширенной матрицы одинаковы и равны 2. Следовательно, две
базисные переменные можно выразить лниейио через другие две свободные. При-
мем за свободные переменные *2 и *s. Тогда
J *1 = 1+*2—*3,
( *4 = 2—*2+2*з(
Д =*2 + *3-
При *2 = 0 и *з=0 базисные переменные *1 = 1, *4 = 2, т. е. имеем первое допус-
тимое решение (1, 0, 0, 2) и Д1 = 0. Увеличение Д можно осуществить прн уве-
личении *з до 1. Тогда при *з = 1, *2 = 0 значения базисных переменных *1=0,
*4 = 4. Новое допустимое решение (0, 0, 1, 4) и Д2 = 1.
Выразим теперь *3 и *4 через *1 и *2:
f *3=1---*1+*2,‘
I *4=4—2*1+ *2,
Д = 1 —*i+2*2.
Увеличение Д возможно при увеличении *2. Увеличение же *2 ие ограничено,
судя по последней системе уравнений. Таким образом, Д будет принимать все
ббльшие положительные значения, т. е. Дтах=-|-оо. Итак, форма Д не ограни-
чена сверху, а потому оптимального решения не существует. ▲
1742. Задана система ограничений: + х2 + 2х3—х4 = 3, х2 + 2х4 = 1
и линейная форма L=5x1—х3. Найти оптимальное решение, миними-
зирующее линейную форму.
А Эту задачу можно было бы свести к задаче нахождения максимума фун-
кции Д1 = —Д, т. е. Д1 = —5*1 + *з, но это необязательно. Рассуждая аналогич-
но предыдущему, ее можно решить, не сводя к максимизации. Данная система
уравнений совместна, так как ранги матрицы системы и расширенной матрицы
одинаковы и равны 2. Следовательно, систему уравнений можно, например, пе-
реписать так:
*1 = 2—2х3-|-Зх4,
х2= 1—2х4,
L — 10— 11Хз-|~ 1бх4.
Здесь за базисные переменные приняты xt и х2, а за свободные х3 и х4. При
х3 = 0 н х4 = 0 первое базисное решение есть х4 = 2, х2=1, х8 = 0, х4 = 0 или
(2, 1, 0, 0), a L!=10. Уменьшение линейной формы L вызывается увеличением
Хз, так как перед х3 в форме L стоит отрицательный коэффициент, причем уве-
личение Хз возможно только до 1, а значение х4 = 0 остается. Если примем xs=l,
то Xi = 0, х2=1, хз=1, х4 = 0 илн (0, 1, 1, 0)—второе базисное решение, при
котором Ь2 =— 1.
Выразим х2 и Хз через новые свободные переменные хх и х<:
f ха=1— 2х4,
I х3=1 — (l/2)xi-f-(3/2)x4i
L = -1 + (11/2)xi-(3/2)x4.
Теперь уменьшение значения формы L зависит от увеличения х4 до х4=1/2
(прн этом х2 неотрицательно), а значение х4 = 0 остается. В этом случае имеем
новое допустимое решение Xi = 0, х2 = 0, xs = 7/4, х4 = 1/2 или (0, 0, 7/4, 1/2),
прн котором L=—7/4.
Выразим х3 н х4через свободные переменные х4 н х2:
( х3 = 7/4— (1/2)х1 — (3/4)х2,
I х4= 1/2—(1/2)х2,
L = -7/4-b(U/2)xi4-(3/4)X2.
Так как дальнейшее уменьшение значения формы L невозможно из-за положи-
тельности коэффициентов при Xi и х2, то допустимое решение задачи (0, 0, 7/4, 1/2)
является оптимальным. Наименьшее значение L равно—7/4. ▲
1743. Максимизировать линейную форму L = 2xx—xt при следу-
ющей системе ограничений:
Х1 + Х2 = 20,
Хз 2х4 5,
— xi -{- Хз Хз 8.
Д Так как система ограничений задана смешанно, то приведем ее к системе
уравнений, введя новую неотрицательную переменную х5 в левую часть второго
условия с отрицательным коэффициентом, а хв—в третье условие с положитель-
ным коэффициентом. Тогда получим систему уравнений
Х1+Х2 = 20,
х2-(-2х4—Xj = 5,
—xi—Хз4-Хз+хв=8.
Приведем эту систему к единичному базису, выбрав за базисные переменные хь
х2, Хз (в силу того, что ранг матрицы системы равен 3):
Xi = 15-]-2x4—х5, Хз = 5—2х4-|-х5, х3 = 28—хв. (*)
Линейная форма тогда примет вид £ = 30-f-3x4—2х5. Прн х4 = 0, х5 = 0,
хв = 0 базисные переменные имеют значения х4 = 15, х3=5, х3 = 28, т. е. первое
допустимое решение (15, 5, 28, 0, 0, 0); прн этом Lj = 30.
Для того чтобы значение L увеличилось, необходимо увеличивать х4, так как
эта переменная входит в выражение для L с положительным коэффициентом.
Увеличение же х4 возможно до х4 = 5/2—это ввдно из второго условия системы
ограничений (*). При х4 = 5/2, х5 = 0, хв = 0 значения других переменных тако-
вы; Xi = 20, х2 = 0, х3 = 28 т. е. получим второе допустимое решение (20, 0,
279
28, 5/2, 0, 0), и линейная функция L примет вид £ = 75/2—(3/2)х2—(1/2)х5,
а при втором допустимом решении ее значение равно £3 = 75/2.
Теперь, поскольку коэффициенты при переменных в L отрицательны, увели-
чение значения L невозможно. Следовательно, Lmax = 75/2 = 37,5. ▲
1744. Для изготовления изделий двух видов имеется 100 кг
металла. На изготовление одного изделия I вида расходуется 2 кг
металла, а изделия II вида—4 кг. Составить план производства,
обеспечивающий получение наибольшей прибыли от продажи изде-
лий, если отпускная стоимость одного изделия I вида составляет
3 ден. ед., а изделия II вида — 2 ден. ед., причем изделий I вида
требуется изготовить не более 40, а изделий II вида — не более 20.
Д Пусть изготовлено х4 изделий 1 вида и х2—11 вида. Тогда имеем следую-
щие ограничения на переменные Xi и х2:
{ Xi «С 40,
х2 < 20,
2xx-j-4x2= 100.
Целевая функция имеетвид £ = 3х1+2ха-Преобразуем смешанную систему ограни-
чений в систему ограничений в виде уравнений, введя новые переменные х3 н xt:
( *1+ *8=40,
< х2 + х4=20,
t xi+2x2 = 50.
Ранг матрицы этой системы
<1 0 1 0\
0 10 1
<1 2 0 0)
равен 3. Выберем за базисные переменные х1( х2, х3 и перейдем к единичному
базису:
Х!= 10 + 2*4,
*2 = 20— *4,
х3 = ЗО—2х4.
Первое допустимое решение получится при х4=0, х1=10, х2 = 20, х3==ЗО. При
этих значениях переменных L = 70. Увеличения значения целевой функции можно
достигнуть путем увеличения х4 до х4=15, судя по третьему уравнению. Тогда
при *4=15, х1 = 40, х2 = 5, х3 = 0 имеем L=130. Второе допустимое решение
(40, 5, 0, 15); х4 = 40—ха, xs = 5+(l/2) ха, х4= 15—(1/2) х3, £,= 130—2х3. Коэф-
фициент прих3в пелевой функции отрицателен, а потому дальнейшее увеличение
L невозможно. Следовательно, оптимальное решение х1 = 40, х2 = 5 и £тах = 130. А
2. Симплексные таблицы. Систему ограничений сведем к единичному базису:
*1+ • • • +Я1»г+1 *r+i+ • • +<hn xn = bi,
*/ + • • • +«/, r+1 *r+l+ • • +«in xn = bi,
, +•+••• ++> r+l*r+l+ • • • +arn xn—br,
а линейную форму L—к виду
^+Yr + i *r + i+ • • • +Y/*/+ • • • +Yn*n = Yo-
280
В виде таблицы эти данные можно 1редставить так:
Базисные перемен* ные Свободные члены *1 xi Xr Xr + i */ Xn
Xi bi 1 0 0 ai, r + 1 an al!t
....... ... ... ... ... ...
Xi bi 0 1 0 ai> r + 1 aij ain
... ...
Xr br 0 0 1 er. r + 1 ... «Г/ ... arn
L Vo 0 0 0 Tr + 1 yj ... Уп
Равенство (1) будем называть приведенным (к свободным переменным) выражением
для функции L, а коэфицненты уу—оценками (индексами) соответствующих сво-
бодных переменных Xj.
1. Выбирают разрешающий столбец ар из условия: оценка ур < 0 и хотя бы
один элемент а;р > 0.
2. Выбирают q-ю разрешающую строку из условия
bq/aqp = min{bi/aip} для aip > 0.
3. Производят пересчет элементов разрешающей q-й строки по формуле
aqk~aqk!aqp (b — Q, 1.....................n).
4. Вычисляют элементы всех остальных строк (при k # р) пэ формуле
a’ik=aik—a'qk<4P (‘=0, 1, •••. <7—1. <? + 1. •••. г).
Следует иметь и виду основную теорему симплексного метода, которую приве-
дем без доказательства.
Теорема. Если после выполнения очередной итерации:
1) найдется хотя бы одна отрицательная оценка и в каждом столбце с
такой оценкой окажется хотя бы один положительный элемент, т. е. Yft > 0 для
некоторых k, и a,h > 0 для тех же k и некоторого I, то можно улучшить реше-
ние, выполнив следующую итерацию;
2) найдется хотя бы одна отрицательная оценка, столбец которой не содер-
жит положительных элементов, т. е. уь < 0, < 0, для какого-то k и всех i,
то функция L не ограничена в области допустимых решений (Lmax "* оо);
3) все оценки окажутся неотрицательными, т. е. для всех k, та
достигнуто оптимальное решение.
1745. Найти наибольшее значение линейной функции L=7xt +
+ 5ха на множестве неотрицательных решений системы уравнений
r 3^2Хз = 19,
2xi -h х< = 13,
3Xg + Х5 = 15,
k 3xi= 18.
281
Л Ранг матрицы системы уравнений
/2 3 1 О О 0\
2 10 10 0]
0 3 0 0 1 0 /
3 0 0 0 0 1/
равен 4. Ранг расширенной матрицы также равен 4. Следовательно, четыре пере*
мениые (базисные) можно выразить через две (свободные), т. е.
х8= 19—2х4—Зха,
х4=13—2xt — ха,
х6 = 15—Зха,
, хв=18—3xj.
Кстати, линейная форма £ = 7х4-|-5ха, нлн L—7xi — 5ха=0 уже выражена через
эти же свободные переменные. Имеем исходную таблицу (табл. 1).
Таблица 1
Базисные переменные Свободные члены *1 X* X» X* xt Xt
xt 19 2 1 0 0 0
3
х4 13 2 1 0 1 0 0
х»
15 0 3 0 0 1 0
X» 18 3 0 0 0 0 1
L 0 —7 —5 0 0 0 Таб 0 лица 2
Базис- ные пере- менные Свободные члены *1 х, х» Х« Xi Xi
Хз
4 2 0 1 0 —1 0
х4 8 2 0 0 1 -1/3 0
ха 5 0 1 0 0 1/3 0
Хв 18 3 0 0 0 0 1
L 25 —7 0 0 0 5/3 0
282
Таблица 3
Базис- ные пере- менные Свободные члены Xt Xi х, *4 Xt X,
Xi 2 1 0 1/2 0 -1/2 6
Xi
4 0 0 —1 1 — 2/3 - 0
Xi 5 0 1 0 0 1/3 0
X» 12 0 0 —3/2 0 3/2 1
L 39 0 0 7/2 0 —11/6 Тг 1( 0 5лица 4
Базис- ные пере- менные Свободные члены Xi х, х» *4 Xt *4
Xi 5 1 0 -1/4 3/4 0 0
Xt 6 0 0 —3/2 3/2 1 0
хг 3 0 1 1/2 -1/2 0 0
х» 3 0 0 3/4 -9/4 0 1
L 50 0 0 3/4 11/4 0 0
Выясняем, имеются ли в последней строке (индексной) отрицательные оценки.
Таких чисел два: —7 и —5. Берем, например, —5 н просматриваем столбец
дли х2, в этом столбце имеем три положительных элемента 3, 1, 3. Делим на эти
числа соответствующие свободные члены: 19/3, 13/1, 15/3, из полученных частных
наименьшее есть 15/3. Следовательно, разрешающим является элемент. 3, стоящий
на пересечении строки для хъ и столбца дли х2. Выделим эту строку и этот
столбец рамками. Новый базис состоит из ха, х4, х2, хв. Для составления следую-
щей таблицы умножим выделенную строку табл. 1 на 1/3, чтобы получить на
месте разрешающего элемента 1, н полученную таким образом строку пишем на
месте прежней. К каждой из остальных строк прибавляем вновь полученную, умно-
женную на такое число, чтобы в клетках столбца для ха появились нули, и пишем
преобразованные строки на месте прежних. Этим завершается I итерация.
Теперь все рассуждении повторяются применительно к табл. 2, т. е. выпол-
няем II итерацию. Новый разрешающий элемент, находящийся на пересечении
строки для хв и столбца для хх, есть 2. Переходим к следующей таблице.
283
То же повторим применительно к табл. 3. Здесь разрешающим является
элемент 2/3, находящийся на пересечении строки для х4 и столбца для х6. Пере-
ходим к табл. 4.
Поскольку в индексной строке нет отрицательных оценок, мы получили
оптимальный план (5, 3, 0, 0, 6, 3) н наибольшее значение линейной формы L
есть ^.щах=50. Д
Найти оптимальные неотрицательные решения, минимизирую-
щие линейную форму:
1746 / xi—2*2 + *з—1»
I *14-Зха+х< = 2,
L = Xi—x3.
1748. {
2Xi +ха—Хз—*4 = 2,
*а—*4= 1,
L = 2xs—х2.
1747.
1749.
*! = 2+2*а—х4,-
х2 = 1+*а—2х4,
*5 = 5—*3+*4,
L = xi + xs.
4*1 + Зх2 + *з — 180,
4х2+9х3 +12*4 = 800,
L = 12*1 + 5х2+Зх3.
1750.
Xl + *4 + 6Xe = 9,
3*1 + х2—4х2+2х, = 2,
*1+2ха+х6+2хв = 6.
L=Хх—ха+*з+*4 + хз—х«.
Найти оптимальные неотрицательные решения, максимизирую-
щие линейную форму:
1751.
(Х1+*з+5ха = 20,
х2 + 2X4 3,
*1+х2—*з 5= 8,
L=2xi+*4.
1752.
{*i—2х2 + Зх3 — 1,
2*1—х2—*з<—1.
L = — xi—2ха — Зха.
1753. Производственная мощность цеха сборки составляет 120
изделий типа А и 360 изделий типа В в сутки. Технический конт-
роль пропускает в сутки 200 изделий того или другого типа (без-
различно). Изделия типа А вчетверо дороже изделий типа В. Тре-
буется спланировать выпуск готовой продукции так, чтобы пред-
приятию была обеспечена наибольшая прибыль.
1754. Для изготовления изделий двух видов склад может отпус-
тить металла не более 80 кг, причем на изделие I вида расходу-
ется 2 кг, а на изделие II вида—1 кг металла. Требуется сплани-
ровать производство так, чтобы была обеспечена наибольшая при-
быль, если изделий I вида требуется изготовить не более 30 шт.,
а изделий II вида не более 40 шт., причем одно изделие I вида
стоит 5 ден. ед., а II вида — 3 ден. ед.1
1755. Для откорма животных употребляют два вида кормов; сто-
имость 1 кг корма I вида — 5 .ден. ед., а корма II вида — 2 ден. ед.
В каждом килограмме корма I вида содержится 5 ед. питательного
вещества А, 2,5 ед. питательного вещества Б и 1 ед. питательного
2S4
вещества В, а в каждом килограмме корма II вида соответственно
3, 3 и 1,3 ед. Какое количество корма каждого вида необходимо
расходовать ежедневно, чтобы затраты на откорм были минималь-
ными, если суточный рацион предусматривает питательных единиц
типа А не меиее 225 ед., типа Б — не менее 150 ед. и типа В—не
менее 80 ед.?
3. Понятие о вырожденном решении. Прн рассмотрении симплексного метода
предполагалось, что Ь, > 0 (см. с. 276) как в исходной системе, так и в системах,
получаемых после очередных итераций. Если же в некоторых уравнениях свобод-
ные члены />|=0, то в соответствующем этой системе опорном решении базисные
переменные, относительно которых эти уравнения разрешены, принимают нулевые
значения. Опорное решение, в котором хотя бы одна из базисных переменных при-
нимает нулевое значение, называется вырожденным решением, а задача линейного
программирования, имеющая хотя бы одно вырожденное решение,— вырожденкой
задачей. Применяя в этом случае последовательные итерации, мы можем вернуть-
ся к ранее встречавшемуся набору базисных и свободных переменных, т. е. появ-
ляется так называемое зацикливание в схеме расчета. Приведем правило для уст-
ранения зацикливания (мы не касаемся теоретического обоснования этого правила,
являющегося специальным вопросом так называемой проблемы вырождения).
Если на каком-либо этапе расчета возникает неопределенность в выборе раз-
решающей строки, т. е. оказывается несколько равных минимальных отношений
bi/aip, то следует выбирать ту строку, для которой отношение элементов сле-
дующего, столбца к разрешающему является наименьшим. Если при этом снова
оказываются равные минимальные отношения, то составляют отношения элемен-
тов следующего столбца, и так до тех пор, пока разрешающая строка не опре-
делится однозначно.
1756. Максимизировать линейную форму L = 4x6-}-2xt при огра-
ничениях: *1 + + х, = 12, ха4-5х6—х, = 30, x3-)-xR—2х, = 6, 2х44-
+3х6—2хв=18, х4^0, ха^0, х3^0, х4^0, хб^0, х,^0.
Д Исходной системе соответствует опорное решение (12, 30, 6, 9, 0, 0) и
значение L — 0. Ниже приводится последовательность итераций симплексного
метода:
Исходная таблица
Xi bi 4 2 bi/aip Qdlfalp
Xi Xi Xt Xi xt
Х1 12 1 1 12
1
Х2 30 1 5 —1 6 -1/5 '
Хз 1 6 —2
6 1 1 —2
х4 18 2 3 —2 6 —2/3
L 0 —4 —2
285
I итерация
Xi 6 1 —1 3 2
ха 0 1 —5 9 0 —5/9
X» 6 1 1 —2
х4 0 —3/4
0 —3 2 4
L 24 4 —10'
II итерация
Xi 6 1 5/4 —3/2 24/5,
Ха 1 0
0 1 7/4 —9/2
1
х6 6 -1/2 1 1
хв 0 —3/4 1/2
L 24 —7/2 5
III итерации
Xi 6 1 -5/7 — | 12/7|
J L
х3 0 4/7 1 — 18/7
х» 6 2/7 —2/7 1
х, 0 3/7 —10/7 1
L 24 2 —4
286
IV итерация
х4 7/2 7/12 —5/12 1
х3 9 3/2 -1/2 1
Хз 7 1/6 1/6 1
хв 5 5/6 -1/6 1
L 38 7/3 1/3
После I итерации получили систему, разрешенную относительно базисных пере-
менных Xi, х2, xt, х6, которой соответствует опорное решение (6, 0, 0, 0, 6, 0)
и значение Lj = 24. II и III итерации не изменяют опорного решения и значения
L2=Z,3 = 24 н только IV итерация дает оптимальное решение (0, 0, 9, 7/2, 7/5)
и Lmax = 38. В данной схеме расчетов зацикливание не появилось, хотя в течение
трех итераций мы как бы «топтались на месте», менялись только базисные н сво-
бодные переменные. В рассмотренном примере в исходной таблице оказалось трн
равных наименьших отношения: Ьц/а^ —b3/a33 = bt/at3 = 6. Поэтому, пользуясь
правилом устранения возможного зацикливания, берем отношения элементов сле-
дующего за свободным столбца: а23/а23 = — 1/5, “36/азэ =—2, “4в/а45 =—2/3.
Наименьшим оказалось отношение “зв/а35 =—2. Следовательно, третья строка
должна быть взята в качестве разрешающей и т. д. (см. таблицы). А
1757. Максимизировать линейную функцию L = 2xi + 4xij при
ограничениях: —2х4 + х2 + х3 = 6, —xt + (3/2) х2 + х4 = 9, —+ 5х2+
+%5 = 30, —Xi + x2 + xt = 12, х^О, х2>0, х3>0, х4>0, х6>0,
х6>0.
§ 4. ДВОЙСТВЕННЫЕ ЗАДАЧИ
Каждой задачей линейного программирования можно сопоставить определен-
ным образом с ней связанную другую задачу, которая называется двойственной
по отношению к первой. •
Так, если исходная задача (задача I) линейного программирования состоит
в минимизации линейной функции Т=с1х1+с2х2++слхп, когда заданы
ограничения в форме неравенств
“u*i+“i2*2 +.,. -t-alnxn bi,
“21^-1+“22^-2 + • • • -\~а2ПХП t>2,
amlxi~\-am2x2~\~ • • • +атпхп
прн условии неотрицательности х^ (k = 1, 2, ... , п), то с ней связана двойствен-
ная задача (задача I'), состоящая в том, что требуется максимизировать
линейную функцию Т= /»1У1 + Ь2уг + • • -\-ЬтУт прн условии ограничений
“111/1 + “211/2 + • • • + “и11//В < с£ >
“121/1+ “221/2 + • • • +“и21/т <с2,
“1п1/1+ “2п1/2+ • • • +атпУт <сп
И неотрицательности (1=1, 2, ... , т).
Заметим, что в задаче I н в двойственной задаче I' матрицы
/“11 “12 * *» “in
Д _[ “21 “22 • • • а2П
/ац a2i ... ami
н А' — I 012 а~2 ’ ‘ ’ атг
flrni ат2 • • • атп
,а1п а2п • • • атп.
287
составленные из коэффициентов при переменных, получаются друг из друга транс-
понированием. В правых частях системы ограничений каждой задачи стоят коэф-
фициенты линейной функции, взятой из другой задачи. В системе ограничений
задачи I (минимизация) все неравенства типа «?а», а в системе ограничений за-
дачи I' (максимизация) все неравенства типа «<;». Понятие двойственности яв-
ляется взаимным, т.е. если задачу Г записать в форме, аналогичной задаче J, то
двойственной к ней окажется исходная задача I. Поэтому задачи I н Г называ-
ются взаимно двойственными, или взаимно сопряженными. Доказывается, что
Z-min= Лпах> а также, что необходимым и достаточным условием оптимальности
решений любой пары двойственных задач является равенство L (х)= Т (у), где
х и у—допустимые решения задач I и I'.
1758. Дать геометрическую интерпретацию следующих взаимно
двойственных задач:
Исходная задача (I): найти неотрицательные значения (х1( х2)
из условий лу + 2х, 4, —х2^—1 и минимизации линейной функ-
ции L = 3x1 + 2x2.
Двойственная задача (Г): найти неотрицательные значения (z/n у2)
из условий У1 + у2^3, 21/,—у2С/2 и максимизации линейной функ-
ции Т = 4у1—у2.
Д Построим систему ограничений задач I и I'. В точке Р (2/3; 5/3) достига-
ется минимум линейной функции L, т.е. Z.min = 3-(2/3)-{-2-(5/3)= 16/3, а в точке
Р' (5/3; 4/3)—максимум линейной функции Т, т.е. 7’шах = 4-(5/3)—4/3=16/3
(рнс. 72). А
1759. Исходная задача (I): найти неотрицательные значения
х3), минимизирующие линейную функцию Л = 3х,4-2х2, если
дана система ограничений 7х, + 2х2^ 14, 4х, + 5х2 20. Составить
двойственную задачу и решить ее.
1760. Исходная задача (I): найти неотрицательные значения
(х,, х2), максимизирующие линейную функцию L = 5x,-|-4x2 при
системе ограничений 4х,4-3х2^24, Зх, + 4х2</24. Составить двойст-
венную задачу и решить ее.
1761. Исходная задача (I): найти неотрицательные значения
(*1, х2), минимизирующие линейную функцию Л = 3х, + 3х2 при
системе ограничений 5х,—4х2^—2, x1-]-2xs,'^G. Составить двойст-
венную задачу и решить ее.
§ 5. ТРАНСПОРТНАЯ ЗАДАЧА
Одной из типичных задач линейного программирования является так назы-
ваемая транспортная задача. Оиа возникает при планировании наиболее рацио-
нальных перевозок грузов. В одних случаях это означает определение такого
28&
плана перевозок, прн котором стоимость последних была бы минимальна, а в дру-
гих—более важным является выигрыш во времени. Первая задача получила на-
звание транспортной задачи по критерию стоимости, а вторая—транспортной
задачи по критерию времени.
Первая задача является частным случаем задачи линейного программирова-
ния и может быть решена симплексным методом. Однако в силу особенностей
этой задачи она решается проще.
Пусть в р пунктах отправления находятся соответственно aj, аг,..., ар
единиц однородного груза, который должен быть доставлен q потребителям в ко-
личествах Z?i, Ьг, ••• , Ьч единиц. Заданы стоимости сц, перевозок единицы груза
из i-го пункта отправления £-му пункту потребления. Обозначим через х;>2э0
(i=l, 2, ... , р; k=l, 2, ... , q) количество единиц груза, перевозимого нз 1-го
склада £-му потребителю; тогда переменные должны удовлетворять следующим
ч р
ограничительным условиям: 1) 2 Xik = «i (i = l, 2,..., р); 2)
ft=i 1=1
(k = 1, 2, ... , р); 3) Xjh^O. Суммарные затраты на перевозки равны Е = СцХц+
+ci2*i’ + • • -\-cpqXpq. Следовательно, требуется найти pq переменных х^, удов-
летворяющих указанным условиям и минимизирующих целевую функцию L.
Решение такой задачи разбивается иа два этапа:
1) определение исходного опорного решения;
2) построение последовательных итераций, т. е. приближение к оптимальному
решению.
1. Определение исходного опорного решения. Пусть мы имеем таблицу исход-
ных данных задачи. Исходное опорное решение будем строить по так называемому
правилу «северо-западного угла».
bk а‘ bi Ьг ... Ьц bq
at 1 С11 | С12 ... | clk
хц %12 Xlk Xlq
аг | С21 | ^22 ... | c2k ... | C2?
ХМ Xlk xiq
• .... .... .... ....
1 с<’1 I СМ ... | cik ... 1 ci'l
хц ХЦ xik Xiq
• .... .... ....
ар 1 СЛ>1 1 СР* ... 1 CPK ... 1 CP4
Xpi хр?. xpk xpq
Заполним вышеуказанную таблицу, начиная с левого верхнего угла, двигаясь
далее или по строке вправо, или по столбцу вниз. В клетку (1, 1) занесем мень-
шее из чисел 1?! и &!, т. е. xn = min{ai, &]}.
Если Hi > &i, то Хц = й1 и первый столбец «закрыт», т. е. потребности пер-
вого потребителя удовлетворены полностью. Двигаемся далее по первой строке,
289
записывая в соседнюю клетку (1, 2) меньшее из чисел а±—н Ьг, т.е. х12 =
= min{ai—bi, Ьг}.
Если же Ьг > а±, то аналогично «закрывается» первая строка н далее перехо-
дим к заполнению соседней клетки (2, 1), куда заносим x2i=min{a2, Ьг—aj.
Будем продолжать этот процесс до тех пор, пока иа каком-то этапе не исчерпы-
ваются ресурсы ар и потребности bq.
1762. В двух пунктах отправления Л и В находится соответст-
венно 150 и 90 т горючего. В пункты 1, 2, 3 требуется доставить
соответственно 60, 70 и 110 т горючего. Стоимости перевозки тонны
горючего из пункта А в пункты 1,2,3 составляют соответственно 6,
10 и 4 ден. ед., а из пункта В — 12, 2 и 8 ден. ед. Составить
оптимальный план перевозок горючего так, чтобы общая сумма
транспортных расходов была наименьшей.
Таблица 1
1 2 3
ai bk 60 70 ПО
1 6 1 10 1 4
150 60 70 20
12 1 2 1 8
90 90
А Запишем исходные данные в табл. 1. Заполнение начнем с клетки (1, 1):
*11 = min (150, 60) =60, первый столбец закрыт. Переходим к клетке (1, 2): Х]2 =
= min {150—60, 70} =70, второй столбец закрыт; далее, переходим к клетке (1, 3):
xls = min{150— 60— 70, 110}=20. Так как в третьем столбце оказался остаток,
равный 90, то переходим к заполнению клетки (2, 3), куда заносим x23 = min{90,
90} = 90. Поскольку остатки по строке и столбцу равны нулю, опорное исходное
решение построено. Этому плану соответствуют затраты в количестве 1 = 6-60 +
+ 10-70 +4-20 +8-90-1860 ден. ед.
В правиле «северо-западного угла» не учитывается величина затрат сц,, а
потому исходное опорное решение часто может быть далеким от оптимального.
Применяют также прием «минимального элемента», в котором учитывается вели-
чина с(>. В этом случае построение исходного опорного решения начинают с клет-
ки с наименьшей величиной с^, в данном примере—с клетки (2, 2), где с22 =
= 2 (табл. 2). В эту клетку заносим x22 = min {a2, />2} = min{90, 70} = 70.
Таблица 2
12 3
bk a‘ 60 70 110 Остаток
•150 60 6 1'° 1 4 90 60,0
90 12 1 2 70 1 8 20 20,0
Остаток 0 0 20,0
290
Остатки по строке и столбцу записываем в соответствующие клетки строки
и столбца остатков. Столбец Ь2 закрыт. Теперь переходим к клетке (1, 3), так
как после cas = 2 наименьшим является с13=4. В клетку (1, 3) заносим xjS =
= min {at—bi, bs} = min{150—60, 110} = 90. Затем переходим к клетке (1, 1):
Xn = min{ai, i>l} = min {150, 60}=60. Наконец, переходим к клетке (2, 3), в ко-
торую заносим x2S = min{as—bit 6s} = min{90—70, 110} = 20.
Применяя это правило, мы получили другой вариант исходного опорного
решения, при котором затраты £=6'60 +4’90 +2-70 + 8'20=1020 ден. ед., т. ё.
сумма затрат ближе к оптимальному плану.
2. Построение последовательных итераций. Получив исходное опорное реше-
ние, перейдем теперь к построению новых опорных решений, улучшающих друг
друга: для этого применим метод потенциалов.
Итак, после построения исходного опорного решения все переменные разбиты
на две группы: х«—базисные н хрЧ—свободные; линейные функции стоимости
перевозок выразятся через свободные переменные так:
2V/>?xw+Vo- (D
Р<7
Для нахождения коэффициентов ypq при свободных переменных сопоставим
каждому пункту отправления Д/ некоторую величину и, (1=1, 2, ... , т), кото-
рую назовем потенциалом пункта А/, н каждому пункту назначения Вj величину
Vj—потенциал пункта Ду. Свяжем эти величины равенством Uft + c'z=c/ez> где
Chi—стоимость перевозки одной тонны груза из пункта Д^ в пункт Вг. Доказы-
вается, что совокупность уравнений u* + c'z = c£z, составленных для всех базисных
переменных, составляет совместную систему линейных уравнений, причем значе-
ние одной нз переменных можно задавать произвольно, и тогда значения осталь-
ных переменных находятся из системы однозначно. Обозначим для свободных пе-
ременных сумму соответствующих потенциалов через c'pq, т. е. up-}-vq = cpq, и
назовем ее косвенной стоимостью (в отличие от данной стоимости cpq). Тогда
коэффициенты при свободных переменных в соотношении (1) определяются с по-
мощью равенства ypq = cpq—cpq.
Если все величины урЧ неотрицательны, то исходное решение является опти-
мальным. Если же средн них имеются отрицательные, то переходим к следующе-
му базису путем увеличения члена с отрицательным коэффициентом, оставляя
другие переменные равными нулю.
Воспользуемся изложенными общими понятиями и продолжим решение задачи
1762. Мы получили исходное опорное решение (следуя правилу «минимального
элемента»): Хц = 60, х12 = 0, xI3 = 90, x2i = 0, х22=70, х2з = 20, £=1020. Для
нахождения потенциалов необходимо решить систему
+ = 011=6, Ui + т’З = С13 = 4, ZZ2 + ^2 = с22 = 2, и24-С'з = 023 = 8.
Значение одного из неизвестных зададим произвольно, например «1=1.
Тогда t'i = 5, с'з = 3, и2 = 5, с2 = —3. Далее вычисляем косвенные стоимости с';
, , г ’
012 = Ui + С’з —2, £-21 = U2 + ^1 = Ю.
Подсчитаем теперь разности ypq=cpq—c'pq:
Vi2=Ci2—-cu= 10—(—-2)= 12, V2i = 02i—Сз1= 12—10 = 2.
Следовательно, выражение L через свободные переменные имеет вид L =
= 1020+ 12xi3 + 2x2f. Среди коэффициентов при переменных в правой части нет
отрицательных. Значит, исходное опорное решение является оптимальным. Таким
образом, правило «минимального элемента» сразу дает оптимальное решение.
Решим теперь эту же задачу при условии, что исходное решение получено
по правилу «северо-западного угла», т. е. хц=60, xiS = 70, xiS = 20, xs3=90,
291
£=1860. Для нахождении потенциалов необходимо решить систему
«i -f- t'i=Сц=6, «i + v2=Ci2 = 10, «1-|-цз=:С1з = 4, u2v2 = Сзз=8>
Полагая «1=1, получим t»i = 5, г2 = 9, vs = 3, «2 = 5.
Вычисляем косвенные стоимости cpq:
c2i = «24-V1 = 10, C22 = u24-t>2=14.
Подсчитаем теперь разности ypq = cpq —срч‘.
y2i =c2i—c2i = 12 —10 = 2, у22=с22—с22 = 2 —14 =—12.
Следовательно, выражение £ через свободные переменные имеет вид L =
= 18604-2*21—12*33. Среди коэффициентов при переменных в правой части есть
отрицательный прн *22, следовательно, можно попытатьси уменьшить L, увеличив
*22 (сохранив нулевое значение *2i). Положим *22 = Х. Поскольку суммы значений
неизвестных по строкам н столбцам должны остаться неизменными, нужно про-
извести следующий балансовый пересчет:
60 70—X t —> 204-Х +
X..., .,..90:—X
Добавление X к *22 компенсируется вычитанием X из х12, а это в свою очередь —
прибавлением X к х12 и т. д. до тех пор, пока мы не вернемся обратно к х22.
Обходя клетки по пунктирной ломаной лииии, в одной из вершии которой нахо-
дится свободная перемеииая *22, а в остальных вершииах—базисные переменные
(причем ие обязательно все), мы получим так называемый цикл пересчета (лома-
ная называется циклом), отвечающий свободной клетке *22. Как видно из табли-
цы, дли неотрицательности перемеииых X можио увеличить до Х = 70, тогда
получим второе опорное решение:
60 0 90
0 70 20
т. е. *ц = 60, *i2 = 0, xiS = 90, *2i = 0, *22 = 70, *23 = 2О.
Значение функции L для него составляет £=1860—12-70=1020, т. е. полу-
чили оптимальное решение (судя по предыдущему решению). Д
Таким образом, правила вычислений по методу потенциалов сводятся к сле-
дующему.
1. Находят потенциалы и^ и V/ всех пунктов отправления А^ и назначе-
ния Вр
2. Выбирают какую-иибудь свободную переменную, для которой сумма по-
тенциалов строго больше соответствующей стоимости, это соответствует элементу
с отрицательным коэффициентом при свободной переменной в правой части функ-
ции £.
3. Для выбраииой в п. 2 переменной находят соответствующий ей цикл пере-
счета и производят сдвиг по этому циклу. Этот сдвиг приводит к новому допус-
тимому решению.
4. Вышеуказанные операции 1—3 повторяют до тех пор, пока ие получат
оптимальный базис, т. е. неотрицательные коэффициенты при свободных перемен-
ных в правой части лииейиой функции £.
292
1763. На двух складах А и В находится по 90 т горючего.
Перевозка одной тонны горючего со склада А в пункты 1, 2, 3
соответственно стоит 1, 3 и 5 ден. ед., а перевозка одной тонны со
склада В в те же пункты — соответственно 2,5 и 4 ден. ед. В каждый
пункт надо доставить по одинаковому количеству тонн горючего.
Составить такой план перевозки горючего, при котором транспорт-
ные расходы будут наименьшими.
1764. В резерве трех железнодорожных станций А, В и С нахо-
дятся соответственно 60, 80 и 100 вагонов. Составить оптимальный
план перегона этих вагонов к четырем пунктам погрузки хлеба,
если пункту № 1 необходимо 40 вагонов, № 2—60 вагонов, № 3—
80 вагонов и № 4—60 вагонов. Стоимости перегонов одного вагона
со станции А в указанные пункты соответственно равны 1, 2, 3,
4 ден. ед., со станции В — 4, 3,2, 0 ден. ед. и со станции С — 0,2,2,
1 ден. ед.
1765. Завод имеет три цеха А, В, С и четыре склада № 1, 2,
3, 4. Цех А производит 30 тыс. шт. изделий, цех В—40 тыс. шт.,
цех С—20 тыс. шт. Пропускная способность складов за то же
время характеризуется следующими показателями: склад № 1 — 20
тыс. шт., склад № 2—30 тыс. шт., склад № 3—30 тыс. шт., склад
№ 4 —10 тыс. шт. Стоимости перевозки 1 тыс. шт. изделий из це-
хами склады № 1, 2, 3, 4 соответственно равны 2, 3, 2, 4 ден. ед.;
из цеха В — 3, 2, 5, 1 ден. ед., а из цеха С — 4, 3,2, 6 ден. ед. Соста-
вить такой план перевозки изделий, при котором расходы на пере-
возку 90 тыс. шт. изделий были бы наименьшими.
1766. На трех складах А, В, С находится сортовое зерно соот-
ветственно 10, 15, 25 т, которое надо доставить в четыре пункта:
пункту № 1—5 т, № 2—10 т, № 3—20 т и № 4—15 т. Стои-
мости доставки одной тонны со склада А в указанные пункты соот-
ветственно равны 8, 3, 5, 2 ден. ед.; со склада В — 4,1, 6, 7 ден. ед. и
со склада С — 1, 9, 4, 3 ден. ед. Составить оптимальный план пере-
возки зерна в четыре пункта, минимизирующий стоимость перевозок.
ОТВЕТЫ
Глава I
4. 1) 8; 2) 3. 5. 1) 1/2; 2) —9/4. в. М (7). 7. С (I), D(3). 8. С (—9), D(-l).
16. 1) 13; 2) 3. 19. 5. 20. (—1; 8), (1; 9), (3; 10). 21. 5 = 0, т. е. точки А, В^С
лежат иа одной прямой. 22. D (17; 12). 23. С(—10; —7). 24. 1^53, У 82, 185.
25. 24 кв. ед. 29. 4(4; л/6); 5(3;—л/2); С (4 У 2 Зл/4)*; _D (2; —л/4);
Е (2 У 2; 4л/3); 5(7; л). 30. А (0; 10); В (— У 2; — У 2 ); С (0; 0);
D (У2/2; — /2/2); Е (— /2/2; — /2/2); Р(~У2/2; У2/2).
31. Ир? + р2—2pip2 cos (01—02). 32. 5. 33. Mt (р; —0). 34. Mt (р; я+0).
35. 1) j(3; 7 л/6), (5; — л/3) и (2; 5я/6); 2) (3; — п/6), (5; —2л/3) и (2; л/6).
36. Mi (р; л—0). 44. у = 2х—1,5. 45. Биссектриса 1 и III координатных углов.
46. Биссектриса II и IV координатных углов447. х2+уа—2х—2у=0. 48. Зх2 +
+ 2ху+3у2—4х—4у=0. 49. р=а. 50. 0=а. 51. p=acos0. 57. Прямая у = 2х.
58. x2/a2+y2/6a= 1 (кривая называется эллипсом). 59. х2/а2—</2/62=1 (кривая
называется гиперболой). 60. Отрезок прямой АВ, где Д(Г, 0), В (0; 1).
61. хг1з-\-уз1з=аг1л. 62. x=a(tsin /4-cost), y=a_(sini—/cost) (кривая иазы-
вается эвольвентой круга). 67. 1) х+2у—2 Уб =0; 2) у = {—1/2) х+/5;
3) х/(2/5)+у//5 = 1; 4) (1 /Уб) х+(2/У 5) у—2 = 0. 68. 135°. 69. 54 кв. ед.
70. Нет. 72. УЗх+у—1=0. 73. x-f-y—4=0. 74. Зх—2у=0. 75. х+у—7=0.
76. х+3=0, у+4=0. 77. х+у—5 = 0, х+у+5=0. 99. tga = 27/ll.
100. х—у=0, 5х+3у—26 = 0, Зх+5у—26 = 0. 101. 14х+ 14у—45=0, 2х—2у+
+ 35 = 0. 102. Зх—«/+14=0, х—бу—14 = 0, х+2у=0. 103. х—2 = 0, у—7 = 0.
104. 4,4. 105; 2,4. 106. т=4. 107. х—у=0, х+5у—14=0, бх+у—14 = 0.
108. л/6. 109. (0; 5) и (4; 3). ПО. (7/8; 0) и (—27/8; 0). 111. 13х+6у—82 = 0,
3*+4у—23=0, 5 = 31,5 кв. ед. 112. Зх—2у = 0, 5х+у+6=0. 113. 5х+4 = 0.
114. 5x+8j/+11=0. 115. 5у+2=0. 116. 17х+Пу=0. 117. х+у+1=0.
118. х=а, у = Ь. 119. х=1; у = х. 120. 30°. 121. <р=53°8'. 122. 5х—Зу+2 = 0.
123. УЗ кв._ед. 125. 5(1; 3), С(11; 6). 126. 1) х/4+у/6=1; 2) х/4(/2 — 0+
+ 1//(-6)(К2+0 = 1; 3) х/(—4) (/2+1)+у/6 (/2 —1) = 1. 127. Зх-4у-
— 9 = 0, Зх—4«/+16=0, 4х+3у—37 = 0 или 4х+Зу+13 = 0. 134. 1) а = 4,
Ь = —3, г = 5; 2) а = —5, 6=2, г — 0; уравнение определяет точку; 3) а = 2,
Ь = —7, г2 = —1; уравнение не имеет геометрического смысла (мнимая окруж-
ность). 135. tg<p = —2,4. 136. (х+1)2 + (у—1)2 = 5. 137. (х—3)2 + (у—4)2 = 25.
138. х = 3,2. 139. Зх—4i/+8=0, 4х—Зу+7=0. 140. (х—2)2+уа= 16.
142. (4; 1,8); (4; —1,8); (—4; 1,8); (—4; —1,8). 143. Ьг/а. 144. 4х+Зу+12 = 0.
145. 16х2+25у2=41. 146. Точка М—вне эллипса; точка N—иа эллипсе; точка
Р—внутри эллипса. 147. e = sin(a/2). 148. М (—5; 7). 149. 3ха+3у2—2ху —
— 2х—2у—1=0. 150. х2/3+уа/4 = 1. 151. Искомая кривая—эллипс. Если на-
править оси координат по сторонам прямого угла (точка А пеж.т иа оси Ох), то
уравнеиие этого эллипса 9ха+36у2 = 4аа. 155. х2/9—у2/8=1. 156. ха/3—у2/5=_1.
157. (—4; —3). 158. х2/64+//48= 1. 159. ?х2—у2 = 8/225. 160. е = 2/УЗ.
161. (—8, 0). 162. х2/4—у2/\2 = 1. 163. 6 и 14. 166. Правая ветвь гиперболы
х2—//3=1. 169. у2=4х. 17O._Af! (2; 4) и М2(2; —4). 171. уа=4х, у2 = —4х.
172. у = ±2У2 х. 173. у2 = У2 х. 174. !М (0; 0), Мг (18; —24). 175. у2 = х,
tg <z=8/15. 179. (3; 2). 180. (8; —6). 183. 1) Ох (1; 2), р = —1/4; х'а = —(1/2)</';
2)О1(1;3); р = —1/2; х'г = -у'; 3) Oi (1/16; 1/8), р =—1/8; у'2 = (-1/4) х';
4) ОН1; —2), р=1/2; у,г=х'. 184. 1) х'«/' = 1/8; 2) х'у' = 13/9; 3) x'j/' = —6/5;
4) х'у'=1/2.187. Окружность (х— 1/2)2+(у— 1 /3)2= 1.188. Эллипс х'2/25+у'2/16=1;
иовое начало О'(1; —1). 189. Гипербола х'2/4—уг!/9=1; новое начало О'(2; 3).
190. Точка О'(2; 1). 191, Мнимый эллипс х'а/(—1)+ «/'*/(—1/4) = 1; х'=х,
294
у'=у-\-\. 192. Гипербола у'2—х'2=1; новое начало О' (3; 0). 193. Парабола
х'2 =— у’’, новое начало О’ (1; 5/2). 194. Прямые х = 2 и х=4. 195. Мнимые
прямые. 205. Совокупность двух параллельных прямых 1 = 0 и 5х +
-\-у—1=0. 203. Совокупность двух слившихся прямых х-{-у-|-1=0. 204. Сово-
купность двух пересекающихся прямых 2х—Зу-|-1=0, 4х—Зу—1=0.
205. х"2/30-|-у*2/5 = 1. 206. х"2/9—у"2/36=1. 207. у"2 = — 2х". 210. х=1/2,
у=1/2. 211. Система противоречива (решений не имеет). 212. x = a-j-b, y—a—b.
213. Система неопределенная (имеет бесчисленное множество решений: х остается
произвольным, а у = —(3/2)х-f-1/12. 214. x—y = z = t. 215. x = cosa, y=sina.
216. x = 2t, y — t, z — 2t. 222. 0. 223. 2. 224. 2 (ad—be). 225. x=l, y = 2, z=3.
226. x = 0, y=0, z = —2. 227. x = 0, y=0, 2 = 0. 228. x = t, y = 2t, z = —3t.
229. x=l, y = —1, 2 = 0. 230. x = t, y=t, z = — t.
Глава II
234. C(5/3; 11/3; 13/3), £> (1/3; 13/3; 17/3). 236. M (3; 1; 3). 237. Пополам.
238. M(0; 0; 17/8). 239. M (16; —5; 0). 246. AM = (b + Xc)/(l-f-X). 248. a* = 0,
ay — 2, az = —2. 249. m24-zn-j-l. 251. a = 3/5; cosa=l/3, cos (5 = cos у = 2/3.
252. 1^!^! = ?; cos a = 2/7, cosj5 = —6/7, cos у = 3/7. 253. b = —2)4-5k или
b = — 2j—5k. 254. M(—4; 4; 4/2). 255. a0 = (1/3) i —(2/3) j—(2/3) k. 268. —96.
269. arccos (17/50). 270. m=l. 271. 547. 272. 4 = Fs = Fs cos<p = 5 /3.
273. (± 1//Ti)(i—3j + k). 274. c = l-|-k или c = (1/3) (—i + 4j—k). 275. 20/3 и
20/7. 276. rjr)=7i4-7j+7k. 279. Нет, так как компланарные векторы ие могут
быть попарно перпендикулярными. 280. а X Ь = —17i-|-7j—к. 281. /65/2 кв. ед.
282. 4. 284. 20 куб. ед.; 4 V510/17.
Глава III
296. 1) (x-\.y—z-2)W3 =0; 12) -3/(5/2)х-(1//2)у+4/(5/2) 2 —
— 7/(5 /2) = 0. 297. б/=13/Э<29; начало координат и точка Мо лежат по раз-
ные стороны от плоскости. 298. d=7/5/3. 299. 1) x-j-y-^-z—5 = 0, 2) 2х-(-2у+
4-г—6 = 0. 300. 7х—Пу—2—15 = 0. 301. М (5; 5; 5). 302. 4х—Зу4-12г—169=0.
303. 5у4-4г = 0^5х—Зг = 0; 4х4-Зу = 0. 304. 6х4-5у—7г—27=0. 305. х/2-f-
4*у/24-г/(± V2)=1. 306. 60°. 307. х4-7у4-10z = 0. 308. х—г = 0. 309. х4-У +
_|_г_3 = 0. 310. 5х4-2у4-5г—9 = 0. 311. У~2х+у-\-г—5=0. 1312. 4х4-3у —
—2г—1=0. 313. (Лх/^а — -4 $7) 4 х 4- (BiD%— В%О1) y-^-(C\D2—^1Са)2=0.
314. х—у+2 = 0. 315. arcsin (5/6). 327. 5y+5z—64 = 0, х = 0(уОг); 5x4-5z —
— 2 = 0, y = 0(x0z); 5x—5y-|-62 = 0, z = 0(xOy). 328. (x4*l)/5 = (y—3)/2 = z/l.
329. cosa = 6/7, cos ₽ = 3/7, cos у = 2/7. 330. (x—1)//2 =(y4*2)/l = (z—3)/(±l).
331. (X—5)/1=(у-Н)/3 = (г+3)/(—11). 332. M (0; 7; —2). 333. (x—3)/(— 1) =
= y/5 = (z+l)/2; x/2 = (y-7)/(-2) = (z+2)/3. 334. x = -3/-l, y=6/+l,
z = Z-[-2. 335. 5 /30/6. 336. (x—3)/3 = (y+l)/(—5) = (z—2)/(—2). 337. cos<p =
= 20/21. 338. x/0=y/l=z/2. 339. (x-4)/2=(y-l)/l =(z4-2)/(—2). 340. x/2 =
= (У-2)/(-1) = (г-1)/0. 341. (x—l)/2 = (y—1)/(—3) = (z —1)/2. 342. x/1 =
=(y—2)/(—l) = (z—1)/(—I). 343. х-5у-2г+11=0. 344. x/(-10) = (y-3,4)/13=
= (z—5,2)/19. 348. 1) C(—1; —2; 0), r = 5; 2) C (2; —3; —1), r = 4; 3) C (0; —1;
3/4), r = 3/4; 4) C(l; 0; 0), r=l; 5) C (0; 0; 2), r=l. 349. 1) Внутри сферы;
2) вне сферы; 3) иа сфере- 350. (х—2)24-(у—l)24-(z-|-2)2=9. 351. (х—1)2 +
+ (у—1)2 = 16, 2 = 0. 352. С (4; 4; —2); г = 8. 356. 1) Круговой пилиидр;
2) эллиптический цилиндр; 3) гиперболический цилиндр; 4) параболический
цилиндр; 5) параболический цилиидр; 6) параболический цилиндр; 7) круговой
цилиндр; 8) ось аппликат х = 0, у = 0; 9) биссектральиые плоскости х=2 и
х = — z; 10) плоскости у = 0 и у = х. 357. 1) x2-j-z2 = 9, у = 3 (окружность);
2) у2 —х2 = 1, 2=1 (гипербола); 3) г2—у2=0, х=0 (две прямые). 358. 1) у2/Ь24-
+ z2/b2—х2/а2 = 0; 2) х2/а24-г2/а2—у2/Ь2 = 0; 3) x2/a2+y2/b2—z2/c2=0.
295
361. 4x2-|-4j/2—(z—2)2 = 0. 362. х2—у2=1, z=l; z-|-l=*2. у= 1; у2= 1 — г,
х=1; у2—х2=1, г = —1. 363. 1) Гиперболический параболоид; 2) конус с вер-
шиной в начале координат. 364. 3z = 2x2+y2. 365. x2/9+j/2/54-z2/1 = 1.
366. х2-}-у2=1, z=l (окружность). 367. 1) Ось ординат; 2) конус с осью Оу
и вершииой в начале координат; 3) конус с осью Ох н вершиной в начале коор-
динат; 4) начало координат; 5) пара плоскостей, пересекающихся по осн Ог.
374. Две плоскости х = у и х = г. 375. Круговой цилиндр (х—2)2-f-(z—2)2 = 4.
376. Прямая х—у=г. 377. Конус второго порядка x2-j-(y—I)2—(г—1)2 = 0
с вершиной S (0; 1; 1). 378. Точка (0; 1; —1). 379. Однополостиый гиперболоид
с каноническим уравнением х'2 + «'2/4 — z'2/4= 1. 380. Двуполостный гиперболоид
с каионическнм уравнением х' -|-г/'2— г'2 = —1. 381. Параболоид вращения
с каноническим уравнением х'г~\-у'г = 4г'. 382. Гиперболический параболоид
с каноническим уравнением х'г — г'2/0 = 2у'.
Глава IV
387. 900. 388. 12. 389. 21 280. 390. а262. 391. х = 1, у = 2, г = 1, /=—1.
392. х=1, у=1, z = 0, / = —2. 393. х=1, у = 2, г = 3, и = 4, t'=5.
394. х=1, у = —1, г = 0, t — 2, 410. (1; 2t\ 3f), где /—произвольное действи-
тельное число. 411. (2/; 2/; t), где t—произвольное действительное число.
412. (0; 0). 413. Прямая x'cosa—у' (
/9 6 6\ /0,1 —0,2 0,7\
415. 6 9 6. 416. 0 0,1 —0,2
\6 6 9 / \0 0 _ 0,1)
7^=11; e1 = (4/K4Di-(5/K41)j, е2
Лз=3, Х3==6; Ti = cc(i—к), г2 = Д(1—Л-
,/'-4 —8 —4\
-f-sina) = 0. 414. 5=^—3 —|—5J.
417. x=l, y=2, z=3. 418. ki = 2,
= (l/|<2)i + (l/K2)j. 419. Xi = —2,
,, r3 = y(i + 2j4-k). 423. x"i/16+z/'2/4=l.
424. х"*!2&—tf2/9= 1.425. у”г = 2 У2 x". 426. x'*-j-у'г/1 —z,2/3= 1 (однополостиый
гиперболоид). 427. 2y’’2-J-Зг"* = 6 x” (эллиптический параболоид). 434. г(Я)=0,
если Х=0; г(Л) = 2, если X # 0. 435. г(Л) = 3. 436. г(Л)=3, базисные миноры
437. г (Л) = 2; базисные миноры
|Н|. |Н|. IJII-
3 81* 21 ’ |? 1 I’ |? з| и ‘ Система совместна, г (Л) = г (Лх) = 2;
Х!=1, х2=1/2. 442. г(Л) = 1, г (Л^ = 2. Система несовместна. 443. Система сов-
местна, г (Л) = л(Л1) = 2. 446. Xi = l, х2=5, х3 = 2. 447. х1 = 1, х2 = 2, х3 = 3,
х4 = 4. 448. Xi = 5, х2 = 4, х3 = 3, х4 = 1, х6 = 2. 449. Система несовместна.
450. х=1,96, у = 2,96, 2 = 5,04. 451. х=1,50, у=1,16, z=l,40. 457. Х!=1,
ха = 2, х3 = 3, х4 = 4. 458. Xi = «, x2 = u-f-l, x3 = u-}-2, x4 = u-f-3. 459. Система
несовместна. 460. г(Л) = 3.
Глава V
463. Да. 464. Нет, так как сумма двух элементов множества не является
элементом этого множества. 465. Нет, так как сумма двух многочленов второй
степени может быть многочленом первой степени илн постоянной величиной.
466. Да. 467. 1) Да; 2) да; 3) да; 4) нет. 468. Да. 469. 1) Лишь в том случае,
если это нуль-вектор; 2) нет, так как в этом пространстве, кроме векторов хну,
должны быть и другие векторы вида Xx-|-gy. 470. Нет, так как в полученном
множестве векторов найдутся векторы, сумма которых равна х, например векторы
(х—У)/2 и (х-(-у)/2. 471. Может. Например, исключив нз множества геометри-
ческих векторов векторы, не перпендикулярные оси Ог, получим множество век-
торов Xi-j-gj, образующее линейное пространство. 473. Нет, так как Х(|4; |2; Ь)
не принадлежит этой совокупности, если X—не целое число. 474. Нет. 475. Нет,
так как противоположные векторы расположены ие в I октанте. 488. Множество
296
всех многочленов не выше n-й степени. 501. х = ех-)-2е2 —Зе3 —4е4. 502. x=ei-|-
+ е2 + ез+ ... +еА. 504. = е^, g2 = а&, gs = pg2. It = ?5з, = 6^. 505. Нет,
так как имеет место равенство ej -±е2-}-е3 = 0, которое невозможно в силу линей-
ной независимости базисных векторов е2 и е3. 506. Может лишь в том слу-
чае, если этим элементом является нуль-вектор. 508. Пересечением является мно-
жество элементов х12 = (0; 0; g3; Е,4), у12 = (0; 0; т)3; т)4), Zi2 = (°; 0; £3; .......
Сумма совпадает с пространством R. 509. d(/?4)=3, d(Z?2) = 3, d(R3) = 2,
d = (Ri) = 4. 510. Нет. 513. R3—множество постоянных величин, /?4—множество
многочленов вида с0/44-с4/2-{-с2/-)-с3. 514. R3—множество всех векторов, парал-
лельных осн Ох, а /?4 = /?. 516. Множество всех четных функций образует под-
пространство, а множество нечетных — нет, так как произведение двух нечетных
функций есть четная функция. 517. Нет, так как любой вектор Ха не принадле-
жит этому множеству, если X—иррациональное число. 522. й = 3; fi = (—1; 0; 1;
0; 0), f2 = (—1; 0; 0; 1; 0), f3 = (0; —1/2; 0; 0; 1), f = (— c4 —c2; — 0,5c3; c4;
c2; c3). 526. Да. 527. Нет, так как равенство | a-f-b |-(a-)-b) = a-a + 6-b не выпол-
няется, если ab 0. 528. Лишь в том случае, если Хо = 0. 529. Лишь прн а = 0.
/а 0 0 ... 0\ /0 1 0 0\
530. Да. 533. ( 0 а 0 ••• 0 j. 536. л = (оОО?)’ 538, ЗА—2В = Е.
\0 0 0 ... а/ \1 0 0 0/
544. —1 1 —1 . 545. A~4 = A. 546. А~1 = ( 7 А ) . 547. 5=2Ecosa.
\—1 —1 1 у V—1
548. Линейное преобразование А не имеет обратного, так как |А| = 0.
549. А~2 = (А_1)2 = (_® q) . 550. Прн Х =—2. 552. 1) Если a # Р, то Х4 — а,
u = c4ei, Xj> = P, v=c2e2; 2) если a = p, то X4=X2 = a, u = c1e1+c2e2. 553. X4 =
= X2 = 2, u = c4 (e4-±e2). 554. 1) Если b 0, то линейное преобразование не имеет
собственных векторов; 2) если 6=0, го X1 = X2 = a, u=c4ei+c2e2. 556. Х = 2,
u=c1(e1 —е3); Х = 3, v=c2 (е4—е2-±е3); Х = 6, w=c3 (е4 + 2е2-|-е3). 558. Х= — 1,
u = c4i-|-c2j. 560. X — 1, u = Ci (е4 е2 -f- е3 е4); Х =—l,.v=c2(e4—е2-|-е3—е4).
561. Х = а4-Р4-у, и —с (ег-}-е2—j-е.з). 563. (х, у)—общая стоимость всех изделий,
выпускаемых заводом. 565. Да. 566. Нет, так как не выполняются условия 2°
и 3°, если X < 0. 567. Да. 569. arccos (1/п). 573. Да. 576. |х| = 5. 577. х/| х | =
=(1/15)е4+(2 К2/15)е2+(КЗ/5)е3+(8/15) е4 + (/57з) е6. 579. х — нормиро-
ванный вектор. 580. <р = л/3. 581. ± 0,5 (е44-е2-}-е3+е4). 582. Х=± 1. 587. Да.
588. Да. 589. При Х=± 1. 590. Да, так как векторы Ае4, Ае2 и Ае3 образуют
ортонормированный базис. 591. Да. 598. х'2/21 +у'2/3= 1. 599. х'2/16—у'2/4=1.
600. х'’/44-±|/'2/4=1.
Глава VI
606. п = 4. 607. 6 = 0,16%. 608. 6 = 0,0005%. 609. 6 = 0,022%; n = 4; S =
= 8765 ±0,1 м2. 617. 1) [—2, 0)0(0, 2] ; 2) [0, 4); 3) (-оо, 0)0(0, +оо) ;
4) х * я(2л+1)/4, n £ Z; 5) (-оо, — 2] (J [2, + оо ); 6) (1/3, +оо) ; 7) [0, 2) .
618.1) [1,+оо); 2) (-оо, 0)и(0, +оо); 3) [-4, 4]; 4) (-оо, 3]; 5) [—2, 4J;
6) (6, 1] . 619. 1) Нечетная; 2) четная; 3) нн четная, ни нечетная; 4) четная;
5) нн четная, нн нечетная; 6) четная; 7) нечетная. 620. 1) 2л/5; 2) 6л; 3) л;
4) л. 657. Г/2. 658. —1. 659. 1/6. 660. —2. 661. —sin а. 662. m/n. 663. sec2x0.
664. — jf2/4. 665. 1/2. 666. оо. 667. 2. 668. 3/4. 669. —1/4. 670. 1/2. 671. 3.
672. р^7/4. 673. 25/9. 674. 1/2. 675. т. 676. 1, если х—►+»; —1, если
х—4—оо. 677. (а—с)/2. 678. 0. 679. 0. 680. 1п 5. 681. 1п (8/7):1п (6/5). 682. 2.
683. 1п 5. 684. 1/4. 685. 1, если х—*--[-0; —1, если х—>—0. 686. -±оо. 687. 2.
688. 0. 689. Не существует. 690. 5/4 . 691. 1п а. 692. е. 693. е3. 694. 1/6.
695. 1п(5/4). 696. 1. 697. —3. 698. 0. 699. 1/2 . 700. е1». 701. /Т. 702. еа~ь.
703. Уе. 708. у ~ х. 709. 2. 710. 1/2. 711. а=о(Р). 712. а ~ р. 713. а ~ р.
714. 1/3. 715. 9/4. 716. —1/2. 717. —1/2. 718. —1/2. 719. 1. 720. 9/25.
297
721. (1п5-1п4)/(1пЗ-1п6). 722. 1,6. 726. х = 2—точка скачка. 727. х=1, х = 5—
точки разрыва II рода. 728. Разрыв 11 рода. 729. х~0—точка устранимого
разрыва. 730. х = 3—точка скачка; х = 5—точка разрыва II рода; х = 0—точка
устранимого разрыва; х = л/24-лп (л £ Z)—точки разрыва II рода. 731. х=Ь
х = 2—точки устранимого разрыва. 732. х =—2, х — —3—точки разрыва II рода;
х =—1—точка устранимого разрыва. 733. Функция иепрерывиа в бесконечном
промежутке (—оо, +оо) . 734. 1) Функция иепрерывиа; 2) имеет одну точку
разрыва II рода; 3) имеет две точки разрыва 11 рода. 735. 1) Функция непре-
рывна; 2) имеет две точки разрыва II рода; 3) имеет четыре точки разрыва
II рода.
Глава VII ,
739. у' = — 2/х3. 740.у'= 2/(3 f/x) . 741. y' = 5cosx—3sinx. 742. у’ =
= 5tg2x. 743. у'= — е*/(е*4-1)2. 744. у' = 2**.2х-In2. 771. у' = ~21/х*.
772. у' = ^х . 773. у' =х2 Кх (1 —х2)2. 774. у' = — х2е~*. 775. у' = 9х2 1п х.
776. у'= (8/9)* In (8/9). 777. у'=х2 cos х. 778. у'=6 (х+l)/(2x2+3xj. 779. у'=
=—Зх/р^! —Зх2. 780. у'= arccos (х/2). 781. у' = 1/(2 Кх)arcsin Vx. 782. у'=
= — cosx. 783. у'= — cos2 (х/3) sin (х/3). 784. у' =cosec (2x41)/2. 785. у'=
= 1/cos х. 786. у' = 2 sec6 2х. 787. у' = 1 /(2 V* ) sin2 V* cos6 Vx . 788. у' =
= 6х/К9х*+1. 789. у> = Уа2—х2._______790. у' = — 2sec2x/Ktgx(4tg х41).
791. у’ = ctg3 (х/2). 792. у' = 1/(х К4х2 —1). 793. у'= 1/J<a2—х2. 794. у'=
= 1/(2 J<1—х2). 795. у'=6х2/(1+х6). 796. у' =6 sgnх/(х2 + 9). 797. ^' =
=—2е~* sin%-*. 798. у'=—1/(2 V1—х2). 799. у'=—6/[(х—1) (х—2) (х—3) (х—4)].
800. у'=3e’in* зж sin 6xsin2 Зх. 801. у'= —241nsinx-ctgx/(41n4slnx—9).
802. y' = secx. 803. y' = cosecx. 804. y'=Vix‘ 805. y' = 10/[x(xs4-2)]. 806. у'=
= 2 sin х/(1-j-cos х)2. 807. у' = cosx/(l-|-sin2 х). 808. у'= cosec2 (х/2) ctg (х/2).
809. у'= (2/х) cos2 (1пх). 810. у' = 5х41п (х5+3). 811. у’ = — х/(| х | Кб—х2 ).
812. у' = Кх2+2ах+3. 813. у'=0. 814. у' = (тх4л)/|/"х242ах4₽.
815. у' = 1/(1 —тх2)3/2. 816. y'=4xcos2x. 817. у'=—2 cosec3 х. 818. у'=
^пЯь^Тхр ' 819, «''=9xsin2 х cos х- 82°- V=2AX КТ+х3)- 821. у' =2е* sin2e*.
822. у'=2/(х2 + 2х+2)2. 823. у' = 1п3х. 824. у' = (|п sin Кх)/(2 К* cos2K*)-
825. у' = 2(Ц-1пх)/(х* + х-*). 826. y' = l/sin6x. 827. у' = cos* x/sln х. 828. у'=
= 1/(3 sin х-|-4 cos х+5). 829. y'=cosxtg3sinx. 830. у' = 1/[х2 (х— 1)].
831. у' = 1/[х(х+1)(х+2)]. 832. y' = 4xtg22x. 833. у'=—2е*/К 1—е2*. 834. у' =
= (In In In х)/(х In х). 835. у'=2е2* (1 —2х)/(х4е2*)2. 836. у'=2 (In х-f-1 )/(х21п2х—1).
837. у'=3/(14-х2). 838. у'=(е2 S,nxcosx):sin(e2 ,1пж/2). 839. y'=asin2x.
840. у'=3sec2xsec4tgx. 841. у' = (—1/х2) arctg х. 842. у' = (—5/х6) 1п х.
843. у' = (1/К2x41) In (2x41). 844. у' = sec х tg х In sec х. 845. у'=
= — 2e^lV^=^x- 846. у'=3-2СО,Э ж-3 со,ж-81п3 х-1п 2. 847. у' = (е*-26*/34*)Х
Х1п(32е/81). 848. у' = 0. 849. у' = х cos 2х. 850. у' = 2е**х (х*4х24 1)/(х24- I)2.
851. y'=xcosx/sin2x. 852. у' = (1/К х) tg2 К х. 853. у' = х*Цх^—а4). 854. у' =
= —4х/Кх44-1- 855. у'=е°’6 sin х tg2x. 856. у' = 8х3/(1-|-х8). 857. у'—
= хе** (2х21п х+21пх+1). 858.у'=0,5 In 2 К2ж/(1 —2*). 859. у' = —1п 2/(2х In2 х).
860. у'=(тх4-л)/К—х2+2ах+р. 861. y'=(2/ln2)ctgx. 862. у'=1/(Кх249 1п а).
863. у' =xarc’in * (у*”* 2 + ЭГ”1П * ) . 864. у' =8 (х— 1)3/(х+ I)6. 865. у' =
=-----2*(х+1)3 /1п2+ 3--------2 _ вдв. ^^/(ixi/T+T5)-
(х—1)2К2х+1 \ *41 х 1 2x4-1/
867. у'= xm cos (л 1п х). 868. y' = (xtgx+lncosx)sec2(xtgx4-lncosx)xsec2x.
869. у' = — хsin х-In (хcos х—sinx). 870. у'= 3cos3(хе*—е*)-хе*. 871. у'=
=—2(1 —2х2)/(|1—2х2| К1 —х2).
Я72 «'-J 1 при х > 0,
’ у 1—1 ПРИ х < 0.
873, у' =>
298
f W при f (x) > 0, J з при X > 5/3, ( e* при x > 0,
(—f’ (x) при f (x) < 0. ' y (—3 при x < 5/3. ' y ( —е-*прих<0,
(—2 при x < 0,
876. у' = < 0 при 0 < х < 2, 877. у' = 2xe*sinx. 878. y' = (xcosx):
( 2 при х > 2.
:У~(х sin x+cos х)г4- 1. 879. у' = х*+11п х (1п х—1)/е*. 880. y' = (ctgx-lncosx +
+ tgx-lnsinx)/ln2cos х. 881. у' = пх»~1/(2 Ух2»Ч- 1). 882. у' —— (log* е)2/х.
883. у'=0. 884. у' = 1/2. 885. у'=0. 886. /=х*(1 + 1пх). 887. у’ = х~*-2*-х2Х
ХОпг+гх-1—1 —1пх). 888. / = 2х1пж-1 1пх. 889./=—** 1 -X
(х—1)3/5х—1
X [4+т/ТХп ~• 893, (arcsec х)'= 1^х УГ^~ 0« (arocosec х)' =
= —1/(х/х2— 1). 894. 4 cosec2х. 898. у' = (х2—у)/(х—уг). 899. у'——(Ах+
+ By+D)/(Bx+Cy+E). 900. у’ = х/(3у). 901. у' = у(у—х\пу)/х(х—у 1пх).
902. у'=—(ycosx-f-sin y)/(xcosy-f-sinx). 903. у'=—(ех—у-2*У.\п2)/(еУ—х-2*7.1п2).
904. у' =2х. 905. у' =у/х. 906. у' = — у/(2х 1пх). 907. у' =— (2xsin у—у3 sin х—2):
:(х2 cos y-|-3y2cos х—3). 909. — ctg t 910. е». 911. 2Кае'Г®. 912. cth t.
914. <z = n/4; y=x-|-l. 917. у—ул = (— у0/р) (х—х0). 918. х—у-{-1=0.
919. х+у— 1=0; х—у=0- 920. х—у-}-2—л/2=0; х^-у—л/2=0. 921. Зх—у—4=0;
х-|-3{/—28 = 0. 923. л/4. 924. Зх—8у4- Ю—61п 2 = 0; 32х+ 12у—15—64 1п 2 = 0.
925. xch/e—1=0. 926. tg<p = 2/3. 927. л/4. 928. л/4; Зл/4. 929. tg<p1==3,
tg <р2=—3. 930. л/2. 933. 1,76м/с. 934. х/= а. 939. л—arctg (1/3). 940. tg<o = (p;
если <р—>-оо, то<о—>-л/2. 941. л/24-ф. 942. 0. 943. arctg (1/m). 944. л—arctg (125/64).
950. / = —44/(х4-5)3. 951. у"=1пх. 952. у" = 2)< 1 —X2. 953. y"=xsin3x.
954. у"=\1У х24-а2. 955. J-cosec4 4- 956. -^ = —4
* 1 dx2 4o 2 dx2
959. —1/3 м/с2.960. /" = l/(x+1)4. 961. y"'=(2 In x—3)/*3. 962. y'" = 105}<2x+3.
963. y'"=4sh2x. 964. /">=^5,7--2;(2n+1)}<x. 965. /»>= •
966. /«> = —1,5-2».cos(2x4-nn/2). 967. /»>= [2*4-(—1)»-2-*] ln« 2. 968. /«> =
= n! (ad—6c)(—c)» 1 969. /П)=й»еЛх. 970. /»> = cos(x4-nzi/2). 971. ^7; =
(cx4-d)n+1 y я кт// dxn
= (_1)«.±. 972. t/ni = t/IV=...=O. 982. dy = /49— x2dx. 983. dy=^436 .
984. dy = th (x/2) dx. 985. dy= ***** . 986. dy= In xdx, d*y=J£$- , <Py=— .
14- x x*
987. ^{/=-~ . 988. by=----ГА\. , dy= — . 989. Ay=0, 0401;
v (Xa_|_4)3/2 ’ x(x4-Ax) x2 » > .
d{/ = 0,04. 990. 34,04 м3. 991. л/4-f-1/13. 992. 0,811. 993. 1,035. 994. 0,078.
995. 1,9938. 1007. 5 = 5/2. 1008. J-где
*e Xo Xo Xo
/?., =tz^-(x0>g<x).l°09./и(}<3; 0). 1010. 0,754. 1011. 4,946. 1012. 1,395.
1013. 2,002. 1614. 0,587. 1024. 3/5. 1025. 2. 1026. 2/3. 1027. 1/3. 1028. 0,18.
1029. 18. 1030. 1. 1031. 0. 1032. 1/2. 1033. oo. 1034. 0. 1035. 1/л. 1036. 1.
1037. 0. 1038. —1/2. 1039. (p—q)/2. 1040. 2/3. 1041. 1. 1042. e~e. 1043. 2.
1044. e1/3. 1055. Возрастает на (—оо, —1) и на (1, +оо), убывает на (—1, 1).
1056. Убывает на (—оо, — 1) , возрастает на (—1, +ao) . 1057. Возрастает на
(—оо, 1), убывает на (1, +оо). 1058. Убывает иа (—оо, —1) и на (1, +оо), воз-
растает на (-1, 1) . 1059. ymin=y (0) = 0, угаах = у (2 ^2/49) = (12/49) ^4/7.
1060. Утах = У (Н/4) =13/4.1061. ymin=y (0) = 0.1062. ymin=у (0) = 1. 1063. ymin=
= y(e) = e. J064. |/max=|/(l) = l/K е,ут\п=у(—1) = —\/У~е. 1065. ymin=^(l)=0.
1066. J/min=!/(3) = 0, »max = y(2) = 3. 1067. Яти=!/(l) = -l- Ю68. ymax =
= (я-124-б/ 3)/12, «/min= (5л—12—б/ 3)/12. 1069. i/max=e3/2, ?/min = e’3/2-
1070. А/наим = 2, А/наиб = 66. 1071. (0 ; 4) и (0; —4). 1072. 25км; 8ч 15мин.
1073. 5^1, 3/2. 1074. 1/4, 1/4. 1075. V = 2л/3/ 3/27. 1076. V= (S/3)/S/(6n).
1077. На расстоянии 9 км от А. 1078. 125 м. 1079. а//2. 1083. Выпукла на
(—оо, —2), вогнута иа (—2, + оо). 1084. (4; 20). 1085. (1; 0). 1086. Точек пере-
гиба иет. 1091. х=0; у=2х. 1092. х = 0; у=—Зх. 1093. у = х—6. 1094. у =
=0,5х-|-лн у = 0,5х. 1095. р=0,5лх4-1 н у=—0,5лх-|-1. 1098. D(y)—(—оо,
—j-oo); функция четная и периодическая с периодом л. Возрастает на (пк,,
л/24-яЛ), убывает на (п/2+пк, п+пк); ут\п = У (xk) = 0, утлх— y(n/2-}-nk) = h
k£Z. Кривая вогнута на (—я/4 + як, п/4+пк) и выпукла на (л/4-f-n^, Зл/44-л£);
точки перегиба (—л/4-|-л£; 1/2) н (л/44-лй; 1/2), AgZ. 1099. £>(у) = (—оо, + оо),
функция нечетная. Убывает на (—оо, —1) и на (1, +оо),, возрастает на (—1, 1);
i/min=y(—1) = —2, г/тах = У(0 = 2. Кривая вогнута иа (—оо, 0) и выпукла на
(О, +ОО); точка перегиба (0; 0). 1100. D(y)= (1, +оо); асимптоты х=1, у = 0.
Убывает во всей области определения. Кривая всюду вогнута. Экстремумов и
точек перегиба нет. 1101. D(y)=(— оо, 0)U(l, -f-oo); асимптоты х=0, х=1,
у = 0. Возрастает на (—оо, 0), убывает на (1,+оо). Кривая всюду вогнута.
Экстремумов и точек перегиба нет. 1102. D(y)= (— оо, — 2)(J(—2, 2)|J(2, + оо);
функция нечетная; асимптоты х=—2, х = 2, у=х. Возрастает на (,—оо, —2/ 3)
и иа (2/ 3, -f-oo), убывает на (—2/ 3, — 2),_(—2, 2), и на (2, 2/ 3); i/min =
= у (2 /3) = 3/ 3, утах = у (— 2/3) = — 3/ 3. Кривая выпукла на (—со, —2)
и на (0.2). вогнута на (—2,0) и на (2, +‘оо); точка перегиба (0; 0). 1103. D (у)=
“(0, +оо); асимптота у = 0. Возрастает на (0, е2), убывает иа (е2, +оо); А/тах =
= р(е2) = 2/е. Кривая выпукла на (0, е&) и вогнута иа (е , +оо); точка пере-
гиба (е8/3; 8е-4?,3/3). 1104. D(y)= (— оо, + оо). Убывает иа (—оо, 1/4), возрас-
тает иа (1/4, +оо);; ут1п = У (1/4) — —27/16. Кривая вогнута на (—оо, 1/2) и на
(1, +оо), выпукла на (1/2, 1); точки перегиба (1/2; —1) и (1; 0"). 1105. D(y) =
-[0,+оо). _ Убывает иа (0,1/3), возрастает на (1/3, +оо); Ут1п=У (1/3) =
=—2/(3 / 3). Кривая всюду вогнута. 1106. D(y)= (— оо, +оо); асимптота у=х.
Убывает на (—оо, 0), возрастает иа (0, +оо); A/min=У (0) = 1 • Кривая всюду
вогнута. 1107. D (у) = (— оо,. + оо); функция нечетная; асимптоты у =—1 и у=\.
Возрастает на (—оо, <+оо). Кривая вогнута на (—оо, 0) и выпукла на (0, +оо);
точка перегиба (0; 0). 1108. О(у) = (—оо, +оо), асимптота у=0. Возрастает_ на
(—оо, 1), убывает иа (1, +оо); утах=у (1)=е. Кривая вогнута иа (—оо, 1—/2/2)
и на (14-/2/2, 4-00), выпукла на (1 — У 2/2, 1-|-/ 2/2); точки перегиба
(14-/2/2; /ё) и (1 — У~2/2; Уе). 1109. О (р) = (-оо, 2) (J (2, + оо); асимп-
тоты х = 2 и у = х-}-4. Возрастает иа (—оо, 2) и на (6, +оо), убывает иа (2, 6);
Ут\п — У (6) —27/2. Кривая выпукла на (—оо, 0), вогнута иа (0,2) и на (2, +»);
точка перегиба (0; 0). 1114. /? = 25/3. 1115. /? = (4а/3) cos (0/2). 1116. А=1/(е/ 2).
1117. (2; 2). 1118. Окружность g24-T]2=l. И21. Первый. 1122. Первый. 1123. Тре-
тий. 1124. Первый. 1125. Третий. 1126. Второй. 1128. Окружность х24-г2 = 1,
у—1. 1129. Прямая, проходящая через начало координат и образующая с осями
координат равные углы. ИЗО. Прямая, параллельная оси Ог и проходящая через
точку (1; 1; 0). 1131. Равнобочная гипербола, лежащая в плоскости хОг.
1134. (i -f-k) sh 2/4- j ch 2/. 1135. 0. 1136. 3 (i2—2/5) i 4-(5/4 —2i) j. 1138. x/(—1) =
= (p—l)/0 = (z— я/3/2)//3, 2x— 2г/3-|-Зл = 0. 1139. ML(0; 0; —1) и
Af2(2/3; —8/9; —1/27). 1140. 70°23'. 1141. x/1 = (у—l)/0= {г— У 2/2)/l, x-|-z —
—У 2/2=0. 1142. (x— 1)/2=(у4-1)/0=(г—1)/1. 1143. (x—l)/2=(y—l)/3=(z—l)/4.
1144. arccos (14/(3/29)). 1146. ds=/ a2-\-b2dt. 1147. h = 2/3 л. 1148. v =
dr d2r
=-//ц——311 sin /4- 3j cos 14- 4k, w=^=—3i cos t—3jsini. 1149, v|(=i = 14"
4-2J4-3k, w|/=i = 2j-|-6k. 1151. t=(5/13)i — (12/13) j sin/4-(12/13) k cos i.
300
1152. r = -(l/3) j + (2/"2/3)k. 1161. (2/3) i + (2/3) j + (l/3)k. 1162. (1/3)1 —
— (2/3) j +(2/3) к. 1163. (—2/3) i + (l/3) J + (2/3)k. 1164. 2/27. 1165. 2/27.
1166. X—2F+2Z—2=0. 1167. 2X —Y—2Z— 7=0. 1168. 2X4-2K-|-Z—19=0.
Глава VIII
1174. x24-y23s 1—часть плоскости вне единичного круга с центром в начале
координат. 1175. Часть плоскости внутри круга ха4-уа < 1. 1176. Полоса между
параллельными прямыми х+у<1 и х4~УЭ=—1- 1177. Концентрические кольца
л/2 5» х2У2 3^ 0, 5л/2 х2+у2 Эг Зл/2. 1178. у>х—полуплоскость, лежа-
щая выше биссектрисы у =х. 1179. Полуплоскость хЗгО. 1180. Шар xa4-y2-f-za<
<а2.1181. Часть пространства вне конусах24-уа—г2 = 0. 1182. Часть пространства
внутри шара xa + ya4-za < 1, за исключением начала координат. 1183. Часть про-
странства над плоскостью х-)-у4-г = 0, включая эту плоскость. 1184. Семейство
параллельных прямых 2х+у=С. 1185. Семейство прямых у=Сх. 1186. Семейство
прямых у = е2Сх, или у = С^ (С > 0). 1187. Семейство парабол у=СУ~~х. 1188. Се-
мейство равнобочных гипербол ху—С (при С # 0); совокупность коордииатиых
осей Ох и Оу (при С = 0). 1189. Семейство плоскостей x-f-y-|-3z=C. 1190. Семей-
ство сфер xa4-ya-|-za = C. 1191. Семейство двуполостных гиперболоидов х2—у2 —
— г2 = С (при С > 0); семейство одиополостиых гиперболоидов ха—у2—г2 = С
(при С < 0); конус х2—у2—г2 = 0 (при С = 0). 1197.
-3x4-2. 1198. -^-=2psta40, 5н=4р2 sin3 0 cos 0.
dp 00
= у-^. *200. -|- = ^^+^(Зх2у4-У3),
1201. ^=2Гх+6у3/?,
дх Y х дУ у dz г
= —^^+4 е-Ч 1203. дг
у2 ' у2 ’ dz у
1 Д-г2
1204.
du du .
=2x—3y—4, ^=4y-
1199. ^=4-1, =
dx у2 у' dy
^-=^<J'’+^)(x»4-3xya).
1202. ^=1^° du
dx у
2xy
.Х/У.______
’ dy~
dz
dx~~ (l + x2)2+y2 ’ dy ~
- ... ... , .*«». -^-=6x2(x34-y2)e<*’+J',)’, ^-=4у(х34-у2)е<ж’+У')’.
(1 + x2)2 + tf &x ' dy y v y ’
1205, ^=(y—z)(2x—У—z), ^=(x—z)(x—2y+z), ^L=(X—y)(—y+2z—x).
1206. ^=(6x-y)e3x‘+2^-^, ff=(4y-x)e3**+2"’-*«'. 1207. ^=xze«* sin-£ +
_|_le«*cos-£-. 1209. p. 1214. dz=i(xd*+ydy). 1215. dz^^~ydx).
X X и xa4-ya xasta(2y/x)
1216. 2(xdx-}-ydy) cos (x24-y2)- 1217. dz = x^ (~dx-f-In xdy] . 1218. du =
..J_____(dr+
)Axa4-j/a \ x-j-j/'x2-
+ cos y-\-xshiy)dx]. 1220. dz=e*-H'{[ (x4-1) cosy-f-y (sin x4-cos x)] dx-f-
4-[x(cosy—stay) + (y+l) sin x] dy}. 1221. <fe= +^”^4 • *222. du =
= eW(yzdx4-xzdy4-xydz). 1223. 1,08. 1224. —0,03. 1225. 1,013. 1226. 3,037.
1227. 1,05. 1232. 6(x4-y). 1233. — sin(x4-y). 1234. —4 cos (2x-|-2y)/staa (2x-|-2y).
1235. 0. 1236. x (x+2y)/(x+r/)2. 1237. у (2- у2) cos xy—xy2 sin xy. 1238. sin у X
Xcos(x+cos y).1239. -^=^[(dy)a-(dx)a]—*240.-cos (x+y) (dx+dy)2.
1241. aeS'[e»sta(ax+e«9—cos(ax+e»)l- *242. 4. 1244. 2[(dx)2—dxdy+(dy)2].
1249. exy[(ydx+xdy)2+2dxdy]. 1250. — f . 1251. --^(ydx-xdy)(dx)2.
1219. dz=e* [(x cos у—sin у) di/-|-(sln у +
301
о
1252. Gdxdydz. 1253. - (4ydx—Зх dy)3 (dy)3. 1254. ex+ff (dx+dy)9. 1257. 4/sin 2x.
у
1258. 2x(3x4-2)/(x24-3x4-l)2. 1259. ~-=2xcos x, ^-=x(2cosx—xsinx).
1260. 0.1261. -ft-=4g, J-=4t]. 1262. J=-|-, . 1268. () =^-.
dg Or] $ 6 Л) r](r]4+1) \dl J м 5
1269. ,27°- (^т)Л1=‘Г 1271’ l£rad“bM = 1/'£ cosa=—x0/r0,
cosP = — Уо/го, cos y== —z0/r0, где г<1 = \/Г4+уо + го- 1272. | grad и|м = 3,
cosa= 1/3, cosB=cos_y==2/3. 1273. 1/3. 1278. —x/y. 1279. y/x. 1280. y' = —y/x,
У=2у/х*. 1281. (у V2ху—х*)1(2у* — х V"2xy). 1282. y/x. 1283. (a2—*2)/(2*2—a2).
1284.
1288.
y/(2x). 1285. (x+y)/(x—y). 1286. 1/(2^ In 2). 1287. y' = — 1, y" = 0.
dz dz_ 1 dz x*—yz dz y*—xz
dx dy x-f-y-1-г— 1 ’ ’ dx za—xy’ dy z*—xy'
dx + (z/y)dy xcos у 4-sinx „ (y4-z)dx4-(x4-z)dy
l+ln(z/y) ’ 1291’ sinx • ’ x+y
1290.
1293. — y—z— ey~x. 1294. 1. 1297. 2x4-2y—z = 1, (x— l)/2==(y— l)/2=(z—3)/(—1).
1298. 2x+2«/—3z4-l=0, (x—2)/2= (y—2)/2=(z—3)/(—3). 1299. z—2x 4-2=0,
(x—l)/2=y/0=z/(—1). 1300. x—y— 2z4-l=0, (x—п/4);1 = (y—я/4)/(—I) =
= (z—1/2)/(—2). 1301. x-j-4y+6z ± 21=0. 1303. (4/3; 4/3; 1/3) и (—4/3; —4/3;
—1/3). 1307. Zmax= 1/64. 1308. Zmin = —125. 1309. Ztnax = 4. 1310. Ztnin = 0.
1311. zmax=a/ 3/9 при x = y = 2a/3. 1315. zmin= 144/25 в точке (36/25; 48/25).
1316. ZHaaM= 16/3, ^нанб=16* 1317. ZHaHM—5, 2нанб=И* 1318. _ZHaaM= 1/2,
гнавб=1/2. _1319. Знаим —1> гнанб==4. 1320. ^иаим — 2(/24*0^ 4,8,
анаиб = 2(/2—1) s 0,8. 1321. zHaHM==0> 2цанб = 3/3/2. 1322. хиаим= 3 при
X~y = 3rc/2, 2Наиб~’И-/ 3/2 При Х=(/ = 5я/6. 1323. ZHaaM =—1/8, Zh3h6=J_’
1324. Равносторонний. 1325. Равносторонний. 1326, Квадрат; ^Наим = 4/5.
1327. Куб; Vmax = (S/6)KS/6.
Глава IX
1337. (2/5) х2 V х+С. 1338. (5/4) >/х44-С. 1339. 2arcsin х—х4-С.
1340. arctgx-f-x— х3/3+С. 1341. г3*-3*/(34-1п 3)4-С. 1342. tgx—x+C.
1343. chx+cosx+C. 1344. х2/2—2х-±1п |х|-±С. 1345. 4tgx—9ctgx—x-f-C.
1346. (1/2) sin (х2)4-С. 1347. In | In x 14-С. 1348. 3 (ax2 4-6)4/s/(8a) 4-C.
1349. (2/3) sin x /sin x-f-C. 1350. —(1/6) cos (a 4- bx) 4- C. 1351, sin (sin x) 4- C.
1368. еу27Т14-С. 1369. —(1/32) (1—2x4)44-C. 1370. (1/3) cos (2—3x)4-C.
1371. (1/10) sh (5x24-3)4-€. 1372. 2arctg/x-f-C. 1373. (1/5) (x24-l)6/24-C.
1374. (1/2) In I x2—1 |4-C. 1375. <l/2) ln]x24-/x^-l l-±C. I?76- (—1/4)X
Xarctg (0,5cos22x)4-C. 1377. (1/f 7)1п| (K x-/7)/(K x + V 7)\ + C.
1378. 2arcsln(e*/2/4)4-C. 1379. In | x+V2+x2 |-harcsln (x/K 2)4- C.
1380. (—2/9) V2- 3x34-C. 1381. —5 V3—x24-3 arcsin (x/V 3) + C. 1382. (1/4)X
Xarctg (x—3V44-C. 1383. 2/3x4-54- V5 In |(/3x4-5—/5)/(/3x4-54-/5)|4-C.
1384. 1/(2/10)arctg (x2/2/5)4-C. 1392. (x2/4) (21nx—1)-±C. 1393. xaroslnx+
4-/1—x24-C. 1394. (x2/3) arctgx—(1/6) x24-(l/6) In (x24-l)4-C. 1395. xex4-C.
1396. — x2cosx4-2xsinx4-2cosx4-C. 1397. (1/2)ext (x4—2x2-±2)4-C.
1398. 0,5 (x/x24-A,4-A,lnjx4-/x24-A,|)±C. 1399. (x4-l)2 slnx4-2(x4-l)cosx+C.
1400. (e2x/5) (sin x4-2_cosx)4-C. 1401. (x/2)(slnlnx—coslnx)-f-C. 1402.—2/xX
Xcos/x4-2sin/x4-C. 1410. — l/[3(x— 1)3J4-C. 1411. —1/[4 (2x-|-3)2]4-C.
1412. (1/3) arctg (x—3)/34-C. 1413. 1/(3/ 2) arctg (x34-1)// 24-C. 1414. (1/2)X
Xln(x2—4x4-7)4-C. 1415. (5/2) In (x24-10x4-29)—! 1 arctg (x4-5)/24-C.
1416. (1/10) In (5x24-2x-f-1)4-(2/6) arctg (5x-f-l)/2-f-C. 1417. x/[8 (x24-2)2] 4.
4-3x/[32 (x24-l)]4-(3 /2/64) arctg (x//2) 4- C. 1418. (x— 7)/[8 (x2 4- 2x4- 5)] +
4-(l/16) arotg (x4-1 )/24-C. 1428. —(2/3) In | x | 4- (5/3) In |x — 31 4- C. 1429.
-(1/2) In(x2+ x+D+3 In | x+2 |+(l//3)arctg (2x+l)//3+C. 1430. l/[2 (x-l)2]+
4-2 in | x—1 l-f-3 In | x—214-C. 1431. (l/12)ln|x—2| — (l/24)ln(x2 + 2x+4) —
—1/(4/3) arctg (x+l)//3+C. 1432. (31/108) In | x—31+ (29/108) In | x+31 +
4- (2/9) In (xa4-9) — (1/54) arotg (x/3) + C. 1433. (1/4) In | x/(x—2) |-(x— l)/[2x (x —
— 2)]+C. 1434. (l/16) [ln (x24- l)/(x24-9)]4-(1/8) arctg x—(1/24) arctg (x/3)4-C.
1435. (1 /4) In [(x24-4)/(x24- 2x4-5)]4- (1 /8) arctg (x/2) 4-(7/32) arotg (x+ l)/2+C.
1436. (1/2) [arctg (x—1) + arctg (x+1)] + C. 1437. x+(9/2) In | x—31-(l/2)x
Xln|x— 1 |4-C. 1438. x«/2+7x+(75/2)ln|x—5|—(1/2) ln[x—l l + C. 1439. x-h
4-(1/2) In | (x—2)/(x+2)|— arctg (x/2) + C. 1440. Зх + ln | x | + 2arctg x+C.
1442. (1/32) In | ex — 2|13 (ex4- 2)74- (3/16) In (e«* + 4) — (3/16) arctg (e*/2)—x+C.
1443. (5/6) In | e* — 1| + (16/5) In (2e* + 1) + (11 /20) In (e2* +1) — (7/5) arctg e*—3x+C.
1453. — /Г=2х—2_/1 — 2x—2 In | y/i^2x— 1 | + C. 1454. (6/5)^/x6—2/x+
+ б|/x—6arctg p/ x+C. 1455. In |x—0,5+/x2—x—1 | +C. 1456. arcsln(x + 1) :
:3+C. 1457. —5У—x2+4x+5+13 arcsin(x—2)/3+C. 1458. 3/x2+x+2+0,51n[x+
+ 0,5+/x2 + x+2| + C. 1459. /x/(x+2) + C. 1460. —arcsin [(x+1):
:(xf3)]+C. 1461. In |x+ | + / 2 In I1 <**+1 I -f-C.
I ^Ит»)
1462. — (x/2+5) K—x2+4x+13arcsin (x—2)/2+C. 1466. з/( jJ/^c+]) _j_
+ In[x/(/x+ 1)3] + C. 1467. 4//x+l [(l/5)(/7+l)a-(2/3)(Kx+l) +
+1] + C. 1468. (1/6) In [(/2+/ +1)/(/2—2/+ 1)]—(1// 3) arctg (2/+1)// 3 + C,
где t= j/l + x3/x. 1469. (1/3) In [(/T+x3— l)2/|x3|] + C. 1470. (l/10)X
x(5x4/3 + 3)3/2 + C. 1471. — (2-x3)2/3/(4x2) + C. 1489. (1/5) ln|5tg(x/2) + 3| + C.
1490. —2/[tg (x/2)— 1] + C. 1491. — (1/17) x+(l/4) In [ sin x|— (1/68) In [ sin x +
+ 4cosx| + C. 1492. In | sinx |—sin x-f-C. 1493. —(2/5) In (1—cosx) +
+ (1/5) ln(cos2x + 2cosx+2)—(6/5) arctg (1 + cos x) + C. 1494. (l/3)cossx—
— cosx+C. 1495. ln|sinxl—sin2 x+(l/4) sin4x + C. 1496. (l/8)x—(l/8)sinx + C.
1497. (3/8)x+(l/4)sln2x + (l/32)sin4x+C. 1498. (2/3) tg® (x/2)—2tg(x/2) + x+C.
1499. (— l/6)ctg23x—(1/3) In I sin 3x l + C. 1500. tgx + (2/3) tg®x + (l/5) tg3x + C.
1501. — (l/3)ctg3x+C. 1502. (1/2) tgxsecx + (l/2) In I tg (x/2+n/4) l + C.
1503. — (1/2) ctgx cosec x— (1/2) In | tg (x/2)| + C. 1504. (1/4) sin 2x—(1/8) sin 4x+C,
1505. (3/5) sin (5x/6)+3sin (x/6)+ C. 1509.x//1—x2 + C. 1510. x/(a2/a2+x2)+C.
1511. (1/2) (arccos (1/x)+ /x2—l/x2) + C. 1512. — (1/6)cos3x+ (1/20) cos 5x +
+ (1/4) cos x+C. 1513. — 2(2х2 + 6х+13)е-ж/2 + С. 1514. — (2 In x+ l)/(4x2)+C.
1515. xarctgx—(3/2) (arctgx)2—(1/2) In (l+x^+C. 1516. (x2—l)sln2x+xcos 2x+C,
1517. (1/4) x2 (21n2x — 21nx+l)+C. 1518. x + ln|e*—3 |+C. 1519. (x+l)arctg/x—
—/x+C. 1520. (2/ln2)(/2х—1—arctg/2x —1)+C. 1521. (l/4)ln|(Z+l)/(/—l)|—
— (1/2) arctg/ + С, где /4 = 1+х”4. 1522. / 2 [0,5 (x—1)/3_+2x—x2 +
+2 arosln (x—l)/2]+C. 1523. sin ex—ex cos ex-\-C. 1524. (1// 5) In | tg x +
+/tg2x +0,4 l + C. 1525. 0,5cos2x(l—21ncosx)+C. 1526. 0,5sln (x2+4x+l)+C.
1527. —0,5(x/sin2x+ctgx) +C. 1528. 2(x—2) /1 + ex —2In [(/Т+г*—
_ !)/(/!+<•*+!)]+ C. 1529. x In (x2+x) + ln |x+1 |—x+C. 1530. —1/x —
— arotgx+C. 1531. (x/2) (cos In x+sin In x) + C. 1532. 12{j//\ +
+ln[(r/x-l)*/rZx]Hc. 1533. ea7(a2 + P2)](aslnPx—P cos 0x) +C.
1534. [e“*/(a2 + ₽2)] (Bsin fix+acosPx) + C. 1535. [!/(«£>)] arctg [(b/a) tgx] +C.
1536. tgx—ctg x+C.' 1537. 0,5 [arctg x+x/(l + x2)]+C.
Глава X
1547. 1/2^1548.6—1. 1549. 0 </<4/27,_1550. л/2</<ел/2. 1551. 0</<l.
1552. 464 / 2/15. 1553. л/8. 1554. e—/e. 1555. ee—e. 1556. (еп/г~ l)/2.
1557. (1пЗ—1)/2. 1558. In 1,5. 1559.0. 1560. 2/5. 1561. л/2. 1562. In (4/3).
1563. (ея/2—1)/2. 1564. 0. 1565. л/2—1. 1572. л2/8. 1573. л/4.
1574 . 256/15. 1575. л, 1576. + оо. 1577. 1/4. 1578. л/6, 1585. Расходится.
303
1586. Сходится. 1587. Расходится. 1588. Сходится. 1589. Расходится. 1590. Схо-
дится. 1591. Расходится. 1596. 4,5 (кв. ед.) 1597. 18 (кв. е/г). 1598. 2/15
(кв. ед.). 1599. (41/2) arosin (9/41) + 20 In 0,8 (кв. ед.). 1600. У 2—1 (кв. ед.).
1601. 8 (кв. ед.). 1602. (9л/4) — У 2-|-4/ 2 ki 2—(9/2) arcsin (1/3) (кв. ед.).
1603. 169л (кв. ед.). 1604. (3/8) ла3. 1605. 8 У 3/3 (кв. ед.). 1£06. (3/2) ла3.
1607. (Зл—8)/32 (кв. ед.). 1608. ла3/12. 1609. л/3+/ 3/2 (кв. ед.).
1613. (1/2)1пЗ. 1614. (20/9)/5/3. 1615. 0,5 [У 2-f-ln (1 + У 2)].
1616. (1/2)1пЗ. 1617. shlasl,17. 1618.12. 1619. /2(л—1). 162О._5л.
1621.72. 1622. [(л3 + 4) Кл24-4—8]/3. 1623. ла. 1624. а (2л-|-3 У 3)/8.
1625. 8. 1628. 16л (5л-[-8)/5 (куб. ед.). 1629. 0,3л (куб. ед.). 1630. л(е2+1)/4
(куб. ед.). 1631. 4л/35 (куб. ед.). 1632 . 72 (куб. ед.). 1633. 2а2Л/3. 1634. лг3/г/2.
1636. л(е3—е"3 + 4) (кв. ед.). 1637. 61п/1728 (кв. ед.). 1638. 2л6 [6 + (а2/с2)Х
Xarcsin (с/а)], гдес2 = а2— Ь2. 1639. 64л/3 (кв. ед.). 1644. Мх = а2 (е2 —е 3-|-4)/8;
Ix = a3(e—e-1)(e3+e-34-10)/24.-1645. Ma=a/i2/6; /а=а£3/12. £646. /х= 1628/105.
1647. /х = аб3/12; /у_=а36/12. 1648. /0==лс/4/32. 1653. х = 0, у = 2г/п (для полу-
окружности); х=0, у=4г/(3л)_(для полукруга). 1654. х = (л—2)/2, у= л/8.
1655. х = 0, 7=8/5. 1656. х = у = 2а/5. 1657. Г=1, 7=2/5. 1658. х= 1, у = л/8.
1659. лг3 (Зл—4)/3. 1661. 480л (куб. ед.). 1670. лр£Г3/г2/4. 1671. npgad3/8.
1672. 51450л Дж. 1673. 547,8л Дж. 1674. 50,7 Дж. 1675. pga/i2/3.
1676. 17,64л кН; 70,56л кН; 158,76л кН; 282,24л кН. 1677. pgnd3/8.
1678. 150 кг. 1679. 1400 м. 1680. х = е13. 1681. 36 м. 1691. 1) y' = shx//ch3x+i;
2) у' =sh3 (х/15) ch3 (х/15); 3) y' = l/chx; _4) y'=l/chex; 5) y' = l/chx;
6) у' = x/sh(x2/2). 1692. М [1п(1 +К 2); У 2]. 1693. yrain = 0 при х = 0.
1694. 1) х3 sh х— 2хchx -t- 2 sh х С; 2) (l/32)sh4x — (l/4)sh 2х -|-6х + С;
3) 2arctg /chx— l-f-C; 4) (1/2) (ch х slnx—shxcosx) + C; 5) th2 (x/2)-|-C;
6) (3/5) ch5 (x/3)—ch3 (x/3) 4-C. 1695. 1) л/6; 2) ln2—0,6; 3) 2(21n3— l)/3.
1696. sh (x—a) = shx ch a—chxsha; ch (x — a) = chx ch a — shxsha.
1697. th (x+a) = (th x-|-tha)/(l + th x th a); th (x—a) = (th x—tha)/(l — th x th a);
th 2x = 2 th x/(H-th2x). 1698. sh (x/2) == ± У (chx—1)/2; ch (x/2) = /(chx+ 1 )/2;
th (x/2) = ±/(ch x—l)/(chx+l). 1699. 2sh0,5(x±y)-ch0,5 (xTy)> 2ch0,5 (x-(-y)X
Xch0,5(x—y), 2 sh 0,5 (x-\-y) sh 0,5 (x—y), sh (x ± y)/(ch x ch y). 1700. shx =
= 2 th (x/2)/[l — th3(x/2)]; chx = [l + th3(x/2)]/[l —th2(x/2)]. 1701. 0,5[sh(x+y)+
4-sh (x—y)]; 0,5 [ch (x+y)4-ch (x—y)]; 0,5 [ch (хЦ-у)—ch (x—y)]. 1702 . 8/5 (кв. ед.).
1703. 1,17a. 1704. a2 (t2—ti)/2. 1705. Дуга эллипса, расположенная над осью
абсцисс. 1706. Луч прямой х—у—1=0, расположенный в I четверти.
1707. cos a = ± 1/ch t; tg а~ ±sh t. 1708. 1. 1709. x2—у2.
Глава XI
1720. Ниже прямой Xj—х2 — 10 = 0. 1721. Треугольник. 1722. Неограничен-
ная область. 1723. Пустая область. 1724. Точка (2; 3). 1725. Областью решений
является трапеция, неравенство (д) можно исключить. 1726. Треугольная пира-
мида. 1727. Трехгранная призма. 1732. £гаах=Ю при хт = 4, х« = 2. 1733. £min=
= —4 при Xj = 0, х2 = 4. 1734. £тах = 18 при Xj=6, х2 = 0. 1735. £тах = 2 при
Х! = 0, х2=1. 1736. £тах = 48 в каждой точке отрезка АВ, где Я (6; 0), В (7; 4).
1737. Lmin = —4 при xj = 2, х2 = 0, х3 = 0. 1738. £шах=33 при Xj = 0, х2 = 3,
х3 = 9. 1739. £гаах = 20 при Xj = 2, х2 = 0, х3 = 0. 1746. (О, 1, 3, 0); £ = —3.
1747. (3/2, 0, 0, 1/2, 11/2); £ = 3/2. 1748. (О, 3, 1, 0); £ = —1. 1749. (О, 50, 30,
215/6); £ = 340. 1750. (О, 5, 3/2, 0, 0, 3/2); £ = —5. 1751. £ = оо. 1752. (О, 4/5,
1/5); £ = —11/5. 1753. (80, 120); £тах = 440. 1754. (20, 40); £гаах = 220. 1755. 15 кг
корма I вида; 50 кг корма II вида. 1757. (5, 7, 9 , 7/2, 0 , 0); £щах=88.
1759. £min=86/9; (10/9, 28/9); 7’max = 86/9; (7/27, 8/27). 1760. £гаах = 216/7;
(24/7 , 24/7); Tmi„ = 216/7; (8/7, 1/7). 1761. £rain = 78/7; (10/7, 16/7); 7'max =78/7;
(27/14, 3/14). 1763. £^-510 ден. ед.; хи-ЗО, х12-60, х21-30, х23,=60.
1764. £,„;„=•=280 ден. ед. Оптимальный план: х12=х24-х33-60, х23-20, х31=40.
1765. 4nin-395 ден. ед. Оптимальный план: хц-25, xi3=x32=20, xi2=x2i»=5,
*23” 35. 1766. £^ = 140 ден. ед. Оптимальный план: xi4“X22“10, x23”X3i=x34“
”5, х33 = 15.