Г. Я. ЛЮБАРСКИЙ
ТЕОРИЯ ГРУПП
И ЕЕ ПРИМЕНЕНИЕ
В ФИЗИКЕ
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1958

АННОТАЦИЯ
В книге дается систематическое изложение
теории представлений групп, изучаются пред-
представления групп, играющих важную роль в фи-
физике, и на этой основе рассматриваются различ-
различные применения теории представлений в теорети-
теоретической физике.
Книга рассчитана на студентов старших курсов
физических факультетов университетов, на аспи-
аспирантов и научных работников.

ОГЛАВЛЕНИЕ
Предисловие	 6
Глава I. Элементы теории групп	 7
§ 1. Группа G). § 2. Подгруппа (9). § 3. Изоморфизм и гомомор-
гомоморфизм групп A1).
Глава II. Некоторые конкретные группы	 13
§ 4. Группа перестановок A3). § 5. Группа вращений A5).
§ 6. Полная ортогональная группа A9). § 7. Евклидова группа B0).
§ 8. Точечные группы B2). § 9. Точечные группы первого рода B3).
§ 10. Точечные группы второго рода B6). § 11. Группы трансля-
трансляций B9). § 12. Сингонии C1). § 13. Симметрия кристаллов C7).
Глава III. Теория представлений групп .	 41
§ 14. Представление группы D1). § 15. Эквивалентные представ-
представления D3). § 16. Функционал усреднения D5). § 17. Приводимые
представления D6). § 18. Неприводимые представления и свойства
ортогональности D9). § 19. Теорема полноты E4). § 20. Теория
характеров E6).
Глава IV. Операции с представлениями групп	 60
§ 21. Произведение представлений F0). § 22. Сопряженное
представление F3). § 23. Вещественные представления F5).
§ 24. Произведение групп F7). § 25. Симметризованные степени
представлений F8). § 26. Фактическое разложение приводимого
представления на неприводимые G2).
Глава V. Представления некоторых групп	 77
§ 27. Представления группы перестановок 5П G7). § 28. Непри-
Неприводимые представления точечных групп (80). § 29. Представле-
Представления групп трансляций (83). § 30. Представления пространствен-
пространственных групп (86).
Г л и в а VI. Малые колебания симметричных систем	 95
§ 31. Главные координаты и собственные частоты (95). § 32. Сим-
Симметрические координаты (97). § 33. Выражение функции Лаг-
ранжа в симметрических координатах A00). § 34. Колебательное
представление A04). § 35. Пример. Молекула СНС13 A08).
Г л п и а VII. Фазовые переходы второго рода	111
§ 36. Постановка задачи A11). § 37. Активные представления A17).
§ 38. Пример A22).
I*

4	ОГЛАВЛЕНИЕ
Г л а в а VIII. Кристаллы	141
§ 39. Звук в кристаллах A41). § 40. Электронные уровни в кри-
кристалле A45). § 41. Тензоры в кристаллах A47).
Глава IX. Бесконечные группы	151
§ 42. Специфические особенности бесконечных групп A51).
§ 43. Элементы теории групп Ли A57). § 44. Инфинитезимальное
представление группы Ли A67).
Глава X. Представление группы поворотов, группы вращений и
полной ортогональной группы	170
§ 45. Неприводимые представления группы поворотов Z A70).
§ 46. Классификация неприводимых представлений группы вра-
вращений A71). § 47. Матричные элементы неприводимых предста-
представлений A77). § 48. Снойства неприводимых представлений группы
вращений A82). § 49. Произведение представлений группы вра-
вращений A86). § 50. Спинорная алгебра A88). § 51. Тензорная алге-
алгебра A94). § 52. Представления полной ортогональной группы A99).
§ 53. Двузначные представления точечных групп B01).
Глава XI. Коэффициенты Клебша — Гордана и коэффициенты
Рака	203
§ 54. Вычисление коэффициентов Клебша —• Гордана B03).
§ 55. Свойства коэффициентов Клебша — Гордана B11). § 56. Коэф-
Коэффициенты Рака B15).
Глава XII. Уравнение Шредингера	224
§ 57. Законы сохраЕЮния B24). § 58. Классификация состояний
^233).
Глава XIII. Уравнения, инвариантные относительно евклидовой
группы движений пространства	236
§ 59. Шаровые функции со спином B36). § 60, Уравнения, инва-
инвариантные относительно группы евклидовых движений простран-
пространства B39). § 61. Пример B44).
Глава XIV. Поглощение и комбинационное рассеяние света . . . 247
§ 62. Квантовомеханическое введение B47). § 63. Правила отбора
для поглощения света атомами и молекулами B50). § 64. Комби-
Комбинационное рассеяние света атомами и молекулами Bо6).
Глава XV. Представления группы Лоренца	259
§ 65. Группа Лоренца B59). § 66. Инфинитезимальные операторы
группы Лоренца B61). § 67. Классификация неприводимых пред-
представлений группы Лоренца B63). § 68. Произведение неприводи-
неприводимых представлений группы Лоренца B65). § 69. Комплексно-со-
Комплексно-сопряженные представления B67). § 70. Спинорная алгебра B69).
§ 71. Тензорная алгебра B71). § 72. Представления полной группы
Лоренца B75).
Глава XVI. Релятивистски-инвариантные уравнения	278
§ 73. Волнопаи функция С-'7Я). § 71. Релятивистски-инвариантные
уравнения (_'Ж>). «j 75. Функции Ллгранжа B86). § 76. Законы со-

ОГЛАВЛЕНИЕ	О
хранения B89). § 77. Спин B94). § 78. Релятивистски-инвариант-
Релятивистски-инвариантная операция инверсии времени и теорема Паули B97). § 79. Урав-
Уравнение Дирака C00).
Глава XVII. Ядерные реакции	305
§ 80. Матрица рассеяния C05). § 81. Угловое распределение про-
продуктов ядерной реакции C09). § 82. Угловое распределение про-
продуктов ядерной реакции (продолжение) C10).
Приложения	314
I. Характеры неприводимых представлений групп перестановок
54, S5, 56 и 57 C14). II. Характеры неприводимых представлений
точечных групп C16). III. Двузначные представления точечных
групп C17). IV. Пространственные группы C18). V. Коэффициенты
Рака C43).
Указатель литературы	345
Предметный указатель	350

ПРЕДИСЛОВИЕ
Предлагаемая книга представляет собой обработку курса лекций,
читавшихся автором в течение ряда лет в Харьковском универси-
университете им. А. М. Горького. Книга предназначается для физиков, спе-
специализирующихся в области теоретической физики. Ее цель—по-
цель—подробно и последовательно изложить в возможно меньшем объеме те
сведения из теории представлений конечных и непрерывных групп,
которые наиболее важны для применений, рассмотреть группы,
представляющие интерес для теоретической физики и, наконец, про-
продемонстрировать принципы применения в теоретической физике
абстрактных понятий и теорем теории представлений. В конце книги
помещены таблицы, дающие подробное описание двухсот тридцати
пространственных групп, и таблицы характеров некоторых групп.
Книга снабжена значительным количеством задач.
У читателя предполагаются знания основ линейной алгебры
в объеме первых двух глав книги И. М. Гельфанда «Лекции по
линейной алгебре».
Несмотря на появление в недавнее время статьи И. М. Гель-
Гельфанда и 3. Я. Шапиро о представлениях группы вращений и статьи
М. А. Наймарка о представлениях группы Лоренца, автор включил
в настоящую книгу главы, посвященные этим вопросам. Это сделано
для удобства читателя и для сохранения цельности книги.
В заключение автор хочет поблагодарить Н. Я. Виленкина,
И. М. Гельфанда, М. Г. Крейна и Е. М. Лифшица за внимание
к его работе и ряд полезных советов. Автор признателен также
О. В. Ковалеву, замечания которого помогли устранить ряд ошибок.

ГЛАВА I
ЭЛЕМЕНТЫ ТЕОРИИ ГРУПП
§ 1. Группа
Группой называется всякое множество О элементов, в котором
выполняются следующие четыре условия:
1. На множестве определено групповое действие — «умножение»,
¦ставящее в соответствии каждой паре элементов / и g некоторый
элемент h из этого же множества; это записывается так:
Элемент h называется произведением элементов / и g, а сами эле-
элементы / и g — сомножителями. Заметим, что произведение двух
•сомножителей зависит, вообще говоря, от их порядка, так что эле-
элементы fg и gf могут отличаться друг от друга.
2. Умножение ассоциативно: если /, g и h — три произвольных
элемента, то произведение элемента / на элемент gh должно рав-
равняться произведению элемента fg на элемент h:
3.	Множество-О содержит единичный элемент е, т. е. такой,
что, каков бы ни был элемент /? G, имеет место соотношение
ef = fe=f.
4.	Вместе с любым элементом / множество содержит элемент/,
обратный данному, т. е. такой, что
Если число элементов группы конечно, то группа называется
конечной; в противном случае группа называется бесконечной. Число
элементов конечной группы называется ее порядком.
Если умножение обладает свойством коммутативности, т. е. для
любой пары элементов fug имеет место равенство fg — gf, то
группа называется коммутативной или абелевой.
Приведем несколько примеров групп.

8	ЭЛЕМЕНТЫ ТЕОРИИ ГРУПП	[ГЛ. I
1.	Совокупность всех поворотов пространства вокруг некоторой фикси-
фиксированной оси образует группу. Произведение двух поворотов на углы аир
определяется как результирующий поворот (на угол a -f- 8).
Заметим, что два поворота пространства, одинаковым образом переме-
перемещающие все его точки, считаются тождественными. Поэтому, в частности,
не различаются повороты на углы 0, ±. 2-я, ±4т., ... Роль единицы в группе
поворотов играет поворот на угол, равный нулю. Взаимно-обратными
являются два поворота в противоположных направлениях на один и тот же
угол.
2.	Совокупность радиусов-векторов всех точек трехмерного пространства
образует группу относительно сложения по правилу параллелограмма. Еди-
Единицей группы служит нуль-вектор. Взаимно-обратными элементами группы
являются равные по величине и противоположно направленные векторы.
Вообще, всякое линейное пространство является группой относительно
сложения.
3.	Совокупность всех поворотов пространства вокруг всевозможных
осей, проходящих через фиксированную точку О, образует группу, назы-
называемую группой вращения. Произведение gtgz двух поворотов g1 и g% опре-
определяется как поворот, который претерпевает пространство, если сначала
осуществить поворот g->, а затем, дополнительно, поворот g^.
4.	Результат параллельного переноса пространства и последующего его
вращения вокруг некоторой точки называется движением пространства.
Под произведением g^2 двух движений пространства gt и g2 подразуме-
подразумевают результирующее движение, причем сначала следует произвести дви-
движение g%, a затем gi. Совокупность всех движений пространства образует
группу — группу движений.
5.	Совокупность всех неособенных линейных операторов, действующих
в некотором линейном пространстве, образует группу относительно обыч-
обычного умножения операторов. Роль единицы в этой группе играет единичный
оператор.
6.	Всякую перестановку п предметов можно записать с помощью сим-
/ 1 2 ... л \
вола (	, который означает, что предмет, находившийся до
\mi Щ •• • тп1
перестановки на первом месте, после перестановки оказывается на месте
с номером ть предмет, занимавший второе место, в результате переста-
перестановки перемещается на место с номером /яг и т. д. Произведение g\g<> двух
перестановок gl и g% определяется как перестановка, получающаяся, если
сначала произвести перестановку g2, а затем перестановку gt. Так, например,
1	2 3 4\ /1 2 3 4у /1 2 3 4^
2	4 3 lJ'll 4 2 ЗУ ^ 42. 1 4 з)'
Совокупность всех перестановок п предметов образует группу. Эта группа
.называется группой перестановок, или симметрической группой, и обозна-
обозначается символом Sn.
7.	Совокупность всех действительных чисел образует группу относи-
относительно сложения, взятого в качестве группового действия. Единицей группы
является число нуль.
Элемент g называется сопряженным элементу h, если найдется
такой элемент х группы, что xgx~l = h. Очевидно, что g сопря-
сопряжен g. Если g сопряжен /г, то и /г сопряжен g, так как из xgx~1 = h
следует, что g = x~1hx=:x~1fi(x~1-)~1. Если g сопряжен /г, то и g~l
сопряжен h~l. Если g. сопряжен /г, и/г сопряжен /, то g сопряжен /.

§ 2]	подгруппа	9
так как из xgx~x = h и yhx*1 — / следует, что f~yxgx~ly~l =
= yxg(yx)~\
Объединяя все взаимно-сопряженные элементы в один класс,
мы получим разбиение всей группы на классы сопряженных эле-
элементов.
Отметим, что класс элементов, сопряженных е, состоит лишь
из е, так как хех~1 = е; у коммутативной группы каждый класс
содержит по одному элементу, так как xgx = g-
Задача I. Доказать, что группа не может содержать нескольких раз-
различных единичных элементов.
Задача II. Проверить, что элемент, обратный произведению/^, есть
произведение g~lf"i-
Задача III. Доказать, что если хфу (х и у — элементы некоторой
группы G), то и х/фу/(/еО).
Задача IV. Доказать, что у каждого элемента группы есть только
один обратный ему элемент.
§ 2. Подгруппа
Подгруппой называется всякое подмножество группы, если оно
в свою очередь является группой относительно того же группового
действия.
Приведем примеры подгрупп.
1.	Целые числа в группе действительных чисел.
2.	Повороты вокруг оси OZ в группе вращений.
3.	Перестановки, оставляющие неподвижными определенные предметы
в группе перестановок.
4.	Совокупность всех вращений вокруг центра куба, которые совмещают
куб с самим собой, очевидно, образуют группу. Эта группа является под-
подгруппой группы вращений.
5.	Множество, состоящее только из одного элемента — единицы группы,
является тривиальной подгруппой „всякой группы.
Подгруппы конечных групп обладают одним замечательным свой-
свойством. Порядок (т. е. число элементов) подгруппы конечной группы
является делителем порядка группы (теорема Лагранжа).
Из этой теоремы следует, например, что группа^ порядок кото-
которой есть простое число, не имеет никаких подгрупп, кроме три-
тривиальной.
Для доказательства теоргмы Лагранжа введем понятие смежных
классов. Пусть Gt есть подгруппа группы G, состоящая из эле-
элементов е, gu g2, ..., и а — какой-либо элемент группы G. Левым
смежным классом подгруппы Glt порожденным элементом а, назы-
называют совокупность элементов
ае = a, aglt ag2, ...
Ьулем сокращенно обозначать левый смежный класс, порожденный
элементом а, символом aGv
Аналогично олределяются правые смежные классы.

10	ЭЛЕМЕНТЫ ТЕОРИИ ГРУПП	[ГЛ. I
Ясно, что число элементов в каждом смежном классе равно
порядку подгруппы.
Смежный класс, порожденный элементом е, совпадает с самой
подгруппой Gv Возьмем теперь какой-либо элемент a?G, не вхо-
входящий в подгруппу Gv Если смежные классы eGx — Gt и a1G1 не
исчерпывают всей группы G, то выберем элемент аъ не содержа-
содержащийся в этих классах, и образуем еще один класс аг0г. Поступая
таким образом, мы получим в конце концов некоторый набор левых
смежных классов
Gv afilt uzG-l, ..., uj_xGx,	(a)
которые в своей совокупности исчерпывают всю группу G (т. е. каж-
каждый элемент группы G содержится хотя бы в одном из этих клас-
классов). Покажем, что смежные классы (а) не пересекаются, т. е. не
имеют общих элементов.
Предполагая противное, мы сможем написать:
—1).
Отсюда следует, что
Так как это противоречит выбору элемента ак, то тем самым
утверждение доказано. Итак, все элементы группы распределяются
по j классам (а). Поэтому общее число элементов группы равно
произведению числа классов на число элементов в каждом из них.
Число j различных смежных классов подгруппы Gt называется
ее индексом.
Важным примером подгрупп являются так называемые цикли-
циклические подгруппы, которые образованы всеми целыми положитель-
положительными и отрицательными степенями какого-либо элемента а группы G.
Если группа не бесконечна, то не все степени ат различны; ска-
скажем, ам = ап, где для определенности /га > п. Тогда ат~п = е, т. е.
существует такая положительная степень k, что ак = е. Пусть наи-
наименьшее из всех таких чисел k есть р; тогда а.Р = е. Элементы
е, а, а2, ..., ар~1 все различны и исчерпывают циклическую под-
подгруппу.
Приведем два примера циклических подгрупп.
1.	Подгруппа поворотов пространства вокруг фиксированной оси на
углы 0°, 60°, 120°, 180° и 240°.
2.	Подгруппа всех целых чисел в группе действительных чисел (груп-
(групповое действие — сложение).
Задача I. Доказать, что элементы, обратные элементам левого смеж-
смежного класса некоторой подгруппы, образуют правый смежный класс той же
подгруппы (правый смежный класс G^a подгруппы G^ определяется как
совокупность всех элементов вида gta (gt 6 Gj ).

§ 3]	ИЗОМОРФИЗМ И ГОМОМОРФИЗМ. ГРУПП	1 1
Задача II. Любой элемент а группы, возведенный в степень порядка
группы, равен единичному: а = е (указание: воспользоваться теоремой
Лагранжа).
Задача III. Пересечение двух подгрупп (т. е. совокупность их общих
элементов) является подгруппой.
§ 3. Изоморфизм и гомоморфизм групп
Взаимно-однозначное соответствие между элементами двух групп
F и G
называется изоморфным, если из любой пары соотношений
fi<-~+gu !г<	>gt (Л. !г^.Р\ gu g2^G)
вытекает соотношение
ЛЛ <—> gigi-
Группы, между элементами которых можно установить изоморфное
соответствие, называются изоморфными.
Всякая алгебраическая теорема, установленная применительно
к некоторой группе О, автоматически распространяется на все
группы, изоморфные G. Именно этим оправдывается введение поня-
понятия изоморфизма групп. Можно сказать, что с точки зрения теории
групп изоморфные группы одинаковы.
Приведем два примера изоморфных групп.
1.	Группа симметрии прямой треугольной пирамиды С8„ изоморфна
группе S3 перестанонок каких-либо трех предметов. Действительно, каждый
элемент g группы С3„ совершает некоторую перестановку вершин треуголь-
треугольника, лежащего в основании пирамиды. Обозначим эту перестановку через Рд.
Легко видеть, что соответствие g<—>Рд. является изоморфным.
2.	Корни п-н степени из единицы ооразуют группу относительно умно-
умножения. Эта группа изоморфна группе поворотов вокруг оси OZ на углы
вь = ^— (k — 0, 1, ..., п—1). Изоморфизм этих групп устанавливается
п
с помощью соответствия % <—> ег?к (k = 0, 1, 2, ..., п — 1).
Группа G называется гомоморфной группе F, если каждому эле-
элементу g? G можно поставить в соответствие некоторый элемент
/ ? F таким образом, что из соотношений
вытекает:
>• ЛЛ (gu gz € О; Л. Л ? П-
Гомоморфное соответствие двух групп отличается от изоморфного
отсутствием требования взаимной однозначности. Изоморфизм, таким
играном, является частным случаем гомоморфизма.

12	ЭЛЕМЕНТЫ ТЕОРИИ ГРУПП	[ГЛ. I
Приведем примеры гомоморфных групп.
1.	Группа целых чисел гомоморфна группе поворотов шестигранника:
е, С6, С\, С\, С\, С% Гомоморфизм устанавливается с помощью соответствия
2.	Группа S3 перестановок трех предметов гомоморфна группе, состоя-
состоящей из двух чисел 1 и — 1 (групповое действие — умножение). Гомомор-
Гомоморфизм устанавливается с помощью соотношений
/1 9 Чч
¦ 1,
1
1
1
2
2
2
2
1
3\
зУ"*
3\
зУ"*"
1
	 1,
/1
V2
/1
ll
2
3
2
3
3U i
2J""'
(з
u
2
1
2
2
3
2
3
1
¦ — 1.
Задача I. Доказать, что все группы, состоящие из трех элементов
изоморфны между собой.
Задача II. Пусть х — фиксированный элемент некоторой группы G.
Доказать, что соответствие
устанавливает изоморфное отображение группы G на самое себя.

ГЛАВА II
НЕКОТОРЫЕ КОНКРЕТНЫЕ ГРУППЫ
§ 4. Группа перестановок
Начнем изучение группы перестановок Sn с анализа отдельной
перестановки s. Если в результате перестановки 5 предмет, стояв-
стоявший на k-м месте, перешел на место с номером тк, то удобно
говорить, что перестановка s переводит число k в число тк. Записы-
Записывается это так: sk = mk. Разобьем с помощью перестановки 5
совокупность чисел 1, 2, ..., п на отдельные циклы. С этой целью
выберем совершенно произвольно какое-либо число то^п, напи-
напишем ряд чисел
т0, ml = sm0, m2 = sm1	mp = smp_1	(a)
и оборвем его, как только последнее написанное нами число тр
окажется равным одному из выписанных ранее чисел. При этом все
числа
т0, mlt т2, . . ., тр_х	C)
будут различными. Следовательно, различными будут и числа
/»!, тг	тр, так как они получаются из чисел C) в результате
перестановки s. Отсюда вытекает, что число тр равно т0, т. е.
Соотношения (а) и (у) показывают, что если расположить числа C)
в вершинах правильного /7-угольника, то действие перестановки s
на эти числа можно наглядно представить в виде поворота этого
многоугольника на угол —'-. Поэтому совокупность чисел C) назы-
называют циклом. Число р называется длиной цикла.
Взяв какое-либо из чисел 1, 2	п, не вошедшее в цикл C),
мы можем построить второй цикл. Этот процесс можно продол-
продолжать, пока не будут исчерпаны.все п чисел.
Ясно, что если указано разбиение чисел 1, 2	п на циклы
и порядок следования чисел в каждом цикле, то тем самым задана

14	НЕКОТОРЫЕ КОНКРЕТНЫЕ ГРУППЫ	[ГЛ. II
перестановка s. Поэтому перестановку s можно записать в виде
s = (m0, mlt ..., rrip^i) (n0, nv .. ., «e_t) • • • {l0, /i	^r-i)>
т. е. в виде произведения циклов.
Если какое-либо число переходит под действием перестановки s
само в себя, то оно образует цикл из одного числа. Такие циклы
принято опускать при записи перестановки в виде произведения
циклов.
В качестве примера запишем перестановки
Л 2 3 4\	/1 2 3 4\	/12 3 4'
Sl"V2 1 4 ЗУ' 52~1з 1 4 2)' $ь~\\ 4 3 2
в виде произведения циклов
sj = A2) C4), 52 - A312), s;! = B4).
Укажем теперь простой способ вычисления перестановок xsx~l
(x?Sn), сопряженных перестановке s. Для этого заметим, что если
перестановка s переводит число тх в т2, то перестановка xsx~l
переводит число хтх в число хт2:
xsx-1 (хт^) — xsm^ = хт2.
Это означает, что любая пара чисел mlt т.,, следующих друг за
другом в одном из циклов перестановки s, переходит под действием
перестановки х в пару чисел хти хт2, которые являются соседями
в одном из циклов перестановки xsx~l. Отсюда следует правило:
для вычисления перестановки xsx~x следует представить s в виде
произведения циклов и заменить затем в циклах все числа т чис-
числами хт. Например, если s=A24)C6); x~ B6) C415), то
((
Произведем разбиение группы перестановок Sn на классы сопря-
сопряженных элементов и определим число этих классов. Предварительно
заметим, что порядок циклов при записи перестановки безразличен.
Условимся располагать циклы в порядке убывания их длин. Общее
количество чисел, входящих во все циклы данной перестановки
(включая и циклы, состоящие из одного числа), равно п. Поэтому
каждой перестановке s соответствует разбиение числа п на сумму
невозрастающих целых чисел, равных длинам циклов перестановки s.
Так, например, перестановкам su s2, s3 отвечают разбиения: 4 = 2-f-2,
4 = 4, 4 = 2+1 + 1-
Сформулированное выше правило составления сопряженной пере-
перестановки xsx-1 показывает, что взаимно-сопряженным перестанов-
перестановкам соответствует одинаковое разбиение числа п. Наоборот, если
двум перестановкам st и s2 соответствуют одинаковые разбиения
числа п, то эти перестановки сопряжены. Чтобы в этом убедиться,
достаточно подписать перестановку s2 под перестановкой st и взять
в качестве х перестановку, переводящую каждое число из верхней-
строки в находящееся под ним число нижней строки.

§ 5]	ГРУППА ВРАЩЕНИЙ	15
Таким образом, каждый класс сопряженных перестановок
группы Sn состоит из всех тех перестановок, которым соответствует
одно и то же разбиение числа п. Количество qn классов сопряжен-
сопряженных элементов группы Sn равно числу различных разбиений. Для
ге—2, 3, 4, о имеем q2=2, q3 = '5, <74 = 5, <75—7-
В заключение укажем на один способ построения подгрупп
группы Sn. Пусть f = f(tl, t2, ..., tn)—некоторая функция п пере-
переменных. Sn можно рассматривать как группу перестановок аргумен-
аргументов этой функции. Легко видеть, что те из перестановок группы Sn,
которые не изменяют вид функции /, образуют подгруппу.
Тем самым каждой функции/^, (г, .. ., tn) сопоставляется неко-
некоторая подгруппа группы Sn. Особо важную роль играет так назы-
называемая альтернативная подгруппа Ап, отвечающая функции
f{t,, U, .... tn)= И (ti — tk).
г <к
Функция / представляет собой произведение всевозможных разно-
разностей ti—tk, взятых по одному разу с тем или иным знаком. Любая
перестановка аргументов либо не изменяет этой функции, либо
меняет только ее знак. Первые перестановки называются четными
(они образуют подгруппу Ап), вторые — нечетными. Произведение
двух перестановок одинаковый четности есть четная перестановка.
Произведение перестановок различной четности есть нечетная пере-
перестановка.
Задача I. Доказать, что число четных и нечетных перестановок
в группе Sn одинаково и что, следовательно, индекс альтернативной под-
подгруппы равен двум.
Задача II. Доказать, что четность перестановки п предметов равна
(—\)п~т, где т. — число циклов, на которые распадается перестановка.
§ 5. Группа вращений
Элементами группы вращений, которую мы будем обозначать
через R, являются всевозможные вращения пространства, оставляю-
оставляющие неподвижными некоторую фиксированную точку О. Каждое
вращение можно характеризовать единичным вектором к, направлен-
направленным вдоль оси вращения, и углом а, на который производится пово-
поворот. Поэтому мы будем обозначать вращения через Си (а). Заметим,
что угол а отсчитывается в направлении, которое является поло-
положительным относительно k.
Произведение двух вращений Ск^о^С^^) определяется как
результирующее вращение Ск(а). Это означает, что если произволь-
произвольный вектор г переводится вращением Ch, (э^) в вектор г', а вектор г'
в результате вращения С^(а2) переходит в вектор г", то произве-
произведение Ск (а) переводит вектор г в вектор г". Формулы, выражаю-
выражающие k и а через fclt at и k2, ac2, весьма громоздки, и мы не будем
их приводить.

16
НЕКОТОРЫЕ КОНКРЕТНЫЕ ГРУППЫ
[ГЛ. II
Пусть Ск (а) — произвольное вращение. Элементарный геометри-
геометрический расчет показывает, что оно переводит вектор г в вектор
r' — Ch{a)r = k{kr){\— cos а) + г cos a-+-[*, r]sina. E,1)
Эта формула значительно упрощается, если угол поворота 8а мал
и можно пренебречь величинами порядка 8аа. Вводя обозначения
Ъг — г'—г и 8a = ?8a, мы получим из E,1) в этом приближении
8r = [5a,r] или г' — г-{-\Ъх, г\.	E,2)
Каждое вращение определяется с помощью трех параметров.
В качестве этих параметров можно взять числа
Й1 = aku a2 = ak2, a3 = ak3,
являющиеся проекциями вектора ak на оси координат. Очень удобно
взять в качестве параметров, характеризующих вращения, так назы-
называемые углы Эйлера 0, ср и ф. Для определения этих углов введем,
помимо неподвижной системы координат XYZ, подвижную систему
;, т], С, связанную с вращаемым
пространством. Прямую, вдоль кото-
которой пересекаются плоскости XOY и
Юг\, назовем осью узлов (рис. 1).
Положительным направлением на
оси узлов будем считать направле-
направление вектора я = [ez, e^] (ег и
ес—единичные векторы, направлен-
направленные вдоль осей OZ и ОС). Обозна-
Обозначим через б угол между осями OZ
и <% @ <; 0 <; тг). Угол между осью
узлов и осью О\ обозначим через «,
угол между осью узлов и осью
ОХ—-через ф. Положительные от-
отсчеты углов сриф указаны на рис. 1 стрелками. Вращение, харак-
характеризуемое углами Эйлера 6, ср и ф, мы будем обозначать
через ^@, ср> $'• Это вращение может быть представлено в виде
произведения трех поворотов: поворота С3 (у) вокруг оси OZ, по-
поворота CiF) вокруг оси ОХ и поворота С3(ф) вокруг оси OZ, т. е.
g F, ?, ф) = С3 (ф) С, F) С3 (с?).	E,3)
Рис. 2 иллюстрирует это соотношение. На нем изображено поло-
положение подвижной системы координат после вращений С3 (сэ)
(рис. 2, а) и Сх F) С3 (») (рис. 2, б); окончательное положение
C3(ty)C1(b)C3(<?) изображено на рис. 1.
Каждое вращение g можно рассматривать как линейный опера-
оператор, переводящий вектор г в вектор г' = gr *). Вычислим матрицу
*) В тех случаях, когда вращение рассматривается как оператор, мы
будем обозначать его g (аналогично, если вращение обозначено другой
буквой).
Рис. 1.

§ 5]
ГРУППА ВРАЩЕНИЙ
17
оператора g в естественном базисе, состоящем из ортов ev e2, е3,
направленных вдоль осей OX, OY, OZ. Ясно, что для поворотов
Сз (») и C3(<J>) вокруг оси OZ эта матрица имеет следующий вид:
/cos о
С3 (ср) = I sin cp
\ 0
Матрица поворота
— sin
— sin о 0\	/cos ф	ф
cos ? 0 1, С3 (ф) = 1 sin ^ cos ф
0 1/	\ О	О
Cj (8) вокруг оси OJV, очевидно, равна
/10	0
d F) = I 0 cos 6 — sin
\0 sin 9 cos 6,
Матрица произвольного вращения g{%, с?, ф) получается согласно E,3)
перемножением этих трех матриц. Произведя вычисление, мы по-
получим:
''cos 9 cos if — cos 8 sin 9 sin 6 — sin 9 cos •} — cos 6 cos <f sin \ sin 1} sin 1
sin 6 cos 9 -)- cos 6 cos 'i/ sin 9 — sin 9 sin & -(- :os 8 cos 9 cos if — cos if sin в |,
1 9 sin 8	cos 9 sin в	cos 6
E,4)
В последнем столбце матрицы E,4) стоят координаты вектора е,.
Мы видим, что задание углов 0 и у вполне определяет вектор е;.
z
б)
Рис. 2.
Поэтому в и i) можно рассматривать также, как координаты точки
(конца вектора е{) на единичной сфере. Если обозначить сфери-
сферические координаты этой точки через 0 и ф, то, как легко видеть,
е=е, ф = ф+^.	E,5)
Выясним, как разбивается группа вращений на классы сопря-
сопряженных элементов. Для этого найдем все вращения Ckl (ах), сопря-
сопряженные произвольному фиксированному вращению Ск(а).

18	НЕКОТОРЫЕ КОНКРЕТНЫЕ ГРУППЫ	[ГЛ. II
Согласно определению сопряженных элементов, вращение С^ (ах)
может быть представлено в виде
где g—некоторый элемент R. Обозначим через пц матрицу вра-
вращения Cfc(a) в базисе е1; е2, въ. Легко видеть, что в базисе
e'j = gej (у=1, 2, 3) эта же матрица изображает вращение Cfcl (at).
Действительно,
Сь, (a0ej = &»W S~le'j = sCh (a)^ = ga.ft = a..e'r
Заметим, что матрица вращения однозначно определяет угол, на
который производится это вращение, и расположение оси вращения
относительно базисных векторов. Поэтому угол а{ равен углу a
и вектор ky имеет в базисе e'j те же координаты, что и вектор k
в базисе еу Это означает, что вектор kt получается из вектора k
путем вращения g. Итак, о^ = a, kx — gk и
gCfc(a)^-1 = Cfffc(a).	E,6)
Полученное соотношение показывает, что каждый класс сопряжен-
сопряженных элементов состоит из поворотов на один и тот же угол a
@<;а<^2т:) вокруг всевозможных осей.
Так как при вращениях пространства сохраняются длины векто-
векторов и углы между ними, то скалярное произведение двух векторов
в результате вращения также не изменяется, т. е. (г, r1) = (gr, gr,).
Это означает, что вращения представляют собой унитарные опера-
операторы. Как известно, определитель любого унитарного оператора
в трехмерном действительном пространстве равен либо -(-I, либо —1.
Вращениям соответствуют только те унитарные операторы, у кото-
которых определитель равен единице. Действительно, поворот на угол,
равный нулю, является единичным оператором; определитель его
равен единице. Отсюда в силу соображений непрерывности опре-
определитель любого поворота также равен единице.
Итак, каждое вращение представляет собой унитарный оператор
с определителем, равным единице. Можно показать, что и, наоборот,
всякий унитарный оператор в трехмерном действительном простран-
пространстве с определителем, равным единице, является вращением.
Если в качестве группового действия взять обычное умножение
операторов, то совокупность всех унитарных операторов в действи-
действительном трехмерном пространстве, имеющих определитель, равный
единице, образует группу. Эта группа изоморфна группе вращений.
Скажем несколько слов о другой трактовке группы вращений,
которая в ряде случаев оказывается предпочтительней. Воспользуемся
тем, что унитарные матрицы можно рассматривать как преобразо-
преобразования координат неподвижных векторов при вращениях системы коор-

§ 6]	ПОЛНАЯ ОРТОГОНАЛЬНАЯ ГРУППА	19
динат. Если орты новой системы координат е', выражаются через
Орты старой системы координат посредством соотношений
то координаты неподвижного вектора преобразуется по закону
Таким образом, одну и ту же унитарную матрицу можно рас-
рассматривать либо как вращение g пространства, либо как враще-
вращение g-1 системы координат. Иными словами, группа унитарных
матриц с определителем, равным единице, изоморфна не только
группе вращений пространства, но и группе вращений системы коор-
координат. В силу этого изоморфизма обе последние группы носят общее
название группы вращений.
Задача I. Используя матрицу E,1), проверить, что
g @, 9, ф) = С3 (* + ф) d (- 6) Cs (* + ч).
Задача П. Показать, что вращения g@, <р, ф) и g(Q,~—!}> г. — у)
нааимно обратиы.
Задача III. Показать, что в группе вращений коммутируют между
собой только те вращения, которые производятся вокруг одной и той же
оси.
§ 6. Полная ортогональная группа
Преобразование пространства, переводящее каждый вектор г
и вектор —г, называется инверсией. Инверсию обычно обозначают
через /. Таким образом, 1г = — г*). Отсюда следует, что инверсия
коммутирует со всеми вращениями:
Ig = gl.	F,1)
Ясно также, что /2 = е. Определитель оператора инверсии равен —1.
Если ко всем элементам группы вращений R присоединить все-
нозможные произведения Ig(g^R), то получится группа. Действи-
Действительно,
8та группа называется полной ортогональной группой. Будем обо-
вначать ее через W. Элементы группы W, не являющиеся враще-
вращением, называются элементами второго рода; вращения называются
Клементами первого рода. Определитель матрицы, соответствующей
любому элементу второго рода, равен —1. Напомним, что для эле-
элементов первого рода этот определитель равен 1.
Выясним геометрический смысл элементов второго рода. Прежде
мсего ясно, что произведение /С^(я) есть зеркальное отражение
*) В тех случаях, когда инверсия рассматривается как оператор, мы
Оудим обозначать ее I.

20	НЕКОТОРЫЕ КОНКРЕТНЫЕ ГРУППЫ	[ГЛ. II
в плоскости, перпендикулярной к вектору к. Обозначим его через о,..
Отсюда следует, что произвольный элемент второго рода
Юн (* + «) = Юк (я) Ch (а) = окСн (а)
есть произведение поворота вокруг некоторой оси на зеркальное
отражение в плоскости, перпендикулярной к этой же оси. Такое
произведение называется зеркальным поворотом и обозначается
через Sfc(a). Таким образом, полная ортогональная группа состоит
из всевозможных поворотов и зеркальных поворотов.
Произведем разбиение группы W на классы. Пусть h — Ig—
элемент второго рода, а g— элемент первого рода. Используя E,6),
получим:
hCk (a) /Г1 = IgCk {a)g-} I = Сдк (a) = С_й* (а),
т. е.
AC*(a)A-1 = C_ft*(a) (h?W, h?R).	F,2)
Подобным же образом получаем соотношения
AS* (a)/Г1 =S_Afc(a), gSh(a)g~l = Sgh(*).	F,3)
Из F,2) и F,3) следует, что совокупность всех поворотов на один
и тот же угол образует класс и что совокупность всех зеркальных
поворотов на один и тот же угол также образует класс.
§ 7. Евклидова группа
Всякое перемещение пространства можно задать с помощью век-
векторной функции а(г), определяющей перемещение а точки с радиусом-
вектором г.
Функция а{г) должна быть такой, чтобы расстояние между любой
парой точек не изменялось в результате их перемещения.
Под произведением двух перемещений пространства понимают
результирующее перемещение. Совокупность всех перемещений обра-
образует относительно этого произведения группу. Эта группа назы-
называется евклидовой группой. Мы будем обозначать ее через П.
Полная ортогональная группа является, очевидно, подгруппой
евклидовой группы. Другой важной подгруппой II является группа
трансляций. Трансляцией называют такое перемещение пространства,
при котором перемещения всех точек одинаковы. Мы будем обозна-
обозначать трансляции символом ta, где а — общее перемещение всех точек
пространства. Ясно, что
ta-tb = ta+b.	G,1)
Из этого равенства следует, что группа трансляций, а также любая
ее подгруппа, изоморфна некоторой векторной группе, т. е. группе,
состоящей из векторов с векторным сложением в качестве группо-
группового действия.

§ 7]	ЕВКЛИДОВА ГРУППА	21
Всякий элемент g группы П может быть представлен в виде
произведения поворота или зеркального поворота л о вокруг произ-
произвольной точки О на некоторую трансляцию ta:
g = *Jo <?€U)-	G,2)
Для доказательства выберем совершенно произвольно точку О и
обозначим через О' точку, в которую переходит О при перемеще-
перемещении g. Рассмотрим теперь перемещение t^ag, где а—вектор, про-
проведенный из точки О в О'. Ясно, что под действием перемещения
t-ag точка О остается неподвижной. Поэтому iZ g является пово-
поворотом или зеркальным поворотом rQ вокруг точки О. Это доказы-
доказывает соотношение G,2).
Можно получить еще более наглядное представление об элемен-
элементах группы ТТ. Для этого рассмотрим сначала случай, когда
го = ск (а)« а * ° и « -L *•
Легко видеть, что при перемещении taCk{o.) (a _[_ k) существует
неподвижная точка О1 и поэтому ^«Cfc(a) является поворотом СьНа)
вокруг этой точки. Если трансляция ta не параллельна оси враще-
вращения k, то ее можно представить в виде ta = tbte, где b\\k и cj_k.
Тогда taCk (a) = tbteCk (я) = tbC$ (a) и мы получаем произведение
поворота вокруг оси на трансляцию вдоль оси. Такое перемещение
называется винтовым, а ось, скользящая при этом движении вдоль
самой себя, называется винтовой осью.
С помощью аналогичных рассуждений можно показать, что произ-
произведение taSk(ot) (a ф 0) является зеркальным поворотом вокруг неко-
некоторой точки и что taSb@) есть произведение отражения в некото-
некоторой плоскости ah на трансляцию вдоль этой плоскости.
Такое перемещение называется скользящим отражением, а пло-
плоскость а*, — плоскостью скольжения.
Таким образом, евклидова группа состоит из поворотов, зер-
зеркальных поворотов, трансляций, винтовых перемещений и скользя-
скользящих отражений.
В заключение приведем, опуская элементарное доказательство,
следующие два тождества:
gtJg-1 = tea>tar0t-a=r0 + a>	G,3)
где g — произвольный элемент группы ТТ, ga — вектор, получаю-
получающийся из а в результате перемещения g, rQ—какой-либо поворот
или зеркальный поворот вокруг точки О, О-\-а — точка, в кото-
которую переходит О при трансляции а.

22	НЕКОТОРЫЕ КОНКРЕТНЫЕ ГРУППЫ	[ГЛ. II
§ 8. Точечные группы
Всякая подгруппа полной ортогональной группы называется
точечной группой. Точечные группы, не содержащие зеркальных
поворотов, называются группами первого рода. Все остальные точеч-
точечные группы — группами второго рода.
Если поворот вокруг некоторой примой С содержится в данной
точечной группе G, то прямая С носит название оси группы G.
Рассмотрим точечную группу G первого рода, имеющую только
одну ось С. Если число элементов такой группы равно п, то ее
обозначают через Сп. Все элементы группы Сп представляют собой
повороты вокруг оси С. При возведении любого элемента группы Сп
в п-ю степень получается единичный элемент (см. задачу 2 § 2).
Поэтому группа Сп может содержать только повороты вокруг оси С
на углы
О, ?.?.2.....?(»-!).	(8,1)
Число этих поворотов равно п, поэтому все они входят в группу Сп
и исчерпывают ее.
Поворот на наименьший угол — вокруг оси Сп обозначают
через С„. Все остальные повороты являются степенями Сп. Поэтому
элементы группы Сп можно записать в виде
е, Сп, Cl	СТ\	(8,2)
Подчеркнем, что группы Сп (п — 2, 3, ...) являются циклическими.
Для того чтобы отличать повороты С„ и Сп , целесообразно рас-
рассматривать ось Сп как направленную прямую, т. е. различать на
ней положительное и отрицательное направления.
Пусть G— произвольная группа, а С — какая-либо ее ось. Сово-
Совокупность всех поворотов вокруг оси С из группы G образует (вместе
с единичным элементом) подгруппу группы О. Эта подгруппа, оче-
очевидно, представляет собой группу Сп. В соответствии с этим ось С
группы G обозначают через С„ и называют осью га-го порядка.
Ось Сп группы G называется двусторонней осью, если повороты С„
и Сп являются взаимно-сопряженными. В противном случае ось Сп
называется односторонней.
Для того чтобы ось Сп была двусторонней, необходимо, чтобы
в группе G содержался поворот на 180° вокруг какой-либо оси,
перпендикулярной к оси Сп, или чтобы группа, G содержала зер-
зеркальный поворот вокруг оси Сп.. Это непосредственно вытекает из
формул E,6) и F,2).
Две оси Сп и Сп группы G называются эквивалентными, если
поворот С'п сопряжен повороту Сп или повороту Си1. Легко видеть,

^ 9]	ТОЧЕЧНЫЕ ГРУППЫ ПЕРВОГО РОДА	23
что условием эквивалентности осей Сп и Сп является наличие в группе G
элемента, переводящего ось Сп в ось С„.
Задача I. Доказать, что зеркальные повороты 5 (а) и S(—а) вокруг
двусторонней оси сопряжены друг другу.
Задача П. Пусть С и С — две эквивалентные оси группы G. Дока-
Доказать, что зеркальный поворот S (а) вокруг оси С сопряжен повороту 5' (а)
(или S'(— а)) вокруг оси С.
§ 9. Точечные группы первого рода
Перечислим все точечные группы первого рода.
1.	Наиболее простыми после групп Сп являются группы О„.
Группа Dn состоит из всех поворотов, совмещающих правильную
л-угольную призму саму с собой. Она имеет одну ось п-то порядка Сп
и п перпендикулярных к ней осей второго порядка. Эти оси обо-
обозначают через ии иг, и3, .. ., ип. Угол между двумя соседними осями и
равен ~-. Таким образом, группа Dn содержит единичный элемент,
2~
{п—1) поворот вокруг оси Сп на углы, кратные —'-, и п поворо-
поворотов на 180° каждый вокруг осей второго порядка, т. е. всего
2и элементов. Благодаря наличию осей второго порядка ось Сп
в группе Dn является двусторонней. Поэтому повороты с\ и С"~
взаимно сопряжены. Если п — четное число, то повороты вокруг
оси Сп разбиваются на (-к-И- ') классов:
( 1-\ 1 ¦ \\ '1
\еI > (^ п> t-> п />•••> [ ^ п > ^п Jib;;'
Если п — нечетное число, то эти же повороты разбиваются на — у-
классов:
Оси ult u3, u~, . . . эквивалентны между собой, так как они пере-
переводятся друг в друга при поворотах Счп (k=\, 2, 3, ...). Точно
так же эквивалентны между собой оси м2, и4, «6	Заметим еще,
что ось Mn_t при повороте Сп совмещается с осью и1 и потому
эквивалентна ей. Отсюда следует, что при п нечетном все оси вто-
второго порядка эквивалентны между собой, а повороты вокруг них
составляют один класс. При четном я повороты ии и2, и3, .. ., ип
распадаются на два класса \ии и3, ..., «„_!} и {и2, ai	ип\.
Обозначая через g(Dn) число классов сопряженных элементов
группы Dn, получаем из приведенных рассуждений
?_(Dn) = -J + 3 (п — четно), q(Dn) = ^±~ (я —нечетно). (9,1)
2.	Группа Т (группа тетраэдра) состоит из всех поворотов,
совмещающих тетраэдр сам с собой.
( п-л n_+_i ^
\г 2 Г 2 \

24
НЕКОТОРЫЕ КОНКРЕТНЫЕ ГРУППЫ
[гл. р
Группа Т содержит четыре оси третьего порядка и три оси вто-
второго порядка. Оси третьего порядка проходят через вершины тетра-
тетраэдра (одна из них изображена на рис. 3). Будем обозначать их
через Сз\ Cf\ C^ и С34)- Оси второго порядка
соединяют середины непересекающихся ребер.
Обозначим эти оси через и12, «13 и ии. Таким
образом, группа Т, кроме единичного элемента,
содержит четыре поворота на 120°, четыре пово-
поворота на 240° и три поворота на 180°, т. е. всего
двенадцать элементов. Оси С3г) (i= 1, 2, 3, 4)
являются односторонними. Все они эквивалентны
друг другу, так как повороты м12, и,а и и
переводят ось С* в оси
Рис. 3.
43 " 4
и Сз соответ-
соответственно. Оси и12, ии и м14 также эквивалентны, так как они пере-
переходят друг в друга при поворотах вокруг осей С3г). Отсюда
следует, что двенадцать элементов группы следующим образом раз-
разбиваются на четыре класса сопряженных элементов:
[е\, {Cf\, {C<iJ}. {«и}-	(9,2)
3. Группа О (группа октаэдра) состоит из всех поворотов,
совмещающих куб сам с собой. Она содержит три оси четвертого
порядка di\ С?] и СЧ\ четыре оси третьего порядка d?\ C32), С33), СD3)
и тесть осей второго порядка и12,
2
..:^.л.:^с'
\ '
\ /
/\
-Х-
\
1 \
1 \
У
«23> «34> «41' М26 И «37 (РИС- 4)- °СИ
четвертого порядка соединяют сере-
середины противоположных граней. Поло-
Положительные направления на них выбраны
так, чтобы они образовывали право-
винтовую систему. Оси третьего по-
порядка проходят через противополож-
противоположные вершины. Будем считать, что они
направлены от вершины с большим
номером к вершине с меньшим. Оси
второго порядка соединяют середины	рис 4>
противоположных ребер.
Кроме единичного элемента, группа О содержит три поворота
на 90°, три поворота на 180° вокруг осей четвертого порядка, три
поворота на 270°, четыре поворота на 120°, четыре поворота на 240°
и шесть поворотов на 180° вокруг осей второго порядка, т. е. всего
24 элемента.
Легко видеть, что все оси одного и того же порядка эквива-
эквивалентны между собой. Кроме того, оси четвертого и третьего порядка
являются двусторонними. Поэтому разбиение элементов группы О
на классы имеет следующий вид:

9]
ТОЧЕЧНЫЕ ГРУППЫ ПЕРВОГО РОДА
25
4. Группа Y (группа икосаэдра) состоит из всех поворотов,
срвмещающих самого с собой пентагональный додекаэдр, т. е. две-
двенадцатигранник с правильными пятиугольными гранями. Число ребер
9того многогранника равно 30, а число вершин — 20. В этом легко
убедиться, если заметить, что на каждую грань приходится в сред-
среднем по 5/2 ребер и 5/3 вершин. Группа икосаэдра состоит из шести
осей пятого порядка С^ (/=1. 2, ..., 6), соединяющих середины
противоположных граней, 10 осей третьего порядка, соединяющих
противоположные вершины, и 15 осей второго порядка, соединяю-
соединяющих середины противоположных ребер.
Группа икосаэдра содержит, помимо единичного элемента, 24 пово-
поворота вокруг осей пятого порядка, 20 поворотов вокруг осей третьего
порядка и 15 поворотов вокруг осей второго порядка, т. е. всего
60 элементов. Все одноименные оси эквивалентны друг другу. Оси
пятого и третьего порядков являются двусторонними. Поэтому группа
икосаэдра распадается на пять классов:
[е], {<#>. СИ. {СГ, СП. № СГЬ И-	0,4)
Можно показать, что рассмотренные группы исчерпывают набор
конечных точечных групп первого рода. Существуют, однако, две
бесконечные группы первого рода (кроме группы вращения). Это —
группы Ссо и Doo- Группа Соо представляет собой группу всех пово-
поворотов вокруг фиксированной оси. Эта группа коммутативна. Группа
Deo состоит из всех поворотов вокруг фиксированной оси ОО' и пово-
поворотов на 180° вокруг всех осей, перпендикулярных к оси ОО'.
В заключение приведем таблицу (см. табл. 1).
Таблица 1
Точечные группы первого рода
Группа
с„
On
т
о
Y
а)
Число 9J
ментов
п
2л
12
24
60
Число классов
п
-у -)- 3 при п — 2k
-±-? ПрИ п = 2k -j- 1
4
5
5
Число осей разных порядков
второго
—
п
3
6
15
третье-
третьего
—

4
4
10
четвер-
четвертого
—
--
—
О
ПЯТОГО
—
—
—
__
—. ! 6
!
шестого
—
—
—
ол-и
1
1
—
—

26
НЕКОТОРЫЕ КОНКРЕТНЫЕ ГРУППЫ
ГЛ. II
§ 10. Точечные группы второго рода
Продолжим обзор точечных групп. Обратимся к группам вто-
второго рода.
1.	Группа S2n состоит из степеней зеркального поворота
S2n~s(—). Она содержит In элементов: е, S2n, Stn, ..., Sa".
Четные степени S2n образуют подгруппу, совпадающую с группой
Сп. S2n является циклической группой.
2.	Группа Cnh состоит из поворотов и зеркальных поворотов
вокруг фиксированной оси 00' на все углы, кратные углу — . Она
содержит, таким образом, 2п элементов:
Скп и оАсЛ=5(^
= 0, 1, 2	п—\).
Здесь <зй означает отражение в горизонтальной плоскости, т. е. пло-
плоскости, перпендикулярной к оси Сп. Группа СпП коммутативна.
Каждый ее элемент сам по себе образует класс.
3. Группа Ст есть группа симметрии правильной «-угольной
пирамиды. Она содержит одну ось п-то порядка С„, совпадающую
с высотой пирамиды, и п «вертикальных» плоскостей зь о2	ап,
проходящих через ось Сп (иными словами, отражения в этих пло-
плоскостях содержатся в группе Cnv).
Если п — нечетное число, то каждая
такая плоскость проходит через
одно из ребер пирамиды и делит
на две равные части противополож-
противоположную боковую грань. Если п — четное
число, то половина этих плоскостей
проходит через взаимно-противопо-
взаимно-противоположные ребра, а вторая поло-
половина— через середины противо-
противоположных граней (рис. 5). Груп-
Группа Cnv содержит 2ге элемен-
элементов: е, Сп, Cl, .... С"~\ ор з2, ..., ап. Группа Cnv изоморфна
группе Dn. Действительно, каждый элемент группы Cnv совершает
некоторую перестановку вершин основания пирамиды. При этом
разным элементам группы Cnv соответствуют разные перестановки.
Точно такие же перестановки над вершинами основания совершают
повороты из группы Dn. Если поэтому сопоставить друг другу те
элементы групп Спо и Dn, которые совершают одинаковую переста-
перестановку вершин, то мы получим изоморфное соответствие
Рис. 5.
&-i -1
¦«* + ,
= 0, 1, 2, ..., я—1). A0,1)

ТОЧЕЧНЫЕ ГРУППЫ ВТОРОГО РОДА
27
В силу изоморфизма групп Cnv и Dn число элементов и классов
у них одинаково, поэтому
(«четно), д(Спс)=
=^±1
(п нечетно). A0,2)
4. Группа Dnh есть группа симметрии правильной «-угольной
призмы. Она содержит 2п элементов группы Cnh, n горизонтальных
осей ии а2	, ип второго порядка и п вертикальных плоскостей
av а2, . . ., ап, проходящих через эти оси, т. е. всего An
элементов.
Отражения в вертикальных плоскостях <зи а3, ...
взаимно сопряжены друг другу, так как эти плоскости
переходят друг в друга при поворотах С„- Точно
так же сопряжены между собой плоскости о2, о4, ...
Отражение яп сопряжено а2. Если п—нечетное число,
то ап~а1 и, следовательно, з1~а2- Поэтому при
нечетных значениях п все отражения в вертикальных
плоскостях образуют один класс; если п четно, то они
разбиваются на два класса [ov з3, ..., on-i}>
(о2, о4, . . ., оп). Эти же рассуждения применимы и к по-
поротам вокруг осей их, а2, ¦ ¦ ¦, ип, которые состав-	Рис. 6.
ляют один класс, если п нечетно, и два, если п четно.
Ось Сп является двусторонней*. Поэтому повороты вокруг оси Сп
разбиваются на классы так же, как и в группе Cnv, т. е.
\г Гп~1\ \сг Гп~2\
Точно так же разбиваются на классы зеркальные повороты
,inCkn (k=\, 2, ..., п). Вспоминая A0,2), получим:
ЯФпь) = я+ 10 (ге четно), q (Dnh) = п -\-5 (п. нечетно).
A0,3)
б. Группа Dnd. Представим себе две одинаковые /г-уголь-
мыс правильные призмы, приставленные друг к другу основаниями
и повернутые одна относительно другой
на угол — (рис. 6). Группой симметрии
такого тела и будет группа Оы. Груп-
Группа Dnd содержит одну зеркально-попорот-
ную ось 52„ порядка 2я, п вертикальных
плоскостей av з2, . . ., ап, проходящих через
ребра призм, и п горизонтальных осей вто-
второго порядка ии и2, ..., ип, проходящих
41-рез точки пересечения /г-уголышков, ограничивающих основания
призм (рис. 7).
При повороте uv плоскость zL переходит в плоскость а.,. По-
^ I ому отражения во всех вертикальных плоскостях составляют один
мисс. С другой стороны, при отражении в плоскости о2 ось и1
игреходит в ось и2. Поэтому повороты вокруг всех горизонтальных
рис 7

28	НЕКОТОРЫЕ КОНКРЕТНЫЕ ГРУППЫ	[ГЛ. II
осей также образуют один класс. Ось S2n является двусторонней.
Степени S2n образуют (ге-)-1) класс
Общее число классов в группе Dnd равно п -j- 3
q{Dnd) = n + Z.	A0,4)
6.	Группа Td есть группа симметрии (-тетраэдра. Она содер-
содержит в качестве подгруппы группу Т. Кроме двенадцати элементов
группы Т, группа Td содержит шесть плоскостей
ai2> ai3> °u> °2з> а24.. а34 (рис. 8) и по два зеркаль-
ных поворота 54 и Si вокруг каждой из трех осей
второго порядка. Более подробно эти зеркальные
повороты мы будем обозначать S±, S3!2K> 5113),
оA3K оB3) о B3K
Итак, группа Td содержит 24 элемента: четыре
р о	поворота на угол 120°, четыре поворота на угол 240°,
три поворота на 180°, шесть зеркальных поворотов
на углы 90° и 270°, шесть отражений в плоскости и единицу
группы. Все оси являются двусторонними, одноименные оси экви-
эквивалентны. Поэтому разбиение на классы имеет следующий вид:
[^j, \Сз , Сз J, \Uij, |O4 , O4 \,-{3ik)-	(IV.O)
Итак, группа Td распадается на пять классов.
7.	Группа Тд получается из группы Т путем прибавления
инверсии и произведений инверсии на все элементы группы Т.
Произведение инверсии на поворот Сз есть зеркальный поворот
вокруг оси dl) на угол 300°, т. е. /Сз0 = SlP5. Подобным же об-
образом /Сз = Se • Итак, все четыре оси третьего порядка пре-
превращаются в зеркально-поворотные оси шестого порядка; это дает
восемь новых элементов. Произведение / на поворот на 180° дает
отражение в плоскости, перпендикулярной к оси поворота. Это
дает нам еще три плоскости о12, а13, аи. Таким образом, общее
число элементов группы Tft равно 24.
Разбиение на классы имеет следующий вид:
\e)i 1^3 (> \Ьз (> \игк]> I1}' Ь'1> )> I"-*!) (> I3!*j- VIU>O;
8.	Группа Oh есть группа симметрии куба. Помимо 24 эле-
элементов группы О, она содержит еще отражения в трех плоскостях
ai> 32> Зз> параллельных граням куба, отражения в шести плоско-
плоскостях, проходящих через диагонали противоположных граней, инвер-
инверсию, восемь зеркальных поворотов S\ , Se, (i=l, 2, 3, 4) вокруг
осей С|г) и шесть зеркальных поворотов вокруг осей с2\ ClP, Cf^
на углы 90° и 270°. Таким образом, группа Oh содержит 48 эле-

§ 11]
ГРУППЫ ТРАНСЛЯЦИЙ
29
ментов. Эти элементы распределяются между двенадцатью классами.
Шесть классов — такие же, как и в группе О. Остальные шесть
получаются из первых путем умножения на инверсию.-Таким образом,
?(Од)=12.	A0,7)
9. Группа Yh есть группа симметрии правильного двенадцати-
двенадцатигранника с'пятиугольными гранями. Она содержит все элементы
группы Y и все произведения этих элементов на инверсию. Поэтому
число элементов группы Yh равно 120, а число классов— 10.
Этими исчерпываются все конечные группы второго рода (см.
табл. 2). Путем предельного перехода из групп Cnh и Cnv можно
получить группы Cccft и Coov Группы Dnh и Dnd «в пределе» пере-
переходят в одну и ту же группу, которую принято обозначать через D^h.
Таблица 2
Точечные группы второго рода
Группа
Cnh
?-»!)
Dnh
Dnd
Та
Th
Oh
h
Число элементов
2л
2л
2л
4л
1л
24
24
48
120
Число классов
2п
2л
¦т,- -+- 3 при п = 2k
л -|- 3 -
—^— при л = 2k -j- 1
л -\-10 при n = 2k
л -р 5 при л = 2k -j- 1
л + З
5
8
12
10
§ 11. Группы трансляций
Как уже упоминалось, трансляцию ta можно мыслить просто как
вектор а, а группу трансляций — как группу векторов с векторным
сложением в качестве группового действия. Мы будем часто пользо-
пользоваться этой точкой зрения.

30	НЕКОТОРЫЕ КОНКРЕТНЫЕ ГРУППЫ	[ГЛ. II
Если все векторы группы векторов параллельны друг другу,
то группа называется одномерной, если они параллельны одной и
той же плоскости, группа называется двумерной; если среди век-
векторов группы найдется тройка некомпланарных векторов, то группа
называется трехмерной.
Группа векторов называется дискретной, если существует поло-
положительное число d такое, что всякий не равный нулю вектор группы
длиннее d.
Структуру трехмерных дискретных векторных групп выясняет
следующая теорема:
Теорема I. Пусть оГ—трехмерная дискретная группа век-
векторов. В сГ содержится три вектора а1; а2, а3 таких, что
всякий вектор а?_§ может быть представлен в виде
а = т1а1-\-т.гаг-\-т3аъ (ти т2, т3 = 0, zfcl, ±2, ...).
Векторы alt а2, и а3 называются основными векторами группы оГ.
Доказательство. Возьмем произвольно какие-либо два не
параллельных друг другу вектора Ьх и Ъг из группы §. Плоскость,
проходящую через эти векторы, обозначим через Р. Обозначим
через «j^gT вектор минимальной длины, параллельный вектору bv
Рассмотрим теперь все векторы группы §, которые лежат в пло-
плоскости Р, но не параллельны вектору av Возьмем из них те век-
векторы, которые имеют минимальную проекцию на прямую, перпен-
перпендикулярную вектору av Один из этих векторов обозначим через а2.
Легко видеть, что, кроме векторов 0, а1; а2 и с1 + а2> ||И один
вектор группы |Г не оканчивается внутри или на границе параллело-
параллелограмма, построенного на векторах а, и а2.
Рассмотрим теперь векторы группы оГ, не лежащие в плоско-
плоскости Р. Возьмем из них те векторы, которые имеют минимальную
проекцию на перпендикуляр к плоскости Р. Один из этих векторов
обозначим через а3. Легко видеть, что конец каждого вектора
группы IT лежит либо вне параллелепипеда Q, построенного на векто-
векторах аг, а2, as, либо совпадает с одной из вершин этого параллеле-
параллелепипеда.
Разложим какой-либо вектор а ?<!Г по векторам аи а2, аъ\
а = [х,
Обозначим через [jx] наибольшее целое число, не превышающее |х.
Ясно, что вектор а0 = [j^] сх -\- [а2] а2 -f- [^з! а* содержится в группе |Г.
з
Поэтому вектор а—а0 = 2 {Pi — IM ) а% также содержится в группе f.
Числа [Xj—[[j^] меньше единицы. Если хотя бы одно из них неравно
нулю, то вектор а — а0 лежит внутри параллелепипеда Q. Так как
это невозможно, то мы приходим к заключению, что коэффициенты
Pi' Рг> Рз являются целыми числами. Это завершает доказательство
теоремы.

§ 12]	сингонии	31
Параллелепипед Q, построенный на основных векторах аи а2, а,3
называется основным параллелепипедом или элементарной ячей-
ячейкой. Из приведенного доказательства вытекает следующая теорема:
Теорема II. Одно из ребер основного параллелепипеда может
быть направлено вдоль любого вектора Ьх ? оГ. Одна из граней
основного параллелепипеда, проходящая через это ребро, может
проходить через любой вектор Ь2^$. Любой параллелепипед, свя-
связанный указанным образом с векторами Ьл и Ь2 и имеющий мини-
минимальный объем, является основным.
Из теоремы I вытекают два следствия.
Следствие I. Объем параллелепипеда, построенного на любой
тройке не компланарных векторов гх, г2, г3 из группы §, не
меньше объема Vo основного параллелепипеда.
Доказательство, Представим векторы rt в виде ri = Ci]iak.
Объем параллелепипеда со сторонами ги г2, г3 равен | (гх [/у3])'.
Подставляя сюда выражения векторов rt (i—1, 2, 3), получим:
V =
2j CuC2kC3l (Cj [акаг]
к, I
2
= V0IDet(Cik):.
2j н2кз1
i, h, I
Так как согласно теореме I все числа С« — целые, то определитель
равен некоторому целому числу. Следствие I доказано.
Следствие II. Объемы всех основных параллелепипедов дан-
данной группы равны между собой.
Это непосредственно вытекает из следствия I.
§ 12. Сингонии
Всякий поворот или зеркальный поворот, который переводит
любой вектор векторной группы оГ в какой-либо вектор этой же
группы, называется элементом симметрии группы JT. Совокупность
нсех элементов симметрии группы |Г образует некоторую точечную
группу К, называемую группой симметрии векторной группы |Г.
Если у двух векторных групп оГ[ и сГ2 одна и та же группа
симметрии, то говорят, что группы Ш1 и §2 принадлежат одной и
той же сингонии. Таким образом, под сингонией (или системой)
понимают совокупность всех векторных групп, имеющих одну и ту же
группу симметрии. Мы покажем сейчас, что существует всего семь
сингонии, соответствующих группам S2, C2h, D2h, D3h, Dib, DEh
и Oh. Эти сингонии называются триклинной (S2), моноклинной (C2h),
ромбической или ортогональной (D2h), ромбоэдрической или триго-
нальной (D3d), тетрагональной или квадратной (Dih), гексаго-
гексагональной (Deh) и кубической (ОЛ).
Пусть §—какая-либо векторная группа, а К—ее группа сим-
симметрии.

32	НЕКОТОРЫЕ КОНКРЕТНЫЕ ГРУППЫ	[ГЛ. II
Так как наряду с каждым вектором a?<f группа сГ содержит
также вектор —а, то ясно, что среди элементов группы К имеется
инверсия.
Выясним, какие оси симметрии может иметь группа К- Пусть
Сп (п — 2, 3, ...) — одна из осей группы К. Обозначим через а?§
какой-либо вектор, не параллельный оси С„. Вектор Сйс0 — а0,
очевидно, не равен нулю и перпендикулярен к оси Сп. Обозначим
через е самый короткий из векторов группы сГ, перпендикулярных
к оси С„. Ясно, что вектор Спе-\-Сп1е, параллельный е, имеет
длину, кратную е и не превышающую 2е. Поэтому
1« = ane (<*„ = —2, —1, 0, 1, 2).
С другой стороны, Спе-\-Сп1е = 2cos— e. Итак,
2 cos — = лп.
Полагая а„ = —2, мы получим га = 2; если ап = —1, то п — Ъ.
Подобным же образом значениям а„=0 и ап=1 соответствуют
п = 4 и п = 6. Значению а„ = 2 не соответствует никакое п, этот
случай невозможен. Таким образом, группа К может иметь оси Сп
только 2-го, 3-го, 4-го и 6-го порядков. В плоскости, перпенди-
перпендикулярной к оси С„, лежит по меньшей мере один вектор группы G.
Установим еще одно свойство группы К-
Лемма. Если группа К содержит подгруппу Сп (п > 2), то
она содержит и подгруппу С„„.
Доказательство. Прежде всего выберем специальным обра-
образом три основных вектора группы К- В качестве аг возьмем самый
короткий из векторов, лежащих в плоскости Р,
перпендикулярной к оси Сп. В качестве а2
возьмем вектор С„а1 (это можно сделать, так
как если бы внутри параллелограмма со сто-
сторонами av a2 помещался какой-либо вектор
а' ? оГ, то хотя бы один из четырех векто-
Рис g	ров а', ах — а', аг — а', a^-j-a^ — а'был бы
короче вектора at (рис. 9)). Выбор третьего
базисного вектора а3 для нас безразличен. Представим его в виде
а3 = я-\-Р(а\}.Сп, $J_Cn). Разность векторов Спа3 — а3 —Cnj3 — §
перпендикулярна к оси (или равна нулю) и принадлежит группе $".
Поэтому вна может быть представлена в виде
Подействуем на это равенство поворотом Си

§ 12]	сингонии	33
Вычтем полученное равенство из предыдущего
Си? + Си1? — 20 = (щ — т2) ак — /ra1C^1a1 + tn2a2.
Так как Cnf3 + C^1p = arep(a,j = 2cos — ) и аналогичное равенство
имеет место для вектора av то последнему равенству можно при-
придать следующей вид:
(а„ — 2) р = (/И! — а„/га1 — /га2) at -f- (^i -f- m2) «г- A2,1)
Рассмотрим случай га = 4. Тогда из A2,1) следует:
—
(а = 4).	A2,2)
Обозначим через av отражение в плоскости, проходящей через ось С4
и вектор ах. Ясно, что <svax = av ava2 = — о2 и ащаз = «з 4~
-f («i + ^^-
TaKUM образом, все три основных вектора при отражении а„ не
выводятся из группы |Г. Это означает, что а„ содержится в группе К-
Так как элементы С4 и av порождают группу Civ, то утверждение
леммы для случая га = 4 доказано.
Аналогичным образом рассматриваются случаи га — 3 и п = 6.
Если просмотреть список всех точечных групп, то легко устано-
шггь, что только семь групп, а именно S2, Cih, DVl, Dsh, Dih, D6h
и Oh обладают следующими свойствами:
1)	они содержат инверсию;
2)	они не содержат осей 5-го, 7-го и более высоких порядков;
3)	вместе с осью 3-го, 4-го или 6-го порядков они содержат
также и плоскости, проходящие через эти оси.
Поэтому существует только семь сингонии.
Перейдем теперь к классификации векторных групп, принад-
принадлежащих одной и той же сингонии.
Две векторные группы, принадлежащие одной и той же синго-
сингонии, называются однотипными, если одна из них может быть пере-
Ш'дсна в другую с помощью непрерывной деформации; при этом
н процессе деформации симметрия векторной группы должна быть
in- ниже, чем симметрия групп данной сингонии.
Мы покажем, что существует 14 типов векторных групп, и
иыясиим, как эти типы распределяются по сингониям.
Заметим, что тройка базисных векторов вполне определяет тип
Ш'кторной группы |Г, поскольку она определяет саму группу t>J.
Векторные группы, принадлежащие триклинной сингонии,
имеют один и тот же тип. Это вытекает из того, что триклинная
3 Зак. 3512, Г. Я. Любарский

34
НЕКОТОРЫЕ КОНКРЕТНЫЕ ГРУППЫ
[ГЛ. II
сингония допускает любые деформации. Этот тип обозначают сим-
символом Tt.
Рассмотрим остальные сингонии.
Моноклинная сингония Сгъ. Всякая векторная группа сГ,
принадлежащая этой сингонии, имеет двумерную подгруппу, лежа-
лежащую в плоскости ah. Для того чтобы в этом убедиться, возьмем
два произвольных вектора Ьх и Ь2 группы оГ, не лежащих в одной
и той же вертикальной плоскости. Векторы by-\-cthb1 и bz-\-ahb-?
лежат в плоскости ah и не параллельны друг другу.
В связи с этим условимся выбирать два основных вектора а»
и аг в плоскости ah.
Представим третий основной вектор в виде аг — л-\-$ (а||С2>
gJ_C2)- Ясно, что С2я3 — «з =^ С2Р — j3 = —2J3 есть вектор, лежа-
лежащий в плоскости orft. Поэтому его можно представить в виде
2|з = тхах-\-тгаг. Итак, вектор а3 равен сумме я-\-™х- ах-\-~-а2-
Воспользуемся тем, что от вектора о3 можно отнять любую цело-
целочисленную комбинацию п1а1-\-п2а2 и полученную разность принять
за третий основной пектор. Выберем а?1 так, чтобы числа т1 и т2
не превосходили единицы и были неотрицательны. Мы получим сле-
следующие четыре возможности:
1) а3 = а, 2) аг = л-\-\ах,
3) а3 = я-\--к
4) а3 =
Второй и третий случаи не отличаются, по существу, от четвертого
случая. Действительно, если в качестве первого базисного вектора
взять аъ а в качестве второго аи то четвертый случай перейдет
во второй. Если же в качестве второго базисного вектора взять
а1-\-а2, то четвертый случай перейдет в третий.
<1'а,- а
Рис. 11.
Поэтому существуют два типа векторных групп, принадлежащих
сингонии Cih. Один из этих типов характеризуется условиями
аи a2j_a3, другой — условиями ait a2j_2a3 — а,- Эти типы обозна-
обозначаются символами Тт и Тт соответственно (см. рис. 10 и 11).

§ 12]
сингонии
35
Заметим, что у типа Гот шестерка векторов z^.a{, zrza2, -*-а3
инвариантна относительно всех элементов группы C2h. У типа Ym
эта шестерка векторов не является инвариантной. Роль инвариантной
шестерки векторов играют у групп типа Ym векторы dzzav ±a2.
rt Ba3 — а2). Объем параллелепипеда, построенного на векторах а1(
а2 и 2а3 — аъ вдвое больше объема элементарной ячейки. Конец
вектора а3 лежит в центре одной из граней этого параллелепипеда.
В центре противоположной грани лежит конец вектора az-\-ai-
Центры остальных' четырех граней параллелепипеда не совпадают
с концами векторов рассматриваемой группы. В соответствии
с этим, Гт называется типом с центрированными основаниями.
Тип Ym называется простым.
Произведя подобный разбор остальных пяти сингонии, легко
получить все 14 различных типов групп трансляций (см. табл. 3).
Сингоиия D2h осуществляется четырьмя типами групп Го, Го, Го
и Го- Типы Го и Го вполне аналогичны типам Ym и Ybm. Для того
чтобы наглядно представить себе тип Го> возьмем шестерку векторов:
rirai, zta2> ±B«з—«1 — #г) (рис. 12), инвариантную относительно
2а,-а,-
2аг-а,
Рис. 12.
Рис. 13.
группы D2h. Параллелепипед, построенный на векторах av a2 и
2а3 — at—а2, имеет объем, вдвое больший объема элементарной
ячейки. Конец вектора аг находится в центре этого параллелепипеда.
Поэтому тип Го называется объемноцентрированным. У типа Го
инвариантную шестерку векторов образуют векторы dz«i,
г±гBа2 — «i), гЬгBа3 — а{) (рис. 13). Объем параллелепипеда, по-
построенного на векторах аи 2а2—av 2а3 — at, в четыре раза больше
объема элементарной ячейки. Все грани этого параллелепипеда
центрированы. Поэтому тип Го называется гране центрированным.
Из остальных типов нуждается в пояснении только тип г?. Роль
шестерки инвариантных векторов играют в группах типа г? векторы
— (ai—а^ и —Bаз—ai — aS- У куба, построенного
3*

Таблица 3
Сингония
Триклинная S2
Моноклинная C2/i
Ромбическая ?>2д
Тетрагональная Z?4;t
Ромбоэдрическая Z?3?j
Гексагональная D6d
Кубическая ' Oh
Типы векторных групп
Тип
простой
простой
г*
' т
с центрированными основа-
основаниями Г^
простой
Го
с центрированными основа-
" ниями Г*
объемноцентрированный
гранецентрированный
простой
объемноцентрированный
простой
простой
простой
гранецентрированный
объемноцентрированный
' 0
г{
а
г,-,,.
г,
гс
у{
оз-
ot I a
а
а
1
1
оз-
1
Основные векторы
любые
а8 J. Oi, o2
а3 —н" а2 -L а1>
Oi j. а2 ± о3 J,
1
(et + e,)!^.*
X Og —~- Oi _L O3 —
Oi
2-L
—
lO2
-i±
(cr
i. Q><i 1_ О3 J_ Oj, й
1 /
о3—2~(ai ' °2^
1 ,
-1 = Я2. О3— 2-(?
Oj J_ Оз J_ O(, <?i
Й2)_[_О1, й^^й2 | О
Ьо2)±о1)й1=й2|
о2
Ol
Ч. о, 1-е,
1
J_ Ol, «1 = й2
li — о2) ± Oi, a2
± аь о2
= в2 = %
1 1
2 у~
1 / , м 1
о3— у (о1+а2) | = — ах

§ 13]	СИММЕТРИЯ КРИСТАЛЛОВ	37
на векторах ах-\~а2, ах — а%, 2а3 — ал—а2, центрированы все
шесть граней (рис. 14).
Будем называть сингонию А подчиненной сингонии В,
если:
1)	группа симметрии сингонии А является подгруппой группы
симметрии сингонии В;
2)	каждый тип сингонии В может быть с помощью сколь угодно
малой деформации основных векторов переведен в один из типов
сингонии А.	.л! i
Таблица 3 показывает, что за одним
2а3-а,-а^	исключением выполнение первого условия
влечет за собой выполнение второго усло-
Рис. 14.	Рис. 15.
вия. Исключение представляет случай A = D3d, B = Deh. Действи-
Действительно, если подвергнуть основные векторы типа Th достаточно малой
деформации, то они не смогут удовлетворить условию
1
обязательному для основных векторов типа Trh. На рис. 15 изобра-
изображена схема подчинения сингонии.
§ 13. Симметрия кристаллов
Говоря о кристалле, мы не будем учитывать его границ, пред-
предполагая кристалл занимающим все пространство. Такой подход
оправдывается тем, что многие физические свойства кристаллов не
зависят от размеров кристалла и его формы.
Две точки кристалла или два направления в кристалле называются
эквивалентными, если все их физические и геометрические свойства
одинаковы после усреднения по времени (предполагается, что кри-
кристалл находится в равновесном состоянии).
Рассмотрим все те элементы евклидовой группы, которые пере-
переводят каждую точку кристалла в эквивалентную ей и каждое на-
направление в кристалле в эквивалентное ему. Совокупность всех этих
элементов образует группу, называемую группой кристалла. Всего
существует 230 различных кристаллических групп. Эти группы
называют также пространственными группами. Они были открыты
Е. С. Федоровым A895 г.) и несколько позже Шёнфлисом.

38	НЕКОТОРЫЕ КОНКРЕТНЫЕ ГРУППЫ	[ГЛ. II
Для группы кристалла характерным является наличие трехмерной
дискретной подгруппы трансляций оГ. Сингония и тип подгруппы 5Г
называются сингонией и типом кристалла.
Рассмотрим теперь симметрию направлений в кристалле. Сово-
Совокупность всех поворотов и зеркальных поворотов, которые пере-
переводят каждое направление в ему эквивалентное, образует точечную
группу F, характеризующую симметрию направлений. Элементы
группы F не обязательно принадлежат группе симметрии кристалла,
так как от них не требуется, чтобы они переводили все точки кри-
кристалла в им эквивалентные.
Группу F можно охарактеризовать следующим образом. Всякий
элемент g группы кристалла G можно представить в виде G,2)
Совокупность всех элементов г, соответствующих элементам g,
образует точечную группу. Эта точечная группа есть не что иное,
как группа направлений F.
Все кристаллы, имеющие одну и ту же группу направлений,
образуют один кристаллический класс. Всего существует, как мы
сейчас увидим, 32 группы направлений и, следовательно, 32 кри-
кристаллических класса.
Заметим, что всякий элемент группы F является в то же время
элементом группы К (К—группа симметрии группы трансляций).
Действительно, если г — какой-либо элемент группы F, а а^, а2,
«з — тройка основных векторов группы JT, то rav ra2, га3 также
являются векторами группы оГ, так как в противном случае опера-
операция г нарушила бы эквивалентность направлений. Поэтому F со-
содержится в К- Так как у семи групп, характеризующих различные
сингонии, существует ровно 32 подгруппы, то число различных
кристаллических классов равно 32. Приведем эти 32 класса:
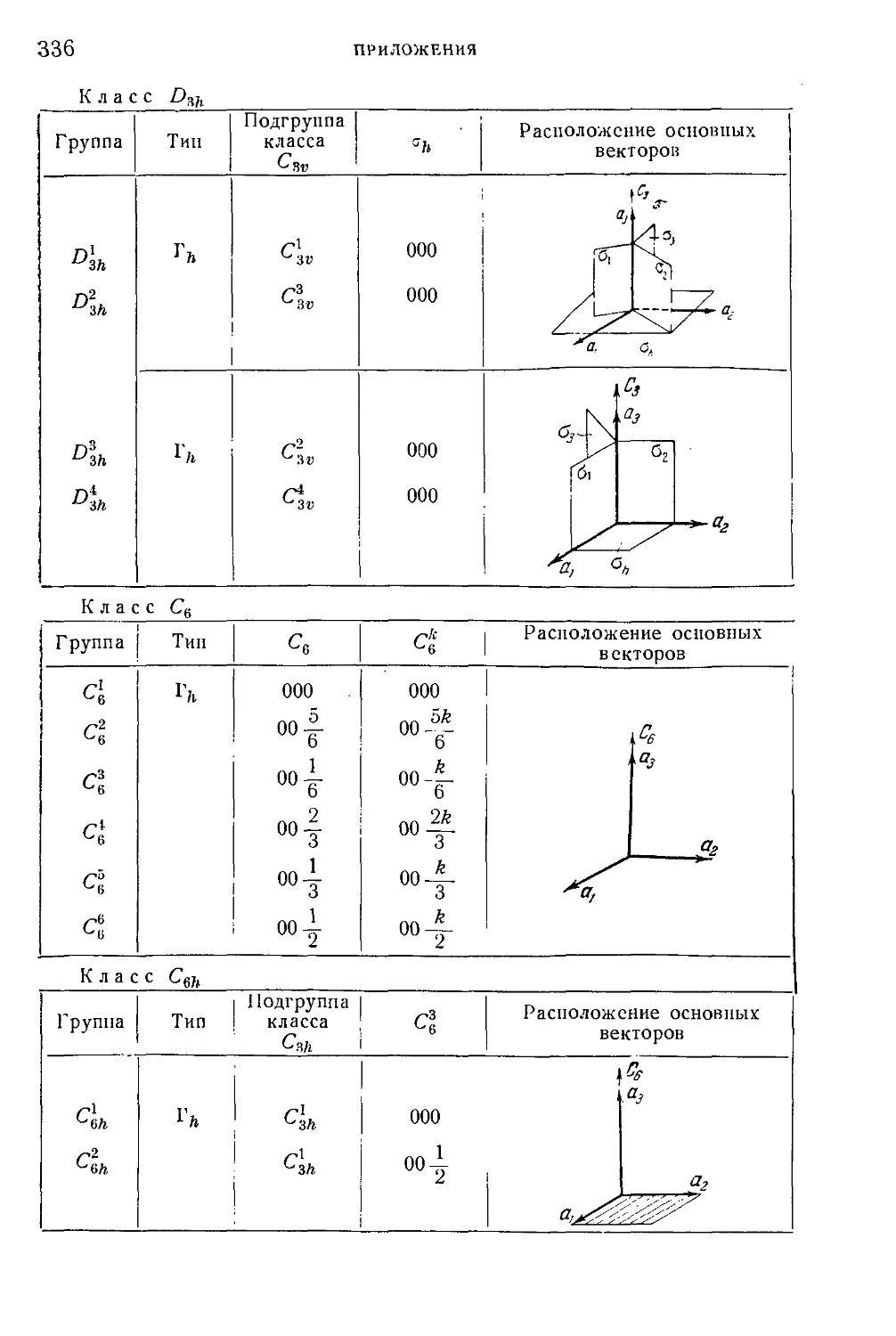
е,, S2, Coh, C2, C2h' C2v, Ц>, O2h, S^, D2(j, C4,
Св> ^6h> Cei>, D6, u^, i, 1Й, Iф O, Ojr
Кристаллический класс F относят к сингонии К, если
1)	группа К содержит группу F;
2)	ни одна сингония Ки подчиненная сингонии К, не содержит
группу F.
В соответствии с этим определением 32 кристаллических класса
распределяются между семью сингониями так, как показано в та-
таблице 4.
Итак, каждая пространственная группа G принадлежит одному
из 14 типов и одному из 32 классов. При этом тип группы в зна-
значительной мере ограничивает ее класс. Выясним, что нужно знать

13]	СИММЕТРИЯ КРИСТАЛЛОВ	39
Таблица 4
Распределение кристаллических классов между сингониями
Сингонии
Триклинная . . .
Моноклинная . .
Ромбическая . .
Тетрагональная .
Ромбоэдрическая
Гексагональная .
Кубическая . . .
е, 52
Coh, С
Civ, D
Si, D2
cs, sa,
T, Th,
2> C2ft
2. D,n
i, Q. Cih,
Cs», Ач> J
л> С3, S6,
Классы
Civ, Dit D^
-* 3?;» ^3» U3d* ^3/p ^3/i> ^-' ^ 6/i> ^ 6U
о группе, помимо ее типа и класса, чтобы иметь возможность
перечислить все ее элементы.
Тип группы G полностью характеризует все элементы
*m1a1 + msa, + m,a, («1, /»2. тЗ = °' =tb =t2' •••)	С13'1)
ее подгруппы трансляций S". Все прочие элементы группы G имеют
вид tar, где г—элементы точечной группы F, характеризующей
класс. Поэтому для задания этих элементов нужно, во-первых,
указать расположение осей и плоскостей группы F относительно
основных векторов av a2, а3 подгруппы трансляций §. Во-вторых,
если класс F состоит из п элементов rlt r2, ..., гп, то нужно
указать п векторов «1( «,	хп таких, что элементы
*«/i. t*s2, ..., tanrn	A3,2)
содержатся в пространственной группе G. Ясно, что каждый элемент
группы G представляет собой произведение одной из трансляций A3,1)
на один из п элементов A3,2).
Заметим, что вектор а, соответствующий единице г = е, всегда
можно взять равным нулю.
Условимся в дальнейшем задавать векторы а с помощью трех
коэффициентов аи а2, а3, фигурирующих в разложении
Заметим, что основные векторы, характеризующие данный тип
векторной группы, можно выбирать самым различным образом.
Поэтому каждый раз, говоря об основных векторах av a2, а3, мы
будем указывать, как именно они выбраны.
Для обозначения пространственной группы принято пользоваться
символом класса данной группы. При этом группы, принадлежащие
одному и тому же классу, отличают друг от друга с помощью

40	НЕКОТОРЫЕ КОНКРЕТНЫЕ ГРУППЫ	[ГЛ. II
верхнего индекса. Таким образом, символ С\н обозначает одну из
групп класса C4h.
В приложении дается описание всех 230 пространственных групп.
В заключение заметим, что если взять в кристалле произвольную
точку О и произвести над ней все трансляции группы оГ, то полу-
полученная таким образом совокупность точек называется решеткой
Браве, а сами точки—узлами решетки Браве.
Ясно, что группа симметрии группы трансляций есть в то же
время группа симметрии решетки Браве.
Параллелепипед, построенный на любой тройке основных век-
векторов группы трансляций кристалла, называется кристаллической
ячейкой.

ГЛАВА III
ТЕОРИЯ ПРЕДСТАВЛЕНИЙ ГРУПП
§ 14. Представление группы
Если рассмотреть наиболее существенные применения, которые-
нашла себе теория групп в физике, то окажется, что в подавляющем
большинстве случаев для приложений используются результаты,,
составляющие один из разделов теории групп, именно, теорию
представлений.
Теория представлений, изучает гомоморфные отображения про-
произвольной группы на всевозможные группы линейных операторов.
Значение теории представлений связано с тем обстоятельством, что
подобные отображения возникают «сами собой», при рассмотрении
задач, обладающих той или иной симметрией.
Мы будем говорить, что задано представление Т группы G
в некотором линейном пространстве L, если каждому элементу g
группы О отвечает оператор T(g) в пространстве L так, что при
этом произведению элементов группы отвечает произведение опера-
операторов, т. е.
Размерность пространства L называют размерностью представле-
представления. Группа может иметь как конечномерные, так и бесконечно-
бесконечномерные представления. Мы, однако, будем изучать только первые..
Рассмотрим некоторые примеры представлений.
1. Пусть частица, находящаяся во внешнем поле U (г), имеет отрицатель-
отрицательную энергию Е. Волновая функция i/ (r) такой частицы удовлетворяет, как
известно, уравнению Шредингера
дМГ> + -|П?-?/(г)Жг) = 0.	A4,2)
Совокупность всех решений этого уравнения при фиксированной энергии Е
образует линейное пространство Z.?, размерность которого равна кратности
вырождения уровня Е.
Предположим, что поле U(г) обладает некоторой пространственной
симметрией. Обозначим через G совокупность всех поворотов и зеркаль-
зеркальных поворотов пространства, которые не изменяют поля U (г), т. е. удовле-
удовлетворяют условию

•42 теория представлений групп	• [гл. ш
Рассмотрим в пространстве LE операторы Т(g)(g?G),	определенные ра-
равенством
'-) = 1Нг-1'-).	A4,3)
Покажем, что* функция fy (g~lr) является решением уравнения A4,2). Дей-
Действительно,
¦« = ^ С) + ^ № - U(r)\ ф (г) = Д6 (g-ir) + ~ [Е - U (g-ir)] 6 (g-V) =
Следовательно, операторы Т (?-) (? ? G) переводят каждую функцию из про-
пространства LE в это же пространство.
Проверим теперь, что Т (gj) T (g«) = T (gig?). Для этого введем обозна-
обозначение
2() 2
Имеем:
т (*i)т Ш Ф С") = т {gl) б2 (г) = ъ (gfV) =
= * (g2"I«rf1'') = ? ((glg2) V) = Т (^2) ^ (г).
Итак, сопоставляя каждому элементу симметрии g- g G оператор Т (g), опре-
определенный равенством A4,3), мы получаем представление группы G в про-
пространстве волновых функций /.?.
2.	Рассмотрим группу трансляций пространства вдоль оси Ог. Пусть
L—-произвольное одномерное пространство. Сопоставим трансляции на вели-
величину г оператор умножения на число eiks в пространстве L, где k — некото-
некоторое фиксированное число. Соответствие
z _> glitz
является, как легко проверить, представлением группы трансляций.
3.	Если элементами грунпы G являются линейные операторы в некотором
линейном пространстве L, то соответствие
g^g	A4,4)
можно рассматривать как представление группы G. Иными словами, группа G
образует представление самой себя. Разумеется, помимо представления A4,4),
группа G может иметь и иные представления.
В качестве важного примера можно указать на точечные группы (см. § 8).
Элементы точечных групп представляют собой линейные операторы
в трехмерном пространстве, и поэтому каждая точечная группа образует
представление самой себя. Это представление мы будем называть вектор-
векторным. Размерность векторного представления равна трем.
4.	Пусть G—-произвольная группа. Сопоставим каждому ее элементу g
единичный оператор Е в некотором пространстве L
Мы получим представление группы G. Это представление называется еди-
единичным.
Часто говорят, что пространство L преобразуется по представле-
представлению Т группы G, подразумевая под этим, что операторы T(g') пред-
представления Т определены в пространстве L.

§ 15]	ЭКВИВАЛЕНТНЫЕ ПРЕДСТАВЛЕНИЯ	43
§ 15. Эквивалентные представления
Одна из задач теории представлений состоит в перечислении
всех возможных представлений данной группы. При решении этой
Вадачи существенную роль играют два понятия: понятие эквивалент-
эквивалентности представлений и понятие приводимости представления. Настоя-
Настоящий параграф посвящается эквивалентности представлений.
Если известно какое-либо представление Т группы в простран-
пространстве L, то нетрудно построить сколько угодно новых представле-
представлений группы G. Для этого следует произвольно выбрать какой-либо
Неособенно линейный оператор А, переводящий векторы из L в какое-
либо пространство Lt того же числа измерений (в частности, Ll
может совпадать с L) и сопоставить элементу g?G вместо опера-
оператора T(g) оператор
Tk(g) = \T(g)L-\	A5,1)
действующий в пространстве Lv
Нетрудно проверить, что соответствие g—>Ti(g') является пред-
представлением группы G. Действительно,
Та (g1 ¦ g2) = AT (g, ¦ g2) A = AT (gl) T (g2) A1 =
= AT Ы a'AT (Ы A'1 = TA Ы TA Ы-
Всякие два представления группы G, связанные соотношением тина A5,1),
называются эквивалентными. Все представления, эквивалентные
данному, эквивалентны между собой. Поэтому все представления
данной группы О распадаются на классы взаимно-эквивалентных
представлений. Если известно хотя бы одно представление из дан-
данного класса, то без труда может быть получено любое другое пред-
представление из этого же класса.
Тем самым задача нахождения всех представлений сводится
к более узкой задаче нахождения всех взаимно-неэквивалентных
представлений.
Так как из каждого класса эквивалентных представлений доста-
достаточно выбрать для дальнейшего изучения только по одному пред-
представителю, то естественно попытаться сделать этот выбор наиболее
рациональным образом.
В настоящей главе рассматриваются только те группы, у которых
каждое представление эквивалентно некоторому унитарному пред-
представлению (т. е. представлению Т, у которого все операторы T(g)
унитарны). При изучении этих групп можно ограничиться рассмотре-
рассмотрением только унитарных взаимно-неэквивалентных представлений.
К таким группам относятся, в частности, все конечные группы.
Иными словами, имеет место следующая теорема.
Теорема. Каэкдый класс эквивалентных представлений конеч-
конечной группы содержит унитарные представления.

44	ТЕОРИЯ ПРЕДСТАВЛЕНИЙ ГРУПП	[ГЛ. III
Доказательство. Будем исходить из некоторого предста-
представления Т из данного класса, действующего в пространстве L. Дока-
Доказательство разобьем на два этапа.
1) Сначала определим новое скалярное произведение в простран-
пространстве L так, чтобы все операторы Т (g) оказались относительно него-
унитарны. Этим свойством обладает скалярное произведение [х, у),
определенное следующим образом:
{х, у}=^-
где круглые скобки (х, у) означают старое скалярное произведение,
а N — число элементов группы. Легко проверить, что выражение
{х, у} удовлетворяет всем требованиям, предъявляемым к скалярному
произведению (линейность и неотрицательность).
Далее,
{T(g)x, T{g)y}=.-^^i(T(h)Tl(g)x, T(A)T(g-).y) =
Так как hg при фиксированном g пробегает вместе с h?G все
элементы группы, то
jf 2 (Т(hg) х, Т(hg)y) = ±- ^ (Т(А) х, Т(h)y) = [x, у},
что и доказывает унитарность операторов T(g) относительно нового
скалярного произведения.
2) Пусть теперь elt е2, ..., es — какой-либо базис, ортонормиро-
ванный относительно старого скалярного произведения, ае'х, е'2>..., e'g —
базис, ортонормированный относительно нового скалярного произ-
произведения. Зададим оператор А согласно правилу Ае =?'(у—1,
2, . . ., s). Ясно то, что (х, у)={Ах, Ау]. Действительно, если x = %iei
и y = t\jej, то
{Ах, Ay} = {i/t, т)в;} — 5Я= <*• -У)'	A5'2>
Построим представление
Используя A5,2), получаем:
(Tx(g)x, Tb(g)y) = (A-
= {Т (g) Ax, T (g) Ay} = {Ах, Ay) = (х, у).
Таким образом, представление Та(#) унитарно, что--и доказывает
наше утверждение.

§ 16]	ФУНКЦИОНАЛ УСРЕДНЕНИЯ	45
В следующем параграфе эта теорема обобщается применительно
к некоторым бесконечным группам.
Задача. Пусть Т (g) и Ti (g) — два эквивалентных представления
группы Q. Представление Т (g) действует в пространстве L, представление
'Ti(g) действует в L\. Пусть еъ е2, ..., es — произвольный базис в L. Пока-
Показать, что в L\ можно выбрать базис
таким образом, чтобы матрицы операторов Tj (g) в этом базисе совпадали
¦с матрицами операторов Т (g) в базисе в\, ?•>,..., es (тем самым переход
от одного эквивалентного представления к другому равносилен переходу от
-одного базиса к другому).
§ 16. Функционал усреднения
Если каждому элементу g группы О сопоставлено некоторое
действительное или комплексное число <?(g), то говорят, что на
группе задана функция ср. Рассматривавшееся в предыдущем пара-
параграфе выражение (T(g-)x, T(g)y) представляет собой пример функ-
функции на группе. Функции 9 (t) действительного переменного t также
можно рассматривать как функции на группе, поскольку совокуп-
совокупность всех действительных чисел образует группу со сложением
в качестве группового действия.
Периодические функции можно трактовать так же, как функции
на группе поворотов плоскости ХО Y вокруг оси OZ. Действительно,
если, например, период функции /@) равен 2я, то число 0 можно
отождествить с поворотом вокруг оси OZ на угол G.
Если группа G конечна, то нетрудно построить так называемый
функционал усреднения М (ср) для функций на группе G.
Функционалом усреднения М (ср) называется линейный функцио-
функционал, обладающий следующими свойствами:
1)	если ср (g) > 0 при всех g^G, то М (ср) > 0;
2)	если cp(g-)=l при всех g?G, то ЛГ(ср)=1;
3)	если cpi (g) = ? (g ¦ h) и ср2(§¦) = ср (h • g), где h — любой эле-
элемент группы G, то Л1(ср1) = Ж(ср2) = Л1(9).
Легко видеть, что на конечной группе функционал усредне-
усреднения М (9) можно задать следующим образом:
Проверим только третье свойство. Имеем:
Этот же метод легко обобщается на некоторые бесконечные группы.
Так, для группы поворотов плоскости XOY вокруг оси OZ можно

46	ТЕОРИЯ ПРЕДСТАВЛЕНИЙ ГРУПП	[ГЛ. Щ
положить:
2г.
М (с) = ~ f ? @) db
о
(ф (б) — периодическая функция 0).
В случае группы вращений сферы вокруг ее центра функ-
функционал М (ср) задается равенством
2г. 2- т.
М (?} = ^ / / / ? (9' '^' ^ Sin
0 0 0
Здесь 0, 61 и ф2—углы Эйлера.
Заметим, что не у всех групп существует функционал усредне-
усреднения *).
При доказательстве теоремы § 15 был использован функционал
усреднения М(о) для построения нового скалярного произведения.
Это построение опиралось только на указанные ранее три свойства,
общие всем функционалам усреднения. Поэтому приведенное в § 15
доказательство автоматически переносится на все группы, обладающие
функционалом усреднения.
§ 17. Приводимые представления
Введение понятия эквивалентных представлений позволило свести
задачу перечисления всех представлений к нахождению только
неэквивалентных представлений.
Подобно этому разделение представлений на так называемые
приводимые и неприводимые еще более сужает поставленную задачу,
сводя ее к нахождению одних только неприводимых представлений.
Это тем более существенно, что именно неприводимые представле-
представления обладают целым рядом специфических свойств, обусловливающих
их ценность в приложениях и облегчающих их нахождение.
Представление Т группы G в пространстве L называется приводи-
приводимым, если в L существует хотя бы одно нетривиальное подпростран-
подпространство Ly, инвариантное относительно всех операторов TH(g)(g? G)**).
В соответствии с этим представление Т группы G в пространстве L
называется неприводимым, если в L не существует ни одного
*) В частности, он отсутствует у группы Лоренца и у группы действи-
действительных чисел. Более подробно об этом см. в § 42.
**) Напомним, что подпространство Lx линейного пространства L назы-
называется инвариантным относительно некоторого оператора А, если этот
оператор, действуя на векторы из подпространства L\, переводит их в век-
векторы, принадлежащие этому же подпространству Ly.
Ах ? Z.J, если х $ L\.
Все подпространства пространства L, кроме самого L и нуль-пространства
называются нетривиальными подпространствами.

§ 17]	ПРИВОДИМЫЕ ПРЕДСТАВЛЕНИЯ	47
нетривиального подпространства Lv инвариантного относительно
всех операторов T(g) (g?G).
Заметим, что в силу этого определения все одномерные представле-
представления являются неприводимыми.
В качестве примера приводимого представления можно указать вектор-
векторное представление группы Dn. Действительно, трехмерное векторное
пространство распадается на два инвариантных относительно труппы Dn
подпространства: одномерное, состоящее из всех векторов, направленных
вдоль оси 07., и двумерное, состоящее из всех векторов, расположенных
в горизонтальной плоскости.
Выясним некоторые свойства приводимых представлений. Пусть Т
есть приводимое представление группы G в некотором пространстве L.
Пространство L содержит нетривиальное инвариантное подпростран-
подпространство, которое мы обозначим через Lv Каждый вектор из Li под
действием операторов T(g) (g"?G) переходит в векторы из этого" же
пространства. Поэтому в пространстве Lx можно определить опе-
операторы Tt (g) (g(zG) с помощью соотношений
).	A7,1)
Оператор Ti {g), определенный таким образом, очень тесно связан
с оператором T(gO, но не равен ему, хотя бы потому, что опера-
оператор Tt(g) определен только в пространстве Llt в то время как
оператор Т (g) определен в пространстве L, имеющем большее
число измерений.
Чтобы подчеркнуть это своеобразное соотношение между
операторами T^gO и T(g), будем говорить, что оператор T(g)
индуцирует в инвариантном подпространстве Lx оператор T^g),
определенный равенством A7,1); оператор Tt{g) будем называть
индуцированным.
Ясно, что соответствие g—>T1(g) является представлением
группы О в подпространстве Lv Будем говорить, что приводимое
представление Т (g) индуцирует в инвариантном подпростран-
подпространстве Z.J представление T-ilg). Индуцированное представление Tt
является унитарным, если унитарно индуцирующее представление Т.
Значение индуцированных представлений заключается в том,
что они в своей совокупности полностью характеризуют то приво-
приводимое унитарное представление, которое их индуцировало. Для того
чтобы это показать, воспользуемся следующей простой теоремой.
Теорема I. Пусть Т—унитарное приводимое представле-
представление группы О в пространстве L, a Lv—инвариантное подпро-
подпространство. Тогда ортогональное дополнение к Lt — подпростран-
подпространство L2 — также инвариантно.
Доказательство. Пусть x?Llt y?Lz. Тогда Т (g)х?Lx
и (Т (g") *, у) = 0. С другой стороны, (Т^)*. у) = {х, T(g)y).
Поэтому T(g)yS_x, т. е. T(g)y?L2, и теорема доказана. Итак,
если пространство L преобразуется по некоторому приводимому

48	ТЕОРИЯ ПРЕДСТАВЛЕНИЙ ГРУПП	[ГЛ. III
унитарному представлению, то оно расщепляется на два взаимно-
ортогональных инвариантных подпространства Lx и L2,
Обозначим через 1\ и Т2 представления, индуцируемые в этих
подпространствах приводимым представлением Т.
Так как каждый вектор z ? L может быть однозначно представлен
в виде суммы векторов из Lx и L2
то задание представлений Tt и Т2 полностью определяет пред-
представление Т. Именно, имеет место очевидное равенство
Если представления Т, Tt и Т2 находятся между собой в ука-
указанной связи, то говорят, что представление Т расщепляется на
представления 1\ и Т2. Представление Т называют также суммой
представлений Tt и Т2.
Если хотя бы одно из представлений 1\ или Т2 приводимо,
то его можно в свою очередь разбить на два представления меньшей
размерности. Продолжая этот процесс, мы неизбежно придем
к неприводимым представлениям, если исходное представление было
конечномерным.
При этом пространство L окажется разложенным на сумму
взаимно-ортогональных инвариантных подпространств
I = Z.<1>-|_lW+ ... +L(m\	A7,2)
каждое из которых преобразуется по некоторому неприводимому
представлению группы G.
Если среди подпространств A7,2) имеется несколько, скажем,
т., подпространств, преобразующихся по представлениям, эквива-
эквивалентным одному и тому же неприводимому представлению х,,
то будем говорить, что представление "cv содержится в приводимом
представлении Т т., раз. Если ни одно из подпространств A7,2)
не преобразуется по данному представлению t,, то говорят, что
представление tv не содержится в представлении Т.
Приведенные рассуждения доказывают следующую важную
теорему.
Теорема П. Всякое приводимое унитарное конечномерное
представление распадается на унитарные неприводимые пред-
представления и может быть из них составлено {т. е. является
их суммой).
Значение этой теоремы состоит в том, что она сводит задачу
нахождения всех представлений к задаче отыскания только непри-
неприводимых представлений.

§ 18] НЕПРИВОДИМЫЕ ПРЕДСТАВЛЕНИЯ И СВОЙСТВА ОРТОГОНАЛЬНОСТИ 49
Заметим в заключение, что если в качестве базиса в простран-
пространстве L взять совокупность базисных векторов инвариантных под-
подпространств A7,2), то матрицы, соответствующие операторам T(g),
принимают квазидиагональный вид.
Задача. Доказать, что если представление Tt эквивалентно представле-
представлению Tj, а Т2 ~> Т2, то Tj -f- T2 ~Tj -j- T'2 (символ'^означает эквивалентность).
§ 18. Неприводимые представления и свойства ортогональности
Как уже указывалось, неприводимые представления обладают
рядом специфических свойств, которые делают их очень ценными для
различных приложений и облегчают их нахождение. В этом параграфе
исследуются свойства неприводимых представлений. Начнем с леммы.
Лемма. Если представление t(g) (g^G) группы G неприво-
димо, то всякий линейный оператор А, коммутирующий со всеми
операторами t(g) {g?G), кратен единичному. Иными словами,
из соотношений
t(?)\ = \t(g) (g?G)	A8,1)
вытекает равенство
А = ХЕ,
где X— некоторое число, а Е — единичный оператор.
Доказательство. Как и всякий линейный оператор в ком-
комплексном пространстве, оператор А имеет по крайней мере одно
собственное число. Обозначим его через X, а подпространство
собственных векторов оператора А, соответствующих числу X,
обозначим через Lv Таким образом, имеем:
Ах —Хх, если x?Lt.	A8,2)
Ясно, что подпространство L1 не пусто (в противном случае число X
не было бы собственным). Покажем, что подпространство Lx
инвариантно. Пусть х — произвольный вектор из Llt a i(g') — один
из операторов неприводимого представления. Вычислим вектор A-c(g)x.
С помощью A8,1) и A8,2) получаем:
At (g) x = -и (g) Ax = t (g) кх = It (g) x.
Таким образом, вектор t (g) x является собственным вектором
оператора А и соответствует собственному числу X. Иными словами,
вектор t(g)x содержится в Lu что и доказывает инвариантность Lv
Так как представление т неприводимо, то инвариантное подпро-
подпространство Lx должно быть тривиальным. Не будучи пустым, оно
совпадает со всем пространством L : Li = L. Равенство A8,1) можно
теперь переписать в виде Ах = ).х, если х?1, т. е. А = ХЕ, что
и завершает доказательство.
Введем теперь чрезвычайно важное понятие функций, порож-
порождаемых представлениями.
4 Зак. 3512. Г. Я. Любарский

50	ТЕОРИЯ ПРЕДСТАВЛЕНИЙ ГРУПП	[ГЛ. Ш
Пусть Т—какое-либо (приводимое или неприводимое) представле-
представление группы О размерности s в некотором пространстве L. Выберем
в L какой-либо базис и сопоставим с его помощью каждому опе-
оператору T(g) (g?G) соответствующую ему матрицу*)
T«(g) (l,k=l, 2	s; g?G).	A8,3)
Получаемые таким образом матричные элементы A8,3) составляют
совокупность s2 функций на группе. Эти функции удовлетворяют
важным алгебраическим соотношениям
S«fe)Iftte	A8,4)
1=1
непосредственно вытекающим из основного	свойства представле-
ния Т(?*) = Т(г)Т(й).
Скалярным произведением двух функций	на группе sp (g) и ф (g)
называется выражение
^2^	A8,5)
Функции cp(g-) и O(g-) называются ортогональными, если их ска-
скалярное произведение **) равно нулю.
Теперь можно сформулировать первую теорему ортогональности.
Теорема I. Неприводимое представление т размерности s
порождает s2 взаимно-ортогональных функций
Hk(g) (*,Л=1. 2	s).
При этом
(.*a,4'k')=jtii,okk'.	A8,6)
Доказательство носит несколько искусственный характер.
С помощью совершенно произвольного линейного оператора В,
действующего в том же пространстве L, в котором определены
операторы представления т (g), строим оператор А по формуле
*) Напомним, что матрица А^, соответствующая оператору А (при
фиксированном выборе базиса е-у, е%,..-, еа), определяется как совокупность
коэффициентов в тождествах Ке^ = 2 Mbfii,- При этом, если х = ^ х^е/е
,• = 1	к -1
S	8
и у = А-г = ^ у^, то у.г = ^ -^ifc-fft-
e = l	i = l
**) Приводимые ниже рассуждения легко переносятся на случай беско-
бесконечных групп, имеющих функционал усреднения. В частности, скалярное
цроизведение следует определить, положив (ср, 40 = М {<р, ^}.

§ 18] НЕПРИВОДИМЫЕ ПРЕДСТАВЛЕНИЯ И СВОЙСТВА ОРТОГОНАЛЬНОСТИ 51
Проверим, что оператор А коммутирует со всеми операторами т(g)
(g?G). Имеем:
•е {g) A = ± 2 * (g) т (A) Вт (A-I) = ^ ^ * igh) Вт (А-*).
Пользуясь свойством инвариантности суммы относительно замены
h-+g~lh (§ 16, свойство 3), находим:
т (g) А = 1
Согласно первому свойству неприводимых представлений это озна-
означает, что оператор А кратен единичному оператору. Итак,
где X—число, зависящее от выбора оператора В. Перейдем от
равенства операторов к равенству матричных элементов
2 (/г) 5х (*-1) Х (В) 8 *}	(' 8>7>
Поскольку оператор t(h) унитарен, то ^й(А~1) = ':зй(Л) и
Х5№.	A8,8)
Для вычисления Х(В) положим в A8,7) i = k и просуммируем по I
обе части равенства:
а (В) * = ^ 2 * (А)"««(*)Я»? = 37 2 ТЭ- (в> В«? = 3-3В-Э = в«-
h g О	h ? G
Выберем теперь оператор В так, чтобы
1, если сг. — р и ^ = 9,
О при всех остальных значениях ее, 3.
Тогда Х(В)= — Зр2 и равенство A8,8) переходит в
что и составляет содержание теоремы.
*) В дальнейшем мы будем опускать знак суммы при суммировании по
дважды встречающимся индексам, если это не может привести к недоразу-
недоразумениям.
4*

52	ТЕОРИЯ ПРЕДСТАВЛЕНИЙ ГРУПП	[ГЛ. Ш
Если группа G имеет порядок N, то максимальное число линейно
независимых функций на группе равно N. В качестве примера N
линейно независимых функций можно указать семейство функций,
определяемых соотношениями
8« Q.k=\, 2, .... N).	A8,9)
Так как взаимно-ортогональные функции линейно независимы, то
s2<,/V.
Первую теорему ортогональности дополняет вторая теорема
ортогональности.
Теорема И. Функции i$(g), порожденные неприводимым
представлением^, ортогональны функциям т^ (g), порожденным
любым другим неэквивалентным неприводимым представлением тB):
Доказательство первой теоремы ортогональности существенно
опиралось на тот факт, что оператор А, коммутирующий со всеми
операторами х (g) неприводимого представления, равен \Е-
Поэтому прежде чем приступить к доказательству второй теоремы
ортогональности, следует выяснить, что можно сказать об опера-
операторе, удовлетворяющем соотношениям
*Q)(g)A = A-zW(g) (g?0)t	A8,11)
где xW(g) и № (g) — операторы двух неприводимых представлений.
Ответ на этот вопрос дает
Лемма Шура. Пусть х^1* и х<2>—два неэквивалентных
неприводимых представления группы G. Операторы, x<J) (g) дейст-
действуют в пространстве Lu операторы x2(g)— в пространстве 1г.
Если линейный оператор А, переводящий векторы- из Ц в Lu
удовлетворяет соотношениям A8,11), то он равен нулю.
Доказательство. Рассмотрим сначала случай, когда раз-
размерность st пространства Lt больше размерности s2 пространства L2.
Обозначим через MczLx область значений оператора А, т. е. сово-
совокупность векторов xv?Llt которые могут быть представлены в виде
Xl — Ax2
Нетрудно видеть, что М образует инвариантное подпространство.
Действительно,
,(i) (g) Xl = xO (g) Ax2 = Ат<2> (g)xz?M.
Следовательно, подпространство М либо совпадает с Ц, либо
состоит только из нуль-вектора. Размерность подпространства М
не превышает s2 и потому меньше, чем sv M поэтому не может
совпадать с Lx и, следовательно, состоит только из нуль-вектора.
Это и означает, что оператор А равен нулю.

§ 18] НЕПРИВОДИМЫЕ ПРЕДСТАВЛЕНИЯ И СВОЙСТВА ОРТОГОНАЛЬНОСТИ 53
Если размерности пространств Ll и L2 одинаковы, т. е. s1=^=s2,
то оператор А должен быть особенным (ибо в противном случае
представления тМ и tj('2) эквивалентны). Поэтому размерность под-
подпространства М меньше, чем sv Отсюда вытекает равенство нулю
оператора А совершенно так же, как и в случае sx > s2.
Пусть, наконец, sx < s2. Оператор А в этом случае является
особенным. Обозначим через NczL2 подпространство, состоящее из
тех векторов x2?L2, которые переводятся оператором А в нуль,
Размерность N не равна нулю, так как оператор А является осо-
особенным. С другой стороны, пространство N инвариантно относи-
относительно операторов t<2>(g-). Действительно,
т. е. t@4g) x2?N, если Xb?N. В силу неприводимости предста-
представления 1B) инвариантное подпространство ./V должно совпадать со
всем пространством L2. Это и означает, что оператор А равен нулю.
Лемма Шура, таким образом, доказана.
Теперь можно провести доказательство второй теоремы ортого-
ортогональности совершенно аналогично доказательству первой теоремы
ортогональности.
Доказательство теоремы II. Пусть В — произвольный
линейный оператор, переводящий векторы из пространства L2 в про-
пространство Lv Построим оператор
который, как легко видеть, удовлетворяет соотношению xW (g) A =
= A4B'(gr) (g?G) и> следовательно, равен нулю. Выберем опера-
оператор В так, чтобы
1, если a = j0 и $ = q,
О, если а Ф р или 3 Ф q.
Тогда из равенства нулю оператора А следует:
Так как тй(А-') = #(<!), то пбследнее равенство можно переписать
в виде (Sy\ ^2')= 0. Теорема, таким образом, доказана.
Задача I. Показать, что единице группы соответствует при неприво-
неприводимом представлении единичный оператор.
Задача II. Доказать, что у абелевых групп все неприводимые пред-
представления одномерны.
Задача III. Представить произвольную функцию на группе в виде
линейной комбинации функций семейства A8,9).

54	ТЕОРИЯ ПРЕДСТАВЛЕНИЙ ГРУПП	[ГЛ. Ш
Задача IV. Пусть Т — приводимое представление группы G, дей-
действующее в пространстве L. Пусть Ltcz L — инвариантное подпространство,
преобразующееся по неприводимому представлению х. Доказать, что если
некоторый оператор В коммутирует со всеми операторами T(g), то под-
подпространство BZ.1, состоящее из всех векторов вида Вх± (хг ? Lt), является
инвариантным и преобразуется по представлению х.
Задача V. Пусть х (g) (g ? G) — унитарное неприводимое представле-
представление. Доказать, опираясь на первую теорему ортогональности, что базис
ортонор.мирован, если все операторы х (g) (g ? G) выражаются в этом базисе
унитарными матрицами.
Задача VI. Пусть х (g) (g ? G) и эквивалентное ему представление
~x(g) = Ax(g) А унитарны и неприводимы. Оператор А нормируем так,
чтобы DetA= 1. Опираясь на задачу I § 15 и предыдущую задачу, доказать
что оператор А унитарен.
§ 19. Теорема полноты
В предыдущем параграфе было показано, что функции "^(g),
порождаемые неэквивалентными неприводимыми представлениями,
взаимно ортогональны (в смысле § 18). Теперь мы докажем следую-
следующую теорему:
Теорема полноты. Совокупность функций
z®(g) (Я=1, 2, ..., q; i, k=l, 2	s«), A9,1)
порождаемых всеми неэквивалентными неприводимыми предста-
представлениями, полна в пространстве всех функций на группе.
Приведем эквивалентную формулировку этой теоремы.
Всякая функция ср (g) на конечной группе О может быть
разложена в сумму
' ?(Й=2С&М'^).	A9,2)
а, г, к
Заметим, что если самый факт возможности такого разложения
доказан, то коэффициенты С$ легко находятся по формулам
C$ = se(?,-$).	A9,3)
Доказательство теоремы полноты. Сопоставим ка-
каждому элементу g группы оператор R(g"), определенный равенством
R (g) Ф (h) = ф № (g, h?G)	A9,4)
(функция fy(hg) рассматривается как функция от h и потому, вообще
говоря, отличается от функции <]>(h)). Обозначим ^(hg) = f(h) и
вычислим R(gi)v(h) (gi(zG). Имеем:
R fei) ф (hg) з= R (g{) ? (h) = о (hgl) = Cf (hglg) = R (glg) i/ {h).

§ 19]	ТЕОРЕМА ПОЛНОТЫ	55
Полученное равенство показывает, если учесть A9,4), что R(g-1)R(g-) =
= R(gig), т. е. что соответствие g—>R(g) является представлением
группы. Это представление называется регулярным представлением.
Регулярное представление, как и вообще всякое представление
конечной группы, можно разложить на неприводимые представле-
представления. Это означает, что пространство всех функций на группе Zy
распадается на подпространства
каждое из которых преобразуется по некоторому неприводимому
представлению т'а) группы G.
Обозначим через
?<•>, <pW	?W	A9,5)
базис в одном из этих подпространств Lri (а=1, 2	р). Так
как любая функция о Ш) на группе G может быть разложена по
функциям вида A9,5), то для доказательства теоремы полноты
достаточно показать, что любая функция A9,5) представима в виде
суммы A9,2). Чтобы это сделать, выберем произвольно одну из
функций A9,5) е(.а>(/г) и подействуем на нее оператором R(g"). Мы
получим:
С другой стороны, но определению оператора R(g) имеем
^f>	f))- Поэтому
Полагая здесь /г = е, получим:
Функция <?W(g) представлена в виде A9,2), и теорема полноты
доказана.
Итак, функции, порождаемые всеми неприводимыми представле-
представлениями, образуют ортогональный базис в пространстве Lf. Поэтому
число этих функций равно размерности Lf. Размерность простран-
пространства Lf равна N (N — порядок группы О). С другой стороны,
общее число функций, порожденных неприводимыми представлениями,
равно сумме квадратов размерностей этих представлений. Отсюда
следует, что
S1 + 4+ ... +s2q = M,	A9,6)
т. е. сумма квадратов размерностей всех неприводимых неэкви-
неэквивалентных представлений равна порядку группы (теорема Бернсайда).

56	ТЕОРИЯ ПРЕДСТАВЛЕНИЙ ГРУПП	[ГЛ. III
§ 20. Теория характеров
В этом параграфе рассматриваются так называемые характеры
представлений. Введение этого понятия в теорию представлений
оказалось чрезвычайно плодотворным. Причины, в силу которых
характер является ценным математическим инструментом, можно
отчасти усмотреть из приводимых ниже свойств характеров.
Характером у (g) представления Т (g) называется сумма диаго-
диагональных элементов матрицы, соответствующей в каком-либо базисе
оператору Т (g). Нетрудно проверить, что произвол в выборе базиса
пространства L, в котором действуют операторы T(g), не отра-
отражается на величине характера %(g).
Выясним некоторые свойства характеров.
1.	Характеры эквивалентных представлений совпадают. Это
свойство устанавливается непосредственным вычислением. Пусть Т
и Т' — два эквивалентных представления. Они связаны соотношением
T'(g-) = AT(g-) Л. Характер -/_' (g) представления Т (g) равен
'/'. (S) = Т« (g) = АЫТ«? (g) Aj? = З.рТ.р (g) = Т„ (g) = x (?).
2.	Характеры неприводимых неэквивалентных представлений
ортогональны между собой. Это непосредственно вытекает из
ортогональности любых матричных элементов неэквивалентных не-
пршюдимых представлений. Из ортогональности характеров непри-
неприводимых неэквивалентных представлений следует, в частности, их
линейная независимость.
3.	Скалярный квадрат характера неприводимого представле-
представления равен единице. Действительно,
s	S3
г, к=^\	j = l	i -1
Последние два свойства характеров неприводимых представлений
можно выразить одним соотношением
3ift.	B0,1)
4. Характер приводимого представления Т(g) равен сумме
характеров всех неприводимых представлений тМ (g)t которые
содержатся в Т (g) (считая каждое представление столько раз,
сколько раз оно содержится в T(g)). Это непосредственно выте-
вытекает из возможности записи матриц Tik (g) в квазидиагоналыюм
виде (см. § 17). Обозначим через т^ число, показывающее, сколько
раз содержится в представлении Т неприводимое представление х^\
имеем, следовательно,
Z(fir) = S«,X(')(«r).	B0,2)

§ 20]	теория характером	57
5. Числа /rev, показывающие, сколько раз входят в представле-
представление Т неприводимые представления tW, определяют представление Т
с точностью до эквивалентности. С другой стороны, соотноше-
соотношение B0,2) можно разрешить относительно mv. Для этого умножим
скалярно обе части B0,2) на у_М. В силу ортонормированности
характеров получаем при этом
Таким образом, характер %(g) приводимого представления позволяет
найти числа /га, и, следовательно, определить Т с точностью до
эквивалентности. Иными словами: два представления, имеющих
одинаковые характеры, эквивалентны.
Заметим, что хотя формула B0,3) непосредственно позволяет
выяснить, на какие неприводимые представления распадается дан-
данное приводимое представление, она не дает никаких указаний отно-
относительно метода разбиения пространства на инвариантные взаимно-
ортогональные подпространства, преобразующиеся по этим непри-
неприводимым представлениям. Такой метод будет указан в § 26.
6.	Равенство B0,2) позволяет указать очень удобный критерий
неприводимости представления. Действительно, из B0,2) следует,
что
(Z. У.) = B /и//.00. 2 т^'А = ^ ml	B0,4)
Поэтому, если представление приводимо, то скалярный квадрат
его характера больше единицы.
7.	У взаимно-сопряженных элементов характеры равны
) (g,x?G).	B0,5)
Действительно,
Z (Kg*'1) = Ъ Т„ (xgx-i) = 2 IV,(х) Т,? (g) T?
Эта свойство характеров означает, что они, собственно говоря,,
являются функциями классов сопряженных элементов. Иными словами,
чтобы определить характер элемента g, достаточно указать лишь
класс Кд, которому принадлежит этот элемент. Таким образом,
можно написать:
8. Совокупность характеров всех неприводимых представле-
представлений является полной в линейном пространстве функций, опре-
определенных на классах сопряженных элементов.

58	ТЕОРИЯ ПРЕДСТАВЛЕНИЙ ГРУПП	[ГЛ. III
Докажем это. Пусть f(g)—произвольная функция классов. Это
означает, что для любой пары элементов g и h имеет место тождество
f{h-*gh)=f(g) (g, л GO).
Разложим функцию j(g) по функциям ^(g), порожденным всеми
неприводимыми представлениями:
f(g)= 2*й(?).
i, к, v
Подставляя сюда h~lgh вместо g, находим:
f(g)= 2 diWih-'gh)^ s сйЕ
i, It, v	i, k, v а, Э
Усредним обе части этого равенства по h
i, к, ч	к, 3	Л f: 6'
Остается вычислить величину
iV л*А	'	N m^	^'	^ '"' n'	Ss,
Подставляя это в выражение для f(g), находим:
что и завершает доказательство.
Следствие. Число q различных неприводимых представле~
ний равно числу классов сопряженных элементов.
9. Из полноты совокупности характеров всех неприводимых
представлений следует так называемое второе соотношение орто-
ортогональности характеров. Чтобы прийти к нему, полезно использо-
использовать следующее положение, доказываемое в линейной алгебре:
Если q2 величин f).{i, k=\, 2	q) удовлетворяют «соотно-
«соотношениям ортогональности» по нижнему индексу
Yftf.^Zij,	B0,6)
a=l

§ 20]	ТЕОРИЯ ХАРАКТЕРОВ	.')!)
то они удовлетворяют подобному же соотношению и по верхнему
индексу
hi-	B0,7)
Рассмотрим теперь р2 величин
fl = V7.Zm(K,) (/, я=1, 2, .... q),
где ра есть число элементов в классе Кг. В силу B0,1) они удовле-
удовлетворяют соотношению B0,6). Следовательно, они удовлетворяют и
соотношению B0,7), которое можно записать в виде
>ЮупЩ)=}лку	B0,8)
Это равенство носит название второго соотношения ортогональ-
ортогональности характеров.

ГЛАВА IV
ОПЕРАЦИИ С ПРЕДСТАВЛЕНИЯМИ ГРУПП
§ 21. Произведение представлений
Пусть Тг, Т2 и Т3— какие-либо представления некоторой
группы О. Если характер представления Т3 равен произведению
характеров представлений Tt и Т2
¦/.s(g) = 7.i(gO*(g) (g?G),	B1,1)
то представление Т3 называется произведением представлений 1\
и 'Г,
Иго :i;iiiiicuk;u тем так:
J3 	 М X 1-2-
Ясно, что произведение представлений не зависит от порядка
сомножителей. Подчеркнем, что существование представления Т3,
характер которого удовлетворяет соотношению B1,1)', отнюдь не
является само собой разумеющимся. Ниже, однако, будет доказано,
что произведение характеров любых двух представлений какой-либо
группы О совпадает с характером некоторого представления
группы G. Иными словами, будет доказано, что можно перемножать
любую пару представлений одной и той же группы.
Рассмотрим два важных примера произведения представлений.
Пусть Lx и L2 — пространства, преобразующиеся по представле-
представлениям Tt и Т2 группы G; е^\ е$\ ..., 4'*' — базис в пространстве Lt;
et\ ef\ ..., е^ — базис в пространстве L2; Т^Ш) — матрица опе-
оператора T1(g)(g^G); T$ (g) — матрица оператора %(g).
Рассмотрим формально линейное пространство L размерности
$! • s2, в котором базис состоит из всевозможных произведений
<№ (/=1,2	Sl; A==l, 2	*2).	B1,2)
Под действием элемента g?G вектор е^1) переходит в вектор
T1(g)e(i) = irrl1)(g)e^), а вектор еР — в вектор T2(g)ef =
а=1

§21]	ПРОИЗВЕДЕНИЯ ПРЕДСТАВЛЕНИЙ	() 1
= 2 Tp2ft (g) ef\ В соответствии с этим положим, что вектор е(ре$
переходит под действием элемента g в вектор
Т (g) W = (Т\ (?) rfO (T2 (у) ef) = 2 ТН (?) Т$ fe)«W. B1,3)
«.3
Соотношение B1,3) ставит в соответствие каждому элементу
линейный оператор T(g), определенный в пространстве L. Легко
видеть, что операторы T(g") удовлетворяют соотношению Т (gt) Т (g)=
= T(g1g2) {gi, g2^.O) и, следовательно, соответствие g—>T(g)
является представлением группы G. Размерность этого представле-
представления равна произведению размерностей представлений Tt и Т2.
Вычислим характер представления Т. Имеем, используя B1,3),
X (?) = .2 ft2 TiV (g) Т(Л (g) = /л (g) -Ь (g).	B1,4)
Соотношение B1,4) показывает, что представление Т является
произведением представлений Tt и Т2 *).
Из рассмотренного примера вытекает, что, каковы бы ни были
представления Tt и Т2 некоторой группы О, существует предста-
представление Т3 группы О, являющееся произведением представлений 1\ и Т2.
Перейдем теперь ко второму примеру. Рассмотрим совокуп-
совокупность L всех линейных операторов, переводящих векторы из про-
пространства L± в пространство L2. Эта совокупность образует линей-
линейное пространство размерности sl ¦ s2, поскольку каждый оператор
может быть представлен в виде матрицы, имеющей st столбцов и s9
строк.
Сопоставим теперь с помощью некоторого элемента g каждому
оператору A?Z- оператор Ag?L, определяемый равенством
Aff = T2(^)AT1(^-1).	B1,5)
Соответствие A->Xff является линейным. Обозначим через T(g")
оператор, осуществляющий это соответствие,
Tfe)A = Ae.	B1,6)
Непосредственная проверка показывает, что операторы Т (g)
~1) образуют представление Т группы О.
Вычислим характер этого представления. Для этого выберем
в качестве базиса в L совокупность операторов вида
......	ft, 1=1, 2, ..., s2,
ft, m= 1, 2, . . ., 5t
*) 1Можно о преде л ить произведение представлений Т^ и Т2 как
представление Т, построенное в рассмотренном примере. Такое определение
эквивалентно приведенному выше.

62	ОПЕРАЦИИ С ПРЕДСТАВЛЕНИЯМИ ГРУПП	[ГЛ. IV
и вычислим матрицу оператора T(g) AB> ft). Имеем
Поэтому
w й) 2 Э $ -1) A1" p>.
Отсюда характер xto) представления Т равен
B1.7)
Рассмотрим некоторые следствия, вытекающие из B1,7). Если
в качестве представления Т2 взять единичное представление, то
соотношение B1,7) примет более простой вид
Мы видим, что наряду с представлением T^g), характер которого
равен /i (g), группа G имеет представление, характер которого
равен yA(g~1)- Такое представление называется сопряженным пред-
представлению Т\ и обозначается Г1\. Свойство сопряженности является
взаимным.
Соотношение B1,7) показывает, что представление Т, по кото-
которому преобразуются операторы, переводящие векторы из про-
пространства Lx в пространство L2 (см. формулы B1,5) и B1,6)),
является произведением представления Т2 на представление '1\.
Рассмотрим более подробно случай, когда представления ТЛ и Т2
являются неприводимыми представлениями х^ и т2- Для того чтобы
произведение ^ X чг содержало единичное представление, нужно,
чтобы существовал такой оператор А, который не изменяется под
действием операторов T(g): T(g)A = A. По определению B1,5),
B1,6) это означает, что t2 (g) At: (g~J) = А или
t2 (g) A = A-Ci to)-
Согласно лемме Шура этот оператор равен нулю, если представле-
представления tt и т2 неэквивалентны. Если же представления -^ и ч2 экви-
эквивалентны, то согласно лемме § 18 оператор А кратен единичному,
т. е. определен с точностью до множителя.
Приведенные рассуждения доказывают следующую теорему.
Теорема. Произведение двух представлений tl X ^г содер-
содержит единичное представление в том и только том случае,
если представления 1г и т2 эквивалентны.

§ 22]	СОПРЯЖЕННОЕ ПРЕДСТАВЛЕНИЕ	ОЛ
Задача I. Доказать, что произведение неприводимого представления
на одномерное неприводимо.
Задача II. Доказать, что взаимно-сопряженные представления имеют
одинаковую размерность.
Задача III. Пусть zu т? и т3—какие-либо три неприводимых предста-
представления группы G, а ъь то и т3— сопряженные им представления.
Доказать, что если имеет место хотя бы одно из следующих трех соот-
соотношений
1)	хг содержится в х2 X х3,
2)	т2 содержится в xt X i3,
3)	т3 содержится в xt X х2,
то имеют место и остальные два.
Задача IV. Доказать, что представление х, сопряженное неприводи-
неприводимому представлению х, в свою очередь неприводимо.
Задача V. Доказать, что произведение двух неприводимых предста-
представлений размерности s-i и s« (sj > s2) не может содержать представления раз-
S-,"
мерности меньшей, чем ¦¦*-.
Задача VI. Если каждый элемент g группы G сопряжен своему обрат-
обратному g~l, то каждое представление группы G сопряжено самому себе.
§ 22. Сопряженное представление
Если нам известны матрицы Т^^) некоторого представления Т,
то матрицы сопряженного представления можно вычислить по сле-
следующей простой формуле:
T«fe) = Tw(g-1).	B2,1)
Непосредственная проверка показывает, что матрицы Т^(^) обра-
образуют представление; характер матрицы Ta(g-) равен Tii(g~1) = ^(g~1).
Это означает согласно определению, что матрицы B2,1) являются
матрицами представления, сопряженного представлению Т.
Обозначим через L и L пространства, в которых осуществляются
взаимно-сопряженные неприводимые представления т и t.
Базисы пространств L и L: еи ег	ен и elt e2, . . ., es, выбран-
выбранные таким образом, чтобы им отвечали матрицы
называются взаимно-контравариантными базисами.
В § 21 было доказано, что произведение неприводимого пред-
представления х на сопряженное ему представление х содержит ровно
один раз единичное представление. Так как совокупность всех сумм
вида
S <W*	B2,2)

64	ОПЕРАЦИИ С ПРЕДСТАВЛЕНИЯМИ ГРУПП	[ГЛ. IV
¦преобразуется по представлению т X t> то коэффициенты Су. можно
подобрать таким образом, чтобы сумма B2,2) была инвариантна
относительно элементов g группы О.
Докажем непосредственным вычислением, что такой инвариантной
суммой является выражение
2 е^ = inv.	B2,3)
i = \
Имеем:
S	3	8
*(g)X4 (g) 1>егег = 2 2 "«(g) t??(g-1) eji? =
il	g
a, 0 = 1
С контравариантным базисом связано еще одно инвариантное
выражение. Пусть аи а2	as — координаты какого-либо век-
вектора а в пространстве L, пусть Ъи Ь2, ..., bs — координаты неко-
некоторого нектора b в пространстве L. Тогда сумма
в
2 «А = inv	B2,4)
i = l
инвариантна относительно одновременной замены вектора а векто-
вектором a' ='V(g)a и вектора Ъ—вектором b='\](g)b. Иными сло-
словами, имеет место равенство
2 аФг = 2 a'i~b'i-
г = 1	г •-1
Для доказательства заметим, что а{ = Tik(g) ак и ~b\ = '1\г (g) bL =
= '^ii(g~x)bi- Отсюда
2 t	2 « (g> ku (g) t
» = 1	i, k, 1 = 1
Это эквивалентно соотношению B2,4).
Если пространство L, на котором определено некоторое пред-
представление Т группы G, состоит из функций, то функции, комплексно-
сопряженные функциям из L, преобразуются по так называемому
комплексно-сопряженному представлению. Операторы T(g") этого
представления определяются равенством
)-	B2,5)
Легко видеть, что операторы T(g') действительно образуют пред-
представление. Если (рх, ф2	фь, — базис в пространстве L, то ^1 ,

§ 23]	иЕщкстикшшк ш'кдг.тлидкпия	(>i
ф2	^s образуют базис в пространстве сопряженных функций Z.
Вычислим матрицу оператора 'V(g) B этом базисе. Имеем:
т. е.
(Ш)* = Т^(г)-	B2,6)
Отсюда следует, ..чтохарактер комплексно-сопряженного представле-
представления определяется формулой
7.(g)-	B2.7)
Заметим, что, если представление Т унитарно, то сопряженное ему
представление Т и комплексно-сопряженное представление Т совпа-
совпадают.
§ 23. Вещественные представления
Пусть нам надо некоторое неприводимое представление группы О
в пространстве L. Если в этом пространстве можно выбрать базис
таким образом, чтобы матрицы всех операторов были веществен-
вещественными, то мы будем говорить, что представление т вещественно.
В ряде случаев весьма важно знать, вещественно ли данное пред-
представление. В этом параграфе мы получим простой критерий, позво-
позволяющий ответить на этот вопрос.
Характер вещественного представления является вещественным
числом. Поэтому представления с невещественным характером безу-
безусловно не являются вещественными представлениями.
Сделаем еще одно простое замечание. Если представление t
вещественно, то
2 1 (g2) j 2 ~ (g2)	2 ~ (g) ~ (g)
» fe) ТИ (g) •
a; i	g; i, к	g;i,k
Вспоминая первую теорему ортогональности, мы можем написать:
ago	а; i, к
где s—размерность представления т. Таким образом, для вещест-
вещественных представлений имеет место соотношение
Докажем, что это соотношение имеет место только для веществен-
вещественных представлений и поэтому может служить необходимым и доста-
достаточным признаком вещественности.
5 Зак. 3512. Г. Я. Любарский

66	ОПЕРАЦИИ С ПРЕДСТАВЛЕНИЯМИ ГРУПП	[ГЛ. IV
Пусть ч— некоторое представление с вещественным характером.
Очевидно, что характер комплексно-сопряженного представления t
равен характеру т и, следовательно, t и ъ эквивалентны
*(g) = Aite)\-1.	B3,2)
Без ограничения общности представление т можно считать унитарным.
При этом и представление t тоже будет унитарным. Вспоминая
задачу VI § 18, мы можем считать, что оператор А тоже унитарен1
A-' = A*.
Переходя к комплексно-сопряженным величинам, получим из B3,2):
%(g) = A4(g)A:ri.	B3 Д)
Подставим B3,3) и B3,2):
или
т. е. оператор АА коммутирует со всеми операторами неприводи-
неприводимого представления. Согласно лемме § 18 это означает, что
АА = ).Я или
А = ХА*.
В матричных обозначениях это можно записать так: Aik = hAki.
Сопоставляя это равенство с равенством Д.;; ~ ).Ail;, находим, что
\ = ± 1. Итак,
А — — А — — А , A j? — A^j.	\<?о,Ц}
Вычислим теперь сумму
Из B3,2) следует, что i!(g) = y,Aiai-:^(g)(A~lKk. Подставляя>это
«, э
выражение в последнюю сумму и пользуясь ортогональностью матрич-
матричных элементов, получим:
z ^
«, Э,/, Й
a, g, j, к	I, fc
i, к

§ 24]	ПРОИЗВЕДЕНИЕ ГРУПП	67
Мы видим, что если имеет место равенство B3,1), то выполняется
условие
А = А\	B3,5)
Покажем, что при этом представление z вещественно. С этой целью
2
введем в рассмотрение унитарный оператор В = А2 такой, что В2 = А
и В = В~' (используя соотношение B3,5), можно доказать, что такой
оператор существует). С помощью оператора В построим предста-
представление
эквивалентное -с. Имеем:
*i (g) = В 7(F) В = Вт (g) В = ВА-: (g) АГ'В1 = Ъ~\ (g)B,
т. е. х1 = ч1. Итак, условие B3,5) является необходимым и доста-
достаточным для вещественности представления т. Если представление х
с вещественным характером не является вещественным, то А = — А
=-1-	B3.6)
§ 24. Произведение групп
Группа G называется прямым произведением или произведением
двух своих подгрупп G1 и G2> если
1)	каждый элемент g группы G может быть представлен, и при-
притом единственным образом, в виде произведения
glg2,
где первый сомножитель принадлежит подгруппе Gv а второй — G2;
2)	элементы, принадлежащие подгруппе Gt> коммутируют с эле-
элементами подгруппы Go-
Заметим, что подгруппы Gx и О2 не предполагаются коммута-
коммутативными.
В качестве примера можно указать на группу Cnh, которая
является произведением подгруппы Сп па подгруппу ah. Другим
примером может служить полная ортогональная группа, являющаяся
прямым произведением группы вращений на группу инверсии.
Произведение двух групп Gx и G2 обозначают через Gt X Ог.
Каждое представление Т (g{) (gi^Gx) группы G± можно есте-
естественным образом дополнить до представления всей группы G. Для
этого достаточно сопоставить каждому элементу g2?G2 единичный
оператор, а произведению gxg2 в соответствии с этим оператор Т^).
Точно так же каждое представление Т (g2) группы G2 можно рас-
рассматривать как представление всей группы G.

68	ОПЕРАЦИИ С ПРЕДСТАВЛЕНИЯМИ ГРУПП	[ГЛ. IV
Перемножая представление группы Gt (рассматриваемые в ука-
указанном смысле как представления всей группы G) на представления
группы G2, получим новые представления группы G.
Если перемножить, таким образом, неприводимое представление
подгруппы Gx и неприводимое представление подгруппы G2, то полу-
получится неприводимое представление группы G.
Задача I. Доказать последнее утверждение для конечных групп.
Задача II. Доказать, что, перемножая неприводимые представления
подгрупп Gi и G2, можно исчерпать все неприводимые представления конеч-
конечной группы.
Задача III. Доказать, что каждый класс сопряженных элементов
группы G состоит из всевозможных произведений элементов одного из клас-
классов группы Gx на элементы одного из классов группы G2.
§ 25. Симметризованные степени представлений
В этом параграфе мы рассмотрим один общий метод разбиения
пространства, преобразующегося по я-й степени представления Т
группы G, на инвариантные подпространства. Представления, кото-
которые индуцирует в этих инвариантных подпространствах представле-
представление Т", называются симметризованними степенями представления Т.
Мы вычислим характеры симметризованных степеней представле-
представления Т.
Пусть Lu L2	Ln — некоторые линейные 5-мерные простран-
пространства, преобразующиеся по одному и тому же представлению Т
группы G. Произведение всех этих пространств L = Lx X 1*г X • • X Ln
преобразуется по представлению Тп. Обозначим через е^
(сс= 1, 2, ..., s) базисные элементы в пространстве Lk(k— 1, 2, ..., п).
Элементы
е , — е0)„И J") („ з	г — 1 2	s4
<-аЗ ... е -— са eg . . . fj	(J., J, ¦ . • , с 	 1, ^, . • • , Л)
образуют базис в пространстве L.
Произвольный элемент пространства L можно представить в виде
А»,3 ... г^аЗ ... е-
Пусть Р—какая-либо группа перестановок п предметов. Каждой
перестановке р?Р можно сопоставить линейный оператор р в L,
положив
.е]е«з... г.	B5,1)
где р[аЗ . . . е] есть совокупность индексов, которая получится, если
над индексами а, р, . . ., е произвести перестановку р.
Легко видеть, что операторы р образуют представление группы Р
в пространстве L. Обозначим это представление через Тр.
Пусть t—какое-либо неприводимое представление группы Р,
содержащееся в Тр. Обозначим через L0 сумму всех неприводимых

§ 25]	СИММЕТРИЗОВАННЫЕ СТЕПЕНИ ПРЕДСТАВЛЕНИЙ	09
подпространств из L, которые преобразуются по представлению t
группы Р.
Ортогональное дополнение к L0 обозначим через L1. Подпро-
Подпространства L0 и L1 инвариантны относительно всех операторов Tn(g)
(g? G). Это вытекает из утверждения задачи IV § 18, если учесть,
что операторы р и ln (g) коммутируют между собой.
Выбирая в качестве т различные неприводимые представления,
входящие в представление Тр, мы получим разбиение пространства L
на инвариантные относительно группы G подпространства.
Обозначим через T°(g) (g? G) представление, индуцируемое
в подпространстве L0 представлением Тв. Вычислим характер y?(g)
представления T°(g'). Для простоты мы будем считать, что предста-
представление t содержится в представлении Тр ровно один раз. Однако
выражения B5,5) и B5,9) для характера y_°(g), которые мы получим
ниже, справедливы в том случае, когда т содержится в Тр несколько
раз.
Введем в рассмотрение прямое произведение групп G и Р. Обо-
Обозначим через y(pg), ~l°(pg) и y}(pg) характеры элемента pg в про-
пространствах L, L0 и L1. Ясно, что
B5,2)
Характер y°(pg) равен
¦/« (pg) = [х (р) Tn (g)}n = zu (p) 1% (g).	B5,3)
Характер ~/}{pg) можно вычислить по аналогичной формуле
¦/} (Рё) = [Т1 (Р) Т1 (g))a — Т\к (р) Т)а (g),	B5,4)
где Т1 (р) и T'(g") — операторы, соответствующие элементам р и g
в подпространстве L1. Подставляя B5,3) и B5,4) в B5,2), получим:
YL (Pg) = ~4j (P) T?i \g) + Tik (P) Ты (g).
Умножим обе части этого равенства на у°(р) и усредним его по
группе Р. Вспоминая соотношения ортогональности, найдем:
РСР
где sQ—размерность представления t, а у°(р) — характер этого
представления.
Нам осталось вычислить характер y(pg)- Подействуем операто-
оператором Тр(р)Тп(g) на базисный элемент eap...z:
tP (P) Tl(g)e.?..., = Tp (p) Ta-a (g) Тр,р (g)... T?,s (g) ea,? ....,=
'3'...s', B5,6)

70	ОПЕРАЦИИ С ПРЕДСТАВЛЕНИЯМИ ГРУПП	[ГЛ. IV
где р(a), pQ), ..., /?(s) — индексы, которые в результате переста-
перестановки р становятся соответственно на место а, |3, . . ., s.
Из равенства B5,6) следует, что
*(pg)= 2 Tep(«)te)T^(W(gr)...Tip(.)(g)- B5,7)
а,3 ... е
Для вычисления этой суммы разобьем перестановку р на циклы
P0*i«2 ••• а«.) ¦•• (TiT2 ••• Те,)
и расположим в соответствующем порядке сомножители
7. (№) = 2 ¦ • • 2 т«*
2	Твл(^)Твд(г) ... Т „а,(
¦•¦f	S TT.Ts(ff)T№(ff)...Tr Т
Суммы, стоящие в	скобках, легко вычисляются:
2	з (ff) .. . Т aj (g) = 2 Ta,a
Поэтому
Z (A?) = Z (««') Z (?*) • • • Z te4').	B5'8)
где x(g) — характер представления Т (g).
Подставляя это выражение в соотношение B5,5), получим окон-
окончательно:
Z° (g) = -^r S Z^ Z С^1) X (^J) • • • z (^),	B5,9)
Р
где grj, ^2» ••¦. 9а — длины циклов перестановки р.
Рассмотрим более подробно важный частный случай, когда
группа Р представляет собой группу всех перестановок п предме-
предметов, т. е. является симметрической группой Sn.
В этом случае все перестановки, имеющие одинаковые длины
циклов, принадлежат одному и тому же классу сопряженных эле-
элементов. Всем таким перестановкам соответствуют в сумме B5,9)
одинаковые слагаемые. Обозначим через {rlqlr2q, ¦ . . rvqv) класс,
состоящий из перестановок, у которых имеется rv циклов длины qv r2
циклов длины q2 и т. д. Число перестановок, содержащихся в классе

§ 25]	СИММЕТРИЗОВАННЫЕ СТЕПЕНИ ПРЕДСТАВЛЕНИЙ	71
••• rv<]-»}> равно 	—-—'-	. Поэтому в случае
rilq[1-rzlq'2*...rjrr4-,
'—Sn формулу B5,9) можно переписать в виде
. . rv<7v}. B5,10)
Суммирование происходит здесь по всевозможным различным раз-
разбиениям числа п
п =
(два разбиения п = r]qi -+-r2q2¦+-...+ r^q^ и п = r[q[ + r'2q'2 + ...
...-|-г^' считаются одинаковыми, если после подходящей пере-
перестановки слагаемых имеют место равенства ri — r[> <7i —<?i> •••
..., г^=.г'^, q^ = q'\. Если P = Sn и представление t является
единичным, то представление Т° называется симметрической п-й
степенью представления Т:
Характер этого представления определяется согласно B5,10) выра-
выражением
2^f^4^.	B6,11)
! ^	! ^
Полагая здесь п =2, 3, 4 и 5, получим:
t/J4 (?)= |Z(§-') + 4 Z fe3) Z(§•) +1Z2(g2)+ j 7.
B5,12)
V/f (g)= j z (r) + t z (?') z te) -f- -J- z fe3) z fe2) +1 z fe3) z2 fe) -+-
+1Z2 fe2) Z ar) + f2 Z fe2) Z3 (g) + щ Z5 (Й-
Если P = Sn и в качестве t взять представление, ставящее в соот-
соответствие каждой четной перестановке единичный оператор Е, а каж-
каждой нечетной перестановке оператор —Е, то представление Т°
называется антисимметрической /г-й степенью представления Т:

72	ОПЕРАЦИИ С ПРЕДСТАВЛЕНИЯМИ ГРУПП	[ГЛ. IV
Характер этого представления определяется согласно B5,10), выра-
выражением
Полагая здесь п =2, 3, 4 и 5, получим:
{у.}4 (г)=-| ¦/№>+ у у. te3) zte)- is /-2 ^>—т у. ^2)/2^)+211
{у.}5 fe)= 7 * te5> - т z ^) z (g)'i- 4 /. fe:!) z (g*) + J
+ 4 7.2 (^2) 7. Or) ~ /2 7. ОТ2)	Г2о
За дача I. Доказать, что если Т = Т1ТТ., то [Т2] = [Т]]5+[Т2]г-f-
! X Т2 и {Т}2 + {Т,}- + Tt X Т.2 + {Т.}2.
§ 26. Фактическое разложение приводимого представления
на неприводимые
Для успешного применения теории представлений групп к раз-
различным прикладным вопросам часто оказывается необходимым произ-
произвести разложение приводимого представления на входящие в него
неприводимые представления. В настоящем параграфе излагается
метод, позволяющий производить такие разложения.
Напомним некоторые относящиеся к этому вопросу факты.
Если Т есть приводимое унитарное представление группы Ог
действующее в пространстве L, то пространство L можно разло-
разложить на сумму инвариантных взаиммо-ортогомальных подпространств.
Z._L1 + /-2+...+Lv)	B6,1)
каждое из которых преобразуется по одному из неприводимых пред-
представлений
Ъ, Ъ. • ... ~а	B6,2)
группы G. Инвариантные подпространства, преобразующиеся по-
неприводимым представлениям, будем называть неприводимыми под-
подпространствами. Разложение пространства L на неприводимые
взаимно-ортогональные подпространства называют полным разложе-
разложением пространства L.
Поставленную задачу теперь можно сформулировать так: найти
все полные разложения (их может быть бесконечно много) простран-
пространства L, преобразующегося но приводимому представлению Т.

§ 26] ФАКТИЧЕСКОЕ РАЗЛОЖЕНИЕ ПРИВОДИМОГО ПРЕДСТАВЛЕНИЯ	7S
Подчеркнем, что все неприводимые представления B6,2) группы О
считаются известными. Более того, мы будем считать, что каждое
из неприводимых представлений задано в матричной форме
(*• ?=1> 2	SP /=!. 2- •••' Я)- B6,3)
Хотя одно и то же представление можно задать в виде разных,.
но, разумеется, эквивалентных матричных представлений, нам будет
удобней при решении поставленной задачи фиксировать сделанный
выбор B6,3) матричных представлений.
Рассмотрим более подробно какое-нибудь полное разложение
B6,1) пространства L. Неприводимые подпространства, фигурирую-
фигурирующие в этом разложении, целесообразно разбить на классы, отнеся
к У-му классу те подпространства, которые преобразуются по пред-
представлению tj(j—\, 2, . . ., q). Ясно, чтоу-й класс содержит столько
неприводимых подпространств, сколько раз представление tj входит
в представление Т.
Напомним, что число nij, показывающее, сколько раз представле-
представление tj входит в представление Т, определяется формулой B0,3)
Щ^{Ъ 7j) G=1, 2, ..., <?)	B6,4)
и, следовательно, одинаково для всех полных разложений простран-
пространства L.
Неприводимые подпространства, составляющие /-й класс, обо-
обозначим через
Ад, LJ2, .... LJmJ.	B6,5)
В каждом из этих подпространств выберем ортогональный базис
таким образом, чтобы оператор Т (g) изображался в каждом из этих
подпространств выбранной заранее матрицей B6,3), т. е. чтобы ¦
имели место соотношения
¦V
Т (g) ehk = 2 -jin (g) ej,,i (a = 1, 2, . . ., my, j = 1, 2, . . ., q;
k.= l, 2, ..., Sj);	B6,6)-
здесь
«fc*G*=l. 2, .... my, j=\, 2, .... q; k-=\, 2, ..., Sj) B6,7)
— базисный вектор с номером к из неприводимого подпростран-
подпространства lir
Выбранный таким образом базис будем называть каноническим.
Еще раз подчеркнем, что в равенстве B6,6) коэффициенты tjudg)
не зависят от индекса а. Это является результатом согласованного
выбора базисов в подпространствах одного класса.
Метод, который мы используем для решения задачи о факти-
фактическом разложении приводимого представления, базируется на сле-
следующей лемме.

•74	ОПЕРАЦИИ С ПРЕДСТАВЛЕНИЯМИ ГРУПП	[ГЛ. IV
Лемма. Оператор
^^T(«") V=1'2	Ч)	B6,8)
оставляет неизменными базисные векторы е^ (и= 1, 2, .. ., ту,
j = 1,2	9) и обращает в нуль все остальные базисные
векторы.
Доказательство получается простой проверкой. Действи-
Действительно, используя B6,8) и B6,6), имеем:
"V" & T
lJ AT
•Отсюда с помощью теорем ортогональности находим:
что и доказывает лемму.
Так как все базисные векторы е^ fc взаимно ортогональны, то
доказанную лемму можно сформулировать еще и так:
Оператор Pj является оператором проектирования на под-
подпространство Ej, представляющее собой линейную оболочку
векторов
Поскольку оператор проектирования Р^ известен, то нетрудно найти
и подпространство Ер на которое он проектирует все векторы из
пространства L. Для этого достаточно взять nij произвольных
векторов из L
.и подействовать на них оператором Pj. Полученные векторы
yi = PjXi (*¦ = 1. 2	mj)	B6,9)
лежат в подпространстве Ej и, как правило, линейно независимы.
Если же, однако, они случайно окажутся линейно зависимыми, то
следует заменить некоторые из векторов х; другими векторами х[.
Во всяком случае, если
аи аъ .... аа

§ 26] ФАКТИЧЕСКОЕ РАЗЛОЖЕНИЕ ПРИВОДИМОГО ПРЕДСТАВЛЕНИЯ	75
¦есть произвольный базис в пространстве L, то линейная оболочка s
лекторов	Ь{ = Р^ (/-1,2, .... s)
совпадает с подпространством Ej.
Итак, из пространства L можно фактически выделить все
подпространства Ej (j = 1, 2, ..., q), причем знание подпространств
Lfaip = 1. 2, ..., mj) не является необходимым для этой цели.
Более полную' характеристику подпространства Ej дает следую-
следующая теорема.
Теорема. Если Lj— какое-либо инвариантное подпростран-
подпространство пространства L, преобразующееся по неприводимому пред-
представлению "Zj, U
еи е.г, . .., е,.
есть канонический базис в Lj, то вектор et содержится в под-
подпространстве Ej.
Наоборот, если е1 есть произвольный вектор из подпростран-
подпространства Ej, то существует неприводимое подпространство Lj, и
притом только одно, содержащее этот вектор и преобразую-
преобразующееся по представлению tj. Вектор et совпадает при этом
¦с первым вектором канонического базиса в пространстве Lj.
Доказательство первой части теоремы. Повторяя выкладки,
приведенные в доказательстве леммы, убеждаемся в том, что вектор ех
инвариантен относительно оператора Pj. Это и означает, что et?Ej.
Доказательство второй части теоремы. Если вектор et
содержится в Ej, то он может быть представлен в следующем виде:
«. = 2^1	B6Л0)
11=1
•(обозначения те же, что и в лемме, с^ — комплексные числа). Наряду
с вектором ех введем в рассмотрение векторы ег, еЛ, ..., es. с по-
помощью равенств
**=2^вм. (k=l,2,...,sj),	B6,11)
с которых коэффициенты с^ заимствованы из соотношения B6,10).
Легко убедиться в том, что линейная оболочка векторов
еу, ег, ..., ed. образует неприводимое пространство, а сами век-
векторы ек играют роль канонического базиса в этом пространстве.
Действительно, имеем:
т.	т. Sj
(g) *ja- = 2 <> 2 tflk (g) e3-,i =
= 2 ijik (g) 2 cjj*i = 2

76	ОПЕРАЦИИ С ПРЕДСТАВЛЕНИЯМИ ГРУНП	[ГЛл IV
Наконец, вектор ех не может принадлежать двум различным,
неприводимым подпространствам Lx и L,, так как их пересечение,
являясь инвариантным подпространством и не совпадая ни с Lu.
ни с Z-2, должно быть пусто.
Теорема доказана полностью.
Существуют простые формулы, связывающие векторы е&.
(& = 2, 3, «. ., Sj) с вектором e1?Ej. Они имеют следующий вид:
eb = Pjbei.	B6.12>
где
^ S ^	(А = 2, 3, . . ., s,.),
и непосредственно вытекают из теоремы ортогональности.
Теперь нетрудно осуществить произвольное разложение про-
пространства L, преобразующегося по приводимому представлению Т.
Для этого следует:
1)	выяснить, сколько раз входит в представление Т каждое
неприводимое представление ¦Zj группы G; полученные числа ту
дадут нам размерности подпространств Fly
2)	найти с помощью операторов Pj (см. A2(>,8)) все подпро-
подпространства IIj, имеющие положительную размерность т_,->¦ 0;
3)	в каждом из подпространств Ilj (mj > 0) выбрать совершенно
произвольным образом ортогональный базис
eju. ej2i, ej31, . . ., eJmy,	B6,13)
4)	применяя формулу B6,12) поочередно к каждому из век-
векторов B6,13), построить неприводимые подпространства, содер-
содержащие эти векторы; полученные таким образом подпространства
взаимно ортогональны и преобразуются по представлению "zy, в сово-
совокупности они дают полное разложение подпространства L.
Заметим, что произвол, который допускается пунктом 3, совер-
совершенно достаточен для того, чтобы указанным метолом могли быть
получены все полные разложения пространства L.
Задача I. Обозначим через Lj сумму всех подпространств LjX,
Zj2, ..., Ljm., преобразующихся по одному и тому же представлению т^_
Доказать, что оператор
является оператором проектирования на подпространство Lj. Этот оператор*
удобен тем, что для его построения достаточно знать только характер /;(g}
представления tj.
Задача П. Пусть е% и fx два взаимно-ортогональных вектора из Еу
Доказать, что неприводимое подпространство, содержащее вектор ех, орто-
ортогонально неприводимому подпространству, содержащему вектор Д.

ГЛАВА V
ПРЕДСТАВЛЕНИЯ НЕКОТОРЫХ ГРУПП
§ 27- Представления группы перестановок Sn
Все неприводимые представления симметрической группы могут
быть найдены с помощью так называемых схем Юнга. Не остана-
яливаясь на доказательстве некоторых утверждений, мы приведем
описание этого метода.
Рассмотрим все возможные разбиения числа п на положительные
целые слагаемые. Два разбиения, отличающихся только порядком
слагаемых, будем считать одинаковыми. Поэтому в каждом разбие-
разбиении можно располагать слагаемые в невозрастающем порядке.
Каждому разбиению соответствует так называемая схема Юнга,
которая представляет собой набор клеток, расположенных но стро-
строкам. Число строк равно числу слагаемых в разбиении; число клеток
в первой строке равно первому слагаемому в разбиении; число
клеток во второй строке равно второму слагаемому и т. д. Общее
число клеток равно, разумеется, числу п. На рис. 16 изображены
•схемы Юнга, соответствующие пяти	г_т_^_,_,
. возможным разбиениям числа 4.	Mill
Сопоставим теперь каждой схеме	4
Юнга некоторое представление сим- i—|—i—i r~j I
метрической группы Sn. Для этого j_J	| I !
рассмотрим какую-либо схему Юнга з*1	<?+* <?+/+/ /+/+/+/
и перенумеруем в произвольном	р .g
порядке все ее клетки.
Группу SH можно рассматривать теперь как совокупность всех
перестановок клеток схемы Юнга. Обозначим через р все те пере-
перестановки, которые оставляют каждую клетку в той строке, на
которой она находилась до перестановки. Подобным же образом
обозначим через q все те перестановки, которые сохраняют в ука-
указанном смысле столбцы рассматриваемой схемы Юнга. Ясно, что
совокупности р и q перестановок для различных схем Юнга раз-
различны.

78	ПРЕДСТАВЛЕНИЯ НЕКОТОРЫХ ГРУПП	[ГЛ. V
Введем в рассмотрение функцию о (s) (s?Sn) на симметрической
группе Sn, которую определим следующим образом:
О, если элемент s не равен
одному из произведений
'	вида qp;
<q, если s— qp;
здесь bq есть четность перестановки q *).
Рассмотрим теперь комплексную линейную оболочку L функций'
ot (s) = сэ (st) (s, t ? Sn)
и определим на этих функциях линейные операторы т(г) (г ? Sn),
положив
x(r)ot(s)=^t(sr).
Так как по определению tpf (sr) = о (srt) = orf(s), то операторы
-с (г) (r?Sn), действуя на функции из L, не выводят их из L. Ясно,
что операторы х (г) удовлетворяют условию ~(/"i) "•(/¦2) = t('/'2}
(rv гг€ "^п) "» следовательно, образуют представление группы Sn.
Приведенная конструкция ставит в соответствие каждой схеме
Юнга некоторое представление. Можно доказать, что получаемые
таким образом представления неприводимы и что представления,
соответствующие различным схемам Юнга, неэквивалентны.
Число различных схем Юнга равно числу различных разбие-
разбиений п. Этому же равно число сопряженных классов группы Sn и,
следовательно, число всех неприводимых представлений группы Sn.
Поэтому схемы Юнга позволяют найти все неприводимые предста-
представления группы перестановок Sn.
В качестве примера рассмотрим представление группы Ss, отве-
отвечающее схеме Юнга
1 i 3 i
L2J ~'
Совокупность перестановок р, сохраняющих строки, состоит из
дв\'Х элементов: е и A3). Совокупность д также состоит из двух
элементов: е и A2).
Легко вычислить все произведения вида qp:
ее = е,	еA3) = (.13),	(\2)е = е,	A2) A3) = A32).
Следовательно, функция cp(s), соответствующая рассматриваемой
схеме Юнга, равна -\-1 на перестановках е и A3), —1 на пере-
*) Иными словами, bq равно -j-1, если q — четная перестановка, и —1,
если q — нечетная перестановка.

§ 27]
ПРЕДСТАВЛЕНИЯ ГРУППЫ ПЕРЕСТАНОВОК
79-
становках A2) и A32), нулю на всех остальных перестановках.
Функцию '«(s) можно записать «табличным» образом (см. табл. 5).
Функция у (s)
Таблица 5
S
*<s)
1
A2)
— 1
B3)
0
A3)
1
A23)
0
A32)
	j
Теперь нетрудно построить остальные пять функций. Они задаются
таблицей 6.
Таблица 6
Функции <fK(s), <p2i,(s). ?i3(s). ?1!з(«). 4iai(s)
?и (s)
<?12з00
<?132 (S)
e
— 1
0
1
0
— 1
A2)
1
0
— 1
0
1
B3)
— 1
1
0
1
— 1
A3)
0
	^
1
	 J
0
A23)
1
— 1
0
— 1
1
A32)
0
1
1
0
Среди построенных таким образом функций есть только две
линейно независимые. В качестве этих функций можно взять, на-
например, функции ср (s) и 9i2(s). Остальные функции выражаются
через них следующим образом:
Т13 ¦
Y132	 Yl2>
Г12-
Эти равенства полезны тем, что позволяют записать первые столбцы
матриц представления. Для того чтобы записать эти матрицы пол-
полностью, заметим, что
'f 12= С? A2) A2) — <?>
"B3) ?12= Г B3) A2) = ?132=
т A 3) ср 12 = ¦— о — cs12,
хA23)?12=>,
тA32)?12= —?1 — ?12f
Г12>

80	ПРЕДСТАВЛЕНИЯ НЕКОТОРЫХ ГРУПП	[ГЛ. V
Итак, матрицы представления группы S3, соответствующего схеме
Юнга B-}-1), в базисе срE)> <?i2(s)> имеют следующий вид:
•Схемы Юнга сокращенно обозначают символами типа 43, 2, 3, 2, I5,
и т. д., символ 43, 2 означает схему Юнга, у которой три строки
из четырех клеток и одна строка из двух клеток; 3, 2, 1Г) означает
.схему Юнга, содержащую одну строку из трех клеток, одну строку
из двух клеток и пять одноклеточных строк.
В приложении приведена таблица характеров неприводимых пред-
представлений групп Sv 55, Se н S7.
§ 28. Неприводимые представления точечных групп
1. Группы Сп и S2n- Группа Сп является абелевой группой.
Поэтому все ее неприводимые представления являются одномерными,
а число их равно порядку группы, т. е. п. Пусть t — одно из непри-
неприводимых представлений этой группы. Так как хп (Сп) — -с (с™) =
==х(е)=1, то % (Сп) принимает одно из значений
с » "(fe = 0, 1	п — 1).
Таким образом, мы получаем все п неприводимых представлений
.труппы Сп
2-ikm
** (С™) = е~~ (ft, m =- 0, 1, . . ., и — 1). B8,1)
Группа 52в изоморфна группе Сгп. Поэтому ее представления
. могут быть найдены по формуле
2r.ikm
fk{SZ) = e~^~	(A, »t = 0, 1, .... 2«—1). B8,2)
2. Группы Dn и Cnv. Метод, с помощью которого мы най-
найдем неприводимые представления группы Dn, очень часто приме-
применяется при отыскании представлений. Поэтому мы изложим его по
возможности подробно.
Пусть х — некоторое неприводимое представление группы Dn>
.a L — пространство, в котором действуют операторы представле-
представления t. Рассмотрим теперь те операторы, которые в представлении т

§ 28]	НЕПРИВОДИМЫЕ ПРЕДСТАВЛЕНИЯ ТОЧЕЧНЫХ ГРУПП	81
соответствуют элементам подгруппы Сп группы Dn. Ясно, что эти
операторы
х(е),х(Сй), х(с2п)	х^Г1)
образуют некоторое представление группы Сп. Если это представ-
представление приводимо, то его можно расщепить на неприводимые пред-
представления. Иными словами, пространство L можно разложить на
подпространства Lu L2	 каждое из которых преобразуется по
одному из неприводимых представлений подгруппы Сп. Так как
все неприводимые представления группы Сп одномерны, то и под-
подпространства Lv L2, ¦ ¦ • также одномерны. Обозначим через ev
е2, ... единичные векторы, лежащие соответственно в Llt L2, ...
По самому определению вектора е1 он преобразуется под дей-
действием оператора х(Сге) по одному из представлений B8,1) группы
•Ыък
Введем в рассмотрение вектор е'^=ч(иЛех. Легко видеть, что
х (а,) е[ = х (и,) -в («,) е, = -с (а\) е, = т (е) ех = ех
Последние два равенства показывают, что векторы еу и е'х преобра-
преобразуются друг через друга под действием операторов x(Mj) и х(Си).
Так как всякий элемент группы Dn может быть представлен в виде
Сп или С«и1( то линейная оболочка векторов е1 и е[ инвариантна
относительно всех операторов представления х. Это значит, что про-
пространство L совпадает с линейной оболочкой векторов ех и е'у Если
е~^~фе «",	B8,3)
то векторы еу и е'г линейно независимы и представление двумерно.
Матрицы, соответствующие в базисе ех и еу операторам х(С„) и
х (aj, имеют следующий вид:
О 1\
. »)• B8-4)
Положение существенно изменяется, если неравенство B8,3) не
выполняется. При этом каждый из векторов el~e[ и ех-\-е'х инва-
инвариантен относительно всех операторов представления х. Поскольку
6 Зак. 3512. Г. Я. Любарский

82	ПРЕДСТАВЛЕНИЯ НЕКОТОРЫХ ГРУПП	[ГЛ. V
представление % неприводимо, то это означает, что один из этих
векторов равен нулю. Таким образом, если k = О или k = -^- (что
возможно только в случае четных п), то ч(иЛех = е^ = ev либо
т(#1)е1= — е1г и мы получаем для каждого из этих случаев два
одномерных представления
1тЛк
2т.д	B8,5)
Итак, если п четно, то группа Dn имеет п — 2 двумерных пред-
представления, определяемых соотношениями B8,4), и четыре одномер-
одномерных представления B8,5). Если п нечетно, то число двумерных
представлений равно а—1, а одномерных—двум.
Группы Cnv изоморфны группам Dn и имеют поэтому те же
представления.
3.	Группы Cnh, Dnh, D2n+l> d. Группа Cnh является прямым про-
произведением группы Сп на группу aft = Coft. Неприводимые пред-
представления Cnh получаются путем умножения неприводимых предста-
представлений группы Сп на неприводимые представления группы Coft
(группа COh изоморфна группе С2).
По этой же причине нет нужды специально отыскивать представле-
представления группы Dnh, являющейся прямым произведением групп DnXCoh,
и группы D2n+lfd = D2n+l X /•
4.	Группы D2nd. Рассуждая так же, как и в случае группы Dn,
находим, что группа D2nd имеет 2«—1 двумерных представлений,
определяемых соотношениями
0 \ *,<*)=Г !
О е W
и четыре одномерных представления
^0 (Sin) == 1 • "О (Sin) == 1 >	^2П (Sin) = — 1, ~2n(Sin) =	 1,
б. Группы T, O, Td. Приведем таблицы характеров неприводи-
неприводимых представлений этих групп (см. табл. 7).
Первый вертикальный столбец как в левой, так и в правой части
таблицы 5 содержит символ группы и обозначения неприводимых
представлений. В одной строке с символом группы стоят символы
элементов группы. Коэффициент, стоящий перед символом элемента

§ 29)
ПРЕДСТАВЛЕНИЯ ГРУПП ТРАНСЛЯЦИЙ
83
Таблица 7
Характеры неприводимых представлений Т, О и T<j
т
ч
То
*з
Т4
е
1
1
1
3
зс2
1
1
1
— 1
4С3
1
3
3
0
1
3
3
0
*2
"з
Т4
to
1
1
2
3
3
8С3
8С3
1
1
— 1
0
0
ЗС2
зс2
1
1
2
— 1
— 1
6С2
¦6od
1
— 1
0
1
— 1
65
1
	^
0
— 1
1
группы, указывает на число элементов группы, сопряженных дан-<
ному элементу.
Чтобы от характеров перейти к представлениям, заметим, что
представление т4 группы Т является векторным представлением. То
же можно сказать о представлении т4 группы Td и представлении т6
группы О. Представление t5 группы Td равно произведению век-
векторного представления ti на любое из представлений t2> "V Предста-
Представление х4 группы О равно произведению представления тб на любое
из представлений т2> ^з-
Двумерное представление х3 группы Td определяется равенствами
/О 1\
2*1
О е
Группы Тй и Oh являются произведениями групп Т и О на группу /.
Мы не выписываем неприводимых представлений групп К и Yh,
так как они, насколько нам известно, не встречаются в прикладных
вопросах.
В приложении приведена таблица характеров неприводимых пред-
представлений наиболее часто встречающихся точечных групп.
§ 29. Представления групп трансляций
Найдем всевозможные представления группы трансляций. Пусть
§ — группа трансляций, пусть ах, а,, а3 — тройка основных векторов
этой группы. Всякое неприводимое представление т группы §~ одно-
одномерно в силу коммутативности группы трансляций. Поэтому опера-
операторы т(?)(^?сГ) являются просто числами. Обозначим
*(taj) = Qj C/=l, 2, 3).	B9,1)
6*

84	ПРЕДСТАВЛЕНИЯ НЕКОТОРЫХ ГРУПП	[ГЛ. V
Ясно, что трансляции а = т1а1-\-т2а2~\-т3а3 соответствует оператор
* D) = вГ'в^е?1.	B9,2)
Таким образом, тройка чисел ди 02, 63 вполне определяет неприво-
неприводимое представление. Задавая различные тройки чисел 0и 62, 63, мы
получим все неприводимые представления группы трансляций. Пред-
Представление будет унитарным, если все три числа 6j, 02 и 63 равны
по модулю единице.
Вместо чисел б1, 02, 63 удобно использовать для характеристики
неприводимого представления вектор k, определяемый условиями
% = eihaj (/=1, 2, 3).	B9,3)
Легко видеть, что, решая уравнение B9,3) относительно k, мы
получим:
3
k ~ ~Ьп ] 1П
B9,4)
где
и _ 2_ [Да, Да]	 А _ 9 [Да. fli]	А .._ 2_ f«i> ^1 _ ,oq 54
2	А 9
^ - ^'V (в1 [О,, С„]) '  — ^ (Я] [fl
— так называемые основные векторы обратной решетки. Любая цело-
целочисленная линейная комбинация этих векторов называется вектором
обратной решетки. Мы видим, что вектор k определен с точностью
до произвольного вектора обратной решетки. Иными словами, двум
векторам kx и k2, которые отличаются на вектор обратной решетки,
отвечает одно и то же неприводимое представление группы транс-
трансляций. Мы будем говорить, что такие векторы эквивалентны друг
другу, и писать k1 = k2-
Формула B9,2) может быть переписана в новых обозначениях
<c(fe)=e**».	B9,6)
Представление, определяемое этой формулой, назовем представле-
представлением тл.
Совокупность всех векторов k, каждый из которых нельзя уко-
укоротить, добавляя к нему какой-либо вектор обратной решетки,
называется первой зоной Бриллуэна или просто зоной Бриллуэна.
Если вектор k короче всех ему эквивалентных векторов, то он
лежит внутри зоны Бриллуэна, если же среди векторов, эквивалент-
эквивалентных k, нет ни одного вектора короче k, но есть векторы, равные
по длине ft, то вектор k лежит на границе зоны Бриллуэна. Отсюда,
в частности, следует, что среди векторов, лежащих внутри зоны,
нет ни одной пары эквивалентных векторов. Наоборот, каждый вектор,
конец которого лежит на границе зоны Бриллуэна, эквивалентен
одному или нескольким векторам, тоже принадлежащим границе зоны.

§ 29]
ПРЕДСТАВЛЕНИЯ ГРУПП ТРАНСЛЯЦИЙ
85
Для нахождения зоны Бриллуэна данной группы трансляций
полезно иметь в виду следующее замечание.
Пусть Ь — какой-либо вектор обратной решетки. Рассмотрим
две плоскости Р+ и Р~, перпендикулярные к Ъ и отстоящие от
начала координат на расстоянии -^-Ь (рис'. 17). Ясно, что у любого
вектора k, пронизывающего плоскость Р+, имеется эквивалентный
ему более короткий вектор fc1 = k—Ь. Поэтому вектор k не может
принадлежать зоне Бриллуэна, которая, таким образом, целиком
умещается в слое между плоскостями Р+ и Р~. Выбирая в каче-
качестве b другой вектор обратной решетки, мы получим другой слой,
Рис. 19.
который также содержит зону Бриллуэна. Пересечение всех таких
слоев совпадает с зоной Бриллуэна.
Рассмотрим для примера плоскую группу трансляций а —
= mxa<i -f- тга<1, причем положим, что aj = a2 и угол между векто-
векторами at и a-i равен -~- (рис. 18). Если через е обозначить единич-
единичный вектор, параллельный вектору [аи а2], то основные векторы
обратной решетки можно записать в виде 6t = 2д. ,"'
—2т-
?
2> е\)
Легко видеть, что bx~b2 и угол между Ьх и Ъг
равен -^-. Взяв Ъ = Ъи мы получим полосу / (рис. 19). Положив
Ь = Ь2, мы получим полосу //. Наконец, выбор b=^bx-\~b2 приведет
нас к полосе ///. Все остальные возможные значения Ъ приводят
к полосам, содержащим заштрихованный шестиугольник, который,
таким образом, и является зоной Бриллуэна рассмотренной группы
трансляций.
Задача I. Показать, что группа симметрии обратной решетки совпадает
с группой симметрии исходной группы трансляций.
Задача II. Показать, что зона Вриллуэна симметрична относительно всех
элементов симметрии группы трансляций.

86	ПРЕДСТАВЛЕНИЯ НЕКОТОРЫХ ГРУПП	[ГЛ. V
§ 30. Представления пространственных групп
В этом параграфе производится классификация неприводимых
представлений пространственных групп и рассматривается задача
о разложении приводимого представления пространственной группы.
Пусть О — пространственная группа, а Т-^-некоторое предста-
представление G в пространстве L. Представление Т можно рассматривать
как представление подгруппы оГ всех трансляций из группы G. При
этом оно распадается на одномерные представления группы 5Г. Каж-
Каждое такое представление характеризуется вектором к. Обозначим
через
ku kz, ... kz
векторы, характеризующие представления группы оГ, содержащиеся
в представлении Т. Набор этих векторов называется звездой пред-
представления Т.
Покажем, что звезда инвариантна относительно всех элементов
группы G. Пусть вектор el^iL преобразуется по представлению kv
Рассмотрим вектор 1i(g)el^L(g^G). Имеем:
Т (У Т <*) о, = Т (tjr) ех = Т («/„-..) ех = Т (g) T (t^a) ex =
C0,1)
Таким образом, если вектор е1 преобразуется при трансляции
по представлению ku то вектор T(g)e1 преобразуется по пред-
представлению gkt. Мы видим, что звезда представления Т содержит
наряду с вектором kx все векторы gfex (g^G). Каждый вектор
звезды представления переводится любым элементом пространственной
группы в вектор, также принадлежащий звезде.
Линейная оболочка всех векторов T^e^^G, ei^iL) образует
подпространство, инвариантное относительно группы G. Поэтому,
если представление Т неприводимо, то это подпространство совпа-
совпадает со всем пространством L и все векторы звезды представления
могут быть получены из вектора ky с помощью операций g?G.
Звезды, обладающие тем свойством, что любые два вектора звезды
могут быть получены один из другого с помощью операций g?G,
называются неприводимыми. Таким образом, звезда неприводимого
представления неприводима (обратное утверждение неверно). Непри-
Неприводимая звезда полностью определена, если известен хотя бы один
ее вектор k. Поэтому неприводимые звезды можно обозначать сим-
символом \k).
Звезда приводимого представления состоит из одной или не-
нескольких неприводимых звезд.
Возьмем какой-либо вектор k звезды представления Т и обозна-
обозначим через Lh подпространство тех векторов из L, которые преоб-
преобразуются по представлению тл группы трансляций.

§ 30]	ПРЕДСТАВЛЕНИЯ ПРОСТРАНСТВЕННЫХ ГРУПП	87
Линейная оболочка подпространств Lh, которые соответствуют
векторам k, принадлежащим одной неприводимой звезде, инвариантна
относительно группы О. Представление, индуцируемое в этой обо-
оболочке представлением Т, имеет, очевидно, неприводимую звезду.
Итак, каждое представление с приводимой звездой легко раз-
разбивается на представления с неприводимыми звездами. Всякое не-
неприводимое представление имеет неприводимую звезду. Поэтому для
классификации неприводимых представлений, так же как и для раз-
разложения приводимых представлений на неприводимые, достаточно
рассматривать только представления с неприводимыми звездами.
В дальнейшем мы будем предполагать, что представление Т
имеет неприводимую звезду.
Для анализа представления Т введем в рассмотрение подгруппу
Gfc cz G, состоящую из тех элементов g, которые либо не изменяют
вектор k, либо изменяют его несущественно, прибавляя к нему
какой-либо вектор обратной решетки. Подгруппу Gft называют
группой вектора k. В силу соотношения C0,1) подпространство Lk
инвариантно относительно подгруппы Gk- Представление группы Ои,
по которому преобразуется Lk, называется малым представлением.
Мы будем обозначать малое представление через Tft.
Покажем, что вектор k и малое представление Т^ однозначно
определяют представление Т, если оно имеет неприводимую звезду.
Придадим вектору k индекс 1, а остальные векторы звезды
обозначим через k2, k3, ..., ka. Выберем из группы G каким-либо
'образом (о—1) элементов g2, g3, ..., g^ так, чтобы
С30'2)
Если е^\ eW	еО)— некоторый базис в подпространстве Lk ,
то векторы
C0,3)
образуют базис в подпространстве Lfc.(/=2, 3, ..., а). Объеди-
Объединяя векторы C0,3), соответствующие всевозможным значениям j,
мы получим базис в пространстве L. Найдем с помощью этого
базиса операторы Т(А) (h?G).
Пусть kj — один из векторов звезды, под действием элемента h
он переходит в некоторый, вообще говоря, другой вектор звезды,
скажем kj',
Составим произведение h° = g7,lhg.. Действуя элементом h° на век-
вектор kv мы получим:

88	ПРЕДСТАВЛЕНИЯ НЕКОТОРЫХ ГРУПП	[ГЛ. V
т. е. элемент h° принадлежит подгруппе GkV Вычислим
используя соотношение h = g.,h°g-1. Имеем:
Т (h) ер = Т (gj.) Т (АО) Т (gj-i) еШ = Т (^.) Т (А») е? =
Итак,
в(Я.	C0,4)
Мы видим, что малое представление Tfej, действительно, однозначно
определяет представление Т группы G, если звезда Т неприводима.
Если малое представление Т* унитарно, то унитарно и пред-
представление Т.
Если малое представление Тк неприводимо, то неприводимо и
представление Т, и наоборот.
Подчеркнем, что для классификации неприводимых представле-
представлений пространственной группы достаточно двух индексов k и р,
где k — векторный индекс, определяющий звезду представления,
а р — номер неприводимого представления zhp группы Gfc. Для раз-
разложения приводимого представления Т достаточно разложить пред-
представление группы О^ на неприводимые представления t/clJ.
Мы не будем останавливаться на простом, но несколько гро-
громоздком доказательстве этих утверждений.
Рассмотрим более подробно представления Т^ группы G&. Любой
элемент g этой группы можно представить в виде произведения
g = tur	C0,5)
некоторой трансляции aL=^<x,(g) на поворот или зеркальный поворот
r — r(g) вокруг некоторой точки О. Точку О мы выберем на
пересечении возможно большего числа осей (простых или винтовых)
и плоскостей группы Ой- Совокупность всех элементов r(g) (g?Gk)
образует точечную группу, которую мы обозначим через G/c. Сопо-
Сопоставим каждому элементу г (g) оператор
г B) -+1 (r) = Tfc(g) e-i"* (g = tj).	C0,6)
Это соответствие является однозначным, несмотря на то, что одному
и тому же элементу г отвечает бесконечное множество различных g.
Операторы T(r) (r?Gk) вполне определяют представление Tk(g)
и, как мы сейчас увидим, удовлетворяют одному простому соотно-
соотношению. Пусть g1 — tairl, gz = t*arz fa, gz^Gh). Произведение glgz
может быть записано в виде
t^+r^/Sz *).
*) Поворот (или зеркальный поворот) г следует отличать от радиуса-
вектора г.

§ 30]	ПРЕДСТАВЛЕНИЯ ПРОСТРАНСТВЕННЫХ ГРУПП	89
Поэтому.
t (/у2) = TAgigz) е~т *>+гл) =
C0,7)
По определению группы Ofc элемент г~1 либо не изменяет век-
вектор k, либо переводит его в эквивалентный вектор путем прибавле-
прибавления некоторого вектора 6Х обратной решетки
Подставляя это выражение для г~'й в C0,7), получим:
Т Оч) t (г2) = t (гЛ) в«л.	C0,8)
Введем понятие нагруженного представления. Если каждому эле-
элементу г некоторой группы сопоставлен оператор Т(г), причем
Т(г1)Т(г2) = Т(г1г2)ф(г1. г2),	C0,9)
где ty{ru r2) — некоторая функция, то такое соответствие будем
называть нагруженным представлением. Если ф=1, то нагружен-
нагруженное представление превращается в обычное представление. Соотно-
Соотношения C0,6) и C0,8) показывают, что обычные представления Тл
пространственной группы Ок тесно связаны с нагруженными пред-
представлениями точечной группы Gu- Прежде чем идти дальше, отме-
•тим два важных частных случая, в которых нагруженное предста-
представление C0,8) сводится к обычному представлению.
1.	Все векторы a (g) (g?G/t) содержатся в подгруппе трансля-
трансляций IT группы G. В этом случае все скалярные произведения Ь&г
кратны 2тг и множитель eib2fX'=l.
2.	Элементы группы Ofc не изменяют вектор k: r~1k=k. При
этом все векторы bl = 0 и e'Va = l. Этот случай имеет место,
в частности, тогда, когда вектор k лежит внутри зоны Бриллуэна.
Действительно, вектор r~lk при этом тоже лежит внутри зоны
Бриллуэна и эквивалентен вектору к. Между тем внутри зоны
Бриллуэна не существует ни одной пары различных эквивалентных
векторов. Поэтому r~lk = k.
Из соотношения C0,6) следует, что каждому неприводимому предста-
представлению xhp группы Од, соответствует неприводимое нагруженное пред-
представление той же размерности tp группы Gh. Индекс р можно рас-
рассматривать как номер нагруженного представления точечной группы О&.
Если Т*; — приводимое представление, то для того, чтобы разло-
разложить его на неприводимые представления, достаточно разложить
нагруженное представление Т(г) на неприводимые нагруженные
представления ip(r). Разумеется, в тех случаях, когда нагруженные

90	ПРЕДСТАВЛЕНИЯ НЕКОТОРЫХ ГРУПП	[ГЛ. V
представления превращаются в обычные, нет никакой необходи-
необходимости рассматривать их как нагруженные представления.
Нахождение неприводимых нагруженных представлений точечных
групп производится весьма просто в каждом конкретном случае.
В § 38 на двух примерах иллюстрируются методы нахождения
нагруженных представлений. Что касается разложения приводимого
нагруженного представления на неприводимые, то оно производится
не сложнее, чем в случае обычных представлений. Для того чтобы
выяснить, как именно это делается, рассмотрим кратко некоторые
свойства нагруженных представлений.
Понятия эквивалентности, приводимости и неприводимости непо-
непосредственно переносятся на нагруженные представления. Каждое на-
нагруженное представление эквивалентно унитарному, если \ty(rlt /-2)|=1.
Это условие выполняется в интересующем нас случае C0,8). Спра-
Справедливость этого утверждения доказывается совершенно так же,
как и для обычных представлений. Поэтому всякое нагруженное
приводимое представление распадается на сумму неприводимых
представлений.
Функция <]>(rlf г2) должна удовлетворять функциональному
уравнению
Л. 'з).	C0>10)
которое немедленно получается из сравнения следующих двух
тождеств:
Т (гх) Т (г2) Т (г,) = Т (гх) Т (г2г3) ф (г2> г,) = Т (r,r2r3) <]> (г2, /¦,) ф (rx, r2r3),
Т (г,) Т (г2) Т (г,) - Т (г1Г2) Т (г,) <|> (rlt r2) = Т (г^Гз) ф (/у2> г3) ф (гх. г2).
Если иметь в виду это уравнение, то легко проверить, что оператор
где В — произвольный оператор, коммутирует со всеми операторами
нагруженного представления. Отсюда для унитарного неприводимого
представления размерности 5 получается соотношение ортогональности
C0,12)
Вывод этого соотношения чрезвычайно похож на вывод соотно-
соотношения ортогональности в обычной теории представлений. Совершенно
аналогично получается соотношение ортогональности для неэкви-
неэквивалентных неприводимых представлений
1
J7
г

§ 30] ПРЕДСТАВЛЕНИЯ ПРОСТРАНСТВЕННЫХ ГРУПП	91
Отсюда. вытекают соотношения ортогональности для	характеров
неприводимых представлений
i 2 у^ = 8.?.	C0,14)
Число та, показывающее, сколько раз неприводимое представле-
представление с характером у№ (г) содержится в приводимом представлении
с характером х(г)> равно
<30-16)
Если известны все неприводимые нагруженные представления чр
точечной группы дк, то легко выяснить, сколько раз произвольное
представление Т» группы Gk содержит неприводимое представле-
представление ihp. Из формул C0,6) и C0,15) следует, что
е-ци,г«) (g = tj). C0,16)
Если среди нагруженных представлений данной группы есть
хотя бы одно одномерное представление /, то между нагруженными
представлениями -zp и обычными представлениями tp существует
.простая связь
kp{r) = x{r)tp(r),	C0,17)
немедленно вытекающая из определения C0,9).
Однако в ряде случаев у группы может не быть ни одного
одномерного нагруженного представления (напомним, что среди
обычных представлений всякой группы всегда имеется по крайней
мере одно одномерное представление, а именно, единичное предста-
представление). В связи с этим возникает очень существенный для теории
кристаллов вопрос, в каких случаях группа Gk не имееу одномер-
одномерных представлений хк. Не имея возможности исчерпывающе решить
здесь этот вопрос, мы приведем следующий простой критерий:
если пространственная группа G имеет хотя бы одну нетривиаль-
нетривиальную винтовую ось или плоскость скольжения и содержит инверсию,
то можно выбрать вектор k так, чтобы все представления %к группы Gk
были многомерными.
Докажем справедливость этого критерия. Пусть gi^_G— какой-
либо винтовой поворот или отражение со скольжением. Обозначим
через Ь один из тех векторов обратной решетки, которые не изме-
изменяются под действием элемента gt. Выберем в качестве вектора k
вектор -н-й: ? = —&. Ясно, что gtk = k и \k——k = k — b. Эти

92	ПРЕДСТАВЛЕНИЯ НЕКОТОРЫХ ГРУПП	[ГЛ. V
соотношения показывают, что элементы gt и / входят в группу (?&.
Запишем теперь gl в виде произведения
где г — какой-либо поворот или зеркальный поворот вокруг центра
инверсии. Вычислим произведение J^l
Если бы у группы Gfc существовало одномерное представление
хк = у, то мы получили бы:
Oxter1)* @=1.
т. е.
ei(k. 2«)= i_	C0,18)
Если gj есть винтовое вращение, то вектор я имеет компоненту
вдоль винтовой оси, причем эта компонента не входит в подгруппу
трансляций. Поэтому Ья ф 2т.т (т — 0, dz 1. • •.) и равенство C0,18)
не может иметь места. Если gr есть плоскость скольжения, то ком-
компонента вектора я в этой плоскости не содержится в подгруппе
трансляций. Поэтому вектор Ь можно выбрать так, чтобы Ъ%ф1ът
(т— 0, z+z 1, ±2, ...) и мы видим, что равенство C0,18) невоз-
невозможно и в этом случае. Полученное противоречие показывает, что
одномерные представления группы Gfc в рассматриваемом случае
отсутствуют.
В заключение параграфа найдем критерий вещественности непри-
неприводимого представления т пространственной группы G.
В § 23 был получен критерий вещественности произвольной
конечной группы. Для того чтобы его можно было применить
к пространственным группам, содержащим бесконечное множество
элементов, необходимо предварительно сделать одно замечание.
Будем пока считать, что векторы k, составляющие звезду пред-
представления, рациональным образом выражаются через основные век-
векторы обратной решетки
При этом количество различных операторов t(g) ig^G) конечно.
Эти операторы образуют группу Ot и одновременно представление
этой группы. Так как группа О] конечна, то к ней можно приме-
применить критерий вещественности. Вычислим сумму, фигурирующую
в этом критерии,
S^iiXig2)	C0,19)

§ 30]	ПРЕДСТАВЛЕНИ ПРОСТРАНСТВЕННЫХ ГРУПП	93
(суммирование производится по всем тем g?G, для которых опе-
операторы t(g) различны). Для этого запишем х(^2) в
fe	(
и подставим в C0,19). Мы получим, изменяя порядок суммирования,
У неприводимой звезды \k) все векторы k равноправны. Поэтому
все слагаемые, стоящие под знаком суммы по J, равны между
собой и, следовательно,
(	<)	C0,20)
где а — число существенно различных векторов в звезде [k].
Учтем теперь, что (х (g2) e\, el\ = 0, если g2ftx ф kx (см. C0,4)).
Поэтому суммирование в C0,20) можно производить только по тем
элементам g, квадрат которых содержится в группе вектора kv
С другой стороны, если gz€.Qkj. то 2 ("= (gz)el> el) = Xhl(S2)- Эти
два обстоятельства позволяют записать сумму C0,20) в виде
Полученную формулу можно значительно упростить, если при-
принять во внимание, что каждый элемент g группы О равен произ-
произведению
g — htiya^. m.2a.,~vi2afi
некоторой трансляции tmia.+mtai+miaa на один из п элементов
hv h2	hn	C0,21)
{п — число элементов точечной группы О).
Ясно, что
g z=z: *«?,«!-гт2й2+ягаалч \(т±а1~т.2аг\ maas)"-
И
7 (Я2) = e^fc" "*j<ll+}Baaii+J«aa«+J«1ha1+niahaI1+™abea)y (fl2).
Перепишем теперь S в виде
р. р, Р3
5-= о S Z* (А) 2 2 2 е<<^ь-^ЯА+«!л+вд), C0,22)
В первой сумме суммирование производится по тем элементам /г из
C0,21), квадрат которых содержится в группе G^.. Внутренняя

94	ПРЕДСТАВЛЕНИЯ НЕКОТОРЫХ ГРУПП	[ГЛ. V
сумма по щ, т2 и тъ представляет собой произведение трех про-
прогрессий, знаменатели которых равны соответственно
01 = е*(*,+ь-Ч. «О, g2 = ei(bI+h-1fc11as)t ^3 = giCfcx-rb-V. »з). C0,23)
Легко видеть, что qT*> = q%* — qf»= 1. Поэтому сумма по mv
т2, т3 в C0,22) равна PiP2p$. если ql = q2 = <73= 1; если же- хотя бы
одно из трех чисел qx, q2, q% отлично от единицы, то сумма равна
нулю. Поэтому
3 % 7.
где суммирование производится по тем элементам из C0,21), кото-
которые обращают в единицу числа qv q2, q3.
Легко, однако, видеть, что числа C0,23) одновременно обра-
обращаются в единицу в том и только в том случае, если
или, что то же самое,
hftlS=s —*!.	C0,24)
Заметим, что из этого условия вытекает соотношение
Окончательно для S получается следующее выражение:
где А/ = npip2pa — число элементов группы Gv
Применяя критерий вещественности, получим:
( 1, если т вещественно;
— V /к (А2) = < 0, если х не эквивалентно х\
hfc,=-fc,	j—j_ если <[ эквивалентно t, но не
вещественно;
суммирование производится здесь по тем элементам C0,21), кото-
которые переводят вектор kl в вектор, эквивалентный — kv
Полученный критерий остается в силе и для неприводимых пред-
представлений с произвольной звездой. Это следует из соображений
непрерывности, если учесть, что в произвольной близости любого
вектора k0 имеется вектор k с рациональными координатами, группа
которого совпадает с группой вектора kQ.

ГЛАВА VI
МАЛЫЕ КОЛЕБАНИЯ СИММЕТРИЧНЫХ СИСТЕМ
§ 31. Главные координаты и собственные частоты
Решение задачи о малых колебаниях механической системы мо-
может быть значительно упрощено, если система обладает той или
иной симметрией. Это упрощение достигается путем применения
методов теории представлений.
Мы будем рассматривать системы, состоящие из конечного
числа точек. Условно будем называть такие системы молекулами,
а точки — атомами. Число атомов в молекуле обозначим через п.
Если молекула выведена из состояния равновесия, то поло-
положения ее атомов можно характеризовать п радиусами-векторами
tj(j=l, 2, ..., га), каждый из которых мы условимся проводить
из равновесного положения соответствующего атома.
Радиусы-векторы rj{J=l, 2, ..., га) в своей совокупности ха-
характеризуют отклонение всей молекулы. Это отклонение мы обо-
обозначим через г, так что г есть совокупность п трехмерных векторов
и поэтому может рассматриваться как вектор в Зя-мерном про-
пространстве. Это пространство мы будем называть пространством
отклонений молекулы и обозначать через М.
Если все атомы молекулы колеблются по гармоническому закону
с одной и той же частотой и фазой
Tj — а$ cos (Ы -f- a),
то такое движение называется главным колебанием. Главное коле-
колебание характеризуется, таким образом, набором амплитуд о,- и ча-
частотой со. Как известно из механики, всякое движение системы, со-
совершающей малые колебания, можно представить в виде
Зп
П = 2 А„а) cos К* + а*),	C1,1)
ft"-1
т. е. в виде суперпозиции Зга главных колебаний
г* = a) cos Ы + ак) (/=1,2,..., Зга).	C1,2)
Коэффициенты Ак и ак определяются из начальных условий.

*96	МАЛЫЕ КОЛЕБАНИЯ СИММЕТРИЧНЫХ СИСТЕМ	[ ГЛ. VI
Частоты
ш1( со2, . . ., шзп,
с которыми совершаются главные колебания, называются собствен-
собственными частотами системы.
Равенства C1,1) и C1,2) можно переписать в виде
rk = ak cos H/+ <**).
з»
1с-1
Будем говорить, что вектор ак?Ж характеризует главное коле-
.бание с частотой шк.
Рассмотрим случай, когда несколько различных главных коле-
колебаний имеют одну и ту же частоту.
Всякая суперпозиция таких колебаний
г — (%Акак) cos (со/ + а)
в свою очередь является главным колебанием с той же частотой
(штрих над знаком суммы означает, что сумма берется только по
главным колебаниям с частотой ш). Отсюда следует, что совокуп-
совокупность векторов, характеризующих главное колебание с данной ча-
.стотой, образует линейное подпространство Мш в пространстве М.
Размерность пространства Мщ называется кратностью частоты со.
Ясно, что пространство М является суммой подпространств Мш,
соответствующих различным собственным частотам со.
Обозначим через G группу симметрии неподвижной молекулы
в состоянии устойчивого равновесия.
Каждый поворот (или зеркальный поворот) g из группы G пере-
переводит выведенную из равновесия Оолекулу одной конфигурации
в некоторую, вообще говоря, другую конфигурацию. При этом
вектор г, характеризовавший отклонение молекулы до поворота, пе-
переходит в результате поворота в некоторый вектор гд.
Если ввести в рассмотрение линейные операторы T(g)(g?G),
.определяемые равенством
и сопоставить каждому элементу g оператор Т (g): g -*¦ Т (g), то мы
получим представление группы G, называемое механическим пред-
представлением. Характер механического представления принимает только
действительные значения.
Если в пространстве М определить скалярное произведение,
доложив
Ci, '¦2)=ij(ry), rf)

§ 32]	СИММЕТРИЧЕСКИЕ КООРДИНАТЫ	97
(здесь (г'.1), К2)) — обычное скалярное произведение), то все опера-
операторы механического представления окажутся унитарными, так как
относительное расположение двух отклонений молекулы гх и г2 не
изменяется при одновременном повороте.
Весьма существенно, что каждое из подпространств Мш инва-
инвариантно относительно операторов T(g)(g ?G). Это следует из того,
что при одновременном повороте или зеркальном повороте всех ато-
атомов их относительное расположение не изменяется. Поэтому, если
до поворота молекула совершала главное колебание с частотой ш,
то после поворота все атомы молекулы будут продолжать колебаться
с той же частотой.
Обозначим через Тщ представление группы G, по которому пре-
преобразуется подпространство Мш. Если представление Тш приводимо,
то его можно разложить на неприводимые представления. В соот-
соответствии с этим подпространство М„> можно разложить на непри-
неприводимые подпространства
м„ = mL1'+mL2) + • • • -+- mS?.
Выбирая в каждом подпространстве Мш' базис
а[», af	а<Л
и объединяя все такие базисы, мы получим базис в пространстве М.
Каждый вектор построенного базиса характеризует некоторое глав-
главное колебание.
Таким образом, мы получаем Зге главных колебаний, каждое из
которых относится к одному из неприводимых представлений группы О.
Тем самым главные колебания классифицируются по неприводимым
представлениям группы О.
§ 32. Симметрические координаты
С помощью теории представлений можно существенно упростить
вычисление собственных частот и нахождение главных колебаний.
Это упрощение достигается путем введения так называемых сим-
симметрических координат. Если функцию Лагранжа молекулы выразить
в симметрических координатах, то она, вообще говоря, распадается
на несколько «элементарных функций Лагранжа», каждая из которых
зависит лишь от части обобщенных координат. Это, как пра-
правило, существенно облегчает нахождение малых колебаний мо-
молекулы.
В этом параграфе мы покажем, как, зная все неприводимые
представления группы О, найти симметрические координаты.
Для того чтобы можно было пользоваться теорией представле-
представлений, расширим формально действительное пространство М до соот-
соответствующего комплексного пространства Мс, которое состоит из
7 Зак. 3512. Г. Я. Любарский

98	МАЛЫЕ КОЛЕБАНИЯ СИММЕТРИЧНЫХ СИСТЕМ	[ГЛ. VI
всевозможных выражений вида rx-f- 1гг(гх, г2?Ж). Два элемента
Г] + /г2 и гх— 1гг(гх, г2?М) будем называть комплексно-сопряжен-
комплексно-сопряженными. Те элементы Мс, которые содержатся в М, будем называть
вещественными. Операторы T{g) доопределим на комплексных эле-
элементах, положив
Т (g) A4 + ir2) = T (g) r, + ГЕ (g) r2.
Из этого определения следует, что
= Т(*)г,	C2,1)
где черта означает переход к комплексно-сопряженному вектору.
Легко видеть, что распространенные таким образом на простран-
пространство Ме операторы t(g) по-прежнему осуществляют представление
группы G.
Разложим пространство Мс на неприводимые подпространства
Мо = Mt + М2 + ... + Мв.	C2,2)
Пусть Mj—одно из таких подпространств. Ясно, что комплексно-
сопряженное подпространство Mj также является неприводимым под-
подпространством. Поэтому подпространства Mj и М^ либо совпадают,
либо не имеют ни одного общего вектора (кроме нуль-вектора).
В первом случае, когда Mj = Mi, в Мг существует действитель-
действительный базис. В самом деле, пусть е\, е\	 е[ —какой-либо базис
в Мг = Мг. Образуем 2sz вещественных векторов
а* =Л?е 4 = -j («* + **>• bk^lme\^~(ei — e'k) C2,3)
(ft=l, 2, .... Sl),
принадлежащих Mj. Каждый вектор а из Мг можно представить
в виде линейной комбинации векторов C2,3)
а =
к	к
Поэтому среди векторов C2,3) существует sz линейно независи-
независимых векторов. Они и образуют вещественный базис в Мг.
Во втором случае, когда Мг ф Мг, сумма подпространств
Mj-f-Mj имеет 2$г измерений. При этом все векторы C2,3) линейно
независимы.
Если представление te, по которому преобразуется подпростран-
подпространство Mj, невещественно, то первый случай не может иметь места.
В самом деле, если Mj = Mj, то в Мг существует вещественный
базис, в котором все операторы представления та выражаются
с помощью вещественных матриц.

§ 32]	СИММЕТРИЧЕСКИЕ КООРДИНАТЫ	99
Условимся в этом случае разложение C2,2) производить таким
образом, чтобы вместе с подпространством Мг оно содержало и
сопряженное подпространство Мг. Базис
pi pi	pi
подпространства Мг будем считать комплексно-сопряженным базису
ег ei	ег
ev ei	еч
подпространства Mj:
4 = 4 (*=1. 2	si).	C2,4)
Если представление ха, по которому преобразуется под-
подпространство Мг, вещественно, то возможны оба случая: Мг = Мг и
Мг ф Мг. В первом случае в пространстве Мг существует, как мы
показали, вещественный базис. Во втором случае мы разобьем
сумму Mj-f-M на два подпространства
где Мг — линейная оболочка векторов агк = -^(е\-\-е\), Мг'—линей-
Мг'—линейная оболочка векторов Ьк = -тр (?к—ек)- Каждое из этих подпро-
подпространств преобразуется по одному и тому же представлению т„.
В самом деле, в силу C2,1) имеем, например:
_
(g) егт = 2 zmk ig) ^m-
2
Итак, Мг и Мг являются неприводимыми подпространствами, имею-
имеющими вещественные базисы. Мы видим, что и в случае Мг ф Mj воз-
возможно такое разбиение пространства Мс, при котором все подпро-
подпространства Мг, преобразующиеся по вещественным представлениям,
имеют вещественные базисы.
В дальнейшем мы будем предполагать, что C2,2) является именно
таким разбиением. Таким образом, мы будем считать, что у под-
подпространств, преобразующихся по вещественному представлению,
базис состоит из вещественных векторов.
Введем обозначения
q\(r) = {r, e\) (ft=l, 2,..., Sl\ /= 1, 2	q). C2,5)
Набор Ъп чисел qk{r) вполне характеризует отклонение г и потому
может служить набором обобщенных координат. Построенные, та-
таким образом, обобщенные координаты называются симметрическими.
7*

100	МАЛЫЕ КОЛЕБАНИЯ СИММЕТРИЧНЫХ СИСТЕМ	[ГЛ. VI
§ 33. Выражение функции Лагранжа в симметрических
координатах
В приближении теории малых колебаний потенциальная энергия
молекулы является однородной квадратичной функцией обобщенных
координат. Выразим ее в симметрических координатах
и = т S ***^*{г) ^Г) *}-	C3> 1}
klk'V
При поворотах g?G (как и вообще при любых перемещениях мо-
молекулы как целого) потенциальная энергия не изменяется, так как
не изменяются расстояния между атомами. Это обстоятельство
существенно ограничивает возможные значения коэффициентов Ь^.
Для того чтобы убедиться в этом, подставим в C3,1) T(g)r = rg
вместо г
U = 1 S *"*>9* {rs) & (^}-	C3>2)
klk'V
Заметим, что
= ( г,
и перепишем C3,2) в виде
(г).
'ig)bllk- qlm (r) qlm> (r).
ЫткЧ'т'
Левая, а следовательно, и правая часть этого равенства не зависит
от g?G. Поэтому, производя усреднение по g и вспоминая свой-
свойства ортогональности матричных элементов неприводимых представ-
представлений, получим:
klmk'l'm'
(а — номер неприводимого представления, по которому преобразуется
подпространство Мг; s* — его размерность).
Обозначая
1k = biV,	C3,3)
к
получим окончательно:
U = T% ]? %Ь1гдгт{г)~дпг).	C3,4)
а I, Г ?ос т
*) Такой вид потенциальной энергии следует из ее вещественности.

§33] ВЫРАЖЕКИЕ ФУНКЦИИ ЛАГРАНЖА В СИММЕТРИЧЕСКИХ КООРДИНАТАХ 101
Запись /, Г?а означает, что каждое из подпространств М^ и
Мг- преобразуется по неприводимому представлению тв группы О.
Обратим внимание на две особенности выражения C3,4) потенциаль-
потенциальной энергии U в симметрических координатах:
1)	потенциальная энергия равна сумме квадратичных форм иа{г),
из которых каждая зависит только от симметрических координат,
связанных с каким-либо одним неприводимым представлением чл
группы О;
2)	квадратичная форма ия(/") в свою очередь распадается на sa
квадратичных форм
и'»=ЛЛ'М <w=i-2	*•>
с совершенно одинаковыми коэффициентами.
Аналогичный вид имеет выражение кинетической энергии Т
в симметрических координатах
Поэтому и функция Лагранжа L=T—U имеет следующий про-
простой вид:
*-=-2М?«. km).	C3,5)
a, >/i
где
Выражение C3,5) для функции Лагранжа поддается дальнейшему
упрощению, если представление Т содержит невещественные пред-
представления. Пусть хл — одно из таких представлений. Пусть Mj—не-
Mj—неприводимое подпространство, преобразующееся по представлению хя,
а Мг — комплексно-сопряженное подпространство. Координаты qm(r)
и фт (г) комплексно-сопряжены при действительных отклонениях
Ягт^ = Я1п(г) (т=1, 2	s,; л?М)	C3,7)
в силу C2,4). Выпишем сумму двух элементарных функций Ла-
Лагранжа, связанных с этими координатами

102	МАЛЫЕ КОЛЕБАНИЯ СИММЕТРИЧНЫХ СИСТЕМ	|ГЛ. VI
Учитывая C3,7), эту сумму можно переписать при действительных
отклонениях так:
Итак, вместо суммы двух элементарных функций мы получили одну
элементарную функцию.
Ввиду того, что функция Лагранжа принимает при действитель-
действительных отклонениях только вещественные значения, коэффициенты
Aw=aiv+aTT и вн'=й
можно считать эрмитовыми. Это означает, что
AVi = Aiy, Bvl = Bw.	C3,8)
Итак, каждому вещественному представлению та размер-
размерности sa соответствует sa элементарных функций Лагранжа
с одинаковыми коэффициентами. Каждая из этих элементарных
функций зависит от аа вещественных симметрических координат
(аа — число, показывающее, сколько раз представление та содер-
содержится в Т).
Каждой паре комплексно-сопряженных невещественных пред-
представлений т„ и ta размерности sa соответствует sa элементар-
элементарных функций Лагранжа. Каждая из этих функций зависит от аг
невещественных симметрических координат.
Общее число координат, от которых зависит функция Лагранжа,
равно Зга, если каждую невещественную координату считать за две
координаты.
Для вычисления собственных частот нужно привести каждую
элементарную функцию Лагранжа L^{qm, qm)^I.am к сумме квад-
квадратов
где Qjm — некоторая линейная функция от симметрических коорди-
нат «4
Qjm = S Cjrfm.	C3,9)
S
Коэффициенты Cji не зависят от т, так как элементарные функ-
функции Лагранжа с одинаковым индексом а и различными индексами т

§ 33] ВЫРАЖЕНИЕ ФУНКЦИИ ЛАГРАНЖА В СИММЕТРИЧЕСКИХ КООРДИНАТАХ 103
имеют одинаковые коэффициенты. По этой же причине числа
и maj не зависят от т. Подставляя C2,5) в C3,9), получим:
= (г, S C$4.) = (г, вЬ).
C3,10)
где
«$»=2с&&.	(зз.П)
Набор векторов
е?„ ej,	е3.в	C3,12)
преобразуется по тому же представлению тв, что и векторы
еь 4	е' • Это следует из того, что коэффициенты С]г не за-
зависят от т.
.Цели представление ta вещественно, то вещественны и числа Q]m.
В этом случае элементарная функция Лагранжа равна
"т — La ~2~ ™т ~~ "Чгб1»/!
а координаты Qjm называются главными.
Если представление х„ невещественно, то числа Qjm являются
комплексными. Вводя обозначение
Qjm = QjjmI ~ lQjm.2,
а3 1 , P*j ГДа!	2
1 )
j j ¦
перепишем Z.aTO в виде
"а
l
В этом случае главными координатами являются Qjml и Qjrm- Всего
мы получаем, таким образом, 2>п главных координат.
Из уравнений Лагранжа следует, что если все главные коорди-
координаты, кроме одной, скажем Qjm\, равны нулю, то молекула совер-
совершает главное колебание с частотой maj.
Отсюда следует, что частота ш^- вырождена «„-кратно, если
представление чл размерности sa вещественно. Если представление та
невещественно, то частота шв^ вырождена 2«а-кратно.
Итак, каждому вещественному представлению ха размер-
размерности sa, если оно содержится в Т оа раз, соответствует aa
частот, каждая из которых вырождена s^-кратно; каждой паре
невещественных представлений ха и ха размерности sa соответ-
соответствует aa частот, каждая из которых вырождена 2sa-Kpamno.

104	МАЛЫЕ КОЛЕБАНИЯ СИММЕТРИЧНЫХ СИСТЕМ	[ГЛ. VI
Мы видим, что, разлагая представление Т на неприводимые,
можно узнать кратности собственных частот молекулы.
Покажем, что для фактического вычисления коэффициентов aw
и Ьц>, характеризующих элементарную функцию Лагранжа Lam, нет
необходимости находить все симметрические координаты. Оказы-
Оказывается достаточным определить только те оа векторов е1х (/?<*),
которые соответствуют представлению та.
Действительно, пусть функция Лагранжа молекулы задана в де-
декартовых координатах Xj, yj, Zj (y=l, 2	п). Будем предпо-
предполагать, что все базисные векторы ет ортонормированы. Тогда про-
произвольное отклонение г молекулы можно представить в виде
г = У, а1 е1 .
,-^J "mm
I, m
С другой стороны, это же отклонение можно записать и так:
где i^ — такое отклонение молекулы, при котором (л-й атом имеет
единичное смещение в направлении оси ОХ, а все остальные атомы
не смещены; аналогичный смысл имеют отклонения Д и k^.
Приравнивая оба эти выражения для г и умножая скалярно по-
полученное равенство на I , находим:
•*v=2?» 04. v)-
I
Таким же образом получаем соотношения
У п. = 2 1т (elk, Л). ^ = 2 Ят («4. kj.
l,m	ltm
Если подставить эти выражения в функцию Лагранжа, а затем по-
положить равными нулю все симметрические координаты, кроме q%
, то получится элементарная функция Lal. Очевидно, что
l
можно сначала положить в выражениях для х^, у^ и z^ все qlm
равными нулю, кроме q\ (/?a), a затем подставить полученные
таким образом выражения
7i №. О. J'. = S Ч\ {е\, /J, ^ = ^q\ (e\, k^) C3,13)
в функцию Лагранжа.
§ 34. Колебательное представление
С точки зрения теории малых колебаний молекулы шесть коор-
координат из общего числа Ъп являются паразитическими, так как они
соответствуют перемещениям молекулы как единого целого без изме-
изменения взаимных расстояний между атомами. В приближении теории

34]	КОЛЕБАТЕЛЬНОЕ ПРЕДСТАВЛЕНИЕ	105
малых колебаний этим координатам соответствуют «частоты», рав-
равные нулю. Естественно, что эти «частоты» и соответствующие им
главные координаты не представляют никакого интереса и должны
быть как можно ранее исключены из рассмотрения.
Займемся сначала поступательными отклонениями молекулы.
Каждое такое отклонение ас М характеризуется тем, что смещения
всех атомов ri{a) равны между собой,
гг(а) = гк(а) (l,k=\,2	п).
Совокупность всех таких отклонений образует трехмерное подпро-
подпространство, которое мы будем обозначать через II. Подпростран-
Подпространство II инвариантно относительно всех операторов Т(g) механиче-
механического представления.
Поэтому, для того чтобы избавиться от трех координат, описы-
описывающих поступательное перемещение молекулы, достаточно рассма-
рассматривать механическое представление не во всем пространстве Мс,
а в ортогональном к П дополнении.
Подобным же образом исключим три координаты, описывающие
повороты молекулы как целого. Отклонение, связанное с поворо-
поворотом молекулы вокруг некоторой оси 00' на малый угол ср> выра-
выражается формулой
где ер—вектор, направленный вдоль положительного направления
оси поворота и равный по величине углу поворота, a /?j—радиус-
вектор i-го атома в положении равновесия, проведенный из точки О.
Так как каждое малое вращение характеризуется с помощью
этой формулы вектором ср, то совокупность всех вращений моле-
молекулы как целого образует в приближении теории малых колебаний
трехмерное линейное пространство. Будем обозначать это подпро-
подпространство через 2.
Подпространство Q—инвариантно относительно всех операто-
операторов T(g) механического представления.
Поэтому подпространство М', являющееся ортогональным допол-
дополнением в пространстве Мс к сумме поступательного и вращательного
подпространств, есть инвариантное подпространство. Размерность
пространства М' равна Зп—6. Представление ТУ, индуцируемое
механическим представлением в подпространстве М', будем назы-
называть колебательным представлением.
Характер %' колебательного представления связан с характером ?
механического представления следующим очевидным соотношением:.
где Zn Uf) и Zsfe') — характеры представлений, индуцируемых меха-
механическим представлением в подпространствах II и 9 Вычислим
характер yf колебательного представления. Для этого определим

106	МАЛЫЕ КОЛЕБАНИЯ СИММЕТРИЧНЫХ СИСТЕМ	[ГЛ. VI
X. Хц и Xs- Выберем в качестве базиса в пространстве Мс введен-
введенные на стр. 104 отклонения
Zm> Jmy km (m—l, 2	n).
Рассмотрим отклонение Т (g)im. Так как при отклонении im была
•смещена только одна точка (точка с номером /я), то при отклоне-
отклонении T(g)?m тоже смещена только одна точка — та, в которую под
действием операции g переходит точка т. Поэтому, обозначая
номер этой последней через т', можем написать:
-	C4,2)
¦Сравнивая это соотношение с тождеством
замечаем, что в столбце, соответствующем базисному вектору 1т
отличны от нуля только три матричных элемента
Поэтому, если т' ф т, то диагональный элемент этого столбца
равен нулю и может не приниматься во внимание при вычислении
следа матрицы T(g). Итак, при вычислении следа матрицы T(g)
следует учитывать только те атомы, узлы которых, т. е. положения
равновесия, остаются на месте под действием операции g.
Пусть g = C9 есть поворот на угол ср и узел атома т непо-
неподвижен относительно этой операции. Если направить ось OZ вдоль
оси вращения, то равенство C4,2) примет следующий вид:
Т (С?) lm = cos ср 1т Ч- sin cp jm.
¦Следовательно, диагональный элемент в строке, которая соответ-
соответствует базисному вектору 1т, равен cos ср. Действуя оператором
поворота Т(С,р) на векторы jm и km, получим:
Т (С,) = — sin cp/TO -+- cos cpym. T (C9) km = km.
Соответствующие диагональные элементы равны cos<p и 1. Таким
образом, сумма диагональных элементов, стоящих в трех столбцах,
соответствующих частице т, равна 1-j- 2 cos ср. Очевидно, что весь
след матрицы Т (С?) равен
X(C?)=-«c(l+2cos?),	C4,3)
где пс есть число атомов, узлы которых остаются неподвижными
при операции поворота Сг

§ 34]	КОЛЕБАТЕЛЬНОЕ ПРЕДСТАВЛЕНИЕ	107
Если операция g есть зеркальный поворот S9 на угол ср и узел т
неподвижен относительно S?, то для подсчета характера хОЯр) сле-
"дует исходить из тождеств
Т (S9) im = cos ср im -f- sin tp jm,
T (S?)ym = — sin cp im + cos ? jm,
которые немедленно приводят к формуле
oscp),	C4,4)
где ns — число атомов, узлы которых остаются неподвижными при
зеркальном повороте.
Вычислим характер Хд (§")• Для этого выберем в пространстве П
в качестве базиса отклонения i, j, k, где / — отклонение, при
котором все атомы смещены на единицу длины в направлении
оси ОХ, аналогичный смысл имеют отклонения j и k. Ясно, что
эти три базисных вектора преобразуются друг через друга как
три взаимно-ортогональных вектора в евклидовом трехмерном про-
пространстве. Поэтому характер хп (g) определяется формулами
/n(C?)=l+2coscp, Xn(ST)=~- l-t-2coscp. C4,5)
Обратимся теперь к представлению в подпространстве 2. Для
вычисления характера этого представления введем в подпростран-
подпространстве 2 базис <рж, cpj/i ?E- Здесь срж означает поворот на единичный
(малый) угол вокруг оси ОХ; соответствующий смысл имеют базис-
базисные векторы еру и срг. Если g = C^ есть поворот молекулы на угол ср
вокруг оси OZ, то, как легко видеть, отклонения ух, срр, срг преоб-
преобразуются так же, как три единичных взаимно-ортогональных вектора
в евклидовом пространстве, т. е. по формулам
i срж= cp^cos ср -j- cpysin ср, |
T(C9)<py= —«Pa-slncp + ^cos?, \	C4,6)
Поэтому
Xa(C,)=l+2cos<p.
Под действием отражения в плоскости XOY поворот срг, очевидно,
не изменяется, а повороты срж и tpw меняют свое направление:
t(°zof) ?» = —

108
Так как
Поэтому
МАЛЫЕ КОЛЕБАНИЯ СИММЕТРИЧНЫХ СИСТЕМ	1ГЛ. VI
то, объединяя эти формулы с C4,6), находим:
<?.„ = — Та, cos ср — ср„ sin ср,
Т) ?„ = <?* sin <р — сру cos ср,
C4,7)
§ 35. Пример. Молекула СНС13
Рассмотрим малые колебания молекулы СНС13. Группой симме-
симметрии её является C3v- Напомним, что C3v состоит из шести элемен-
элементов: е, С3, С3, з1, <з2 и а3. По формулам предыдущего параграфа
определяем характеры xM(g0> Xn(g)> Xq(S) и х'(g). Получаем табл. 8.
Таблица 8
Характеры хм> Хп> Х2 и х'
Таблица 9
Характеры неприводимых
представлений группы С3„
-х
м
*
X'
е
15
3
9
с,, с»
0
0
0
0
• з
1
— 1
3
с.
"$ л
у
е
1
1
2
Г С2
1
1
	 1
1
— 1
3
Рядом для удобства помещена таблица 9 характеров всех трех не-
неприводимых представлений группы С3„. С помощью формулы B0,3)
вычисляем, сколько раз содержится
каждое из неприводимых представле-
представлений в представлениях Тм, ТП,Т2 и Т'.
Получаем таблицу 10.
Из последнего столбца этой таб-
таблицы видно, что молекула СНС13 имеет
три невырожденные частоты и три
двукратно вырожденные частоты. Из
этого же столбца таблицы 10 видно,
что в процессе решения задачи о малых
колебаниях придется решить два ха-
характеристических уравнения третьей
степени.
Приступим к нахождению симметрических координат. Простран-
Пространство М' распадается на три одномерных подпространства, преоб-
Та
блица 10
Анализ представлений
Тм, Тп, Т2
та
ТМ
4
1
5
т„
' 1
0
1
и V
тв
0
1
1
V
3
0
3

35]
ПРИМЕР. МОЛЕКУЛА CHClg
109
разующихся по единичному представлению, и три двумерных, пре-
преобразующихся по представлению у3. Обозначим эти пространства
через Мь М2, М3 и М4, М5, Мв. Базисные векторы в первых трех
пространствах легко найти непосредственно; так как они не изме-
изменяются при всех движениях группы С31), то соответствующие им
отклонения обладают полной симметрией равновесной молекулы.
Рис. 20.
Эти отклонения изображены на рис. 20, причем смещения выбраны
так, чтобы все три отклонения были ортонормированы.
Подчеркнем, что геометрическая сумма смещений всех атомов
равна нулю в каждом из этих отклонений, как оно и должно быть,
так как все они перпендикулярны к подпространству II.
Для вычисления коэффициентов элементарной функции Ла-
гранжа Z.t следует в полную функцию Лагранжа подставить со-
согласно C3,13) следующие выражения:
1
/3 ч
7(з)
7(з)
г» = г	Ф
2	/30
г, = —— а1
3	У 30Ч
A).
Построим теперь векторы ef\	eft и ef*. С этой целью выпишем
первые диагональные элементы	матриц двумерного представления
группы С3„
С$	Со &\ ^9 ^3
ZTI	Z~L l ZT ZX
2	2 2 2

110	МАЛЫЕ КОЛЕБАНИЯ СИММЕТРИЧНЫХ СИСТЕМ	[ГЛ. VI
Оператор Рг (см. B6,8)), следовательно, равен
Pi = у Iе+т (Oi) ~i т (С^~ т т (аа) - т т (°з)) •
Применим его к трем произвольным отклонениям из М'. Возьмем
отклонения аи аг и а3, изображенные на рис. 21.
Рис. 21.
Числа а и 3 следует подобрать так, чтобы момент всех смеще-
смещений у вектора Р^ равнялся нулю. Это равносильно условию орто-
ортогональности Pta2 подпространству Q. Теперь остается ортонорми-
ровать три вектора P1fli, Pja2 и P^j и получить, таким образом,
векторы е?\ ef] и ef] (рис. 22).

ГЛАВА VII
ФАЗОВЫЕ ПЕРЕХОДЫ ВТОРОГО РОДА
§ 36. Постановка задачи
Как известно, у кристаллов существует два типа фазовых пере-
переходов. Фазовые переходы первого рода сопровождаются поглоще-
рнием или выделением скрытой теплоты, фазовые переходы второго
хода происходят без подобного выделения или поглощения и сопро-
сопровождаются скачкообразным изменением теплоемкости, коэффициента
теплового расширения и других производных от термодинамических
величин.
Общая термодинамическая теория фазовых переходов второго
рода была разработана Л. Д. Ландау [Ц. Он показал, в частности,
что изменение симметрии кристалла играет существенную роль
в этих переходах и что далеко не всякое изменение симметрии кри-
кристалла может иметь место при фазовых переходах второго рода.
Е. М. Лифшиц [4] подробно рассмотрел кристаллы и выяснил, какие
изменения класса кристалла могут сопровождать фазовый переход
второго рода.
В настоящей главе частично излагаются работы [1>4j и рассмат-
рассматривается метод расчета возможных изменений симметрии кристалла.
Симметрию кристалла можно охарактеризовать с помощью функ-
функции плотности р(х, у, z), определяющей вероятность р(х, у, z)dV
нахождения частицы в объеме dV; если кристалл состоит из частиц
нескольких сортов, то необходимо ввести несколько функций р4> по
одной функции на каждую частицу.
В дальнейшем мы будем говорить об одной функции р(х, у, z),
имея в виду, что в случае необходимости под р можно подразуме-
подразумевать многокомпонентную функцию.
Совокупность всех преобразований координат, оставляющих
функцию р инвариантной, образует пространственную группу кри-
кристалла.
Изменение давления р и температуры Т влечет за собой, вообще
говоря, изменение функции р. При фазовом переходе второго рода
плотность изменяется непрерывно, однако таким образом, что сим-
симметрия кристалла до и после перехода различна.

112	ФАЗОВЫЕ ПЕРЕХОДЫ ВТОРОГО РОДА	[ГЛ. VII
У замкнутой системы, т. е. у системы, не взаимодействующей
ни с какими внешними телами, состоянию термодинамического равно-
равновесия соответствует, как известно, максимум энтропии. Если система
не является замкнутой, но находится в некоторых фиксированных
внешних условиях, то в состоянии термодинамического равновесия
достигает экстремума не энтропия, а некоторая другая термодина-
термодинамическая функция.
В интересующем нас случае, когда фиксированы температура и
давление внешних тел, такой функцией является так называемый
термодинамический потенциал, равный
F = E—TS + pV,
где Е, S и V — энергия, энтропия и объем единицы массы. В состоя-
состоянии равновесия термодинамический потенциал принимает наименьшее
значение. Принцип минимальности термодинамического потенциала
означает, что при фиксированных давлении и температуре плот-
плотность р должна быть такой, чтобы выражение
F = F(p, T, р)
<было минимальным. Этот принцип позволяет проследить, как изме-
изменяется вид функции р при изменении р и Т.
Пусть р0, То—какая-либо точка на линии фазовых переходов
второго рода. Обозначим через ро(х, у, z) плотность кристалла при
р = р0, Т=Т0. Группу симметрии ро(х, у, z) обозначим через G.
Рассмотрим точку р, Т, близкую к точке р0, То, и обозначим плот-
плотность кристалла в этой точке через р (х, у, z). Так как при фазо-
фазовом переходе второго рода плотность изменяется непрерывно, то
можно написать:
р(х, у, г) = ро(х, у, z) + op(x, у, z),
где So стремится к нулю, когда р, Т-+р0, То.
Подействуем на функцию Ьр(г) всевозможными элементами
группы О. Мы получим инвариантное семейство функций fy(g~lr)
(g?G). Линейная оболочка всех этих функций образует простран-
пространство L, преобразующееся по некоторому представлению группы О
Расщепляя это пространство на инвариантные неприводимые под-
подпространства Lj и выбирая в каждом из них произвольный орто-
нормированный базис cp(-fc) (k = \, 2	 s}), мы получим базис
в пространстве L.
Функцию 8р(г) можно, как и всякую функцию из L, разложить
по элементам указанного базиса
Если представление tj, по которому преобразуется подпростран-
подпространство Lj, не вещественно, то функции cpt*) принимают невеществен-

§ 36]	ПОСТАНОВКА ЗАДАЧИ	113
ные значения. В этом случае мы объединим функции срС'1') с ком-
плексно-сопряженными функциями и обозначим через tj-\-tj пред-
представление, по которому преобразуется 2sj функций I»'.*', yffiX.
Представление tj-\-"Zj мы будем называть физически-неприводимым.
Можно считать, что в выражении C6,1) для ор суммирование
производится по неприводимым вещественным представлениям и по
физически неприводимым представлениям. При этом ввиду веще-
вещественности 8р коэффициенты Cjk при комплексно-сопряженных функ-
функциях yW (r) в свою очередь комплексно сопряжены.
При изменении р, Т изменяется 8р, а вместе с ним изменяется
пространство L и базисные функции <pW (г). Таким образом, функ-
функции tpt*) (r) зависят от р, Т.
Учитывая малость 8р, можно разложить термодинамический потен-
потенциал в ряд
Ф(р, Г.р) = Ф(р, Т, ро) + Ф1(р. Т, Ро, 8р) + Ф2(р, Т, ро,8р)+...,
где Ф1— линейный функционал относительно 8р, а Ф2 и Ф3 — функ-
функционалы второй и третьей степени. Используя C6,1), получим:
Термодинамический потенциал Ф, разумеется, инвариантен относи-
относительно любого поворота системы координат. Если произвести пре-
преобразование системы координат с помощью одного из элементов
группы G, то функции tp^J (У—фиксировано, k=\, 2, . . ., Sj) пре-
преобразуются друг через друга. Согласно C6,1) это линейное преоб-
преобразование функций о'/' можно трактовать как линейное преобразо-
преобразование коэффициентов С^.
Итак, при поворотах координат с помощью элементов группы Q
коэффициенты Cjk преобразуются по физически неприводимым пред-
представлениям группы О, а потенциал Ф остается инвариантным. Отсюда
следует, что Ф может зависеть только от инвариантных комбинаций
коэф ициентов С^.
Среди линейных функций от Cjk есть только один инвариант С°о,
т. е. коэффициент при функции ср«, инвариантной относительно всех
преобразований группы О. Поэтому
®i(P> Т, р0, Ьр) = С^,Ф1\р, Т, р0, еру).
Инварианты второго рода имеют следующий вид:
'J
8 Зак. 3512. Г. Я. Любарский

114	«ГАЗОВЫЕ ПЕРЕХОДЫ ВТОРОГО РОДА	[ГЛ. VII
Поэтому функционал Ф2 можно представить в виде
Ф2 (р. Т. Ро> Зр) = ^ Aj (p, T) 2 | Cjk p.
j	к
В точке р0, То все коэффициенты Cjk равны нулю, так как Зр = 0.
Воспользуемся теперь тем, что всякое изменение коэффициен-
коэффициентов Cjk может только увеличить потенциал Ф; это означает, как
легко видеть, что при р—р0, Т=Т0 коэффициент Ф1 = 0, а все
коэффициенты Aj(p, T) неотрицательны:
AjiPo. То)>0.
Если бы, однако, все коэффициенты Aj были строго положительны,
то они оставались бы такими и в некоторой окрестности Q точки
р0< То и, следовательно, в этой окрестности все коэффициенты Cjk
равнялись бы нулю и симметрия кристалла была бы одинаковой во
всех точках Q. Это противоречит предположению о том, что точка
р0, То лежит на кривой фазового перехода второго рода. Итак,
хотя бы один из коэффициентов Aj(pQ, То) (У =? 0) равен нулю.
Если точка р0, То не лежит на пересечении двух или нескольких
линий фазовых переходов второго рода, то, вообще говоря, только
один из коэффициентов, скажем А1(р0, Г()), равен нулю
А (А>. Т0)=0,	C6,2)
а остальные положительны. Действительно, уравнение C6,2) можно
рассматривать как уравнение линии фазовых переходов. Если бы
в точке р0, То обращалось в нуль несколько коэффициентов Aj, то
точка р0, То лежала бы на пересечении нескольких линий фазовых
переходов.
Равенство C6,2) означает, что, как правило, коэффициент А^(р, Т)
при переходе точки р, Т через линию фазовых переходов изменяет
свой знак. По ту сторону линии, где At > 0, все коэффициенты-
Cjk — 0 (f ф 0) и плотность о имеет ту же симметрию, что плот-
плотность р0 в точке р0, То. По другую сторону линии фазовых пере-
переходов плотность имеет следующий вид:
где функции cpW (r) преобразуются по некоторому неприводимому
вещественному представлению 1 = ^ или физически-неприводимому
представлению Т — ^ -f- x*.
В дальнейшем для краткости мы будем опускать индекс 1 так, что
Группа симметрии кристалла после фазового перехода О' есть-
подгруппа G, состоящая из тех ее элементов, которые не изме-

§ 3G|	ПОСТАНОВКА ЗАДАЧИ	115
пяют плотность р. Для того чтобы найти группу G', необходимо
знать коэффициенты Ск. Между тем не все наборы значений воз-
возможны для коэффициентов 0%, так как не каждый возможный набор
значений обращает в минимум термодинамический потенциал. Рас-
Рассмотрим этот вопрос более подробно.
Термодинамический потенциал Ф имеет с точностью до членов
пятого порядка следующий вид:
Ф = Ф04-Фг(С1; р, T) + <I>4(Q; p, T),
где Фо не зависит от Q, Ф2 — полином второй степени относительно
коэффициентов Q, Ф4 — полином четвертой степени. Члены третьей
степени отсутствуют в этом разложении, так как наличие этих
членов приводит к сдвигу точки фазового перехода.
Функции <$1 можно считать вещественными, так как каждое физи-
физически-неприводимое представление вещественно. Поэтому они обра-
образуют базис, который контравариантен самому себе. Как уже гово-
говорилось, можно считать, что под действием элементов группы G
преобразуются не функции cpj> a коэффициенты С;. Эти коэффи-
коэффициенты также образуют контравариантный самому себе базис.
Поэтому единственный квадратичный инвариант имеет следующий
пид:
Ф2(С,; р, Т) = Аг(р, 7-)SCi
(коэффициенты Q вещественны). На симметрию функции р влияют
только отношения коэффициентов Q. Поэтому мы будем считать,
что коэффициенты нормированы:
При такой нормировке изменение потенциала Ф связано в рассма-
рассматриваемом приближении только с членами четвертой степени. Эти
члены представляют собой некоторую линейную комбинацию инва-
инвариантов четвертой степени. Поэтому для определения возможных
значений коэффициентов Q следует найти все инварианты четвертой
степени, которые можно построить из коэффициентов Cj.
Покажем теперь, что далеко не всякое представление может быть
ответственно за понижение симметрии кристалла при фазовом пере-
переходе второго рода.
Прежде всего необходимо, чтобы в разложении Ф отсутствовали
члены третьей степени относительно Cjc. Для того чтобы разложение
термодинамического потенциала не содержало членов третьей сте-
степени, необходимо, вообще говоря, чтобы из них нельзя было со-
составить инвариант. В терминах теории представлений это означает,
что представление IT]3 не содержит единичного представления.
Далее, если в выражении для плотности заменить коэффициенты С^
некоторыми медленно меняющимися функциями координат, то плот-
плотность р не будет соответствовать кристаллу, так как она потеряет

116	ФАЗОВЫЕ ПЕРЕХОДЫ ВТОРОГО РОДА	[ГЛ. VII
свойство периодичности. Из устойчивости кристаллического состоя-
состояния следует, что термодинамический потенциал всего кристалла,
Л/
рассматриваемый как функция от производных -г-^ (/ = ], 2, 3),
1 дС
дСк
принимает наименьшее значение, когда все производные -~ равны
нулю. Для этого необходимо, чтобы интеграл от Ф по объему кри-
кристалла не содержал слагаемых, линейно зависящих от производ-
производных -з-;-. Заметим что, если представить Ф в виде
т- с> ё)=ф°(/7> т' с)+2ф*^-
кЛ
k,k',l
у li; . _ Г, дСь
к, к', I
то после интегрирования получим:
ft,ft',г
Так как термодинамический потенциал всего красталла инвариантен
относительно всевозможных преобразований координат, то в правой
части последнего равенства могут стоять только те слагаемые, кото-
которые инвариантны относительно всех элементов группы G. Таким
образом, для возможности фазового перехода, связанного с пред-
представлением Т, необходимо, чтобы в линейной оболочке выражений
вида
(/—1, 2, 3; к, *'=1, 2	s)
не было ни одного инварианта. Это означает, что антисимметри-
антисимметрический квадрат {Т}2 не должен содержать ни одного неприводимого
представления, которое входило бы в векторное представление
группы G.
Полученные два условия весьма сужают совокупность возможных
изменений симметрии при фазовых переходах второго рода. В сле-
следующем параграфе производится подробный анализ этих условий.

I 37]	АКТИВНЫЕ ПРЕДСТАВЛЕНИИ	117
§ 37. Активные представления
В предыдущем параграфе было показано, что изменение симмет-
симметрии кристалла при фазовых переходах второго рода может быть
связано только с теми неприводимыми вещественными представле-
представлениями Т = х и теми физически-неприводимыми представлениями
Т = х-|-х*, которые удовлетворяют двум условиям:
1)	{Т}2 не имеет с векторным представлением ни одного общего
Представления,
2)	|Т]3 не содержит единичного представления.
Такие представления мы будем называть активными. Представле-
Представления, не удовлетворяющие хотя бы одному из условий 1), 2), назовем
пассивными.
Выясним, как узнать, удовлетворяет ли данное представление
условию 1).
Напомним, как строится базис, преобразующийся по неприводи-
неприводимому представлению х группы G.
Пусть &J — один из I векторов звезды К представления х,
n Gx— группа этого вектора. Обозначим через
еп> «12. ••¦. еи>	С37-1)
те базисные векторы, которые при трансляциях ta?G умножаются
на elfci«. Линейная оболочка этих векторов Lx инвариантна относи-
относительно всех операторов х (gt) (gi^ Gt). Представление xW (g^igx^ OJ
группы Gt, по которому преобразуется пространство Llt является
неприводимым.
Как известно, каждый вектор звезды К можно получить из век-
вектора kv действуя на kt тем или иным элементом группы О. Выберем
произвольно 1-Х элементов группы G
g"i2> Sw • • • > Sn
таким образом, чтобы
gij^^kj (у = 2, 3	/).
Если положить
^(gij)Cun^ eJm G^2, 3, ..., /; т=\, 2, ..., s), C7,2)
то совокупность I векторов е^т и образует базис представления х.
Если предстапление х вещественно, то среди векторов звезды К
найдется вектор, скажем k2, эквивалентный вектору — k{.
и — и
»2 = К1
(т. е. k2 = — *! + *. 1'Де Ь—один из векторов обратной решетки).
Ясно, что у векторов kv и k2 одна и та же группа симметрии GX=~GZ.
Рассмотрим 'теперь представление {х}2. Базис пространства, пре-
преобразующегося по этому представлению, состоит из векторов
е}-тРУт'	e.'m'ajni'

118	ФАЗОВЫЕ ПЕРЕХОДЫ ВТОРОГО РОДА	[ГЛ. VII
где djm—базис, однотипный базису ejm. Звезда К2 представле-
представления {тр состоит из всевозможных векторов вида kj -f-ky (kj и ky—век-
ky—векторы звезды К представления -z). Если среди этих векторов нет
нуль-вектора, то представление {т}2 заведомо не имеет общих
представлений с векторным представлением, так как звезда послед-
последнего содержит только нуль-вектор. Таким образом, вопрос о выпол-
выполнении условия 1) остается открытым только для тех представлений т,
звезды которых содержат наряду с каждым вектором kj и вектор k^,
эквивалентный вектору — kj. Если т — такое представление, то
звезда К1 представления {т}2 распадается на две звезды. Одна из
них-содержит только нуль-вектор, другая — все остальные векторы.
В соответствии с этим представление {тр распадается на два пред-
представления То и Т1( причем только То может иметь общие предста-
представления с векторным представлением группы О.
Базис представления То состоит из векторов
Рjmm' = ejmPhm' — ej<mi3jm	U <C Уl)>	C7,3)
где j\—номер того вектора звезды К, который эквивалентен век-
вектору— kj. Если каждый вектор kj эквивалентен вектору — kj, то
j = j\ и индекс j пробегает в C7,3) / значений; если же kj ф — kj,
т0 3 Ф]\ и индекс j пробегает только -я-1 значений.
Для того чтобы представление ГГО имело хотя бы одно общее
представление с векторным представлением, необходимо и доста-
достаточно, чтобы сумма
5 = W 2 Zo (g) У (g) (g = t*f € О)	C7,4)
(Xo u У — характеры представления То и векторного представления V,
N	- порядок группы F) была положительна.
Обозначим через Xoj(s) «клад в выражение для характера Хо(^)>
который вносится базисными векторами pjmm,(j—фиксировано).
Можно написать:
Хо (g) = 2 loj (g)-
j < h
Подставляя эту сумму в C7,4), мы получим:
Так как все векторы kj звезды К совершенно равноправны, то все
слагаемые, стоящие под знаком внешней суммы, равны друг другу.
Поэтому
5 ~ 2 Zoi (g) У (g) (g = t<f€ О).	C7,5)

¦§ 37]	активные шч;лстлбл1'Пия	119
Если элемент g Переводит вектор kt и вектор gku не эквива-
эквивалентный ни вектору ftj, ни вектору — ku то XoifgO — O- Поэтому
-в C7,5) остаются только элементы g^G1 и элементы g, переводя-
переводящие вектор kx в вектор — ku
•5~ 2 7j»i(g)V(g) ig=tJ?G).	C7,6)
Рассмотрим отдельно два случая.
1. Пусть — kt^kv В этом случае суммирование в C7,6) произво-
производится по элементам группы Gl
re о.
а базисные векторы pim)re/ имеют следующий вид:
Ясно, что jj)i(g) является в этом случае характером представле-
представления {тО)}2 группы О:. Поэтому
). C7,7)
2. Пусть — ftjS&j. 13 этом случае сумму C7,6) можно переписать
в виде
S { (^) V (g) + Xoi (g-«g) V (^2g)},	C7,8)
где g = taf? Gu
Векторы pimm/ записываются так:
Pimm/ = e\m?2m'	e2m'°l?ra-
Для вычисления Xoi (§") и ZoiGS'iag') над° выяснить, как преобра-
преобразуются базисные векторы plmm/ под действием элементов g и g12g-
Имеем:
^ iS) еШ = '«m (ff) еш	t (g-12g") «и» = *nm
1W = "«'m' (^Гг
»' = I! ignggri) elm' = tn/j»' {gliggn) eln'-
Отсюда следует, что
Ч (?") Plmm' = ^ш (g) 'n'm' (gwggu) ?lnn',
t
iz) Pln'n-

120	ФАЗОВЫЕ ПЕРЕХОДЫ ВТОРОГО РОДА	[ГЛ. VII
Теперь легко вычислить
7-0. (S) = ^ш (Я)
/01 (gi2g) =^ — "m'm (g) tmm' (gizggu) = ~ X^ (giiggizg)-
Подставляя эти выражения в сумму C7,8), мы получим:
*A)WzA) (snsg12)v(g)~z'1»(g12gg12g)v(gl2g)}
(gi2*i=-*i, gu€G, g^tafZGJ.	C7,9)
Если представление т вещественно и— ktE^kz, то базисные
векторы е2т преобразуются но представлению х'2), комплексно-со-
комплексно-сопряженному представлению t^K Так как
то в этом случае Xw (gyilggl.,) = '/^1)(g) и сумма C7,9) принимает
следующий вид:
5 '-= Ш S ^ ! 7-A) ^)i2 ^(^) - /.0) (S-i2^.2ff) ^ ^i2ff)] • C7,10)
fcf}.
Итак, для того чтобы неприводимое представление t удовле-
удовлетворяло условию 1), необходимо и достаточно, чтобы равнялась нулю
сумма C7,7), если — kL=kb или сумма C7,9), если—fti=&2.
Если представление t вещественно, то в этом критерии можно
заменить сумму C7,9) суммой C7,10). Если звезда представления т
не содержит вектора, эквивалентного вектору — kv то представле-
представление заведомо удовлетворяет условию 1).
Теперь нетрудно выяснить, когда физически-неприводимое пред-
представление 'Г = t--J-t* удовлетворяет условию 1).
Согласно задаче I § 25 представление {Т}2 равно сумме трех
представлений:
(Tf=[T]4K}- + -Xx'.
Для того чтобы {Т}2 ме имело общих представлений с вектор-
векторным представлением, необходимо и достаточно, следовательно, чтобы
каждое на трех представлений {т}2, {т*J и t X "* обладало этим же
свойством.
Рассмотрим представление % X х* группы G. Согласно задаче III §21
у него и у векторного представления V имеются общие предста-
представления лишь при условии, что т содержится в 1 X V. Звезда пред-
представления х X V такая же, как и у представления х. Поэтому доста-
достаточно рассмотреть малые представления группы вектора kt, связанные
с представлениями т X V и х. Если tWfiWXV, то x?xXV, и
наоборот. Согласно той же задаче соотношение xA>?x^XV озна-

§ 37]	АКТИВНЫЕ ПРЕДСТАВЛЕНИЯ	121
чает, что у представлений т(') X ^A)* и V имеется по крайней мере
одно общее представление. Это в свою очередь означает, что сумма
положительна. Итак, необходимым и достаточным критерием отсут-
отсутствия у т X * и V общих представлений является равенство нулн>
суммы C7,11).
Заметим, что представление tW X xC1)* обязательно содержит
единичное представление группы Gv Поэтому, если группа Gx
такова, что ее векторное представление содержит единичное пред-
представление, то Т = т-|-т* пассивно. Перечислим те группы С?!, век-
векторное представление которых не содержит единичного представле-
представления, т. е. группы, не оставляющие неподвижным ни одного вектора-
Из тридцати двух групп, характеризующих кристаллические классы,
этим свойством обладают двадцать две группы:
Cj, C2)V ^2> ^2h< $2> D2a> Cih, Dt, Dih, Sv Dx,
As<z> C3ft, D3h, Ceh, D6, Dsh, T, Th, Td, O, Ok.
Каждая из этих групп имеет в качестве подгруппы одну из сле-
следующих пяти групп:
Сь П2, S.v D3, CSh.	C7,12)
Поэтому представление Т — t + x* может быть активным только
при условии, что вектор kx звезды невещественного представления <с
инвариантен относительно хотя бы одной из подгрупп C7,12).
В частности, представление Т = '!-|-т* пассивно, если все эле-
элементы группы (?! оставляют вектор kv строго неподвижным. Каж-
Каждый вектор kx-f~-O, лежащий внутри зоны Бриллуэпа, короче любого
эквивалентного ему вектора. Поэтому группа Gt такого вектора
оставляет его строго неподвижным и не содержит ни одной из под-
подгрупп C7,12). Это означает, что векторы звезды всякого активного
представления Т=т-)-т* достигают границы зоны Бриллуэпа.
Если сумма Sn равна нулю, то следует проверить, не имеют ли
представления {tj2 и V общих представлений (аналогичная проверка
для представления (-с*]2 излишня, так как оно сопряжено пред-
представлению {t}2, a V— вещественное представление). Иными словами,
следует проверить, удовлетворяет ли представление т условию 1).
Несколько выше мы подробно объяснили, как это делается.
В заключение приведем без доказательства два полезных правила,
относящихся к вещественным представлениям при условии, что
— *, = *„.
1. Если среди элементов группы G имеются инверсия I или
произведение tj, а векторное представление группы Gt содержит
единичное представление, то т пассивно.

122	ФАЗОВЫЕ ПЕРЕХОДЫ ВТОРОГО РОДА	[ГЛ. VII
Из этого правила вытекает, что в случае Т = т,—?j=?2
представление Т может быть .активным только при условии, что
вектор &! инвариантен, по крайней мере относительно одной из сле-
следующих четырех групп:
D2, S,, D,, C3h.	C7,13)
В самом деле, если из тридцати двух точечных групп выделить те,
которые не содержат инверсии и не имеют среди своих подгрупп
ни одной из четырех групп C7,13), то окажется, что векторные
представления этих групп содержат единичное представление..
2. Если векторы звезды представления t лежат внутри зоны
Бриллуэна и не равны, нулю, то представление т пассивно.
Что касается условия 2), то для его выполнения достаточно,
чтобы звезда представления -с не содержала ни одной тройки век-
векторов kj, kj', kj«, сумма которых эквивалентна нулю:
Если существует одна или несколько троек таких векторов,
то следует вычислить характер у3 представления, по которому пре-
преобразуется совокупность всех элементов вида
и составить сумму
Если эта сумма положительна, то представление Т пассивно;
если же эта сумма равна нулю—представление Т удовлетво-
удовлетворяет условию 2).
§ 38. Пример
Рассмотрим в качестве примера кристаллы с пространственной груп-
группой C\h. Пользуясь результатами предыдущего параграфа, найдем все актив-
активные представления группы C\h, а затем выясним, какие изменения симмет-
симметрии кристалла могут быть связаны с этими представлениями.
Группа С^ принадлежит тетрагональной сингонии D , ее решетка
Бравэ объемноцентрированного типа Г*. Основные векторы решетки а^, а2, а3
удовлетворяют условиям (см. приложение II, таблица класса С4;,):
а1 = ач = 'ая> «1 + а2 -L Oi + из -L дз -+" а1-
Каждый элемент группы С^й представляет собой произведение трансля-
Ц™ <»11«,+тА!-т#а (mv т2' тз^0' ±1<---) на-один из следующих восьми
элементов:
е, Sv C\, S% taoh, tj, taCit taCl	C8,1)
где
а = Та1 + Та2+1"аз-	C8>2)

§ 38]	пример	123
Векторы ,Ci, а2, ct3 преобразуются друг через друга под действием эле-
элементов Sit C± и ай группы направлений С^ следующим образом:
= — Oi — а2 — «з>
C4«l = — Оз.	С4«2 = Я1 + «2 + «3.	С4аЗ = — «2.
Векторы обратной решетки согласно B9,5) равны
[a2a8], б2 =
-1 - «ц [а2а3]) I-™'  - (в1 [0,08]) L^1J>  ~ («1 [а2а8]
Они преобразуются под действием элементов S , С , С\ и cft следую-
следующим образом:
S461 = — Ь-о	S462 ~ ^3 — ^2> ^4^3 == ^1	^!>
^3-	C8,33
Найдем звезды возможных активных представлений. Начнем со звезд,
у которых каждый вектор kj эквивалентен вектору —Лу. Из условия
kj = — kj следует, что 2й^ = 0, т. е. с точностью до эквивалентности kj
принимает одно из следующих восьми значений:
-б!, l&j, -iftl,, yFt + &2), ^Fl + &3),
С помощью соотношений C8,3) легко находим, что вектор -^ 6j не изме-
изменяется (существенно) только при инперсии. Этой означает, что точечная
группа G^ вектора -.- Ъ± есть Ct — /. Действуя поочередно на вектор -^- Ьх во-
восемью элементами C8,1), мы получим звезду Кь состоящую из четырех
векторов:
Вектор 7j- 6 не изменяется при инверсии, повороте С\ и отражении
в плоскости aft. Это означает, что точечная группа этого вектора есть С2;,.
Звезда /С2, содержащая вектор -^ й8, состоит из двух векторов:

124	ФАЗОВЫЕ ПЕРЕХОДЫ ВТОРОГО РОДА	[ГЛ. VIj
Вектор -а- (fi% -\- &2 + &з) инвариантен относительно всех элементов
группы G. Поэтому он сам по себе образует звезду Ks\
То же относится и к вектору k^ — 0.
Теперь займемся векторами k, ф—k,. Так как группа C\h содержит
инверсию, то согласно предыдущему параграфу пектор kj ф—kj звезды
активного представления должен быть инвариантен относительно хотя бы
одной из групп C7,13): D2> S4, A* Q/i- Из этих четырех групп только S4
содержится в С^,. Поэтому нам остается найти векторы, инвариантные отно-
относительно зеркального поворота S^.
Представим искомый вектор в виде
Так как вектор k определен с точностью до произвольного вектора
обратной решетки, то без ограничения общности можно положить:
— -ту < И> ,а:> fti. < — •	C8>4>
Согласно C8,3) вектор S4ft равен
S^ft = ЦЗ&! — (щ -)- (i2 -f- (л,,) Ь2 -I (х2Ья.
Разность
& S4ft = ((ii — Цз) &1 + (Р-1 + 2,"-2 "Г ^з) &2 + (^3 — М-2) бЗ
должна быть равна одному из векторов обратной решетки. Это означает,
что числа р.|—(х3, (J4 ~|- 2;j.s -4- а3, >а3 - а3 являются целыми. Принимая
во внимание условие C8,4), мы заключаем, что ij^ = [л3, ;j.3 = jx^ и 4;j.t = — 1,
О, 1, 2. Таким образом, получаются четыре решения:
a) nt = (i2 = (л3 = — , б) [Л! = ,а2 = (Aj = — — ,
в) [х? = [i2 = ;х3 = 0, г) р.х =- ;j.2 = [x3 — -^ ,
Решения в) и г) приводят к уже найденным векторам k^ и k^\ Остав-
Оставшиеся решения дают нам два вектора:
образующих неприводимую звезду Л'-. Точечная группа Gj'-* вектора k^
есть 54. Перечислим теперь все неприводимые представления, имеющие
одну из наиденных пяти звезд. С этой целью найдем нагруженные предста-
представления точечных групп
Звезда {ft'1', 4!)> ^з0- *1')}- Точечная группа Й'/' = С. вектора k[])
содержит два элемента. Поэтому набор ее нагруженных представлений

38]
ПРИМЕР
125
исчерпывается двумя одномерными представлениями. Для того чтобы их
найти, вычислим нагрузку ф (/, /)• Имеем:
= е
Отсюда следует, что -с (/) т (/) = 1х (/2) = /, и мы получаем два нагру-
нагруженных представления точечной группы д[1^ вектора к[1^ (см. табл. 11).
Звезда {kf\ ft!,2'}. Точечная группа G(,2)
вектора
есть С„.. Она состоит из четырех
2ft.
элементов и поэтому имеет либо четыре одно-
одномерных нагруженных представления, либо одно
двумерное. Вычислим нагрузку
). Для этого заметим, что
Таблица 11
Нагруженные пред-
представления группы О1/'
-ai2» —ь3,
Поэтому
—»,
равны единице.
хи
:(»
Х12
е
1
1
/
ui
ici
-«*
Все остальные значения
Из тождества
" (Зй)т (-0 = т (afc0 = т Caft) ~ — т (О х (ah)
•следует, что одномерные представления отсутствуют. Группа С2^ имеет
¦единственное неприводимое представление, которое мы обозначим через т^1'.
Размерность Ц1' равна двум.
Если ~2' рассматривать как представление подгруппы С = а,, то оно
является обычным представлением. При естествешюм выборе базиса матрица
оператора Ц1' совпадает с одной из следующих трех матриц:
/1 0\ /1 0\ / —1 0\
\0 —V' V0 \)' \ 0 —\)'
Последние две матрицы следует отбросить, так как они коммутируют
со всеми матрицами. Поэтому
х'2 ^"Чо —:
Обозначим -\ > (I) =	) и воспользуемся тождеством
\г 5/
Л1ы получим:
или
о —
— 17'
-Y —ЬУ V—Y
т. е. а = О, S = 0. Так как, кроме того, Г-:У'(/)|2 = —Е, то
o
o

126
т. е. Py ==
Итак,
ФАЗОВЫЕ ПЕРЕХОДЫ ВТОРОГО РОДА	[ГЛ. VII
— 1. Без ограничения общности можно положить 3 = 1, f = — 1.
Теперь легко вычислить матрицу
Собирая полученные таким образом операторы, составим таблицу
h
х2 (/г)
е
/1 Ох
UlJ
/
( °
Ui
о)
с
С1
U
°\
-J
/ОЬ
(л о)
Звезда {А3}. Для нахождения нагруженных представлений точечной
группы С\ = Cih предварительно вычислим величину ег *-Л к к' "' (см.
табл. 12).
Таблица 12
Вычисление
е
I ^2
-26,
-2*8
!1 -1 1
-2&2
— 1
by
-6i+6o-J
— 1
— 1
Числа, стоящие в последней строке этой таблицы, показывают, что на-
нагрузка ty (h^, h2) равна —1, если hx = S , S|, о , / и /г2 = С^ Cv од, /.
Для всех остальных пар элементов нагрузка равна единице.
Из сопоставления двух равенств
следует, что у группы С4& нет одномерных представлений с рассматривае-
рассматриваемой нагрузкой. Поэтому группа С4Й имеет два двумерных представления.
Пусть -z — одно из этих представлений. Если рассматривать его как
представление подгруппы С4, то оно вырождается в обычное представление
и поэтому может быть разложено на одномерные представления группы С4
(см. табл. 13).
Оператор - (С^) коммутирует со всеми операторами - (Л) (h g CJi). Это
означает, что он кратен единичному оператору. Поэтому имеется две воз-
возможности:
0\	^	/1 0\
при этом т(С )=
2)
— 1 0
0 —1
при этом т (С4) =
0
.о -

§ 38]
ПРИМЕР
127
Теперь нетрудно найти оператор х (/). Из C8,5) следует, что"-: (/) х (СА) =
: — x(C4)t(O- Подставляя сюда хя(/) = ( \ получим:
« -f
т. е. а = 0, 3 = 0. Равенство
х (/) х (/) = — х (е) показывает, что
Py = -—1- Без ограничения общности
мы можем положить р = f = /. Итак,
0	I
1	0
Умножая оператор х (/) на ранее
найденные операторы, получим два
двумерных представления (см. табл.
14).
Таблица 13
Неприводимые представления
группы Ci
Q
ч
ч
хз
е
1
1
1
1
с,
1
/
— /
С2
Ь4
1
1
	 1
— 1
Г3
1
	 J
— /
/
Таблица 14
Нагруженные представления группы
•С 31
Х32
е
/1 0\
V0 17
(о 17
г о
V—1
оД
]ч /.
оД
с2
1
0
-1
0 —
°v
l)(
si
0
	 ^
0 —
1
'V
оХ
Ь /
1
Q/ \^
а
0
i
0-
1
о)
о)
[i
/0
07
i\
о)
/1 0\
lo-J
// 0\
Vo-J
c3
^ 1
v. 0 —
/	/
\ 0
°\
17
l)
Звезда {АD'= 0}. Нагруженные представления группы С^ совпадают
с обычными представлениями, так как k^ = O. Поэтому группа С^ имеет
восемь неприводимых представлений (см. табл. 15).
Звезда jft^, k^}- ^ак виД«о из C8,1), элементы точечной группы S4
.содержатся в С®Л. Поэтому нагрузка 4 равна единице, и нагруженные пред-
представления вырождаются в обычные представления группы 54. Приведем
для удобства таблицу этих представлений (см. табл. 16).
Итак, мы обнаружили семнадцать неприводимых представлений:
"ll> T12! X2'i T3t> "82! X41> "i1> 3> "i4> Tiu> X4B> "iT Xi$< '51 • T52> T53. T54-
Выясним, какие из этих представлений вещественны, и объединим попарно
комплексно-сопряженные представления.
Прежде всего ясно, что представления
t48 попарно объединяются в фи-
фи'41> ~i2> 3'
вещественны, а представления x^j, X47 и х46,
зически-неприводимые представления
5 + Т47> 6 + Т48-
Для того чтобы исследовать остальные представления, выпишем матрицы
соответствующих им малых представлений (см. табл. 17).

128
ФАЗОВЫЕ ПЕРЕХОДЫ ВТОРОГО РОДА
[ГЛ. VII
Таблица 15
Неприводимые представления группы C4j,
Х41
Х42
Чп
¦44
Х45
^46
Х47
Х48
е
1
1
1
1
1
1
1
1
s4
1
	1
— 1
1
1
	^
— /
/
С2
Ь4
1
1
1
1
	]
— 1
	 |
— 1
S3
°4
1
— 1
— 1
1
— 1
1
i
— 1
X
1
— 1
1
	\
1
— 1
1
— 1
/
1
	j
1
— 1
	j
1
— 1
1
с4
1
1
— 1
— 1
/
— 1
— 1
г3
С4
1
1
— 1
— 1
— /
— /
1
1
Таблица 16
Неприводимые представления
группы Si
xW
xf,2
X53
X54
e
1
1
1
1
st
1
	1
I
— I
c2
1
1
—-1
— 1
s3
1
— 1
— i
I
Таблица 17
Неприводимые представления групп векторов
ft»), kf\ k^\ ft»)
1
,(D
xli
X12
1
1
tj
— 1
1
Gf
xm
2
. t
/1 Ox /
Vo i) V-
V ( )
Vl
-2
оУ
Gf
M)
X51
X52
X(D
X63
X54
1
1
1
1
s>
1
— 1
I
— 1
c2
1
1
— 1
	J
si
1
	J
-/

§ 38]
пример	129
Продолжение табл. 17
of)
'31
Х32
I
u
С
ГХ
l A
0
— i
0
—1
V
oA
I)(
C2
1 0\ /
о iA
~o-i)(
si
0 Л
-г oJ
о-ь
1 ОУ
( °
I i
/ 0 -
oJ
r°
li
(i
i
o)
1)
I 0
(;
i)
tuc*
{—I
{ 0
/— 1
V 0
J
Из приведенных таблиц сразу видно, что представления tu, т12 и т32
являются вещественными. Действительно, в этих представлениях веществен-
вещественные матрицы соответствуют всемдтоворотным элементам и всем трансляциям.
Воспользуемся теперь критерием вещественности представлений про-
пространственных групп (см. § 30). Применим его к представлениям т;1, -::л,
':58> Я">4- Из восьми элементов группы направлений четыре элемента: /, гЛ,
С4> С\ — переводят вектор kf^ в —Щ'\ Квадраты соответствующих эле-
элементов пространственной группы tj, t^h, /aC4, taC\ равны е, ta +a ,
Составим таблицу характеров этих элементов в малом представлении
(см. табл. 18).
Таблица 18
Характеры малых представлений
уA) „A)	'
yd) у'!)
'$!• Л52
yd) yd)
'-53 > Л51
е
1
1
— 1
— 1
t с2
la^i
I
— I
t С2
	^
i
Мы видим, что сумма характеров у каждого из четырех представлений равна
нулю. Это означает, что ни одно из представлений не эквивалентно своему
сопряженному. Для того чтобы получить физически-неприводимые предста-
представления, следует попарно объединить комплексно-сопряженные предста-
представления
1 + *58> "ХЛ + 4-
Применяя этот же критерий к представлениям т2 и т81, убеждаемся в том,
что они вещественны.
Таким образом, мы получили четыре физически-неприводимых предста-
представления и девять неприводимых вещественных представлений:
Т11» Х1°> *& "81 > Т82! ^41 > Т42> 3' ":44> Х45 + Т47> 6 + Т48! Т51 + " " + Т
Т51
Выясним, какие из этих представлений являются активными. Ясно, что
представления со звездами Къ Къ Кз и Кг, удовлетворяют условию 2), так
как никакая тройка векторов, входящих в любую из этих звезд, не дает
сумму, эквивалентную нулю. Что касается представлений с нулевой звездой,
то 1:41 не удовлетворяют условию 2), а остальные семь представлений удо-
удовлетворяют этому условию.
9 Зак. 3512. Г. Я. Любарский

130
ФАЗОВЫЕ ПЕРЕХОДЫ ВТОРОГО РОДА,
[гл. vr
Рассмотрим теперь условие 1). Начнем с представления тп. Так как это
представление вещественно и вектор k\ эквивалентен вектору — Al5 то сле-
следует пользоваться критерием C7,7). В данном случае под знакам суммы стоят
два слагаемых, соответствующих элементам е и S4, / — 4, N = 8. Значения
характеров '/.$ (е), х'У (S4) и XiV (^4) берем из таблицы 11 и убеждаемся,
что сумма C7,7) равна нулю. Это означает, что представление -п активно.
Таким же образом находим, что и представление т12 активно.
Рассмотрим представление ~2. Оно вещественно, векторы А^ и —¦ k^
эквивалентны. Поэтому следует пользоваться критерием C7,7). Замечая, что>
= '«
C8,6>
и пользуясь таблицей 11, легко находим, что сумма C7,7) равна двум и,
следовательно, представление т2 пассивно.
Совершенно так же убеждаемся в том, что представление т3| пассивно,
a tjh активно. При подсчете суммы C7,7) полезно иметь в виду соотно-
соотношения C8,6) и
,j. r> ч2	 ^ r?l (t /\2	j	?.2
Что касается представлений т42, з и ~44> то они активны. В самом деле,
они одномерны, а из одномерного представления, очевидно, нельзя построить
антисимметрический квадрат.
Представление ~„5 -f- Х47 активно. В самом деле произведение 145 X ^47
есть единичное представление и не содержится в векторном представлении!
группы С"Л. Поэтому нужно лишь проверить, что представление ч удовле-
удовлетворяет условию 1). С этой целью вычисляем сумму C7,7) и убеждаемся
в том, что она равна нулю.
Таким же способом находим, что и представление -46 + т48 активно.
Рассмотрим, наконец, представления zbl -\- -г,8 и 2Т~Т34- Проверим, удо-
удовлетворяет ли представление i^ условию 1). Так как k\^ ф — kf\ то теперь
следует пользоваться критерием C7,9). В качестве элемента gi2 можно,
взять tj.
Вычисление суммы C7,9) можно расположить в виде таблицы (см.
табл. 19).
Таблица 19>
Вычисление суммы C7,9)
8
yS}) (g)
-i
/(-V (gv^Sgu)
gnggng
V (SnSgnS)
V(g) = — V(giSg)
e
1
e
1
e
1
3
6
1
— /
'a+a+afl
— I
— 1
2/
C2
1
t c2
	1
	1
— 1
2
1
^ 53
I
t c2
i
— 21

§ 38]	пример	КИ
В последней строке стоит вклад элемента g в сумму C7,9). Легко ви-
видеть, что эта сумма положительна. Это означает, что представление т51,
а вместе с ним и представление -хл + трз, пассивно.
Совершенно так же убеждаемся в том, что представление -52 -\- -г4 пас-
пассивно.
Итак, у группы С|А есть восемь активных представлений:
~'Л< 'isi Т3?> ~4*i Т43> Т44> Т45 ~Г" ~47> Т46 "Ь ~4Ч-
Выясним какие изменения симметрии кристалла связаны с этими предста-
представлениями.
Начнем с одномерных представлений:
~1Ь '*)> Т44>
имеющих нулевую звезду. В результате фазового перехода второго рода
плотность р принимает следующий вид:
Р = fo + ci-ft (г),
где функция tpj (r) преобразуется по одному из этих представлений. Так
как *(*' — 0, то при всех трансляциях функция <f t "e изменяется. Это озна-
означает, что все трансляции группы С4Й входят в группу G' симметрии кри-
кристалла после фазового перехода. Объем элементарной ячейки решетки Бравэ
при этом не изменяется. Что касается поворотных элементов, то при фазо-
фазовых переходах, связанных с представлением -^, функция <ух не изменяется
под действием элементов taCv C\, taC^ и изменяет свой знак под действием
элементов 5,, Sj, t^y и tj. Это означает, что группа симметрии G' со-
состоит из всех трансляций *тов+то„ )тоа и их произведений на элементы
Группа G' принадлежит, таким образом, классу С4, который содержится
в сингонии D .. Тип группы G' есть Г^. Согласно таблице групп класса Ci
(см. приложение IV) G = С\.
Итак, представление т42 связано с переходом
Таким же образом находим переходы, связанные с представлениями т43 и
Обратимся к двумерным представлениям т4Г, -)- ~i7 и т4е + t^. В резуль-
результате фазового перехода, связанного с представлением т46 -f х47 функция р
приобретает следующий вид:
Р = РО + Ci?l + С2<?2.
где tp! преобразуется по представлению т45, a <f« преобразуется по сопря-
сопряженному представлению. Так как плотность р принимает только веществен-
вещественные значения, то сх = с2 и cpi = <p2- Согласно таблице 15 сумма
ci?i + «2?2 = 2 Re cltpi
9*

132	ФАЗОВЫЕ ПЕРЕХОДЫ ВТОРОГО РОДА	[ГЛ. VII
не изменяется под действием элемента ^зл и изменяет свой знак под дей-
действием элемента С\. Поэтому элемент t^. входит в группу G', а элемент С|
не входит. Рассмотрим элемент taCt. Под его действием сумма переходит в
tctfi — 1сгъ = —2 1га
Если предположить, что Re crfi = — Im Ci9ii то получится, что функция tfj
только постоянным множителем отличается от вещественной функции. Это,
однако, невозможно, так как представление т45 невещественно. Таким обра-
образом, элемент tJZ± не содержится в группе О'. Группа G' принадлежит
поэтому классу Cs — aft. С помощью таблиц пространственных групп опреде-
определяем, что G' = С^.
Итак, представление ~4ъ-\-'ц связано с переходом
Таким же образом находим, что представление в~г"3 связано с перехо-
переходом
Clh-* S2 (т — Т46 + тш>
Рассмотрим теперь двумерное представление т3о. Плотность р после фазо-
фазового перехода принимает такой вид:
р = |
причем функции -ft и ?о преобразуются по представлению -т<>. При трансля-
tmlal+m.ia,i+та, каждая из этих функций умножается на
	 i	j i	t
Если сумма т^ -\- т<, -\- ms является четным числом, то плотность р не изме-
изменится. Поэтому группа G' содержит все трансляции вида
'mIa1.|-m1as+m,a!1 (тI + т"- + тЪ = °> ±2, ±4, ±6, ...).
В качестве основных векторов подгруппы трансляций .можно выбрать
три взаимно-перпендикулярных вектора
о, = Оо -f- ач, о, = a, 4- с,, a, = а, 4- a9 ( л, = д9> ^ wt
Объем ячейки, построенной на этих векторах, «двое ботьше объема ячейки
до фазового перехода.
Найдем теперь поворотные элементы группы G'. Для этого, как было
показано и предыдущем параграфе, следует построить из коэффициентов Cj
все линейно независимые инварианты четвертой степени.
В качестве первого шага разложим представление [т^р на неприводи-
неприводимые представления.
Звезда представления [t3,]2 состоит из одного вектора 2k^\ эквивалент-
эквивалентного нулю. Поэтому [t3o]3 можно рассматривать как представление группы
направлений F. Характер этого представления легко посчитать, пользуясь
формулой B5,12). Так, например,
У. , «я = -/J2 It a + 1Z 2 (It a J) =
= ° + j '/-32 (x-!-«.,) = e% ' Я'+аа = !• "

§ 38]	пример	133
Вычисляя таким образом характеры остальных поворотных элементов и
отождествляя их с элементами группы направлений С^, получим следующую
таблицу:
е S,
3—13—1111 1
Мы видим, что
= T4t "Г Т4
Линейные комбинации функций <fi> cpj<p2, ?2> преобразующиеся по этим
представлениям, можно найти с помощью оператора B6,8). Простой подсчет
приводит к выражениям
?1 — У2> Yi + У2>
Таким же образом, очевидно, преобразуются и величины
с\-с% с] + 4 Clcz.
Так как представления т41, -с^?. и "чз вещественны и унитарны, то квад-
квадраты этих величин инвариантны
(ci — ctf — inv> (с? + сгJ = inv> cic2 = inv-
Легко видеть, что третий инвариант линейно выражается через перьые
два. Поэтому общий вид функции Ф4 таков:
Ф
= 5, (р/) (с? + 4J + S2 (P. IT) {c\ - с^.
ъ
Нам нужно найти минимум этого выражения при условии с\-\-с\= 1. Ясно,
что при ??2 (/>, Т) > 0 этот минимум достигается, если
Сц = ± С;.
Если же В-, (р, Т) <[ 0, то минимум достигается при
et = 0 или с2 = 0.
Если Во (/^, Т) = 0, то для определения Cj и с2 необходимо рассмотреть члегы
более высокой степени в разложении термодинамического потенциала. Мы
не будем рассматривать этот случай, так как его можно считать практически
невозможным.
Если Cj = Со, то р = ро -L- Cj (tfj -\- tf2). Сумма тi-j-?2 П°Д действием эле-
элементов группы Cbih преобразуется следующим образом (см. таблицу пред-
представления -32 на стр. 129):
с\ sl tjh tj tac, tac\
Т32 (g) (у 1 + fi) j — V" 2 + У1— У1 — Y? <f 2— Yl — Y2 — fl Y? "f Yl <f 1 ~ <f 2 ~ Tl + Y2
Мы видим, что сумма у^+тг остается инвариантной при операциях

134	ФАЗОВЫЕ ПЕРЕХОДЫ ВТОРОГО РОДА	[ГЛ. VH
Группа G' принадлежит в рассматриваемом случае классу С2л- Она имеет
плоскость скольжения, ее решетка не центрирована. Эти свойства одно-
однозначно определяют G' как группу С^.
Таким же образом находим, что и при ct = — с2 группа G' совпадает
с C\h.
Если Сх = 0, то плотность р инвариантна относительно операций ta C\ ,
tа +.С4 и t^Cl- Группа G' в этом случае равна С\. Такой же результат
получается и в случае с2 = 0.
Итак, с представлением т32 могут быть связаны следующие фазовые
переходы:
f~»H	f*J	Г\Я	/^2	Пр 	 т \
°1/г~>(-2й' и4й">с4 К} — "ггУ
Рассмотрим, наконец, представления tu и т12. Прежде всего вычислим ма-
матрицы, соответствующие элементам C\h в этих представлениях. Исходя из
тождеств
положим:
8=S g = C\ g=S
gu=S>.
Введем далее обозначения:
" (gn) «1 = еъ -с (gn) е1 = еь, -. (gu) ех = е4 (ч = ха, -!12),
где ei — вектор, преобразующийся по представлению т'1'. Найдем матрицу
элемента S4 в базисе е^ ег, ел, е±. Имеем:
= ег, х (S4) ег = t
Итак,
/0010
I i n n n I
C8,7)
Матрица элемента tj находится несколько сложней. Имея в виду тож-
тождество Ik»Ezk«, вычислим произведение
Полученное равенство можно переписать в виде
Теперь легко вычислить вектор " (/а/) e<i
хitj)е-г = - (gl2) '. (t -«О t (tj) -.-I (gl2) e.2 = -. (gl2) ~. (t-,.) t (tj) et =

§ 38]	пример	135
Подсчитывая таким же методом векторы т (tj) е% и - (tj) e±, находим матрицу,
соответствующую элементу tj:
C8,8)
{верхний знак берется для представления "ц, нижний — для представле-
представления -:1?).
Комбинируя C8,7) и C8,8), получим все остальные матрицы представле-
представлений -п и т12:
1
0
0
0
0
	1
0
0
0
0
—1
0
0
0
0
—1
= ±
(х = х1и т12).	C8,9)
Плотность р после перехода, связанного с одним из этих представлений
имеет следующий вид:
Р = Ро = cm + с??г + сз?в + С4?4.
причем функции <fi> ?2> *?з и ?i принимают только вещественные значения.
Так как функция р вещественна, то вещественны и коэффициенты с±, с2, с3> с^.
Выясним, какие наборы значений возможны для коэффициентов Cj, C2,
^з, ^4- С этой целью найдем все инварианты четвертой степени, которые
можно построить из сii с2, Сд, с^. В качестве первого шага рассмотрим пред-
представление [т]2.
Базис этого представления состоит из двенадцати функций:
(в скобках указан вектор k, характеризующий представление подгруппы
трансляций, по которому преобразуются базисные функции). Мы видим, что
свезда представления [т]2 состоит из трех звезд К±, звезды Кг и звезды Л.
Проанализируем представления, связанные с этими звездами.

136
ФАЗОВЫЕ ПЕРЕХОДЫ ВТОРОГО РОДА
[ГЛ. VII
Звезда /С4. Зная представление - (см. C8,7)—C8,9), легко определить
матрицы, но которым преобразуются функции =р
О 0 1 0\
(,)
<?\, 9j> 'i\-
Выпишем характеры представления Т4
С\
/4
4 О О О
0
/„С,
О
О
и разложим, используя формулу B0,3), Т4 на неприводимые представления:
Т4 = 1 + '43 + ~4в + ЧЧ-
С помощью оператора B6,8) легко найти линейные комбинации
преобразующиеся соответственно по представлениям т41, -in, т46 и -с^. Мы
получаем, таким образом, три инварианта четвертой степени:
/J i „2 I „2 I ,„2\2 /„2 „2 „2 , „2\2 /,„2 „2\2 . ЛЛ2 ,Л2\2
Аналогичные выражения, составленные из коэффициентов съ с5, с3 и ci
(c* + c* + cl + <*f, {cl-cl-cl h ci), (С?-фЧ(с!-с?J( C8,10)
также являются инвариантными.
Рассмотрим теперь функции, относящиеся к звезде А^,
?1?8. ?!?4' <?1?2. ?3?4-	C8,11)
Они преобразуются по представлению т2, так как у звезды Кг нет других
четырехмерных представлений. С помощью C8,7) — C8,9) легко убедиться
в том, что все матрицы представления т2 в базисе C8,11) вещественны. Это
означает, что базис C8,11) сопряжен самому себе, так как представле-
представление fr]2 унитарно. Поэтому единственный инвариант, квадратичный отно-
относительно функции C8,11), имеет следующий вид:
В соответствии с этим инвариантом является также выражение

§ 38]	пример	137'
Рассуждая таким же образом, легко получим, что из коэффициентов
можно построить только один инвариант четвертой степени:
44 + 44-	C8,13),
Из C8,10), C8,12) и C8,13) следует, что
Ф, = В, D + 4 + с\ + С2J + В2 (с\ - 4 -4+ ctf +
+ bs [D - clJ+D - сщ + в, D4 + 44 - ь с\с\ \- с\§ +в, D4 +44).-
Найдем минимум этого выражения при условии
4+4 + 4 + 4=1-
Для этого перепишем Ф4 в виде
Ф4 = В, {1 - 2у - 2г)« +ВяЦ2х + у + г—\Г- + (у-г)*] +
-|- В4 (у + г) A — у — г) + ?5 [* A — х — у — г) + у г] + const,
где
9	9	9	9
х = с\, у = Cj, г = Cj, 1 — л: — у — г = сJ.
Для отыскания минимума выражению Ф4 удобно придать следующую форму:
Рассмотрим отдельно две возможности.
1. В3 — — fi5>0. При любых фиксированных значениях у иг вели-
величина х определяется из условия
Ясно, что этот минимум равен нулю и достигается при
х==^(\—у — г).
Далее, при фиксированном значении суммы у + г произведение уг
должно быть максимальным. Иными слонами, должно иметь место равенство
у = г.
Учитывая последние два соотношения, перепишем Ф4 в виде
Ф4 = 4 D5, - Д,) у2 + 2 (- 4В.г + В1 + 1 В5) у + const
или
Ф4 = 4 DВ2 — В4) (у — уоу- + const,

138
где
ФАЗОВЫЕ ПЕРЕХОДЫ ВТОРОГО РОДА
Я	] R 1 Я
[ГЛ. VII
Если 4В2 —В4>0, то
f 0 при у0<0,
_ I уй при 0<у0<
_1_
2 '
ПрИ тГ<У0.
Если же 4б2 — 54 < О, то
у при Уо < -j ,
О при у0 > -j .
-Мы получили, таким образом, три возможных случая:
1) У = г = 0, * = у , т. е. с2 = с, = 0, Ci =
2) у = z = —•, л: = 0, т. е. с» = ± с3, d = с4 = О,
3) у = г,
1
х = у — у, т. е. с2 = ± с3, ct = ± с4.
2. В3	^-бГ)<^0. При фиксированных значениях у и г минимум Ф4
достигается при максимальном значении Bх-{-у-\-г — IM, т. е. при
х — 0 и дг=1—у — z.
В любом из этих случаев функция Ф4 равна
1
¦ + (У +
+ S3 - В4 - 1 Вв
+ 2) (- 4S2 + В4 + I B5
const.
Ясно далее, что при фиксирозанном значении суммы у -\-z произведе-
произведение уг должно быть минимальным. Эго означает, что либо у = 0, либо z = 0.
Подставляя в Ф4г = 0, получим:
Ф4 = DВ2 + 2В3 - Bi ~ ~ Вь) (у - ytf- Ч- const,
где

¦§ 38]	пример	139
Если 4В„
Если же
-Мы получили еще восемь возможных	случаев:
4)	х = О,	у = 0,	z — 0,	т. е.	ct = с2 = с3 = О,
5)	* = О,	у ф О,	г = 0,	т. е.	d = с3 = О,
6)	х = 0,	у = 1,	г = 0,	т. е.	Ci = с3 = с4 = О,
. 7) лг = 0,	у = 0,	г ^= 0,	т. е.	ct = с2 = ci = О,
e)jc=O,	у = 0,	г=1,	т.е.	с1 = с2 —с4 = 0,
9) х = 1,	у = О,	г = О,	т. е.	с2 = cs = с4 = О,
1О)лг=1 — у,	у^=0,	г = О,	т.е.	с3 = с4 = 0,
\\)х = \ — z,	у = 0,	г^О,	т.е.	с2 = с4 = 0.
Зная коэффициенты сь с-,, ся, ct, нетрудно определить группу симметрии
Кристалла. Рассмотрим, например, случай с^ = с4, с2 = с3 = 0. Функция плот-
плотности р имеет при этом следующий вид:
Р = Ро + ci ("ft + <р4)-
При трансляциях *OTiei + nl!iaj+OTaej функция «pi умножается на
¦ЛИ) m , „ m \
Л ' ia'+ J1 ^ = (-1Г',
а функция 94 умножается (— \)та+таш Отсюда следует, Зчто плотность р
не изменяется только при трансляциях вида
*та -т1а1 + т3а1(т1 = °> ± 2> ±4, ...; /И2 + тЛ = 0, ±2, ± 4, . . . ).
Ясно, что эти услозия уменьшают в четыре раза плотность узлов решетки
Бравэ. Поэтому объем элементарной ячейки решетки Бравэ увеличивается
в четыре раза.
В качестве трех основных векторов можно взять
Вектор а\ перпендикулярен к векторам а!2 и а3. Векторы а2 и о3 имеют
одинаковую длину и составляют одинаковый угол с о;.

140
"ФАЗОВЫЕ ПЕРЕХОДЫ ВТОРОГО РОДА
[гл. vii;
Найдем теперь поворотные элементы, не изменяющие функцию р. Если
рассматриваемое представление есть Хц, то согласно формулам C8,7), C8,8)
и C8,9) получаем:
g
t I
С3
V4
ТИ (g) (?1
Отсюда вытекает, что
ТЧ
Мы видим, что в рассматриваемом случае группа О' принадлежит классу Сгй,
имеет плоскость скольжения, а решетка Бравэ группы G' центрирована.
Эти свойства однозначно определяют G' как группу С\^.
Если с\ = — cit c2 = c3=O, то получается такой же результат.
Итак, в случае 1) представление хц связано с фазовым переходом
Решетка Бравэ переходит из типа Г" в тип Г^, а объем элементарной
ячейки учетверяется.
Производя подобным образом исследование всех остальных случаев, мы
получаем таблицу 20.
Таблица 20
Фазовые переходы, связанные <
"и и t12
Случай
• G'
Объем элемен-
элементарной ячейки
1
г6
4
2
Г6
Ь2Л
4
3
c2/l
о
4
с)
^2
2
5
*2
4
: представлениями
6
2
7
s\
4
8
ol
°2
2
9
10
•ч
cl
^2
4
и
cl
62
4
Такие же фазовые переходы связаны с

ГЛАВА VIII
КРИСТАЛЛЫ
§ 39. Звук в кристаллах
Целью настоящего параграфа является рассмотрение тех особен-
особенностей звуковых волн в кристаллах, которые связаны с кристалли-
кристаллической симметрией.
Мы будем пользоваться некоторыми результатами главы VI.
Хотя эти результаты были получены в предположении, что группа
симметрии есть конечная точечная группа, они, тем не менее, спра-
справедливы и в тех случаях, когда группа симметрии является про-
пространственной группой. Кратко сформулируем эти результаты.
1.	Пространство Мс всех отклонений системы от равновесного
положения можно разбить на неприводимые относительно группы
симметрии G подпространства Mj таким образом, что любой век-
вектор s любого из этих подпространств характеризует некоторое
главное колебание. Напомним, что главным колебанием механической
системы называется такое ее движение, при котором все точки
колеблются с одной и той же частотой по гармоническому закону.
В комплексной фэрме главное колебание описывается соотношением
г = ее*»* (г^Ю,	C9,1)
где со — частота колебания, а г — вектор, характеризующий данное
главное колебание.
В случае точечных групп индекс j пробегает конечное множество
значений, в случае пространственных групп множество значений
индекса j является континуальным.
2.	Все главные колебания, связанные указанным образом с одним
и тем же неприводимым подпространством JVI/, имеют одну и ту же
,частоту.
Используем первое из этих свойств для классификации главных
¦колебаний кристалла. Рассмотрим одно из подпространств М^- про-
пространства Мс. Обозначим через "Zkv неприводимое представление
пространственной группы О, по которому преобразуется Mj. Век-
Вектор к является одним из векторов звезды этого представления,
адискретный индекс р характеризует неприводимое представление ip

142	КРИСТАЛЛЫ	[ГЛ. VIII
группы Gfc вектора k. Обозначим через sp размерность предста-
представления тр и через
ъ ъ	ъ
1 > **2» • • • » п'ч
все существенно различные векторы звезды представления thp.
В подпространстве Mj можно выбрать базис гкрг (fe = A1> k2, •-.,.
k4; 1=1, 2	sp) так, что при трансляциях ta?G вектор zkpi
умножается на eiha
=eikazhpl,	C9,2)
а под действием элементов группы Gfc векторы &крг (k, р фикси-
фиксированы, 1=1, 2, ..., sp) преобраззются друг через друга по пред-
представлению ~р группы Gfc. Таким образом, каждый базисный эле-
элемент екрх, а вместе с ним и соответствующее главное колебание
кристалла характеризуются тремя индексами k, р и /. Пара индек-
индексов k и р характеризует неприводимое представление ъир группы G,
с которым связано данное главное колебание. Индекс k сам по себе
характеризует представление подгруппы трансляций S" cz О и назы-
называется волновым вектором.
Два главных колебания, имеющих одинаковый волновой вектор'
и различные значения р или /, называются различно поляризован-
поляризованными. Таким образом, пара индексов р, I характеризует поляриза-
поляризацию колебания. Помимо волнового вектора и поляризации, сущест-
существенной характеристикой главного колебания является частота о>.
Выясним физический смысл вектора k. Для этого разобьем'
мысленно кристалл на кристаллические ячейки так, чтобы начала
координат, выбранное произвольно, оказалось внутри одной из ячеек.
При этом внутри каждой кристаллической ячейки окажется конец
одного и только одного вектора а из группы трансляций !Г. Таким
образом, все кристаллические ячейки можно «перенумеровать» с по-
помощью векторов группы трансляций. Обозначим через ./V число
атомов, которые в положении равновесия находятся в одной кри-
кристаллической ячейке. Перенумеруем атомы так, чтобы любые два
атома, положения равновесия которых могут быть совмещены с по-
помощью трансляции из группы §Г, имели одинаковый номер. Такие
атомы естественно называть эквивалентными. Обозначим через гап
(taCzS', n=\, 2, ..., N) отклонение атома с номером п, находя-
находящегося в кристаллической ячейке а. Отклонение г кристалла харак-
характеризуется набором векторов гаг.
При трансляции ta'(z& атом, находившийся в ячейке а — а',
перейдет в ячейку а, сохранив свой номер. Поэтому отклонение г\
получающееся из отклонения г в результате трансляции кристалла,
на вектор а', характеризуется набором векторов
_/
an	а—о'п*

§ 39]	ЗВУК В КРИСТАЛЛАХ	143-
Если отклонение г совпадает с отклонением гкрг, то согласно C9,2)
г' =eika'r .
an	an
Сопоставляя последние два равенства, получаем:
Га'п = e-ika'ron (я = 1, 2, .. ., N, ta-c &);» C9,3)
Таким образохт, главное колебание ekpi представляет собой дискрет-
дискретный аналог плоской волны, а вектор ft играет роль волнового
вектора.
Рассмотрим теперь все отклонения кристалла, зтювлетворяющие
условию C9,3) (вектор ft фиксирован). Очевидно, что совокупность
таких отклонений образует ЗЛ/-мерное подпространство простран-
пространства Мс. Это подпространство мы обозначим через Мк. Число
линейно независимых главных колебаний с данным волновым векто-
вектором k равно размерности М*, т. е. равно ЗЛ/. Обозначим через
I»!(ft). Mft). •••. Щя{к)	C9,4)
частоты, отвечающие этим главным колебаниям. Частоты C9,4)
являются периодическими функциями вектора к, причем периодами
служат векторы обратной решетки.
Совокупность значений, принимаемых w>l(fr, называется первой
полосой частот, w2(?)— второй полосой частот и т. д. Эти
полосы могут, вообще говоря, перекрываться. Наибольшее и наи-
наименьшее значения u>v(A) (v=l, 2, ..., ЗЛ/) называются краями
полосы. Ясно, что на краях полосы выполняется условие
Если механическое представление 7м содержит некоторое неприво-
неприводимое представление т^;, то sp (sp—размерность представления хр}
главных колебаний с волновым вектором k0, отвечающих этому
представлению, имеют одинаковую частоту. Это непосредственно
вытекает из сформулированного в начале параграфа второго свойства
малых колебаний. В этом случае говорят, что sp полос соприка-
соприкасаются при k = k0, а соответствующая этим колебаниям частота sp,
кратно вырождена.
Таким образом, для того чтобы выяснить, соприкасаются ли
несколько полос при некотором значении волнового вектора к, сле-
следует определить, содержит ли механическое представление 7м
хотя бы одно многомерное представление хкр. Число ткр, показы-
показывающее, сколько раз представление хкр пространственной группы О
содержится в представлении 7м, определяется фО[мулой-C0,15)
C9,5>

144	кристаллы
ГЛ. VIII
где Nk— порядок точечной группы Gfc вектора k, %р— характер
нагруженного представления кр этой же группы, ук—характер
представления группы Gft вектора k, индуцируемого механическим
^представлением в подпространстве Мл,.
Характер Xfo(g") = Xft(V) определяется по формуле
Zfc(^) = (l+2coscpJ««eifca, если г = С(ср), C9,6)
a6jr
Хй V«r) -= (— 1 + 2 cos ?) 2 «»«**", если r = S (<p). C9,7)
Здесь rca обозначает число атомов ш/утри нулевой кристаллической
ячейки, которые под действием элемента tar?Gk, не изменив своего
номера, перешли в кристаллическую ячейку а(а^3').
Формулы C9,6), C9,7) совершенно аналогичны формулам C4,3),
C4,4).
Если группа G;Si не имеет одномерных малых представлений, то
при k — kt каждая полоса частот обязательно соприкасается с одной
или несколькими соседними полосами.
Отметим одно следствие, вытекающее из формул C9,5), C9,6)
и C9,7). Представим себе, что вектор k изменяется непрерывно
и притом так, что его группа Gk остается неизменной. При этом
в формулах C9,5), C9,6) и C9,7) изменяются только множители
е-%(к,га) и eiua и> следовательно, число nihp изменяется непрерывно.
Это, однако, означает, что число ткр не изменяется вовсе, так как
оно является целым числом.
В главе о малых колебаниях было показано, что вектор &крь
комплексно-сопряженный вектору &кр1, характеризует главное коле-
колебание, имеющее ту же частоту, что и колебание гкрг. Поэтому, если
векторы &hpi и гкрх не принадлежат одному и тому же неприво-
неприводимому подпространству Mj, то мы получаем некоторое дополни-
дополнительное совпадение частот, не учтенное в предыдущих рассуждениях.
Заметим, что если векторы ehpi и efc;jj принадлежат одному и
тому же неприводимому пространству Mj, то в пространстве Mj
существует вещественный базис
Поэтому подпространство M.j преобразуется по вещественному
представлению thp.
Отсюда следует, что каждому невещественному представлению tkp
соответствует пара (или несколько пар) подпространств Mj и М^.
Частоты (о, связанные с подпространствами М/ и М^, одинаковы.
Таким образом, невещественному неприводимому представле-
представлению tfcj, размерности s соответствует 25-кратно вырожденная частота.
Вещественные представления легко отличить от невещественных
с помощью критерия § 30.

§ 40]	ЭЛЕКТРОННЫЕ УРОВНИ В КРИСТАЛЛЕ	145
В заключение параграфа упомянем о разделении ЗЛ/ частот u>v(A)
и соответствующих им главных колебаний на акустические и опти-
оптические.
Акустическими называются те три частоты, скажем u)x(fe), o>2(fe)
и A>3(?), которые при k—> 0 стремятся к нулю. Все остальные ЗЛ/ —3
частоты и соответствующие им колебания называются оптическими.
Покажем, что при k=0 три частоты обращаются в нуль. Для
этого заметим, что подпространство Жк=о содержит среди прочих
перемещений три линейно независимых трансляции всего кристалла
как целого. Потенциальная энергия при таких перемещениях остается
постоянной. Поэтому три частоты, соответствующие этим переме-
перемещениям, равны нулю.
§ 40. Электронные уровни в кристалле
Настоящий параграф посвящен классификации состояний элек-
электронов в кристалле. Мы будем исходить из так называемой одно-
электронной теории, которая заменяет взаимодействие электронов
кристалла некоторым эффективным полем. Таким образом, эта
теория рассматривает каждый электрон кристалла как электрон,
находящийся в заданном внешнем потенциальном поле U(r). Поле
U(г), разумеется, обладает той же симметрией, что и кристалл.
Волновая функция ф(г), описывающая стационарное состояние
такого электрона с энергией Е, удовлетворяет уравнению Шре-
дингера:
|1	ф = 0.	D0,1)
В § 14 было показано, что совокупность ?д всех решений урав-
уравнения Шредингера является линейным пространством, которое
преобразуется по одному из представлений Т_е группы симметрии
потенциальной энергии. Разложим пространство LE на неприводи-
неприводимые подпространства Lhp. Индексы k и р указывают на неприво-
неприводимое представление tkP, по которому преобразуется Lhp. В каждом
подпространстве Lhp выберем базис
ф^ (* = *i, k2, ..., kz; 1=1, 2	sp),	D0,2)
где kb k2, ..., ka—векторы, образующие звезду представления thp,
s. sp — размерность представления ip, связанного с т^.
Функции tyhpi выбраны так, что при трансляциях ta?§ они
D0,3)
Совокупность всех таких функций образует полную систему. Любая
волновая функция электрона в кристалле является суперпозицией
этих функций.
10 Зак. 3512. Г. Я. Любарский
умножаются на eika:

146	КРИСТАЛЛЫ	[ГЛ. VIII
Индексы k, р характеризуют то представление пространствен-
пространственной группы G, с которым связана функция ф^. Индекс k указы-
указывает на соответствующее представление группы трансляций § и
называется квазиимпульсом электрона.
Из соотношения D0,3) следует, что функция fupi = ^upi?~ikr
не изменяется при трансляциях ta из группы оГ. Иными словами,
функция <fhpi является периодической функцией. Поэтому волновая
функция tjjfcp/ может быть представлена в следующем виде:
(г) =?*я(г) «***"•	D0,4)
Мы видим, что волновая функция ^крх представляет собой некото-
некоторую обобщенную плоскую волну, которая получается из обычной
плоской волны, если заменить постоянную амплитуду периодиче-
периодической функцией (?крг.
Из соотношения D0,4) следует, что волновая функция <bhp]
является решением следующей краевой задачи:
Найти внутри кристаллической ячейки функцию, удовлетворяю-
удовлетворяющую уравнению Шредингера D0,1) и краевому условию: функция
tyhi,ie~ihr вместе со своей нормальной производной принимает оди-
одинаковые значения в соответственных точках противоположных граней
кристаллической ячейки.
Собственные числа Е этой задачи образуют дискретный набор
значений
\ЕЦк), E2(k), .... ?„(*)		D0,5)
являющихся периодическими функциями квазиимпульса k. Когда k
пробегает все возможные значения, En(k) пробегает некоторое
множество значений, которое называется л-й полосой энергетиче-
энергетического спектра. Различные полосы энергетического спектра могут,
вообще говоря, перекрываться. На краях каждой полосы имеет
место равенство*
Если при некотором значении квазиимпульса k = ko~ '¦ нескольким
различным волновым функциям электрона соответствует одна и
та же энергия Е, то говорят, что несколько энергетических полос
D0,5) соприкасаются при k = k0.
Такое соприкосновение может быть следствием симметрии кри-
кристалла. Действительно, пусть tyk^i — волновая функция, отвечающая
уровню энергии E(k0). Все волновые функции, принадлежащие
тому же неприводимому подпространству Lkp, что и tykph отвечают
этому же уровню энергии. В пространстве LhoP есть sp линейно
независимых функций с тем же квазиимпульсом k0, что и у функции
tykopi- Поэтому, если размерность sp представления tp точечной
группы Gfc, больше единицы, то при k — k0 соприкасаются sp

§41]	ТЕНЗОРЫ В КРИСТАЛЛАХ	147
энергетических полос. Наоборот, если группа Gho имеет только
одномерные представления, то приведенные рассуждения не дают
основания ожидать соприкосновения полос при k — k0.
Если подгруппа Ofco не имеет одномерных представлений т&0,
то каждая энергетическая полоса соприкасается в точке k = k0
с одной или несколькими соседними энергетическими полосами.
Такое явление «принудительного» соприкосновения имеет место,
в частности, у всех кристаллов, группа которых содержит инвер-
инверсию и хотя бы одну нетривиальную винтовую ось или плоскость
скольжения. Это вытекает из сделанного в § 30 замечания об
отсутствии у таких групп одномерных представлений th при неко-
некотором выборе вектора k.
Существует еще одна причина, приводящая к вырождению энер-
энергетических уровней. Действительно, если волновой функции %pi(r,t)
отвечает некоторая энергия Е, то и комплексно-сопряженной функ-
функции 'bupiir, —t) отвечает та же энергия. Это непосредственно выте-
вытекает из уравнения Шредингера.
Из равенства D0,4) следует, что функция ф^ отвечает состоя-
состоянию с квазиимпульсом —k. Поэтому, если векторы k и —k отли-
отличаются друг от друга лишь несущественно и линейная оболочка
функций difcpz (k, р фиксированы, /=1, 2	sp) не совпадает
с линейной оболочкой функций ohpl, то в точке k имеет место
соприкосновение 2sp полос (а не sp полос, как можно было бы
заключить, если не учитывать вырождения, связанного с симметрией
относительно знака времени).
Легко видеть, что линейные оболочки функций tyhpi и tykpi
A=1, 2	sp) не совпадают друг с другом, если представление
Гщ не является вещественным.
§ 41. Тензоры в кристаллах
Такие физические свойства кристаллов, как теплопроводность,
электропроводность, упругость и др., характеризуются с помощью
тензоров *). Хорошо известно, что наличие у кристалла симметрии
направлений приводит к некоторым зависимостям между компонен-
компонентами тензора. Эти зависимости остаются в силе при любом физиче-
физическом воздействии на кристалл, если оно не влияет на симметрию
направлений в кристалле. Таким образом, симметрия кристалла при-
приводит к тому, что не все элементы тензора независимы.
Если тензор при некоторых перестановках его индексов не изме-
изменяется или умножается на — 1, то это обстоятельство может допол-
дополнительно уменьшить число независимых компонент тензора.
*) Тензорами называются величины, которые при вращениях пространства
преобразуются по л-й степени векторного представления; число п называется
рангом тензора.
10*

148	КРИСТАЛЛЫ	[ГЛ. VIII
Результаты, полученные в § 25, позволяют легко определять
число независимых компонент тензора с учетом симметрии его
индексов и симметрии среды.
Рассмотрим более подробно этот вопрос. Пусть F— точечная
группа симметрии направлений анизотропной среды. При всяком
повороте или зеркальном повороте g?F совокупность всех возмож-
возможных тензоров т-го ранга преобразуется по представлению \т группы
F (V—векторное представление группы F). Так как под дей-
действием преобразований g?F все направления кристалла переходят
в эквивалентные направления, то тензор A%_..t, характеризующий
данный кристалл, не изменяется при всех перемещениях
Иными словами, тензор А%..., преобразуется по единичному пред-
представлению группы F. Предположим, что единичное представление
группы F содержится в тензорном представлении к раз. Это озна-
означает, что среди тензоров wi-ro ранга есть к линейно независимых
тензоров
Л$..... 4?1...	 А§\..„	D1,1)
инвариантных относительно группы F. Всякий другой тензор, инва-
инвариантный относительно группы F, представляет собой линейную
комбинацию тензоров D1,1). В частности,
Мы видим, что задание к параметров сх, с2	ск вполне опреде-
определяет тензор A^_s. Это и значит, что среди компонент тензора
А%...е есть ровно k линейно независимых компонент.
Итак, тензор Л^р... е имеет столько линейно независимых ком-
компонент, сколько раз единичное представление группы F содержится
в ее тензорном представлении Vй. Это число равно
где N — порядок группы F, a x(s)—характер векторного пред-
представления группы F. Он равен
X(C9) = l+2coscp, ZE9) = — l+2cos?.	D1,3)
Заметим, что если вместо тензора мы имеем делэ с псевдотензором,
то к следует вычислять по формуле
signg= ,Z.<? ()
При выводе формулы D1,2) мы не учитывали возможной симметрии
4
тензора ^4ар...« относительно перестановок его индексов. Если такая

§41]	ТЕНЗОРЫ В КРИСТАЛЛАХ	149
симметрия имеет место, то формула D1,2), вообще говоря, стано-
становится неверной.
Поэтому следует рассмотреть случай, когда компоненты тензора
А° не изменяются при некоторых перестановках его индексов.
Совокупность всех таких перестановок образует некоторую группу Р.
Очевидно, что тензор А0 следует искать теперь только среди таких
тензоров т-го ранга, которые симметричны относительно пере-
перестановок Р. Подпространство таких тензоров мы обозначим через Lp.
Это подпространство инвариантно относительно группы F и пре-
преобразуется по представлению Т0^). Характер этого представления
равен (см. B5,9))
Y^ (РЛ = 	 у V 1 J0* I V ( Р* 9 I	7 I сг П	(А\ R\
где Np — порядок группы Р, у_— характер векторного представле-
представления группы F, определяемый по D0,3), а 1Х, /2	If — длины
циклов перестановки р?Р- Тензор А^,_,е имеет столько линейно
независимых компонент, сколько раз представление Т° содержит
единичное представление группы F. Это число согласно B0,3)
равно
Ъ№)-	D1.6)
Предположим теперь, что тензор А0 не изменяется при всех
четных перестановках индексов из группы Р и умножается на — 1
при всех нечетных перестановках из Р. Обозначим через L°_\ под-
подпространство всех таких тензоров. Характер представления, по кото-
которому преобразуется это пространство, определяется формулой
(см. B5,9))
где [р] — четность перестановки \р. Число k в этом случае равно
* = ~^.,(г).	D1,8)
Рассмотрим некоторые конкретные примеры.
1. Тензор диэлектрической постоянной Bik. Этот тензор
симметричен относительно своих индексов sik = eui. Группа Р состоит из
двух перестановок: е и A, 2). Формула D1,5) принимает в этом случае
следующий вид:

150	КРИСТАЛЛЫ	[ГЛ. VIII
Более подробно это можно записать в виде
/С0 (С,) = ^ A + 2 cos ?)» +1 A + 2 cos 2?),
У.0 (S,) = i (- 1 + 2 cos 9J + I A + 2 cos 2ч).
Если кристалл принадлежит классу Civ, то согласно D1,6) получаем:
k = \ {/.° («) + х° (С,) + 2у.о (So)} = 3,
т. е. тензор диэлектрической постоянной в кристалле класса C*v имеет три
независимые компоненты.
Подобным же образом можно рассмотреть другие кристаллические
классы.
2. Тензор упругости Я;ига. Тензор упругости симметричен отно-
относительно перестановок A2), C4), A3), B4) и их произведений. Таким обра-
образом, группа Р состоит в этом случае из восьми перестановок:
в, A2), C4), A3) B4), A2) C4), A4) B3), A423), A324).
В соответствии с этим характер х°(?) равен
Xй (g) = 4 G.4 (?) + 2Х (?2) /.- (g) + 3Х» (?а) + 2/. (?4)}-	D1,9)
Рассмотрим какой-либо кристалл класса D2. Группа D2 имеет четыре эле-
элемента: е, С2, «1, «2- Согласно формуле D1,9) имеем:
X°(e)=jC< + 2.32 + 3. 32 + 2-3) = 21,
Подставляя эти значения в формулу D1,6), получим:
т. е. тензор ^упругости в кристалле класса ?>2 имеет девять независимых
компонент.

ГЛАВА IX
БЕСКОНЕЧНЫЕ ГРУППЫ
§ 42. Специфические особенности бесконечных групп
Приступая к изучению бесконечных групп, целесообразно выяс-
выяснить, какие из результатов, полученных при рассмотрении конечных
групп переносятся в том или ином виде на бесконечные группы.
Остановимся вкратце на трех основных теоремах, относящихся
к представлениям конечных групп.
Теорема I. Каждое представление конечной группы является
неприводимым или распадается на сумму неприводимых предста-
представлений.
Эта теорема вскрывает структуру приводимого представления
и лежит в основе всех или почти всех приложений теории предста-
представлений. Кроме того, она делает обозримой совокупность всех пред-
представлений данной групгул, сводя ее, по сути дела, к совокупности
только неприводимых представлений.
Представляется чрезвычайно трудной задача разобраться во всех
представлениях группы, у которой некоторые приводимые предста-
представления не распадаются на неприводимые.
Так как унитарное представление всякой группы почти автомати-
автоматически распадается на неприводимые представления, то доказательство
теоремы I сводится в основном к установлению того замечательного
факта, что каждое представление конечной группы эквивалентно
некоторому унитарному представлению (см. § 15).
Этот последний факт вытекает из того, что для каждой конеч-
конечной группы О можно построить функционал усреднения функций
на группе (см. § 16).
Итак, при доказательстве теоремы I конечность группы была
использована только для построения функционала усреднения.
Поэтому, переходя к изучению бесконечных групп, естественно
начать с вопроса о существовании функционала усреднения функций
на группе.
Для того чтобы приобрести некоторую ориентировку в этом
вопросе, рассмотрим один пример. Возьмем группу всех целых
чисел
А = 0, ±1, ±2, ...	D2,1)

152	БЕСКОНЕЧНЫЕ ГРУППЫ	[ГЛ. IX
и попытаемся определить функционал усреднения, положив
со
2 ?(«)•	D2,2)
При этом, однако, результат усреднения функции tp(/i)=l не
только не равен единице, но вообще лишен смысла. Более того,
ни один характер рассматриваемой группы вида
у(п) = е**п	D2,3)
не поддается усреднению, так как ряд D2,2) при о — Z расходится.
Поэтому использование функционала D2,2) не дает возможности
доказать разложимость приводимых представлений, составленных
из нескольких одномерных представлений D2,3).
Единственный плодотворный способ определения функционала
усреднения на группе целых чисел дается соотношением
к
М (с?) = 11m -g-rby У <? («)•	D2,4)
*+°° /Л+ \~
При таком определении имеем:
М A) = 1, М (еЫп) = О, М (е1лп ¦ е»"») = Ьтп.
Таким образом, функционал D2,4) можно применять к характерам
одномерных представлений и к их произведениям. Тем не менее —
и в этом заключается существеннейшее отличие рассматриваемой
группы от любой конечной группы—функционал М можно приме-
применять далеко не ко всем функциям группы D2,1). Так, например,
функции
<р(я) = я, <${п)=п2, ср(я) —е-«
усреднению не поддаются.
Обозначим через L тот класс функций, которые поддаются
усреднению с помощью функционала D2,4).
Напомним, что при доказательстве теоремы об эквивалентности
всякого представления унитарному мы применяли функционал усред-
усреднения к скалярному произведению вида (T.(g)x, T(g)y), т. е., по
сути дела, к произведению матричных элементов оператора T.(g).
Поэтому с помощью функционала М удается доказать разложи-
разложимость только тех представлений, у которых попарные произведения
матричных элементов поддаются усреднению или, что то же, содер-
содержатся в классе L.
Используя аппарат так называемых периодических функций,
можно показать, что такими представлениями являются все предста-
представления, матричные элементы которых ограничены.
К счастью, в приложениях встречаются главным образом такие
представления, поэтому вопрос о разложимости приводимых пред-

§ 42]	СПЕЦИФИЧЕСКИЕ ОСОБЕННОСТИ БЕСКОНЕЧНЫХ ГРУПП	15S
ставдений группы целых чисел можно считать решенным. Следует,
однако, иметь в виду, что представления группы целых чисел
не исчерпываются представлениями с ограниченными матричными
элементами. Легко построить представление с неограниченными
матричными элементами. Для этого рассмотрим две функции:
сро(и)=1,
t?l(n) = n,
и сопоставим каждому целому числу k оператор Тд., определенный
равенствами
(я) = То (« -Ь Ь) = ?о (л).
Совершенно очевидно, что матрица оператора Tft имеет следующий
вид:
Мы видим, что не все ее матричные элементы ограничены.
Представление, осуществляемое операторами Т^ (k = Q, rt I, . . .),
является приводимым, так как функция <р0 инвариантна относительно
всех операторов Tft. Тем не менее оно не разлагается на сумму
двух инвариантных одномерных подпространств, так как уравнение
имеет, как легко видеть, только одно решение Х= 1, |3 = 0. Это
не противоречит сделанным ранее утверждениям, так как матрица
оператора '1\. имеет один неограниченный матричный элемент.
Положение вещей, с которым мы столкнулись в этом примере,
типично для всех бесконечных групп: для каждой группы G можно
определить функционал усреднения, однако класс L функций, под-
поддающихся усреднению с помощью этого функционала, далеко не
исчерпывает всех функций на изучаемой группе. В соответствии
с этим, удается доказать разложимость не всех приводимых пред-
представлений группы.
Впрочем, в приложениях большей частью встречаются унитарные
приводимые представления, для которых вопрос о разложимости
на неприводимые представления всегда решается в положительном
смысле.
Теорема П. Матричные элементы двух неприводимых не-
неэквивалентных представлений конечной группы взаимно орто-
ортогональны.
Доказательство этой теоремы опиралось на лемму Шура и на
использование функционала усреднения. Лемма Шура справедлива
для всех групп, как конечных, так и бесконечных. В этом
легко убедиться, просмотрев ее доказательство. Поэтому теорема

154	БЕСКОНЕЧНЫЕ ГРУППЫ	[ГЛ. IX
•ортогональности справедлива в случае бесконечных групп только для
тех представлений, у которых произведения матричных элементов
поддаются усреднению.
Что касается ортогональности матричных элементов, относящихся
к одному и тому же неприводимому представлению, то здесь,
помимо операции усреднения, было использовано предположение
об унитарности рассматриваемого представления. Как мы видели,
это предположение всегда выполняется для представлений, у которых
попарные произведения матричных элементов усредняемы. Таким
образом, и здесь все сводится к возможности применять к рас-
рассматриваемому представлению функционал усреднения. Следует заме-
заметить, что в приложениях часто вместо соотношений ортогональности
можно использовать непосредственно лемму Шура, которая имеет
значительно большую общность.
Теорема III. Каждая функция на конечной группе может
быть представлена в виде суммы матричных элементов всех
неприводимых представлений, взятых с соответствующими коэф-
коэффициентами.
Доказательство этой теоремы опиралось на теорему I. Поэтому
и теорема III не может быть автоматически перенесена в теорию
бесконечных групп.
В течение последних десятилетий были достигнуты серьезные
успехи в обобщении в той или иной форме теоремы III на беско-
бесконечные группы. Эти успехи связаны в основном с именами мате-
математиков Петера и Вейля, Хаара, Понтрягина, Неймана, Гельфанда
и Райкова.
Не имея возможности охарактеризовать методы, использованные для
обобщения теоремы III, попытаемся сформулировать некоторые из получен-
полученных результатов. Для этого разделим все бесконечные группы на две
категории: дискретные группы и непрерывные группы. Группа G называется
непрерывной, если множество ее элементов образует так называемое топо-
топологическое пространство. Это означает, что каждому элементу g^O ставится
в соответствие бесконечное число подмножеств FcG, называемых окрест-
окрестностями элемента g. Это соответствие должно удовлетворять некоторым
естественным условиям, на которых мы не будем останавливаться *).
Для иллюстрации понятия окрестности рассмотрим группу вращений Я.
Путь gr=Ck (<f) есть поворот на угол у вокруг некоторого вектора
А (|*| = 1). Произвольно выбирая два положительных числа ег и е?, рас-
рассмотрим множество Ftitt, состоящее из всех поворотов Ск, (?'), для которых
выполняются неравенства
\* — V\<*i, l?-'f'l<4-
Каждое такое множество Ft t является окрестностью поворота Ch (tp). При-
Придавая числам г1 и s2 различные значения, мы получим бесчисленное мно-
множество окрестностей элемента Ск (<р).
*) Точное определение непрерывной группы можно найти в книге
Л. С. Понтрягина «Непрерывные группы».

§ 42]	СПЕЦИФИЧЕСКИЕ ОСОБЕННОСТИ БЕСКОНЕЧНЫХ ГРУПП	155
Функция f(g) на группе G называется непрерывной на элементе gt ? G,
если для каждого положительного числа.Ь существует такая окрестность F
элемента git что для всех элементов g из F выполняется неравенство
I/(*)-/<ft) К» (g?F)-
Непрерывная группа G называется компактной, если каждая функция f(g),
непрерывная на всех элементах группы G, является ограниченной.
Так, например, группа всех действительных чисел х (—оо <^ х <С оо)
не компактна, так как существуют непрерывные, но не ограниченные функ-
функции f(x) (скажем f(x) = х).
Наоборот, группа поворотов вокруг фиксированной оси компактна.
Компактной является также и группа вращений. Группа Лоренца не является
компактной.
Заметим тут же, что класс L поддающихся усреднению функций вклю-
включает в себя все непрерывные функции, если группа О компактна.
Для компактных групп справедлива следующая теорема:
Теорема IV. Пусть G — компактная группа, a f(g) (g?G)—
произвольная непрерывная функция. Тогда функцию f(g) можно аппро-
аппроксимировать с произвольной точностью г > 0 конечными суммами вида
2 2 <Mlw (« = i,2,...).
1 = 1 i, ft=l
Здесь tp^ (^) —• матричные элементы, порождаемые неприводимым предста-
представлением хг группы G.
Ясно, что эта теорема является обобщением приведенной выше тео-
теоремы III.
Гельфанд и Райков, отказавшись от требования компактности непре-
непрерывной группы и заменив его более слабым требованием так называемой
локальной компактности *), сумели установить следующее положение:
Теорема V. Если группа G является локально-компактной, то
она имеет достаточное количество неприводимых унитарных предста-
представлений в бесконечномерном гильбертовом пространстве.
Выражение «достаточно много» следует понимать в том смысле, что,
каков бы ни был элемент gt, существует неприводимое представление -. (g)"
такое, что -с (gt) Ф Е.
В соответствии с этой теоремой Гельфанд и Наймарк нашли все уни-
унитарные бесконечномерные представления группы Лоренца и некоторых дру-
других локально-компактных групп.
Видоизменения, которые испытывают рассмотренные три теоремы
в теории бесконечных групп, связаны, как уже указывалось,
с отсутствием у бесконечных групп универсального функционала
усреднения.
Этим, однако, не исчерпываются особенности теории бесконечных
групп. Не ставя перед собой задачу сколько-нибудь подробно осве-
осветить этот вопрос, мы ограничимся рассмотрением одной наиболее
важной для физики особенности теории представлений непрерывных
групп.
*) Группа О называется локально-компактной, если каждая непре-
непрерывная на ней функция ограничена в каждой окрестности любого элемента
g ? G. Группа всех действительных чисел является, согласно этому опре-
определению, локально-компактной группой. Группа Лоренца также является
локально-компактной.

156	ЬЕСКОНЕЧНЫЕ ГРУППЫ	[ГЛ. IX
Если рассматривать всевозможные непрерывные функции, опре-
определенные на группе G, то среди них могут оказаться многозначные
функции. Подчеркнем, что ни у дискретных, ни, тем более, у конеч-
конечных групп многозначные функции не возникают иначе, как искус-
искусственным путем механического объединения нескольких однозначных
функций в одну многозначную.
Наоборот, у непрерывной группы может встретиться непрерыв-
непрерывная многозначная функция, которая не может быть без нарушения
непрерывности сделана однозначной «насильственным путем», т. е.
путем отбрасывания лишних значений у каждого элемента g?G.
В качестве примера можно привести функцию
«5-
на группе поворотов. Так как каждый поворот на угол 0 можно
рассматривать и как поворот на угол 6-j-2rc, то функция прини-
принимает для поворота на один и тот же угол два значения:
Если отбросить второе значение, то функция /(б) стала бы раз-
разрывной в точке 0 —О = 2тг.
Группы, у которых существуют непрерывные многозначные
функции, называются многосвязными.
Рассмотренный пример показывает, что группа поворотов является
многосвязной. Группа вращений также является многосвязной. В этом
проще всего убедиться, рассмотрев, например, функцию
/Iе'к(«I = sin -|->
которая, безусловно, является непрерывной, если ее трактовать как
двузначную функцию. Всякая попытка рассматривать эту функцию
как однозначную осуществляется ценой превращения ее в разрыв-
разрывную функцию.
Наличие у некоторых непрерывных групп многозначных функ-
функций позволяет ожидать, что некоторые непрерывные представления
у этих групп являются многозначными. Мы увидим впоследствии,
что группа вращений, например, имеет бесчисленное множество дву-
двузначных представлений. Эти представления нельзя игнорировать
хотя бы потому, что они играют важную роль в некоторых физи-
физических приложениях. С другой стороны, на них нельзя автомати-
автоматически переносить теоремы, справедливые для обычных однозначных
представлений.
Для преодоления этой трудности мы воспользуемся тем обстоя-
обстоятельством, что каждая многосвязная группа G является гомо-
гомоморфным образом некоторой односвязной группы Gv Группу Gx
можно выбрать таким образом, чтобы ни одна ее односвязная

§ 43]	ЭЛЕМЕНТЫ ТЕОРИИ ГРУПП ЛИ	157
подгруппа не имела группу G своим гомоморфным образом. Выбран-
Выбранная так группа Gx называется универсальной накрывающей группой.
Доказательство существования у каждой многосвязной группы
универсальной накрывающей группы выходит за рамки настоящей
книги.
Рассмотрим в качестве примера группу поворотов. Для нее
универсальной накрывающей группой является односвязная группа
всех действительных чисел. Гомоморфизм задается соотношением
х -> 0 = х — 2тг Г^Л *) (— оо <х <со, 0<6<2тг).
Оказывается, что каждое непрерывное представление группы G
(в том числе и каждое многозначное представление) можно рассма-
рассматривать как однозначное непрерывное представление универсальной
накрывающей группы G^, представления группы G, получаемые та-
таким образом, исчерпывают все непрерывные представления группы G.
Если представление t группы G ставит в соответствие каждому
элементу группы О т различных операторов, то представление z
называется т-значным.
Обозначим через
hu h2, ...	(а)
элементы группы Gt, переходящие при гомоморфизме в единицу
группы О. Предположим, что число таких элементов конечно
и равно п. Тогда группа G называется п-связной. Если в некото-
некотором представлении хх группы G^ элементам (а) соответствует п раз-
различных операторов, то в соответствующем представлении z группы G
единице будет соответствовать п различных операторов. Предста-
Представление будет /г-значным.
Если элементам (а) в представлении хх соответствует т. различ-
различных операторов (т < п), то, как легко показать, число т является
делителем числа п. Поэтому если группа G имеет от-значное пред-
представление, то число т является делителем числа п.
В частности, если число п является простым, то все непрерыв-
непрерывные представления группы G являются либо однозначными, либо
и-значными.
§ 43. Элементы теории групп Ли
Среди непрерывных групп важную роль играют так называемые
группы Ли**). Особое место, занимаемое этими группами, обу-
обусловлено тем, что группы Ли, с одной стороны, представляют со-
собой достаточно обширный класс групп, охватывающий важнейшие
Г х Л	х
*) Символ кг означает целую часть от числа =—•
**) Софус Ли A842—1899) — норвежский математик, одним из первых
обративший внимание на класс групп, получивших впоследствии его имя.

158	БЕСКОНЕЧНЫЕ ГРУППЫ	[ГЛ. IX
непрерывные группы, которые встречаются в геометрии, математи-
математическом анализе и физике, с другой же стороны, каждая группа Ли
удовлетворяет целому ряду жестких требований, которые делают
возможным применение для ее изучения методов теории дифферен-
дифференциальных уравнений.
Непрерывная группа О называется группой Ли, если каждый ее
элемент g?G может быть задан с помощью конечного числа пара-
параметров. Минимальное число параметров, достаточных для этой цели,
называется размерностью группы Ли.
Дадим более строгое определение группы Ли. Пусть G — некото-
некоторая непрерывная группа. Рассмотрим какую-либо окрестность V единицы
этой группы. Предположим, что с помощью т вещественных парамет-
параметров О], я2, ..., ат можно задать любой элемент окрестности V таким
образом, что
1)	различным наборам значений параметров alt а», ..., ат соответствуют
различные элементы g из V;
2)	при непрерывном изменении параметров элемент g изменяется непре-
непрерывно, и наоборот, при непрерывном изменении элемента g непрерывно
изменяются и характеризующие его параметры;
3)	если элементы gu g« и gtg2 лежат в окрестности V, то параметры
произведения gigi являются непрерывными и дифференцируемыми функ-
функциями от параметров сомножителей.
При выполнении перечисленных условий группа О называется груп-
группой Ли.
Группа R вращений является группой Ли, так как каждый пово-
поворот может быть охарактеризован тремя параметрами, скажем углами
Эйлера (см. § 5). Поскольку эти параметры независимы в том смысле,
что каждый из них может изменяться, в то время как остальные
два остаются без изменения, то число измерений группы вращений
равно трем.
Другим важным примером является группа Лоренца. Это — группа
преобразований, испытываемых согласно теории относительности
пространственно-временными координатами х, у, z, t при переходе
от одной инерциальной системы к другой. Размерность группы
Лоренца равна шести, так как для исчерпывающей характеристики
взаимного движения двух инерциальных систем нужно шесть пара-
параметров: три проекции скорости начала координат второй системы
отсчета относительно первой и три угла, характеризующих пово-
поворот осей второй системы координат относительно первой.
Пусть G е,сть некоторая группа Ли размерности т и
«1. Ч	<*т	D3,1)
— набор т параметров, характеризующих элементы этой группы.
Условимся выбирать эти параметры так, чтобы единице е группы G
соответствовали нулевые значения параметров.
В дальнейшем мы будем интересоваться только теми предста-
представлениями Т группы О, операторы которых являются дифференцируе-
дифференцируемыми функциями параметров я,, а2	ат. Более точно это озна-

§ 43]	ЭЛЕМЕНТЫ ТЕОРИИ ГРУПП ЛИ
чает следующее. Так как задание параметров D3,1) однозначно
определяет элемент группы, то оператор T(g) можно рассматривать
как функцию от параметров D3,1):
Т(g) = T (oj. а2	О === Т(а).	D3,2)
Выберем произвольно базис в пространстве L, в котором действуют
операторы Т(^) (g? G), и сопоставим с его помощью оператору T(g}
матрицу Tiu(g-) (i, k= 1, 2	s). Каждый матричный элемент Tik(g}
в свою очередь является функцией от параметров D3,1).
Будем называть представление Т дифференцируемым, если все
матричные элементы
Tift(ai. О2,_..., ат) (i, k=\, 2	s)
являются дифференцируемыми функциями от параметров группы
ai> а2	ат.
Оператор, изображаемый матрицей
(с)
будем называть производной от оператора Т(а) по параметру
и обозначать через
Пусть Т — дифференцируемое представление группы в простран-
пространстве L. Введем фундаментальное понятие инфинитезимальных опера-
операторов. Инфинитезимальным оператором \j, соответствующим пара-
параметру oij, называется производная от оператора T.(g) по о^, взятая
при g = e, т. е. в точке at = а2 =....= ат = 0.
Заметим, что при вычислении оператора 1^- можно до дифферен-
дифференцирования положить все параметры ад.(& Ф j) равными нулю.
Таким образом, представление T(g) имеет т инфинитезималь-
инфинитезимальных операторов, т. е. число инфинитезимальных операторов равно
размерности группы.
Рассмотрим в качестве примера векторное представление z группы
вращений. Каждый поворот будем характеризовать тремя парамет-
параметрами: а^ а2, а3> которые определим следующим образом. Сопоста-
Сопоставим произвольному повороту g вектор, направленный по положи-
положительному направлению оси поворота и равный по величине углу
поворота. Ясно, что такой вектор однозначно характеризует пово-
поворот g. Поэтому три его проекции на оси координат можно выбрать
в качестве параметров группы. Именно их мы и возьмем в качестве а.и
ссг, а3. Для вычисления оператора lt достаточно продифференциро-
продифференцировать оператор т^, 0, 0) по at. Так как вращение g(zR
с параметрами a.lt 0, 0 является поворотом вокруг оси ОХ

160
БЕСКОНЕЧНЫЕ ГРУППЫ
[ГЛ. IX
в положительном направлении на угол a,lt то в обычном декартовом
базисе оператор т^, 0, 0) изображается матрицей
Отсюда
«!, 0, 0)
д- (*!, 0, 0)
0 —sin ах —cos
О cos at — sin at
и, следовательно,
Вводя обозначения
/1 О О
б11= О О О
\О О О.
перепишем последнее равенство в виде
D3,3)
= ?32	г
23-
D3,4)
Отсюда круговой перестановкой индексов получаем выражения для
остальных двух инфинитезимальных операторов:
lj = S13 S31, l3 = ?21 ?12"	Do,0)
Разумеется, эти соотношения можно было бы получить незави-
независимо от соотношения D3,4) прямым вычислением.
В известной мере роль инфинитезимальных операторов вскры-
вскрывается следующей теоремой.
Теорема I. Пусть Т и TL — два представления группы G,
действующих в одном и том оке пространстве L, и пусть они
имеют одинаковый набор инфинитезимальных операторов, тогда
представления Т и Т1 совпадают.
Доказательство. Для доказательства этой теоремы пока-
покажем, что инфинитезимальные операторы \t(j=l, 2, ..., т) одно-
однозначно определяют операторы T(g) (g?G). С этой целью выберем
совершенно произвольно вектор jc(t и введем обозначение
y(g) = T (g) x.	D3,6)
Ясно, что вектор у (g) является функцией (и притом дифференци-
дифференцируемой) параметров а^(у=1, 2	/га). Если нам удастся опре-
определить эту функцию, то в силу произвольности вектора х тем самым

§ 43]	ЭЛЕМЕНТЫ ТЕОРИИ ГРУПП ЛИ	161
будут определены все операторы T(g). Покажем, что y(g) удо-
удовлетворяет некоторой системе дифференциальных уравнений, коэф-
коэффициенты которой зависят только от инфинитезимальных операто-
операторов и которая имеет единственное решение.
С этой целью заменим в последнем равенстве элемент g элемен-
элементом g-1 и подействуем на обе части полученного равенства опера-
оператором Т(Л) (h?G). Мы получим:
T(h)y(g-i) = T(h)T(g-l)xT(hg-i)x = y(hg-i). D3,7)
Если обозначить
то равенство D3,7) можно переписать в виде
T(fg)y(g-1) = y(f)-	D3,8)
Обозначим через яг(/), 0Lt(g) и a^fg) параметры, характеризующие
элементы /, g и fg. Так как задание параметров cq(/) и a.i(g)
(/=1, 2, ..., т) однозначно определяют элементы/ и g, то они
определяют и их произведение fg, а следовательно, и параметры
ai(fg)- Последние, таким образом, являются функциями 2т пара-
параметров a-iif), a-iig)
= «Pi l*i (/)• Я2 (/). •••.«» (/); «i (ff). «a (ff)	«TO (g) 1- D3,9)
Ясно, что вид функций (р4(/=1, 2	/re) определяется исключи-
исключительно способом задания умножения на группе О и выбором пара-
параметров щ, характеризующих элементы группы, и не зависят от рас-
рассматриваемого представления Т.
Продифференцируем теперь соотношение D3,8) по ocj(f) (j= I,
2	т) при фиксированном элементе g:
т
2U да, (fg) daj (/) У* > — d*j (/) '
и положим g=f~1. Тогда производные ^—^у перейдут в соот-
соответствующие инфинитезимальные операторы и мы получим:
D3,10)
где введено обозначение
о / f,	d<tj (fg)
К системе дифференциальных уравнений первого порядка D3,10)
можно присоединить вытекающее из соотношения D3,6) начальное
условие
у(е) = х
11 Зак. 3512. Г. Я. Любарский

162 БЕСКОНЕЧНЫЕ ГРУППЫ	[ГЛ. IX
или, если заменить элемент е соответствующим	ему набором пара-
параметров,
, 0, .... 0) = х.	D3,12)
Рассмотрим сначала первое из уравнений D3,10), положив в нем
сс2 = <х3 = ... = а.т — 0. Получим:
Это уравнение вместе с начальным условием D3,12) однозначно
определяет функцию
«i. 0	0) = F1(a1).	D3,13)
Выпишем теперь второе из уравнений D3,10), положив в нем
аз — а* = • • • = ат — 0,
та
0,..., 0) ^^5(a а2> о, .... 0)/^(а1, «2> 0, .... 0).
г ---1
Величину ах можно рассматривать здесь как некоторый пара-
параметр, так как дифференцирование по ах отсутствует. Мы получили
обыкновенное дифференциальное уравнение с начальным усло-
условием D3,13). Оно однозначно определяет функцию _у(аь а2, 0, .. ., 0) =
= /72(а1, а2).
Продолжая это рассуждение, убеждаемся в том, что система
уравнений D3,10) вместе с начальным условием D3,12) однозначно
определяет функцию y(g).
Следовательно, инфинитезимальные операторы lj(J~ 1.2	т),
построенные с помощью представления Т, в свою очередь одно-
однозначно определяют это представление. Теорема I доказана.
Следует подчеркнуть, что при доказательстве теоремы фактически
показано, как по инфинитезималы:ым операторам построить пред-
представление Т. Тем самым задача нахождения представлений Т сво-
сводится к нахождению соответствующих инфинитсзимальных опера-
операторов.
Эта последняя задача значительно облегчается теоремами II и III.
Теорема II. Инфинитезималъные операторы lj(J — 1,2, . .., т),
соответствующие какому-либо представлению Т группы G, удов-
удовлетворяют следующим перестановочным соотношениям:
т
¦у*—и.,-=2ед.	D3,14)
где постоянные С^к не зависят от выбора представления Т.
Доказательство немедленно вытекает из рассмотрения системы
уравнений D3,10). Заметим, что это система уравнений заведомо

§ 43]	ЭЛЕМЕНТЫ ТЕОРИИ ГРУПП ЛИ	163
разрешима: ее решение дается функцией D3,6). Поэтому должно
выполняться необходимое условие разрешимости системы D3,10),
д"-у	д*у
гарантирующее равенство вторых производных -=—itr~= да да '
Покажем, что это условие эквивалентно соотношениям D3,14).
С этой целью вычислим ^—^—. Имеем, опуская аргумент / у пара-
параметров ос{(/=1, 2, ..., т),
Меняя порядок индексов j и k, получаем:
i, «'=1
та
Приравняем теперь полученные выpaжeflия для смешанных произ-
производных
и положим здесь f=e. Тогда, учитывая соотношение
и начальное условие D3,12), получим:
ал
В силу произвольности вектора х из этого векторного равенства
вытекает равенство операторов
где коэффициенты
/л.9-й dS,4\
не зависят, разумеется, от выбора представления Т. Теорема II
доказана.
11*

164	БЕСКОНЕЧНЫЕ ГРУППЫ	[ГЛ. IX
Из соотношения D3,15) видно, что коэффициенты Су& анти-
антисимметричны относительно двух последних индексов
Cijk = — Cikj (i, k, j=l, 2, .... m).	D3,16)
Прежде чем переходить к те'ореме III, получим вспомогательное
тождество
?Si}Ug) d-t^m=Sik{f)'	D3>17)
которое будет использовано при доказательстве этой теоремы.
Рассмотрим произведение fgg\(f, g, gi?O) и обозначим fg — h
и ggi = h1; тогда справедливо равенство hgl—fhl. Следовательно,
<р{ [а (ft), а (gl) 1 = ?i [а (/), а (Лх) ] (а (Л) ~ at (Л), а2 (Л), .... ага (ft)).
D3,18)
Кроме того, можно написать
Продифференцируем теперь D3,18) по aft(/), предполагая элементы g
и gi фиксированными. Получим:
d-n(fhx)
daj(h) ' dak(f)	d*k(f) •
Положим в этом тождестве g1 = (fg)~1 = h~l и, следовательно,
Л! = ggi=f~1. Вспоминая определение D3,11) матрицы S(f), полу-
получим тождество D3,17).
Теорема III. Если какие-либо линейные операторы
определенные в некотором пространстве L, удовлетворяют тем
оке перестановочным соотношениям
т
AjAj, — AkAj = 2 СтАь	D3,19)
i — I
что и инфинитезимальные операторы \и 12	\т, то опера-
операторы Aj являются инфинитезимальными операторами некото-
некоторого действующего в L представления Т группы О.
Доказательство опирается на тот известный факт, что для
разрешимости системы уравнений
^-^V^fe)	(«.20)

§ 43]	ЭЛЕМЕНТЫ ТЕОРИИ ГРУПП ЛИ	165
условие совпадения смешанных производных
д*У (g) = д*у (g)
doij daft daj. до-j
является не только необходимым, но и достаточным. Так как это
условие имеет вид D3,19), то система D3,20) имеет решение, и
притом единственное, соответствующее начальному условию у(е) = х,
где х — произвольный вектор из L. В силу линейности системы D3,20)
оператор Tx(g), ставящий в соответствие вектору х вектор y(g),
является линейным. Покажем, что соответствие ?"->TA(g") является
представлением группы О. Для этого достаточно установить соот-
соотношение TA(g7*) = TA(g")T(/;) для любой пары элементов g, h
группы G. Это соотношение, если его применить к вектору х,
принимает следующий вид:
и означает, что вектор y(gh), рассматриваемый как функция от g
при фиксированном h, также является частным решением системы
дифференциальных уравнений D3,20), но удовлетворяет другому
начальному условию
То, что последний факт действительно имеет место, совершенно
очевидно. Поэтому остается только проверить, что у (gh) удовле-
удовлетворяет уравнениям D3,20).
С этой целью вычислим -J~y-r> Имеем:
т
__ у ду (gh) d?s (gh) _ у d?s (gh) „
8=1	J, 8=1
Используя только что полученное тождество D3,17), находим:
Итак, функция y(gh) удовлетворяет уравнению D3,20) и,.следова-
и,.следовательно, операторы T±(g) дают представление группы G.
Найдем в заключение инфинитезимальные операторы, связанные
с этим представлением. Имеем:
дТл (g) __ dy(g)

166	БЕСКОНЕЧНЫЕ ГРУППЫ	[ГЛ. IX
Мы видим, что инфинитезимальные операторы, порожденные
представлением Та, совпадают с операторами А. Это завершает
доказательство теоремы III.
Значение теорем II и III состоит в том, что они устанавливают
эквивалентность задачи разыскания инфинитезимальных операторов
всевозможных представлений и задачи разыскания всевозможных
совокупностей операторов
Av A2, .... Ат,
удовлетворяющих заданным соотношениям коммутации D3,14).
Три теоремы настоящего параграфа сводят к этой последней
задаче задачу разыскания всевозможных дифференцируемых пред-
представлений группы G.
Заметим в заключение, что если Т и Т — два сопряженных
представления, а ех, ег	es и еъ е2	es—взаимно-контра-
вариантные базисы, то матрицы инфинитезимальных операторов I
и I относительно этих базисов связаны соотношением
Г« = — hi-	D3,21)
Если Т — представление, комплексно-сопряженное представлению Т
то инфинитезимальный оператор I может быть определен соотно-
соотношением
Ц = Ц.	D3,22)
В соответствии с этим матричные элементы инфинитезимальных
операторов I и I в комплексно-сопряженных базисах связаны соот-
соотношением
T T«.	D3,23)
Задача I. Найти перестановочные соотношения для инфинитезималь.
ных операторов группы вращения.
Задача II. Показать, что всякий оператор А, коммутирующий со всеми
операторами некоторого представления группы Ли, коммутирует со всеми
инфинитезимальными операторами этого представления. Показать, что обрат-
обратное утверждение также справедливо.
Задача III. Пусть Tt и Т?—-два представления группы Ли, действую-
действующих в пространствах Lx и Ц. Пусть
i(») i(») . i(i) (i _ i 91
¦—инфинитезимальные операторы, связанные с представлением Т.;(/ = 1, 2).
Обозначим через Е^ и Е5 единичные операторы в пространствах Z.t и L*.
Доказать, что инфинитезимальные операторы Jt, J2, ••¦, Sm, связанные
с произведением представлений ТгХТ2, действующим в пространстве LtXL2,
имеют следующий вид:
+ E142) (*=1, 2	т).

§ 44]	ИНФИНИТЕЗИМАЛЫЮЕ ПРЕДСТАВЛЕНИЕ ГРУППЫ ЛИ	167
Задача IV. Доказать, что инфинитезималыше операторы унитарного
представления являются антиэрмитовыми,'т. е. удовлетворяют соотношениям
!* = -!*¦
Наоборот, если все тшфинитезимальные операторы представления Т являются
антиэрмитовыми, то представление унитарно.
Задача V. Пусть g(alt a2, ..., ат) — элемент группы Ли. Доказать,
что
= -1*.
Задача VI. Доказать, что пространство L, преобразующееся по не-
неприводимому представлению группы Ли, не имеет ни одного нетривиального
подпространства, инвариантного одновременно относительно всех инфините-
зимальных операторов рассматриваемой группы.
§ 44. Инфинитезимальное представление группы Ли
Пусть Т есть некоторое представление группы G в линейном
пространстве L размерности s. Совокупность всех линейных опера-
операторов, действующих в пространстве L, образует линейное простран-
пространство L2 размерности s2. Каждому элементу g?G можно сопоставить
в пространстве L2 оператор Tz(g), определенный равенством
Как показано в § 21, операторы T2(g) осуществляют в простран-
пространстве L2 представление группы G, эквивалентное произведению пред-
представления Т на сопряженное ему представление Т
Пусть группа G является группой Ли размерности т, а 1и
12	1т — ее инфинитезимальные операторы. Каждый из опера-
операторов 1к (&=1, 2	т) можно рассматривать как элемент про-
пространства L2.
Обозначим через IczL2 линейную оболочку всех инфинитезималь-
ных операторов группы G.
Теперь можно сформулировать основную теорему настоящего
параграфа.
Теорема. Линейная оболочка I ияфанитезимальных опера-
операторов представления Т группы G образует в L2 инвариантное
подпространство относительно представления Т2 —ТХТ. Пред-
Представление группы G, индуцируемое в I, не зависит от выбора
представления Т, если только размерность I равна размер-
размерности т группы G.
Представление* индуцируемое в подпространстве /, называется
инфинитезимальным.

168	БЕСКОНЕЧНЫЕ ГРУППЫ	[ГЛ. IX
Изучение инфинитезимального представления оказывается полез-
полезным при нахождении неприводимых представлений группы Ли,
а также при решении ряда прикладных вопросов. В квантовой меха-
механике инфинитезимальные операторы выступают в роли операторов,
отвечающих тем или иным физическим величинам. Поэтому пред-
представляет интерес характер их преобразования под действием эле-
элементов группы G; сформулированная теорема показывает, что эти
операторы преобразуются по инфинитезимальному представлению.
Доказательство. Начнем с инвариантности подпростран-
подпространства /. Для доказательства инвариантности подпространства / до-
достаточно проверить, что все операторы
; k=\, 2, .... т)
содержатся в /.
Так как по определению \к
T(ff)I*T(ff-i) = g^{T(ff)T(/)T(^-1)}ree,	D4,1)
то естественно рассмотреть более подробно выражение
^)- D4>2)
Введя обозначение
h = gfg~1.
можем написать:
„. . dak(f) •
Подставляя в это равенство /=е, получим в силу D4,1) и D4,2)
h=e ""kv/
т. е.
т
Т2 (g) h = T ig) \k'l (g~i) = 2 Cjk (g) lj,	D4,3)
где
D4,4)
f=e
Соотношение D4,3) доказывает инвариантность подпространства /.
Коэффициенты Cjk(g) вполне определяют оператор T2(g") в под-
подпространстве /. Как показывает равенство D4,4), эти коэффициенты
не зависят от выбора представления Т.

§ 44]	ИНФИНИТЕЗИМАЛЬНОЕ ПРЕДСТАВЛЕНИЕ ГРУППЫ ЛИ	169
Если операторы 1^- (у=1, 2	т) линейно независимы в про-
пространстве L2, то они образуют базис подпространства /. В этом
случае коэффициенты Cjk(g) не просто определяют оператор Tz(g),
а являются матричными элементами этого оператора, который, та-
таким образом, не зависит от выбора представления Т. Теорема до-
доказана полностью.
Задача I. Обозначим через Jj, J2, ..., im набор инфинитезимальных
операторов, связанных с инфинитезимальным представлением. Доказать фор-
формулу
JaIj = I&Iy — Ь1д-
Задача II. Доказать, что инфинитезимальное представление группы
вращения эквивалентно векторному представлению.

ГЛАВА X
ПРЕДСТАВЛЕНИЕ ГРУППЫ ПОВОРОТОВ, ГРУППЫ ВРАЩЕНИЙ
И ПОЛНОЙ ОРТОГОНАЛЬНОЙ ГРУППЫ
§ 45. Неприводимые представления группы поворотов Z
Группой поворотов Z называется подгруппа группы вращений,
состоящая из всевозможных поворотов вокруг оси OZ.
Так как группа Z коммутативна, то все ее неприводимые пред-
представления одномерны (см. задачу II § 18). Найдем непрерывные и
дифференцируемые неприводимые представления группы Z. Пусть
Х(«р) есть характер какого-либо, быть может, и многозначного пред-
представления группы Z. Тогда в силу одномерности представления
можем написать:
Дифференцируя это равенство по (|> и полагая затем ф^О, полу-
получим:
Отсюда следует, что ?(-.?) = е<?/-'@). Число m = ix'{0) называют ин-
индексом найденного представления, характер представления с инде-
индексом т будем обозначать через ут («). Таким образом, мы имеем:
Х« (?) = «"'""•	D5>!)
Если индекс т — целое число, то представление у^т однозначно.
В противном случае мы получаем многозначное представление.
Группа Z имеет, таким образом, континуум неприводимых предста-
представлений. Представления с действительными индексами являются унитар-
унитарными, все остальные не унитарны.
Инфинитезимальный оператор, соответствующий углу ср, равен
— e~imf — — lm. Поэтому
df	?=o	J
Задача. Найти произведение двух неприводимых представлений
группы Z с индексами т1 и яг2.

§ 46]	НЕПРИВОДИМЫЕ ПРЕДСТАВЛЕНИЯ ГРУППЫ ВРАЩЕНИЙ	171
§ 46. Классификация неприводимых представлений
группы вращений
Прежде чем приступить к отысканию неприводимых представле-
представлений группы вращений, перечислим некоторые установленные ранее
факты.
1.	Характер векторного представления определяется формулой
X(CT)=l+2cos?;	(a)
здесь С<р —С(ср) обозначает поворот вокруг какой-либо оси на
угол ср.
2.	Параметры группы вращений можно ввести следующим обра-
образом. Сопоставим каждому повороту вектор, направленный вдоль
оси поворота в сторону, откуда поворот кажется происходящим
в положительном направлении, и равный по величине углу поворота.
Проекции этого вектора на оси координат обозначим через alt a2
и a3, а сам поворот обозначим через g[oLlx2'x3). Полученные таким
образом числа alt а2 и а3 могут служить параметрами группы вра-
вращений.
3.	Инфинитезимальные операторы, соответствующие параметрам
ax> a2 и a3, определяются в векторном представлении матрицами
(см. D3,4), D3,5))
*1 := ?32 е23> *2 == г13 S31> *3 == S21 S12-	(б)
4.	Инфинитезимальные операторы векторного представления,
а значит, и любого другого представления удовлетворяют следую-
следующим перестановочным соотношениям:
lib —W^UAl^s. [Ыз1 = 11, [Wil = b-	(в)
5.	Инфинитезимальное представление группы вращений эквива-
эквивалентно векторному представлению. При этом роль базисных векто-
векторов i, j и k играют соответственно операторы 1и 12 и 13.
6.	У группы вращений существует функционал усреднения. Если
воспользоваться углами Эйлера 8, о и if, то функционал усредне-
'ния можно записать в виде
М (f) = ~ J J J /@, <?, ф) sin 0 db d? dif.	(г)
Группа вращений является компактной группой, поэтому каждое непрерыв-
непрерывное однозначное представление этой группы имеет эквивалентное себе уни-
унитарное представление. Оказывается, что у группы вращений универсальная
накрывающая группа также компактна, поэтому этим же свойством обладают
и неоднозначные представления группы вращений.
Перейдем теперь к отысканию неприводимых представлений
группы вращений, которые мы. будем считать унитарными в соот-
соответствии со сделанным замечанием.

172	ПРЕДСТАВЛЕНИЯ ГРУПП	[ГЛ. X
Пусть D(g) (g?R) есть некоторое неприводимое представление
группы вращений, действующее в s-мерном пространстве L, и пусть
'i> h и 'з — порожденные этим представлением инфинитезимальные
операторы.
Представление D(g) является в то же время представлением
группы Z поворотов вокруг оси OZ. Так как все неприводимые
представления группы Z одномерны, то представление D, рассма-
рассматриваемое как представление группы Z, разбивается на s одномер-
одномерных представлений. Соответствующие этим представлениям одно-
одномерные подпространства можно охарактеризовать, выбрав в каждом
из них по вектору. Таким образом, мы получаем ортогональную
совокупность s векторов emi, ет%, ..., emg. Здесь ти т2, ..., ms
обозначают индексы представлений группы Z. Операторы D [0, 0, а3],
соответствующие всевозможным поворотам вокруг оси OZ, изобра-
изображаются в этом базисе следующим простым образом:
О	... О
О	e-tms«3 ... О
D [0, 0, а3] =
D6,1)
10	0	... е~гтак
Подобную же процедуру произведем с инфинитезимальными опе-
операторами, введя в рассмотрение операторы
Ао = 13,	D6,2)
преобразующиеся под действием поворотов вокруг оси OZ по не-
неприводимым представлениям группы Z с индексами 1,—1 и 0.
Согласно равенству D6,2) имеем:
AoeOTv = hem, = — im^ (ч=1,2, .... s)	D6,3)
и
[Ao\k] = — tk\k (ft=0,±l),	D6,4)
[AiA.J = 2/Ao-	D6,5)
Рассмотрим теперь вектор Ахетч. Легко видеть, что если он не
равен нулю, то он преобразуется по произведению представлений
группы Z с индексами 1 и /и.,. Действительно,
Ч"-\етч === "-т\гет^ "I A1J emi ==
Точно так же вектор А_1ете>1 если только он не равен нулю, пре-
преобразуется по представлению группы Z с индексом mv—1 (v=l,
, ..., s).

§ 46]	НЕПРИВОДИМЫЕ ПРЕДСТАВЛЕНИЯ ГРУППЫ ВРАЩЕНИЙ	173
Обозначим через ] наибольшее из чисел mv щ	ms и через
¦e^L — вектор (или один из векторов), преобразующийся по пред-
представлению группы Z с индексом J.
Построим последовательно векторы
^_i = A_1fy ej_2 = A_1ei_1	ej_r = A_1ej_r+1,... D6,6)
Среди этих векторов имеется не более s отличных от нуля.
Действительно, все не равные нулю векторы fy_ft (& = 0, I, .. .)
линейно независимы и даже ортогональны, так как преобразуются
по неэквивалентным неприводимым представлениям группы поворо-
поворотов Z. Если г — число отличных от нуля векторов D6,6), то
ej-r+i — последний не равный нулю вектор и
ej_r = A_1ej_r+1 = 0.	D6,7)
Подпространство Lr, состоящее из всевозможных линейных комби-
комбинаций взаимно-ортогональных векторов
ejt ej_lt .... ej_r+1,	D6,8)
инвариантно относительно оператора А_х в силу соотношений D6,6)
и D6,7). Оно инвариантно и относительно оператора Ао в силу
соотношений D6,3), которые применительно к векторам D6,8) за-
записываются в виде
V* = -'*«* {k^j,j—\	j — r + Y). D6,9)
Рассмотрим теперь векторы, получающиеся в результате примене-
применения оператора At к векторам D6,8). Прежде всего имеем А1е;- = 0,
так как в противном случае в пространстве L существовал бы век-
вектор Аф Ф 0, преобразующийся по представлению группы Z с ин-
индексом /-|~1, что невозможно в силу выбора индекса J. Далее,
имеем:
A1ei_1 = A1A_1<?i = A_1A1ei + [A1A_1]ei.	D6,10)
Первое слагаемое в правой части этого равенства есть нуль. Вто-
Второе слагаемое согласно D6,5) равно 2iAoe,- = 2jej. Равенство D6,10)
принимает следующий простой вид:
A1ej__1 = 2jej.	D6,11)
Теперь нетрудно вычислить вектор А^_2- Имеем:
Ai^-2 = А1А_1^_1 = A_1A1eJ_1-\-2tA0pJ_1 = 2jei_l-\-2 (j— 1) et_v
т. е.
A1ej_2±=2Bj—l)ej_1.
Легко видеть, что, последовательно вычисляя векторы А1е^_3,
A-t^j-i, • • •. мы получим соотношения вида
(m = j, j— 1, ..., j — r + 1), D6,12)

174	ПРЕДСТАВЛЕНИЯ ГРУПП	[ГЛ. X
где )^j — некоторые числа. Значения Xj, Xj_t, Xj_2 нами уже найдены:
\f = 0. Х,_, = 2/, Х,_2 = 2BУ—1).
Равенства D6,12) показывают, что подпространство Lr инвариантно
не только относительно операторов Ао и А_х, но также и относи-
относительно оператора Av Это означает, что подпространство Lr инва-
инвариантно относительно всех трех инфинитезимальных операторов 11(
12 и 13 и, следовательно, относительно всех операторов рассматри-
рассматриваемого представления D(g) группы вращения. Поэтому Lr совпа-
совпадает со всем пространством L, число r = s и векторы D6,8) обра-
образуют базис в пространстве L. Равенства D6,6), D6,9) и D6,12)
определяют операторы A_i, Ao и kv Остается выяснить, какие
значения может принимать число j и числа \т для того, чтобы
определенные этими равенствами операторы удовлетворяли необхо-
необходимым перестановочным соотношениям. Как только эта задача будет
решена, мы получим возможность перечислить все неприводимые
дифференцируемые представления группы вращений, придавая j и \т
разрешенные совокупности значений.
Нетрудно видеть, что соотношения D6,4) удовлетворяют при
любом выборе чисел 1т и j.
Для того чтобы операторы Ао, A_t и Аи определенные равен-
равенствами D6,6), D6,9) и D6,12), удовлетворяли также и перестано-
перестановочному соотношению D6,5), должны выполняться следующие ра-
равенства:
2т = 1т_1 — lm (m = j, 7—1, ..., J —
О = kle}_s = X^_g^ _e+1.
К этому следует присоединить условие
выражающее тот факт, что в представление D не входит ни одно
представление группы поворотов с индексом, большим чем j.
Итак, мы получили систему разностных уравнений
К-1 — >™=2л»	D6,13)
вместе с дополнительными условиями
Х,= 0, >*_в=0.	D6,14)
Решая уравнение D6,13) с учетом первого из усло"вий D6,14)
находим:
— »(m+l).	D6,15)
Поэтому для выполнения второго условия D6,14) необходимо и
достаточно, чтобы

§ 46]	НЕПРИВОДИМЫЕ ПРЕДСТАВЛЕНИЯ ГРУППЫ ВРАЩЕНИЙ	175
Число ] может быть, таким образом, любым целым или полуцелым
числом (т. е. половиной нечетного числа).
Проведенное рассуждение показывает, что каждое из значений
числа j
j=0, I, 1, 1, 2, ...	D6,16)
определяет, и притом единственным образом, представление группы
вращений; размерность этого представления равна s—2/-J-1.
Отсюда следует, что с точностью до эквивалентности группа
вращений имеет ровно по одному неприводимому представлению
каждой размерности.
Неприводимое представление группы вращений удобно характе-
характеризовать числом у, называемым его весом.
Размерность s представления веса j равна
s=2/+l.	D6,17)
Представление группы вращений веса j принято обозначать через Oj.
Используя формулу s = 2j-\-l, можно переписать соотноше-
соотношение D6,1) в виде
*Ja> ... О 1
D, [0, 0, <х8] =
[О
D6,18)
Заметим, что матрицы, соответствующие в базисе D6,8) опера-
операторам Dj[av ос2, а3] унитарного представления Dj, не являются уни-
унитарными, поскольку этот базис хотя и ортогонален, но не норми-
нормирован. Так как часто бывает более удобно иметь дело с унитарными
матрицами, то целесообразно произвести нормировку базиса D6,8).
Пусть векторы
ет = *тет (т = ~J> ~J + l	Л	D6,19)
образуют нормированный базис. Для вычисления коэффициентов рт
проще всего воспользоваться результатом задачи IV § 43, в силу
которого необходимым и достаточным признаком унитарного пред-
представления является антиэрмитовость всех его инфинитезимальных
операторов. В нашем случае это означает, что операторы /I1( i\2
и il3 являются эрмитовыми. Поэтому оператор А*, сопряженный
оператору kv равен
'*m\em+V em+V == \"-lem' em+l)z=\em> ^-lem+l) == \ет> ет)>

176	ПРЕДСТАВЛЕНИЯ ГРУПП	[ГЛ. X
Учитывая соотношение D6,19), получаем отсюда:
V-m + i	\V-m\
Фаза нормирующих множителей совершенно произвольна. Если взять
в качестве [ато (/и = —j, ..., j) положительные числа, то послед-
последнее равенство можно переписать в виде
Выразим операторы A_lf Ао и Ах в новом базисе. Используя
соотношения D6,6), получаем:
т. е.
или, окончательно,
А
~ вт-\ ~
	Н-от-1 /
1) — т(т— 1)в^_,.	D6,20)
Подобным же образом находим:
Будем называть базис
е' ., е' , ,, .... е'.	/ар, оо\
каноническим базисом. Он состоит из ортонормированных векто-
векторов е'т{т=^—j	j), каждый из которых осуществляет непри-
неприводимое представление группы Z индекса т. Операторы A_v Ао и Ах
определяются в каноническом базисе формулами D6,20) и D6,21).
Инфинитезимальные операторы связаны с операторами A_v Ao и At
соотношениями
Если ввести обозначения
aim = Vj(j-\-l) — m(m— 1),	D6,24)
то соотношения D6,20) и D6,21) можно переписать в виде
д		 j	д		 	 .	д		 j	,.П OCX
(штрих над ет_1г ет и ет+1 опущен).

§ 47]	МАТРИЧНЫЕ ЭЛЕМЕНТЫ НЕПРИВОДИМЫХ ПРЕДСТАВЛЕНИЙ	177
В заключение подчеркнем, что в настоящем параграфе произведено
перечисление всех неприводимых представлений oJj=zQt —, 1, ... j
группы вращений и найдены матрицы инфинитезимальных операто-
операторов в так называемом каноническом базисе.
Кроме того, приведенные в этом параграфе рассуждения дока-
доказывают следующую теорему.
Теорема. Пусть llt I2, 13—-три произвольных оператора,
определенных в некотором пространстве L и удовлетворяющих
перестановочным соотношениям
Обозначим через X1^zi\l —12, A_] = ilt —j—12> Ao = I3. Тогда
1)	среди собственных векторов оператора Ао найдется век-
вектор ej такой, что \tej = 0;
2)	собственное число j, отвечающее вектору ej, является
целым или полуцелым;
3)	векторы ^ и векторы ej_v ej_2, •¦-, e_j, построенные
с помощью рекуррентных соотношений
1)«„_1 (» =7. J— 1	—1 +
преобразуются следующим образом под действием операторов
и Ао:
В следующем параграфе будут вычислены матрицы Dj(g) в кано-
каноническом базисе.
Задача. Показать, что
I2=lf + «2+ 'з = Aj-lcAjiA-i-t- A-jAi)- -JU+ 1)Е, D6,26)
где Е—единичный оператор.
§ 47. Матричные элементы неприводимых представлений
В настоящем параграфе мы вычислим матричные элементы непри-
неприводимого представления D, как функции от углов Эйлера 8, ср, ф.
Определим прежде всего зависимость DJtpF, ср, ф) от углов ср
и f Из тождества E,3) g-@, ср, ф) = С3 (ф)Сг @)С3 (ф) следует, что
D^ (в, ср. '»-?>Ш}(С3(ф))^(С1F))О<!|)(Сз(ср)).
Вспоминая, что матрица, соответствующая повороту вокруг оси OZ,
имеет вид D6,18), можно написать:
D& (С, (<|>)) = З^е-**. ОЙ> (Ся (?)) = 5„ге-
12 Зак. 3512. Г. Я. Любарский

178	ПРЕДСТАВЛЕНИЯ ГРУПП	¦	[ГЛ. X
Подставляя эти выражения в предыдущее равенство, получим:
рф)	?)РИ,1,F),	D7,1)
где
^•u(°)=D«(Ci@)).	D7,2)
Отсюда следует, что
8.	D7,3)
Для определения функций Ры>?-@) выведем дифференциальное урав-
уравнение, которому удовлетворяют матричные элементы D/?i (б, ср, ф).
Сопоставим каждому элементу h группы вращении оператор t{h),
действующий на матричные элементы Djji (g) (g?R)'-
D7,4)
Так как D$ (gk^ = D{i?b{g)D{Ja (к), то последнее равенство можно
переписать так:
Отсюда видно, что семейство функций D(-m(g) (k фиксировано,
m——j, ..., j) инвариантно относительно всех операторов t(h)
(h?R). В базисе em==D{^ (g) оператору t(/z) соответствует мат-
матрица D\i\(h). Это означает, что операторы t(/z) образуют пред-
представление Dj группы вращений, а функции D$m(g) (т = —j	у)
играют роль канонического базиса.
Вычислим инфинитезимальные операторы этого представления.
Возьмем в качестве вращения h поворот вокруг оси ОХ на угол at.
Равенство D7,4) можно при этом переписать в виде
t [о., О 0] Di-f F, ф, ф) = D® F (at), 9 (a,), ф(a,)),	D7,5)
где б (at), cp (at), ^(a,) — углы Эйлера, характеризующие произведе-
произведение вращений gh. Дифференцируя тождество D7,5) по ал и полагая
затем ах = 0, получим:
«,=о
«,-=о-
Мы видим, что инфинитезимальный оператор It является оператором
дифференцирования:
, дО (cxt) д , ду (cti) д , db (oe-i) д	.,- «.
|t = v wJl--[- TV i/jl^^tv "	D7,6)
Вычислим входящие сюда производные , ^ , ^	. Для
этого воспользуемся тождеством
X! О 0),	D7,7)

§ 47]	МАТРИЧНЫЕ ЭЛЕМЕНТЫ НЕПРИВОДИМЫХ ПРЕДСТАВЛЕНИЙ	179
где gik(fi, <?. 40 — известная нам матрица E,4). Полагая здесь /==3,
А = 3, получим:
cos6 («!)==—
sinat
@, <р> ^
Дифференцируя это соотношение по at и полагая затем а( = О,
найдем:
^-^ =—g32(b, ср, ф} = —sin 6 cos ср.
i «,=о
Отсюда следует, что
а,=О
cos ср. Полагая в D7,7) г = 3,
& = 2, найдем подобным же образом, что
Ааконец, взяв 1=1, k — З, получим, что
= —ctgf 6 sin ср.
	sin 9
sin i
Операторы 12 и 13 могут быть подсчитаны этим же методом.
В результате получаются следующие выражения:
д
с>6
.	д . о • д i s'n 9 д
• I, = cos Ф 3F — ctg о sin ср з—	h: -^г,
1	т с>6 s "dtp cos в dfy
От операторов I,, 12, 13 легко перейти по формулам D6,2) к опе-
операторам A_i, Ao^Ajt
Ах = ,
D7,8)
Применим теперь общие соотношения D6,20) D6,21) к нашему слу-
случаю. Получим:
sinT
(m
D7,9)
12*

180	ПРЕДСТАВЛЕНИЯ ГРУПП	[ГЛ. X
Подставим сюда выражение D7,1) для D^:
/д . mcos8—fe\p _ уу
В частности,
/ д у cos 6 — k
\Ж	sufi
Общее решение последнего уравнения имеет следующий вид:
phj,j Ф) = ск 8Ы-* | cosJ+* |- (А = —7	У). D7.11)
Для определения всех остальных функций Pkmj обратимся к пер-
первому рекуррентному соотношению D7,10). Если сделать замену
переменных
т-к	т+к
,	), D7,12)
то это рекуррентное соотношение примет следующий простой вид:
¦уА>я»-1 =	,/¦...... . ,ч*~3—*	D7,13)
УуО + 1) — т{т — 1) rfjx
Отсюда следует, что
ТТ^Г	D7'14>
Ц /Уи + 1)-л(я-1) .**
n=m+l
Функцию vkj легко посчитать с помощью D7,11):
vkj (Jf) - с*?"' A — ix)^fc (I + tf+k.
Подставляя это выражение в D7,14) и используя D7,12), получим:
X
D7.15)
Неизвестные пока коэффициенты ск должны быть определены из
условия Pftfcj.'@)=T(CM. D7,3)).
^Имеем-.j

§ 47]	МАТРИЧНЫЕ ЭЛЕМЕНТЫ НЕПРИВОДИМЫХ ПРЕДСТАВЛЕНИЙ	181
Полагая здесь 6 = 0, ц = 1, получим:
H ^
=л+1
Отсюда следует, что
Подставляя это выражение в D7,15), получим окончательно:
2jU ~k)\
m—k	m+k
_	~2-X
D7,16)
Функции Ойда (б, ср, ф) называются обобщенными сферическими
"функциями у-го порядка.
Итак, мы доказали, что матричные элементы
где функции P/cmjfi) определяются соотношением D7,16).
Приведем вычисленные по формулам D7,1) и D7,16) матрицы
представлений D\ и Dt:
Т
А (б. ?. ф) =
s б)	i= ег> sin G iei(-V-T)
/	y2	2
L *>»> sin б	cosO	^
2
jL *> sin б	cosO	^=<
/2	У 2
—cos 6)	^e-Hsine — е-* (Ф+т) A + cos 6)
V 2	.2
¦!(?+¦) в	. |(Ф-?) . в
e2 c°s-o- —/e	sm

182	ПРЕДСТАВЛЕНИЯ ГРУПП	[ГЛ. X
Из соотношения D7,16) следует, что функции Po,-m-,j(®) про-
пропорциональны присоединенным функциям Лежандра
Р? (cos 0) = -?- sin» б	dm+J . jcos26 — l/. D7,17)
•*	2'/!	{d cos 8)га+'	7	'
Именно, имеет место соотношение
Л). -та; j @) = f"» ]/ ((j ~g| Pf (cos 6).	D7,18)
Поэтому матричные элементы D,{ .OT(8, о) пропорциональны сфери-
сферическим функциям
Yjm (9. ?) = W* eim*Pf (cos 6);
Екм(в. ср).	D7,19)
Задача I. Доказать с помощью соотношения D6,26), что функции Ркт, j
удовлетворяют дифференциальному уравнению
2 — 2mk cos в
Задача П. Показать, что
P^TjW = (- l)m-& Pftm, j (8).
Задача III. С помощью D6,25) и D7,9) показать, что
§ 48. Свойства неприводимых представлений группы вращений
Выводы, полученные в двух последних параграфах, позволяют
ответить на ряд вопросов, относящихся к неприводимым предста-
представлениям группы вращений.
Выясним прежде всего, все ли неприводимые представления
группы R являются однозначными. Для этого напомним, что углы
Эйлера 6, ср и ф, характеризующие вращения, изменяются в пределах
0<8<тс, 0<с?^2я и 0<ф<2т:. При этом вращения g(б, 0, ф)
и gF, 2тс, ср) совпадают между собой; подобным же образом совпа-
совпадают вращения g-@, ср, 0) и g(b, cp, 2ir). Если матрицы представле-
представления Dj удовлетворяют условиям D,-(G, 0, ^) = Dj@, 2тс, ^) и
D^F, cp, O) = D^@, ср, 2тс), то мы имеем дело, очевидно, с однознач-
однозначными представлениями, в противном случае представление D^- не
является однозначным. Согласно формуле D7,1), мы можем написать:
2«. ^) = e-2"JD$(G, 0, ф), ,
ср, 2ъ) = е-ЫкО(Ц{Ъ, ср, 0).

§ 48]	СВОЙСТВА ПРЕДСТАВЛЕНИЙ ГРУППЫ ВРАЩЕНИЙ	183
Числа / и k являются целыми или полуцелыми одновременно с чис-
числом j. Поэтому, если вес представления j есть целое число, то
представление однозначно. Если же представление имеет полуцелый
вес, то вращениям g@, О, <1>) соответствуют два оператора d=D^ @, 0, <]>).
Отсюда следует, что и всякому другому вращению соответствуют
два оператора ±Dj(g). Таким образом, представления с целым
весом являются однозначными, представления с полуцелым весом —
двузначными.
.Мы видели, что произведение двух вращений с углами Эйлера 9,
ср, ^ и 9, тс— 6, тс—9 равно единице. Поэтому произведение
IX;(9, ср, 6)Dj@, тс— i>, тс — cs) равно единичному оператору Е, если
представление Dj однозначно. В случае двузначного представления
это произведение равно либо Е, либо — Е:
Выясним, какой знак следует взять в правой части этого равенства.
Переходя к матричным элементам и используя D7,1), напишем:
j
2 e-i W+4)PaJ (G) <.-*№=-«*+*¦=-•»*>/>, ; F)== ±hm-
Устремим здесь угол 0 к нулю, имея в виду, что ЯиД0) = 8й.
Мы получим:
Так как мы рассматриваем полуцелые значения j, то 1т является
нечетным числом и в правой части последнего равенства следует
взять знак минус. Таким образом,
Dj(b, <p, ty)Dj(b, тс — ф, п—<?) = е2гЛ№.	D8.1)
Рассмотрим теперь операцию перехода к сопряженному пред-
представлению. Так как взаимно-обратные вращения g и g-1 осущест-
осуществляют поворот на один и тот же угол (вокруг противоположных
осей), то они сопряжены друг другу. Поэтому (см. задачу VI § 21)
каждое представление группы R сопряжено самому себе. Имея это
в виду, можно следующим образом сформулировать теорему § 21
применительно к группе вращений:
Произведение двух неприводимых представлений Dj и Dj>
с различным весом (j -f= f) не содержат единичного представления.
Квадрат каждого неприводимого представления Dj содержит
ровно один раз единичное представление.
Найдем в пространстве^-, в котором действуют операторы Dj(g),
базис
e-i, e~i+l	ei,	D8,2)
контравариантный каноническому базису.

184	ПРЕДСТАВЛЕНИЯ ГРУПП	[ГЛ. X
Оператор Dj(g) в силу унитарности изображается в этом базисе
матрицей, которая комплексно сопряжена матрице оператора Dj(g)
в каноническом базисе *). Поэтому инфинитезимальные операторы
также изображаются комплексно-сопряженными матрицами. Легко
видеть, что при этом в силу соотношений D6,2) матрицы операто-
операторов Ао, А+], A_t в контравариантном базисе комплексно сопряжены
матрицами операторов соответственно — Aq, —А+1, —A_t в кано-
каноническом базисе. Учитывая это, получаем из D6,20) и D6,21):
-l) — /и(да —
/C/ + 1) —я*(да-г- \)ет^, >	D8,3)
= imem.	J
Последнее равенство показывает, что индекс вектора ет равен — т.
Поэтому можно написать:
е'» = Тте_от(яг=— j, ..., j; \im\ = \).
Подставляя это выражение в D8,3), получаем:
^	— m(m+l)e_m_v
Сравнивая это соотношение с соотношением D6,20), находим, что
Т»г+1— — Тда и> следовательно, ~\т = const (— \f~m. Поэтому векторы
em = (—iy-me_m (т. = - j, —j + 1	j) D8,4)
образуют базис, контравариантный каноническому базису.
Будем называть компоненты вектора fl^t в каноническом базисе
ковариантными компонентами и обозначать их через
Компоненты этого же вектора в контравариантном базисе D8,4)
будем называть контравариантными компонентами и обозначать
их через ат (—j*Cm^.j). Таким образом,
а = ате^ — (— \)j~mame_m.
Из этого равенства видно, что между ковариантными и контрава-
контравариантными компонентами вектора в пространстве Lj существует
простая связь:
«-» = (— DJ~mam.	D8.5)
*) Отсюда следует, что векторы контравариантного базиса D8,2) совпа-
совпадают с комплексно-сопряженными векторами исходного базиса D6,22), если
для последних определена операция перехода к комплексно-сопряженному
вектору.

§ 48]	СВОЙСТВА ПРЕДСТАВЛЕНИЙ ГРУППЫ ВРАЩЕНИЙ	185
Обозначим через fm канонический базис в некотором пространстве А^,
преобразующемся по представлению D^-. Согласно § 22 имеют место
соотношения
2 emfm — m\, 2 a"»*w = inv.	D8.6)
j	j
С помощью равенств D8,4) и D8,5) эти соотношения можно пере-
переписать в виде
2 (- 1/~W «-«/m = inv, 2 (- i)J'm a-J>m = inv. D8.7)
m—i	m--j
Применительно к пространствам [) и/., эти соотношения принимают
Т
следующий вид:
e_ifi—e±f_}_ = inv>	a_iAl— fll* i=inv,|
~ i ~2 ~I	~2 2 ? ~1	у D8.8)
e_iA — e0/0 + ej_i = inf, a_i6i — ao^o-f-a^i^inv. j
Нетрудно установить связь между векторами канонического базиса
в трехмерном евклидовом пространстве и ортами i, j и к. Прежде
всего ясно, что можно положить
так как оба эти вектора не изменяются при поворотах вокруг оси OZ~
Далее, согласно D6,25) имеем:
С другой стороны,
А_,к = (И, —12) k = —\lj+0. Atft - Oil -I-18) ft = —
Сравнивая эти соотношения, находим:
«_i = —y=-(f-R0. eo = k, e1==-J=.y_y). D8,9)
В соответствии с этим координаты ?_[, ?0, ^ в каноническом базисе
равны
ix + ly). D8.10>
Если подставить эти выражения в D8,8), то получится:
«"-К/У -f **'= inv
и

186 ПРЕДСТАВЛЕНИЯ ГРУПП	[ГЛ. X
Последнее соотношение выражает хорошо известное свойство инва-
инвариантности скалярного произведения двух трехмерных	векторов.
Соотношения D8,7) удобно записывать в виде
gbA/m=inv, gW*fc&OT = inv.	D8,11)
где введена матрица
(-1^~т5*,-т-	D4,12)
Эту матрицу иногда называют метрическим тензором. Для j = -^
матрица ?^ш равна
/ 0 1\
(_i о)	D8>13)
для j— 1 она равна
/О О IX
(	D8,14)
В естественном базисе эта матрица согласно D8,9) равна единичной
матрице
gnm-^hm-	D8,15)
В заключение заметим, что характер -ц (?) поворота вокруг
оси OZ на угол ср в представлении Ц^- равен
V^	sln(y + -o-)?
\ У	D8,16)
Sin -jr- Ф
m=-j	2
Это непосредственно вытекает из формулы D6,18) для опера-
оператора Dj[00a3]. Полученная формула D8,16) справедлива, разумеется,
для поворота вокруг любой оси, так как повороты на один и тот же
угол вокруг различных осей сопряжены друг другу.
Задача 1. Показать, что в силу D8,1) и унитарности матрицы Djii{g)
имеет место соотношение
Задача II. Опираясь на D8,4), показать, что
§ 49. Произведение представлений группы вращений
При решении ряда прикладных вопросов оказывается полезным
разложить на неприводимые представления произведение двух или
нескольких неприводимых представлений группы вращений. В на-
настоящем параграфе решается задача о таком разложении.

§ 49f
ПРОИЗВЕДЕНИЕ ПРЕДСТАВЛЕНИЙ ГРУППЫ ВРАЩЕНИЙ
187
Рассмотрим произведение двух представлений D, и D/. Для
этого обозначим через
-j, e_J+1
е}
канонический базис в пространстве Lj, в котором действуют опе-
операторы представления D.,-, и через
*-j" f-j'+i	sУ
— канонический базис в пространстве Ly, в котором действуют
операторы представления Dj>.
Базис пространства LjX^-j'> B котором действует представле-
представление Dj X Dy, состоит из векторов
D9,1)
ejf-f+i<
ejff-
Каждый из векторов D9,1) преобразуется по неприводимому пред-
представлению группы Z. При этом вектор e_jf_y преобразуется по
представлению с индексом —j— /, векторы e_jf_j-+1 и e_j+if_y —
по представлению с индексом —j — _/'-j-l и вообще век-
вектор emfm> преобразуется по представлению с индексом т-\- т'.
Ясно, что векторы, расположенные в таблице D9,1) на одной диа-
диагонали, преобразуются по представлениям группы Z с одним и
тем же индексом.
Предположим для определенности, что j^.j'. Выясним, сколько
раз в представлении D^-X D^', рассматриваемом как представление
группы Z, содержится представление индекса /к^-0. Обозначим
это число через <?(т)- Из D9,1) видно, что
[ 0,
<? (и) = | j +/ + 1
! 2/-4-1,
если /к>
т. если / —./ < m < j +/, D9,2)
если 0 </»</—• j.
Учтем теперь, что каждое неприводимое представление группы вра-
вращений веса \ъ^.т содержит ровно одно представление группы Z
индекса т, а представление веса [а < т не содержит ни одного
представления индекса т. Поэтому ср (т) равно числу неприводимых
представлений с весом jj. ^> т, содержащихся в представлении Dj X
X Of-. Разность
? (от) — ? (т-4-1).

188	ПРЕДСТАВЛЕНИЯ ГРУПП	[ГЛ. X
очевидно, равна числу представлений веса р = т, содержащихся
в представлении D^XD/. Из D9,2) следует, что
0,	если т >у+у',
1,	если У— у</к<у'+у,
О, если 0^от<у'—у.
Иными словами, если у'<у', то представление D., X Dy содержит
по одному разу представления с весами
v-=f—j. /-У+1. ••-./+;
и не содержит никаких иных неприводимых представлений.
Ясно, что при у > У в приведенном утверждении следует поме-
поменять местами у и у'. Следующая формулировка объединяет оба
случая:
Произведение Dj X Dj' двух неприводимых представлений
группы вращений с весами у и у' содержит по одному разу непри-
неприводимые представления D^ (jx = | у — у' |, | у — у' | + 1	у -{- у')
и не содержит никаких иных неприводимых представлений.
Таким образом, справедлива формула
З'+З'
D*XD,,= % D.	D9,3)
v-=\i-i'\
Из этой формулы вытекает, что произведение двух двузначных
представлений есть однозначное представление.
Задача. Доказать, что произведение D, X Dy, X D^ содержит |один
раз единичное представление Do, если наибольшее из чисел j, j\ и /2 не
превосходит суммы двух других, и не содержит единичного представления
в противном случае.
§ 50. Спинорная алгебра
В различных областях физики и математики важную роль играют
величины, которые при вращении пространства преобразуются ли-
линейным образом или, в частности, остаются инвариантными. В каче-
качестве примеров таких величин можно указать скалярные величины
(расстояние между двумя точками пространства, угол между двумя
прямыми, потенциальная энергия точки в центрально-симметричном
поле, температура в данной точке пространства и пр.), векторы
(радиус-вектор точки, сила взаимодействия между двумя точками,
скорость точки, однородные линейные полиномы относительно коор-
координат х, у, z и пр.), тензоры второго ранга (тензор инерции,
тензор проводимости и пр.) и много других величин.
Возможные значения каждой такой величины образуют некоторое
линейное пространство (например, возможные значения скалярной

§ 50]	СПИНОРНАЯ АЛГЕБРА	189
величины заполняют одномерное действительное или комплексное
пространство, значения векторной величины образуют трехмерное
векторное пространство и т. п.).
Каждое такое пространство L, естественно, порождает некоторое
представление группы вращений.
Рассмотрим это утверждение более подробно. Пусть произведено
некоторое вращение g?R (R— группа вращений). Тогда каждый
элемент х из L переходит в некоторый, вообще говоря, другой
элемент xgQ_L, причем соответствие
х-+хд.
как уже говорилось, является линейным. Таким образом, каждому
вращению g?R, естественно, сопоставляется линейный оператор Т (g),
определяемый равенством
Так как два последовательных вращения g и gt физически экви-
эквивалентны результирующему вращению g)g, то элемент хв1д, в кото-
который переходит х под действием вращения g^, совпадает с элемен-
элементом Ту^:
отсюда следует, что
и, следовательно, соответствие g->l(g) является представлением
группы вращений.
Итак, исходя из пространства L и учитывая физическую природу
его элементов, мы пришли к представлению Т. Будем называть Т
представлением, порожденным или связанным с пространством L.
Будем также говорить, что элементы из пространства L преобразуются
по представлению Т.
Если некоторая физическая величина преобразуется при враще-
вращениях линейным образом, то она преобразуется по некоторому
представлению Т группы вращений. Классификация величин по
представлениям группы вращений оказывается очень целесообразной
с точки зрения физики. Эта классификация лежит в основе спинор-
ной и тензорной алгебры.
Введем теперь важное понятие спиноров. Спинором веса j *)
называется всякая физическая величина, которая при вращении про-
пространства преобразуется по неприводимому представлению D^-
группы R.
Согласно этому определению спинор веса 0 есть скаляр,
веса 1—вектор, веса 2, как будет показано, — симметричный
*) Этот термин не является общераспространенным.

190	ПРЕДСТАВЛЕНИЯ ГРУПП	[ГЛ. X
тензор и т. д. Волновая функция электрона в нерелятивистском
приближении является спинором веса -к-. Спиноры веса -=- мы будем
называть просто спинорами, как это обычно и делается.
Спинором ранга п называется всякая физическая величина, пре-
преобразующаяся по представлению D1?, которое является я-ой степенью
Т
представления Di группы вращений.
Т
Условимся о выборе базиса в пространстве спиноров я-го ранга.
Обозначим через LA), Z,B)	L(n) n пространств, элементы кото-
которых суть спиноры (веса -g-l. Перемножение этих двумерных про-
пространств дает пространство L спиноров ранга п. В каждом из п
пространств L<-k\k=\, 2, ..., п) выделим канонический базис
еф. е(к\
2
Составляя всевозможные произведения типа
еф. е(к\.	E0,1)
2	2
мы получим базис в пространстве L. Элементы этого базиса пре-
преобразуются по формуле
** - %и<*)<м ... V	E0-3)
где
(j, i = ±Y,
Ясно, что в каждом пространстве спиноров и-го ранга (незави-
(независимо от их физической природы) можно выбрать базис, однотипный
с базисом E0,2)*).
Элементы такого базиса условимся по-прежнему обозначать
через е4 ¦ . , хотя они не обязательно выражаются формулой E0,2).
Соотношение E0,3) при этом остается в силе. Каждый спинор А
ранга п можно представить в виде линейной комбинации базисных
элементов
*) Если в двух пространствах L и U заданы два эквивалентных пред-
представления Т и Т' и базисы
ev е2 ..., еп и е[, е'2	еп
в этих пространствах выбраны так, что каждому элементу g б G соответ-
соответствует в представлениях Т и Т' одна и та же матрица, то эти базисы
называются однотипными.

§ 50]	СПИНОРНАЯ АЛГЕБРА	191
Координаты Aii . преобразуются при вращениях по закону
А. . . —а. .а	а. . А. . .,	E0,4)
т. е. так же, как и произведения координат п спиноров первого
ранга. Ясно, что всякие 2П чисел, преобразующиеся при враще-
вращениях по закону E0,4), являются координатами некоторого спинора.
Поэтому совокупность таких 2п чисел является спинором.
Рассмотрим два основных действия со спинорами: умножение
и свертку. Умножая спинор ранга т с координатами А({ { , на
спинор ранга п с координатами В.. . , мы получим спинор С
ранга т-\-п с координатами
c*A...v.A-i. = ^.-'.B^-v	E0>5)
Числа С действительно являются компонентами спинора (т-\-п)-то
ранга, так как они преобразуются так же, как и произведения ком-
компонент m -\-n спиноров первого ранга.
Свертка спинора Л*,,-,...,- по индексам /t и 1г состоит в пере-
переходе от этого спинора к спинору
i4W....*fB = «rvAl.iA...V	E0>6)
ранг которого равен т—2; матрица g\ i определена равенством D8,13).
Проверим, что числа Д^...» действительно являются компо-
компонентами спинора. Для этого заметим, что числа giiAii i пре-
преобразуются по тому же закону, что и числа giiA{BiCi •¦¦Fi ,
где А, В, С, . . , F — спиноры первого ранга.
Согласно соотношению D8,11), произведение giiAiBi инва-
инвариантно и, следовательно, эти числа преобразуются как произведения
компонент Ci:i...Fi (т — 2) спиноров первого ранга, т. е. как
компоненты спинора (т—2)-го ранга.
Свертку спинора Л^,...» можно производить по любой паре
его индексов. Операцию свертки можно разбить на две элементар-
элементарные операции: операцию подъема индекса, т. е. перехода к компо-
нентам	л<1
и операцию упрощения, т. е. суммирования компонент с одинако-
одинаковыми значениями индексов ii и i2
?ijAjih-..im-
С помощью матрицы g можно поднять несколько или даже все
индексы спинора.
Поднятые индексы называются контравариантными в отличие
от расположенных внизу индексов, которые называются ковариант-
ными.

192	ПРЕДСТАВЛЕНИЯ ГРУПП	. [ГЛ. X
Теорема. Спиноры re-го ранга, координаты которых сим-
симметричны по всем своим индексам, образуют инвариантное под-
подпространство, преобразующееся по неприводимому представлению
группы вращений веса j = — n.
Значение приведенной теоремы связано с тем, что она позволяет
в простой форме записать матрицы представлений любого веса, если
известны матрицы представления веса -у»
Доказательство теоремы вытекает из следующих трех заме-
замечаний. Во-первых, подпространство L' спиноров п-ro ранга, имею-
имеющих симметричные по всем индексам координаты, инвариантно отно-
относительно всех операторов представления D". Действительно, если
есть такой спинор и g?R, то спинор
.« <xiA(g)a.M,(g)
2
имеет координаты
также симметричные по всем индексам. Отсюда следует, что подпро-
подпространство U порождает некоторое представление Т группы вращений
Во-вторых, спинор я-го ранга е\ \ \, очевидно, входит в про-
Т?""Т
странство U и осуществляет представление группы Z индекса -^п.
Отсюда следует, что представление Т содержит по крайней мере
одно представление с весом, не меньшим -к- п.
Наконец, в-третьих, размерность подпространства U равна n-f-1.
Действительно, если известны координаты
^_1_± _!• Al_±_± _!*¦*¦' A1L L
2 2 ¦"' 2	2 2"~У •¦	2 2 '" 2
спинора из L', то известны все его координаты.
Поскольку размерность L' равна п-\-\, то представление Т не
может содержать представлений D^ с весом j > -^. Значит, оно
содержит ровно одно представление Dra и не содержит никаких дру-
21?
гих представлений. Иными словами, Т—Dn , что и доказывает тео-
-.Т
рему.,

§ 50]	СПИНОРНАЯ АЛГЕБРА	193
Очень простая реализация пространства L' получается, если ото-
отождествить спиноры ?(i'\ еB)	e(in) и спиноры е(х\ , еB\ , ..., е(и\,
	У	~2	~~г ~~2	2
т. е. положить
а = е{к\, v = eV (Л = 1. 2	я).	E0,7)
2	2
Тогда базис в пространстве L' принимает следующий простой вид:
и», un~lv, ..., uvn~l, vn.	E0,8)
Инвариантность пространства U относительно вращений при таком
определении очевидна. Ясно, далее, что каждый из спиноров
un-kvk (?=^0, 1, ..., п) осуществляет неприводимое представление
группы Z, индекс которого равен k—-~ . Отсюда получается, что U
есть пространство спиноров веса j =--л, а базисные спиноры E0,8)
отличаются от спиноров канонического базиса самое большее число-
числовым множителем
em = 9mul+mvj-m.	E0,9)
Для вычисления коэффициентов рда подействуем на обе части
равенства оператором A_t. Используя формулу D6,20) и результат
задачи III § 43, получаем:
—!)*„_! - РмU
) ^ V
"гге-1
Отсюда
_ ,/17 + 1) — т(т^Л) _ ,/"/?даТ
EолО)
Формулы E0,9) и E0,10) дают простую связь между спинорами
веса j и спинорами веса -к-.
В частности, канонический багис векторного представления Dt
выражается следующим образом через спиноры е i n e\\
~Т ?
е_1==е2_ь eo = V2'e_iei, e1 = e\.	E0,11)
2	2 2	2
13 Зак. 3512. Г. Я. Любарский

194	ПРЕДСТАВЛЕНИЯ ГРУПП	[ГЛ. X
§ 51. Тензорная алгебра
Тензором п-то ранга (ге = 0, 1, 2, ...) называется всякая физи-
физическая величина, которая при вращении пространства преобразуется
по представлению D", т. е. по ге-й степени векторного предста-
представления.
Согласно этому определению тензор нулевого ранга есть скаляр,,
тензор первого ранга — вектор. Представление D" называется тен-
тензорным представлением п-ro ранга. Характер х" тензорного пред-
представления равен характеру векторного представления, возведенному
в л-ю степень:
X? (С (?)) = A + 2 cos <?)".	E1,1)
В пространстве тензоров и-го ранга обычно выбирают базис,,
который преобразуется при вращениях как произведение
базисных элементов пространства Lv При этом в качестве базиса
пространства Lx выбирают вещественный ортогональный базис
ех, е2, е3.	E1,3)
Каждый тензор n-го ранга А задается в базисе E1,2) или в одно-
однотипном с ним базисе 3" координатами Л,-^..,^
Ясно, что произведение двух тензоров рангов шип есть тензор
ранга (ш-\-п). Координаты этого тензора получаются в результате
перемножения координат перемножаемых тензоров.
Над каждым тензором А ранга выше первого можно произвести,
операцию свертки, вполне аналогичную операции свертки над спи-
спинорами. Нужно лишь иметь в виду, что в качестве матрицы gkm
следует взять единичную матрицу (см. D8,15))
gkm = \т-
Поэтому операция свертки тензоров сводится к операции упрощения,
т. е. к операции перехода от тензора Л^,-,... ,• к тензору Ащя...{
В результате свертки тензора по какой-либо паре индексов полу-
получается тензор, ранг которого на две единицы меньше ранга исход-
исходного тензора.
Если ранг тензора А равен двум, то в результате свертки мы
получим число, равное сумме его диагональных элементов.

§ 51]
"тензорная алгебра
Тензорное представление D" является приводимым, если ft
Пользуясь формулой D9,3), легко находим, что
195
> 1.
и т. д. Результаты подобных подсчетов для я=1, 2, 3, 4, 5 и 6
сведены в таблицу 21.
Таблица 21
Произведения представлений группы вращений
Di
D?
Df
D?
D«
Do
0
1
1
3
6
15
Dx
1
1
3
6
15
36
D2
0
1
2
6
15
40
D3
0
0
1
3
10
29
0
0
0
1
4
15
D,
0
0
0
0
1
5
D6
0
0
0
0
0
1
Рассмотрим более подробно соотношение Di —Do + D1 + D2. эт0
соотношение означает, что произведение L\ X ^-1 двух пространств
Lx и Z.2. преобразующихся по представлению D1; может быть разло-
разложено на сумму трех взаимно-ортогональных подпространств
преобразующихся по представлениям Do, Dt и D2. Обозначим через
аи й2, о3 и Ьи Ьг, Ъъ вещественные ортогональные базисы в про-
пространствах L\ и L\. Тогда совокупность девяти величин
афъ
E1,4)
образует базис в пространстве L\ X ^-2, преобразующемся по пред-
представлению Dx X D2- Мы уже знаем, что сумма
е0 = a1bl + агЪ% + афъ
инвариантна относительно вращений пространства и потому осуще-
осуществляет единичное представление Dc, содегжгщеехя в произведении
13*

196	ПРЕДСТАВЛЕНИЯ ГРУПП	[гЛ- X
Dt X Di- Заметим, что коэффициенты элемента е0 образуют единич-
единичную матрицу (eo)ik. Поэтому одномерное подпространство Lo состоит
из всех тех элементов, координаты которых образуют матрицу,
кратную единичной матрице.
Для выделения представления Dl из Dt X Di заметим, что согласно
перестановочным соотношениям для инфинитезимальных операторов
в сражения
Ь'з— Ь'г> Mi — Мз и Ii'a — Mi
преобразуются при вращениях как операторы 1(, 12 и 13. Так как
эти операторы образуют базис однотипный с базисами а{, а2, а3
и bu b2, Ь3, то мы приходим к выводу, что линейная оболочка Z,,
элементов
v1 = a2b3— a3b2, t/2 = a3?i — «1*3. ^з = аА— афх
преобразуется при вращениях по представлению Dt. Поэтому эле-
элементы vu vt, я)ъ и все прочие элементы из Lt могут рассматриваться
как трехмерные векторы.
Возьмем теперь произвольный вектор х = х^а^ из пространства L\
и произвольный вектор y=yfij из пространства L\ и составим их
произведение
з
ху= ^ Xiyjuibj.
Проекция этого произведения на подпространство LyczL\ Xii, являю-
являющаяся вектором, называется векторным произведением векторов х
и у. Для того чтобы убедиться в том, что это определение совпа-
совпадает с известным определением векторного произведения, вычислим
какую-нибудь координату этого произведения. Имеем:
з	\ з
«^3 — 8гз^а) = -*^з — x3y2
что доказывает сделанное утверждение.
Возьмем произвольный элемент из L
Ti KaiPi — азЬ2) -t- 72 (Mi — Мз) -h Тз (Ma — аф^.
В базисе E1,4) этот элемент изображается следующей матрицей
координат:
О Тз — Тг>
—Тз О	Tl
Т2 — Ъ О
Мы получили общий вид антисимметричной матрицы третьего порядка.
Таким образом, подпространство Lxc:LiX^b преобразующееся

§51]	ТЕНЗОРНАЯ АЛГЕБРА	197
по представлению D], состоит из всех элементов пространства L.[ X L,[',
координаты которых образуют антисимметричные матрицы. Иными
словами, антисимметричные тензоры второго ранга можно рассмат-
рассматривать как векторы.
Теперь нетрудно выделить пятимерное подпространство Lx. Если
23	E1,6)
32 а
— матрица элемента из L2, то в силу ортогональности подпро-
подпространств Lo, Lx и L2 должны выполняться условия
Тз (ai2 — a2i) + Та
— 4i) + Ti (ягз — «зг) =
Так как последнее условие выполняется при любых значениях чисел
7i> Тг и 7з> т0 имеют место равенства
а12 == а21>	а13 == а31>	а23 ^^ а32-
Полученные' соотношения показывают, что матрица E1,6) имеет
равный нулю след и является симметричной матрицей. Пространство
всех элементов, имеющих такие матрицы, пятимерно и совпадает
с подпространством L,-
Обратим теперь внимание на первый столбец таблицы 21, ука-
указывающий на число линейно независимых тензоров данного ранга,
не изменяющихся при вращениях пространства. Таблица показывает,
что существует только один такой тензор второго ранга—это еди-
единичный тензор oik или, что то же, тензор
, «I	-" -	1 • А '	d •
Точно так же существует только один тензор третьего ранга,
не изменяющийся при вращениях пространства.
Проще всего найти этот тензор, если заметить, что он содер-
содержится в произведении пространства Lx на пространство Lx . Таким
образом, этот тензор имеет следующий вид:
ах а2 аг
Ъх Ь2 Ь3
где сх, с2, св—естественный базис в пространстве L\ .

198	ПРЕДСТАВЛЕНИЯ ГРУПП
Полученный определитель можно переписать в виде
[ГЛ. X
al a2 a3
bx b2 b3
cl C2 C3
: 2^
где
0,	если i = k, или г = /, или & = /;
1,	если перестановка I.,,,) четна;
-1, если перестановка I .. | нечетна.
Таким образэм, тензор третьего ранга е^м инвариантен относительно
вращений. Все инвариантные тензоры третьего ранга равны рЕда-
где р — численный коэффициент.
Итак, мы располагаем двумя инвариантными тензорами: тензором
второго ранга 8iA. и тензором третьего ранга eikl.
Составляя всевозможные произведения типа
hlfilnfinp> ^ikHmri' sikl°mnp, • • •.
мы будем получать инвариантные тензоры высших рангов. Так,
например, тензоры
образуют набор линейно независимых инвариантных тензоров чет-
четвертого ранга. Этот набор является полным, так как согласно таб-
таблице 21, представление Dt, по которому преобразуются тензоры
четвертого ранга, содержит единичное представление только три
раза. В теории инвариантов доказывается следующая фундаменталь-
фундаментальная теорема.
Теорема. Каждый инвариантный тензор Т
ранга п равен сумме тензоров вида
..
...in
четного
где числа ар а2, . ., а„ суть написанные в произвольном порядке
числа 1, 2,.. ., п.
Каждый инвариантный тензор Tilit...in нечетного ранга п
равен сумме тензоров вида
Эта теорема чрезвычайно облегчает поиски инвариантных тен-
тензоров данного ранга, сводя их к выделению из тензоров вида E1,7)
или E1,8) нужного количества линейно независимых тензоров.

§ 52|	ПРЕДСТАВЛЕНИЯ ПОЛНОЙ ОРТОГОНАЛЬНОЙ ГРУППЫ	199
Задача I. Тензор tiji^mnv является инвариантным тензором шестого
ранга. Представить его в виде суммы тензоров вида ^>ц^>цЬ{ ..
Задача II. Разложить тензоры ^ikiEtmn и цы^Ыт на сумму произве-
произведений тензоров oqp.
§ 52. Представления полной ортогональной группы
После того как найдены все неприводимые представления группы
вращений R, не составляет никакого труда перечислить все непри-
неприводимые представления полной ортогональной группы W. Для этого
достаточно воспользоваться следующим простым рассуждением.
Пусть х(Л)(й?1^)— какое-либо неприводимое представление
труппы W. Так как инверсия / коммутирует со всеми элементами
группы W, то оператор х (/) должен коммутировать со всеми опе-
операторами х(/г) <7г? W). Поэтому в силу леммы § 18 оператор х(/)
кратен единичному оператору
Так как Р = е, то >.2=1 и
т(/) = Е или х (/)== — Е.	E2,1)
Представление х группы W является в то же время представлением
группы вращений RczW. Представление х, рассматриваемое как
представление группы вращений, также неприводимо, так как каж-
каждый оператор х (/г) либо совпадает с одним из операторов пред-
представления группы вращений (если h?R), либо отличается от него
знаком (если h?R).
Итак, представление t(g)(g^,R) является неприводимым пред-
представлением группы вращений и совпадает с одним из представле-
представлений D,
*(g) = Djlg) (ff€*)-	E2,2)
Используя это соотношение и E2,1), получаем:
*(h) = x(g)-t(I) = ±Di(g) (g = hr?R).	E2,3)
Формулы E2,2) и E2,3) полностью определяют представление х (h).
Если j—целое число, то различный выбор знака в E2,3) при-
приводит к двум разным представлениям группы W, которые мы будем
обозначать через
D/ и DJ (У=0, 1, ...)¦
Эти представления являются однозначными.
Несколько иное положение получается, если,/ — полуцелое число.
В этом случае каждому элементу g?R отвечают два оператора Dj(g),
отличающиеся только знаком. Поэтому и каждому элементу h — gf
будут отвечать те же два оператора независимо от выбора знака

200	ПРЕДСТАВЛЕНИЯ ГРУПП	(ГЛ. X.
в формуле E2,3). Поэтому полная ортогональная группа имеет
только одно представление, соответствующее данному полуцелому
значению у. Это представление мы будем обозначать, так же, как
и представление группы R, символом Dj.
Итак, полная ортогональная группа имеет по два однозначных
представления D/ и DJ" каждого целого веса и по одному двузнач-
двузначному представлению Dj каждого полуцелого веса.
Представления DJ и D/, рассматриваемые как представления,
группы вращений, эквивалентны одному и тому же представлению Dj.
Формула E2,3) показывает, что спиноры целого веса j могут
вести себя по-разному относительно группы W: одни из них не
меняются при инверсии, другие изменяют свой знак. Это означает,
что с точки зрения группы W оказывается целесообразной дальней-
дальнейшая классификация спиноров. Принято называть просто спинорами
спиноры нечетного веса, если они меняют свой знак при инверсии,
и спиноры четного веса, если они не меняют свой знак при инвер-
инверсии. В соответствии с этим спиноры называются псевдоспинорами,
если они при инверсии, имея нечетный вес, не меняют свой знак
или, имея четный вес, меняют свой знак:
[(—1)" еп, если еп — спинор,
\{—1)ппеп, если еп — псевдоспинор.
Представление Df веса 1 называется векторным, а предста-
представление Djr — псевдовекторным. Скаляр не меняет свой знак при
инверсии, а псевдоскаляр — меняет. Поэтому единичное представле-
представление, порождаемое скаляром, обозначается через D+.
Представление, эквивалентное произведению нечетного числа
псевдовекторных представлений и любого числа векторных, назы-
называется псевдотензорным представлением соответствующего ранга.
Для спиноров полуцелого веса подобного разделения не суще-
существует. Оно не существует также для спиноров нечетного ранга.
Рассмотрим теперь вопрос о произведении неприводимых пред-
представлений группы W. Произведение двух однозначных представле-
представлений D/ и DJ> определяются очевидными формулами
j X Dp = Dj X D/ = 2
irr-\j-i
i\5'
) X D7' = D7 X Dp = 2
E2,4)
Произведение однозначного представления на двузначное также
очевидным образом разлагается на неприводимые двузначные пред-

§ 53]	ДВУЗНАЧНЫЕ ПРЕДСТАВЛеНИЯ ТОЧЕЧНЫХ ГРУПП	201
ставления:
d/xd^JNz(/=o( i,.../=44---)-E2>5>
Несколько сложней обстоит дело с произведением двух двузнач-
двузначных представлений. Это произведение является однозначным пред-
представлением и определяется одной из следующих двух взаимно-исклю-
взаимно-исключающих формул:
i ¦<¦!'
DjXDj,= 2 Df.
Какая из этих двух формул справедлива — зависит в каждом
конкретном случае от способа составления произведения предста-
представлений (ясно, что двузначные представления можно перемножить
двумя различными способами).
Задача I. Показать, что о,7? является тензором, ещ--псевдотензором.
Задача II. Определить число линейно независимых тензоров третьего
ранга, все координаты которых являются псевдоскалярами.
§ 53. Двузначные представления точечных групп
Каждую точечную группу G можно рассматривать как подгруппу
полной ортогональной группы W. Пусть D — какое-либо двузначное
представление W. Каждому элементу группы W это представление
ставит в соответствие два оператора. В частности, каждому эле-
элементу g?G соответствуют два оператора
g-*±D(g).	E3,1)
При этом для любой пары элементов gv g2 выполняется одно из
двух соотношений:
или DWDte) —D(№)" E3,2).
Соответствие E3,1) при условии E3,2) называется двузначным пред-
представлением группы G. Двузначное представление не является пред-
представлением в строгом смысле этого слова, так как каждому эле-
элементу g группы G соответствует не один, а два оператора.
Двузначные представления точечных групп представляют значи-
значительный интерес с физической точки зрения. Это связано с тем,
что при всевозможных движениях пространства из группы О спи-
спиноры нечетного ранга (например волновые функции электрона)
преобразуются по двузначному представлению.
Каждое двузначное представление группы G можно рассматривать,
как обычное представление некоторой вспомогательной группы 0^

202	ПРЕДСТАВЛЕНИЯ ГРУПП	[ГЛ. X
имеющей вдвое больше элементов и называемой поэтому двойной
группой.
Такой вспомогательной группой Gt является группа матриц
,	,	2 | E3,3)
-о (?-« . е
^	n
•где тройка чисел F, <?> ф) принимает всевозможные значения, соот-
соответствующие элементам точечной группы G. Так как углы ср и ф,
•соответствующие некоторому повороту (или зеркальному повороту),
определены лишь с точностью до целого кратного 2тс, то каждому
элементу g соответствуют две матрицы D i (9, о, ф), отличающиеся
1
друг от друга только знаком. Обозначим одну из этих матриц
через g+, а другую—через g_. Ясно, что совокупность 2ге матриц
{g+, ?¦_} (g?G) образует группу. Ясно, далее, что всякое дву-
двузначное представление группы G является однозначным обыкновен-
обыкновенным представлением построенной указанным образом двойной
группы Gt *).
Итак, каждое двузначное представление точечной группы G
можно рассматривать как обычное представление двойной группы Ох,
состоящей из двумерных матриц.
Условимся для определенности понимать под g+ ту матрицу
-LF, ср, ф), которая получится, если в качестве о и <|> взять углы,
лежащие в интервале 0 ^ «, 6 < 2тс.
В приложении приведена таблица характеров двузначных пред-
представлений некоторых точечных групп.
A 3
^ = ~2"' ~2 '
2
¦ тг , • • • ) группы матриц Dx (8, 9, ф) является однозначным. Если мы огра-
Т
дичимся рассмотрением только тех поворотов g, которые содержатся
,в группе G, то это представление останется, разумеется, однозначным.

ГЛАВА XI
^КОЭФФИЦИЕНТЫ КЛЕБША—ГОРДАНА И КОЭФФИЦИЕНТЫ
РАКА
§ 54. Вычисление коэффициентов Клебша—Гордана
В § 49 мы выяснили, на какие неприводимые представления раз-
разлагается произведение Од X Dj2 двух неприводимых представлений
группы вращений R. Теперь мы фактически произведем это разло-
разложение и изучим свойства возникающих при этом коэффициентов
Клебша — Гордана.
Пусть ет (—7\ ^.т^ j\) — канонический базис в пространстве Lu
преобразующемся по представлению D^. Векторы канонического
'базиса в пространстве L2> которое преобразуется по представле-
представлению Dj-2, обозначим через fm(—J2-*Cm^j2).
Рассмотрим теперь произведение этих представлений.
Базис в пространстве Ll X L2, в котором действует это предста-
представление, состоит из Bj\-\- 1) By2-j- 1) векторов eTOi/TO2 (—j\ < ml^.jl;
—A^m2-CA)' По доказанному в § 49 пространство L1 X Ц
разлагается на сумму инвариантных подпространств, в которых
-действуют неприводимые представления с весами j(\j\—AI^C/-^
^Cj\-\-J2)- Канонические базисы в этих подпространствах обозна-
обозначим через g-^, где значок наверху указывает на вес неприводимого
представления, действующего в данном подпространстве.
При фиксированном т каждый из векторов gi! (\j\—Л|-<С/^
-«С71+Л) является собственным вектором Ао в пространстве L1 X L%,
•отвечающем собственному значению —1т. Поэтому векторы gi
представляют собой линейные комбинации тех базисных векторов
етfmi, которые являются собственными векторами Ао с тем же
собственным значением, т. е. emjm-mi.
Положим
Числа UiJ2.mimz\J'n) называются коэффициентами Клебша — Гор-
Гордана. Мы получим явное выражение для этих коэффициентов и
установим некоторые их свойства.

204 КОЭФФИЦИЕНТЫ КЛЕВШЛ	ГОРДАНА И КОЭФФИЦИЕНТЫ РАКА [ГЛ. XI
Канонический базис g^ определен лишь с точностью до множи-
множителя, зависящего от j и равного по модулю единице. Поэтому
соотношения E4,1) недостаточно для однозначного определения
коэффициентов Клебша — Гордана. Для устранения этой неоднознач-
неоднозначности мы введем дополнительное условие
ШУ1Щ\М)>0.	E4,2)
Это условие, вообще говоря, не симметрично относительно чисел j\
и j2. Поэтому целесообразно отличать друг от друга базисные
векторы
gm =^gm= 2
mJmi-	E4,3).
Так как коэффициенты Клебша — Гордана связывают между собой
два ортонормированных базиса, то матрица, составленная из этих
коэффициентов, является унитарной, т. е.
2 иигЩЩ I Jm) UdWh . У in') = Ojj-lmm-.	E4,4)
/и,
Заметим, что в формуле E4,4) можно опустить черту, означающую
переход к комплексно-сопряженной величине, поскольку, как выяс-
выяснится ниже, все коэффициенты Клебша — Гордана действительны.
Разрешая соотношения E4,1) относительно emjm%, мы получим:
rm2)gm1+m3- E4,5),
Коэффициенты Клебша—Гордана равны нулю, если сумма j\-\-
-\-J2~\~j не является целым числом или если не выполняется условие
Числа j\, j\ и j входят в это условие симметрично. Действительно,.
E4,Ь) есть условие существования треугольника со сторонами _/,,.
j2 и j. Таким образом, если никакой треугольник не соответствует
числам j\, j% и j, то {jJimxm2\jm)=^Q.
Для того чтобы упростить вычисление коэффициентов Клебша—
Гордана, мы воспользуемся одним вспомогательным приемом.
Введем в рассмотрение пространство L, преобразующееся по
неприводимому представлению вес»у (|7\ — jz\ <СУ ^y'l-f-A)- Пусть
*m(—J^mjCJ) — канонический базис в пространстве L. Вспоми-
Вспоминая (§ 48), что произведение двух неприводимых представлений
с весами j' и ] содержит представление веса 0 только при условии
j'=j, заключаем, что произведение пространств Ц X L2 X L содер-
содержит ровно одно подпространство, преобразующееся по неприводи-

•§ 54]	ВЫЧИСЛЕНИЕ КОЭФФИЦИЕНТОВ КЛЕБШЛ	ГОРДАНА	205
мому представлению веса 0. Из § 48 мы знаем, что вектор а° =
¦=BJ-\-\) 2 2 (—^ymgmh-m лежит в этом пространстве. Норма
m=-j
вектора а0 равна единице. Подставляя выражение E4,1) для век-
вектора g->m и заменяя т на —т, получаем отсюда:
af>= 2 u(jlj2jmlm2m)emjm.1hm,	E4,7)
где
\j — m).	E4,8)
Мы видим из E4,7), что коэффициенты u(jlj.ijmlm2m) являются
координатами единичного инвариантного вектора а0 из пространства
Ll X L2 X ?¦ в базисе em.finjim. Это свойство определяет коэффи-
коэффициенты u(jj2jm[nt-,m) с точностью до множителя, равного по
модулю единице и не зависящего от /и,, от2 и т- Заметим, что пары
чисел y'jmj, y2w2 и у'зт2 входят в это определение симметрично.
Поэтому коэффициенты и{)^J]т,1тгт) fie изменяются по абсо-
абсолютной величине при любых перестановках пар ]±ти ]гтг и jtn.
В § 55 этот вопрос будет подробно рассмотрен.
Для дальнейшего нам понадобится соотношение
{—lftmuUJJj\m2m)^>0,	E4,9)
которое вытекает из E4,2) и определения E4,8).
Для того чтобы с помощью равенства E4,7) вычислить коэффи-
коэффициенты и (JiJ2Jmim->'n)> следует найти в явной форме вектор а0.
•Это удается легко сделать, если реализовать пространства Lv L2
и L с помощью спиноров.
Пусть {м1; Vi), \u2, v2) и [и, v)—канонические базисы в трех
пространствах, преобразующихся по представлениям веса --. По-
•строим пространство Lv положив (см. § 50)
j_
Ul Vl	E4 }
+ mi)! (A-«
Подобным же образом построим базисы в пространствах L2 и L:
hm=[W.
Bj)!	It J+m -m
j U V '
E4,П)

206 КОЭФФИЦИЕНТЫ КЛЕБШЛ	ГОРДАНА И КОЭФФИЦИЕНТЫ РАКА [ГЛ. Xf
Пространство LlX ЦУС L можно теперь рассматривать как сово-
совокупность линейных комбинаций векторов вида
В частности, в Lt X Ц X ^ содержится вектор
(u2v— uv2)j+j^Jl(uv1 — u^t'-^u&z
Этот вектор инвариантен, так как инвариантен каждый из его со-
сомножителей, и мы можем написать:
=Р(У1. Л. Л(«2«
X (av1 — u1v)i+il-Jt(tt1V2 — u2Vl)il+h-}, E4,12>
где р — нормирующий множитель.
Вычисление модуля коэффициента р (весьма громоздкое) приво-
приводит к следующему результату:
\pUi. h, J)\ =
IT
О-1 J
Сравнивая полученное для вектора а0 выражение E4,12) с выра-
выражением E4,7), мы вычислим коэффициенты и (JiJ2Jmim2m)- Подста-
Подставляя E4,10) и E4,11) в E4,7), находим:
u(j1jJm1m2m)X
Y Г	B/i)! BЛ)! Bj)!	if y
L0'i + mi)!0'i — Я1)!0'г+и,)М/:- m?)! 0' +"OK/ — m)\ \ ^
X ui+m'v{i-m'u{t+n'tvlt-m'u?-imv1-m.	E4,14)
С другой стороны, раскрывая скобки в E4,12), получим:
— Л — нУ- ^! (; + Л—Л — я«
Суммирование производится здесь по всем значениям av a2 и а,
для которых аргументы факториалов являются целыми неотрицатель-
неотрицательными числами. Произведи замену индексов суммирования в полу-
полученном выражении:

§ 54]	ВЫЧИСЛЕНИЕ КОЭФФИЦИЕНТОВ КЛЕБША	ГОРДАНА	207
Получим:
e°=-p (Л+У — JiV-U+Ji—J2V- (Л+Л—/)i X
X 2 (_1J'-''-Л+».-*.и{1-жЧ>{1+Я1'х.
X (г+У — Л + «1)!(Л — «1 — г)!]-1 E4,15>
Приравнивая коэффициенты в равенствах E4,14) и E4,15), находим:.
v Г
1
(А + »»i)! (Л - «i)! (/? + »»?)! (Л - м?)! (У + т)\ (j - т)\ IT
J
Х Ъг\ (h+кЧ-гУ-
(z+J—h—щУ- G2 + Щ—гУ- (z+j—j
E4,16)
/	_]		I ^ 	 Л\
Нам осталось определить аргумент числа р так, чтобы выполня-
выполнялось условие E4,9). При подстановке в E4,16) ml~j1 сумма в пра-
правой части E4,16) сводится к одному слагаемому, которое положи-
положительно. Отсюда
(мы воспользовались тождеством ml-\-т2-\-т= О и учли, что
m^^ji). Подставляя это выражение для р и используя E4,13),
получаем окончательно:
ГО'г + 7 —7'i)! G + А —7?М Gi +72 —7)!
L	С/1 + Л+У+1)!
X
X (Л4- «2 — ^)! B-W—/2 + «i)I (Л — «1 — z)I]-1 E4,17>.
= 0).

*208 КОЭФФИЦИЕНТЫ КЛЕБША	ГОРДАНА И КОЭФФИЦИЕНТЫ РАКА [ГЛ. XI
Отсюда, вспоминая связь E4,8) между коэффициентами
u(JiJ2Jmim2m) и коэффициентами Клебша — Гордана, находим:
.U\j2mlm2\jm) =
X (У, + Щ)! (Л — «i)'• (Л + Щ)! (Л — Щ)! (У + «)! (У — »)П 2 X
.у V	<=!>!
А ZJ2! (Ji+h—j ~гУ- {z+j—h—nhI- (h+"h—z)\ (z-\-j-j«+m{)\ (Ji — Щ—г)\
z
(m = mi-\-m2).	E4,18)
Заметим, что под знаком суммы z пробегает неотрицательные
целые числа не меньшие, чем т2 -\-j\—/ и у2—J — т1 и не боль-
большие, чем y'i+Л—J< /2~hm2 и Л — mi- Поэтому число слагаемых
в E4,18) превышает на единицу наименьшую из девяти сумм:
Л —m2, Ji + mlt jz — h+j, j + m, j — m, jy-{-j — j2,
Л4-Л— J- Ь + Щ> Ji — Щ-
Приведем значения коэффициентов Клебша — Гордана в некоторых
наиболее важных частных случаях. Используя общую формулу E4,18),
легко находим:
! у/и) = -(j—^y X
f
x Lc/i +7e+/ +1)! c/ +/i —A)!"</i -к/i—7)! с/г + «.)u ( ' '
{m=ji-\-m2),
Uih — У>2! jm) = {/+туГ Х
fBJ + 1) (Л +J —/i)' BЛ)! (Л + w»)l 0" + m)l (J — тЩТ -4 9n
L(/i + Л + j + 1)! (A + Л -У)' (Л —к + У)! Os - ms)!J ' "' ^ ' '
(те = — j\-\-m2),
г IУ1
_ Г	BЛ)'-BЛI(/ + дIС/-/я)!	IT ft.. 9,
"" L BУ)! (A + /»i)! (A - «I)! (/j + ЩI (h - ЩI J ¦ K ' >
i	1 \j-m
{jjm — m | 00) = y=== •	E4,22)
*) В этой и последующих формулах следует считать -^ — °> если
к — целое отрицательное число.

§ 54]
ВЫЧИСЛЕНИЕ КОЭФФИЦИЕНТОВ КЛЕБШЛ —ГОРДЛНЛ
20(.»
Весьма важным является случай, когда вес одного из перемно-
перемножаемых представлений равен 1. При фиксированных значениях
]2~^>\ и т2 числа j и т пробегают значения j = j2—1. Л> Л+Ь
т = т2—1, щ, т2-\-1 (разумеется, если какое-либо из чисел
т2— 1, т2 или ш2-\- 1 превосходит по модулю j, то оно не является
возможным значением т). Так как наименьшее из чисел /i+У —/2
и Ji-\-J2—У »e превосходит единицы, то сумма E4,18) в рассма-
рассматриваемом случае содержит не более двух слагаемых. Результаты
подсчета удобно расположить в виде матрицы
= к
= Л
+1) t/V-»O _ -./~(h+m+l)(h—m) ¦. /"(Л+от-Н) (/
2)B"/, + П' V	2/,(/,4-П Г	2/,B/,4-
Г	/¦ /_ _!	 1 4
2/jB/2+l)
*¦>) O'o — m")
2/,(/, +
'2—от)
2.Ы2Л +
77?! — 1.
E4,23)
С помощью формул E4,19) и E4,20) составляем подобную ма-
1
трицу и для случая j\ — -су , j2 ^- -к
¦ , Ь
1
Приведем без доказательства еще одно соотношение:
(—1) 7
П
0, если L нечетно;
E4,24)
2 "
•Bj+l) (L—2jt)! (L—2j\)\ (L—2j)\]T
(T+Tj!	~J '
если L четно,
E4,25)
здесь положено L=jx-\-j2-\-j.
В заключение параграфа сделаем одно замечание, относящееся
к сферическим функциям.
14 Зац. 3512. Г. Я. Любарский

210 КОЭФФИЦИЕНТЫ КЛЕКШЛ	ГОРДЛНЛ И КОЭФФИЦИЕНТЫ РАКЛ [ГЛ. ХЕ
Если подействовать на обе части равенства E4,5) оператором,,
соответствующим вращению h, то получится соотношение
У
^m'm W Dm'm (Л) ^'4' =
1™2
Подставляя сюда выражения для gim из равенства E4,1) и при-
приравнивая коэффициенты при е -f -, находим:
- т'г) (ЛЛ^1«21М + т2) ?>^+ц	(А).
E4,26).
Если в качестве вращения h взять поворот на угол 0 вокруг
оси ОХ, то получим:
m\m\< i\	m.,m2, j2^	j	2	" '
X (]\}гт\.тг \JmiJrm-i) P '_ ' . ¦ Ф)- E4,27>
Задача 1. Доказать с помощью E1,27) следующие тождества:
X (ЩХ)! У0) yrf)B F, 9) («=«! + m,),.
2 («. г) - -^у=^- 2j К	2J.-JT1	X
X (ЛЛ — «1^2 I Ум) (У1У2ОО 1У0) К/м @, ?) (т = ти2 —
Задача II. Доказать тождества:
2jD^ ,(ti){hk
mvm m\m\

§ ~.5]	СВОЙСТВА КОЭФФИЦИЕНТОВ КЛЕБШЛ	ГОРДАНА	211
§ 55. Свойства коэффициентов Клебша — Гордана
В предыдущем параграфе мы установили, что коэффициенты
и (.}\}2jmxm2m) должны обладать определенной симметрией относи-
относительно своих аргументов. Рассмотрим теперь этот вопрос более
подробно.
Будем исходить из формул E4,12) иE4,14). Используя соотно-
соотношение р=|р|(—1)Л-/-Л, перепишем E4,12) в виде
| р | (U2V — U
X (wvi — и.{о)}+)*~3-'(U]V2 — u2vly'^Ji~i. E5,1)
Это выражение показывает, что при замене величин jv j2, j, av vx,
u2, v2, u, v величинами j2, /t, j, u2, v2, uy, vx, a, v вектор а0 умно-
умножается на (—l)Ji+3i-J. Легко видеть также, что замена jv j2, j, uv
vv u2, v2, u, v—*j, j2, j\, u, v, u2, v2, ux, vx приводит к умноже-
умножению вектора а0 на (— \)h+U-\-i. Символически это можно записать так:
A,
A,
Имея в виду эти соотношения, произведем замену A, 2) в равен-
равенстве E4,14). Мы получим, изменяя обозначения индексов суммиро-
суммирования:
^	m.m) X
v Г	BЛ)! BА) Bj)l	¦__-хт
Л Шх + ЩУ- (Л - ячI O"s + mj)! (к — *1°У- (J + m)l (j ~т)\\ А
Сравнивая это равенство с равенством E4,14), находим:
) = (— \)h+h~j и {j1J2Jm.im2m).	E5,3)
Таким же образом, производя замену A,0) в равенстве E4,14),
получим:
и (Лгкт-ЩЩ) = (— W^+J и (jxi2jmxm2m).	E5,4)
Комбинируя E5,3) и E5,4), можно получить еще три соотношения,
которые мы не будем выписывать.
Из равенства E4,12) и E4,14) вытекает еще одна группа соотно-
соотношений симметрии. Действительно, если произвести в E4,12) замену
«!, vu u2, v2, и, v-^vv ax, v2, и2> v' и, то вектор а0 перейдет
14*

212 КОЭФФИЦИЕНТЫ КЛЕБША	ГОРДАНА И КОЭФФИЦИЕНТЫ РАКА [ГЛ. XI
в вектор (—l)J'+J'+Ja°. Поэтому из равенства E4,14) следует, что
X
Г	BЛ)! B/t)! B;)!	I
Lt/i + «i)! (А - mi)! O's + я,)! (h - «s)! (У + m)\ (j — m)\ J
Производя здесь замену индексов суммирования т1 -> — /я,,
«12—>• — tn2, m —> — /те и сравнивая полученное выражение с E4,14),
найдем еще одно соотношение
и UJzJ — Щ — тг — т) = (— 1 y'^J'+J и О'иУЩЩт). E5,5)
Комбинируя его с ранее найденными соотношениями, получим еще
пять соотношений.
Вспоминая связь E4,8) между коэффициентами u{jlj.ijmlmim)
и коэффициентами Клебша — Гордана, мы можем переписать E5,3),
E5,4) и E5,5) в виде
UJ2 — mmi Л — m\) — ( — l)^"™2 у L _j_ t (jj>mlm21 у/я), E5,6)
(/, i9 — ttij — m,a I / —- tri) = (— 1 )ii~rJ'~3 (j. j.,/n,ntn in.
В этих формулах положено m — ml-\-m2. Комбинируя соотноше-
соотношения E5,6), можно получить еще восемь соотношений симметрии.
Отметим, что из E5,6) непосредственно вытекают следующие
«правила отбора»:
U\jlm1tn1\jm) = 0, если 2j\ — j нечетно; |
(ЛУ200|У0) = 0, если Л+у2+у нечетно. ) E5J)
Первое из равенств E5,6), можно переписать в обозначениях E4,3)
следующим образом:
?т = (~ ^V^'-^g^.	E5,8)
Заметим еще, что с помощью E5,6) можно придать равенству
E4,4) следующий вид:
S(juimxm.a | jm) (hj2m.[nt21 jm) — -2/ + ]¦ Ь. .,8 /. E5,9)
7i mi»»,
i i i
Между коэффициентами Клебша — Гордана существует целый ряд
рекуррентных соотношений. Мы получим их, исходя из равенства
54,1): g3m = 2и^гЩЩ ' Jm) emjmi, и используя услзвиг E4,2)-

§ 55]	СВОЙСТВА КОЭФФИЦИЕНТОВ КЛЕБША	ГОРДАНА	213
Для того чтобы получить первое рекуррентное соотношение,
подействуем на E4,1) преобразованием Aj(cm. D6,25))
aii+lgii+l = 2 U'lhmim2\Jm){^m1-!iemi+lfnh + ^+iemJmSL\i}-
т,+т2=т
Левая часть этого равенства может быть записана в виде
«то-н 2 U\J2m1m2'Jm+\)emJm.2.
Сравнивая коэффициенты при emjma в левой и правой частях, нахо-
находим рекуррентное соотношение
aJm+i UJ z*"-\mz \ J
= «и, UJ-iPii — 1 т2 jm) -\- r*H и^2тхт2 — 1 | jm). E5,10)
Подобным же образом действуя на равенство E4,1) преобразова-
преобразованием А_!, получим второе рекуррентное соотношение
\jm). E5,11)
Третье рекуррентное соотношение легко получить, исходя из
E4,12) и E4,14). Согласно этим равенствам мы можем написать:
(u2v — uv^^J'-i' (uvt — h
где
j —	!	v
I m,m,m
X и и'иУщщт)' E5,13)
Воспользуемся теперь тождеством
(u2v — uv2)i*J'~il («ft — uxv)i-l--
^+i'i~j X
X (u2v — uv/+ >"*-%(uv,-Ulv)j"+:"~^{uxvt-u

214 КОЭФФИЦИЕНТЫ КЛЕБША	ГОРДАНА И КОЭФФИЦИЕНТЫ РАКА [ГЛ. XI
Если все показатели, встречающиеся в этом тождестве, положи-
положительны, то его можно переписать с помощью E5,12) в таком виде:
я»!+?»,-; т = 0 ' '
.' .1 .'	.'	' .'	Г .Г	II	1.1	1,1	I
3JJ 3+m J-i-m, 3., + m2 j.2~m2 j +m j -m
x
=0
„ 2 „
+ +m =0
it it	ff ir n n n rr rr r/
Приравнивая в этом равенстве коэффициенты при члене
^Н ,yj1,uj1 ^32
получаем:
,т„т
E5,14)
m' ~-m" = m
j^Cj\-\-j-2.— 1- Тогда можно полэжить fl=j'2 = -jt
у'= 0, и мы получим:
ч	1.1.
1 1 „ I 1	1
0 »»?»i
LLn * -L ¦¦ _L ¦
2 2	„/' ~ 2 •'" ~ 2 3	/CC 1 K\
i i T i i • (oo.io)
Вспоминая определение коэффициентов ^ и и, можно придать этому
равенству вид рекуррентного соотношения
-[2/. 1
\	1
; 2
2 [(У1 + к -Л (Л + Л
Л ^ +
E5,16)

•¦§ 56|	коэффициенты рака	215
В заключение приведем без доказательства четвертое рекуррент-
соотношение
+Ji+h+V U+Jv-fi+l) (У+jW.+I) Ui+J-r-ЩТ v
(>" -H 1Я B/ + 1) By H- 3)	J A
X U\iim\.mt \i+ I'm) -+-
, r(;+w) (./ ~m) (Я-> —7i) (У+У1 — />) ih 4- У? —/+1) (it+y? 4-У -j-im v
"Т.	" У2B/-1)BН-1)	J A
X {jJ-гЩЩ |y— 1 «) = 0. E5,17)
§ 56. Коэффициенты Рака
¦Шри рассмотрении ряда вопросов квантовой механики естественно
возникают так называемые коэффициенты Рака. Для того чтобы
дать их алгебраическое определение, воспользуемся следующей си-
системой обозначений.
Пусть Lj^ Lj2, Ljt, ...—пространства, преобразующиеся по
представлениям D^, D^, D^, •.. группы вращений. Произведение
пространств Ly, X Lj,2 можно разложить на неприводимые подпро-
подпространства, которые мы будем обозначать символами LO'J*); здесь
(ЛЛ) есть число, пробегающее значения \j\—j2\, \j\—У2 j —)— 1. •••
•••> Ji +Л- Ясно что
Подобным же образом неприводимые подпространства, на кото-
которые распадается произведение ^зф) X ?/2. мы будем обозначать
через LlOiiib'al. Эта форма записи удобна тем, что она указывает на
происхождение рассматриваемого пространства. Так, например,
l_\Uih)(hu)\ означает пространство, преобразующееся по представле-
представлению веса l(j\j\) UjS] и содержащееся в произведении пространств
LU.h) у LUJ,).
Рассмотрим теперь два различных вида разложения пространства
Lj\ X Lj, X Lj3 на неприводимые подпространства:
Lj. X Lh X Lh = 2 LU.h) X Lh --= 2 WM U.
UJ.)	UMIUJ,)M
4, X LJt X Lh = L3i X 2 ИШ = 2 LU> tf.«l.
(hh)	и,ШММ\
Построим канонические базисы в подпространствах ^КЛЛ) JJ и
LliiUMl. Пусть ет, fm и кщ — канонические базисы в Ljt, Lh и Lit.
Обозначим через gi™ и g^ векторы канонического базиса в про-

216 КОЭФФИЦИЕНТЫ КЛЕБША	ГОРДАНА И КОЭФФИЦИЕНТЫ РАКА [ГЛ. XI
странствах W>№ и №*<) (j\2=(jj2), Jn=(j2j-i))- Векторы кано-
канонического базиса в ?ДЛ-М*1 обозначим через /ЖМ' (у' = lUiJz) Js])-
Индекс у указывает здесь на вес представления, по которому пре-
преобразуется базис g^'*) ¦>, заключенный- в скобку индекс у12 частично
характеризует происхождение этого базиса. Индекс у12 = (ЛЛ) п0~
ставлен слева от j, потому что в произведении LWii») X Lj., подпро-
подпространство iWiia) играет роль левого сомножителя. В соответствии
с этими соображениями векторы канонического базиса пространства
[\)Лиш мы (Зудем обозначать через g}m .
Вспоминая определение коэффициентов Клебша — Гордана, мы
можем написать:
gfc, = 2 ии'гЩЩ ! /12^12) emjnh,
mia -r m3 = m
Исключая из этих формул векторы gi™ , мы получим:
)J	2	l2jumnmz\jm)eluJmihmi. E6,1)
Подобным же образом можно написать:
2	h,n,	E6,2)
-	E6>3>
Векторы giy*) являются собственными векторами операторов I
и Ао, отвечающими собственным значениям —у" (у —)— 1) и —int
соответственно. Всякий собственный вектор из Lx X L2 X ?3 опеРа"
торов I2 и Ао, отвечающий тем же собственным значениям, является
линейной комбинацией векторов g^J^ (j и т фиксированы; |у—у\ |<!
^•J23JCJ-\-J\)- В частности, таким образом могут быть выражены
векторы gU,*)j
j = S < ЛЛ Ua) hi IЛЛЛ (Лв) J > g^- E6-4>
i
i3
Входящие в это выражение коэффициенты <у'1у2 (j\2) jJ \ jJJ-z (J23) У >
не зависят от т. В этом проще всего убедиться, Подействовав на
обе части последнего равенства оператором А_! или Аг.
Теперь можно определить коэффициенты Рака W (JiJ2jJz\ Л2./23)
с помощью равенства
U Л2Лз) = ^МЩ^М^.	E6,5)
У B+1) B/+1)

§ 56]	КОЭФФИЦИЕНТЫ РАКА	217
Из определения коэффициентов Рака легко вытекает их связь-
с коэффициентами Клебша — Гордана.
Действительно, из E6,2) и E6,3) следует:
2
j
Отсюда вытекает, что
em.fnhhm:i = 2 ШзЩЩ ! Лзт23) ии\ъпЧЩз \ М) gJm °ю)-
Подставляя это выражение в E6,1), мы найдем:
gm*K —¦	2	и^гЩГПъ \ ji2ml2) (jvij3ml2m3 \ jm)
Л j' от+г+пг
2
Лз. j'; от,+яг3+пг3 -т
X иУ
Отсюда, сравнивая с E6,4), получаем:
2 иигЩМг I ЛгЯЧг) Ц^зЩгЩ \ М) X
X (УгУз^г^
^ 5jj' < У1У2 (У1г)УзУ 1У1У2У3 (Угз)У > =
Это соотношение показывает, что коэффициенты Рака действи-
действительны.
Формуле E6,6) можно придать более симметричный вид, если'
просуммировать обе ее части по т в пределах от —/ до j и раз-
разделить на 2y~j-l. Левая часть при этом не изменится, поскольку
она, как было показано, не зависит от т, и мы, обозначая индекс-
суммирования т через — тА, получим:
W (JJJj3; У12У23)-
X	иЩ ! y«) и^Щ IУ — ««) X'
= 2/+1
X {к)%тгтъ | у23т23) {)х]гъ^\тч.ъ! У — т4)- E6,7У
Из формулы E6,7) следует, что коэффициенты
(У1У2 (У12)УзУ I hhh (Угз)У)
равны нулю, если хотя бы одной из троек чисел
JiJiiJ> J2J3J23' J1J2J1Z' J12J3J

218 КОЭФФИЦИЕНТЫ КЛЕБШЛ	ГОРДАНЛ И КОЭФФИЦИЕНТЫ РАКЛ [ГЛ. XI
не соответствует какой-либо треугольник или если ни одна из сумм
Л+Лз+Л Л-г-Л+Л:). Л-г-Л+Ло. Лг + Уз+У
не является целым числом.
Полученная связь между коэффициентами Рака и Клебша—-Иор-
Клебша—-Иордана позволяет перенести свойства симметрии коэффициентов Клебша—
Гордана на коэффициенты Рака. Для того чтобы это сделать,
удобно придать формуле E6,7) еще более симметричный вид,
заменив в ней коэффициенты Клебша — Гордана коэффициентами
U(jJ2J3mlm2m3) (СМ- § 54)'
При этом мы получим:
hrw UJJU У.2У23) = 2 f — 1 )ia+Sa''' m'~m*u и^зМпщъ) х
X и ииУ^ЩЩЩ + /к4) и и^^'гъЩЩЩ + mi) X
X и ии'гзУщЩ + т3т^.	E6,8)
Под знаком суммы здесь стоит произведение четырех функций.
Число у\ входит в качестве аргумента во второй и четвертой мно-
множители. Мы это обозначим, написав j\—-[2, 4]. Легко видеть,
что У2 ~ [2, 3], у'з — [1, 3] и у—[1, 4] (если положить j = J');
- У12 ^— 11» 2] и у23 --—^ [3, 4]. С помощью этих обозначений любой из 24
перестановок чисел 1, 2, 3 и 4 можно сопоставить перестановку
шести чисел j\, }г, /:!, j, y12l y23. Так, перестановка A2) переводит
пару чисел [2, 4] в {1, 4]; в соответствии с этим A2) переводит у, в у.
При каждой такой перестановке слагаемые под знаком суммы E6,8)
либо не изменяются, либо меняют свой знак согласно соотноше-
соотношениям E5,3) и E5,4). Поэтому каждая из указанных 24 перестановок
аргументов коэффициентов Рака равносильна умножению на 1 или — 1.
Проведем вычисления, соответствующие перестановке A2). Имеем:
W (//злу,; у12у23) -	2	(- 1)*':*¦'¦'»¦-»'> X
X и UviJ2j\mi-{-m3tn2m1) и {jj3j\2mim.iml + тг) X
X и (УзУгУг -,ЩЩЩ + «4) « (JJ2jimimz + w3m4).
С помощью соотношений E5,3) и E5,4) перепишем это в виде
wшли jm = 2 (-1 ia4isгт'~тз х
.X uUJ2j\2fn1m2m3-{-mi)(— 1K1+:'+3"ии^Ущ-\-т2т3Щ)- X
X (~ l)j"+S°+ju (ЛУзЛ*тг«зЯ1Ч- «*) (— 1)-'-+л+л X
X « Шгз]ЩЩ + ЩЩ)(— lf+j"+:i.
Собирая вместе все степени — 1 и учитывая, что
ге4 = О,

¦§ 56]	коэффициенты рака	219
получим:
Отсюда, если вспомнить E6,8) видно, что
W UhJJi, ЛгЛз) = w UJJU JM-	E6,9)
Таким же способом, используя подстановки C4), A4) и A3), мы
«ридем к тождествам
^ UJiJJ» Ji2J2i) = W U'-JJJ; JvJn) =
=- (— 1 f'**»-'•-¦>< W(JJnh,Л: hJ)- E6,10)
Комбинируя между собой соотношения E6,9) и E6,10), можно
получить все 24 соотношения симметрии (включая в это число и
тождественное соотношение).
Приведем некоторые тождества, непосредственно вытекающие
из определения коэффициентов Рака.
Из унитарности матрицы (JihUidJ.iJlJJ-J.iUzilJ) следует
тождество
2 U\h UliU'JlJlJJ.i Uii)J) (Л Л {h'i)JJ\JlJ2J;l U-ii)J) = S,-
«(так как элементы этой матрицы действительны, то в этой фэрмуле
<нет необходимости писать знак комплексного сопряжения). Вспоми-
тая определение коэффициентов Рака, получаем отсюда
BУ12 -т- 1) B/2i +1)W (JJiJU Уи/м) X
X ^ (/,Л//а; W = s, ,- • E6,11)
•'12J12
Для получения второго тождества введем в рассмотрение век-
векторы g^J'** и g^")J и напишем два тождественных соотношения
<см. E6,4)):
g(U.)J = 2 (у,;! (У21) УЙУ | у2Лув (У13) У) ^4°'13) •
g^j = 2 (ЛУз (Л3)У2У: У|У:,Л (Лг)У> «&U:t)-
Согласи® E5,8) мы можем написать:

220 КОЭФФИЦИЕНТЫ КЛЕБША	ГОРДАНА И КОЭФФИЦИЕНТЫ РАКА [ГЛ. XU
Из последних пяти соотношений вытекает, что
6«|	\	'	от
х (— i)*+*--' UiMji3)j2j\jjJ
т. e.
gldM = 2 (- 1)*+*"-'-Л-А-*.-Л. X
Ла. Л»
X (У2У1 U21) J'J I У2У1Л Uvd J) Uih U\i) J'J,' У1ЛУ2 Оаг)/) Si'/'23' •¦
Сравнивая это равенство с E6,4), получаем:
Uih Un)jy | JJ2J3 (У23)У> =
= 2(— ^ltt~i'1%~Jt~Ja~JnU2JiU2x)JvJ\hhhU^j) х
^J) (hi=Ji2> Угз^Уяа)- E6,12).
Переходя в этом соотношении к коэффициентам Рака, мы полу-
получим следующее тождество:
2(- 1)*+'»+^*+*'+*'B/13+ 1) X
J',3
X w UJJU У12У1:!) w UJJJ2\ JM- E6,1 з>
Для получения третьего тождества
UizJaJJv У123У34) W (У1У2УУ84; Ji2J2sd^=
= 2 BУ28 + !) ^ UJoJmU JM X
X W UJ23JU JaJtu) W (У2УУ234/4; УгзУи) E6,14>
рассмотрим произведение четырех пространств L = L^X^, X
X ^-3 X ^,. преобразующихся по представлениям с весами j\, jit ya
и j\. Пространство L можно разложить на неприводимые: подпро-
подпространства следующими пятью способами:
V L{[U,h)Js\j.} _ v
У i{i/' [0'зЛ)-'ч]> = 2 ^^'u" u'it)]}=2
Обозначим через gVJ'iiihMt o-UiUJa)\j, p-JAiM^J*] аЗЛШМ?
и g\U,n)U.u)\ векторы канонических базисов в подпространствах
[iW]^} {\ЛШ\} {\Uh)i	j\jU

«•§ 561	коэффициенты рака	221
Эти векторы связаны между собой следующими соотношениями:
2 (ЛЛа UmJiw! з з	? ЛЛ)Л], E6,15)
л ш» Л1 = 2 (у2у:1 f y2:S) у4у2,4 [ ЛЛЛ (У«) Л34> gi '
(У12 = (ЛЛ). Угз = (УгУа). 712:! = [(У^Уг^Уз!.
7i234 = {\h (У2У3)] У4} = {Л КУгУз) J*\})
g\UMh\ J, = 2 (У12У3 (У123) 74712341 ЛгУзУ* (У») Л
Зм	E6,16)
ff 1ОЛ) UJ,)] = 2 (ЛЛ G,2) 7347i234 IУ1У2У34 (У234) У1234) gjrk{J2 UJl)l ¦
J23I
Исключая из равенств E6,15) векторы glh(hh)]u и gi^MMM, полу-
получим:
giUMh] J, = 2 (У1У2 (У12)У3У1231ЛУ2У3 (Угз) У123} X
X (У1У2З Ul2a)Jij'l23l 'JiJwJl G234O1234/ X
X (У2У3 G23O47234 I У2У3У4 G.«O234> ^
Подобным же образом из E6,16) получаем:
g[U,h)M U ~ 2 (У12У3 (Уиз) 747,234 1 ЛгУзЛ (Уз*) Аш) X
7з]> Jim
X (ЛУ2 G,2)У34У12341ЛУ2У34 (Угз.)У1234) g'l}
Сравнивая последние два равенства, мы найдем:
G127з G*123O471234 |7127з7*4 G*34) 7*1234) X
X \7l72 (Jl2> JuJl2U \JlJ2Jn G234Ol234) ==
= 2 Gi7*2 (У12) У3У123! У1У2У3 (Угз) Уиз) X'
X G1/23 (Уш) 7*47*1234 I717W4 G234O*1234) X
X (УгУз (УгзO*47234 I УгУзУ* (Уз*) Угз4>•
Вспоминая определение E6,5) коэффициентов Рака, мы видим,
что это равенство эквивалентно соотношению E6,14).

222 КОЭФФИЦИЕНТЫ КЛЕБША	ГОРДЛНЛ И КОЭФФИЦИЕНТЫ РАКА (ГЛ. XI
Как показал Рака, коэффиценты W{Jijzjjz\ У12У23) могут быть
вычислены по следующей формуле:
W UiJ2JU У12У23) =
— l)z+*+*+J+* (z + 1)! A (jiM?) А О'-Уя/т)А (ААгУ) А (А«У?У) х
— Л — к — Л?)! (* — Л — Уз — hsY- (z—h — Аз—У)! B —Jn—Js—JY-
г
Х (Л	E6!
(Л + к + к + /-*)! (А + Уз + Ju+Jw-zy- (Л -Н У
где
[<-t»att?*e±-«]V E6,18>.
Сумма в E6,17) берется по тем значениям z, которые не меньше,,
чем числа-
Лг. Л+Л+Лз. Л+Лз+У и Л
и не больше чисел
И У2+У+У12+У23-
Поэтому число слагаемых в E6,17) на единицу превышает наимень-
наименьшую из следующих двенадцати разностей:
У +Уз — У12> У1+У - У23. У2+У3 — У*з. У1+У2 — У12. ]
Уз+Угз- У2. Л-Г-У12—Л. Уз + У'12—Ум. У1+У23— У12. | E6,19>
Уз- I
У Н-Ум — Ур У +У12- У:!. У0 + У12 — У1. Уг+Уга—Уз
Если хотя бы одна из этих разностей равна нулю, сумма E6,17)
сводится к единственному слагаемому. Пусть, например, _/12 =j\-\-J2-
тогда с помощью E6,17) легко находим:
W UiJ'iJU У1+У2У23) "=
-- lBy\)! BЛ)! (Л -г Уг -г У + У3 + 1)! (Л + У2 + У — Л)!' X
1
X 1Bу\ + 2Л+ 1)КУ+У3—у\ —ЛЖЛ-Ьу -Ла)! X
X
Все остальные случаи сводятся к этому, если использовать
соотношения симметрии.
Если хотя бы один из аргументов W равен нулю и W Ф 0, то
среди остальных аргументов найдется пара одинаковых и. можно,

§ 5C]	КОЭФФИЦИЕНТЫ РАКА	223-
следовательно, воспользоваться формулой E6,20). Пусть, например,
J2=Q и W Ф 0. Тогда j\—jl2 и Лз—Л- Применяя соотношение
E6,20), мы получим:
WUiOJU jju) = [B/, + 1 MBу„ + 1 )]*'.	E6,21)
С помощью соотношений симметрии можно получить отсюда
выражения для коэффициентов Рака в случае равенства нулю любого
другого аргумента.
Значения всех коэффициентов Рака для j12 — -х- и 1 приведены
в приложении.
В заключение выведем одну формулу, которая играет важную
роль при рассмотрении ядерных реакций (см. § 80—82). Умножая
обе части E6,6) на UiJ2bmim2-i \j т) и суммируя по }' от \j\—y23j;
до Л + Лз получим:
X
Теперь, используя первые два соотношения E5,3), придадим^
этой формуле следующий более симметричный вид:
\b X
X (ШиЩ — Щг! Л — mi) =
7Шг1ущ^^ W(jlj2jj,, y12y23). E6,22)
Заметим, что суммирование в левой части можно формально рас-
распространить на индексы т12 и тл, так как при этом в левой части
не появится дополнительно ни одного отличного от нуля слагаемого.

ГЛАВА XII
УРАВНЕНИЕ ШРЕДИНГЕРА
§ 57. Законы сохранения
В этой главе рассматриваются некоторые общие методы изучения
жвантовомеханической системы, обладающей той или иной симметрией.
Начнем с установления связи между группой, характеризующей
-симметрию квантовомеханической системы, и законами сохранения,
имеющими место для данной системы.
Как известно, в наиболее важных случаях состояние квантово-
квантовомеханической системы, состоящей из п частиц, характеризуется ее
волновой функцией
У=$(Ги г2, .... rn, t).	E7,1)
Волновая функция удовлетворяет уравнению Шредингера
!$=Нф.	E7,2)
где Н — некоторый линейный оператор, не содержащий производных
по времени, называемый оператором Гамильтона. Конкретный вид
оператора Н для нас сейчас безразличен. Заметим только, что при
изменении внешних условий изменяется и оператор Н.
Так как оператор Н не содержит производных по времени, то
задание волновой функции <Ь в некоторый момент времени t — t0
ф(ги г2, ..., rn, t0) = ф0(ги г2	гп)
однозначно определяет функцию i во все последующие и предыду-
предыдущие моменты времени.
Значения, принимаемые волновой функцией, могут быть либо
числами, либо элементами некоторого линейного о-мерного про-
пространства А. В последнем случае, выбирая в Л ортонормированный
базис, можно записать вектор-функцию E7,1) в виде совокупности а
компонент
ЬЛ, r2,...,rn,t) G=1,2	а).	E7,3)

§ 57]	законы сохранения	225
Уравнение E7,2) в этом случае может быть записано в виде
Существенную роль в квантовой механике играет скалярное произ-
произведение (ср, ф) двух волновых функций ср и ф, которое определяется
следующим образом:
(?• тО = Г У Ъ(ri- гг< ••¦- гп- *)tyfa, r2	rn
J fZ	'	E7,5)
Каждой физической величине а соответствует согласно кванто-
квантовой механике некоторый линейный оператор А; при этом выражение
-/М1	E7,6)
трактуется как среднее значение величины а в состоянии ф. Так
как среднее значение каждой физической величины в любом состоя-
состоянии является во всяком случае действительным, то оператор А,
соответствующий физической величине, должен быть эрмитовым.
В частности, должен быть эрмитовым оператор Гамильтона Н, так
как согласно квантовой механике он соответствует энергии системы.
Таким образом,
(Нф. ф) = (ф. Щ).	E7,7)
Если волновая функция <|> является собственной функцией опера-
оператора А
Аф = Хф,	E7,8)
то согласно квантовой механике в состоянии ф физическая вели-
величина а имеет совершенно определенное значение X. Разумеется,
в этом случае среднее значение величины с также равно X.
Уравнение Шредингера E7,2) будем называть инвариантным
относительно некоторого оператора g, если всякое решение ф этого
уравнения переходит под действием оператора g в функцию
f=g*.	E7,9)
которая также удовлетворяет уравнению Шредингера *)
j^g—Нф'.	E7,10)
Совокупность всех таких операторов образует группу. Эта группа,
а также любая ее подгруппа называются группой уравнения E7,2).
*) Если волновая функция ф, помимо уравнения Шредингера, должна
удовлетворять некоторым граничным условиям, то мы потребуем, чтобы
функция ф' = gф также удовлетворяла этим условиям.
15 Зап. 3512. Г. Я. Любарский

226	УРАВНЕНИЕ ШРЕДИНГЕРА	[ГЛ. XII
В дальнейшем мы будем предполагать, что операторы g являются
линейными и коммутируют с операцией дифференцирования по вре-
времени:
мени:
В этом случае можно утверждать, что операторы g коммутируют
с оператором Гамильтона. Действительно, подставляя E7,9) в E7,10)
и используя E7,11) и E7,2), получим:
.. ¦ 1 д ,	1 д<1> „ .
Hg* = T^g* = gT-^ = gH*.
Итак,
Hg^ = gH^,	E7,12)
если ф — волновая функция, т. е. какое-либо решение уравнения
Шредингера E7,2). Из последнего соотношения вытекает, что и опе-
оператор g*, сопряженный оператору g, также коммутирует с опера-
оператором Н:
Поэтому эрмитовы операторы
gi = Y(g + g*) и S2=^f(S~ g*)
также коммутируют с оператором Н:
и Hg2^ = g2H<l>.	E7,13)
Покажем, что эти операторы соответствуют сохраняющимся физи-
физическим величинам. Под этим подразумевается следующее:
1) если в некоторый момент времени t = t0 среднее значение
оператора gt равнялось
то и в любой другой момент времени среднее значение оператора gx
будет равно qy;
2) если в некоторый момент времени t = t0 волновая функция tj*
являлась собственной функцией оператора gt
то и в любой другой момент она будет собственной функцией этого
оператора.

57|	законы сохранения	227
Для доказательства вычислим производную ^-(g1<!>. ф). Имеем:
** «=(«•&• ¦)+(«*#)=
Это доказывает первое утверждение.
Рассмотрим функцию
y(rv г2, ..., rn, t) = gd(rvr2, .... г,,, 0 — ЩГг, г2, .... г„. О-
Она удовлетворяет уравнению Шредингера и обращается в нуль
при t = t0. Поэтому волновая функция о тождественно равна нулю
во все моменты времени. Это означает, что
r2, ..., rn, t) = l<b(rv г2, .... rn, t).
Факт существования сохраняющейся физической величины носит >id-
звание закона сохранения этой величины. Каждому элементу группы
уравнения Шредингера соответствует некоторый закон сохранения
(именно, закон сохранения «комплексной» физической величины
gt-4-/g2). Ясно, однако, что не все эти законы независимы. Так,
закон сохранения величины f = gfi вытекает из законов сохранения
величин g и h. Поэтому возникает вопрос, как выделить из всех
законов сохранения, доставляемых нам группой уравнения Шредин-
Шредингера, некоторое, по возможности небольшое, число законов сохра-
сохранения так, чтобы остальные законы сохранения вытекали из них.
Этот вопрос особенно актуален для непрерывных групп *), которые
приводят к континуальному множеству законов сохранения.
Мы рассмотрим с этой точки зрения только группы Ли и уста-
установим справедливость следующей теоремы.
Теорема. Пусть группа операторов G уравнения Шредин-
Шредингера есть группа Ли размерности т. Пусть alt а2, . . ., ат—па-
ат—параметры группы G, a lv I2, ..., \т — инфинитезимальные опера-
операторы, соответствующие этим параметрам. Тогда
1)	каждый инфинитезимальный оператор соответствует не-
некоторой сохраняющейся физической величине;
2)	все законы сохранения, связанные с элементами группы G,
являются следствием т законов сохранения, связанных с т инфи-
нитезимальными операторами.
Эта теорема показывает, что с точки зрения законов сохранения
можно полностью игнорировать группу G и учитывать только ее
инфинитезимальные операторы, как это часто и делается в курсах
квантовой механики.
*) Для конечных групп он рассмотрен А. В. Соколовым и В. П. Широ-
ковским [А, 6].
15*

228	УРАВНЕНИЕ ШРЕДИНГЕРА	[ГЛ. XII
Доказательство теоремы. Продифференцируем тождество
)	E7,14)
по параметру aj (/=1, 2	т) элемента g и положим затем
g = e. Получим:
1^НФ = Htyb.	E7,15)
Это доказывает первую часть теоремы. Для доказательства второй
части покажем, что из условий E7,15) вытекают условия E7,14).
С этой целью перепишем уравнения D3,10) в виде
').	E7,16)
где ф — произвольная функция. Подставляя в E7,16) вместо ф функ-
функцию Яф, получим:
т
= V 5ад (gr) 14вНф.	E7,17)
Применим к обеим частям равенства E7,16) оператор Н и восполь-
воспользуемся перестановочными соотношениями E7,15)
Вычтем полученное равенство из E7,17)
т
— (gH—ни <|. = 2 % (g) i4 (gH - Hg) ф.
Таким образом, функция
удовлетворяет системе уравнений
и очевидному начальному условию
Повторяя рассуждения, подобные рассуждениям § 43, легко убе-
убеждаемся в том, что функция y(g) тождественно равна нулю. Это
завершает доказательство теоремы.
Рассмотрим некоторые применения этой теоремы.

§ 57]	законы сохранения	229
1. Пусть К—квантовомеханическая система, находящаяся в по-
постоянных внешних условиях. Все моменты времени для такой системы
физически равноправны. Поэтому, если <b (t) есть какая-либо волно-
волновая функция системы К, т. е. какое-либо решение уравнения Шре-
дингера E7,2), то все функции
а) (— схэ<а<оо)
также будут удовлетворять уравнению Шредингера. Итак, в рас-
рассматриваемом случае группа операторов Т(а), определяемых равен-
равенством
Т (а) ^ (t) = d» (t -\- а) (— со < а •< со),
представляет собой группу уравнения Шредингера. Эта группа
является однопараметрической группой Ли. Единственный инфини-
тезимальный оператор, связанный с этой группой, имеет следую-
следующий вид:
А — ^ (О
Закон сохранения, связанный с однородностью времени, называется
законом сохранения энергии, в соответствии с этим в квантовой
механике оператор
Ai_ А А
i	/ dt
называется оператором энергии. Множитель й введен для того,
чтобы оператор имел размерность энергии.
2. В качестве второго примера рассмотрим систему К, находя-
находящуюся в однородных внешних условиях. Это означает, что потен-
потенциальная энергия системы не изменяется при перемещении ее «как
целого» в пространстве. В частности, такой системой является
всякая замкнутая система.
Если
т"(Г1' Г2< • • •> ГП< О
— какая-либо волновая функция системы К, то функция
'Mri + e. г2-\~а, .... rn-\-a, t)
также будет волновой функцией рассматриваемой системы. Это
является непосредственным следствием однородности пространства.
Таким образом, совокупность операторов Т(а), определяемых
равенствами
Т(с)ф(Г[, г2	rn, t) = ty(rl-\-a, r2-\-a	rn-\-a, t),
образует группу G уравнения Шредингера. Эта группа — группа
параллельных переносов — является трехпараметрической группой Ли.
В качестве параметров можно взять проекции
av аг и а3

230	УРАВНЕНИЕ ШРЕДИНГЕРА	[ГЛ. XII
вектора а. Этим параметрам соответствуют три инфинитезимальных
оператора lv I2 и 13 и, следовательно, три закона сохранения, назы-
называемые, как известно, законами сохранения проекций импульса.
Вычислим инфинитезимальные операторы 1и \г и 13. Имеем:
г, г) = -з— Т (а) Ф (г,, г.,, ..., г„,
и /	фа^	/ т \	^	и
а=О
Итак,
Подобным же образом находим, что
ь^^-ч-^--1- ••• -4-/-.
дух оу2	' 0>'п
Операторы
называются операторами проекций импульса.
3. Рассмотрим, наконец, квантовомеханическую систему, нахо-
находящуюся в центрально-симметричном поле с центром в некоторой
точке О.
Для простоты предположим сначала, что система состоит из одной
частицы и поэтому волновая функция системы
зависит только от одного радиуса-вектора г и времени t.
Кроме того, для наглядности будем считать, что значения, при-
принимаемые волновой функцией ф(г, t), суть векторы. Таким образом,
в каждый данный момент t волновая функция ф(г, t) образует неко-
некоторое векторное поле: каждой точке с радиусом-вектором г ста-
ставится в соответствие вектор ф(г, t). Будем представлять себе век-
вектор ф(г, t) отложенным от точки г. Конец этого вектора находится
в точке г' —г-|-ф(г, /). Произведем вокруг центра О какой-либо
поворот g пространства вместе с волновой функцией ф (г, f). Это
означает, что мы одновременно поворачиваем точку приложения г
вектора ф, переводя ее в точку gr, и поворачиваем вектор ф, пере-
переводя его в вектор gtj*. Вектор gi|> отложен от точки gr, конец век-
вектора g^ совпадает с точкой gr'.

Ч) 57]	ЗАКОНЫ СОХРАНЕНИЯ	231
В результате такого поворота мы получим новую функцию
ф' (г, t). В силу сферической симметрии внешних условий функция
<ji' (г, t) также будет удовлетворять уравнению Шредингера. Таким
образом, оператор Т (g) (g ? R), переводящий волновую функцию <|>
в волновую функцию if', принадлежит группе уравнения Шредингера.
По построению функции ф' она удовлетворяет условию
т. е.
f (r,t) = tff(g-*. rt),	E7,18)
или
T(g)«Kr. O=g*(g-1r. t).	E7,19)
Если волновая функция зависит от радиусов-векторов нескольких
частиц, то при вращениях пространства она преобразуется, очевидно,
Следующим образом:
ТЧвЖ/-!, г2, ...,г„. 0=^(8"^. g-lr2	g-irn. О-
Наконец, если значения волновой функции суть не векторы, а эле-
элементы более общего линейного пространства L, преобразующегося
по некоторому представлению S группы вращений, то последнее
равенство принимает следующий вид:
1. г2. .... гп. 0 = S(g)*(g-1r1. g-1^, .... g-irn, 0. E7,20)
Совокупность операторов Т (g) образует, разумеется, представление
группы вращений R. Вычислим инфинитезимальные операторы 1Х,
\v, 1г, соответствующие параметрам лх, ау и аг, группы вращении.
Начнем с вычисления оператора 1г. Положим в последнем равенстве
?г —g-[0 0 яг], т. е. возьмем в качестве элемента g поворот вокруг
оси OZ на угол аг. Вводя цилиндрические координаты рк, zk, cp&
(fe=l, 2	п), перепишем соотношение E7,20) в рассматривае-
рассматриваемом случае в виде
Т [0 0 а-] ф (р:, zv cpi; р2, г2, ср2; . ..; рп, г„, с?»: 0 =
= S[0 0 a,]^(Pi. «1. ?l —«г! Рг- г2. 'f2 —V. •••; Р«- «». ?» —аг; 0.
Дифференцируя это равенство по а3 и полагая затем ccz = O, получим
1г<1» (rt> r2, . . ., гп, ¦ „0 = \2t? (rv r2, .. ., г„, 0 —
Здесь через I* обозначен инфинитезимальный оператор, соответ-
соответствующий параметру аг в представлении S.
Вводя эрмитовы операторы
п
l	М	»^
E7,21)

232	УРАВНЕНИЕ ШРЕДИНГЕРА	[ГЛ. XII
перепишем последнее равенство в виде
•W» = (S, + M,)«|>.	E7,22)
Физическая величина, изображаемая эрмитовым оператором 5Z, сохра-
сохраняется, так как оператор Jz только постоянным множителем /ft отли-
отличается от инфинитезимального оператора 1г группы уравнения Шре-
дингера. Эта физическая величина называется проекцией полного
момента на ось OZ.
Равенство E7,22) показывает, что проекция Jz полного момента
на ось 07. слагается из двух величин: величины Sz, называемой
проекцией спина на ось OZ, и величины Мг, называемой проекцией
орбитального момента на ось OZ.
Оператор Sz зависит от представления S, по которому преобра-
преобразуется пространство L значений волновой функции. Наоборот, опе-
оператор Мг не зависит от представления S. В том частном случае,
когда волновая функция <j> является скаляром, представление S является
единичным, оператор S3 равен нулю, а оператор проекции орбиталь-
орбитального момента М„ совпадает с оператором проекции полного момента J,.
Таким образом, различие между операторами Мг и J2 возникает
только в тех случаях, когда пространство L преобразуется по пред-
представлению группы вращений более сложному, чем единичное пред-
представление.
Оператор Мг может быть записан в декартовых координатах
в виде
К
Совершенно аналогично приходим к проекциям полного момента
системы на две другие оси координат
J^S^+JVL,,, J^S^+AV	E7,24)
где
Sx = ih\%, Sy = ihly,
Таким образом, мы получили три закона сохранения 5Х, Jy и J2,
связанных с изотропией пространства.
Заметим в заключение, что перестановочные соотношения для
введенных операторов немедленно получаются из перестановочных
соотношений для инфинитезимальных операторов. Действительно,
•М» - -У* = - h2 ('А - W = - й% = ihh-
Подобным же образом можно получить остальные перестановочные
состюшения, например
МуМг — MjMj, = ihJAx, SZSX — S^Sg = ihSy.

§ 58]	КЛАССИФИКАЦИЯ СОСТОЯНИЙ	233
§ 58. Классификация состояний
Пусть О — какая-либо группа уравнения Шредингера. В преды-
предыдущем параграфе было показано, что наличие группы G влечет за
собой существование законов сохранения. Теперь мы увидим, что
волновые функции естественно классифицируются по неприводимым
представлениям этой группы.
Совокупность всех волновых функций, рассматриваемых в неко-
некоторый момент t0, образует линейное пространство L, преобразую-
преобразующееся по некоторому представлению Т группы G. Разлагая Т на
неприводимые представления, мы расщепляем пространство L на
неприводимые инвариантные подпространства. В каждом из этих
подпространств можно выбрать базисные функции. Любую волновую
функцию можно мыслить как суперпозицию этих базисных функций.
С другой стороны, каждая базисная функция принадлежит тому или
другому неприводимому представлению группы G. Таким образом,
базисные функции можно классифицировать по неприводимым пред-
представлениям группы О.
Эта классификация не представляла бы, пожалуй, никакого инте-
интереса, если бы не то обстоятельство, что если волновая функция ф
в некоторый момент t0 преобразуется по некоторому неприво-
неприводимому представлению группы G, то во все последующие моменты
она преобразуется по этому же представлению.
Докажем это утверждение. Пусть LQ — некоторое неприводимое
инвариантное относительно группы О подпространство, а ф^, .. .
.... фМ— какой-либ базис в этом подпространстве. Под действием
элементов g?G функции ф*,1'	ф<в) преобразуются друг через
друга:
2
Обозначим через ф*1), ..., ф'*) волновые функции (т. е. решения
уравнения Шредингера), равные в момент t — tQ соответственно функ-
функциям ф^1', .. ., ф^*). Введем в рассмотрение функцию
Эта функция удовлетворяет уравнению Шредингера (так как каждое
слагаемое правой части удовлетворяет этому уравнению) и при t = t0
обращается в нуль. Отсюда следует, что функция ф=0, что и до-
доказывает наше утверждение.
Рассмотрим теперь какую-либо квантовомеханическую систему К,
находящуюся в поле с центральной симметрией. В этом случае

234	УРАВНЕНИЕ ШРЕДИНГЕРА	[ГЛ. XII
в качестве группы О можно взять либо группу вращений R, либо
группу поворота Z вокруг некоторой фиксированной оси OZ.
В первом случае волновые функции ф можно классифицировать
A	3	\
j = 0, -к- > 1 > -к-, .. . ) группы
вращений. Если j— вес представления, по которому преобразуется
функция ф, то говорят, что система К в состоянии ф имеет момент j
{в единицах й).
Во втором случае волновые функции классифицируются по не-
неприводимым представлениям хт группы поворотов Z. Индекс пред-
представления т совпадает с собственным значением проекции момента
на ось OZ, если система К находится в состоянии ф, преобразую-
преобразующемся по представлению пт.
Рассмотрим теперь случай, когда система К состоит из двух
подсистем Ki и К2, причем в момент времени ^ = ^0 взаимодействие
между системами пренебрежимо мало и каждая из подсистем имеет
свою волновую функцию. Обозначим эти функции через ф1 и ф2
и предположим, что функции фх отвечает момент jv а функции
ф2 — момент у2. Волновая функция всей системы ф = ф1ф2 может быть
разложена по волновым функциям ^, отвечающим определенному
значению момента всей системы К. Легко сообразить, что эта раз-
разложение содержит только конечное число членов. Действительно,
произведение ф^ф^ преобразуется по произведению представле-
представлений D,, X Ол = D|jWa| -j-Di./.-^i+i-f- .. . _j_Dj]+^. Поэтому функ-
функция ф записывается в виде суммы
Согласно квантовой механике это означает, что измерение момента
системы К может привести только к одному из следующих значений:
IЛ —Л |. IЛ —к 1-Й	к +Уз
(теорема сложения моментов).
Если функции ф! и ф2 отвечают определенным значениям т1 и т2
проекции момента на ось OZ, то, так как tmi X tm' = -zm'+m*, вол-
волновая функция системы ф = ф1ф2 отвечает значению ml-{-mi проек-
проекции момента на ось OZ.
Если система Я\ находится в состоянии с моментом j\ и проек-
проекцией момента т.у, а состояние системы К2 характеризуется значе-
значениями jt и т2, *то нетрудно вычислить вероятность найти систему К
в состоянии с моментом j(\j\—k\-^.j-^.j\-{~k)-
В самом деле, функция ф1 является вектором канонического
базиса е^ пространства, преобразующегося по представлению группы

§ 58]	классификация состояний	235
вращений веса j\. Подобным же образом функцию ф2 можно рас-
рассматривать как вектор е/«. Поэтому (см. § 54) произведение t|> = t';1^2
представимо в виде
где (jj^m^.^l jml -J-m2)—коэффициенты Клебша—Гордана. Из
последнего равенства следует, что вероятность найти систему К
в состоянии с моментом j равна
wi = I иигМ\Щ 1

ГЛАВА XIII
УРАВНЕНИЯ, ИНВАРИАНТНЫЕ ОТНОСИТЕЛЬНО ЕВКЛИДОВОЙ
ГРУППЫ ДВИЖЕНИЙ ПРОСТРАНСТВА
§ 59. Шаровые функции со спином
Если в каждой точке пространства задано значение некоторой
физической величины Ч" (температуры, скорости, тензора деформаций
и т. п.), то говорят о поле величины Ч". В качестве примера можно
указать поле скоростей и давлений в гидродинамике, электромагнит-
электромагнитное поле в электродинамике, электронное поле в квантовой элек-
электродинамике и т. д.
Поля подразделяют на скалярные, векторные, тензорные, спи-
норные и более сложные поля. Так, температурное поле является
скалярным, поле скоростей — векторным, электронное поле в нереля-
нерелятивистском приближении — спинорным, поле деформаций — тензор-
тензорным. В основе этой классификации лежит поведение величины W,
взятой в любой фиксированной точке, при вращениях вокруг этой
точки. Мы видели в § 50, что если при этих вращениях компоненты
величины 47 преобразуются друг через друга линейно, то они пре-
преобразуются по некоторому представлению Т группы вращений. Если
T = D0, то поле называется скалярным, если T = Di—спинорным,
~г
если T = Dt — векторным, если T = D? — тензорным. Если предста-
представление Т совпадает с неприводимым представлением Ds, то мы будем
говорить о спинорном поле веса 5. В общем случае произвольного
представления Т мы будем говорить о Т-поле. Т-поле может быть
представлено в виде суммы спинорных полей, если представление Т
приводимо.
При вращении g вокруг начала координат поле Ч"(г) переходит
в поле 47'(г), равное
Т'С) = T(g)V(g-1r)	E9,1)
(ср. E7,19)).
Рассмотрим совокупность всех спинорных полей одного и того же
веса s на сфере единичного радиуса. При вращениях вокруг начала
координат эти поля преобразуются друг через друга в соответствии
с формулой E9,1), по некоторому бесконечномерному представлению.

•§ 59]	шаровые функции со спином	237
Это представление может быть разложено на неприводимые конечно-
конечномерные представления D/. Спинорные поля веса s, преобразующиеся
по неприводимому представлению веса J, называются шаровыми
функциями со спином s порядка J. Те спинорные поля, которые
образуют канонический базис, называются основными шаровыми
функциями; мы будем обозначать их следующим образом:
В частности, если s = 0, то с точностью до постоянного множителя
основные шаровые функции совпадают с обычными сферическими
функциями YJM{%, с^-
Поставим задачу найти явный вид всех шаровых функций со спи-
спином s порядка J. При этом мы выясним, какие представления Dj
и сколько раз содержатся с бесконечномерном представлении, по
которому преобразуется совокупность всех спинорных полей веса s,
рассматриваемых на единичной сфере.
При вращении g вокруг начала координат функция Xjjt g пере-
переходит в функцию
7.JM,. С) =M,S j DJM,M (g) y,JMi „ (r).
С другой стороны, согласно E9,1) имеем:
Сопоставляя эти два равенства, получим:
2
или
7jm, s is'1') - | D'L'M (S) Ds (g-1) 7.JM,, s (r).	E9,2)
Положим в этом соотношении г —А, где k — орт, направленный
вдоль оси OZ, и возьмем в качестве вращения g поворот С3(а)
вокруг оси OZ на произвольный угол а. Мы получим, вспоминая,
= е~Ш^8 (cs (-«)) 7jM, s
Переходя в этом равенстве к компонентам, находим:
У-Тм, s (*) = еНт-Щ.Ум,. (*)• (m = — s.—s-\-l	s).
Отсюда следует, что
(*) = 0, если Мфт.	E9,3)
8

238 уравнения, инвариантные относительно евклидовой группы [гл; хш
Это соотношение показывает, что если в E9,2) положить r =
g-1 = h, hk
и перейти к компонентам, то получится:
r, з = minE, /)),
если J—5 — целое число; если же J — s — полуцелое число, то все
члены в правой части E9,2) обращаются в нуль после подстановки
г = k. Это означает, что порядок шаровых функций является
целим или полуцелым числом одновременно с их весом.
Мы видим, что задание Bз -)— 1) чисел у^м s(k) однозначно опре-
определяет все функции 7.JMif.(f)- С другой стороны, простая проверка
показывает, что при любом выборе этих чисел функции, определяе-
определяемые равенством E9,4), являются шаровыми функциями со спином s
порядка J. Отсюда вытекает, что среди шаровых функций со спи-
спином s существует Bа —|— 1) линейно независимых инвариантных
семейств, каждое из которых преобразуется при вращении про-
пространства вокруг начала координат по представлению Dj, если
J—s—целое число.
Из E9,4) следует, что всякое спинорное поле веса 5, преобра-
преобразующееся при вращениях вокруг начала координат по представле-
представлению Dj, имеет следующий вид:
2
М' = — а
—r, j =
E9,5)
где м]Г (/•) —произвольные функции.
Формуле E9,4) можно придать более удоб-
Рис. 23.	ный для применений вид. С этой целью рас-
рассмотрим на единичной сфере триэдр, одна
из осей которого О'С, направлена по вектору г, а две другие оси
О'\ и O'tj — по касательным к меридиану и параллели в точке г
(рис. 23). Если сферические координаты вектора г равны 6 и ср,
то вращение Л, поворачивающее оси триэдра OXYZ параллельно
осям триэдра O'srf,, характеризуется эйлеровыми углами Oj = 0,
Введем в рассмотрение в пространстве значений величины W базис:
«™ = D.(A)«« (« = -*. —s+1, .... s).

§ 60] УРАВНЕНИЯ, ИНВАРИАНТНЫЕ ОТНОСИТЕЛЬНО ЕВКЛИДОВОЙ ГРУППЫ 239
где ет — канонический базис. Ясно, что базисные векторы е'т обра-
образуют канонический базис относительно осей O'\t{,. Мы будем назы-
называть его местным базисом. Обозначим через ^J^ й (г) координаты
функции yJM s(r) в местном базисе е'т. Координаты $™м>11 легко
выражаются через у™м и:
Лиг —V Г)" (h~l\-/m'
M
Подставляя сюда выражение E9,4) для функций у^ s, находим:
= r, o = min(s, 7)). E9,6)
О,	если | /и | > а,
Это соотношение можно переписать в виде
fjM, s (9, i) = «}^ ¦ (-0m+:tf еш?Ртл:,./(9) (! т ! < а), E9,7)
где M™g — произвольные константы.
Таким образом, в местном базисе шаровые функции со спином s
выражаются через функции Ртм, j( \ т [С а)-
Всякое спинорное поле Ч-" веса s, преобразующееся по предста-
представлению Dj, является согласно E9,7) линейной комбинацией следую-
следующих полей:
*7*. 8 (г) = и% (г) (- f)m+M е™* ¦ РтМ, j @)
(!mj<3, M = — J, —J-\-l, .... J). E9,8)
§ 60. Уравнения, инвариантные относительно группы
евклидовых движений пространства
Всякая система уравнений, описывающая какой-либо процесс
в пустоте или в безграничной однородной изотропной среде, должна
иметь одинаковый вид в любой прямоугольной системе координат.
Мы попытаемся найти общий вид таких уравнений в предположении,
что они линейны. Что касается поля xV(r), описывающего рассма-
рассматриваемый процесс, то мы будем считать его некоторым Т-полем
(см. § 59). Иными словами, значения функции lF принадлежат неко-
некоторому р-мерному пространству L, которое преобразуется по пред-
представлению Т группы вращений вокруг начала координат.
Без ограничения общности можно считать, что система уравнений,
определяющая компоненты функции W, содержит производные только
первого порядка. В сгдоом деле, этого всегда можно достичь, рас-
рассматривая некоторые первые производные как самостоятельные ком-
компоненты.

240 УРАВНЕНИЯ, ИНВАРИАНТНЫЕ ОТНОСИТЕЛЬНО ЕВКЛИДОВОЙ ГРУППЫ [ГЛ\ XIII
Для простоты мы будем считать, что производные по времени
в уравнении не содержатся. Такие «укороченные» уравнения полу-
получаются, когда ищут решения вида
47(г, 0 = ^('")е1ш*-
Таким образом, мы будем рассматривать уравнения
=^ (/=1.2	Р). (бол)
где tyft— компоненты функции 47.
В силу однородности пространства коэффициенты аЦ, /Щ, 41'
не зависят от координат.
Выясним, какими должны быть эти коэффициенты для того,
чтобы система уравнений F0,1) была инвариантна относительно вра-
вращений.
Для этого условимся прежде всего о выборе компонент фй. Разобьем
пространство L на неприводимые подпространства. Каждое из непри-
неприводимых подпространств будем обозначать символом Lsn, где индекс s
указывает на вес представления Ds, по которому преобразуется под-
подпространство L8 (, а индекс п нумерует различные подпространства,
преобразующиеся по одному и тому же представлению Ds. Канони-
Канонический базис в Lsn обозначим через
«8»,« (m = — s.—s+l	s).	F0,2)
В соответствии с этим компоненты функции W обозначим через х^
так, что
ч7= У, уте
*-* A-ns 8п, т
s, m,n
Целесообразно также ввести дифференциальные операторы
+ 'V d '? d4
/2 V д.*	ду)	dz	Y'2\dx^ ду) К '
которые преобразуются при вращениях пространства так же, как и
координаты в каноническом базисе (см. D8,10)).
Уравнения F0,1) можно теперь переписать в виде
, ? , Hs»m. s'n'm'^-lXnV "+" Afnm, в', п'. т'доУ™'8' +
а',п , т'
,S'n-m'y$A = 4ns- F0.4)
Учтем теперь, что 3Bs-j-l) величин
д vm' r) vm> д ут'.
0-lXnV "obi's" °1'я'|'

§ GO] УРАВНЕНИЯ, ИНВАРИАНТНЫЕ ОТНОСИТЕЛЬНО ЕВКЛИДОВОЙ ГРУППЫ 241
(s'n' фиксированы, т' = — s', —s'-\-\, ..., s') преобразуются по
произведению представлений Di X Ds'- Если s' = s— I, s, s-\-l,
то существует линейная комбинация этих величин
2 (ls'pm' \sm)dj^,,	F0,5)
которая преобразуется при вращениях так же, как и ^™. В силу
инвариантности уравнения F0,4) его левая часть должна состоять
только из сумм вида F0,5). Поэтому каждая система уравнений,
инвариантная относительно вращений, имеет следующий вид:
2 2 А8п> а,п, 2, A *>»' I sm) djC$a. = 4Z. F0,6)
8 =8—1, S, S + 1 И	(I, TO
причем коэффициенты А6П,„>„- совершенно произвольны. Подчеркнем,
что либо все индексы 5 являются целыми, либо все они являются
полуцелыми.
Часто бывает полезно переписать систему уравнений в сфери-
сферических координатах. Для этого нужно совершить не только замену
,	д д д
дифференциальных операторов д^ операторами -г-, -^-, ^-, но и
сделать переход от координат у^8 в каноническом базисе к коор-
координатам t]>™ в местном базисе (см. § 59). Координаты y^s и фто
связаны между собой соотношением
или
*/W* tf\	/~)й (h\ diW (r\	(C\C\ 7^
^ns V' — mm' *¦ ' Тгг^ I' '•	I1-"-'' ' )
Аналогичным соотношением связаны друг с другом операторы
д^ = Dlp.> (h) d'j.',	F0,8)
где
(расположение осей O'^rf, указано на рис. 23).
Производные по &, tj, С легко выразить через производные по
г, 6, ср. Именно
_а	j__a_ a _ i а _а__ _й
а? г ae' arj г sin в а^' ас дг'
Поэтому
F0,9).
16 Зак. 3512. Г. Я. Любарский

242 УРАВНЕНИЯ, ИНВАРИАНТНЫЕ ОТНОСИТЕЛЬНО ЕВКЛИДОВОЙ ГРУППЫ [ГЛ. XIII
Подставим в уравнения F0,6) выражения F0,7) и F0,8) для у™а
и д^ Мы получим:
2 Л«..'я' 2 A *V»' I sm) Dlv-' W К'°™'р' (А) Ф5'»' =
u', n'	|a, »»', jj.', p'
ИЛИ
s', n'	[i, m', у-', p', »i
= x^e.	F0.10)
С помощью второго тождества задачи II § 54 внутреннюю сумму
можно записать в виде
или
V-'	X	Р'
Вспоминая результат задачи III § 47, легко находим, что
D8' (А) д+ 1 D8' (А) = —V= fAs-1 — i ctg бАо']-
J -	rVt
где All, Ao ¦ Af —операторы D6,25). Кроме того, ясно, что
d0D3(A)=0.
Теперь можно следующим образом переписать уравнение F0,10):
Am..'»'
и', п'
Подставим в это уравнение значения D6,25) матричных элемен-
элементов операторов All, Ао , А? :
+ (р + 1) ctg 6) фР+1 + о?+1ф?,в.
— —^--^	(р—l)ct? в) iPr)-\-а*'4>р, И = х<У>. F0,11)

$ 60] УРАВНЕНИЯ, ИНВАРИАНТНЫЕ ОТНОСИТЕЛЬНО ЕВКЛИДОВОЙ ГРУППЫ 243
Мы получили общий вид системы уравнений, инвариантной от-
относительно евклидовой группы движений, в сферических коорди-
координатах.
Рассмотрим совокупность всех решений, удовлетворяющих этой
системе при некотором фиксированном значении •/. Ясно, что эта
совокупность образует некоторое линейное пространство. Обозна-
Обозначим его через Lx. Пространство Lx инвариантно относительно всех
вращений вокруг начала координат и, следовательно, преобразуется
по некоторому представлению этой группы. Расщепим пространство L%
на неприводимые подпространства и обозначим одно из них
через Lj. Индекс J указывает на то, что Lj преобразуется по пред-
представлению D/. Обозначим через
VjM(r) (M = — J, —У+1. .... У)
поля, играющие роль канонического базиса в пространстве Lj. Вспо-
Вспоминая выводы, полученные в предыдущем параграфе, мы можем
написать:
м. ns (г) = иУ, т (г) (- [)т+ме**чРтм. j F). | * К о.
|>о (o = min(s. 7)).
где ffiv, пя—компоненты поля XYJM в местном базисе.
Мы видим, что угловая зависимость функций ^'jm (г) получается
из общих соображений и не зависит от конкретного вида урав-
уравнений F0,11).
При подстановке ^™„ = $УМ П8 в уравнение F0,11) все множи-
множители, зависящие от углов, должны взаимно сократиться, а сами
уравнения станут обыкновенными дифференциальными уравнениями.
Таким образом, задача отыскания полей Ч-'^(г) сводится к нахо-
нахождению функций и™ пв (г), удовлетворяющих системе обыкновенных
дифференциальных уравнений.
Производя фактически подстановку <^='\ljM ns в уравнении F0,11),
мы получим с помощью рекуррентных соотношений D7,10) следую-
следующую систему обыкновенных дифференциальных-уравнений:
где о4 = уГуG+1)— m(m— 1).
16*

244 УРАВНЕНИЯ, ИНВАРИАНТНЫЕ ОТНОСИТЕЛЬНО ЕВКЛИДОВОЙ ГРУППЫ [ГЛ. XIH
§ 61. Пример
Рассмотрим в качестве примера уравнения Максвелла
rot?= — H, — то\Н=—Е	F1,1)
с	с
для электромагнитного поля с частотой ш.
Электромагнитное поле в данной точке характеризуется двумя векторами
Е(г) и Я (г). Поэтому шестимерное пространство L значений доля f рас-
распадается в данном случае на два неприводимых подпространства L\\ и L^,
каждое из которых преобразуется по векторному представлению Dj. Индекс s
принимает, таким образом, только одно значение s = 1, и мы будем в даль-
дальнейшем его опускать. Индекс п пробегает два значения л = 1, 2.
Роль компонент электрического поля в каноническом базисе играют
величины
?	^ (? + /?) Е Е Е	{Е1Е)
Аналогичный вид имеют компоненты магнитного поля в каноническом базисе
Нетрудно переписать уравнения Максвелла в новых обозначениях. Так, на-
например, получаем:
!^Hl = — {Hx~ 1Ну) = -i= (rot, Е-1то1уЕ)=>
се	у I
1 / дЕг дЕу
у 2 \ dy dz
дЕх dEz
+
dy
т. e.
d^Eo-d&^^Ht.	F1,2)
С
Подобным же образом можно получить остальные пять уравнений. Однако
для нахождения коэффициентов Asn>atn,, фигурирующих в уравнении F0,6),
достаточно одного лишь уравнения F1,2). В самом деле, сравнение F0,6)
с F1,2) показывает, что
Л21-о,A110|11)~ Y Z о,
(индексы s = s' = 1 опущены). С другой стороны, из уравнений Максвелла
F0,1) непосредственно видно, что
Ап = Ai2 = 0, Ап = — Ап.
Зная коэффициенты АП11,, нетрудно записать уравнения Максвелла в форме
F0,11), т. е. в сферических координатах. Фигурирующие в F0,11) компо-
компоненты поля в местном базисе — 4*из имеют простой физический смысл:

§ 01]
ПРИМЕР
245
где Ег, Е$, ??, Нг, Щ, Я9 — проекции векторов Е, //на сферические орты
еп еь и ег
Поставим задачу найти электромагнитные поля, преобразующиеся по
представлению Dj группы вращений. Для определенности будем считать,
что />1.
Используя результаты предыдущего параграфа, мы можем компо-
компоненты
такого поля записать в виде
= -l, 0, 1).
При этом функции u'j^ ns — и™ удовлетворяют уравнениям F0,12), которые
в рассматриваемом случае принимают следующий вид:
da
-1
dr
¦ =	и
-l
К	(О
= 	 К,.
e -
Исключая из этих уравнений функции «J и И2> получим систему из четы-
четырех уравнений:
F1,3)
1 г' [ 2/-a со cJMll+ 2r2 — «1 — °.
, /(/+1) в „-!_„
2г2 со
Положим теперь
И = U
и\-\- «f1 +ttj, W =
— «2 — И
—«Г1—

246 УРАВНЕНИЯ, ИНВАРИАНТНЫЕ ОТНОСИТЕЛЬНО ЕВКЛИДОВОЙ ГРУППЫ [ГЛ. ХШ
Складывая все четыре уравнения F1,3), найдем:
1	г
и'	«+ Г
——s—	\v = 0.
2	]
с
Подобным же образом получаем еще три уравнения:
Мы видим, что существуют два типа волн: и, 1>ФО, р, q = 0 и a, v = О,
^O. Вычислим функции и, f. Исключая и, находим:
civ ,\
2 ,
Мы получили уравнение вида
общее решение которого выражается с помощью функции Бесселя Jn{x)
и функции Неймана Nn(x) следующим образом:
где Сх и с2 — произвольные постоянные (см. Янке и Эмдс, «Таблицы функ-
функций», Гостехиздат, 1948).
В нашем случае у=1> <х = ~~"9'> Р ==—• n==^~rir- Таким образом,
Если точка г = 0 входит в рассматриваемую область, то коэффициент с2
следует положить равным нулю, так как функция Неймана N- г обра-
обращается в нуле в бесконечность.
Теперь нетрудно вычислить и функцию и.
Система уравнений, которым удовлетворяют функции р и q, ничем не
отличается от только что рассмотренной системы. Поэтому
где с3 и с4—^произвольные постоянные.

ГЛАВА XIV
ПОГЛОЩЕНИЕ И КОМБИНАЦИОННОЕ РАССЕЯНИЕ СВЕТА
§ 62. Квантовомеханическое введение
Квантовая теория излучения света существенно использует тот
факт, что энергия взаимодействия между веществом (атомом, молеку-
молекулой, кристаллом) и электромагнитным полем весьма мала. Это позво-
позволяет в нулевом приближении рассматривать поле и вещество незави-
независимо друг от друга и говорить о фотонах и стационарных состояниях
вещества. Учет энергии взаимодействия в первом приближении обна-
обнаруживает возможность перехода вещества из одного стационарного
состояния в другое. Эти переходы сопровождаются появлением или
исчезновением одного фотона и представляют собой поэтому те эле-
элементарные акты, из которых слагаются процессы излучения и погло-
поглощения света веществом.
Если Ei и Ef — энергии стационарных состояний вещества до
и после перехода и ?^ << Ер то частота v поглощенного кванта
равна v = -t-(?/. — Е{), где h — постоянная Планка. Это соотношение
используется для экспериментального изучения энергетических уров-
уровней стационарных состояний вещества.
Согласно теории возмущений вероятность перехода в единицу
времени пропорциональна квадрату матричного элемента энергии
взаимодействия, соответствующего начальному и конечному состоя-
состояниям. В интересующем нас случае матричный элемент энергии взаи-
взаимодействия пропорционален интегралу *)
\ i	/
где ej и Tj — заряд и радиус-вектор у-й точки поглощающей системы
(атома, молекулы, кристалла), <J>4 и tyf — волновые функции этой
системы до и после поглощения света, k — волновой вектор погло-
поглощенного фотона, п — единичный вектор, параллельный электриче-
электрическому полю фотона, Vj — градиент, относящийся к координатам
*) См. [!], стр. 120, формулы C), (За).

248	ПОГЛОЩЕНИЕ И КОМБИНАЦИОННОЕ РАССЕЯНИЕ СВЕТА [ГЛ; XIV
у-й частицы, интегрирование производится по всем координатам погло-
поглощающей системы.
Если интеграл F2,1) равен нулю при всех значениях k и п, то
переход ^-э-fy., сопровождающийся поглощением одного фотона,
не осуществляется. В этом случае говорят, что уровни ?^ и Ef не
комбинируют между собой (относительно поглощения). Ниже будет
показано, что наличие запрещенных переходов является следствием
симметрии системы.
Рассмотрим более подробно матричный элемент F2,1) в пред-
предположении, что поглощающей системой является атом. Мы будем
считать, что энергия поглощенного фотона йш недостаточна для
вырывания электрона, т. е. по порядку величины не превосходит
Z—(Ze — заряд ядра атома, а — «радиус» атома). Из неравенства
Йш-^ Z— следует, что ka-^Z -~г = т-^? (& = —> с—скорость света).
о>	си \о/ \	с	I
Таким образом, для атомов с небольшим зарядом ядра Z можно
с большой точностью положить eika=l.
Волновые функции ijij и fy практически равны нулю для' тех зна-
значений координат электрона, которые превышают размеры атома.
Поэтому в интеграле F2,1) можно заменить множитель ег г: едини-
единицей, после чего получится:
Это приближение становится неудовлетворительным, если выраже-
выражение F2,2) равно нулю. В этом случае следует разложить eihr в ряд
eikv ==\_^_ikr_}_. (ftrJ _|- . . .
и удержать первый неисчезающий после интегрирования член. Таким
образом, мы получим матричный элемент перехода в виде
Поглощение, определяемое формулой F2,2), называется дипольным
поглощением. Поглощение, определяемое формулой F2,3), назы-
называется мулътипольным поглощением. Если /и=1, то поглощение
называется квадрупольным.
Формулы F2,2) и F2,3) справедливы и для молекул. В следую-
следующем параграфе мы выясним, в каких случаях симметрия атома или
молекулы приводит к тому, что выражение F2,2) или выражение
вида F2,3) оказываются равными нулю.
Рассмотрим теперь так называемое комбинационное рассеяние,
т. е. процесс, заключающийся в том, что атом (молекула или кри-
кристалл), поглощая фотон энергии fiu>, переходит из состояния с энер-

« 62]
КВАНТОВОМЕХАНИЧЕСКОЕ ВВЕДЕНИЕ
249
гией Ei в состояние с энергией Ef и одновременно испускает фотон
с энергией йю. Частота со испущенного фотона связана с часто-
частотой ш0 поглощенного фотона соотношением
значением
выражающим закон сохранения энергии. Если воспользоваться обо-
Ef-Et
L—i— = v, то последнее paBeiiciBO можно переписать в виде
ш = оH
Опыт показывает, что атом, находящийся в стационарном состоя-
состоянии, не мажет, вообще говоря, перейти в результате этого процесса
в любое другое стационарное состояние. Те пары состояний, между
которыми возможен указанный переход, называются комбинирую-
комбинирующимися. Уровни энергии, соответствующие этим состояниям, также
называются комбинирующимися. Если какие-либо два уровня не ком-
комбинируются друг с другом, то это часто является следствием симмет-
симметрии атома (молекулы или кристалла). Для того чтобы иметь воз-
возможность подробно исследовать это явление, выпишем матричный
элемент И'', соответствующий переходу из состояния фг в состоя-
состояние ({у при комбинационном рассеянии:
НА1И1Е
?n — Б,- — hta
н =
F2,4)
где [а—масса покоя электрона, k0 и k — волновые векторы погло-
поглощенного и испущенного фотонов, п0 и п — единичные векторы,
направленные параллельно электрическому полю поглощенного и
испущенного фотонов, ^„— волновая функция конечного состояния
вещества (атома, молекулы или кристалла), ^ — волновая функция
начального состояния, ЕЩ = ЕО — ck0 — Ег, Еп= Ео — Et — ck, ЕП:,
Е^ и Еп—энергия вещества в начальном, промежуточном и конеч-
конечном состояниях. Матричные элементы Hai, Hah, Hif>
деляются формулами
опре-
опре/2
Hjjp =
F2,5)
У

250	ПОГЛОЩЕНИЕ И КОМБИНАЦИОННОЕ РАССЕЯНИЕ СВЕТА [ГЛ. XIV
Суммирование в F2,5) производится по всем заряженным частицам,
составляющим атом, молекулу или кристалл.
Если комбинационное рассеяние происходит на атомах или моле-
молекулах, то множители eikr и e~ikr несущественно отличаются от еди-
единицы и формулы F2,4), F2,5) можно переписать в более простом
виде:
ч B
и т-д-
F2,6)
Заметим, что если в результате комбинационного рассеяния энер-
энергия атома или молекулы изменяется, то матричный элемент Hi, равен
нулю. В дальнейшем мы всегда будем предполагать, что имеем дело
именно с таким случаем.
§ 63. Правила отбора для поглощения света атомами
и молекулами
Найдем условия, достаточные для того, чтобы матричный элемент
з
характеризующий интенсивность дипольного излучения (и поглоще-
поглощения), обратился в нуль. Иными словами, выясним, как находить неком-
бинирующиеся между собой относительно поглощения уровни энергии.
Обозначим через g какое-либо преобразование координат,
оставляющее инвариантным гамильтониан поглощающей системы.
Совокупность всех таких преобразований образует группу. Обозна-
Обозначим через О какую-либо подгруппу этой группы.
Зафиксируем проекции пх, пу и пг вектора п и произведем
в интеграле F3,1) замену переменных, соответствующую какому-либо
преобразованию координат g из группы О. Величина интеграла F3,1)
при такой замене, разумеется, не изменится. Это означает, что
интеграл F3,1) либо преобразуется по единичному представлению
группы О, либо равен нулю.
С другой стороны, мы знаем, что функции ^ и fy. можно рас-
рассматривать как элементы некоторых линейных пространств L^ и Lp
которые преобразуются по представлениям Г4 и 7^ группы G. Сумма
2ejVj преобразуется по векторному представлению V группы О.
Вследствие этого интеграл F3,1) преобразуется под действием
элементов G по представлению 1г X V X Т^. Поэтому, если пред-
представление f j X V X Tf не содержит единичного представления, то ин-

§ 63]	ПРАВИЛА ОТБОРА ДЛЯ ПОГЛОЩЕНИЯ СВЕТА	251
теграл F3,1) равен нулю и переход <Jij-»-<Jy в рассматриваемом при-
приближении запрещен.
Согласно § 21 для того, чтобы представление Т» X V ХТ7 со-
содержало единичное представление, необходимо и достаточно, чтобы
произведение V X Т^ содержало хотя бы одно представление, вхо-
входящее в Tj, т. е. чтобы
VXTfnT,?=0.
Этому критерию удобно придать несколько иную форму:
TiXVflT^O	F3,2)
(см. задачу III § 21).
Если условие F3,2) не выполняется, то переход ф4—>-(|у запрещен.
Рассмотрим некоторые следствия из правила F3,2).
1. В качестве группы G можно взять группу R всех вращений
атома или молекулы как целого. Если начальное состояние имело
полный момент /, то на языке теории групп это означает, что функ-
функция ф{ преобразуется по представлению D^ группы вращений. Век-
Векторное представление V, по которому преобразуется сумма 2 еЛ.
есть представление Dv Согласно D9,3) имеем:
если / ^- 1.
Поэтому конечное состояние ф1 должно отвечать моменту /, /it 1
или быть суперпозицией состояний, из которых по крайней мере одно
отвечает моменту /, /zt 1. Таким образом, при поглощении одного
фотона полный момент атома или молекулы (в единицах й) должен
измениться на единицу или остаться неизменным.
2. Сузим группу G до группы поворотов вокруг некоторой
оси OZ. Пусть в начальном состоянии проекция полного момента
на ось OZ равна М. Это означает, что функция i/i преобразуется
по представлению т-? группы поворотов Z с индексом М. Векторное
представление V распадается на три представления группы Z:
Поэтому согласно § 45 получаем:
т» X V = Iм-1 +тя + хм+1 ¦
Это означает, что при поглощении фотона проекция полного момента
на ось OZ может либо не измениться, либо измениться на -+- 1.
3. Расширим группу О до полной ортогональной группы. Если
волновая функция <|>{ при инверсии умножается на itl> то это озна-
означает, что она преобразуется по представлению DT. Векторное пред-
представление полной ортогональной группы есть Df. Согласно E2,4)
имеем:
D; X ОГ - D7-, + DJ + DJ+1; DJ X Df = D/

252	ПОГЛОЩЕНИЕ И КОМБИНАЦИОННОЕ РАССЕЯНИЕ СВЕТА [ГЛ. XIV
Отсюда следует, что характер инверсии в результате поглощения
фотона изменяется на противоположный.
4. Рассмотрим малые колебания атомов (или ионов) в молекуле.
Благодаря тому, что эти колебания мало отражаются на состоянии
электронов молекулы, можно считать, что атомы (ионы) молекулы
колеблются в заданном внешнем поле электронов. Возьмем группу
симметрии этого поля в качестве группы О.
Найдем полную систему стационарных состояний колеблющейся
молекулы, определим, какие представления группы G связаны с ее
уровнями энергии, и укажем затем способ отыскания запрещенных
переходов.
Воспользуемся главными координатами Q", Q"	Q"a. Qi> Q2, • •
.... Qg , ... Координаты, имеющие одинаковый верхний индекс, под
действием элементов группы О преобразуются друг через друга по
некоторому неприводимому представлению t этой группы. Среди
представлений та, тр, ... могут быть и эквивалентные. В главе VI
был указан способ, позволяющий найти представления "са, tg, ...
В приближении малых колебаний уравнение Шредингера распа-
распадается на 5а -)- s$ -\- ... обыкновенных дифференциальных уравнений *)
*AQf
где [j.a и ша — приведенная масса и собственная частота, соответ-
соответствующие при классическом рассмотрении главной координате Qy.
Эти уравнения имеют не возрастающие на бесконечности решения
только для следующих значений Еа:
(« = 0. 1,2. ...)•	F3,3)
Нормированные функции, соответствующие этим значениям энергии,
равны
где Нт(х)(т = 0, 1, ...) — полиномы Эрмита.
Волновая функция молекулы равна произведению всех найденных
функций:
здесь Q обозначает совокупность всех координат Q"., QL . .., a v —
совокупность всех индексов m.j, tij, ...
*) По поводу этого уравнения, а также формул F3,3) и F3,4) см. [3],

§ 63]	ПРАВИЛА ОТБОРА ДЛЯ ПОГЛОЩЕНИЯ СВЕТА	253
Энергия колебательного движения, соответствующая этой волно-
волновой функции, равна
+ 
от = 2 m^, ft = 2 «/• • •
Отсюда следует, что кратность вырождения уровня Ет,п>_,, равна
числу способов, которыми можно удовлетворить равенствам
• т = 2 ttij, n — 2 %¦ • • •
при фиксированных значениях от, и, ... с помощью произвольных
целых чисел /я^, «,-, . . .
Выясним, по какому представлению группы О преобразуется
произведение ТТ<!^ .(Q")- Согласно соотношению F3,4) оно преоб-
преобразуется так же, как и функция
(индекс а при координате Qj здесь опущен). Каждое такое произ-
произведение является полиномом степени т относительно переменных Qj.
Эти полиномы вполне определяются своими старшими членами
ТГ Qp-
F3,6)
Поэтому функция F3,5) преобразуется по тому же представлению,
что и произведение F3,6). Легко видеть, однако, что это послед-
последнее преобразуется по симметризованной от-й степени представле-
представления ха, т. е. по представлению [ta\m. Поэтому представление Тмп...,
по которому преобразуются все волновые функции, отвечающие
энергии Етп.,., является произведением представлений
КГ X Ы1 X ...	F3,7)
Таким образом, если молекула в результате поглощения света
переходит из состояния с энергией Етп... в состояние с энер-
энергией Ет/„г..., то представления Т* и Tf, связанные с начальным
и Конечным состояниями, определяются по формуле

254
ПОГЛОЩЕНИЕ И КОМБИНАЦИОННОЕ РАССЕЯНИЕ -СВЕТА [ГЛ. XIV
Применяя критерий F3,2), легко определим, какие переходы запре-
запрещены в рассматриваемом приближении.
Рассмотрим в качестве примера молекулу СН3, обладающую
группой симметрии C^v Напомним, что группа C3v имеет шесть
элементов: е, С3, С2., ot, o2, о3, которые разбиваются на три класса:
{е}, |С3, С2} и {а^ а2, а3}. Характеры трех неприводимых пред-
представлений А, В и Е этой группы представлены в таблице 22.
Таблица 22
Характеры неприводимых представлений
группы С8и
А = тх
В = т2
Е =т,
1
1
2
С С2
1
1
_1
°1> 32- аЗ
1
— 1
0
1
Легко видеть, что векторное представление V состоит из двух
неприводимых представлений А и Е:
Представления А, В и Е перемножаются следующим образом:
А2 = А, АВ = В, АЕ = Е,
В2 = А, ВЕ = Е, E2
F3,8)
Из этих формул вытекает, что если представление Т$ содержит Е,
то переход ф4—>(()> разрешен. Действительно, произведение EX V =
= ЕХА + Е2=2Е-)-А + В содержит все неприводимые пред-
представления группы Czv. Поэтому всякое неприводимое представление,
содержащееся в Tf, входит также в произведение Tj X V и усло-
условие F3,2) выполняется. Таким же образом можно показать, что
переход разрешен, если представление Ту содержит Е. Если ни одно
из представлений Tj, T^ не содержит представления Е, то для возмож-
возможности перехода необходимо, чтобы Tj и Т^ оба содержали пред-
представление А или чтобы Т^ и Ту оба содержали представление В.
Таким образом, переход запрещен только в том случае, когда одно
из представлений Tj, T^ содержит только представления А, а дру-
другое— только представления В. Выясним, в каком случае представление

§ 63]	ПРАВИЛА ОТБОРА ДЛЯ ПОГЛОЩЕНИЯ СВЕТА .	255
содержит только представление А. Из формул F3,8) следует, что
для этого среди представлений
КГ. h?ln, •••
не должно быть ни одного, содержащего Е.
Поэтому ни одно из представлений tx, 1^, ... не должно со-
совпадать с Е *).
Итак, если представление Т4 не содержит Е, то оно является
одномерным представлением и совпадает с А или В. Обозначим
через щ сумму квантовых чисел, соответствующих колебаниям, анти-
антисимметричным относительно плоскостей av o2, о3 (эти колебания
преобразуются по представлению В). Ясно, что
Tj = A, если у.4 четно, и 7^ = 5, если щ нечетно.
Обозначим через х^ сумму тех же квантовых чисел в конечном
состоянии, тогда
Ту=А, если v.f четно, и Т,. = В, если %f нечетно.
Поэтому, если щ и х^ имеют различную четность, то переходы
между невырожденными уровнями запрещены. Иными словами, за-
запрещенными являются переходы между невырожденными уровнями,
волновые функции которых имеют различную симметрию относи-
относительно отражений в вертикальных плоскостях оь о2> <з3. Остальные
переходы разрешены.
Скажем несколько слов о квадрупольном поглощении. Со-
Согласно F2,3) матричный элемент, соответствующий квадруполыюму
излучению, имеет вид
*) Число k, показывающее, сколько раз представление Е содержится
в представлении [Е]га, равно согласно B0,3)
Согласно формуле B5,8) получим:
6
Так как характер любого элемента не превосходит размерности предста-
представления, то фигурные скобки, стоящие в правой части последнего равенства
неотрицательны. Скобка, соответствующая специальному распределению
числа п — п-\, имеет вид 2« — х»(С3) = 2» — (—1)»>0 и, следовательно,
положительна. Поэтому 4>0и представление [Е]" содержит Е.

256	ПОГЛОЩЕНИЕ И КОМБИНАЦИОННОЕ РАССЕЯНИЕ СВЕТА [ГЛ. XIV
Выражение 2^'^(^'"^ преобразуется по квадрату векторного пред-
представления V2. Если в качестве группы О взята группы вращений,
то
Зто означает, что при квадрупольном поглощении момент погло-
поглощающей системы либо не изменяется, либо изменяется на±1, ~+~ 2.
Если в качестве группы G взять группу поворотов, то
V2 = (х-1 -И° + -с1J = х-2 + 2ч-1 + Зх° + 2ч1 +12-
Поэтому проекция момента на ось OZ при переходе из состояния ^
в состояние i]^ изменяется на ±1, ±2 или не изменяется вовсе.
•§ 64. Комбинационное рассеяние света атомами и молекулами
Обозначим через О какую-либо группу преобразований коор-
координат, которые оставляют инвариантным гамильтониан атома или
молекулы.
Рассмотрим, как преобразуются произведения матричных эле-
элементов HjjHip и HaiiHiif под действием элементов g"?G.
Все волновые функции ф, отвечающие данному энергетическому
уровню Е, преобразуются друг через друга по некоторому предста-
представлению Т группы О. Поэтому, если в интегралах сделать замену
переменных, соответствующую преобразованию g"?G, то функ-
функция iftht перейдет в линейную комбинацию функций
Ттп (g) фтеи-
Каждая компонента вектора 2^fy преобразуется по векторному
лредставлению V. Наконец, волновые функции промежуточных со-
состояний tyn. перейдут в функции
4iW	F4,1)
Так как, однако, по всем промежуточным состояниям производится
суммирование, причем выбор этих состояний несуществен при усло-
условии, что волновые функции промежуточных состояний ортонормиро-
ваны, то преобразование F4,1) не изменяет величины суммы и его
можно игнорировать.
Отсюда следует, что сумма F2,4) преобразуется по представле-
представлению Т° X V X V X Т = Т° X V2 X Т, где Т — представление, отве-
отвечающее конечному состоянию, а V2 — тензорное представление.
Рассмотрим некоторые частные случаи.
1. Возьмем в качестве О группу всех вращений атома или моле-
молекулы как целого. Если начальное состояние имело момент j, то пред-
представление T°—Dj. Тензорное представление группы вращений есть

§ 64] КОМБИНАЦИОННОЕ РАССЕЯНИЕ СВЕТА АТОМАМИ И МОЛЕКУЛАМИ 257
ПоэтомуТ° X V*=Dy.X (Do-f-D^+D,,) =
jjj D^ + D^+2. Отсюда следует, что полный
момент атома или молекулы после комбинационного рассеяния может
принимать значения j, /it I, j-+-2.
2.	Сузим группу вращений до группы поворотов вокруг неко-
некоторой оси OZ. Пусть в начальном состоянии проекция полного
момента на ось OZ равна М. Это означает, что функция <]^ преоб-
преобразуется по представлению tw группы поворотов Z. Тензорное пред-
представление группы поворотов равно
V2 = (-c-1 + 'c0 + 'e1)X ('с-1Ч--с0-|-т:1)=-с-2-|-2х-1-|-Зт:0-1-2-с1-|-'с2.
Поэтому проекция полного момента на ось 07. может иметь после
комбинационного рассеяния только значения М, М±1, М±2.
3.	Если расширить группу О до полной ортогональной группы,
то легко убедиться в том, что четность волновой функции относи-
относительно инверсии не изменяется в результате комбинационного рас-
рассеяния.
4.	Рассмотрим малые колебания атомов (или ионов) в молекуле.
Возьмем в качестве G группу симметрии эффективного поля, созда-
создаваемого электронами молекулы (см. пример 4 § 63). Мы видели,
что колебательные энергетические уровни молекулы определяются
соотношением
Етп> Л — mhi»1-{- nhio2-\-
а соответствующие этим уровням представления группы G равны
«•Поэтому для того, чтобы обнаружить запрещенные при комби-
комбинационном рассеянии переходы, нужно разложить тензорное пред-
представление группы О на неприводимые представления и умножить
его на представление 1°. Если произведение Т° X V2 не будет иметь
ни одного общего неприводимого представления с представлением Ту,
то соответствующий переход запрещен.
Особенно просто выглядит это правило, если одно из состояний,
например начальное, соответствует основному (невозбужденному)
состоянию молекулы, а другое — состоянию с т=1 и п = 0, ...
Переход
Фоо... ->tio...
будет запрещен, если представление tj не содержится в тензорном
представлении. В этом случае говорят, что уровень Е10_,, не является
активным относительно комбинационного рассеяния. Заметим, что
уровень Е2о- ¦ ¦ и более высокие уровни ?„,<)... могут быть при
этом активными.
17 Зак. 3512. Г. Я. Любарский

258
ПОГЛОЩЕНИЕ И КОМБИНАЦИОННОЕ РАССЕЯНИЕ СВЕТА
'ГЛ. XIV
Рассмотрим в качестве примера молекулу СНС18. Группа симметрии этой
молекулы есть C%v. Она имеет три неприводимых представления (см. § 63,
табл. 22). Характер тензорного представления равен квадрату векторного
представления и определяется таблицей 23.
Таблица 23
Характер тензорного представления
группы CSv
С
Разлагая тензорное представление V2 на неприводимые представления,
получим:
V* = 2А + В + ЗЕ.
Мы видим, что тензорное представление в рассматриваемом случае
содержит все неприводимые представления. Поэтому все уровни энергии
молекулы СНС13 являются активными относительно комбинационного рас-
рассеяния.

ГЛАВА XV
ПРЕДСТАВЛЕНИЯ ГРУППЫ ЛОРЕНЦА
§ 65. Группа Лоренца
По терминологии, принятой в теории относительности, совокуп-
совокупность трех прямоугольных координат х, у, z и времени" t назы-
называется событием, «происшедшим» в точке х, у, z в момент времени t.
Числа х, у, z и t называются четырехмерными координатами
события.
Согласно специальной теории относительности координаты одного
и того же события в различных инерциальных системах координат
выражаются друг через друга линейным образом, и притом так, что
интервал
Sab = Vc2 (tA — tB) — (xA — xBf — (yA —yBf — (zA — zB)*
между любыми двумя событиями А(хА, уА, zA, tA)nB(xB,yB,zB, tB)
Одинаков во всех этих системах.
Для того чтобы прийти к понятию группы Лоренца, следует
выделить из всех инерциальных систем совокупность тех систем,
начала которых в некоторый момент времени совпадали, и принять
Этот момент за начало отсчета времени во всех этих инерциальных
системах. В дальнейшем, говоря об инерциальных системах, мы
будем подразумевать именно такие системы.
Ясно, что событие с координатами @, 0, 0, 0) в одной из инерци-
инерциальных систем имеет те же координаты в любой другой инер-
циальной системе. Поэтому зависимость между координатами неко-
некоторого события в различных инерциальных системах является
не только линейной, но и однородной. Обозначим матрицу, осу-
осуществляющую переход от координат в системе К к координатам
в системе К' через ац(К'К), так что
х^а^(К'К)х, (/,/*= 0, 1, 2, 3; )
17*

260	ПРЕДСТАВЛЕНИЯ ГРУППЫ ЛОРЕНЦА	[ГЛ. XV
Если в системе К" координаты того же события обозначить
через л^'(/ —0, 1, 2, 3), то можно написать:
х'1 = ау {КГК) xj и х'{ = «„ {К"К') х\.
Из этих равенств и из F5,1) следует, что
ау {К"К) = а„ {К"К') ац (К'К).	F5,2)
Мы видим, что матрицы а образуют группу относительно обыч-
обычного матричного умножения. При этом
а(К'К).	F5,3)
Эта группа называется полной группой Лоренца. Мы будем обо-
обозначать ее буквой j^.
Полная группа Лоренца имеет в качестве подгруппы так назы-
называемую собственную группу Лоренца. Она получается если из всех
инерциальных систем выделить только левые (или только правые)
системы координат. Операторы, соответствующие переходам из одной
левой системы в другую левую систему, образуют, очевидно, группу.
Эта группа и называется собственной группой Лоренца (или просто
группой Лоренца) и обозначается через _2Y
В полной группе Лоренца содержится оператор инверсии I,
определяемый равенствами
\х — — х, \у = — у, Vz = — z, lt = t.	F5,4)
Этот оператор осуществляет переход из произвольной системы К
в неподвижно с ней связанную систему К', оси которой направлены
в стороны, прямо противоположные осям системы К. Ясно, что
квадрат оператора инверсии равен единичному оператору. Оператор I
изображается матрицей
F5,5)
Приведем в явном виде матрицу ai!c для одного важного част-
частного случая. Пусть система К' имеет оси, параллельные осям си-
системы К, и движется относительно последней со скоростью V,
направленной параллельно оси ОХ. Как известно, формулы пере-
перехода в этом случае имеют следующий вид:
1
0
0
0
0
— 1
0
0
0
0
	1
0
0
0
0
— 1
¦ = y, z' = z, ?= -_JL^ F5,6)

1961
ИНФИНИТЕЗИМАЛЬНЫЕ ОПЕРАТОРЫ ГРУППЫ ЛОРЕНЦА
261
У i-
р
Vi-
0
0
rf-
У 1—^2
1
Y\-P
0
0
- 0
1
0
0
0
1
и называются преобразованиями Лоренца. Согласно .F5,6) матрица а.1к
в этом случае равна
1	В
F5,7)
Группа Лоренца jg^1 является группой Ли. В качестве параме-
параметров этой группы можно выбрать три проекции скорости системы К'
относительно системы К и какие-либо три параметра, характе-
характеризующие поворот, который надо произвести над осями системы К,
чтобы они стали параллельны одноименным осям системы К'¦ Та-
Таким образом, общее число параметров в группе Лоренца ^'1 равно
шести.
§ 66. Инфинитезимальные операторы группы Лоренца
Имея в виду использовать инфинитезимальный метод Ли для
разыскания всех неприводимых конечномерных представлений группы
J2?lt найдем перестановочные соотношения для инфинитезимальных
операторов этой группы.
Условимся о выборе параметров. Оператор а.(К'К) зависит
исключительно от относительного движения систем отсчета К и К'.
Это движение можно полностью задать, указав три проекции ах,
ау, аг «вектора» поворота системы К' относительно системы К и
три проекции vx, vy, vz скорости v начала системы К' в си-
системе К-
Инфинитезимальные операторы, соответствующие шести пара-
параметрам аж, а,у, <xz, (Зд, = —, $y=JLt рз = ii > мы обозначим через
¦1> '2> '3> "М> •'2' ^З'
Так как элементы группы Лоренца являются операторами
в четырехмерном векторном пространстве, то они сами по себе
образуют представление группы Лоренца. Это представление назы-
называется векторным.
Легко вычислить оператор Ju в векторном представлении. Для
этого продифференцируем выражение F5,7) по ^ и положим 3 = 0.
Мы получим:
0—100
-1	0 0 0
0 0 0 0
0 0 0 0
F6,1)

262
ПРЕДСТАВЛЕНИЯ ГРУППЫ ЛОРЕНЦА
[ГЛ. XV
где sift(/, k = 0, 1, 2, 3) — матрица, у которой элемент, стоящий
на пересечении j-й строки и &-го столбца, равен единице, а все
остальные элементы равны нулю.
Производя в F6,1) круговую перестановку индексов 1, 2, 3,
получим:
"<2 ==	?02	S20> J3 === S03 S30-	(DO,2)
Для вычисления Ij будем исходить из соотношений
х' ~ х, У = ycos я, —|— г sin а, г' = — ^s'na~r~zcosa> ? =t F6,3)
между координатами события в системе К и системе К', поверну-
повернутой относительно К на угол а вокруг оси Ох. Из F6,3) следует,
что матрица л^, соответствующая такому повороту, равна
1
0
0
0
0
1
0
0
0
0
cos a
— sin а
0
0
sin а
cos а
Дифференцируя это равенство по а и полагая затем а = 0, получим,
что It = е23— е32. Выражения для 12 и 13 можно теперь получить
с помощью круговой перестановки. Таким образом, мы находим:
h = е2з — аз2> 'г —S3i — si3> 1з = а12— e2i- F6,4)
С помощью выражений F6,1), F6,2) и F6,4) легко находим все
перестановочные соотношения:
= Ji, [I3J1]= >>2>
11,12] = —Ij, [I2I,] = —I,, HaliJ = — I2,
[J,J2] = I,, [J2J3] == It. [J3JJ = I2.
Наряду с операторами 1к, }к (А=1, 2, 3), удобно пользоваться
операторами
* = —уA* —«*) (ft =1,2,3).
F6,6)
Перестановочные соотношения для этих операторов имеют особенно
. простой вид:
[А,А*] = е,мА„ [B,Bft] = eiMB,, [AiBft] = 0	F6,7)
(У, ft, Z=l, 2, 3);
они вытекают из перестановочных соотношений F6,5).

§ 67] КЛАССИФИКАЦИЯ НЕПРИВОДИМЫХ ПРЕДСТАВЛЕНИЙ ГРУППЫ ЛОРЕНЦА 263
Подчеркнем, что перестановочные соотношения, которым под-
подчиняются операторы \k(k= 1, 2, 3), такие же, как и у инфинитези-
мальных операторов группы вращений. То же относится и к опе-
операторам Bft.
§ 67. Классификация неприводимых представлений
группы Лоренца
Для отыскания всевозможных неприводимых представлений
группы jg?x достаточно найти все реализации операторов \к, ih
(& — I, 2, 3), удовлетворяющие перестановочным соотношениям F6,5).
Эта задача равносильна построению операторов кк,Ък (k—\, 2, 3),
удовлетворяющих значительно более простым перестановочным
соотношениям F6,7). Для построения этих'операторов целесообразно
использовать теорему § 46.
Пусть L — линейное пространство, преобразующееся по некото-
некоторому неприводимому представлению t группы Лоренца. Введем
обозначения
А+ = *А! — А2, А_ = /А1-г-А2, А0 = А3, |
В+ = гВ1—В2, В_ =/B1-j-B2, B0 = B3. J
Согласно теореме в L есть вектор е такой, что
Boe = Qe, iB+e = 0,	F7,2)
где Q—некоторое целое или полуцелое число. Обозначим через Lq
подпространство всех тех векторов из L, которые удовлетворяют
условию F7,2). Это подпространство инвариантно относительно
операторов А+, А_, Ао, так как они коммутируют с операторами
В + , В_, Во. Поэтому в подпространстве Lq существуют векторы
{	1.
которые под действием операторов А+, А_, Ао преобразуются
по формулам
ту	Р
ae	ke = zxcij)+XQ I	•
{pi,о)
Построим теперь векторы
iK(p = — P....;P;q = — Q	Q)	F7,4)
с помощью рекуррентных соотношений
В_в„ = а^вя_1.	F7,5)
Согласно терреме имеем:
Z^ , Воет = — lqeM.	F7,6)

264	ПРЕДСТАВЛЕНИЯ ГРУППЫ ЛОРЕНЦА	[ГЛ. XV
Если к равенствам F7,3) применить оператор (В)^~3> то мы получим:
*' J	F7,7)
Формулы F7,5), F7,6) и F7,7) показывают, что линейная оболочка
векторов F7,4) инвариантна относительно операторов А^, В&.
Поэтому она совпадает с пространством L. Векторы F7,4) образуют
в L базис, а соотношения F7,5), F7,6), F7,7) полностью опреде-
определяют операторы А±, Ао, В + , Во в пространстве L.
Мы видим, что инфинитезимальные операторы вполне определены,
если заданы числа Р, Q. Следовательно, каждой паре чисел
, QyP, Q = 0, -^ , 1, ... J
отвечает неприводимое представление
группы Лоренца, и притом только одно. Мы будем обозначать это
представление через Xpq. Размерность представления tpQ равна
B/*—(— 1)BQ-|- 1). Единственным одномерным представлением группы
Лоренца является Tqq. Пару чисел Р, Q мы будем называть весом
представления -zpq. Базис F7,4) называется каноническим.
Можно показать, что представление "Zpq является однозначным,
если P-\-Q есть целое число. Если же P-j-Q — полуцелое число,
то представление tPQ двузначно.
В заключение скажем несколько слов о бесконечномерных не-
неприводимых представлениях группы Лоренца, найденных И. М. Гель-
фандом и М. А. Наймарком.
Каждое неприводимое бесконечномерное представление i^k^
группы Лоренца ^х определяется двумя индексами k0 и kv Индекс'&а
может принимать все целые или полуцелые значения
«о== "i —"» — ¦ • • • >
индекс kt может принимать все значеЕЖЯ, в том числе и комплексные.
Однако, если разность kt—kQ является целым числом, то описы-
описываемое представление вырождается в конечномерное. Мы будем
считать в дальнейшем, что разность kt—k0 не равна целому числу.
В пространстве L, в котором действуют операторы представле-
представления x(kQ, kx), выберем базис
fp(p=k, k—\, ..., — k; k=\ko\, I&ol-M. •••)
и определим с помощью этого базиса инфинитезимальные операторы
группы Лоренца. Нам будет удобнее вместо инфинитезимальных
операторов 1г, ^(/=1,2,3) задать следующие шесть операторов:
=— Jlt F+ = — J3 — U2, F' = —

§ 68] ПРОИЗВЕДЕНИЕ НЕПРИВОДИМЫХ ПРЕДСТАВЛЕНИЙ ГРУППЫ ЛОРЕНЦА 265
Неприводимое представление х (k0, kx) определяется формулами
2F°S* = -
где
f
Пары чисел Ao, &t и —й0, —ftt определяют эквивалентные пред-
представления. Во всех остальных случаях мы получаем неэквивалентные
представления.
Представление х (k0, fej) унитарно, если kt чисто мнимо или
если &0=0 и kl вещественно. Нетрудно убедиться, что в этих
случаях операторы \к, ik антиэрмитовы, что свидетельствует об уни-
унитарности представления (см. задачу IV § 43).
§ 68. Произведение неприводимых представлений
группы Лоренца
Рассмотрим произведение двух неприводимых представлений хр „
и Хр„ группы Лоренца и разложим его на неприводимые пред-
представления.
Обозначим через ир&' и vF&' канонические базисы в простран-
пространствах Lx и L2, преобразующихся по представлениям хр„ и -срп.
¦Произведения up^vPi(^ образуют базис в произведении этих про-
пространств.
Рассмотрим сначала случай Q1 = P2 —0. Напомним, что
где С—любой инфинитезимальный оператор или линейная комбина-
комбинация таких операторов. С помощью этой формулы легко убедиться
в том, что матрицы операторов Ао, А±, Во, В+ совершенно одинаковы
в базисе еВщ и в базисе и™ • v$q. Это означает, что произведение

266
представлений х^ X
однотипен базису ер
ПРЕДСТАВЛЕНИЯ ГРУППЫ ЛОРЕНЦА
эквивалентно представлению
[ГЛ. XV
. Базис
Этот результат сводит задачу разложения произведений общего
типа к задаче разложения произведений fpoX'Epo и ^оо X tQn • ^ти
разложения производятся буквально так же, как и разложения
представлений Dp, X Ора группы вращений. Поэтому можно сразу
написать:
Связь между базисными векторами выражается с помощью коэф-
коэффициентов Клебша — Гордана:
**>= 2 (
Теперь легко перемножить представления -Ср„ и TpQ . Имеем:
X "«oft —
X
2j
2j
т. е.
2
Из этой формулы следует, что произведение хр„ Х^рп coдepжиf
единичное представление в том и только том случае, когда Pt = Р2
и QX=:Q2' T- е- когда перемножаемые представления эквивалентны.
Векторы е%? канонического базиса в подпространстве LPq, пре-
преобразующемся по представлению -с™, выражаются через u?&vp*Q>
следующим образом:
=	2
+
4'^m:- F8-4)
Это следует из соотношений F8,1) и F8,2). В силу унитарности
коэффициентов Клебша — Гордана равенство F8,4) можно пере-
переписать в виде
«ай1 «wh = ^2
(
РР) (ЯгЯгйгЯг I Qq) «м	F8,5)
Формулы F8,3) и F8,4) полностью решают задачу разложения
произведения представлений.

§ 69]	КОМПЛЕКСНО-СОПРЯЖЕННЫЕ ПРЕДСТАВЛЕНИЯ	267
Рассмотрим некоторые следствия из полученных соотношений.
5 ^	^
р	р	у
Пусть 5 и^1 и 71йд3г'«а^2 —два произвольных вектора из про-
проL В	?
странств L, и L,. Вектор ? ri ир&щр&* можно представить в виде
p. e
Отсюда следует, что выражения
ъ F8>6)
являются координатами некоторого вектора из пространства, пре-
преобразующегося по представлению тр„.
Приведем важный частный случай формулы F8,4), который
получается, если положить Р1 = Р2, Q1 = Q2, P = Q = 0;
еы=	2	(РхРхPiРг I 00) (Q&qfa \ 00)u™v™.
Вспоминая выражение E4,22) для (PiPiPiP21 00), получим:
2 (- 1)р+в-«-«в^г^_д = inv.	F8,7)
Р'Ч
Аналогично из соотношения F8,6) следует:
2(-l)p+«-*-Vi_p_e = inv.	F8,8)
В заключение выясним связь между представлениями группы
Лоренца и группы вращений.
Группа вращений является подгруппой группы Лоренца. Поэтому
каждое представление группы Лоренца является в то же время
представлением группы вращений. Рассмотрим с этой точки зрения
представление %FQ. У этого представления операторы Blt B2 и В3
равны нулю и, следовательно, А^ — — 1^ (k=l, 2, 3; см. F6,6)).
Собственные числа оператора 13 принимают значения —Р	Р.
Это означает, что представление тро, рассматриваемое как предста-
представление группы вращений, эквивалентно представлению Dp. Таким же
образом убеждаемся в том, что представление iqq эквивалентно Dq.
Поэтому представление хр„=хро X tOg эквивалентно представлению
DPXDQ=	S	D,-
\P-Q\<j<P+Q
группы вращений.
§ 69. Комплексно-сопряженные представления
Рассмотрим представление, комплексно-сопряженное представле-
представлению Трд. Обозначим его через тр^. В комплексно-сопряженном
базисе матрицы инфинитезимальных операторов комплексно сопря-
сопряжены матрицам соответствующих инфинитезимальных операторов

268	ПРЕДСТАВЛЕНИЯ ГРУППЫ ЛОРЕНЦА	[ГЛ. XV
исходного представления
Юм = hi' A*)т = Jki-
Опуская индексы матриц, получаем отсюда:
1	i	= - у (I* — ih) = Bft,
Далее,
2 v« г ™ы — — 2
Подобным, же образом можно вычислить операторы А+, В_, В + .
В результате получим следующие соотношения:
Bo = Ao b~=-a в =-a ¦	F-9Л)
Обозначим через epq канонический базис в пространстве Lv
преобразующемся по представлению хрд. Комплексно-сопряженные
векторы epq образуют базис в пространстве L, преобразующемся
по представлению ъР„. С помощью равенств F7,5), F7,6) и F7,7)
легко выяснить, как действуют операторы F9,1) на векторы epq.
После простых вычислений получаем:
Q —	* —	Q —
ХрИ!от *+!.м~ «ввя-ь F92)
Первый столбец показывает, что векторы ev являются собственными
* „*	ч
векторами операторов Ао и Во- Поэтому они с точностью до мно-
множителя совпадают с векторами канонического базиса u_q_p
Мы видим, что первый индекс пробегает BQ-|-1) значение,
а второй — BР-|-1) значение. Поэтому представление *р(, эквива-
эквивалентно представлению "¦*¦"'
Определим коэффициенты Xpq с помощью второй пары равенств F9,2).
Имеем:
™--еР1 == kpqA-U-1 -2>— '~pqZ-qu-q-l, -p =
Q —	Q
ie1o

§ 70]
СПИНОРНАЯ АЛГЕБРА
269
q =
Отсюда следует, что
р	*
a
Итак, окончательно,
,= (-!)¦
O+P-g-я
Вспоминая соотношения F8,7) и F8,8), получаем отсюда:
и
¦¦= inv.
p,q
F9,3)
F9,4)
F9,5)
§ 70. Спинориая алгебра
Собственная группа Лоренца в отличие от группы вращений
имеет два двумерных представления tj и х i . Двумерные век-
2°	°У
торы, преобразующиеся по этим представлениям, называются спино-
спинорами первого /4i \ и второго /х Л рода. Векторы канонического
базиса в пространстве спиноров принято сокращенно обозначать сле-
следующим образом:
G0,1)
Выпишем для справок формулы, определяющие действие операто-
операторов Aot. Bo+ на эти векторы:
1 .	.	1 .
= Ao±ei = Bo±e-i = Bo±ei = °.
j —А_е_х=В^е{ =^B_e_-j =0,
'-Г
G0,2)

270	ПРЕДСТАВЛЕНИЯ ГРУППЫ ЛОРЕНЦА	[ГЛ. XV
Компоненты спиноров обозначают соответственно через %_lt $t
В теории спиноров существенную роль играют соотношения
G0,3)
е1и_1 — e_1M1 = inv, е\и_\—е-\и\ = inv>
j- y] 	 с Т\ ' 1TIV	С * Т\ * 	t * *f) * ¦- ~~- lllV
которые являются частными случаями равенств F8,7) и F8,8). Если
ввести в рассмотрение матрицу
)(	\	G0 4)
то соотношения G0,3) можно переписать в виде
Skiekui = inv- ёыей и I = inv- )	7Q
Всякий элемент пространства, преобразующегося по представле-
представлению /4i V /х Л', называется спинором ранга ml-\~nt2. Так,
например, элемент, преобразующийся как произведение
р0)/г)Лз) Мр(ь)
е\ ei e-\eie\ •
является спинором ранга 3 + 2. Его принято обозначать следующим
образом: еи_1^.
При буквенных обозначениях индексов спинора ранга тх-\-тг
точек над буквами не ставят; вместо этого первые тх индексов
обозначают буквами аи а2, а3, ..., anh, a остальные т2 индексов —
буквами pif p2	Э»»ч:
е«л ¦¦¦ «».,. РА •¦• 3,„2-
Произведение двух спиноров рангов тх-\-тг и пх-\-пг является
спинором ранга (тх-\-п1)-\-(тг-\~пг). Поэтому, если
являются коэффициентами двух спиноров, то их произведения
С	. с'< --'-' =
= с"
V2-Vi-V?2'-W2
являются коэффициентами спинора ранга (/га -(- от') + («-)-л').

§ 71)	ТЕНЗОРНАЯ АЛГЕБРА	271
Помимо умножения спиноров, существует операция упрощения
спиноров. Рассмотрим ее. Пусть Сл ... «ТОЗА •.¦ 3„— какой-либо
спинор (т-\-п)-го ранга. Он преобразуется так же, как произ-
произведение двух спиноров первого ранга и спинора {(т — 2)-|-ге}-го
ранга
&«1'»taC«!1...oW за... з„-
Поэтому выражение
ё*лС*л--- *т> Э.Эа ¦ •• 3„
преобразуется так же, как и выражение
g^faC'* •¦¦*„.?! ¦¦¦?„ = inv • С«з • • • «m. 3i • • • Р„>
т. е. как спинор ранга {(т — 2)-\-п). Переход от спинора
С.,... ат, р,... р„ к спинору С,... аю, з,... рп называется упрощением
спинора по индексам ах, а2. Упрощение можно производить также
по любой другой паре индексов а или любой паре индексов р.
В результате упрощения ранг спинора уменьшается на две единицы.
Матрицу gkl называют метрическим тензором. Между спино-
спинорами Св1...« ,р, ...з и векторами, преобразующимися по предста-
представлению "сши, имеется простая связь, устанавливаемая следующей тео-
теоремой.
Теорема. Подпространство спиноров Caj...o , p,...p. сим-
симметричных относительно всех перестановок индексов ах	о.т
и относительно всех перестановок индексов р1; . . ., |3П, преобра-
преобразуется по представлению smn.
Доказательство проводится так же, как и в § 50.
§ 71. Тензорная алгебра
Подобно тому как спиноры (т-\-п)-го ранга строятся на базе
представлений 11 и т i, тензоры л-го ранга строятся с помощью
"г"	° г"
четырехмерного векторного представления. Рассмотрим это пред-
представление более подробно. Легко видеть, что как представление
группы вращений оно распадается на D, и Do в соответствии
с разделением координат четырехмерного вектора на три простран-
пространственные и одну временную. Так как ни одно из этих подпространств
(х, у, z, 0) и @, 0, 0, t) не инвариантно относительно группы
Лоренца, то векторное представление неприводимо и, следовательно,
совпадает с представлением xi i *).
	2" ~2
*) Два других неприводимых четырехмерных представления 13 и х 3
7° ° Т
не могут совпадать с векторным представлением хотя бы потому, что они
являются неприводимыми представлениями группы вращений.

272	ПРЕДСТАВЛЕНИЯ ГРУППЫ ЛОРЕНЦА	[ГЛ. XV
Установим связь между каноническим базисом е \ \ предста-
представления tj 1 и «естественным» базисом
? ~2
ео = {\ 0 0 0), е1 = @ 1 0 0), ег = @ 0 1 0), е3=@ 0 0 1).
G1,1)
С этой целью найдем в естественном базисе какой-нибудь общий
собственный вектор операторов 13 и J3.
С помощью формул F6,2) и F6,4) запишем:
О, J3^3 = —ео-
Отсюда следует, что
13 (ег — iet) — i (ег — iej, J3 (e2 — lej = О
Сравнивая эти соотношения с формулами F7,6), F7,7), мы видим,
что вектор е2 — ie1 параллелен вектору е\ \. Поэтому положим
ТТ
Применяя к этому равенству операторы А_ и В_, легко выразим
остальные векторы канонического базиса через векторы естествен-
естественного базиса. В результате мы получим:
-т-т V5"
2 2
G1,2)
Запишем также выражение для векторов естественного базиса через
векторы канонического базиса:
¦¦zn^(e\ 1 —в 1 А.
У 2 \ it "Т~2/
2 2
= — ^= f«_ii — eL Л.
У 2\ 2 2	22/
G1,3)
Таким образом, переход от естественного базиса к канониче-
каноническому осуществляется по формуле
е% = Pi, Ыек1'

ТЕНЗОРНАЯ .АЛГЕБРА
273
где
=-0	12 3
0 i	7 О) к = \-,
i- 0	0 — I
-i 0	0 —I
О —/ 1 0
ft = -o.
/ = ¦
/ 	 	 J^
к — 2 '	2
G1.4)
д —. 2 *	2 *
Дадим теперь определение тензора п-то ранга.
Тензором п-го ранга называется каждый элемент пространства Ln,
преобразующегося по представлению 1\ j группы Лоренца. Базис
пространства Ln, однотипный базису
*М	41 ' (А = 0. 1. 2. 3; Z = 1, 2	я).
будем называть естественным базисом и обозначать через
еР,Р>--.рп-	G1-5)
Каждый тензор e = CPlPi...p вр^...])	вполне определяется сово-
совокупно стыо своих координат
Сйй...ря.	G1.6)
которую также называют тензором и-го ранга. Обозначим через
aik(g) (gtiJZ'v i' k = 0, 1, 2, 3) матрицу оператора tj_ j_ (g-)
2 2
в естественном базисе. Ясно, что под действием оператора "с™ i (g)
~ Т
векторы естественного базиса пространства Ln преобразуются по
формуле
2 2
¦¦¦ V
V.
в соответствии с этим, координаты тензора Z i i(g)e
ii ?
через координаты тензора е по формуле
С ,=я, (?¦)... a, (g)CPllk...p.
Pf- I'n	plpl	Pnpn
выражаются
G1,8)
Наоборот, всякая совокупность 4П чисел, преобразующаяся при пере-
переходе к новой системе координат по формуле G1,8), представляет
собой тензор и-го ранга. Поэтому произведение двух тензоров
рангов т и п является тензором ранга т-\-п.
18 Зак. 3512. Г. Я. Любарский

274	ПРЕДСТАВЛЕНИЯ ГРУППЫ ЛОРЕНЦА	[ГЛ. XV
Введем теперь операцию упрощения тензоров, аналогичную упро-
упрощению спиноров. Будем исходить из инвариантности выражения
i_±_±1 _±_± _1А± — inv-
~2 ~ 2 ~ 2 2	2  2~ ~Y	~ 2 "~2 2 2
С помощью векторов, составляющих естественный базис, это соот-
соотношение можно переписать в виде
где
A 0	0	Оч
0—1	0	0\
о о	-1	о • <71'9>
0 0	0	—1/
Отсюда следует, что
Переходя в этом тождестве к обратным матрицам, получим:
Ъ'*. = Т«««'ОТ) ***.&)•	G1.11)
Равенство G1,10) иногда бывает полезно переписать в виде
Рассмотрим теперь выражение iudki...p и выясним, как оно-
преобразуется при преобразовании группы Лоренца. Имеем согласно
G1,11;
Таким образом, совокупность 4"~2 чисел
преобразуется как компоненты тензора (п—2)-го ранга. Переход
от тензора «-го ранга Сш...Р к тензору TikCikl	называется
прощением тензора по индексам i, к. Совершенно аналогично про-
производится упрощение тензора по любой другой паре индексов.

§ 72]	ПРЕДСТАВЛЕНИЯ ПОЛНОЙ ГРУППЫ ЛОРЕНЦА	275
§ 72. Представления полной группы Лоренца
В этом параграфе мы найдем все конечномерные представления
полной группы Лоренца. При решении этой задачи нам понадобятся
перестановочные соотношения между оператором инверсии и опера-
операторами Ао±, Во±. Для их вывода удобно воспользоваться равен-
равенством
1а@ 0 Ог^О 0)Г' = а@ 0 0 — vx0 0).	G2,1)
? этого равенства заключается в том, что компоненты скоро-
скорости v в системах К и /С' -= I/C равны по величине и противопо-
противоположны по знаку. Формально равенство G2,1) легко получить, пере-
перемножая матрицы F5,5) и F5,7).
Если операторы t (g) (g ? J3*) осуществляют какое-либо предста-
представление группы J2*. то из соотношения G2,1) следует, что
т(/)х@ 0 0г»ж0 0)т(/~1) = т@ 0 0 — vx0 0).
Дифференцируя это равенство по vx и полагая затем vx = 0,
получим:
-c(/)J1t(/-1) = -Ji.
Так как все направления в пространстве равноправны, то мы
можем написать:
• x(/)JAx(r1) = —J* (*= 1,2,3).	G2,2)
Заметим, что оператор т (/) коммутирует с инфинитезимальными опе-
операторами lk (At = 1, 2, 3):
(r1) = l4.	G2,3)
так как оператор инверсии коммутирует со всеми вращениями. Из
равенств G2,2) и G2,3) следует, что
t(I)Akt^{I) = Bb, -c(/)Bfct-1(O = Ak G2,4)
x(/)Ao±t-i(/) = Box. x(/)BOtT-4/) = Ao±. G2,5)
Пусть i — какое-либо неприводимое представление группы _g\
Рассматриваемое как представление подгруппы Jgr, оно содержит
по меньшей мере одно неприводимое представление хр„ этой под-
подгруппы. Обозначим через Нх подпространство, преобразующееся
по представлению trQ. Пусть epq(—Р~~Ср^.Р, —Q^.Q^.Q) —
канонический базис в Hv Рассмотрим векторы
Имеем:
к/п = Аох'' W ePZ ^ х (/) В«вР« == -/^ (/) еп = - iqe'n
18*

276	ПРЕДСТАВЛЕНИЯ ГРУППЫ ЛОРЕНЦА	[ГЛ. XV
\е'ш — 1Кч
Производя подобные вычисления, получим в результате:
V« —^я. А+^ = ав+1^+1> А_^ = «в^„1. 1
Во?я==-^' "-ь'я^^/р^- В-вЯ=^-1«' I
Соотношения G2,6) показывают, что подпространство Н[, являю-
являющееся линейной оболочкой векторов е' , преобразуется по предста-
представлению Тдр, причем роль канонического базиса играют векторы
Линейная оболочка 2 BР-\- 1) BQ—(— 1) векторов ep(Z и uqp инва-
инвариантна относительно элементов собственной группы Лоренца. Кроме
того, в силу равенств
'№« = «« и -c.(/)i«qp-Vi-	G2>8)
вытекающих из G2,7), эта оболочка инвариантна также относи-
относительно оператора инверсии. Поэтому она инвариантна относительно
полной группы Лоренца и, следовательно, совпадает с простран-
пространством L, в котором действует представление т. Рассмотрим теперь
отдельно два случая.
1.	РфС?- В этом случае представления тр„ и т„р неэквивалентны
и, следовательно, векторы epq и uqp линейно независимы. Поэтому
они образуют базис в пространстве L. Этот базис будем называть
каноническим базисом. Оператор х(Г) определяется равенствами G2,8).
Представление i мы будем обозначать через х^ =% Размер-
Размерность представления xpo{Pj=Q) равна 2B/3 —|— 1)BQ —|— 1). Рассма~
триваемое как представление собственной группы Лоренца, оно
распадается на представления %р„ и ъ„р.
2.	P = Q. Теперь уже нельзя утверждать, что векторы epq и uqp
образуют линейно независимую систему векторов. Наоборот, легко
показать, что
Чтобы это показать, рассмотрим совокупность векторов
Согласно формулам F7,3) и G2,6) имеем:
и аналогичные формулы для операторов Во • Кроме того, вспоми-
вспоминая G2,8), мы видим, что
= eqp it uqp =

§ 72]	шч;дстлнлении полной группы лоренца	277
Обозначим через И+ линейную оболочку векторов v+ и через Н_ —
линейную оболочку векторов v . Полученные соотношения показы-
показывают, что подпространства Н+ и Н_ инвариантны относительно
всех элементов полной группы Лоренца. Поэтому либо Н+ == L
и tf._ = 0, либо H_ = L и Н+ = 0. В первом случае up7 = epq и
ч О evi ^ ечр- Во вт°ром случае арч = — ет и <с (/) epq == — ggp.
Таким образом, существуют два различных представления т^ и tp
группы Лоренца, каждое из которых, если его рассматривать как
представление собственной группы Лоренца, совпадает с предста-
представлением хрр. Оператор, соответствующий в этих представлениях
инверсии, определяется равенствами
G2,9)
Размерность представлений tp- и Тр равна B/3 —{— IK.
Представление т+ называется скалярным, представление т~ —
псевдоскалярным; величины, преобразующиеся по этим представле-
представлениям, называются скалярами и псевдоскалярами. Представление т~
называется векторным в соответствии с тем, что по нему преобра-
преобразуются обычные векторы четырехмерного пространства — времени
представление т+ называется псевдовекторным. Соответствующие
величины называются векторами и псевдовекторами.
Величины, преобразующиеся по представлениям (tI+)m(x~)n, назы-
называются тензорами (т-\-п)-го ранга. Легко видеть, что ("^тJ —(^it) •
Поэтому существует только два вида тензоров п-го ранга: одни
преобразуются по представлению (ч,Т2)п. вторые — по представлению
ч+ (t.y)™- Последние называются псевдотензорами в отличие от
величин первого типа, которые называются просто тензорами.
Заметим еще, что т~ X ъ* = ч? и V X ч* = т*. Если рассма-
рассматривать скаляр как тензор нулевого ранга, то можно сформулиро-
сформулировать следующее очевидное правило: произведение двух псевдотен-
псевдотензоров является тензором, произведение тензора на псевдотензор
является псевдотензором.

ГЛАВА XVI
РЕЛЯТИВИСТСКИ-ИНВАРИАНТНЫЕ УРАВНЕНИЯ
§ 73. Волновая функция
Согласно классической теории элементарных частиц (электронов,
различных сортов мезонов и др.) состояние всякой свободной эле-
элементарной частицы можно характеризовать с помощью волновой
функции ty(x) = ty(x0, xv x2, x3). Функция ф может иметь одну,
несколько или даже бесконечное множество компонент. Если число
ее компонент конечно, то мы будем обозначать его через а.
С помощью волновой функции строится функция Лагранжа частицы
как некоторый квадратичный функционал
Вид этого функционала для различных частиц, вообще говоря, раз-
различен. Интеграл от функции Лагранжа по всему четырехмерному
пространству— времени называется- действием 5. Согласно теории
имеет место принцип наименьшего действия, в силу которого вол-
волновая функция удовлетворяет уравнению 3S—0. Это уравнение
сводится к системе линейных однородных дифференциальных урав-
уравнений, которые всегда могут быть приведены к виду
МкШ + wh^O (Л ft-l. 2	з; у=0. 1.2,3). G3,1)
В силу однородности пространства и времени, коэффициенты Aik
и %ik не зависят ни от координат, ни от времени.
С помощью функции Лагранжа можно выразить энергию и
импульс частицы (или их средние по времени значения) через вол-
волновую функцию ф.
В механике и электродинамике величины, характеризующие дви-
движение материи (скорость, энергия, электрическое и магнитное поля
и др.), принимают в различных системах координат различные зна-
значения. В полном соответствии с этим состояние элементарной
частицы характеризуется в различных системах координат различ-
различными волновыми функциями. Весьма существенно, что преобразова-
преобразование, которое испытывает волновая функция при переходе от одной

§ 73]	волиовля функция	279
системы координат к другой, является линейным. Более подробно
это означает следующее. Рассмотрим какую-либо точку, скажем
х = _у = 2 = 0, ?=0. Пусть К! — какая-либо система координат,
начало которой в момент времени ?=0 совпадало с началом исход-
исходной системы К- Если обозначить через <{/ компоненты волновой
функции в системе К', то линейный характер преобразования выра-
выражается равенствами
f.@, 0, 0, O)=Tik(g)<tk(O- 0. °. 0).	G3,2)
Здесь Tik(g) — квадратная матрица, имеющая а строк и столбцов,
g — элемент полной группы Лоренца, соответствующий переходу от
системы К к системе К'.
Докажем, что матрицы Tik(g) (gl^L) осуществляют представле-
представление полной группы Лоренца. Для этого введем в рассмотрение еще
одну систему координат К", начало которой также совпадало
с началом системы К в момент t-—0. Обозначим через gl переход
от системы К' к системе К" и через h переход от системы К
к системе К". Тогда по определению группы Лоренца имеем h—g^g.
С другой стороны, для компонент ty'j волновой функции в системе К"
мы можем написать равенства
j и <l>;Wr№(A)^.
Сопоставляя эти два соотношения с G3,2), мы получим:
TttW-TyfoKVs). т. е. T(glg)^T(gl)T(g).
Это равенство показывает, что набор а чисел Ьг(х) (i ¦-¦ 1, 2, . . ., з)
при фиксированном х можно рассматривать как компоненты неко-
некоторого вектора 'Ь(х) из з-мерного пространства /;', осуществляю-
осуществляющего представление Т полной группы Лоренца.
Разумеется, выбор координат вектора ф неоднозначен: изменяя
базис в пространстве Е, мы перейдем от старых координат к новым,
являющимся линейными комбинациями старых. Весьма естественным
и удобным для приложений является выбор базиса, связанного с раз-
разложением пространства Е на неприводимые подпространства
?=2?TS.	G3,3)
т, а
Здесь т—неприводимое представление группы L, по которому
преобразуется подпространство E.s. Индекс s служит для нумера-
нумерации подпространств, преобразующихся по одному и тому же пред-
представлению t. Выделим теперь в каждом пространстве E.s канони-
канонический базис e.gti^e-Stpg. Совокупность всех векторов exS г обра-
образует базис в ?.
Координаты ^-8 I, связанные с этим базисом, мы и будем в даль-
дальнейшем использовать в качестве компонент волновой функции.

280	РЕЛЯТИВИСТСКИ-ИНВАРИАНТНЫЕ УРАВНЕНИЯ	[ГЛ. XVI
§*74. Релятивистски-инвариантные уравнения
В силу принципа эквивалентности всех инерциальных систем
уравнение поля G3,1) должно иметь одинаковый вид (и, следова-
следовательно, одинаковые коэффициенты) во всех инерциальных системах
координат. Уравнения, обладающие этим свойством, называются
релятивистски-инвариантными. В настоящем параграфе выводится
общий вид таких уравнений.
Прежде всего заметим, что поскольку коэффициенты уравне-
уравнения G3,1) не зависят от координат х, у, z, t, то инвариантность
его в одной только точке, скажем @, 0, 0, 0), влечет за собой
инвариантность во псех точках. Поэтому мы будем рассматривать
левую часть уравнения G3,1) только в точке @, 0, 0, 0).
Для простоты мы будем считать, что матрица у.й имеет обрат-
обратную. В этом случае без дополнительного ограничения общности
можно положить %ik = кЪцс (* ф 0). Таким образом, мы рассмотрим
систему
Л*Й} + *тЧ=0'	G4,1)
или в новых обозначениях
/\р , , ,,, тт'87'	 ,	G4 2)
Рассмотрим сначала, какие требования налагает инвариантность отно-
относительно собственной группы Лоренца Jgx. Выясним, как преобра-
преобразуются числа ¦—-г-^— при переходе от одной инерциалыюй системы
координат к другой. Согласно G3,2) имеем:
Мы видим, что 4а чисел *8 (х', s' фиксированы) преобра-
преобразуются как координаты из пространства, осуществляющего предста-
представление T'Xti 1 •
 2~
Если представление i'Xii i не содержит представления т, то
никакая линейная комбинация величин •—^—— не преобразуется, так
же как фтзг. Поэтому те уравнения системы G4,2), которые в пра-
правой части содержат 6rsj (t фиксировано), не содержат в левой части
производных — ^—, если т не содержится в т X ч i i •
0xi	J ?

§ 74]	РЕЛЯТИВИСТСКИ-ИНВАРИАНТНЫЕ УРАВНЕНИЯ	28 Г
Будем называть представление х' зацепляющимся с представле-
представлением х, если произведение х' X ^ i 1 содержит х. Теперь можно-
17
Следующим образом сформулировать полученный результат: если
Представление %' не зацепляется с представлением х, то все коэф-
коэффициенты А^и,а,г, равны нулю.
Из сказанного вытекает вывод: если представление х содержится
в Т, то в Т содержится хотя бы одно из зацепляющихся с х пред-
представлений. Действительно, в противном случае левые части уравне-
уравнений G4,2), соответствующих данному -с, не содержали бы ни одного
слагаемого и мы пришли бы к абсурдному выводу, что ф.^ = 0.
Если представление х' зацепляется с х, то произведение х' X 11 i
содержит представление х только один раз, как это следует из
формулы F8,3). Поэтому с точностью до множителя, не зависящего
от / и /', при фиксированных х' и s' существует только один набор
линейных выражений
Р'Л,'--%^- (/=1.2	sj,	G4,3)
которые преобразуются так же, как и набор компонент ^TSf
(/=1, 2	sT). Поэтому релятивистски-инвариантные уравнения
могут быть записаны в виде
%^	„ = 0,	G4,4)
причем коэффициенты Z-Jx-d' произвольны, если не требовать инва-
инвариантности уравнения относительно инверсии.
Согласно формуле F8,3) два представления tpg и tp'Q' являются
зацепляющимися друг с другом, ее ли ] Р — Р' \ = -к- и \Q — Q' | = -к •
Иными словами, с представлением т = pq зацепляются четыре пред-
представления
если Р Ф О, Q Ф 0. С представлением Ход (Q ?= 0) зацепляются только
два представления Xi i, Xi i. Аналогично этому с предста-
влением хра (Р =у^ 0) зацепляются представления х i i и х i i.
р+~2 ' 1 р~~г' 1
Наконец, с единичным представлением Хда зацепляется только одно
представление Xi i.
ТТ
Если два представления х и х' сцеплены, то суммы индексов
этих представлений P-\-Q и Р'-\-Q' являются одновременно либо
целыми, либо полуцелыми числами.

282
РЕЛЯТИВИСТСКИ-ИНВАРИАНТНЫЕ УРАВНЕНИЯ
[ГЛ. XVI
Вычислим коэффициенты P{h.tl ¦ Мы видели, что операторы -г—
(/=0, 1, 2, 3) преобразуются как компоненты 4-вектора в естест-
естественном базисе. Используя матрицу G1,4) перехода от естественного
•базиса к каноническому, легко получить операторы
д , х = / jL _i_ A
2 2
1 _±
2 ' 2
L, 1
1
дх\
G4,5)
которые преобразуются так же, как компоненты вектора в канони-
каноническом базисе. Выражение G4,3) можно теперь переписать в виде
dxj
Согласно F8,4) коэффициенты P™"i< равны
G4,6)
G4,7)
где P, Q — вес представления x; P', Q' — вес представления х',
p, q — индексы базисного вектора ty.sX\ p', q' — индексы базисного
вектора i^vr-
Подставляя в G4,4) выражение G4,6) и используя G4,5) и G4,7},
получим:
P'Q's'p'q'
X
= 0- G4,8)
Входящие сюда коэффициенты Клебша — Гордана были вычислены
в § 54. Подставляя найденные там значения в G4,8), находим

§ 74]	РЕЛЯТИВИСТСКИ-ИНВАРИАНТНЫЕ УРАВНЕНИЯ	283
окончательно:
Д y<*4w
Д
м-О, G4,9)
где u, = sign (P — P') и ч = sign (Q — Q') *).
Если в этом уравнении положить х = 0, то оно, разумеется,
останется релятивистски-инвариантным.
Отметим некоторые свойства симметрии коэффициентов Р-л-.ч' • Из
равенства G4,7) следует, что P™"i', не изменяется при замене P^lQ,
P'*iQ', p*^q, p'+^q', m+Z-ti. Это можно записать так:
P^r=P~~~.lt.	G4,10)
где i — tpQ, ^--=.Тд.р, / — (р, q), 1—(q, р) и т. д. Если в G4,6)
подставить явные выражения G4,5) для дтп и затем приравнять
коэффициенты при производных =— , то получится:
DO		,-П 2 a	/П2 	pi		/П~Т~1 	 iPZ^
"ti t	т(х J	xji ('	-hi	-dx'l	±!	! /уд i -|\
_— _i / i L	1?	_1_ l	I
P2		 n 2 2 I . »2	D3		,-n~Y~2 I /p~2 "	I
Произведем в этих равенствах замену т—>-:, t'->T/, /->Л /'->/"' и
учтем симметрию коэффициентов Р^"г; мы получим:
Р^,--Я~Г^, PL,r = pl^r '7 = 1,2,3). G4,12)
Далее, коэффициенты Клебша—Гордана обладают следующим
свойством (см. E5,6)):
и) = (—iy.+Л-^ (jj2mim21 Ут).
*) Sign х =\, если х > 0, и sign х — — 1, если jr < 0.

284	РЕЛЯТИВИСТСКИ-ИНВАРИАНТНЫЕ УРАВНЕНИЯ	[ГЛ. XVI
Поэтому
Обращаясь опять к равенствам G4,11), находим отсюда
)
,. (? = 2. 3). J
Для дальнейшего нам понадобится одно общее соотношение
между коэффициентами А^ уравнения G4,1)- В силу релятивистской
инвариантности этого уравнения функция 6^ = Tw (g) фг должна удо-
удовлетворять уравнению
или
= 0-	.G4.14)
С другой стороны, уравнение G4,1) можно переписать в виде
Заменяя здесь / на / и умножая на Ta(g), получим:
U |t*.+хгйф, = о:
Сравнение этого равенства с G4,14) показывает, что
или, опуская матричные индексы,
T{g-1)kxT(g) = A\?(g).	G4,15)
В частности, при f = 0
Продифференцируем это равенство по §х = — и положим затем
Учитывая F6,1), получим:
^ — A1.
Ввиду эквивалентности осей х, у и z можно написать более
общее соотношение:
А* = [JftAO] = 4А° — A<>Jft (А = 1, 2, 3).	G4,16)

§ 74)	РЕЛЯТИВИСТСКИ-И1ШАРИАНТНЫЁ УРАВНЕНИЯ]	285
Выясним теперь, при каких условиях уравнение G4,1) инвариантно
относительно инверсии.
Напомним, что оператор инверсии переводит всякий базисный
вектор e.pq, преобразующийся по представлению х = хрд собствен-
собственной группы Лоренца, в базисный вектор и~ , преобразующийся по
представлению x = xQp. Если P = Q, то представление х эквива-
эквивалентно представлению х. В этом случае оператор инверсии опреде-
определяется равенством \e^vq = e^qp или равенством lezpq = — exqy Отсюда
следует, что пространство Е волновых функций содержит одинаковое
число подпространств, преобразующихся по представлениям х и х.
Условимся нумеровать их таким образом, чтобы подпространства Е.а
и Е~а, имеющие один и тот же номер s, переходили друг в друга
под действием инверсии. Таким образом, если х ф х, то
1е — е~
tspg	-сsqp
Если же <5 = т, то, очевидно,
или
Этим трем равенствам можно придать одинаковую форму:
\е_, =^=sign'ce~i ,	G4,17)
если ввести обозначение
1, если х =-- хр„, Р i=[Q,
1, если x — tf,	G4,18)
-1, если т —Тр.
Соотношение G4,15), как это следует из его вывода, должно
иметь место и при ?" = /, если уравнение G4,1) инвариантно относи-
относительно инверсии пространства. Так как аоо(/)— 1, аа (/) = а22 (/) —
= а33(/) = —1, то при g—I и у = 0, 1, 2, 3 соотношение G4,15)
сводится к
V1A°I = A°. \-xk*\ = -k\ (k=l, 2, 3). G4,19)
Иными словами, для инвариантности уравнения G4,1) относительно
инверсии необходимо и достаточно, чтобы матрицы А0 коммутиро-
коммутировала с оператором инверсии, а остальные три матрицы А1, А2 и А3
антикоммутировали с ним.
Выясним, как сказываются условия G4,19) на коэффициентах Z~ ¦
Заметим, что последние три равенства G4,19) вытекают из условия
А°1 = 1А°. Действительно, в § 72 было показано, что оператор
sign х = sign x =

286	РЕЛЯТИВИСТСКИ-ИНВАРИАНТНЫЕ УРАВНЕНИЯ	[ГЛ. XVI
инверсии аптикоммутирует с инфинитезимальными операторами^, J2, J3.
Поэтому
A*I = (JfeAo — A°Jft) I = — I (JAA° — A°JA) = — I A* (ft = 1, 2, 3).
Рассмотрим условие А°1 == IA°. Применяя обе части этого опера-
операторного равенства к базисному вектору eTSj и учитывая G4,17),
получим:
Так как А°?И1 = 2?ч/\'Гт1«х'«>т. T0 отсюда следует:
sPеsign t''zs'sP° e~ ~
Приравнивая коэффициенты при е^8,р и учитывая, что, Я~^~у =
= — Px'v-zi, находим следующее условие инвариантности уравне-
уравнения G4,1) относительно инверсии:
?.	G4,20)
§ 75. Функция Лагранжа
Согласно теории элементарных частиц, функция Лагранжа эле-
элементарной частицы имеет следующий вид:
0М).	G5,1)
где ф—волновая функция частицы, Г (& —0, 1, 2, 3) — о-мерные
матрицы. Выражение (ср, <|)) есть билинейная форма, которую можно
представить в виде
(Ч.<?) = Вц<р&	G5,2).
(по индексам I, j подразумевается суммирование от 1 до а).
Выясним, какими должны быть матрицы Г* и коэффициенты Вц
для того, чтобы функция Лагранжа была инвариантной и чтобы
принцип наименьшего действия
8S = 8 Г Ldx0 dxy dx2 dx3 = 0
был эквивалентен уравнениям G4,1).
Вычислим 85. Имеем:

§ 75]	функция ллгранжа	287
где Тк' — матрица, сопряженная матрице Гк относительно билиней-
билинейной формы G5,2) *).
Первый интеграл в правой части последнего равенства равен
нулю, если 8ф обращается в нуль вне некоторого объема в четырех-
четырехмерном пространстве — времени, и мы получаем:
Ввиду произвольности 8ф отсюда следует:
Из этих соотношений вытекают дифференциальные уравнения G4,1),
если билинейная форма G5,2) невырождена **) и если
Итак, мы видим, что только те дифференциальные уравнения G4,1)
могут быть следствием принципа наименьшего действия, у которых
коэффициенты-матрицы А являются антиэрмитовыми относительно
билинейной формы G5,2):
А**-=-А*.	G5,3)
Рассмотрим теперь условие инвариантности функции Ла-
гранжа G5,1)- Заметим, прежде всего, что выражение Г*-т-— •-=
= Апреобразуется так же, как и функция ф. Это обеспечи-
АА
дхк
вается релятивистской инвариантностью уравнения G4,1). Поэтому,
если операторы А выбраны так, как указано в предыдущем пара-
параграфе, то для инвариантности функции Лагранжа достаточно, чтобы
билинейная форма G5,2) была инвариантной.
Запишем форму G5,2) более подробно в виде
= 2
Компоненты ty-js'i' преобразуются по представлению, сопряжен-
сопряженному ¦?'. Поэтому (см. § 69) из произведений вида y-sity-'s'i' (^ <5' фи-
фиксированы) можно составить инвариантное выражение только в том
*) Иными словами, каконы иы ни были а-мерные векторы у и ty, имеет
место равенство (Г*9, Ф) ~ (?! Г**Ф).
**) Форма (у, 6) называется невырожденной, если для любого вектора
у фО можно подобрать такой вектор 6, чтобы (<р, ^) Ф 0.

88;	РЕЛЯТИВИСТСКИ-ИНВАРИАНТНЫЕ УРАВНЕНИЯ	[ГЛ. XVI
хлучае, когда t' = x. Подчеркнем, что функции ср и i> должны пре-
преобразоваться по одному и тому же представлению не только соб-
-ственной, но и полной группы Лоренца.
В § 69 было показано, что таким инвариантным выражением
¦является сумма
Поэтому инвариантную билинейную форму можно представить в виде
(?,t) = 2 2s,ss'S<P^	G5,4)
х s, s' ?т	Р,Я.
тде коэффициенты fiT8<j' совершенно произвольны.
Условием невырожденности формы (ср, ф) является существование
для каждого t и s такого s'o, чтобы"
В^фО.	G5.5)
Для того чтобы действие 5 принимало только вещественные зна-
значения, форма (ср, i|i) должна быть эрмитовой, т. е. удовлетворять
¦условию (ty, ср) = (ср, ф). Поэтому коэффициенты BXda> обладают свой-
свойством эрмитовости
!В«-. = В^.	G5,6)
Рассмотрим в заключение условие инвариантности формы, (ср,'})
¦относительно инверсии. Учитывая соотношение G4,17), получаем:
а?, но = 2 2 /w 2 тея^„
х 88'	р, q	**
х ее'	j), g	**^
-Изменяя обозначения индексов суммирования, найдем:
a?, i^)-2!2fi?a8.2 «^„«h.'gp.
•Отсюда следует, что инвариантность формы (ср, ф) относительно
инверсии эквивалентна требованию
%*.• = *«.'.	G5-7)
Равенство G5,4) определяет невырожденную инвариантную относи-
относительно полной группы Лоренца эрмитову форму, если коэффи-
коэффициенты Bzes удовлетворяют условиям G5,5), G5,6) и G5,7), а'в осталь-
остальном совершенно произвольны.
*) Напомним, что если t = tp_, то под т мы подразумеваем представле-
представление zQPt

§ 76]	ЗАКОНЫ СОХРАНЕНИЯ	289
§ 76. Законы сохранения
Эквивалентность всех инерциальных систем обусловливает нали-
наличие по крайней мере одиннадцати законов сохранения в любой реля-
релятивистски-инвариантной теории. Не все эти законы независимы друг
от друга. Так, например, постоянство рх, ру и Мг является след-
следствием постоянства рг, Мл, и Му (р — импульс замкнутой системы,
М — ее момент).
Попытаемся выяснить, какую форму принимают эти законы для
поля ф, характеризуемого уравнением G4,1) и представлением Т.
С этой целью вычислим, как преобразуется поле ф при переходе
от одной инерциальной системы к другой.
Начнем с трансляций. Если система К' получилась из К путем
трансляции ta (a — четырехмерный вектор), то координаты одного
и того же события в этих системах связаны между собой соотно-
соотношением
x'i — xt — flj.	G6,1)
Поэтому волновая функция ф(лг) переходит в системе К' в функ-
функцию У (х1), равную
ф'(*')-=ф(*) = ф(*'-г-я)-	G6,2)
Группа трансляций является, очевидно, четырехпараметрической
группой. В качестве ее параметров естественно выбрать компоненты
вектора а, характеризующего трансляцию ta. Вычислим инфините-
зимальные операторы Y& (fe = 0, 1, 2, 3), соответствующие этим
параметрам. Соотношение G6,2) можно переписать в виде
Дифференцируя это равенство по а^ и полагая затем а = 0, полу-
получим:
Ъ^(х')=^Р.	G6,3)
Рассмотрим теперь «повороты» в четырехмерном пространстве —
времени, т. е. преобразования из полной группы Лоренца. Связь
между координатами х'к и хк одного и того же события в системах
отсчета К' и К выражается формулой
х'к = Ч1{К'К)хг.	G6,4)
Вычислим функцию ф' (х') в системе К', в которую переходит за-
заданная в К волновая функция ф(х). Для этого рассмотрим какую-
либо точку хк в системе /С. Координаты этой же точки в системе/Г
равны
xk' = 4i(K'K)xl	G6,5)
19 Зак. 3512. Г. Я. Любарский

290	РЕЛЯТИВИСТСКИ-ИНВАРИАНТНЫЕ'УРАВНЕНИЯ	[ГЛ. XVi
Введем теперь-^две вспомогательные системы -отсчета Ко и Ко,
которые получаются из систем К и К' с помощью 'Трансляций
ч = *1—*?, ?; = *;—*°\	G6,6)
Формулы перехода от Ко к К^ имеют следующий вид:
Они получаются, если из соотношения G6,4) вычесть G6,5). Обо-
Обозначим через 6° ($) и ф°'(?') волновые функции в системах К{) и 'ко-
Согласно G6,2) и G6,6) можно написать:
$(°) = Ых°). W(°) = ?i«)-	G6,7)
Связь между величинами !у?@) и ф?'@) имеет следующий вид:
^Ф) = Тц AСК) ^j@)	G6,8)
по определению G3,2) представления Т.
Объединяя равенства G6,7) и G6,8) и опуская индекс нуль,
получим:
/	0fy(*)-	G6,9)
Обозначим через h тот элемент группы Лоренца, который осуще-
осуществляет переход от системы К к системе К'. Так как hx = x', то
последнее равенство можно переписать в виде
^ (х') — Tij (A) fy (А~ V)	G6,10)
или
Мы видим, что представление Tt, по которому преобразуется полеФ,
не совпадает, вообще говоря, с представлением Т. В качестве про-
простого примера, иллюстрирующего подобное положение вещей, при-
приведем векторное поле f(r) = г, которое остается инвариантным при
вращениях системы координат вокруг ее начала, в то время как зна-
значение этого поля в любой фиксированной точке г преобразуется
при вращениях вокруг этой точки по векторному представлению Dt
группы вращений.
Пусть М — какой-либо оператор из группы трансляций или пол-
полной группы Лоренца, переводящий функцию ф в ф по формуле G6,2)
или G6,10). Волновое уравнение G4,1), которому удовлетворяет
функция ф, мы запишем в векторной форме:

§ 76]	ЗАКОНЫ СОХРАНЕНИЯ	291
В силу эквивалентности всех инерциальных систем этому же урав-
уравнению удовлетворяет функция ij/ = М^
Из этих двух равенств вытекает важное соотношение
^(А*Мф.ф) = О.	G6,12)
Действительно, так как А** = — Ак, то
= — у. (мо, ¦#+¦" (м ;•, о) = о.
Оператор М пробегает континуальное множество операторов,
соответствующих всевозможным трансляциям и преобразованиям из
полной группы Лоренца, и мы получаем бесконечное множество
соотношений вида G6,12). Однако не все они независимы. Для того
чтобы получить конечное число соотношений вида G6,12), из кото-
которых вытекали бы все остальные,перейдем от операторов М к инфи-
нитезимальным операторам.
Если продифференцировать равенство G6,12) по одному из пара-
параметров as, от которых зависит оператор М, то получится:
^.ф) = О.	G6,13)
где Is — инфинитезимальный оператор, соответствующий параметру as.
Добавим к G6,13) соотношение
А(/Аф,ф) = 0,	G6,14)
которое получается, если в G6,12) положить М = /Е (множитель I
добавлен для того, чтобы выражения (/Aft<j>) <!/ были вещественными).
Если речь идет о группе Лоренца, то, как легко показать, из
соотношений G6,13) и G6,14) вытекают все соотношения G6,12).
В случае полной группы Лоренца к равенствам G6,13) и.G6,14)
следует добавить еще одно:
^(А*1ф. ф) = 0,	G6,15)
где I означает оператор инверсии.
Соотношения G6,13 , G6,14) и G6,15) называются законами со-
сохранения. Им можно придать вид уравнения непрерывности .
gg + div ./=<),	G6,16)
19*

292	РЕЛЯТИВИСТСКИ-ИНВАРИАНТНЫЕ УРАВНЕНИЯ [ГЛ. XVI
где
р = 1(А<>1ф, ф), А=(А*1ф. ф) (Л=1. 2, 3), G6,17)
I — любой инфинитезимальный оператор, единичный оператор или
оператор инверсии.
В интегральной форме соотношение G6,16) имеет вид
~{fpdv=—[jds.	G6,18)
V	S
Таким образом, величины (Aftty, ty) (k = 1, 2, 3) можно рассматри-
рассматривать как компоненты потока величины —(А°1ф, ^).
Заметим еще, что, устремив в G6,18) V и S к бесконечности,
мы получим:
j pdV^=const.	G6,19)
Рассмотрим более подробно законы сохранения, связанные с груп-
группой трансляций. Согласно G6,3) соотношения G6,13) можно запи-
записать в виде
MA.ii ф\=о.
дхк \ к dxi т/
Вводя обозначения
G6,20)
мы получим:
^М- = 0.	G6,21)
дхк	[
Величины Ты (k, 1 = 0, 1, 2, 3) образуют тензор, называемый тен-
тензором плотности энергии — импульса. Равенство нулю четырехмерной
дивергенции этого тензора выражает закон сохранения энергии
и импульса.
Для того чтобы убедиться в том, что величины Тм образуют
тензор, произведем переход от системы отсчета К к системе от-
отсчета К'. Учитывая G4,15), получим:
Т; -,. = Re ( /А*' ~?- f ) = Re (/A*' T (g) j|, T (g) ^ av, (g) =
= avl (g) Re (iT (g-') A*'T (g)^. «) =
= «Z'Z (ff) aft'ft (g-) Re (/A* ^, ^ = агг (g-) ak,k(g) Tw,
что и доказывает тензорный характер величин Tw.
Рассмотрим теперь законы сохранения, связанные с собственной
группой Лоренца. Для того чтобы получить эти законы в наиболее

§ 76J	ЗАКОНЫ СОХРАНЕНИЯ	293
симметричном виде, целесообразно изменить выбор параметров, ха-
характеризующих элементы группы Jgx.
Запишем общее преобразование Лоренца в виде
x'i = xi + lik4sxs<	G6,22)
где fife — матрица G1,9), a eks— параметры, характеризующие данное
преобразование. Эти параметры связаны условием
~ixkXiXk == 1ikxixk-
Если eks— малые величины, то с точностью до величин высшего
порядка малости последнее условие означает, что
sfts =¦" — esfc-
Таким образом, число независимых параметров efts равно, как и сле-
следовало ожидать, шести. В качестве этих параметров можно принять
какую-либо независимую шестерку чисел eks. Соответствующие этим
параметрам инфинитезимальные операторы обозначим через lkg. Ясно,
что
U---I*s (ft. s = 0, 1. 2, 3).
Согласно § 44 выражение Т(^Г~1I^Т(§") является линейной ком-
комбинацией инфинитезимальных операторов 1к/8/, причем коэффициенты,
стоящие при 1й/8/, не зависят от представления Т. Подсчитав эти
коэффициенты для векторного представления ti i , мы получим со-
отношение
Т (g-1) h8 T (g) - аш (g) ^»> (g) \ш' (g G J?i). GC.23)
справедливое для любого представления Т собственной группы Ло-
Лоренца.
Операторы 1,.ь, связаны с операторами Гг, Jz (/ — 1, 2, 3) следую-
следующим образом:
112 =—1з> 123 = — Ii> 131 = — 'г>
IOi = Jp I02 = 	J2> 1оз :r= 	^З-
В этом легко убедиться непосредственным вычислением.
Вычислим теперь, как действует инфинитезимальный оператор \ка
на волновое поле ty(x). Для этого продифференцируем равенство
G6,11) по параметру eks элемента /г и положим затем h = e. Мы
получим, согласно задаче V § 43,
'	^^\	G6,24)
dyidska(h J) \n--e
где \кя и \к11 — инфинитезималь'ные операторы, связанные с предста-
представлениями 1\ и Т, у — к~Ах. Вычислим
дуг

294	РЕЛЯТИВИСТСКИ-ИНВАРИАНТНЫЕ УРАВНЕНИЯ	[ГЛ. XVI
Будем исходить из тождества
У1 = *г -Ь Ilk Ч* (h~l) xs.
Дифференцируя его по eks(h~l), получим:
Подставляя это выражение в G6,24), найдем:
7Л> Ш
Теперь можно записать шесть законов сохранения, связанных с груп-
группой Лоренца jg'^ Согласно G6,13) имеем:
0,	G6,26)
OXj
где
, b) -f./ Gzsx, — ТгЛ) (А^, *j . G6,27)
Числа J^.s образуют тензор третьего ранга. Это немедленно выте-
вытекает из соотношений G4,15) и G6,23). Тензор Jjks называется тен-
тензором плотности момента. Он антисимметричен относительно
второго и третьего индексов
Jj*e=-J*ft-	G6-28>
Соотношение G6,26) выражает закон сохранения момента в реля-
релятивистски-инвариантной форме.
Тензор момента состоит из двух слагаемых:
G6,29)
Первое слагаемое называется тензором плотности спинового мо-
момента, второе—тензором плотности орбитального момента.
Закон сохранения, соответствующий инверсии, имеет, очевидно,
следующий вид:
j-(A4'b(x0, — *1( — х2, — х3), Цх0, xlt х2, х3))=0.
Он называется законом сохранения частности.
§ 77. Спин
Понятие спина тесно связано с нерелятивистским понятием
момента. Как известно, компоненты ix, 5y, iz вектора плотности
момента / совпадают с компонентами J023, J031 и •'(иг четырехмерного
тензора плотности момента.

§ 77]	спим	295
Учитывая G6,27), можно написать:
4 = / (А°123*. ф) ¦+- *у (A» g, •>) - te (АО g, if).	G7,1)
Соответствующие равенства для Jy и У2 получаются из G7,1) путем
круговой перестановки х, у, z.
Поэтом}' вектор плотности момента можно записать в виде
J = S + M,	G7,2)
где
5 = (А0»ф. ф), Л1 = (А» [/¦/>] ф, ф)	G7,3)
и
(-1.2, 3; /» = /Jr).	G7.4)
Вектор S называется плотностью спинового момента частицы, век-
вектор М — плотностью орбитального момента, если функция ^ норми-
нормирована так, что
J°6, b)dV=l.	G7,5)
Заметим, что условие G7,5) выполняется во все моменты времени,
если оно выполнялось в некоторый начальный момент времени. Это
следует из равенства G6,19).
В соответствии с принятым в этом параграфе нерелятивистским
подходом мы будем рассматривать представление Т как представле-
представление группы вращений R. Если g?R есть вращение, то из G4,15)
следует, что
(	G7,6)
Обозначим через Ео совокупность всех векторов из Е, которые
переводятся оператором А0 в нуль:
АЧ =0 (ф ? Ео).
Из соотношения G7,6) вытекает, что подпространство ?0 инвариантно
относительно группы вращений. Обозначим через То представление
группы вращений, по которому преобразуется ?0. Выделяя из Т
представление То, мы получим:
Подпространство, преобразующееся по представлению Tg, обозначим
через Е±.
Запишем <]> в виде ф ^ ф0-j— 6Х ('^о€^о> ^iG^i)- Имеем:
S = (Ao<j6, 6) = (А°з^, if) = — {9ifu k^) =
,).	G7,7)

296	РЕЛЯТИВИСТСКИ-ИНВАРИАНТНЫЕ УРАВНЕНИЯ	[ГЛ. XV]
Итак, в выражение для плотности спинового момента входит только
составляющая i|»j волновой функции 6. Поэтому оператор <т можно
заменить оператором j1; связанным с представлением Ts.
Оператор сгг называют оператором спина, оператор [г, р] — опе-
оператором орбитального момента.
Если представление Tg содержит (один или несколько раз) только
одно неприводимое представление хр группы вращений, то вес Р
представления хр называется спином рассматриваемой частицы. Если
представление Ts содержит неприводимые представления различных
весов Рх, Р2, ... , Рк, то эти веса естественно рассматривать как
возможные значения спина частицы *).
Если волновая функция Ф принадлежит одному из неприводимых
подпространств ExaEv то говорят, что спин частицы в состоя-
состоянии 6 равен Р, где Р — вес представления т, по которому пре-
преобразуется подпространство Е..
Пусть волновая функция if является плоской волной с четырех
мерным импульсом р, т. е.
G7,8)
Рассмотрим те плоские волны
G7>9>
у которых р1 = /л, = />3 = 0. Подставляя это выражение в уравне-
уравнение G4,1), получим:
(*А%-Ьх)<!>0 = 0.	G7,10)
Обозначим через В (р0) подпространство, состоящее из всех тех
векторов ф0> которые удовлетворяют уравнению G7,10). Легко видеть,
что подпространство Е(р^) инвариантно относительно всех враще-
вращений. Действительно, учитывая соотношение G7,6), получим:
(/А% + *) Т (g) % = Т (g) (t\°p0 + у) % = 0 (g? R). ¦
Разобьем подпространство Е(р0) на неприводимые подпростран-
подпространства. Пусть 60 принадлежит одному из таких подпространств ?"т
(т—Тр). Тогда волновая функция G7,9) характеризует состояние
частицы, в котором значение спина равно Р, а четырехмерный
импульс равен (р0, 0, 0, 0). Так как подпространство Е^ имеет
BР-\-1) измерений, то, следовательно, существует BР-\- 1) линейно
независимых состояний с данным импульсом и данным значением Р
спина.
*) Следует, однако, отметить, что до настоящего времни не обнаружены
частицы с переменным спином.

§ 78] ОПЕРАЦИЯ ИНВЕРСИИ ВРЕМЕНИ И ТЕОРЕМА ПАУЛИ 297
§ 78. Релятивистски-инвариантная операция инверсии
времени и теорема Паули
Как известно, уравнения механики инвариантны относительна
инверсии времени, т. е. замены t на —t. Уравнения электродинамики
, „	1 дН	, „ 1 дЕ . 4-
rot Е=	з--,	rot Н——тгН	pt>,
с dt	с at ' с '
инвариантны относительно замены
'	%
также содержащей инверсию времени.
Поставим задачу найти общий вид релятивистски-инвариантной
линейной операции
t^ — t, 6^M6,	G8,1)
содержащей инверсию времени.
Пусть волновая функция if в системе отсчета К переходит в </
в системе К'
(вектор а характеризует поворот системы К' относительно К,
V—скорость начала координат К' относительно системы К). В силу
релятивистской инвариантности операции G8,1) функция M'-ji должка
переходить в системе К' в функцию М'У. После инверсии времени
вектор а не изменился, а скорость v изменила направление на про-
противоположное, поэтому
Подставляя сюда if' из G8,2), получим:
МТ(а, к) = Т(«, —«ОМ.	G8.3)
Дифференцируя это равенство по параметрам собственной группы
Лоренца, находим:
Из формул, связывающих операторы АА, Ък с операторами IA, Jk
(/г=1, 2, 3), вытекает теперь, что
ААМ = - 1 (I, + ih) М = — ~ М (Is — iik) = MB,,
т. е. Ак!Л = MB,. »Так же получается соотношение ВАМ =
Далее,
А+М — (lAt — А2) М = М (/Bt — В2) = МВ+,
А_М = МВ_, А0М = МВ0, В ±М = МА±, В0М = МА0.

298	РЕЛЯИВИСТСКИ-ИНВАРИАНТНЫЕ УРАВНЕНИЯ	(ГЛ. XVI
Пусть tytspq — одна из компонент волновой функции ф., отвечающая
¦базисному вектору ezspq представления % = хр. группы Лоренца:
zspq
Согласно G8,5) имеем:
Мы видим, что вектор Me^spq преобразуется как и~ , где и- ' — век-
вектор канонического базиса в представлении -с = т„р
Для определения коэффициентов )>pq подействуем на это равенство
операторами А+ и В + . Так как А+М = МВ+, то MB+eXSM = ^2>дА+и~
или
"О i и_ = X ав и- .
'--¦"' тд-i-lp pq g+1 tq+lp
Отсюда следует, что ^Pq+i = ^pq, т. е. числа Хр1[ не зависят от q.
Они не зависят и от р, в чем легко убедиться, подействовав на
-обе части равенства G8,6) оператором В + . Итак, Xpq = 'k. Поэтому
из соотношения G8,6) следует, что линейный оператор М, удовле-
удовлетворяющий условию G8,4), имеет вид
:?>,,,...„.	G8,7)
тде M-cs'x — совершенно произвольные коэффициенты. Применяя опе-
оператор М к функции ф, получим:
МФ= S Ф M , e~ , ,
1ТЖТ	^J f i zSp'i  do' ~i <lp
т. е.
Выясним, можно ли подобрать таким образом коэффициенты Л4,33',
чтобы релятивистски-инвариантное уравнение G4,4) было инвариант-
инвариантным и относительно инверсии времени. Подставляя в левую часть
равенства G4,4) вместо функции ty-si(xQ, xv x2, x3) функцию
2 ^m'+VT (—*<>. ху х2, х3)
а'
и используя соотношения
sign xZ-v-b = — sign -c'Z,,-4e

§ 78]	ОПЕРАЦИЯ ИНВЕРСИИ ПРКМКНИ И ТЕОРЕМА ПАУЛИ	299
легко находим, что уравнение G4,4) инвариантно относительно
инверсии времени, если
Мта8- = MTo«d< и blgnxM. — — sign t'Mz'	G8,9)
для любой пары сцепленных представлений.
Так как всякая замкнутая цепочка сцепленных представлений
всегда состоит из четного числа представлений, то условие G8,9)
никогда не является противоречивым. В дальнейшем мы будем счи-
считать его выполненным. Кроме того, мы положим, что все коэффи-
коэффициенты Жт равны
М, = ±1.
Проследим, как изменяется плотность заряда р = е(А°у, у) и
плотность энергии частицы г = 1А°;з-^, у) ПРИ инверсии времени.
Имеем согласно G5,4)
Мр = е (А°Му, Мб) = е 2 В..,й> (A°My)_sZ (Mybs.p =
Заменяя здесь т, / на т, / и имея в виду, что В , = В~ ,
А0 , , „,,, ^- — A°~~r~t ,л„, получим:
~.Л- б I"	-. а I -.'б I"	J
2 M,;4vr*:^hi
Tj'J9 16 I
= -е1>В^ь,(А^^71МхМ~.	G8,10)
Вычислим произведение Ж_Л1Г = sign тМ,. sign xAf~. Так как при
переходе от какого-либо представления -с к сцепленному с ним т'
величина sign-cM- изменяет свой знак, то, очевидно, произведе-
произведение М,М~ равно
М_М~=(— 1)\
где v — число шагов, которые необходимо совершить для того,
чтобы перейти от представления х к представлению т. При каждом
шаге индекс Р изменяется на -к-. Поэтому число необходимых шагов
является четным, если Р — Q целое число, и нечетным, если Р — Q-—
полуцелое число. Иными словами, v—четное число, если спин
частицы целый, и v — нечетное число, если спин частицы нецелый.
Вынося постоянное произведение М_М~ за знак суммы G8,10),
получим:
Мр = (—ly+V	G8,11)

300	РЕЛЯТИВИСТСКИ-ИНВАРИАНТНЫЕ УРАВНЕНИЯ	[ГЛ. XVI
Совершенно аналогично получаем:
Ме = (—l)ve.
Из этих равенств вытекает теорема Паули.
Теорема Паули. Плотность энергии частицы с полуцелым
спином может принимать как положительные, так и отрица-
отрицательные значения.
Плотность заряда частицы с целым спином может прини-
принимать как положительные, так и отрицательные значения.
§ 79. Уравнение Дирака
Если рассмотреть релятивистски-инвариантные уравнения, которым
удовлетворяет волновая функция, преобразующаяся по представле-
представлению Т = ti + х 1, то мы получим уравнения Дирака для электрона.
Прежде всего найдем вид этих уравнений. Для этого восполь-
воспользуемся формулой G4,9). В рассматриваемом случае каждое из непри-
неприводимых представлений, содержащихся в Т, входит в Т по одному
разу. Поэтому индекс s, который нумерует подпространства, пре-
преобразующиеся по одному и тому же представлению, не нужен в рас-
рассматриваемом случае. С представлением ii сцеплено только одно
представление т i. С представлением т i также сцеплено только
одно представление. Поэтому суммирование по Р', Q', s' в нашем
случае отпадает. Индексы, характеризующие компоненты волновой
функции, целесообразно упростить. Мы положим:
Ф 1 1 = Фч. Ф 1	1 = ^ 1. Ф 1 1 = <1> 1* . Ф 1	1 = Ф i •
Y{oio ^ Цо-10 '-1 'olol -I 'olo-T '-1
Положим теперь в G4,9) Р = \, Q=--0, Р'= 0, Q' = ^> P = -J •
q = 0. Мы получим следующее уравнение:
Подобным же образом получаем остальные три уравнения:
V 2 о у -io Ц dx ^^ (?х/ т1 \ djf ' ^/ Т11 ' ' *

§ 79]
УРАВНЕНИИ ДИНЛКА
301
Условие G4,20) инвариантности уравнения относительно инверсии
Дает:	7, . _ 7 _
Поэтому мы положим Z\ 1
следующую систему уравнений:
дх
; — У 2, Z 11 =У2и получим
°1Т°
1
з
- i
i ' их, '
L i /•L
^ 0
' "л1^ г av " 1
дх0
G9,1)
Таким образом, матрицы операторов
следующий вид:
А° =
А2 =
(У=0, 1, 2, 3) имеют
/
U
/о
0
0
0
0
¦ 1
0
0
0
- i
0
0
- i
0
0
I
0
0
-1
0
0
0
0
0
о/
0\
i
0
o!
G9,2)
(строки и столбцы отвечают следующему порядку индексов: —1, 1,
-1, 1).
Для того чтобы получить уравнения Дирака в обычной форме
о о о i\
0 0 10
0—100
\—l 0 0 0/
где Yo> Yi- Тг. Тз — матрицы Дирака:
То-
1
0
0
0
0
1
0
0
0
0
0
¦i
0
0
i
0
0
0
-1
0
0
I
0
0
0
0
0
	J
/'
0
0
0.
0 0 1
0\
0 0 0—1
— 10 0 0
0 10 0/

302	РЕЛЯТИВИСТСКИ-ИНВАРИАНТНЫЕ УРАВНЕНИЯ	[ГЛ. XVI
достаточно перейти от компонент 0_j, fy, ф_ j. tyi к их линейным
комбинациям:
G9,3)
Построим теперь инвариантную билинейную форму G5,2). Со-
Согласно формуле G5,4) в рассматриваемом случае она имеет следую-
следующий вид:
Условие эрмитовости G5,6) означает, что В \ = В \. Что же
касается условия инвариантности относительно инверсии G5,7), то
оно сводится к равенству В i—Bi . Несложная проверка показы-
показывает, что матрицы А& являются антиэрмитовыми относительно инва-
инвариантной формы, как оно и должно быть.
Итак,
(<?. 40 = 'r1iii + ?_1l-i + 'fi^-b?-it-1- G9-4)
Рассмотрим некоторые свойства электрона, вытекающие из урав-
уравнений G9,1) и вида инвариантной формы G9,4).
Представления xi и х i, рассматриваемые как представления
~z	° T
группы вращений, совпадают с представлением Xi. Это соответ-
i"
ствует тому, что спин электрона равен -=-. Далее, согласно G6,14)
четырехмерный вектор тока электрона равен jk = i'(А*ф, 0), или
в компонентах:
л=]ф^1 i2—;^i i2—i^ir^i^i!2-
По формуле G6,20) вычислим плотность энергии

§ 79]
УРАВНЕНИЕ ДИРЛКЛ
В частности, если волновая функция соответствует стационар-
стационарному состоянию, т. е. имеет следующий вид:
(•j = t],O(*,, x2, xs)eiEx°,
то из последней формулы следует:
Таким образом, Е играет роль энергии, приходящейся на единицу
плотности.
С помощью формул G6,20) и G6,27) можно вычислить осталь-
остальные компоненты тензора энергии импульса, а также все компоненты
тензора момента. Мы, однако, не будем на этом останавливаться.
Построим оператор спина.
Для этого, прежде всего, нужно отделить от пространства Е
подпространство Ео тех векторов, которые переводятся в нуль
оператором А0 (см. § 77). Однако оператор А0 не является особен-
особенным (его определитель равен единице), и подпространство Ео отсут-
отсутствует. Компоненты оператора спина равны, следовательно,
— /Ij, — П2 и — /J3>
где lu \2 и 13 — инфинитезимальные операторы, связанные с пред-
представлением T = Ti -f-т 1-
7°	°2
Выпишем в явном виде оператор проекции спина на ось OZ
= — /I, =
i °
0 0
0 0
о о
о о
— 4r о
Отсюда следует, что в состояниях b проекция спина на ось OZ
1 т_ i '
/О
равна —-у, а в состояниях | 0 | проекция спина равна -^-.

304
РЕЛЯТИВИСТСКИ-ИНВАРИАНТНЫЕ УРАВНЕНИЯ
[ГЛ. XVI
Рассмотрим теперь те решения системы уравнений G9.1), кото
рые имеют вид плоской волны:
Подставляя это выражение в G9,1). получим:
(Pi + iP-г) Ф_ 1 + (Ро + Р8) «I» I
=0.
Определитель этой системы должен быть равен нулю:
*	0	Ро — Рз Pi — iPi
0	у. р1_-\-1рг
Ро + Рз —Р\-\~1Рг	*	0
— Pi —<Рг Ро —Рз	°	*
Раскрывая определитель, получим уравнение
Таким образом, если состояние электрона описывается плоской
волной, то между его энергией р0 и импульсом р = ipl -\-jp2 + */':,
существует простая зависимость
Из этого соотношения следует, что величина х равна энергии покоя,
т. е. энергии электрона, импульс которого равен нулю.

ГЛАВА XVII
ЯДЕРНЫЕ РЕАКЦИИ
§ 80. Матрица рассеяния
В настоящей главе рассматриваются некоторые общие свойства
ядерных реакций типа А-\-Р — B~\-Q, связанные с изотропией про-
пространства. При этом не делается никаких предположений относи-
относительно характера ядерных сил.
Рассмотрим столкновение двух частиц А и Р (под частицей мы
подразумеваем либо элементарную частицу, либо ядро). В резуль-
результате столкновения может образоваться одна или несколько частиц.
Мы ограничимся случаем, когда образуются две частицы В и Q.
Такой процесс принято обозначать следующим образом:
A + P = B-\-Q.	(80,1)
Разумеется, одно лишь указание на сорт частиц В и Q, полу-
получившихся в результате реакции, отнюдь не характеризует ее исчерпы-
исчерпывающим образом. Для полной характеристики реакции необходимо
определить волновую функцию W системы B-\-Q в зависимости от
волновой функции 47 системы А-\-Р.
В силу линейности уравнения Шредингера lPv линейно зависит
от W. Поэтому, если ввести ортонорм-ированный базис Wj в про-
пространстве Ч:"-функций и базис W. в пространстве функции W, то
координаты С- функции W (W = 2 С'Л''.) выразятся через коорди-
координаты Cj функции Ф D7 = 2 Cft'j) c помощью некоторой матрицы 5:
C'r=YiSrfij.	(80,2)
з
Матрица S полностью характеризует реакцию (80,1) и называется
матрицей рассеяния.
Изотропия пространства налагает на коэффициенты матрицы
весьма существенные ограничения *). Ниже мы найдем общий вид
матрицы S, совместимый с изотропией пространства, и получим
*) Подобно тому как симметрия кристаллов налагает известные ограни-
ограничения на тензоры, характеризующие его физические свойства (см. § 41).
20 Зак. 3512. Г. Я. Любарский

306	ЯДЕРНЫЕ РЕАКЦИИ	[ГЛ. XVII
некоторые следствия, относящиеся к угловому распределению продук
тов реакции.
Займемся построением базиса Wj. Прежде всего заметим, что ,к>
столкновения (т. е. в период, когда частицы А и Р настолько уда
лены друг от друга, что энергией их взаимодействия можно npv
небречь) гамильтониан системы можно записать в виде
Н = На + Нр -f- Нкин,
где Н^ — гамильтониан частицы А в системе отсчета, в которой
покоится центр масс частицы А; соответствующий смысл имеет Нр;
НКИн — гамильтониан двух материальных точек с массами, равными
массам частиц Л и Р. В системе отсчета, где покоится центр масс
частиц А и Р, Нкин имеет, как известно, следующий вид:
пкий — 2A а/.2,
где (х — приведенная масса частиц Л и Я, г = гЛР — вектор, соеди-
соединяющий частицы А и Р. Волновую функцию Wj можно искать в виде
Ч> = ФХ.	(80,3)
причем
где е— сумма внутренних энергий частиц А и Р в состоянии ф,
а Е—кинетическая энергия относительного движения этих частиц.
Полная энергия ЕЛоли равна
Всевозможные стационарные функции ф двух изолированных
частиц можно классифицировать с помощью индексов s, ma и я,
где s — суммарный спин частиц А и Р, ms — проекция спина на ось OZ,
а—совокупность всех остальных квантовых индексов, необходимых
для полной классификации функций ^. Эта совокупность индексов
выбирается так, чтобы при поворотах системы координат значение а
не изменялось.
Итак, ф=ф6.та- Функцию у можно .характеризовать с помощью
энергии Е, орбитального момента I и его проекции mt на ось OZ.
Как известно *), функция у, соответствующая энергии Е, мо-
моменту / и проекции момента т^ имеет в сферических координа-
координатах г, 8 и ср следующий вид:
См., например, ['], часть 1, § 33.

§ 80]	МАТРИЦА РАССЕЯНИЯ	307
где k=~y -—	волновой вектор, Z i (kr) — некоторая цилиндри-
2
ческая функция полуцелого порядка Z-|—„> YimA®> f) — сферическая
функция. При больших г нормированная функция у приближенно
равна
¦Хл1т1С-^9) = 7у=е-^У1щ(В.9) (ftr^/ + l). (80,4)
Умножая ф на Хеш ¦ ПОЛУЧИМ Функции
S	1
Эти функции образуют полную ортонормированпую систему. Состоя-
Состояния Ч'. системы B-j-Q выбираются совершенно аналогично:
', ,, ,,.=b', , /у,, ,,,	(80,6)
s т I т,а Е	l s т а **1 т, Е	v
о	С	в	I
где
1
Выясним теперь, каков общий вид матрицы рассеяния в выбран-
выбранном базисе (80.5), (80,6).
Функция ф8ОТ а преобразуется при вращениях пространства по
неприводимому представлению Ds, функция Xi,n в преобразуется
по неприводимому представлению D;. Поэтому базисная функ-
функция Wsm гт„в преобразуется по представлению Ds X D;, которое,
Ь I
вообще говоря, приводимо.
С помощью коэффициентов Клебша — Гордана функцию 4"sm imi<,E
можно представить в виде суммы функций, каждая из которых пре-
преобразуется по одному из неприводимых представлений группы вра-
вращений:
%ш 1т.«Е = 2 (*/«,«» | JM) QjM8ue.	(80,8)
* ' /, и
где
q		 ^1 {с!гц т I 11\/[\ ^t*	(RQ Q^
mg, mt
Заметим, что суммы в (80,8) и (80,9) не являются, собственно
говоря, двойными, так как коэффициенты (slmsmr | JM) отличны
от нуля только при условии ms-\-mi= M.
Обозначим через S',,,, „, ,„, функции, связанные с Ч"', , ,
равенствами, аналогичными равенствам (80,8) и (80,9).
Предположим, что система до столкновения находилась в состоя-
состоянии QjMdaE- При этом полный момент системы равнялся у
20*

308	ЯДЕРНЫЕ РЕАКЦИИ	[ГЛ. XVII
а проекция полного момента на ось 07. равна М. Так как полный
момент J и его проекция М в силу изотропии пространства сохра-
сохраняются, то после реакции система должна иметь тот же полный
момент и ту же величину его проекции. Поэтому волновая функ-
функция W после столкновения должна иметь следующий вид:
2 4j*.T.4^jjr,T.'B'	(80,10)
s'l'a'E'
(по индексам У и Ж суммирование не производится!).
Здесь Дйля, s'z'a'.E—-некоторые коэффициенты, вычисление кото-
которых невозможно без знания ядерных сил.
Если произвести произвольный поворот g системы координат,
то функция QjMsiaE перейдет в функцию 2ом'лг(?) Yjm^ue- Подоб-
Ш'
ным же образом изменится и функция Ч;/. Поэтому в новой системе
координат реакция Ч-' -> Ч-"' имеет следующий вид:
JL D_M'3l(g) Qjm'sl«E-+ 2 A*l*E, s'l'a'E' DM'M(g)QjM'j'l'*'Er •
W	М'б'1'л'Е'
Разумеется, такая же реакция может произойти и в старой
системе координат ввиду равноправности всех систем координат.
С другой стороны, из (80,10) в силу линейного характера связи
между 1Г и Ч'' следует, что
JjDM'M(g)QjMsialE—>- 2j DM-M(g) AetaEt s'l'a'E^JM's'l'oi'E'-
M'	M's'l'a'E'
Сравнивая два последних равенства, находим, что
.JM	,JM'		 ,J
AslaE, b'l'a'E' -— ЛЛо.Е, б'1'а.'Е' 	 ЛЛо.Е, $'1'о.'Е'>
т. е. коэффициенты AjZxe, s'Va'E' не зависят от индекса М. Выразим
матрицу рассеяния через коэффициенты Л^е, аг7'«'В'-
Используя линейный характер связи между волновыми функ-
функциями до и после столкновения, мы можем написать:
2
J,M
2, (si\) 2	,
J, M	S'l'a'E'
=	2	{slm№\JM)A^.a.Va.E,(s'l'myi\ML'
S l
„	, ,	„smlmf-E
Зто равенство показывает, что коэффициент о / / , г , < мат-
матрицы рассеяния равен
S/f/Тш^Е' = ^ (slm^ | JM) A<laEt s,ra,?, (s'l'mX | JM). (80,11)
& t	J, M.

§ 81]	УГЛОНОЕ РАСПРЕДЕЛЕНИЕ ПРОДУКТОВ ЯДЕРНОЙ РЕАКЦИИ
309
С формальной точки зрения эта формула выражает матрицу
с двенадцатью индексами через матрицу с девятью индексами.
Таким образом, учет изотропии пространства значительно сокра-
сокращает число известных параметров, характеризующих ядерную
реакцию.
§ 81. Угловое распределение продуктов ядерной реакции
Пусть волновая функция Ч"', характеризующая состояние частиц В
и Q после столкновения, равна
t , Т^, , , s m ,l m, a E s от I т,л В
*• ' '
8 от г то, а Я
&	I
Предположим, что нас интересуют только те реакции, в резуль-
результате которых частицы В и Q оказываются в состоянии с опреде-
определенным значением а и произвольными s', т'а, Г, т^ (величина Е'
однозначно определяется значениями остальных индексов). Тогда
волновую функцию 'Г' можно согласно (80,6) заменить функцией
а	^U s
хр'
l ш7
i
Поэтому на больших расстояниях угловое распределение о@, ср)
потока интересующих нас частиц равно
pi
У С .. ¦ .Л. ¦ .Y. -@,
'V "Ч
mgl „ч
(81,2)
Здесь интегрирование производится по всем внутренним коорди-
координатам частиц В и Q. Учитывая ортонормированность функций ф > • <,
получим:
em.
г w.
Подставим сюда выражение коэффициентов С через коэффи-
коэффициенты С
рF. cp) =
I m
s «» J t»ji S a»bJ,m^E \ I 14-1
Если до столкновения система, состоящая из частиц А и Р,
находилась в состоянии с определенным спином s и проекцией

310	ЯДЕРНЫЕ РЕАКЦИИ	[ГЛ. XVII
спина тп8, то в последней формуле исчезает суммирование по s
и tns и мы получаем:
P«,<e.-*)=J?I 2 sr^,s.c у^.
amg\ I mllml	* l	l	•
Предположим теперь, что мы имеем дело не с одной частицей Л
и одной частицей Р, а с потоком частиц А, падающим на мишень,
состоящую из большого числа частиц В.
Выясним, какой вид должно иметь угловое распределение ча-
частиц Q, если как в падающем пучке, так и в мишени все напра-
направления спинов частиц встречаются одинаково часто (полностью депо-
деполяризованные пучок и мишень).
Ясно, что для получения углового распределения в этом случае
следует усреднить выражение (81,3) по всем возможным значениям s
и ms:
a m
I
Лт-,
(81,4)
На практике обычно волновая функция, описывающая относи-
относительное движение падающих частиц Р, есть плоская волна eikr.
Если ось OZ направить по вектору k, то каждая частица будет
находиться в состоянии с »гг = 0. Поэтому в дальнейшем мы будем
полагать ягг=0 и опускать суммирование по тг. Вспоминая фор-
формулу (80,11), перепишем (81,4) в виде
(в. ?> = ^ 2
s, m	s , m I
Суммирование по яг' и jM является здесь чисто формальным, так
как при Мфтп или т'фпг —т' выражение, стоящее под знаком
1	S	бое
внутренней суммы, обращается в пуль. Однако дальнейшие выкладки
оказываются более простыми, если сохранить суммирование по от^и М.
§ 82. Угловое распределение продуктов ядерной реакции
(продолжение)
В сумме (81,5), дающей угловое распределение частицы Q, от
индексов mg, т'в, m't и М зависят только коэффициенты Клебша —
Гордана и сферические функции.
Если, изменив порядок суммирования, вынести за знак суммы
но mg, m'a, т'г и М все множители, не содержащие этих индексов,

§ 82] УГЛОВОЕ РАСПРЕДЕЛЕНИЕ ПРОДУКТОВ ЯДЕРНОЙ РЕАКЦИИ	311
то останется сумма, не зависящая от характера ядерных сил. Мы
вычислим эту сумму и, таким образом, существенно упростим полу-
полученное в предыдущем параграфе выражение для углового распре-
распределения.
Сумму (81,5) можно переписать в виде
>- Т) — 2so+l ^ *Л Л^аЛ, .' I а' Е'К^Е, в l[ «' Е Х
а, я' IjJJji
X ClOaEC^EK(s, I, lv s', V, 1[, У, У,), (82,1)
где
K(s, I, lv s',l',l'v /, У,) =
X {s'l[m'm'n | JlMl) Y,m,{ht 9)Y^. T). (82,2)
Приступим к вычислению A^(s, Z, /j, s', I', l'v У, УЛ. В качестве пер-
первого шага заменим произведение сферических функций линейной
комбинацией сферических функций:
( ¦*) 1//о;' i 1 л i о и i 1 > х
х
(см. задачу 1 § 54). Мы получим:
K(s, I. lv s',l', l[, J, У,) =
j, m
X J] (в/»в0|УЖ)(я/1/и1@|У1Л11)Х
X
x (s'/^x I лж0 W—mum'i I у™)- (82 >4a)
Преобразуем сумму по /га^, m'v m'u так, чтобы к ней можно
было применить формулу E6,22). Для этого, используя свойства

312	ЯДЕРНЫЕ РЕАКЦИИ	[ГЛ. XVII
симметрии E5,6) коэффициентов Клебша — Гордана, напишем:
(s'l'm'm[ | УМ) = (— 1)аЧ l' J {l's'm\m^ \ JM).
Подставляя это выражение во внутреннюю сумму и заменяя (—1)' и
t	tt
на (—1) ' s = (—1)	а. получим:
n in-,m\
Применяя формулу суммирования E6,22), находим:
/B/; + 1)Bу+1) {lJ l
Подставляя в (82,4) вместо внутренней суммы это выражение,
получим:
^VV— >¦)	А
4яBУ +
J, ш
X ^ (—l)Ml(slms0\JM){sl1ms0\J1M1)(J1J—M1M\jfn). (82.5)
Для вычисления внутренней суммы по ms, M, Mt перепишем коэф-
коэффициенты Клебша — Гордана в виде
(slms0 | JM) = (— 1)а+г-J+s+ '"• лГЦ±±. (Js — Mms \ 10),
(sl.mO | JM) = (- l)~s +Ii+».-
После подстановки этих выражений внутренняя сумма приобре-
приобретает следующий вид:
X (sAme - Mv |
Согласно формуле E6,22) это выражение равно
штт (y/i - m01Ю) w (y7i/s; y/i)-

§ 82] УГЛОВОЕ РАСПРЕДЕЛЕНИЕ ПРОДУКТОВ ЯДЕРНОЙ РЕАКЦИИ	313
Подставляя его в (82,5), получим окончательно:
S
2/i
W(Jxs'jT; l[J) W{JJxls; У/j) (82,6)
j
суммирование по т. исчезло, так как при тфО коэффициент
(Jlx — otOI/0) обращается в нуль).
Формулы (82,1) и (82,6) дают самый общий вид углового рас-
распределения, если проекция орбитального момента падающих частиц
равна нулю. Коэффициенты А зависят от характера ядерных сил,
а коэффициенты С — от вида волновой функции, характеризующей
относительное движение частиц А и Р.
Из полученного выражения для K[s, I, lv s', I', l'v У, УЛ вытекают
некоторые следствия. Прежде всего, видно, что угловое распреде-
распределение не зависит от угла ср, т. е. является аксиально-симметричным.
Для того чтобы получить второе следствие, предположим, что
в падающей волне играют роль только те компоненты, которым
соответствует орбитальный момент Z^Zo(/o=0, 1, 2, ...). Тогда
в (82,1) суммирование по / и 1Х можно производить от 0 до /0.
Если j > 2/0, то j">li.-\-l и коэффициент (j, /х00[Ю) обращается
в нуль. Это означает, что в (82,6) суммирование по j можно про-
производить в пределах от 0 до 21. Угловое распределение о (8) оказы-
оказывается в этом случае линейной комбинацией полиномов Лежапдра
степени не выше 2/0. Поэтому р@) само является полиномом от cos 9
степени не выше 2/0.
Этот вывод .чрезвычайно важен при обработке эксперименталь-
экспериментальных данных, полученных при наблюдении ядерных реакций.

ПРИЛОЖЕНИЯ
I. ХАРАКТЕРЫ НЕПРИВОДИМЫХ ПРЕДСТАВЛЕНИЙ
ГРУПП ПЕРЕСТАНОВОК S4, S5> S6 и S7
1'р
Схемы
Юнга
4
1*
1,3
п
у п п а
Классы
1*
1
1
3
1
12,2
1
-i
6
1,3
1
J
8
22
1
1
— 1
3
4
1
— 1
— 1
6
Схемы
Юнга
22
13,2
п
Классы
1*
2
3
1
12,2
— 0
1
6
1,3
1
	1
8
22
2
1
3
4
0
— 1
6
Число п перестановок, содержащихся в каждом классе, указано в последней
строке таблицы.
Группа S5
Схемы
Юнга
5
15
4,1
3,2
3,12
1,22
1»,2
п
15
1
1
4
5
6
5
4
1
18,2
1
— 1
2
1
0
— 1
— 2
10
Р,3
1
1
1
— 1
0
	. J
1
20
Классы
1,22
1
1
0
1
— 2
1
0
15
1,4
1
— 1
0
— 1
0
1
0
30
2,3
1
— 1
— 1
1
0
1
1
20
5
1
1
— 1
0
1 1
-1
— 1
24
Группа
Схемы
Юнга
6
1»
5,1
2,1*
4,2
22,12
4,12
3,13
32
23
3,2,1
п
Классы
1»
1
1
5
5
9
9
10
10
5
5
16
1
1*,2
1
— 1
3
— 3
3
— 3
2
	2
1
— 1
0
15
13,3
1
1
2
9
0
0
1
1
— 1
— 1
— 2
40
12,22
1
1
1
1
1
1
	9
— 2
1
1
0
45
12,4
1
— 1
1
	1
— 1
1
0
0
— 1
1
0
90
1,2,3
1
— 1
0
0
0
0
— 1
1
1
1
0
120
1,5
1
1
0
0
— 1
— 1
0
0
0
0
1
144
23
1
— 1
— 1
1
3
— 3
	о
2
— 3
3
0
15
2,4
1
1
— 1
— 1
1
1
0
0
— 1
	1
0
90
32
1
1
— 1
	 |
0
0
1
1
2
2
— 2
40
6
1
— 1
— 1
1
0
0
1
— 1
0
0
0
120

Груп
Схемы
Юнга
7
V
6,1
2,1s
5,2
2^,13
5, I2
3,1*
,3
2»,1
4,2,1
I2
4,1»
3?, 1
3,22
п
п a S
1?
1
1
6
6
11
14
15
15
14
14
35
35
20
21
21
1
7
18,2
1
— 1
4
— 4
6
— 6
5
— о
4
— 4
5
— 5
0
1
— 1
21
I4, 3
1
1
3
3
2
2
3
3
— 1
— 1
— 1
	1
2
— 3
	з
70
13,22
1
1
2
2
2
2
	1
	1
2
2
— 1
— 1
— 4
1
1
105
is, 4
1
— 1
2
— 2
0
0
1
— 1
	2
2
— 1
1
0
	1
1
210
I5, 2,3
1
	1
1
	1
0
0
— 1
1
1
	1
	1
1
0
1
	]
420
12,5
1
1
1
1
	1
	1
0
0
— 1
	 1
0
0
0
1
1
504
Классы
1,23
1
— 1
0
0
2
— 2
— 3
3
0
0
1
— 1
0
— 3
3
105
1,2,4
1
1
0
0
0
0
— 3
	1
0
0
1
1
0
— 1
	 1
630
1,32
1
1
0
0
— 1
	1
0
0
2
2
— 1
	1
2
0
0
280
1,6
1
— 1
0
0
— 1
1
0
0
0
0
1
— 1
0
0
0
840
22,3
1
1
— 1
	 1
2
2
	, j
— 1
— 1
	1
— 1
	1
2
1
1
210
2,5
1
	1
— 1
1
1
— 1
0
0
	1
1
0
0
0
1
— 1
504
3,4
1
	1
— 1
1
0
0
1
	1
1
	1
— 1
1
0
— 1
1
420
7
1
1
1
1
0
0
1
1
0
0
0
0
— 1
0
0
720

316
ПРИЛОЖЕНИЯ
II. ХАРАКТЕРЫ НЕПРИВОДИМЫХ ПРЕДСТАВЛЕНИЙ
ТОЧЕЧНЫХ ГРУПП
Cic!
Со
Cs = s
ч
ч
е
е
е
1
1
1
Со
а
1
	|
ч
"Со
ч
е
1
1
1
с3
1
в"
« 3
1
« 3
С»й
Со
08
Х1
X»
т3
-4
е
е
е
1
1
1
1
Со
Со
Со
1
	у
1
	1
а1

1
— 1
— 1
1
X
(Jo
Ио
1
1
— 1
— 1
Cv
Da
Ч
¦с»
¦с»
в
г
1
1
2
Со
с,
1
1
— 1
а
1
— 1
0
с.
54
Т1
То
ч
е
е
1
1
1
1
с4
1
— 1
/
— 1
С2
и4
с2
1
1
— 1
— 1
г3
С4
оЗ
Л4
1
— 1
,	 ?
civ
оы
ч
ч
ч
ч
е
е
е
1
1
1
1
2
Со
С2
с2
1
1
1
1
	2
с4
с4
54
1
1
	\
— 1
0
а1
«1
и
1
	1
1
— 1
0
Зо
Мо
а
1
— 1
— 1
1
0
Се
Ч
То
ч
Х5
1
1
1
1
1
1
С6
1
	j
2т:г
е 3
4лг
¦иг
е~
е~3~
Г2
1
1
4ici
« 3
2м
« 3
2тсг
в 3
4тсг
г3
1
— 1
1
— 1
— 1
ct
1
1
2«
е~
4r.i
Г3"
4г»
в 3
2кг
Г5
1
— 1
4*г
Г3
2*i
e~f
br.i
ia'
r.i
C6V
Ч
Ч
Ч
Ч
ч
ч
е
е
р
1
1
1
1
2
2
С3
Г3
1
1
— 1
— 1
2
— 2
с2
с2
1
1
1
1
— 1
— 1
с6
6'6
1
1
— 1
— 1
— 1
1
и,
а1
и
1
— 1
1
— 1
0
0
мг
°2
О
ti
1
— 1
— 1
¦ 1
0
0

ПРИЛОЖЕНИЯ
317
,.
ч
ч
е
1
1
1
3
и
1
1
1
	1
с.
1
р~Т
4-г
е з
0
Г2
°з
1
4м
2ici
0
0
ld
~1
т2
т8
'4
1
1
2
та со
сз
1
1
— 1
0
0
с2
и
1
1
2
— 1
и
а
1
— 1
0
1
— 1
с4
1
1
0
	J
1
HI. ДВУЗНАЧНЫЕ ПРЕДСТАВЛЕНИЯ ТОЧЕЧНЫХ ГРУПП
Сп
/
ЪтЛк ™
е "
ртп
	g И
,13 1
^2
г'
е+
2
е-
0
и2±
0
4,
0
?>з
zi
г
Т2
/
'з
1
1
2
	j
— 1
— 2
Г С2
°3+' °3-
	j
	j
1
Г Г2
Ь3-' °3+
1
1
— 1
«+
— г
0
и_
— 1
1
0
Об
"l
/
*з
2
2
2
е-
— 2
— 2
— 2
С2±
0
0
0
с с2
1
1
— 2
V Г1
_!
	 1
2
С64-, С6-
Уз-
— Уз
0
с5 с
64-' 6 —
-Уз-
Уз
0
0
0
0
и'т
0
0
0
о4
е+
2
2
е-
— 2
— 2
С2-
0
0
С С3
у?
-У 2"
с|\, с4_
— У 2"
У?
«4- [ М±
0
0
0
0
т
'"I
ъ
2
2
2
— 2
	2
	2
1
2r.i
? 3
¦lJti
^ 3
с2+
_1
4,-!
— в 3
2г.г
-^ «
С3-
_1
2-г
	е 3
4r.i
-^3
с2
1
4«
б S
2гг.
3
С2±
0
0
0
О
\
г
""А
е+
2
2
4
е~
— 2
— 2
— 4
с3+> с2
1
1
— 1
С2 , С
— 1
— 1
1
С1±
0
0
0
с44., cj_
У?
-У 2
.0
-/2
У2"
0
с2±
0
0
0

318
ПРИЛОЖЕНИЯ
IV. ПРОСТРАНСТВЕННЫЕ ГРУППЫ
Триклинная сингония
Класс Со- Класс содержит одну группу Сд, состоящую только из трансля-
трансляций. Группа принадлежит типу Г(.
Класс 52 = С{. Класс содержит одну группу Sf2, состоящую из трансля-
трансляций и произведений трансляций на инверсию. Группа принадлежит типу Г,.
Моноклинная сингония
Класс а,, = С„.
Группа
С1
С2
cl
с4
Тип
Г™
Г*
000
7»
000
100
Расположение основных векторов
Тройки чисел 000, -=• 00 означают коэффициенты аь я2, ад вектора
определяющего трансляцию ta, на которую нужно умножить ofl для того,
чтобы получить элемент t№ ид соответствующей пространственной группы.
Так как единице группы всегда соответствует вектор « = 0, то в этой
и всех последующих таблицах столбец, отвечающий единице, опущен.

ПРИЛОЖЕНИЯ
319
Класс
Группа
С1
С2
Тип
г.
ТО
с.
0
0
0
0
0
0
0
1
2
0
Расположение основных
векторов
а,
Класс C2ft
Группа
Тип
Расположение основных
векторов
000
000
000
000
1 „„
loo
000
loo
г*
иг
000
000
000
loo
000
loo

320
ПРИЛОЖЕНИЯ
Ромбическая сингония
Класс CV
Группа
Г1
Чо
Г2
Чо
г3
Чо
Г*
ч«
с5
Чо
Чо
г7
Чо
Q8o
г9
ь 2о
Чо
Г12
Чо
с13
Чо
Тип
Го
г6
000
ooi
000
ioo
i-oo
Т°-2"
-2-2°
1 1 1
III
il°
000
00-1
000
°1
000
000
00 2-
ioo
ioo
1 1
2 2
ioo
ioo
000
000
ooi
000
~2
ooi
000
2
ooi
000
oio
1 1
oii
000
oo -o-
Расположение основных
векторов
ь
в, Л

ъ>—4
>
р

321
Продолжение
Группа
cu
1 -15
' 2v
f 17
'• 2»
/18
2u
c\l
2v
/^21
Тип
¦'¦о
г»
c2
000
000
000
000
000
00 i
000
 "°
000
000
-2-T°
00 i-
2
1 1 1
2 2 2
000
oio
000
000
000
00^-
1 1 1
2 2' 2
000
loo
000
-2Y°
o1-!
2 2
Расположение основных
векторов
/I /<
v\ ,
a3
--4
/
21 Зак. 3512. Г. Я- Любарский

322
ПРИЛОЖЕНИЯ
Класс ?><.
Группа
Тип
«1
Расположение основных
векторов
D\
D\
D\
000
000
li
000
ооЛ
44»
i i
000
col
000
000
000
000
ч
000
000
000
000
)] '
2 2"
000
Класс ZJ;,. Каждый элемент группы Z)?ft принадлежит подгруппе D-,
или является произведением инверсии на элемент из ?>». В соответствии
с этим каждая пространственная группа класса D«^ содержит в качестш-
подгруппы одну из пространственных групп класса ?>о. Поэтому для характе-
характеристики пространственных групп класса D«j, вполне достаточно указать соот-
соответственную группу из класса ?>, и выписать вектор я, соответствующим
инверсии.

ПРИЛОЖЕНИЯ
323
Группа
D\h
D\h
Din
<
D\h
Тип
Го
Dm
D\h
D\n
D\h
nlo
Dth
л"
U2h
n\2
U2h
Л13
U2h
ulh
D211
D-ih
Подгруппа
класса
D\
Dl
D3
D$
I
000
1 1 1
2 2 2"
00 i
iio
2 2
000
IT0
i00
2"
000
1 1 1
2 2 
2
1 1
¦ Ik-
000
Расположение основных
векторов
f
ti? аг
("

324
ПРИЛОЖЕНИЯ
Группа
Продолжени
Тип
Подгруппа
класса
Расположение основных
векторов
Л
000
D\
000
00 г
1 1 1
112
2h
u
u-
26
-ih
-id
1o
000
1 1 1
4 4 4

ПРИЛОЖЕНИЯ
Тетрагональная сингония
325
К л а с
Группа
С1
С2
с3
с4
с-
с Q
Тип
Г"
9
с4
000
«4
00 —
2
ooi
000
3 1 1
4 4" 
сУ
000
~2
000
000
000
000
с3
000
•4
2
<
000
3 1 1
4 ТУ
Расположение основных
векторов
с
Л
'а,
/ \
/
'а.
Класс 54
Группа
51
5.1
Тип
000
000
Расположение осношшх нектором
(
/
—^
t\\ ,--7
/

326
ПРИЛОЖЕНИЯ
§
с
«з4
1
8?
-И! 8
о
•—см	— см
— см
о —|^<—.|^
со h? — 1ч*
¦—см	— см
|
см
I — ;см
¦ |см
о — ;см — !см о о — |см — |с
ч-*1	О	О	О	О
О — |<N r-i \-> 1
CO IT ГО 1-Ч-
о о 8
о о
8 8
.— |CN -- [(N
8
— CM — |CN
(о

К л а с
Группа
С1
С2
Cth
С5
Ч'л
с Ч(»
Тип
¦Jit)
000
000
000
000
000
000
с2
ч
000
000
000
000
000
000
*1
000
000
000
000
000
осо
ч
000
«4
1 1 1
000
3 1 1
4 4 2
с3
000
001
0
2 2
1 1 1
2 2 "
000
3 1 1
4 4 '2
000
«4
1 1 \_
~2 ~2 2
000
1J 1
4 4 2
000
111
 2 2
000
ill
4 4 2
Расположение основных
векторов

Класс D9d
Группа
Тип
Ola
Ola
Ot
ta
Ota
Ola
Ol
la
с2
000
000
000
000
000
000
000
000
000
000
000
000
000
000
000
000
000
000
000
000
000
000
000
000
000
00 4-
1 1 1
У У 2"
000
ooi
1 1 1
2 2 2
000
оо I
1 1 1
" 2 2
000
00 у
1 1 1
2" У У
000
ool
1 1 1
2" У 2'
000
оо I
1 1 1
2" 2 2
000
jLJ 1
2 2" 
000
оо 1
1 1 1
2 2 2
Расположение основных
векторов
ш
A
СЛ
оо

П родолжение
Группа
D!
10
D
ы
D
Тип
000
000
000
000
000
000
000
1 1 1
2  2
000
000
000
000
000
000
000
111
4 4 2
000
111
222
000
1 3 1
Y 4" 2"
Расположение основных
векторов

Класс
руппа
D\
D\
D,
10
Тин
000
000
«4
«4
00 у
«4
oo 4-
4
000
_3 J_ J^
T 4 2
000
000
«4
00 -1
000
000
00 —
000
000
000
000
001
00-g-
col
000
47
000
22°
000
000
'2 У°
000
000
000
Ho
2 2
00-
00-
4
111
~ ~2 4
1

111
2 2 2
«4
11 3
2 2 
000
l
4 4
000
ool
111
000
«4
Hi
2 2 2"
000
000
l
2 2
00
3
4
111
2 2 4
ooi
1	1
Y 2"
00'
111
2	2 4
000
Расположение основных
векторов

ПРИЛОЖЕНИЯ
Класс Dih
Группа
Тип
Подгруппа
класса
Расположение основных
векторов
о
4ft
D*
u
17
18
ill
19
D20
uih
i12
Jzti
-,13
Jth
D%
Dl
D
12
2ft
13
D2b
U2h
D28
D24
U2h
000
«1
000
«.i
000
oo I
000
«.1
000
ool
000
00 i-
000
ool
000
000
000

332
ПРИЛОЖЕНИЯ
Ромбоэдрическая сингония Dsd и гексагональная сингония D6h
Класс Са
Класс 56
Группа
С1
С2
Тип
г*
с3
000
»¦§
000
с2
000
00 т
00 2
00 з
000
Расположение основных i
векторов ?
Л
С3 "у
/^120° \
а*
Л
\
Сз
\
Группа
S1
Тип
000
000
Расположение основных векторон
аз
а

Класс D3
Группа
D\
D\
D\
D\
D\
D\
Тип
гй
000
¦1
000
1
• 0° T
000
r2
000
00 !.-
о
»4
000
oo 4-
о
2
00-3-
000
и,
000
«4
ооэ
2
оо з-
000
000
«4
000
«4
1
оо 4
000
"з
000
000
000
000
000
оэо
000
Расположение основных
векторов
0,
аз
п
а' 1и2 ' "'
аз
Оз
1
щ

Класс С,
С*:
о;
Расположение основных
векторов
а,к. '

III*II In* I МИН
К л асе 1)ы
Группа
Тип
Г i.
3d
DZd
Dld
Подгруппа
класса
sl
sl
sl
si
sl
s«
000
T
000
«4
000
1 1 1
2 2 2
Расположение основных
векторов
'У
1
о-
а
>
ajk\
а>\\
ф
-Jf
а.
К л а с
Группа
С1
с С зд
Тип
Подгруппа
класса
000
Расположение основных
векторов

336
ПРИЛОЖЕНИЯ
Класс D
nh
Группа
Тин
Подгруппа
класса
Расположение основных
векторов
С1
ЬЗИ
Г3
Г4
°3l>
000
000
000
000
К л ас
Группа
С1
С2
С1
с*
с Се
Тип
rh
Со
000
«4
оо 4
001
ск
000
oof
00 4-
b
00 -f
ооА
Расположение основных
векторов
Се
аз
	аг
Класс C6h
Группа
С1
С\п
Тип
у
11одгруппа
класса
Сзй
С1
С1
с\
000
00 -i-
Расположение основных
векторов
а s%-

ПРИЛОЖЕНИЯ
337
Класс Се
Группа
I
| Подгруппа
Тип ' класса
Ся
Расположение основных
векторов
С1
Класс ?N
000
00 Т
000
001
а,
Подгруппа
класса
Расположение основных
векторов
Г2
r5
c6
Класс
pynna
Тип
Подгруппа
класса
000
000
000
000
000
000
!	I
000 i 000 000
1
13
000
00
oo 4
001
000
00 -i
000
а-.
Расположение основных
векторов
fdT
• в,
22 Зак. 3512. Г. Я. Любарский

338
ПРИЛОЖЕНИЯ
Кубическая сингония Oh
Класс Т
Группа
тг
Т*
тз
Тип
Подгруппа
класса
D\
!
Dl
Q
000
000
000
000
000
Расположение основных
векторов
/
/
и,* а,
А
\
/
и. /
/
о,
"
с
ьиз /^
У
Ц,
1

ПРИЛОЖЕНИЯ
339
: л а с с Th
i Подгруппа
Группа Тип { класса
I
Tl
n
Th
D
гъ.
D
2h
Л15
U2h
Расположение ¦ основных
векторов
000
000
000
000
000
000
7-7
1 h
-.25
U2
2h
000 I 000
000
000
ooa ooo
000
000
¦—.-4—.-. ^,U
/ а3
22*

340
ПРИЛОЖЕНИЯ
Класс
Группа
п
Тип
Подгруппа
класса
Т
тг
000
1 1 1
2 2 2"
Расположение основных
векторов
"з,
Z.U.
/
а,
5
/''¦: а,
000
2 2 2
000
ill ;
2 2 2.1

ПРИЛОЖЕНИЯ
341
Класс О
Группа
О1
О2
о6
о7
о3
О*
о5
о8
Тип
Подгруппа
класса
Т
Т1
Т1
74
Г*
Г2
Г2
г3
С3
000
1 1 1
z z z
3 3 1
Т 4 4
1 1 3
4 4 4
000
1 1 1
4 4 4
000
ooi
Расположение основных
векторов
с* с3
as /У
/
аг
/
\
/
/
и, У %
ъ4^г
\у.
w
о,
23 Зак. 3512. Г. Я. Любарский

342
ПРИЛОЖЕНИЯ.
Класс О/,
Группа
Тип
Подгруппа
класса
О
Расположение основных
векторов
о\
о\
о\
о\
Ч
г;
О1
о1
о2
о2
000
ill
2 2 2
ill
2 2 2
000
О3
О3
О1
О*
О6
О8
000
111
2 2 2
000
111
2 2 2
000

со
¦tf
СО
г
I
г
I
г (I
1
(е + !
-V + V-
<е +
У + 7)A
+ Уг)A
/¦z)(i + yz)(i +
-7>te + V + V-
Уг)(т + У)A +
+ У + У-7)A
+ У)(е + Уг)A
+У+У+7—
1
У) (У) (i — Уг) (i — Уг) \>
- 7) (l 4- У — У + 7) (У —
j G/ V L Г У / \ L 1^ 1 (j' IV
+ У + У + 7-)(г + У +
+ Уг)A + У)(е + Уг)*
fe + V + V+7)(c + V +
+ v = «,
У+ 7)
У+ 7)
У+ 7)
1
а-,
У == ^7
G1 .'
Г (l
.Ш7 —
J-
A + Уг)(Уг)(г + Уг)A + УгЛ
(У + У —7)(i + V —У + 7) J-
Vs) (i + Уг)
r(s + !
УгI
J
iL d + 7 - V + У) (z + 7 +»/ + У) J
G у .*VW
ихнаи'пиФФеом -л

344
ПРИЛОЖЕНИЯ
к
я
¦ч
о
=f
о
о,
С
*~»
II
С*
~1д»
' ''*
Ч1
+
ч1
1
7-
1
1
Ч4
+
4-
т
ч1
1
1
т
+
чг
+
+
+
+
+
<
7-
г—<
+
<
>**
)_
N.
г*
+
II
*—4
+
1
+
г+а
+
V
Ч1
7-
+
*~S
1—1
+
+
7
s
i
Ч*
ч1
1!
J-
Ч1
1
+
ч
+
+
1
f 1)(
¦
ч1
+
ч1
4-
1
i
7
i
Ч"
+
7
<
II

4-
г
ч;
+
7
+
-г
	1
I
>

УКАЗАТЕЛЬ ЛИТЕРАТУРЫ
(в алфавитном порядке)
А. МОНОГРАФИИ, УЧЕБНИКИ И ОБЗОРЫ ПО ТЕОРИИ
ПРЕДСТАВЛЕНИЙ ГРУПП
1.	Ван-дер-Варден Б. Л., Метод теории групп в квантовой механике,
ДНТВУ, Харьков, 1938.
2.	Вей ль Г., Классические группы, их инварианты и представления, ИЛ,
М., 1947.
3.	Мур наган Ф., Теория представлений групп, ИЛ, М., 1950.
4.	Понтрягин Л. С, Непрерывные группы, Гостехиздат, 1954.
5.	Смирнов В. И., Курс высшей математики, т. III, ч. 1, Гостехиздат,
1949.
6.	Соколов А. В. и Широковский В. П., Метод теории групп
в квантовой физике твердого тела, УФН 60, вып. 4, стр. 617, 1956.
7.	Bhagavantam S., Venkatarayudi Т., Theory of groups and
its application to physical problems, Andhra University, 1948
8.	Boerner H., Darstellungen von Gruppen, Berlin, J. Springer 1935.
9.	Weyl H., Gruppentheorie und Quantenmechanik, Leipzig, 1928.
10. Wlgner E., Oruppentheorie und ihre Anwendungen auf die Quanlen-
mechanik und Atomspektren, Braunschweig, 1931.
В. ЛИТЕРАТУРА, ОТНОСЯЩАЯСЯ К ОТДЕЛЬНЫМ ГЛАВАМ
К главе I
1.	Баумгартнер Л., Теория групп, ОНТИ, М. —Л., 1934.
2.	Курош А. Г., Теория групп, Гостехиздат, М. — Л., 1944.
3.	Шмидт О. Ю., Абстрактная теория групп, ОНТИ, М. — Л., 1933.
4.	Speiser A., Die Theorie der Gruppen von endlicher Ordnung, Berlin,
J. Springer, 1927.
К главе II
1.	Белов Н. В., Структурная кристаллография, АН СССР, М., 1951.
2.	Б р э г г У. Л., Кристаллическое состояние, ОНТИ, М. — Л., 1938.
3.	Гельфанд И. М. и Ш а пиро 3. Я., Представления групп вращений
трехмерного пространства и их применения, § 1, УМН, 10, вып. 3, 1955.
4.	Делоне Б., Паду ров Н., А л екс а нд ро в А., Математические
основы структурного анализа, ОНТИ, М. — Л., 1934.
5.	Ландау Л. Д. и ЛифшицЕ. М., Квантовая механика, Гостехиздат,
М. — Л., 1948.
6.	Ландау Л. Д. иЛифшиц Е. М., Статистическая физика, Гостех-
Гостехиздат, М. —Л., 1951.

346	УКАЗАТЕЛЬ ЛИТЕРАТУРЫ
7.	Т а в г с р Б. А. иЗайцев В. Н., О магнитной симметрии кристаллов
ЖЭТФ 30, 564, 1956.
8.	Федоров Е. С, Симметрия и структура кристаллов. Основные работы,
АН СССР, М., 1949.
9.	Шубников А. В., Симметрия, АН СССР, М. — Л., 1940.
10.	Ш у б н и к о в А. В., Атлас кристаллографических групп симметрии, АН
СССР, М. —Л., 1946.
11.	Burkchardt J. J., Die Bewegungsgruppen der Kristallographie, Basel,
1947.
12.	Sc h oenf 1 ie s A., Theorie der Kristallstructur, Berlin, 1923.
13.	Speiser A., Die Theorie der Gruppen von endlicher Ordnung, Berlin,
J. Springer, 1927.
К главам III и IV
1.	В а н-д ер-В а р д е н Б. Л., Современная алгебра, ч. I и'П, Гостехиздат,
М. —Л., 1947.
2.	Компанеец А. С, О нахождении колебательных обертонов много-
многоатомных молекул, ЖЭТФ 10, 1175, 1940.
3.	Шмидт О. Ю., Абстрактная теория групп, ОНТИ, М. —Л., 1933.
4.	Frobenius, Schur J., Berliner Berichte 186, 1906.
5.	L i 111 e w о о d, The theory of group characters and matrix representations
of groups, Oxford, Clarendon Press, 1950.
К главе V
1.	Ландау Л. Д. иЛифшицЕ. М., Квантовая механика, Гостехиздат,
М. —Л., 1948.
2.	Н е г г i n g С, Character tables for two space groups, Journ. of Franklin
Inst. 233, 525, 1942.
3.	Herring C, Effect of time-reversal symmetry on energy bands of
crystals, Phys. Rev. 52, 361, 1937.
4.	Little wood, The theory of group characters and matrix represantations
of groups, Oxford, Clarendon Press, 1950.
5.	Rutherford D. E., Substitutional analysis, Edinburgh, 1948.
6.	Seitz F., Ann. of Math., 37, 17, 1936.
7.	Wintgen O., Zur Darstellungstheorie der Raumgruppen, Math. Ann. 118,
195, 1941.
S. Zia-ud-Din, The characters of the symmetric group of order 11, Proc.
Lond. Math. Soc. B), 39, 200, 1935.
S. Z i a - ud - D i n, The characters of the symmetric group oi order 12, 13, Proc.
Lond. Math. Soc. 39, 347, 1935.
К главе VI
1.	Волькенштейн М. В., Эльяшевич Н. А., Ст еп ано в Б. И.,
Колебания молекул, Гостехиздат, М.— Л., 1949.
2.	Компанеец А. С, О нахождении колебательных обертонов много-
многоатомных молекул, ЖЭТФ 10, 1175, 1940.
3.	Ландау Л. Д. и Лифшиц Е. М., Квантовая механика, Гостехиздат,
М, —Л., 1948.
4.	Ландау Л. Д. и Пятигорский Л. М., Механика, Гостехиздат,
М. —Л., 1940.
5.	Barriol J., Applications de la theorle des groupes a l'etude des vibra-
vibrations moleculaires et cristallines, Paris, 1947.
6.	R о s e n t h a 1 J. E., Murphy О. Н., Group theorie and the vibrations
of polyatomic molecules, Rev. Mod. Phys. 8, 317, 1936.

УКАЗАТЕЛЬ ЛИТЕРАТУРЫ	347
К главе VII
1.	Л а н д а у Л. Д., Фазовые переходы второго рода, Sow. Phys. 11, 545, 1937.
2.	Л а ндау Л. Д. и Лифшиц Е. М., Статистическая физика, Гостех-
издат, М. —Л., 1951.
3.	Л е в и ч В. Г., Введение в статистическую физику, Гостехиздат, М.—Л.,
1954.
4.	Лифшиц Е. М., К теории фазовых переходов-второго рода, ЖЭТФ 11,
255, 269, 1941.
К главе VIII
1.	Борн М. и Гепперт-Мейер, Теория твердого тела, ОНТИ, М. — Л.,
1938.
2.	Г е р м а н В. Л., Некоторые теоремы об анизотропных средах, ДАН 48,
55, 1945.
3.	Ферми Э., Молекулы и кристаллы, ИЛ, М., 1947.
4.	Barrio! J., Applications de Ja theorie des groupes a 1'etude des vibrations
moleculaires et cristallines, Paris, 1947.
5.	В о u с k a r t L. P., S m о 1 u с h о w s k i R., W i g n e r E., Theory of
Brilloin zones and symmetry properties of wave functions in crystals, Phys.
Rev. 50, 58, 1936.
6.	During W., Z e h 1 e r V., Oruppentheoretische Untersuchung der Elec-
tronenbander im Diamantengitter, Ann. der Phys. 13, 214, 1953.
7.	Elliot R., Theory of the effect of spin-orbit coupling on magnetic reso-
resonance in some semiconductors, Phys. Rev. 96, 266, 1954.
8.	H e r r i n g C, Role of low-energy photons in thermal conduction, Phys.
Rev. 95, 954, 1954.
9.	Herring C, Effect of time-reversal symmetry on energy bands of
crystals, Phys. Rev. 52, 361, 1937.
10.	Herring C, Accidental degeneracy in the energy bands of crystals, Phys.
Rev. 52, 365, 1937.
11.	Jahn, Zeitschr. d. Kristallographie 98, 191, 1937.
12.	P a r m e n t e r R. H., Symmetry properties of the energy bands of the zine
blende structure, Phys. Rev. 100, 573, 1955.
К главе IX
1.	Чеботарев Н. Г., Теория групп Ли, Гостехиздат, М. — Л., 1910.
2.	Эйзенхарт Л. П., Непрерывные группы преобразовании, ИЛ, М.,
1947.
К главе X
1.	В и ленки н Н. Я., К теории присоединенных сферических функций
ДАН Ш, 742, 1956.
2.	Г е л ь ф а н д И. М. и Ш а п и р о 3. Я., Представления группы враще-
вращений трехмерного пространства и их применения, УМН 10, вып. 3, 1955.
3.	Bell D. С, Group theory and crystall lattices, Rev. Mod. Phys. 26, 311.
1954.
4.	Lit tie wood, The theory of group characters and matrix representation s
of groups, Oxford, Clarendon Press, 1950.
5.	Opechowski W., Sur les groupes cristallographique «doubles», Physica
7, 552, 1940.

348	УКАЗАТЕЛЬ ЛИТЕРАТУРЫ
К главе XI
1.	Biedenharn LC, В 1 a 11 J. M., Rose M. E., Properties of Racali
coefficients, Rev. Mod. Phys. 24, 249, 1952.
2.	Racah G. Theory of Complex Spectra 1, 11, Phys. Rev. 61, 186, 1942; 62,
438, 1942.
К главе XII
1.	Блохинцев Д. И., Основы квантовой механики, Гостехиздат, М. — Л.,
1949.
2.	Л а н д а у Л. Д. и Л и ф ш и ц Е. М., Квантовая механика, Гостехиздат,
М. —Л., 1948.
К главе XIII
1.	Берестецкий В. Б., Долгинов А. 3., Мартиросян К. А.,
Угловые волновые функции частиц со спином, ЖЭТФ 20, 527, 1950.
2.	Г е л ь ф а н д И. М. и Шапиро 3. Я., Представления группы вращений
трехмерного пространства и их применения, УМН 10, вып. 3, 1955.
3.	Петрашень Г. И., Динамические задачи теории упругости в случае
изотропной сферы, Уч. зап. ЛГУ 114, вып. 17, 1949.
К главе XIV
1.	Га йт л ер В., Квантовая теория излучения, Гостехиздат, М. — Л., 1940.
2.	Д а в ы д о в А. С, Теория поглощения света в молекулярных кристал-
кристаллах, Изд. АН УССР, Киев, 1951.
3.	Л а н д а у Л. Д. и Л и ф ш и ц Е. М., Квантовая механика, Гостехиздат,
М. —Л., 1948.
4.	С a b a n n e s J., Introduction a I'etude de l'effet Raman dans les cristaux,
Rev. Scient. n° 3205, fevrier 1942.
5.	PI aczek Q., Rayleigh Streuung und Raman Effect, Handb. der Radiologie
1V/2, Leip2ig, 1934.
6.	Tisca, Zur Deutung der Spectren Mehratomiger Molekiile, Zeits. Phys.
82, 48, 1933.
К главе XV
1.	Гельфанд И. М. и Наймарк М. А., Унитарные представления
классических групп, Труды Матем. ин-та им. Стеклова 36, 1950.
2.	Гельфанд И. М. и Наймарк М. А., Унитарные представления
группы Лоренца, Изв. АН СССР, матем. 11, 411, 1947.
3.	Наймарк М. А., Линейные представления группы Лоренца, УМН 9,
4, 19, 1954.
4.	Румер Ю. Б., Спинорный анализ, ОНТИ, М.—Л., 1936.
5.	В a d e W. L., J e h I e H., An introduction to spinors, Rev. Mod. Phys. 25,
714, 1953.
6.	W i g n e r E. P., On unitary representations of inhomogeneous Lorentz
group, Ann. of Math. 40, 149, 1939.

УКАЗАТЕЛЬ ЛИТЕРАТУРЫ	31У
К главе XVI
1.	Ахиезер А. И. и Берестецкий В. Б., Квантовая электродинамика,
Гостехиздат, М., 1953.
2.	ГельфандИ. М. и Яглом А. М., Общие релятивистски инвариантные
уравнения и бесконечномерные представления группы Лоренца, ЖЭТФ
18, 703, 1948.
3.	Гельфанд И. М. и Я г л о м А. М., Теорема Паули для общих реля-
релятивистски инвариантных уравнений, ЖЭТФ 18, 1096, 1948.
4.	Гельфанд И. М. и Яглом А. М., Зарядная сопряженность для об-
общих релятивистски инвариантных уравнений, ЖЭТФ 18, 1105, 1948.
5.	Паули В., Релятивистская теория элементарных частиц, ИЛ, М., 1947.
К главе XVII
1.	Ландау Л. Д. иЛифшиц Е. М., Квантовая механика, Гостехиздат,
М. — Л., 1948.
2.	В 1 a 11 J. M., The angular distribution of scattering and reaction cross-
sections, Rev. Mod. Phys. 24, 208, 1952.

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Алгебра спинорная 269 и д.
—	тензорная 194 и д., 271 и д.
Базис в пространстве спиноров 190
—	канонический 73
	представления группы враще-
вращений 176
Базисы пространства взаимно-кон-
травариантные 63
Векторы обратной решетки 84
	 основные 84
—	основные группы векторов 30
Вес неприводимого представления
группы вращений 175
Вращение пространства 15
	, матрица оператора вращения
	, произведение вращений 15
Вычисление сопряженных перестано-
перестановок 14
Группа 7
—	абелева 7
—	бесконечная 7
—	векторная (группа векторов) 29
и д.
	, векторы основные 30
	, группа симметрии ее 31
	 двумерная 30
	 дискретная 30
	 одномерная 30
	, параллелепипед основной 31
	, сингония ее 31
	, тип ее 33, 35, 36
	, — гранецентрированный 35, 36
	, — объемноцентрированный 35,
36
	, — простой 35, 36
	 трехмерная 30
	, элемент симметрии 31
—	—, ячейка элементарная 31
—	векторов см. Группа векторная
Группа вращений 15 и д.
—	евклидова 20 и д.
—, единичный элемент 7
—	икосаэдра (К) 25
—	коммутативная 7
—	конечная 7
	, порядок ее 7
	, представление регулярное
—	кристалла 37
—	Ли 158
	, размерность ее 158
—	Лоренца 260
	, законы сохранения 294
	, инфинитезимальные операторы
261, 262
	, полная 260 и д.
—	¦—, представление векторное 2(il
	, представления неприводимые
263
	 собственная 260
—	многосвязная 156, 157
—	накрывающая универсальная 1Г>7
—	направлений кристалла 38
—	октаэдра (О) 24
—	перестановок 13 и д.
—	полная ортогональная 19 и д.
	, классы сопряженных эле-
элементов 20
	, элементы второго рода 1!)
	—, — первого рода 19
—	произведение групп 67, 68
—, разбиение на классы сопряжен-
сопряженных элементов 9
—	симметрии кристалла 38
	 векторной группы 31
	куба 28, 29
	правильной п-угольной призмы
27, 29
—	— тетраэдра 28
—	точечная 22
	второго рода 22, 26 и д.
—	C»h 26, 29

пи'.дмктный указан:Л1.
351
Группа точечная второго рода Cnv
26,	29
	Dnd 27, 29
	Dnh (группа симметрии
правильной л-уголыюй призмы)
27,	29
	Оь (группа симметрии
куба) 28, 29
	Та (группа симметрии
тетраэдра) 28
	Y\ 29
	первого рода 22, 23 и д.
	 икосаэдра (Y) 25
	октаэдра (О) 24, 25
	тетраэдра (Т) 23, 25
	Dn 23, 25
		^ 99 91!
—	трансляций 20, см. также Группа
векторная
—	уравнения Шредингера 225
—, элемент обратный 7
	, сопряженный данному 8
Группы гомоморфные 11
—	изоморфные 11
—	первого рода бесконечные 25
—	пространственные 37 и д., 318 и д.
сингония гексагональная 332
и д,
—	кубическая 338 и д.
—¦ моноклинная 318 и д.
—	ромбическая 320 и д.
—• ромбоэдрическая 332 и д.
—	тетрагональная 325 и д.
—	триклинная 318
Длина цикла перестановки 13
Законы сохранения 227, 229, 230, 232,
289, 292, 294
Звезда представления 86
	 неприводимая 86
Звук в кристаллах 141 и д.
	—, края полосы частот 143
Зона Бриллуэна 84
Инверсия времени 297 и д.
—	пространства 19
	, определитель ее 19
Индекс подгруппы 10
Класс левый смежный подгруппы 9
—	правый смежный подгруппы 9
Классификация представлений непри-
неприводимых группы вращений 171 ид.
—	состояний 233 и д.
Классы кристаллические 38
—	сопряженных вращений 18
	 перестановок 15
	 элементов 9
	¦ полной ортогональной груп-
группы 20
—	эквивалентных представлений
группы 43
Колебание атомов молекулы главное
95
	, нахождение 97
	СНС13 108 и д.
Координаты симметрические 97
—	события четырехмерные 259
Коэффициенты Клебша — Гордана 203
	, свойства 211 ид.
	, связь с коэффициентами
Рака 217
—	Рака 216, 342
	, вычисление 222
	, свойства 218 и д.
	, связь с коэффициентами Клеб-
Клебша—Гордана 217
Кристалл 37 и д.
—, группа его 37 и д.
—, — направлений его 38
—, — симметрии его 38
—, направления эквивалентные 37
—, тензор диэлектрической постоян-
постоянной 149
•—, — упругости 150
Матрица оператора вращения 17
—	представления сопряженного 03
—	рассеяния 305 и д.
—	унитарная 19
Матрицы представлений неприводи-
неприводимых группы вращений 177
Направления в кристалле эквивалент-
эквивалентные 37
Оператор вращения 18
—	Гамильтона 224
—	индуцированный 47
—	инфинитезимальный 159, 160
—	унитарный 18
—	энергии 229
Операторы инфинитезимальные груп-
группы Лоренца 261, 262
—	проекций импульса 230
Ось точечной группы 22
	 двусторонняя 22
	 односторонняя 22
—	, порядок ее 22
—	узлов 16
Отражение скользящее 21

352
Ш>1!ДМ1'Л'!1ЫЙ УКАЗАТЕЛЬ
Параллелепипед основной группы
векторов 3
Перестановка нечетная 15
—, цикл ее 13
—	четная 15
Переходы фазовые первого рода
111
	 второго рода 111
Плоскость скольжения 21
Поглощение света дипольное 248
—	— квадрупольное 248, 255
	 мультипольное 248
Подгруппа 9
—, индекс ее 10
—, левый смежный класс ее 9
—	перестановок альтернативная 15
—t правый смежный класс ее 9
—	циклическая 10
Подпространство неприводимое 72
—	топологическое 154
Подчинение сингоний 37
Поле векторное 236
—	скалярное 236
—	спинорное 236, 238, 239
—	тензорное 236
—	физической величины 236
Полоса частот звука в кристалле
143
	—, края ее 143
—	энергетического спектра кристалла
146
	, соприкосновение полос
146, 147
Порядок группы конечной 7
—	шаровой функции 237, 238
Правила отбора для поглощения света
атомами и молекулами 250 и д.
Представление группы 41
	 активное 117
—	— векторное 42
	дифференцируемое 159
—	¦— единичное 42
	, звезда его 86 и д.
—	— индуцированное 47
	инфинитезимальное 161 и д.
	 колебательное 105
	, характер его 105
	конечной 151, 153, 154
	 регулярное 55
	Ли инфинитезимальное 167
и д.
	 малое 87
•— — механическое 96
	/я-значное 157
	нагруженное 89 и д.
—	— неприводимое 49
	 пассивное 117
Предстаи.'к'иш: группы полной орто
тональной некторное 200
	 псевдовекторное 200
	 — — псевдотензорное 200
	, порожденное пространством
189"
	, произведение представлений (id
и д.
—	—, размерность его 41
—	¦— сопряженное 62, 63 и д.
•	, матрица его 63
	, степень его антисимметриче-
антисимметрическая л-я 71
	, ¦	симметрическая л-я 71
	 точечной 42
—	— унитарное 43
—	— физически-неприводимое 113
	, характер его 56
Представления групп вещественные
65
	, критерий вещественности
67
	зацепляющиеся 281
	компактных 155
	 локально компактных 155
—	— неприводимые 47
—	— приводимые 46
•	пространственных 86
—	— точечных двузначные 201 и д.,
317
—	— — неприводимые 80 и д.
—	— трансляций 83 и д.
—	— эквивалентные 43
—	группы вращений неприводимые
базис кононический 176
вес 175
матрицы 177 и д.
произведения 186 и д.
свойства 182 и д.
—	— —, связь с представлениями
группы Лоренца 267
—	— Лоренца неприводимые 263,264
—	бесконечномерные 264-
—	, произведение 265 и д.
—	комплексно-сопряженные
267
—	полной 275
—	— — псевдоскалярные 277
—	, связь с представлениями
группы вращений 267
—	скалярные 277
—	— перестановок 77 и д.
—	неприводимые 77
—	— поворотов неприводимые 170
—	— полной ортогональной непри-
неприводимые 199 и д.

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
353
Произведение вращений пространства
—	групп 67, 88
—	представлений 60 и д.
	группы вращений 186 и д.
—	функций на группе скалярное 50
—	элементов группы 7
Производная оператора 159
Пространство отклонений молекулы
Уо
Псевдоспинор 200
Псевдотензоры 277
Разбиение группы на классы сопря-
сопряженных элементов 9
Разложение приводимого представле-
представления на неприводимые 72
—	пространства полное 72
Размерность группы Ли 158
—	представления 41
Распределение продуктов ядерной
реакции 309 и д.
Рассеяние света комбинационное 248,
256
Расщепление представления 48
Решетка Браве 40
	, узлы ее 40
Свертка спинора 191
	, операция подъема индекса 191
	, — упрощения 191
—	тензора 194
Свойства коэффициентов Клебша —
Гордана 211 ид.
—	неприводимых представлений
группы вращений 182 и д.
Связь между представлениями группы
Лоренца и группы вращений 267
Симметрия кристаллов 37 и д.
Сингония гексагональная 31 и д.,
332 и д.
—	квадратная 31 и д.
—	кубическая 338 и д.
—	моноклинная 31 и д., 34, 318 и д.
—	ортогональная 31 и д.
—	ромбическая 31 и д., 320 и д.
—	ромбоэдрическая 31 ид., 332 и д.
—	тетрагональная 31 и д., 325 и д.
—	тригональная 31 и д.
—	триклинная 31 и д., 318
Событие 259
—, координаты его четырехмерные
259
Соответствие элементов двух групп
изоморфное 11
Соприкосновение энергетических по-
полос кристалла 146, 147
Состояния атома комбинирующиеся
249
Спин 294 и д.
Спинор ве.са / 189, 200, 269
— индексы ковариантные 191
—, — контравариантные 191
—, ранг 190, 270
—, свертка его 191
—, умножение спиноров 191
—, упрощение 271
Способ вычисления сопряженных пе-
перестановок 14
Степени представлений симметризо-
ванные 68 и д.
Степень представления антисимметри-
антисимметрическая 71
	симметрическая 71
Столкновение двух частиц 305
Сумма представлений 48
Схема Юнга 77 и д.
Тензор 294
—	диэлектрической постоянной кри-
кристалла 149
—	метрический 271
—, ранг 194, 273
—, свертка 194
—, упрощение 274
—	упругости кристалла 150
Тензоры 277
—	в кристаллах 147 и д.
Теорема Бирсайда 55
—	Паули 300
—	полноты 54
Теория представлений 41
—	характеров 56 и д.
Теплопроводность кристалла 147 и д.
Точечная группа, представление ее 42
Трансляция 20, 21, 29 и д.
Умножение спиноров 191
Упругость кристалла 147 и д.
Уравнение Дирака 300 и д.
—	Шредингера 224
	инвариантное относительно опе-
оператора 225
	, группа его 225, 229
Уравнения инвариантные
тельно вращений 240
—	Максвелла 244
—	релятивистски-инвариантные 280
Уровни электронные в кристалле 145
Функции на группе, произведение
скалярное 50
—	шаровые 237
	основные 237
	, порядок 238
относи-

354
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Функционал усреднения функций на
группе 45
	бесконечной 151, 152
Функция волновая 278
—	Лагранжа 286 и д.
	 в симметрических координатах
101 и д.
—	многозначная на группе бесконеч-
бесконечной 156
—	на группе 45, 161
	, функционал усреднения 45
Характер представления 56
	 колебательного 105
	, свойства 56, 57
Характеры неприводимых предста-
представлений групп перестановок 314 ид.
	точечных 316
Цикл перестановки 13
	, длина его 13
Частоты собственные молекулы 104
	системы 96
	, вычисление 97 и д.
Число независимых компонент тен-
тензора' кристалла 148
Эквивалентность представлений 43
и д.
Электропроводность кристалла 147
и д.
Элемент группы единичный 7
	, обратный данному 7
	 сопряженный данному 8
Ячейка элементарная группы векто-
векторов 31

Любарский Григорий Яковлевич
ТЕОРИЯ ТРУПП И ЕЕ ПРИМЕНЕНИЕ В ФИЗИКЕ
Редактор М.-М. Горячая
Техн.|редактор Е. А. Ермакова
Корректор И. С. Цветкова
Сдано в набор 8/IX 1958 г.
Подписано к печати 10/XII 1958 г.
Бумага бОх 92/16. -*-Физ.'иеч. л. 23,25. Усл. печ. л. 22,25.
Уч.-изд. л.' 22,37. Тираж 5000. Т-11575.
Цена книги 13 pi 20 к. Заказ 3512.
Государственное издательство физико-математической
литературы
Москва, В-71, Ленинский проспект, 15
Типография № 2 им. Евг. Соколовой
УПП Ленсовнархоза.
Ленинград, Измайловский пр., 29.