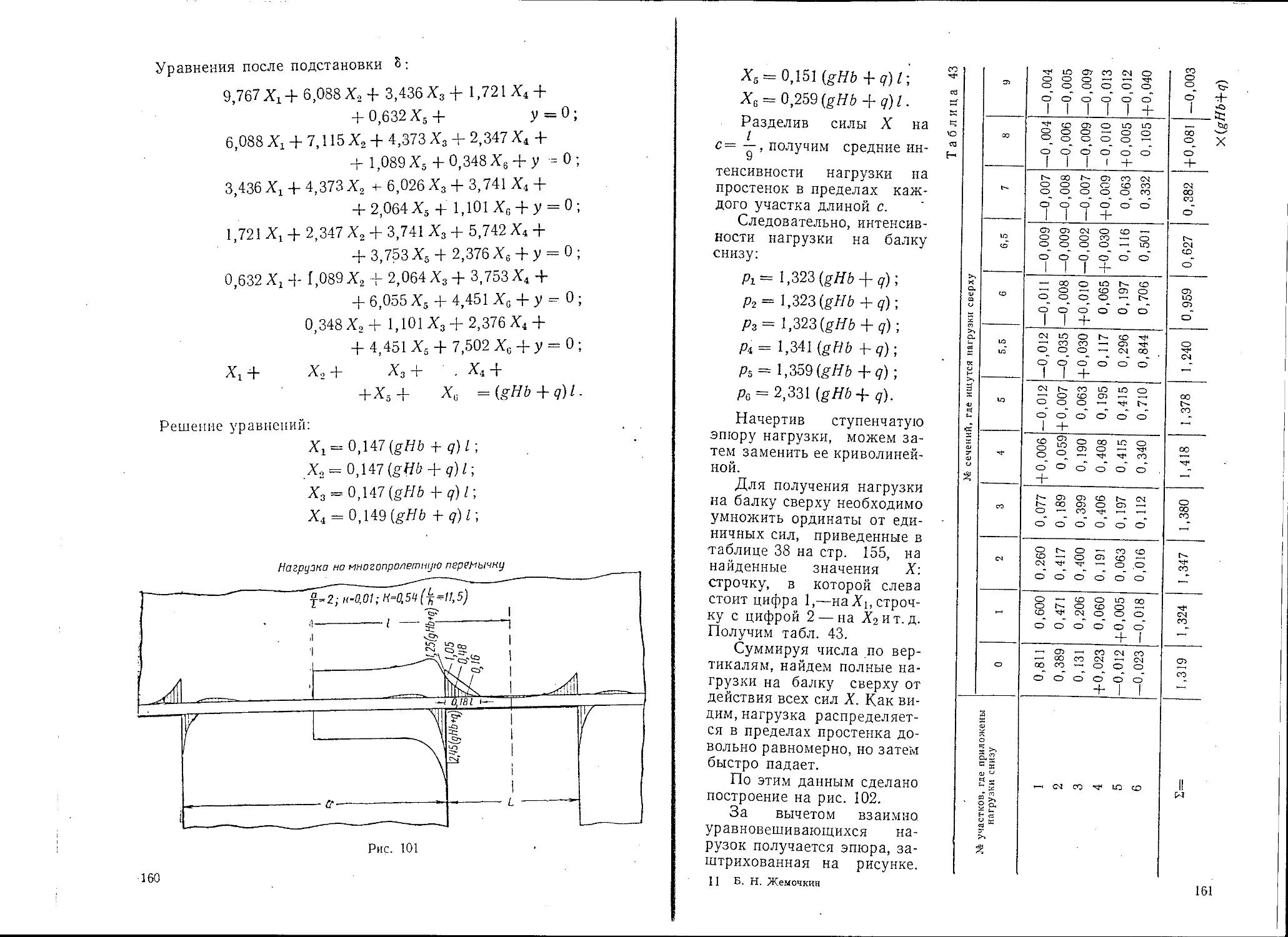
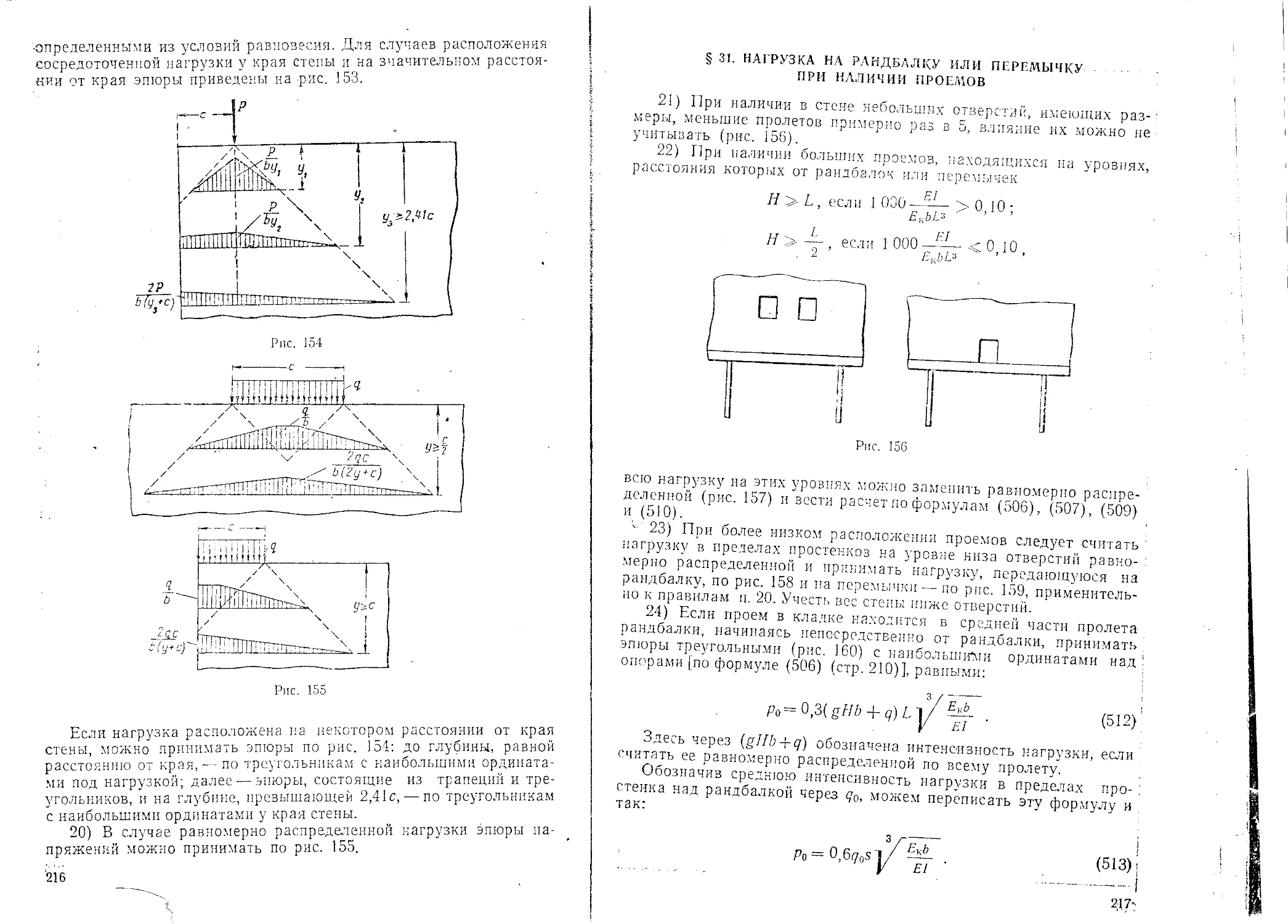
Text
Б. Н. ЖЕМОЧКИН
проф. д-р техн, наук
6 OZ
Щ-53
РАСЧЕТ РАНДБАЛОК
И ПЕРЕМЫЧЕК
' лс пр^.гТ^гй. ;
, OC\^“TXj//OO.*c<:rX’ ’ ’ »
Atz':5Г>:ьс^, ngn ГЬВтюградонд. 32j
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ЛИТЕРАТУРЫ ПО СТРОИТЕЛЬСТВУ, АРХИТЕКТУРЕ
И СТРОИТЕЛЬНЫМ МАТЕРИАЛАМ
Москва — I960
Научный редактор инж. В. Л. Шадурский
Книга посвящена вопросу об определении нагрузок на ранд-
балки и перемычки,
. Разобран ряд частных случаев: рандбалки и перемычки
при стенах ограниченной высоты, наличие отверстий в стенах
над рандбалками. и перемычками, влияние’ сосредоточенных
сил, приложенных к стенам, рядовые перемочки и т. д.
Задачи, приведенные в книге, решаются методами' теории
упругости.. .
Особая глава содержит рекомендации для расчета. Пред-
лагаемые способы расчета настолько просты, что могут непо-
средственно, без затруднений применяться на практике.
Книга предназначена для инженеров-проектировщиков,
строителей и специалистов, работающих в области теории
упругости,
ВВЕДЕНИЕ
Под рандбалкой подразумевается достаточно длинная,
многопролетная балка, лежащая на колоннах и поддерживающая
кирпичную или каменную кладку стены (рис. 1,а). Перемыч-
кой называется короткая балка, перекрывающая отдельный
пролет.
В настоящей книге не охватывается полностью вопрос о расче-'1
те рандбалок и перемычек. Мы ставим своей целью исключительно,
определение нагрузок на них, без чего нельзя находить изгибаю-
щие моменты. Проектирование же делается общепринятыми спо-л
собами, однако в конце работы немного сказано о подборе сечений.
Те результаты, которые мы получим, будут относиться не толь-
ко к случаям, когда стена состоит из малых элементов (кирпичей
или камней)-, но и к случаям кладки из крупных блоков. Однако
они не будут приложимы к панельным конструкциям.
Вопрос об определении нагрузок на перемычки при проектиро-
вании жилых зданий, имеющих ;в стенах только небольшие отвер-
стия, является мало актуальным.
Но в зданиях общественного и промышленного назначения в.
случае, если в их стенах имеются отверстия значительных размер
ров, приходится определять нагрузки на рандбалки и перемычки.'
Исследование, приведенное в книге, носит теоретический харак-
тер. Экспериментов в этой области очень мало, опыты до сих пор
насчитываются единицами. Оно и понятно: организация опытов с
конструкциями в натуральную величину представляет большие за-
* з
труднения вследствие их громоздкости; -модели же не могут дать
исчерпывающих данных. ' ’
Кроме того, проверить экспериментально решения для всех ча-
стных случаев, которые здесь- разобраны, просто невозможно. Но
то, что имеющиеся опыты подтверждают основные положения тео-
рии -в простейших случаях, вызывает доверие к выводам и в дру-
гих случаях.
__Раньше принималось, что эпюры нагрузок на ранд балки и пере-
мычки имеют вид треугольников с наибольшими ординатами в се-
фединах пролётовдрис. 2), причем эпюры не зависят от высоты
кладки.^и _от„нагрузок, передающихся на стену.
Рис. 2
Еще вД.9.37~г.1-автором-была доказана ошибочность такого
взгляда; им было найдено, что наибольшие ординаты эпюр не в се-
рединах пролетов, а, наоборот, у опор. Это вполне согласовывалось
с опытами, которые производились в то время. Ссылка -на необхо-
димость принимать эпюры с наибольшими ординатами у опор име-
лась и в книге проф. Л. И. О и и щ и к а1 2.
Здесь мы займемся более подробным исследованием вопроса,
рассмотрим целый ряд частных случаев. В результате будем в со-
стоянии дать некоторые практические рекомендации для проекти-
рующих (см. главу V). Очень важно, чтобы эти рекомендации бы-
ли достаточно простыми и указывали бы на приемы, вполне до-,
ступные для применения, хотя бы они основывались на очень слож-
ных математических выкладках. ;
Задачи, нами разбираемые, целиком относятся к области тео-
рии упругости. Поэтому настоящая книга, с одной стороны, имеет
назначение оказать посильную помощь проектирую-
щим, но, с другой стороны, она может рассматриваться как сбор-
ник решений. таких задач теории упругости, в которых учи-
тывается совместная работа.разнородных мате-
риалов (балка и кладка).
Исследование будем вести в таком порядке: сначала разберем
более простой случай рандбалки (рис. 3,п), предполагая ее с бес-
конечным числом пролетов и рассматривая средние пролеты.
1 См. Б. Н. Жем очкин, Плоская задача расчета бескОнечно-ДЛикйой бал-
ки на упругом основании, М„ ВИА, 1937.
2 Л. И. ОнищиК, Каменные конструкции, Сгройиздат, 1939.
4
Далее перейдем к перемычкам.
Однако прежде чем говорить об однопролетных ’ перемычках,'
рассмотрим предварительно балки, проходящие непрерывно над
проемами и простенками (рис. 3,6). Такие балки по существу так-
же относятся к рандбалкам, но мы назовем их для удобства мно-
гопролетными перемычками. .
Основное различие между рандбалками и мнбгопролетнымй
перемычками мы будем полагать в том, что рандбалки имеют уз-
кие опоры (стальные или железобетонные), а потому опорные
°) 6)
Рис. 3
реакции в большинстве случаев можно принимать сосредоточен-
ными; у многопролетных же перемычек опорами служат более или
менее широкие простенки, выполненные из кладки, и, следователь-
но, опорные реакции являются распределенными.
Хотя многопролетные перемычки иногда и могут применяться
в строительстве, но нами они здесь рассматриваются преимущест-
венно для того, чтобы на них более просто исследовать разнооб-
разные случаи соотношений размеров и жесткостей и'сделать соот-
ветствующие выводы. Эти выводы мы отнесем и к однопролетным
перемычкам. Очевидно, что работа многопролетных перемычек, не
должна существенно отличаться -от работы однопролетных балок,
надежно заделанных концами в кладку, так как в пределах про-
стенков многопролетные балки на изгиб почти не работают.
Тем не менее мы проверим свои выводы на ограниченном числе
свободно лежащих, а также заделанных концами однопролетных
перемычек (рис. 3,в и 3,г). . . :
Наконец, рассмотрим еще случай отсутствия балок, когда 'про-
емы перекрыты рядовыми перемычками (рис. 3,6). , .... л?..г:
'.<5
Большой интерес представляет также исследование ряда допол-
нительных задач: влияние касательных напряжений, влияние высо-
ты стены над перемычкой, учет сосредоточенной вертикальной на-
грузки при малой высоте стены, влияние проемов, определение
напряжений в кладке и т. п.
Такие исследования мы проведем в основном “для рандбалок,
где это сделать проще (рис. 4), и полученные выводы распростра-
ним и на перемычки, сделав для них только ограниченное число
проверок. . ' ,
К тому же для -перемычек можно лишь получить самые общие
данные: расположение нагрузок и проемов бывает самое разнооб-
разное.
Не исключено, что на практике появится необходимость в ре-
шении иных задач, сходных с разобранными здесь. Чтобы облег-
чить решение таких задач, мы будем в дальнейшем изложении да-
вать подробные выкладки и приводить примеры с указанием хода
вычислений, В первых примерах даже будут даны 'практические
указания по суммированию рядов.
Конечно при чтении, если в том не встретится надобности, та-
кие места могут быть пропущены.
Здесь необходимо сделать следующее замечание.
Решения, приведенные в дальнейшем изложении, получены ме-
тодами теории упругости, рассматривающей все тела как идеально
упругие. Между тем при значительных напряжениях строительных
материалов наблюдается отклонение от закона Гука о пропорцио-
нальности между напряжениями и деформациями.
Поэтому при больших напряжениях, близких к предельным, на-
грузки на рандбалки и перемычки должны отличаться от найден-
ных в настоящем исследовании, вследствие чего при расчете кон-
струкций по разрушающим нагрузкам неизбежно должны возни-
кать некоторые затруднения.
Однако если принять, что более слабым звеном конструкции
должны быть рандбалки и перемычки, т. е. принять, что при раз-
6
рушающей нагрузке в первую очередь должны исключаться из ра-
боты рандбалки и перемычки, а не кладка, то нагрузку на них сле-
дует определять в упругой стадии работы кладки, подбор же их
сечений можно делать по разрушающим нагрузкам. Но, конечно,
жесткость рандбалок и перемычек необходимо принимать при на-
пряжениях в них, близких к предельным.
Таким образом, можно вполне пользоваться приводимыми да-
лее данными, но все же не мешает иметь в виду приближенность
расчетов.
(
ГЛАВА I
РАНДБАЛКИ ПРИ СТЕНЕ БОЛЬШОЙ ВЫСОТЫ
§ L НАГРУЗКА НА РАНДБАЛКУ
Разберем сначала простейший случай, когда стена, ' опираю-
щаяся на рандбалку, имеет достаточно большую высоту (рис. 5).
К верхнему краю стены приложена равномерно распределенная
нагрузка.
а) Основные данные
Примем начало координат над одной из опор и направим ось X
вправо и ось У вверх. Реакции опор будем считать сосредоточенны-
ми. Касательными напряжениями по линии контакта рандбалки и
стены будем пренебрегать.
Введем следующие обозначения:
I — полупролет;
8
L — пролет (в дальнейшем так будет обозначаться отверстие
в свету); -
Н — высота стены;
b — толщина стены;
q— равномерно распределенная нагрузка, приходящаяся на
единицу длины, по верхнему краю стены;
g—собственный вес кладки в единице объема;
р —нагрузка на единицу длины, передающаяся на рандбалку
от кладки;
— нормальные напряжения в кладке над рандбалкой в го-
ризонтальном направлении;
ау—нормальные напряжения в вертикальнОхМ направлении;
т— касательные напряжения;
и — перемещения в кладке в горизонтальном направлении;
v — перемещения в вертикальном направлении (положитель-
ные вверх);
w — ‘перемещения (прогибы) рандбалки (положительные
ВНИЗ);
£к— хМодуль упругости кладки;
EI— жесткость рандбалки.
б) Функция напряжений
Основное уравнение (уравнение совместности) плоской задачи
имеет вид1:
[. О + =о
ах4 dx2dy2 dyi
(1)
Входящая в уравнение функция <?—так называемая «функция
напряжений».
Напряжения выражаются через эту функцию так:
__ д2?
у дх2 ’
д2ъ ,
Т = — —+ gX .
дхду
(3)
(4)
(знак у gx поставлен с учетом направления осей).
Зададимся функцией - в виде следующего тригонометрическо-
го ряда с гиперболическими функциями и с добавлением полинома
2 и 3 степени:
ОО
<Р = COS (ах) [(?! sh (ау) + С2 ch (ау)' + С3у sh (ау) + С4у ch (ау)] +
+ D-.X2 + Д:;ху + D-y2 + Dsx3 + D„x2y + D10xy2 + Duy2. (5)
i См. Б. H. Же м очкин, Теория упругости, Госстройиздат, 1957.
9
Здесь sh и ch — гиперболические функции; — коэффи-
циенты, зависящие от порядковых номеров членов; D — постоян-
ные коэффициенты.
Через а обозначено:
Легко убедиться, что функция принятая в таком виде, удов-
летворяет уравнению (1).
. Производя дифференцирование, найдем напряжения:
~ JL? — V a cos (а х) [Cj sh (а у) + C2ch (а у) -ф
ду2 I [
1
+ С3у sh (а у) + С4у ch (а у)] + 2 [С3 ch (х у) 4- C4sh(xy)] | +
4-2D74-2£>10x4-6Dny; (7)
а = Д2. = — У а2 cos (а х) [С sh (а у) + С2 ch (а у) +
у дх%
1
4- С3у sh (а у) + С4у ch (а у)] 4- 2 £>5 4~ 6 Dsx 4- 2 D3y ; (8)
со
т =----—р gx = X1 а sin (а х)|а {Сх ch (а у) ф- С2 sh (а у) +
дхду 4—1 I
4- С3у ch (а у) + С4у sh (а у)] 4- [С3 sh (я у) 4-
+ C4ch(xy)]|—Db — 2D}x- 2Z?10y 4- gx. (9)
В дальнейшем нам придется иметь дело с перемещениями. По-
этому найдем и их.
Перемещение и определим из условия:
= -jr (°ж — Rj) • (10)
ОХ г* [с
Подставляя сюда значения <*х и и производя интегриро-
вание, получим:
со
и •-=> — V sin (а х) !(1 4~ [1) а [Сх sh (а у) 4~ С2 ch (а у) +
4- С3у sh (а у) + С4у ch (а у)] + 2 [С3 сh (7. у) 4- С4 sh (а у)]| 4-
4~ ту“ [2 Z)7 4~ Ч* 6 ОцУ (2 4~ 3 D$x 4-
Ек
+ 2^)14-^ (у), (Н)
где Ei (у) —некоторая функция от у; появляющаяся при интег-
рировании, . .
10
При перемене знака у х в силу симметрии должен , меняться
знак и у и. Отсюда следует, что:
Л(Л = 0. (12)
Для перемещения v используем условие:
еу = ~ = 7- (°У — РЛс) • (13)
йу £к
После подстановки и.ау и интегрирования:
со
v *=----У cos (ах) I (1 + р) а [Cj ch (ау) 4- С2 sh (ау) 4~
Ек I
1
4- С3у ch (а у) + С4у sh (а у)] — (1 — у) [С3 sh (а у) +
+ ch (а у)] | -|- ~ [2 £)5 + 6 Dsx + /Ху — р (2 D7 4~
J Ек
4- 2 D10x 4- 3 Duy)] 4~ (Л)» (14)
причем Е2(х) может быть или функцией х, или постоянной вели-
чиной.
Докажем, что Е2(%) постоянная величина. Вспомним уравнение
теории упругости:
dy "I" дх Ек '
Если подставим сюда значения v и т и сделаем сокращения,
го придем к уравнению:
4~ ~~ [6 £)п — 2 р 4- 4 (1 + у) О9 — 2(1 4- у) g] +
дх Ек
+ ^[бО8-2р.О10+4(1 4-(л)О10] + Д-Г+Д6 = 0. (16)
Ек Ек
Ниже найдены коэффициенты D. После их подстановки получим:
. _ _ДлЦЕ = о1 (17)
дх
А
Следовательно, F2(x) постоянная величина. Обозначим Г2(х)=В.
Примем, что в начале координат (х==0, у=0) перемещение
V равно нулю. Тогда должно соблюдаться условие:
со
-Г-Ую +р)«С1-(1-1л)(?4] + S = °. (18)
1
Следовательно:
OQ
+ Ю«СХ —(1 — ^)С4], (19)
Ек
1
"11
а потому:
----—У cos (a x) [ (1 4- |i) a [CjCh(ay) 4-C2sh(ay)4-
£k I »
i
4- Сгу ch (ay) + C4ysh(ay)] — (1 — p.) [C3sh (ay) 4-C4ch (ay)]I +
QO
+ ^У [’(i + rt^-a-toc,] + o-[2Z)s+
1
4- 6 D%x + £^y — p (2 D4 4" 2 4" 3 Dny)] .
(20)
в) Определение коэффициентов D
Найдем сначала коэффициенты О5—Dn.
При перемене знака у х не должны изменяться знаки у и °у-
Это дает: О8 = 0; (21) Dw = 0. (22)
При перемене знака у х должен измениться знак у т . Следова-
тельно: Da = 0; (23)
При x—/ Так как * =0. sin (a/) = sin = S1'n («^ = 0, то — 2 D,l + gl - 0 . (24)
Отсюда: D,= f. (25)
Далее в любом горизонтальном сечении (у — const) вертикаль-
ные усилия должны уравновешиваться с нагрузкой. Это дает
условие -f0 bdx = [gb(H-y) + q]l. (26) 0
Знак минус введен потому, что за положительные а приняты
напряжения растяжения.
Получим:
Е a [sin (a I) — sin 0] • [Сй sh (a y) 4- C2 ch (ay) 4~ C3y sh (ay) 4*
1
+ C4ych(ay)]&-2D56/-2-|-6/y=[g6(^-y) + ?]^ (27)
I2
Поскольку
sin (а/) — 0, .
— 2Dbb — gby = gbH — gby + q, (28)
а потому
D„ = —J- (gH + 4). • (29)
z \ о /
Для сечения на опоре (х=0) ив середине пролета (х = I) по
условиям симметрии w = 0.
Получим:
00
““У Sin (а/) [(1 4- |х) а [Схsh (а у) + C2ch(ay) 4-С3у sh(ay) -f-
i
+ C4y ch (ay)] 4- 2 (C3ch(ay) + C4 sh (ay)]} 4-
+ ^[2D7 + 6Du^ + l-4i£W+4)‘~2!J'vd==0 <3°)
EK L 2\ & / 2 j
или:
2D7 + pfgW + 4)+y(6Du-pg)=0. (31)
Это условие должно удовлетворяться при любых значениях у.
Следовательно
D7 = ~4fgH+4); (32)
2 \ b /
£>п = 4 . (33)
О
Таким образом все коэффициенты D найдены. Для удобства
дальнейшего подставим их в формулы (7) — (9), (11) и (20).
cos (a x^afCjSh (ay)-|- C2 ch(a у) + C3 у sh (a у) + C4ych(a у)] +
+ 2 [C3ch (ay) + C4 sh (ay)])-p [g (Д - у) + 4] ;
J L о I
ay = — S a2cos (a x) C4 sh (ay) -}-C2 ch (a у) + C3 у sh (a y) 4-
— g (H — У) + 4b
0 J
т = S a sin (a x) }a [С\ ch (a y) 4-^2 sh (a У) + Сз У ch (a y) 4-
4~C4ysh(ay)] 4-{C3sh(ay)+C4ch(ay)]};
+ С4у Ch (а у)
(34)
(35)
(36)
13
у, - — V sin (а х) f(l + р-) а sh (а у) Д ^2ch (а У) ж
£к I
1
/- + С3у sh (а у) + С1У ch (а у)] 4~ 2 [C3ch (ау)о + C4sh (ay)]j; (37).
и =----— У cos (а х) [(1 + Р1)а [Ci(а У) + C^sh (а у) +
Ч,.: . £к . I
1
4-C3ych(ay) + C4ysh(ay)] —(1 — fi) [C3sh(ay) + C4ch(ay)]j +
OO
+ т-У [(i + rta^-d-nJCJ-
I
_ C1 fl )y... g /я---2-Л JL . pg)
£к L \
Можно сделать проверку и убедиться, что все вышеприведенные
условия удовлетворяются.
г) Определение коэффициентов С
Перейдем теперь к определению коэффициентов С, зависящих
от порядковых номеров членов ряда. Для этого учтем условия по
нижнему краю стены и по верхнему.
Первое условие таково: по нижнему краю стены по линии кон-
такта с рандбалкой вертикальные перемещения кладки должны
быть равны прогибам рандбалки.
Для прогибов удобнее принять положительное направление
вниз. Поэтому прогибы рандбалки равны перемещениям кладки
при у ^0, но с обратным знаком.
Получим:
и> = —о = 4- -РУ cos (ax) [(1 + н) aCi — (1 у.) С4] —
У=0 —
, со
1
со
. . =-Р-У [l-cos(ax)]-[(l+1i)aC1-(l-OC4], (39)
1
Нагрузка на балку (на единицу длины):
: a b — + b S a2 cos (а х) С2 + (gHb 4- q). (40)
Ь = 0) 1
14
- Для 'балки
ругой кривой:
можно написать дифференциальное уравнение уп~
d^w р
= -Г- — " ,
dx* El
(41)
Знак введен в соответствии с принятыми нами положительными
направлениями для w и р.
На основании формулы (41) напишем, уравнение:
00
+ 7“У«4cos(ax) [(1 + (1 — |х)С4] = '
1
со 1
= +~-^a2^{a-x)C2+^-(gHb + q). (42)
Ei Е1
1
Необходимо член —(gHb + q) ' также разложить в ряд по cos,
El
Для этого воспользуемся известной формулой:
2 £ cos (я ср) = — 1 , ; (43)
действительной в пределах ср от 0 до 2~.
3 нашем случае вместо<? надо подставить <р= — . Предельное
значение при х— I равно таким образом, формулу можно при-
менить. Умножая обе части равенства (43) на
77- (gHb+q), по-
лучим:
1 О
- 77 (gHb + <?) = — (gHb + g) У COS (а х).
Ei El
1
Уравнение (42) примет вид:
(44)
со
1
да 00
— + 77 Ц “2 cos (ах) С2 — ~~(gHb + q) У cos(ax)
1 1
(45)
или:
а4
[(1 + h)«G-(1 - |i) с4]-
«2 О ч
- — bC^i-{gHb + q) 1 = 0.
JC1 . ч Е1 , J ы
(46)
15
. Для того чтобы сумма бесконечного ряда равнялась нулю, не-
обходимо и достаточно, чтобы каждый член суммы равнялся ну-
лю. .Следовательно:
1 2
+ А.а1 [(1 + (1) а С1-(1 —И)СИ -~ЬС2 +
Ек ' EI
+ (gHb + q) = 0 . (47)
л
Это уравнение приводится к виду:
+ *S 6(1 +0С1-«г^С2-а4(1-ЛС1=-^(^ + <?). (48)
Таким образом, одйо условие нами учтено.
Второе условие состоит в том, что (поскольку мы решили пре-
небрегать касательными усилиями между рандбалкой и кладкой
стены) при у=0 должно быть *с==0, т, е.
fasin(xx)(aC1-pC4) = 0. (49) *
1
Опять каждый член суммы должен быть равен нулю; следова-
тельно
аС1 + С4 = 0. (50)
Для верхнего края стены при у=Н должно быть
— oyb^q. (51)
Получим уравнение:
5 a2 COS (а х) [С. Sh (а Н) + С2 ch (а Я) + С3Н sh (а Я) +
+ С1ЯсЬ(аЯ)]6 + -£--* = ?- (52)
ь
Отсюда
Су sh(аН) + С2ch (а II) 4-C3tfsh(atf) + C4tfch(a/Z) = 0. (53)
Наконец, для верхнего края стены при у^Н должно быть т=0
или:
S a sin (а х) | а [Cj ch (а Н) -f- С2 sh (а Н) + С3Н ch (а Н) +
1 I
+ С4Н sh (а Я)] + [C3sh(a/Z) + С4 ch (а//)]} =0. (54)
Это дает уравнение:
aCiCh(a /7) + а С2 sh (а 77) + [(а /7) Ch (а Н) + sh(a77)]C3 +
+ [(“/7) sh(а/7) + ch(^ 77)] С4 = 0. (55)
16
Итак, для нахождения коэффициентов С мы имеем 4 уравнения
(48), (50), (53) и (55):
«41 + н) ci - С2 - (1 - р) С4 =(gHb + 9); (56)
я Сх + С4 = 0; (57)
С4 sh (« Н) + С2 ch (я Н) + С3 Н sh (а И) + С4Я ch (а Н) = 0; (58)
а С\ Ch (сс Я) + а С2 sh (а Н) + [(а Я) ch (а Я) + sh (« Я)] С3 +
+ [(а И) sh (аЯ) ’+ ch (а Я)] С4=0. (59)
К этим уравнениям в общем виде мы еще вернемся в дальней-
шем. Здесь же будем иметь в виду, что Я достаточно велико, и, сле-
довательно, можно принять
sh (а Я) = ch (а Н) . \ои;
с
Тогда уравнения:
“5(1 +и)Сх-«2^
Е1
Е1
(61)
(62)
(64)
Решая совместно эти уравнения, получим:
El \ Ъ
а» [2аЗ 4--^
L El J
2(sH+ -3-
Г WEI \
a2 • -j"
L EKb
(65)
-С4 = -
gH А
Ь
адТ
3 ( —-
El J
2(g//+4-|
\ b /
, 2 ^EI J
л 1
I E*b J
(66)
Подставим значения С в формулы (34) — (38):
2кя+ -у)
-г9"—;---7 [“ sh (а у)4-ch (а у)-а у sh (а у) +
2 a3El I
а2
ЕКЬ
J
+ «уch(ay)] + 2 [— ch(ay) + sh(ay)] р. я(Я — у) +=
J Ь
2 Б. H. Жемочкин
17
00
2SfjsrLi|sh(“”-ch,<>’)-
---------[_. I
1 L ЕкЬ J
— ay sh(ay) + ay ch (ay)] --p. 4- p. gy ;
(67)
= — S a2 cos (a x) —
— [—sh(ay) 4” ch (ay) — a у sh (ay) 4-
2сЛЕ7
. ЕкЬ
4-aych(ay)]— g(H — y) + 4" =
b
a2
Г2о-3£7
1
COS (a x) sh + ch (a _
~ a у sh (a y) 4- a у ch (a y)] 4~ 1 + gy ;
(68)
т = £ a2 sin (ax)
i
Г2 a3£/
a 2 -----
L E*b
= 2
О sin
/ . ;2a3£/
az&d I 4~
i I EKb
(69)
1 °° 2 +
и sin (a л)—_ f(l + |i) [—sh(ay) + ch(ay) —
ьк i 2 ^zj/ I
A о i 1
— a^sh(ay) + ay ch (ay)] 4- 2 [—ch (az/) + sh (a y)j j ==
2 (gH 4- .
\ b / \ ’ sin (ax) (f. x r i / ч 1 / м
= - ----- Л ------------7 Ш - H) [sh (a у) - C h (a y)] +
’ +1J
+ (l 4- [i)ay [— sh(ay) 4-ch(ay)] }; (70)
18
— S a cos (a x) —
1 ,2
a*2
2 a3El
— st У ch (a y) + a у sh (a y)] — (1 — p) [— sh (a y) + ch (a y)]} +
2 gff + ^~
\ b
[2a3EI
" ------ + 1
E*b
4-u) — (1 — [x)] —
a-
cos (ax)
'2 a3EI
. EKb
+ (I + p) a У [ — ch (ex y) + sh (a y) I
{[— 2 ch (a y) 4- 2 sh (a y) +
+ 1
(1 — ^2) у (1 — (±2) y2
2 EK 2
/
Обратим внимание на то, что
еаУ д_ е—*у _ е~^у
ch (а у) — sh (а у) =--;-------------------— в .
2 2
Для упрощения формул введем обозначение
(71)
(72)
(73)
2г.^Е/
Этот коэффициент (в отвлеченных ме^ах) хорошо характери-
зует упругие свойства раидбалки и кладки. Мы будем им пользо-
ваться в нашем исследовании, так как введение его в этом случае
представляет большие удобства.
Здесь через EI обозначена жесткость раидбалки. При реаль-
ном проектировании железобетонных рандбалок их жесткости сле-
дует определять с учетом арматуры, а иногда и с учетом возмож-
ности снижения жесткостей из-за трещинообразования.
Одновременно будем применять и другую упругую характери-
стику
(74)
19
Такой вид упругой характеристики удобен для практических
расчетов.
Очевидно, что между коэффициентами k и К должна быть за-
висимость:
1 000--^-= Д^А = 2,016й. (75)
2Лз 1б~з ’ 4 7
Итак: коэффициент k удобен для исследования, коэффициент
же Л удобен для практических расчетов.
Если ввести коэффициент k, то выражения, входящие в знаме-
натели формул, примут такой простой вид:
о
EI
— = n3k .
Е^Ь
(76)
д) Формулы в
После всех преобразований
о
окончательном виде
получим окончательно:
/п~х \ пт-У "
cos --- I
\ ! (п~у . 1\ в
(tl3k +1)
п-у
— [А
+ ц gy;
(77)
а,
пт.х \
cos ----
\ / / {пку
(«3^4-1)
ппу ~
—
I
е
(78)
x = -2(gW + ^-
[ПКХ \
м sin I ~ I у п~у
-----V 7 g~~7"
(n3k 4- 1)
(79)
2 gff + -гН
\ ь
и — —--------------—
1
/ п^х
sin -----
п (n3k 4-1)
1
21 ёЯ + 711
\ о
V =-----------—
£кл
е 1
(80)
\ 1 Гп {tWX
7 t ------- 2 — COS -----
7й п О3£4-1) I \ 1
20
+ Р-) + 2 е ] +
1 J J
'i
j (1 -^)
21 | "Г 2 £к
Нагрузка на балку:
Р = — Су ь -
'(У = 0)
Она равна:
(81)
(82)
(83)
со
Р =~- kgHb -г 7) [2 [V cos -------------------1 + 1 )
6 Пр U / (пЧг 4-1) J J
1
Наибольшая ордината эпюры нагрузки на балку должна быть
над опорой (х=0):
СО
Pa = (gHb+q) [2 [у;—Н1+ 1)-
I L («3« 4- 1) J )
I
(84)
Прежде чем перейти к числовым примерам, свяжем упругую
характеристику k с высотой рандбалки.
Предположим, что. рандбалка выполнена из железобетона и
имеет прямоугольное сечение. Ее пролет, равный 2Z, обозначим че-
рез L.
Мы не предполагаем здесь делать подбор сечений рандбалок, нам
нужно только найти способ определять высоты рандбалок, хотя бы
и очень грубо, ради наглядности чертежей, из рассмотрения кото-
рых ясна была бы связь нагрузок на рандбалки с их высотами.
Поэтому, не заботясь о точности, условно примем жесткость
рандбалки равной
Тогда:
Отсюда:
3 ’
Т = ’ ! (86)
h. у ок
Отношение модулей упругости может колебаться в широких
пределах, примерно от 5 до 20. Но нас это отношение интересует не
<41
с точки зрения расчета определенной конструкции, а только с точ-
ки зрения наглядности чертежа. Поэтому остановимся на некото-
Е
ром среднем значении — = 10 (например, £=200 000 кг/см2 и £к=
£к
= 20 000 кг/см.2, или £=150 000 кз/сьи2 и £к=15 000 кз/з.п2).
Тогда:
или:
L _ 7,45
h 3__________
V k.
Если мы имеем дело с коэффициентом К, то:
, bh3
к = 1 ооо -12.= р_ Г ~
ЕКЫ* . 12 \ L ) Ек
Получим:
(89)
(90)
На всех эпюрах нагрузки мы будем для наглядности показывать
балки, высоты которых определены по формулам (88) или (90),
§ 2. ПРИМЕРЫ
Сделаем три расчета для различных значений упругой харак*
теристики; примем &=0,05, /г=0,5, /г=5.
Этим характеристикам соответствуют характеристики /<, равные
0,10, 1,01 и 10,1; отношения —по формуле (88) 20,2,9,4 и 4,4.
h
Таким образом, мы охватим те случаи, какие могут встретиться
на практике.
1) k = 0,05 или К = 0,10 (— = 20,2 ).
\ h /
Найдем наибольшую ординату над опорой.
По формуле (84)
со
Po=(g^ + 7)[2[S-——•] 4- 1). (91)
( [*“ 4-1)1 I
: 1
'22
Вычисление удобнее вести в табличной форме. Порядок вы-
числения виден из табл. 1.
п л3
1 1
2 8
3 27
4 64
5 125
6 216
7 343
8 512
9 729
10 1000
11 1331
Таблица 1
0,05 л3+1 0,05л3+1
1,05 0,95238
1,40 0,71429
2,35 0,42553
4,20 0,23810
7,25 0,13793
11,80 0,08475
18,15 0,05510
26,60 0,03759
37,45 ' 0,02670
51,00 0,01961
67,55 0,01480
2=2,78196
Ряд сходится довольно медленно; необходимо вычислить боль-
шое число членов. Можно поступить так: до некоторого члена, ко-
1
торому соответствует малое значение---:, принимать поряд-
0,05 л3 -f" 1
ковые п, когда каждое последующее п больше предыдущего на
единицу. После этого принимать п с интервалами, по мере даль-
нейших вычислений все возрастающими.
Например, для /2=60:
----------= 0,000093 ;
0,05«a4-l
——1-------= 0,000058.
0,05 п3 + 1
1
» /г=70:
Среднее значение---------:---- в этом интервале равно:
0,05 гс3 4~ 1 *
0.000093 + 0,000058 =
2
Следовательно, на весь интервал придется 0,000075* 10—0,00075.
Дойдя таким образом до п—100, далее примем /г=120, 150, 200,
250, 300, 400, 500, 1000 и т. д.
1
При больших интервалах, когда разница в величине ——-——
г 0,05 п3 -j- 1
в начале и конце интервала велика, среднее значение лучше нахо-
дить делением не на 2, а на 3.
23
Например: , '
i _5
Для п = 1 000 - - = 0,002 • 10 ;
О, (to л3 1
, п == 2 000 1 ..— = 0,00025 • Ю“5.
0,05 п3 4-1
Среднее значение
0’001±.0’00025, . ю-s = 0,00075-10~5.
На весь интервал:
0,00075-10^5-1 000 = 0,75- Юг5 = 0,00001 .
Г
Продолжать вычисления для //>2 000 нет смысла.
Суммируя цифры, полученные в последней графе таблицы, по-
лучим:
У--- —• = 2,78196.
0,0э п3 4- 1
1
Подставим в формулу (91) и округлим реультаты:
Ро = (gblb + q) {2 • 2,78196 4- 1} = 6,564 (gHb + q).
Округление необходимо потому, что вычисления у нас велись до
5-го десятичного знака; следовательно, можно ручаться только за
4-й знак. Но мы умножаем результат на 2 и тем самым снижаем
точность, поэтому достоверным следует признать только 3-й деся-
тичный знак.
Оказывается, что при большой высоте стены безразлично, яв-
ляется ли нагрузка, внешней, приложенной на верху стены, или
создается собственным весом самой стены.
Примем теперь х=0,1 I и определим соответствующую ординату
эпюры нагрузки на рандбалку по формуле (83), которая теперь
примет вид:
/ т т /-.I \ (q \ / пг. 0,1 I \ 1
Ро.и = (йя6 + 9) 2 lcos -----7— ктгттт +1 .
I L \ * / (и,ц3 4~ 1/J J
Заметив, что
cos/------— } =cos(0,1 пк) = cos\п 18 ),
опять составим таблицу (табл. 2), используя частично данные пре-
дыдущей таблицы.
При знакопеременных рядах нет особенной надобности в вычис-
лении очень большого числа членов.
24
В данном случае вычисления следует довести только до 60-го
члена.
Таблица 2
п 1 0,05п3+1 / п~х \ cos — cos(n*18’) \ 1 ) inzx\ 1 cos . I I J (0,05-n3+n
1 0,95238 cos 18°— 4-0,95106 +0,90577
2 0,71429 cos 2-18°= cos 36°— 4-0,80902 4-0,57787
3 0,42553 cos 3‘ 18°= cos 54°— 4-0,58778 4-0,25012
4 0.23810 cos 4.18°= cos 72°= 4-0,30902 4-0,07358
5 0,13793 cos 5-18°— cos 90°— 0 0
6 0,08475 cos 6-18°— —cos 72°— —0,30902 —0,02619
7 0,05510 cos 7 18°= — cos 54°= —0,58778 —0,03239
8 0,03759 cos 8- IS0— —cos 36°= -0,80902 —0,03041
9 0,02670 ccs 9-18°— —ccs I8°— —0,95106 —0,02539
10 0,011'61 cos 10-18°— —cos 0°= — 1 —0,01961
11 0,01480 cos il -18°— —cos 18°= -0,95106 -0,01408
•
Ордината эпюры нагрузки:
Po.iz = {2• 1,65586 + 1} = 4,312 (gHb + q).
Далее вычисляем ординаты для других значений х до х=/.
На основе полученных данных можем вычертить эпюру нагруз-
ки на рандбалку (рис. 6).
25
2) 6=0,5; Л = 1,01 (у-= 9,4).
Для ординаты над опорой имеем по формуле (84):
й = (гН4 + ,){2[у;— -1^ ] и). (92)
1
Получим:
Таблица 3
1 1 1,5 0,66667
2 8 5 0,2
3 27 14,5 ’ 0,06897
4 64 33 0,03030
5 125 63,5 0,01575
6 216 109 0,00917
Этот ряд сходится быстрее, чем в -предыдущем случае; следо-
вательно, можно ограничиться меньшим числом членов. Ордината:
pQ= (gf/& ?) {2-1,01486 + П - 3,030 (gHb + 7).
Далее переходим к вычислению других ординат.
Эпюра нагрузки приведена на рис. 7.
' 26
3) k - 5 ;
Аналогично поступаем при вычислениях для этой упругой ха-
рактеристики.
Как видно из табл. 4, составленной для ординаты над опорой,
сходимость в данном случае еще лучше. Достаточно ограничиться
20 членами, а дальше вести вычисления с интервалами до п=200.
Таблица 4
5п3 +1
____
5/Н + I
1 1 6 0,16667
2 8 41 0,02439
3 27 136 0,00735
4 64 321 0,00312
5 125 626 0,00160
6 216 1081 0,00093
Л
4-0,20643
Ордината над опорой:
Ро = (gHb + q) {2-0,20643 4- 1} = 1.413 (gHb + q).
Эпюра нагрузки приведена на рис. 8.
27
Сделаем теперь выводы на основании полученных данных. Из
чертежей видно, что ни о какой треугольной эпюре с наибольшей
ординатой в середине пролета не может быть и речи. Наоборот, на-
грузка увеличивается к опорам, причем при гибкой рандбалке на-
грузка непосредственно над опорами велика, но распространяется
на небольшие участки. В серединах пролетов по линии контакта
кладки и рандбалки может быть даже растяжение в вертикальном
направлении1.
При жесткой рандбалке нагрузка над опорами снижается и
на остальном протяжении нагрузка приближается по мере увеличе-
ния жесткости к равномерно распределенной. Очевидно, что в
крайнем случае абсолютно жесткой рандбалки нагрузка будет в
точности равномерно распределенной.
Выведенные нами формулы показывают, что нельзя нагрузку
на рандбалку считать не зависящей от высоты стены или от ее веса,
как получается в предположении эпюры в виде треугольников с
наибольшими ординатами в серединах пролетов. В действительно-
сти же нагрузка на рандбалку увеличивается пропорционально
внешней нагрузке.
Необходимо заметить, что, поскольку нагрузка сосредоточи-
вается у опор, моменты в рандбалке вообще невелики, причем в
гибкой рандбалке моменты меньше, чем в жесткой. Это показыва-
ет, что не всегда целесообразно увеличивать сечение рандбалки
при больших нагрузках; хорошие результаты могут быть получены
и при гибкой рандбалке, что даст достаточно большой простор про-
ектировщикам при подборе сечений.
Но вместе с тем не следует упускать из виду, что поперечная
сила у опор не зависит от жесткости 'рандбалки.
Из-за поперечной силы иногда приходится усилить рандбалку у
опор и давать вуты. В некоторых проектных организациях, где при-
меняли изложенный здесь способ расчета, делали вуты вверх и да-
вали им прямоугольное очертание для удобства возведения кир-
пичной кладки (рис. 9).
1 В опытах б. ЦНИПС еще в 1935 г. с однопролетными балками, поддер-
живающими кирпичные стены, иногда замечалось в середине пролета растяжение.
'28
. § 3. МОМЕНТЫ И ПОПЕРЕЧНЫЕ СИЛЫ
Моменты можно найти, исходя из дифференциального уравне-
ния упругой кривой:.
d~w _ М
dx- “ EI 1
<93)
где w прогиб рандбалки.
Формулу для прогибов получим или из формулы (39), подставив
в нее значения С, или из формулы для вертикальных перемеще-
ний (81) (стр. 21), положив в пей у = 0 и изменив знак на обрат-
ный, так как ось ординат у нас направлена вверх, между тем как
положительные прогибы предполагаются направленными вниз.
Итак:
1
п (п3& -р 1)
О Q /72 * -X
2— 2 cos —
\ /
4(gHb + д) I f VT 1 fi __
' EK~b 12j /г(/г3£ф 1) [ \ I /JJ ’
(94)
Дифференцируя дважды, найдем M:
EI^L fy cos piL'l 1 =
dx* EK~b (ZJ \ I ) nP(n?k^-\) }
Oo
A , rTf , 4 Eire v1 fax \ n
= -4(gHb + q)-~-^C0S(~r], • <95
£K6Z \ I / (n?k 4- 1)
Входящий в формулу (95) коэффициент на основании формулы
(73) (стр. 19):
EI* №
ЕКЫ 2гЛ
(96)
Поэтому:
М = — <2(gHb + q)
<х>
kt* v
---------У cos
1
п^х \ п
или:
С»
М = - 0.2026 (gHb + ?) kP У cos (—4—.
\ I / [nrR. + 1)
1
(97)
(98)
29
Поперечную силу получим, дифференцируя выражение для М:
dM , TTt । \ . !п~х\ п2
Q = — = + 0,2026 (gHb + q) — 2j sin — , „7 =
dx I \ I / 4-1)
i
□O
= 0,6365 (gHb + q)kl^ sin (99)
1
Наибольший по абсолютной величине момент над опорой при
х — 0. Он равен:
00
м = - 0,2026 (gHb + q')kP^j
(ПУК -f- 1 )
1
(ЮО)
Наибольшая поперечная сила у опоры (справа), что можно
установить непосредственно.
. Она равна
\Q = (gHb + д)1\ . .(101)
при любых /г.
§ 4. НАПРЯЖЕНИЯ В КЛАДКЕ
Ошибочно принимая нагрузку на рандбалку в виде треуголь-
ника с наибольшей ординатой в середине пролета, обычно счита-
ют, что в кладке появляются трещины, и представляют себе, что
часть ее в середине пролета отделяется от всей стены и непосред-
ственно нагружает рандбалку.
Проверим это предположение и выясним, действительно ли в
кладке возникают растягивающие напряжения такой величины,
что они могут вызывать трещины.
Найдем сначала вертикальные нормальные напряжения в клад-
ке в середине пролета, затем горизонтальные напряжения в том же
сечении и, наконец, горизонтальные напряжения по линии сопря-
жения кладки с рандбалкой. Вычисления проведем для упругих
характеристик /е=0 (случай рядовой перемычки, когда балка от-
сутствует) /г=0.05, /г=0,5 и k=2.
Основная цель, которую мы преследуем, состоит не в расчете
кладки, а в выяснении, какой порядок имеют напряжения в ней.
А. Вертикальные нормальные напряжения в кладке
в середине пролета
Общая формула (78)
в кладке имеет вид:
(стр. 20) для вертикальных напряжений
со
— (g/7-ф—cosM
\ ъ / ( [_ \ Z /
1
1
(n^k Д- 1)
30
_ п~'-'
4 1) е
+ 1} + gy.
(102)
Для середины пролета, когда х=1: .
— — [gH4- [2 У [cos (п тс) —5-4
\ м I Y l +1) \ 1
mty
+ 1 j -4 1 j -4 gy • (ЮЗ)
С целью упрощения вычислений в нашем исследовании будем
учитывать только собственный вес кладки, принимая нагрузку
<7 = 0.
Следовательно:
со
%- = —gH f2 £|cos(ns) —+ Й e
I L (n3k 4 1) \ l /
+ 1 1 +gy. (104)
1) = 0 (отсутствие рандбалки).
В этом случае:
Оу = — RH [2
00
+ 1 + gy •
(105)
Для точки на уровне у =0,2/:
°у == ~ gH j 2 cos (п ~) (0,2 п п 4 1) £-о,2«-
(Ю6)
Для точки на уровне у = 0,4/:
S = ~ gH {2 S [cos (пт:) (0,4 П т: 4 1) ] 4 1 j 4 0,4 gl (107)
И т. д.
Приводим начало таблицы для вычисления Сумм (табл. 5).
После суммирования получим следующие результаты.
Для у ~ 0,2 Z:
5, ==“£#{—2.0,49050 4 1} +0,2о7 =
= —0,01900 gH 4 0,2g/. (108)
Для z/=0,4/:
ау=х—^Я{—2-0,43826 4 1) + 0,4g/
= —0,12348 gH 4 0,4 gl (109)
и т. д.
31
ст
cos (лк) (0,4лк+1)Х —0,4 mt Xe CO t'- CT -Ф O -Ф • • CJ IO О ЮЮ (MK- OO n -T • • ТГ oo о CO ~ Q co CT —> о о о • • o"o о о о о • • 1 + 1 4- 1 + • СО ст СО СО II м
° £ e: o* 1 - nw — о СТ СО СО со со о о ю со ст • • гг _ то <о — о оо со ст о о о • woo ОСО о о о о о о
0,4 /;ic+ 1 ТГ b- —> -гр со СТ < со см ст СТ —< со ’ • со со <ст со ст ст LO — СО СТ 00 СО • ’ О IЛ N О W 1Л ф ст ст ст со ст оэ .
1 0,4 пк ст — ст со ст СО СТ СТ ьО — СО * ' СО со СТ СО со ст . ю — со ст ос со ст ю ст о ст ю . —, ст со ю со ст .
. cos (лк) (0,2 пк + 1)х —0,2 mt Хе ст ст ст г- со ст • ст ст о ст ст ст СО ст СО ст со ст • • со ст со со ст о со ст ст Ст —1 —> • о о* о о о о • - 1 + 1 + 1 + . . —0,49050 |
сч o* i 3 Z 0“ сг> »-< СТ О —г СТ СТ СТ со о ст о СО СТ —> со со . . со СО СТ СО ст ст ст — о О СТ - . оо'о’ст'о'ст . .
| 0,2 rtit+1 ст ст г- ст — . , СО со ст ст ст ст СО СО -st1 со -- СТ . . СТ СТ со — Kf со СО СТ 00 Ст . —СТ СТ со -Ф .
0,2 mt Ст -Ф ст ст — со со Ст ст ст ст • ' со со -Ф со —1 ст ст ст СО —' -Ф СО • * со Ст со CT г- О — СТ СО со
5? g ! + !+(+'
e — СТ СО -Ф ст СО * '
Таблица
Переходя к вычислению на-
пряжений, зададимся следующи-'
ми данными: полупролет 1=6 я
(пролет А=12 ж). Высота стены
Н — 10 я и Н = 20 я. Объемный
вес кладки g = 1,6 т/ж3.
Таким образом, например,
для у=0,2/ и Н = 10 я, получим:
Су = —0,01900 1,6-10 +0,2 X
X 1,6 - 6 — 1,62 т/м2 = 0,16 'кг/см2.
Результаты выписаны в табл.
6 (растягивающие напряжения
имеют знак плюс, сжимающие —
знак минус).
2) k= 0,05(—= 20,2
’ \ h
Формула:
а
ллу
1 (^У. 4- 1Ь~~
(0,05л»+1)\, I I
+ 1] + ёУ •
(НО)
На уровне у = 0 (по линии со-
пряжения с рандбалкой):
Со
ау = — g+2 У [cos (п^) х
1
(111)
На уровне у = 0,2/ (табл. 7):
00
5у = —cOS(ttir)X
1 L
1
(0,05/г3+ 1)
(0,2 n тс +
—0,2лгс
+ l} + 0,2gZ (112)
и T. Д.
32
Таблица 6
УН а При H — IO м У в кг'см4 а При Н-20 .W в кг[см2
0 0 0
0,2 +0,16 +0,13
0,4 +о, 18 -0,02
0,6 +0,09 -0,39
0,8 —0,03* —0,84
I —0,11 — 1,18
1,2 —0,11 — 1,37
1.6 +0,06* —1,41
Таблица 7
п п1 0,05л1 + + 1 cos (пг) COS {П~') х 1 у — о 2Z
0,2п % 4- 1 ‘ 1 (,—0,2/7 ~ । , V 1 cos (ZJ-) X 0,05n! + 1 X Ю 2.ч k-l l) e~0 2/z“
X О.Ойл* + 1
1 1 1,05 —1 -0,95238 1,62832 0,53349 —0,82733
2 8 1,4 4-1 +0,71429 2,25664 0,28461 + 0,45876
3 27 2,35 —1 -0,42553 2,88495 0,15184 —0,18640
4 _ i 64 4,20 + 1 +0,23810 3,51327 0,08100 +0,06776
S « -0,51169 * £ — — 0,50516
Для зл ^О:
оу - ~~gH{— 2-0,51169+ I} = + 0,02338g//. (ИЗ)
Для v = 0,2/:
Оу 2-0,50516 + 1} + 0,2 g/ =
- + 0,01032 g// + 0,2g/ (114)
и т. д.
Напряжения равны (табл. 8):
Таблица 8
yi ау при Н = Ю м в кг см- ст У при /7-20 м в кг см2
0 +0,04 + 0,08
0,2 + 0,21 +0,22
0,4 + 0,21 +0,04
0,6 + 0,09 —0,40
0,8 -0,05 —0,86
1 -0,13 — 1,21
1,2 —0,13 — 1,40
1,6 +0,06 — 1,42
3)k = 0,5 (— = 94'
Поступаем аналогично предыдущему. * 3
* На верху стены зу — 0; между тем почти у верхнего края стены оказалось
растяжение. Неточность объясняется тем, что при выводе формул мы приняли
sh (а//) = ch (а/7) (см. стр, 17), что справедливо только при большой высоте
стены.
3 Б. Н. Жемочкин
33
Результаты вычислений (табл. 9):
Таблица 9
У'Л о при Н~Ю м в кг см1 при Н-20 м в кг'см*
0 +0,05 +0,10
0.2 4-o.li +0.03
0.4 -0.01 —0,40
0.6 -0.15 -0,88
0.8 —0.25 -1,26
1,0 • -0,27 — 1,49
1,2 —0.22 — 1,59
1,6 +0,02 —1,59
4)/s=2f— = 5,9
t /г
Результаты вычислений (табл. 10):
Табл и ща 19
У Л при /-/ = 10 м в кг см' а ( при //-20 м в кг см*
0 —0,68 — 1,36
0,2 -0,58 — 1,36
0,4 —0.58 — 1,55
0.6 -0,57 —1,72
0,8 —0.53 —1,84 -
1 —0 45 — 1,86
1,2 -0,33 — 1 ,82
1 + —0,02 — 1,58
На рис, 10 приведены эпюры вертикальных нормальных напря-
жений для рассмотренных случаев. Сплошными линиями пока-
заны эпюры для //=10 м и пунктирными для //=20 м.
Как видим, растягивающие напряжения появляются только
внизу, причем, они ничтожно малы. Здесь напряжения пропорцио-
нальны высоте стены и, следовательно, нагрузке. 1
Увеличив нагрузку, мы все же не получим таких напряжений,
которые способны превысить предел прочности.
Ввиду этого заключаем, что, если в особых исключительных слу-
чаях горизонтальные, трещины и могут появиться, то только внизу
кладки у рандбалки1. Появление же горизонтальных трещин на
некоторой высоте, где уже возникает сжатие, по-видимому, не-
вероятно.
1 Далее,
ния кладки с
в § 6, выясним возможность появления трещин по линии сопряже-
балкой в результате сдвига из-за больших касательных напряжений.
34
Следовательно принимать треугольные эпюры с наибольшими
ординатами в серединах пролетов совершенно неправильно: это не
соответствует действительной работе конструкции.
Вертикальные нормальные напряжения бу 8 кладке 8 середине
пролета (6 кг/см2)
----Зпюры напряжений для случая Высоты стены Юм
---- « » - •> •» 20 м
н-0(£ = ъ) «=0,05 (%-20,2) н=0,5(^9,Ч) n-2(j-5t9)
Рис. 10
Б. Горизонтальные нормальные напряжения в кладке
в середине пролета
Общая формула (77)
ний имеет вид:
(стр. 20) для горизонтальных
напряже-
cos
п~х
1 ппу
+ 1) V 1
п~у
Г
-1)е
— I1 1 + pgy
(И5)
Для середины пролета в случае, если <7=0:
СТ
1
П~У
1 /п~у
\ I
(116)
Опять решим задачу для различных упругих характеристик.
а
I
~ - Н + ш
3*
35
1) k~0 (отсутствие рандбалки)
В этом случае:
Ч-Р’Й/-
Внизу кладки (у—0):
сх = gH {— 2 S cos (n ~) — рь).
(117)
(118)
На высоте у—0,2/:
or= gH 12 [cos (п д) (0,2 л д — 1) £-°-2zki] Д + H‘g‘0,2/ (119)
И Т. Д. .
Для вычислений примем коэффициент Пуассона р — 0,2.
Тогда для у =0:
= ^/7 { — 2S eos (/2тс) —0,2} —'0,8gH* . (120)
Для у =0,2/: * 1 ; л
2 Е [cos (я я) (0,2 га я - 1) с-0-2"" | — 0,2] + 0,04 gl. (121)
И т. д.
Опять сделаем вычисления для /=6 м;
Н — Юл« и И ~ 20 At; g = 1,6 т/лР.
Результаты вычислений приведены в табл. 11 (растягивающие
напряжения со знаком плюс, сжимающие — со знаком минус).
Таблица 11
У// а при Н -10 м в кг см1 при /7-20.И в кг см1
0 + 1,28 -1-2,56
0,2 4-0,38 4-0,72
0,4 -0+3 —0,53
0,6 -0,47 —1,06
0,8 —0 48 —1,12
I — 0,40 —0,98
1,2 —0,28 -0,80
1,6 —0,10 —0,50
Необходимо заметить, что при выводе формул мы предполага-
ли опоры (стойки) несмещающимися. Это соответствует случаю,
* Ввиду того, что
СО j
Е COS (и к) =----------
1 2
36
когда сумма горизонтальных нормальных усилий в любом верти-
кальном сечении не равна нулю: в кладке возникает продольная
сжимающая сила.
Если же смещение опор возможно, то растягивающие напряже-
ния ах должны увеличиваться; сжимающие, наоборот, уменьшать-
ся. Внизу напряжения будут равны:
а, = gH. (122)
Здесь наблюдается то же явление, что и в балках-стенках1.
Подобный вопрос не возникает в случае рандбалок (&#^0), так
как рандбалки препятствуют перемещению опор в горизонтальном
направлении.
2) 6 = 0,05 (—= 20,2 Y
' п /
Здесь:
00
j = gH [2 V fcos (/г *) —-----------------г f—
I Д’ L (°-05 "3 + В X 1
1
rm у
— 1)е ‘ +
Внизу кладки;
оо
'з gH | — 2 v cos (п -)---------------- — р .
х Ь I — V '(0,05 л* + 1)J )
1
На высоте у -0,21'.
(123)
(124)
со
5 = gH (2 У [cos (п z)------------------- (0,2 п г. — I) е
I к '(0,05 гс3 + 1)
1
Ч~ I1 g'0,21
(125)
И т. д.
После подстановки р получим:
для
У=0:
□
1
(0,05 гР+1)
— 0,2 ;
(126)
для
у = №
а
1
-------------(0,2 п тт 1) е
(0,05 п3 -В 1)
— 0,2 + 0,04 gl
(127)
и т. д.
1 См. Б. Н. Же мо ч кин, Теория упругости, Госстройиздат, 1957,
37
Результаты вычислений для тех же данных, что и выше., приве-
дены в табл. 12.
Таблица 12
с при Н- 10 м в кг см2 ПРИ ^—“2® м в см?
0 4-1,32 4-2,63
0.2 4-0,37 4-0,71
0.4 — 0.26 —0,59
0.6 —0.49 — 1,09
0,8 —0,48 — 1,12
1 -0,39 -0,97
1,2 —0,27 —0,78
1,6 —0,09 —0,49
Ведем вычисления аналогично предыдущему.
Результаты вычислений (табл. 13):
Таблица 13
yll а при Н- 10 Л( в кг см1 а при Я” 20 м в кг см-
0 4-1,33 4-2,66
0.2 4~0,17 4-0,30
0.4 -0,34 —0,74.-
0,6 —0.45 — 1,02
0,8 —0,41 —0,97
1 —0,32 -0,83
1 2 - 0,22 —0.68
1,6 —0,07 -0,45
Результаты вычислений (табл. 14):
Таблица 14
У/1 с при Н-10 .и в кг'см1 при /7=20 м в кг; см2
0 4-0,60 4-1,20
0.2 -0,06 —0,16
.0.4 —0,30 -0,68
0.6. —0,34 -0,79
0.8 —0,29 -0,73
1 —0,23 -0.64
1.2" —0.16 -0.54
1,6 —0,04 —0,39
38
На рис. И приведены эпюры горизонтальных нормальных на-
пряжений. Сплошными линиями показаны эпюры для случая
Я=10 м и пунктирными — для случая Н=20 м.
Напряжения внизу не зависят от величины пролета и почти оди-
наковы при любых значениях k; уменьшаются только в случае
очень жесткой рандбалки (&=2).
В общем напряжения внизу несколько велики, хотя для нор-
мальной кладки они ниже предела прочности. Так, например, в
Горизонтольные нормальные напряжения 6Х в кладке
в середине пролета (кг/см2)
Рис. 11
случае раствора марки 50 кг/см2 нормативное сопротивление рас-
тяжению при изгибе по перевязанному сечению равно б кг/см2. Да-
же с учетом коэффициента однородности, равного 0,5, будем, иметь
3 кг/см3.
Полученные нами напряжения не достигают этой величины.
Правда, по наклонным направлениям (разрушение по косой штра-
бе) сопротивление кладки меньше, но и напряжения по таким на-
правлениям меньше.
Конечно, если стена будет очень высокой или к стене будет
приложена большая нагрузка, то напряжения увеличатся и могут
дойти до предела прочности.
Однако следует иметь в виду, что при принятой нами расчетной
схеме, когда опоры предполагаются очень узкими, нагрузка лими-
тируется также напряжениями сжатия в кладке над опорами.
В табл. 15 сопоставлены вертикальные сжимающие напряжения
над опорами и горизонтальные напряжения в середине пролета.
Анализируя результаты, можно сделать вывод, что в отдельных
случаях все-таки возможно появление трещин в кладке. Но нас
39
Таблица 15
Упругая характеристика k /Ч-тЮх // = 20 м
Вертикальные на- пряжения над опорами Горизонтальные напряжения в се- редине про/Сета Веэтикальные на- пряжения над ОПО.’ЭМИ Горизонтальные напряжения в се- редине пролета
0,05 0,5 — 10,50 — 4,85 + 1,32 + 1,33 —21,00 — 9,70 +2.63 +2,66
здесь интересует не прочность кладки, а распределение нагрузок
на рандбалку, между тем на распределении нагрузок наличие тре-
щин заметно не может отразиться. Впоследствии мы увидим, что не
только трещины, но да Же крупные проемы в стене не меняют суще-
ственно распределения нагрузок.
В заключение отметим, что в исследовании мы предполагаем от-
сутствие касательных напряжений между кладкой и рандбалкой;
при этом возможен сдвиг кладки по рандбалке. При наличии каса-
тельных напряжений эпюры горизонтальных нормальных напряже-
ний, как это увидим далее, изменяются, но величина этих напряже-
ний остается примерно того же порядка.
В. Горизонтальные нормальные напряжения по линии
сопряжения кладки с рандбалкой
Напряжения должны вычисляться по приведенной выше Форму-
ле (115) (стр. 35). В этой формуле следует теперь рассматривать
как переменное х, координату же у принять равной нулю.
Формула будет:
С* п~х
' cos ------
1
1
(128)
---------- — р,}.
(пЧ 4-1) J I
Нет надобности исследовать вопрос при различных упругих ха-
рактеристиках, достаточно выяснить только общую картию/ рас-
пределения напряжений. Поэтому ограничимся рассмотрением слу-
чая, когда А=0,5; [— = 9,41
\ Л /
После подстановки k и и, в формулу (128) она примет вид:
— (gH-\- — И2 [cosl-^l
\ Ъ) ( - L \ I )
1
1
(),5пз + 1)
+ 0,2).
(129).
Будем давать величине х различные значения.
Получив выраженными через [gH 4—— j, далее вычислим на-
пряжения для случаев Я=10 м и Я=20 м при отсутствии нагрузки
q (табл. 16).
40 . .
Таблица 16
1 з* при Н — 10 м в кг'см2 при Н—20 м в кг'см2
0 —2,229 —3,57 -7,13
0,1 —1,860 —2,98 —5,95
0,2 — 1.272 -2,04 —4,07
0,4 —0,222 —0,36 —0,71
0,6 +0,427 +0,68 + 1,37
0,8 +0,741 + 1,19 +2,37
1,0 +0,831 + 1,33 +2,66
Рис. 12
На рис. 12 приведена эпюра напряжений; ординаты эпюры вы
ражены через (£#+—) (4-растяжение, — сжатие).
\ Ъ /
§ 5. ПРИБЛИЖЕННЫЕ ФОРМУЛЫ
Та задача, которую мы себе поставили, решена: найдено, что
нагрузка на рандбалку наибольшая над опорами и уменьшается к
середине пролета; эпюра нагрузки криволинейная, ее характер за-
висит от упругой характеристики. Для полноты исследования мы
нашли и напряжения в кладке в целях освещения вопроса о воз-
можности появления трещин. ?
Однако использование приема, изложенного в § 2, связано с
оольшой вычислительной работой и потому для практических це-
пей не пригодно.
41
Решение должно быть значительно упрощено; только б этом
случае оно может сделаться применимым на практике.
Изучение эпюр нагрузок, приведенных на рис. 6, 7 и 8, показы-
вает, что без большой ошибки криволинейные эпюры могут быть
заменены треугольными (рис. 13) с наибольшими ординатами над
опорами. Постараемся найти эти ординаты.
В работе автора «Плоская задача расчета бесконечно-длинной
балки на упругом основании» (ВИА, 1937 г.) предлагалась такая
упрощенная формула для определения реакции упругого основа-
ния в месте приложения к балке сосредоточенной нагрузки:
Более точно:
Р0=0,31Р-|/
р0= 0.3055Р
]R=7
(130)
(131)
Поскольку решаемая нами задача имеет много общего с за-
дачей, рассмотренной в вышеуказанной работе, естественно попро-
бовать применить ту же формулу и в данном случае.
Вместо Р следует подставить продольное усилие в колонне;
оно равно:
P = (gHb J-7)L. (132)
Таким образом:
р0 = 0,3055 (g/7& + q)-L
(133)
Длину эпюры d найдем из условия равновесия:
= (gHb + <7) •
(134)
42
г
Отсюда:
q) L __ (rHb + q)L / El
Pq 0,3055 {gHb -f- q) L у EKb
(135)
или:
El
E«b
d =
(136)
г
>F
Вычисления по этим формулам не представляют никаких за-
труднений.
Посмотрим, насколько правильно применить формулы для ранд-
балок.
Для удобства исследования введем упругую характеристику
[см. формулу (73) (стр. 19)]
, 2г.3 EI
я =------.
£к W3
Очевидно:
£к Ь _ 2гз
Е1 ~~ /г/3
(137)
(138)
Следовательно:
р0 = 0,3055 (g776 + <7) '2Z1Z — - (139)
у kt3
или:
£
f -
p0=2,418(g/76 + </) —4—
Vk
(МО)
Г
i.
Аналогично найдем и d:
d_JrHb + q)L
Ро
2 (gWb 4- д') I
или:
з__
d = 0,8271/V k
(Ml)
(142)
г
Й;
Может случиться, что длина эпюры d окажется больше полу-
пролета Z; эпюры будут накладываться одна на другую (рис. 14).
В этом случае в средней части пролета ординаты придется сло-
жить, эпюра будет здесь ограничена горизонтальной прямой.
При большой жесткости рандбалки, когда d >21, надо принять
равномерно распределенную нагрузку.
43
Исследование приведем, как и в § 2, для упругих характеристик
6—0,05; 0,5 и 5. “
На рис. 15, 16 и 17 приведены эпюры, взятые из § 2; па этих
рисунках прямыми линиями показаны приближенные эпюры, для
построения которых использованы формулы (140) и (142).
Как видим, приближенные треугольные эпюры вполне могут за-
менить более точные криволинейные.
Построением эпюр мы не можем ограничиться. Необходимо еще
осветить вопрос и об изгибающих моментах в неразрезной ранд-
балке.
44
Учитывая, что пролет равен 2/ и применяя уравнение 3 момен-
тов (при бесконечно большом числе пролетов), напишем1:
М0ПЛ + 2А4О„ (Л+Л) + MOnL = - — 2 (143)
или:
6MonL — — ,
(144)
1 Индекс оп означает слово «опорный».
45
откуда
ЛДи
(145)
Здесь Л40П —момент на опоре;
— площадь эпюоы моментов для свободно лежащей
балки (рис. 18).
«>=2- — • + —
4 6 6
-2d) = p0-g-(2L-d). (146)
Момент найдем равным:
(72/ я \
Чп=-Ро-ТГ(2-—). (147)
Но, так как
-^- = W+<7)4~. <148)
(gHh 4- q}L(i 19________rf
on in I " r
(И9)
Формулу (149) можно использовать для нахождения момента в
любом сечении, что важно для правильного конструирования ранд-
балки.
На расстоянии от опоры х, если x<dt изгибающий момент ра-
вен (см. рис. 18):
Л4х = Моп+^Дх--^-. l_x--^(d-x)^-.’f =
= маа + (3d2 - 3dx + л=). (150)
Далее при х > d:
мх = Мт + . (151)
6
Для суждения о размерах погрешности, даваемой приближен-
ными формулами, приводим таблицу абсолютных величин опорных
моментов, вычисленных по формуле (100, стр. 30) и по приближен-
ной формуле (149) при различных упругих характеристиках* 1
(табл. 17).
L
1 При k~ 5 формула (149), строго говоря, неприменима, так как4>'у
мы рассматриваем эту формулу как приближенную.
46
Таблица 17
k По формуле (100) По приближенной фор- муле (14Л Ошибка в %
0.05 0,0897 0,0938 4,6
0,5 0,1862 0,1829 1.8
5 0,2980 0,3047 2,2
XfeWf X(gHb+q)?
Из таблицы видно, что приближенной формулой вполне можно
пользоваться.
Замена криволинейной эпюры треугольной практически вполне
оправдана и значительно упрощает вычисление.
При расчете раидбалки необходимо также проверять сжимаю-
щие напряжения в кладке над опорами, где они достигают наиболь-
шей величины.
Так как концентрация напряжений наблюдается только на ко-
ротких участках, можно повысить допускаемые напряжения или
снизить коэффициент запаса.
Не лишен интереса вопрос о распределении напряжений в клад-
ке в предельном состоянии. Можно предложить такую довольно
условную схему работы конструкции. Когда напряжения над опо-
47
рами дойдут до предельных разрушающих, они дальше увеличи-
ваться не будут, но зона пластичности станет распространяться в
стороны. В результате в стадии разрушения кладки эпюра нагруз-
ки на рандбалку изобразится трапециями, или проще — прямо-
угольниками с ординатами, равными Rb (рис. 19,а), где/? — предел
прочности, а b — толщина стены.
Если вести расчет по допускаемым напряжениям, то, когда на-
пряжения над опорами превысят допускаемые, эпюры можно ус-
ловно принять в виде трапеций. Ординаты их будут соответство-
вать допускаемым напряжениям; углы же наклона эпюр по их кон-
цам примерно равны углам наклона соответствующих треугольных
эпюр (рис. 19,6). Площади эпюр должны быть равны опорным ре-
акциям.
§ 6. УЧЕТ'КАСАТЕЛЬНЫХ НАПРЯЖЕНИЙ
Во всех предыдущих выводах мы принимали, что между ранд-
балкой и вышележащей кладкой отсутствуют силы сцепления или
трения, что кладка может свободно скользить по рандбалке. Нам
необходимо теперь проверить, насколько такое допущение обосно-
вано.
Поэтому разберем более сложный случай, когда скольжение
кладки по рандбалке невозможно и по линии контакта возникают
касательные напряжения.
а) Основные данные
Предварительно следует вывести некоторые формулы, которые
будут нужны в дальнейшем,
48
Обозначения.оставим те же, что и в § 1 (рис. 20). Положитель-
ные направления напряжений указаны на рисунке.
Двумя параллельными сечениями выделим из рандбалки эле-
мент длиной dx (рис. 21).
К этому элементу помимо мо-
ментов (слева Л4, справа M+dM) и
поперечных сил (Q и Q-h^Q) при-
ложены еще продольные силы, выз-
ванные касательными усилиями:
слева N и справа N+dN.
От кладки на рандбалку пере-
дается вертикальная нагрузка ин-
тенсивностью р; на длину dx при-
дется pdx. Кроме того, к элементу
приложена горизонтальная сила tdx,
где t касательное усилие при
Рис. 21
Напишем уравнения равновесия
выделенного элемента.
Возьмем сумму моментов отно-
сительно точки В:
ЕЛ4„ = О. (152)
М-(М +dM) + Qdx — pdx~ + tdx- = 0. (153)
Сделаем сокращение и отбросим бесконечно малую .второго по-
рядка:
— dM + Qdx + tdx-~- = 0. (154)
Отсюда:
_"L = Q + f* (155)
dx 2 .
Спроектируем теперь силы на вертикальную ось (£У=0):
q „ (Q + dQ) — pdx = 0 : (156)
Отсюда известная’формула:
dQ
(157)
Далее возьмем проекции сил на горизонтальную ось (2Л^0):
(/V dN) л-tdx^Q. (158)
Отсюда:
dN
dx
(159)
4 Б. Н. Жемочкин
.49
Дифференциальное уравнение упругой кривой рандбалки;
-^- =-------" (1б0)
dx* EI , х 7
Знак минус объясняется тем, что мы считаем прогибы положи-
тельными, если они направлены вниз.
От момента необходимо перейти к нагрузке. С этой целью два
раза продифференцируем это выражение и воспользуемся форму-
лами (155) и (157):
d2M 1 / dQ . h di \ .
dx* El dx* El \ dx 2 dx j 7
Таким образом:
П4 w _ 1 / Л di \
dx^ “ EI 2 dx 1
(162)
Поскольку рандбалка и кладка работают совместно, перемеще-
ния точек верхнего волокна рандбалки и нижнего волокна кладки
одинаковы. Это мы и учтем в дальнейшем, сейчас же нам нужно
установить связь между горизонтальными перемещениями в верх-
нем волокне рандбалки и нагрузкой..
Напряжение в верхнем волокне рандбалки:
где F— площадь поперечного сечения рандбалки.
Относительное удлинение:
С другой стороны:
где Uq — перемещение точки внизу кладки при у^О.
/ М —
dun _ 2__________У
dx Е V I F
Продифференцируем дважды:
ds и0 _ 1 /___d2M__________1 (/ТУ
rfx3 ~ Е 2/ ‘ dx* F ' dx2
(164}
(165)
(166)
(167)
На основании формул (155), (157) и (159):
_ 1______/? IdQ h dt \____1 dt '
dx* E _ 21 \ dx 2 dx ) F dx
50
— ( — О 4-• -— ---• —
2/ \ л 2 dx) F dx
1 Г . * f h2 . 1 \ dtl
— + —P—-----------— •
E [ 2Г ( 41 F dx
(168)
Предположив рандбалку прямоугольного сечения, будем иметь:
(169)
Поэтому
d2 h h2 d<
- - —---— р — ——.-----
dx2 2Е1 н ЗЕ! dx
(170)
б) Функция напряжений
Зададимся функцией напряжений того же вида, что и раньше
[формула (5) (стр. 9)]:
<f> = s COS (ах) [Ci sh (ау) ф- С2 СЙ (ау) + С3 у sh (ау) 4- Ci у ch (ау)] +
+ D5x2 + D,xy + ZXy2 4- 4- D^y 4- Dicxy2 4- Dny*. (171)
Общие формулы для напряжений и перемещений останутся те
же, как и в случае отсутствия касательных усилий между рандбал-
кой и кладкой. Следовательно, будут справедливы формулы (7) —
(20).
в) Определение коэффициентов D
Условия для определения коэффициентов D остаются -прежними.
Ввиду этого можно взять готовые формулы (34) — (38) (стр. 13
и 14) для напряжений и перемещений из § 1:
~ £ 1 cos (ах) а [С2 sh (ау) 4~ С2 ch (ау) 4- С3 у sh (ау) С4 у ch (ау)] 4-
+ 2 [С8 ch («у) + С, sh («/)]] - 4^ - У) + 441 (172)
а у ~ — £ а2 cos (ах) [С3 sh (ау) -ф С2 сН(ху)фС3у sh(ay) 4-С4 у ch(ay)] —
h
(173)
т = £ a sin (ax) [Ci Ch (ay) 4" C2 sh (ay) 4- C3 У ch (ay) 4-
+ Ci у sh (ay)] + [c3 sh (ay) -ф C4 ch (ay)] ; (174)
4*
51
и = — 2 sin (ах) f (1 J- р.) а [Сх sh (zy) 4- C2 ch (ay) 4~
£k i I
(175)
V =-----— S COS (ax) [ (1 J- р.) a [Cj ch (ay) 4- C2 sh (ay) +
1 .1
+
Ee[(1 +Я)аС1-(1-н)СЛ
_ (1 _4-~
L I 2 T 6
(176)
Е,
г) Определение коэффициентов С
Условия по нижнему краю в данном случае отличаются от тех
условий, которые мы имели в § 1.
Первое условие состоит .в том, что вертикальные перемещения
кладки и раидбалки в месте их сопряжения одинаковы. Исполь-
зуем дифференциальное уравнение упругой кривой [формула (162)]:
d^w 1 / д & \
dx* Е1\ 2 dxl
Входящий сюда прогиб w мы получим из формулы (176), при-
няв в ней у=^0 и изменив знак:
ш - - V - — s COS (zX) [(1 4- p.) a C\ - (1 - (i) G] -
i
-A-S[(l +P)aC,-(l-|l)C1] =
=----“ S [1 — cos (ax)] • [(1 + ЛаС1 —(1 —OCJ •
''K 1
Нагрузка на балку на основании формулы (173):
Р = — °у(у=0)b = b£ [a2cos (ax) Cz\ + (gHb + q).
Далее: - 1
' 4 = &4 =6X«.2cos(ax)[aCI + Cil] .
(178)
(179)
(180)
(у=Щ 1
52
Подставляя найденные значения в уравнение (177) и произво-
дя четырехкратное дифференцирование в левой ’части, получим:
— S a4cos(/%) [(1 + р-)а<?г — (1 — р.) С4] =
£к J
- (бX[<ха cos (ах) С.1 + (gHb + а)- COS (ах) [aCj+Cj
El i “ 2 ,
(181)
Каки раньше (стр. 15), разложим в ряд по cos величину
(gHb + q)-.
(gft6+ <?) = —+ <?) Xcos(ax). (182)
1
Подставим в уравнение (181).
Все члены его представят теперь разложение по cos. Объеди-
ним их:
Seos (ах) К1 + Iх) а ~ Iх) £*]---------С"2 +
1 I Ек EI
+ 47(^ + <?) + а*-^-[аС1 + сф = О.' (183)
Е1 J
Для того чтобы сумма бесконечного ряда равнялась нулю, не-
обходимо и достаточно, чтобы каждый член равнялся нулю. Сле-
довательно:
— а4 [(| + и) аС1 - (1 _ ц) С4] - -f-ЬС2 +
£к
4- ту (&7/^ 4- q) + or 0 "у (aCi 4~ ~ 0 -
Е1
Это уравнение приводится к виду:
(1 + Л as+«!-^r’ СХ-^^С2-
J hl
(1. _ а) а> _ а2 АД11 Ci =--(„нь + а) .
(184)
(185)
Учтем теперь условие, что горизонтальные перемещения точек
верхнего края раидбалки и нижнего края кладки одинаковы. Это
условие выражено формулой (170):
-АА_ = _А_ р--------. (186)
dx* 2EI 3£/ dx
Входящее сюда w0 по формуле (175) равно:
"о = " 0)= 2rSsin(ax)f (1 + р.)аС2 +2С3 1. ’ (187)
u Ек j ( )
-53
Подставляя в уравнение (186) значения uOt р и , получим:
-----— S a3 cos (ах) [(1 + р.) а С2 ф- 2С3] ~ - Й а2 cos (ах) С2 ф
1 2Е1 1
+ (gHb + q)
Сделав замену
(gHb J-7) = —2 (gHb 4- 7) Seos (ax), (189)
i
Sa2COS (ax) [a Сг ф-C4] . (188)
приведем уравнение к виду:
Seos (ax) [(1 + pj a C2-b 2C3] — C8 +
I ( 2£i
• H90)
Ы oEJ J
Отсюда следует:
- 4 [(’ + O*C2 + 2C3] - a2 C2 + A(gHb 4- q) +
hh%
+ a* ФФ <aCi + C<> = 0 (191)
oE.1
или в более удобной форме:'
3~ГС1~И1 +о+*2
ЗЕ1 |_
£к bh ~
2Е1
С2-2а3 с3 +
+ *г С* = - -^гteHb + *?)•
ЗЕ1 El
(192)
Следующее условие состоит в том, что для верхнего края сте-
ны при у~Н\
-oyb^q, (193)
. Получим уравнение: ' С'
S a2 cos (ах) b [Q sh (a/Y) + С2 ch (аЯ) +
+ C^Hsh^.H) 4- С4 Z/ch(a/Y)] 4- q = q. (194)
Отсюда;
Cz sh (a/7) 4- c2 ch (аЯ) + C3 H sh (аЯ) + с, H ch (аЯ) - 0 . (195)
Как и раньше, остановимся только на случае, когда Я доста-
точно велико, и примем
зЬ(аЯ) сИ(аЯ). (196)
Й
Тогда’по сокращении:
Сх 4- С2 4- С3 Н + С Л = 0.
Наконец, учтем, что в верху стены при
Е a sin (ах)| а [Ci ch аЯ) 4* С2 sh (аЯ) 4"
1 t
(197)
4- С3 Н ch (аЯ) 4- С4 Н sh (аЯ)] 4- [С3 sh 4- С4 ch (а//)] = 0. (198)
.Опять, -принимая гиперболические синус и косинус величины
(аЯ) равными между собой, получим уравнение:
а Сх 4- а С2 4- (аг/ 4- 1) С3 4" (^Я 4- 1) С4 — 0 . (199)
Итак имеем систему из 4 уравнений:
(1+(1)а5 + азД^]С1_а2Щ^С2_ .
-[(i-rf«4-«2^-]c4 = -2-^-(gW6 + <7); (200)
[ J hl
oizl -czsJ
-2asC3 + a2^C4 = --^(^6 + <7); (201)
3E1 El
C, + C2 + Cs H + Ci H = 0 ; (202)
aCi + aC2 + (atf + 1) C3 + (all + 1) Ct = 0 . (203)
Решая совместно эти уравнения, получим:
C^-C^^lglJ+^X
а3 \ о /
Г El , El 1
.— 24а--- — 6(1 — р.) а2-г — 1
_________:______EHbh2_________EKbh J____________ (204)
(El)2 El El El ' \ I
12(14-д)(3-(ф4Щ-‘+24z—— + 12(1-^2— +8a3 —-+1
E b2h2 EKbh- £Kbh EKb
к
Г. £1 1 е a + с -2) -1 ЕКЬ№
(El)2 El El El
12(1+^) +24s-—П2(1-;х)а2-— 4-8a3— +i
E:.b2h2 EKbh2 EKbh - EKb
(205)
Введем применявшуюся нами ранее упругую характеристику
[формула (73) (стр. 19)]
9Г3 рг
(206)
. . ........ .. Ек Ы3 _ _______ ______
' 55
Очевидно, что в формулах придется сделать замену:
(207)
£кй 2.-.S
Палее учтем, что:
а = -у- . (208)
Наконец, для упрощения письма примем обозначение:
V = Л_ . (209)
тт/г
Тогда наши формулы примут вид:
сх = — с, = — fff/7+ -Ч X
“ а2 Ь )
у, _____________f— — ЗЦ . (2
[3(1 +ЖЗ-н)'^2''2Ч- 12лгЛ >2 6( 1 — 1и.)л2Ь-р4кЗ/г+ lj ’
C3 = -C4 = -^-(g//+4-)x '
у ________________[3(1 + и.) л/г (/г — 2-Q -- 1]__________ (211)
Х [3 (1 + и) (3 - р-) /Лг2/2 + 12лг/г + 6 (1 - р.) п№ + WU + 1] * '
д) Формулы в окончательном виде
Найденные значения С можем подставить в формулы для на-
пряжений и перемещений (172) — (176) (стр. 51—52).
Ограничимся здесь только определением нагрузки на рандбал-
ку р, определением касательных напряжений по линии контакта
рандбалки и кладки и горизонтальных нормальных напряжений
в низу кладки
Формула (179) (стр. 52) даст нагрузку на рандбалку:
р = Sa2cos(7.x) ЬС2 4- (gHb J- q). (212)
i
После подстановки получим:
Р = (gHb + q)/2 V cos(~—) x .
11 \ 1 /
'112 + 3(1 —u.) -+ 11 . p
[3(1 + jj.) (3 — p.) rpk~ 'i2 -j- 12/гА’ v2 + 6(1 — jj ) /z2 X v -t- 4/i3Zt’ + 1] 1
56
Касательные напряжения по линии контакта рандбалки и клад-
ки на основании формулы (174):
То — s a sin (ал) (а С\ + С4) ~ 2 gH + — 'j S sin (ах)Х
1 ' b ! 11
— [—12^2 — 3(1 -p.) zz2^ — 1]-— [3(1 + ^)nk^ (n- 2'4—1] '
X-------------------------:------------------------------. (214)
[3 (1 -f- (j.) (3 — у.) n4j2 'J2 Д- 12п г v2 -j~ 6(1 — p) n2k ч 4- 4;z3£ -p 1]
Получим:
T0 = - 12 gH^ -4 VsinjXX x
b / j \ I /
________________nfr ч Щ 4~ (1 — 1X) ”4_
^[3\1 4- p) (3 — p.) л4Л2'/2+ 1‘/2 4-6 (1 — ;i) tfk w ~p4/z3A + 1]
Горизонтальные нормальные напряжения в низу кладки на ос-
новании формулы (172):
с — 2 a COS (ах) (а С2 4~ 2С3) — [gH + —) =
j ! L \ ь /
= (gH Ф Ь £ а cos (а%)Х
\ ь / ( !
1 , 2
— [12ггЛ 'A]-3(l — y}n2k '> 4- 1] + — [3(1 4-p)/z£'> (rz —24)—1]
а а
[с(1 4- р.) (3 — а) /£4А'2 '^2 4“ 12/zA v2 4~ 6( 1 — и.) _|_ 4/i3?t 4~ 1]
После преобразований:
' Г3(3,4- ч) —12irt.^'^ —И___________________________]
у.) л4/?2 '/2 4- 12«V v2 4-6(1 — u) п21?') 4~ 4/z3/? 4- 1 j J
[3(1 4-(3
е) Пример
Вычисления по вышеприведенным формулам чрезвычайно слож-
ны и, конечно, эти формулы на практике совершенно не примени-
мы. Пример, который мы здесь разберем, имеет цель выявить толь-
ко общую картину для возможности оценки влияния касательных
напряжений.
Примем для примера некоторое среднее значение упругой ха-
рактеристики £=0,5 или /С=1,01.
57
. Этой характеристике соответствуют данные:
отношение длины пролета к высоте раидбалки по формуле (88)
(стр. 22)
-=^^- = 9,38 — 9,4;
Л з______
]Л),5
коэффициент
/ L 9,38 , .nQ
. v ~---- = ----- = ---- = 1 493 ;
г./г 2г h 2л
Нагрузка на рандбалку будет определяться по формуле (213),
которая примет вид:
2 S cos
1
Р = (glib + <?)
_______[1,792^4- 13,374л 4-1]______
[5,617л4 4- 2/4 4- 3,583л2 + 13,374л 4-1]
(218)
Опуская вычисления, дадим только окончательный результат,
изображенный на рис. 22. Здесь сплошной линией показана эпюра
нагрузки^на рандбалку в предположении, что между рандбалкой
и кладкой возникают касательные напряжения.
Для сравнения на чертеже дана эпюра, взятая из рис. 7 (стр. 26)
и вычерченная пунктиром, в предположении отсутствия касатель-
ных напряжений.
Как .видим, разница между эпюрами невелика. Наибольшая
ордината над опорой при наличии касательных напряжений рав-
на 3,28 (gHb+q)t а в случае их отсутствия 3,03 (gHb + q), Таким
образом, расхождение составляет 8%, что, .безусловно, для подоб-
,58
ных расчетов следует признать малой величиной. Но это расхож-
дение относится к ординате над опорой; в других ординатах разни-
’ * ца меньше.
На рисунке показана и треугольная эпюра, построенная по при-
ближенным формулам § 5. Она одинаково хорошо заменяет и одну
и другую криволинейные эпюры.
На основании анализа полученных результатов приходим к за-
ключению, что наличие касательных напряжений очень мало от-
ражается на характере эпюры нагрузки на рандбалку и практиче-
ски ими можно пренебрегать. Поэтому впредь мы уже не будем
возвращаться к-тому же вопросу и все дальнейшие исследования
будем вести без учета касательных напряжений.
Попутно необходимо выяснить, какова величина касательных
напряжений и насколько реально их существование.
Для касательных напряжений используем формулу (215), ко-
торая для нашего примера примет вид:
(i СО / _ л <
£#+ —) S Sin IX
ь / 1 \ / /
_________[0,746^ 4-0,892^______ .
Х [5,617л4 4- 2л3 4- 3,583/г2 Д- 13,374л 4- 1] * 1 '
Эпюра касательных напряжений приведена на рис. 23. Наиболь-
шая' ордината равна 0,99 (gH~]—~ ,
\ Ь / ”
Если мы обратим внимание на то, что в месте тотах приложе-
на значительная вертикальная нагрузка, которая обеспечивает си-
лу трения, то придем к выводу, что существование касательных
напряжений вполне реально. Эти напряжения могут погашаться не
только сцеплением, но даже силами трения, А потому появление
горизонтальных трещин как результата сдвигов кладки по ранд-
59
балке хотя при каких-либо особых условиях и не исключено, но в
общем мало вероятно.
Если касательные напряжения мало отражаются на нагрузке-
на рандбалку, а следовательно, и вообще на вертикальных нор-
мальных напряжениях в кладке, то влияние их на горизонтальные
нормальные напряжения, наоборот, весьма значительно.
Эпюры, которые были приведены на рис. И и 12 (стр."39 и 41)
для освещения вопроса о порядке величин напряжений, уже не
соответствуют действительности,
Горизонтапьные нормальные напряжения 6:
---------- с учетом касательных напряжений
•— без учета касательных напряжений
1'2,23 (дН + р)
Рис. 24
Раньше мы получили в низу кладки растяжение (в горизон-
тальном направлении) в середине пролета и сжатие на опорах.
Теперь же при отсутствии сдвигов кладки по рандбалке в середине
пролета должно быть сжатие, а на операх растяжение.
Горизонтальные нормальные напряжения по ли-
нии сопряжения кладки с рандбалкой можно найти по формуле
(217), которая примет вид:
°Xj= \gH + I2 £ cos
X----------{Л1_ббпз-2,б-оя-1|-------— 02). (220)
[5,617/11-t 2n3 4-3,5S3№ + 13,374/1 + Ц J
Эпюра напряжений, вычерченная сплошной линией, приведена
на рис. 24. Здесь же пунктиром показана эпюра, взятая из рис. 12,
для случая, когда касательные напряжения отсутствуют. Знаки
ординат стали другими, но порядок величин напряжений примерно
прежний.
Если в кладке и появится вертикальная трещина, то не в сере-
дине пролета, а над опорой. Наличие такой трещины не отразится
заметно на нагрузке на рандбалку.
ГЛАВА II
НЕКОТОРЫЕ ЧАСТНЫЕ СЛУЧАИ РАСЧЕТА РАНДБАЛОК
§ 7. РАСЧЕТ РАНДБАЛОК ПРИ СТЕНЕ ОГРАНИЧЕННОЙ ВЫСОТЫ
а) Нагрузка на рандбалку
До сих пор мы предполагали, что кладка стены имеет очень
большую высоту, намного превышающую пролет. Теперь же нам
надлежит исследовать случай стены ограниченной высоты (рис. 25).
Функцию напряжений примем ту же, как и в § 1. Коэффициен
ты D будут такими же. Но для нахождения коэффициентов С сле-
дует взять уравнения в общем виде [формулы (56—59) (стр. 17)]
без сокращения гиперболических функций, что было справедливо
при Я, стремящемся к оо .
Эти уравнения:
а5 (1 + ц) С,-«2 ££С2- а*(1 - |х) С4=' -(gHb + <?); ' (221)
bl с/
' а С, + С4 = 0 ; (222)
61
Ci sh (аЯ) + C2 ch (аЯ) 4~ C3 ЯзЬ (аЯ) + C4 Я ch (аЯ) = 0 ;......(223)
a Cj ch (аЯ) 4- a C2 sh (аЯ) 4~ [(%H) ch (аЯ) 4- sh (a//)] C3 4~
4- [(a//) sh (аЯ) 4- ch (аЯ)] C4 - 0 . (224)
Решив уравнения, получим:
>i —
MHEI
2^з EI
(225)
EKb
E}<b
a2
2a4 HEl 1
E^b
27.3 El
~T— (^ + О + “2^(1“Ф2)
E^b
(226)
2(T+~M
c3 =---------------------------------------------
Г 2a4 HFl \ 2ct3 El
a ф2(" ' ^---1 ~ - (аЯ + |) + а2Я2(1-ф2)
L \ ' E«b / EKb
2 fg/y -£~\ [ф _{_ a// (1 _ ф2)]
C4---------------------------4—------------------------------ (228)
Г / 2a* HEl \ 2a3 El
4И —PT— — 1) — -~(aH 4- Ф) T a2//2 0 “ Ф2)
L \ EKb / EKb J
Здесь через ф обозначено
= th (=Я) = • (22Э>
Ch (a/7)
Ограничим свою задачу только определением нагрузки на ранд-
балку. Так как в формулу для нагрузки входит коэффициент С2, то
дальнейшие преобразования проведем для этого коэффициента.
Введем для удобства упругую характеристику k [формула (73)
(стр. 19)]
2кз EI
ЕКЫ3
(230)
Следовательно:
EI _ ^/3
ЕКЬ “ 2гсЗ
(231)
Кроме того, подставим
mz
a — ------.
Z
(232)
62
Тогда:
П2-2//2.
--------- (1 — б2)
/2 . )
Решая конкретную задачу, мы будем принимать определенное
отношение высоты кладки к полупролету. Обозначим это отношение
( = -у-. • (234)
Поэтому:
: . , с'2 х .......................
\ ь /
х_______________________________________________________ (235)
П2 7г2 [ф2 Гь.С £ _ пЧ д2=2 Ц - q,2) j
Коэффициент б является переменной величиной, зависящей от
порядковых номеров членов ряда. Преобразуем выражение для Сг,
пользуясь тем, что:
ф — th (аЯ) —
sh (оН}
ch (я/У).
(236)
— Q
еаН + е-аН
Таким образом:
C2 = fg^+-^p2X ’
\ о /
2 пМ2 1 —
еаН~е~аИ \ 2~
2
е-н_ е~аН
еаИ~е~аИ V
е^Н ... е-аН ) J
/ ' е*н ~е~аН
n3k ( п 4-----------
е^н _е~аН т
е^н ^е~аН )
63
Умножим числитель и знаменатель на (еаН + е~аН)2: .
C2 = (gW+^-)/2X
2 f4rt2TC2^—-g-a/92]________>
п2 т> J (ес// — e~aii )2 (п4 v£k — 1)->
-+------------------------------------------------- . (238)
[/ьх- (еаЛ/ + е *H)2 + {е^н — е 2aW)] -|-4n2 *2;2}
Далее, умножим числитель и знаменатель на е~2лИ:
С2 — X
X___________2 [4/Z2 л2;2 е-^н — (1 — е~2а/у)2]__
П2Л2 [(1 — k __ (j е-2аН)*+
----------------------------— . (239)
+ + (1 - e“w)] + № *~2а"!
Наконец, сгруппируем иначе слагаемые в знаменателе, сделав
соответствующие преобразования. Получим:
C2 = lgH-i-^-\pX
\ о /
2 [(1 _ е-2аИ}2~4п2т^ е~2аН]
х---------------ill!—-----------------'——L__-----------. (240)
«2тс2 [п3/г [4я л; е 2a/v+(l—е 4a//)j—4ч2 к2;2 е~ 2а//-|- (1—е—2аА/)2|
Нагрузку на балку
р^~оуЬ (241)
при У=0 найдем по формуле (40) (стр. 14):
р — b £ a2 cos (ах) С2 + -j- q) =
1
= b sа2cos (ах) [gH4- —) /2 X
( 1 \ Ь /
__________________2 [(1 - с"2*")2 ~
п2к2{п3А[4/г е~2аИ 4- (1 —е—4а/у)] —4^2 к2;2 е~~2а^-{- (1—е“2а//)2}
(242)
Окончательно получим:
Р — + q) 2 X cos
I 1
(243)
-2^)2„ 4z22r^2e-2^]
/Xn^k [4/г е"2пгЛ+ (1 ~ 4^Ve-2n^+(\
€4
Вследствие сделанных нами преобразований входящий в фор-
мулу ряд имеет хорошую сходимость.
Если принять £ = оо (для очень высокой стены), то, поскольку
получим формулу (83) (стр. 21).
б) Примеры
Разберем случаи упругих характеристик 6 = 0,05 и 6=0,5 при
различной высоте стены. .
1) k = 0,05 ; к = 0,10 (— = 20,
n L
При высоте стены, равной полупролету, т. е. когда Я = — / и
— ~ — — 1 , 1, формула (243) примет вид:
р= (gHb + у) 2 Seos —7
1 \ *
2«-
0,05/г3 [Ч/гке 2пг'
—4^2-2 с
-4^)] _ ^2-2 е-^
+ 1 .(244)
Если высота стены равна четверти пролета, т. е. Н = — и
I
2
, /7
— = — = 0,5, то:
7 /
Р = (gHb + <?) 2
0,05л3
(245)
В этих рядах при увеличении порядкового номера п числитель
быстро приближается к 1. В формуле (244) уже при /г=3 числи-
тель равен 0,999998 и в формуле (245) та же величина числителя
будет при п = 6. Начиная с этих значений п, знаменатель становит-
ся равным (/гб + 1), а потому при вычислениях можно пользовать-
ся дальше данными примеров из § 2.
Опуская вычислительный процесс, дадим только окончательные
результаты.
На рис. 26 приведены эпюры нагрузок, причем сплошной линией
Н 1 я 1
дана эпюра для — = — и пунктирной — для — = — .
Эпюру для случая Н = оо показать на чертеже нельзя, так как
она совершенно сливается с эпюрой для Н~'~~. Да и расхожде-
ние между эпюрами для Н = и Н = ~- чрезвычайно мало.
5 Б. Н. Жемочкин
65’
Таким образом, оказывается, что при высоте стены, равной да-
же четверти пролета, распределение нагрузки на рандбалку такое
же, как и при стене неограниченной высоты.
Следовательно, вполне можно применять приближенный способ,
изложенный в § 5.
Рис. 27
36
Формулы для этого случая отличаются от-формул для случая
6=0,05.только тем, что в знаменателях вместо коэффициента 0,05/Р
должен быть поставлен коэффициент 0,5/г3. Сходимость рядов здесь
лучше, чем в предыдущем случае.
Результаты приведены на рис. 27.
Оказывается, что эпюра при Н = — почти та же, что при Н= оо.
Однако эпюра при Н=~~ уже заметно отличается от эпюры
при В наибольших ординатах разница доходит до 15%.
Очевидно, что если высота стены будет еще меньше, то эпюра на-
грузки приблизится к эпюре нагрузки, равномерно распределенной.
в) Изгибающие моменты
Решающими факторами при подборе сечения рандбалки яв-
ляются изгибающие моменты и поперечные силы.
Моменты можно находить дифференцированием уравнения уп-
ругой кривой. Но тогда придется установить значения коэффициен-
тов С] и С4.
Чтобы избежать этого, найдем моменты интегрированием на-
грузки, пользуясь тем, что:
М = — Л pdx2. (246)
По формуле (40) (стр. 14):
р ~ — Gvfy_0) 6 = 6 S [с? COS (ах) С2] + (gHb 4- q). (247)
Момент равен
М == — С С [a2 cos (ах) С2| — (gHb -f- <?)| dx2 =
J J ( 1 J
00 у2
= byl[cos(,ax)Ci]-(gHb + q)^- + Ах+в. (248)
1 *
Произвольное постоянное А найдем из условия, что в середине
пролета при х—7
Q = = 0 . (249)
dx
Получим:'
— b S [a sin (а/)С2] — (gHb + q) I + Л = 0 . (250)
1
Так как
sin (а/) = sin (пт) ~ 0 , (251)
5*
67
то:
(252) -
ЧТО ПЛО-
Для нахождения постоянного В воспользуемся тем,
щадь, ограниченная эпюрой моментов, равна нулю (как и во всякой
неразрезной балке, фиктивные опорные реакции на всех промежу-
точных опорах равны нулю).
Следовательно:
(253)
Получим уравнение:
J i 1
о
Интегрируем:
i
+ (gHb + q) Iх 4- £? I dx — 0.
(254)
sin (ах) С2 —(gHb q) ~ -6 (gHb ф- q)^+ Зх! =0.
(255)
Далее:
I д
Отсюда:
1 /3 ГА )
I “ (gHb + д)~± (glib + д) 4- Bl - 0..
(256)
в = •- (gHb 4- 7)— .
О
(257)
Таким образом:
М = b £ [cos (ах) С2] — (gHb + q) — -f-
1 2
+ (gHb 4-7 lx~(gHb + q) у
О
= ь E [C s (ax) c2j — (gHb 4- q)
i
х2
2
(258)
Это выражение можно
образование:
X2 /2
— — /х + — -
2 3
2/2 /
упростить, если сделать следующее пре-
2/2 / ~2Х2 __ 7^2 lx , 7t2 /2
К2 (, 4/2 2/2 6/2
2/2
ТИ2 ( 4/2
2/
(259)
i
о
— Iх 4 — •
О 1
Но есть некоторый угол
тсх
? = ~
(260)
68
причем
О < О .
Таким образом:
х2 , , /2 2/2 / <р-
~~— lx Н-----= — ~
2 3 'к 4
Известна формула:
V । _т
'пЬ ~ 4 2*6
I
(261)
(262)
Поэтому:
2/2
00 cos ___ 2Z- y, , И “ x , I 1 00 = 2 V — cos (ax), П~ a2 (263)
1 1 Момент: oo Qo zVI = b У [cos (rix'} C2] — 2 У — cos (ax) {gHb + q) = ““ a~ i i
co = £ COS(ax) 1 Г 9 1 bc.~^ (gHb + q) . a- I- J (264)
Подставим сюда значение С2 по формуле (240):
М = S cos (ах) !(gZ/6 + q) р X ,
. 2 [(1 — е~-“О3 - 4л» е~Ы1\______________
tf-т? [«'* [4л л5г~2’"+(1 — г_4’я)[ — 4л2л=е2е-2аН+(1 — е-2’«)2|
— у,- (gHd + q) j = 2 (gHb + q) E cos (ах) X
r _____________[(1 e-^H] p
tait2 \ri>k [4n те? e~2“"+ (1 — e~4aH)l — 4a2 ^2 g-2aH-j- (1 — e~2’w)2)
_-£_)-!ftOT + 0i(S^M.x
n2 к2 J it1 V ii"
x - tfk [(1 + 4n TtS 1 .
n?k [4n e“2aW-f- (1 —e~.4a/y)] — 4n27i262£“2a//4- (1 —£~2a/7)2J
69
Окончательно
(266)
В частном случае, когда £ = со, эта формула переходит в фор-
мулу (97) (стр. 29).
Поперечных сил мы здесь не касаемся, поскольку у опор опи
не зависят от упругих характеристик.
Сделаем вычисления моментов на опоре (х = 0) для тех же слу-
чаев, которые мы разобрали раньше.
В следующей таблице (табл. 18) выписаны абсолютные значе-
ния моментов по точной (условно) формуле (266) и по приближен-
ной формуле (149) (стр. 46).
Таблица 18
k К L h н L По формуле (2GG) По приближен- ной формуле (149) Ошибка в %
0,05 0,10 20,2 со 0,5 0,25 0,0897 0,0907 0,1045 | 0,0938 < 4,6 3,4 10,2
0,5 1,01 9,4 оо 0,5 0,25 0,1862 0,1909 0,2339 0,1829 J 1,8 4,2 21,8
и X (gHb + 7) Z2 X(g//6-b(7)/2
Анализ таблицы показывает, что при гибкой рандбалке, с упру-
гой характеристикой k^0,05 или К = 0,10, приближенную формулу
можно применять в том случае, когда высота стены превышает l/i
пролета ^т. е. — ^,25 или с = у- = уу — . Для более
жесткой раидбалки, когда /г=0,5 или К= 1,01, лучше считать преде-
I Н z е Н Н ж
лом высоту, равную полупролету — = 0,5 или = — = — = 1 .
JLy JLz JLrj £ т
При промежуточных значениях упругих характеристик предель-
ные высоты стены имеют промежуточные значения.
В практических расчетах можно предложить придерживаться с
некоторым запасом следующего очень упрощенного правила.
70.
Принимать нагрузку на рандбалку по треугольным эпюрам,
определяемым приближенными формулами, если упругая характе-
ристика К (см. формулу 74 стр. 19), равная
1000
EI
EKbL3 ’
(267)
меньше или равна ОДО (К< ОДО) при стене высотой большей или
равной четверти пролета j ; если же упругая характери-
стика больше ОДО (К>0,10), то приближенные формулы приме-
нимы при стене высотой равной или большей полупролета .
Если высота стены меньше указанных пределов, следует рас-
считывать рандбалку на равномерную нагрузку.
Конечно, если от расчета не требуется большой точности, мож-
но перейти эти пределы и применять приближенные формулы при
меньших высотах стены.
г) Влияние способа производства работ
Во всем предыдущем изложении мы как бы подразумевали, что
кладка стены и рандбалка сначала выполнены, а затем.они начи-
нают работать на вес стены и внешнюю нагрузку. В действительно-
сти так не бывает: кладка возводится постепенно .и внутренние
силы в ней по 'мере возведения непрерывно изменяются.
Когда на рандбалку положены только первые ряды кладки, то
они дают равномерно распределенную нагрузку; последующие ряды
нагружают рандбалку больше у опор. Переход от равномерно
распределенной нагрузки к нагрузке по треугольной эпюре, заме-
няющей эпюру криволинейную, совершается постепенно.
Канд. техн, наук М. Я. Пильди-йН приводит интересные дан-
ные о результатах опытов с возведением стены из керамических
блоков на стальной однопролетнои ''Валке пролетом 3,5 ж из швел-
лера № 18.
Из графиков, помещенных в статье, видно, что до того момента,
как был уложен 3-й ряд кладки (высота примерно 0,9 м, что соот-
ветствовало четверти пролета), прогибы балки были такие же, как
и от равномерно распределенной нагрузки. Далее нарастание про-
гибов замедлялось, что свидетельствовало о начале совместной ра-
боты балки и кладки. После укладки 6-го ряда (высота примерно
равнялась полупролету) нарастание прогибов становилось почти
равномерным. Значит нагрузка уже концентрировалась у опор,
как это должно быть при затвердевшей кладке большой высоты.
В результате обработки наблюдений и теоретического исследо-
вания автор статьи приходит к выводу, что до высоты, равной про-
1 Влияние условий производства работ иа расчет балок, несущих каменные
стены, «Строительная промышленность» № 2, 1949.
71
лету, нагрузку следует считать равномерно распределенной и рав-
ной некоторой условной нагрузке, определяемой данными автором
формулами. Последующую нагрузку принимать по треугольным
эпюрам (формулы для треугольных эпюр несколько отличаются от
выведенных нами). Полученные эпюры от обеих нагрузок нужно
сложить.
Нам представляется такой путь, связанный с использованием
довольно сложных формул, практически мало удобным.
Графики, приведенные в статье, показывают, что очень резкое
уменьшение прогибов наблюдалось после укладки третьего ряда,
при высоте, равной 74 пролета, что хорошо увязывается с изложен-
ным выше и должно было наблюдаться при гибкой балке (в опы-
тах балка была гибкой, упругая характеристика /( = 0,02).
Поэтому мы предложили бы другой прием, не особенно точный,
но практически удобный. До высоты, равной — пролета при гибкой
4
рандбалке (/( <0,10), или до высоты, равной пролета при жест-
кой (/(>0,10), принимать нагрузку от собственного веса кладки
равномерно распределенной; всю же дальнейшую нагрузку считать
передающейся по треугольным эпюрам. Конечно, затем надо прямо-
угольную и треугольные эпюры сложить.
Если под рандбалкой предполагается поставить временные стой-
ки, то надобность в расчете на равномерно распределенную нагруз-
ку вообще отпадает; эпюры нагрузок можно принять треугольными.
Постановку временных стоек особенно следует рекомендовать
при зимней кладке методом замораживания.
§ 8. УЧЕТ СОСРЕДОТОЧЕННОЙ СИЛЫ В ПРОЛЕТЕ
а) Нагрузка на стену
Предположим, что в серединах всех пролетов рандбалки к стене
ограниченной высоты приложены сосредоточенные силы (рис. 28).
Найдем нагрузку на рандбалку только в результате действия сос-
редоточенных сил, собственный вес стены учитывать не будем, так
как его влияние нам уже известно.
Для решения задачи необходимо сосредоточенные силы заме-
нить равномерной нагрузкой, распределенной на участке сколь
угодно малой длины и разложить нагрузку в ряд по cos (рис. 29).
Обозначим равномерно распределенную нагрузку в пределах 2с
через q, нагрузку же, выраженную рядом и распределенную по
всей длине, через <?(х).
Формула для разложения функции (в данном случае функции
нагрузки) в ряд такова:
. </(х) = Ло + I Ап cos = а0 4- £ Аг cos (ах). (268)
1 . . 1 7 1
'72
Найдем коэффициенты:
—а I
q COS (ax) dx + i q cos (ax) dx =
Лп— — j q COS (ax) dx = —
—l —I a
q ’
= — + sin (—ай) — sin (—aZ) + sin (aZ)—sin[(aa) ==
aZ [
=-------sin (ай).
al V
(заметим, что sin (aZ) = sin (—) = 0).
(270)
73
Таким образом, нагрузка на стену:
q (х) = q fl------—) — V — sin (ац) cos (ах) =
\ Z / а/
1
СО
с 2а V1 cos(ах) . ( .
=--q-------г- L------’--Sln М =
/ / а
1
00
q Г „ V cos (ах) . . х ,л_,.
= — с—2 У-----------------— sin (аа) . (271)
I а J
1
Если в целях проверки мы станем вычислять нагрузку по этой
формуле, то увидим, что в середине пролета на длине 2с нагрузка
равна q, на остальном же протяжении она равна нулю.
б) Функция напряжений
Функцию напряжений примем такую же, как ii b § 1 [форму-
ла (5) (стр. 9)]. Выпишем оттуда формулы для напряжений
[формулы (7—9)]:
= S a cos (ах) [а [Сх sh (ау) + С2 ch (ау) ф- С3 у sh (ау) +
+ С4 У ch (ау)] + 2 [С3 ch (ау) + С4 sh (ау))'] +
+ 2D7 4- 2D10x + 6Dut/; (272)
ау = — S а2 COS (ах) [Сх sh (ау) ф- С2 ch (а//) ф- С3 у sh (ау) ф-
ф- С4 у ch (ау)] 4~ 2ZD5 4" 6D8x 4- 2Е)9 у ; (273)
т ~ S а sin (ах) {а [Сг ch (ау) ф- С % sh (ау) ф- С3у ch (ау) ф-
+ с4 у sh (ау)] 4- [C3sh (ау) ф- C4ch(ay)]} —
— Dg — 2Dg х — 2£)10 у . (274)
Учитывать собственный вес в формуле (9) не нужно. Перемеще-
ния [формулы (11 и 20) (стр. 10 и 12)]:’
Ц = sin (ах) [(1 + jx) а [С\ sh (at/) 4- C2ch (ay) 4~
1
+ C3y sh(ay) + C4y ch (ay)] + 2 [C3ch (ay) -f- C4 sh (ay)]] -f-
+ 4" [207 + O10 x + 6Ony — [x (2D5 + 3O8x + 2D,y)] ; (275)
^K
~ — E cos (ax) {(1 4" p-) a. [Ci ch (ay) 4~ C2 sh (ay) 4- C3y ch (ay) +
Ek i
74
+ Ct у sh (ay)] — (1 — (x) [c3 sh (at/) + C4 ch (ay)]) +
+ у* £ [(1 + P) * Сг - (1 - (x) C4] + -2- [2D5 + 6Dsx + D,y -
- |x (2£>, + 2D10x + 3Duy)] . (276)
Вертикальные перемещения нижних точек стены или прогибы
раидбалки, равные —У(У=О):
w = + -i- 2 c°s (ax) ( (1 + |Х) a [Сх] — (1 — 0 [C4]i —
Ск 1 I )
1
=------К 2 11 - COS (ax)] • ](1 +H) aC\ - (1 - p.) C4] . (277)
1
в) Определение коэффициентов D
Относительно некоторых коэффициентов можно сразу сказать,
что они равны нулю.
Так как при перемене знака у х нормальные напряжения не
должны менять знака, знак же у касательных напряжений дол-
жен измениться, то:
Dg - Ds = D10 - 0 . (278)
При х = / т=0. Значит
D, = 0 . (279)
Далее учтем, что в любом горизонтальном сечении сумма вер-
тикальных усилий должна быть равна внешней нагрузке с обрат-
ным знаком
i
— ^ayb dx — qc . (280)
b
Получим:
—У — Isin (a0— sin (7-0)1 ’ [G sh (ay) -г C2 ch (ay) 4-
[ a
1
4- C3 у sh (ay) + у ch (ay)] 4- 2D5 6/j = qc., (281)
Так как sin(aZ)=0, а потому и все выражение суммы, равно
нулю, то
(282)
75
Для сечения в середине пролета по условиям симметрии а = 0:
— S bin (а/) ((1 + р.) а [Сх sh (ау) ~r С2 ch (ау) Д- С3 у sh (ау) +
1 I
+ С4 у ch (ау)] + 2[С3 ch (у.у) ф- С4 sh (ау)] | +
+ 4- (2D7 + 6Dn-V - 2а D5] = 0 (283)
Ек
или: *
2DT Н- 6Пп у — 2у Г)5 - 0 . (284)
Это условие должно удовлетворяться при любых значениях у.
Следовательно:
(285)
2bl
Du - 0 . (286)
После подстановки найденных значений D в формулы (272) —
(274) и (277) будем иметь:
00 (
= S a cos (ах) а [Ci sh (ау) Д С2 ch (ау)Д С5 у sh (ау) Д
1 <
+ С4 у ch (ау)] + 2 [С3 ch (ау) + С4 sh (ау)] )— ; (287)
) О*'
— Sa2 cos (ах) [Сх sh (ay) Д С2 ch (ау) Д С\ у sh (ау) Д
1
+ C4ych(ay)I-----%- (288)
ы
со (
't = s a sin (ах) а [С\ ch (ay) + С2 sh (ау) + С3 у ch (ау) +
I t
+ С4у sh(ay)] + [C3sh(ay) + c4ch(ay)]j ; (289)
^=--yS[l-c< s(ax)] [(l + ^aCj —(1 — p.)c4] . (290)
Нагрузка на рандбалку:
P= — ау(у=тЬ = b S a2 COS (ax) C2 + . (291)
г) Определение коэффициентов С
Для линии контакта стены и рандбалки условие равенства вер-
тикальных перемещений кладки и прогибов рандбалки дает урав-
нение:
d* W р
dx^ ~~ Е/
(292)
76
После подстановки:
“ S ct4 cos (ах) [(1 + ii) a Ct — (1 — у) С4] =
Ек 1
= Л?агСО8(м)(?з+._££_. (293)
El j Еi I
Сделаем замену (см. стр. 15):
--~Г = +-Т7Г S COS И). (294)
Ell Е11 ।
Тогда:
— £ a4 cos (хх) [(1 Н- у-) я С\ — (1 — р.) С4] —
Ек j
= — Sа2cos (ах) ЬСг--— Scosp.x). (295)
El t Ell j
Это дает:
1 а2 ^ае
4-И(1 +1*)^-(!-:•№] - —6С2+-^- = 0 (296)
Ек El Ы1
или:
а5(1 + H)Ci-*2^7C2-a4(l-l<)Cl= - (297)
г.1 Lil
Следующее условие состоит в том, что при у —0 х=0:
£ а sin (ах) (аС\ + С4) ~ 0 (298)
1
или:
а С4 + С4 = 0 . (299)
Для верхнего края стены при у~Н должно быть
— ауЬ == q (х) . (300)
Получим уравнение:
Sa2 cos (ах) b [С4 sh (а Н) + С2 ch (а Н) + С3 Н sh (а И) 4- С4 И ch (а//)] 4-
+ ^L = ^_[c_2y_££H^sin(aa)
I Z а
1
(301)
Оно приводится к виду:
а26 [С\ sh (а И) + С2 ch (а Н) + Са И sh (а Н) + CJ/ ch (« Я)] =
= — sin (а а) (302)
а/
77
или:
Сг sh (а И} + С2 ch (а И) + С3Н sh (а И) + С4Я ch (а Я) =
—-----—sin (а а). (303)
а36/
Наконец, вверху 0:
S sin (а х) | а [С\ ch (а Н) 4- С2 sh (а И) + С3Н ch (а И) 4~
+ C4//sh(atf)] + [С3 sh (а/7) + C4ch (а//)]| == 0. (304)
Это дает:
а (\ ch (7. И) + 7. С2 sh (7. Н) + [(7. Н) ch (а Н) 4- sh (7. Н)] С3 4- •
+ [(7. Н) sh (а Н) + ch (а Н)] С^О. (305)
Итак, имеем 4 уравнения:
а5 (1 + О Сх - а2 С2 - а* (Г— ц) С4 = - . (306)
EI ЕН
аСх + С4 = 0; (307)
Сг sh (а Я) + с2 ch (7. Я) + С3Н sh (7. Я) + CJ1 ch (а Я) =
= — (308)
а Сх ch (а Я) + а С2 sh (а Я) + [(а Я) ch (7. Я) +
+ sh (а Я)] С3 + [(7 Я) sh (а Я) + ch (7 Я)] С4 = 0.
Решение этих уравнений:
2rf ( sin (аа) 1
q __ Ы (а СП /7 Н) J
1”' И,«/2“4ЯЕ/ \ 2аЗЕ/ , 1
’ И -Г— -1 — (a//+i) + I=W"-(l-W
L \ Дк0 / ЕКЬ
‘Iq (2 ЕI sin (ал)
77 7Т “ 77, <a// + W + с 1°^(1 -<р)-ф=)
bi \ iz^b сп (?Н)
2 а*НЕ1
ЕКЬ
2
—— (аЯ+^)+а2№ (1-^)
2д-Ь Г sin (па)
Ы а ch (пН)
/ 2аЗ£7\ ( 1
аН —------- -4- iy с
ЕЛ 1 1
,J2^HEI \ 2аЗЕ/
<и —г— - 1) — — (а^ 4-ф) 4-«W2 (1 — <р)
\ ЕКЬ 1 ЕКЬ
2q ( sin (аа)
ir(aTrbr(ii//+w+c№+a//(1-WI
а ф2
2*НЕ1
2 п?Е/
(а/г 4- 44 4-<х*№ (1 — Ф2)
(309)
(310)
(311)
78
Как и раньше, принято:
4> = th(aH) = Sh ("Я)‘
1 7 ch (аЯ)
Сделаем преобразования, аналогичные преобразованиям в § 7,
только для С2.
В формуле (226) (стр. 62) множитель 2 [ g/Y + — ], в формуле
\ б /
же (311) во втором члене множитель ; поэтому на основании
Ы
формулы (240) (стр. 64) мы сразу можем написать второй член
числителя и знаменатель. Что же касается первого члена числи-
теля, то учтем, что в процессе преобразований мы множили числи-
тель и знаменатель на /2, затем на (еаИ 4- е-аН)2 и, наконец, на е~2с<н
Кроме того, в числителе и знаменателе изменили знаки.
Получим:
4qEla2 sin(an)
(314)
ЕКЬЧ
а =
С1з(аЛ7)_______________________
д2т.2 { П3 k |Ч 2аН
е-^н
е
-4г?т2 е е~2*и
(315)
~^Н\1
Преобразуем
4 qElz2
ЕКЬЧ
4qEIn2K2
~ EKbW
первый член числителя:
S‘nfa0) (а Я + ’i)/=(<?’"
ch (а//)
sin (ад) , . - । . .о /
• -----—— (а Н 4- б) Z2 (е
Ch(atf) ? 17 V
__ 2^z2/2 2 гЛ£/
кЬ ЕКЫ3
<—iH у =
sin (ап)
ch (а Н)
2
,аН t _—а
—аН \2л—2аН
еаП-е~'и
е*н , е-*н
+ й—и )2 е-^н sin (а а) =-- 4?д^;г [Л (е’« + е-"н) +- '
4- еаН — е~*н ] е~2аИ sin (а а) = 4 [а // (j е-2«я j _|_
4- (1 — е-2-н)] е—и sin (а а) (316)
Подставим найденные значения в формулу для нагрузки (291)
(стр. 76):
Р = S qf-cos (я х) X
1
79
---j | _|_ е ( I — е 2аН) j е нН s|n (да) _|_
Х > „:i /г [ -I п^е-^ 4- (1 — j - -
(317)
- + 12L [ (1 _ е-2.Ну _ 4 „2 п2 у г-2«И1 ;2
_______I _______________________1 .
--4/г2т:2а2й-2аН+(1-^2^)2} '
Окончательно:
(318)
д) Примеры
а
и — =
/
Опять разберем случаи упругих характеристик /г -^ 0,05 и & =
= 0,5. Высоту стены примем равной Н = I = п Н ~ ~ ~ .
Сосредоточенную нагрузку заменим равномерно распределенной
на длине 2ct равной 0,1 пролета. Таким образом,—0,1
= 0,9. Поэтому: о
. sin (а а) — sin sin (0,9 п т?) = sin {п -162°).
1) £-0,05;Л-0,10/—==20,2 V
. \ h • . I
фор-
1 =
т
в
Если высота стены равна полупролету, т. е. //=/=-—, то
Н
мулу следует подставить^ = — ~ 1 . При высоте стены Н =
= — S = — = 0,5 .
> 4 .1 '
Опуская вычисления, приведем только результаты. На рис. 30 и
31 показаны эпюры нагрузки на рандбалку.
Из рисунков видно, что при Н — I эпюра нагрузки на ранд-
30
* балку такая же, как и в случае Н = со, При меньшей высоте Н ==*
;== нагрузка на опоре снижается, но вместе с тем появляет-
ся максимум в середине пролета.
Поскольку эпюра для случая Н = не отличается от эпюры,
6 Б. Н. Жемочкин
81
На грузна на рандбалку при Н=^
ТТГТГП
--^1
I
L
Рис. зз
82
построенной ранее (см. рис. 6) для стены бесконечно большой вы-
соты, можно применить приближенные формулы (133), (136) (стр.
42 и 43), но вместо (gHb-\-q )в формулу (133) следует подставить
Очевидно, что эта величина представляет интенсивность равно-
мерно распределенной по всему пролету нагрузки, равнодействую-
щая которой равна данной сосредоточенной нагрузке.
При Н — можно также применить приближенные формулы,
но результат будет менее точным.
2) 6 = 0,5; К = 1,01 (—=9,4').
' h /
Результаты видны из рис. 32 и 33.
Здесь при высоте
Н = —
2
очень резко повышается нагруз-
ка в середине пролета. Поэтому применение в этом случае прибли-
женных формул не оправдывается.
е) Изгибающие моменты
Для полноты исследования найдем и моменты в рандбалке.
Воспользуемся формулой (264) (стр. 69), но заменим в ней
(gHb 4- q) выражением — , Это мы можем сделать на основании
аналогии между формулами (247) и (291):
ею
М ~ У cos (а х)
1
Подставим сюда С2:
ьс2 —
2qc 1
J
(319)
00
М = В cos (я х) X
1
—------ [аН (14-е 2а^) 4- 11 — е 2«wj j е а.н sjn
п2 л2 { г? k [4 п -6 е 2аЯ4-(1 — е ] —
4- 2 [(1 - е~2аИ)2 - 4 п2 *2 Е2 e~2gJ/]
— 4 п2 я2 С2 е~2аИ + (1 — 2аН j21 а2^
(320)
6*
83
После соответствующих преобразований окончательно получим:
2qkcl ((п"Х \ . .
М =--------1> cos ------------ X
т;2 • I— \ I )
-► + п [(1 — ) + 4/171^ 2/37tcj
4п2 к2 £2 Ч- (1 — е-2л-£ j2
(321)
Абсолютные значения моментов, вычисленных для х = 0 по этой
формуле и по приближенной формуле (149) (стр. 46), в которой
вместо (gHb + q) взято у-, приведены в табл. 19.
Таблица 19
k К L h н L По формуле (321) По приближенной формуле (149) Ошибка в %
0,05 0,10 20,2 оо 0.5 0,25 0,0897 0,0940 0,1198 0,0938 4,6 0,2 21,7
0,5 1,01 9,4 оо 0.5 0,25 0,1862 0,2148 0,3177 0,1829 - 1.8 14,9 42,4
X qcl X qcl
На основании изучения таблицы можем сделать такой вывод.
Если упругая характеристика 0,10, то при высоте стены
LT L
it > — можно сосредоточенную нагрузку заменить нагрузкой, рав-
номерно распределенной по всему пролету и приложенной к верх-
ней грани стены. Тогда можно пользоваться приближенными фор-
мулами для треугольных эпюр. Если упругая характеристика Л >
> 0,10, такую замену можно сделать только при высоте стены
L.
Когда высота стены меньше указанных пределов, сосредото-
ченную нагрузку следует считать приложенной непосредственно к
рандбалке. При этом можно применить общеупотребительный при-
ем, состоящий в том, что сосредоточенная нагрузка считается рас-
пределенной на некоторой длине (см. следующий параграф).
84
Если не требуется большой точности, можно принять более низ-
кие пределы: при гибкой рандбалке до Н > — и при жесткой
рандбалке — до
Мы разбирали случай, когда сосредоточенные силы расположе-
ны в серединах пролетов. Но если нагрузки приложены около опор
или даже над опорами (рис. 34), то они также вызывают изгиб
раидбалки. Для таких нагрузок оставим в силе только что уста-
новленное правило.
§ 9. РАСПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ В КЛАДКЕ
Как сказано в предыдущем параграфе, при небольшой высоте
кладки над рандбалкой можно заменить сосредоточенную нагрузку
нагрузкой, распределенной
по некоторой длине и прило-
женной непосредственно к
рандбалке. Исследуем этот
вопрос, и выясним, как вооб-
ще распределяются напря-
жения в кладке от сосредо-
точенной силы.
Предположим, что по
верхней грани, безгранично
идущей в обе стороны и вниз
полуплоскости, приложена
сосредоточенная сила (рис.
35). . . . , .
По формуле, вытекающей
из решения Фламана,
вертикальные нормальные
напряжения в горизонталь-
ных сечениях:
Рис. 35
ДДсоз4в. (322)
85
Но
Следовательно:
2Р у* 2Pv3
<j ---------------i------ =---------:---- .
у кЪу (х2 ~j- у'2)2 к Ъ (х2 4- у2)2
(323)
(324)
Проведем ряд горизонтальных сечений и, вычислив вертикаль-
ные нормальные напряжения в различных их точках, построим
эпюры напряжений <зу (рис. 36).
Из рисунка видно, что напряжения распространяются в области,
приблизительно ограниченной прямыми, проведенными под углом
к горизонту, тангенс которого равен-. Эти линии показаны пунк-
1,5
тиром. Эпюры же можно считать треугольными с наибольшими
ординатами, определяемыми условиями равновесия-
Средняя ордината такой упрощенной эпюры на глубине у най-
дется из условия равновесия:
<зУ‘Зу Р
2 Т‘
Отсюда
д =0,67 —.
у by
(325)
(326)
86
Между тем по формуле (324) эта ордината должна быть (по
абсолютной величине):
Оу = _2Л'8-..= о,б4 -Д
У кд(0 + у2)2 by
(327)
Разница невелика.
Однако считать распределение напряжений под углом, тангенс
которого равен — , можно только в случае полуплоскости, т. е.
в случае, когда стена имеет достаточно большую высоту. Иначе
должно быть, если под кладкой стены находится основание с дру-
гими упругими свойствами.
Напряжения п0 линии контакта с жестким основанием
Рис. 37
При податливом основании эпюра нагрузки на него будет иметь
большую протяженность.
При жестком основании эпюра нагрузки будет короче и на-
грузка окажется более сосредоточенной.
На рис. 37 приведена эпюра напряжений по линии контакта с
абсолютно жестким основанием.
Здесь ближе к истине считать распределение напряжений под
углом, тангенс которого равен 1. Эпюру напряжений опять можно
считать треугольной со средней ординатой, которая находится из
условия равновесия:
2 у _ Р
2 ” “7*
(328)
откуда:
(329)
87
Между тем значение этой ординаты по точной формуле при р- •=
0,2 должно быть
< = 0,82 —.
У .by
(330)
Рассмотрим еще случай, когда сосредоточенная сила приложена
у края стены (рис. 38).
Вертикальные нормальные напряжения в точке с координатами
х и у*:
ЖЕ 4 РУ2
У (гЛ— 4)
(331)
На рис. 39 показаны эпюры вер-
тикальных нормальных напряжений
на различных уровнях.
В этом случае опять можно счи-
тать распределение напряжений под
углом, тангенс которого равен 1, и
принимать эпюры треугольными.
При таком расчете наибольшая
ордината у края стены на глубине у
найдется из условия:
М __ Р
2 b ’
откуда:
По формуле же (331):
г — 4 рУ2гУ _ 4Рк ^2 14 Р
у (п2 — 4) ь (0 4- у2^2 (Л2 —4)бу ' by '
(334)
То, что в разных случаях приходится принимать различный ха-
рактер распределения напряжений, представляет большое неудоб-
ство. Нам нужен наиболее простой, хотя и грубо приближенный
способ.
Поэтому примем для всех случаев, независимо от условий, в ко-
торых находится стена, распределение напряжений под углом 45°
и эпюры треугольными.
Тогда для рассмотренных выше случаев эпюры будут согласно
рис. 40, 41 и 42. На этих рисунках пунктиром показаны криволи-
нейные эпюры, полученные на основании точного расчета, для воз-
можности сравнения.
* Приводим формулу без доказательства. Формулу можно получить, рассмат-
ривая крайний случай клина (с прямым,углом), нагруженного силой в вершине.
88
р
Рис. 40
89
90
91
В том случае, когда сосредоточенная сила расположена от края
стены на расстоянии, меньшем у, можно принять эпюру, показан-
ную на рис. 43,а. Крайняя ордината найдется из условия, что
площадь эпюры, умноженная на толщину стены, равна нагрузке.
Если в эпюре под силой получится*входящий угол, принимать
эпюру треугольной (рис. 43,6). Это должно быть при
y>o(]/2d-l) или у > 2,41 с.
Иногда приходится иметь дело с нагрузкой, равномерно рас-
пределенной на некоторой длине. Хотя для этого случая нетрудно
получить точное решение,
однако мы и-здесь применим
приближенный, но удобный
на практике способ.
Приняв для каждого эле-
мента нагрузки qdx такое
же распределение напряже-
ний, как и для случая сосре-
доточенной силы, получим
эпюру по рис. 44.
Упрощая эпюру, заменим
ее трапецеидальной (рис.
45).
Если протяженность за-
глубины, то эпюра будет тре-
Рис. 47
груженного участка меньше двойной
угольной (рис. 46).
По аналогии можем построить эпюру, когда равномерная на-
грузка расположена у края стены. Если длина участка загружения
больше глубины, эпюра будет по рис. 47.
Если же длина участка
загружения меньше глу-
бины, то эпюра будет по
рис. 48.
Установленные нами
правила мы сможем при-
менять для определения
нагрузки на рандбалку
при наличии сосредото-
ченной силы или равно-
мерно распределенной на-
грузки, когда кладка сте-
ны имеет небольшую вы-
соту. Тех же правил мы будем придерживаться и далее при реше-
нии вопроса о нагрузке на перемычки.
Но не следует забывать, что, применяя такие приемы определе-
ния нагрузок на рандбалки и перемычки, мы получаем очень гру-
бые решения, обычно дающие некоторый запас. В этом, например,
можно убедиться, если попробовать найти указанными приемами
нагрузку на рандбалку для схем по рис. 30, 31, 32 и 33.
92
Следовательно, применять их следует только тогда, когда более
точных решений не существует.
§ 10. НАГРУЗКА НА РАНДБАЛКУ В СЛУЧАЕ ПРОЕМОВ В СТЕНЕ
В СРЕДНИХ ЧАСТЯХ ПРОЛЕТОВ
а) Постановка задачи. Ход решения
Если стена над рандбалкой имеет проемы, то меняются как на-
пряжения в стене, так и нагрузка на рандбалку.
Рис. 49
Нас не интересует случай небольших отверстий (рис. 49), так
как очевидно, что их наличие отражается очень мало на нагрузке,
передающейся рандбалке. Поэтому изучим только влияние боль-
ших отверстий, повторяющихся во всех пролетах (рис. 50).
В расчете примем высоту каждого проема //—со, т. е. будем
рассматривать рандбалку, нагруженную кладкой стены у опор
(рис. 51), без учета связи между простенками по сторонам проемов.
Ширину проемов примем равной —- пролета.
3
Решение задачи будем вести в таком порядке1.
Отделим мысленно кладку от рандбалки и поставим между ни-
ми условные жесткие связи-стержни (рис. 52). Другими словами,
предположим, что контакт между кладкой и рандбалкой осущест-
вляется только в отдельных точках, где поставлены стержни, пере-
дающие усилия. Для неизменяемости системы необходимо еще до-
бавить горизонтальные опорные стержни. В дальнейшем никакой
роли они не будут играть.
Если мы найдем усилия в условных связях-стержнях, то нагруз-
ка на балку станет известной и задача будет решена.
' Очевидно, что здесь мы имеем статически неопределимую систе-
му и расчет ее будем вести точно так же, как расчет любой стати-
чески неопределимой системы.
Вертикальные стержни поставим на равных расстояниях с и
будем считать, что каждый стержень передает усилие, которое рав-
номерно распределяется на длине с соответствующего участка.
1 Этот порядок является основным при расчете перемычек (см. главу III).
93
Рис. 50
—L -
Рис. 51
Рис. 52
Применим так называемый смешанный способ решения. Разре-
жем или лучше отбросим мысленно все стержни (рис. 53) и заме-
ним действие стержней действием неизвестных сил Х2,.., Чтобы
система была неизменяемой, надо добавить закрепление1.
Напишем теперь уравнения деформаций, выражающие условия,
что суммарные перемещения по направлениям неизвестных сил рав-
ны нулю, т. е. что рандбалка и кладка в местах контакта не расхо-
дятся и не сближаются.
Перемещение по направлению какой-либо силы Xk зависит от
всех сил Х2,.... Кроме того, поскольку у нас теперь кладка и
рандбалка не связаны между собой, надо еще добавить перемеще-
ние всей кладки в целом или перемещение заделки уо.
Таким образом, уравнение, выражающее, например, условие,
что суммарное перемещение по направлению силы Xk равно нулю,
должно быть таким:
+ Л3\,34“ • • • + Xkbkk + - • • + у0 — 0. (335)
Здесь под ......... понимаются перемещения по направлению
силы X k от единичной силы Xj = 1, от единичной силы Х2 = 1 и т. д.
Уравнений такого вида будет столько, сколько неизвестных сил.
Кроме того, составим уравнение равновесия: сумма неизвестных
сил равна внешней нагрузке.
Учитывая симметрию системы, будем рассматривать одновре-
менно по две силы, расположенные симметрично относительно опор
раидбалки.
При решении поставленной задачи разобьем кладку по длине
на 12 участков (по 6 с каждой стороны опоры). В полупролете ока-
1 Закрепление мы показали умышленно достаточно высоко, чтобы не вносить
усложнений в вычисление перемещений.
95
жутся 9 участков (включая и 3
(см. дальше рис. 58 и 59).
Следовательно, будем иметь
перемещение у0. Канонические
строительной механики:
участка до середины отверстия)
6 неизвестных сил и 1 неизвестное
уравнения смешанного способа
+ ^2^12 4- *з*13 -И + Я5315 4~ ХДб + у0 = 0;
^/’21 4* ^2^22 4- -^3 '23 4“ Хр24 4" ^5°25 4* + Уо = О •
Я Ах 4- ^2?J32 4- Лз^зз + 4- Яй335 4~ ХДб 4- Уо = 0;
4" ^2^2 + ^3%3 4- ХЛ* + Х5''45 4~ ^6?J4G 4" Уо ~ 0 *>
^i^5i + ^2^52 + ^3^53 4- ЯД4 4- Х5о-5 4- ХДЙ + у0 — 0 ;
ХАх 4" ^2^62 4- Хз%з 4- Я4364 4“ X5oG5 4- Xt36G 4- уо “ 0;
Хх 4-*2 4-Хз 4-Х 4-Х5 4-Х6 =(^64-^)Z.
Под (gHb-^rq) подразумевается интенсивность нагрузки, если
считать последнюю равномерно распределенной по всему пролету.
Единичные силы должны быть приложены и к кладке, и к ранд-
балке. Поэтому перемещения, т. е. коэффициенты уравнений, будут
состоять каждое из двух слагаемых: одно зависит от деформации
кладки, а другое — от изгиба рандбалки (рис. 54).
Таким образом, перемещение по направлению силы X f, т. е. в
точке k> вызванное приложением единичной силы Х^ 1, равно:
§ki ~ vki 4- • (337)
Перемещения примем для удобства уменьшенными в ------раз.
Екк3Ь
Итак, видим, что для решения задачи нам нужно находить пе-
ремещения кладки v и прогибы рандбалки w.
б) Деформации кладки
Занумеруем участки, в серединах которых были поставлены
условные связи-стержни, по порядку, начиная от опоры рандбалки,
или, что то же, от середины кладки (рис. 55).
Расстояние единичной силы, вызывающей деформацию, от оси
обозначим через £с, а расстояние от оси до середины участка, где
ищется перемещение, — через, Здесь с—длины участков, на
которые разбита кладка, или расстояния между стержнями.
Вычислению перемещений для кладки ниже будет посвящен
специальный § 17. Возьмем со стр. 143 готовую таблицу (табл. 20).
В этой таблице помещены не абсолютные перемещения, а раз-
ности перемещений различных точек и некоторой точки, находя-
щейся на произвольной, но достаточно большой высоте вверху (так,
чтобы расстояния от нее до всех точек внизу кладки можно было
принять одинаковыми).
96
Нс ^1
I I I
---?C~----*4 P-----
Рис. 56
7 Б. H. Жемочкин
97
Таблица 20.
участков, где прило- жены нагрузки С № участков, где ищутся перемещения
1 1 2 3 4 5 6
0.5 1,5 2.5 3,°5 4,5 5,5
1 2 3 4 5 6 0,5 1,5 2,5 3,5 4,5 5,5 5,259 2,638 3,890 1,269 1,940 3,499 0,571 0,878 1,760 3,499- 0,180 0,391 0,878 1,940 3,890 0 0,180 0,571 1,269 2,638 5,259
Кроме того, таблица переработана так, что минимальное пере-
мещение равно нулю. По существу это равносильно преобразова-
нию канонических уравнений, состоящему в том, что ко всем коэф-
фициентам уравнений (кроме коэффициентов последнего уравне-
ния) прибавлено одно и .то же число. Такое преобразование воз-
можно в тех случаях, когда у одного из неизвестных (уо) коэффи-
циенты во всех уравнениях одинаковые (см. ниже § 17 и 19).
Но в таком случае вместо Уо придется принять другое неизвест-
ное у, которое будет уже совершенно условной величиной. После
решения уравнений у вообще не понадобится.
в) Прогибы раидбалки
Выделим из раидбалки один пролет (рис. 56) и предположим,
что на расстояниях от опор приложены две единичные силы.
Требуется найти прогиб щ в точке, отстоящей от опоры на расстоя-
нии ЦС.
Чтобы использовать симметрию, будем одновременно находить
сумму прогибов слева и справа.
Как известно, для нахождения прогибов необходимо перемно-
жить две эпюры: эпюру от заданной нагрузки и эпюру от единич-
ных фиктивных сил, приложенных по направлениям искомых про-
гибов (рис. 57). К нагрузке добавим и опорные моменты. Мы най-
дем их из условия, что площадь эпюры от нагрузки для свободно
лежащей балки равна площади эпюры опорных моментов. Следо-
вательно:
2^y- + (L -2Сс)Сс= М0Ь.
(338)
Отсюда опорный момент по абсолютной величине:
Предположим, что C<*q.
98,
Перемножая эпюры, получим:
2ш£/ = ^. 4-Cc-2 + [(CCtV>Og-^)2H-
2 3 2
/г о \ 1 — 2гс) ]Л
-4* (L, — 2 д с) д с ч с 7jC (fl \ С с
о
= — (Сс)3 + [OicJM'^+L V-2(V)2Hc —
3
- (L - V)t( J1 - Д-V с = -+ (С С)= j-, с) -
= С3'2 С—L _|_ JL 'I.
L М з ' ' L )
(340)
Мы приняли с = — . Поэтому:
(341)
Разделим, как мы условились, прогиб на --------- и введем
Е к7,3^
гую характеристику k [по формуле (73) (стр, 19)].
упру-
w~ — z-3£,<-- :з(18т]-^~бс
2-93-18.16£7 V '
_ /зо
2 ~3Е7
---------Ч2 (1 8 Д — Д2
93-18.16 k
- —..-------7 (18 т] — д2 — 6 ч)
93-18.16-/? >
0.004579 .о,10 о
=-----------,“(18 д — т —6,).
к
(342)
Для случая, когда ч>д, без вывода напишем:
0,004579
k
д2(18с —ч2 —6д)
(343)
w —
По этим формулам вычислены прогибы, помещенные в двух таб-
лицах для k = 0,05 (табл. 21) и /г- 0,5 (табл. 22). '
7*
99
г- < - —1
Рис. 57
100
Таблица 21
k= 0,05; К = 0,10
№ участков, где ищутся прогибы
№ участков, 1 2 3 4 6 6
где приложены нагрузки с
0,5 1.5 2,5 3,5 4,5 5,5
1 2 3 4 5 6 0,5 1,5 2,5 3,5 4,5 5,5 0,132 0,498 3,245 0,819 6,130 13,594 1,093 8,603 20,463 33,376 1,322 10,664 . 26,187 44,595 62,590 1,505 12,312 30,766 53,570 77,427 99,040
Таблица 22
k = 0,5; К — 1,01
№ участков, где приложены нагрузки с „М участков, где ищутся прогибы
> 2 1 3 1 4 1 5 1 6
7i
0,5 1.5 2,5 3,5 4,5 5,5
1 2 3 4 5 6 0,5 1,5 2,5 3,5 4,5 5,5 0,013 0,050 0,325 0,082 0,613 1,359 0,109 0,860 2,046 3,338 0,132 1,066 2,619 4,459 6,259 0,151 1,231 3,077 5,357 7,743 9,904
г) Примеры
1) /г = 0,05; К -0,10
Расчетная схема показана на рис. 58 и основная система — на
рис. 59.
Общий вид уравнений приведен выше [формула (336) (стр.
96)].
Вычислим перемещения по формуле (337), пользуясь табли-
цами.
6ц = 5,259 + 0,132 = 5,391;
В12= 2,638+ 0,498 = 3,136;
о13= 1,269 + 0,819= 2,088;
814 = 0,571 + 1,093= 1,664;
8,5= 0,180+ 1,322= 1,502;
8W = 0 + 1,505 = 1,505;
о,2 = 3,890 + 3,245 = 7,135 ;
В23 = 1,940 + 6,130 = 8,070;
В24 = 0,878 + 8,603 = 9,481 ;
S25 = 0,391 + 10,664 = 11,055:
326 = 0,180 + 12,312 = 12,492
101
S33 = 3,499 + 13,594 = 17,093 ;
834 = 1,760 + 20,463 = 22,223 ;
835 = 0,878 + 26,187= 27,665;
= 0,571 + 30,766 = 31,337;
344 = 3,499 + 33,376 = 36,875 ;
84. = 1,940 + 44,595 = 46,535
о40 = 1,269 + 53,570 = 54,839
866 = 3,890 + 62,590 = 66,480 ;
о56 = 2,638 + 77,427 = 80,065:
86С = 5,259 + 99,040 = 104,299
После подстановки уравнения будут:
5,391 Х1+ 3,136 Х2 + 2,088 Л3 + 1,664 %4 + 1,502 %5 +
+ 1,505 X, +у = 0;
3,136 хг + 7,135 %. + 8,070 %3 + 9,481 %4 + 11,055%3 +
+ 12,492 %с +у = 0;
2,088%! + 8,070%. + 17,093 %3 + 22,223 %4 + 27,065 Х3 +
+ 31,337 %с + у = 0 ;
1,664 %! + 9,481 %. + 22,223 %3 + 36,875 %4 + 46,535 %3 +
+ 54,839 %„ +у = 0;
1,502 %! + 11,055 %2 + 27,065 %3 + 46,535 %4 + 66,480 %5 +
+ 80,0б5%6 + у = 0;
1,505 %! + 12,492 %2 + 31,337 %3 + 54,839 %4 + 80,065 %5 +
+ 104,299 %6 +у = 0;
+ %2 + %3 + %4 + %5 +
+' = (gHb + q) I.
104
Ввиду взаимности коэффициентов (коэффициенты, расположен-
ные симметрично относительно нисходящей диагонали, взаимно
равны) можно было бы для сокращения письма оставить половину
таблицы незаполненной.
Решив уравнения, найдем неизвестные:
Хх = + ( ,6387(gtf& + ?)Z;
Х2 = + 0,2807 +
= + 0,0984 {gHb + q) Z;
+ 0,0223 (gHb + q) Z;
+ 0,0037 {gHb + q)l>,
X6 = —0,0438 {gHb + q)l.
Сумма неизвестных равна (gHb+q)l.
Неизвестное у, представляющее совершенно условную величи-
ну, здесь не приведено.
Разделим каждое неизвестное на длину с, равную
В ре-
с = —.
9
зультате получим интенсивности нагрузки на рандбалку в преде-
лах участков длиной с\
Pi = + 5,74 {gHb + 7);
р2—+2,53 fe/7&+7);
Рз — + 0,89 {gHb + q) ;
= + 0,20 (^Л/Ь + 7) ;
Рз ~ + 0,03 {qHb + q);
Рз — 0,39 {gHb + q).
На рис. 60 показана ступенчатая эпюра нагрузки на рандбалку, по-
строенная по полученным данным.
Эта эпюра затем заменена криволинейной.
На рисунке показана также треугольная эпюра, построенная по
приближенным формулам (133) и (136) или (140) и (142) (стр. 42
и 43). В эти формулы надо подставить среднюю интенсивность на-
грузки (gHb+q), равномерно распределенной по всему пролету и в
сумме равной той нагрузке, которая передается через кладку про-
стенков.
Как видим, разница между криволинейной и треугольной эпю-
рами невелика.
Разница в величинах опорных моментов, вычисленных для той
и другой эпюры, составляет 3,4%, причем треугольная эпюра дает
больший момент.
- 9,4).
2) k = 0,5; К = 1,01 f-
Расчетная схема и основная система остаются те же, что и в пре-
дыдущем случае- : . ' -г. .-
103
Перемещения:
8И= 5,259+0,013 = 5,272;
8И = 2,638+ 0,050 = 2,688;
013= 1,269 + 0,082 = 1,351 ;
Неизвестные X равны:
Х1= + 0,3335 {gHb + q)l;
Х2= +0,2613 {gHb + q) l\
Х3 = +0,1911 {gHb + q)l\
Х4 = + 0,1307 {gHb + q)l;
X5 = + 0,0861 {gHb-\-q)l;
Xe = —0,0027 (gHb + q)l.
Интенсивности нагрузки:
Pi= + 3,00 {gHb +7);
p2 = +2,35(gHb + 7);
p3= + l,72(gffb + 7);
pt = + 1,18 {gHb + 7);
104
Pi = + 0,77 (gHb + q);
p6 = — QfiZtgHb + q).
Результаты приведены на рис. 61.
Разница в величинах моментов от нагрузки по криволинейной и по
треугольной эпюрам составляет 4,1% (треугольная эпюра дает мо-
мент больше).
д) Выводы
Исследование показывает, что в случае проема в средней части
пролета можно пользоваться приближенными формулами, дающи-
ми треугольную эпюру нагрузки на рандбалку и выведенными для
случая сплошной кладки стены.
105
Рп+Ра \
2 /
В формулы надо подставлять интенсивность равномерно рас-
пределенной по всему пролету нагрузки, которая заменяет задан-
ную нагрузку, передающуюся через простенки.
Если основание треугольной эпюры превышает размеры участка,
на котором расположена кладка, можно сделать так. Ординату над
опорой ро принять по приближенной формуле (рис. 62) и, предпола-
гая эпюру трапецеидальной, ординату у края кладки найти из
условия равновесия:
а = (gHb + q)L. (344)
Если окажется, что ра >ро, то следует принять нагрузку на
балку равномерно распределенной в пределах простенка.
§ 11. НАГРУЗКА НА РАНДБАЛКУ В СЛУЧАЕ ПРОЕМОВ
НАД ОПОРАМИ
а) Постановка задачи. Ход решения
Здесь мы решим задачу, имеющую сходство с только что рас-
смотренной. Предположим, что проемы находятся над опорами, так
что кладка степы расположена только в средней части пролета
(рис. 63).
Узкие простенки-столбы, опирающиеся на рандбалку, представ-
ляют мало интереса; нагрузку от них можно считать равномерно
распределенной или даже сосредоточенной. Поэтому рассмотрим
случай, когда в каждом пролете рандбалки стена занимает длину,
равную 7з пролета, и такая схема повторяется во всех пролетах.
Будем придерживаться того же порядка решения, как и в пре-
дыдущем параграфе.
Предположим, что между рандбалкой и кладкой стены постав-
лены условные связи-стержни на равных расстояниях с (рис. 64).
К основной системе перейдем, отбросив стержни и заменив их
действие действием неизвестных сил Х2,... Кроме того, добавим
заделку в верху кладки (рис. 65).
Уравнения будут иметь тот же вид, что и в §Д0. Так же будем
находить и перемещения.
Если мы разобьем простенок нач12 частей, то будем находить
перемещения кладки по таблице на стр. 98, но теперь начало коор-
динат поместим в середине пролета и от этой точки будем вести
нумерацию сил и участков.
Для прогибов же рандбалки придется составить новые табли-
цы, так как раньше у нас был отсчет от опоры.
б) Прогибы рандбалки
Нам нужно находить прогиб в точке, отстоящей от середины
пролета на расстоянии?] с, от единичной нагрузки, приложенной
на расстоянии Сс (рис. 66). Будем учитывать, как и раньше, две
симметричные силы. '
106
Рис. 65
107
Используем прежнюю формулу (343) (стр, 99), относящуюся
к случаю С < tj по обозначениям рис, 66. Но, в ней надо заменить
Сс через (/—[Сс) или С через ------- , a ус через [(/ — ус) или у
\ с /
/ т С \ I
через (I и учесть, что "
Тогда:
'0,004579 II--;тС\2 Г .'(/ -Се) //-Сс\2 п _ riC
w —----Z--- ----- 1 °--------‘— ------ — о I-----
к \ cj / L с \>с/ \ с /
Щ^(9-т1)Ч18(9-С)-(9-С)2-6(9-7))] =
0,004579
k
(9-71)2(27 —С2+ 6 7]).
Если С> т], то:
0,004579
k
(9 — Q2 (27 — т]2 4* 6 Q .
(346)
Результаты вычислений единичных прогибов w для значений
/г —0,05 и k = 0,5 приведены в табл. 23 и 24.
/г = 0,05; К = 0,10
Таблица 23
№ участков, где приложены нагрузки С № участков, где ищутся прогибы
1 2 3 4 . 5 6
0,5 1,5 2,5 3,5 4,5 5.5
1 2 3 4 5 6 0,5 1,5 2,5 3,5 4,5 5,5 196,850 184,165 173,862 161,545 153,806 138,329 132,284 126,744 115,662 99,040 99,681 95,972 88,554 77,427 62,590 67,032 64,789 60,301 53,570 44,595 33,376
108
Таблица 24
6 = 0,5; К = 1,01
№ участков, где приложены нагрузки с № участков, где ищутся прогибы
1 2 3 4 5 6
0,5 1,5 2.5 3,5 4,5 5,5
1 2 3 4 5 6 0,5 1,5 2,5 3,5 4,5 5,5 19,685 18,417 17,386 16,154 15,381 13,833 13,228 12,674 11,566 9,904 9,968 9,597 8,855 7,743 6,259 6,703 6,479 6,030 5,357 4,459 3,338
в) Примеры
Разобьем длину простенка на 12 участков; с каждой стороны от'
оси будет по 6 неизвестных.
На основании таблицы 20 на стр. 98 и только что составленной
перемещения для случая & = 0,05 или /( = 0,10 равны:
= 5,259 + 196,850 = 202,109;
о12 - 2,638 + 184,165 = 186,803 ;
З33 = 1,269 + 161,545 = 162,814;
= 0,571 + 132,284 = 132,855;
315 = 0,180 + 99,681 =99,861;
В1С = 0 + 67,032 = 67,032;
Общий вид уравнений тот же, что и на стр. 96. После реше-
ния уравнений найдем интенсивности нагрузки на рандбалку. По-
лученную ступенчатую эпюру нагрузки заменим криволинейной
эпюрой.
Опуская вычисления, дадим только окончательные результаты.
На рис. 67 построена эпюра нагрузки для £=0,05 и на рис. 68
для £=0,5.
На рисунках показаны также треугольные эпюры, построенные
по приближенным формулам (133) и (136) или (140) и (142)
(стр. 42 и 43). В эти формулы следует подставить среднюю интен-
сивность нагрузки в простенках 7о, т. е. для принятой длины прос-
тенков в ~ пролета (gHb + q) ----, где (gHb + q) средняя интен-
3 — L
3
сивность нагрузки, которая равномерно распределена по всему
пролету и заменяет заданную нагрузку.
109
Таким образом:
3 1 1
Ро = 2,418-4- (gHb + q) = 2,418 <?„—*— =
У й О
/т /т
= 0,305 9oLj/ 44- .
3 ___
2 г— 2 f El
d - 0,8271- —/т/ k = 3,27-—1/ —
3 У ’ 3 V Ekb
(347)
(348)
Как видим, треугольные эпюры значительно отличаются от
криволинейных и особенно при гибкой рандбалке. По концам
кладки замечается концентрация нагрузки.
Нагрузка по треугольным эпюрам является менее благоприят-
ной, так как равнодействующая нагрузки в этом случае смещает-
ся к середине пролета.
Это становится особенно ясным, если найти изгибающие опор-
ные моменты.
Моменты над опорами по абсолютной! величине равны:
если k = 0,05, то
при криволинейной эпюре
„ треугольной• эпюре
(разница 26%)
если k — 0,5, то
при криволинейной эпюре
„ треугольной эпюре
(разница 6,2%)
М = 0,169 (gHb+qjl2-,
Л1 = 0,213(gH5 + q)i2;
M = 0,239(g//6-H)/2.
г) Выводы
Применяя способ, изложенный в настоящем параграфе, мы не
могли получить точных данных о величине концентрации нагрузки.
Этот способ позволяет лишь установить общий характер эпюр.
Вследствие значительной концентрации нагрузки у концов клад-
ки здесь может быть достигнут предел прочности материала и про-
изойти местное смятие, сопровождающееся неупругими деформа-
циями. Поскольку такое повреждение бу^ет носить местный харак-
тер, оно не отразится на прочности кладки в целом, но вызовет
перераспределение нагрузки на рандбалку. Эта нагрузка умень-
шится у краев, но распространится на большую длину. Эпюры бу-
дут ближе к треугольным эпюрам, построенным по приближен-
ным формулам.
Эти соображения позволяют рекомендовать применение при-
ближенных формул, которые упрощают расчет и вместе с тем в
случае местного смятия кладки даже лучше отображают действи-
тельную работу конструкции. Не следует также забывать, что рас-
хождение в моментах на 26% при расчетах конструкций, подобных
только что рассмотренным, нельзя признать чрезмерным, тем бо-
лее что треугольные эпюры дают некоторый запас.
ИО
§ 12. ОДНОПРОЛЕТНАЯ БАЛКА
Разберем случай однопролетной балки-перемычки, опирающей-
ся концами на колонны и несущей кладку стены (рис. 69).
Результаты решения можно будет применять и для расчета
крайних пролетов рандбалок.
Как и раньше, поставим между кладкой и балкой условные
связи-стержни на равных расстояниях с (рис. 70).
Отбросим стержни, заменим их действие действием неизвестных
сил Xi, Х2?... и добавим заделку в верху кладки (рис. 71).
Напишем уравнения, выражающиеусловия, что суммарные пе-
ремещения по направлениям неизвестных сил равны нулю, и одно
уравнение равновесия.
Для перемещений кладки будет справедливой прежняя табли-
ца на стр. 98. Прогибы же балки придется найти вновь.
Предположим, что две единичные силы приложены на рассто-
яниях tc от середины пролета и требуется найти прогиб в сечении
на расстоянии цс от середины пролета (рис. 72), причем С < д.
Для этой цели нужно перемножить две единичные эпюры
(рис. 73), что даст двойной прогиб.
Получим:
п / L у 1 2
2 wEl =------т] с] • — • —
12 / 2 3
+ [Л — (^ + С) с] (т] - Q с -Ь (L- 2Сс)Сс
112
5 Б. Н. Жемочкин
из
—hi2 - 4 L Tjc+4 if ^+6 L •>) c — 6 L С c —
— б^ + бС^ + бЬСс—12C2c2] =
= / £~?У \ [p + 2 L -n c — 2 x2c2 — 6 CV1. (3491
\ 12 J * J 4’-/
Если мы хотим пользоваться прежними таблицами, то полу-
пролет придется разделить на 6 частей, т. е. принять L=2Z=12c.
Тогда:
2wEl =--------— [41s + 41-П — —2-n2/—\2_
12 L 6 \ 6 ./
— 6С2(—У1 = l3[4 + 4-5-------2 ———
\ 6 / J ( 36 / L 6 36 6.
= /’ (B-648[72 + 12t)--3C2]. (350)
Разделим прогиб на ~~~ и введем упругую характеристику
k [формула (73) (стр. 19)]?
ю = -—Е-кЬ (6 — 71) (72+ 12iq —-п2 — ЗС2) =
2-648.ЕЛ 16 м 11 '
тс®
~7 • 7^7 (6 - ^1) (72+ 12т] —V]2 —ЗС2) =
2тс3£/ 648-16
= —2-----(6 _ (72 + 12 7) - т>2 - 3 С2) =
648-16.А ' 1
= -^^-(6-7j)(72+ J2T] —7)2-3i;2). (351)
Если С>т|, то w = -0-09273- (6 — С) (72 + 12С — С2 — 3т;2). (352)
ft-
По этим формулам вычислены единичные прогибы ш только
для ^=^0,5 (табл. 25).
Таблица 25
А» ==-0,5; К = 1,01
№ участков, где приложены нагрузки с № участков, где ищутся прогибы
1 2 3 ! 4 5 6
0,5 1.5 2.5 3.5 4.5 5,5
1 2 3 4 5 6 0,5 1,5 2,5 3,5 4,5 5,5 78,539 72,605 67,598 61,663 57,769 49,980 46,827 44,045 38,482 30,136 29,209 27,540 24,202 19,194 12,518 9,922 9,365 8,253 6,584 4,358 1,576
114
Перемещения на основании таблицы 20 на стр. 98 и только что
-оставленной:
8и = 5,259 + 78,539 = 83,798 ;
В12 = 2,638 + 72,605 = 75,243 ;
813- 1,269 + 61,663 — 62,932 ;
= 0,571 + 46,827 - 47,398 ;
815 = 0,180 + 29,209 - 29,389 ;
816 = 0 + 9,922 - 9,922;
Подставим найденные значения в уравнения, которые имеют
тот же общий вид, как и в предыдущих случаях. После решения
уравнений определим интенсивности нагрузки на балку.
Дадим только окончательные результаты.
На рис. 74 приведена эпюра нагрузки для случая £=0.5.
Как видим, у опор наблюдается значительная концентрация на-
грузки по сравнению с много пролетной ранд балкой. Точную ве-
личину концентрации, применяя изложенный здесь способ, мы не
можем установить.
Этот способ является приближенным, поскольку таблица пере-
мещений кладки (стр. 98) составлена, как это будет показано
далее, для случая неуравновешенных горизонтальных нормаль-
ных напряжений.
8* 115
На рис. 74 приведены также треугольные эпюры, построенные
’по приближенным формулам. Очевидно, что нагрузка, определен-
ная по этим формулам, должна давать преувеличенное значение
изгибающего момента в середине длины балки.
Следовательно, на практике можно вполне пользоваться при-
ближенными формулами § 5, выведенными для многопролетных
рандбалок.
§ 13. РАСЧЕТ РАНДБАЛОК В СЛУЧАЕ ШИРОКИХ ОПОР
В предыдущем исследовании мы принимали опорные реакции
как сосредоточенные силы, что может иметь место только при очень
случай, когда реакции распределяются па протяжении участков
длиной а (рис, 75). Через L обозначим теперь не пролет, а отвер-
стие в свету, равное (2/—а).
Предположим реакции равномерно распределенными. В дей-
ствительности должна наблюдаться концентрация реактивных уси-
лий у граней опор, что не может не отразиться на распределении
нагрузки, передающейся на рандбалку от вышележащей кладки.
Чем шире опора, тем больше влияние концентрации. Поэтому рав-
номерное распределение реакций нельзя предполагать при очень
широких опорах. Вопрос этот исследован в главе III.
а) Вывод формулы
В своем исследовании мы воспользуемся данными, полученны-
ми нами в § 1.
Нагрузка на рандбалку сверху по формуле (83) (стр. 21) при
сосредоточенных реакциях:
р = (gHb + q')h Г£ cospy-) —К— 1 + 1 1
i
(353)
И 6
или:
Разобьем эпюру реактивных сил на участки длиной dr (рис. 76).
Рассмотрим сначала действие одной элементарной силы, представ-
ляющей реактивное усилие,
приходящееся на длину dr.
Через расстояние 2/ к
рандбалке будет приложена
такая же сила. Элементар-
ные силы будут периодиче-
ски повторяться. Картина
будет та же, что и для ранд-
балки с пролетами 21 при
сосредоточенных реакциях.
Поэтому мы имеем право
применять формулу (354).
Но каждая элементарная
сила будет уравновешивать-
ся не со всей внешней на-
грузкой интенсивностью (gHb + q), а только с частью этой пагруэ
ки, во столько раз меньшей, во сколько dr меньше ширины эпюры а
Найдем нагрузку на рандбалку в сечении, отстоящем от ось
опоры на расстоянии х, при условии, что реакция, являющаяся
элементарной силой, приложена на расстоянии г от оси опоры, так
что между точкой приложения реакции и точкой, где мы имеем
нагрузку, расстояние s = x—г.
НГ
Эта нагрузка по формуле (354):
Д.+ 9). Г2у cos (as)-Д— + 11 dr. (356)
а ь* (п3я + 1)
I С
Подставим значение 5:
dp = (^ь+-^ р у cos [а (x — r)] —+ 11 dr. (357)
а (. Щ3/г +1) }
Учтем теперь элементарную силу, расположенную симметрично
относительно оси опоры (рис. 77). Тогда от двух сил, симметрично
расположенных и периодически повторяющихся:
dp = (2 у COS [а (х— г)] 1 + 11 dr +
а I " \п3к 4- 1) J
1
+ р у cos [а (X + г)] - Г -- + 11 dr =
а ( \п3я +Ц )
1
= < 2 V f cos [а (х — г)] +
а 1^1
1
+cos [а(х + г)] 1 —+ 21 dr. (358)
J (n3k I) )
Чтобы узнать нагрузку на рандбалку в сечении, находящемся
на расстоянии х от оси опоры, но при наличии всей реакции, надо
взять интеграл в пределах от г=0 до г
а
~2J
г — а
2 со
р — + J £ {cos [а (х — г)] 4-
r=0 1
+ COS [а (х + г)] 2 W. (359)
Дл3Л + 1) )
Интегрируя, получим:
а
г — --
2 со
р = / 2 У |----1. sin [а (х — г)] +
г^О 1
: ' + -Д sin [а (х + г)] 1 3. С-- + 2 г / =
а J (п3к -р 1) /
00
„ (gHb + д')
а
а х---------
\ 2 t
(g^+_?L(2y_L(_sin
а [ а (
1
+ —)
2 Л
СО
S1 . / аа \ f . 1
--sin '— COS (а X) • ---
а \2/ (п3Л+1)
1
СО
/ПГ.Х \ 1
COS ----- -------—
\ I J (^4-1).
1
Введем обозначения:
п (п3/г -{- 1)
(361)
(362)
Тогда окончательно:
(363)
1
(п3Ь + 1)
а
х
а
Формула была выведена в предположении, что х>“, но она
сохраняет силу и для х < —- . У—' Г 7 i 1
б) Примеры
Кроме упругой характеристики k, равной [по формуле (73)
(стр. 19)]
мы условились вводить в практические расчеты также характери-
стику К, равную [по формуле (74) (стр. 19)]
К = 1 000 . (365)
£Kit’
Зависимость между коэффициентами k и К была установлена
формулой (75). Но в данном случае, ввиду' того, что пролет 2/ не
равен отверстию в свету L, зависимость будет другая.,
110
Из формулы (364):
— = —. (366) ЕКЬ 2 гз
Подставим в формулу (365): 1 .L а \з k\—" + —
юоо-Л— = 2лЗ/.з 1 0С0 -Т X —3 = 1 ОООДШЫГ (367) 2 КЗ АЗ * 16тсЗДз
или:
К = 2,016 k [ 1 + —
Отношение отверстия в свету L к высоте балки по формуле
(90) (стр. 22):
L _ 9,41
h у~у (369)
или также:
А _______________________ = 2^ . 1 . (370)
|/ 2,016/ф + у-) У k (/+ /J
Сделаем расчет для 4 случаев:
Х = 4 = 5; y- = Y; * = 0,05; /( = 0,14; Щ = 18,2;
Х= — =2,5; -У = 4-1 6=0,05;/( = 0,20; ~ = 16,2;
a L 4 h
Х = _С==5; -4 = 4; 6 = 0,5; Л= 1,38; 4 = 8>4 1
a L 9 h
Х= 2-= 2,5; 4 = 4; 6 = 0,5; /(=1,97; 4 = 7-5'
a L 4 h
Эпюры нагрузки на рандбалку для этих случаев приведены на
рис. 78—81.
в) Выводы
Анализируя результаты и сравнивая эти эпюры с эпюрами, по-
лученными нами ранее (рис. 6 и 7), видим, что чем шире опоры, тем
более снижается концентрация нагрузки над осями опор, эпюры
становятся более плавными; нулевые точки эпюр смещаются, хотя
и незначительно, к серединам пролетов.
Поскольку, как и раньше, нас интересует возможность исполь-
зования приближенных формул, посмотрим, удовлетворяют ли нас
формулы (133) и (136) или формулы (140) и (142) (стр. 42 и 43).
120
Очевидно эти формулы без введения поправок здесь применять
нельзя. В самом деле, ординаты треугольных эпюр над опорами
должны получаться завышенными. С другой стороны, длины эпюр
(основания треугольников) не зависят от размеров опор, а потому
. а
может случиться, что а окажется меньше—, т. е. эпюра нагрузки
расположится в пределах опоры, что не соответствует действитель-
ности.
Ввиду этого применим формулу (133), но условимся считать,
что ордината относится не к оси опоры, а к ее грани.
Формула (133):
(371)
Для исследования удобно ввести упругую характеристику k.
По формуле (366):
£к6 = Д;
£/ №
(372)
Подставим в формулу (371):
р0 ~ 0,3055 (gHb + д) L
з __
г V 9
= 0,3055 (gHb ^q)L
3
/ v ~k
= 0,3055 (gHb
0,3055 (gHb +
(373)
или:
Po = 2,418 (gHb + 9)-— - -7
(CL \
1+T V
(374)
121
Для длины эпюры d оставим прежние формулы (136) и (142):
d = 3,27
El
ЕкЬ
(375)
или:
з ______
<7 = 0,8271/]/" k ,
(376)
но так же будем откладывать d не от оси опоры, а от ее грани.
Fla рис. 78—81 эпюры, построенные на основании формул (374)
и (376), показаны пунктиром:
Д4ы видим, что для гибкой балки (6=0,05) ордината р0 является
сильно завышенной, но длина эпюры d оказывается найденной
удачно.
Поэтому, оставив для определения d формулы (375) или (376),
для нахождения ро применим другой прием. Многочисленные под-
счеты показывают, что во многих случаях удовлетворительной
является ордината, равная средней величине из интенсивностей на-
равна
грузки выше раидбалки и ниже ее в пределах опор.
Средняя интенсивность нагрузки выше раидбалки
(gnb + q), ниже раидбалки —--------—
а
Средняя величина из этих двух интенсивностей:
,и, 1 л 1 ^Hb + 2Z Л - д
(gT/b + 9) + ’ 1 +
Ро -------------------------- (gHb + q) ±
ИЛИ'
p0 = (gHb+q)ll + ±\.
\ 2а /
(377)
(378)
Эпюры, построенные на основании этой формулы, показаны на
рисунках сплошными прямыми.
На рис. 78 ордината р0, подсчитанная по. формуле (378), мень-
ше, чем ордината, подсчитанная по формуле (374), но она все же
велика. На рис. 79 при более широкой опоре разница между орди-
натами, подсчитанными по той и другой формуле, довольно зна-
чительная и эпюра, показанная сплошной прямой [по формуле
(378)], ближе подходит к действительной эпюре.
На рис. 80 при узкой опоре ордината, подсчитанная по форму-
ле (378), больше ординаты, подсчитанной по формуле (374). Здесь
лучше остановиться на пунктирной эпюре. Но на рис. 81 разница
между обеими ординатами меньше. Несомненно, что, если опте
увеличить ширину опоры, сплошная линия пройдет уже ниже
пунктирной.
122
123
Нагрузка на рандбалку 8 случае широких опор
Рис. 81
ф 124
Подводя итоги, приходим к заключению, что длину эпюры, от-
считываемую от грани опоры, следует определять по формуле (375),
в практических расчетах более удобной чем (376):
з
‘'-«’/Д- <379>
Ординату у грани опоры необходимо вычислить и по формуле
(371):
з ____
Ро = 0,3055(^6 4-9)11/ (380)
у с.1
и по формуле (378):
Pa=(gHb + q)(l+ (381)
и остановиться на меньшей величине.
При вычислении моментов может потребоваться эпюра и в
пределах опоры. Тогда необходимо продолжить наклонную пря-
мую, ограничивающую треугольную эпюру, до оси опоры.
ГЛАВА III
МНОГОПРОЛЕТНЫЕ ПЕРЕМЫЧКИ
§ 14. ПОСТАНОВКА ЗАДАЧИ
В предыдущих главах рассмотрены рандбалки, опирающиеся
на узкие опоры. Теперь же перейдем к изучению таких случаев,
когда опоры балок, несущих кладку стены — простенки, имеют ши-
рину того же порядка, как и
пролеты балок, т. е. перейдем
к изучению перемычек.
Будем считать отверстия и
простенки чередующимися и
образующими совместно бес-
конечно длинную систему (рис.
82); Те результаты, которые мы
получим, можно распростра-
нить с некоторым приближени-
ем и на случай одного отвер-
стия, перекрытого перемычкой.
Решение задачи, нами по-
ставленной, связано с больши-
ми затруднениями вычисли-
тельного характера. Поэтому
мы ее упростим. Примем, что
пролеты перекрываются не от-
дельными балками-перемычка-
ми, а одной бесконечно длин-
ной балкой, проходящей че-
рез неограниченное число пролетов (рис. 83).
Такую балку мы условились (стр. 5) называть многопролет-
ной перемычкой.
При хорошей заделке отдельных балок в кладку их работа не
будет значительно отличаться от работы бесконечно длинной бал-
ки, так как очевидно, что в серединах простенков бесконечно
длинная балка должна мало работать на изгиб, причем нагрузки
на нее сверху и снизу взаимно уравновешиваются. Но не исключе-
126
на возможность существования и реальной многопролетной пере-
мычки.
Как уже отмечено во введении, нам удастся по отношению к
многопролетным перемычкам провести более полное исследование
и разработать практические рекомендации. Мы их проверим затем
на однопролетных перемычках со свободным опиранием на опоры
или с заделкой по концам.
Итак, предположим, что бесконечно длинная балка перекры-
вает пролеты длиной L (отверстия в свету) и опирается на про-
стенки шириной а (рис. 83). На балке расположена кладка, имею-
щая собственный вес и, кроме того, несущая нагрузку интенсив-
ностью q.
Примем, что кладка достаточно большой высоты — не меньше
половины пролета.
Поставим себе цель найти расчетную нагрузку на балку.
Расчеты сделаем для самых разнообразных случаев соотноше-
ний величин а и L и жесткостей кладки и балки. Анализ результатов
даст возможность сделать выводы и установить простые зависимо-
сти, пригодные для непосредственного применения при проектиро-
вании.
Будем пользоваться такими же упругими характеристиками,
как и раньше, а именно: коэффициентом k, удобным для исследо-
вания [формула (73) (стр. 19)], и коэффициентом А, удобным для
практических расчетов [формула (74)]:
k = ~~ , (382)
ЕКЫ* к 7
FI
К = Ю00-Ц-. (383)
EKbLz
Зависимость между ними была установлена формулой (368)
(стр. 120):
К = 2,016/гр + — Y . (384)
На рисунках будем изображать балки высотой, соответствую-
щей упругим характеристикам. По формуле (369) (стр. 120)
у = 4^ (385)
или по формуле (370)
Ниже разработаны следующие варианты, указанные в таблице
26 на стр. 128.
127
Таблица 26
а L k к L h
2 0,01 0,54 11,5
0,05 2,72 6,7
0,5 0,01 0,07 23,1
0,05 0,34 13,5
2 0,50 3,40 6,3
=0,29 7 0,05 0,21 15,7
Как видим, пределы отношений размеров и упругих характери-
стик взяты довольно широкими, в них укладываются практически
встречающиеся случаи.
§ 15. ОБЩИЙ ПОРЯДОК РАСЧЕТА
В расчете будем пренебрегать трением между балкой и клад-
кой и учтем только нормальные напряжения. Приемы расчета при-
меним аналогичные тем, какие мы уже применяли в § 10, 11, 12.
Но здесь придется осветить некоторые детали, которых мы не
касались, и составить таблицы, частично использованные ранее.
За расчетную схему примем показанную на рис. 84. Предпо-
ложим, что между балкой и простенком поставлен ряд жестких
стержней на равных расстояниях а.
Усилия между балкой и простенком будут передаваться толь-
ко через эти стержни; в пределах же каждого участка длиной с
предположим распределение напряжений по верхней грани про-
стенка равномерным.
Перейдем к основной системе. Отбросим стержни и заменим их
действие на балку и кладку действием неизвестных сил X2l Х3...
По оси простенка предположим где-либо по высоте заделку
(рис. 85).
Ввиду симметрии системы силы справа и слева от оси простен-
ка должны быть одинаковыми и симметрично расположенными.
Вследствие той же симметрии изгиб балки будет симметричным.
Вертикальное смещение места заделки в действительной сис-
теме обозначим через
Напишем теперь условия деформаций: по направлению каждой
из сил X суммарные перемещения равны нулю. Эти перемещения
зависят от всех сил X и от осадки верхней части системы у0.
Уравнения будут такого вида:
А\оп + Л2в12 + Х3о13 +...............+ у0 = 0;
+ А"2522 + х3в2з +.............+ Уо — 0;
+ А^2В32 + Х3633 -В........+ у0 = 0;
/
(387)
128
Кроме того, составим еще одно уравнение равновесия:
+ * * * = (gH b + q)l.
• (388)
Силы X мы берем только с одной стороны простенка, но пере-
мещения 8 следует принимать от групповых сил, так как фиктив-
ная заделка, помещенная на некоторой высоте, не препятствует
силам, расположенным слева от оси, вызывать перемещения по на-
правлению сил, расположенных справа.
Перемещения 8 состоят из двух слагаемых: перемещений верх-
ней грани простенка под балкой v и перемещений балки, а также
кладки над балкой w.
Как увидим далее, в формулы для осадок входит постоянный
множитель, равный ------ . Чтобы не вводить этого множителя в
Ек-зь
вычисления, выделим его.
Поскольку мы имеем дело с плоской задачей, абсолютные вели-
чины перемещений найти нельзя; в плоской задаче можно гово-
рить только о разностях перемещений. Ввиду этого в выражения
перемещений войдут некоторые произвольные постоянные.
Таким образом, например, полное перемещение по направле-
нию силы Xk от единичной силы Х1 равно:
4------4“ ^2- (389)
EK^b EK^b
Здесь Bi и B2 — произвольные постоянные, a vki и wki — пе-
ремещения, определенные по формулам, в которых отброшены эти
постоянные, а также множители и которые приведены дальше.
9 Б. Н. Жемочкин
129
После подстановки Qki в k-oe уравнение получим:
у / 16 । D 1 16 1 LJ \ 1
р 3, vki + 81 + " wkt 4 82 4-
\Екк3Ь Ект^Ь /
4 Х2 ( -1-6 ,- ^2 4 8Х + „-16— wk2 4- В21 +
\Ект^Ь Ект^Ь „ }
4 Vk3 4 4 г ~ 4 ^2) 4 ’ '' 4 Уо = 0- (390)
\ЕК^Ь Ект^Ь )
Сделаем преобразования:
Х-i {pki 4- 4 Х2 (^A2 4 шлг) 4 Х3 (vk3 4- wft3) 4- • • +
+ [(Х1 + Х2+Х3+ -)(81+5ЯУо1^ = 0- (391)
I J 16
Так как S= (gHb+q)l, то выражение в фигурных скобках
не зависит от X. Обозначим это выражение вместе с множителем
одной буквой у. Это будет некоторая условная осадка, которая
войдет в выражение как вспомогательная величина, но для окон-
чательных результатов она совершенно не нужна.
Таким образом, уравнение примет вид:
4 X2bk2 -f- АУдз4 • - 4- У = 0, (392)
причем:
^ki ~ vki + wki> (393)
Решив уравнения, найдем все силы X. Разделив их на длины
участков с, найдем интенсивности нагрузки на простенок в преде-
лах каждого участка. Полученную ступенчатую эпюру заменим
затем криволинейной.
Кроме того, найдем усилия, возникающие между балкой и вы-
шележащей кладкой, или, иначе, нагрузку на балку.
130
Следовательно, для возможности решения задачи нам необхо-
димо предварительно проделать следующее:
а) найти вертикальные перемещения верхней грани простенка
v от действия единичных сил;
б) найти вертикальные перемещения балки и вышележащей
кладки w от действия единичных сил;'
в) найти нагрузку на'балку сверху от действия единичных сил,
приложенных к балке снизу;
г) составить соответствующие таблицы.
§ 16. ДЕФОРМАЦИИ ПРОСТЕНКА ОТ ДЕЙСТВИЯ ЕДИНИЧНЫХ СИЛ
Примем, что все простенки настолько большой высоты, что их
можно считать идущими вниз бесконечно далеко.
Рис. 86
При деформации простенка в вертикальном направлении он де-
формируется одновременно и в горизонтальном направлении. При-
меним приближенный способ. Примем, что боковые грани простенка
со стороны проемов не деформируются в горизонтальном направле-.
нии и остаются вертикальными. Это требует, чтобы к ним были
приложены горизонтальные нагрузки.
Между тем, в действительности таких нагрузок нет. Следова-
тельно, мы допустим некоторую ошибку1. Можно ожидать, что
ошибка эта невелика, так как горизонтальные нагрузки, которые
будут по боковым граням простенка, малы по сравнению с верти-
кальными нагрузками. Кроме того, нас не интересуют напряжения
в простенке и его деформации сами по себе. Деформации нам нуж-
ны лишь как вспомогательные величины для определения нагрузки
на балку сверху. Допускаемая нами ошибка отразится на этой на-
грузке незначительно. Да и ошибка должна быть преимущественно
для деформаций простенка только вблизи боковых граней.
Все эти соображения указывают на полную возможность при-
менения приближенного способа. Уточнение расчета было бы до-
1 В настоящее время имеется решение для прямоугольной пластинки, нагру-
женной как угодно без введенных нами упрощений. См. М. М. Филоненко-Боро-
дич «Об одной системе функций*, Прикладная математика и механика, т. X.
Однако применение таких им функций вызвало бы большие затруднения при
составлении таблиц, почему нам приходится останавливаться на приближенном
решении.
9* 131
стигнуто очень дорогой ценой, так как вызвало бы ничем не оправ-
данное усложнение.
Итак, примем, что боковые грани простенка не деформируются
в горизонтальном направлении. Йо в таком случае для определения
перемещений в вертикальном направлении нам придется задаться
расчетной схемой бесконечно длинной стенки, нагруженной перио-
дически повторяющейся нагрузкой (рис. 86). В местах сопряжения
отдельных участков длиной а в такой стенке как раз и будут со-
блюдаться условия отсутствия горизонтальных перемещений. Раз-
мер а будет равен ширине простенка. К каждому из участков дли-
ной а должны быть приложены две единичные силы, симметрично
расположенные, в соответствии с изложенным в § 15.
Если некоторая сила Р повторяется через промежутки а, то пе-
ремещение — упругая осадка верхней грани упругой полуплоскости
в точке, отстоящейют силы Р на расстоянии s (рис. 87), равна1
Р .
V ~ ----- 1п
2[l-cos—]
L a/2j
---— In 2 1 — cos — В.
[ д/2
(394)
а/2
Член В является некоторым произвольным постоянным. Ввиду
того, что простенок предполагается бесконечно большой высоты,
мы не можем получить, как это уже выше отмечено, абсолютной
величины осадки, а только разность осадок данной точки и некото-
рой другой точки, находящейся на произвольном расстоянии d в
горизонтальном направлении, или, что по существу то же самое, на
некоторой произвольной глубине d по вертикали. Если эта глубина
1 См. формулу (382) работы автора «Плоская задача расчета бесконечно
длинной балки иа упругом основании». Обозначения соответствующим образом
изменены.
132
достаточно велика, то В будет одинаковым для всех точек по по-
верхности упругой полуплоскости1.
1 Поскольку в упомянутой выше работе предполагается, что достаточно
удаленная точка находится на поверхности, не мешает сделать вывод для точки,
находящейся на глубине d по вертикали.
За исходную следует принять формулу (100), взятую из этой работы.
Перемещение в вертикальном направлении
(здесь изменены обозначения, вместо / взято а/2, подставлено а и принято £7=^0).
Для поверхности у — 0. Для точки, находящейся на глубине rf, у == d. Раз-
ность осадок точек с у = 0 и у = d:
(1+|х)^ + 2
а/2
С увеличением d выражение в малых фигурных
скобках стремится к нулю.
Чтобы убедиться в этом, достаточно доказать, что
аП
al
стремится
нулю.
., nr.d
Обозначив для упрощения U. — —— , получим:
а/2
limUe~JJ— lim -~г —lim
t/^oo eu u-^<x
U t/2 t/з
------!_ -----_J_ —.
1 2! 3!
Поэтому:
-lim
1
U
2!
= 0.
U
к
.133
В формуле (394) предполагается, что толщина полуплоскости
равна 1. Если же у нас толщина простенка Ь, то очевидно, что от
той же силы Р осадка будет в b раз меньше.
Сила Р предположена на расстоянии z ото оси простенка; заме-
ним s через (х—z):
In 2(1 — cos Г-^—4- В.
I L а/2 Л
(395)
От двух сил Р, расположенных симметрично относительно оси
простенка,
р ( г
v~------- In 2 1—cos
I I
-j- In 2
~(x — z) Ъ
«/2 Г
(396)
Здесь также произвольное постоянное, равное 2В. Это про-
извольное постоянное опустим, так как по соображениям, изложен-
ным на стр. 130, оно в вычисления не войдет.
Сделаем некоторые преобразования, учитывая, что
o ? I T (X -
—- 2 sin2, —
— cos
I a/2
P 1 (
v=----------In {4 sin2
EKvb I I
(in 4 + 2h
EKT.b 1
p (o 1 • Г T- c
------(2 In sin —
PKr-b I
2P f. .
=--------In sin
— 1 + In U sin2
+ In 4 + 2 In sin
4- 2 In sin
' r, (x z)'
-p 2 In 2 4- 2 In 2} ~
(397)
a J
~ (x — 2) '
a
a
a
a
a
a
В дальнейшем при решении задачи нам придется принимать, что
на простенок передаются единичные силы, распределенные равно-
мерно в пределах участков длиной с (рис. 88).
На такие участки мы разобьем для расчета ширину простен-
ка а.
7
1
Первый член примет вид
Р 1 1
Г /г
cos \а/2! j
n EKa
- —in 2 1 — cos ( —)
д/2/.
Р
2 1 - cos
\a/2/_
Второй член зависит от произвольного d\ следовательно, его величина произ-
вольная. В результате получим формулу (394). '
134
Так как нагрузка, распределенная на длине с, равна 1, то интен-
1
сивность нагрузки — .
В формулу (397) придется вместо г ввести -новое переменное
г—расстояние до элементарном- силы-—' dr, поставить вместо Р
с
1 , [ с \ .
величину —dr к проинтегрировать в пределах от 2-------- до (д4
с \
— где г-теперь уже расстояние до середины загруженного
участка (напомним, что каждой элементарной силе — dr соответ-
с
ствуст такая же сила, расположенная симметрично, формула же
(397) у нас и выведена для двух сил, что определяет пределы ин-
тегрирования).
Осадка точки, находящейся на расстоянии х от оси простенка,
от действия единичной распределенной нагрузки будет равна:
2 Дг
ЕклЬс
In sin
-ф 2 In 2
с
г = ?4---
2
2 Л [ Гл (л- — г)
...... In Sill —-----------------
Erxbc J ( Iй
с
г-г— --
2
+ In sin
Н-2 In 2 Jr (398)
Найдем нужные нам интегралы отдельно.
При вычислении первого интеграла сделаем для облегчения за-
мену U —. Очевидно, что в этом случае dr=—~ dU. Во
й Я
втором интеграле сделаем замену , здесь dr^x.— dU.
а ’ л
135
Получим:
In sin U dU ==
_ _1_ у'Sin (2^) _ у ln 2
2 n2
1
Подставим пределы:
2гЦл — г —— — х-р г — ~
2а
— c In 2
COS
2 пл (х — 2)
а
(400)
136
1 n
— 2 cos
/г2
Xsin
2a
£.y^-cosk^±^
к n2 [ a
i
2
J- 21n2dr = 21n2- ^z+ — z +-у) = 2c In 2. (402)
,=г- Л
2
137
Таким образом:
2
V ~--------
EKitbc k
— cos
Г (х— г) 1 , (ппс\) _
------------- Sin ------ — С In 2—
а
СО
1
i
а
sin I—)!— c In 2 + 2c ln2
\ а /I
2a
EKT.2bc
S-cos
4J П2
" 2/itc (x—z4-x+zY
----COS
~2п~ (x—z-~x—z)
п~с
2а
2а
sin
\ а
4а
Ек^2Ьс
1
п2
{пкс\ /2ппх\ [2mtz
sin — cos ---------- cos -------
\ а / \ а 7 \ я .
(403)
Формула (403) пригодна
как для определения осадок
в точках, лежаших вне за-
груженного 'участка, так и в
точках, находящихся внут-
ри этого участка.
Расстояния х придется
принимать до середин уча-
стков длиной с и определять
осадку только в этих точ-
ках.
Но лучше иметь дело не
с осадкой в середине какого-
либо участка, а со средней осадкой в пределах этого участка. Это
несколько повысит точность решения, а вместе с тем, как увидим
дальше, улучшит сходимость рядов.
Для этого, перейдя к новой переменной проинтегрируем по-
лученное значение для v в пределах от ^х--|-j до ^х + -|~j и ре-
зультат разделим на длину участка с (рис. 89).
Получим:
с
2 со
4a f 3
E^bc2 J
, c 1
f=X— —
2
. /2n^t\ i'2n~z\ <
sin — cos ------------ cos -------- at =
\ a \ a \ a /
c
t—x -J- ——
2
4a I
Екк2Ьс2 I
t-x——
2
00
V 1 . /пкс \ а . /2ляг/
\ ----- Sin ------- )• ------sin ---------
п2 \ а 7 2/гтс \ а
1
2пт?
а
138
2a2
EKn3bc2
2д2
£’к~35с2
— sin
Xsin
4a2
EKr3bc2
•cos
, 2cos
sin
2a
1
Введем такие обозначения:
rf = — (405)
С
C = — (406)
c
Тогда:
v =
4а2
Е^Ьс2
cos
/2/ггх\
cos ------- cos
\ a j
(404)
(x — расстояние от середины участка, для
которого ищется осадка, до оси);
(z — расстояние от середины загруженно-
го участка до оси). •
СО
V 1 . о /п~с\ / 2п~ъс \ [ 2пг£с \
У — sm2 — cos -----------— cos --------- .
^/z3 \ a j \ a ] \ a )
1
(407)
Из шести разобранных ниже примеров расчета в пяти половина
ширины простенка — делится на 6 частей, т. е. отношение —
2 с
- 12.
Поэтому:
СО
576 1 с/== Екк3Ь * СТ 1 . п /П|и \ ! \ /ЛЛО\ У —sin2 — cos — cos — . (408) "J п3 \ 12 j \ 6 / \ 6 / 1
В одном примере половина ширины простенка делится на 2
части.
139
Здесь — =4, а потому:
с
64 v 1 •*> /лтс \ /лтс'пХ /лХ
о — ---------У— sin2 — cos —! cos —•
£кх86 X \ 4 У \ 2 / \ 2 ,
(409)
~ длина"
Осадки получаются в мерах ------.
сила
Мы уже отмечали выше (на стр. 129), что в выражениях для
перемещений верха простенка и балки имеется общий множитель
16
. Разделив полученные нами выражения на эту величину и
EKr^b
оставив прежнее обозначение для и, примем окончательно: для слу-
чая, когда половина ширины простенка делится на шесть частей
V1 1 \ /л'7)) MX
v — 36 У—sin- —cos р—1 cos—
/i3 \ 12 / \ 6 / \ 6 ,
1
для случая деления на две части
СО
1 . о /ЛК \
v =4 >, — sm2 — cos —1 cos — .
л3 \ 4 У \ 2 У \ 2 У
1
(410)
(411)
Теперь v—в отвлеченных мерах.
§ 17. ТАБЛИЦЫ ОСАДОК ПРОСТЕНКА
Покажем, как практически находятся упругие осадки верха
простенка.
Пусть требуется найти осадку У53 в предположении, что нагруз-
ка приложена в третьем участке от оси простенка, осадка же
ищется в пятом участке (рис. 90).
В данном случае и С—относительные безразмерные расстоя-
ния до середины участков — равны: rj == 4,5, С = 2,5.
Формула (410) примет вид
Рис. 90
v53 = 36 2-Vin2(-’5°)X
* /г3
1
X cos (п - 135°) cos (п -75е).
(412)
Составим такую таб-
лицу (табл. 27).
Окончательные значе-
ния v желательно иметь с
140
третьим десятичным
знаком. Для уверен-
ности в третьем знаке
следует их вычислять
до четвертого знака. Но
так как для получе-
ния v надо сумму чле-
нов ряда умножить на
36, то, следовательно,
члены ряда приходится
вычислять с шестью
знаками. Это впол-
не можно сделать,
имея пятизначные таб-
лицы тригонометриче-
ских величин, так как
произведения этих ве-
личин делятся на п3.
Производя вычисле-
ния членов ряда при-
мерно до 60-го, най-
дем сумму равной
—0,021532. Умножая
на 36, получим
——0,7752' или, округ-
ляя, и53 = —0,775.
Аналогично прове-
дем вычисления и для
других V.
Конечно, при со-
ставлении таблиц воз-
можны упрощения, так
как некоторые вычис-
ления повторяются. Не
следует пренебрегать и
различными поверками.
Так, например, осадка
во 2 участке от единич-
ных сил, приложенных
одновременно в 1 и во
2 участках (слева и
справа от оси простен-
ка) , равна осадке в 1
участке от единичных
сил, приложенных в 1
и в 3 участках. В са-
мом деле, в первом слу-
чае расстояния сил от
середины 2 участка
0.021532
141
равны 0, с, 2 с и 3 с\ те же расстояния и во втором слу-
чае.
Таким образом, должны соблюдаться соотношения:
’ ^12 4“ 022 = ^11 4~ ^13 >
013 4" 023 = ^12 4" ^14j
^14 4- у24 = ^1з 4- ;
01; 4- о>5 = ^4 + ^iC;
V22 4" ^23 “ V11 4*
02з 4- 033 = uu + ul5;
024 4- ^34 = ^12 4- t>iC;
y23 4 ^24 “ У12 4" t>i5;
033 + ^34 = 0ц 4- fiG;
024 4" ^25 = ^13 4- 0ЦЬ
0ц = 0(>(>;'
012 = 05C;
0i3 = 04G;
014 = 036;
015 ~ 02Ci
’ 022 = 0551
023 = 045*.
024 = 035;
033 = 044-
Самая простая поверка: сумма и для одного и того же С равна
нулю.
Чтобы не иметь дела в вычислениях с отрицательными значения-
ми v, лучше будет наименьшее v принять за нуль, другие же соот-
ветственно увеличить. Такая операция равносильна изменению
произвольного постоянного; она не отразится на значении неизвест-
ных сил X, а только лишь на значении совершенно условной вели-
чины у.
Наименьшее =— 1,653. Поэтому р53 примем равным ^53 =
= —0,775-Т 1,653 = 0,878. Величину 1,653 приложим ко всем и.
После соответствующей обработки всех v получим таблицу пере-
мещений верха простенка от единичных сил для. случая, когда
половина ширины простенка делится на 6 частей длиной с (табл.
28).
Половина таблицы не заполнена, так как по теореме о взаим-
ности перемещений vtk.
Поступая совершенно таким же образом, в случае, когда поло-
вина ширины простенка делится только на 2 части, получим
другую таблицу (табл. 29).
142
Таблица 28
Осадки простенка у для случая с =
а
?2
№ участков, где приложены нагрузки С № участков, где ищутся осадки
1 2 3 4 5 6
Ч
0,5 1.5 2,5 3,5 4,5 5,5
1 2 3 4 5 6 0,5 1,5 2,5 3,5 4,5 5,5 5,259 2,628 3,890 1,269 1,940 3,499 0,571 0,878 1,760 3,499 0,180 0,391 0,878 1,940 3,890 0 0,180 0,571 1,269 2,638 5,259
Таблица 29
а
Осадки простенка v для случая с — —
4
№ участков, где приложены нагрузки С № участков, где ищутся осадки
1 2
0,5 1.5
1 2 0,5 1,5 2,104 0 2,104
Напоминаем, что абсолютных величин осадок получить нельзя;
v дают только разность осадок данной точки на поверхности и не-
которой точки на глубине. Разность осадок двух каких-либо точек
на поверхности мы можем получить, взяв разность соответствую-
щих V.
Поскольку мы делали расчет в условных единицах, для получе-
ния, если потребуется, действительных v надо вводить множитель.
16
В том случае, когда нагрузки не единичные, следует умножать и-
на эти нагрузки.
(см. стр. 140).
§ 18. ДЕФОРМАЦИИ КЛАДКИ, РАСПОЛОЖЕННОЙ НАД БАЛКОЙ
Если кладка достаточно большой высоты, то мы имеем как бы
перевернутую схему бесконечно, длинной балки на упругой полу-
плоскости, нагруженной периодически повторяющимися нагрузка-
ми (рис. 91).
Для такого случая решение имеется, мы его и применим.
143:
Осадка балки на упругом основании (или перемещение) в точке,
отстоящей от сосредоточенной силы Р (повторяющейся периодиче-
ски) на расстоянии s (рис. 92), равна:
COS
(413)
[см. формулу (102) упомя-
нутой выше работы; обозна-
чения приняты применитель-
но к нашему случаю].
Поскольку величина про-
извольного постоянного В не
имеет никакого значения, в
дальнейшем В опустим.
.Если толщина стены рав-
на Ь, надо w разделить на Ь.
Раньше мы условились
вводить в расчеты упругую характеристику k, равную:
2кЗ£/
Ек6/3
(414)
£1
Поэтому удобнее формулу (413) переписать так:
2Р
Ект.Ь
00 nr,S
cos —
\ /
П(/23^4" 1)
1
(415)
Вместо s введем (х—z).
144
От двух сил P, расположенных симметрично относительно оси
простенка:
СО
2P V
w =--------- У
ЕккЬ
1
cos
+cos '»ТС(±±Д]1 (416)
Перейдем к единичной нагрузке, распределенной на длине с
(рис. 93). Для этого вместо z введем как переменное г. Вместо Р в
1
формулу (416) подставим —dr и возьмем интеграл в пределах от
2
Получим:
г=г+ —
2 оо
w
2
1
'w (x —
ЕккЬс J п (n3k
с 1
Г ~ Z— -—
2
с
Г-Z-'r <—
2 оо
cos
COS
2
Е^кЬс
------sin
(x —
. * -
_]----- sin
ПК
00
21
EK^bc
— sin
1
/ С
пк I х—z— —
-
с I
2
z
I
dr =
1
z
/ с
п~ 1х4-гН-
— sin
с
z— —
2
Z
Ю Б. Н. Жемочкин
145
4/V 1 n (п~Х\ /41-74
-------) ,-------------sin — 2 cos — cos — . (417)
EK~~bc n2 (n:ik -p 1) \ 2/ / \ / / \ I /
Рис. 94
Перейдем теперь к среднему перемещению в пределах участка
длиной с, середина которого отстоит на х от оси простенка
(рис. 94).
Для этого введем новую переменную /, проинтегрируем в пре-
делах от t~x--до t=x + ~~ и результат разделим на с.
146
2
8/
w =--------------
t-
/ ПТС\
•SIH — COS
\ 2/ /
n~t\ Ьгтг\
--- COS -----!
8/2
ЕктЛЬс2
1 . птс\ .
------------ Sin — Sin
И \2/ /
ЬгтЛ
№
Ект3Ьс2
/птс\ .
sin -----
\ 2/
sin
пт.
8/2
— sin
/ птг
CQS ---
v 1 . (птс
\ ----------sin —
— пЧп^- 1) \ 2/ ,
1
птх , . /птс\
2 COS ---- SIH ----- COS
\ / I 2/ !
ПТ2
16/2
Ект-Ьс2 *
i
о / П TC
sirr-----
\2Z
cos
tlTZ
(418)
Применим обозначения:
(419)
(420)
(421)
2
2
2
1
1
1
77 тг
с
т
/
И
c
" 2
I
X
с
с
2
С
отбросим, как условились раньше (стр. 129)
Тогда получим окончательно:
16
, множитель ------
1 . о
-------------Slrr
n3 (n3k + 1)
ПТТ}
COS -----
\ x
/птЛ\
cos -----
I X /
(422)
Нагрузка на балку снизу может быть только в пределах простен-
ка, в этих же пределах нужно находить и деформации кладки, так
как нам придется сравнивать перемещения простенка и кладки. По-
10*
147
этому т] и С могут меняться в пределах от 0,5 до 5,5. Для X мы
возьмем значения X =9 и X =18. Коэффициент k в различных слу-
чаях будем брать £=0,01, £=0,05 и Д=0,50.
§ 19. ТАБЛИЦЫ ПЕРЕМЕЩЕНИЙ КЛАДКИ
Предположим, что нам нужно найти перемещение кладки в 5
участке {от оси простенка) от нагрузки, приложенной в 3 участ-
ке. В этом случае С =2,5 ит{--4,5 (рис. 95). Пусть длина /=9с, т. е.
Х=9, а упругая характеристика £=0,05.
Формула (422) примет вид:
^53
со
1
«3(0,05^4- 1)
1
sin2 (л -10°) cos (п- 90°) cos (п -50°). (423)
Составим таблицу (табл.
30).
Сходимость здесь гораз-
до лучше, чем при вычисле-
нии о, достаточно 20 членов.
Умножая полученную
сумму на 92 = 81, получим
^53= + 81-0,000288 - +0,0233
или, округляя, й”53=+0,023.
Составляя таблицу для
всех w, опять наименьшее w
примем для упрощения за нуль, остальные же аг соответственно из-
меним.
Для проверки можно использовать следующие зависимости:
®12 + W22 — “’ll 4~
®13 + ^23 = W12 + ^14;
®14 + ®13 4~
^15 + — ®!4 4
ш22 + +?3 = + О+ь
w23 + ^33 : • “’ll + ^’15;
®24 + “'12 4-
®23 + КЦ1 “12 + ^'15
~33 + ®3l = “11 4~ ^16 >
®24 + №25 — “13 + ^16’
Для различных исследованных нами случаев составлено не-
сколько таблиц перемещений кладки, и следовательно, прогибов
балки (табл. 31, 32, 33, 34 и 35). Половина таблиц не заполнена
вследствие взаимности перемещений:
143
0,000288
.
со
о
о Ю о
со сч ' ' о
СТ) О ОО LO
Ct СЧ СО ' Ь-
О О о со О О СО о
сл к
о ° о . . о
V. | 1
с
<Л
О Ю СО О СЧ —< СЧ
о Г- СО О О О ’’ СО О'
1X0 СЧ со СО О СЧ TF СЧ
ТГ Г"- СО со ХГ ‘со
со — со о со оюсо
К — - № —- к.
из О о о О О о ООО,
-Г 1 1 1 1 '. 1 1 + .
о
СП О — О — О *0-0 *
g. 1 4- * • * 4~
v>
о
Г О Ю со о со СЧ ’ СЧ О СЧ
— О О — 00 О О ио
О со о со со ’ * со о <ю
Ct со — ю — СО 00 Ю 00
О — СЧ "Ч4 Ю ’ ’ 00 С- ю
й
’сЛ о о О О о 'ООО
о Ю СЧ ОМ1 О СО тн
со о с- О со о о
со СЧ сч со о со со
£* ТГ т* СО " СП СО со
— СО ю со Г- . . СП QO Г"-
с О О о О С . .ООО
[/) 4“ 4“ Н“ + + . . ~г 4“ “Г
—
+ ю ю ю ь- Г- ।
Г) t; О СЧ -ч4 ОО СЧ . ОЭ СЧ 00
LO ----- о о ю
О — — со оо CD . .О’—'CQ, 1
о" — СО СО О О LQ ’’f * ‘
СЧ о .00 — 01
СО
Ct : 1 .
Ct — СЧ со
— СЧ СО СО — — —
149
Перемещения кладки
Таблица^ 31
а) А 9( /г — 0,01
№ участков, где приложены нагрузки с № участков, где ищутся перемещения >
1 2 3. 4 5 ' 6 :
Ч
0,5 1.5 2,5 3,5 4,5 5,5
< СЧ СО Tf LQ СО 0,5 1,5 2,5 3,5 4,5 5,5 5,242 3,495 3,630 1,883 2,548 3,066 0,936 1,319 2,176 2,814 0,372 0,564 1 ,067 2,017 2,737 b i 0,120 0,406, 0,990 2,017 2,814
•Таблица. 32
б) Л--- 9, k — 0,05
№ участков, где приложены нагрузки С № участков, где ищутся перемещения
1 2 3 4 5 1 5 !
ri
0.5 1,5 2,5 3,5 4.5 5,5
1 2 3 4 5 6 0,5 1,5 2,5 3,5 4,5 5,5 4,508 3,450 3,225 2,167 2,433 2,527 1,150 1,469 1,981 2,243 0,452 0,698 1,186 1,813 2,165 0 0,168 0,530 1.107 1,813 2,243
с
Таблица 33
в) Х = 18, k = 0,01
>6 участков, где приложены нагрузки- № участков, где ищутся перемещения
1 2 3 4 5 6
*1
0.5 1.5 2,5 3,5 4,5 5,5
- . -у — — ir 1 —• см со ю с© /0,5 . 1,5 - 2,5 —З/б’-" 4,5 -5,5 » - 4,481 ' 3,589 3,312 с 2,420 2,556 2,514 1,387 1,622 1,967 - 2,-076- г 0,589 0,798 1,184 1,631 1,810 0 0,151 0,462 0,918 1,414 1,629
050
Таблица 34
г) X = 18, k = 0,05
№ участков, № участков, где тщутся перемещения
I i 2 3 4 5 | 6
где приложе- ны нагрузки с 7
0,5 1,5 2,5 3,5 | 4,5 5,5
1 2 3 4 5 6 0,5 1,5 2,5 3,5 4,5 5,5 3,053 2,636 2,405 1,988 1,926 1,727 । 1,278 1,310 1,326 1 ,219 0,600 0,678 0,802 0,907 0,879 0 0,092 0,258 0,462 0,634 0,661
Таблица 35
д) X = 18, k = 0,50
№ участков, где ищутся перемещения
№ участков, < 1 2 3 1 4 5 6
где приложе- ны нагрузки с У
0,5 1,5 2,5 3,5 ' 4,5 5,5
1 0,5 1,308 1,198 1,003 0,750 0,463 0,159
2 1,5 1,113 0,945 0,715 0,446 0,156
3 2,5 0,326 0,642 0,409 0,148
4 3,5 0,519 0,343 0,127
5 4,5 0,237 0,082
6 5,5 0
Если бы мы захотели находить истинные величины перемещений
кладки или, правильнее, разности перемещений, так как их абсо-
лютные величины найти нельзя, то табличные данные пришлось бы
16
умножать на коэффициент ------- (см. стр. 147) и на нагрузку.
Ект^Ь
§ 20. НАГРУЗКИ НА БАЛКУ (РЕАКЦИИ КЛАДКИ) ОТ ЕДИНИЧНЫХ СИЛ
Нашей конечной целью является определение нагрузки на балку
сверху. Для этого сначала нужно найти реакции кладки от единич-
ных сил, приложенных к балке снизу и представляющих силы вза-
имодействия между балкой и простенками (рис. 96).
Как и раньше, мы имеем здесь бесконечно длинную балку на
упругом основании, нагруженную периодически повторяющимися
нагрузками.
Мы можем воспользоваться теми данными, которые нами были
получены для рандбалок.
151
Нагрузка на рандбалку была установлена формулой (83)
(стр. 21):
ОО
p = (gm> + ?){2[Vcosp^—] + 1 !• <424)
V [ Лшяш \ I / \11УК “1“ 1) }
Эта же формула остается и для определения нагрузки на балку
от вышерасположенной кладки, если снизу приложены силы, пе-
риодически повторяющиеся через 2/. По формуле можно найти на-
грузку на балку в сечениях, отстоящих от сосредоточенных сил на
расстояниях х.
Рис. 96
Но в формуле (83) предполагалось, что реактивные сосредото-
ченные силы (на опорах) равны (gHb + q)2l. В нашем же случае
следует принять единичные силы; следовательно, нагрузка р долж-
на быть в (gHb+q)<2l раз меньше.
Поэтому:
(425)
Удобнее обозначить расстояние от единичной силы до сечения,
где мы хотим найти нагрузку на балку сверху, через s:
р- — 2
А 2/1
(426)
+ lj •
В § 2 были решены раидбалки для упругих характеристик
Д=0?05 и /г=0,5 (см. рис. 6 и 7). Таким образом, для этих упругих
характеристик данные уже имеются. Для £=0,01 придется сделать
вычисления вновь.
Покажем, как находить нагрузку на балку по данным, найден-
ным для рандбалок.
Допустим, например, что расстояние I мы предполагаем разде-
лить на 9 участков длиной с; упругая характеристика ДО,05.
152
Ордината эпюры нагрузки на рандбалку в месте расположения
сосредоточенной силы была нами найдена равной ро ~ 6,564 X
X(gHb + q). В разбираемом случае мы получим:
р0 = 6,564 — = 3,282- — .
г ’ 21 I
Подобным образом мы можем, используя имеющиеся данные,
найти интенсивности нагрузок для любых сечений.
Обозначая
S S
Х=~ = Т’
9
(427)
получим такую таблицу нагрузок на балку, вызванных единичной
силой, приложенной снизу (конечно, для Л=0,05 и с= -—-j(табл. 36).
Мы дошли только до середины пролета, так как эпюра нагруз-
ки симметричная.
Таблица 36
X р X Р
0 0,5 1 1,5 2 2,5 3 3,5 + 3,282 +2,758 + 1,971 + 1,324 +0,795 +0,445 +0,217 +0,077 4 4,5 5 5,5 6 6,5 7 7,5 8 8,5 9 оооооооооо ооооооооооо 1 1 1 1 1 1 1 1 1 1
Обозначим расстояние от силы до оси простенка через г и рас-
стояние от сечения, где мы ищем нагрузку на балку сверху, до оси
простенка через х (рис. 97).
Введем обозначения:
(428)
X
Д = — -
с
(429)
Сечения будем нумеровать 0, 1, 2, расстояния между ними
равны с. У грани простенка для повышения точности возьмем
сечения через 0,5 с.
153
Определяя -ординаты р, мы должны учитывать две силы, распо-
ложенные симметрично относительно оси простенка.
Предположим, что нам нужно для случая н —9 и /^=0,05 найти,
ординату эпюры нагрузки р в сечении № 5 (д=5) от нагрузки, на-
ходящейся в 3-м участке (С=-=2,5). Для одной силы расстояние
s=-2,5 с и для другой силы у =7,5.
Тогда получим:
р = (0,445 — 0,017)-С = 0,428—.
/ /
В некоторых случаях придется учитывать не левую силу данно-
го простенка, а левую силу следующего. Так, например, предполо-
жим, что нужно найти ординату эпюры нагрузки в сечении № 6
(д=6) от единичной силы, приложенной в 6-м участке (С =5,5).
От правой силы это сечение отстоит на л=0,5 с и * =0,5, для ле-
вой силы данного простенка расстояние s= 11,5 с, т. е. больше /;
тогда учтем левую силу следующего простенка, до которой s=^6,5c
и х=6,5.
Получим:
р = (2,758- 0,031)--у- = 2,727- у-;
Произведя вычисления для различных 7 и k, составим таблицы
ординат эпюр нагрузок на перемычки (табл. 37—42).
Если мы хотим получить действительные ординаты эпюры реак-
ций от единичных сил, то табличные данные следует делить на I
(см. стр. 153).
§ 21. ПРИМЕР
' Покажем на конкретном примере, как вести вычисления.
Предположим, что мы хотим решить задачу для того случая, ко-
гда ~~~ 2 и k = 0,05 (рис. 98). J .
154
Таблица 37 а) X = 9, k = 0,01 № сечений, где определяются нагрузки на балку о Сб о ю ея ' — Ю СО 1 03 о о О О o' О EJ № сечений, где определяются нагрузки на балку СП р" о> т* тг ся ос со (N о? со ОО S иО О О О О О •— o' о о о" o' о" 1 1 I 1 1 —
ОС' 6,5 7 8 0 0 —0,005 —0,028 —0,071 —0,067 Т а б СО 00 —0,029 —0,043 —0,061 —0,070 + 0,033 0,406
юоосос^ со С'ГШ'О?)^ о о о о г- о о о' о о о 1111 + г- г~- ОО О 7—1 О О g LQ iG О —• ОО о о о О о" -2
ю СС 0 —0,015 —0,046 —0,081 + 0,165 1,870 I 6,5 6‘9 м _1 О 04 тГ — Tf со СО -г-н О Ь- со О О О СТ
1 ( 2 3 4 | 5 5,5 6 0 1 2 3 4 5 5,5 6 —0,005 —0,028 —0,066 —0,039 -00,718 3,808 LO ю 4 | 5 5,5 6 Ю <D G G N N N Ю СО СО О 04 OOOTGN О О О О 04 1 IO
—0,015 -0,016 —0,081 НО,165 1,870 । 5,612 ; 0,05 ОС' О1 о 00 S? VQ О О G4 G- СП 04 О О о О СО
со со СП оо сс со го со О —< О О ОО О S X X О О О О С? со 1 1 1 4_ Я cGCOOOCNO’—1 СО 'Т О) 1 "'Г Т С О G X t- N о 04 04
I —0,094 —0,044 + 0,718 3,808 3,808 +0,718 б) 2 +0,038 0,401 1 1,293 2,741 2,746 1,312
- -0,105 +0,690 3,803 3,808 -НО,718 -0,039 1 со G l lG 'Ч4 Ь- СО СН ОС — 04 О со i-Q О) 1— О- СО 'TF О " О) 04 1 О
+0,679 3,742 3,780 +0,713' -0,039 -0,066 С-1 СП L.O СП О TF О СО СО !—• СО 'О ' ь» ОС ь. 04 о 04 О О И’
4,526 3,769 +0,652 —0,067 -0,071 —0,028 —1 4,082 3,203 1,401 ' 0,406 +0,033 —0,070
СО СО 00 CN О О 73 + 5? + Зр° <7 о — С X О ’ТСООЭ yr СП LG Г'-' <эо Ю 04 О О О О
lO lQ iG lQ lO LQ О *— 04 CO Ю *-7 Ю Ю Ю Ю lG Ю О —< 04 СО тг Ю
Н1ГИЭ эпньинигэ ннажогиби эта ‘ЯОНТЭЕЬХ $ч ея co -гг ig co Н1ГИЗ Э1ЧННИНИГЭ ннажоь’ибв ага ‘аоядэиьХ ' СЧ СО ’«Г tG *4D
155
в) X = 9,
(для случая
№ участков, где приложен единичные силы С № сечений, где определяется
0 1 1,5 2 - 2.5 3
Л
0 1. 1,5 2 2,5 3 ‘
1 2 0,5 1,5 5,516 2,648 г 4,082 3,203 2,766 3,498 1,769 1,835 1,012 1,971 0,522 1,285
г) X = 18 ,
№ участков, где приложены единичные силы ч № сечений, где определяются
0 . 1 1 2 3 4 5 5,5 6 6,5
0 1 2 3 4 5 5,5 6 6,5
1 2 3 4 5 6 0,5 1,5 2,5 3,5 4,5 5,5 « 9,820 5,40.8 2,380 0,750 +0,056 —0,144 7,011 6,100 3,079 1,157 +0,301 —0,040 3,894 5,285 4,9В 2. 32 1,177 + 0,324 1,5'5 2,737 4,838 4,837 2+53 1,155 4-0.342' 1,113 2,831 4,859 4,875 2,084 —0,039 1-0,302 1,139 2,669 4,890 4,900 —0,123 + 0,089 0,673 1,855 3,795 5, (ЮЗ —0,145 —0,018 +0,340 1,170 2,6.91 4,907 —0,145 —0,030 4-0,123 0,ь93 1 877 3,803
д) X- 18,
>5 сечений, где определяются
Ns участков, 0 1 2 3 4 1 5 5,5 6 15,5
где приложены единичные силы С *1
0 1 2 3 4 5 5,5 6 6,5
1 0,5 6,310 1 5,548 4,009 2,649 1,644 0,935 0,663 0,461 0,294
2 1,5 4,786 4,771 4,188 3,004 1,940 1,170 -0,866 0,641 0,446
3 2,5 3,232 3,423 3,766 3,479 2,530 1,645 1,324 1,009 0,750
4 3,5 2,036 2 227 2,717 3,292 3,185 2,369 1,932 1,572 1,277
5 4,5 1,222 1,357 1,753 2,423 3,131 3,111 2,711 2,345 1,927
6 5,5 0,748 0,748 1,063 1,592 2,349 3,107 3,237 3,114 2,721
е) Х.= 18,
Ns участков, № сечений, где определяются
. 0 1 2 3 4 5 5,5 6 6,5
где приложены единичные силы С ' 71
0 1 2 3 1 4 5 5,5 6 6.5
- 1 0,5 3,030 2,856 2,622 2,297 1,940 1,608 1,462 1,325 Г, 195
2 1,5 2,770 2,733 2,551 2,255 1,9/5 1,657 1,502 1,354 1,215
3 2,5 2,474 2,445 2,381 2,229 1,9 32 1,711 1,5:5 1,423 1,286
4 3,5 2,120 2,117 2,113 2,098 1,975 1,748 1,634 1,515 1,391
5 4,5 1,760 ' 1,788 1,834 1,859 1,864 1,779 1 693 1,5Я- 1,490
6 5,5 1,456 1,477 1,534 1,600 1,663 1,707 1,691 1,650 1,577
156
Таблица 39
6—0,05
a 2 к
~L^~
нагрузки на пялку
4 5 6 7 8 9
4 5 6 7 8 9
+0,038 0,401 -0,083 +0,046 —0,075 —0,056 —0,048 —0,056 —0,029 —0,043 * 4' -0,024 —0,034
Таблица 40
Л=0,01
нагиузки на палк •
7 8 9 ю . 11 12 13 14 15 16 17 18
7 .8 9 10 11 12 13 14 15 16 17 18
—0,124 —0,035 —0,055 —0,030 —0,013 —0,004 —0,001 0 0 0 0 ' 11 —, 0
-0,107 —0,С93 —0,0 Д -0,038 —0,021 —0,010 —0,003 —0,001 0 0 0 0
+0,013 —0,082 —0,076 —0,052 —0,035 —0,020 —0,010 —0,003 -0,001 0 0 0
0,Зг5 +0,030 -0,073 -0,073 —0,051 —0,035 -0,020 —0 010 —0,003 —0,001 0 0
1.18? 0,374 + 0,033 —0,072 —0,073 -0,051 —0,035 —0,020 —0,010 —0,003 —0,001 0
2.703 1,190 0,375 4-0,033 —0,072 —0,073 -0.051 —0,035 -0,020 —0,010 —0,003 —0.001
Таблица 41
6—0,05
iraгрузки на балку
7 8 9 10 1 11 12 13 14 15 16 17 18
л
7 ! 8 9 10 11 12 13 14 15 16 17 18
0,167 + 0,005 —0,068 -0,092 —0,039 —0,074 -0,059 0,045 —0,034 -0,027 -0,022 —0,020
0,300 + 0,093 —0,018 —0,065 -0,077 -0,074 —0,060 -0,018 -0,038 —0,029 -0,025 -0,024
0,557 0,276 +0,096 —0,003 —0,050 —0,063 -0,063 -0,053 0,043 —0,036 -0,031 - 0,0'30
0,935 0,570 0,291 +0,111 + 0.011 —0,039 -0,055 -0,058 -0,051 -0,045 -0,041 —0,038
1,575 1,000 0,585 0,305 0,122 + 0,018 -0,034 -0,054 —0,060 —0,056 -0,052 —0,052
2,360 1,590 1,014 0*593 0,312 0,127 + 0,020 -0,036 —0,0а9 -0,067 -0,067 —0,066
Таблица 42
Л=0,50
нагрузки на балку
7 8 9 10 11 12 13 14 15 16 17 18
71 -
7 8 9 10 11 ' 12 . 13 14 15 16 17 18
1,071 • 0,837 0,641 0,484 0,355 0,250 0,159 0,086 +0,0‘33 -0,004 -0,021 -0,024
1,091 0,875 0,680 0.512 0,379 0,264 0,177 0,106 0,049 +0,016 —0,007 -0,018
1,158 0,934 0,746 0,575 0,421 0,305 0,211 0,140 0,089 0,046 +0,019 + 0,010
1,266 1,029 0,829 0,655 0,502 0,358 0,269 0,194 0,137 0,092 0,033 0,055
1/386 1,161 0,938 0,756 0,t02 0,4с5 0,351 0,266 0,197 0,154 0,129 0,116
' 1,485 1,295 1,088 0,885 0,719 0,585 0,462 0,354 0,283 0,234 0,207 0,202
157
Здесь нам удобно разделить на 6 участков длиной с, а I —
на 9 частков. При этом X =9. Длина L будет иметь 6 участков.
Разделив ™ на 6 участков длиной с, в серединах участков по-
местим между балкой и простенком условные связи-стержни. На
Отбросим стержни и заменим их действие действием неизвестных
сил Х2.. По оси простенка поместим условную заделку. Ос-
новная система приведена на рис. 100.
Уравнения составим, исходя из условий, что суммарные пере-
мещения по направлениям сил X равны нулю [см. формулу (387)
(стр. 128)]. Кроме того, будет одно уравнение равновесия [фор-
мула (388)].
4- Х2^12 + *3^3 + ^4^14 + ^5^15 + + У “ 0 *,
-^1^21
+ "V 1 У7
^2°22 “Г ^3°23
"Г ^4^24 + ^5^25 + ^6°2С
+ у -- 0 ;
^1^31 + ^2^32 + ^33 + -^4^34 + ^5^35 + -^36 + У = 0 ",
+ ^2^42 + -^3^43 + ^4^44 + ^5^45 + -^6^46 + У — 0 ;
158
ХДх + ^2^52 + ^3°53 + Хс§и + у = 0 ;
^61 + ^2°б2 + ХД,; + ХД-4 + Х:уй5 + Х35! + у = 0 ;
+ *з + Х4 + X- + XG = (gHb + q) I.
Перемещения В слагаются из перемещений простенка и пере-
мещений балки вместе с кладкой [формула (393) (стр. 130)].
^ki — vkt + wkt • (430)
Для v используем таблицу 28 на стр. 143 и для w таблицу 32 на
стр. 150. ‘
Получим:
8И = 5,259 + 4,508 = 9,767 ; 833 = 3,499 + 2,527 - 6,026 ;
В12 = 2,638+ 3,450 = 6,088; 834 = 1,760 + 1,981 = 3,741 ;
813 = 1,269 + 2,167 = 3,436 ; 835 = 0,87,8 + 1,186 = 2,064 ;
314 = 0,571 + 1,150 = 1,721 ; о36 = 0,571 + 0,530 = 1,101 ;
815 = 0,180 + 0,452 = 0,632 ; 8М = 3,499 + 2,243 = 5,742 ;
836 = 0+ 0= 0 ; 345 = 1,940 + 1,813= 3,753;
822 = 3,890 + 3,225 =7,115; В46 = 1,269 + 1,107 = 2,376;
823 = 1,940 + 2,433 = 4,373;
824 = 0,878 + 1,469 = 2,347 ; 85. = 3,890 + 2,165 = 6,055 ;
825 = 0,391 + 0,698 = 1,089 ; о56 = 2,638 + 1,813 = 4,451 ;
о2с = 0,180 + 0,168 = 0,348 ; 866 = 5,259 + 2,243 = 7,502 ;
159
Уравнения после подстановки &:
9,767 Х1 + 6,088 Х2 + 3,436 Х3 4- 1,721 Х4 4-
+ 0,632Х5+ у = 0;
6,088 Ха + 7,115 Х2 4- 4,373 Х3 + 2,347 Х4 4-
+ 1,089 Х34- 0,348 Х6 + у =0;
3,436 Хг + 4,373 Х2 +- 6,026 Х3 4- 3,741 Х4 4-
+ 2,064 Х3 + 1,101 Хс 4-у = 0;
1,721 Xj 4- 2,347 Х2 + 3,741 Х3 4- 5,742 Х4 4-
4- 3,753Х3 4- 2,376Х6 4- У = 0 ;
0,632 Хх 4- 1,089 Х2 4- 2,064 Х3 4- 3,753 Х4 4-
4~ 6,055 Х3 4" 4,451 XG 4" У — 0;
0,348 Х24- 1,Ю1Х3 + 2,376Х44-
+ 4,451 Х5 4- 7,502Хс4-У = 0;
Xi 4- Х2 4- Х3 4- . Xi 4-
+Х34- XG ^(gHb + q)l.
Решение уравнений:
^ = 0,147(^6 + </)/;
Х2 = 0,147(g^4-<?)/;
Х3 = 0,147 (gHb
X, = 0,149 (gHb+q) /;
160
Х5 = 0,151 (gHb + 7) I
X6 - 0,259 + q)l.
Разделив силы X на
I
получим средние ин-
тенсивности нагрузки на
простенок в пределах каж-
дого участка длиной с.
Следовательно, интенсив-
ности нагрузки на балку
снизу:
Л = 1,323 (gHb + ?);
р2 = 1,323 (gHb + 0;
р3 = 1,323(^6 + 0;
р4= 1,341 (gHb + 0;
Рь = 1,359 (gHb + 0 ;
р0 = 2,331 (g/f6+0.
Начертив ступенчатую
эпюру нагрузки, можем за-
тем заменить ее криволиней-
ной.
Для получения нагрузки
на балку сверху необходимо
умножить ординаты от еди-
ничных сил, приведенные в
таблице 38 на стр. 155, на
найденные значения X:
строчку, в которой слева
стоит цифра 1,—на Xi, строч-
ку с цифрой 2 — на Х2ит.д.
Получим табл. 43.
Суммируя числа по вер-
тикалям, найдем полные на-
грузки на балку сверху от
действия всех сил X. Как ви-
дим, нагрузка распределяет-
ся в пределах простенка до-
вольно равномерно, но затем
быстро падает.
По этим данным сделано
построение на рис. 102.
За вычетом взаимно
уравновешивающихся на-
рузок получается эпюра, за-
штрихованная на рисунке.
И Б. Н. Жемочкин
СО Tf Ю СТ' СО СМ О со
о О О —« —<
4Л о о о о о о
СХЗ о о о о о о со т|-
Ef 1
К
СО СТ о ю ю
о о о — о о оо '
чо со (Q c~?i со X
03 а. а»
о о о со о О
| I | 1 4- 4~
N + N о со с;
о о о о со со см
о о о о о со оо
a, ль аъ а. гэ
со со со со о о со
от от см со СО —’
to со СО СО СО со J4"—ц
0 0 0 0 — 0 см
а. а. а. со
СО СО СО СО СО СО со
к" —' оо О ю Г- со
Q. -0-000 СО
4) to о о о о - > LQ
03 ОТ
со со со о о о **
о
.. —- — .
СМ 1-0 СО Ь- со
и to — со о — о м*
«3 X to СО СО СО СМ оо
• W о со со о со со •*
1 1 4- Р--и
3 СМ Г- СО Ю LO со
к -ООО-- оо
to О О О — ь
со
О О О СО О О
1 4“
X О S О ОО Ю о СО 0? ОТ со — оо
от со ^4, со м <
о ° о о с о
2 4“
Ь- ОТ ОТ <о OI
co Ь- оо От со ст —< со — оо < оо со
со со со со со со ТН-»
О Г"- СО — со со
СО —‘ СО ст со —'
см ТГ ТГ — о .О со
со со со со со со ♦-—f
о — С О to (X)
О N О О о —
1—< с + <?4 о о о СМ
** а. а. Л а со
СО СО СО СО СО О
—j
— СП — + о; со
— СО СО 04 — 04 от
о оо со — о О О
со
со со со со о со + 1 1
к
си
я
о
е;
& = к
и о
II
- 04 СО + Ю С II
* ~ И
и >>
° си м г*
f- я
° К «
5*
r’l
161
§ 22. РЕЗУЛЬТАТЫ ВЫЧИСЛЕНИЙ И ВЫВОДЫ
Само собой понятно, что на основании одного примера нельзя
сделать надежного заключения. Поэтому способом, изложенным в
предыдущем параграфе, проделан целый ряд расчетов для раз-
личных отношений длины простенка к длине лроема — и
1—1
для
раз-
личных упругих характеристик А, равных [формула (73) стр. 19)]
2г^е1
ЕКЬР
(431)
Соответственно упругие характеристики
К - 1000
EI
EKbL*
(432)
Результаты приведены на рис. 101 —106. Эпюры нагрузки на
балку снизу на этих рисунках показаны не ступенчатыми, а соот-
ветствующими криволинейными.
Заштрихованы эпюры, получающиеся после вычета взаимно-
уравновешивающихся частей эпюр.
Высоты балок определены по формуле (385) (стр. 127) или
(386). Эти высоты относятся к железобетонным балкам прямо-
угольного сечения. Но нужно иметь в виду, что они в значительной
степени условны и показаны только для возможности наглядного
сравнения жесткостей в различных случаях.
162 *•
'Нагрузка-на мяогопролегпную перемычну
Рис. 104
11*
163
Нагрузка на многопролетную перемычку
Рис, 105
Нагрузка на многопралетную перемычну
Рис. 106
164
Рассмотрение рисунков позволяет сделать некоторые выводы.
Во всех случаях нагрузка на балку вообще небольшая и может
быть приближенно представлена треугольниками с наибольшими
ординатами у граней простенков.
Формулы, определяющие размеры этих треугольников, выведен-
ные нами для рандбалок, когда реакции принимались сосредото-
ченными (рис. 107), здесь не подходят.
Но в § 13 мы уже имели возможность убедиться, что при ши-
роких опорах (рандбалок) иногда удачное решение получается, ес-
ли наибольшую ординату у граней опор принимать равной полу-
сумме средних интенсивностей нагрузки на рандбалку сверху и.
Рис. 107
снизу [см. формулу (378) (стр. 124)]. Попробуем тот же прием
применить в данном случае и принять ординату у грани опоры рав-
ной (рис. 108):
Po = (gHb+q)(l+±-y, (433)
длину же эпюры найти по формуле (375): \
з
d=3'27/s (434>
или по формуле (376): •'
з __ г
d = 0,8271 l/k . (435)
Оказывается, что в перемычках ординаты у опор еще меньше
и приблизительно равны средним интенсивностям нагрузок на пе-
ремычки сверху. При узких простенках эти ординаты больше. По-
этому правильнее будет принять с некоторым запасом ординаты у
опор равными полусумме интенсивностей нагрузки сверху и сни-
зу и вычислять их по формуле (433).
Длины же эпюр определяются формулами (434) или (435) до- .
вольно точно.
165
Для суждения о том, насколько удачно принимать треуголь-
ные эпюры, построенные изложенным способом, на всех рисунках
101—106 показаны такие треугольные эпюры.
Далее оказывается, что после вычитания взаимно уравновеши-
вающихся частей эпюр остаются реакции снизу у граней простен-
ков по криволинейным треугольникам, причем длины эпюр в
пределах простенков не превышают полуторных высот балок. На
остальном протяжении нагрузки почти нет. Исключением является
балка, приведенная на рис. 105, нагруженная снизу по всей ши-
рине простенка. Но эта балка принята настолько жесткой/ что в
практике проектирования конструкций вряд ли может встретиться.
Конечно, почти полное отсутствие нагрузки в серединах про-
стенков не свидетельствует еще об отсутствии моментов. Моменты
здесь имеются, но они меньше, чем вблизи граней простенков, так
как балки в пределах простенков получают почти равномерную
осадку и изгиб балок здесь очень мал.
Если мы разрежем балку, проходящую через несколько проле-
тов, удалим части ее в пределах простенков И перейдем к ряду од-
нопролетных балок-перемычек, заделанных в кладку простенков, то
хотя и изменим работу конструкции, но изменим ее немного. Во
всяком случае можно ожидать, что благодаря уменьшившейся
жесткости балок нагрузка па них должна также уменьшиться.
Поэзому, принимая эпюры по треугольникам, о которых сказано
выше, мы получим некоторый запас. Правда, при применении од-
нопролетных балок увеличиваются моменты в пролете, но они
вообще невелики. Да и решающим фактором при расчете перемы-
чек часто являются не столько моменты, сколько поперечные
силы.
•При хорошей заделке концов балок в степы на глубину, при-
мерно равную двойной высоте балок, вполне можно считать их как
защемленные на опорах на условную треугольную нагрузку. Вви-
ду некоторого запаса за расчетный пролет можно принимать от-
верстие в свету.
Если же балки имеют не вполне надежную заделку, лучше их
. рассчитывать как свободно опирающиеся на опоры. Однако железо-
бетонные балки должны быть заармированы на опорах на отри-
цательные моменты.
Наконец, отметим, что, как видно из рисунков, наибольшее
давление на кладку простенков у их граней приблизительно раза
'в два больше, чем средняя интенсивность нагрузки на простенки.
Это замечание может быть полезным при расчете опорных частей
'балок.
' РезТоМируя все вышеизложенное, приходим к следующим вы-
водам.
'J) ,Нагрузка на перемычки может приниматься по треугольным
эпюрам,: расположенным у опор.
Длина каждого треугольника применительно к обозначениям
' рис. 108:
466
(436)
где El — жесткость балки;
Ек—модуль упругости кладки;
Ь — толщина стены.
Наибольшая ордината у опоры:
(437)
2) Перемычка может считаться заделанной на опорах, если
глубина заделки не менее ее двойной высоты. Расчетный пролет ра-
вен отверстию в свету. При меньшей глубине заделки перемычку
следует считать как свободно опирающуюся на опоры.
3) Наибольшее давление на кладку у края простенка в два раза
больше среднего сжимающего усилия в простенке:
Ртах = 2 (gHb +<7)1
(438)
Правда, наибольшее давление должно несколько снижаться за
счет пластических свойств кладки. Может быть удобно было бы
вводить в расчет повышенный предел прочности для краевых на-
пряжений. Но величина такого повышения должна быть норми-
рована.
§ 23. РАСЧЕТ ПЕРЕМЫЧЕК ПРИ СТЕНЕ ОГРАНИЧЕННОЙ ВЫСОТЫ
Выше, в § 7, при расчете рандбалок мы установили ту пре-
дельную высоту стены, при которой еще допустимо принимать на-
грузку на рандбалку по треугольникам. Можно предполагать, что
и для перемычек остаются в силе выведенные нами зависимости.
Проверим это предположение, сделав расчет для случая пере-
167
мычки, опирающейся на простенки, когда стена, к которой прило-
жена нагрузка, небольшой высоты (рис. 109).
Необходимо, однако, заметить, что эта задача является более
сложной, чем задача, разобранная в § 7. Поэтому опустим необхо-
димые доказательства и укажем только общий ход решения.
Рис. 110
Поступим так, как и в предыдущих параграфах. Отделим пере-
мычку от простенков и поставим условные связи-стержни. Расчет-
ная схема приведена на рис. ПО.
Разрежем или отбросим эти стержни и приложим неизвестные
силы Х2. Основная система будет по рис. 111.
Уравнения составим, как обычно; они будут выражать условия,
что перемещения по направлениям неизвестных сил равны нулю:
+ ^2^2 + + • • • = 0. (439)
Кроме того, будет одно уравнение равновесия:
+ Х2 + Х3 + • • • = {gHb + q)l. (440)
Перемещения должны состоять из двух слагаемых: из переме-
щений простенка v и перемещений кладки над балкой w
*ki = vki + wki. (441)
Перемещения или упругие осадки простенка от единичных сил
нами были найдены раньше (для случаяс = — на стр. 143).
Для определения перемещений кладки над балкой воспользу-
емся данными, относящимися к рандбалке (рис. 112). На рис. 112
168
-W-Ak Ц- -ЛАО
Рис. 112
Рис. 113
169
схематически показаны единичные сосредоточенные силы и соот-
ветствующая им нагрузка на балку сверху.
По формуле (39) (стр. 14) перемещения:
СО
да J_y [1 —с°з(ал:)] • [(1 .(1 — р.)С4] . (442)
Ек. "
1
Коэффициенты (Д и С4 определены в § 7 [формулы (225) и
(228) (стр. 62)]. Подставив их, найдем выражение для перемещений
нижних точек кладки или верхней поверхности балки, принимая
точку, приложения сосредоточенной силы за неподвижную. Сделаем
преобразование такое же, как и на стр. 152.
Мы можем найти перемещения от действия одной и той же силы:
перемещение какой-либо точки нижней поверхности кладки и пере-
мещение по оси простенка. Вычтя одну величину из другой, найдем
перемещение по отношению к оси простенка. Далее учтем силу, рас-
положенную симметрично (рис. 113).
Получив общую формулу, сделаем преобразования. Для повы-
шения точности, а также для улучшения сходимости рядов заме-
ним сосредоточенные силы нагрузками, равномерно распределенны-
ми на участках длиной а где с — расстояния между условными
стержнями.
В целях дальнейшего улучшения сходимости рядов перейдем к
среднему перемещению в пределах каждого участка длиной с, как
мы делали и раньше в § 18.
16
Опустив по-предыдущему множитель --------- , получим:
Екг^Ь
со
1 9 V1 9/ \ / \ I \ х z
W == X2 7,sm2 -- COS ---- COS --- X
\2 х / \ х ; \ х /
1
I ™ +
«3 / n3'k [4 ПК е-^и + (1 -
//2 Ч
— 4 п2 г? е-2“" +(1 - е-2“")2
Здесь приняты обозначения:
С
X
с
С=-,
с
(443)
(444)
(445)
(446
170
причем z — расстояние от середины участка, где приложена сила,
до оси простенка; х — расстояние от середины участка, где ищется
перемещение, до оси простенка.
Разделим длину I на 12 участков длиной с; таким образом, при-
мем Х=12.
. В формуле (443) уже учтено, что положительные перемещения
должны быть направлены вверх, т. е. по направлениям сил X.
Вычислим по формуле (443) перемещения для какого-либо кон-
кретного случая и составим таблицу.
После этого мы сможем найти перемещения бАг и подставить
их в уравнения.
Решив уравнения и найдя неизвестные, перейдем ко второй час-
ти задачи: определению нагрузки на перемычку.
И здесь будем исходить из данных, относящихся к рандбалке
(рис. 112). Формула для нагрузки на рандбалку была выведена
выше [формула (243) (стр. 64)].
Поскольку нам нужно знать нагрузку на рандбалку при еди-
ничной сосредоточенной силе, вместо (gHb + q) примем — t
Заменим сосредоточенную силу, приложенную к балке снизу,
нагрузкой, равномерно распределенной на длине с. Тогда окон-
чательно:
Здесь
(447)
где х— расстояние от середины участка, на кото-
ром приложена нагрузка на балку снизу, до точки, где ищется на-
грузка на балку сверху.
Можно еще улучшить сходимость, если находить не интенсив-
ность нагрузки в какой-либо-точке, а среднюю интенсивность в
пределах участка длиной с.
Далее перейдем к двум единичным силам, расположенным сим-
метрично относительно оси простенка (см. рис. 113).
Составив таблицу, аналогичную таблицам, приведенным на
стр. 155—157, умножим числа каждой строчки таблицы на значение
соответствующего неизвестного. Получим в итоге ординаты искомой
эпюры нагрузки на перемычку.
171
Поскольку мы не собираемся делать подробного исследования,
а хотим только проверить наше предположение о том, что и на
перемычки распространяются правила, выведенные для рандба-
лок, нам достаточно разобрать только один числовой пример.
Примем для расчета ширину простенка равной отверстию в све-
ту, т. е. примем -— = !. Для удобства сравнения сделаем расчет,
предполагая Н “ со , Я = — п Н = ~ .
Нагрузка на многолролетную перемычку д случае стены неограниченной высоты
Упругой характеристикой зададимся £=0,05. При этом упругая
характеристика
а \з
( + — 3
К = 1000-&- .....-Г = 1 000-0,05 (1 +.1)3. =0,81.
16 тс3 16 л3
Отношение отверстия в свету к высоте железобетонной балки
равно [формула (90) (стр. 22)]:
—= 9-1 - = 10,1.
h 3 ________
/0,81
Таким образом, мы имеем здесь условия, близкие к тем, какие
были взяты в § 7 при £=0,5 (/С=1,01; — =9,4).
h
На рис. 114 приведена эпюра для случая Я=оо, на рис. 115 для.
Я = у и на рис.. 116 для Я= .
172
Нагрузка на мпогопролетну^ перемычку 6 случае стены ограниченной высоты
l~l; Н-?; п'0,05; К‘0.81 ;(fc-IO,l)
Рис. 116
173
На этих же рисунках показаны и треугольные эпюры, построен-
ные на основании приближенных форАмул (436) и (437) (стр. 167).
Анализ результатов показывает, что при Я— — эпюры на-
грузки вполне можно считать треугольными.
Но при И = — эпюры значительно отличаются от треугольных.
Следовательно, здесь повторяется та же картина, как и в случае
рандбалок. Ввиду этого аналогично правилу, установленному для
рандбалок, будем считать возможными принимать треугольные эпю-
ры при упругой характеристике К >0,1, если Н> — .При упругой
же характеристике К < 0,1 треугольные эпюры примем, если
н> — .
4
Если высота кладки меньше указанных пределов, нагрузку
нужно считать равномерно распределенной.
В- случае сосредоточенных сил или сил, распределенных на ко-
ротких участках и приложенных к стене небольшой высоты, будем
придерживаться правила, изложенного в § 8.
ОДНОПРОЛЕТНЫЕ ПЕРЕМЫЧКИ
§ 24. СВОБОДНО ЛЕЖАЩАЯ ПЕРЕМЫЧКА
а) Общие данные
Исследуя вопрос о расчете многопролетных перемычек, мы при-
шли в § 22 к заключению, что и для однопролетных перемычек
можно применять те же
формулы (436) и (437)
(стр. 167), как и для мно-
гопролетных.
Теперь нам надлежит
проверить это положение
и рассмотреть однопро-
летную перемычку, шар-
нирно опирающуюся на
опоры (рис. 117). Изобра-
женная на чертеже схема,
конечно, весьма условна,
так как всегда балка бу-
дет частично заделана
концами в кладку. Следовательно, в действительности будет нечто
среднее между свободно опирающейся балкой и многопролетной.
б) Порядок расчета
При решении задачи будем предполагать чередующиеся отвер-
стия в стене, перекрытые однопролетными балками; однако предус-
мотрим простенки достаточно широкими, именно примем, что, ши-
рина простенка а вдвое больше отверстия L.
Сделаем горизонтальный разрез над балками и поставим в раз-
резе вертикальные связи-стержни. Таким образом, расчетная схема
.будет по рис. 118.
Разрежем или отбросим стержни и заменим их действие дейст-
вием неизвестных сил Х2,..., Ха.
175
Придется еще добавить заделки: две заделки в кладке на оси
простенка вверху и внизу и заделку балки в середине пролета.
Основная система показана на рис. 119.
Обозначим осадку верхней заделки по оси простенка через у$
(вверх); это есть изменение расстояния между верхней и нижней
заделками, далее в середине пролета балки осадку обозначим че-
рез у; (вниз). Нижнюю заделку будем считать неподвижной.
Рис. 119
176
Составим 10 уравнений, выражающих условия, что суммарные
перемещения по направлениям неизвестных равны нулю. Кроме
того, будет два уравнения равновесия.
+ Х2 S12 + 43 + • •' + ХА о1Л 4- у0 _ 0 ;
*1821 + Х2 S22 + Х'Л 523 ----Ь ХА °2А + Уо ~ 0 >
Перемещения по направлениям сил Л\, Х2,..., Л4 от тех же
единичных сил слагаются из перемещений — осадок простенка
, ^59 и перемещений вышележащей кладки wi2,..., Щ55:
sn = ;
°12 ~ V12 4" ^12 >
S55 = ЩЬ + 45 •
(449)
Перемещения по направлениям сил Х2,..., Х5 от единичных сил
Ле, Х7, Х8 и Х9 равны только перемещениям вышележащей кладки:
о16 — ;
В17 = ш17;
» й V • »
556 = ^56 -
(450)
Обратно: перемещения по направлениям сил Хб, Х7, Х8г Х9 от
единичных сил -^2, ...,^5 также равны только перемещениям
вышележащей кладки, причем
°1б — ^6i 5
%6 “ ^65 >
(451)
Перемещения по направлениям сил Хб,. .,Х9 от этих же единич-
ных сил слагаются из перемещений вышележащей кладки <^66,
ш67,..., tt>99 и прогибов балки/С6,/еь .. ♦ ,/99
12 Б. Н. Жемочкии
177
°66 — >
o67 — -f- ; (452)
Ogg ~ Wgg 4~ •
Перемещения по направлению Хл от сил X2t.,.,X^ равны
осадкам простенка
p6l; U62 ’> , . - . (453)
r 3Л5 = Uo5-
Перемещения по направлению Хлот сил Хб1 Х7, Х8 и Х9 равны
прогибам балки
тив JV,)
о <
со знаками минус (положительные прогибы про-
(454)
Наконец, перемещение.по направлению Хлот силы Хл.равно
3 — Г) J- f
АА и66 ' /66 *
(455)
Таким образом, для решения задачи нам нужно знать:
осадки простенка — и;
перемещения вышележащей кладки — ш;
прогибы консольной балки —
Поскольку для деформаций простенка v мы уже имеем данные,
перейдем к определению w и/.
в) Деформации вышележащей кладки
Для перемещений w можно использовать выведенную ранее
формулу (407) (стр. 139), относящуюся к простенку. Однако в фор-
муле надо заменить ~ через I или а через 21.
Следовательно:
у
Ек тА Ьс2
1
пкс \ i2n^Ti€\ i-2nntc
— cos ----------— cos ———
21 \ 21 \ 21
(456)
1.73
Здесь
с — длины участков, на которые мы разбили нашу конструк-
цию;
Се — расстояние от оси простенка до середины участка, где
приложена единичная сила;
ус — расстояние от оси простенка до середины участка, где
ищется перемещение.
Мы будем делить длину I на 9 участков длиной с.
Поэтому:
4 (2.9с)2
W = —----------
Ек кЗ Ьс2
/ п~с \ /2п с\
----- COS ------—
\2-9c/ \ 2-9с }
COS
2п с \
2-9с /
16-81 V 1 • о / \
•------- ) ,---Б1П“ —-1
£к г.3 Ъ л3 \ 18 7
1
COS
(457)
16
Разделив на ------- , как это мы делали раньше, получим:
Ек т2Ь
w — 81 V-Г sin2 (п-10°) cos (лг-г] • 20°) cos («С • 20°). (458)
п3
1
Результаты’ вычислений по этой формуле приведены в табл. 44.
Таблица 44
участков, где приложе- ны нагрузки с № участков, где ищутся перемещения
1 2 3 4 5 6 7 8 9
0,5 1,5 2,5 3.5 4,5 5,5 6,5 7,5 8,5
I 2 3 4 5 6 7 8 9 0,5 1.5 2,5 3,5 4,5 5,5' 6,5 7,5 8,5 6,285 3.634 4,850 2,199 2,835 4,317 1.400 1,666 2.463 4,0j3 0,867 1,029 1,412 2,304 3,986 0,495 0,613 0,870 1,334 2,304 4,063 0,241 0,336 0,536 0,870 1,412 2.463 4,317 0,082 0,164 0,336 0,613 1,029 1,666 2,835 4,850 0 0,082 0,241 0,495 0,867 1,400 2,199 3,634 6,285
При составлении таблицы наибольшее пр абсолютной величине
отрицательное перемещение принято за нулевое, и, таким образом,
в таблице исключительно положительные данные.
г) Прогибы консольной балки
Предположим, что надо найти прогиб, вызванный единичной си-
лой, отстоящей от оси простенка на расстоянии С с, в сечении, от-
12* 179
стоящем от оси простенка на расстоянии г[С (рис. 120). В нашем
случае 7j и С могут принимать только значения 5,5, 6,5, 7,5 и 8,5.
Для нахождения прогиба надо перемножить две эпюры от еди-
ничных сил и результат разделить на жесткость.
Получим:
J EI 2 ' ' 3
= (9 - 7])2 (18 - з; + r(). (459)
Разделим на —— :
р* 7^3 ЬгЗ
/=-4f77-(9-^)2(18-3C4-7i). . (460)
Введем упругую характеристику k [формула (73) (стр. 19)]:
, 2r3 EI
k =--------.
£KW’
(461)
180
Из этой формулы
Е«Ь _ 2~$
EI ~ /л3
Следовательно:
9тй гЗ
/=тг~(9-^3(18“3': + ^)-
Так как мы делили I на 9 частей длиной с, то:
„ 2тг° г3 .
— (9 ™ тО 2 (18 — ЗС + rj
7 96 А(9г)3 и
у 6
= а/ш (9 —^)2 (18 — ЗС + 7l)-
48*94
Таким рбразом:
г 0,02747о v /1 q or t \
/ =-----7—О —т^(18 — 3; + 7,)
k
(462)
(463)
(464)
(465)
По этой формуле составлены таблицы для k = 0,01 (табл. 45) и
k = 0,05 (табл. 46). Соответствующие упругие характеристики
[формула (74) (стр. 19)].
К = 1 С00 - ,. (466)
Ек ЬЕ^
равны К = 0,54 и К = 2,72.
Таблица 45
k = 0,01
№ сечений, где приложены нагрузки с № сечений, где ищутся прогибы
6 7 8 9
д
5,5 6,5 7,5 8.5
6 7 8 9 5,5 6.5 7,5 8,5 235,598 137,375 85,859 4» 55,637 37,091 18,546 6,869 4,808 2,747 0,687
k = 0,05 .
Таблица 46
№ сечений, где ищутся прогибы
№ сечений, где г 6 1 8 9
приложены нагрузки ч
5,5 6,5 7,5 8.5
6 5,5 47,120 27,475 11,127 1,374
7 ' 6,5 17,172 7,418 0,962
8 7,5 3,709 0,549
9 8,5 0,137
18Г
д) Примеры
Сделаем два расчета для упругих характеристик k = 0,01 и k =
= 0,05.
Для k = 0,01 отношение отверстия в свету к высоте балки в
предположении, что она из железобетона [по формуле (386) (стр.
127)], равно:
^- = —---------------= 115_.
h з________
У О, 01II +~— j
Расчетная схема приведена была раньше на рис. 118 и основная
система на рис. 119.
Вычислим перемещения, пользуясь таблицами 28 (стр. 143),
44 (стр. 179) и 45 (стр. 181).
о17 = + щ,, = 5,259 + 6,285 = 11,544;
512 = »J2 + ^12 = 2,638 + 3,634 = 6,272 ;
81S = vj3 + щ13 = 1,269 + 2,199 == 3,468;
8И = + “’ll = 0,571 + 1,400 = 1,971
8 = v 15 + w,,= 0,180 + 0,867 = 1,047 ;
?jig = “ig = 0,495 ;
o17 = w17 = 0,241 ;
°i8 ~ ^18 “ 0,082 ;
^19 ~ - 0 ;
o22 “ ^2 4“ ^22 3,890 4~ 4 850 8 740 *
S23 — v03 4“ ^23 ~ 1,940 2 835 ~ 4,775 *
824 = t>24 + C!24 = 0,878 4- 1,666 = 2,544 ;
€2S = y,5 + w2s =0,391 + 1,029 = 1,420;
S2G = K)2G = 0,613 ;
827 = a>27 = 0,336;
82g = ^28 = 0,164;
o29 = ш29 = 0,082 ;
'°2A~ V26 = 0, 180 ,
o33 = v33 + w33 = 3,499 + 4,317 = 7,816 ;
834 = ^ + ^= 1,760 + 2,463 = 4,223;
B35= ц35 + и>86= 0,878+ 1,412 = 2,290;
‘830 — ®36 = 0,870;
182
837 = а'37 = 0,536;
°зз = ^38 ~ 0,336 ;
°39 = *-^39 ~ 0,241 ‘
гзл = 1’зб = 0>571 ;
= vu + к'м — 3,499 + 4,063 = 7,562 ;
845 = ^5 + ®45 = 1,940 + 2,304 = 4,244 ;
g4g = = 1,334 ;
s47 = = 0,870 ;
843 = ®4.s = 0,613;
o49 = = 0.495 ;
34л = У46 ~ 1,269;
+5 = = 3,890 + 3,986 = 7,876 ;
85C= №5g = 2,304;
s57= ^57--= 1,412;
^8 = w.s = 1,029;
^59 = +33 = 0,867;
8,. = o„ - 2,638 ;
5Д 56 ’ J
866 = wGe + /cc = 4,063 + 235,598 = 239,661 ;
8U7 = tt’67 + /G7 = 2,463 + 137,375 = 139,838 ;
%8 = wGS + /C8 = 1,666 + 55,637 = 57,303;
3G9 = ^9+ Ao = 1,400 + 6,869 = 8,269; '
%л = -Аб=~ 235,598;
O77 = W-. +fn = 4,317 + 85,859 = 90,176 ;
o78 = w7S + /78 = 2,835 + 37,091 = 39,926 ;
^9 = ^79 +/79 ==2,199 + 4,808 = 7,007;
87Л =-Л6 = -137,375;
S88 = wss + /88 = 4,850 + 18,546 = 23,396 ;
*89 = ^89 + /89 = 3,634 + 2,747 = 6,381 ;
38л = -/86=-55,637;
о9э = uj09 /99 = 6,285 + 0,687 = 6,972 ;
89л = -/96=-6>869;
Злл= ^6 +/б3 = 5,259 + 235,598 = 240,857.
123
Уравнения:
11,544Xi + 6,272X2+ 3,468XS+ 1,971Х4 4 1,047Х5 4
4 0,495Х6-+0,241Х7 4 0,082Х8 4у0 = 0;
6,272Хх 4 8,740Х2 4 4,775Х3 4 2,544Х4 4 1,420Х5 4
4 0,61 ЗХС4 0,336Х7 4 0,164Х8 4 0,082Хэ4 0,180Хл 4уо=0;
3,468X1 + 4,775Х2 4 7,816Х3 4 4,223Х4 4 2,290Xs 4
4 0,870Х6 4 0,536Х7 4 0,336Х84 0,241Х94 0,571Хл4 уо=0;
1,971X1 + 2,544Х2 4 4,223Х3 4 7,562Х4 4 4,244Х5 4
4 1,334Х6 + 0,870Х7 4 0,613Х8+ 0,495Х94 1,269ХЛ4 уо=О;
1,047X1 4 1.420Х, + 2,290Х3 4 4,244Х4 4 7,876Х5 4
4 2,304Х6 + 1,412Х7 4 1,029Х8+ 0,867Х94 2,638ХЛ4 у0= 0;
0,495X1 4 0,61 ЗХ2 + 0,870Х3 4 1,334Х4 4 2,304Хй 4 -
+ 239,661Xfi+ 139,838Х7+57,303Хй+8,269Х„-235,598Хл4уп4У> = 0-
0,241Хг +- 0,336Х2 + 0,536Х3 + 0,870Х4 + 1,412ХЙ +’
+ 139,838Х6+ 90,176Х7+39,926Хй+7,007Х9—137,375Хл+уо+у1=0;
0,082X1 + 0,164Х2 + 0,336Х3 + 0,613Х4 + 1,029Х6 +
+57,303Х6+39,92бХ7 + 23,39бХ8+ 6,381ХЭ —55,637ХЛ +у0-]-у1 =0;
0,082Х2 + 0,241Х3 + 0,495Х4 + 0,867Xs +
+ 8,269Х6 + 7,007Х7 + 6,381Х8 4 6,972Х9- 6,869ХЛ4 у0 4 у, = 0 ;
0,180Х2 4 0,571Х3+ 1,269Х4 4 2,638Х5 —
—235,598Х6—137,375Х7—55,637Xg — 6,869Х9 4 240,857Хл —У1 = 0 ;
+ ^2 + Хз + Х4 + Х5 + Хс 4 X, 4 Х8 4 Хэ = (gHb + q)l-
x6 4 х7 + Х8 4 Х9 — хл = о.
В процессе решения такой системы уравнений можно все коэф-
фициенты в пяти левых столбцах верхних пяти строчек умножить
на 100; коэффициенты же в правых столбцах верхних строчек
и в пяти левых столбцах нижних строчек умножить на 10.
Решение уравнений дает:
Х1 = 0,151(§Я&4^)/;
Х2= 0,151 (gHb + q)l-,
X3 = 0,151(gtf&4 7H;
Х4 = 0,157 (gHb 4 q)l-,
= 0,155 (gHb+ q) I ,
Хй = 0,223 (g Hb + q) I ; . ..
'Ш
Х7 = 0,022 + 7)/;
Х8 = 0,001 (gW& + 9)/.
Ха= -0,011 (gHb + q)l-,_
*л = 0,235(glib + q) I.
Чтобы получить интенсивности нагрузки на отдельных уч. стках,
надо силы X разделить на с = — . Получим:
1,36(°7П> + 9);
р2= 1,36 (glib + q)
Рз = 1,36 (gHb + q) ;
А = 1,41 (gHb + q) ;
Ps = l,40(gH& + ^);
рй = 2,01 (gHb+ q)- '
p, = 0,20 (gHb + q);
Ps = 0,01 (gHb + q) ;
p9 = — 0,10 (gHb + 9);
PA= 2,12 (gHb+ q).
Эпюры нагрузки на балку и усилий в кладке простенка показа-
ны на рис. 121.
.. Далее на рис. 122 приведены эпюры для случая упругой харак-
теристики k — 0,05. •
185
Задача решается тем же порядком, как в только что разобран-
ном примере. Отношение отверстия в свету к высоте балки
------= 6,7.
Л * ______ с,2
V 0,05/1 4- — )
На обоих чертежах показаны треугольные эпюры, построенные
по приближенным формулам (436) и (437) (стр. 167).
Рис. 122
Как видим, эти формулы дают запас, а потому они вполне при-
менимы.
У опор балок мы получили нагрузку на простенки равномерно
распределенной. Это является следствием принятого условного
предположения о шарнирном опирании балок и предположения о
том, что в пределах участков длиной с нагрузка равномерно рас-
пределенная. Было естественно поэтому принять приближенно, что
через условный шарнир и через какую-то плиту под ним опорное
давление передается на кладку равномерно.
В действительности как бы ни была мала заделка балки в
кладку, в заделке возникает момент, а тогда эпюра давления от
балки на край простенка будет средней между той, какая получена
здесь, и той, какая была найдена в предыдущей главе.
§ 25. ПЕРЕМЫЧКА С ЗАДЕЛАННЫМИ КОНЦАМИ
а) Общие данные
Решим теперь другую задачу. Предположим, что однопролетная
балка, представляющая перемычку, жестко заделана своими кон-
цами в кладку (рис. 123).
186
Но абсолютно жесткая заделка предполагает, что та среда, в
которую заделаны концы балки, сама является абсолютно жесткой.
Ввиду этого мы вынуждены ввести дополнительное условие, что
кладка ниже линии АВ абсолютно жесткая и не деформируется.
Конечно, на практике это
невозможно.
Однако в некоторых слу-
чаях, например, при очень
толстой стене ниже перемыч-
ки, при стене из другого, бо-
лее жесткого материала
(например, из бетона), при
отверстии малой высоты
и большой протяженности
(рис. 124), перемычка по ус-
ловиям своей работы будет
приближаться к перемычке с
концами, заделанными в аб-
солютно жесткую среду.
Поэтому исследование случая заделки, как крайнего, представ-
ляет известный интерес.
б) Порядок расчета
Расчетную схему получим, если сделаем горизонтальный раз-
рез над балкой и поставим условные связи-стержни (рис. 125). Для
решения задачи необходимо будет считать отверстия, перекрытые
перемычками, повторяющимися.
Расстояние между осями простенка и пролета будем делить на
9 равных частей длиной с, но отношение ширины простенка к от-
Л Q Н
верстию в свету будем принимать различным: — = z и — — и,о.
Для перехода к основной системе разрежем или отбросим
стержни и заменим их действие действием неизвестных сил Хь Х2,...
187
j
(нумерацию начнем от оси простенка). Заделку расположим вверху j
на оси простенка (рис. 126). '!
Уравнения составим аналогично прежнему. j
Рис. 125
Рис. 126
Девять уравнений будут выражать условия, что суммарные пе-
ремещения по направлениям неизвестных сил равны нулю и деся-
тое уравнение будет уравнением равновесия.
Для нахождения перемещений необходимо иметь данные о пере-
мещениях кладки w и о прогибах балки/.
188
Первые данные возьмем из таблицы 44 на стр. 179. Необходимо
дополнительно исследовать только вопрос о прогибах балки.
1
в) Прогибы балки
Нам нужно находить прогиб, вызванный единичной силой, при-
ложенной на расстоянии tc от начала координат, т. е. от оси про-
стенка, в сечении, отстоящем от оси простенка на-расстоянии ъс
(рис. 127).
Половину ширины простенка обозначим через ^с.
Будем для облегчения находить прогибы сразу в двух симмет-
рично расположенных точках и результаты разделим на 2.
Прогибы получим, перемножая две эпюры: от двух единичных
сил, из которых левая приложена на расстоянии от начала коорди-
натС с, и от единичных сил, из которых левая приложена на рас-
стоянии rtc (рис. 127).
Эпюры будем чертить для свободно лежащей балки, но учтем
опорный момент Л40:
Этот момент можно получить из равенства площадей эпюр для
свободно лежащей балки от сосредоточенных сил и от опорных мо-
ментов с учетом знака:
L+ [А-2(С-Х)с] . , _ ,
2 ’Ь
189
Отсюда:
(468)
Перемножая эпюры, получим.:'
2EIf =
(С-Х)2с2 2 _ х (71-))с+(г_Х)С
2 ' 3 1 1 2 Л
X К7! — Х)с — G — Х)с] (С —А)с-2 + (-/]— Х)с. [Л —2(т] —Х)С]Х
Xfi-X) с + | ,2 + (т]-Х) с [Л-2(7] - X) ф X
xU(c-X)ch-(!;-X)-M}
I J
(469)
Так как мы решили делить расстояние от оси простенка до оси
пролета на 9 частей, то:
= 9с - Хс• (470)
или:
L = (18 - 2Х) с. (471)
Подставим это значение L и произведем необходимые преобра-
зования, несколько сократив писание формул.
( 9
2£7/ = ф (; - Х)з + (г - X) [(т] - Х)= - (С—
\ о
+ G-X) (1)-Х)[18-2Х-2(71-Х)]_
- (С - X) (т] - X) [(/] -X) + 18- 2Х - 2(т) - X)] .[1 -
С-Х
18 — 2Х
"1
2 I
+ (7) - X) (18 - 2rJ - (7] - X) [ 18 - 7) - X] 08 ~ 2Х -С+ х)-
1о —
+ 2(т) — X) (9 —г;) -
-(/]-X) (18 - т]-X)
« n Х)2 t~ + 2СХ - 36Х + X2 -U 54т] - Зт)2] . (472)
Таким образом:
f = I - 18С + - 36Х + х2 + 54т' “ Зт(2]. (473)
1Z (У —* •<) tz!
190
(475)
(476)
(477)
Разделим на -—— :
£к т3Ь
_ гЗ (Г __), \2 р 3 А
/== iFi t~ 18С + 2U - 36k + Х2 + 547i “ 3тЛ <474>
12 16 (У — А; bl
Выше [формула (462) (стр. 181)] было указано, что:
EJ> _ 2-з
El kt3
Поэтому:
f = —V------—------ - 18r, + 27 — 36Х 4- + 54т] — з-л2] .
12-16(9 Л)/2Л 1 ill 1 j
Подставляя I = 9с, окончательно получим: '
л 0,013737! (С —X)2 о г,
7 —---------•——— [ — 1Ь. + 2,Л — ЗоХ + л- -f- 54т] — Зт] .
При выводе формулы мы предполагали, что у >£,. Очевидно, что
если < С, в формуле надо вместо С, подставить т] и вместо под-
ставить С
В тех двух примерах, которые мы далее рассмотрим, половина
простенка будет делиться на 6 частей (X = 6) и на 3 части (X = 3).
Если X = 6, то:
0,013737 (С —6)2 r ior,9. Q 21 ’
/ _ --------—___ j _ 2Ч. 6 — 36-6 + о -г 54т] — 3vj =
О 0Р737
----— (С —6)2 [18v] — 2С — V!3 — 60] . (478)
k
Если X = 3, то:
О 01 0737 (Г _4)2
f = -~Г I- 18С + • 3 - 36 • 3 + З2 + 54т] - 3v4 =
к (У — о)
= 0,ППВ869 (С - З)2 [187] - 4С - - 33]. (479)
k
Результаты вычислений приведены в таблицах 47 и 48:
Таблица 47
а / L
~ ^2(Х=6), k 0,05 —-6,7
L \ h
Л-! участков, где прилож НЫ нагрузки с , Хе участков, где ищутся прогибы
7 8 9
*1
6,5 7,5 8,5
7 8 9 6,5 7,5 8,5 0,120 0,395 2,318 0,532 3,555 6,439
191
Таблица 48
а • ( L
— ™0,5 А = 3), Д-0,05—=13,5
Д \ Л
№ } часткив, где ищутся прогибы
№ участков. 4 5 6 “7 8 9
где приложены нагрузки С
3,5 4,5 5,5 6,5 7,5 8,5
Ю ОО -Ч 05 Сл Ф» 3 5 4.5 5.5 6.5 7.5 8,5 0,129 0,472 3,014 0,747 5,486 11,806 0,953 7.341 16.957 26,505 1,090 8,577 20,391 33,236 43,814 1,159 9,189 22,109 36,602 49,377 57,139
г) Примеры -
Разберем только два примера, представляющие крайние случаи:
один пример для — == 2 и k — 0,05 и другой — для = 0,5 и k =
д д
- 0,05.
л / Д
Расчетная схема и основная система для случая — =2 — —
Д \ h
= 6,7) приведены ранее на рис. 125 и 126.
Перемещения найдем, пользуясь таблицей 44 перемещений вы-
шележащей кладки (стр. 179) и таблицей 47 прогибов (стр. 191).
Осадки простенка, принятого нами абсолютно жестким, равны нулю.
8ц = 6,285;
612 = 3,634;
813 = 2,199;
Ы= 1,400;
81S = 0,867;
81в = 0,495;
§17 = 0,241 ;
В18 = 0,082;
819= 0;
822 = 4,850;
823 = 2,835;
824 = 1,666;
825 = 1,029;
8„й = 0,613;
827 — 0,336;
8щ = 0,164 ;
829 = 0,082 ;
833 = 4,3 1 7 ;
= 2,463;
835= 1,412;
836 = 0,870;
637 — 0,536;
°38 ~ 0,336;
8ЗЭ = 0,241;
= 4,063;
845 = 2,304;
846 = 1,334 ;
192
§47 = 0,870; §67 = 2,463;
§48 = 0,613; S68 = 1,666;
§43 = 0,495 ; ос9 = 1,400 ;
§55 = 3,986; S77 = 4,317 + 0,120 = 4,437 ;
§56 = 2,304 ; 378 = 2,835 + 0,395 = 3,230;
357 = 1,412 ; 879 = 2,199 + 0,532 = 2,731 ;
868 = 1,029;
§s9 = 0,867; 388 = 4,850 + 2,318 = 7,168;
§89 = 3,634+ 3,555 = 7,189;
866 = 4,063;
99 = 6,285 + 6,439 = 12,724. '
Уравнения:
6,285Xx + 3,634X2 + 2,199X3 + l,400X4 + 0,867Xs + 0,495X6 +
+ 0,241X7 + 0,082X8 + у = 0 ;
3,634ХХ + 4,850X2 + 2,835X3 + 1,666X4 + 1,029Xs +
+ 0,613X6 + 0,336X7 + 0,164X8 + 0,082X9 + у = 0;
+ X2 + Xs + X4 + X5 + X6 + X7 + X8 + X9 = {gHb + q)l.
Решив уравнения, найдем:
Х1 = 0,116(£//6 + <7)/;
X2=0,I17(g^ + 7H;
Х3 = 0,118(^7/6 + q)l;
Х4 = 0,119(^7/6 + q) I-
X5 = 0,123 (gHb + q)l-t
Xc = 0,136 (gHb + </)/;
X7 = 0,163fe//6 + 7)Z;
X8 = 0,075 (gHb + <?)/;
X9 = 0,033 (gHb + q)l.
Чтобы получить интенсивности нагрузки, разделим силы X на
Pi = 1,04 (gHb + q) ;
Р2 = 1,05 (gHb + q) ;
p3= 1,06 (gHb + q)-
13 Б. Н. Жемочкин
193 •
Pi — 1,07 (gHb + q);
Ps — \,\\(gHb + q);
Pe = 1,22 (gHb + q);
Pi = 1,47 (gHb + q);
ps = 0,68 (gHb + q);
Ps = 0,30 (gHb + q).
Нагрузка на однопролетную перемычку
Рис. 128
Нагрузка на однопролетную перемычку
Эпюра нагрузки на балку и на простенки изображена на рис,
128. Эпюра в пределах простенка даст только нагрузку на уровне
верха балки. Распределение же усилий в простенке на более низ-
ких уровнях должно быть иное, так как в месте заделки балки к
поверхности простенка приложены момент и сосредоточенная сила,
направленная вниз и равная опорной реакции.
Аналогично решаем задачу и для случая — = 0,5 и k =
.Zin
= 0,05 ( — = 13,5).
h
Результаты приведены на рис. 129.
На обоих рисунках начерчены также треугольные эпюры, полу-
ченные по приближенным формулам (436) и (437) (стр. 167).
Треугольные эпюры оказываются расположенными внутри кри-
волинейных. Следовательно, приближенные формулы не только не
обеспечивают запаса, а, наоборот, дают преуменьшенную нагрузку.
Однако учтем, что абсолютно жесткого простенка в действитель-
ности не существует и мы рассматривали только крайний случай; в
реальных же конструкциях должно быть нечто среднее между за-
делкой и опиранием по схемам главы III.
В исключительных случаях особенно жесткой стены ниже пере-
мычки можно рекомендовать умножать р0 и d по приближенным
формулам на некоторый коэффициент, равный в крайнем случае
стены абсолютно жесткой 1,3.
Рис. 129
§ 26. РЯДОВАЯ ПЕРЕМЫЧКА
а) Общие данные
Здесь мы рассмотрим случай, когда перемычка отсутствует и в
передаче нагрузки на простенки участвует вся вышележащая клад-
ка (рис. 130).
Предположим, как это часто бывает, что арматура снизу рядо-
вой перемычки ставится конструктивно.
Как и раньше, примем, что проемы чередуются с простенками.
194
13*
195
б) Порядок расчета
Задачу будем решать в таком порядке.
Сделаем горизонтальный разрез АВ и поставим связи-стержни
между простенком и вышележащей кладкой (рис. 131).
Рис. 131
Разрежем или отбросим стержни и заменим их действие действи-
ем неизвестных сил Х2;... (рис. 132). Добавим заделку вверху
по оси простенка.
Рис. 132
Составим уравнения, выражающие условия, что суммарные пе-
ремещения по направлениям неизвестных сил равны нулю. Кроме
того, будет одно уравнение равновесия.
196
Осадки простенка даны в табл. 28 на стр. 143. Перемещения
вышележащей кладки также были найдены, но здесь эту работу
придется повторить. •
Выше мы делили расстояние между осью простенка и серединой
пролета на 9 частей; если на половине простенка будет 6 частей
(именно для такого случая и составлена таблица 44 на стр. 179), то
на половину проема придется 3 части. Между тем, в данной задаче
нас не столько интересуют напряжения в простенке, сколько напря-
жения в вышележащей кладке. Поэтому ширину простенка можно
признать достаточной, проем же надо увеличить. Будем делить рас-
стояние между осью простенка и серединой проема не на 9, а на
12 частей; тогда на половину проема придется 6 частей, что являет-
ся уже приемлемым.
в) Деформации вышележащей кладки
Исходной будет формула (456) (стр. 178), но в нее надо под-
ставить /= 12 с\
4(2-12 с)2
га ~ ------—
Ект3Ьс2
S1 - о/ п~с \ [2п~ъс\ / 2 пп&
---(---------- COS ------- COS ---------
п3 \2-12c/ \2*12с/ ( 2.12 с
1
Здесь
Се— расстояние от оси простенка до середины участка,' где при-
ложена единичная сила;
ус— расстояние от оси простенка до середины участка, где ищет-
ся перемещение.
Разделив, как и раньше, га на ----- , получим:
16
4(24 с)2-Ект?Ь
Екп3Ьс2‘ 16
1
зш2 — cos —L cos ---------
\ 24 / \ 12 / \ 12
(481
п~
Таким образом:
OQ
w — 144 У-1. sin2 (ц- 7,5е) cos (и у-15°) cos (я С -15°).
п3
1
(482)
Величины т] и £ должны меняться в пределах от 0,5 до 5,5
(только для точек в пределах простенка).
Результаты вычислений приведены в табл. 49.
При составлении таблицы наименьшее значение га принято рав-
ным нулю; поэтому все га положительные.
19?;
Таблица 49
№ участков, где приложены нагрузки с № участков, где ищутся перемещения
1 2 1 3 4 5 6
Т]
0,5 1,5 2,5 3,5 4,5 5,5
1 2 3 4 5 >6 0,5 1,5 2,5 3,5 4,5 5,5 5,961 3,304 4,501 1,844 2,471 3,921 1,011 1,265 2,040 3,593 * 0,431 0,579 0,935 1,789 3,404 0 0,102 0,328 0,746 1,653 3,316
г) Определение нагрузки на простенок
Задавшись отношением •— =1, исследуем только этот случай.
Перемещения найдем, пользуясь таблицей 28 на стр. 143 и толь-
ко что составленной:
Зп = 5,259 + 5,961 = 11,220;
= 2,638 + 3,304 = 5,942 ;
о13= 1,269 + 1,844 = 3,113;
314 = 0,571 + 1,011 = 1,582;
315 = 0,180 + 0,431 = 0,611 ;
^16 = 0 + 0=0 ;
822 = 3,890 + 4,501 = 8,391 ;
823 = 1,940 + 2,471 = 4,411 ;
824 = 0,878+ 1,265 = 2,143;
325 = 0,391 + 0,579 = 0,970 ;
S,G = 0,180 + 0,102 = 0,282;
833 = 3,499 + 3,921 = 7,420;
834= 1,760 + 2,040 = 3,800;
835 = 0,878 + 0,935= 1,813;
836 = 0,571 + 0,328 = 0,899 ;
§44 = 3,499 + 3,593 = 7,092;
§45 = 1,940 + 1,789 = 3,729;
оад= 1,269+.0,746 = 2,015;
8S5 = 3,890 + 3,404 = 7,294 ;
Ав = 2,638+ 1,653 = 4,291 ;
366 = 5,259 + 3,316 = 8,575 .
198’
Составив уравнения и решив их, найдем:
X1 = 0,145(g/ft> + <z)/;
X2 = 0,146(gtf& + ?)/;
Х3 = 0,148 (gHb + q)l;
Xt ~ 0,155 (glib + q) l;
X5 = 0,\58(gHb + q)l‘,
X6 = 0,248 (gHb + q)l.
Разделив силы X на длину участков с = получим интенсив-
ности нагрузки.
Эпюра нагрузки на простенок приведена на рис. 133.
Как видно из рисунка, нагрузка в средней части простенка ма-
ло отличается от равномерно распределенной. Но у краев прое-
мов наблюдается значительная концентрация нагрузок и, следова-
тельно, напряжений.
Наибольшее напряжение примерно в 2 раза больше равномер-
ного. Здесь можно высказать те. же соображения, как и выше на
стр. 167.
д) Напряжения в кладке над проемом
Особенный интерес представляет вопрос о напряжениях в клад-
ке над проемом.
Кладку стены можно рассматривать как упругую полуплос-
кость, к которой приложены найденные нами силы X— силы взаи-
модействия между кладкой и простенками.
Мы можем использовать здесь уже имеющееся решение на
стр. 20. Но поскольку в данном случае отсутствует балка, в форму-
лах (77), (78), (79) следует положить k == 0.
199
Таким образом:
Здесь предполагается, что опорные реакции представляют со-
средоточенные силы, повторяющиеся через 2/ (рис. 134).
Поскольку Р равны нагрузке на длине 2/, то
Р (gHb g- q) -2.1.
Поэтому
Сделаем замену в формулах (483)—'(485):
00
av = g-• (2 У [cos (а х) (а у — 1) е~^У] — Д + р. gy ; (486)
2 lb ( J
1
СО
s = — ~~ Ь У [cos (я х) (а у + 1) e~“-v] + 1 j + gy ; (487)
Я lb { J
1
00
т —-------— У [ sin (а х) ау • е^У] . (488)
lb “
1
200
Отбросим члены ygy, зависящие от собственного веса.
Предположим теперь, что нагрузка снизу не. сосредоточенная, а
равномерно распределенная на длине с (рис. 135).
Введем переменное г. Элементарные силы будут — ^г,так как в
с
дальнейшем нам следует заменить силы Р единичными силами.
Придется интегрировать в пределах от г — х — до г = х +
с
r = X-i---
2 оо
°х= J £ [cos (а г) (а у —
С
------
2 '>-
-К- I 2 У [Д- sin (а г) (ссу —
2Z&C / |_ а м Л
С 1
1)
СО
1 (о V 1 Ь Г / I с . Г 7
= -----{2 У— {sin а х4--------------—sin а (х
21Ьс\ а ( L \ 2 /J ' 113
1 (л \ 1 > ( &С \ . 1 \ '
~ 14 у, — sin 1 — 1 COS (а X) (а у — 1) е~яУ
оо
-^сЬ489)
1
201
с
Г-Х+ ----
2 <х
f----------^2 [cos (а г) (а у + 1) е~^] + 1
ОО
Т7~ (4 lj[~sin(v)cos О У + е~*У
2 Ibc ( *—
1
(490)
2
Ibc
(491)
Примем теперь во внимание две единичные силы, расположен-
ные симметрично относительно оси простенка (рис. 136).
{cos [а (х — z)] + cos [а (х +
+ г)]} • (ау — 1) — 2 у с
'202
Т = — I — sin sin [x(x —z)] 4- sin [a(x +
ibc a \ 2 Д
1 k
z)]ky • c~ay 1“----— У
J Ibc
1 . / ac \ , z x { .
— sin — sin (z x) cos (a z) a у •
a \ 2 /
' 1
4 V Г I • /зС V , , /4
--------/ i —-sin — sin (zx) cos (az) ay • e~a? .
xbc n \2 I
i
Наконец учтем, что 12c. Тогда окончательно:
co
[ — У — sin (гг- 7,53) cos (nr[ -15°) cos (п С -15°) X
lb ( к [ п
1
(494)
(495)
— H ;
□о
1 t 44 хх Г 1
Ъ =----------{— / , — sin (п 7,5’)cos(nT| • 15°) -cos(zzC- 15°)X
lb I к |_ n
1
203
Для нижних волокон кладки на уровне верха проема напряжения
^==-ф(1“Н) (498)
lb
во всех участках, кроме того, в котором действует распределенная
единичная сила. В этом же последнем
аЛ = 4(-Н-0- (499)
lb
Для того, чтобы найти напряжение в какой-либо точке, надо,
пользуясь этими формулами, вводить множителями величины най-
Напрятения б рядобой перемычке
Рис. 137
денных ранее сил X (каждой силе соответствует свое расстояние
С) и сложить результаты.
Зная нормальные и касательные напряжения, можно затем най-
ти главные напряжения и установить характер траекторий напря-
жений.
На рис. 137 приведены эпюры нормальных напряжений в неко-
торых вертикальных и горизонтальных сечениях, а на рис. 138-
траектории главных растягивающих и сжимающих напряжений.
За положительные приняты напряжения растяжения.
При вычерчивании эпюр и траекторий не учтено, что собствен-
ный вес кладки вызывает дополнительно растягивающие напряже-
ния, т. е. кладка в нижней части принята невесомой.
На следующем рис. 139 сделаны построения эпюр для частного
случая, когда нагрузка создается собственным весом стены высотой
204
20 я, причем пролет перемычки (отверстие в свету) равен 6 я. Вес
кладки в нижней части здесь учтен. В этом случае к напряжениям
о* следует добавить а к напряжениям добавить gy.
Анализируя результаты вычислений, можно заметить, что наи-
большие растягивающие напряжения возникают по нижней поверх-
Траектории напряжений 6 рядовой перемычке
Напряжения б рядовой пере ми/чне при высоте стены 20 гч
Рис. 139
205
но-сти перемычки в горизонтальном направлении. Они не зависят
от пролета и равны:
°шах= (1—И) (gH + Y-).
\ Ь )
Если опоры могут получать незначительные смещения, то наи-
большие напряжения внизу должны увеличиться и стремиться к
значению:
атах = ~ •
ь
В вертикальном направлении могут появляться значительные
растягивающие .напряжения только при очень больших, практиче-
ски не выполнимых, проле-
f__________________________________~_тах. Решающими нужно
/ считать горизонтальные на-
пряжения в низу перемычки.
/ [ I Оказывается, что пере-
I i)j I мычки и больших, и малых
пролетов находятся почти в
одинаковых условиях. Если
I кладка нормального качест-
1 ____ L— ____________________ ва может выдержать напря-
жения, определяемые фор-
Рнс- 140 мулой (495), то ее прочность
обеспечена.
Если же напряжения окажутся выше предела прочности, неиз-
бежно появление одной или нескольких вертикальных трещин
(рис. 140). Эти трещины не должны идти далеко вверх, так как
растянутая зона имеет небольшую высоту. Правда, при появлении
трещины растянутая зона должна переместиться выше, но макси-
мальные напряжения будут меньше. В пределе, при трещине, рас-
пространяющейся далеко вверх, кладка уже должна работать как
арка, растянутой зоны (в горизонтальном направлении) вообще не
будет.
Однако даже при больших вертикальных трещинах нижняя
часть кладки не может оторваться от верхней вследствие того, что
раствор имеет некоторую прочность на растяжение; вертикальные
же напряжения ничтожно малы.
Приведенные соображения позволяют поставить на очередь воп-
рос о возможности применения рядовых перемычек при несколько
больших пролетах, чем это принято в настоящее время.
Но конечно кладка перемычки должна вестись на растворе
надлежащей прочности, качество кладки должно быть вполне удов-
летворительное, перемычку следует вводить в работу после за-
твердения раствора.
Остается осветить еще вопрос о распорном действии рядовой
перемычки на поддерживающие ее простенки. Это становится осо-
206
•бенно важным тогда, когда нет уверенности, что кладка может вос-
принимать растягивающие напряжения.
Для нахождения распора необходимо использовать эпюру гори-
зонтальных нормальных напряжений в пределах простенка у
края отверстия.
Оказывается, что распор существенно зависит от того, являются
ли опоры совершенно неподвижными в горизонтальном направле-
нии или могут смещаться.
Эпюра о, для первого случая приведена на рис. 141, а, для вто-
рого—на рис. 141,6.
Рис. 141
Если принять опоры совершенно неподвижными, то суммарная
горизонтальная сила окажется весьма завышенной. Не забудем,
что чем на более высоких уровнях мы определяем горизонтальные
нормальные напряжения* тем они все больше приближаются к
пределу
(500)
= P'S ‘
Учитывая, что абсолютная неподвижность опоры может быть
только при такой массивной кладке, для которой распор не имеет
значения, мы должны признать более правильным остановиться на
эпюре по рис. 141,6.
Если отбросить часть эпюры с напряжениями растяжения и счи-
тать, что распор определяется площадью части эпюры с напряже-
ниями сжатия, то распор окажется приблизительно равным:
^=.0,08 (gHb + q)L.
(501)
Но в случае, если кладка в пределах пролета не будет рабо-
тать на растяжение и появятся вертикальные трещины, то распор
должен увеличиться. Аналогично этому в арке с затяжкой, если
207
произойдет обрыв затяжки, распор, передающийся на опоры, будет
равен усилию в затяжке.
Следовательно, необходимо учесть также растягивающие на-
пряжения в сечении посередине пролета. Нижнюю ординату теперь
надо считать (в отличие от того, что показано на рис. 137) равной:
Эх = -7-) •
\ ь )
(502)
В результате, определяя площадь эпюры, установим, что рас-
пор получит приращение:
R2 = 0,14(^76 + q)L. (503)
Суммируя jRi и найдем полный распор. Мы исходили из
предположения, что кладка совершенно не работает на растяжение,
т. е. принимали крайний, в сущности маловероятный случай. По-
этому для практических расчетов можно несколько уменьшить
полный распор и остановиться на величине его:
R = 0,2(gHb + q)L. (504)
В том случае, когда в низу перемычки уложена арматура, вос-
принимающая растягивающие усилия, распор будет меньше.
Округляя, примем:
R^0,UgHb + q)L.
(505)
Определяя по эпюрам высоту, на которой проходит равнодей-
ствующая, можем установить, что распор приблизительно распола-
гается от нижней поверхности перемычки на высоте, равной
L
12 *
ГЛАВА V
РЕКОМЕНДАЦИИ ДЛЯ РАСЧЕТА
Сделаем теперь выводы из всего, исследования и разработаем
конкретные рекомендации, которыми можно было бы пользоваться
при проектировании.
§ 27. ОБЩИЕ ДАННЫЕ. УСЛОВНЫЕ ОБОЗНАЧЕНИЯ
Будем в дальнейшем различать:
а)* рандбалки, представляющие неразрезные балки, которые
поддерживают кладку и имеют настолько узкие опоры, что опорные
реакции можно считать сосредоточенными (рис/ 142);
Рис. 142
Рис. 143
б) перемычки многопролетные и однопролетные, опирающиеся
на широкие опоры—простенки (рис. 143).
В приводимых ниже форму-
лах приняты следующие обо-
значения:
q — равномерно распреде-
ленная вертикальная
нагрузка, приложенная
к стене вверху или
другом уровне, но
высоте достаточно
леко от рандбалки
перемычки (см. п.
на
по
да-
или
13);
14 Б. Н. Жемочкин
209
g — собственный вес кладки в единице объема;
L — пролет раидбалки или отверстие в свету перемычки;
b — толщина стены;
Н—- высота стены над рандбалкой или перемычкой;
EI—жесткость раидбалки или перемычки; при железобетонных
'рандбалках и перемычках она должна определяться с
учетом арматуры, а также, если потребуется, с учетом
возможности трещинбобразования;
модуль упругости кладки стены.
§ 28. НАГРУЗКА НА РАНДБАЛКУ ИЛИ ПЕРЕМЫЧКУ ПРИ СТЕНЕ
БОЛЬШОЙ ВЫСОТЫ
1) Эпюру нагрузки на рандбалку можно принять состоящей из
треугольников (рис. 144).
Наибольшие ординаты эпюры р0 над опорами [формула
(стр. 42)] равны (коэффициент в формуле округлен):
Ро - 0,3 (gHb + q)Lj/ .
lz L I
Длины полуоснований треугольников [формула (136)]:
.3
(133)
(506)
d = 3,3 |/—
V ЕкЬ
2) Если длина d превышает половину пролета, то треугольники
в средней части пролета накладываются один на другой (рис. 145).
При d> L нагрузка на рандбалку равномерно распределенная,
что возможно только при очень жесткой рандбалке.
3) На крайних опорах длина d меньше, чем получается по фор-
муле (507), а ордината pQ больше, чем получается по формуле
(506).
Практически можно принимать ту же эпюру нагрузки.
4) Поперечная сила у опоры равна половине опорной реакции.
5) Наибольший по абсолютной величине момент на опоре. Он
равен [формула (149) (стр. 46)]:
(507)
d
210
Если L и d в м, а нагрузка в кг[м, то /И в кгм.
6) При р асчете рандбалок должны быть обеспечены:
а) прочность кладки над опорами, причем в данном случае
имеет место не сжатие, а смятие, так как концентрация нагрузки
наблюдается на небольших
участках; при напряжениях,
превышающих допускаемые,
или при расчетах но предель-
ному состоянию, превышаю-
щих расчетные сопротивления,
можно применить такой услов-
ный прием: ограничить эпюру
над опорой нагрузкой, соответ-
ствующей допускаемому на-
пряжению или расчетному соп-
ротивлению, но расширить
эпюру в стороны так, чтобы сохранилась ее площадь; наклонные
прямые провести под теми же углами (рис. 146); в первом случае
мы получим эпюру при эксплуатационной нагрузке на рандбалку,
во втором — при нагрузке в предельном состоянии;
б) прочность раидбалки на изгибающий момент и поперечную
силу; часто высота сечения на опоре зависит не от момента, а от
поперечной силы, к
7) Эпюры нагрузки на перемычки как однопролетные, так и
многоттролетные можно принимать состоящими из треугольников
(рис. 147).
Наибольшая ордината у края простенка равна полусумме сред-
14
211
них интенсивностей сжимающих усилий выше и ниже перемычки.
Это-дает [формула (437) (стр. 167)]
. Po = (gHb + q)(\+ -М (509)
\ д d •
Длина основания каждого треугольника [формула (136)]:
(5Ю)
При вычислении моментов наклонные линии эпюр могут быть
продолжены в стороны простенков .до сечений, которые принимают-
ся опорными в зависимости от условий заделки (при неглубоких
заделках однопролетных перемычек до середин -опор).
Рис. 147
3) В и. 7 предполагается, что стена выше и ниже уровня пере-
мычки имеет одинаковую толщину и выполнена из одного и того
же материала. Если же ниже_ перемычки _ стена. боле_е..._жесткая
(имеет большую толщину, выполнена из материала с большим мо-
дулем упругости, проем малой высоты и т. п.), ордината р0 и дли-
на d должны быть увеличены. При абсолютно жесткой стене ниже
уровня перемычки р0 и d должны быть умножены на коэффи-
циент 1,3.
9) Однопролетная перемычка может рассчитываться как заде-
ланная на опорах, если глубина заделки не менее двойной высоты
перемычки. При меньшей глубине заделки надежнее считать пере-
212
мычку шарнирно опертой, но в железооетонных перемычках пре-
дусмотреть арматуру, работающую на отрицательный момент.
10) При многопролетных перемычках и однопролетных с хоро-
шо заделанными, концами на 1----2 высоты (рис. 148) наибольшее
давление на кладку у края простенка равно удвоенной средней ин-
тенсивности давления в простенке [формула (438) (стр. 167)], если
не устраиваются специальные опорные конструкции.
Таким образом:
Ртах = 2 + 9) — V (511)
Поскольку это давление возникает только в крайних волокнах,
сопротивление кладки может считаться здесь повышенным. Вели-
чина повышения должна быть нормирована.
11) В случае неглубоко заделанных перемычек давление на
кладку простенка зависит от глубины заделки и от конструкции
опорных частей.
12) При конструкциях, занимающих среднее положение между
рандбалками и перемычками, когда опоры имеют небольшую ши-
рину, но реакции нельзя считать сосредоточенными (рис. 149), сле-
дует сделать два варианта расчета: как для рандбалки [по форму-
лам (506) и (507) (стр. 210)], но отсчитывать длину d от края про-
стенка и ординату ро относить к краю простенка, и как для пере-
мычки [по формулам (509) и (510) (стр. 212)]*
Принять эпюру с меньшей ординатой.
§ 29. НАГРУЗКА НА РАНДБАЛКУ ИЛИ ПЕРЕМЫЧКУ ПРИ СТЕНЕ
МАЛОЙ ВЫСОТЫ
13) Эпюры нагрузок можно считать треугольными и применять
формулы (506), (507), (509) и (510) и при небольшой высоте стены
над рандбалкой или перемычкой (рис. 150), но при условии, что
Я> — , если 1 000-^->0,10;
2 £кЬ£з
—, если 1 000 < 0,10.
4 , EKbL3
15 Б. Н. Жемочкин
213
14) При меньшей высоте стены следует ' считать нагрузку на
рандбалку или перемычку от внешней равномерной нагрузки и от
собственного веса также равномерно распределенной.
15) В предыдущих пунктах предполагается, что рандбалка или
перемычка начинает нести нагрузку после того, как кладка затвер-
дела и может работать как одно целое. Если же рандбалка или пе-
ремычка нагружается постепенно еще не затвердевшей кладкой, то
нагрузку от веса первых рядов кладки следует считать равномер-
но распределенной до высоты, равной
если 1 000—— > 0,10 ;
EKbL3
EI
если 1 000---<010.
E«bL?
Вышележащая кладка будет давать нагрузку на рандбалку или
перемычку по треугольникам.
При расчете следует сложить эпюры: одну эпюру прямоуголь-
ную от веса н-ижних рядов кладки и другую, состоящую из тре-
угольников, от веса вышележащей кладки и от внешней нагрузки.
При стене большой высоты или несущей большую нагрузку мож-
но, конечно, в зависимости от требуемой точности расчета прене-
брегать прямоугольной эпюрой и считать, что вся нагрузка дает
треугольные эпюры.
Не учитывать прямоугольную эпюру следует и тогда, когда под
рандбалкой или перемычкой ставятся временные стойки.
16) Если в верху стены высотой Н или на высоте Н над ранд-
балкой или перемычкой приложена сосредоточенная нагрузка
(рис. 151), то она может быть заменена равномерно распределен-
ной по длине пролета L нагрузкой, когда сохраняют силу формулы
(506), (507), (509) и (510), но при условии, что
Н > L, если 1 000 -EL. > 0,10 ;
Н>Е если j 000 —— <010.
' 2 ’ EKbL3
214
Если в пролете несколько грузов (3 и более), предельные высо-
ты могут быть снижены до указанных в п. 13.
17) Указания предыдущего п. 16 следует учитывать и в том -слу-
чае, когда сосредоточенная нагрузка приходится над опорой ранд-
балки.
Рис. 151 Рис. 152
18) В случаях, когда расстояние по высоте от рандбалки или
перемычки до места приложения сосредоточенной нагрузки меньше
пределов, указанных в п. 16, сосредоточенную нагрузку следует
считать приложенной к рандбалке или перемычке, но распределен-
ной согласно п. 19 (рис. 152). Прием, предлагаемый в п. 19, можно
применить как очень приближенный и при большой высоте, превы-
шающей пределы, указанные в п. 16, если это не вызывает утяже-
ления рандбалки или перемычки.
Если при перекрытии проемов перемычками сосредоточен-
ная нагрузка находится на высоте меньшей, чем указано в п. 16, и
располагается-над простенком, то она должна быть учтена
приемом, приведенным в п. 19.
§ 30. РАСПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ В КЛАДКЕ
19) Распределение вертикальных нормальных напряжений в го-
ризонтальных сечениях стены от сосредоточенной нагрузки можно
считать вообще под углом 45° к горизонту, эпюры же на различ-
ных уровнях считать треугольными с наибольшими ординатами,
15*
215
-определенными из условий равновесия. Для случаев расположения
сосредоточенной нагрузки у края стены и на значительном расстоя-
нии от края эпюры приведены на рис. 153.
Рис. 154
Рис. 155
Если нагрузка расположена на некотором расстоянии от края
стены, можно принимать эпюры по рис. 154: до глубины, равной
расстоянию от края,— по треугольникам с наибольшими ордината-
ми под нагрузкой; далее — эпюры, состоящие из трапеций и тре-
угольников, и на глубине, превышающей 2,41с,— по треугольникам
с наибольшими ординатами у края стены.
20) В случае равномерно распределенной нагрузки эпюры на-
пряжений можно принимать по рис. 155.
'216
§ 31. НАГРУЗКА НА РАНДБАЛКУ ИЛИ ПЕРЕМЫЧКУ
ПРИ НАЛИЧИИ ПРОЕМОВ
21) При наличии в стене небольших отверстий, имеющих раз--
меры, меньшие пролетов примерно раз в 5, влияние их можно не
учитывать (рис. 156).
22) При наличии больших проемов, находящихся на уровнях,
расстояния которых от рандбалок или перемычек
H>L, если 1 030 —Ш >0,10:
£к^3
всю нагрузку на этих уровнях можно заменить равномерно распре-
деленной (рис. 157) и вести расчет по формулам (506), (507), (509)
и (510). :
; ' 23) При более низком расположении проемов следует считать ’
нагрузку в пределах простенков на уровне низа отверстий равно-
мерно распределенной и принимать нагрузку, передающуюся на
рандбалку, по рис. 158 и на перемычки — по рис. 159, применитель-
но к правилам и. 20. Учесть вес стены ниже отверстий.
24) Если проем в кладке находится в средней части пролета
раидбалки, начинаясь непосредственно от раидбалки, принимать ’
эпюры треугольными (рис. 160) с наибольшими ординатами над i
опорами [по формуле (506) (стр. 210)], равными:
p^0,3(gHb + q)L]/. (512)
Г
Здесь через (gHb + q) обозначена интенсивность нагрузки, если
считать ее равномерно распределенной по всему пролету.
Обозначив среднюю интенсивность нагрузки в пределах про- :
стенка над рандбалкой через д0, можем переписать эту формулу и
так:
Ро^О.б^]/^~ • (513):
217-
1 Ю к
219
218
Длина эпюры в пределах половины ширины простенка:
(514)
25) Если длина эпюры d больше половины ширины простенка s
(рис. 161), следует принимать эпюру по трапеции с ординатой у
края отверстия, определенной из условия равновесия:
(515)
Если ра^> ро, принимать нагрузку равномерно распределенной.
26) При расчете перемычек можно применить аналогичные при-
емы (рис. 162).
Ординату у края нижнего простенка принять по формуле (509)
(стр. 212) равной:
Ро = <?)1 +
(516)
Здесь через [gHb + q) обозначена интенсивность нагрузки, если
считать ее равномерно распределенной по всей длине стены.
Обозначив среднюю интенсивность нагрузки в пределах верх-
него простенка через 7о, можем также написать:
Длина эпюры:
’ к ДО '
27) Если длина эпюры d больше, чем х, следует принимать эпю-
ру по трапеции с ординатой у края отверстия равной (рис. 163):
(519)
-Если ра>Ро, принимать нагрузку равномерно распределенной.
28) Если отверстия расположены у опор, так что рандбалки или
перемычки несут нагрузку от простенков, находящихся в пролете
(рис. 164), эпюры можно считать треугольными.
Наибольшая ордината будет у края отверстия. Она равна:
(520)
Через 7о обозначена средняя интенсивность нагрузки в преде-
лах верхнего простенка.
220
221
Длина эпюры с каждой стороны:
з
EI
ЕКЬ
(521)
Если сГ>2з, нагрузку в пределах верхних простенков считать
равномерно распределенной.
§ 32. РАСЧЕТ РЯДОВОЙ ПЕРЕМЫЧКИ
29) В случае рядовой перемычки, выполненной из кладки, когда
балка отсутствует (рис. 165), наибольшее давление у края простен-
ка приблизительно равно удвоенному среднему давлению в про-
стенке. Таким образом, справедлива формула (511) (стр. 213).
30) Наибольшее горизонтальное растягивающее напряжение в
нижних волокнах перемычки равно:
°„акс=(1-Л (522)
Предполагается, что кладка имеет достаточно большую высоту
над проемом, не меньшую, чем пролет.
При расчете крайней рядовой перемычки, а также в случаях,
когда или нагрузки или отверстия в свету смежных рядовых пере-
мычек различны, следует учитывать распор, передающийся на про-
стенок, по формуле (504) (стр. 208):
£ = 0,2(gtf& + g)L. (523)
Если внизу перемычки уложена арматура, воспринимающая
растягивающие напряжения, то распор по формуле (505):
R = 0,}(gHb + q)L. (524)
Арматура в таком случае должна рассматриваться не как кон-
структивная, а как рабочая. Ее следует рассчитывать на усилие
R = 0t\A(gHb + q)L. (525)
Точку приложения распора следует принимать на высоте ~ от
нижней поверхности перемычки.
§ 33. НЕКОТОРЫЕ ДАННЫЕ ДЛЯ ПОДБОРА СЕЧЕНИЙ
При проектировании рандбалок и перемычек, как правило,
приходится подбирать сечения путем последовательных
проб. Для облегчения этой довольно сложней операции (так как
приходится делать несколько попыток) ниже приводится несколько
приближенных формул, относящихся к железобетонным балкам
прямоугольного сечения и к стальным двутавровым балкам.
222
В приводимых далее формулах приняты обозначения:
\gH+ —) —нагрузка, передающаяся на стену (включая собст-
£ /
венный вес стены), в т/ж2; при расчете по СНиП
нагрузку следует брать умноженной на коэффициен-
ты перегрузки (расчетная нагрузка) и разделенной
на коэффициент условий работы (или на произведе-
ние коэффициентов условий работы);
Ро — ордината эпюры нагрузки на перемычку у края
проема;
L, b, Н — размеры в ж;
f— прогиб в середине пролета перемычки в см;
/г — высота сечения в сж;
W—суммарный момент сопротивления всех попадающих
в поперечное сечение стальных балок, перекрываю-
щих проем в стене, в си3; _
/— их суммарный момент инерции в см4;
R — расчетное сопротивление в кг/см2;
Ек— модуль упругости кладки в кг! см2;
Е—модулу упругости материала рандбалки или перемыч-
ки в кг/см2.
31) Если высоту прямоугольного сечения железобетонной
рандбалки можно выразить формулой
где а—коэффициент, обычно приводимый в справочниках для
заданных марок бетона и стали и определенного процента
h
армирования, но умноженный на отношение ---- 1,05—
h—а
—1,10, то требуемая высота сечения может быть определе-
на по формуле:
з
з / т:—\2 /
h =
(527)
60
£
b
Здесь Е — условный модуль упругости железобетона. Он равен
жесткости В, определенной с учетом арматуры (если
нужно, то и с учетом возможности трещинообразова-*
ч v т bhz
ния) и деленной на / = —- :
В
ЫгЧ 12 *
(528)
223
Следует сначала задаться Е, найти Л, подобрать сечение, вычис-
лить жесткость В и, определив уточненное значение Е, -повторить
расчет.
Предположим, например, что пролеты рандбалки Е — 6 м, тол-
щина кирпичной стены равна 0,51 м, высота стены— 10 м. Нагрузка
слагается из собственного веса кладки стены и временной нагрузки
вверху стены q = 2 т!м. Требуется подобрать сечение рандбалки.
Нагрузка с учетом коэффициентов перегрузки:
= 16-101,1 +-Д— -1,3 = 22,7г0и2.
Коэффициент условий работы примем равным единице.
Предположим, что расчетные сопротивления:
бетона при изгибе 7?и = 80 кг!см2'
стали 7% = 2 1 00 кг! см2
Примем армирование в количестве 0,75%.
По справочнику с учетом коэффициента 1,05:
а - 0,265-1,05 - 0,278.
Зададимся модулями упругости:
Ек = 10 000/<г/слг2
Е - 200 000 кг/сл?
Таким образом:
^=j™l = 005
Е 200 000
По формуле (527):
— 55 см .
Предположим, что после подбора сечения выяснилась необходи-
мость принять условный модуль упругости равным 120 000 кг1см\
Повторим расчет.
Теперь & Юмо
Е
= 0,083.
120000
з______
г 140-22,7-6 Ио,083 лл
П — --------------------------- = 49 см.
I | 3_______2
60 7Г^Г0,083 ) +22,7
\ U,2/0 . I
224
Уточнять высоту сечения дальше надобности нет. Следует перей-
ти к проектированию рандбалки и к проверке ее прочности, учиты-
вая и собственный вес рандбалки.
32) Для стальной рандбалки можно применить фор-
мулу:
— = 500 000 (gH + -у? -bz-L3
h \ b /
(529)
ФЪрмула не дает непосредственно высоту балки, а только величину
~ . Следовательно, следует дальше подбирать сечение путем проб.
Предположим, например, что нужно запроектировать рандбалку
для условий, приведенных в предыдущем пункте.
Приняв расчетное сопротивление стали Д = 2 100 кг!см2, по-
лучим:
— = 500 000-22,73-0,512-63 Д-1212Ж = 7451 смъ.
h ’ 10000-2 1003
Если будет уложено 2 двутавра, то для одного двутавра следует
взять — в 4 раза меньше, т. е.— — 1 863 смь. Подходит сечение
h h
№ 20а, у которого
U72
к
= 2 808 см5.
33) Для подбора сечения как железобетонной, так и
стальной п ер ем ыч к и (однопролетной или многопролетной),
к сожалению, нельзя вывести удобных аналогичных формул.
Здесь приходится вести расчет исключительно путем последова-
тельных проб, задаваясь сечениями. Опыт проектирования показы-
вает, что обычно перемычки не нуждаются в больших сечениях.
Однако, нельзя переходить некоторых границ. Во-первых, пере-
мычка должна быть достаточно жесткой и ее прогиб должен соот-
ветствовать нормативным указаниям; во-вторых, перемычка слабо-
го сечения переходит собственно в арматуру рядовой перемычки.
Во избежание трещин в кладке желательно, чтобы перемычка была
рассчитана не только на изгиб, но и на растяжение по формуле
(525).
34. Для проверки жесткости и определения прогиба желе-
зобетонной перемычки прямоугольного сечения можно
применить формулу:
225
(\ / \ / 3 /--\ 2
т)(4Ш|/ 4)- (530>
L г*Т
При определении — принять для L и h одинаковые меры. Пред-
h
положим, например, ро = 2О т/лг, 6 = 0,51 ж, А = 6 м, 6 = 30 см, Е^=
= 120 000 кг!см2, Ек= 10 000 кг! см2.
Тогда:
(\ / \ / 3 /------. 2
J2222L =1,0^.
0,51/\ 30/ 120 000 ХУ 10 000 /
К прогибу от нагрузки надо добавить прогиб от собственного _
веса перемычки.
35) Для нахождения'п р о г и б а стальной перемычки
можно применить формулу:
з _______
/= 1030 /-М Р]/ —-— . (531)
\Ь / У Е-кЕ1
Здесь L — в м, суммарный момент инерции в см4.
Предположим, например, что для предыдущих данных спроек-
тирована перемычка из двух двутавров № 24а с / = 4 570 см4.
f = 1 030 f—Уб2 \ f--------—--------- = 1,0 см.
J [о,51/ У 10 000-’-2 100 000-4 570.2
ч
ОГЛАВЛЕНИЕ
Стр.
Введение ............................................................ 3
Глава I. Рандбалки при стене большой высоты.......................... 8
§ 1. Нагрузка на рандбалку..................................... .....
§ 2. Примеры...................................’..............; 22
§ 3. Моменты и поперечные силы.................................. 29
§ 4. Напряжения в кладке......................................... 30
§ 5. Приближенные формулы........................................ 41
§ 6. Учет касательных напряжений................................. 48
Глава II. Некоторые частные случаи расчета рандбалок................ 61
§ 7. Расчет рандбалок при стене ограниченной высоты........... .....
§ 8. Учет сосредоточенной силы в пролете........................ 72
§ 9. Распределение напряжений в кладке.......................... 85
§ 10. Нагрузка на рандбалку в случае проемов в стене в средних ча-
стях пролетов................................................... 93
§ II. Нагрузка на рандбалку в случае проемов над опорами .... юб
§ 12. Однопролетная балка....................................... Ц2
§ 13. Расчет рандбалок в случае широких опор.....................116
Глава III. Многопролетные перемычки.................................. 126
§ 14. Постановка задачи........................................ ..
§ 15. Общий порядок расчета . . ..«..............................128
§ 16. Деформации простенка от действия единичных сил.............131
§ 17. Таблицы осадок простенка . ................................140
§ 18. Деформации кладки, расположенной над балкой................143
§ 19. Таблицы перемещений кладки............................... 148
§ 20. Нагрузки на балку (реакции кладки) от единичных сил .... 151
§ 21. Пример.................................................... 154
§ 22. Результаты вычислений и выводы.............................162
§ 23. Расчет перемычек при стене ограниченной высоты.............167
Глава IV. Однопролетные перемычки...................................175
§ 24. Свободно лежащая перемычка ........................... . . ___
§ 25. Перемычка с заделанными концами............................186
§ 26. Рядовая перемычка..........................................195
Глава V. Рекомендации для расчета...................................209
§ 27. Общие данные. Условные обозначения....................... .....
§ 28. Нагрузка на рандбалку или перемычку при стене большой высоты 21 о
§ 29. Нагрузка на рандбалку или перемычку при стене малой высоты 213
§ 30. Распределение напряжений в кладке'....................... 215
§ 31. Нагрузка на рандбалку или перемычку при наличии проемов . . 217
§ 32. Расчет рядовой перемычки.................................. 222
§ 33. Некоторые данные для подбора сечений.........................._
Жемочкин Борис Николаевич
РАСЧЕТ РАНДБАЛОК И ПЕРЕМЫЧЕК
* * *
Госстройиздат
Москва, Третьяковский проезд, д. 7
* * *
Редуктор издательства Э. М. Бударина
Технический редактор П. Г. Гиленсон
Сдано в набор 3/VI1I 1959 г. Подписано к печати 22/ХП 1959 г.
Т-14130. Бумага 60х92/(6 д. л.-7,12 бум. л.—14,25 печ. л., (13,20 уч.-изд. л.).
Тираж 6 000 экз. Изд. № VHI-3337 Зак. № 1774 Иена 6 р. 60 к.
Переплет №5 цена 1 р. 25 к.
Типография № 1 Государственного издательства литературы
по строительству, архитектуре и строительным материалам,
г. Владимир
ОПЕЧАТКИ
Стра- ница Строка Напечатано Должно быть ' -
20 3 снизу -И+;(+ + > ** <1++"-++ , ' \ tf
43 f 1 51 4 сверху 2 снизу -(**){ [• х/ И Е«ь (ох) {ар-
63 4 сверху . /2 п№Н& и2л//2 '* \ /4-2л’ ” ' /2 /2"4л4#&3 ' П2Лг#а \ /4-2л3 *” /а
65 10 сверху ••• 1,1, ••• С
68 8 снизу ' + (gH b + q lx*** + (gHb + q) lX* • •
111 4 сверху 9 е- * • со | to 11 • 4
131 3 снизу таких им .таких
141 Табл. 27, графа 6, строка 4 сверху + 0,70711 — 0,70711
141 То же, графа 7, строка 6 сверху — 0,63726 ‘ +0,63726
111 То же, строка 6 снизу + 0,01226 —0,01226 ;
165 12 сверху (стр. 124) (стр. 122): •
i?