54
54
В Н. ПРОКОФЬЕВ, ю. Л. ДАНИЛОВ, Л. А КОНДАКОВ. А С ЛУГАНСКИЙ и |(» А ЦЕЛ11Н
АКСИАЛЬНО-ПОРШНЕВОЙ РЕГУЛИРУЕМЫЙ ГИДРОПРИВОД
Под редакцией д-ра техн наук проф. В. Н. //РиКиФЬЕВА
ИЗДАТЕЛЬСТВО .МАШИНОСТРОЕНИЕ.
Москва
1969
Дксиально поршневой регулируемым гидропривод 11 р о-ьофьсвВ Н п ДР Пол РУЛ Лра техн наук пр. ф В Н. Прокофьево. At, «Машиностроение». 1969, 196 стр
R кгатте рассматривается устройство и действие, расчет и проектирование, технология изготовления и организация про итнодств.т отечественных аксиально поршневых гндромашни большое внимание уделяется свойствам рабочей жидкости особенно упругости тт вязкости, а также уплотнениям, часто олредезяюшим ресурс гидропривода. Подробно исследуются метаиизмы упрлвлетнтя автоматизированным гидроприводом дается анатиз их динамических свойств, излагаются взгляды’ ни снижение уровни шума гидропривода, приводятся способы реиипия нешнеиных задач о работе нтдропрцвода на нижнем претеле диапазона регулирования, Когда возникают автокоде-оянпя.	'
-г» ;== rz,
'тиаетке г, оргзш.ззтши производства гидромашни акснальио-
поршневого типа
Киша предназначена для работников производства, конструкторских бюро и научно исследовательских организаций, занимающихся вопросами гидроприводов Она может быть полезна также студентам машиностроительных вузов. Табл. 47. илл 312, бпбз 130 назв
книжный фонд""—
ЬИЬЛИГХТ.М моги. ЭНЕРГ.
^-£1195 64
Редснзепт д р техн. наук про()) £ Гордеев
3-1-Л
177-69
ПРЕДИСЛОВИЕ
Книга «Аксиально-поршневой регулируемый гидропривод» написана группой авторов, в течение многих лет занимающихся созданием и совершенствованием машин этого вида.
При выборе материала авторы учитывали зарождение специализированной отрасли промышленности — гидропередач общего назначения, поэтому в первую очередь обращались к тем разработкам, которые могут представить интерес при создании и внедрении в машиностроение новых гидроприводов.
Конкретизация содержания разделов, посвященных применению материалов, оборудования и оснастки, способу изготовления, а также рассмотрению вопросов организации производства, была достигнута выбором единого объекта — различных модификаций гаммы II отечественных гидроприводов, получивших широкое распространение в машиностроении и, особенно, в автоматических приводах. Понимая, что все связанное с процессом изготовления машин нового типа определяется масштабами производства, имеющимся оборудованием, опытом обслуживающего персонала и многими иными обстоятельствами, допускающими многозначные решения в основу написания гл 13—15 положен опыт серийного производства. Такой способ выбора содержания глав, посвященных раз личным вопросам технологии изготовления, представляется обязательным также из-за отсутствия литературы и установившихся способов изложения технологии изготовления гидроприводов.
При компоновке гидропривода на базе изготовляемых гидромашин его динамические свойства в большой степени обусловливаются возможностями механизма управления, поэтому глава об устройствах управления составлялась с подробностями, относящимися к выбору, расчету и, особенно, к оценке динамических свойств тех электро- и гидромеханических преобразователей, которые чаще всего применяются в современных машиностроительных автоматических приводах.
Непосредственно примыкающие к содержанию этой главы задачи	.
синтеза автоматических приводов в книге не рассматривались, по	.
скольку их решением занимаются специалисты, не участвующие	|
в конструировании и изготовлении гидромашин.	s
Г
3
ппнямика гидропривода в большой мере
Ресурс, надежность и динам	и рациональном конструк-
определяются вь^ром рабочс.	с возможн()й степенью под-
цин уплотняющих устройся. 5'Содрржа1|11е этих глав окажется ж*“ г""|,авл,"ет"‘уп-
иь. —cssxsz: машин роторною типа < аксиалыю-поршневых гидромашпп SaSaHHoJo'^a и для многих иных поршневых и плунжерных ГИДПоиХвие фактических материалов и технических характеристик но наиболее распространенному типу отечественных гидроприводов сопровождается многочисленными справочными материалами по иным близким к ним конструкциям.
В книге анализируются различные задачи динамики гидропривода, однако только в линейной постановке, если не считать решения нелинейной задачи о работе гидропривода на нижнем пределе диапазона регулирования. В настоящее время при изучении динамики гидропривода обязательно исследуются и автоколебания, возникающие на малых скоростях движения.
В книге компактно изложен способ оценки динамической ошибки гидропривода. Этот, ло-видимому, наиболее простой способ определения ошибки привода с разомкнутой системой управления может быть использован применительно к любому приводу динамические свойства которого задаются линейным дифферент! альным уравнением	дицхреренци-
За последние годы внимание исследователей и конструкторов
“лерж,,т в ис"от"°“ »₽""'•
вопросам гидропривода ' существующую литературу по
а~< Ч? ”~
£	™ л. шд’ж’-йя
Мес™ с Ректором, которому пп^я?Л"НЬ,М: гЛ' 2 ~ им сов-непамТВр1гьИ РсдактсР выражают глубок^'1 остальной материал, помощь, отшшуюИНУ’ В' А' СакОвУ « ВЮНРХа(теЛЬН0СТЬ инже-
ую ПРИ создании этой книги нову за Ценную
Д-Р »аук проф. „ н П(юкофьи
к


Глава /
акспально-поршневыь ГИДРОМА 1ПШПЛ
§ 1. 1. КОНСТРУКТИВНЫЕ ФОРМЫ И ТЕХНИЧЕСКИЕ ХАР ХКТЕРИСТИКИ АКСИАЛЬНО-ПОРШНЕВЫХ
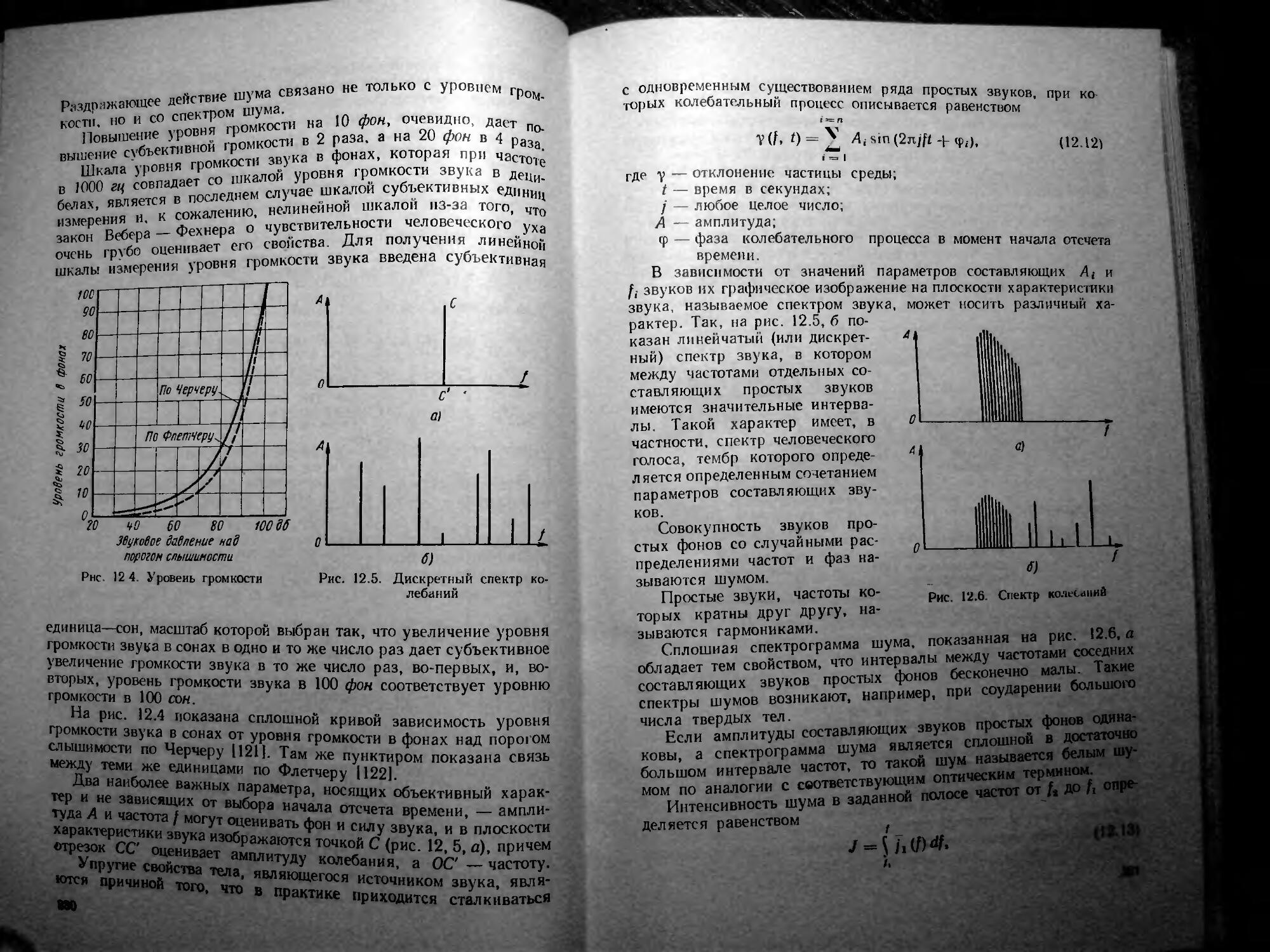
ГИДРОМАШИН
В машиностроении получили распространение три группы аксиально-поршневых гидромашин: 1) с двойным несиловым карданом, 2) с силовым карданом и 3) бескарданные гидромашнны. Столь же широко распространены аксиально-плунжерные гидро-машины, в которых отсутствуют шатуны. Чаще всего различия этих машин не являются принципиальными шли даже существенными, а их предельные характеристические возможности в первую оче-редь определяются выбором геометрических форм, материалов, способов обработки и иными технологическими особенностями
Подавляющее распространение в аксиально-поршневых гидромашинах получило торцовое распределение рабочей жидкости, осе-
вое распределение используется лишь в порядке исключения, поскольку приводит к повышенным утечкам, существенно зависимым от времени и режимов эксплуатации.
Наибольшее распространение, особенно в автоматических приводах, имеют аксиально-поршневые гидромашины с двойным несиловым карданом (рис. 1 1). Упорный диск /, выполненный как одно целое с валом 7, шарнирно связан со сферическими головками шатунов 2. Вторые сферические головки шатунов шарнирно заделаны в поршнях 3, которые совершают возвратно-поступательное движение в блоке цилиндров 4, приводимом во вращение от вала 7 через двойной кардан 6. Магистрали присоединяются к распределителю 5, с изменением положения которого на угол у относительно вала 7 изменяется ход каждого поршня, а значит, и
подача.
Основной нагружающий момент компенсируется усилиями, действующими через штоки 2, а кардан 6 нагружается только моментом, затрачиваемым на вращение блока цилиндров (для установившегося движения — момент потерь).
Относительно меньшее распространение, главным образом из-за больших весов и моментов инерции вращающихся частей, получили аксиально-поршневые гидромашины с силовым карданом ’Р^с-  )• который нагружается основным моментом. Блок цилиндров в этом конструкции непосредственно соединен с валом.
такой гндромаш"нь1	полУчивщий
Другой вариант	тор СКОрости (УРС), принципиально
название УН”ре^'Хго то-пько пропуском вала через у1юрный отличается от предыд>
ДИСК
Рис. I I Схема аксиально поршневой гидромашины с несиловым карданом
Рис. 1.2. Схема аксиально-поршневой гидромашпны с силовым карданом
Карданное сочленение только в отдельных случаях обеспечивает полную синхронизацию вращения упорного диска с блоком цилиндров. Полная синхронизация вращения достигается в гидромашинах с постоянной производительностью при использовании зубчатой передачи 6 (рис. 1.4). Однако в этом случае необходимо предусмотреть восприятие соответствующего радиального усилия
Рис. 1.4. Схема аксиально-поршневой гидромашины с синхронизацией вращения блока цилиндров зубчатой передачей
типа
,^1г^Х|ныК21^нЬнН°П0₽ш
-о регулятора скор^^
стей ИмеюцШе небольшойР°МаШИНЫ беекарданного У нас °лучнли широкое oacnnnM°MeHT инеРДии вращающихся ча-КонсттИСПОЛьзуются вРстооитТранеНИе в послеДНие годы I48J.
на Рис. lPfiKlv Я |<ас°са с двойиыеЛЬНО’А<’РОЖном машиностроении.
Опорный дцск ВЬ|ПП нссиловым карданом приведена
6	днец как одно целое с приводным
цапф 6 и подшипников. Опорой блока цилиндров является ос?// с подшипником, закрепленная в люльке насоса и проходя??
распределитель 8. Ось с подшипником центрирует блок цилиндров относительно распределителя Между концом оси // и блоком цилиндров 4 размещена пружина 12, обеспечивающая предварительный поджим блока цилиндров к распределителю Между подшипником и блоком цилиндров 4 имеется некоторый радиальный зазор в пределах которого блок может совершать небольшие угловые перемещения, обеспечивающие ----------- -
к распределителю. Синхронное вращение блока цилиндров с упорным диском обеспечивает двойной кардан 2. Карданный валик имеет сфе-
надежное прилегание его торца
Рис. 1.6. Конструкция аксиальнопоршневого насоса «Виккерс» с двойным несиловым карданом
Рис. 1.5. Схема аксиальнопоршневой гидромашины с ша тунным ведением блока цилиндров (бескардаиного типа)
рические концы, в которых
рические концы, в которых запрессованы пальцы, проходящие через центр сферы, имеющей плоские скосы, перпендикулярные оси пальцев. На пальцах установлены два скользящих сегмента, входящих в прорези втулкп-буксы, установленной в блоке цилиндров. Шатун 3 одним концом установлен в бронзовом гнезде упорного диска, а другим, также через бронзовый вкладыш, закреплен в поршне. В этих насосах блок цилиндров изготовляется из бронзы, а распределитель — из закаленной стали, гак же, как шатуны и поршни. Бронзовые вкладыши на сферы шатунов заваль цовываются, а затем запрессовываются в тело поршня и гнездо упорного диска. Через соответствующие каналы. выполненные на торце крышки люльки, жидкость поступает к uan(N	X
она следует в магистраль. В каналах люльки скорость ""и не должна превышать определенно»! величины, поэтому про* Д
7
о
$
п вариант такс"’ ^“сХ^ЛрС), прпн шит налево ЛяЙниЛ^ЬНЬ'” РД тпькС пропуском вала через упорНый *ЙЙ <* "^yiucro
Рис. 1.1 Схема аксиально-поршневой гидромашины с несиловым карданом
Рис. 1.2. Схема аксиально-поршневой гпдромашины с силовым карданом
Карданное сочленение только в отдельных случаях обеспечивает полную синхронизацию вращения упорного диска с блоком цилиндров. Полная синхронизация вращения достигается в гидромашинах с постоянной производительностью при использовании зубчатой передачи 6 (рис. 1.4). Однако в этом случае необходимо предусмотреть восприятие соответствующего радиального усилия.
Рис. 1.3. Схема аксиально-порш невой гидромашииы — универсального регулятора скорости (УРС)
Рис. 1.4. Схема аксиально-поршневой гидромашины с синхронизацией вращения блока цилиндров зубчатой передачей гидромашины бескарданного типа пой момент инерции вращающихся ча-
Аксиально-поршневые гид
(рис. 1.5), имеющие небольшой	™
v^J.' П0ЛуЧИЛИ шиРокое распространение в последние годы (481. а^оии используются в строительно-дорожном машиностроении.
на пнЛГГ Наа5а с дойным несиловым карданом приведена р i p- Упорный диск выполнен как одно целое с приводным
в
валом / Блок цилиндров 4 с поршнями 5 установлен в качающейся люльке 7, которая смонтирована в корпусе насоса при цапф 6 и подшипников. Опорой блока цилиндров является ось / с подшипником закрепленная в люльке насоса и проходящая через распределитель 8. Ось с подшипником центрирует блок вдпиндпов относительно распределителя. Между концом оси 11 и'бпоком цилиндров 4 размещена пружина 12, обеспечивающая предварительный поджим блока цилиндров к распределителю. Между подшипником и блоком цилиндров 4 имеется некоторый радиальный зазор в пределах которого блок может совершать небольшие угловые ............................."	..	- торца
перемещения, обеспечивающие к распределителю. Синхронное вращение блока цилинд-
надежное прилегание
его
ров с упорным диском обеспечивает двойной кардан 2. Карданный валик имеет сфе
Рис. 1 6. Конструкция аксиальнопоршневого насоса «Виккерс» с двойным несиловым карданом
Рис 1.5. Схема аксиальнопоршневой гидромашяны с ша тунным ведением блока цилиндров (бескарданного типа)
рические концы, в которых запрессованы пальцы, проходящие через центр сферы, имеющей плоские скосы, перпендикулярные оси пальцев. На пальцах установлены два скользящих сегмента, входящих в прорези втулки-буксы, установленной в блоке цилиндров. Шатун 3 одним концом установлен в бронзовом гнезде упорного диска, а другим, также через бронзовый вкладыш, закреплен в поршне. В этих насосах блок цилиндров изготовляется из бронзы, а распределитель — из закаленной стали, так же, как шатуны и поршни. Бронзовые вкладыши на сферы шатунов заваль-цовываются, а затем запрессовываются в тело поршня и гнездо упорного диска. Через соответствующие каналы, выполненные на торце крышки люльки, жидкость поступает к цапфе 6, от которой она следует в магистраль. В каналах люльки скорость жидкосгм не должна превышать определенной величины, поэтому проходи**
7
сечения должны быть выбраны соответствующими. Это увеличивает габариты люльки и всего иасоса, повышает время реверсирования насоса, требует более мощного механизма управления.
Конструкция насоса довольно сложная из-за наличия большого количества деталей, требующих точного выполнения. Габариты и вес насосов и гидромоторов резко различаются.
Точная сравнительная оценка различных конструкций гидро-машин затруднена ограниченностью опубликованных материалов. Кроме того, очень мало проводилось сравнительных испытаний гидромашин в одинаковых условиях эксплуатации, особенно испытаний на надежность и долговечность, требующих большой затраты времени. Однако представления о существующем техническом уровне современных аксиально-поршневых гидромашин могут быть получены путем сопоставления кратких технических характеристик конструкций, экспонируемых на международных выставках последних лет.
Таблица 1.1
Давление в кГ1сч*
Число оборотов вала в минуту
. а
Д о
Модель
»Е
I

2
5 Е
Е
о
С
С
Насосы
PV-2003 РУ-2008 PV-20I2
PV-2020
PV-2O32
PV-2050
PVA-120
MF-2003 МН-2008 MF-20I2 МН-2020 MFA-50
МГ-2050
MFA-I20
16
40
62
98
156
245
388
16
40
62
98
156
245
388
переменной производительности
140
140
140
140
140
140
140
140
140
140
140
210
140
210
210 210 210 210 210 210 210 Гил 210 210 210 210 350 210 350	1800 1200 1200 1200 1200 1200 1200 роме 1800 1200 1200 1200 1200 1200 1200	)тор ь 4400 3300 2700 2300 2400 1600 1800	28,6 48,0 74,4 117,5 187,0 294,0 466,0 28,6 48,0 74,4 117,5 187,0 294,0 466,0	6,54 11,0 17,0 27,0 42,7 67,2 106,5 6,54 11,0 17,0 27,0 64,2 67,2 160,0	20 39 64 98 155 247 400 13,4 23,0 34,0 50,0 68,5 194,0	3,06 3,54 3,76 3,63 3,63 3,68 3,76 1,22 1,35 1,26 0,78 1,02 1.21
В настоящее время утвержден ГОСТ 13824—68, предусматривающий в качестве главного параметра ряда гидромашин объемного типа геометрическую подачу (т. е. подачу без учета утечек) на один оборот ротора (упорного диска или блока цилиндров в завис и-ь
мости от того, кто из них непосредственно связан с валом) поэтом^ в таблицах технических характеристик каждый типоразмер гадм машины сопровождается значением главного параметра о в сЖ
В системе СИ используется характерный объем, т е среднее раХ'Г Ге°МетрнЧескОЙ подач" ПР« повороте ротора'на одвд
® = 2л 9 смг!рад.
(11)
Технические характеристики насосов переменной производительности, показанных на рис. 1.6, и гидромоторов аналогичных конструкций приведены в табл. 1.1.
Имеется модификация гидромоторов для авиационных гидросистем. Эти машины более быстроходны, форсированные по давлению и обладают меньшим удельным весом (табл. 1.2).
Табшца 1.2
Модель	Подача в см3/об	Давление в кПсиЗ		Число оборотов вала в минуту		Номинальная производительность В .t/MUH 1		I Номинальная мощность а кет	S и V о СО	Удельный пес в кг/квт
		номинальное 			максимальное	номинальное	максимальное ,				
				Гндромоторы					
906	1.56	210	315	6060	9100	9,46	3,23	1,18	0.355
907	3.08	210	315	4840	7245	14,9	5,07	1,63	0.322
909	6,02	210	315	3860	5800	23,2	8,08	2,68	0.332
911	9.8	210	315	3280	4920	32,2	11.0	3.86	0.351
913	15.58	210	315	2820	4230	43,9	14,1	5,44	0,37
915	24,9	210	315	2820	4230	70.2	23,55	7.98	0,338
918	38,5	210	315	2400	3610	92,5	31.6	Н.1 13,6	0.351
921	60.2	210	315	2080	3120	125,5	42,6		0,320
Конструкция регулируемого насоса, выполненного по кинематической схеме, показанной на рис. 1.5, приведена иа рис. 1-Л а на рис 1.8 — аналогичная конструкция гидромотора.
Использование сферического распределения п03“° скорость скольжения на оси окон распределителя, котораясущ ственно смещена к оси вращения. В конструкциях ^свально поршневых гидромашин бескардаиного типа шир к	Q
гидростатическая разгрузка, например, на <ИР сЛепическом упорного диска, на сферических головках
распределителе, в разгрузочные канавки и ^л д^ Подасти с ком-изводится впрыск рабочей ’«идкосги из напорной
мутационной частотой (произведени  позволила повькить цилиндров). Совокупность таких меро р
Рис J.7. Регулируемым аксиально-поршневой насос с шатунным ведением поршней
10
ресурс (гарантированное время эксплуатации) распределителя настолько, что общий ресурс гидромашины стал определяться работой ее упорного подшипника.	1
Блок цилиндров центрируется при помощи специального валика (рис. 1 7), а первоначальный прижим обеспечивается специальной поджимной пружиной, установленной на этом валике.
Корпус грушеобразной формы вместе с люлькой замыкает на себя силовые воздействия и разгружает опоры. Наряду с достоинствами такого конструктивного оформления гидромашины приходится считаться и с недостатком — увеличение момента инерции поворачивающихся при изменении производительности частей.
Блок цилиндров в этих гидромашинах выполняется бронзовым, а распределитель из специальной стали. Поршень с шатуном закрепляется при помощи разжимного кольца, а большие сферические головки шатунов в упорном диске — при помощи винтового соединения.
Таблица (.3
Модель		Подача в cw3/od	Число обор в мин номинальное	отов вала уту максимальное	Номинальная производительность в Л/.пин	Номинальная мощность в кет	Вес в кг	Удельный вес в кг1квт
VII	01г 				Н а со 12 16 20 25 32 40 50 12 16 20 25 32 40 50 55	с ы п е 11,6 28,1 54,8 107 225 468 915 Н,6 28,1 54,8 107 225 468 915 1210	ре м е н 1450 1450 1450 1450 970 970 730 Гн 1450 1450 1450 1450 970 970 730 730	ной пр 4500 3550 2800 2240 1800 1400 1120 д р о и о 5000 4000 3150 2500 ‘2000 1600 1250 1120	О И 3 В О д 16,8 40.8 79,5 155 218 454 668 торы 16,8 40.8 79.5 155 218 454 668 885	и т е л ь 4,78 11.78 22,81 44,6 62,6 130 191,5 4,37 10,7 20.9 40.8 57,4 119 175 231	т о ст и 13 28 49 109 257 450 700 5,5 12,5 23 44 88 195 328 486	2,72 2,36 2,14 2,44 4,10 3,46 3,65 1,26 1,17 1,1 1,07 1,53 1,63 1,87 2,1
Технические характеристики насосов "ер«« Г'таб^.З. n?H°m”^cS“3aatoaCT с имивальнин »ен^ 175 кГ/ci^ и допускаемой кратковременной пеРзгр).3^1 и дояуска*-а гидромоторы - соответственно сдаменнемJ60 «Г/« Ж мой кратковременной перегрузкой 320 w /см .								
Таблица 1.4
Модель	Подача СИЛ[об	Чцгло оборотов валов в минут»		Номинальная производительность в л/ wtt«	Номинальная мощность в кет	Вес и лг	Сдельный вес в Kt/квт
		номинальное	максимальное				
Насосы		перем	е п и о 0	производительности			
НАР-32 НАР-40	225 450	1000 1000 750 600 500 395	1500 1200 1000	225 450 675	55,1 110,2 165	250 460 850	1,54 4,16 5,15
НАР-50	900		750	1080	261	1570	5,95
НАР-63	1800		600	1800	440	2900	6,6
НАР-80 НАР-ЮО	3600 7200		500	2700	663	5500	8,3
		Гидромоторн					
НАМ-27 НАМ-32 НА М-40 НА М-50 НАМ-63	133,2 233 460 900 1808	1500 1000 1000 750 600	2000 1800 1500 1200 900	200 233 460 675 1090	49 57,2 112 165 267	75 120 220 400 800	1,53 2,1 1,96 2,42 3
НА М-72	2715	500	750	1350	330	2500	7,58
НАМ-80	3670	375	60	1370	335	2500	7,44
Имеются конструкции гидромоторов, блок цилиндров которых с при помощи конической зубчатой пары. Техническая характеристика гидромашин, аналогичных по конструкции приведенным на рис. 1.7 и 1.8, но изготовляемых другой фирмой, работающих при номинальном давлении 150 и 200 к/7с.м2 и кратковременной перегрузке, приведены в табл. 1.4.
Зависимость ресурса в часах одного из насосов переменной производительности от угла наклона люльки в процентах от его наибольшего значения у>П1ВХ показана на рис. 1.9; зависимость ресурса разных насосов при Y,najI от давления нагнетания — на рис. 1.10.
Выпускаются аксиально-поршневые гидромашины бескарданного типа с центральным прижимом распределителя к блоку цилиндров (рис. 1.11). В этой более сложной конструкции усилие прижима блока цилиндров к распределителю пропорционально
упорным диском связываются
Рис 1.10 Ресурс насосов в часах при Углах в зависимости от давления
Рис. 1.11. Аксиально-поршневой насос бескарданного типа с центральным прижимом распределителя к блоку цилиндров
Рис 1.12. Гидроыашина с центральным прижимом блока цилиндров к распределителю
13
гяпактеристпки насосов пере-=S5=S₽-,ss:x „нем 100л/ "f ид	Таблица 1.5
в табл. 1.5-
Удельный пос в кг! кет
Число оборотов пали в минут?
Модель
Подача R
СЛ<8/О#
Насосы
поминальное
максимальное
Номинальная производительность и Л/ W//H
Номинальная мощность в К(1ГП
Вес п
переменной производительности
HR12 HRI6 IIR20 HR25 HR30 HR36
7,9
17,0
33,0
59,0
101.0
137,0
1450
1450
1450
970
970
970
11,4
25,0
48,0
57,2
98,0
1,915 4,05 7,87
9,4 16,0
24,8
34
9'2
187
6,27
8,38
6,6
9,8
9,45 7,55
Гидромоторы
HS12
HS16
HS20
HS25
HS30
HS35
9,3
20.0
39,0
70.0
119,0
185,0
1450
1450
1450
970
970
970
2000 2000
2000 1750 1750
1450
13,5
29,2
57,0
68,0
179,5
оо
4,78
9,35
18,9
29,0
8,9 15,0 28,0 47,0 70,0
102,0
4,04
3,15
3,0
4,24
4,2
3,52
Таблица 1.6
Модель	Подача в см^/об	Число оборотов вала в минуту		Номинальная производительность в л/ чин	Номинальная мощность в кет	Вес в кг	Удельный вес в кг! кет
		номинальное	максимальное				
	Насосы переменной производительности						
СТ-10	42	3200	3200	135	31	114	3,68
СТ-15	66,4	1500	1500	100	22,9	152	6,65
СТ-25	102	1500	1500	153	35	200	5,7 1,27 1,99
СТ-50	236	1200	1800	285	65,5	125	
СТ-90	404	1000	1500	404	92,5	184	
			Гидро моторы				
СТ-10 СТ-15 СТ-25 СТ-50 СТ-50	42 66,4 102 216 404	3200 1500 1500 1200 1000	3200 1500 1500 1800 1500	135 100 153 285 404	31 22,9 35 65,5 92,5	40 56 78 114 169	1,29 2,44 2,23 1,17 1,83
——— - - -		—							
Изготовляются аксиально-поршневые гидромашины яняп. ные изображенным на Рис. 1.7, но отличающиеся дополнительным гидростатическим прижимом блока цилиндров к распределю за счет использования центрирующей оси в качестве поршня под который подается рабочая жидкость из полости нагнетания (рис. 1.12). Предпола1ается. что в этой конструкции обеспечивается постоянный зазор между блоком цилиндров и плоским распределителем. Технические характе-
рпсгикп насосов переменной производительности, показанных на рис. 1.12, и гидромоторов аналогичной конструкции приведены в табл. 1.6. Гидро-машпны работают при номинальном давлении 140 кГ /см2, допуская кратковременную перегрузку до 320 кГ!см2.
Подробные материалы по аксиально-поршневым гидро-машинам бескарданного типа с установленным на подшипнике блоком цилиндров (рис. 1.!3) приведены в работах 166] и [631. Сведения по аксиально-поршневым гидромашинам с силовыми карданами можно найти в работе |48|.
Очень большое распространение, кроме гидромашин больших мощностей, получили аксиально-поршневые
Рис. 1.13. Гидромашина «Брюнингхауз»
наиболее старого образца с точеч-, показанном на рис. 1-15,
гидромашины плунжерного типа, в которых упорный диск выполняет обязанности пространственного кулачка. Схема ---- ,
ным касанием головок плунжеров показана на рис. 1.14. 1акие гидромашины в варианте исполнения, показанном на рис Но, могут обладать свойством самовсасыванкя. Примененная гидростатическая разгрузка, принципы расчета которой приведены в гл. Ь, получила в последние годы большое распространение. Эти гидро-маЛты выполняются также н со
(рис. 1.16) и с размещением плунжеров по конической
(рис 1.17), позволяющим использовать действие центробеж сил в процессе всасывания и обеспечивающим боле? благояр ицтно* действие нагружающего изгибающего момента 114‘
Характерной особенностью рассматриваемых nt poм«Ш ляются значительные силы трения плунжера о стенки
опкной составляющей силы достигает 36% от осевой (величина ради • ’ давления).
силы гидростатическ го Д	получили самое широкое рас.
Гидромашины Да,™"ке зарубежного гидромашиностроения в пространение в пр i
Рис. 1.14. Схема аксиально-плун жерной гидромашины
Рис. 1.15. Аксиально-плунжерная гидромашина с гидростатической разгрузкой головок плунжеров
последние 10—16 лет вследствие простоты конструкции, малых весов и габаритов, большой мощности при небольшом весе в малой стоимости.
Широко известны гидромашины с гидростатической разгрузкой головок плунжеров и размещением блока цилиндров в наружном шарикоподшипнике, в пределах зазора которого возможно
угловое перемещение блока, обеспечивающее самоустанавливаемость на плоской поверхности распределителя (рис. 1.18). Замена лишь одной крышки с упорным диском позволяет превратить насос переменной подачи в гидромашину с постоянной подачей, различие в весах которых незначительно. Гидромашина имеет только один разъем корпуса, что уменьшает технологическую неточность выполнения плоскости распределителя перпендикулярно оси вращения блока цилиндров. Размещение опор упорною диска в смен-
Рис. 1.18. Аксиально-плунжерный иасос «Лукао
пой крышке и выполнение их ня поппшт»,.,.
лист сократить габариты гидромашины. Размещен™'^ пшГ машины со стороны распределителя гюзволяе? осущеХятьХ сборку и разборку без отсое-	осуществлять ее
дннеппя от приводного двигателя п магистралей.
Гпдромоторы, построенные по данной конструктивной силовой схеме, имеют один существенный недостаток — невозможность работы на малых оборотах под нагрузкой. Имеются сведения, что гидромотор 1М 500 при давлении в полости нагнетания 210 кГ/см2 имеет наименьшее число оборотов 350 в минуту.
Блоки цилиндров этих гидромашнц выполнены из бронзы с напрессованным кольцом, являющимся внутренним кольцом подшипника. Торец блока имеет серебряное ные. Плунжеры — стальные, сти. Башмаки плунжеров—бронзовые, имеющие серебряное покрытие на рабочем торце. Корпуса насосов — поковки из алюминиевых сплавов. Упорный диск выполнен из стальной поковки. Опоры диска выполнены в виде стальной ленты, на которую нанесен антифрикционный материал типа найлона. Лента устанавливается в цилиндрическую расточку крышки насоса.
покрытие. Распределители — сталь-закаленные до высокой твердо-
Таблица 1.7
Модель
Давление в
Число оборотов вала в минуту
Насосы постоянной производительности
IP60 1Р125 1Р500
IP 1000 1Р3000
4,55
9,3
38,0
76.0
225,0
280
210
210
210
170
350
280
280
280
246
4000
3000
3000
3000
2000
6000
4000
4000
3000
2000
18.2
28,0
43,5
228,0
450,0
8,5
9,6
39.2
78,5
125,0
4,08
6,35
16.1
27.4’<
0,48 "56 0.41 и б О.к>
609561
Тпб.1цца /g
Модель
Поляча п емЧоб	Пяпзсннр в кПсм‘		Число оборотов вала в минуту		Номинальная произ- 1 водительность в 1 Л; MUH	1	Номинальная мощность в кет	Вес в кг	। Удельный вес в кг/кет
	номинальное	максимальное	1 номинальное 		о 3 rt X rt X				
С Т II
производители!
о
Насосы п е р с ч с н в о fl
IP60
IP 125
IP500
IP 1000
IP3000
4,57
36. 1
76.2
218,7
280
210
210
280
280
3.50
280
380
350
3.50
3.500 3800
1750 17.50 1750
6000
1000 touo
3600
1 2.500
IM60 1ЛИ25 1М500 1 Ml ООО I.M3000
	Г	1 Д Р О	мотор	ы
4,57	280	350	4000	6000	21.5
9,51	210	280	4000	5000	39.8
38,1	210	280	4000	5000	106.4
76,2	280	35(1	3000	4801)	256,7
218,7	280	3.50	9000	31KJJ	5011.0
14,0
30.7
121,9
370.9
7,36	9	1,22
11,4	13	1,14
26,5	36	1,36
61,8		1,05
191,2	135	0,705
7,64	9	1,18
11,2	13	1,16
47,7	36	0.756
101,5	65	Ц.66
195,4	135	0.69
Технические характеристики насосов постоянной производительности, показанных иа рис. 1.18, приведены в табл. 1.7. Техннче-
Рис. 1.19. Аксиально-плунжерный иасос «Клайн гидравлик»
ские характеристики насосов переменной производительности и гидромоторов, аналогичных по конструкции, но изготовляемых другой фирмой, приведены в табл. 1.8.
На рис. 1.19 показан регулируемый насос, отличающийся тем, что опора блока цилиндров расположена на валу. Это сферический поясок, центр сферы которого совпадает с точкой приложения результирующей радиальной силы от сил давления жидкости на плунжеры. Вал насоса проходит через распределитель и упорный Диск. Опоры вала расположены в крышках насоса. Силы трения в соединении вала с блоком ци-
вилка.
‘упенчатым. От вспомогательного на-
18
сося к большему отверстию подводится рабочая жидкость поп „яо леиием, действуя на площадь уступа, она создает сипу прижимаю щую плунжер к упорному диску. а блок Ц11ЛИ11 *7аР"лТ телю. Пружинный поджим плунжеров и блока цилиндров к Кое делителю отсутствует.	р распре-
Основные характеристики таких насосов приведены в табл 1 9 Материалы по аксиально-плунжерным гидромашинам используемым главным образом в грузоподъемных машинах различных типов, можно найти в работе (66].
Таблица 1.9
Модель	Подача В СМ3/об	Давление в кГ/см*		Число оборотов пала в минуту		Номинальная производительность в л/ »ш«	Номинальная мощность в кет
		номинальное	максимальное	номинальное	максимальное		
1205	18,30	210	350	1200	1801)	28	7,57
1210	35,1	210	350	1200	1800	42	14,85
1220	78	210	350	1200	1800	93,5	33
1210	158	210	330	1200	1800	190	65,5
Выпускаются аксиально-плунжерные насосы переменной производительности упрощенной конструкции (рис. 1.20). Технические характеристики таких насосов и гидромоторов приведены в табл. 1.10.
Таблица 1.10
Модель	Подача в <? И:,/об’	Давление в кГ1ся~		Число оборотов вала в минуту		Номинальная производительность в л/мин	Номинальная мощность в кет	Вес в кг	Удельный вес в кг 1 кет
		номинальное	максимальное	номинал ь- иое	максимальное				
Насосы переменной					производительности				
PVB-5	10,4	140	210	1440	3600	15	3,5	7	2
PVB-6	14	140	210	1440	3600	20	4,55	7	1,54
PVB-10	21	140	210	1440	3600	30	7	14	2 1,27
PVB-15	33	140	210	1440	3600	47	11	14	
PVB-20	42,5	140	210	1440	3600	61	14	21,5	1,74 1,22
PVB-29	61	140	210	1410	3600	88	20	24,5	
PVB-45	90,5	105	210	1440	2200	130	22,5	49,5	2,2
			Гидромоторы						
MFB-5	10,4	105	210	1800	3600	18,7	3,21	5 9,5	1,56 1,46 1,3 1,31
МРВ-10	21	105	210	1800	3200	37,8	6,5		
MFB-20 MFB-29	42 61	105 70	210 140	1800 1800	2400 2400	75,6 ПО	13 12,6	11 17	
ia
Наименьший	Хроспстемах, ’’регулируемы”’’^^
=тайт("г^--о лаянию (р..с. L2,)'67's
Рис 120 Аксиально-плунжерный Рис 1.21. Аксиально-плунжерный ,1асос насос «Виккерс»	«Ьендикс»
сведения, что их ресурс не превышает 500 ч. Технические характеристики этих насосов, работающих при номинальном давлении 210 кПсм* и допускающих перегрузку до 280 кГ'см2, приведены в табл. 1.11.
Таблица 1.Ц
Модель	Подача в см*/оС	Число обсрслов вала в МЙН)Ту		Номинальная производительность в я/мин	Номинальная МОЩНОСТЬ в кет	Вес в кг	Удельный лес в кг/ кет
		номинальное	максимальное				
Р38	6,24	8000	11 000	50	17,1	3	0.175
Р56	9,31	7000	10000	65	22,3	3,68	0.165
Р105	16,4	5000	8 000	82	28,1	5,36	0,19
Р175	28,7	4000	6 000	115	39,5	7,31	0,185
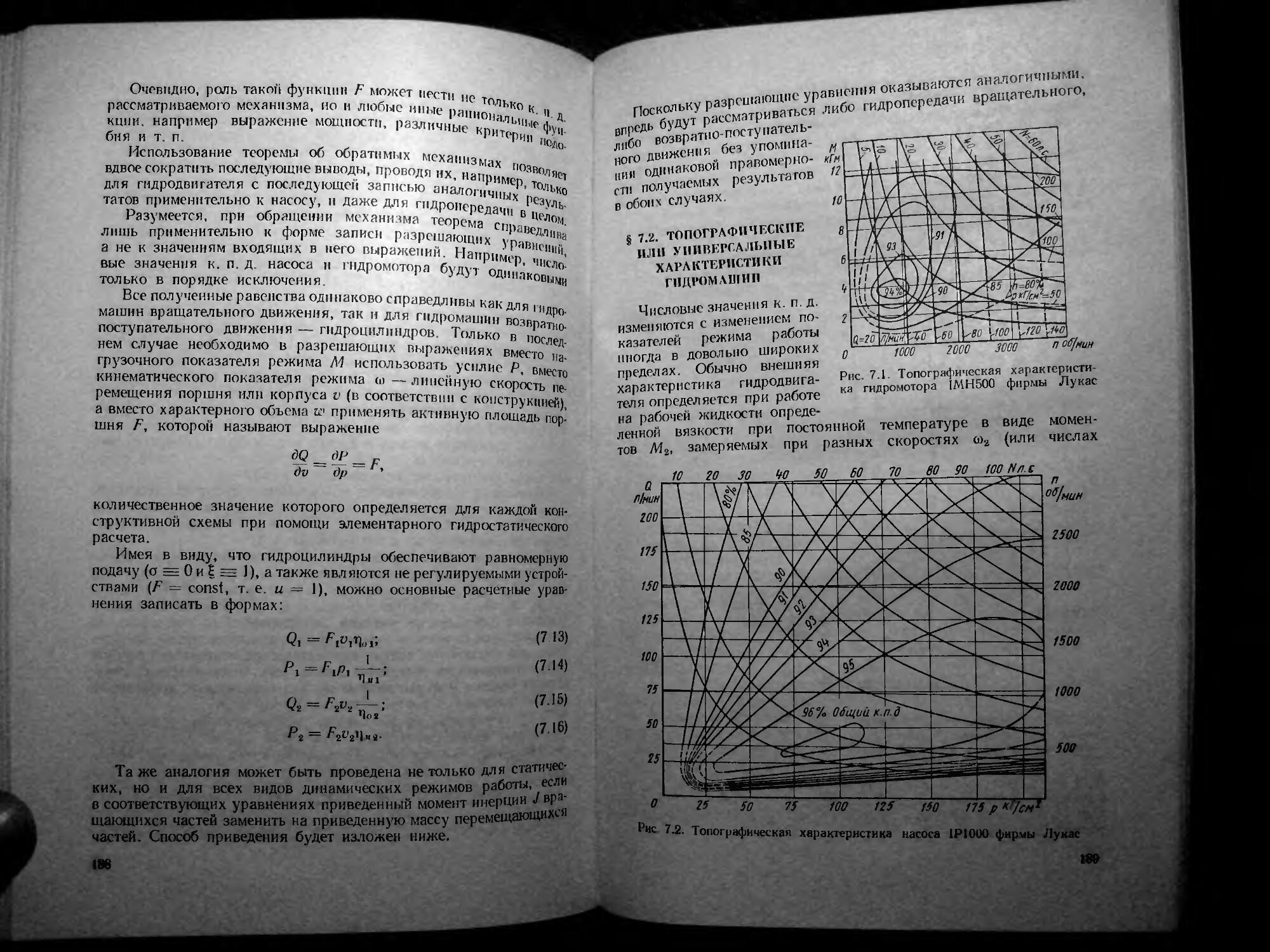
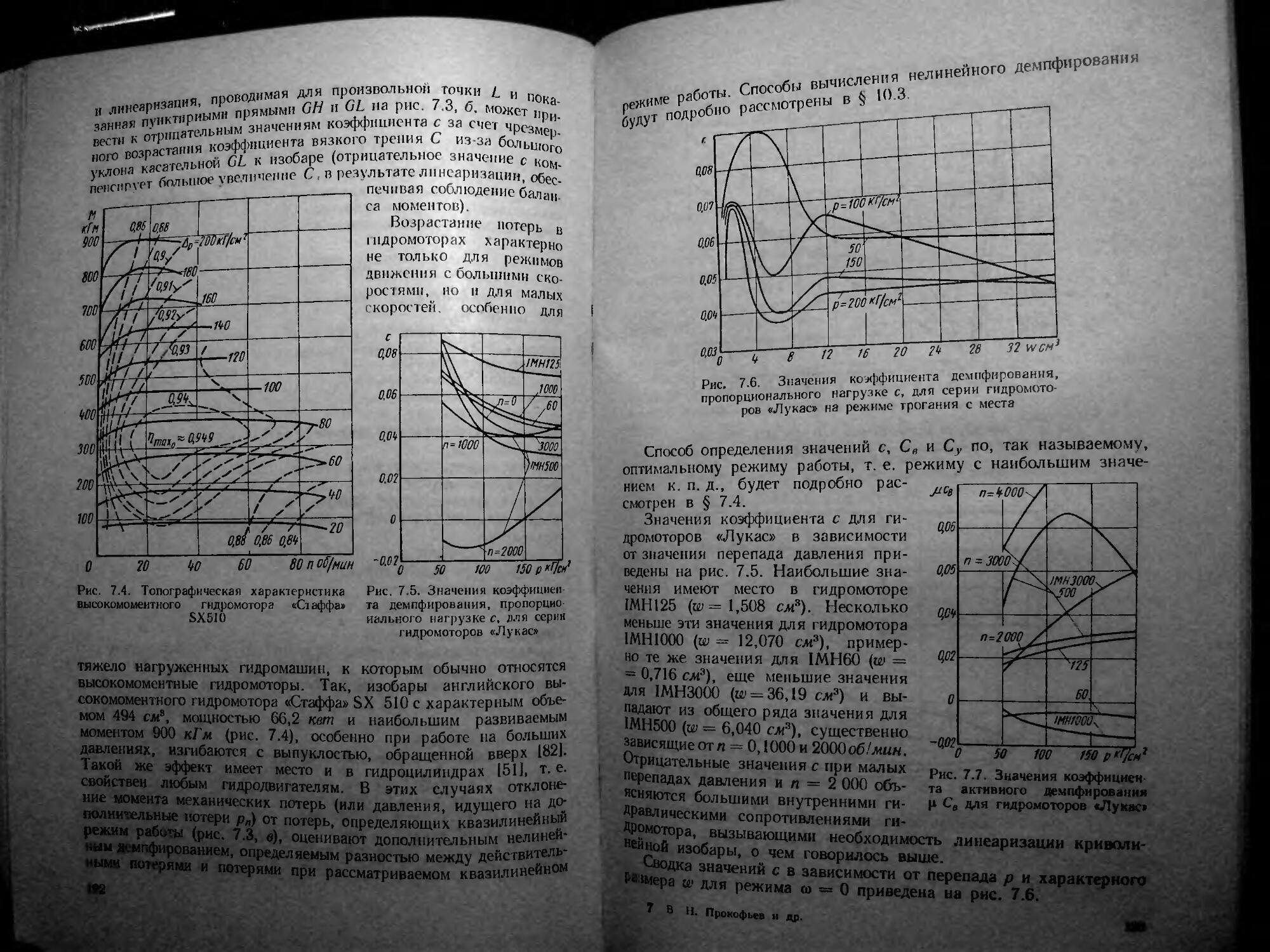
§ 1. 2. ОСНОВНЫЕ КОЛИЧЕСТВЕННЫЕ СООТНОШЕНИЯ ГИДРОМАШИН ОБЪЕМНОГО ТИПА
жЯт«₽СИ^Л«пГП^РШНеВЫе гидР°машины, как и другие, принадле-паботять n РОТОРНЫХ’ принципиально обратимы, т. е. могут НаС0С0В И "роторов (48]. Зная техниче-мотора можно лпети ГИДР°МаШИНЬ1’ В1>1полнеьной в качестве гидро-зований в качестве насоса тоТьт °ценить ее свойства при исполь-соотношениями гинг>™ ’ ПОлвзУясь основными количественными подсчеты могут быть поовепг. °6ЪСМН0Г0 типа' В частности, такие веденным в табл. 1 1 Р] o/Vo пРименительн0 к материалам, при-значения к. п. д. cobd’cmpuu ‘д’ 1Л’ , 5’ 16 и поскольку меняются мало.	ых гидРомашин рассматриваемых типов
20
характерного объема w, можно записать утечек,
выражение геометрической подачи, т. е. подачи без учета любой гндромашнны объемного типа	'	-
Q, — К®
Обозначая объемный к. п. д. насоса 1
(1-2)
n Ci
П'’1~0г1’	(13)
где Qi п Q 1 — соответственно действительная подача рассматриваемого насоса и его геометрическая подача, получаем
<?i = u,wlto,ilol,	(1.4)
кд где ы, — -— параметр регулирования насоса;
мд — текущее значение характерного объема насоса переменной подачи.
Для насосов постоянной производительности w = и)ь поэтому = 1.
Применительно к гидродвигателю выражение действительной подачи записывается в форме
Qa — ^2^2 — >	(1-5)
ЧО2
поскольку утечки приводят к увеличению расхода Q2, проходящего через гидродвигатель.
Любые потери в гидромашине, не являющиеся объемными (утечками), называются механическими [48|, поэтому механический к. п. д.
(1.6)
Чо
где 1] — полный к. п. д. гидромашины.
При отсутствии потерь в гидромашине гидравлический (индикаторный) момент на ее валу
Мг = uwp,	(1 -7)
где р — перепад давления в гидромашине.
Сравнивая выражения (1.2) и (1.7), можно убедиться, что характерный размер w является коэффициентом связи как в уравнении связи (1.2) между кинематическими показателями режима, так и
1 Здесь я дальше величины с индексом 1 будут относиться к насосу. Отсутствие индекса будет означать запись выражения применительно к гидро-двигателю. В отдельных случаях отсутствие индекса может также одинаковую правомерность записанного выражения для насо а Д ₽ двигателя В случае противопоставления или сравнения выражений, записи ваемых применительно к насосу и гидродви! ателю, использование индексоа 1 и 2 обязательно.
В»
оои /1 71 между нагрузочными показателями режима ‘	да» об
<18>
ды др
Записывая уравнение энергий применительно к насосу
= QiPi
с ясжяиоиня». рабств " <'®- ““ У^«'т чт°
м, - ““’'Л	(L9>
для гидромотора
(МО)
М2 —
На самом деле у подавляющего большинства гндромашпп const, поэтому рассмотренные выражения применяются в порядке первого приближения. Переменность значения w учитывается соответствующими коэффициентами, рассматриваемыми в следующей главе.
§ 1. 3. НАСОСЫ, ГИДРОМОТОРЫ II ГИДРОПРИВОДЫ ГАММЫ п
Основным объектом исследования в данной работе является получившая большое распространение в машиностроении, особенно в автоматических приводах, гамма II отечественных аксиальнопоршневых гидроприводов, выполняемая во многих модификациях.
Аксиально-поршневые насосы типа ПД (дистанционного управления) или типа ПР (ручного управления) вместе с гидромоторами постоянной подачи типа ИМ являются элементами гидравлических приводов и предназначены для работы в качестве силовых исполнительных агрегатов в различных схемах автоматического и полуавтоматического дистанционного или местного и ручного управления. Все три типа гидромашин предназначены для работы при 160 давлении 100 кГ/см* с допускаемой перегрузкой до
При помощи гидромашин этих типов компонуются гидроприводы олного^нп^0 исполнения НД-Н, включающие насос и гидромотор н2й аггегатРГпиеР1 ” "Редставляюи«е собой законченный автоном-размероН№ о£-2О) аГреГа™ ВЫПУС™ шести типо-нястсТвЫтеке^лМучНзй°хЙ пР°ИЗВОДительности типов ПД и ПР приме-расхед рабочей жилкосты°ГДа НУЖНО быстро и точно регулировать ваемой гидросистеме П° 86/1114,11,6 и направлению в обслужи-
постояв-
(1.8)
(1.9)
(1.10)
II
ляется юбенно
-я в по-'ывается следую-
ы при кой до
” Режима *:ти |48|.
типо-
лужи-
Рис. 1.22. Нераздельный гидропривод типа ПД-Н
> что
:ациях. управ-торами ческих испол-[ полу-
Гидроприводы, составляемые из насоса и гидромотора, служат для плавного (бесступенчатого) регулирования скорости вращения ведомого вала и связанного с ним обслуживаемого агрегата по заранее заданному или желаемому закону при постоянной или мало меняющейся скорости вращения приводного двигателя. Кроме такого способа использования гидропривода-гидроусилителя, применяют гидромотор и насос (обычно постоянной производительности) в качестве трансмиссии (гидравлический вал).
Гидромашины ПД, HP, ИМ и ПД-Н одинаковых номеров имеют одинаковые основные узлы и собираются из одинаковых деталей.
Насосы ПД малых номеров (Ке 0,5—2,5) отличаются по исполнению от насосов больших номеров так же, как и гидромоторы.
Насосы переменной подачи ПД (№ 5—50) составляются по одинаковой гидравлической схеме (рис 1.23), предусматривающей возможность регулирования подачи при помощи маломощных электрогидравлических механизмов управления, рабочий процесс и расчет которых подробно рассмотрен в гл. 11. Конструкции допускают переключение насосов ПД на ручное управление без использования вспомогательных устройств.
Магистрали а и б насоса / (рис. 1.23) присоединяют к гидравлическому исполнительному органу (гидромотор или гидроцилиндр). Давление в приемной магистрали создается вспомогательным насосом 4 постоянной производительности, который одновременно обслуживает основные узлы гидроавтоматики. Рабочая жидкость из насоса 4 подается через фильтр 7 к крану переключения 9, включающему дистанционное или ручное управление, и к подпиточным клапанам 2, обеспечивающим избыточное давление в приемной линии 8—9 ат.
Избыточное количество рабочей жидкости удаляется через сливной клапан 6, а давление подпитки ограничивается предохранительным клапаном 5 (настраивается на давление 20 ат).
Производительность насоса изменяется при помощи управляющего золотника 12 и исполнительных гидроцилиндров 13, поворачивающих люльку насоса 3.
При падении давления подпитки, благодаря срабатыванию запорного клапана 11 в клапанной коробке 10, силовые цилиндры 8 нирЬУпДТВИТеЛЯ СТавЯТ ЛЮЛЬКУ насоса 3 в нейтральное положе-устаиявпш^гНИТеЛЬНЬ1е клапаны гидроприводов этого размера устанавливаются в гидромоторах.
навливаютсяР иешГ Д° № 2,5 пРедохРанительные клапаны 1 уста-^Х5 втнХТДСгееНН° В "аС0Се (РИС- L24)- подпиточный систему подпитки и шестеРенным> а шиберным, обслуживающим coca.	Ц ИНДРЫ управления производительностью ка-
литочным насосом1/ чеоез ппп^ обслуживаются шестеренным полна избыточное давление 2	клапаны 4, настраиваемые
давление 2 ат. Сливнои клапан 3 настраивается на
Рис. 1.23. Гидравлическая схема насосов 11Д № 5-
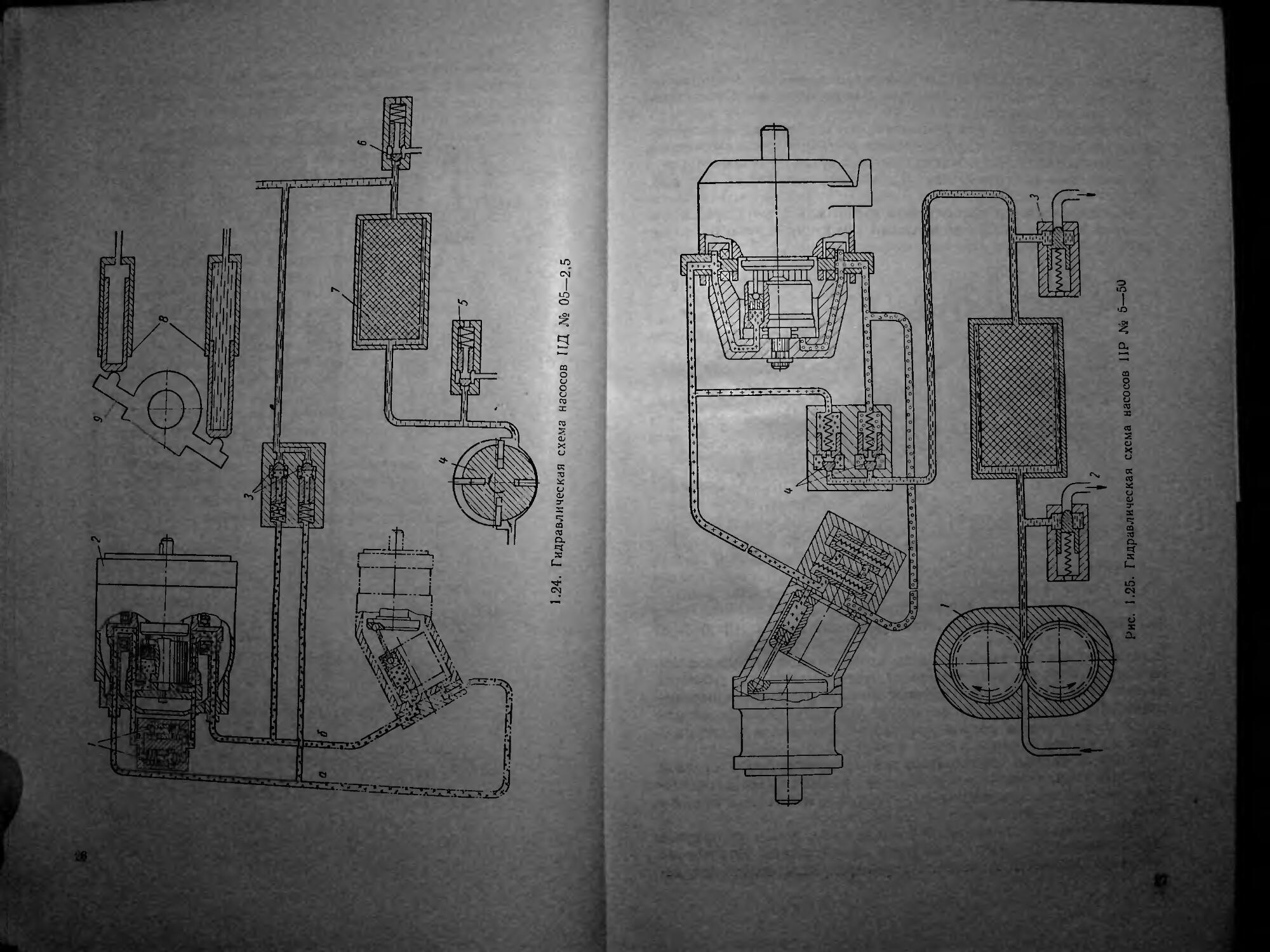
1-24. Гидравлическая схема насосов ЦД № 05—2,5
давление 11 utn, предохранительный клапан 2 системы подпитки — на 20 сип, а предохранительные клапаны устанавливают па исполнительном гидродвигателе.
Гидравлические схемы соответствующих номеров гидроприводов IIH получаются присоединением к гидравлическим схемам участков гидравлических исполнительных органов (гидромоторов), которые показаны условным пунктиром соответственно на рис. 1 23 и 1.24.
Наиболее сложной является кинематическая схема управления насосами ПД (рис. 1.26). Вал насоса 15, вращаемый приводным лви-
Рис. 1.26. Кинематическая схема системы управления насосов
ПД № 5—50
гателем, через карданный механизм вращает блок цилиндров 16-На валу насоса укреплена шестерня /, которая связана с зубчатым колесом 7, сидящим на выступающем конце приводного валика шестеренного насоса. На этом же валике укреплена коническая шестерня 6, вращающая посредством другой конической шестерни 5 валик вибратора 4.
Вибратор служит для создания между золотником и втулкой золотника осциллирующих перемещений, регулируемых по амплитуде, которые при соответствующей амплитуде и частоте повышают чувствительность золотникового устройства.
При уменьшении перекрытий в золотнике с целью увеличения его чувствительности могут возникнуть автоколебания. Наличие же вибратора позволяет иметь величину перекрытий золотника, га-28
рантирующую от возникновения автоколебаний, и одновременно получить его высокую чувствительность.
Валик вибратора 4 имеет на своем конце шейку с резьбой ось которой расположена эксцентрично относительно оси валика’ На шейку валика с резьбой навернута и законтрена глухая гайка вибратора, имеющая цилиндрический палец. Ось пальца, в свою очередь, эксцентрична относительно оси гайки, при этом величина эксцентрицитетов гайки и валика вибратора одинакова. Поэтому при повороте гайки относительно валика вибратора их эксцентрицитеты алгебраически складываются, изменяясь в сумме от нуля до максимального значения, позволяя изменять амплитуду вибрации, передаваемой на втулку золотниковой коробки гидроусилителя 9 при помощи тяги 8, насаженной на палец гайки вибратора.
Управление люлькой насоса производится путем поворота валика управления 11, связанного с рычагом 2, который посредством тяги 10 перемещает золотник гидроусилителя. Рычаг 2, соединенный одним концом через тягу 10 с золотником гидроусили-
теля, другим через тягу 3	Р'|С- I-27- Кинематическая схема системы
с ЛЮЛЬКОЙ гидронасоса, об- управления насосов ПД № 0,5-2,5
разует вместе с рычагом
валика управления 11 механический рычажный дифференциал. Поэтому перемещение золотника гидроусилителя всегда будет равно алгебраической сумме перемещений (углов поворота) валика управления и люльки. А так как расстояние точки крепления тягиЗ на люльке от ее оси поворота равно расстоянию между осями крепления на рычаге 2 тяги 10 и тяги 3, и при среднем положении рычага 2 ось валика управления совпадает с осью крепления тяги 10 на рычаге 2, то угол поворота люльки (при неподвижном золотнике) точно соответствует углу поворота валика управле-
Таким образом, при повороте валика управления перемещается золотник гидроусилителя, открывая доступ рабочей жидкости в соответствующий гидроцилиндр.'Люлька, поворачиваясь, через рычажный дифференциал перемещает золотник к нулевому иол°*^ нию до тех пор, пока угол поворота люльки не будет равен углу поворота валика управления. Этот процесс слежения люльки_за валиком управления благодаря малой постоянно усилителя происходит непрерывно с очень малой оши >
которой может быть рассчитана при использовании материалов, приводимых в гл. 3.
При ручном управлении отклонение люльки осуществляется с помощью силового вала 12 с укрепленной на нем шестерней, сцепляющейся с зубчатым сектором 13, связанным с люлькой на coca. Передаточное отношение шестерни и зубчатого сектора равно 1 : 4, поэтому при ручном управлении полному повороту люльки на угол 30° соответствует угол поворота силового вала на 120
Кинематическая схема насосов ПР № 5—50, в отличие от рассмотренной, включает в себя те же элементы за исключением ва лика управления, приводных шестерен вибратора и рычажного дифференциала.
Значительно проще кинематическая схема насосов ПД мень ших номеров (рис 1.27). В этих конструкциях поворот люльки 1
Рис. 1.28. Кинематическая схема системы управления гидроприводом 11Д-Н Ks 5—20
^Т™ЯетСЯ непосРеДственным поворотом валика ручного vn равления 4 ня vmn ____i-	ручного yn-
(8 на рис. 1.24 и 3 на рис. 1.27) Р щи гиДроцилиндров ния^ПД-'нм’б-го приХипи™РьноРГ1е°Да иераздельного исполнена рис. 1.26, поскольРкГа^
машин ПД н ЦМ в общем корпусе (рис L28) К°МПОНОВКУ ГИДР°-
« 1. 4. КОНСТРУКЦИЯ НАСОСОВ НД № 5-50
“	ПД № 5—50 <р„с. ,.29).
7“УС ‘ К‘’РЙ5ЧаИЙ	о Х'Гь"
зуется как резервуар для рабочей жидкости. С передней и задней сторон корпус закрыт крышками 10 и 20 из алюминиевого сплава. Места разъемов крышек и выходящих наружу деталей уплотняются кольцами из маслостойкой резины, а выходной вал, вал силового управления и валик для дистанционного управления уплотнены манжетами 12. В центральной расточке корпуса 8 помещается приводной вал 13 (вал ротора) насоса, укрепленный в шариковых (или
роликовых) подшипниках 7 и 11. Конец вала ротора, находящийся внутри насоса, выполнен в виде диска, в расточках КОТ°РОГ°’ р“ положенных равномерно по окружности, укреплено семь (или девять) шатунов с поршнями 21.	^.„^поГютяны
Шатуны выполнены из цементуемой стали и тер”^р®^
до высокой твердости. Сферическая головка шатуна замльцотана во вкладыше из бронзы Бр. АЖ9-4, который, в СВОД очере^‘ S лен в расточке вала ротора при помощи^ развальцовки. На другой головке шатуна завальцован бронзовый поршень 21 из бронзы Бр. АЖ 9-4.
3!
"Z’Xy»S^№«»"»CTb «о&лно поворачивать™ в порш. ”” В^ХХ^насоса^Гапф^	укреплена люлька 2
сплотненьУ пртГпомощи комбинированных уплотнении из фторопласта и резины 4 Рабочая жидкость через каналы в крышке 19 люльки, каналы в юльке 2 и отверстия в цапфах 5 подводится к неподвгж-Z фланцам /, установленным на верхней и нижнеп плоскостях
Рис. 1.30 Кодовая часть насоса:
1 — вал насоса; 2 — букса блока цилиндров; 3 — блок цилиндров; 4 — распределитель.
5 — упор блока; 6 — валик кардана; 7 — упор (сферическая опора) вала; 8 — букс» вала
корпуса насоса. В центральной расточке крышки 19 люльки укреплена ось 17, па которой на шарикоподшипнике 15 установлен блок цилиндров 14. Блок на шарикоподшипнике устанавливают с зазором, дающим возможность блоку самоустанавливаться и тем самым сохранять постоянное прилегание торца блока к торцу распределителя 18.
Распределитель 18 выполнен из бронзы Бр. ОСН 10-2-3, торцы его о ра отаны с высокой точностью (допускаемая неплоскостность не должна превышать 5 лис).
В отверстия блока цилиндров с зазором 0.013—0,045 мм (в за-nonvc^TL°T размеР°Б машчны) входят бронзовые поршни. Поле S сумме обычип Т?ВЛеНИе °™ерс™я в блоке цилиндров и поршня в сумме обычно не превышает 15—20 /ик.	F
Детали ходовой части показаны на рис 1 30 пРужХХИвп?“пТОЙННО П₽-ЖЭТ К определителю усилием
Р р оты насоса олок дополнительно прижимается
к распределителю усилием давления жидкости а обеспечения длительном и нормальной работы ° усилйе д-™ в пределах 1 — 1,5% от суммарного усилия пяпп! °Са выбиРается поршни.	У “Я давлен11Я жидкости (1а
Люлька насоса, с закрепленными на ней шатии.
силовых гидроцилиндров управления произиоиХ С П0Ршня«и зава на рис. 1.31.	производительностью, пока-
Синхроииое вращение блока цилинлппп
люльки насоса обеспечивается двойным ! лгобь,х Отклонениях состоящим из валика с за- Явош,ым карданом (рис. 1.32,
прессованными в него двумя пальцами и надетыми на них сегментами. Сегменты входят в пазы буксы 3
fl).
Рис. 1.31. Люлька
й)
Рис 1.32. Двойной кардан:
1 — конструкция с сегментами; б — конструкция с роликами
(см. рис. 1.29) блока цилиндров и буксы 9 вала ротора. Положение валика кардана относительно точки пересечения оси вала ротора с осью блока цилиндров определяется установкой упора в блоке Цилиндров 16. Угол наклона люльки насоса, при котором карданный механизм работает синхронно, примерно равен 28 В этом случае работа трения в сочленениях карданного механизма оказывается наименьшей. Для обеспечения нормальной работы карданный механизм в насосах подвергается принудительной смазке подводимой к нему рабочей жидкостью, отбираемой от сливного клапана.
В последнее время сегментный кардан (на рис. 1.32, а. 1 — валик Кардана, 2 — палец и 3 — сегмент) па всех моделях маиИШ
О, В И Прокофьев и цр — 154
заменяется роликовым карданом (рис. 1.32, б), хорошо заршюмец. девавшим себя при многочисленных испытаниях. В роликовом кардане вместо сегментов применяют ролики из термообработаннои стали ШХ15, все остальные детали - буксы, упоры, также нзготов-
ЛЯЮШестереиный насос, примененный в насосах № 5-50, и шибер-ный (рис 1 33). примененный в насосах № 0,5—2,5, приводятся от вала насоса. Шестеренный насос крепят на передней стенке насоса и соединяют трубопроводом с расточкой в корпусе, в которой
помещается фи л ы р.
В последнее время на всех моделях машин применяются металлокерамические фильтры (см. гл. 13 и 14), которые значительно превосходят по качеству очистки рабочей жидкости щелевые, обеспечивая тонкость фильтрования до размера частиц 20—30 мк.
Рис. 1.33 Шиберный подпиточный насос
Сливной клапан состоит из стакана, в котором под действием пружины перемещается цилиндрический клапан с запирающей конической частью. Клапан регулируется на давление 11—\2 кГ/см2 при полной производительности шестеренного насоса.
Предохранительный клапан шестеренного насоса по конструкции аналогичен сливному клапану и отрегулирован на давление coca СМ 063 Клапана УСТанавливают в расточках в корпусе на-кла?аномТОнЧНппЙ Клапа~н ыСТ0ИТ из стального стакана с коническим 2 5 ^Й П РУ Н0И’ КлаПаН РегУлиРУется на давление 1,5— нем и ™м ж7ТОЧНЫепК?Паны (рис' L34) Установлены в верх-из полости ЛипыгпяЦаХ а^0Чая жидкость к клапанам подводится
Гидроусилители ^трубопроводам и каналам в корпусе насоса, стью насоса поспепгтп Ужащии для управления производительно-золотника, 4 — вибпатоп^ и Р° КИ’ 2 ~ 30л°тник, 3 — втулка Р Р) механического рычажного дифферен-34
циала конструктивно выполнен в виде отдельных узлов (на рис. 1 ЗЬ: / — силовые гидроцилиндры и 2 — поршень со штоком нульустанови геля с пружиной).
Рис. 1.34. Фланец насоса и подпиточный клапан
Золотниковая коробка представляет собой стальную коробку, укрепленную на корпусе насоса, в которой помещена втулка золотника. На втулке шарнирно закреплена тяга, соединяющаяся с вибратором.
Внутри втулки золотниковой коробки размещен золотник, соединенный системой рычагов с валиком управления. Золотниковая
/
Рис. 1.35. Золотниковая коробка с вибратором
коробка трубопроводами соединена с распределительной коробкой и силовыми гидроцилиндрами.
Золотниковая коробка является основным узлом, от работы которого зависит работа всего следящего устройства насоса.
Зазоры между втулкой и золотником как радиальные, так и особенно осевые — между проточками, должны точно выдержи-
„	Уменьшение или увеличение осе-
ваться в определенных пр Д :	к снижецию быстродействия
вых зазоров приводит в од У появление самовозбуждения к ошибкам, » другому может помечь"	»uf„,p„TbCT
„ „„бра,,,,,,.	VrXro расширения, так кок кто
с различными коэффиц пРЧ«Льтатам при различных темпера-приводит к «и»	Т”герХ ». втулки - сталь
ЖИзакда"а»‘до твердой 40-45 единиц ио Роквеллу, золот-Й-S 2ПХ. цементованная по наружному диаметр) и за-"Хияая™ тДдмтп 56-62 «Инины ио Роквеллу, или закале,,.
Рис 1.36. Силовые гидроцнлиндры с иульустановителе.м
ная сталь ШХ15. Золотник и втулка должны быть подвергнуты термообработке для исключения поводок и изменения размеров (обработка холодом).
Силовые цилиндры представляют собой стальной корпус, в котором перемещается шток с поршнем, соединенный с люлькой (рис. 1.36). Зазор между поршнем и корпусом выбирается наименьшим, исходя из расчета, что при максимальной температуре рабочей жидкости между поршнем и корпусом еще есть зазор. Максимальная величина зазора зависит от поля допусков на изготовление.
Силовые цилиндры конструктивно выполнены в одном корпусе с нульусгановителями (см. рис. 1.36). Нульустановитель представляет собой поршень со штоком, перемещающийся в стальном корпусе. од поршня ограничен крышкой, в отверстие которой прохо-Д”!„УГГОК‘ На °°Рщень воздействует расположенная внутри него Пгш	КотоР0^ Достаточно для поворота люльки насоса.
Р чении насоса жидкость подается в корпус перед поршнем
86
Рис 1.37. Распределительная коробка
Рис. 1.38. Насос 11Д № 5—50 со снятой передней крышкой
Рис 1.39. Насос НД № 0.5—2,5 со снятым колпаком
37
л..о.,таТ1,ГЯ сжимая пружину. При этом
и заставляет поршень веР мешать повороту люльки.
штоки утапливаются чтоб,	ми„ль„ая коробка. пристав-
ст» ”»» корпус, а котором расположены золоти,,к
с пружиной И клапан. „ппптн,,|( перемешается, сжимая пру-
ГШФОП..ЛННДРОН „ нульустановителя.
Рис. 1.40. Гидропривод нераздельного исполнения ПД-Н № 0,5—2,5 без корпуса
На рис. 1.38 показан насос ПД № 5—50 со снятой передней крышкой, что позволяет видеть размещение шестеренного насоса, золотниковой коробки, силовых цилиндров, распределительной коробки и трубопроводов, соединяющих их. Ясно видны силовые гидроцилиндры в насосе ПД № 0,5—2,5 со снятым колпаком (рис. 1.39). Эти гидроцилиндры являются единственными узлами гидроавтоматики в насосах малых номеров.
На рис. 1.40 показан нераздельный гидропривод типа ПД-Н № 0,5—2,5 без наружного корпуса — кожуха.
Сопоставляя рис. 1.22, 1.28 и 1.40, можно достаточно точно представить конструкцию гидропривода ПД-Н, общую компоновку и положение соединительных трубопроводов.
§ 1. 5. РАБОТА НАСОСОВ ПД № 5-50
®апЛц=Са Вместе с поРи1,,евой группой вращается от привод-цилинппов Л” Че13е3 каРдаиный валик передает вращение блоку цилиндров и шестеренному насосу, засасывающему рабочую жид-
кость из корпуса насоса и подающему ее через фильтр клапаны подпитки (давление настройки 1,5—2 кГ/см2) в рабочие полости насоса п соединенною с ним гидромотора (или другого исполнительного элемента). Рабочие полости заполняются жидкостью, пока давление возрастает до 11 кГ 1см2, после чего открывшийся сливной клапан пропускает избыток рабочей жидкости обратно в корпус насоса	'
В начальный момент работы насоса ось блока цилиндров и вала с поршневой группой составляют одну прямую, так как пружины нульустановителя удерживают люльку в среднем положении. При возрастании давления свыше 6 кГ/см1 открывается золотник в распределительной коробке и, сжимая пружину, перемещается в крайнее заднее положение. При этом рабочая жидкость, поступая в нульустановптели, перемещает поршни, сжимая пружины, а штоки поршней нульустановителей, погружаясь в гидроцилиндры, освобождают люльку. Одновременно рабочая жидкость начинает поступать в золотниковую коробку и ранее соединенные полости гидро-цилиндров разобщаются. В этом положении насосом можно управлять при помощи валика управления. Поворачивая валик управления в ту или другую сторону от нулевого положения, заставляют перемещаться золотник гидроусилителя, который открывает доступ рабочей жидкости в один из гидроцилиндров.
Поршень гидроцилиндра под действием давления рабочей жидкости перемещается, поворачивая люльку, а второй поршень вытесняет находящуюся под ним рабочую жидкость через золотниковую коробку в корпус насоса. При повороте люльки рычаг механического дифференциала возвращает золотник золотниковой коробки в среднее положение, прекращается доступ рабочей жидкости в гидро-цилиндр и люлька перестает поворачиваться.
Поворот люльки создает наклон оси блока цилиндров к осн вала насоса, и поршни совершают относительное возвратно-поступательное движение в цилиндрах, всасывая и вытесняя рабочую жидкость. Величина хода поршней в цилиндрах зависит от величины угла отклонения люльки насоса от среднего «нулевого» положения.
Управление насосом может производиться при помощи вала силового управления, который через сидящую на нем шестерню поворачивает зубчатый сектор и скрепленную с ним люльку. Для этого устанавливают кран переключения режимов работы в положение ПА. При этом прекращается доступ рабочей жидкости к распределительной коробке и золотник под действием пружины возвращается в крайнее переднее положение.
Переместившийся золотник замыкает полости гидроцилиндров между собой и соединяет полости под поршнями нульустановителей с корпусом насоса. Поршни нульустановителей под действием пру жин выдвигаются и устанавливают люльку в нейтральное положение. Поэтому при управлении насосом через силовой вал люлька,
3»
плвопачиваясь Давит на штоки и сжимает пружины нульустанови. ХТпрн прекращении воздействия люлька опять устанавливается пп\7жинэми в нейтральное положение.
Р>В некоторых случаях применения насосов бывает необходимо остановить вал гидромотора, несмотря на то, что валик управления остается повернутым на некоторый угол. Для этого люльку устанавливают в среднее положение при помощи вала силового управления преодолевая усилие силовых гидроцилиндров. При этом рабо-чая жидкость перепускается из одного гидроцилиндра в другой через клапан в распределительной коробке, отрегулированный на давление 25 кГ/см2.
При прекращении вращения приводного вала давление подпиточного насоса падает, срабатывает золотник распределительной коробки, сообщая полости нульустановителен с баком, штоки нульустановителей выдвигаются и устанавливают люльку в нулевое положение.
большими восприни-
S 1. 6. ОСОБЕННОСТИ КОНСТРУИРОВАНИЯ И ИСПОЛЬЗОВАНИЯ АКСИАЛЬНО-ПОРШНЕВЫХ ГИДРОМАШИН ГАММЫ II
Основным назначением гидромашин гаммы II является их применение в схемах дистанционного управления. Поэтому при выборе конструктивно-силовой схемы основным требованием являлось создание гидромашин с высокими регулировочными качествами и широким диапазоном изменения скоростей. В то же время эти машины должны быть пригодны для применения в любых схемах объемного или дроссельного регулирования там, где требуется широкий диапазон бесступенчатого изменения скорости с ' ускорениями, высокая удельная мощность и способность мать значительные динамические перегрузки.
Производственные и эксплуатационные соображения, связанные с выгодой иметь ряд машин от самых малых до самых крупных, построенных по единому принципу, из одинаковых по форме, назначению и материалу деталей, также наложили свой отпечаток на выбор конструктивно-силовой схемы. Для получения высоких регулировочных качеств одним из основных требований является о еспечение высокого объемного коэффициента полезного действия, не изменяющегося или изменяющегося незначительно в зависимости Ра^очей жидкости, нагрузок и времени работы ма-пав^хГ^^ТиТЬ'^’ПЛУ,,ЖерНЬ,е ГИдРомашины имеют при прочих вЛ±еМНЫЙ К- п- Д- На 3~6% ниже- чем машины чески разгочженпых пат? Дополнительнь1Х утечек из-под гидравли-ный диск МинимальнаяК0Т°РЬ,МИ плУнжеры опираются на наклон-построенных по этим схемам^около^О°30°o6/В°а ГидромотоР°В1 моделей машин даже 260 об/мин 2°~3° ^1мин' & У некотоРь,х 40
Аксиально-плунжерные гидромашины с силовым замыканием поршней хорошо компонуются, имеют малые габариты и в₽с на единицу мощности, однако диапазон регулирования таких машин невелик, а регулировочные свойства ниже, чем машин других типов. Тем не менее во многих случаях применения, в том числе и в некоторых схемах дистанционного управления с низкими требованиями к точности, они с успехом могли бы быть использованы.
Группа гидромашин с упорным диском и точечным касанием головок плунжеров обладает высокими регулировочными качествами, однако не может работать на самовсасывании без дополнительных устройств (например, установка пружин под плунжерами). Осуществление по этой схеме машин большой мощности весьма затруднительно.
Гидромашины, в которых для передачи крутящего момента между валом и кривошипным диском применен силовой карданный механизм, строятся начиная с определенных размеров. Построить машины с силовым карданом малой мощности, а следовательно, малых габаритов, очень сложно и дорого, к тому же каких-либо ощутимых преимуществ такие машины не имеют.
Наиболее приемлемой конструктивно-силовой схемой, по которой можно построить как насосы, так и гилромоторы универсального применения широкого ряда мощностей с очень высокими регулировочными качествами, является схема с наклонным блоком цилиндров. Однако насосы, построенные по этой силовой схеме имеют принципиальный недостаток: необходимость отвода рабочей жидкости под давлением от подвижной качающейся люльки к неподвижным маслопроводам. Такое устройство несколько усложняет конструкцию, делает ее тяжелее и увеличивает габариты. Поэтому гидромашины, построенные по этой схеме, не всегда являются лучшими в тех или иных случаях применения. Однако проектирование и изготовление специальных гидромашин, наиболее удобных и выгодных для каждого случая применения, привело бы к созданию очень большого количества различных типов машин, сильно затруднило производство, снабжение запасными частями и
эксплуатацию.
Гамма II гидромашин состоит из 35 типоразмеров, в которые входят восемь типоразмеров насосов для дистанционного управления типа ПД, восемь типоразмеров насосов для ручного управления типа ПР, шесть типоразмеров нераздельных гидроприводов для дистанционного управления типа ПД-Н, четыре типоразмера нераздельных гидроприводов для ручного управления iтипа I Р-Н и девять типоразмеров гидромоторов типа ИМ, К0ТОР“ работать также и в качестве насосов постоянной производительн -Технические характеристики этих машин приведены в та пь  •
Рассматриваемые гидромашины обладают стабильными харак тер„™м», яеаависямнмн ОТ ИИ- температур,,ых у«о«п» (температура окружающей среды допускается от -аО до -г ои ы.
41
—т~		'		_	Номера гидромашнн								
	0.6	Ъ5	25	Я.5Л	&	» 1	20	30	|	50
Pacxv' гидромотора и подам касоса в елг’гоб		3	9	16	32	71	142	251	501	790
Наибольшее число оборотов вала я минуту: приводного насоса и гидропривода 		2950	2950	29.50		1440	1440	1440	980	980
выходного гидропривода и гидромоторэ . . .	,	± 2930	± 2930	± 2950	+ 1440	+ 1440	+ 1440	± 1440	+ 980	+ 980
Наибольшие производительность насоса и расход гидромо-1 торов (теоретические/ в л мин	9	26.5	47	46	102	204	361	491	774
Момент, развиваемый на валу, в кГм- гидромотора при перепаде давления 100 кГ\см* . .	0,4	1,2	2,1	4,2	10,5	21	37	1	74	1П
гидропривода (номинальный) 		0,33	1.0	1.75	—	95	19	34			
Момент инерции вращающихся частей в кГ. см. сек-’. наСоса и входного вала гидропривода 		0,001	0.004	0.01		0,06	0.193	0.47	1,6	4,26
гидромоторэ и выходного вала гидропривода	0.0009	0.004	0.009	0 02	0,0.56   *	0.175	0.415 ' . 1	1,5 —	3,74
Продолжение табл. 1.12
Номера п-ирамашнч
Показатели	0.5	|	1 5	25	2.5А	5	to	Л)		1 к
Минимальное время изменения производительности от нуля до максимального значения в сек	 Момент трогания валика уп-	0,1 15	0.12 20	0Л5 ‘25	—	0.2 0,35	0.3 0.7	0.35 0.9	0,4 1.2	0,5 1,5
Максимально допустимые моменты: иа валике управления в	100	300	400		10	10	10	10	10
иа валу силового унравле-	1	3	4	——	5	10	20	25	50
| Вес гидромашнн без рабочей 1 жидкости В К.”	10	17,5	29		95	160	238	410	580 535	[
	10	17,5	29	—-	75	140	198	330	
гмиротфиводов 11Д-Н . . >. • ГНДрИПрН» • 40» UP"H	13,5 13	25.7 25,1 4,64	43 42/ 7,0	14,7 1	_	177 152 29	282 52,4	429 79	!21 1	р 1 1 i	.
„ Уяпяктеристики должны быть станагрузок, вибрации и толчко> . ар , Р J30 _)4(r с ЧТ() соответ. Сильными при изменен^i_r^e^ жидкости в 300-400 раз. ствует изменению вязкост Р характеристики заключается Один из способов	X, вместо обычно приме-
в изготовлении блока и Р наоборот, изготовления порш-няющейся для этой целир’ у коэффициент теплового „ей из бронзы вместо стальных.^ Так как^ Повышении темпера_ т^маТишТрабочей жидкости зазор между блоком цилиндров Хршнем Уменьшается. Поэтому, несмотря на значительное уменьшение вязкости рабочей жидкости при нагреве утечки в зазоре
между поршнем и цилиндром
Рис. 1.41. Зависимость утечек через зазор между поршнем и цилиндром, выполненными из разных материалов, от температуры
почти не меняются.
На рис. 1.41 показан характер изменения утечек через этот
Рис. 1.42. Зависимость объемного к. п. д. гидромотора № 20 от давления при разных температурах (работа в насосном режиме)
зазор при изменении температуры при постоянном давлении. Первоначальная величина рассматриваемых зазоров выбирается из условия возможности местного перегрева до температуры НО_
120 С, при которой не должно происходить заклинивания поршней в цилиндрах. Принимая начальную температуру ф- 20° С (темпе-?лло	нагРев деталей может превзойти ее на величину до
1W С. Переохлаждение же деталей относительной той же началь-X ™РГУРЬ’ ?льше’ Чем на 70°С- ПРИ КОТОРОМ может закли-
Р нь в бронзовом блоке цилиндров, вряд ли возможно S*bS ZTT1’2 ~50°Ф Пи7“у ''маль"“й 3"°t’ ° "Z cL,™ Т™1” 7 6Р°“’«“ЫЙ поршень должен ванна-пот,™, п™ паре бР°«»=ий блок цилиндров - стальной XXZT”1 блока ВДЛ“""|’“ “ "а™ р2У5шХВл“ ₽а“К7Г"а""’е“"х	« Уларам»
слабым местом гидромотооов /и t. atOKe испытании показали, что «стающих с риЕГ=.* насосов а некоторых случаях), ра-валу, является кинематическаТцепочка,а“"он"ы“" нагрузками на X почка, передающая вращение от
ТО?
вала блоку цилиндров. Особенно часто ломались у бронзовых бло ков цилиндров выступы для установки буксы блокаРЕ5 ntne‘ даюшпе крутящий момент.	««усы»), пере-
расчет карданного механизма насосов и гидромоторов ведется по инерционным нагрузкам, которые возникают при резкой оста
новке вала гидромотора за время 0,02—0,05 сек.
Рис 1 43. К. п. д. гидроприводов нераздельного исполнения при разных скоростях:
а — для № 0,5—2,5; б — для № 5—20; I — полный к. п. д.; II — объемный к. п. д.
Давление нагнетания
Рис. 1.44. К. П. д. гидромоторов ИМ в зависимости от давления для № 5—50
Использование разности коэффициентов теплового расширения бронзы н стали для компенсации утечек через зазоры и другие меры, как, например, выбор степени гидравлического уравновешивания между блоком цилиндров и распределителем (коэффициента прижима), позволили изготовлять машины с высокими регулировочными качествами и стабильными параметрами.
На рис. 1.42 показана зависимость объемного к. п. д. гидромотора № 20 при работе его в насосном режиме от давления нагнетания при разных температурах рабочей жидкости. Диапазон регулирования скорости вращения вала гидромотора при работе с насосом того же номера
достигает 1 : 1000. В конце гарантийного срока объемный ж п. д. гидромашин в большинстве случаев, как правило, остается в преде Ла%а3ваисХЫс™Добщего°и объемного к. п. д. гидроприводов нераз-ЯМХ исполнения тиноа НД-Н-ПМ ». Р— нения, состоящих из насосов типа НА	Р
ИМ, приведены на рис. 1.43 и 1.44.	гипплсистемы в
Гидравлические машины могут включатьс	Р „ниЯ
различных сочетаниях. В обычную схему машинного рсгу.шроаани.
45
гидропривод нераздельно ^полпенни, при размещении которого как гидропривод Раздельного ’™'е™Я;еРте РуДобном для обслу-насос с приводным дви '	на приводимом им механизме,
при эксплуатации благодаря тому, что насос, гидромотор и связы-ваХе ю; трубопроводы тщательно очищаются и промываются на заводе-изготовителе.	,
Однако компоновочные соображения обычно приводят к выбору раздельного варианта привода.
Гидравлические устройства исключительно чувствительны к засорениям, поэтому подготовка узлов к монтажу, особенно трубопроводов, качество проведения самого монтажа существенно влияют на дальнейшую работоспособность и надежность гидроприводов
Особенно частой ошибкой, допускаемой при монтаже гидрома шин, является небрежная подготовка трубопроводов. Случается, что машины выходят из строя в первые часы работы из-за сильного абразивного износа. Причиной может быть то, что после гибки, пайки или сварки труб и фланцев была применена дробеструйная или пескоструйная очистка, частицы дроби или песка не могли быть полностью удалены из стыков между фланцами и трубами и попали в рабочую жидкость; трубы с множеством изгибов нагревались при гибке, образовалась окалина, которая не была полностью удалена, а после окончательной промывки, при транспортировке труб или их монтаже трубы подвергались ударам и окалина попала в рабочую жидкость.
Для компенсации температурных изменений объема рабочей жидкости в гидросистему должен быть включен пополнительный бак.
Пополнительный бак обычно состоит из литых алюминиевых корпуса и крышки, уровня со смотровым стеклом, используемым пК?ИВКе раб0Че” жндкости- горловины с фильтром для заливки ния ИДК0“СТИ’ а также Сапуна’ предназначенного для сообще-баТ™ ГвыбиОппополнитедьного бака с атмосферой. Объем роси™ L™S V УЧеТ°М °бъема раб0Чей «скости в гид-Ц	олр““й
КОСТИ ^Де°мХаа^вХЬ?п1аКИМ °бра30М> Чтобв! уРовень жид-Иногда это условие полностьюРвмп™ НаСОСе и во в£еи гидросистеме. Дусмотреть меры, гарантипуюшие нельзя. Тогда нужно пре-и зная, что узлы системы нйспг.п, пеРеполнения бака жидкостью, заполнены воздухом, пре^усмотре тТмепь^ чтоТ УР°ВНЙ бЭКа’ буДуТ нормальной работе системы и рь ’ чтобы воздух не помешал
Иногда «„oawySS v„,,X бМТЬ ™ У®®»-гидроцилиндрами, в котопых ппИИ С си,П0ВЫМи несимметричными которых при перемещении штока из бака в
цилиндр и обратно перекачиваются большие объемы рабочей жид кости. В бак в этом случае поступает много воздуха и образуется значительное количество конденсата, который при температупе ниже нуля замерзает, образовавшийся лед попадает в фильтры золотники и другие элементы, нарушая работу системы В этих слу' чаях пополнительные баки должны иметь специальную конструкцию, включающую в себя упругий герметичный элемент, разделяющий рабочую жидкость с атмосферным воздухом. ‘
Кроме бака в гидравлическую схему привода должны быть вклю-
чены предохранительные устройства — клапаны. Насосы малых номеров № 0,5—2,5 включают в себя предохранительные клапаны, смонтированные внутри насосов, а насосы от № 5 до 50 таких устройств не имеют. Предохранительные клапаны для машин № 5—50
Рис 1.45. Детали клапанной коробки устанавливают на крышках гидромоторов, если же в систему не входят гидромоторы, клапанные коробки устанавливают в другом месте и соединяют с магистралями насосов.
При использовании гидромоторов в качестве насосов постоянной производительности клапанные коробки (рис. 1.45) с гидромоторов должны быть сняты во избежание очень быстрого перегрева при работе и установлены в более удаленных точках системы. Клапанные устройства типа ПК специально спроектированы для работы С "в^^ыТу^Хвах режимы работы г»лропр»«=« ковы, ч™ дХкы^допускать „чек., резки, «такоики тора. При этом скорость нарастания давления достигает № т,ю кГ/см2 в секунду. Поэтому предохранительные клапаны ™жкы бЫТЬ^ ОЧеНЬ^ОМСТроД.ЙСТвуюЩНИИ, НО На^абрнР^^^’^^ как вибрация вызывает быстрое разру У прямОГО действия, более быстродействующими	" и Х1е£ие пере-
однако они имеют очень крутую хар Р расхода. Двухкас-пуска таких клапанов очень сильно зависит от расхода, иву
кадные клапаны имеют пологую характеристику, герметичны, однако время срабатывания у них относительно велико. Клапаны типа ПК представляют собой дифференциальные клапаны прямого действия, у которых для исправления характеристики исполь зуется реакция струи жидкости, проходящей через клапан. Благодаря этому клапаны типа ПК обладают достаточным быстродейст вием, а характеристика клапана сделана пологой.
Общий вид такой клапанной коробки и ее детален показан на рис. 1.45, а характеристики — на рис. 1.46.
Насосы должны соединяться с приводными двигателями при помощи эластичной муфты н монтироваться на жестком основании Насосы малых номеров № 0,5—2,5 приспособлены для соединения со встроенным электродвигателем типа АВ, для которого делается специальный корпус и вал. В этом случае электродвигатель может
Рис. 1.46. Характеристики клапанных коробок ПК
иметь только один подшипник на конце вала, противоположном насосу. Второй конец вала электродвигателя, имеющий внутренние шлицы, надевается на шлицевой конец вала насоса. Такая компоновка значительно сокращает габариты всей установки.
Для управления насосами существует целый ряд механизмов управления, построенных по различным схемам. На рис. 1.47 и 1.48 показаны насосы типа ПД № 20 и 2,5 с установленными на них механизмами управления.
На насосах типа ПД № 5—50 с гидроусилителями из корпуса выведен валик управления, максимальный момент на котором не должен превышать 10—40 кГ-см. Поэтому механизм управления должен соединяться с валиком управления через безлюфтовое упругое звено, ограничивающее передаваемый момент при всех углах поворота до 30° во избежание поломок. При установке на насосы ™?ПД № 5 ограничителей мощности или регуляторов для ра оты по схеме с постоянным давлением эти устройства также должны соединяться с управляющим валиком через упругое звено» и ™.“УЯ насось1 в схемах с ручным управлением, необходимо ня вяпикГДУ>г,ЧТ° У насосов типов ПД и ПР величина мертвой зоны на валике управления не превышает 5-6 угловых минут. Поэтому 48
попытки сделать механизм для ручного управления с четкой установкой на нулевое положение часто кончаются неудачей. Для того чтобы все же иметь возможность устанавливать насос в нуле-
Рис. 1 47. Насос ПД № 20 с установленным на нем механизмом управления
Рис. 1.48. Насос 1Щ № 2,5 с установленным на нем механизмом управления
вое положение и исключить «ползучую» скорость гидромотора, иногда идут па ухудшение характеристик всего привода, включая дроссель между рабочими полостями и создавая таким образом внутренние перетечки для увеличения мертвой зоны.
Рис. 1.49.; Схема питающей установки с гидромотором, работающим в качестве насоса постоянной производительности
При расчете автоматических или ручных механизмов управления нужно учитывать, что несмотря на возможность некоторого повышения быстродействия насосов, время изменения производительности от нулевой до максимальной не должно делаться меньше рекомендуемого каталогами и руководствами. Если это время умгиь
4»
л.п,^п. ппсти подпиточного насоса будет недоста-ШИТЬ’ л^яП£пе= слишком быстрого перемещения гидроци-ХХдр^силителя, что может привести к разрушению насоса ВХТисп^ьзоваании в раздельном приводе машин разных номе-ров (обычно насоса с гидромотором большего номера) получают гидравлическую редукцию. В таких случаях необходимо иметь « JhZ что чем крупнее машина, тем большие у нее утечки Поэтому, если например, составить гидропривод с насосом № 2,5 и гидро-мотором № 20, то может оказаться, что в некоторых, даже не особенно жестких режимах работы, подпиточный насос не сможет восполнять утечки и поддерживать давление в полости всасывания на необходимом уровне, т. е. в этом случае также могут наступить явления кавитации. Поэтому, составляя привод из машин разных номеров, необходимо проверять возможные режимы работы.
Очень часто гидромоторы используются в качестве насосов постоянной производительности. В этом случае необходимо обеспечить хорошее всасывание. С этой целью устанавливают всасывающие трубопроводы большего диаметра, размещают бак выше насоса, уменьшают, по возможности, длину всасывающего трубопровода, сокращают до минимума различные колена и изгибы трубопровода. При работе гидромотора в качестве насоса скорость вращения приводного вала должна быть уменьшена в полтора раза против допустимой для гидромотора. Часто для улучшения всасывания, особенно в условиях низких температур, применяют инжекторы^ подводя к ним часть потока жидкости из линии слива. Иногда масляный резервуар используется как корпус для создания питающей насосной установки, в которую помещают также фильтр клапаны и другие узлы. На рис. 1.49 приведена схема такой установки а на рис. 142 к. п д. гидромотора при работе в качестве насоса с постоянной подачей.
Глава 2 кинематика аксиально-поршневых гидром дшин
§ 2. 1. КИНЕМАТИКА ОБОБЩЕННОЙ АКСИАЛЬНО-ПОРШНЕВОЙ ГИДРОМАШИНЫ
Получение точных аналитических зависимостей между углом поворота ведущего вала (а значит, и ротора гидромашины) и относительным перемещением поршня гидромашины в большинстве случаев затруднительно из-за весьма громоздких алгебраических выкладок, несмотря на то, что путь получения точного решения очевиден.
Чаще всего в технической литературе рассматриваются приближенные зависимости между углом поворота вала а и относительным перемещением поршня в цилиндре х только в тех случаях, когда шток поршня находится в общей меридиональной плоскости с осью поршня, или когда рассматривается плунжерная аксиальнопоршневая гидромашина.
Работы, где рассматривается точная задача о кинематике относительного перемещения поршня аксиально-поршиевой гидромашины [481 и [901, исследуют вариант с неизменным значением угла наклона упорного диска у относительно блока цилиндров, т. е. относятся к так называемым статическим исследованиям, не позволяющим установить существование динамической подачи [75J, которая в связи с этим будет специально рассмотрена в § 2.2.
С целью установления точной зависимости х = х (а) рассмотрим обобщенную схему механизма аксиально-поршневой гидромашины, показанную на рис. 2.1. В этой схеме ведущий вал 2 в опоре вра щается с угловой скоростью <о =	, а блок цилиндров 3, ось кото
рого наклонена под углом у к оси приводного вала, вращается с уг левой скоростью Q = вокруг собственной оси. Поскольку поршни 4 при помощи штоков 5 шарнирно связаны с' У”°Р^д цилинд-то они совершают возвратно-поступательные д
Р Рассматриваемый механизм бда^0Да^
и £2 не определена (упорный диск 2 с бл „п„хплы Чтобы этот чески не связаны) обладает двумя
механизм мог быть основой аксиально-поршневой гидром
SI
. „гтяновпть кинематическую завиСп.
«,-лппмо любым способом J ста	ль1Ю.ПОрШпевых гидрома,
"пет. межДУ углами а п ₽• ;пнвЯЮТ синхронный пли асин-Хнах с силовым карданом 5ста ||аЛ1>но.ПОршпевых гпдро. ровный кардан (Л' «а Р''^JнОм устанавливают аспнхро,,. машинах с двойным нес.<« Рально-поршневых гидромашииах ный кардан. В бескарданнь^	сь на юбку порп.ня 4, при.
с ведущими шатУн'™'1ааютУ определенную связь между углами а нудптельно устанавливают f акС11альн0.плунжерных гидрома-,,-р ,701. 1891 и 190J. Вак	ь на упорны.. диск, также
шипах головки п. } И ’ углами а и Р-делают определенной связь между )
Рис. 2.1. Обобщенная схема аксиально-поршневой гидромашины
Используя методы векторной алгебры (90], можно конкретизировать зависимость относительного перемещения поршня в цилиндрах от угла поворота вала а:
*= — 2 Z>sinycosa +/со$ф,	(2.1
при этом
____________ cos <p =
= 1/ 1 ~ Р''1 ~	S'"’ “ ~ р2 (rD - “s v)' “s!« - Зр’Лп X
X |(eos1acosT+sin=a)(l	2usi„
где p =	,	^2,2
2lkD - безразмерный параметр;
чей в упорномНдиске,РаЗМеЩеНИЯ головок ПОРШ' ‘ Длина шатуна-
h _ ы
U’ ~ Дезаксиал;
52
D' ~ “ке;°КРУЖН0СТИ РЙЗМещения ocefi Цилиндров — ₽ — угол отставания блока цилиндров от пов-шневои группы;	1
<р — угол между осями поршня и шатуна
В начальный момент нагнетания при а = 0 поршень в цилиндре находится в наиболее близком положении к поверхности упорного диска и тогда начальная координата будет	н
D .
= — ~2 SI" У + / COS ф0,	(2.3)
а относительное перемещение поршня в цилиндре при повороте поршневой группы на угол а
li = % —	= 2 sin у (1 — cos а) + / (cosip — cos<pn). (2.4)
Приближенные значения h можно получить в предположении, что блок цилиндров и поршневая группа вращаются синхронно, т. е. ф = а — [3 = 0. Считается, что для аксиально-поршневой гпдромашины с двойным несиловым карданом это условие примерно справедливо. Тогда
й = у sin у(1 — cos а) +
+ / [1 Г1 —	l)2sin2a — ра(1 — йо cos у)2 cos2 a —
— ]Л1 — р2(1 — AD cos у)2| = у sin у(1 — cos а) +
+ ' [\/ 1	-*ocosy)2-yl(*D- D2-d-*dCOSY)2]x _
I»	X (1 — cos2 а)
_	1 _р2(1 _АоСО8у)2}_	(2.5)
Если считать, что подрадикальные выражения близки к единице (равносильно предположению о малости угла q>), то раскладывая радикалы в ряд и пользуясь лишь двумя первыми членами, можно получить более простое приближенное выражение перемещения поршня
h= ?{siny(l -cosa) + g^X
X f(l - kD cos Y)2 - (kD - I)2] (1 - cos2 Y)}.	<26)
Следовательно, перемещение поршня в блоке цилиндров мо^ рассматривать в виде суммы двух движений (й из которых часто называют основным
й' = у siny(l — cosa),	* '
наклоном оси блока цилиндров относительно обусловленным толь. г ~ д0П0ЛнИТельным упорного диска, । t
л„ <2-8>
АЛ = Шр''
оси штока поршня от оси цилиндра, обусловленным отклонен допоЛнИтеЛьного перемещения пор.
Разумеется, это^выр	ПОСКОЛЬКу оно не учиты-
S'r«X"y“«»ro перемещения &»-«»	"ТНо-
С"Х”Л»=ь"ч“' при «зегаиле 4». удовлетворяющем условию
_	2
~ 1 + cosin’
(2-9)
дополнительное движение обращается в нуль. °
Дифференцированием полученных уравнении определяют скорость относительного движения поршня в цилиндре и, умножая ее иа площадь поперечного сечеиия поршня, пол)чают расход Однако при таком способе определения производительности полагают у = const, тогда как в регулируемых гидроприводах у =# const, поскольку именно эта величина и является параметром регулирования и изменение подачи будет определяться также изменением значения у Иначе говоря, рассматриваемая система при у =^= const имеет две входные координаты: угол поворота поршневой группы а и угол поворота оси блока цилиндров относительно оси поршневой группы у.
§ 2.2. ПОЛНАЯ ГЕОМЕТРИЧЕСКАЯ ПОДАЧА ГИДРОМАШИНЫ ОБЪЕМНОГО ТИПА
ока^ыва^отсяЬсправед*ивНыми0иеОСНТеЛЬНОГС) Перем«я поршня гидромашии, иоРи дпя роторн'ыхХг^ АЛ" аксиальн°-п°Ршневых типов, поскольку перемещения	гилРОмашин иных
совершаются либо по ХХмонХ™316'"6” ТаКИХ гидР°машин ляюг собою сумму мХапЕХХ °МУ ЗЭКОНу’ ЛИб° "Р^тав-определенным образом связанными ппХ Перемещен”й с разными, гармониками |93|.	ДРУГ с другом (обычно кратные),
«»« ™»ромащшё““ ’SSS'"” п,’’шиеГ| в акснально-плунжер-причем в обеX ИзмененнымКкоэ(^иРц№нЯтомеппП,,СЬ,ВаЮТСЯ равен' м матическои схемы гидрома°шикX^XhoV на
рис. 2.2, и кинематической схемы одного из поршней этой гилоп-машины — на рис. 2.3 (номера позиций иа рис. 2.2 и 2.3 одинаковые).
Одновременное действие нескольких замыкателей, каждый из которых принимает участие в работе в течение конечного весьма краткого промежутка времени, делает подачу дискретной.
При использовании гидромашины в качестве насоса ведущей деталью обязательно должен быть водитель 2 (рис. 2.2), который вращаясь с угловой скоростью <ог, заставляет синхронно вращаться
Рис. 2.2 Схема поршневой роторной гидромашины с плоскостной кинематикой и плоской направляющей:
эксцентрично установленный ротор 3, что вынуждает замыкатель / совершать возвратно-поступательные движения в роторе 3, а также относительно плоской направляющей водителя 2 (481.
Рис. низма машины
2 3 Кинематическая схема меха-одйого из поршней роторной гидро-с плоскостной кинематикой И плоской направляющей
а — кинематическая сх ма гидромашины; б — кинематическая схема механизма изменения подачи, Г — поршень' 2 — плоская направляющая;
3 — ротор. « — распределительная ось; 5 — механизм изменения хода поршня
В случае использования ротора 3 в
в цилиндрах ротора 1481.	„__пи изменением эксцентриаж-
Управление подачей осуществляется изменением
тета е между осями вращения водителя 2 и ро р
^вт.„(1-
(2-Ю)
где
е
(2.И)
w
горизонтальное положе-Е«	- Г”“' ” ОТ''ОС',1еЛЬ’
д =р„1а,-р е(
Г, vinee расстояние поверхности плоской Р " Ха^яюшей от осн вращения блока ц„-П /=льшее значение текущего расстояния; Р«*= еп>=» ' д _расстояние той же поверхности от оси вращения водителя;
эксцентрицитет, т. е. расстояние между осями вращения водителя и блока цилпнд-ров;
Етах _ наибольшее значение эксцентрицитета, « =	— параметр регулирования;
f пт
/ — номер рассматриваемого поршня; а. — Ы| /—угол поворота поршня.
Таким образом,' наибольший полный ход поршня S = 2етах, наибольшая подача любого одного поршня за полный оборот ротора 2ffnia, (где F— площадь поперечного сечения поршня), а удельный объем гидромашины
q = 2Ftmmz см3, об, где г — число поршней.
Очевидно характерный объем гидромашины 1	— z F
2Л ? ~ п remax-
Дифференцируя равенство (2.10) по времени в предположении, что не только «, = а, ((), но и и = и (t), получим выражение скорости относительного движения поршня
vf = Xi = ии>х£тах sin а,- -|- йе1пах (1 — cos a,).	(2. ] 2)
Умножая последнее равенство на площадь поперечного сечения поршня F и суммируя полученное произведение для всех попш ней, одновременно участвующих в по™.» "	ОрШ'
действительной подачи	Д 4 ’ "°Лучим сражение
= «егамШ1^ sin a,. + етахД й ^ (1 _ cos a() =
— UWU).
Z +	5-\ (! _cusai)
(2-13)
56
Первое слагаемое, широко используемое во
дяется обычкой статической подачей; втопое ™ работах- яв-упускают, представляет собой так называем™ Р°е чаще ««его ,’=чу 1751. Эта подача адппкает . «Х’
привода и может быть как незначительной так ^уЛИрования гидро-юшей на динамические процессы системы в завгсим^ст^л”0 Вдия‘ изменения параметра регулирования, структурной с™бЫстроты привода и параметров его составляющих Дементов 1851 ГИДР°'
При равномерном размещении цилиндров в бпок₽ „
осей цилиндров относительно нейтральной оси определяе^я™“и поворо । а «!, a2 = а, + -£ , ..а для Лго порш„я а. == + _ - о 2Г-
В полости нагнетания (одна полуплоскость относительно нейтральной оси) при нечетном числе цилиндров может быть k = **1 поршней; при четном k = -у.
Различными способами (481 можно убедиться, что
,	11 л I
г — I) — I sin —
. П sin — 2
, z	л	2л
k = ив интервале
cosfa! —4^ у sin а,- =
Il
sin
При z четном
(2.14)
в интервале
при г нечетном
будет k = ki — поршней и
. л sin — 2
О < a. — В полости нагнетания
k
cos sin a, = —
> • п
I sin .г
(2.15)
а в интервале
Z - I	о
= —2~ поршней и
k
z
B полости нагнетания будетA
cos — ~2
2sul 22
Графические изображения выражений (2 14) — (2 16) приведены на рис. 2.4, причем графические изображения выражений (2.15) и (2.16) повторяют яруг друга • по фазе на угол ‘ t
со СДВИГОМ
IJ sinBl
Рис 2.5. Графическое изобра-* жение У, cos а,-:
I = I
а — при четном г. б — при нечетном г
Рис. 2.4 Графическое июбраже k
ние J] sin at: i = I
a — при четном г: б — при нечетном з
а среднее значение суммы рассматриваемых синусоид определяется выражением
Аналогично можно получить выражения сумм косинусоид
*
,	л . fen
cos сц-Н^-- 4— s,n —
п sm — Z
; (2.18)
при г четном и А = -|- в интервале O^ajjg —
(2.19)
ппп z нечетном и k — R
nP"	2 в интервале 0
а при z
нечетном и
(2.21)
Графические изображения выражений (2.19) — (2.21), представляющие собой функции, которые претерпевают разрыв,' показаны на рис 2.5, причем их среднее значение равно нулю. Несмотря на то, что все три функции являются синусоидами, при сколько-нибудь значительном числе поршней их изображения так незначительно отличаются от прямых, что в практических расчетах обычно принимаются прямолинейными участками.
Аналогично можно получить для z четного (481
У, sin 2а/ = 0,	(2 22)
для г нечетного
\ Л	sin ('2а, — —
7,sin 2«. = —-—;	(2.23)
—J	2 cos"
»	z
кроме того,
^sin’a,»^- 4-1 Л sin 2а,;	(2.24)
к
У, cosaa4 = ~ ± 1 4-1 A sin 2а,.	(2.25)
н
Сравнив первую часть выражения (2.13) с выражениями (2.14) — (2.16), можно убедиться, что статическая подача гидромашииы неравномерна. Эта неравномерность подачи, оцениваемая коэффициентом неравномерности	’
а = Omax-Cmln,
Цпаж	*
будет тем меньше, чем большее число поршней имеется в гидроме-шине с моногармоническим движением поршней. --------------------------------------------------------------
„ «я по пользуются выражением
В тех случаях, когда значение о мало, п
, Смитах ~~~ (2min 0
° = Qcp
(при 2 -* оо обязательно о' -* о).
При z четном
о.
моногармоннческом движении поршней „ , л 125 .
a = 2sin22-^ 22 ,
(2.28)
при 2 нечетном
Л 500
(У = 2 sin2 4_ А=> -г-
(2.29)
Поскольку статическая подача неравномерна, то и значение характерного*объема w меняется по тому же закону, оцениваемому коэффициентом равномерности подачи £, используя который в ра-венстве (2.26), можно получить
. |min
При этом действительное (в смысле мгновенное) значение ш, определяется через его среднее значение
(2.30)
при помощи выражения
и>м = &,	(2.31)
=	(2.32)
I'	0 w
вХажГнК^пТ?^073 Р°Т0Ра гидР°маш«ны '751- Сравнивая
P (а.31) и (2.13), а также имея в виду равенство 19 171
(2.33)
6 —г / sln о. ,
МП, „ я, •	’	о«мо Среднего
г»д„р,м“	«яикяовеяя, вы„ужде„„ь1х
частота колебания ? по»..
КОМ^та“ойПчастотойНОВ В 220)1 ~ прн 2
rpy™	«яН“Т'Ь,Ю “
вается равной его угловой скорости <0 |48|
явление может привести к существенному сш1же^° "Желательное ' машин В гидроприводе дистанционного Хоп" ^есур« гидро-гидропривод является низкочастотной системой ’ ^скольку достигать значения его резонансных частот В К°ТОрой <0 м°жет ционных частот из-за фильтрующих свойств’гиппо"СТВИе коммута-чески остается незаметным.	идропривода практи-
Подставляя в равенство (2.33) выражения (2.14) - (2
получить при г четном и 0<а,^_	’ Можно
cos — а \
Е _	\ Z Ч
z	. Л ’
sin —
г

при г нечетном и О а, sg
Функции £ периодические, причем в первом случае £ (at) = = | а, + п , а во втором £ (aj = £ (ai +	• где « — любое
целое число.
При решении задач о вынужденных колебаниях, вызываемых неравномерностью подачи гидромашины, методом гармонического анализа параметры составляющих гармоник отыскиваются при помощи выражения при г четном
У, Bk sin kzu>t = | — 1,	(2.34)
k = 1
а при г нечетном
у Bk sin 2 kzwt = 5- 1.	(2.35)
* = i
Определение коэффициентов разложения в ряд Фурье в равенствах (2.34) и (2.35) не представляет труда с учетом выражений ранее определенной статической подачи.
Если дополнительная подача не равна нулю, например, при использовании насоса переменной производительности в ^качестве гидромотора, то она учитывается в форме дополнительной составляющей, определяемой по дополнительной скорости поршня при помощи выражения (2.8):
А/| —	1(1 — До cos у)8 — (kD— l)8Jsinaa = --
=	f (1 — kD cos у)2 — (kD — I)2) sinaa,
_	= <oZpS 1(1cos >)2 —	— । )2I s’n 2fI- (2 36)
— rit 2
При определении действующих усилий приходится обращаться к выражению
м _ ^ = «,*104(1 -kn cosy)2-(kD- 1)2I cos 2ct (2 37)
Однако проще не разделять статическую подачу на основную и динамическую и при значениях у, отличающихся от тех, которые удовлетворяют уравнению (2.9), а выяснять неравномерность вращения блока цилиндров из-за того, что карданное сочленение становится асинхронным. Способ определения этой неравномерности приведен в работе 148]. Очевидно учет неравномерности вращения блока цилиндров, возникающей из-за асинхронности карданного сочленения, равносилен учету дополнительной подачи. По существу введение понятия дополнительная подача и есть способ учета асинхронности карданного сочленения. В той же работе [48| показан соответствующий способ оценки неравномерности подачи
S 2.3. НЕРАВНОМЕРНОСТЬ ДИНАМИЧЕСКОЙ ПОДАЧИ
Динамическая подача, согласно равенству (2.13), может быть выражена
н
(j _cosa.) = l2w	(2.38)

= 7^, (1 — cos а,-). < = 1
При четном числе поошней , „„
Р ей ?, одновременно участвующих
в подаче^!, а VCOSu. = "L
ылД соответствии с равенством (2-19), поэтому
= 1 _ £ 2 Sil] « г
(2.39)
62
Сомножитель второго члена уравнения (9 пт
собой сумму косинусов, изображен сплошной ли^РеДСТаадя^иЙ Ег0 умножение на 7<1 уменьшает произведени " 2Д а С суммой S cos а, (показано пунктигюм , е П° срав,!ению —	Уэйром на том же рис. 2.6, fl)
Вычитая произведение нз единицы, получим ..
коэффициента равномерности показанное на с^ачение Следовательно, величина опоелепя^ Р 2'6’6-
ного числа поршней, колеблется равномерно ^'ИЯнием к°неч-равного положительной единице, и может оцениватмТан^и^о
равномерности динамической подачи при четном г
и динамической подач от числа поршней
тому, как оценивалось изменение коэффициента равномерности статической подачи £, при помощи коэффициента неравномерности подачи
“(Umax +
(2.40)
так как
2	/»• \ i । 2
G<,)n.ln = 1 - 7; «	= 1 + Г’
Следовательно, колебания величины коэффициента Ь около положительной единицы весьма существенны, о чем можно судить по величине коэффициента неравномерности аа, значения которого показаны на рнс. 2.7 и там же приведены величины отношений , которые показывают во сколько раз колебание коэффициента Ь больше колебания коэффициента Несмотря на то, что с увеличением г величина этого отношения возрастает, следует увеличивав» * так как при этом уменьшаются значения о<> и о.

„ ,л отелиться, ЧТО при г почетном п Аналогичным способом можно уоедитьс
(2.41)
а при г нечетном и	г _ ] _ 1 — А
Л 2 sin
ZZ
Графическое изображение полученных результатов приведено Р 4 98 б На рис. 2.8, а даны соответствующие исходные 	Г	41П ПИП ЛПП^ПППО.
на рис
Йшо;
Icosa.
a-ul
tiCOSH
ai
2
'7
fl

V-Cjf
динамическом подачи при нечет
выражения для определения Ед. и.
Коммутационная частота динамической подачи при ! четном и г нечетном определяется одинаково произведением угловой скорости гндромашпны на число поршней
Кроме того, коэффициент неравномерности динамической подачи при г четном и z нечетном опре-
деляется одним и тем же
уравнением (2.39).
Рис. 2 8. Определение коэффициента равномерности ----------—......... —.... -
пом г
§ 2.4. ФИЗИЧЕСКИЙ СМЫСЛ ДИНАМИЧЕСКОЙ подачи
На рис. 2.9 показан поршень 7, находящийся в цилиндре ротора 2 при нулевом значении параметра регулирования (е ~ и = = 0), имеющем место при совпадении центров О п на рис. 2.2 и 2.3.
При Q и вращении ротора гидромашины (щ
2.9. Относительное перемещение порш ня в Цилиндре 1
около среднего noXX^OcT	°Т 061 Д0 11 обР™
те ЛЛТСТКУ часть объема ц„Т'Т ДВИЖенин заштриховаи-Йть5 ?!ует В ГЮдаМ, будет при ка^тп6^В,',ЯЮщаяся Рабочсй
Я И3 Лод™ нагнетания в noS в °Р°те ротора пе»’ен0*
И	‘ ь ^асывания и обратно.
Как только параметр регулирования НЯи„
граница нерабочего объема аа, отстоящая от соели₽еНЯТЬСя ~ л*>ая на расстоянии х — г, начнет перемещаться Д его ПОложрния 00 нерабочий ооьем, за счет которого и создаётДЗМеНЯЯ ПР» ^ом динамическая подача.	г создается Дополнительная
С“’Г,’СТ"	гра„„цы аа, я«,яющаяся
вытеснения рабочего объема, будет х = de . .
(It = Kema*.
скоростью
Так как в подаче одновременно „р„„к„ает у,апж , й (использование этого значения правомерно в спя™ с 2 ба1„,я рассматриваемой подачи учитываются коэ^Х^ТГ то среднее значение динамической подачи будет W ЦИентом
Qn = й у emaxf = йш 4,
поскольку <?! 2ли» — 2emax Fz, что совпадает с соответствующей частью выражения (2.38).
Совпадение решений, полученных двумя разными способами, позволяет трактовать дополнительную динамическую подачу как результат изменения нерабочих объемов в цилиндрах гидромашины. Поэтому расчет гидроприводов по осредненным значениям параметров I пдромашпн, используемых в системах автоматического регулирования, следует вести по характерному объему w. исправленному безразмерным множителем р = 1 + > нли в изображениях по Лапласу р = 1 + ^-s = 1 + ТjS .
В ряде случаев значение постоянной времени Тг>- оказывается столь малым по сравнению с остальными постоянными времени [ 4-= ^^оказывается вне полосы частот пропускания), что
\ Гд	л
ее влиянием можно пренебречь. Однако могут встретиться многоконтурные системы, в которых при расчете высокочастотных кон-туров пренебрегать значением Тд окажется невозможным 1851.
8 2. 5. О ВЫБОРЕ НЕКОТОРЫХ ГЕОМЕТРИЧЕСКИХ РАЗМЕРОВ АКСИАЛЬНО-ПОРШНЕВЫХ ГИДРОМ ШИН
В аксиально-поршневых сидромашипах постоянно* лоИ» можно выбрать значение дезаксиала ko так, чтОб“	V? '
чтобы удовлетворялось условие (2-9). Тогда Довални^пм^а.-, обращается в нуль и относительное движение поршне	Ш
приближается к моногармоническому-. <	'
Для гидромашин с регулируемой	ми
значения у нельзя выбрать такое значение деа^>ц Дополнительная подача обращается в нуль.
3 U Н Прокофьев И ДР	-	• Vх*
Г®
„..спала показана на рис. 2 10. значения дезакснала, при кото-
с переменной подачей п для гидромоторов с постоянной подачей по-разном) выбирают значение дезакснала.
Зависимость дополнительного перемещения поршня \h от значения у при разных значениях дезакснала показана на рис. 2 ю Для гпдромоторов выбирают такие значения дезакснала, при которых ДЛ = 0, т. е. в соответствии с равенством (2.9) в зависимости от значения угла у = у0.
Для насосов с переменной подачей выбирают значение kp так, чтобы Д/; при наибольшем возмож-yu было равно по абсо-но отлн-
Рис 2 11 Зависимость <р, <рх и <pv 01 угла и поворота поршневой
группы при kD= 1,07 ир =
2 kD
ном угле у.
ПОТНОЙ величине Aftm.ix,
Рис 2.10. Зависимость дополнительных перемещений поршни от у при различных значениях дезакснала kD
Для насосов с у„ = 30 выбирают kp = 1,055 -и 1,072, для 1идромоторов с у = 30 kp — 1,072, для гидромоторов с у = 45° принимают йи = 1,175.
При выборе диаметра шатуна необходимо убедиться в том, что он не задевает за кромку цилиндра. Точная оценка действительного положения шатуна может быть произведена вычислением значения угла наклона оси шатуна но отношению к оси цилиндра при помощи уравнения (2.2) с учетом того, что разным значениям угла поворота поршневой группы соответствуют разные положения поршня в цилиндре.
Более пр< т поверочный приближенный расчет значения v™ р радианах, к которому обращаются при мРалых значе иях Я ; ^.нхропном вращении блока цилиндров с поршневой 1	_ р 0) в тех случаях, когда при компоновке гидром™",
ведомо оказывается невозможным касание штока кромки цилиндра „блоке. Сущность этого приема заключается в приближенном оп£ делении ума <Р по двум составляющим <рх и <ру:
(2.42)
где
cpv p(kn— l)sina н <pv = p (&n cos-p — l)cosa (2.43)
Графики изменения углов <рд., ср,, и ср в зависимости от угла поворота поршневой группы а при kD = 1,07 ир = ~ (I = D) при. ведены на рис. 2.11. Наибольшее значение <р = р (kD — 1) имеет л место при a = y-
к
Глава 3
НЕКОТОРЫЕ ВОПРОСЫ РАСЧЕТА РАБОЧИХ ОРГАНОВ АКСИАЛЬНО ПОРШНЕВЫХ ГИДРОМ -AUIIIII
§ 3.1. ОПРЕДЕЛЕНИЕ ОСНОВНЫХ РАЗМЕРОВ БЛОКА ЦИЛИНДРОВ
Основные размеры блока цилиндров роторной аксиально-поршневой гидромашипы должны обеспечить получение заданного удельного объема q см3 об при определенных допустимых параметрах (прочность блока, скорость скольжения, удельные давления). При этом следует стремиться
Он------
достижению минимальных размеров блока, так как его размеры существенно влияют на размеры всей гидромашипы и определяют момент инерции вращающихся частей. Зависимость удельного объема q или характерного размера/^ от диаметра поршня d„, диаметра делительной окружности упорного диска Dp и угла наклона оси блока цилиндров у определяется уравнением q=Dv = zFnDp sin у =
Л(/п
= -^-zDpsiny. (3.1)
Основные расчетные размеры блока цилиндров показаны на рис. 3.1.
Рис. 3.1 Основные расчетные размеры блока цилиндров
Прочность стенки цилиндра оценивается приближенно по известной зависимости напряжения от растяжения стенок толстостенной трубы, внутри которой действует давление р,
П-Л‘+Г<_ Аа4-1 ’ р& — гг ~ р Л!— 1 ’
(3-2)
где
А = - =
Г dn
Суммарное напряжение о на внутренней поверхности цилиндра определяется из равенства
„ _ „ -А12	2А»
Р №~гг~ р А*~ Г
(3 3)
Соотношение между прочностью материала блока цилиндров и аКсимальным допустимым давлением р дано в табл. 3.1.
Прочность материала
Сталь, одоп — 1-500 кГсм-Ьронза, ааоп = 600 кГ/сл«
Таблица 3 I
Макимально допустимое давление р » ,r/ot, [ при А
	1.3	Ь4	I.S	16 [
•	306 123	ЗС18 147	416 166	456
110ДСТЭВЛЯЯ в уравнение (3.1), определенное из Л ОВС (рис. 3.1) соотношение Dlf sin — — dn 4- b = R 4- г. получаем зависимость диаметра поршня от удельного объема или характерного размера Dg гидромашины
3 dn = К<7  |
8 sin —
________£_______ j г) •
nze sin у {A + 1) ~ n v’
где — размер dn в долях от характерного размера Dg; а
(3-4)
о  Л
8 sin — z
F	jue sin у (Д 4- 1) ‘
аналогично диаметр делительной окружности блока Л _ Л + 1 _ Л £) . Ua - 2	. я
sin -Z
цилиндров
(3.5)
наружный диаметр блока цилиндров
+ dn+ 2b~DHDq-
(3.6)
ход поршня
(3.7)
h — Dp sin у = eDu sin у = bDq.
Таким образом, все основные размеры поршневой группы: dH, Dlt, DH и h, закономерно выражаются в долях от характерного размера Dt/ или от диаметра поршня dn. Так как в выражении (3.4) влияние А на dn мало, диаметр поршня зависит в основном
(3.6)
_________________ dn = az ", где а = 1,82 для А == 1,5; у ₽ 30°.
Относительные размеры блока цилиндров „
в табл. 3.2. Из таблицы следует, что число поршне# мйЗн> ал*
Таблица 3.2
Рдзморы F ДОЛЯХ 01 характер-	г - 7	А = г = 9	= 1.3 г=Н	г=13	г7	А =	1.4 г-П	г- 13	А = г 7	।	„	1 1	II	01 °
него	0.50 1.34	1	 0,43 1,44	0,39 1,52	0.34 1,62 1 74 2.06 1,18 0.87	0,50 1,37 1,47 2,07 0,67 0.72	0.42 1,49 1.59	0,38 1,57 1.68	0,33 1,67 1,79	0.49 1,41 1,51	0.42 1,52 1 63
a-l Ь t>| * ж чэ :	1,44 2.00 0.68 0.12	1,54 2,00 0.88 0,77	1 83 2,02 1,02 0.82			2,08 0.90 0,80	2,09 1,05 0.84	2,14 1,20 0,89	2,14 0,68 0,75	2,14 0 90 0,81
Размеры в полях от характер ного	А =	= 1.5		А =	1.6			д =	= 1.7		
	г=Н	г= 13	г = 7	« = 9	г- И	г =13	г-7	2 = 9	г = II	z== 13
d .	0.36	0,33	0,48	0.41	0,36	0,32	0,48	0,41	0.35	0,32
С 5Г «  IQ |С	1,62 1,74	1,71 1,84	1,45 1,55	1.56 1,67	1,66 1,78	1,75 1,89	1,48 1,59	1,8 1,72	1,7 1,82	1,79 1,92
	2,17	2,21	2,22	2,22	2,24	2,27	2,30	2,29	2,30	2,32
д	1,07	1,20	0,68	090	1,08	1,24	0,66	0.90	1,10	1,26
л	0.87	0.92	0.78	0,84	0,89	0,94	0,80	0,85	0,91	0.96
на наружный диаметр блока D,, существенно влияет на диаметр поршня d„ и на диаметр внутренней полости блока De, в которой располагаются карданный механизм и подшипник блока. При проектировании необходимо учитывать, что головка карданного механизма имеет размер D, = (0,8 ч- 0,9) Dq и необходимо обеспечить DK «£ D„. При выборе размеров блока цилиндров следует проверить, разместятся ли на упорном диске вала головки и опоры шатунов. Размеры больших головок шатунов d,„ = (1	1,08) dn и тем больше,
чем больше заданное максимальное давление в гидромашине.
S 3. 2. ПОРЯДОК ПРОЕКТИРОВАНИЯ БЛОКА ЦИЛИНДРОВ
1. По заданным расходу Q и числу оборотов п определяют необходимые удельный объем q и характерный размер ZX При X
«.	л (табл. 3.1)
поршней г для углаР наклона	ТабЛ' 32 вь1биРают число
вести расчет но уравнениям (34)-°(3.8)™ ДРУГ”Х V Необходнмо
70
пияметр поршня dn желательно округлять до ближайшего Д но ГОСТу 6636-60 (ряд Ra 40): dn = 8-9-10-()_ 3"аЧП -14 -15—16—17—18—Ю—20—21 -22 - 24 - 25 - 26 -28-12 32—34 -36—38 40—45 м и т. д.
30''' гидромашин малых размеров часто приходится применять
>тпы через I мм в интервале до 20 мм
диаме I ’’ ерЯЮТ размещение головок шатунов (d,„) в упорном *’• па н кардана в блоке цилиндров. После этого окончательно диске j у и рассчитывают все остальные размеры по урав-выбираю , «.
пениям (3.1)	1° ‘>
§ 3.3.	МОМЕНТ НА НАЛУ II ОСНОВНЫЕ СИЛОВЫЕ НАГРУЗКИ АКСИАЛЬНО ПОРШНЕВОЙ ГИДРОМАШПНЫ
С НАКЛОННЫМ КЛОКОМ ЦИЛИНДРОВ
Момент на валу создается силами давления на поршни, которые через шатуны воздействуют на упорный диск. Составляющие сил давления в опорах создают крутящий момент, который без учета
Рис. 3.2 Схема дейсгвуюших сил
потерь можно определить, пользуясь схемой на рис. 3 2. На каждый поршень полости нагнетания действует гидростатическая сила рг„. 11ри отклонении оси вала от оси блока на угол у эта сила направ-
71
лена поп углом 90 — у + «г к упорному лиску вала, где"
между осью шатуна и осью цилиндра, определяемый по фор‘п°'’1 (2 42). Пржкиня силы давления, создающая момент от од, поршня, равна	0,0
А., = р1" sin (У — фг)
Подставляя угол % из выражения (2.43) и принимая cos «г- cos <&. вследствие малости углов <р и <р,„ получаем момент, н(>зГ нпкающпн от действия одного поршня,
Л/, — pF„	S И) у S111 «, —
— pF"	сOs 1* — oos«; sin
Все поршни полости нагнетания создают мгновенный момент Ми-
ь,
Mt t — pFn у sin у sin а, —
i = I
г L>p I Dj, \	\S
pFn 8 ii^r/^,cosV— 1) J sin 2а,.	(3 9)
Среднее значение момента определим, воспользовавшись нениями (2.17) и (2.22) для сумм синусов углов одной Так как? Vsina,!^ я« - |	др = о, го г
момента от действия поршней полости нагнетания
урав-полостп. sin 2а, jcp = 0, то среднее значение
ср —	» 3
__ PiFnDp sin у 1 у~ •
Следовательно, с учетом ческих сил, действующих на тания, будет
выражения (3-1) момент от гидростати-поршнн, находящиеся в полости нагие*
М
2л-
Аналогично определяется момент М2 от гидростатических сил, действующих на поршни в полости всасывания, где давление равно ри. Этот момент направлен противоположно А1,
Результирующий момент на валу
Л1» М, ~ М, - W-S	Ро) w.	(3.10)
-на валу будет отличаться на величину момента механических потерь.
ТО ‘	-
Коэффишк-нт неравномерности мсш^
определяют без учета влияния угла „Л "а ВадУ пщпомя практически величина максимального ч?'3 И'атуна в уравнении (3 ..)) не превосходит 0 4%	втоРого чл
налу. Коэффициенты неравномерности мХ,,£ДНего м™™та ковы;	,,с"та и подачи
о н = ——'____'1_ । S sin а
Л f	• == 1 —____!т»п
П|а*	IX sin а —
’шах
Для нечетного числа поршней о = |2-'% 300%	м га . для
G|J z2
так как второго члена
...а на одина-
(3.11)
четного
I;
I.
И
§ 3. 4. ОСНОВНЫЕ СИЛОВЫЕ НАГРУЗКИ В ПОРШНЕВОЙ ГРУППЕ
Основными силовыми нагрузками в поршневой группе являются-
1)	силы давления на поршни, передающиеся на упорный диск вала, создающие момент на валу и реакции в подшипниках;
2)	силы давления в направлении оси блока цилиндров, прижимающие блок цилиндров к распределителю и действующие через распределитель на корпус гидромотора или люльку насоса; дополнительно к этим силам действует пружина блока, уравновешивающая силы, отрывающие блок цилиндров от распределителя при низком давлении;
3)	силы трения, из которых основные:
а)	силы трения блока по распределителю, создающие момент трения, воспринимаемый синхронизирующей передачей (карданным механизмом);
б)	силы трения поршней по цилиндрам и головок шатунов в опорах поршней н упорного диска вала, создающие силы, опрокидывающие блок цилиндров относительно распределителя;
в)	силы трения в подшипниках вала.
Координаты векторов сил давления, действующих иа вал, показаны на рис. 3.3. В первом приближении можно считать векторы всех сил, передающихся шатунами, параллельными, прене per небольшим углом <р между осями цилиндра и шатуна.
Со стороны полости нагнетания действует сила пая иод углом у к диску вала, а вдоль оси сила од> р
л 'ДО в период поворота вала на угол	я
^Удет а при повороте на угол — г При дальнейшем повороте- вала провесе циклическ
1
'-I
направлен-этом
(3.12)
поршней г-1 г-5-
Координаты
'юф<’р”у“и
13. n
Dr „	,. -{^cosa, - координаты
' sina,. Ifi — 2
каож опоры
где x штока.
После подстановки средней величины cj'Mm полз’чим средние координаты равнодействующей А = ')р; }' = 0.
Л
V"in«<|rp ~
При повороте вала величина сумм меняется н
*	••	_____„г. А«.плт нмртц КООрДННЛТЫ,
мгновенное дна-сметающиеся
чение равнодействующей будет иметь
SL П У
Рис. 3.3. Векторы сил давления, действующих на вал
по двум кривым вблизи ТОЧКИ ; о], Со стороны полости вытеснения
(рнс. 3.3):
заштрихованной на рис. 3.2. действует осевая сила Ро0
~ pFп—2’ cosy
(3.14)
со средними координатами jr0 , у0 — q РезультируЮщая этих двух сип Р - р in
мается упорным подшипником а~ Рао восприии-
pe«.fejd£±£o)iI	1
(3 15)
74
В. 16) реакций в Под.
Средние координаты осевой силы
" 'WV*0
Эти координаты необходимы для 0ППрпо
)Нцпниках вала в плоскости XOZ р(-деления Величину и координаты равнодействующ"
ствуютеи на люльку насоса или корпус ги™ СНЛ Давления, дей-бдока-цилиндров, определяют аналогиЧныУ о^ра “ стороны цилиндре полости нагнетания действует сила nF В ка*Дом гнетанпя возникает результирующая сила лавп» ‘ гГ пол°сти ла-вытеснения результирующая сила Р„ гп г-, я а в полости « средними координатами
Х л- ^0:
Рр — РР п 2 '• Рр — РпР п~2~
Их равнодействующая Рг, вдоль оси блока равна
Р j *	в Р ~Ь Pd Г | 4- Р— Ре 1
6	2 I ~^(/' + р»Н
(3.17)
(3 18)
н имеет координаты
=	(3-U)
Эти координаты необходимы для расчета блока цилиндров на опрокидывание относительно распределителя и для определения усилия, действующего на регулирующий орган (люльку) насоса.
§ 3. 5. МОМЕНТ НЛП УСИЛИЕ НА РЕГУЛИРУЮЩЕМ ОРГАНЕ
Момент или усилие, действующие на регулирующий орган, — важнейшая характеристика регулируемой гидропередачи, необходимая для выбора гидроусилителя или других устройств для управления гидропередачей. Усилие, действующее на регулирующий орган, является -основной составляющей внешнего воздейств!Гя, необходимого для перемещения регулирующего органа или удержания его в покое. В аксиалыю-поршиевом насосе регулирующий орган (люлька) является опорой блока цилиндров и местом расположения каналов для подвода рабочей жидкости к торцевому распределителю и отвода ее. Люлька -поворачивается относительно оси Цапф (рис. 3.4), изменяя подачу насоса.	
Силы, действующие на регулирующий орган, разделяются к три группы: силы, определяемые гидростатическим давление смоченные рабочие органы; реактивное сопротивление, опредмгг Мое массой и ускорением деталей, и активное сопротнвлен > Р Деляемое силами трения в местах соприкосновения деталей
»— - —
"а Равнодействующая	Так как м?но-
“« М‘тс’
среднего положения л •
; мгно-смещаются относительно JL происходит смеще-
за время
, то
Рис. 3.5. Схема сил, действующих на регулирующий орган

Рис. 3.4. Схема люльки
ние Рг, из точки а в точку b (рис. 3.6, о), затем следует мгновенное перемещение в точку с и смещение за время в точку d. Далее цикл повторяется. В результате воздействия сил давления в опорах регулирующего органа (люльки) создаются реакции, вызывающие трение при его движении. Мгновенное смещение равнодействующей г 4 от плоскости XOZ вызывает — цапф, разного
(3.20)
появление момента относительно
^xt = (р — р0) Рп J1 cos о
Цапф, является з?шопеременнойСНЛЫ 5авле11ия относительно оси период колебания7^	~*Й
мента равно нулю Rr W Р ‘ 3’6’ С₽сднее значение мо-„	₽	ВСЗД*	ЧАСТОТЫ гае6ан„й, срав„„.
Рис. 3.6. Гидростатические усилия в цилиндрах
на участках	2 2 - 2’ и Z - 3 и т. д. может вызывать
сползание незакрепленной люльки в крайнее положение если остальные действующие силы будут незначительны.
Рис. 3.7. Момент от неточности изготовления
Неточность выполнения некоторых размеров регулирующего органа может значительно изменить момент вектора равнодействующей силы Р„. Если ось цапф люльки XX повернута или смещена относительно оси распределителя X' X' (рис. 3.7), то координ
V
где Д'/ - плечо
цапф АХ;
д»' — плечо, гелию оси ряслрокл"’»"
(3.22)
,11вно.ейст«'п.'Х'- П булут ;= = ":= — S'"'	»">
Л “	 ..„wh относительно осн
вектора равнодействующей
осн цапф относп-'• опредсляеж. У^а J * вектора силы /ф,
лЛ Д'/ = Аб IMj.
да в_уго. оли^ьиог»	О—"
’ Мнение (МО -«"»
м-ол7' ” ’Z.
А.Р’Ч"-'
Тогда момент /Ид будет
Л4Д = А?д (р + Ро) £)«>
где /ИА = я/^"А-)1 — безразмерный коэффициент.
Для насосов с характерным размером 1,6—3,2 см и плечом Др = 0,1 леи коэффициент /Ид = 0,001 -е 0,003.
Направление действия момента Л1д зависит от направления вращения вала насоса, которое определяется положением плеча Др' в полости нагнетания. Если ось цапф отклонена от оси ОХ' в направлении вращения вала насоса, составляющая момента Мд от Др' уменьшает угол наклона люльки у. Если ось цапф отклонена в сторону, противоположную направлению вращения вала насоса, то составляющая момента/Ид стремится повернуть люльку в крайнее положение. Смещение оси цапф параллельно оси О'Х' на величину Др создает момент, стремящийся повернуть люльку в какое-то одно крайнее, либо нулевое положение. Значение величины угловой ошибки 6 и смещения Др устанавливается допусками на изготовление. При расчете момента на регулирующем органе необ-
м“?™ТЬ момент ПРН неблагоприятном сочетании допусков. давпения°пчяК^е искУсственн0 смещать равнодействующую сил
На HenoLLJ.ТеНИЯ М°МеН™ На Роллирующем органе, действующей силы лявпе лируюВ1ИВ °Рган помимо момента равно-шатунов. Большие гопов™8 деиствУет момент трения в головках плоскости XOY (см оие ч г*уагунов поворачиваются относительно Ротора. При Э1ом шатун впашяя Г°Л 2 (v + %') 32 каждый оборот а1ун вР2^а«ся И вокруг своей оси. Малые /о
и1(„ шатунов также поворачиваются относительно вкладышей гол() лей но на угол 2 3 .
скольку на сферическую головку шатуна передается сила
1 /я" действующая па поршень, в опорах ротора возникает давпС1П трецця, пропорциональный давлению Этот момент пере-моМе"т Я1£пьке посредством добавочного бокового давления порш-даетСЙ Стенки цилиндров.
цеп !и ое давление головок шатунов на опоры больше давления
УДе'П пах При таких удельных давлениях не может быть обес-в цилиндр дкОСТ1Юе трепне. Поэтому момент трения в большой шатунов М Uli приближенно может быть определен по фор роповке ш у муле	(I
M‘lui = iutFnp-^
(3.23)
f __ коэффициент трения в опоре; гДЧ'"_ площадь поршня в см ;
j ' пиаметр большой головки шатуна в
и" 7м найти составляющую момента трения относительно оси необходимо определить направление момента трения иапф шатуне Затем моменты Л м.
см.
Рис 3 8. Схема движения ша гуна
мла ротора
- можно прене-
В Иа1шДМ ^каждом шатуне необ-сложить. используя изложеи-
НУЮКХеат“‘Хсительного движения шатуна показана на рис. 3.8. Гжду радиусом OS и осьюэ шат^ координатными осями и Р_^У ns (8 = 90 — «; и = а> —	’
05 (о - уо . f	шатуна
между радиусом и ось > SQ (62 = 90 + <р/ В 9г°ол nj+p и = -у ф- <pv), где от У	определяемые
Ф, и V-составляющие угла <Р.	9 даЛЬнейшем можнм
(2.42),	(2.43). Однако Угла^И ^тиошений аналитической бречь. На основе известны-	гла ф-_
получим формулу для опред •	ipnSCt	(3.24)
с„ьЧ1-еоЧ90»-г + <’->с“ •
В опоре большой ™ов« ^7"-
Mlui, направленный против д ендикуляром к_ ^костИ, прохо-совпадает по направлению с nepHpaBHeHiie этой плоское , ходящей через прямые Оо Дящей через начало координа	m — 0.
Xeost + Seob1.+ ^“’'-
(3.27)
..лмента грення в оольшой г_
между напр	_~j1^cosa	cOS ah	(3.26)
Mud . tP2 V a
зменателе дает незначительное изменение Л4„„.
и может быть принят	на регулирующий орган
Рассмотрим действие мо	,я в больШОЙ головке шатуна.
Чтобы преодолеть сопротивле^ £ьдоЛЖ„о быть приложено боковое к другой головке на СовмесТНОе воздействие всех этих боко-усилие Ршхь Равиое L ’
• а плече0*'cos a sin у создает момент Мш, поворачи-вых усилии на плече  ваюший люльку относительно оси цапф XX.
мш =	cos2 "* •
i = I
Среднее значение суммы 2 cos2 а равно Поэтому без учета знакопеременной части момента Мш, используя обозначения на рис. 3.4. получаем
Мш = /и (р + Ро) ЛД sin yz 1(“ .	(3.28)
В этой формуле можно заменить D4 = D^ko и записать
Мш = (р + pjALDJsiny,	(3.29)
где Мш = ~~ • у • sirl — безразмерный коэффициент, в котором коэффициент трения /ш — величина, меняющаяся с режимом трения в опоре шатуна.
Коэффициент трения зависит от характеристического числа Рш ГДе вязкость; сош — угловая скорость; рш — контактное Давление в опоре). Режим трения в опоре — граничный, поэтому эффициент трения уменьшается с увеличением скорости проскальзывания	(1) JI VBP.nHUUaaPTna Г, _______ .	_ _	_____
Л давления рш |..„Момент тРени« “в больших
Трение малых головок г ~ момент Мй в каждой опоре:
ML ~р!ш Fnd~
Г“ "“-“"«Р головки „ см 80
и увеличивается с увеличением контактного
I '2 п ‘	—
J . Примерные значения даны в табл. 3.3. --------------------------1 головках шатунов стремится установить регулирующий орган в нулевое положение.
пение mqpliv	шатунов об опоры в поршнях создает
р*
кГ/си-"		_ Угол "акяона п грал.		
	0	10	20
10 50	0,100 0.125	0.075 0 100	0.0.50
100	0.150	0,110	0,060 0.080
Таблица 33
30
0.025
0.030
0.050
Составляюшая вектора этого момента огносительно^и~ОХ определяется углом <рл, аналогично моменту М,и-.
M,ui .= Мш cos фх = М”и	. ~Р~— sin a.	(3.30)
Рассматривая рис. 3.8, можно установить, что моменты трения во всех малых головках шатунов имеют одинаковое направление. Поэтому моменты М,Ш1 во всех опорах однозначны и при сложении дают М'ш'-
М'ш — (р + р0) fu Fn~ •	. JL— V sjna
4 L kD
I = - , to zFnDp sin yM-q и уравнение момента
Так как
трения может быть записано в виде М’ш = М’ш(р + р0) D\,
—	< diu	1
где М’ш = 1ш-£-~^
(3.31)
sjn  — безразмерный коэффициент. Момент трения в малых головках шатунов относительно мало действует на регулирующий орган, так как d'lu — 0,26 ч- 0,3; L = = 1,5-? 1,7; k[)— 1	0,07. Коэффициент М’и имеет величину
порядка 0,001, что на порядок меньше коэффициента Л4Ш ДЛЯ момента трения в больших головках шатунов.
Так как ось шатуна отклоняется от оси цилиндра на угол ф, то на стенки цилиндров действуют боковые составляющие сил давления на поршни (рис. 3.9). Относительно оси цапф люльки каждый поршень создает момент
Mvxl = pFп ф,	cos at sin у.	(3-32)
Подставляя в эту формулу значение ф, из выражения (2.43) и суммируя для всех поршней полости нагнетания, получае
М -dF	sin у V cos^a,.
- ргп 2L kD	t
ш
Среднее значение момента Мг для обеих полостей м =(г+	(з33)
где Л/ =zF„D„	т -безразмерный
“ Г>‘' r Dq-
Так как .11 зависит от угла у, то направление момента совпа : напрзнленпем момента М „ при у < уп и противоположно Дйет |’> У». но около ус —21 6’ величина <р,, очень мала	ПРИ
о
У
I? а/
Рис 3.9. Момент от боковых составляющих сил давления на поршни
На поршень действуют боковые составляющие сил давления Р„ и РЧ1., центробежные силы Рц и силы от трения в шатунах Рш. Эти силы прижимают поршень к стенке цилиндра и вызывают появление сил трения в зоне контакта поверхностей. Кроме того, поршень может быть снабжен уплотнениями, прижимающимися к стенке цилиндра. Наконец, при движении поршня возникает сила вязкого трения жидкости в зазоре.
Сила трения в каждом цилиндре полости нагнетания направ-ВдаЛЬ оси в ^ОР011}' распределителя. Момент сил трения сип пя^п1ЬН° °СИ ЦаП<^ может быть определен аналогично моменту ствуют по оси в днлиидРа*> если полагать, что силы трения дей-цилиндпе зависит отДа Однако величина силы трения в каждом ное выражение силы трения0В°Р0Та Р°Тора Запишем приближен-
ие Р и р ₽" = <P/o+p/uSina)DJ,	(3.34)
с = 1 сл/“ относительные силы трения (для гидромашин
Момент сил трения поршней относительно
оси цапф
Г) VI	"
Л1/л- = К/п _/* cos-а, ф sin2oj. (3.35)
Среднее значение сумм cos2 а,- и sin 2а( равно нулю поэтому силы трения поршней не создают момент на регулирующем органе
В результате воздействия сил давления в опорах регулирую' 1Цего органа создаются реакции /?, и /?2, вызывающие трение в подшипниках. При повороте регулирующего органа необходимо преодолеть сумму моментов трения в обеих опорах и уплотнениях цапф (см. рис. 3.4).
Момент трепня состоит из двух составляющих:
Л-1/ = Л4„ |- .VI,.,	(3.36)
где Мп — Л1„1 4- М,л — момент трения в подшипниках цапф;
Mv = Мм + Л1V2 — момент трения в уплотнениях цапф. Момент трения в обоих подшипниках
Мп = (Rc + Ъ)-	(3.37)
Подставив вместо реакций /?г и К2 выражение равнодействующей сил давления Ри из равенства (3.18), получим
Л1 = I Р„ 1У1п I п 2 г б’
(3.38)
где f„ — приведенный коэффициент трения подшипников;
d0 — расчетный (внутренний) диаметр подшипника в см.
Приведенный коэффициент трения подшипников качения для нормального режима работы принимают 0,002—0,008. Подшипники регулирующего органа работают при очень малых скоростях поворота и значительной пульсирующей нагрузке, поэтому при расчетах момента на регулирующем органе коэффициент трения fn принимается 0,008—0,015.
Момент M,t можно выразить через общие параметры насоса, подставив относительные размеры диаметра поршня dn и диаметра подшипника люльки du —	, равного для типовых гидроприводов
0,68 —0,945,
Мп = Мп(р + р0) D3q,	(3-39)
где Мп = fn~?cPaz — безразмерный коэффициент, равный для типовых гидроприводов (0,20—0,28) fn-
Уплотнение цапф состоит из резинового эластичного к или кольца из фторопласта.
83
При действии трения, который такта равным дав
пав пения жидкости уплотнение создает Мо м5жно определить, полагая давление в месте Кон ленпю жидкости
M^f^hp,
(3.40)
где _ коэффициент трения; и — диаметр цапфы в см, д______высота уплотняющего
Коэффициент трения резины в уплотнениях цапф изменяется
Рис. 3 10. Зависимость коэффициента трения от давления.
I — фторопласт по стали; 2 и 3 — резина по стали
кольца в см.
и фторопласта по ста пи при работе с изменением давления и при дВн женин с малой скоростью имеет величину, показанную на рцс 3.10.
Снижение коэффициента трения резины и фторопласта при повышении давления можно объяснить наличием смазочной пленки между трущимися поверхностями. При понижении давления происходит дискретный контакт поверхностей и масляная пленка вытесняется в углубления поверхностей. При повышении давления увеличивается поступление масла под давлением в неплотности стыка и масло из углублений распространяется по всей поверхности, создавая условия для гра ничного трения.
Введя относительный диаметр цапфы d — (для типовых •'Я
приводов 0,95—1,26) и относи-
кольца h =	(0,06—0,08) в
уравнение
тельную толщину уплотняющего равенство (3.40), получим общее
=	+	(3-41)
где Му ~ fhdfa — безразмерный коэффициент, равный при четырех уплотнительных кольцах (0,19—0,32)/.
Если в рабочем режиме насоса давление меняется в сравни-тг^,Н° Узком интервале, то берется среднее значение коэффициента мий р ?.° гРаФику РИс- 3.10. При значительном интервале давле-ппинвмЯст^еНТ "ачала движения расчетный коэффициент трения по ста пи 0 2 Равным для фторопласта по стали 0,1, для резины
84
u неподвижный регулирующий орган действуют моменты- от
на 1Я равнодействующей сил давления Л4Д, от трения в боль
сМе головках иг»гунов Л4Ш, в малых головках шатунов М"ш и от iu"x ,х составляющих сил давления Л4^. Структура уравнений б(ЖоВ д0Г0 из этих моментов в обобщенном виде одинакова 1урав-ДЛЯ ,<а (3.21), (3.28), (3.30) и (3.33)1, поэтому результирующий цегп,я '
м°мснт = MiuSinT М"и -у-Мр sin-у) (Р + Ро) D?r (3.42)
и личина этого момента может существенно изменяться в зави-, ОТ направления моментов Л4Д, Мщ, A4q, и Л4щ.
cl,Mr[t и движении регулирующего органа появляются моменты тре-Р опорах Мп и уплотнениях Му, действующие против направ-
ИИЯця движения; поэтому момент Мр равен:
Мр = ±Мро+Мп+Му.	(3.43)
Направление действия и величины составляющих моментов, пропорциональных давлению в системе, даны в табл. 3.4.
Таблица 3.4
	—		 Со.-тавляюише момента	Коэффициент Л1	Направление действия	I момента	|
От сил трения в подшипниках	Л1п = 0.002 — 0.0028 при /=0.01	_	Против движения	1 люльки	1
От сил трения в уплотнениях	/й,, = (0.19-0.32)/	То же	!
От сил трения в шатунах	/ИШ = О.27/Ш /ш-0'1	В сторону уменьшения угла наклона люльки
От боковых составляющих сил давления	Т в град. 1 о Ю 21 30 д|# 0 0.009 0 —0.004	То же
От смещения равнодействующей вследствие неточности изготовлении, проворот оси распределителя в на-|	правлении враше- |	ния ротора то же, против направления вращения ротора смещение оси	МЛ = 0.001 4-0.003 при Ду = 0,1 ММ	То же В стороне увеличения угла наклона люльки Определяется ком Ду 			
Неподвижный регулирующий орган испытывает действие це побежных сил поршней и сил тяжести при отклонении цапф от вер тикатн Силы инерции поршней в переносном движении мо>к' не учитывать, так как они воспринимаются упорным диском, ц Па реп пирующий орган действуют только весьма незначительные 11х составляющие, перпендикулярные осп цилиндров.
При движении регулирующего органа начинает действовать гироскопический момент и момент инерции, пропорциональный ускорению поворота регулируй, щего органа.
Из указанных сил напболыщ значение имеют цецтробежн схема их действия показана рис. 3.11 Каждый штоком угловой действие р = ^п “ g
г?
Рис. 3.11. Схема действия центре-оежлых сил
iee Ые;
На со с
поршень при вращении ротора v скоростью со испытывает центробежной силы Рч;
=	(3.44)
P4cosat
Си g масса поршня с
где т, шатуном в кг.
Момент силы Рц относительно осн цапф XX равен
Л4„,-= cos2 a; sin у, (3.45) где I — координата центра тяжести (см. рис. 3.11). Центробежные силы действуют на все поршни, поэтому, суммируя моменты Л4Ч<, получим общий момент
Ми = Рп £ у* sin у У cos2 а,	(3.46)
;=1 г
где Seos2а —сумма cos2а для всех поршней ротора. Среднее значение величины
У cos2a(-
__ г
~ 2’

86
поэтому момент от действия центробежных сил / D*
Л4Ц — тп ~ со2 siny.
(3.47)
(3.48)
удельн°й массы насоса
(3.49)
4g Ч =6-ЮЛ примерно до 3 . до »
। поворачивает
<Ю
	- щ,,тоб-
уравнение можно выразить через общие павами ^ьзу» выражение массы „ Д1)лях „ ,*£**»•. насос,.
Р<! и заменив Оц па Du — ^ч;
1’v 4g
= 4^4 °)2 Sin у О’,
п Y ' Q 2 »	^7П =-Qr-T
где "«	£ к
для насосов малых размеров с Dq = 2~ 3 см
а для насосов больших размеров уменьшается пр„1ИС.
Момент от действия центробежных сил поршней по— регулнрУющи” орган в направлении увеличения угла у. '
При движении регулирующего органа с ускорением -ходимо преодолеть момент инерции
Л4 — I dQ Vy I <^1 _.
~ J* ~dt =	D;>’	(3 50)
где Jx =	—момент инерции регулирующего органа с при-
соединенными массами гидроусилителя относительно оси цапф;
Jx — безразмерная величина, для типовых гидроприводов 7Х = 250 -г- 600.
При повороте регулирующего органа со скоростью й рад'сек развивается гироскопический момент
Mj~ JzaQ =	(3.51)
где Jг = J 7У‘Ч — момент инерции блока цилиндров ^поршнями относительно оси вращения OZ в кГ-см-сек2;
7 — относительная величина, для типовых гидроприводов I. = 32 4- 40.
Однако этот момент действует в плоскости оси цапф и вызывает лишь незначительное изменение реакций Rt и R. в опорах.
При наклоне оси цапф от вертикального положения на угол в силы тяжести создают момент, стремящийся переместить регулирующий орган в одно из крайних положений. Этот момент имеет значение для объектов, подверженных качке
Л1е — G ,zx sin 0,	(3.52)
где G., — вес люльки с деталями;	уу
— координата центра тяжести люльки относительно оси Л.
В результате воздействия на регулирующий орган массовых сил создается момент, пропорциональный пятой степени хар Р
87
кого размера Dv. Особенно заметно воздействие массовых сил гндромашин большой мощности, а также для высокоскорост^4” насосов, поскольку момент Мц пропорционален квадрату уг„ ”Ь|* скорости вращения ротора ю, а момент Мч пропорционален °В°® скорости.	Эт°й
Суммарное воздействие массовых сил на регулирующий описывается уравнением	РГан
Ме
Dg Ы2.
(3 53)
Второй член в скобках мал и достаточно вести расчет только с учетом момента от действия центробежных сил._
Уравнение дпя определения суммарного воздействия моментов от всех нагрузок (кроме и М"„ вследствие их неопределенности) находится из равенств (3.36), (3.42) (3.43) и (3.53):
М = |(Л4Ш + sin у 4-+ Л4/1 (р + Ро) Dq + + w2siny£)'.
(3 54)
в
Для правильной оценки знаков выражении (3.54) необходимо рассмотреть диаграмму моментов Л4 = f (у) при р = const. Знаки составляющих определяются с помощью табл. 3 4 На рис. 3.12 показано поле моментов для насо-са с Dq = 1 см и со = 315 рад/'сек, которое получается при положительном знаке моментов, направленных против часовой стрелки.
Общая зависимость момента М от давления и угла наклона у нелинейная. Нелинейность имеет
ке насоса	место: 1) при перемене направ-
ления движения, 2) в области около у = 0, где имеется некоторая мертвая зона, 3) в области вблизи у = уЛ.
Для расчета нагрузки на гидроусилитель при движении в одном направлении можно пользоваться линеаризированным уравнением М = (а + by)(p + р0) Dq — cy Dq,	(3.55)
где у— угол наклона регулирующего органа в рад', а, Ь, с — коэффициенты, определяемые по уравнению (3.54) при р0 = 0; sin у — у.
88
Прй изменении направления ДВНЖ(11
"эМ£н^агрузка на валу гидромо	К°*^нтов
нЯССой перемещаемых частей, то да^^яется в
ляется скоростью движения Люлькн fi ^приводе Опре°м
_ , 2л </<о ,	dt • Имея в Bifnv
(Где у2_момен	ДУ. «гго
ралу гидромотора), и подставляя это ВЬ1Па РЦИи нагРУзки на
получаем	выражение в формулу (3
где А н В — коэффициенты.

(3.56)
Иногда в каталогах момент на регулирующем органе задают висимостп от времени tp равномерного поворота люльки от угла в L 0 до ум Эта зависимость выражается гиперболической кривой, так как при ™ уравнение (3.56) превращается в
М = A'J* +cyDg. 'р
(3.57)
§ 3. 6. ПРИМЕР РАСЧЕТА МОМЕНТА НА ЛЮЛЬКЕ
Определить нагрузку на гидроусилитель насоса с удельным объемом <7 = 100 см3 об (D4 = 4,65 см) в режиме I слежения при ря» ^рП1ах и при повороте люльки на угол -у = 30° за 0,25 сек (режим II).
Гидромотор привода имеет q2 — 100 см3/об и вращает нагрузку с моментом инерции J2 = 5 кГ-см-сек? и угловой скоростью шП)ах = 150 рад!сек. Давление в гидроприводе при разгоне
Артак = Р — Р„ = J2 -7^- ~ = 5 ‘ 0^55 • 100 • 0,9 - 2,0 КП0**-
Давление в гидроприводе при режиме слежения Др = р — р0 = =	— 52 Ориентировочно момент, необходимый для по-
ворота люльки, подсчитывается с помощью безразмерных коэффициентов, помещенных в табл. 3.4, и диаграммы на рис. 3 12.
В режиме слежения при р + р0 = 52 + 8 = 60 кГсм нео -ходимо преодолеть момент трения
Mf = {Мп + Му) (р + р0) D* = (0,018 + 0,002) 60-100 = 120 кГсм\
момент от трения в шатунах при ум — 30°
Ми- = (Р + Ро) sill у„ = 60 • 0,027 • 100  0,5 = 81 кГсм,
8»
составляющих сил давления При
момент от действия боковых т = 0; 10. 20; 30
АД (Р + Рп} D<’ Л,ЧР = °’
М 1(1 = 0,009  60 100 = 54 кГсм, Alf21, = 0;
' м = _ 0,004  60 • ЮО = — 24 кГсм, момент от действия центробежных сил при у = 30 Мц = £ Л/„ w*D;, sin у = 5- 10 е  150s • 4,65s- 0,5 = 25 кГсм. Резутьтируюшнй момент 44 в режиме слежения, определенный по уравнению (3.54), в зависимости от угла у изменяется от 120 до 248 кГсм. Так как изменение Л4м здесь невелико, то можно считать, что в режиме слежения нагрузка на гидроусилитель зависит только от давления в гидроприводе.
При остановке люльки момент М уменьшается до величины Л10 = Мш + Мч — Мц = 64 кГсм при у = 20°. При движении в обратном направлении момент меняет знак и уменьшается по абсолютной величине на 2 (Мш ± /И,( — Л4|(). При повороте люльки от у = 0 до у = 20° (режим II) момент возрастает от 480 д0 720 кГсм.
Ориентировочный (в порядке первого приближения) расчет необходим для предварительного выбора гидроусилителя и других элементов гидропривода. После окончания проектирования поршневой группы насоса производится более точный расчет момента на регулирующем органе с использованием уравнений (3.20) — (3.57), в которых коэффициенты определяются по конкретным размерам Dl, L, dui и т. д.).
РПИИ блока цилиндров с диаметром делительной пр11 вра,п Ход, скорость и ускорение поршня;
Я°СТЙ	хп = -/ (1 — cos af) tg у,
t>„ = w sinaf.
окруж-
(3.58)
(3.59)
tg Y w2 cos a,.	(3.60)
УД“""“Й °6М" ’ "	Р»з«Р о.
На плунжер действует сила давления Р = пР кптппо pi п, которая создает
наклонном диске реакцию *'	'	п__ _____
поршня можно ввести к.
на трение
N = ——-. Для учета потерь на п.
cosy
д. Т]п = 0,98; тогда Р = pr)„F,
VI
Fl
§ 3. 7. МОМЕНТ НА РЕГУЛ ИР> ЮЩЕМ ОРГАНЕ АКСИАЛЬНО-ПЛУНЖЕРНЫХ НАСОСОВ
Рассмотрим силовые воздействия на регулирующий орган в насосе с плунжерами без опорных башмаков, в котором головки плунжеров свободно опираются о упорный диск (см. рис. 1.15).
Схема силовых воздействий и основные кинематические соотношения показаны на рис. 3.13.
В этом типе насосов плунжер имеет сферическую головку с р3‘ диусом г, опирающуюся на диск, наклоненный к оси вращения блока цилиндров на угол у. Ось цапф ОХ обычно совпадает с плоскостью расположения центров сфер Aj, либо незначительно смещается от этой плоскости на величину е (например, за счет неточности изготовления деталей). Основные кинематические соотношения легко установить, рассматривая движение центров сфер А 90
Рис. 3.13. Схема силовых воздействий на регулирующий орган аксиально-плунжерного насоса
Как видно из рис. 3.13, б центры сфер располагаются по эллипсу, а точки А',- касания плунжеров с наклонным диском смещены от осей плунжеров на величину г sin у. При вращении блока цилиндров плунжеры проскальзывают относительно наклонного Диска, создавая силу трения. Для уменьшения проскальзывания обойма наклонного диска вращается на опорном подшипнике.
На неподвижный регулирующий орган действуют силы реакции плунжеров N, силы трения Т, возникающие в месте контакта. Для удобства расчета составляющая реакции Л’ от сил инерции плунжеров в переносном движении рассматривается отдельно, о результате действия системы сил в опорах регулирующего органа иозникают реакции /?, и /?2, вызывающие трение в подшипниках.
При повороте регулирующего органа необходимо пРеоЛ<^^ сумму моментов трения в опорах, неуравновешенный иа регулиру Щем органе от действия системы сил, инерционный и гирос
W
ческий моменты. Вее это создает на гидроусилителе или дру^
Ц«Х “«»«"	"-’>'яж'г“‘ "агае™ «ст»;
ляюших (рис. 3.13, а)
Mpl =PQ2U cus а‘
(Г)	f>
^tgycosa J;-y
Все поршни полости нагнетания создают момент к
Г) VI	.Г» sin V Z
= Р 2^ у i COS a + Рв™* у Г О 62) i = I
Во всасывающей полости будет соответственно Л1 2, создавав мый силой Pa = PvFrn,. Так как среднее значение .2 cos и = о, то среднее значение результирующего момента будет
Мр = (р + р0) Fn i]„ у •	.	(3.63)
Знак этого момента определяется направлением смещения е относительно плоскости центров сфер А. Когда ось цапф смещена от этой плоскости к опорной плоскости диска, момент Мр направлен на уменьшение угла наклона у. Если ось цапф смещена от опорной плоскости, то момент Мр направлен на увеличение угла наклона у. Это свойство можно использовать для корректирования момента на регулирующем органе или для его самоустановления в положение у = О при отключенном гидроусилителе. Момент Мр можно выразить через общие параметры насоса:
MP = (p + p0)MpD>g±,	(3.64)
где Мр = dne гт]„ — безразмерный коэффициент; </,, = -5; е = —, Знакопеременная часть момента сил давления Mpt определяется по методике § 3.5 при помощи уравнения (3.20) и (рис. 3.6). Она вызывает высокочастотные колебания незакрепленного регулирующего органа.
Неточность изготовления деталей может привести к смещению оси цапф относительно оси блока цилиндров на величину At/ и к повороту оси симметрии распределителя на угол 6, что вызовет 9оЛе1а^МОМента ^л’ КОТОРЫ*1 был определен в § 3.5 по уравнению (3 22).^ Этот момент может поворачивать регулирующий орган как в крайнее, так и в нулевое положение.
Силы инерции плунжеров в переносном движении воспринимаются упорным диском и должны быть учтены при расчете момента на регулирующем органе. Силы инерции в секторах плоскости XOY
92
о ДО a = 90 ’ и от a = 180 до a 97По
с л а в секторах от а = 90 до a = %0 “Явлены п 360'" они складываются с силами Р. у'?? и от « - 270 ™*
^жения плунжера	скорение относительного
ln ~ 2~ 0)2 cus О tg у,
Рцcos« — плечо.
ГДС мирУя для всеХ плУ”жеР0В "Ри помощи равенства (3.47), полу чаем	z
V . D4	Di ,
Mg = 2, m„j„i ? cos a,- =- m„ щ <n2x I I
xtgy v	(3 65)
или
Mg=- fco2tgy,	(3.66)
, IDA2
где J no — mn I “2 ) 2—полярный момент инерции плунжеров относительно оси вращения в кГ -см сект.
Этот момент действует в направлении увеличения угла наклона у.
Уравнение (3.66) можно выразить через общие параметры насоса:
Mg — kg <о2 tg у О£,	(3.67)
где kg = JgJno —коэффициенте размерностью кГ -секАсм*', Jno — безразмерный коэффициент, выражающий Jm
в долях от условного момента инерции насоса.
Силы трения поршней действуют в плоскост»! наклонного диска, смещенной на величину г от оси цапф. Величина этих сил трения от действия давления на плунжеры (см. рис. 3.13, а)
T=fNigy-
Точка касания плунжера А, и центр сферы А, находятся в одной плоскости, перпендикулярной оси цапф. Направление проскальзывания у всех плунжеров полости совпадает, поэтому создаваемые каждой силой Т на плече г моменты Мт = Тг будут складываться.
М т = г V 7 =	tg у.	(3.68)
»= t
Вводя общие параметры насоса, получим уравнение
= +	(3.69)
9Э
где 4jz= л /z rd', —безразмерный коэффициент;
Ветчину коэффициента трения сферического плунжера по диску при работе в масле можно определить^экспериментально, папрн. мер. на четырехшариковой машине (I ( CI J4JU о()). До возникновения критических температур и предельных нагрузок смазочная пленка обеспечивает коэффициент трения в пределах 0,08 0,13
Дополнительные силы трения плунжеров от действия па ц|1х сил инерции в переносном движении можно не учитывать, так как эти силы в первой и четвертой четвертях уменьшают силы реакции плунжеров Л;, а во второй и третьей четвертях увеличивают их Поэтому суммарное воздействие дополнительных сил трения незначительно.
Глава 4 бочие Жидкости
« 4. 1. ФУНКЦИИ РАБОЧИХ ЖИДКОСТЕЙ И условия ЭКСПЛУАТАЦИИ ГИДРОПРИВОДА °ВИЯ
рабочая жидкость выполняет в гидроприводе важные и много стороинне функции. Она является рабочим телом гидропередачи вспомогательных и управляющих приспособлений, а также при’ воров. Благодаря большой энергоемкости жидкости возможно создание легких и компактных гидропередач. Выполнение этой цервой функции определяется прежде всего упругими свойствами рабочей жидкости и позволяет рассматривать ее в качестве элемента гидропривода 1511.
Возможность передачи энергии или сигналов обусловливается возможностью герметизации всех трактов гидропередачи. Поэтому нельзя рассматривать свойства рабочей жидкости безотносительно к средствам уплотнения и, во всяком случае, без рассмотрения материалов уплотнительных устройств.
Третья основная функция рабочей жидкости — обеспечение работоспособности и надежности всех узлов гидропригода. Для этого, в частности, рабочая жидкость выполняет функции смазочного и охлаждающего агента, защищает детали от коррозии, позволяет удалять из системы продукты износа. Успешное решение широкого комплекса задач с помощью одной жидкости — одна из причин известных преимуществ гидроприводов.
Можно утверждать, что повсеместное распространение гидроприводов в значительной степени обязано наличию ассортимента рабочих жидкостей, решивших поставленные задачи.
Такими жидкостями оказались прежде всего состоящие из угле водородных полимеров минеральные масла нефтяного происхождения. В последнее время число рабочих жидкостей пополняется синтетическими маслами на основе сложных эфиров, фтороуглерод пых полимеров и некоторых других веществ. Рабочий процесс гидромашины определяется такими свойствами жидкости, как ма сжимаемость, способность выдерживать без разрушения пРа*^™ любые давления, способность не распадаться при пр в Дросселирующих щелях с большими перепадами да ’ собность выдерживать без кавитации разряжения пену.
Объемные и механические потери, износ трущихся| ляются трением и утечками в зазорах. Это связано прежде все
с вязкостью ЖИДКОСТИ и ее способностью образовывать на поворх. ностях адсорбированные пленки. Вязкость жидкостей, н особе.,110 минеральных масел, значительно меняется при изменении т₽мНе. РаТКооме перечисленных выше свойств, рабочая жидкость гидр0. привода должна удовлетворять следующим требованиям, должна быть стабильна в течение установленного срока хранения и работы, тетостойка не взрывоопасна и не пожароопасна, не токсична, совместима с применяемыми в гидроприводе материалами, особенно с материалами уплотнении. Исключительно важное значение имеет обеспеченность производства рабочих жидкостей сырьем и ее стон-мосты
Условия эксплуатации гидропривода характеризуются прежде всего диапазоном температур окружающей среды п соответствующими рабочими температурами, режимами нагрузки (давление, скорости) и требуемым сроком работоспособности. При выборе рабочей жидкости гидропривода температура работы оказывает влияние на процессы износа в трущихся парах и на процессы старения полимерных материалов (масла, материала уплотнений, элект-ронзоляции и лакокрасочных покрытий). Последние играют большую роль в обеспечении высокой надежности гидропривода.
Стремление конструктора сделать машину компактной приводит к повышению рабочей температуры, но оно вызывает резкое ускорение старения полимеров. Согласно известному правилу Вант — Гоффа, можно ориентировочно ожидать, что увеличение температуры на каждые 10е С вызовет увеличение скорости старения полимеров вдвое. Поэтому выбор рабочей жидкости, являющийся одним из исходных пунктов проектирования гидропривода, требует тщательного анализа режимов работы, ограничения рабочих температур и расчетов стабильности примененных полимерных материалов.
§ <4.2. КЛАССИФИКАЦИЯ ГИДРОПРИВОДОВ ПО УСЛОВИЯМ ЭКСПЛУАТАЦИИ
По условиям эксплуатации гидроприводы можно разделить на следующие укрупненные группы.
1. Приводы, работающие в закрытых отапливаемых помещениях, обычно на промышленных предприятиях и кораблях. Приводы должны работать 5—15 тыс. ч. без ремонта, смена масла должна производиться не ранее чем через 2—5 тыс. ч работы.
Решение этой задачи облегчается узким диапазоном изменения температуры, так как обычно в помещениях температура колеблется в пределах 0—35' С. Это позволяет применять масло высокой вязкости (тьо = 25—40 сст) с повышенными теплостойкостью, стабильностью и смазывающими свойствами. Следует использовать водяное охлаждение и ограничивать верхний предел рабочей температуры 50 60 С. При воздушном охлаждении этот предел повы-96
п0 70-80° С, что снизит сроки смены Масла и п с-тСЙ н1ДР0,1РивоДа БОЛее высокая Рабочая темпРпРабОТОСП0с°б-И^Д^ивающего псРсонала и вызывает очень	°пасна
*"£ов уплотнении, а также самого п олзреии. <КаИИ™ ™ЛР01Ч'“в°м "» «ькокнх тотто,,1"™ эКС Пировать с металлическими или высокотемпсватупяГ Нужн° <2 и тяжелыми минеральными или синтетиЙЕи™ УПЛОЪ
МПривоДы, работающие на открытых неотХХХ^Г-яХ весьма разнообразны по областям применения. К ним ™о £я: различные транспортные и строительно-дорожные машХ юдвижные полевые объекты, палубные корабельные установки
1 попарные полевые сооружения и т. д.	У ки’
СТ Можно выделить три климатические зоны, в которых работают оти приводы:
а)	крайне холодные зоны, характеризующиеся морозами до _55° С (исключительные морозы до —85° С обычно не рассматриваются);
б)	умеренная зона с морозами примерно до —35° и летними температурами до +35° С с длительными осенними и весенними периодами при температурах в пределах ±15° С;
Выбор рабочей жидкости и проектирование гидроприводов, работающих без смены масла во всех этих зонах, является крайне трудной задачей, так как общий интервал изменения температуры может достигать 150—160° С, а вязкость такой всепогодной жидкости должна находиться в регламентированных пределах. Первой проблемой является обеспечение запуска гидропривода при крайне низкой температуре, что возможно при вязкости не более 5000 сст, и нормального функционирования гидропривода на морозе, возможного при вязкости не более 1500 сст. Второй проблемой является работа гидропривода при наиболее высокой рабочей температуре, что по условиям сохранения смазочной пленки и увеличения утечек возможно при минимальной вязкости масла не ниже — сст.
Обычно приводы подвижных объектов могут иметь только в душное охлаждение с расчетом на перегрев до 40 Св длв режиме и до 60° С в кратковременных форсированных Р ’ Поэтому верхний предел рабочих температур мож nal<eTHOg 110° С (эти значения выше для гидроприводов авиавВ1 ЭКсплуа-техники). Напряженный тепловой режим сокращает р тации гидроприводов подвижных °^ъе1^Яв и СР которые обычно не превышают 1000—2000 ч.	я /меха-
3. Гидроприводы объектов периодическо 'пр^ стационарные низмы аварийного обслуживания, подвиж	ыми стоян-
попевые объекты и т. д.) характеризуются Д овреМенными ками при постоянной готовности к действ Цяст0 такие гидро-периодами работы в форсированных режима .
В. Н. Прокофьев и др.
ппппояы по тепловому балансу нельзя использовать продолжу X"X," я за короткий период работы происходит увеличе1|1е _атТ'-< ло максимально допустимой из условии в ipi,lliOo е ио тн ма .а пли выхода из строя материалов уплотнений. При использовании минеральны* масел в этом случае обычно донуСка,^ нагрев до 150 (, а при использовании синтетических масел д0 200 С и даже до 300 С.
Важнейшими свойствами рабочей жидкости для объектов Лли. тельного хранения являются антикоррозионная защита, гндролитн. некая стабильность, совместимость с материалами гидропривода Для решения комплекса этих вопросов необходимо более подробное знакомство со свойствами рабочих жидкостей различного химического состава.
§ 4.3. НЕКОТОРЫЕ ФИЗИЧЕСКИЕ СВОЙСТВА РАГ.ОЧИХ ЖИДКОСТЕЙ
Объемный вес у в кПсмя или в н/м* (вес единицы объема) ддЯ минеральных масел находится в пределах 0,00085—0,0009 кГ!см\ для синтетических масел достигает 0,00105 кГслс'. Удельный вес Tai _ отношение веса масла при 20е С к весу воды того же объема
4
при 4 С. Для минеральных масел узо =0,84-1- 0,90, для некото-4
рых синтетических масел Т-о достигает 1,02.
Плотность р в кг/мл в кг!смс* — масса единицы объема. Очевидно р = ^кГ-сек2/см\ где g = 981 см!сек2 — ускорение силы тяжести. Определение плотности и объемного веса производится по ГОСТу 3900—47.
Объем V при нагревании увеличивается практически пропорционально изменению температуры:
ЛГ=аУ0Д/,	(4.1)
где Уо _ начальный объем, который обычно относят к температуре k = 15- С;
А/ = / -
а — коэффициент температурного расширения, который для минеральных масел находится в пределах от 0,00060 до 0,00086, уменьшаясь для более тяжелых масел:
Вязкость или внутреннее трение —	-
кости, проявляющееся при относительном 'дви^ СВ0ЙСТВ0 »ид-Различают два рода вязкости - объемную L ее час™Ц-
Объемная вязкость проявляется при сжата. танг* н««альную кости, вызывая сдвиг фаз между объемной лейхюм-Ра™;"И11 «ид! „ рассеяние энергии при упругих колебаниях Or "РИ " давлением рабочих жидкостей гидросистем изучена недостятл "ая вязк°сть учитывается при технических расчетах. v'dTO4Ho я обычно не
Гапгенниальная вязкость, котовая в ляп,.,,.-
ватьея просто вязкостью, обусловлена силами внуХш!его Г"(> между взаимно перемещающимися слоями жилкоет. ? Р ИЯ современным представлениям, „а основе которых в работе H7I создана молекулярно кинетическая теория вязкости₽	71
жидкости временно соединяются в небольшие агрегаты, нападиХ 1Ц„е кристаллическую решетку, но не имеющие правильной <Смы Агрегаты меняют положение одно относительно другого а\юле кулы жидкости в своем тепловом движении совершают колебания относительно своего «оседлого» положения. Некоторым молекулам удается случайно набрать необходимую энергию V и вырваться из окружения, переселившись в другое место. При ламинарном движении поток жидкости может быть представлен как движение отдельных топких слоев, перемещающихся друг относительно друга. Переход отдельных молекул вследствие молекулярного движения из слоя в слой вызывает возникновение сил трения между слоями. Возникающие при этом тангенциальные напряжения т определяются законом Ньютона Петрова. Сила сопротивления сдвигу одного слоя жидкости относительно другого равна
п r dv	Р,. dv
P^VFdh' x=P=^dh'
где р — коэффициент пропорциональности, называемый динамическим коэффициентом вязкости в н -сек езг;
F — площадь в см2. по которой происходит сдвиг;
— градиент скорости по нормали к поверхности слоя в Мсек.
Широкое распространение имеет коэффициент вязкости в единицах системы СГС, называемых пуазами (пз). I пз соответствует ™ле трения /ф = 1 дн при F = 1 см2. g = 1/™ Очевидно соотношение величии р : 10,2 нсек'см3 = 1 кГ сек.'смг = 1О .Л°ях при 20° С имеет вязкость 0,01 из или сантипуаз (слз).^ Р жа течения жидкости константой, определяющей xapas р «вляется не величина р, а отношение называемое кинематическим коэффициентом вязкости v;
р _ рд v - Р V
(4.2)
(4.3)
99
Единица v (1 см*/сек) называется стокс (от). Обычно применяют бопее удобную величину — сантистокс (сот), равный 0,01 Сщ Кинематический коэффициент вязкости определяется по ГОСТу 33__gg при помощи вискозиметра Пинкевича. 11ри обозначении
вязкости обязательно указывают температуру, при которой она замерена, например vb0 ПРП 50 С, v-«> ПРИ "*0 Часто вязкость выражают в условных единицах путем сравнения времени нстече ния 200 сл8 масла при температуре / С со временем истечения 200 см3 дистиллированной воды при 20 С в вискозиметре типа ВУ (ГОСТ 6258—52). Величина этого отношения выражается как число условных градусов В У (раньше обозначалась в градусах Энглера Е '). Перевод единиц вязкости из градусов Энглера в стоксы можно производить по формуле
v = 0,0732£° 0,0631
(4.4)
Е°
Жидкости, у которых коэффициент вязкости в уравнении (4.2) постоянен при всех градиентах скорости, называются ньютоновскими. К ним относятся вода, керосин, незагущенные минеральные масла, большинство синтетических рабочих жидкостей. Загущенные минеральные и синтетические масла, консистентные смазки, гели, некоторые минеральные масла при низких температурах не подчиняются уравнению (4.2).
Вязкость рабочих жидкостей изменяется с давлением и, особенно сильно, с температурой. На рис. 4.1, а показана зависимость кинематического коэффициента вязкости некоторых распространенных масел от температуры. Изменение вязкости с температурой столь значительно, что для уменьшения масштаба по оси ординат откладывается величина lg v. На рис. 4.1, б вязкость этих же масел отложена по оси ординат в масштабе Iglg v, а по оси абсцисс откладываются IgT = 1g (273 + Г). В таком масштабе кривые вязкости практически спрямляются, поэтому для определения вязкости может применяться уравнение
или
lg lg(v + 0,6) = A-BlgT
(4.5)
lg(v + 0,6)=^.
Построенные в двойной логарифмической [ГхЛгТГ	Л I — —
______г-------- А^мииим логарифмической сетке номограммы, подобные рис. 4.1, б, широко используются в инженерной практике. Вязкостно-температурные свойства минеральных масел имеют определенную зависимость от удельного веса и химического состава. Легкие минеральные масла имеют более пологую кривую вязкости. Например, для масла АУ у =0,89,	= 625, а для керосиновой
V100
фракции Т-5 ? = 0,84,	= 27.
viw
100
Рис. 4.1. Зависимость вязкости от температуры
На основе изложенных выше представлений молекулярно-кинетической теории Я. И. Френкелем получена формула для коэффициента вязкости капельных жидкостей, которая после объединения Ряда параметров может быть представлена в виде
= ае'чТ,	^4'6)
где а =	— определяется периодом т0 колебания молекул, рас
гтоянием 6 между молекулами, постоянной k Больцмана, * определяется энергией V, необходимой для освобождения молекулы из узла решетки.	экспериментальными
п₽о а зав1,симость качественно совпадает	Р уравнением
Результатами, однако в соответствии с эмпир
(4.5) минеральные ^с.—кие^-па №	„
?ЗГ,П ЧТО объясняется особенностью их молек^ляр^ СТРДчя расчетов различных процессов в узлах гидромашин, на мер изменения вязкости жидкости в зазоре с учетом тепловыделени
трении, желательно использовать более удобные, чем уравнщ,.,’ 4 5) зависимости вязкости от температуры. При этом достаточно рассматривать процесс в более узком интервале изменения теМПе. патгР и использовать эмпирические уравнения с коэффициентам,, дчя ограниченного интервала температуры.
Заменяя прямом в некотором интервале температур от /, 4 вязкостно-температурную кривую Igp = / (4), получим нение
I До УРав-
Mr = Bo^-S" " '0>.	(4 7)
где р, — вязкость при температуре
ре — начальная вязкость при температуре /0;
s — коэффициент, значение которого для некоторых МЯГВп дано в табл. 4.1.
	 Тиб ища 4.1					
Интервал температуры в сС	100-80	80—10	•10-10	от ю до — 20	-40 -5U
Очень легкие фракции типа топлива Г-5	 Загущенные масла типа АМГ-10 Масла типа АУ	"	"	0.014 0,020	0.016 0,022 0.030	0.028 0.030 0.050	0,035 (>,040 0,080	0070 0,090
ncnfnb4v^604?X ж!1дкостей в интервале температур 30-100° С используют также формулу vr(П = v50 50п,	(4.8) где п имеет следующие значения:					
V60	в сст	2,8	6,3	9	11,8	21	29	37
Л		,		1,39	1,59	1,72	1,79	1,99	2,13	2,24
Вязкость рабочих жидкостей на нефтяной и синтетической основе увеличивается сдавлением, что объясняется уменьшением расстояния между молекулами [см. член а в уравнении (4.6)]. Изменение ни
„гости рабочих жидкостей с давлением можно описывать
Урав-
l’z’3 '	(4 9»
где 6 — коэффициент, равный для Da6
0,до25 (несколько уменьшается с увеличь *ИДК°СТей 0,00!—
Масло	, АУ	Турбин,,()е м, Н ем ТеМпеРатУРЫ):
О слг'/w при 2О’(, 0,0024	0.0025	(Х,- Сил|Ыыювое
0.0014
Обычно при расчетах изменения вязкости в и„
до 300 лТ/ся- берут два первых члена ряда (Экгп™Г;рваде явлений мула Гурвича, где о =0,01 смЧн) <™спЧ>иментальная фОр. Объединяя уравнения (4.7) и (4.9), МОЖно
вязкости or давления и температуры:	у ь зависимость
f0p " ~ Р° 7Нг-г0> ’
(4 10)
При низких температурах вязкость многих минеральных масел -величина непостоянная вследствие выделения твердых парафинов и появления аномалии вязкости, свойственной дисперсным системам.
Застыванием масла называют условный критерий, оценивающий потерю подвижности его частиц. При этом масло не превращается в твердое тело. Температурой застывания по ГОСТу 1929—51 называют такую наиболее высокую температуру, при которой поверхность уровня масла в стандартной пробирке не перемещается при наклоне пробирки на 45° в течение 5 глин. В трубопроводах малых сечений вследствие возрастания вязкости масло может терять подвижность при температурах на 10—15° С выше температуры застывания.
При нагревании минеральных масел углеводородного состава происходит их испарение, особенно интенсивное при температуре выше температур вспышки. Пары, смешиваясь с воздухом, образуют воспламеняющуюся смесь. Минимальная температура, до которой необходимо нагреть масло, чтобы пары его образовали с воздухом горючую смесь; воспламеняющуюся при поднесении в ней пламени, называется температурой вспышки. Температура вспышки определяется по ГОСТам 6356—52 и 4333 48 в специальных аппаратах закрытого или открытого типа. В приборе закрытой типа вспышка происходит при температуре на 7—20 С меньшей, чем в приборе открытого типа, поэтому температура вспышки указывается с упоминанием метода испытаний. Обычно температура вспышки повышается с повышением плотности минерального ”а<^я Для легких масел в закрытом тигле она равна 85 и , средних масел — 120—165° С. В закрытых ГИДРОС’™^’ * масло не соприкасается с воздухом и нет опасности ор _егкИ, г°рючей смеси, иногда допускают кратковременную р У
минеральных масел при температуре на 10 20° С выше темпера. ТУРСинХХие масла отличаются более высокой температур вшышм , часто дополняемой невоспламеняемостью „ Огнес£"
Однако при высоких температурах, близких к пределу Те11Ло. стойкости, синтетические масла склонны к окислению и деполиме-рвзации, иногда с выделением твердых веществ. Например, пекото-пые силиконы при температуре свыше 200 С окисляются, увеличи вая вязкость, образуя формальдегид и уксусную кислоту и загу. стевая вплоть до превращения в гель. Синтетические диэфпры при 250__300° С разлагаются, образуя твердую себациновую кислоту.
Температура самовоспламенения масла зависит от многих условий и не регламентируется стандартом. Для легких минеральных масел отмечалось самовозгорание на горячей поверхности Прп температурах порядка 250 С, для масла 350 С. Таким образом, с учетом температуры вспышки температурный предел работоспособности легких минеральных масел ограничивается в закрытых системах 120° С. Значительно меньшую огнеопасность представляют синтетические масла, которые обеспечивают температурный предел работоспособности до 200—250 С. В последнее время появился ряд рабочих жидкостей с более высокими пределами температур.
Теплоемкость и теплопроводность характеризуют условия отвода тепла от трущихся пар, температуру в зазорах, зависимость нагрева гидроагрегатов по времени. Теплоемкость минеральных масел (количество тепла в ккал/кг, необходимое для повышения температуры на ГС) лежит в пределах 0,4—0,6 ккал /кг °C и зависит от температуры. Теплоемкость с в ккал /кг СС нефтепродуктов понижается по мере повышения плотности и может ориентировочно определяться по формуле
с = (0,345 + 0,000886/) (2,1 —у16),
(4.11)
где у1ь — удельный вес при 15° С.
Легкие минеральные масла обеспечивают значительно лучший теплоотвод от трущихся пар и более пологую кривую нагрева гидропривода, чем синтетические масла типа силиконов и фосфорных эфиров. Теплоемкость с в ккал/кг^О. и теплопроводность X в кал /см-сек°С- 10 8 рабочих жидкостей гидропередач, воды и некоторых материалов 155, 591 в зависимости от температуры представлены в табл. 42.
Коэффициент теплопроводности минеральных масел X в кал/см -сек°С — количество тепла в калориях, которое проходит в 1 сек через площадь 1 см2 слоя толщиною 1 см. Среднее значение теплопроводности рабочих жидкостей близко к 0,3 ккал/см-сек С, с повышением^ температуры от Одо 12O'JCX уменьшается примерно в линейной зависимости. Коэффициент теплопроводности
, „-„VKIOT n MianSSOHE тсилсратру 0 — 200 ’ с с Точностью ±So-“ "»»« «"O-W- "° ’“">'Р''ет" *'P“y™. денной в работе 1551:
z = в (1 -0.00054/°) ккал/м ч °C.	(4
Ti*
Минеральные масла имеют высокую тептотворную способность опвз ю к 11 Ш«кал!кг п являются опасным горючим (наир11К1 ’ кретенное масло выделяет 10 890 ккал/кг, машинное масло 22 10 900 ккаткг).
Смазываюшая стп собность рабочей жидкости характеризуй прочность масляной пленки на поверхности металлов н друг11Х твердых тел. Смазывающая способность должна проявляться, но-первых в обеспечении наименьшего граничного трения и износа во-вторых, в предотвращении возможного задира трущихся пар пр» высоких нагрузках. Между этими двумя функциями есть некоторая разница. Смазывающие свойства масел обусловливаются способностью молекул полимеров образовывать во взаимодействии с поверхностью металлов граничные адсорбционные пленки, обладающие высокой механической прочностью н относительно малым сопротивлением поперечному скольжению [61.
В большинстве случаев масла можно рассматривать как растворы малой концентрации полярных поверхностно-активных веществ в неполярной углеводородной среде. Неполярная среда облачает хорошей смазывающей способностью в гидродинамических условиях при обеспечении достаточно больших зазоров между трущимися парами (примерно больше 0,5 лк). При повышении нагрузок и уменьшении зазоров наступает переход к граничному трению, характеризующемуся соприкосновением граничных пленок, которые предотвращают контакт чистых металлов и их схватывание. Износ поверхности при легких режимах граничного трения характеризуется процессом образования, последующего разрушения н удаления пленок продуктов взаимодействия поверхностно-активных кислородосодержащих элементов масла и металла.
ри этом протекают различные физико-химические процессы, в частности, окислительно-восстановительные реакции, которые ипр^РйИТгЛЬ1,°г CTvIIeHH определяют силы трения и износ поверх ногтям т,ЮСТЬ м?сла транспортировать кислород к поверх-KHciono 1чпг11ЯлИМСеТ 6°ЛЬШ0е значение, поэтому при нарушен1111 деталей "mn аланса в масле наблюдается увеличение износа г<рмстизипг1пяии°ЯВ«ЯеТСЯ’ иаг,РймеР. при заполнении полостей Содержание в ЭК°В гидР°систем Вместо воздуха азотом (1051-вкеащием шютипгш? повеРх,|О^тно-активных веществ повышаю* бы.ю евсд ние в мш?10СНЬ1Х |,рисадок- Первоначальным способ®* время	'ТЛЪПЬ1а Масла кислот, в насюяше?
включает <жислешшеп₽исадок значите чьяо расширился и
Т	продукты нефтепереработки {напрИ^Р-
W6
s мГ ’
IB 1,0 ti
Рис
Mill 1-5), органически» соединения сейм S' («»«,) к ар.	Ыеплтогенать, л
' При высоких удельных давлениях на трущих,.
„роисходит местное разрушение граничных ипено? n0Bf'P™”<™x ' ЛЫ1ЫХ вспышек высоких температур и возм  ВЛен,,е л<>-ванне металлов пары. В масла, смазывающие ТХ " 3„аДир- CBaP«-механизмы, вводятся специальные пргггивозаХ?, ГРУЖе,",ые ^держапще химически актив-	шриые присадки.
l(I,ie вещества серу, хлор, фос-ф.р, кш пород В зонах высо- 4 ких температур происходит ; разложение противозадирной присадки и взаимодействие ее с металлом с образованием на металле слоя сульфида, хлорида или фосфида, что обеспечивает устранение задиров и заеданий |105|. Типичным представителем присадок такого типа является трикрезил-фосфат. Смазывающая способность жидкостей при работе с различными металлами трущихся пар оценивается многими способами, однако все они трудно сопоставимы с реальными условиями эксплуатации. Для гндромашин более реальные показатели дают испытательные машины, построенные на принципе трения скольжения ролика о колодку (типа МИ-1М, Альмеца, Боулена и др.). На рис. 4.2 показаны полученные на машине трепня типа МИ-1М кривые износа бронзовых колодок по лом АУ ИЛИ !	л v Г. п
существенное ул.-.„_
Противозадирные 'bipexuiapHKouofi лишние Пдтно износа в месте г. стпа масла, а нагрузка, при
1
Кривые износа, полученные на 1	__ _____АЛЫ 1
~ о
Рнс 4.2.	---- ----„
машине трепня скольжения типа МИ1-М

Z/crftW НПф/Мй
Рис 4.3. Кривые излом, полученные ва четырехшариковой машине:
I — при сухом трении; ! — миелр без присадки; 3 — масло с аитиэадиркоб (фасадной:
4 — завнощость диаметра питии упругой де формации от нагрузка
аыл	стати при смазке минеральным мас-
маслоы А У с присадкой МНИ-5, демонстрирующие "меньшение износа nprt введении в масло присадки-свойства жидкости лучше сравнивать на че-ко‘ ------------- "трения (ГОСТ 9490—60), на которой вместе
нтакта шариков создается очень высокое контактное давление. C1J-T,,° изн°са в месте контакта характеризует смааывающие свой-масла, а нагрузка, при которой во время испытания произошло сЛ?Ивание трущихся шариков, характеризует противоэадиркмё (uf2,CT8a масла. На рис. 4.3 показаны кривые, снятые на четырех-триковой машине.
миг
§ 4 4. РАБОЧИЕ ЖИДКОСТИ ИЛ НЕФТЯНОЙ ОСНОВЕ нечаемые переработкой нефти, называют минерадь Жидкости, получаемы нн предсТавляют собою чрезвычайно „ыми масламн,\, X’углеводородов, то первым шагом при пр0Из. сложные смес,’^Хя разгонка нефти на фракции, в состав кото-водстве м^^Хдороды примерно одинакового молекулярного РЫХ входят Углевод Р	температура кипения нефтяных
веса. Эго вОЗМ®кЛп1,3|.теп;но пропорциональна их молекулярным УГЛеВХРвТфР— наХ-о-я дистиллятами, а полученные Из ннхаМмас“а-дистиллятными. После отбора в соответствующей очистки дистиллятов получают основу масла, свойства которой затем улучшают введением различных присадок. Для понимания эксплуатационных свойств и возможностей масла необходима хотя бы самая краткая характеристика группового состава его ос-НОВВходящие в состав масла углеводороды имеют обилие изомерных форм которые состоят из трех основных классов:
алкановых или парафиновых углеводородов, построенных в виде прямых или разветвленных цепей звеньев СН2. Это насыщенные углеводороды, имеющие формулу С„Н2п+2;
нафтеновых или циклановых углеводородов, в молекулы которых входят замкнутые кольца звеньев СН2, соединенные простыми валентными связями; общая формула нафтенов СпН2п;
ароматических углеводородов, имеющих в молекулах бензольные ядра CGHG с различными боковыми цепями. Высококачественные масла после очистки состоят в основном из нафтенов с боковыми парафиновыми цепями и некоторого количества ароматических и парафиновых углеводородов.
Наиболее легкие фракции с температурой выкипания 200— 315" С имеют удельный вес порядка 0,84 Г 1см3, вязкость v20 я» 4 сст, очень пологую вязкостно-температурную кривую с индексом вязкости порядка 110 и температуру застывания ниже — 60е С.
Такие фракции являются основой для получения загущенных рабочих жидкостей, применяемых в температурном диапазоне от -60 до +120° С.
По мере повышения температуры выкипания получаются фракции с последовательно возрастающими удельным весом, вязкостью, температурой застывания и вспышки. При этом растет крутизна вязкостно-температурных кривых v = f (Г), которые на графике рис. 4.1 смещаются вправо. На характер этих кривых существенно влияет также способ очистки и соотношение классов углеводородов в масляных дистиллятах основы. Поэтому для производства масел п^оНраТ НС^Т- опРеделеНн°го состава или производят комбини-L ,,”ГФРаКЦИИ ,двух неФтей, чтобы обеспечить определенное соот-допочои пТУ КОЛ11чеством нафтеновых и ароматических углево-Р • Д. получения более однородных свойств масла жела-
108
Телыю применять «узкие» фракции с небольшой оазняпрь температурах начала и конца выкипания.	разницей в
Процессы очистки имеют целью дальнейшее разделение vrn дородных компонентов масла уже по типу молекул в отличи₽В°' разделения по весу молекул, производящегося при первоначал разгонке нефти.	ьнои
Очистка дистиллятов состоит главным образом в удалении из них нежелательных или неустойчивых компонентов. Для удаления парафинов, которые, выделяясь в виде твердых частиц, ухудшают поведение масла при низких температурах, производится депарафинизация. Для удаления асфальтов и смол, которые дают отложение на деталях и вызывают коррозию, для удаления ароматических углеводородов с целью улучшения индекса вязкости, а также для повышения стабильности масла применяют сернокислотную или селективную очистку. Затем фракция подвергается очистке от технологических продуктов и фильтрации для удаления оставшихся смолистых компонентов. С увеличением степени очистки масла количество ароматических углеводородов уменьшается, что проявляется в повышении индекса вязкости, но еще не означает комплексное улучшение эксплуатационных свойств масла. Глубоко очищенные масла, лишенные ароматических углеводородов, поверхностноактивных веществ — жирных и нафтеновых кислот, смолистоасфальтовых веществ и сернистых соединений, обладают недостаточными смазочными свойствами. Поэтому в масле желательно получить оптимальное соотношение между группами углеводородов.
Соотношение между классами углеводородов в масле оценивает анилиновая точка, которой называют критическую температуру растворения смеси углеводородов в анилине. Этот показатель имеет большое значение для ориентировочной оценки поведения резиновых уплотнений и резиновых рукавов в масле. В рабочих жидкостях на нефтяной основе хорошо ведут себя резиновые детали, изготовленные на основе синтетического дивинилнитрильного (нитриль-ного) каучука. В СССР выпускаются три типа такого каучука. СКН-18, СКН-26 и СКН-40.
Температурные пределы работоспособности резин на основе этих каучуков совпадают с температурными пределами работоспособности минеральных масел. Наиболее морозостойкие резины получаются на основе СКН-18. Они работоспособны в маслах с анилиновой точкой 80—90° в диапазоне температур от —55 до +«и (кратковременно до 120° С). На основе СКН-26 получаю р ^ работоспособные в маслах с анилиновои точкой 75-?0овДиа!а30”! температур от -40 до +90° С (кратковременно д<ю120 С). Масда стойкая резина из нитрильных каучуков, У»^Р“™ тающая в данном минеральном масле, буде	₽ковой анили-
жр идЛиуянир r ппугих минеральных маслах с один же иабухание в других минер что ароматические углеводороды новой точкой. Это объясняется тем,	пяпаЛиновые
проникают в резину и вызывают ее набухание, а парафин
.	-^5
бнннруя состав ' масла с минимальным воздействием группы резин подощ	па
Чиновая топка
находится в преД^« тоЧК0Й около 80" С, будет сильно набуТат, В масле с анилино	oft 70—75° С и терять вес в маслах с ани’
в маслах с анилине,	Обычно допускают изменение веса ре
•ПИН0В« маГпе в'пределах от + 5 до —2 "<», что лимитирует возможны. ЗИНЫ в масле в 11	состава масла.
К°ЛЧисНтые гидравлические масла обладают высокой химической «Гн.льнТстью прекрасно защищают металлические детали от Хпозноиных процессов и умеренно воздействуют на неметалличе. ские мТтериалы резиновые уплотнения и электрическая изоляция).
Пон правильной эксплуатации гидропередачи, спроектированной с счетом изменения свойств гидравлических масел во времени, можно обеспечить ее работоспособность в течение многих лет.
Изменение качества масла в процессе эксплуатации, сопровождающееся изменением вязкости, повышением кислотности, изменением цвета, выпадением осадков и коррозией металлов, связано прежде всего’с процессом окисления масла. В масле растворяется в нормальных условиях по объему 7—10% воздуха, который богаче кислородом, чем атмосферный воздух. Окисление углеводородов, из которых состоит основа масла, приводит к образованию нафтеновых, муравьиной, уксусной кислот и других продуктов, которые вызывают появление отложений и коррозии.
В процессе окисления различают два периода. В индукционном периоде заметных изменений в масле нет. Затем наступает период интенсивного окисления, при наступлении которого масло в гидропередаче необходимо заменять. Индукционный период резко сокращается за счет: 1) накопления в масле продуктов износа деталей гидропередачи, особенно частичек бронз, содержащих медь и свинец и оказывающих каталитическое действие на процессы старения; 2) длительной работы гидропередачи при высокой температуре, особенно в режимах дросселирования масла на больших перепадах давления с большой кратностью циркуляции; 3) соприкосновения масла с атмосферным воздухом в открытых резервуарах, сопровождающегося проникновением в масло атмосферной пыли, воды и агрессивных промышленных газов. Особенно опасна местная концентрация^ воды и кислот на парах разнородных металлов при Дчи" льнои остановке гидропередачи, сопровождающаяся возникнове-=Л30ГаЛЬВаНИЧеских коррозионных процессов. Для попы-сел и miv м Л?НОСТИ И коррозионной защиты гидравлических ма
Лействно°аит антиокислитель11ые и антикоррозионные присадки-образованию ИОКИСлительных присадок основано на препятствИ образованию перекисных цепей углеводородов за счет вступления НО
„ реакции молекул присадки. Поэтому присадка в процессе .
Р^хОДУетСЯ ” ДОЛЖ,,а в Ряд* случаев возобновляв та,1В качестве антиокислительиых присадок приме X ? П11(ьениламип, фенотиазин, ионол, альфанафтол и дпЮтд™раок“-эиониые присадки главным образом образуют на по^рхнДде талей гидропередачи прочные адсорбированные пленки „редохрачяют металл от воздействия продуктов окисления м°™ ,/атмосферных примесеи Некоторые присадки изолируют проник шУю в масло воду, образуя крупные капли воды, покрытые зашит ной поверхностно-активной пленкой присадки. Присадки обладают комбинированным действием, улучшая помимо антикоррозионной зашиты смазывающие свойства масла.
Антиокислительные и антикоррозионные присадки входят в состав большинства современных минеральных масел (например, АГМ, АМГ-10). Введение этих присадок в масло повышает его работоспособность в 2—3 раза. Контроль за состоянием масла в процессе эксплуатации осуществляется с помощью стандартных критериев — стабильности и кислотного числа Стабильность оценивается по стойкости масла против окисления кислородом воздуха по ГОСТу ggl__55 методом ВТИ и характеризуется процентом осадка, кислот-
ным числом и содержанием водорастворимых кислот в масле, подвергнутом искусственному старению при пропускании через масло воздуха (например, при 120е С в течение 67 ч). Кислотным числом масел называют количество милиграммов едкого кали (КОН), требующегося для нейтрализации 1 г масла. Оно определяетсяпо ГОСТу 5985—59 или потенциометрическим методом по lOCly 1784_47. Кислотное число зависит от наличия в масле свободных
жирных кислот и присадок, поэтому само по себе не СВ|1Д1^ЛВС™У^ о разложении масла. В свежем масле без присадок к	,,
обычно равно 0,1-0,2 мг КОН, а в маслах с "Р^ 0,35 мг КОН. Важно изменение кислотного числа е>пР°дВ“	У
тации масла, отражающее процесс 0™^™эксплуатации следует мами для кислотного числа масла в проц	У именены
считать 1.5 а,а КОН «л» в масле нет «>» »
детали из стали. Присутствие 0,5 с д р и деталей сплавов вает скорость коррозии металлов, на Р процессы- Поэтому меди и свинца также усиливает к0РР 3	Р q 5—0,6 мг
принято допускать увеличение
КОН после чего масло необходимо за ‘ 0ТЛ0Жение смол на
При высоких температурах усиливаете^ чТ0 неблагоприятно поверхностях гидропередачи смывае	. золотниковых систем-
сказывается на работе резиновых уплотнении
§ 4. 5. ЗАГУЩЕННЫЕ МИНЕРАЛ^Ы^“пХваюиИ« ра-
Свойства загущенных минеральных * ом диапазоне, боту гидроприводов в широком щенное масло представ-» Ряд существенных особенностей- у
>п1.мепной вязкостной присадки в маловязкой Лег. собою раствор полимерно! ываЛ0СЬ) чт0 легкие маслянЬ1е КОЙ масляной OCH^V„ ВЯЗКОСтно-температурную характеристику фракции имеют пологую	ю теМпературу застывания, 2
(« Р"С- Ч	высоких температур недостаточна ш удо„”
ИХ вязкость в5б^С™ гидропривода. Вязкостная присадка к Та. летворительной раооты и нь вязкости полученного загу. SZTae7”xp=»e=
owomS кТаелу“^ученному аагущеннем основы, описываемой КР”£а1я5ЛУ для 6ол« тяжелого незагущенпого масла, прохо.
Кр /LX,VK>ТОЧКУ А, имеет значительно более крутой подъем. "b"XS ’Ж« предок используются высокомолекуляр. ные соединения цепного строения с молекулярным весом от 3000 до 30 000 и выше. Чем выше молекулярный вес присадки, тем более по-ногой получается кривая вязкости при меньшем количестве присадки.
Наиболее распространенной стабильной и проверенной в эксплуатации вязкостной присадкой является вин и пол (полимер винил-н-бутилового эфира). Применяются также полиметакрилаты — полимеры сложных эфиров акриловой кислоты и полиизобутилены, из'которых первые дают наилучшие вязкостно-температурные кривые масла. Свойства некоторых загущенных масел, широко применяемых в гидросистемах, видны из табл. 4.3.
Под воздействием энергичного перемешивания и высоких скоростей сдвига происходит разрушение высокомолекулярных составляющих вязкостных присадок, в результате чего снижается вязкость масла. Наиболее интенсивное снижение вязкости загущенного масла вследствие деструкции загущающей присадки наблюдается в течение первых 50—100 ч эксплуатации. Считают допустимым снижение вязкости на 20—30% вязкости при 50° С, установленной техническими условиями.
Загущенным маслам свойственна зависимость вязкости от градиента скорости сдвига При низких градиентах скорости сдвига (например, в капиллярных вискозиметрах) вязкость имеет большое значение, при высоких градиентах скорости сдвига наблюдается временное снижение вязкости, которая может приближаться к вязкости основы. Временное снижение вязкости загущенного масла — явление обратимое, поэтому при прекращении движения, вязкость лКчиГьНЭД МПЮВенно восстанавливается до первоначальной ве-счетмеханичёскпй пМвеТ ничего o6u*ero с уменьшением вязкости за при длительной ®СТ₽УКЦИИ полимерной присадки, наблюдаемой мХи3ХйДКпС™УаТаЦИИ зонных масел.
скорости сдвига можнпВЯЗКОСТНОЙ пРисадки при малых градиентах наглядно представить следующим образом
U8
Таблица 4.3
Наименование масел		АМГ-10	ЛГМ	A1R 3520	АУ	Индустриальное 20
Номера ГОСТа		6794—53		—	1642—50	1707—51
Удельный вес у при 20°		0.85	0.85	0.85	—	0.88—0,9
Условная вязкость при 50°С		1,85	1,8	1,85	2,1—2,2	2,6—3,2
Кинематическая вязкость в сст при температуре в °C	100 50 20 0	4,6 10 16 42	4,0 9 26 70	5,0 10	4,5 12—14 47 180	5,5 17—23 75 260
	—20 —40 —50 -60	130 450 1200	260 1250 4000	520 1540 2500	1250 4070 (при —30°)	II II
Температура застывания в °C		—70	-60	-67	—45	-20
Температура вспышки в °C в приборе	открытом закрытом	92	НО	107	165	170
Основа масла		Нефтяная с присадками, загущенная	Нефтяная с присадками, загущенная	Нефтяная с присадками	Нефтяная (с присадками АУП)	Нефтяная
Область	применения, климатическая зона		Транспортные установки, все зоны		Авиация, все эоны	Суда, зоиыуме-ренного климата	Машины, работающие в помещениях
Анилиновая точка °C		80—85	78—85	Г-	78-85		
113
Продолжение табл и, * '«о
Трансформатор”06 082—56	| вис 0 89—0-95	жгм	Шелл 27	MK-S
		—	—	6-157- fig
		0.91 LlZZ	0.87	п.88
0.89				
	—	1,86		3,7		——
9.6 96	10.4 40	6,2 23	7,2 27 400	8,5 25 91
600 8500	440 1060	150 300	2440	528 7000
-45	-70	—	—43	- 55
135	120	108	195	115 — 165
Нефтяная	Силиконовая	Силиконовая с маслом АМГ-10	Нефтянан	Нефтяная
Млшнны, работающие в помещениях	Авиация, все зоны		Машины, работающие в помещениях	ТРД, все зоны
—	—		80—85	80—85
В исходном состоянии молекулы основы, имеющие относительно короткие цепи, перемешаны с беспорядочно ориентированными молекулами загущающего полимера, имеющими очень длинные Х™1,1 цепочки с короткими ответвлениями. Подобие решетки, соиииоовян^.1иЛИННЬ1МИ молекУлами загущающей присадки с ас-лекул основы мИспЛекула”И основы- задерживает движение мо-повышению вязкости. ” ДеистВует эквнвалентно соответствующему «каркаса из^агес™'™*11’ В КОТОРЫХ масло располагается внутри стями Хл вдя • хаРактеРизУются ‘иными закономерно-Ш1я молекулШз1пщш^е7аппис^пРОСТИ СДВИГа ПРОНСХ°ЛИТ ориента-новы, вследствие они ^КИ ВД0ЛЬ 0си потока молекул ос-щ	они меньше ему препятствуют, что нрояв-
ется в уменьшении вязкости затушенного масла при больших „^центах скорости сдвига.
рис. 4.4 приведен график изменения вязкости в зависимости от 7 6 (<<« для масла SAE10 и трех загущенных масел, полученных наего основе [27], из которого видно, что уже при ~ = 150 000 J-рязкость некоторых загущенных масел приближается к вязкости основы. В гидроприводах приходится встречаться с очень большими градиентами скорости сдвига. Например, в зазоре распределителя аКсиалыю-поршневого насоса диаметром 100 мм при скорости вращения 3000 об мин и зазоре 10 мк градиент скорости сдвига оу дет 1,6-10" 1 сек. Вязкость загущенных масел при больших градиентах скорости сдвига определяется при помощи ротационного вискозиметра, тарируемого на дистиллятных маслах с известной вязкостью. Такой вискозиметр представляет собою подвижный цилиндр, вращающийся относительно коаксиального неподвижного цилиндра, на котором замеряется момент от трения в заполненном испытуемым маслом зазоре.
Работа гидропривода на загущенном масле при низких температурах отличается следующими юобенпостями. При неработающем приводе вязкость масла велика, что
уменьшении утечек через различные зазоры и уплотнения. В момент запуска в основных трущихся парах за счет градиента скорости сдвига происходит резкое снижение вязкости и сил трения, что облегчает условия запуска гидропривода (при этом температура в приводе продолжает оставаться практически первоначальной). При работе гидропривода в условиях нормальной и высоких температур фактическая вязкость масла во многих зазорах трущихся пар близка к вязкости основы масла, т. е. меньше первоначальной в 2—3 раза.
Зависимость вязкости загущенных масел от градиента скорости сдвига имеет большое значение для энергетических и динамических характеристик многих классов гидроприводов, в которых применяются эти масла, так как они отличаются нелинейностью закона вязкого трения. При расчете динамического нли кинематического коэффициента вязкости можно исходить из следующих представлений Считая вя кость смеси основа — присадка обратно провор-
Рис. 4.4. Вязкость загущенных масел в зависимости от градиента скорости сдвига:
I — основа; 2—4 загущенные масла: -5 — незагущенное масло
благоприятно сказывается на
п. ипГ, Iinomani проекций молекул присадки на перпенц,Ку шюнллыюи ио ц	а сКорость ориентации молекул
са н и пропори пональной градиенту скорости потока, можно noj"’ Хься при определении вязкости р загущенного масла следуй щен зависимостью:
р = Ро — (Ро~НоИ1 ~~е ”')	(4.13)
где цо _ пехотная вязкость смеси при очень малых градиентах скорости сдвига;
_ вязкость смеси, определяемая экспериментально и уста, навливающаяся при очень больших градиентах скорости (она несколько больше вязкости основы р0(?н);
— постоянная времени процесса ориентации молекул, опре. деляемая экспериментально в сек;
V— ----------градиент скорости сдвига в 1/сек.
Из графика рис. 4.4 можно заметить, что ф имеет очень малую величину (if = I -н 3-10-5 сек).
Следовательно, в отличие от закона Ньютона—Петрова (4 2) напряжение сдвига загущенных масел будет описываться уравнением
т=|рв + (Ро-М«)е * ]	<414)
Это уравнение качественно отличается и от уравнения, описывающего напряжения сдвига таких неньютоновских жидкостей, как консистентные смазки и гели, которое имеет вид
г = те + р^,	(4-15)
где т0 — напряжение в каркасе загустителя, которое необходимо преодолеть в момент начала движения.
На рис. 4.5 показаны графики зависимости удельной силы трения от градиента скорости сдвига (/ — для ньютоновских жидкостей; 2 — для загущенных масел; 3 — для основы загущенных масел; 4 — для консистентных смазок).
Нелинейная зависимость вязкого трения от скорости отразится на зависимости потерь от скорости также в области полу-жидкосгного и граничного трения (на зависимости момента трения от угловой скорости Mf = f (ц>) или силы трения от скорости для ™лр?^а пИНЫ’ Работа,ощ.ей на незагущенной основе и загущенном к гпяннинп »ТОР°М СЛГае наблюДается более быстрый переход В об пасти бАеТТ (минимум кривой) и более пологая кривая в ооласти более высоких скоростей.
Фракций'позво^ип чяВ°ВаННП В технологии переработки нефтяных ные жидкости с иск чюТитеТВрвМЯ получить новые углеводород-следует полагать что вабоиия0 аднными свойствами [111]. Поэтому не	’	* чие жидкости на нефтяной основе в даль-
IieiiiiicM будут находить еще более широкое применение, что обусловлено перепек твои улучшения их эксплуатационных характеристик, низкой стоимостью и неограниченными сырьевыми ресурсами Некоторые фракции нефтяных углеводородов обладают очень хорошей смазывающей способностью и стабильностью в области температур До 370 С. Существенное улучшение свойств нефтяных жидкостей было достигнуто: 1) подбором надлежащего сырья с оп-____ гтт НЫШТ гпги'сотп О»СГ1  О\
Рис. 4.5. Зависимость напряжения сдвига т от градиента скорости сдвига жидкости

тпмальпыми свойствами; 2) применением методов углубленной переработки с отбором «узких» фракций; 3) улучшением стабильности этих фракций и приемистости к присадкам при помощи гидрогенизации; 4) глубокой депарафинизацией для улучшения температуры застывания.
Одним из примеров такой жидкости является MLO7415, имеющая вязкость v 18 = 1000 сап, v38 = 9 can, v2(i0 — 1,1 сап, температуру вспышки 229° С, температуру воспламенения 257° С, температуру застывания — 34° С и удельный вес 0,88 Г/см*. В гидросистемах, из которых был удален воздух, масла углубленной переработки во время испытания при 37Г С показали лучшие, чем синтетические жидкости, результаты по устойчивости к образованию осадков и по устойчивости к разложению (111].
§ 4. 6. СИНТЕТИЧЕСКИЕ РАБОЧИЕ ЖИДКОСТИ
В последние два десятилетия большое внимание уделялось изысканию и исследованию новых синтетических рабочих жидкостей, причем успехи химии полимеров позволили создать широкий ассортимент таких жидкостей. Некоторые из них нашли применение в тех гидросистемах, в которых требования к высокотемпературным свойствам и негорючести не позволяют применять минеральные масла. Основным препятствием к широкому применению синтетических жидкостей является их высокая стоимость, ограниченность сырьевых ресурсов, необходимость замены материалов уплотнений на дефицитные и дорогие материалы. Кроме того, многие синтетические жидкости, обладая рядом уникальных свойств, не обеспечивают комплекс остальных требований. Поэтому синтетические жидкости применяются в тех случаях, когда их особые преимущества окупают неизбежные недостатки.
Многие сложные эфиры (продукты взаимодействия органических спиртов с органическими кислотами) представляют собою маслянистые жидкости и обладают свойствами, сходными со смазочными
117
n качеСтвс смазочных масел и рабочих жидкостей ГцЛр маслами. В?а*с™ 1р0С1-раНены диэфиры (например, дц-2-э/"' сктем наишлее	/работоспособны в температуру £
гексила-батшат)	отличаются очснь хорошей смазыва *'
вазоне от - Д удовлетворительную вязкостно-темп< /' теп слос<^н/ диэфвры, являясь кислородными соединениям,,' SSX устойчивы К окислению и требуют применения а||/ окТпХышх присадок (последние ограничивают термостойкость Киры плохо совмещаются с антрильными резинами, вызывая повышенное набухание и поэтому требуют прн^неипя дефицит,,Ых резин па основе фторорганнческих каучуков (СКФ). Металлические пары при применении диэфиров должны тщательно проверяться на коррозионную стойкость, так как диэфиры плохо совместимы с кадмием, пинком, свинцом и медью.
Примером этих жидкостей могут служить дпэфпры Эссо MIL—L-7808.
Полисилоксаны (силиконы) являются полимерами, в основе которых лежит силоксановая группировка
—Si—О—Si —О—Si —
К свободным боковым связям кремния могут быть присоединены различные органические радикалы, образующие полиметил-, полиэтил-, полифенил-снлоксаиы. Силиконы обладают наиболее пологими вязкостно-температурными характеристиками из всех рабочих жидкостей и низкой температурой застывания. Они негорючи, но при температуре свыше 200 С могут разлагаться, образуя гели. Смазочные свойства силиконов при граничном трении значительно хуже всех остальных классов масел. Нитрильные резины в силиконах теряют вес и снижают сроки работоспособности. Так как силиконы дороги и дефицитны, они чаще применяются для улучшения вязкостно-температурных свойств нефтяных масел в количестве 20 30%. Иногда для улучшения смазывающих свойств к силиконам добавляют минеральные масла. Хорошими смазывающими и вязкостно-температурными свойствами обладают смеси силиконов с органическими эфирами. Примером такой жидкости является 7-50-СЗ— С/йСЬппИЛНК°На С °Рганическ™ эфиром и противоизносной присад-тур’о?- №елоа4В9ППИГ1ИПННЫХ гидР°системах [1051 для темпера-кости 7-50 СЗ в // ° С Вязкостно-температурные свойства жид-01 г60» 1 ‘“’°с "₽ает“-струировании |илпоппи/п> г "а неФтянои основе. При кон-вые жидкости по₽сра₽внени В необходимо учитывать, что силиконо-чаются значительно большой С маслами на нефтяной основе отли-ностным натяжением (19—20 вмее-Г,И очень низким поверх-врименяются в качестве антмпо/1? 30 ^чн/см). Поэтому силиконы честве антипеннои присадки к маслам
Вторым классом распространенных кремнийорганических жид |(Остей являются жидкости на основе эфиров кремниевой кислоты Они имеют низкую летучесть, очень хорошие вязкостно-температурные свойства, отличаются высокой термической стабильностью. ]]о использование этих жидкостей помимо высокой стоимости и дефицитности затрудняет подверженность их гидролизу, особенно в присутствии щелочей. В присутствии воды они распадаются с образованием юля и при высоких температурах выделяют твердые продукты двуокиси кремния. По стойкости к окислению и смазывающим свойствам эфиры кремниевой кислоты близки к углеводородным жидкостям па нефтяной основе, поэтому в них необходимо вводить антпокиелнтельные и противоизносные присадки. При наличии присадок такие жидкости удовлетворительно работают при температурах до 260 С. Уплотнения из нитрильных резин при таких высоких температурах неработоспособны, кроме того, они не могут длительно храниться в среде жидкостей на основе крем-нпйоргаиических эфиров. В этих жидкостях работоспособны уплотнения из резин на основе фторорганических (СКФ) или фторсили-коновых каучуков, однако первые не обеспечивают работу при температурах ниже —25° С, а вторые не обладают необходимой прочностью. Резины на основе этих каучуков дороги и дефицитны. Смешением нескольких различных продуктов часто удается получить жидкость, превосходящую по своим свойствам любой из ее компонентов.
11рпмером жидкости на основе эфиров кремниевой кислоты может служить жидкость оронайт 8515 (технические условия ВВС США M1L-H-8446), применяемая для гидросистем сверхзвуковых самолетов п ракет. Эта жидкость является смесью дисилоксана, полисилоксана и 15% диэфира с присадками. Она применяется в диапазоне температур от —54 до + 232’ С, имеет вязкость v.6O = 2360ccm, v,„ = 24 сст, v176 = 3,4 сст, v204 = 2,6 сст, плотность у = = 0,930 Г'см3, температуру вспышки 202° С, температуру самовоспламенения 402° С.
§47 ПРИМЕРЫ ВЫБОРА РАБОЧЕЙ ЖИДКОСТИ И ЕМКОСТИ БАКОВ ДЛЯ ГИДРОПРИВОДА
Гидропривод, включающий насос и гидромотор ««ьне-поршневого типа с торцовым распределением (рис. .. ),’ Р чается для использования в различных условиях. э У вода> этом допускается выпуск специальных исполне	выбрать
сохраняя конструкцию основных элементов. п_.,ования ГИд-наиболее целесообразную для каждого 5’У4^” конструктивные ропривода рабочую жидкость и решит ,'	ьног£ исэдмв
изменения необходимы для гидроприводе
ния. Насос и гидромотор имеют( УД^ьный объе°	' g U₽uef.
ность на один оборот вала) у - 10 сд<8^
“ с-СКОРБЬ »раЩИ,„ЯМла рост 1642 29W об!миН	эксплуатации в произвол-
НаТг дропР11ВОД "^монта в течение 2 лет и 4000 ч работы при Условиях без ремонт g качестве рабочей жидкости СТвенпых > иой мощности 1 Заменителямп могут быть маета-
S»	умозрения пз ошоп Марк,,
о гпппоприводе могу Г быть г	совместимой с указавшими
Т’ты 1	Дм оЛепеченпя Мигель.
Рмс. 4.6. Блок-схема гидропривода:
/ — насос; 2 — гндродвигатель;
3 — приводной двигатель; 4 — нагрузка; 5 — бак
ной работоспособности масла и уплотнений температуру гидропривода ограничим 60 С при температуре в помещении 25 С. В парах трения скольжения должны быть умеренные нагрузки с удельной работой трения порядка 10—15 кГм слгсек в торцовом распределителе и 20—30 кГЛ! см2 сек в остальных узлах трения. Для обеспечения хорошего теплоотвода от пар трения и длительной работоспособности масла, его объем в гидроприводе должен быть достаточно большим. Отношение расхода циркулирующего масла к его объему в системе называется кратностью циркуляции. Принято выбирать объем масла в гидросистеме равным 2—3-кратной минутной производительности насоса. В нашем случае циркуляция масла в системе насос — бак происходит за счет вспомогательного насоса, производительностью 4 л/мин, емкость резервуара насоса 2,5 л. Поэтому выбираем бак емкостью 10 л и кратность циркуляции 20 раз в час.
Для поддержания необходимой температуры масла производим тепловой расчет гидропривода, при котором найдем поверхность теплоотдачи при воздушном охлаждении. Количество выделяемого гидроприводом тепла Q, ккал1ч определяется мощностью потерь Nf. Отдаваемая гидроприводом мощность N = 1 кет, а потребляемая мощность N, = * (п _ « к п д поэтому>
Qf = 860/Vf ккал!ч.	(4.16)
Подставляя N = 1
Qe = 370 ккал/ч. Это теп^’ 11 = °’7- получим тепловыделение при температурном пеоепяп^^о быть Рассея1!0 с площади F * 1ао	урном перепаде Ы° и коэффициенте теплоотдачи
ккал1^“'г^ (пРи воздушном охлажлРн.„, Л *10-1-16). Следовательно,	Деним гидроприводов
Qf = KF№-,
М = ~р.
KF'	(4.17)
Задаваясь /\	14 и перепадом температуры М = fin ос
35 С, определим необходимую поверхность то„„ ' W ~ 25 = гРх> V76 как "аетс
Промотор F2 - 0,15 м2, прочие механизмы F3 = 0,1 А2 не’Х’ „нмо иметь поверхность бака не менее F6 = 6 76 - 0 5S -= О,21Л12.
2. Гидропривод предназначен для периодической работы на транспортной машине в крайне холодной и умеренной зонах (okdv-жающая температура от 55 до + 40° Q. Необходимо обеспечить межремонтный ресурс работы 600 ч в течение 4 лет эксплуатации без замены масла и уплотнений. Один цикл работы гидропривода может продолжаться 2 ч, при этом максимальная отдаваемая мощность достигает 5 кет, а эффективная мощность равна 3 кет. По заданию в гидроприводе применены рассмотренные выше элементы (насос q — 10 см3/об), а вес и габариты гидропривода желательно уменьшить за счет бака.
Для данного случая применения гидропривода необходима всепогодная рабочая жидкость, имеющая хорошие вязкостные характеристики (примерно г 55 = 1000 -ь 1500 сст, v100 = 3 сст), обеспечивающая надежную антикоррозионную защиту, хорошие смазывающие свойства и совместимая с нитрильными резинами группы 1 (табл. 5.5). Если ограничить верхний предел температуры 100—110° С, то заданным условиям соответствуют загущенные масла на нефтяной основе с полным комплексом присадок типа масла АМГ-10 (см. табл. 4.3). Смазывающие свойства загущенных масел с присадками несколько хуже, чем у незагущенных нефтяных масел с присадками, но не уступают маслу АУ, на котором был испытан гидропривод в течение 4000 ч. Широкое применение масла АМГ-10 в аналогичных авиационных гидросистемах подтверждает возможную работоспособность гидропривода при повышенной в раза мощности. Однако скорость износа будет при этом соответственно интенсифицирована, что и учтено снижением ресурс работы до 600 ч.
При проектировании гидропривода необходимо Г1Р(7|’^вес™ Ораторные испытания пар трения распределитель дельных шине трения при соответственно повышенных в Р теОнадов работах трения, а также произвести проверку осн теплоотдачи на коррозию в выбранном^ масле. Выбор n0BePxvHXaroeS^ Fм2 произведем из условия обеспечения темпер ур привода к концу 2-часового цикла работы до 11
По.
Л12, А!.
(4.18)
Тепловыделение по уравнению (4.16), где Л' = 3 KRIIl< () о равно	’
= 86оХ(1—0.75) = 860 ккал/ч. и,/о
Перепад температур Л/ = 110- 40 = 70 С, иеобходцМап верхность теплоотдачи должна быть раина	вдая
"=1S) = 0’83 и2
Так как поверхность гидропривода без бака равна о ге необходимо иметь поверхность бака -- 0,88 — 0,55 = п'ц Объем бака выберем равным 4 л при кратности Циркуляции ' в час.	J() Раз
Однако за 2 ч работы гидропривода температура может стнгнуть установнвигегося значения, так как текущий' "е ж происходит согласно уравнению:	пеР°грев
1 -Лг(
где/ —время с пачача нагрева в часах;
т = постоянная времени нагрева в ч (с  — трпп,»
В Тпас гРад' Gi~Macca материала гидропривода в хг) _ В рассматриваемом гидроприводе масса стальн^
17,5кг, алюминиевых деталей G = 75	* сталей GCT =
Теплоемкости, согласно табл 4 2 оавныепАт * ' масла G« ~ 6 кг. С“ = 0,224; см = о,55 ккал/к<’ g nfX	= 0. 116;
/ка град, поэтому постоянная времени т = 1 с‘°1_ _ 7,02
т	= 0,57 Ч.
Температуру 110° г
сового цикла работы.	только к концу 2-ча-
До температуры 40 4--L д/ ' Р3 ТЬ1 гнлРопривод нагреется пературы нагрева и охлажГ " +	‘ ?° = 84' С’ ГРаФ,,к тем‘
ТгХпеТа Времеии Х^иХ’ПРИВОДа Обходим для после-периодическое п°а. = 1 с^я/об) ппРпИаЛ°В уплотнений и масла. во всех клнмати слУЖивания на vctJ дназначе,< Для механизма Работы по 20 Задах. НеобхопГ^^’ Э|<сплУатчрующихся ~ 5 кет. Вес и гяг 8 Лет Эксплуаташп?Мп обеспечить 300 циклов ?*ет повышен” бариты Должны Полезная мощность N = 6?тке спеЦиальногоНагрева 'адроппип'ТЬ "Радино уменьшены за РУктивных Детад „ Исполнения гилпоДа ПрИ Работе. При разра-e^eHHe ST 3aMFHe^ «а аХПРИВ°Да большинство кон-м£л.10	gu. ал7п,1,шевые сплавы, что дало
• ИеобходИмвго’ Умеиьщен д0 чо ’ М и увеличило тепло-12й	компенсации ,,„Л’ ВКЛЮчая емкость бачка
менения объема при коле-
6а11ни температуры на 200° С. Пары трения г
тзк как гидропривод ранее проверен ппи Сохране«ы прежними с передачей мощности 5 квт. Поверхность ТепК°ВрСМе,1№й Ра<й лась до F = 0,50 м*.	Р °сть тепл00ТДаЧи умеР
Прежде чем выбрать рабочую жидкость и	‘
ний. произведем ориентировочный тепловой пя РИЛлы Упл°™е-(4.16) при /V = 5 квт, п = о,75 тепловХХ^вно0 УРаВНению
860 (Г75
При длительной работе установившаяся температчпа по цепню (4.17)	миература по урав-
= 5О + Д/° = 5о+ >«2550
14-0,50 ~	•
(1	0,75) = 1430 ккал/ч.
Расчет нагрева гидропривода производят согласно уравнению (4.18), в котором, принимая для масла с = 0,5 ккал/кг град постоянная времени равна
Zf.lzi 10-(),И6-|- 10,1.0,224 + 3 0,5
т — '/</-	м.пч------------= 0,7 ч или 42 мин.
14-0,5
Рис.
4.7. Температурные характеристики гидропривода
Поэтому через 42 мин работы гидропривод нагреется до температуры 180 С, а к концу заданного цикла работы до 150е С (кривая / на рнс. 4.7). В температурном диапазоне от — 55 до +150 С может быть применена одна из синтетических жидкостей, например 7-50-СЗ, проверенная в отношении смазывающих свойств в аналогичных условиях применения, или оронайт 8515 [105]. Переход на синтетическую жидкость потребует замены материала уплотнений на соответствующие высокотемпературные смеси,	''яла уплот-
морозостойки п потребуют коренной перера >	зировать
пений. Поэтому вполне целесообразно зан0 р ,,величИТЬ вес всю проблему. Вероятно имеет смысл «ескапько >величи№ и габариты гидропривода с целью Увели^™ нагрева до 120-верх пости теплоотвода, снижения темпер' Ур оезИны. В рассмК-125 С и применения уплотнении из нитри Р концу цикл» Риваемом примере снижение температуры Д1 объема масл» может быть достигнуто за счет уве. g g » («рназя i и* АМГ-10) до 5 л и поверхности теплоот^ ДОы. рис. 4.7). При этом расчетный вес гидр пр -
смеси, которые недостаточно
22% (с 23 до 28 л<’)- Олнако СРОК эксплуатации гидропривода Необ ходимо проверить расчетом и ускоренными испытаниями уплОт ,жй в заданном режиме, что, возможно, потребует некоторого его сокращения.
(4.19)
§ 4. 8. УПРУГИЕ СВОЙСТВА РАВОЧПХ ЖИДКОСТЕЙ
Пои деформации жидкости меняется расстояние между молеку. ламп и считается, что при малых деформациях реактивное давление пропорционально относительной деформации:
dV	.	ilV
dp = — Кжа |,ЛП “Р Км-и ы >
где V — объем;
и хжи— адиабатический и изотермический модули объемной упругости соответственно.
При быстропротекающих процессах, когда из-за инерционности тепловых свойств рабочей жидкости теплообмен, обеспечивающий тепловое равновесие и равновесие возможных дополнительных процессов, не успевает устанавливаться, обращаются к кма, в противном случае, при медленно протекающих процессах, обращаются к значению
Наиболее достоверный и точный способ определения хжп заключается в замере скорости распространения плоской волны ультразвука 1101], имея в виду общеизвестное соотношение
са
(4.20)
где са — скорость звука в жидкости и р — массовая плотность.
Оптимальный диапазон частот упругих колебаний жидкости для замера са лежит в пределах от 20 кгц до 100 мгц, поскольку на низких частотах фронт волны перестает быть плоским, а на более высоких частотах возникнет явление дисперсии (зависимость са от частоты), а длина волны может оказаться соизмеримой с расстояниями между молекулами.
В МВТУ 1831 значение v-ка определялось импульсным методом с однократным пробегом цуга упругих волн. При помощи импульсного генератора / типа Г5-4Б (рис. 4.8) формируются прямоугольные импульсы, которые по экранированному проводу поступают на передающий пьезокристалл 2, установленный в рабочей камере 4. v приемного пьезокристалла 5 электрический сигнал поступает на вертикально-отклоняющие пластины осциллографа 7 типа ПО-4, тающего в ждущем режиме. Синхронизирующий импульс, зятый с клемм второго канала генератора, поступает по проводу 6 ОсциллогРаФ и запускает в работу блок развертки, а иа экране появляется изображение цуга упругих волн (рис. 4.9). 1М
Замер времени прохождения сигнала через рабочую жидкость 3 пне. 4.8 производится при помощи переключателей линии за-"апжки генератора. Если время задержки равно нулю, то момент пег	импульса генератора определяется точкой 1
генератора определяется точкой / на рис. 4.9, соответствующей приходу синхроимпульса на осциллограф. Тогда точка 2 соответствует моменту прихода сигнала
выхода основного
10
us
Рис. 4.8 Схема усгановки для определения скорости распространения ультразвука в жидкости импульсным методом с однократным пробегом цуга упругих волн
п
с приемного пьезокристалла на вертикально-отклоняющие пла
Рис. 4 9. Изображение цуга упругих волн на экране осциллографа
стины осциллографа 7, и расстояние между этими точками определяет время Т пробега цуга упругих волн. Зная расстояние s ме-s
жду поверхностями пьезокристаллов, определяют са = у.
Положение точки 3 относительно 2 на рис. 4.9 определяется
свойством пьезокристалла, не меняется в диапазоне давлений от О
до 400 кг!см2 и температурах от 20 до 80° С и может быть протариро-вано при помощи дистиллированной воды, упругие свойства которой определены весьма точно. Использование времени Тк позволяет более точно определить значение иЖа.
Давление в камере 4 (см. рис. 4.8) изменяется при помощи ручного пресса 12 и контролируется манометром 10. Для обеспечения чистоты замеряемой рабочей жид-
Рис. 4.10. Схема пикнометра высо кого давления для определения
кости используется переходная диа-	плотности жидкости
фрагмная камера 11, а стабиль-
ность температуры обеспечивается термостатом 8 и контролируется термометром 9.	и	<--«
Значение адиабатического модуля объемной упругости работе
жидкости хжа может быть вычислено при помощи равенства ( -*w
m определения плотности рабочей жидкости 11р1, только после точного ong; объема пикнометра 1 на рнс. 4 ' помошн заранее тарирова	ура которого контролируй
помешенного в теР^сТ0дим^ давление создается ручным прессомз термометром 5, а необх°д1ю камсру 2	Запертыи	Ш1КН
„ерез переходную	,апит11чсских весах, что позволяет опрё.
взвешивается на точ11ь1Х входя1ДСй в дифференциальное урав. делить значение плотности I.
пение	dp	,4 9|
, nnnvueHO из уравнения (4.19) при помощи вы-которое может быть пс. у 	_ const Замена в последнем-
ражепия "“1”я""?.сдовл„мется тем. что процесс заполнения „ Хра»я‘ пнХпра в термостате происходит при постоя,« "ТмХз,«™,Х"Левиным. то интеграл уравие™, (4 19) будет	р_ра
у = voe *жи •
которым можно пользоваться в случаях, когда |р — рп|<Сх^„.
На самом деле х^-,. зависит от давления и температуры. Считается 1401, что модуль объемной упругости хх„ с достаточной точностью описывается равенством
х^, = X k> Р + S л/ <z* — П'1 , । I L /=1	J
причем ki{iy ^, а при Г <200 С также и лу+1 «4(1 = ’<
2, 3, ...; j — 1, 2, 3, ...). Поэтому в порядке первого приближения можно принять
хж0 = 1р + Л1 0* —01.
где tt — температура разрушения жидкости, 5 < Л] < 30 /сг'слт’х со
Хград, a— S Пу — t)1 ——р* — предел устойчивости жидкости.
Применительно к минеральным маслам и рабочим жидкостям линейная зависимость модуля объемной упругости от давления при заданной температуре экспериментально подтверждается. Однак0 о иаруживается зависимость fclt и притом нелинейная, от темпера' туры.
Результаты замера х«а при разных температурах и давлениях S пиГ1₽п ЬН0Г° МЭСЛа ГМ’50И сказаны сплошными линиями ТУ МХП 491ИкчлЛГ полнметилсилоксановой жидкости № 5 (ПД1С-ния	На РИС’ ^ам Же пунктиром показаны значе-

Впредь будет использоваться линейная зависимость и ™ давления-	*п
хж« — АаР + Ва,
f-де Aos^l« а = ^1л1 (I* — О-Подставляя равенство (4.22) в (4.19) и проводя получим уравнение состояния жидкости
(4.22)
интегрирование,
или
(/> + £ V''o=(p0 +
\	ж ' /Ла/ жо
(4.23)
В, ГДе А. вечно.
А
V = V \ аг • яго I
Апрд 4- В„ б пр 4 Ва р*, Ра и V«<o— начальные давление
и объем соответст-
Аналогично и для изотермического сжатия. В частности, применяя тот же прием к плотности и имея в виду закон сохранения
Рис. 4.11. Адиабатический xw„ и изотермический иж„ модули объемной упругости минерального масла ГМ-50И при разных давлениях и температурах
Рис. 4.12. Адиабатический нжа и изотермический х^.,, модули объемной упругости ПМС-5 при разных давлениях и температурах
массы О' = pgV = const, где g — ускорение сил тяжести, можно получить
1
Ро“
(4.24)
или
Р — Ре
>'/"Аир + Ви г Ацри -)- Ви '
127
поскольку
Х„	,л
(4.25)
Существование адиабатического и изотермического МОд , тоугости рабочих жидкостей обусловливается зависимостью 611 1.‘я объемной упругости не только от давления, но и от темнел’0' туры, И скорости деформации поэтому	Ра-
dv.^___дхж । дпж л di
dp ~ др ' dt° dp ’
(4.26)
Для изотермического процесса, при котором /° = const Iх» _ а	’ °'р ='
=-^ и отличается при динамических процессах, которые сопро вождаются местными изменениями температуры.
Наиболее точное определение xw„ осуществляется при помош фазометра — тарированного цилиндра с нагружаемым поршнем перемещения которого при нагружении и разгружении и подлеж ’ замеру.	ат
Значительно большую погрешность дает использование значе ний, замеренных при помощи пикнометра и используемых в выоа женин, получаемом в результате логарифмирования равенства (4.24)'
=	+	+Й)’	(4.27)
Подбирая значение при котором графическое изображение шаетсяНнГппГВеНСТВа В логаР”Фмических осях координат обращается в прямую, можно найти значение Аи по наклону этой пря-
"£>2 приведены значения Л. и В. значениям р = р (г °М по экспериментально полученным
Использование известного соотношения
У'жа -	(1 +	(4.28)
чаще всего оказывается сведений по значению трптРУдннтельным из-за недостаточности стоянном объеме с,. Кроме тпг^К°СТ^ Рабочей жидкости при по-коэффициента термической ’ не°йх°димо знать точное значение Р «ческой деформации рабочих жидкостей
а== _Ро — Р Po«“-Q
, п	гои ~1о>
(в последнем ряввнетпр
в градусах	Шатура Г в oq а в предыдущем —
Менее точная, однако vn^r
128	Ная ПРИ Решении многих задач в слу-
чае небольшого диапазона измененья [непринятая линейная аппроксимация
давлений и температур об
Р = Р<» 11 — а (/° — /0) — ₽ (р — р0)|,	(4.30)
еде значения р могут быть выбраны при помощи параметров А„ и В„.
Таблица 44
Наименование масла	! Iараметр			 1 С			
			20	40	60	so
Минеральное масло ГМ-5011	р.	г< см'	0.850 20	0.8.39 19,125	0.821 18.625	0.798 16,875 13 600
	^«1	кГ1см‘	18 900	17 950	16 050	
		Aft	12,00	11,00	10.125	8.50
	^«1	кГ,см-	12 150	11 700	10 800	9600
Минеральное	р,	г/с.мя	0.835	0.823	0.802	0.779
масло АМ1 -10		Ап	12,75	12,375	10.925	9.875
	Ва.	h Г/см'	16 800	14 950	13 330	11 850
		А„	9,98	10.25	9,25	7,60
	в„	кГ]см-	14 970	13 100	11 600	10 100
Индустриальное	р.	г!см3	0.872	0.861	0.845	0.822
20 ГОСТ 1707—51		А„	15,75	12,62	12,00	10.00
	в.„	кГ/см‘	18 800	17 400	15330	12550
		А„	12,75 15 900	10.7	9,26	7,75
	в Hi	кГ'!сма		15 000	13 800	И 900
Г илравлпческос	р.	г)см3	0.887	0.877	0.859	—
летнее для строи-		А„	12,5	11.6	1<>.О	—
тельно-дорожных		кГ1смя	20 600	18 350	15600	—
машин		Л„	1U.7	9,07	7.42	—
	в„.	к Г/ем-	17 500	14 300	11 560	—
Гидравлическое	р.	г1см3	0.841	0,832	0.814	—
зимнее для строи-		Л,	11,5 17 400 13,25	12,5	1Д9	—
тельно-дорожных машин	в„,	кГ1см‘ А„		15 400 11,5	1 1 400 10.0	—
	Вц>	кГ/см‘	14 600	12 700	10800	—
ПМС-5 полиметилсилоксановая жидкость № 5	р. Во,	?1смя Ла к Г} cm-д..	0,910 11,58 9 100 8,13	0,893 11.11 7 850 7,77	0.871 11,72 6630 7,63	0,845 10.78 5 4.50 7,38
	Вт	кГ1смг	8050	7 100	6 050	5 200
Из-за различия значений Аи и В„ процессы при разных частотах будут отличаться друг от друга (модуль объемной упругости рабочей жидкости зависит не только от давления и температуры, по и от частоты), что может сделать использование частотных методов расчета динамических процессов некорректным. Однако материалов о зависимости модуля объемной упругости от частоты применительно к реальным установкам пока еще недостаточно.
12»
б В Н. Прокофьев и др.
________________________«.ПЧЫЗКОГО и изо-.^(жичсского модулей объемной упругости при разных давлениях и различном содер
жании фазы Г
§ 4.9.	ДВУХФАЗНЫЕ РАБОЧИЕ ЖИДКОСТИ
ыр материалы по значениям х«п и хи.„ относятся к ра. Приведенные ма Р’	поставки.
бочим жидкостям 1в со ст	содержится растворенный воздух.
что он не меняет значении р, „ х<« ,841;	- липкости работающего гидропривода всегда имеется
В рабочей жидкости I ырьк0В> количественное содержание газовоздушная (раза f и "	которых оценивается вели-
чиной т0 = рЩ, где V ,о и Уг0 — объемы в начальных условиях газовоздушной фазы и смеси соответственно. При изменении режима работы значение т0 меняется, обычно составляя 0,015—0,025. При остановке гидропривода пузырьки газовоздушной составляющей поднимаются и при достаточном давлении растворяются.
Значение т0 определяется при взятии под давлением пробы регламентированного герметически запертого объема и замере давления через определенные промежутки времени. Из-за растворения пузырьков газовоздушной составляющей давление уменьшается и через 50—60 сек стабилизируется (стабилизация не происходит в случае недостаточной гер-м«тио пп«л,	метизации). Если в момент
«ше	был,, р,. „ Т„ а дав-
т0=------—	1	________
•4- т-у—-—_(*лси 4- Pi) 7\
+ а <7, - ро) (Л + 1) <pi _pi} Та vnpTSTLSe" щ Принятых за начальные, для №•
(4.31)
Уравнение состояния газовоздушной составпяющей
(Р+1)И;_(Ро+|)^,	(4 32)
гДе для адиабатического процесса принимают 1 4 а для ичп. термического k = 1 (учет влияния давления на k желателен) Поскольку обе фазы рабочей жидкости одновременно подвеп-гаются сжатию. выражение модуля объемной упругости смеси можег быть записано в форме
l+i
ТГф
+ ll Vж
— объем жидкой фазы, причем
'1УЖ
(4.33)
где И
(4.34)
Уго _	">о
Ужо I то
Обращаясь к уравнению состояния для адиабатического про-
цесса (4.23), можно получить равенства
* /7 i Г"
Yiг. — "'о
Уж 1 — 1П0
и
лтщздд.____:
1 /	В а
' АаР + Ва
у
Уж
£ Л,
(4.33) дает
(1 — ff’0)x
Л, * использование которых в уравнении
Xro = k (Р + (А.1Р + Вп) |)(i —m0)x« А,
X
'« im Л/ Ро + 1 а +ГПо \ Р+1
xv ^r€+^A-p+B->i/
Аналогично для изотермического процесса в соответствии с равенством (4.24)
У г __________________
dV, _ Уг Аир + Вц
ЯУЖ уж р +1
(4.35)
и» (Ро + О
и
* И - (р + V (^"Р + В») X А____________________
/1 — т ) 1" А"/>в	4- т В» + 1
~ —___________ • (4.36)
х -----" , S + »'<. GW + в„) 'А+1
(r+l)(l-'"o>j А„р + В„	/’+1
пллсчета х „ ДЛЯ минерального масла ГМ 5011 при
Результаты сп^4 ли" ых значениях т0 показаны сплошными температуре	пунктирными для хг/г
линиями на рис.	> ft жидкости, для которой >
В ” ™>«! я«о™№«Р » »>. неравеис™, нарушает™, >Г"’Х“ да’ которых	» 3"ачт ° 5ТОМ
данантетх процессов становятся В этом смысле корректными.
§4.10. ПРИВЕДЕННЫЙ МОДУЛЬ ОБЪЕМНОЙ УПРУГОСТИ
При распространении сигнала в упругой трубе, заполненной рабочей жидкостью, происходит деформация не только жидкости, но и стенок, которая может быть учтена применением приведенного (на деформации стенок упругой трубы) модуля х объемной упругости жидкости.
Рассмотрим отрезок круглой упругой трубы длиной А/ с внутренним диаметром D„, с концентрнчно размещенным в ней недефор-мируемым цилиндром диаметра d (например, плунжер в гидроцилиндре) и заполненным рабочей жидкостью с модулем х,„- объемной упругости, значение которого учитывает и характер процесса и газовоздушную составляющую.
Объем, занятый жидкостью, будет
nD-‘
V =-ф,	(4.37)
где
ф = 1-^ °!'
объ^оп^адХ^^аж^м” ЖИДКОСТИ в рассматриваемом
(4.38)
-г^аь«'длнвисти^заК0н1^Яр”дН0к тРУбопровода в предположении
=	(4.39)
гДе о — напряжения в стенках трубопровода, вызванные линейными деформациями;
Е — модуль Юнга материала стенок трубопровода, D — некоторый средний диаметр стенок рассматриваемой трубы. Из теории упругости известно, что для толстостенных труб
Da + De'
(4.40)
где О„ — наружный диаметр трубы; а = (Da — DR)— толщина
стенок.
Считая, что стенки трубопровода длиною Д/ и площадью поперечного сечения 2«Д/ находятся под воздействием разрывающего усилия dP — D„Aldp, можно определить выражение изменения напряжений в форме
, dp D„ .
da = 2Дд7 = 2о dP-
Используя полученное выражение в равенстве (4.39), окончательно получим
,n _D D„._D„ Dh + D".
dDe ~ Ё' 2adp~ E ‘	— D* dp
(очевидно для тонкостенных трубопроводов средний диаметр D а-At О,„ поскольку при а -> 0 обязательно D -> £>„, а для толстостенных D„ < D < D„).
Дополнительная деформация внутреннего объема рассматриваемого трубопровода из-за деформации его стенок из того же закона Гука определяется очевидным соотношением
dVr= лПвфд/ = лД;^-£д/.	(4.41)
Поэтому выражение суммарной деформации объема будет
Средняя сжимаемость на единицу объема, которую обычно называют просто сжимаемостью и обозначают через 0 = *, является
отношением суммарной деформации объема к первоначальному объему и перепаду давления. Таким образом, средняя сжимаемость — это относительная деформация на единицу изменения Давления
1 SdVi___________________1_ I] _l . D . Д = —	(4.42)
~ £>“ Х«Л	W
133
или
1
к = X
1 I ХЛ« .	. —
1 + Е а 1|>
Следовательно, значение приведенного модуля об госта меньше, как меньше и приведенная скорость пя РЛ1Н°й ynDv упругих колебаний	1 пРостра1)ен1^
с.-)/?-
Сж
Поскольку в различных участках тракта гидропривода значения Е и а а иногда и D„, разные, то и скорость распространения упру, гих колебаний в различных участках будет^разная.
Однако весь проведенный элементарный (одномерный) вывод, совпадающий с имеющимся в литературе 1101] для случая ф = )’ получен без учета сил инерции материала стенок трубы, т. е. применим для задач статики, а не динамики.
Дополнительный перепад давления, обусловленный действием сил инерции материала стенок трубы Дри, определяется выражением
dpB = apTj = ~ap Td^,	(4.44)
где рт — плотность материала стенок трубы (площадь внутренней, движущейся с ускорением поверхности равна л£>„Д/); nD„a&l — объем стенок; ррЮ^Д! — масса.
Умножая массу стенок на j, получим силу, а относя ее к внутренней поверхности, получим искомое выражение dpu и ускорение / радиальных перемещений внутренней поверхности трубы.
Применительно к гармоническим колебаниям с частотой Я последнее выражение принимает форму
dptt = ~jQiapTdDl>
(дифференциальные урав-
X dpi = dp _р dpu —
—,2et’ h DI) \
ч -DDX~Pr^^dDe.
убедиться, что увдтЧвлияниВЫ₽ажение с Равенством (4.39), можно в®! "слученных	инеРиионных свойств стенок трубы во
•««ртяйщего мяожителяЫ₽аЖеНИЯХ ОсУш-ествляется введением

т е. заменой х на его приведенное значение хлр, причем хпр = х
L)DB
(4.45)
Поскольку исправляющий множитель безразмерный, то произведение^^ имеет размерность квадрата угловой частоты й0. являющейся квадратом собственных радиальных колебаний стенок трубы, причем
У° = 2Кр7Щ, ИЛИ =	<446)
где /о — частота собственных радиальных колебаний стенок трубы, т. е. число пробегов волны упругих колебаний в поперечном сечении стенок рассматриваемой трубы.
Учет влияния частоты внешнего воздействия f на значение са, очевидно, необходим тогда, когда длина волны X невелика. Для длинных волн, когда X =	л1)в зависимостью са от й.
т. е. эффектом дисперсии, можно пренебречь.
Окончательные выражения приведенного значения модуля объемной упругости или приведенной скорости распространения упругих колебаний будут:
X ~ у.ж
____1________
2*ж	4“ ^в)
и
(4.47)
Са =
сж
(4.48)
нуль, что
При возрастании й уменьшается са с обращением в экспериментально подтверждено. Физический смысл этого явления заключается в том, что при й = й0 наступает эффект резонанса, при котором перемещение рассматриваемой плоской волны становится невозможным.
Строго говоря, при учете эффекта деформации стенок трубы Фронт волны перестает быть плоским (при двухмерном решении задачи), и перемещение такого возмущения в круглой упругой тРубе называют волной Кортевега [102].
Помимо волны Кортевега имеют место и иные формы перемещения периодических возмущений, определяемые иными решениями дифференциального уравнения, решаемого методом Фурье ПОН-При Й й0 соответствующие возмущения, например винтовые
13S
т а поэтому И не учитываются. ОдНако
Алгтоо затухают, a in все этн многочисленные BOJ1,' ^чет’нях «. с0113МХюшнх иным решениям разрешающего u 3иЛ типов, соответствен яТСЯ определяющими по финального =«еХЯёнию, чем и обусловливается стрему,. ^яс^нногГзиачения са к «^ьный член (добавка к едини,.) ВЫ S обозначить ^‘S)" (4.48), учитывающих вл„я„и’ в знаменателе выражен^ 1ерез vT. то соотношение величин сжи. деформации стенок pj
маемости будет	1 = ₽ (i + vr), г > Л
Р X
пичем приведенное значение сжимаемости составной магистрали ^стоящей из т участков круглых упругих труб, будет определяться
равенством
₽s = Ро У, + vn) Г01,
2*.« (Оь + D=)
<4S01
При исследовании динамических процессов в гидропередачах в предположении существования сосредоточенных параметров рас-ход сжатия определяют, основываясь на законе Гука, dV=^dp = Wodp
или
О =p.v _ av
Услг г и» d------— .
(4.51)
Если магистраль состоит из т участков круглых упругих труб, для каждого из которых справедливы ранее записанные равенства, то суммарный расход сжатия определяется выражением
т	т
S	=S Pl VotPi
i=l	i=l
p не зависит от номера участка.
iyOf- через Уад и назовем относительным объемом участка безразмерное отношение
Очевидно pi =
Обозначим 2 у
(4.52)
где отличие множителей 1 + vTi от единиц обусловливается деформацией стенок магистралей.
В заключение следует заметить, что рассмотрено частное значение модуля объемной упругости, поскольку более общая зависимость имеет форму
<tp _ х d V dt	у dt ’
где / — время, а модуль объемной упругости х[р, Проявление зависимости х от называется эффектом релаксации. Для адиабатического процесса ха = х (р, оо), а для изотермического х„ = х (р, 0).
Поскольку при экспериментальном определении х замеряют р и V, а не то возможно вместо непосредственного использования равенства (4.19) обращение к промежуточному соотношению л ли Др =— х ~у,
где Др = р, — р, ДП = Г1 — V. а р и V — параметры началь-и х определяется очевидными равенствами
' _ 1 f’ Х ~ AV' J V
ного состояния.
Связь между х'
Ар
bi
₽
или Ар-*0 х = х'. При х(р) обязательно
V —	— Гр,
Vl ~ £УЫ ~ Уо1 •
Тогда расход сжатия, обусловливающий критерий унрУ гидропривода, определяется равенством
При X = Const 1 ... —г . _	. 1>рг, ^\р) иииза1ельно
х^>х',еслн Др>0, и наоборот. Особенно велико превышением' чад х при Др<^0 и малых значениях Рх>0.
= /)Уох Рц У, U + vn) ^о«>
1-1
Глава 5
УПЛОТНЕНИЯ
§ 5.1.	ПРИНЦИП ДЕЙСТВИЯ УПЛОТНЕНИЙ
Все элементы гидропривода объемного типа имеют заполненные рабочей жидкостью внутренние полости, находящиеся под постоянным или переменным высоким давлением (до 350 кГ/см2), и полости находящиеся под гидростатическим давлением рабочей жидкости’ Кроме того, в гидроприводе имеются различные управляющие и механические устройства, в полостях которых рабочее давление обычно находится в пределах 5—30 кГ/см2.
Необходимо отсутствие внешних утечек по всем подвижным и неподвижным наружным соединениям во время остановки и хранения гидропривода. При работе гидропривода обычно допускаются весьма ограниченные наружные утечки или просачивание только по уплотнениям валов насосов и гидромоторов. Для внутренних уплотнений, герметизирующих узлы гидропривода в заполненных рабочей жидкостью корпусах, могут быть допущены только такие утечки и перетечки, которые практически не влияют на характеристики гидропривода.
Используются четыре степени оценки герметичности: абсолютная герметичность (полное отсутствие просачивания жидкости или газа через соединение), отпотевание (не обнаруживается невооруженным глазом), просачивание без образования капель (количественно не оценивается) и утечки, оцениваемые количеством жидкости или газа за определенный промежуток времени.
Достигнуть абсолютной герметичности, проверяемой специальными способами, в разъемных и подвижных соединениях машины чрезвычайно трудно, поэтому в работающей гидромашине обычно имеется некоторое отпотевание в местах соединений. Так как это масло при нагретом гидроприводе испаряется, в помещении с работающими гидроприводами обычно имеются пары масла в воздухе.
Уплотнения играют в гидроприводе очень большую роль, определяя пределы допустимых рабочих давлений, скоростей, диапазон температуры, ресурс безремонтной работы и надежность.
п насосах и гВДромоторах применяются преимущественно сле-сгС>пии1оВИДЬ1 Уплотне,,ий- Наружные и внутренние неподвижные (пис к 1*ИЯ Уг'лотпяются эластичными резиновыми кольцами Гпмс	’ Реже металлическими кольцами или прокладками
• ) Внутренние подвижные соединения герметизиру10ТСЯ
<38
Рис. 5.1 Уплотнения неподвижных разъемов
Рис. 5.2.
Уплотнения деталей.
вратно-поступательное
совершающих движение
воз-
эластичными нпрованнымп (рис. 5.2, б н
5'2' ”> теме,,.
<р-
резиновыми уплотнениями (рис.
резиновыми кольцами с защитными в), резинотканевыми уплотнениями
Рис 5.4. Торцовые уплотнения валов
Рис
5.5. Уплотнения поворачивающихся деталей
за счет обеспечения малых зазоров между деталями (например, между поршнями и цилиндрами) или за счет гидростатических уплотнений (например, в распределителе). Валы герметизируются радиальными манжетными уплотнениями (рис. 5.3) или торцовыми уплотнениями (рис. 5.4), подробно рассматриваемыми в дальнейшем.
Подвижные (допускающие поворот соединяемых деталей) соединения маслопроводов герметизируются специальными уплотнениями цапф (рис. 5.5). При необходимости абсолютного уплотнения непрерывно вращающихся валов применяются винтовые уплотнения (рис. 5.6) или гидравлические замки (381, принцип действия которых
с.	заключается в том, что за-
р между неподвижным корпусом 5 и вращающимся валом уплотняется на участках / и 2 разнонаправленной нарез-_ г, подаюЦ1еи рабочую жидкость к центральной части зазо-м а °п давлД“ием — &Pi + р, где р — давление уплотняе-ды- Отсутствие непрерывного протока рабочей жидкости . ля'Дмт к большому нагреву жидкости, запирающей герметизиро-
ванную полость, а реверс или прекращение вращения вала 4 может привести к утечке уплотняемой жидкости. Так как винтовое уплотнение не может герметизировать вал при остановке и реверсе, в
конструкцию узла необходимо вводить дополнительное стояночное
уплотнение.
Существует три вида герметизирующих сопряжений поверхностей: сопряжение поверх постен с натягом (рис. 5.7, а), при котором за счет внешнего усилия происходит деформация поверхностей с внедрением одного поверхностного слоя в другой; сопряжение поверхностей с зазором который заполняется рабочей жидкостью или газом (рис. 5.7, б); граничное сопряжение уплотняющих поверхностен (рис. 5.7, в), при котором происходит соприкосновение адсор
бированных на металлических поверхностях пленок.
Характер просачивания жидкости или газа через соединение с зазором определяется величиною зазора б, перепадом давления АД' Др, формой сопрягаемых поверхностей (коэффициент формы у),
физической природой жидкости и материала сопряжения.
Последние характеризуются прежде всего вязкостью ц жидкости и поверхностным натяжением о.
При наличии достаточного зазора и перепада давления течение вязкой жидкости следует законам классической гидродинамики. Для ламинарного течения расход утечки в см3,'сек определяется выражением
где В — ширина щели; / — ее длина;
р — в пз;
&р - в кГ /см2,
6 — в см.
141
В случае зазора между поршнем и цилиндром диаметра Л = лО; I — длина поршня; е — эксцентриситет, k == L+1,% 6 ”
Для расчета расхода утечки Q't. при зазорах, соизмеримы шиной адсорбированных на поверхности пленок, в работе Т М Ст<к'1' та, Л. М. Кудряшова и В. В. Трофимова (191 предложена I ^аЦ|’
где b — доля сечения зазора, занятая пленкой. Соотношение действительным расходом и расходом, определяемым по vna МеЖдУ (5.1), имеет вид	УР^нению
о,.	(5.3)
При очень малых перепадах давления начинает проявля влияние поверхностного натяжения.	' ТЬся
Рис. 5.7. Виды герметизируемых сопряжений поверхностей
Закономерности традиционной гидравлики макропотоков теряют силу при уменьшении зазоров до долей микрона. В этом случае частицы жидкости в зазоре подвержены действию силовых полей поверхности металла, которые очень сильны непосредственно иа поверхности, но быстро ослабевают по мере удаления от нее. В поверхностных слоях жидкость приобретает некоторые свойства твердого тела, в частности упругость формы. Так как поверхность металла хаотически рельефна, в зазоре не может быть однородного состояния жидкости: имеют место отдельные контакты металлических поверхностей, участки с соприкосновением граничных пленок М2
„ „ участки со впадинами, в середине которых жидкость *,,ЛКОС « а обычном состоянии Поэтому просачивание жидкости ’,аХ0ДИ™аничпые сопряжения пока не поддается количественному 4f^e.neX, а закономерности трения зависят от критерия режима °прр ия и“- Между цилиндрическими поверхностями обычно суще-^Тют зазоры более 3 мк и утечки подчиняются уравнению (5.1). СТВУ	Таблица 5.1
Класс чистоты поверхности	4	5	6	7	8	9	10	11	12	13	14
Цг в мк	40	20	10	0,3	3,2	1,6	0,8	0,4	0,2	0,1	0,05
Среднее арифметическое отклонение профиля Ra в мк	10	5	2,5	1,25	0,63	0,32	0,16	0.08	0,04	0.02	0,01
В случае сопряжения тщательно обработанных (плоских) поверхностей при отсутствии движения обычно наблюдается граничное состояние с участками полусухого трения. При движении эти участки смазываются, что проявляется в снижении трения. Дальнейшее увеличение скорости движения приводит к возникновению гидродинамических эффектов за счет натекания жидкости на наклонные микронеровности. При этом отмечается увеличение зазора до микрона и более, постепенное увеличение трения со скоростью, появление утечек в соответствии с гидродинамическими закономерностями. Между грубо обработанными поверхностями неподвижных соединений также имеются зазоры за счет поверхностных неровностей и неправильной геометрической формы. Высота неровностей Rt по ГОСТу 2789—59 указана в табл. 5.1.
Уменьшая зазор и повышая чистоту обработки, можно достигнуть граничного сопряжения и прекращения утечек. Однако такой метод уплотнения требует трудоемких доводочных работ и может применяться только в исключительных случаях. Между сопряжен-
” *‘талями может быть введена прокладка из мягкого металла ки зЕииЛаТ!Р"аЛ0В’ ПрИ достаточном сжатии материал проклад-соединмие ОиЛ₽ ” повеРхностные неровности, создав герметичное нений Гопа^л пн ЭТ° ПрИГ0ДН0 только Д™ неподвижных соеди-Щих элементов из? решается ПРИ применении уплотняющих элементов из эластичных материалов.
f 5.2. МЕХАНИЗМ ДЕЙСТВИЯ ЭЛАСТИЧНЫХ УПЛОТНЕНИЙ ииальнойУ канавке?ппЫМИ сопРягаемыми поверхностями в спе-интельный элемент "° ад°чном месте — устанавливается уплот-рис 57 Л т т из эластичного материала (рис 5 7 г и ваются эластомеКХиаТП?1Ьпп7ЛеЗИНЫ ИЛИ их соединения назы-Р • ри монтаже уплотнение деформируется и
143
юностях возникает определенное контактное на сопряженных поверх™ )М парамсТром, определяющим давление, которое ™™%еЛИЧНна контактного давления должна механизм герметичности.	не,|ИЯ вдавЛнвался в поверхност-
быть такой, чтобы матерн > овую посадку При низком дав_ ныс неровности и	яемой полости контактное давление
.пенни жидкости в > • vnDvr0cTbio деформированного уплотни Рк = Р. создается тольк У деформа11„и должна превосходить тельного элемента. Вели от).лоне^11Я от геометрической формы поверхностные	’ т0ВЛеНие сопряжения, относительные
В пределах допусков на или
перемещения (Л на рис. 5.7, б) поверхностей, которые всегда бывают в работающей машине. Сверх этого деформация уплотнения должна обеспечивать минимальное контактное давление рк min порядка 2,0 кГ см* для предотвращения просачивания жидкости при очень малых давлениях. Для газов ркт1п = 2,5	3,0 кПсм2.
Эластомерные материалы склонны к старению и ограничены по температурному диапазону применения. Поэтому контактное давление от упругости материала постепенно уменьшается, что приводит к потере герметичности Для предотвращения этого явления в конструкции уплотнений вводят пружинящие элементы (см рис. 5 3, а). Механизм действия эластичного уплотнения проще всего рассмотреть сначала на примере колец / прямоугольного сечения применяемых ^я уплотнения неподвижных торцовых разъемов (рис. 5.8) трубопро-сжатн₽ВмЬ1^К0Г0 давления- Контактное давление рк = pt создается ное сжатий НИЕ К°ЛЬЦа П0 высотс на величину th (е — относительной пастет г ю С? Рав,10весный модуль упругости резины Д<л «ей повелхностм пРсне^Регая некоторым выпучиванием внутреннем поверхности кольца, можно определить контактное
р‘ = Р> ~
Ue Кф ‘	Формы 1 для в<0>3)
давление
(5.4)
„лтгти пав пение р становится достаточ
К»г«.	элемента. его материал неяез
бХ етльио вязкой жидкости. При этом на уплотняемых "»етях “оХлежнно возрастает контактное давление
""Р	p.~p + Pi-	<S51
Материал уплотнения находится в состоянии всестороннего J™S способен выдерживать практически любые давления Ис-Чтение составляет только часть кольца (показано на рис 5 8, ) Уступающая в зазор 6 между уплотняемыми поверхностями. При некотором давлении среды уплотнение начнет выдавливаться в зазор. Выдавливаемый материал по поверхности растягивается и может разрываться, так как прочность резины на разрыв не велика. Явление носит усталостный характер и зависит от количества пульсаций давления.
Таким образом, для обеспечения герметичности при низком давлении основную роль играет сохранение необходимого контактного д|вления рк = pi. Для обеспечения работоспособности уплотнения при высоком давлении основную роль играет процесс выдавливания кольца в зазор. Это выдавливание будет тем меньше, чем выше твердость резины Н и меньше зазор 6.
Кольца прямоугольного сечения удовлетворительно герметизируют фланцы трубопроводов при давлениях до 200 кг/см2 и зазорах до 0,1 —।0,15 мм. При более высоких давлениях необходимо приме-^Р^Мр^^
₽:3n„“ закрь,ва,от заз°р" п^отвРа-™7д=ий XvX0,"' 1ЮСТОЯ""°	поддействнем
пластические материалы но лрименень’не обладающие упругостью давления без специального нажУУ^10006'^' ,УПЛОТНЯТЬ очень низкие создание р;.	го УстР°иства, обеспечивающего
которые наиболееешироко,УрилГеНН5потК°ЛЬЦаМИ кРУГлого сечения, своей универсальности (они moi-vt СЯ В констРУкИиях благодаря Ильных, подвижных и нёпХИжиыРИМеНЯТЬСЯ В ториовых и ра-Радиальное неподвижна vSnТ	Упло™ениях).
оказано на рис. 5.9. У Нение кольцом круглого сечения
ЙХГ	Тдствне деф°р—
АииФ°РМуЛ Теории ГеРца-Беляева ил бЫТЬ олределено с по-^ается ” J уплотнение давления среды п "риме™ьн°- При
я кольцо деформируется, но некотс
силами трения (рис. 5.9, б) затем смещаетс удерживается с""бХчуя зазор (рис. 5.9, в) и iiapyuja51
Kp’S "«4'S s юовь »'*°рм"р1,<;тс’"° герметичность.
Рис. 5.9. Уплотнение кольцом круглого сечения
нию, принимая форму канавки и восстанавливая герметичность. Ширина контактной поверхности b зависит от давления среды р и твердости резины Н. Вследствие трения уплотнения о стенки
'• Контактное давление при уплотняющих кольцах фасонной формы
сил давления на уплотнение затрачивается на деформацию повеРхность кольца в углах канавки может находиться в растянутом состоянии. Поэтому среднее контактное давление здесь
менее вычисляемого по формуле (5.5), что учитывается ^ЙГипентом Ф передачи давления'
рк-Р1 + ЧР-	(5.6)
Коэффициент Ф является функцией твердости материала Н и ппиия о Для мягких резин практически <р — 1 при р >50 кГ см , Дпя твердых резин <р = 1 при р > 100 кПсм*. При меньших даваниях можно считать Ф = 0,9.
Уплотнение кольцами более сложных профилен сечения, например X-образными (рис. 5.10, а) или U-образными (рис. 5 10, б), имеют более сложные изменения формы при действии давления. чт0 существенно меняет кривую распределения контактного давления.	„
Как будет показано ниже, для хорошей работы уплотнения очень важную роль имеет профиль сечения уплотнительного кольца и кривая распределения контактного давления. Знание механизма уплотнительного действия помогает правильному конструированию уплотнений.
§ 5.3. ХАРАКТЕРИСТИКА РЕЗИНЫ КАК УПЛОТНЯЮЩЕГО МАТЕРИАЛА
Сточки зрения эксплуатационных свойств резина является своеобразным конструкционным материалом. Высокая эластичность, амортизационная способность, стойкость к воздействию различных химических веществ делают ее незаменимым материалом уплотнений и многих других деталей. По своим механическим свойствам резины качественно отличаются от низкомолекулярных твердых и жидких тел характером зависимости напряжения от времени действия силы (релаксация напряжения), а также протеканием процесса старения который резко усиливается под воздействием тепла и света.
Маслостойкие резиновые смеси приготовляются на основе синтетических каучуков, которые смешиваются с рядом веществ, придающих резине необходимые качества. Эта смесь, называемая сырой, не обладает необходимыми упругими свойствами. Резиновая смесь подвергается вулканизации, в результате которой она становится эластичной. Основные свойства резины — морозостойкость, теплостойкость, химическая стойкость и, в частности, маслостойкость — определяются в основном каучуком. Для повышения упругих и прочностных свойств резины в смесь вводят активные наполнители (о ычно сажи), играющие большую роль в изменении формы молекул каучука в резине и межмолекулярных связей.
Процесс вулканизации осуществляется при нагреве резиновой ее сп В прес^Ф°Рме за счет реакции вулканизатора (обычно серы и мает ж^НеНИИ ’ С молекУлами каучука. В результате деталь прини-Молрй РМУ пРессФ°Рмы. а в материале получаются длинные цепные Шие гийЫ' связанные в единую пространственную систему, обладаю-
костью и эластичностью. Существует определенное коли-
147
смесп при котором прочность и ynnvr чеетво	наибольшими, определенное количество
резины стан<«ятся	обеспечения необходимой струКТу^
„изатора. _ вулканизации, при использовании ' ' ” определенная тс»	pejIlllbi оказываются наплучшнми тТ
рой механш„я смеси и режим вулканизации опред^ н0Л°Г^нейшХ поведение материала уплотнения, поэтому до Bfe гп контролироваться Если увеличивать количество вулканИз“Ы СТР пемёси резина при вулканизации будет получаться все б02 ГОдёёее твердой и хрупкой, пока не превратится в эбонит. LoXc может протекать и в некоторых случаях эксплуатаций уплотнений, например при работе резиновых детален в осерНе11„Ых Ма<Лпя повышения маслостойкости резины в смесь вводят пассивные наполнители, для улучшения пластичности при низких температурах — пластификаторы. Молекулы резины подвержены процессу старения, который носит окислительный характер для уменьшения процесса старения в резиновую смесь вводят стабилизаторы, для уменьшения коэффициента трения—фторопласт-4 и другие антифрикционные вещества.
Процессы старения резины связаны главным образом с распадом (деструкцией) молекул или с образованием новых связей (структурированием) в процессе окисления. Кроме того, при высоких температурах происходят процессы термического разложения, не идентичные окислению. Температурный режим играет решаю цую роль при эксплуатации резиновых деталей Дтя каждого сорта резин существует определенный температурный диапазон возможной работы. Если при нормальных условиях уплотнение может находиться в изделии многие годы, то при предельной температуре работы она может сохранять необходимые свойства только десятки часов. При низких температурах твердость резины постепенно возрастает до тех пор, пока резина не становится хрупкой (эту температуру называют температурой стеклования резины). Изменение механических свойств резин с температурой показано на рис. 5.11.
Поведение резин в рабочих жидкостях определяется взаимодействием ее молекул с молекулами углеводородов минеральных масел или полимерами синтетических жидкостей. Стойкие в минеральных маслах резины изготовляются на основе бутадиен-нитрильных каучуков (СКН). Отечественная промышленность выпускает СКН-18, идущий на приготовление наиболее морозостойких (до —60е С) резин, СКН-26, идущий на приготовление умеренно морозостойких резин (до 45 С); СКН-40, идущий на приготовление мало морозостойких (до—25 С), но более маслостойких резин. Общее свойство резин из СКН — понижение маслобензостойкости с повышением морозостойкости.
СКНР1Я ^а4УРС до 60—70э С уплотнения из резин на основе СКН-26 способны работать несколько тысяч часов и хра-
148
Изменение механических резины с температурой на основе силиконового кау __________ 2 — резина на основе ни-трильного каучука СКН; 3 — резина на основе этмленпропнленового каучука С КЭП; 4 — резина на основе фторорганн ческого каучука (СКФ, вайтон)
я несколько лет, а при температуре порядка 120 С только ||1,ТЬ)Пько десятков часов. Предельной температурой применения "“их ре,,ч| яялястся —'5^ С, при которой происходит быстрое та1^пческое разрушение уплотнении. Резины имеют очень низкий т‘Схьнннспт теплопроводности (порядка 0,3- 10 3 кал!см сек' С), ''"этому кратковременно (доли минуты) могут работать даже при контактировании с горячими газами при температуре до 600— 700 С.
Для уплотнении, работающих при более высоких температурах в среде теплостойких синтетических жидкостей п минеральных масел, применяются резины на основе фторорганпческих каучуков (СКФ). Выпускаемые отечественной промышленностью СКФ-32 и СКФ-26, а также зарубежные вайтон, кель-F и другие каучукоподобные сополимеры позволяют получать резины с исключительной стойкостью к действию масел, топлив, кислот и даже некоторых растворителей. Они не могут гореть, озоностойкн, сохраняют эластичность во время длительной работы при высокой температуре. Резины на основе СКФ-32 длительно работоспособны при 150— 200' С и могут работать несколько десятков часов при 250 С. Резины на основе СКФ-26 длительно работоспособны при 200—250 ' С и могут работать
несколько часов при 300 С. Основной недостаток резин на основе фторорганпческих каучуков — ограниченная морозостойкость (примерно до —25' С). Частично этот недостаток может быть устранен при конструировании уплотнений введением металлических упругих элементов. Резины на основе СКФ недостаточно работоспособны при радиационном облучении, они более интенсивно накапливают остаточную деформацию при умеренных температурах, чем резины на основе СКН. Наконец, резины на основе СКФ дороги и нетехнологичны, поэтому применяются преимущественно для гидроагрегатов, работающих с синтетическими и агрессивными жидкостями.
Процесс деформации резины по времени существенно влияет на работу уплотнения. Для резины характерна зависимость иапря-
14»
Рис. 5.11. свойств
1 — резина чука С КТ;
жения в образце от времени действия силы и от скорОст
цин. Процесс деформации резинового образца по времен И ДеФ°Рмя ложенни и святи нагрузки Р показан на рис. 5.12 рИ При пр,9' ственны три основные составляющие деформации под РЗи,,е сво;' упругие (главный вид высокочастотных деформаций с ма НаГрУ3Кой' тудой), высокоэластичные, сопровождающиеся релакса! Л°'1 аМпЛц жения (главный вид деформаций с большой амплитуд01Ие” Напря. ленных процессах), а также необратимые пластические ” "" ционные, связанные с процессом старения.	и
пРи Мед. дестРук-
Рис. 5.12. Механические свойства резины
трех ви-
В действительности процесс является сочетанием всех трех видов, но каждый из ннх характерен временем проявления. Например, на рис. 5.12, а упругая деформация проявляется на участке 4 — /ь высокоэластичная деформация на участке — /г завершается через десятки часов, а остаточная деформация Л/ практически выявляется через несколько месяцев.
Явление постепенного спада напряжения (рис. 5.12, в) в деформированном образце называется релаксацией напряжения. Этот спад происходит до некоторого конечного значения, которое называется равновесным. Релаксация при высокоэластичной деформации связана с перегруппировкой звеньев цепных молекул без изменения среднего расстояния между ними. Релаксационные процессы, связаны также с энергией ван-дер-ваальсового взаимодействия между звеньями цепных молекул: они зависят от соотношения этой энер-г.. ргии елового движения звеньев, поэтому при повышении ервгуры релаксационные процессы усиливаются.
r условиях ограниченного растяжения — сжатия связь между Ь ным напряжением о,Л и относительной деформацией е описы-
,,сТ,1'д после достижения равновесного состояния соотношением 03	о.,. = е Егу.,	(5.7)
£ ___равновесный модуль эластичности в кГ/см2.
ГДеПри испытаниях образцов резин обычно определяют напряжение, относя силу растяжения к первоначальному сечению образца, g этом случае зависимость (5.7) нелинейна.
Механические свойства резин в условиях динамического нагружения обычно исследуются при синусоидальном напряжении
= о0 sin at.	(5.8)
В этом случае необходимо рассматривать динамический модуль резины, равный отношению амплитуды напряжения к амплитуде деформации. Деформация всегда несколько отстает от соответствующего напряжения на угол сдвига фаз <р:
е = е0 sin (at — q>).
Вследствие сдвига фаз между напряжением и деформацией в резине имеется динамический гистерезис (рис. 5.12, б), механические потери и нагрев от теплообразования.
Динамический модуль Е* выражается комплексным числом 1921 £* = £+i£’,	(5.9)
<о2т2 где Е =———вещественная часть модуля, характеризующая упругость;
(Ео — Е^) <от
£ =—— — мнимая часть модуля, характеризующая внутреннее трение (значения £', Е" см. на рис. 5.12, г), с — постоянная времени релаксационной кривой.
Прочность резин по ГОСТу 270—64 характеризуется напряжением и, при разрыве образца, соответствующим относительным удлинением ел% при разрыве и остаточным удлинением <?°о образца после разрыва. Эти критерии не дают достаточного представления о работе материала в уплотнениях, но служат способом контроля производства и сравнительной оценки резин.
Особым вопросом является испытание резины на прочность в динамических режимах. Выявление усталостно-прочностных свойств производится при циклическом многократном нагружении.
Твердость — важнейший показатель, оценивающий совокупность основных упругих свойств резин. Измерение твердости производится двумя методами. Наиболее распространен метод оценки твердости в условных единицах по шкале в 100 единиц, заключающийся в замерах деформации пружины при вдавливании иглы твер-омера в испытуемый образец. Чем меньше глубина погружения глы и соответственно больше ее нагрузка, тем выше твердость и
1*1
, пя Так определяется твердость по Ц]Пп вязания прпоорл-	тм.<2 Второй метод основан ня . У
ГОСТу 263'53 "а пр1,жс^ия в резиновый образец стально*
И по ' бипы ft погр) . р При 9Т0М показателем тн(>п„ £ приоре ТШМ-2,
СТН, определяем кГ/(М2 за рубежом распространен аналогу, величина П = л dh с0 Так как пересчет твердости с одной НЫЙ твердомер типа	весьма затрудНе11, были приняты
сНОемы измерен'<и ' Н ис0 в которых теПерь градуируЮтся международные един1	НИИРП. По ИСО твердость оЦе.
твердомеры типа Дж	нц> практическн совпадающей со шКа.
нивается по шка	свыше 40 единиц.
лой Шора для тверд и ы непосредственно в деталях в по Для оценкИ ^паботаны и начинают применяться микротвердо-следнее время разр	я п0 ис0. В мнкротвердомерах за счет
меры, кот°Рь’енТетм шарика и усилия вдавливания в несколько уменьшения Диам^ Р погружения иглы, что и дает возможность ра3	твердости резины не на специальных образ-
производить измер _	широкие возможности использования
цах, а на деталях. ,.питпППЯ готовых изделий и исследования
° "ро““е
ции.
Принято называть резины мягкими, если твердость по ИСО (ТМ-2) Н < 50, средними при твердости Н — 50 4- 70, твердыми при Н = 70 4- 88 и очень твердыми при Н > 88.
Соотношение между твердостью и модулем эластичности резин [92] примерно соответствует данным, приведенным ниже:
Твердость по ИСО	70	75	80	85	90	95
Модуль Ev_ в кГ1смя	55	75	95	120	200	350
Обычно для уплотнений применяют твердые резины с Н = 75 4- 85.
Очень важен расчет возможного срока эксплуатации и складского хранения с учетом процесса старения резин. В настоящее время уже используется методика расчета гарантированных сроков хранения уплотнений в агрегатах на основании данных ускоренных испытаний на термостарение [52].
Процесс старения резины заключается главным образом в процессе окисления молекул эластомера. Метод ускоренного определения сроков хранения резиновых деталей сводится к пересчету по принципу экстраполяции старения резин при высоких температура* на температуру склада или эксплуатации изделия. Для процесса окисления оказался в основном справедливым экспериментально установленный закон изменения напряжения о (и соответственно контактного давления р,) со временем /:
и1 = сое~(5.Ш) ’де k — константа скорости окисления (старения).
мПературная зависимость этой константы Р уравнению химической кинетики
няется yt	v
формально подчи
k — Ае RT ’
(5.Н)
„п„ А — постоянная,
гл у __ кажущаяся энергия активации процесса старения, р — газовая постоянная;
f — абсолютная температура.
На основании этих уравнений строятся номограммы типа
. L=|g/___а (рис. 5.13), позволяющие производить указанные
расчеты. Этот метод еще несовершенен и дает лишь ориентировочные результаты, но, очевидно, будет положен в основу инженерной методики расчета на надежность и долговечность уплотнений неподвижных соединении.
§ 5.4. КОНСТРУИРОВАНИЕ ПОСАДОЧНЫХ МЕСТ
ДЛЯ УПЛОТНЕНИЙ КОЛЬЦАМИ КРУГЛОГО СЕЧЕНИЯ
Наиболее распространены уплотнения неподвижных соединений кольцами круглого сечения, установленными в канавки с деформацией сжатия, создающей контактное давление за счет упругих сил кольца. Существуют четыре типа уплотнения, требующие разного выбора колец и посадочных мест: радиальное уплотнение наружной поверхности (рис. 5.14, а); радиальное уплотнение внутренней оверхности (рис. 5.14. б); торцовое уплотнение плоского разъема при действии давления среды изнутри (рис. 5.14, в)- то же при действии давления среды снаружи (рис. 5.14, г).
В первом случае кольца устанавливаются в канавку с натягом РеЛ^ТреННеМу диаметРУ« 80 втором — по наружному диаметру.
мендуется контролировать рабочий размер Dp перед сборкой
153
Кольцо для торцовых уплотнений устанавлив • к	от направления действия давления V*
зависимое в канав1<е под давлением (см. рИс 1аЛ Если давление р действует изцутп2‘ кольцо должно устанавливаться в ‘’ вавке по наружному диаметру о Л в противном случае — по внутре||^ му диаметру D.
Кольца изготовляются с допуска-ми, указанными в табл. 5.2, поэтому для правильной установки кольца очень важно сочетание допусков коль-ца и канавки. Разница в размерах посадочного диаметра кольца и канавки должна компенсироваться за счет растяжения кольца на 1—5% или за счет обжатия кольца по наружному диаметру (рис. 5.14, бив) до 3°о.
При высоком давлении повреждение кольца и потеря герметичности наступают вследствие выдавливания кольца в зазор (см. рис. 5.9, д). При циклической пульсации давления этот процесс носит усталостный количеством циклов пульсаций давле-
соединения в канавке в чтобы оно не перемешалось

а
в
Л
в
D----
—i п

' В)
t— DA-
—1 В
Рис. 5.14.
для колец
a)
р
д)
Prui
1 е)
Посадочные места круглого сечения
и определяется
ни^д^^начала потери герметичности или до начала повреждения
кольца.
Таблица 5.2	Таблица 5.3
Внутренний диаметр D в мм	Допуск на Du %	Диаметр сечения d в им		Давление р в кг/см%	Зазор на сторону (с учетом деформации) в мм при твердости резины по ИСО		
До 20 20—30 30—50 50—90 90-120 Свыше 120 мм	-3 —3 —2,5 -2,5 —2,0 -1,5	2 + 0,07 2,5 + 0,1 3 + 0,1 4 + 0,15 5 + 0,15 6 + 0,2			70	КО	to
				0—50 50—100 100—150 150—200	0,10 0,06 0,03 0,02	0.12 0.08 0,06 0,04	0,15 0,10 0,06 0,04 —
Давление р, зазор б и выносливость т кольца связаны линейной зависимостью типа
Igm-=а —pigp,	(5.12)
где коэффициенты аир являются функцией зазора и твердости Р зины (увеличение зазора резко уменьшает выносливость). Дл предотвращения повреждений колец при циклической нагрузке и
1М
,ИЯ выносливости более 10 млн. циклов практикой вырабо-Рбеспече‘ имые величины зазоров, указанные в табл. 5.3.
та)|^Д0 обеспечения работы уплотнений при давлениях свыше ^Лгсмг рекомендуется устанавливать защитные шайбы из пласт-
200 К! ока3аННЫе на рис. 5.14, д ие. Часто применяют защитные шай-|'|асС’3'1фторопласта-4, которые под действием давления закрывают 6lJop и предотвращают выдавливание колец.
Таблица 5.4
Показатель	Внутр»ппий дням-тр В ЯМ				
	Радиальные уплотнения				Торцовые уплотнения
	До 10	10 20	20 -70	Свыше 70	
Растяжение при установке кольца в канавке в %	4—6	3—4	2—3	2	—
/<,	0,95	0,97	0,98	0.98	—
К, при -40—50' С	0.99	0.99	0.99	0,99	0.99
	0.94	0.96	0.97	0,97 	—«	0.99 ,	
Диаметр сечения кольца d увеличивается с увеличением внутреннего диаметра кольца D примерно в соответствии с табл. 5.2 (сортамент колец устанавливается ГОСТом 9833—61 или нормалями).
Кольцо должно располагаться в канавке свободно. Объем кольца должен быть на 5—10°о меньше объема канавки с учетом неблагоприятного сочетания допусков. Это условие учитывает объемное набухание кольца до 5%. Для резин, имеющих большое объемное набухание в рабочей жидкости, необходимо соответственно увеличивать объем канавки. Объем кольца Vo должен определяться по формуле тороида
W = 4 (^max "Т dmax) <2?цах»	(5.13)
где D,nax — наибольший внутренний диаметр кольца; dmax — наибольший диаметр сечения кольца.
Размеры канавки должны обеспечить деформацию сжатия кольца по сечению для создания требуемого контактного давления при всех очетаниях допусков на размеры канавки и кольца. При низких лениях герметичность обеспечивается при минимальном среднем контактном давлении р, порядка 2,0 кГ/см*.
и еличина Pi определяется относительной деформацией сжатия и Мало зависит от диаметра сечения d;
6==£_Люоо/0,
(8.14)
ш
ГЛР сумма высоты канавки и зазора между детяпг, наибольшем эксцентрицитете.	' та*Ями
При разнородных материалах учитывается увелич >	*
из-за температурных деформаций, а при тонких стен?"16 3азОп деформации, происходящих под воздействием давпеищ Х Из.
Начальная относительная деформация р,п1п Дад ни- а минимальное контактное давление z>, n,jn при Л|Обой “d ()бссПеч,.ъ пературе в течение всего времени эксплуатации П Да,|||ой Те,ь е,пы требует учета зависимости эластичных своие™’* В|^п температуры и времени. При низких температурах |ХЧ|<ны ства резины ухудшаются (см. рис. 5.11), что проявчяе^» ,ЧНЫе нин контактного давления рн уплотнения п. < „ в УмецЬп ' контактное давление при 20'С, пли в неполном 2? ГДе высоты образца после снятия нагрузки Болес правипТаН0ВЛеи«'« характеризует вел,„„„а	„„ „обгтК1 „зж,ришй ™
пользоваться коэффициентом восстанавливаемости Д' == ''г — h
°СТаТО',Н°Й	"Г" низкой темц'ери^"’
Ао — Aj
С учетом накопления остаточной деформаций в нр„цес« (см- ₽"'• 5.13) определяют минимальное контакт " “iZZr П₽" НИЗКОЙ к концу возмож,™
Pi min — Pio Кй (1	Д/)»
(5.15)
где pi0 — начальное контактное давление, определяемое по формуле pi0 = Е-^фг,	(5.16)
где Кф — коэффициент формы, учитывающий зависимость результатов экспериментального определения модуля эластичности от формы образца; для колец круглого сечения К.ф = 1,3.
Опыт эксплуатации уплотнений показал, что при низкой температуре удовлетворительно могут работать резины с коэффициентом восстанавливаемости не ниже Кв = 0,15, а остаточную деформацию к концу срока эксплуатации можно допускать до 70% (А/ -— 0,7). Для обеспечения герметичности необходимо контактное давление plmin > 1 кПсм2. Так как обычно для уплотнений применяются резины твердостью 80—85 единиц ИСО, которые имеют равновесный модуль 100 кПсм2, величина elnin должна быть равна 10 12%>. Это значение несколько увеличивают для уплотнений неподвижных соединений.
Верхний предел е1пах определяется сочетанием допусков. Накоп-лен2^ остаточной деформации происходит медленнее при в = 20 т •«- 30/о. При е = 22 4- 25% наблюдается наибольшая выносливость 156
Характеристики некоторых резин
колец при циклической нагрузке. Таким образом, с учетом и < члвать:
)лец при HllK.’iHicviwn	.... ........, v. J4C1OM Доп
старения резины необходимо для наружных уплотнений об^06
_ A^niin % ах
®Щ|П -- f1
"mln
^max ^nihi
Етях —	,1
"так
"100%; emin^15%;
100%; Ещлх ==== 35%.
(5.17)
Поправочный коэффициент /< = К^К^К-, (см. табл. 5.4) V4. вает сплющивание колец радиальных уплотнении вследствие пя ТЬ1' жения колец в канавках (коэффициент Л\), изменение размера с?1” ния кольца на морозе (коэффициент ^2), изменение размера сечен** кольца вследствие набухания (растворения) резины в масле (КГЛЯ фициент Ks).	Ф'
Последний коэффициент учитывается только для сортов резин уменьшающих объем в рабочей жидкости. Если коэффициент объем него набухания ДЕ = ^51°, изменение диаметра сечения будет
d + М = d У Г±ДГ d ± V';	(5Л8)
„ d + bd . АИ Лз =~— = 1 ± 3-.
Кольца круглого сечения для неподвижных соединений низкого давления изготовляются из резины средней твердости (по ТМ-2 (ИСО) 65—75 единиц]. Резина должна сохранять эластичность в течение примерно удвоенного срока эксплуатации, иначе не будет обеспечена необходимая степень надежности. Резина должна быть очень термостабнльна и морозостойка. Не рекомендуется применять резину с отрицательным набуханием в масле и объемным набуханием свыше 8%.
Применяются следующие марки резины (81: 8190, В-14, 98-1, 8075, а также теплостойкие резины ИРП-1054, ИРП-1078 и др. (резина ИРП-1054 имеет повышенное набухание в масле АМГ-10 и требует увеличения канавки по ширине). Для колец круглого сечения при высоких давлениях применяют резину с твердостью 75—85 единиц по ТМ-2 (ИСО). Очень часто применение разных марок резин в одном агрегате вызывает производственные трудности, поэтому кольца, рассчитанные на высокие и низкие давления, приготовляют из одной резины. Характеристики некоторых марок резины даны в табл. 5.5.
| 6.5. УПЛОТНЕНИЯ ПАР ВОЗВРАТНО-ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ
Конструкции уплотнений пар возвратно-поступательного движения показаны на рис. 5.2 и 5.15. Механизм действия эластомерны* уплотнений пар возвратно-поступательного движения, выполняв-
,х с помощью колец круглого, Х-образного или U-образного сече-ПРИ неподвижном штоке или поршне рассмотрен выше. При дрижении штока относительно }шлотнения (или поршня относительно цилиндра) между уплотняемыми поверхностями образуется щель, через которую некоторое количество масла может выноситься наружу- Часть этого количества масла при обратном ходе штока 1зновь возвращается в цилиндр и лишь их разность образует утечку При таком режиме работы поверхность уплотнений отделена от контртела пленкой масла, что резко снижает трение и износ обеспечивая длительную работу уплотнения при незначительной’ утечке.
уплотнения при
незначительной утечке.
Стремление получить сухой шток приводит к быстрому износу уплотнений.
Вследствие гидродинамического действия пленки жидкости на эластичную уплотняющую кромку она принимает конусообразную форму.
В гидромеханике задача о распределении давления и величине зазора решается для случая заданной постоянной формы поверхности и приводит к уравнению Рейнольдса
дР _Rllr) M-v) — Ао _ /и
где h (х) — высота щели вдоль координаты х\ h0 — высота щели в точке
₽'W-*=0.
В случае эластичных уплотнений форма щели меняется пол Мй* вием гидродинамического давления, но величина h (х) очез* шма
(5.19)

(1 — 10 лл-) по сравнению с предварительной дефорМац „ нения, поэтому в первом приближении считают, что расПт?. ^п,,|от давления по уплотняющей поверхности при движении uitoi ня) мало отличается от распределения давления при Heno<a *,IOPUi-состоянии. Это предположение значительно упрощает заДапПи>К||<л деляя распределение давлений по уравнению (5 19), котор0мУ’ 0,1Ре-придать форму	У Мо>кио
—/? + 1 =0,
где h =	— безразмерный зазор, при помощи которого
деляется значение й0.
После первого расчета может быть произведен повторный с использованием найденных 1г (х) в качестве начальных который дает уточненную форму пленки 138].
Для определения толщины пленки
Расчет Условий,
(5.20)
необходимо знать производную р'(х) кривой давления в точке пере, гиба эпюры распределения давлений (см рис. 5.9 и 5.10).
р' (х) = ~k, где k — поправочный коэффициент.
Приближенно
Безразмерный параметр а определяется соотношением размеров уплотняющей поверхности и несколько зависит от давления (в среднем а = 0,25 для колец круглого сечения). Следовательно, величина
пленки существенно зависит от формы кривой контактного давления, которая определяется профилем сечения уплотнения. Знание высоты щели й01 при прямом (насосном) и й02 при обратном (двигательном) ходе штока позволяет рассчитать величину утечки через уплотнение с диаметром штока D и ходом L за один двойной
ход:
Qy^^(h01-h02).	(5-21)
Как видно из рис. 5.15, с и б, величина утечки зависит в основном от профиля сечения уплотнения, определяющего крутизну нарастания контактного давления, и мало зависит от давления в цилиндре-Очевидно, для работы без утечки уплотнение должно иметь такую форму кривой контактного давления, при которой h01 я» йог за счет смещения максимума кривой контактного давления ближе к полости давления р (рис. 5.15, в).
Отсюда следует, например, что универсальные уплотнения с симметричной формой кривой собственного давления р, (кольца О- и X-образного сечения) принципиально более склонны крбра-зованию утечек при работе под давлением, чем рационально спро' ектнрованные манжетные уплотнения.
собственного давления уплотнения
Рис. 5.16. Значения коэффициента трения уплотнений при обеспеченной смазке
Таблица 5.6
Давление р в кГ/см-	Менее 20	20-70		Свыше 70	
Твердость резины	Большая	Средняя	Большая	Средняя	Большая
Относительная ширина контакта b/d	0,4	0.6	0.55	0,8	0.75
Для определения коэффициента трения могут быть получены ашь литические зависимости на основе решения уравнения (о. ) ДЛ гидродинамического режима работы и эмпирические формулы для остальных режимов. При расчетах можно пользоваться графиком, показанным на рис. 5.16 (/ — фторопласт; 2 — резина с антифрикционным наполнителем; 3 — резина на основе СКН)-
6 В н. Прокофьев и др.
s 5.6. УПЛОТНЕНИЯ ВРАЩАЮЩИХСЯ ВАЛОВ
Наибольшее распространение получили радиальные у валов армированными манжетами (см. рис. 5.3) с браелЛ°ТНенця жимной пружиной 3. Такне манжеты делаются в основ07"0*' На-типов. Манжеты для уплотнения наружных валов копГ|Н,°М ДвУх давлением доО,5—1 кГ 1см2 выполняются с пыльником (см. рц1СцВ "°Д защищающим шейку вала от пыли и влаги. Если ° ние в корпусе может превышать 1 кГ'см\ применяются маш Давле-пыльника (см. рис. 5.3, а) с шайбой 2, предохраняющей мС1Ыбез от деформации при действии внутреннего давления. Рад^' ^У эластичное уплотнение отличается наличием нажимной пп адьное поддерживающей контактное давление на уплотняющей к>К1,НЬ|’ в необходимых пределах. Так как усилие пружины практи'04^ не меняется в процессе эксплуатации, потеря эластичности n4eCKl1 вследствие старения не оказывает решающего значения на пе3,Ины манжеты. Для обеспечения длительной работы манжеты необход применение рациональной формы кромки и правильный выбор у ° лия нажимной пружины.	"с,|‘
При вращении вала необходимы гидродинамическая смазывающая пленка на поверхности вала и хороший отвод тепла от трущейся поверхности, что существенно повышает ресурс работы при малом износе и незначительных утечках. При неподвижном вале механизм уплотняющего действия аналогичен механизму уплотняющего действия рассмотренных выше уплотнений. При расчетах используют удельную силу контактного давления Р, отнесенную к 1 см длины
кромки:
Р = Ри + Ри + Рп 4- Рр,	(5.23)
где Рм — составляющая от растяжения конической губки манжеты;
Ри — составляющая от деформации изгиба этой губки вследствие эксцентричной посадки манжеты относительно вала;
Рп — составляющая от растяжения пружины;
Рр — составляющая от давления жидкости на профиль манжеты.
При вращении вала точки кромки перемещаются в радиальном направлении вследствие воздействия микронеровностей поверхности вала и его биения из-за динамического эксцентрицитета. Кроме того, силы трения смещают кромку в направлении вращения. В результате этого точки уплотняющей кромки совершают сложные движения, траектории которых близки к эллипсам, а между валом и уплотняющей кромкой появляется гидродинамическая пленка масла. Однако толщина этой пленки весьма мала и обычно не превышает 1 мк, поэтому для расчета манжеты может быть использовано равенство (5.23). Для обеспечения герметичности необходимо иметь удельную силу Р > 0,2 кПсм, при которой наблюдается просачи ванне масла без каплепадения, или утечки в количестве 3—5 капел

(5.24)
,, Р > 0,4 кПсм обычно происходит нарушение смазки 6 чаС возникновение сухого трения. Значения Р уточняются эк-03/13 ментально для конкретных случаев Упругие свойства рези-сГ,еР i губки в процессе эксплуатации ухудшаются за счет релакса-"°В°и старения с постепенной потерей составляющей силы Рч, 11,1 тому основную роль в работе манжеты имеет усилие Рп пружины, П°влияние Р« необходимо по возможности уменьшать.
3 рассмотрим отдельно члены формулы (5.23). При отсутствии эксцентрицитета 1убка манжеты деформируется подобно тонкостенной трубке, на которую по уплотняющей кромке изнутри действует равномерно распределенное усилие Рм Распределение напряжений в уплотняющей губке соответствует этой модели, так как длина губки / примерно равна полуволне распределения напряжений в трубке. Поэтому для расчета удельной силы Р„ может быть применено равенство
F F ‘ м	2»
где AD — деформация растяжения губки;
— равновесный модуль эластичности резины;
F — площадь сечения губки;
D — диаметр вала (все обозначения показаны на рис. 5.17, а).
Усилие Рр на уплотняющей кромке, создаваемое давлением масла на внутреннюю полость манжеты, равно Рр^2 (рг— р2) = = 2Лр. Это усилие учитывается при определении Р только при расчете работы трения При определении минимального значения Р, обеспечивающего герметичность, рассматривается случай работы уплотнения при отсутствии избыточного давления внутри корпуса давзени^Р^т nf ~ Р1 ~	= °' СоставляюШая силы удельного
” растяжения пружины связана с усилием растяжения пружины Рс соотношением Рп = 2%. Пружина растяжения имеет трапецеидальную характеристику (рис. 5.17, б)
рс= />«, + с А/,
ГДб Рс° ~ вагшово^кеУС^Ие ВСЛедствие внутренних напряжений с ~ жесткостьКпруВжины^аЮЦ1ИХ "РИ НаВИВКе "PyW
Pr°	= Ф ет,т-	(5.25)
Деляющий, Такую™'Р у<^анаВливаемый коэффициент, опре-Усилия пружины /ппа f0 ^оставляет от предельно допустимого “№« ф1оН|™,<™У№нных при терЧюоврабо^еадх.™ * 0,33);	’	°’15, для неотпущеиных пружин <р » 0.25 +
(/„ — днимстр проволоки, d, — срецннй диаметр витка пружины; a — коэффициент, зависящий от отношения dn
„ = ] 35 для обычно принимаемого соотношения .
</.,	’*5 -i. е
т - предельно допустимое тангенциальное напряжен., * Ь;
териале (т = 0.5 ое 100 кГ/мм2).	1е в Мд,
Kwvw\aaaaaaaaaaa/wwJ dl
Рис. 5.17 Расчетные размеры манжетного уплотнения
Жесткость пружины с, имеющей пружины
Zo	,
i = витков на длине ь0 “п
(5.26)
где G = 800 000 кПсм' — модуль t
Удлинение пружины определяется ходимо для гх---
откуда
модуль сдвига материала пружины. ----г°делястся по усилию Рс, которое необ-
обеспечения заданного Р:
р	_(P-PM)D d . А,
&L = L — Lo = л (ДД + дпп)1	(5.28)
длина пружины в рабочем состоянии, L = л (£>, + I состоянии, которую необходимо О17) и (5.28).	*
(5.27)
где L —	, j...и. о раиочем <
L# — длина пружины в свободном сос определить из уравнений (5.26), (5.27)
ИН
Объединив при этом все параметры в одном коэффициенте kL, учим Lo = ki-L. Практически kL = 0,88 -е- 0,93, поэтому при
Г четах выбирают kL = 0,9. Допуски на изготовление манжеты раСаметр D, площадь сечения F) и пружины довольно велики, поэму получить необходимое удельное давление кромки манжеты т вал очень трудно. Это вынуждает производить подбор параметров ”оуЖины за счет изменения ее начальной длины Lo и удлинения д/ Для этого пружины должны проверяться на величину усилия р на рабочей длине L. За счет широкого допуска на Lo при этом возможна подрезка пружины. После установки пружины на манжету рекомендуется проверить величину удельного давления на специальном приборе. Контроль за Р в процессе производства дает при эксплуатации уплотнений большой эффект, повышая ресурс в 2—3 раза и устраняя такой серьезный дефект, как износ вала под манжетой.
Биение шейки вала вследствие динамического эксцентрицитета оказывает большое влияние на герметичность радиального уплотнения, вызывая дополнительную деформацию изгиба губки манжеты и появление инерционных сил. Все это проявляется в высокочастотных пульсациях контактного усилия в каждой точке уплотняющей кромки.
Деформация элементов уплотняющей губки и сила ее давления на вал определяются методами теории тонких оболочек с учетом динамического модуля упругости резины и запаздывания напряжения. Такие исследования выполнены, например, Ф. Хирано [621, который получил уравнения эллиптических траекторий точек кромки, величину давления на вал. Оказалось, что существует определенная величина эксцентрицитета ео при которой уплотняющая кромка начинает отставать от вала и уплотнение теряет герметичность
2ес I I
ДО = |^|(1+6),	(5.29)
где 6 — модуль сложной комплексной функции, зависящей от массы и размеров губки, окружной скорости и других параметров.
Следовательно, необходимо обеспечивать условие
По исследованиям Ф. Хирано, при очень малых окружных скоростях предельный эксцентрицитет не зависит от скорости, и губка надежно следит за валом. Затем величина е, оказывается зависимой от скорости до о) (где т — постоянная времени релаксационной кривой [уравнение (5.9)]. При скоростях  величина ее не зависит от окружной скорости, пока мало ее отношение к скорости звука (до 30—46м/сек). Кроме ухудшения герметичности, эк, йПГТМ цитет вала усиливает усталостные процессы в материале крог ‘ может вызывать отслоение резины от арматуры. Поэтому дли
высокоскоростных гидромашин допускают возможно сцентршштеты, значение которых приведено в табл 5 7’аль1е зк.
Г°0л,(1{0 5?
	Окружная скорость в м/сек	До 2	2-4	4-8	8-15
С	Допускаемая несоосность вала посадочным гнездом манжеты	0.2	0.10	0.10	0.08
в в	Допускаемое радиальное биение мм	0.15	0.10	0.05	0.03
Для работы манжет очень важное значение имеет выбор резинь с меньшим коэффициентом трения и улучшение условий теплоотвода с трущихся поверхностей, так как высокая температура в зоне тре-ния является основной причиной ускоренного старения резины приводящего к растрескиванию уплотняющей кромки и появлению утечек. Вследствие плохой теплопроводности резины отвод тепла происходит практически полностью через вал и большое значение имеет теплопроводность покрытия вала.
Момент трения Мт равен
MT = ^fP,	(5.30)
где f — коэффициент трения, являющийся функцией безразмерного
Ц<1) критерия режима s = —.
Рк
По данным Ф. Хирано 162) зависимость [ от критерия режима s выражается уравнением
f = ф j^s,	(5.31)
где коэффициент Ф несколько зависит от числа оборотов. Обычно коэффициент трения при работе уплотнения находится в пределах 0,2—0,3, а в момент пуска после длительной остановки вала возрастает до 0,6—1,0. Меньшим коэффициентом обладает резина, подвергнутая специальной обработке — фторированию — или резина, в состав которой введены фторопласт-4, углеграфит и другие антифрикционные вещества. В этих материалах f — 0,154-0,25, а при пуске f = 0,3 4- 0,5.
Расчет температуры кромки производится по уравнениям теории теплопередачи, принимая, что весь теплоотвод происходит только через вал, а вал представляет собою стержень неограниченной длины. В нормально работающем радиальном уплотнении температура кромки обычно превышает температуру корпуса гидромашины на 10 15° С (учитывается при расчете старения материала у плот* нения),
1вв
ы пол манжеты должны иметь высокую чистоту обработки
ЬЯ'еПах v9—уЮ, дня тихоходных валов \ 8. 1 вердость поверх-Р „вала должна быть не ниже HRC 30. Лучшую износостойкость Н<К.ют валы с цементированной шейкой, закаленной до твердости
52—60. Из соображений коррозионной защиты валы хромируют (хром твердый).
§ 5.7. ТОРЦОВЫЕ УПЛОТНЕНИЯ ВАЛОВ И ПОВОРАЧИВАЮЩИХСЯ ДЕТАЛЕЙ
Торцовые уплотнения валов с эластичным уплотняющим элементом не получили широкого распространения, хотя они имеют ряд принципиальных преимуществ по сравнению с радиальным уплотнением — допустимость больших радиальных биений вала, лучшие условия теплоотвода. Для гидромашин с повышенным ресурсом работы (свыше 3000 ч) и для специальных тяжелых условий наиболее ответственных изделий применяют торцовые уплотнения, в которых уплотняющим элементом являются два притертых диска. Примеры конструкции таких уплотнений показаны на рис. 5.4. Уплотнение, нормализованное НИИ Гидромашем (см. рис. 5.4, а), имеет установленный на вал корпус 2 с гайкой 3, в котором расположены все вращающиеся детали: стальной уплотняющий диск 6, нажимная пружина 4 с шайбой 7, уплотняющее резиновое кольцо 5. Диск 6, опирается на углеграфитовый неподвижный диск 7, закрепленный в корпусе машины (однако этот диск имеет возможность
самоустанавливаться в перпендикулярное валу положение за счет эластичности кольца 8). На рис. 5.4, б показано уплотнение, в котором применена плоская волнообразная нажимная пружина 3, сокращающая габариты уплотнения.
Большим преимуществом торцовых уплотнений является возможность работы при высоких давлениях в корпусе гидромашины. Это позволило в некоторых случаях применять гидросистемы без дренажных трубопроводов, допуская в корпусах насосов и гидромоторов давление до 35 кГ/см2.
Герметичность и долговечность работы торцового уплотнения определяются состоянием масляной пленки между трущимися поверхностями. Если эта пленка возобновляется в результате некоторого просачивания жидкости, в зазоре наблюдается режим жидкостного трения с низкими потерями на трение. Однако в большинстве случаев торцовые уплотнения работают в режиме граничного или полусухого трения (в последнем случае происходит значительный износ дисков).
Различными исследованиями установлено также, что режим тре-Яц<о Уплотнении определяется безразмерным критерием режима ~~ Рк ’ пРичем в области s >• 10 ’ отмечается типичный для гидродинамических подшипников характер зависимости кепффиц—пв
	-_	гидродинамического режима РГ1 F {s). Вознчк«ове 1ПШ пле„ки до 1-5 мк. (>бъ ' трения_________увеличен ™ С11ЛЫ ч0 счет ппрод.шамичезд
пР^^пЛенне», под^	к0В, волнистости поверх,,^
няетея взаНмного	проектирования торцовых уПлот.
«ГмикроклиньеЛдВ;
И Голубева 1221 и ряд других работ 162] на1ИЧ посвяшена книга А- '	' J лотнян>щнй диск, показана Иа
не Схем? сил, ^йс1Т2 я трения и износа дисков желательно иметь Сч 18 Для уменьшения тр	ния, пр11 котором раснреЛеле_
Г»«Р”»™“ХТп«.ке близки « >*"» „ ер»,,,, ние давления в к-
Рис. 5.18. Схема сил, действующих па диск торцового уплотнения
ление в зазоре близко к 0,5 р. В этом случае при выборе размеров площадей F3 и F2 пользуются приближенным равенством
pFt — kpF2 + Рс—Т = рк F2,	(5.32)
где pFj — сила давления на диск внутри корпуса;
kpF2 — сила противодавления пленки в зазоре (kp— среднее давление в зазоре с учетом нелинейности его распределения);
Рс — усилие нажимной пружины;
Т — сила трения в уплотняющем кольце;
р,;— контактное давление, равное избыточной прижимающей силе, отнесенной к площади уплотняющей поверхности.
Усилие нажимной пружины выбирают из условия обеспечения минимального давления рк на трущейся поверхности в пределах 1,5—2,5 к.Г!смг (при отсутствии давления р в корпусе). Это давление может несколько меняться для разных материалов трущихся пар.
Один из дисков обычно выполняется из стали наивысшей твердости и износостойкости (например, из PI8, Х12Ф1). Второй диск при работе всухую выполняется из углеграфитов (например, марки ПКО, АГ-1500) или специальных керамик. При работе в среде масел применяют высококачественные бронзы (например, Бр. ОСН 10-2-3, ОЦС 6-6-3). Диски по рабочей части должны иметь чистоту обработки ПО—VI1 и отклонение от плоскостности не более 0,5—1 лк. Столь высокие требования к обработке поверхности должны соблюдаться и для уплотнений больших диаметров.
Пример подвижного уплотнения магистрали был приведен на рис. 5.5 (цапфы люльки 1 регулируемого насоса). К ним относятся уплотнения люльки 1 (см. рис. 5.5, а) регулируемого насоса с на" 1Ь8
м бпоком, которая поворачивается относительно неподвиж-кдонинм на у’гпл 30 этИ уплотнения находятся внутри кор-"wJi ^поэтому могут допускать утечки в пределах нескольких "Xf3’ не влияющие на характеристики насоса. Уплотнение ра-сМ nt ного типа в насосах с низким рабочим давлением (до 80 кГ/см2) Ложет выполняться кольцами 2 (см. рис. 5.5, а) из твердой резины. Кольцо устанавливается с натягом по наружному диаметру и тор-к ' ’цТ0 обеспечивает начальное контактное давление р,-. Давление жидкости р, подведенной внутрь кольца, создает дополнительный поджим кольца, в результате чего контактное давление рк = р + 4- р,. Износ кольца происходит прежде всего за счет его выдавли-ваггия в зазор, так как конструкция насоса не позволяет сделать этот зазор менее 0,1 мм. В насосах на рабочие давления до 200 кГ/см? уплотняющие кольца выполняют из фторопласта-4, который вследствие большой твердости меньше подвержен выдавливанию в зазор.
Для создания начального давления на контактной поверхности иногда применяют комбинированные уплотнения (см. рис. 5.5, б), состоящие из уплотнительного пластмассового кольца 4 (фторопласт-4) и резинового кольца 2, создающего начальный натяг с давлением Pi- При давлениях 150—200 кГ/см2 наблюдается постепенное выдавливание фторопласта-4 в зазор, что ограничивает срок службы таких уплотнений. Поэтому для насосов, создающих высокие давления до 250—350 кГ/см2, применяют торцовые уплотнения, показанные на рис. 5.5, в. В неподвижном корпусе насоса 3 устанавливается стакан 4, поджимаемый усилием нажимной пружины 5 и силой давления р на торец Fr к сферической шайбе 2, притертый торец которой опирается на торец втулки 1 в поворотной люльке. Площадь этой опоры Е, больше площади Fx для того, чтобы в зазоре происходило некоторое просачивание масла и возникала сила, уравновешивающая силу pFj давления. Принцип действия и расчет этого уплотнения и рассмотренных выше торцовых уплотнений валов аналогичны.
Особенностью проектирования торцовых уплотнений цапф насоса являются высокие контактные давления на трущихся поверх-КОТ°РЬ^ требуют выбора соответствующих материалов TwnZ™ ,Пар‘ °ДНа И-3 детадей паРы Делается из стали наивысшей Я оК?СГОИКОСТИ: ВТОрая из твеРдой бР°нзы (например, Р- VK 9-4) или закаленной стали с твердостью HRC 50_55 Для
м™дХтьеКя°НлТоКТН0Г0 давления на трущейся поверхности F3 ная дедаться Дополнительная опорная поверхность F,, отделен-УплотаяюшейНЯЮЩеИ ПОВеР£нос™ Дренажной канавкой. Выбор Упдотняющеи^ поверхности Е2 производится по формуле kF. = 2F., ’ • i.J уменьшается при увеличении рабочего давления.
Глава 6
ГИДРОСТАТИЧЕСКАЯ РАЗГРУЗКА
§ 6.1. УРАВНЕНИЯ ДИНАМИКИ ПЛ М1АЮЩЕИ ГИДРОСТАТИЧЕСКОЙ ОПОРЫ
Во многих гидромашинах используется гидростатическая раз. грузка, чаще всего обеспечивающая регламентированную раздели-тельную пленку между трущимися поверхностями. Обычно гидростатическая разгрузка применяется для уменьшения механических потерь за счет некоторого увеличения утечек. Задача нахождения условий минимальных суммарных потерь решалась Шюте и Тэри-буллом 148]. Однако главные задачи гидростатического уравновешивания: снижение механических потерь на малых («ползучих») скоростях движения, когда они особенно велики и могут вызвать нежелательные автоколебания, и увеличение ресурса гидромашины за счет гарантированного разделения трущихся поверхностей пленкой рабочей жидкости.
Имея в виду, что общие вопросы гидростатического уравновешивания рассмотрены более или менее подробно |48, 74]. ограничимся анализом так называемой обобщенной плавающей гидростатической опоры (рис. 6.1), поскольку она при очень небольших ограничениях обращается либо в самоустанавливающуюся гидростатическую опору, обычно применяемую на головках аксиально-плунжерных гидромашин (см. рис. 1.16 и 6.2), либо в поджимной стакан, применяемый в торцовых распределениях высокомоментных гидромоторов или обычных радиально-плунжерных гидромашин (рис. 6.3). Так в устройстве, показанном на рис. 6.1, меняя размеры подводящего канала (/ — длина и f— площадь поперечного сечения), центральной камеры (В — отношение диаметра этой камеры к наружному диаметру D торцовой опоры) и устраняя поджимающую пружину, можно получить различные варианты используемых плавающих гидростатических опор.
Размеры и форма устройства, жесткость пружины и динамический коэффициент р вязкости рабочей жидкости определяют зависимость зазора от давления р1# (здесь, как и в дальнейшем, индекс в виде звездочки внизу будет относить величины к стационарному режиму работы, для которого а* = О для любой величины тоТ же индекс вверху относит любую величину к нестационарному Р6' жиму работы).
170
. ^пьчование плавающей »« ™овке
ГО
0-
Р
й гидростатической опоры, например. поршня аксиально-поршневой гид-
Рис. 6.2. Гидростатическая опора на головке плунжера
v
Рис. 6.1. Схема обобщенной плавающей гидростатической опоры
Ромашины (48] (рис. 6.3), требует выяснения величины наибольшей амплитуды колебания зазора 6', поскольку давление под поршнем
с- 6.3, Поджимной егаця
r°SX рас~— верной .ядро-
р1 меняется п ... is*с см|™“»
проходных пиро
Очевидно, выбираемый при помощи статического
зор б» должен удовлетворять неравенству	1 асчета За
। >“*”	(6.1)
импий допустимый зазор, величина которого опре. где - наимеХ"тями поверхностей и размерами возможных деляется шсрохо	рабочей жидкости.
инородных включещи в I ..СтВа - сравнительно высокое значе.
Особенность работы j	со6сгве11|1ых незатухающих коде-
ние первой (наименышо)	в11СШН1,х воздействий Q.
баннй йд " ^ь^вовсдение поверочного динамического расчета
При Q <	ПР°';П„11К нмест смысл только для таких, которые
для последующих гармонику	м
имеют порядковый номер i -
I й’

(6.2)
где Q =о и д’ — V .
I
При малых изменениях (колебаниях) торцового зазора переходные процессы рассматриваемой системы (см. рис. 6.1) в случае ламинарного движения рабочей жидкости в подводящем канале и торцовой щели описываются системой четырех дифференциальных уравнений
р* — Р* =	и* + р И'*\
Р*=- (6^1п £ ю* ~ Р '*>1п £
— л£)б*	— Fb* — "8, р* = 0;
Мб* + рНб* + с„ (6* - б0) 4- /ф (Fi -f)- Р: (фР - f) = 0.
(6.3)
где в первой строке — уравнение потерь в подводящем канале, во второй — уравнение потерь в торцовой щели, в третьей — уравнение расхода и в четвертой — уравнение равновесия гидростатической пяты обобщенной плавающей гидростатической опоры, причем;
Р* — давление в центральной камере;
скорость рабочей жидкости в подводящем канале;
Р — плотность рабочей жидкости;
и’* скорость рабочей жидкости на выходе из торцовой щели,
4	’
А V
~ х — коэффициент сжатия;
V объем рабочей жидкости в центральной камере,
«72
„ _ модуль объемной упругости рабочей жидкости (обычно адиабатический, если только частота колебаний не чрезмерно мала);	• .
д) — масса (включая и соответствующую долю массы пружины) гидростатической пяты;
j-j_отношение площади боковой трущейся поверхности к
среднему значению радиального зазора,
и _ жесткость пружины и ее предварительный натяг;
" р_____активная площадь (находящаяся под воздействием гид-
ростатическою давления).
В последнем равенстве член р0* (tyF — f) является значением гидростатического отжимающего усилия, причем величина исправляющего коэффициента ф будет зависеть от закона изменения давления в торцовой щели по радиусу. Эта закономерность, рассмотренная, например, в работе 1481, будет зависеть в случае не слишком малого зазора (адиабатический ламинарный поток), в том числе, от вязкости рабочей жидкости, ее теплоемкости, упругости, теплообмена, формы и размера торцовой щели.
Возможны случаи, когда сравнительно небольшое изменение значения ф может существенно изменить динамические свойства и «жесткость» рассматриваемой системы, поскольку некоторые параметры разрешающего линеаризованного дифференциального уравнения зависят в том числе от разности F, — ф/7. Чем ближе отноше-ние у к единице, тем точнее должен вычисляться исправляющий коэффициент ф, разумеется, при условии значимости влияния членов разрешающего дифференциального уравнения, зависящих от значения Fr — фр.
Первое уравнение, представляющее собою выражение потерь в цилиндрическом канале при неустановившемся режиме движения (при ускорении, отличном от нуля), и третье — уравнение расхода— в одинаковой мере справедливо как при постоянном р14!, так и переменном значениях pf, и в каких-либо ниях не нуждаются 148].
Иначе обстоит дело со вторым (потери напора при протекании ламинарного потока через торцовую щель) и четвертым (уравнение равновесия гидростатической пяты) уравнениями, которые при сколь-нибудь значительных амплитудах перестают быть справедливыми, поскольку возникающее из-за колебания пяты поле давлении в торцовом зазоре изменит характер распределения давления счшДТу Н ЭТ° ? пеРвУю очередь приведет к нарушению (и вероятно, у юственному) правомерности четвертого уравнения системы (6.3). той естественн0 в качестве критерия справедливости приня-BenmivA Ь.\ расчета выбрать проверку справедливости именно четвертою уравнения.
и з"'-' РекоменДУемЬ1е и применяемые в настоящее время у нас РУ ежом способы расчета гидростатических опор и торцовых
173
специальных обоснова-
уплотнений исходят из предположения справедливости гилп ческого расчста. Естественно считать, что если бы это пред СТати’ нне не оказалось справедливым (разумеется, за исключени°10>кр' неудачных случаев, когда разрешаются контактирующие i/' Тех пости, что возможно только при неудачно выбранных парамо то это сейчас же бы выявилось, имея в виду очень большой применения гидростатических устройств.	°ПЬ1Т
Поскольку зафиксированы весьма небольшие отклонения держивающего гидростатического усилия, вписывающиеся в ГП°^' тезу о неизотермнческом щелевом потоке, то естественно счит'00 что справедливость четвертого уравнения подтверждена инжене^ ным опытом всех стран. В литературе отклонения не отмечены
Поскольку практика подтверждает справедливость четвертого уравнения, то можно считать справедливым и второе уравнение
На самом деле постоянное значение зазора существовать не может, поскольку в действующих установках рабочие параметры не постоянны. Внешнее усилие на гидростатические опоры всегда меняется, в торцовых уплотнениях практически не бывает постоянного (не колеблющегося) давления жидкости и т. д.
Следовательно, несмотря на существование обязательно колеблющихся торцовых зазоров, факты несправедливости четвертого уравнения при замерах средних значений действующих усилий не обнаружены, за исключением неправильно спроектированных. Под неправильно спроектированными понимаем такие, которые разрушались из-за чрезмерно больших амплитуд.
Более того, если признать, что предлагаемая схема расчета неприменима, то тогда придется признать, что все существующие рекомендации по расчету гидростатических устройств не справедливы. Кроме того, из-за отсутствия точного способа расчета придется признать неприменимыми все существующие приемы расчета.
В этом и заключается обоснование справедливости принятой схемы расчета, которая рассматривает так называемый квазистацио-нарный режим с малыми колебаниями параметров потока.
Второе уравнение системы (6.3) представляет собой результат интегрирования уравнения энергий одномерного потока в торцовом щели для нестационарного движения (имеются в виду малые колебания зазора, о чем говорилось выше):
—я Рй,*\г = с±^	(6Л)
\ dr 2r р ) пй*а ‘
Справедливость записанного равенства для статического потока (ю* — 0) очевидна. Для случая, когда й>* ф 0, было доказано 1681. что дополнительное усилие, возникающее из-за разгона жидкости в канале произвольной формы, определяется произведением плотности на координату, среднее значение площади поперечного сечения и ускорение в центре тяжести. Поэтому потеря давления, отне-
174
аЯ к координате, будет определяться произведением плотности ^а" ускорение.
Поскольку произведение скорости на радиус 1ля торцовой щели постоянно, скорость на любом радиусе определяется выражением 0w*-1 а значит ускорение будет и?*. Именно эта величина и вычи-2г др* тается из в рассматриваемом уравнении.
Разумеется, вращательное относительное движение одной поверхности относительно другой или любое иное относительное движение, а значит любые гидродинамические эффекты не рассматриваются и исследуются только i ндростатические устройства.
Таким образом, рассматриваемый способ расчета является дальнейшим развитием существующих общепринятых приемов расчета и в первом приближении позволяет учесть влияние динамических факторов.
В статических условиях работы, когда 6* = 6* = 0, система уравнений (6.3) принимает форму
8лц/ .. . _	In 5 ... .
Pi* До* —	у*' Ро*	6=	w*'
vJ=nD6.w„	(6’5)
сп 0* — 6О) + Pi* (Л — Г) = Ро* ОН — /)•
Исключая из первых трех уравнений V* и получим известное соотношение между р0* и р1+, не зависящее от вязкости рабочей жидкости:
-4-^у)р0*=(1—Ф)р01!,	(6.6)
использование которого в четвертом уравнении (6.5) позволяет найти зависимость между статическим зазором 6* и постоянным значением давления питания
6* = 60 + <$£-/)-(1-Ф) (Г,—/) (1-Ф)с„	Р1*‘
(6.7)
§ 6.2. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ ОБОБЩЕННОЙ ПЛАВАЮЩЕЙ ГИДРОСТАТИЧЕСКОЙ ОПОРЫ
При рассмотрении малых колебаний можно принять, что значения 6*, V*, to*, pZ и р* отличаются от соответствующих значений статического процесса, описываемого системой уравнений (6.5), величинами вариаций, обозначаемых теми же буквами, но без индексов в виде звездочек, которые должны удовлетворять условиям: о = 6* — 6Ф < 6e; v = и* — о» < u,; w — w* — и»»	ш*.

pt, — po — Po* Pn* H Pi В1 P* Po, = pi* = 0), или, что то же самое, б* <26*, o*<2t»*, щ* 2щ*,
Р’Оо* 11 РГ<2/Н*.
Используя эти условия и уравнения (6.5) в системе диффеп циальных уравнений (6.3), можно после проведения обычной л ин " ризации второго и третьего уравнений получить систему линейны" дифференциальных уравнений, описывающих малые колебани* пяты обобщенной плавающей гидростатической опоры в вариациях-
8лр/
Pi - Ро = ~f- + Р /г)>
6р£> , t D. . . . 12р£) .
Ро = — 7Г ln — Р 2 ,П е W + ~ЪТ~ П б;
vf — nD H>*w — л Dw* 6 — Fb — $гРо = 0, Mb + р Н 6 + cnb + pi (Fi — f) — ра (фр — f)=0.
(6.8)
где
Во р / 0гб#
в.
г'7?л-,|,) = хртч 96nv3 , _2_( 7’ltJL — yy-g ж + та /lnl
I2v/	— Ф);
.Г) I bl \ t-\—f	1
ФР—/ 1
И1* —J- 1
1 p
л — [48.TW ft, ,V1 6J |
I (\>Hv‘	+ -1-14с» + 8лрда*(4'В-
А = м(<('	’ Р1'
П 4г + 94aF Ргс« + П “
1 1 bi) \Tf^:	_
24ц w* 01В—Л1 ГВ |nt 1;
сп — м I л J'
Д2 =
2лб
pH I 96л v2 7vi I fbi
(6 Ю)
Линеаризация второго уравнения осуществляется подстановкой
Во* + Ро = — /777 1п + щ) — р In £щ = 0.
Имея в виду, что
“(Йж 111 ^’* +
_,6цР Ing (,	W\(	_

\ W*
6p£> In g /,
/ b \2	n 6	„ w6
! = по сравнению с членом 2 = и члена z —
ввиду малости члена !
по сравнению с членами— н 2 а также используя второе урав-нение системы (6.5), получим второе линеаризированное уравнение
вариаций системы (6.8).
Исключая вариации давления в центральной камере р0, а также вариации скорости v и w, получим передаточную функцию обобщенной плавающей гидростатической опоры, позволяющую по колебанию давления рх оценить колебания зазора б:
W (б, рх) =	= Т х
Pi (s)
у____а* + e,s* + б18 + бр __________ (6.9)
s8 -|- a4s‘ Ass3 -f- A2s* 4- ^is + Ao ’
ft2p' I Itlg/! Щ ft I6n2v6*
лбЛ , I Ing/ "Г M
х| — .	96nv2 .
4 = W +
Н
Р
,	. /2л	3 \ . |iH
^4 —4v -f -t~6J+	;
T Л1 ’ ф=Гф = ±.^
1	3 ring
и s = tQ — переменная Лапласа, причем Q — частота колебания входной координаты рг.
§ 6. 3. ЧАСТОТНАЯ ХАРАКТЕРИСТИКА ГИДРОСТАТИЧЕСКОГО
БАШМАКА
Применительно к гидростатической пяте на головке плунжера (ин РИС’ 6'2) в с,лУчае' еслн П°Д плунжером установлена пружина аче во всех разрешающих уравнениях следует принять ся — 0), зазоп° »спользовать ляя проверки малости колебаний вариации
Ра о выражение (6.9), имея в виду, что давление под поршнем
меняется по закону «прямоугольного» синуса, а наибольшие ции давления очевидно будут	ВаРиа-
Ртах — (Р1)тях Pl* л (Р1т Рщ) X
X sinfl/4-у sin3Q/4-у sin5Q/4-...
(6.Ц)
где Pim — давление настройки ограничителя момента (предох-ранительного клапана);
р1п — давление подпитки при достаточной производительности подпиточного насоса;
о = со — угловая скорость гидромашины.
Для оценки необходимого числа членов последнего равенства, которое должно быть использовано при расчете (обычно удается ограничиться только первым членом), т. е. для оценки фильтрующих свойств рассматриваемой системы обращаются к изображению логарифмической амплитудно-частотной характеристики. С этой целью определяют коэффициент усиления передаточной функции W (6, Р1):
/(фР-/Д + Ф(Г1-/)
Z 0	/	-ш / р
(1 — Ф) сп + — 48лр (4’Р -/) И* у -
(6.12)
по которому проводят статические расчеты, а выражение передаточной функции (6.9) раскладывают на элементарные множители. Так, характеристическое уравнение может быть представлено в виде произведени я трех сомножителей:
A (s) = (s + с) (s + 2n(1s + Qo) (s2 -ф 2n„s + £4) = 0	(6.13)
методом итераций.
Для определения значения с в качестве первого приближения можно принять q = ~?, а для последующих (i 2г 2, где i — порядковый номер прибли?кения) используется 1771 равенство
с. = -т— —-----------—° ..  _____________ (6.14)
ci-i {-4а I Дя ~~ е1-1	— Cj_i)]}
так, чтобы в пределах точности вычислений это равенство обрати" лось в тождество. Тогда, поделив характеристический полином A (s) на s ~г с, получим полином четвертого порядка
* (S) “ ГГе = S4 4- Сп5« + Cass 4- C,s 4- со,	<6-19)
дяя которого в первом приближении можно принять 2nai
178
с. а „.гелолуй-е прЛиже.шя (для i -2. пр,.
__________________;
Cs-^)/-i	f<?8 —	(6 16)
Ci - (£«), 1JG — <2я«Х 11_-.
2п„; = Cj __ (<yj. j _ (2^),- , [С3 — (2п„); И
Разлепив полином R (s) на элементарным трехчлен 2п .<? получим второй элементарный трехчлен s* -J-2ng -Означит частоты собственных незатухающих колебании Q« и Qft Н показатели степеней экспонент затухания с обратными знаками „ и Z по значениям которых вычисляются добротности (в теории колебаний так называют относительную амплитуду на сооственнои частоте)	.
Ь <617’
Существо дела не изменится, если окалкется. что па Q, или В этом случае под частотой Q„ или Q6 будем понимать обратную величину постоянной времени апериодического элемента второго порядка, и соответствующие полюсы на плоскости корней, размещаясь на действительной оси, окажутся взаимно сопряженными относительно окружности с радиусом Qa или Qft (sols„2 =? Q,’ и sblsb2 = Щ).
Очевидно, теми же приемами можно разложить на элементарные сомножители и числитель передаточной функции (оператор воздействия) и представить ее в форме
IB fd. п.} =___А(1 + Bes) (I -р Tds -р f|s2)
(1 + rcs) (1 + 2^ Ta + /««») 11 -p 2£ьГ6з -I- 7	•
где	T — — T — 1 н T 1
По значениям постоянных времени Т,„ Т,„ Т Г пТ а тэкжа ^аыХТоЯК°ЭфФНЦИеНТа уСИЛення * "Р” помощи оби^известных «	иогарафм,,ча:кой
«гением коэффицие нта '«иле^я“к	' опРед<ляется
Щег0 — порядком мнпж«-г1п	Уклои каждого последую-
времеин Tt начала этого уйаст^'^”61*10™ нндексом постоянной Рйстического уравнения соотеетг ’ ТаК’ сомножителем характеры в 20 дб на декаде °°тветствует отрицательный уклон ас«мп-«а декаду для сомножителя	Иерв0г0 гюРяд*а и 40 дб
==
,„аоиРНия (6.11) и логарифмической амплитудН0.ио ПО”Ои^пактеристнкн, можно установить их большую или мощ,^’ иои характеристик^,^ данамического перемещения опоры b^*° ^Точная оценка динамической амплитуды осуществляется п
1 очная о;	та усиления на амплитуду входной коопп.
наш нЯдвнамийск1>е коэффициенты определяющие соответствуй щие ординаты амплитудно-частотном характеристик!.
(6.18)
ГДе k — порядковые значения действительных нечетных чисел. Обычно 6з>б5>..-, и всегда влияние амплитуд колеба-
Рис. 6.4. Логарифмическая амплитудно-частотная характеристика обобщенной плавающей гидростатической опоры
ния зазора для k 7 несущественно.
Рассматриваемая система, особенно при малых объемах центральной камеры и отсутствии газовоздушной составляющей в рабочей жидкости, низкочастотна, и при сколь-нибудь значительных частотах возбуждения колебаний, например, у насосов, динамическая амплитуда даже первой гармоники оказывается незначительной. Иначе обстоит дело с гидромо-торами, которые работают на переменных скоростях и могут иметь очень малые скорости. В
этих случаях иногда приходится вести расчет по трем первым гармоникам (k — 1, 3 и 5) и при конструировании необходимо уменьшать ординаты амп пит-,,,, всеми „Доступными средствами мплитудно-частотной характеристики и умень-
шать ее полосу пропускания.	емятся
Наиболее эффективны два мероприятия. Во-первых, СТР так подобрать параметры системы, чтобы постоянные вРе1^н11Ь1ци и Та оказались возможно меньшими по сравнению с посте
ни T„, T„ и Tr, а если это окажется невозможным, то стре-яреме свесП| к минимуму разность между каждой из двух первых МЯТтоянных времени и постоянными времени Та и Т h.
п0СВо-вторых, стремятся «затрубить» (задемпфировать) систему па уменьшения возможных резонансных всплесков.
ЛЛ При решении первой части задачи можно воспользоваться приближенными аналитическими выражениями разложения на множи-ЯеЛ11 полинома «я + B2.s2 + B,s + В„ в случае, если В{ > Во {12]:
X
s3 + B2s2 + B,s + Bn
x(1+£S
___!___S2
В1~
(6.19)
Если В? Во, то можно воспользоваться приближенным равенством
S3 -|- B2s2 + BjS> ф- Bu «« Во х
*(' + »?)(' + Ss+i4 <6201
При выборе значений параметров проектируемой системы, обеспечивающих ее «загрубление», обращаются к выражению передаточной функции
= W (&, v), v(s) ' ’ >'
(6.21)
предполагая, что меньшая добротность рассматриваемой системы при рассмотрении скорости питания v в качестве входной координаты одновременно обеспечит меньшую добротность применительно к входной координате рг.
Передаточная функция (6.21) имеет более низкий порядок по сравнению с передаточной функцией (6.9), и при дг = 0 характеристическое уравнение имеет второй порядок, причем коэффициент демпфирования и постоянная времени Т„ будут определяться выражениями
____—
____________г п (фД — ppi 1п |
I ^2|.36у-.<Ё спй, 1Г 2лМ6,	|
’ л I й; I л р (фВ-Z-j) 1п|Ц р(фВ-В1)1пи
(6.22)
Tv
В- В,) Ing
(6.23)
Г 2л|^1/£ +_______Д I
I к Л ЛВя-ф/^lnd
та Ta™M °бРазом> желаемое уменьшение колебаний й достя™-> г м иже таким выбором параметров, при котором увеличнеаен в
значениеЕ„ В частности, наиболее простыми оказываются ме тия по приближению значения Л* к одному из критических 3|Р°ПР,,Я'
" (^*Х'Р> определяемых уравнениями	и ,ачепнй
/Л и — Р Ing/'nl’F—Ft)
,О»Ч - >л.и
(6.24)
и
(6.25)
/Л1‘ = 6 1/ ' *'*Р I	с„
которые не могут быть достаточно небольшими (а значит, недостижимы) потому, что в этом случае рассматриваемые колебания не будут малыми и тогда использование последних четырех равенств не будет правомерным.
При больших нагрузках на пяту, когда значения ft*, и (6*)» становятся недопустимо малыми приходится переходить на использование замкнутых гидростатических опор и уплотнителей [48].
Глава 7 тШФПРуЮ1НИЕ свойства ГИДРО1МЛ1ППН
рл. основы	ПОДОБИЯ РОТОРНЫХ
Обычно используемые в качестве основных элементов объемны, п1Дропередач роторные гидромашины характеризуются больший поверхностями трения, механические и объемные потери на “ото рых превалируют над остальными, и поэтому в качеств матемХ ческой модели роторной гидромашины принимается такая в которой рассматриваются потери только в зазорах между упомянутыми поверхностями Разумеется, принятие такой модели не исключает существование и иных видов потерь (например, гидравлические потери, потери в уплотнениях, на перемешивание рабочей жидкости и т. д.), которые чаще всего раздельно не рассматриваются. Поскольку коэффициенты потерь определяются экспериментально, то соответствующим их корректированием можно с достаточной для практических целей точностью описывать рабочий процесс.
Вблизи оптимальных по к. п. д. режимов работы числовые значения коэффициентов потерь меняются столь незначительно, что аналитические выражения потерь описываются линейными уравнениями и вся область работы гидромашины, в которой возможно использование таких линейных выражений, называется квазилинейной и подлежит рассмотрению.
Возможно расширение квазилинейной области работы гидрома-шин при помощи различных приемов линеаризации, в„кои^°“ счете сводящихся к корректированию числовых значений коэффициентов членов, описывающих механические потери.
Если предположить, что указанные выше виды потерь явля *°ТСя настолько превалирующими, что можно рассматрива
качестве единственных с последующей к0РР^~РуВ*°х Мишке (|оНт^!ьных коэффициентов, как это делали в МВТ
63], а в США - Вильсон [120, 128], то рабочий £ подобных гидромашин описывается номинальным хараетер
« размером D = некоторым эквивалентны^
Опп ГДа °6Разно называют допусковым размере ) Р давлена* Р^еляемым тремя переменными факторами: п Р «Щом 0ВОЙ ск°Ростью гидромашины ш в динамическим ко-чм-
Пои изменении номинального размера D гидромаипшы Не of затепьно пропорционально меняется размер эквивалентного заз’яа б Чаще всего связь между D и б устанавливается в виде степени? зависимости
(7.2)
& = Sy<D,	(71)
обычно используемой в различных системах допусков В зави мости от числового значения <р по-разному меняются свойства 1Ил ромашин с изменением характерного размера D 148, 63]. Поэтов применительно к серии геометрически подобных гидромашин чаще всего приходится говорить о номинальном подобии, имея в виду переменность коэффициентов, определяющих демпфирующие свойства гидромашин.
Подача насоса без учета потерь, т. е так называемая геометрц-ческая подача, будет = со(£)|, и поэтому индикаторная мощность насоса определяется выражением
А/; = (OjD'p, где р — перепад давления.
В соответствии с законом Ньютона о потерях на вязкое трение в эквивалентном зазоре 6 теряется мощность
(7.3) где k„ коэффициент, предполагающийся постоянным для серии геометрически подобных гидромашин.
В последнем равенстве площадь трущихся поверхностей про-порциональна D), а градиент скорости — -у—.
Потери мощности на кулоново трение или, как их правильнее называть, потери, пропорциональные перепаду давления, определяются выражением
Nf = cfo^D,’ = cNh	<7-4)
поскольку pDj пропорционально усилию, создаваемому гидростатическим перепадом давления, tdjDj — скорости относительною перемещения трущихся поверхностей и с — коэффициенту кулонов трения.
Если считать расход просачивания через эквивалентную и ламинарным, то мощность, теряемая на утечки, будет определят выражением
к,|7”
б; поскольку расход утечек пропорционален выражению p-jp Если бы рассматриваемые потери были единственными, то было бы ожидать, что коэффициенты k4 и kv будут иметь
184
значение для серии геометрически подобных гидромашин. Од-*е оказывается невозможным подобрать такое значение эквивалентного зазора б,, для которою k„ и /г,, были постоянными глав-Ш.1М образом из-за того, что выбранная модель чрезмерно грубая. Так, значение р в малых зазорах реальных гидромашин не совпадает со значением динамического коэффициента вязкости в магистралях, а тем более в сборном баке. Кроме того, на характер течения в щелях существенно влияют термические эффекты |48| и даже сжимаемость рабочей! жидкости.
Поскольку значения коэффициентов ke и kY не постоянны, то предлагаемую модель явления следует рассматривать только в качестве аппроксимирующей и перейти к укрупненным коэффициентам потерь, оценивающим их в долях индикаторной мощности. Так, сравнивая выражения (7.2) и (7.3), можно записать
N^kJh.^N^C^N,,	(7.6)
где Са = k0 — коэффициент потерь на вязкое трение.
Безразмерный параметр о, называемый иногда функцией Зом-мерфельда [48), представляет собою критерий, оценивающий характер потока в узкой щели:
О = “1Й.
Р
Этот безразмерный параметр о называют также критерием изогональное™ потому, что если в двух геометрически подобных по номинальным размерам гпдромашинах значения о окажутся одинаковыми, го в эквивалентных зазорах этих гидромашин суммарные профили скоростей потоков фрикционного (увлекаемого движущейся стенкой) и просачивания (вызванного перепадом давления) окажутся подобными.
Сравнивая выражения (7.2) и (7.5), можно получить соотношение между Nv и N , в форме равенства
Л\, =	% — Ni = Cv- Ni.
-	' D\ pco! ' v a 1
Поскольку коэффициент утечек Cv содержит множитель *. причем б, £),, то значение Су на несколько порядков меньше единицы. Наоборот, коэффициент Св, содержащий множитель у, много больше единицы.	'
В связи с затруднениями в оценке значения вязкости рабочей жидкости непосредственно в зазорах часто пользуются выражениям)! --г и рСа, тем более что ряд закономерностей, описывающих Демпфирующие свойства гидромашин, определяется произведением
Cv
() pC. = CrC„. непосредственно не зависящим От
бочей жидкости.	Пя3|(остц ра>
Числовые значения коэффициентов Су и иС Ппг
к	п	>'	ГИДР°«а1и1111
«Брюнингхауз» и «Лукас» различных размеров содерж-
боте [81J и частично будут приведены ниже.	атся в Ра-
Очевидно, для установившегося режима (статически I насоса его к. п. д. определяется выражением ' °' l,a6°Ti.i
। С'
111	/У, + Л7Ч-^	1+<Ч-С^	(7.7)
или
. Cv р
I — -- • —
П,=-------
1 + с + |<с„ —
причем объемный к. п. д. насоса будет
. б'у С,, р
По1=1 ~ - =1-	(7.8)
а механический к. п. д.
Аналогично можно получить для гидродвигателя
Nj-Nf-Ne _ \~с~С„а _ 1 ~ с ~ flC« р Ni + 7V,,	[ Су	Су р '
а	' р. cj
(7.10)
(7 11)
и
’!>« = 1 _с_С«а = 1 — с —рСв ".	(7 12)
Получение трех последних выражений из равенств (7.7), (7-8) и (7.9) соответственно может быть основано на общей теореме об обратимых машинах и механизмах, по которой алгебраическая запись характеристических уравнений для насоса и гидромогора сохраняется, как и для любых обратимых машин, за исключением того, что знак при показателе степени к. п. д. меняется на обратный. Разумеется, при обращении гидромашииы знаки членов потерь меняются иа обратные.

Пол обращением машины или мехами ;ма щжимлю» гр»-ьр»м» е\ ведущих звеньев в ведомые или на /	1!р> иитклмю
н"е Вгом\ характеристическому уравнению это < сх/глмсгвует од-к ЛК)менному изменению знаков всех нагрузочных показателя* ре ,оВ'1 п | неизменных знаках кинематических показател й р< яма '’'"^^одновременному изменению знаков всех кинематических по-11Л" eJ)eIj режима при неизменных знаках нагрузочных показате-ь3?аТ,еЖ11ма. Очевидно, при этом меняются знаки произведений лс" ю нагрузочного показателя режима на сопряженный с ни* л,матнческ1П1 показатель режима, т е. меняется знак мощности """Соответствует превращению ведущих звеньев в ведомые или "Сворот Под сопряженными показателями режима понимают та-н"е произведения которых дают мощность на соответствующем
Зиен*--	-
Целесообразно выбирать направление движения и направление „eiicTBUH моментов так, чтобы указанные произведения для ведущих звеньев были положительными. Для этого необходимо принять в качестве положительных направлений скорости и действия момента приводного двигателя. В справедливости отмеченной закономерности можно убедиться при алгебраической (т. е. с учетом правила знаков) записи равенств (7.7) и (7.10), которые приведены в модульной (арифметической, т. е. без учета знаков) форме. При этом для роторною насоса ведущим звеном будет приводной вал (показатели режима «iq и М,), а для гидромотора — поток рабочей жидкости (показатели режима Q2 и р2).
Отмеченная закономерность не случайна и является следствием более общей теоремы об обратимых механизмах, приведенной в работе [65], где обобщенная форма обозначения кинематических казателеп режима — Q, а нагрузочных — ¥
Если какая-либо рациональная функция показателей режима и к. п. д k механизмов его составляющих у (q,. q±.	q*- ▼«.
Qtl, Q;> ... c>z) тождественно равна функции Г, .
%. £o.	... , Q;), где индексы о, b, .... I относят пемазатеп
режима к одноименным звеньям рассматриваемого меха дома, ж» одновременное изменение знаков всех нагрузочных показателем режима при неизменных знаках кинематических показателей ре»'-** либо одновременное изменение знаков всех кинематических аскэ-эателей режима при неизменных знаках нагрузочных пок .. гД-** режима приведет к соответственным равенствам
F(-¥o, -Т6, .... -v,. Йя, е».....
-<• £.......... I,, т.. т.......т„ -С- -«► • •».
ИЛИ
f(4a.	.....-Qe. -Я».	-0,»~
**ф(—— — Т — *F —£ \П>’ п»....... ч*’	”	'	•
Очевидно, роль такой функции F может нести не только к рассматриваемого механизма, но н любые иные ранцОН;1Л1 ”  д. кипи, например выражение мощности, различные критерии ыу" бия и т. п.	1ОЛо'
Использование теоремы об обратимых механизмах гюзвоп вдвое сократить последующие выводы, проводя их, например топ?01 для гндродвнгателя с последующей записью аналогичных рСз‘?(° татов применительно к насосу, п даже для гидропередачи в целом
Разумеется, при обращении механизма теорема справедлив лишь применительно к форме записи разрешающих уравнении а не к значениям входящих в него выражении. Например, чНСЛо' вые значения к. п. д. насоса п гндромотора будут одинаковыми только в порядке исключения.
Все полученные равенства одинаково справедливы как для гидро, машин вращательного движения, так и для гидромаипш возвратно-поступательного движения — гндроцилпндров. Только в последнем случае необходимо в разрешающих выражениях вместо нагрузочного показателя режима М использовать усилие Р, вместо кинематического показателя режима w — линейную скорость перемещения поршня или корпуса v (в соответствии с конструкцией), а вместо характерного объема щ применять активную площадь поршня F, которой называют выражение
б© _	= F
dv~ ()р	’
количественное значение которого определяется для каждой конструктивной схемы при помощи элементарного гидростатического расчета.
Имея в виду, что гидроцилиндры обеспечивают равномерную подачу (о = 0 и | = 1), а также являются не регулируемыми устройствами (F = const, т. е. и = 1), можно основные расчетные уравнения записать в формах:
Qi — F	(7 13) (7 14)
Р-г =	(7.15) (7.16)
Та же аналогия может быть проведена не только для статических, но и для всех видов динамических режимов работы, если в соответствующих уравнениях приведенный момент инерции J вращающихся частей заменить па приведенную массу перемещающих1 частей. Способ приведения будет изложен ниже.
186
Поскольку разрешающие
уравнения
впредь будут рассматриваться либо возвратно-поступательного движения без упоминании одинаковой правомерности получаемых результатов в обоих случаях.
§ 7.2. ТОПОГРАФИЧЕСКИЕ ИЛИ УНИВЕРСАЛЬНЫЕ
ХАРАКТЕРИСТИКИ ГИДРОМАП1ИИ
Числовые значения к. п. д. изменяются с изменением показателей режима работы иногда в довольно широких пределах. Обычно внешняя характеристика гидродвигателя определяется при работе на рабочей жидкости опреде-
оказываются
аналогичпыми, вращательного,
либо гидропередачи
Рнс. 7.1. Топографическая харакгеристи ка гидромотора IMH500 фирмы Лукас
ленной вязкости при постоянной тов /И2, замеряемых при разных
температуре в виде момен-скоростях со2 (или числах
»8»
Оборотов в минуту «»)- Обычно на такой характеристике „а. носятся линии постоянных перепадов давления р, (изобары) и пинии постоянных расходов (?2 — const (рис /1) На таком изображении каждой точке графика соответствуют легко ЧИта мне значения М2, <•>.. р» и <?»• Если одновременно на график нанесены линии равных значении к. п. д. т)->, аналогичные «сре. зам» на чертеже лопасти гидромашипы, имеющей пространственную форму, или линиям, расположенным на одной высоте на топографической карте, то такое изображение характеристики называют топографическим.
Иногда на топографической (или универсально!!) характер», стике наносят линии постоянной мощности. В случаях, ьо1Да какие-либо области поля характеристики не определялись экспе
риментально, например при малых скоростях, на которых пр0. ведение эксперимента затруднительно, а устойчивость движения
в)
Рис. 7.3. Определение значений ко*|фи-циентов демпфирования по топографической характеристике гидродвигателя
иногда невозможно обеспечить, осуществляют экстраполяцию изобар, линий равных расходов и равных к. п д., отличая эти участки пунктирными изображениями (рис. 7.1).
По тем же самым принципам строятся топографические или универсальные характеристики насосов (рис. 7 2).
§ 7.3. ОПРЕДЕЛЕНИЕ ЧИСЛОВЫХ ЗНАЧЕНИЙ КОЭФФИЦИЕНТОВ ДЕМПФИРОВАНИЯ
Проще всего числовые значения коэффициентов демпфирования определять по изобарам и линиям постоянных расходов на топографической характеристике.
В области квазилинейных
режимов работы гидромашины как изобара, так и линия постоянного расхода из-за ли-_	ценности уравнений (7.2) —
(т .о) прямые (FF и А В на рис. 7.3, а соответственно), причем отличие коэффициентов Св и Cv от нуля приводит к соответственным отклонениям изобары от горизонтали и линии постоянного
расхода от вертикали.

Переходя в равенствах (7.2), (7.4) и (7.6) от выражений мощностей к выражениям моментов, можно записать выражение сво бедного момента на валу насоса в виде
= Мг — Mf — М„ — pw2 — cpw2 — Свора)2. (7.17)
Если топографическая характеристика гидромотора снималась при постоянном значении вязкости (а обычно так и делается), то, откладывая по осп ординат отрезок OD = pw2, получим выражение коэффициента с, определяющего демпфирование, пропорциональное нагрузке
с =	=	(7.18)
где р, — доля перепада давления, затрачиваемая на демпфирую щпй момент М,.
, ,2[роя горизонталь через точку К в соответствии с равенством (7.17), получим графическое изображение момента вязкого трения М „ = C„upw2, или	н
г _ Р Л|" __ Р вк _ Р« — w Мг ~ ы OD ~ ы ’
где р„ — доля перепада давления, затрачиваемая на демпфирующий момент М„.
Легко видеть, что уклон изобары в определенном масштабе изображает величину рС„.
Строя вертикаль АС, можно горизонтальными расстояниями между прямыми	-------
гидромотора:
(7.19)
Дщ = Ывг — (1).
(7.20)
где <1>2- — число утечек.
Следовательно, угол между прямыми АВ и А чение коэффициента утечек С,„ поскольку ВС — точки В соответствует определенному значению
uvv IVH11H 71МП ---к
АВ и АС определить потерянные числа оборотов
И>2 ” Р И ’
оборотов гидромотора, a Qv = pw2 — расход
и АС определяет зна-~ . Дш, а положение перепада давления р
=	(7.21)
и р '
т. е. значение — определяется потерянной угловой скоростью, от* несенной к единице перепада давления (рис. 7.3).
Возрастание гидравлических потерь происходит не точно по линейной закономерности, что особенно заметно на больших скоростях движения, где потери момента становятся пропорциональными квадрату скорости, превращая изобару в параболу. В этом случае режим работы гидромашины перестает быть квазилинейным 17 J,
,мая для произвольной точки L и ПОка. оа11НЯ проводим3” А	и GL иа рис. 7 3, б, может при-
и линезр«3 т ’,ыми прямымI	к0Эфф1П1Пента с за счет чрезмер-
занная пр Льным зна я 01*.о тре1шя С из-за большого вести К,пястанпя коэфф»и11СН	® (отрицательное значение с ком-
"ог° В°Гясатёльной GL к нз^еДД..пЬтате линеаризации, обес-уклона к |ое увеличение >. пеЧ1)вая соблюдение балаи. пенснРУ6'
почивая соблюдение баланса моментов).
Возрастание потерь в шдромоторах характерно не только для режимов движения с большими скоростями, но и для малых скоростей, особенно для
wo
700
600
900
ш
300
100
Л
900
80 n o5jnuH
О 70	90	60
Рис. 7.4. Топографическая характеристика высокомомеитного гидромотора «Ст аффа» SX510
200№^
Рис. 7.5. Значения коэффициента демпфирования, пропорцио иального нагрузке с, для серин гндромоторов «Лукас»
тяжело нагруженных гидромашин, к которым обычно относятся высокомоментные гидромоторы. Так, изобары английского высокомоментного гидромотора «Стаффа» SX 510 с характерным объемом 494 см8, мощностью 66,2 кет и наибольшим развиваемым моментом 900 кГм (рис. 7.4), особенно при работе на больших давлениях, изгибаются с выпуклостью, обращенной вверх 182]. 1акои же эффект имеет место и в гидроцилиндрах 151], т. е. свойствен любым гидродвигателям. В этих случаях отклоне-™!?°МеНТа меканических потерь (или давления, идущего на до-пежим^йЛ,Ь^,П/)ТеРИ-чо °Т потеРь- определяющих квазилинейный гым я мгЖип РИС‘ 7	в)’ Оце11ивают дополнительным нелиней-
нымЛпт?™аНИеМ’ опРеДе-'!яемым разностью между действитель-? и потерями при рассматриваемом квазилинейном
*2
Риг 7 6 Значения коэффициента демпфирования, пропорционального нагрузке с, для серии гидромоторов «Лукас» на режиме трогания с места
Способ определения значений с, Ся и Су по, так называемому, оптимальному режиму работы, т. е. режиму с наибольшим значе-
Рис. 7.7. Значения коэффициента активного демпфирования р Св для гидромоторов «Лукас»
нием к. п. д., будет подробно рассмотрен в § 7.4.
Значения коэффициента с для гидромоторов «Лукас» в зависимости от значения перепада давления приведены на рис. 7.5. Наибольшие значения имеют место в гидромоторе IMH125 (№=1,508 ел3). Несколько меньше эти значения для гидромотора IMH1000 (w = 12,070 см3), примерно те же значения для IMH60 (te, — = 0,716 см3), еще меньшие значения Для IMH3000 (№ = 36,19 см3) и вы-падают из общего ряда значения для МН500 (ы — 6,040 ел3), существенно зависящие от л = 0,1000 и 2000об/мин. Отрицательные значения с при малых перепадах давления и л = 2 000 объясняются большими внутренними ги-I пТЧеСКИМИ сопР°™влениями ги-Нейно?изобХЫТТмМИ необходимость линеаризации криволи-
Cnnnv ° Р ’ ° чем гов°рилось выше.
Размера w д^^ежима*5 аависвмости от перепада р и характерного для режима со = 0 приведена на рис. 7.6.
7 в Н. Прокофьев и др.
Рис 7.8 Значения и С„ ния для серии
J W
коэффициента активного демпфнрова-
гидромоторов «Лукас» при 500 оборо-
тах в минутУ
194
J ско-ГИДроМОТОрОВ при Пу ~
Рис. 7.10. Значения —С,, и —Cvl< w И у И уу для гидромоторов «Брюнингхауз» которых нет гидростатической раз----------------- --------- су, но бо-
чначеиия коэффициента активного (пропорционального 3 \ демпфирования *‘С" для тех же гадромотопов п™
РоСсТоп об1*ин пРиведе"ы ^500 w77 и 7.8 в виде на Р"С В’зависимости от дромаши,1ь1-	с
Коэфф,,и,,ен 1 уТеЧеК V лт« и зависит от перепада тя * я цз-за применения
Дапомтатическои разгруз-ГТРояпако меняется не в очень широких "Ределах-S не считать П,ДР°МО-тора самого малого разме-р3 Иные 7значения коэффициентов демпфирования гидромоторов «Бр™инг-хауз» (см. рис. 7.10), в	____________________
грузки и поэтому наблюдаются меньшие значения -<
оигпкчр значения нСй, изменяющиеся в сравнительно широ-лее вы	ком диапазоне из-за колебания за-
зоров в пределах одного и того же типоразмера.
₽ис. 7.11. Значения коэффициентов активного демпфирования для гидромоторов «Брюннигхауз»

Су в зависимости от харак-
Пределы изменения коэффииие	ко1Ором показаны
терного размера w показаны на рис. • •
7
также используемые при расчетах значения—? обладают^, большей стабильностью по отношению к значению w
Значительно больше значения коэффициентов активного дем фнрования цС„ у гидромоторов «Брюнннгхауз» (рис. 7.11). фнциенты демпфирования, пропорциональные нагрузке с, для . р же гидромоторов «Брюнннгхауз» при п = 500 об!мин показаны на рис. 7.12, причем пунктиром — для образцов с наибольшими суммарными механическими потерями, а сплошными линиями — йр,, наименьших суммарных потерях.
Те же гидромоторы на режиме трогания с места имеют значения с, равные 0,05—0,06 при перепаде р = 25 кГ!см2, 0,035— 0,046 при р = 50 кГ'см2, 0,03—0,04 при р — 75 кГ/см2, 0,0275— 0,038 при /7—100 кГ 'см2 и 0,026—0,036 при р = 125 кПсм2.
§ 7.4. ОПТИМАЛЬНЫЙ РЕЖИМ РАБОТЫ ГИДРОМАШИПЫ
Безразмерные выражения к. п. д. как насоса, так и гидромотора, записанные в форме уравнений (7.7) и (7.10), являются функциями одного безразмерного коэффициента — критерия изого-
нальности о, при некотором значении о = о* которого к. п. д. принимает наибольшее значение (здесь, как и в дальнейшем, индекс в виде звездочки вверху справа будет относить соответствующие величины к оптимальному режиму работы гидромашины, т. е. тому режиму, при котором к. п. д. принимает наибольшее значение). Значение о* можно
Рис. 7.13. Закономерность изменения к. п. д гидромотора от критерия изогональности на квазилинейном режиме работы
определить, взяв производную от к п. д. по о и приравняв ее нулю. Так, применяя индекс 1 для насоса и индекс 2 для гидро
мотора, можно получить:
и
<7 23)
Поскольку для лучших современных гидромашин подкоренные выражения достигают значений порядка 1 000 и более, то при подсчете значений t]f и т|* можно пользоваться приближенными значениями критериев изогональности, получаемыми из выражении
196
22) и (7.23) отбрасыванием единиц
Ь» „ за„юч««ым» » ф,„ур„„е	» •«
С» (1 -|- с) >
W}
(7.24)
ьв I ‘ — С)'
Помимо того, что значения of и о? соотпет че1|Ням последних двух выражений, хара^Т™? близвд*<зНа. висимостеи П. - •)> (о.) и Пг = Пг ( } f ZT "t°,,ML№,x за’ пения К. п. д., как это показано на рис 7 13 стремальн°го заделает ошибки при определении rtf и rtf иичтп^ гВДР°Двигателя
Используя выражения (7.7) и (7.10) П 24? „? <7^МИ’ приближенные выражения оптимальных’ кпд Л25ПОЛУЧИМ
(7 25)
равенств:
(1 +с)г]*
СвСу
(7.26)

СвСу
1 — с
(7.27)
причем Vj и v2 весьма близки к единице.
Поскольку функции (7.2G) и (7.27) симметричные, то
1 - (1 +н П?
1 +(1 +с>П?
i-JL
3 -	I — с
ф V2^--
*+л
(7 28)
(7 29)
С помощью элементарных подстановок можно убедиться, что на режимах, отличающихся от оптимальных, значения к. и. д. бу-ДУт меньшими. Они определяются при помощи выражении
(7.30)
(7 3П
UH
Обычно значения коэффициентов Се, Сг и с определяют по о тимальному режим) работы, для которого бывают известны тольк два параметра д* » °*- Как правило, более стабильно при Изме нении параметров режима работы гпдромашины значение С,,, По этому его определяют в первую очередь для любого режима работы для которого известны значения о и объемного к. п. д. цо2;
1 r _ ® ! 1	_ 1 \
р ’’ р \ч<>г	’	(7 32)
Зная С,., можно определить С„ и с, отыскивая 1 — с и С„ из двух уравнений:
-с-(“1) “
о решая которые, получим:
т)?	С.	! р* \2
Q = ”лн НС* =-jf	(7.33)
и
/ С.А	/ Cv р*\
с = 1-ПЙ1 +2 0<) »лн С= +2 Д-г) (7.34)
Таким же способом можно получить аналогичные выражения и для насоса.
§ 7.5. ВЛИЯНИЕ ДЕМПФИРУЮЩИХ СВОЙСТВ ГИДРОМАШИН НА ПЕРЕХОДНЫЕ ПРОЦЕССЫ ГИДРОПРИВОДА
Переходные процессы гидропривода описываются уравнением нагрузки и уравнением расхода.
Уравнение нагрузки гидродвигателя применительно к квазилинейному режиму работы записывается в форме
pw2 (1 —с) = Мо -|- С<о + J <Ь,	(7 35)
где Л40 — статическая нагрузка;
J — приведенный момент инерции нагрузки вместе с момент-том инерции всех вращающихся частей;
С — коэффициент активного сопротивления, включая активное демпфирование в гидромоторе, равное рСвш2, как это следует из равенств (7.2) и (7.6).
Поскольку с и С„ определяются для оптимального режима работы, а в довольно широкой квазилинейной области работы гидропривода значение к. п. д. меняется, то следует либо соответственно менять значения коэффициентов с и Се, либо принимать их постоянными и равными тем значениям, которые получаются из равенств (7.33) и (7.34), а дополнительные потери учитывать при помоши переменного значения момента / нелинейного демпфирования, сло-
гов
ипеделення которого приведен в § ю.З В соб оПР.1е Haipy3KH принимает форму	следнем случае
)'р	/W'JI — С) = Л4„ ФСо)+ J(1) + f
(7.36)
«яя оказывается справедливой не только в области vD Coro режима работы. В частности, такая форм;Записи Н Сгрузк" используется при анализе гидропривода при в"й ползучих» скоростях (см. ГЛ. Ю).	1
нЭ Пои исследовании режимов работы гидродвигателя с изменением
_ скорости оказывается удобным объединение членов pw«c и f ^записью уравнения нагрузки в форме [861
pw2 = MQ + См + J <0 -[-с, signor,	(7.37)
значение с7 =# с и с достаточной степенью точности может быть ^инято постоянным
пр Уравнение расхода записывается в форме
Q„ = Qrt + Q,+<U
—	геометрическая подача насоса;
—	параметр регулирования насоса;
—	его характерный размер;
—	его угловая скорость;
геометрическая подача гидромотора;
— угловая скорость гидромотора,
О — расход утечек;	„
_ расход, вызванный деформацией рабочей жид-
Расход утечек в гадромоторе в соответствии с выражением (7.5) можно записать в форме
I ~	(7.38)
Аналогично записывается выражение расвдм
где Q.-i =
K'j
Wj
Q?2 =
(1).,
e,,=i С,(7 39)
Г*
причем для дистанционных гидропередач р, > р8 из-за потерь в магистралях.
Суммарный расход утечек определяется выражением
Q, = о,.,+а„-~е-'<р + в 'е'р'~
<!М1
н
где
(741;
им
причем
Суг Ъ
Г— М ®’2'	(7.42)
Расход QCM_, вызванный деформацией рабочей жидкости, в с ответствии с законом Гука определяется выражением
<?€.« = 'МР-
где fl =	—критерии упругости гидропривода;
V — объем жидкости в напорной магистрали;
х — приведенное значение модуля объемной упругости ЖИДКОСТИ, СПОСОб ВЫЧИСЛеНИЯ КОТОРОГО был цОд. робно рассмотрен в § 4.10
Таким образом, переходные процессы гидропривода с разомкнутой схемой управления в квазилинейной области могут исследоваться при помощи системы уравнений
—р1 и — m ф- тшр + flw/5; pw (1 — с) — Мо + См ф J ы. (7.43)
При исследовании таких переходных процессов, при которых знак скорости гидродвигателя не меняется и существует нелинейное демпфирование, используют систему уравнений
и — и> + xwp 4- -&wp; pw{l — с) = Л40 + / + Cm + J ш.
(7-44)
При исследовании переходных процессов с изменением знака скорости применяют систему уравнений
и = с) + xwp + Ащ/); pw — Мо + Cm ф- J ы ф- cf sign ш.
(7.45)
Во всех трех последних системах уравнений индекс при членах соответствующих гидродвигателю для упрощения записи, как это часто будет делаться и впредь, опущен.
Глава 8
дТИЧЕСКПЕ ХАРАКТЕРИСТИКИ ГИДРОПРИВОДА
5 8Л. предельная характеристика гидропривода в машиностроении чаще всего применяется ги„п
де гидроусилителя (приводной двигатель с	В №
!,да оборотов. О "ОСОТОМ переменой npoSXj™Т“" дпомотором постоянной производительности) ИЛИ гиппя^и ГИ’ вала с гидромашинами постоянной производительности КжТГ™ дроприводе используется гидромотор переменной производитель ности главным образом из-за трудности управления им ocSo в многодвигательном приводе. Гидропривод с гидромотором пере мениои производительности обладает существенно иной динами ческой характеристикой, применительно к которой оценка устойчивости движения оказывается иной по сравнению с гидроприводом, составляемым по традиционной схеме.
Помимо демпфирующих свойств гидромашин, особенно при их дистанционном размещении, потери энергии в соединительных магистралях также отразятся на значении к. п. д.
Механическим к. п. д. трактов гидропередачи шение
Ч«з-Л.
где рг и р} — соответственно перепады давления я насосе, а объемным к. п. д. — отношение
Чоз = с* •
где Q, и — соответственно расходы гидромотора
всего Q2 <; Qx не из-за утечек, а из-за отбора части расхода служиваиие элементов контроля или управления.	ипппя
Очевидно, выражения общего объемного к. п. Д. гидропривода
По = ЧоЛаЧоз. общего механического к. п. д. гидропривода коэффициента трансформации
— АД «»»»
называют отно-
(8.1)
на гидромоторе
(8.2)
и насоса. Чаще на оо-
(8-3)
(8.4)
(85)

*21	0>| 11г1Чг
(8.6)
и полного к. п. Д-
Т] == ki-n	(8.7)
, т1. получены при помощи записи баланса расходов, легко могут быть полу ч
моментов ”	„ых размеров гидромашин гидропривода
1РИ Вп2шым значением коэффициента трансформации обра-с гарантиров.а в случае необходимости обеспечения определенного значения передаточного отношения - к равенству (8'6Поедеаьнымн характеристиками гидропривода называют такие, которые ссхяветствуют наибольшему статическому давлению рабочей жидкости в магистралях, т. е. давлению, соответствующему настройке ограничителя момента. Очевидно, в этом случае моменты на валах насоса и гидромоторэ будут наибольшие. Меньшим значениям статического давления будут соответствовать меньшие значения моментов, а значит, недогрузка основных элементов гидропривода.
Рассмотрим предельные статические характеристики гидропривода (р = Pn,ax= const), работающего с постоянной скоростью приводного двигателя w, = const, отдельно для зоны управления Л, характеризующейся условиями иг = 1 и их =£ const, и отдельно для зоны управления В, в которой иА — const и u.2 #= const. Разумеется, при изменении скорости приводного двигателя Wj соответственно изменяется масштаб оси абсцисс.
Зона А соответствует гидроприводу, выполненному по традиционной для машиностроения схеме.
учета'потерьВ1(рмсИ 8 ^)сдельнУю статическую характеристику без что^изм₽нп?ирбаЛаНС расходов зоны А и Л„ можно убедиться, pampa peryaa'pS™ ,™сХ“'"°ра	па’
W2 = Uj f при этом момент на нас
доомпт3 регУлпр°вания^ыМеняется пропорционально значению па-w, _ бУДет постоянным U,WlPrn’ а момент, развиваемый ги-^ги то Мг1 ~ /у и притом наибольшим. Поскольку причи^й ДвигателемУ иЛСгилппС0ВМестной Раб°ты гидропривод» Риа,1та eoc"Zt,^P°w-'<> распой.3 с нагрузкой и послужил*1 авления »идропривоп1>СТранения рассматриваемого ва-в машиностроении..
Расширение области изменения <ог может быть достигнуто изменением производительности гидромотора (зоны S и в, на рис 8 1) Из баланса расходов можно убедиться, что в этом случае (и = 1 и wj = const) скорость гидромотора будет обратно пропорциональна его параметру регулирования, причем
M'.toi I Const О>, —	- — =-----------,
2 W2 и2 «2
Очевидно, в тех же зонах при неизменном значении Ма момент на валу гидромотора также будет изменяться обратно пропорционально о)2, поскольку он пропорционален параметру регу
Рис. 8.1. Статическая характеристика гидропривода без учета потерь
лирования и2 (Мг2 = u2w2t»2).
Поскольку построенные на рис. 8.1 статические характеристики определялись без учета потерь, то они в соответствующем масштабе изображают не только момент, но и перепад давления на соответствующей гидромашине.
Рис. 8.2. Статическая характеристика гидропривода с учетом потерь
Из-за существования механических потерь действительный момент на валу насоса Мг > M.-t (mtp вместо Okl на рис. 8.2), а на валу гидромотора меньше М2 < М22 (dlf вместо abc на рис. 8.2,. Поскольку перепад давлений на гидромоторе пропорционален моменту, во втором квадранте рис. 8.2 можно построить зависимость расхода утечек Qy от перепада р (oq на рис. 8.2), которая в опредк ленных масштабах будет изображать зависимость потерянной «.КО рости с>3 от нагружающего момента Ма. Смещая в этих масштаба* границу рассмотренных зон 0'1 в положение O'g, а харакгериспь ческую кривую If в положение gh, можно получить статическую рактеристнку гидропривода, границу эоны В (точка Л на рж г • •
а значит, предельную скорость ю2лр гпдромотора и 1( допустимее значение параметра waml„ регулирования гцдп МеНьи,ре но достижении которого момент на валу гидромотора об °Мот°Ра, в нуль.	Ра"1аетх;я’
Рис 8.3. Статическая характе ристина гидропривода с насосом переменной прои iводительпости и ограниченной мощностью при водного двигателя
ПРИ ОГРАП»*',:,,,,ОЙ МОЩНОСТИ
5 8.2. П1ДР0ПРП^Яодн01,о ДЮ1ГАТЕ.,1Я
„ лглбенно НЯ самоходных и самодвижущцхсп В ряде «>чае°.	Л||Ческяе приводы-трансмиссии с ДЩ1.
пп'пями oSi'iwHHOfi мощное™ И насосом переменной производительности МЛ11||)()СТЬ приводного двигателя приводит к ие-обходнмости	мощи трансмиссии, от которой тре-
буют обеспечение определенного енло-,	'^2.' max
вого диапазона а — -------.значение
'"s?niln
которого, в зависимости от типа и класса машин колеблется в широких пределах и может доходить до значения, равного 12 1481, 1721 В случае использования в качестве трансмиссии гидропривода с гидромотором постоянной производительности и насосом переменной производительности проявляется один из недостатков такого привода, составленного по традиционной схеме — невозможность
обеспечить необходимый силовой диапазон. В этом случае получение необходимого силового диапазона достигается за счет существенной недогрузки гидропередачи, как показано на статической характеристике гидропривода, приведенной на рис. 8.3. Эта характеристика, ради упрощения принципиальной стороны анализа, построена без учета потерь.
Момент гидромотора Мп на рис. 8.3 показан горизонталью LLV, а момент на валу насоса - прямой OGA. При учете влияния гмнпри^ЧКИ D " А сместятся в D' и А' соответственно, причем а спниг вертикали происходят за счет механических потерь, а сдвиг влево — за счет утечек.
мость noTv«X°«Tb мощности приводного двигателя н необходимости огра|1иче1шГиаХзки wBOr° диапазона приводят к необх<> рг, а!рузки трансмиссии, показанной гиперболой причем ^/ = d_ силоюй диапазон
ся произведен ием^аибмп 'идрамичссК|,х агрегатов определяет-нием наибольшего момента гадромогора на наиболь-
Vio его скорость, поэтому связь между установочной мощностью '!!' , ндравлическпх а1регатов и мощностью приводного двигателя определяется соотношением
лг ___ '^im.ixco.2inax _ ^У
<>	Cl ~ сГ
(8.8)
Следовательно, чем больше силовой диапазон трансмиссии, тем большей мощности должны устанавливаться гидравлические агрегаты, используемые при этом с большей недогрузкой и в невыгодных режимах по к. п. д Так,
при 0 ==£ <»г <	- давление
в гидропередаче наибольшее (06 на рис. 8 3), ас дальнейшим увеличением скорости оно снижается пропорционально ординатам гиперболы ЕН, соответствующей изображению постоянной мощности двигателя, и гидромашины больше не нагружаются (прямая GK на рис. 8.3).
При использовании составных, параллельно соединенных гидромоторов, с выклю
Рис. 8.4. Статическая характеристика гидропривода, составленного из насоса переменной производительности и г пар одинаковых гидромоторов постоянной производительности
чением отдельных из них с соответстве и и ы м у вел и че и не м скорости движения и уменьшением суммарного развиваемого момента происходит сближение гиперболы установочной мощности N* с кривой мощности двигателя Nd, как
показано на рис. 8.4 для гидравлической трансмиссии, составленной из насоса переменной производительности и г пар одинаковых гидромоторов постоянной производительности. Гидромоторы последовательно отключаются по мере разгона, например, при помощи распределительного золотника Разумеется, это означает исполь-
зование ступенчатого переключения.
Однако в отличие от механической трансмиссии здесь каждая ступень имеет бесступенчатую прогрессивную характеристику и легко переключается рычагом управления производительностью насоса, например, посредством телескопического золотинка, имеющего столько положений, сколько ступеней в трансмиссии. Последующая ступень включается тогда, когда рычаг управления достигает крайнего положения. Переключение ступеней должно сопровождаться автоматической установкой такой производительности
оотВРТГТВует скорости, достигнутой на предЬ|Ду.
н8С0СЯп.пнЩ Я” ' составлена из регулируемого насоса и г Пар "lfnvr трансмиссиясостав	8 4 ступенчатой линией П()К₽
nLoBbix гидре»’070!108- 'парного момента гидромоторов з; "»«от "ixX-™" “ с»™’™’»™* »р. «'
-л» «ажил оставшаяся зд.
чнная с перво i,	гЛ-пиживает диапазон скорости
„ пяп гидромотпр08 w •3	г •
нйния пар	„ложена угловая скорость <о2 ведущего
Поскольку по оси аоси чптается велцчпна суммарного момента колеса, по осн °Р ное отношение между их валами и веду-щдромоторов (перед )це) же характеристика справсд-щнми колесам" Рентных гидромоторов, встроенных в колеса Л"Ва ^нрлсс'щ) У которых в различных комбинациях выключаются ОТЛй XxU слХях мощность выбираемого насоса определяется точками/ 2’ •	-• г' пР1,чем координаты любой i-и точки
будет:
i	хх г~ Ч Д4
<O2J = - <Bimax; M2i = ---- /VJiinax,
(8.9)
(8.Ю)
а величина установочной мощности насоса
л/ Ф-О- 1)]д4 IV yi —----“jj	шахматах*
Если г — четное число, наибольшее значение установленной
мощности окажется при i* = у и = у + 1
2 | 2
Л у max г Л12 дахСО^ щах = N у.
(8.Н)
Если t — нечетное число, при i* =	-
^vtnax	MjniaxWjnitix — N*.
(8.12)
ВСех иных значениях i насос будет иметь неко-дой из остальны1°ДаЧИ’ позволяющий повысить скорость на каж-возможного ппнп (показано штрих-пунктиром), величин ППИ шмт,. приращения скорости Ло>„ будет:
ДО),; = I_Z + 2
при четном г
при нечетном г
•тЛПйХ»
(8.13)
<4,«[.-Д+1>2	i
max*
(8.Н)
206
Произведение M2max <о2тахоценивает величину установочной мощности насоса при г = 1 Множители при М2тах и>2таж в равенствах (8 11) и (8 12) указывают, какую долю составляют установочные мощности Wj при заданном г по сравнению со значением при г = I (табл 8.1).
Габлица 8.1
Отношение	z							
	1	2	3	4	5		7	Я
Nv Ny	i.ouo 6.000	0,500 3,000	0.445 2,670	0.375 2,370	0.360 2,160	0.333 2,000	0,327 1,960	0,313 1,875
Уменьшение установочной мощности N* по сравнению с той, N*
которая была при г = 1, приближает отношение — к единице. Ма
Увеличение г свыше четырех мало изменяет относительную мощ-
ность /V* = _, величина которой при г ->оо асимптотически стрелу
мится к 0,25, что, например, соответствует полуторной мощности двигателя универсального сельскохозяйственного трактора (при d = 6).
Рассмотренный способ выбора составных гидромоторов требует достаточного значения силового диапазона d, которое должно быть равным или большим критической величины dK, когда пунктирная гипербола /-// должна будет пройти через точку /" (см. рис. 8.4). При четном г это условие имеет вид ,	,	4
(8.15)
а при нечетном г, но не меиьшем двух.
4
(8.16)
Так как знаменатели в последних выражениях ие бывают больше единицы, dK 4. Например, при силовом диапазоне универсального трактора d = 6 мощность насоса всегда будет достаточна для передачи мощности приводного двигателя. Для гусеничного трак-тора d 3, и использование неравенств (8.15) и (8.16) обязатгтьн 
Трансмиссия с составными гидромоторами одиакового Рае*' ра позволяет несколько расширить скоростной диапазон при работе на ступенях, относительно удаленных от средних, причем '
„1ЯЧ1)тельнее, чем больше номер ступени ОТЛи. расширение тем зла	те исходи) некоторое перекрытие
SSX284)-О запасе мощности насоса. Следу
стремиться к снижению этого запаса с тем, чтобы уменьшить вес и стоимость трансмиссии.
Очевидно, наименьшее значение установочной мощности можно получить в том слу чае, когда каждая включенная ступень гидромоторов будет иметь одинаковую мощность н не будет перекрывать скоростные диапазоны соседних ступеней Такой способ выбора размеров составляющих пар гпдромоторов назовем способом равнонагру-женных ступеней.
На рис. 8.5 пунктирной гиперболой /-// показана величина постоянной мощности двигателя N, = ^тах^тах °	d '
а штрих-пунктирной гипербо-равнонагруженпых ступеней
Рис 8.5 Статическая характеристика гидропривода, составленного из насоса переменно!! производительности н г лар равнонагружениых гидромоторов
лой /' — 2' — постоянная мощность гидромоторов Эти условия описываются двумя системами уравнений, состоящих: первая пз г уравнений:
шахматах ___
d	— Лз21<!>2 (/-1)
0 = 2, 3............г),
(8.17)
вторая — из г — ] уравнений:
= Л122ю2, = мг1юг1 (i — 2, 3, .... г— 1), (8.18)
содержащих 2 (г — 1) неизвестных о)г,-(г - I, 2........ г	— I) и
d....г>‘ решеиия систем (8.17) и (8.18) имеют вид:
=	(8.19)
у а* *
(' = 1,2......г) (8 20)
И величина установочной мощности в этом случае
d ’ d — d — const. (8.21)
Чем больше г и d (для некоторых видов самоходных строительных и дорожных машин и для тяжелых гусеничных тракторов силовой диапазон может достигнуть значений d = 10 -ь 12), тем ближе к единице величина относительной мощности
А*
/V** "а
= V d .
Расчеты, проведенные по уравнению (8.21), показывают, что при малых силовых диапазонах (d = 4) выигрыш от использования равпопагруженных ступеней невелик и имеются все основания в таком случае выбрать составные гидромоторы одинакового размера. Тогда при двух ведущих колесах вряд ли стоит применять более трех пар одинаковых гидромоторов.
Для универсального сельскохозяйственного трактора (d = 6) прН г = 4 (по два гидромотора на каждом из четырех ведущих колес) можно на 70% уменьшить величину мощности насоса по сравнению с вариантом использования одинаковых гидромоторов. Для трансмиссий с большим силовым диапазоном (d = 12) установленная мощность при г Зг 3 уменьшается более чем вдвое по сравнению с мощностью при использовании одной пары гидродвига-челей в трансмиссии
Исходные данные для выбора размеров ж	.
нонагруженных ступеней можно получить из равенства (8.20)
Так, для
рабочих объемов рав-
первой пары
AAlt —' Л421 — Af23 = AIJmax
для
второй
.. 1
ДМ2 — М.м — М23 — А1зт,х
для
1-Й
ДА!1 = Af3max z___
(8.22)
для
(i = 1, 2, .... z—1) последней (z-й)	(
AA1- = АД max г___
(8.23)
Выигрыш в величине установочной
уменьшение размеров гидромашин и “ подобных маши» веса (поскольку в каждой серии ^метричеош
с уменьшением размера снижается опноагоегатиого высоко-
Методика выбора размеров
моментного гидромотора может бы	пя л те явных.агрегатов-
ких гидромоторов, применяемых в нде Р
Можно показать, что величина номинальной мощности кажп пары паромоторов, кроме последней, одна и та же /ранеиг,°Й (8.19), (8.20) и (8.22)1:	‘ClBa
_____1
Л ^4 maxc,,i mix	| ‘
а для последней ступени (равенство (8.23)1
АЛ7_ <о —. Лп|лх(,>2 Л1ЛУ ~ •— .V**,
Следовательно, номинальная мощность насоса равна ной мощности последней пары гидромоторов и больше ной мощности всех остальных пар:
N, = JVJ* = 2Л(И > 2Nti
M1,W,
= №, .* /1 — ,
(8.25)
помппаль-помниаль-
(8.26)

где । = 1.2......z — 1 
Номинальная мощность гидромашпны объемного типа реализуется полностью, если угловая скорость от будет иметь наибольшее значение, обусловливаемое' допустимой наибольшей величиной коэффициента |48|
Сш = <> 1' W.
Так как мощность
N = юДртахО) —	I ЬУ2
н рабочий объем насоса
(8-27)
(8.28)
u>,
, (8.29)
соотношение размеров насоса и гидромоторов w,: wu: w2l =
(8.30)
§ 8. 3. СТАТИЧЕСКИЕ КРИТЕРИИ СРАВНЕНИЯ ГИДРОМАИШН ОБЪЕМНОГО ТИПА И ВЫБОР ИХ РАЗМЕРА
Непосредственно из уравнений, описывающих статические характеристики, следуют статические критерии сравнения гидромашин объемного типа. Использование при этом характерного объема гидромашины w или характерного размера D = yfw = у/ <7 по" зволяет обобщить методы сравнения гидромашин, сопоставляя образцы, конструктивно не похожие друг на друга, для определе-210
SyCZa“P",PHCTBa К°НСТРУКЧИИ "° конкрет-
Скорости в гидромашине, например, скорости скольжения и поверхности распределителя или любой иной трущейс* ™"а пости, скорости рабочей жидкости в любом из каналов и таХ’ лее „с должны превосходить определенных заранее заданных пое делов в первом случае во избежание взносов или обеспечения опое’ деленного ресурса работы гидромашины, а во втором случае- для предупреждения возникновения кавитационных процессов или ради того, чтобы гидравлические потери не ухудшали значение меха Н11ЧССКОГО к п. д.
Сравнение гидромашин в любом исполнении вне зависимости от их конструктивных форм облегчается введением уже ранее использованного понятия обобщенной скорости или коэффициента скорости
см = ю = wD s (Сш	(8.31 j
которые не должны превосходить предельного значения сш
Очевидно, что скорости в любых участках гидромашин пропорциональны с<„, а для серий геометрически подобных гидромашин коэффициенты пропорциональности между значениями любой местной скорости и обобщенной скорости сш одинаковы. Поэтому предельное значение обобщенной скорости си - может служить мерой совершенства гидромашины. Чем больше значение см, которое может быть допущено при эксплуатации гидромашипы, тем более она быстроходна, т. е. допускает работу с большей скоростью при том же значении характерного объема ш.
Существование предельного значения обобщенной скорости с^, означает, как это следует из условия (8.31), необходимость эксплуатации гидромашин больших размеров обязательно на меньших скоростях.
Современные гидроприводы работают на гидромашинах с Сы = 450 -ь 490. Рассматриваемая гамма гидроприводов имеет cQ = 470, аксиально-поршневые гидромашины «Лукас» имеют са до 680.	.
Поскольку помимо характерного объема используется удельный объем, а скорости измеряются в оборотах в минуту, применяются еще две формы выражений обобщенных скоростей:
с„ = п Vq сПпр и cD = п y/w < сояр,
причем связь между разными формами записи обобщенных скоростей определяется очевидными равенствами.
сп 30 yi = 17,65со> и Со = Jc» = 9-5б£'«-Значения обобщенной мощности
= /?(1> y^W *= рСа РтчСаяр “ c*v
to
Кшнй'топустнмын перепад давления р.„ах (пли соответствуют^ ему давление в напорной липин). Значение cNfi/i определяется ре. сурсом работы гндромашнны. Чем меньше значение ртах> тем & ше ресурс 163/. Поскольку мощности в любом звене гндромашнны пропорциональны значению c.v, возможно при помощи этого коэф, фнцпепта оценивать удельные мощности трения в наиболее напри
.. поэтому высокие значения сл- в гпдромашцЯах
женных узлах '\п”т°^’ер,;;ецСтве. В тех случаях, когда ресурс >ляется ресурсом ее опор качения (обычно длЯ
гндромашпн ФРГ 1661), сле-
свидетельствуют о
гндромашнны опреде.
Рис. 8.6. Удельные веся гидромоторов и электродвигателей серии НП.
дует обращаться к иным критериям оценки, применяемым в курсе «Детали машин» для опор качения Для рассматриваемых гидроприводов cN ~ = (7,2 <- 7,84)  К)'.
Важность весовых характеристик гидромашнн привела к широкому распространению так называемого удельного веса гндромашнны, т. е. веса, отнесенного к мощности гидромашины в кет '.
G = -^ KZiKetn. (8.34)
Разумеется, существует некоторая неопределенность этой и соответствующих иных
характеристик, поскольку могут быть использованы значения
различных мощностей, например наибольшая допустимая, номинальная (определяющаяся при некоторых заранее оговоренных условиях), или такая, которая соответствует определенному ресурсу гидромашины. Сравнение гидромашин различных типов должно проводиться при помощи идентичных (равноправных) значений мощности.
Для рассматриваемых гидромашин с регулируемой производительностью G ~ 2,4 + 3,6 кг,'кет, причем большие значения соответствуют большим образцам, а для гидромашин постоянной производительности О' = Д5 4- 0,9 кг/кет. Для гидроприводов нераздельного исполнения G = Б ч- 7 кг /кет.
Значения удельного веса для рассматриваемых гидромоторов приведены на рис. 8.6, на котором через СА обозначены значения, соответствующие действительным значениям мощностей, отличаю-
212
щимся от приводимых в каталогах для малых номеров гидромашин из-за того, что в них сообщаются сведения применительно к синхронным числам оборотов приводных электродвигателей. Там же дня сравнения приведены значения удельных весов приводных электродвигателей серии НП, отмеченные соответствующим индексом Gs. который и впредь будет использоваться для сравнения.
При сравнении аксиально-поршневых гидромашин с высокомоментными гидромоторами используется понятие — удельный момент
С“ = °М кг кГм-	(8.35)
Для гидромоторов рассматриваемого типа G., Эг 0,28 кг!кГм.
Рис 8.7. Сравнение гидромоторов постоянной производительности с приводными электродвигателями серии П
Определенное представление о габаритах конструкции и ее совершенстве дает понятие — металлоемкость конструкции 1481, которой называют отношение объема стали, имеющей вес гидромашины к ее характерному объему
с= ®.Ю»	(8-36)
i,oW
Значения металлоемкости v для рассматриваемых гидромоторов постоянной производительности приведены на рис. •• •
При оценке гидроприводов в нераздельном ИСПОД«^И"’ “ торых насос и гидромотор разных размеров, вы^е“^м^°“ водится по характерному объему гидромотора. Для гидромоторо
„ - 70 031—0,059) 10 3, для насосов Пе. рассматриваемого ти"8 । v = (0.09 ч- 0,43) 10 3, а для ги, ременной пРо’13^р"3дельном исполнении V = (0,22	0,58) . Н)-\
дропрнводов в НСризн
s к. 4. ПРИЕМИСТОСТЬ П1ДРОДВП. АТЕЛЯ
Аттил пвигатсля называют его способность разгонять Приемистостью	способность зависит от величины раз.
впвасмого ^момента	момента инерции вращающихся („ли воз-
нпятно поступательно движущихся) частей.
Р НесХя на то, что приемистость относится к динамическим свойствам гидродвигателя, она рассматривается здесь в связи с тем, «то в конечном счете определяется статическими характеристиками гидродвнгателя п его конструкцией (через момент инерции вращающихся частей).
При расчете конкретного объекта со всеми заданными параметрами, например при заданном передаточном отношении между приводным двигателем и нагрузкой, оценка способности разгонять инерционную нагрузку сравниваемых двигателей производится при помощи отношения развиваемого момента к моменту инерции вращающихся частей двигателя
х - Э
(8.37)
Исполнительный двигатель, у которого значение больше, обеспечивает большее значение ускорения инерционной нагрузки. Рассматриваемые гидромоторы меньших размеров имеют значение и<> в 160 раз, а большие в 50 раз выше, чем значение и,-> для электрических двигателей той же мощности [731. Именно это обстоятельство и является главной причиной широкого распространения гидроприводов.
При проектировании привода, когда заранее еще не известно r'iwnpv0 пеРедаточвого отношения i между исполнительным дви-поскснн™нагРУ3кои’ использование критерия х() нецелесообразно, миссии изменит^”110 Г1араметРов м'> и к любому звену трансмиссии изменит значение этого отношения 1481:
_____	Мд	Xd ^пр__Ud	i
поскольку приведенный	момент	М	ня	_
ношением i межлс ним и . "г на звене с передаточным от-между ним и исполнительным двигателем будет
Мпр = ^Мд,	(8.39)
а приведенный момент инепнии .
него двигателя	р вращающихся частей исполнитель-
~ ,s Jд-
(8.38)
(8.40)
214
Независимость соотношения М„„ и Jпр может быть достигнута использованием критерия	7
/; _ Я, ° fjd'	(841)
iioci ольку в этом случае
^пр Л4,}
Vinp^Vrrk^w	(8-42*
Этот критерии широко используется при расчете конкретных систем автоматического управления, не вызывает трудностей при неизбежном изменении значения i в процессе проектирования и для рассматриваемых гидромоторов имеет значение в 7,5—10 раз большее по сравнению с электрическими двигателями [731 и 1711
Несмотря на известные преимущества при использовании критериев п kf> при проектировании приводов, для сравнения серий подобных исполнительных двигателей, включая и электродвигатели, безотносительно к их размерам приходится обращаться к третьему критерию, не зависящему, например, от размера гидродвигателя и представляющему собою величину, пропорциональную отношению наибольшего возможного ускорения инерционной нагрузки к корню квадратному из мощности исполнительного двигателя 171]:
П =	Л'й—.	(8.43)
Г	п|ах
Так, если исполнительный двигатель с моментом инерции вращающихся частей Jo соединен через редуктор (передаточное число редуктора <) с инерционной нагрузкой, момент инерции которой JH, то наибольшее возможное ускорение инерционной нагрузки 0* будет при I* = у/~у и определяется равенством
б* = KMajjd лГ м»	(8.44)
в котором и JH учитывают моменты инерции соединяющих валов, вращающихся частей трансмиссии и т. п. Таким образом, достижение наибольшего возможного ускорения инерционной нагРУзки осуществимо тогда, когда приведенный к исп™н^еть"омУ '^иг телю момент инерции инерционной нагрузки бтд р инерции его вращающихся частей.	и кп.
При вычислении значения П по каталожным ^о^иач^ торых иногда приводится вместо <1><тт.х меньшее си Р	га_
ние (в соответствии с числом оборотов привод	Р
теля) желательно уточнение действительного значения	по
215
fltoT значения Пл. причем индекс указывает „а которому и вычисляют
уточнение. ирИИ„ П>ПА вовсе нс означаюг возможности ' Повышенные значения/ орения инерционной нагрузкн получения большего знамен*	дополнительныи множитель
поскольку В выражение
’ ЛНаЮоис 8 7 показано отличие П от ПА и для сравнения ПрИве. дены значения приемистости П, приводных электродвигателей се-' Выбор передаточного отношения i редуктора, отличного от значения I* = приведет к уменьшению значения наибольшего ускорения инерционной нагрузки
гмх < °* • Это уменьшение может быть оценено выражением по работе [76]
Й
гдеГ = £ и ё= 6|р.
Сравнение приемистости рассматриваемых гидромоторов постоянной производительности с приводными электродвигателями серии П различных размеров приведено иа рис. 8.7 и 8.8, причем там же приведены значения „	п	/п\	/п\
отношении	—,	Nr	и	= ,
G	\G)a	\GIs
которые более стабильны для серии различных исполнительных двигателей одного и того же типа. Эта величина
3 f И 30 50 100 П,Л'кОт
Рис. 8.8. Сравнение динамических свойств гидромоторов постоянной производительности с приводными электродвигателями серии П
позволяет в определенной мере судить о добротности исполнительного двигателя одновременно и по динамическим, и по весовым характеристикам [71].
Приемистость гидромотора не является независимой от гидравлических параметров гидромотора характеристикой. Так, момент инерции гидромотора, выраженный через коэффициент момента инерции J, будет
J ~ w,	(8.46)
причем для аксиально-поршневых гидромотороз J = 0,001 + 0,006. Для рассматриваемых гидромоторов постоянной производительности значения J приведены иа рис. 8.7. Для авиационных гидро-216
моторов «Виккерс» и бескарданных гидромашин типа «Гидроматик» |6(5| эти значения почти вдвое меньше, однако главным образом за счет комплектующих деталей значения J обычно несколько возрастают для образцов самых больших размеров. Именно этим обстоятельством объясняется падение приемистости гидромоторов больших размеров, и при необходимости осуществления привода с высокими динамическими свойствами приходится обращаться к многодвигагелыюму приводу, составленному из нескольких ги дромоторов, каждый из которых обладает более высокой приеми стостью, чем приемистость одного гидромотора суммарной мощ-HOCTI
Подставляя уравнение (8.46) в (8.43), а также имея в виду, что М msn = wpm^-, получим
Ч м
П = 1	— = 1 / т-,	(8.47)
\/ w<ortma!lJ у
причем ориентировочные значения г]я приведены на рис. 8.7.
Последнее выражение объясняет непрерывные поиски конструкторами такого гидромотора, момент инерции вращающихся частей которого был бы наименьшим, а перепад давления — наибольшим. Тенденция развития современных гидромоторов — создание исполнительного гидродвигателя с наибольшей приемистостью.
Глава 9
ИНЛМПЧЕСКЙЕ	1Е2П!2^а
§ 9.1. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕН!!» ГИДРОПРИВОДА
Структурная схема обобщенного гидропривода с простейшей формой обратной связи (рис. 9.1, а), в котором выходной коорд,,. натои будет угол 0 поворота вача гндродвигатечя, описывается тремя уравнениям! Первое из них — уравнение обратной связи и = Л> —К.Д	(9.1)
где и — параметр регулирования насоса;
х — входная координата;
— коэффициент усиления по входной координате;
/(„ — коэффициент усиления обратной связи.
Если гидропривод составляется из регулируемого насоса и гн-дромотора, то уравнение расхода будет
+ «И'] 2	= к’ю^2 +	+ ®ы2р,	(9.2)
где и — параметр регулирования насоса;
_ dfl
(i»j и <й — — скорости насоса и гидромотора соответственно;
и — коэффициенты равномерности подачи насоса и гидромогора соответственно;
Li — коэффициент равномерности динамической подачи насоса;
т — параметр герметичности гидропривода, опре-депяемый уравнением (7.42);
~ параметр упругости;
Пт. Р перепад давления на гидромотоое веает	"“«""брааво обращение к ра-
нить членом С„0 описываюш™«У’ КОТОрое Целесообразно допол-'«ворога гилромокра ОрДЗ	У™У
- -»x::x+c"“+c'+jS+a,"+/- м
с - коэффициент активиойХ"°рРуЦзкиНаЛЬНЬ1Х НагРу3ке;
J—приведенная к вал а‘рузки, вместе со всеми'Bnan1^OMOTOpa инеРЦи°нная нагрузка МИ “РаЩа^Щимися частями.
218
Рассматривая х в качестве входной координаты, а 0 — в честве выходной, можно, исключая из равенств (9 1) (9 2) и (Q р и и, получить два дифференциальных уравнения системы ctdvk турная схема котором показана на рис. 9.1, а. Первое уравнение, справедливое при 0 > 0, записывается в форме
тЛ4„ + aj + о.,6 + а3ё -р а40 xf _р =
= Bi J (£г — с) х +	_ С)х,	(9.4)
а второе, справедливое при 6 <0, отличается знаком при коэффициенте с > 0:
т/Ип + Oj6 ф- а20 4- а30 4- а40 _|_ xf 4.	=
= X’ «1 (&2 + с) х 4- U % & 4- с) х,	(9.5)
где
а|=ВЛ1о)1Ко+-тСя,
«2 == В. " Ко + ТС 4- 0СЯ + & + с),
а3 = tJ 4* и а4 = 9J.
При изменении знака 0, т. е. в местах перехода из одной области в другую, неизбежны определенные отклонения, аналогичные эффекту Гиббса, определяемые выражением ^[1 (Z)sign 6] [112] и 1861.
При отсутствии обратной связи (рис. 9.1, б) дифференциальные уравнения получаются из равенств (9.2) и (9.3) исключением выражения перепада давления р. Так, при 0 > 6, дифференциальное уравнение принимает форму
тМ0 4- Ьо6 4- bj 4- b.fi 4- М + V + У =
<9-6’
а при 0 < О
тЛ10 4- М 4- bfi + Ь26 4- Ь3ё 4-	=
= Ъ & + с) 4- (U + с) у 2 «•	(9
где
Ьо = тС„, t>i = тС 4- ЪСп 4- $2 (£а -+- с)>
Ь3 = tJ 4- bt = &J-
При отсутствии шарнирного момента (Ся — щение разрешающего уравнения переходом наты 0 к выходной координате ы » 0 (рис. 9.1,
Наиболее простую форму приобретает дифференциальное некие в случае Е, =	। — ?2 = 1, которым обычно и польз ^ав'
при рассмотрении процессов с неизменным знаком скопосУ1°7Сп При исследовании процессов, происходящих с переходом 311/И '°' w через нуль, целесообразно обращаться к равенствам (7 45? щ1"1
Таким образом, дифференциальное уравнение гндравлпч » трансмиссии при <о > 0 записывается в форме	Ск°й
тЛ10 + (I — с + тС) ы + (г./ + ОС) <>>	0.7 о» ф т/ j Of =
= (!-.)--.,„ + (! _с)^й (9р)
Влияние статической нагрузки проще всего учитывать при помощи так называемой статической ошибки, переходя при рассмо-тренин динамических процессов к использованию в качестве выходной координаты приведенной скорости
О/ _
1 — с + тС
которая при отсутствии статической нагрузки совпадает с действительной, почему соответствующий индекс зачастую опускают. Также может быть опущен индекс при включении статической нагрузки в нелинейное демпфирование |80|
, xJ + ОС . . 0J  , т/ “ + Т37+тсы+ Г-г-НС*" + 1^4 w, .	•
-0-е) Vc + tC--	0.9)
Весьма удобно использование этого дифференциального уравнения в безразмерной форме 1801, которая будет приведена в следующей главе для насоса, допускающего изменение производительности без изменения кинематики (отсутствует последний член правой части).
Наконец, при отсутствии нелинейного демпфирования или использования каких-либо приемов линеаризации передаточная функция гидропривода принимает форму
U7 =	- А’(I + 7»
u(s)	7'sS2>
где коэффициент усиления
(9.10)
постоянная опережения
(9.12)
(9.13)
постоянная времени
Kt
(9.16)
а £ и Г будут иметь те же выражения, что и в случае использования в каче-
коэффициент демпфирования t =
(9.14)
Режимы работы гидропривода, для которых справедливо уравнение (9 Ю), называются квазилинейными.
Имея в виду, что при быстроходных приводных двигателях Tf, Т, ее следует учитывать в случаях, когда исследуется система, содержащая высокочастотный контур (например, гидропривод с автоматом мощности) 1851, при работе на малых скоростях приводного двигателя, а также для дистанционных приводов с малыми значениями постоянной времени Т.
В тех случаях, когда в качестве входной координаты рассматривается скорость приводного двигателя <oIt а выходной — скорость исполнительного двигателя о> (гидравлический вал), передаточная функция при квазилинейном режиме работы будет (рис. 9.1, г).
=	= F+'StjTs-l- W (915)
где коэффициент усиления
WjU А» — /	_
г)
Рис. 9.1. Структурные схемы гидроприводов объемного типе
стве гидропривода гидроусилителя. Следовательно, при исполь зовании гидропривода в качестве гидроусилителя или Г1*ДРа®’ лического вала характеристическое уравнение на квазилинейном режиме одинаково.
§ 9.2. ПОСТОЯННАЯ ВРЕМЕНИ И КОЭФФИЦИЕНТ ДЕМПФИРОВАНИЯ ГИДРОПРИВОДА
Обычно в системах автоматического УпРа^'1И*’ ней мощности гидравлический исполнительный™ наибольшее значение постоянной времени ₽ времеингад| остальными элементами системы. Поэто“У"°^ . оп[)меаяя пе привода является важнейшей характери - еастеМи, ный процесс и точность работы рассматр
, „ П что критерий упругости гидропривода Вспоминая (гл П,
w/u'x’	(9.17)
, момент ННЧ.ОН" »"П»'»" «	18'4’
j==Uf, = Uu'i w,	(9.18)
ГПР /_ поперечное сечение магистрали,
Д к коэффициент поперечного сечения,
./ — коэффициент момента инерции вращающихся частей ги-
можно разверну^Г’выражение постоянной Т времени (уравнение ( Подставляя выражения для #и J в равенство (9 12), получим
т = I 1? I /Х = I / kf	|Л1
|	1 — с + тС и I (I — с + тС) । w f“max ’ и *
поскольку при разгоне инерционной нагрузки J ГИшах = ВДрп111х.
Таким образом, естественно стремление конструкторов создавать гидропривод форсированный по давлению, особенно при необходимости обеспечения высоких динамических качеств привода, оцениваемых, в том числе, по наибольшему ускорению инерционной нагрузки.
Для высококачественного привода 1— с -фтС близко к единице, поэтому, пользуясь материалами гл. 7, можно убедиться, что
Т = (0,045-ь 0,077) |
При проекшрованин, когда приходится многократно изменять значения л, I и х (например, учитывая изменения давления, тем-пфатуры, а также и самой рабочей жидкости), удобно использо-. п_..ятие - эталонный гидроусилитель, отмечая его параметры nu^n i	о. /0 = 25 ОИ и х0 = 15 000 кПсмг.
т 0,0445	= 1 = 38 5	22,5 1/сек или
тпон^.гп₽1И^22„1°ЯН1,ая вРемени ПРИ любых соотношениях па-
вать понятие — 
индексом Oi например, >.о = 2; lt
Тогда Т„ 0,026 +
6.14 < " -
раметров будет опраделят^ся^^^
Т
где
'Г Т 1 и1 >
(9.19)
X
рис. 9.2, а и свиде?^ьствуетПоРспМе1Ра 7 от х и х z приведена на > равнительно небольшом влиянии х
х= * «о-
на значение Т Наиболее существенно влияние I. принимающее большие значения при удалении насоса и гидромотора.
Рис. 4.2. Зависимость безразмерных параметров гидропривода Т и J от х, Ъ- И
Выражение коэффициента демпфирования в форме равенства (9.13) можно переписать
где
с© __ р€, _ м *7 £ ^С xj ф и> Су v j
(9 201
г материалами гл. 7 в случае, когда активное соПро «ХВпеГСТ(сопроп1впеи..е, пропорциональное скорости) только'в гндромоторе.	ю	.	рСв
дпя гидромоторов «Лукас»	0,01 +
0 025 (первое значение для машин меньшего размера). ПрИНи
/ °’о ь - 1 - 2 / = /п, х = х„ и А = Ао = 2, получим Д. J L 0 041^ 0,0175, а при малых нагрузках Д£ 0,082 - 0.1225. Пня гидромоторов «Брюнннгхауз» Д£ = 0,10 - 0.0,
Д При изменении параметров /, А и х можно в порядке перВДго приближения не учитывать изменения Д{. То.да выражение коэф, фициента демпфирования принимает вид
и I 1 ’
(9.21)
ь 2 0
Весьма важно, что I х, так же как и 7, т. е. изменение инерционной нагрузки одновременно и в одинаковое число раз (через значение А) меняет и постоянную времени, и коэффициент демпфирования, который обычно считается независящим от на-
грузки.
Используя ранее приведенные значения определяющих коэффициентов, можно получить для гидромоторов «Лукас» \ = 4 ' б /о = 45 -ь 90 и для гидромоторов «Брюнннгхауз» =11 -з- 22,5.
= 45 -\ /о
Таким образом, значение £ может оказаться весьма большим, если только привод не будет дистанционным, особенно для гидромоторов «Лукас», в которых гидростатическая разгрузка осуществляется за счет существенного увеличения демпфирующих свойств. Очевидно, главной причиной увеличения £ являются утечки, которые стали особенно существенными в последнее десятилетие из-за повсеместного применения приводов хотя и более 1ерметич-пХ^НаКОф?рсИрова,,н,Ь1х по Давлению. При переходе на режимы иемс пппрпТ°И НаГРуЗК°Й значение £ существенно падает, по-преж-поенебпеж/нирЯСЬ упругими свойствами гидропривода. Разумеется, ^Ревебрежение значением 0 делает невозможным точное опреде-тапью^можишТюз^и1^ММЬ'Х СКОРОСТЯХ Движения делает не деляет их характер пп кновсние автоколебаний, но также опре-томсоновского типа достюоч7оПревращает гидропривод в систему мощи консервативной системы 1°ЧН° аппРокс"Мируемую при по-ции гипотезы фильтра при ана\и«,ачиТ’ не требующей реализа-ризации.	к Р нализе методом гармонической линеа-
сравнительно малым Тлщ Д^м°лебаНИЙ уже нельзя пренебрегать ляться более высоким прибл! 2	" значе1и,с I. должно опреде-
224	ириближенпем, т. е. с учетом Д£.
Так же, как и при определении постоянной времени Т удобно пользоваться при проектировании выражением

(9.22)
где коэффициент демпфирования £п соответствует значениям ?.Г1 = 2 /0 = 25 см и х0 = 15 000 кГ1смг (или каким-либо иным заранее выбранным) и графиком, приведенным на рис. 9.1, б.
8 9.3. ДИНАМИЧЕСКАЯ ОШИБКА ГИДРОПРИВОДА
Известно, что если на вход любой линейной стационарной системы подается сигнал описываемый полиномом (или любой функцией, которая в интервале 0 <Tj <Т„, где — время, а Тп — время переходного процесса, раскладывается в ряд Тейлора, сходящийся в этом интервале к самой функции), то отклик на выходе можно представить в виде полинома {87J:
о> (/„) = Р„Ф (*„) + Н1Ф (М + 14 т + Из +  -, (9.23)
где

(9.24)
Р (tJ — импульсная переходная функция, а динамическая ошибка системы е в tn момент времени определяется разностью
е = Км - от = ср (<„)-«(/„),	(9.25)
причем Ки = ср (tn) — входной сигнал.
Поскольку динамическая ошибка является характеристикой установившегося режима, то выходная функция определяется частным решением дифференциального уравнения. Коэффициенты щ определяются только параметрами системы и не зависят от формы входного сигнала, поэтому целесообразно выбрать вид входного сигнала ср = ср (/) таким, чтобы определение щ было наиболее простым.
Полагая, что входной сигнал ср = <р (/) можно описать полиномом второй степени, определим первые три параметра р0> щ и р8 ряда (9.23) при помощи простейшей степенной функции
ф(о = 4’ ф<о=* и ф(^=1-	(9,2б)
Поскольку корни характеристического уравнения (9.Ю) отличны ог нуля:
4±|гР=г. г,*°.
289
8 В. Н. Прокофьев в др.
„ искать в форме уравнения решение слслх	+
(9.28)
л—2£7;
(9.29)
(9 27) очМи.нпентов которою можно получить подстановку значение коэффишк	д такжс ф „ ф нз уравнении (9 26)
пг" °»Ш“ЮЙ С1СПИ"’'" "Р“>«
н левой частях-	(	_ _2L__2£7' и
Cfl = ‘J 	1	2<l>!
C,= 2E7(2£7-2;)-T-.
Подставляя равен™» (9.21» » ИЯ- т™>«™ со = 2С(1([ + с, q + С2ч ,
и, сравнивая полученное выражение с искомым рядом (9.23), окон чательно запишем:
р0 == 2С„ = 1; Р1 = С1 = <
^ = 2С2 = ЦТ^Т-£
При использовании насоса без динамической подачи, т. е. такого, регулирование которого обеспечивается без изменения кинематики замыкателей (например, регулирование распределением), множитель-^- в равенствах (9.10) и (9.29) превращается в нуль, и отклик на выходе объемного гидропривода будет
“ (Q = ЧР (U - ЦТ ф (1Я) + 2Тг (4^ -1) ф (/„).	(9.30)
Таким образом, динамическая ошибка гидропривода объемного типа с разомкнутой схемой управления при отсутствии нелинейного демпфирования определяется только параметрами системы £ и 7 и не зависит от значения коэффициента усиления. Но тогда динамическая ошибка такого гидропривода меняется с изменением инерционной нагрузки.
riant!3 Равенства (9.10) видно, что рассматриваемая система не об-’ т а^татизмом относительно управляющего воздействия и поэ-р нципиально не может без ошибки отрабатывать сигнал типа <р (/) = '
Передаточная функция ошибки е (s) будет
Фе	= ЧГйф) ’
ГДенТ адГва°нТЯтеорееТмы	равенства <910)-
к которому стремится ошибка*"^™ °М Значении Функции, предел, 22g	°К времени, выражается через пере-
(9.31)
даточную функцию ошибки. и входное в выражением	ущение определяется
lime (Г) = lim s<bt (s) (si
z —00	,_0 «WW)	(9.32)
„ли, имея	в виду, что •мо = ?	ИЛИ ф(5)= 1 S8 •
получим	lim е(() = linis < — OQ	s — 0		1 1_ к __ 1 + w (s) S2 s» ~ °°
Аналогично можно получить и для входного сигнала вида <р (/)= == t или <р (-'>) = s2
lime (0 = — = оо. / — СО	s
Таким образом, если входной сигнал задает постоянную скорость, то скорость на выходе будет меньше заданной. Поэтому разность между задаваемым положением исполнительного органа и его действительным положением (ошибка) будет непрерывно возрастать, и управление гидроприводом нуждается в обязательной компенсации увеличивающейся ошибки.
§ 9.4. ГИДРОПРИВОД С УПРАВЛЯЕМЫМ ГИДРОМОТОРОМ
Динамика гидромотора описывается следующими уравнениями расхода и нагрузки с учетом применяемых ранее обозначений:
Qj =	+ w й* у х +
u*wp* + wp* й -у— = Mo + cwp* + Cw* J to*,
(9.33)
где индекс * относит величины к нестационарному движению; и — параметр регулирования гидромотора;
Qi — подача насоса;	,
X — функция кинематических свойств гидромашины, Р^^ Щаяся в положительную единицу в случае зависимости кине от значения и и в нуль для гидромашин, pei улирован ₽ обеспечивается без изменения кинематики (например, коммутации при повороте РаспР1^"^)оегулнроВания и,
Используем малые вариации параметра р у Р"	,
пада давления р и скорости ©, полагая, что и ”	.
Р = р* - р* <р>, <0 = <0* - <0* < относит величины к статическим режимам ра
(9 33) в вариациях после линеаризации принимают форму «,<> +и + syx) + M7’(T + <ls) = °;
К'/1 («* — И -<’ (о + sJ) — K'w/\ (1 + s 2^-x) = 0,
где s — Hi — переменная Лапласа;
q___частота колебаний входной координаты.
Исключая из равенств (9.34) перепад давления р и принимая в качестве входной координаты параметр pei улирования гпдромо-тора и, а выходной — скорость о>, получим дифференциальное уравнение второго порядка с оператором воздействия второго порядка
T2ii> + 2£7'<•» + °> = A<f> + А Ф + *P>
(9.35)
где q = Ки — приведенная входная координата;
К — коэффициент усиления;
Т — постоянная времени;
£ — коэффициент демпфирования, причем
К =	=	<°:
7 = |'----------= I	А17— = -L т 0 ;
I тС + и* (“* — с) ' 1 — с + тС Ук
ь тС + », (и,—с) , _О.
А------Г^- с-НС- • v"~ k'
т — т м«||« 11_______**»“* — *>** 
"	\	«»/’ «74 I- П»«’
(9.36)

зависимости то в этом случае энергично возрастает г’”""— соответственно увеличивая
где 0„ — приведенное значение критерия упругости1, То = const — постоянная времени гидропривода при и„ = • (случай составления гидропривода по традиционной схеме);
Чо* — объемный к. п. д.
Поскольку значение k = k (иф) по параболической падает с уменьшением ut, го " ста™ . постоянная времени гидропривода Т, с------
время переходных процессов. В той же пропорции для гидропривода с короткими магистралями увеличивается и коэффицие11т демпфирования.
228
Очевидно, нижний предел значения параметра регулирования должен превышать значение с.
Коэффициент усиления увеличивается обратно пропорционально коэффициенту k и в соответствии со значениями параметров системы, а также (что очень важно) в соответствии с величиной статической нагрузки по различным закономерностям меняются значения параметров оператора воздействия Д, и Дг, поскольку т]0, определяется значением статической нагрузки. Переходные процессы могут исследоваться при помощи традиционной схемы (с нерегулируемым гндромо тором) при использовании приведенного «замороженного» значения критерия упругости 0п= * 0 с соответствующей заменой
критерия герметичности т на увеличенное значение
Подобный способ исследования упоминается в связи с тем, что его использование неизбежно, поскольку в действительных системах значение модуля упругости рабочей жидкости меняется не только с изменением давления 184), но и с содержанием нерастворениых воздуха и газовых составляющих.
Поскольку силовой электрогидропривод должен проектироваться как устойчивая система, а постоянная времени не очень мала, то время переходного процесса, возникающего при изменении вида управляющего сигнала или при его скачкообразном изменении, невелико. Поэтому точность воспроизводства управляющего сигнала, определяемая динамическими ошибками, становится важной оценкой управляемости рассматриваемой системы, имея в виду ее использование с разомкнутой схемой управления главным образом в качестве привода транспортных машин, когда обязанности обратной связи песет водитель (или машинист).
Используя изложенный в предыдущем параграфе прием определения динамической ошибки, можно записать для входного сигнала выражения:
ф(()=2, <р(/)=/иф(/)=1.	(У37)
а для выходной координаты
ш = CnP + QZ + Са.	(9.38)
Обращаясь к равенству (9.23), устанавливаем, что о) = 2С0ф + Cj ф -|- Саф,
причем
Со = ' • Ci = А, - 2£Т и Cs = — Л» — 2СТ (Лг - 2ИЭ >&
откуда
Ро = 2Со — 1 > л
г _Li2ie*--2?T<0;
Р1 = с'- тп
р, = 2Сг = Л
о + тт- х 2(0*_____2?;т
О

нлп
л й+*о;х
ЦТ Кй(1„) +
2<о*т,
__2^Т
0 + ^	I
—-^-2£Г КЙ(/„).
* п	'
(9 40)
Полученная методом «замораживания» коэффициентов количественная оценка динамической ошибки у называет на значительное отличие рассматриваемой схемы от традиционной, заключающееся в существенной переменности коэффициента усиления const, входящего в каждый член ряда (9.23). Это означает существенное изменение управляемости трансмиссии при использовании разных значений параметра регулирования и*, к чему обязательно должен приучаться водитель или машинист, особенно при маневрировании на разных скоростях движения.
Для гидромоторов, кинематика которых не зависит от значения (т. е. х = 0),
п г- Ё___21Т =___________Ё_______________т£+_Ё^_
т»	т__<0*ы* I1__£_\ ТС + и* (и* — с)
\ uj
(9.41)
Следовательно, искажение при отработке командного сигнала за счет члена pj<p (/„) существенно меняется с изменением его значения и в нуль обращался не может, поскольку каждый член выражения И! отрицателен.
Все члены выражения р2 положительны и при всех доступных ”™ЯХ Реж,1ма работы не проходят через нулевое значение. Поэтому р2 > 0 и в нуль не обращается.
чем ппы\^-1г?бпЛЮ™ые значения коэффициентов р) и р2 больше, гилпомяпгии ™ 0Эт0мУ использование в качестве регулируемых не меняется п ИХ’ КОТОРЫХ в процессе управления кинематика женную отп'аботи°ЛЯеТ полУчать в большинстве случаев менее искаженную отработку командного сигнала.
230
Свойства рассматриваемой системы, которые определяются Хао?рсш>и"ЦИМИ СЛуЧа"НЫИ хаРактеР- нуждаются в otXhoJ °' Гидропривод находится под воздействием целого ряда помех которые, вообще говоря, могут поступать на разные входы Напои мер, колебания подачи насоса и гидромотора из-за дискретности подачи, осуществляемой каждым отдельным поршнем вследствие непрерывного изменения давления, вызванного несовершенством распределения, изменения утечек, вызванного непрерывными колебаниями различных механических узлов гидромашин, имеющих различные собственные частоты, неточности изготовления узлов замыкателей тдромашин, которые должны обеспечивать строгую цикличность работы и т. п. Особенно увеличиваются помехи, если в качестве приводного двигателя вместо электродвигателя используется двигатель внутреннего сгорания. Самыми большими помехами, носящими случайный характер, являются колебания нагрузки при использовании гидропривода на транспортной машине.
Если бы колебания подачи не сопровождались перечисленными дополнительными процессами, то они относилисьбы к регулярным помехам, рассмотренным применительно к насосу в работе 1751. Однако при работе такого насоса на гидромотор с дискретной, а значит, неравномерной подачей, главным образом при <0! =£= ы, перечисленные выше дополнительные процессы, особенно при длинных маги-
стралях, приводят к возникновению помех, определенная часть которых носит случайный характер и может быть задана в виде спектральной плотности S„ (9).
Хотя помехи поступают на разные входы, для линеаризированной модели рассматриваемой системы они при помощи элементарных приемов всегда могут быть приведены ко входу управляющего воздействия в форме некоторых эквивалентных помех, поступающих вместе с управляющим воздействием на один вход. Будем считать, что спектральная плотность S„ (й) характеризует именно эти эквивалентные помехи, приводящие к дополнительным изменениям скорости гидромотора, а значит, и дополнительным ошибкам отработки управляющего сигнала и дополнительным динамическим нагрузкам. Очевидно, что в гидроприводе рассматриваемые помехи являются стационарными случайными функциями, поэтому среднее значение квадрата ошибки гидропривода, вызванной помехами, определяется выражением (791
fl« = 1 J S„ (Q) | W (»Q) 1* dQ.	0-42)
0
где U7 (tQ) — передаточная функция гидропривода, определяемая из равенства (9.35):
1V,, , cii(s) у 14- А* + Ар1	(9-43)
лпя гидромоторов с кинематикой, зави-причем, что очень важно. ЛЛ^г^р	Q
сящен от значения «.	нтные помехи, носящие случайный
Для гидроприводаI Э	в В11Де суммы двух типов помех;
характер, можно рассм	с0 спектральной плотностью с2,
помехи,	(«) = s„ («)-<-:
и помехи, задаваемыесп ^да среднее значение квадрата ошибки гпдропрдаода°|13-за помех, задаваемых белым шумом, определяется выражением
6== с° J С
(9.44)
причем значение интеграла
1 е	л2
/(«) = - \ |w(/Q)i2dfi =	(9.45)
б
меняющейся
служит мерой фильтрующих свойств гидропривода, с изменением входного сигнала и, от значения которого существенно зависят ряд параметров дифференциального уравнения (9.35).
Рассмотрим работу привода при условии й = 0; Л1п = 0 и С = 0, принимая в качестве выходной координаты ускорение привода. Тогда передаточная функция будет
(s) = 9.W (s), а среднее значение квадрата ошибки ускорения будет
(9.46)
ы2=	(s) |2 dfi,
о
и в соответствии с равенством (9.33)
р*(0=,„ J sm(0
'	(u, — с) w ' '
ИЛИ
(9.47)
(9.48)
00
(I
(9.49)
Поскольку при у. =#= 0 полиномы и числителя, и знаменателя W (з) имеют один и тот же порядок, то интеграл
СО
1 = | J о
не сходится, что свидетельствует о неуправляемости линеаризированной модели гидропривода. При практическом использовании 232
рассматриваемого гидропривода колебания давления из-за помех будут конечными вследствие нелинейностей системы, в том числе из-за периодических травлений предохранительных клапанов, обычно называемых oi раничителями момента.
Таким образом, неустойчивость гидропривода из-за помех, носящих случайных характер, требует использования в рассматриваемой схеме гидромотора, кинематика которого не меняется с изменением параметра регулирования (например, при помощи поворачивающегося распределителя), т. е. требует использования гидромоторов, ранее считавшегося менее совершенным.
Примечательно, что постоянная времени практически не определяется утечками, поскольку они входят только в виде слагаемого в знаменателе (тС < 1) 181].
Значение этого слагаемого можно оценить при помощи равенства
т — CJ. L = I ®>’н\ _ £у (। I р w pw \ ' Qy / pw \ ' CyW j ’
где QVh и Qy — утечки в насосе и гидромоторе соответственно; Су» и Су — коэффициенты утечек в насосе и гидромоторе соответственно;
Ь — коэффициент учета влияния утечек в насосе.
Также ограничено число степеней свободы при выборе параметров системы, обеспечивающих желаемое значение коэффициента демпфирования. Так, из третьего и четвертого равенств (9.36) можно записать	_____
/ kfllJ
9гт - tJ+®C =(b^S + —(9.50) *(1 —с + тС) \ р S /Л(1 — с + тС)
или
£ = -Т 2
ЬСу Св
2 УЪ (1 — с -р тС)
(9.51)
где
. (9.52)
х »/—
— у да =
5 =
Значение динамического параметра гидропередачи S определяет коэффициент демпфирования и удельный вес утечек и сжимаемости в демпфирующих свойствах. Так, при возрастании значения S увеличивается роль утечек, но уменьшается влияние сжимаемости.
Проводя исследование на экстремум, можно убедиться, что наименьшее значение коэффициента демпфирования будет при
„„.«„мое значение коэффициента демпфирования л х И отмсти J при выборе гидромотора более совершенного типа) б'ДеТ + г	..
2j FcT^T+bCyCtj
,	,-с	(9 53>
' * I 1 + ьсясу
Значение определяется совершенством конструкций используемых гидромашин, а величина k в соответствии с равенством (9 .36) существенно изменяется в процессе регулирования, увеличивая £ при уменьшении значения параметра регулирования.
Динамические свойства рассматриваемой системы на малых («ползучих») скоростях движения, которые могут привести либо к автоколебаниям, либо к остановке гидромотора из-за нелинейностей типа «отрицательного сопротивления» (подробно рассмотрены в гл. J0), не отличаются от свойств силового электропривода, осуществляемого по традиционной схеме, поскольку при этом и, = 1, а поэтому не нуждаются в самостоятельном рассмотрении.
Также ничего принципиально нового не вносит работа гидропривода при самых малых значениях и*, поскольку нелинейное демпфирование из-за гидравлических сопротивлений при высоких значениях «о, невелико, а способ его учета аналогичен способу учета гидродинамической составляющей силового электрогидропривода, выполненного по традиционной схеме (7].
Глава Ю
работа ГИДРОПРИВОДА ИД «ползучих» СКОРОСТЯХ
§ 10.1. ОСОБЕННОСТИ РАБОТЫ ГИДРОПРИВОДА НА «ПОЛЗУЧИХ» СКОРОСТЯХ
При уменьшении подачи насоса переменной производительности, когда она окажется меньше некоторого критического значения, скорость гидромотора не сможет быть постоянной и ее колебания окажутся значительно большими тех, которые обусловливаются незначительными колебаниями характерного объема гидромотора w. Такие колебания скорости гидромотора обусловливаются существованием сопротивления, уменьшающегося с увеличением скорости дви-жения («отрицательного» сопротивления) |4], и являются автоколебаниями, т. е. генерируются самой системой, находящейся на границе устойчивости. Скорости гидромотора (или гидроцилиндра), при которых возможно возникновение автоколебаний, называются «ползучими».
Существуют две причины появления нелинейностей типа «отрицательное» сопротивление. Силы кулоновского трения, пропорциональные нагрузке и направленные в сторону, противоположную относительному движению, оказываются зависимыми от относительной скорости, а частная производная от силы сопротивления по этой скорости меньше нуля. Второй причиной, действие которой, однако, существенно меньше, являются отклонения сил вязкого трения от’закона Ньютона, о чем говорилось в гл. 4 применительно
к загущенным маслам.
Имея в виду вторую причину, следует считаться с тем, что автоколебательные процессы принципиально возможны и в систем х, в которых используется гидростатическая разгрузка 174| и Г/BJ, хотя весьма часто, например в направляющих тя* пежлеиИя гидростатические опоры применяются с целью р У Р возможности возникновения автоколебании.	пипятыьное»
Таким образом, нелинейное сопротивление типа «ощательно® сопротивление — экспериментально установле	> nqq|fnM
щий место не только при кулоновом трении I , ичении ско_ трении, причем падение силы сопротивлен ₽ у с «омен’л рости относительного движения‘	так и с момента Дуст*-
возникновения относительного двиЖ® ’ пвижения. В после* женин определенной скорости относится . го сспрот»«ле»о<» нем случае закономерность изменения нелинейного сспр
имеет один экстремум пша максимум пли два экстремума: перпнй читая во направлению возрастания скорости относительного ДШ1.
L . я) - типа минимум, а второй - типа максимум.
Процесс автоколебаний гидропривода с разомкнутой схемой управления имеет тот же характер и описывается теми же уравнения, мн что и процесс колебания тока в цепи вольтовой дуги |4|
По мере уменьшения Q ио сравнению с его критическим зпачс-пнем (?, амплитуда колебания ы увеличивается, п если эти колебания близки к гармоническим, то частота колебании мало отличается от частоты собственных колебаний. При дальнейшем уменьшении колебаний становятся заметными влияния последующих гармоник, а увеличение амплитуды автоколебаний в конце концов приводит к периодическим остановкам гндродвигателя, т. е. к возникновению релаксационных колебаний при Q > Qu > Qi (861
Чем меньше значение коэффициента демпфирования гидропривода (чем больше добротность системы), т. е. чем ближе гидропривод к томсоновской системе, тем больше диапазон изменения Q, при котором автоколебания близки к гармоническим, и тем более точно они могут аппроксимироваться гармоническими колебаниями.
Нелинейное демпфирование системы типа «отрицательное» сопро-тнвденне не поддается расчету и должно определяться экспериментально. Поскольку такого рода сопротиаления в одинаковой степени существуют как для гидромоторов, так и гпдроцилиндров, то существуют принципиально одинаковые возможности возникновения автоколебаний как в гидроприводах вращательного движения, так и в гидроприводах возвратно-поступательного движения.
(Ю.1)
(Ю.2) и и = 1;
f 1(1.2. .'РАВНЕНИЯ СВЯЗИ ПРИ НАЛИЧИИ НЕЛИНЕЙНОГО ДЕМПФИРОВАНИЯ
Уравнения расхода и нагрузки с учетом демпфирующих свойств гидродвигателя в случае, если он является гидромотором, при зада-ном постоянном значении параметра управления будут 176]:
uQx = око + tw2p +
Mr = pw = Mu + f + epw + Сш + J ш, где Qx — подача насоса при отсутствии нагрузки w — характерный объем гидромотора;
т =	— параметр герметичности;
Q,. — утечки;
р перепад давления на гидромоторе;
Ми — момент статической нагрузки;
f момент нелинейного сопротивления;
с нКа°*ЦИеНТ ДемпФиРованИя> пропорционального
236
С — коэффициент активного сопротивления-
.1 — приведенный момент инерции нагрузки’и вращаю шнхся частей гидромотора.
Теми же уравнениями можно пользоваться в случае, когда ищродвигателем будет гидроцилнидр, если w заменить на Г — активную площадь Iидроцилиндра, w — на и — скорость поршня /П„ па Ро — усилие статической нагрузки и У — на т — приведению массу нагрузки вместе с поступательно-двнжущимися частями , идроцилиндра. В этом случае f будет являться нелинейным сопротивлением движению, имея размерность усилия.
Дифференциальное уравнение движения гидродвигателя получается исключением р из уравнений (10.1) и (10.2):
тд|. ,	. тУ-J-OC . . ОУ » . ту
+ Г-f + тс'” + 1 - с фтС<0 + I - с фтС
,	&	- « 0*0-0
’ 1 — е ф тС w (1 — с 4- тС)'
Ф
(10.3)
При у = 0, й = 0 и f = 0 скорость движения Д<о (статическая ошибка) определяется равенством
Ди =
тМ0
1 - С + тС
(Ю.4)
Тогда, пользуясь понятием приведенной скорости
о„ = со — Дсо,	(10.5)
можно уравнение (10.3) переписать в безразмерной форме 1801 ю + (2?+Уг)3 + ^Г + /==и’	(10.6)
\ тГ </ы/ dt dt1
где
Q„W (1 — С фТС) (!-<№
ОУ
— е ф тС ’
________f t = —
(l-С) Qxf> Т’
(Ю.7)
Выяснение условий, при которых возможно устойчивое движение на заданном значении и при и = 0 и со=0, целесообразно проводить при помощи безразмерных скорости у и нелинейного сопротивления Ф, под которыми понимаются выражения
„ _ и. _ со„м>(1 — сфтС) . ф _ 7 _	г
у—и~ uQx(\-c) ' и и<?х(1-е)'-использование которых в
/ д d<t>\ dy У +	+ iTlfr) dt
(10.8) уравнении (10.6) придает ему форму ^ + Ф-1. (Ю-W
Ф статического режима работы (при обра-Координаты р, и о отвыходнОй координаты у) проще всего “pXS" точюЛ ктрм”А ’а”"с"	1 ~11"ф
ренесем нач^°=к^р^ дф тО1-даУравенство (10 9) превращается в
У У" /1 i 4-/2С 4 — —+-^ =°, (’ + rf+( ТГ Л/Л Л' а при его линеаризации переходом к началу координат, т. е в случае г -► 0
rfz + £2 = 0.	(10.10)
dt df>	'
Для того чтобы движение было устойчивым, необходимо в соответствии с критериями Гурвипа одновременное удовлетворение двух условий
| >о; о
(10.11)
0.
'о '
Удовлетворение первого условия обеспечивает устойчивость, а второго — свидетельствует о достаточности коэффициента демпфирования С Для гашения колебательных процессов в положении статического равновесия при отсутствии внешних возмущений.
В дальнейшем подлежит исследованию случай удовлетворения условия (10.11) при нарушении условия (10.12), когда при отсутствии внешних возмущений могут возникнуть колебательные движения системы.
Указанные условия движения могут возникнуть только при определенных сочетаниях параметров рассматриваемой системы, определяемых наклоном касательной к кривой, изображающей — Ф 0/)> в точке, определяющей возможный в некоторых условиях режим работы с t/ = 0. На рис 10.1 эта точка обозначена птТош/’ а На рис ^‘2 30111,1 областей различных видов я разделены радиусами 0kt и Ok2 с изображением четырех шкал измерения А, В, и №-\ с -
ПеР/В/ф\И третья и,калы определяются
НИем \ Л) •т- е- углом ф = arctg \ ной, а вторая и четвертая — г---*
j У Ф наклона касательной будет размещаться в области расходящимся, если в области
fi = 2t +
(10.12)
статическую
в пределах от —оо до 4°о.
—I только числовым значе-наклона указанной касатель-зависят от параметров гидропривода.
«-«-vu 1 v*41»nu
Ф« в 2 п) ~ Движение будет
R» и <Р>Фл~ arctg^^, где	(т е в = 0) -
двпжение будет устойчивым. Если же касательная размещается в
то возможно возникновение авто-
колебаний, подлежащих исследованию. Следовательно чем мпШ демпфирующие свойства гид-	’	е
ропривода тем больше область R2, положение нижней границы которой определяется критерием
,z _ lrif\ _'J
>-У
1-и
областей не-
Рис. 10.2. устойчивых
Положение _______
устоичиоил движений (/?>>. неустойчивых в малом (Rs) и устойчивых (/?») в зависнмостн от <р = arctg I I и значений параметров гидропривода
(10.13)
4-arct^L
1	\

Рис. 10.1. Определение статического условия работы гидропривода при помощи графического решения безразмерного уравнения
Следовательно, необходимым условием возникновения автоколебаний является наличие падающей закономерности изменяют нелинейного сопротивления.
§ 10.3. ОПРЕДЕЛЕНИЕ ЗНАЧЕНИЙ НЕЛИНЕЙНОГО ДЕМПФИРОВАНИЯ ГИДРОДВИГАТЕЛЯ
Обычно приводимые материалы по характеристическим алЛ-ствам гидродвигателей не содержат числовых «качений нетям* кого демпфирования и требуют проведения расчетов.
В случае, когда нелинейное демпфирование значмнмшмйр Ml показывают соответствующими отклонениями изобар (аимй1. ввв> . *•
ветствующпх постоянным перепадам давления в гидромоторе) от прямых изображающих развиваемый момент (на статическом режиме работы) на топографических характеристиках (см. рис. 7.4),
Из-за трудностей проведения точных экспериментов изобары часто показываются в виде экстраполирующих прямых (см рис. 7.1), т. е. неточно в области малых значений скоростей. В этом случае использование экстраполированных линий равных к. п. д. оказывается достаточным для определения f.
Демпфирующие свойства гидродвигателя при отсутствии нелинейного демпфирования (для режима с наибольшим значением к. п. д. ц = т)*) оцениваются тремя коэффициентами потерь с, CpnCt (C„ и С,,—коэффициенты вязкого трения и утечек соответственно), один из возможных способов определения которых приведен в работе [76]. причем к. п. д.
где индекс л указывает на отсутствие нелинейного демпфирования (/ = О, линеаризированная система) ио =	— критерий изого-
нальное™, характеризующий режим работы гидромашины.
При существовании нелинейного демпфирования к. п. д. уменьшится, причем
I — с — Сос ——
4 =-------------— <ПЛ-	(Ю.15)
1 + |сх
(10.16)
я характеристика гидромотора d л0 нанесена изобара для задан-р — const, т. е. зависимость
Вычитая уравнение (10.14) из уравнения (10.15), можно получить выражение, позволяющее вычислять значение f при помощи топографической характеристики гидромотора
f = ®р(1 +	—т])-
Пусть задана топографическая (рис. 10.3, с), на которой прямой АА ного значения перепада давления	. --------— —
свободного момента от скорости в соответствии с равенством (10.2):
M — pw(i—с) —110,10(15.	(10.17)
Прямолинейность изобары свидетельствует о том, что влияние f на малых скоростях не учитывалось. Тангенс угла наклона изобары определяется отношением по определению коэффициента вязкого трения. Допуская, что линии равных к. п. д. (т|*, т/> ’Г'...)• показанные пунктиром на рис. 10, а, достоверны, при-
ведем корректировку изобары в области малых скоростей для любого 240
выбранного значения скорости от = 0D Тогда
для соответствующей точки А значение п ги-unon П° топогРамме отрезка ОВ на рис. 10.3, б и
вертикалью ССС). Используя равенство НО in°C (показано OF^f. и строим кривую f = FE для ряда точек » каждой из которых соответствует точка из числа F F' F" ’ лежащая на соответствующей одной горизонтали ’	’ ’ ...
Очевидно, искомое значение f, определяющее необходимое onvc какие соответствующего участка изобары, определяется точкой полученные значения нелинейного демпфирования нелинейным сопротивлением нагрузки, можно опре-
встречи биссектрисы OF'" угла COO'" с кривой FE Складывая --------------
гидромотора с
Рис. 10.3. Уточнение положения изобары в области «ползучих» скоростей
делить зависимость Ф = Ф (у), изображенную на рис. 10.1 и входящую в основное расчетное уравнение (10.9), при помощи которого ведется анализ исследуемого движения.
Оказывается, что при иных «уровнях» давления, т. е. для изобар с иными значениями перепада давления (например, рв на рис. 10.3, а) значение / будет иным, поскольку f = / (to, р):
(10.18) dt да ' др da'
Если при возникновении периодических движений системы окажется что	, т. е. если локальная и субстанциональная
’ др da da'	,df
производные в равенстве могут считаться одинаковыми то такие колебательные движения называются малыми и подлежат
обследованию.	____ „ иапинРй-
Поскольку нелинейное демпфирование в гидром р	из
ное сопротивление нагрузки складываются, ка	соцро-
равенства (10.2), то в дальнейшем будем Раа“^ривРМп<Ьн"овании тивление нагрузки в виде составляющей гидродвигателя, соответственно исправляя з	«•
Я*1
Периодические движения с большими амплитудами колебания давления являются предметом отдельного рассмотрения, а мерой малости автоколебаний должна слу жить амплитуда колебания давления в системе, определяющая, motjt или нет локальная и субстанциональная производные в равенстве (10.18) считаться одннако-<1/	м / „	"Р	e‘f\
выми. Если можно принять^«к। пли riw 1/(л , то нелинейное демпфирование может рассматриваться в качестве функции только ю Поэтом\ решение задачи об автоколебаниях должно сопровождаться выяснением значений колеблющегося давления, которые сравниваются с положением кривых, изображающих зависимости f — / (<о) или Ф = Ф (<->) для разных значений «уровней» давления, т е перепадов давления, соответствующих статическим режимам работы и определяемым положениями точек Л, В, С,.... на рис. 10.1. Каждой из этих кривых соответствует своя изобара на рис, 10.3, а.
$ 10.4. ПРИБЛИЖЕННОЕ РЕШЕНИЕ НЕЛИНЕЙНОГО ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ
Имея в виду, что линейная часть системы обладает свойствами фильтра низкой частоты, и предполагая линейность обратной связи (утечки и сжимаемость), можно считать возможным применение метода гармонической линеаризации в рассматриваемой форме, поскольку исследоваться будут только малые автоколебания 161] и 182].
Метод гармонической линеаризации с равным правом можно применять к дифференциальному уравнению, записанному в безразмерной форме (10.6) и в размерной форме (10.3). Однако в первом случае придется проводить пересчет экспериментально определяемого графика f = / (<о) в i рафик Ф = Ф (у), который будет иметь разные масштабы при изменении параметра регулирования, а также сдвигаемую ось абсцисс в соответствии со значением статической нагрузки. Поэтому целесообразно применять метод гармонической линеаризации к уравнению (10.3).
Приняв все указанные выше допущения, линеаризуем функцию
f = wqB + wqt(1>a,	(10.19)
где in
<7о = 2^,	+ A sin u) du;	(10.20)
<1
1 anw
ы — ‘"о- + ыв — u>u ф ц sinu = ш0 ф a sin	(10.22)
242
«я
f (% + a sin и) sin и du\	(10.21)

причем йо — постоянная часть решения m
решения, Q„ и а - частота и амплитуда пев^и^РеМенная "асть
соответственно.	у еРеменнои части решения
Использование уравнений (10.19) — НП 9-л
нении (Ю.З) позволяет записать его в форме В исходном УРав-
С + W<71
а/ ..
tn
С + W91
j т (,Мо + w?o> + (> — с + тС) <>» _ »<Z
1 — С	W
(10.23)
поскольку <п = <п„ и w = «>„.
В рассматриваемой системе возможен статический режим работы ----- *	' )а = 0). Полагая в равенстве (10.22) wo = 0, получим выражение постоянной части искомого
(m = const, чему соответствует to
<1'я = «'а решения
„   0 —с) uQx	г (Л10 -р «0|	. „ „.
° w(l—с-ртС)	1— r-prC '	(10.24)
Однако этот режим может оказаться неустойчивым. Для суждения об устойчивости подставим найденное выражение ы0 в дифференциальное уравнение (10.23) и получим однородное дифференциальное уравнение для переменной составляющей скорости
11
с + т (С 4- ш91)) ыа = 0.
(10.25)
Периодическое решение должно соответствовать движению на границе устойчивости, что соответствует прохождению кривой Михайлова (годограф характеристического уравнения) через начало координат и означает обращение в нуль показателя экспоненты затухания линеаризированного уравнения, т. е.
тУ
Wi = — о — С-
(10.26)
1
а частота автоколебаний
(10.27)
значение которой будет вещественным при (Т^ГР 1
инерции
выражение критерия упругости О (83], а также момента поскольку выр^йются выражениями.
е.Л.Л;	(10 29)
V ии,2 ИИ' / К»

(10.30)
1/_ объем жидкости в соединительной магн-где	v стралн А я» 2 — коэффициент, учитываю-
щий приведенный моментинерции нагрузки, ,	/• га юкоэффициент момента инерции вращаю-
J = (1	°'	щнхся деталей гидродвпгателя;
_ коэффициент поперечного сечения маги-1	стр ал ей;
/	— площадь поперечного сечения магистралей;
/	— длина напорной магистрали;
к _ приведенное значение адиабатического модуля объемной упругости рабочей жидкости. Следовательно, увеличением утечек можно устранить автоколебания, если они возможны, и снизить нижнюю границу устойчивых скоростей.
§ 10.5. ГРАФО-АНАЛИТИЧЕГ.КПП СПОСОБ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ АВТОКОЛЕБАНИИ
Поскольку при автоколебаниях скорость состоит из двух составляющих: постоянной ш0 и переменной то существование квази-гармонического колебания составляющей <оа означает существование квазигармоннческого колебания давления, также состоящего из двух составляющих: постоянной р0, к которой относится ранее использованный термин — «уровень» давления и переменной составляющей ра, подлежащей в дальнейшем выяснению. Очевидно, постоянная составляющая р0 определяет характер изменения нелинейного демпфирования f = / (р0, ш).
Поскольку значение нулевого коэффициента гармонической пИглгпоЗЭЦИИ еще Не опРеДелено> то пока можно говорить только сованных значениях <о0 и рв, определяемых равенствами uQr
w’ = -V~Wo;	(Ю.31)
Л10 + wqB + С
wp° =—ггг+гс™-.	(10.32)
(. • ), а второе — из равенства (10.2) после
подстановки в него уравнений (10.31) „ (Ю 19) при условии ,, -т е Ма = °- а значит, и> - о	~
' ЗМ1К»«™ ». « M. + w,. от р.	1м рм ,04
W	w*(1-c + tC).
причем ОВ > ОТ], позволяющие получить для любого выбван кого значения р0 OG согласованные значения со ~ он МП + “?<> = °'К	°
Поскольку wgn>0, то автоколебания при С > 0 и
CuQ"x га2 (I — с -|- тС)
Рис. 10.4. Согласованные значения и Л10 + ПРИ заданном уровне давления р0

возможны лишь при отрицательной статической нагрузке Л^.
Задаваясь любым произвольным * значением р0 и находя соответственные согласованные значения Мо + wq0 и ш0 (рис 10.4), можно графическим интегрированием найти амплитуды предполагаемых автоколебаний а0 и alt обеспечивая необходимые значения wq0 и wqy соответственно, как показано на рис. 10,5. Индекс при обозначении амплитуды показывает, какому значению из двух коэффициентов q0 или гармонической линеаризации удовлетворяет полученное значение амплитуды автоколебаний а0 или О].
Строя f = / (to) (кривая ЕС на рис. 10.5) и о) = to (и) для какого-либо значения амплитуды а0 (кривая SFZ на горизонтали ОА = 0'S
значений и = (УС откладывают величину fn = CH = DE =
— too), для каждого из ряда
где СВ принято за единицу измерения нелинейного члена.
Тогда площадь под кривой KHL, обозначаемая через г0, поз ляет найти выражение • которое в соответствии с уравнением (10.20) должно удовлетворять условию
1 f ; /„ fo G du~^.	(10 331
<h = 2^ V du	J tn M 21tv>
о	°
М3
. р „с удовлетворяет этому условию,
Если полученное значи	значение а„ имея в виду,
то необходимо соответстве
что увеличение а0 уменьшает Fo, и наоборот (штрих-пунктирная н пунктирная линии соответственно на рис. 10.5).
Для кривая
нахождения амплитуды at строится на том же рис. 10J5 O'TPRN, ординаты
Рис 10.6. Зависимость значений подсчитываемых амплитуд колебания скорости от постоянной части решения
(10.34), могут оказаться
которой GT = DE • MF. Площадь Ft этой подкривой (с учетом правила знаков) должна удовлетворять условию
2л
1	(’ Г	J
о. =----- I f sin и du =
0
2л
_ _/о_
а,лш J	а1лто
о
= -.TJ-—,	(10.34)
VW w ’

для чею проверяется ряд значений at.
Полученные два значения а„ и аи удовлетворяющие условиям (10.33) и о невепнл BuiAno_ не одннаковыми, что свидетельствует
логичный подсчет повторяется ^авления р<> <или поэтому ана-ряется для ряда значений р0 с изображено
„нем получаемых при этом величин an=oc(<o0) и а, = а, (<«„), как оказано на рис. 10.6. Очевидно, точка встречи этих кривых, обеспе-
п°2а10щая равенство оп аг = а, дает значение wn, а значит и «уро-Ч1'нь» давления рп и необходимое значение М0-фwqn в соответствии °е 1С Ю 4 Возможны несколько точек встречи кривых а0 == а0 (<п0) с Р* Oj (<,)0), что означает существование нескольких предельных И 11 лов. определяемых формами экспериментально получаемых зависимостей f = f (ра. «).
§ 10.fi. ПРОВЕРКА УСТОЙЧИВОСТИ ДВИЖЕНИЯ
Для проверки устойчивости анализируемого периодического Тения необходимо определение зависимости qx = qA (а).
^Известно, что система находится на границе устойчивости, если годо1раф характеристического уравнения 1821
T(s) =
+ т (С + «ч,) + Ы (ф +	» + «s’ = 0. года
переменная Лапласа, проходит через начало коорди-н	--------- существование равенств
= 1 —С
HaVlnMCHHO это условие и определяет /10 24) и (10.25)1.
' Известно что рассматриваемое движение находится на границе устойчивости если годограф характеристического уравнения удовлетворяет Двум требова	личении амплитуды о на
малую положительную ®™ч“Хт “ва« погваф полинома Г (s) — и * ” начало координат и движение устойчива
2. При уменьшении амп^итУга же малую величину Да годограф того же полинома Т (s) = 0 не	|Ьн
координат и движение веУ	означает
полнение первого требов	ен11
Г
Рис Ю 7. Зависимость величины первого коэффициента гармонической линеаризации от амплитуды автоколебаний
существование отрицательной вадастя „идаветше
7(S) = O ил»	“ТГ
второго требования су	мИ условия -§- +
„ой час™ корней УР»в«=™«	оим„«ют«.
, С + w (<д - Д'/iL 0. Очевидно, оба треи т~ J если удовлетворяется условие да
о,
мт
„оамом случае параметры т, ft, J и С положи, поскольку в Рассм\Т,;Хматр||васмоГО случая постоянны гельвы, II ПРНТО".А™НЫМ11 значениями ыр и pt, можно приемами, Пользуясь найден шыли	заВ|1С11М0СТИ первого коэффцццента
показанными на pncjiw	, от амплнтудь| автоколебаний
гармонической niiHeapi (() 7) н уСтан0В|1ТЬ справедливость в подавляющем большинстве случаев для
ХХЙ>““"е сМУ’юд"етс”'
§ 10.7. ОЦЕНКА ВАРИАЦИИ ДАВЛЕНИЯ
Рассмотренный приближенный расчет автоколебаний нуждается в оценке вариаций давления р„ относительно р„, поскольку при чрезмерно больших отклонениях р„ от р0 нелинейная функция / не может рассматриваться зависимой только от выходной координаты ы (субстанциональная производная будет отличаться от локальной и условиебудет нарушено), автоколебания будут большими. отличаясь величиной амплитуды и формой колебаний.
Подставив в равенство (10.2) условия р = рп -|- ра< и _ =	+ <л„, f = wqn + шдрла, а также имея в виду уравнение (10.26),
можно получить
(I — С) = - -у сод + J wo,	(10.37)
поскольку
шр0(1 -c) = A40 + tcg0 + C(oc (при ра = <о„ = 0).
Принимая закономерности изменения ра и <но от времени моно-гармоническимн и рассматривая равенство (10.37) применительно к амплитудам pi, и ш'а в качестве векторного равенства, можно записать очевидное соотношение
₽-infer fev) (|О-38) или выражение амплитуды колебания давления через динамический коэффициент цо |771:
’-«infers.	(10.39)

(10.40)
Pd= J/ 1
Правомерность обращения к использованному способу количественной оценки амплитуды колебания давления р'а, обычно применяемой при оценке установившихся вынужденных колебаний, является следствием того, что и при оценке малости автоколебаний 248
И при проведении противокавитационипт н
сЯВ11га фаз не требуется. Однако в случае нужд^Т опРеделе„11Я дяек’Я по известным каноническим правиламГ фаз °"Реде-
(10.38).	Ри помощи равен-
В отличие от амплитуды автоколебаний а и постоянной части скорости <ii0, которые могут иметь различные значения, частота розможных автоколебаний определяется равенством (10.27) однозначно, и поэтому амплитуда переменной части давления будет _________________________________ /оЕй | г) n<h«)2 I
п	а । J
Р“	w V 0(1
0(1 -с)
/оГо
ЛЕ' о + J 1 W(l-c) ’
(10.41)
или через конструктивные параметры гидродвигателя, принимая например, в соответствии с работами 1811 и (83|
получим
= - ----------5-U«-0 ________________
/ЬС,,х|<w	цсТ\ . — -------- ’
nw —---------Ь-77— I к kf/J (1 — с)
\ llk/l у/ 111
Обращаясь к графику, изображенному на рис. 10.1, устанавливают, насколько может изменяться значение нелинейного демпфирования f = f (to, р0) при полученном значении статической скорости to to(l из-за квазигармонического колебания давления с амплитудой ра и насколько при этом будет справедливо условие dm dm ’
Кроме того, обязательно выясняется невозможность возникновения кавитационных явлений при помощи неравенства
Pti Ра^ Рь
где р, — упругость газовых составляющих и паров рабочей жидкости, имея в виду, что подпиточные клапаны системы могут не сработать при полученной частоте квазигармонических колебаний переменной составляющей давления ра.
S 10.8. ПРОВЕРКА ПРАВОМЕРНОСТИ ПРИМЕНЕНИЯ МЕТОДА ГАРМОНИЧЕСКОЙ ЛИНЕАРИЗАЦИИ
Известно, что применение метода гармонической линеаризации, Т- е. аппроксимация исследуемой системы некоторой линейной 111] и [61] справедлива либо при реализации гипотезы фильтра, либо при реализации гипотезы авторезонаиса.
249
, пмон схемы исследуемой системы, опи-
Нсполкзование стР\1'.а п „ ПО 2) как это следует из нзображе-сываемой уравнениями (КМ '	|(е „03ВОЛяет без структурных
ния приведенного на рис ' ’ ова1(||е фильтрующих свойств преобразовании замел _	просматривается»)
(говорят, структурная схе	№ва11ИЯ фильтрующих свойств
Аналитическая	нз уравнений (101) и (10.2) при
ццествляется "ск-пЮЧ"слСДуЮТся периодические решения при
асу— обращении Q в ННЬ постоянном подаче)
о)
(10.42)
А"1(1 + П -9 _ ф
т____и 7 — 19 —постоянная временифильт-
пашш системы' а коэффициент демпфирования Си постоянная времени гидропривода Т определялись ранее при помощи равенств ^Соотношения Г, и Т выявляются из равенств (10.10) и (10.12), из которых следует возможность существования автоколебании при удовлетворении неравенства
К,-21Т'е =
Следовательно, при анализе автоколебаний соотношение постоянных времени Т и 7\ определяется неравенством
Г , 1
Г, 2Г
обычно соответствующим Т > Т} для дистанционного гидропривода, составленного из высококачественных гидромашин (томсоновская система), а для гидропривода нераздельного исполнения с недостаточно высокими значениями объемного к. п. д. Т < Т\.
Правая часть равенства (10.42), будучи линейной, описывает фильтрующие свойства исследуемой системы. Ее логарифмические амплитудно-частотные характеристики показаны на рис. 10.9 В случае Т> 7\, когда £ мало (большой и острый «всплеск», показанный пунктиром на рис. 10.9, а для томсоновской системы), одновременно И гипотеза фильтра и гипотеза авторезонанса, что тельствует о достоверности аппроксимации системы при помощи некоторой консервативной системы, имея в виду, что составляется' К°‘Да ГИДРОПРИВ°Д нераздельного исполнения К. п. д. резонансный'и-МаШИН С невысоквм значением объемного ром, невелик и	П0к?занный на рис. 10.9., б пункти-
Ф рующие свойства могут оказаться иедоста-250
T0 ТСЯ решение методом гармонической линеаризации, окажется ЛЫПеЙ R TriV rnvunax КПГПЯ Т -- I Т- ТТПП\7ГТЧЛ*ГГУ u^hahi/mwm.
ине г’*~ п0сравнению
ымп несмотря на то, что первая гармоника, по которой и про-
-.-.j В тех случаях, когда Т | Г], допустимо использова-метода гармонической линеаризации, однако, чем меньше Т с I Г,, гем более существенными окажутся последующие гармоники и тогда следует прибегать к асимптотическим методам решения нелинейного уравнения, описывающего автоколебания.
Рис 10.8.
12 ". Структурная схема исследуемой системы
Рнс 10.9. Логарифмические амплитудно-частотные характеристики фильтрующих свойств гидропривода, работающего при постоянном входном сигнале
Меж,» — ™ ™'"Sr структурного анализа блок сх . вненИЯМи (10.1) и •) описываемый дифференциальными^	ш (т + М а
На этой структурной схеме W'i — Ю(1 — с)’
/По+Л^Ь-
оператор нелинейного члена <•)« янИЯ линейных one Применяя обычные	“’10.8,6.
раторов, как последовательно пока^ано^ св0Йства линейной час™ и 10.8, г, можно определить фил^^чн0Й функции, совпадают исследуемой системы в виде пр .
с ранее полученным выражен ( •
<S «0.9. ОБЩИЕ ЗАКОНОМЕРНОСТИ ГИДРОПРИВОДА ПРИ НЕЛИНЕЙНОМ ДЕМПФИРОВАНИИ В ГИД РОД В 111 АТЕЛЕ
И ЖЕСТКО ПРИСОЕДИНЕННОЙ К НЕМУ НАГРУЗКЕ
Решение задач об автоколебаниях гидропривода в коиечн счете сводится к решению системы уравнений	ом
— со 4- ти'р -f-pw = / + Ссо 4 ./<;>,
(10.43)
где л _	_ скорость холостого хода, а / включает статическую
нагрузку и демпфирование, пропорциональное р, а значит, и куло-ново трение. В етих уравнениях три переменных: командный сигнал и, выходная координата со и функциональная координата р. Исключая р, получают разрешающее уравнение, в котором только одна переменная со, поскольку решаются задачи применительно к случаю и — const. На самом деле в этой системе в скрытой форме содержится еще одна координата — возмущающее воздействие М, действие которого обычно определяют при и = 0. Так, если / = = М + cpw, то разрешающее уравнение в изображениях будет
i \	(1 — с) <о,.	, ,
•"(s)- |i_f + (T + fisHC + ys)i“(s) —
IT + 0.4	. . . .
|l — С + (T + fts) (С4-/s)|	(10.44)
Использование последнего равенства, к которому всегда обращаются при анализе автоколебаний, правомерно только тогда, когда со =/= 0. При переходе значения си через нуль полученное при помощи равенства (10.44) решение перестает быть точным, и к нему можно обращаться только тогда, когда время А/ остановки в процессе периодических движений много меньше периода Т„ этих движений.
В момент остановки гидродвигателя решение должно быть получено из системы (10.43) путем исключения выходной координаты ш:
Р О ~ W11 - < 4-Тт 4-	(С +7s7jи	+
+ W [I - С 4- (т 4- 0s) (С 4- Js)JМ	(10.45)
Последнее равенство также ограниченно справедливо, и к нему следует обращаться только при р Ф 0. Следовательно, точное решение должно получаться «склеиванием» двух решений, получаемых из равенства (10.44) и (10.45), к которому следует обращаться при использовании вычислительных машин.
Можно пользоваться приближенным решением уравнения (10.44) тогда, когда соблюдается неравенство
^тах < Тп,
(10.46)

где А/n.ax наибольшее время остановки гпк.
„ прохождении оз через нуль. При Hanvi?6cTDeHHo™ движения периодические движения подучаютсР п^^У'нении условия (Я применение вычислительных машин по™Е?°НИческим”. и ЗД затруднения, го обращаются к числений "ричинам вы3ь1вает (10.45) методом гармонической линеаризации с тре,иению Уравнения гармоники, принимая /И =/.	Ни и с точностью до третьей
Можно показать, что при соблюдении неравенств
~ 2с J ш 2С происходит остановка гидродвигателя и во впемя пад давления меняется в пределах время остановки пере-
W \ w ,	(10.48)
причем выход значения р за пределы .
водит к возобновлению движения	Х неРавенств при-
Во время остановки гидродвигателя происходит изменение дав-ления, которое на фазовой плоскости р - р в безразмерных координатах описывается уравнением	и *«юрди
Р = (и~“Р)(1 +₽|р| + р').
где
(10.49)
7,— dp т — “’i‘°ixoc t л w
P~~dT'	Р=сР<
а = —w—;	Р = ——; и = А (| р | + рп) + х0;
(DlWj	Г X0W	М К 1 * Н,У ‘ °’
Д
рг = — рп и рп — давление подпитки. хо
Следовательно, фазовая траектория гидропривода с разомкнутой схемой управления, который является четырехполюсником, изображается на двух листах фазовой плоскости, причем в момент остановки гидродвигателя изображающая точки переходит на лист р — р.
Можно показать, что наибольшее возможное время остановки гидропривода определяется выражением
л/	2U 
Д^тах ---------л
uwu>xA
(10.50)
Поскольку —-	1, то пользуясь первым членом ряда In (1 -НО—
СО
_ у (- !)
получим
получение малых скоростей дви-
Поэтому падение	командного сигнала и увеличение
уменьшении значс ни»	ГВСЛИЧнть наибольшее воз-
Хема жидкости Г могут суш^беино для гидроприводов с ма-можное время остановки	вадеНие значения х„ имеет место
,пым значением w.	рабочей жидкости газовой фазой,
при уменьшении р и "^ебаниях определяется выражением
Значение /я ПРИ	-----—---------
£ ^Т„ = 2л |' nrr+T(C+wJ’
Значение
а поскольку
то
w — с
®<7i = ~	’
2л гг _
fi, - "
или, имея в виду, что О нить более сильным неравенством
Л
с~^ . /^7 fl
2nfi
J -t!
можно неравенство ()0.46) заме-wax0 ’
(10.52)

Очевидно, что при несоблюдении последнего неравенства, общепринятое описание кулонова трения при помощи характеристики репейного типа перестает быть корректным нз-за конечного времени остановки. Однако несмотря на то, что кулоново трение не может вызвать автоколебаний, значение коэффициента этого трения определяет форму колебаний, которые при увеличении значения с перестают быть моногармоническими.
Хотя амплитуда автоколебаний гидропривода с незамкнутой схемой управления зависит от постоянной части периодического решения, частота автоколебаний не зависит от этой скорости и определяется только параметрами привода. Это не случайность Аналогичным свойством обладает также и гидропривод с жесткой отрицательной обратной связью, описываемый уравнениями
ишх = 6 -р пар + (tep;
wp = C6 + jfi-p М + /; и = Кхх - Ко6,
(10.53)
где х — входная координата;
6 — выходная координата (6 = ш);
ной связи соотХ1:таенноИТМожиоаМЯЮЩеГО УстРойства и обРат'
М = const =/= 0 автоколебания показать- что при х = const и «ютоколебания невозможны, а при х = cxt, где
254
cv = const, а / — время, при достаточном значении «отрицательного» сопротивления возникают автоколебания с частотой
= |/гет [1 - Т + К(1 - 7	• (10-54)
если верный коэффициент i армонической линеаризации достигает значения
' L-L[-т^+4*го]+
+ И О 7У+4т<^Л0}.	(10.55)
Можно еще более обобщить решаемую задачу. Пусть гидропривод, снабженный механизмом управления, электромеханическим преобразователем и корректирующими устройствами, обладает нелинейностью типа «отрицательного» сопротивления в гидродвигателе и жестко соединенной с ним нагрузке. Предположим, что неравенство (10.52) удовлетворяется, а любое изменение выходной координаты а2 приводит к изменению возмущающего момента, а значит, может при соблюдении определенных условий служить причинен возникновения автоколебания. Тогда в изображениях выходная координата а2 (s) определяется равенством
а2 (s) = Фа (s) a, (S) + Ф.„ (s) М (s),	(10.56)
где Фа (s) = при М = 0 и ФЛ1 (s) = при аг = 0.
Равенство (10.56) при достаточности фильтрующих свойств системы приводится к характеристическому уравнению
1 + sO,M (s) q (а, йа) = 0,	(10.57)
где q (a, Q,,) — первый коэффициент гармонической линеаризации, действи гельное число, значение которого зависит от амплитуды автоколебаний и скорости <оо.
Годограф линейной части системы на плоскости комплексного переменного представляет собой некоторую кривую, которая для разомкнутою гидропривода начинается с действительной осина правой полуплоскости и при й -> оо приходит в начало координат. В случае астатизма первого порядка годограф начинается в начале координат и образует замкнутую кривую, а в случае астатизма второго порядка при аналогичной конфигурации имеет выпуклую часть в левой полуплоскости.
При (п0 = 0 годограф нелинейной части (кулоново трение и «отрицательное» сопротивление) размещается на действительной оси в левой полуплоскости и имеет точку встречи с годографом линейной части только в случае астатизма второго порядка. Очевидно, что точка встречи определяется выражением Фл (?)> т. е. от
Ж5
. « части не зависит. Такой точке встрече параметров нелннейнои	,e. весьма низкочастотные авто-
соотвстствхют мало исслсд
колебания.	ЦРпнненной части расслаивается, причем сос-
При о>о=/=0 годограф  размешается на действительной оси в ле-тавляюшаяьулоноватр^ 1ая начала координат, а составляющая вон полуплоскости, нс "	_ на действительной оси в правой
«отрицательного» сопр	)|ачала координат. В этом случае
полуплоскости, также .	ются точкой встречи годографа
параметры -™ых чнеел^правой полуплоскости, если в эТу с осью дй'с™,т^  п годограф «отрицательного» сопротивления. Координаты такой точки определяются только параметрами линей-ной части пр.вода и не зависят ни от параметров нелинейной части.
от Рачения £. Именно в этом смысле следует понимать утверж-Рние о том, что автоколебания происходят на собственных часто-ТаХНа'СсТаСмом деле явление усложняется тем, что рассматриваемая нелинейность есть функция и скорости, и нагрузки f (го, р) или, что то же самое, / (ы, <о). Само значение нелинейного сопротивления зависит от со и обязательно имеется петля гистерезиса (зависимость от знака й). При увеличении скорости от нулевого значения сухое трение заменяется полусухим, а затем переходит в жидкостное с проявлением гидродинамического эффекта. Однако при уменьшении скорости гидродинамические эффекты сохраняются, обладая своеобразна'! инерцией, и /п при ыо = ч>ь не равно fb, если и>аы1: О В этом случае нелинейный член в равенстве (10.57) q (а, й„) будет уже не действительным числом, а комплексным и соответствующая точка встречи с годографом системы уже не будет совпадать с осью действительных чисел. Тогда нельзя говорить о том, что автоколебания происходят на собственных частотах системы.
Существование петли гистерезиса в «отрицательном» сопротивлении разными исследователями подтверждено экспериментально и затрудняет проведение точных расчетов из-за недостаточной повторяемости численных значений / (ш, ш).
Г лава 11
АНАЛИЗ И РХСЧЕТ ЭЛЕКТРОГНДРАВЛПЧЕСКИХ МЕХАНИЗМОВ УПРАВЛЕНИЯ НАСОСАМИ ПЕРЕМЕННОЙ ПРОИЗВОДИТЕЛЬНОСТИ
§ II 1 ОСНОВНЫЕ СХЕМЫ II КОНСТРУКЦИИ МЕХАНИЗМОВ УПРАВЛЕНИЯ
В системе управления насосом переменной производительности (рис. 11.1) сшнал рассогласования, усиленный электронным усилителем (пли усилителем другого типа), поступает на вход механизма управления насосом. В механизме управления электрический сигнал в зависимости од его величины и полярности преобразуется
5	6	7 в	9
Рис. 11.1. Принципиальная схема электрогпдравлической следящей системы с гидроприводом машинного регулирования:
/ — приводной электродвигатель; 2 — насос переменной производительности; 3 — механизм управления насосом; 4 — гидродвигатель; 5 — усиди 1ель; 6 — принимающий тахогенератор; 7 — сельсин-приемиик; 8 — силовой редуктор; 9 — задающее устройство; 10 — дающий тахогенератор;
II — сельсин датчик: 12 — нагрузка
в положение или скорость перемещения люльки (обоймы, чашки) насоса. Тем самым осуществляется бесступенчатое регулирование скорости вращения вала гпдродвнгателя и связанной с ним нагрузки.
Механизм управления насосом обычно состоит из электромеханического преобразователя и гидроусилителя; в случае использовании электромеханического преобразователя достаточной мощности нали чие гидроусилителя не обязательно.
В качестве электромеханических преобразователей применяются электродвигатели небольшой мощности постоянного и перемен*»1-' тока или электромагниты поворотного и поступательною тяиип.
9 В. Н. Прокофьев и др.	№
1-.х-
Электродвигатели соединяются с регулирующим элементом гидро-vcimnen или тюльки насоса через зубчаты.. редуктор ) правляю-ши Гснгиал полается на входэлемродв...-.теле., малой мощности, пегулинующих положение люльки насоса с помощью гидроуенли-тепей от электронных, крист .ллическпх пли магнитных усилителей Лтя управления электродвигателями большой мощности, непосредственно перемещающими люльку насоса, применяются эпектромашннные пли тиратронные усилители.
Электромагниты обычно соединяются непосредственно с регу лирующим элементом iндроусилптеля и получают управляющий сигнал от электронных, кристаллических или магнитных усилителей.
В механизмах управления насосами используются как одно-так и двухкаскадные гидроусилители. Для управления люлькой насоса применяются почти исключительно золотниковые гидроу силн-телн. В качестве вспомогательного каскада усиления в двухкаскадных гидроусилителях наибольшее распространение получили устройства типа «сопло-заслонка». Питание гидроусилителей осуществляется от вспомогательною насоса, вал которого соединен зубчатой передачей с валом основною насоса переменной производительности.
В настоящее время получили широкое распространение два типа электро, идравлнческнх следящих систем, включающих в себя гидроприводы объемного регулирования: скоростные системы щ двумя интегрирующими звеньями), в которых величине и знаку рассогласования пропорционально ускорение вращения вала гидродвигателя, и позиционные системы (с одним интегрирующим звеном), в которых величине и знаку рассогласования пропорциональна скорость вращения нала гидродвигателя
Скоростные следящие системы, ошибки в которых зависят главным образом от ускорения вращения задающего вала, применяются Для управления объектами, основным режимом работы ко.о-рых является движение с постоянными скоростями и малыми ускорениями. Обладая структурной неустойчивостью, скоростные следящие системы требуют введения эффективных средств для стаби-u™UIH' ЧЙ< г,10сти’ в качестве стабилизирующего сигнала широко п_^етСЯ сигнаЛ’ пропорциональный скорости перемещения низы vnnan°Ca’ полУчаемь|й от тахогенератора, встроенного в механизм управления.
в оГновштмНл?,1^^ПадЯЩИе сис,емы> ошибки в которых зависят почти полней и ю /’ОС1И вращения задающего вала и могут быть тахоенепатопя компенсиРова|,ы с помощью си. пала дающею режимом котопыхР1НЛ1'1ЯЮТСЯ ДЛЯ УРавлеиия объектами, основным Прениями Г МСЯ ДВ"™е с Евшими скоростями и сма?рОив^гьЬв\ачест°ве^з^^а^ЪпМН^1 ° ре'УлиРования можно Рас’ вена с одной степенью ас.атизма, характер
зависимости между законом движения вада i идродвигателя ц ветчиной рассо1ласования на входе следящей системы определяется выбором принципиальной схемы механизма управления насосом
В скоростных следящих системах механизм управления имеет интегрирующее звено (электродвигатель или гидроуенлигель) не охваченное обратной связью по положению (рис. 11.2, а)
В позиционных следящих системах применяют четыре способа умепыиспия степени асгатизма.
Рис. 112 Струм урные схемы лкекгрогидравлическич _ле-дящих систем:
а — скоростного типа; б — позиционного типа v электрической обратной связью на усилитель; о — позиционного типа с механической обратной связью от j идродвигателя: г — позиционного типа с комбинированной обратной сршью; д — позиционного типа с внутренней механической обратной связью; 1 — сельсинная паре, 2 — усилитель; 3 — механизм управления насосом; 4 — гидропрн вод объемного регулирования
Первый способ заключается во введении электрической обратной связи но положению между люлькой насоса и усилителем (рис. 11.2, б). Этот способ сравнительно прост и получил достаточно широкое распространение, особенно в механизмах с электромагнитным управлением. Однако в этом случае необходимо введение в механизм управления электрического датчика углового положения люльки, а также суммирующего устройства в усилитель и дополнитель-ных связей между усилителем и механизмом управления, Значн ные углы поворота люльки (до ±30°) существенно затруд
»»
е-
р датчиков углового положения, которые наряд,,
схемы механизмов управления
Рис 11.3. Принципиальные схемы механизмов управления с электродвигателем без гидроусилителя: ратиол’свя^ью'на усилитель- "оло*еннк>: 6 - с электрической об ОТ гндродьигателн ? еЛ^’ в механ веской обратной свизью 1 — тахогенсватоо 2	КомбиниРованиой обратной связью;
СИН о6ратиойРсВязРи 4 -УпЛачк,г п-Щ?Й элекЛр0АВ'" атеЛЬ; 3 ~ “ль" насоса. 7 — валик ₽А 5 ~ диФФеРснциал; 6 — люлька валик обратной связи от гидроднигателя
обратной связи мржп ючается во введении жесткой механической ^АУ валом гидродвигателя и люлькой насоса
26и
(рис. 11-2. fl), в этом случае в механизм управления вводится дифференциал, алгебраически суммирующий углы поворота валов управляющего электродвигателя и гидродвигателя (рис. 11.4,6). Такой способ позиционирования весьма сложен и практически применяется только в тех случаях, когда гидродвигатель расположен в непосредственной близости к насосу.
Третий способ заключается в использовании комбинированной обратной связи, включающей жесткую механическую обратную связь между валом гидродвигателя и люлькой насоса, а также
Рис. 11.4. Принципиальные схемы механизмов управления с электродвигателем и однокаскадным гидроусилителем.
и _ без обратной связи по .положению;^
связью: 1 — тахогенератор^ 2 > Р	дифференциал; 6 — золотник:
сельсин обратион связи. J реДУ P.	Д V 8— рычажная система до
поёГвительмой^'обр'атно^ХзЙ ~а насоса; <0 - силовые гндро-
электрическую обратную связь по положению «ежДУ люлькой cMUKipu ice у к J	случае рассматриваемая система
способ позиционирования,включают в себя диффер
тоический датчик обратной связи (рис. • ,	D i. Стлан ней меха-
Последний способ основывается на введении у р	,(Ия
нической обратной связи в i идроу^“^зН„ея Следящей сш темы (пис 112 <91 Этот способ позиционирования ел д
приводит к некотором} усложнению	<М*
(пис. 11.5, в), однако позволяет исключить электри*	jj)|M
углового положения люльки, что сущесгвенн у •
управления в целом и электронный усилитель, а также повьш надежность и долговечность этих устройств.	,ает
Необходимо отметить, что в механизмах управления с маломо ным электродвигателем и гидроусилителем все эти методы по нноннрованпя рассматриваются применительно только к элект-3'1 двигателю. В механизмах такого типа гидроусилитель всегда о ^°* чен дополнительной внутренней ____	-	___Ва*
что обеспечивает пропорциональность электродвигателя и углом поворота люльки
й механической обратной связью, между углом поворота валика (рис. 11.4).
о/	б)	б)
Рнс 11.5. Принципиальные схемы механн imob управления с электромагнитом и однокаскадиым гидроусилителем:
и — без обратной связи по положению; б — с электрической обратной связью на усилитель; в — с внутренней механической обратной связью; / — управляющий электромагнит;
2 — обмотка возбуждении; 3 — обмотка управления; 4 — золотник; 5 — электрический датчик углового положения люльки; 6 — пружина обратной связи; 7 — рычажная система обратной связи; 8 — люлька иасоса; 9 — силовые гндроцилиндры
То же относится и к механизмам с электромагнитом и двухкаскадным гидроусилителем, в которых обратные связи рассматриваются применительно ко второму каскаду гидроусилителя, а первый каскад имеет дополнительную внутреннюю обратную связь или позиционирован с помощью пружины (рис. 11.6 и 11.7).
Таким образом, электрогидравлические механизмы управления насосами переменной производительности можно классифицировать по следующим главным отличительным признакам: типу электромеханическою преобразователя, числу каскадов гидроусилителя и способу введения основной обратной связи по положению (рис. 1J.8). В этой классификации дополнительные обратные связи в гидроусилителях не рассматриваются.
На рис. 11.3 и 11.7 показаны наиболее характерные схемы механизмов управления, нашедшие применение в различных системах 282
Рис 11.6. Принципиальные схемы механизмов управления с электромагнитом и двухкаскадным гидроусилителем:
а — без обратной свази по положению; б — с электрической обратной связью, / — управляющий электромагнит: 2 — сопло; 3 ~~ дроссель; 4 — позиционирующая пружина; 5 — золотник; 6 — люлька иасоса; 7 - электрический датчик углового положепн i люльки; а — силовые ГИДРОЦИЛиндры
механизмов управления с электромагнитом, внутренней механической обратной ссязыс
_	I4UH uvpaiu«»>	д
© — золотник; 7 - .
зого каскада гидроусилители;
Рис. 11.7. Принципиальные схемы двухкаскадным гидроусилителем и
О-с упругой обратной связью; 6-е жесткой обратной	угч>“'J“
-----	>	1 сопло; 3 _ дроссель; * - пру жвиад обрати ой	I
— рычажная системе обратной связи. 9 — ел *аш г•Д*’ * ,	1, .
дроуевлителн; 9 — валик; 10 — люлька иачоса. Ч цилиндры
11.8. Классификация механизмов управления насосами переменной производительности
264
автоматическою регулирования. На рис. 11.3, а приведен простейший механизм управления, состоящий из электродвигателя 2 тахогенератора 1 и зубчатого редуктора 4. При подаче управляющею сигнала на электродвигатель 2 его ротор начинает вращаться и через редуктор 4 перемещает люльку 6. Поскольку электродвигатель 2 является интегрирующим звеном, эти механизмы применяются в скоростных следящих системах, причем для стабилизации этих систем используется сигнал обратной связи по скорости перемещения люльки, вырабатываемый тахогенератором 1118].
В этих механизмах электрическая обратная связь осуществляется с помощью сельсина 3 (рис 11.3, б), сигнал которого, пропорциональный углу поворота электродвигателя 2, поступает в усилитель, суммируется с сигналом рассогласования и позиционирует систему автоматического регулирования.
В механизме управления с механическим дифференциалом (рис. 11.3, в) управляющий сигнал, поступающий на вход электро-двш атсля 2, заставляет его ротор вращаться и через дифференциал 5 перемещать люльку насоса 6.
Как только люлька насоса выходит из нейтрального положения, вал гидромогора и связанный с ним зубчатой передачей валик обратной связи 7 приходят во вращение. Дифференциал 5 алгебраически суммирует углы поворота валов электродвигателя 2 и гидромотора, и в тот момент, когда скорости их вращения сравняются, движение люльки 6 прекратится. Таким образом, в рассматриваемом механизме угол поворота люльки, а следовательно, и скорость вращения вала гидромотора пропорциональны величине и знаку управляющего сигнала [16], [118].
Механизм управления для позиционных систем с комбинированной обратной связью (рис. 11.3, ?), кроме электродвигателя 2 и тахогенератора /, включает механический дифференциал 5 и сельсин обратной связи 3.
При повороте сельсина-датчика и появлении рассогласования на входе следящей системы ротор электродвигателя 2 начинает вращаться, отклоняя с помощью дифференциала^5 люльку . д временно сигнал обратной связи, поступающий на вход системы :Р!Хна 3	.ЕТГпХ
до НУЛЯ, в результате чего управляющий электГ’одв“г“ поворота иувщись на угол, равный или пропорциональный углу поворота сельсииа-датчика, останавливается. Отклонение лтьки 6 вызывает вращение вала гидродвигателя, который ^^«XZroH^t ференциала 5 поворачивается на угол, равный ил р ЛЮЛЬка ный углу поворота вала электродвигателя 2, после; чего ли* устанавливается в нейтральное положение, и вращение вал •• мы выбирают таким образом, чтобы процесса угол поворота нагрузки, связанной с гидродви равен углу поворота вала сельсина-датчг .
Ня пне 11 4 а показан механизм управления состоящий пз аЧектпо?вигателя2, тахогенератора 1 и охваченного дополнительной механической обратной связью золотникового гидроусилителя. Пои подаче ' правдяюшего сигнала вращение ротора электродвигателя 2 через редуктор 4 и рычажную систему 8 преобразуется в поступательное перемещение золотинка 6, который сообщает полость одного из силовых гидроцилиндров Юс полостью нагнетания вспомогательного насоса, а полость другого силового гидроцп-линдра-со сливной магистралью Под действием разноси, сил давления люлька 9 начинает перемещаться и через рычажную систему 8 уменьшает скорость перемещения золотинка. Как только скорость вращения люльки 9 станет равной или пропорциональной скорости вращения вала электродвигателя 2, движение золотника прекратится, площадь открытия его рабочих окон станет неизменной, вследствие чеголюлькаРбудетпродолжать поворачиваться с постоянной скоростью. Этот механизм управления применяется в скоро-стных следящих системах, поскольку входному сигналу пропорциональна скорость перемещения люльки насоса переменной нроиз-водительности 15], (118).
Позиционирование следящих систем с механизмами такого типа выполняется также с помощью сельсина обратной связи, дифференциала или путем их совместного использования На рис. 11.4, б показан механизм управления, предназначенный для работы в позиционных следящих системах с комбинированной обратной связью 11181.
Принципиальная схема механизма управления, включающего в себя позиционный электромагнит 1 и золотниковый гидроусилитель без обратной связи показан на рис. 11.5, а. При подаче управляющего сигнала в обмотку управления 3 электромагнита / его ротор вместе с присоединенным к нему золотником 4 выходит из нейтрального положения, рабочая жидкость под давлением р0 поступает в один из силовых гидроцилиндров 9, и люлька 8 начинает перемещаться Скорость перемещения люльки пропорциональна смещению золотника и, следовательно, управляющему сигналу на входе механизма управления. Механизмы такого типа применяют в скоростных следящих системах (51 ].
В механизме управления, представленном на рис. 11.5, б, ско-я ^Т“ИЯ лю^ьки та,<же пропорциональна разности токов с датчикя и?™ВЛеНИЯ ,лектР°магнита 1. Однако в этом механизме лителя пост\-паетГсиПиЛОЖеНИЯ люльки на ВХ°Д электронного уси-Этотсигнал яшрбпя' 3/11 пРопоРциональнь1й углу поворота люльки, в результате чегг^пяя е<ЖИ с^ммнруется с сигналом рассогласования, магнита / уменьшается^ В обмотках управления 3 электро-ником 4 возвращаются » ?0Т0Р электромагнита вместе с золот-люлька насоса оказыяяртеНеИТраЛЬНОекПаЛожение- Таким образом, сигналу рассогласования ” повеРнУтой на угол, пропорциональный ния на входе электронного усилителя 151], 1123]. ад>
На рис 11.5, в показана принципиальная схема механизма управления с электромагнитом, однокаскадным золотниковым гидроусилителем и внутренней механической обратной связью. В механизмах такого типа при перемещении люльки 8 деформируется пружина обратной связи 6, что приводит к изменению суммы сил, действующих на золотник 4. Вследствие этого золотник возвращается в нейтральное положение, и люлька насоса 8 устанавливается иа угол, пропорциональный величине управляющего сигнала в обмотках управления 3 электромагнита / 1107].
В механизмах управления, приведенных на рис. 11.6, а и б, введен дополнительный каскад гидравлического усиления, позволяющий использовать электромагниты меньшей мощности. Электрический датчик обратной связи 7 работает так же, как и в механизме управления с однокаскадным гидроусилителем (рис. 11.5,6) 116].
Механизм управления с двухкаскадным гидроусилителем и внутренней механической обратной связью, показанный на рис. 11.7. л, работает следующим образом. При появлении разности токов в обмотках управления электромагнита 7 его ротор вместе с закрепленной на нем заслонкой поворачивается на некоторый угол, что вызывает изменение давлений в междроссельных полостях перед соплами 2. Вследствие этого нарушается равновесие сил, действующих на торцы золотника 6, и золотник начинает перемещаться, сообщая полость нагнетания вспомогательного насоса с рабочей полостью одного из силовых гидроцилиндров 11, а полость другого силового гидроцилиндра — со сливной магистралью. Под действием момента, создаваемого силовыми гидроцилиндрами, происходит перемещение люльки 10 и связанных с ней рычажной передачей 7 толкателей 5. При этом деформируются пружины обратной связи 4, вследствие чего золотник возвращается в нейтральное положение, и движение люльки 10 прекращается 125].
В механизме управления, показанном на рис. 11.7,6, разность давлений в междроссельных полостях вызывает перемещение силовых гидроцилиндров первого каскада гидроусилителя и связанного с ними валика 9 до тех пор, пока разность усилий деформируемых пружин, установленных в силовых гидроцилиндрах 8,„ не уравновесит разность сил давления. Золотник 6, соединенный рычажной системой с валиком 9, выходит из нейтрального положения, и люлька 10 начинает перемещаться. При некотором угле поворота люльки рычажная передача возвращает золотник в нейтральное положение, и движение люльки прекращается ]25].	„
К механизмам управления насосами переменной производит иости предъявляются следующие основные требования.
статическая характеристика (зависимость угла скорости перемещения люльки насоса от управляюш должна быть линейной во всем диапазоне;	и авм*
ширина петли гистерезиса ствтической характеристики
нечувствительности должны быть минимальными,
.вменение крутизны статической характеристики и дрейф нуля должны быть минимальными во всех температурных условиях экс-ПЛ'пеТреходный процесс должен быть монотонным, а постоянная племени возможно меньшей,
статические п динамические характеристики должны оставаться стабильными в течение всего периода эксплуатации;
конструкция механизмов должна быть возможно более надежной и простой, а их вес и габариты — минимальными
Линейность статических характеристик механизмов управления достигается путем применения электромеханических преобразователей и датчиков углового положения с линейными статическими характеристиками, введением жесткой обратной связи в гидроусилителях, а при отсутствии обратной связи посредством использования гидроусилителей дифференциального типа (т. е. гидроусилителей, в которых перемещение исполнительного элемента происходит под действием разности сил давления в рабочих полостях).
Для уменьшения ширины петли гистерезиса и зоны нечувствительности на вход электромеханических преобразователей подается дополнительный осциллирующий сигнал переменного тока. Под действием осциллирующего сигнала уменьшается магнитный гистерезис электромеханических преобразователей, снижается сухое трение и выбираются люфты в гидроусилителях и рычажных системах. Если вследствие инерционности электромеханического преобразователя осциллирующее воздействие не передается на гидроусилитель, в конструкцию насоса вводят специальный механический вибратор, сообщающий осциллирующее движение золотнику или золотниковой втулке.
При изменении температуры окружающей среды и рабочей жидкости характеристики электромеханических преобразователей изменяются вследствие температурного изменения сопротивления их обмоток. Одновременно изменяются характеристики гидро-усилителен, не имеющих механической обратной связи, вследствие ’зменения вязкости рабочей жидкости и связанного с этим измене-X2xSSOr° С0Пр0ТИВЛеНИЯ Рабочих окон распредели-в обмотках ЭТОГО явления применяют стабилизаторы тока ”В“б>™ия электромеханических преобразователей или магнитами. УменьшеТ₽Тп™СКИе пРеобРазователи с постоянными кости на работу гидроусмитХй ИЗ“еНения вязк°с™ рабочей жид-Дифференциальных схем 066^^™™™* *УТСМ »спользования таческнх характеристик ’ я В ЮЩИХ стабнльность нуля ста-кое трение в рабочих о’кня» Ке Путем Уменьшения потерь на вяз-
Быстродействие механизмов3*^™Делительнь,х устройств, пользования малоинерционних У равления Достигается путем ис-с
эд	ями, непосредственно перемещаю-
щнми пюльку насоса и имеющими вследствие большой мощности значительный момент инерции ротора, применяются только венете мах, от которых не требуется большого быстродействия
Постоянная времени маломощных электродвигателей, применяемых в механизмах управления с однокаскадными гидроусилителями, значительно меньше, что обусловило широкое применение механизмов такого типа. Еще большим быстродействием обладают маломощные электромагниты, которые применяются для управления насосами малой мощности с однокаскадными гидроусилителями и насосами большой мощности с двухкаскадными гидроусилителями
Стабнльность характеристик механизмов управления в течение периода эксплуатации достигается главным образом путем подбора материалов трущихся пар с высокой износостойкостью, применения в дросселирующих элементах гидроусилителей материалов, стойких к размыванию потоком жидкости при больших скоростях истечения, а также посредством введения устройств для выбора люфтов в рычажных передачах.
Конструктивное выполнение механизмов управления весьма разнообразно. Они выполняются или в виде отдельных блоков, устанавливаемых на насосы переменной производительности, или встраиваются непосредственно в корпусы насосов. Первый способ позволяет устанавливать на насос механизм управления различной конструкции, второй — несколько уменьшить вес и габариты насосного агрегата в целом.
§ 11.2. ЭЛЕКТРОМЕХАНИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
Преобразование электрических сигналов управления в механическое перемещение люльки насоса или регулирующего элемента гидроусилителя, как уже указывалось выше, осуществляется с помощью электродвигателей’ переменного и постоянного тока или позиционных электромагнитов.
В качестве исполнительных двигателей переменного тока почти исключительно применяются асинхронные
с полым немагнитным короткозамкнутым ротором 1УЫ, ПОЗ], liioi.
На рис. 11.9 приведены регулировочные и механические характеристики электродвигателей такого типа. Как видно Рисунка, в рабочем диапазоне характеристики практически линейны у быть аппроксимированы следующим уравнением:
। де М j — момент, развиваемый электромеханическим преобразователем;
iv — ток управления;	.ми»
— угловая скорость вращения вала vuxTpcw*.x ww ского преобразователя;
q U с2 — постоянные коэффициенты, определяемые конструк ткаными параметрами и обмоточными данными элек-тромехани чес кого п реобр азовате л я
Для нагруженного электродвигателя
ри _ коэффициент вязкого трения нагрузки, приведенный к валу электромеханического преобразователя;
Л — момент инерции ротора электромеханического преобразователя;
Л — момент инерции нагрузки, приведенный к валу электромеханического пр еоб р а зов а тел я
Рис. 11.9. Статические характеристики электродвигателей переменного тока
Дифференциальное уравнение динамики нагруженного электродвигателя принимает вид
Ыу == (Сг + FH) Q, + (J, + J н) =
+	+	О’-2)
где <j>B — угол поворота вала электромеханического преобразователя.
Переходя к преобразованию Лапласа при нулевых начальных условиях, получим Ср, (S) = (С, 4- FH) «р, (s) + (J. + J J s*q>, (s).
«М
где /<д ==
постоянная времени
Т
где
а передаточная функция нагруженного электродвигателя
U7S (s) =	's> =____ ч	,,
c'v(s) (Ci+FH)S +7VPOT ~ repair 1М-3>
С +\~ коэффициент усиления электродвигателя по скорости;
^а + JH
Сг + F~ ~ =*лекгРомеханическая электродвигателя
Для ненагруженного электродвигателя
117,(8) =
(I + f»s)s ’
и Гэ=4
С2	С2
Для электродвигателей переменного тока коэффициенты^ и С мало зависят от температуры обмоток, что является важным преимуществом электродвигателей такого типа.

Рис. 11.10. Статические характеристики электродвигателей постоянного тока
Электромеханическая постоянная времени ненагруженных асин хронных двухфазных машин с полым ротором составляетотри частое 50 гц т; = 0,006 -ь 0,03 сек, а при частоте 400 гц Та =» 0,0» ч- 0,1 aw I114J.	я________
Для электродвигателей переменного тока постоянная г выходного каскада усилителя, нагруженного обмоткой улрм. существенно меньше Т'3. и ее влиянием м динамике».км< механизмов управления можно пренебречь.
R качество электродвигателей постоянного тока, как правило, применяют машины с независимым параллельным возбуждением (по представлены регулировочные и механические хапактеристнкн электродвигателей такого типа. Как видно из шкунка указанные характеристики линенны во всем диапазоне.
Упавнение статических характеристик для электродвигателей постоянного тока отличается от соответствующего уравнения для машин переменного тока (111) переменностью коэффициентов С и С, существенным образом зависящих от тока возбуждения.
1 Прц2малых токах возбуждения, когда магнитная цепь машины ненасышена. С, = Д,/,! G- В2Ц, где В. ч В.. - постоянные коэф-фнцненты, определяемые
Рис 11 11. Зависимость коосррицпентов С] и Сг от тока возбуждения
конструктивными параметрами и обмоточными данными элек громеханическо-го преобразователя.
Для уменьшения влияния тока возбуждения на статические в динамические свойства электродвигателей постоянного тока и повышения тем самым температурной стабильности их характеристик параметры ма
шин выбирают таким образом, чтобы при номинальном токе возбуждения насыщение магнито-
провода было достаточно большим. На рис. 11.11 приведены кривые изменения коэффициентов С} и С2 в зависимости от тока воз-
буждения для электродвигателей такого типа.
Передаточную функцию выходного каскада усилителя, нагруженного управляющей обмоткой, определяют из выражения
UV>^sT=r+%.	(4.4)
где	I/ — напряжение на входе выходного каскада уси-
лителя;
Ку — коэффициентуеиления выходного каскада усилителя по току;
Л1 ~ ^,-р	~ постоянная времени выходного
каскада усилителя;
Ls индуктивность обмотки управления электро-механического преобразователя;
Kj активное сопротивление обмотки управления электромеханического преобразователя;
у — активное сопротивление выходного каскада усилителя.
272
- * £.
Позиционные поворотные электромагниты, преобразующие управляющий сигнал в угол поворота ротора, выполняют с пением от постоянного магнита или с возбуждением от независимого источника постоянного тока.
Позиционирование осуществляется путем введения специального немагнитного зазора в статоре либо путем подпружинивания ротора с помощью торсиопа.
Регулировочные и нагрузочные характеристики позиционного электромагнита представлены на рис. 11.12. Как видно из рисунка, характерно тики практически линейны во всем диапазоне и могут быть описаны уравнением
M, = Ctiy-C2<f>s.	(11.5)
Коэффициенты Ct и С2 в электромагнитах с постоянными магнитами стабильны во всех рабочих режимах. В электромагнитах с воз-1
Рис. Л. 12. Статические характеристики позиционных электро-
магнитов
буждепнем от независимого источника эти коэффициенты существенным образом зависят от тока возбуждения (рис. 11.11). Для нагруженного электромагнита
м. - с„ф, + (Л. + ЛЛ + <i3 + JJ ,
где Сн — жесткость торсионной составляющей нагрузки, привезенной к валу электромеханического преобразователя;
F3 — коэффициент вязкого трения электромеханического преобразователя.	 j
Поэтому дифференциальное уравнение динамики нагрулсеилгго позиционного электромагнита принимает вид
-(Сг , C„i<₽, i- ГЛ	-r.V, г	,Ндй
- -	- • мм*	|ДЯйГ|^
Переводя к лргсбр»"»""»	"Р“ ,'y“”b‘X
’Тч^77С.>,.<я) + (Г. + г.).^(«) + (А + 4)яЧ<д). а „«Х™.«я фу™« «ягру»»"»™ позяцяокяого «еятромаг-нита запишется в виде
Г,'= Т^Г = (^ +	+ ,л-’ + ^>s + ('9 + 7и) s’ ~
Кя ___	(11.74
= T+C,7>+^’’	(	>
где
и
к_____Li  Т
К>~ С2 +
г
н
где
2/Сг/э
г
2К(С, + С„) (Л + Л) '
Для йена груженного элетромагнита к;
^(s) - ] + 2£;r;s + (qm ’
Ki = ^; г’ ь2
Для позиционных элетромагнитов, применяемых в механизмах управления, Т'а = 0,002 ч- 0,005 сек.. При работе электромагнита в масле — 0,5 [24]. Передаточная функция выходного каскада усилителя, нагруженного управляющей обмоткой электромагнита, определяется выражением (П.4).
$ 11.3. ЗОЛОТНИКОВЫЕ ГИДРОУСИЛИТЕЛИ
Золотниковые гидроусилители, управляющие органами регулирования насосов переменной производительности, состоят из четырехкромочного золотникового распределительного устройства, силовых гидроцилиндров и системы обратной связи.
Подвод питания осуществляется от вспомогательного насоса. Давление питания обычно выбирается в пределах 10—25 кГ/см2. Поэтому перепад давления на рабочем окне (золотниковой щели) гидроусилителя не превышает 12 кГ/см2.
Расход жидкости Q, протекающей через рабочие окна распределительных устройств гидроусилителей, определяется выражением
Q =	(Ц.8)
где F — площадь рабочего окна;
И — коэффициент расхода;
р плотность жидкости;
ор — перепад давления на рабочем окне.
274
Для золотниковою распределительного устройства (рис. 11 13)
/г = ()
F = л<7фята (X — а)
при при
Х^а- 1
X>a, j
(119)
где	— диаметр золотника;
ф = । л arcs 11 0 коэффициент открытия периметра золотника;
а — величина начального перекрытия;
b — ширина перемычки золотниковой втулки;
« — угол скоса кромки золотника;
X — перемещение золотника относительно его нейтрального положения.
Обычно применяют золотники с прямоугольными кромками (а = 90 ), имеющие коэффициент открытия периметра ф — 1 или ф = 0,5.
На рис. 11.14 приведены расходные характеристики рабочего окна золотникового распределительного устройства, имеющего d — 1,4 см, ф = 0,5, a = 90°, а = 0 и F = const. Испытания проводились на веретенном масле АУ ГОСТ 1642—50 при температуре 35__40° С; коэффициент кинематической вязкости v = 0,2 см21сек,
плотность р = 9 -10 7 кГ -секшем*.
На рис. 11.15 приведены подсчитанные значения р. в зависимости от перемещения золотника X и числа Рейнольдса Re (р изменяется от 0,65 до 0,75 и для приближенных расчетов может быть принят равным 0,7). Число Рейнольдса Re определили по формуле
XV V
где и — периметр истечения;
и — скорость истечения жидкости.
При Re>300 коэ|)фициент расхода меняется незначительно, совпадая с данными В. А. Хохлова 1112].	„ппичполитель-
В механизмах управления насосами передвои производитель ности для устранения возможности залипа”“ или золот. вышения чувствительности гидроусилителя з	У высокой
никовой втулке сообщается осцилли^ующ	зш<угники выпол-
частоты (аксиальная осцилляция). В этом слу	ЧУВСТВИтель-
няют с положительными перекрытиями, а P УУ_ подучаютп¥" ность гидроусилителя при сохранении его УС™«“™ "^лирова-тем регулирования амплитуды 0С1^“лл”Хест^ино уменьшить вязание амплитуды осцилляции позволяет СУ^	гидро^силктед»-
ние технологических допусков на хар Р телямн
В механизмах управления с
осцилляция создается с помощью р У РУ
Рис. 11.13. Схема рабочего окна золотникового распределител ьного устройства
Рис. 11.14. Расходные характера стики рабочего окна при отсутствии осцилляции
Рис. 11.15. Коэффициент расхода рабочего окна при отсутствии осцилляции
Рис. 11.16. Схема определения эквивалентной пло
связанного рычажной передачей с золотин™», втулкой и приводимого во вращение чевез ,vfi. ЗОДо™*ТО1юй вала насоса переменной производительности У УЮ пеРрДачу от
В механизмах управления с электоомагнитя».
BpeM^"°m УПраВЛЯЮЩИМ подается перем^нный^ °Д”°’ той 50-100 гц, который способствует сужениюпХ электромагнита и позволяет создать оспиллирХщее
При этом амплитуда осцилляции золотника переменного тока, подаваемого на управляющие обмотки электромагнита.
Аксиальная осцилляция существенно влияет на расходные характеристики рабочих окон золотниковых распределительных устройств, особенно при положительных перекрытиях. Если частота осцилляции достаточно велика, а амплитуда сравнительно мала, то колебания расхода и давления весьма незначительны. Проведенные эксперименты на насосах гаммы II гидроприводов показали, что при частоте осцилляции 30—100 гц и амплитуде 0,03—0,05 см люлька движется практически плавно.
Фактический расход через рабочее окно
ток часто-петли гистерезиса - движение регулируется силой
При ОСЦИЛЛЯЦИИ ЗОЛОТНИКОВОГО распреде- щади рабочего окна лительного устройства за достаточно боль-
шой отрезок времени определяется по тому же уравнению (11.8), однако с иным значением коэффициента расхода
Q, =	V Др,	(П.Ю)
где Q, — осредиенный расход через рабочее окно;
F, — эквивалентная площадь рабочего окна;
р' — коэффициент расхода осциллирующего рабочего окна.
Мгновенный расход жидкости Q (/), протекающей через периодически открывающееся рабочее окно в некоторый момент времени t,
Q(f) = F(t)p' j/y У Др,	(И-Н)
где F (/) — площадь рабочего окна в момент времени t.
При синусоидальном движении золотника относительно втулки с амплитудой А и периодом Т около некоторого положения X площадь рабочего окна запишется в виде
F (t) = 0 при X + A sin -2" I <в;
F(t) = лг/ф s*n « ( V + Л sin у / — aj (11.14
V л	„
при A A sib
vn
На рис. H .I6 покачан характер изменения положения золотника в течение периода колебании 7\ Очевидно, открытие рабочего окна происходит в момент времени т. е. в тот момент, когда рабочие кромки золотника и втулки совпадают. При дальнейшем движении золотника площадь рабочего окна вначале увеличивается, затем начинает убывать, и в момент времени /2 рабочее окно вновь закрывается.
Количество жидкости d\7 = Q (/) dt, прошедшей через рабочее окно за время dt, в соответствии с уравнениями (1111) будет
dV = 0
Ч (11 12)
при X + /4 sin
dV = nd^ sina XЛ sin— a p'
р 1 Apdl при -Y -J- A sin у. t g\ Количество жидкости И, прошедшей через рабочее окно Т, составляет
(11.13)
за время
lz = j dV = ndip sin ap'
sin
(H.14)
ниемЖ! б^ИР°ВаНИЯ ° СООТ™“” с рис. 11J6
и
уравне-
или
А + Л sin ~ (12 = а
= iarcsin - л~
Подставив значения / <. / п вав, получим	1 4 В ВЬ|Раже|1ие (11.14) и проинтш риро-
V = ndty sin up'
/ __ Т Т . а_______________у
1 ~	~ 2? arcs,n тг
(11.15)
(j+^arcsin^
с
•'-е.т-г.к
(11.16)
7 ИДр7\
(11.17)
F„= ndipsiuaX
Приравнивая выражения (11.16) и (11.17), получим 1,1	. X - « , ,
,4— arcsin —т—1 + 2 л	А I
т\2
-1 = ndtysinuX,,,
Л
(H.18)
при ЭТОМ
X,- /|
Здесь X — эквивалентное перемещение золотника т расстояние между рабочими кромками золотника и Хк/ Д ТаК<* ром площадь рабочего окна равна F	втулки, при кото-
В соответствии с рис. 11.16, выражение Н1 10\ „ для периодически открывающейся золотниковой щ!|и ^тТЕ условии а — А X а А.	•*-е. при
П_.. V п Л /X и __	\
— 1 I рабочее
Х—а А
• (H.19)
....."\ А
тым в течение всего периода колебаний и, следовательно X = О
При Х^-" ‘ л‘Х~а Л '
осцилляция не влияет на величину осредненного расхода Q3. В этом случае Х3 = X — а.
Из выражения (11.19) следует, что величина Х° является ,	„	Х-а п„	А
функцией только —д—. Действительно, раздел и в обе части равенства
(11.19) на А, получим
ф = 0
А
Хэ _Х
А
окно остается закры-
А 1) рабочее окно не закрывается и
при
X— а
(11.20-
I	V
„ arcsin _" л	д
. X — а arcsin —-.—
А
2
1;
’ А
Х-а при
Х—а А
X, _ А ~
На рис. 11.17 дано графическое изображение выражения (11.20/ характеризующего изменение эквивалентного перемещения золи; ника X, в зависимости от перемещения X, амплитуды осцилляции А и величины перекрытия а. Если известны величины a, d, ф, в. А, то при помощи такой кривой искомую зависимость F. (X) мвЖДв построить простым изменением масштаба осей коердмкм.
Искомую зависимость F, (X) строят в такой
сти (рис. 11.18):
1) строят ломаную F (X), характеризующую *****e}?*r’WRHp рабочего окна при отсутствии оедкддяин* (при Л — ЧВ
Y-n нт one 11 18 проводят вспомогательную
°’K|T" Г00*™ ”“"a 6>*r i’afc,,ero
Puc. 11.17. Зависимость безразмерного эквивалентного перемещения золотника от безразмерного действительного перемещения
3) на графике с началом координат в точке X — и строят кри-с .J	.. X, г/Х-а\
bjio /„(A—а), которая получается из кривом —А = [ I—д—j
Рис. 11.18. чего окна
Зависимость эквивалентной площади рабо-
<л перемещения золотника и амплитуды осцилляции
умножением абсциссы каждой к точки м	д а
ч,я„„а1 Л. м „рияВД1!ние
g Kai™пеР^наинльных осей
г;«).	‘ в точте л = 0) дает искомую зависимость
На рис. 11-18 приведено семейство кривых F. (X), соотвегствчю-Щ11Х разным значениям А, построенных указанным способом для рабочего окна золотникового распределительного устройства, имею-щего лг/'Г 1 см’ и  а 6,02 см.
На рис. 11.19 показаны расходные характеристики рабочего окна золотникового распределительного устройства, аналогичные показанным на рис. 11.14, но полученные при аксиальной осцилляции с амплитудой 0,009 см и частотой 70 гц.
Рис 11.19. Расходные характеристики рабочего окна при наличии осцилляции
Эксперименты показали, что изменение частоты осцилляции от 20 до 80 гц практически не влияет на расходные характеристики. Результаты обработки полученных экспериментальных данных приведены на рис. 11.20. Следовательно, при наличии осцилляции коэффициент расхода ц' в рабочем диапазоне более стабилен и может быть принят равным 0,62.
Некоторое уменьшение коэффициентов расхода можко объяснить тем, что при наличии осцилляции необходима дополнительная wipe-та энергии на деформацию жидкости, истекающей из рабочегч * «
При работе гидроусилителей с положительными персжрмяМ^ *5ак правило, одновременно открыто два рабочих оая»• Поскольку механизмы управления работают ин вмМШД' ы • утечки в них малы, поэтому ими и сжимаемостью бочих полостях, имеющих малые объемы, <ЛЛК>
При сделанных допущениях окна принимают вид
= \2
Qt = Р^' |Г р
уравнения расходов через рабочие
1 Р« — Pi~~ Р*»
(11.21)
1 pi — Phi ,
|ле Q' _ Qt = qh — расход в силовых гидроцилпндрах гидроусилителя
н рг _ давления в полостях силовых гидроцилиндров; ри р,.о — потери давления в каналах гидроусилителя, Г,1 и Рл — эквивалентные площади рабочих окон распределительною устройства
Обозначим
Д, - Pi = Рн Н Phi + Phi = Рк,	(11.22)
где р„ — перепад давления на органе регулирования производительности насоса,
р,. — суммарные потери давления в каналах гидроусилителя.
Момент на органе управления насосом записывается в виде двух составляющих, одна из которых зависит от скорости перемещения органа регулирования, а вторая — от его ускорения. Поэтому
Рн = Ре+Ру,	(11.23)
где р, — перепад давления на органе регулирования, зависящий от скорости;
Рг — перепад давления на органе pei улирования, зависящий от ускорения.
В статическом режиме pt = 0 и
Pi - Рг = Pc-	(11.24)
Из выражений (11 21), (11 22) и (11.24) получим
<2я = ^Рр'}/ р V рр,	(11.25)
где Fv ~ расчетная площадь рабочих окон;
Рр - расчетный перепад давления на рабочих окнах, F — _ F'nFa
р VW	<1126>
Рр~Ро — Р. — рк.
Расчетная площадь рабочих распределительного устоойствя и золотника. Для построе.п-я криЖ^^У^^'Т^ пе тельно построить кривые F(X) и /vi необ*адимо значения X по уравнению (11 26) М W1 И;
(11.27) окон определяется параметрами является функцией перемещения ....................э предвари-• а звтсм для каждого вычислить Fp.
Результат такого постпоения показан на рис. 11 22 для золотникового распредели тельного устройства механиз-^’а Управления насосом №2,5 nm(d^ (1-7с^11’ = 0,5; а1 = ’ <	^ = 0>(>2 см; Д =
— 0,02 cjh)
Величины р., Рг и рм оп. редел яющие расчетный перепад давления на рабочих ок
нах р;1 зависят от скорости перемещения органа регули рованпя или, что то же самое.
от расхода в силовых гидроцилиндрах Q„.
Давление питания р0 определяется характеристикой сливного клапана. С увеличением Q, расход через сливной клапан уменьшается и
давление питания р0 несколько падает.
Перепад давления на органе регулирования рс обычно
определяется экспериментально для каждого типоразмера насоса. С увеличением скорости перемещения органа регулирования перепад давления рс возрастает.
Суммарные потери давления в каналах гидроусили-
теля
„ __ V су. V Su». I
+ ,28 vvQnV>. (И 28)
’л g —
I
_ коэффициент сопротивления 1-го канала;
— площадь поперечного сечеиия »-го канала;
11к— длина i-re капала, din — дивмет? i-m
ею
11.23 приведены кривые
изменения величин р,„ иловых гндроцилнндрах
Рс, QH
Рк if1 р/в зависимости от расхода
Рис. 11.21 Схема золотникового гидроусилителя
Рис. II 22. Определение расчетной площади рабочих окон механизма управления насосом № 2.5
для насоса № 2,5 НД, работающего на веретенном масле АУ при температуре рабочей жидкости 35—40 С (v 0,2 см2/сек). С уве-/П ГК'Г Л Пгх 1 Г ГОСС
личением QH от 0 до 150 ел? сек расчетный перепад давления на рабочем окне уменьшается более чем вдвое.
Рис. 11.23 Расчетный перепад давления на рабочих окнах t идроусилителя
Рис. 11.24. Расходная характеристика гидроусилителя механизма управления насосом № 2,5 1Ш
пос^стмннмГисп^аСХ0ДН0Й хаРак,еРис'Г||ки гидроусилителя не-^ Х“|Хй ц^^ВаНИе вь,Ражения (И .25) невозможно, гак Р ти кроме величины Fp, зависящей только от X,
стоит расчетный перепад рр, зависящий от величины Он, подлежащей определению. Вместо этого задаются различными значениями Qh и по кривой рр (Q„) (рис. 11.23) определяют соответствующие значения рр. Затем с помощью выражения (11.25) для каждого значения QH вычисляют величину Fp и по кривой F, (X) (1122) определяют искомые значения X.
Расходную характеристику удобно строить графо-аналитическим методом, используя все четыре квадранта (рис 11.24). Во втором квадранте строят кривую Q,, (рр) — обратную характеристику Рр (Q:<) (Рис- И.23). В четвертом квадранте наносят зависимость FP (X).
Задаваясь различными значениями Q„, по кривой Q„ (рр) определяют рр и с помощью выражения (11.25) вычисляют соответствующие значения Fp.
Результаты расчета строят в третьем квадранте в виде зависимости Fp (рр), по которой в четвертом квадранте определяют значения X, позволяющие строить в первом квадранте расходную характеристику гидроусилителя (это построение на рис. 11.24 показано стрелками для QH = 80 см3,сек). Расходная характеристика близка к линейной для гидроусилителей всех насосов гаммы II гидроприводов, свидетельствуя о возможности ее линеаризации. Поэтому при анализе динамики механизмов управления принимают
<?„=СЯХ.	(11.29)
Для рассмотренного гидроусилителя крутизна расходной характеристики С3 = 1400 см-/сек.
Реактивная сила Pim , действующая на золотник со стороны потока жидкости, в соответствии с рекомендациями, данными в работах [6], 1112], определяется из равенства
Ог
Pem^PQv COS 6=р^-COS6,
где v _ скорость истечения жидкости через рабочее окно;
Q = 69° — угол между осью струи и осью золотника
Суммарная сила, действующая на четырехкромочный золотник, при наличии аксиальной осцилляции
Fcm = pQJ cos 6	4-^У.
(И 30)
Все величины, входящие в правую часть равенства, опр что позволяет легко построить зависимость Рс„ (Л), по на рис. 11.25 для механизма управления насоса № -  J > ния, проведенные для механизмов УПР^*®Н««	Щ =.
типоразмеров, свидетельствуют о возможное	« Р	«rgy
= С4Х, причем для рассматриваемого механизм-. G»
При работе гидроусилителя в динамических режимах выражение (11.25) принимает вид
I'Po - (Pc + Рк + Ре) signA 	(И.31)
В насосах переменной производительности инерционная составляющая момента сопротивления органа регулирования производительности значительно меньше скоростной составляющей. Вслед-
ции струи от перемещения золотника для механизма управления насосом № 2,5 ПД
ствне этого давление в силовых гидро-цилиндрах не [превышает давления питания р0, что подтверждено экспериментально. Поэтому в выражении (11.31) знак sign можно опустить н записать
Qh^FiP' р 1 Pr — Pv (И 32)
Для вывода передаточной функции гидроусилителя используем выражение приращения расхода
AQ„ = ^AX +
Поскольку pv невелико и его среднее значение равно нулю, можно принять =
Для вычисления частной производной ренцируем выражение (11.32) по (р — pv) = const):
. Qu _
X
"Р°ДИ(М,е-
при Fp = const (X =
QK
2<Р₽—Ру) ’
d<Pp — Pyl	2V/'p — Pv
Численное значение производной —p у зависит в основном от Q„ и рр (рг мало), т. е. в конечном счете от того значения X, в окрестностях которого определяется производная.
Среднее значение производной будет при Х=-"у5- и Pv = оно принимается и для дальнейших расчетов:
( <4 1 _ « _г l^p- ₽v> U
где Q1 расход через силовые гидроцилиндры при X = -
‘max *
2 '
Рр — расчетный перепад давления на рабочих окнах при V ^тах
Л ~	1~ 
Для рассмотренного выше гидроусилителя Q* = 80 слг'/сек-рр = 7,8 кГ/см2; Св = 5,1 см°/(кг -сек).
Так как расчетный перепад давления на рабочих окнах определяется положением золотника X, а при X = const, рр = const и Др/, = 0, го
Ь(рР Ру) = — Хру
Подставляя полученные значения частных производных и приращений переменных в выражение (11.33), имеем
&QH = C,&X-C6bpy.	(11.34)
Ту же величину можно получить из геометрических соображений (см. рис. 11.21):
_ л£>» р d (Ду)
~ 4 dt ’
Д<2«
где £> _ диаметр силового гидроцилиндра;
/1 — расстояние от оси силового гидроцилиндра до оси органа регулирования;
у _ угол поворота органа регулирования.
Кроме того,
4J d* (Ду)
&Ру~ nD3h dt* '
где J — момент инерции органа регулирования.
Поэтому
„ . v	nD*h d (Ду) , 4C6J d* (Ду)
С3АЛ — 4 dt ‘ nD*h dt*
(11.35)
или
С,ЛХ и s <Лт1 (»)+Si,
где s — переменная Лапласа, а передаточная функция гидроусилителя без обратной связи
/ х Ду(«)_______Кр
AA (s) ~ (I + Tps)s '
(11.36)
где коэффициент усиления
/г 4С» nD*h
и постоянная времени
т J6CU
* р"
(11.37)
в рассматриваемом примере С;| = 1400 см-/сек; Св = =	- бел»; J = 0,3 кГ -см -сек*; К 39,31 (сек -см);
Тг Пепёшаточная функция золотникового гидроусилителя с обратной связью 11 (х) определяется обычными методами, в зависимости от характера и типа обратном связи K8I.
Так, например в гидроусилителе с жесткой обратной связью уравнение обратной связи будет
ДЛ (s) = AZ(s) —A'nAy(sl,
где Л7 — перемещение входного элемента;
— коэффициент обратной связи.
Поэтому из равенства (11.36) ip __________________Ду Is!—__ Aj--------
1г j(s) - д/ (S) - 1 +	+ T‘S* •
(11.39)
(11 40)
где коэффициент усиления
«‘i.
(11.41)
постоянная времени

Л'рЛ'о
(11.42)
(11.43)
и коэффициент демпфирования
t -	1
В рассматриваемом примере при /<(| = 0,8 см Кз — 1,25, Т, = 0,007 сек и = 2,3.
Поскольку > 1, то
't7j(S) = (T+7>)(N- 7>)«
где Т', = 0,03 сек; Т", = 0,0025 сек.
На динамические характеристики гидроусилителей большое влияние оказывает производительность источника витания.
В насосах объемного регулирования производительность вспомогательного насоса выбирают из условия необходимости компенсации объемных потерь основного насоса и обеспечения заданного времени перемещения люльки. Чрезмерное увеличение производительности вспомогательного насоса лимитируется тепловым режимом, размерами фильтра и к. п. д. гидропривода в целом. Поэтому про-рм^Д«ТС1ЬНССТЬ источника питания гидроусилителей насосов объ-envulo п^УЛИР°ВаНИЯ являе'ГСЙ величиной ограниченной. В этом баний nJ подаче„на ВХОД гидроусилителя синусоидальных коле-р деленной частоты и амплитуды производительность вспо-
288
moi ателыгого насоса может оказаться недостаточной для отпаботки заданного сигнала, и движение исполнительного органа гидроусилителя будет происходить по закону, отличному от синусоидального.
Скорость силового исполнительного органа гидроусилителя без обратной связи при синусоидальном сигнале на входе и ограничен-
Рис. 11.26. Влияние производительности источника питания на фазовый сдвиг и амплитуду отработки органа регулирования:
1 — при неограниченной производительности;
2 _ при ограниченной производительности
ной производительности источника питания вследствие насыщения расходной харак-тернстн и будет изменяться по кривой, близкой к синусоиде со срезанными вершинами. При этом происходит дополни ильное уменьшение амплитуды отработки, а фазовый сдвиг остается прежним. Для построения частотных характеристик гидроусилителя в этом случае можно воспользоваться одним из методов линеаризации существенных нелинейностей, например методом гармонической линеаризации, считая, что выражение передаточной функции, постоянная времени и фазовый сдвиг не меняются, а коэффициент усиления (амплитуда отработки) становится меньше в результате уменьшения крутизны расходной характеристики гидроусили-
При помощи метода гармонической линеаризации можно определить крутизну расходной характеристики при наличии насыщения 161]
2	। Х„ X
Сзг = — С:11 arcsin + х,
Где Сзг — линеаризованная крутизна расходной характеристики X , — ходР^от™"на линейном участке расходной характеристики;
Хн — максимальный ход золотника.	„ об-^тной
Скорость исполнительного органа ГИД₽°УС“ ()Гоаниченнои гро-
связью при синусоидальном сигнале на вх д ₽ сЯ (|О изводительности источника питания буд ппямых Гггис состоящей из отрезков синусоиды и наклонных прямых (р-с <
(11.44)
10 в. Н. Прокофьев и др.
Следовательно, насыщение расходной характеристики гидроусилителя с обратной связью приводит к возникновению дополнительного фазового сдвига, а при увеличении частоты входного сигнала и к уменьшению амплитуды отработки.
Однако метод I армонической линеаризации как это следует из выражений (11.40) и (11.43), позволяет приближенно оценить только фазовый сдвиг, поскольку в выражение для коэффициента усиления гидроусилителя с обратной связью (II 41) крутизна расходной характеристики не входит Поэтому для построения частотных характеристик гидроусилителя с обратной связью при ограниченной производительности источника питания используют графо-аналитический метод, позволяющий с достаточной точностью определить как фазовый сдвиг, так и амплитуду отработки входного сигнала.
Пусть золотник перемещается по синусоидальному закону X = X* sin a>f, при этом <о много меньше частоты осцилляции, а амплитуда колебаний X* существенно больше амплитуды осцилляции А.
При неограниченной производительности вспомогательного на-
соса орган регулирования производительности основного насоса (насоса переменной производительности) будет также совершать синусоидальные колебания с той же частотой со. Колебания органа регулирования в этом случае будут линейными.
Положение органа регулирования у в каждый момент времени t будет описываться равенством
Т = Ул = т1(<о/-|-фД
(И 45)
где у, — расчетное значение перемещения органа регулирования; у,* — амплитуда линейных колебаний органа регулирования;
—фазовый сдвиг между положениями золотника и органа регулирования.
Величины уЛ и вычисляют по передаточной функции гидроусилителя U7, (s) путем подстановки /со вместо s в выражение (11.40) или находят с помощью частотных характеристик. Фазовый сдвиг <Рл определяют непосредственно по фазо-частотной характеристике, а амплитуду колебаний у* из выражения
б,	rt=K,Z*H„,	(11.46)
де Юге модуль амплитудно-фазовой характеристики гид-роусилителя при линейных колебаниях; уменьшение амплитуды линейных колебаний в дб, ия?5?еЛЯ-емое 110 логарифмической амплитудно-Вепичнии, m ча™ои характеристике.
усилителя (геометрическимиеЛпя^ТСЯ рабочими параметрами гидро-тельного устройства плотяРаЗМераМИ ра6очих окон распредели-»»JU.
Максимальная угловая скорость органа регулирования необ холимая для отработки заданного закона движения, будет
П,, = у*ш К,ХН,(л,	(11.47)
где — максимальная угловая скорость органа регулирования при линейных колебаниях с частотой <о и амплитудой входного сигнала X.
При работе гидроусилителя от источника питания ограниченной производительности максимальная угловая скорость, которую может развить орган регулирования,
= _±СЛ<_
н Jtb'h ’
(11.48)
где QM — производительность источника питания.
Если -гг-<С1. то производительность вспомогательного насоса не будет влиять на динамические характеристики гидроусилителя, и движение органа регулирования насоса переменной производительности будет описываться равенством (11.45). Если^->1, то система нелинейна.
На рис. 11.26 показаны гармонические входные сигналы X (t) с периодами 7\ и Т2. Движение органа регулирования при неограниченной производительности источника питания показано также в виде гармонических кривых /, сдвинутых относительно входного сигнала X (/) на величину <р.„
Движение органа регулирования при ограниченной производительности источника питания показано на том же графике кривыми 2. Это движение происходит с постоянной скоростью и характеризуется прямыми, которые при малом значении отношения
касаются синусоиды, а при достаточно большом значении этой величины проходят таким образом, что отсекают от верхней и нижней части синусоиды равные отрезки, отстоящие от
оси на расстоянии
При условии > 1 появляется дополнительный фазовый сдвиг между положениями золотника и органа регулирования насоса переменной производительности (рис. 11.26, а), а при > амплитуда нелинейных колебаний органа Per^MP0BXnaU«S новится меньше ее значения определяемого по передаточн функции гидроусилителя (рис. 11.26, б). ^„„un,,uuprKOM вход-
Рассмотренные нелинейные колебания при р	. в Эб
ном сигнале характеризуются уменьшением амплитуды L. и фазовым сдвигом <f«.
Под амплитудой нелинейных колебаний ун будем понимать наибольшее отклонение органа регулирования от нейтрального по-ложеиия. Уменьшение амплитуды L„, как и при линеиныхколеба-ниях определяется выражением L„ — 20 lg пн on, где Нн модуль’ амплитудно-фазовой характеристики гидроусилителя при нелинейных колебаниях,
=	(11.19)
AZ.
Умножая числитель и знаменатель на амплитуду линейных колебаний у*. получаем
^=5 =
где /7Й =	— отношение амплитуд нелинейных и линейных коле-
баний, поэтому
LH = 20 lg Н„НД = 20 lg Н, + 20 lg H,t = + Lg, (11.50)
где Ld = 20 lg Но — дополнительное уменьшение амплитуды коле-
ста источника питания и La и фй зависят только
баний, определяемое производительностью источника питания.
Фазовый сдвиг при нелинейных колебаниях будем определять в момент прохождения органа регулирования через нейтральное положение. Величину фазового сдвига можно представить как сумму двух величин (см. рис. 11.26):
фн = <Pj + Фа, (11.51) где <р^ — дополнительный фазовый сдвиг между положениями органа регулирования и золотника, определяемый производительностью источника питания.
Можно показать, например, посредством графического построения (см. рис. 11.26), что при
ограниченной производительногармоническом входном сигнале величины от отношения ~.
шения РИС показаны зависимости этих параметров от отно-
— пК^*НлРЧиа
(11.52)
источника
нескольких по уравне-вычпсляют
Эти закономерности получены в результате обработки оезмпь татов графических построений, показанных па рис, 11.26 для различных значений отношения Используя такие графики, можно учесть влияние производительности источника питания на динамические свойства гидроусилителя.
Частотные характеристики строят в следующей последовательности:
1)	по передаточной функции гидроусилителя W, («) строят частотные характеристики L, (о>) и ср, (со), соответствующие неограниченной производительности питания;
2)	дл я । значений со нию (11.52)
Q отношение
3)	по кривым, приведенным на рис. 11.27, для выбранных частот по соответствующим от-
Q, ношениям ,у- опреде-л я ют и строят величины L,) (со) и (со);
4)	в соответствии с равенствами (11.50) и (11.51) графическим суммированием полученных кривых определяют частотные характеристики гидроусилителя LH (со) и ф„ (о>) при ограниченной производительности источника питания.
На рис. 11.28 показаны частотные характеристики с обратной связью и । «“ 0,03 сек, = 1
Z* = 0,2 см и Z? = 0,4 см.
Рис 11.28. Влияние производительности источника питания на частотные характеристики золотникового гидроусилителя с обратной связью
.еричнпн ЗОЛОТНИКОВОГО ГИДрОуСИЛНТеЛЯ
- " гзь=су&’.т°=
150г>/«« и Двух значениях амплитуды входного сигиада
БчХ^ 7оХм амплитудах входного сигнала «—• производительности источника питания на	ым
ристики гидроусилителя становится весьма сущ	Л14ТвлвЛ
К качеству изготовления золотниковой пары г У насосов переменной производительности, ра
тепьно низких давлениях (до 25 кГ/см2), предъявляются менее высокие требования, чем к аналогичным устройствам систем высокого давления.
Золотники и подвижные золотниковые втулки изготовляют из
Неподвижные золотниковые втулки, запрессовы-
цементуемых сталей 20Х или 12ХНЗА с закалко! до твердости HRC 56__62. Неподвижные золотниковые втулки, запрессовы-
вающиеся в корпусе, выполняют из стали 40Х с твердостью HRC 40—45.
Цилиндрическая поверхность золотника должна иметь чистоту не менее V Н, а сопряженная поверхность втулки не менее Ц). чистота обработки торцовых поверхностей поясков золотника и расточек во втулке должна быть не менее V 7.
Радиальный зазор между золотником и втулкой выбирают в пределах 8—16 мк на диаметр, при этом овальность и конусность цилиндрических поверхностей не должна превышать 3—5 мк.
Осевые размеры поясков золотника выполняют по фактическим значениям размеров проточек или пазов во втулке с допуском 0,02—0,05 мм.
При проектировании золотников и золотниковых втулок особое внимание следует обращать на обеспечение их жесткости. Длина золотников не должна превышать (5—6) d, а диаметр штока должен составлять не менее 0,7 d. Крепление золотниковой втулки в корпусе должно осуществляться таким образом, чтобы крепящие детали не создавали какого-либо усилия вдоль оси втулки.
При соблюдении этих условий золотниковые гидроусилители насосов переменной производительности надежно работают в течение нескольких тысяч часов.
Расчет золотниковых гидроусилителей заключается в выборе давления питания, вычислении максимального расхода, потребляемого гидроусилителем QM, а также в определении диаметра поршня D, его расстояния от оси органа регулирования h и диаметра золотника d.
Давление питания выбирается из условия создания необходимого давления в полости всасывания насоса переменной производительности, обеспечения устойчивой работы подпиточных клапанов и получения приемлемых размеров силовых гидроцилиндров. Давление в полости всасывания обычно составляет 5— \0 кГ/см2, перепад давления на подпиточных клапанах — 2—6 кГ/см2.
выбравдНрХымР11\гВ°ПРИВ0ДаХ ГаММЫ П давление ПИтан11Я лотниковы^гиппп^2713’ ЧТ0 обеспечения надежной работы зо-ности нелесопВпГа Усилителен насосов переменной производитель-Р но выбирать конструктивные параметры силовых ZZrWOB таКИМ °бра30М> чгобы*-->£^. где Ppmln-ния При Q^ei0Ho.4eHHe расчетн0г0 давления, а рон — давление нита-
2И
Как видно из рис. 11.23, расчетное давление имеет миним значение при максимальной скорости перемещений опто,г регулирования производительности. Обычно при этом давление питания рП1< уменьшается „а 2 кГ/см*. а сопротивление кантов гидроусилителя рк составляет 1-2 кПсм\ Поэтому при расчете можно принять p₽min = pc 4-3,5 ^Лон, где	_ ма1ад)ма_
льпый перепад давления на органе регулирования.
Таким образом,
где Л4тах максимальный момент па органе ре,улирования.
Соотношение между D и h выбирают из конструктивных соображений, исходя из компоновки насоса и геометрии органа регулирования производительности. Если размеры силовых гидроцилиндров получаются чрезмерно большими, необходимо увеличить давление питания.
Расход, потребляемый гидроусилителем, определяется по заданному времени изменения производительности насоса t, которое обычно составляет 0,2—0,4 сек.
Очевидно, что
Qmux — h tg Утах С
где ушах — максимальный угол поворота органа регулирования. Максимальная скорость рабочей жидкости между золотниковой втулкой и штоком золотника выбирается равной 4 м/сек.
Учитывая, что <1Ш = 0,7 d, получим d = 0,08 р Q„.
Положительные перекрытия выбирают в пределах 0,1—0,5 мм, в некоторых случаях на поясках золотника вводят дополнительный конусный участок, позволяющий снизить крутизну расходной характеристики гидроусилителя при малых открытиях рабочих окон и тем самым повысить устойчивость гидроусилителя. Обеспечение чувствительности гидроусилителя при сохранении его устойчивости достигается подбором амплитуды аксиальной осцилляции.
§ 11.4. ГИДРОУСИЛИТЕЛИ «СОПЛО — ЗАСЛОНКА»
Гидроусилители «сопло—заслонка» в механизмах управления насосами переменной производительности используются в качестве промежуточного гидравлического каскада усиления между электромагнитом и золотниковым гидроусилителем. Давление питания подводится также от вспомогательного насоса. Как видно из рис. и 11.8, в схемах механизмов управления вспомогательный кас£ ц гидравлического усиления не охвачен обратной связью и поэто» необходимы большая линейность и стабильность регулиро
Crtl-2
53)
(11.54)
где Л],»
Рис. 11.29. Схема гидроусилителя «Дроссе л ь—сопло—заело и ка»
распределительного устройства вспомогательною каскад? определяющего аналогичные параметры механизма управ-ЛСНрЯе"олыДжп1д™а протекающей через рабочие окна дросселирующих элементов гидроусилителя «сопло-заслонка, (рис 11.29), I определяются выражениями 
р 1 Pa~Pli'
. Г 2 । ---
Q, 12 = лфх12н. | р । /’i2.
4- л__зазоры между соплами и заслонкой |
v — зазор между соплами и заслонкой при ней-° тральном положении заслонки;
х — перемещение заслонки;
q , _ расход жидкости через дроссель;
Q — расход жидкости через сопло;
d. — диаметр дросселя;
d — диаметр сопла;
р , — коэффициент расхода дросселя;
р — коэффициент расхода сопла;
р|я„—давления в междроссельных полостях.
Величины с индексом 1 относятся к левой полости гидроусилителя. с игдексом 2 — к правой. Здесь, как и в дальнейшем, верхний знак в формуле соответствует первому индексу, нижний знак — второму.
На рис. 11.30 и 11.31 показаны значения коэффициентов расхода в зависимости от перепадов давления на рабочих окнах и чисел Рейнольдса (получены для масла А У при 35—40е С и А К-10 ГОСТ 1862—60 при разных температурах). Эти расхода достаточно стабильны и можно принимать
0,7. Такие же значения рекомендуются в работах 135], 142] и 1441.
Осцилляция заслонки не оказывает существенного влияния на не закг>к1п«™-о‘ ' ------- потому, что при этом рабочее окно
фициенты оасхлля°Л,1ОСТЬЮ' Г ри малых числах Рейнольдса коэф-сиввее чем бол? существенно уменьшаются, причем тем интен-ясняется влиянием Длина Дросселирующих элементов, что обгоняется влиянием входных и выходных участков щели.
коэффициенты
= 0,68 и
коэффициенты расхода сопел
Рис 11.31. Коэффициенты расхода сопла с параметрами dc =0,22 см; 1С = 0,1 см, 13= 0,02 см,
Поскольку сжимаемостью жидкости и утечками пренебрегаем, то в статическом режиме при х = const
Qdl.S— Qrl.2-	(11.55)
Из выражений (11.53) и (11.54) с учетом равенства (11.55) определяем безразмерное давление в междроссельных полостях
На рис. 11.32 дано сравнение расчетных и экспериментальных значений безразмерного давления при различных отношениях полученных для масла АУ при 35—40° С, начальном давлении р0 = И кГ!см\ диаметре дросселя, равном 1 мм. Изменение значений достигалось соответствующим выбором диаметров сопел
Из равенства (11.56) легко получить уравнение безразмерной регулировочной характеристики — зависимости безразмерной разности давлений в междроссельных полостях — Р1 от безразмер-
Ро
ного перемещения заслонки у-:
Если принять = Цй, что допустимо для работы при нормаль ной температуре и больших числах Re, то выражение (11.57) упро
На рис. 11.33 приведены расчетные и экспериментальные безразмерные регулировочные характеристики при =1,6 и раз-
личных значениях-^.
Выражение крутизны безразмерной регулировочной характе-ристики получается делением выражения (11.57) на отношение -т-: ас
ИЛП для линейного участка (в частности при х = 0)
се =
<1.
На линейном участке крутизна регулировочной характеристики зависит только от двух безразмерных конструктивных параметров
и а разрешающее выражение имеет вид г!с
р2 — Pt — CapQ
(Н.59)
Регулируемые насосы, предназначенные для широкого использования, должны надежно и устойчиво работать при изменении тем-
пературы окружающей
среды в пределах от —50 С до +90 С, что соответствует изменению вязкости даже специально подобранных рабочих жидкостей от 0,04 до 14 см-/сек, т. е в 350 раз.
В то же время геометрические размеры дросселирующих элементов должны быть выбраны таким образом, чтобы обеспечить линейность регулировочной характеристики механизма управления во всем рабочем диапазоне, максимальную разность давлений в междроссельиых
Рис. 11 32 Зависимость безразмерного давления в междросселъной полости от безразмерного перемещения заслонки
полостях (для наилуч-“ л использ°вания вспомогательного каскада усиления), а также интрпкяпрСТЬ кР^тазнЬ1 Регулировочной характеристики в рабочем кости пябоиейп5ратуР‘ Кроме того, значительное увеличение вяз-действие ruApoycoSiV.16 А0ЛЖН° Существенно Ухудшать быстро-наи^3^нХыТН1ХтокТег™иоо М°Ж^ убедиться’ ЧТ° будет при	участок регулировочной характеристики
800
% = 1,64-2,0; ^ = 0,14-0,125,
Рис. 11.33. Безразмерные регулировочные ха рактеристики распределительного устройства dс	I г
лсопло—заслонив» при = 1,о da
причем меньшему значению отношения соответствует большее значение £ В этом случае р1н = р2н= 0,35ро, где Р1„, Ргн _ дав. лспия в междроссельных полостях при нейтральном положении заслонки в кГ/см2.
Снижение быстродействия гидроусилителя при увеличении вязкости рабочей жидкости связано с уменьшением коэффициента расхода рабочих окон дросселирующих элементов, поэтому для уменьшения влияния вязкости на расходные характеристики необходимо максимально уменьшать длину рабочих отверстий. Ширину рабочей кромки сопла I, (рис. 11.34) следует выполнять равной
0,05—0,1 мм, а длина цилиндрической части сопла 1С не должна превышать (0,5—0,8) d,. Для уменьшения потерь на вязкое трение при входе в цилиндрическую часть сопла и при выходе из дросселирующего зазора между соплом и заслонкой внутренний и наружный углы конусности сопла щ и аа принимаются равными 30°.
Наибольшая стабильность регулировочной характеристики с сохранением ее линейности получается при
А=16: 4^=0,125; ds ’ d'
k =0,8-4- 1. dd
в соединительных каналах их — возможно меньшей. —з, практически не влияния Тастатаческие" характеристики, пРиД°^тпкк^ ‘нию габаритов гидроусилителя и массы, находите	°
рабочей жидкости, что ухудшает динамические характер •
801
Рис. 11.34. Дросселирующие элементы
Для исключения влияния потерь диаметр d* должен быть не менее 4 dc, а длина
Дальнейшее увеличение оказывая влияния । личению  лах I механизма управления.
Геометрические размеры и рабочие параметры дросселирую,цих элементов распределительного устройства «сопло - заслонка» ре-
комендуются следующие:
Начальный°мзор между соплом и заслонкой..........
Длина дросселя ..................................
Длина цилиндрической части сопла ................
Ширина рабочей кромки сопла......................
Угол сопла: внутренний ......................................
наружный.................................... ‘ ’
Диаметр каналов.........................•	  • • •
Давление в междроссельной полости при нейтра льном положении заслонки...............................
dF = х„ = 0,125</с
/с= (0,8-$-1.0)^ /3 = (1.05 4-0,10 мм
а, = 30"
ак == 30" dK = 4 dc
Pih~ Ран = О,35ро
При использовании рекомендуемых геометрических размеров Се = 7,5 и р2 —р, = 7,5р0	, а расход, потребляемый вспомога-
тельным каскадом гидроусилителя,
Q, = 2Q.t =	ро ] Г~f Vp^Th = 128(М5 Г(11.60)
и при р0 = 11 кГ 1см* будет Q, = 4250 d„*.
Усилие воздействия потока жидкости на заслонку можно разложить на две составляющие 127], [43]:
1) усилие, возникающее в результате изменения количества движения рабочей жидкости, вытекающей из сопла;
2) усилие, создаваемое давлением рабочей жидкости на площади выходного сечения сопла, в зазоре между торцем сопла и заслонкой, а также в зазоре между заслонкой и наружным конусом сопла.
Первая составляющая усилия в предположении поворота потока на 90° будет
^1.4 = pQc 1.4^ 1.4»
где /?)|2 —реакция потока жидкости на заслонку;
w с г» скорость рабочей жидкости в цилиндрическом участке сопла.
Вторую составляющую можно определить путем интегрирования эпюры гидростатического давления по площади заслонки:
Ло ^*1в<=2л $ ргхягdr, о
где ₽|.г усилие, создаваемое давлением жидкости на заслонку; го — расстояние от центра сопла до края заслонки;
При большо^'г^НчипЖИДКОлТИ И«а Расст°янии г от центра заслонки, чение происходит без обпя?8604611 Ж11АКОС™ и малых зазорах нсте-утьшй“Ха? и 2«к?ВаНИЯ ВИХ₽еЙ и зоны разрежения. При щкть истечения становится иас-адько^м™ Рьабочей ЖИДКОС™ ско" астолько большой, что непосредственно
за рабочей кромкой сопла возникает зона разрежения, которая вследствие отрыва потока от наружного конуса сопла может распространиться на значительное расстояние.
Увеличение скорости истечения приводит к более резкому падению давления вблизи рабочей кромки сопла и увеличению разрежения.
В центре заслонки давление распределено равномерно и по величине равно давлению в междроссельной полости р12, уменьшенному па величину потерь в цилиндрическом участке сопла
тической вязкости рабочей жидкости
Обработка и осреднение экспериментальных данных вает, что при изменении давлений в междроссельных полостях в пр -делах 2—12 кГ/см3 и относительных зазоров^ в пределах
0,05-0,25 для определения полного усилия R, действующего ВД заслонку со стороны потоков жидкости, исте ем с достаточной точностью можно пользоваться выр
(11.61)
К = С^(Рг-Р1)< 0,004 la +	до' —“а?
‘8—2~~ С, = 0.9 + 0,25---------
н. рнс. П.35 приввле».
ческими размерами.	w
где
(11.62)
При работе гидроусилителя в динамическом режиме уравнения расходов жидкости в’ рабочих полостях принимают вид
Qif 1,2 ~ Qi- I S Ч~ Qn 	(11.63)
где О,расход жидкости, поступающей под золотник.
Для вывода передаточной функции гидроусилители вычислим приращения расходов AQd, &QC и \Qn:
1	2
___ <	------«и_АР„;
2) Рп—/’1,8	- IPo Pl,a’
Л<?и., = -^ЛХ1.8 + ^И Л'’>» гл 1,2	<7’1,2
= ^-£Ь^Д.г+^ЛЛ,2;
’ О — Л	ZP1,2
л/л — я'/а d
~ 4	~ ’
где <^12 и Q! 1а — установившиеся значения расходов через дроссели и сопла.
Подставляя эти выражения в равенство (11.63), получаем
/ЦЬХ)
dt •
= -ь^£Ь2_Дх + -°*1-= Лп — л(/а -х0±х ЬХ+^ЬР^-1- 4 
— Q*i,t~ Qi.u, можно убедиться, что
- /’1,»)
Учитывая, что QH
Д (А — Pi) = Дра — Др, = ’Й (’ “ й)]Дг
После окончания переходного процесса ^ = 0, тогда
ЦРг - Pi) = 2р0 Г-J— . ₽!• (1 _ Р*\ .
1-4 —Л- рй\ рг, 1^
У&2«"ЮчтоЛМУ,И"0' ““₽«» ‘ равенством (11.59). можно
3—. р»
-X ₽о
п -С р0
(11.64)
. 1 Х/-Т*
мой ^рактерист1щиПкоэффициент пт Не^“ом Учасгке регулировоч-и w 9а»нСИт о^^ло^еиия^заслод^и л:^1*0110186	П°'
. Л. Pt
I
Поскольку крутизна регулировочной характеристики
в пределах ее линейного участка то „ Рис™ьи постоянна
ce=4rf; h _ М vo Ро Ро /
(11.65)
2 I Ра [I /
9л^а Ро z 4 Оу
р
4 ~0у'
Преобр уя коэффициент при— — rit
Л \ , Л
р« I <?г
р? I Pi I Ро рй I
где условный расход через дроссель при перепаде давления ва нем, равном /;0
гу п det 	2 1 
Qy = - 4~ ^p - I Ро,
получим
С8 = 2
/?а |/~ । _	। Pi i r j__________Pi 1
Po F Po Po F Po ]
Поскольку можно показать, что при работе на линейном участке регулировочной характеристики коэффициент С8 остается практически постоянным, то его можно определять при любом значении х, в том числе при х — 0, когда Pi = р^ — р».
С. = 4-^1-^1-^-.	(11.66)
8 Po F Ро
(11.67)
Подставляя полученные значения коэффициентов в выражение (11.64), получаем
. ,	.	С.	. л<Р p0Ct 4(ЛХ)
Л (Ра ~ Pi) — ас Ро^ 4 ' Qy ’ fit '
Запишем уравнение сил, действующих на золотник,
(11.68)
где X — жесткость пружины:
р — кож])фициент вязкого трения золотника о втулку, т — масса золотника.
Обработка экспериментальных данных показывает,а
Из выражений (11.67), (11.68) и (11.69) можно получить
Лх = (2Z + С4) ЛХ 4-	+ 0,1 d |	+ т АЛ)
или в изображениях по Лапласу при нулевых начальных условиях Лх (s) = (2Х + Q Д X (s) +
+I + °'Ы1sAX <s) + ^S“AX <0-
Поэтому передаточная функция гидроусилителя
„„ , , AXts)	AV		(11.70)
где		
		
	Ас 4dc(2X + Cd) ‘	(11-71)
	Т 1/ m .	(11.72)
	7 ~ V 21 + С4 ’	
	^^+0,lrf	(11.73)
	Г. =		—			
	2У«(2Л + С<1)	
Например, при р0 = 11 кГ'см2; d = 0,7 ом; С4 = 1,75 кГ/см;
К = 2,7 кПсм; dc = 0.14 см; dr) — 0,09 см; = 0,35; т = Ро
= 1 -10 5 кГ -сек'см2 получим С, = 7.2; С8 = 1,13; Qy — 21,3 см/сек, откуда Кс = 49; Тс = 1,2 -10 3 сек; £ = 9,5.
Поскольку £> 1, то
сУ) (i + r;s)(i + rc's) 
где Т'с — 22 40'® сек; Г" = 5 40 6 сек.
При работе электромагнита совместно с распределительным устройством «сопло — заслонка» уравнение (11.5) записывается в виде
(11.74)
где h3 — расстояние от оси электромагнита до оси сопел.
В статическом режиме
М„=Rh„ = С, "J (р„ - Р1) h,.	(П -75)
Из выражений (11.74) и (11.75) с учетом (11.59) можно получить
Л-Л------------лэ-	<I1W
'	**в**<Ро
В реальных условиях работы насосов переменной производительности ток возбуждения управляющего электромагнита ^fcconst. Следовательно, коэффициенты Ct и С2, входящие в выражение (11.76), не остаются постоянными, что вызывается изменением напряжения на клеммах обмотки возбуждения электромагнита вследствие ограниченной мощности источника питания и температурного изменения сопротивления обмотки возбуждения.
Как следует пз выражения (11.76), изменение коэффициентов Cj и Сг приводит к изменению крутизны регулировочной характеристики механизма управления.
Рнс 11.36. Зависимость крутизны регулировочной характеристики от величины тока возбуждения
11.36 приведены расчетные и экспериментальные кри-'* ''•'"’"’'oent/vrUIZU ПЯГППР-.сопло — заслонка», работающего сов-; омагнитом, в зависимости от тока возбуждения громагнита i, при различных значениях h3. При h3 = 1 см п3 = 1,8 см изменение крутизны регулировочных характеристик рабочем диапазоне изменения тока возбуждения довольно значи-‘	' л — чоирирнио минимально и зна-
р* ~Pl (ie) совпадают между собой в точках, соот-у- -	pup и 3R) в этом случае
На рис. 1..OV,	--- г_____
вые изменения крутизны регулировочной характеристики распределительного устройства «сопло - -------сов-
местно с электромагнитом, электромагнита 1в и Л- =	‘
В раиичем ДМапалипс	........
тельно. Однако при h3 = 1,4 см это изменение минимально
чения функции
ветствующих iemin й »впих (см. Рис- Н-36). В этом случае с;	,Cj______
лД’ ‘ C'd „ nd* CZd. .
—+ -^—	лас, 4 + ЛаСвРв
гДе С[ и С2 — значения коэффициентов Сй и Са при ia = (««ы
С|' и С2 — значения коэффициентов Q и С, при i, = 6 шм
ям
Поэтому
,а4 c;cs"-c[G 1/	’
| л С," - С, I	' ?)
Таким образом, выбор расстояния между осью электромагнита и осью сопел h, в соответствии с выражением (11.77) позволяет практически исключить влияние изменения тока возбуждения электромагнита на крутизну регулировочной характеристики механизмов управления.
Для вывода передаточной функции гидроусилителя «сопло — заслонка», работающего совместно с электромш нитом, восполь-

Рис. 11.37. Структурная схема распределительного устройства «сопло—заслонка», работающего совместно с электромагнитом
зуемся структурной схемой, приведенной на рис. 11.37, полученной на основании выражений (11.6), (11.67), (11.68) и (11.75), в предположении, что Сн = 0; F„ = 0; J„ — 0, поскольку трение и инерция заслонки ничтожно малы.
Проводя обычные структурные преобразования [58], получаем
U? (s) = А*— =_______,s> К'г <8) К'3 (s)	<s)	/II 7М
1 + W's(s, MZs(sl U/4(s)+ re(s) W', (s) U7,(s)’
где
898
ft7! (S) = K. = Cx; W2 (S) = _ ___________-
Wa(s) = Ks^=C^.
К»
c«’
; ^(5)=к4=с,^л>-,
^2 ’
т “4" "»’•
U7.(s) = -________K,_________ .
1 + 2C» f,s + 7'
F
С.4-2Л’ 2£б7в	1в-
^7(s) = /C,=^.£^k.
4 Qy
ftl
C4 + 2X *
После преобразований
I +Z’lS+*2'2 + *3Sa4-ft4S4 •
(11.79)
где
£Z ___
I _L IS ISIS
___________яС1С,Лэг/*р0
fc, - 2tBTB + 2^-1	= f ,
1 + KtK-tKt	C44-2Z,+
Zl I n2C»rf4Po 1	4C2
ci 16 (c4 + Щ "4С2 + лСвС/<;Л‘р(4 ’
_____П________I 2$a Ft (2t;6 ?c+AbA'oAT;)_
' 4" K2K3Ki I 4~ A'a/CgA^
IJ । FFa , n»C,d«p0F, ]
L 3 <G 4-	+ 16 (Ct 4- 21) Qv J
4
b^Ti
in
C4 -|- 2X L
(11.80)
X
l _ 27~27~B (^jlt 4- s«72i 4~ КъК3К,Т^ _
3	1 4” sKj
FJ, 4- mF, nC„rl,/>nl, 1________________4Ca________.
C4(C,4-21) l6C4 (C\4--’X) Qy ] 4С24-лС6С/сЛ»р0 ’
, Г| Г% ___________	4C-2rriJ, _______
°* “ I 4- KJ<3Kt ~ c2 (C4 4- 21) (4CS 4- лС^/ДЧ) 
Для практических расчетов двухкаскадных механизмов управления можно пренебречь инерцией и трением в электромагните, а также массой золотника и положить 7, = 0; J, = 0; m = 0.
Тогда ir2(s) = K2, ^<,(8) = -!^-:, ;7’в = с^21 и выражение (11.79) принимает вид
^-(’)=ттЬ-’
где
Т Т ' -L. Къ^еК,--------_______|_
‘ 6 + Т+А4А'зК4 4- 21 т t	n3C2Co^Vo__________
+4 (С4 4-21) (Л ОЦ. 4- лСеС,ДсЛ’р„) 
Для рассмотоенног; выше гидроусилителя = 0,035 кГ см.'ма, С2 = 11,7 кГ -см рад. h, -1,1 К, = 0,035 кГ -см.'ма; К2 = 0,1 рад, кг; К3 = 0,017 см3; Кь = 0,385 см3; К, = 0,14 см,кг; К Те = 0,01 сек; Кк = 0,053 см.'ма; Тк = 15,4 -1U
Для обеспечения необходимого быстродеист	г^[1М
управления параметры вспомогательного каскад _ образом, чтобы потребляемый им расход рабочей
ЗОН
(11.81)
при С] = см. получим = 567 кг см3. Kt = = 0,2 кг -сек'см3, сек.
„ q-l_4« от расхода, потребляемого золотниковым гидроуСИли. S? Qi = (0.35 - 0,45) Q„, поэтому в соответствии с выражением (11.60)	0-
0,028	(Н.82)
j Ро
а при р0 = И кГ!см* de = 0,015 KQi -
Дальнейший расчет гидроусилителя проводится при помощи выражения (11.77), в соответствии с рекомендациями на стр. 302.
Сопла и дроссели изготовляют из стали 40Х, закаленной д0 твердости HRC 32—38. Дросселирующие отверстия выполняют по 2-му классу точности, с чистотой V 7. Для обеспечения стабильности характеристик сопла и дроссели уплотняют резиновыми кольцами. Заслонки изготовляют из стали ЗОХГСА, закаленной т. в. ч до твердости HRC 40—45 Чистота поверхности заслонок V8.
Заслонку крепят на оси электромагнита и устанавливают строго перпендикулярно осн сопел. Начальный зазор х0 регулируют поворотом сопел, имеющих резьбовой участок. Величина зазора определяется по давлениям в междроссельных полостях. После регулировки сопла контрят контргайками. Возможность засорения сопел и дросселей исключается благодаря наличию фильтра на выходе из вспомогательного насоса.
§ 11.5. ДИНАМИКА МЕХАНИЗМОВ УПРАВЛЕНИЯ
Динамические свойства механизмов управления насосами переменной производительности при малых амплитудах входного сигналами наличии осцилляции с достаточной точностью описываются линейными дифференциальными уравнениями. При больших амплитудах входного сигнала начинает проявляться влияние ограничения производительности источника питания.
Динамика механизмов управления с электродвигателями без УвгюнениемТЛ 1*91 Cri РИС’ °писывается Дифференциальным беч пбпат “	’ ' Передаточная функция механизма управления
\™“ЙЗН С-УЧТМ выходног° каскада усилится, нагру-вателя, имеет ви^^ обмоткой электромеханического преобразо-
а?(8)	КуКв1
Т1 + МТГ-ПТЛТ ’	(11.83)
гателя и ор^^м^гул^ова^Гм133 МСЖДУ ВаЛОМ электРодвИ' Структурные схемы L./” производительности насоса.
рис. 11.38, где напряжение с«М0В такого ТИпа показаны на эффиадент усиления ?ахогенеп»топ^Ла^браТНОЙ Связн; К°с ~ К°' ния сельсина обратной связи- ? тора’ — коэффициент усиле-тора обратной связи. ’ 8 передаточное отношение редук-
810
Динамические свойства механизмов управления с электродвигателями и однокаскадными гидроусилителями (см. рис. 11.4) описываются системой дифференциальных уравнений (11.2), (11.35) и (11.39). Передаточная функция механизма управления без обратной связи записывается в виде
Ду (s)	KfKn>Ks
W <s> = W) = (1 + M (‘ + W1 + 2№ +	( 1
(см. структурные схемы на рис. 11.39).
Динамика механизма управления с позиционным электромагнитом и однокаскадным гидроусилителем без обратной связи (см.
№
а)
(t'JpS)S
Рис. 11.40. Структурные схемы механизмов управления с электромагнитами и однокаскадными гидроусилителями
?ик?1;571<?)о^ИСЬ1Вается системой ДиФФеренциальных уравнений ¥*_’ Им 1 ь’ пРичем в выражении (11,6) С„ = 0, FH = Fft, никя	~ Расстояние от оси электромагнита до оси золот-
ника. Ю1да передаточная функция будет
117 (<-) _ AY ГО _ ' ' А«/(з) ~
= _____________КуКв^ьКр
(' + Ту) (1 -I- 2tBfes	(11 -85)
(см структурную схему на рис. 11.40, а).
схема аналогичного меха'
однокаскадиого гидроусилителя ^“тояще|'0 из электромагнита и jig	механической обратной связью
СЛ=(C.+с.) Ф.+(F.+F,>	++J J a, +
где Сн — ^h'',
X — жесткость пружины обратной связи;
д0 — коэффициент обратной связи.
Структурная схема механизма такого типа приведена ня рис. 11.40, в, а передаточная функция
И «>- XV(S> -	К
К &U(s) (I -|- Tvs) il + b.^ + b^+b^' где
h —	4~ CH .
1 CHKPKO '
(IP + -C C) (C2 -J- CH)
-	CJ<pKo	’
C^r,rp+7;)(4 + Q.
°3-	C„KPKO
. rirp(C2 + CH)
CHKPKO •
Поскольку величины ТЛР, Т‘, Г,ТР невелики и их влияние проявляется на высоких частотах, для которых «^руже объемный гидропривод является фильтром, при проведении р тических расчетов выражение (11.85) можно записать
W/ /а Ду (s)_______________01 -86)
W7<S) = WJ

где
(Гр + 2£,О(С2 + См) ,
Cs + Си фа 
Структурные схемы механизмов	с ““Три™"м
и двухкаскадными гидроусилителями (  Р
представлены на рис 11.41 и 1L ’	функция механизм»
Как видно из рис. 11.41. а перед	свЯЭИ будг
с двухкаскадным гидроусилителем	Р
Ду (s)	...	.	А1 м
w (s) = Д77(5)=	+-₽
Для аналогичного механизма с жесткой обратной связью (рис. 11.41. в) передаточная функция записывается в виде выра. жения
KvKk~^Ks
.... Л у (s)	__"s________. _
и <s> =	= O + W’+W1 +	+ Tls”) ’
где /7j — расстояние от оси поршня первого каскада гидроусилителя до оси валика;
— расстояние от оси валика до оси золотника.
Рис. 11.41. Структурные схемы механизмов управления с позиционными электромагнитами и двухкаскадными гидроусилителями
В формулы для подсчета Кк и Тк следует подставлять диаметра золотника d диаметр поршня первого каскада d„
вместо
СТ₽УКТЕт^м7п“иХйУоРб:ГеИ2Я С	гидро-
« и пружинной обратной связью

ной связью приведена на* mic3Mi .У$’авления с пружинной обрат-
914	Р •	. 2 и составляется при помощи
«равнений (11 5), (11.35), (11.67)
(11.67) и (И.68) принимают вид
и (И.68), причем
Уравнения
п т _ Сб/’« л V nfl2p«c* л х nd" . b(p2~PJ — dc 4Qj,	4Qy-AV-
-^A(p2-p1) = (2X + C4)AX+Fd-^ + + tn —+ 2ХКоДу.
(11.88)
(11.89)
где dm — диаметр толкателя;
Kn коэффициент обратной связи между толкателем и органом регулирования.
Передаточная функция механизма управления
W (s) = &у Ф —
Al/(s)~
IF,, (s) VFj (s) VFS (S) IF, (it uz6 (si \F, (s) Wp (s)
= ц4Г^аи) UZJs) IF4 (s)J JI 4- Wets}Wp(s) VFe(s)]-|-lF6(sMFe(s)|W'7(s) + (Fp(s)Vr,W|’
где
U/8 (s) =/Cgs; fr8 =	; W, (s) = Ko = 2MC0.
После проведения элементарных преобразований получаем
Ч7 (s) = (l + TyS} (l +	+ м+,
Ку^КЛ
. 1 .
1 “ к,крк» + (i+WQа:.’
Т'е + Тр	КъКч
Ь'г = KiKpKt + (\+КгКМКРК,;
Тр Г . KtKtKi ]
/C^Ai'lTe+ l +
Поскольку коэффициент 63 невелик и его влияние проявляется на высоких частотах, то для практических расчетов можно пользо-
вался более простым выражением
К_________ (11.90)
(s) = (T+T^Hi+ajrs + r***)'
где
2ir тдаг+(ТтЙ8и^:
т, + тр
ЛГвАрЛв П 4“	’
Рис. 11.44. Зависимость крутизны регулировочной характеристики механизма управления с двухкаскадным гидроусилителем и пружинной обратной связью от температуры
-0.6-
Рис. 11.43. Регулировочная характеристика механизма управления с двухкаскадным гидроусилителем и пружинной обратной связью
механизма управлеии* с' nnv Фазочастотиь1е характеристики Хжии^ЖяаСКТЫМ гидр°ус*™ем и ирутиинои обратной связью
Рассмотрим в качестве примера динамические свойства механизма управления с двухкаскадиым гидроусилителем и пружинной обратной связью, имеющею параметры элементов, приводимых в качестве примера в предыдущих параграфах при условии что
= 0,7 см; К» 0,8 см; Kv = 50 ма/в; Ту = 3 - КН сек.
Раисе было получено Кг = 0.035 кГ  см; Кг = 0 1 МкГ К = = 567 кГ/см3; Ку 0,017 см3; К-а = 0,385 см'; Кв = 0,14'смкГ
= 0,2 кГ • сек см3; КР 39,3 Мсек-см; Тр = 1,5 -10"3 сек; Ть — 0,01 сек Затем вычисляем коэффициенты К„ и К„; Кв = = 0,16 кГ • сек/смг; Кв = 4,15 кГ, откуда К = 4,8 рад/в ; Т — 2ТК у |0'3 сек; £ = 0,95.
На рис 11.43 показана регулировочная характеристика механизма управления с двухкаскадным гидроусилителем и пружинной обратной связью, имеющего параметры, приведенные в примере расчета. На рис. 11.44 показан характер изменения крутизны регулировочной характеристики от температуры рабочей жидкости. Как видно из графиков, регулировочная характеристика линейна во всем диапазоне работы, имеет узкую петлю гистерезиса, а крутизна регулировочной характеристики мало меняется с температурой. Уменьшение крутизны регулировочной характеристики механизма управления при отрицательных температурах компенсируется увеличением крутизны характеристики электронного усилителя, сопротивление нагрузки которого (управляющей обмотки электромагнита) при отрицательной температуре падает.
На рис. 11.45 приведены расчетные (сплошные кривые) и экспериментальные (точки) амплитудно- и фазочастотные характеристики рассматриваемого механизма (совпадение расчетных данных и результатов эксперимента хорошее).
Глава 12
СНИЖЕНИЕ АКУСТИЧЕСКИХ ЭФФЕКТОВ И ВИБРАЦИИ В ГИДРОПЕРЕДАЧАХ
§ 12.1. АКУСТИЧЕСКИЕ ЭФФЕКТЫ РАБОТ МОЩНА ГИДРОПЕРЕДАЧ
Повышение мощности, быстроходности, давления и быстродей ствия, а также снижение веса и габаритов гидропередач, что является естественными тенденциями развития техники, привело к повышению уровня воздушного шума и вибраций в гидропередачах.
Испытание серийного образца регулируемого радиально-поршневого насоса завода народного предприятия «Гидравлик» в города Рохлиц (ГДР), работавшего на давлении в 100 кГ/см2 при 1450— 1500 об/мин с производительностью 56 л/мин (наибольшая произво дительность 100 л/мин при эксцентрицитете 8 мм), имеющего 12 поршней диаметром в 18 мм, позволило замерять уровень шума в 90 <36 [125], что соответствует уровню шума интенсивного уличного движения, мощного вентилятора или громкого крика на расстоянии 1 м.
Имея в виду, что гидромашины при увеличении мощности и, особенно быстроходности, повышают уровень воздушного шума и вибраций, становится ясной необходимость изыскания путей его снижения.
Воздействие воздушного шума и вибраций на человеческий организм повышает раздражительность, мешает сосредоточиться, приводит к энергичному расходу нервной энергии, существенной потере работоспособности, ослабляет внимание, замедляет реакции и поэтому приводит к травмам, а также снижает производительность труда до 40—60%. Вредные последствия шума тем больше, чем продолжительнее его действие, чем выше его уровень.
Высокий уровень шума свидетельствует об определенных дефектах рабочего процесса гидромашины, является косвенным свидетельством недостаточной надежности машины, имеющей поии-жегппИцоч^РС ^живУчесть)- Борьбу с шумом в гидропередачах в дн 11201 рассматривают в качестве важной социальной задачи.
в последние 7—8 лет появилось много сообщений, свидетель-
!!! 4 ° Том* что в основных капиталистических странах начаты и	П° снижению уровня воздушного шума и вибраций
повышАыиае^,аЧаХ АЛЯ повышення надежности, увеличения ресурса, роизводительности труда обслуживающего персонала 318
и ДЛЯ увеличения комфорта пассажиров мяпш» к гидропередачами.	р машнн- обслуживаемых
В 1958 г. на Конгрессе по промышленной г докладывалась совместная работа фИпм J1LГИДравлаке в США Виккерс 11271 п» создкнк.о	»
ным уровнем воздушного шума для аксиально „о г,0™жен-машин с двойным несиловым карданом РешениеРбылоЫХ ™Др0‘ при помощи регламентированных утечек через спр.^Т получено солирующие канавки Можно отметать, что те же поХГ ДР0С’ уровня воздушного шума для аналогичных, но бескарданиы? Гидро машин были применены Западногерманскими фирмами ГидроЯк Манесмен-Меер Н Ашвенрарск°й фирмой Айзенверке Кпус
США была опубликована работа [124], излагающая многочисленные мероприятия по снижению уровня воздушного шума и вибраций в гидропередачах и системах гидроавтоматики Во Франции в I960 г. выдано несколько патентов фирме Ситроен по снижению уровня воздушного шума в регулируемых аксиально-поршневых гидромашинах. В ГДР в 1961 г. была опубликована большая работа Института станков по снижению уровня воздушного шума в регулируемых радиально-поршневых насосах [125].
Образцы гидропередач, экспонированные в 1961 г. на Международной ярмарке в Ганновере (ФРГ), свидетельствуют о том, что дальнейшее повышение давления в гидропередачах приводит к созданию новых конструктивных форм основных элементов гидропередач — насосов и гидродвигателей, созданию новых методов расчета, к возникновению иных взглядов на их рабочий процесс [66]. Так, фирмы Бош и Урах (ФРГ) и Тоулер (Англия) предпочли отказаться от принудительного распределения, свойственного роторным гидромашинам и перешли на клапанное распределение быстроходных гидромашин, предназначенных для работы на высоких давлениях. Аналогичные взгляды имеются и в ГДР [125].
В последующие годы появился еще ряд работ, в которых анализируются различные особенности воздушного шума и вибрации гидропередач, описываются приспособления, снижающие эти эффекты и повторяющие основные принципы процесса, проанализированные в перечисленных работах.
§ 12.2. КРАТКИЕ СВЕДЕНИЯ ИЗ АКУСТИКИ
В самых различных явлениях природы приходится сталкиваться с возникновением колебательных явлений. Непрерывность материи приводит к -тому, что колебание одних частиц вызывает колебательное движение соседних с ними, т. е. приводит к распространению колебательного движения с какой-то конечной скоростью.
Исследованием процесса распространения подобных колебании занимается наука, называемая акустикой.
Копебатопьное движение оценивается частотой, причем колейн^ секунду называется частотой в герцах и обозначав бУКн2датоя на большое развитие акустики, ею задачи разрешаю^ в предположении малых амплитуд колебании, но с учетом сжимае. мести среды В этом смысле акустику называют газодинамикой малых амплитуд, которая в большей степени развита примени, тельно к газам и в меньшей степени к жидким телам, особенно находящимся под воздействием высоких давлении. Вот почему следует проявлять осторожность при переносе выводов, полученных в акустике на основе решения волнового уравнения, к явлениям в которых используются жидкости, особенно столь сложные, как рабочие жидкости гидропередач, а также в тех случаях, когда амплитуды колебаний не могут считаться малыми.
При помощи приборов при правильно поставленном эксперименте можно дать объективную оценку колебаний, пользуясь абсолютными величинами.
Поскольку колебания определенных частот и определенной силы могут ощущаться человеческим ухом, приходится помимо объективных единиц, оценивающих колебания, применять еще и относительные единицы, связанные со свойствами человеческого организма и человеческого уха.
Очевидно, что такие относительные единицы носят субъективный характер, определяемый физиологическими и психиологиче-скими свойствами человеческого организма. Эти единицы достаточно точно позволяют замерять объективные явления природы, существующие вне нас.
Неправильно было бы делать вывод о том, что если ощущение определенных колебаний есть свойство человеческого организма, то эти колебания существуют только в ощущениях человека. Просто человеческий организм является прибором, могущим проводить замеры и имеющим определенную «полосу пропускания». Что же касается того обстоятельства, что единицы измерения определяются свойствами применяемых при замерах приборов, то с этим приходится встречаться во всех областях техники и во многих областях ”зу,ки- 1<7?ОВе1^^С^ое Ухо спос°бно воспринимать колебания с часто-епчпям^ Д° 6	20 000 гц, если эти колебания достаточны для
”У,<0“ГО МЮе™”' Такие КИ|аба™Я “
a kSJkw’ таеХТсвыше 2oS'> ”азывают<:’ »ифразвуко№ Вся облягтк	выше zU ООО гц называются ультразвуком.
частот охватывает кол^ания^	ТРИ 3°"Ы- 3°На
от 500 до 1000 гц н зона высокL .° Д 500 г,Ц' 30113 сРедних часТ0Т
Интервал ча^ в ЧаСТ0Т ОТ 1000 до 20 0°0 гЧ-другой, соответствует олнлй₽г>М °ДНа гРаница вдвое отличается от одна граница отличается от доугой^еа«ННТерВаЛ частот’ В КОТОр°М и от другой в десять раз, соответствует декаде.
Рис. 12.1. Субъективная высота тона в мел
Свойства человеческою уха таковы, что ощущение звуков паз ных частот воспринимается по-разному. Увеличение частоты при низких частотах легче различается человеческим ухом, нежели изменение высоких частот. Поэтому была установлена субъективная высота тона в мелах, выбранных так, чтобы количественное изменение высоты тона, выраженное в этих единицах, соответствовало количественному изменению ощущения органов слуха человека, т. е. субъективно дающих линейную шкалу изменения высоты топа. Для установления этой шкалы высоту тона частоты в 1000 гц приняли равной в 1000 мел, а затем шкалу соответствия этих новых единиц частоте в герцах деформировали так, чтобы изменение высоты тона в мелах соответствовало количественному изменению ощущения высоты тона органами слуха.
На рис. 12.1 показана зависимость между субъективной высотой тона в мелах и частотой в герцах в логарифмическом и линейном масштабах. Пользуясь этой шкалой, можно оценить, во сколько раз звук заданной частоты имеет более высокий или более низкий тон с точки зрения субъективного его восприятия человеческим ухом.
В основе современной акустики лежит волновое уравнение, которое получается в ре
зультате совместного решения трех уравнений: движения, неразрывности среды и деформаций.
При выводе волнового уравнения делаются следующие до у-
щения:
1) движение безвихревое;	л , п
2) возникающие деформации среды малы, а связь между деформациями и напряжениями, их вызывающими, динеина (закон ГуК3))’среда однородна без перехода вещества из одной фазы в другую;
I	«ЙСТ»У«Я на сред» только через ее границы.
7) объемные силы в среде отсутствуют,	„лемеии
8) скорости как постоянные так и	РД^
а также их градиенты должны быть малы (п р ростями распространения звуковых колебании).
И В Н. Прокофьев и др-
Волновое уравнение записывается в одной из двух следу^
форм:	()2ф с2Дф=-^!-	(12.1)
или	д"р =	(12.2)
1 г v- _скорость распространения звуковых полн;
рх — модуль объемной упругости среды;
р — плотность;
Дф — лапласиан потенциальной функции скорости;
t — время;
Др — лапласиан давления.
Волновое уравнение свидетельствует о том, что при отличии в некоторый момент времени давления pj в любой точке от давления рг в окрестностях этой же точки величина рх изменяется, приближаясь к величине р2.
Применяя волновое уравнение для случая движения плоской волны, т. е. такого движения, при котором изменение состояния происходит только от одной плоскости к другой (в каждой точке рассматриваемой плоскости вектор скорости к ней перпендикулярен), получим скорость распространения упругих колебаний.
Интегрирование волнового уравнения дает зависимость между давлением р и скоростью движения частиц среды щ;
p = pci’i,	(12.3)
причем давление при любой форме импульса пропорционально скорости частицы среды и находится с ней в одной фазе.
Расстояние между двумя соседними точками, находящимися в одинаковой фазе (речь идет о периодическом процессе), называется длиной волны X.
Если частота / импульсов в герцах (число колебаний в секунду) и длина волны каждого импульса X, то
kf=c
(12.4)
X Т ’ где Т = j период импульса.
Свя'зь^ме^^'Тп Час3°та> тем коРоче длина волны, и наоборот. n'Sa^a^X ?2%В0ЛНЫ И В ГеРцах РазНЫХ называемым Хо°вымКтамбЛ^Ты2ВИЖеНИЙ ПОЛЬЗ*ЮТСЯ ТаК тлим к, которым называют ь____________________2л w
~ X ~~• • де ю — nf — угловая частота колебаний 822
(12-5)
Волновое число — вектор, имеющий направление скорости распространения звука с.
Очевидно, что последняя зависимость имеет смысл для гармонических колебаний, имеющих угловую частоту колебаний <о постоя II ной.
Так как величина давления р (уравнение (12.3)1 колеблется в соответствии с колебанием скорости щ, то можно рассматривать наибольшее давление (иногда его называют амплитудным)
Ра ~ или эффективное давление
(12.6)
Pf	у 2 Р°'
Под эффективной величиной любого переменного параметра понимается величина равноценного ему по энергии и постоянного во времени параметра.
Энергия, проходящая через единицу площади плоской волны в 1 сек, называется интенсивностью звука
J= Л
рр р J PVS dt  о
В случае гармонических колебаний
> (VsaPa)
Рис. 12.2. Связь между длинами волн и частотой для разных сред
или после подстановки vsa из равенства,(12.6)
J-lPp°e (12.7)
Интенсивность звука является векторной величиной, впервые полученной
в 1874 г. русским физиком	.
Умовым (вектор Умова). Она измеряется в эрг слт-сек или в вт
При использовании эффективного давления р, вместо амплитудного значения давления (уравнение (12.6)1 получим г —	= (vsy рс = pt
(».•)
₽<'
В дальнейшем при оценке интенсивности звука или сиыы будут использоваться эффективные значения давления и <л©;
.о AvnvT записываться без индекса е. Чаще всего величии, которые бУд>т Оцецивается в барах (принято до появле " chwmh CM), т е. в динах на квадратный сантиметр (1 кГ
* Итак^силой звука называется количество звуковой Эцерп1|1 пвоходяшей в 1 сек через поверхность сечения плоской волны в 1 Сл?’ "величину pc = R называют удельным акустическим сопрот,1|ь пением или сопротивлением изучения среды, поскольку для непрерывного излучения звука требуется непрерывный подвод энергии которая тратится на передачу колебательного движения новым порциям среды. Измеряется в акустических омах (акусти-ческий ом — сопротивление, при котором сила в I дн вызывает скорость в 1 см!сек).
Значения р, х, с и /? = ре для некоторых сред приводятся в табл. 12.1, причем для стали, латуни и свинца приводится скорость распространения продольных упругих колебаний в стержнях.
Таблица 12.1
.Материал	р в г/см*	« в д/см-	с в с it/сек	Л’ = рс г.си-сек
Воздух при 0“ С и 760 лл	1,29- 10-’	1,43- 10»	3,33- 104	43
рт. ст.				
Воздух при 20" С и 760 лл	1,20- 10-’	1,43- 10°	3,43- 1 О’	41
рт. ст.				
Водород при 0 С и 760 лл	0.09  IO*’	1,43. 10®	12,6- 104	11
рт. ст.				
Углекислота при О' Си 760лл	1,98  10~«	1,43. Ю8	2,58  104	51
рт. ст.				
Дистилдирован-ная вода при	0.999	2,04- Ю1®	1,43  105	1,43- 10s
Морская вода при Ю'С	1,03	2,32- 10,и	1,5 - 10®	1 5 . j Q5
Минеральное пасло при 20' С Ртуть	J,85—0,92	П,6—1,8.5). iqio	(1,2—1,44) . 10я	(1,2—1,45)  10®
Этиловый спирт Сталь Латунь Свинец	13,6 0.79 7,8 8,5 Н,4	25,6 • Ю1с 1,3 • 10'® 1,8- Ю,а 1,05- Ю1г 0.5. 10’»	1,46- 101, 1,18- 10® 5,05  10® 3,42. Ю® 1,2-10®	19,8 • 10® 0,93 • 10® 39.3 • 10® 29,0- 10® 13,7- 10®
SB^"Ka-™np««XpTH"a S™" колеба""й л«	’™"^рТвю3втеу™°”?овод -«“ s: Ж	’ «аических усов				в ЖИДКОСТЯХ ность, тепло-не, происхо-ьемной упру-иях. Именно
поэтому говорят об адиабатическом процессе сжимаемости жидкости, отличая соответствующее значение х от хст, полученного в статических условиях (изотермический модуль объемной упоу гости).	J
Рассмотрим различие в параметрах звуковой волны для разных сред Пусть пластина разделяет воду от воздуха. Если пластина придет в колебательное движение, то опа может стать источником звуковых колебаний, причем скорости среды по обеим сторонам пластины будут одинаковы по величине. Поэтому, пользуясь равенством (12.8), можно записать
/?1 = ipc), /?2	(р<-)2 ’
где индексы 1 и 2 соответственно относят величины к воде и воздуху. Пользуясь числовыми значениями табл. 12.1, можно записать
= I , <_1° = 3490, /•>»	43
т. е. при одной и той же скорости движения частиц среды давления в воде будут в 3490 раз больше. Очевидно, в этом случае сила звука по одну и другую стороны пластины будет разная.
Если же в тех же средах распространяется звук одной и той же силы, то из того же уравнения
£• = 1/А = 1Л££к =	= 58,3,
рг V Яг I (рс)2 V 43
т. е. при одной и той же силе звука звуковое давление в воде будет в 58,3 раза больше, чем в воздухе.
§ 12.3. ПОВЕРХНОСТЬ слышимости
Высота простого звука (гармонические колебания определенной частоты и силы) или простого тона (иногда основного) / в гц и сила звука J в эрг/см2 - объективные показатели звуковых коле-бЭНДля того чтобы человеческое ухо могло воспринимать звук, необходима не только определенная частота но должна быть еще достаточная величина звукового давдени . Наименьшая величина мости, зависит от высоты тона и при f = 1000 гц достигает шего значения в 2-10 4 бар.	нижний порог
Значение звукового ДавлДния ^Р^™^ентальиым данным слышимости, зависит от частоты олъем порога слышимости на Мансона [99] приведена на рис. 12.3 Подъем1 порог;
низких частотах и в меньшей степ^ ппганизма в течениг многих татом приспособляемости человеческо> р	ческог0 уха при
поколений. Понижение чувствительности челове
следствие защиты слухового аппарата От низких частотах J^ ^биения, кровообращения и физиологи^ шумовых эффек ческого тела.
скпх колебаниН Уморительность человеческого уха и при высоких
Понижается чувств	чТО если бы при высоких частотах
частотах. Скучик U неизменной, то ощущались бы колеба-чувствительность он ( что соответствует сотой части диаметра 11НЯ с амплнтуДО» в • сл	всегда были бы Под воздействием
атома. В этом,слу	1 ким движением молекул воздуха.
Ш’'при ^..чении силы звука наступают болевые ощущения, Опре. дел^	~етси —р—
ель—™, на которой нанесены кривые одинаковых слуховых °Ш Шкала L Уровня громкости основана на законе Вебера - Фех-неоа по которому чувствительность человеческого уха пропорцио-наль'на логарифму силы звука J, не завися от первоначального уровня и тона. Таким образом, субъективное ощущение одинаковости повышения силы звука соответствует возрастанию силы звука (или звукового давления) на одинаковую величину
(12.9)
откуда
L=a\np-.	(12-10)
Ро
Если в последнем равенстве принять а = 1, то величина L будет измеряться в неперах.
Если положить а — 20 1g е, то
L = 201gA = ioig(-£ У = 101g	(12.11)
Ро	\Ро /
и уровень громкости звука будет измеряться в децибелах.
Соотношение между децибелом и непером определяется выражением
1:201g е = 1:8,68.
или 1 иепер равен 8,68 Об.
И децибел и непер — относительные единицы, определяющие не абсолютные значения громкости, а различие в громкостях. В качестве нулевого звукового давления обычно принимается порог слышимости, для которого громкость принимается равной нулю.
Несмотря на то, что и децибел, и непер — относительные еДИ-*“^иизме₽ени.я- °ИИ явлиются объективными единицами, незавй-™ °₽ганов слУ*а- нач^о отсчета этих еЖ ИТГОМ ““шимости, является величиной субъ-шнвнм (точнее, субъективно выбранной).
Я -
На самом деле закон Вебера — Фехнера неточен. Уже ранее приходилось встречаться с тем, что чувствительность органов слуха человека при разных силах звука, не говоря уже о разных частотах, различная. При высоких, и особенно при самых низких, чувствительность понижается.
В качестве примера можно указать, что при средних частотах громкость звука в 50 дб над порогом слышимости примерно соответствует громкости тихой речи. Зато при низких частотах громкость звука в 50 до над порогом слышимости вызывает болевые ощущения. Вот почему пришлось ввести субъективные единицы
Рис. 12.3. Поверхность слышимости
уровня громкости в Ф°,,ах пР“сП°2°зЦ^анкень1 Х"ы°Х: ^ни7уровня°гГромХкаости звука на поверхности слышимости по опытам Флетчера и Мансона.	гпг,МИОгти на пис 12.3 по-
Линии Равных ощущении уровня П>омко^
строены через 10 дб при частоте / =*	4- тем же ьоличе-
линии уровень громкости звука оценивается од	ровшо гром-
ством фонов, которое при частоте / = 1000
кости в децибелах и не равно при » гвомкости в объектив-
Следовательно, чтобы оценить УР восп0ЛЬзОваться экспериментах единицах — децибелах, нуж	/рис. 12.3), на кото-
тально полученной поверхность! VDObhh громкости всубъек рой нанесены линии равных ощущении уровня iPom тивных единицах — фонах.
100 фон
от 110
Можно нязоатк	Считается, что
кости звука - И» «“	’ ганяэмом посредством оценки Ко.
“?Х«”Импульсов. поступающих в мозговые це„тры B 'rZ— звука » « П» гоответс 1ВуеТ 1000 верим	“еоответствует поступлению одного
nynSTl «к « воспринимается как уровень громкости звука „а Хз”"1!""''™ может бить произведена по шеста укрупненным шумовым группам.
’ 1) тишина — уровень громкости от 0 ДО 30 фон (от 0,001 до °'4 2)Р°слабъш шум —уровень громкости от 40 до 50 фон (от 1 до з/'умереннын — уровень громкости от 60 до 75 фон (от 4 до 4) громкий шум — уровень громкости от 80 до 90 фон (от 18 до 40 гро);
5) очень громкий шум — уровень громкости от 90 до (от 40 до 90 гро);
6) оглушительно громкий шум — уровень громкости до 130 фон (от 200 до 1200 гро).
Определенное представление об ощущении различных шума и шумов каждой из перечисленных шести укрупненных шумовых групп дает содержание табл. 12.2.
Воздействие шума на человека зависит от очень многих причин и не всегда носит объективный характер. Отмечено, например, что работающим на шумных аппаратах шум мешает меньше, чем у занятых рядом работой на машинах, уровень громкости шума которых ниже.
Считается, что шум с уровнем громкости ниже 40 фон не может вызвать раздражение здорового человека.
приятны*0	громкости в 40—70 фон может при неблаго-
тельного отпых^ИЯт ВЫЗвать Усталость, которая потребует дли-продолжительным choT уСТаЛ0СТЬ 061514110 снимается глубоким 70 фонов может^ри^сти^к '//Ма С уровнем громкости свыше ниям слухового аппарата Хот Ъективн0 констатируемым пораже-к длительному воздействию организм и может приспособиться лишь за счет потерь чувствитрп^?13 таКого Уровня громкости, но
Шум с уровнем громкости ЯпЛол?! К любым иным шумам, утомляет и раздражает	96 $Он при Длительном действии
солее высокие vixm*
Мьццаы сРеДнего уха что связано0/7 ВЫзвать судорожное сжатие В	ВЯ8аН0 с 1ютсрей чувства равновесия.
уровней
Таблица 12.2
Уровень громкости звука		Характер и источник звука, слуховой порог
в фонах	в гро	
0-10 10 20 20 20 30 30 30—40 40 40—50 40 50—60 60—65 60—70 70—75 70—80 80 80—85 80—90 90 90—95 90—100 100 100—110 110—115 110—120 120—130 130—140 Более 140	П.001—0.01 0.01—0,1 0.1 0.1—0.4 0,4 0,4—1,0 1,0 1 2 2 2-4 4—6 4-8 8—12 8—18 18 18—28 18—40 40 40—65 40—100 90 90—200 200-320 200—500 500—1200 1200—3000 Более 3000	Пирог СЛЫШИМОСТИ Шум листвы, шум слабого ветра Ход карманных часов на расстоянии 1 .и Шепот на расстоянии 1 м Читальня, тихая квартира Очень тихая музыка (по радио), шум в жилых помещениях Шепот на расстоянии 0,3 ,« Шум в комнате с окнами на улицу Разговор в полголоса на расстоянии 1 м Тихая речь Разговор средним по громкости голосом на расстоянии I м Громкая речь на расстоянии нескольких метров Средний уличиый шум при оживленном движении, машинописное бюро Воспроизведение музыки громкоговорителем, шум в цехе с работающими металлорежущими станками Громкая речь на расстоянии 1 м, аппаратные телеграфа Шум проходящего на расстоянии 1 м грузового автомобиля, станки-автоматы Шум интенсивного уличного движения Громкий крик на расстоянии 1 м, мощный вентилятор Вагон метро, автоматно-револьверные цехи Шум в большом заводском сборочном цехе, машинное отделение на судне, мотоцикл без ГЛ Лесопильные цехи, шум в кабине самолета Оркестровая музыка (фортиссимо) Пневматическая клепка листового металла, шум пневмодвигателей без глушителей, быстро Х°Шум Работающего пневматического инмру-МеШум на расстоянии 3 м от работающего вит. самолета, порог болевого	игатеяя м Шум работающего реактивного двигателя * расстоянии 1 м от сопла (сбоку) Р Шум работающей ракетной установки стоянии 20 м
раздражающее действие шума связано не только с уровнем гРом. ^вы^	р^’наТЕ’вТ -
вы=да^ ° *~р;
В 1000 гц совпадает со шкалой уровня громкости звука в д * белах является в последнем случае шкалой субъективных ед„НИ1 измерения и, к сожалению, нелинейной шкалои из-за того, ЧТо закон Вебера — Фехнера о чувствительности человеческого уха очень грубо оценивает его свойства. Для получения линейной шкалы измерения уровня громкости звука введена субъективная
единица—сон, масштаб которой выбран так, что увеличение уровня громкости звука в сонах в одно и то же число раз дает субъективное увеличение громкости звука в то же число раз, во-первых, и, во-вторых, уровень громкости звука в 100 фон соответствует уровню громкости в 100 сон.
На рис. 12.4 показана сплошной кривой зависимость уровня громкости звука в сонах от уровня громкости в фонах над порогом слышимости по Черчеру 1121]. Там же пунктиром показана связь между теми же единицами по Флетчеру 1122].
Два наиболее важных параметра, носящих объективный характер и не зависящих от выбора начала отсчета времени, — ампли-и частота / МОГУТ оценивать фон и силу звука, и в плоскости ото?™РГГ'ИКИ ЗВуКа изобРажаются точкой С (рис. 12, 5, а), причем ^Уппугир ДЦГИВаеТ амплитУдУ колебания, а ОС — частоту, ются причиной то* ЯВЛЯЮ1цегося источником звука, явля-. что в практике приходится сталкиваться 8»
(12.12)
Рис. 12.6. Спектр колесаний
с одновременным существованием ряда простых звуков, при ко торых колебательный процесс описывается равенством
Д< sin (2njft + ф(),
где Y — отклонение частицы среды;
t — время в секундах;
/ — любое целое число;
А — амплитуда;
Ф — фаза колебательного процесса в момент начала отсчета времени.
В зависимости от значений параметров составляющих А, и А звуков их графическое изображение на плоскости характеристики звука, называемое спектром звука, может носить различный характер. Так, на рис. 12.5, б показан линейчатый (или дискретный) спектр звука, в котором между частотами отдельных составляющих простых звуков имеются значительные интервалы. Такой характер имеет, в частности, спектр человеческого голоса, тембр которого определяется определенным сочетанием параметров составляющих звуков.
Совокупность звуков стых фонов со случайными пределениями частот и фаз i зываются шумом.
Простые звуки, частоты I торых кратны друг другу, : зываются гармониками.
Сплошная спектрограмма
про-рас-на-
ко-на-
с.плишпал Luvn.p.w, .._ .j__ г	12.6, Д
обладает тем свойством, что интервалы между частотами соседних составляющих звуков простых фонов бесконечно малы. Такие спектры шумов возникают, например, при соударении большого числа твердых тел.
Если амплитуды составляющих звуков простых фонов одинаковы, а спектрограмма шума является сплошной в достаточно большом интервале частот, то такой шум называется белым шумом по аналогии с соответствующим оптическим термином.
Интенсивность шума в заданной полосе частот от ft до определяется равенством
шума, показанная на рис.

(ft 131
ГЛР Т _ спектральная плотность интенсивности шума. которой
Л чывают отношение интенсивности составляющею прост звука к соответствующей ему ширине полосы частоты Д /
Очевидно, что для белого шума /, (/) const, а интенсивность белого шума - среднее значение белого шума.
В машиностроении очень часто приходится сталкиваться со смешанными спектрограммами шума (рис. 12.6, б).
Для получения спектрограммы воздушного шума необходимо после записи осциллограммы Z = Л (/) осуществить ее гармонический анализ, позволяющий по осциллограмме найти значения амплитуд (обычно звуковых давлений р„) и частот для каждого из составляющих простых звуков. Такое нахождение осуществляется специальными акустическими анализаторами.
Таблица 12.3
Класс шума	Характеристика класса	Допу< Тимый уровень громкост.1 в фонах
1 (особо низкочастотные)	Наибольшие уровни шума в спектре ниже частоты 60 гц, выше которой они понижаются не менее 5 дб на каждую последующую октаву (шумы в легковых автомобилях)	100
2 (низкочастотные)	Наибольшие уровни шума в спектре расположены ниже частоты 350 гц с понижением на более высоких частотах (шумы тихоходных машин неударного действия, шумы, проникающие через звукоизолирующие преграды в виде стен, кожухов и перекрытий)	90
3 (среднечастотные)	Наибольшие уровни шума в спектре, расположенном ниже частоты 800 гц, выше которой они понижаются (шумы большинства машин и агрегатов неударного действия)	85
4 (высокочастотные)	Наибольшие уровни шума в спектпе расположенном выше 800 гц:	’ а) с понижением уровней на частотах повышающихся от 1600 гц-поГ™ГНИем Уровней «а частотах, повышающихся от 4000 гц	80 75
----------------- --------I_____________1
шума.ЗАеИСТВИе ШУМа Иа человека существенно зависит от спектра
332
Редкие, но громкие импульсы более неприятны, чем непрерывно девствующий шум Особенно раздражающе действуют высокие звуки Поэтому уменьшение звуков высоких тонов в спектре шума приносит большое облегчение
В зависимости от характера спектра шумы разделяются на четыре класса, характеристика каждого из которых с указанием допустимого уровня громкости в фонах приведена по материалам Славина 1991 в табл 12.3.
Имея в виду, что шум должен оцениваться частотой тона с наибольшим уровнем громкости, обязательным падением уровня громкости (не меньше, чем на 5 дб на 1 окт) на более высоких частотах п соответствующим допустимым уровнем громкости, как это следует из табл. 12.3, можно оценивать допустимый уровень громкости при помощи графика, показанного на рис 12.7 по материалам Славина 1991.
Рис. 12.7. Понижение уровня громкости
, сплошная линия на этом графике соответствует• опре-допустимому уровню громкости по отношению к спектру азмещенному слева от этой линии. Так, на этом^ р Ф пунктиром спектр шума, для которого допустимый уровень
Хен™ ЗЫКОВЫХ волн папьзуются плотности потока звуковой энерги , РУ
Хенне “пропорционально :а, поэтому звуковое давление определяется средним квадратичным из . твлении каждою .><. —--- 	источников
те
Каждая
деленному допустимому у|Жтз, .рт--„я чтом гоаФике
шума, размещенному слева от этой линии. Так, на этом р показан i	'
громкости равен 80 фон.	----
При на----
сивности звука и излучает источник звука
Звуковое  I интенсивности звука источников звука < . новых давлений каждого из	ух источников игуш.
При подсчете уровня ;р°“К“7оот^енио равны 4, * U
. / в децибелах (рис. 12.8) в зависимость !ГЛВ„,	Л ^„ВГОГ1| д L _ I, - L.. .. тогда
” I”’"0"" ”	(12.Ц,
„ гх ммировать уровень громкости нескольких истец.
ЕсЛ" Тто нумеруют их в порядке убывания величин ур0Вней ников шума, то
громкости
о пппсчета L первых двух источников шума проводят Сум. п после подсч ' 0*г0 ,,р0ВНя громкости £, источника, ЭКВ|1. вМХтноД первым двум источникам шума с уровнем громкости третьего источника шума и т. д.
Разность уровней еромкости
Рис. 12 8 Прирост уровня громкости
Можно также при суммировании уровней громкости двух источников шума пользоваться табл. 12.4. В этой таблице подчеркнут случай суммирования двух одинаковых источников шума. В этом
случае суммарное звуковое давление будет больше звукового давления одного источника на 41%, а уровень силы звука повысится наЗдб. Соответствующие значения в табл. 12.4 даны жирным шрифтом.
Из рассмотрения табл. 12.4 вытекают два вывода:
. Использование шкалы в децибелах весьма удобно из-за того, что встречающийся в природе Диапазон интенсивности звука от Т„Л“НЫХ Туков до ОглУшительных (более сильных во много миллиардов раз) размещается в диапазоне от 0 до 140 дб смь1ЫГРучитыМватГ°иетпИ ЗВук0В нескольких источников не имеет источника с наибольшейНИКИ’-СИЛа звука которых отличается от
0РГа'
нении звуков с разныадспектп^и1 возмо>кных ошибок при срав-мость арифметического сложрнм о ’ указать на недопусти-звуков шума, выраженных и УРовнеи громкости составляющих ьагься только для ^HHeap ^0Hax- которые должны использо-8М	еаризации» масштабной шкалы уровня гром-
человека. °ТИОШе,,И1° К Субъе™<ым	органов
слуха
Таблица 12 4					
Разность уровней силы звука AL п	Отношение сил звуков Л Л	Отношение звуковых давЛенин Р1 Ря	Разность уровней сипы звука Д/. п дб	Отношение сил звуков । Л Jo	Отношение звуковых давл нин Pi Р2
0 0,5 1 2 3 4 5 6 7 8 9 10 II 12 13 14 15 16 17 18 19 20	1.00 1,12 1,26 1,58 2,00 2,51 3,16 3,98 5,01 6,31 7,91 10.00 12,60 15,8 20,0 25,1 31,6 39,8 50,1 63,1 79,4 100.0	1,00 1.06 1.12 1,26 1,41 1,58 1,78 2,00 2,24 2,51 2,82 3,16 3,55 3,98 1.47 5,01 5,62 6,31 7,08 7,94 8,91 10.0	21 22 23 24 25 26 27 28 29 .30 46 50 60 70 80 90 100 НО 120 (	130 140	126,0 158,0 200.0 251,0 316,0 .398,0 501,0 .3.31,0 754,0 10' 10' ю-10" 10’ 10" 10“ 10*" 10" 10'* 10” 10“	11,2 12,6 14,1 15.8 17,8 20.0 22,4 25.1 28,2 31,6 101>.0 316,0 10" 3.16- 10’ 10* 3,16- 10* 10- 3,16- 10s 10“ 3,16- 10“ КУ
Субъективное ощущение уровня громкости воздушного шума органами слуха человека может сопровождаться раздражающим влиянием на его организм. Объективная оценка уровня неприятности ощущения звука не существует, хотя субъективная количественная оценка уровня неприятности звуков была проведена в тридцатых годах Лэйрдом.
Количественная оценка уровня неприятности звука осуществляется нанесением линий равного раздражающего действия на плоскости «уровень громкости (в фонах) — частота (в герцах)», как это показано на рис. 12.9 по материалам Паркинсона [1261.
Опять за исходные точки оценки уровня неприятности звука приняты уровни громкости через 10 дб при частоте в 1000 гц.
Можно заметить, что человеческий организм с меньшим раздражением воспринимает звуки низких частот, чем высокочастотные звуки. В этом случае можно раздражающее действие звука оценить разностью ординат линий равных уровней громкости и уровней неприятности звука, имеющих одно и то же число фонов при частоте в 1000 гц. Очевидно, что в этом случае превышение ординаты линии равной громкости над линией равного уровня
999
разных частотах, но и при разных уровнях громкости звука, как это показано на рис. 12.10 для уровней громкости звука в 30, 60 и 100 фон.
Также по-разному воспринимаются организмом человека вибрации, которые, кроме всего прочего, являются еще источниками воздушного шума.
1ш(!!х™ВиТМ' .11281 сУществУют шесть степеней воздействия йена в тяб/ ?Р'?НИЗМ человека, характеристика которых приве* дхпд и 1аиЛ. 14.0.
На рис. 12.11 дана оценка амплитуды вибрации в мм в соот ретствни с материалами табл. 12.5 для разных частот в гц причем частоты обычно не бывают большими из-за значительных масс колеблющихся узлов машин.
При оценке вибрации пользуются колебательной скоростью вибрирующей поверхности v„ в см/сек, а способ оценки такой же. что и Для звука при помощи разности логарифмов оцениваемой скорости вибрации и пороговой скорости вибрации. Если в качестве пороговой скорости вибрации принята скорость в 0,031 см/сек, то уровень вибрации будет выражен в палах:
Рв = 20 'g ( 3 | . Щ-2
(12.15)
По Анциферову вибрация замеряется в децибелах над порогом в 5-10 *’ см/сек. Этот порог соответствует порогу слухового восприятия и позволяет
Заглушение одного звука другим называется маскировкой. Маскировка звуков происходит вследствие повышения порога слышимости под воздействием звуков на органы слуха.
Маскирующий зв\ к любой тональности повышает порог слышимости не только для частоты маскирующего звука, ио и для соседних частот в достаточно широком диапазоне, как это показано на рис. 12.12 для простых тонов с частотами 200, 1000 н 4000 гц по Флетчеру [122].
Повышение порога слышимости зависит не только от уровня силы звука, но и от частоты простого тона.
Наибольшее маскирующее действие оказывают при достаточном Уровне силы звуки простого тона низкой частоты, причем в больше
степени заглушаются звуки более высоких тонов и в меньшей степени — звуки низких тонов.
Частота наскируеного тона
Рис. 12.12. Маскировка звуков
Простые звуки высоких тонов поднимают порог слышимости в более узкой полосе частот и практически не заглушают звуки низких частот.
Х'.ТЛ.*" ШУ“	шириной
""'Критической шириной полосы частот называют такую полос-v частот белою шума А/, увеличение ширины которой не приводит К маскировке чистого тона размещенного в центре расеХои васмой полосы	•
Критическая ширина в децибелах представляет собой 10 lg Д/ ,10 отношению к 1 гц, а в герцах - А/ в виде ширины полосы Значения критической ширины в децибелах и герцах показаны по Флетчеру на рис. 12.13. Ширина каждой такой полосы равна количеству децибел, на которое простой тон должен быть поднят над уровнем белого шума, чтобы быть слышимым.
Для заглушения простою тона маскирующий шум должен превосходить его па 15—25 дб. При очень больших уровнях звука (до 1Ю—фон) по Славину 1991 эта величина опускается до 5—Ю дб.
Вместе с тем для шумов и тонов, близких по частоте, взаимная маскировка создает впечатление меньшей громкости. В этом случае общая громкость меньше суммарной громкости, полученной при помощи приемов, рассмотренных выше. Поэтому при подсчете общей громкости следует учитывать эффект маскировки.
§ 12. 4. УСЛОВИЯ ЗАМЕРА ВОЗДУШНОГО ШУМА РАБОТАЮЩЕЙ МАШИНЫ
Идеальные условия дня определения уровня воздушного шума и вибрации могут быть получены только при проведении испытания машины в специальной акустической камере, которая должна создать условия изоляции от воздушного шума и вибраций, проходящих извне и поглощать, но не отражать звуки, создаваемые в этой камере испытуемой машиной.
Только при выполнении этих условий можно рассчитывать на высокую точность замеров, особенно необходимую при выяснении причин возникновения шумов и вибраций в машинах.
Чаще всего приходится сталкиваться с необходимостью исследования машины, которую по каким-либо причинам нельзя установить в подобной акустической камере, как это и было в исследованиях Клауса 11251 в ГДР, и тогда приходится проводить испытания в обычных условиях эксплуатации машины или условиях лаборатории.
Для получения в достаточной мере объективных данных испытуемая машина должна быть установлена на амортизаторах, связана с приводными двигателями и потребителями энергии аморти зирующими упругими звеньями, не должно быть шумовых•Д от других источников звука и из-за отраженных звуков. _ если окажется возможным, испытуемую машину следует в какой-то степени экранировать звукопоглощающими щитами.
При замерах уровня шума необходимо 199), чтобы он ходил уровень иомех (уровень посторонних шумов и ото-, Прев0ь звуков) на 6—8 дб и тогда ошибка прп замерах не бу„>КС|,|1Ых восходить 0,5—1,0 дб.	<г пре.
Желательно сопровождать результаты акустических указанием на уровень помех, а при замере спектра щуМа _JaMePoe ром помех.	С[)ект.
Очевидно, что уровень помех определяется замером шума при выключенном источнике замеряемых звуков ^1,ОвНя
При замерах уровня шума проверка искажении от уровг проводится двумя замерами:	1,51 Поме*
1. Замер разности уровней шума Д£„ при включении чении источника замеряемого
2. Замер разности уровней мера ненаправленного шума и
Рис. 12.14 Увеличение суммарного уровня шума
не искаженный
уровне помех
выклю.
шума.
шума А£р в выбранном месте за-в месте, имеющем двукратное уд0 ление по сравнению с выбранным местом замера
Величина Д£„ оценивает влияние уровня помех, а Д£р — влияние отраженных звуков.
Если в результате замеров окажется, что Д£„ =5 6—8 дб, а Д£р еу 6 дб, то можно считать, что замеряется уровень звука.
При высоком .	___
можно, пользуясь графиком, приведенным па рис. 12.14, вносить поправки, которые должны исключить влияние уровня помех, так как по оси ординат откладывается увеличение суммарного уровня замеряемого шума в зависимости от уровня помех в децибелах.
Для уменьшения влияния уровня помех микрофон устанавливается в непосредственной близости от источника замеряемого шума и определяется место замера, для которого будут получены удовлетворяющие указанным выше требованиям величины Д^л и L^Lp.
замеРс уровня шума, создаваемого малыми агрегатами, >ет ^станавливать замеряющее устройство на расстоянии возможносткИС™?Ч"1,Ка Ш^ма' Д-Ля крупных агрегатов, чтобы иметь ж -it
водить замеры0в'пазп^ vL,tnbH“e исг°чники шума, следует про-« тщательно анализиповя™ Ках’ окРУжающих отдельные узлЫ-визировать результаты замера («проводить зон-
ДИ>'14з-за обязательного влияния помещения пя
в „ем звуковой энергии замеров уровня шума на больших рХо^
1 flX от источника следует избегать.	расстоя-
" При замере спектра шума нужно следить за тем чтобы он бып
6-8 дб выше спектра помех на всех частотах, иначе в замеряв mom спектре могут появиться несуществующие составляющие а вывод1'1- сделанные на основании исследования спектра шума’ moi 5т оказаться неправильными.	у '
Лучше всего сравнивать замеренный спектр шума со спектром помех.
Считается допустимым не снимать спектра помех, если уровень шума исследуемого агрегата на 20—25 дб выше уровня помех 199).
При анализе спектра шума некоторую ориентировку дает значение частот собственных колебаний отдельных деталей. Эти частоты, как и затухание колебаний при вибрациях, можно определить выстукиванием.
При замерах шума микрофон должен защищаться от вибраций и от действия ветра, который может создать дополнительный, иногда с весьма высоким уровнем, собственный аэродинамический шум.
Если уровень такого ветрового шума не превышает уровень исследуемого шума, то ослабление помех ветра достигается обертыванием микрофона куском легкой ткани 1991.
При высоких уровнях ветрового шума микрофон следует закрывать обтекаемым экраном из легкого шелка или муслина, натянутых на проволочный каркас.
§ 12.5.	ВОЗНИКНОВЕНИЕ ШУМА В МАШИНАХ
Работа любой машины сопровождается вибрациями и воздушным шумом. Чаще всего и воздушный шум, и вибрации (если только речь не идет о сиренах в иных сигнальных устройствах или о специально сделанных вибраторах) — явления нежелательные.
Можно назвать ряд машин или условий, в которых они работают или испытываются, когда уровень и характер шума является важным, а порою и единственным показателем исправности машины. Иногда именно шум является обобщающим показателем ее Динамических свойств.
Ведь воздушный шум и вибрации порождаются физическими свойствами машины, характером и особенностями ее рабочего процесса, а значит, являются формой выражения определенных свойств машины и ее рабочего процесса, порождаются ими, а порой даже иМи и определяются. Несомненно, что рабочий процесс машин и порожденный ею шум не только взаимно связаны, но часто имно обусловливают друг друга.
Ml
- nnnmecc требующий повышения главных Па
Технический прогр^ ^ь моЩНОСТЬ, энергоемкость, Про£ метров машин (быстр' т к СОЗДанию более шумных MauilIH водительность и т п. щ внбрац„й в подавляющем болыи11Нс • Чрезмерный уровень^Ством несовершенства рабочего Про случаев ЯВЛ^ТС”МСВ' щественно ограничивается область ее При. цесса машины, чем чаекя возможность ее использования менення, а иногда и •	и вибрацняМ11 заставляет Соз:
lW= ы « « г*™, «нова™» яа »"«». ГОК|). давать машины и У 1	прОцесса, и поэтому с развитием
"и многие' шумные машины и технологические процессы вц. меняются мш.ее шумными А это, в свою очередь, служит делу ^лХТколХ^ьные процессы в машине являются источи, ками возникновения воздушного шума и вибрации. Каждая машина вставляет собою сложную систему напряженных элементов, каждый из которых, а иногда и отдельные его части имеют свое значение частоты собственных колебании. Поэтому колебания нагрузок, напряжении и т. п„ а также любые возникающие шумы и вибрации заставят резонировать в разной степени, в зависимости от соотношения частот, фаз и просто силовых воздействий, каждый участок любого из элементов машины. В этом случае опять возникнут дополнительные шумы и вибрации, в том числе и за счет отражения звуковых волн.
Следовательно, процесс возникновения шумов и вибраций весьма сложен, обусловливается взаимным влиянием друг на друга разных, весьма сложных по рабочему процессу, элементов. Более того, работающая машина не может рассматриваться отдельно от того, где она размещена. Работающая машина с точки зрения шума и вибраций должна рассматриваться как часть всего окружающего ее комплекса, который также будет уже иным, если рассматриваемая машина будет из него изъята.
Все в значительной мере еще более усложняется субъективными свойствами органов слуха человека.
И вместе с тем в большем числе случаев можно говорить о том, что является главной причиной возникновения воздушного шума и вибраций, влияние каких сторон рабочего процесса, каких воз действий будет в этом случае решающим.
iilVMnnTOMy/-СТрем,ЯТСЯ класснфчиировать причины возникновения шумов и вибраций в виде двух категорий:
вибпаии^ми11 «Т ШУМЫ’ ^““новение которых обусловливается виорациями и ударами твердых тел;	У
ленной нктабильн™КИе Шумы’ возникающие вследствие опреде-всего	ТО™Й' ""₽« или газов.
Не всегда удается п П^И с*зыве вихрей пульсации потока, новения шуМовУ и вибраЗ^Втп ТЙКИМ СПособом причины возник-виорации. В том числе, когда каждая из причин
рТ примерно равноценные по результатам
^можно разделить эти причины из-за сложна™ п гР0С™ "^есса, на*, например, в некоторых kohctdvkh^ Рабочего Предохранительных клапанов, работающих подУ большимТпере-"^п'ДРОпередачах особенно часто приходится сталкиваться со с,учаями. когда указанное выше и широко распространенное раз еденпе причин возникновения шумов и вибраций затруднено о все же эта классификация полезна и поэтому используется повсеместно. главным образом, из-за того, что в обоих случаях способы борьбы с причинами, их порождающими, различны.
Для уменьшения шумов и вибраций применяются активные и пассивные методы шумоглушения.
Активный метод шумоглушения, наиболее естественный и радикальный, заключается в устранении различными способами первопричин возникновения воздушного шума и вибраций.
Пассивные методы шумоглушения заключаются в применении средств изоляции шума и средств его поглощения. Эти методы бопее просты в исполнении, имеют наибольшее распространение и не всегда могут быть строго разделены из-за того, что, как правило, средство изоляции шума в какой-то степени поглощает шум, а средство поглощения шума обладает в определенной степени и изолирующими по отношению к шуму свойствами.
Наконец, многие гидравлические устройства снабжаются узлами и агрегатами, широко распространенными во многих Других отраслях машиностроения В их числе можно назвать опоры, зубчатые передачи и т. п. Очевидно, что при решении любых вопросов, связанных с уменьшением воздушного шума и ви PJ^hh, в возникновении которых они принимают большее или “ участие, следует познакомиться с тем, как те же задачи р в других смежных областях техники.	«„-.„иый ме-
Наиболее сложен радикальный по результатам изучение тех год борьбы с шумом. В его основе ле*^ первопричинами сторон рабочего процесса, которые связаны Р анизм воз-возиикновения воздушного шума и ви6Рациидят ти изменения, никновения нежелательных явлении, д пабочего про-«ршевствоввкяя, а заачит.	Sa-
цесса машины, и в процессе создания но ,	пациональным
шины, либо устраняют, либо ослабляют, ли	и вибраций.
способом размещают источники воздушнспособов борьбы
Любые, даже скромные Успехи а^ сов шеНной машины, с Шумом, не только приводят к созданию	(сооком службы) в
как правило, обладающей большим ресУР стеПени облегчает большой надежностью, но и в сушес	в виде испольэо-
шумоглушение при помощи пассивны иЯ шума, который »««»« средств изоляции и средств
8 этом случае должен иметь более
где
(12.17)
за счет срыва вихрей возникают коЛебяь
При обтекании тел з н0Й ВОЗНпкновения JByKa ианч« Частота аэР°д^"аМ"оер?коменДОШ1ЯМ ряда авторо? [99??*^
/ = 0,185 * /,
относительная скорость потока;
характерный размер мнделева сечения (прое цпя тела на плоскость, перпендикулярна направлению скорости потока);
. _ । 2 3 ___номера обертонов (обычно слабо выражении^
при i > 2).
Это уравнение представляет собою форму выражения числа Струхаля
где d — характерный размер;
v — относительная скорость потока.
Для тел различной формы будут справедливы разные значения числа Струхаля и значение 0,185 обычно получается при обтекании некоторых удобообтекаемых тел, в том числе и цилиндра.
Далее будет дано аналогичное уравнение для клапанных щелей, для которых число Струхаля будет в несколько раз меньше.
Уровень громкости шума в децибелах при обтекании тела определяется при помощи уравнения
L=10
где | — коэффициент лобового сопротивления;
г — расстояние до источника звука;
v относительная скорость обтекания;
г ~ bh. площадь прямоугольника, описанного около миде-лева сечения;
Ь наибольшая ширина миделева сечения; УпнпРии~Наиб°ЛЬШая ВЬ1СОта миделева сечения.
В аналити??? V п°ВЬ1Шаег Уровень громкости L на 15—18 дб. гель степени пои	^ейтхила показано, что показа-
поздних работах 1119]’’даны ^лжен бить Равен восьми. В более шести до восьми ncJrrJj” показатели степени, меняющиеся от в качестве приближенного? РЗВНеНИе ^121^ бедует рассматривать шумами не дают юопошихСП,?С°бЬ1 боРьбь1 с аэродинамическими к пассивным Ыерам ES результатов и приходится прибегаТЬ 1ВУкоизоляции. рьб оутем использования глушителей й И4
(12.18)
При выходе потока из клапанных щелей ритмические звуки «щелевых» тонов 199| 2С^ТСЯ «Ро-
/ = 0,055 "	,<ОТ°РЫХ
d '	(12.19)
1<оэфф"чиент пропорциональности может R г
^ьшнх пределах меняться в зависимости от reoSeX??° №' оТОка.	’ щелевого
Если выбрасывается поток из пневматической мЯ .„ательпого движения, то уровень шума может Jr? машины вРа-‘ 115—120 фон для пневматических двигателей) Эт??™ ВЫСОК быть осл аблеи глушителями.	‘ntl0- Этот шум может
’ во всех опубликованных за рубежом работах, посвящение проблеме снижения уровня воздушного шума в потоп?,?
содержится утверждение о гом.’что гл₽аЗ“ S возникновения шума в них является несовершенство пропса переноса рабочей жидкости из приемной полости в полость от дающую и обратно Подчеркивается, что особо нежелателен пеп вый процесс.	и
Если в момент открытия рабочей клетки давление в ней не равно давлению в камере, в которую затем открывается рабочая метка, то происходит перераспределение энергии, сопровождаемое различного рода потерями энергии и ударными явлениями (своеобразное «выстреливание» рабочих клеток), являющимися причиной возникновения звуковых волн.
Исследования высокочастотных спектров воздушных шумов роторных гидромашин, проведенные в разных странах (США, ГДР и т. д.), показали, что составляющие простые тоны, имеющие наиболее высокие уровни громкости звука, кратны частотам «выстреливания» рабочих клеток.
Можно назвать много работ, в которых не только указывается эта причина возникновения шума в качестве главной, но и сообщается об экспериментальной проверке различных способов борьбы с возникновением такого шума.
Вместе с тем обращает на себя внимание тот факт, что нигде не называется какая-либо иная причина возникновения шумов в роторных гидромашинах в качестве главной.
В роторных гидромашинах процесс подачи осуществляется переносом рабочих клеток из приемной полости в отдающую. Такая рабочая клетка либо возникает в приемной полости, либо прихо-Днт в нее из отдающей полости, затем герметично отделяется от полостей, проходя через перевальное пространство, и открывается в отдающую полость. Аналогичное явление происходит и при оо-Ратном возвращении рабочей клетки из отдающей полости в прием-
Разумеется, в зависимости от типа гидромашины и ее *°нструк и объем рабочей клетки при переходе через перевальн Р
346
ранство может либо оставаться неизменным, либо монятг эго бывает в большинстве регулируемых роторных гцдп Ся' Как
В поршневых роторных гидромашинах закон псремеи, '"«Ч поршня относительно дна цилиндра весьма близок к синус 6111,11 у ному, как это показано на рис. 12.15. Так как перемещения 0,,Даль' относительно цилиндра пропорционально вытесняемому ПЗр,,|«я причем коэффициентом пропорциональности является ч °бъеМу, площадь Л то на рис. 12.15 по оси ординат откладываетеК™Вная цилиндра, а начало отсчета выбрано так, чтобы произвел*1 °бъем было равно действительному объему рабочей -	нир г
ченному в цилиндре (объем abedefghika).
г\ жидкости Зяк Ч ’ закЛК).
По оси абсцисс откладывается время /= —0, или линейные ।
Р/?, где У? — радиус цилиндри-машин S'= fir °СИ ЦИЛИНДР°в, а для н > где г — радиус осевого
'мЛ	Среднего «можем» таре
шестпр11 ееличины параметра nervn еТ СВОего положения при из-рвение Зависят величинР
и, от которого су-0 к и мертвого Vo объемов
определяющие0^6 регУлиР°вания точКИ начальный момент вытесни-
Св0СЛучае и начальный момент певемАпта, '—"япутъ о кпиа^Г° пол°жения не меняют-понижения щумн<^е ТОчек и В в nn«KUHH’ в котоР°й исполь-В уп°МЯнУТОЙ вын ГИДрОмац>ины р Цессе РегУДирования ДЛ* также рассматриваются
угол 0 поворота цилиндра или аксиально-поршневых машин S	°СИ ЦИЛ”ндра №
ческой поверхности, Л* .- рк- ГДе ‘ радиально-поршневых „_°ТОрои„Разл?еЩены распределителя).
Для регулируемых
Р«УПгтгг»л Я Л Ж 1	“
менении величины -
Цилиндра.
А	«Ромашт
°Диако можно поршня, зуетея перемеще° упомя»Уть о к
« В
Vn°MSHyTo£ ВЫП1А '^О"“ШЙНЫ.
,ЛЛнр°вания1)а^ХиЛауСа f,25j и В.	’ дающие г-ирп-о,	paucMarpMBaiviv
«ещеиие тех же двух опорных
Положение окна поршня на перемычке п₽
„„ при отсутствии перекрытия ПАА пеРевальногп ^изображении размер окна Цилиндр*3™^ ряс 12.11,°^ „еремычки.	р точности раеен - На
'При положительном перекрытии S\n	РУ
„ер перемычки больше половины размера Г1Т>ТВе'Гст,1УюЩий Раз Тщательном перекрытии S' < 0 _ меньше ц')Л™Дра, а
Очевидно, что перекрытия, которые
„линейных величинах S, либо в углах 0,	”°*Н° ,,змеР«ть либо
^опорных точек А и В либо симметричный Гибп П° СТОР°™ Будем обозначать угол перекрытия опопноТ НеСИММетР”чными чиваюшеи заблаговременную отсечку нипияп к" А’ обрспе-J ^линдра в конце процесса
Рис. 12.16. Перекрытие перемычкой распределителя
всасывания, через 0, (эта величина может быть в том числе мень-еи нуля, и тогда она будет оценивать запаздывание закрытия цилиндра), а запаздывание открытия цилиндра для той же опорной чки, т. е. для начала процесса нагнетания, через 0г.
е же величины для опорной точки В будем отмечать индексом виде звездочки справа вверху, т. е. 0* — угол отсечки цилиндра конце процесса нагнетания и 0* — запаздывание открытия ци-ЦЦДра в начале процесса всасывания.
олная величина перекрытия определяется для опорной точки л выражением
08 = 0т + 02.
4 Для опорной точки В
Е	0з* = 0Г + 0«*.
если
0.=0, = ^08 и 0? = 0Г = 40?.
Перекрытия называются симметричными.
насоеп*6 обознзчения применяются и для радиально-поршн в« как показано на рис. 12.17.
Рассмотрим закон изменения дево.м перекрытии, т. е. при рз =
/у
Рис. 12.17. Цапфенное распределение

давления в цилиндре при р* = 0 (график, изобража ''У' закон изменения давления"' цилиндре в зависимости 6 угла поворота п„линдрОв блока, назовем по апалощ с обычными поршневыми 11а" сосами индикаторной д„а граммом).
При проходе окна Ци. линдра через перемычку На опорной точке А произойду
,	« жидкости ИЗ области низкого давления р, в об-
переход объема Д	приведет к возникновению удар.
\ (|2|)" <И2>-
Распределителя Мы симметричного «змек„„е юмеиия м
__	___pi
Внезапное	золения на величину рз — Р*
(рис. 12.18, а) и является причиной возникновения шума. й3
Аналогичное явление происходит и при переходе цилинДР области нагнетания в приемную область.
М8
утверЖДаЮТ, что С|<ачок давления ня ™
„ переходе из приемной области в р"ой т°чке А .
|1(1' чКи зрения шумовых эффектов >, T;ia,0UW, более А С
01 Хотя при таком утверждении какие-либо « ссы,пки »а соответствующую экспериментальную'пг?бражен"я или едятся, в его справедливости можно убедиться "е ПР“ „еретических соображении, которые будут щ” "л Элеме^арнЫх щем параграфе.	' приведены в следую.
Некоторую роль играет также и то обстоятельно
„плиидра 6 конце пеР"оДа всасывания и в кон,Т ’ ЧТ° Отсечка гания происходит при разных объемах цилиндра ТтоТ На'не’ дичину градиента давления.	др ’ что меняет ве-
Индикаторная диаграмма при положительны*
перекрытиях в обеих опорных точках показана на риТТГГб Следует обратить внимание на то, что градиент измен ения давл₽ п„я В защемленном объеме для опорной точки А менЛ! Д 0Юр„ой точки В. что объясняегся^иным
„ото объема рабочей жидкости (изменение давления пропорю^ нально относительной деформации). Количественная оценка этого изменения давления будет дана в следующем параграфе.
Характер протекания процесса в защемленном объеме определяется следующими соображениями.
При отсечке цилиндра в конце процесса всасывания (точка 1 на рис. 12.18, б) на первом угле flj перекрытия поршень будет продолжать движение вверх и понизит давление в цилиндре за счет упругости рабочей жидкости. Самое малое давление будет в опорной точке А (точка 2 на рис. 12.18, б), и соответственное понижение давления Д/?31 может быть определено кинематическими соотношениями, геометрией и упругими свойствами рабочей жидкости .
Из-за утечек понижение давления будет иным (показано пунктиром на рис. 12.18), причем величина утечек практически не зависит от числа оборотов машины, поэтому с увеличением числа оборотов пунктирная и сплошная кривые будут сближаться.
При переходе через опорную точку А поршень начнет входить в Цилиндр, и знак градиента изменения давления изменится при неизменном знаке утечек, поэтому отличие процессов без учета >течек и при их учете будет больше.	D„nuu«
Очевидно, что без учета влияния утечек изменение да при перемещении цилиндра от опорной точки А до м°“ен™ здывания открытия цилиндра в отдающей области, ОПР®Д _ .
>гл°м ₽2, будет то же, что и в предыдущем случае Др8, Р» поэтому скачок давления при открытии цилиндр гнетания будет
ря = Pi — Рг

fivn„T проходить процесс при переходе цИЛи
АнаЛОП'Т°о&па?т>1 в область приемную (окрестности о'п>а „з отдающей обл‘	СПЛОШноп кривой 5—6—7—8 на рИс. 12 ’М
точки В), ка« пОказ^У_2б'-7'-5-в случае учета влияния v 8'6 " "рсл™ пренебречь малым влиянием утечек, то можно заме^-чтоп” положительном симметричном перекрытии, одинаковом^ что при полож	удалось уменьшить скачка даГи,/я
л. 3=™»=“™""на' °"0|,иых точках X »? да’аа предай <*“ в воторО11 ,геняли“ молетия нулевом перекрытии.
Кроме того, дополнительное изменение давления Др* в За щемленном объеме для опорной точки В соответственно увеличило нагрузку на узлы гидромашины, а значит, несколько увеличило интенсивность шума
Если представить себе, что несимметричное перекрытие может понизить скачок давления р3, то нужно иметь в виду, что для реверсивных машин одинаковость рабочих процессов при обоих направлениях вращения требует применения симметричных распределителей, а это делает невозможным понижение скачка давления Рз-
Значительное превышение изменения давления Ар*, = Дд|2 над изменением давления Ар31 = &р32 объясняется меньшей величиной объема жидкости, участвующей в процессе упругой деформации, как об этом говорилось ранее и будет подробно рассмотрено ниже.
Если от гидромашины не требуется реверс, то можно подобрать несимметричный распределитель, существенно понижающий скачки давления р3 и р3 при открытии цилиндра в отдающей области приемной области (рис. 12.19, а).
инпичатпД В”ду’ ЧТ0 хаРактеР изменения давления на участках матикой р днагРаммы 1—2—3 и 4—5—6 определяется кине-что подробно пТ- И уг|ругими свойствами рабочей жидкости, так подобпать vr^w°rpeH° 6 следУюш-ем параграфе, можно всегда ₽.	~ — лавле»
значения иамешшня^и^ИЯТИЯлГ,Оэва'1яют на самом леле выбирать •Уоше ска”и даМе Р я: д	" М’- а
₽. = р.-ла, + Др>!_/,!. .
Рз — Pt ф- Дп®,_д n« /	(12.^ I
могут имел, любые желае! М ~ Р1 ’
явлений Р1 и рг в „0еХойаЧеНИЯ- значения, зависящие kohctoJ/3^^ Режима вабо”°ТДаЮЩей областях, будут ме‘ для лющ^ИИ с ‘^Ременными угля?*1 гидР°Машины, поэтому только ков давлен ₽ежимов Работы по пЛ” ПеРекРЫтия могут обеспечить Давления р, и	Давлению заданные значения ска*
К сожалению величины измене™
М' и аРз2 зависят также и ПерепаДов давлен„ А е)улнрования гидромашины, пр„ и значения парам^Л31’ меняются первоначальный объем рабочп ’ КОтоР°го cS ра и Скорости и перемещения поршня	** Жид^ 'и, от^Т"0
При постоянных значениях л ’	игельные
„«„„«тричные перекрытия „	Собрать
рнои диаграммы
р

\j}=wt



ж
Рис. 12.19. Индикаторные диаграммы несимметричного распределителя
с нулевыми значениями скачков давления рз^и^рз, казано на рис. 12.19,6 для случая Pi 7 поошневыми гидро
В американских исследованиях с акс“	чт0 гидромашина
машинами фирмы Виккерс 112^1 Р^оКазана на рис. 12.19,6, с такой индикаторной диаграммой, ка будет работать бесшумно.	„о1.1и;1ется на работах института
По мнению Клауса, который оснi в выполнение указанного станков в городе Карл-Маркс-Штадте . мнению не требования необходимо, но недостато ‘ каторнОй диаграмм быть не только скачка давления н	рекомендовано
в скачка градиента давления, ДДЯ
i.
Жясоннымп канавками вУсика., небольшими 4 спечить плавное изменение щать перем» J е должны С пуНктпром на рис. 12,|Л п О ТД 71 ГII I [ ^ 1	з^/Д'^оказано на рис. 12.20, 0, н;«б.
»'с"га ®’абе То „ыт” я. «астияво открытого „р„ „ * в	"'“а	X Оставшийся горыет,™,™ уЧап«
^	обозначена чере3 „оМ 6.2? =	г
•>с,‘"ида	из' рк/ре»“игели’’ етабжи"'ОТ0 Л.
ПП’Г£”т'Я"« „гомеяпото для опытного насоса, кот„м
шу ""*•*1,1
должен бил ра	и11СТнтуте станков в городе Кар.п.
РИСЭтот насос	испьпанпй будут приведены ниже.
Маркс-Штадте 11251-

и
г А
Jkut
Рис. 12.20. Коррекция
Опорная точкой
Опорная тсчМ А
индикаторной диаграммы при помощи «усиков»
а)
Совместные экспериментальные исследования фирм Дженерал Электрик и Виккерс [127] не подтвердили мнения [125] о роли регламентированных утечек на распределителе, хотя также показали, что таким способом удается существенно снизить величину скачка давления при изменении режима работы гидромашины, что будет рассмотрено ниже.
Если геометрия распределителя подобрана для определенного режима работы гидромашины, то любое изменение давления Рг потребует иных значений несимметричного перекрытия р-> и поэтому нужно либо поворачивать распределитель, меняя тем спосоМбпмЛппПереКрЬ,ТИЙ	и ₽*• -™бо менять каким-нибудь
выппп,?оти Ние опорных точек А и В, либо одновременно диаграммы ИПепвый И ДРУ10Й спос2б н изменения индикаторном боте Клауса 11251 и пСпосо6 настройки насоса разбирается в ра’ торы?применись пТ™ В Работах Фирмы Виккерс [1271, в к<> работы на строго пег спределители с разными геометриями ДО
Второй способ РнХМХ™Р?“Н_ИЫХ давлениях.
точек А и В ракмотве?ТКИ“ 1идромашины смещением опорных Р осмотрен в той же работе Клауса [125].
Третий способ настройки насоса п процесса регулирования, запатентов"РеДусмотРен в самп 1|;1|<о Из-за того, что в некоторых ,, М фирм°й Си п СПособе точек А и В в последней конструк^Овиях смещени?*"’ Од лается изменением подачи, констпчЛ. 0ДН0бРеменно г порнь'х у"»”- ....................“г ЙС*
закономерностью изменения подачи « о?0/0 регла«ентирЕ^ Изменение закономерности потребует 1 и.зме^«‘<я давдР°;а ной Л1Пеля или иных параметров п.л™ геомегр11И .	Я--
третьему способу. Р "фашины, выполненной^'
Иная индикаторная диаграмма получаете перекрытии, которое также может быть к" сРИ отрида^ьном несимметричным.	ть Ка1< симметричным, так
Рис. 12.21. Распределитель
Очевидно, можно подобрать отрицательные значения перекрытий, при которых на заданном числе оборотовi и р ма давлениях pt и р.г будет подходящая индикатор скачков давления, как это показано на Рис- • ’ заключается
Основной недостаток такой системы расп^двде"аИ^ в падении в обязательном повышении утечек или, ч
значения объемного к. п. Д.	„«пипАимення. Одно из
Но есть и достоинства такой системы р р этОй системы них заключается в определенной приспосаблива^	отрицатель-
к изменению давления. Так, при	лдаграмму
ных перекрытиях повышение рг измени & а п0ИИжение —• так, как это показано пунктиром на рис. • • диаграмме.
так, как показано штрих-пуиктиром в будут-соб'гветеП’оваТ> Разумеется, большим градиентам да низкиезначения к. »• 3 большие расходы утечек, а значит, более низкие зн
12 В Н. Прокофьев и ДР-
n.₽M участке индикаторной Диаграммы, в
Кроме того, во BCJ" давления, защемленного объема*0' тором происходит	проточную камеру будет * £
будет. и ЧСРХЬ рабочая жидкость из отдающей Камер W рывио перетекав ь	в
приемную. отрицательном перекрытии расход утечек буДст При малом 01Р1,и гпялиент давления и может принкУ понижен, что Умень'0|.азаР0 „а рис. 12.22 сплошной кривой. Т" К давлению Ps, как оборОТов понизит давление в цилиндре впЛот.
Ъ’пнТточк Л (показано на рис. 12.22 пунктиром) и Л0ВЫс ДО опорном ТОЧКИ » \	ег0 после опорной ТОЧКИ Д
так как дополнительный рас’ ход, выдавливаемый из ци. линдра, должен увеличить градиент давления. В этом случае величина скачка давления уменьшится.
Уменьшение числа оборотов насоса даст обратное действие (штрих-пу нктирная кривая на рис. 12.22).
Очевидно, что увеличение параметра регулирования в
этом случае эквивалентно некоторому увеличению числа оборотов, а уменьшение параметра регулирования — наоборот.
Следует специально отметить, что расчет давления в защемленном объеме при положительном перекрытии основывается на упругих свойствах рабочей жидкости, а при отрицательном — на расчете утечек, но все же при обязательном учете сжимаемости рабочей жидкости в цилиндре.
При положительном перекрытии индикаторная диаграмма весьма мало зависит от числа оборотов гидромашины, и поэтому целесообразно проверить такие распределения в разных вариантах в первую очередь для гидродвигателя, который обычно эксплуатируется в весьма широком диапазоне изменения чисел оборотов.
а почтпми3*!0^ эксплУатиРУ10тся на постоянном числе оборотов, верить все воЛп2УЮ Очередь применительно к ним следует преньем перекрытием. Н0С™ применения Распределения с отрицатель-
*12-6- энергетический скачок
в камеру, объем жидкостей 2™ да^”;Иием Р мгновенно откроется Если сжатие ТидХи й ^°Р°И И Давлен^ Р-
354	оих объемах подчиняется закону
rv«a то величина энергии, котопяа Леньшей величиной дамеиия.
л «и/	ыРажением у
Ас =____J'v
2*(I
(12.21)
где рс — разность первоначальных давлений
объемов;	1Ии обоих соединяемых
х — модуль объемной УПРУГОСТИ паЛ^ 
Величина А, называется величиной , ЖиДкости.
Если V — объем цилиндра « моХ"
камеры, в которую он открывается, а также все £тя„ ~ °бъем с ней соединяемые, то )’га>(/, и расчетное ^- ! 'е тического скачка соответственно упрощается: П ,Ие энеРге-
А - -р? v
r 2xv>	(12.22)
Можно предположить, что потери энергии при «выстреливании» рабочей клетки в отдающую камеру насоса пропорциональны личине энергетического скачка Ас так же, как величина энергии затрачиваемая на создание звуковой волны.
Поэтому можно записать величину потерь энергии в течение 1 сек работы гидромашины в виде выражения
nzn*
/V = ^V-	(’2-23)
где £ — коэффициент потерь, зависящий в том числе от геометрии открываемого отверстия, свойств рабочей жидкости и значений соответствующих критериев динамического подобия;
п — число оборотов гидромашины в минуту;
z — число рабочих клеток.
Можно определ ять потерю энергии в виде потери напора в метрах столба рабочей жидкости. Для этого нужно отнести потерю энергии к весу подаваемого в 1 сек объема рабочей жидкости.
_ г 2L	(12.24)
“ Ь 2ах '
где
Л’60 aV’zn
(12.25)
а — у
коэффициент учета мертвого объема, т. е. объема, возвращаемого в приемную камеру.
Аналогично определяется величина энергии, идущая на
Дание звуковой волны:
..	► nzPi и	(AW
где Ki и
Vniax
Кроме того,
пнтеПЯ должен вестись так, чтобы ЭИе
Расчет распределителя д Очевидно, его величина 6v^ ческпй скачок был	а нз приемной камеры в отда1оУ^
разной^” ^ем в ^ВОМ	°б°ЗНа^
"ер°езР гГ’а "°"вТОрОМ ' Vp
Понятно, что	^-1- 17 = V04-wVmax,
__ величина мертвого объема,
1,3 пр"емной в отдающую.
V1= V0 + 4(l-«) Vmax,
«меть в виду что поршень в цилиндре совершает возвратно-поступагельное движение около плоскости, положение которой не меняется в процессе регулирования подачи.
Если обозначить в соответствии с равенством (12.25) величину
с =	=	(12.27)
1 атах °
(коэффициент использования цилиндра), то величина отношения энергетических скачков на соответствующих режимах работы будет
'Р™\2	(12.28)
Д2 _	1 + иа
Л1 1 + | (1 - и) а
В случае симметричного распределителя и и = 1
— (1 + а) ^i, означая, что энергетический скачок при «выстреливании» цилиндра в отдающую камеру насоса будет в десятки раз больше, чем при его «выстреливании» в приемной камере. Именно поэтому первый случай и представляет наибольший интерес.
При и = — равенство (12.28) принимает форму
/ О,. \2
очень мадТ^может^казаться8	яараметРа регулирования
объема V, цилиндпа состав’ ЧТ° А* А1' но ПРИ этом величина Можно ГказХ* что поиепТ/ИШЬ ПОЛОВИНу °т
и -*= 1 по 1	’	₽ РегУлировании насоса в пределах от
объема V ап 8631141,113 У2 больше, чем самое большое значение ₽ ЭТИХ режимах работы и возникают наиболее
(12.29)
fl-at
«не УРовНИ шуМа’ Именно ПОЭТ°МУ «выстреливание» цилиндпа HSuy” камеру?' является наяб°лее нежелательным явлемем р°тЛ лоте роторной гидромашины.	ием
при Ра
§ 12. 7- КОЛЕБАНИЕ СИЛОВЫХ ВОЗДЕЙСТВИЙ в РЕГУЛИРУЕМОЙ роторной гидромашине
, я В виду, что наиболее подробное исследование возникно-воздушного шума в роторных гидромашинах проведено при-веИИЯ н0 к радиально-поршневым регулируемым насосам 1128], менител считаясь с тем, что наибольшие знакопеременные усилия а такж х раВных условиях имеют место именно в радиально-при ПР „ -.«.чоиях ПЯССМОТПИМ колебания СИЛОВЫХ ВГгаППЫГТпий поршневых - для
a также при 1  i .
именно
машинах, рассмотрим колебания силовых воздействий этого типа гидромашин.
X

pf
V

pfC0S[/i>vl

V a)
Рис.
12.23. Определение силовых
воздействии
лмп пракиии кольцевой на-
Приближенная схема "вия^р	12.Я.?.
правляющеи на головки иир
гусю ппиАпиженная потому,
Приближенная
-----------------------------------заХ "ле линии действия схема приближенная воТОМу’ я™ нТ через центр ротора, а через каждого из усилий pf проходи!-----„иоНШО
центр кольцевой направляющ . центрИцитета е по ера_
Однако, имея в виду малость эксценр^ в порядке первого с радиусом кольцевой направл н’ыМИ выражениями, приближения воспользоваться у	ппошеиь-
при анализе малых подач.	действий на головки
Суммируя проекции силовы ков, можно записать
' О числа поршней от Р-где р — меняется для четног
г _ число поршней;
1; 3® "рав"° ”ул'0, то Г ч""°" ** проводить от , = 0 до , _
поп 6 меняющемся от 0 до г
Ппи нечетном числе поршней суммирование следует проводИть от.=Р0до/=_£_4 при 0, меняющемся от Одо
Если предположить, что давление в отдающей полости м,1ого больше давления в приемной полости, то можно суммированием усилий В приемной полости пренебречь.
' Тогда при четном числе поршней проекции усилии на оси д
и У будут:
(12.30)
График изменения вертикальной Y и горизонтальной X составляющих показан на рис. 12.23, б, причем пунктиром показаны зоны, в которых имеет место защемленный объем, являющийся причиной возможного соответственного изменения усилий.
Наиболее неприятно знакопеременное изменение горизонтальной составляющей от значения ф- pf до — pf. Такие изменения возникают в момент перехода цилиндра из приемной области в отдающую и могут вызывать вибрации тех деталей, частота собственных колебаний которых наиболее близка к частоте колебания усилия X (так называемая коммутационная частота):
г__ nz
' ~ 60 
наппайпаПЛ,т1ПрЯЖеННЫХ деталей находятся кольца подшипников, осьЧастота Л0ЛЬЦ° И консольно укрепленная распределительная выяснению РРпТВеННЬ1Х колебаний всех этих деталей подлежит уровнем громкости цЯГСПеКТре Шума бУдУт тональности с высоким там или числам им к™™ которых бУдет близка указанным часто-что колебания соответс™^’ Т° будут основания предполагать, этих участков спектра щу^* деталей являются источнике риментально при^зменТ пр5дположения легко проверяется экспе при Измененной частоте собственных колебаний де'
||йеп положительно являющейся источником™
т*""’ ГЕсли после этого удастся получить более ^Г^ТВующих ёмкости шума, ТО принятое выше предположен^ ^УР°Ве,,ь 'Р « справедливым.	,е может счи-
тЯТПоЛная величина силового воздействия определяется из послед
p = x’+r, = -l-.rt_co„sl sin
(12.31)
поэтому знакопеременное колебание горизонтальной составляю-“ PH может быть представлено в виде результата плавного пере-решения конца вектора Р по дуге АВ (рис. 12.24, а) из точки А
Рис 12 24 Определение силовых воздействий при помощи «качающегося ‘	вектора» г
. точку В с последующим	Ч-
вектора Р из точки В в точку А в л область.
линдров из приемной области в отда	у роекции на вертикаль
При указанном движении вектора	пр“К3равенств (12.30),
и горизонталь будут теми же, какие получаются Р
и показаны на рис. 12.23, б. эП„„яюшце уравнения При нечетном числе поршней разрешающие^
pf (12-32)
Ф.
4
-й колебания гори-	12.24,6).
t действующи* с
(12-331
X =
2 sin -5-
4
изменятся так же, как и Читальной X и вертикальной . *:____________________ . '
будет
cos р—ф У = —~ 2 sin
график, изображающий Р-й У составляющих (рис-тальноц Л и вертикальной 1 v прктооа Лрйс Абсолютное значение суммарно
р _________L pf ~ const.
2 sin
Сота „ерем»™»	Нс. 12А
чктота >'С""Й «
₽а- ,:
нужденных
сдвинутые по
колебаний с одинаковыми частотами / = Но фазе на половину периода. При рассмотрении совместного действия обоих видов колебаний считают, что есть лигць один вид колебаний с удвоенной частотой, что на самом деле справедливо только при одинаковых закономерностях изменения давления в защемленном объеме.
Рис. 12.25. Модель силовых воздействий
§ 12.8. ИСТОЧНИКИ ВОЗДУШНОГО ШУМА ОСНОВНЫХ ЭЛЕМЕНТОВ
ГИДРОПЕРЕДАЧ
Источники шумов в гидропередачах наиболее подробно были перечислены в работе Хоена и Питерсона [124]. Там же были указаны и способы борьбы с этими шумами.
Как уже не раз отмечалось
______	выше, в качестве главной причины вехопо паО-НМ шума указано влияние скачка давления при пе-Там же^тпоп11 клетки из вриемной области в отдающую и обратно. шума вю,|икая м
f 60 пг.
Хоена и Петерсонами 241°Т(ЭЧеН° И в исследованиях Клауса [1251, U16I, что наибольшее значений подчеРКивают, так же, как и Эрнст области, иллюстрируя ппы имеют скачки давления в напорной римента. ю ,1ри Этом соответствующие результаты экспе-р^™^Гпе^	благодаря тому, что у них
НИЯ иТеЛЬН0 велики, имеют НЯибез изменений объема, а утечки и. как следствие, наХХ^*10 величину скачка давлб"
3<Ю	наименьший уровень шума
Наоборот, в шестеренных насосах труднее всего регламентировать закон изменения давления в защемленном объеме В насосах этого типа наибольшие скачки давления и, как следствие, наиболее высокий уровень шума. Вероятно, еще большее значение имеет «выстреливание» межзубовых пространств, переходящих из приемной камеры в отдающую.
Для шестеренных насосов уровень шума увеличивается с увеличением давления в отдающей камере, размера насоса и числа оборотов.
Неуравновешенность узлов механизма является источником шума на частотах соединительного вала и на высших гармониках.
Одним из источников возникновения специфического шума является конденсация пузырьков пара, возникших вследствие кавитации. Очевидно, место возникновения таких очагов шума будет первый же участок за кавитационной зоной, после которого имеется достаточное повышение давления.
Считается, что повышение содержания газовой составляющей способствует развитию кавитационных явлений и таким способом повышает уровень шума [1241.
Обычные способы эксплуатации гидропередач предусматривают создание условий, делающих невозможным возникновение кавитационных явлений. Иногда кавитация все же может оказаться неизбежной в защемленном объеме. Возможно, что именно этим обстоятельством следует объяснять повышенный шум в шестеренных гидромашинах. Однако и в этом случае очаг шума должен возникать либо в приемной полости насоса, либо в герметически замкнутой рабочей клетке, в том числе и при раскрытии ее в отдающей камере.
В той же работе имеется прямое утверждение о том, что уже имеются насосы, которые могут работать бесшумно в определенных условиях а также возможно создание насосов, автоматически настраивающихся на бесшумную работу в менения эксплуатационных параметров [127]. Это весьма важное утвепждение может рассматриваться в качестве свидетельства о том, что у американских инженеров имеется полная увереншктъ в вильности их точек зрения на причины возникновения шуь«ц Тем сшым лишний раз подтверждается факт решающего влияния скачка давления на возникновение шума^ п„оводиться в том
Утверждается, что ВЬ1^Р Н^“ветДствующихР режимах работы числе и по величине шума на соответс У V	оцени-
в соответствии с допустимым уровнем у •	распространи
вать „о еп> спектру е	"yZ^S^ » Г
НИЯ не только по воздуху, но также и ГУ	эти обстод.
бочей жидкости в трубопроводах <иЛ диапазоне изменения тельства должны выясняться в р Ирования для регул* Давлений, чисел оборотов, параметр р У нствалях (при сяо-руемых гидром—.
бодном выборе размера	однозначна), ее вязкости
лирования от скорости жидкости не одиозначн
qTVnI1 Изменение этих многочисленных фактОрОв , температуры.	влияние на возникновение шуМа
0К‘н3асос вместе с приводным двигателем должны быть сбап
Насос вм овпень1 на амортизаторах, действие Л.8’1' “от” зрения заглушения шума считается весьма сущ*; ^Рекомендуется [124] выбирать систему крепления так, собственная частота системы креплении не превышала 1/3 низкой частоты всего агрегата.	°и
В отличие от аэродинамических систем считается, что ВСЯк изменения проходного сечения магистралей, плохообтекаемые фОв.11е границ потока, не говоря уже о резких изменениях направдев1Ь1 потока, отводы и тройники при турбулентных потоках являют/ источником создания шумов с широким диапазоном частот днмо, это является свидетельством высокого уровня собственное шума указанных устройств по сравнению с остальными шуМамц° вызываемыми в магистралях гидропередачи. Такие утвержден/ следует рассматривать в качестве утверждения важной роли аэродинамических шумов в гидропередачах.
Трубопроводы могут не только передавать звуковые волны через рабочую жидкость, т. е. могут быть не только' волноводами но и резонировать, превращаясь вследствие этого в мощный источник шумов. Кроме того, стенки трубопровода также могут быть волноводами, излучая при этом воздушный шум.
Рекомендуется [1241 не допускать в магистралях скорости выше ; м.сек а отводы должны иметь радиус кривизны, по крайней мере, в 5 раз больше диаметра трубопровода в свету.
обляляХ6 врименять шланги, а не трубопроводы, так как шланги менение шпямгДеЛеНН°И заглУшаюшей способностью. Если при-применить во каким;либ° причинам невозможно, следует прокладки, которыеЦлучшеУби°ПРОВОДа упругие звукоизолирующие Звукоизолиоуюпшр пп ше установить возможно ближе к насосу, магистраляхУв том	следует устанавливать на любых
на сливных ’трубопроводахДУЩИХ К системам управления, и даже жидкости из картера’ предназначенных для слива рабочей шинь1 — использование^юбп трУб°пР°вода от корпуса гидрома-
Покрытие трубопроволя чп/ЗНЫХ ги^Ких (резиновых) участков, ер, стеклянная ткань) сушесУпК°П°ГЛ0Щ'аюЩ'им материалом (напри-У в7иХУ^чаТРУ^Пр0®°д”Нм° УМеНЬШаеТ УР°ВеНЬ BOMylUHOrfl тель)<ОипРУбОПрс)ВС)АЬ1 и основнырВ°ЗДуШНОго шУма могут быть не РекомендуетрН°ГИе ИНЫе элементы гЭЛементы (насос и гидродвига-развитыеУотиЯ обра,Дать внимание ИДросистемы. В первую очередь аккУмуляторыЬ1ТЫе поверхности как Т« элемепты- которые имею «и,	Р '	’ к’ Например, холодильники 11
Очевидно, что холодильникам свойственны аэпппииа lUyMbi, и для их устранения следует улучшать проточХИЧеСКИе Если переделка холодильника по каким-либо причи ам Хч можна, следует обращаться к звукоизолирующим кожуХаМ
ДЛЯ снижения шума клапанов следует использовать жидкостное илИ фрикционное демпфирование, если только при этом не Чпе? мерно понизится быстродействие.	р
В серводвигателях возвратно-поступательного движения шумы обычно возникают в начале и конце каждого хода. Уровень шума определяется нагрузкой и быстротой изменения скорости.
[Дум может вызываться силами трения, особенно при дефектах монтажа или при неправильных компоновках гидросистемы из-за возникновения поперечно-действующих усилий. Эти усилия нередко вызывают шум с высокочастотными составляющими высокого уровня громкости.
При очень малых скоростях движение колебания сил трения (при возможных кратковременных остановках колебания сил трения возникают, в том числе из-за различия коэффициентов трения покоя и движения) вызывают кратковременные шумы в соответствии с изменениями режимов работы механизма. Уменьшение шума в этом случае может быть достигнуто изменением компоновки системы, если изменение компоновки может обеспечить устойчивость работы системы.
В некоторых случаях устойчивость работы системы обеспечивается применением плавающих (самоустанавливающихся) поршневых уплотнений в тех участках, в которых нестабильность действия боковых усилий вызывает возникновение шума.
Большое значение, с точки зрения возникновения шума, имеет недостаточность давления в каких-либо участках гидросистемы, особенно в случае, когда из-за этого в рабочую жидкость может попасть воздух. Именно в этом случае возникает недопустимый специфический шум в виде дребезжания. Для пРед0™Р*“евн™ возникновения следует следить за достаточностью дав^ ‘ия в "^ напорных участках гидросистемы, которое обычно поддерживаете при помощи специальных подпиточных насосов
При проектировании гидросистем следует пРедУвР^^сХ можность возникновения вакуума, а если в каю Утизации гидросистемы он неизбежен, следует позаботиться о герметиз ц ""’дэ^ические шумы в
спектром широкочастотного типа и устраняются голы® У У нием форм проточной части.	..иягтки спектра шума
Отдельные, особенно	„SXhx глушителе»,
могут гаситься при помощи акти . пяпагоафе.
которые рассматриваются в следую РТСР частотой собствен-
Воздушный шум опор качении “Р^Хегся У«Р»“ W ных колебаний деталей подшипников и визы ков и роликов о кольца и сепара р.
3®
сплетает с увеличением числа оборотов „ уровень шума возраi	выПОЛНеНии, почти не заВнс ра*-
мера подшипника при х г	не зависит от Ч|1сла с т От
нагрузки, а спектр Д	опорь1 скачьЖенпя понижает
Замена опор качен очастотНые составляющие из crS? 15—25 дб и устраняй в	ектРа
шума‘ п смазки существенно влияет на уровень щума щар
Характер смазки 5	пОДШИПНИК без смазки имеет ур^
подшипников 1ак, и виях подшипник, смазанный жИпк1 Ь шума 65 дб, а	,ровень шума 57 дб. Замена *2?
машинным масло,	|Ррматорное дает уровень шума
пХХе Х»“°™»а" w0Be"b шума еще "а 2 а
«аз™ M3e™“a:.™cz° “ “""°го “сла ««
касторового масла понижает уровень шума до 52 дб.
Уровень шума существенно зависит от качества установки опоры качения (не должно быть перекосов, следует обеспечить правильность геометрических форм гнезда и цапфы вала, предусмотреть защиту от загрязнения), которая должна иметь минимальный диаметр и тугую посадку.
Необходима эластичная прокладка в месте крепления узлов опоры качения для уменьшения передачи вибрации на корпус машины.
Большое значение имеет качество изготовления, изготовления беговой дорожки подшипника качения (неточности даже порядка в 0,5 ж сказывается на акустических свойствах опоры), неодинаковость размера шариков или роликов, и даже повышенные «зазоры плавания» сепаратора, приводят к возникновению значительного воздушного шума и вибраций.
1ШпиииеЛИЧИНе ЭТИ»Х ВибРаЦИЙ можно судить по уровню вибра-образователяТчкТ1' В Аецибелах тРех типов опор судового пре-ооразователя 136], указанных на nur юэк шум работающих двумя причинами:
2) SSS Ж " на них;
Соударение зхбкеп И зу^чатых колес.
дает тональную составляющую с частотой
Рис. 12.26. Уровень вибраций
Неточность
указанных на рис. 12.26.
7"‘ сопРяженных зубчатых колес вызывается
1) соударением зубьев
Соударение
ГДе " - число оборотов г “ Число зубьев.
в
i - nz
' «о « минуту;
(12.34)
Вибрация зубьев дает высокочастотную составляют™ . являющуюся частотой собственных колебаний У У
Кроме того отдельные детали (стенки корпуса,' валы, зубчатые колеса и т. п.) имеют свои частоты ff собственных колебаний которые не должны совпадать с частотой вынужденных колебаний
Понижение шума достигается уменьшением окружных скоро стен, улучшением качества обработки и сборки.
Понижение скорости достигается уменьшением диаметров зубчатых колес, в том числе за счет увеличения ширины зубьев.
По Славину 1991 снижение уровня громкости зубчатых колес при понижении окружной скорости от значения иг до значения м определяется при помощи эмпирического уравнения
D»231g£.	(12.35)
и2
Хорошие результаты дает селективная подборка шестерен.
Свободная посадка одной из двух сопряженных шестерен понижает уровень громкости шума на 3—4 дб.
Существуют оптимальные зазоры между зубьями зубчатых колес, так как чрезмерно малые зазоры приводят к заклиниванию, а при больших зазорах неравномерная нагрузка приводит к отрыву зубьев с последующими ударами, что также повышает шум [130].
Величины оптимальных зазоров приведены в табл. 12.6 для крупных зубчатых колес трех классов точности изготовления, использовавшихся до введения ГОСТа 1643—55.
Таблица 12.7
колес весьма велик и во многих ма-
Таблица 12.6
Модуль шестерни в мм	Оптимальный зазор в мм		
	Классы точности изготовления зубьев шестерен		
	I	п	ш
2 4 6	0.07 0,12 0,15	0,012 0.15 0.20	0,15 0,20 0,25
Уровень шума зубчатых _________ ______________________
шинах они определяют спектр шума. О том, как велик этот шум, можно судить по значениям допустимого уровня шума в децибелах, приведенным в табл. 12.7 для косозубых шестерен семи классов точности, применявшиеся до введения ГОСТа 1643—56с дмаэвтрахи °т 40 до 200 мм, с модулями от 2 до 7 мм и углами наклона аубье» от 0 до 40°.
Для прямозубых П0 сХ^н«0ГО С- , „„ЙЙь «»"Ф»Р“аМ,еМ
Рис. 12.27. Демпфирование зубчатого колеса
Металлическая или деревянная прижимная шайба
Шестерня
Шайба из листовой резины толщиной 5'10 нм
болт
считается звукозаглушение
, колес допустимый уровень громкости ЩуМа ,б' -гния уровня громкости шума МожНо СН вибрации зубьев и диска шестерни использовании демпфирующих риалов (текстолит, пластмасса и т Л за счет понижения прочности. За -,т ’ счет удается снизить уровень i р0/. кости на 4— Ю дб, а высокочастотны* составляющих даже на 10—12 дб Хорошие результаты дают демп фнрующие резиновые шайбы, при>ка. тые к торцам диска (рис. 12.27), Или неплотно запрессованные чугунные кольца в ободе шестерен.
Из-за значительно большего внут-реннего трения чугуна по сравнению со сталью уровень громкости шума чугунных шестерен на 2—4 дб ниже, чем для стальных. Наоборот, закалка и цементация увеличивают уровень громкости шума на 2—3 дб.
Наиболее эффективным способом понижения шума зубчатых колес ? при помощи специальных кожухов. Нередко кожух облицовывается листовой резиной для заглушения воющего звука редуктора.
§ 12.9. ГЛУШИТЕЛИ ШУМА
Из-за невозможности полного устранения первопричины возникновения звуковых излучений соответствующим улучшением рабочего процесса гидравлических, а также «аэродинамических» (так условно назовем машины или их узлы, рабочей средой которых будут газы в широком смысле слова, включая воздух и пар) машин нередко применяют звукоизолирующие кожухи.
ели рассматриваемые машины соединяются магистралями спуцярп!ПАп^аи1ИНаМИ или аппаратами, то эти магистрали в ряде магистоалг пп» проходить сквозь звукоизолирующий кожух, а тогда Хае? необхолХ^ННО буДет волвводом В этом случае воз-стралях. доя чего hohLT^111^1^ звУК0ВЫХ колебаний в маги-должны уничтожить ипы няю* спеииальные глушители, которые гистрали, являющейся* н₽<^Ла^ИТЬ колебательные процессы в ма-ником возникновения ЛЬК° ВОЛНОВОДОМ, но нередко и источ-
Задача создания подобнптНОГ° ШуМа и вибРаций.
няегся еще и вследствие т?°да глУШителей существенно уело»' вд	°> цто в гидропередачах приходите
сталкиваться с шумами более высоких ™
новыми колебаниями малых длин волн °СТей' т- е. со 3BV
При малых длинах волн звукових	У'
с размерами сечений потоков звуковые^,™ По Мнению в центральной части потока и влияние вХнГТ прОхо«ить а также физических свойств стенок магистпапи Ф°РМ "Занижается. Именно поэтому во всех сие.тяп? сУЩественно по-[1301 подчеркивается необходимость вы&ра Da3tpa6°Tax 110’1 и токов такими, чтобы они были меньше попоЛ^ а сечений по' звуковой волны. Этим своеобразным «масштабним0°^1ТСТВуК)Щей дует объяснить то обстоятельство что в некптп Эффектом сле-воды, полученные применительно к аэродинамичХ* случаях ВЬ|' оказываются неприменимы к магистралям гидропереда^™"8^’
Кроме того, в четыре с лишним пазя бппХ D Р Д распространения звуковых колебав,,!, и с^вввтел^ГнХьХ
И все же вопросы акустики обследованы аналитически и экспе риментально в аэродинамических устройствах более основательно чем аналогичные вопросы в гидропередачах, где пришлось столкнуться с решением акустических задач лишь в последние годы. Ознакомление с опубликованными в последние годы работами [116| и (124] убеждает в том, что во многих случаях принципиальные пути решения задач уменьшения шума в гидропередачах те же, что и в аэродинамических машинах и устройствах, если не считать отдельных специфических особенностей и нюансов, к сожалению, довольно многочисленных из-за сложности рассматриваемых явлений. Именно поэтому, решая новые задачи борьбы с шумом в гидропередачах, нужно стараться использовать достаточно большие накопленные материалы в соответствующих областях аэродинамических машин и устройств.
Вместе с тем очевидно, что нельзя механически переносить указанные способы решения основных задач борьбы с шумом в гидравлические устройства не только из-за иных относительных размеров длин звуковых волн и иных физических свойств среды, но также, и это очень важно, из-за высоких давлений (как правило, более 100 кГхм1), во много раз большей массовой плотности среды, много большего удельного акустического сопротивления R — рС очень высоких давлений звуковой волны, большой мощности, расходуемой на создание шумов и т. д. Все эти особенности в очень большой степени затрудняют нахождение путей решении новых и сложных задач, а также создание соответствующих констру' •
Наконец, существует еще одно весьма важное различи• чающееся в том, что использование глушителя на ма™\₽ няет характеристику гидропередачи, особенно исп^” реходных процессах систем передачи энергии и> шипп обстоятельство заставляет взвешивать все воз
кН гидропередачи, вызванные установкой „ ния хараЛТеРпПится применять только некоторые Допусти^-шителя ПРИХОД7Я ” I известных типов глушителя или пере* варианты использова*	Таким образом, выбор	глущИтад
к глушителям ины<	ограННЧНваеТся
гидропередачи с ^et	действия глушителей:
1ГХошеХ звуковой энергии с превращением ее в теплОву|0;
2) отражение ^ву^^Лренция звуковых волн.
3) искусственн * душитель, основанный на одном из ука
В 0ТДтоехЬпринШ1пов, может в существенно меньшей степе^ 3аННЫХп ?ть заглушение также и по другим принципам. Т0Гд наименование глушителя применяется в соответствии с тем Прин. пипом действие которого имеет наибольший удельный вес в общем балансе заглушающих действии глушителя.
Глушитель, основанный на поглощении звуковой энер!ии с превращением ее в тепловую, называется активным, имеет наибольшее распространение и в настоящее время, видимо, стал применяться в США в виде шлангов и трубопроводов со специальной оплеткой 1124].
Глушитель, основанный на отражении звуковых волн, называется реактивным глушителем. По своему' действию аналогичен электрическим фильтрам, получившим широкое распространение в электротехнике. Судя по работе Эрнста, такие устройства давно привлекают внимание американских инженеров и ученых, а в последние годы ими стали интересоваться и в Англии. Сейчас появились сообщения о том, что в США создаются специальные конструкции таких глушителей для гидропередач [124].
Интерференционные глушители по своему принципу действия наиболее просты, однако применимы в тех случаях, когда в спектре шума имеется небольшое число простых тонов с высоким уровнем громкости звука при стабильной частоте подлежащего заглушению простого тона.
Все ВИДЬ' глУшителей из-за неудобообтекаемых форм проточной громкостиЯ«ТСЯ ИСТОчником аэродинамического шума, степень потока По ™Р°Г° пропоРциональна шестой степени скорости шум глушителя ^noiST*1116 ЗВука имеет пРеДелом «собственный» дувкой стационаоным^пт громк°сти которого определяется про-шума снижается уменм.™*^' ^ровень громкости «собственного из уравнения (12.18) ением скорости потока, как это следует энергии с превращен]^L<^H0BaHHbIe на поглощении звуковой легко поддаются расчету к ^ТВпловУю энергию, наиболее прост . уст^7ИВНЫе глУшители В?ффективны в широкой области частот-У	и ми°го матепия^е,,Я,0ТСЯ Аавно в аэродинамически*
Работе Славина [99]. ₽ ЙЛа по глУШителям такого типа собраВ
В простейшей форме активный глушитель представляет с магистраль с облицовкой омываемых потоком среТы с= f М01 лотающим материалом.	р дь стенок звуко-
ПС Величина заглушающих свойств магистралей обратно пропоп циональна гидравлическому радиусу, поэтому для увеличения X (Ьективиости активного фильтра уменьшают величину гидравлического радиуса чаще всего уменьшением размеров сечения магистрали Для того чтобы гидравлические сопротивления при этом не возросли, соответственно увеличивают число каналов, применяя так называемые «сотовые» магистрали.
Не требуют большого места камерные глушители, семь схем которых показаны на рис. 12.28. При использовании таких глу-
глушителей
Рис- 12.28. Схемы камерных

шителей необходимо иметь в виду, что они вносят большое гидравлическое сопротивление, которое несколько понижается увеличением площади прохода между ребрами экранов и стенками.
Такие камеры при работе на воздухе должны иметь звукоизоляцию не менее 25—30 дб для каждых перегородок и экранов.
Из-за больших гидравлических сопротивлений глушители ставятся на воздушных магистралях при скоростях потока не более 6—7 м/сек.
При использовании таких, а также перечисленных ниже глушителей на потоках жидкостей следует иметь в виду, что каждое из местных сопротивлений одновременно является местом возник новения срыва вихрей, а значит, является источником вихревого шума.
Если обозначить ослабление шума в элементе активногоиглу-шителя через ДА, а увеличение уровня громкости из-за Л возникающего источника вихревого шума через v, величина не должна быть меньше второй, и их разность Добротностью активного глушения
ДА - ДА„>0-
r том числе от физических „
Добротность ° Мяться экспериментально
греды н допжна fZ.ie справедливо для воздушных магиСТр.
Р Последнее УРавве^ерJ активного глушения (рис. 12.29)
Расширительные к 1 высокиХ звукОв с длинами вол изменяются ДЛЯ заг‘ '	ь
Шнми размеров камер _ звукн н„зКОЙ частоты иное, Так
Действие таких ка 1 ая камера работает в качестве РРа? в этом случае расш.^ акустического фильтра. рабочий про -
тивного глхшител . еТ рассм0Трен ниже.
РеаГ™вНЬ’* 'то воздушных магистралей добротность расширь ной Херы опр^яется при помощи приближенного уравнения,
\yw*v*v*v*i
Рис 12.29. Схемы глушителей с расширительными камерами
основанного на предположении равномерного распределения ковоЙ энергии в объеме камеры:
D = 10 Igu
зву-
где а — коэффициент звукопоглощения стенок камеры;
FK — полная внутренняя поверхность камеры;
F — живое сечение магистрали.
Это уравнение используется в тех случаях, когда поперечные размеры превышают половину длины звуковой волны. Так, при диаметре камеры 20—30 см и работе на воздухе уравнение применимо для частот, больших 830—550 гц. Расчет заглушающего действия таких камер при частотах, меньших указанных, будет дан в следующем параграфе.
„р..При	однов камеры не удается ослабить шум больше,
динеины* пп б’ П0зТ0мУ используют несколько таких камер, сое-
В этом с?едОВаТе*Г,ЬН°’ как сказано на рис. 12.29 в центре-шения звука X*na В03Никает возможность дополнительного глУ магистрали относителыГ"16”’ ДЛЯ Чего НУЖИО сместить ось одно справа Таад “	° Другой- как э™ показано на рис. 12^9
частотной части спектпя°ВаНИе 0006011110 эффективно для высо
Поворот каналя п/ хаРактеРизУемой короткими длинами во  ковки обладает добпотно^^ гз°Вании звукоизолирующей 06 °^ств облицовк^ ГпХЮЯ 4 " 6 аб- в зависимости размера канала
«пи
сюоборот, при отсутствии Облицовки стенок применительно Игнстралям гидропередач считается Ц24], что отводы с пово-
к М0Г магистрали на 90 при турбулентных потоках имеют отри-роТ°м * ю добротность и являются источниками вихревого шума 11атсль1 У диапазоном частот. Поэтому в магистралях гидропередач сгШ’Р0 мендуют применять скорости рабочей жидкости свыше не РеК . диаметр должен быть, по крайней мере, в пять раз больше 3>t/C2na магистрали в свету.
д»0Ме 1 етСЯ, что при использовании ряда последовательно сое-Сш’та за’глушающих устройств суммарное заглушение равно дпнениЫ еннй всех элементов. Таким образом, индукция эле-сумме за‘ уен11Я практически отсутствует.
центов - ’0Jlbj что и активные глушители, играют широко распро-ТУ Жене звукоизолирующие втулки, применяемые в месте вывода стравеннь >	&	12.30), причем величина заглушения такой
’^ТХпориио^л-.ка ее длине.
нтУдК"	ный глушитель, основанный на отражении звуковых
РеЭ 1 оказывает препятствий прохождению потока с неизменными ВОЛН, не окаэ
6)
Я,
и, It) htt)
(12.37)
Дополнительная втулка
Рис. 12.30. Звукоизоляция вала
Звукопоглои дающий материал
7>ь-ва/7
воздушный '—заязг-'
Стенка кожуха
I
'410 1,М
Аналоги фильтров на основе

Рис- ^ ртаюивны"1 глушителей
параметрами. Простейшим видом та^°гГ°чН0У уравнительной башне установленный на магистрали	«дар-
гидростанции (рис. 12.31, о)-	гидравлического уд Р
При возникновении в магистрали ди
ная волна отразится от оака_ птношению к удар»0 гИдрав-Следовательно, такой бак по °™Ш рная
ляется реактивным фильтром.	что и звуявлич£ски«
лическом ударе носит тот же характеР^	ые гидравли^
с тем лишь отличием, что колебания,
УДаром, не являются гармония вЯЗкостного трену»
Аналогично действие пружин и	изображу-’
Даче колеблющихся усилии чер
„ гнгтему сопротивлений /?,, /?а и /?31 а т
Рк 12.31.«. « ?с№„1икаТОров В электрической цс„„ »<», емкостей G- С» н ’	12.31, в.	Ъ
которой показана на Р	эквивалентны бакам Г11др
Емкости G в	Пружин д, и Ъ механической cxZ
wS “тырехпйхэеиик (рис. ,2.31. „) „Мто
При пропуске через ^„яния на пропуск тока. При проПу°1? тока емкости не к Уа параметры U2 (О " 4 (П будут 0 N к< колеблющегося ci •	. тока /, (!) по-разному n
пяться напряжением Щ (О и спим	' ' ' н ^у, в За.
Умости от емкости конденсаторов , и С2.
В С щество щие сопротивлений во всех трех случаях дает По_ твою энергии. поэтому изображенные устройства должны рас. сманиваться в качестве активных, а не реактивных глушителей.
Рис. 12.32. Аналоги фильтров низкой частоты
Иное дело, если в гидравлической схеме будет усилено влияние массы жидкости в соске фильтра (длинная и тонкая трубка в калом элементе на рис. 12.32, а). Влияние такой массы оценивается отношением массы т f живого сечения:
среды в соске фильтра к квадрату площади
Таким образом,
т = Л =Plfj-P~.	(12.38)
усилено увеличение В ГИДравлическ°й схеме это влияние будет ской схеме будет усилено^ В€ЛНЧИН тъ и т3, в механиче-(Рис. 12.32, б), а вУэлектоиХИЯ1'Ие МаССЫ зве['ьев М1г Мг и элементе индуктивность I ^Л011 схеме будет увеличена в кажд<’л1 Гидравлические схемк> L 2 И La (рис- 12-32, в).
чаются также и тем tPHC‘ i2’31’a и Р^. 12.32, а о™*1' объемом V. деля ko« ня Р°“ Wy4ae бак заменен замкнуть151 372	d Мо^Уль объемной упругости и fia>U
реактив-с тем, что частоты
Колеоания, частоты которых больше частоты f =« 2/0 среза не проходят через реактивный фильтр и отражаются обратно. Степень
(12.39)
ч„м величину, называемую акустической поДатЛивогт , ^..чина играет гу же роль, что и статическое	?
крутость пружины q и индуктивность L Во все, ДЭВление в баке i чаях имели место- канал в ма( истрали и Трех "P^yuinx проявляется действие массового рЛда	В к<^
винительных участков и тормозов в мех»™^ прУ*”«. дуктивиость, которая в какой-то степени cvinS Схеме и № электрическом элементе.	существует в каждом
Усиление влияния массы потока при применении „
малого диаметра происходит погому, что ускопрм Длиннои тРУбки рагно пропорционально площади его живого сечениЛ "°ТОКе °б‘
Каждая из рассматриваемых ячеек несет обязанности кого глушителя пли фильтра низкой частоты в связи г колебания с частотами, меньшими удвоенной резонансной /„ ячейки, беспрепятственно проходят через фильтр
Колебания, частоты которых больше частоты f =• ।, " . .
заглушения акустическою фильтра низкой частоты в децибелах определяется из равенства
D = 40 1g-?/-Al
поэтому характеристика фильтра должна была бы определяться величиной /0.
Однако каждая изображенная на рис. 12.32 схема при любой форме ее выполнения имеет потери энергии, поэтому реактивный фильтр в какой-то степени одновременно является и активным фильтром, поскольку электрический четырехполюсник обязательно имеет сопротивление R 0, в механической цепи всегда есть силы трения S 0 и в гидравлическом или акустическом фильтре всегда есть гидравлические или аэродинамические сопротивления, определяемые коэффициентом потерь £.
Видимо, в определенной степени это справедливо также нД-тя рассмотренных ранее активных глушителей, в какой-то мере обладающих также и свойствами реактивных глушителей.
Физические явления в сплошных средах отличны от аналогач Ных явлений в механической и электрической цепях в том • и потому, что переменность параметров потока по е™ . в очонь большой степени усложняет характер	тог0
йЧе™”х процессов. Так, из-за этого возникает	и
Чтобы линейные размеры сечений глушителя -
®ины Длины звуковой волны, подлежащей У будут через JTO условие не соблюдается, то звуковые коиебания буду Душитель проходить насквозь.	глушятел®.
Чем ниже частота / среза, тем больше Р	ддя по-
меньше реактивный глушитель, пред
оглушает колебания высокочастотные н яв.чення низких частот аа,л>.тот При увеличении частоты уМе,1ь. цястнчио колебания ср^н”^ Н11С перестает монотонно увеличи. Хекя Длина волны. « за Л^однт периодическое возрастание или Хкя Вместо этого "P0HC0* ценное чередование полос гаще. ослабление глушения т ° 1 поэтому применяют последОва. S. и полос пропускания^ ячеек реакТивного глушителя, тельное соединение н^ол	полос гашения „ пропуска-
каждая из которых имеет с	заключается в максимальном
Задач»	X ,я"в даракее заданной облает,, чапи.
расширении полос.заглуше	происхОДЯЩ|1н в любой из
Рассматривая Ф113"4/ пнЛ(Ьереициальное уравнение, устанавли-ячеек, можно ^^^Хтрам’’ входной X и выходной Y ве-пВ,ш1шеЭтоЯ диф^енХльное уравнение второго порядка имеет Ф°рму 1	+2L2L + у = кх, (12.40)
ш« dt2 ' “о dt
где <оо - круговая частота собственных колебаний или резонансная
I _ относительный коэффициент демпфирования;
КруТХ*^	колебаний - это резонансная
частей ячейки реактивного фильтра, которая для электрической схемы будет
1 /1С ’
где L — электрическая индуктивность;
С — электрическая емкость.
Для акустического фильтра резонансная угловая частота будет 1
ш0 =	—
VT^Ca

(12.41)
(12.42)
где La = tn
уравнение (12.38)]; податливость;
ячейки реактивного акустического глУ'
Г х
акустическая инертность, которая представляет собою массу среды в соске ячейки реактивного акустического глушителя, отнесенную к квадрату жи-вого сечения ]см. упавнри uo /1 ° от 1
= — акустическая
V — объем камеры
шителя.
Имея в виду, что
W4
c2== 2L
f ’
I
(12.44)
моя<но получит резонансную угловую частот-v ячр&гги .душителя в виде выражения	У ячейки реактивного
<n0 = C-±L. = fdVn
Viv	чуiv ’
где d — диаметр соска ячейки реактивного глушителя
Так как частота f среза ячейки реактивного глушителя равна
' = 2'-='=^Ж = 0-Ж-^Г.	(12.43}
так как	°-282 
При расчете ячейки реактивного глушителя заданным значениям частоты среза / и с соответствуют разные значения остальных трех подлежащих определению величин d, I и V.
Многозначность выбора снимается, если заданы допустимые пределы потери напора в магистрали л -1 1 ^р = р^-а--т, где X — коэффициент потерь;
v — скорость в соске фильтра.
Последним условием для получения однозначного выбора всех трех искомых величин d, I и V будет условие получения желаемых динамических свойств гидросистемы, на которой должен устанавливаться подлежащий расчету фильтр. В большой степени эти свойства описываются передаточной функцией, представляющей собою отношение преобразования Лапласа от выходного сигнала к преобразованию Лапласа от входного сигнала (см., например, § 9.1 и 9.2).
Передаточная функция может иметь разную форму в зависимости от гидравлической схемы гидропередачи, для которой [шс-считывается фильтр, и от значений параметров этой схемы. Эта передаточная функция будет зависеть от упругих свойств системы и поэтому не безразлично, как выбирать величину V. При решении задачи можно в той или иной степени учесть отдельные пожелания по динамическим свойствам рассчитываемой гидропередачи.
Может случиться, что не всегда окажется возможным польз ваться в полной мере всеми тремя указанными УсЛ0®^ лины с тем, что размеры соска не должны быть больше п волны:	_
(12-45)
Поэтому, в соответствии с этим дополнительным Уменьшается число свободы выбора основных пар метр реактивного глушителя.
В настоящее время появились активные и реактивные гсли, специально предназначенные для гидропередачи (124?У1Ц|1' торые рекомендуется устанавливать возможно ближе к цГ7. ’ Ко-°Ч||ИКу
ШУИ в этом случае глушители оказываются эффективными I11VM0B с большим диапазоном частот.
^Интерференционные глушители, предназначенные ДЛя 3 шения небольшого числа простых тонов с высоким уровнем rpoj. X™ звука, даже при стабильной частоте заглушаемого простого тона чаше всего нуждаются в настройке из-за крайне узкой полоС11,
3аГНУяТбо^ простая форма интерференционного глушителя по-Наиболее п Параллельно присоединенная дополнительная
SZZ	01 ”'Т '• «-
Застряли между умзе-помн присоединении отвода.
Рис 12.33. Принципиальная схема ннтер ференционного глушителя
Рис. 12.34. Интерференционные глушители
Размеры участков должны выбираться с соблюдением следующих условий:
z> 4-(п + ур-;| 4+4 = nk, /
(12.46)
где п — 0; 1; 2; 3; ... — любое целое число;
X — длина волны.
И в этом случае ослабление более эффективно, если поперечный размер сечения меньше половины длины волны. Чем ниже частота, тем лучше работает глушитель.
Несколько лучше из-за крутых поворотов на высоких частотах заня^ внтеР^?Ренционный глушитель, схема которого пока-лана на рис. 12.34, а,
за™^рГНл/еЙСТВИе "единенного тупика (рис. 12.34, б), тону) ответвления0 Ч-г'?°™и’ Равной собственной частоте (основному шает волну с ллиипй К°И интеРФеРенционный глушитель загЛУ а также обертоХ w ’ равной Учетверенной длине ответвления. ™ обертоны основного тона, длины волн которых будут 091
376
На главной магистрали можно установить несколько тупиковых ответвлении разной длины в соответствии с подлежащими S-|||С1Н1Ю простыми тонами.
Чисто тупиковые ответвления, как и байпасы, размещают в звукопоглощающем кожухе, как показано пунктиром на рис. 12 34
§ 12.10. регулирование индикаторной диаграммы
Для каждого заданного режима работы гидромашины можно так подобрать распределитель (моменты отсечки и открытия), что за счет изменения объема цилиндра при его прохождении через перемычку давления в нем к моменту открытия окажется равным давлению в камере.
Однако работа цилиндра при одном и другом направлении вращения не одинакова из-за необходимости использования несим-метрн ч но го рас предел ител я.
Из-за то| о, что режимы работы гидромашины могут меняться, необходимо использование какого-либо регулирующего органа, которым мог бы в благоприятную сторону менять индикаторную диаграмму.
Большого успеха в изменении индикаторной диаграммы достигли в США в результате совместных работ фирм Дженерал Электрик и Виккерс 11271, проверявших действие и установивших способ расчета профилированных дросселирующих канавок. Благодаря утечкам, канавки существенно снижают скачки давления при изменении режима работы.
Те же способы регулирования индикаторной диаграммы применяются в ФРГ.
Похожие устройства без расчета и специального подбора применялись в ГДР 1125], причем автор исследования из Дрезденского института станков дает неверное объяснение действия этих утечек. Ниже этот способ регулирования индикаторной диаграммы будет рассмотрен подробно.
Возможно регулирование индикаторной диаграммы поворотом распределителя, хотя считается, что для аксиально-поршневых гидромашин конструктивное оформление этого> способа'регул' ' вания весьма сложно. В ГДР были подробно обследованы возмож-ности такого способа регулирования в работе Клауса	₽
ложен простой способ возвратно-поступательных пер . пределителя по двум взаимно перпендикулярным «апРа^ который эквивалентен по своему действию повороту р р
Сущность такого способа регулирования заключается в том. что смещение перемычки в другой участок ХОДВУ ^яет менять степень сжатия рабочей жидкости и за этот с
Давление в цилиндре в момент открытия. и„плп.вместо
Французская фирма Ситроен предложилi	и*»
поворота распределителя эквивалентное д
Клона оси регулирующего устройства.
п л TA Knavca упоминается об изменении индикатор,,»., В методом «впрыска», т. е подводом рабочей ж„ДкР ° диаграммы методом • егО ИСТОчника непосредственно на п0д Дарением от п J автОматнческОе регулирование давл мычку. Считается, очнике слОЖНо.	я
В TS жХХе сообщается о безуспешном использовании уп
В той же рао	уТем присоединения ДОнолнптельик..
SS’k’Sp»»’» Отсутствие успеха объяснялось главным обра юм ZiraUiHM быстродействием устройства при переходу процессах.
Рнс. 12.35. Кинематическая схема аксиально-поршневой гидромашины «Ситроен»
Рис. 12.36. Кинематические соотношения
цузской ЛипмыТпеСН0 пРИНЦИПиаЛьн0 новое предложение фран-перемычкахРпезг>иятТрОеН’ к°торая рекомендует использование на В патенте Ситпоен Вп работающих на резонансных режимах.
машина с точечным касанием361™ аксиальн°-поршневая гИДр0’ ной шайбы, как это показано ня Смещ^ной осью поворота наклон-струкции ось поворота наклонной*? Л'35’ °' В предлагаемой коН‘ распределителя угол ф а пп Н°И шаибы составляет с плоскостью рачиваться вокруг этой оси °СК0Сть наклонной шайбы может пово-
Соответствую^ее?Хем^иПОА ра3ными Углама У-
Ромашины показано на пис ”3°бра>кение конструкции гид-Рассмотрим кинем Р
наиСп	центровУ предлагаем°г° механизма. Пусть Ра‘
°иной шайбы наклонена пол^°В В цилинДР°вом блоке г, ось 878	углом ф к поверхности торцового
распределителя, как показано на рис. 12.36, а прЯмая, перпендикулярная к оси АВ. проходящая через центр наклонной шайбы и совпадающая с ее поверхностью, параллельна плоскости распределителя.
для рассматриваемого случая точка А будет опорной точкой, соответствующей началу процесса вытеснения рабочей жидкости, а точка В — второй опорной точкой, соответствующей началу процесса приема рабочей жидкости.
Примем опорную точку А в качестве начала отсчета угла поворота осп цилиндра:
P = ®t,	(12.47)
где <о — угловая скорость цилиндрового блока в рад!сек-, t — время в сек.
При повороте цилиндрового блока на угол 0 стопорной точки А точка контакта поршня на верхней проекции сместится в положение ЛБ, а на нижней — из Л, в А2. Очевидно, что в этом случае
ОА4 = OtAa = О4А2 cos р = г cos р.
Расстояние точки ЛБ контакта от нейтральной плоскости, проходящей параллельно плоскости распределителя через центр наклонной шайбы О, измеряется отрезком Л5Л4 образующей цилиндрической поверхности, на которой размещаются оси цилиндров.
Из прямоугольного треугольника ОА4А6 можно определить указанное расстояние
Л6Л4 = х0 = (M4tgq>.
Подставляя в полученное равенство выражение OAt, окончательно получим
х0 = л tg ф cos Р,	(12.48)
откуда ход поршня
Хотах Хо т|п = 2г tg ф.	(12.49)
Если же принять за начало отсчета положение поршня в опорной точке А, то относительное перемещение поршня в цилиндре определяется выражением
Хо = Хотах —*о=='lg ф(1—COS ₽).	(12.50)
Повернем поверхность наклонной шайбы на угол у относительно оси АВ, как показано на рис. 12.37. В этом случае линия встречи с цилиндрической поверхностью, на которой размещаются оси поршней плоскости наклонной шайбы, будет выглядеть на верл-ней проекции уже не в виде прямой АВ, а в виде аллинса.
При повороте оси цилиндра от опорной точки А на угод ₽ “ положение оси цилиндра будет определяться точкой Л» айеотг. Aj,
плоскостью, перпендикулярно!! плоскости Рассечем цилиндр "• Q л Тогда точка контакта поршня гРас‘ преде-пителя и РМ > >на ей проекции в точке Дп, прЯмая клоннои шайбой ^Д л1111К0Г, поверхностн с радНуСОм А будет образуюик? увеличение расстояния точки контакта’ а отрезок ЛИ* ' ' * по нению со случаем у = 0. Если бу2 Не"^новьюажениедля отрезка Дх, то его прибавление к величине? лТт искомое^расстояние точки контакта до нейтральной плоское^ знаЧит определит кинематику механизма.
Обозначил! точку встречи секущей плоскости с осью АВ через д, ио	и построим треугольник А,А Л
(рис. 12.38, п).	’
Рис. 12.38. Определение соотношений углов
= OAsin В =Д <Jn°R треУгольнике сторона ЛВЛ7 = Л2Л8 = Р и поэтому искомый отрезок образующей
О	“ ЛьЛв = Л6Л, tgy' = г tgy sin р.
вокруг оси АВ итьУГОлТ через угол у поворота наклонной шайбы прямой ЛБД7 построим плос-плоскостъ Д^^ цифпой / м паРадлельна оси Л В. Назовем эту ного положения поверхнос-н?0’ 2'38, Плоскость первоначаль-вем цифрой 2, а плоск аНаклонной шайбы при у = 0 назо-шаибы, в которой лежат^тп^МаТлИВаем0|° положения наклон-Л’л‘£- на“““ П“ФР°Й Л
ость. перпеиддкудяркую оси”!» на угол V. то строя в точке А 880	получим плоскость 4, в к°’
. будут размещены точки Л7К1Л5, так как по построению отре-Т°Р°Л д перпендикулярен оси АВ. Точку выбираем в плоско-з°к д а поэтому отрезок A(,Kt параллелен оси АВ, углы Д7ДГ>К, и сТИ. д прямые, так же как и углы ВАтКх и ВД7Д5, а поэтому угол ^46д“ также прямой.
^‘’Очевидно, угол между плоскостями 2 и 3 будет измеряться углом л К = у,’а угол ДЙД7ДВ = у' отличается от угла у из-за наклона ди на угол ф к плоскости распределителя.
0111 Имея в виду, что плоскость /, в которой лежат точки ДИв^ь ерпепдикулярна отрезку ДГ1Д7, можно записать
ДЬК1= Д5Д^Ь45ДЛ1 = Д.Д^у; 1
Д6Д0 = A.nA^gLAbAiAe = AbAi tgy'. )
Так как в треугольнике Д5Д0/(1 угол дд д прямой а M5X8 равен ф, то
cos <р = Mt = AdilSY
Л/Ч Л6Д, tg у' • и окончательно

откуда
Ax = ^sin0.
COS (f r
(12.52)
Поэтому расстояние точки Ав (см. рис. 12.37) от нейтральной плоскости будет определяться равенством
х = х0 + Ах = (sin ф COS 0 + tg у sin 0).	(12.53)
Возьмем за скобки в полученном выражении такой множитель К, чтобы были справедливы равенства
CosO = -^V <1; sin0 = T^_<l,	(12.54)
К	/fcostp	'
что возможно при условии
ИЛИ
К = ГоБф 1 sin’ф-Mg* у,	(12.55)
и тогда
x = r/Ccos(P-fi).	(12.56)
Сравнивая полученное равенство с уравнением (12.48), вира* знм величину множителя К через tg тогда окончательно
х » г tg 4> cos (0 — 8)»	(M S?)
где
1
6 = arcsin	sin* <г »
02.58)
Ф =
I tg2 V ’Р=агШ(5Ш1А,пЧ + 1е’у).|
Таким образом, поворот наклонной шайбы на угол у Ирн ее оси на угол <р равносилен изменению хода поршня от веЛ1 2 ffi ф до величины 2К = 2 tg ф и смещению опорной точки > направлению вращения цилиндрового блока на угол 0.	* "°
Следовательно, вместо поворота распределителя на угол , можно повернуть наклонную шайбу, ось которой наклонена П( углом ф.
Если конструкцию гидромашины выполнить так, чтобы можно было произвольно изменять углы поворота наклонной шайбы и угол наклона осн ф в качестве независимых переменных, тод.1я любого заданного значения параметра регулирования, или, что то же самое, для любого значения хода поршня,
2 tg ф = 2К =	/sin^ + tg2v = а,	(12.59)
и можно получить необходимое значение угла смещения опорной точки	1
б — arcsin
— b,
(12.60)
если, решая совместно последние два равенства, найти удовлетворяющие их значения углов <р и у.
Рассмотрим случай, когда при у = 0 и а> 0 распределитель мешен так, что при (3=0 = 0 происходит отсечка цилиндра, опопной'п'^моЛ0СК0СТЬ) в которой осуществляется наклон осн называться гпягГна“СК0СТЬЮ регУлиРова"ия. Такая плоскость будет того является ппо^ ПЛОскостью регулирования, если она, кроме
Л па Л	плоскостью начала отсчета углов В и 0.
подачи отличается на™ Р®спред^ителя угол 0 отсечки в начале сывания, и поэтому кпэдн/™3 6 Отсечки Цилиндра в начале вса-ницы всегда, когда 0 ФФ‘1циент т]0 подачи будет отличен от еди-ходит не на опорной точке! ЭТ°М случае отсечка цилиндра пропс
Легко показать что
подачи	’ У‘ол ® определяет величину коэффиш1е1Гга
i> „л	Ло = cos б.
° соответствии г
"««ж,, „0^7™“ <‘2 S7) ход поршня 2г tg 0, = ‘>* 882	первого уравнения (12.54) можно полУ
Г’	*°Р«г ротора
[3 ВИД’ - — I
•lofs = 2f г tgi|)T]„ =2f г tgi|)cose=2rf tg«p.
Вог почему угол ф можно назвать углом подачи, а угол у-углом сжатия, так как его величина определяет величину сжатия рабочей жидкости в запертом цилиндре при угле перекрытия отличном от нуля.
Полученные результаты позволяют сформулировать несколько утверждений.
Утверждение 1. Регулирование аксиально-поршневой гидромашипы с торцовым распределением при помощи изменения угла подачи и угла сжатия эквивалентно по кинематике аналогичной щдромашине, у которой угол подачи равен нулю, а опорные точки смещены относительно опорных точек распределителя на угол сдвига, косинус которого равен отношению тангенса угла подачи к тангенсу действительного угла поворота регулирующего органа.
Утверждение 2. Изменение рабочего объема аксиально-поршневой гидромашины с торцовым распределением, у которой угол подачи лежит в главной плоскости регулирования, определяется только этим углом.
Утверждение 3. Изменение угла сжатия аксиально-поршневой гидромашины с торцовым распределением, у которой угол подачи лежит в главной плоскости регулирования, не меняет подачу гидромашины, по меняет сжатие в цилиндре при положительном перекрытии.
Следствие. При использовании аксиально-поршневои гидромашины с торцовым распределением, у которой угол подачи лежит в главной плоскости регулирования, изменения подачи следует производить только при помощи угла <р подачи, а угол у сжат i должен выбираться в соответствии с заданным режимом' умения так, чтобы получить наименьший скачок давления в момент откры
Попядок расчета По заданным рабочим давлениям plt р? «ахо-«я^оХщке значения 0 я 0« Для нескольких значении умов П'Р№Р™6ра₽нвымЧ;аче„Иям углов 0 и «• —" —£» значения у?ла у сжатия для ™ пары = М
"качки лай— а момеи™ откры-’“Й^ЛекТВиселеДОван„? в
(рис. 1₽2^9ГнаНр°0ДН0ГО предприятия в городе Рохлиц, для которого и проводилась работа.	„паяпяились в лаборатории
Такие же по теме исследования	Выоием тех«-
кафедры металлорежущих станков Р

родством проф. Бартельса, в том Чи
, липшие под РУко.^ом высшем учебном заведении вМег
дииломнь1е работь°в
дипломных про	12.39) показана ось, ОКолп
1960 гг. ппоекиии внизу ( •	12.40), несущая кольцевс®
^поворачивается „Генного подшипника. Поворот КОТОР „яюШУЮ тяжело нагруи {показано в верхней части Пра. НепъРгТпри помощи ходового в	кОльцевую направляющ^
серЬ " оекции иа рис- Определителя, несущей цилиндро. "Х-о	i »»№ртш.тег ротора „о w
>”	SnP»”»«*=S'
шению К кольце
Рис. 12.40 Регулирующая серьга
Рис 12.39 Раднально-поршиеван гидромашина
На кинематической схеме регулирующей серый (рис. 12.40) показано несовпадение оси кольцевой направляющей в серьге / относительно оси распределителя 2 на величину Ь, отсчитываемую по вертикали.
Серьга 1 поворачивается относительно поворотной оси 3, меняя эксцентрицитет распределителя относительно направляюще10
ТО изменение эксцентрицитета происходит вследствие того, чается^пясс^и ₽аспРеделителя от центра поворотной оси отливом напрадляюи1ейИЯПМе>ВДУ центРом поворотной оси и осью кольце мчалью»	6,^“®““"“ "°ложении
b = r — l.	(12.61)
цитет. мснении угла поворота серьги будет меняться эксцентрй'
«г	J
торной г«ДРомадиадТХю,?ДдР.У€МОЙ радиально-поршневой Р® аи	с кольцевой наПравляющей и ТОЧеЧИым касз-
Кольцевая направляющая, ОА = R, где А - -----
размещается так, что ее центра ротора.
При повороте блока точки контакта А будет
рМ показана на рис. 12.41 Около центра О, вращается блок Н'ппндров, ось цилиндра которого 0,4 наклонена под углом р ^горизонтальному диаметру, причем
Р = ®1.	(12.62)
радиус беговой дорожки которой — точка контакта поршенька с беговой дорожкой,  центр смещен на (RO = е относительно цилиндров в соответствии со смещением меняться величина отрезка OtA = S, за счет чего и будет происходить возвратно-поступательное относительное перемещение поршня в цилиндре.
Рис. 12.41. Кинематическая схема гидромашины
Проектируя ломаную О,ОА на писать
отрезок прямой OtA, можно за-
S = в cos Р Ч- /? cos т, причем S = Smax при р = т = О, поэтому ^тах — В + R, а относительное перемещение поршня в цилиндре
— COS Р —- cos т).
X — *^niax
Из прямоугольного треугольника АОВ
R cos т = р/?2 — е2 sin8 р,
причем ~ величина малая по сравнению с единицей. Кроме того, разрешающие уравнения будут использоваться главным образом 13 В Н. Прокофьев и др.
.„пенного объема, который имеет место па пе при расчете зашемле11^шенн11]х лпбо „а опорных Гочк<1Р’а-Ч. „нх И«’Ра"с™’^рР„,,в точек углы Р равны 0 „ п, тоТОву Л
е"ХПью'^«™ °“КТО РМ"КаЛа
е2
COST-I пользоваться только первыш двум» членами ряда разложен,,, COST= l--^sill2P-
Поэтому относительное перемещение поршня в цилиндре буДет
x = efl-cos₽+-^-sin2p)	(i2.G3)
или, заменяя sin2 0 через двойной угол,
х = е(1 -cosp) + ^-(l — cos 20).	(12.64)
Скорость относительного перемещения поршня, которая обусловливает подачу, определяется производной во времени от выражения
=w	i'2'65’
На рис. 12.17 показана распределительная ось в момент отсечки цилиндра, находящегося в начальный момент нагнетания. В этом случае ось цилиндра проходит через опорную точку А, а угол р3 перекрытия совпадаете углом 02 запаздывания открытия цилиндра (открытие цилиндра произойдет при его повороте на угол 03, когда точки 2 совпадут с точками 2' и перейдут через них, а отсечка произошла на кромке в точке /).
Регулирование индикаторной диаграммы поворотом распределительной оси показано на рис. 12.42. Верхнее изображение показывает обычный способ регулирования гидромашины изменением эксцентрицитета е, т. е. таким смещением распределительной оси пягпп»?ЛЬНО кольцевой направляющей, при котором радиусы остаются™.^Я’ Иа КОТОРЫХ размещаются опорные точки А и В, расппепелиз^яаепНЬ1МИ ^ЭКС1};ентРицитет меняется смещением оси прямая ппохпп«^Ь ОПОРНОЙ Оси)’ В этом СЛУ436 опорная ось, т. е. кольцевой ианпанпя черД3 063 центРа (распределительной оси и
распределителя^ ’ Не меняет своего положения относи-отсечки и вапазпыТяИи^К0М РегУлиРовании соответствующие УгЛЬ1 ;	открытия остаются неизменными:
= РГ + р*^0*.	(12.66)
Л86
Направления перестановки
При поюрои распределителя па угол ₽,+ | пр0„
то’^ То - "Й Ея и при переходе цилиндра из отдающей полости в Прием^ Можно добиться тех же результатов если смещать 0Сь 0 невой Управляющей относительно оси (\ распределителя одНос Хо по двум взаимно перпендикулярным направлениям, £ показано на рис. 12.43, внизу. В этом случае опорная ось Л00*в окажется повернутой на тот же угол 0j 4- Р8( а пол ный эксцеНтри. цитет будет определяться геометрической суммой смещений По обоим направлениям:
е = рЛБ| 4- eg.
Во втором случае также отсечка цилиндра произойдет при повороте цилиндра на угол Pt после прохождения через опорную точку Л, и поворот цилиндра еще на угол ₽3 откроет его, соединив с отдающей камерой.
В той же работе Клауса 1125] дан подробный расчет изменения давления в запертом цилиндре.
Для определения изменения давления в запертом цилиндре обозначим его объем при среднем положении поршня (рис. 12.44, с) через Vo. Тогда объем цилиндра в начальный момент нагнетания при р = О будет
Vo + ef.
При повороте блока цилиндров на угол р = со/ =#= О поршень вытеснит из цилиндра объем
так как по
Вычитая выражение рота блока
V.«m =Х/ = ef (1 — cos р +	sin2 р),
уравнению (12.63) перемещение поршня х-Ц1 — cosP4-~ sin2py
из начального объема вытесненный объем, получим текущего значения объема в виде функции угла пов цилиндров:
V = V04-ef(cosp— ® sin’p).	<12,б7)
Отсечка цилиндра перед его вступлением в отдающую область происходит при вначении угла- « <р1<0, если принять за на-быть положитедьным0 съЧКУ И считать> что перекрытие Д03*"# » положительным. Открытие цилиндра в отдающей области пр>» Я81
положительном перекрытии происходит уже в диапазоне углов характеризующем запаздывание открытия цилиндра 'с. 12.44, б).
Для каждого из углов щ и р2 можно записать выражение объема причем объем в цилиндре при Р = ₽j будет начальным, и на осно-ваНни закона Гука (предполагается, что х = const)
где
поэтому
Др = Др31 - Др32 = х ,
Vi = Vo + ef (cos Pi — ^-sin2p^; '
Va = V0+ef (cosp2 —2~sin2p2),
cos Pi — cos p2 + A (sin2 p2 — sin2 p^
Др = x--------p-----------------------
+ cos P, - Asin2 p,
(12.68)
Имея в виду правило знаков, связь между углами р3 перекрытия, р! отсечки в конце всасывания и р2 запаздывания открытия, можно записать
Р2 = Р1 + Рз	(12-69)
и тогда выражение величины повышения давления в защемленном объеме примет форму
СОЗ ₽, — COS (р, + ps) + A [Sinl (Pt + ра) _ sin» pj]
Да> = х--------------р-------. (12.70)
А» Ч-совРз-Аsin2₽1
Если бы рабочая клетка переходила из отдающей камеры в приемную, то абсолютная величина изменения перепада давления осталась бы той же, но знак изменения перепада давления изменился бы.
Сущность регулирования защемленного объема заключается в таком выборе pt и р8, при которых заданным значениям plt pt и в будут соответствовать наименьшие скачки давлений р3 и а значит, будут получены определенные значения изменений давлений в защемленных объемах, поскольку
р9 = Р1 + Лр + ра; Р1 = Л + ЛР* + Р»-	(12.71)
Рассмотрим возможности регулирования изменением угла 0S перекрытия pj = 0. Этот случай соответствует отсечке цилиндра а опорной точке и запаздыванию открытия на угод 0».
„ пяпрнство (12.70) значения ₽, = о Подстановка Р	д форму	рОц«ет
разрешающее уравнение, д
1—cosPs + 2# si,,S03
ЛР = Х JZTZ '	<>2.72)
е/
Из подученного равенства можно найти значение угла переКрь|. тпя X обеспечивающего заданное значение изменения давления в защемленном объеме.	___
cosP3 = -4±K(’? + 1)“2x’^	+1) 02.73)
(для минерального масла при температуре в 50 С принято, что модуль объемной упругости х= 16150 кГ см2) 1125]. Расчетное уравнение упрощается в связи с тем, что второй член под радикалом много меньше первого. Поэтому, взяв из-под радикала множитель 1 R _р 1, разложив радикал в ряд и воспользовавшись только первыми двумя членами ряда разложения, получим разрешающее уравнение в форме
+ (12.74)
Таким образом, cos ра запаздывания открытия линейно связан с изменением давления в защемленном объеме, а зависимость от эксцентрицитета гиперболическая.
Чем меньше первоначальный объем, т. е. чем меньше мертвый объем цилиндра, тем меньше может быть запаздывание открытия цилиндра при заданном изменении давления Ар.
Влияние изменения эксцентрицитета е обратное, и чем он меньше, тем ольше при прочих равных условиях требуется угол (щ-
’|а‘ПС,ГИЧ-Н0 Решается задача для случая перехода цилиндра g _ ющеи области в приемную, которая начинается с углов уравнений 7m ДЛЯ ЭТ°Г° случая ₽> = л и ₽з = № из тог0 же (.	) можно получить разрешающее уравнение в форме
Ап*- л	-Л sin’ р*
ар = — Ар = х-----------2/?	(12.75)
1
которая после аналогичных упрощений приводится к равенству
j]	(12.76)
ЛМ		ьЛ+1 ’
Подсчет необходимых значений косинусов углов 6, и 6? nene- I крытня, которые дают необходимые значения изменения давления V О 5^1 0^ 0-Э2 2ПеГоМ7оаЛ4 5°rs nHROCa кс7эксцентРивитетами е = 0,5, 1,0, AU, Z.Z, д,О, 1,0, 4,5, 5,0; 6,0 и 6,7 дал значения которые изображены на рис. 12.45. На нем пунктирными линиями „оказаны зависимости cos р? = f (Др*), а сплошными - cos Р = ^/(М-
Объектом испытании был насос с параметрами: начальный объем цилиндра Vo = 4,276 см3, активная площадь поршня f = 4,02 си2 радиус сферической голов-  кп поршня г — 45 мм и модуль объемной упругости рабочей жидкости х
16 150 кГ /см2.
На рис. 12.46 приведены аналогичные зависимости, только по оси ординат вместо cos рз и cos р отложены необходимые углы ра и Рз перекрытия в градусах.
Легко видеть, что
сколь-нибудь малых значениях эксцентрицитета в для получения значительных изменений давления требуется осуществление больших углов ря и Рз перекрытия, что особенно заметно на рис. 12.47, где необходимые значения этих углов построены в зависимости от эксцентрицитета
для разных значений изменения давления в защемленном объеме. И в этом случае, как и раньше, пунктирные линии относят величины для необходимых значений угла р$, а сплошные — для необходимых значений угла рэ.
Изменение углов перекрытия рз и р* конструктивно очень трудно осуществить. Проще менять углы Рх и Р* при постоянных значениях углов перекрытия рз и р*, что легко осуществимо или поворотом распределителя (см. рис. 12.42), или смещением оси кольцевой направляющей относительно оси распределителя одновре-риНН°2П° ДВУМ взаимн0 перпендикулярным направлениям (см
Для того чтобы не делать громоздких выкладок и иметь возможность воспользоваться уже проделанными расчетами, рассмотрим график изменения давления в защемленном объеме в зависимо-
381
Рис. 12.45. Оценка изменения давления
при
стн ОТ угла 0а открытия цилиндра в предположении, Что цилиндра была осуществлена при 0 = 0 (уравнение zioTcei,Ka рис. 12.48].	(,2-74) и
Поскольку изменение давления по закону Гука пропорци относительной деформации, тот же самый график изобража0На,ПЬ110 си тельные деформации.	ет °тно.
Для случая отсечки цилиндра при 0 = 0 график в опрел масштабе будет изображать абсолютные деформации. Р деленном
В рассматриваемом случае при угле 0, ф 03 откпы линдра (см. рис. 12.42 и 12.43) относительные деформа0'” Ци‘ меряются отрезком bd
Открытие цилиндра при Уг. ле 0! поворота блока цилиндров приведет к относительным д₽ формациям, измеряемым отрез ком ас на рис. 12.48.	1
ft
10
$ tpac 18
ipet Ц
?00кГ/смг 150
Р=200Щн
2
Чкнсныш tabtaui '««ггз»"™
4	6	8 с чн
Эксцентрицитет
мч Значения давления p2 ври p зличных значениях эксцентрицитета


100^ P2=50ir/[Mi
“то“” Р	Р™вЧи°п “а УГЛаХ
0» -Г ₽« а от^СЛен из Уравнении^; т5\ИЧем отРезок bd = Api+s £•	П = д₽1 из того же7уояаменой угла ₽s на У?
4 ДЛ. шэска^’ В 9Т0М случае искпм уравнення заменой угла 0з «•’’Ряжениям У ^ит^ьнз”С“™ая величина Др = Др>+5 + ’	Деформация пропорциональна
Применяя эти утверждения к уравнению (12.74), можно записать —/?
cos Pi - cos (Р, + р8) =	(V0/8f + 1 )-j-5-.	(12.77)
Г*+1
Неточпость рассуждения заключается в том, что график на ,1С 12.48 изображает относительные и абсолютные деформации топько в том случае, если отсечка цилиндра действительно произошла при р = 0. Если же отсечка цилиндра была осуществлена только при Р = Рь то объем цилиндра при тех же значениях абсолютных деформаций будет меньше, как показано на рис. 12.48.
Приводя левую часть последнего равенства к виду, удобному для логарифмирования, получим разрешающее уравнение в тригонометрической форме
Рис. 12.48. Рабочий участок индикаторной диаграммы
2х sin
(12.78) 7/?+1
давления Ар и гипер-
откуда видна пропорциональность синуса необходимого угла поворота оси распределителя желаемому изменению болическая зависимость от эксцентрицитета.
Разумеется, запаздывание с отсечкой цилиндра при повороте распределителя приводит к уменьшению подачи из-за уменьшения рабочего хода, что оценивается коэффициентом подачи г)0.
Только следует иметь в виду, что величина т]0 указывает на относительную потерю подаваемого объема рабочей жидкости, а не на потерю энергии. Большая часть этой энергии рекупируется за счет превращения на некоторых участках хода цилиндра гидромашины из насоса в гидродвигатель.	* f
Аналогичному тому, как было сделано ранее, результаты подсчета величины sin psj в зависимости от величины изменения Давления Др для того же самого экспериментального насоса с углами р3 = р* = ]4 показаны на рис. 12.49 для эксцентрицитетов ' = 0,5; 0,7; 1,0; 2,0; 2,2; 3,0; 4,0; 4,5; 5,0; 6,0 и 6,7 мм.
Пользуясь материалами графика, изображенного иа рис. 12.49, можно подсчитать соответствующую величину необходимого угла Pi
Оборота оси распределителя, которая показана на рис. 12.50. На М же графике пунктиром показана необходимая величина угла
8М
й* поворота при расчете перехода цилиндра из отдающей камеры в приемную. Как и в предыдущем случае, необходимые значения углов РТ оказываются меньшими (пунктирные линии на рис. 12.50) углов Pi. что объясняется большими относительными деформациями (меныпая величина первоначального объема рабочей жидкости) при переходе цилиндра из отдающей камеры в приемную.
Наконец, на рис. 12.51 показана зависимость необходимого уГЛа поворота оси распределителя в зависимости от эксцентрицитета для величин изменений давления Ар = 0; 50; 100; 150 и 200 кГ!смг для того же самого опытного насоса с 03 = 03 = 14°.
§ 12.11. ИСПОЛЬЗОВАНИЕ РЕГЛАМЕНТИРОВАННЫХ УТЕЧЕК ДЛЯ ИЗМЕНЕНИЯ ИНДИКАТОРНОЙ ДИАГРАММЫ
По утверждению Клауса (1251, для того чтобы не возникали звуковые волны необходимо, чтобы не было энергетического скачка, а было плавное изменение давления и плавное изменение градиента давления.
Рис. 12.52. Форма и размеры распределителя
Сколь убедительны вторые два утверждения — неясно, тем более, что опыты Клауса не дали прямого подтверждения. Вместе с тем, хотя регламентированные утечки понизили градиент давления и Дали плавное изменение давления, но они в еще большей степени уменьшили энергетический скачок, и поэтому нет оснований считать, что понижение уровня шума достигнуто именно за счет первых обстоятельств.
Обычно регламентированные утечкн создаются при помощи канавок — «усиков».
3W
»»»»»« to,b“c значение терекрод, Обращает н	является свидетельством того, что J
ппдао^лся для’работы с пониженным уровнем шума. СОс ПР<Значнтельно большие по размеру калиброванные проходы Пре. дусмотрены на распределителе другого насоса (рис. 12.52).
Особенно мала здесь перемычка (Рз) Можно видеть, что па опор, ной точке А имеется даже отрицательное в 1 мм перекрытие. Правда,
Рис. 12.53. Разгружающие усики
калиброванные проходные зазоры’ особенно на подходе к перемычке, весьма малы.
Малое отличие размеров г и I [уравнение (12.61)1 приводит к тому, что при увеличении эксцентрицитета происходит опускание центра направляющего кольца по отношению к центру распределительной оси, как показано на рис. 12.52 при помощи дуги. Рассмотрим дифференциальное уравнение, определяющее давление в запертом цилиндре при существовании регламентированных утечек.
На рис. 12.53 показан цилиндр, в котором поршень совершает возвратно-поступательное движение около среднего положения сс.
Пусть в начальный момент времени торец поршня будет в положении аАаъ давление в цилиндре р, а давление в камере, с которой цилиндр соединен при помощи «усика», рк. Через промежуток времени dt торец поршня переместится из положения в положение 22 величи||У уменьшая при этом величину объема под поршнем на величину	3
dVJ, = fdx = fod/<0,
(12.79)
сложенная де^°1)мация объема рабочей жидкости, обу-f-?K=e кинематикой механизма;
' _ ™тивная площадь поршня-
За этот жеСИг^мНаЯ СКОР°СТЬ поршня.
жидкости через «усик^/^н вРемени из-за протекания рабочей рабочей жидкости dV закпЛИНЛР пР°пикнет определенный объем Уравнение расхода’имр^°1еННЬ1Й межДУ сечениями и bsbr в '-лода имеет форму [69]
dVy •= sign (р
р^^У~\р~рк\ dt.
(12.80)
при p_Pl>0 „	при
p — коэффициент расхода;
fy - площадь живого сечения «усика» в месте хода расхода утечек в цилиндр;
р = —плотность рабочей жидкости;
у — объемный вес рабочей жидкости;
g — ускорение сил тяжести.
Из-за сжатия рабочей жидкости в цилиндре давление в нем повысится на величину dp, которая определяется по закону Гука из выражения
=	= —^(dV^ + dVy), (12.81)
где х — модуль объемного сжатия рабочей жидкости;
Уо — первоначальный объем рабочей жидкости, при котором р = Ро-
Если за начало отсчета давлений было принято давление р0 = О в цилиндре в момент отсечки, то величина р будет определять избыточное давление в цилиндре.
Подставляя выражения (12.80) и (12.79) в равенство (12.81), получим дифференциальное уравнение защемленного пространства
^= — [tf — sign(p-pK)p^	р,с|]. (12.82)
Рис. 12.54 Схема аксиально-поршневой гидромашины
Приближенное значение (однако с высокой степень относительной скорости поршня v в цилиндре можно п у рассмотрения схемы механизма (рис. 12.54). Поршневая группа П вращается с постоянной угловой скоростью а = си/, где а — угол поворота и со — угловая скорость.
Угол поворота блока цилиндров Б, в котором на радиусах г равномерно размещены оси цилиндров, обозначим через 0. Точки А и В являются опорными точками.
На распределителе (рис. 12.55)
размещены, в соответствии с ука-	пг>иемная а и
завным направлением вращения блока цилиндр ’ Р11ИЛИВДрОВ. отдающая б канавки, по которым перемещают ктяром# Геометрия окна показана на той же фигуре ш Р У
Принимая г = R cos у (рис. 12.56), получим
ОВС8 « О»с, « О»с» = f cos 0.	__
и относительное перемещение поршня можно опргДе, КОМ	,ПЯТь Отп„
х ССа = ВС2 tg у = г (1 + cos |3) tg у.
Относительная скорость перемещения порНШя 0	^2'83*
произвс'днон по времени от относительного Перемсщсп ПредеЛяетс положении постоянства угла наклона блока цплнпдпо"51 Х 13 пРедЧ величина производной от 0 по времени /, позволяющая В п°ЭтоД пень равномерности п вращения блока цилиндров* 0°це,||,ть сТе.
„ г-—ч	кинематической ззп1|).еДС'ПЯетсч
«е»Д> удом ™
А X---!—'^L /	ПОППШрплй^^^
1 11 У’ломв ЦПЛИНдрод
1 Руппы
л
поршневой группы
поворота блока i
ЕСЛИ блок ЦИЛппдпон ' водится от поршневоТ Р"’
-Ч? н-
с
б
А
д Ж
F к
/
Mj км
В
Рис 12.55. Угловые размеры
перемычки
При помощи кардана, то Уравнением
ГДе
6 ~
машины связь между угламп о и ₽ описывается
Если б	tga = cosytg0.
SS ™рда™“ ™ cZ? ^ХгроуХ“ям" "ри ™”“" « и p описывается уравне-
tga^^gP.	(12.84)
причем величина k пп
ось п™ршне2°Гпа	на котопо^* ЗНачениях ?• Vi « Ь
^^-соответсХшо а П',яма« оЛ П0Р”МаЯ/И0 изобРажаеТ Очевидно, ЧТО ппи УГЛЫ поворота пепп блока цилиндров, при	первого и второго карданов.
«ХТ км*«иевд	-ТГ	„г.®)
№ BUC°t’a Vra“B°ro SZ“,b„?Ma"a Рав"»» единице при дного кардана относительно
гоп? как это и делается в нерегулируемых аксиапьно-поршне-гид’ромаишнах с двойным несиловым карданом.
вь|Чнпя возможности регулирования головка кардана О2 в блоке п„|1Лров делается фиксированной (00г = q = const и 0х02 = I =
11Н-onst), а вторая головка кардана в поршневой группе — сколь-*icii опирающейся при помощи сферической опоры на пружину (рис. 12.58).
Рис. 12.57. Положение осей двойного кардана
Рис. 12.58. Схема двойного кардана
При изменении угла у шаровая головка кардана 0t сместится, соответственно деформируя пружину, и тогда связь между углами yt п у.2 может быть определена при помощи теоремы синусов
sin Yj = sin (у, + у2) = у sin у,	(12.86)
а угол поворота второго кардана
Y« = Y-Ti-	(12.87)
Так как условие (12.85) имеет место только при определенном значении угла у = у, которое можно найти из условия (12.86), то
y = arccos4-.	(12.88)
При любых иных углах у =/= у поворота оси блока цилиндров относительно оси поршневой группы можно установить связь между углами поворота поршневой группы а и блока цилиндров ₽ в виде равенства
<12-89>
сравнивая которое с равенством (18.84), можно записать
^^cosy^	(12.90)
cos	'
После применения равенства (12.83) можно найти зависимость угловой скорости блока цилиндров от углов у и р:
< « Й =	(12.91)
на Графи*'^изображающий зависимость св и Q « Q (р), приведен
от
ченных на рис
делить l_
и и
const.
fi
Рис 12.59 Неравномерность угловой скорости ведомого вала кардана
на„мда. ~~ -'ЗХГ —
При р= °- а наименьшая Р	2
й = йт« = ^<о: fi = Q-'" = cosv<->. (1292) п vrnax v не превосходящих 30 кривая. изображаю^, При углах у, Г • „сидров, может быть с точностью до о То уг„,-ю<к»Р»™“»7“мД «„„„уймы в предела/^ аппроксимирована пр	о
значений углир. Р»™« 0 » 7 Поэто">' "	»₽»,
..,_ 12 59волнистыми линиями, можно приближенноопре.
величину угловой скорости блока цилиндров при помощи } J	интерполяционного урав.
нения
5 -«-W-
— I)cos2₽ + 1]ш, (12.93) где
k = —. cosy
Наибольшие относительные (а не абсолютные) ошибки при определении разности угловых скоростей Q — ш будут иметь место при значениях углов р, близких к " и л. Однако при этих значениях углов р величина множителя cos 2 р в равенстве (12.93) мала, а поэтому и при этих значениях углов можно с большой степенью точности пользоваться тем же интерполяционным уравнением.
™пиЛеЛИЧИНах иеРавномеРиости вращения блока цилиндров можно У по величине коэффициента неравномерности
° = -Т = «(₽. Y).
» табд. 12.8.
рис. 12.59, может иметь лг^АОрИТЬ’ ЧТ0 гРаФик, изображенный иа симости от положении ^°е Начало отсчета по оси абсцисс в зави-тельно места присоединения Ра“матРИваемого цилиндра относн-Таким образом для каРДана в блоке цилиндров.
ном (например, консточкпшлТРпКЦИЙ с двойным несиловым карДа' тием — вквивалви ' «Виккерс») можно пользоваться поня-„	у™ 7.	мады8 з«аче«й»
(12.94)
Таблица 12.8
	₽ в град							
	0	15	30	45	60	76	90	
1 л	0.015	0,013	0,008	одни	—0.008	—0.013	-0,016	45“10'
iv 9Л	0,060	0,052	0.032	0.002	—0.031	—0.056	—0.065	45-52'
ЧЛ	0,134	0,120	0,076	0,007	—0,065	-0.126	— 0,155	47”04'
ли 35 —	0,181	0,163	0,107	0,020	—0,090	—0,185	—0,222	47°46'
тлов уэ с достаточной степенью точности заменять угловую скорость блока цилиндров угловой скоростью приводного вала
Й =	(12.95)
Возможны разные формы «усиков». На рис. 12.60 показаны трехгранные «усики», для которых площадь живого сечения в соот-
Рис. 12.60. Угловые размеры перемычки Рис. 12.61. Конфигурация усика с разгружающим усиком
ветствии с обозначениями на рис. 12.61 будет:
f	l ЬП110 nj
'у	2 ₽J р ’
(12.96)
а для прямоугольных усиков
f, =	₽	(12.97)
Общее выражение
(, = /(₽-₽,if.	(12.98)
где = const — угол поворота блока цилиндров до начального момента открытия дросселирующей щели (угол начала отсчета
(12-99)
В рассматриваемом докладе [131] есть указание о дросселирующих щелей трехтранной формы принЯТНР	„
значения коэффициента Pacx°№ 1‘ в виде зависимости epeMeH1Jj" 0,65+ 0,2 4
Р.ч практически не изменило результатов расчета.
Имея в виду, что градиент давления dp _ <tp dp dt dp dt ’
а также имея в виду равенства (12.83) и (12 98) дифференциальное уравнение градиента давления Л’ЗД<Н° зац11Сят линдре в форме	Б 3аг,ерТ0Л| 01
dn	R
W = A sin ₽ + -^-sjgn (p _ Ph} (p _
Л	,K 1 ’
(12.100)
где
Ц> ’ . Г 2 х б = р/ Г 7 V
Для конструкций, не обладающих постоянным значением угловой б/В
скорости блока цилиндров , приходится пользоваться равенством (12.93).
Следует оговориться, что равенства (12.101) записаны в соответствии с принятыми у нас взглядами на рабочий процесс аксиально-поршневых гидромашин.
В совместной работе фирм Дженерал Электрик и Виккерс 11271 использованы близкие к ним, однако иные выражения коэффициентов уравнения
(12.101)
д __А*со2к_________
J?
COS₽V0(1 +tg!₽) 2 sinXtg
В -- |u2a!	I
„	/(₽- ₽vl)u I
где «-угол открытая «усика»;
X — угадав веотш^НИЯ центРов штоков в поршневой группе; т —угол открыта ячейка сечении Дросселирующей щели;
следовательно в па У '
• Рассматриваемой работе было принято «Х"’С0!,р'
«2	’ угол’ определяющий перекрытие Р> ^0 ’
(12.102)
чет проводится числовым способом и в указанной работе РЯС ц« меж I подсчитываемыми точками была равной Г (рас-^подверглись 15—20 точек).
чс'У верждается, что расчет индикаторной диаграммы требует 1 т 2 н так как расчет каждой точки требует около 8—10 мин.
оК°Расчет проводился для давления в отдающей камере р0 = 4000 фунтов на квадратный дюйм и подсчитывалось только избы-6ое давление, т. е давление в приемной камере было принято
^'начало отсчета
Время перекрытия цилиндра было
t„ — — сек. п п
Использование всех условий расчета образца гидромашины, размер которой, к сожалению, не известен, дал уравнению (12.82) форму
= Q ± с,2 К К «2.	(12-103)
где
С, = 6,773-102п; 1
С2 = 2,199- 104п2. /
К сожалению, коэффициенты Gj и С2 (размер в дюймах, а усилия в фунтах) размерные, чем и объясняется оставление принятой в оригинале размерности используемых величин.
Имеется указание на то, что в одном из расчетов применительно к маслу mi 1-0-5606 модуль объемной деформации был принят
х = 250 000 фунт/дюйм2,
и в этом случае не удалось получить удовлетворительного совпадения расчета с экспериментом.
Однако при помощи косвенной проверки возможных значений модуля объемной деформации была получена величина
х = 145 000 фунт/дюйм2
и ее использование в расчетах дало вполне удовлетворительное совпадение с результатами эксперимента,
В этом же месте работы [1271 содержится прямое утверждение ° том, что расчету и экспериментальному обследованию подлежала гидромашина, предназначенная для работы с давлением рй --“= 3000 фунт!дюйм2 при п = 3600 об/мин.
Так же имеется утверждение о том, что бесшумный насос может °Ыть получен при проектировании распределителя на опрецелеиные значения давления и числа оборотов. Изменение же эксплуатационных параметров приведет к возникновению шума.
„ ,0 ПНПАМПЧЕГКИП МЕТОД РЕГУЛИРОВАНИЯ ДАВДРц,,
« 12.12. ДИНАМ|£1ДПКАТОР11оИ ДИАГРАММЫ	'Й"Я
„ А «> Кпя\'са [125] приведена конструкция распред»,.,, fnnc Р12 S Имеющего дополнительные объемы, присоед,^я (рис.	елителя. Давления в промежуточных Ка. '*
насоса на строго определенном режиме.
Всякий переход работы насоса на другой режим прИво несоответствию давлений /м и />м получающейся инд„като Л диаграмме и снижение уровня громкости шума прекращал^
Таким образом, обследование регулирования индикаторной дн. аграммы посредством «впрыска» в запертый объем по-настоящее
не проведено, и первые испытания, которые были проведены в ГДР и о которых очень скудно говорится в работе Клауса [1251, следует считать только начальными поисковыми исследованиями. Патент фирмы Ситроен на использование резонаторов, присоединенных к перемычкам распределителя аксиально-поршневой гидромашины, показывает важность динамических явлений в запертом
цилиндре и в присоединенном к нему промежуточном объеме, что не учитывалось в исследованиях Клауса, которые тем самым в какой-то степени обесценивались.
На рис. 12.63 к перемычке распределителя (развертка по окру*4’ ности с радиусом гк, на которой размещены оси окон цилиндров) j через трубку регулируемой длины / присоединен цилиндр 2, кущению попшнГчИгаТОрОМ РегУлиРУемого объема благодаря перем^ ние поошня nJ В патентном описании предполагается перемеш ние поршня резонатора от регулятора).
АЛЛ
Г—2?'.
Рис. 12.63. Схема резонатора «Ситроен»
л я в виду, что вентральный угол р„ окна цилиндра, цеит-угол Р« + ₽з перемычки, где рз — вентральный угол пере-РвЛ^)Я* / АР — вентральный угол выхода трубки резонатора на К|? сМычку (АР = у-). можно построить диаграмму abcdef (рис. 12.64) "Ягнения давления на выходе трубки резонатора, где на угле "3= р3 зоны 1 цилиндр будет перекрыт перемычкой.
в зоне II, определяемой центральным углом рп = ^(рц — Р3 + 4- АР) резонатор будет соединен с отдающей камерой, давление в которой Рг-
В зоне ///.определяемой центральным углом рш = -----Рч,
где z — число цилиндров, резонатор будет закрыт.
В зоне /V, определяемой центральным углом piv = Рп = = -2- (₽ч — Рз + д Р) > Резонатор будет соединен с приемной камерой, давление в которой
Периодически действующее давление в магистралях и ps будет возбуждать колебания в резонаторе, и если бы эти внешние по отношению к резонатору колебания были бы гармоническими, т. е. подчинялись бы закономерности р = ра sin <о/ (по
казано в виде кривой / на рис. 12.64), то перемещения частиц жидкости в трубке резонатора описывались бы уравнением х — - х0 sin (о)/ —-ф), где х0 — статическое перемещение жидкой частицы в трубке резонатора, a ф — сдвиг фазы, причем

,	. 2ыа
где ш0 — частота собственных колебаний резонатора (подробно рассмотрена в разделе о реактивных фильтрах); — = т— промежуток времени, за который из-за потерь амплитуда свободных колебаний станет равной + = о,37 первоначальной величины.
Наконец, скорости частиц жидкости, определяемые производной °т перемещения, будут сдвинуты по фазе еще на-£. Таким образом, меняю!1шйДК0СТИ’ постУпающий из резонатора в цилиндр, а значат. «сияющий в нем градиент давления в соответствии с дифференциала
s2) W»t "° *S3e " l4"“* ' »
vr«»"«""eM ’„ J; M,„0MM»0"y““™r°“"as™“P«y,w
ПНС 12.M на УГ0Л 2
P п Л	пронатора по сравнению с pa3Mepa
(ЕРш за малости	момент соединения цилиндра с Мап.
Jwanefl расход из него ® м магнстралн. Зато при 3aruipa
М3 п^ю не изменит Давл^н11Т „ нем давление, и подбирая пара.
CTCwa этот же расход' измену	ься ТОго, чт0 скачок давле.
“ётр« Центов система мож * достат0чно малой
Рис. 12.64. Колебания давления
Хотя внешние возбуждающие усилия не являются гармоническими функциями, они могут быть представлены в виде ряда гармонических функций, что позволит определить свою закономерность изменения расхода из резонатора.
Отличие такого регулирования индикаторной диаграммы от pei улирования использованием дросселирующих каналов заключается в том, что в рассматриваемом случае изменение давлений pi 11 Р2 пропорционально изменит и расход из резонатора, а значит, и величину градиента давления, если одна из величин pi или Pt останется неизменной (обычно так и работают гидропередач). Следовательно, изменение перепада не приведет к возникновению скачка давления. Именно в этом и заключается преимущество рассматриваемого регулирования.
ofn рм°«ёТОГ°’ ПрИ изменении параметра регулирования измените’’ ертого цилиндра, в котором может быть снят скачок А
ш
, nnvroM расходе из резонатора. Расход придется изменить ^""еГобьема V,, и длины /
За <- рв11дно, величина сдвига фазы ф определяется величинами пости р 'Де 1 — Длина, a f — площадь поперечного сече-
/бки резонатора, и акустической податливости — , где Vp— еМ резонатора их — объемный модуль упругости рабочей жид-К0Суказанные две величины определяют отношение действующей систему силы к вызываемому ею перемещению, так называемый, Импеданс системы.
В частности, можно отметить, что собственная частота резонатора определяется выражением
_ cVf
<Пп —	/--
и если сдвиг фазы ф меняться не должен, то регулирование следует проводить так, чтобы IVP = const (ы = const и ш0 = const). Поэтому нужно одновременно менять и Vp и /, а изменение /, как это следует из рис. 12.64, затруднительно.
Если же при изменении параметра регулирования желают менять сдвиг фазы, то условие Vpl = const не может быть соблюдено.
Из четырех имеющихся зон работы резонатора только в одной (зона /) он может регулировать давление в запертом цилиндре, поднимая его от значения до значения р2. Кроме того, в зоне /// резонатор попросту заперт, чем затрудняется его работа.
На второй перемычке распределителя имеются аналогичные четыре зоны и только в одной из них будет работать второй резонатор, на этот раз снижая давление от р2 до рх.
Было бы желательно обслужить при помощи одного резонатора одновременно обе перемычки, заставляя резонатор работать и на одном, и на втором участках индикаторной диаграммы. Решая такую задачу, а также желая получить возможность изменять
в широких пределах акустическую инертность р у без потери герметичности, та же фирма Ситроен применила вихревой резонатор, обладающий постоянной величиной акустической гибкости
VP
X 
П(1ГВих[)евой РезонатоР представляет собою цилиндр 1 (рис. 12.65) вар^Я"Н0Г° объема’ в котором соединительная трубка 2 заканчи-ностъ ЫЧК0М 3’ CO3AaiOu*HM вихрь в резонаторе, причем интенсив-i хря, существенно изменяющего акустическую инертность ₽7‘ будет зависеть от положения язычка 3.
Одновременное присоединение резонатора к обеим позволяет переводить энергию расширения из одИогПерем,1,ч>< в энергию сжатия во втором цилиндре, что повышает к ° 4,и1Иц1 чает работу резонатора.	’ п- 4. и
Разумеется, такая система может работать в только с нечетным числом поршней. Кроме того / ИДР°1',а,4и относительно обеих перемычек присоединение вих'рев ММетРичц^ тора требует их симметричной работы несмотря на то , °Г0 Резон? в
Рис. 12.65. Схема вихревого резонатора
из опорных точек, размещающихся на перемычках, объемы цилиндров разные. Это различие в объемах компенсируется при помощи двух дополнительных объемов 6 и 4, величины которых меняются при помощи поршней 7 и 5, кинематически связанных с рычагом { и одновременно перемещающихся относительно опорной шайбы, изменяющей производительность гидромашины.
К сожалению, подробности о расчете динамического способа регулирования индикаторной диаграммы, в частности, о вихревом резонаторе, равно как и результаты экспериментов с такой гидромашиной, не публиковались.
§ 12.13. НЕКОТОРЫЕ ЭКСПЕРИМЕНТАЛЬНЫЕ РАБОТЫ НО ПОНИЖЕНИЮ УРОВНЯ ВОЗДУШНОГО ШУМА
В РОТОРНЫХ ГИДРОМАШИНАХ
На рис. 12.39 был показан один из образцов регулируе^ радиально-поршневого роторного насоса с кольцевой наПРаа' щей народного предприятия «Гидравлик» в городе Рохлин, ко был подвергнут подробному испытанию в институте станков роде Карл-Маркс-Штадте (ГДР) с целью понижения возду й шума. Отдельные выборки из результатов этих испытаний опубликованы Клаусом 11251.
408
пелью испытаний было нахождение путей понижения Тя1< Кпсов выпускаемых предприятиями ГДР, то были осуще-в'Ума “Некоторые конструктивные усовершенствования, цель ко-сТвЛеНЬ1аключалась в уменьшении действия причин возникновения < есто обычно применяемого в насосах такого типа числа порш-И = 7 9 11, а иногда и 13 были изготовлены блоки цилиндров
Сличенным (15 и 18) числом поршней.
С 'для устранения колебания регулирующей серьги система ее ворота была переделана и заменена замкнутой системой нагру-Л°нных звеньев Точность установки желаемого значения эксцентрицитета обеспечивалась при помощи эксцентрикового меха-"ИЗразмеры г и I [равенство (12.61) и рис. 12.40)1 выполнялись так, что их разность не превышала 1 мм.
Проверялись различные варианты перекрытия на распредели
теле.
Каждое из этих мероприятий в отдельности не давало сколь-нибудь значительного понижения шума, однако одновременное удвоение числа поршеньков, применение регулировки при помощи эксцентрикового механизма и смещение оси распределителя относительно оси кольцевой направляющей на 1 мм (г — 1=1 мм), а также установка несимметричных распределителей позволили добиться существенного снижения уровня воздушного шума. Все эти мероприятия были применены в насосе, который условно назван насосом II.
Таблица 12.9
Наименование конструктивного параметра	Номер насоса		
	I	П	ш
Производительность в л/мин при но.минальном числе оборотов Номинальное число оборотов в минуту Наибольшее давление в кГ см* Наибольший эксцентрицитет в мм число поршней в одном ряду Число рядов поршней Диаметр поршня в мм вадиус головки поршня в мм Размеры подшипника Ширина окна в мм	63 1450 250 (при нулевой подаче) 6,7 9 2 16 40 170 х 230 8	100 1450 250 7,5 18 1 18 .12 150 х 210 12	100 1450 90 8,0 9 2 1» 45 170x230 i 6 I
И 1^адХ2итад?к?тоППЫ Испытаний три насоса: I. Ц *2-52 соответственно На т РЫХ Г1оказаны н» рис. 12.62. 12 17 и "“°' На тех же рисуных мю/раэжры г н
Наименование параметра
с
-700
-ЧОО
=3
К
Рис 12.67. Мгновенные значения перестановочного уси-лия
подшипник, несущий обя-кольцевой направляю'
Размеры пояшппника
Частота /лi импульсов в гц
Частота /ла импульсов в гц Частота /к собственных колебаний внутреннего кольца в гц
рыс определяют закон смешения кольцевой из
счтельно распределителя в процессе регулир0Вя?,РаВЛт1КХ11Рх Насос I с регулированием индикаторной ли	' Ч
точными камерами снабжен зубчатым подпитой ГрЭМмЫ
Иасос II не имел под.пнточного насоса чш HWM Насоеп степень влияния этого насоса на уровень пп, ?Озволало u ’
Насос IK был обычным серийным насосом^Ц'Н°Г0 ШумЧсЧ мерно в I мм.	ыиеом с nepPhp( умя. 11
«Г дан"“е ° т,’“ „асосах
Установка насоса на испытательиомстенле	Pn‘!Wl 6
сгевд жтт (юкшт Мек~^"а₽»с-'Ч
стенде При помощи
и соединенный	н' рт,;э;'П>ро
Упругую муфту).	нас°оом
мощи аморбти'заторКоРвеплен ПР« по. и СП№^умаа,^^ УРовеяь ;™7^Г0ЖЕ""„“
места замера. ССТВе Основн°го Фона было Bbi6nfT Насоса ло микро-
НаибХ SaBHb,M0=^ НИКОМ UIVIWM ^есгвенным источ-₽егУлир0Вания °^зался механизм ство ее пепо. Я ^СеРьга Р устрой-
Р Мещепия)-
является пТ нагРУ>кенной деталью , -"ЧСЯ Полшипи,.., ________к В I
ЗНННОСГИ Щей.
собственныу°ДСЧиТапы частоты Д
'сльным пео™~..уМпУльс°в на внешнем > кольда го
Рис. 12 % э
жаетс^ш19 Ко ВиУтреннйИТСЛьным пеоем^ ИМпУЛЬс°в на внешнем TaK>J S₽MKatol (или пп МУ кадьцу ко^ЩеНИем этого кольда по ко-’ьца бдп^ ПоДечитаиаП'1НКами)-Эта ЧаДрО^ попеременно нагру-*2.-10, ^ш,11’Иика f an^0rH4Hao «>> Т°Га обозначена через /ли 4	"г‘ РезУльуатц rJWa и для внутреннего
™	Ы Счетов сведены в т?бл.
Таблица 12.10
Номера насоса
I	II	111
170 X 230	150 X 210	170 X 230
458	408	458
517	<Ш5	517
4650	8400	4650
Горизонтальная составляющая сил, действующих на блок цилиндров от поршней из-за реакции кольцевой направляющей, приведена на рис. 12.67 при пулевом перекрытии, нулевом эксцентрицитете и девяти поршнях.
На рис, 12.68 показаны наибольшие перестановочные усилия в статике Pstmax, наименьшие перестановочные усилия в статике PvZmin и средние значения
,J г *	6 atw
Рис. 12.68. Зависимость перестхгновач» ного усилия от эксцентрицитету
перестановоч-

пРе°лолеватьИ1^°р™Гуд^фдРвв1ещення в КОТ€>₽ь» необх®АИМа Рощ этих усилий УА Р “ии гадР0маашяы.
^ наСОса превосходив^
“« достаточно больших зксщштрици-
пги ЛЁвяп|8^оо1(л<я1^введены лля нУлево«> оедеюытвя
Величины сил инерции, точнее, сил, которые при кольцевой направляющей затрачивались на преодоление поршней, показаны пунктирной кривой на рис. 12.68 ИНеРЦц^
Учет силы Pj позволяет определить Действительные п ' вочные усилия Рт^, РсР и р™><" правда, без учета ереСтац_
Результаты испытания в виде зависимости уровня пЛ’Ч в дб от давления в кГ см2 для насоса /, имеющего наименып % крытие, а значит, наиболее склонного к возбуждению -ч^е колебаний из-за больших скачков давлений, приведены на пЛЧ Испытания проводились при эксцентрицитетах et — 2 2 » Hes = 6.75 мм при замерах на трех расстояниях от насоса- q *45 = 25,0 и о, = 50 мм. Там же приведены результаты замера у '2'5-
Рис. 12.69. Результаты замера уровня воздушного шума на насосе /
громкости шума помех, т. е. уровня громкости шумов, которые вызываются не гидромашиной в помещении, в котором она испытывалась.
Испытуемый насос при небольших эксцентрицитетах, например е = 2,2 мм, на малых давлениях до 100 кГ/см2 давал уровень громкости воздушного шума ниже, чем при больших эксцентрицитетах. При более высоких давлениях уровень громкости воздушного шум* насоса, работающего с малым эксцентрицитетом, энергично возра стает, достигая значений, близких к 100 дб. Такое явление бул понятным, если вспомнить, что для сжатия рабочей жидкости в линдре при его запирании необходим достаточный ход зависящий не только от угла перекрытия, но и от эксцентрик которому пропорционален ход поршня.	пенн°м
Если мал эксцентрицитет, то мало и сжатие в заше^ияДли объеме, велик скачок давления, а значит имеются все основа возникновения высокого уровня шума.
412
oWpoe падение градиента уровня шума на очень высоких
, ^иях (от 150 до 200 кГ1смг) следует объяснять благоприятным ^ПЛе нем утечек в распределителе, которые играют ту же роль что вЛ”яНтоК рабочей жидкости через фасонные калиброванные «усики». 11 Законен, запертые камеры благодаря их аккумулирующей спо-
оСТИ несколько улучшают характер индикаторной диаграммы с°б1,высоких давлениях, и это обстоятельство также должно способ-вР1’ вать снижению роста уровня громкости воздушного шума. сТВПри больших эксцентрицитетах изменение уровня громкости постом давления много меньше, что подтверждает благоприятное Сияние сжатия рабочей жидкости в защемленном объеме, которое будет более существенным на больших эксцентрицитетах.
Рис. 12.70. Спектрограмма уровня воздушного шума насоса /
Все же результаты испытания показывают, что сжатие рабочей жидкости в защемленном объеме недостаточно и его нужно увеличить.
Промежуточные камеры, о которых уже говорилось ранее, понижают уровень громкости шума только на режимах работы, Для которых специально были отрегулированы давления р8Д и в промежуточных камерах. Изменения режима работы гидромашины сопровождались таким повышением уровня громкости воздушного Ум*1, какой был в машине без промежуточных камер.
Небольшое влияние увеличения числа оборотов на повышение мипВНЯ гРомкости воздушного шума было объяснено влиянием акку-У ирующего действия промежуточных камер.
и и - Ж1Ш^а иасоса/ при работе с эксцентрицитетом в « 2,2 мм Давление °б,Мин показаны на рис. 12.70 для четырех режимов ния, параметры каждого из которых приведены в табл. 12.11.
413
				5,,
		Избыточное давление в кГ(см*		
Номер режима		Ps		
		200	130	
1	0	100	65	0
2 3	0 0	0 У ровен!	0 помех	0 0
Спектры воздушного шума при других эксцентрицИТет причемхарактер их изменения аналогичен характеру Изме Ч ссютветствуюших кривых уровня громкости воздушное приведенных на рис. 12.69.
Р Наиболее высокие уровни громкости тонов были обнару>КР на частотах 460; 680, 920; 1160; 1380 и 2300 гц, а частоты [г L *
/з = 675; Д = 920;7 =~]g: /„=1350 и /1и = 2250 * весьма близки к ним. 4
Наиболее высокий уровень громкости имеет место на частотах, близких к частотам /б и /„.
Некоторые расхождения значений указанных выше частот вполне могут быть объяснены, во-первых, неточностями, которые всегда могут быть допущены при расшифровке спектрограмм и, во-вторых, неточностями в удержании числа оборотов насоса и при их замере.
Повышение числа оборотов насоса дало аналогичные
a)	6)
Рис. 12.71. Результаты замера уровня воздушного шума на насосе 11
результаты, подтверждающие основное значение эффектов, сопровождающих открытия цилиндров в отдающей камере.
Замеры уровня воздушного шума для насоса II при эксцентри-, цитетах 6j = 1,4 и е2 = 2,8 мм и п = 1500 об/мин показаны ДО рис. 12.71. Причем штрих-пунктирная кривая с пониженным уровнем громкости воздушного шума была получена при заполнен® корпуса насоса рабочей жидкостью за счет утечек. Чем выше ДДО дение, тем больше снижается уровень громкости воздушного шум за счет наполнения корпуса насоса рабочей жидкостью, котор очень быстро нагревается.
шДТмчТй 9Кар™на была получена и при больших t >3 и 6,2 мм), но несколько меньшем диапазоне
4Ц
эксцентр!1' изменен*1*.
Рис. 12.72. Результат замера уровня воздушного шума при е — 2,9 мм и разных числах оборотов
/рис 12.71,6), который устанавливался вынужденно ^"'.’ёдопус।имост" перегрузок.
цз-3? .рдаря более благоприятной геометрии распределения уда-
1’'Па'п1естве11Но понизить уровень громкости шума, в том числе л<*ь С\]алых эксцентрицитетах, и сделать его мало зависящим от " 11Рч|П1Ы давления в отдающей камере.
в*Л'этмечсио, что заполнением корпуса насоса рабочей жидкостью
, уТече'к удавалось добиться значительного понижения уровня 381'' Однако такой режим работы приводил к быстрому нагрева-НИЮ рабочей жидкости.
Влияние числа оборотов насоса II на уровень громкости воздушного шума в децибелах при работе с эксцентрицитетом Е= 2,9 мм показано на рис. 12.72 (сплошной липин соответствует /?2 = 0, а пунктирной — р2 = ЮОкГ/слт2). Получающееся некоторое повышение уровня громкости воздушного шума с ростом числа оборотов следует объяснять тем, что величина расхода через калиброванные фасонные «усики» практически не зависит от числа оборотов, а сжатие рабочей жидкости в цилиндре зависит от них, а поэтому при изменении числа оборотов появляется рассогласование действия обоих факторов, которое было согласовано только для определенного числа оборотов.
Следовательно, регулирование индикаторной диаграммы поворотом распределителя при использовании эксцентрикового вания позволило снизить уровень шума на 6 дб.
Спектры воздушного шума насоса II при работе с эксцентриците-2 \ькГ2Оо" тоо-Т/ °б'МиН показаны на Рис- 12.73 для давлении (В К1 СМ ) 200, 100, 0 (сплошная, пунктирная и штрих-пунктио-” Пр" УР°ВНе ГрОМКОс™ шума^омёх. при частотах 228°^ Ум^И лял°М<^СТИ В0ЗДУШН0ГС шума были
« 1340 <1360): 2300; 3750 “ « при Даменпк Тоо™/?£л ' ° "аСТОТЫ- Г"ИУ"™‘ I. =	™ SIT Ll Zg6-= 45°- f> = 67S-
близки к ним. ’ 10	0’ 17 ~ 3825 и ~ 9225 гц весьма
снижает уровень гпомё^тИе индикатоРной Диаграммы не только Дельных тонов, кратных ^ол^в' Н° И приводит к появлению от-бУ^Даемых рабочими	KllM гармоникам частот, воз-
“Останов™ более SXS* ''«Рок-аишны. Спектр
механизма регулиро-
Рис. 12.73. Спектрограмма уровня воздушного шума насоса Ц
зоне давлений от 0 до 150 кГ/см2 при числах оборотов 1209- 1500 и 1800 в минуту.
Так, на рис. 12.74, а показан уровень громкости воздушного шума в децибелах при указанных ' ----------------
выше числах оборотов в минуту и эксцентрицитете 4,6 мм. Зависимость, полученная при л = = 1500 об/мин мало отличается от зависимостей, полученных при тех же числах оборотов и эксцентрицитетах 2,8 и 6,9 мм.
Градиент уровня громкости воздушного шума на высоких давлениях, особенно свыше 150 кГ/см*, уменьшается, что свидетельствует о благоприятном влиянии утечек, которые в определенной степени улучшают индикаторную диаграмму и уменьшают получающийся при открытии цилиндра скачок давления-
Проверка влияния числа оборотов на уровень громкости н эксцентрицитете е = 4,6 мм показала, что при разных дам ниях (р, = 0,50; 100 и увеличение числа оборотов вес
416
675, /4 = 900, f,, = 1125 и /„ = 1350 гц
Рис. 12.75. Спектрограмма воздушного шума насоса /// при 1500 об/мин
лит К повышению уровня громкости воздушного шума, дй ^""повышается также с повышением давления (рис. 12.74,6). ьогоры»воздушного шума насоса III (п — 1500 об мин) пока-
(П<л пне 12 75 для четырех режимов работы: / — е — 4,6 мм
100 кГ см2; 2 — в = 4,6 мм и р.2 = 0; 3 — в = 0 и р.2 == 0;
11 уровень громкости воздушного шума помех.
Изпболсе высокие уровни громкости тонов были обнаружены густотах 225; 450 (460); 680; 915 (920); 1140 и 1390 гц, а частоты ( 225, /2 = 450, Л весьма близки к ним.
Наиболее высокий вровень громкости имеет место на частотах, близких к частотам /2, /3 и Д.
Понижение уровня громкости сопровождается расширением спектра частот и приводит к появлению более высоких тональностей.
Исследования в институте станков в городе Карл-Маркс-Штадте показали, что главной причиной возникновения шума является несовершенство индикаторной диаграммы защемленного объема.
»»».ХКХ^яТ“"-рузок
нагрузкой деталей.	стальных нагруженных переменной
SU	р'™““ "’««епия дав-
Результат еРЩе 'Х Скости воздуШно₽гоИщРу Д^дели^я удалось ""Ликаторной пи, поДтвердадает ведущее Насосе 11 Такой
С вьХкиДм 5раммы на нздученне^и “аЧение ««^шенсто УР0?СПадь308а»иеУРпОпомееМ Громкости. дромашиной воздушного :=^=~=Н»г===
изменения нагрузок

ними В исследованных насосах относятся к высОк(
пп.1 11П1ВНИ.11ОМ конструировании машин vpoBlllI г Чм ШУМ,'М у Рбыть снижены до 80 дб.
fT1| 111) «1.1 М0|>	1500 об мин ДОЛЖНО СЧ||Тат>
делмым ??очкн зрения уровня громкости воздушного ,'<1'1г!авным для насосов с пониженным уровнем громкости „ мш.юиштма и вибраций является точность геометрии рас ' Ч-X i устройст с помощью которых осуществляется вза|^ пепемёшевнс распределителя н кольцевой направляющей jX нуждаются в обеспечении высокой точности нзгоТ0ВЛе|11|^
При проектировании наиболее важно провести расчеты Вт можного влияния углов Pi П Р.Ч на pei улирование индикатора диаграммы н суметь выбрать оптимальный вариант.
Регулирование индикаторной дншраммы должно проводиться в зависимости от того, будет ли гпдромашипа работать при иещ. менпых эксплуатационных параметрах, или они будут изменяться в каком-нибудь заранее заданном диапазоне. Это регулирование должно проводиться либо выбором геометрии распределителя, либо ее автоматическим поворотом пли за счет подходящего В1ибора кинематики рейдирующего устройства. Решение должно быть разное в зависимости от назначения гидромашины Гак, для реверсивных и нереверсивных насосов или гидромашни, которые должны работать и в качестве двигателя, и осуществлять плавное торможение, решения могут быть разные.
Управляемое регулирование индикаторном диаграммой требует создания кинематически сложных устройств. Зато насосы с клапанным распределением более просты и в то же время в принципе должны работать с пониженным уровнем громкости шума.
По мнению Клауса — автора исследования — создание насосов с клапанным распределением в настоящее время становится главной задачей.
§ 12. 14. ИНДИКАТОРНЫЕ ДИАГРАММЫ АКСИАЛЬНО-ПОРШНЕВЫХ ГИДРОМАШИП 110 ОПЫТАМ ФИРМ ДЖЕНЕРАЛ
ЭЛЕКТРИК И ВИККЕРС
В докладе на пленарном заседании Конгресса по промышлен, ной гидравлике в Чикаго в 1958 г. 1127] сообщалось не т0ЛЬ ши расчете индикаторной Диаграммы и проверке расчета при п0 электрического моделирования, но также и результаты экспер тальиой проверки этих расчетов.	v авле.
Обследованию был подвергнут насос, работавший при . ииях 1000; 3000 и 5000 фунтов на квадратный дюйм и loOU* 3600 « 4500 об/мин.
41В
8P/cn. 320\
р=350
a
\п=3600°б/нин ,
280,
'-О
p=210
740
Р=2/0
200
160,
/20,
80
<fO\
ВНЛЯ задача, которая решалась при помощи электрическою чарования, — нахождение оптимальных форм дросселирующих
“‘‘Подсчет каждого режима работы защемленного объема на счет машине Внивок-120 проводился в течение 10 сек.
"^Применяя ранее принятые обозначения, можно так формулиро-И пять задачу.
 Отсечка цилиндра происходит при его проходе через опорную Н точку. Поэтому угол отсечки цилиндра fi, = 0. Запаздывание 6т-м>щня цилиндра определяется углом 02 = f}3. Расчету подвер-тется переход цилиндра через перемычку' распределителя, содержащую опорную точку А, т. е. рассчитывается переход из приемной помети в отдающую полость.
Результат расчета без учета утечек показан в виде кривой а на рис. 12.76.
Через «усик» трехгранной формы будет проходить расход утечек, которые увеличат давление в цилиндре тогда, когда оно окажется меньше давления в отдаю-дав’чен^™ наоб°Р°т. Уменьшат Давление, когда его величина пп₽ взойдет величину давления ПР Дающей полости У пс ня в от-«Р»м	™ =
правление утечек cfkaw учаях »а-«Усик» • был 0ЯсГ ТС” РаЗНЫМ‘ ^У тидромашиР JC4fiTa» на ра-2Юк//Сл2 при Л = з6лав^нием Результатом поавипг °61миц. геометрии ‘У& подбора
~ку"с uS'*" «’уГЛГТ* ™'мм-S S'Z'4;n”	“h запаэд—
” ДаМе""Я
лИЧине У^ет иметь мес-^а	гг ^,а Рис 19
«4-
г — ''"°ве-
’''7о - 77 кГ окуптеин
0
/7	20^4°
А.--------4
Рис. 12.76. Давление в запертом объеме при различных давлениях в напорной линии
Г ™Ятрпыю применение «усиков» понизило скачок „
Спедова • Kric'M2 и существенно снизило градиент Jt/3®'’1''-Н11Я с /7	™	камере в 35() кГсм, 1 корос1|1
Л ПР" повышают давление в цилиндре и при его откр11Тни'ъ'Л»
РЬШ= 15 )’ Давление в цилиндре окажется равным 2С2
>орпрт к скачку давления />я — 350 26 — 88 кГ с.м2
ЧТОЕПсРпГбы «усика» не было, то давление в цилиндре 0Каз бы равным 147 кГ см*, и скачок давления оказался бы М11о,о *£
Рис. 12.77. Давление в запертом объеме при разных углах перекрытия
Рис. 12.78. Давление в запертом объеме при разных числах оборотов насоса
шим (рз = 350—147 = 203 кПсм*). Величина же градиента давления в этом случае меняется мало.
О том, насколько значительно уменьшается скачок давления Рз — Рг — р, {pt — давление в цилиндре в момент его открытия), особенно при повышении давления р.г в отдающей камере, по сравнению с расчетным значением, можно судить из графика, приведен ного на рис. 12.77. Сплошная кривая дает зависимость скачка дав ления в момент открытия цилиндра при отсутствии «усика», а пун тарная — при существовании утечек через него.	.
Величина расхода утечек не зависит от времени и числаОТОР тов гидромашины, но объем рабочей жидкости, прошедший че| «усик», пропорционален времени.	др
Чем больше число оборотов гидромашины, тем быстрее „й будет проходить через перемычку, тем меньше времени оста
420
твориое действие «усика», тем меньше поднимается давлена благо в|’е1|1|Ю с давлением в цилиндре, работающем с распреде-
не имеющим «усика» (рис. 12.78).
^Так при расчетном числе оборотов, для которого и подбиралась истр’ия «усика», скачок давления в момент открытия цичиндра
Гдвсн нулю (точка С на рис. 12.78) вместо давления 147 кГ см1, которое было бы при отсутствии усика (точка С' на рис. 12.78).
Уменьшение числа оборотов до 1800 в минуту приведет к положительному значению скачка давления ря — 9 кГ см2, а увеличение до 5400 в минуту к отрицательному скачку давления 13кГ'см2.
Величина скачка давления ря при отсутствии «усика» на перемычке не будет зависеть от числа оборотов гидромашипы (показано сплошной кривой на рис. 12.79), а утечки через специально в -10
-w
30
-50
т—3---1 
Qu+0,№6
0у=0;/3=15'
Pi=2l0
200
160
120
60
<fO
О
xP/cS
2<t0
4.
12
4-------
эксПеРимента₽е3ультатами
п=3600 °^/мин firO
п	3500 ~1^ooi^fn
₽“-	а.,„ „ие,1ия
\ "одобранный «усик» y™ Х°ноГо ZL060^0^ И’ДеЛЭЮТ
•Легко видеть°из3""' “>н»<т1
Срытия цилин„п РИС- ]2-78	'
Как показано штри/0 16° Уменьшит' и7м“*СМИе угла
° 'пом, как пРИХ'пУНктирной ип. ИаМедение скачка ~«““чния ЙНИТСЯ С{<ачокИпЯУВеЛИЧении Ума п₽И На ₽ИС‘ 79 ДаВДе»ия,
" л = Х00Яо22 ₽«воп. „а
АЗД/кна
га““=™н»™нУа™:чтгния ”»»• пи. ?оНМиР°м на рис. 12 ™ уменьшают Что УВелнчение угпг»
... У ла запзздывания
<at
u.Tufl 6, = Р» = 15 при Р'- Если >ке Venn „меть угол г,рР^'Рь „Хенения давления в отдающей ма1|(с2П|1« эксплуатации требуют	1С а также могут меняться и
№Р“'’“™я *|& ««**««г оборотов, то J
образным.	эдяченнй углов перекрытия, можно iionV4llTl
Г,'’0ВеЕ”’еР^ки зр“нИ» тех или иных требований ,тем'* оптимальное с перСкрытия.
цИИ значение >гла ментально проверив ряд распредели^ Накои^пв какой мере величина скачка давления при можно выяснигь т на урОве11Ь шума. Использование таких открытии ШЕ™Р находить оптимальную геометрию раС1|рвде. материалов позвол величины возможного понижения ур0В11я лителя, оценивая р	матрИВаемых вариантов.
шума для кажд , ‘ РПроведена проверка точности расчета, ре. пьтаты°которо о п^каХь, пунктирной кривой на рис. 12.80.
X же кдамм показаны результаты эксперимента, имеющие Там же кружкам!	результатами расчета. Поэтому можно
очень большое с расчета работы распределителя с заданной к любым уеловпям эксплуа™™ ™щ». геометрия "Г"*""т"ие «ультата» таках подсчетов гм™ ра“»™вать на создание' гндромашнны с пониженным уро.» шума.
Глава 13
МАТЕРИАЛЫ И НЕКОТОРЫЕ ТЕХНОЛОГИЧЕСКИЕ ПРОЦЕССЫ, ПРИМЕНЯЕМЫЕ ПРИ ИЗГОТОВЛЕНИИ АКСИАЛЫ1О-ПОРШНЕВЫХ ГИДРОМАШИН
§ 13.1. МАТЕРИАЛЫ
При изготовлении аксиально-поршневых гидромашин используют сравнительно небольшое число марок сталей, цветных металлов и других материалов
В табл. 13.1 приведены механические свойства проката из сталей 35 и 45, закаленных при 860 С и отпущенных при 200" С, стали 20Х, закаленной при 860 С и отпущенной при 560°G
стали 40Х, нормализованной и отпущенной при 650 С, стали I8XHBA, закаленной при 870' С и отпущенной при 460 С, стали 60С2А, закаленной при 850 С и отпущенной при 400 С, стали 50ХФА, закаленной при 850° С и отпущенной при 420” С, стали 65С2ВА, стали ШХ15, отожженной и закаленной при температуре 840 С и отпущенной при 150° С. В таблице он — предел прочности на растяжение; от — предел текучести; 6 — относительное удлинение в %; а„ — ударная вязкость, существенно меняющаяся при низких температурах; ф — относительнее сужение в °п.
Тио.тци 13.1
Марка стали	^8	°7	6	Ф		ан в кГм!им-		при /	£
	В кГ[мм*	В кГ/ и и*	В %	В %	+20	-10	-40	- 0	1 50
35 45 20Х 40 X 12ХНЗА 18ХНВА 60С2А 50ХФД . 65С2ВА U,X15 (огож-inxTIHa’" (после закалки)	55 65 80 117 56 125 160 150 190 66 220	33 37 65 109 40 111 140 130 40 170	25 22 11 14 26 14 5 12	52 50 45 55 73 58 20 40 20	6.4 4.7 6,0 12 24 13 2.5 4,5 0,5	4.7 4,0 20.0 । 		9 20.0 1U.3 2,4	1 4,6 * 19 9	1.4 7.0 1 18 9 2,1 I
Некоторые Н1Ы ~Г,объемн ,я в М X	физич ый вес — коз	еские в г/сл *ффищ	С ВОЙС! и3; а -<ент Ti	гва ст - K03(j *ПЛОП]	—L_Lj приведены в хрициент линейно! говодности в ка.1 г			табл. 13.2, "о рисшир,--мегк ’грш) ;	
емкость в кал'г град.-, Ас, — нижняя Кп» с _ удельная тс"л<^твс1ттвую1цая началу превращения , Вт,,% екая точка в % (° шин; Ас, - верхняя критическая в аустенит при на £	|)Ю превращения перлита в Т°**а
соответствующая	ичеСкая точка, соответствующая
в С; Аг, -№рх”Я 1 в перлит при охлаждении в » С; > превращения ayci	соответствующая окончанию mJ1"
нижняя сЕ!т‘> в перлит при охлаждении в ° С. Ю Пр('%а
Таблии,,
Марка стали	1 , В ЦС"*	° X в 1/грД”	X в кал)см  сек -град	с в кал1г • град	Критические точки >> с			
					Лс,		Дг3	Лг,
35 4э 40Х	7.81 781	11,1 11.6	0.18 0.115	0.112 0.112	725 725	805 770	720	690 690
	78'2	13,4	0.11	—	743	782	730	693
I2XH3A	7,88	11,8	0.074	—	710	820	725	660
18ХНВА	7,94	14,5	0.11	—	700	810	—		
60С2А	—	—	—	-—	75э	810	770	700
5(1 ХФ А	7,8	12,4	—	—	7.>2	788	746	688
ШХ15	7.8	14	•—	—	/43	—	—	700
хвг	—	—	—	—	750	940	—	710
Использование цветных металлов ограничивается бронзами марок Бр.АЖ9-4 (основа — Си, А1 —8,0—10,0%; Fe — 2,0— 4,0% и примесей не более 1,7%), Бр.ОСН 10-2-3 (основа—Си Sn- 9,0-11,0%; Pb — 2,0—3,25%; Ni — 3,0—4,0% и примесей не более 1,2%) и Бр.ОФЮ-1 (основа—Си, Sn — 9,0—11,0%, Р — 0,4 — 1,0% и примесей 0,9%), а также алюминиевыми сплавами АЛ2 (основа Al, Si — 10,0—13% и примесей 2,2—2,8%) и АЛ9 (основа Al, Si—6,0—8,0% и Mg—0,2—0,4%). Механические и физические свойства этих сплавов приведены в табл. 13.3.
Бронза Бр,АЖ9-4 имеет температуру заливки 1120—1140°С при литье в кокиль и 1060—1100° С при литье в землю. Процесс расплавления ведется под слоем древесного угля. Линейная усадка ujiHrnL ъемная —3,6%. Атмосфера при плавлении нейтральная иием , °КИСЛительная- Эта бронза хорошо обрабатывается давле-750° С	пР0Катки 700—650° С, прессования — 850—
калка’с трмп^пИ шт?моП0ВКИ - 840-650 ' С). Термообработка: за-жиг^при температуре 700-75?С	°РИ ТемПераТуре С "
припоями с^пимм^4. ПоДвеРгается пайке мягкими и твердым" поверхностей Она еМ предваРИтельного омеднения спаиваемы с присадкой из оенД^ИВается газов°й сваркой и электросварку 4а1	И3 °LH0BHoro «еталла и применением флюсов, содер-
ристае и
,ч (ЬториС‘ „мнительная, полиру
<iel УДОВЛ	Таблиц»
реза	___________—
роШаЯ- ,Чагернвл	7 л л кГ/Я-"2	О гносите энное удлинение 8 в %	НВ	т , в г/с и3	Коэффициент лииейиеГО расширения в t = 20 -j- ln0 С	Предельная нагрузка в кГ/си- При скорости скольжения 0.9 л/сек. и обильной смазке марки АФ-70
					10,8	450.0
Бр. АЖ9-1	50 •>'>	Ь,0=1^1’	НО - 18»	7,5		430.0
/прессованные iipy™ii)	40	а,„ = ю	ПО	7,5	19,8	
Бр. АЖ9-4		° 10	75	8,6	18,8	70О.0
(литье) Ер.	25	1|0 = 5			18. 1	600.0
ОСН Ю-2-3	22	л — 3	80	8.7		
Бр. ОФЮ-1		«10 — °				
(литье в землю) АЛ2	14—16	6. = 24-4 К = 1Ю	50 50	2,65 2,66	21,1 23,0	—
АЛ9 (без термообработки) АЛ9 с термообработкой по ре-	16					
						
						
жиму: Т-2	14	8. = 2	45	2,66	23.0	—
Т-4 Т-5	18 20	IIII 0 in in *© «С	50 60	2,66 2,66	23.0 23.0	—
Бр.ОСН10-2-3 расплавляется под слоем древесного угля, температура заливки в водоохлаждаемый кокиль 1100—1200° С. Для этой бронзы обработка давлением не применяется. Она хорошо сваривается диффузионной сваркой (сварка плавлением не применяется), паяется мягким и некоторыми твердыми припоями, обрабатывается резанием.
Бр. ОФЮ-1 расплавляется под слоем древесного угля (температура заливки 1100—1150 С). Линейная усадка ее 13___14°
няютсГоия °бработка> ковка и прессование этой бронзы не приме-свариваться газовой ваяется„мягКИМИ и твердыми припоями, может чо обрабатывается пмянРК°И И электРосваРкой, удовлетворитель-
Алюминиевый сплав АЛ9 пб°Р°Ш° полиРуется и притирается, ствами, допускает все випы пи хорошнми литейными свой-75°С, температурный интепв^’ ^мператУра его заливки 680-линейная усадка — 0 5<>/ и^еРвал кристаллизации — 600—577° С*
притеняют тержобрХтеуГадёржка^рн
j щдержка при температуре
9—4 ч, охлаждение на воздухе, а 11Пп 300+10 С в тече neii__c печью. Термической o6pafiKpyn-вых тонкостей пых е Сплав плохо обрабатывается реза^* сплав не -'"^ХТ^азовой и аргоно-дуговой сваркой”•> хороню сварпвае	имеет хоро1и1И- литейные СВойг
Алюминиевый сплав я исталл„зации G10-5770 с
Температурнып^ с ли11ейная усадка 1,0, а объемная - з"^' тура литья 680 • ’вных реЖима термообработки:	,в'°.
Просияет '<«1	деталей, требующих сох|М№
U3 -	'Г™'"1’8”'1* 300 ± Ю С.'*
р „Ро 4 и и охлаждение с печью,
ЧеНпеж\.м Т-4 - закалка с нагревом при температуре 535 + 5е С в течение 2-6 ч и охлаждение в воде, нагретой до температуры RO-100 С для деталей сложной формы, или в воде комнатной температуры для деталей простой формы (применяется с целью повышения пластических свойств);
режим Т-5 — закалка по режиму Т-4 с последующим старением при температуре 150 + 5’С в течение 2—3 ч и охлаждением на воздухе. Предназначен для нагруженных деталей (например, корпусов). Сплав сваривается газовой и аргоно-дуговой сваркой, обрабатывается резанием удовлетворительно.
Манжеты изготовляются из резины 8075, имеющей предел прочности иа разрыв 100 кГ'см\ относительное удлиненение после разрыва не более 140%, остаточное удлинение после разрыва не более 10%, твердость по твердомеру ТМ-2 75—85 условных единиц, коэффициент старения после выдерживания в термостате при 70 ±2° С в течение 240 ч не менее 0,6, морозостойкость не менее —40 С, изменение веса после воздействия масла в течение 240 ч при 70 + 2 С не более — 3% для сорта масла АГМ и не более 2,5% для сорта АУ.
Сталь 35 Л-I используется для изготовления корпуса насоса, сталь 35 — люльки и угольника крепления трубопровода.
Сталь 20Х применяют при изготовлении шатунов, валика кардана, корпуса золотниковой коробки, золотников, штоков нульуста-насс>ТеЛЯ Н гидроУсилителя> а также зубчатых колес шестеренного
Сталь Х12Ф1 используют для изготовления блока цилиндров. HVJiKv,-rP0Tbl kp' АЖ9-4 изготовляют поршни, вкладыши, поршни рённого насо^1” И гидроУСилителя- а также прокладки шесте-
Распределитель изготовляется из бронзы Бр. ОСНЮ-2-3.
« 13.2. ТЕРМООБРАБОТКА
ство деталей^ак^шиГ”’ которым Должны удовлетворять болынин-шествления теомопПп^0 поршнев°й гидромашины, требуют осу-я ^рмообработки высокого качества и большой культур* 426
производства Особенно это относится к деталям ходовой части Так. шатуны подвер! аются многократным нагревам и охла,кдеииям! цементация, улучшение (закалка и высокий отпуск) и окончательная закалка, а припуск под окончательную обработку с чистотой поверхности V составляет 0,05 мм Такая малая величина приписка требует сохранения высокой чистоты поверхности после всех этих операций, полного отсутствия коррозии и разъедания поверхности сферы Это, в свою очередь, требует отсутствия за-1рязненнн карбюризатора разъедающими примесями при цемента min, а также высокой чистоты соляных ванн и качественного раскисления при операциях улучшения и закалки. Ведь даже операция промывки после закалки в соляной вание может вызвать значительную глубину коррозии, для выведения которой припуск на доводку может оказаться недостаточным. Малая величина припуска накладывает также высокие требования и на чистоту поверх ности деталей, поступающих на термическую обработку. Глубокие риски и забоины в исходном состоянии совершенно недопустимы, так как после термообработки они не выводятся и такие детали являются окончательным браком.
Первостепенное значение имеет также сохранение стабильности размеров деталей в процессе эксплуатации. Наиболее ответственные детали ходовой части гидромашин изготовляются из высоколегированных сталей 20Х, 12ХНЗА, 18ХНВА, ШХ15, Х12Ф1, которые подвергаются цементации и закалке п содержат после этого в структуре значительное количество остаточного аустенита.
Так, после закалки и охлаждения до +20 С остаточного аустенита в цементированной стали 20Х оказывается 10—25%, в цементированной стали 18ХНВА 20—45% в стали ШХ15 9 28% и в стали Х12Ф1 25%
Гидромашины зачастую работают в условиях значительного циклического колебания температур (обычно от —50 до +90 С), которые способствуют распаду остаточного аустенита.
Если не принять мер по сокращению количества остаточного аустенита, то его самопроизвольный распад в процессе эксплуатации приведет к изменению размеров деталей и нарушению иормаль-ного рабочего процесса машины или даже выходу ее из строя. Эффективным средством сокращения количества остаточно у иита является обработка деталей при температуре ниже
Наивысшая температура, при которой	$ марок
низкотемпературную обработку, различна для р	аннЫх
сталей и зависит от температуры закалки Для
салей 20Х. I2XH3. .а ™кж<; =
с температуры 1050 С. низкотемпературна и производиться при температуре “ обпяботки ПРИ отрицательной температуре также с.~ 2висит от интервала времени между закалкой и	'Д
но! обработкой и оценивается приростом количеств	-
ияе немедленною охлаждения после зак *	oSei производится в течение времен,. ври 20 С рзбл. 13.4).							
Мярка Стали	Те мпсратура закалки В сС	Количество мартенсита в % после охлажл™’” до 4-20° С	Прирост количества мартенсита после выдержки				» 96
			0	1 *	24 ч	4 6 суток	10 'Уток
111X15 Х12Ф1 Х12Ф1 ЦЛНВА 12Х2Н4А I2X2H4A	8'0 1050 1150 S50 790 850	90.0 81.4 36.2 70.0 88,0 74,5	3,0 9.6 41,8 21,0 4,0 16,0	2,0 8,7 40.8 22,0 1.0 14,5	0 39,8 0	0,7 18,6 9,5	0,0 14,4
Допустимая продолжительность выдержки закаленных деталей „„ ипмиятной температхре до обработки холодом до 3 ч, если детали ™XUP12XH2rA » I8XHBA. до 2 « - „з „мя, ХГ ШХ15 и Х12Ф1 и до 30 мин — для цементированных деталей из сталей 20Х и 15Х. Таблица 13.5							
Наименование свойств	Единица измерения	Материал			
		Бронза	Нержавеющая сталь	Нейзильбер	Никель
Пористость °в °сж 8 Способность к осадке ^Теплопроводность при Удельная теплоемкость при 20" С Коэффициент линейною расширения axlO-’	°/о А'Г и.1Г кГ мм* 7о 7о кал/см • сек • град кал)г  град 1/'С	30-40 4—6 4—6 15 0,05 0.082 18,4	50—60 2—5 3—5,5 2—5 5 0,015 0.12 18,5	30—40 2—4 1,6—5,4 2-4 15 0,035 0.093 10,6	30 -40
Для закалки блоки цилиндров укладываются в железные ящики размером 150 х 150 х 150 мм (для блока цилиндров № 5 ф90 мм) и засыпаются незагрязненным отработанным твердым карбюризатором. Торцы блока защищаются от попадания в отверстия карбюризатора листовым асбестом. Ящики закрываются крышками, замазываются глиной и ставятся в нагретую печь По окончании выдержки ящики выгружаются из печи, блок цилиндров освобождается от карбюризатора и охлаждается на воздухе в течение
428
а 10 сек я затем охлаждается в масле. ИИТепвап „ балкой и «обработкой холодом», а также =1 ремени между зЯло отпуска не дол кем превышать 30-40 лХ ЗТ°" Грации " Последовательное ,ь операций следующая. Подпев л0 гемпературь* 860 4- 10 Св отработанном KaX^L Р" Закалке д° 90 мин и затем нагрев в течение того же вЛ. Р атоРе в течете 1050 ± 10 С Затем охлаждение на воздух?'??',? Тем"ера‘ Охлаждение в ма.ле при температуре не болг? т г № 9 сек ?0_|5л««, после чего следует 10-минутная по™» С В Течение Swpo-Я*'»°7: 00 С- Поокэдюща, kXXXXLTJ1'’" ботка при -70 С продолжается 3 ч, после чего с	^Р3’
0ТПуск в масле при температуре 160-200 С И^п^000" закалкой и «обработкой холодом» не более 30-40 J‘r Между проводится проверка на трещины и определяется твеХТ™''01”6 кости, которая должна быть ///?С 62—65	РДОС ь поверх-
Один из возможных видов брака - пониженная твердость яв ляющаяся следствием несоблюдения режимов термической обо? ботки, исправляется повторной закалкой после предварительного отжига. Трещины чаще всего возникают из-за значительных пев? падов температур при переходе от операций закалки к низкотемпературной обработке и от низкотемпературной обработки к отпуску. Точное выполнение рекомендуемых режимов обработки обычно предохраняет от возникновения трещин. При использовании в качестве хладоагента твердой углекислоты необходимо предупредить непосредственный контакт кусочков углекислоты с поверхностью блока цилиндров. При использовании в качестве хладоагента смесей ацетона, спирта и т. п. с твердой углекислотой необходимо производить предварительное охлаждение блока до температуры — 40—50° С.
Шатуны из стали 20Х подвергаются цементации, после которой производится улучшение (закалка при температуре 860 ±10° С и высокий отпуск при температуре 700 ±20 С). После сверления отверстий и зачистки сфер производится окончательная закалка при температуре 810±z 10' С, низкотемпературная обработка и отпуск для снятия напряжений. Контроль шатунов сводится к проверке отсутствия разъедания поверхности сфер и проверке твердости, которая должна составлять HRC 56—62.
Буксы вала и блока цилиндров, изготовляемые из стали 20 л, подвергаются перед цементацией гальваническому меднению, исключением поверхностей рабочих пазов, по которым двигаются сегменты кардана После цементации производится снятие меди " высокий еХуек при температуре 680 ±10” С. Закалка КЗ цилиндров производится полностью, а букс вала местьая (только Рабочего паза). Далее следует низкотемпературная обраоотканит пУск для снятия напряжений. После мехзничесм	шт
прока "дитси кскусетаекное старение при температур.	1«Г С
в течение 2 ч.	л '	4В>
„згООТЛЕНПЕ ТГМ;О1,Г,11«,Л(,В
,, трубопроводы изготовляются из чолоднотя Магистраль^ ' Он11 имеют изогнутую форму. к ''^х стальных (сталь Л W
На фланцах чз> стали	ся гибке в горячем состоя,..,,, р
3аГОТОВКаЛнсокой частоты. Окалина, образ} ющаяся пр., с нагревом током ^ сОляной к„слоте после предварИтель ве. УД^яется трзвленн	Соединение трубы с	о
обезжиривания в Р I	долже1, составлять 0,05-0 I . ‘
резьбовое при ’ а‘ Рьбы „а трубе и фланце, а также сборка трубопровода "РО—	”аЙК0Й' П^
ЖХе^ХиоНапр-тпоя из латунной проволоки марки Д62 д,а. метром 2-3 мм надевают на трубу до упора во фланце. Собран^ S вводят в индуктор и нагревают током высокой частоты До расплавления припоя. В качестве флюса используется смесь из 50% плавленой буры и 50%. борной кислоты. Глубина пропая должна быть не менее 60%. длины резьбы. Далее опаивают фаску, производят дробеструйную очистку внешней поверхности трубопровода и запиливают наплывы припоя. Категорически запрещается очистка металлической (чугунной) дробью внутреннего канала трубопровода, ввиду того, что внедрившиеся в стенки трубы мельчайшие металлические частицы в процессе технологической очистки полностью не удаляются, но в процессе работы машины они вымываются рабочей жидкостью (маслом) и, попадая в зазоры поршневой пары и между цилиндровым бпоком и распределителем, вызывают заклинивание поршней и повышенный износ распределительной пары.
Дальнейшая обработка трубопроводов заключается в очистке внутреннего канала от окалины и жировых загрязнений, для чего трубопроводы сначала обезжиривают в уайт-спирите, а затем химическим путем. После промывок в горячей и холодной проточной воде производится травление в соляной кислоте и декапирование, авершается технологическая обработка магистральных трубопроводов промывкой в проточной воде, обработкой в содовомыль-СУШКО" и смазкой, погружением в масло. Хранят-тр. опроводы в железных ящиках, наполненных маслом АГМ.
S 13.4. ПОКРЫТИЯ
Я nOKpJjf'pj^ r->
ВУк> эмаль ПФ-223 ОБДР^НОстей корпуса применяют пентафтале-и Деталей из алюминия ,.рЫТИе этой эмалью стальных детален „^Ривания’ обдувки ежнт "° сплавОв производится после обез-п. л|!>Иеания’ "оотирки ппг ^ЗДУХом, грунтовки, сушки, за-нроводится местное ши’	в случае необходимости
«0	“"'“клевание. Затем деталь повторно зашЫ
ют сушат- протирают и только после этого проводят первую Рива ку эмалью с последующей сушкой. После сушки проводится СЬеП>е зашкуривание, протирка и вторая окраска с последующей ^Обезжиривание производится уайт-спиритом или дру|им орга-ческим растворителем. Для грунтования стальных деталей ис-Н^пьзуются грунты ГФ-020 или № 138. Для грунтования деталей ”з алюминия и его сплавов применяются грунты КФ-030 и ГФ-031 g качестве разбавителей используются для грунта ГФ-020 каменно-игольный сольвент или ксилол (может также применяться смесь одного из них с уайт-спиритом в пропорции 1:1), для грунта № 138 применяют каменноугольный сольвент, а для грунта КФ-030 и ГФ-031 смесь ксилола с уайт-спиритом в пропорции 1:1.
Грунт наносится на поверхность детали пульверизатором или кистью. Сушка грунта ГФ-020 при температуре 18—23 С продолжается 48 ч или 35 мин при t = 100—110 С Для грунта № 138
при тех же температурах продолжительность сушки соответственно 24 ч и 35 мин Грунт КФ-030 требует 40 ч сушки при t = 18 -ь ж 23е С и 4 мин при t — 70 -г- 80 С, а грунт ГФ-031 —2,5 ч при температуре в 100' С.
В случае необходимости производится шпаклевание составом ПФ-00-2 с последующей сушкой в течение 24 ч при температуре окружающею воздуха или 1 ч при 80 С.
Эмаль ПФ-223 наносится пульверизатором или кистью с последующей сушкой в течение 30—36 ч при температуре окружающего воздуха или 3—5 ч при температуре 70—80 С.
Внутренние поверхности корпусных деталей, постоянно смоченные минеральным маслом, покрываются глифталевым лаком ГФ-95 с последующей сушкой в течение 48 ч при температуре окружающего воздуха или в течение 1,5—2 ч при температуре 100—110е С
Все детали ходовой части, а также детали, работающие в масле, подвергаются химическому оксидированию. В ряде случаев химическому оксидированию подвергаются сварные детали, а также детали сложной формы. Необходимо иметь в виду, что электролит, попавший в поры сварного шва в глухие и глубокие полости, часто не удается удалить даже при весьма тщательной промывке. Остатки электролита в дальнейшем вызывают коррозию деталей (например, проволочные фильтры). Электролит практически не удается полностью удалить из впадины резьбы перекрытой проволокой, а также из пор сварного шва и из зазора в месте стыка заглушек с трубой корпуса фильтра. Поверхности пружин для защиты от коррозии покрываются цинком или кадмием.
б 13. 5. ТЕХНОЛОГИЯ ДИФФУЗИОННОЙ СВАРКИ
При изготовлении биметаллического блока цилиндров с целые получения надежного соединения бронзовой шэйбы со стальным корпусом применяется разработанный Н. Ф Казаковым метод
диффузионной сварки. Иные способы получения такого неразъемного соединения оказываются ненадежными.
Для осуществления диффузионно» сварки необходимо образование и развитие физического контакта свариваемых поверхностен, что требует создания удельных давлений 1,0 — — 2,0 кГ мм'2 и температур, со-
Рис. 13.2. Установка для диффузной ной сварки
Рис. 13.1 Биметаллический блок цилиндров
ставляющнх 0,6 — 0,8 температуры плавления, что обеспечивает пластические деформации металла в зоне сварки. Диффузионная сварка производится в вакууме.
При сварке стали со сталью необходимо удельное давление 2,0 кГ мм2 и температура 1000°С, меди с медью — 0,7 кГ/мм1 и 850°С, стали с медью 0,6 кГ/мм* и 900вС.
Подготовительные операции перед сваркой заключаются в тщательной очистке свариваемых поверхностей. Наилучшим способом очистки стальных деталей является отжиг в вакууме, однако хорошие результаты получаются и в случае обработки свариваемых поверхностей резцом непосредственно перед загрузкой в вакуумную камеру. Медь, кроме того, можно также очищать травлением в кислоте.
гпо1^°СЛеД0ВаТельН0СТЬ онерации при проведении диффузионной варки следующая. Промываются в бензине а затем в спирте мошиЦп?,оВДРОВ 2 На ₽ИС- ,31- г^ьзы 1 и’шайба 3. При постам ксmm™ пРесса запрессовываются гильзы, на токари0 блока и слбпаЮТС” выстУпаюш.ие концы гильз и торен к0Рпу‘: камеру устянпвННЬ1И ^°К цилиндров помещают в вакуумнУ камеру установки диффузионной сварки (рис. 13.2).
432
350
440
12(1
. .	180
п двух диа пазо-
50— 1000
. . 1000—10 00!)
10
130.9 2—25 (2-10)-.
25
установки без высо-
6
5-7
1450
1000
1900
450
даовиые ««»»««« данные уетаноенн А306.04
«—""Г ".................
диаметр 	................................
размеры’сварйв’аемых деталей, мм;
диаметр ..... ...	............
свариваемых’ деталей (плавно регулируется
пах), «Г-первый диапазон...................
второй диапазон.......................
максимальный ход при сжатии, мм..............  •
Максимальная температура нагрева свариваемых деталей. С Время сварки (регулируется ступенчато), мин..........
Остаточное давление воздуха в камере, мм pm. cm......
Выходная мощность источника нагрева свариваемых детален (высокочастотного генератора И060.011). кет
Потребляемая электрическая мощность кочастотиого генератора, кет ....
Расход охлаждающей воды. л]мин . . .
Габаритные размеры, мм;
длина ....	................
ширина .......................
высота .......................
Вес, кГ..........................
Последовательность дальнейших операций такова: создается вакуум, контактное давление, включается нагрев, осуществляется выдержка, охлаждение, отключается нагрев, деталь охлаждается до температуры 100—120°С, снимается контактное давление сбрасывается вакуум, открывается камера и свариваемые детали выгружаются.
§ 13.6. ИЗГОТОВЛЕНИЕ ФИЛЬТРОВ
ЩеЛеИ>Г° ™Па- чаще
которой нарезана резьба вКп!™ "азами’ по ВнешнемУ Диаметру Разность между ^аРгом резьбьГи лп'^Р631368' уЛОЖена пР<”™окаУ дичину фильтрующего зазора (щелЭТ ‘1Р°Вадоки «Являет
качеством щелевых фильтров являет
Положительным|)С потоку рабочей жидКости 'Па1<Т|) чески нулевое сопро.доемКость нзгоишления, Лег необходимо "меть._,Латочную тонкость фильтрации.	п0.
ареждаемость и неД тся применение пористых метаЛло
Перспективным 1|3|0ТОВЛеН11Я пористых фильтрующ*0^ ческих фильтров. м ются пороц|К|1 со сферической /*Меи. Т0В ЧГХечиваюишх легкость промывки и рсгепераци^ частпи. wecne4 ЧРГ0 не достигается при пспользоваш,.. „?"< трующих свсч ’ в случае применения сферических попп^"1* неправильнойДРМcJ3a|| с максиДЛЬНЬ)МХ R^kOb ч^сД пропускаемых через фильтр, соотношением d 0 ''J Матепп^ом Для пзютовленпя сферических порошков сл . So нержавеющая сталь, оловянистая бронза, а также ппугие металлы, сплавы и неметаллические материалы "«
В насосах применяются металлокерамические фильтры, 111го товляемые из бронзового порошка имеющего химический состав олово - 7,5-9,5%, фосфор — 0.15—0,2 «, медь — остальное, с диаметром гранул 0,2—0,3 лги В этом случае обеспечивается максимальный размер пропускаемых частиц равный 30—35 ж
Свойства металлокерамических материалов фильтров приве-дены в табл. 13.5. Пористость составляет 30—70%, предел прочности при растяжении оя = 2	6 кГ мм1, cooti етственно при
сжатии пс> = 1,6-г 7,0 кГ'мм2, а относительное удлинение б = = 2ч- 6%.
Фильтр состоит из фильтрующею элемента в форме стакана с небольшим конусом и двух латунных втулок. Соединение этих деталей проводится пайкой припоем ПОС-40 Долговечность металлокерамического фильтра определяется допустимым перепадом давления, повышающимся при засорении Для i идромашин, работающих при температурах до — 50 С, этот перепад составляет 2 и 1 кГ см1 при 20 С, а долговечность достигает 1000 ч при условии регулярной промывки через каждые 100 ч работы
есьма эффективным способом промывки фильтров является прод\вка сжатым воздухом под слоем бензина или уайт-спирита пяктАп.^1.еНИИ’ пРОт|1ВОПОЛО'К11ом направлению фильтрования Ха-пволапжит1НеНИЯ пеРепада Давления на фильтре в зависимости от каждые 10(^H°L™ Ра^0ТЬ| с учетом регулярных промывок через ломаной соотпрЭКСПЛуаТЭЦИИ показан на рис. 13.3 (верхние точки но после опреде\7нн^ величине перепада давления непосредствен-точки кривХ соответстХСп0а ЧЭѰ работЫ Д° ПРОМЫВКИ’ 3 “***“
Тонкости ж, тоетственно после промывки) керамическогоФ35Ь2аиИИ пРОвол°чного фильтра 85 мк, металл °'4 кГ см\ регТяе^’ "!Р!Паддавления соответственно 0,0 и 0. боты — неогг)йнииоР11руемОСТЬ ~ полная и частичная, режим Р Вибропрочность фильтоо1 i0?°4’ УДаРО|1рочность низкая и высока  ость фильтров обоих типов высокая и одинаковое ДВ»'
W1
давления от времени эксплуатации фильтра
рушения в 30—35 кГ'см*. Исходным материалом для н» лен|;е 'пня фильтров является бронзовая дробь Изготовление ю(Ц||Х элементов производится путем спекания в формах насыпанной дроби.
1 На рис. 13.4 показана форма для спекания фильтров. Материа-мдля изготовления форм служит нержавеющая сталь IX 18119 Г;
Л°жет также применяться сталь 1\|3. Оформляющие поверхности (|к)рмы должны быть Обработаны не ниже у 9
Перед началом работы новые формы окисляются при лемнсра-туре 600—550 С в течение 1—2 ч. Образующаяся при этом на стали пленка окиси хрома препятствует в дальнейшем спеканию бронзовых гранул со сталью. Спекание фильтров производится в водородной или вакуумной печи с выдержкой при температуре 850 ± 10 С в течение
50—60 мин. Охлаждение производится под током водорода или в ва-к)уме до температуры 60 80 С, после чего формы выгружаются пз печи и готовые фпльтроэлементы извлекаются из форм.
Механическая обработка фильтроэлементов заключается в подрезке полученною стакана со стороны открытого конца до требуемой
Рис 13 4 Форма для спекания фильтра
длины, а также в расточке посадочных мест под втулки. Соединение филыроэлементов со втулками производится пайкой припоем ПОС-40 с применением бескислотных флюсов.
После пайки фильтры промываются в бензине или уайт-спирите. Консервация фильтров производится в масле, на котором они Должны работать.
Глава 14
n314)WBJIEHHH ГПДР()ПРНВОд0и тк\нол<>н»и=----------	—•
дКРДЗМВНЫЕ МАТЕРИАЛЫ ДЛЯ ОБРАБОТКИ { 14.1. АЫАЗШ ДБТАЛЕ11 маШПП
пртяли гидромашин должны иметь твердость Мол Некоторые д , ябоТКИ не менее 7—14-го класса, овальнг5С 58_б2. ч”ст°Т5цХндрических отверстий до 0,010-0,015 И ЕкЕЕть до 0,005 мм. Поэтому при изготовлении та’ 3 неплоскостн» ис пользование абразивных материалов ’ ^Минимальные припуски на шлифование при диаметре Опока „ ли ми — не менее 0,2 мм, от 90 до 120 мм 2>0,3 «д-rs s «-»w -" °т 140 200 -- <« s Шпнфовапьный круг для шлифования торца блока цилиндра полжен быта изготовлен из монокорунда М на керамической связке форма круга IН поГОСТу 2424-60 (размеры определяются станке и окружной скоростью). Допускается использование круга избе-лого электрокорунда ЭБ. Зернистость 40 (допускается 32) по ГОСТу 3617—59, а твердость Ml или М2 (допускается М3 и СМ1) по ГОСТу 3751-47.
Шероховатость обрабатываемой поверхности перед шлифованием должна быть не ниже 6-го класса.
Окружные скорости черновых и чистовых проходов 20—25 м'ак, продольная подача 12—20 м/мин, поперечная подачаО.6—0,8 мм!ход, вертикальная подача для черновых проходов 0,01 мм, а для чистовых 0,005 мм.
При шлифовании торцовой поверхности блока цилиндров рекомендуется обильное охлаждение водой, содержащей 1,5% кальцинированной соды и 0,5% нитрита натрия.
Шлифование осуществляется на плоскошлифовальных станку высокой точности с прямоугольным столом (например, станок 31 завода «Красный борец»). Осевое и радиальное биение щпияД станка дмжно быть не более 0,005 мм.	Л
ным ЕП°Ка “° ^ифовать и без охлаждения, но сгобяз^ фования гл'НИеМ указанных выше режимов резания. 11осЛ^ соВ, следует ’ еспечиваюц1его чистоту поверхности 8—9-го
При шлиЖг3 С° снягием слоя не менее 0,02 мм.
избежания волнистости^ ПЛОскошлиФовальных станках димо тщательно А0Сти пл°скости торца блока цилиндро ,	||й
тщате.пьно балансировать и править круг. Для п0ЛУ
436
кЛасса чистоты и точности обрабатываемых поверхностей рисоког изготовления деталей осуществляются доводочные one-fl "Р011^ применением абразивных паст. Доводке обычно подвер-PaU,II,fl цилиндры и торцовые поверхности блоков цилиндров. га1°11илиндрические отверстия после абразивного шлифования обращаются мпогошпиндельными юловками с чугунными прити-^аТЬ< £ применением порошка карбида бора № 260—280 и оконча-^пьно обрабатываются на токарных станках (шлифовальных бабках) притирами с применением того же порошка.
Предварительная и окончательная обработка торцовой поверхности производится на разных станках. Для предварительной обработки используется абразивный микропорошок М10—М14 (ГОСТ 5744—62), а для окончательной — от М5 до М7 (ГОСТ 5744—62). При доводке диск станка покрывают тонким слоем абра-знвно-стеарпновой смеси (одна часть абразивного микропорошка и одна часть стеарина, разведенных на керосине до вязкого состояния).
Для обеспечения чистоты поверхности и точности доводки диск станка промывают керосином не реже трех раз в неделю. Неплоскост-ность доводочных кругов должна быть не более 0,01 мм и проверяться не реже 2—3 раз в месяц. Диск изготовляется из чугуна АК4-1 с НВ — 140 —200. Во избежание высушивания рабочей
поверхности диска в процессе доводки ее периодически смачивают керосином.
При предварительной доводке на чугунных притирочных дисках достигается чистота 9-го класса, применение микропорошка марки М5—М7 обеспечивает чистоту торцовой поверхности блока цилиндров до 10—12-го классов. Для получения зеркальной поверхности (13—14-го классов чистоты) торцов блоков цилиндров из стали Х12Ф1 применяется алюминиевый диск, покрытый слоем смолы толщиной 8—10 мм (2 части канифоли и 1 часть каменноугольного песка и битума). Размеры круга и скорость вращения должны быть такие же, как и у чугунного диска. Перед началом работы рабочая поверхность круга смачивается раствором 1% нитрита натрия и 1—2°о окиси хрома в дистиллированной воде. В процессе работы круг периодически смачивается 1%-ным раствором нитрита натрия в дистиллированной воде.
При доводочной обработке может возникнуть неплоскостность торца (брак) из-за неплоскостности доводочного диска при несоблюдении требований его контроля, а также риски от абразива, остающегося на блоке после шлифования. Применение пасты АСМ5 (паста из синтетических алмазов) повышает производительность в 2—2,5 раза и обеспечивает требуемую чистоту поверхности
Установлено, что обработка пастами из синтетических алмазов не ухудшает эксплуатационные свойства деталей. При применении таких паст необходимо тщательно промывать детали, а притирочный Диск должен быть значительно с меньшей твердостью, чем обрабатываемая деталь.
гПТКд СФ1ТПЧЕСКПХ ПОВЕРХНОСТЕЙ
t 14 2. 0БрА150	, А
’	„лети сначала обрабатывают На То
ОЬернческне поверхн« кярданоп „а скарном станке
СКИХ поверхностен |
Рис. 14 I Резей лая обточки сферы
1аблЧЦа Ц.,
1	9,4	24	0.5	9 9+0.05	1,4
9	12,4	26	0.7	3,94-0,05	1,4
3	13,4	26	0.7	4,5+0,05	1,8
1	1Ь,1	30	1 >	4,9н,-<	1,4
5	18.4	35	1,2	5,91" 1	1,4
6	22,4	40	1.2	7,4Т“*	2,0
7	30.4	50	1,2	7,4+',-i	9 9
8	38,05	62	2,0	13,0+°-«	2,2
0,3 0,3 0.3
0.3 0.3 0.5 0.5
0,5
12
14
16
Окончательная доводочная обработка сферических поверхностей производится на станке с помощью притиров из чугуна СЧ 12-40 р	в	(рис. 14.2 и 14.3). Для этого об-
стаика
раба гываемая деталь 1 зажимается во вращающемся приспособлении 2, а притир 3 закрепляется в опоре 4 с приводом 5 и прижимается к обрабатываемой сферической поверхности пружп-
Рис. 14.3. Притир для образки сферы
микропоР01И011
16 П
11
М7 (Г(ХТ 4647-54^ ЛСПи'1ЬЗуется паста ГОИ и микропор'
Диаметр сферы Ровные размеры притиров следующие: - » ? If I? К
4
5
7
8
НЯ рис. 14.4 показаны размеры резцов для обработки внутрен-„гЛ сферической поверхности в поршнях (/ - винт, 2 - державка
Тиб.ища 14.2
диаметр дфйбаты-пармоп сферы	Дп.1М С гр притира (заготовки	L
.——				К w W	
35А	38	55
ЗОА	32	55
25А	28	55
22А	24	55
11,5 А	14	55
»лг- Дотекаете» ленточка не более Q02
ql
--Г7Л
\2a_J.
Рис 14.-1 Резец для обработки внутренних сферических поверхностен


Рис. 14.5. Притир для доводки внутренней сферы
3— резец). Окончательная обработка осуществляется притирами /(табл. 14.2 и рис. 14.5) из текстолита ПТК ГОСТ 5—52, укрепленными на державке 2 из стали 45. При притирке применяется автол К) (АК-10).
Контроль сферических поверхностей производится рычажной скобой (пассаметром) с точностью до 0,002 мм.
Расстояние между центрами проверяется индикаторным прибором (рис. 14.6), в котором индикатор 6 при помощи призмы 4
через пружину 5 фиксирует контролируемую деталь 3 на неподвижной призме 2, закрепленной на основании 1
mi
И*с. 14.6 Индикаторный прибор для контроля расстояния «жду венграми
«в
КраС1<У'	§ 143. ПРОВЕРКА ГЕРМЕТИЧНОСТИ
Корпусные детали не должны иметь раковин газовых пуЗЫрей тпеши и других дефектов и поэтому подвергаются В11ешн' « CCMOTPV и испытанию на герметичность. С этой целью внутренни полости запивают керосином или уайт-спиритом на 20 мин: дефекть, обнаруживаются по пятнам на наружной поверхности, подкраше1,. ной водным раствором мела
Рис 14 7. Стенд для проверки деталей на герметичность
Более ответственные корпусные детали закрывают заглушками и внутри создают давление от 0,5 до 4 ат: затем их помешают в ванну с водой на 2—3 мин и по пузырькам воздуха обнаруживают дефектные участки.
Детали, работающие под давлением (трубы, люльки и их крышки, и»о.Шлл |”ЛРОМОТОРОВ и др.), опрессовываются маслом под давлением 40-400 ат в течение 5 мин.
н чяпие™ испРавляются газовой и дуговой сваркой, пайкой н заливкон эпоксидными смолами.
или сайт спнпеНД ЛЛЯ пРовеРки герметичности с помощью керосина ленная на Z? ,1а рНС' 14'7- В К)""е I люлька 5, укре»; механизма4РКепп ИНе2’П°В0|?ачивается ПР” "ОМОШИ поворотной (показана штпих^т”"’ залитЬ1Й в установленную на люльке Де1а вороте люльки ' унктиР°м)> удаляется после испытания при рис. ц/ КинфииповоРОТНЬ1м столом 7 на роликах 5 показан На установленный внстп°СЛе испытания сливается в сборный ба 
нныи внутри каркаса 2. К баку через шланг поДа101С 440
керосин и через магистраль — сжатый п
при помощи крана 3 и редуктора 4	КОТОрь,й ™Дводитгя
детали керосином и слива его
воздушное сети
Рис. 14.8. Стенд с поворотным столом для проверки деталей на герметичность
Герметичность корпусов и фланцев проверяется опрессовкой воздухом под давлением 0,5 ат на сварном стенде (рис. 14.9). На корпусе / укреплена ванна8, залитая водой с добавкой триэтаноламина (6 а на 10 л воды). Деталь устанавливают в ванне при помощи
Рис. 14.9. Стенд для проверки деталей на герметичность под давлением
гидравлического зажима 4, работающего от центр^*н°Г°„даыв-10, подающего воду из бака 3 через фильтр 2 н клапан 9 в управл
ЛИ. Управление кнопочное (5 на рис. 14.9), Л етаем <&—*»« Редуктор 7, давление воздуха контролируется Р сто присоединения манометра).
4»
s И 4 УСТРАНЕНИЕ БРАКА OT.UIIHOI, КОР11Ус0ц ГИДРОМ U1IHII
Раковины, трещины, ужнмы « места отливок, требующие „Ов ностной наплавки на высоту не более толщины стенки, отмечаЙ? мелом пли цветным карандашом (рекомендуется одНОврем^ся фиксация в цеховом журнале) и разделываются до здорового Мет., я ла фрезерованием, сверлением, шарошкой, ппевмозубплом „ , Разделанные места должны иметь чашеобразную форму jja ДР пинах трещин сверлятся отверстия диаметром 3—6 мм. 'Ра-
Дефекты, выявленные в отливках до механической o6pa(j0 и после предварительной обработки, заваривают с продпаритеп. JKtl подогревом до 180—200 С и последующим отпуском дЛя c,IB напряжений при 620—650 С (продолжительность отпуска зав,?'1 от толщины детали).	С|,т
После заварки дефектные места зачищают, осматривают испытывают на герметичность.	Или
Дефекты, выявленные при проверке на герметичность окончательной механической обработки можно заваривать’Т(П°СЛе в том случае, если удается сохранить необходимые размеры >ЛЬК°
В случае невозможности применения электродуговой или газояп-сваркп, для заделки пороков отлпвок можно применять эпоксипи.» смолы. Для работы с эпоксидными смолами должен привлекалея только квалифицированный персонал в присутствии представ,™
П”,УЧе""Я ра3|",""и"	«™«РУ™р,»
»этр«мP»B"lo“X’™iS“e toS"" л°д"е1,гаются А*»™ я»-отливки в количестве нр «пн &0Лее з толщины стенки стальной трех на всей ХхнХТЯДВУХ ДефеКТ0В НЭ 100	” не более
а также все ви^Х™^0™4"0 ” для чугунных отливок), 8 № мм на каждой обработанной^1’' КОТОРОИ не превышают участков на отливке. Р<Юотаннон поверхности, но не более двух
же способом, есл,? оазм₽пТЛИВ°К весом Д° ЮО кг заделывают тем и количество пористыхХтПТ70С™ Не "Ревышает 50 X 50 мм
Для более тяжечых чю	6°Лее тРех-
заделываемых мест допжнм'\ННЬ'Х Отливок размеры и количество см ДЛ1Заделки Ракови^ппимСТаИаВливаться индивидуально.
в весп дибутилфталата еняют тШательно размешанную смесь Этиле ЫХ пР°П0РЦИях 100 |сП0^Иэ™ленполиамина и наполнителя
д 'яП°ЛИаМИН) Добавляете^,; 8 : ‘°0' пРичем отвердитель (поли-Для алюминиевы» последним
еГСЯаЛ"мин еваяХр "1ХВ КаЧе"ве наполнителя пспользу;
442	Ра'Для чу| Уна - , рафи г, для стали - Ш*£НТ
и для медных сплавов — бронзов
заделывают оез наполни геля. "УДРа Глубокие раковин» Перед заделкой поверхностг п л
ОЧНЩаЮТ ОТ ОКИСЛОВ и Грязи ппо К™ЫХ УЧаСТКОВ ТШатрпк.
„ поры разделывают до здорового м™/ ТК0Й’ а Р^овины фрезой. Затем места дефектовобезжирнваХ )б"ЛОМ’ сввРчом или после чего выдерживают на воздухе?5? ^СТОНом Ил» бензином растворителя	Д)Х( <5—20 мин ДЛя yW]eH”-
Раковины заполняют замя.»
чтобы заполняющая масса поднимала.'? J ПОЫОщью шпателя так суш,, м возду„ , те“““м 2~3
наждачной шкуркой или напильником vnP 2 ~ 5 С- после чего Состав изготовляют перед заделкой Т Излишки состава. 45 60 мин после пр.ГготовлениГон
Дефекты размером меньше 3 5 «« н непригодным, отливках заделывают под вакуумом скв°зные раковины в прешХХм	в 2 р„
§ 14.5. ТЕХНОЛОГИЯ ОБРАБОТКИ КОРПУСНЫХ ДЕТАЛЕЙ
* ТОЧНОСТ" изготовления деталей очень сложной формы предъяв ляются высокие требования. Так, основные отверстия дадХ пппрЬп2 З и КЛассы точнос™ н 6-й класс чистоты. Привалочные плоскости имеют допуск на неплоскостность до 0,05 мм и 7-й класс чистоты Отклонение от соосности отверстий допускается до 0 01 ям
При базировании заготовок корпусных деталей в принятых технологических процессах в основном совмещаются базы механической обработки, измерительные и сборочные. Базирующие поверхности обрабатываются по разметке, что обеспечивает наиболее равномерное распределение припусков при последующей обработке. Вначале обрабатывают базирующие поверхности и основные отверстия начерно, а также крепежные отверстия, которые могут быть использованы при последующей установке. Заделывают пороки штья, после чего проводят повторную чистовую обработку плоских базовых поверхностей и основных отверстий. Затем обрабатывают буршки, платпки, выточки, рассверливают и нарезают резьбу под крепеж. После окончательной обработки детали контролируют и испытываю г на герметичность, после чего наносят покрытие.
Корпус гпдромотора изготовляется из чугуна ВЧ 45-5 ГОСТ 7293—54 (заменители — чугун ВЧ 40-10 ГОСТ 7293—54, сталь 35Л-1 и сталь 25Л-1, ГОС? 977—65). Центральные посадочные отверстия обрабатывают по 2-му классу точности и 6-му классу чистоты; эксцентрицитет относительно центральных отверстий — до 0,05 мм. Привалочные плоскости торцов обрабатывают по 7-му Классу точности и 6-му классу чистоты; неперпендикулярность к посадочным поверхностям — не более 0,1 мм. Уплотнительные
44а
no S-mv классу точности и (5-му к„ канаСки	поверхности - по 7-му классу точное^
чистоты, а своб°Д Ш|ГТОТЫ Литейные поверхности выполняю?" 3—4-му классам чпстот»1	,g55_55) и чнстоты.
по 3-му классу то	деталей гидромоторов методом ли™
Изготовление KOp" АП2 вместо стальных, отпитых в зем?” ПОД давлением И	сть изготовления гидромо горов. в
позволяет снизит Р ПОДШ11Пники паромоторов № 5, |0 Л ZZt сталытымп стаканами, а отверстия под сливные 11роб° кн втулками; ио наружным боковым сторонам корпусов и фланцев предусмотрены ребра жесткости толщиной Ь ЛЛ4 (рнс 14.10).
Рис. 14.10. Чертеж корпуса гидромотора
Перед механической обработкой одна заготовка из партии проверяется на разметочной плите.
Механическая обработка начинается со слесарной зачистки напильником базовой поверхности квадратного торца (со стороны меньшего выступа).	г	1	'
пийм₽атпТ0КаРНОМ станке П0Дрезают торец, обтачивают наружный Ласки1?/ Г1ротачиваю'1 канавку, растачивают отверстия, снимают обоабатывя?т^ПЛЯЮТ 0СТ(1Ь|С кРомки (рис. 14.11, а). Затем корпус
Стороны (РИС- ,4Л1> б)- Работа выполняется ЕХТ/ Ш1астннками из сплава Т15К6.
НОМ станке с испо₽Л °ТКЭ производится на радиально-сверлиль-на фланцах па™п°?аНИеМ кондУ*<торов. Зачищают отверстия (рис. 14.11 е) Сно?п *ВаЮТ И зенкуют 6 отверстий под резьбу знак, зенкеруют отвел?™? зе,НкУюг два отверстия под товарный Фаску и нарезают i!Lr> И обРабатывают торец бобышки, зенкукЛ ^перпендикулярность п?ч г отверстин бобышки (рис. 14.Н.г>-пределах до 0,1 лиц q Р Зьбы к тоРиу должна выдерживаться метчиками нарезают пр, 'л На резьбонарезном станке нормальным •нести отверстиях лл« vb В отвеРстиях под товарный знак и
Для крепления фланца (рис. 14.11, д).
Рис. 14.11. Технологический процесс обработки корпуса гидромотора
Годную деталь смазывают тонким слоем 561—60, смешанной с веретенным маслом (по бО"'?' в тару.
После указанных операций зачищают облой притупляют острые кромки и клеймят деталь ’к111,Ма,°Тз меры детали и испытывают на герметичность ппп „
0,5 ат в течение 2 мин.	Д Давление^ К'т Раз
™“к" Hr 8?“ - « »».«« >» ''Ю;
тг
Conti® 8 ?omti®6

Рис 14.13. Технологический процесс обработки фланца гидромотора
Заготовка фланца (рис. 14.12) поступает на механнче^ обработку после дробеструйной и термической обработки^^^^ стие большого диаметра выполняется по 2-му классу а малою диаметра — по 3-му, причем оси отверстий дол в л1сйо« секаться в точке Б под углом 30 ± 10J. Расхождение осеи^^ направлении допускается не более 0,1 мм. Привалочна торна со стороны большего отверстия обрабатывается
1 лом, а со стороны меньшего отверстия — с го1}НОд],т]0чные цЛ° н'ьлоскостнос гь допускается не более 0,05 мм. При
44в
кости обр омываются по 6-му классу чистоты „
утлом 30 ± 10 относительно дру/дру™ " Разлагаются
Свобошы поверхности обрабатываются по 7-му классе той „ости и по 5 му классу чистоты. Литейные поверхности вин/ ются по 3-му классу точности (ГОСТ 1855-55) и чистоты '
Перед механической обработкой размеры одной заготовки из партии проверяются на разметочной плите. Механическая обработка начинается с зачистки напильником на слесарном верстаке базовой поверхности горца со стороны большею отверстия (рис 14 13 т Затем фланец обрабатывают на токарном станке со специальным приспособ тепнем нормальными резцами с пластинами из сплава ВКб Сначала со стороны мепынего диаметра (рис. 14.13, б) подрезают торен фланца, растачивают отверстия, делают фаску и протачивают канавки, затем растачивают внутренний диаметр (рис. 14.13, в). На вертикально-сверлильном станке через кондуктор (рис 14.13, г) зенкеруют и зенкуют четыре отверстия под резьбу MI6, сверлят два отверстия диаметром 6А, и шесть отверстий диаметром 8А7 (для гидромотора №5).
Токарная обработка фланца со стороны большого диаметра (рнс. 14.13, д) проводится аналогично
Зснкерование четырех отверстий под резьбу (рис. 14.13, е) осуществляется на вертикально-сверлильном станке по кондуктору. Зенкуют 4 фаски на этих отверстиях и рассверливают на ребре отверстия диаметром 18Ае.
Резьбу в восьми отверстиях фланцев нарезают на резьбонарезном стайке метчиком (рис 14.13, з).
Зачистка заусенцев, облоя, притупление острых кромок производится напильником. После этого деталь клеймят и контролируют геР тегичность и размеры.
§ 14. 6. ОБРАБОТКА ЛЮЛЬКИ
Центральное отверстие основания люльки (рпс. 14.14) обрабатывается по 3-му классу точности и 6-му классу "аст®™н ' 'Рю валочная поверхность торца основания обрабатывается точность ±1,5 лип, по 7-му классу чистоты и допуском на 0,5 : 172. Отверстия в проушинах обрабатываются по 2 му У точности, 6-му классу чистоты, несооыюсть отверс т ЛЮлыот не более 0,01 мм Оси отверстий в "РО>Ш"НО^	-
должны находиться в одной плоскости (Д У
не более 0,2 мм).	^„оЛятыпяются по 5-му классу
Торцовые поверхности проушин ₽	неперпеидикулярно-
точности и 6-му классу чистоты с обеспечением неперп ид у сти к оси посадочных отверстии до . ' няегся по 4-му класту
Обработка уплотнительных кана^“ ® vluKa - по 5-му кжсу точности и 6-му классу чистоты_'1л0^Оскосп.ость - До **• точности и 5-му классу чистоты, неплоск
— п<
отверг (отверстию в основании лкХ^Т?Ьиопент ному от^ ^ ость платина обрабатывается 1ю 7.м ’
дат—"’"" °™
С™гвХ« ^абаГЫ— ™ 7-му
С”поск'"Ургз2и на горизонталь,к,-фре,ер„„„	‘
11ОСЛГ Р	„„.nuuifH НЯ основании пгп,,„...	. “Ке <

<Т|5Кб”%«“"» лнтникн „а основании отливки ',а* W на ироуша^нах (рис. 14 15. б), с боковых и торцоои
*
(рис. 14.15, в), а затем с наружной поверхности (рис. I4.IM-после отливки размечаются для последующей обрабол
Следующей операцией является предварительная, a 3aTtN ™ст°вая обработка торца и отверстия (рис. 14.15, е). За
"анке свеРлят и рассверливают отверстия • наружны”’ 4’ 5’ж)> после предварительной расточки no^J. вают 6onwТОрсц пР°УШины, обтачивают бобышку по верху, Р й. вают меньпн*0 ВНУТреннюю ВЬ1ТОЧку, затем предварительн Р^, , После удалей ВЫточкУ и подрезают внутренний торен 1 400 агпц Ппп я 3аУСеннев детали опрессовывают пой
д и промывают.	К|
станке в такой °бработка производится на вертикально ФР । СКие повепхнаетПОС/1едовагельнС)СТ11: окончательно ФР
Р*ности между проушинами (рис. 14.15, з). ве₽
нижнюю плоскости платиков (рис 14 15 » у (рис 14 15, ?), эти же уступы с паружнь,; „опп 14.15,л); а затем платик, вначале ио большому Пя ?' ni>°Vn X напроход и начерно по меньшему радиусу и Д усУ (piiC ''Ч внутренние торцы проушины и после переустаи"аК°1,ец ФгЧ’Ч руют закругления на четырех углах торца оснп«КИ Деталц >> ляют заусенцы, проводят контроль и, в CJ1V ани«. ЗатЛс% заделывают раковины.	У ае необхОД| 1 fta-
Следующая операция —шлифование плос (рис. 14.15,0). Затем деталь размагничивают зач*^™ ^ова контролируют деталь по обработанным размерам п Т 3аУс<?«| " вертикально-фрезерном станке фрезеруют паз (рис' *ог0, (рис. 14.15, /г), наружные плоскости ушка (рис 14 15 vX"3 начисто (рис. 14.15, н), затем снимают заусенцы, поит Р ’ ПЛаТ11^ кромки И проводят контроль.	’ р ^ПЛЯ1°ТоСТр|?0
После этого на радиально-сверлильном станке све стия по кондуктору, зенкеруют н развертывают согла^ ваниям чертежа. На вертикально-расточном станке г> '° два отверстия в платинах, четыре отверстия со стороны тоГ"'8310’ вания (рис. 14.15, с), отверстия в проушинах (нессюсность оХ две выточки меньшего диаметра с подрезкой торца, снимают тели две фаски и окончательно растачивают две большие с подрезкой торца (рис. 14.15, т). Неперпендикулярнопь Z допускается не более 0,05 мм, а несоосность с отверстиями не fc лее 0,01 мм.
Затем нарезают резьбу в отверстиях, снимают заусенцы, Лрц. тупляют острые кромки, пропиливают паз, сжатым воздухомочи-щают все отверстия от стружки, после чего окончательно проверяют герметичность.
Обработанную люльку, промытую от масла в керосине в просушенную на воздухе, клеймят и сдают ОТК.
§ 14.7. ОБРАБОТКА БЛОКА ЦИЛИНДРОВ
Блоки цилиндров изготовляются из бронзовых сплавов» I высоколегированных сталей (рис. 14.16) в зависим свойств гидромашины. Предпочтительны бронза рр-СТаПриХоб^аботке бронзовых блоков пРимен^2ф^пХБр риалов недопустимо, а при обработке стали^Х^ определяетI них шлифовальных кругов и притироч	й Однако при
обработки торцовых поверхностей и Р	?
требуется тщательная промывка.	й обработку •
Глухие отверстия труднее поддаются ° дКИ му в процессе шлифования и последу! дедах 0.010^уi?-'1 чить погрешность формы цилиндр	Р^е блока из
причем диаметры цилиндров одног
450
могут Of пчаться один от Другого на 0 10—0	п
Филипп бронзовых сплавов точность пбппл ’ °	' ПРИ исполь-
Малые габариты гидрометр до Й°™ Выше-а.рсгатнпх станков для одновременной обп1кУДНЯКУГ С0зда,|ие отверстий и усложняют шлифование. Колебание^ нескольких дров .ндромашмн № 5 и больших номеров созТаеТзатпудн^нГГ балансировке расточных приспособлений nn«innuL РУД ия при
Те«.,.,„рА
размер-. I. является «новым. «примято, материмом “X”'™ производства (массовое, серийное или единичное). И характеРом
Общин допуск па обработку определяется 5-м классом точности Неплоскосгность торцовои поверхности, прилегающей к раеппеде-дителю должна быть не более 0,005 мм - выпуклость не допускается. Несоосность «усов» с центральным отверстием допускается до 0,01 мм, радиусных пазов до 0,1 мм. Неперпендикулярность торна к образующей центрального отверстия допускается до 0,03 мм Чистота обработки: торца V 10—V 14; цилиндров — V 9; центрального отверстия и «усов» — V7; радиусных пазов — V6; остальные поверхности обрабатываются по 4-му классу.
11ервая группа шести токарных операций проводится на станке
1 К(>2 в такой последовательности:
1)	подрезка торца, обточка наружной поверхности и черновая сверловка большого отверстия до уступа и малого — напроход (рис. 14.17, а);
2)	подрезка торца и черновая обточка второй наружной no-вер хнеюти (рис. 14.17, б);
3)	расточка центрального отверстия и притупление острых кромок (рис. 14 17, в);
4)	расточка канавки (рис. 14.17, г);
5)	обточка конуса, наружной поверхности и окончательная обточка фаски (рис. 14.17, <?);
6)	подрезка торца, обточка наружной поверхности наибольшего диаметра, расточка выточки и отверстия напроход и притупление острых кромок (рис. 14.17, е).
Затем на вертикально-сверлильном станке по кондуктору р-лят отверстия со стороны торцовой поверхности блока цилиндров (Рщ 14.17, ж), на специальном агрегатном станке сверлят цилинд-РЫ нГто^арном'станке растачивают циливдрн затем фаски (рис, 14.17, к) и канавки (рис., . ,*ьно фр^руил вертикально-фрезерном станке начерно окна цилиндров (рис. 14.и, м и н,.	.
выступы (рис. 14.17,о), а затем ФаскУ ^р на Токарном станке
После предварительной подрезки ^ЯД(ОВЫМИ номерами наснимают фаску (рис. 14.17, р). кле" " Рдяют контроль» «тем линдры, зачищают заусенцы и “У^ деталь подвергается термической р
«1
На плоскошлифовальном станко тппиА«
Меряют твердость поверхности затем на	<<усов>>- из'
,<е типа ЗА25О шлифуют центральное OT^cwt зачитают торец от окалины и продувают сХш R<S, ’ Ч7’с)’ этого на внутришлифовальном станке типа чк» возДУхом. После ры (рис 14.17,/п), причем овапьХт! 250 ш^фуют цилинд-НС более 0.010-0,015^. Далее деталь контр^^Хгавд старению в масле и промывают в бензине. У ’ подвеРгают
Последующее шлифование выступа (рис. 14.17, у) проводится на заточном станке. На специальном станке шлифуют окна поЕ тему и меньшему радиусам (рис. 14.17, н) и на плоскошпифоваль-пом станке шлифуют торцовую поверхность (рис. 14.17, ф), причем допускается биение не более 0,03 мм, после чего притупляют острые кромки (наружные кромки окон — 0,1 лои, остальные — 0,3 лл) и деталь поступает на контроль.
На модернизированном вертикально-сверлильном станке с мно-гошппндельной головкой цилиндры притираются (рис. 17,17, х), затем на токарном станке доводят овальность и конусность до 0,012 мм (технологический размер), контролируют и на специальном станке притирают торец (рис. 14.17, ш) до чистоты V 9.
Твердость измеряют после промывки в бензине; на магнитном дифектоскопе осуществляют контроль на трещины, затем размагничивают, промывают и продувают сжатым воздухом, после чего производят тщательный контроль чистоты обработанной поверхности, окон, притупления острых кромок и твердости торцовой поверхности каждой детачи.
Затем осуществляют окончательную притирку торцовой поверхности до \7 10—14 на специальном доводочном станке; неплоско-сгность при этом допускается не более 0,005 мм (выпуклость не допускается); обработанные блоки цилиндров контролируют, тщательно промывают и упаковывают.
s 14.8. ПРИМЕНЕНИЕ ЗЛЕКТРОЭРОЗИОННОГО ШЛИФОВАНИЯ И АЛМАЗНОГО ХОНИНГОВАНИЯ ДЛЯ ОБЕСПЕЧЕНИЯ ВЗАИМОЗАМЕНЯЕМОСТИ ПОРШНЕЙ
Рассмотренный способ ®P*O™	20\
гарантирует диаметральный	поршня - 0.0® «).
с конусом и овалом до 0,015 м ( должны отличаться боаее, диаметры цилиндров одного блока не должны
чем на 0,1—0, 15и плпшневой паре, с учетом гочвосЯ Гарантированный заз0Р в обеспечивается 15-35 мн изготовления цилиндра и п р ’
дом селективной сборки (рис- - (• цилиндров одного Одам
Штучное время шлифованияI се ~ мин. В баГЬШИЛ* с гавл яет 170 мин, притирки Iк	в цилиндрах дастигэсг <*
случаев после шлифования ко у
,.п0В цилиндров блока, конусности » ПТ1 поненпя РазмеР°„11е после притирки цилиндров, ДиаИ Ь0Л1’”,,,С "затрудняй’1 менее чем на 0,1 лл, что не доПуска £ овальности^ ’отличались бы_ о.о алмазного хонингован,,,1 метры KOT"JWBUCoKonpon3BOA''	ттакЖе конт роль деталей р0Та;
применения	меровзатр>Д , ж Большая трудое^1
БаПЬ'ми,Гко^рь’е ,,мСЮ\Тожает „х стоимость и требует вложенИя метрами, м 1.локов удорожает оборуДование.
„зготов-пе! каПИтаПы1ЫХ затра отклонениями по диаметр,, ЗНаПп7 изготовлении иилинДР> 5 а пор,1]Ней с отклонениям,;
11|1И 10 м с овалом и кону	в пор111„евон группе, Соб.
,у 4 ж гаРант1’2 взаимозаменяемости, будет составлять ’принципу ПОЛ 15 + 4 = 29 лк п
15 + 0 = 15 лк.
равными по диаметру ранной по I
Ал,ах ~ Ю 4"
АтШ = 0 4"
При селективной сборке
Атах = 5 4"
15 4- 4 = 24 мк и Amin = 15 МК.
При существующем методе обработки Атах — 35 лк и Дт|П = с= 15 ж, где Л = д, 4" б2 4~ б3 (рис. 14.18). Кроме того, повышение
Рис. 14.18. Структура зазора между поршнем и стенками цилиндра (4, — допуск на размер отверстия; 6г — минимальный гарантированный затор; 63 — допуск на размер поршня; N — номинальный размер отверстия)
Рис. 14.19. Схема электроэрознонного шлифования цилиндров гпдромашины № 5;
/ — блок цилиндров; 2 — электрод* инструмент; J — шпиндель станки
шение тп3аИЧОЗамсНяемос1ьРппи ЗВг°Ляет повысить к. п. д. и обеспе-электоо- Ч,,осто обработки цил111<’б°РКе поРшнезой группы. Поны э^м^7оХоГ° ШЛ,,Ф°ва»ия ДР0В обес,,ечпвается применением
питаемо^К0Г0	осУ114ествляется периферией JJ’
‘“‘’’ифонанрТОКОм низкого нлп СКтРода’Инструмента (рис. 141^ нь,е UMMdmn- НС,1ОДьзУ*отсЯ пеп112л'е11ии' ДЛя электроэрозионяо^ Фо адьные станки реоБоРУДованные серийные абрази
Скорость съема металла и чистота поверхности детали, получаемая при использовании смеси масел МС и индустриального 20 (1 : 1), а также трансформаторного масла, примерно одинаковы, □днако в первом случае при напряжении 19 в процесс нестабилен, ввиду большой вязкости. При токах короткого замыкания менее 60 а происходят частые короткие замыкания, электрод-инструмент омедняет деталь и получается шероховатость поверхности иа класс ниже, чем при обработке с применением трансформаторного масла. Износ электрода-инструмента составляет 10—15% от веса снятого металла.
Применение электродов из специальных сплавов на медной основе целесообразно, так как повышается производительность и уменьшается износ электрода-инструмента.
Технологические характеристики изучались при иапряжеииях 12, 19 и 24 в. На первом режиме процесс нестабилен. Характернсти-
Рис 14.20. График съема металла V и шероховатости поверхности в зависимости от силы тока короткого замыкания
Рис. 14.21. Профилограмма поверхности, полученной при режимах: a—V'=19«. /кэ=И7а; б-К=19«./Л ,=«Л
a -V=ISe, lKJ =8 а
ки напряжений 19 и 24 в показаны иа рис. 14.20. Съем металла при напряжении 24 в на токах короткого замыкания выше = 10в, больше, чем при 19 в. Однако в первом случае чистота поверхности значительно хуже, поэтому для уменьшения припуска под алмазное хонингование рекомендуется применять напряжение 19 в.
Профилограммы обработанных поверхностей при напряжены 19 в /к. з. — 117, 40 и 5 показаны на рис. 14.21.
При напряжении 19 в чистота поверхности на класс выше не грубых режимах и иа 2—3 класса выше иа мягких режимах, чем при обработке под напряжением 24 в при равных значениях/», j.
После обработки зона термического влияния состоит из белого •^травящегося слоя, слоя вторичной закалки (мартенсит и карбиды;
456
и отпущенного мартенситного слоя с
Структура основного металла состоит из мяпТ"0® твеРД°стьЮ. (рис 14.22, а—ж).	*оит из ^ртенсита и карбидов
При электроэрозионном Шлифовании и
обработки образуются трещины различной глубин^? °Т режима - 19«	120ИО,,., достигают”»™ а £ ТакЛ’"1' =
ствуют вообще.	— 5 а отсут-
Установлено, что зона теомичрскпт ппгш.,
же после электроэрозионного шлифования а трещины^Т СРЭЗу несколько позже Это дает возможность по^едующи шлифованием на более мягком режиме снимать слой вторичной^каХ и S накладывать на предыдущий слой термического влиянияотойкХ ческого влияния последующего режима. Производя этот поонТс можно окончательно снять слой вторичной закалкн от предыдущих режимов и практически свести образование трещин к нулю (на мягких режимах они отсутствуют).
Установлено, что старение блоков в масляной ванне при 160 ± ±10 Св течение 3 ч уменьшает глубину трещин на 20—50% по сравнению с их глубиной при электроэрозионном шлифовании без старения.
Старение после обработки V = 19 в н током с /кз. = 20 а устраняет появление трещин, тогда как без старения они отсутствуют только после обработки током с /к. 3. = 10 а.
При обработке блоков гпдромашин № 5 последовательно на нескольких режимах, начиная от грубого (на V = 19 в и токе 1к.з.= 117 а) и кончая мягким режимом (/к. 3. = 5 а), выявлено, что овальность и конусность отверстий составляли 2—6 мк и определялись в основном точностью станка.
При двухконтурном шлифовании производительность повышается на несколько десятков процентов при сохранении той же чистоты, что и при одноконтурном.
Положительные результаты дает шлифование отверстий сегментным раздвижным электродом-инструментом, который имеет форму конусной разрезной цанги с напаянными медными брусками электродами (сегменты). Такой способ электроэрозионного ш™Фовапвя позволяет разрабатывать станки с полной автоматизацией обработки отверстий, включая контрольные операции.	чистовой
Алмазное хонингование рекомендуется пчипнного шлифо-операции при обработке цилиндров после электрозионного фо-ВЗ,1ИЯ-	„ nnxvuv отвеостий небольшого
Алмазное хонингование у стали ₽Х12Ф1 проводится диаметра (до 20-30 ДдТ^оф_3 ЧисЛо оборотов шпинделя на серийных станках ОФ-ЗЬ А н • „.пинлеля до 230, 350 и 500 в минуту, скорость движения	до 5
И давление насоса, обслуживающегор обеспечивающем две Деталь устанавливается в приспособлении, ooeui степени свободы перемещений.
«п
vnunHrosaHHii цилиндров брусками ДСй9г При черновом хон	машинное время С(Ml
и снимаемом ПРИВ> з8д „ 5 мин — на станке Оф-3 и'В,'1Ярт
3 мин на станке ОФ-^а	• ЧнСТ0Та
|2ГЛТч«“и - v9- п1’°‘'з=°А^Х; на ст у___g блоков № 5 в смену.
СИП«№ ХОЖ.ВГовавия рассе,.ванне размеров диаметров ш„Янд Р° СкорТсТе^е°м^тал°ла дефектного слоя, остающегося П0(71е эпектроэрознонного шлифования, зависит от режима шлифоСа1]1|я Например, скорость съема при хонинговании после шлифОван|(

Рис 14.23 Циклограмма электроэрозионного шлифования и алмазной хонингования
чеГиопп/1 /к-5,= 117 й в течение первых 30 сек в 6 раз bi* иЛппи ” шл,,фования ПО режиму с /« = 5 и с обеспечен'^ кий выбог>ПпязеШНОСТИ Ф°РМЫ отверстия. Поэтому возможен W назначенииРтрЛИЧ11ЫХ Рсжнмов шлифования и хонингования
при назначь°Л01ИЧеСК0Г0 пРоцесса обработки блоков. Bpe циклограмм ппп И“ режима обработки целесообразно ™Х₽В ХТ0““ Т 14-23>- На '-ряф"”'	№•
определении мя,,..,и СЛОЯ’ МикРонеровности и треш'1 пинаемого металла «Н0Г° време,,и съема припуска по 00 01ifp$’ ностями. а Умывается заполнение профиля ми*Р°иег
г?0'.
» «.». ТЕХНОЛ„Г„Я 0Ер
» ИЙХ “«• Валики кардана изготовп
после изготовления имеют „ ЮТСя стали 20Y
SXЖ ssr™нкс ю~62 |р™
ности и чистотой V 5 —77 6 .Г перпендикулярность осей отвел стий под палец должна быть Je более 0,005 мм. Несимметричность «лысок» к сфере должна быть в пределах 0,02 мм.
Шатуны изготовляются из стали 2ОА. Сферы шатунов обрабаты-
Рис 14.24. Вадик кардииа
вают по 2-му классу точности с чистотой V7 in п
должна быть в пределах до 0 005 ГЬт °' П()ГРешность формы батывают по 5-7-mvклассам™ , ° ЛЬНЫе повеР™«™ обра-/ му классам точности с чистотой 4
Заготовки валиков кардана и шатунов получают методом штам ХиНаг~Х"Т'‘'"“' Прк“’ Пер« “™— к«“ы товки нагревают на электрокоитакпюй установке в течение 2—5 тек
1
Рис 14 25. Технологический процесс обработки валика карлт при силе тока 1000—2000 а и напряжении 6—11 и. Перея^е^^ головок карданов и шатунов на эксцентриковом пр каждой заготовки проверяется на стиллоскопе.
Валики (рис. 14 24) после высидки пмояж (рис. HAfl Рабатывают в такой последовательное». ' ff);
а)	заготовку центруют с двух конив fr
б)	обтачивают сферы вначале	11Д5>
»том выдерживают межцентровое расе
в)	протачивают шейку (рис. 14
г)	скругляют радиусы бруском ГОСТ 24о6- 67 (ри
д обрабатывают четыре бобышки подиаметру (р„с1Р^'	125
После цементации на глубину 0,7—1,0 мм н заЧИс,25-«и и карпом станке сверлят центральное отверстие (р„с.	ца £
валик кардана подвергается закалке с обработкой ,/п3)' валик	,д ///?С 58-62. После зачистки довоппЗДо^д
₽ л А ,	"° Размеру и чистоте V 9 (рис. 14 сфер4 ,
. AZ7X	ПЛОСКОСТИ ГОЛОВОК шишк... '	И).
Плоскости головок шлифую*/'^0’и>)-шлифовальном станке (рис. 14 25 к\й Плосьо-выдерживают параллельность 0 01 * ’ nf>w ^04 тричность 0,02 лл, а острые кромки ЭКС1Ш (0,03 мм) бруском ГОСТ 2456—52 р,1тУПляют фуют и доводят плоскости бобышек 3аТРМ Шл"-деталь промывают в бензине и пя™, ПОсле Ч(-Го ™ui,o	1 i/no ----- ’
_.г____,UIV/O в сЬч
снимают фаски. Обработанный валик промываютТбенз ТВерстия -вают сжатым воздухом и клеймят, после чего его поп "Не' "Р°Д5‘ рению в масляной ванне при 160 С в течение 3 ч и □<>./ ргают ста-ГЛ VI/Y1* 1454 TftADTUULI f ггхч	- u " JdTeM КОНтролц.
консервируют и
и
Рис. 14.26. Шатун
На токарном станке модели 1К62 сверлят отвер'стТ'ННчива|от. растачивают канавки, (рис. 14.24), затем прочищают ™ В С(1’в,”“ вают сжатым воздухом и клеймят, после чего его руют на трещины. После оксидирования детали упаковывают.
Рис. J4.27. Технологический
с)	м)
процесс обработки шатуна
Шатуны (рис. 14
токарном станке модели вь'с;'дки головок (рис. 14.27, о) на новом (рис. 14 2/,	61 Центруют с двух концов с переус^’
Расстояний (рис. 14’27 ИВаютсферыс выдержкой межцентровй Гуляют зенковку (ри/ ш ?£Та?ИВают шейкУ (Р',с- П.27, г) ПР«
‘	' д) и контролируют обработанну10
станке™6 '₽ИС‘ 14 убННу 1.0 мм сверлят центральна ется ЯГп°Луавтомате. На /',аМе!Ром 2~3 мм на спецпаль^ ловкой ГаТНа« г°ловка „иар"ой станине этого станка разМе рабатык Шпиндельная баб четь,Рехшпи,1дельной сверлнльН° ^ать<ваеМвд детал»ая бабка для закрепления и врашенИЯ
Число Хро^^^^^^	по четыре детали.
ляет 310 в минуту.	обрабатываемыми деталями, состав-
После сверления шатуны закаливают до HRC 58—г ^щеи °бРаб0ТК0Й холо*ом и прочищают Антральное Sp-
На круглошлифовальном станке шлифуют сферы с чистотой об-работт н 7. Шатуны размагничивают, промывают в чистом бензине продувают сжатым воздухом и оксидируют. После оксидирования па специальном станке доводят сферы, промывают в бензине с тщательной очисткой центрального отверстия, смазывают и укладывают в тару.
§ 14.10. ТЕХНОЛОГИЯ ОБРАБОТКИ РАСПРЕДЕЛИТЕЛЯ
Распределители изготовляются из бронзовых сплавов или высоколегированных сталей (рекомендуется бронза Бр.ОСНЮ-2-3 и сталь X12Ф1); точность изготовления распределителей должна быть очень высокой (рпс. 14.28). Центральное отверстие обрабатывается по 2-му классу точности и \7 7, радиусные пазы — по 5-му, а остальные размеры по 7-му классу точности. Неплоскостностъ торцов должна быть не более 0,005 мм, а выпуклость не допускается. Кромки проточек и пазов на торце А (соприкасающегося с торцом блока) должны быть острыми без заусенцев, остальные кромки притуплены. Эксцентрицитет пазов по отношению к центральному отверстию допускается не более 0,05 мм для одного и 0,1 мм для другого. Эксцентрицитет выточек по отношению к центральному отверстию допускается до 0,08 мм. Чистота бронзовых торцов V 8, стальных — V 1°. а кромок и пазов —V6. остальные поверх-,ЮСТребуемая чистота и допустимая погрешность торца бРОнз°в°-го распределителя достигается шабровкой с обеспечением 20 точек на квадрате со стороной 25 мм по контрольной плите 1-го класса
распределителей «брайтываюте» торцовой поверхности стального блока иили^-слепредваритель-зового распределителя отличается отуказа то 0М Станке отре-ного сверления центрального отверст	Р 14.29, а);
зают заготовку от отливки изброизь. Бр.<ХН 10
подрезают торец с чиСТОТО“япУ2е 0" Стие; подрезают № кромки. Затем растачиваютwaMerpt снижают фаску, раста-рой торец, обтачивают нару RnD0TO4Ke меньшего диаметра {рис. чивают выточку, клеймят торец Д в проточе	надер
14.29, б), повторяют переходы на ДРУ* и
462
плавки на проточке меньшего диаметпя и
(рис. 11.29,«) Затем па протяжном станке ппотГ™™™ размеРь> |4.29, г) и на вертикально-сверлильном станкгг”ВаГОТ Пазн (рис-панроход (рис. 14,29, д).	ке свеРлят отверстия
Па вертикально фрезерном станке фрезеруют четыг^ торце /1 и после переустановки - два паза на торце В [рис 14 М заТем зачищают заусенцы, предварительно фрезеруют 4 У’ (рис. 14.29, ж) и затем начисто с обоих торцов. Поме снятия lavcet цев, сохраняя острые кромки проточек и пазов торца А 13мят деталь в проточке меньшего радиуса торца В	клеймят
Контре^ распределителя производится после зенкования двух углов (1о _ ) (рис 14.29,3); затем деталь подвергается старению в масляной ванне при 280' С в течение 2 ч. Торец В клеймят буквоп <<Т», деталь промывают в бензине, продувают сжатым воздухом н подрезают торцы с чистотой V 7 (допускаемое отклонение от параллельности — 0,05 лги). Затем на торце А снимают заусенцы, при этом кромки проточек и пазов остаются острыми (при необхо-димосги углы исправляются), после чего распределитель промывают в бензине, продувают сжатым воздухом и контролируют.
Окончательные операции — подрезка торцов с обеих сторон (рис. 14.29, и), непараллельность до 0,02 мм, чистота V 8 и не-плоскостность — До 0,005 мм (выпуклость не допускается) и контроль после шабровки торца А (20 точек в квадрате со стороной 25 см).
Готовый распределитель промывают в бензине, продувают сжатым воздухом, смазывают веретенным маслом и упаковывают
§ 14.11. ТЕХНОЛОГИЯ ОБРАБОТКИ БУКС
Токарная обработка буксы (рис. 14.30) выполняется на токарновинторезном станке модели IK62. При этом отрезают заготовку, подрезают торцы, обтачивают цилиндрическую и коническую поверхности затем (рис. 14.31, а) обтачивают наружную поверхность, рассверливают и растачивают отверстие, снимают фаску и притупля-
ной поверхности и закруглении (р) .	’ aTbPQ05 мм. Снимают
разЕьФ(РР«р»-
нием эксцентрицитета не	’ и фрезеруют на том же ста жг
заусенцы, притупляют острые^кромки с Фрма^Узаусенцы, притуг.ля-торцовой паз. После	к^ХТверлильном ст= OMMJT
ют острые кромки и на ^"заусенцев в отверста Нр-С* Два отверстия напроход с „ных операций буксы п ’  31, е). После проведения указанных
464
гтарснню в масле при 200г С, затем
„ снимают фаски.	Р пиливают пазы (рис 14 31
Готовые буксы промывают в бензине	’ Ж)
<оМ „ после контроля н такой же очисткТ еТЭЮТ Сжатым в°зду-маслом и упаковывают.	гки созывают веретенным
§ 14.12. ОБЩИЕ ТРЕБОВАНИЯ К ПРОЦЕССУ СБОРКИ
И ЕЕ ПОСЛЕДОВАТЕЛЬНОСТЬ
При сборке для согласования размещения стыкуемых узлов широко используются компенсационные кольца Так для совме шения осей вала и отверстия люльки с точностью до 0,1 мм, обеспечивающей необходимую равномерность подачи, используют компенсационные кольца, которые устанавливают под внутренние обоймы шарикоподшипников, связывающих цапфы люльки с корпусом насоса Толщину компенсационных колец подбирают или подгоняют шлифовкой по кольцу-калибру. Непараллельность плоскостей компенсационных колец должна быть не более 0,02 мм. Одновременное соосностью осей обеспечивается и осевой зазор люльки в направлении оси цапф до 0,04 мм при осевой нагрузке, равной 20 кГ (здесь, как и в дальнейшем — для гидромотора и насоса №5).
Для сборки крышки с люлькой используют калибр на соосность оси отверстия крышки (под ось блока) с осью центрального отверстия люльки. Затем крышку присверливают, закрепляют штифтами .
В сборе ось вибратора с осью стакана должна совпадать (допуск до ±0,5 мм). Предусматривается специальный калибр для проверки соосности осей кронштейна вибратора, шестеренчатого насоса и стакана валика управления. Одновременно обеспечивается параллельность этой осн осям цапф, а также размер между этими осями (для гидронасоса №5 этот размер равен 85,5 ±0,09 мм). При установленном калибре на корпусе насоса закрепляют штифтами стакан валика управления, корпус кронштейна вибратора и шестеренчатый насос.
га	‘Xpisre
„„„„„е „ оси и»фи
компенсационных колец при	под „агрузкой 75/сГ)
Зазор С (0,15 + °’® J5* Лп^ионными кольцами и проверят* также обеспечивается компенсЖелателен селективный подборке» калибрами-приспособлениями. Ж мехаНических цехах < иски»' пенсациониых колец, изгоняемых.^нрки
чением подшлифовки колец Р и напрессовКи дуплемкрт**'
Сборка гидромоторов	33 о)13атемопредаПРо4*
Пых подшипников 6 на вал 1 (рис. . "5 при осевой н»гру*г  ческий размер компенсационного кольцу к
16 В Н. Прокофьев И ДР• — 164
вал 500 кГ (создается кольцо, запрессовывают кольцо, проверяют размер
специальным приспособлением), шлифую, Дп с поршнями в корпус 2 до упора '
А. Затем устанавливают зазор Ме>к подшипником 3 и наружным устуцом корпуса 2 за счет подшлпфовки втул К11 4 при осевой нагрузке 75 кГ (со, здается специальным приспособлением). После этого запрессовывают подшипник 6 п навертывают гайку Следующая операция заключается в закреплении корпуса на поворотном столе, после чего вкладывают уплотнительное кольцо в буксу вала 7, вводят пружину 8 п большой упор 9, Вставляют вал в сборе 14, буксу 25 в блок цилиндров (рис. 14.33, б), устанавливают кардан 26 до отказа в сферу большого упора 9, а в буксу 25 вкладывают компенсационную шайбу 11 и малый упор 12. Размер С доводится подшлифовкой компенсационной шайбы. После сдачи ОТК промывают уайт-спиритом все детали блока цилиндров, продувают сжатым воздухом и смазывают рабочей жидкостью. Операция завершается сборкой блока цилиндров с распределителем и закреплением его штифтом 15.
В крышку гидромотора запрессовывают штифты 16 и 22 и по калиб-
Рнс. 14.32. Ходовая часть на- ру совмещают оси отверстия крыш coca	ки 21 и фланца 10. На сверлильном
станке сверлят и развертывают отвер стия фланца под штифты и закрепляют двумя штифтами крышку на фланце 10. После проверки совмещения осей крышки и фланц сборка проверяется ОТК. Соединение блока цилиндра 13 с пор ними проводится на поворотном столе.
На том же поворотном столе начинается вложение УГ1Л0'Т тельных колец 24 в выточки пробок 23, затем ввертывают пр в отверстия фланца 10, вкладывают уплотнительное кольцо > надевают крышку 21 на ось 14 и закрепляют ее четырьмя 1)0Л га со стопорными шайбами. Уплотнительное кольцо надевают на пер 9, ввертывают в отверстие, затем надевают гайку 20 с упл ВИВм- Наконец, в выточки крышки вкладывают уплотнения, 33 а т отверстия технологическими крышками, а в резьбовые ^апХиТИВВТЬ1ваЮтчетыРешп«льки- На шпнльках уКЙием ую коробку 18, после чего специальным приспособ
466
Я1ОТ момент вращения ходовой группы. Затем уплотнитель-^юльцо 30 вводят в выточку передней крышки 29 (рис. 14.33, в), н°с к ссовывают манжету 28 и крышку в сборе привертывают к запрет: Алтами со стопорными шайбами. Затем надевают наруж-корпу ушку 27, привертывают винтами, которые закрепляют в ИУ^пах в ДВУХ точках-
111)1 Собранный гнДромотор подвергается приемно-сдаточным испы-м согласно специальным техническим условиям. Момент пово-
Тота вала в собранном гидромоторе не должен превышать 35 кПсм.
ю
IS и
б 7
8 9
12
13
15
16 П

Рис. 14.33. Технологический процесс сборки гидромотора
После сборки суммарные утечки рабочей жидкости через сопряженные торцы блока цилиндров, распределителя и крышки, через вкладыш вала и из-под поршней при статическом давлении 150 + + 10 кГ1смг не должны превышать 800 смЛ!мин. Утечки по плоскостям разъема корпуса клапанной коробки и крышки не допускаются (здесь и далее для гидромотора № 5).
После проверки суммарных утечек и утечки по плоскостям разъема, гидромотор обкатывают по режимам, приведенным в табл. 14.3.
Затем гидромотор подвергают гидравлическим испытаниям по режимам, приведенным в табл. 14.4, совместно со штатным или технологическим насосом № 5.
Общая продолжительность испытании составляет 2 После испытания по режиму VI11 гидромотор, работающий в паре с на Сосом должен иметь следующие показателир полости нагие-а) момент на валу гидромотора при давлении в полос™
тания 40 ± 5 кПсм* ~~ 2,5 к.1 м,

. екопости вращения вала гидромотора при да
б) падение скорое l± g	по срав1и НИ10 со с »щ
в полости нагнетания 40 нагруЗК[, _ не более 25 об/мин Р В,,° вращения при Раи~ вращения вала гидромотора при Пяп„
В) наименьшая скорость вр±£.	должпа Р UaBne.
Уб’обда^прн^том вал должен вращаться без остановки. °е
Тиб'ЧЦа
Режим	Давление нагнетания в кГ/см'2	Скорость Вращения вала гидромотора В об,МПН	Направление вращения вала гидромотора	Время обкатки В ч
1	Холостой ХОД	300 + 15 300 + 15	Против часовой стрелки По часовой стрелке	1 1
		600 + 30 600 ±30	По часовой стрелке Против часовой стрелки	1 1
		1000 + 50 1000 + 50	Против часовой стрелки Но часовой стрелке	1 1
		1440 + 75 1440 + 75	Против часовой стрелки По часовой стрелке	1 I
11	20 + 5	300 +15 300 + 15	Против часовой стрелки По часовой стрелке	1 1
		600 + 30 600 + 30	По часовой стрелке Против часовой стрелки	1 1
		1000 + 50 ЮОО + 50	Против часовой стрелки По часовой стрелке	1 1
		1440 + 75 1440 + 75	Против часовой стрелки По часовой стрелке	1 1 		-—-
		Общая продолжительность обкатки		16
давлениев ппп^.?ЫТаНИЯ П0 Режимам. приведенным в табл.
этом утечки пял И ?сасывания Должно быть равно lOi.'jW' сМ ' , „0 местам разъем °Ч6И ж,,Дкости из корпуса гидромотора нарУ*)
" "P«fc« "« допускаю™; допус
и подтеков уХ пР0Сачивание масла без образования капе Допускается не болЖ. Ma™e™?e уплотнение вала гидр°“а^о. ^ра.ХлненвТ °’к СМУ“- Утеч™ из неработающего кГ/сл2, не допускаютс^ап°ЧеИ жидкостью под давлением . ^ра. зования капель и подтек^°П^СКаеТСЯ пР°сачиваНИе MacJld
468	°В‘
-	 решим	Давление нагнетания в кГ/см”	Скорость вращения пала гндромотора в об 1 мин	Направление вращения вала гндромотора	Время испытаний в мин
1 11	Холостой ход	1440 +50 1440 _t 50	По часовой стрелке Против часовой стрелки	10 10
111 IV	4(1 х 5	1440 + 50 1440 + 50	Против часовой стрелки По часовой стрелке	30 30
V VI	60 ±5	960 + 30 960 + 30	По часовой стрелке Против часовой стрелки	10 10
VII vlll	100 + 5	450 + 20 450 + 20	Против часовой стрелки По часовой стрелке	5
IX X	40+5	1440 + 50 1440 + 50	По часовой стрелке Против часовой стрелки	5 5
После проведения указанных испытаний гидромотор разбирают для проведения контрольного осмотра. Разбирают и гидромоторы, не удовлетворяющие техническим требованиям по результатам испытаний.
На трущихся поверхностях деталей гидромотора допускается нарушение покрытий. Суммарный осевой зазор шатуна во вкладыше и в поршне допускается не более 0,08 мм под нагрузкой 6кГ, при этом осевой зазор вкладыша в развальцовке с валом и его поворот не допускаются.
После устранения дефектов гидромотор вновь предъявляется для приемки по тем же техническим условиям, как и при изготовле-
нии нового гндромотора.
Обкатка в этом случае проводится под давлением нагнетания, вавным 20 + 5 кГ'см*, и скоростях вращения указанных выше. В качестве рабочей жидкости при испытаниях применяют веретенное мягпл А V ГОСТ 1642—50 Масло должно иметь паспорт завода-изг <-“ ±У КХвии паспорт» по быть проверено на сооиетствие ГОСТу и сваожено р
иа”"ет,,и
не ниже 2,5.	ОЛГ,аетгя линамометром или подякзи*
Момент поворота вала про Р новки на вал манжетного ванием груза на полном обороте до усг
Уплотнения.	„„овтгя на специальном стенд
Суммарная утечка пР°®ер нЫМ выше, производят
Обкатку по режимам, ;У	приведена на рис. 14.34.
Рекомендуемая схема котор
пппгскается охлаждение обкатки Доп>сквв полжен быть водой Гидромотор Должен
гидромотора, насоса и Tpvr заполнен рабочей жпдК0Ст?"р0' соединен дренажным Х” проводом с баком насоса °' НИТКИ	П°А-
Испытаиия по 5 казанным в табл 1} 4	’
изводят па стенде соспеодХ ними приспособлениями '
Испытания по каждому |)е. жиму должны проводиться непрерывно. Допускается остановка и охлаждение гид-ромотора, насоса и трубопроводов между испытаниями по каждому режиму.
Время одного оборота при проверке скорости вращения вала гидромотора при давлении в полости нагнетания 40 ± 5 кГ !сн? определяется по секундомеру; давление в полости нагнетания при этом устанавливают при наибольшей скорости вращения вала гидромотора. Скорость вращения вала гидромотора замеряется тахометром или счетчиком оборотов.
Утечка из неработающего гидромотора, заполненного рабочей жидкостью под давлением 0,5 + 0,1 кГ/ож2, проверяется в течение 10 мин. Рабочая жидкость подводится через одно из сливных от верстий во фланце гидромотора; дренажное отверстие при этом заглушают.
При проведении обкатки и испытаний должны быть соблюдены следующие условия:
а) нагрев рабочей жидкости выше 90' С не допускается; ncnnL™PaKTepHC™KH при всех виДах проверок и испытании Р
Во темпеРатУРе рабочей жидкости 15—40° С.	ь10
заливают ” хране,1У1я и транспортирования гидромотор по заливают маслом ДУ ГОСТ 1642—50 покрывают «e повеРхнос™ гидромотора, не защищенные крае* покрываются смазкой АФ-70 ГОСТ 2967—52.
Рис. 14.34. Принципиальная схема стен да для обкатки и испытаний гидромотора:
/ — приводной двигатель; 2 — муфта; 3 — насос; 4 — переключатель; 5 — манометр низкого давления; 6 — манометр высокого давления; 7 — подпиточные клапаны; 8 — фильтр; 9 — манометр для определения давления в корпусе гидромотора; 10 — испытуемый гидромотор; 11 — вагружатель; 12 — охлаждаю щнй резервуар; 13 — змеевик охлаждения; 14 — предохранительные клапаны; /5 — сливной клапан; 16 — бак; 17 — фильтр; 18 — насос подпитки; 19 — фильтр; 20 — термопары
Глава 15
ОТ, АПИЗАЦПЯ ПРОИЗВОДИВ ГИДРОПРИВОД
§ 15.1. МЕХАНИЧЕСКИЙ ЦЕХ ХОДОВЫХ ЧАСТЕЙ
В механическом цехе ходовых частей изготовляют детали удовлетворяющие высоким требованиям по точности выполнения й чистоте обработки (поршни, блоки цилиндров, распределители, валы, шатуны, валики карданов, детали распределительной коробки и т. п.).
Этот цех целесообразно подразделять на восемь основных участков: 1 — механической обработки; 2 — шлифования; 3 — промывки и ультразвуковой обработки; 4 — старения; 5 — антикоррозионной обработки; 6 — доводочный с отделением предварительной доводки и отделением окончательной доводки; 7 — точной обработки; 8 — сборочный.
Заготовки поступают из заготовительного цеха в виде прутков и поковок, литые детали — из литейного цеха (бронзовый распределитель, крышки и т. д.), крепежные детали — из цеха нормалей, а подшипники — через службу снабжения.
Участок механической обработки имеет тот же характер, что и одноименные участки обычных машиностроительных предприятий.
Для изготовления деталей повышенного класса точности ре-
комендуются соответствующей точности токарно-винторезные станки. Изготовление валов целесообразно вести с применением высокопроизводительных полуавтоматов специальной конструкции. При обработке блоков используются агрегатные станки для сверления отверстий (рис. 15.1); модернизированные вертикально-сверлильные станки с многошпиндельными головками для одновременной притирки отверстий (рис. 15.2), станки групповой притирки и Доводки торцовых поверхностей (рис. 15.3) и другое!
чзводительное оборудование. При изготовлении	центрикв.
ческим участком Р изолированном помещ Распространения пыли.
е «ости от шлифовального участка в ппсоедственной бл „язмещается участок старения. Этот В Хм помещении ра^ ованпя для СИЯТ11Я термически >'з°лПР0ВпХчает Детали п^дс ШвФием участка являются ванны участок по » ОсЯовным о0ор)"пятором для поддержания задан-НаПХооподогревом и J^a Обычная операция старения - выдер. СЭЛ т₽мпепатурного режима, и	, в котороп поддерживается
н0Га°; течение Зч в маслйИ“ егрев опасен из-за возможности
П("’ заги'“е “едует 11С’“““"Ь специальную тарУ’
600
2W0
Рис. 15.1. Станок для одновременного сверления трех отверстий в блоках: 1 — станина; 2 ~ силовая головка; 3 — шпиндельная головка; 4 — деталь;
б — зажимное приспособление
Доводочный участок пя в изолированном пометив "°Л^еТСЯ всл™ за участком старения вентиляцией. Поскольку по и\^°РУДОВанном приточно-вытяжной нои доводок необходима r-Ш предварительной и окончатель-размещается в непосредстпЛ,” т^втельна(1 промывка, этот участок Установка промывочного ^ И близ0сти от участка промывки. икс- участке нежелательна РУдования непосредственно на доводоч-пЧЗСТ0к с °^еспеченирм°гК0ЛЬКу Необх°дим единый промывоч-Хлк₽ерации В Со<'РоХтелкТ^ГОЙ ФиксаНИИ каждой промывоч-недопХТ0РЦС)ВЬ1х поверхностей r0H Карте- Это особенно важно при при Xlr?'0 попадание абпазипбЛОКОВ цилиндров, когда совершенно и окон а °ТКе г'РитиРОчнЫми 5НЫХ частиц с предыдущих операции ДовододЛщ>Н“°Й Д0В0Дки- кругами в процессе предварительной сост1веЧпа?ЬН°Й	НЭ отделения предварительной
ваниечиЛ ’ изготовляе.,’.^аддое из которых работает на своем ^еобхоли ТКа спинальные / центРализованно. Основное оборуД0' водимая авещенХ^ (рис- 15-3), а также фирменные станки.
ть Участка — 300 лк.
п непосредственной близости от участка доводки располагается < пение участка для промывки и антикоррозионной обработки п°мС рй Оба этих участка требуют одинаковых условий освещения, детал и т д в помещении участка должны устанавливаться,
Рнс. 15.2. Модернизированный сверлильный станок для доводки отверстий в блоках:
I — редуктор; 2 — электродвигатель; 3 ~ механизм подачи нметру-мента; 4 — станина; 5 — головка крепления и вращения инструмента; Ь — подъемный стол по крайней мере, две ванны для первичной и вторичной промывок, после которых следует продувка в специальных продувочных шкафах, которые, так же как н ванны, оборудуются вытяжной вентиляцией. Промывка деталей производится в авиационном бензине (ГОСТ 1012—54). Отделение ультразвуковой обработки оборудуя ультразвуковыми генераторами УЗГ-10, УЗГ-10М, ультразвуковой ванной УЗВ-15 и моечными машинами.
В отделении антикоррозионной обработки
НЫ для обезжиривания, ванны для обработки нятрито П»  «3
„„талей проточной водой, электрические Печ _ лпя промывки детале	^^цваются вытяжной венщ.
ваН ^кн деталей, причем в	нитритом натрия устанавливав
суик отделении обрабо_	и кальцинированной соды, Вап.
SX’e нитрн»растра «о с. ны оборудуются V ______________________
2 3 Ч
Рис. 15.3. Станок для притирки торцев блоков:
/ — основание; 2 — плита; 3 — притирочный диск; 4 — кожух; 5 — сепаратор; 6 — водило; 7 — редуктор; 8 — кожух: 9 — электродвигатель; 10 — кронштейн; // — редуктор; 12 — электродвигатель
В отделении устанавливаются сушильные шкафы для сушки деталей после нитритной обработки при температуре 100—120' С.
Участок точной обработки комплектуется оборудованием повышенного класса точности.
ц ^а,сборочном Участ»<е осуществляется сборка только ходовой лен1*1(поршневой гРУппы). В отдельной комнате оборудуется отде-\'станппиПРеСС0ВКИ’ имеюЩее гидравлический и винтовой прессь, установку для контроля запрессовки и т. д.
В механическом	ЦЕХ К°РПУСНЫХ ДЕТАЛЕЙ
погоТза^™’ кР°нштейнРы и^^ £еталей изготовляют корпуса, П0Рядке кп °ВИТельНого Нехоп -д-Заготовки поступают из литеи-режущий „0Г’ераци«, поступав Литье и поковки, поставляемые в вспомогатеп..ИЗМерительнь1й инг ? С центРального склада завода, завода ЬНЫе Материалы об₽ТРУМент’ тех пологи чес кую оснастку, да.	1 налы обеспечивают соответствующие слу^ы
474
Для изготовления Деталей в корпусном основном о гл ивки из углеродистой стапи/ ис"ользуются в 977—65), отливки из чугуна (ГОСТ 7904	35Л~1 Гост
сплавов (ГОСТ 2685-63).	'	7293-54) и алюминиевых
Детали, обрабатываемые в цехе Konnvr
сложные геометрические формы пои и>™Х деталей- имеют К механическому цеху корпусных деталей пп КЛЭССе Точности-кие требования по культуре производств? редьявляются высо-
Освещениость на рабочих местах должна быть не менее 300 Окраска стен, оборудования, стеллажей для хранения деталей поп на соответствовать нормам промышленной эстетики ЕточнТвы тяжиая вентиляция должна обеспечивать нормальные условия рХ ТЫ иа участках цеха. Исключительно большое внимание в X уделяется созданию н работе промывочного участка
Увеличение производительности достигается использованием аг-peiaTHo-расточных станков, применением конвейерных линий на окраске, сушки в терморадиационных печах, зачистки в специальных камерах, снабженных вентиляционными установками и инструментом (шарошками, щетками, фрезами и т. д.) с пневмо- или электроприводом. Операции, выполняемые абразивными инструментами, должны проводиться в изолированных помещениях. При заточке инструмента из твердых сплавов следует использовать круги из синтетических алмазов.
Точность и высокая производительность изготовления деталей досгшается использованием координатно-расточных станков, применением пневматических патронов и пневматических тисков, струйной промывки корпусов, сваркой в защитной атмосфере, пневматической проверкой герметичности и заделкой литья эпоксидными смолами. Необходима организация внутрицеховой транспортировки обрабатываемых деталей и узлов при помощи напольных и подвесных устройств (кран-балки, электротельферы грузоподъемностью до 1 т, электрокары, ручные тележки).
Участки цеха размещаются в соответствии с последовательностью технологических операций, а их организация основывается по предметно-замкнутому циклу.
Участки сварочный, заделки эпоксидными смолами, приготовлен, i я эмульсии заточки, притирки (доводки), окраски, травления и обезжиривания следует размещать в’ я^«₽°“ниых помещенИ * оборудованных	иметь разнооб-
Механический цехкорп.сн “ "	альной точности, по-
разный парк металлорежущих , 7СЯ по 2—3-му классам скольку большинство'ДО™ включать в себя токарные, фрезерные, точности. Этот парк ДОЛ ж	натИО.расточные, сверлильные.
Горизонталь но- расточ н ые, .	ые> круглошл ифовальные станки
резьбонарезные, п‘пос!?оШп,1.^,.кции. Например, arPecra/.H^„"j^ и станки специальной	отверстий (^ис. 15,4). снекиаль-
для двусторонней расточки соосных н
„опрчйнпя конической резьбы и для заверти
* ”,“есгсн“<"'
пытания на герме комплектуется постами газовой, электпп„
Сварочнь.1 )ча	Для поДогрева теплоемких Р°Ду
говой и арго’'^ с автоматическим регулятором темпера™!" £Тр=тяжелыми деталями используется кран-ук^Х
Рис. 15 4. Станок с алмазно-расточными головками:
1 — коробка скоростей: 2 — подставка; 3 — алмазно-расточная головка АР-35;
4 — плита; 5 — станина; 6 — электродвигатель; 7 — подставка
Участок изготовления трубопроводов обеспечивает пять основных производственных циклов: 1 — заготовка труб; 2 — гибка труб с подгонкой по макету или контрольному приспособлению; 3 — слесарная сборка с подгонкой; 4 — пайка; 5 — травление и гальваническое покрытие или окраска наружных поверхностей. Обеспечение каждого из этих циклов требует отдельного помещения.
Помещение для заготовки труб оборудуется металлическими Si(2000Х600Х85°) с я«! для' инструмента и приспо-слесапны’мпСТеЛЛ,аЖаМИ ДЛЯ хРанения заготовок труб, обыч  а вХТиХЛе1\СТакаМИ- станк°м Для отрезки труб при помощи рамбовки Х ”Г,разивиЬ1х кругов и установкой для 3ac“nK”veTCfl HaJS	полостей труб, которая оборудуй
для ™6ки ТРУ<5
X150 - 200) с отв₽ Т‘ в' ч- Устанавливается чугунная пли д^лизИ плиты размещается'СТИЯМИ для опРавок под гибку ТР> ’ я труб Р мацается ванна с проточной водой для охлаждения
47©
Рис. 15 5. Установка для завертывания заглушек в крышках гидроприводов:
/ — станина; 2 — пневмоцилиндр; 3 — пневмораспределитель; 4 — рычаг; 5 — система возврата; 6 — храповик; 7 — пневмокран; 3 — зажим; 9 — деталь; 10 — переходная втулка; II — головка; 12 — маховик
Рис. 15.6. Стенд для
«-»— ssr“ *“* по 4UU Ы !<"* •
з — плунжерный пасе-лД стол: 5 — манометр. доотДелнтел« У — I*" — стальной сварной J вмозолотннк. 6 привод; 5 ~ 1ШС
в процессе выполнения гибочной операции Помещение o6onvn слесарными верстаками, а также необходимыми стеллажами / инструмента, шаблонов, макетов и контрольных приспособлен -Обязательна приточно-вытяжная вентиляция.	п,иц)
В непосредственной близости от отделения для гибки тр\б п мешается заготовительное отделение, в которое и поступают tdvf.3 после гибки для отрезки припусков и последующей траиСпопТ' ровки в помещение сборки, где трубы снабжают фитингами (штуп рами или фланцами) и подгоняют по макетам гидромашнн. е
Сборочное отделение оборудуется слесарными верстаками, стан ком для нарезки резьбы на трубах, станком для снятия внутренних и наружных фасок, стеллажами для заготовок труб и готовой про дукцни (600x1800x2000), шкафом для комплектации деталей макетами гидромашин для подгонки собранных труб, плитой для догпбки труб и приспособлением для гибки труб.
После сборки труб с фланцами они поступают обратно в отделе ние гибки для пайки. Запаянные трубы поступают в отделение сборки труб на проверку, а в случае необходимости — и на догпбку на макетах гидромашин. Подогнанные трубы направляются на химическое травление и покрытие.
Участок термической обработки получает и возвращает после проведения производственных операций детали в механические цехи, около которых он и должен размещаться.
Участок обеспечивает осуществление следующих операции: отжиг и нормализацию, закалку в печах и ваннах, закалку токами высокой частоты, отпуск, цементацию в твердом карбюризаторе, а о-тирование, обработку холодом и зачистку шлифовальными кругами.
Существенное увеличение производительности труда на участке гальванических покрытий достигается установкой универсальной гальванической линии с программным управлением для оксидиро-ногяйяпТаЛЬНЬ1Х яетапев- Такая линия позволяет обрабатывать крупного Tnv^b.'e5етали тесом до 200 кг с минимальной затратой руч-неболыппгп , <спечивает высокую культуру производства. Ввиду в обычных ван^аТ ^аб°Т анод,1Рование целесообразно проводить чать в°себя ванныгальванических покрытий должно вкдю-У800 мм ваннп Р°маслввання с внутренними размерами 1500Х 1500 у80о’ мм ХОЛОДнов промывки с внутренними размерами размерами юбОу^ОП* х,1МИческого обезжиривания с внутренними и ванны пассивипппя ванны осветления, ванны анодирования
Участок довоЕ Т С ?нУтРенними размерами 1000x800 ММ. Деления во избежяии<?еТаЛеИ гиДР°машин разделяется на два °т водку, проводимую Попадания абразивов на окончательную Д оборудование для ХПя ВГОР°М отделении, и имеет необходим мых деталей, сепаоятпг,еНИЯ а®Разивных материалов, обрабатыва соблений, горюче-смяя °В’ вРитиР°чных станков, съемных присп 478 I че сма30ЧНЬ1х материалов и т. д.
§ 15.3. ОБОРУДОВАНИЕ И НЕнотпрчк-дли механическое' овелвотк!
Пр. обработке корпусных деталей применяется как ное. так и специально разработанное оборудование и
Плоские поверхности обрабатываются на продольно-фпезео ных двухшпиндельных, вертикально-фрезерных и гориз^Ео фрезерных станках.	риаишально-
Плоские поверхности с повышенной точностью обрабатываются на плоскошлпфовальных станках.
Доводочные станки (см. рис. 15.3), снабженные специальными сепараторами, используются для одновременной доводки торцовых поверхностей восьми блоков цилиндров или распределителей из стали Х12Ф1 диаметром до 135 мм. Станок состоит из тумбы с приводом на доводочный диск, который, в свою очередь, через зубчатую передачу внутреннего зацепления приводит в движение центральное зубчатое колесо, на котором эксцентрично оси вращения установлен палец с сепаратором для установки деталей. Одинаковые траектории всех точек сепаратора получаются благодаря специальному устройству — стабилизатору сепаратора. При равномерном вращении доводочного (притирочного) диска сепаратор совершает плоскопараллельное движение по окружности с диаметром 100 мм. Вследствие разности чисел оборотов доводочного диска и чисел колебаний сепаратора траектория движения обрабатываемых деталей на доводочном диске повторяется только через 55 оборотов и образует сетку с шагом 4 мм.Число оборотов в минуту доводочного диска равно 32, скорость притирки — 63 м/мин, число колебаний сепаратора в минуту—43, мощность приводного двигателя — 1,7 кет.
Обработку основных отверстий в корпусных деталях производят на универсальных горизонтально-расточных, токарных и координатно-расточных станках.
Для двусторонней расточки соосных отверстий в люльках и кронштейнах разработан специальный агрегатный станок (рис 15.4). Обрабатываемую деталь крепят на установочное пРи“^ен“е поперечного суппорта. В шпинделях двух алмазно-расточных головок АР-35 устанавливают регулируемые‘
в специальных сварных Ф абразивную пыль. Для деталей отсасывающей металлич У 0П1ЧНЫе шкафы с отодвигающейся весом до 500 кг применяют анало.
верхней крышкой.
ocnvnocTH шкафов облицовывают звуков Внутренние поверх'^™ резиной и т. д.).	УКоп°^о1Ца.
ющим материале,леТапеи весом до 50 кг от стружки и загрЯзнс Для проД)ВК1 А	специальные сварные шкафы Д eilllii
® 50» «сад01»1 вытяжной “/“^догичные шкафы (рис. 15.7), снабженные " *с Z«PZ«M« Хр««"» детален а прессе обр^* S?JZa—K« «ер™»"" «Г»-"'»-™"-
еречпсленное оборудование снабжается универсальной ос-а™ои И инстРУментом- В необходимых случаях оборудование nvuiYin*40 специальнь1ми установочными приспособлениями, конным 4 Сп<'циальнь1м режущим, измерительным и вспомогательным инструментом.
ЛЮл^ЯппиТ“ВаНИЯ заглУшек с конической резьбой в крышках на котопом илиЮТ станок специальной конструкции (рис. 15.5), вливается в пят!?3 зажимается пневмотисками. Заглушка устана-создается пнев^™’ ИмеюЩ'ИЯ осевое перемещение, a BPauieH''^ (усилие на штокеЦ^ИщпоМ При ПОМ°ШИ храпового м^аИИ\
Конические пХ н°° *Г' КР™Й момент - ДО 480 М стРукции (вис 1Г. я, наРезают полуавтоматом специальной Деталь с усилием 1100 С^ппорт которого зажимает обрабатыва У речное и продольное ПрИ давлении воздуха в сети 4 ат. Арами с усилим попяи?ере^Щения осуществляются пп6131^011*1^^-шем патроне, смонтиппп Д° 90	' Метчик устанавливают в пл'	0.
Двигэтель главного лви анном в шпинделе передней бабки. Э . оборотов шпинделя до 20еНИЧоМОи1НОСТЬ1° 4’5 квт обеспечива^ щЙ-деля и Детали'п^^О в минуту. Параллельность ос ^ну 480	Р *°т вкидывающейся липеикои, а У
резьбы регулируют по упору п п подается охлаждающе-смазывающ"
В серийном производстве при св. лесообразнс применять специальные ками (см. рис 15.1). Блоки
при сверл™
З.ЖИМВЮ,™
Рис. 15.8. Полуавтомат для нарезания конических резьб:
I — станина; 2 — силовая головка; 3 — режущая головка; 4 — инструмент: 5 — деталь; 6 — зажим; 7 — пульт управления; 8 — система охлаждения
соблением с усилием 650 кГ. Глубину сверления устанавливают перемещением упоров, расположенных на салазках силовой головки. Сверление производят спиральными сверлами, имеющими отверстия для подвода охлаждающей жидкости на режущую кромку. При сверлении предусмотрены три автоматические операции: быстрый подвод сверла, сверление отверстий при заданных режимах резания и быстрый отвод сверл. В процессе сверления блок переустанавливают.
§ 15. 4. СБОРОЧНО-ИСПЫТАТЕЛЬНЫЙ ЦЕХ
Сборочно-испытательный цех имеет ,,1ИР°^1Я^!ерИР0ВаН‘'е с цехами-изготовителями дет^л^ "усные* детали, сборочный цех Из цеха, уготовляющего	кроиштейны,
получает корпуса нас , крЬ1Шки к насосам и гидромьпл люльки насосов и крышки к ним, “Р“7детгией.
рам трубопроводы и целый ряд ДРУ	получае, детая - и > ы»
Р йз цеха ходовых	и Хики, корпусные дан
ходовой части гидромашин, валы
ПРЙ ЦИЛИНДР» и поршни клапаны, вклады,,,„ установителей, пяльпЫ, осп и т. д.
"'вплки. шатун». в*ова,,,,ые в межцеховую технологнческу,о И ВВсе детали н узль1,>пан°НтовоЧнь1п склад сборочного цеха. 5 ° таох поступают на комп	пзготовлнющии оснастку „ Пр|1.
^Инструментальныйi не	1тельный и режущим инструмент,
способления, поставляют	(приспособления). испытатель-
сборочно-техналопшеску д ,цЖ| обсспсч„вает упаковочной таро,,, ные стенды. Цех Д Р пяется широкая связь с отделами „ Сборочным цехом осущест
службами завода. помещениям сборочно-испытательного цеха
К производственнь “ боваж1Я п0 культуре производства, предъявляются высок * оизводцтся сборка и стендовые испы-
Помешения, в ко /п ,11боров и узлов, изолируют от вспомога-тания гидравлически ^борочнь1Х помещениях должна отсутство-№ьзасоПештетъ и запыленность воздуха. Проверку запыленности ПР°пХ™яеполове, о5рскаРст3еан и потолка помещений должны быть явочными и обеспечивать влажное удаление пыли. Трубопроводы ^электропроводку защищают материалами, допускающими влажную протарку. При этом следует обратить внимание на то, чтобы протирка Электропроводки и осветительной арматуры проводилась при соблюдении правил техники безопасности.
Перед входом в помещение необходимо иметь пылесосы и влажные половики для очистки одежды и обуви, а также шкафы для хранения спецодежды. Вход в помещение без специальной одежды и обуви как работающим, так и посетителям не разрешается.
Окна в производственных помещениях должны быть герметич-ными и содержаться в чистоте. Поток воздуха приточно-вытяжнои вентиляции должен проходить через фильтры, обеспечивающие требования санитарии по запыленности воздушной среды.
В помещениях сборки и испытания гидромашин нельзя производить пайку, механическую обработку деталей и узлов (припиловку, сверление, развертывание, нарезание резьбы и т. д.). Станочное оборудование для выполнения технологических операции механической обработки следует размещать в изолированных помещениях. Отдельные помещения необходимо отводить для приема пищи, хранения спецодежды, средств уборки и т. Д.
При организации рабочих мест и проектировании специального оборудования и технологической оснастки следует учитывать особенности производства гидромашин. Конструкции рабочих столов и испытательных стендов должны быть простыми, по возможное обтекаемой формы, а отделка — обеспечивающей возможность вла нои протирки. Съемные стендовые приспособления, баки, маслопроводы, фильтры и гидравлическую арматуру перед монта 0 испытуемого прибора промывают в чистой проточной жидкое технологии завода-изготовителя.
«2
Хранение и транспортирование
в пределах цеха производится = дегалеи- узлов и инет™ быть простой, обтекаемой формы с ХатГ™0? таРе- Тара должна щеп периодическую очистку Для «Х °И 0ТДелк^, допускаю блоков цилиндров, распределителей6 доХ”1*"™*деталей типа используют специальную тару. е ’ ^^никовых пар и т д.
Новые или разобранные узлы (летаптЛ
крытых стеллажах, а крупные узлы - Л храниться в за-
“ .LT:д-’6“’ь"“™
Детали, узлы и приборы неокончательно собранные, подлежащие сборке или разобранные, должны быть смазаны рабочей жидкгстою При этом особенно тщательно смазывают ходовые части подшипники и закрытые полости узлов. В таком состоянии узлы й приборы могут храниться на сборочном участке не более трех суток. В случае более длительного хранения детали, узлы и приборы консервируют, завертывают в пергаментную бумагу и не реже, чем один раз в 10 дней ОТК производит проверку консервации указанных деталей и узлов.
Гидромашины должны храниться залитыми чистой рабочей жидкостью до верхнего уровня маслоуказателя. При длительном хранении (свыше 30 суток) гидромашины должны быть залиты рабочей жидкостью до верхней крышки. Гидравлические трубы хранят в закрытой емкости, заполненной маслом АУ или АГМ.
Применение сжатого воздуха в сборочно-испытательном цехе допускается только при наличии специальных очистительных и влагопоглотительных фильтров и систематической проверки состава воздуха на влагу и механические примеси. Утечка воздуха из трубопроводов, проходящих на участке сборки и испытании, не допускается.
Для определения влажности и масла в сжатом
аспиратор Мигунова, аналитические весы, аЛЛ0“Ж“ (пр гофрированный), резиновые трубки, хлористый кали ₽ > ват,. Простой ““«TnSSSi ’Л ванный — хлористым кальцием. Пер д у Р	веса,
шиваются при температуре окс^° педовательио: первый — При отборе проб аллонжи соедини	и масла, второй —
аллонж с ватой для поглощения влаги (частнчн 1	гм.
аллонж с хлористым	«’ J™""» раиновых
Соединен» аллонжем "Р01™ „р0„уск«от Юл воауха»^' Через аллонжи в
ростью 0,5 л мин.	плати и масла в 1 л воздуха- ₽	*
рассчитывают содержави	й лаборатории не реже
производят сотрудники завод	-
в неделю.	' * ‘
", пех должен включать в себя комплск г^почнолюпытательный ‘ сние с участками промывки Дега.
3 к-пал. сб°Р°ЧНмеханический, сборки насосов п1Дром товочнып ск изделии, мсха‘ .,. узлов, отделения обкатки п
V^cJkob ЗИПа. механика и £ Р°тяН2 окраски. 5па1^ ’рганвзанпоннон структуры щ,ха , X Такая^мплектн^ть^ия	предметио-замкнутому Г1р„и.
воляег органчзова	означается для складирования
Комплектовочный склад	детале11 „ узЛов, узлоп
поступающих из цеховлж	центральных складов завода. Все
рации и различных^ *ды и детали должны быть законсервиро-поступающие на складтД „логической таре Для удобства работы ваны п находиться в ты в следует нспользовать специальные при раскладке детален ^лерь1.укладчнкн в комплексе со стел-транспортные тележки	тппа и т д Помещение должно
лажами, стеллажи Jл 'иым, отапливаемым п вентилируемым быть сухим, хорош й11НОп температуры).
(с поддержанием	ес6ороЧно-испытательногоцеха произ-
Накомплектовочн ^ей на определенныЁ узел с укладкой водится комплек	определяется удобством производства.
ИХ Укомплектованные партии деталей поступают в промывочное отделение*^где они разупаковываются и промываются. Затем детали «вают на специальный поддон и промывают в специальных камерах уайт-спиритом. Первую промывку производят без спе-ных фильтров на сливе жидкости. Вторая промывка производится в течение 10 мин с контролем на одном слое батиста на поддоне, установленном на сливе. Степень загрязнения батиста сравнивается с эталоном.
Детали со сложными внутренними каналами промывают в специальных происпособлениях, причем промывка ведется также в два этапа.
Внутренние полости деталей сложной конфигурации и маслопроводы промывают потоком рабочей жидкости. Ванны и бачки с промывочной жидкостью закрывают крышками. Промывочную жидкость ежедневно проверяют на отсутствие загрязненности и со ответственно заменяют.
Промытые и проконтролированные детали укладывают, согласно графика разбивки соответствующего технологического процесса, в специальную тару (каждая деталь в свое гнездо) и отправляют на сборочный участок. Резино-технические детали и детали не таллических материалов промывку не проходят.
Участок промывки деталей, располагающийся по технолога cfcn™y “У Д° Сборки и Участок промывки изделии ~ п° nnnMKinuu°‘™HbI ,УД0Влетв°рять общим требованиям. На У > деталей деталей производят обезжиривание (расконсер е Деталей и промывку либо в горячем масле, либо в уайт-спирите
484
Особенно тщательно, в трех п...
части.	Р ва""ах. промываются детали
Целесообразна ппомыпкя	' х°Довой
плн камерах, в которых провоДП,ХХлелПРОМЬ,ВОЧНЫХ ма,™иа* тщательно очищенным сжатым воздухом ДУЮЩЗЯ Сушка Сдувом
Рис. 15.9. Шкаф для сушки деталей:
1 — каркас; 2 — механизм поворота стола; 3 — приставной роль ганг; 4 — поворотный стол с рольгангами; 5 — проемы для рук;
6 — проем с дверьми для постановки деталей
Сушка обдувом проводится в специальных шкафах (рис. 15.9) или под зонтами с вытяжной вентиляцией.
Промывочная машина представляет собой шкаф, в котором через систему трубопроводов осуществляется промывка изделия струями уайт-спирита. Уайт-спирит стекает через воронкообразное отверстие с фильтром в сборный бак. При помощи отстойника и системы сеток уайт-спирит регенерируется, вновь поступает в питающий насос и оттуда через фильтры тонкой очистки опять используется для промывки. Качество промывки определяется по чистоте батиста, через который пропускается в воронкообразном отверстии уайт-спирит.	g
При небольших объемах производства участки промывки объединяются с участком испытании
Механический участок, предназначенный для сверления отверстий под штифты, токарной обработки и шлифования
г™олируютбве^яТпредуМпар^ения загрязнения, >
пОСЛС работы закрывают чехлами или укладывают в специальную тару vnx-пмогабарнтных изделий проводят на стационарных
Сборку кР>п"°6га J ,-ндромашин до двадцатого номера включи-рабочих местах. Сборка'_псременных линиях.
^Слбпанн'ые^гидромашины поступают в отделение испытаний.
Собранные гидро	проводят обкатку с повторной
где пРов^Хмапны\Р Улечек, испытание на герметичность, лове-ПР°нВыРеКвИспытания элементов гидроавтоматики и. в заключении, Р „от комплексные испытания гидроприводов.
ПР°Рабочне места оборудуются сварными столами, накрытыми текстолитом и снабженными желобами для стока масла.
^^Комплектующие детали хранятся в сварных шкафах. Более кпупные детали комплектуются и хранятся на сварных стеллажах со шторкой из перка™. Оснастка хранится в сварных шкафах, окрашенных молотковой эмалью.
Рабочие места обеспечиваются подставками и тумбами для различного вида крупногабаритной оснастки. Вся площадь участка обеспечивается передвижными грузоподъемными устройствами.
Подача и вывоз гидромашин в боксы с акустической изоляцией, каждый из которых предназначен для испытания только одной машины, должна быть механизирована. Управление выполняется дистанционно.
Желательна такая организация процесса испытания, которая делала бы невозможным перемешивания воды с маслом. К стендовым плитам подводится энергопитание, очищенный и осушанный сжатый воздух, вода, чистое масло. Стендовый зал обслуживает кран-балка грузоподъемностью не менее 1 т. Верстаки, шкафы и подставки в стендовом зале применяют те же, что на участке сборки. Повышенные требования предъявляют к промывке внутренних полостей и трубопроводов централизованной системы подачи рабочей жидкости к испытательным стендам гидромашин. Эта система состоит из верхнего бака с футерованной венипластом внутренней поверхностью и системы трубопроводов из нержавеющей стали, предназначенных для подачи рабочей жидкости к испытательным стендам через металлокерамические фильтры. Перед сдачей в эксплуатацию проводится предварительная и окончательная промывка.
й.?п^ари1ельную ПР°МЫВКУ проводят горячим 20%-ным содо-поомР=РОМ Г,ри темг1ературе около 70° С в течение 24 ч. Затем духом noonviulu11 ГОрячей водой и в течение 5 ч, продувают воз-му пр*омнняи1т ‘Г Ч-ерез масловодо°тстойник. И наконец, систе-С заливкой мяспРаб°ЧеИ ЖИДКостью (маслом АУ) в течение 150 ч мощи насоса coV,?563 Каждые 50 4 Промывку производят при по-2 м сек. Общее кппиР0СТЬЮ движения рабочей жидкости не мен быть не менее 600 1Чес.ТВ0 заливаемой в систему жидкости должн менее 600 (в завиеимости от	емкости системы).
[При этом очистка жидкости производится через блок фильтров который подключается в систему.
Окончательная промывка проводится уайт-спиритом После слива рабочей жидкости из системы внутреннюю поверхность бака промывают и протирают батистом, смоченным уайт-спиритом. Каналы трубопроводов промывают свободным потоком уайт-спирита, залитого в верхний бак в количестве 60—80 кг. После этого систему промывают в течение 3 ч циркулирующим потоком уайт-спирита, общее количество которого должно быть не менее 600 кг. Промывку уайт-спиритом проводят через фильтр тонкой очистки с ячейками 10 —16 мк.
Заключение о пригодности системы для заливки рабочего масла дается на основании результатов проверки чистоты батиста и анализа уайт-спирита на наличие механических примесей (весовым методом).
Профилактическую промывку системы в процессе эксплуатации производят для поддержания надлежащей чистоты в ее внутренних полостях. Эта промывка проводится циркулирующим потоком уайт-спирита в течение 3 ч аналогично проведению этой операции при чистовой промывке. Профилактическую промывку проводят по утвержденному графику, но не реже одного раза в полгода.
Выполнение работ, связанных с промывочными операциями централизованной системы подачи рабочей жидкости, должно вестись в строгом соответствии с правилами техники безопасности и соблюдением противопожарных условий.
Поставка минерального масла производится в бидонах из белой жеои, по диаметру которых наносится красная полоса. Емкость бидонов 7 и 20 I. Вкладыш заливного отверстия бидона запаивается.
Бидоны должны храниться на стеллажах пробками вверх в местах, защищенных от действия прямых солнечных лучей и атмо-
сферных осадков.
Банки с маслом, завезенные со склада, рекомендуется промывать уайт-спиритом и хранить на цеховом складе. Не менее чем за сутки перед заливкой масла в системы, банки с маслом данной партии должны быть внесены в помещение с температурой 15— 30 С и протерты чистой ветошью, смоченной уайт-спиритом. Затем банки вскрываются и немедленно отбираются пробы масла с целью проверки на присутствие воды и механических примесей.
До получения положительных результатов анализа выдача масла в цех не допускается, а при получении отрицательных результатов масло не допускается в производство. Выданные в цех банки с маслом АГМ после проверки пломбируются. Заливка одной гидромашины маслом АГМ разных партий запрещена.
ЛИТЕРАТУРА
, ,	„ и О В В н И др. Исследование рабочего процесса элементов
о^ных передач Цномощи индикаторных диаграмм. Сборник «Гвдр0. автоматика» М , "Няз-кэ». А' |аШ10нНые топлива, смазочные материалы н спе-2Аксснов	1965
цпальные^идкостн. М-.^ТР®нљД’3 я в е т „ t1 ДО. А. Производство гидро-"РТанДР^ГГа.’.'в'итт А. А. и X айкни С. Э. Теория ко-лебанин. • Ф|,ам£' ‘р Практика следящих систем. М., Госэнергопздат, 1960.
6. Ахматов А С. Молекулярная физика граничного трения. М., Фнз-МЭТГ73’Ба6ранов В Н.. Захаров IO. Е. и П р о к о ф ь е в В В. Динамика силового гидропривода, нагрузка которого имеет гидродинамическую составляющую. Сборник «Теория машин-автоматов и пиевмогидропрнводов». М. (Машиностроение^, 1966.
8.	Б а шт а Т. М. Машиностроительная гидравлика. М., Машгиз, 1963.
9.	Белянин П. И. и Черненко Ж. С. Авиационные фильтры и очистительные гидравлические системы. М., «Машиностроение», 1964.
10.	Бергман Л., Ультразвук и его применение в науке и технике. М., Изд во иностр, лит., 1957.
II.	Бесекерский В А «Попов Е. П. Теория систем автоматического регулирования. М., «Наука», 1966.
12.	Б л е и з Е. С. и др. Динамика электромашинных следящих систем. М., «Энергия», 1967.
13.	Б о р и с о в а Н. Л. Статические и динамические характеристики гидропривода сопло — заслонка — гидроцилиндр». Труды МАИ. Вып. 134. М., Оборонгиз, 1961.
14.	Борисова Н А. Перестановочное усилие на шайбе аксиально-«HajKa60^^04'3 ПРИ малых Углах наклона. Сборник «Гндроавтоматика». М-, млн5'»/а м ы н н и Н. С. Гидроусилитель типа «сопло — заслонка». Труды МАИ. Вып. 134. М„ Оборонгиз. 1961.
Оборонгиз2 ?962И ” Н С' Основь1 следящего гидравлического привода. М., 18 Гиптп^Л Э В"зкость «едкостей. М., Гостехиздат, 1935.
12. М.'Машгиз 1947И с’нциклопедическии справочник «Машиностроение». Т. ние>, 196(^РОПРИВОД и гидроавтоматика в машиностроении. М., «Машннострое-ши построение»? 1964^ Исследование и расчет гидравлических систем. М., ‘Ма-рия газов иРжидк^ейе м Д7? К е р т и с с Ч., Б е р т Р. Молекулярная тео-м 22. Голубев А и’сп?'В° ИН0СТр‘ лит'' 196L	М
Машгиз, 1963	’ ’ современные уплотнения вращающихся валов, м..
23 Г о '
в плоской модели уплот.Л./ Ф е л ьд м а н г и Исследование напряжений 1963, № 4.	ельиого кольца круглого сечения. «Каучук и резина .
488
струн на органах типа
----- заслонка». «Автоматика и телемеханика»' 1956 №6
2R ПпптплпГП и о... ------- ’  и'
ких контактных давлениях. «Машиноведение», 1966 № 5.
ОО Плыппп,. ..г> IV/ - -
издат, 1957.
30. Жиль
'ваюлсй с магнитной Пружйпо^Тр™ и"' МАИ Вы7Р^еХ??»ИЧеЛКИХ пР«>бразо-25. Д а н и л о в Ю. А ЭпектпХапшт... » М ’ 134' 0б°Ронгиз. 1%1
Р< улнровапия производительности насосов эл1к?тога^Ие механизмы Сборник статей < Гидропривод и гидпоявто шти» Р°гидравлических систем, шнностросние», 1966. Р гиЛРОавтоматпка в машиностроении» М„ «Ма-нчла?6 !^ ° Р " >К " К’ М°ТОрнь,е масла и смазк” Двигателей. М , Гостоптех-
27.	Д м и т р и е в В Н. и Шашков А. Г. Силовое действие заслонку в пневматических и гидравлических управляющих «сопло заслонка». «Автоматика н телемеханика», 1956, № 6.
28.	Дроздов Ю. Н. Коэффициенты трения скольжения при очень высоких контактных давлениях «Машиноведение», 1966, № 5.
29.	Доклады на IV Международном нефтяном конгрессе. Т. 7. М., Гостоптех-издат. 1957.
Ж , П е л ь г р е н М. и Д е к о л ь н П. Теория и техника следящих систем М , Машгиз, 1961.
.31	. Жуковский Н Е., О гидравлическом ударе в водопроводных трубах Полное собрание сочинений. Т. VII. М., ОНТИ НКТП, 1937.
32.	Захаров Ю. Е. Определение гидродинамической силы на золотниках гидравлических сервомеханизмов. Труды МВТУ. Вып. 99. М., Оборонгиз, 1959.
33.	Квартальное Б. В Динамика электроприводов с упругими связями М , «Энергия», 1965.
34.	Кениг Г, и Б л е к у э л л В. Теория электромеханических систем. М , «Энергия, 1965.
35.	Кичин И. Н. Определение коэффициентов гидравлических потерь для дроссельных сопротивлений в системах автоматики. «Автоматика и телемеханика», 1957. № 1.
36.	Клюкин И. И., Борьба с шумом и звуковой вибрацией на судах.
М” 37ДКРсГгТ’н Ч’ М. и Нарспдзе К- М. Двухфазная асинхронная машина с тонкостенным ротовом. «Автоматика и телемеханика» 19лЗ № Z
38.	К о н д а к о в Л. А. и Прокофьев В. Н. Современная уплотни
тельная техника. «Вестник машиностроения», 1967. № 	т i
39	Конструкционные материалы. Энциклопедический справоч и -
М , «Советская энциклопедия», 1963.	„„—„а м Глстехиэдат.
40.	К о р н ф е л ь д М. Упругость и прочность жидкостей. М, Гостехиэдат, 195*41. К р а г е л ь с к п й И. В. В и н о г р а д о в а И. Э. Коэффициенты трения. М., Машгиз, 1962	- Б г Коэффициенты расхода гидра-
“i-.—. *—-
процессов», I960, № 3.	г Силовой эффект струи в гидравлн-
флигеле0 «сИопл^-^лРон^. Автоматика и -механика» 1^.
№ ’'44- К Р 3 С СногВо гидр^вличХ: ус— f«—L—амкЛ ^лотХТЖник маип1ностроеиия.^9б1, №менты	аотомотичеекого
45. К Р а с с о в И. м- « "ДР
регулирования. М-, Машгиз, 19 коэффицнентв трения в тяже*» ₽# контак'теК«УВестник машииост^оешгя^^954^^ ®^иогооПределеии«1«Рач*,’*,,ы1 сроков хранения' «Каучук и	констру-Р—
и Лй К v Л а Г И Н А. О- " ДЮ	| оса	.	— вея»
48	М «Высшая школа», ‘--„„ого теплового
гидропередач. М., о	Мст(1ды ускоренно!
49. Л е ж н е в н.
М , Госхимиздат, 195<-
заслонка». «Автоматизация производственных
п Д ..ппавлпческие следящие Приводы для автоматц. 50. Л £ ш е и к 0	10( 9
зашш станков. М., Машгиз, ' х Гидравлические системы управления. ,Ц 51. Льюис Э. истер
«Мир». I966- п и и до Методы ускоренного определения гарантий-52. Л ю б ч е н к о Д И и др Д	1963, № 4.
иых сроков хранения резин .«к ! >	► в снстемах автоматического управле-
53 М е л к о з е р о в и. с-
ния. М., «Энергия». 1966 распрОстраиение ультразвуковых волн в жид-
54. М и х а и л о в 11.1- г и
НеДродТ^’Справочник. Под ред Б В Лосикова. М . «Химия», I956- и т и н О Ф О регулировании подачи аксиальио-порщиевых насосов поворотом торцевого распределителя. Сборник «Гидроавтоматика». М, ♦Наука», 1965^	Влияние низких температур на работоспособность
57. Носов у	])7 м , 06opOHnl3i 1959
'П1°58.еОсновы автоматического регулирования Под ред. проф. В В Солодовникова. ЛЕ. Машпи ,^1954 р g f 0 3 п н н д Технический словарь-справочник по топливам и маслам. М., Гостоптехиздат, •963.
60.	Пономаренко Ю. Ф. и Рогов Л Я. Радиально поршневые высокомоментные гидромоторы М., «Машиностроение», 1964
61.	Попов Е. П. и П альтов И. П., Приближенные методы исследования нелинейных автоматических систем. М., Машгиз, 1960.
62.	Проблемы современной уплотнительной техники. Под ред. В. Н. Прокофьева и Л. А. Кондакова. Сборник докладов на 2-й Международной конференции по уплотнениям. ЛЕ, «Мир», 1967.
63.	Прокофьев В Н. Основы функциональной взаимозаменяемости гидропередач Сборник «Взаимозаменяемость и технические измерения в машиностроении», № 4. М , «Машиностроение», 1964.
64.	Прокофьев В. Н. О вязкости смазочных масел и жидкостей, применяемых в машинах и гидросистемах. «Вестник машиностроения», 1944, № 3—4.
65.	Прокофьев В. Н. Основы теории гидромеханических передач. ЛЕ, Машгиз, 1957.
66.	Прокофьев В. Н. Гидравлические передачи на Ганноверской ярмарке (ФРГ) в 1961 г. «Станкостроительная промышленность». 1961, № 6.
„ > Р 0 к 0 Ф ь е в Н. Объемные гидропередачи в ГДР. М., ЦИНТИ-МАШ. Серия 111, 1962.
68. П р о к о ф ь е в В. Н. Учет взаимодействия потока с ограничивающими его стенками при анализе переходных процессов. «Известия АН СССР. «Энергетика и транспорт», 1963. № 3.
о_ П Р ° о ° Ф ь е в В- Н- Новое направление исследований гидропередач за рубежом. «Вестник машиностроения», 1963 №5.
Некотопыр ппппл0<^ Ь е В В Н’’ Б ° д Р а ш е в а Г. Ф. и Си и ев А. В. «Известия «Л С|?,кииематикибескаРДанных аксиально-поршневых гидромашии. «известия вузов. Машиностроение», 1964, № 4.
ренциалом.Р«Элек^рич^', l^Kfe Ч™” Пр“ВОДа С механнческим ДИ<И>е' трансмиссии ° Л ®Ы^°Р оптимальной схемы объемной гидро-и электрификация сониал^т0,, сельско*ОЗЯЙСТЕенного трактора. «Механизация
73. П ро кофьеТ R иК%° ссльского хозяйства». 1965, № 1. исполнительных двигателей «Л. Количественная оценка эффекта дробления ♦Наука», 1965.	следящих систем Сборник «Гидроавтоматика». М-,
♦Известия ву°зов°мХностроеиии71^6 ДРОСТаТИЧССКОГО УРавиовешиваНИЯ характеристику объемнее инЛ.,? влиянии динамической подачи на частотную ФРФ	ДР РИЕ°ла.«Автоматика и телемеханика», 1966, As 8-
подпятника.
|я и устойчивость
В. Н. и 3 а х а р о в Ю. Е. Условия возникно-гидроприводах. «Известия вузов. Машиностроение», В. Н, и К и к о т ь В. С. Влияние размера исполни-на динамику гидропривода. «Известия вузов. Машиио-
76.	П рокофьев В. И. Влияние демпфирующих свойств гидвомотоппп па динамику силового электрогидропривода «Электричество» 1966 № 9 Р
77.	Прокофьев В. Н. Расчет динамики гидростатического подпятника с центральной камерой. «Вестник машиностроения», 1967 № 5 «""|ника
78.	Прокофьев В Н. О динамике гидростатического Вестник машиностроения», 1968, № 8.
79.	П р о к о ф ь е в В. Н. Основные динамические свойства электрогидро-приводов с управляемым гидродвигателем. Сборник «Колебание •• — ’ машин М., «Наука», 1967.
80.	II р о к о ф ь е в пения автоколебаний в 1967, № 8.
81.	Прокофьев 1СЛЫЮГО гидродвигателя строение», 1967, № 1.
89 Прокофьеве. Н. и Кузнецов В. Д. Автоколебания гидропривода. «Известия вузов. Машиностроение», 1966, № 5.
83. Прокофьеве. Н. и Л у з а н о в а И. А. Определение критерия упругости гидропривода. «Известия вузов. Машиностроение», 1966, № 7.
'	’84 Прокофьев В Н. и др. Экспериментальное исследование упругих
свойств двухфазных рабочих жидкостей гидроприводов объемного типа. «Известия вузов Машиностроение», 1968, № 2.
85.	Прокофьев В. Н. иНеймаи В. Г. Решение задачи динамики
автоматической гидрообъемной трансмиссии при помощи метода линейных графов. Известия вузов. Д1ашииостроение», 1966, № 11.
86. П р о к о ф ь е в В. Н., Нейман В. Г. и Л у з а и о в а И. А.
Влияние давления рабочей жидкости на динамические свойства гидропривода. «Известия вузов», 1968, № 1.
87. Прокофьев В Н. и Рябова-Орешкова А. П. Оценка качества у праяляемости гидрообъемной трансмиссии. «Известия вузов. Машино-
строение», 1967, № 9.
88.	Прокофьев В. И. и др. О синхронизации распределения нагрузок я многодвигательном приводе при стационарном режиме работы. «Известия вузов Машиностроение», 1967, № 5.
89.	Прокофьев В. Н. и С и н е в А. В. Геометрия реверсивной аксиально-поршневой гидромашины бескарданного типа. «Известия вузов. Машиностроение, 1963, № 11.
90.	Прокофьев В. Н. и С и н е в А. В. Кинематические связи в бес-карданиых аксиально-поршневых гидропередачах. «Вестник машиностроения», 1964, №11.
91.	Раздолии М В. Уплотнения авиационных гидравлических агрегатов. М., «Машиностроение», 1965.
92.	Резниковский М. М. нЛукомская А. И. Механические испытания каучука и резины. М , «Химия», 1964.
93.	Роторные насосы. Энциклопедический справочник «Машииостроецие».
Т. 12. М., Машгиз, 1948.	nuuruuiiu ioki
94.	Савин И. Ф. Объемные гидроприводы. М., ЦИНТИМАШ.
95.	Садове к и й БД. Гидропривод. Ч. 1. М.. МВТУ. 1И66.
96	Садовский И. М. Асинхронный серводвигатель как элемет пямее регулирования. ^Автоматика и телемеханика», 1952. № 6-
97.	С е м и и и д о и др. О некоторых особенных г^^ия в «V ’мопаре смазочных масел с полимерными присадками. Сборник «Теорнх
"«• -» ’с г>*
ДС|1С99а С А .А	шу» и борьба с ***
— -> -«-«
ред. Д. Траксела. М.. Энергоиздат. 1962.
р Основы акустики. Т. I в П М, Изд-во иностр
101. Ску чнк Е. и	.	. . т. 1. МГУ. I960
Специальный^^	электрических сч«ио-
решаюшнх Д^Не^е^	в “ехан,,',еск,,х 11 “Рическнх
rurJvax СД1° нзд-во иностр- лит - 19°2 новые матсриалы М , Наука». 1965 ?05 Теория смазочного денсгш  газов. Энциклопедический спра-}и Техническая механика "ств Маш1,„. 1948	ра
ночник «.Машиностроение». э ектроГидравлическпе и эл< кгроппевм.ппческпе ,07 Толчеев 1~‘1ого действия. Основы автоматического рсгулирова следящие системы непрерывное
„„я. Т 3. М„ Машгпз, !«>'„ ная усталость материалов для зубчатых 108. Т р V о и и ।  1'-
колес. М., Машгпз, 196- Гидравлика. М-, Энергоиздат, 1956.
109. Френкель п. пр11В0ЛЫ и гидроавтомат ка станков М НО. X а й м о в и ч ь. /н । |шг г
Машгиз. Ira ° н р £ Жидкости для гидравлических систем. М., «Химия», 1965 12 Хохлов В Л Электрогидравлическпй следящий привод М. йНа'пЗ ’ чТч е т Ю. С. Управляемый асинхронный двигатель с полым ротором М„ Энергоиздат.^ Электр))ЧескиеЫ|1КрОмашины автоматических устройств. М ’ Пб.^Чи л пТи и М. Г. Корытин А. М. и Прокофьев В Н. Силовой электрогидропрнвод. М., Энергоиздат, 1955.
116.	Эр и ст В. Гидропривод и его промышленное применение. М., Машгпз, 1963
117.	Юферов Ф. М. Электрические двигатели автоматических устройств. М.. Госэнергоиздат, 1959.
118	Яворский В. Н. п др. Проектирование инвариантных следящих приводов. М., «Высшая школа», 1963.
119.	Adams Н. W. Mechanical engineer's Solution for noise suppression. ASME Paper, № 59—AV—30 for meeting march 8—12, 1959.
120.	Blackburn J F., Reethof G., Shearer J. L. Fluid Power Control, N. J ., I960.
121.	Churcher B. G. A loudeness scale for industrial noise measurements. «Journal ol the Acoustical Society of America», 1935, 6, 216.
122.	Fletcher H. Loudeness, masking and their relation to the hearing process and the problem of noise measurement. «Journal of the Acoustical Society of America», 1938, 9.
123.	H i m m 1 e r C. R. Construction and performance data on some French — developed servo systems. «Applied Hydraulics», 1957, № 10.
124.	Hoene H. J., Pietersen G. H. Hydraulic Sistem noise. •Machine Design». 1962, 3.
sehinfnb^i1 V? Gerau,schuntersuchungen an Radial kolbenmascbinen. Ma-19fib p hn‘MVtB Verlag Technik), 1961, Heft 7, 10.
127’ P eMh V г" Л ‘Noise Control», 1954, № 1.	(
of fluid onwer rnnirJi G ’Goth C. W. Machine computation in the Development Hydraulic USA 1958 cornPonents and systems. National Conference on Jndustrial
129. W i I s о n™ uf"	Rubbers. 1950, October.
Pitman Publishing corp., 1950^*3 6 DisPlacemcnt Pumps and Fluid Motors.
e 11 e r W. Technigne de la defense contre le bruit. Paris, 1954.
ОГЛАВЛЕНИЕ
Предисловие ...	.....................
Глава 1 Аксиально-поршневые гидромашины......................
§ I 1 Конструктивные формы и технические характеристики аксиально поршневых гпдромашин.........................
§ 1.2. Основные количественные соотношения гидромашин объемного типа .	...........................................
§ 1	3. Насосы, гидромоторы и гидроприводы гаммы И
§ 1.4	Конструкция насосов ПД № 5—50....................
§ 1.5.	Работа насосов 11Д № 5— 50.................
§ 1.6.	Особенности конструирования и использования аксиально-поршневых гидромашин гаммы II..................................
Г л а в а 2 Кинематика аксиально-поршневых гидромашин ..........
§ 2.1.	Кинематика обобщенной аксиально-поршневой гидромашииы
§ 2.2.	Полная геометрическая подача гидромашииы объемного типа
§ 2.3.	Неравномерность динамической подачи...................
§ 2.4.	Физический смысл динамической подачи..................
§ 2.5.	О выборе некоторых геометрических размеров аксиально-поршневых гидромашин...........................................
Глава 3. Некоторые вопросы расчета рабочих органов аксиально-поршневых гидромашин.............................. .................
§ 3.1.	Определение основных размеров блока цилиндров........
§ 3.2.	Порядок проектирования блока цилиндров...............
§ 3.3.	Момент на валу и основные силовые нагрузки аксиально-поршневой гидромашииы с наклонным блоком цилиндров.............
§ 3.4.	Основные силовые нагрузки в поршневой группе.........
§ 3.5.	Момент пли усилие на регулирующем органе.............
6 3.6.	Пример расчета момента на люльке.......... •
§ 3.7.	Момент на регулирующем органе аксиально плунжерных насосов	....................
Г л а в а 4. Рабочие жидкости ........................
§ 4.1.	Функции рабочих жидкостей и условия эксплуатации гидро-
6 4 ^Классификация гидроприводов по условиям
6 4 3 Некоторые физические свойства рабочих жидкое*» М'4 рХиеР жидкости иа нефтяной основе . . - - -6 4 5. Загущенные минеральные масла............
§ 4*6. Синтетические	«емкости«аио» *лв
§ 4.7. Примеры выбора рабочей жидкост......... ...
8 4 8 Упругие свойства жидкостей .  •
§ 4.9. Двухфазные рабочие	упругость < • - •
§ 4.10. Приведенный модуль о
3
5
5
20
22
30
38
40
51
51
54
62
64
65
68
68
70
71
74
75
83
г л к В Я 5. Уплотнения .	.......
6 5.1 Принцип действия уплотнении .......
«52 Механизм действия эластичных уплотнении
6 53 Характеристика резины как уплотняющего материл ц	,
6 5.4 Конструирование посадочных меег для уплотнении кольцами круглого сечения...............
§ 5.5 Уплотнения пар возвратно поступательного движения
6 5.6 Уплотнения вращающихся валов...................... .	. .
§ 5.7. Торцовые уплотнения ватов и поворачивающихся деталей
Гчаваб Гидростатическая раирузка ....	................... .
6 6 1 Уравнения динамики плавающей гидростатической опоры .
j 6 2 Передаточная функция обобщенное плавающей гц уростати-ческон опоры ..............................  .	. .	........
§ 6.3 Частотная характеристика гидростатического башмака
Г л а в а 7. Демпфирующие свойства гидромащии................
§7.1.	Основы линейной теории подобия роторных гидромащии
§ 7.2.	Топографические нлн универсатьиые характеристики гидромашин ............................................ ............
§ 7.3.	Определение чистовых значений коэффициентов демпфирования ......................................... ...............
§ 7.4	Оптимальный режим работы гндромашнны
§ 7.5.	Влияние демпфирующих свойств гидромащии на переходные процессы гид/юиривода...............................
138
138
141
147
153
158
162
167
170
170
183
183
189
190
196
198
Главав. Статические характеристики гидропривода........................ 201
§ 8	1 Предельная характеристика гидропривода..................... 201
§8 2.	Гидропривод при ограниченной мощности приводного двигателя 204
§ 8.3.	Статические критерии сравнения гидромашин объемного типа и выбор их размера....................... . . ............... ....	210
§ 8	4 Приемистость гидродвигателя ............................... 214
Г л а в а 9. Динамические характеристики гидропривода.............
6 9.1	Дифференциальное уравнение гидропривода............. .
§ 9.2.	Постоянная времени и коэффициент демпфирования гидропривода ........................................................
§ 9.3.	Динамическая ошибка гидропривода....................
§ 9.4.	Гидропривод с управляемым гндромотором................
Г л а в а 10. Работа гидропривода на «ползучих» скоростях.........
§ 10	1. Особенности работы гидропривода на «ползучих» скоростях
§ 10.2.	Уравнения связи при наличии нелинейного демпфирования
§ 10.3.	Определение значений нелинейного демпфирования гпдродвп-гателя ......................................................
§ 10.4.	Приближенное решение нелинейного дифференциального у равнения .......................................................
§ 10.5	Графо аналитический способ определения параметров автоколебаний ................ ..................................
§ 10.6.	Проверка устойчивости движения........................
§ 10.7.	Оценка вариаций давления .............................
§ 10.8.	Проверка правомерности применения метода гармонической линеаризации ................................................
§ 10.9.	Общие закономерности гидропривода при нелинейном демпфировании в гидродвигателе и жестко присоединенной к нему нагрузке Г л а в а 11 Анализ и расчет электрогидравлических механизмов управления насосами переменной производительности ...........................
! 11.1.	Основные схемы и конструкции механизмов управления.
i 1.2. Электромеханические преобразователи .... t ... • «4
218
218
221
225 227
235
235
236
239
242
244
247
248
249
262
257
257
269
г
Kill 'ототвиковые гидроусилители . . . к 11 R п1|ДГ>пУсилигели «сопло - заслонка». '.............. '
9 115 Динамика механизмов управления
aJ2 Снижение акустических эффектов и вибраций в гидропередачах Лкусгнчеекне а^^кты работающих гидропередач KpdfKHe сведения из акустики ...
Поверхность слышимости ..................
Условии замера воздушного шума работающей машины В >зникнов1 пне шума в машинах . .жчвческпй скачок.................... .... . . . ........
Колебание силовых воздействий в регулируемой роторной гид
пав;
§ 12.1.
§ 12.2.
§ 12 .1
§ 12.4.
6 12	5 Воэн
§ 12.6.	Эпер,
§ 12.7.	Г
Ромашине
§ 12.8.	Источники возду итого шу ма основных элементов гидропередач
§ 12.9.	Глушители шума ........................................
§ 12	10 Регулирование индикаторной диаграммы ...................
§ 12	11 Использование регламентированных утечек для изменения индикаторной диаграммы ..........................................
§ 12.12 Динамический метод регулирования давления индикаторной
274
295
310
318
318
319
325
339
341
354.
35?
360
366
377
395
диаграммы ...............................................  404
§ 12 13 Некоторые экспериментальные работы по понижению уровня воздушного шума в роторных гидромашннах ................... 408
§ 12 14. Индикаторные диаграммы аксиально-поршневых гндромашин по опытам фирм Дженерал Электрик и Виккерс . -	.	418
423
423 126 430 430 431
433
430 436 Ш 440 .442 443 447
450
453 4W 451
§ § § § § §
13.1.
13.2.
13.3.
13.1.
13.5.
13.6.
Глава 13. Материалы и некоторые технологические процессы, применяемые при изготовлении аксналыю-поршиевых гидромашин . . Материалы....................................................
Термообработка ....	............ ................
Изготовление трубопроводов Покрытия ......................... ...................
Технология диффузионной сварки .......................
Изготовление фильтров.................................
Глава 14. Технология изготовления гидроприводов .................
§ 14.1. Абразивные материалы для обработки деталей машйп ... " 14.2. Обработка сферических поверхностей...............-
14.3. Проверка герметичности ........................
14.4. Устранение брака отливок корпусов гидромашнн 14 Д. Технология обработки корпусных деталей.........
14 6. Обработка люльки ........................   ’	 -  
14 7. Обработка блока цилиндров .	• • •	’I
14 8. Применение электроэрозионного шлифования и алмазного «р пингования для обеспечения взаимозаменяемое*лорши**/ 7 * • *
14.9. Технология обработки валиков кардана и шатун®» - vt _______
14 10 Технология обработки распределителя........
1й:
а 15. Организация производства гидроприводов	g
. Механический «»	’й ‘ * . ? • . , .	 - • 1К
ии1- ™ '-------------------- • •  «•.
§
§
§
§
§
§
§
§
§
§
§
ГЛа| !5-1- Меха-ическин цех
I
§ ^очноТ^^льный цех
Литература
Владимир Николаевич Прокофьев Юрий Анатольевич Данилов Лев Анатольевич Кондаков
АКСИАЛЬНОПОРШНЕВОЙ РЕГУЛИРУЕМЫЙ гидропривод
Редакторы издательства Ю. А. Зарянкан и Л1. Н. Журавлева Технический редактор А. Ф. Уварова Корректор В. Воробьева
Переплет художника £. В. Бекетова
Сдано в производство 16/Х 1968 г. Подписано к печати 24/VII 1'469 г. Т-05925. Тираж 8200 экз. Печ. л. 31,0 Бум. л. 15.5. Уч изд. л. 32,0. Формат б0Х90,/|«. Цена 1 р. 88 к. Зак. № 271
Издательство «МАШИНОСТРОЕН И Е ».
Москва. Б-66, I-й Басманный пер.. 3
Ордена Трудового Красного Знамени Ленинградская типография № 1 «Печатный Двор» имени А. М. Горького Главполиграфпрома Комитета по печати прн Совете Министров СССР. Ленинград. Гатчинская ул., 26.
Отпечатано с готовых матриц в типографии № 6 Главполиграфпрома Ленинград, ул Моисеенко, 10